Похожие
Текст
ТЕХНИЧЕСКИЙ
СПРАВОЧНИК
ЖЕЛЕ 3 НОДОРОЖН И КА
ТЕХНИЧЕСКИЙ
СПРАВОЧНИК
ЖЕЛЕЗНОДОРОЖНИКА
РЕДАКЦИОННАЯ КОЛЛЕГИЯ
А. Ф. БАРАНОВ, Д. Д. БИЗЮКИН,
М. И. ВАХНИН, Б. Н. ВЕДЕНИСОВ,
И. В. ИВЛИЕВ, В. И. ПОПОВ,
Е. Ф. РУДОЙ, я. и. соколинский,
В. Н. СОЛОГУБОВ, В. А. ШИЛОВСКИЙ
Главный редактор
Е. Ф. РУДОЙ
*
ГОСУДАРСТВЕННОЕ ТРАНСПОРТНОЕ
ЖЕЛЕЗНОДОРОЖНОЕ ИЗДАТЕЛЬСТВО
оИ о с к в а • 4 а 5 4.
ТЕХНИЧЕСКИМ
СПРАВОЧНИК
ЖЕЛЕ 3 НОДОРОЖН И КА
Том 1
ЧЪ?!
ФИЗИКО-
МАТЕМАТИЧЕСКИЙ
Ответственный редактор тома
проф., докт. техн, наук
Н. И. БЕЛОКОНЬ
МХ:СР
РВЩ : iff!!.:
(..Г. >! ’.ОЦ
ГОСУДАРСТВЕННОЕ ТРАНСПОРТНОЕ
ЖЕЛЕЗНОДОРОЖНОЕ ИЗДАТЕЛЬСТВО
о ск в а •
АВТОРЫ ТОМА
И. М. ВОРОНКОВ, проф., д-р техн, наук; Б. В. КЛИМЕНКОВ, доц., канд.
техн, наук; К. В. КОНСТАНТИНОВА; Н. А. КУТЫРИН, доц., канд. техн, наук;
Н. В. ЛЕВИН, инж.; Г. Л. ЛУНЦ, доц., канд. физ.-мат. наук; Г. М. ПАНЧЕН-
КОВ, проф., д-р хим. наук; М. А. ПЕТРОВ, проф., докт. техн, наук; В. И. ЧЕР-
НИКИН, доц., канд. техн, наук; А. Р. ЯНПОЛЬСКИЙ, доц., канд. техн. наук.
4
РЕЦЕНЗЕНТЫ
А. П. ЮШКЕВИЧ, проф., докт. физ.-мат. наук; А. 3. РЫВКИН; К. А. СЕМЕНДЯЕВ,
доц., канд. физ.-мат. наук (математика); К. Ф. ЖИГАЧ, проф., докт. хим. наук (химия);
В. Г. ГОГОЛАДЗЕ, проф., докт. техн, наук; А. У. ГАЛЕЕВ, доц., канд. техн, наук (механи-
ка); И. А. ЧАРНЫЙ, проф., докт. техн, наук; Я. 3. РАБИНОВИЧ, доц., канд. техн, наук
(гидромеханика); И. И. МЕНЩИКОВ, доц,, канд. техн, наук; М. Д. НАХОДКИН, доц. (ос-
новы электротехники); В. К. КОШКИН, проф., докт. техн, наук; В. М. ТАРЕЕВ, проф.,
докт. техн, наук (теплота); В. С. ЛЕВИЦКИЙ, доц., канд. техн, наук (графический материал).
*
РЕДАКЦИЯ ТОМАг
Н. И. БЕЛОКОНЬ, М. Л. РУДОЙ, В. Я. ЧЕРНЯВСКИЙ
СОДЕ РЖАН И Е
Стр.
От редакционной коллегии ................... 6
От редакции первого тома ................... 9
АЛФАВИТ ЛАТИНСКИЙ.......................... 12
АЛФАВИТ ГРЕЧЕСКИЙ ......................... 12
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ . . 13
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ..................... 15
МАТЕМАТИКА доц., канд. физ.-мат. наук
Лунц Г. Л. и доц., канд. техн, наук Ямполь-
ский А, Р................................ 91
Арифметика и алгебра ..................... 91
Геометрия . ..................' ... . 108
Тригонометрия....................... 117
Диференциальное исчисление ........ 127
Интегральное исчисление . ................ 135
Бесконечные ряды.................... 156
Диференциальные уравнения , 165
Вариационное исчисление .................. 177
Аналитическая геометрия .................. 179
Диференциальная геометрия ................ 194
Векторное исчисление ..................... 207
Теория функций комплексного переменного 212
Теория вероятностей и метод наименьших
квадратов ............................ 222
Эмпирические формулы...................... 230
Приближённые вычисления............. 233
Приближённое решение алгебраических и
трансцендентных уравнений........... 236
Исчисление конечных разностей и интерпо-
лирование ............................ 244
Численные и графические методы анализа . 254
Номография.......................... 262
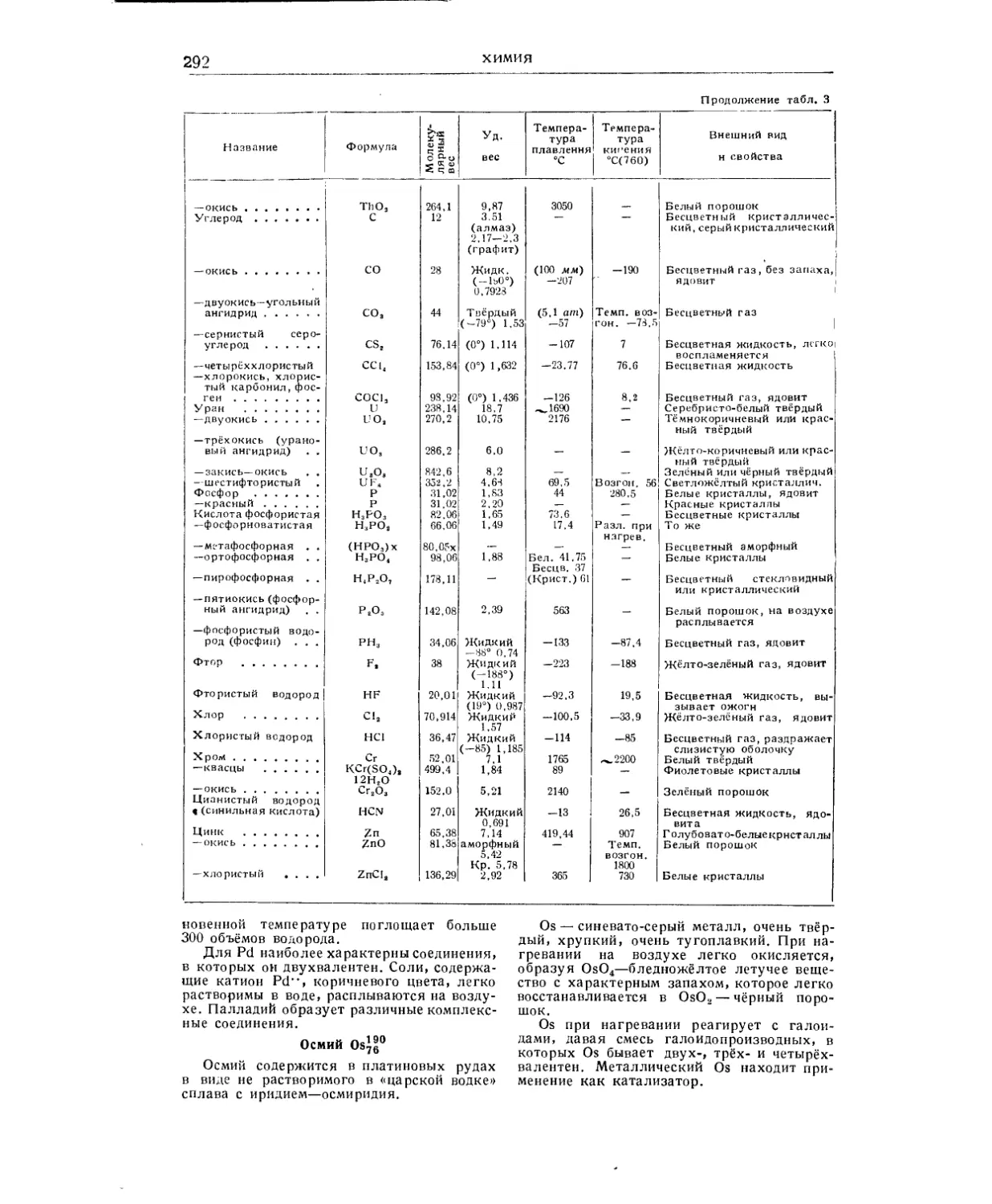
ХИМИЯ (проф., д-рхим. наукПанченковГ.М. 269
Периодическая система элементов .......... 269
Неорганическая химия (Константинова К- В.) 272
Органическая химия ....................... 294
Физическая химия (Панченков Г. М. проф.,
докт. хим. наук и канд. хим. наук Кли-
менков Б. В.-) 315
Коллоидная химия.......................... 349
МЕХАНИКА (проф., докт. техн. наук Во-
ронков И. М. и инж. Левин Н. В.) , , . 357
Основные определения . .................. 357
Статика..................ф................ 357
Стр.
Кинематика ............................ 368
Динамика................................ 375
Центр тяжести и моменты инерции........ 390
Трение.................................. 398
ГИДРОМЕХАНИКА (доц., канд. техн, наук
Черникин В. И.)...................... 404
Физические свойства жидкостей.......... 404
Гидростатика.......................... 408
Гидродинамика идеальной жидкости .... 413
Гидродинамика реальной (вязкой) жидкости 420
Движение жидкости по трубам ........... 422
Расчёт трубопроводных систем........... 428
Местные сопротивления . ............... 432
Равномерное движение жидкости в открытых
руслах............................... 437
Водосливы . 443
Неравномерное движение жидкости в откры-
тых руслах . .......................... 449
Удар жидкости.......................... 458
Истечение несжимаемых жидкостей при по-
стоянном уровне........................ 461
Истечение несжимаемых жидкостей при пе-
ременном уровне........................ 465
Внешнее обтекание тел.................. 467
Движение грунтовых вод................ 469
Аэро- и газодинамика................... 474
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ (проф.,
докт. техн, наук Петров М. А.)...... 480
Магнитное поле ..................... 480
Электрическое поле.................. 486
Постоянный ток .................... 490
Переменный ток...................... 497
ТЕПЛОТА (доц., канд. техн, наук Кутырин
Н. А.).................................... 510
Общие тепловые свойства тел............... 510
Термодинамика . ... . 527
Газы............ .... ......... 531
Водяной пар • 546
Течение газов и паров по трубам, истечение
из резервуаров .................... . 568
Теплопередача ............................ 574
ЕДИНИЦЫ ИЗМЕРЕНИЙ .......... 605
АЛФАВИТНЫЙ УКАЗАТЕЛЬ....... 615
ОТ РЕДАКЦИОННОЙ КОЛЛЕГИИ
ТЕХНИЧЕСКОГО СПРАВОЧНИКА ЖЕЛЕЗНОДОРОЖ НИКА
Огромные изменения, происшедшие на железнодорожном транспорте за последние
15 лет со времени выхода в свет Технического справочника транспортника, настоя-
тельно требуют издания нового справочного руководства для железнодорожников.
Сталинские пятилетки коренным образом преобразили железнодорожный транс-
порт СССР. Советский железнодорожный транспорт в результате оснащения новой
техникой и развития стахановского движения стал передовой отраслью народного
хозяйства. Это позволило транспорту в годы Великой Отечественной войны с
честью выдержать нагрузку, с которой, как отметил товарищ Сталин, едва ли
справился транспорт любой другой страны.
Организованный партией Ленина — Сталина после победоносного окончания
Великой Отечественной войны новый мощный хозяйственный и культурный подъём
позволил железнодорожному транспорту в короткие сроки не только залечить раньц
нанесённые войной, но и двинуться вперёд по пути дальнейшего технического
прогресса и обеспечения потребностей народного хозяйства передвижными сред-
ствами.
Превысив в 1948 г. довоенный уровень грузооборота, железнодорожный транс-
порт успешно выполняет послевоенный пятилетний план.
Благодаря повседневным заботам партии, советского правительства и лично
товарища Сталина железные дороги оснащаются во всё возрастающих количествах
новой высокопроизводительной отечественной техникой.
Подвижной состав пополняется новыми конструкциями паровозов, тепловозов,
электровозов, грузовых и пассажирских вагонов. Путевое хозяйство значительно
усиливается усовершенствованными механизмами.
Широко механизируются трудоёмкие работы. Растёт число механизированных
сортировочных горок. Всё в больших размерах на транспорте находят применение
радио, телеуправление, различные устройства, улучшающие безопасность движения
поездов и увеличивающие пропускную н провозную способность железнодорожных
линий.
В депо, на заводах, стройках, станциях, дистанциях растёт производственная
культура, совершенствуются технологические процессы.
В Техническом справочнике железнодорожника обобщены и систематизирова-
ны важнейшие справочные данные по основным вопросам техники и экономики
железнодорожного транспорта.
Коллектив авторов, рецензентов и редакторов справочника стремился создать
пособие, отвечающее требованиям современного развития науки и техники в области
транспорта, с учётом достижений передовых людей железнодорожного транспорта
в использовании транспортной техники и организации технологического процесса.
В связи с этим в Техническом справочнике железнодорожника получили широкое
отражение вопросы новой техники по каждой отрасли железнодорожного хозяй-
ства; в нём помещены также расчётные данные и технические формулы, которые
могут быть использованы как производственниками, так и проектировщиками при
ОТ РЕДАКЦИОННОЙ КОЛЛЕГИИ
7
решении технических вопросов эксплоатации и развития железнодорожного транс-
порта.
Справочник рассчитан на лиц, имеющих высшее и среднее специальное образо-
вание. В связи с этим в справочнике приводятся понятия, определения и формулы,
как правило, без объяснения их, за исключением особо сложных случаев. В гла-
вах, посвящённых машинам и технологии, наряду со справочными данными, приво-
дится также описательный материал, разъясняющий схему действия машины и
технологический процесс.
Сведения, которые относятся к различным отраслям железнодорожной работы,
помещены в целях избежания дублирования, как правило, в одном томе, например:
«Насосы», «Инженерная геология», «Электрическое освещение» и т. п.
Справочные данные по физико-математическим и общетехническим дисциплинам
помещены в первых двух томах. Конкретные вопросы железнодорожного транспорта
вынесены в специальные тома, например, в первом томе приведены общие тепловые
свойства тел, основные законы термодинамики и теплопередачи, в III томе строи-
тельная теплотехника, а в V томе—описание и тепловой расчёт паровой машины.
Таким образом, несмотря на специализацию,отдельные тома находятся во вза-
имной связи и дополняют друг друга.
Ссылки на материалы других томов и глав должны помочь читателю ориентиро-
ваться в размещении справочных материалов по томам.
Для удобства и облегчения пользования справочником в начале каждого тома
дано содержание по главам, а в конце каждого тома—алфавитные указатели.
Для ориентировки в размещении материала ниже приводится перечень основ-
ных разделов каждого тома.
I том — Физико-математический. Греческий и латинский алфавиты. Математи-
ческая символика. Математические таблицы. Математика. Химия. Механика.
Гидромеханика. Основы электротехники. Теплота. Единицы измерений и перевод-
ные таблицы.
II том — Технические расчёты. Сопротивление материалов. Теория упругости
и пластичности. Статика сооружений. Динамика сооружений. Расчёт тонкостенных
стержней. Механика грунтов. Детали машин. Сортамент и расчётные характери-
стики некоторых материалов. Топливо. Электрические машины. Электрическое
освещение. Паровые машины. Двигатели внутреннего сгорания. Паровые тур-
бины. Газовые турбины. Ветряные двигатели. Насосы. Холодильные установки и
льдозаводы. Геодезия. Инженерная геология- Метеорология. Электрические изме-
рения. Измерение температуры. Измерение расхода жидкости, пара и газов. Изме-
рение давления, числа оборотов, мощности и веса.
III том — Проектирование и постройка железных дорог. Габариты железных
дорог. Проектирование железных дорог. Экономические изыскания. Постройка
железных дорог. Основания и фундаменты. Расчёт металлических, деревянных,
бетонных, железобетонных и каменных конструкций. Здания на железнодорожном
транспорте (конструктивные элементы зданий, строительные работы). Строительные
механизмы и инструменты.
IV том—Путь и путевое хозяйство. Земляное полотно. Верхнее строение.
Устройство рельсовой колеи. Соединение путей. Основы расчёта пути на прочность
и устойчивость. Путевой инструмент. Механизация путевых работ. Текущее содер-
жание пути. Борьба со снегом, водой и песком. Ремонт и реконструкция путей.
Карьерное хозяйство.
Мостовые переходы. Опоры мостов. Деревянные, каменные, бетонные, желе-
зобетонные и металлические мосты.Постройка мостов.Определение грузоподъёмности
мостов. Усиление, ремонт и переустройство мостов. Проектирование и постройка
тоннелей. Метрополитены.
V том—Подвижной состав. Классификация и основные характеристики парово-
зов. Конструкция и тепловой расчёт паровозного котла. Паровая машина паровоза.
Парораспределение. Экипаж. Тендер. Вписывание пароврзов в кривые. Динамиче-
ский паспорт паровоза. Паровозы узкоколейных железных дорог.
8 ОТ РЕДАКЦИОННОЙ КОЛЛЕГИИ
Классификация, основные характеристики и конструкции тепловозов. Тепло-
возные двигатели. Холодильные установки тепловозов. Конструктивное оформление
передач тепловозов.
Классификация, основные характеристики вагонов. Конструкции товарных и
пассажирских вагонов. Динамика вагонов. Прочность вагонов. Тормоза. Автосцепка.
Тяговые расчёты (сопротивление поезда, сила тяги’, тормозная сила, уравнение
движения поезда, расчёт времени хода,тормозные'задачи, расход воды и топлива).
VI том — Локомотивное и вагонное хозяйство. Организация паровозного
хозяйства. Водоснабжение и водоподготовка. Организация тепловозного хозяйства.
Организация вагонного хозяйства. Организация производства на паровозоремонт-
ных и вагоноремонтных заводах. Технические условия, технология и справочные
данные по ремонту паровозов, тепловозов и вагонов. Технология сварки, литейного
и кузнечно-прессового производства. Обработка металлов резанием. Металлорежу-
щие станки. Металлорежущий инструмент. Допуски и посадки.
VII том — Сигнализация, централизация, блокировка и связь. Сигнализация
на железнодорожном транспорте. Полуавтоматическая блокировка. Механическая
централизация и станционная блокировка. Диспетчерская централизация. Автобло-
кировка. Электрическая централизация. Автостопы и кэб-сигнализация. Оповести-
тельная сигнализация.
Теория связи. Воздушные линии связи. Кабельные линии. Избирательная
связь. Телеграф. Радио на железных дорогах. Измерения и измерительная аппара-
тура. Защита линий связи. Эксплоатация устройств связи.
VIII том — Электрификация железных дорог. Тяговые подстанции (тяговые
трансформаторы, ртутные выпрямители, моторгенераторы, коммутационная аппара-
тура). Контактная сеть (опоры, схемы соединений, расчёт сети, проектирование,
эксплоатация).
Основные характеристики электровозов и моторвагонных секций. Тяговые
двигатели и их характеристики. Вспомогательные машины, электрическая аппара-
тура, аккумуляторные батареи, тормоза. Электровозное и моторвагонное депо.
Ремонт электроподвижного состава.
Потребление энергии и источники энергоснабжения железных дорог.ЦЭС,ТЭЦ,
электростанции узлов и депо, передвижные электростанции.
IX том—Эксплоатация железных дорог. Коммерческая эксплоатация желез-
ных дорог. Железнодорожные станции и узлы. Организация работы станций и
узлов. Организация движения поездов. Планирование и регулирование движением
на железнодорожном транспорте. Пассажирские перевозки. Правила технической
эксплоатации и обеспечение безопасности движения поездов. Структура органов
управления железнодорожным транспортом и их задачи. Координация работы
железных дорог и других видов транспорта.
X том—Экономика и планирование на железнодорожном транспорте. Значение
железнодорожного транспорта в системе социалистического хозяйства СССР. Произ-
водственно-финансовое планирование хозяйства социалистического транспорта.
Тарифы на грузовые и пассажирские перевозки. Труд и заработная плата на
железных дорогах. Бухгалтерский учёт на железнодорожном транспорте. Железно-
дорожная статистика.
Подробное содержание всех разделов приводится в каждом томе.
Редакционная коллегия просит всех читателей направлять свои замечания и
пожелания в Трансжелдориздат для использования их в дальнейшей работе над
материалами Технического справочника железнодорожника.
ОТ РЕДАКЦИИ ПЕРВОГО ТОМА
Содержание первого тома Технического справочника железнодорожника, как
тома физико-математического, определяется общими задачами технических справочни-
ков и специальными требованиями последующих томов ТСЖ,
Первый том ТСЖ объединяет справочные материалы по наиболее общим раз-
делам.
Математические таблицы даны, соответственно обычной практике тех-
нических справочников, в нижеследующем объёме: степени, корни, натуральные
логарифмы, длины окружностей, площади кругов и обратные величины (табл. 1),
мантиссы десятичных логарифмов (таблица 2), натуральные значения тригономет-
рических функций (табл. 3), характеристики дуг (табл. 4—6), специальные
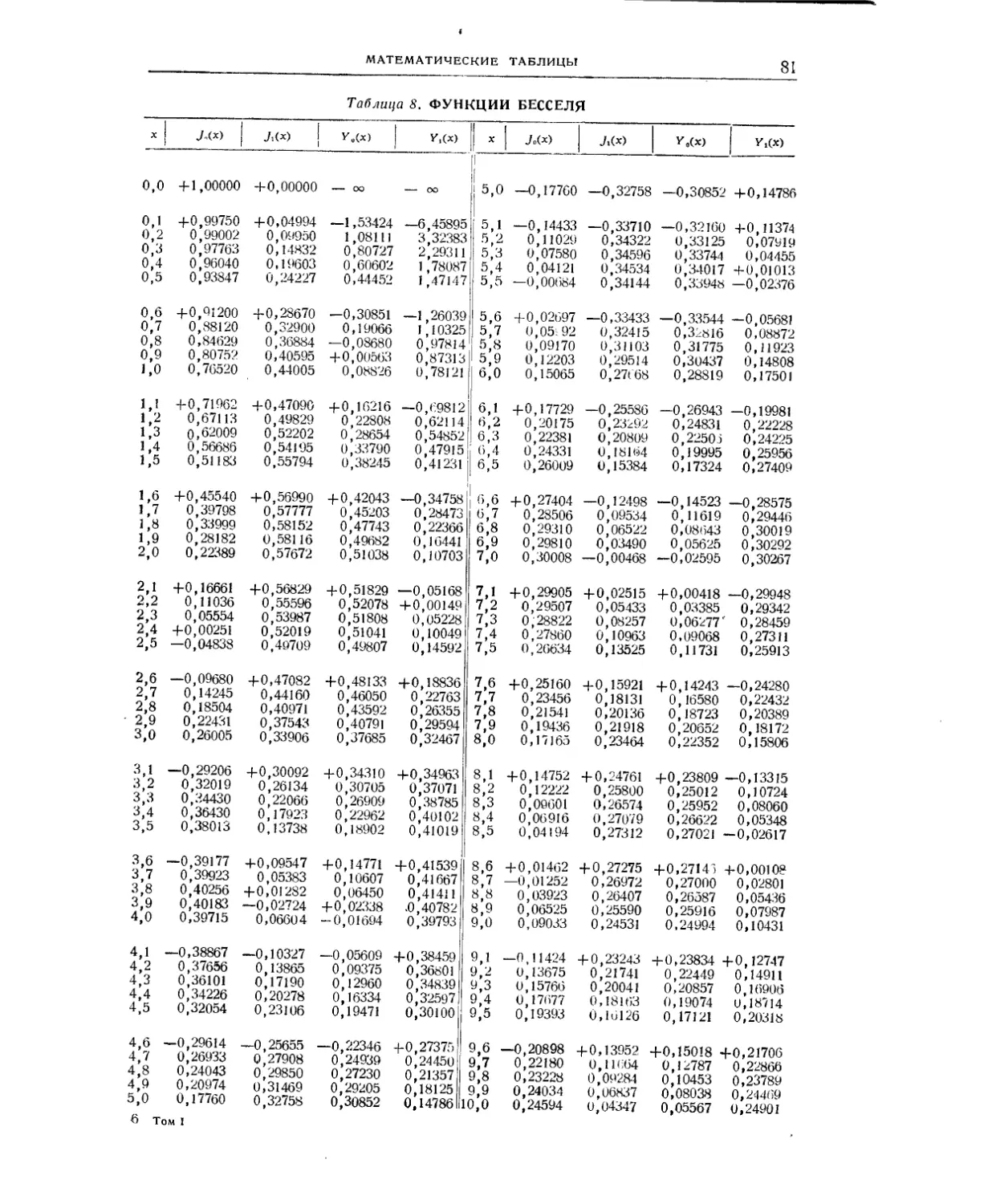
функции (табл. 7 и 8), важнейшие постоянные (табл. 9) и сводка расчётных харак-
теристик плоских фигур и тел (табл. 10 и 11).
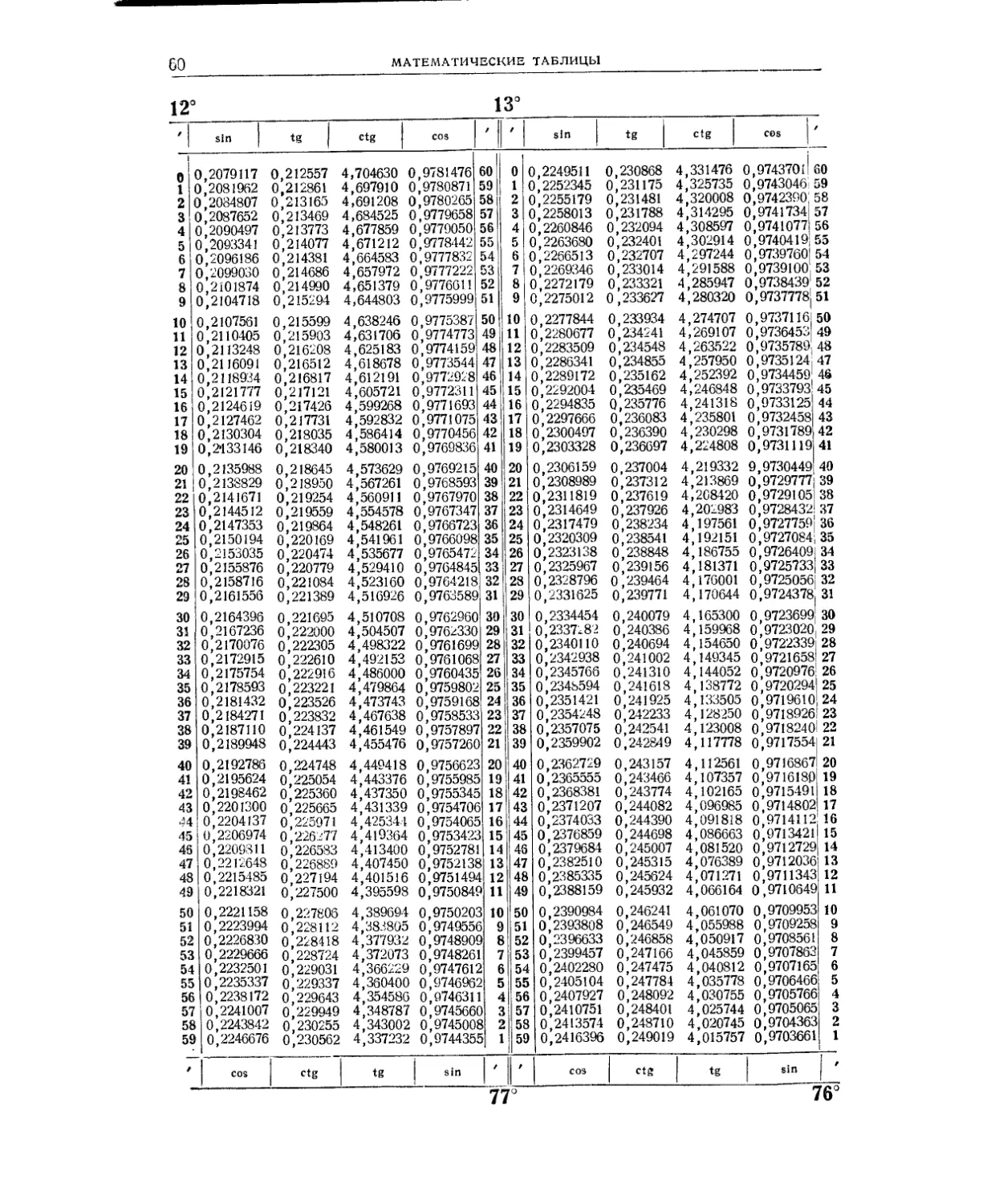
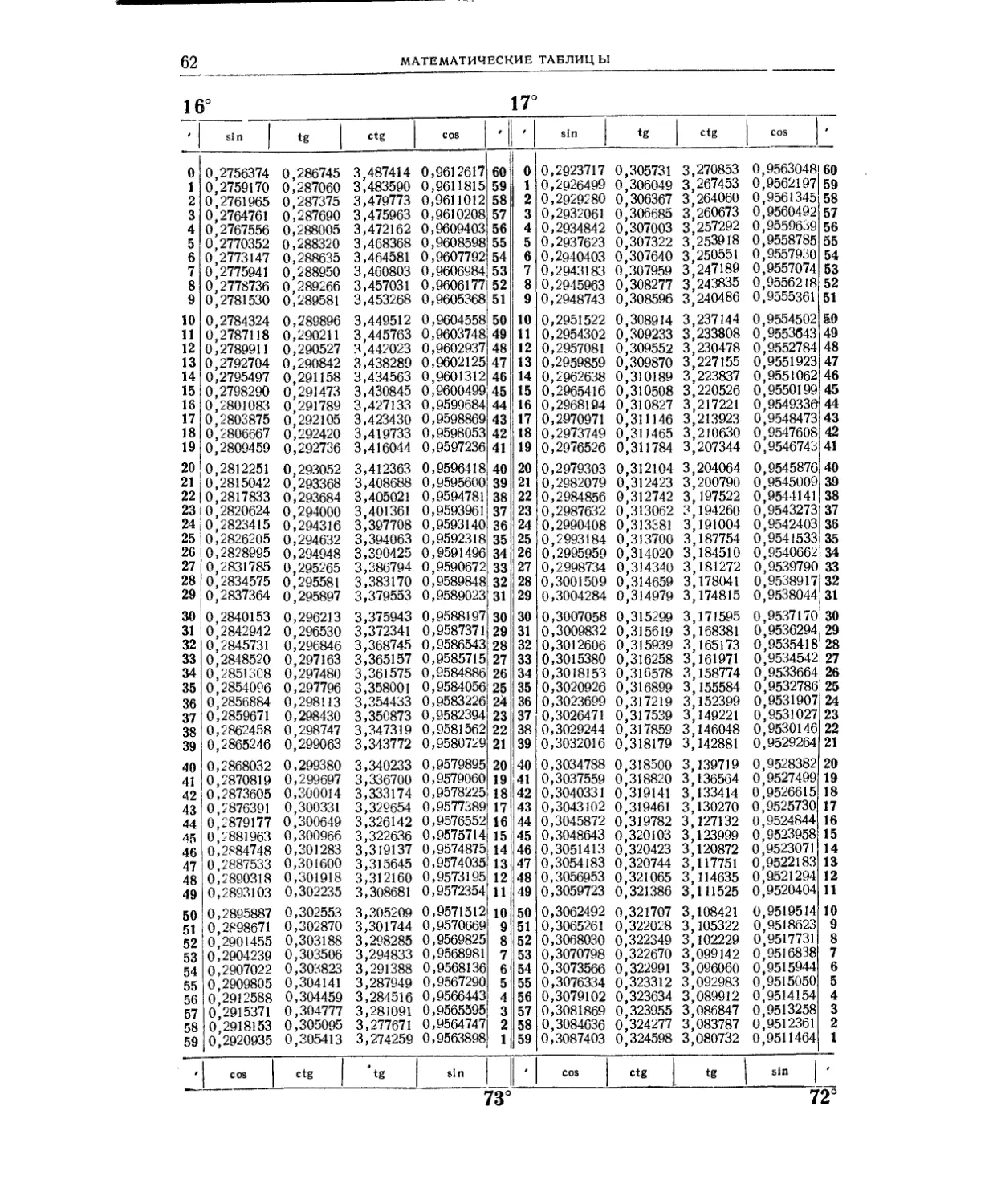
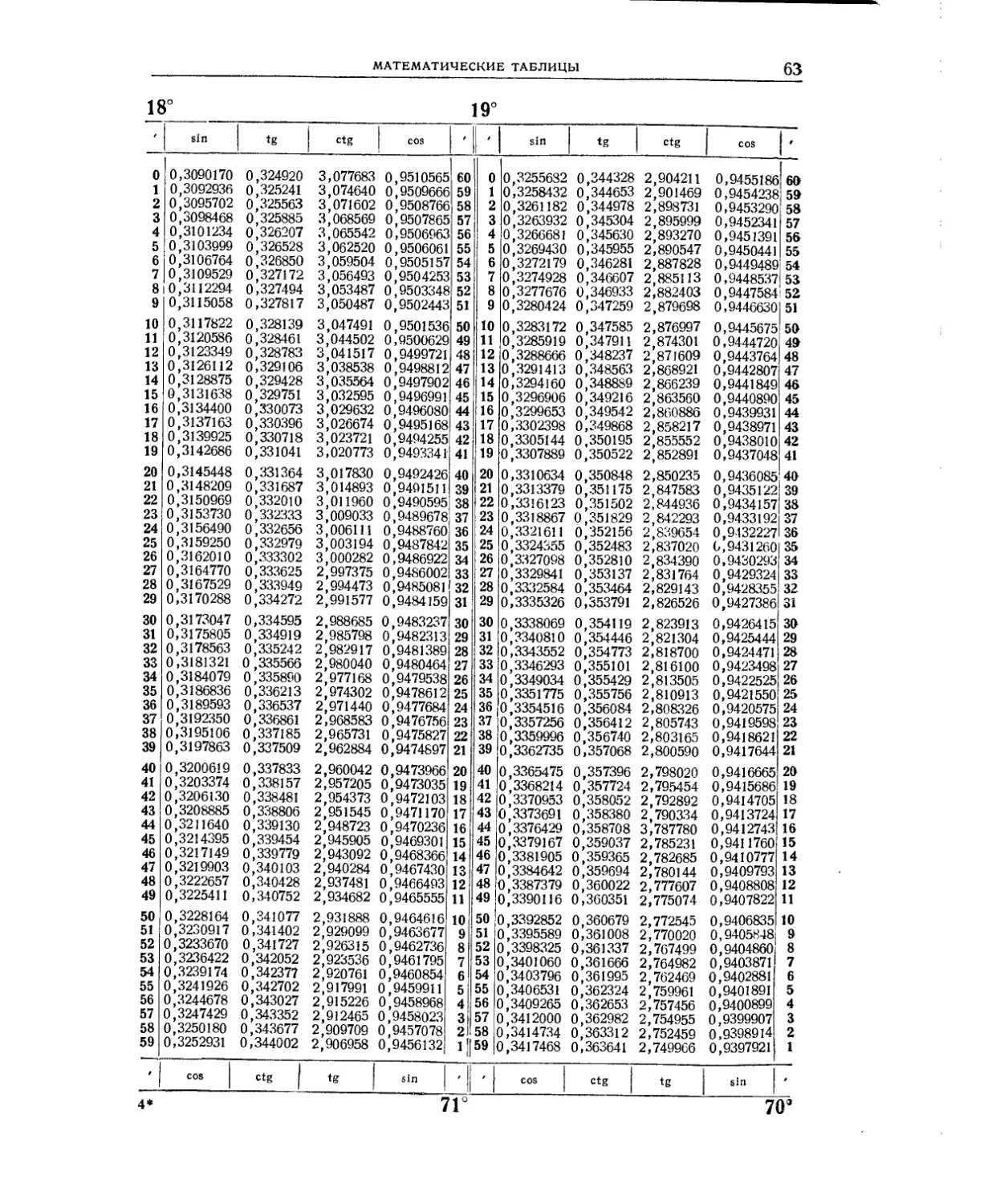
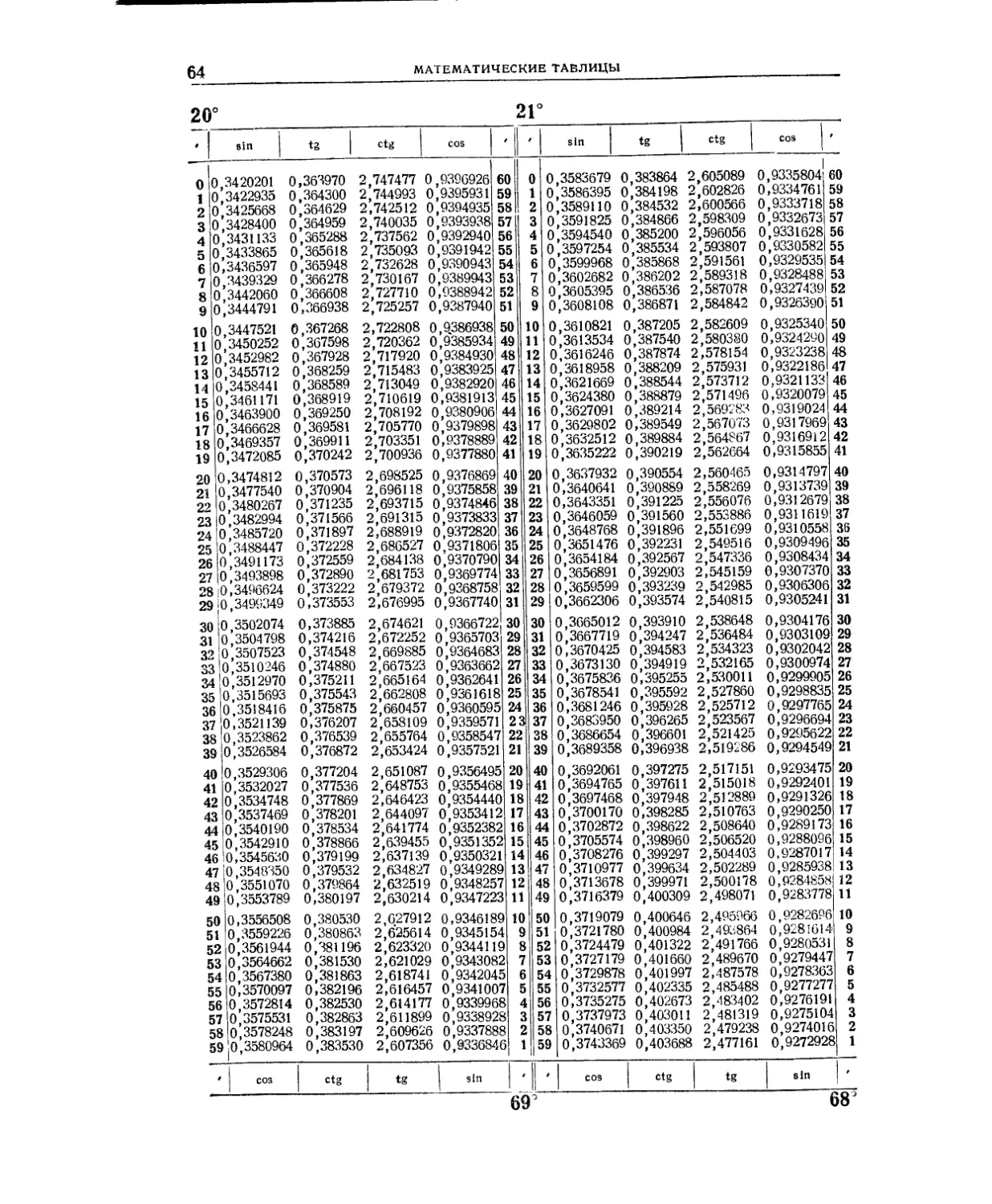
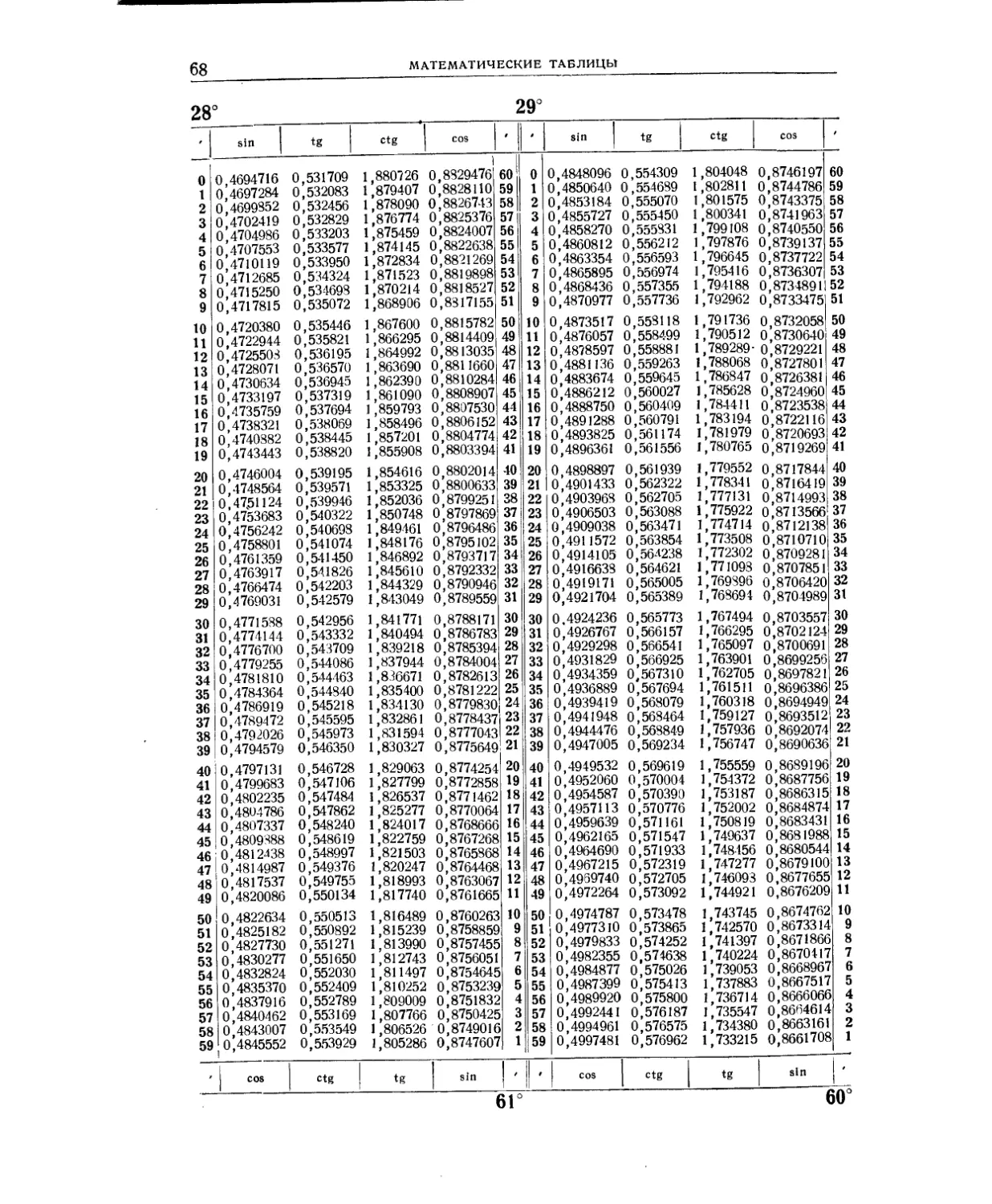
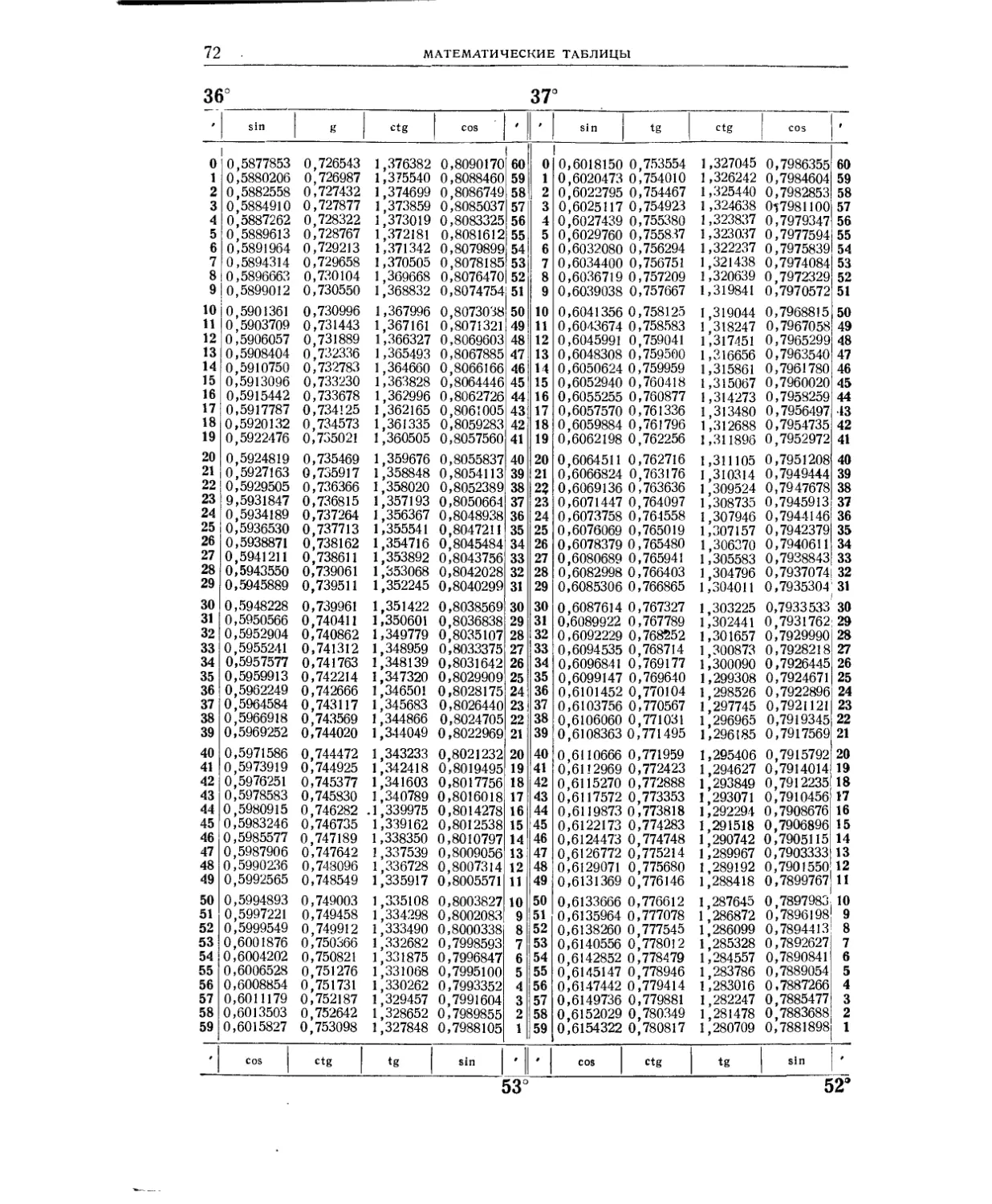
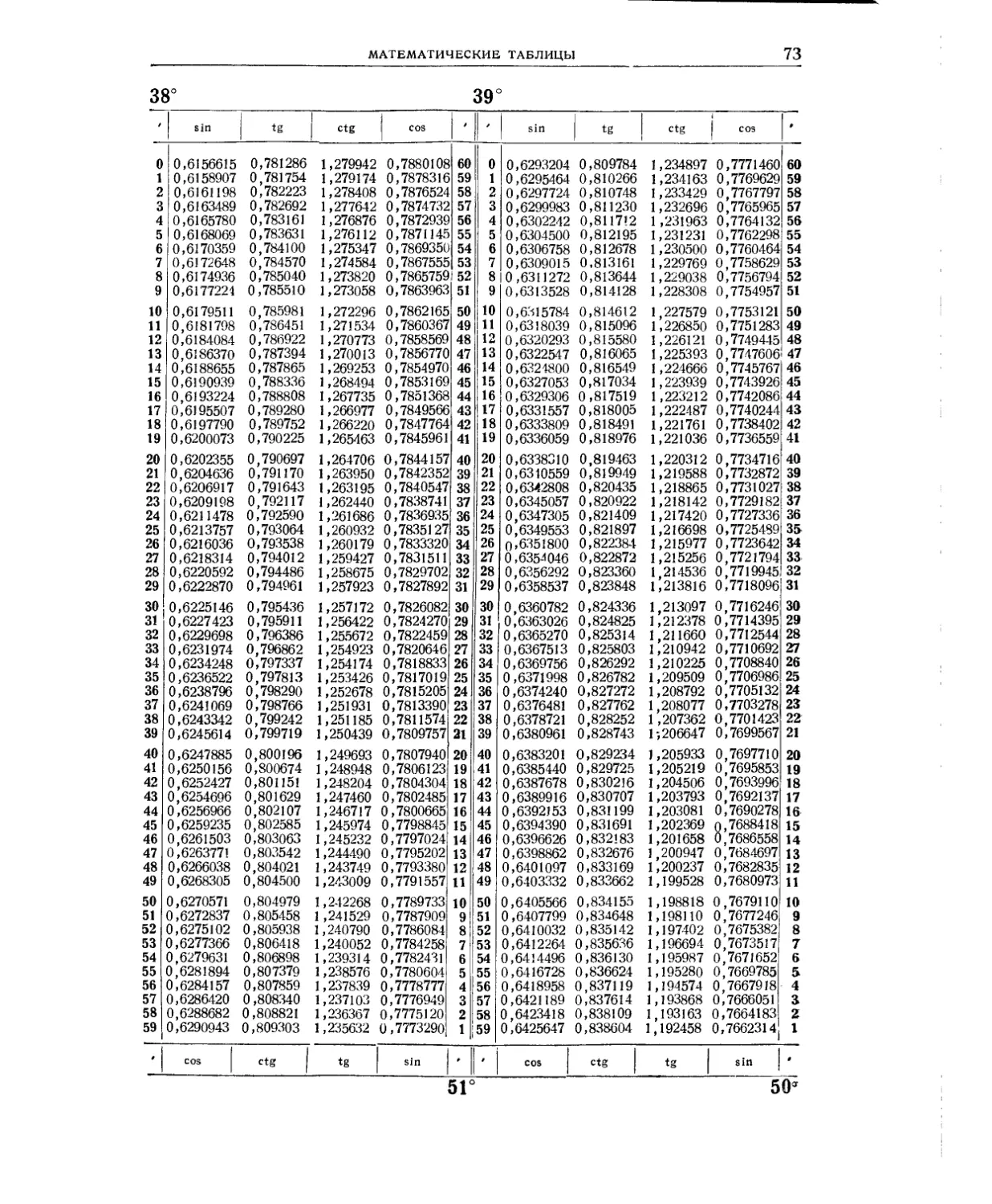
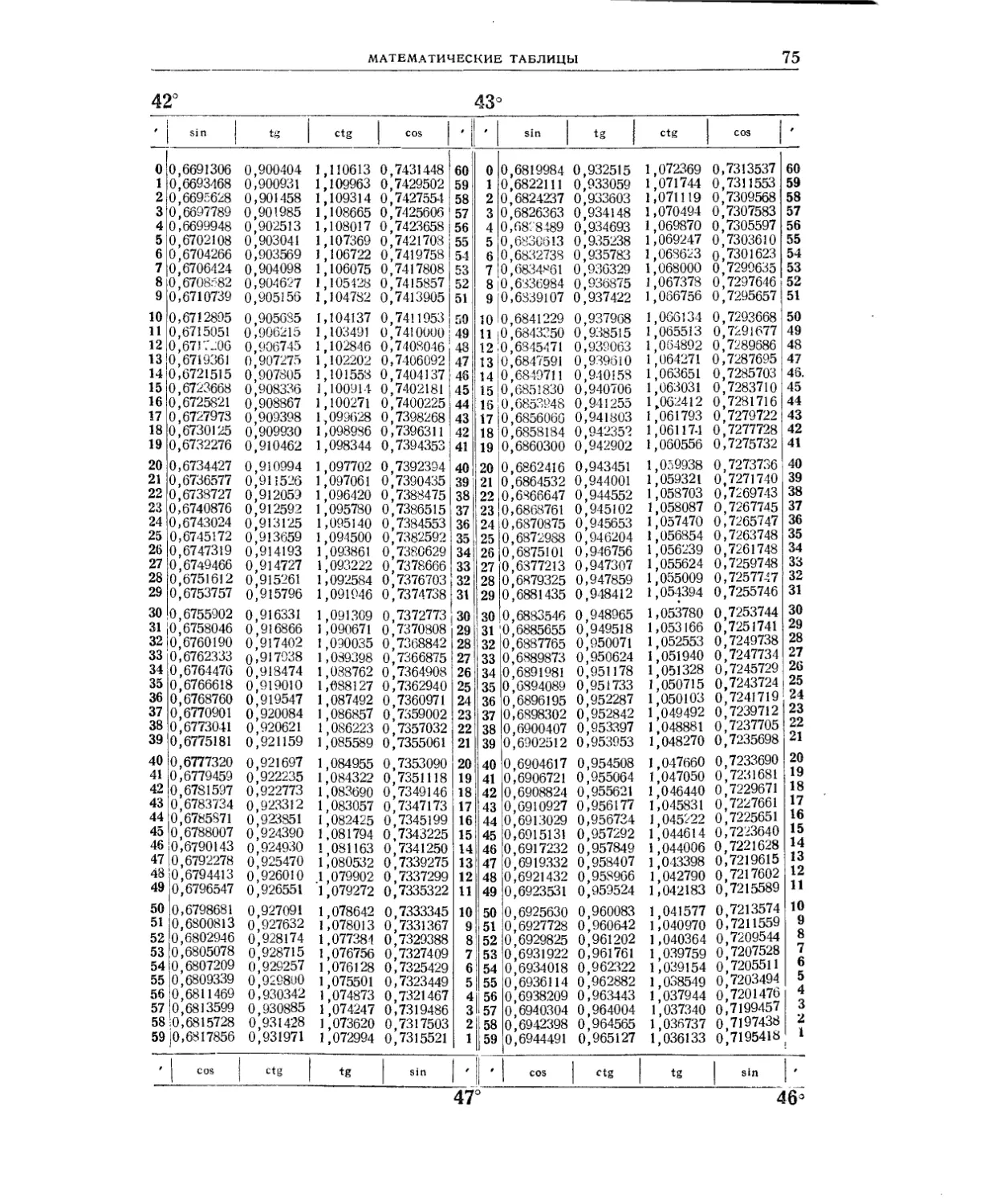
Мантиссы десятичных логарифмов (табл. 2) и натуральные значения тригоно-
метрических функций (табл. 3) даны в расширенном объёме: шестизначные мантиссы
десятичных логарифмов для аргументов от 1 до 10 000, шести-и семизначные таб-
лицы тригонометрических функций через 1'. Столь подробные таблицы исключают
необходимость применения специальных математических справочников и позволяют
осуществлять с необходимой точностью даже наиболее строгие вычисления по гео-
дезии, механике, электротехнике и т. п.
Математика охватывает общие и специальные дисциплины математического
анализа: арифметику и алгебру, геометрию, тригонометрию, диференциальное и
интегральное исчисления, ряды, диференциальные уравнения в полных и частных
производных, вариационное исчисление, аналитическую и диференциальную гео-
метрию, векторное исчисление, теорию функций комплексного переменного и эле-
менты прикладного анализа; теорию вероятностей и метод наименьших квадратов,
приближённые вычисления, построения эмпирических формул и номографию.
Относительно широкий состав математических дисциплин, начиная от арифме-
тики и геометрии, обусловлен требованиями специальных разделов железнодорож-
ной техники и преследует цели совмещения справочных материалов по математике
для наиболее широкого круга специалистов и технического персонала железнодо-
рожного транспорта.
Химия дана в объёме общих основ, неорганической, органической и физи-
ческой химии, включая основы термохимии и коллоидной химии; в целях усиления
прикладной роли справочных материалов по химии приведён обзор основных свойств
химических элементов и важнейших соединений (кислоты и соли).
Механика изложена наиболее кратко и сжато: статика и графостатика,
кинематика, динамика точек и системы; прикладные задачи механики кратко осве-
щены лишь в части теории трения, так как специальным задачам механики (напри-
мер, теории тяговых расчётов и т. п.) посвящены самостоятельные разделы после-
дующих томов ТСЖ.
10
ОТ РЕДАКЦИИ ПЕРВОГО ТОМА
Гидромеханика объединяет справочные материалы по гидростатике,
гидродинамике идеальной и вязкой жидкостей, газодинамике и прикладной
гидравлике, включая задачи гидравлики трубопроводов, движения в открытых
руслах, истечения жидкостей и подземной гидравлики (движение грунтовых вод);
справочные материалы по гидротехнике широко иллюстрированы и, по возможности,
систематизированы в форме справочных таблиц, чем обеспечено наиболее сжатое
изложение теоретического и экспериментального материала.
Основы электротехники, как и механики, даны весьма сжато—магнит-
ное поле, электрическое поле', постоянный ток, переменный ток, так как специ-
альные вопросы электротехники подробно освещаются в соответствующих разделах
ТСЖ (электротяга, связь и т. п.).
Теплота включает основы технической термодинамики и теплопередачи;
справочный материал этого раздела первого тома ТСЖ дан в наиболее распростра-
нённой редакции, характерной для технических справочников.
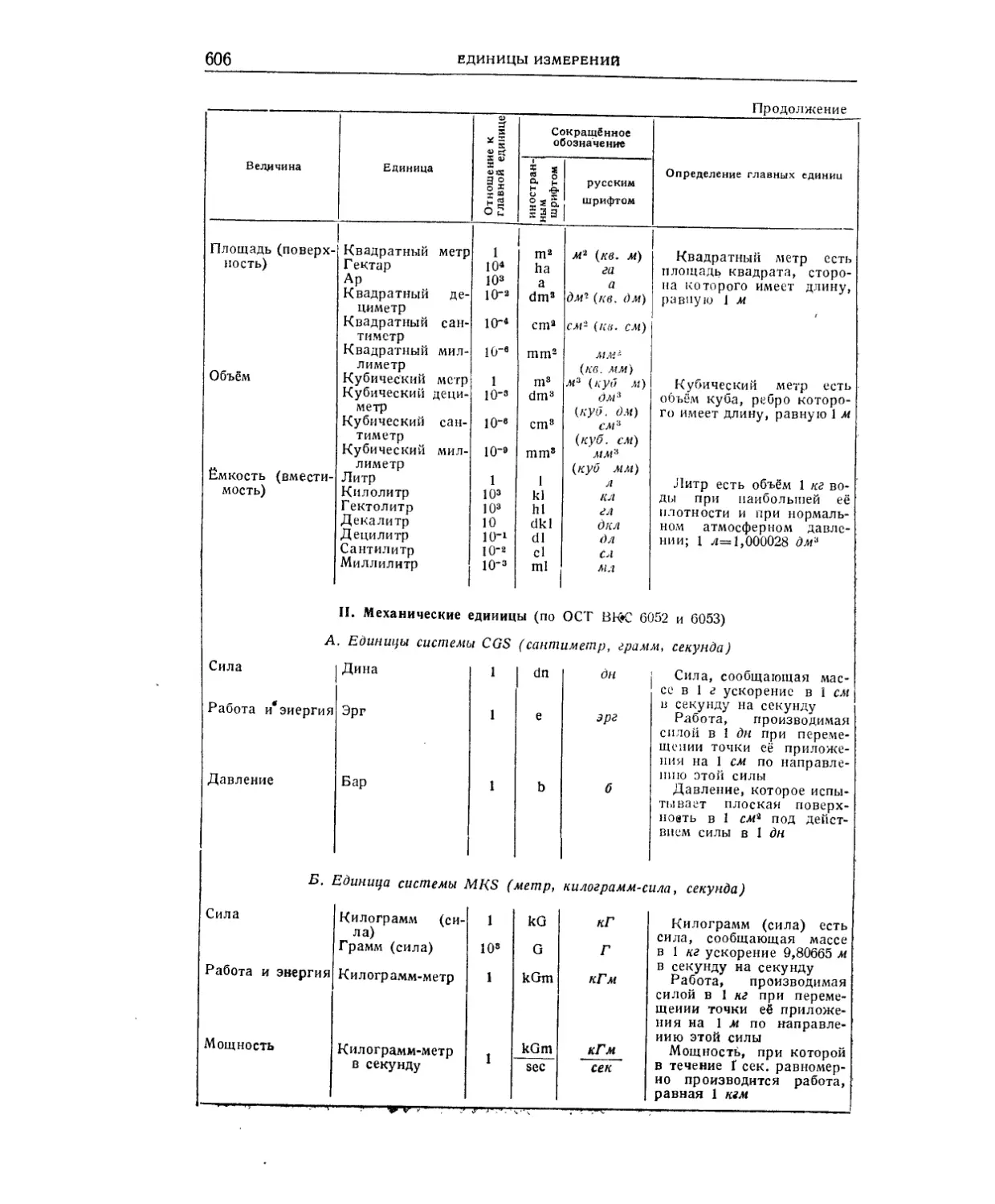
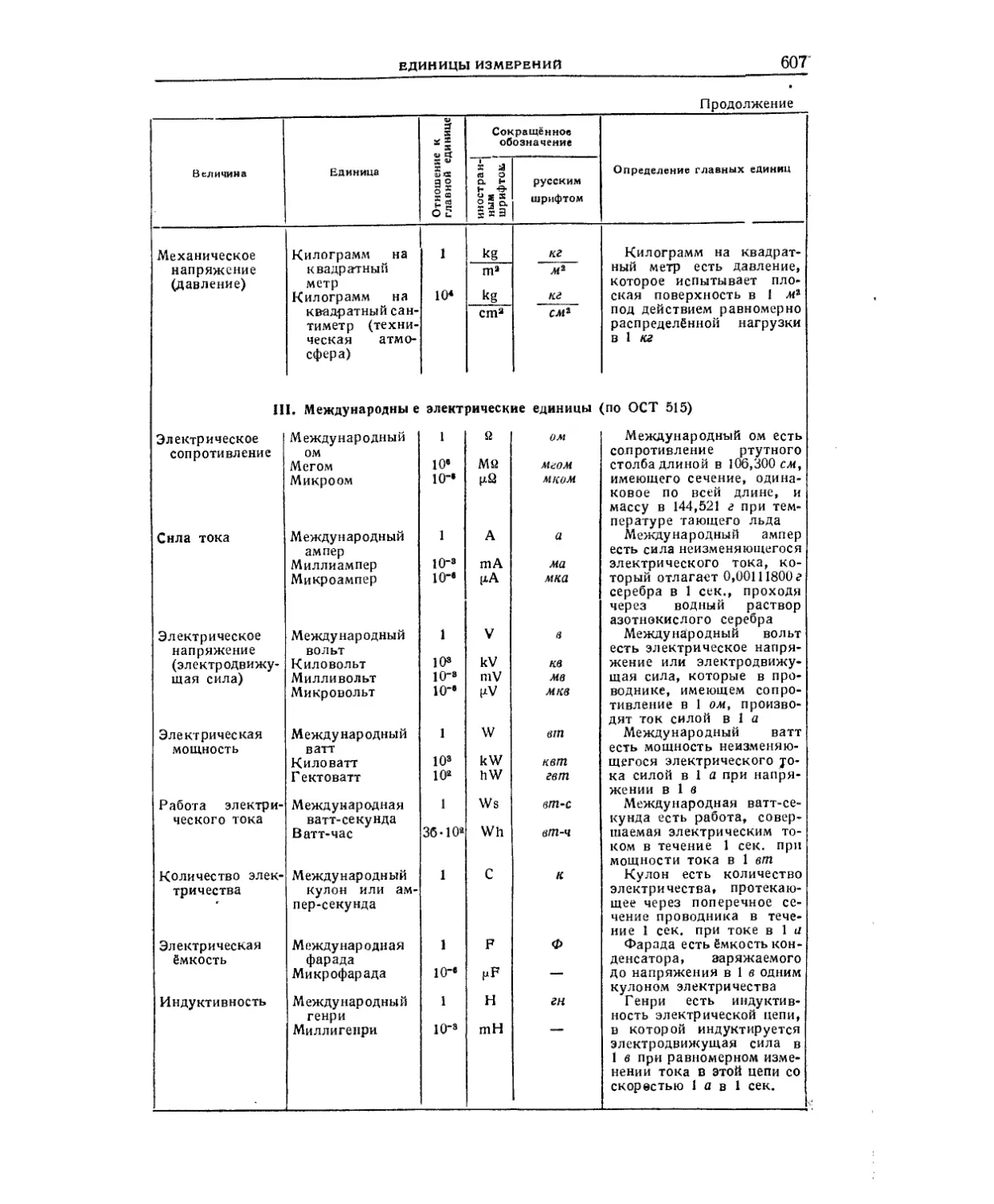
Единицы измерений даны в точной редакции соответствующих стандартов.
Наиболее трудные разделы первого тома ТСЖ, по возможности, иллюстри-
рованы примерами.
Первый том ТСЖ не может заменить специальных руководств и предполага'ет на-
личие необходимой подготовки у читателей; для облегчения пользования справочником
в случае ведения специальных расчётов в конце каждого раздела I тома ТСЖ
приведён указатель рекомендуемой литературы и важнейших первоисточников.
ТЕХНИЧЕСКИЙ
СПРАВОЧНИК
ЖЕЛЕ 3 НОДОРОЖН И КА
ТЕХНИЧЕСКИЙ
СПРАВОЧНИК
ЖЕЛЕЗНОДОРОЖНИКА
РЕДАКЦИОННАЯ КОЛЛЕГИЯ
А. Ф. БАРАНОВ, Д. Д. БИЗЮКИН,
М. И. ВАХНИН, Б. Н. ВЕДЕНИСОВ,
И. В. ИВЛИЕВ, В. И. ПОПОВ,
Е. Ф. РУДОЙ, я. и. соколинский,
В. Н. СОЛОГУБОВ, В. А. ШИЛОВСКИЙ
Главный редактор
Е. Ф. РУДОЙ
*
ГОСУДАРСТВЕННОЕ ТРАНСПОРТНОЕ
ЖЕЛЕЗНОДОРОЖНОЕ ИЗДАТЕЛЬСТВО
оИ о с к в а • 4 а 5 4.
ТЕХНИЧЕСКИМ
СПРАВОЧНИК
ЖЕЛЕ 3 НОДОРОЖН И КА
Том 1
ЧЪ?!
ФИЗИКО-
МАТЕМАТИЧЕСКИЙ
Ответственный редактор тома
проф., докт. техн, наук
Н. И. БЕЛОКОНЬ
МХ:СР
РВЩ : iff!!.:
(..Г. >! ’.ОЦ
ГОСУДАРСТВЕННОЕ ТРАНСПОРТНОЕ
ЖЕЛЕЗНОДОРОЖНОЕ ИЗДАТЕЛЬСТВО
о ск в а •
АВТОРЫ ТОМА
И. М. ВОРОНКОВ, проф., д-р техн, наук; Б. В. КЛИМЕНКОВ, доц., канд.
техн, наук; К. В. КОНСТАНТИНОВА; Н. А. КУТЫРИН, доц., канд. техн, наук;
Н. В. ЛЕВИН, инж.; Г. Л. ЛУНЦ, доц., канд. физ.-мат. наук; Г. М. ПАНЧЕН-
КОВ, проф., д-р хим. наук; М. А. ПЕТРОВ, проф., докт. техн, наук; В. И. ЧЕР-
НИКИН, доц., канд. техн, наук; А. Р. ЯНПОЛЬСКИЙ, доц., канд. техн. наук.
4
РЕЦЕНЗЕНТЫ
А. П. ЮШКЕВИЧ, проф., докт. физ.-мат. наук; А. 3. РЫВКИН; К. А. СЕМЕНДЯЕВ,
доц., канд. физ.-мат. наук (математика); К. Ф. ЖИГАЧ, проф., докт. хим. наук (химия);
В. Г. ГОГОЛАДЗЕ, проф., докт. техн, наук; А. У. ГАЛЕЕВ, доц., канд. техн, наук (механи-
ка); И. А. ЧАРНЫЙ, проф., докт. техн, наук; Я. 3. РАБИНОВИЧ, доц., канд. техн, наук
(гидромеханика); И. И. МЕНЩИКОВ, доц,, канд. техн, наук; М. Д. НАХОДКИН, доц. (ос-
новы электротехники); В. К. КОШКИН, проф., докт. техн, наук; В. М. ТАРЕЕВ, проф.,
докт. техн, наук (теплота); В. С. ЛЕВИЦКИЙ, доц., канд. техн, наук (графический материал).
*
РЕДАКЦИЯ ТОМАг
Н. И. БЕЛОКОНЬ, М. Л. РУДОЙ, В. Я. ЧЕРНЯВСКИЙ
СОДЕ РЖАН И Е
Стр.
От редакционной коллегии ................... 6
От редакции первого тома ................... 9
АЛФАВИТ ЛАТИНСКИЙ.......................... 12
АЛФАВИТ ГРЕЧЕСКИЙ ......................... 12
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ . . 13
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ..................... 15
МАТЕМАТИКА доц., канд. физ.-мат. наук
Лунц Г. Л. и доц., канд. техн, наук Ямполь-
ский А, Р................................ 91
Арифметика и алгебра ..................... 91
Геометрия . ..................' ... . 108
Тригонометрия....................... 117
Диференциальное исчисление ........ 127
Интегральное исчисление . ................ 135
Бесконечные ряды.................... 156
Диференциальные уравнения , 165
Вариационное исчисление .................. 177
Аналитическая геометрия .................. 179
Диференциальная геометрия ................ 194
Векторное исчисление ..................... 207
Теория функций комплексного переменного 212
Теория вероятностей и метод наименьших
квадратов ............................ 222
Эмпирические формулы...................... 230
Приближённые вычисления............. 233
Приближённое решение алгебраических и
трансцендентных уравнений........... 236
Исчисление конечных разностей и интерпо-
лирование ............................ 244
Численные и графические методы анализа . 254
Номография.......................... 262
ХИМИЯ (проф., д-рхим. наукПанченковГ.М. 269
Периодическая система элементов .......... 269
Неорганическая химия (Константинова К- В.) 272
Органическая химия ....................... 294
Физическая химия (Панченков Г. М. проф.,
докт. хим. наук и канд. хим. наук Кли-
менков Б. В.-) 315
Коллоидная химия.......................... 349
МЕХАНИКА (проф., докт. техн, наук Во-
ронков И. М. и инж. Левин Н. В.) , , . 357
Основные определения . .................. 357
Статика..................ф................ 357
Стр.
Кинематика ............................ 368
Динамика................................ 375
Центр тяжести и моменты инерции........ 390
Трение.................................. 398
ГИДРОМЕХАНИКА (доц., канд. техн, наук
Черникин В. И.)...................... 404
Физические свойства жидкостей.......... 404
Гидростатика.......................... 408
Гидродинамика идеальной жидкости .... 413
Гидродинамика реальной (вязкой) жидкости 420
Движение жидкости по трубам ........... 422
Расчёт трубопроводных систем........... 428
Местные сопротивления . ............... 432
Равномерное движение жидкости в открытых
руслах............................... 437
Водосливы . 443
Неравномерное движение жидкости в откры-
тых руслах . .......................... 449
Удар жидкости.......................... 458
Истечение несжимаемых жидкостей при по-
стоянном уровне........................ 461
Истечение несжимаемых жидкостей при пе-
ременном уровне........................ 465
Внешнее обтекание тел.................. 467
Движение грунтовых вод................ 469
Аэро- и газодинамика................... 474
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ (проф.,
докт. техн, наук Петров М. А.) ...... 480
Магнитное поле ..................... 480
Электрическое поле.................. 486
Постоянный ток .................... 490
Переменный ток...................... 497
ТЕПЛОТА (доц., канд. техн, наук Кутырин
Н. А.)................................... 510
Общие тепловые свойства тел............... 510
Термодинамика . ... . 527
Газы............ .... ......... 531
Водяной пар • 546
Течение газов и паров по трубам, истечение
из резервуаров .................... . 568
Теплопередача ............................ 574
ЕДИНИЦЫ ИЗМЕРЕНИЙ .......... 605
АЛФАВИТНЫЙ УКАЗАТЕЛЬ....... 615
ОТ РЕДАКЦИОННОЙ КОЛЛЕГИИ
ТЕХНИЧЕСКОГО СПРАВОЧНИКА ЖЕЛЕЗНОДОРОЖ НИКА
Огромные изменения, происшедшие на железнодорожном транспорте за последние
15 лет со времени выхода в свет Технического справочника транспортника, настоя-
тельно требуют издания нового справочного руководства для железнодорожников.
Сталинские пятилетки коренным образом преобразили железнодорожный транс-
порт СССР. Советский железнодорожный транспорт в результате оснащения новой
техникой и развития стахановского движения стал передовой отраслью народного
хозяйства. Это позволило транспорту в годы Великой Отечественной войны с
честью выдержать нагрузку, с которой, как отметил товарищ Сталин, едва ли
справился транспорт любой другой страны.
Организованный партией Ленина — Сталина после победоносного окончания
Великой Отечественной войны новый мощный хозяйственный и культурный подъём
позволил железнодорожному транспорту в короткие сроки не только залечить раньц
нанесённые войной, но и двинуться вперёд по пути дальнейшего технического
прогресса и обеспечения потребностей народного хозяйства передвижными сред-
ствами.
Превысив в 1948 г. довоенный уровень грузооборота, железнодорожный транс-
порт успешно выполняет послевоенный пятилетний план.
Благодаря повседневным заботам партии, советского правительства и лично
товарища Сталина железные дороги оснащаются во всё возрастающих количествах
новой высокопроизводительной отечественной техникой.
Подвижной состав пополняется новыми конструкциями паровозов, тепловозов,
электровозов, грузовых и пассажирских вагонов. Путевое хозяйство значительно
усиливается усовершенствованными механизмами.
Широко механизируются трудоёмкие работы. Растёт число механизированных
сортировочных горок. Всё в больших размерах на транспорте находят применение
радио, телеуправление, различные устройства, улучшающие безопасность движения
поездов и увеличивающие пропускную н провозную способность железнодорожных
линий.
В депо, на заводах, стройках, станциях, дистанциях растёт производственная
культура, совершенствуются технологические процессы.
В Техническом справочнике железнодорожника обобщены и систематизирова-
ны важнейшие справочные данные по основным вопросам техники и экономики
железнодорожного транспорта.
Коллектив авторов, рецензентов и редакторов справочника стремился создать
пособие, отвечающее требованиям современного развития науки и техники в области
транспорта, с учётом достижений передовых людей железнодорожного транспорта
в использовании транспортной техники и организации технологического процесса.
В связи с этим в Техническом справочнике железнодорожника получили широкое
отражение вопросы новой техники по каждой отрасли железнодорожного хозяй-
ства; в нём помещены также расчётные данные и технические формулы, которые
могут быть использованы как производственниками, так и проектировщиками при
ОТ РЕДАКЦИОННОЙ КОЛЛЕГИИ
7
решении технических вопросов эксплоатации и развития железнодорожного транс-
порта.
Справочник рассчитан на лиц, имеющих высшее и среднее специальное образо-
вание. В связи с этим в справочнике приводятся понятия, определения и формулы,
как правило, без объяснения их, за исключением особо сложных случаев. В гла-
вах, посвящённых машинам и технологии, наряду со справочными данными, приво-
дится также описательный материал, разъясняющий схему действия машины и
технологический процесс.
Сведения, которые относятся к различным отраслям железнодорожной работы,
помещены в целях избежания дублирования, как правило, в одном томе, например:
«Насосы», «Инженерная геология», «Электрическое освещение» и т. п.
Справочные данные по физико-математическим и общетехническим дисциплинам
помещены в первых двух томах. Конкретные вопросы железнодорожного транспорта
вынесены в специальные тома, например, в первом томе приведены общие тепловые
свойства тел, основные законы термодинамики и теплопередачи, в III томе строи-
тельная теплотехника, а в V томе—описание и тепловой расчёт паровой машины.
Таким образом, несмотря на специализацию,отдельные тома находятся во вза-
имной связи и дополняют друг друга.
Ссылки на материалы других томов и глав должны помочь читателю ориентиро-
ваться в размещении справочных материалов по томам.
Для удобства и облегчения пользования справочником в начале каждого тома
дано содержание по главам, а в конце каждого тома—алфавитные указатели.
Для ориентировки в размещении материала ниже приводится перечень основ-
ных разделов каждого тома.
I том — Физико-математический. Греческий и латинский алфавиты. Математи-
ческая символика. Математические таблицы. Математика. Химия. Механика.
Гидромеханика. Основы электротехники. Теплота. Единицы измерений и перевод-
ные таблицы.
II том — Технические расчёты. Сопротивление материалов. Теория упругости
и пластичности. Статика сооружений. Динамика сооружений. Расчёт тонкостенных
стержней. Механика грунтов. Детали машин. Сортамент и расчётные характери-
стики некоторых материалов. Топливо. Электрические машины. Электрическое
освещение. Паровые машины. Двигатели внутреннего сгорания. Паровые тур-
бины. Газовые турбины. Ветряные двигатели. Насосы. Холодильные установки и
льдозаводы. Геодезия. Инженерная геология- Метеорология. Электрические изме-
рения. Измерение температуры. Измерение расхода жидкости, пара и газов. Изме-
рение давления, числа оборотов, мощности и веса.
III том — Проектирование и постройка железных дорог. Габариты железных
дорог. Проектирование железных дорог. Экономические изыскания. Постройка
железных дорог. Основания и фундаменты. Расчёт металлических, деревянных,
бетонных, железобетонных и каменных конструкций. Здания на железнодорожном
транспорте (конструктивные элементы зданий, строительные работы). Строительные
механизмы и инструменты.
IV том—Путь и путевое хозяйство. Земляное полотно. Верхнее строение.
Устройство рельсовой колеи. Соединение путей. Основы расчёта пути на прочность
и устойчивость. Путевой инструмент. Механизация путевых работ. Текущее содер-
жание пути. Борьба со снегом, водой и песком. Ремонт и реконструкция путей.
Карьерное хозяйство.
Мостовые переходы. Опоры мостов. Деревянные, каменные, бетонные, желе-
зобетонные и металлические мосты.Постройка мостов.Определение грузоподъёмности
мостов. Усиление, ремонт и переустройство мостов. Проектирование и постройка
тоннелей. Метрополитены.
V том—Подвижной состав. Классификация и основные характеристики парово-
зов. Конструкция и тепловой расчёт паровозного котла. Паровая машина паровоза.
Парораспределение. Экипаж. Тендер. Вписывание пароврзов в кривые. Динамиче-
ский паспорт паровоза. Паровозы узкоколейных железных дорог.
8 ОТ РЕДАКЦИОННОЙ КОЛЛЕГИИ
Классификация, основные характеристики и конструкции тепловозов. Тепло-
возные двигатели. Холодильные установки тепловозов. Конструктивное оформление
передач тепловозов.
Классификация, основные характеристики вагонов. Конструкции товарных и
пассажирских вагонов. Динамика вагонов. Прочность вагонов. Тормоза. Автосцепка.
Тяговые расчёты (сопротивление поезда, сила тяги’, тормозная сила, уравнение
движения поезда, расчёт времени хода,тормозные'задачи, расход воды и топлива).
VI том — Локомотивное и вагонное хозяйство. Организация паровозного
хозяйства. Водоснабжение и водоподготовка. Организация тепловозного хозяйства.
Организация вагонного хозяйства. Организация производства на паровозоремонт-
ных и вагоноремонтных заводах. Технические условия, технология и справочные
данные по ремонту паровозов, тепловозов и вагонов. Технология сварки, литейного
и кузнечно-прессового производства. Обработка металлов резанием. Металлорежу-
щие станки. Металлорежущий инструмент. Допуски и посадки.
VII том — Сигнализация, централизация, блокировка и связь. Сигнализация
на железнодорожном транспорте. Полуавтоматическая блокировка. Механическая
централизация и станционная блокировка. Диспетчерская централизация. Автобло-
кировка. Электрическая централизация. Автостопы и кэб-сигнализация. Оповести-
тельная сигнализация.
Теория связи. Воздушные линии связи. Кабельные линии. Избирательная
связь. Телеграф. Радио на железных дорогах. Измерения и измерительная аппара-
тура. Защита линий связи. Эксплоатация устройств связи.
VIII том — Электрификация железных дорог. Тяговые подстанции (тяговые
трансформаторы, ртутные выпрямители, моторгенераторы, коммутационная аппара-
тура). Контактная сеть (опоры, схемы соединений, расчёт сети, проектирование,
эксплоатация).
Основные характеристики электровозов и моторвагонных секций. Тяговые
двигатели и их характеристики. Вспомогательные машины, электрическая аппара-
тура, аккумуляторные батареи, тормоза. Электровозное и моторвагонное депо.
Ремонт электроподвижного состава.
Потребление энергии и источники энергоснабжения железных дорог.ЦЭС,ТЭЦ,
электростанции узлов и депо, передвижные электростанции.
IX том—Эксплоатация железных дорог. Коммерческая эксплоатация желез-
ных дорог. Железнодорожные станции и узлы. Организация работы станций и
узлов. Организация движения поездов. Планирование и регулирование движением
на железнодорожном транспорте. Пассажирские перевозки. Правила технической
эксплоатации и обеспечение безопасности движения поездов. Структура органов
управления железнодорожным транспортом и их задачи. Координация работы
железных дорог и других видов транспорта.
X том—Экономика и планирование на железнодорожном транспорте. Значение
железнодорожного транспорта в системе социалистического хозяйства СССР. Произ-
водственно-финансовое планирование хозяйства социалистического транспорта.
Тарифы на грузовые и пассажирские перевозки. Труд и заработная плата на
железных дорогах. Бухгалтерский учёт на железнодорожном транспорте. Железно-
дорожная статистика.
Подробное содержание всех разделов приводится в каждом томе.
Редакционная коллегия просит всех читателей направлять свои замечания и
пожелания в Трансжелдориздат для использования их в дальнейшей работе над
материалами Технического справочника железнодорожника.
ОТ РЕДАКЦИИ ПЕРВОГО ТОМА
Содержание первого тома Технического справочника железнодорожника, как
тома физико-математического, определяется общими задачами технических справочни-
ков и специальными требованиями последующих томов ТСЖ,
Первый том ТСЖ объединяет справочные материалы по наиболее общим раз-
делам.
Математические таблицы даны, соответственно обычной практике тех-
нических справочников, в нижеследующем объёме: степени, корни, натуральные
логарифмы, длины окружностей, площади кругов и обратные величины (табл. 1),
мантиссы десятичных логарифмов (таблица 2), натуральные значения тригономет-
рических функций (табл. 3), характеристики дуг (табл. 4—6), специальные
функции (табл. 7 и 8), важнейшие постоянные (табл. 9) и сводка расчётных харак-
теристик плоских фигур и тел (табл. 10 и 11).
Мантиссы десятичных логарифмов (табл. 2) и натуральные значения тригоно-
метрических функций (табл. 3) даны в расширенном объёме: шестизначные мантиссы
десятичных логарифмов для аргументов от 1 до 10 000, шести-и семизначные таб-
лицы тригонометрических функций через 1'. Столь подробные таблицы исключают
необходимость применения специальных математических справочников и позволяют
осуществлять с необходимой точностью даже наиболее строгие вычисления по гео-
дезии, механике, электротехнике и т. п.
Математика охватывает общие и специальные дисциплины математического
анализа: арифметику и алгебру, геометрию, тригонометрию, диференциальное и
интегральное исчисления, ряды, диференциальные уравнения в полных и частных
производных, вариационное исчисление, аналитическую и диференциальную гео-
метрию, векторное исчисление, теорию функций комплексного переменного и эле-
менты прикладного анализа; теорию вероятностей и метод наименьших квадратов,
приближённые вычисления, построения эмпирических формул и номографию.
Относительно широкий состав математических дисциплин, начиная от арифме-
тики и геометрии, обусловлен требованиями специальных разделов железнодорож-
ной техники и преследует цели совмещения справочных материалов по математике
для наиболее широкого круга специалистов и технического персонала железнодо-
рожного транспорта.
Химия дана в объёме общих основ, неорганической, органической и физи-
ческой химии, включая основы термохимии и коллоидной химии; в целях усиления
прикладной роли справочных материалов по химии приведён обзор основных свойств
химических элементов и важнейших соединений (кислоты и соли).
Механика изложена наиболее кратко и сжато: статика и графостатика,
кинематика, динамика точек и системы; прикладные задачи механики кратко осве-
щены лишь в части теории трения, так как специальным задачам механики (напри-
мер, теории тяговых расчётов и т. п.) посвящены самостоятельные разделы после-
дующих томов ТСЖ.
10
ОТ РЕДАКЦИИ ПЕРВОГО ТОМА
Гидромеханика объединяет справочные материалы по гидростатике,
гидродинамике идеальной и вязкой жидкостей, газодинамике и прикладной
гидравлике, включая задачи гидравлики трубопроводов, движения в открытых
руслах, истечения жидкостей и подземной гидравлики (движение грунтовых вод);
справочные материалы по гидротехнике широко иллюстрированы и, по возможности,
систематизированы в форме справочных таблиц, чем обеспечено наиболее сжатое
изложение теоретического и экспериментального материала.
Основы электротехники, как и механики, даны весьма сжато—магнит-
ное поле, электрическое поле', постоянный ток, переменный ток, так как специ-
альные вопросы электротехники подробно освещаются в соответствующих разделах
ТСЖ (электротяга, связь и т. п.).
Теплота включает основы технической термодинамики и теплопередачи;
справочный материал этого раздела первого тома ТСЖ дан в наиболее распростра-
нённой редакции, характерной для технических справочников.
Единицы измерений даны в точной редакции соответствующих стандартов.
Наиболее трудные разделы первого тома ТСЖ, по возможности, иллюстри-
рованы примерами.
Первый том ТСЖ не может заменить специальных руководств и предполага'ет на-
личие необходимой подготовки у читателей; для облегчения пользования справочником
в случае ведения специальных расчётов в конце каждого раздела I тома ТСЖ
приведён указатель рекомендуемой литературы и важнейших первоисточников.
АЛФАВИТЫ
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ
и
ТАБЛИЦЫ
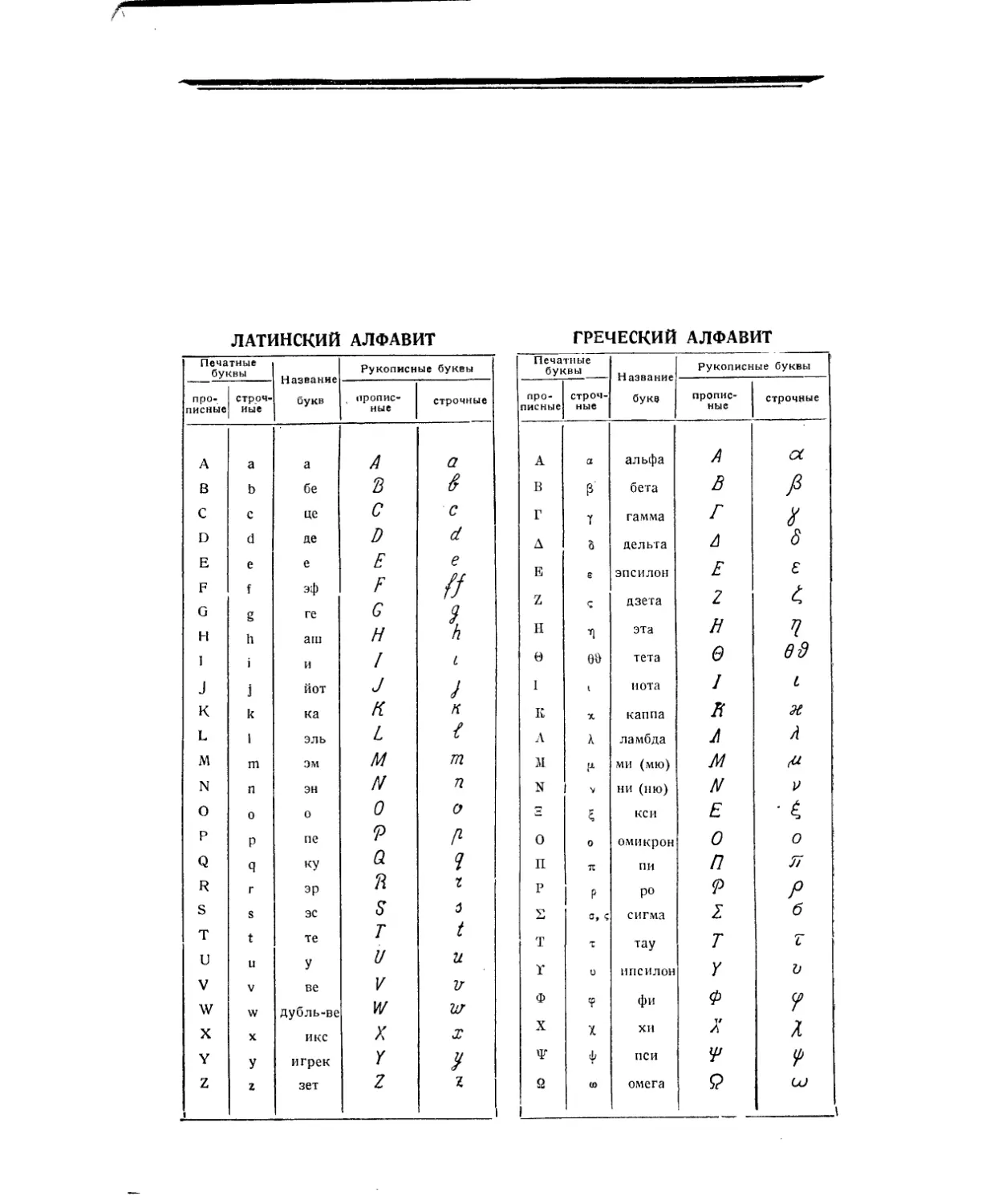
ЛАТИНСКИЙ АЛФАВИТ
ГРЕЧЕСКИЙ АЛФАВИТ
Печатные буквы Название букв Рукописные буквы
про- писные строч- ные пропис- ные строчные
А а a А а
В ь бе В 3
С с це С с
D d де D d
Е е е Е е
F f эф F ff
G g ге G %
Н h аш Н h
I i и / L
J j йот J
К k ка К к
L 1 эль L /
М m эм М тп
N n эн N п
О 0 О 0 0
Р p пе ? л
Q q ку а
R r эр В г
S s эс S л
т t те Т t
и u У и и
V V ве V V
W w дубль-ве W W
X X ИКС X X
Y У игрек Y у
Z z зет Z 1
Печатные буквы Название букв рукописные буквы
про- писные строч- ные пропис- ные строчные
А а альфа А ос
В ₽ бета В
Г т гамма р «У
д 3 дельта А 8
Е е эпсилон Е £
Z С дзета Z
н *1 эта Н п
0 о» тета в ед
1 1 йота I 1
к X каппа В эе
л л ламбда л А
JI ми (мю) м
N ч ни (ню) N и
2 г. кси Е • <
О О омикрон О О
п тс пи п Л
р р ро <р Р
S О» S сигма Z б
т т тау т Г
У и ипсилон Y V
ф ? фи Ф
X X хи X X
ф- ф пси ф
2 1 со омега со
I____________________________________________________________________________________________________________
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ (ОСНОВНЫЕ) ОСТ 573
(Редакция 1931 г.)
I. Обозначения чисел
В многозначном целом числе цифры раз-
биваются на группы по три справа налево,
причём группы отделяются друг от друга
промежутками; например : 1 411 312.
Десятичная дробь отделяется от целой ча-
сти запятой; при отсутствии целой части
на её место ставится нуль. В случае боль-
шого числа десятичных знаков они разби-
ваются на группы по три слева направо про-
межутками; например: 13,563 93.
Для обозначения обыкновенной дроби при-
меняется горизонтальная черта; например:
7
22
Примечание. Для удобства печатания до-
пускается косая черта, если это не вызывает не-
доразумений.
В смешанном числе правильная дробь ста-
вится непосредственно за целой частью; на-
2
пример: 7 -j-
% — процент
°/оо — промилле
Положительный характер числа знаком не
отмечается, кроме тех случаев, когда это
требуется отметить; в этих случаях ставит-
ся впереди знак + (плюс); например: 4- 5
Отрицательный характер числа обозна-
чается поставленным впереди знаком (ми-
нус); например: —5
Абсолютное значение числа обозначается
двумя вертикальными чертами; например:
| - 5 |
II. Обозначения соотношений
= равно
s тождественно или тождественно равно
(применяется в случае, когда желательно
особо отметить тождественность обеих ча-
стей равенства)
неравно
к приближённо равно
< меньше
> больше
< меньше или равно (не больше)
> больше или равно (не меньше)
< мало сравнительно с
> велико сравнительно с
III . Обозначения основных действий
+ (плюс) сложение
— (минус) вычитание
• или х умножение
Знак умножения обычно не ставится пе-
ред числом, обозначенным буквой, и перед
скобками.
: или ----------- деление
ат а в степени т
у/ квадратный корень
i квадратный корень из—1;/= j/” — 1
mz- —
у корень степени т при т -А 2
log6 логарифм при основании Ь.
Примечание. В тех случаях, когда нет на-
добности указывать основание, соответствующий
подстрочный значок при leg опускается.
1g логарифм при основании 10 (обыкновен-
ный или десятичный логарифм)
In логарифм при основании е = 2,718 28...
(натуральный логарифм)
Для обозначения степени логарифма пока-
затель степени ставится при знаке логариф-
ма, например: logj; а
( ) круглые
[ ] квадратные
| } фигурные
скобки
IV . Геометрические обозначения
| перпендикулярно
|| параллельно
равно и параллельно
~ подобно
Л треугольник; например: Л АВС
/ плоский угол; например: / АВС
Примечание. В тех случаях, когда могут
возникнуть недоразумения, для обозначения угла
можно применять более сложный знак
14
МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ
/л или о дуга; например: о АВ, АВ
° — градус
* — минута
3 — секунда
при обозначении величины
плоского угла или дуги;
например: 2° 3' 4*
Если обозначение ° (градус), ' (минута)
или • (секунда) относится к числу, содер-
жащему десятичную дробь, то оно ставится
над запятой; например: 3°,41; 6°5',27;
8° 4' 2',9.
л — отношение длины окружности к диа-
метру; л = 3,141 59 . . ,
V. Обозначения тригонометрических
и гиперболических функций
Тригонометрические функции:
sin синус
cos косинус
tg тангенс
ctg котангенс
sec секанс
cosec косеканс
Для обозначения степени тригонометри-
ческой функции показатель степени ставит-
ся при знаке этой функции; например: sin2x.
Для обозначения обратных тригономет-
рических функций перед вышеуказанными
обозначениями ставится arc (arcus — дуга);
например: arcsinx— дуга, синус которой
равен х
arc sin арксинус
arc cos арккосинус
arc tg арктангенс
arc ctg арккотангенс
Гиперболические функции:
sh синус гиперболический
ch косинус гиперболический
th тангенс гиперболический
cth котангенс гиперболический
Для обозначения степени гиперболической
функции показатель степени ставится при
знаке этой функции; например: sh2x
Для обозначения обратных гиперболиче-
ских функций перед вышеуказанными обо-
значениями ставится Ar (area — площадь);
например: Arsh х —площадь, соответствую-
щий гиперболический синус которой равен х
Ar sh арсинус гиперболический
Arch аркосинус гиперболический
Ar th артангенс гиперболический
Ar cth аркотангенс гиперболический
VI. Обозначения математического анализа
Постоянные числа обозначаются преиму-
щественно первыми буквами латинского ал-
фавита; например: а, Ь, с, ....
Переменные числа обозначаются преиму-
щественно последними буквами латинского
алфавита; например: х, у, z, и, . . .
Функция одного или нескольких перемен-
ных обозначается одним из знаков: / ( ),
<? ( ), Ф ( ), • • •; например: / (х), / (х,
У. *)•
const постоянное
оо бесконечность
lim предел
—> стремится к; например х —> а,
А приращение
d диференциал
8 вариация
• • •> iv v обозначения последовательных
производных от функции одного перемен-
ного; например: /'(х), у', / iv(x), yV.
Примечания: 1. Если порядок производной
обозначается буквой или арабской цифрой, то эта
буква или цифра ставится в скобках; например:
/з) /а)
/ (ЭС), /(у)*
2. Для обозначения первой или второй произ-
водной в особых случаях допускается применение
одной или двух точек, помещаемых над зависи-
мой переменной, например; г, х
d
-^первая производная от некоторой функции
по переменному х: например:
dy_
dx' dx'
dn
производная
п-го порядка при п<1 от
некоторой функции по переменному х; напри-
d2/ d3y
мер: dx2’ dx3’
fx’ iy'ixx’ixy
д У d2L &L
dx' dy' dx2’ dxdy
частные производные от функции /
нескольких переменных х, у, z........
X сумма, например: ц=их-|-ц24- . . -+ип
К=1
J интеграл
ь
J определенный интеграл от нижнего пре-
а
дела а до верхнего предела Ь.
П произведение; например:
П ик . . . ип
к=1
и! факториал; п! — 1 • 2 • 3 . . . п
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
15
Таблица 1. СТЕПЕНИ, КОРНИ, НАТУРАЛЬНЫЕ ЛОГАРИФМЫ, ДЛИНЫ
ОКРУЖНОСТЕЙ, ПЛОЩАДИ КРУГОВ И ОБРАТНЫЕ ВЕЛИЧИНЫ
1—50
п л* п3 In /Юп 3;~ Vп In п пп‘ ЯЛ2 4 1000 п п
1 1 1 1,00000 3,16228 1,00000 0,00000 3,1416 0,7853981000,000 1
2 4 8 1,41421 4,47214 1,25992 0,69315 6,2832 3,14159 500,000 2
3 9 27 1,73205 5,47723 1,44225 1,09861 9,4248 7,06858 333,333 3
4 16 64 2,00000 6,32456 1,58740 1,38629 12,566 12,5664 250,000 4
5 25 125 2,23607 7,07107 1,70998 1,60944 15,708 19,6350 200,000 5
6 36 216 2,44949 7,74597 1,81712 1,79176 18,850 28,2743 166,667 6
7 49 343 2,64575 8,36660 1,91293 1,94591 21,991 38,4845 142,857 7
8 64 512 2,82843 8,94427 2,00000 2,07944 25,133 50,2655 125,000 8
9 81 729 3,00000 9,48683 2,08008 2,19722 28,274 63,6173 111,111 9
10 100 1000 3,16228 10,0000 2,15443 2,30259 31,416 78,5398 100,000 10
11 1 21 1 331 3,31662 10,4881 2,22398 2,39790 34,558 95,0332 90,9091 11
12 1 44 1 728 3,46410 10,9545 2,28943 2,48491 37,699 113,097 83,3333 12
13 1 69 2 197 3,60555 11,4018 2,35133 2,56495 40,841 132,732 76,9231 13
14 1 96 2 744 3,74166 11,8322 2,41014 2,63906 43,982 153,938 71,4286 14
15 2 25 3375 3,87298 12,2474 2,46621 2,70805 47,124 176,715 66,6667 15
16 2 56 4 096 4,00000 12,6491 2,51984 2,77259 50,265 201,062 62,5000 16
17 2 89 4913 4,12311 13,0384 2,57128 2,83321 53,407 226,980 58,8235 17
18 3 24 5832 4,24264 13,4164 2,62074 2,89037 56,549 254,469 55,5556 18
19 3 61 6 859 4,35890 13,7840 2,66840 2,94444 59,690 283,529 52,6316 19
20 400 8000 4,47214 14,1421 2,71442 2,99573 62,832 с >14,159 50,0000 20
21 441 9 261 4,58258 14,4914 2,75892 3,04452 65,973 346,361 47,6190 21
22 484 10 648 4,69042 14,8324 2,80204 3,09104 69,115 380,133 45,4545 22
23 529 12 167 4,79583 . 15,1658 2,84387 3,13549 72,257 415,476 43,4783 23
24 5 76 13 824 4,89898 15,4919 2,88450 3,17805 75,398 452,389 41,6667 24
25 6 25 15 625 5,00000 15,8114 2,92402 3,21888 78,540 490,874 40,0000 25
26 6 76 17576 5,09902 16,1245 2,96250 3,25810 81,681 530,929 38,4615 26
27 729 19 683 5,19615 16,4317 3,00000 3,29584 84,823 572,555 37,0370 27
28 784 21 952 5,29150 16,7332 3,03659 3,33220 87,965 615,752 35,7143 28
29 8 41 24389 5,38516 17,0294 3,07232 3,36730 91,106 660,520 34,4828 29
30 900 27000 5,47723 17,3205 3,10723 3,40120 94,248 706,858 33,3333 30
31 9 61 29 791 5,56776 17,6068 3,14138 3,43399 97,389 754,768 32,2581 31
32 10 24 32 768 5,65685 17,8885 3,17480 3,46574 100,53 804,248 31,2500 32
33 10 89 35 937 5,74456 18,1659 3,20753 3,49651 103,67 855,299 30,3030 33
34 11 56 39 304 5,83095 18,4391 3,23961 3,52636 106,81 907,920 29,4118 34
35 12 25 42875 5,91608 18,7083 3,27107 3,55535 109,96 { 162,113 28,5714 35
36 12 96 46 656 6,00000 18,9737 3,30193 3,58352 113,10 1017,88 27,7778 36
37 13 69 50 653 6,08276 19,2354 3,33222 3,61092 116,24 1075,21 27,0270 37
38 1444 54 872 6,16441 19,4936 3,36198 3,63759 119,38 1134,11 26,3158 38
39 1521 59 319 6,24500 19,7484 3,39121 3,66356 122,52 1194,59 25,6410 39
40 16 00 64 000 6,32456 20,0000 3,41995 3,68888 125,66 1256,64 25,0000 40
41 1681 68 921 6,40312 20,2485 3,44822 3,71357 128,81 1320,25 24,3902 41
42 1764 74 088 6,48074 20,4939 3,47603 3,73767 131,95 1385,44 23,8095 42
43 1849 79507 6,55744 20,7364 3,50340 3,76120 135,09 1452,20 23,2558 43
44 19 36 85 184 6,63325 20,9762 3,53035 3,78419 138,23 1520,53 22,7273 44
45 20 25 91 125 6,70820 21,2132 3,55689 3,80666 141,37 1590,43 22,2222 45
46 21 16 97 336 6,78233 21,4476 3,58305 3,82864 144,51 1661,90 21,7391 46
47 22 09 103823 6,85565 21,6795 3,60883 3,85015 147,65 1734,94 21,2766 47
48 23 04 110 592 6,92820 21,9089 3,63424 3,87120 150,80 1809,56 20,8333 48
49 24 01 117 649 7,00000 22,1359 3,65931 3,89182 153,94 1885,74 20,4082 49
50 2500 125 000 7,07107 22,3607 3,68403 3,91202 157,08 1963,50 20,0000 50
Л п‘ п* l'n /1Оп In п пп яЛ1 1000 л п
16
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
50—100
п п‘ п* р 10п Э,- V" Inn пП ппа 4 1000 п п
50 2500 125 000 7,07107 22,3607 3,68403 3,91202 157,08 1963,50 20,0000 50
51 26 01 132 651 7,14143 22,5832 3,70843 3,93183 160,22 2042,82 19,6078 51
52 27 04 110 608 7,21110 22,8035 3,73251 3,95124 163,36 2123,72 19,2308 52
53 28 09 148 877 7,28011 23,0217 3,75629 3,97029 166,50 2206,18 18,8679 53
54 29 16 157 464 7,34847 23,2379 3,77976 3,98898 169,65 2290,22 18,5185 54
55 30 25 166 375 7,41620 23,4521 3,80295 4,00733 172,79 2375,83 18,1818 55
56 31 36 175616 7,48331 23,6643 3,82586 4,02535 175,93 2463,01 17,8571 56
57 32 49 185 193 7,54983 23,8747 3,84850 4,04305 179,07 2551,76 17,5439 57
58 33 64 195Н2 7,61577 24,0832 3,87088 4,06044 182,21 2642,08 17,2414 58
59 3481 205 379 7,68115 7,74597 24,2899 3,89300 4,07754 185,35 2733,97 16,9492 59
60 3600 216 000 24,4949 3,91487 4,09434 188,50 2827,43 16,6667 60
61 37 21 226 981 7,81025 24,6982 3,93650 4,11087 191,64 2922,47 16,3934 61
62 38 44 238 328 7,87401 24,8998 3,95789 4,12713 194,78 3019,07 16,1290 62
63 39 69 250 047 7,93725 25,0993 3,97906 4,14313 197,92 3117,25 15,8730 63
64 40 96 262 144 8,00000 25,2982 4,00000 4,15888 201,06 3216,99 15,6250 64
65 42 25 274 625 8,06226 25,4951 4,0-073 4,17439 204,20 3318,31 15,3846 65
66 43 56 287 496 8,12404 25,6905 4,04124 4,18965 207,35 3421,19 15,1515 66
67 44 89 300 763 8,18535 25,8844 4,06155 4,20469 210,49 3525,65 14,9254 67
68 46 24 314 432 8,24621 26,0768 4,08166 4,21951 213,63 3631,68 14,7059 68
69 47 61 328 509 8,30662 26,2679 4,10157 4,23411 216,77 3739,28 14,4928 69
70 4900 343000 8,36660 26,4575 4,12129 4,24850 219,91 3848,45 14,2857 70
71 50 41 357 911 8,42615 26,6458 4,14082 4,26268 223,05 3959,19 14,0845 71
72 51 84 373 248 8,48528 26,8328 4,16017 4,27667 226,19 4071,50 13,8889 72
73 53 29 389 017 8,54400 27,0185 4,17934 4,29046 229,34 4185,39 13,6986 73
74 54 76 405 224 8,60233 27,2029 4,19834 4,30407 232,48 4300,84 13,5135 74
75 56 25 421 875 8,66025 27,3861 4-21716 4,31749 235,62 4417,86 13,3333 75
76 57 76 438 976 8,71780 27,5681 4,23582 4,33073 238,76 4536,46 13,1579 76
77 59 29 456 533 8,77496 27,7489 4,25432 4,34381 241,90 4656,63 12,9870 77
78 60 84 474 552 8,83176 27,9285 4,27266 4,35671 245,04 4778,36 12,8205 78
79 62 41 493 039 8,88819 28,1069 4,29084 4,36945 248,19 4901,67 12,6582 79
80 64 00 512 000 8,94427 28,2843 4,30887 4,38203 251,33 5026,55 12,5000 80
81 65 61 531 441 9,00000 28,4605 4,32675 4,39445 254,47 5153,00 12,3457 81
82 67 24 551 368 9,05539 28,6356 4,34448 4,40672 257,61 5281,02 12,1951 •82
83 68 89 571 787 9,11043 28,8097 4,36207 4,41884 260,75 5410,61 12,0482 83
84 70 56 592 704 9,16515 28,9828 4,37952 4,43082 263,89 5541,77 11,9048 84
85 72 25 614 125 9,21954 29,1548 4,39683 4,44265 267,04 5674,50 11,7647 85
86 73 96 636 056 9,27362 29,3258 4,41401 4,45435 270,18 5808,80 11,6279 86
87 75 69 658503 9,32738 29,4958 4,43105 4,46591 273,32 5944,68 11,4943 87
88 77 44 681 472 9,38083 29,6648 4,44796 4,47734 276,46 6082,12 11,3636 88
89 79 21 704 969 9,43398 29,8329 4,46475 4,48864 279,60 6221,14 11,2360 89
90 81 00 729 000 9,48683 30,0000 4,48140 4,49981 282,74 6361,73 11,1111 I 90
91 82 81 753 571 9,53939 30,1662 4,49794 4,51086 285,88 6503,88 10,9890 91
92 84 64 778 688 9,59166 30,3315 4,51436 4,52179 289,03 6647,61 10,8696 92
э:- 86 49 804 357 9,64365 30,4959 4,53065 4,53260 292,17 6792,91 10,7527 93
9<1 88 36 830 584 9,69536 30,6594 4,54684 4,54329 295,31 6939,78 10,6383 94
90 25 857 375 9,74679 30,8221 4,56290 4,55388 298,45 7088,22 10,5263 95
9( 92 16 884 736 9,79796 30,9839 4,57886 4,56435 301,59 7238,2?. 10,4167 96
9Г 94 09 912 673 9,84886 31,1448 4,59470 4,57471 304,73 7389,81 10,3093 97
91 96 04 941 192 9,89949 31,3050 4,61044 4,58497 307,88 7542,96 10,2041 98
9 3 98 01 970 299 9,94987 31,4643 4,62607 4,59512 311,02 7697,69 10,1010 99
10 ) 10000 1000 000 10,00000 31,6228 4,64159 4,60517 314,16 7853,98 10,0000 100
3 — ЛПа 1000
л п1 пэ /п У Wn Уп In п ПП ~4~ п п
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
17
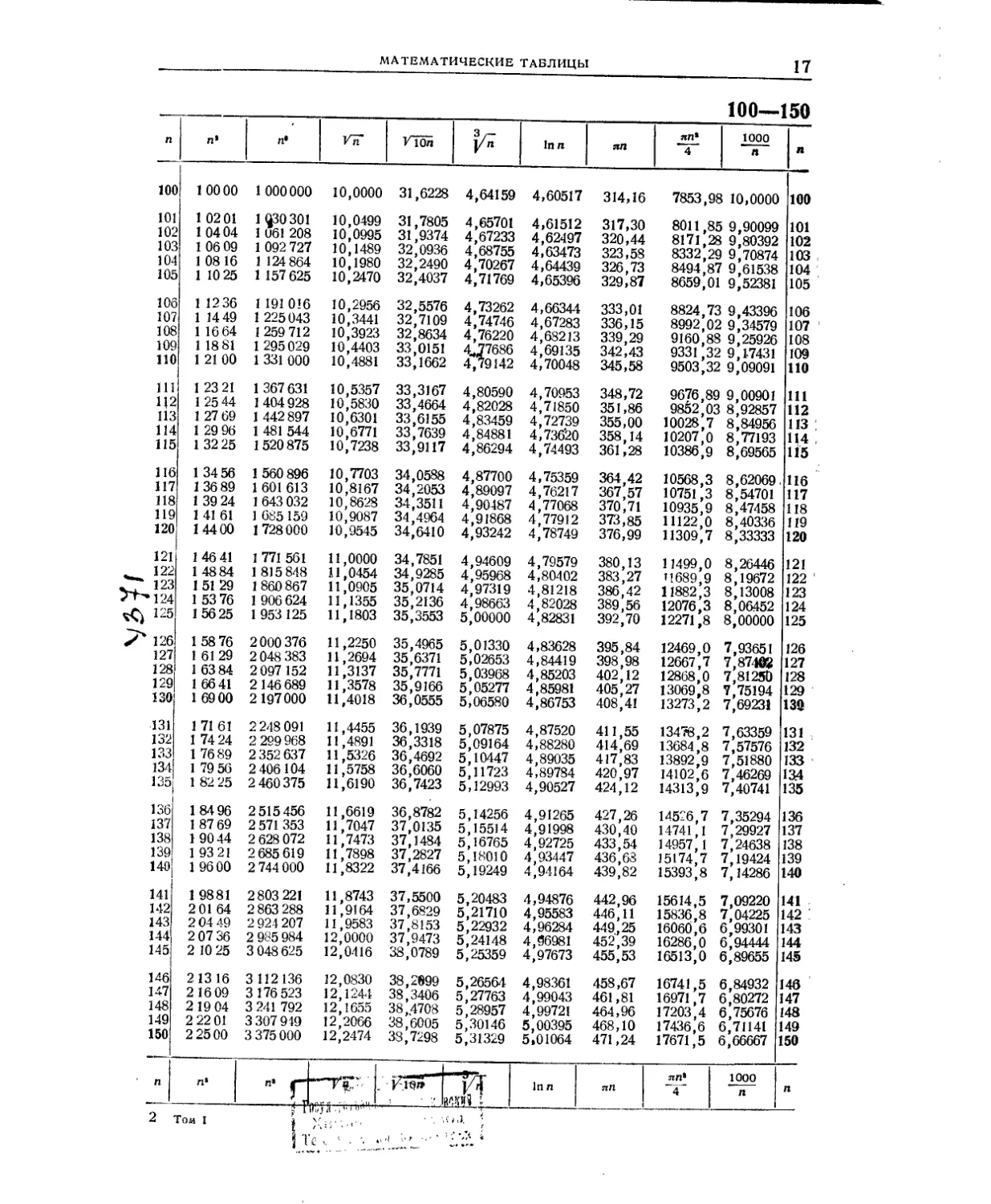
100—150
п п> п* У7Г /Той In It an an* 4 1000 n n
100 10000 1 000000 10,0000 31,6228 4,64159 4,60517 314,16 7853,98 10,0000 100
101 1 02 01 1030301 10,0499 31,7805 4,65701 4,61512 317,30 8011,85 9,90099 101
102 10404 1 061 208 10,0995 31,9374 4,67233 4,62497 320,44 8171,28 9,80392 102
103 1 06 09 1 092 727 10,1489 32,0936 4,68755 4,63473 323,58 8332,29 9,70874 103
104 1 08 16 1 124 864 10,1980 32,2490 4,70267 4,64439 326,73 8494.87 9.61538 104
105 1 10 25 1 157 625 10,2470 32,4037 4,71769 4,65396 329,87 8659,01 9,52381 105
106 1 12 36 1 191 016 10,2956 32,5576 4,73262 4,66344 333,01 8824,73 9,43396 106
107 1 1449 1 225043 10,3441 10,3923 32,7109 4,74746 4,67283 336,15 8992,02 9,34579 107
108 1 16 64 1 259 712 32,8634 4/76220 4,68213 339,29 9160,88 9,25926 108
109 1 18 81 1 295029 10,4403 33,0151 4Л7686 4779142 4,69135 342,43 9331,32 9,17431 109
ПО 1 21 00 1 331 000 10,4881 33,1662 4,70048 345,58 9503,32 9,09091 110
111 1 23 21 1 367 631 10,5357 33,3167 4,80590 4,70953 348,72 9676,89 9,00901 111
112 1 2544 1 404 928 10,5830 33,4664 4,82028 4,71850 351,86 9862.03 8.92857 112
113 1 27 69 1 442 897 10,6301 33,6155 4,83459 4,72739 355,00 10028,7 8,84956 113
114 1 29 96 1 481 544 10,6771 33,7639 4,84881 4,736’20 358,14 10207,0 8,77193 114
115 1 32 25 1520875 10,7238 33,9117 4,86294 4,74493 361,28 10386,9 8,69565 115
116 1 34 56 1 560 896 10,7703 34,0588 4,87700 4,75359 364,42 10568,3 8,62069. 116
117 136 89 1 601 613 10,8167 34,2053 4,89097 4,76217 367,57 10751,3 8,54701 117
118 1 39 24 1 643 032 10,8628 34,3511 4,90487 4,77068 370,71 10935,9 8,47458 118
119 1 41 61 1 685 159 10,9087 34,4964 4,91868 4/77912 373,85 11122,0 8,40336 119
120 144 00 1728 000 10,9545 34,6410 4,93242 4,78749 376,99 11309,7 8,33333 120
121 1 46 41 1 771 561 11,0000 34,7851 4,94609 4,79579 380,13 11499,0 8,26446 121
122 1 4884 1 815 848 11,0454 34,9285 4,95968 4,80402 383,27 ’1689,9 8,19672 122
123 15129 1860867 11,0905 35,0714 4,97319 4,81218 386,42 11882,3 8,13008 123
124 1 53 76 1 906 624 11,1355 35,2136 4,98663 4,82028 389,56 12076,3 8,06452 124
125 156 25 1 953 125 11,1803 35,3553 5,00000 4,82831 392,70 12271,8 8,00000 125
126 1 58 76 2000 376 11,2250 35,4965 5,01330 4,83628 395,84 12469,0 7,93651 126
127 1 61 29 2 048 383 11,2694 35,6371 5,02653 4,84419 398,98 12667,7 7,87402 127
128 1 6384 2 097 152 11,3137 35,7771 5,03968 4,85203 402,12 12868,0 7,81250 128
129 1 66 41 2146 689 11,3578 35,9166 5,05277 4,85981 405,27 13069,8 7,75194 129
130 1 69 00 2197000 11,4018 36,0555 5,06580 4,86753 408,41 13273,2 7,69231 130
131 1 71 61 2 248 091 11,4455 36,1939 5,07875 4,87520 411,55 13478,2 7,63359 131
132 1 74 24 2 299 968 11,4891 36,3318 5,09164 4,88280 414,69 13684,8 7,57576 132
133 1 7689 2 352 637 11,5326 36,4692 5,10447 4,89035 417,83 13892,9 7,51880 133
134 1 79 56 2 406104 11,5758 36,6060 5,11723 4,89784 420,97 14102,6 7,46269 134
135 1 82 25 2 460375 11,6190 36,7423 5,12993 4,90527 424,12 14313,9 7,40741 135
136 184 96 2 515 456 11,6619 36,8782 5,14256 4,91265 427,26 14526,7 7,35294 136
137 1 87 69 2 571 353 11,7047 37,0135 5,15514 4,91998 430,40 14741,1 7,29927 137
138 1 9044 2 628 072 11 7473 37,1484 5,16765 4,92725 433,54 14957,1 7,24638 138
139 1 93 21 2 685 619 11,7898 37,2827 5,18010 4 93447 436,68 15174,7 7,19424 139
140 1 9600 2 744 000 11,8322 37,4166 5,19249 4,94164 439,82 15393,8 7,14286 140
141 1 9881 2 803 221 11,8743 37,5500 5,20483 4,94876 442,96 15614,5 7,09220 141
142 2 01 64 2 863 288 11,9164 37,6829 5,21710 4,95583 446,11 15836,8 7,04225 142
143 204 49 2 924 207 11,9583 37,8153 5,22932 4,96284 449,25 16060,6 6,99301 143
144 2 07 36 2 985 984 12,0000 37,9473 5;24148 4,96981 452,39 16286,0 6,94444 144
145 2 10 25 3 048 625 12,0416 38,0789 5,25359 4,97673 455,53 16513,0 6,89655 145
146 21316 3112136 12,0830 38,2699 5,26564 4,98361 458,67 16744,5 6,84932 146
147 2 16 09 3 176 523 12,1244 38,3406 5,27763 4,99043 461,81 16971,7 6,80272 147
148 2 19 04 3 241 792 12,1655 38,4708 5,28957 4,99721 464,96 17203,4 6,75676 148
149 2 22 01 3 307 949 12,2066 38,6005 5,30146 5,00395 468,10 17436,6 6,71141 149
150 2 2500 3 375 000 12,2474 38,7298 5,31329 5,01064 471,24 17671,5 6,66667 150
an* 1000
п п* Г” In n an ~4~ n n
*4
2 ТОМ I |
I Т£ .
18
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
150-200
Л» л* 3,- j/л In л яЛ лп* 4 1000 п
150 2 25 00 3 375000 12,2474 38,7298 5,31329 5,01064 471,24 17671,5 6,66667 150
151 228 01 3 442 951 12,2882 38,8587 5,32507 5,01728 474 38 17907,9 6,62252 .51
152 2 31 04 3 511 808 12,3288 38,9872 5,33680 5,02388 477,52 18145,8 6,57895 152
153 234 09 3581 577 12,3693 39,1152 5,34848 5,03044 480,66 18385,4 6,53595 153
154 237 16 3 652 264 12,4097 39,2428 5.36011 5,03695 483,81 18626,5 6,49351 154
155 240 25 3 723 875 12,4499 39,3700 5,37169 5,04343 486,95 18869,2 6,45161 155
156 243 36 3 796 416 12,4900 39,4968 5,38321 5,04986 490,09 19113,4 6,41026 156
157 2 46 49 3 869893 12,5300 39,6232 5,39469 5,05625 493,23 19359,3 6,36943 157
158 2 49 64 3 944 312 12,5698 39,7492 5,40612 5,06260 496,37 19606/7 6,32911 158
159 2 52 81 4 019 679 12,6095 39,8748 5,41750 5,06890 499,51 19855,7 6,28931 159
160 2 5600 4 096 000 12,6491 40,0000 5,42884 5,07517 502,65 20106,2 6,25000 160
161 2 59 21 4 173 281 12,6886 40,1248 5,44012 5,08140 505,80 20358,3 6,21118 161
162 2 62 44 4 251 528 12,7279 40,2492 5,45136 5,08760 508,94 20612,0 6,17284 162
163 2 65 69 4330 747 12,7671 40,3733 5,46256 5,09375 512,08 20867,2 6,13497 163
164 2 68 96 4 410 944 12,8062 40,4969 5,47370 5,09987 515,22 21124,1 6,09756 164
165 2 7225 4 492125 12,8452 40,6202 5,48481 5,10595 518,36 21382,5 6,06061 165
166 2 75 56 4 574 296 12,8841 40,7431 5,49586 5,11199 521,50 21642,4 6,02410 166
167 2 78 89 4 657 463 12,9228 40,8656 5,50688 5,11799 524,65 21904,0 5,98802 167
168 2 82 24 4 741 632 12,9615 40,9878 5,51785 5,12396 527,79 22167,1 5,95238 168
169 2 85 61 4 826 809 13,0000 41,1096 5,52877 5 12990 530,93 22431,8 5,91716 169
170 28900 4 913000 13,0384 41,2311 5,53966 5,13580 534,07 22698,0 5,88235 170
171 292 41 5000 211 13,0767 41,3521 5,55050 5,14166 537,21 22965,8 5,84795 171
172 2 95 84 .5088 448 13,1149 41,4729 5,56130 5,14749 540,35 23235,2 5,81395 172
173 2 99 29 5 177 717 13,1529 41,5933 5,57205 5,15329 543,50 23506 2 5,78035 173
174 3 02 76 5 268 024 13,1909 41,7133 5,58277 5,15906 546,64 23778,7 5,74713 174
175 3 06 25 5 359 375 13,2288 41,8330 5,59344 5,16479 549,78 24052,8 5,71429 175
176 309 76 5 451 776 13,2665 41,9524 5,60408 5,17048 552,92 24328,5 5,68182 176
177 313 29 5 545 233 13,3041 42,0714 5,61467 5,17615 556,06 24605,7 5,64972 177
178 316 84 5 639 752 13,3417 42,1900 5,62523 5,18178 559,20 24884,6 5,61798 178
179 3 20 41 5 735 339 13,3791 42,3084 5,63574 5,18739 562,35 25164,9 5,58659 179
180 3 24 00 5 832 000 13,4164 42,4264 5,64622 5,19296 565,49 25446,9 5,55556 180
181 3 2761 5 929 741 13,4536 42,5441 5,65665 5,19850 568,63 25730,4 5,52486 181
182 3 31 24 6 028 568 13,4907 42,6615 5,66705 5,20401 571,77 26015,5 5,49451 182
183 3 34 89 6 128 487 13,5277 42,7785 5,67741 5,20949 574,91 26302,2 5,46448 183
184 338 56 6 229 504 13,5647 42,8952 5,68773 5,21494 578,05 26590,4 5,43478 184
185 3 42 25 6 331 625 13,6015 43,0116 5,69802 5,22036 581,19 26880,3 5,40541 185
186 345 96 6 434 856 13,6382 43,1277 5,70827 5,22575 584,34 27171,6 5,37634 186
187 349 69 6 539 203 13,6748 43,2435 5,71848 5,23111 587,48 27464,6 5,34759 187
188 353 44 6 644 672 13/7113 43,3590 5,72865 5,23644 590,62 27759,1 5,31915 188
189 3 57 21 6 751 269 13,7477 43,4741 5,73879 5,24175 593,76 28055,2 5 29101 189
190 3 61 00 6 859 000 13,7840 43,5890 5,74890 5,24702 596,90 28352,9 5,26316 190
191 3 64 81 6 967871 13,8203 43,7035 5,75897 5,25227 600,04 28652,1 5,23560 191
192 3 68 64 7 077888 13,8564 43,8178 5,76900 5,25750 603,19 28952,9 5,20833 1.92
193 372 49 7 189 057 13,8924 43,9318 5,77900 5,26269 606,33 29255,3 5,18135 193
194 3 76 36 7 301 384 13,9284 44,0454 5,78896 5,26786 609,47 29559,2 5,15464 194
195 380 25 7 414 875 13,9642 44,1588 5,79889 5,27300 612,61 29864,8 5,12821 195
19€ 38416 7 529 536 14,0000 44,2719 5,80879 5,27811 615,75 30171,9 5,10204 196
19' 3 88 09 7 645 373 14,0357 44,3847 5,81865 5,28320 618,89 30480,5 5,07614 197
193 3 92 04 7 762 392 14,0712 44,4972 5,82848 5,28827 622,04 30790,7 5,05051 198
194 39601 7 880 599 14,1067 44,6094 5,83827 5,29330 625,18 31102,6 5,02513 199
20( 40000 8 000 000 14,1421 44,7214 5,84804 5,29832 628,32 31415,9 5,00000 200
п Л* Л3 V л" /Тбл In л ЛП ЯЛ® ~4~~ 1000 п Л
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
19
200—25G
п п* п‘ Vn К'1Сл 3,- Vn In n ЛП ЯП* 1000 п п
200 4 0000 8 000000 14,1421 44,7214 5,84804 5,29832 628,32 31415,9 5,00000 200
201 4 04 01 8120 601 14,1774 44,8330 5,85777 5,80330 631,46 31730,9 4,97512 201
202 408 04 8 242 408 14,2127 44,9444 5,86746 5,30827 634,60 32047,4 4,95050 202
203 4 12 09 8 365 427 14,2478 45,0555 5,87713 5,31321 637,74 32365,5 4,92611 203
204 41616 8 489 664 14,2829 45,1664 5,88677 5,31812 640,88 32685,1 4,90196 204
205 4 20 25 8 615 125 14,3178 45,2769 5,89637 5,32301 644,03 33006,4 4,87805 205
206 4 24 36 8 741 816 14,3527 45,3872 5,90594 5,32788 647,17 33329 2 4,85437 206
207 4 28 49 8 869 743 14,3875 45,4973 5,91548 5,33272 5/33754 650,31 33653,5 4,83092 207
208 4 32 64 8 998 912 14,4222 45,6070 5,92499 653,45 33979 5 4,80769 208
209 4 36 81 9129 329 14,4568 45,7165 5,93447 5,34233 656,59 34307,0 4,78469 209
210 4 41 00 9 261 000 14,4914 45,8258 5,94392 5,34711 659,73 34636,1 4,76190 210
211 4 45 21 9 393 931 14,5258 45,9347 5,95334 5,35186 662,88 34966,7 4,73934 211
212 4 49 44 9 528 128 14,5602 46,0435 5,96273 5,35659 666,02 35298,9 4,71698 212
213 4 53 69 9 663 597 14,5945 46,1519 5,97209 5,36129 669,16 35632,7 4,69484 213
214 4 57 96 9800344 14,6287 46,2601 5,98142 5,36598 672,30 35968,1 4,67290 214
215 4 62 25 9 938 375 14,6629 46,3681 5,99073 5,37064 675,44 36305,0 4,65116 215
216 4 66 56 10077 696 14,6969 46,4758 6,00000 5,37528 678,58 36643,5 4,62963 216
217 4 70 89 10218313 14,7309 46,5833 6,00925 5,37990 681,73 36983,6 4,60829 217
218 4 75 24 10 360232 14,7648 46,6905 6,01846 5,38450 684,87 37325,3 4,58716 218
219 4 79 61 10 503 459 14,7986 46,7974 6,02765 5,38907 688,01 37668,5 4,56621 219
220 4 84 00 10 648 000 14,8324 46,9042 6,03681 5,39363 691,15 38013,3 4,54545 220
221 4 88 41 10 793 861 14,8661 47,0106 6,04594 5,39816 694,29 38359,6 4,52489 221
222 4 92 84 10 941 048 14,8997 47,1169 6,05505 5,40268 697,43 38707,6 4,50450 222
223 4 97 29 11 089 567 14,9332 47,2229 6,06413 5,40717 700,58 39057,1 4,48430 223
224 501 76 11 239 424 14,9666 47,3286 6,07318 5,41165 703,72 39408,0 4,46429 224
225 506 25 11 390 625 15,0000 47,4342 6,08220 5,41610 706,86 39760,8 4,44444 225
226 510 76 11 543176 15,0333 47,5395 6,09120 5,42053 710,00 40115,0 4,42478 226
227 51529 11 697 083 15,0665 47,6445 6,10017 5,42495 713,14 40470,8 4,40529 227
228 519 84 11 852 352 15,0997 47,7493 6,10911 5,42935 716,28 40828,1 4,38596 228
229 5 24 41 12 008 989 15,1327 47,8539 6,11803 5,43372 719,42 41187,1 4,36681 229
230 5 2900 12 167 000 15,1658 47,9583 6,12693 5,43808 722,57 41547,6 4,34783 230
231 533 61 12 326 391 15,1987 48,0625 6,13579 5,44242 725,71 41909,6 4,32900 231
232 538 24 12487168 15,2315 48,1664 6,14463 5,44674 728,85 42273,3 4,31034 232
233 5 42 89 12 649 337 15,2643 48,2701 6,15345 5,45104 731,99 42638,5 4,29185 233
234 5 47 56 12 812 904 15,2971 48,3735 6,16224 5,45532 735,13 43005,3 4,27350 234
235 5 52 25 12 977 875 15,3297 48,4768 6,17101 5,45959 738,27 43373,6 4,25532 235
236 556 96 13144256 15,3623 48,5798 6,17975 5,46383 741,42 43743,5 4,23729 236
237 5 61 69 13 312 053 15,3948 48,6826 6', 18846 5,46806 744,56 44115,0 4,21941 237
238 566 44 13 481 272 15,4272 48,7852 6,19715 5,47227 747,70 44488,1 4,20168 238
239 5 71 21 13651 919 15,4596 48,8876 6,20582 5,47646 750,84 44862,7 4,18410 239
240 576 00 13824000 15,4919 48,9898 6,21447 5,48064 753,98 45238,9 4,16667 240
241 580 81 13 997 521 15,5242 49,0918 6,22308 5,48480 757,12 45616,7 4,14938 241
242 585 64 14 172 488 15,5563 49,1935 6,23168 5,48894 760,27 45996,1 4,13223 242
243 590 49 14 348 907 15,5885 49,2950 6,24025 5,49306 763,41 46377,0 4,11523 243
244 5 95 36 14 526 784 15,6205 49,3964 6,24880 5,49717 766,55 46759,5 4,09836 244
245 600 25 14 706 125 15,6525 49,4975 6,25732 5,50126 769,69 47143,5 4,08163 245
246 6 05 16 14 886 936 15,6844 49,5984 6,26583 5,50533 772,83 47529,2 4,06504 246
247 610 09 15069 223 15,7162 49,6991 6,27431 5,50939 775,97 47916,4 4,04858 247
248 615 04 15 252 992 15,7480 49,7996 6,28276 5,51343 779,11 48305,1 4,03226 248
249 6 20 01 15 438 249 15,7797 49,8999 6,29119 5,51745 782,26 48695,5 4,01606 249
250 6 25 00 15 625 000 15,8114 50,0000 6,29961 5,52146 785,40 49087,4 4,00000 250
п п* п* У’п /10п Inn лП ЯП* 4 1000 п п
20
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
250-300
п п* п' У" УТбп К Inn пП лп* ~4~ 1000 п
250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 265 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 293 299 зоо 62500 15625000 15,8114 50,0000 6,29961 5,52146 785,40 49087,4 4,00000 6 30 01 15 813 251 15,8430 50,0999 6,30799 5,52545 788,54 49480,9 3,98406 63504 16003008 15,8745 50,1996 6,31636 5,52943 791,68 49875,9 3,96825 64009 16 194 277 15,9060 50,2991 6,32470 5,53339 794,82 50272,6 3,95257 645 16 16387064 15,9374 50,3984 6,33303 5,53733 797,96 50670,7 3,93701 65025 16581 375 15,9687 50,4975 6,34133 5,54126 801,11 51070,5 3,92157 6 55 36 16 777 216 16,0000 50,5964 6,34960 5,54518 804,25 51471,9 3,90625 6 60 49 16 974 593 16,0312 50,6952 6,35786 5,54908 807,39 51874,8 3,89105 66564 17 173512 16,0624 50,7937 6,36610 5,55296 810,53 52279,2 3,87597 6 70 81 17 373 979 16,0935 50,8920 6,37431 5,55683 813,67 52685,3 3,86100 67600 17576000 16,1245 50,9902 6,38250 5,56068 816,81 53092,9 3,84615 681 21 17779581 16,1555 51,0882 6,39068 5,56452 819,96 53502,1 3,83142 68644. 17984 728 16,1864 51,1859 6,39883 5,56834 823,10 53912,9 3,81679 691,64 18 191 447 16,2173 51,2835 6,40696 5,57215 826,24 54325,2 3,80228 69696 18399744 16,2481 51,3809 6,41507 5,57595 829,38 54739,1 3,78788 7 0225 18609625 16,2788 51,4782 6,42316 5,57973 832,52 55154,6 3,77358 7 07 56 18 821 096 16,3095 51,5752 6,43123 5,58350 835,66 55571,6 3,75940 7 12 89 19 034163 16,3401 51,6720 6,43928 5,58725 838,81 55990,2 3,74532 7 18 24 19 248 832 16,3707 51,7687 6,44731 5,59099 841,95 56410,4 3,73134 7 2361 19465 109 16,4012 51,865’2 6,45531 5,59471 845,09 56832,2 3,71747 7 29 00 19 683 000 16,4317 51,9615 6,46330 5,59842 848,23 57255,5 3,70370 734 41 19 902 511 16,4621 52,0577 6,47127 5,60212 851,37 57680,4 3,69004 73984 20123648 16,4924 52,1536 6,47922 5,60580 854,51 58106,9 3,67647 745 29 20 346417 16,5227 52,2494 6,48715 5,60947 857,65 58534,9 3,66300 7 50 76 20 570 824 16,5529 52,3450 6,49507 5,61313 860,80 58964,6 3,64964 7 56 25 20 796 875 16,5831 52,4404 6,50296 5,61677 863,94 59395,7 3,63636 761 76 21 024576 16,6132 52,5357 6,51083 5,62040 867,08 59828,5 3,62319 76729 21 253933 16,6433 52,6308 6,51868 5,62402 870,22 60262,8 3,61011 7 7284 21 484 952 16,6733 52,7257 6,52652 5,62762 873,36 60698,7 3,59712 7 78 41 21 717 639 16,7033 52,8205 6,53434 5,63121 876,50 61136,2 3,58423 7 84 00 21 952 000 16,7332 52,9150 6,54213 5,63479 879,65 61575,2 3,57143 78961 22 188041 16,7631 53,0094 6,54991 5,63835 882,79 62015,8 3,55872 79524 22425768 16,7929 53,1037 6,55767 5,64191 885,93 62458,0 3,54610 8 00 89 22 665 187 16,8226 53,1977 6,56541 5,64545 889,07 62901,8 3,53357 80666 22906304 16,8523 53,2917 6,57314 5,64897 892,21 63347,1 3,52113 8 1225 23 149125 16,8819 53,3854 6,58084 £>,65249 895,35 63794,0 3,50877 8 1796 23393656 16,9115 53,4790 6,58853 5,65599 898,50 64242,4 3,49650 8 23 69 23 639903 16,9411 53,5724 6,59620 5,65948 901,64 64692,5 3,48432 82944 23887872 16,9706 53,6656 6,60385 5,66296 904,78 65144,1 3,47222 83521 24 137569 17,0000 53,7587 6,61149 5,66643 907,92 65597,2 3,46021 84100 24 389000 17,0294 53,8516 6,61911 5,66988 911,06 66052,0 3,44828 8 46 81 24 642 171 17,0587 53,9444 6,62671 5,67332 914,20 66508,3 3,43643 85264 24897088 17,0880 54,0370 6,63429 5,67675 917,35 66966,2 3,42466 85849 25 153757 17,1172 54,1295 6,64185 5,68017 920,49 67425,6 3,41297 8 64 36 25 412 184 17,1464 54,2218 6,64940 5,68358 923,63 67886,7 3,40136 8 70 25 25 672 375 17,1756 54,3139 6,65693 5,68698 926,77 68349,3 3,38983 8 7616 25 934 336 17,2047 54,4059 6,66444 5,69036 929,91 68813,4 3,37838 8 8209 26 198 073 17,2337 54,4977 6,67194 5,69373 933,05 69279,2 3,36700 88804 26463592 17,2627 54,5894 6,67942 5,69709 936,19 69746,5 3,35570 89401 26 730899 17,2916 55,6809 6,68688 5,70044 939,34 70215,4 3,34448 9 0000 27 000 000 17,3205 54,7723 6,69433 5,70378 942,48 70685,8 3,33333 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 п
п п’ ч пг У'п 1Л0П 3/- 1/п In п лП лП* "4- 1000 ” п
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
21
300—350
И п‘ п’ /п }/10п Inn ЯП ЯП* ~4~ 1000 и и
300 90000 27000000 17,3205 54,7723 6,69433 5,70378 942,48 70685,8 3,33333 300
301 906 01 27 270901 17,3494 54,8635 6,70176 5,70711 945,62 71157,9 3,32226 301
302 912 04 27 543 608 17,3781 54,9545 6,70917 5,71043 948,76 71631,5 3,31126 302
303 9 18 09 27818 127 17,4069 55,0454 6,71657 5,71373 951,90 72106,6 3,30033 303
304 9 24 16 28 094 464 17,4356 55,1362 6,72395 5,71703 955,04 72583,4 3,28947 304
305 930 25 28 372 625 17,4642 55,2268 6,73132 5,72031 958,19 73061,7 3,27869 305
306 9 36 36 28 652 616 17,4929 55,3173 6,73866 5,72359 961,33 73541,5 3,26797 306
307 9 42 49 28 934 443 17,5214 55,4076 6,74600 5,72685 964,47 74023,0 3,25733 307
308 9 48 64 29 218 112 17,5499 55,4977 6,75331 5,73010 967,61 74506,0 3,24675 308
309 9 54 81 29 503 629 17,5784 55,5878 6,76061 5,73334 970,75 74990,6 3,23625 309
310 9 61 00 29 791 000 17,6068 55,6776 6,76790 5,73657 973,89 75476,8 3,22581 310
311 9 67 21 30080 231 17,6352 55,7674 6,77517 5,73979 977,04 75964,5 3,21543 311
312 9 73 44 30 371 328 17,6635 55,8570 6,78242 5,74300 980,18 76453,8 3,20513 312
313 9 79 69 30 664 297 17,6918 55,9464 6,78966 5,74620 983,32 76944,7 3,19489 313
314 985 96 30959144 17,7200 56,0357 6,79688 5,74939 986,46 77437,1 3,18471 314
315 9 92 25 31 255 875 17,7482 56,1249 6,80409 5,75257 989,60 77931,1 3,17460 315
316 9 98 56 31 554 496 17,7764 56,2139 6,81128 5,75574 992,74 78426,7 3,16456 316
317 1004 89 31 855 013 17,8045 56,3028 6,81846 5,75890 995,88 78923,9 3,15457 317
318 10 11 24 32 157 432 17,8326 56,3915 6,82562 5,76205 999,03 79422,6 3,14465 318
319 10 1761 32461 759 17,8606 56,4801 6,83277 5,76519 1002,2 79922,9 3,13480 319
320 10 24 00 32 768000 17,8885 56,5685 6,83990 5,76832 1005,3 80424,8 3,12500 320
321 10 30 41 33 076161 17,9165 56,6569 6,84702 5,77144 1008,5 80928,2 3,11526 321
322 10 36 84 33 386 248 17,9444 56,7450 6,85412 5,77455 1011,6 81433,2 3,10559 322
323 10 43 29 33 698 267 17,9722 56,8331 6,86121 5,77765 1014,7 81939,8 3,09598 323
324 1049 76 34 012 224 18,0000 56,9210 6,86829 5,78074 1017,9 82448,0 3,08642 324
325 10 56 25 34 328125 18,0278 57,0088 6,87534 5,78383 1021,0 82957,7 3,07692 325
326 10 62 76 34 645 976 18,0555 57,0964 6,88239 5,78690 1024,2 83469,0 3,06748 326
327 10 69 29 34 965 783 18,0831 57,1839 6,88942 5,78996 1027,3 83981,8 3,05810 327
328 10 75 84 35 287 552 18,1108 57,2713 6,89643 5,79301 1030,4 84496,3 3,04878 328
329 10 82 41 35 611 289 18,1384 57,3585 6,90344 5,79606 1033,6 85012,3 3,03951 329
330 10 89 00 35 937000 18,1659 57,4456 6,91042 5,79909 1036,7 85529,9 3,03030 330
331 10 95 61 36 264 691 18,1934 57,5326 6,91740 5,80212 1039,9 86049,0 3,02115 331
332 11 02 24 36 594 368 18,2209 57,6194 6,92436 5,80513 1043,0 86569,7 3,01205 332
333 11 08 89 36 926037 18,2483 57,7062 6,93130 5,80814 1046,2 87092,0 3,00300 333
334 11 15 56 37 259 704 18,2757 57,7927 6,93823 5,81114 1049,3 87615,9 2,99401 334
335 11 22 25 37595 375 18,3030 57,8792 6,94515 5,814,13 1052,4 88141,3 2,98507 335
336 И 28 96 37 933056 18,3303 57,9655 6,95205 5,81711 1055,6 88668,3 2,97619 336
337 1135 69 38 272 753 18,3576 58,0517 6,95894 5,82008 1058,7 89196,9 2,96736 337
338 114244 38 614 472 18,3848 58,1378 6,96582 5,82305 1061,9 89727,0 2,95858 338
339 11 49 21 38 958 219 18,4120 58,2237 6,97268 5,82600 1065,0 90258,7 2,94985 339
340 11 56 00 39 304 000 18,4391 58,3095 6,97953 5,82895 1068,1 90792,0 2,94118 340
341 116281 39 651 821 18,4662 58,3952 6,98637 5,83188 1071,3 91326,9 2,93255 341
342 11 69 64 40 001 688 18,4932 58,4808 6,99319 5,83481 1074,4 91863,3 2,92398 342
343 11 7649 40 353 607 18,5203 58,5662 7,00000 5,83773 1077,6 92401,3 2,91545 343
344 11 83 36 40 707 584 18,5472 58,6515 7,00680 5,84064 1080,7 92940,9 2,90698 344
345 11 90 25 41063625 18,5742 58,7367 7,01358 5,84354 1083,8 93482,0 2,89855 345
346 И 97 16 41 421 736 18,6011 58,8218 7,02035 5,84644 1087,0 94024,7 2,89017 346
347 1204 09 41 781 92г 18,6279 58,9067 7,02711 5,84932 1090Л 94569,0 2,88184 347
348 1211 04 42 144 192 18,6548 58,9915 7,03384 5,85220 1093,3 95114,9 2,87356 348
349 12 1801 42 508 549 18,6815 59,0762 7,04058 5,85507 1096,4 95662,3 2,86533 349
350 1225 00 42 875 000 18,7083 59,1608 7,04730 5,85793 1099,6 96211,3 2,85714 350
И п* ns /п р Топ К In п ЯП ЯП* 4 1000 п п
22
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
350-400
п п' п' рп р юп р/п 1п п ЯП лп.1 1000 п п
350 12 2500 42 875000 18,7083 59,1608 7,04730 5,85793 1099,6 96211,3 2,85714 350
351 123201 43 243 551 18,7350 59,2453 7,05400 5,86079 1102,7 96761,8 2,84900 351
352 12 39 04 43 614 208 18,7617 59,3296 7,06070 5,86363 1105,8 97314,0 2,84091 352
353 12 46 09 43 986 977 18,7883 59,4138 7,06738 5,86647 1109,0 97867,7 2,83286 353
354 12 53 16 44 361 864 18,8149 59,4979 7,07404 5,86930 1112,1 98423,0 2,82486 354
355 12 60 25 44 738875 18,8414 59,5819 7,08070 5,87212 1115,3 98979,8 2,81690 355
356 12 67 36 45 118 016 18,8680 59,6657 7,08734 5,87493 1118,4 99538,2 2,80899 356
357 12 74 49 45 499 293 18,8944 59,7495 7,09397 5,87774 1121,5 100098 2,80112 357
358 12 81 64 45 882 712 18,9209 59,8331 7,10059 5,88053 1124,7 100660 2,79330 358
359 12 88 81 46 268 279 18,9473 59,9166 7,10719 5,88332 1127,8 101223 2,78552 359
360 12 96 00 46 656 000 18,9737 60,0000 7,11379 5,88610 1131,0 101788 2,77778 360
361 13 03 21 47 045 881 19,0000 60,0833 7,12037 5,88888 1134,1 102354 2,77008 361
362 13 10 44 47 437 928 19,0263 60., 1664 7,12694 5,89164 1137,3 102922 2,76243 362
363 13 17 69 47 832 147 19,0526 60,2495 7,13349 5,89440 1140,4 103491 2,75482 363
364 13 24 96 48 228544 19,0788 60,3324 7,1-4004 5,89715 1143,5 104062 2,74725 364
365 13 32 25 48 627 125 19,1050 60,4152 7,14657 5,89990 1146,7 104635 2,73973 365
366 13 39 56 49 027896 19,1311 60,4979 7,15309 5,90263 1149,8 105209 2,73224 366
367 13 46 89 49 430 863 19,1572 60,5805 7,15960 5,90536 1153,0 105785 2,72480 367
368 13 54 24 49 836032 19,1833 60,6630 7,16610 5,90808 1156,1 106362 2,71739 368
369 13 61 61 50 243 409 19,2094 60,7454 7,17258 5,91080 1159,2 106941 2,71003 369
370 13 69 00 50 653 000 19,2354 60,8276 7,17905 5,91350 1162,4 107521 2,70270 370
371 13 76 41 51 064 811 19,2614 60,9098 7,18552 5,91620 1165,5 108103 2,69542 371
372 13 83 84 51 478 848 19,2873 60,9918 7,19197 5,91889 1163,7 108687 2,68817 372
373 13 91 29 51 895 117 19,3132 61,0737 7,19841 5,92158 1171,8 109272 2,68097 373
374 13 98 76 52 313 624 19,3391 61,1555 7,20483 5,92426 1175,0 109858 2,67380 374
375 14 06 25 52 734 375 19,3649 61,2372 7,21125 5,92693 1178,1 110447 2,(56667 375
376 14 1376 53 157 376 19,3907 61,3188 7,21765 5,92959 1181,2 111036 2,65957 376
377 14 21 29 53 582633 19,4165 61,4003 7,22405 5,93225 1184,4 111628 2,65252 3/7
378 14 28 84 54010 152 19,4422 61,4817 7,23043 5,93489 1187,5 112221 2,64550 378
379 14 36 41 54 439 939 19,4679 61,5630 7,23680 5,93754 1190,7 112815 2,63852 379
380 14 4400 54 872 000 19,4936 61,6441 7,24316 5,94017 1193,8 113411 2,63158 380
381 14 51 61 55 306 341 19,5192 61,7252 7,24950 5,94280 1196,9 114009 2,62467 381
382 14 59 24 55 742 968 19,5448 61,8061 7,25584 5,94542 1200,1 114608 2,61780 382
383 14 66 89 56 181 887 19,5704 61,8870 7,26217 5,94803 1203,2 115209 2,61097 383
384 14 74 56 56 623104 19,5959 61,9677 7,26848 5,95064 1206,4 115812 2,60417 384
385 1482 25 57 066 625 19,6214 62,0484 7,27479 5,95324 1209,5 116416 2,59740 385
386 14 89 96 57 512 456 19,6469 62,1289 7,28108 5,95584 1212,7 117021 2,59067 386
387 14 97 69 57 960 603 19,6723 62,2093 7,28736 5,95842 1215,8 117628 2,58398 387
388 15 05 44 58411 072 19,6977 62,2896 7,29363 5,96101 1218,9 118237 2,57732 388
389 1513 21 58863 869 19,7231 62,3699 7,29989 5,96358 1222,1 118847 2,57069 389
390 15 2100 59 319 000 19,7484 62,4500 7,30614 5,96615 1225,2 119459 2,56410 390
391 15 28 81 59 776 471 19,7737 62,5300 7,31238 5,96871 1228,4 120072 2,55754 391
392 15 3664 60 236 288 19,7990 62,6099 7,31861 5,97126 1231,5 120687 2,55102 392
393 15 44 49 60 698 457 19,8242 62,6897 7,32483 5,97381 1234,6 121304 2,54453 393
394 15 52 36 61 162 984 19,8494 62,7694 7,33104 5,97635 1237,8 121922 2,53807 394
395 1560 25 61 629 875 19,8746 62,8490 7,33723 5,97889 1240,9 122542 2,53165 395
396 15 68 16 62 099 136 19,8997 62,9285 7,34342 5,98141 1244,1 123163 2,52525 396
397 15 7609 62 570 773 19,9249 63,0079 7,34960 5,98394 1247,2 123786 2,51889 397
398 15 8404 63044 792 19,9499 63,0872 7,35576 5,98645 1250,4 124410 2,51256 398
399 15 92 01 63521 199 19,9750 63,1664 7,36192 5,98896 1253,5 125036 2,50627 399
400 16 00 00 64 000000 20,0000 63,2456 7,36806 5,99146 1256,6 125664 2,50000 400
3/- 1000
п п« п» V'n' Р Юп уп 1п п ЯП 4 п п
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
23
400—450
Л п* и* /л /10л In л пп ЯП1 1QOQ п п
400 1600 00 64000 000 20,0000 63,2456 7,36806 5,99146 1256,6 125664 2,50000 400
401 16 08 01 64 481 201 20,0250 63,3246 7,37420 5,99396 1259,8 126293 2,49377 401
402 16 16 04 64 964808 20,0499 63,4035 7 38032 5,99645 1262,9 126923 238756 402
403 16 24 09 65 450827 20,0749 63,4823 7.38644 5,99894 1266,1 127556 2,48139 403
404 16 32 16 65 939 264 20,0998 63,5610 7,39254 6,00141 1269,2 128190 2,47525 404
405 16 40 25 66 430 125 20,1246 63,6396 7,39864 6,00389 1272,3 128825 2,46914 405
406 16 48 36 66 923 416 20,1494 63,7181 7,40472 6,00635 1275,5 129462 2,46305 406
407 16 56 49 67 419 143 20,1742 63,7966 7,41080 6,00881 1278,6 130100 2,45700 407
408 16 64 64 67 917 312 20,1990 63,8749 7,41686 6,01127 1281,8 130741 235098 408
409 16 72 81 68417 929 20,2237 63,9531 7,42291 6,01372 1284,9 131382 2,44499 409
410 168100 68 921 000 20,2485 64,0312 7,42896 6,01616 1288,1 132025 2,43902 410
411 lfj.89 21 69 426 531 20,2731 64,1093 7,43499 6,01859 1291,2 132670 2,43309 411
412 13 97 44 69 934 528 20,2978 64,1872 7,44102 6,02102 1294,3 133317 2,42718 412
413 17 05 69 70 444997 20,3224 64,2651 7,44703 6,02345 1297,5 133965 2,42131 413
414 17 1396 70 957 944 20,3470 64,3428 7,45304 6,02587 1300,6 134614 2,41546 414
415 17 22 25 71 473 375 20,3715 64,4205 7,45904 6,02828 1303,8 135265 2,40964 415
416 17 30 56 71 991 296 20,3961 64,4981 7,46502 6,03069 1306,9 135918 2,40385 416
417 17 38 89 72 511 713 20,4206 64,5755 7,47100 6,03309 1310,0 136572 2,39808 417
418 17 47 24 73 034 632 20,4450 64,6529 7,47697 6,03548 1313,2 137228 2,39234 418
419 17 55 61 73 560 059 20,4695 64,7302 7,48292 6,03787 1316,3 137885 2,38663 419
420 17 64 00 74 088000 20,4939 64,8074 7,48887 6,04025 1319,5 138544 2,38095 420
421 17 72 41 74 618 461 20,5183 64,8845 7,49481 6,04263 1322,6 139205 2,37530 421
422 17 80 84 75 151 448 20,5426 64,9615 7,50074 6,04501 1325,8 139867 2,36967 422
423 17 89 29 75686 967 20,5670 65,0385 7,50666 6,04737 1328,9 140531 2,36407 423
424 17 97 76 76 225 024 20,5913 65,1153 7,51257 6,04973 1332,0 141196 2,35849 424
425 18 06 25 76 765 625 20,6155 65,1920 7,51847 6,05209 1335,2 141863 2,35294 425
426 18 14 76 77 308 776 20,6398 65,2687 7,52437 6,05444 1338,3 142531 2,34742 426
427 18 23 29 77 854 483 20,6640 65,3452 7,53025 6,05678 1341,5 143201 2,34192 427
428 18 31 84 78 402 752 20,6882 65,4217 7,53612 6,05912 1344,6 143872 2,33645 428
429 18 40 41 78 953 589 20,7123 65,4981 7,54199 6,06146 1347,7 144545 2,33100 429
430 18 49 00 79 507 000 20,7364 65,5744 7,5478-1 6,06379 1350,9 145220 2,32558 430
431 18 57 61 80 062 991 20,7605 65,6506 7,55369 6,06611 1354,0 145896 2,32019 431
432 18 66 24 80 621 568 20,7846 65,7267 7,55953 6,06843 1357,2 146574 2,31481 432
433 18 74 89 81 182 737 20,8087 65,8027 7,56535 6,07074 1360,3 147254 2,3094’7 433
434 18 83 56 81 746 504 20,8327 65,8787 7,57117 6,07304 1363,5 147934 2,30415 434
435 18 92 25 82 312 875 20,8567 65,9545 7,57698 6,07535 1366,6 148617 2,29885 435
436 1900 96 82 881 856 20,8806 66,0303 7,58279 6,07764 1369,7 149301 2,29358 436
337 1909 69 83 453 453 20,9045 66,1060 7,58858 6,07993 1372,9 149987 2,28833 437
438 1918 44 84027 672 20,9284 66,1816 7,59436 6,08222 1376,0 150674 2,28311 438
439 19 27 21 84 604 519 20,9523 66,2571 7,60014 6,08450 1379,2 151363 2,27790 439
440 19 36 00 85 184 000 20,9762 66,3325 7,60590 6,08677 1382,3 152053 2,27273 440
441 1944 81 85 766 121 21,0000 66,4078 7,61166 6,08904 1385,4 152745 2,26757 441
442 19 53 64 86 350 888 21,0238 66,4831 7,61741 6,09131 1388,6 153439 2,26244 442
443 19 62 49 86 938 307 21,0476 66,5582 7,62315 6,09357 1391,7 154134 2,25734 443
444 19 7136 87 528 384 21,0713 66,6333 7,62888 6.09582 1394,9 154830 2,25225 444
445 19 80 25 88 131 125 21,0950 66,7083 7,63461 6,09807 1398,0 155528 2,24719 445
446 19 89 16 88 716 536 21,1187 66,7832 7,64032 6,10032 1401,2 156228 2,24215 446
447 19 98 09 89 314 623 21,1424 66,8581 7,64603 6,10256 1404,3 156930 2,23714 447
448 200704 89 915 392 21,1660 66,9328 7,65172 6,10479 1407,4 157633 2,23214 448
449 20 16 01 90 518 849 21,1896 67,0075 7,65741 6,10702 1410,6 158337 2,22717 449
450 20 2500 91 125 000 21,2132 67,0820 7,66309 6,10925 1413,7 159043 2,22222 450
И И’ п’ /7Г р 10л 3/— V п In п | ЯП пп* "V 1000 п п
Й4
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
450—500
п п‘ п« Уп /10л 3 у п In п пп ЯП* 1000 п п
450 202500 91 125 00С 21,2132 67,0820 7,66309 6,10925 1413,7 159043 2,22222 150
451 20 34 01 91 733 851 21.2368 67,1565 7,66877 6,11147 1416,9 159751 2,21729 451
452 20 43 04 92 345408 21.2603 67,2309 7,67443 6,11368 1420,0 160460 2,21239 452
453 20 52 09 92 959 677 21,2838 67,3053 7,68009 6,11589 1423,1 161171 2,20751 453
454 20 61 16 93576664 21,3073 67,3795 7,68573 6,11810 1426,3 161883 2,20264 454
455 20 70 25 94196 375 21,3307 67,4537 7,69137 6,12030 1429,4 162597 2,19780 455
456 20 7936 94 818 816 21,3542 67,5278 7,69700 6,12249 1432,6 163313 2,19298 456
457 20 88 49 95443993 21,3776 67,6018 7,70262 6,12468 1435,7 164030 2,18818 457
458 20 9764 96071912 21,4009 67,6757 7,7082^ 6,12687 1438.8 164748 2,18341 458
459 2106 81 96 702579 21,4243 67,7495 7,71384 6,12905 1442,0 165468 2,17865 459
460 21 16 00 97 336000 21,4476 67,8233 7,71944 6,13123 1445,1 166190 2,17391 460
461 21 2521 97972 18 21,4709 67,8970 7,72503 6,13340 1448.3 166914 2,16920 461
462 21 3444 98611 128 21,4942 67.9706 7,73061 6,13556 1451,4 167639 2,16450 462
463 21 43 69 99 252847 21,5174 68.0441 7,73619 6,13773 1454.6 168365 2,15983 463
464 21 52 96 99897344 21,5407 68.1175 7,74175 6,13988 1457.7 169093 2,15517 464
465 21 62 25 100544625 21,5639 68,1909 7,74731 6,14204 1460,8 169823 2,15054 465
466 21 71 56 101 194 696 21,5870 68,2642 7,75286 6,14419 1464,0 170554 2,14592 466
467 21 80 89 101847563 21,6102 68,3374 7,75840 6,14633 1467,1 171287 2,14133 467
468 2190 24 102 503 232 21,6333 68,4105 7,76394 6,14847 1470.3 172021 2,13675 468
469 21 99 61 103 161 709 21,656* 1 68,4836 7,76946 6,15060 1473.4 172757 2,13220 469
470 2209 00 103823 000 21,6795 68,5565 7,77498 6,15273 1476,5 173494 2,12766 470
471 22 18 41 104487111 21,7025 68,6294 7,78049 6,15486 1479,7 174234 2,12314 471
472 22 2784 105154048 21,7256 68,7023 7,78599 6,15698 1482,8 174974 2,11864 472
473 22 37 29 105 823 817 21,7486 68,7750 7,79149 6,15910 1486,0 175716 2,11416 473
474 22 46 76 106496424 21,7715 68,8477 7,79697 6.16121 1489,1 176460 2,10970 474
475 22 56 25 107171875 21,7945 68,9202 7,80245 6,16331 1492,3 177205 2,10526 475
476 22 65 76 107 850 176 21,8174 68,9928 7,80793 6,16542 1495,4 177952 2,10084 476
477 2275 29 108531 333 21,8403 69,0652 7,81339 6,16752 1498,5 178701 2,09644 477
478 22 84 84 109215352 21,8632 69,1375 7,81885 6,16961 1501,7 179451 2,09205 478
479 22 94 41 109 902239 21,8861 69,2098 7,82429 6,17170 1504,8 180203 2,08763 ,479
480 23 04 00 110592000 21,9089 69,2820 7,82974 6,17379 1508,0 180956 2,08333 480
481 23 1361 111 284 641 21,9317 69,3542 7,83517 6,17587 1511,1 181711 2,07900 481
482 23 23 24 111 980168 21,9545 69.4262 7,84059 6,17794 1514,2 182467 2,07469 482
483 23 32 89 112 678 587 21,9773 69.4982 7,8460 6,18002 1517,4 183225 2,07039 483
484 23 42 56 113 379904 22,0000 69,5701 7,85142 6,18208 1520,5 183984 2,06612 484
485 23 52 25 114084 125 22,0227 69,6419 7,85683 6,1841. 5 1523,7 184745 2,06186 485
486 23 61 96 114 791 256 22,0454 69,7137 7,86222 6,18621 1526,8 185508 2,05761 486
487 23 71 69 115501 303 22,0681 69,7854 7,86761 6,18826 1530,0 186272 2,05339 487
488 23 81 44 116214272 22,0907 69,8570 7,87299 6,19032 1533,1 187038 2,04918 488
489 23 91 21 116930169 22,1133 69,9285 7,87837 6,19236 1536,2 187805 2,04499 489
490 24 01 00 117649000 22,1359 70,0000 7,88374 6,19441 1539,4 188574 2,04082 490
491 2410 81 118 370771 22,1585 70,0714 7,88909 6,19644 1542,5 189345 2,03666 491
492 24 20 64 119095488 22,1811 70,1427 7,89445 6,19848 1545,7 190117 2,03252 492
493 24 30 49 119 823 157 22,2036 70,2140 7,89979 6,20051 1548,8 190890 2,02840 493
494 24 40 36 120553784 22,2261 70,2851 7,90513 6,20254 1551,9 191665 2,02429 494
495 24 5025 121 287 375 22,2486 70,3562 7,91046 6,20456 1555,1 192442 2,02020 495
496 24 6016 122 023936 22,2711 70,4273 7,91578 6,20658 1558,2 193221 2,01613 496
497 24 70 09 122 763 473 22,2935 70,4982 7,92110 6,20859 1561,4 194000 2,01207 497
498 24 80 04 123505 992 22,3159 70,5691 7,92641 6,21060 1564,5 194782 2,00803 498
499 24 90 01 124 251 499 22,3383 70,6399 7,93171 6,21261 1567,7 195565 2,00401 499
500 25 0000 125000000 22,3607 70,7107 7,93701 6,21461 1570,8 196350 2,00000 500
п п* п? У10п з 1/ п In п пп пп* 4 1000 п п
I
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
85
500—550
п п‘ п3 Vn У Юп 3,- ]/« In п ЯП ЯП’ 4~ 1 000 п п
500 25 00 00 125 000 000 22,3607 70,7107 7,93701 6,21461 1570,8 196350 2,00000 500
501 2510 01 125 751 501 22,3830 70,7814 7,94229 6,21661 1573,9 197136 1,99601 501
502 25 2004 126 506 008 22,4054 70,8520 7,94757 6,21860 1577,1 197923 1,99203 502
503 25 3009 127 263 527 22,4277 70,9225 7,95285 6,22059 1580,2 198713 1,98807 503
504 25 4016 128 024 064 22,4499 70,9930 7,95811 6,22258 1583,4 199504 1,98413 504
505 255025 128 787 625 22,4722 71,0634 7,96337 6,22456 1586,5 200296 1,98020 505
506 256036 129 554 216 22,4944 71,1337 7,96863 6,22654 1589,6 201090 1,97628 506
507 25 70 49 130323 843 22,5167 71,2039 7,97387 6,22851 1592,8 201886 1,97239 507
508 258064 131 096 512 22,5389 71,2741 7,97911 6,23048 1595,9 202683 1,96850 508
509 259081 131 872 229 22,5610 71,3442 7,98434 6,23245 1599,1 203482 1,96464 509
510 26 01 00 132 651 000 22,5832 71,4143 7,98957 6,23441 1602,2 204282 1,96078 510
511 2611 21 133 432 831 22,6053 71,4843 7,99479 6,23637 1605,4 205084 1,95695 511
512 26 21 44 134 217 728 22,6274 71,5542 8,00000 6,23832 1608,5 205887 1,95312 512
513 26 31 69 135005 697 22,6495 71,6240 8,00520 6,24028 1611,6 206692 1,94932 513
514 26 41 96 135 796 744 22,6716 71,6938 8,01040 6,24222 1614,8 207499 1,94553 514
515 26 52 25 136 590 875 22,6936 71,7635 8,01559 6,24417 1617,9 208307 1,94175 515
516 26 62 56 137 388 096 22,7156 71,8331 8,02078 6,24611 1621,1 209117 1,93798 516
517 26 72 89 138188 413 22,7376 71,9027 8,02596 6,24804 1624,2 209928 1,93424 517
518 26 83 24 138 991 832 22,7596 71,9722 8,03113 6,24998 1627,3 210741 1,93050 518
519 26 93 61 139 798 359 22,7816 72,0417 8,03629 6,25190 1630,5 211556 1,92678 519
520 27 04 00 140608000 22,8035 72,1110 8,04145 6,25383 1633,6 212372 1,92308 520
521 27 1441 141 420761 22,8254 72,1803 8,04660 6,25575 1636,8 213189 1,91939 521
522 27 24 84 142 236 648 22,8473 72,2496 8,05175 6,25767 1639,9 214008 1,91571 522
523 27 35 29 143 055 667 22,8692 72,3187 8,05689 6,25958 1643,1 214829 1,91205 523
524 2745 76 143 877824 22,8910 72,3878 8,06202 6,26149 1646,2 215651 1,90840 524
525 27 56 25 144 703125 22,9129 72,4569 8,06714 6,26340 1649,3 216475 1,90476 525
526 27 66 76 145 531 576 22,9347 72,5259 8,07226 6,26530 1652,5 217301 1,90114 526
527 27 77 29 146363183 22,9565 72,5948 8,07737 6,26720 1655,6 218128 1,89753 527
528 27 8784 147197952 22,9783 72,6636 8,08248 6,26910 1658,8 218956 1,89394 528
529 27 9841 148 035 889 23,0000 72,7324 8,08758 6,27099 1661,9 219787 1,89036 529
530 28 0900 148 877000 23,0217 72,8011 8,09267 6,27288 1665,0 220618 1,88679 530
531 28 19 61 149 721 291 23,0434 72,8697 8,09776 6,27476 1668,2 221452 1,88324 531
532 28 3024 150 568 768 23,0651 72,9383 8,10284 6,27664 1671,3 222287 1,87970 532
533 28 40 89 151 419437 23,0868 73,0068 8,10791 6,27852 1674,5 223123 1,87617 533
534 28 51 56 152 273304 23,1084 73,0753 8,11298 6,28040 1677,6 223961 1,87266 534
535 28 6225 153130 375 23,1301 73,1437 8,11804 6,28227 1680,8 224802 1,86916 535
536 28 72 96 153990656 23,1517 73,2120 8,12310 6,28413 1683,9 225642 1,86567 536
537 28 83 69 154 854 153 23,1733 73,2803 8,12814 6,28600 1687,0 226484 1,86220 537
538 28 94 4Z4 155 720872 23,1948 73,3485 8,13319 6,28786 1690,2 227329 1,85874 538
539 29 05 21 156 590 819 23,2164 73,4166 8,13822 6,28972 1693,3 228175 1,85529 539
540 29 16 00 157 464 000 23,2379 73,4847 8,14325 6,29157 1696,5 229022 1,85185 540
541 29 26 81 158 34 0 421 23,2594 73,5527 8,14828 6,29342 1699,6 229871 1,84843 541
542 29 37 64 159 220 088 23,2809 73,6206 8,15329 6,29527 1702,7 230722 1,84502 542
543 29 48 49 160 103007 23,3024 73,6885 8,15831 6,29711 1705,9 231574 1,84162 543
544 29 59 36 160989184 23,3238 73,7564 8,16331 6,29895 1709,0 232428 1,83824 544
545 29 7025 161 878 625 23,3452 73,8241 8,16831 6,30079 1712,2 233283 1,83486 545
546 29 81 16 162 771 336 23,3666 73,8918 8,17330 6,30262 1715,3 234140 1,83150 546
547 29 92 09 163 667323 23,3880 73,9594 8,17829 6,30445 1718,5 234998 1,82815 547
548 3003 04 164 566 592 23,4094 74,0270 8,18327 6,30628 1721,6 235858 1,82482 548
549 3014 01 165 469 149 23,4307 74,0945 8,18824 6,30810 1724,7 236720 1,82149 549
550 30 25 00 166 375 000 23,4521 74,1620 8,19321 6,30992 1727,9 237583 1,81818 550
п‘ п» Vn V Юп ]/п In п пп ЯП* 1000 п
26
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
550—600
п п1 * п3 1 3,- VlOn }/п In п пп пп* 4 WOQ п п
550 30 25 00 166 375 000 23,4521 74,1620 8,19321 6,30992 1727,9 237583 1,81818 >50
551 30 36 01 167 284 151 23,4734 74,2294 8,19818 6,31173 1731,0 238448 1,81488 551
552 30 4704 168 196 608 23,4947 74,2967 8,20313 6,31355 1734,2 239314 1,81159 552
553 30 58 09 169 112 377 23,5160 74,3640 8,20808 6,31536 1737,3 240182 1,80832 553
554 3069 16 170 031 464 23,5372 74,4312 8,21303 6,31716 1740,4 241051 1,80505 554
555 30 80 25 170 953 875 23,5584 74,4983 8,21797 6,31897 1743,6 241922 1,80180 555
556 30 91 36 171 879 616 23,5797 74,5654 8,22290 6,32077 1746,7 242795 1,79856 556
557 31 02.49 172808 693 23,6008 74,6324 8,22783 6,32257 1749,9 243669 1,79533 557
558 31 13 64 173 741 112 23,6220 74,6994 8,23275 6,32436 1753,0 244545 1,79211 558
559 3124 81 174 676 879 23,6432 74,7663 8,23766 6,32615 1756,2 245422 1,78891 559
560 31 36 00 175 616 000 23,6643 74,8331 8,24257 6,32794 1759,3 246301 1,78571 560
561 3147 21 176 558 481 23,6854 74,8999 8,24747 6,32972 1762,4 247181 1,78253 561
562 31 5844 177504 328 23,7065 74,9667 8,25237 6,33150 1765,6 248063 1,77936 562
563 3169 69 178 453 547 23,7276 75,0333 8,25726 6,33328 1768,7 248947 1,77620 563
564 3180 96 179 406 144 23,7487 75,0999 8,26215 6,33505 1771,9 249832 1,77305 564
565 31 92 25 180 362 125 23,7697 75,1665 8,26703 6,33683 1775,0 250719 1,76991 565
566 32 03 56 181 321 496 23,7908 75,2330 8 27190 6,33859 1778,1 251607 1,76678 566
567 32 14 89 182 284 263 23,8118 75,2994 8,27677 6,34036 1781,3 252497 1,76367 567
568 32 2624 183 250 432 23,8328 75,3658 8,28164 6,34212 1784,4 253388 1,76056 568
569 32 3761 184 220 009 23,8537 75,4321 8,28649 6,34388 1787,6 254281 1,75747 569
570 32 4900 185 193 000 23,8747 75,4983 8,29134 6,34564 1790,7 255176 1,75439 570
571 32 60 41 186 169 411 23,8956 75,5645 8,29619 6,34739 1793,8 256072 1,75131 571
572 32 7184 187 149 248 23,9165 75,6307 8,30103 6,34914 1797,0 256970 1,74825 572
573 3283 29 188 132 517 23,9374 75,6968 8.30587 6,35089 1800,1 257869 1,74520 573
574 32 94 76 189 119 224 23,9583 75,7628 8,31069 6,35263 1803,3 258770 1,74216 574
575 33 06 25 190 109 375 23,9792 75,8288 8,31552 6,35437 1806,4 259672 1,73913 575
576 331776 191 102 976 24,0000 75,8947 8,32034 6,35611 1809,6 260576 1,73611 576
577 33 29 29 192 100 033 24,0208 75,9605 8,32515 6,35784 1812,7 261482 1,73310 577
578 33 40 84 193 100 552 24,0416 76,0263 8,32995 6,35957 1815,8 262389 1,73010 578
579 33 52 41 194 104 539 24,0624 76,0920 8,33476 6,36130 1819,0 263298 1,72712 579
580 33 64 00 195 112 000 24,0832 76,1577 8,33955 6,36303 1822,1 264208 1,72414 580
581 33 75 61 196122 941 24,1039 76,2234 8,34434 6,36475 1825,3 265120 1,72117 581
582 33 87 24 197137 368 24,1247 76,2889 8,34913 6,36647 1828,4 266033 1,71821, 582
583 33 98 89 198 155 287 24,1454 76,3544 8,35390 6,36819 1831,6 266948 1,71527 583
584 34 10 56 199 176 704 24,1661 76,4199 8,35868 6 36990 1834,7 267865 1,71233 584
585 34 22 25 200 201 625 24,1868 76,4853 8,36345 6,37161 1837,8 268783 1,70940 585
586 34 33 96 201 230 056 24,2074 76,5506 8,36821 6,37332 1841,0 269703 1,70648 586
587 34 45 69 202 262 003 24,2281 76,6159 8,37297 6,37502 1844,1 270624 1,70358 587
588 34 57 44 203 297 472 24,2487 76,6812 8,37772 6,37673 1847,3 271547 1,70068 588
589 34 69 21 204 336 469 24,2693 76,7463 8,38247 6,37843 1850,4 272471 1,69779 589
590 34 8100 205 379 000 24,2899 76,8115 8,38721 6,38012 1853,5 273397 1,69492 590
591 34 92 81 206 425 071 24,3105 76,8765 8,39194 6,38182 1856,7 274325 1,69205 591
592 35 04 64 207 474 688 24,3311 76,9415 8,39667 6,38351 1859,8 275254 1,68919 592
593 35 16 49 208 527 857 24,3516 77,0065 8.40140 6,38519 1863,0 276184 1,68634 593
594 35 28 36 209 584 584 24,3721 77,0714 8,40612 6,38688 1866,1 277117 1,68350 594
595 35 40 25 210 644 875 24,3926 77,1362 8,41083 6,38856 1869,2 278051 1,68067 595
596 35 52 16 211 708 736 24,4131 77,2010 8,41554 6,39024 1872,4 278986 1,67785 596
597 35 64 09 212 776 173 24,4336 77,2658 8,42025 6,39192 1875,5 279923 1,67504 597
598 35 76 04 213 847 192 24,4540 77,3305 8,42494 6,39359 1878,7 280862 1,67224 598
599 36 88 01 214 921 799 24,4745 77.3951 8,42964 6,39526 1881,8 281802 1,66945 599
600 36 00 00 216 000 000 24,4949 77,4597 8,43433 6,39693 1885,0 282743 1,66667 600
п и» | п* Vn | р Т6Ч | In п 1 пп 1 ЯП* "4“ 1000 1 п п
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
27
€00 — 650
п п* ! п* Уп У 10п 3,- Vя In It пп пп* 1000 п п
600 3600 00 216000 000 24,4949 77,4597 8,43433 6,39693 1885,0 282743 1,66667 600
601 36 1201 217081 801 24,5153 77,5242 8,43901 6,39859 1888,1 283687 1,66389 601
602 36 24 04 218 167 208 24,5357 77,5887 8,44369 6,40026 1891,2 284631 1,66113 602
603 36 36 09 219 256 227 24,5561 77,6531 8,44836 6,40192 1894,4 285578 1,65837 603
604 36 48 16 220 348 864 24,5764 77,7174 8,45303 6,40357 1897,5 286526 1,65563 604
605 3660 25 221 445 125 24,5967 77,7817 8,45769 6,40523 1900,7 287475 1,65289 605
606 36 72 36 222 545 016 24,6171 77,8460 8,46235 6,40688 1903,8 288426 1,65017 606
607 36 84 49 223 648 543 24,6374 77,9102 8,46700 6,40853 1906,9 289379 1,64745 607
608 36 96 64 224 755 712 24,6577 77,9744 8,47165 6,41017 1910,1 290333 1,64474 608
609 37 08 81 225 866 529 24,6779 78,0385 8,47629 6,41182 1913,2 291289 1,64204 609
610 37 21 00 226 981 000 24,6982 78,1025 8,48093 6,41346 1916,4 292247 1,63934 610
611 37 33 21 228 099 131 24,7184 78,1665 8,48556 6,41510 1919,5 293206 1,63666 611
612 37 45 44 229 220 928 24,7386 78,2304 8,49018 6,41673 1922,7 294166 1,63399 612
613 37 57 69 230 346 397 24,7588 78,2943 8,49481 6,41836 1925,8 295128 1,63132 613
614 37 69 96 231 475 544 24,7790 78,3582 8,49942 6,41999 1928,9 296092 1,62866 614
615 3782 25 232 608 375 24,7992 78,4219 8,50404 6,42162 1932,1 297057 1,62602 615
616 37 94 56 233 744 896 24,8193 78,4857 8,50864 6,42325 1935,2 298024 1,62338 616
617 380689 234 885 113 24,8395 78,5493 8,51324 6,42487 1938,4 298992 1,62075 617
618 381924 236 029 032 24,8596 78,6130 8,51784 6,42649 1941,5 299962 1,61812 618
619 38 31 61 237 176 659 24,8797 78,6766 8,52243 6,42811 1944,6 300934 1,61551 619
620 38 44 00 238 328 000 24,8998 78,7401 8,52702 6,42972 1947,8 301907 1,61290 620
621 38 56 41 239483 061 24,9199 78,8036 8,53160 6,43133 1950,9 302882 1,61031 621
622 ,38 68 84 240 641 848 24,9399 78,8670 8,53618 6,43294 1954,1 203858 1,60772 622
623 38 81 29 241 804 367 24,9600 78,9303 8,54075 6,43455 1957,2 304836 1,60514 623
624 38 93 76 242 970 624 24,9800 78,9937 8,54532 6,43615 1960,4 305815 1,60256 624
625 39 06 25 244140 625 25,0000 79,0569 8,54988 6,43775 1963,5 306796 1,60000 625
626 39 18 76 245 314 376 25,0200 79,1202 8,55444 6,43935 1966,6 307779 1,59744 626
627 39 3129 246 491 883 25,0400 79,1833 8,55899 6,44095 1969,8 308763 1,59490 627
628 39 43 84 247 673 152 25,0599 79,2465 8,56354 6,44254 1972,9 309748 1,59236 628
629 39 56 41 248 858 189 25,0799 79,3095 8,56808 6,44413 1976,1 310736 1,58983 629
630 39 6900 250 047-000 25,0998 79,3725 8,57262 6,44572 1979,2 311725 1,58730 630
631 39 81 61 251 239 591 25,1197 79,4355 8,57715 6,44731 1982,3 312715 1,58479 631
632 39 94 24 252 435 968 25,1396 79,4984 8,58168 6,44889 1985,5 313707 1,58228 632
633 40 06 89 253 636 137 25,1595 79,5613 8,58620 6,45047 1988,6 314700 1,57978 633
634 40 19 56 254 840104 25,1794 78,6241 8,59072 6,45205 1991,8 315696 1,57729 634
635 40 32-25 256 047 875 25,1992 78,6869 8,59524 6,45362 1994,9 316692 1,57480 635
636 40 44 96 257 259 456 25,2190 79,7496 8,59975 6,45520 1998,1 317690 1,57233 636
637 40 57 69 258 474 853 25,2389 79,8123 8,60425 6,45677 2001,2 318690 1,56986 637
638 40 70 44 259 694 072 25,2587 79,8749 8,60875 6,45834 2004,3 319692 1,56740 638
639 40 83 21 260 917 119 25,2784 79,9375 8,61325 6,45990 2007,5 320695 1,56495 639
640 40 9600 262 144 000 25,2982 80,0000 8,61774 6,46147 2010,6 321699 1,56250 640
641 4108 81 263 374 721 25,3180 80,0625 8 62222 6,46303 2013,8 322705 1,56006 641
642 41 21 64 264 609 288 25,3377 80,1249 8,62671 6,46459 2016,9 323713 1,55763 642
643 41 34 49 265 847 707 25,3574 80,1873 8,63118 6,46614 2020,0 324722 1,55521 643
644 41 47 36 267089 984 25,3772 80,2496 8,63566 6,46770 2023,2 325733 1,55280 644
645 41 60 25 268 336 125 25,3969 80,3119 8,64012 6,46925 2026,3 326745 1,55039 645
646 41 7316 269 586 136 25,4165 80,3741 8,64459 6,47080 2029,5 327759 1,54799 646
647 41 86 09 270 840 023 25,4362 80,4363 8,64904 6,47235 2032,6 328775 1,54560 647
648 41 99 04 272 097 792 25;4558 80,4984 8,65350 6,47389 2035,8 329792 1,54321 648
649 42 1201 273 359 449 25,4755 80,5605 8,65795 6,47543 2038,9 330810 1,54083 649
650 42 25 00 274 625 000 25,4951 80,6226 8,66239 6,47697 2042,0 331831 1,53846 650
п п8 п* УТ )/Тбп In п пп 4 1000 п п
28
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
650 — 700
п п* п’ 1 П 3/~ 1/ п Inn пП пП1 4 1000 п п
650 42 25 00 274 625 000 25,4951 80,6226 8,66239 6,47697 2042,0 331831 1,53846 650
651 42 38 01 275 894 451 25,5147 80,6846 8,66683 6,47851 2045,2 332853 1,53610 651
652 42 51 04 277 167 808 25,5343 80,7465 8,67127 6,48004 2048,3 333876 1,53374 652
653 42 6409 278 445 077 25,5539 80,8084 8,67570 *6,48158 2051,5 334901 1,53139 653
654 42 77 16 279 726 264 25,5734 80,8703 8,68012 6,48311 2054,6 335927 1,52905 654
655 42 90 25 281 011 375 25,5930 80,9321 8,68455 6,48464 2057,7 336955 1,52672 655
656 4303 36 282 300 416 25,6125 80,9938 8,68896 6,48616 2060,9 337985 1,52439 656
657 4316 49 283593 393 25,6320 81,0555 8,69338 6,48768 2064,0 339016 1,52207 657
658 43 29 64 284 890 312 25,6515 81,1172 8,69778 6,48920 2067,2 340049 1,51976 658
659 43 42 81 286 191 179 25,6710 81,1788 8,70219 6,49072 2070,3 341084 1,51745 659
660 4356 00 287 496 000 25,6905 81,2404 8,70659 6,49224 2073,5 342119 1,51515 660
661 43 69 21 288 804 781 25,7099 81,3019 8,71098 6,49375 2076,6 343157 1,51286 661
662 4382 44 290 117 528 25,7294 81,3634 8,71537 6,49527 2079,7 344196 1,51057 662
663 43 95 69 291 434 247 25,7488 81,4248 8,71976 6,49677 2082,9 345237 1,50830 663
664 44 08 96 292 754 944 25,7682 81,4862 8,72414 6,49828 2086,0 346279 1,50602 664
665 44 22 25 294 079 625 25,7876 81,5475 8,72852 6,49979 2089,2 347323 1,50376 665
666 44 35 56 295 408 296 25,8070 81,6088 8,73289 6,50129 2092,3 348368 1,50150 666
667 44 48 89 296 740963 25,8263 81,6701 8,73726 6,50279 2095,4 349415 1,49925 667
668 44 62 24 298 077 632 25,8457 81,7313 8,74162 6,50429 2098,6 350464 1,49701 668
669 44 75 61 299 418 309 25,8650 81,7924 8,74598 6,50578 2101,7 351514 1,49477 669
670 44 89 00 300 763000 25,8844 81,8535 8,75034 6,50728 2104,9 352565 1,49254 670
671 45 02 41 302111 711 25,9037 81,9146 8,75469 6,50877 2108,0 353618 1,49031 671
672 45 15 84 303 464448 25,9230 81,9756 8,75904 6,51026 2111,2 354673 1,48810 672
673 45 29 29 304 821 217 25,9422 82,0366 8,76238 6,51175 2114,3 355730 1,48588 673
674 45 42 76 306182 024 25,9615 82,0975 8,76772 6,51323 2117,4 356788 1,48368 674
675 45 56 25 307 546 875 25,9808 82,1584 8,77205 6,51471 2120,6 357847 1,48148 675
676 45 69 76 308 915 776 26,0000 82,2192 8,77638 6,51619 2123,7 358908 1,47929 676
67? 45 83 29 310 288 733 26,0192 82,2800 8,78071 6,51767 2126,9 359971 1,47710 677
678 45 96 84 311 665 752 26,0384 82,3408 8,78503 6,51915 2130,0 361035 1,47493 678
679 46 1041 313 046 839 26,0576 82,4015 8,78935 6,52062 2133,1 362101 1,47275 679
680 46 24 00 314 432 000 26,0768 82,4621 8,79366 6,52209 2136,3 363168 1,47059 680
681 46 37 61 315 821 241 26,0960 82,5227 8,79797 6,52356 2139,4 364237 1,46843 681
682 46 51 24 317 214 568 26,1151 82,5833 8,80227 6,52503 2142,6 365308 1,46628 682
683 46 64 89 318 611 987 26,1343 82,6438 8,80657 6,52649 2145,7 366380 1,46413 683
684 46 7856 320 013 504 26,1534 82,7043 8,81087 6,52796 2148,8 367453 1,46199 684
685 46 92 25 321 419 125 26,1725 82,7647 8,81516 6,52942 2152,0 368528 1,45985 685
686 47 05 96 322 828 856 26,1916 82,8251 8,81945 6,53088 2155,1 369605 1,45773 686
687 47 19 69 324 242 703 26,2107 82,8855 8,82373 6,53233 2158,3 370684 1,45560 687
688 47 3344 325 660 672 26,2298 82,9458 8,82801 6,53379 2161,4 371764 1,45349 688
689 47 47 21 327 082 769 26,2488 83,0060 8,83228 6,53524 2164,6 372845 1,45138 689
690 47 61 00 328 509 000 26,2679 83,0662 8,83656 6,53669 2167,7 373928 1,44928 690
691 47 74 81 329 939 371 26,2869 83,1264 8,84082 6,53814 2!70,8 375013 1,44718 691
692 47 88 64 331 373 888 26,3059 83,1865 8,84509 6,53959 2174,0 376099 1,44509 692
693 48 02 49 332 812 557 26,3249 83,2466 8,84934 6,54103 2177,1 377187 1,44300 693
694 48 16 36 334 255 384 26,3439 83,3067 8,85360 6,54247 2-180,3 378276 1,44092 694
695 48 30 25 335 702 375 26,3629 83,3667 8,85785 6,54391 2183,4 379367 1,43885 695
696 48 4416 337153536 26,3818 83,4266 8,86210 6,54535 2186,5 380459 1,43678 696
697 48 58 09 338 608 873 26,4008 83,4865 8,86634 6,54679 2189,7 381553 1,43472 697
698 48 72 04 340068392 26,4197 83,5464 8,87058 6,54822 2192,8' 382649 1,43266 698
699 48 86 01 341 532 099 26,4386 83,6062 8,87481 6,54965 2196,0 383746 1,43062 699
700 490000 343000000 26,4575 83,6660 8,87904 6,55108 2199,1 3848451 “ 1,42857 700
п п* И1 1/п р'10п 3/- 1/ п Inn пп пп1 4 1000 п п
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
29
700 — 750
Л л’ и3 Vn ^Юп 3,- V п Inn ЯП ЯП9 4 1000 л п
700 49 0000 343000000 26,4575 83,6660 8,87904 6,55108 2199,1 384845 1,42857 700
701 4914 01 344 472101 26,4764 83,7257 8,88327 6,55291 2202,3 385945 1,42653 701
702 49 28 04 345 948408 26,4953 83,7854 8,88749 6,55393 2205,4 387047 1,42450 702
703 49 42 09 347428 927 26,5141 83,8451 8,89171 6,55536 2208,5 388151 1,42248 703
704 49 5616 348 913 664 26,5330 83,9047 8,89592 6,55678 2211,7 389256 1,42045 704
705 49 70 25 350 402 625 26,5518 83,9643 8,90013 6,55820 2214,7 390363 1,41844 705
706 49 84 36 351895 816 26,5707 84,0238 8,90434 6,55962 2218,0 391471 1,41643 706
707 49 98 49 353 393 243 26,5895 84,0833 8,90854 6,56103 2221,1 392580 1,41443 707
708 50 12 64 354 894 912 26,6083 84,1427 8,91274 6,56244 2224,2 393692 1,41243 708
709 50 26 81 356400829 26,6271 84,2021 8,91693 6,56386 2227,4 394805 1,41044 709
710 50 41 00 357 911 000 26,6458 84,2615 8,92112 6,56526 2230,5 395919 1,40845 710
711 50 55 21 359 425 431 26.6646 84,3208 8,92531 6,56667 2233,7 397035 1,40647 711
712 50 69 44 360944 128 26,6833 84,3801 8,92949 6,56808 2236,8 398153 1,40449 712
713 50 83 69 362 467 097 26,7021 84,4393 8,93367 6,56948 2240,0 399272 1,40252 713
714 50 97 96 363 994 344 26,7208 84,4985 8,93784 6,57088 2243,1 400393 1,40056 714
715 51 12 25 365 525 875 26,7395 84,5577 8,94201 6,57228 2246,2 401515 1,39860 715
716 51 26 56 367061 696 26,7582 84,6168 8,94618 6,57368 2249,4 402639 1,39665 716
717 51 40 89 368 601 813 26,7769 84,6759 8,95034 6,57508 2252,5 403765 1,39470 717
718 51 55 24 370 146 232 26,7955 84,7349 8,95450 6,57647 2255,7 404892 1,39276 718
719 51 69 61 371 694 959 26,8142 84,7939 8,95866 6,57786 2258,8 406020 1,39082 719
720 51 84 00 373 248 000 26,8328 84,8528 8,96281 6,57925 2261,9 407150 1,38889 720
721 51 98 41 374 805 361 26,8514 84,9117 8,96696 6,58064 2265,1 408282 1,38696 721
722 52 12 84 376 367 048 26,8701 84,9706 8,97110 6,58203 2268,2 409415 1,38504 722
723 52 27 29 377 933 067 26,8887 85,0294 8,97524 6,58341 2271,4 410550 1,38313 723
724 52 41 76 37950342' 26,9072 85,0882 8,97938 6,58479 2274,5 411687 1,38122 724
725 52 56 25 381 078 125 26,9258 85,1469 8,98351 6,58617 2277,7 412825 1,37931 725'
726 52 70 76 382 657 176 26,9444 85,2056 8,98764 6,58755 2280,8 413965 1,37741 726
727 52 85 29 384 240 583 26,9629 85,2643 8,99176 6,58893 2283,9 415106 1 37552 727
728 52 99 84 385 828 352 26,9815 85,3229 8,99588 6,59030 2287,1 416248 1,37363 728
729 53 1441 387 420 489 27,0000 85,3815 9,00000 6,59167 2290,2 417393 1,37174 729
730 53 29 00 389 017 000 27,0185 85,4400 9,00411 6,59304 2293,4 418539 1,36986 730
731 53 43 61 390 617 891 27,0370 85,4985 9,00822 6,59441 2296,5 419686 1,36799 731
732 53 58 24 392 223 168 27,0555 85,5570 9,01233 6,59578 2299,6 420835 1,36612 732
733 53 72 89 393 832 837 27,0740 85,6154 9,01643 6,59715 2302,8 421986 1,36426 733
734 53 87 56 395 446 904 27,0924 85,6738 9,02053 6,59851 2305,9 423138 1,36240 734
735 54 02 25 397065 375 27,1109 85,7321 9,02462 6,59987 2309,1 424293 1,36054 735
736 54 16 96 398 688 256 27,1293 85,7904 9,02871 6,60123 2312,2 425447 1,35870 736
737 54 31 69 400 315 553 27,1477 85,8487 9,-03280 6,60259 2315,4 426604 1,35685 737
738 54 46 44 401 947 272 27,1662 85,9069 9,03689 6,60394 2318,5 427762 1,35501 738
739 54 61 21 403 583 419 27,1846 85,9651 9,04097 6,60530 2321,6 428922 1,35318 739
740 54 76 00 405 224 000 27,2029 86,0233 9,04504 6,60665 2324,8 430084 1,35135 740
741 549081 406 869 021 27,2213 86,0814 9,04911 6,60800 2327,9 431247 1,34953 741
742 55 05 64 408 518 488 27,2397 86,1394 9,05318 6,60935 2331,1 432412 1,34771 742
743 5520 49 410 172 407 27,2580 86,1974 9,05725 6,61070 2334,2 433578 1,34590 743
744 5535 36 411 830 784 27,2764 86,2554 9,06131 6,61204 2337,3 434746 1,34409 744
745 55 50 25 413 493 625 27,2947 86,3134 9,06537 6,61338 2340,5 435916 1,34228 745
746 55 65 16 415160 936 27,3130 86,3713 9,06942 6,61473 2343,6 437087 1,34048 746
747 55 80 09 416 832 723 27,3313 86,4292 9,07347 6,61607 2346,8 438259 1,33869 747
748 55 95 04 418 508 992 27,3496 86,4870 9,07752 6,61740 2349,9 439433 1,33690 748
749 56 10 01 420 189 749 27,3679 86,5448 9,08156 6,61874 2353,1 440609 1,33511 749
750 56 25 00 421 875000 27,3861 86,6025 9,08560 6,62007 2356,2 441786 1,33333 750
п п« п' Jzn /Ж 3,- j/n In n ЯП ЯП* 4 1000 ' п п
, 30
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
750 —800
п п* п» J/n In п пп ЯП8 £000 п * л
750 56 2500 421 875000 27,3861 86,6025 9,08560 6,62007 2356,2 441786 1,33333 750
751 56 4001 423 564 751 27,4044 86,6603 9,08964 6,62141 2359,3 442965 1,33156 751
752 56 5504 425 259 008 27,4226 86,7179 9,09367 6,62274 2362,5 444146 1,32979 752
753 56 70 09 426 957 777 27,4408 86,7756 9,09770 6,62407 2365,6 445328 1,32802 753
754 56 8516 428 661064 27,4591 86,8332 9,10173 6,62539 2368,8 446511 к, 32626 754
755 570025 430368 875 27,4773 86,8907 9,10575 6,62672 2371,9 447697 1,32450 755
756 571536 432 081 216 27,4955 86,9483 9,10977 6,62804 2375,0 448883 1,32275 756
757 5730 49 433 798 093 27,5136 87,0057 9,11378 6,62936 2378,2 450072 1,32100 757
758 57 4564 435519 512 27,5318 87,0632 9,11779 6,63068 2381,3 451262 1,31926 758
759 57 60 81 437 245 479 27,5500 87,1206 9,12180 6,63200 2384,5 452453 1,31752 759
760 57 7600 438 976 000 27,5681 87,1780 9,12581 6,63332 2387,6 453646 1,31579 760
761 57 91 21 440 711 081 27,5862 87,2353 9,12981 6,63463 2390,8 454841 1,31406 761
762 58 06 44 442 450 728 27,6043 87,2926 9,13380 6,63595 2393,9 456037 1,31234 762
763 58 21 69 444194 947 27,6225 87,3499 9.13780 6,63726 2397 0 457234 1,31062 763
764 58 36 96 445943 744 27,6405 87,4071 9,14179 6,63857 2400,2 458434 1,30890 764
765 5852 25 447 697125 27,6586 87,4643 9,14577 6,63988 2403,3 459635 1,30719 765
766 58 6756 449 455 096 27,6767 87,5214 9,14976 6,64118 2406,5 460837 1,30548 766
767 58 82 89 451 217 663 27,6948 87,5785 9,15374 6,64249 2409J5 462041 1,30378 767
768 58 98 24 452 984 832 27,7128 87,6356 9,15771 6,64379 2412,7 463247 1,30208 768
769 591361 454 756 609 27,7308 87,6926 9,16169 6,64509 2415,9 464454 1,30039 769
770 59 2900 456 533 000 27,7489 87,7496 9,16566 6,64639 2419,0 465663 1,29870 770
771 59 44 41 458 314 011 27.7669 87,8066 9,16962 6,64769 2422,2 466873 1,29702 771
772 59 59 84 460099 648 27,7849 87,8635 9,17359 6,64898 2425,3 4680S5 1,29534 772
773 59 75 29 461 889 917 27.8029 87,9204 9,17754 6,65028 2428,5 46929.8 1,29366 773
774 59 90 76 463 684824 27,8209 87,9773 9,18150 6,65157 2431,6 470513 1,29199 774
775 60 06 25 465 484 375 27,8388 88,0341 9,18545 6,65286 2434,7 471730 1,29032 775
776 60 21 76 467 288 576 27,8568 88,0909 9,18940 6,65415 2437,9 472948 1,28866 776
777 60 37 29 469 097 433 27,8747 88,1476 9,19335 6,65544 2441,0 474168 1,28700 777
778 60 5284 470 910 952 27,8927 88,2043 9,19729 6,65673 2444,2 475389 1,28535 778
779 60 68 41 472 729139 27,9106 88,2610 9,20123 6,65801 2447,3 476612 1,28370 779
780 60 8400 474 552 000 27,9285 88,3176 9,20516 6,65929 2450,4 477836 1,28205 780
781 6099 61 476 379 541 27.9464 88,3742 9,20910 6,66058 2453,6 479062 1,28041 781
782 61 15 24 478 211 768 27,9643 88,4308 9,21303 6,66185 2456,7 480290 1,27877 782
783 61 30 89 480 048 687 27,9821 88,4873 9,21695 6,66313 2459,9 481519 1,27714 783
784 61 46 56 481 890304 28,0000 88,5438 9,22087 6,66441 2463,0 482750 1,27551 784
785 61 62 25 483 736625 28,0179 88,6002 9,22479 6,66568 2466,2 483982 1,27389 785
786 61 77 96 485 587 656 28,0357 88,6566 9,22871 6,66696 2469,3 485216 1,27226 786
787 61 93 69 487 443 403 28,0535 88,7130 9,23262 6,66823 2472,4 486451 1,27065 787
788 6209 44 489 303 872 28,0713 88,7694 9,23653 6,66950 2475,6 487688 1,26904 788
789 62 25 21. 491 169 069 28,0891 88,8257 9,24043 6,67077 2478,7 488927 1,26743 789
790 62 41 00 493 039 000 28,1069 88,8819 9,24434 6,67203 2481,9 490167 1,26582 790
791 62 56 81 494 913 671 28.1247 88,9382 9,24823 6,67330 2485,0' 491409 1,26422 791
792 62 72 64 496 793 088 28,1425 88,9944 9,25213 6,67456 2488,1 492652 1,26263 792
793 62 88 49 498 677 257 28,1603 89,0505 9,25602 6,67582 2491,3 493897 1,26103 793
794 63 04 36 500 566184 28,1780 89,1067 9,25991 6,67708 2494,4 495143 1,25945 794
795 63 2025 502 459 875 28,1957 89,1628 9,26380 6,67834 2497,6 496391 1,25786 795
796 63 3616 504 358 336 28,2135 89,2188 9,26768 6,67960 2500,7 497641 1,25628 796
797 6352 09 506 261 573 28,2312 89,2749 9,27156 6,68085 2503,8 498892 1,25471 797
798 63 68 04 508 169 592 28,2489 89,3308 9,27544 6,68211 2507,0 500145 1,25313 798
799 63 84 01 510 082 399 28,2666 89,3868 9,27931 6,68336 2510,1 501399 1,25156 799
800 6400 00 512 000000 28,2843 89,4427 9,28318 6,68461 2513,3 502655 1,25000 800
п п‘ пг Уп У 10п | 3 1 In п аП ЯП’ 1000 ' п п
МАТЕМАТИЧЕСКИЙ ТАБЛИЦЫ
31
800 — 850
п2 и8 Vn j/10n 3/“ In п лп лп1 ~4~ 1000 п
800 64 0000 512 000000 28,2843 89,4427 9,28318 6.68461 2513,3 502655 1,25000 800
801 641601 513 922 401 28,3019 89,4986 9,28704 6,68586 2516,4 503912 1,24844 801
802 64 32 04 515 849 608 28,3196 89,5545 9,29091 6,68711 2519,6 505171 1,24688 802
803 64 48 09 517 781 627 28,3373 89,6103 9,29477 6,68835 2522,7 506432 1,24533 803
804 64 64 16 519 718464 28,3549 89,6660 9,29862 6,68960 2525,8 507694 1,24378 804
805 64 80 25 521 660125 28,3725 89,7218 9,30248 6,69084 2529,0 508958 1,24224 805
806 64 96 36 523 606616 28,3901 89,7775 9,30633 6,69208 2532,1 510223 1,24069 806
807 65 12 49 525 557943 28,4077 89,8332 9,31018 6,69332 2535,3 511490 1,23916 807
808 65 28 64 527514112 28,4253 89,8888 9,31402 6,69456 2538,4 512758 1,23762 808
809 65 44 81 529 475129 28,4429 89,9444 9,31786 6,69580 2541,5 514028 1,23609 809
810 65 61 00 531 441 000 28,4605 90,0000 9,32170 6,69703 2544,7 515300 1,23457 810
811 65 77 21 533 411 731 28,4781 90,0555 9,32553 6,69827 2547,8 516573 1,23305 811
812 65 93 44 535 387 328 28,4956 90,1110 9,32936 6,69950 2551,0 517848 1,23153 812
813 66 09 69 537 367 797 28,5132 90,1665 9,33319 6,70073 2554,1 519124 1,23001 813
814 66 25 96 539 353 144 28,5307 90,2219 9,33702 6,70196 2557,3 520402 1,22850 814
815 66 42 25 541 343 375 28,5482 90,2774 9,34084 6,70319 2560,4 521681 1,22699 815
816 66 58 56 543 338 496 28,5657 90,3327 9,34466 6,70441 2563,5 522962 1,22549 816
817 66 74 89 545 338513 28,5832 90,3881 9,34847 6,70564 2566,7 524245 1,22399 817
818 66 91 24 547 343432 28,6007 90,4434 9,35229 6,70686 2569,8 525529 1,22249 818
819 67 07 61 549 353 259 28,6182 90,4986 9,35610 6,70808 2573,0 526814 1,22100 819
820 67 24 00 551 368 000 28,6356 90,5539 9,35990 6.70930 2576,1 528102 1,21951 820
821 67 40 41 553 387 661 28,6531 90,6090 9,36370 6,71052 2579,2 529391 1,21803 821
822 67 56 84 555 412 248 28,6705 90,6642 9,36751 6,71174 2582,4 530681 1,21655 822
823 67 73 29 557 441 767 28*6880 90,7193 9,37130 6,71296 2585,5 531973 1,21507 823
824 67 89 76 559 476 224 28,7054 90,7744 9,37510 6,71417 2588,7 533267 1,21359 824
825 68 06 25 561 515 625 28,7228 90,8295 9,37889 6,71538 2591,8 53-1562 1,21212 825
826 68 22 76 563 559 976 28,7402 90,8845 9,38268 6,71659 2595,0 535858 1,21065 S26
827 68 39 29 565 609 283 28,7576 90,9395 9,38646 6,71780 2598,1 537157 1,20919 827
828 68 5584 567 663 552 28,7750 90,9945 9,39024 6,71901 2601,2 538456 1,20773 828
829 68 72 41 569 722 789 28,7924 91,0494 9,39402 6,72022 2604,4 539758 1,20627 829
830 68 89 00 571 787 000 28,8097 91,1043 9,39780 6,72143 2607,5 541061 1,20482 830
831 69 05 61 573 856191 28,8271 91,1592 9,40157 6,72263 2610,7 542365 1,20337 831
832 69 22 24 575 930 368 28,8444 91,2140 9,40534 6,72383 2613,8 543671 1,20192 832
833 69 38 89 578 009 537 28,8617 91,2688 9,40911 6,72503 2616,9 544979 1,20048 833
834 69 55 56 580 093 704 28,8791 91,3236 9,41287 6,72623 2620,1 546288 1,19904 834
835 69 72 25 582182875 28,8964 91,3783 9,41663 6,72743 2623,2 54759’9 1,19760 835
836 6988 96 584 277 056 28,9137 91,4330 9,42039 6,72863 2626,4 548912 1,19617 836
837 70 05 69 586 376 253 28,9310 91,4877 9 42414 6,72982 2629,5 550226 1,19474 837
838 70 22 44 588 480 472 28,9482 91,5423 9,42789 6,73102 2632,7 551541 1,19332 838
839 70 39 21 590 589 719 28,9655 91,5969 9,43164 6,73221 2635,8 552858 1,19190 839
840 70 56 00 592 704 000 28,9828 91,6515 9,43539 6,73340 2638,9 554177 1,19048 840
841 70 72 81 594823 321 29,0000 91,7061 9,43913 6,73459 2642,1 555497 1,18906 841
842 70 89 64 596 947 688 29,0172 91,7606 9,44287 6,73578 2645,2 556819 1,18765 842
843 71 06 49 599 077 107 29,0345 91,8150 9,44661 6,73697 2648,4 558142 1,18624 843
844 71 23 36 601 211 584 29,0517 91,8695 9,45034 6,73815 2651,5 559467 1,18483 844
845 7140 25 603 351 125 29,0689 91,9239 9,45407 6,73934 2654,6 560794 1,18343 845
846 71 5716 605 495 736 29,0861 91,9783 9,45780 6,74052 2657,8 562122 1,18203 846
847 71 74 09 607615 423 29,1033 92,0326 9,46152 6,74170 2660,9 563452 1,18064 847
848 71 91 04 609 800 192 29,1204 92,0869 9,46525 6,74288 2664,1 564783 1,17925 848
849 72 08 01 611 960 049 29,1376 92,1412 9,46897 6,74406 2667,2 56611о 1,17786 849
850 72 25 00 614125 000 29,1548 92,1954 9,47268 6,74524 2670,4 567450 1,17647 850
па л3 /п VlOn К in п пп лПа 1000 п
32
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
850 — 900
п п* п» Vn /ion 3/- 1/ и Inn пп пп* Т 1000 п п
850 72 25 00 614 125 000 29,1548 92,1954 9,47268 6,74524 2670,4 567450 1,17647 850
851 7242 01 616 295 051 29,1719 92,2497 9,47640 6,74641 2673,5 568786 1,17509 851
852 72 5904 618 470 208 29,1890 29,2062 92,3038 9,48011 6,74759 2676,6 570124 1,17371 852
853 72 7609 620 650477 92,3580 4,48381 6,74876 2679,8 571463 1,17233 853
854 729316 622 835 864 29,2233 29,2404 92,4121 9,48752 6,74993 2682,9 572803 1,17096 854
855 731025 625 026 375 92,4662 9,49122 6,75110 2686,1 574146 1,16959 855
856 73 27 36 627 222 016 29,2575 92,5203 9,49492 6,75227 2689,2 575490 1,16822 856
857 734449 629 422 793 29,2746 92,5743 9,49861 6,75344 2692,3 576835 1,16686 857
858 73 61 64 631 628 712 29,2916 92,6283 9,50231 6,75460 2695,5 578182 1,16550 858
859 7378 81 633 839 779 29,3087 92,6823 9,50600 6,75577 6,75693 2698,6 579530 1,16414 859
860 73 96 00 636 056 000 29,3258 92,7362 9,50969 2701,8 580880 1,16279 860
861 74 13 21 638 277 381 29,3428 92,7901 9,51337 6,75809 2704,9 582232 1,16144 861
862 743044 640503 928 29,3598 92,8440 9,51705 6,75926 2708,1 583585 1,16009 862
863 7447 69 642 735 647 29,3769 92,8978 9,52073 6,76041 2711,2 584940 1,15875 863
864 7464 96 644 972 544 29,3939 92,9516 9,52441 6,76157 2714,3 586297 1,15741 864
865 7482 25 647 214 625 29,4109 93,0054 9,52808 6,76273 2717,5 587655 1,15607 865
866 74 99 56 649 461896 29,4279 93,0591 9,53175 6,76388 2720,6 589014 1,15473 866
867 75 16 89 651 714363 29,4449 93,1128 9,53542 6,76504 2723,8 590375 1,15340 867
868 7534 24 653 972 032 29,4618 93,1665 9,53908 6,76619 2726,9 591738 1,15207 868
869 7551 61 656 234 909 29,4788 93,2202 9,54274 6,76734 2730,0 593102 1,15075 869
870 7569 00 658 503 000 29,4958 93,2738 9,54640 6,76849 2733,2 594468 1,14943 870
871 75 86 41 660 776 311 29,5127 93,3274 9,55006 6,76964 2736,3 595835 1,14811 871
872 76 03 84 663 054 848 29,5296 93,3809 9,55371 6,77079 2739,5 597204 1,14679 872
873 76 21 29 665 338 617 29,5466 93,4345 9,55736 6,77194 2742,6 598575 1,14548 873
874 7638 76 667 627624 29,5635 93,4880 9,56101 6,77308 2745,8 599947 1,14416 874
875 7656 25 669 921 875 29,5804 93,5414 9,56466 6,77422 2748,9 601320 1,14286 875
876 76 73 76 672 221 376 29,5973 93,5949 9,56830 6,77537 2752,0 602696 1,14155 876
877 76 91 29 674 526133 29,6142 93,6483 9,57194 6,77651 2755,2 604073 1,14025 877
878 7708 84 676 836152 29,6311 93,7017 9,57557 9,57921 6/77765 2758,3 605451 1,13895 878
879 77 26 41 679151 439 29,6479 93,7550 6 77878 2761,5 606831 1,13766 879
880 77 44 00 681 472000 29,6648 93,8083 9,58284 6,77992 2764,6 608212 1,13636 880
881 77 61 61 683 797841 29,6816 93,8616 9,58647 6,78106 2767,7 609595 1.13507 881
882 77 79 24 686128968 29,6985 93,9149 9,59009 6,78219 2770,9 610980 1,13379 882
883 77 96 89 688 465 38г 29,7153 93,9681 9,59372 6,78333 2774,0 612366 1,13250 883
884 7814 56 690.807104 29,7321 94,0213 9,59734 6,78446 2777,2 613754 1,13122 884
885 78 32 25 693154 125 29,7489 94,0744 9,60095 6,78559 2780,3 615143 1,12994 885
886 78 4990 695 506456 29,7658 94,1276 9,60457 6,78672 2783,5 616534 1,12867 886
887 7867 69 697864 103 29,7825 94,1807 9,60818 6,78784 2786,6 617927 1,12740 887
888 78 85 44 700 227 072 29,7993 94,2338 9,61179 6,78897 2789,7 619321 1,12613 888
889 79 03 21 702 595 369 29,8161 94,2868 9,61540 6,79010 2792,9 620717 1,12486 889
890 79 21 00 704 969000 29,8329 94,3398 9,61900 6,79122 2796,0 622114 1,12360 890
891 79 3881 707 347 971 29,8496 94,3928 9,62260 6,79234 2799,2 623513 1,12233 891
892 79 56 64 709 732 288 29,8664 94,4458 9,62620 6,79347 2802,3 624913 1,12108 892
893 79 74 49 712 121 957 29,8831 94,4987 9,62980 6,79459 2805,4 626315 1,11982 893
894 79 92 36 714 516 984 29,8998 94,5516 9,63339 6,79571 2808,6 627718 1,11857 1,11732 894
895 80 10 25 716 917375 29,9166 94,6044 9,63698 6,79682 2811,7 629124 895
896 80 2816 719 323 136 29,9333 94,6573 9,64057 6,79794 2814,9 630530 1,11607 896
897 804609 721 734273 29,9500 94,7101 9,64415 6,79906 2818,0 631938 1,11483 897
898 80 64 04 724150 792 29,9666 94,7629 9,64774 6,80017 2821,2 633348 1,11359 898
899 808201 726 572 699 29,9833 94,8156 9,65132 6,80128 2824,3 634760 1,11235 899
900 81 00 00 729 000000 30,0000 94,8683 9,65489 6,80239 2827,4 636173 1,11111 900
п п* п» Уп /Топ 1/п . In п пп ЯП* 1000 п п
________________МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ 33
900 — 950
п \ п‘ п3 1 п | /ion 3,- j/n In п лП ЯП* ~4~ 1000 п п
900 । 81 00 00 729 000 000 30,0000 94,8683 9,65489 6,80239 2827,4 636173 1,11111 900
901 81 1801 ,731 432 70 30,0167 94,9210 9,65847 6,80351 2830,6 637587 1,10988 901
902 81 36 04 733 870 808 30,0333 94,9737 9,66204 6,80461 2833,7 639003 1,10865 902
903 81 54 09 736 314 327 30,0500 95,0263 9,66561 6,80572 2836,9 640421 1,10742 903
904 81 72 16 738 763 264 30,0666 95,0789 9,66918 6,80683 2840,0 641840 1,10619 904
905 81 90 25 741 217 625 30,0832 95,1315 9,67274 6,80793 2843,1 643261 1,10497 905
906 82 08 36 743 677 416 30,0998 95,1840 9,67630 6,80904 2846,3 644683 1,10375 906
907 82 26 49 746 142 643 30,1164 95,2365 9,67986 6,81014 2849,4 646107 1,10254 907
908 82 44 64 748613312 30,1330 95,2890 9,68342 6^81124 2852,6 647533 1,10132 908
909 82 62 81 751 089 429 30,1496 95,3415 9,68697 6,81235 2855,7 648960 1,10011 909
910 82 81 00 753 571 000 30,1662 95,3939 9,69052 6,81344 2858,8 650388 1,09890 910
911 82 99 21 756 058 031 30,1828 95,4463 9,69407 6,81454 2862,0 651818 1,09769 911
912 83 17 44 758 550 528 30,1993 95,4987 9,69762 6,81564 2865,1 653250 1,09649 912
913 83 35 69 761 048497 30,2159 95,5510 9,70116 6,81674 2868,3 654684 1,09529 913
914 83 53 96 763 551 94^ 30,2324 95,6033 9,70470 6,81783 2871,4 656118 1,09409 914
915 83 72 25 766 060 875 30,2490 95,6556 9,70824 6,81892 2874,6 657555 1,09290 915
916 83 90 56 768 575 296 30,2655 95,7079 9,71177 6,82002 2877,7 658993 1,09170 916
917 84 08 89 771 095 213 30,2820 95,7601 9,71531 6,82111 2880,8 660433 1,09051 917
918 84 27 24 773 620 632 30,2985 95,8123 9,71884 6,82220 2884,0 661874 1,08932 918
919 84 45 61 776 151 559 30,3150 95,8645 9,72236 6,82329 2887,1 663317 1,08814 919
920 84 64 00 778 688 000 30,3315 95,9166 9,72589 6,82437 2890,3 664761 1,08696 920
921 84 82 41 781 229 961 30,3480 95,9687 9,72941 6,82546 2893,4 666207 1,08578 921
922| 8500 84 783 777 448 30,3645 96,0208 9,73293 6,82655 2896,5 667654 1,08460 922
923 85 19 29 786 330 467 30,3809 96,0729 9,73645 9,73996 6,82763 2899,7 669103 1,08342 923
924) 85 37 76 788 889 024 30,3974 96,1249 6,82871 2902,8 670554 1,08225 924
925 85 56 25 791 453 125 30,4138 96,1769 9,74348 6,82979 2906,0 672006 1,08108 925
9261 85 74 76 794 022 776 30,4302 96,2289 9,74699 6,83087 2909,1 673460 1,07991 926
927 85 93 29 796 597 983 30,4467 96,2808 9,75049 6,83195 2912,3 674915 1,07875 927
928 86 11 84 799 178 752 30,4631 96,3328 9,75400 6,83303 2915,4 676372 1,07759 928
929 86 30 41 801 765089 30,4795 96,3846 9,75750 6,83411 2918,5 677831 1,07643 929
930, 86 49 00 804 357 000 30,4959 96,4365 9,76100 6,83518 2921,7 679291 1,07527 930
931 86 67 61 806 954 491 30,5123 96,4883 9,76450 6,83626 2924,8 680752 1,07411 931
932 86 86 24 809 557 568 30,5287 96,5401 9,76799 6,83733 2928,0 682216 1,07296 932
933 87 04 89 812 166 237 30,5450 96,5919 9,77148 6,83841 2931,1 683680 1,07181 933
934 87 23 56 814 780 504 30,5614 96,6437 9,77497 6,83948 2934,2 685147 1,07066 934
935' 87 42 25 817 400 375 30,5778 96,6954 9,77846 6,84055 2937,4 686615 1,06952 935
936 87 6096 820 025 856 30,5941 96,7471 9,78195 6,84162 2940,5 688084 1,06838 936
937 87 79 69 822 656 953 30,6105 96,7988 9,78543 6,84268 2943,7 689555 1,06724 937
938 939 87 98 44 825 293 672 30,6268 96,8504 9,78891 6,84375 2946,8 691028 1,06610 938
88 17 21 827 936 019 30,6431 96,9020 9,79239 6,84482 2950,0 692502 1,06496 939
940 88 36 00 830 584 000 30,6594 96,9536 9,79586 6,84588 2953,1 693978 1,06383 940
941 88 54 81 833 237 621 30,6757 97,0052 9,79933 6,84694 2956,2 695455 1,06270 941
942 88 73 64 835 896 888 30,6920 97,0567 9,80280 6,84801 2959,4 696934 1,06157 942
943 88 92 49 838 561 807 30,7083 97,1082 9,80627 6,84907 2962,5 698415 1,06045 943
944 8911 36 841 232 384 30,7246 97,1597 9,80974 6,85013 2965,7 699897 1,05932 944
945 89 30 25 843 908 625 30,7409 97,2111 9,81320 6,85118 2968,8 701380 1,05820 945
946 89 4916 846 590 536 30,7571 97,2625 9,81666 6,85224 2971,9 702865 1,05708 946
947 948 89 68 09 849 278 123 30,7734 97,3139 9.82012 6,85330 2975,1 704352 1,05597 947
89 87 04 851 971 392 30,7896 97,3653 9,82357 6,85435 2978,2 705840 1,05485 948
949 950 90 06 01 854 670 349 30,8058 97,4'66 9,82703 6,85541 2981,4 707330 1,05374 949
90 25 00 857 375 000 30,8221 97,4679 9,83048 6,85646 2984,5 708822 1,05263 950
п п‘ Vn /Той 3 /п In п ЛП лПа ~~4~ 1000 п п
Том I
з
34
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
950—1000
п п8 Vn р'юп f7" In п пп пп1 1000 п п
950 90 25 00 857 375 000 30,8221 97,4679 9,83048 6,85646 2984,5 708822 1,05263 950
951 90 44 01 860 085 351 30,8383 97,5192 9,83392 6,85751 2987,7 710315 1,05152 951
952 90 63 04 862 801 408 30,8545 97,5705 9,83737 6,85857 2990,8 711809 1,05042 952
953 90 82 09 865 523 177 30,8707 97,6217 9,84081 6,85961 2993,9 713306 1,04932 953
954 91 01 16 868 250 664 30,8869 97,6720 9,84425 6,86066 2997,1 714803 1,04822 954
955 91 20 25 870 983 875 30,9031 97,7241 9,84769 6,86171 3000,2 716303 1,04712 955
956 91 39 36 873 722 816 30,9192 97,7753 9,85113 6,86276 3003,4 717804 1,04603 956
957 91 58 49 876 467 493 30,9354 97,8264 9,85456 6,86380 3006,5 719306 1,04493 957
958 91 77 64 879 217 912 30,9516 97,8775 9,85799 6,86485 3009,6 720810 1,04384 958
959 91 96 81 881 974 079 30,9677 97,9285 9,86142 6,86589 3012,8 722316 1,04275 959
960 92 16 00 884 736 000 30,9839 97,9796 9,86485 6,86693 3015,9 723823 1,04167 960
961 92 35 21 887 503 681 31,0000 98,0306 9,86827 6.86797 3019,1 725332 1,04058 961
962 92 54 44 890 277 128 31,0161 98,0816 9,87169 6,86901 3022,2 726842 1,03950 962
963 92 73 69 893 056 347 31,0322 98,1326 9,87511 6,87005 3025,4 728354 1,03842 963
964 92 92 96 895 841 344 31,0483 98 1835 9,87853 6,87109 3028,5 729867 1,03734 964
965 9312 25 898 632 125 31,0644 98,2344 9,88195 6,87213 3031,6 731382 1,03627 965
966 93 31 56 901 428 696 31,0805 98,2853 9,88536 6,87316 3034,8 732899 1,03520 966
967 93 50 89 904 231 063 31,0966 98,3362 9,88877 6,87420 3037,9 734417 1,03413 967
968 93 70 24 907 039 232 31,1127 98,3870 9,89217 6,87523 3041,1 735937 1,03306 968
969 93 89 61 909 853 209 31,1288 98,4378 9,89558 6,87626 3044,2 737458 1,03199 969
970 94 09 00 912 673 000 31,1448 98,4886 9,89898 6,87730 3047,3 738981 1,03093 970
971 94 28 41 915 498 611 31,1609 98,5393 9,90238 6,87833 3050,5 740506 1,02987 971
972 94 47 84 918 330 048 31,1769 98,5901 9,90578 6,87936 3053,6 742032 1,02881 972
973 94 67 29 921 167 317 31,1929 98,6408 9,90918 6,88038 3056,8 743559 1,02775 973
974 94 86 76 924 010 424 31,2090 98,6914 9,91257 6,88141 3059,9 745088 1,02669 974
975 95 06 25 926 859 375 31,2250 98,7421 9,91596 6,88244 3063,1 746619 1,02564 975
976 95 25 76 929 714 176 31,2410 98,7927 9,91935 6,88346 3066,2 748151 1,02459 976
977 95 45 29 932 574 833 31,2570 98,8433 9 92274 6,88449 3069,3 749685 1,02354 977
978 95 64 84 935 441 352 31,2730 98,8939 9,92612 6,88551 3072,5 751221 1,02249 978
979 95 84 41 938 313 739 31,2890 98,9444 9,92950 6,88653 3075,6 752758 1,02145 979
980 96 04 00 941 192 000 31,3050 98,9949 9,93288 6,88755 3078,8 754296 1,02041 980
981 96 23 61 944 076 141 31,3209 99,0454 9,93626 6,88857 3081,9 755837 1,01937 981
982 96 43 24 946 966 168 31,3369 99,0959 9,93964 6,88959 3085,0 757378 1,01833 982
983 96 62 89 949 862 087 31,3528 99,1464 9 94301 6,89061 3088,2 758922 1,01729 983
984 96 82 56 952 763 904 31,3688 99,1968 9,94638 6,89163 3091,3 760466 1,01626 984
985 97 02 25 955 671 625 31,3847 99,2472 9,94975 6,89264 3094,5 762013 1,01523 985
986 97 21 96 958 585 256 31,4006 99,2975 9,95311 6,89366 3097,6 763561 1,01420 986
987 97 41 69 961 504 803 31,4166 99,3479 9,95648 6,89467 3100,8 765111 1,01317 987
988 9761 44 964 430 272 31,4325 99,3982 9,95984 6,89568 3103,9 766662 1,01215 988
989 97 81 21 967 361 669 31,4484 99,4485 9,96320 6,89669 3107,0 768214 1,01112 989
990 98 01 00 970 299 000 31,4643 99,4987 9,96655 6,89770 3110,2 769769 1,01010 990
991 98 20 81 973 242 271 31,4802 99,5490 9,96991 6,89871 3113,3 771325 1,00908 991
992 98 40 64 976 191 488 31,4960 99,5992 9,97326 6,89972 3116,5 772882 1,00806 992
993 98 60 49 979 146 657 31,5119 99,6494 9,97661 6,90073 3119,6 774441 1,00705 993
994 98 80 36 982 107 784 31,5278 99,6995 9,97996 6,90174 3122,7 776002 1,00604 994
995 99 00 25 985 074 875 31,5436 99,7497 9,98331 6,90274 3125,9 777564 1,00503 995
996 99 20 16 988 047 936 31,5595 99,7998 9,98665 6,90375 3129,0 779128 1,00402 996
997 99 40 09 991 026 973 31,5753 99,8499 9,98999 6,90475 3i32,2 780693 1,00301 997
998 99 60 04 994 011 992 31,5911 99,9000 9,99333 6,90575 3135,3 782260 1,00200 998
999 99 80 01 997 002 999 31,6070 99,9500 9,99667 6,90675 3138,5 783828 1,00100 999
1000 100 00 00 1000 000 000 31,6228 100,0000 10,00000 6,90776 3141,6 785398 1,00000 1000
п п' пг /п /Той ! п п пп лпа 1000 п п
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
35
Таблица 2. МАНТИССЫ ДЕСЯТИЧНЫХ ЛОГАРИФМОВ ЦЕЛЫХ ЧИСЕЛ ОТ 1 ДО 1000
Для отыскания логарифма четырёхзначно-
го числа следует, не обращая внимания на по-
ложение^запятой, отыскать по таблицам ман-
тиссу и прибавить к ней характеристику. Ха-
рактеристика логарифма числа, большего
единицы, меньше числа знаков перед запятой
на одну единицу; если же число меньше еди-
ницы, то характеристика его логарифма
равна числу нулей, предшествующих первой
значащей цифре (включая и нуль, стоящий
перед запятой) со знаком минус (стр. 107).
Так, например:
1g ПО, 1 =2+0,041 787= 2,041 787;
1g 0,01101 =—2 + 0,041 787=2,041787 =
= — 1,958 213.
Пользование таблицами логарифмов для
вычислений основано на том, что переход от
чисел к их логарифмам понижает порядок
алгебраических действий (стр. 107), а именно:
lg(a’*)= nlga; IgV^a =^lga;
lg(a&)=lga+lg&; lg-“=lga— lg6.
b
Если логарифм числа известен, то само
число определяется следующим образом: в
таблицах отыскивается мантисса, ближайшая
к данной, по ней определяется число, кото-
рому она соответствует, и в найденном числе
ставится запятая так, чтобы число знаков
перед запятой было на единицу больше харак-
теристики, если она положительна; если же
она отрицательна, то слева приписывается
соответствующее количество нулей.
Для отыскания логарифма пятизначного
числа и для отыскания числа с пятью знача-
щими цифрами по данному его логарифму в
конце каждой страницы даны поправки, осно-
ванные на линейной интерполяции (стр. 248).
Вычисление логарифма пятизначного числа
производится по следующей схеме: находится
мантисса логарифма по первым четырём зна-
кам данного числа, вычисляется так называе-
мая табличная разность между этой мантиссой
и следующей за ней в таблице и отыскивается
поправка, соответствующая при найденной
табличной разности пятому знаку данного
числа; прибавив эту поправку к ранее най-
денной мантиссе, получим искомую мантиссу
пятизначного числа.
Пример. Найти мантиссу 1g 72 017.
Мантисса 1g 7201 равна 857 393, следующая
за ней мантисса 857453, табличная разность
857453 — 857393 = 60. Для табличной разности
60 поправка на последний знак данного
числа (7) равна 42 и искомая мантисса
857393 + 42 = 857435.
Если по данной мантиссе логарифма тре-
буется найти число с пятью значащими циф-
рами, то отыскивают сначала в таблице бли-
жайшую мантиссу, меньшую данной, по ней
определяют первые четыре знака искомого
числа, далее вычисляют табличную разность
между этой мантиссой и следующей за ней,
а также разность (поправку) между данной
мантиссой и той, которой мы воспользовались
для определения первых четырёх знаков
искомого числа. Найдя в таблице поправок
для вычисленной табличной разности по-
правку, ближайшую к найденной, слева чи-
таем пятую цифру искомого числа.
Пример. Найти число, если мантисса его
логарифма равна 857 410.
Найденная по таблицам ближайшая, мень-
шая данной, мантисса 857393 соответствует
числу 7201. Табличная разность 857 453 —
—857 393= 60. Поправка 857 410-857 393 = 17.
В таблице поправок для табличной разности
60 поправка, ближайшая к найденной (18),
соответствует числу 3, которое и является
пятой цифрой искомого числа 72013.
На первых страницах по техническим
причинам даны поправки не для всех таблич-
ных разностей; здесь следует при вычисле-
нии поправок пользоваться ближайшей таб-
личной разностью; нужно, однако, иметь в
виду, что за шестой знак мантиссы вычис-
ляемого логарифма при этом ручаться нельзя.
Для вычисления мантисс логарифмов
шестизначных чисел следует пользоваться
более точными интерполяционными форму-
лами (стр. 246). •
1 —99
N 1g ilN 1 1g i| N 1g | N 1g 1 N Ig N Ig
0 .— I 17 23 04 49 34 53 14 79 51 70 75 70 68 8325 09 I 84 92 42 79
1 00 00 00 18 25 52 73 35 54 40 68 52 71 60 03 69 83 88 49 85 92 94 19
2 30 10 30 19 27 87 54 36 55 63 03 53 72 42 76 70 84 50 98 86 93 44 98
3 47 71 21 20 3010 30 37 56 82 02 54 73 23 94 71 85 12 58 87 93 95 19
4 60 20 60 21 32 22 19 38 57 97 84 55 74 03 63 72 85 73 32 88 94 44 83
5 69 89 70 22 34 24 23 39 59 1065 56 74 81 88 73 86 33 23 89 94 93 90
6 77 81 51 23 36 17 28 40 60 20 60 57 75 58 75 74 86 92 32 90 95 42 43
7 84 50 98 24 38 02 11 41 61 27 84 58 76 34 28 75 87 50 61 91 95 90 41
8 90 30 90 25 39 79 40 42 62 32 49 59 77 08 52 76 88 08 14 92 96 37 88
9 95 42 43 26 41 49 73 43 63 34-68 60 77 81 51 77 88 64 91 93 96 84 83
10 00 00 00 27 43 1364 44 64 34 53 61 78 53 30 78 89 20 95 94 97 31 28
11 041393 28 44 71 58 45 65 32 13 62 79 23 92 79 89 76 27 95 97 77 24
12 07 91 81 29 46 23 98 46 66 27 58 63 79 93 41 80 90 30 90 96 98 22 71
13 11 39 43 . 30 47 71 21 47 67 20 98 64 80 61 80 81 90 84 85 97 98 67 72
14 14 61 28 31 49 1362 48 68 12 41 65 81 29 13 82 91 38 14 98 99 12 26
15 1760 91 32 50 51 50 49 69 01 96 66 81 95 44 83 91 90 78 99 99 56 35
16 2041 20 33 51 85 14 50 69 89 70 67 82 60 75
N 1 1g 1 N Ig N ig N | ig N | Ig j N | ig
3*
36
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
100—150
N 0 1 2 3 1 4 . 5 , 6 1 7 8 1 9
100 00 00 00 04 34 08 68 1301 1734 21 66 25 98 30 29 34 61 38 91
101 43 21 47 51 51 81 56 09 60 38 64 66 68 94 73 21 77 48 81 74
102 86 00 90 26 94 51 98 76 *03 00 *07 24 *11 47 *15 70 *19 93 *24 15
103 01 28 37 32 59 36 80 41 00 45 21 49 40 53 60 57 79 61 97 66 16
104 70 33 74 51 78 68 82 84 87 00 91 16 95 32 99 47 *03 61 *07 75
105 02 11 89 16 03 20 16 24 28 28 41 32 52 36 64 40 75 44 86 48 96
106 53 06 57 15 61 25 65 33 69 42 73 50 77 57 81 64 85 71 89 78
107 93 84 97 89 *01 95 *06 00 *10 04 *1408 *18 12 *22 16 *26 19 *30 21
108 03 34 24 38 26 42 27 46 28 50 29 54 30 58 30 6230 66 29 70 28
109 74 26 78 25 82 23 86 20 90 17 94 14 98 11 *02 07 *06 02 *09 98
ПО 04 13 93 17 87 21 82 25 76 29 69 33 62 37 55 41 48 45 40 49 32
111 53 23 5714 61 05 64 95 68 85 72 75 76 64 80 53 84 42 8830
112 9218 96 06 99 93 *03 80 *07 66 *11 53 *15 38 *19 24 *23 09 *26 94
113 05 30 78 34 63 38 46 42 30 4613 49 96 53 78 57 60 61 42 65 24
114 69 05 72 86 76 66 80 46 84 26 88 05 91 85 95 63 99 42 *03 20
115 06 06 98 10 75 14 52 18 29 22 06 25 82 29 58 33 33 37 09 40 83
116 44 58 48 32 5206 55 80 59 53 63 26 66 99 70 71 74 43 7815
117 81 86 85 57 89 28 92 98 96 68 *00 38 *04 07 *07 76 *11 45 *15 14
118 07 18 82 22 50 26 17 29 85 33 52 3718 40 85 44 51 48 16 51 82
119 5547 59 12 62 76 66 40 70 04 73 68 77 31 80 94 84 57 88 19
120 91 81 95 43 99 04 *02 66 *06 26 *09 87 *13 47 *17 07 *20 67 *24 26
121 08 27 85 31 44 35 03 38 61 42 19 45 76 49 34 52 91 56 47 60 04
122 63 60 67 16 70 71 74 26 77 81 81 36 84 90 88 45 91 98 95 52
123 99 05 *02 58 *06 11 *09 63 *13 15 *1667 *20 18 *23 70 *27 21 *30 71
124 09 34 22 37 72 41 22 44 71 48 20 51 69 55 18 58 66 .'>2 15 65 62
125 6910 72 57 76 04 79 51 82 98 86 44 89 90 93 35 96 81 *00 26
126 10 03 71 0715 10 59 14 03 1747 20 91 24 34 27 77 31 19 34 62
127 38 04 41 46 44 87 48 28 51 69 55 10 58 51 61 91 65 31 68 71
128 72 10 75 49 78 88 82 27 85 65 89 03 92 41 95 79 99 16 *02 53
129 11 05 90 09 26 12 63 15 99 1934 22 70 26 05 29 40 32 75 36 09
130 39 43 42 77 46 11 49 44 52 78 56 11 59 43 62 76 66 08 69 40
131 72 71 76 03 79 34 82 65 85 95 89 26 92 56 95 86 99 15 *02 45
132 12 05 74 09 03 12 31 15 60 18 88 22 16 25 44 28 71 31 98 35 25
133 38 52 41 78 45 04 48 30 51 56 54 81 58 06 61 31 64 56 67 81
134 7105 74 29 77 53 80 76 83 99 87 22 90 45 93 68 96 90 *00 12
135 13 03 34 06 55 09 77 12 98 16 19 19 39 22 60 25 80 29 00 32 19
136 35 39 38 58 41 77 44 96 48 14 51 33 54 51 57 69 60 86 64 03
137 67 21 70 37 73 54 76 71 79 87 83 03 86 18 89 34 92 49 95 64
138 98 79 *01 94 *05 08 *08 22 *11 36 *14 50 *17 63 *20 76 *23 89 *27 02
139 14 30 15 33 27 36 39 39 51 42 63 45 74 48 85 51 96 55 07 58 18
140 61 28 64 38 67 48 70 58 73 67 76 76 79 85 82 94 8603 89 11
141 9219 95 27 98 35 *01 42 *04 49 *07 56 *10 63 *13 70 *16 76 ♦19 82
142 15 22 88 25 94 2900 32 05 3510 3815 41 20 44 24 4728 50 32
143 53 36 56 40 59 43 62 46 65 49 68 52 71 54 74 57 77 59 80 61
144 83 62 86 64 89 65 92 66 95 67 98 68 *01 68 *04 69 *07 69 ♦10 68
145 16 1368 16 67 19 67 22 66 25 64 28 63 31 61 34 60 37 58 40 55
146 43 53 46 50 49 47 52 44 55 41 58 38 61 34 64 30 67 26 70 22
147 7317 76 13 79 08 82 03 84 97 87 92 90 86 93 80 96 74 99 68
148 17 02 62 05 55 08 48 11 41 14 34 17 26 2019 23 И 26 03 28 95
149 31 86 34 78 37 69 40 60 43 51 46 41 49 32 52 22 55 12 58 02
150 60 91 63 81 66 70 69 59 7248 75 36 78 25 81 13 84 01 86 89
Р.Р. 430 420 410 400 390 380 370 360 350 340 330 | 320 310 300 290
1 43,0 42,0 41,0 40,0 39,0 38,0 37,0 36,0 35,0 34,0 33,0 32,0 31,0 30,0 29,0
2 86,0 84,0 82,0 80,0 78,0 76,0 74,0 72,0 70,0 68,0 66,0 64,0 62,0 60,0 58,0
3 129,0 126,0 123,0 120,0 117,0 114,0 111,0 108,0 105,0 102,0 99,0 96,0 93,0 90,0 87,0
4 172,0 168,0 164,0 160,0 156,0 152,0 148,0 144,0 140,0 136,0 132,0 128,0 124,0 120,0 116,0
5 215,0 210,0 205,0 200,0 195,0 190,0 185,0 180,0 175,0 170,0 165,0 160,0 155,0 150,0 145,0
6 258,0 252,0 246,0 240,0 234,0 228,0 222,0 216,0 210,0 204,0 198,0 192,0 186,0 180,0 174,0
7 301,0 294,0 287,0 280,0 273,0 266,0 259,0 252,0 245,0 238,0 231,0 224,0 217,0 210,0 203,0
8 344,0 336,0 328,0 320,0 312,0 304,0 296,0 288,0 280.0 272,0 264,0 256,0 248,0 240,0 232,0
9 387,0 378,0 369,0 360,0 351 ,0 342,0 333,0 324,0 315,0 306,0 297,0 288,0 279,0 270,0 261,0
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
37
151—200
N 0 1 3 4 5 i 6 7 8 9
151 17 89 77 92 64 95 52 98 39 *01 26 *04 13 *06 99 *09 86 *12 72 *1558
152 18 18 44 21 29 24 15 27 00 29 85 32 70 35 55 38 39 41 23 44 07
153 46 91 49 75 52 59 55 42 58 25 61 08 63 91 66 74 69 56 72 39
154 75 21 78 03 80 84 83 66 86 47 89 28 92 09 94 90 97 71 *00 51
155 19 03 32 06 12 08 92 11 71 14 51 1730 20 10 22 89 25 67 28 46
156 31 25 34 03 36 81 39 59 42 37 4514 47 92 50 69 53 46 56 23
157 59 00 61 76 64 53 67 29 70 05 72 81 75 56 78 32 81 07 83 82
158 86 57 89 32 92 06 94 81 97 55 *00 29 *03 03 *05 77 *0850 *11 24
159 2013 97 16 70 19 43 22 16 24 88 27 61 30 33 33 05 35 77 • 38 48
160 41 20 43 91 46 63 49 34 5204 54 75 57 46 6016 62 86 65 56
161 68 26 70 96 73 65 76 34 79 04 81 73 84 41 8710 89 79 92 47
162 95 15 97 83 *00 51 *0319 *05 86 *08 53 *11 21 *1388 *16 54 *1921
163 21 21 88 24 54 27 20 29 86 32 52 35 18 37 83 40 49 43 14 45 79
164 48 44 51 09 53 73 56 38 59 02 61 66 64 30 66 94 69 57 72 21
165 74 84 77 47 80 10 82 73 85 36 87 98 90 60 93 23 95 85 98 46
166 22 01 08 03 70 06 31 08 92 11 53 14 14 16 75 19 36 21 96 24 56
167 27 16 29 76 32 36 34 96 37 55 40 15 42 74 45 33 47 92 50 51
168 53 09 55 68 58 26 60 84 63 42 66 00 68 58 71 15 73 72 76 30
169 78 87 81 44 84 00 86 57 89 13 91 70 94 26 96 82 99 38 *01 93
170 23 04 49 07 04 09 60 12 15 14 70 17 24 19 79 22 34 24 88 27 42
171 29 96 32 50 35 04 37 57 4011 42 64 4517 47 70 50 23 52 76
172 55 28 57 81 60 33 62 85 65 37 67 89 70 41 72 92 75 44 77 95
173 80 46 82 97 85 48 87 99 90 49 92 99 95 50 98 00 *00 50 *03 00
174 24 05 49 07 99 10 48 12 97 1546 17 95 20 44 22 93 25 41 27 90
175 30 38 32 86 35 34 37 82 40 30 42 77 45 25 47 72 50 19 52 66
176 55 13 57 59 60 06 62 52 64 99 67 45 69 91 72 37 74 82 77 28
177 79 73 82 19 84 64 87 09 89 54 91 98 94 43 96 87 99 32 *01 76
178 25 04 20 06 64 09 08 И 51 13 95 16 38 1881 21 25 23 68 26 10
179 28 53 30 96 33 38 35 80 38 22 40 64 43 06 45 48 47 90 50 31
180 52 73 55 14 5755 59 96 62 37 64 77 67 18 69 58 71 98 74 39
181 76 79 79 18 81 58 83 98 86 37 88 77 91 16 93 55 95 94 98 33
182 26 00 71 03 10 05 48 07 87 10 25 12 63 1501 1739 19 76 22 14
183 24 51 26 88 29 25 31 62 33 99 36 36 38 73 41 09 43 46 45 82
184 48 18 50 54 52 90 55 25 57 61 59 96 62 32 64 67 67 02 69 37
185 71 72 74 06 76 41 78 75 81 10 83 44 85 78 88 12 90 46 92 79
186 9513 97 46 99 80 *02 13 *04 46 *06 79 *09 12 *11 44 *13 77 *16 09
187 27 18 42 20 74 23 06 25 38 27 70 30 01 32 33 34 64 36 96 39 27
188 41 58 43 89 46 20 48 50 50 81 53 11 55 42 57 72 60 02 62 32
189 64 62 66 92 69 21 71 51 73 80 76 09 78 38 80 67 82 96 85 25
190 87 54 89 82 9211 94 39 96 67 98 95 *01 23 *03 51 *05 78 *08 06
191 • 28 10 33 12 61 14 88 17 15 19 42 21 69 23 96 26 22 28 49 30 75
192 3301 35 27 37 53 39 79 42 05 44 31 46 56 48 82 51 07 53 32
193 55 57 57 82 60 07 62 32 64 56 66 81 69 05 71 30 73 54 75 78
194 78 02 80 26 82 49 84 73 86 96 89 20 91 43 93 66 95 89 98 12
195 29 00 35 02 57 04 80 07 02 09 25 11 47 13 69 15 91 18 13 20 34
196 22 56 24 78 26 99 29 20 31 41 33 63 35 84 38 04 40 25 42 46
197 44 66 46 87 49 07 51 27 53 47 55 67 57 87 60 07 62 26 64 46
198 66 65 68 84 71 04 73 23 75 42 77 61 79 79 81 98 84 16 86 35
199 88 53 90 71 92 89 95 07 97 25 99 43 *01 61 *03 78 *05 95 *08 13
200 30 10 30 12 47 14 64 16 81 18 98 21 14 23 31 25 47 27 64 29 80
р. р. 290 285 280 275 270 265 260 255 250 245 240 235 230 225 1 220 215
1 29,0 28,5 28,0 27,5 27,0 26,5 26,0 25,5 25,0 24,5 24,0 23,5 23,0 22,5 22,0 21,5
2 58,0 57,0 56,0 55,0 54,0 53,0 52,0 51,0 50,0 49,0 48,0 47,0 46,0 45,0 44,0 43,0
3 87,0 85,5 84,0 82,5 81,0 79,5 78,0 76,5 75,0 73,5 72,0 70,5 69,0 67,5 66,0 64,5
4 116,0,114,0 112,0 1 10,0 108,0 106,0 104,0 102,0 100,0 98,0 96,0 94,0 92,0 90,0 88,0 86,0
5 145,0 142,5 140,0 137,5 135,0 132,5 130,0 127,5 125,0 122,5 120,0 117,5 115,0 112,5 110,0 107,5
6 174.01171.0'168.0 165.0'162,0 159,0 156,0 153,0 150,0 147,0’144,0 141,0 138,0 135,0 132,0 129,0
7 203,0 199,5 196,0 192,5 189,0 185,5 182,0 178,5 175,0 171,5 168,0 164,5 161 ,0 157,5 154,0 150,5
8 232,0 228,0 224,0 220,01216,0 212,0 208,0 204,0 200,0 196,0 192,0 188,0 184,0 180,0 176,0 172,0
9 261,0 256,5 252,0 247,5 1243,0 238,5 234,0 229,5 225,0 220,5 216,0 211,5 207,0 202,5 198,0 193,5
38
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
201—250
N 0 1 2 3 4 5 6 7 8 9
201 30 31 96 34 12 36 28 38 44 40 59 42 75 4491 47 06 49 21 51 36
202 5351 5566 57 81 5996 6211 64 25 66 39 68 54 70 68 72 82
203 74 96 77 10 79 24 81 37 83 51 85 64 87 78 89 91 92 04 94 17
204 9630 98 43 *00 56 *02 68 *04 81 •06 93 *09 06 *1 18 ►13 30 *1542
205 31 17 54 19 66 21 77 23 89 26 00 28 12 30 23 32 34 34 45 36 56
206 3867 40 78 42 89 44 99 47 10 49 20 5130 53 40 55 51 57 60
207 5970 61 80 63 90 65 99 68 09 70 18 72 27 74 36 76 46 78 54
208 80 63 82 72 84 81 86 89 88 98 91 06 93 14 95 22 97 30 99 38
209 32 01 46 03 54 05 62 07 69 09 77 11 84 13 91 15 98 18 05 20 12
210 22 19 24 26 26 33 28 39 30 46 32 52 34 58 3665 38 71 40 77
211 42 82 44 88 46 94 48 99 5105 5310 55 16 57 21 59 26 6131
212 63 36 6541 67 45 69 50 71 55 73 59 75 63 77 67 79 72 81 76
213 83 80 85 83 87 87 89 91 91 94 93 98 9601 98 05 *00 08 *02 11
214 33 04 14 0617 08 19 10 22 12 25 14 27 16 30 18 32 20 34 22 36
215 24 38 26 40 28 42 30 44 32 46 34 47 36 49 38 50 40 51 42 53
216 44 54 4655 48 56 50 57 52 57 54 58 5658 58 59 60 59 62 60
217 64 60 66 60 68 60 70 60 72 60 74 59 76 59 78 58 80 58 82 57
218 84 56 86 56 88 55 90 54 92 53 94 51 96 50 98 49 *00 47 *02 46
219 34 04 44 06 42 08 41 10 39 12 37 14 35 16 32 18 30 20 28 22 25
220 24 23 26 20 28 17 30 14 32 12 34 09 36 06 38 02 39 99 41 96
221 43 92 45 89 47 85 49 81 51 78 53 74 55 70 57 66 59 62 6157
222 63 53 65 49 67 44 69 39 71 35 73 30 75 25 77 20 79 15 81 10
223 8305 85 00 86 94 88 89 90 83 92 78 94 72 96 66 98 60 *00 54
224 35 02 48 04 42 06 36 08 29 10 23 1216 14 10 16 03 17 96 19 89
225 21 83 23 75 25 68 27 61 29 54 31 47 33 39 35 32 37 24 39 16
226 4108 43 01 44 93 46 85 48 76 50 68 52 60 54 52 56 43 58 34
227 60 26 6217 64 08 65 99 67 90 69 81 71 72 73 63 75 54 77 44
228 79 35 81 25 83 16 85 06 86 96 88 86 90 76 92 66 94 56 96 46
229 98 35 *00 25 *02 15 *04 04 *05 93 *07 83 *09 72 *11 61 *13 50 *15 39
230 36 17 28 19 17 21 05 22 94 24 82 26 71 2859 30 48 3236 34 24
231 36 12 38 00 39 88 41 76 43 63 45 51 47 39 49 26 51 13 53 01
232 54 88 56 75 58 62 60 49 62 36 64 23 66 10 67 96 69 83 71 69
233 73 56 75 42 77 29 79 15 81 01 82 87 84 73 86 59 88 45 90 30
234 92 16 94 01 95 87 97 72 99 58 *01 43 *03 28 *0513 *06 98 *08 83
235 37 10 68 12 53 14 37 16 22 18 06 1991 21 75 23 60 25 44 27 28
236 29 12 30 96 32 80 34 64 36 47 38 31 40 15 41 98 43 82 4565
237 47 48 49 32 51 15 52 98 54 81 5664 58 46 60 29 62 12 63 94
238 65 77 67 59 69 42 71 24 73 06 74 88 76 70 78 52 80 34 82 16
239 83 98 85 80 87 61 89 43 91 24 93 06 94 87 96 68 98 49 *0030
240 38 02 11 03 92 05 73 07 54 09 34 11 15 12 96 14 76 16 56 18 37
241 20 17 21 97 23 77 25 57 27 37 29 17 30 97 32 77 34 56 3636
242 3815 39 95 41 74 43 53 45 33 47 12 48 91 50 70 52 49 54 28
243 56 06 5785 59 64 61 42 63 21 64 99 66 77 68 56 70 34 72 12
244 73 90 75 68 77 46 79 23 81 01 82 79 84 56 86 34 88 11 89 89
245 91 66 93 43 95 20 96 98 98 75 *00 51 *02 28 *04 05 *05 82 *07 59
246 39 09 35 11 12 12 88 1464 1641 18 17 19 93 21 69 23 45 25 21
247 26 97 28 73 30 48 32 24 34 00 35 75 37 51 39 26 41 01 42 77
248 44 52 46 27 48 02 49 77 51 52 53 26 55 01 56 76 5850 60 25
249 61 99 63 74 65 48 67 22 68 96 70 71 72 45 74 19 75 92 77 66
250 79 40 81 14 82 87 84 61 86 34 88 08 89 81 91 54 93 28 95 01
Р. Р. 215 210 205 200 195 190 185 180 178 176 174 172 170
1 21 >5 21,0 20,5 20,0 19,5 19,0 18,5 18,0 17,8 17,6 17,4 17,2 17,0
2 43’О 42,0 41,0 40,0 39.0 38,0 37,0 36,0 35,6 35,2 34,8 34,4 34,0
3 64, 5 63,0 61,5 60,0 58,5 57,0 55,5 54,0 53,4 52,8 52,2 51,6 51 ,0
4 86,0 84,0 82,0 80,0 78,0 76,0 74,0 72,0 71,2 70,4 69,6 68,8 68,0
5 107,5 105,0 102,5 100,0 97,5 95,0 92,5 90,0 89,0 88,0 87,0 86,0 85,0
6 129^0 126,0 123,0 120,0 117,0 114,0 111,0 108,0 106,8 105,6 104,4 103,2 102,0
7 150,5 147,0 143,5 140,0 136,5 133,0 129,5 126,0 124,6 123,2 121,8 120,4 119,0
8 1 72 ’ 0 168,0 164,0 160,0 156,0 152,0 148,0 144,0 142,4 140,8 139,2 137,6 136,0
9 193; 5 189,0 184, 5 180,0 175,5 171 ,0 166,5 162,0 160,2 158,4 .156,6 154,8 1 53, U
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
39
251—300
N 0 - 1 2 3 4 5 6 7 8 9
251 39 96 74 98 47 *00 20 *01 92 *03 65 *05 38 *07 11 *08 83 *10 56 *12 28
252 4014 01 15 73 17 45 19 17 20 89 22 61 24 33 26 05 27 77 29 49
253 31 21 32 92 34 64 36 35 38 07 39 78 4149 43 20 44 92 46 63
254 48 34 50 05 51 76 53 46 55 17 56 88 58 58 60 29 61 99 63 70
255 65 40 67 10 68 81 70 51 72 21 73 91 7561 77 31 79 01 80 70
256 82 40 84 10 85 79 87 49 89 18 90 87 92 57 94 26 95 95 97 64
257 99 33 *01 02 *02 71 *04 40 *06 09 *07 77 *09 46 *11 14 *12 83 ♦1451
258 41 1620 1788 19 56 21 24 22 93 24 61 26 29 27 96 29 64 3132
259 33 00 34 67 36 35 38 03 39 70 41 37 43 05 44 72 46 39 48 06
260 49 73 51 40 53 07 54 74 56 41 58 08 59 74 61 41 63 08 64 74
261 66 41 68 07 69 73 71 39 73 06 74 72 76 38 78 04 79 70 81 35
262 83 01 84 67 86 33 87 98 89 64 91 29 92 95 94 60 96 25 97 91
263 99 56 *01 21 *02 86 *04 51 *0616 *07 81 *09 45 *11 10 *12 75 *14 39
264 42 1604 17 68 19 33 20 97 22 61 24 26 25 90 27 54 29 18 30 82
265 32 46 34 10 35 74 37 37 39 01 40 65 42 28 43 92 45 55 47 18
266 4882 50 45 5208 53 71 55 34 56 97 58 60 60 23 61 86 63 49
267 65 11 66 74 68 36 69 99 71 61 73 24 74 86 76 48 78 И 79 73
268 8135 82 97 84 59 86 21 87 83 89 44 9106 92 68 94 29 95 91
269 9752 99 14 *00 75 *02 36 *03 98 *05 59 *07 20 *08 81 *10 42 *12 03
270 43 13 64 15 25 16 85 18 46 20 07 21 67 23 28 24 88 26 49 2809
271 29 69 31 30 32 90 34 50 36 10 37 70 39 30 40 90 42 49 44 09
272 45 69 47 29 48 88 50 48 52 07 53 67 55 26 56 85 58 44 60 04
273 6163 63 22 6481 66 40 67 99 69 57 71 16 72 75 74 33 75 92
274 77 51 79 09 80 67 82 26 83 84 85 42 8701 88 59 90 17 91 75
275 9333 94 91 96 48 9806 99 64 *01 22 *02 79 *04 37 *05 94 *07 52
276 44 09 09 10 66 12 24 13 81 15 38 16 95 18 52 20 09 21 66 23 23
277 24 80 26 37 27 93 29 50 31 06 32 63 34 19 35 76 37 32 38 89
278 40 45 42 01 43 57 45 13 46 69 48 25 49 81 51 37 52 93 54 49
279 56 04 5760 59 15 60 71 62 26 63 82 65 37 66 92 68 48 70 03
280 7158 73 13 74 68 76 23 77 78 79 33 80 88 82 42 83 97 85 52
281 87 06 88 61 90 15 91 70 93 24 94 78 96 33 97 87 99 41 *00 95
282 45 02 49 04 03 05 57 07 11 08 65 10 18 11 72 13 26 14 79 16 33
283 17 86 19 40 20 93 22 47 24 00 25 53 27 06 28 59 30 12 31 65
284 33 18 34 71 36 24 37 77 39 30 40 82 42 35 43 87 45 40 46 92
285 4845 49 97 5150 53 02 54 54 5606 57 58 59 10 60 62 62 14
286 63 66 6518 66 70 6821 69 73 71 25 72 76 74 28 75 79 77 31
287 78 82 80 33 81 84 83 36 84 87 8638 87 89 89 40 90 91 92 42
288 9392 95 43 96 94 98 45 99 95 *01 46 *02 96 *04 47 *05 97 *07 48
289 46 08 98 10 48 11 98 13 48 14 99 16 49 17 99 19 48 20 98 22 48
290 23 98 25 48 26 97 28 47 29 97 3146 32 96 34 45 35 94 37 44
291 38 93 40 42 41 91 43 40 44 90 4639 47 88 49 36 50 85 52 34
292 53 83 55 32 5680 58 29 59 77 61 26 62 74 64 23 65 71 67 19
293 68 68 70 16 7164 73 12 74 60 76 08 77 56 79 04 80 52 82 00
294 83 47 84 95 86 43 87 90 89 38 9085 92 33 93 80 95 27 96 75
295 98 22 99 69 *01 16 *02 63 *0410 *05 57 *07 04 *08 51 *09 98 *11 45
296 4712 92 14 38 15 85 1732 18 78 20 25 21 71 23 18 24 64 26 10
297 27 56 29 03 30 49 31 95 33 41 34 87 36 33 37 79 39 25 40 71
298 4216 43 62 45 08 46 53 47 99 49 44 50 90 52 35 53 81 55 26
299 56 71 58 16 59 62 61 07 62 52 63 97 65 42 66 87 68 32 69 76
300 71 21 72 66 74 11 75 55 77 00 78 44 79 89 81 33 82 78 84 22
р. р. 174 172 170 168 166 164 162 : 160 158 156 | 154 152 150 148 146 144
1 17,4 17,2 17,0 16,8 16,6 16,4 16,2 16,0 15,8 15,6 15,4 15,2 15,0 14,8 14,6 14,4
2 34,8 34,4 34,0 33,6 33,2 32,8 32,4 32,0 31,6 31,2 30,8 30,4 30.0 29, 6 29,2 288
3 52,2 51,6 51,0 50,4 49,8 49,2 48,6 48,0 47,4 46,8 46,2 45,6 45,0 44,4 43,8 43,2
4 69,6 68,8 68,0 67,2 66,4 65,6 64,8 64,0 63,2 62,4 -61,6 60, 8 60,0 59,2 58,4 57,6
5 87,0 86,0 85,0 84,0 83,0 82,0 81,0 80,0 79,0 78,0 77,0 76,0 75,0 74^0 73,0 72,0
6 104,4 103,2 102,0 100,8 99,6 98,4 97,2 96,0 94,8 93,6 92,4 91,2 90,0 88,8 87,6 86Л
7 121,8 120,4 119,0 117,6 116,2 114,8 113,4 112,0 110,6 109,2 107,8 106,4 105,0 103,6 102,2 100,8
8 139,2 137,6 136,0 134,4 132,8 131,2 129,6 128,0 126,4 124,8 123,2 121,6 120,0 118,4 116,8 115,2
9 156,6 153,0р51,2jl49,4 147,6 145,8 144,0 142,2 140,4 138,6 136,8 135,0 133,2 131,4 129,6
40
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
301—350
N ° 1 1 2 3 | 4 5 1 б 7 8 9
301 47 85 66 87 11 88 55 89 99 91 43 92 87 94 31 95 75 97 19 98 63
302 48 00 07 01 51 02 94 04 38 05 82 07 25 08 69 10 12 11 56 12 99
303 14 43 15 86 17 29 18 72 20 16 21 59 23 02 24 45 25 88 27 31
304 28 74 30 16 31 59 33 02 34 45 35 87 37 30 38 72 40 15 41 57
305 43 00 44 42 45 85 47 27 48 69 50 11 51 53 52 95 54 37 55 79
306 57 21 58 63 6005 61 47 62 89 64 39 65 72 67 14 68 55 69 97
307 71 38 72 80 74 21 75 63 77 04 78 45 79 86 81 27 82 69 84 10
308 85 51 86 92 88 33 89 74 91 14 92 55 93 96 95 37 96 77 98 18
309 99 58 *00 99 *02 39 *03 80 *05 20 *06 61 *08 01 *09 41 *1081 *12 22
310 49 13 62 15 02 16 42 17 82 19 22 20 62 22 01 23 41 24 81 26 21
311 27 60 29 00 30 40 31 79 3319 34 58 35 97 37 37 38 76 4015
312 41 55 42 94 44 33 45 72 47 11 48 50 49 89 51 28 52 67 54 06
313 55 44 56 83 58 22 5960 60 99 62 38 63 76 65 15 66 53 67 91
314 69 30 70 68 72 06 73 44 74 83 76 21 77 59 78 97 80 35 81 73
315 83 11 84 48 85 86 87 24 8862 89 99 91 37 92 75 94 12 95 50
316 96 87 98 24 99 62 *00 99 *02 36 *03 74 *05 11 *06 48 *07 85 *09 22
317 5010 59 11 96 13 33 14 70 16 07 17 44 18 80 20 17 21 54 22 91
318 24 27 25 64 27 00 28 37 29 73 31 09 32 46 33 82 35 18 36 55
319 37 91 39 27 40 63 41 99 43 35 44 71 46 07 47 43 48 78 5014
320 5150 52 86 54 21 55 57 56 93 58 28 59 64 60 99 62 34 63 70
321 65 05 66 40 67 76 69 11 70 46 71 81 7316 74 51 75 86 77 21
322 78 56 79 91 81 26 82 60 83 95 85 30 86 64 87 99 89 34 90 68
323 92 03 93 37 94 71 96 06 97 40 98 74 *00 09 *01 43 *02 77 *04 11
324 5105 45 06 79 08 13 09 47 1081 12 15 13 49 14 82 16 16 17 50
325 18 83 2017 21 51 22 84 2418 25 51 26 84 28 18 29 51 30 84
326 32 18 33 5 Г 34 84 36 17 3750 38 83 40 16 41 49 42 82 44 15
327 45 48 46 81 48 13 49 46 50 79 52 11 53 44 54 76 56 09 57 41
328 58 74 60 06 61 39 62 71 64 03 65 35 66 68 68 00 69 32 70 64
329 71 96 73 28 74 60 75 92 77 24 78 55 79 87 81 19 82 51 83 82
330 85 14 86 46 87 77 89 09 90 40 91 71 93 03 94 34 95 66 96 97
331 98 28 99 59 *00 90 *02 21 *03 53 *04 84 *06 15 *0745 *08 76 *1007
332 52 11 38 1269 14 00 15 30 1661 17 92 19 22 20 53 21 83 2314
333 24 44 25 75 27 05 28 35 29 66 30 96 32 26 33 56 34 86 3616
334 37 46 38 76 40 06 41 36 42 66 43 96 45 26 46 56 47 85 4915
335 50 45 51 74 53 04 54 34 55 63 56 93 58 22 59 51 6081 62 10
336 63 39 64 69 65 98 67 27 68 56 69 85 71 14 72 43 73 72 75 01
337 76 30 ' 77 59 78 88 80 16 81 45 82 74 84 02 85 31 86 60 87 88
338 89 17 9045 91 74 93 02 94 30 95 59 96 87 98 15 99 43 *00 72
330 53 02 00 03 28 04 56 05 84 07 12 08 40 09 68 10 96 12 23 1351
340 14 79 16 07 17 34 18 62 1990 21 17 2245 23 72 25 00 26 27
341 27 54 28 82 30 09 31 36 32 64 33 91 3518 36 45 37 72 38 99
342 40 26 4153 42 80 44 07 45 34 46 61 47 87 49 14 5041 51 67
343 52 94 54 21 55 47 56 74 58 00 59 27 60 53 61 80 63 06 64 32
344 65 58 66 85 68 11 69 37 70 63 71 89 73 15 74 41 75 67 76 93
345 78 19 79 45 80 71 81 97 83 22 84 48 85 74 86 99 88 25 89 51
346 90 76 92 02 93 27 94 52 95 78 97 03 98 29 99 54 *00 79 *02 04
347 54 03 29 04 55 05 80 07 05 08 30 09 55 1080 12 05 1330 1454
348 15 79 17 04 18 29 19 53 20 78 22 03 23 27 24 52 25 76 2701
349 28 25 29 50 30 74 31 99 33 23 34 47 35 71 36 96 38 20 39 44
350 40 68 4192 43 16 44 40 45 64 46 88 4812 49 36 5060 51 83
Р. Р. 146 144 142 1 40 138 136 134 132 130 129 128 127 126 125 124 123
1 14,6 14,4 14,2 14,0 13,8 13,6 13,4 13,2 13,0 12,9 12,8 12,7 12,6 12,5 12,4 12,3
2 29,2 28,8 28,4 28.0 27,6 27,2 26,8 26,4 26,0 25,8 25,6 25,4 25,2 25,0 24, 8 24,6
з 43,8 43,2 42,6 42,0 41,4 40,8 40,2 39,6 39,0 38,7 38,4 38,1 37,8 37,5 37,2 36,9
4 58,4 57,6 56,8 56,0 55,2 54,4 53,6 52,8 52,0 51 ,6 51,2 50,8 50,4 50,0 49,6 49,2
5 73,0 72,0 71,0 70,0 69,0 68,0 67,0 66,0 65,0 64,5 64,0 63,5 63,0 62,5 62,0 61,5
6 87,6 86,4 85,2 84,0 82,8 81,6 80,4 79,2 78,8 77 ,4 76,8 76,2 75,6 75,0 74,4 73,8
7 102,2 ЮО, 8 99,4 98,0 96,6 95,2 93,8 92,4 91,0 90,3 89,6 88,9 88,2 87,5 86, 8 86,1
8 116,8 115.2 113,6 112,0 110,4 108,8 107,2 105,6 104,0 103,2 102,4 101,6 100,8 100,0 99,2 98,4
9 131,4 129.6 127,8 126,0 124,2 122,4 120,6 118,8 117,0 116,1 115,2 114,3 113,4 112,5 111,6 110, т
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
41
351—400
N ° 1 2 3 4 5 6 7 8 9
351 54 53 07 54 31 55 55 56 78 58 02 59 25 60 49 61 72 62 96 64 19
352 6543 66 66 67 89 69 13 70 36 71 59 72 82 7405 75 29 76 52
353 77 75 78 98 80 21 81 44 82 67 83 89 85 12 86 35 87 58 88 81
354 90 03 9126 92 49 93 71 94 94 96 16 97 39 98 61 99 84 *01 06
355 55 02 28 03 51 04 73 05 95 07 17 08 40 09 62 10 84 12 06 13 28
356 14 50 15 72 16 94 18 16 1938 20 60 21 81 23 03 24 25 25 47
357 26 68 27 90 29 11 30 33 31 55 32 76 33 98 35 19 36 40 37 62
358 38 83 40 04 41 26 42 47 43 68 44 89 46 10 47 31 48 52 49 73
359 50 94 52 15 53 36 54 57 55 78 56 99 58 20 59 40 60 61 61 82
360 63 03 64 23 65 44 66 64 67 85 69 05 70 26 71 46 72 67 73 87
361 75 07 76 27 77 48 7868 79 88 81 08 82 28 83 49 84 69 85 89
362 8709 88 29 89 48 90 68 9188 93 08 94 28 95 48 96 67 97 87
363 99 07 *00 26 *01 46 *02 65 *03 85 *05 04 *06 24 *07 43 *08 63 *09 82
364 56 11 01 1221 13 40 14 59 15 78 16 98 18 17 19 36 20 55 21 74
365 22 93 2412 25 31 26 50 27 69 2887 30 06 31 25 32 44 33 62
366 34 81 3600 37 18 38 37 39 55 40 74 41 92 43 11 44 29 45 48
367 46 66 47 84 49 03 50 21 51 39 52 57 53 76 54 94 5612 57 30
368 5848 59 66 60 84 62 02 63 20 64 37 65 55 66 73 67 91 69 09
369 70 26 71 44 72 62 73 79 74 97 76 14 77 32 78 49 79 67 80 84
370 82 02 8319 84 36 85 54 86 71 87 88 89 05 9023 91 40 92 57
371 93 74 94 91 96 08 97 25 9842 99 59 *00 76 *01 93 *03 09 *04 26
372 57 05 43 06 60 07 76 08 93 10 10 11 26 12 43 13 59 14 76 15 92
373 17 09 18 25 19 42 20 58 21 74 22 91 24 07 25 23 26 39 27 55
374 28 72 29 88 3104 32 20 33 36 34 52 35 68 36 84 3800 39 15
375 40 31 41 47 42 63 43 79 44 94 46 10 47 26 48 41 49 57 50 72
376 51 88 53 03 54 19 55 34 56 50 57 65 5880 59 96 61 11 62 26
377 6341 64 57 65 72 66 87 68 02 69 17 70 32 71 47 72 62 73 77
378 74 92 76 07 77 22 78 36 79 51 80 66 81 81 82 95 84 10 85 25
379 86 39 87 54 88 68 89 83 90 97 92 12 93 26 94 41 95 55 96 69
380 97 84 98 98 *00 12 *01 26 *02 41 *0355 *04 69 *05 83 *06 97 *08 11
381 58 09 25 10 39 11 53 12 67 13 81 14 95 16 08 17 22 18 36 19 50
382 20 63 21 77 22 91 24 04 2518 26 31 27 45 28 58 29 72 30 85
383 31 99 33 12 34 26 35 39 36 52 37 65 38 79 39 92 41 05 42 18
384 43 31 44 44 45 57 46 70 47 83 48 96 50 09 51 22 52 35 53 48
385 54 61 55 74 56 86 57 99 59 12 60 24 61 37 6250 63 62 64 75
386 65 87 67 00 68 12 69 25 70 37 71 49 72 62 73 74 74 86 75 99
387 77 11 78 23 79 35 80 47 81 60 82 72 83 84 8196 86 08 87 20
388 88 32 89 44 90 56 91 67 92 79 93 91 95 03 96 15 97 26 98 38
389 99 50 *00 61 *01 73 *02 84 *03 96 *05 07 *06 19 *07 30 *08 42 *09 53
390 59 10 65 11 76 12 87 13 99 1510 1621 17 32 18 43 19 55 20 66
391 21 77 22 88 23 99 25 10 26 21 27 32 28 43 29 54 30 64 31 75
392 32 86 33 97 35 08 36 18 37 29 38 40 39 50 40 61 41 71 42 82
393 43 93 45 03 46 14 47 24 48 34 49 45 50 55 51 65 52 76 53 86
394 54 96 56 06 57 17 58 27 59 37 60 47 61 57 62 67 63 77 64 87
395 65 97 67 07 6817 69 27 70 37 71 46 72 56 73 66 74 76 75 85
396 76 95 78 05 79 14 80 24 81 34 82 43 83 53 84 62 85 72 86 81
397 87 91 89 00 90 09 91 19 92 28 93 37 94 46 95 56 96 65 97 74
398 98 83 99 92 *01 01 *02 10 *03 19 *04 28 *05 37 *06 46 *07 55 *08 64
399 6009 73 10 82 11 91 12 99 14 08 15 17 16 25 17 34 18 43 19 51
400 20 60 21 69 22 77 23 86 24 94 26 03 27 11 28 19 29 28 30 36
Р.Р. 124 123 122 121 120 119 118 117 116 115 114 113 112 | 111 110 109; 108
1 12,4 12,3 12,2 12,1 12,0 И ,9 11,8 11,7 11,6 23,2 11,5 И ,4 11,3 11,2^11 , 1 22,4 22,2 1 1,0 10,9 10,8
2 24,8 24,6 24,4 24,2 24,0 23,8 23,6 23,4 23,0 22,8 22,6 22,0 33,0 21,8 32,7 21 ,0
3 37,2 36,9 36,6 36,3 36,0 35, 7 35,4 35,1 34,8 34,5 34,2 33,9 33,6 33,3 32,4
4 49,6 49,2 48,8 48,4 48,0 47,6 47,2 46,8 46,4 46,0 45,6 45,2 56,5 44,8 44,4 44,0 43,6 43,2
5 62,0 61,5 73,8 61,0 60,5 60,0 59,5 59,0 58,5 58,0 57,5 57,0 56,0 55,5 67,2 66,6 55,0 54.5 54,0
б 74,4 73,2 72,6 72,0 71,4 70,8 70,2 69,6 69,0 80,5 68,4 67,8 66,0 65,4 64,8
7 86,8 86,1 85,4 84,7 84,0 83,3 82,6 81,9 81,2 79,8 79,1 78,4 77,7 77,0 76,3 75,6
8 99,2 98,4 97,6 96,8 96,0 95,2 94,4 93,6 92,8 92,0 91,2 90,4 89,6 88,8 88,0 87,2 86,4
У 111,6,110,7 1 109,8 108,9 108,0 107,1 106,2 105,3 104,4 103,5 102,6 101,7,100,8 99,9 | 1 99,0 98,1 97,2
42
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
401—450
N 0 ' 1 2 3 4 5 6 7 8 9
401 603144 32 53 33 61 34 69 35 77 36 86 37 94 39 02 4010 41 18
402 42 26 43 34 44 42 45 50 46 58 47 66 48 74 49 82 50 89 51 97
403 53 05 54 13 55 21 56 28 57 36 58 44 59 51 60 59 61 66 62 74
404 63 81 64 89 65 96 6704 68 11 6919 70 26 71 33 72 41 73 48
405 74 55 75 62 76 69 77 77 78 84 79 91 80 98 82 05 83 12 84 19
406 85 26 86 33 87 40 8847 89 54' 90 61 91 67 92 74 93 81 9488
407 95 94 97 01 98 08 99 14 ♦00 21 »01 28 *02 34 *03 41 *04 47 *05 54
408 61 06 60 07 67 08 73 09 79 10 86 11 92 12 98 14 05 15 11 16 17
409 17 23 18 29 19 36 20 42 21 48 22 54 23 60 24 66 25 72 26 78
410 27 84 28 90 29 96 31 02 32 07 33 13 34 19 35 25 36 30 37 36
411 38 42 39 47 40 53 41 59 42 64 43 70 4475 45 81 4686 47 92
412 48 97 5003 51 08 52 13 53 19 54 24 55 29 56 34 57 40 58 45
413 59 50 6055 61 60 62 65 63 70 64 76 65 81 66 86 67 90 68 95
414 70 00 71 05 72 10 73 15 74 20 75 25 76 29 77 34 78 39 7943
415 80 48 81 53 82 57 83 62 84 66 85 71 86 76 87 80 88 84 89 89
416 90 93 91 98 93 02 94 06 95 11 96 15 97 19 98 24 99 28 *00 32
417 62 01 36 02 40 03 44 04 48 05 52 06 56 0760 08 64 09 68 10 72
418 1176 12 80 13 84 14 88 15 92 16 95 17 99 19 03 20 07 21 10
419 22 14 23 18 24 21 25 25 26 28 27 32 28 35 29 39 30 42 3146
420 32 49 33 53 34 56 35 59 36 63 3766 38 69 39 73 40 76 41 79
421 42 82 43 85 44 88 45 91 46 95 47 98 49 01 50 04 51 07 52 10
422 53 12 54 15 5518 56 21 57 24 58 27 59 29 60 32 61 35 62 38
423 63 40 64 43 65 46 6648 67 51 68 53 69 56 70 58 71 61 72 63
424 73 66 74 68 75 71 76 73 77 75 78 78 79 80 80 82 81 85 82 87
425 83 89 84 91 85 93 86 95 87 97 89 00 90 02 91 04 92 06 93 08
426 9410 95 12 96 13 97 15 98 17 99 19 *0021 *01 23 *02 24 *03 26
427 63 04 28 05 30 06 31 07 33 08 35 09 36 10 38 11 39 12 41 13 42
428 14 44 15 45 16 47 17 48 18 49 1951 20 52 21 53 22 55 23 56
429 24 57 25 59 26 60 27 61 28 62 29 63 30 64 31 65 3266 33 67
430 34 68 35 69 36 70 37 71 38 72 39 73 40 74 41 75 42 76 43 76
431 44 77 45 78 46 79 47 79 48 80 49 81 50 81 51 82 52 83 53 83
432 54 84 5584 56 85 57 85 58 86 59 86 6087 61 87 62 87 6388
433 64 88 65 88 66 88 67 89 68 89 69 89 7089 71 89 72 90 73 90
434 74 90 75 90 76 90 77 90 78 90 79 90 8о 90 81 90 82 90 83 89
435 84 89 85 89 86 89 87 89 88 88 89 88 90 88 91 88 92 87 93 87
436 94 86 95 86 96 86 97 85 98 85 99 84 *00 84 *01 83 *02 83 *03 82
437 64 04 81 05 81 06 80 07 79 08 79 09 78 10 77 11 77 12 76 13 75
438 14 74 15 73 16 72 17 71 18 71 19 70 20 69 21 68 22 67 23 66
439 24 65 25 63 26 62 27 61 28 60 29 59 30 58 31 56 32 55 33 54
440 34 53 35 51 36 50 37 49 38 47 39 46 40 44 41 43 42 42 43 40
441 44 39 45 37 46 36 47 34 48 32 49 31 50 29 51 27 52 26 53 24
442 54 22 55 21 56 19 5717 5815 59 13 6011 61 10 62 08 6306
443 64 04 65 02 66 00 66 98 67 96 68 94 69 92 70 89 71 87 72 85
444 73 83 7481 75 79 76 76 77 74 78 72 79 69 80 67 81 65 82 62
445 83 60 8458 85 55 86 53 87 50 88 48 89 45 90 43 91 40 92 37
446 93 35 94 32 95 30 96 27 97 24 98 21 9919 *00 16 *01 13 *0210
447 65 03 08 04 05 05 02 05 99 06 96 07 93 08 90 0987 1084 11 81
448 12 78 13 75 1472 15 69 16 66 17 62 18 59 19 56 20 53 21 50
449 22 46 23 43 24 40 25 36 26 33 27 30 28 26 29 23 30 19 31 16
450 32 13 33 09 34 05 3502 35 98 36 95 37 91 38 88 39 84 40 80
Р. Р. 109 108 107 106 105 104 103 102 101 100 99 98 97 96
1 10,9 10,8 10,7 10,6 10,5 10,4 10,3 10,2 10,1 10,0 9,9 9,8 9,7 9,6
2 21,8 21 ,б 21 ,4 21,2 21 ,0 20,8 20,6 20,4 20,2 20,0 19,8 19,6 19,4 19,2
3 32,7 32,4 32,1 31,8 31,5 31,2 30,9 30,6 30,3 30,0 29,7 29,4 29,1 28,8
4 43,6 43,2 42,8 42,4 42,0 41,6 41,2 40,8 40,4 40,0 39,6 39,2 38,8 38,4
5 54,5 54,0 53,5 53,0 52,5 52,0 51,5 51,0 50,5 50,0 49,5 49,0 48, 5 48,0
б 65,4 64,8 64,2 63,6 63,0 62,4 61,8 61,2 60,6 60,0 59,4 58,8 58,2 57,6
7 76,3 75,6 74,9 74,2 73,5 72,8 72,1 71,4 70,7 70,0 69,3 68,6 67.9 67,2
8 87,2 86,4 85,6 84,8 84,0 83,2 82,4 81,6 80,8 80,0 79,2 78,4 77,6 76,8
9 98,1 97,2 96,3 95,4 94,5 93,6 92,7 91,8 90,9 90,0 89,1 88,2 87,3 86,4
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
43
451—500
N 0 1 2 3 4 5 б 7 8 9
451 65 41 77 42 73 43 69 44 65 45 62 46 58 47 54 48 50 49 46 50 42
452 51 38 52 35 53 31 54 27 55 23 56 19 57 15 58 10 59 06 60 02
453 60 98 61 94 6290 63 86 64 82 65 77 66 73 67 69 68 64 69 60
454 70 56 71 52 72 47 73 43 74 38 75 34 76 29 77 25 78 20 79 16
455 8011 81 07 82 02 82 98 83 93 84 88 85 84 86 79 87 74 88 70
456 89 65 90 60 91 55 92 50 93 46 94 41 95 36 96 31 97 26 98 21
457 99 16 ‘ООН *01 06 *02 01 *02 96 *03 91 *04 86 *05 81 *06 76 *07 71
458 66 08 65 09 60 10 55 11 50 1245 13 39 14 34 15 29 16 23 17 18
459 1813 19 07 20 02 20 96 21 91 22 86 23 80 24 75 25 69 26 63
460 27 58 28 52 29 47 30 41 31 35 32 30 33 24 34 18 35 12 36 07
461 37 01 37 95 38 89 39 83 40 78 4172 42 66 43 60 44 54 45 48
462 4642 47 36 48 30 49 24 50 18 51 12 52 06 52 99 53 93 54 87
463 55 81 56 75 57 69 58 62 59 56 60 50 61 43 62 37 63 31 64 24
464 65 18 66 12 67 05 67 99 68 92 69 86 70 79 71 73 72 66 73 60
465 74 53 75 46 76 40 77 33 78 26 79 20 80 13 81 06 81 99 82 93
466 83 86 84 79 85 72 86 65 87 59 88 52 89 45 90 38 91 31 92 24
467 93 17 94 10 95 03 95 96 96 89 97 82 98 75 99 67 *00 60 *01 53
468 67 02 46 03 39 04 31 05 24 0617 0710 08 02 08 95 09 88 10 80
469 11 73 12 65 13 58 14 51 15 43 16 36 17 28 18 21 19 13 20 05
470 20 98 21 90 2283 23 75 24 67 25 60 26 52 27 44 28 36 29 29
471 ’ 30 21 31 13 32 05 3297 33 90 34 82 35 74 36 66 37 58 3850
472 39 42 40 34 41 26 4218 43 10 44 02 44 94 45 86 46 77 47 69
473 48 61 49 53 50 45 51 37 52 28 53 20 54 12 55 03 55 95 56 87
474 57 78 58 70 59 62 60 53 61 45 62 36 63 28 64 19 65 11 66 02
475 66 94 67 85 68 76 69 68 70 59 71 51 7242 73 33 74 24 7516
476 76 07 76 98 77 89 78 81 79 72 80 63 81 54 8245 83 36 84 27
477 85 18 86 09 8700 87 91 88 82 89 73 90 64 91 55 92 46 93 37
478 94 28 95 19 96 10 97 00 97 91 98 82 99 73 ‘00 63 *01 54 *0245
479 68 03 36 04 26 0517 06 07 06 98 0789 08 79 09 70 10 60 11 51
480 1241 13 32 14 22 15 13 16 03 16 93 1784 18 74 19 64 20 55
481 21.45 22 35 23 26 2416 25 06 25 96 26 86 27 77 28 67 29 57
482 30 47 31 37 32 27 33 17 34 07 34 97 35 87 36 77 37 67 38 57
483 39 47 40 37 41 27 4217 43 07 43 96 44 86 45 76 46 66 47 56
484 4845 49 35 50 25 51 14 52 04 52 94 ’ 53 83 54 73 55 63 56 52
485 5742 58 31 59 21 6010 61 00 61 89 62 79 63 68 64 58 65 47
486 66 36 67 26 6815 69 04 69 94 70 83 71 72 72 61 73 51 74 40
487 75 29 76 18 77 07 77 96 78 86 79 75 80 64 81 53 82 42 83 31
488 84 20 85 09 85 98 86 87 87 76 88 65 89 53 90 42 91 31 92 20
489 93 09 93 98 94 86 95 75 96 64 97 53 98 41 99 30 *00 19 *01 07
490 69 01 96 02 85 03 73 04 62 05 50 06 39 07 28 0816 09 05 09 93
491 1081 11 70 1258 13 47 14 35 15 24 16 12 17 00 17 89 18 77
492 19 65 20 53 21 42 2230 2318 24 06 24 94 25 83 26 71 27 59
493 2847 29 35 30 23 31 11 3199 32 87 33 75 34 63 35 51 36 39
494 37 27 3815 39 03 39 91 40 78 41 66 42 54 43 42 44 30 45 17
495 46 05 46 93 47 81 48 68 49 56 5044 51 31 52 19 53 07 53 94
496 54 82 55 69 56 57 5744 58 32 59 19 60 07 60 94 61 82 62 69
497 63 56 64 44 65 31 66 18 67 06 67 93 68 80 69 68 70 55 71 42
498 72 29 73 17 74 04 74 91 75 78 76 65 77 52 78 39 79 26 80 14
499 81 01 81 88 82 75 83 62 84 49 85 35 86 22 87 09 87 96 88 83
500 89 70 90 57 91 44 92 31 93 17 94 04 94 91 95 78 96 64 97 51
Р.Р. 96 95 94 93 92 91 90 89 88 87 86
1 9,6 9,5 9,4 9,3 9,2 9,1 9,0 8,9 8,8 8,7 8,6
2 19,2 19,0 18,8 18,6 18,4 18,2 18,0 17,8 17,6 17,4 17,2
3 28,8 28,5 28,2 27,9 27,6 27,3 27,0 26,7 26,4 26,1 25,8
4 38,4 38,0 37,6 37,2 36,8 36,4 36,0 35,6 35,2 34,8 34,4
5 48,0 47,5 47,0 46,5 46,0 45,5 45, 0 44,5 44,0 43,5 43,0
6 57,6 57,0 56,4 55,8 55,2 54,6 54,0 53,4 52,8 52,2 51,6
7 67,2 66,5 65,8 65, 1 64,4 63,7 63,0 62,3 61,6 60,9 60,2
8 76,8 76,0 75,2 74,4 73,6 72,8 72,0 71,2 70,4 69,6 68,8
9 86,4 85,5 84,6 83,7 82,8 81,9 81,0 80,1 79,2 78,3 77,4
44
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
501—550 ______________
NO 12 3 456789
501 69 98 38 99 24 *00 11 *00 98 *01 84 *02 71 *03 58 *04 44 *05 31 *06 17
502 70 07 04 07 90 08 77 09 63 10 50 11 36 12 22 13 09 13 95 14 82
503 15 68 16 54 1741 18 27 1913 19 99 20 86 21 72 22 58 23 44
504 24 31 25 17 26 03 26 89 27 75 28 61 29 47 30 33' 31 19 32 05
505 32 91 33 77 34 63 35 49 36 35 37 21 38 07 38 93 39 79 40 65
506 41 51 42 36 43 22 44 08 44 94 45 79 46 65 47 51 48 37 49 22
507 50 08 50 94 51 79 52 65 53 50 54 36 55 22 56 07 56 93 57 78
508 58 64 59 49 60 35 61 20 62 06 62 91 63 76 64 62 65 47 66 32
509 67 18 6803 68 88 69 74 70 59 71 44 72 29 73 15 74 00 74 85
510 75 70 76 55 77 40 78 26 79 11 79 96 80 81 81 66 82 51 83 36
511 84 21 85 06 85 91 86 76 87 61 88 46 89 31 90 15 91 00 91 85
512 92 70 93 55 94 40 95 24 96 09 96 94 97 79 98 63 99 48 *00 33
513 71 01 17 02 02 02 87 03 71 04 56 05 40 06 25 07 10 07 94 08 79
514 09 63 10 48 11 32 12 17 1301 13 85 14 70 15 54 16 39 17 23
515 1807 18 92 19 76 20 60 21 44 22 29 23 13 23 97 24 81 25 66
516 26 50 27 34 28 18 29 02 29 86 30 70 31 54 32 38 33 23 3407
517 34 91 35 75 36 59 37 42 38 26 39 10 39 94 40 78 41 62 42 46
518 43 30 44 14 44 97 45 81 46 65 47 49 48 33 49 16 50 00 50 84
519 51 67 52 51 53 35 5418 55 02 55 86 56 69 57 53 58 36 59 20
520 60 03 60 87 61 70 62 54 63 37 64 21 6504 65 88 66 71 67 54
521 68 38 69 21 70 04 70 88 71 71 72 54 73 38 74 21 75 04 75 87
522 76 71 77 54 78 37 79 20 80 03 80 86 81 69 82 53 83 36 84 19
523 85 02 85 85 86 68 87 51 88 34 89 17 90 00 90 83 91 65 92 48
524 93 31 94 14 94 97 95 80 96 63 9745 98 28 99 11 99 94 *00 77
525 720159 02 42 03 25 04 07 04 90 05 73 06 55 07 38 08 21 09 03
526 09 86 1068 11 51 12 33 13 16 13 98 14 81 15 63 16 46 1728
527 18 11 18 93 19 75 20 58 2140 22 22 23 05 23 87 24 69 25 52
528 26 34 2716 27 98 28 81 29 63 30 45 31 27 32 09 32 91 33 74
529 34 56 35 38 36 20 3702 3784 38 66 3948 40 30 41 12 41 94
530 42 76 43 58 44 40 45 22 46 04 46 85 47 67 48 49 49 31 50 13
531 50 95 51 76 52 58 53 40 54 22 ' 55 03 55 85 56 67 57 48 58 30
532 59 12 59 93 60 75 61 56 62 38 63 20 64 01 64 83 65 64 66 46
533 67 27 68 09 68 90 69 72 70 53 71 34 72 16 72 97 73 79 74 60
534 75 41 76 23 7704 7785 78 66 79 48 80 29 81 10 81 91 82 73
535 83 54 84 35 85 16 85 97 86 78 87 59 88 41 89 22 90 03 90 84
536 91 65 92 46 93 27 94 08 94 89 95 70 96 51 97 32 98 13 98 93
537 99 74 *00 55 *01 36 *02 17 *02 98 *03 78 *04 59 *05 40 *06 21 *07 02
538 7307 82 08 63 09 44 10 24 1105 11 86 12 66 13 47 14 28 15 08
539 15 89 16 69 17 50 18 30 19 11 19 91 20 72 21 52 22 33 23 13
. 540, 23 94 24 74 25 55 26 35 2715 2796 28 76 29 56 30 37 31 17
541 31 97 32 78 33'58 34 38 3518 35 98 36 79 37 59 38 39 39 19
542 39 99 40 79 41 60 42 40 43 20 44 00 44 80 45 60 46 40 47 20
543 48 00 48 80 49 60 50 40 51 20 5200 , 52 79 53 59 54 39 55 19
544 55 99 56 79 57 59 58 38 59 18 59 98 60 78 61 57 62 37 63 17
545 63 97 64 76 65 56 66 35 6715 6795 68 74 69 54 70 34 71 13
546 71 93 72 72 73 52 74 31 7511 75 90 76 70 77 49 78 29 79 08
547 79 87 80 67 81 46 82 25 83 05 83 84 84 63 85 43 86 22 87 01
548 87 81 88 60 89 39 90 18 90 97 91 77 92 56 93 35 94 14 94 93
549 95 72 96 51 97 31 98 10 98 89 99 68 *00 47 *01 26 *02 05 *02 84
550 74 03 63 04 42 05 21 06 00 06 78 07 57 08 36 09 15 09 94 10 73
p.p. 87 86 85 84 83 82 81 80 79 78
8,7 8,6 8,5 8,4 8,3 8,2 8,1 8,0 7,9 7,8
2 17,4 17,2 17,0 16,8 16,6 16,4 16,2 16,0 15,8 15,6
3 26,1 25,8 25,5 25,2 24,9 24,6 24,3 24,0 23,7 23,4
4 34,8 34,4 34,0 33,6 33,2 32,8 32,4 32,0 31 ,6 31,2
5 43,5 43,0 42,5 42,0 41,5 41,0 40,5 40,0 39,5 39,0
6 52,2 51,6 51,0 50,4 49,8 49,2 48,6 48,0 47,4 46,8
7 60,9 60,2 59,5 58, 8 58,1 57,4 56,7 56,0 55,3 54,6
8 69,6 68,8 68,0 67,2 66,4 65,6 64,8 64,0 63,2 62.4
,9 78,3 77,4 76,5 75,6 74,7 73,8 72,9 72,0 71,1 70,2
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
45
551-600
N 0 1 2 3 4 5 6 7 8 1 9
551 74 11 52 12 30 1309 13 88 14 67 15 46 16 24 1703 1782 18 60
552 19 39 20 18 20 96 21 75 22 54 23 32 24 11 24 89 25 68 26 47
553 27 25 28 04 28 82 29 61 30 39 31 18 31 96 32 75 33 53 34 31
554 3510 35 88 36 67 37 45 38 23 39 02 39 80 40 58 41 36 42 15
555 42 93 43 71 44 49 45 28 46 06 46 84 47 62 48 40 49 19 49 97
556 50 75 51 53 52 31 53 09 53 87 54 65 55 43 56 21 56 99 57 77
557 58 55 59 33 60 И 60 89 61 67 62 45 63 23 6401 64 79 65 56
558 66 34 67 12 67 90 6868 69 45 70 23 71 01 71 79 72 56 73 34
559 74 12 74 89 75 67 76 45 77 22 78 00 78 78 70 55 80 33 81 10
560 81 88 82 66 83 43 84 21 84 98 85 76 86 53 87 31 88 08 88 85
561 89 63 9040 91 18 91 95 92 72 93 50 94 27 95 04 95 82 96 59
562 97 36 98 14 98 91 99 68 *00 45 *01 23 *02 00 *02 77 *03 54 *04 31
563 7505 08 05 86 06 63 07 40 08 17 08 94 09 71 10 48 11 25 12 02
564 12 79 13 56 14 33 1510 1587 16 64 1741 18 18 18 95 19 72
565 20 48 21 25 22 02 22 79 23 56 24 33 25 09 25 86 26 63 27 40
566 28 16 28 93 29 70 30 47 31 23 32 00 32 77 33 53 34 30 35 06
567 35 83 36 60 37 36 3813 38 89 39 66 40 42 41 19 41 95 42 72
568 43 48 44 25 45 01 45 78 46 54 47 30 48 07 48 83 49 60 50 36
569 51 12 51 89 52 65 53 41 54 17 54 94 55 70 56 46 57 22 57 99
570 58 75 59 51 60 27 6103 61 80 62 56 63 32 64 08 64 84 65 60
571 66 36 67 12 67 88 68 64 69 40 70 16 70 92 71 68 72 44 73 20
572 73 96 74 72 75 48 76 24 7700 77 75 78 51 79 27 80 03 80 79
573 81 55 82 30 83 06 83 82 84 58 85 33 86 09 86 85 87 61 88 36
574 89 12 89 88 90 63 91 39 92 14 92 90 93 66 94 41 95 17 95 92
575 96 68 97 43 98 19 98 94 99 70 *00 45 *01 21 *01 96 *02 72 *03 47
576 76 04 22 04 98 05 73 06 49 07 24 07 99 08 75 09 50 10 25 11 01
577 11 76 1251 13 26 14 02 14 77 15 52 16 27 17 02 17 78 18 53
578 19 28 20 03 20 78 21 53 22 28 23 03 23 78 24 53 25 29 26 04
579 26 79 27 54 28 29 29 04 29 78 30 53 3! 28 3203 32 78 33 53
580 34 28 3503 35 78 36 53 37 27 38 02 38 77 39 52 40 27 41 01
581 41 76 42 51 43 26 44 00 44 75 45 50 46 24 46 99 47 74 48 48
582 49 23 49 98 50 72 51 47 52 21 52 96 53 70 54 45 55 20 55 94
583 56 69 57 43 58 18 58 92 59 66 60 41 61 15 61 90 62 64 63 38
584 64 13 64 87 65 62 66 36 67 10 67 85 68 59 69 33 70 07 70 82
585 7156 72 30 73 04 73 79 74 53 75 27 76 01 76 75 77 49 78 23
586 78 98 79 72 80 46 81 20 81 94 82 68 83 42 84 16 84 90 85 64
587 86 38 87 12 87 86 88 60 89 34 90 08 90 82 91 56 92 30 93 03
588 93 77 94 51 95 25 95 99 96 73 97 46 98 20 98 94 99 68 *00 42
589 77 01 15 01 89 02 63 03 36 04 10 04 84 05 57 06 31 07 05 07 78
590 08 52 09 26 09 99 10 73 11 46 12 20 12 93 13 67 14 40 15 14
591 15 87 16 61 17 34 1808 1881 19 55 20 28 21 02 21 75 22 48
592 23 22 23 95 24 68 2542 26 15 26 88 27 62 28 35 29 08 29 81
593 30 55 31 28 32 01 32 74 33 48 34 21 34 94 35 67 36 40 37 13
594 37 86 38 60 39 33 40 06 40 79 41 52 42 25 42 98 43 71 44 44
595 45 17 45 90 46 63 47 36 48 09 48 82 49 55 50 28 51 00 51 73
596 5246 53 19 53 92 54 65 55 38 5610 56 83 57 56 58 29 59 02
597 59 74 60 47 61 20 61 93 62 65 63 38 64 11 64 83 65 56 66 29
598 67 01 67 74 68 46 69 19 69 92 70 64 71 37 72 09 72 82 73 54
599 74 27 74 99 75 72 76 44 77 17 77 89 78 62 79 34 80 06 80 79
600 81 51 82 24 82 96 83 68 84 41 85 13 85 85 86 58 87 30 88 02
Р.Р. 79 78 77 76 75 74 73 72
1 7,9 7,8 7,7 7,6 7,5 7,4 7,3 7,2
2 15,8 15,6 !5,4 15,2 15,0 14,8 14,6 14,4
3 23, 7 23,4 23,1 22,8 22,5 22,2 21,9 21,6
4 31,6 31,2 30.8 30,4 30,0 29,6 29,2 28,8
5 39,5 39,0 38,5 38,0 37,5 37,0 36,5 36,0
. 6 47,4 46,8 46,2 45,6 45.0 44,4 43,8 43,2
7 55,3 54,6 53,9 53,2 52,5 51,8 51,1 50,4
8 63,2 62,4 61,6 60,8 60,0 59,2 58,4 57,6
9 71,1 70,2 69,3 68,4 67,5 66,6 65,7 64,8
46
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
601—650
N 0 1 2 3 i 4 1 5 6 7 8 9
601 77 88 74 89 47 90 19 90 91 91 63 92 36 93 08 93 80 94 52 95 24
602 95 96 9669 97 41 98 13 98 85 99 57 *00 29 *01 01 *01 73 *02 45
603 78 03 17 03 89 04 61 05 33 06 05 06 77 07 49 08 21 08 93 09 65
604 10 37 11 09 11 81 12 53 13 24 1396 14 68 15 40 1612 1684
605 17 55 18 27 18 99 1971 20 42 21 14 21 86 22 58 23 29 24 01
606 24 73 2544 26 16 26 88 27 59 28 31 29 02 29 74 3046 31 17
607 31 89 32 60 33 32 34 03 34 75 35 46 36 18 36 89 37 61 38 32
608 3904 39 75 40 46 41 18 41 89 42 61 43 32 44 03 44 75 45 46
609 46 17 46 89 47 60 48 31 49 02 49 74 5045 51 16 51 87 52 59
610 53 30 54 01 54 72 55 43 56 15 56 86 57 57 58 28 58 99 59 70
611 60 41 61 12 61 83 62 54 63 25 63 96 64 67 65 38 66 09 66 80
612 67 51 68 22 68 93 69 64 70 35 71 06 71 77 72 48 73 19 73 90
613 74 60 75 31 76 02 76 73 77 44 78 15 78 85 79 56 80 27 80 98
614 81 68 82 39 83 10 83 81 84 51 85 22 85 93 86 63 87 34 88 04
615 88 75 89 46 9016 90 87 91 57 92 28 92 99 93 69 9440 95 10
616 95 81 96 51 97 22 97 92 98 63 99 33 *00 04 *00 74 ♦01 44 ♦02 15
617 79 02 85 03 56 04 26 04 96 05 67 06 37 07 07 07 78 08 48 09 18
618 09 88 10 59 11 29 11 99 12 69 1340 1410 14 80 15 50 16 20
619 16 91 1761 1831 1901 19 71 20 41 21 11 21 81 22 52 23 22
620 23 92 24 62 25 32 26 02 26 72 27 42 28 12 28 82 29 52 30 22
621 30 92 31 62 32 31 33 01 33 71 34 41 35 11 35 81 36 51 37 21
622 37 90 38 60 39 30 40 00 40 70 41 39 42 09 42 79 43 49 44 18
623 44 88 45 58 46 27 46 97 47 67 48 36 49 06 49 76 5045 51 15
624 51 85 52 54 53 24 53 93 5463 55 32 56 02 56 72 57 41 58 11
625 58 80 59 49 60 19 60 88 61 58 62 27 62 97 63 66 64 36 65 05
626 65 74 66 44 67 13 67 82 68 52 69 21 69 90 70 60 71 29 71 98
627 72 68 73 37 74 06 74 75 75 45 76 14 76 83 77 52 78 21 78 90
628 79 60 80 29 80 98 81 67 82 36 83 05 83 74 84 43 85 13 85 82
629 86 51 87 20 87 89 88 58 89 27 89 96 90 65 91 34 92 03 92 72
630 93 41 94 09 94 78 95 47 96 16 96 85 97 54 98 23 98 92 99 61
631 80 00 29 00 98 01 67 02 36 03 05 03 73 04 42 05 И 05 80 06 48
632 07 17 07 86 08 54 09 23 09 92 1061 11 29 Н 98 1266 13 35
633 14 04 14 72 1541 16 09 16 78 17 47 18 15 18 84 19 52 20 21
634 20 89 21 58 22 26 22 95 23 63 24 32 25 00 25 68 26 37 27 05
635 27 74 28 42 29 10 29 79 30 47 31 16 31 84 32 52 33 21 33 89
636 34 57 35 25 35 94 36 62 3730 37 98 38 67 39 35 40 03 40 71
637 41 39 42 08 42 76 43 44 4412 44 80 45 48 46 16 46 85 47 53
638 48 21 48 89 49 57 5025 50 93 51 61 52 29 52 97 53 65 54 33
639 55 01 5569 56 37 57 05 57 73 58 41 59 08 59 76 60 44 61 12
640 61 80 62 48 63 16 63 84 64 51 6519 65 87 66 55 67 23 67 90
641 68 58 69 26 69 94 70 61 71 29 71 97 72 64 73 32 74 00 74 67
642 75 35 76 03 76 70 77 38 78 06 78 73 79 41 80 08 80 76 81 43
643 82 11 82 79 83 46 84 1-1 84 81 85 49 86 16 86 84 87 51 88 18
644 88 86 89 53 90 21 90 88 91 56 92 23 92 90 93 58 94 25 94 92
645 95 60 96 27 96 94 97 62 98 29 98 96 99 64 *00 31 *00 98 *01 65
646 81 03 33 03 00 03 67 04 34 05 01 05 69 06 36 07 03 07 70 08 37
647 09 04 09 71 10 39 11 06 11 73 1240 13 07 13 74 14 41 15 08
648 15 75 16 42 17 09 17 76 1843 19 10 19 77 20 44 21 11 21 78
649 22 45 23 12 23 79 24 45 25 12 25 79 2646 2,7 13 27 80 28 47
650 29 13 2980 30 47 31 14 31 81 32 47 33 14 33 81 34 48 35 14
р.р. 73 72 71 70 69 68 67 66
1 7,3 7,2 7,1 7,0 6,9 6,8 6,7 6,6
2 14,6 14,4 14,2 14,0 13,8 13,6 13,4 13,2
3 21,9 21,6 21,3 21,0 20,7 20,4 20,1 19,8
4 29,2 28,8 28,4 28,0 27.6 27,2 26,8 26,4
5 36,5 36,0 35,5 35,0 34,5 34,0 33,5 33,0
6 43,8 43,2 42,6 42,0 41,4 48,3 40,8 40,2 39,6 .
7 51 , 1 50,4 49,7 49,0 47,6 46,9 46,2
8 58,4 57,6 56,8 56,0 55,2 54,4 53,6 52,8
9 65,7 64,8 63,9 63,0 62,1 61,2 60,3 59,4
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
47
651 —700
N 0 1 2 3 4 5 6 7 8 9
651 81 35 81 36 48 3714 37 81 38 48 3914 39 81 40 48 41 14 41 81
652 42 48 4314 43 81 44 47 45 14 45 81 46 47 47 14 47 80 48 47
653 49 13 49 80 5046 51 13 51 79 52 46 53 12 53 78 5445 55 11
654 55 78 56 44 57 11 57 77 58 43 5910 59 76 60 42 61 09 61 75
655 62 41 63 08 63 74 6440 65 06 65 73 66 39 67 05 67 71 68 38
656 69 04 69 70 70 36 71 02 71 69 72 35 73 01 73 67 74 33 74 99
657 75 65 76 31 76 98 77 64 78 30 78 96 79 62 80 28 80 94 81 60
658 82 26 82 92 83 58 84 24 84 90 85 56 86 22 86 88 87 54 88 20
659 88 85 89 51 9017 9083 91 49 92 15 92 81 93 46 94 12 9478
660 95 44 9610 96 76 97 41 98 07 98 73 99 39 *00 04 *00 70 *01 36
661 82 02 01 02 67 03 33 03 99 04 64 0530 05 95 06 61 07 27 07 92
662 08 58 09 24 09 89 1055 11 20 11 86 1251 13 17 13 82 1448
663 1514 15 79 16 45 17 10 17 75 1841 1906 1972 20 37 21 03
664 21 68 22 33 22 99 23 64 24 30 24 95 25 60 26 26 26 91 27 56
665 28 22 28 87 29 52 3018 30 83 31 48 32 13 32 79 33 44 34 09
666 34 74 35 39 36 05 36 70 37 35 38 00 38 65 39 30 39 96 40 61
667 41 26 41 91 42 56 4321 43 86 44 51 4516 45 81 46 46 47 11
668 47 76 48 41 49 06 49 71 50 36 51 01 51 66 52 31 52 96 53 61
669 54 26 54 91 55 56 56 21 56 86 57 51 5815 58 80 59 45 60 10
670 60 75 61 40 62 04 62 69 63 34 63 99 6464 65 28 65 93 66 58
671 67 23 67 87 68 52 69 17 69 81 70 46 71 11 71 75 72 40 73 05
672 73 69 74 34 74 99 75 63 76 28 76 92 77 57 78 21 78 86 79 51
673 8015 80 80 81 44 8209 82 73 83 38 8402 8467 85 31 85 95
674 86 60 87 24 87 89 88 53 89 18 89 82 90 46 91 11 91 75 92 39
675 93 04 93 68 94 32 94 97 95 61 96 25 96 90 97 54 98 18 98 82
676 99 47 *00 11 *00 75 *01 39 *02 04 *02 68 *03 32 *03 96 *04 60 *05 25
677 83 05 89 06 53 07 17 0781 08 45 09 09 09 73 1037 11 02 И 66
678 12 30 12 94 13 58 1422 1486 15 50 16 14 1678 17 42 18 06
679 18 70 19 34 19 98 20 62 21 26 21 89 22 53 23 17 23 81 24 45
680 25 09 25 73 26 37 27 00 27 64 28 28 28 92 29 56 30 20 3083
681 31 47 32 11 32 75 33 38 34 02 34 66 35 30 35 93 36 57 37 21
682 37 84 38 48 39 12 39 75 40 39 41 03 41 66 42 30 42 94 43 57
683 44 21 44 84 45 48 46 11 46 75 47 39 48 02 48 66 49 29 4993
684 50 56 51 20 51 83 52 47 53 10 53 73 54 37 5500 55 64 56 27
685 56 91 57 54 58 17 58 81 59 44 60 07 60 71 61 34 61 97 62 61
686 63 24 63 87 64 51 65 14 65 77 66 41 67 04 67 67 68 30 68 94
687 69 57 70 20 70 83 71 46 72 10 72 73 73 36 73 99 74 62 75 25
688 75 88 76 52 7715 77 78 78 41 79 04 79 67 8030 80 93 81 56
689 82 19 82 82 83 45 84 08 84 71 85 34 85 97 86 60 87 23 87 86
690 88 49 89 12 89 75 9038 91 01 91 64 92 27 92 89 93 52 9415
691 94 78 95 41 96 04 96 67 97 29 97 92 98 55 9918 99 81 *00 43
692 84 01 06 01 69 02 32 02 94 03 57 04 20 04 82 05 45 06 08 06 71
693 07 33 07 96 08 59 09 21 09 84 10 46 11 09 11 72 1234 1297
694 13 59 14 22 14 85 15 47 16 10 16 72 17 35 17 97 1860 19 22
695 19 85 20 47 21 10 21 72 22 35 22 97 23 60 2422 24 84 25 47
696 26 09 26 72 27 34 27 96 28 59 29 21 29 83 30 46 31 08 31 70
697 32 33 32 95 33 57 34 20 34 82 35 44 36 06 36 69 37 31 37 93
698 38 55 39 18 39 80 40 42 41 04 41 66 42 29 4291 43 53 4415
699 44 77 45 39 46 01 46 64 47 26 47 88 48 50 49 12 49 74 50 36
700 50 98 51 60 52 22 52 84 53 46 5408 5470 5532 55 94 56 56
р.р. 67 66 65 64 63 62
1 6,7 6,6 6,5 6,4 6,3 6,2
2 13,4 13,2 13,0 12,8 12,6 12,4
3 20,1 19,8 19,5 19,2 18,9 18,6
4 26,8 26,4 26,0 25,6 25,2 24,8
5 33,5 • 33,0 32,5 32,0 31,5 31 ,0
6 40,2 39,6 39,0 38,4 37,8 37,2
7 46,9 46,2 45,5 44,8 44,1 43,4
8 53,6 52,8 52,0 51,2 50,4 49,6
9 60,3 59,4 58,5 57,6 56,7 55,8
48
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
701—750
N 0 1 2 3 4 5 1 6 7 ' 8 9
701 84 57 18 57 80 58 42 59 04 59 66 60 28 60 90 61 51 6213 62 75
702 63 37 63 99 64 61 65 23 6585 66 46 67 08 67 70 68 32 68 94
703 69 55 70 17 70 79 71 41 72 02 72 64 73 26 73 88 74 49 75 11
704 75 73 76 34 76 96 77 58 78 19 78 81 79 43 80 04 80 66 81 28
705 81 89 82 51 83 12 83 74 84 35 84 97 85 59 86 20 86 82 87 43
706 88 05 88 66 89 28 89 89 90 51 91 12 91 74 92 35 92 97 93 58
707 94 19 94 81 95 42 96 04 96 65 97 26 97 88 98 49 99 11 99 72
708 85 00 33 00 95 01 56 02 17 02 79 03 40 04 01 04 62 05 24 05 85
709 06 46 07 07 07 69 08 30 08 91 09 52 10 14 10 75 11 36 11 97
710 12 58 13 20 13 81 14 42 15 03 15 64 16 25 16 86 17 47 18 09
711 18 70 1931 19 92 20 53 21 14 21 75 22 36 22 97 23 58 2419
712 24 80 25 41 26 02 26 63 27 24 27 85 28 46 29 07 29 68 30 29
713 30 90 31 50 32 11 32 72 33 33 33 94 34 55 35 16 35 77 36 37
714 36 98 37 59 38 20 38 81 39 41 40 02 40 63 41 24 41 85 42 45
715 43 06 43 67 44 28 44 88 45 49 46 10 46 70 47 31 47 92 48 52
716 49 13 49 74 50 34 50 95 51 56 52 16 52 77 53 37 53 98 54 59
717 55 19 55 80 56 40 57 01 57 61 58 22 58 82 59 43 60 03 60 64
718 61 24 61 85 62 45 63 06 63 66 64 27 64 87 65 48 66 08 66 68
719 67 29 67 89 68 50 69 10 69 70 70 31 70 91 71 52 72 12 72 72
720 73 32 73 93 74 53 75 13 75 74 76 34 76 94 77 55 78 15 78 75
721 79 35 79 95 80 56 81 16 81 76 82 36 82 97 83 57 8417 84 77
722 85 37 85 97 86 57 87 18 87 78 88 38 88 98 89 58 90 18 90 78
723 91 38 91 98 92 58 93 18 93 79 94 39 94 99 95 59 96 19 96 79
724 97 39 97 99 98 59 9918 99 78 *00 38 *00 98 *01 58 *02 18 *02 78
725 86 03 38 03 98 04 58 05 18 05 78 06 37 06 97 07 57 0817 08 77
726 09 37 09 96 10 56 11 16 11 76 12 36 12 95 13 55 14 15 14 75
727 15 34 15 94 16 54 17 14 17 73 18 33 18 93 19 52 20 12 20 72
728 21 31 21 91 22 51 23 10 23 70 24 30 24 89 25 49 26 08 26 68
729 27 28 2787 28 47 29 06 29 66 30 25 30 85 31 44 32 04 32 63
730 33 23 33 82 34 42 35 01 35 61 36 20 36 80 37 39 37 99 38 58
731 39 17 39 77 40 36 40 96 41 55 42 14 42 74 43 33 43 92 44 52
732 4511 45 70 46 30 46 89 47 48 48 08 48 67 49 26 49 85 50 45
733 51 04 51 63 52 22 52 82 53 41 54 00 54 59 55 19 55 78 56 37
734 56 96 57 55 58 14 58 74 59 33 59 92 60 51 61 10 61 69 62 28
735 62 87 63 46 64 05 64 65 65 24 65 83 66 42 67 01 67 60 68 19
736 68 78 69 37 69 96 70 55 71 14 71 73 7232 72 91 73 50 74 09
737 74 67 75 26 75 85 76 44 77 03 77 62 78 21 78 80 79 39 79 98
738 80 56 81 15 81 74 82 33 82 92 83 50 84 09 84 68 85 27 85 86
739 86 44 87 03 87 62 88 21 88 79 89 38 89 97 90 56 91 14 91 73
740 92 32 92 90 93 49 94 08 94 66 95 25 95 84 96 42 97 01 97 60
741 98 18 98 77 99 35 99 94 *00 53 *01 11 *01 70 *02 28 *02 87 *03 45
742 87 04 04 04 62 05 21 05 79 06 38 06 96 07 55 08 13 08 72 09 30
743 09 89 10 47 11 06 11 64 12 23 1281 13 39 13 98 14 56 15 15
744 15 73 16 31 16 90 17 48 18 06 18 65 19 23 19 81 20 40 20 98
745 21 56 22 15 22 73 23 31 23 89 24 48 25 06 25 64 26 22 26 81
746 27 39 27 97 28 55 29 13 29 72 30 30 30 88 31 46 32 04 32 62
747 33 21 33 79 34 37 34 95 35 53 36 11 36 69 37 27 37 85 38 44
748 39 02 39 60 40 18 40 76 41 34 41 92 42 50 43 08 43 66 44 24
749 44 82 45 40 45 98 46 56 47 14 47 72 48 30 48 88 49 45 50 03
750 50 61 51 19 51 77 52 35 52 93 53 51 54 09 54 66 55 24 55 82
р. р. 62 61 60 59 58 57
1 6,2 6,1 6,С 5,9 5,8 5,7
2 12,4 12,2 12,0 11,8 11,6 11 ,4
3 18,6 18,3 18,0 17,7 17,4 17,1
4 24,8 24,4 24,0 23,6 23,2 22,8
5 31,0 30,5 30,0 29,5 29,0 28,5
6 37,2 36,6 36,0 35,4 34,8 34,2
7 43,4 42,7 42,0 41,3 40,6 39,9
8 49,6 48,8 48,0 47,2 46,4 45,6
9 55, 8 54,9 54,0 53,1 52,2 51,3
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
49
751 87 5640 56 98 57 56 5813 58 71 59 29 59 87 60 45 61 02 61 60
752 62 18 62 76 63 33 63 91 64 49 65 07 65 64 66 22 66 80 67 37
753 67 95 68 53 69 10 69 68 70 26 70 83 71 41 71 99 72 56 73 14
754 73 71 74 29 74 87 75 44 76 02 76 59 77 17 77 74 78 32 78 89
755 79 47 80 04 80 62 81 19 81 77 82 34 82 92 83 49 84 07 84 64
756 85 22 85 79 86 37 86 94 87 52 88 09 88 66 89 24 89 81 90 39
757 90 96 91 53 92 11 92 68 93 25 93 83 94 40 94 97 95 55 96 12
758 96 69 97 26 97 84 98 41 9898 99 56 *00 13 *00 70 *01 27 *01 85
759 88 02 42 02 99 03 56 04 13 04 71 05 28 05 85 06 42 06 99 07 56
760 08 14 08 71 09 28 09 85 10 42 10 99 11 56 12 13 12 71 13 28
761 13 85 14 42 14 99 15 56 1613 16 70 17 27 17 84 18 41 18 98
762 19 55 20 12 20 69 21 26 21 83 22 40 22 07 23 54 24 11 24 68
763 25 25 25 81 26 38 26 95 27 52 28 09 28 66 29 23 29 80 30 37
764 30 93 31 50 32 07 32 64 33 21 33 77 34 34 34 91 35 48 36 05
765 36 61 37 18 37 75 38 32 38 88 39 45 40 02 40 59 41 15 41 72
766 42 29 42 85 43 42 43 99 44 55 4512 45 69 46 25 46 82 47 39
767 47 95 48 52 49 09 49 65 50 22 50 78 51 35 51 92 52 48 53 05
768 53 61 54 18 54 74 55 31 55 87 56 44 57 00 57 57 58 13 58 70
769 59 26 59 83 60 39 60 96 61 52 62 09 62 65 63 21 63 78 64 34
770 64 91 65 47 66 04 66 60 67 16 67 73 68 29 68 85 69 42 69 98
771 70 54 71 11 71 67 72 23 72 80 73 36 73 92 74 49 75 05 75 61
772 76 17 76 74 77 30 77 86 7842 78 98 79 55 8011 80 67 81 23
773 81 79 82 36 82 92 83 48 84 04 84 60 85 16 85 73 86 29 86 85
774 8741 87 97 88 53 89 09 89 65 90 21 90 77 91 34 91 90 92 46
' 775 93 02 93 58 94 14 94 70 95 26 95 82 96 38 96 94 9750 98 06
776 98 62 99 18 99 74 *00 30 *00 86 *01 41 *01 97 *02 53 *03 09 *03 65
777 89 04 21 04 77 05 33 05 89 06 45 07 00 07 56 08 12 08 68 09 24
778 09 80 10 35 1091 11 47 12 03 12 59 1314 13 70 14 26 14 82
779 15 37 15 93 1649 17 05 17 60 18 16 18 72 19 28 19 83 20 39
780 20 95 21 50 22 06 22 62 23 17 23 73 24 29 24 84 25 40 25 95
781 26 51 27 07 27 62 28 18 28 73 29 29 29 85 30 40 30 96 31 51
782 32 07 32 62 33 18 33 73 34 29 34 84 35 40 35 95 36 51 37 06
783 37 62 3817 38 73 39 28 39 84 4039 4094 41 50 42 05 42 61
784 43 16 43 71 44 27 44 82 45 38 45 93 46 48 47 04 47 59 48 14
785 48 70 49 25 49 80 50 36 50 91 51 46 52 01 52 57 5312 53 67
786 54 23 54 78 55 33 55 88 56 44 56 99 5754 58 09 58 64 59 20
787 59 75 60 30 60 85 61 40 61 95 62 51 63 06 63 61 64 16 64 71
788 65 26 65 81 66 36 66 92 67 47 68 02 68 57 69 12 69 67 70 22
789 70 77 71 32 71 87 7242 72 97 73 52 74 07 74 62 7517 75 72
790 76 27 76 82 77 37 77 92 7847 79 02 79 57 80 12 80 67 81 22
791 81 76 82 31 82 86 83 41 83 96 84 51 85 06 85 61 8615 86 70
792 87 25 87 80 88 35 8890 89 44 89 99 90 54 91 09 91 64 92 18
793 92 73 93 28 93 83 94 37 94 92 95 47 96 02 96 56 9711 97 66
794 98 21 98 75 99 30 99 85 *00 39 *00 94 *01 49 *02 03 *0258 *03 12
795 90 03 67 04 22 04 76 05 31 0586 0640 06 95 07 49 08 04 08 59
796 09 13 09 68 10 22 10 77 11 31 11 86 12 40 12 95 13 49 14 04
797 14 58 15 13 15 67 16 22 16 76 1731 17 85 18 40 18 94 19 48
798 20 03 20 57 21 12 21 66 22 21 22 75 23 29 23 84 24 38 24 92
799 25 47 26 01 26 55 27 10 27 64 28 18 28 73 29 27 29 81 30 36
800 30 90 31 44 31 99 32 53 33 07 33 61 34 16 34 70 35 24 35 78
р. р. 58 57 56 55 54
1 5,8 5,7 5,6 5,5 5,4
2 11,6 11,4 11,2 11,0 10,8
3 17,4 17,1 16,8 16,5 16,2
4 23,2 22,8 22,4 22, О 21,6
5 29,0 28,5 28,0 27,5 27,0
6 34,8 34,2 33,6 33,0 32,4
7 40,6 39, 9 39,2 38,5 37,8
8 46,4 45,6 44,8 44,0 43,2
9 52,2 51,3 50,4 49,5 43,6
4 Том 1
50
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
801—850
N 0 1 2 3 4 5 6 7 8 9
801 90 36 33 36 87 37 41 37 95 38 49 39 04 39 58 4012 4066 41 20
802 41 74 42 29 42 83 43 37 43 91 44 45 44 99 4553 46 07 46 61
803 4716 47 70 48 24 48 78 49 32 49 86 50 40 50 94 51 48 52 02
804 52 56 53 10 53 64 5418 54 72 55 26 5580 56 34 56 88 5742
805 57 96 58 50 59 04 59 58 60 12 60 66 61 19 61 73 62 27 62 81
806 63 35 63 89 64 43 64 97 65 51 66 04 66 58 6712 67 66 68 20
807 68 74 69 27 69 81 70 35 70 89 71 43 71 96 72 50 73 04 73 58
808 74 11 74 65 75 19 75 73 76 26 76 80 77 34 77 87 78 41 78 95
809 79 49 80 02 80 56 81 10 81 63 8217 82 70 83 24 83 78 84 31
810 84 85 85 39 85 92 86 46 86 99 87 53 88 07 88 60 8914 89 67
811 90 21 90 74 91 28 91 81 92 35 92 89 93 42 93 96 94 49 95 03
812 95 56 9610 96 63 97 16 97 70 98 23 98 77 99 30 9984 *00 37
813 91 00 91 01 44 01 97 02 51 03 04 03 58 04 11 04 64 0518 05 71
814 06 24 06 78 07 31 07 84 08 38 08 91 09 44 09 98 10 51 11 04
815 11 58 1211 12 64 13 17 13 71 14 24 14 77 15 30 15 84 16 37
816 16 90 1743 17 97 18 50 19 03 19 56 20 09 20 63 21 16 21 69
817 22 22 22 75 23 28 23 81 24 35 24 88 25 41 25 94 26 47 27 00
818 27 53 28 06 28 59 29 13 29 66 30 19 30 72 31 25 31 78 32 31
819 32 84 33 37 33 90 34 43 34 96 35 49 36 02 36 55 37 08 37 61
820 3814 38 67 39 20 39 73 40 26 40 79 41 32 41 84 42 37 42 90
821 43 43 43 96 44 49 45 02 45 55 46 08 46 60 47 13 47 66 48 19
822 48 72 49 25 49 77 50 30 50 83 51 36 51 89 52 41 52 94 53 47
823 54 00 54 53 55 05 55 58 56 11 56 64 5716 57 69 58 22 58 75
824 59 27 59 80 60 33 60 85 61 38 61 91 62 43 62 96 6349 64 01
825 64 54 65 07 65 59 6612 66 64 67 17 67 70 68 22 68 75 69 27
826 6980 70 33 70 85 71 38 71 90 72 43 72 95 73 48 74 00 74 53
827 75 06 75 58 76 11 76 63 77 16 77 68 78 20 78 73 79 25 79 78
828 80 30 80 83 81 35 81 88 82 40 82 93 83 45 83 97 84 50 85 02
829 85 55 86 07 86 59 87 12 87 64 88 16 88 69 89 21 89 73 90 26
830 90 78 91 30 91 83 92 35 92 87 93 40 93 92 94 44 94 96 9549
831 96 01 96 53 97 06 97 58 98 10 98 62 99 14 99 67 *0019 *00 71
832 92 01 23 01 76 02 28 0280 03 32 03 84 04 36 04 89 05 41 05 93
833 06 45 06 97 07 49 08 01 08 53 09 06 09 58 10 10 10 62 11 14
834 11 66 1218 12 70 13 22 13 74 14 26 14 78 15 30 15 82 16 34
835 16 86 1738 17 90 1842 18 94 1946 19 98 20 50 21 02 21 54
836 22 06 22 58 23 10 23 62 24 14 24 66 2518 25 70 26 22 26 74
837 27 25 27 77 28 29 2881 29 33 29 85 30 37 30 89 31 40 31 92
838 32 44 32 96 33 48 33 99 34 51 3503 35 55 36 07 36 58 37 10
839 37 62 3814 38 65 39 17 39 69 40 21 40 72 41 24 41 76 42 28
840 42 79 43 31 43 83 44 34 44 86 45 38 45 89 46 41 46 93 4744
841 47 96 4848 48 99 49 51 50 03 50 54 51 06 51 57 52 09 52 61
842 53 12 53 64 54 15 54 67 55 18 55 70 56 21 56 73 57 25 57 76
843 58 28 58 79 59 31 59 82 60 34 60 85 61 37 61 88 6240 62 91
844 63 42 63 94 64 45 64 97 65 48 66 00 66 51 67 02 67 54 68 05
845 6857 69 08 69 59 70 11 70 62 71 14 71 65 72 16 72 68 7319
846 73 70 74 22 74 73 75 24 75 76 76 27 76 78 77 30 77 81 78 32
847 78 83 79 35 79 86 80 37 80 88 81 40 81 91 82 42 82 93 83 45
848 83 96 84 47 84 98 85 49 86 01 86 52 87 03 87 54 88 05 88 57
849 89 08 89 59 90 10 90 61 91 12 91 63 9215 92 66 9317 93 68
850 94 19 94 70 95 21 95 72 96 23 96 74 97 25 97 76 98 27 98 79
Р. Р. 55 54 53 52 51
1 5,5 5,4 5,3 5,2 5,1
2 11,0 10,8 10,6 10,4 10,2
3 16,5 16,2 15,9 15,6 15,3
4 22,0 21,6 21,2 20,8 20,4
5 27,5 27,0 26,5 26,0 25,5
6 33,0 32,4 31,8 31,2 30,6
7 38,5 37,8 37,1 36,4 35,7
8 44,0 43,2 42,4 41,6 40,8
9 49,5 48,6 47,7 46,8 4 5,9
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
51
851—900
851 92 99 30 9981 *00 32 *0083 ♦01 34 *01 85 *0236 *02 87 *03 38 *03 89
852 93 04 40 04 91 05 42 ®5 92 06 43 06 94 0745 0796 08 47 08 98
853 09 49 1000 1051 11 02 11 53 12 04 1254 13 05 13 56 14 07
854 14 58 1509 15 60 1610 16 61 17 12 1763 1814 18 65 1915
855 19 66 2017 20 68 21 18 21 69 22 20 22 71 23 22 23 72 24 23
856 24 74 25 24 25 75 26 26 26 77 27 27 2778 28 29 28 79 29 30
857 29 81 30 31 3082 31 33 31 83 3234 32 85 33 35 33 86 34 37
858 34 87 3538 35 89 36 39 36 90 3740 37 91 3841 38 92 39 43
859 3993 40 44 4094 41 45 41 95 42 46 42 96 43 47 43 97 44 48
860 44 98 4549 45 99 46 50 47 00 4751 48 01 48 52 49 02 49 53
861 5003 50 54 51 04 51 54 52 05 52 55 53 06 53 56 54 06 54 57
862 55 07 55 58 56 08 56 58 57 09 5759 5809 58 60 59 10 59 60
863 60 11 60 61 61 11 61 62 62 12 62 62 63 13 63 63 64 13 64 63
864 65 14 65 64 6614 66 65 6715 67 65 6815 6865 6916 69 66
865 7016 70 66 71 17 71 67 72 17 72 67 7317 73 67 74 18 74 68
866 7518 75 68 Гб 18 76 68 7718 7769 7819 78 69 79 19 79 69
867 80 19 80 69 81 19 81 69 8219 82 69 83 20 83 70 84 20 84 70
868 85 20 85 ’/0 86 20 86 70 87 20 87 70 8820 88 70 89 20 89 70
869 90 20 90 70 91 20 91 70 92 20 92 70 93 20 93 69 94 19 94 69
870 9519 95 69 9619 96 69 97 19 97 69 9819 98 69 99 18 99 68
871 94 0018 00 68 01 18 01 68 02 18 02 67 0317 03 67 04 17 04 67
872 05 16 05 66 06 16 06 66 0716 0765 0815 08 65 09 15 09 64
873 1014 1064 11 14 11 63 1213 12 63 13 13 13 62 14 12 14 62
874 15 11 1561 16 11 16 60 17 10 1760 18 09 18 59 19 09 19 58
875 20 08 20 58 21 07 21 57 22 07 22 56 23 06 23 55 24 05 24 55
876 25 04 25 54 26 03 26 53 27 02 27 52 28 01 2851 29 01 29 50
877 30 00 30 49 30 99 31 48 31 98 32 47 32 97 33 46 33 96 34 45
878 3495 35 44 35 93 36 43 36 92 3742 3791 38 41 38 90 39 39
879 39 89 40 38 40 88 41 37 41 86 42 36 42 85 43 35 43 84 44 33
880 4483 45 32 45 81 46 31 46 80 47 29 4779 4828 48 77 49 27
881 49 76 50 25 50 74 51 24 51 73 52 22 52 72 53 21 53 70 54 19
882 54 69 5518 55 67 56 16 56 65 5715 5764 58 13 58 62 5912
883 59 61 6010 60 59 61 08 61 57 62 07 62 56 63 05 63 54 64 03
884 64 52 65 01 65 51 66 00 66 49 66 98 6747 67 96 68 45 68 94
885 69 43 69 92 7041 70 90 71 40 71 89 72 38 72 87 73 36 73 85
886 74 34 74 83 75 32 75 81 76 30 76 79 7728 77 77 78 26 78 75
887 79 24 79 73 80 22 80 70 81 19 81 68 82 17 82 66 83 15 83 64
888 84 13 84 62 8511 85 60 86 09 86 57 8706 87 55 88 04 88 53
889 89 02 89 51 89 99 90 48 90 97 91 46 91 95 92 44 92 92 93 41
890 93 90 94 39 94 88 95 36 95 85 96 34 96 83 97 31 97 80 98 29
891 98 78 99 26 99 75 *00 24 *00 73 *01 21 *01 70 *02 19 *02 67 *03 16
892 95 03 65 04 14 04 62 05 11 05 60 06 08 06 57 07 06 07 54 08 03
893 08 51 09 00 09 49 09 97 1046 10 95 11 43 11 92 1240 12 89
894 13 38 13 86 14 35 14 83 1532 15 80 16 29 16 77 17 26 17 75
895 18 23 18 72 19 20 19 69 20 17 20 66 21 14 21 63 22 11 22 60
896 23 08 23 56 24 05 24 53 250? 25 50 25 99 26 47 26 96 2744
897 27 92 28 41 28 89 29 38 29 86 30 34 30 83 31 31 31 80 32 28
898 32 76 33 25 33 73 34 21 34 70 35 18 35 66 36 15 36 63 3711
899 3760 38 08 38 56 39 05 39 53 40 01 40 49 40 98 41 46 41 94
900 4243 42 91 43 39 43 87 44 35 44 84 45 32 45 80 46 28 46 77
р р. 52 51 50 49 48
1 5,2 5,1 5,0 4,9 4,8
2 10,4 10,2 10,0 9,8 9,6
3 15,6 15,3 15,0 14,7 14,4
4 20,8 20,4 20,0 19,G 19,2
26,0 25,5 25,0 24,5 24,0
6 31,2 30,6 30,0 29,4 28,8
7 36,4 35,7 35,0 34,3 33.6
8 41,6 40,8 •40,0 39,2 38,4
9 46,8 45,9 -15,0 44,1 43,2
^4*
52
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
901—950
N 0 1 2 3 4 5 6 7 8 9
901 95 47 25 47 73 48 21 48 69 49 18 4966 50 14 50 62 51 10 51 58
902 52 07 52 55 53 03 53 51 53 99 54 47 54 95 55 43 55 92 56 40
903 56 88 57 36 57 84 58 32 58 80 59 28 59 76 60 24 60 72 61 20
904 61 68 62 16 62 65 63 13 63 61 64 09 64 57 65 05 65 53 66 01
905 66 49 66 97 67 45 67 93 68 40 6888 69 36 69 84 70 32 70 80
906 71 28 71 76 72 24 72 72 73 20 73 68 74 16 74 64 7512 75 59
907 7607 76 55 77 03 7751 77 99 78 47 78 94 79 42 79 90 80 38
908 8086 81 34 81 81 82 29 82 77 83 25 83 73 84 21 84 68 85 16
909 85 64 8612 86 59 87 07 87 55 88 03 88 50 88 98 89 46 89 94
910 90 41 90 89 91 37 91 85 92 32 92 80 93 28 93 75 94 23 94 71
911 9518 95 66 96 14 96 61 97 09 97 57 98 04 98 52 99 00 99 47
912 99 95 *00 42 *00 90 *01 38 *01 85 *02 33 *02 80 *03 28 *03 76 *04 23
913 9604 71 05 18 05 66 06 13 06 61 07 09 07 56 08 04 08 51 08 99
914 09 46 09 94 10 41 10 89 11 36 1184 1231 12 79 13 26 13 74
915 14 21 14 69 15 16 15 63 16 11 16 58 1706 17 53 18 01 18 48
916 18 95 19 43 19 90 20 38 20 85 21 32 21 80 22 27 22 75 23 22
917 23 69 2417 24 64 2511 25 59 26 06 26 53 27 01 2748 27 95
918 28 43 28 90 29 37 29 85 30 32 30 79 31 26 31 74 32 21 32 68
919 33 16 33 63 34 10 34 57 3504 35 52 35 99 36 46 36 93 37 41
920 3788 3835 38 82 39 29 39 77 40 24 40 71 41 18 41 65 42 12
921 42 60 43 07 43 54 44 01 44 48 44 95 45 42 45 90 46 37 46 84
922 47 31 4778 48 25 48 72 49 19 49 66 5013 50 61 51 08 51 55
923 52 02 52 49 52 96 53 43 53 90 54 37 54 84 55 31 55 78 56 25
924 56 72 5719 57 66 58 13 5860 59 07 59 54 6001 60 48 60 95
925 61 42 61 89 62 36 62 83 63 29 63 76 64 23 64 70 65 17 65 64
926 66 11 6658 6705 67 52 67 99 68 45 68 92 69 39 69 86 70 33
927 70 80 71 27 71 73 72 20 72 67 73 14 73 61 74 08 74 54 75 01
928 75 48 7595 76 42 76 88 77 35 77 82 78 29 78 75 79 22 79 69
929 80 16 80 62 81 09 81 56 82 03 82 49 82 96 83 43 83 90 84 36
930 84 83 85 30 85 76 86 23 86 70 8716 87 63 88 10 88 56 89 03
931 89 50 89 96 90 43 90 90 91 36 91 83 92 29 92 76 93 23 93 69
932 94 16 94 63 95 09 95 56 96 02 96 49 96 95 97 42 97 89 98 35
933 98 82 99 28 99 75 *00 21 *00 68 *01 14 *01 61 *02 07 *02 54 *03 00
934 97 03 47 03 93 04 40 04 86 05 33 05 79 06 26 06 72 0719 0765
935 0812 08 58 09 04 09 51 09 97 10 44 1090 11 37 И 83 12 29
936 12 76' 13 22 13 69 14 15 1461 15 08 15 54 1601 16 47 16 93
937 17 40 17 86 18 32 18 79 19 25 19 71 20 18 20 64 21 10 21 57
938 2203 2249 22 95 23 42 23 88 24 34 24 81 25 27 25 73 26 19
939 26 66 27 12 27 58 2804 28 51 28 97 29 43 2989 30 35 30 82
940 31 28 31 74 32 20 32 66 33 13 33 59 34 05 34 51 34 97 35 43
941 35 90 36 36 36 82 37 28 37 74 38 20 38 66 3913 39 59 40 05
942 40 51 40 97 41 43 41 89 42 35 42 81 43 27 43 74 44 20 44 66
943 4512 45 58 46 04 46 50 46 96 4742 4788 48 34 48 80 49 26
944 49 72 50 18 50 64 51 10 51 56 52 02 52 48 52 94 53 40 53 86
945 54 32 54 78 55 24 55 70 5616 56 62 57 07 57 53 57 99 58 45
946 58 91 59 37 59 83 60 29 60 75 61 21 61 67 62 12 62 58 63 04
947 63 50 63 96 64 42 64 88 6533 65 79 66 25 66 71 6717 67 63
948 68 08 68 54 69 00 69 46 69 92 70 37 70 83 7129 71 75 72 20
949 72 66 7312 73 58 74 03 74 49 74 95 75 41 75 86 76 32 76 78
950 77 24 7769 78 15 78 61 79 06 79 52 79 98 80 43 80 89 81 35
р. р. 49 48 47 46 45
1 4,9 4,8 4/7 4,6 4,5
2 9,8 9,6 9,4 9,2 9,0
3 14,7 14,4 14,1 13,8 13,5
4 19,6 19,2 18,8 18,4 18,0
б 24,5 24,0 23,5 23,0 22,5
6 29,4 28,8 28,2 27,6 27,0
7 34,3 33,6 32,9 32,2 31,5
8 39,2 38,4 37,6 36,8 36,0
9 44,1 43,2 42,3 41,4 40,5
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
951—1000
N 0 1 2 3 4 5 б 7 8 9
951 9781 81 82 26 82 72 83 17 83 63 84 09 84 54 85 00 85 46 85 91
952 86 37 86 83 87 28 87 74 88 19 88 65 89 11 89 56 90 02 90 47
953 90 93 91 38 91 84 92 30 92 75 93 21 93 66 94 12 94 57 95 03
954 95 48 95 94 96 39 96 85 97 30 97 76 98 21 98 67 99 12 99 58
955 98 00 03 00 49 00 94 01 40 01 85 02 31 02 76 03 22 03 67 04 12
956 04 58 05 03 05 49 05 94 06 40 06 85 07 30 07 76 08 21 08 67
957 09 12 09 57 10 03 10 48 10 93 И 39 11 84 12 29 12 75 13 20
958 1366 14 И 14 56 1501 15 47 15 92 16 37 16 83 17 28 17 73
959 18 19 18 64 19 09 19 54 20 00 20 45 20 90 21 35 21 81 22 26
960 22 71 2316 23 62 24 07 24 52 24 97 25 43 25 88 26 33 26 78
961 27 23 27 69 28 14 28 59 29 04 29 49 29 94 30 40 30 85 31 30
962 31 75 32 20 3265 33 10 33 56 34 01 34 46 34 91 35 36 35 81
963 36 26 36 71 37 16 37 62 38 07 38 52 38 97 39 42 39 87 40 32
964 40 77 41 22 41 67 42 12 42 57 43 02 43 47 43 92 44 37 44 82
965 45 27 45 72 4617 46 62 47 07 47 52 47 97 48 42 48 87 49 32
966 49 77 50 22 50 67 51 12 51 57 52 02 52 47 52 92 53 37 53 82
967 54 26 54 71 55 16 55 61 56 06 56 51 56 96 57 41 57 86 58 30
968 58 75 59 20 59 65 60 10 60 55 61 00 61 44 61 89 62 34 62 79
969 63 24 63 69 64 13 64 58 65 03 65 48 65 93 66 37 66 82 67 27
970 67 72 68 17 68 61 69 06 69 51 69 96 70 40 70 85 71 30 71 75
971 7219 72 64 73 09 73 53 73 98 74 43 74 88 75 32 75 77 76 22
972 76 66 7711 7756 78 00 78 45 78 90 79 34 79 79 80 24 80 68
973 81 13 81 57 82 02 82 47 82 91 83 36 83 81 84 25 84 70 85 14
974 85 59 86 04 86 48 86 93 87 37 87 82 88 26 88 71 89 16 89 60
975 90 05 90 49 90 94 91 38 91 83 92 27 92 72 93 16 93 61 94 05
976 94 50 94 94 95 39 95 83 96 28 96 72 97 17 97 61 98 06 98 50
977 98 95 99 39 99 83 *00 28 *00 72 *01 17 *01 61 *02 06 *02 50 *02 94
978 99 03 39 03 83 04 28 04 72 05 16 05 61 06 05 06 50 06 94 07 38
979 07 83 08 27 08 71 09 16 09 60 10 04 10 49 10 93 11 37 11 82
980 12 26 12 70 13 15 13 59 14 03 14 48 14 92 15 36 1580 16 25
981 16 69 1713 17 58 18 02 18 46 18 90 19 35 19 79 20 23 20 67
982 21 11 21 56 22 00 22 44 22 88 23 33 23 77 24 21 24 65 25 09
983 25 54 25 98 26 42 26 86 27 30 27 74 28 19 28 63 29 07 29 51
984 29 95 30 39 30 83 31 27 31 72 32 16 32 60 33 04 33 48 33 92
985 34 36 34 80 35 24 35 68 36 13 36 57 37 01 3745 37 89 38 33
986 38 77 39 21 39 65 40 09 40 53 40 97 41 41 41 85 42 29 42 73
987 43 17 43 61 44 05 44 49 44 93 45 37 45 81 46 25 46 69 47 1S
988 47 57 48 01 48 45 48 89 49 33 49 77 50 21 50 65 51 08 51 52
989 51 96 52 40 52 84 53 28 53 72 54 16 54 60 55 04 55 47 55 91
990 56 35 56 79 57 23 57 67 5811 58 54 58 98 59 42 59 86 60 30
991 60 74 61 17 61 61 62 05 62 49 62 93 63 37 63 80 64 24 64 68
992 65 12 65 55 65 99 66 43 66 87 67 31 67 74 68 18 68 62 69 06
993 69 49 69 93 70 37 70 80 71 24 71 68 72 12 72 55 72 99 73 43
994 73 86 74 30 74 74 75 17 75 61 76 05 76 48 76 92 77 36 77 79
995 78 23 78 67 79 10 79 54 79 98 80 41 80 85 81 29 81 72 8216
996 82 59 83 03 83 47 83 90 84 34 84 77 85 21 85 64 86 08 86 52
997 86 95 87 39 87 82 88 26 88 69 89 13 89 56 90 00 90 43 90 87
998 91 31 91 74 92 18 92 61 93 05 93 48 93 92 94 35 94 79 95 22
999 9565 96 09 96 52 96 96 97 39 97 83 98 26 98 70 99 13 99 57
1000 00 00 00 0043 00 87 01 30 01 74 02 17 02 60 03 04 03 47 03 91
р. р. 46 45 44 43
1 4,6 4,5 4,4 4,3
2 9,2 9,0 8,8 8,6
3 13,8 13,5 13,2 12,9
4 18,4 18,0 17,6 17,2
5 23,0 22,5 22,0 21,5
6 27,6 27,0 26,4 25,8
7 32,2 31,5 30,8 30,1
8 36,8 36,0 35,2 34,4
9 41,4 40,5 39,6 38,7 *
54
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
sin
tg
ctg
cos
sin
tg
Ctg
cos
Таблица 3. НАТУРАЛЬНЫЕ ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
0° 1°
О 0,0000000
1 10,0002909
2!0,0005818
3 0,0008727
4 0,0011636
0,000000 OO
0,000291 3437,747
0.000582 1718.873
5
6
7
8
9
0,0014544
0,0017453
0,0020362
0,0023271
0,0026180
0,000873
0,001164
0,001454
0,001745
0,002036
0,002327
0,002618
145,916
859,4363
687,5489
572,9572
491,1060
429,7176
381,9710
10
11
12
13
14
15
16
17
18
19
0,0029089
0,0031998
0,0034907
0,0037815
0,0040724
0,0043633
0,0046542
0,0049451
0,0052360
0,0055268
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
0,0058177
0,0061086
0,0063995
0,0066904
0,0069813
0,0072721
0,0075630
0,0078539
0,0081448
0,0084357
0,0087265
0,0090174
0,0093083
0,0095992
0,0098900
0,0101809
0,0104718
0,0107627
0,0110535
0,0113444
0,0116353
0,0119261
0,0122170
0,0125079
0,0127987
0,0130896
0,0133805
0,0136713
0,0139622
0,0142530
0,0145439
0,0148348
0,0151256
0,0154165
0,0157073
0,0159982
0,0162890
57 0,0165799
58 0,0168707
59 = 0,0171616
0,002909
0,003200
0,003491
0,003782
0,004072
0,004363
0,004654
0,004945
0,005236
0,005527
0,005818
0,006109
0,006400
0,006691
0,006981
0,007272
0,007563
0,007854
0,008145
0,008436
0,008727
0,009018
0,009309
0,009601
0,009891
0,010181
0,010472
0,010763
0,011054
0,011345
0,011636
0,011927
0,012218
0,012509
0,012800
0,013091
0,013382
0,013673
0,013964
0,014254
0,014545
0,014836
0,015127
0,015418
0,015709
0,016000
0,016291
0,016582
0,016873
0,017164
343,7737
312,5214
286,4777
264,4408
245,5520
229,1817
214,8576
202,2187
190,9842
180,9322
171,8854
163,7002
156,2591
149,4650
143,2371
137,5074
132,2185
127,3213
122,7740
118,5402
114,5887
110,8921
107,4265
104,1709
101,1069
98,21794
95,48948
92,90849
90,46334
88,14357
85,93979
83,84351
81,84704
79,94343
78,12634
76,39001
74,72917
73,13899
71,61507
70,15335
68,75009
67,40185
66,10547
64,85801
63,65674
62,49915
61,38291
60,30582
59,26587
58,26117
1,000000
1,000000
0,9999998
0,9999996
0,9999993
0,9999989
0,9999985
0,9999979
0,9999973
0,9999966
0,9999958
0,9999949
0,9999939
0,9999928
0,9999917
0,9999905
0,9999892
0,9999878
0,9999863
0,9999847
0,9999831
0,9999813
0,9999795
0,9999776
0,9999756
0,9999736
0 9999714
0 9999692
0,9999668
0,9999644
60
59
58
57
56
55
54
53
52
51
0
1
2
3
4
5
6
7
8
9
0,9999619
0,9999593
0,9999567
0,9999539
0,9999511
0,9999482
0,9999452
0,9999421
0,9999389
0,9999357
0,9999323
0,9999289
0,9999254
0,9999218
0,9999181
0,9999143
0,9999105
0,9999065
0,9999025
0,9098984
0,9998942
0,9998900
0,9998856
0,9998812
0,9998766
0,9998720
0,9998673
0,9908625
0,9998577
0,9998527
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
0,0174524
0,0177432
0,0180341
0,0183249
0,0186158
0,0189066
0,0191974
0,0194883
0,0197791
0,0200699
0,0203608
0,0206516
0,0209424
0,0212332
0,0215241
0,0218149
0,0221057
0,0223965
0,0226873
0,0229781
0,0232690
0 0235598
0,0238506
0,0241414
0,0244322
0,0247230
0,0250138
0,0253046
0,0255954
0,0258862
0,0261769
0,0264677
0,0267585
0,0270493
0,0273401
0,0276309
0,0279216
0,0282124
0,0285032
0,0287940
0,0290847
0,0293755
0,0296662
0,0299570
0,0302478
0,0305385
0,0308293
0,0311200
0,0314108
0,0317015
0,017455
0,017746
0,018037
0,018328
0,018619
0,018910
0,019201
0,019492
0,019783
0,020074
0,020365
0,020656
0,020947
0,021238
0,021529
0,021820
0,022111
0,022402
0,022693
0,022984
0,023275
0,023566
0,023857
0,024148
0,024439
0,024731
0,025022
0,025313
0,025604
0,025895
0,026186
0,026477
0,026768
0,027059
0,027350
0,027641
0,027933
0,028224
0,028515
0,028806
0,029097
0,029388
0,029679
0,029970
0,030262
0,030553
0,030844
0,031135
0,031426
0,031717
57,28996
56,35059
55,44152
54,56130
53,70859
52,88211
52,08067
51,30316
50,54851
49,81573
49,10388
48,41208
47,73950
47,08534
46,44886
45,82935
45,22614
44,63860
44,06611
43,50812
42,96408
42,43346
41,91579
41,41059
40/91741
40,43584
39,96546
39,50589
39,05677
38,61774
38,18846
37,76861
37,35789
36,95600
36,56266
36,17760
35,80055
35,43128
35,06955
34,71511
34,36777
34,02730
33,69351
33,36619
33,04517
32,73026
32,42129
32,11810
31,82052
31,52839
0,9998477; 60
0,9998426: 59
0,9998374 58
0,9998321
0,9998267
0,9998213
0,9998157
57
56
55
54
0,9998101 53
0,9998044 52
0,9997986 51
0,9997927, 50
0,99978671 49
0,9997807 48
0,9997745’ 47
0,9997683 46
0,9997620
0,9997556
0,9997492
0,9997426
0,9997360
0,9997292
0,9997224
0,9997155
0,9997086
0,9997015
0,9996943
0,9996871
0,9996798
0,9996724
0,9996649
0,9996573
0,9996497
0,9996419
0,9996341
0,9996262
0,9996182
0,9996101
0,9996020
0,9995937
0,9995854
0,9995770
0,9995684
0,9995599
0,9995512
0,9995424
0,9995336
0,9995247
0,9995157
0,9995066
0,9994974
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
50
51
52
53
54
55
56
57
58
59
0,0319922
0,0322830
0,0325737
0,0328644
0,0331552
0,0334459
0,0337366
0,0340274
0,0343181
0,0346088
0,032009
0,032300
0,032591
0,032882
0,033173
0,033465
0,033756
0,034047
0,034338
0,034630
31,24158
30,95993
30,68331
30,41158
30,14462
29,88230
29,62450
29,37111
29,12200
28,87709
0,9994881
0,9994788
0,9994693
0,9994598
0,9994502
0,9994405
0,9994308
0 9994209
0,9994110
0,9994009
10
9
8
7
6
5
4
3
2
1
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
55
3°
ctg cos
sin tg
ctg
cos
о
1
2
3
4
5
6
7
8
9
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
29
30
31
32
33
34
35
36
37
38
39 j
40'
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
0,0348995
0,0351902
0,0354809
0,0357716
0,0360623
0,0363530
0,0366437
0,0369344
0,0372251
0,0375158
0,0378065
0,0380971
0,0383878
0,0386785
0,0389692
0,0392598
0,0395505
0,0398411
0,0401318
0,0404224
0,0407131
0,0410037
0,0412944
0,0415850
0,0418757
0,0421663
0,0424569
0,0427475
0,0430382
0,0433288
0,0436194
0,0439100
0,0442006
0,0444912
0,0447818
0,0450724
0,0453630
0,0456536
0,0459442
0,0462347
0,0465253
0,0468159
0,0471065
0,0473970
0,0476876
0,0479781
0,0482687
0,0485592
0,0488498
0,0491403
0,0494308
0,0497214
0,0500119
0,0503024
0,0505929
0,0508835
0,0511740
0,0514645
0,0517550
0,0520455
cos
0,034921
0,035212
0,035503
0,035795
0,036086
0,036377
0,036668
0,036960
0,037251
0,037542
0,037834
0,038125
0,038416
0,038707
0,038999
0,039290
0,039581
0,039873
0,040164
0,040456
0,040747
0,041038
0,041330
0,041621
0,041912
0,042204
0,042495
0,042787
0,043078
0,043370
0,043661
0,043952
0,044244
0,044535
0,044827
0,045118
0,045410
0,045701
0,045993
0,046'84
0,046576
0,046867
0,047159
0,047450
0,047742
0,048033
0,048325
0,048617
0,048908
0,049200
0,049491
0,049783
0,050075
0,050366
0,050658
0,050949
0,051241
0,051533
0,051824
0,052116
ctg
28,63625
28,39940
28,16642
27,93723
27,71174
27,48985
27,27149
27,05656
26,84498
26,63669
26,43160
26,22964
26,03074
25,83482
25,64183
25,45170
25,26436
25,07976
24,89783
24,71851
24,54176
24,36751
24,19571
24,02632
23,85928
23,69454
23,53205
23,37178
23,21367
23,05768
22,90377
22,75189
22,60201
22,45410
22,30810
22,16398
22,02171
21,88125
21,74257
21,60563
21,47040
21,33685
21,20495
21,07466
20,94597
20,81883
20,69322
20,56911
20,44649
20,32531
20,20555
20,08720
19,97022
19,85459
19,74029
19,62730
19,51558
19,40513
19,29592
19,18793
0,9993908
0,9993806
0,9993704
0,9993600
0,9993495
0,9993390
0,9993284
0,9993177
0,9993069
0,9992960
0,9992851
0,9992740
0,9992629
0,9992517
0,9992404
0,9992290
0,2992176
0,9992060
0,9991944
0,9991827
0,9991709
0,9991590
0,9991470
0,9991350
0,9991228
0,9991106
0,9990983
0,9990859
0,9990734
0,9990609
0,9990482
0,9990355
0,9990227
0,9990098
0,9989968
0,9989837
0,9989706
0,9989573
0,9989440
0,9989306
0,9989171
0,9989035
0,9988899
0,9988761
0,9988623
0,9988484
0,9988344
0,9988203
0,9988061
0,9987919
0,9987775
0,9987631
0,9987486
0,9987340
0,9987194
0,9987046
0,9986898
0,9986748
0,9986598
0,9986447
tg sin
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
0,0523360
0,0526264
0,0529169
0,0532074
0,0534979
0,0537883
0,0540788
0,0543693
0,0546597
0,0549502
0,0552406
0,0555311
0,0558215
0,0561119
0,0564024
0,0566928
0,0569832
0,0572736
0,0575640
0,0578544
0,0581448
0,0584352
0,0587256
0,0590160
0,0593064
0,0595967
0,0598871
0,0601775
0,0604678
0,0607582
0,0610485
0,0613389
0,0616292
0,0619196
0,0622099
0,0625002
0,0627905
0,0630808
0,0633711
0,0636614
0,0639517
0,0642420
0,0645323
0,0648226
0,0651129
0,0654031
0,0656934
0,0659836
48 I 0,0662739
49 0,0665641
50
51
52
53
54
55
56
57
58
59
0,0668544
0,0671446
0,0674349
0,0677251
0,0680153
0,0683055
0,0685957
0,0688859
0,0691761
0,0694663
cos
0,052408
0,052699
0,052991
0,053283
0,053575
0,053866
0,054158
0,054450
0,054742
0,055033
0,055325
0,055617
0,055909
0,056200
0,056492
0,056784
0,057076
0,057368
0,057660
0,057951
0,058243
0,058535
0,058827
0,059119
0,059411
0,059703
0,059995
0,060287
0,060579
0,060871
0,061163
0,061455
0,061747
0,062039
0,062331
0,062623
0,062915
0,063207
0,063499
0,063791
0,064083
0,064375
0,064667
0,064959
0,065251
0,065543
0,065836
0,066128
0,066420
0,066712
0,067004
0,067296
0,067589
0,067881
0,068173
0,068465
0,068758
0,069050
0,069342
0,069635
19,08114
18,97552
18,87107
18,76775
18,66556
18,56447
18,46447
18,36554
18,26765
18,17081
18,07498
17,98015
17,88631
17,79344
17,70153
17,61056
17,52052
17,43139
17,34315
17,25581
17,16934
17,08372
16,99896
16,91503
16,83191
16,74961
16,66811
16,58740
16,50746
16,42828
16,34986
16,27217
16,19523
16,11900
16,04348
15,96867
15,89454
15,82110
15,74834
15,67623
15,60478
15,53398
15,46381
15,39428
15,32536
15,25705
15,18935
15,12224
15,05572
14,98978
14,92442
14,85962
14,79537
14,73168
14,66853
14,60592
14,54383
14,48227
14,42123
14,36070
I
Ctg I tg
0,9986295
0,9986143
0,9985989
0,9985835
0,9985680
0,9985524
0,9985367
0,9985209
0,9985050
0,9984891
0,9984731
0,9984570
0,9984408
0,9984245
0,9984081
0,9983917
0,9983751
0,9983585
0,9983418
0,9983250
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
0,9983082! 40
0,9982912 39
0,9982742 38
0,9982570 37
0,9982398 36
0,9982225 35
0,9982052 34
0,9981877 33
0,9981701 32
0,9981525 31
0,9981348
0,9981170
0,9980991
0,9980811
0,9980631
0,9980450
0,9980267
0,9980084
0,9979900
0,9979716
0,9979530
0,9979343
0,9979156
0,9978968
0,9978779
0,9978589
0,9978399
0,9978207
0,9978015
0,9977821
0,9977627
0,9977433
0,9977237
0,9977040
0,9976843
0,9976645
0,9976445
0,9976245
0,9976045
0,9975843
sin
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
87
86
56
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
4° 5°
см со © «о г- со © о т-* см со © со г> оо © © см ео © со t* оо © © г- см со © © г> ао оз © см ео © © г* ао © © см со © © t* оо о
ГМ w* W4 CM CM CM CM CM CM CM CM CM N СО СО ео СО СО СО СО ео СО СО ТГ ”3* Tf ТГ ю ю ю © © © © © © ©
sin tg ctg COS / / sin tg ctg cos | '
0,0697565 0,069927 14,30067 0,9975641 60 0 0,0871557 0,087489 11,43005 0,9961947 60
0,0700467 0,070219 14,24113 0,9975437 59 1 0,0874455 0,087782 11,39188 0,9961693 59
0,0703368 0,070511 14,18209 0,9975233 58 2 0,0877353 0,088075 11,35397 0,9961438 58
0,0706270 0,070804 14,12354 0,9975028 57 3 0,0880251 0,088368 11,31630 0,9961183 57
0,0709171 0,071096 14,06546 0,9974822 56 4 0,0883148 0,088661 11,27889 0,9960926 56
0,0712073 0,071389 14,00786 0,9974615 55 5 0,0886046 0,088954 11,24171 0,9960669' 55
0,0714974 0,071681 13,95072 0,9974408 54 6 0,0888943 0,089248 11,20478 0,9960411,54
0,0717876 0,071973 13,89405 0,9974199 53 7 0,0891840 0,089541 11,16809 0,99601521 53
0,0720777 0,072266 13,83783 0,9973990 52 8 0,0894738 0,089834 11,13164 0,99598921 52
0,0723678 0,072558 13,78206 0,9973780 51 9 0,0897635 0,090127 11,09542 0,9959631)51
0,07'26580 0,072851 13,72674 0,9973569 50 10 0,0900532 0,090421 11,05943 0,9959370 50
0,0729481 0,073143 13,67186 0,9973357 49 11 0,0903429 0,090714 11,02368 0,9959107:49
0,0732382 0,073435 13,61741 0,9973145 48 12 0,0906326 0,091007 10,98815 0,9958844 48
0,0735283 0,073728 13,56339 0,9972931 47 13 0,0909223 0,091300 10,95285 0,9958580'47
0,0738184 0,074020 13,50980 0,9972717 46 14 0,0912119 0,091594 10,91777 0,9958315 46
0,0741085 0,074313 13,45663 0,9972502 45 15 0,0915016 0,091887 10,88292 0,9958049 45
0,0743986 0,074605 13,403’87 0,9972286 44 16 0,0917913 0,092180 10,84892 0,9957783 44
0,0746887 0,074898 13,35152 0,9972069 43 17 0,0920809 0,092474 10,81387 0,9957515 43
0,0749787 0,075190 13,29957 0,9971851 42 18 0,0923706 0,092767 10,77967 0,9957247 42
0,0752688 0,075483 13,24803 0,9971633 41 19 0,0926602 0,093061 10,74569 0,9956978 41
0,0755589 0,075775 13,19688 0,9971413 40 20 0,0929499 0,093354 10,71191 0,9956708 40
0,0758489 0,076068 13,14613 0,9971193 39 21 0,0932395 0,093647 10,67835 0,9956437 39
0,0761390 0,076361 13,09576 0,99709721 38 22 0,0935291 0,093941 10,64499 0,9956165 38
0,0764290 0,076653 13,04577 0,9970750 37 23 0,0938187 0,094234 10,61184 0,9955893 37
0,0767190 0,076946 12,99616 0,9970528 36 24 0,0941083 0,094528 10,57890 0,9955620 36
0,0770091 0,077238 12,94692 0,9970304 35 25 0,0943979 0,094821 10,54615 0,9955345 35
0,0772991 0,077531 12,89806 0,9970080 34 26 0,0946875 0,095115 10,51361 0,9955070 34
0,0775891 0,077824 12,84956 0,9969854 33 27 0,0949771 0,095408 10,48126 0,9954795' 33
0,0778791 0,078116 12,80142 0,9969628 32 28 0,0952666 0,095702 10,44911 0,9954518' 32
0,078’691 0,078409 12,75363 0,9969401 31 29 0,0955562 0,095995 10,41716 0,9954240i31
0,0784591 0,078702 12,70620 0,9969173 30 30 0,0958458 0,096289 10,38540 0,9953962 30
0,0787491 0,078994 12,65912 0,9968945 29 31 0,0961353 0,096583 10,35383 0,9953683 29
0,0790391 0,079287 12,61239 0,9968715 28 32 0,0964248 0,096876 10,32245 0,9953403 28
0,0793290 0,079580 12,56600 0,9968485 27 33 0,0967144 0,097170 10,29126 0,9953122 27
0,0796190 0,079873 12,51994 0,9968254 26 34 0,0970039 0,097464 10,26025 0,9952840 26
0,0799090 0,080165 12,47422 0,9968022 25 35 0,0972934 0,097757 10,22943 0,9952557 25
0,0801989 0,080458 12,42883 0,9967789 24 36 0,0975829 0,098051 10,19879 0,9952274 24
0,0804889 0,080751 12,38377 0,9967555 23 37 0,0978724 0.098345 10,1683.3 0,9951990 23
0,0807788 0,081044 12,33903 0,9967321 22 38 0,0981619 0,098638 10,13805 0,9951705 22
0,0810687 0,081336 12,29461 0,9967085 21 39 0,0984514 0,098932 10,10795 0,9951419 21
0,0813587 0,081629 12,25051 0,9966849 20 40 0,0987408 0,099226 10,07803 0.9951132 20
0,0816486 0,081922 12,20672 0,9966612 19 41 0,0990303 0,099519 10,04828 0,9950844 19
0,0819385 0,082215 12,16324 0,9966374 18 42 0,0993197 0,099813 10,01871 0,9950556 18
0,0822284 0,082508 12,12006 0,9966135 17 43 0,0996092 0,100107 9,989305 0,9950266 17
0,0825183 0,082801 12,07719 0,9965895 16 44 0,0998986 0,100401 9,960072 0,9949976 16
0,0828082 0,083094 12,03462 0,9965655 15 45 0,1001881 0,100695 9,931009 0,9949685 15
0,0830981 0,083386 11,99235 0,9965414 14 46 0,1004775 0,100989 9,902112 0,9949393 14
0,0833880 0,083679 11,95037 0,9965172 13 47 0,1007669 0,101282 9,873382 0,9949101 13
0,0836778 0,083972 11,90868 0,9964929 12 48 0,1010563 0,101576 9,844817 0,9948807 12
0,0839677 0,084265 11,86728 0,9964685 11 49 0,1013457 0,101870 9,816414 0,9948513 11
0,0842576 0,084558 11,82617 0,9964440 10 50 0,1016351 0,102164 9,788173 0,9948217 10
0,0845474 0,084851 11,78533 0,9964195 9 51 0,1019245 0,102458 9,760093 0 9947921 9
0,0848373 0,085144 11,74478 0,9963948 8 52 0,10221-38 0,102752 9,732171 0,9947625 8
0,0851271 0,085437 11,70450 0,9963701 7 53 0,1025032 0,103046 9,704407 0,9947327 7
0,0854169 0,085730 11,66450 0,9963453 6 54 0,1027925 0,103340 9,676800 0,9947028 6
0,0857067 0,086023 11,62476 0,9963204 5' 55 0,1030819 0,103634 9,649347 0,9946729 5
0,0859966 0,086316 11,58529 0,9962954 4 56 0,1033712 0,103928 9,622049 0,9946428 4
0,0862864 0,086609 11,54609 0,9962704 3 57 0,1036605 0,104222 9,594902 0,9946127 3
0,0865762 0,086902 11,50715 0,9962452 2 58 0,1039499 0,104516 9,567907 0 9945825 2
0,0868660 0,087196 11,46847 0,9962200 1 59 0,1042392 0,104810 9,541061 0,9945523 1
cos ctg tg sin / / COS Ctg tg sin
85° 84°
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
57
6° 7°
7 sin tg ctg COS / 7 sin tg ctg COS | 7
0 0,1045285 0,105104 9,514364 0,9945219 60 0 0,1218693 0,122785 8,144346 0,9925462 60
1 0,1048178 0,105398 9,487815 0,9944914 59 1 0,1221581 0,123080 8,124807 0,9925107 59
2 0,1051070 0,105692 9,461412 0,9944609 58 2 0,1224468 0,123375 8,105360 0,9924751 58
3 0,1053963 0,105987 9,435153 0,9944303 57 3 0,1227355 0,123670 8,086004 0,9924394 57
4 0,1056856 0,106281 9,409038 0,9943996 56 4 0,1230241 0,123966 8,066739 0,9924037 56
5 0,1059748 0,106575 9,383066 0,9943688 55 5 0,1233128 0,124261 8,047565 0,9923679 55
6 0,1062641 0,106869 9,357235 0,9943379 54 6 0,1236015 0,124557 8,028480 0,9923319 54
7 0,1065533 0,107163 9,331545 0,994307Q 53 7 0,1238901 0,124852 8,009483 0,9922959 53
8 0,1068425 0,107458 9,305994 0,9942760 52 8 0,1241788 0,125147 7,990576 0,9922599 52
9 0,1071318 0,107752 9,280580 0,9942448 51 9 0,1244674 0,125443 7,971755 0,9922237' 51
10 0,1074210 0,108046 9,255303 0,9942136 50 10 0,1247560 0,125738 7,953022 0,9921874 50
И 0,1077102 0,108340 9,230163 0,9941823 49 11 0,1250446 0,126034 7,934376 0,9921511 49
12 0,1079994 0,108635 9,205156 0,9941510 48 12 0,1253332 0,126329 7,915815 0,9921147 48
13 0,1082885 0,108929 9,180284 0,9941195 47 13 0,1256218 0,126625 7,897340 0,9920782 47
14 0,1085777 0,109223 9,155544 0,9940880 46 14 0,1259104 0,126920 7,878949 0,9920416 46
15 0,1088669 0,109518 9,130935 0,9940563 45 15 0,1261990 0,127216 7,860642 0,9920049 45
16 0,1091560 0,109812 9,106456 0,9940246 44 16 0,1264875 0,127512 7,842419 0,9919682 44
17 0,1094452 0,110107 9,082107 0,9939928 43 17 0,1267761 0,127807 7,824279 0,9919314 43
18 0,1097343 0,110401 9,057887 0,99396101 42 18 0,1270646 0,128103 7,806221 0,9918944 42
19 0,1100234 0,110695 9,033793 0,9939290 41 19 0,1273531 0,128399 7,788245 0,9918574 41
20 0,1103126 0,110990 9,009826 0,9938969 40 20 0,1276416 0,128694 7,770351 0,9918204 40
21 0,1106017 0,111284 8,985984 0,9938648 39 21 0,1279302 0,128990 7,752537 0,9917832 39
22 0,1108908 0,111579 8,962267 0,9938326 38 22 0,1282186 0,129286 7,734803 0,9917459 38
23 0,1111799 0,111873 8,938673 0,9938003, 37 23 0,1285071 0,129582 7,717149 0,9917086 37
24 0,1114689 0,112168 8,915201 0,9937679 36 24 0,1287956 0,129877 7,699573 0,9916712 36
25 0,1117580 0,112463 8,891850 0,9937355 35 25 0,1290841 0,130173 7,682077 0,9916337 35
26 0,1120471 0,112757 8,868621 0,9937029 34 26 0,1293725 0,130469 7,664658 0,9915961 34
27 0,1123361 0,113052 8,845510 0,9936703 33 27 0,1296609 0,130765 7,647317 0,9915584 33
28 0,1126252 0,113346 8,822519 0,9936375 32 28 0,1299494 0,131061 7,630053 0,9915206 32
29 0,1129142 0,113641 8,799645 0,9936047 31 29 0,1302378 0,131357 7,612866 0,9914828 31
30 0 1132032 0,113936 8,776887 0,9935719 30 30 0,1305262 0,131652 7,595754 0,9914449 30
31 0,1134922 0,114230 8,754246 0,9935389 29 31 0,1308146 0,131948 7,578718 0,9914069 29
32 0,1137812 0,114525 8,731720 0,9935058 28 32 0,1311030 0,132244 7,561757 0 9913688 28
33 0,1140702 0,114820 8,709308 0,9934727 27 33 0,1313913 0,132540 7,544870 0,9913306 27
34 0,1143592 0,115114 8,687009 0,9934395 26 34 0,1316797 0,132836 7,528057 0 9912923 26
35 0,1146482 0,115409 8,664822 0,9934062 25 35 0,1319681 0,133132 7,511318 0,9912540 25
36 0,1149372 0,115704 8,642747 0,9933728 24 36 0,1322564 0,133428 7,494651 0,9912155 24
37 0,1152261 0,115999 8,620783 0,9933393 23 37 0,1325447 0,133725 7,478058 0,9911770 23
38 0,1155151 0,116294 8,593929 0,9933057 22 38 0,1328330 0,134021 7,461536 0,9911384 22
39 0,1158040 0,116588 8,577184 0,9932721 21 39 0,1331213 0,134317 7,445085 0,9910997 21
40 0,1160929 0,116883 8,555547 0,9932384 20 40 0,1334096 0,134613 7,428706 0,9910610 20
41 0,1163818 0,117178 8,534017 0,9932045 19 41 0,1336979 0,134909 7,412398 0,9910221 19
42 0,1166707 0,117473 8,512594 0,9931706 18 42 0,1339862 0,135205 7,396159 0 9909832 18
43 0,1169596 0,117768 8,491277 0,9931367 17 43 0,1342744 0,135502 7,379991 0,9909442 17
44 0,1172485 0,118063 8,470065 0,9931026 16 44 0,1345627 0 135798 7,363892 0,9909051 16
45 0,1175374 0,118358 8,448957 0,9930685 15 45 0,1348509 0,136094 7,347861 0,9908659 15
46 0,1178263 0,118653 8,427953 0,9930342 14 46 0,1351392 0,136390 7,331899 0,9908266 14
47 0,1181151 0,118948 8,407051 0,9929999 13 47 0,1354274 0,136687 7,316005 0,9907873 13
48 0,1184040 0,119243 8,386252 0,9929653 12 48 0,1357156 0,136983 7,300178 0,9907478 12
49 0,1186928 0,119538 8,365554 0,9929310 11 49 0,1360038 0,137279 7,284418 0,9907083 11
50 0 1189816 0,119833 8,344956 0,9928965 10 50 0,1362919 0,137576 7 268725 0,9906687 10
51 0,1192704 0,120128 8,324458 0,9928618 9 51 0,1365801 0,137872 7,253099 0,9906290 9
52 0,1195593 0,120423 8,304059 0,9928271 8 52 0,1368683 0,138169 7,237538 0,9905893 8
53 0,1198481 0,120718 8,283758 0,9927922 7 53 0,1371564 0,138465 7,222042 0,9905494 7
54 0,1201368 0,121013 8,263555 0,9927573 6 54 0,1374445 0,138761 7,206612 0 9905095 6
55 0,1204256 0,121308 8,243448 0,9927224 5 55 0,1377327 0,139053 7,191246 0,9904694 5
56 0,1207144 0,121604 8,223438 0,9926873 4 56 0,1380203 0,139354 7,175944 0,9904293 4
57 0,1210031 0,121899 8 203524 0,9926521 3 57 0,1333089 0,139651 7,160706 0 9903891 3
58 0,1212919 0,122194 8,183704 0,9926169 2 58 0,1385970 0,139948 7,145531 0 9903489 2
59 0,1215806 0,122489 8,163979 0,9925816 1 59 0,1388850 0,140244 7,130419 0,9903085 1
СОЗ | ctg tg sin / 7 COS ctg tg sin t
83
82°
58
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
8° 9°
/ sin 1 tg ctg cos / / sin tg ctg COS t
0 0,1391731 0,140541 7,115370 0,9902681 60 0 0,1564345 0,158384 6,313751 0,9876883 60
1 0; 1394612 0,140837 7,100383 0,9902275 59 1 0,1567218 0,158683 6,301887 0,9876428 59
2 0,1397492 0,141134 7,085457 0,9901869 58 2 0,1570091 0,158981 6,290065 0,9875972 58
3 0,1400372 0,141431 7,070593 0,9901462 57 3 0,1572963 0,159279 6,278287 0,9875514 57
4 0,1403252 0,141728 7,055790 0,9901055 56 4 0,1575836 0,159577 6,266551 0,9875057 56
5 0,1406132 0,142024 7,041048 0.9900646 55 5 0,1578708 0,159876 6,254859 0,9874598 55
6 0,1409012 0,142321 7,026366 0,9900237 54 6 0,1581581 0,160174 6,243209 0,9874138 54
7 0,1411892 0,142618 7,011744 0,9899826 53 7 0,1584453 0,160472 6,231601 0,9873678 53
8’ 0,1414772 0,142915 6,997182 0,9899415 52 8 0,1587325 0,160771 6,220035 0,9873216 52
9 0,1417651 0,143212 6,982678 0,9899003 51 9 0,1590197 0,161069 6,208511 0,9872754 51
ю1 0,1420531 0,143508 6,968233 0,9898590 50 10 0,1593069 0,161368 6,197028 0,9872291 50
и 0,1423410 0,143805 6,953847 0,9898177 49 11 0,1595940 0,161666 6,185587 0,9871827 49
12; 0,1426289 0,144102 6,939519 0,9897762 48 12 0,1598812 0,161965 6,174186 0,9871363 48
13 0,1429168 0,144399 6,925249 0,9897347 47 13 0,1601683 0,162263 6,162827 0,9870897 47
14 0,1432047 0,144696 6,911036 0,9896931 46 14 0,1604555 0,162562 6,151508 0,9870431 46
15 0,1434926 0,144993 6,896880 0,9896514 45 15 0,1607426 0,162860 6,140230 0,9869964 45
16 0,1437805 0,145290 6,882781 0,9896096 44 16 0,1610297 0,163159 6,128992 0,9869496 44
17 0,1440684 0,145587 6,868738 0,9895677 43 17 0,1613167 0,163458 6,117794 0,9869027 43
18 0,1443562 0,145884 6,854751 0,9895258 42 18 0,1616038 0,163756 6,106636 0,9868557 42
19 0,1446440 0,146181 6,840820 0,9894838 41 19 0,1618909 0,164055 6,095517 0,9868087 41
20 0,1449319 0,146478 6,826944 0,9894416 40 20 0,1621779 9,164354 6,084438 0,9867615 40
21 0,1452197 0,146776 6,813123 0,9893994 39 21 0,1624650 0,164652 6,073398 0,9867143 39
22 0,1455075 0,147073 6,799356 0,9893572 38 22 0,1627520 0,164951 6,062397 0,98666701 38
23 0,1457953 0,147370 6,785645 0,9893148 37 23 0,1630390 0,165250 6,051434 0,9866196 37
24 0,1460830 0,147667 6,771987 0,9892723 36 24 0,1633260 0,165549 6,040510 0,9865722 36
25 0,1463708 0,147964 6,758383 0,9892298 35 25 0,1636129 0,165848 6,029625 0,9865246 35
26 0,1466585 0,148262 6,744832 0,9891872 34 26 0,1638999 0,166147 6,018777 0,9864770 34
°7 0,1469463 0,148559 6,731334 0,9891445 33 27 0,1641868 0,166446 6,007968 0,9864293 33
23 0,1472340 0,148856 6,717889 0,9891017 32 28 0,1644738 0,166745 5,997196 0,9863815 32
29 0,1475217 0,149154 6,704497 0,9890588 31 29 0,1647607 0,167044 5,986461 0,9863336 31
30 0,1478094 0,149451 6,691156 0,9890159 30 30 0,1650476 0,167343 5,975764 0,9862856 30
31 0,1480971 0,149748 6,677868 0,9889728 29 31 0,1653345 0,167642 5,965104 0,9862375 29
32 0,1483848 0,150046 6,664631 0,9889297 28 32 0,1656214 0,167941 5,954481 0,9861894 28
33 0,1486724 0,150343 6,651445 0,9888865 27 33 0,1659082 0,168240 5,943895 0,9861412 27
34 0,1489601 0,150641 6,638310 0,9888432 26 34 0,1661951 0,168539 5,933345 0,9860929 26
35 0,1492477 0,150938 6,625226 0,9887998 25 35 0,1664819 0,168838 5,922832 0,9860445 25
36 0,1495353 0,151236 6,612192 0,9887564 24 36 0 1667687 0,169137 5,912355 0,9859960 24
37 0,1498230 0,151533 6,599208 0,9887128 23 37 0,1670556 0,169437 5,901914 0,9859475 23
38 0,1501106 0,151831 6,586274 0,9886692 22 38 0,1673423 0,169736 5,891508 0,9858988 22
39 0,1503981 0,152129 6,573389 0,9886255 21 39 0,1676291 0,170035 5,881139 0,9858501 21
40 0,1506857 0,152426 6,560554 0,9885817 20 40 0,1679159 0,170334 5,870804 0,9858013 20
41 0,1509733 0,152724 6,547767 0,9385378 19 41 0,1682026 0,170634 5,860505 0,0857524 19
42 0,1512608 0,153022 6,535029 0,9884939 18 42 0,1684894 0,170933 5,850241 0,9857035 18
43 0,1515484 0,153319 6,522340 0,9384498 17 43 0,1687761 0,171233 5,840012 0,9856544 17
44 0,1518359 0,153617 6,509698 0,9.884057 16 44 0,1690628 0,171532 5,829817 0,9856053 16
45 0,1521234 0,153915 6,497104 0,9883615 15 45 0,1693495 0,171831 5,819657 0,9855561 15
46 0,1524109 0,154213 6,484558 0,9883172 14 46 0,1696362 0,172131 5,809531 0,9855068 14
47 0,1526984 0,154510 6,472059 0,9882728 13 47 0,1699228 0,172430 5,799440 0,9854574 13
48 0,1529858 0,154808 6,459607 0,9882284 12 48 0,1702095 0,172730 5,789382 0,9854079 12
49 0,1532733 0,155106 6,447202 0,9881838 11 49 0,1704961 0,173030 5,779359 0,9853583 11
50 0,1535607 0,155404 6,434843 0,9881392 10 50 0,1707828 0,173329 5,769369 0,9853087 10
51 0,1538482 0,155702 6,422530 0,0880945 9 51 0,1710694 0,173629 5,759412 0,9852590 9
52 0,1541356 0,156000 6,410263 0,9880497 8 52 0,1713560 0,173929 5,749489 0,9852092 8
53 0,1544230 0,156298 6,398042 0,9880048 7 53 0,1716425 0,174228 5,739599 0,9851593 7
54 0,1547104 0,156596 6,385866 0,9379599 6 54 0,1719291 0,174528 5,729742 0,9851093 6
55 0,1549978 0,156894 6,373736 0,9879148 5 55 0,1722156 0,174828 5,719917 0,9850593 5
56 0,1552851 0,157192 6,361650 0,9878697 4 56 0,1725022 0,175127 5,710126 0,9850091 4
57 0,1555725 0,157490 6,349609 0,9878245 3 57 0,1727887 0,175427 5,700366 0,9849589 3
58 0,1558598 0,157788 6,337613 0,9877792 2 58 0,1730752 0,175727 5,690639 0,9849086 2
59 0,1561472 0,158086 6,325660 0,9877338 1 59 0,1733617 0,176027 5,680945 0,9848582 1
COS ctg tg sin / f COS Ctg tg sin /
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
59
sin tg ctg
cos
ctg
cos
10
11°
О 0,1736432
1 0,1739346
2; 0,1742211
3 i 0,1745075
41 0,1747939
510,1750803
б I 0,1753667
7 10,1756531
8 | 0,1759395
9'0,1762258
0,176327
0,176627
0,176927
0,177227
0,177527
0,177827
0,178127
0,178427
0,178727
0,179028
10
11
12
13
14
15
16
17
18
19
0,1765121
0,1767984
О,1770847
0,1773710
0,1776573
0,1779435
0,17822.98
0,1785160
0,1788022
0,1790884
20
21
22
23
24
25
26
27
28
29
0,1793746
0,1796607
0,1799469
0,1802330
0,1805191
0,1808052
0,1810913
0,1813774
0,1816635
0,1819495
30
31
32
33
34
35
36
37
38
39
0,1822355
0,1825215
0,1828075
0,1830935
0,1833795
0,1836654
0,1839514
0,1842373
0,1845232
0,1848091
40
41
42
43
44
45
46
47
48
49
0,1850949
0,1853808
0,1856666
0,1859524
0,1862382
0,1865240
0,1868098
0,1870956
0,1873813
0,1876670
50
51
52
53
54
55
56
57
58
59
0,1879528
0,1882385
0,1885241
0,1888098
0,1890954
0,1893811
0,1896667
0,1899523
0,1902379
0,1905234
0,179328
0,179628
0,179928
0,180229
0,180529
0,180819
0,181130
0,181430
0,181731
0,182031
0,182332
0,182632
0,182933
0,183234
0,183534
0,183835
0,184136
0,184437
0,184737
0,185038
0,185339
0,185640
0,185941
0,186242
0,186543
0,186844
0,187145
0,187446
0,187747
0,188048
0,188349
0,188651
0,188952
0,189253
0,189555
0,189856
0,190157
0,190459
0,190760
0,191062
0,191363
0,191665
0,191966
0,192268
0,192570
0,192871
0,193173
0,193475
0,193777
0,194078
5,671282
5,661651
5,652052
5,642484
5,632947
5,623442
5,613968
5,604525
5,595112
5,585730
5,576379
5,567057
5,557766
5,548505
5 539274
5,530072
5,520900
5,511758
5,502645
5,493560
5,484505
5,475479
5,466481
5,457512
5,448571
5,439659
5,430775
5,421919
5,413091
5,404290
5,395517
5,386772
5,378054
5,369363
5,360699
5,352063
5,343453
5,334870
5,326313
5,317783
5,309279
5,300802
5,292350
5,283925
5,275525
5,267152
5,258803
5,250481
5,242184
5,233912
5,225665
5,217443
5,209246
5,201074
5,192926
5,184803
5,176705
5,168631
5,160581
5,152556
0,9848078
0,9847572,
0,9847066
0,9846558
0,9846050,
0,9845542
0,9845032
0,9844521
0,9844010
0,0843498
0,9842985
0,9842471
0,9841956
0,9841441
0,9840924
0,9840407
0,9839889
0,9839370
0,9838850
0,9838330
0,9837808
0,9837286
0,9836763
0,9836239
0,9835715
0,9835189
0,9834663
0,9834136
0,9833608
0,9833079
0,9832549
0,9832019
0,9831487
0,9830955
0,9830422
0,9829888
0,9829353'
0,9828818
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
0,9828282] 22
0,9827744'21
0,9827206
О,9826668
0,9826128
0,9825587
0,9825046
0,9824504
0,9823961
0,9823417
0,9822873
0,9822327
20
19
18
17
16
15
14
13
12
11
о
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
0,1908090
0,1910945
0,1913801
0,1916656
0,1919510
0,1922365
О,1925220
0,1928074
0,1930928
0,1933782
0,1936636
0,1939490
0,1942344
0,1945197
О,1948050
О,1950903
0,1953756
'0,1956609
0,1959461
0,1962314
0,194380
0,194682
0,194984
0,195286
0,195588
0,195890
0,196192
О,196494
0,196796
О,197099
0,197401
О,197703
0.19S005
0,198308
0,198610
0,198912
0,199215
0,199517
0,199820
0,200122
5,144554
5,136576
5,128622
5,120692
5,112785
5,104902
5,097043
5,089206
5,081393
5,073602
5,065835
5,058091
5,050369
5,042670
5,034993
5,027339
5,019708
5,012098
5,004511
4,996946
0,9816272
0,9815716
0,9815160
0,9814603
0,9814045
0,9813486
0,9312927'
0,9812366*
60
59
58
57
56
55
54
53
0,9811805, 52
0,9811243! 51
0,9810680] 50
0,9810116| 49
0,9809552
0,9808986
0,9808420
0,9807853
0,9807285
48
47
46
45
44
0,9806716] 43
0,9806147] 42
0,9805576] 41
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
0,1965166
0,1968018
0,1970870
0,1973722
0,1976573
О,1979425
0,1982276
0,1985127
0,1987978
О,1990829
0,1993679
0,1996530
0,1999380
0,2002230
0,2005080
0,2007930
0,2010779
0,2013629
0,2016478
0,2019327
0,2022176
0,2025024
0,2027873
0,2030721
0,2033569
0,2036418
0,2039265
0,2042113
0,2044961
0,2047808
0,9821781
0,9821234
0,9820686
0,9820137
0,9819587
0,9819037
0,9818485
0,9817933
0,9817380
0,9816826
10
9
8
7
6
5
4
3
2
1
50
51
52
53
54
55
56
57
58
59
0,2050655
0,2053502
0,2056349
0,2059195
0,2062042
0,2064888
0,2067734
0,2070580
0,2073426
0,2076272
0,200425
0,200727
0,201030
0,201333
0,201635
0,201938
0,202241
0,202544
0,202847
0,203149
0,203452
0,203755
0,204058
0,204361
0,204664
0,204967
0,205271
0,205571
0,205877
0,206180
0,206483
0,206787
0,207090
0,207393
0,207697
0,208000
0,208304
0,208607
0,208911
0,209214
0,209518
0,209822
0,210126
0,210429
0,210733
0,211037
0,211341
0,211645
0,211949
0,212253
4,989403
4,981881
4,974382
4,966904
4,959447
4,952012
4,944599
4,937207
4,929836
4,922486
4,915157
4,907849
4,900562
4,893296
4,886050
4,878825
4,871620
4,864436
4,857272
4,850128
4,843004
4,835901
4,828817
4,821754
4,814710
4,807685
4,800681
4,793696
4,786730
4,779784
4,772857
4,765949
4,759060
4,752191
4,745340
4,738508
4,731695
4,724901
4,718126
4,711369
0,9805005
0,9804433]
0,9803860
0,9803286
О 9802712
0,9802136
0,9801560
0,9800983]
0,9800405:
0,9799827,
0,9799247
0,9798667
0,9798086
0,9797504
0,9796921
0,9796337
0,9795752
0,9795167
0,9794581
0,9793994
0,9793406
0,9792818
О 9792228
0,9791638
0,9791047
0,9790455
0,9789862
0,9789268
0,9788674
0,9788079
0,9787483
0,9786886
0,9786288
0,9785689
0,9785090
0,9784490
0,9783889
0,9783287
0,9782684
0,9782080
7 | cos | ctg tg sin / cos Ctg tg sin
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
79
78
60
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
12° 13°
/ sin tg Ctg cos / t sin tg ctg COS /
0 0,2079117 0,212557 4,704630 0,9781476 60 0 0,2249511 0,230868 4,331476 0.9743701 so
1 0,2081962 0,212861 4,697910 0,9780871 59 1 0,2252345 0,231175 4,325735 0,9743046 59
2 0,2084807 0,213165 4,691208 0,9780265 58 2 0,2255179 0,231481 4,320008 0.9742390,1 58
3 0,2087652 0,213469 4,684525 0,9779658 57 3 0,2258013 0,231788 4,314295 0,9741734 57
4 0,2090497 0,213773 4,677859 0,9779050 56 4 0,2260846 0,232094 4,308597 0,9741077 56
5 0,2093341 0,214077 4,671212 0,9778442 55 5 0,2263680 0,232401 4,302914 0,9740419 55
6 0,2096186 0,214381 4,664583 0,9777832 54 6 0,2266513 0,232707 4,297244 0;9739760 54
7 0,2099030 0,214686 4,657972 0,9777222 53 7 0,2269346 0,233014 4,291588 0,9739100 53
8 0,2101874 0,214990 4,651379 0,9776611 52 8 0,2272179 0,233321 4;285947 O’,9738439 52
9 0,2104718 0,215294 4,644803 0,9775999 51 9 0,2275012 0,233627 4,280320 0^9737778 51
10 0,2107561 0,215599 4,638246 0,9775387 50 10 0,2277844 0,233934 4,274707 0,9737116 50
11 0,2110405 0,215903 4,631706 0,9774773 49 11 0,2280677 0,234241 4,269107 0’,9736453 49
12 0,2113248 0,216208 4,625183 0,9774159 48 12 0,2283509 0,234548 4,263522 O;9735789 48
13 0,2116091 0,216512 4,618678 0,9773544 47 13 0,2286341 0,234855 4,257950 0,9735124 47
14 0,2118934 0,216817 4,612191 0,9772928 46 14 0,2289172 O’235162 4,252392 0,9734459 46
15 0,2121777 0,217121 4,605721 0,9772311 45 15 0,2292004 0,235469 4;246848 0,9733793 45
16 0,2124619 0,217426 4,599268 0,9771693 44 16 0,2294835 0,235776 4,241318 Ci 9733125 44
17 0,2127462 0,217731 4,592832 0,9771075 43 17 0,2297666 0,236083 4,235801 0,9732458 43
18 0,2130304 0,218035 4,586414 0,9770456 42 18 0,2300497 0,236390 4,230298 0,9731789 42
19 0,2*133146 0,218340 4,580013 0,9769836 41 19 0,2303328 0,236697 4;224808 0,9731119 41
20 0,2135988 0,218645 4,573629 0,9769215 40 20 0,2306159 0,237004 4,219332 9,9730449 40
21 0,2138829 0,218950 4,567261 0,9768593 39 21 0,2308989 0,237312 4/213869 0^9729777 39
22 0,2141671 0,219254 4,560911 0,9767970 38 22 0,2311819 0,237619 4,208420 0,9729105 38
23 0,2144512 0,219559 4,554578 0,9767347 37 23 0,2314649 0’237926 4,202983 0^9728432 37
24 0,2147353 0,219864 4,548261 0,9766723 36 24 0,2317479 0;238234 4,197561 0,9727759 36
25 0,2150194 0,220169 4,541961 0,9766098 35 25 0,2320309 0,238541 4,192151 O’9727084 35
26 0,2153035 0,220474 4,535677 0,9765472 34 26 0,2323138 0’238848 4,186755 0^9726409 34
27 0,2155876 0,220779 4,529410 0,9764845 33 27 0,2325967 0,239156 4,181371 0'9725733 33
28 0,2158716 0,221084 4,523160 0,9764218 32 28 0,2328796 0,239464 4;176001 0,9725056 32
29 0,2161556 0,221389 4,516926 0,9763589 31 29 0,2331625 0; 239771 4,170644 0’,9724378 31
30 0,2164396 0,221695 4,510708 0,9762960 30 30 0,2334454 0,240079 4,165300 0 9723699 30
31 0,2167236 0,222000 4,504507 0,9762330 29 31 0,2337282 O’, 240386 4;159968 0’9723020 29
32 0,2170076 0,222305 4,498322 0,9761699 28 32 0,2340110 0,240694 4,154650 0,9722339 28
33 0,2172915 0,222610 4,492153 0,9761068 27 33 0,2342938 O', 241002 4,149345 0’9721658 27
34 0,2175754 0,222916 4,486000 0,9760435 26 34 0,2345766 0^241310 4,144052 0,9720976 26
35 0,2178593 0,223221 4,479864 0,9759802 25 35 0,2348594 0,241618 4,138772 O', 9720294 25
36 0,2181432 0,223526 4,473743 0,9759168 24 36 0,2351421 0,241925 4; 133505 0’9719610 24
37 0,2184271 0,223832 4,467638 0,9758533 23 37 0,2354248 0,242233 4,128250 0’9718926! 23
38 0,2187110 0,224137 4,461549 0,9757897 22 38 0,2357075 0,242541 4;123008 0 9718240! 22
39 0,2189948 0,224443 4,455476 0,9757260 21 39 0,2359902 0,24-2849 4’117778 O’, 9717554 21
40 0,2192786 0,224748 4,449418 0,9756623 20 40 0,2362729 0,243157 4,112561 0,9716867 20
41 0,2195624 0,225054 4,443376 0,9755985 19 41 0,2365555 0,243466 4,107357 0,9716180 19
42 0 j 2АУ&46.2 0,225360 4,437350 0,9755345 18 42 0,2368381 0^243774 4,102165 0’9715491 18
43 0,2201300 0,225665 4,431339 0,9754706 17 43 0,2371207 Ci244082 4,096985 0,9714802 17
44 0,2204137 0,225971 4,425344 0,9754065 16 44 0,2374033 0,244390 4; 091818 0,’9714112 16
45 0,2206974 0,226277 4,419364 0,9753423 15 45 0,2376859 0,244698 4,086663 0,9713421 15
46 0,2209811 0,226583 4,413400 0,9752781 14 46 0,2379684 0,245007 4,081520 0,9712729 14
47 0,2212648 0,226889 4,407450 0,9752138 13 47 0,2382510 0,245315 4;076389 0,9712036 13
48 0,2215485 0,227194 4,401516 0,9751494 12 48 0,2385335 0,245624 4,071271 0,9711343 12
49 0,2218321 0,227500 4,395598 0,9750849 11 49 0,2388159 O;245932 4,066164 0,9710649 11
50 0,2221158 0,227806 4,389694 0,9750203 10 50 0,2390984 0,246241 4,061070 0,9709953 10
51 0,2223994 0,228112 4,383805 0,9749556 9 51 0,2393808 0,246549 4,055988 0,9709258 9
52 0,2226830 0,228418 4,377932 0,9748909 8 52 0,2396633 0,246858 4,050917 0,9708561 8
53 0,2229666 0,228724 4,372073 0,9748261 7 53 0,2399457 0,247166 4,045859 0,9707863 7
54 0,2232501 0,229031 4,366229 0,9747612 6 54 0,2402280 0;247475 4’040812 0,9707165 6
55 0,2235337 0,229337 4,360400 0,9746962 5 55 0,2405104 0,247784 4;035778 0,9706466 5
56 0,2238172 0,229643 4,354586 0,9746311 4 56 0,2407927 0,248092 4,030755 0,9705766 4
57 0,2241007 0,229949 4,348787 0,9745660 3 57 0,2410751 0,248401 4;025744 0,9705065 3
Ь8 0,^24384'2 0,230255 4,343002 0,9745008 2 58 0,2413574 0,248710 4,020745 0,9704363 2
59 0,2246676 0,230562 4,337232 0,9744355 1 59 0,2416396 0^249019 4,015757 0,9703661 1
t COS ctg tg sin t / COS ctg tg sin f
'°
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
61
14° 15°
/ sin tg Ctg COS / sin tg Ctg COS e
0 0,2419219 0,249328 4,010781 0,9702957 60 0 0,2588190 0,267949 3,732051 0,9659258 60
1 0,2422041 0,249637 4,005816 0,9702253 59 1 0,2591000 0,268261 3,727713 0,9658505 59
2 0,2424863 0,249946 4,000864 0,9701548 58 2 0,2593810 0,268573 3,723385 0,9657751 58
3 0,2427685 0,250255 3,995922 0,9700842 57 3 0,2596619 0,268885 3,719066 0,9656996 57
4, 0,2430507 0,250564 3,990992 0,9700136 56 4 0,2599428 0,269197 3,714756 0.9656240 56
5 0,2433329 0,250873 3,986074 0,9699428 55 5 0,2602237 0,269509 3,710456 0,9655484 55
6 0,2436150 • 0,251183 3,981167 0,9698720 54 6 0,2605045 0,269821 3.706165 0.9654726 54
7 0,2438971 0,251492 3,976271 0,9698011 53 7 0,2607853 0,270133 3,701883 0,9653968 53
8 0,2441792 0,251801 3,971387 0,9697301 52 8 0,2610662 0,270445 3,697610 0,9653209 52
9 0,2444613 0,252111 3,966514 0,9696591 51 9 0,2613469 0,270757 3,693347 0,9652449 51
10 0,2447433 0,252420 3,961652 0,9695879 50 10 0,2616277 0,271069 3,689093 0,9651689 50
11 0,2450254 0,252729 3,956801 0,9695167 49 11 0,2619085 0,271382 3,684847 0,9650927 49
12 0,2453074 0,253039 3,951961 0,9694453 48 12 0,2621892 0,271694 3,680611 0,9650165 48
13 0,2455894 ' 0,253348 3,947133 0,9693740 47 13 0,2624699 0,272006 3,676384 0,9649402 47
14 0,2458713 0,253658 3,942316 0,9693025 46 14 0,2627506 0,272319 3,672166 0,9648638 46
15 0,2461533 0,253968 3,937509 0,9692309 45 15 0,2630312 0,272631 3,667957 0,9647873 45
16 0,2464352 0,254277 3,932714 0,9691593 44 16 0,2633118 0,272944 3,663757 0.9647108 44
17 0,2467171 0,254587 3,927930 0,9690875 43 17 0,2635925 0,273256 3,659566 0,9646341 43
18 0,2469990 0,254897 3,923156 0,9690157 42 18 0,2638730 0,273569 3,655384 0,9645574 42
19 0,2472809 0,255207 3,918394 0,9689438 41 19 0,2641536 0,273882 3,651211 0,9644806 41
20 0,2475827 0,255516 3,913642 0,9688719 40 20 0,2644342 0,274194 3,647047 0,9644037 40
21 0,2478445 0,255826 3,908901 0,9687998 39 21 0,2647147 0,274507 3,642891 0,9643268 39
22 0,2481263 0 256136 3,904171 0,9687277 38 22 0,2649952 0,274820 3,638744 0,9642497 38
23 0,2484081 0,256446 3,899452 0,9686555 37 23 0,2652757 0,275133 3,634606 0,9641726 37
24 0,2486899 0,256756 3,894743 0,9685832 36 24 0,2655561 0,275446 3,630477 0,9640954 36
25 0,2489716 0,257066 3,890045 0,9685108 35 25 0,2658366 0,275759 3,626357 0,9640181 35
26 0,2492533 0,257377 3,885357 0,9684383 34 26 0,2661170 0,276072 3,622245 0,9639407 34
27 0,2495350 0,257687 3,880680 0,9683658 33 27 0,2663973 0,276385 3,618141 0,9638633 33
28 0,2498167 0,257997 3,876014 0,9682931 32 28 0,2666777 0,276698 3,614047 0,9637858 32
29 0,2500984 0,258307 3,871358 0,9682204 31 29 0,2669581 0,277011 3,609961 0,9637081 31
30 0,2503800 0,258618 3,866713 0,9681476 30 30 0,2672384 0,277325 3,605883 0,9636305 30
31 0,2506616 0,258928 3,862078 0,96.80748 29 31 0,2675187 0,277638 3,601815 0,9635527 29
32 0,2509432 0,259238 3,857454 0,9680018 28 32 0,2677989 0,277951 3,597754 0,9634748 28
33 0,2512248 0,259549 3,852840 0,9679288 27 33 0,2680792 0,278265 3,593702 0,9633969 27
34 0,2515063 0,259859 3,848236 0,9678557 26 34 0,2683594 0,278578 3,589659 0,9633189 26
35 0,2517879 0,260170 3,843642 0,9677825 25 35 0,2686396 0,278891 3,585624 0,9632408 25
36 0,2520694 0,260480 3,839059 0,9677092 24 36 0,2689198 0,279205 3,581597 0,9631626 24
37 0,2523508 0,260791 3,834486 0,9676358 23 37 0,2692000 0,279519 3,577579 0,9630843 23
38 0,2526323 0,261102 3,829923 0,9675624 22 38 0,2694801 0,279832 3,573570 0,9630060 22
39 0,2529137 0,261413 3,825371 0,9674888 21 39 0,2697602 0,280146 3,569568 0,9629275 21
40 0,2531952 0,261723 3,820828 0,9674152 20 40 0,2700403 0,280460 3,565575 0,9628490 20
41 0,2534766 0,262034 3,816296 0,9673415 19 41 0,2703204 0,280773 3,561590 0,9627704 19
42 0,2537579 0,262345 3,811773 0,9672678 18 42 0,2706004 0,281087 3,557613 0,9626917 18
43 0,2540393 0,262656 3,807261 0,9671939 17 43 0,2708805 0,281401 3,553645 0,9626130 17
44 0,2543206 0,262967 3,802758 0,9671200 16 44 0,2711605 0,281715 3,549685 0,9625342 16
45 0,2546019 0,263278 3,798266 0,9670459 15 45 0,2714404 0,282029 3,545732 0,9624552 15
46 0,2548832 0,263589 3,793783 0,9669718 14 46 0,2717204 0,282343 3,541789 0,9623762 14
47 0,2551645 0,263900 3,789311 0,9668977 13 47 0,2720003 0,282657 3,537853 0,9622972 13
48 О',2554458 0,264211 3,784848 0,9668234 12 48 0,2722802 0,282971 3,533925 0,9622180 12
49 0,2557270 0,264523 3,780395 0,9667490 11 49 0,2725601 0,283286 3,530005 0,9621387 11
50 0,2560082 0,264834 3,775952 0,9666746 10 50 0,2728400 0,283600 3,526094 0,9620594 10
51 0.2562894 0.265145 3,771518 0,9666001 9 51 0,27.31198 0,283914 3,522190 0,9619800 9
52 0,2565705 0,265457 3 767095 0,9665255 8 52 0,2733997 0,284229 3,518295 0,9619005 8
53 0,2568517 0,265768 3,762681 0,9664508 7 53 0,2736794 0,284543 3,514407 0,9618210 7
54 0,2571328 0,266079 3,758276 0,9663761 6 54 0,2739592 0,284857 3,510527 0,9617413 6
55 0.2574139 0,266391 3,753881 0,9663012 5 55 0,2742390 0,285172 3,506655 0,9616616 5
56 0.2576950 0,266702 3,749496 0,9662263 4 56 0,2745187 0,285487 3,502792 0,9615818 4
57 0.2579760 0,267014 3,745121 0,9661513 3 57 0,2747984 0,285801 3,498936 0,9615019 3
58 0,2582570 0,267326 3,740755 0,9660762 2 58 0,2750781 0,286116 3,495087 0,9614219 2
59 0,2585381 0,267637 3,736398 0,9660011 1 59 0,2753577 0,286431 3,491247 0,9613418 1
| cos | ctg tg sin / / COS ctg tg sin
75 74°
62
МАТЕМАТИЧЕСКИЕ ТАБЛИЦ Ы
16°
17°
• sin tg ctg COS t sin tg ctg COS •
0 0,2756374 0,286745 3,487414 0,9612617 60 0 0,2923717 0,305731 3,270853 0,9563048 60
1 0,2759170 O;287060 3,483590 0,9611815 59 1 0,2926499 0,306049 3 267453 0,9562197 59
2 0,2761965 0,287375 3,479773 0,9611012 58 2 0,2929280 0,306367 3 264060 0,9561345 58
3 0,2764761 0,287690 3,475963 0,9610208 57 3 0,2932061 0,306685 3.260673 0,9560492 57
4 0,2767556 0,288005 3,472162 0,9609403 56 4 0,2934842 0,307003 3,257292 0,9559639 56
5 0,2770352 0,288320 3,468368 0,9608598 55 5 0,2937623 0,307322 3,253918 0,9558785 55
6 0,2773147 0,288635 3,464581 0,9607792 54 6 0,2940403 0,307640 3.250551 0,9557930 54
7 0,2775941 0,288950 3,460803 0,9606984 53 7 0,2943183 0,307959 3,247189 0,9557074 53
8 0,2778736 0,289266 3,457031 0,9606177 52 8 0,2945963 0,308277 3,243835 0,9556218 52
9 0,2781530 0,289581 3,453268 0,9605368 51 9 0,2948743 0,308596 3,240486 0,9555361 51
10 0,2784324 0,289896 3,449512 0,9604558 50 10 0,2951522 0,308914 3,237144 0,9554502 50
11 0,2787118 0,290211 3,445763 0,9603748 49 11 0,2954302 0,309233 3,233808 0,9553643 49
12 0,2789911 0,290527 3,442023 0,9602937 48 12 0,2957081 0,309552 3,230478 0,9552784 48
13 0,2792704 0,290842 3,438289 0,9602125 47 13 0,2959859 0,309870 3,227155 0,9551923 47
14 0,2795497 0,291158 3,434563 0,9601312 46 14 0,2962638 0,310189 3,223837 0,9551062 46
15 0,2798290 0,291473 3,430845 0,9600499 45 15 0,2965416 0,310508 3,220526 0,9550199 45
10 0,2801083 0,291789 3,427133 0,9599684 44 16 0,2968104 0,310827 3,217221 0,9549336 44
17 0,2803875 0,292105 3,423430 0,9598869 43 17 0,2970971 0,311146 3,213923 0,9548473 43
18 0,2806667 0,292420 3,419733 0,9598053 42 18 0,2973749 0,311465 3,210630 0,9547608 42
19 0,2809459 0,292736 3,416044 0,9597236 41 19 0,2976526 0,311784 3,207344 0,9546743 41
20 0,2812251 0,293052 3,412363 0,9596418 40 20 0,2979303 0,312104 3,204064 0,9545876 40
21 0,2815042 0,293368 3,408688 0,9595600 39 21 0,2982079 0,312423 3,200790 0,9545009 39
22 0,2817833 0,293684 3,405021 0,9594781 38 22 0,2984856 0,312742 3,197522 0,9544141 38
23 0,2820624 0,294000 3,401361 0,9593961 37 23 0,2987632 0,313062 3,194260 0,9543273 37
24 0,2823415 0,294316 3,397708 0,9593140 36 24 0,2990408 0,313381 3,191004 0,9542403 36
25 0,2826205 0,294632 3,394063 0,9592318 35 25 0,2993184 0,313700 3,187754 0,9541533 35
26 10,2828995 0,294948 3,390425 0,9591496 34 26 0,2995959 0,314020 3,184510 0,9540662 34
27 0,2831785 0,295265 3,386794 0,9590672 33 27 0,2998734 0,314340 3,181272 0,9539790 33
28 0,2834575 0,295581 3,383170 0,9589848 32 28 0,3001509 0,314659 3,178041 0,9538917 32
29 0,2837364 0,295897 3,379553 0,9589023 31 29 0,3004284 0,314979 3,174815 0,9538044 31
30 0,2840153 0,296213 3,375943 0,9588197 30 30 0,3007058 0,315299 3,171595 0,9537170 30
31 0,2842942 0,296530 3,372341 0,9587371 29 31 0,3009832 0,315619 3,168381 0,9536294 29
32 0,2845731 0,296846 3,368745 0,9586543 28 32 0,3012606 0,315939 3,165173 0,9535418 28
33 0,2848520 0,297163 3,365157 0,9585715 27 33 0,3015380 0,316258 3,161971 0,9534542 27
34 0,2851308 0,297480 3,361575 0,9584886 26 34 0,3018153 0,316578 3,158774 0,9533664 26
35 0,2854096 0,297796 3,358001 0,9584056 25 35 0,3020926 0,316899 3,155584 0,9532786 25
36 0,2856884 0,298113 3,354433 0,9583226 24 36 0,3023699 0,317219 3,152399 0,9531907 24
37 0,2859671 0,298430 3,350873 0,9582394 23 37 0,3026471 0,317539 3,149221 0,9531027 23
38 0,2862458 0,298747 3,347319 0,9581562 22 38 0,3029244 0,317859 3,146048 0,9530146 22
39 0,2865246 0,299063 3,343772 0,9580729 21 39 0,3032016 0,318179 3,142881 0,9529264 21
40 0,2868032 0,299380 3,340233 0,9579895 20 40 0,3034788 0,318500 3,139719 0,9528382 20
41 0,2870819 0,299697 3,336700 0,9579060 19 41 0,3037559 0,318820 3,136564 0,9527499 19
42 0,2873605 0,300014 3,333174 0,9578225 18 42 0,3040331 0,319141 3,133414 0,9526615 18
43 0,2876391 0,300331 3,329654 0,9577389 17 43 0,3043102 0,319461 3,130270 0,9525730 17
44 0,2879177 0,300649 3,326142 0,9576552 16 44 0,3045872 0,319782 3,127132 0,9524844 16
45 0,2881963 0,300966 3,322636 0,9575714 15 45 0,3048643 0,320103 3,123999 0,9523958 15
46 0,2884748 0,301283 3,319137 0,9574875 14 46 0,3051413 0,320423 3,120872 0,9523071 14
47 0,2887533 0,301600 3,315645 0,9574035 13 47 0,3054183 0,320744 3,117751 0,9522183 13
48 0,2890318 0,301918 3,312160 0,9573195 12 48 0,3056953 0,321065 3,114635 0,9521294 12
49 0,2893103 0,302235 3,308681 0,9572354 11 49 0,3059723 0,321386 3,111525 0,9520404 11
50 0,2895887 0,302553 3,305209 0,9571512 10 50 0,3062492 0,321707 3,108421 0,9519514 10
51 0,2898671 0,302870 3,301744 0,9570669 9 51 0,3065261 0,322028 3,105322 0,9518623 9
52 0,2901455 0,303188 3,298285 0,9569825 8 52 0,3068030 0,322349 3,102229 0,9517731 8
53 0,2904239 0,303506 3,294833 0,9568981 7 53 0,3070798 0,322670 3,099142 0,9516838 7
54 0,2907022 0,303823 3,291388 0,9568136 6 54 0,3073566 0,322991 3,096060 0,9515944 6
55 0,2909805 0,304141 3,287949 0,9567290 5 55 0,3076334 0,323312 3,092983 0,9515050 5
56 0,2912588 0,304459 3,284516 0,9566443 4 56 0,3079102 0,323634 3,089912 0,9514154 4
57 0,2915371 0,304777 3,281091 0,9565595 3 57 0,3081869 0,323955 3,086847 0,9513258 3
58 0,2918153 0,305095 3,277671 0,9564747 2 58 0,3084636 0,324277 3,083787 0,9512361 2
59 0,2920935 0,305413 3,274259 0,9563898 1 59 0,3087403 0,324598 3,080732 0,9511464 1
cos
ctg
’tg
sin
cos
ctg
tg sin
73
72
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
63
18°
19°
t sin tg 1 Ctg COS • • sin tg Ctg COS
0 0,3090170 0,324920 3,077683 0,9510565 60 0 0,3255682 0,344328 2,904211 0,9455186 6»
1 0,3092936 0,325241 3,074640 0,9509666 59 1 0,3258432 0,344653 2,901469 0,9454238 59
2 0,3095702 0,325563 3,071602 0,9508766 58 2 0,3261182 0,344978 2,898731 0,9453290 58
3 0,3098468 0,325885 3,068569 0,9507865 57 3 0,3263932 0,345304 2,895999 0,9452341 57
4 0,3101234 0,326207 3,065542 0,9506963 56 4 0,3266681 0,345630 2,893270 0,9451391 56
5 0,3103999 0,326528 3,062520 0,9506061 55 5 0,3269430 0,345955 2,890547 0,9450441 55
6 0,3106764 0,326850 3,059504 0,9505157 54 6 0,3272179 0,346281 2,887828 0,9449489 54
7 0,3109529 0,327172 3,056493 0,9504253 53 7 0,3274928 0,346607 2,885113 0,9448537 53
8 0,3112294 0,327494 3,053487 0,9503348 52 8 0,3277676 0,346933 2,882403 0,9447584 52
9 0,3115058 0,327817 3,050487 0,9502443 51 9 0,3280424 0,347259 2,879698 0,9446630 51
10 0,3117822 0,328139 3,047491 0,9501536 50 10 0,3283172 0.347585 2,876997 0,9445675 5»
11 0,3120586 0,328461 3,044502 0,9500629 49 11 0,3285919 0,347911 2,874301 0,9444720 49
12 0,3123349 0,328783 3,041517 0,9499721 48 12 0,3288666 0,348237 2,871609 0,9443764 48
13 0,3126112 0,329106 3,038538 0,9498812 47 13 0,3291413 0,348563 2,868921 0,9442807 47
14 0,3128875 0,329428 3,035564 0,9497902 46 14 0,3294160 0,348889 2,866239 0,9441849 46
15 0,3131638 0,329751 3,032595 0,9496991 45 15 0,3296906 0,349216 2,863560 0,9440890 45
16 0,3134400 0,330073 3,029632 0,9496080 44 16 0,3299653 0,349542 2,860886 0,9439931 44
17 0,3137163 0,330396 3,026674 0,9495168 43 17 0,3302398 0,349868 2,858217 0,9438971 43
18 0,3139925 0,330718 3,023721 0,9494255 42 18 0,3305144 0,350195 2,855552 0,9438010 42
19 0,3142686 0,331041 3,020773 0,9493341 41 19 0,3307889 0,350522 2,852891 0,9437048 41
20 0,3145448 0,331364 3,017830 0,9492426 40 20 0,3310634 0,350848 2,850235 0,9436085 40
21 0,3148209 0,331687 3,014893 0,9491511 39 21 0,3313379 0,351175 2,847583 0,9435122 39
22 0,3150969 0,332010 3,011960 0,9490595 38 22 0,3316123 0,351502 2,844936 0,9434157 38
23 0,3153730 0,332333 3,009033 0,9489678 37 23 0,3318867 0,351829 2,842293 0,9433192 37
24 0,3156490 0,332656 3,006111 0,9488760 36 24 0,3321611 0,352156 2,839654 0,9432227 36
25 0,3159250 0,332979 3,003194 0,9487842 35 25 0,3324355 0,352483 2,837020 6,9431260 35
26 0,3162010 0,333302 3,000282 0,9486922 34 26 0,3327098 0,352810 2,834390 0,9430293 34
27 0,3164770 0,333625 2,997375 0,9486002 33 27 0,3329841 0,353137 2,831764 0,9429324 33
28 0,3167529 0,333949 2,994473 0,9485081 32 28 0,3332584 0,353464 2,829143 0,9428355 32
29 0,3170288 0,334272 2,991577 0,9484159 31 29 0,3335326 0,353791 2,826526 0,9427386 31
30 0,3173047 0,334595 2,988685 0,9483237 30 30 0,3338069 0,354119 2,823913 0,9426415 30
31 0,3175805 0,334919 2,985798 0,9482313 29 31 0,3340810 0,354446 2,821304 0,9425444 29
32 0,3178563 0,335242 2,982917 0,9481389 28 32 0,3343552 0,354773 2,818700 0,9424471 28
33 0,3181321 0,335566 2,980040 0,9480464 27 33 0,3346293 0,355101 2,816100 0,9423498 27
34 0,3184079 0,335890 2,977168 0,9479538 26 34 0,3349034 0,355429 2,813505 0,9422525 26
35 0,3186836 0,336213 2,974302 0,9478612 25 35 0,3351775 0,355756 2,810913 0,9421550 25
36 0,3189593 0,336537 2,971440 0,9477684 24 36 0,3354516 0,356084 2,808326 0,9420575 24
37 0,3192350 0,336861 2,968583 0,9476756 23 37 0,3357256 0,356412 2,805743 0,9419598 23
38 0,3195106 0,337185 2,965731 0,9475827 22 38 0,3359996 0,356740 2,803165 0,9418621 22
39 0,3197863 0,337509 2,962884 0,9474897 21 39 0,3362735 0,357068 2,800590 0,9417644 21
40 0,3200619 0,337833 2,960042 0,9473966 20 40 0,3365475 0,357396 2,798020 0,9416665 20
41 0,3203374 0,338157 2,957205 0,9473035 19 41 0,3368214 0,357724 2,795454 0,9415686 19
42 0,3206130 0,338481 2,954373 0,9472103 18 42 0,3370953 0,358052 2,792892 0,9414705 18
43 0,3208885 0,338806 2,951545 0,9471170 17 43 0,3373691 0,358380 2,790334 0,9413724 17
44 0,3211640 0,339130 2,948723 0,9470236 16 44 0,3376429 0,358708 3,787780 0,9412743 16
45 0,3214395 0,339454 2,945905 0,9469301 15 45 0,3379167 0,359037 2,785231 0,9411760 15
46 0,3217149 0,339779 2,943092 0,9468366 14 46 0,3381905 0,359365 2,782685 0,9410777 14
47 0,3219903 0,340103 2,940284 0,9467430 13 47 0,3384642 0,359694 2,780144 0,9409793 13
48 0,3222657 0,340428 2,937481 0,9466493 12 48 0,3387379 0,360022 2,777607 0,9408808 12
49 0,3225411 0,340752 2,934682 0,9465555 11 49 0,3390116 0,360351 2,775074 0,9407822 11
50 0,3228164 0,341077 2,931888 0,9464616 10 50 0,3392852 0,360679 2,772545 0,9406835 10
51 0,3230917 0,341402 2,929099 0,9463677 9 51 0;3395589 0,361008 2,770020 0,9405848 9
52 0,3233670 0,341727 2,926315 0,9462736 8 52 0,3398325 0,361337 2,767499 0,9404860 8
53 0,3236422 0,342052 2,923536 0,9461795 7 53 0,3401060 0,361666 2,764982 0,9403871 7
54 0,3239174 0,342377 2,920761 0,9460854 6 54 0,3403796 0,361995 2,762469 0,9402881 6
55 0,3241926 0,342702 2,917991 0,9459911 5 55 0,3406531 0,362324 2,759961 0,9401891 5
56 0,3244678 0,343027 2,915226 0,9458968 4 56 0,3409265 0,362653 2,757456 0,9400899 4
57 0,3247429 0,343352 2,912465 0,9458023 3 57 0,3412000 0,362982 2,754955 0,9399907 3
58 0,3250180 0,343677 2,909709 0,9457078 2 58 0,3414734 0,363312 2,752459 0,9398914 2
59 0,3252931 0,344002 2,906958 0,9456132 1 59 0,3417468 0,363641 2,749966 0,9397921 1
f cos ctg tg sin • COS ctg tg sin •
4*
71
70е
64
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
20°
sin
Ctg
cos
sin
tg
ctg
cos
0,3420201
0,3422935
0,3425668
0,3428400
0,3431133
0,3433865
0,3436597
0,3439329
0,3442060
0,3444791
0,3447521
0 3450252
0,3452982
0,3455712
0,3458441
0,3461171
0,3463900
0,3466628
0,3469357
0,3472085
0,3474812
0,3477540
0,3480267
0,3482994
0,3485720
0,3488447
0,3491173
0,3493898
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27, .
28 10,3496624
29 10,3499349
0,3502074
0,3504798
0,3507523
0,3510246
0,3512970
0,3515693
0,3518416
0,3521139
0,3523862
0,3526584
0,3529306
0,3532027
0,3534748
0,3537469
0,3540190
0,3542910
0,3545630
0,3548350
0,3551070
0,3553789
0,3556508
0,3559226
0,3561944
0,3564662
0,3567380
0,3570097
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 0,3572814
57 0,3575531
58 0,3578248
59 0,3580964
0,363970
0,364300
0,364629
0,364959
0,365288
0,365618
0,365948
0,366278
0,366608
0,366938
0,367268
0,367598
0,367928
0,368259
0,368589
0,368919
0,369250
0,369581
0,369911
0,370242
0,370573
0,370904
0,371235
0,371566
0,371897
0,372228
0,372559
0,372890
0,373222
0,373553
0,373885
0,374216
0,374548
0,374880
0,375211
0,375543
0,375875
0,376207
0,376539
0,376872
0,377204
0,377536
0,377869
0,378201
0,378534
0,378866
0,379199
0,379532
0,379864
0,380197
0,380530
0,380863
0,381196
0,381530
0,381863
0,382196
0,382530
0,382863
0,383197
0,383530
2,747477
2,744993
2,742512
2,740035
2,737562
2,735093
2,732628
2,730167
2,727710
2,725257
2,722808 0,9386938 1
2,720362 0,9385934 .
2,717920 0,9384930 •
2,715483 0,9383925 .
2,713049 0,9382920
2,710619 0,9381913
2,708192 0,9380906
2,705770 0,9379898
2,703351 0,9378889
2,700936 0,9377880
2,698525 0,9376869
2,696118 0,9375858
2,693715 0,9374846
2,691315 0,9373833
2,688919 0,9372820
2,686527 0,9371806
2,684138 0,9370790
2,681753 0,9369774
2,679372 0,9368758
2,676995 0,9367740
2,674621 0,9366722
2,672252 0,9365703
2,669885 0,9364683
2,667523 0,9363662
2,665164 0,9362641
2,662808 0,9361618
2,660457 0,9360595
2,658109 0,9359571
2,655764 0,9358547
2,653424 0,9357521
2,651087 0,9356495
2,648753 0,9355468
2,646423 0,9354440
2,644097 0,9353412
2,641774 0,9352382
2,639455 0,9351352
2,637139 0,9350321
2,634827 0,9349289
2,632519 0,9348257
2,630214 0,9347223
2,627912 0,9346189
2,625614 0,9345154
2,623320 0,9344119
2,621029 0,9343082
2,618741 0,9342045
2,616457 0,9341007
2,614177 0,9339968
2,611899 0,9338928
2,609626 0,9337888
2,607356 0,9336846
0,9390926
0,9395931
0,9394935
0,9393938
0,9392940
0,9391942
0,9390943
0,9389943
0,9388942
0,9387940
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
. 25
- 24
23
22
21
> 20
1 19
i 18
! 17
! 16
! 15
14
) 13
' 12
! 11
10
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2,605089
2,602826
2,600566
2,598309
2,596056
2,593807
2,591561
2,589318
2,587078
2,584842
2,582609
2,580380
2,578154
2,575931
2,573712
2,571496
2,569283
2,567073
2,564867
2,562664
2,560465
2,558269
2,556076
2,553886
2,551699
2,549516
cos
ctg
tg
sin
0,3583679
0,3586395
0,3589110
0,3591825
0,3594540
0,3597254
0,3599968
0,3602682
0,3605395
0,3608108
0,3610821
0,3613534
0,3616246
0,3618958
0,3621669
0,3624380
0,3627091
0,3629802
0,3632512
0,3635222
0,3637932
0,3640641
0,3643351
0,3646059
0,3648768
0,3651476
0,3654184
0,3656891
0,3659599
0,3662306 0
0,3665012 0
0,3667719 0
0,3670425 0
0,3673130 0
0,3675836 0
0,3678541 0
0,3681246 0
0,3683950
0,3686654
0,3689358
0,3692061
0,3694765
0,3697468
0,3700170
0,3702872
0,3705574
0,3708276
0,3710977
0,3713678
0,3716379
0,3719079
0,3721780
0,3724479
0,3727179
0,3729878
0,3732577
0,3735275
0,3737973
0,3740671
0,3743369
383864
384198
384532
384866
385200
385534
385868
386202
386536
386871
387205
387540
387874
388209
388544
388879
389214
389549
389884
390219
390554
390889
391225
391560
391896
392231
392567 2,547336
392903 2,545159
393239 2,542985
393574 2,540815
393910 2,538648
394247 2,536484
394583 2,534323
394919 2,532165
395255 2,530011
395592 2,527860
395928 2,525712
396265 2,523567
396601 2,521425
396938 2,519286
397275 2,517151
397611 2,515018
397948 2,512889
398285 2,510763
398622 2,508640
398960 2,506520
399297 2,504403
399634 2,502289
399971 2,500178
400309 2,498071
400646 2,495966
400984 2,493864
401322 2,491766
401660 2,489670
401997 2,487578
402335 2,485488
402673 2,483402
403011 2,481319
403350 2,479238
403688 2,477161
0,9335804 ।
0,9334761
0,9333718 !
0,9332673
0,9331628
0,9330582
0,9329535
0,9328488
0,9327439
0,9326390
0,9325340
0,9324290
0,9323238
0,9322186
0,9321133
0,9320079
0,9319024
0,9317969
0,9316912
0,9315855
0,9314797
0,9313739
0,9312679
0,9311619
0,9310558
0,9309496
0,9308434
0,9307370
0,9306306
0,9305241
0,9304176
0,9303109
0,9302042
0,9300974
0,9299905
0,9298835
0,9297765
0,9296694
0,9295622
0,9294549
0,9293475
0,9292401
0,9291326
0,9290250
0,9289173
0,9288096
0,9287017
0,9285938
0,9284858
0,9283778
0,9282696
0,928’614
0,9280531
0,9279447
0,9278363
0,9277277
0,9276191
0,9275104
0,9274016
0,9272928
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
cos
Ctg
tg
sin
69
68°
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
65
23°
• sin tg ctg COS • r sin tg ctg COS t
0 0,3746066 0,404026 2,475087 0,9271839 60 0 0,3907311 0,424475 2,355852 0,9205049 60
1 0,3748763 0,404365 2,473015 0,9270748 59 1 0,3909989 0,424818 2,353948 0,9203912 59
2 0,3751459 0,404703 2,470947 0,9269658 58 2 0,3912666 0,425162 2,352047 0,9202774 58
3 0,3754156 0,405042 2,468882 0,9268566 57 3 0,3915343 0,425505 2,350148 0,9201635 57
4 0,3756852 0,405380 2,466819 0,9267474 56 4 0,3918019 0,425849 2,348252 0,9200496 56
5 0,3759547 0,405719 2,464760 0,9266380 55 5 0,3920695 0,426192 2,346358 0,9199356 55
6 0,3762243 0,406058 2,462703 0,9265286 54 6 0,3923371 0,426536 2,344467 0,9198215 54
7 0,3764938 0,406397 2,460649 0,9264192 53 7 0,3926047 0,426880 2,342579 0,9197073 53
8 0,3767632 0,406736 2,458599 0,9263096 52 8 0,3928722 0,427224 2,340693 0,9195931 52
9 0,3770327 0,407075 2,456551 0,9262000 51 9 0,3931397 0,427568 2,338809 0,9194788 51
10 0,3773021 0,407414 2,454506 0,9260902 50 10 0,3934071 0,427912 2,336929 0,9193644 50
11 0,3775714 0,407753 2,452464 0,9259805 49 11 0,3936745 0,428256 2,335050 0,9192499 49
12 0,3778408 0,408092 2,450425 0,9258706 48 12 0,3939419 0,428600 2,333175 0,9191353 48
13 0,3781101 0,408432 2,448389 0,9257606 47 13 0,3942093 0,428945 2,331302 0,9190207 47
14 0,3783794 0,408771 2,446356 0,9256506 46 14 0,3944766 0,429289 2,329431 0,9189060 46
15 0,3786486 0,409111 2,441326 0,9255405 45 15 0,3947439 0,429634 2,327563 0,9187912 45
16 0,3789178 0,409450 2,442298 0,9254303 44 16 0,3950111 0,429979 2,325697 0,9186763 44
17 0,3791870 0,409790 2,440274 0,9253201 43 17 0,3952783 0,430323 2,323834 0,9185614 43
18 О', 3794562 0,410130 2,438252 0,9252097 42 18 0,3955455 0,430668 2,321974 0,9184464 42
19 0,3797253 Oi410470 2,436233 0,9250993 41 19 0,3958127 0,431013 2,320116 0,9183313 41
20 0,3799944 0,410810 2,434217 0,9249888 40 20 0,3960798 0,431358 2,318261 0,9182161 40
21 О'3802634 0,411150 2,432204 0,9248782 39 21 0,3963468 0,431703 2,316408 0,9181009 39
22 0,3805324 0,411490 2,430194 0,9247676 38 22 0,3966139 0,432048 2,314557 0,9179855 38
23 0,3808014 0,411830 2,428186 0,9246568 37 23 0,3968809' 0,432393 2,312709 0,9178701 37
24 0,3810704 0,412170 2,426182 0,9245460 36 24 0,3971479 0,432739 2,310864 0,9177546 36
25 0,3813393 0,412511 2,424180 0,9244351 35 25 0,3974148 0,433084 2,309021 0,9176391 35
26 0,3816082 0,412851 2,422181 0,9243242 34 26 0,3976818 0,433430 2,307180 0,9175234 34
27 0,3818770 0,413191 2,420185 0,9242131 33 27 0,3979486 0,433775 2,305342 0,9174077 33
28 0,3821459 0,413532 2,418192 0,9241020 32 28 0,3982155 0,434121 2,303506 0,9172919 32
29 0,3824147 0,413873 2,416201 0,9239908 31 29 0,3984823 0,434467 2,301673 0,9171760 31
30 0,3826834 0,414214 2,414214 0,9238795 30 30 0,3987491 0,434812 2,299842 0,9170601 30
31 0,3829522 0,414554 2,412229 0,9237682 29 31 0,3990158 0,435158 2,298014 0,9169440 29
32 0,3832209 0,414895 2,410246 0,9236567 28 32 0,3992825 0,435504 2,296188 0,9168279 28
33 Qi3834895 0,415236 2,408267 0,9235452 27 33 0,3995492 0,435850 2,294365 0,9167118 27
34 0,3837582 0Л15577 2,406291 0,9234336 26 34 0,3998158 0,436197 2,292544 0,9165955 26
35 О'3840268 0,415919 2,404317 0,9233220 25 35 0,4000825 0,436543 2,290726 0,9164791 25
36 0,3842953 0,416260 2,402346 0,9232102 24 36 0,4003490 0,436889 2,288910 0,9163627 24
37 0,3845639 0,416601 2,400377 0,9230984 23 37 0,4006156 0,437236 2,287096 0,9162462 23
38 0,3848324 0,416943 2,398-112 0,9229865 22 38 0,4008821 0,437582 2,285285 0,9161297 22
39 0,3851008 0,417284 2,396449 0,9228745 21 39 0,4011486 0,437929 2,283476 0,9160130 21
40 0,3853693 0,417626 2,394489 0,9227624 20 40 0,4014150 0,438276 2,281669 0,9158963 20
41 0,3856377 0,417967 2,392532 0,9226503 19 41 0,4016814 0,438622 2,279865 0,9157795 19
42 0,3859060 0,418309 2,390577 0,9225381 18 42 0,4019478 0,438969 2,278064 0,9156626 18
43 0,3861744 0,418651 2,388625 0,9224258 17 43 0,4022141 0,439316 2,276264 0,9155456 17
44 0,3864427 0,418993 2,386676 0,9223134 16 44 0,4024804 0,439663 2,274467 0,9154286 16
45 0,3867110 0,419335 2,384729 0,9222010 15 45 0,4027467 0,440011 2,272673 0,9153115 15
46 0,3869792 0,419677 2,382785 0,9220884 14 46 0,4030129 0,440358 2,270881 0,9151943 14
47 0,3872474 0*420019 2,380844 0,9219758 13 47 0,4032791 0,440705 2,269091 0,9150770 13
48 0,3875156 0,420361 2,378906 0,9218632 12 48 0,4035453 0,441053 2,267303 0,9149597 12
49 0,3877837 0,420704 2,376970 0,9217504 11 49 0,4038114 0,441400 2,265518 0,9148422 11
50 0,3880518 0,421046 2,375037 0,9216375 10 50 0,4040775 0,441748 2,263736 0,9147247 10
51 0,3883199 0,421389 2,373107 0,9215246 9 51 0,4043436 0,442095 2,261955 0,9146072 9
52 0,3885880 0,421731 2,371179 0,9214116 8 52 0,4046096 0,442443 2,260177 0,9144895 8
53 0,3888560 0,422074 2,369254 0,9212986 7 53 0,4048756 0,442791 2,258402 0,9143718 7
54 0,3891240 0,422417 2,367332 0,9211854 6 54 0,4051416 0,443139 2,256628 0,9142540 6
55 0,3893919 0,422759 2,365412 0,9210722 5 55 0,4054075 0,443487 2,254857 0,9141361 5
56 0,3896598 0,423102 2,363495 0,9209589 4 56 0,4056734 0,443835 2,253088 0,9140181 4
57 0,3899277 0,423445 2,361580 0,9208455 3 57 0,4059393 0,444183 2,251322 0,9139001 3
58 0,3901955 0,423788 2,359668 0,9207320 2 58 0,4062051 0,444532 2,249558 0,9137819 2
59 0,3904633 0,424'132 2,357759 0,9206185 1 59 0,4064709 0,444880 2,247796 0,9136637 1
в COS ctg tg sin ! COS ctg tg sin I •
5 Том I.
67
66
66
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
24° 25°
* sin tg Ctg COS * • sin tg Ctg COS | '
0 0,4067366 0,445229 2,246037 0,9135455 60 0 0,4226183 0,466308 2,144507 1 0,9063078 60
1 0,4070024 0,445577 2,244280 0,9134271 59 1 0,4228819 0,466662 2,142879 0,9061848' 59
2 0,4072681 0,445926 2,242525 0,9133087 58 2 0,4231455 0,467016 2,141254 0,9060618' 58
3 0,4075337 0,446275 2,240772 0,9131902 57 3 0,4234090 0,467371 2,139630 0,9059386 57
4 0,4077993 0,446624 2,239022 0,9130716 56 4 0,4236725 0 467725 2,138008 0,9058154; 56
5 0,4080649 0,446973 2,237274 0,9129529 55 5 0,4239360 0,468080 2,136389 0,90569221 55
6 0,4083305 0,447322 2,235528 0,9128342 54 6 0,4241994 0,468434 2,134771 0,90556881 54
7 0,4085960 0,447671 2,233784 0,9127154 53 7 0,4244628 0,468789 2,133156 0,9054454 53
8 0,4088615 0,448020 2,232043 0,9125965 52 8 0,4247262 0,469144 2,131542 0,9053219' 52
9 0,4091269 0,448369 2,230304 0,9124775 51 9 0,4249895 0,469499 2,129931 0,9051983! 51
10 0,4093923 0,448719 2,228568 0,9123584 50 10 0,4252528 0,469854 2,128321 0,9050746'50
11 0,4096577 0,449068 2,226833 0,9122393 49 11 0,4255161 0,470209 2,126714 0;9049509 49
12 0,4099230 0,449418 2,225101 0,9121201 48 12 0,4257793 0,470564 2,125108 0,9048271' 48
13 0,4101883 0,449768 2,223371 0,9120008 47 13 0,4260425 0,470920 2,123505 0,9047032 47
14 0,4104536 0,450117 2,221643 0,9118815 46 14 0,4263056 0,471275 2,121903 0,9045792 46
15 0,4107189 0,450467 2,219918 0,9117620 45 15 0,4265687 0,471631 2,120303 0,9044551 45
16 0,4109841 0,450817 2,218194 0,9116425 44 16 0,4268318 0,471986 2,118706 0,9043310 44
17 0,4112492 0,451167 2,216473 0,9115229 43 17 0,4270949 0,472342 2,117110 0,9042068' 43
18 0,4115144 0,451517 2,214754 0,9114033 42 18 0,4273579 0,472698 2,115516 0,9040825' 42
19 0,4117795 0,451868 2,213038 0,9112835 41 19 0,4276208 0,473054 2,113925 0,9039582' 41
20 0,4120445 0,452218 2,211323 0,9111637 40 20 0,4278838 0,473410 2,112335 0,9038338' 40
21 0,4123096 0,452568 2,209611 0,9110438 39 21 0,4281467 0,473766 2,110747 0,903709.! 39
22 0,4125745 0,452919 2,207901 0,9109238 38 22 0,4284095 0,474122 2,109161 0,9035847 38
23 0,4128395 0,453269 2,206193 0,9108038 37 23 0,4286723 0,474478 2,107577 0,9034600137
24 0,4131044 0,453620 2,204488 0,9106837 36 24 0,4289351 0,474835 2,105995 0,9033353! 36
25 0,4133693 0,453971 2,202784 0,9105635 35 25 0 4291979 0,475191 2,104415 0,9032105! 35
26 0,4136342 0,454322 2,201083 0,9104432 34 26 0,4294606 0,475548 2,102837 0,90308561 34
27 0,4138990 0,454673 2,199384 0,9103228 33 27 0,4297233 0,475905 2,101261 0,9029606' 33
28 0,4141638 0,455024 2,197687 0,9102024 32 28 0,4299859 0,476262 2,099686 0,90283561 32
29 0,4144285 0,455375 2,195992 0,9100819 31 29 0,4302485 0,476619 2,098114 0,9027105] 31
30 0,4146932 0,455726 2,194300 0,9099613 30 30 0,4305111 0,476976 2,096544 0,902585! 30
31 0,4149579 0,456078 2,192609 0,9098406 29 31 0,4307736 0,477333 2,094975 0,9024600 29
32 0,4152226 0,456429 2,190921 0,9097199 28 32 0 4310361 0 477690 2,093408 0,9023347 28
33 0,4154872 0,456781 2,189235 0,9095990 27 33 0,4312986 0,478047 2,091844 0,9022092 27
34 0,4157517 0,457132 2,187551 0,9094781 26 34 0,4315610 0,478405 2,090281 0,9020838 26
35 0,4160163 0,457484 2,185869 0,9093572 25 35 0,4318234 0,478762 2,088720 0,9019582 25
36 0,4162808 0,457836 2,184189 0,9092361 24 36 0,4320857 0,479120 2,087161 0,9018325'24
37 0,4165453 0,458188 2,182512 0,9091150 23 37 0,4323481 0,479477 2,085604 0,9017068 23
38 0,4168097 0,458540 2,180836 0,9089938 22 38 0,4326103 0,479835 2,084049 0,9015810 22
39 0,4170741 0,458892 2,179163 0,9088725 21 39 0,4328726 0,480193 2,082495 0!9014551 21
40 0,4173385 0,459244 2,177492 0,9087511 20 40 0 4331348 0,480551 2,080944 0,9013292 20
41 0,4176028 0,459596 2,175823 0,9086297 19 41 0,4333970 0,480909 2,079394 0,9012031 19
42 0,4178671 0,459949 2,174156 0,9085082 18 42 0,4336591 0,481267 2,077846 0,9010770 18
43 0,4181313 0,460301 2,172491 0,9083866 17 43 0,4339212 0,481626 2,076301 0,9009508 17
44 0,4183956 0,460654 2,170828 0,9082649 16 44 0,4341832 0,481984 2,074757 0,9008246 16
45 0,4186597 0,461006 2,169168 0,9081432 15 45 0,4344453 0,482343 2,073215 0,9006982 15
46 0,4189239 0,461359 2,167509 0,9080214 14 46 0,4347072 0,482701 2,071674 0,9005718 14
47 0,4191880 0,461712 2,165853 0,9078995 13 47 0,4349692 0,483060 2,070136 0/9004453 13
48 0,4194521 0,462065 2,164198 0,9077775 12 48 0,4352311 0,483419 2,068599 0,9003188 12
49 0,4197161 0,462418 2,162546 0,9076554 11 49 0,4354930 0,483778 2,067065 0”9001921 11
50 0,4199801 0,462771 2,160896 0,9075333 10 50 0 4357548 0,484137 2,065532 0,9000654 10
51 0,4202441 0,463124 2,159248 0,9074111 9 51 0,4360166 0,484496 2,064001 0,8999386 9
52 0,4205080 0,463478 2,157601 0,9072888 8 52 0 4362784 0,484855 2,062472 0,8998117 8
53 0,4207719 0,463831 2,155957 0,9071665 7 53 0,4365401 0,485214 2,060944 0,8996848 7
54 0,4210358 0,464185 2,154316 0,9070440 6 54 0 4368018 0,485574 2,059419 0,8995578 6
55 0,4212996 0,464538 2,152676 0,9069215 5 55 0,4370634 0,485933 2,057895 0,8994307 5
56 0,4215634 0,464892 2,151038 0,9067989 4 56 0,4373251 0,486293 2,053373 0,8993035 4
57 0,4218272 0,465246 2,149402 0,9066762 3 57 0,4375866 0,486653 2,054853 0,8991763 3
58 0,4220909 0,465600 2,147768 0,9065535 2 58 0,4378482 0,487013 2,053335 0,8990489 2
59 0,4223546 0,465954 2,146137 0,9064307 1 59 0,4381097 0,487373 2,051818 0,8989215 1
COS ctg tg sin * COS ctg tg sin *
65° 64;
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
67
26° 27°
* sin tg ctg COS sin tg ctg COS r
0 0,4383711 0,487733 2,050304 0,8987940 60 0 0,4539905 0,509525 1,962610 0,8910065 60
1 0,4386326 0,488093 2,048791 0,8986665 59 1 0,4542497 0,509892 1,961200 0,8908744 59
2 0,4388940 0,488453 2,047280 0,8985389 58 2 0,4545088 0,510258 1,959791 0 8907423 58
3 0,4391553 0,488813 2,045771 0,8984112 57 3 0,4547679 0,510625 1,958384 0,8906100 57
4 0,4394166 0,489174 2,044263 0,8982834 56 4 0,4550269 0,510992 1,956978 0,8904777 56
5 0,4396779 0,489534 2,042758 0,8981555 55 5 0,4552859 0,511359 1,955574 0,8903453 55
6 0,4399392 0,489895 2,041254 0,8980276 54 6 0,4555449 0,511726 1,954171 0,8902128 54
7 0,4402004 0,490256 2,039752 0,8978996 53 7 0,4558038 0,512093 1,952771 0,8900803 53
8 0,4404615 0,490617 2,038252 0,8977715 52 8 0,4560627 0,512460 1,951371 0,8899476 52
9 0,4407227 0,490978 2,036753 0,8976433 51 9 0,4563216 0,512828 1,949973 0,8898149 51
10 0,4409838 0,491339 2,035256 0,8975151 50 10 0,4565804 0,513195 1,948577 0,8896822 50
11 о;4412448 0,491700 2,033761 0,8973868 49 11 0,4568392 0,513563 1,947183 0,8895493 49
12 0^4415059 0,492061 2,032268 0,8972584 48 12 0,4570979 0,513930 1,945790 0,8894164 48
13 О’4417668 0,492422 2,030777 0,8971299 47 13 0,4573566 0,514298 1,944398 0,8892834 47
14 0^420278 0,492784 2,029287 0,8970014 46 14 0,4576153 0,514666 1,943008 0,8891503 46
15 03422887 0,493145 2,027799 0,8968727 45 15 0,4578739 0,515034 1,941620 0,8890171 45
16 0 3425492 0,493507 2,026313 0,8967440 44 16 0,4581325 0,515402 1,940233 0,8888839 44
17 0,4428104 0,493869 2,024829 0,8966153 43 17 0,4583910 0,515770 1,938848 0,8887506 43
18 0 3430712 0,494231 2,023346 0,8964864 42 18 0,4586496 0,516138 1,937464 0,8886172 42
19 03433319 0,494593 2,021865 0,8963575 41 19 0,4589080 0,516507 1,936082 0,8884838 41
20 0,4435927 0,494955 2,020386 0,8962285 40 20 0,4591665 0,516875 1,934702 0,8883503 40
21 0 3438534 0,495317 2,018909 0,8960994 39 21 0,4594248 0,517244 1,933323 0,8882166 39
22 0,4441140 0,495679 2,017433 0,8959703 38 22 0,4596832 0,517613 1,931946 0,8880830 38
23 0,4443746 0,496042 2,015959 0,8958411 37 23 0,4599415 0,517982 1,930570 0,8879492 37
24 0,4446352 0,496404 2,014487 0,8957118 36 24 0,4601998 0,518351 1,929196 0,8878154 36
25 0,4448957 0,496767 2,013016 0,8955824 35 25 0,4604580 0,518720 1,927823 0,8876815 35
26 0,4451562 0,497130 2,011548 0,8954529 34 26 0,4607162 0,519089 1,926452 0,8875475 34
27 0 3454167 0,497492 2,010081 0,8953234 33 27 0,4609744 0,519458 1,925082 0,8874134 33
28 0,4456771 0,497855 2,008615 0,8951938 32 28 0,4612325 0,519828 1,923714 0,8872793 32
29 0,4459375 0,498218 2,007152 0,8950641 31 29 0,4614906 0,520197 1,922347 0,8871451 JI
30 0,4461978 0,498582 2,005690 0,8949344 30 30 0,4617486 0,520567 1,920982 0,8870108 30
31 0,4464581 0,498945 2,004229 0,8948045 29 31 0,4620066 0,520937 1,919619 0,8868765 29
32 0,4467184 0,499308 2,002771 0,8946746 28 32 0,4622646 0,521307 1.918256 0,8867420 28
33 0,4469786 0,499672 2,001314 0,8945446 27 33 0,4625225 0,521677 1,916896 0,8866075 27
34 0,4472388 0,500035 1,999859 0,8944146 26 34 0,4627804 0,522047 1,915537 0,8864730 26
35 0 3474990 0,500399 1,998406 0,8942844 25 35 0,4630382 0,522417 1,914179 0,8863383 25
36 0,4477591 0,500763 1,996954 0,8941542 24 36 0,4632960 0,522787 1,912824 0,8862036 24
37 0,4480192 0,501127 1,995504 0,8940240 23 37 0,4635538 0,523158 1,911469 0,8860688 23
38 0,4482792 0,501491 1,994055 0,8938936 22 38 0,4638115 0,523528 1,910116 0,8859339 22
39 0,4485392 0,501855 1,992609 0,8937632 21 39 0,4640692 0,523899 1,908764 0,8857989 21
40 0,4487992 0,502219 1,991164 0,8936326 20 40 0,4643269 0,524270 1,907415 0,8856639 20
41 0,4490591 0,502583 1,989720 0,8935021 19 41 0,4645845 0,524641 I,906066 0,8855288 19
42 0,4493190 0,502948 1,988279 0,8933714 18 42 0,4648420 0,525012 1,904719 0,8853936 18
43 0,4495789 0,503312 1,986839 0,8932406 17 43 0,4650996 0,525383 1,903374 0,8852584 17
44 0 3498387 0,503677 1,985400 0,8931098 16 44 0,4653571 0,525754 1,902030 0,8851230 16
45 0 3500984 0,504041 1,983964 0,8929789 15 45 0,4656145 0,526125 1,900687 0,8849876 15
46 0,4503582 0,504406 1,982529 0,8928480 14 46 0,4658719 0,526497 1,899346 0,8848522 14
47 0,4506179 0,504771 1,981095 0,8927169 13 47 0,4661293 0,526868 1,898007 0,8847166 13
48 03508775 0,505136 1,979663 0,8925858 12 48 0,4663866 0,527240 1,896669 0,8845810 12
49 0,4511372 0,505502 1,978233 0,8924546 11 49 0,4666439 0,527612 1,895332 0,8844453 11
50 0,4513967 0,505867 1,976805 0,8923234 10 50 0,4669012 0,527984 1,893997 0,8843095 10
51 0 3516563 0,506232 1,975378 0,8921920 9 51 0,4671584 0,528356 1,892663 0,8841736 9
52 0,4519158 0,506598 1,973953 0,8920606 8 52 0,4674156 0,528728 1,891331 0,8840377 8
53 0,4521753 0,506963 1,972530 0,8919291 7 53 0,4676727 0,529100 1,890001 0,8839017 7
54 0,4524347 0,507329 1,971108 0,8917975 6 54 0,4679298 0,529473 1,888671 0,8837656 6
55 0,4526941 0,507695 1,969687 0,8916659 5 55 0,4681869 0,529845 1,887344 0,8836295 5
56 0,4529535 0,508061 1,968269 0,8915342 4 56 0,4684439 0,530218 1,886017 0,8834933 4
57 0,4532128 0,508427 1,966852 0,8914024 3 57 0,4687009 0,530591 1,884692 0,8833569 3
58 0,4534721 0,508793 1.965436 0.8912705 2 58 0,4689578 0,530963 1,883369 0 ,'8832206 2
59 0,4537313 0,509159 1,964023 0,8911385 1 59 0,4692147 0,531336 1,882047 0,8830841 1
/ COS ctg tg sin > f COS ctg tg sin f
63° 5* 62’
68
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
28°
29°
• sin tg ctg COS • t sin tg ctg COS /
0 0,4694716 0,531709 1,880726 0,8829476 60 0 0,4848096 0,554309 1,804048 0,8746197 60
1 0,4697284 0,532083 1,879407 0,8828110 59 1 0,4850640 0,554689 1,802811 0,8744786 59
2 0,4699852 0,532456 1,878090 0,8826743 58 2 0,4853184 0,555070 1,801575 0,8743375 58
3 0,4702419 0,532829 1,876774 0,8825376 57 3 0,4855727 0,555450 1,800341 0,8741963 57
4 0,4704986 0,533203 1,875459 0,8824007 56 4 0,4858270 0,555831 1,799108 0,8740550 56
5 0,4707553 0,533577 1,874145 0,8822638 55 5 0,4860812 0,556212 1,797876 0,8739137 55
6 0,4710119 0,533950 1,872834 0,8821269 54 6 0,4863354 0,556593 1,796645 0,8737722 54
7 0,4712685 0,534324 1,871523 0,8819898 53 7 0,4865895 0,556974 1,795416 0,8736307 53
8 0,4715250 0,534698 1,870214 0,8818527 52 8 0,4868436 0,557355 1,794188 0.8734891152
9 0,4717815 0,535072 1,868906 0,8317155 51 9 0,4870977 0,557736 1,792962 0,8733475 51
10 0,4720380 0,535446 1,867600 0,8815782 50 10 0,4873517 0,558118 1,791736 0,8732058 50
И 0/722944 0,535821 1,866295 0,8814409 49 11 0,4876057 0,558499 1,790512 0,8730640 49
12 О;4725508 0,536195 1,864992 0,8813035 48 12 0,4878597 0,558881 1,789289 0,8729221 48
13 О;4728071 0,536570 1,863690 0,8811660 47 13 0,4881136 0,559263 1,788068 0,8727801 47
14 0,4730634 0,536945 1,862390 0,8810284 46 14 0,4883674 0,559645 1,786847 0,8726381 46
15 0,4733197 0,537319 1,861090 0,8808907 45 15 0,4886212 0,560027 1,785628 0,8724960 45
16 0,4735759 0,537694 1,859793 0,8807530 44 16 0,4888750 0,560409 1,784411 0,8723538 44
17 0,4738321 0,538069 1,858496 0,8806152 43 17 0,4891288 0,560791 1,783194 0,8722116 43
18 0,4740882 0,538445 1,857201 0,8804774 42 18 0,4893825 0,561174 1,781979 0,8720693 42
19 0,4743443 0,538820 1,855908 0,8803394 41 19 0,4896361 0,561556 1,780765 0,8719269 41
20 0,4746004 0,539195 1,854616 0,8802014 40 20 0,4898897 0,561939 1,779552 0,8717844 40
21 0,4748564 0,539571 1,853325 0,8800633 39 21 0,4901433 0,562322 1,778341 0,8716419 39
22 0,47,51124 0,539946 1,852036 0,8799251 38 22 0,4903968 0,562705 1,777131 0,8714993 38
23 0,4753683 0,540322 1,850748 0,8797869 37 23 0,4906503 0,563088 1,775922 0,8713566 37
24 0,4756242 0,540698 1,849461 0,8796486 36 24 0,4909038 0,563471 1/774714 0,8712138 36
25 0,4758801 0,541074 1,848176 0,8795102 35 25 0,4911572 0,563854 1,773508 0,8710710 35
26 0,4761359 0,541450 1,846892 0,8793717 34 26 0,4914105 0,564238 1,772302 0,8709281 34
27 0,4763917 0,541826 1,845610 0,8792332 33 27 0,4916638 0,564621 1,771098 0,8707851 33
28 0,4766474 0,542203 1,844329 0,8790946 32 28 0,4919171 0,565005 1,769896 0,8706420 32
29 0,4769031 0,542579 1,843049 0,8789559 31 29 0,4921704 0,565389 1,768694 0,8704989 31
30 0,4771588 0,542956 1,841771 0,8788171 30 30 0.4924236 0,565773 1,767494 0,8703557 30
31 0,4774144 0,543332 1,840494 0,8786783 29 31 0,4926767 0,566157 1,766295 0,8702124 29
32 0,4776700 0,543709 1,839218 0,8785394 28 32 0,4929298 0,566541 1,765097 0,8700691 28
33 0,4779255 0,544086 1,837944 0,8784004 27 33 0,4931829 0,566925 1,763901 0;8699256 27
34 0,4781810 0,544463 1,836671 0,8782613 26 34 0,4934359 0,567310 1,762705 0,8697821 26
35 0,4784364 0,544840 1,835400 0,8781222 25 35 0,4936889 0,567694 1,761511 0,8696386 25
36 0,4786919 0,545218 1,834130 0,8779830 24 36 0,4939419 0,568079 1,760318 0,8694949 24
37 0,4789472 0,545595 1,832861 0,8778437 23 37 0,4941948 0,568464 1,759127 0,8693512 23
38 0,4792026 0,545973 1,831594 0,8777043 22 38 0,4944476 0,568849 1,757936 0,8692074 22
39 0,4794579 0,546350 1,830327 0,8775649 21 39 0,4947005 0,569234 1,756747 0,8690636 21
40 0,4797131 0,546728 1,829063 0,8774254 20 40 0,4949532 0,569619 1,755559 0,8689196 20
41 0,4799683 0,547106 1,827799 0,8772858 19 41 0,4952060 0,570004 1,754372 0,8687756 19
42 0,4802235 0,547484 1,826537 0,8771462 18 42 0,4954587 0,570390 1,753187 0,8686315 18
43 0,4804786 0,547862 1,825277 0,8770064 17 43 0,4957113 0,570776 1,752002 0,8684874 17
44 0,4807337 0,548240 1,824017 0,8768666 16 44 0,4959639 0,571161 1,750819 0,8683431 16
45 0,4809888 0,548619 1,822759 0,8767268 15 45 0,4962165 0,571547 1,749637 0,8681988 15
46 0,4812438 0,548997 1,821503 0,8765868 14 46 0,4964690 0,571933 1.748456 0,8680544 14
47 0,4814987 0,549376 1,820247 0,8764468 13 47 0,4967215 0,572319 1,747277 0,8679100 13
48 0,4817537 0,549755 1,818993 0,8763067 12 48 0,4939740 0,572705 1,746093 0,8677655 12
49 0,4820086 0,550134 1,817740 0,8761665 11 49 0,4972264 0,573092 1,744921 0,8676209 11
50 0,4822634 0,550513 1,816489 0,8760263 10 50 0,4974787 0,573478 1,743745 0,8674762 10
51 0,4825182 0,550892 1,815239 0,8758859 9 51 0,4977310 0 /73865 1,742570 0,8673314 9
52 0,4827730 0,551271 1,813990 0,8757455 8 52 0,4979833 0,574252 1,741397 0,8671866 8
53 0,4830277 0,551650 1,812743 0,8756051 7 53 0,4982355 0,574638 1,740224 0,8670417 7
54 0,4832824 0,552030 1,811497 0,8754645 6 54 0,4984877 0,575026 1,739053 0,8668967 6
55 0,4835370 0,552409 1,810252 0,8753239 5 55 0,4987399 0,575413 1,737883 0,8667517 5
56 0,4837916 0,552789 1,809009 0,8751832 4 56 0,4989920 0,575800 1,736714 0,8666066 4
57 0,4840462 0,553169 1,807766 0,8750425 3 57 0,4992441 0,576187 1,735547 0.8664614 3
58 0,4843007 0,553549 1,806526 0,8749016 2 58 0,4994961 0,576575 1,734380 0,8663161 2
59 0,4845552 0,553929 1,805286 0,8747607 1 59 0,4997481 0,576962 1,733215 0,8661708 1
COS ctg tg sin f COS ctg tg sin
61
60
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
6.9
30°
31
' | sin tg ctg COS • sin tg ctg COS’ | '
0 0,5000000 0,577350 1,732051 0,8660254 60 0 0,5150381 0,600861 1,664279 0,8,571673 60
1 0,5002519 0,577738 1,730888 0,8658799 59 1 0,5152874 0,601257 1,663183 0,8570174159
2 0,5005037 0,578126 1,729726 0,8657344 58 j 2 0,5155367 0,601653 1,662088 0,8568675 58
3 0,5007556 0,578514 1,728565 0,8655887 57 3 0,5157859 0,602049 1,660994 0,8567175; 57
4 0,5010073 0,578903 1,727406 0,8654430 56 4 0,5160351 0,602445 1,659902 0,8565674; 56
5 0,5012591 0,579291 1,726248 0,8652973 55 5 0,5162842 0,602842 1,658810 0,8564173 55
6 0,5015107 0,579680 1,725091 0,8651514 54 6 0,5165333 0,603239 1,657719 0,8562671 54
7 0,5017624 0,580068 1,723935 0,8650055 53 7 0,5167824 0,603635 1,656629 0,8561168 53
8 0,5020140 0,580457 1,722780 0,8648595 52 8 0,5170314 0,604032 1,655541 0,8559664 52
9 0,5022655 0,580846 1,721626 0,8647134 51 9 0,5172804 0,604429 1,654453 0,8558160 51
1.0 0,5025170 0,581235 1,720474 0,8645673 50 10 0,5175293 0,604827 1,653366 0,8556655 50
И 0,5027685 0,581625 1,719322 0,8644211 49 11 0,5177782 0,605224 1,652281 0,8555149 49
12 0,5030199 0,582014 1,718172 0,8642748 48 12 0,5180270 0,605622 1,651196 0,8553643 48
13 0,5032713 0,582403 1,717023 0,8641284 47 13 0,5182758 0,606019 1,650113 0,8552135 47
14 0,5035227 0,582793 1,715875 0,8639820 46 14 0,5185246 0,606417 1,649030 0,8550627 46
15 0,5037740 0,583183 1,714728 0,8638355 45 15 0,5187733 0,606815 1,647949 0,8549119 45
16 0,5040252 0,583573 1,713583 0,8636889 44 16 0,5190219 0,607213 1,646869 0,8547609 44
17 0,5042765 0,583963 1,712438 0,8635423 43 17 0,5192705 0,607611 1,645789 0,85460991 43
18 0,5045276 0,584353 1,711295 0,8633956 42 18 0,5195191 0,608010 1,644711 0,8544588 42
19 0,5047788 0,584743 1,710153 0,8632488 41 19 0,5197676 0,608408 1,643634 0,8543077 4i
20 0,5050298 0,585134 1,709012 0,8631019 40 20 0,5200161 0,608807 1,642558 0,8541564 40
21 0,5052809 0,585524 1,707872 0,8629549 39 21 0,5202646 0,609205 1,641482 0,8540051 39
22 0,5055319 0,585915 1,706733 0,8628079 38 22 0,5205130 0,609604 1,640408 0,8538538 38
23 0,5057828 0,586306 1,705595 0,8626608 37 23 0,5207613 0,610003 1 639335 0,8537023 37
24 0,5060338 0,586697 1,704459 0,8625137 36 24 0,5210096 0,610403 1,638263 0,8535508 36
25 0,5062846 0,587088 1,703323 0,8623664 35 25 0,5212579 0,610802 1,637192 0,8533992 35
26 0,5065355 0,587479 1,702189 0,8622191 34 26 0,5215061 0,611201 1,636122 0,8532475 34
27 0,5067863 0,587870 1,701056 0,8620717 33 27 0,5217543 0,611601 1,635053 0,8530958 33
28 0,5070370 0,588262 1,699924 0,8619243 32 28 0,5220024 0,612001 1,633985 0,8529440 32
29 0,5072877 0,588653 1,698793 0,8617768 31 29 0,5222505 0,612401 1,632918 0,8527921 31
30 0,5075384 0,589045 1,697663 0,8616292 30 30 0,5224986 0,612801 1,631852 0,8526402 30
31 0,5077890 0,589437 1,696534 0,8614815 29 31 0,5227466 0,613201 1,630787 0,8524881 29
32 0,5080396 0,589829 1,695407 0,8613337 28 32 0,5229945 0,613601 1,629723 0,8523360 28
33 0,5082901 0,590221 1,694280 0,8611859 27 33 0,5232424 0,614002 1,628660 0,8521839 27
34 0,5085406 0,590613 1,693155 0,8610380 26 34 0,5234903 0,614402 1,627598 0,8520316 26
35 0,5087910 0,591006 1,692031 0,8608901 25 35 0,5237381 0,614803 1,626537 0,8518793 25
36 0,5090414 0,591398 1,690908 0,8607420 24 36 0,5239859 0,615204 1,625477 0,8517269 24
37 0,5092918 0,591791 1,689786 0,8605939 23 37 0,5242336 0,615605 1,624418 0,8515745 23
38 0,5095421 0,592184 1,688665 0,8604457 22 38 0,5244813 0,616006 1,623360 0,8514219 22
39 0,5097924 0,592577 1,687545 0,8602975 21 39 0,5247290 0,616408 1,622303 0,8512693 21
40 0,5100426 0,592970 1,686426 0,8601491 20 40 0,5249766 0,616809 1,621247 0,8511167 20
41 0,5102928 0,593363 1,685308 0,8600007 19 41 0,5252241 0,617211 1,620192 0,8509639 19
42 0,5105429 0,593757 1,684192 0,8598523 18 42 0,5254717 0,617613 1,619138 0,8508111 18
43 0,5107930 0,594150 1,683077 0,8597037 17 43 0,5257191 0,618015 1,618085 0,8506582 17
44 0,5110431 0,594544 1,681962 0,8595551 16 44 0,5259665 0,618417 1,617033 0,8505053 16
45 0,5112931 0,594937 1,680849 0,8594064 15 45 0,5262139 0,618819 1,615982 0,8503522 15
46 0,5115431 0,595331 1,679737 0,8592576 14 46 0,5264613 0,619221 1,614932 0,8501991 14
47 0,5117930 0,595725 1,678626 0,8591088 13 47 0,5267085 0,619624 1,613883 0,8500459 13
48 0,5120429 0,596120 1,677516 0,8589599 12 48 0,5269558 0,620026 1,612835 0,8498927 12
49 0,5122927 0,596514 1,676407 0,8588109 11 49 0,5272030 0,620429 1,611788 0,8497394 11
50 0,5125425 0,596908 1,675299 0,8586619 10 50 0 5274502 0,620832 1,610742 0,8495860 10
51 0,5127923 0,597303 1,674192 0,8585127 9 51 0 5276973 0,621235 1,609697 0,8494325 9
52 о 5130420 0.597698 1,673086 0,8583635 8 52 0’5279443 0,621638 1,608653 0,8492790 8
54 0.5132916 0,598093 1,671982 0,8582143 7 53 0’5281914 0,622042 1,607609 0,8491254 7
54 0,5135413 0,598488 1,670878 0,8580649 6 54 0,5284383 0,622445 1,606567 0,8489717 6
55 0,5137908 0,598883 1,669776 0,8579155 5 55 0,5286853 0,622849 1,605526 0,8488179 5
56 0,514040- 0,599278 1,668674 0,8577660 4 56 0 5289322 0,623253 1,604486 0,8486641 4
57 0,5142899 0,599674 1,667574 0,8576164 3 57 0 5291790 0,623657 1,603446 0,8485102 3
58 0,5145393 0,600069 1,666475 0,8574668 2 58 0 5294258 0,624061 1,602408 0,8483562 2
59 0,5147887 0,600465 1,665377 0,8573171 1 59 0,5296726 0,624465 1,601371 0,8482022 1
* cos ctg tg sin • COS ctg tg sin I '
59
58
70
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
32° 33°
' | sin tg ctg cos ' j ' sin tg ctg cos '
ft 05299193 0,624869 1,600335 0 8480481 60 0 0,5446390 0,649408 1,539865 0,8386706 60
1 0 5301659 0,625274 1,599299 0 8478939 59 1 0,5448830 0,649821 1,538885 0,8385121 59
2 0 5304125 0,625679 1,598265 0’847739758 20,54512690,650235 1,5379050,838353658
3 05306591 0,626083 1,597231 0 8475853 57 3 0,5453707 0,650649 1,536927 0,8381950 57
4 0 5309057 0,626488 1,596199 0 8474309 56 4 0,5456145 0,651063 1,535949 0,8380363 56
5 0 5311521 0,626894 1,595167 0847276555 5 0,5458583 0,651477 1,534973 0,837877555
6 0 5313986 0,627299 1,594137 0847121954 6 0,5461020 0,651892 1,533997 0,837718754
7 0,5316450 0,627704 1,593107 0 8469673 53 7 0,5463456 0,652306 1,533022 0,8375598 53
8 0,5318913 0,628110 1,592078 0 8468126 52 8 0,5465892 0,652722 1,532048 0,8374009 52
9 0,5321376 0,628516 1,591051 0,846657951 9 0,5468328 0,653136 1,531075 0,837241851
10 05323839 0,628921 1,590024 0 8465030 50 10 0 5470763 0,653551 1,530102 0,8370827 50
11 05326301 0,629327 1,588998 0,846348149 11 0,5473191? 0,653966 1,529131 0,836923649
12 0;5328763 0,629734 1,587973 0846193248 12 0,5475632 0,654382 1,528160 0,836764348
13 05331224 0,630140 1,586949 0,8460381 47 13 0,5478066 0,654797 1,527190 0,8365050 47
14 05333685 0,630546 1,585926 0,8458830 46 14 0,5480499 0,655213 1,526222 0,8364456 4S
15 05336145 0,630953 1,584904 0,845727845 15 0,5482932 0,655629 1,525253 0,836286245
16 0,5338605 0,631360 1,583883 0,845572644 16 0,5485365 0,656045 1,524286 0,8361266144
17 0,5341065 0,631767 1,582863 0 8454172 43 17 0,5487797 0,656461 1,523320 0,8359670143
18 0,5343523 0,632174 1,581844 0,8452618 42 18 0,5490228 0,656877 1,522355 0,8358074 42
19 0,5345982 0,632581 1,580825 0,845106441 19 0,5492659 0,657294 1,521390 0,835647641
20 05348440 0,632988 1,579808 0,8449508 40 20 0,5495090 0,657710 1,520426 0,8354878 40
21 0,5350898 0,633396 1,578792 0,8447952 39 21 0,5497520 0,658127 1 519463 0,8353279 39
22 0,5353355 0,633804 1,577776 0,8446395|38 22 0,5499950 0,658544 1*518501 0,835168038
23 0,5355812 0,634211 1,576761 0,8444838 37 23 0,5502379 0,658961 1 517540 0,8350080 37
24 0,5358268 0,634619 1,575748 0,8443279 36 24 0,5504807 0,659379 1 516580 0,8348479 36
25 0,5360724 0,635027 1,574735 0,844172035 25 0,5507236 0,659796 1’515620 0,834687735
26 0,5363179 0,635436 1,573723 0,8440161 34 26 0,5509663 0,660214 1,514661 0,8345275 34
27 0,5365634 0,635844 1,572713 0,8438600 33 27 0,5512091 0,660631 1 513704 0,8343672 33
2810,5368089 0,636253 1,571703 0,843703932 28 0,5514518 0,661049 1,512747 0,834206832
29 0,5370543 0,636661 1,570694 0,8435477 31 29 0,5516944 0,661467 1,511790 0,8340463 31
30 0,5372996 0,637070 1,569686 0,8433914 30 30 0,5519370 0,661886 1 510835 0,8338858 30
31 0,5375449 0,637479 1,568678 0,8432351 29 31 0,5521795 0,662304 1’509881 0,8337252 29
32 0,5377902 0,637888 1,567672 0,843078728 32 0,5524220 0,662723 1’508927 0,833564628
33 0,5380354 0,638298 1,566667 0,842922227 33 0,5526645 0,663141 1*507974 0,833403827
34 0,5382806 0,638707 1,565662 0,842765726 34 0,5529069 0,663560 1*507022 0,833243026
35 0,5385257 0,639117 1,564559 0,8426091 25 35 0,5531492 0,663979 1*506071 0,833082225
36 0,5387708 0,639527 1,563656 0,842452424 36 05533915 0,664398 1*505121 0,832921224
37 0,5390158 0,639937 1,562655 0,842295623 37 o’5536338 0,664818 1*504172 0,832760223
38 0,5392608 0,640347 1,561654 0,842138822 38 05538760 0,665237 1*503223 0,8325991 22
39 0,5395058 0,640757 1,560654 0,841981921 39 0^5541182 0,665657 1/02275 0,832438021
40 0,5397507 0 641167 1 559655 0,8418249 20 40 0,5543603 0,666077 1 501328 0 8322768 20
41 0,5399955 0,641578 1,558657 0,8416679 19 41 0 5546024 0,666497 1 500382 0 8321155 19
42 0,5402403 0,641989 1,557660 0,8415108 18 42 о’б548444 0,666917 1 499437 0*,8319541 18
43 0,5404851 0,642399 1,556664 0,8413536 17 43 o’555O864 0,667337 1 498492 0 8317927 17
44 0,5407298 0,642810 1,555669 0,8411963 16 44 0 5553283 0 /67758 1*497549 o’,8316312 16
45 0,5409745 0,643222 1,554674 0,8410390 15 45 0 5555702 0,668179 1 496606 0,8314696 15
46 0,5412191 0,643633 1,553681 0,8408816 14 46 0 5558121 0,668599 1 495664 0 8313080 14
47 0,5414637 0,644044 1,552688 0,8407241 13 47 05560539 0,669020 1 494723 0,8311463 13
48 0,5417082 0,644456 1,551696 0,8405666 12 48 0,5562956 0,669442 1 493782 0,8309845 12
49 0,5419527 0,644868 1,550705 0,8404090 11 49 0,5565373 0,669863 1,492843 0,8308226 11
50 0,5421971 0,645280 1,549715 0,8402513 10 50 0.5567790 0.670284 1.491904 0.8306607 10
51 0,5424415 0,645692 1,548726 0,8400936 9 51 0,5570206 0,670706 1 490966 08304987 9
52 0,5426859 0,646104 1,547738 0,8399357 8 52 0.5572621 0,671128 1 490029 0.8303366 8
53 0,5429302 0,646516 1,546751 0,8397778 7 53 0.5575036 0,671550 1.489092 0.8301745 7
54 0,5431744 0,646929 1,545765 0,8396199 6 54 05577451 0,671972 1,488157 0,8300123 6
55 0,5434187 0,647342 1,544779 0,8394618 5 55 o’5579865 0,672394 1 487222 0,8298500 5
56 0,5436628 0,647755 1,543795 0,8393037 4 56 0,5582279 0,672817 1,486288 0,8296877 4
57 0,5439069 0,648168 1,542811 0,8391455 3 57 05584692 0,673240 1,485355 0,8295252 3
58 0,5441510 0,648581 1,541828 0,8389873 2 58 0.5587105 0.673662 1.484423 0.82936281 2
59 0,5443951 0,648994 1,540846 0,8388290 1 59 0,5589517 0,674085 1,483492 0,8292002 1
• cos Ctg tg sin cos ctg tg sin
57
56
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
71
34
35°
• sin tg ctg i | cos • ' sin tg ctg cos *
0 0.5591929 0,674509 1,482561 0 8290376 60 0 0,700208 1,428148 0,8191520 60
1 0,5594340 0,674932 1,481631 0 8288749 59 1 0,5738147 0,700641 1,427264 0,8189852 59
2 0.5596J51 0,675355 1,480702 0 8287121 58 2 0,5740529 0,701075 1,426381 0,8188182 58
3 0,5599162 0,675779 1,479774 0 8285493 57 3 0,5742911 0,701509 1,425499 0,8186512 57
4 0,5601572 0,676203 1,478846 0 8283864 56 4 0,5745292 0,701943 1,424617 0,8184841 56
5 0,5603981 0,676627 1,477920 0 8282234 55 5 0,5747672 0,702377 1,423736 0,8183169 55
6 0,5606390 0,677051 1,476994 0 8280603 54 6 0,5750053 0,702812 1 422856 0,8181497 54
7 0,5608798 0,677475 1,476069 0 8278972 53 7 0,5752432 0,703246 1,421977 0,8179824 53
8 0,5611206 0,677900 1,475144 0 82773401 52 8 0,5754811 0,703681 1,421098 0,8178151 52
9 0,5613614 0,678324 1,474221 0 8275708] 51 9 0,5757190 0,704116 1,420220 0,8176476 51
10 0,5616021 0,678749 1.473298 0 8274074 50 10 0,5759568 0,704551 1,419343 0,8174801 50
11 0,5618428 0,679174 1,472376 0 8272440'. 49 11 0,5761946 0,704987 1,418466 0,8173125 49
12 0,5620834 0,679599 1,471455 0 8270806 48 12 0,5764323 0,705422 1,417590 0,8171449 48
13 0 5623239 0,680025 1,470535 0 8269170 47 13 0,5766700 0,705858 1,416715 0,8169772 47
14 0,5625645 0,680450 1,469615 0 8267534 46 14 0,5769076 0,706294 1,415841 0,8168094 46
15 0,5628049 0,680876 1,468697 0 8265897 45 15 0,5771452 0,706730 1,414967 0,8166416 45
16 0,5630453 0,681302 1,467779 0 8264260 44 16 0,5773827 0,707166 1,414094 0,8164736 44
17 0,5632857 0,681728 1,466862 0 8262622 43 17 0,5776202 0,707603 1,413222 0,8163056 43
is 10,5635260 0,682154 1,465945 0 8260983 42 18 0,5778576 0,708039 1,412351 0,8161376 42
19 0,5637663 0,682580 1,465030 0 8259343 41 19 0,5780950 0,708476 1,411480 0,8159695 41
20 0,5640066 0,683007 1,464115 0 8257703 40 20 0,5783323 0,708913 1,410610 0,8158013 40
21 0,5642467 0,683433 1,463201 0 8256062 39 21 0,5785696 0,709350 1,409740 0,8156330 39
22 0,5644869 0,683860 1,462287 0 8254420 38 22 0,5788069 0,709788 1,408872 0,8154647 38
23 0,5647270 0,684287 1,461375 0 8252778 37 23 0,5790440 0,710225 1,408004 0,8152963 37
24 0,5649670 0,684714 1,460463 0 8251135 36 24 0,5792812 0,710663 1,407137 0,8151278 36
25 0,5652070 0,685142 1,459552 0 8249491 35 25 0,5795183 0,711101 1,406270 0,8149593 35
26 0,5654469 0,685569 1,458642 0 8247847 34 26 0,5797553 0,711539 1,405404 0,8147906 34
27 0,5656868 0,685997 1,457733 0 8246202 33 27 0,5799923 0/711977 1,404539 0,8146220 33
28 0,5659267 0,686425 1,456824 0 8244556 32 28 0,5802292 0,712416 1,403675 0,8144532 32
29 0,5661665 0,686853 1,455916 0 8242909 31 29 0,5804661 0,712854 1,402811 0,8142844 31
30 0,5664062 0,687281 1,455009 0 8241262 30 30 0,5807030 0,713293 1,401948 0,8141155 30
31 0,5666459 0,687709 1,454103 0 8239614 29 31 0,5809397 0,713732 1,401086 0,8139466 29
32 0,5668856 0,688138 1,453197 0 8237965 28 32 0,5811765 0,714171 1,400224 0,8137775 28
33 0,5671252 0,688567 1,452292 0 8236316 27 33 0,5814132 0,714611 1,399364 0,8136084 27
34 0,5673648 0,688995 1,451388 0 8234666 26 34 0,5816498 0,715050 1,398503 0,8134393 26
35 0,5676043 0,689425 1,450485 0 8233015 25 35 0,5818864 0,715490 1,397644 0,8132701 25
36 0,5678437 0,689854 1,449583 0 8231364 24 36 0,5821230 0,715930 1,396785 0,8131008 24
37 0,5680832 0,690283 1,448681 0 8229712 23 37 0,5823595 0,716370 1,395927 0,8129314 23
38 0,5683225 0,690713 1,447780 0 8228059 22 38 0,5825959 0,716810 1,395070 0,8127620 22
39 0,5685619 0,691143 1,446880 0 8226405 21 39 0,5828323 0,717250 1,394213 0,8125925 21
40 0,5688011 0,691572 1,445980 0 8224751 20 40 0,5830687 0,717691 1 393357 0,8124229 20
41 0,5690403 0,692003 1,445081 0 8223096 19 41 0,5833050 0,718132 1,392502 0,8122532 19
42 0,5692795 0,692433 1,444183 0 8221440 18 42 0,5835412 0,718573 1,391647 0,8120835 18
43 0,5695187 0,692863 1,443286 0 8219784 17 43 0,5837774 0,719014 1,390793 0,8119137 17
44 0,5697577 0,693294 1,442390 0 8218127 16 44 0,5840136 0,719455 1,389940 0,8117439 16
45 0,5699968 0,693725 1,441494 0 8216469 15 45 0,5842497 0,719897 1,389088 0,8115740 15
46 0,5702357 0,694156 1,440599 0 8214811 14 46 0,5844857 0,720339 1,388236 0,8114040 14
47 0,5704747 0,694587 1,439705 0 8213152 13 47 0,5847217 0,720781 1,387385 0,8112339 13
48 0,5707136 0,695018 1,438811 0 8211492 12 48 0,5849577 0,721223 1,386534 0,8110638 12
49 0,5709524 0,695450 1,437919 0 8209832 11 49 0,5851936 0,721665 1,385684 0,8108936 11
50 0,5711912 0,695881 1,437027 0 8208170 10 50 0,5854294 0,722108 1,384835 0,8107234 10
51 0,5714299 0,696313 1,436136 0 8206509 9 51 0,5856652 0,722550 1,383987 0,8105530 9
52 0,5716686 0,696745 1,435245 0 8204846 8 52 0,5859010 0,722993 1,383139 0,8103826 8
53 0,5719073 0,697177 1,434355 0 8203183 7 53 0,5861367 0,723436 1,382292 0,8102122 7
54 0,5721459 0,697610 1,433466 0 8201519 6 54 0,5863724 0,723879 1,381446 0,8100416 6
55 0,5723844 0,698042 1,432578 0 8199854 5 55 0,5866080 0,724323 1,380600 0,8098710 5
56 0,5726229 0,698475 1,431691 0 8198189 4 56 0,5868435 0,724766 1,379755 0,8097004 4
57 0,5728614 0,698908 1,430804 0 8196523 3 57 0,5870790 0,725210 1,378911 0,8095296 3
58 0,5730998 0,699341 1,429918 0 8194856 2 58 0,5873145 0,725654 1,378067 0,8093588 2
59 0,5733381 0,699774 1,429033 0 8193189 1 59 0,5875499 0,726098 1,377224 0,8091879 1
COS ctg tg sin • COS ctg tg sin
55°
54
72
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
37°
• sin g ctg COS f sin tg ctg COS
0 0,5877853 0,726543 1,376382 0,8090170 60 0 0,6018150 0,753554 1,327045 0,7986355 60
1 0,5880206 0,726987 1,375540 0,8088460 59 1 0,6020473 0,754010 1,326242 0,7984604 59
2 0,5882558 0,727432 1,374699 0,8086749 58 2 0,6022795 0,754467 1,325440 0,7982853 58
3 0,5884910 0,727877 1,373859 0,8085037 57 3 0,6025117 0,754923 1 ,324638 057981100 57
4 0,5887262 0,728322 1,373019 0,8083325 56 4 0,6027439 0,755380 1,323837 0,7979347 56
5 0,5889613 0,728767 1,372181 0,8081612 55 5 0,6029760 0,755837 1,3230.37 0,7977594 55
6 0,5891964 0,729213 1,371342 0,8079899 54 6 0,6032080 0,756294 1,322237 0,7975839 54
7 0,5894314 0,729658 1,370505 0,8078185 53 7 0,6034400 0,756751 1,321438 0,7974084 53
8 0,5896663 0,730104 1,369668 0,8076470 52 8 0,6036719 0,757209 1,320639 0,7972329 52
9 0,5899012 0,730550 1,368832 0,8074754 51 9 0,6039038 0,757667 1,319841 0,7970572 51
10 0,5901361 0,730996 1,367996 0,8073038 50 10 0,6041356 0,758125 1,319044 0,7968815 50
11 0,5903709 0,731443 1,367161 0,8071321 49 11 0,6043674 0,758583 1,318247 0,7967058 49
12 0,5906057 0,731889 1,366327 0,8069603 48 12 0,6045991 0,759041 1,317451 0,7965299 48
13 0,5908404 0,732336 1,365493 0,8067885 47 13 0,6048308 0,759500 1,316656 0,7963540 47
14 0,5910750 0,732783 1,364660 0,8066166 46 14 0,6050624 0,759959 1,315861 0,7961780 46
15 0,5913096 0,733230 1,363828 0,8064446 45 15 0,6052940 0,760418 1,315067 0,7960020 45
16 0,5915442 0,733678 1,362996 0,8062726 44 16 0,6055255 0,760877 1,314273 0,7958259 44
17 0,5917787 0,734125 1,362165 0,8061005 43 17 0,6057570 0,761336 1,313480 0,7956497 43
18 0,5920132 0,734573 1,361335 0,8059283 42 18 0,6059884 0,761796 1,312688 0,7954735 42
19 0,5922476 0,735021 1,360505 0,8057560 41 19 0,6062198 0,762256 1,311896 0,7952972 41
20 0,5924819 0,735469 1,359676 0,8055837 40 20 0,6064511 0,762716 1,311105 0,7951208 40
21 0,5927163 0,735917 1,358848 0,8054113 39 21 0,6066824 0.763176 1,310314 0,7949444 39
22 0,5929505 0,736366 1,358020 0,8052389 38 22 0,6069136 0,763636 1,309524 0,7947678 38
23 9,5931847 0,736815 1,357193 0,8050664 37 23 0,6071447 0,764097 1,308735 0,7945913 37
24 0,5934189 0,737264 1,356367 0,8048938 36 24 0,6073758 0,764558 1,307946 0,7944146 36
25 0,5936530 0,737713 1,355541 0,8047211 35 25 0,6076069 0,765019 1,307157 0,7942379 35
26 0,5938871 0,738162 1,354716 0,8045484 34 26 0,6078379 0,765480 1,306370 0,7940611 34
27 0,5941211 0,738611 1,353892 0,8043756 33 27 0,6080689 0,765941 1,305583 0,7938843 33
28 0,5943550 0,739061 1,353068 0,8042028 32 28 0,6082998 0,766403 1,304796 0,79370741 32
29 0,5945889 0,739511 1,352245 0,8040299 31 29 0,6085306 0,766865 1,304011 0,7935304 31
30 0,5948228 0,739961 1,351422 0,8038569 30 30 0.6087614 0,767327 1,303225 0,7933533 30
31 0,5950566 0,740411 1,350601 0,8036838 29 31 0,6089922 0,767789 1,302441 0,7931762; 29
32 0,5952904 0,740862 1,349779 0,8035107 28 32 0,6092229 0,768252 1,301657 0,7929990 28
33 0,5955241 0,741312 1,348959 0,8033375 27 33 0,6094535 0,768714 1,300873 0,7928218 27
34 0,5957577 0,741763 1,348139 0,8031642 26 34 0,6096841 0,769177 1,300090 0,7926445 26
35 0,5959913 0,742214 1,347320 0,8029909 25 35 0,6099147 0,769640 1,299308 0,7924671 25
36 0,5962249 0,742666 1,346501 0,8028175 24 36 0,6101452 0,770104 1,298526 0,7922896 24
37 0,5964584 0,743117 1,345683 0,8026440 23 37 0,6103756 0,770567 1,297745 0,7921121 23
38 0,5966918 0,743569 1,344866 0,8024705 22 38 0,6106060 0,771031 1,296965 0,7919345 22
39 0,5969252 0,744020 1,344049 0,8022969 21 39 0,6108363 0,771495 1,296185 0,7917569 21
40 0,5971586 0,744472 1,343233 0,8021232 20 40 0,6110666 0,771959 1,295406 0,7915792 20
41 0,5973919 0,744925 1,342418 0,8019495 19 41 0,6112969 0,772423 1,294627 0,7914014 19
42 0,5976251 0,745377 1,341603 0,8017756 18 42 0.6115270 0,772888 1,293849 0,7912235 18
43 0,5978583 0,745830 1,340789 0,8016018 17 43 0,6117572 0,773353 1,293071 0,7910456 17
44 0,5980915 0,746282 .1,339975 0,8014278 16 44 0,6119873 0,773818 1,292294 0,7908676 16
45 0,5983246 0,746735 1,339162 0,8012538 15 45 0,6122173 0,774283 1,291518 0,7906896 15
46 0,5985577 0,747189 1,338350 0,8010797 14 46 0,6124473 0,774748 1,290742 0,7905115 14
47 0,5987906 0,747642 1,337539 0,8009056 13 47 0,6126772 0,775214 1,289967 0,7903333 13
48 0,5990236 0,748096 1,336728 0,8007314 12 48 0,6129071 0,775680 1,289192 0,7901550 12
49 0,5992565 0,748549 1,335917 0,8005571 11 49 0,6131369 0,776146 1,288418 0,7899767 11
50 0,5994893 0,749003 1,335108 0,8003827 10 50 0,6133666 0,776612 1,287645 0,7897983 10
51 0,5997221 0,749458 1,334298 0,8002083 9 51 0,6135964 0,777078 1,286872 0,7896198 9
52 0,5999549 0,749912 1,333490 0,8000338 8 52 0,6138260 0,777545 1,286099 0,7894413 8
53 0,6001876 0,750366 1,332682 0,7998593 7 53 0,6140556 0,778012 1,285328 0,7892627 7
54 0,6004202 0,750821 1,331875 0,7996847 6 54 0,6142852 0,778479 1,284557 0,7890841 6
55 0,6006528 0,751276 1,331068 0,7995100 5 55 0,6145147 0,778946 1,283786 0,7889054 5
56 0,6008854 0,751731 1,330262 0,7993352 4 56 0,6147442 0,779414 1,283016 0.7887266 4
57 0,6011179 0,752187 1,329457 0,7991604 3 57 0,6149736 0,779881 1,282247 0,7885477 3
58 0,6013503 0,752642 1,328652 0,7989855 2 58 0,6152029 0,780349 1,281478 0,7883688 2
59 0,6015827 0,753098 1,327848 0,7988105 1 59 0,6154322 0,780817 1,280709 0,7881898 1
* COS ctg tg sin * » COS ctg tg sin *
53
52е
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
73
38° 39°
| sin tg ctg | cos sin tg Ctg i | cos
0 0,6156615 0,781286 1,279942 0,7880108 60 0 0,6293204 0,809784 1,234897 0,7771460 60
1 0,6158907 0,781754 1,279174 0,7878316 59 1 0,6295464 0,810266 1,234163 0,7769629 59
2 0,6161198 0,782223 1,278408 0,7876524 58 2 0,6297724 0,810748 1,233429 0,7767797 58
3 0,6163489 0,782692 1,277642 0,7874732 57 3 0,6299983 0,811230 1,232696 0,7765965 57
4 0,6165780 0,783161 1,276876 0,7872939 56 4 0,6302242 0,811712 1 ,231963 0,7764132 56
5 0,6168069 0,783631 1,276112 0,7871145 55 5 0,6304500 0,812195 1,231231 0,7762298 55
6 0,6170359 0,784100 1,275347 0,7869350 54 6 0,6306758 0,812678 1,230500 0,7760464 54
7 0,6172648 0,784570 1,274584 0,7867555 53 7 0,6309015 0,813161 1,229769 0,7758629 53
8 0,6174936 0,785040 1,273820 0,78657591 52 8 10,6311272 0,813644 1,229038 0,7756794 52
9 0,6177224 0,785510 1,273058 0,7863963 51 9 0,6313528 0,814128 1,228308 0,7754957 51
10 0,6179511 0,785981 1,272296 0,7862165 50 10 0,6315784 0,814612 1,227579 0,7753121 50
11 0,6181798 0,786451 1,271534 0,7860367 49 11 0,6318039 0,815096 1,226850 0,7751283 49
12 0,6184084 0,786922 1,270773 0,7858569 48 12 0,6320293 0,815580 1,226121 0,7749445 48
13 0,6186370 0,787394 1,270013 0,7856770 47 13 0,6322547 0,816065 1,225393 0,7747606 47
14 0,6188655 0,787865 1,269253 0,7854970 46 14 0,6324800 0,816549 1,224666 0,7745767 46
15 0,6190939 0,788336 1,268494 0,7853169 45 15 0,6327053 0,817034 1,223939 0,7743926 45
16 0,6193224 0,788808 1,267735 0,7851368 44 16 0,6329306 0,817519 1,223212 0,7742086 44
17 0,6195507 0,789280 1,266977 0,7849566 43 17 0,6331557 0,818005 1,222487 0,7740244 43
18 0,6197790 0,789752 1,266220 0,7847764 42 18 0,6333809 0,818491 1,221761 0,7738402 42
19 0,6200073 0,790225 1,265463 0,7845961 41 19 0,6336059 0,818976 1,221036 0,7736559 41
20 0,6202355 0,790697 1,264706 0,7844157 40 20 0,6338310 0,819463 1,220312 0,7734716 40
21 0,6204636 0,791170 1,263950 0,7842352 39 21 0,6310559 0,819949 1,219588 0,7732872 39
22 0,6206917 0,791643 1,263195 0,7840547 38 22 0,6342808 0,820435 1,218865 0,7731027 38
23 0,6209198 0,792117 1,262440 0,7838741 37 23 0,6345057 0,820922 1,218142 0,7729182 37
24 0,6211478 0,792590 1,261686 0,7836935 36 24 0,6347305 0,821409 1,217420 0,7727336 36
25 0,6213757 0,793064 1,260932 0,7835127 35 25 0,6349553 0,821897 1,216698 0,7725489 35
26 0,6216036 0,793538 1,260179 0,7833320 34 26 0,6351800 0,822384 1,215977 0,7723642 34
27 0,6218314 0,794012 1,259427 0,7831511 33 27 0,635-4046 0,822872 1,215256 0,7721794 33
28 0,6220592 0,794486 1,258675 0,7829702 32 28 0,6356292 0,823360 1,214536 0,7719945 32
29 0,6222870 0,794961 1,257923 0,7827892 31 29 0,6358537 0,823848 1,213816 0,7718096 31
30 0,6225146 0,795436 1,257172 0,7826082 30 30 0,6360782 0,824336 1,213097 0,7716246 30
31 0,6227423 0,795911 1,256422 0,7824270 29 31 0,6363026 0,824825 1,212378 0,7714395 29
32 0,6229698 0,796386 1,255672 0,7822459 28 32 0,6365270 0,825314 1,211660 0,7712544 28
33 0,6231974 0,796862 1,254923 0,7820646 27 33 0,6367513 0,825803 1,210942 0,7710692 27
34 0,6234248 0,797337 1,254174 0,7818833 26 34 0,6369756 0,826292 1,210225 0,7708840 26
35 0,6236522 0,797813 1,253426 0,7817019 25 35 0,6371998 0,826782 1,209509 0,7706986 25
36 0,6238796 0,798290 1,252678 0,7815205 24 36 0,6374240 0,827272 1,208792 0,7705132 24
37 0,6241069 0,798766 1,251931 0,7813390 23 37 0,6376481 0,827762 1,208077 0,7703278 23
38 0,6243342 0,799242 1,251185 0,7811574 22 38 0,6378721 0,828252 1,207362 0,7701423 22
39 0,6245614 0,799719 1,250439 0,7809757 21 39 0,6380961 0,828743 1-, 206647 0,7699567 21
40 0,6247885 0,800196 1,249693 0,7807940 20 40 0,6383201 0,829234 1,205933 0,7697710 20
41 0,6250156 0,800674 1,248948 0,7806123 19 41 0,6385440 0,829725 1,205219 0,7695853 19
42 0,6252427 0,801151 1,248204 0,7804304 18 42 0,6387678 0,830216 1,204506 0,7693996 18
43 0,6254696 0,801629 1,247460 0,7802485 17 43 0,6389916 0,830707 1,203793 0,7692137 17
44 0,6256966 0,802107 1,246717 0,7800665 16 44 0,6392153 0,831199 1,203081 0,7690278 16
45 0,6259235 0,802585 1,245974 0,7798845 15 45 0,6394390 0,831691 1,202369 0,7688418 15
46 0,6261503 0,803063 1,245232 0,7797024 14 46 0,6396626 0,832183 1,201658 0,7686558 14
47 0,6263771 0,803542 1,244490 0,7795202 13 47 0,6398862 0,832676 1,200947 0,7684697 13
48 0,6266038 0,804021 1,243749 0,7793380 12 48 0,6401097 0,833169 1,200237 0,7682835 12
49 0,6268305 0,804500 1,243009 0,7791557 11 49 0,6403332 0,833662 1,199528 0,7680973 11
50 0,6270571 0,804979 1,242268 0,7789733 10 50 0,6405566 0,834155 1,198818 0,7679110 10
51 0,6272837 0,805458 1,241529 0,7787909 9 51 0,6407799 0,834648 1,198110 0,7677246 9
52 0,6275102 0,805938 1,240790 0,7786084 8 52 0,6410032 0,835142 1,197402 0,7675382 8
53 0,6277366 0,806418 1,240052 0,7784258 7 53 0,6412264 0,835636 1,196694 0,7673517 7
54 0,6279631 0,806898 1,239314 0,7782431 6 54 0,6414496 0,836130 1,195987 0,7671652 6
55 0,6281894 0,807379 1,238576 0,7780604 5 55 0,6416728 0,836624 1,195280 0,7669785 5
56 0,6284157 0,807859 1,237839 0,7778777 4 56 0,6418958 0,837119 1,194574 0,7667918 4
57 0,6286420 0,808340 1,237103 0,7776949 3 57 0,6421189 0,837614 1,193868 0,7666051 3
58 0,6288682 0,808821 1,236367 0,7775120 2 58 0,6423418 0,838109 1,193163 0,7664183 2
59 0,6290943 0,809303 1,235632 0,7773290 1 59 0,6425647 0,838604 1,192458 0,7662314 1
* COS ctg tg sin COS ctg tg sin t
51
50
7,1
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
40° 41°
f sin tg ctg | COS * • sin tg ctg COS •
0 0,6427876 0,839100 1,191754 0,7660444 60 0 0,6560590 0,869287 1,150368 0,7547096 60
1 0,6430104 0,839595 1,191050 0,7658574 59 1 0,6562785 0,869798 1,149693 0,7545187 59
2 0,6432332 0,840092 1,190347 0,7656704 58 2 0,6564980 0,870309 1,149018 0,7543278 58
3 0,6434559 0,840588 1,189644 0,7654832 57 3 0,6567174 0,870820 1,148343 0,7541368 57
4 0,6436785 0,841084 1,188941 0,7652960 56 4 0,6569367 0,871332 1,147669 0,7539457 56
5 0,6439011 0,841581 1,188240 0,7651087 55 5 0,6571560 0,871843 1,146995 0,7537546 55
6 0,6441236 0,842078 1,187538 0,7649214 54! 6 0,6573752 0,872356 1,146322 0,7535634 54
7 0.6443461 0,842575 1,186837 0,7647340 53 7 0,6575944 0,872868 1,145649 0,7533721 53
810.6445685 0,843073 1,186137 0,7645465 52 8 0,6578135 0,873.381 1,144976 0,7531808 52
9 0,6447909 0,843571 1,185-137 0,7643590 51 9 0,6580326 0,873894 1,144304 0,7529894 51
10 0,6450132 0,844069 1,184738 0,7641714 50 10 0,6582516 0,874407 1,143633 0,7527980 50
11 0,6452355 0,844567 1,184039 0,7639838 49 11 0,6584706 0,874920 1,142961 0,7526065 49
12 0,6454577 0,845066 1,183340 0,7637960 48 12 0,6586895 0,875434 1,142291 0,7524149 48
13 0,6456798 0,845564 1,182642 0,7636082 47 13 0,6589083 0,875948 1,141621 0,7522233 47
14 0 6459019 0,846063 1,181945 0,7634204 46 14 0,6591271 0,876462 1,140951 0,7520316 46
15 0,6461240 0,846562 1,181248 0 ,7632325 45 15 0,6593458 0,876976 1,140281 0,7518398 45
16 0,6463460 0,847062 1,180551 0,7630445 44 16 0,6595645 0,877491 1,139613 0,7516480 44
17 0,6465679 0,847562 1,179855 0,7628564 43 17 0,6597831 0,878006 1,138944 0,7514561 43
18 0,6467898 0,848062 1,179160 0,7626683 42 18 0,6600017 0,878521 1,138276 0,7512641 42
19 0,6470116 0,848562 1,178464 0,7624802 41 19 0,6602202 0,879037 1,137609 0,7510721 41
20 0,6472334 0,849062 1,177770 0,7622919 40 20 0,6604386 0,879553 1,136941 0,7508800 40
21 0,6474551 0,849563 1,177076 0,7621036 39 21 0,6606570 0,880069 1,136275 0,7506879 39
22 0,6476767 0,850064 1,176382 0,7619152 38 22 0,6608754 0,880585 1,135609 0,7504957 38
23 0,6478984 0,850565 1,175689 0,7617268 37 23 0,6610936 0,881102 1,134943 0,7503034 37
24 0,6481199 0,851067 1,174996 0,7615383 36 24 0,6613119 0,881619 1,134277 0,7501111 36
25 0,6483414 0,851568 1,174304 0,7613497 35 25 0,6615300 0,882136 1,133612 0,7499187 35
26 0,6485628 0,852070 1,173612 0,7611611 34 26 0,6617482 0,882653 1,132948 0,7497262 34
27 0,6487812 0,852573 1,172921 0,7609724 33 27'0,6619662 0,883171 1,132284 0,7495337 33
28 0,6490056 0,853075 1,172230 0,7607837 32 2810.6621842 0,883689 1,131620 0,7493411 32
29 0,6492268 0,853578 1,171539 0,7605949 31 29 0,6624022 0,884207 1,130957 0,7491484 31
30 0,6494480 0,854081 1,170850 0,7604060 30 30 0,6626200 0,884725 1,130294 0,7489557 30
31 0,6496692 0,854584 1,170160 0,7602170 29 31 0,6628379 0,885244 1,129632 0,7487629 29
32 0,6498903 0,855087 1,169471 0,7600280 28 32 0,6630557 0,885763 1,128970 0,7485701 28
33 0,6501114 0,855591 1,168783 0,7598389 27 33 0,6632734 0,886282 1,128309 0,7483772 27
34 0,6503324 0,856095 1,168095 0,7596498 26 34 0,6634910 0,886802 1,127648 0,7481842 26
35 0,6505533 0,856599 1,167407 0,7594606 25 35 0,6637087 0,887321 1,126987 0,7479912 25
36 0,6507742 0,857104 1,166720 0,7592713 24 36 0,6639262 0,887842 1,126327 0,7477981 24
37 0,6509951 0,857608 1,166033 0,7590820 23 37 0,6641437 0,888362 1,125667 0,7476049 23
38 0,6512158 0,858113 1,165347 0,7588926 22 38 0,6643612 0,888882 1,125008 0,7474117 22
39 0,6514366 0,858619 1,164662 0,7587031 21 39 0,6645785 0,889403 1,124349 0,7472184 21
40 0,6516572 0,859124 1,163976 0,7585136 20 40 0,6647959 0,889924 1,123691 0,7470251 20
41 0,6518778 0,859630 1,163292 0,7583240 19 41 0,6650131 0,890446 1,123033 0,7468317 19
42 0,6520984 0,860136 1,162607 0,7581343 18 42 0,6652304 0,890967 1,122375 0,7466382 18
43 0,6523189 0,860642 1,161923 0 7579446 17 43 0,6654475 0,891489 1,121718 0,7464446 17
44 0,6525394 0,861148 1,161240 0,7577548 16 44 0,6656646 0,892012 1,121062 0,7462510 16
45 0,6527598 0,861655 1,160557 0,7575650 15 45 0,6658817 0,892534 1,120405 0,7460574 15
46 0,6529801 0,862162 1,159875 0,7573751 14 46 0,6660987 0,893057 1,119750 0,7458636 14
47 0,6532004 0,862669 1,159193 0,7571851 13 47 0,6663156 0,893580 1,119094 0,7456699 13
48 0,6534206 0,863177 1,158511 0,7569951 12 48 0,6665325 0,894103 1,118439 0,7454760 12
49 0,6536408 0,863685 1,157830 0,7568050 11 49 0,6667493 0,894627 1,117785 0,7452821 11
50 0,6538609 0,864193 1,157149 0,7566148 10 50 0,6669661 0,895151 1,117130 0,7450881 10
51 0,6540810 0,864701 1,156469 0,7564246 9 51 0,6671828 0,895675 1,116477 0,7448941 9
52 0,6543010 0,865209 1,155790 0,7562343 8 52 0,6673994 0,896199 1,115823 0,7446999 8
53 0,6545209 0,865718 1,155110 0,7560439 7 53 0,6676160 0,896724 1,115171 0,7445058 7
54 0,6547408 0,866227 1,154432 0,7558535 6 54 0,6678326 0,897249 1,114518 0,7443115 6
55 0,6549607 0,866736 1,153753 0,7556630 5 55 0,6680490 0,897774 1,113866 0,7441173 5
56 0,6551804 0,867246 1,153075 0,7554724 4 56 0,6682655 0,898299 1,113215 0,7439229 4
57 0,6554002 0,867756 1,152398 0,7552818 3 57 0,6684818 0,898825 1,112563 0 7437285 3
58 0,6556198 0,868266 1,151721 0,7550911 2 58 0,6686981 0,899351 1,111913 0,7435340 2
59 0,6558395 0,868776 1,151044 0,7549004 1 59 0,6689144 0,899877 1,111262 0,7433394 *
COS | ctg tg sin • COS ctg tg sin
49
48
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
75
43°
sin tg I Ctg cos * * sin tg Ctg cos
о
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
,6691306
,6693468
,6695628
,6697789
,6699948
,6702108
,6704266
,6706424
,6708582
,6710739
,6712895
,6715051
,6717206
,6719361
,6721515
,6723668
,6725821
,6727973
,6730125
|,6732276
1,6734427
,6736577
1,6738727
56740876
56743024
1,6745172
1,6747319
1,6749466
1,6751612
1,6753757
1,6755902
1,6758046
1,6760190
1,6762333
1,6764476
1,6766618
1,6768760
1,6770901
1,6773041
1,6775181
1,6777320
1,6779459
1,6781597
1,6783734
1,6785871
1,6788007
1,6790143
1,6792278
1,6794413
9,6796547
0,6798681
0,6800813
,6802946
,6805078
6807209
0,6809339
0,6811469
0,6813599
0,6815728
0,6817856
0,900404
0,900931
0,901458
0,901985
0,902513
0,903041
0,903569
0,904098
0,904627
0,905156
0 905635
0,906215
0,906745
0,907275
0,907805
0,908336
О 908867
0,909398
0,909930
0,910462
0,910994
0,911526
0,912059
0,912592
0,913125
0,913659
0,914193
0,914727
0,915261
0,915796
0,916331
0,916866
О 917402
0,917038
О 918474
0,919010
0,919547
0,920084
О 920621
0,921159
0,921697
0,922235
0,922773
0,923312
0,923851
0,924390
0,924930
0,925470
0,926010
0,926551
О 927091
О 927632
0,928174
О 928715
0,929257
0,929800
0,930342
О 930885
О 931428
0,931971
1,110613 0,7431448
1,109963 0,7429502
1,109314 0,7427554
1,108665 0,7425606
1,108017 0,7423658
1,107369 0,7421708
1,106722 0,7419758
1,106075 0,7417808
1,105428 0,7415857
1,104782 0,7413905
1,104137 0,7411953
1,103491 0,7410000
1,102846 0,7408046
1,102202 0,7406092
1,101558 0,7404137
1,100914 0,7402181
1,100271 0,7400225
1,099628 0,7398268
1,098986 0,7396311
1,098344 0,7394353
1,097702
1,097061
1,096420
1,095780
1,095140
1,094500
1,093861
1,093222
1,092584
1,091946
1,091309
1,090671
1,090035
1,089398
1,088762
1,088127
1,087492
1,086857
1,086223
1,085589
1,084955
1,084322
1,083690
1,083057
1,082425
1,081794
1 081163
1,080532
1,079902
1,079272
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
43
42
41
О
1
2
3
4
0,6819984
0,6822111
0,6824237
0,6826363
0,6828489
5 0,6830613
6 0,6832738
7 0,6834861
8 10,6336984
9 [0,6839107
10 10,6841229
11(0,6843250
1210,6845471
1310,6847591
14
15
16
17
18
19
0,6849711
0,6851830
0,6853248
0,6856066
|0,6858184
0,6860300
0,932515
0,933059
0,933603
0,934148
0,934693
0,935238
0,935783
0,936329
0,936875
0,937422
0,937968
0,938515
0,939063
0,939610
0,940158
0,940706
0,941255
0,941803
0,942352
0,942902
1,072369
1,071744
1,071119
1,070494
1,069870
1,069247
1,068623
1,068000
1,067378
1,066756
1,066134
1,065513
1,064892
1,064271
1,063651
1,063031
1,062412
1,061793
1,061174
1,060556
0,7313537
0,7311553
0,7309568
0,7307583
0,7305597
0,7303610
0,7301623
О 7299635
0,7297646
0,7295657
0,7293668
0,7291677
0,7289686
0,7287695
0,7285703
0,7283710
0,7281716
О 7279722
О 7277728
0,7275732
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46.
45
44
43
42
41
0,7392394
0,7390435
0,7388475
0,7386515
0,7384553
0,7382592
О 7380629
0,7378666
0,7376703
0,7374738
0,7372773
0,7370808
0,7368842
0,7366875
0,7364908
0,7362940
0,7360971
0,7359002
0,7357032
0,7355061
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
0,6862416
0,6864532
0,6866647
0,6868761
0,6870875
[0,6872988
0,6875101
0,6877213
0,6879325
0,6881435
0,6883546
0,6885655
0,6887765
0,6889873
0,6891981
0,6894089
0,6896195
0,6898302
38 0,6900407
39 0,6902512
0,943451
0,944001
0,944552
0,945102
0,945653
0,946204
0,946756
0,947307
0,947859
0,948412
0,948965
0,949518
0,950071
0,950624
0,951178
0,951733
0,952287
0,952842
0,953397
0,953953
0,7353090
0,7351118
0,7349146
0,7347173
0,7345199
0,7343225
0,7341250
0,7339275
0,7337299
0,7335322
20
19
18
17
16
15
14
13
12
11
40
41
42
43
44
45
46
47
48
49
0,6904617
0,6906721
0,6908824
0,6910927
0,6913029
0,6915131
0,6917232
0,6919332
0,6921432
0,6923531
0,954508
0,955064
0,955621
0,956177
0,956734
0,957292
0,957849
0,958407
0,958966
0,959524
1,078642 0,7333345
1,078013 0,7331367
1,077384 0,7329388
1,076756 0,7327409
1,076128 0,7325429
1,075501 0,7323449
1,074873 0,7321467
1,074247 0,7319486
1,073620 0,7317503
1,072994 0,7315521
10
9
8
7
6
5
4
3
2
1
50
51
52
53
54
55
56
57
58
59
0,6925630
0,6927728
0,6929825
0,6931922
0,6934018
0,6936114
0,6938209
0,6940304
0,6942398
0,6944491
0,960083
0,960642
0,961202
0,961761
0,962322
0,962882
0,963443
0,964004
0,964565
0,965127
1,059938
1,059321
1,058703
1,058087
1,057470
1,056854
1,056239
1,055624
1,055009
1,054394
1,053780
1,053166
1,052553
1,051940
1,051328
1,050715
1,050103
1,049492
1,048881
1,048270
1,047660
1,047050
1,046440
1,045831
1,045222
1,044614
1,044006
1,043398
1,042790
1,042183
1,041577
1,040970
1,040364
1,039759
1,039154
1,038549
1,037944
1,037340
1,036737
1,036133
0,7273736
0,7271740
0,7269743
0,7267745
0,7265747
0,7263748
0,7261748
0,7259748
0,7257747
0,7255746
0,7253744
0,7251741
0,7249738
0,7247734
0,7245729
0,7243724
0,7241719
0,7239712
0,7237705
0,7235698
0,7233690
0,7231681
0,7229671
О 7227661
0,7225651
0,7223640
0,7221628
0,7219615
0,7217602
0,7215589
0,7213574
0,7211559
0,7209544
О 7207528
О 7205511
0,7203494
0,7201476
0,7199457
О 7197438
0,7195418
cos Ctg tg sin | '
cos ctg tg
sin
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
47
46
76
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
44° 44°
'1 sin tg | ctg | COS sin | tg | ctg | cos | f
0 0,6946584 0,965689 1,035530 0,7193398 60 30 0,7009093 0,982697 1,017607 0,7132504 30
1 0,6948676 0,966251 1,034928 0,7191377 59 31 0,7011167 0,983269 1,017015 0,7130465 29
2 0,6950767 0,966814 1,034325 0,7189355 58 32 0,7013241 0,983842 1,016424 0,7128426 28
3 0,6952858 0,967377 1,033724 0,7187333 57 33 0,7015314 0,984414 1,015833 0,7126385 27
4 0,6954949 0,967940 1,033122 0,7185310 56 34 0,7017387 0,984987 1,015242 0,7124344 26
5 0,6957039 0,968504 1,032521 0,7183287 55 35 0,7019459 0,985560 1,014651 0,7122303 25
6 0,6959128 0,969067 1,031920 0,7181263 54 36 0,7021531 0,986134 1,014061 0,7120260 24
7 0,6961217 0,969632 1,031319 0,7179238 53 37 0,7023601 0,986708 1,013471 0,7118218 23
8 0,6963305 0,970196 1,030719 0,7177213 52 38 0,7025672 0,987282 1,012882 0,7116174 22
9 0,6965392 0,970761 1,030120 0,7175187 51 39 0,7027741 0,987857 1,012293 0,7114130 21
10 0,6967479 0,971326 1,029520 0,7173161 50 40 0,7029811 0,988432 1,011704 0,7112086 20
11 0,6969565 0,971892 1,028921 0,7171134 49 41 0,7031879 0,989007 1,011115 0,7110041 19
12 0,6971651 0,972458 1,028323 0,7169106 48 42 0,7033947 0,989582 1,010527 0,7107995 18
13 0,6973736 0,973024 1,027724 0,7167078 47 43 0,7036014 0,990158 1,009939 0,7105948 17
14 0,6975821 0,973590 1,027126 0,7165049 46 44 0,7038081 0,990735 1,009352 0,7103901 16
15 0,6977905 0,974157 1,026529 0,7163019 45 45 0,7040147 0,991311 1,008765 0,7101854 15
16 0,6979988 0,974724 1,025931 0,7160989 44 46 0,7042213 0,991888 1,008178 0,7099806 И
17 0,6982071 0,975291 1,025335 0,7158959 43 47 0,7044278 0,992465 1,007592 0,7097757 13
18 0,6984153 0,975859 1,024738 0,7156927 42 48 0,7046342 0,993043 1,007006 0,7095707 12
19 0,6986234 0,976427 1,024142 0,7154895 41 49 0,7048406 0,993621 1,006420 0,7093657 11
20 0,6988315 0,976996 1,023546 0,7152863 40 50 0,7050469 0,994199 1,005835 0,7091607 10
21 0,6990396 0,977564 1,022951 0,7150830 39 51 0,7052532 0,994778 1,005250 0,7089556 9
22 0,6992476 0,978133 1,022356 0,7148796 38 52 0,7054594 0,995357 1,004665 0,7087504 8
23 0,6994555 0,978703 1,021761 0,7146762 37 53 0,7056655 0,995936 1,004081 0,7085451 7
24 0,6996633 0,979272 1,021166 1,020572 0,7144727 36 54 0,7058716 0,996515 1,003497 0,7083398 6
25 0,6998711 0,979842 0,7142691 35 55 0,7060776 0,997095 1,002913 0,7081345 5
26 0,7000789 0,980413 1,019979 0,7140655 34 56 0,7062835 0,997676 1,002330 0,7079291 4
27 0,7002866 0,980983 1,019385 0,7138618 33 57 0,7064894 0,998256 1,001747 0,7077236 3
28 0,7004942 0,981554 1,018792 0,7136581 32 58 0,7066953 0,998837 1.001164 0,7075180 2
29 0,7007018 0,982126 1,018200 0,7134543 31 59 0,7069011 0,999418 1,000582 0,7073124 1
30 0,7009093 0,982697 1,017607 0,7132504 30 60 0,7071068 1,000000 1,000000 0,7071068 0
cos | ctg I tg | sin I ' || ' I cos | ctg | tg | sin | '
‘“45° 45s
Таблица 4. ПЕРЕВОД ГРАДУСНОЙ МЕРЫ В РАДИАННУЮ
(длина дуг окружности радиуса 1)
Угол Дуга Угол Дуга | Угол Дуга Угол | Дуга Угол Дуга Угол Дуга
1" 0,000005 20" 0,000097 | 7' 0,002036 2° 0,034907 20° 0,349066 120° 2,094395
2" 0,000010 30" 0,000145 8' 0,002327 3° 0,052360 30° 0,523599 150° 2,617994
3" 0,000015 40" 0,000194 9' 0,002618 4° 0,069813 40° 0,698132 180° 3,141593
4" 0,000019 50" 0,000242 10' 0,002909 5° 0,087266 50° 0,872665 200° 3,490659
5" 0,000024 1' 0,000291 20' 0,005818 6° 0,104720 60° 1,047198 250° 4,363323
6" 0,000029 2' 0,000582 30' 0,008727 7° 0,122173 70° 1,221730 270° 4,712389
7" 0,000034 3' 0,000873 ' 40' 0,011636 8° 0,139626 80° 1,396263 300° 5,235988
8" 0,000039 4' 0,001164 50' 0,014544 9° 0,157080 90° 1,570796 360° 6,283185
9" 0,000044 5' 0,001454 1° 0,017453 10° 0,174533 100° 1,745329 400° 6,981317
10" 0,000048 6' 0,001745
Таблица 5. ПЕРЕВОД РАДИАННОЙ МЕРЫ В ГРАДУСНУЮ
Ради- Градусная мера Ради- Градусная мера Ради- Градусная мера Ради- Градусная мера
анная анная 1 анная анная
мера ° 1 1 * мера ° 1 1 " мера ° 1 ' 1 и мера “ 1 ' 1 -
1,о 57 17 44,8 0,07 4 0 38,5 0,004 0 13 45,1 0,0002 0 0 41,3
0,9 51 33 58,3 0,06 3 26 15,9 0,003 0 10 18,8 0,0001 0 0 20,6
0,8 45 50 11,8 0,05 2 51 53,2 0,002 0 6 52,5 0,00009 0 0 18,6
0,7 40 6 25,4 0,04 2 17 30,6 0,001 0 3 26,3 0,00008 0 0 16,5
0,6 34 22 38,9 0,03 1 43 7,9 0,0009 0 3 5,6 0,00007 0 0 14,4
0,5 28 38 52,4 0,02 1 8 45,3 0,0008 0 2 45,0 0,00006 0 0 12,4
0,4 22 55 5,9 0,01 0 34 22,6 0,0007 0 2 24,4 0,00005 0 0 10,3
0,3 17 11 19,4 0,009 0 30 56,4 0,0006 0 2 3,8 0,00004 0 0 8,3
0,2 11 27 33,0 0,008 0 27 30,1 0,0005 0 1 43,1 0,00003 0 0 6,2
0,1 5 43 46,5 0,007 0 24 3,9 0,0004 0 1 22,5 0,00002 0 0 4,1
0,09 5 9 23,8 0,006 0 20 37,6 0,0003 0 1 1,9 0,00001 0 0 2,1
0,08 4 35 1,2 0,005 0 17 11,3
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
77
Таблица б. ДЛИНА ДУГИ И ХОРДЫ, СТРЕЛКА И ПЛОЩАДЬ СЕГМЕНТА
ДЛЯ КРУГА РАДИУСА, РАВНОГО ЕДИНИЦЕ
Центр, угол в град. Длина Дуги 1 Стрел- ка Л J- Л Длина хорды $ Площадь сегмента Центр, угол В град. Длина дуги 1 Стрел- ка h 1 h Длина хорды S Площадь сегмента
1 0,0175 0,0000 458,36 0,0175 0,00000 51 0,8901 0,0974 9,14 0,8610 0,05649
2 0,0349 0,0002 229,19 0,0349 0,00000 52 0,9076 0,1012 8,97 0,8767 0,05978
3 0,0524 0,0003 152,79 0,0524 0,00001 53 0,9250 0,1051 8,80 0,8924 0,06319
4 0,0698 0,0006 114,60 0,0698 0,00003 54 0,9425 0,1090 8,65 0,9080 0,06673
5 0,0873 0,0010 91,69 0,0872 0,00006 55 0,9599 0,1130 8,49 0,9235 0,07039
6 0,1047 0,0014 76,41 0,1047 0,00010 56 0,9774 0,1171 8,35 0,9389 0,07417
7 0,1222 0,0019 64,01 0,1221 0,00015 57 0,9948 0,1212 8,21 0,9543 0,07808
8 0,1396 0,0024 56,01 0,1395 0,00023 58 1,0123 0,1254 8,07 0,9696 0,08212
9 0,1571 0,0031 50,96 0,1569 0,00032 59 1,0297 0,1296 7,94 0,9848 0,08629
10 0,1745 0,0038 45,87 0,1743 0,00044 60 1,0472 0,1340 7,81 1,0000 0,09059
11 0,1920 0,0046 41,70 0,1917 0,00059 61 1,0647 0,1384 7,69 1,0151 0,09502
12 0,2094 0,0055 38,23 0,2091 0,00076 62 1,0821 0,1428 7,56 1,0301 0,09958
13 0,2269 0,0064 35,28 0,2264 0,00097 63 1,0996 0,1474 7,46 1,0450 0,10428
14 0,2443 0,0075 32,78 0,2437 0,00121 64 1,1170 0,1520 7,35 1,0598 0,10911
15 0,2618 0,0086 30,60 0,2611 0,00149 65 1,1345 0,1566 7,24 1,0746 0,11408
16 0,2793 0,0097 28,04 0,2783 0,00181 66 1,1519 0,1613 7,14 1,0893 0,11919
17 0,2967 0,0110 27,01 0,2956 0,00217 67 1,1694 0,1661 7,04 1,1039 0,12443
18 0,3142 0,0123 25,35 0,3129 0,00257 68 1,1868 0,1710 6,94 1,1184 0,12982
19 0,3316 0,0137 24,17 0,3301 0,00302 69 1,2043 0,1759 6,85 1,1328 0,13535
20 0,3491 0,0152 22,98 0,3473 0,00352 70 1,2217 0,1808 6,76 1,1472 0,14102
21 0,3665 0,0167 21,95 0,3645 0,00408 71 1,2392 0,1859 6,67 1,1614 0,14683
22 0,3840 0,0184 20,90 0,3816 0,00468 72 1,2566 0,1910 6,58 1,1756 0,15279
23 0,4014 0,0201 20,00 0,3987 0,00535 73 1,2741 0,1961 6,50 1,1896 0,15889
24 0,4189 0,0219 19,17 0,4158 0,00607 74 1,2915 0,2014 6,41 1,2036 0,16514
25 0,4363 0,0237 18,47 0,4329 0,00686 75 1,3090 0,2066 6,34 1,2175 0,17154
26 0,4538 0,0256 17,71 0,4499 0,00771 76 1,3265 0,2120 6,26 1,2313 0,17808
27 0,4712 0,0276 17,06 0,4669 0,00862 77 1,3439 0,2174 6,18 1,2450 0,18477
28 0,4887 0,0297 16,45 0,4838 0,00961 78 1,3614 0,2229 6, 11 1,2586 0,19160
29 0,5061 0,0319 15,89 0,5008 0,01067 79 1,3788 0,2284 6,04 1,2722 0,19859
30 0,5236 0,0341 15,37 0,5176 0,01180 80 1,3963 0,2340 5,97 1,2856 0,20573
31 0,5411 0,0364 14,88 0,5345 0,01301 81 1,4137 0,2396 5,90 1,2989 0,21301
32 0,5585 0,0387 14,42 0,5513 0,01429 82 1,4312 0,2453 5,83 1,3121 0,22045
33 0,5760 0,0412 13,99 *0,5680 0,01566 83 1,4486 0,2510 5,77 1,3252 0,22804
34 0,5934 0,0437 13,58 0,5847 0,01711 84 1,4661 0,2569 5,71 1,3383 0,23578
35 0,6109 0,0463 13,20 0,6014 0,01864 85 1,4835 0,2627 5,65 1,3512 0,24367
36 0,6283 0,0489 12,84 0,6180 0,02027 86 1,5010 0,2686 5,59 1,3640 0,25171
37 0,6458 0,0517 12,50 0,6346 0,02198 87 1,5184 0,2746 5,53 1,3767 0,25990
38 0,6632 0,0545 12,17 0,6511 0,02378 88 1,5359 0,2807 5,47 1,3893 0,26825
39 0,6807 0,0574 11,87 0,6676 0,02568 89 1,5533 0,2867 5,42 1,4018 0,27675
40 0,6981 0,0603 11,58 0,6840 0,02767 90 1,5708 0,2929 5,36 1,4142 0,28540
41 0/7156 0,0633 11,30 0,7004 0,02976 91 1,5882 0,2991 5,31 1,4265 0,29420
42 0,7330 0,0664 11,04 0,7167 0,03195 92 1,6057 0,3053 5,26 1,4387 0,30316
43 0,7505 0,0696 10,78 0,7330 0,03425 93 1,6232 0,3116 5,21 1,4507 0,31226
44 0,7679 0,0728 10,55 0,7492 0,03664 94 1,6406 0,3180 5,16 1,4627 0,32152
45 0,7854 0,0761 10,32 0,7654 0,03915 95 1,6581 0,3244 5,11 1,4746 0,33093
46 0,8029 0,0795 10,10 0,7815 0,04176 96 1,6755 0,3309 5,06 1,4863 0,34050
47 0,8203 0,0829 9,89 0,7975 0,04448 97 1,6930 0,3374 5,02 1,4979 0,35021
48 0,8378 0,0865 9,69 0,8135 0,04731 98 1,7104 0,3439 4,97 1,5094 0,36008
49 0,8552 0,0900 9,50 0,8294 0,05025 99 1,7279 0,3506 4,93 1,5208 0,37009
50 0,8727 0,0937 9,31 0,8452 0,05331 100 1,7453 0,3572 4,89 1,5321 0,38026
78
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Продолжение
Центр, угол в град. Длина ДУГИ 1 Стрел- ка h J- h Длина хорды S Площадь сегмента Центр, угол в град. Длина Дуги 1 Стрел- ка h h Длина хорды S Площадь сегмента
101 1,7628 0,3639 4,84 1,5432 0,39058 141 2,4609 0,6662 3,69 1,8853 0,91580
102 1,7802 0,3707 4,80 1,5543 0,40104 142 2,4784 0,6744 3,67 1,8910 0,93135
103 1,7977 0,3775 4,76 1,5652 0,41166 143 2,4958 0,6827 3,66 1,8966 0,94700
104 1,8151 0,3843 4,72 1,5760 0,42242 144 2,5133 0,6910 3,64 1,9021 0,96274
105 1,8326 0,3912 4,68 1,5867 0,43333 145 2,5307 0,6993 3,62 1,9074 0,97858
106 1,8500 0,3982 4,65 1,5973 0,44439 146 2,5482 0,7076 3,60 1,9126 0,99449
107 1,8675 0,4052 4,61 1,6077 0,45560 147 2,5656 0,7160 3,58 1,9176 1,01050
108 1,8850 0,4122 4,57 1,6180 0,46695 148 2,5831 0,7244 3,57 1,9225 1,02658
109 1,9024 0,4193 4,54 1,6282 0,47845 149 2,6005 0,7328 3,55 1,9273 1,04275
но 1,9199 0,4264 4,50 1,6383 0,49008 150 2,6180 0,7412 3,53 1,9319 1,05900
111 1,9373 0,4336 4,47 1,6483 0,50187 151 2,6354 0,7496 3,52 1,9363 1,07532
112 1,9548 0,4408 4,43 1,6581 0,51379 152 2,6529 0,7581 3,50 1,9406 1,09171
113 1,9722 0,4481 4,40 1,6678 0,52586 153 2,6704 0,7666 3,48 1,9447 1,10818
114 1,9897 0,4554 4,37 1,6773 0,53806 154 2,6878 0,7750 3,47 1,9487 1,12472
115 2,0071 0,4627 4,34 1,6868 0,55041 155 2,7053 0,7836 3,45 1,9526 1,14132
116 2,0246 0,4701 4,31 1,6961 0,56289 156 2,7227 0,7921 3,44 1,9563 1,15799
117 2,0420 0,4775 4,28 1,7053 0 57551 157 2,7402 0,8006 3,42 1,9598 1,17472
118 2,0595 0,4850 4,25 1,7143 0,58827 158 2,7576 0,8092 3,41 1,9633 1,19151
119 2,0769 0,4925 4,22 1,7233 0,60116 159 2,7751 0,8178 3,39 1,9665 1,20835
120 2,0944 0,5000 4-, 19 1,7321 0,61418 160 2,7925 0,8264 3,38 1,9696 1,22525
121 2,1118 0,5076 4,16 1,7407 0,62734 161 2,8100 0,8350 2,37 1,9726 1,24221
122 2,1293 0,5152 4,13 1,7492 0,64063 162 2,8274 0,8436 3,35 1,9754 1,25921
123 2,1468 0,5228 4,11 1,7576 0,65404 163 2,8449 0,8522 3,34 1,9780 1,27626
124 2,1642 0,5305 4,08 1,7659 0,66759 164 2,8623 0,8608 3,33 1,9805 1,29335
125 2,1817 0,5383 4,05 1,7740 0,68125 165 2,8798 0,8695 3,31 1 ,9829 1,31049
126 2,1991 0,5460 4,03 1,7820 0,69505 166 2,8972 0,8781 3,30 1,9851 1,32766
127 2,2166 0,5538 4,00 1,7899 0,70897 167 2,9147 0,8868 3,28 1,9871 1,34487
128 2,2340 0,5616 3,98 1,7976 0,72301 168 2,9322 0,8955 3,27 1,9890 1,36212
129 2,2515 0,5695 3,95 1,8052 0,73716 169 2,9496 0,9042 3,26 1,9908 1,37940
130 2,2689 0,5774 3,93 1,8126 0,75144 170 2,9671 0,9128 3,25 1,9924 1,39671
131 2,2864 0,5853 3,91 1,8199 0,76584 171 2,9845 0,9215 3,24 1,9938 1,41404
132 2,3038 0,5933 3,88 1,8271 0,78034 172 3,0020 0,9302 3,23 1,9951 1,43140
133 2,3213 0,6013 3,86 1,8341 0,79497 173- 3,0194 0,9390 3,22 1,9963 1,44878
134 2,3387 0,6093 3,84 1,8410 0,80970 174 3,0369 0,9477 3,20 1,9973 1,46617
135 2,3562 0,6173 3,82 1,8478 0,82454 175 3,0513 0,9564 3,19 1,9981 1,48359
136 2,3736 0,6254 3,80 1,8544 0,83949 176 3,0718 0,9651 3,18 1,9988 1,50101
137 2,3911 0,6335 3,77 1,8608 0,85455 177 3,0892 0,9738 3,17 1,9993 1,51845
138 2,4086 0,6416 3,75 1,8672 0,86971 178 3,1067 0,9825 3,16 1,9997 1,53589
139 2,4260 0,6498 3,73 1,8733 0,88497 179 3,1241 0,9913 3,15 1,9999 1,55334
140 2,4435 0,6580 3,71 1,8794 0,90034 180 3,1416 1,0000 3,14 2,0000 1,57080,
Радиус г для заданной длины дуги I н стрелки h определяется по формуле r=l'.l0, где f0—
длина дуги, которая при радиусе, равном 1, соответствует заданному отношению l:h. Если г—
радиус круга и е—центральный угол в градусах, то имеем:
1) длина хорды : s = 2г sin J
2) стрелка : h=т (1—cos-^— ) = tg = 2r sin3 ;
3) длина дуги : / = лг —~т=О,О17453г<? ^1/ sa4—h3 (приблизительно);
I ©U f 3
4) площадь сегмента равна 9“ sin 9 h
2 \180 /
5) » сектора равна №=0,00872665?ra.
6) ( = r соответствует <p=57°17'44,8O6" = 57,2957795° = 2O6 264,806".
7) arc 1° : 180=0,017 453 292 52; Ig arc l°=0,241877368-2;
8) arc 1' : 10800 = 0,000 290 *88 21; Ig arc l' = 0,463726117-4;
9) arc 1"=я : 648000=0,000004 848 14; Ig arc l" = 0,685574867-6.
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
79
Таблица 7. ПОКАЗАТЕЛЬНЫЕ И ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
X е* shx chx thx х | е* | е х | shx chx | thx
0,00 1,00000 1,00000 0,00000 1,00000 0,00000 01 1,01005 0,99005 0,01000 1,00005 0,01000 02 1,02020 0,98020 0,02000 1,00020 0,02000 03 1,03045 0,97045 0,03000 1,00045 0,02999 04 1,04081 0,96079 0,04001 1,00080 0,03998 05 1,05127 0,95123 0,05002 1,00125 0,04996 Об 1,06184 0,94176 0,06004 1,00180 0,05993 07 1,07251 0,93239 0,07006 1,00245 0,06989 08 1,08329 0,92312 0,08009 1,00320 0,07983 09 1,09417 0,91393 0,09012 1,00405 0,08976 0,10 1,10517 0,90484 0,10017 1,00500 0,09967 11 1,11628 0,89583 0,11022 1,00606 0,10956 12 1,12750 0,88692 0,12029 1,00721 0,11943 13 1,13883 0,87810 0,13037 1,00846 0,12927 14 1,15027 0,86936 0,14046 1,00982 0,13909 15 1,16183 0,86071 0,15056 1,01127 0,14889 16 1,17351 0,85214 0,16068 1,01283 0,15865 17 1,18530 0,84366 0,17082 1,01448 0,16838 18 1,19722 0,83527 0,18097 1,01624 0,17808 19 1,20925 0,82696 0,19115 1,01810 0,18775 0,20 1,22140 0,81873 0,20134 1,02007 0,19738 21 1,23368 0,81058 0,21155 1,02213 0,20697 22 1,24608 0,80252 0,22178 1,02430 0,21652 23 1,25860 0,79453 0,23203 1,02657 0,22603 24 1,27125 0,78663 0,24231 1,02894 0,23550 25 1,28403 0,77880 0,25261 1,03141 0,24492 26 1,29693 0,77105 0,26294 1,03399 0,25430 27 1,30996 0,76338 0,27329 1,03667 0,26362 28 1,32313 0,75578 0,28367 1,03946 0,27291 29 1,33643 0,74826 0,29408 1,04235 0,28213 0,30 1,34986 0,74082 0,30452 1,04534 0,29131 31 1,36343 0,73345 0,31499 1,04844 0,30044 32 1,37713 0,72615 0,32549 1,05164 0,30951 33 1,39097 0,71892 0,33602 1,05495 0,31852 34 1,40495 0,71177 0,34659 1,05836 0,32748 35 1,41907 0,70469 0,35719 1,06188 0,33638 36 1,43333 0,69768 0,36783 1,06550 0,34521 37 1,44773 0,69073 0,37850 1,06923 0,35399 38 1,46228 0,68386 0,38921 1,07307 0,36271 39 1,47698 0,67706 0,39996 1,07702 0,37136 0,40 1,49182 0,67032 0,41075 1,08107 0,37995 41 1,50682 0,66365 0,42158 1,08523 0,38847 42 1,52196 0,65705 0,43246 1,08950 0,39693 43 1,53726 0,65051 0,44337 1,09388 0,40532 44 1,55271 0,64404 0,45434 1,09837 0,41364 45 1,56831 0,63763 0,46534 1,10297 0,42190 46 1,58407 0,63128 0,47640 1,10768 0,43008 47 1,59999 0,62500 0,48750 1,11250 0,43820 48 1,61607 0,61878 0,49865 1,11743 0,44624 49 1,63232 0,61263 0,50984 1,12247 0,45422 0,50 1,64872 0,60653 0,52110 1,12763 0,46212 51 1,66529 0,60050 0,53240 1,13289' 0,46995 52 1,68203 0,59452 0,54375 1,13827 0,47770 53 1,69893 0,58860 0,55516 1,14377 0,48538 54 1,71601 0,58275 0,56663 1,14938 0,49299 55 1,73325 0,57695 0,57815 1,15510 0,50052 56 1,75067 0,57121 0,58973 1,16094 0,50798 57 1,76827 0,56553 0,60137 1,16690 0,51536 58 1,78604 0,55900 0,61307 1,17297 0,52267 59 1,80399 0,55433 0,62483 1,17916 0,52990' io,60 1,82212 0,54881 0,63665 1,18547 0,53705 61 1,84043 0,54335 0,64854 1,191890,54413 62 1,85893 0,53794 0,66049 1,19844 0,55113 63 1,87761 0,53259 0,67251 1,205100,55805 64 1,89648 0,52729 0,68459 1,211890,56490 65 1,91554 0,52205 0,69675 1,218790,57167 66 1,93479 0,51685 0,70897 1,225820,57836 67 1,95424 0,51171 0,72126 1,232970,58498 68 1,973«8 0,50662 0,73363 1,240250,59152 69 1,99372 0,50158 0,74607 1,247650,59798 0,70 2,01375 0,49659 0,75858 1,255170,60437 71 2,03399 0,49164 0,77117 1,262820,61068 72 2,05443 0,48675 0,78384 1,270590,61691 73 2,07508 0,48191 0,79659 1,27849 0,62307 74 2,09594 0,47711 0,80941 1,286520,62915 75 2,11700 0,47237 0,82232 1,294680,63515 76 2,13828 0,46767 0,83530 1,302970,64108 77 2,15977 0,46301 0,84838 1,311390,64693 78 2,18147 0,45841 0,86153 1,319940,65271 79 2,20340 0,45384 0,87478 1,328620,65841 0,80 2,22554 0,44933 0,88811 1,337430,66404 81 2,24791 0,44486 0,90152 1,346380,66959 82 2,27050 0,44043 0,91503 1 35547 0,67507 83 2,29332 0,43605 0,92863 1,364680,68048 84 2,31637 0,43171 0,94233 1,37404 0,68581 85 2,33965 0,42741 0,95612 1,383530,69107 86 2,36316 0,42316 0,97000 1,393160,69626 87 2,38691 0,41895 0,98398 1,402930,70137 88 2,41090 0,41478 0,99806 1,412840,70642 89 2,43513 0,41066 1,01224 1,422890,71139 0,90 2,45960 0,40657 1,02652 1,433090,71630 91 2,48432 0,40252 1,04090 1,443420,72113 92 2,50029 0,39852 1,05539 1,453900,72590 93 2,53451 0,39455 1,06998 1,464530,73059 94 2,55998 0,39063 1,08468 1,475300,73522 95 2,58571 0,38674 1,09948 1,486230,73978 96 2,61170 0,38289 1,11440 1,497290,74428 97 2,63794 0,37908 1,12943 1,50851 0,74870 98 2,66446 0,37531 1,14457 1,519880,75307 99 2,69123 0,37158 1,15983 1,53141 0,75736 1,00 2,71828 0,36788 1,17520 1,543080,76159 01 2,74560 0,36422 1,19069 1,55491 0,76576 02 2,77319 0,36059 1,20630 1,566890,76987 03 2,80107 0,35701 1,22203 1,579040,77391 04 2,82922 0,35345 1,23788 1,591340,77789 05 2,85765 0,34994 1,25386 1,603790,78181 06 2,88637 0,34646 1,26996 1,61641 0,78566 07 291538 0,34301 1,28619 1,629190,78946 08 2,94468 0,33960 1,30254 1,642140,79320 09 2,97427 0,33622 1,31903 1,655250,79688 1,10 3,00417 0,33287 1,33.565 1,66852 0,80050 11 3,03436 0,32956 1,35240 1,681960,80406 12 3,06485 0,32628 1,36929 1,695570,80757 13 3,09566 0,32303 1,38631 1,709340,81102 14 3,12677 0,31982 1,40347 1,723290,81441 15 3,15819 0,31664 1,42078 1,73741 0,81775 16 3,18993 0,31349 1,43822 1,75171 0,82104 17 3,22199 0,31037 1,45581 1,766180,82427 18 3,25437 030728 1,47355 1,780830,82745 19 3,28708 0,30422 1,49143 1,795650,83058
80
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Продолжение
X ех shx chx thx X е* е-х shx chx thx
1,20 3,32012 0,30119
21 3,35348 0,29820
22 3,38719 0,29523
23 3,42123 0,29229
24 3,45561 0,28938
25 3,49034 0,28650
26 3,52542 0,28365
27 3,56085 0,28083
28 3,59664 0,27804
29 3,63279 0,27527
1,50946 1,81066 0,83365
1,52764 1,82584 0,83668
1,54598 1,84121 0,83965
1,56447 1,85676 0,84258
1,58311 1,87250 0,84546
1,60192 1,88842 0,84828
1,62088 1,90454 0,85106
1,64001 1,92084 0,85380
1,65930 1,93734 0,85648
1,67876 1,95403 0,85913
2,00 7,38906 0,13534
10 8,16617 0,12246
20 9,02501 0,11080
30 9,97418 0,10026
40 11,023180,09072
50 12,18249 0,08208
60 13,46374 0,07427
70 14,87973 0,06721
80 16,44465 0,06081
90 18,17415 0,05502
3,62686
4,02186
4,45711
4,93696
5,46623
6,05020
6,69473
7,40626
8,19192
9,05956
3,76220
4,14431
4,56791
5,03722
5,55695
6,13229
6,76901
7,47347
8,25273
9,11458
0,96403
0,97045
0,97574
0,98010
0,98367
0,98661
0,98903
0,99101
0,99263
0,99396
1,30 3,66930 0,27253
31 3,70617 0,26982
32 3,74342 0,26714
33 3,78104 0,26448
34 3,*81904 0,26185
35 3,85743 0,25924
36 3,89619 0,25666
37 3,93535 0,25411
38 3,97490 0,25158
39 4,01485 0,24908
1,40 4,05520 0,24660
41 4,09596 0,24414
42 4,13712 0,24171
43 4,17870 0,23931
44 4,22070 0,23693
45 4,26311 0,23457
46 4,30596 0,23224
47 4,34924 0,22993
48 4,39295 0,22764
49 4,43710 0,22537
1,69838 1,97091 0,86172
1,71818 1,98800 0,86428
1,73814 2,00528 0,86678
1,75828 2,02276 0,86925
1,77860 2,04044 0,87167
1,79909 2,05833 0,87405
1,81977 2,07643 0,87639
1,84062 2,09473 0,87869
1,86166 2,11324 0,88095
1,88289 2,13196 0,88317
1,90430 2,15090 0,88535
1,92591 2,17005 0,88749
1,94770 2,18942 0,88960
1,96970 2,20900 0,89167
1,99188 2,22881 0,89370
2,01427 2,24884 0,89569
2,03686 2,26910 0,89765
2,05965 2,28958 0,89958
2,08265 2,31029 0,90147
2,10586 2,33123 0,90332
3,00 20,08554 0,04979
10 22,19795 0,04505
20 24,53253 0,04076
30 27,11264 0,03688
40 29,96410 0,03337
50 33,11545 0,03020
60 36,59823 0,02732
70 40,44730 0,02472
80 44,70118 0,02237
90 49,40245 0,02024
4,00 54,59815 0,01832
10 60,34029 0,01657
20 66,68633 0,01500
30 73,69979 0,01357
40 81,45087 0,0122'8
50 90,01713 0,01111
60 99,48432 0,01005
70109,9472 0,00910
80 121,5104 0,00823
90 134,2898 0,00745
10,01787 10,06766 0,99505
11,07645 11,121500,99595
12,24588 12,28665 0,99668
13,53788 13,57476 0,99728
14,96536 14,99874 0,99777
16,54263 16,57282 0,99818
18,28546 18,31278 0,99851
20,21129 20,23601 0,99878
22,33941 22,36178 0,99900
24,69110 24,71135 0,99918
27,28992 27,30823 0,99933
30,16186 30,17843 0,99945
33,33567 33,35066 0,99955
36,84311 36,85668 0,99963
40,71930 40,73157 0,99970
45,00301 45,01412 0,99975
49,73713 49,74718 0,99980
54,96904 54,97813 0,99983
60,75109 60,75932 0,99986
67,14117 67,14861 0,99989
1,50 4,48169 0,22313 2,12928
51 4,52673 0,22091 2,15291
52 4,57223 0,21871 2,17676
53 4,61818 0,21654 2,20082
54 4,66459 0,21438 2,22510
55 4,71147 0,21225 2,24961
56 4,75882 0,21014 2,27434
57 4,80665 0,20805 2,29930
58 4,85496 0,20598 2,32449
59 4,90375 0,20393 2,34991
2,35241 0,90515
2,37382 0,90694
2,39547 0,90870
2,41736 0,91042
2,43949 0,91212
2,46186 0,91379
2,48448 0,91542
2,50735 0,91703
2,53047 0,91860
2,55384 0,92015
5,00148,4132
10164,0219
20181,2722
30 200,3368
40 221,4064
50 244,6919
60 270,4264
70 298,8674
80330,2996
90 365,0375
0,00674 74,20321 74,20995 0,99991
0,00610 82,00791 82,01400 0,99993
0,00552 90,63336 90,63888 0,99994
0,00499 100,1659 100,1709 0,99995
0,00452110,7009 110,7055 0,99996
0,00409122,3439 122,3480 0,99997
0,00370135,2114 135,2150 0,99997
0,00335 149,4320 149,4354 0,99998
0,00303 165,1483 165,1513 0,99998
0,00274 182,5174 182,5201 0,99999
4,95303
5,47395
80 6,04965
90 6,68589
1,60
70
2,57746
2,82832
0,20190 2,37557
0,18268 2,64563
0,16530 2,94217 3,10747
0,14957 3,26816 3,41773
0,921671
0,93541
0,94681
0,95624|
6,00 403,4288
30 544,5719
0,00248 201,7132 201,7156
0,00184 272,2850 272,2869
0,99999
0,99999
Определения показательной и гиперболических функций:
chx =
+ е х
"2
х2, 21
”2! + 4!
shx ех — е х х3 2xs 17х’
chx - е* + е-х = х —~ЗГ + Т5 — ’3?5 +
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
81
Таблица 8. ФУНКЦИИ БЕССЕЛЯ
X | + (Х) | У,(х) 1 Х ЛОО Л(х) уо(х) У,(х)
0,0 + 1,00000 +0,00000 — оо — оо 1 5,0 —0,17760 —0,32758 —0,30852 +0,14786
0,1 +0,99750 + 0,04994 —1,53424 —6,45895 5,1 —0,14433 —0,33710 —0,32160 +0,11374
0,2 0,99002 0,09950 1,08111 3,32383 5,2 0,11029 0,34322 0,33125 0,07919
0,3 0,97763 0,14832 0,80727 2,29311 5,3 0,07580 0,34596 0,33744 0,04455
0,4 0,96040 0,19603 0,60602 1,78087 5,4 0,04121 0,34534 0,34017 + 0,01013
0,5 0,93847 0,24227 0,44452 1,47147 5,5 —0,00684 0,34144 0,33948 —0,02376
0,6 + 0,91200 + 0,28670 —0,30851 —1,26039 5,6 + 0,02697 —0,33433 —0,33544 —0,05681
0,7 0,88120 0,32900 0,19066 1,10325 5,7 0,05-92 0,32415 0,32816 0,08872
0,8 0,84629 0,36884 —0,08680 0,97814 5,8 0,09170 0,31103 0,31775 0,11923
0,9 0,80752 0,40595 + 0,00563 0,87313 5,9 0,12203 0,29514 0,30437 0,14808
1,0 0,76520 0,44005 0,08826 0,78121 6,0 0,15065 0,27668 0,28819 0,17501
1,! + 0,71962 + 0,47090 + 0,16216 —0,69812 6,1 + 0,17729 —0,25586 —0,26943 —0,19981
I,2 0,67113 0,49829 0,22808 0,62114 6,2 0,20175 0,23292 0,24831 0,22228
1,3 0,62009 0,52202 0,28654 0,54852 6,3 0,22381 0,20809 0,22503 0,24225
1,4 0,56686 0,54195 0,33790 0,47915 1 6,4 0,24331 0,18164 0,19995 0,25956
I,5 0,51183 0,55794 0,38245 0,41231 6,5 0,26009 0,15384 0,17324 0,27409
1,6 +0,45540 +0,56990 + 0,42043 —0,34758 1 h.V + 0,27404 —0,12498 —0,14523 —0,28575
1,7 0,39798 0,57777 0,45203 0,28473 6,7 0,28506 0,09534 0,11619 0,29446
1,8 0,33999 0,58152 0,47743 0,22366 6,8 0,29310 0,06522 0,08643 0,30019
1,9 0,28182 0,58116 0,49682 0,16441 6,9 0,29810 0,03490 0,05625 0,30292
2,0 0,22389 0,57672 0,51038 0,10703 7,0 0,30008 —0,00468 —0,02595 0,30267
2,1 +0,16661 +0,56829 + 0,51829 —0,05168 7,1 + 0,29905 + 0,02515 + 0,00418 —0,29948
2,2 0,11036 0,55596 0,52078 + 0,00149 7,2 0,29507 0,05433 0,03385 0,29342
2,3 0,05554 0,53987 0,51808 0,05228 7,3 0,28822 0,08257 0,06277' 0,28459
2,4 +0,00251 0,52019 0,51041 0,10049 7,4 0,27860 0,10963 0.09068 0,27311
2,5 —0,04838 0,49709 0,49807 0,14592 7,5 0,26634 0,13525 0,11731 0,25913
2,6 —0,09680 + 0,47082 +0,48133 +0,18836 7,6 +0,25160 + 0,15921 + 0,14243 —0,24280
2,7 0,14245 0,44160 0,46050 0,22763 7,7 0,23456 0,18131 0,16580 0,22432
2,8 0,18504 0,40971 0,43592 0,26355 7,8 0,21541 0,20136 0,18723 0,20389
2,9 0,22431 0,37543 0,40791 0,29594 7,9 0,19436 0,21918 0,20652 0,18172
3,0 0,26005 0,33906 0,37685 0,32467 8,0 0,17165 0,23464 0,22352 0,15806
3,1 —0,29206 +0,30092 +0,34310 +0,34963 8,1 +0,14752 + 0,24761 +0,23809 —0,13315
3,2 0,32019 0,26134 0,30705 0,37071 8,2 0,12222 0,25800 0,25012 0,10724
3,3 0,34430 0,22066 0,26909 0,38785 8,3 0,00601 0,26574 0,25952 0,08060
3,4 0,36430 0,17923 0,22962 0,40102 8,4 0,06916 0,27079 0,26622 0,05348
3,5 0,38013 0,13738 0,18902 0,41019 8,5 0,04194 0,27312 0,27021 -0,02617
3,6 —0,39177 +0,09547 + 0,14771 + 0,41539 8,6 + 0,01462 + 0,27275 +0,27143 +0,00108
3,7 0,39923 0,05383 0,10607 0,41667 8,7 —0,01252 0,26972 0,27000 0,02801
3,8 0,40256 + 0,01282 0,06450 0,41411 8,8 0,03923 0,26407 0,26587 0,05436
3,9 0,40183 —0,02724 + 0,02338 .0,40782 8,9 0,06525 0,25590 0,25916 0,07987
4,0 0,39715 0,06604 -0,01694 0,39793 9,0 0,09033 0,24531 0,24994 0,10431
4,1 —0,38867 —0,10327 —0,05609 +0,38459 9,1 —0,11424 + 0,23243 + 0,23834 + 0,12747
4,2 0,37656 0,13865 0,09375 0,36801 9,2 0,13675 0,21741 0,22449 0,14911
4,3 0,36101 0,17190 0,12960 0,34839 9,3 0,15766 0,20041 0,20857 0,16906
4,4 0,34226 0,20278 0,16334 0,32597 9,4 0,17677 0,18163 0,19074 0,18714
4,5 0,32054 0,23106 0,19471 0,30100 9,5 0,19393 0,10126 0,17121 0,20318
4,6 —0,29614 —0,25655 —0,22346 +0,27375 9,6 —0,20898 + 0,13952 +0,15018 +0,21706
4,7 0,26933 0,27908 0,24939 0,24450 9,7 0,22180 0,11664 0,12787 0,22866
4,8 0,24043 0,29850 0,27230 0,21357 9,8 0,23228 0,09284 0,10453 0,23789
4,9 0,20974 0,31469 0,29205 0,18125 9,9 0,24034 0,06837 0,08038 0,24469
5,0 0,17760 0,32758 0,30852 0,14786 10,0 0,24594 0,04347 0,05567 0,24901
6 Том I
82
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Определение функций Бесселя см. на стр. 171.
2п 2п
Рекуррентные формулы: Jn+i(x) = — Jn (х)— Jn-i(x); Ул+1(х) =—Yn (х) —Ул-1(х).
Асимптотические формулы (для больших значений х):
х +
х +
где Ро (х) = 1
- 3 + 105 _
2! (8х)2 + 4!(8х)4
Qo(x) =
1 , 15
1! 8х + 3! (8х)3
РХ(Х)= 1 +
15
2! (8х)2
14175
4!(8х)4
Qi (х) - и 8х — 3! (8х)3 + • • •
Таблица 9. НЕКОТОРЫЕ ПОСТОЯННЫЕ ВЕЛИЧИНЫ
Величина п 1g п | Величина п Ign п л!
Z 3,141593 0,49715 1 0,318310 1,50285 1 1
К 0,785398 1,89509 4 1,273240 0,10491 2 2
iio< =1О) 0,017453 2,24188 180° (=1 радиан) 57°,2958 1,75812 3 6
л2 9,869604 0,99430 1 0,101321 1,00570 4 24
У л 1,772454 0,24857 0,564190 1,75143 5 120
/1 0,886227 1,05246 /4 1,128380 0,05246 6 720
Ут 0,723600 1,85950 /4 1,38198 0,14050 7 5040
з,— 1/ к 1,464592 0,16572 г тс 0,682784 1,83428 8 40320
е 2,718282 0,43429 1 е 0,367879 1,56571 9 362 880
ег 7,389056 0,86859 1 е2 0,135335 1,13141 10 3 628 800
Ут 1,648721 0,21715 /4- 0,606531 1,78285 И 39 916 800
М = Ige 0,434294 1,63778 — = /п 1° 2,302585 0,36222 12 479 001 600
g 9,80665 0,99152 1 g 0,101972 1,00848 13 6 227 020800
g2 96,1703 1,98304 1 К2 0,010398 2,01696 14 87 178 291 200
УТ 3,13156 0,49576 /т 0,319330 1,50424 15 1 307 674 368 000
У2ё 4,42869 0,64628 У 0,225801 1,35372
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
83
Таблица 10. ПЕРИМЕТРЫ И ПЛОЩАДИ ПЛОСКИХ ФИГУР
Фигура । Обозначение размеров Периметр Р; площадь F
Треугольник (стр. 109—111) / Ид \ ! ‘>Лт4 ‘ 3^1 а, Ъ, с — стороны; а, (3, у — углы; h — высота из вершины 1; р » (а + b + с) — полупе- риметр; г — радиус описанной окружности р — радиус вписанной окружности /П1, т9, т3 — медианы; S “ -^-(mi + тг + /п8); (Xl.yO; (Ха- У.); (х„ Уз) - КООРДИ- наты вершин в прямоугольной системе координат. Р => а + b ч- с; F •=> -A- ah 1 * -у- ab sin у да sin р sin у 2 sin а = Р (.Р — а) (р — 6) (р — с) “ 2 г’ sin a sin р sin у а В у = р’ Ctg — Ctg -у Ctg —у- = рр abc = ~4~Г~ = ~V S(S - mJ (S - ma) (S - ms) X, У1 1 = ± -L. X, Уз 1 ; 2 X3 ys 1 1 x, у, 2 хв у, если третья вершина находится в начале координат (х8 — Уз " °)-
Прямоугольный треугольник (стр. 111) а, b — катеты; с — гипотенуза; а —угол, противолежащий стороне а. а » „ « • - Ml 8 u .. -S М .5 + -о w о о и ь г а ~ Н "Н "И II И II II II й. ь
Четыреугольник (стр. 111) 4-- £ Г \ у 1 i а, b, с, d — стороны; Dl} Da — диагонали; (р — угол между диагоналями; т — длина линии, соединяющей середины диагоналей; hlt Л2 — длины перпендикуляров, опущенных из вершин В и D на диагональ Вх; 5, 7 — два противолежащих угла четыреугольника; р — полупериметр. 1 P = a + &+ c + d; F = D1 -= —~ Di Ds sin <f> = 1^ (p — а) (p — Ь) (p- c) (p — d) 6 + Y == abed cos2—y-!—
84
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Продолжение
Фигура Обозначение размеров Периметр Р; площадь F
Трапеция (стр. 112) b a, fy— основания; с, d — боковые стороны; Di, Е>2 — диагонали; с — угол .между диагоналями; тп — средняя линия.* Л — высота. ч г о и и и п I Э о ы о М1 5 + 0 |ст + ст =• о + е> + „ <л с». 4- 5’ ’* »
/ т \rf
а
Параллелограм (стр. 11 2) а, Ь — стороны; h— расстояние между сторонами Ь; 7 — угол параллелограма; Dj, D3 — диагонали; — угол между диагоналями. Р = 2 (а + &); F = bh — ab sin 7 = D, D, sin <?
Прямоугольник (стр. 112) а, b — стороны; D — диагональ; <р — угол между диагоналями. Р == 2 (а + &); F = ab =» __L Da sin <р 2 Y
Ромб (стр. 112) а — сторона; 7 — угол ромба; Dt, О8 — диагонали. Р = 4 а; F аа sin 7 - О, D,
Многоугольник (стр. 109) 4, ая,..., ап — стороны; («и У1); (ха, У1); ( хп , уп ) _ координаты вершин в прямоуголь- ной системе координат. Р »» ау + а3 + ... 4- ап« F “ ± "1г[( ХяУ1 ' Х1Уа) + (ХаУа ” ХвУэ)-Ь 4-...4-( хп Уп—1—" хл—1Ул)-Ь(х1Уп хп , Площадь F может быть определена также путём разделения многоугольника диагона- лями на треугольники.
Правильный многоугольник (стр. 112—113) г — радиус вписанного круга; R — радиус описанного круга; а = iV— г2 — сторона; п — число сторон; а = 180° — 2 — угол многоуголь- ника, 180° где ср = s п Р = па = 2 nr tg <р = 2 nR sin <р; F =-4- naa ctg 9 = nr2 tg 9 nR* sin 2 9 1
Круг (табл. 1 и стр. 113) г — радиус; d— диаметр. P = 2 It r = rt d = 3,141593 d; p =□ к ra 1 an — — я a« 4 = 0,785398 d2
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
85
Продолжение
Фигура Обозначение размеров Периметр Р; площадь Р
Ь Сруговое ко %// \ г^. к—а—- * D — ЛЬ цо г—внутренний радиус; 7? — наружный радиус; d — внутренний диаметр; D — наружный диаметр; г + 7? р = 2 средний радиус; Й е=» 7? -- г — ширина кольца Т 13 II II II II II KJ 1 я а м я 't'! г’ С "2 :1 О? » _1_ О ° ! + -U « 1 G + I
Круговой сегмент (табл. 6 и стр. ИЗ) - s - Q г — радиус; ср — центральный угол в градусах; 1 — длина дуги; S — длина хорды; h — высота стрелки. Р = / + S; р=4- r° (;so -sin ?) _ + sh ~ ’ 2 ; Площадь сегмента меньшего полукруга 2 г. h3 h-~3 Sh + ^T- Площадь сегмента , дуга которого меньше 50° я 2- sh.
Круговой сектор (стр. 113) г — радиус; ср — центральный угол в градусах; 1 = —Х-т,—г—длина дуги. 1 ои Р = 1 + 2г; '’=4-/г .. зсо
Часть кругового кольца г — внутренний радиус; 2? — наружный радиус; г + R р =* — средний радиус; о = R — г — ширина кольца; ср — центральный угол в градусах. р = -Т80- (/? + г>; = 180 р
Круговой серп г — радиус; ср — центральный угол в градусах; 1 — расстояние между центрами. Р = 2 т. г; Р = ГЯ ( Л80^)“Га’1- где . = к + sin ¥ Значения т] в зависимости от 2:
1 2г 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
О,4о|о,79| 1, is|l ,5б| 1,91|2,25 2,55 2,81 3.02
86
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Фигура
Обозначение размеров
Продолжение
Периметр Р; площадь F
Эллипс
(стр, 184)
а — большая полуось;
где Е — эллиптический интеграл 2-го рода
(стр. 149).
Гипербола
(стр. 184)
Парабола
(стр. 185)
Синусоида
4
b — малая полуось;
триситет;
х, у — расстояния точки М на
эллипсе от осей.
а — вещественная полуось;
Ъ — мнимая полуось;
х, у — расстояния точки М на
гиперболе от осей.
р — параметр параболы;
х — высота параболического
сегмента;
2 у — основание параболического
сегмента.
а—основание сегмента (парал-
лельное оси синусоиды);
h—высота «егмента.
г ab>
Площадь эллиптического сегмента MAN
х
F ab arc cos--------------ху.
а
Площадь эллиптического сектора OMAN
х
F — ab arc cos---
Площадь гиперболического сегмента AMN
F^Xy- ab in (-А. +
Площадь гиперболического сектора OMAN
F = ab in ( А- + -£-)
__aftln (j?--------
Длина дуги M0N
2х
Р
~ V у« + р« + р in-
Р
Площадь параболического сегмента 0MN
Р = “ ху
Длина дуги MAN
[*9 / ft \а те* / ft \ <1
1 + 4 a j — S^ajJ»
h
если----мало.
а
Площадь сегмента MAN
2
к ah
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
87
Таблица 11. ПЛОЩАДИ ПОВЕРХНОСТЕЙ И ОБЪЁМЫ ТЕЛ
Т ело Обозначение размеров Площадь боковой поверхности S& площадь полной поверхности S; объём тела V.
Призма (стр. 115) F — площадь основания; Q — площадь сечения, перпенди- кулярного ребру; h — высота; 1 — боковое ребро; Р — периметр сечения, перпен- дикулярного ребру. = S = V == PZ; Pl 4- 2 F; Fh; QI-
Прямая призма (стр. 115) F — площадь основания; 1 — ребро; Р — периметр основания. s,-> = Pl; S = Pl + 2 F; V = Fl.
Прямой прямоугольный параллелепипед (стр. 115) а, Ь, с — рёбра. 5=2 (tzb be tze); V = abc.
Куб (стр. 115) а — ребро. ' Il 11 1 | i 6 aa; a3.
Призма, усечённая непараллельно осно- ванию 1 — длина отрезка, соединяющего центры тяжести оснований; Q — площадь сечений, перпен- дикулярно к 1. V = Ql
Трёхгр усеч раллел К ан ённ ьн пая п ая не оснс Г зизма, па- ванию С, а, Ь9 с — параллельные ребра; Q — площадь сечения, перпенди- кулярного рёбрам. V= 3 ( ° + & + c )<?
С
1
Пирамида (стр. 115) F — площадь основания; fi — высота. V = - TFil
Треугольная пирамида (Х,,у,.zj; (xs,y3,z,); (xs,y,,z3)— три вершины в прямоугольной системе координат; четвёртая вершина — в начале координат. v - ± 4- о X, У! Zj xs y2 2a X3 ya z3
Усечё! ( <ная пирамида ?тр. 116) гтг7\ F, / — площади параллельных оснований; h — высота (расстояние между )
л основаниями); Л, а — две соответственные стороны оснований. = [ ! (4)4
А
Обелиск
4 a, b, bj—стороны прямоуголь- ных оснований; Л—высота. V = -g- л £^2 a + Qi )"+(2 at 4- л j bi J
88
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Продолжение
Тело Обозначение размеров Площадь боковой поверхности площадь полной поверхности S; объём тела V.
Клин а а, ь—стороны основания; ах—верхнее ребро; h—высота. V « —^2 a + Oi j bh.
Цилиндр (стр. 116) F — площадь основания; Q — площадь сечения, перпенди- кулярного образующей; Л — высота; 1 — образующая; Р—периметр сечения, перпен- дикулярного образующей. S, - Pl; 6 S = pi + 2 F; V = Ffl - Qi
Прямой цилиндр (стр. 116) F — площадь основания; / — образующая; Р—периметр основания. S6 = pp’ S - Pl + 2 F; V - Fl
Прямой круговой цилиндр (стр. 116) г — радиус основания; h — высота. S = 2 r. rh 0 S = 2 *r (h + r); V = к r* h
Цилиндр, усечённый непараллельно основанию 1 — длина отрезка, соединяющего центры тяжести оснований; Q — площадь сечения, перпен- дикулярного к 1. V - QI
Прям цилинд непа ОС эй круг р, усе1- раллея нованр г овой ённый ЬНО 1Ю п 1' г — радиус основания; Й1 и Л8 — наименьшая и наиболь- шая из образующих. S6 = r.r(.hi+h.i); V = - "Г8 (h, + h, j
Поль h 1Й цилиндр R — наружный радиус; г — внутренний радиус; Л — высота; 5 — R — г — толщина; /? 4" р „ .— средний радиус. S, = 2r/i (R + r) = 4 т:Лр; S= 2n(R + r)(h+R-f) = 4 np (ft + 6); V = r.h (R‘ - r*) — кЛЗ (2 R — 5) = rM (2 R + — 2 uWp
Цилиндрическая подкова /31 h — высота; г—раднус основания; 2a — прямая сторона; Ь — длина перпендикуляра, опущенного из основания высоты на прямую сторону; 2 ср — центральный угол основания в градусах. s« --.-[(• -')-&+] » 2rh (если в основании полукруг); V--Ma (Зг3- ) + И г) Iso-] = -3- r‘h (если в основании полукруг)
Конус (стр. 116) F — площадь основания; Л — высота. V = -’-F/1
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
89
Продолжение
Тело 1 Обозначение размеров Площадь боковой поверхности S, • площадь полной поверхности S; объём тела V
Прямой круговой конус (стр. 116) г — радиус основания; h — высота; Z = У r‘ + h* — образующая. S6 = У г’ + h> = кг/; кг (г 4- О; V « —nr*h
Усечённый круговой конус (стр. 117) R и г — радиусы оснований; й — высота; ст = R 4- г; <5 •= R — г: i == V йа + /р __ образующая. S _ =я Hl (R 4- Г) => к/ст; S ~ ТС [R3 + Г3 + 1 (R + Г)]; v "" ~з~ + ra + RO =4(Зз,+г-)
Шар (стр. 117) г — радиус; d — диаметр. S — 4 тга . r.d2; 4 V = TtT3 1 e ___ nd3 6 =» 0,523599 d3
Полый шар R — наружный радиус; г — внутренний радиус; D — наружный диаметр; d — внутренний диаметр. S - 4 к (R3 4- г9) = те (ZJ» 4- da); у к ^R*-
Шаровой сегмент 0 Л — высота сегмента; г — радиус шара; а Vh(2 г — h) — радиус осно- вания. n II I II 11 ,, I _ I я a M 1 a g. а с Г » 7 ® 57 +
Шаровой пояс / р \ ^22~ ~т '“'2^ й — высота пояса; а и b — радиусы оснований (а>Ь); Л Г 9 , а* — Ь9 — йа г “ У а2 + 2— ра- диус шара. S _ = 2 r.rh; S = n (aa + b2 + 2 гй); V = T.h (3 a! + 3 fe> + /I*) = Vz + ~ 6 где V! — объём вписанного в шаровой пояс усечённого конуса, радиусы основания которого — а и Ъ, высота — й и образую- щая — 1.
Шаровой сектор Xi// h—высота сегмента; а—радиус основания сегмента; г—радиус шара. S = г.г (а 4-2 й); 2 V = —
Тор (цилиндрическое кольцо) г—радиус поперечного сечения; R—расстояние центра попереч- ного сечения от оси вращения; D=2R; d = 2r S =- 4 K«Rr = Dd = 9,8696 Dd; V - 2 na Rra e _L Dd2 4 «» 2,4674 Dd“
90
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Продолжение
Т е Л О Обозначение размеров Площадь боковой поверхности площадь полной поверхности S; объём тела V
Эллипсоид (стр. 192) а, Ь, с — полуоси. 4 V = —п abc
Эллипсоид (стр. вращения 192) (d>h); а 1) ось вращения — 2 а; 2) ось вращения — 2 Ь. с о • Itf arc sine \ 1) S = 2 r.ao ( у i — ea 4- : I; V = -А- к ab’; 2) S = 2 к a‘+ —Л**.. tn _£<1+ e) . s b V = v.azb
Параболоид (стр. \ л вращения 192) г — радиус основания; h — высота. V = К r‘h
Усечённый параболоид вращения R и г — радиусы параллельных оснований; h — высота. V = -A- r.h (!?’ + r!)
Бочка tf о D — диаметр среднего сечения; d — диаметр доньев; h — высота. V = -A. Tt/1 ( 2 D‘ + Dd + -A- d« \-для 15 \ 4 / параболической клёпки; V = -A- 7th [2 O‘ + d!) - для круговой клёпки
Квдка и (усечённый ский ли чаи эллиптиче- <онус) Параллельные основания — эл- липсы с полуосями а, Ъ и alt &г: /1 — высота. Если at «а = 0 — эллиптический конус. V = -A- r.h £ 2 ( ab + 0,6, j + abt + d.hj
Теоремы Гюльдена для вычисления объёмов и поверхностей тел вращения
1. Если А -- площадь плоской фигуры, которая вращается около оси, лежащей в плоскости этой
фигуры и не пересекающей её, х0 — расстояние центра тяжести фигуры от оси вращения, то объём полу-
ченного тела вращения равен произведению длины окружности, описываемой центром тяжести, на пло-
щадь фигуры:
V = 2 г. x0F.
2. Если s—длина дуги плоской кривой, которая вращается около оси, лежащей в плоскости этой
дуги и ие пересекающей её, х0 — расстояние центра тяжести дуги от оси вращения, то площадь по-
верхности полученного тела вращения равна произведению длины окружности, описываемой центром
тяжести, на длину дуги:
S «= 2 тс xos.
МАТЕМАТИКА
АРИФМЕТИКА И АЛГЕБРА
алгебраические действия
И ИХ СВОЙСТВА
Обозначения шести алгебраических действий
и соответствующие термины
Действия Данные величины Резуль- тат
а b с
Сложение а + b = с Вычитание а — b «=в с Умножение = с Деление а : Ъ =» с Возведение в степень Ъ а — с Извлечение корня Ъ V* а = с Слагаемое Уменьшаемое Множимое (сомножи- тель) Делимое Основание степени Подкоренное количество Слагаемое Вычитае- мое Множи- тель (сомножи- тель) Делитель Показа- тель степени Показа- тель корня Сумма Разность Произве- дение Частное Степень Корень
Результат нескольких выполняемых дей-
ствий может зависеть от порядка действий.
В случае отсутствия скобок сначала произ-
водят действия возведения в степень и
извлечения корня, потом'—умножения и
деления и, наконец, сложения и вычитания.
Действия, которые должны быть выполнены
раньше других, выделяются при помощи
скобок.
Наряду с простыми (круглыми) скобками
употребляются квадратные [ ] и фигурные
| } скобки. Вычисление выражений, содер-
жащих такие скобки, производится в сле-
дующем порядке: сначала производятся вы-
числения внутри всех круглых скобок, за-
тем— внутри квадратных скобок, далее —
внутри фигурных скобок и, наконец, выпол-
няются оставшиеся действия.
Действие сложения обладает свойст-
вами:
переместительности (коммута-
т ивности)
а + b = b + а
и сочетательности (ассоциатив-
но с т и)
а + (Ь + с) = (а + 6) + с = а + b + с.
Действие умножения обладает свой-
ствами:
переместительности
а b = b • а,
сочетательности
а-(Ь-с) = (а-Ь)-с = а-Ь-с
и распределительности (дистри-
бутивности)
(а + Ь)-с = а-с + b-с.
Действие деления обладает следую-
щими свойствами:
т : (abc) = [(т : а) : б] : с;
(abc) : т = (а : m) be;
(ат) : (Ьт) = а :Ь; (а : т) : (Ь : т) = а : Ь.
ДЕЛИМОСТЬ ЧИСЕЛ
Число, на которое делится данное число
без остатка, называется его делителем.
Число, которое не имеет никаких дру-
гих делителей, кроме единицы и самого
себя, называется простым. Простых чисел
бесчисленное множество; простые числа от
1 до 1013 приведены в табл. 1.
Таблица j
Простые числа от 1 до 1013
Q 61 149 239 347 443 563 659 773 887
3 67 151 241 349 449 569 661 787 907
5 71 Т>7 251 353 457 571 673 797 911
7 73 163 257 359 461 577 677 809 919
11 79 167 263 367 463 587 683 811 929
13 83 173 269 373 467 593 691 821 937
17 89 179 271 379 479 599 701 823 941
19 97 181 377 383 487 601 709 827 947
23 101 191 281 389 491 607 719 829 953
29 103 193 283 397 499 613 727 839 967
31 107 197 293 401 503 617 733 853 971
37 109 199 307 409 509 619 739 857 977
41 ИЗ 211 311 419 521 631 743 859 983
43 127 213 313 421 523 641 751 863 991
47 131 227 317 431 541 643 757 877 997
53 137 229 331 433 547 647 761 881 1009
59 139 233 337 439 557 653 769 883 1013
Числа, которые имеют другие делители,
кроме единицы и самого себя, называются
составным и или с л о ж н ы м и.
92
МАТЕМАТИКА
Всякое составное число можно единст-
венным образом представить в виде произ-
ведения простых множителей (разложить на
простые множители), испытывая в качестве
множителей в последовательном порядке
простые числа: 2, 3, 5, 7, 11 и т. д.
Общим делителем нескольких чи-
сел называется число, являющееся делите-
лем каждого из них.
Наибольший из общих делителей назы-
вается общим наибольшим дели-
теле м.
Общий наибольший делитель нескольких
чисел находится путём разложения каждого
из данных чисел на простые множители и
перемножения тех из множителей, которые
входят во все данные числа.
Числа, не имеющие общих делителей
(кроме единицы), называются взаимно
простыми.
Если число а делится нацело на другое
число Ь, то а называется кратным Ь.
Число, служащее кратным для несколь-
ких данных чисел, называется общим
кратны м данных чисел.
Наименьшее из общих кратных несколь-
ких чисел называется их общим наи-
меньшим кратным. Для нахождения
общего наименьшего кратного нескольких
чисел нужно разложить данные числа на
простые множители и взять произведение
всех простых множителей, которые входят
хотя бы в одно из данных чисел.
Признаки делимости чисел
ница, называется знаменателем дроби,
а число, показывающее сколько таких час-
тей взято, называется числителем дро-
а
би. Обозначение дроби: у, где а — числи-
тель, а b— знаменатель.
Дробь называется правильной, если
числитель меньше знаменателя (а < Ь), и не-
правильной, если числитель больше
или равен знаменателю (а > Ь).
Сумма целого числа и правильной дроби
называется смешанным числом.
Неправильную дробь можно обратить
в смешанное число, выделив целую часть
путём деления числителя на знаменатель.
Остаток от деления даёт числитель дроб-
ной части:
где п — целое частное, с — остаток от деле-
ния а на Ь.
Для обращения смешанного числа в не-
правильную дробь целая часть умножается
на знаменатель и складывается с числите-
лем дробной части; это даёт числитель не-
правильной дроби, знаменатель же остаётся
прежний:
а п-b + а
п 6 — b
Величина дроби не изменится, если раз-
делить или умножить числитель и знамена-
тель на одно и то же число:
Дели-
тель п
На гг делятся числа, которые:
а _ а : с а а-с
b ~~ b : с ’ b Ь-с'
3
4
5
6
7
8
9
10
И
25
100
1 000
I
оканчиваются на 2, 4, 6, 8, О (чётные
числа);
имеют сумму цифр, делящуюся на 3;
оканчиваются двумя нулями или у ко-
торых последние две цифры обра-
зуют число, делящееся на 4;
оканчиваются нулём или 5;
делятся одновременно на 2 и на 3;
имеют разность между числом десят-
ков и удвоенной последней цифрой,
делящуюся на 7, или равную нулю;
оканчиваются тремя нулями или у ко-
торых последние три цифры обра-
зуют число, делящееся на 8;
имеют сумму цифр, делящуюся на 9;
оканчиваются нулём;
имеют разность между суммой цифр,
стоящих на нечётных местах (начи-
ная с правого края), и суммой цифр,
стоящих на чётных местах, равную
нулю или делящуюся на 11;
оканчиваются двумя нулями или у ко-
торых последние две цифры обра-
зуют число, делящееся на 25;
оканчиваются двумя нулями;
оканчиваются тремя нулями.
ПРОСТЫЕ ДРОБИ
Др о б ь ю называется одна пли несколько
равных частей (долей) единицы. Число, по-
казывающее, насколько частей разделена еди-
Первая из этих формул применяется для
сокращения дроби (с есть общий дели-
тель чисел а и Ь), а вторая при приведе-
нии дробей к общему знаменателю.
Общим знаменателем нескольких
дробей называется общее наименьшее кратное
знаменателей этих дробей. Чтобы привести
г @1 ^2
дроби ,
. . к общему знаменателю,
нужно числитель и знаменатель каждой из
них умножить на соответствующий допол-
нительный множитель, являющийся
частным от деления общего знаменателя на
знаменатель рассматриваемой дроби.
ДЕЙСТВИЯ с ПРОСТЫМИ ДРОБЯМИ
При действиях с дробями целое число
можно рассматривать как дробь со знаме-
нателем, равным единице.
При. сложении или вычитании
дробей с одинаковыми знаменателями скла-
дываются или вычитаются числители, а
знаменатель остаётся прежний. Если знаме-
натели дробей разные, то сперва нужно при-
вести дроби к общему знаменателю:
а , с _ ad ± Ьс
’Ь±7 bd
При сложении или вычитании смешанных
чисел отдельно складывают или вычитают
целые и дробные части.
При умножении дроби на дробь по-
лучается дробь, числитель которой равен
АРИФМЕТИКА И АЛГЕБРА
93
произведению числителей сомножителей, а
знаменатель — произведению знаменателей
сомножителей:
а с __ас
l)'d~bd'
Если среди сомножителей встречаются
смешанные числа, то их следует предвари-
тельно обратить в неправильные дроби.
При делении на дробь делимое умно-
жается на дробь, обратную делителю:
а с a d ad
b ' d ~~ b ' с be'
Как и при умножении, смешанные числа
предварительно обращаются в неправиль-
ные дроби.
ДЕСЯТИЧНЫЕ ДРОБИ
Десятичные дроби — дроби со
знаменателями, являющимися целыми сте-
пенями числа 10(10, 100, 1 000 и вообще 10”).
При записи десятичной дроби пишется сна-
чала целая часть, затем ставится запятая,
после чего пишется дробная часть, первая
цифра которой означает число десятых до-
лей единицы, вторая — сотых, третья—ты-
сячных и т. д. Цифры, стоящие после за-
пятой, называются десятичными зна-
ками. Если десятичная дробь не содержит
целой части, то перед запятой ставится
нуль.
Десятичная дробь не изменится, если к
ней справа приписать любое число нулей
или отбросить нули, стоящие справа в её
конце (после запятой).
Десятичная дробь увеличивается (или
уменьшается) в 10, 100, 1 000 и т. д. раз,
если запятую перенести на один, два, три
и т. д. знака вправо (влево).
Сложение и вычитание десятич-
ных дробей выполняется по тем же прави-
лам, что и для целых чисел, причём скла-
дываемые или вычитаемые дроби подписы-
ваются одна под другой так, что единицы
приходятся под единицами, десятые доли
под десятыми долями и т. д.
Умножение десятичных дро-
б е й также производится по тем же прави-
лам, что и для целых чисел. В произведе-
нии ставится запятая таким образом, чтобы
число знаков после запятой равнялось об-
щему количеству знаков после запятой во
всех сомножителях.
Деление десятичных дробей
производится следующим образом: отбрасы-
вается запятая в делителе, в делимом запя-
тая переносится вправо на столько знаков,
сколько было десятичных знаков в делителе,
затем находится сначала целое частное, после
которого ставится запятая и далее десятые,
сотые, тысячные и т. д. доли частного:
125,469 : 2,7 = 1 254,69 : 27= 46,47.
Для обращения простой дроби в десятич-
ную нужно разделить числитель на знаме-
натель по правилу деления десятичных
дробей.
При делении десятичных дробей, а также
при обращении простой дроби в десятичную
может случиться, что представляющая част-
ное десятичная дробь будет иметь, начиная
с некоторого места, бесчисленное множество
периодически повторяющихся десятичных
знаков Такая десятичная дробь называется
периодической.
Если повторение начинается с пер-
вой значащей цифры, то дробь называется
чистой периодической, в против-
ном случае — смешанной периодиче-
ской.
Чтобы обратить правильную чистую пе-
риодическую дробь в простую, нужно её
период сделать числителем, а в знаменателе
написать цифру 9 столько раз, сколько цифр
в периоде со столькими нулями, сколько
нулей между запятой и периодом.
Пример:
12 4
0.1212...=О,(12) = --= зз-
Чтобы обратить правильную смешанную
периодическую дробь в простую, нужно
числителем взять разность между числом,
стоящим до второго периода, и числом, сто-
ящим до первого периода, а в знаменателе
написать цифру 9 столько раз, сколько цифр
в периоде, со столькими нулями, сколько
Цифр между запятой и первым периодом.
Пример:
5,3222...= 5,3(2) = 5 ^2=5
23,17236236 ... = 23,1 7 (236) =
,1О 17 236- 17 17 219
“ 99 900 99 000 '
ПРОЦЕНТЫ
Процентом называется сотая часть
числа. Процент обозначается символом %.
Выражение величины а в процентах другой
а
величины b определяется числом • 100%.
Если величина а составляет р % вели-
чины Ь, то
Ьр 100а
а = 100“ и 6 = р •
Изменение числа а за год, выраженное
в процентах, называется годовым про-
центом. Если приращение за каждый год
не влияет на приращение последующих лет,
то число а за t лет при р % годовых об-
ращается в число А, определяемое равен-
ством (формула простых процен-
т о в):
Число а за t лет при р % годовых в слу-
чае сложных процентов обращается в число
А, определяемое равенством (формула
сложных процентов):
( Р \с
А = а 1 + юоу .
Если приращение р % начисляется т
раз в году (через равные промежутки вре-
мени), то
А = а 1 +
94
МАТЕМАТИКА
ОТНОШЕНИЯ и ПРОПОРЦИИ
Отношением (геометрическим) числа
а к числу Ь называется частное от деления
а на Ь: •
а
а : b или ,
при этом делимое а называется предыду-
щим членом отношения, а делитель b—
последующим.
Пропорцией называется равенство
двух отношений:
а : b = с : d
или
а__ с
b ~~d ’
при этом and называются крайними
членами пропорции, а Ь и с—с редкими
членами.
Основное с в о й с т в о п р о п о р ц и и:
произведение крайних членов пропорции
равно произведению её средних членов
ad = be.
Если известны три члена пропорции, то
может быть найден неизвестный четвёртый
член х: если х— крайний член, то он равен
произведению средних членов, делённому
на известный крайний член, а если х — сред-
ний член, то он равен произведению край-
них членов, делённому на известный сред-
ний член, т. е. если дана пропорция
, be
х : b = с : d, то х = . ;
d '
если
ad
а : х = с : d, то х = — .
с
В непрерывной пропорции (про-
порции с двумя равными крайними или
двумя равными средними членами)
х : а = b : х или а : х = х : b
имеет место равенство
х = Vab.
Две взаимно зависимые величины назы-
ваются пропорциональными, если
отношение их значений остаётся неизмен-
ным. Это отношение носит название к о э-
фициеита пропорциональности.
Две величины, зависящие друг от друга
так, что при увеличении одной в некоторое
число раз другая уменьшается во столько
же раз, называются обратно пропор-
циональными. 1
В пропорции можно менять местами сред-
ние или крайние члены или те и другие,
т. е. одновременно справедливы пропорции:
— — а _ ь
ь а ’ с ~ а ; ь ~~ ~^г
Кроме того, из основной пропорции
а : b = с : d можно получить ряд так назы-
ваемых производны х пропорций:
а ± b b а
c±d~~d~ с’
а + b а — b
с + d~ с — d '
Из равенства нескольких отношений:
_______________«з _
bl Ь2 ^3__________________*
следует:
+ Дз + Оз 4~ • • • ~Ь _ o_i
bi + Ь2 4- Ь3 + . . . + Ьп Ь2
Если имеется п чисел: х2, х2, х3..х„,
то их среднее арифметическое хат,
среднее квадратическое xqm,
среднее геометрическое х„т и
среднее гармоническое х^т опреде-
ляются равенствами:
_ *2 ~1" • • ~Н Х>1 .
Aflm л ’
xqn = ]/" X; + х| + х| + . . . + xj;
n
x^m — И XjX2x3. . . x„;
1 1 I 1 L 1 , 1 1\
xhm Л \Xj X2 X3 xn J
В частности, различные средние двух ве-
личин хх и х2 находятся из равенств:
_ xi + х2 ф
хат 2 ’
xqm Xj 4- х| ;
^gm — V ^1^2 >
2ххха
*hm = Xi + х3 •
ПРОГРЕССИИ
Арифметическая прогрессия
есть такая последовательность чисел аг, а2,
а3, ..., ап, ... (членов прогрессии), в кото-
рой каждое последующее число получается
из предыдущего путём прибавления к нему
некоторого определённого числа d, называе-
мого разностью прогрессии. При d > О
члены прогрессии увеличиваются с увеличе-
нием номера и прогрессия называется воз-
растающей, при d<0 члены прогрес-
сии уменьшаются и прогрессия называется
убывающей.
Общий вид арифметической прогрессии:
агг, а1 ~ d~, а1 2 dj аг 4- 3 dj. . .
Здесь aj —первый член, d — разность
прогрессии.
Общее выражение л-го члена арифмети-
ческой прогрессии
а„ = аг 4- (л — О
Сумма л первых членов арифметической
прогрессии
Sn = л [2 Q1 + (Л - 1) </].
Геометрическая прогрессия
есть такая последовательность чисел Oj, а2,
а3, . . . , ап,. . . (членов прогрессии), в ко-
торой каждое последующее число получается
из предыдущего путём умножения его на
некоторое определённое число q, называемое
знаменателем прогрессии.
АРИФМЕТИКА И АЛГЕБРА
95
При I q | > 1 прогрессия называется воз-
растающей, при | <? | <1—убываю-
щей.
Общий вид геометрической прогрессии:
ч-5-й1, а1Ч; arf-, а^3,. . .
Здесь Oj — первый член, q— знаменатель
прогрессии.
Общее выражение п-го члена геометриче-
ской прогрессии:
Сумма п первых членов геометрической
прогрессии
qn - 1 1 — qn
sn-ai q_1 - «1 •
Если число членов убывающей прогрес-
сии безгранично растёт, то Sn стремится к
пределу S:
а,
S = lim Sn = j—.
n->oo 1 ч
При помощи последней формулы можно
преобразовать любую десятичную периодиче-
скую дробь в простую (стр. 93):
12
12 1 , 100 _ 12 _ 4
+ 100 ‘ ТОО5 + ‘ ’ = 1 99 33 ’
100
НЕКОТОРЫЕ КОНЕЧНЫЕ ЧИСЛОВЫЕ РЯДЫ
1) 1+2 + 3+..,+(п-1) + п =
_ п (п + 1)
“ 2 ’
2) Р+ (Р + 1) + (Р + 2) +. . ,+(р+п-2) +
, и(2р + п—1) .
+ (Р + П — 1)— 2 ’
3) 1+3 + 5 + .. ,+ (2п—3) + (2п—1) = п2;
4) 2+4 + 6+ ...+(2п — 2) + 2п =
= п (п + 1);
' 5) I2 + 22 + 32 + . . . + (п — I)2 + п2 =
п (п + 1) (2 п + 1)
“ g ,
6) р + З2 + 52 + . . . + (2 п — I)2 =
п (4 ni — 1)
= 3 ;
7) Р + 23 + З3 + . . . + (п — I)2 + п3 =
п2(п + I)2
~ 4 ;
8) 13+3»+53+ . . . + (2п—1)3=п2 (2 п2—1).
ДЕЙСТВИЯ НАД ОТНОСИТЕЛЬНЫМИ
ЧИСЛАМИ
Абсолютной величиной (моду-
лем) числа а (обозначение: | а I) называется
число, равное а (если а положительное) или
полученное из а изменением знака (если а
отрицательное). Абсолютная величина есть
число положительное (или нуль).
При сложении двух чисел с одинаковыми
знаками складываются их модули и перед
суммой ставится их общий знак. При сло-
жении двух чисел с разными знаками из мо-
дуля большего из них вычитается модуль
меньшего и ставится знак большего числа.
Вычитание одного числа из другого мож-
но заменить сложением, при этом уменьшае-
мое берётся со своим знаком, а вычитаемое
с обратным.
При умножении двух чисел умножаются
их модули и перед произведением ставится
знак плюс, если знаки сомножителей одина-
ковы, и знак минус, если они разные.
При делении одного числа на другое
делят модуль первого на модуль второго и
перед частным ставят знак плюс, если знаки
делимого и делителя одинаковы, и знак ми-
нус, если они разные.
Абсолютная величина суммы или разно-
сти (алгебраической суммы) двух
чисел больше или равна разности абсолют-
ных величин этих чисел и меньше или равна
сумме их абсолютных величин:
I а I — I & К | a ± b I < | а | + | & |.
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
Алгебраическим выражением
называется одна или несколько алгебраиче-
ских величин (букв или чисел), соединён-
ных между собой знаками алгебраических
действий и знаками последовательности этих
действий (скобками). Два алгебраических
выражения, соединённых знаком равенства,
образуют ра венство.
Тождеством называется такое равен-
ство, которое остаётся верным, если вместо
входящих в него букв подставить любые ве-
личины; равенство, которое верно только
при подстановке некоторых определённых
значений входящих в него букв, называется
уравнением. Получение из одного ал-
гебраического выражения другого, тождест-
венно равного ему, называется тождест-
венным преобразованием.
Классификация алгебраических выраже-
ний производится по отношению к буквен-
ным величинам, принятым за основные, в
зависимости от действий, которые произ-
водятся над ними. Различают выражения:
целые рациональные (в которых над
основными величинами производятся только
сложение, вычитание, умножение и возведе-
ние в целую положительную степень),
дробные рациональные (к перечис-
ленным действиям присоединяется деление
или возведение в целую отрицательную сте-
пень) и иррациональные (присоеди-
няется ещё извлечение корня или возведе-
ние в дробную степень).
Алгебраическое выражение, в котором
последним по порядку действием не являет-
ся сложение или вычитание, называется о д-
н о член ом, например:
а-, а (2 Ъ — Зс).
Числовые или буквенные множители, не
содержащие величин, принятых за основ-
ные, называются коэфициентами.
96
МАТЕМАТИКА
Одночлены называются подобными,
если они одинаковы или отличаются только
коэфициентами, например Зй2& и 5а2Ь.
Сложение одночленов сводится к преобра-
зованию суммы к более простому виду. Сум-
ма подобных членов равна подобному им вы-
ражению с коэфициентом, равным сумме
коэфициентов слагаемых. Такая замена на-
зывается приведением подобных
членов, например:
5 х3у 4- 3 х3у — 2 х’у = б х3у.
Если коэфициентами являются буквен-
ные выражения, то производят вынесение
за скобки общих множителей, например:
аху2 + Ьху2 — сху3 = (а 4- b — с)ху2.
При умножении одночленов коэфициенты
перемножаются, показатели одинаковых
букв складываются, а прочие буквы с их
показателями переписываются в произведе-
нии без изменений, например:
Зх3у-( — 5xz2) = — 15х8уг3.
Для деления одночлена на одночлен ну-
жно коэфициенты разделить, а показатели
одинаковых букв вычесть, например:
24xBy‘z : 6x8z = 4х2у4.
Сумма или разность одночленов назы-
вается многочленом. Сложение и вычи-
тание многочленов сводятся к образованию
нового многочлена путём приписывания к
первому многочлену членов остальных с их
знаками (в случае сложения) или с обрат-
ными знаками (в случае вычитания), после
чего производится приведение подобных
членов, если это возможно.
Пример.
(5 х’у + 7 х’у* — 13 ху“) + (2 х’у — 7 х'у!) —
— (5 х’у* — 12 ху“)~ 7 х’у — б х’у’ — ху».
При умножении и делении многочлена на
одночлен нужно каждый член многочлена
умножить или разделить поочерёдно на од-
ночлен и результаты сложить.
Пример 1.
(8 а°Ья — 9 аЧ>в + б ab*)-2 аЬя -»
- 16 а‘Ь* — 18 а‘Ь‘ + 12 а‘Ь‘.
Пример 2.
д
(8 а‘Ьг — 9 а’Ь' + 6 аЬ‘) : 2 ab‘ = 4 а‘ — — ab + 3 Ь*.
При умножении многочлена на многочлен
нужно каждый член множимого умножить
на каждый член множителя и результаты
сложить.
Пример.
(5 а‘Ь — 3 аЬг + 2 -2 6)-
- 5 а'Ь — 3 а‘Ь‘ + 2 ab" — 10 а‘Ь’ + б ab" — 4 i>* -
- 5 а‘Ь — 13 а‘Ь‘ + 8 aba — 4t>‘.
При делении многочлена на многочлен
нужно расположить их по убывающим сте-
пеням какой-либо буквы и разделить стар-
ший член делимого на старший член дели-
теля; получим старший член частного.
Его следует умножить на весь делитель, по-
лученное произведение вычесть из дели-
мого и старший член остатка опять разде-
лить на старший член делителя; полу-
чим второй член частного. Так следует
продолжать до тех пор, пока не получится
в остатке нуль или пока степень старшего
члена остатка не будет меньше степени стар-
шего члена делителя. Последний случай
представляет собой деление с остатком.
Пример.
_2х3 + 5 х2 +13 х+ 4
2 хэ + 4 х3 + 6 х
_ X8 + 7 х + 4
____х8 + 2 х + 3
5 х + 1
Следовательно
I х8 + 2 х + 3
I 2х + 1
(2 х3 + 5 х8 + 1 3 х + 4) : (ха + 2 X + 3) -
5 х + 1
“ 2 х + 1 + + 2 х + 3 ’
В некоторых случаях умножение и деле-
ние многочленов можно производить с ис-
пользованием так называемых формул сокра-
щённого умножения и деления.
ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ
И ДЕЛЕНИЯ
а2 — b* = (a 4- Ь) (а — Ь);
й8 + bs = (а ± &) (а3 Т ab 4- 62);
(й ± й)2= й2 ± 2аЬ + 62;
(а + b + с)2 = а2 4- &2 4- с2 4-
+ 2 ab -|- 2 ас 4- 2 Ьс;
(й! 4- а, 4- ... 4- ап)2 = а3 -Н4 4-... 4- а3 4-
4- 4* 2 4* • • • 4- 2 otan 4-
4- 2 й2 йа 4- • • • + 2an_1 ап>
(й ± Ь)3 = а»± Зп26 +Зй62 ± Ь3;
пп
и --и П— 1 , П—2 , .
а — b “ а
. П—3
4- й^-Ч»"-1
Й2И 2»— 1_ 2П—2
--------- = а т а о 4-
а ± Ъ
4- а2""3 &2 Т ... +а&2”-2Т &2П~Г
Д2П+1 ft2n+l
о + ft — а —а b 4-
+ й2И->-... -й&^-Ч»2”-
РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ
ВЫРАЖЕНИЯ
Различают целые и дробные рациональ-
ные выражения (стр. 95). Всякое целое ра-
циональное выражение можно преобразо-
вать к виду многочлена:
Р (X) = ЙОХ" 4- 4-
4- fl2x 8 4- ••• 4- ап~1 х 4- ап>
где х—основная величина, а й0, at, at, . .., ап—
коэфициенты многочлена.
Корнем многочлена Р(х) назы-
вается такое значение х — а, которое при
подстановке в многочлен вместо х обращает
его в нуль: Р (а) = 0. Например, один из
корней многочлена Р(х) = х2— 6x4-8 ееть
х = 4, так как Р(4) = 0.
Всякий многочлен имеет по крайней мере
один корень (основная теорема ал-
гебр ы).
Во многих случаях можно произвести
разложение многочлена на множители, т. е.
представить многочлен в виде произведения
АРИФМЕТИКА И АЛГЕБРА
97
простых множителей—одночленов и много-
членов.
Пример 1. Вынесение за скобки:
4а az‘ + 6 aaza = 2 aaza (2 а + 3 z).
Пример 2. Группировка:
х’ + ах + Ьх. + аЬ = (х1 + ах) + (Ьх + аЬ) =
= х(х + а) + 6(х + а) = (X + а) (х + Ь).
Пример 3. Применение формул сокращённого ум-
ножения:
5 х‘ — б у* — 5 (х* — у‘) = 5 (х* + у’) (х* — у1) «
= 5(х> + У)(х +у)(х - у).
Всякое дробное рациональное
выражение можно преобразовать в
отношение двух многочленов, не имеющих
общих множителей:
О (х)
* W = Нс) =
1+ Ь2хт 2+ ... -F Ьт_уХ-^-Ьт
~ айхп+ а^х11^ + а2хп~2+ ... + «П-1Х + ап
где х — основная величина, а а0, а2, а2, ...,
&0, &1, bs, ... — коэфициенты.
Коэфициент при старшем члене знамена-
теля можно всегда сделать равным единице,
разделив на него числитель и знаменатель
дроби.
Отношение двух многочленов называется
правильной рациональной
дробью, если степень числителя меньше
степени знаменателя (т < п), и непра-
вильной, если степень числителя больше
или равна степени знаменателя (т > п).
Любая неправильная рациональная дробь
может быть путём деления числителя на
знаменатель представлена в виде суммы
многочлена и правильной дроби (стр. 96):
Д(х) =
2хМ- 5х’ + 13 х + 4
X1 + 2х + 3
2х + 1 +
5х + 1
Xй + 2х + 3
Теорема Безу
Остаток от деления многочлена
Р (х) = айхп + а1х”^' + а2хп~2 + . . . + ап
на х — а равен значению многочлена при
х = а, т. е.
Р(х) = (X — а) Pj (X) + Р (а),
где Pj(x) —многочлен степени п— 1.
В случае, когда Р (а) =0 (т. с. а — корень
многочлена), деление совершается без
остатка:
Р(х) = (х — я) Р^х).
Если alt а2, а3, . . . , ап — корни данного
многочлена, то многочлен А-.ожет быть пред-
ставлен в виде произведения линейных
(первой степени) относительно х множите-
лей:
Р (х) = «о (X — ах)(х — а2) (X — а„) . . . (х — а„).
Если в разложении многочлена множи-
тель х—а встречается к раз, то а называет-
ся корнем многочлена кратности к.
В случае, когда коэфициенты многочлена
ай, alt а2, ... , ап действительны, каждые
два множителя, соответствующие сопряжён-
7 том I
ным комплексным корням (стр. 99), можно
заменить квадратным трёхчленом
х2 + рх + q,
где р и q — действительные числа1.
Поэтому в самом общем случае имеем:
Р(х) = а0(х — аД*' (х — a2)fcl . . . (х2+
+ Р1Х + 91)S1 (Х« + Р2Х + q2)Sa . ..,
где klf к2, . . . — показатели кратности дей-
ствительных корней;
з2, . . . — показатели кратности со-
пряжённых пар комплекс-
ных корней.
Всякая правильная несократимая дробь
о = Q(* * * * * * * * * x> = box'” + ь1Хт 1 + .,, +
Р(х) хл + а1хп-1 +. . ,+а„
может быть единственным образом разло-
жена на сумму элементарных (простей-
ших) дробей вида
А Сх + Р /р4 \
(х — или (х2 + рх + q)a {4 ~ 9 < °}’
где к и s — целые положительные числа:
QW = ь<>хт + М"1"1-]-... + ьт =
р (х) (X—я1)/<*... (x’+PiX + tfi)51 ...
Ai А2 А».
---------1--------------F ... +-------------—j- +
X — «1 (X— aj2 (X — ai)ft‘
Ctx + Dx ,______C2x + P2__
• • + x2 + p2x +?i (x2 + p1x+?1)2
C, x -F P.
+ • • • H----1— + • • •
(X2 + P1X + q2)Sa
Величины Alt A2, . . . , Ak , Bj, B2, . . .,
Bka, Cp C2,. . . , С и т. д. определяются
методом неопределённых коэф и-
ц и е и т о в.
Для этого складывают все простые дроби,
приняв в качестве общего знаменателя зна-
менатель исходной дроби, числитель полу-
ченной суммы располагают по убывающим
степеням х и приравнивают коэфициенты
при одинаковых степенях х этого числителя
и числителя исходной дроби (в силу тожде-
ственности этих числителей).
х__ з
Пример. Разложить дробь - на простей-
шие.
Так как х3 — х = х (х — 1) (х 4- 1), то
х — 3 _ А В С
х3—х ~ х х — 1 х -f- 1 ’
откуда
х - 3 = А(хг - 1) + Вх(х + 1) + Сх(х - 1)
или
х-3 = (А + В + С)х2 + ( В - С) х - А.
Сравнивая коэфициенты при одинаковых степе-
нях х в левой и правой частях равенства, получим:
А + S + С = О;
В — С ~ 1;
- А = - 3,
1 Если а4-М —корень многочлена с действитель-
ными коэфициентами кратности к, то а — bi тоже
корень этого многочлена и притом той же кратно-
сти.
98
МАТЕМАТИКА
откуда А — 3, В —— 1; С = — 2 и, следовательно,
X - 3 _ _3____________1 _ 2
Xs — X X х-1 х + 1
Аналогично
Зх* + х* + 4Х1 + 1 Зх* + х* + 4Х1 + 1 =
’ х® + 2х* + х " х(х* + 1)* “
2,2х + 1_______1
" х + х" + 1 (х« + !)• •
ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
Всякое иррациональное выражение мож-
но привести к простейшему (так называ-
емому нормальному) виду различны-
ми алгебраическими преобразованиями,как
то: сокращение показателя, вынесение за
знак корня и уничтожение иррациональ-
ности в знаменателе.
Сокращение показателя:
у^81 (х«—4 х7 + 4 х») = у^92хе(х — 2)2 =
4
= К 9х3 (х—2).
Вынесение за знак корня:
Зг------- 3Z----------
у 81 х’у6 = 3 х2у у 3 ху2.
Уничтожение иррациональности в знаме-
нателе:
Действия над степенями (при любых по-
казателях степеней):
ат -а" = ат+" ;
а" :ап = ат~п ;
(т\п тп
а ) = а ;
(а-Ь)п = апЬп-,
/а\" а"
\b) = ь~п-
КОРНИ (РАДИКАЛЫ)
Корень нечётной степени имеет тот же
знак, что и подкоренное выражение, напри-
2п+1,— 2п+1,-----
мер: у 1 = 1, у — 1 = — 1.
Корень чётной степени из положитель-
ного числа имеет два действительных зна-
чения, отличающихся одно от другого
2п,—
знаком, например у 1 = ± 1.
Корень чётной степени из отрицательного
числа не имеет действительных значений.
Ниже приводятся формулы, относящиеся
к степеням и корням и к действиям над
ними.
СТЕПЕНИ
Возведение числа а (основания) в сте-
пень при показателе степени л целом и по-
ложительном:
ап = а-а-а-а... а(п раз);
(+ а)2п = + а2п;
(— а)2" = + а2";
(+ а)2"-1 = + а2"-1 ;
(_ й)2«-1 = _ а2"-1 ;
в частности: 0” =0; (+ 1)” = + 1;
(_1)2п=+1; (—1)2п~1= — 1.
При показателе степени, равном нулю
(л = 0, а 0):
а9 = 1.
При показателе целом и отрицательном
(п = - т):
________L-
а ~ ат •
При показателе дробном и положитель-
Уничтожение иррациональности в зна-
мевателе дроби
п,-----
а а у/ Ьп т ,
п/---ь ’
У Ьт
a
Vb ± V с Ь — с
Преобразование выражения V А ± Ув
]/а ± Кв = |/Ч
+ т -I/ А — т
2 ± Г 2 ’
а q = yfa?.
При показателе дробном и отрицательном
где т = К А2 — В.
Пример» Преобразование выражения
Кг - /S':
m — У а* - в - Ул- з- 1;
р
АРИФМЕТИКА И АЛГЕБРА
99
Извлечение квадратного корня.
Извлечение квадратного корня из чисел
производится по схеме, показанной ниже.
Пример 1, Извлечь квадратный корень из числа
|/12'39'О4 = 352
9
65 ] 339
5 I 325
702 I 1404
2 | 1404
Разбиваем число справа налево иа грани по две
цифры в каждой грани: 12'39'04 (первая грань мо-
жет оказаться неполной, т. е. состоящей из одной
цифры). Из первой грани (12) извлекаем корень
точно или приближённо с недостатком (1^12~3 )\
полученное число (3) есть первая цифра искомого
корня. Из 12 вычитаем 3’ и к остатку (3) приписы-
ваем следующую грань (39). Затем, удвоив получен-
ную первую цифру корня (2*3=6), приписываем её
слева от полученного числа (339), оставляя между
обоими числами свободное место ещё для одной циф^
ры; оба числа отделяются друг от друга вертикальной
чертой. Деля число десятков (33) на 6, получаем вто-
рую цифру (5) искомого корня (она может быть и
нулём). Её записывают в трёх местах: в ответе, ря-
дом с цифрой 6 и ниже; полученные слева от черты
два числа перемножаются (65*5 -» 325) и склады-
ваются (65 + 5 70). Произведение вычитаем из
339 и к остатку (14) приписываем следующую грань
(04). Если окажется, что вычитаемое больше умень-
шаемого, то вторую цифру берут на единицу мень-
ше. Нахождение третьей из следующих цифр произ-
водится подобным же образом; так как в последнем
остатке получился нуль, то число 352 является
точным значением квадратного корня:
/ 123 904 - 352.
Пример 2. Извлечь квадратный корень из деся-
тичной дроби 1239,04.
Разбиваем дробь на грани (по две цифры в каж-
дой грани) в обе стороны от запятой: 12' 39', 04';
если крайняя правая грань окажется неполной,
нужно приписать справа нуль. Далее производим
вычисления по той же схеме, что и для целых чисел,
не обращая внимания на запятую. Результат содер-
жит столько цифр до запятой, сколько полных или
неполных граней содержало до запятой данное
число:
/ 1239,04 = 35,2.
Если десятичная дробь не содержит целой час-
ти, то и квадратный корень из неё ие содержит це-
лой части и имеет после запятой столько нулей,
сколько полных граней, состоящих из нулей, справа
от запятой, имеет даниая десятичная дробь:
Y 0,00'00'12'39'04 = 0,00352.
Пример 3. Извлечь квадратный корень из числа
123 906.
Применив ту же схему, получаем в остатке
2, и 352 является не точным, а приближённым (с
недостатком) значением корня: ^1~М’90б7*'352.
/12'39'06-352
9
65 |3 39
5 |3 25 __
702 1 14 06
2| 14 04
2
В этом случае для получения большей точности
следует в подкоренном количестве приписать после
запятой нужное число нулей и продолжать вычис-
ление по схеме для извлечения корня из десятичной
дроби
ДЕЙСТВИТЕЛЬНЫЕ, МНИМЫЕ
И КОМПЛЕКСНЫЕ ЧИСЛА
Все числа, которые могут быть получены
путём сложения, вычитания, умножения и
деления натуральных чисел 1, 2, 3, 4, 5,
называются рациональными, напри-
мер: у, — у ; 2,512; все прочие числа
называются иррациональными, на-
пример: Yi, yf 5, л. Рациональные числа
могут быть изображены конечными или
периодическими десятичными дробями:
j = 0,25; у = 0,333 ....
Каждое число можно приближённо (с лю-
бой точностью) изобразить конечной деся-
тичной дробью с достаточно большим числом
знаков.
Числа рациональные и иррациональные,
как положительные, так и отрицательные,
называются действительными (веще-
ственными).
Формально, введя новую единицу счис-
ления, так называемую мнимую еди-
ницу, определяемую равенством
/2 = — 1 или i = Y — It
получим общее выражение для чисто мни-
мого числа:
Y — - ь Y^i - ы,
где Ъ — действительное число.
Пример 1.
/—~4 _ 2 /~1 -2 1.
Пример 2.
У~з - /3 * - i /з.
Число вида а + &Z, где а и Ь — действи-
тзльные числа, называется комплекс-
ным числом, а —
его действительной
частью, Ы — мнимой,
b — коэфициентом
при мнимой части.
Комплексные чис-
ла содержат в себе
действительные и
мнимые числа как
частные случаи: при
b = 0 комплексное
число а + Ы превра-
щается в действи-
тельное число а, при
а = 0 в чисто мнимое
число Ы.
Фиг. 1
Комплексное число z=a-|-&z изображается
на плоскости точкой М с координатами
а и b (фиг. 1) или вектором ОМ (радиусом-
вектором точки М).
При этом действительные числа изобра-
зятся точками на оси ОХ (действитель-
ная о с ь), а чисто мнимые числа — точка-
ми на оси 0Y (мнимая ось).
Число z^=a—bi изображается точкойN,
симметричной с точкой М относительно
действительной оси, и называется сопря-
жённым с z = a + М.
Два комплексных числа равны между
собой, если отдельно равны их действитель-
ные н мнимые части;
если
ai + bii = as + bti,
= а, и bt = bt.
7*
МАТЕМАТИКА
100
г
о
Фиг. 2
между этим
жительным
Комплексное число равно нулю, если
равны нулю его действительная и мнимая
части:
а + Ы = О,
если
а — 0 и 6 — 0.
Тригонометрическая форма комплексного
числа
z = а + Ы = г (cos ср + i sin ср);
г называется модулем комплексного
числа и обозначается символом |z|,y назы-
вается аргументом комплексного числа
и обозначается символом
arg z:
г= tg <р =
Модуль комплексного
числа равен длине ОМ
радиуса-вектора точки М
(фиг. 2), аргумент—углу
радиусом-вектором и поло-
направлением действитель-
ной оси. Угол отсчитывается от положи-
тельного направления действительной оси
против часовой стрелки.
Число с модулем г и аргументом ср может
быть также записано в форме rel<f> (показа-
тельная форма)1, где е = 2,718 . . . (стр. 129).
Например, число 1 4-t'Fr3 (алгебраическая
форма) может быть представлено в тригоно-
метрической форме в виде
/тс тс
21 cos -3 + i sin у
< тс
и в показательной форме в виде 2е8 .
Сложение и вычитание комплексных чи-
сел. При сложении или вычитании ком-
плексных чисел отдельно складываются или
вычитаются их действительные и мнимые
части;
(01+ &1О ± (о.+ b2f) = (аг ± а2) + (bt ± 6,)г.
Радиус-вектор суммы и разности двух
комплексных чисел строится как геометри-
ческая сумма или разность радиусов-векто-
ров этих чисел (стр. 208).
Сумма двух сопряжённых комплексных
чисел есть число действительное:
(о + bi) + (а — М) == 2 а.
Умножение двух комплексных чисел
(Oj +b1i)(at + b,/) =
•= (ага2 — bib2) 4- (Hib2 + a2bt) i,
или в тригонометрической форме:
[rj(cos cpi + i sin cpHllMcos <p2 + i sin <p2)] =
= nrjcos^! + <p2) + i sin (T1 + <p2)],
т. e. модуль произведения равен произве-
дению модулей сомножителей, а аргумент—
сумме аргументов сомножителей.
Произведение сопряжённых комплексных
чисел равно квадрату модуля:
z z = (а + М) {а — Ы) = аг + Ьг,
* См. формулу Эйлера, стр. 213.
Деление двух комплексных чисел
01 + bji _ (<M2 4- Ь1Ь2) + (д2&! — fltbg)I
а, + b2i а* +
или
Гд (cos ср-д 4- i sin срд)
г, (cos <р2 4- i sin -fa) =
= rjT [С08(<рг—cp2) + f sin(<p, —<p2)J,
т. e. модуль частного равен частному моду-
лей сомножителей, а аргумент — разности
аргументов сомножителей.
Возведение в степень комплексного числа
[г (cos <р 4- i sin <p)ln = rn (cos n у + i sinn tp)
(формула Моав pa), т. e. модуль воз-
водится в n-ю степень, а аргумент умно-
жается на и. В частности:
(-4т = ]. ^4т+1 = ^4т+2_^ _
—целое)
Извлечение корня из комплексного числа
Vr( COS ср + i sin ср) =
nz— ( ? + 2 к л ср 4- 2 к тс \
= У г I cos----~----+ i sin----------),
где к — 0, 1, 2, 3,. . . , п— 1.
Различные значения корня изобража-
ются геометрически вершинами правильного
n-угольника, вписанного в круг с радиусом
Пу--
у г.
Пример.
3.---3.---------------
V — 1 — F 1(COS тс+i SilJTC) >
тс 4- 2л тс . тс + 2к тс
- cos —------+ г sin -----.
Полагая к — О, 1, 2, получим три значения
1 . УТ . ,. 1 i/з
2 + 1 2 ’ 11 2 2 •
СОЕДИНЕНИЯ (КОМБИНАТОРИКА)
Соединениями называются всевоз-
можные группировки данных предметов (эле-
ментов).
Различают следующие виды соединений:
Размещения — соединения, содержа-
щие одинаковое число элементов (например,
т элементов из и данных) и отличающиеся
Друг от друга или элементами (по крайней
мере одним) или порядком элементов. На-
пример, размещения из трёх элементов а,
b и с по два: ab, ас, be, ba, са, cb.
Перестановки — соединения, содер-
жащие все данные элементы и различаю-
щиеся друг от друга только порядком вхо-
дящих в них элементов. Например, переста-
новки из трёх элементов: abc, bca, cab, acb,
bac, cba.
Сочетания — соединения, содержа-
щие одинаковое число элементов (например,
т элементов из п данных) и отличающиеся
друг от друга только самими элементами
(по крайней мере одним). Например, соче-
тания из трёх элементов а, b и с по два:
ab, ас, Ьс.
АРИФМЕТИКА И АЛГЕБРА
101
Число размещений из п элементов
по т:
А™-п(п — 1)(п — 2). . . (п — т+ 1) =
и!
= (п — ту. ’
где символом п\ (п факториал) обозначено
произведение натуральных чисел от 1 до п.
Таблица факториалов (и!) приведена на
стр. 82 (0! принимают равным единице).
Число перестановок из п эле-
ментов
Рп = 1 -2.3-4 . . . п = п! = А„.
Число сочетаний из п элементов
по т:
ст =
" \тГ~рт
п(п— 1) (п — 2). . . (п — т + 1)
“ 1 • 233 777т =
и!
= т! (п — т)! •
В частности: С* = п; С" = С° = 1.
Основное свойство сочетаний:
рт__рп—т
'-п
Число размещений из п различных эле-
ментов пот, при условии, что среди этих m
один или несколько могут повторяться, вы-
числяется по формуле числа размеще-
ний с повторениями
А АД7 = пт.
Число перестановок из п элементов а, Ь,
с,. . ., среди которых имеются одинаковые
(а повторяется а раз, b — (3 раз, с — 7 раз
и т. д.), определяется формулой числа
перестановок с повторениями
, Рп п!
Р (а, ₽, 7, . . .) - р -р^ . . . - а! pi 71 . . . >
где
а + Р + 7 + ... = П.
Число сочетаний из п различных элемен-
тов по т, при условии, что среди этих m
один или несколько могут повторяться, вы-
числяется по формуле числа сочетаний
с повторениями
ppm _ pm _ (п -f- m —1)!
п •'n + m-l т!(гЗЗ)Г’
БИНОМ НЬЮТОНА
Биномом Ньютона называется фор-
мула, представляющая выражение (а + Ь)п в
виде многочлена при целом и положитель-
ном п (другие случаи см. стр. 161):
(а + Ь)п = ап + пап~' Ь + ~ а П~2 68 +
t- (Л —1)! о +
+ . . . + nabn—1 + Ьп.
Общее выражение к-го члена бинома
Ньютона:
П(п- - к+ 2) к+х к_х
(к—1)1 а b
= Ск~' ап~к+1 Ьк~1
Основные свойства биномиальных
коэфициеитов
1) Коэфициенты в разложении бинома
Ньютона возрастают до середины формулы
и затем убывают;
2) коэфициенты членов, равноотстоящих
от начала и от конца разложения, равны
между собой;
3) сумма коэфициеитов в биноме n-й сте-
пени равна 2”;
4) сумма коэфициеитов членов нечётного
порядка равна сумме коэфициеитов членов
чётного порядка, причём каждая из этих
сумм равна 2П—1.
Определители
Определитель (детерминант)
п-го порядка
• • • °1п
a21fl22 • • • °2а
^П2 • • •
содержит п2 элементов, расположенных
в п строках и п столбцах.
Минором некоторого элемента опреде-
лителя п-го порядка называется определи-
тель порядка п — 1, получаемый из данного
определителя вычёркиванием той строки и
того столбца, которым принадлежит рассма-
триваемый элемент.
Алгебраическим дополнением
(адъюнкт ой) элемента определителя
называется его минор, умноженный на
(—1)г+^ , где i — номер строки, а / — номер
столбца рассматриваемого элемента.
Определитель равен сумме произведений
элементов какой-либо строки или столбца
на соответствующие алгебраические дополч
нения (разложение определителя
по минорам); так, например, если Alkt
102
МАТЕМАТИКА
Д21, .. . , Ащ — алгебраические дополнения
элементов первого столбца, то
2. Если все элементы какой-либо строки
(или столбца) равны нулю, то определитель
flu <iia • • • aifi
<?21 ^22 • • • Оап
равен нулю:
. . . I . . .
ап1 Опа. • • апп
= ОцАц + а21^21 +
A &t С]
л 2 Ь 2 А
ООО
= 0.
+ ат Ли-
3. При перестановке двух строк (или
столбцов) определитель изменяет знак:
Это свойство позволяет свести вычисле-
ние определителя порядка п к вычислению
определителей порядка п—1.
Для вычисления определителя второго
порядка | 1 надо из произведения элемен-
тов, расположенных на главной диаго-
нали, вычесть произведение элементов,
расположенных на второй диагонали;
\a12b\ \ =aibi — a2bi-
I A &i I = _ I А А I .
I а2 ba I I лх I ’
01 Ь1С1
d п bС
а3 ba с3
oa ba ca
01 bl Cl
А Ьз C8
4. Если определитель имеет две одинако-
вых строки (или столбца), то он равен нулю:
Для вычисления определителя третьего
порядка можно применить один из следую-
щих способов:
а) Общий способ (разложение по
минорам элементов какой-либо строки или
столбца):
| fli bi I _ п.
I 01 &11 - и’
01 bl Ci
01 bi Ci
«з »8 A
= 0.
5. Общий множитель всех элементов
какой-либо строки (или столбца) можно вы-
нести за знак определителя:
fll&iCi
йаЬаСа
а»ь^»
~ а1 (^2С3
+ Ci («2&з — Мз)
= «1
Al h I a2C2 I I r i a2b2 I
A I 01 I а8Сз I + 1 I o,b, I
&A) — bi (AA — O,Ca) +
albac, — a1b„ca — aab1c> +
+ a,&iC2 + — a,bacr
Oi fti I = X
Ха2 Х&2I
Хда
о,
01 »11 ,
Оа Ьа I *
01 bi Ci
оа ьа са
оа Ьа са
б) Способ Саррюса. Подписывают
под определителем две первые строки и со-
ставляют алгебраическую сумму произведе-
ний элементов, взятых по три, расположен-
ных. по диагоналям определителя и их па-
раллелям, причём произведения по диаго-
нали aa, Ьг, с, (главной диагонали) и по её
параллелям берут со знаком +, а осталь-
ные со знаком —.
6. Определитель, у которого элементы
какой-либо строки (или столбца) пропор-
циональны соответствующим элементам дру-
гой строки (или столбца), равен нулю:
I ai bi I _ п.
I Ха, X&JI и>
01 Ь1 Ci
Хах Х&! Xcj
о» ьа с8
= 0.
Пример.
3 2 —1 |
1 —2 0-18-1 + 0—8-0 + 6-15.
7. Если к элементам какой-либо строки
(или столбца) прибавить элементы другой
строки (или столбца), умноженные на одно
и то же число, то величина определителя
не изменится:
01 bi Ci
оа Ьа са
О, ь3 с,
101 bi I _ I A + X аа
I аа ba I I А
bl + X &2 I
01 + X Qa bi -f- X ba Cj + X c2
oa ba ca
o3 ba ca
В частности, если элементы какой-либо
строки (или столбца) представляют собой
линейную комбинацию соответст-
вующих элементов остальных строк (или
столбцов), то определитель равен нулю:
Вместо строк можно аналогичным обра-
зом приписывать столбцы.
Основные свойства определителей
1. Определитель не изменит своей вели-
чины, если все строки его заменить соответ-
ствующими столбцами (свойство равноправ-
ности строк и столбцов):
I А Ь1 I = I А А I.
I и8 b21 I ba ba |
а1 bi Ci I
oa ba ca
аг b, cs I
AAA
Ь1 b2 ba
C1 c2 A
Ха2 + р. а,
02
о.
х ьа + р ьа
Ь2
ь»
X са -f- р с8
О?
= 0.
с»
8. Если определители разнятся между
собой только элементами какой-либо одной
строки (или столбца), то можно складывать
между собой такие определители, причём
в сумме получается определитель, у кото-
рого элементами соответствующей строки
(или столбца) будут суммы элементов опре-
АРИФМЕТИКА И АЛГЕБРА
103
делителей — слагаемых, а остальные элемен-
ты — те же, что у слагаемых:
ai 1 4 а2 &S 1 1 fl) a b\ 1 = ft 2 1 Qi + a'l a3 bt + ft' b3
01 ftj Ct a, ft. c.
а2 fts с2 -+ a2 ft2 -2 =»
«з ^з ^з 3
a, +a, ь + bl Ci + с'.
<*2 ft. c2
a3 b3 c3
9. Сумма произведений элементов какой-
либо строки (или столбца) на алгебраиче-
ские дополнения соответствующих элемен-
тов другой строки (или столбца) равна
нулю. Например, ftjAt + b2A2 + bsAa = 0
(Alt А2 и А,— алгебраические дополнения
элементов alt а2 и а3).
УРАВНЕНИЯ
УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
Алгебраическим уравнением с одним не-
известным называется равенство Двух алгеб-
раических выражений, которое верно (удов-
летворяется) только при определённых зна-
чениях входящей в него неизвестной вели-
чины х. Эти значения х,, х2, х3, ... назы-
ваются корнями уравнения. Решить
уравнение — значит найти его корни.
Например, уравнение х!—5 х + 6=0 имеет корни:
Х, = 2 и х,=3, так как 2а—5-2 + 6 = 0 и 3!—5-3 + 6=0.
Равносильными называются урав-
нения, имеющие одни и те же корни.
При решении уравнения применяются
следующие основные приёмы:
1. Замена одного выражения другим,
равным ему тождественно.
2. Перенос слагаемых из одной части
уравнения в другую с переменой знака на
обратный.
3. Умножение или деление обеих частей
уравнения на одно и то же выражение. При
этом может, впрочем, оказаться, что новое
уравнение не будет равносильно исходному,
если выражение, на которое умножают или
делят обе части уравнения, содержит неиз-
вестное и может быть равным нулю.
Например, разделив обе части уравнения
(х-3) (х+3)=4 х+12 на x-j-З, получаем уравнение
х— 3=4 их=7 будет его единственным корнем. Меж-
ду тем исходное уравнение имело два корня: х=7 и
х=—3, что легко проверить подстановкой. Наобо-
рот, при переходе от второго уравнения к первому
(путём умножения на х+З) появился бы лишний
корень х=-3.
4. Возведение обеих частей уравнения
в пипу и ту же степень или извлечение
корня одной и той же степени. И в этом
случае возможно появление лишних или по-
теря корней.
Например, уравнение /х+7 = 2 х-4 при возве-
дении в квадрат переходит в х-7^4 ха—4 х + 1 или
4 хг— 5 х—6=0, которое имеет два корня: Xj=2 и
Xj=—-- ; между тем исходному уравнению удов-
летворяет только корень х=2.
Проверка решения уравнения осуществ-
ляется путём подстановки найденных кор-
ней в исходное уравнение.
Всякое алгебраическое уравнение можно
при помощи алгебраических преобразований
привести к так называемой канониче-
ской форме, т. е. к уравнению вида:
аохп + аре"-1 + а2хп~2 + .. . +
+ a„_i х + ап = 0.
Показатель степени п называется сте-
пенью уравнения.
Уравнения первой степени (линейные).
Всякое уравнение первой степени с одним
неизвестным можно привести к виду:
ах + ft = О (канонический вид),
b
откуда х = — — , т. е. линейное уравнение
имеет один действительный корень (если
а =# 0).
Уравнения второй степени (квадратные).
Приведённое уравнение х3 + рх + </= 0:
Уравнение общего в и д а ах2 + Ьх 4-
+ с = 0:
_ — ft + 'Кб2 — 4 ас
ХЬ2-----------у---------
« £• U
Уравнение с чётным средним коэфициен-
том ах2 + 2 тх + с = 0:
v _ — т ± Ут2 —ас
ЛI О —1 11 ' • ' •
Неполное уравнение вида ах2 + Ьх = 0:
„ Ь
Xi = 0; х2 = — - .
Неполное уравнение вида ах2 + с = 0:
Свойства корней квадратного
уравнения. Если хг и х2 — корни урав-
нения х2 + рх + q = 0, то
*1 + = — р; XjX2 = q.
Соответственно для уравнения ах3 + ftx+
+ с = 0:
ft с
Х1 + Х2 = -> ^1^2 = д •
Исследование корней квад-
ратного уравнения. Выражение
«2
q — с- (для приведенного урав-
4 ас — ft2 или
нения) обозначается через А и называется
дискримина нтом квадратного урав-
нения.
Если А < 0, то корни действительные и
разные; если А = 0, то корни действитель-
ные и равны между собой; если А > 0, то
корни мнимые.
Преобразования трёхчлена
второй степени. Если хх и х2 — корни
трёхчлена ах2 + Ьх + с, то
ах2 + Ьх + с = а (х — хх)(х — х2).
104
МАТЕМАТИКА
Всякий трёхчлен второй степени можно
представить также в виде:
ах2 + Ьх + с =
= а
' , Ь V ('Vb3 —4ас\"
+ 21J ----2а----/ __ *
Уравнения третьей степени (кубические).
Корпи кубического уравнения в приве-
дён ной форме
х3 + рх + q = О
находятся по формуле
х =
а) Если
то
хг = А + В;
х2 = - 1 (А + В) + i (А - В);
*3 = - 4 (А + В) - i (А - В),
Z 2,
где А и В — действительные значения ку-
бичных корней, входящих в формулу.
б) Если
3
= 0,
в) Если
то А = В, х, = 2 А, х2 = х3 = — А.
/ а V / nV
< 0 («н епр вво-
димый случай»), то в действительной
форме корни выражаются по формулам:
<Р
Xj = 2 г cos у ;
Х2 = 2 г cos ----g
Хз = 2 г cos ----J
где
3 q
। и cos <р — — •
Уравнение третьей степени общего
вида
ах3 + Ьх3 у сх + d = О
можно преобразовать к приведённой форме
У’ + РУ + Q = 0, разделив обе его части на а
в выполнив подстановку
'1 b
* = у- з
Возвратные уравнения третьей
степени
ах3 + &х2 ± Ьх ± а — О
можно представить в виде:
(х ± 1) [ах3 + (& =F а) х + а] = О
и свести к решению уравнений первой и
второй степени.
Уравнения четвёртой степени. Корни
уравнения четвёртой степени
х4 + Ьх3 + сх2 + dx + е = О
совпадают с корнями двух квадратных урав-
нений:
Xs
где А = ± 8 у + &2— 4с, а у — какой-ни-
будь действительный корень кубического
уравнения
8у3 — 4 су2 + (2 — 8 е) у +
+ е (4 с — &2) — d2 = 0.
Корни биквадратного уравнения
ах4 + Ьх3 + с = 0
определяются по формуле
х1, 2, 3, 4
— Ь ± -уАЬ3 — 4 ас
~2а '
Возвратные уравнения четвёртой сте-
пени
ах4 ± Ьх3 + сх3 + Ьх + а = О
путём деления всех членов уравнения на х’
и подстановки
1
х + "х = у
сводятся к уравнению
ay3 ± by + (с — 2 а) = О,
откуда * _______________
_ У b ± У Ь3 — 4ас + 8а2
2а
и, следовательно,
V _ У ± /у3~4
*1, 2, 3, 4----g'
Если уравнение имеет вид
ах4 ± Ьх3 + сх3 Т Ьх + а — О,
то производится подстановка
1
Двучленные уравнения- Корни двучлен-
ного уравнения
хп — а = 0
определяются по формуле
п,— Г 2кп 2 к те 1
х = у a cos —— + i sin ——
(к = 0, 1,2,..., п— 1).
Трёхчленные уравнения. Трёхчленное
уравнение вида
ах2п + Ьх'1 + с = 0
подстановкой х" = у сводится к квадратно-
му уравнению
ay3 + by + с = 0.
Уравнения степени п. В общем случае
уравнение степени п при п > 4 не может
АРИФМЕТИКА И АЛГЕБРА
1 От-
быть решено в радикалах. Способы отыска-
ния приближённых решений указаны на
стр. 236—244.
Свойства корней. Если Xj, х2> • • • »
Хп—корни уравнения
х" + o1x""’1 + о2х'1“2+ ... + а„_! х+ ап = О,
то:
ai — — (xi + х2 + *3 + • 4- хп);
о2 = х2 х2 + Xj х3 + х± х4 ... + х2 х3 +
+ х2х4+ ... + хп_! хп ;
«3 = — (XiX2X3 + XjX2X4 + ... + XiX2X„ +
+ х2х3х4 + х2х3х5 + ... + Хп_2 х„_! хп);
= (— 1)Л XjX2X3 ... х„_, х„ .
СИСТЕМЫ УРАВНЕНИЙ
Система л алгебраических уравнений
' /1(х, у....z)=0,
. /2 (х,у, ..., z) = О,
/п (X, у, ..., 2) = 0
может иметь одно, несколько или бесчис-
ленное множество решений, а также может
быть несовместной (не иметь решений).
Решением системы называется группа
значений неизвестных х, у, ..., z, обращаю-
щая в тождества все уравнения системы.
Система двух линейных уравнений с дву-
мя неизвестными. Общий вид системы двух
линейных уравнений с двумя неизвестными:
О1Х + b3y = с1г
а2х + Ь2у = с2.
Путём исключения одного из неизвестных
любым из указанных ниже способов реше-
ние этой системы можно свести к решению
одного уравнения с одним неизвестным.
Решив это уравнение и подставив найден-
ное решение в любое из исходных уравне-
ний, можно определить второе неизвестное.
Способ сравнения. Каждое урав-
нение разрешается относительно у (или х) и
полученные для у (или х) выражения при-
равниваются:
С1 — Д1Х _ с2 — Д3Х
bi Ь2
Способ подстановки. Выражение,
полученное для у (или х) из одного уравне-
ния, подставляется в другое:
Способ сложения и в'ы ч и т а н и я.
агх + Ьг у = Cj I (умножаем на Ь2);
__агх + Ьг у = с2 | — Ьг (умножаем на — bj);
a2&i)x = ctb3 — с2Ь1 (складываем).
Решение с помощью определителей.
Если Д“|а2^И0’ Т0
Дз = 1 I с, bi I . 4? = ± ! Ai Ci I
“ А д I с2 b21 ’ у Д А [а, с2|'
Пример, Решить систему уравнений:
2х - 3 у = 1;
Зх + у = 7.
В дальнейшем предполагается, что оба
неизвестных действительно входят в систему,
т. е. хотя бы один коэфициент при каждом
из них отличен от нуля.
В случае А = | | = 0 формулы для-
определения неизвестных при помощи опре-
/ А Ау\
делителей х = -д-; У=-у1 теряют смысл.
Если одновременно с равенством А —О
имеет место неравенство Ах 4= 0 (тогда и
Д 0), то система несовместна (не
имеет решения). Если же одновременно
с Д = 0 имеет место равенство = Av = 0,
то система неопределённая (имеет
бесчисленное множество решений). В этом
случае
а2 Ь2 с2
и одно из уравнений является следствием вто-
рого и может быть отброшено. Любая пара
значений х и у, удовлетворяющих оставшему-
ся уравнению, даёт решение системы
Система двух линейных однородных урав-
нений
Я1Х+ Ьгу = 0,
о2х + Ь2у = 0
либо неопределённая (при А = 0), либо
имеет единственное решение (нулевое: х =
== у = 0 при А =#= 0). Случай несовместности
для однородной системы исключается. Если
система однородных уравнений неопределён-
ная, то она имеет, кроме нулевого, бесчис-
ленное множество решений, содержащихся
в формуле
х : у — — bj : аг = — b2: а2.
Система трёх линейных уравнений с тремя
неизвестными
О1Х biy + С]2 — dlt
а2х-\- Ь2у + с2г = d„,
а%х + Ь3у с32 — d3,
если
А =
Oi bj Ci
о2 b2 с2
Ь3 с3
О,
решается при помощи определителей по фор--
мулам:
Av 1 СГ
х = ^ = д’ d2b2c2
^3 ^3 Сз
у = д^ 1 д’ dt ^2 Сз
й3 ^3 ^3
А.
2~д ~ А ^3 Gj &3
106
МАТЕМАТИКА
В дальнейшем предполагается, что все
три неизвестные действительно входят в си-
стему, т. е. хотя бы один из коэфициентов
при каждом из них отличен от нуля.
В случае Д = 0 приведённые формулы
теряют смысл. Если при Д = 0 среди опре-
делителей Дх, Ду, Дг есть по крайней мере
один, не равный нулю (тогда и остальные
отличны от нуля), то система несовместная
(не имеет решения); если же одновременно
с Д = 0 все три определителя Д^, Ду, Д,
равны нулю, то система неопределённая
(имеет бесчисленное множество решений).
В последнем случае по крайней мере одно
из уравнений системы является следствием
оставшихся двух и может быть отброшено.
Любая тройка значений х, у и z, удовлет-
воряющая оставшимся двум (или одному)
уравнениям, даёт решение системы.
Пример 1.
х+ 2у — z = 2;
5 х— 4 у + z = 0;
2 х + у — 3z» - 5.
х — у + 2 z « 2;
2х — у — 3 z = 3;
4 х — Зу + z -= 7
(Д + Ot система совместна и
имеет единственное решение).
1 2-1
5 О 1
2-5-3
32
(Д « дх а Ду == м о, система
неопределённа).
Умножив обе части первого уравнения на 2 и
еяожив их с соответствующими частями второго,
получают третье уравнение, которое, таким обра-
зом, является следствием первых двух и может
быть отброшено.
Система двух однородных линейных уравг
нений с тремя неизвестными
atX + &1У + ciz = °,
«2х + b2y + c2z = О
имеет бесчисленное множество решений, ко-
торые определяются по формулам:
где t— произвольная величина (предпола-
гается, что не все определители, входящие
в формулу, равны нулю).
Пример. Решив систему уравнений:
х + у — г - О,
Зх—3у+г — О,
получим:
|_з з!‘“~4';
г “ | 3 -3 р - " 6 '
где 1 произвольно.
Положив t —------получим решение:
1=1, у = 2, г=3;
положив 1=1, получим другое решение:
х = — 2, у = — 4, г = — бит. д.
Система трёх однородных линейных урав-
нений с тремя неизвестными
«1Х + Й1У + CjZ = 0;
а2х + b.2y + с„г = 0;
<13х + ЬзУ + c3z = О
либо имеет единственное решение (нулевое,
при Д =/= 0), либо неопределённая (при Д=0).
В последнем случае одно или два уравне-
ния могут быть отброшены как следствия
остальных. Если только одно уравнение
отбрасывается (Д = 0, но по крайней мере
один из его миноров не равен нулю), то
задача сводится к решению системы двух
независимых однородных уравнений с тремя
неизвестными (см. выше). Если же два
уравнения являются следствием третьего
(Д = 0 и все его миноры также равны нулю),
то любая тройка значений, удовлетворяю-
щих этому третьему оставшемуся уравнению,
даёт решение системы.
Система п линейных уравнений с п неиз-
вестными
а11Х1 + а12Х2 + ••• + °1П Хп= Р1>
ИгЛ + а22х2 + ... + а2Пх”= р2,
ani. *1 + ал2 х2+ ... + апп хп= рп
является совместной, если определитель си-
стемы (Д) не равен нулю:
«11 «12 ain
<121 fl22 • •• а2Ч
0.
ат апг •• апп
В этом случае решение системы имеет вида
At А2 Дл
Xi д ; х2 - д ,..., х„ - д ,
где
Pl «12 ... «1Л
Pl «22 а2П
Рп ат •• апп
Иц Pi •• •«1л
д2 = р2.. • а1П
ani Рп •• hn
<111 «12 • Р1
Дд = «21 «22 • Pl
• Рп
НЕРАВЕНСТВА
Два алгебраических выражения, соеди-
нённые знаком > (больше) или < (меньше),
образуют неравенство. Решить нсра-
венсто Р(х)>/(х) или Р(х) < /(х), где
F(x) и / (х) — выражения, содержащие неиз-
вестное х, значит определить, при каких
значениях х неравенство имеет место.
Два неравенства называются равно-
сильными, если они справедливы при
одних и тех же значениях неизвестного х.
Прибавление или вычитание из обеих
частей неравенства одного и того же числа
АРИФМЕТИКА И АЛГЕБРА
107
или выражения, а следовательно, и перенос
любого выражения из одной части неравенст-
ва в другую с изменением знака, приводят
к неравенству, равносильному исходному.
При умножении или делении обеих ча-
стей неравенства на одно и то же положи-
тельное число получается неравенство, рав-
носильное прежнему; при умножении и де-
лении обеих частей неравенства на одно и
то же отрицательное число следует, для
получения неравенства, равносильного пер-
воначальному, изменить смысл неравенства
на обратный (> на < или < на > ).
Неравенства 1-й степени реша-
ются при помощи указанных выше преоб-
разований.
Пример,
2 х 4-3 > 5 х + 18; -Зх>15 и х < - 5.
Неравенства 2-й степени (квад-
ратные) могут быть приведены к одному
из видов:
х2 + рх + q > 0
или
хг + рх + q < 0.
а) х2 + рх + q > 0.
Если корни Xj и х2 многочлена х2 + рх + q
мнимые (т. е. р2—4 </<0), то неравенство имеет
место при всех значениях х(— <х> < х < °°).
Если корни х, и х2 действительные и
хх = х2 (т. е. р2 — 4 q — 0), то неравенство
справедливо при всех значениях х, кроме
х = хх = х2.
Если корни хх и х2 действительны и раз-
личны (т. е. р2 — 4 q > 0), причём хх < х2,
то неравенство имеет место при х < хх и при
X X
б) х2 + рх q < 0.
Если корни хх и х2 мнимые (р2 — 4 q < 0),
то неравенство противоречиво.
Если хх = х2 (р2 — 4 q = 0), то неравен-
ство тоже противоречиво.
Если хх и х2 действительны и различны
(р2 — 4q > 0) и хх<х2, то неравенство имеет
место при хх < х < х2.
Пример 1. х* — 5 х 4- б > О; корни трёхчлена
Xi = 2, х8 =« 3 (действительные) и, следовательно,
х < 2 или х > 3.
Пример 2. х1 — х 4- 2 < О; р* — 4 q >» — 7 < О
(корни мнимые) и неравенство противоречиво.
ЛОГАРИФМЫ
Логарифмом числа N при основании
а (обозначение: logalV) называется показа-
тель степени х, в которую надо возвести
основание а, чтобы получить число N, т. е.
если а* = N, то х = log0N.
При любом положительном основании,
кроме единицы, всякое положительное число
имеет свой логарифм.
При основании а — 10 логарифмы назы-
ваются десятичными и обозначаются
символом 1g. При основании а=е = 2,7...
(стр, 129) логарифмы называются нату-
ральными и обозначаются символом In.
Соотношения между десятичными и на-
туральными логарифмами: lnN = In 10 • IgN
и IgN = 1g e InN.
Числа M *= 1g e — j™ уд и 0,43429 и =•
= In 10 x 2,30259 называются модулями
перехода от десятичных логарифмов к
натуральным и обратно.
Вообще для перехода от системы лога-
рифмов с основанием а к системе с основа-
нием b можно пользоваться формулой
logAN = М \ogaN,
где М = logft Д iog — модуль перехода.
Нахождение логарифма данного числа
называется логарифмированием; на-
хождение числа по его логарифму — потен-
цированием.
ОСНОВНЫЕ СВОЙСТВА ЛОГАРИФМОВ
1) Логарифмы отрицательных чисел при
положительном основании мнимы.
2) Логарифм пуля — бесконечен:
loga 0 = — оо при а > 1,
1 oga 0 = 4- оо при а < 1.
3) Логарифмы положительных чисел,
меньших единицы, при основании, большем
единицы, отрицательны.
4) Логарифм единицы при любом основа-
нии (а ф 1) равен нулю:
loga 1 = 0.
5) Логарифмы чисел, больших единицы,
при основании а > 1 положительны,
6) Логарифм основания равен единице:
loga а = 1; 1g 10 = 1; In е = 1.
7) С увеличением чисел их логарифмы
при основании а>1 возрастают и loga х~> оо,
когда хоо.
ОСНОВНЫЕ ТЕОРЕМЫ О ЛОГАРИФМАХ
loga(NiN2) = logaNi + logalV2;
/NA
loga\N~2) = IoSa “ 108a N2>
loga = n loga N;
loga^N ) = 4 l°ga IV.
ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ
Десятичные логарифмы записываются в
виде десятичной дроби с точностью до опре-
делённого десятичного знака; её целая часть
называется характеристикой лога-
рифма, а дробная — м а н т и с с о й; напри-
мер, 1g 285 = 2,454845, здесь 2 — характери-
стика, а 454845— мантисса. Если число боль-
ше единицы, то характеристика положи-
тельна и на единицу меньше числа его
цифр, стоящих перед запятой; если число
меньше единицы, то характеристика отри-
цательна и по абсолютной величине равна
числу нулей слева, включая и нуль целых.
Мантисса отыскивается по таблицам лога-
рифмов, причём на положение запятой и на
нули слева и справа не обращают внимания,
так как числа, получающиеся из данного
путём умножения или деления на 10 имеют
одинаковые мантиссы. Мантисса всегда бе-
рётся положительной, поэтому если логарифм
отрицательный, то знак минус ставится над
характеристикой (3,820714= —3-J-0,820714=»
---- 2,179286).
108
МАТЕМАТИКА
ВЫЧИСЛЕНИЯ ПРИ ПОМОЩИ ЛОГАРИФМОВ
С помощью логарифмов удобно находить
численные значения одночленных выраже-
ний.
Для этого следует прологарифмировать
(пользуясь свойствами логарифмов) подле-
жащее вычислению выражение и найти при
помощи таблиц логарифмов логарифм иско-
мой величины. Далее, пользуясь таблицами
логарифмов, находят искомую величину по
её уже известному логарифму.
Если значение вычисляемого выражения
отрицательно, то следует указанным спосо-
бом определять его абсолютную величину и
в результате изменить знак.
Пример.
„ 11,08s • 0,02154
IV — --------------- •
р 3,425
Имеем
lg N = 3 1g 11,08 + 1g 0,02154 - ~ 1g 3,425.
По таблицам десятичных логарифмов находим:
1g 11,08 = 1,044540;
1g 0,02154 = 2,333246;
lg 3,425 = 0,534661
lg N = 1,199536.
По мантиссе этого логарифма с помощью таблиц
находим число N (запятую ставим после второй циф-
ры, так как характеристика равна единице):
N - 15,83.
ГЕОМЕТРИЯ
ПЛАНИМЕТРИЯ
ЛИНИИ И ОТРЕЗКИ
Часть прямой линии, ограниченная с
обеих сторон, называется отрезком.
Часть прямой, ограниченная с одной
стороны, называется лучом или полу-
прямой.
Последовательность отрезков, располо-
женных так, что конец первого служит нача-
лом второго, конец второго — началом треть-
его и т. д. называется ломаной линией;
отрезки, образующие ломаную, называются
её сторонами, а общие точки сторон —
вершинами.
Ломаная линия называется выпуклой,
если она вся расположена по одну сторону
от каждого из составляющих её отрезков,
продолженного неограниченно в обе сто-
роны.
Если начало первого и конец последнего
отрезков, составляющих ломаную, совпа-
дают, ломаная называется замкнутой.
УГЛЫ
Фиг. 3
Углом называется фигура (фиг. 3), об-
разованная двумя полупрямыми (лучами)
О А и ОВ, исходящими из одной точки О.
Лучи ОА и ОВ называ-
ются сторонами угла,
точка О — его верши-
н о й.
Два угла называются
равными, если они мо-
гут быть совмещены при
помощи наложения. Вооб-
ще, две геометрические фигуры называются
равными, если они могут быть совмещены
при наложении одна на другую.
В геометрии обычно употребляется гра-
дусная система измерения углов, в кото-
рой за единицу измерения, называемую
градусом, принимается поворот луча на
1/360 часть одного полного оборота. Градус
подразделяется на 60 минут, а минута —
на 60 секунд. Обозначение; 37° 14'27" озна-
чает 37 градусов 14 минут 27 секунд. Пол-
ный оборот, таким образом, составляет 360°;
»/4 его часть, равная 90°, называется пря м ым
углом (фиг. 4,а) и обозначается буквой d.
Угол, меныпий 90°, называется острым
(фиг. 4,6), а больший 90°—т у п ы м (фиг. 4,в).
Прямые, образующие прямой угол, назы-
ваются перпендикулярными одна
другой.
Фиг. 4
Смежными углами (фиг. 5) называется
пара углов АОВ и ВОС, у которых одна
сторона ОВ общая, а две другие ОА и ОС
составляют продолжение одна другой. Сумма
двух смежных углов составляет 180° или
2d.
Вертикальными углами называется
пара углов, у которых общая вершина, а
стороны одного составляют продолжение
сторон другого. На фиг. 6 изображены две па-
ры вертикальных углов (/_ АОВ и / COD, а
Фиг. 5
Фиг. б
также /_ ВОС и /_ DO А). Вертикальные углы
равны между собой.
Биссектрисой угла называется пря-
мая, делящая угол пополам. Биссектрисы
ОМ и ON вертикальных углов АОВ и COD
составляют продолжение одна другой
(фиг. 7а). У смежных углов биссектрисы
ОМ и ON взаимно перпендикулярны (фиг.76).
Две прямые (фиг. 8) называются парал-
лельными, если они лежат в одной пло-
скости и не пересекаются. Расстояние меж-
ду параллельными прямыми определяется
длиной отрезка перпендикуляра MN к пря-
мым, заключённого между ними. Этот отре-
зок имеет постоянную длину. При пересече-
ГЕОМЕТРИЯ
109
нии двух параллельных прямых секущей PQ
образуется восемь углов (7, 2, 3, 4, 5, 6,7,8):
фиг. 7а Фиг. 76
1) соответственные углы (7 и 5;
2 и б; 3 и 7; 4 и 8) равны между собой
(Z. 7 = 5; 2 2 = Z 6 и т- л-);
2) внутренние накрест лежа-
щие углы (4 и 5; 3 и б) также равны;
3) внешние накрест лежащие
углы (7 и 8; 2 и 7) также равны;
4) внутренние односторонние
углы (3 и 5; 4 и б) в сумме составляют 180°
(Z 3 + Z 5 = 180°; 2 + 2 6= 180°);
5) внешние односторонние углы
(7 и 7; 2 и 8) в сумме составляют 180°
(2? + Z7 = 180°; 2 2+ /_8 = 180°).
Углы с соответственно параллельными
или перпендикулярными сторонами либо
равны друг другу, либо в сумме составля-
ют 180°.
Параллельные прямые отсекают на сто-
ронах угла (фиг. 9) пропорциональные части:
ОА АВ ВС
О'А' А'В' В'С"
МНОГОУГОЛЬНИКИ
Многоугольником называется плос-
кая фигура, ограниченная замкнутой лома-
ной линией. Например, фигура АВСРЕ
есть пятиугольник (фиг. 10а). Точки А, В,
С, Р и Е называются вершинами мно-
гоугольника. Отрезки AC, AD, BD, BE и
СЕ называются диагоналями много-
угольника. Сумма длин сторон АВ+ВС-|-
+ CD + DE+EA называется перимет-
ром многоугольника.
Многоугольник выпуклый, если все
его диагонали лежат внутри него (фиг. 10,а),
в противном случае многоугольник нев ы-
пуклый (фиг. 10,6).
Во всяком выпуклом многоугольнике с
числом сторон, равным л, сумма внутрен-
них углов равна 180°-(л—2), а сумма внеш-
них углов (стр. ПО, фиг. 15) равна 360°.
Многоугольники АВСРЕ и A'B'C'D'E'
(фиг. 11) подобны, если их углы соответ-
ственно равны, а сходственные стороны про-
порциональны, т. е. если выполнены усло-
вия:
2 а = 2 Д'; 2 в = 2 В'; LB = L С';
2o = zo'; Z Е = Z Е'
и
АВ ВС _ СР _ РЕ _ ЕА
А' В' ~~В' С'~ С’ О'О' Е' ~ Е' А"
Площади подобных многоугольников от-
носятся как квадраты сходственных линей-
ных элементов (сторон, радиусов вписанных
или описанных кругов и т. д.).
Вписанным в круг многоугольником
называется такой многоугольник, вершины
которого лежат на окружности (фиг. 12);
окружность, проходящая через вершины
многоугольника, называется описанной
около многоугольника.
Описанным около круга многоуголь-
ником называется такой многоугольник,
стороны которого касаются окружности
(фиг. 13); окружность, касающаяся сторон
многоугольника, называется вписанной
в многоугольник.
ТРЕУГОЛЬНИКИ
Треугольником называется много-
угольник с тремя сторонами (фиг. 14).
Различают треугольники: остроуго ль-
ные (если все три угла острые), прямо-
угольные (один из углов прямой) и
тупоугольные (один из углов тупой).
В прямоугольном треугольнике стороны,
составляющие прямой угол, называются
катетами, а сторона, лежащая против
прямого угла, называется гипотену-
зой. Кроме того, различают треугольники
равносторонние (если все три сторо-
ны равны), равнобедренные (две
по
МАТЕМАТИКА
стороны равны) и разносторонние (все
три стороны не равны между собой). Во
всяком треугольнике против большей сто-
роны лежит больший угол; против равных
сторон лежат равные углы и обратно, по-
этому равносторонний треугольник одно-
временно является и равноугольным. Каж-
дая из сторон треугольника меньше суммы
и больше разности двух других сторон
(Ъ — с < а < b + с). Сумма углов всякого
треугольника равна 180°; в равностороннем
треугольнике каждый угол павен 60°.
Фиг. 14
Фиг. 15
Угол, образованный одной из сторон
треугольника с продолжением другой сто-
роны, называется внешним (фиг. 15); он
равен сумме двух внутренних углов с ним
не смежных (/. CBD = /. ВАС + Z АСВ).
Медианой треугольника называется
отрезок, соединяющий вершину с серединой
противоположной стороны треугольника
(фиг. 16). Медианы треугольника пересе-
каются в одной точке (центр тяжести тре-
угольника) и делятся этой точкой в отно-
шении 2:1, считая от вершины угла.
Длина медианы, проведённой на сторону а,
1 ______-________
та = ~2 7/ 2(62+ с2) —а2.
Биссектрисой треугольника назы-
вается отрезок биссектрисы угла треуголь-
ника от вершины до пересечения с противо-
лежащей стороной (фиг. 17). Биссектрисы
Фиг. 16
треугольника пересекаются в одной точке,
являющейся центром вписанной окружно-
сти. Биссектриса делит противоположную
сторону на части, пропорциональные двум
другим сторонам.
Длина биссектрисы угла А
В. = bc(b + c)a — а2
НА b + с
Высотой треугольника называется
отрезок перпендикуляра, опущенного из
вершины на противоположную сторону (ос-
нование) треугольника (фиг. 18). Высоты
треугольника пересекаются в одной точке,
называемой ортоцентром.
Длина высоты, проведённой из верши-
ны А______________________________
ъ _ 2-/р(р —а) (,р-Ъ)(р-с)
иа “------------------------,
а
где р — полупериметр:
а + Ь + с
Р=—^Т-
Перпендикуляры к сторонам треуголь-
ника, проведённые через их середины
(фиг. 19), пересекаются в одной точке О,
служащей центром описанного круга.
В равнобедренном треугольнике медиана,
биссектриса и высота, опущенные на осно-
вание, а также перпендикуляр, проведён-
ный через середину основания, совпадают
друг с другом; в равностороннем треуголь-
нике это имеет место для всех трёх сторон.
Во всех остальных случаях ни одна из этих
линий не совпадает с другой.
В равностороннем треугольнике точки
пересечения медиан (центр тяжести), биссек-'
трис (центр вписанного круга) и высот
(ортоцентр), а также центр описанного кру-
га совпадают между собой. Во всех осталь-
ных случаях ни одна из этих точек не сов-
падает с другой.
Фиг. 18 Фиг. 19
Два треугольника равны, если выпол-
няется одно из следующих условий (приз-
наки равенства):
1. Три стороны одного треугольника
соответственно равны трём сторонам второго
треугольника.
2. Две стороны и угол, заключённый
между ними, одного треугольника соответ-
ственно равны двум сторонам и углу между
ними второго треугольника.
3. Одна сторона и два прилежащих к
ней угла одного треугольника соответствен-
но равны стороне и двум прилежащим к
ним углам второго треугольника.
Два треугольника подобны (фиг. 20), т. е.
соответственные углы у них равны и сход-
ственные стороны пропорциональны, при
выполнении одного из следующих условий
(признаки подобия):
Фиг. 20
Фиг. 21
1. Три стороны одного треугольника про-
порциональны трём сторонам другого:
а b с
а' = Ь' ~ с’ ’
2. Два угла одного треугольника равны
двум углам другого, например:
Z.A-ZA' и =
3. Две стороны одного треугольника про-
порциональны двум сторонам другого тре-
ГЕОМЕТРИЯ
111
угольника, а заключённые между ними углы
равны, например:
а b
р-р^С^С'.
Площади подобных треугольников отно-
сятся, как квадраты сходственных линей-
ных элементов (сторон, высот и т. д.).
Прямоугольные треугольники подобны
(фиг. 21), если гипотенуза и катет одного
треугольника пропорциональны гипотенузе
и катету другого, например:
с а
с' ~ а' '
Ниже приводятся формулы для вычисле-
ния элементов треугольника.
Прямоугольный треугольник
(фиг. 22): /_ С = 90°; с — гипотенуза; А +
+ /_ В = 90°; а и Ь— катеты, лежащие про-
тив углов соответствующих наименований;
точка D — основание перпендикуляра, опу-
щенного из вершины прямого угла С на ги-
потенузу с; S — площадь треугольника.
1) а!- ii!- с! (теорема Пифагора);
AD DC.
DC ~ DB ’
АВ _ AC АВ _ СВ
3> AC ~ AD ’ СВ~ DB’
аЬ
4) S = у .
Равносторонний треугольник
(фиг. 23): а — сторона; h — высота; R—ра-
Фиг. 22
Фиг. 23
дйус описанной окружности; г— радиус
вписанной окружности; S — площадь.
1) Й =
2) а = /?<3 = 2г/3;
3) S = = 3/?2У"3 = 3 Г2 ><3?
Равнобедренный треугольник
(фиг. 24): 21 А=В = а; 21 С = 180°—2а;
АС = ВС = а; h — высота; с — основание;
S — площадь.
1) h = у/4а2 —с2;
„ ch с ,-----------------------
2) 8 = у- = у уЛ 4 а2 — с2.
Косоугольный треугольник (об-
щий случай): R — радиус описанной окруж-
ности; г —вписанной; a + b-\-c = 2p; S —
площадь.
О ZA+21B+21C = 180°;
2) если А — острый угол, то
а2 = &2 -|- с2 — 2с • AD (фиг. 25а),
если А — тупой угол, то
а2= й2 + с2 + 2с-АО (фиг. 256);
С
Фиг. 24 Фиг. 25
3) S = -у = <р(р — а)(р — Ь)(р — С) =
abc
Г - j/<P — <0 (Р — &) (Р — с).
abc
ft S -у- ---- .
4V р(р —а) (р—Ь)(р —с)
ЧЕТЫРЁХУГОЛЬНИКИ
Четырёхугольником называет-
ся многоугольник с четырьмя сторонами
(фиг. 26). Сумма его углов равна 360°. Пло-
щадь его
S = у (fti + й2) di,
где dt— одна из диагоналей, а /г, и Л2—
длины перпендикуляров, опущенных на эту
диагональ из двух не лежащих на ней вер-
шин четырёхугольника.
В четырёхугольник можно вписать окруж-
ность (фиг. 27) только тогда, когда суммы
длин его противоположных сторон равны
а + с = b +</.
Фиг. 26
Около четырёхугольника можно описать
окружность (фиг. 28), если сумма его про-
тивоположных углов равна 180°:
ZA + 21C=(/-B+Zd = 180°.
Для вписанного выпуклого четырёхуголь-
ника имеет место соотношение между его
сторонами и диагоналями (теорема Пто-
л о м е я):
ас + bd = did2.
Площадь вписанного четырёхугольника
S = /(р —а)(р—&)(р —с) (р —d),
где
q “f- b -}-• с “I- d
р= 2 •
112
МАТЕМАТИКА
Различают следующие частные виды че-
тырёхугольников:
а) параллелограм — четырёхуголь-
ник с попарно параллельными (и равными)
противоположными сторонами;
б) ромб — параллелограм, у которого
все стороны равны;
в) прямоугольни к— параллелограм,
у которого все углы прямые;
г) квадрат — ромб, у которого все
углы прямые (прямоугольник, у которого
все стороны равны);
д) трапеция —четырёхугольник с двумя
параллельными противоположными сторона-
ми, называемыми основаниями трапе-
ции. Непараллельные стороны трапеции на-
зываются её боковыми сторонами,
расстояние между основаниями — высо-
той, а отрезок прямой, соединяющей сере-
дины боковых сторон,—с редней линией
трапеции (средняя линия трапеции парал-
лельна её основаниям).
Фиг. 28 Фиг. 29
Ниже ппиводится сводка основных свойств
я формул для вычисления элементов квад-
рата, ромба, параллелограма, прямоуголь-
ника и трапеции.
Обозначения: R — радиус описанной ок-
ружности; г—вписанной; h— высота; d—
диагональ; 8 — площадь.
Квадрат (фиг. 29).
d = а /2; R = ; г = у ;
г— d2
а =* R у 2; S = а1 = у = 2 R2 = 4 г2, где fl-
сторона квадрата.
Ромб (фиг. 30). Диагонали ромба взаим-
но перпендикулярны и делят углы ромба
пополам;
d2 4- d2 — 4 а2 ; 8 = ah = ,
где ' — сторона; dlt d2— диагонали.
Фиг. 31
Параллелограм (фиг. 31). Диаго-
нали параллелограма делятся в точке пе-
ресечения пополам;
dj + d* = 2 (а2 + ft«); S = ЪП,
где а и Ь — стороны; d1( d2 — диагонали;
h — высота, опущенная на основание Ь.
Прямоугольник (фиг. 32). Диаго-
нали прямоугольника равны между собой;
d2 = «2 + b2, S = ab.
Фиг. 33
О а С
Обозначения те же, что и
лограма.
для паралле-
Трапеция (фиг. 33).
а + b
т = -у-
„ а + ь
S = —у- h = mh,
где а и b — параллельные стороны; h — вы-
сота; т — средняя линия.
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Многоугольник называется правиль-
ным, если все его стороны и углы равны.
Ниже приводятся фор-
мулы для вычисления 4______
элементов правильного / \
многоугольника, причём / в \
приняты обозначения (фиг. А X
34): ап— сторона; R — ра- \«/Т\ /
диус описанной окружно- \л Г \/у
сти; г — вписанной (апо- с а„ г.
фема); л — число сторон; фИ£. 34
9 — центральный угол,
опирающийся на сторону;
а — внутренний угол; р— внешний угол
многоугольника и 8— площадь.
в
„ 360°
О ? = —;
180°
2) « = — (п-2)= 180°
360°
з)3=уг;
4) ап = 2 //?’ —г2;
частности,
а3 = R >Лз7 at = R /2? ав = R
«ю ='2 (/5*-1);
или
5) a22n = 2R2-Ry^R2-a2n
(формула удвоения числа сторон пра-
вильного вписанного многоугольника);
1
6) 8 = у папг.
Данные об элементах отдельных правиль-
ных многоугольников приведены в табл. 3.
ГЕОМЕТРИЯ
113
Элементы правильных многоугольников
Таблица 3
п "а № 8 ~ап /? г а п ~R~ а _п г г ~R г
3 0,4330 1,2990 5,1962 0,5774 2,0000 1,7321 3,4641 0,5000 0,2887
4 1,0000 2,0000 4,0000 0,7071 1,4142 1,4142 2,0000 0,7071 0,5000
5 1,7205 2,3776 3,6327 0,8507 1,2361 1,1756 1,4531 0,8090 0,6882
6 2,5981 2,5981 3,4641 1.000U 1,1547 1,0000 1,1547 0,8660 0,8660
7 3,6339 2,7364 3,3710 1,1524 1,1099 0,8678 0,9631 0,9010 1,0383
8 4,8284 2,8284 3,3137 1,3066 1,0824 0,7654 0,8284 0,9239 1,2071
9 6,1818 2,8925 3,2757 1,4619 1,0642 0.6840 0,7279 0,9397 1,3737
10 7,6942 2,9389 3,2492 1,6180 1,0515 0,6180 0,6498 0,9511 1,5388
12 11,196 3,0000 3,2154 1,9319 1,0353 0,5176 0,5359 0,9659 1,8660
15 17,642 3,0505 3,1883 2,4049 1,0223 0,4158 0,4251 0,9781 2,3523
16 20,109 3,0615 3,1826 2,5629 1,0196 0,3902 0,3978 0,9808 2,5137
20 31,569 3,0902 3,1677 3,1962 1,0125 0,3129 0,3168 0,9877 3,1569
24 45,575 3,1058 3,1597 3,8306 1,0086 0,2611 0,2633 0,9914 3,7979
32 81,225 3,1214 3,1517 5,1011 1,0048 0,1960 0,1970 0,9952
48 183,08 3,1326 3,1461 7,6449 1,0021 0,1308 0,1311 0,9979 7,6285
64 325,69 3,1365 3,1441 10,190 1,0012 0,0981 0,0983 0,9988 10,178
ОКРУЖНОСТЬ
Окружностью (фиг. 35) называется
геометрическое место точек плоскости, рав-
ноудалённых от некоторой точки, называе-
мой центром.
Отрезок, соединяющий центр с любой
точкой окружности, называется радиусом
(обозначается обычно буквой Z? или г). Часть
Фиг. 35
окружности (например, АтВ) называется
дугой. Прямая PQ, проходящая через
две точки М и N окружности, называется
секущей, а отрезок её MN, лежащий
внутри окружности, называется хордой.
Хорда, проходящая через центр, называется
диаметром (обозначается буквой D или
d). Диаметр равен двум радиусам (D = 2/?).
Круг есть часть плоскости, ограничен-
ная окружностью. Прямая, имеющая с
окружностью одну общую точку, называется
6
Фиг. 3 7
О
Ф:.1 . 38
касательной. Касательная перпенди-
кулярпа к радиусу ОА в конце его А
(фиг. 36), лежащем на окружности (точка
касания). Из точки Р вне круга можно про-
вести две касательные к окружности, длины
которых равны между собой (PM == PN).
Сегментом называется часть круга,
ограниченная дугой ADB и стягивающей
её’хордой АВ (фиг. 37). Перпендикуляр CD,
восставленный из середины хорды АВ до
пересечения с дугой, называется стрел-
кой дуги АВ или высотой сегмента.
8 Т ом I
Сектором называется часть круга, огра-
ниченная дугой АВ и двумя радиусами
ОА и ОВ, проведёнными к концам дуги
(фиг. 38).
Длина дуги, описываемой концом ради-
уса, пропорциональна величине соответст-
вующего центрального угла, поэтому дуги
одной и той же окружности можно измерять,
как и углы, градусами, принимая за 1°
часть окружности, т. е. дугу, на кото-
рую опирается центральный угол в 1°. Вся
окружность имеет 360°. Длина дуги пропор-
циональна также длине радиуса.
Углы в круге измеряются следующим
образом:
1) центральный угол (фиг. 39) измеряется
дугой, на которую он опирается, т. е. со-
держит столько же градусов (угловых),
сколько его дуга (дуговых): __ АОВ — АВ;
2) вписанный угол (фиг. 40):
АВС = АС;
3) описанный угол (фиг. 41):
/, АРВ = 2 (АтВ — 'Апв);
4) угол между хордой и касательной
(фиг. 42): _ АВС = АтВ;
114
МАТЕМАТИКА
5) угол между хордами (фиг. 43):
/, ВАС = ± (св + еЬ);
6) угол между секущими (фиг. 44):
ВАС = ^(de — ВС);
7) угол между касательной и секущей
(фиг. 45): / ВАС = | (6В — бв).
Если М— точка внутри круга, а АВ и
CD — проходящие через неё хорды (фиг. 46),
то
АМ-МВ = CM-MD.
Если М— точка вне круга, МА и МВ —
проходящие через неё секущие, а МТ —
касательная (фиг. 47), то
МА-МА' = МВ-МВ' = МТ2.
Отношение длины окружности С к её
диаметру d есть величина постоянная, рав-
ная 3,141592653... Это число иррациопаль-
ное, оно не может быть выражено конечным
числом десятичных знаков; сокращённо оно
обозначается греческой буквой л:
С
d - ">
откуда длина окружности
С = Ttd х 3,1416 d,
или
С = 2nR к 6,2832 R.
Длина дуги в 1°
r.d _ kR
s = 360 = 180 •
Длина дуги в а° (фиг. 48)
И£г = Т8Т - 0,01745Ra.
Длина хорды
I = 2yr2hR~iC.
Высота сегмента (стрелка)
h = R-^ R*-lL.
Площадь круга S пропорциональна квадра-
ту его диаметра или радиуса и равна
r.d*
S = = KR2 « 0,78539 4(2= 3,1416 R2.
Площадь сектора с углом в а°
Площадь cei мента
s = 1[R(S __/) + //,].
СТЕРЕОМЕТРИЯ
ПРЯМЫЕ И ПЛОСКОСТИ
Две прямые называются параллель-
ными, если они не пересекаются и лежат
в одной плоскости (непересекающиеся пря-
мые, не лежащие в одной плоскости, назы-
ваются скрещивающимися).
Две плоскости называются параллель-
ными, если они не пересекаются.
Прямая называется параллельной
плоскости, если она не пересекает пло-
скость.
Прямая называется перпендикуляр-
но й к плоскости, если она перпендикулярна
ко всем пересекающим её прямым, лежащим
в данной плоскости.
Угол между двумя прямыми, не лежащи-
ми в одной плоскости, измеряется углом
между параллельными им прямыми, прове-
дёнными из одной точки.
Проекцией (ортогональной) отрезка
прямой на плоскость называется отрезок,
лежащий в этой плоскости, соединяющий
основания перпендикуляров, опущенных из
концов данного отрезка на плоскость.
Угол между прямой и плоскостью изме-
ряется углом между прямой и её проекцией
на плоскость (фиг. 49).
Двугранный угол — угол между
двумя плоскостями — измеряется его л и-
н е й н им углом АВС (фиг. 50), т. е. углом
Фиг. 49 Фиг. 50
между перпендикулярами к ребру MN дву-
гранного угла, восставленными в обеих
плоскостях (гранях) из одной точки В.
Признаки параллельности и перпендику-
лярности прямых и плоскостей следующие:
1. Прямая параллельна плоскости, если
она параллельна одной из прямых, лежа-
щих в этой плоскости.
2. Две плоскости параллельны между со-
бой, если две пересекающиеся прямые, ле-
жащие в одной плоскости, соответственно
ГЕОМЕТРИЯ
115
параллельны двум пересекающимся прямым,
лежащим в другой плоскости.
3. Прямая, перпендикулярная к двум пря-
мым, лежащим в плоскости, перпендикуляр-
на к самой плоскости.
4. Прямая, лежащая в плоскости и пер-
пендикулярная к проекции наклонной на эту
плоскость, перпендикулярна к самой наклон-
ной и обратно: если прямая, лежащая в
плоскости, перпендикулярна к наклонной, то
она перпендикулярна и к проекции этой на-
клонной на плоскость.
Многогранный угол ОABCDE
(фиг. 51) образуется несколькими плоско-
стями (граням и), проходящими через одну
точку. Многогранные углы называются рав-
ными, если при наложении они совпадают;
многогранные углы равны, если соответст-
венно равны их двугранные и плоские углы.
Многогранный угол называется выпу к-
л ым, если он расположен по одну сторону
от каждой его грани. Сумма плоских углов
любого выпуклого многогранного угла мень-
ше 360°.
Трёхгранные углы равны, если они имеют:
а) по одному равному двугранному углу,
заключённому между двумя соответственно
Фиг. 51 Фиг. 52
равными и одинаково расположенными пло-
скими углами;
б) по одному равному плоскому углу,
заключённому между двумя соответственно
равными и одинаково расположенными дву-
гранными углами;
в) по три соответственно равных и оди-
наково расположенных плоских угла;
г) по три соответственно равных и оди-
наково расположенных двугранных угла.
Телесным углолг (фиг. 52) назы-
вается часть пространства, ограниченная по-
верхностью, образованной движением полу-
прямой, одна из точек которой (вершина)
неподвижна, а другая движется по данной
кривой. Телесный угол измеряется пло-
щадью, вырезаемой им на сфере единичного
радиуса с центром в вершине.
МНОГОГРАННИКИ
Обозначения: V — объём, Fn— полная по-
верхность, F6— боковая поверхность, F—
площадь основания, h — высота.
Многогранником называется тело,
ограниченное плоскостями.
Призмой (фиг. 53) называется много-
гранник, основания которого — равные мно-
гоугольники, а боковые грани — параллело-
грамы. Если рёбра перпендикулярны к пло-
скости основания, то призма прямая. Пря-
мая призма, в основании которой правильный
многоугольник, называется правильной-
Для всякой призмы:
V = FA; Fn = F6 + 2F; F6 = pl,
где I — ребро, р— периметр сечения призмы
плоскостью, перпендикулярной к ребру.
Параллелепипедом (фиг. 54) назы-
вается призма, у которой основания — па-
раллелограмы. В параллелепипеде все четы-
ре диагонали пересекаются в одной точке и
делятся в ней пополам.
Фиг. 53 Фиг. 54
Прямой параллелепипед, основания кото-
рого—прямоугольники, называется прямо-
угольным. В прямоугольном параллеле-
пипеде (фиг. 55) все диагонали равны. Если
а, b и с—рёбра прямоугольного параллеле-
пипеда, d— его диагональ, то:
«Р = а2 + й2 + с2; Fn = 2 (ab + Ьс + са);
V — abc.
Куб. а = b = с; = За2; Fn = 6а’;
V = а3.
Пирамида (фиг. 56) — многогранник,
в основании которого многоугольник, а бо-
ковые грани — треугольники, сходящиеся в
одной точке (вершине). Пирамида называется
n-угольной, если её основание — п-угольник.
Треугольную пирамиду называют также
тетраэдром.
Сечение пирамиды плоскостью, парал-
лельной основанию, есть многоугольник,
подобный основанию пирамиды, и
SA, _ SBi _ SCj _ _ SOi
AiA ~ BrB CiC = •" = OiO:
площадь ABCDE / 0S\’
площадь AiB1C1£)1E1 ~ \Ог5у
(OS—высота пирамиды).
Объём пирамиды:
Фи1, 55 Фиг. 56
Пирамида называется правильной
(фиг. 57), если её основание — правильный
многоугольник, а перпендикуляр, опущен-
ный из вершины па плоскость основания
(высота пирамиды), проходит через его центр.
1
F6 - 2 ра,
8»
116
математика
где р — периметр основания, а — апофема
правильной пирамиды, т. е. высота какой-
либо сё боковой грани.
Для усечённой пирамиды (пло-
скости оснований параллельны между собой,
а боковые рёбра при продолжении пересе-
каются в одной точке, фиг. 58):
V=4ft(F+/ + /F/),
где F и f — площади оснований, /г —высота.
Фиг. 56
Цилиндр (фиг. 61) — тело, ограничен-
ное цилиндрической поверхностью, направ-
ляющая которой — замкнутая кривая, и
двумя параллельными плоскостями (осно-
ван и я м и цилиндра)
Fe=pft = sZ; V = Fft = QZ,
где р — периметр основания; F—площадь
основания; s — периметр сечения, перпен-
дикулярного к образующей; Q—его площадь;
I — длина образующей.
Прямой круговой цилиндр имеет в ос-
новании круг, а его образующие перпенди-
кулярны к плоскости основания (фиг. 62);
F6 = 2 тс Rft = тс Oft; Fn = 2 тс R (R + ft) =
1 TC£)2ft
= тс D (D + 2 ft); V = тс R2ft = —,
где R и D — радиус
и диаметр основания.
Если усечённая пирамида правильная,
где Р и р— периметры оснований, а — апо-
фема.
Многогранники, у которых все
грани — равные правильные многоугольники
и все многогранные углы равны, называют-
Коническая поверхность
(фиг. 63) — поверхность, образованная пря-
мой линией (образующей) с неподвиж-
ной точкой (вершина), перемещающейся
вдоль кривой линии (направляюще й).
Фиг 59
ся правильными. Всего имеется пять
правильных многогранников (фиг. 59).
Таблица 4
Элементы правильных многогранников
(а—длина ребра)
Название много- гранника Грани (их число и форма) Число Полная поверх- ность Объём V
рёбер I вер- шин 1
Тетраэдр Куб Октаэдр Додекаэдр Икосаэдр 4 треу- гольника 6 квадра- тов . . . 8 тре- угольни- ков . . . 12 пяти- угольни- ков . . . 20 тре- угольни- ков . . . 6 12 12 30 30 4 8 6 20 12 1,7321 а* 6 аа 3,4641 а2 20,6457 а2 8,6603 а3 0,1179 а3 аэ 0 ,4714 а3 7,6631 а3 2,1817 а3
КРУГЛЫЕ ТЕЛА
Обозначения: V — объём; Fn —полная по-
верхность; F6 — боковая поверхность; ft —
высота.
Цилиндрическая поверхность
(фиг. 60)—-поверхность, образованная пря-
мой линией (образующей), перемещаю-
щейся параллельно самой себе вдоль неко-
торой кривой (направляющей).
Фиг. 62
Вершина
Фиг. 63
Конус (фиг. 64) ограничен конической
поверхностью с замкнутой направляющей и
плоскостью (плоскость основания)
V = ^Fft,
где F — площадь основания.
Фиг. 64 Фиг. 65
Прямой круговой конус (фиг. 65)
имеет в основании круг, а его высота про-
ходит через центр основания:
Fe = тс RI = "2 тс DI = тс R y^R* + ft2;
Fn =tcR(R + /);
ТРИГОНОМЕТРИЯ
117
V = у Г. R- h = r. D*h 0,2618 D*h,
где R и D — радиус и диаметр основания, а
/—длина образующей.
Усечённый прямой круго-
вой конус (фиг. 66)—тело, ограничен-
ное поверхностью прямого кругового кону-
са, его основанием и плоскостью, парал-
лельной этому основанию:
/ = /F+ (R — г)!;
тс I
Гб = тс/(Я + г) =~2 (D + rf);
Шаровым сектором (фиг. 68) на-
зывается тело, образованное вращением пло-
ского сектора около оси симметрии:
а* = h(2R—h); Fn = тсR(2It + а);
2тс
« 2,0944 R2ft.
Шаровым
ся часть шара,
параллельными
слоем (фиг.
заключённая
плоскостями;
69) называет-
между двумя
слой ограни-
Fn = F6 + тс (R2 + г2) = F5 + (D*+d*y,
V = у (R2 + г2 + Rr) =
= ^тсй(О2 + d2 + Dd).
Сфера (поверхность шара). R — радиус
шара; D = 2R— диаметр шара (фиг. 67).
Фиг. 69
чей двумя кругами и частью поверхности
шара, которая называется шаровым поя-
сом.
/а2 —b2 —ft2\2
R2 = a2+ ----ут---- (а > b);
F5—2т: Rh', Еп = тс (2 Rft + а2 + b2);
V = | тс h (3 а2 + 3 b2 + Л2).
Всякое сечение сферы плоскостью есть круг.
Большой круг — круг, получающийся
от сечения сферы плоскостью, проходящей
через её центр. Через всякие две точки А и
В сферы (не являющиеся противоположны-
ми концами диаметра) всегда можно прове-
сти (и при том только один) большой круг.
Поверхность сферы и объём шара:
F = 4 тс R2 = тс D2 » 12,56637 R2 = 3,14159 D2;
4 1
V = 7ttcR8=-jtc D8=tc 4,18879 D3~0,5236 D8.
u 0
/ ft2\
Если а = R, то V = тсй IR2 — I .
Шаровым сегментом (фиг. 70) на-
зывается часть шара, отсечённая плоскостью:
а2 = ft (2 R —ft); F6 = 2тс Rft = тс (а2 + ft2);
Fn = тс (2 Rh + а2) = тс (ft2 + 2 а2);
V = тс ft2 (3 R — ft) = тс ft (За2 + Л2).
ТРИГОНОМЕТРИЯ
ПРЯМОЛИНЕЙНАЯ ТРИГОНОМЕТРИЯ
РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВ
Центральный угол, опирающийся на ду-
гу, длина которой равна радиусу окружно-
сти, называется радианом
Центральный угол, опирающийся на дугу
окружности произвольного радиуса, изме-
ряется в радианах отношением длины дуги
s к длине радиуса R:
s
а = у (радианов).
Переход от градусной меры угла (стр. 108)
к радианной и обратно совершается по фор-
мулам:
а (радианов) = ^а0;
180
а0 = — а (радианов);
в частности:
-g (радианов) = 30°; = 45°; % = 90е;
тс= 180°; 2тс = 360° и т. д.
Один радиан равен
180°
---- « 57° 17'45" » 57°, 2958;
ТС
в одном градусе содержится ® 0,017453
радианов.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Если взять тригонометрический круг (ра-
диус R = 1; фиг. 71) и условиться измерять
положительный угол а от неподвижного
радиуса О А до подвижного радиуса ОМ в
направлении, обратном движению часовой
118
МАТЕМАТИКА
стрелки, то тригонометрические функции
угла а определяются длинами следующих
отрезков, называемых тригонометрическими
линиям»:
sina =NM (синус),
cos а = ON (косинус),
tga-- АР (тангенс),
ctg а = CQ (котангенс),
sec а — ОР (секанс),
cos<‘c а = OQ (косеканс).
Для острого угла а тригонометрические
функции могут быть определены также и из
прямоугольного треугольника (фиг. 72):
Знаки тригонометрических функций. В
зависимости от того, в какой четверти три-
гонометрического круга находится подвиж-
ной радиус ОМ (см. фиг. 71), тригонометри-
ческий! функциям приписывается положи-
тельный или отрицательный знак (табл. 5).
В табл, б приведены значения тригоно-
метрических функций некоторых часто
встречающихся углов, в табл. 7—пределы
изменения тригонометрических функций при
изменении угла от 0° до 360° (от 0 до 2 л).
Таблица 5
Знаки тригонометрических функций
Таблица 6
Значения тригонометрических функций
некоторых углов
'^\^Угол а Функции'''\ О“ 30° 45“ 60° 90"
sin а О 1 2 I сч ! j tol — j co 1 I 1
COS а 1 4/2 1 2 0
tg а О 1 « — 1 К 3 00
Ctg а 00 V 3 1 1 co ~|co 0
sec а 1 СЧ |со V 2 2 00
cosec а оо 2 1 са СЧ 1
Таблица 7
Графики тригонометрических функций
даны на фиг. 73—78.
Тригонометрические функции углов, до-
полнительных до 90°. Угол (3 = 90°— а, до-
полняющий угол а до 90°, называется по
отношению к углу а дополнительным
углом. Между тригонометрическими функ-
циями угла а и дополнительного угла 90° —а
имеют место соотношения:
si п (90° — а)= cos а;
tg (90° — а) == ctg а;
sec (90 — а) = cosec а;
cos (90° —а) = sin а;
ctg (90° — а) =tg а;
cosec (90° —- а) = sec а
ТРИГОНОМЕТРИЯ
119
Периодичность тригонометрических функ-
ций. Тригонометрические функции являются
Периодичность тригонометрических функ-
ций выражается равенствами:
sin а = sin (а ± 360° п); cos а= cos (а ± 360°л);
tg а = tg (а ± 180° л); ctg а = ctg (а ± 180° л);
sec а =sec(a±360°n); cosec a=cosec(a±360° л);
где л= 0, 1, 2, 3, ...,
или (в радианной мере):
sin а — sin (а ± 2 те л); cos а = cos (а ± 2 те л):
tg а = tg (а ± те л); ctg а = ctg (а ± те л);
sec а = sec (а ± 2 те л); cosec а = cosec (а±2тел).
Фиг. 75. График функции у >= tg X
Фиг. 78. Гр афик функции у — cosec х
Соотношения между тригонометрическими
функциями положительного и отрицатель-
ного углов
sin (— а) = — sin а; cos (— а) = cos а;
tg(—а) = —tga; ctg(— а) = — ctg а;
sec (— а) = sec а; cosec (— а) = — cosec а.
Фиг. 77. График функции у ~ sec х
периодическими функциями. Период синуса,
косинуса, секанса и косеканса в градусной
мере 360°, а в радианной 2 те. Период тан-
генса и котангенса соответственно 180° и те.
Приведение тригонометрических функций
любого угла к функциям острого угла. Три-
гонометрические функции любого угла мо-
гут быть выражены через функции острого
угла; для этого нужно из аргумента (если
он больше периода) вычесть целое число
периодов и применить данные в табл. 8
формулы приведения.
Пример.
COS (- 1360°) = cos 136O°=cos (360°.3+280°) «
=» eos 280°=cos (270°+ 10°)=sin 1O°=O,1 73648.
ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
Между тригонометрическими функциями
одного и того же угла а имеют место сле-
дующие соотношения:
sin а
sin2 а + eos2a= 1; tga = —— ;
Luo <*
cos а 1
ctg а = —-- ; sec а =---- :
s sin а ’ cos а ’
1
cosec а = ; tga-ctga = 1;
1 1
1 + “ = cos^cT ’ 1 + ctgS а= •
При помощи этих соотношений каждая
тригонометрическая функция острого угла а
может быть выражена через любую другую
его функцию по формулам, приведённым в
табл. 9.
120
МАТЕМАТИКА
Формулы приведения
Таблица 8
Угол Функция 90°—a 90°+a 180°—a 180° J-a 270е—a 270*+a 360*—a
sin + cosa 4-COS a + sin a —sin a —COS a —cos a —Sin a
cos +sin a —Sin a —cos a —cos a —sin a + sin a + cos a
tg + ctg a -ctga -tg a + tg a + ctg a -ctg a —tg a
ctg + tg a —tg a -ctg a + ctg a +tg a -tga —Ctg a
sec +cosec a — cosec a — sec a — sec a —cosec a +cosec a -f-sec a
cosec +sec a +sec a +cosec a —cosec a —sec a —sec a | —cosec a
Выражение одних тригонометрических функций через другие
Таблица 9
sin a cos a tg a ctg a sec a cosec a
Sill a — yf 1—cos1 a tg a / l+tg’ a 1 У1 +ctg’ a ~yf sec1 a—1 sec a 1 cosec a
COS a У 1—sin’ a 1 V l+tg’ a Ctg a 7/ 1+ctg’a 1 sec a ~y/ cosec’ a—1
cosec a
tg a » Sin a 'yf 1— sin» a ~у/ 1—cos’ a cos a 1 Ctg a 'yf sec’a—1 1 cosec’a—1
Ctg a — 1—sin1 a sin a COS a 1—cos’ a 1 tga 1 secBa—1 ~y/ cosec’a—1
sec a — 1 'yf 1—sin’ a 1 COS a >/ l+tg’ a V 1+ctg’a ctg a cosec a yf cosec’a —1
cosec a — 1 sin a 1 / 1— COS* a У 1 ttg1 a tg a y" 1+ctg* a sec a 'yf sec’ g—1
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ СУММЫ
И РАЗНОСТИ УГЛОВ^ КРАТНЫХ
и половинных углов
sin 3a = 3 sin a — 4 sin3 a;
cos 3 a = 4 cos3 a — 3 cos a;
sin (а ± 0)= sin a-cos 0 ± cos a-sin 0;
cos (a ± 0) = cos a-cos 0 T sin a-sin 0;
tg(a±0) =
tg a ± tg 0 .
1 T tga.tg0 ’
Ctg (a ± 0) =
ctga-ctg0 T 1
ctg0 ± ctg a
sin 2a — 2 sin a-cos a;
cos 2 a — cos2 a — sin2 a == 2 cos2 a — 1 =
= 1 — 2 sin2 a;
2 tg a _ 2
tg2a j — tg2 a ctg a—tga ’
9„ _ ctg2 a - 1 __ ctga —tga
Ctg 2a - 2 ctga ~ ’
sin 4a = 8 cos3a-sin a — 4 cos a-sin a;
cos 4 a = 8 cos4 a — 8 cos2 a + 1;
sin/1 a = n cos"-1 a-sin a —
— C3 cos"-3a-sin3 a +
+ Cocos'1-5a-sin5 a —
cos n a = cos" a — C3 cos"-2 a sin2 a +
+ C4 cos"-4 a sin4 a — C® cos"-6a sin6 a -s ...
где
,c m(m—l)(m —2) . .(m—fc-t-1)
1-2-3-4 . . -Л 1
2
ТРИГОНОМЕТРИЯ
sin (m 4 1)а = sin m a cos а 4 sin a cos m a;
cos (m 4 1) a = cos m a cos a — sin a sin m a;
x / . tg m a 4- tga
tg (m 4- 1) a = ——j----b.-- ;
' ' 1 — tg m a-tg a ’
a 4- p a — В
cos a 4- COS 3 = 2 COS —Q— COS —2— ;
„ a 4- В a — В
cosa—cos p=—2 sin——.sin - r);
а
sin -
— cos а ,
а
COS —
cos a .
2 ’
1 — cos a 1 — cos a
1 4- cos a sin a
1 4 cos а ’
Ctg — =1/ 1 + C0Sg = 1 + C0Sa :
2 r I — cosa sina
sin a
— 1 — COS a ’
ФОРМУЛЫ ПРОИЗВЕДЕНИЙ И СТЕПЕНЕЙ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
1
sin a-sin р= [cos (а — р) — cos (а 4- р)];
1
cosa-cos[3= 2'[cos(a — В) 4- cos (а 4- 3)];
1
sina-cos 3 — 2“ [sin(а — [3)4-sin («4-3)1;
1— cos2a 1 4- cos 2 a
sin2 a =---2--- ! cos2 a = ---------J
3sina— sin 3 a
sin3 a —-------;
. cos 3 a 4- 3 cos a
cos3 a =-------7------ .
tg a ± tg [3 =
Ctg a ± ctgp;
1 4- sin a :
1 — sin a =
1 4- cos a =
sin (a + (3)
cos a- cos ,6 ’
sin (3 4 a)
sin a-sin 3 ’
/ a
2 cos2 ( 45° — -2~
/ a \
2 sin2 I 45° — -g-l
a
2 cos2 ;
a
1 — cos a = 2 sin2 ;
sin a 4 cos a = 2 sin 45° sin (a 4 45°);
a
sin a 4- tg a = 2 tg a cos2 J
2
ctg«4tga=sTn2- ;
ctg a — tg a = 2 ctg 2 a;
a 4 3
sin a 4- sin 3 & 2
sin a — sin 3 ~ a — 3 ’
tg ”~2—
cos a — cos 3 a 4 3 3 — a
cos a 4- cos 3 ~ tg 2 2 >
ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ
ФУНКЦИЙ УГЛА
ЧЕРЕЗ ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ ПОЛОВИННОГО УГЛА
а
a a 2tg а
sina = 2 sin ту cos ту —----------
z а
14-tg2 2
а а 1 tg2 о
cosa = cos2 ~2 — sin2-^- =---------- ;
1 + J ’
a a
2 tg 1 —tg2 -7
tg a =---------; ctg a =-----------“ .
x a
1 —tg2 J 2 tg у
ФОРМУЛЫ СЛОЖЕНИЯ и ВЫЧИТАНИЯ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
а 4 5 а —
sina 4- sin В = 2 sin —cos —у— ;
a 4 (3 a — p
sin a — sin 3 = 2 cos —2-sin —2— ‘
ctg «41
~r—"“T = ctg (45° — a);
ctga — 1 6 v "
sin2 a — sin2 p = sin (a 4 p) sin (a — p);
COS2 a — cos2 3 = sin (a 4 3) sin (3 — a);
4 sin 45° sin (45° ± a)
cosec a± sec a= -
m sin ( a 4 p)
m sin a4 n cos a = -—cos g------,
n
где tg3= — .
Если A 4 В 4 C — 180° (А, В, C — углы
треугольника), то:
sin A 4 sin В 4 sin C —
ABC
— 4 cos cos cos ;
cos A 4 cos В 4 cos C =
ABC
= 4 sin 2’ sin ~2 sin > 4 1;
sin2 A 4 sin2 В 4 sin2 C =
-- 2 cos A cos В cos C 4 2;
cos2 A 4 cos2 В 4 cos2 C =
=— 2 cos A cos В cos C 4 1;
sin 2 A 4 sin 2 В 4 sin 2C =
= 4 sin A sin В sin C;
122
МАТЕМАТИКА
cos 2А + cos 2B + cos 2C =
= — 4 cos A cos В cos C — 1;
tg A + tg В + tg C = tg A 'g В tg C;
ABC
ctg -2“ + ctg -y + ctg -2~ =
ABC
= Ctg -2 ctg -2“ ctg -y •
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ
(КРУГОВЫЕ) ФУНКЦИИ
Определения обратных тригонометриче-
ских (круговых) функций:
если х = sin у, то у = Arc sin х (арксинус);
если х = cos у, то у =Arc cos х (арккосинус);
если x = tgy, то у = Arctgx (арктангенс);
если х = ctg у, то у = Arc ctg х
(арккотангенс);
если х = sec у, то у = Arc sec х (арксеканс);
если х = cosec у, то у= Arc cosec х
(арккосеканс).
Обратные тригонометрические функции
обычно измеряются в радианах. Например,
1 л 5л 7
Arc sin ~2~ — -g- или ~б~ или — q л
и т. д.;
вообще,
Arc sin = п - + (— 1)" -g- ,
где п = 0, ± 1, ± 2, . . .
Функции Arc sin х и Arc cos х определены
для значений х, не превосходящих по абсо-
лютной величине единицы; функции Arc tg х
и Arc ctg х определены для всех значений х,
a Arc sec х и Arc coscc х для значений х, кото-
рые по абсолютному значению больше или
равны единице.
Обратные тригонометрические функции
многозначны (стр. 128), их главные
значения обозначаются через arc sin х,
arc cos х и т. д. и заключены в пределах:
О < arc cos х < л:
л л
- -2- < arc tg х < ;
О < arc ctg х < л.
Между значениями обратных тригономе-
трических функций и их главными значени-
ям:: имеют место соотношения:
Arc sin х = п - + (— 1)" arc sin х;
Arc cos х = 2п л ± arc cos х;
Arc tg х = п л + arc tg х;
Arc ctg х = п л + arc ctg х
(п — целое число).
Графики обратных тригонометрических
функций даны на фиг. 79— 82. Главные
значения на графиках обозначены сплош-
ными линиями.
Соотношения между обратными тригоно-
метрическими функциями положительного и
отрицательного углов:
arc sin (— х) = — arc sin х;
arc cos (— х) = л — arc cos х;
arc tg (— х) = —- arc tg х;
arc ctg (— х) = л — arc ctg х.
Фиг. 79. График
функции y=arc sin х
Фиг. 80. График
функции y=arc cos X
Фиг. 82. График функции у *=• arc etgx
Основные тригонометрические соотноше-
ния в применении к обратным тригономет-
рическим функциям приводят к равенствам:
sin (arc sin х) = х;
sin (arc cos x) = 1^1 — x2;
x
sin (arc tg x)
¥ 1 + x2
ТРИГОН ОМЕТРИЯ
123
1
cos (arc sin x) = К1 — x2;
cos (arc cos x) = x;
1
cos (arc tgx) = :
cos (arc ctgx)= y/'. I
tg (arc sin x) у ] v., !
1/ I _ v2
tg (arc cos x) =----------- j
tg (arc tgx) = x;
tg (arc ctg x) = — ;
тЛ I___
ctg (arc sin x)= —---------
ctg (arc cos x) = yy^f !
1
ctg (arc tgx) = i
ctg (arc ctg x) = x.
Из соотношений между тригонометриче-
скими функциями дополнительных углов
следует:
arc sin х + arc cos х—
arc tg х + arc ctg x = .
Главные значения обратных тригономет-
рических функций связаны соотношениями,
указанными в табл, 10 (при этом следует
иметь в виду, что формулы, взятые в квад-
ратные скобки, верны только для положи-
тельных значений х, так как пределы глав-
ных значений определены для различных
функций по-разному).
Таблица 10
Соотношения между обратными тригонометрическими функциями
arc sin x arc cos x arc tg x arc ctg x
arc sin х=» [arc cos V 1—x1 ] X arc tg , V 1-x’ arc ctg У L x
arc cos х- arc sin V 1—x1 x V l-xa arc tg — L x , x arc ctg — / 1-x’
arc tg х “ arc sin — / 1+x* 1 1 arc cos — — / l+xa arc ctg — X
arc ctg х » 1 arc sin — V 1+x* X arc cos • V 1+x’ [arc tg JL]
РЕШЕНИЕ ПЛОСКИХ
ТРЕУГОЛЬНИКОВ
Решить треугольник — значит найти пу-
тём вычислений все его элементы (стороны,
углы, площадь).
Формулы для решения прямоуголь-
ных треугольников (фиг. 83) даны в табл.
11.
Таблица 11
Решение прямоугольных треугольников
Данные элементы Формулы для определения остальных элементов
Гипотенуза и острый угол (с, А) Б= 90°—А; а = с sin А; п =с cos А
Катет и острый угол (а, А) Б = 90°~-A; b=a ctg А; а sin А
Катет и ги- потенуза (а ,с) sin А-=--; &=»с cos А; с В ~ 90 й-А
Два катета (а, &) tg А = — -—• 6 & ’ smA’ Е=90°—А
Обозначения: а, b — катеты; с—гипоте-
нуза; А, В, С —углы против сторон а, Ь, с
(угол С — прямой).
Фиг. 84
Фиг. 83
Соотношения между сторонами и углами
любого треугольника (фиг. 84)
= _2_ = = 2/?
sin A sin В sin С 4
(теорема синусов)1,
где R — радиус описанной окружности;
а2 = с2 + b2 — 2&CC0S А
(теорема косинусов);
А 4- В
---
а b 3----------2
а ~ b = А — В
2“
(теорема тангенсов);
124
МАТЕМАТИКА
А —В А — В .
о + Ь cos- 2- cos—2—
с ~ А +в~ . С ’ I
cos 2 sin2 I (формулы
А —В . А —В } М о л ь-
а—& sin 2“ Sln 2~ I вейде)
___ д ; |
sin 2— cos -у ।
SinA = 1/ (Р - Ь> ;
2 г Ьс
2 т Ьс
is А = 1/(Р~ &) (Р-сГ
g 2 У р(р-а) ’
где
а + b + с
Р =----2------
полупериметр треугольника);
asin В
А = с — a cos В *
Плошадь
S = -у ab sin С = 2R2 sin Asin Bsin C=rp=
= Ур(р —a) (p — b)(p — c) ,
где r — радиус вписанной окружности.
Формулы для решения косоугольных
треугольников даны в табл. 12. Обозначения:
А, В, С —углы против сторон а, Ь, с;
а + b + с
р=------2--- •
ВЫЧИСЛЕНИЕ ДЛИН НЕКОТОРЫХ ОТРЕЗКОВ
СВЯЗАННЫХ С ТРЕУГОЛЬНИКОМ
Высота из вершины А
ha = b sin С = с sin В.
Медиана из вершины А
та = -4 Vb2 + с2 + 2bc cosA.
Биссектриса угла А
А
be cos
₽a = b + *
Радиус описанной окружности
а b__________с
R ~ 2 sin А ~ 2 sin В ~ 2 sin С
Радиус вписанной окружности
r = S _ -/ (Р — а)(р — Ь)(р~=гс) =
р У р
АВС
= ptg^--tg-2--tg-y =
А В . С
•= 47? sin -г,- sin -у sin -g-.
Таблица 12
Решение косоугольных треугольников
Данные элементы Формулы для определения остальных элементов
Сторона и два угла (а,А,В) С- 180°-А—В; b д -~sln В- ; Sin А a sin С „ 1 С *= —: ; 3 = —— ab Sin С Sin А ’ 2
Две стороны и угол между ними (а,Ь,С) 1-й способ: с—У а* + Ья— 2 ab cos С» , _ b sin С sin В = ; с ’ А—90°—В —С; 8=-?-sin С. 2-й способ: Углы А и В находятся из системы двух уравнений: ~ (А + В) = 90°— £ . a sin С „ 1 sin А : & 2 abs,nC
Две стороны и угол против одной из них (а,Ь,А) Sin В - . а Если а > Ь, то В < QO0 — имеется одно решение. Если b sin А > а, то решение не- возможно. Если b sin А «= а, то имеется одно решение В = 90°. Если bsinA<a, то решений два: В| и Вг; причём В» = 180°—Вх С = 180°- А - В; b = “ г П.С: sin А S — sin С
Три стороны (а^с) 1-й способ: д» + с» _ COSA“ 2bc ’ sin В = C=90°- A-В; a fjQ ~ .— — 8= - sin A = у p(p—a) (.p-bt(p-c). 2-й способ: tgA = <Pr£>_; 2 V P (P-a) tg-®- = ЛГ <P-a) (P-c) ; 2 V p (.p-b) C = 90° — A — B; S = sin A = -yTp (p—a) (p-b) (.p-c)
ТРИГОНОМЕТРИЯ
125
ГИПЕРБОЛИЧЕСКАЯ ТРИГОНОМЕТРИЯ
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Гиперболические функции определяются
через показательные функции по формулам:
е'° — е~ч (гиперболический
sh -у = 2 сипу с);
(Я 4- е~~v (гиперболически и
ch у = 2 косинус);
e'f — е~'? (гиперболический
th ? = е—f тангенс);
4- е—? (гиперболический
cth? = котангенс);
2__(гиперболический
scl1 ' ~ е: + е~^ секанс);
2 (гиперболический
csch ? — _ е—¥ косеканс).
Гиперболические функции для деистви
тельных значений аргумента ? геометриче
ски могут быть изо-
бражены длинами
некоторых отрезков
в равноосной гипер-
боле с полуосями,
равными единице
(фиг. 85), подобно
тому, как тригоно-
метрические функ-
ции изображаются
длинами отрезков в
круге с радиусом,
равным единице, а
именно:
sh ? = NM, ch ? = ON, th 9 = АР.
Аргумент ? гиперболических функций
геометрически представляет собой удвоен-
ную площадь гиперболического сектора
ОАМ подобно тому, как аргумент а триго-
нометрических функций может быть истол-
кован как удвоенная площадь кругового
сектора ОАМ (см. фиг. 71).
При действительных значениях аргумен-
та ? имеют место неравенства:
ch? > 1; — 1 < th ? < -f- 1; I cth? I > 1,
a sh ? может иметь какие угодно значения
как положительные, так и отрицательные.
Соотношения между гиперболическими
функциями отрицательного и положитель-
ного аргументов:
sh (— ?) = — sh ?; ch (— ?) = ch ?;
th (— ?) = — th ?; cth (— ?) — — cth ?.
Фш. 86. График
функции у = sh х
Фиг. 87 График
функции у = ch х
Таблицы значений гиперболических функ-
ций для действительных значений аргумен-
та см. на стр. 79—80.
Фиг. 85
Графики гиперболических функций см. на
фиг. 86 - 89.
ОСНОВНЫЕ ФОРМУЛЫ ГИПЕРБОЛИЧЕСКОЙ
ТРИГОНОМЕТРИИ
Между гиперболическими функциями су-
ществуют соотношения, аналогичные соот-
ношениям между тригонометрическими функ-
циями.
Таблица 13
Выражение одних гиперболических функций через другие
sh ср ch ср th 9 cth cp
sh <р =» f ell2 — 1 th cp 1
У* 1 — th* cp f ctha cp — 1
ch ср = У* sha ср + 1 1 V 1 - th" p cth <p у cth" p — 1
th <? = sh ср / sh" <f> + 1 У ch* <p — 1 ch cp 1 cth cp
cth ср = 1/ sh" р + 1 sh ср ch <p / ch1 cp — 1 1 th cp
126
МАТЕМАТИКА
Между функциями одного и того же ар-
гумента имеют место следующие соотноше-
нии:
ch2 ® — sh2 <р> = 1;
1 — th2 ср = sch2 <р;
cth2 <p — 1 = csch2 <p;
sh <₽
cH“=thtf:
ch cp
sh <p
— cth cp;
sh <p csch <p = I;
ch ср-sch cp =- 1;
th ср-cth cp = 1.
При помощи этих соотношений каждая
гиперболическая функция аргумента <? мо-
жет быть выражена через любую другую
функцию этого же аргумента (табл. 13).
Гиперболические функции суммы и раз-
ности двух аргументов, двойных и половин-
ных аргументов:
sh (-р + ф) = sh <р ch ф ± ch ср sh ф;
ch (ср ± ф) = ch ср ch ф + sh ср sh ф;
th ср + th ф
th ± Ф) = 1 ± thfih ^ >
1 + cth ср cth ф
cth (р + ф) = -^pTTthlT ’
sh 2 ср = 2 sh cp-ch ср;
ch 2 ср = ch2<p 4- sh2cp = 2 sh2cp 4- 1 =
= 2 ch2 cp — 1;
~~ 1 + th2 cp
1 4- cth2 cp
cth 2 cp = —A—-
T 2 cth cp
•hl - /jilZLl ; ch J - / СЦ±1
th 1 ; cth 1 = 1/с11Г1О' .
2 V ch cp 4-1 2 V chep — 1
Суммы и разности гиперболических функ-
ций:
ср + ф ср + ф
sh ср + sh ф = 2 sh ~2~ ch Т '2 ’
щ -Г ф — ф
ch ср 4- ch ф = 2 ch2—е,— ch 1—2 ~ I
ср 4- ф с₽ — ф
ch ср — ch ф = 2 sh - 2 " sh —2~- ;
sh (ср ± б)
th ? ± th ф = ch ? ch . .
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Определение обратных гиперболических
функций:
если x==shy, то y=Arshx (ареасииус);
если x=chy, то y=Archx (арсакосинус);
если x=thy, то y=Arthx (ареатангенс);
если x=cthy, то у—Ar cth х (ареакотангенс).
Графики обратных» гиперболических функ-
ций см. на фиг. 90— 93.
Выражение обратных гиперболических
функций через логарифмы:
Ar sh х = In (х 4- Ух2 4- Т);
Ar ch х = In (х ± Ух2 — 1);
. .. 114-х
Ar th х = -тг In :-— ;
2 1 — х ’
Фиг. 90. График
функции у= Ar sh х
Фиг. 91. График
функции у = Ar chx
Фиг. 92. График Фиг. 93. График
функции у = Ar th х функции у = Ar 6th х
СООТНОШЕНИЯ
МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ
И ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ
На формулах Эйлера:
eix ~ cos х 4- i sin х, е~1Х = cos x — i sin x.
где i = У — 1, основаны соотношения меж-
ду тригонометрическими и гиперболически-,
ми функциями:
4- e~ix
cosx =-----2----= ch z’x>
ch х = cos ix,
gix ___ g—ix
sin x =---2/---= — i sh ix;
sh x = — i sin ix,
eix _ e—ix
tg x = - -i ,x ._e = - i th ix;
£ i e
th x = — i tg ix;
eix e~ix
Ctg x = 1 fix __ ix = ‘ Cth iX’
cth x =-- i ctg ix;
arc cos x = — i In (x + i УI — x2)e-=
= — i Ar ch ix;
arc sin x = — i In (/I — x2 4- (*) =
= — i Ar sh ix;
1 1 4~ ix
arc tg x — ~27 ln) zx = — ' Ar fil ix;
1 ix — 1
arc ctg x 27 ln foT+~l = 1 Ar cth ix'
ДИФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
127
Ar ch х = ± i arc cos ix\
Ar sh x = — i arc sin ix;
Ar th x = — i arc tg ix-,
Ar cth x = i arc ctg ix.
СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ
Меньшая дуга большого круга на сфере
(фиг. 94), соединяющая две точки А и В,
является кратчайшей линией на поверхно-
сти сферы (геодезическая линия) и
играет на сфере такую же роль, как пря-
мая на плоскости. Если принять за единицу
измерения дуги АВ = а радиус сферы (7? =
= 1), то изображённый угол z АОВ=а, из-
меренный в радианах, равен длине дуги:
а = а.
Сферический треугольник (фиг. 95) обра-
зуется пересечением дуг трёх больших кру-
cos а = cos & cosc = ctg 0 etgy;
cos b = cos 0 sin y tg c ; cos 0= ; ' tg a ’
COS с = cos 7 tg b ; COS -== ; tga ’
sin 0
sin 0 = sin b sina ;tg0 = -M; ° ‘ sine ’
sin у =-- sin c sin a fa C ; tgy = b 1 sin b
Для решения косоугольных сферических треугольников пользуются формулами:
sin a sin b sin a = sin 3 == sin c ~ sin y (теорема синусов)
Фиг. 94
Фиг. 95
cos а ~ cos b cos с + \
+ sin b sin с cos а; ( (теоремы ко-
cos а = — cos р cos у + Г синусов)
+ sin р sin у cos а; ’
sin a cos b == cos a sin b cos ( + sin c cos 0;
sin a ctg b = ctg b sin у + cos a cos y;
sin a cos 0 — cos b sin у — cos c sin 0 cos a;
sin a ctg 0 = sin c ctg b — cos c cos a;
sin -a .= ]/zZ^iS S CI|S ,
2 r sin 0 sin у
гов на сфере. Длины его сторон а, Ь, с
измеряются плоскими углами трёхгран-
ного угла О а 0 у.
Сферический треугольник может быть ре-
шён по любым трём из его шести элементов
(трёх сторон и трёх углов), так как его
углы не связаны таким соотношением, как
в прямолинейной тригонометрии. Сумма уг-
лов сферического треугольника всегда боль-
ше т:, поэтому вводится понятие сфери-
ческого избытка сферического тре-
угольника:
е = (а + 0 + 7) — я.
Величина е определяется из формулы
a = 1 / cos (a — 0) cos (j — y) .
2 r sin 0 sin у
a / sin (p — b) sin (p — c) .
2 V sin & sin c ’
а Г sin p sin (p — й)
2 V sin & sin c
ctg ±- =
или
с b
ctgj + ctg 2~ + cos t
siny
Площадь сферического треугольника
S = г В2,
где е — сферический избыток, а 7? радиус
сферы.
'r4- -
Фиг. 96
где
Для решения прямоугольных сфе-
рических треугольников с пря-
мым углом а и гипотенузой а (фиг. 96)
применяются следующие формулы:
Площадь сферического двух-
угольника (фиг. 97), образованного
двумя дугами большого круга,
S= 2 с /?2,
где <р измеряется в радианах.
ДИФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
ВВЕДЕНИЕ В АНАЛИЗ
Всякое действительное значение перемен-
ной величины х может быть изображено
при помощи точки па числовой прямой (осп
ОХ) с абсциссой х. Множеству значений х
соответствует множество точек на прямой.
В частности, совокупность значений х, за-
ключённых между двумя постоянными зна-
128
МАТЕМАТИКА
чениями х=а и х=Ь, изображается при по-
мощи отрезка (фиг. 98).
Если концы отрезка, т. е. значения х=а
и х=Ь, принадлежат данному отрезку, т. е.
совокупность состоит из всех значений х,
для которых жх<&, то отрезок называется
замкнутым или сегментом; обо-
значение: [а, &].
о а Ь
Фиг. 98
Если концы отрезка ему не принадле-
жат, т. е. а < х < Ь, то отрезок называется
открытым, или интервалом; обозна-
чение: (а, &).
Отрезок, которому принадлежит только
один из его концов, т. е. а < х < b или
а<х<Ь, называется полусегментом
или полуинтервалом; обозначения:
[а, &); (а, &].
Окрестностью точки х = х0 назы-
вается всякий отрезок, для которого точка
х„ является внутренней.
Величина у называется ф у н к ц и е и не-
зависимой переменной величины (аргу-
мента) х, если всякому значению вели-
чины х, принадлежащему некоторой сово-
купности, соответствует вполне определён-
ное (действительное) значение у.
Обозначение: y=f (х) (х —аргумент, у —
функция, / — символ функциональной зави-
симости).
Областью существования
функции называется совокупность зна-
чений аргумента, для которых эта функция
определена.
Пример. Областью существования функции
V X - 1 .. ...
j>= —• является полусегмент [1,4) (1 < х < 4).
У 4 - X
Если задано такое соотношение между х
и у, что каждому (пли некоторым) значе-
нию х соответствует более чем одно значе-
ние у, то такое соотношение определяет не
одну, а несколько функций, или, как гово-
рят коротко, многозначную функцию
(каждая из функций, объединяемых этой
.многозначной функцией, называется её
ветвью). .
Пример 1. Равенство у8=х+5 определяет дву-
значную функцию у = ± ] х 4- 5 , т. е. две
функции: у = ] х 4- 5 и у= — Ух 4- 5.
Пример 2. Равенство у == Arc sin х определяет
бесконечнозначную функцию
у = т.п 4- (— l)n arc sin х,
где п = О> 1, ±2, . . .
Всякая функция может быть геометриче-
ски изображена при помощи графика, если
значения аргумента х и функции у интер-
претировать, как координаты точки на пло-
скости.
Функция / (х) называется чётной, если
/ (— х) = / (х) (например: cos х; Зх4 + х2 — 2)
и нечётной, если /(—х) = — / (х) (на-
пример: • sin х; х3 — 2х).
График чётной функции симметричен от-
носительно осн OY, график нечётной функ-
ции симметричен относительно начала коор-
динат.
Заданная при помощи некоторой форму-
лы функциональная зависимость называется
неявной, если она имеет вид F (х,у) =0,
явной, если у=/(х), и параметриче-
с к о й, если аргумент х и функция у выра-
жены через вспомогательную переменную
величину t (параметр): x==^1(Z), y=tp2(0.
Если формула, определяющая функцию,
такова, что над аргументом совершается
конечное число алгебраических действий
(сложение, вычитание, умножение, деление,
возведение в степень, извлечение корня,
решение алгебраического уравнения), то
функция называется алгебраической,
в противном случае она называется транс-
цендентной (тригонометрические и об-
ратные тригонометрические функции, лога-
рифмическая функция, показательная функ-
ция и др.).
Алгебраические функции делятся на ра-
циональные и иррациональные.
Функция рациональна, если для её вычи-
сления нужно произвести над аргументом
конечное число арифметических действий
(сложение, вычитание, умножение, деление,
возведение в целую степень), в противном
случае функция иррациональна.
Рациональная функция называется ц е-
л о й или многочленом (полино-
мом), если для её вычисления можно не
прибегать к делению па выражение, содер-
жащее аргумент (и к возведению аргумента
в отрицательную степень), в противном слу-
чае она является рациональной
дробью.
Функции, для определения которых над
аргументом совершается конечное число так
называемых элементарных действий (к чи-
слу элементарных действий относятся все
алгебраические, а также логарифмирование,
потенцирование и действия, определяемые
тригонометрическими и обратными тригоно-
метрическими функциями), называются
элементарными функциями.
Число & называется пределом функ-
ции /(х) при х, стремящемся к а (обозначе-
ние: lim/(x) = 6), если, как мало бы ни
Х-.а
было положительное число г, к нему можно
подобрать столь малое положительное чи-
сло 8, что для всякого значения х, удов-
летворяющего условию |х — а\<§, имеет ме-
сто неравенство \](х)—&|<е.
Равенство lim/(x)= b обозначает, что ко
X оо
всякому положительному числу е можно
подобрать столь большое число А, что для
всякого х, удовлетворяющего условию х. А,
имеет место неравенство | /(х) — Ь| < s.
Равенство lim/(x) = oo (в этом случае
х -.а
lim/(x) не существует) имеет тот смысл,
х , а
что каково бы ни было сколь угодно большое
число В, можно подобрать столь малое по-
ложительное число 8, что из | х — а I < о
следует /(х) > В.
Аналогичным образом определяется смысл
равенств:
lim/(x)=&; lim/(x)= —со;
х — ос х -t. а
lim / (х) = ± оо; lim / (х) = + со.
X 00 X — .о.
ДИФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
129
Определение левого и правого
пределов функции см. ниже.
Пределом последовательно-
сти чисел аг, а2, ..., ап называется lim ап.
П СО
Если этот предел существует (и конечен), то
последовательность называется сходя-
щейся, в противном случае последова-
тельность расходящаяся.
Величина /(х) называется ограничен-
н о й, если существует такая постоянная А,
что I /(х)| <А, и неограниченной в про-
тивном случае.
Бесконечно малой называется пе-
ременная величина, предел которой равен
нулю.
Бесконечно большой называется
переменная величина, предел абсолютного
значения которой равен бесконечности. Ве-
личина, обратная бесконечно большой, есть
бесконечно малая, и величина, обратная
бесконечно малой, есть бесконечно большая.
Простейшие свойства бесконечно малых:
1. Сумма конечного числа бесконечно
малых есть бесконечно малая.
2. Произведение конечного числа беско-
нечно малых, а также произведение ограни-
ченной величины на бесконечно малую есть
бесконечно малая.
Если а(х) и р(х) — бесконечно малые при
х—>- а, то они называются бесконечно ма-
лыми одинакового порядка мало-
а (х)
сти з случае, если lim х-,—г-= А, причём
х_>а Р W
А =/= 0 и ] А | gb оо.
Если А=0, то а(х) — бесконечно малая
более высокого порядка, чем ₽(х); если
|А| = оо, то а(х) имеет порядок малости
ниже, чем ₽(х).
В случае, когда А=1, а(х) и ₽(х) назы-
ваются равносильными (эквива-
лентными) бесконечно малыми (обозна-
чение: aoofj).
а (х)
Если lim 0 и |А| =^оо),
то а является бесконечно малой порядка к
относительно ₽.
Порядок малости произведения несколь-
ких бесконечно малых выше, чем каждого
из сомножителей.
Сумма нескольких бесконечно малых
различных порядков имеет порядок наиниз-
шего (в отношении порядка малости) сла-
гаемого и равносильна этому слагаемому
(оно называется главной частью суммы).
Если a cv р, то а — [i бесконечно малая
более высокого порядка, чем аир.
Если arv'/.j и p^pt, то
lim
Простейшие теоремы о пределах (а — ве-
личина конечная или бесконечная):
limc=c (если с постоянная);
lim [(х) + /2(х) + ... + /,г(х)] =
= Чш/1(Х) 4-xlim/2(х) + ... -|-lim/„(x);
х х-*а
lim [Л(х) /2(х) ... /„(х)] =
х^а
== Hm/^xj-lim/2(х) л. lim/„(x);
х-'-а х^а х^а
Ит[с/(х)] =clim/(x) (с — постоянная);
Х-,а Х-Ла
.. 1 (*) ____ х^-а
х " a ?(*) ~ ’ еСЛИ Нт ? (Х) * °’
х^а х_>0
Некоторые пределы
.. Sinx tgx
lim —— = hm-~ = 1
л X->0 x
х->0
i • / 1\л
Пт 1+ - = e = 2,71828 ...
П-. + ОО \ “ /
(X
!+ —) =ex-,
и у
{co при a > 1,
1 при a = 1,
О при 0 < a < 1;
(1пх)'г xm
'ЛЬДА—= 0. lim Дт=0 (m-любое
x x-f-co e число);
nl r-—
lim —г~ " = V 2
n-^oo nn e nyn
(формула Стирлинга);
lim Inx = — co; lim
X^O
ln(l 4-x)
X I;
lim ]/n= 1; lim ]/a = 1 (a>0 и постоян-
нее п->сю ная).
Правило Лопиталя для вычисле-
ния пределов см. на стр. 132.
Функция /(х) называется непрерыв-
ной в точке х = х0, если в этой точке
lim Ду = 0. где (фиг. 99) Д х = х — х0
д х о
(приращение аргумента) и Ду =
=7(*)—/(*о)= /(х04-Д х) — /(х0) (п р и р а щ е-
ние функции).
Условие непрерывности /(х) в точке
х -= х0 можно записать также при помощи
равенства lim/(х) =/(х0).
х->х0
Функция непрерывна на отрезке, если
она непрерывна во всех точках этого от-
резка.
Точки, в которых условие непрерывно-
сти нарушается, называются точками раз-
ры в а функции.
Левым и правым пределами функ-
ции в точке х==х0 называются числа, опре-
деляемые равенствами-.
/ (х0 — 0) = 1 пн /(Хо — s) (® >0);
s—>0
( (х0 + 0) = Нт /(Хо + (®>0).
Если эти пределы существуют (и конечны),
но не равны между собой, то точка х, на-
9 Том 1
130
МАТЕМАТИКА
зывается точкой разрыва 1-го рода. Если
хотя бы одни из этих пределов не сущест-
вует, то х0—точка разрыва 2-го рода.
Примеры.
а) Лх)
х0 = О — точка разрыва 1-го ро-
да <фиг. 100);
б) /(х) = 2х 3; х0=3 — точка разрыва 2-го рода
(фиг. 101);
здесь /(3 — 0)=0; /(34-0)=оо;
в) /(x)^sin^ ; хо=О — точка разрыва 2-го рода
(фиг. 102);
здесь /(— 0) и /(4-0) не существуют.
Фиг. 102
Если Дх0 — 0) = /(Хо+0) + /(х0), то точка
х0 называется точкой устранимого
разрыва.
Непрерывность некоторых
элементарных функций
1. Непрерывны при всех значениях аргу-
мента следующие функции:
а) всякая целая рациональная функция;
б) показательная функция у=ах\
в) тригонометрические функции:
у = sin х; у = cosх;
г) обратные тригонометрические функ-
ции:
у = arc tg х; у = arc ctg х.
2. Непрерывна при всех положительных
значениях х функция
у = 1п X .
3. Непрерывны при всех значениях х от
— 1 до + 1 функции:
у = arc sin х; у = arc cos х.
4. Претерпевают разрыв следующие функ-
ции:
а) дробные рациональные функции при
значениях аргумента, обращающих знамена-
тель в нуль, если дробь несократима;
б) тригонометрические функции:
у = tgx
TZ
при х=п п ± ;
у = etgx
при Х=±тс П.
ПРОИЗВОДНАЯ
Производной функции у = /(х) на-
зывается предел, к которому стремится
отношение приращения функции к прира-
щению аргумента, когда приращение аргу-
мента стремится к нулю:
Д у
У' = lim т- = Иш
Ах-^О “ х Лх^О
Другие обозначения
dy d
dx ’ dx
/ (x + Д x) - /(x)
Д x
производной: /' (x);
Нахождение производной или диферен-
циала (стр. 132) называется дифере нци-
рованием.
Для того чтобы при некотором значении
аргумента функция была диференцируемой
(т. е. имела производную), необходимо (но
недостаточно), чтобы она была при данном
значении аргумента
непрерывной.
Производная фун-
кции у=/(х) равна
тангенсу угла нак-
лона касательной к
графику функции в
точке М(х, у) к оси
ОХ (фиг. ЮЗ):
dy <
=
Второй производной функции у=
=/(х), или производной второго порядка,
называется производная от её производной.
Обозначения второй производной: у";
<12у
f"(x); . Аналогично определяются про-
изводные любого порядка.
Обозначения производной п-го пррядка:
у<">; _<*"у .
dxn
Производные основных элементарных
функций (аргумент обозначен через х):
1) С' = О (С — постоянная);
2) (хпУ = пхп~\
в частности:
х'=1, (/х)'= ;
3) (ахУ а-Ппа,
в частности (ехУ = ех;
4) (logax)'=-’-logae = х1!п ~ ,
I
в частности (In х)' - — ;
5) (sin х)' = cos х;
6) (cos х)' — — sin х;
(tg х) = cos2x ’
1
8) (etgx)' « - ;
1
9) (arc sin x)' = ;
У 1 — x2
10) (arc cos^c)' = — г — ;
ДИФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
131
11) (arctgx)'= j +"ха ;
1
12) (arc ctg x)' = —
13) (sh x)' = ch x;
14) (ch x)' = sh x;
15) (thX)'~-~- ;
16) (cth x)' = - ~ ;
17) (Arshx)'=y=^ ;
18) (Archx)'=-^=y 1
19) (Ar th x)'= ’>
20) (Ar cth x)' = “i'r j •
Производные высших порядков некоторых
функций
1) (хп )<"> = т(т — 1)... (т - п + 1) хт~п ;
2) (logax)<n)= (- I)"-1 feW- ^7 ,
till С* }
в частности (lnx)(n> = (— 1)'!—'(n—1)! 1
3) (ax)(,I)= ах(1па)п ,
в частности ( ех )(п) = ех ;
4) (sin x)(n) = sin ^х+ ’-j- j ;
5) (cos ху ’ — COS ^х-г -у j ’
sh х при п чётном,
chx при п нечётном;
_ ( chx при п чётном,
7) (chx)<">= ] shx п;„ п !3.чёТЕ0М
б) (sh х)<"> =
Правила дифгренциреваиия
и, V, W— функции аргумента х, но которо-
му производится диференцирование:
1) (и + и)' — и' + и' (ироизводная суммы);
2) (uv)' = u'v + uv' (производная произве-
, дсния)?
(ue)(n) = uwv + (?) + и<-п~2\" +
+ ... + :
в частности, если с — постоянная, то
(си)' = си'; (си)^ = си1-^:
3) (uv)’ — vuv~1 u'+uv in u-v' (ироизводная
общей показательной функции);
4) если у=/(и) и и =<р (х), то / = /'(«) с'(х)
dy dy du
или dx~du’dx <пРавило Диференцирова-
ния функции от функции).
В более общем случае, если у = /(ц),
U=!f(y), у = ф(х), то
dy___dy du dv
dx ~ du ‘ dv ‘ dx
и т. д.
Пример.
(sin1 5x)' = (u1)- A (sin®) j1- (5x)=3«*,cos v*5 —
= 15 sin*5x-cos 5x
(здесь y=u*; u=sin v; ®=5x).
5) Если переменная у задана, как функция
аргумента х, неявно уравнением F(x, у)=0,
то её производные могут быть найдены с по-
мощью частных производных (определение
частных производных см. стр. 133):
dy = .
dx р1
у
d^y^_ Fxx (^у)2- 2PxyFxFy +Fyy (Fx)2
PyyW)
6) Если зависимость между у и х дана в
параметрической форме: x=<p(t); у=ф(О> то:
dy dx d2y dy d2x
dy _ dt а2у _dt ’ dF ~ dt ' dP
dx dx ’ dx1 ‘dx V ’ *
dt (dT )
7) Если равенство y=/(x) рассматривать,
как определяющее неявно функцию х=?(у),
то символы / и ср определяют, как говорят,
две взаимно обратные функции. Про-
изводные таких функций связаны между
собой соотношением:
, . . 1 dx 1
?z(y)=7^- «ли =
dx
Теорема Ролля. Если функция /(х) непре-
рывна на сегменте [а, &], диференцируема
в интервале (а, Ь) и 1(a) = f(b), то найдётся
в этом интервале по крайней мере одна
точка х=с, в которой /'(с) = О [касательная
к графику функции в точке х-С параллель-
на оси ОХ (фиг. 104)].
Тсьрсиа Лагранжа (теорема о конеч-
ном приращении). Если функция /(х) непре-
рывна на сегменте [а, й] и диференцируема
в интервале (а, Ь), то в этом интервале
найдётся по крайней мере одна точка х = с
такая, что имеет место равенство
Kb) - f(a) = (b-a) f'(c).
Геометрический смысл теоремы Лагран-
жа состоит в том, что касательная к кривой
У=1(х) в точке с абсциссой х=с параллель-
на хорде, соединяющей точки с абсциссами
х—а и х —ft (фиг. 105).
9*
132
математика
Обобщением формулы Лагранжа является
формула Тейлора:
/(х) = /(а)+ (х — а) +
+ Цр(х- ау- + . . . + (X - о)'Ч
+ (х - a)"+1 ,
(и + 1)! V
где 0<б< 1 (см. также стр. 160).
При а = 0получаем формулу Макле-
ре н а.
Правило Лопиталя для вычисления пре-
делов (для раскрытия неопред е-
л ё н н остей).
Если lim /(x)=lim <? (х) = О или lim / (х)=
Х-)Л х->а х-^-а
t (х)
= ± со, limy (х) = ± оо, то lim —7-7 =
х-+а х-^а т W
Пример.
Ineos X —tg X ,, cos’X !
lim ——— = Um -g— = lim ---------------------- = - 77 •
X->0 X X-»-0 1!x X.,0 2 J
Возрастание и убывание функций. Если
для любых точек хх и х2 интервала (а, Ь) из
неравенства хх<х2 следует, что /(хх)</(х2),
то функция /(х) называется в этом интер-
вале возрастающей. Если из нера-
венства хх<х2 следует /(хх) > /(х2), то функ-
ция называется убывающей.
Функция называется монотонной в
интервале, если она в этом интервале воз-
растает (монотонно возрастающая функция)
или убывает (монотонно убывающая функ-
ция).
Для того чтобы функция /(х) в некото-
ром интервале возрастала (убывала), доста-
точно, чтобы во всех точках этого интер-
вала /'(х)>0 [/'(х)<0].
экстремум
Точка х0 называется точкой максиму-
ма (минимума) функции /(х), если су-
ществует такая окрестность этой точки, что
для всякой точки х этой окрестности (х^=х0)
имеет место неравенство /(х0) > /(х) [/(х0) <
< /(*)]•
Общее название для максимума и мини-
мума — экстремум.
В точке экстремума производная данной
функции /'(х) либо равна нулю (фиг. 106),
либо (фиг. 107) не существует (н еобхо-
димое условие экстремума).
Если х0—корень уравнения /'(х)=0 [или
если /'(х0) не существует] и имеется такая
окрестность точки х0, что во всех точках
этой окрестности слева от х0 производная
/'(х) имеет один знак, а во всех точках
справа от х0—противоположный знак, то
точка х0 является точкой экстремума (до-
статочное условие). При этом изме-
нение знака (слева направо) с + на — со-
ответствует точке максимума, ас — на +
точке минимума.
Другое достаточное условие: если /'(х0)=
= 0, /" (х0) < 0, то х0 — точка максимума;
если /'(хо)=О и /"(хо)>0, то х0—точка ми-
нимума.
В более общем случае, если /'(х0) = 0 и
первая из неравных нулю в точке х0 произ-
водных функции /(х)—чётного порядка, то
точка х0 является точкой экстремума, а
именно: точкой максимума, если упомяну-
тая производная в точке х0 отрицательна,
и точкой минимума, если она положительна.
Пример.
f(x)=(x — I)4. Из необходимого условия получаем
уравнение /’(х)=4(х — 1)»=о, которое имеет корень
IV
х0 - 1. Далее f (1) « f ' (1) = 0; f (1) = 41 > 0;
х=1 — точка минимума.
ДИФЕРЕНЦИАЛ
Диференциалом функции у = Дх) [обоз-
начения: dy, d/(x)J называется произве-
дение её производной на приращение аргу-
мента
dy = /' (х) Д х = у' Д х.
Разность между приращением функции
и её диференциалом является бесконечно
малой более вы-
сокого порядка,
чем Дх. Диферен-
циал аргумента
dx равен его при-
ращению Дх и,
следовательно,
dy=y'dx.
Эта формула
инвар иантна,
т. е. сохраняется
и в том случае,
когда х не яв-
ляется независимым переменным: х==р(1).
Геометрически диференциал изображается
приращением ординаты точки на касатель-
ной к графику функции (фиг. 108).
Диференциал второго порядка — дифе-
ренциал диференциала: d2y=d(dy) и т. д.
Формулы для диференциалов высших
порядков:
tPy = y"dx2, d3y = у''-dx'1, ...,
dn у y<n> dxn ,
имеют место, если x — аргумент; если же
x=-tp(l) [причём функция 9 (1) — нелиней-
ная], то эти формулы перестают быть спра-
ведливыми.
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Функцией переменных х, у, Z, ... назы-
вается такая величина и [обозначение: и =
= /(х, у, Z, ...)], которая принимает опре-
делённое значение, когда даны значения не
зависящих друг от друга аргументов х,
у, z, ... Совокупность значений аргумен-
тов, для которых функция определена, об-
ДИФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ.
133
разует область существования
функции. Если имеется функция, зави-
сящая от двух аргументов, z — f(x, у), то
геометрически она может быть интерпрети-
рована при помощи некоторой поверхности,
координаты точек которой обращают в тож-
дество данную зависимость между х, у и г.
Каждая пара значений аргументов (х, у)
может быть изображена при помощи точки
М (х, у) плоскости ОХУ и функцию двух пе-
ременных можно рассматривать как функ-
цию точки в плоскости OXY: z=f(M);
область существования такой функции—не-
которая область в плоскости ОХУ.
Пример. Область существования функции z =
= I I — № — у1 есть круг Xs + уг -< 1.
В качестве окрестности точки
(х0,у0) принято брать либо прямоугольник с
центром в этой точке и сторонами, парал-
лельными координатным осям (т. е. сово-
купность значений х и у, удовлетворяющих
неравенствам |х — х0| < h, [у—уа\ < к, 'где
2й и 2к—стороны прямоугольника), либо
круг с центром в данной точке [(х — х0)2 4-
+ (у — у0)2 < р2, где р — радиус круга].
Число с называется пределом функ-
ции Дх, у) при х, стремящемся к а, и у,
стремящемся к b
[обозначение: lim/(x, у) = с],
х^а
У-»Л
если, как мало бы ни было положительное
число 8, к нему можно подобрать столь ма-
лые положительные числа h и к, что для
всех значений х и у, удовлетворяющих
условиям: ix — а\ < h и !у— bi < к, имеет
место неравенство i/(x, у) — с| < 8.
Подобным образом определяется понятие
предела для функции любого числа аргу-
ментов.
Смысл символов: lim / (х, у) = с;
Х->-ОО
у-*ь
lim f (х, у) = ± оо; lim / (х, у) = ± со
х-»-а х-^оо
ун.6 у->(|
и т. д. аналогичен смыслу соответствующих
символов для функции одного аргумента
(стр. 128).
Функция /(х, у) называется н е п р е-
р ы в н о й в точке (х0, у0), если
у) = /(х0, Уо).
У-гУо
Функция, непрерывная во всех точках
некоторой области, называется непрерыв-
ной в этой области.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ
Частной производной по аргументу х
функции u=f (х, у, z, ...) называется про-
изводная этой функции, вычисленная в пред-
положении, что все аргументы, кроме х,
постоянны:
ди f(x+&x, у, z, ...) —/(х, V, г,...)
дхТо- '
Другие обозначения частной производ-
ной по х функции и=дх, у, Z, ...);
й/ , д
дх' 1х’дХ1<х’ У’ г’ -')
Если функция двух переменных z=f(x, у)
изображена при помощи поверхности, то
dz
— tg а, где а — угол между касательной
в данной точке поверхности к кривой, по-
лученной в сечении этой поверхности пло-
скостью, параллельной плоскости OXZ,n
положительным направлением оси ОХ
dz
(фиг. 109); аналогично = tg [5.
Для производных высших поряд-
ков применяются обозначения:
д / df \ 02f
дх дх у == дх2 ~ ’
д t'Of \ д2'
Ф'!йх / дхду ”fxy » т- д-
В случае, если подлежащие вычислению
производные непрерывны, то результат много-
кратного диференцирования не зависит от
порядка диференцирования; та::, например,
fxy = fух •
Прсизззцпая в данном направлении. Про-
изводной функции Дх,у) В ТСЧлН М(х, у)
/ \
по направлению I ^ооозначение: I на-
зывается предел (фиг. ПО)
д1 г LW-/(?!)
dl "“nIm MN
Если а— угол между направлением I и
положительным направлением оси ОХ, то
й/ й/ df .
дГ^дхС05а + ду&1П^
Аналогично определяется производная
функции /(х, у, z) в данном направлении I
в пространстве. Если при этом а, р, f —
углы, образованные направлением I с поло-
жительными направлениями соответствую-
щих координатных осей, то
df df df
~dl = йх cos a + dy C03 p +
df
dz
Дифзрепциревание сложных
функций. Если z = ffx, у,
==?i(u- v, ...); y="2(u, v, ...), .
COS f.
и неявных
...) и x =
., то
dz
du
df dx df dy
dx du dy du +
В частности, если x---^(f); У ='PaU
dz dz dx dz dy
lit ' ox lit 'oy dt
134 _________________
МАТЕМАТИКА
Если равенство /(х, у, г, ...) = 0 опреде-
ляет неявно Z, как функцию аргументов х,
у.... то
. д2
дх Гг ’ ду fz ’ —
ЭКСТРЕМУМ
точкой о к с-
если сущест-
что для всех
имеет место
Точка (х0, у0) называется
тремума функции /(х, у),
вует такая её окрестность,
точек (х, у) этой окрестности
одно из неравенств /(х0, у0)>/(х, у) (в слу-
чае максимума) или /(х0, у0) </(х, у) (в слу-
чае минимума). Аналогично определение
экстремума для функции /(х, у, ...) любого
числа аргументов.
В точке экстремума частные производ-
ные функции по всем аргументам равны
нулю (если эти производные существуют):
д/ df
йГ=°; дг = 0’ -
(необходимые условия экстремума).
В случае функции /(х, у), зависящей от
двух аргументов, способ определения точек
экстремума следующий. Если х0, у0 — одно
из решений системы = 0; - = 0 и
л _ УоУ R _ 62 У»1
А ~ дх2 ’О- дхду
г _ дг/(х0, У»)
е ~ ду3
то следует составить дискриминант
Д — АС—В3 и применить правило: точка
(х0, у0) является точкой экстремума, если
Д>0 (и притом точкой максимума, если
А<0, или, что то же, С<0, и точкой мини-
мума, если А > 0, или, что то же, С>0) и
не является точкой экстремума, если Д < 0.
Случай, когда Д = 0, требует дальнейшего
исследования.
Пример.
Ах, у) = ху (я - х — у).
Решив систему fx (х, у) у (а — 2.x — у) = о,
fy(x, у) = х (я — х — 2у) -= 0, определи л четыре точ-
ки (О, О); (0, а); (я, С); ( з~ , з)
Здесь
/хх = — 2у; fxv — а — 2х — 2у и fyy — 2х.
В первых трёх точках А = АС — В* < О и пни яе яв-
ляются точками экстремума функции. В точке
/ а а \ аг
13’ 3 I имеем А = 3 > О и она является точкой
2а
эч.’трелц'ма; так как при этола А ==* С= — 3 , то это
точ са есть точка максимума, -спи а > 0, и точка ми-
ni-...-ума, если а < О.
Для отыскания экстремума функции п
переменных / (х, у, 2, ...) в случаях, когда
аргумшты х, у, z, ... связаны между собой
при помощи к условий (к<п):
<д(х, У, z, ...)=0;
?2(х, у, Z, ...) = 0; ...;оь(х, у, г, ...) = 0
(ус л о п п ы й экстрему м),
следует составить вспомогательную функ-
цию:
F(x, у, z, ...) =
= /(Х, у, 2, ...) + М1(Х, у, Z, ...) +
+ А2?2(х, у, 2, ...)+ ... +АКУ>; (X, у, 2, ...)
(/,, Хг, ... , Хк — постоянные, так называемые
множители Лагранжа).
Система п+к уравнений с п+к неизвест-
ными (х, у,
?i
0F
дх
z> ^i> ^2> ^-k)'
= 0; = 0; <?k = 0;
др дР
= °; ду = °; Tz - °- -
даёт необходимые (но недостаточные)
условия условного экстремума.
ДИФЕРЕНЦИАЛ
Полным д и ф е р е н ц и а л о м функ-
ции 2—/(х, у, ...) аргументов х, у, ... на-
зывается выражение
dz = fx(x, у, ...) Дх+/'(х, у, ...)Ду + ...,
где Дх, Ду, ... — приращения аргументов.
Диференциалы аргументов равны их при-
ращениям:
dx == Д х, dy = Д у, ...
и dz == fxdx + fydy + ...
Эта формула инвариантна, т. е.
сохраняется и в том случае, если х, у, ...
не являются аргументами: х=<р1(ц, v, ...);
у = ?2(ц, р,...);„. Выражения fxdx, fydy,...
называются частными диференци-
а л а м и:
dfZ = f'x dx; d vz = {ydy,...
Полный диференциал функции dz отли-
чается or полного приращения
Дг = /(х+ Дх, у + Ду...) —/(х, у, ...)
на бесконечно малую более высокого поряд-
ка, чем уДД х)2 + (Д у)2 + ...
Для того чтобы выражение М (х, у) dx +
4- N (х, y)dy, линейное относительно dx и
dy, было полным диферепциалом некоторой
функции переменных х и у, необходимо и
достаточно, чтобы имело место тождество
дМ dN
ду ~~ дх '
Выражение Р (х, у, z) dx + Q(x, у, z)rfy+
у, z)dz является полным диферен-
цг.а.том некоторой функции переменных х,
у, z, если
ад дР . — ,J-P-
ду~ ~ ~dz~; 7>z = дх ’ дх — Оу
Вообще выражение
/1(хг, xJt/XxH- /г(Х1, Х2, ...»
4* х2> •••> xn)dxn
является полным диф?ренциалом некоторой
функции переменных xt, х», ..., хп, если для
всех / и /
(Z = 1, 2, 3..п; j == 1, 2, 3, ..., п)
выполнены равенства:
«/'(хг, х2..х„) 0//(Х1, х„, х,;)
дх, ~ dxt
Геомттрически полный диференциал dz
функции двух переменных изображается
при помощи приращения апликаты каса-
тельной плоскости в данной точке к поверх-
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
135
ности z—/ (х, у), соответствующего при раще-
ниям аргументов dx и dy (фиг. 111).
Фиг. 111
Формулы для диференциалов выс-
ших порядков (для функции двух
аргументов):
d2z ff’z
dsz = d (dz) = dx* 4-2 dxdy 4-
, дгг Id О V
+ ay dy)z> •••;
. , / д д \п
dnz = d(d z) = Idx 4- ~dy dy \ z
справедливы, если x и у—аргументы или
если х и у зависят от аргументов и, и,...,
линейно.
Формула Тейлора для функции
двух переменных (в символической записи):
7 (* 4- h, у 4- к) = / (х, у) 4-
. 1 / д д \
+ П (dT h + wf <х- у) +
. 1 / д д \з
+ 2! (dx h + ду к) f (х> у) + ••' +
1 [ д д \п
+ пЦдГ h + <)ук} ^х’ У) +
Г / д д \ч+1
+ (7ГИ)\дТ й + дук) /(х4-01й,у+0а/.)>
где 0 < Oj < 1; 0 < 02 < 1.
При х = у =0 получаем формулу Ма-
клер е н а (см. также стр. 160).
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Функция F(x) называется первооб-
разной (примитивной) для функции
/(х), если F'(x) = / (х). Если Ег(х) и Г2(х)
первообразные для одной и той же функ-
ции /(х), то разность Fj(x) — F2(x) посто-
янна. Совокупность всех первообразных для
некоторой функции /(х) называется не-
определённым интегралом от этой
функции и обозначается символом j /(х) dx,
где §— знак интеграла, f (х) —подиптеграль-
ная функция, /(х) dx—подинтегральное вы-
ражение.
Таким образом, | / (х) dx = F (х) 4- С, где
F(x) — одна из первообразных функции /(х),
а С—произвольная постоянная
(постоянная интегрирования).
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
1) I dx = х 4- С;
2) xndx=*---------+С — 1);
J /2 4“ 1
Г dx
3) j — = In X 4- С;
t‘ dx -i x
V J F+Fa = Tarctg </ +C;
(' dx 1 x — a
J x3 — a2 = 2a In x’+'a 4- C =
( 1 x
I-----Y Ar th ~ 4- С, если x < a,
) 1 . x
I — a Ar cth ——С, если x > a;
C dx x
6) J y^rF -arcsin u +o>
7) f —— = In (x 4- ,rx- 4- a) 4- C —
J у x2 4- a
I Ar sh —4- С, если a > 0,
1 Va
1 X
I Arch -7.-^4- С, если a < 0;
\ /-a
8) J exdx = e 4- C;
9) J axdx = + C;
10) J sin x dx — — cos x 4- C;
11) j cos x dx = sin x 4- C;
12) J tg x dx = — In cos x + C;
13) J ctg x dx = In sin x 4- C;
f dx x
14> J ITnT =ln ‘g -2 +C’
C dx / x , n \
15) = 111 tg “2' + ‘4 J + C;
C dx
16> J siFF = -ctsx + ^
(’ dx
17> J ^=^ + C’
18) J sh x dx = ch x 4- C;
19) [ chx dx shx 4- C;
J
20) I th x dx — In cii x 4- C;
136
МАТЕМАТИКА
21) ) cth х dx = In sh x+C;
f dx
22) Th=x~ = -cthx + C;
_ C dx
23> J dKT = th ИС-
ПРАВИЛА ИНТЕГРИРОВАНИЯ
О [/1 (x)±/2 (x)]dx=J/i(x)dx± /2 (x) dx:
2) af (x) dx — a J / (x) dx (a—постоянная);
3) i u (x) du (x) =?- u (x) v (x) — Jy (x) du (x)
(правило интегрирования по
частям);
4) если х = c?(t), то /(x)dx= С f[z(t)]p(t)dt
(правило замены переменной или
правило подст а нов ки).
Пример 1. Найти ( х cos х dx.
Пользуясь правилом интегрирования по частям,
полагаем u=xt dv— cos х dx, откуда du ~ dx, sin х
и j х cos х dx=x sin х — j sin x dx = x sin x + cos x+C.
Пример 2.
J sin ax dx = J sin t d~- = “ J sin t dt =
— — — cos t + C = — -• cos ax + C
a a
^подстановка ax « t, откуда adx= dt, dx = j.
Пример 3.
J }~(x) dX = J ” In Z + c = ln /(x) + С (подста-
новка f (x) « t, откуда f (x)dx = dt).
Пример 4.
J /1 — X‘ dx= J cos’ t dt = 1 j (1 +ccs 2 О dt .=
“ht 1 + 4 sin 2< + c = у (arc sin x+x/1—x!) + c
(подстановка x = sin t, dx = cos t dt).
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ
ФУНКЦИЙ
1) J (ax + b)n dx = yyyyyy (ax+&) "+1 + c
(«¥=-!);
f dx 1
2> J oF+b= Vln<ax+ b>> + c’
3) C___1 j c
’ J (ax + bp (n \ ) a (ax4-b)n 1
(n=M);
(‘ dx 1 <47
4) |--------= -7-— arc tg 1/ -- x + C
J ax3 + b /ab ь Г b
(ab > 0);
C dx 1 iPab — ax
5) 1--------= ~ 1 n —y—---- 4- C
J axx—b 2Vab -fPab + ax
(ab > 0);
_ч f dx 1 x 4- & ,
C) J (7+аУ(хТ b) = a-b in x+ a + C
(a - b)\
ъ dx____________If_______<+ ________
7 l ax24- bx+c a 1 ( by 4ac -- b2
J J ^+2д/ + ~"4a3—
( 2 2ax 4- b
77e^arc‘sV«r=T> +c’
если 4ac — &2 > 0;
= 1 2ax4-& - т/b2 — 4ac
—7===—In-------z-----x-=r-_-- + C,
a у b2 — 4ac 2ax-yb + jPb2 — 4ac
если 4ac — b2 < 0;
2
( “ 2ax 4- b + C’ если 4flC ~
f Mx 4- N M
8) J ax2 +bx +c dx = 2a 111 + bx + +
2aN — Mb_ Г______dx____.
"i" 2a 1 ax2 4- bx 4- c ’
Г_____dx
9) J (ax2 4- bx 4- cP ~
________ 2ax 4- &______________ ,
(n — 1) (4ac - b2) (ax2 4- &x4-c),!'~!
2(2n — 3)a___ C_____d^_ ____
(n — 1) (4ac — b2) J (ax24-6x4-е)"'1
(n ¥= 1);
b
можно также подстановкой x 4- va =
= Y-lgc ~b" tg t (4ac ~ b2 > 0) привести к
2a
виду) cos2m tdt (стр. 140);
f Mx + N
10) J —(ax2+Tx4- cp dx =
_______________________________+
2(n - - l)a(ax2 4- bx 4- cp1 1
2aN — bM d dx
2a (axM7bx 4- cp - !)-
Интегрирование рациональных дробей
в общем случае. Если рациональная дробь
Р(х)
неправильная [т. е. степень много-
члена Р(х) больше или равна степени мно-
гочлена Q(x)], то, разделив Р(х) на Q(x) по
правилу деления многочлена на многочлен,
можно представить дробь ’ виде суммы
некоторого многочлена и правильной раци-
г Л (х)
овальной дроби
Правильную рациональную дробь q^)
можно разложить на сумму простейших
дробей (стр. 97), которые интегрируются,
как указано выше.
1 Для вычисления интеграла эта формула должна
быть применена n— 1 раз (рекуррентная фор-
мула).
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
137
В частности, если все корни многочлена
Q(x) действительны и различны, то
Q(x) = (x —Xi) (х —х2) ... (х —х„)
и
Pj{x) Д2____________А2 А„ '
Q(x) х — х1 х—х„ ••• + х-х,.г’
где коэфициенты А/ могут быть определены
из формул:
Pi(Xi) . Pi(x2)
A1 - Q4XJ ’ “ ” Q'(х>) ’ ’
JaSx^
Ап “ Q' (xn) ‘
Метод Острсградсксго. Метод Остроград-
ского позволяет свести интегрирование про-
извольной рациональной дроби к интегри-
рованию дроби, знаменатель которой имеет
только простые корни. Для этого знамена-
тель правильной дроби
F{x)
Q О)
следует представить в виде
Q (х) = (х) Х-, (х)... X? (х),
где Xi (х) — произведение линейных и квад-
ратичных множителей, соответствующих
простым корням, а Хг- (х) — произведение
линейных и квадратичных множителей,
соответствующих корням кратности i. Тогда
ГГ(х) Н(х) CG(x)
J Q (х) dx - U (xj + J V~(x) dX’
где
U(x) = X2X' ... XP-1 ;
V (x) = XLX2... Xp,
а H (x) и G (x) — многочлены с неопределён-
ными коэфициентами степеней соответст-
венно на единицу меньше, чем степени
многочленов U (х) и V (х).
Многочлены U (х) и V (х) можно найти,
не производя разложения Q (х) на простей-
шие множители: U (х) есть общий наиболь-
ший делитель многочленов Q (х) и Q' (х), а
Коэфициенты многочленов И (х) и G (х)
можно найти путём днференцирования ра-
венства (*), что приводит к равенству
(UH'-HU')V
F = ----------— + GU,
в обеих частях которого следует сравнить
коэфициенты при одинаковых степенях х.
Пример. Вычислить
Здесь;
Q (х) = (х*1 + х + 1)а;
Q' (х) = 2 (х5 + X + 1) (3 ,е -1 1);
U (х ) — х5 + х -I- 1;
г 4 х‘ - 1 . Н (х) О (X)
J X !)’ dx ’ F+7+“i + J Хь х < dx-
Положив:
Я (х) = а„ х« + а, х2 + п. х‘ а- щ х + Щ;
G (х) = Ь„ х4 + Ь, х5 + Ь, х‘ + Ь,х + Ь„
имеем
4 х= — 1 ~ (х6 + х+ 1) (Ь„х‘ + 0, Xs + Ьгх‘ + Ьах + Д.) -Г
+ (х“ я- х + 1) (4 аох« + 3 а,х2 + 2а,х + -.:а)
— (5 х4 Г 1) (а„х4 a- a,xs -!- «.№ + о,х J- а,).
Сравнив коэфициенты при одинаковых сте н нях
х в обеих частях последнего равенства, находим
а, = а, = са = а, - О; г, — — 1;
Ь„ = Ь, = = »3 = ba = О
и
(• 4 х“ — 1 . х
I ..----------------------dx -----------------------
J (Xs + X + I)2 X + X + 1
ИНТЕГРИРОВАНИЕ АЛГЕБРАИЧЕСКИХ ИРРАЦИОНАЛЬНОСТЕЙ
1) + b dx = (j/ax + б)3 + С; 2)^ах + b dx = ija' ([/ах 4- ’ 4- C;
3)j /А + ЧС
(’ dx n inf-------\ n-1
5) I n------ /йх+И +C;
J j/ax + b '
f dX n fnr---------\n-m
flX+H +C;
r Mx + N 2 r____
1) I -T"---- dx == —- (3Na -- 2Mb + Max) г/ax + & + C;
J / ax -J- b 3a-
8)
r - = ~7~ ln (2ax + b + 2 i/ a if ax2 +&x+ c ) + С, если a > 6;
у ax- 4- &x 4- c )/ a
1 2 ax 4- b
— Ar sh —--------— 4- С, если a > 0 и 4 ас — b'1 > 0:
|/ а у 4 ac -- b2
1 2 ax 4- b
— r-~ Ar ch ——_p q если a > 0 и 4 ас -- b: < 0:
у a / b2 — 4 ac
1 2ax 4 b
— —= arc sin ":------e=.~ С, если a < 0;
Y — a у b2 — 4 ac
138
МАТЕМАТИКА
Мх + N М г—--------,-----,
dx = — у ах2 + Ьх 4- с 4
зх2 + Ьх + с а
2aN — Mb Г________dx_______
2а j ax' + bx + с
С X>1 clx X>1 1 УГах'2 + bx + с _________________(п — 1)с _________хп 2dx
10) J /"ах2 4- Лх 4- с па па J /"ах2 4- Ьх +~с
(2п - 1)&
2па
X ______— й2 ________
11) l/’x2 4- а2 dx = -у У х2 4- а2 4- у 1п(х 4- /х2 4- а2 ) 4- С =
xn ldx
У ах2 4- Ьх 4- с
%_________д 2 %
= у /х3 4- а2 4- у Ar sh -- 4- С;
12) J угх2 — а2 dx — * - уг х2 — а1 — у In (х 4- т^х2 — а2) 4- С =
%__________
= у /х2 — а2 — у Ar ch а~ 4- С;
/ * . % _ ______ (I & %
13) I у а" — х2 dx ” а2 — х2 4- arc sin у 4- С;
з
14) 1 х )/ х2 ± a3 dx = у (х2 ± п2) 2 4- С;
С____________ ! _3
15) \ х у^а2 — х2 dx =----о- (а2 — х2)2 4- С;
г/ -3
Р ___________ __________________& 2 _________ __________________
16) х2 рлх3 ± а2 dx = у /"(х2 + а2)3— у [ х -/х2 ± а2 4- а2 In (х 4- угх2 ± а2)] 4- С=
— у /(х2±л2)3—у х /~х- ± а2 4- а2 Ar sh yj 4- С;
з
17) j х2 уГа2 — х2 dx = — у (а2 — х2) 2 4- у (х уГа2 ~ х2 4- а2 arc sin ~ 1 4- С;
18) ( ^х*.+ а'2 dx =/хМ^- a in ± + Z?2_±_gl 4- С;
J X X
С -уГ№ л* ,------- а
19) I _Е-------- ах = Jх2 — а2 — a arc cos — + С;
J X X
20) f dx =/55-=y?- a in A±Z“ZHZ. + C;
J x x
f*-------------- 2ax 4- b .----------------, 4jc — b2 f dx
21) i у ax2 + bx + c dx = ~z;— у ax2 4- bx 4-c 4----— I y=v4 1
J 4a °a J у/ ax2 + bx + c
b
можно также, положив x 4- у = t>
привести к одному из видов 11, 12 или 13;
Г dx
22) | ----——---------- ..._ . приводится к
J (х — а)п у/ ах2 + Ьх + с
1
виду 10 подстановкой х — а = у ;
или, в частном случае,
п ( т, тр 1
J R х, (ах 4- Ь)ъ,(ах 4- b) пр j tlx>
где R —рапиональыая функция от аргумен-
тов, обозначенных внутри фигурной скобки,
a mlt т.2, ..., тр, п2, ..., пр — целые
числа, приводится к интегралу от рацио-
„ ах 4- b N
нальнои дроби подстаиовкои ~х =
(в указанном частном случае ах 4- b ~ tN),
где N — общее наименьшее кратное чисел
П1, п„, ..., пр.
Пример 1. _____
„ 1 — X
Полагая ,—— = р, имеем
1 + х
и
dx =»
- 4tdt
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
139
откуда
(“ 1 — х dx = Г — 4t‘dt
J V 1 + х х J (1 - 4*“)(1 + 4*) ‘
Разложив подинтегральное выражение на сумму
простых дробей, получим
44* 1 i 2
(1 +t)(l -t)(l + 4*) ~ 1+4' l-f + 1 + 4’
и далее
J VГГх~ г = 2 arc tg ' ~ ln u + ° + ln(1 “ ° +
....... ,1 /Т^'х" . , /Г + х'- /1 — X
+ С = 2 arc tg !/ —---Р In - ;—= + С.
ЬГ 1 + х /1 + х + }/ 1 - х
Пример 2.
С________________dx_______
J J/'Г^+^Г+Х •
Полагая 1 + х = г9, имеем dx = 6 t^dt и
___ dx_______Р 6tbdt
?rrs+ ', + /a
t3dt
Г+ 1
= 2P - 3ia + Gt — 6 In (f + 1) + C ==
= 2 V f + x - 3 ,У 1 + x + 6 Л1 + x -
r ►
— 6 In 1 + x + 1) + C;
24) j R (x, / ax3 + bx + c)dx, где R—рацио-
нальная функция от хи /ax3 + bx~+~c, при-
водится к интегралу от рациональной дроби
одной из следующих трёх подстановок (и о д-
с т а н о в к и Эйлер а):
а) у/ ах'3 +~Ьх + с = t ± х /ТГ (а > 0),
6) уГах3 4- Ьх 4- с = tx ± уТ (с > 0),
в) /ах2 + + с = t (х — а) (4 ас— Ь3 < 0),
где а—один из корней трёхчлена ах24-&х4;С.
j R (х, /ах3 4- bx 4- с) dx можно привести
также к j ^(sint, cos t) dt (стр. 140) при
помощи тригонометрических подстановок:
у/~Ь3 ~ 4ас
2а
у/~Ь3 — 4ас
2а
х+ 2а =
sin t
(а < О, 4ас— &2<0);
cos t
у/~ b3— 4ас
2а
у/~Ь3 — 4ас
2а
sec t
(а>0, 4ас—&2<0);
cosec t
В первом случае, если р > 0, получаем
сумму степенных интегралов, если же р<0,
то подстановка х = zN, где N — общий зна-
менатель дробей т и п, приводит к инте-
гралу от рациональной функции.
Во втором случае полагаем ахп 4- b = г2,
г
где s— знаменатель дроби р = — •
В третьем случае пользуемся подстанов-
кой ахп 4- b = zs хп.
Пример 1. J х1Ч 1 + Зх’/а)‘/з dx.
~ т + 1
Здесь —-— =» 2 и, следовательно, полагаем
3/
14-Зх 3 = 23, откуда
(Zs _!)*/» 1/3
х = 1-----~---, dx = — (z® — 1) /* z'dz и
3 J3 2
J X1/» (1 + Зх*ls)x ‘dx = J z3 (z* — 1) dz —
z* z* , „ (1 + 3x’/»)’/a
’14 8 + “ “14
(1+Зха/;.)*/3 , „
8 +
(* dx
Пример 2. I _____________- .
J x*1 У 1 + x1
Здесь + P “ ~~ 3; положив 1 + x1 •> z*x*t
имеем:
1 . zdz
x --------—— , dx — —------------——
(z> - 1) 2(z* — ))
и
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ
ФУНКЦИЙ
т, n, р, q — целые положительные числа.
(’ 1 ’
1) I stn2x dx — — -д sin 2х 4- у X 4- с;
[’ 1 1
2) I cos2xdx = у sin 2х 4- 2“ х
3) I sin х cos х dx = у sin’x 4- С;
y/^ac-b3 tg t
2а (а > 0, 4ас— 62>0);
7/±£HEctgf
2а ь
4)
25) j хт (ax"+b)p dx (интеграл от биноми-
ального д и ф е р е н ц и а л а) выражается
через элементарные функции только при вы-
полнении одного из следующих условий (у с-
л о вия Чебышева интегрируемости би-
номиального диференциала):
т 4- 1
а) если р целое, б) если —— целое, в) ес-
sin(m — n)x
sin mx sinnxdx = —„7 —-—
2(m — n)
т 4- 1
ли-------4- р целое.
п
sin mx cos nx dx
cos (m — n)x
2(т — 1УГ
cos (m 4- n) x
~' 2(m 4- n)
4-C; (m n);
sin (m 4- n)x
2(m 4-и) +C,
(m n);
(• sin(m — n)x
6) 1 cos mx cos nx dx = —2(m' — n)—
, sin ( m 4- n)x
+ ~“2(m“+7i) + C; (m n);
МАТЕМАТИКА
+ j sin p+ “X cos'7x dx;
Р dX А
8) \ ;-----------= — ctg .. + С;
' ' 1 — COS X ° 2 1
С dx _____________
9) ) а -Т- b cos х ~
20) t sinp X cos ?x dx=
sinp+1xcos ,+ 1x
Q J* sini’x cos q+2x dx;
21) 1 sinrx cos4'xdx приводится к сумме сте-
пенных интегралов подстановкой sinx = z,
если s > О и нечётное, и cos х = z, если
г > 0 и нечётное.
(если а2 < Ь2);
cos х dx _ х а р dx
а + Ъ cos х " b b J 1+ b cos~x~ ’
sin a dx _
а + b cos х
1
=------у- 1 п (й + b cos х} + С;
cos x sinr! lx
_ (_
। Л 1 С ц___________2
H------— I sin xdx;
Пример,
sinsx dx _ Д (1 — cossx) sin xdx _ p 1 — z’
pcosx J l^cosx J J^z
= — 2z‘/s + z‘/> + C = — 2 cos'lax +
+ cos’^x + C.
Э
В частности, вместо формул 12, 13, 14,
15, 18, 19, 20, если п, р или q нечётные,
удобнее употреблять указанную подстановку.
В случае, если оба числа г и s чётные и
положительные, можно вместо общей фор-
мулы 18 понизить степень, применяя тож-
дества:
1 cos2x 1 cos2x
cos2x = "I* —2—’ sin?x = ~2------)— >
1г>) j ccs”x dx —-------------
4-
* to” 1 X
14) j tg 'xc.'A- ;j _ (
П — 1 Г ,
n— I cos x dx;
— J tg”-2 x dx;
f Ctff^ ‘ C
15) I ctg"xdx = — —n^=~l-------j ctg”-2xdx;
16)
dx_
Sl'nz,X
sin x cos x = -y sin 2x;
cos x
(n — 1) sin”-1x Г
n — 2 p dx
+ n-lj sin "'A
____ sin x
(n — 1) cosf!—
+ n "2 C_____________
n—1 J cos,!~2x
22) J tgrx sec”xrfx, j ctgrx stc”x dx,
J tgrx cosec” x dx, J ctgr x cosec” dx,
где n>0 и чётное, a r — любое, приводятся
к сумме степенных интегралов: первые два—
подстановкой tgx = z, вторые два — под-
становкой ctg х = z (следует при этом учи-
тывать тождества:
sec3x = 1 + tg2x, cosec2 х = 1 4- ctg2x).
В частности, этим способом удобно вы-
числять интегралы 16 и 17 в случае, если
п чётное.
IS) I sin^X COS'7X O’X —
sinp+,x cos'7 b: .
/» 1_____ р* 1 A.
Пример. I у etgx sec«x dx~ | ___- sec3x dx =»
J Jr tgx
= ( l-t— dz = 2z‘/a 4- a/5 2+ C =»
J Vz
= 2 tg‘/»x + »/s tgs4x + C;
+ ,—- 1 sinp x cos'7 2x dx =
p + q J
'xcos '7+1x
p + q
+ -------I sinp-2x cos? xdx;
p + q J
19) I sin pxcos'7xdx =
sin p+1xcos!,+,x
p-1
23) j R (sin x, cos x) dx, где подиптегральпая
функция R рациональна относительно sin х
и cosx, приводится к интегралу от рацио-
х
нальиой дроби подстановкой tg -5 г; при
этом:
2dz 2z
dx = Г4_-г , sin х = ,
1 — z2
cos * = 1 + •
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
141
ИНТЕГРИРОВАНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
С 1 1
1) 1 sh2 х dx = -у sh х ch х — у х 4- С;
С 1 1
2) I ch2 х dx = -у sh х ch х + — х + С;
С 1 , п — 1 С „ □
3) I sh"x dx = — shn 1 х ch х — --— I shn 2 xdx, (n > 0);
4) J ch”x dx = у ch'1-1 x sh x + у -J ch""2 xdx, (n > 0);
C dx x C dx r „
5) J sh“x = lnth~2~+C; 6) j ch x ~ 2 arctg + C;
0 dx 1 , „ n— 2 f dx
7> J sW= П=^ sh1 "xchx- n—j J —2y (n > 1);
f* dx 1 , „ n — 2C dx
8) J dft E^l ch xsilx + n~i J ch'! 2x (n > 1):
9) J th2x dx = x — th x 4- C;
10) | cth2 x dx = x — cth x + C;
C i i
11) j sh ax sh &x dx = ryyy-sh (a 4-&) x—7цу_ у sh (a— 6)x 4-С (a2-A 62);
f 1 i
12) 1 ch ax ch bx dx = 2(^4, b) sh (a + &)х+з (a — &) sh <-a ~b^x + (a? A: b2);
C 1 1
13) I sh ax ch bx dx = 2(a + b) ch (a + b^x + 2(a_b) cil(a~ b)x + C (c2 =A b2).
ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ ФУНКЦИЙ
!) J аге sin xdx = x arc sin x 4- /Е — x2 4- С;
2) Jarccos xdx = xarc cosx — 1 — xa 4- C;
C 1
3) 1 arc tgxdx = x arc tg x— у In (1 4- x2) 4- C;
4) J arc etgx dx = x arc ctg x + -4- In (1 4- x2) 4- C;
[' 1 r r-___
5) i x arc sin x dx = у [(2x2—1) arc sin x + x 7/ 1—x2] 4-C;
e 1 r z____,
6) I x arc cos x dx = у [(2x2—1) arc cos x — x у 1—x2J 4- C;
7) j x arc tg x dx = у [(x2 4- I) arc tg x — x] 4- C;
8) ^x arc ctgxdx = у [(x2 4- 1) arc ctg x + x] -4 C;
9) I x”arc sin x dx 1 ^x',+ 1 arc sin x Г x',+ 1dx
n + 1 J У'Т^х2
10) j x"arc cos x dx 1 / K+l x arc cos x 4- 1’ xn+1dx
Л + 1 J y<l — X2
11) 12) xr'arc tg x dx = x"arc ctg x dx 1 ~ « +1 1 ^x"+1arc tg x - / x”+1arc ctg x x',+ 1dx \ 1 4- x2 ; Г xn+ldx
~ n + 1 4" 1 1 4- x2
142
МАТЕМАТИКА
13) I Ar sh x dx = x Ar sh x —p/1 + x2 +
14) j Ar ch x dx = x Ar ch x — x2 — 1 4- C;
C 1
15) I Ar th x dx = x Ar th x 4- -y In ( 1 — x2) 4- C;
16) I x Ar sh x dx = [(2x2 4- 1) Ar sh x — х/14х’]4-С:
17) f x Ar ch x dx — -д- [(2x2
1) Ar ch x — x у x2 — 1 ] 4- C;
= x In x — x 4- C;
(In x)r‘dx = x(lnx)" —(lnx)n~’dx;
xn In x dx =x',+ 1 (n’+TJ2
(1пх)^(1п^
22) j TTnx =ln!nx + c;
23) I sin In x dx = -y (sin In x— cos In x) 4- C;
24) cos (n x dx — -y (sin In x 4- cos In x) 4- C;
C ’ 1
25) I x sin ax dx =— x cos ax 4- sin ax 4- C;
26) x cos ax dx = ~ x sin ax — cos ax 4- C;
27) J x”sin ax dx = — x"cos ax 4- ~ J x'i—1 cos ax dx;
28) I x'! cos ax dx == ~ x'1 sin ax— ( x'1-1 sin ax ax;
f 1 1
29) I x sh ax dx = x ch ax—-7 shax4-C;
f 1 1
30) j xchaxdx=- л sh ax — chax+C;
31) J x" sh ax dx == xn ch ax — a”J" хП~1 ch ax
C 1 и C 1
32) I x^chaxdx™ „ х’г sh ax—- 1 xn~ ‘ sh ax dx;
J a ° J
33) j xeax dx = (ax — 1) 4- C;
34) xneax dx =--;x,!eax—" j xn~1 eav dx;
C e"x
35) I eax sin (to x 4- <p) dx = Ia sin (« x 4- 4) — a cos (co x 4- tp)] 4- C;
a eax
36) cos (co x 4-cp) dx —j [a cos (w x 4-<p) 4-<o sin (co x 4-tp)] + С;
C xeax
31) j xe,ix sin (co x + cp) dx ~ [n sin (co x 4- <,) — ш cos (co x 4- -p)] —
£ax
— (Q2“qr^2)2 [(a2 — co2) sin (co x 4- U) — 2a co cos (co x + <p)] 4- C;
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
143
р Хейл;
38) I хеал' cos (со х 4- <?) dx = ^~ы2" [a cos (со х + ?) + w sin (со х -ф ^)] —
еах
— (а= + ^ф [(°2~ о2) cos (со х + ср) + 2а со sin (со х + ср)] фС;
39) J sh ах sin bx dx — д8 (a ch ах sin bx — b sh ax cos bx) + C;
40) J ch ax cos bx dx = fl!i -^2 (a sh ax cos bx + b ch ax sin bx) + C;
41) J sh ax cos bxdx = —2-^ур- (a ch ax cos bx -f- b sh ax sin bx) + C;
42) J ch ax sin bx dx == J; ^2~ (a sh ax sin bx — b ch ax cos ox) + C.
НЕКОТОРЫЕ ИНТЕГРАЛЫ, HE ВЫРАЖАЮЩИЕСЯ
ЧЕРЕЗ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
С ех dx х2 vs
’> J Т = C + ln x + x + 2.2! + 3^f+ - ;
(* dx (Inx)2 ,
2)1 j - = C + In In x + In x + -^2|- +
, (Inx)3 ,
+ 33! + ...;
3) J e-sdx = c + x -3JV+ Г),, -2L-+ • ;
6)
sin xdx „ x3 x6 xi
x = C + x — 3.3! + 5.5! ~7j)+
xdx x3 7x6 pi x’
linT = C+x+ X3! +3.5.5f + 3.7.7!+
cos x dx x2 x4 Ye
' = C +1 nx— +44Г -g-— +
X
xdx „ x- x4 5х6 «су8
cos~x ~ c + т+^гГ+бЛ! +873T +
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
ОПРЕДЕЛЕНИЕ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Пусть дана функция /(х), непрерывная
на сегменте [а, Ь], а числа х0, хг, х,, ...,х,;
выбраны так, чтобы:
а = х0 < х, < х2 < ... < хп_1 < хп Ь,
если b > а;
а ~ х0 хг )> х2 > ••• У*хп_। хп ~ о,
если b < а.
Выбранные таким образом точки делят
отрезок, (а, Ь) на п элементарных промежут-
ков. Внутри или на границе каждого такого
элементарного промежутка (х{_,, х ) выби-
рается произвольное число 5/ так, что:
Хо < gj < Хг, X, < < хг, ...,
хп-1 < < Хц' если b > а,
Хо > ?! > X], Xi > > X», ....
х„_] > £,п > хп, если b < а.
1 Этот интеграл приводится к предыдущему под-
становкой х = е* .
Положив
Xj — х0 “ Д хг, Хо — X] — Дх2, •••»
Хп — x„_j = А х„,
п
составляют сумму 2 /($/) А х,- (и н т е г р а л ь-
7 = 1
пая сумма).
Предел этой суммы, когда наибольшая
из величии | А X/1 стремится к нулю (а, сле-
довательно, п—>-оо), называется опреде-
лённым интегралом функции /(х)
в пределах от а до Ь:
Ь п
\f(x)dx= lim У./(5<)Ах;.
J, тах | ixi | -+ ° 1
Если функция /(х) непрерывна на сег-
менте ]о, &], то предел в правой части этого
равенства существует и не зависит от вы-
бора чисел:
Xi, х2, ..., xzl_j ; 5Х, ••> 5л
(теорема существования определён'
ноги интеграла).
Числа а и b назы-
ваются соответственно
п и ж п и м и вер х-
II и м предел ам и ин-
теграла, отрезок [а,6]—
отрезком интегриро-
вания, /(х) — подии-
тегралыюй функцией,
/(х) dx — подинтеграль-
ным выражением, х—
переменной интегриро-
вания.
Величина интеграла
менной интегрирования:
ь ь
f/(x) dx = l'/(Z) dt.
а а
Если функция /(х) имеет постоянный
знак внутри отрезка интегрирования, то
ь
| t(x) dx может быть геометрически изобра-
а
жён площадью криволинейной трапеции,
ограниченной графиком подинтегралы-юй
функции у=^/(х), осью ОХ и прямыми х — а
и х~Ь (фиг. 112).
144
МАТЕМАТИКА
b
При этом] /(x)dx положителен, если
а
Дх) > 0 на отрезке [a, ft] и b > а или /(х) < О
и ft < а; если же Дх)>0 и Ь<а или Дх)<0
ь
и Ь>а, то f /(х) dx отрицателен.
СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
!>
1) ( dx = ft — а-,
а
Ь а
2) f Дх) dx = — ( Дх) с/х;
а ь
3) J /(х) dx = 0;
а
b с с
4) [ /(х) dx + С Дх) dx = У /(х) с/х;
а b а
b Ь
5) fc/(x)dx=cf /(x)dx<c —постоянная);
а а
b
6) У [/1(A) ± /Дх)] dx =
а
b b
= у /Дх) dx ± У /2(x)dx.
а а
Производная определённого интеграла
но верхнему пределу
X
Л У f(f)c/t= /(х);
dx Ja
. Ip(?c)
JL I /(/)d/ = / [<p(x)]?'(x).
dx "
Диференцирование определённого
интеграла по параметру
* f /(х, a)dx=f dx;
daJ £ да
. d f /(х, a) dx Г .дКХ>. aL dx +
x(«) da
dX (a) dx (a)
+ /[X (a), a] ~y~ — /[X (a), a] •
1-я теорема о среднем. Если /(х) и ср(х)
непрерывны на сегменте [a, ft] и, кроме
того, Дх) не изменяет знака на этом отрезке,
то по крайней мере для одного числа jj
в интервале (а, Ь) имеет место равенство:
ь ь
У Дх) ? (х) dx = Д5) J <? (х) dx.
а а
В частности, положив <р(х)=1, имеем:
ь
У Дх) dx = (ft — a)/ (5).
а
Геометрически в этом частном случае
теорема утверждает равенство площадей
криволинейной трапеции ABCD и прямо-
угольника AB'C'D (фиг. 113).
/11________
О а £ b
Фиг. 113
2-я теорема о среднем. Если Дх) и ср (х)
непрерывны на сегменте [a, ft] и 'р(х)— мо-
нотонна, то
ь t ь
У /(х) Дх) dx = <p(a) у /(х) dx+ <p(ft) J Дх) dx,
a a £
где 5—принадлежит сегменту [a, ft].
Вычисление определённого интеграла.
Если Е(х) — первообразная для функции Дх)
[т. е. Е'(х) = Дх)], то
ь
J Дх) dx = E(ft) - F(a).
а
Применяя так назы-
ваемый символ под*
становки
ь
F(x) \ — F(b) — F(a),
а
получаем:
& ь
У /(X) dx = Е(х) | .
а а
Правило интегрирования по частям
ь
Г И(х) dx =
J dx
» b
= и(х)Дх) I —f (/(x)00'^/ dx,
a a 4X
Пример.
\ 1 *,
J xex dx = xex | — j ex dx = e — e + 1 = I.
') 0 i!
Правило замены переменной. Если х =
ь р
= ?(О> ТО У /(х) dx= У / [<p(t)J <p'(t) dt, где
а а
a = ср (a), ft = <р(₽).
1
Пример, у У1 — х1 dx.
О
Полагая х= sin t (f =» arc sin x), получаем:
1_______ arc sin 1
j — x1 dx = j VI — sina£ cos t dt —
0 arc sin 0
it it
2 2
= J cosBZ dt = у J (I 4- cos 20 dt =i
0 0
it
2
= 4-[/ + -?-sin 2/) ’j
b
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Интегралы с бесконечными пределами
оо ъ
] Дх) dx = Пгпу /(х) dx.
а Ь^оо а
Если указанный в этом определении не-
собственного интеграла предел существует и
конечен, интеграл называется сход я-
щимся; в противном случае говорят, что
интеграл расходится.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
145
Аналогичным образом определяются ин-
тегралы вида
ь оо
J/(x)tfx и \ f(x)dx.
— оо — bo
Пример 1,
интеграл сходится.
Пример 2.
Ь
dx С dx .. . .
— = lim i —• «» lim In b = oo,
x b^CQ J x b~>oo
1
расходится.
2. Трапеция ограничена графиком функ-
ции x = F(y), осью ОУ и прямыми у = а,
У = Р (фиг. 114):
Р §
S = J х dy = [ F(y) dy.
а а
Площадь криволинейного сектора. Пло-
щадь ограничена кривой р = p(tp) и лучами
<р = <Pi, ? = tf>2 (фиг. 115):
Та
s = 4" j* р2
<?1
интеграл
Интеграл от неограниченной функции.
Если функция /(х) неограничена в окрест-
ности точки Ь, то
Ь b—s
f /(x)dx = lim Г /(x)dx (s>0).
а а
Аналогичным образом определяется не-
собственный интеграл, если /(х) неограни-
чена в окрестности точки а.
Случай, когда /(х) неограничена в точке
с, находящейся внутри интервала интегри-
рования, сводится к предыдущим при помо-
щи равенства:
Ь с Ь
j /(х) dx = J /(х) dx + J /(х) dx =
а а с
с—Si Ъ
= lim f /(x)dx + lim f /(x) dx,
s,^0 a s,-H)
где с,>0 и г3 > 0.
Пример 1.
[ = Ит f d* = lim (2-2 ^Г) = 2,
’J. Ух s~>0 j ух e->0
0 s
интеграл сходится.
Пример 2.
1 1
p dx ( ax ,
= lim ----= - lim ln: = oo,
x s ^0 J X e-^O
интеграл расходится.
ПРИЛОЖЕНИЯ К ГЕОМЕТРИИ И МЕХАНИКЕ
Площадь криволинейной трапеции. 1. Тра'
пеция ограничена графиком знакопостоян-
ной1 на отрезке [а, &] функции у=/(х), осью
ОХ и прямыми х=а и х=Ь (см. фиг. 112):
ь ь
S = j* у dx — j /(х) dx.
а а
Если уравнения кривой даны в парамет-
рической форме:
х = <p(t), у =ф(1) и а=<?(tj), b = <p(t2),
то
s=) Ф(П?'(О<в-
t,
• Если /(х) энакопеременна, то формулу для вы-
числения площади следует применять отдельно для
каждого отрезка, где /(X) сохраняет знак, и сло-
жи,ть абсолютные значения полученных величин.
Фиг. 114
Фиг. 115
Длина дуги плоской кривой. Уравнение
кривой в явной форме:
у = /(х) или х = В(у);
в параметрической форме:
х = »(/), у = ф(0-
Координаты начальной и конечной точек
дуги: А (а, а), В (&, Р) (фиг. 116).
Значения параметра г, соответствующие
точкам А и В:
t = /t, f = G,
Ь___________3________________
£ = / /1 + [/'(х)Р dX=f/l + [F'(y)Pdy =
а а
= ? /Жор+Т/аЯ5" at.
к
Уравнение кривой в полярных коорди-
натах:
Р = Р (?)•
Г
Значения полярного угла в начальной
и конечной точках дуги:
= ¥1, ¥ =
d?.
Площадь поверхности вращения, а) Осью
вращения служит ось ОХ (фиг. 117). Урав-
нение кривой, образующей поверхность вра-
щения:
у = /(X)
10 1 ом I
146
МАТЕМАТИКА
или в параметрической форме:
х = <р(Г), у = ФСО-
Абсциссы начальной и конечной точек
дуги: х = а, х=Ь. Соответствующие этим
точкам значения параметра /:
t = tI( t = t2,
t
S=2zJ f(x) /1 + [/'(*)]2dx =
a
f a______________________
= 2k J ф (0 / [<p'(OP+ [Ц/ (f)]2 d*.
t,
а) Осью вращения служит ось OY
(фиг. 118). Уравнение кривой, образующей
поверхность вращения:
х = F(y).
Ординаты начальной и конечной точек дуги:
У = “. у = р,
? _______________________________
S=2z j F (у)/ 1 + [F'(y)]2 dy.
a
Объём тела вращения, а) Осью вращения
служит ось ОХ (фиг. 117). Фигура, образу-
Фиг. 119
ющая тело вращения, ограничена графиком
функции у = /(х), осью ОХ и прямыми х=а
и х = Ь.
ь
V = r.\ [/(х)]Мх.
а
б) Осью вращения служит ось OY
(фиг. 118). Фигура, образующая тело вра-
щения, ограничена графиком функции х =
=Е(у), осью OY и прямыми у = а, у = р.
3
V = rj‘ [F(y)J2 dy.
а
Объём тела произвольной формы. Если
тело заключено между плоскостями х=а и
х=Ь, перпендикулярными к оси ОХ, и пло-
щадь сечения, перпендикулярного к этой оси
S=S(x), дана, как функция от х, где х —рас-
стояние плоскости этого сечения от точки О
(фиг. 119), то объём тела вычисляется по
формуле
ь
V = j S(x) dx.
а
Путь, пройденный точкой, движущейся со
скоростью v — v (t) за время от t = т до
t = T,
т
S = J v (t)dt.
Работа силы F = F(x) при перемещении
точки по прямой ОХ от х = а до х= Ь, если
направление силы совпадает с направлением
оси ОХ,
ъ
А — | F(x) dx.
а
СТАТИЧЕСКИЕ МОМЕНТЫ, КООРДИНАТЫ
ЦЕНТРА ТЯЖЕСТИ И МОМЕНТЫ ИНЕРЦИИ
а) Дуги плоской кривой. Обозначения:
уравнение кривой у = у(х) или х = х(у), на-
чальная точка дуги А (а, а), конечная точка
В (Ь, р) (фиг. 120).
Статические моменты; относи-
тельно оси ОХ
ь
Sr = J у(х) / 1-Ну'(х)Р dx =
а
₽ _________________
= J у /i+[x'(y)P dy;
относительно оси OY
ъ_____________
Sy = \ xjF 1 + [у'(х)]2 dx =
а
₽ ________________
= J Х(У) / 1 + [х'(У)]2 dy.
а
Координаты центра тяжести
где L—длина дуги.
Моменты инерции: относительно
оси ОХ
ъ_____________________
Ix = J [У(х)]2 / 1+[у'(х)]2~ dx =
а
Р _______________
= J у2/1 + [х'(у)]2 dy;
а
относительно оси OY
ь
1у = \ х* /1 + [у'(х)Р dx»=
а
Р ___________
= J [х(У)]2 /1 + [х'(у)Р dy;
а
относительно начала координат
/о ” h 4- у =
ь ______________
= J { х2+[у(х)]2 } У 1 + [y'(x)]2'dx =
а
₽ ____________________________
= П [х(У)Р + У2 } / 1 + [х'(У)]2 dy.
а
б) Площади плоской фигуры. Обозначе-
ния: х = а и х = b — наименьшее и наиболь-
шее значения х на границе фигуры, у = а и
у = Р — наименьшее и наибольшее значения
у на границе фигуры, х(у) — длина сечения,
параллельного оси ОХ, проведённого на рас-
стоянии у от неё, у(х) — длина сечения, па-
раллельного оси OY, проведённого на рас-
стоянии х от неё (фиг. 121).
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
147
Статические моменты: относи-
тельно оси ОХ
Sx = f ух(у) dy,
а
относительно оси OY
ь
Sy = J ху(х) dx.
а
Координаты центра тяжести.
X - • v - -л-
Лс~ S ’ Ус~ S •
где S — площадь фигуры.
Моменты инерции: относительно
оси ОХ
Р
/r = J y*x(y)dy,
а
относительно оси OY
ft
ly = J' х*у(х) dy',
а
относительно начала координат
Л> = 1х + 1У-
А (а, а)
Фиг. 120
S
1-я теорема Гюл
ь д е н а. Если дуга
плоской кривой длины / вращается около
оси, не пересекающей эту дугу и лежащей
с ней в одной плоскости, то площадь по-
верхности образованного при этом тела вра-
щения вычисляется по формуле S — 2r:d-l,
где d—расстояние центра тяжести дуги от
оси вращения.
2-я теорема Гюльдена. Если пло-
ская фигура площади S вращается около
оси, не пересекающей эту фигуру и лежащей
с ней в одной плоскости, то объём образо-
ванного при этом тела вращения вычи-
сляется по формуле
v = 2п d-S,
где d — расстояние центра тяжести площади
фигуры от оси вращения.
НЕКОТОРЫЕ ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ
оо
С dx п
1) \------- = —(а > Ь>0);
J axs + b 2y/lb
О
оо
( ДС ТС
2)jrr?rfx =---------
о bsin-y
00
Csinaxdx те
3) J — 2 (fl > 0);
0
00
Г cos ax
J x
о
dx = co;
5)
J V X
J dX __ (главное значение);
о
2
8) sin2"+1 х
о
о
_ 2.4.6... 2п
“3.5.7... (2ц + 1)
2
С cos2n+1 х dx
(n > 0 и целое);
ТС я
"2 2
О о
1.3.5... (2/7 — 1) те
= -9- (" > О и целое);
2
10) f sin2m+l х cos2 n+1x dx= —-/n
о
(т > 0, п > 0, т и п— целые);
11) J sin2 х cos2
о
(определение функции Г
00
12) J e~xdx = 1;
о
13) J е~х* dx = ;
о
оо
14) xne~xdx = п\
о
оо
15) у е~~аХ sin bxdx =
о
,6)Je-"=o.tea,_
о
00
17) Je_fl*x* cos bx dx
о
dx= r<M-l)T (3+1)
2 Г (a + p + 2)
см. на стр. 149);
(п>Ои целое);
b
а ,
_ b'
y/~it e 4a‘
__ ___ ;
10*
148
МАТЕМАТИКА
18)
In х dx ______те2
x — 1 ~ “6
In x dx
X + Г
J 8in*dL = Si X =
0
X3 , X5
=x —3?3f+ 5.5f
X’
7?71
(интегральный синус)
оо
С cos х dx
21) I --~--= Cl X =
X
X2 X4 x’
= c + In X —^21-4*4^ 6.6!
(интегральный косинус);
X
f dx
22) j l—=hx =
0
, ln2x ,
=C'+ln (—In x) T- 221 >*
ln3x
+ 2~3| + (0<x<l)
(интегральный логарифм),
где С = 0,5772156649 ... (эйлерова и о-
4- с т о я н н а я);
X
23) Jе~ах‘(1х приводится к интегралу
о
вероятности (табл. 14) подстановкой
+ ••• Y_ _?_____.
Таблица 14
Интеграл вероятности
Ф(х)
е
2
dt
X Ф (X) X Ф (X) X Ф(х) X Ф(Х) X Ф (X) X Ф(х)
0,00 0,0000 0,40 0,3108 0,8^ 0,5763 1,20 0,7699 1,60 0.8904 2,00 я 0.9545
01 0,0080 41 0,3182 81 0,5821 21 0,7737 61 0.8926 05 0,9596
02 0,0160 42 0,3255 82 0,5878 22 0,7775 62 0.8948 10 0,9643
03 0,0239 43 0,3328 83 0,5935 23 0,7813 63 0.8969 15 0,9684
04 0,0319 44 0,3401 84 0,5991 24 0,7850 64 0,8990 20 0,9722
05 0,0399 45 0,3473 85 0,6047 25 0.7887 65 0,9011 25 0,9756
06 0,0478 46 0,3545 86 0,6102 26 0,7923 66 0,9031 30 0,9786
07 0,0558 47 0,3616 87 0,6157 27 0,7959 • 67 0,9051 35 0,9812
08 0,0638 48 0,3688 88 0,6211 28 0,7995 68 0,9070 40 0,9836
09 0,0717. 49 0,3759 89 0,6265 29 0,8029 69 0.9090 45 О.У857
0,10 0,0797 0,50 0,3829 0,90 и,6319 1,30 0,8064 1,70 0.9109 2,50 0,9376
11 0,0876 51 0,3899 91 0,6372 31 0,8098 71 0,9127 55 0,9892
12 0,0955 52 0,3969 92 0,6424 32 0,8132 72 0,9146 60 0,9907
13 0,1034 53 0,4039 93 0,6476 33 0,8165 73 0,9164 65 0,9920
14 0,1113 54 0,4108 94 0,6528 34 » 0,8198 74 0,9181 70 0,9931
15 0,1192 55 0,4177 95 0,6579 36 0,8230 75 0,9199 75 0,9940
16 0,1271 56 0,4245 96 0,6629 36 0,8262 76 0,9216 80 0,9949
17 0,1350 57 0,4313 97 0.6680 37 0,8293 77 0,9233 85 0,9956
18 0,1428 58 0,4381 98 0,6729 38 0,8324 78 0,9249 90 0,9963
19 0,1507 59 0,4448 99 0,6778 39 0,8355 ’ 79 0,9265 95 0,9968
0,20 0,1535 0,60 0,4515 1,00 0,6827 1,40 0,8385 1,80 0,9281 3,00 0.99730
21 0,1663 61 0,4581 01 0,6875 41 0,8415 81 0,9297 10 0,99306
22 0,1741 62 0,4647 02 0,6923 42 0,8444 82 0,9312 20 0,99863
23 0,1819 63 0,4713 03 0,697и 43 0,8473 83 0,9327 30 0,99903
24 0,1897 64 0.4778 04 0,7017 44 0,8501 84 0,9342 40 6,99933
25 0,1974 65 0.4843 05 0,7063 45 0,8529 85 0,9357 50 0,99953
26 0,2051 66 0,4907 06 0,7109 46 0,8557 86 0,9371 60 0,99961
27 0,2128 67 0,4971 07 0,7154 47 0,8584 87 0,9385 70 0,99978
28 0,2205 68 0,5035 08 0,7199 48 0,8611 88 0,9399 80 0,99986
29 0,2282 69 0,5098 09 и,7243 49 0,8633 89 0,9412 90 0.99990
0,30 0,2358 0,70 0,5161 1,10 0,7287 1,50 0,8664 1,90 и,9426 4.00 0/09994
31 0,2434 71 0,5223 11 0,7330 51 0,8690 91 0,9439
32 0,2510 72 0,5285 12 0,7373 52 0,8715 92 0,9451 4,417 1-Ю-5
33 0,2586 73 0,5346 13 0,7415 53 0,8740 93 0,9464
34 0,2661 74 0,5407 14 0,7457 54 0,8764 94 0,9476 4,892 1-Ю-6
35 0,2737 75 0,5467 15 0,7499 55 0,8789 95 0,9488
36 0,2812 76 0,5527 16 0,7540 56 0,8812 96 0,9500 5.327 1—10~7
37 0,2886 77 0,5587 17 0,7580 57 0,8336 97 0,9512
38 0,2961 78 0,5646 18 0,7620 58 0,8859 93 0,9523
39 1 0,3035 79 О,57о5 19 0,7660 59 0,8832 99 0.9534
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
149
Эллиптические интегралы 1-го рода; Е(.1г, <р), k — sin а
Таблица 15
а 0" 10° 20 30° 40° 60° 60° 70е 80° 90е
0* 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
10 0,1745 0,1746 0.1746 0.1748 0,1749 0,1751 0,1752 0,1753 0.1754 0,1754
20 0,3491 0,3493 0,3499 0,3508 0,3520 0,3533 0 ,3545 0,3555 0,3561 0,3564
30 0,5236 0,5243 0,5263 0,5294 0,5334 0,5379 0,5422 0,5459 0,5484 0,5493
40 0,6981 0,6997 0,7043 0,7116 0,7213 0,7323 0,7436 0,7535 0,7604 0,7629
50 0,8727 0,8756 0,8842 0,8982 0,9173 0,9401 0,9647 0,9876 1,0044 1,0107
60 1,0472 1,0519 1,0600 1,0896 1,1226 1,1643 1,2125 1,2619 1,3014 1.3170
70 1,2217 1,2286 1,2495 1,2853 1,3372 1,4068 1.4944 1,5959 1,6918 1,7354
80 1,3963 1,4056 1,4344 1,4846 1,5597 1,6660 1,8125 2,0119 2,2653 2,4362
90 1,5708 1,5828 1,6200 1.6858 1.7868 1,9356 2,1565 2,5046 3,1534 ОО
Таблица 16
Эллиптические интегралы 2-го рода: Е (й, <р), А* = sin а
а 0° 1 | 10° 20е 30° 40° 50° 60° 70° 80° 90°
0е 0,0000 и, 0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
10 0,1745 0,1745 0,1744 0,1743 0.1742 0,1740 0,1739 0,1733 0,1737 0,1736
20 0,3491 0,3489 0,3483 0,3473 0,3462 0.3450 0,3438 0,3429 0,3422 0,3420
30 0,5236 0,5229 0,5209 0,5179 0,5141 0,51и0 0,5061 0,5029 0,5007 0,5000
40 0,6981 0,6966 0,6921 0,6851 0,6763 0,6667 0,6575 0,6497 0,6446 0,6428
50 0.8727 0,8698 0,8614 0,8483 0,8317 0,8134 0,7954 0,7801 0,7697 0,7660
60 1,0472 1,0426 1,0290 1,0076 0,9801 0,9493 0,9184 0,8914 0,8728 0,8660
70 1,2217 1,2149 1,1949 1,1632 1,1221 1,0750 1,0266 С,9830 0,9514 0,9397
80 1,3963 1,3870 1,3597 1,3161 1,2550 1,1926 1,1225 1,0565 1,0054 0,9848
90 1,5708 1.5589 1,5238 1,4675 1,3931 1,3055 1.2111 1.1184 1.0401 1,0000
Эллиптические интегралы. Интеграл 1-го
рода (табл. 15):
sin <р
j' _______dx______
) J / (1 —
о
С de
= I .. ^==г = F (к, ср).
J / 1 —k2 sin2 О т
о
Интеграл 2-го рода (табл. 16):
sin с
О
/ 1 — /с2 sin2 0 d0 = Е(к, ср).
О
Эйлеровы интегралы. Интеграл 1-го рода:
1
26) j х*"1 (1 — х)р-1 dx = В (а, ₽).
О
Интеграл 2-го рода (гамм а-ф у н к ц и я)
(табл. 17):
оо
27) J х'-1 е~х </х = Г(1).
о
Эйлеровы интегралы 1-го и 2-го рода
связаны соотношением
В («, ₽) =
Г (а) Г(|3)
Т(« + р)
Таблица 17
Гамма-функцн я
X Г (X) X г (х) X Г (х) X Г (X)
1,00 1,00000 1.25 0,90640 1,50 0,88623 1.75 0,91906
01 0,99433 26 0.90440 51 0,88659 76 0,92137
02 0.98884 27 0,90250 52 0,88704 77 0.92376
0’3 0.98355 28 0.90072 53 0,88757 78 0,92623
04 0,97844 29 0,89904 54 0,88818 79 0,92877
1,05 0,97350 1.30 0,89747 1.55 0,88887 1,80 0,93138
06 0,96874 31 0.89О0О 56 0,88964 81 0,93408
07 0,96415 32 0,89464 57 0,89049 82 0.93685
08 0,95913 33 и,89338 58 0.89142 83 0.93969
09 0.955Л- 34 9,89222 59 0,89243 84 0,94261
1.10 0,95135 1,35 0,89115 1,60 0,89352 1,85 0,94561
11 0,94741' 36 0,80018 61 0,89468 86 0,94869
12 0 у43'9 37 0,88931 62 0.89592 87 0,95184
13 0,93.193 38 0,88854 63 0,89724 88 0,95507
14 0,93642 39 0,88735 64 0,89864 89 0,95838
1.15 0.93304 0,83726 1.65 0,90012 1,90 0,96177
16 0,929-Ф ,1 U.88G76 66 0,00107 91 0,96523
17 0,926?!; 0,88636 67 ’/,90330 92 0,96877
18 0,92373 -13 0,886(4 68 0,90500 93 0,97240
19 0,92с-,У 44 0,88581 (4) 0,90678 94 0.97С10
1,20 0,91817 1,45 0.885G6 1,70 0,90864 1,95 0,97988
21 0,у155« 46 0,88560 71 0,91057 96 0,98374
09 0.9131i 47 0,88563 72 0,91258 97 0,98768
23 0,91075 48 0,88575 73 0,91467 98 0,99171
24 0.90852 i 49 0.88595 74 0,91683 99 0,99581
Основные свийст па функции Г (х):
i (!)= 1; Г(х+ 1) = хГ(х):
Г (л + 1) = и!, если п > 0 и целое;
Г (— п) = ± со (п = О, 1, 2, 3,
150
МАТЕМАТИКА
График функции Г (х) см. на фиг. 122.
КРАТНЫЕ ИНТЕГРАЛЫ
Двойной (двукратный) интеграл
функции /(х,у), распространённый на об-
ласть (S) плоскости OXY ^обозначение:
, определяется таким образом.»
(S)
Область (S) разбивается произвольно на
элементарные части, площади которых обо-
значаются через A SJ( Д S2, . . ., Д Sn
(фиг. 123); внутри или на границе каж-
дой такой элементарной области с площадью
Д Si выбирается произвольная точка А1/(х/,у/)
и составляется сумма (интегральная сумма)
п
i=l
Предел, к которому стремится эта сумма,
когда наибольший из диаметров1 элементар-
ных площадок стремится к нулю, и назы-
вается двойным интегралом:
(S)
dS = lim 2 / д
1 = 1
Если функция /(х,у) во всех точках
области (S) имеет одинаковый знак, то
/ (Х>У) даёт величину объёма тела, or-
is)
раниченного поверхностью z — f (х, у), пло-
скостью OXY и цилиндрической поверхно-
стью с образующей, параллельной оси OZ,
пересекающей плоскость OXY вдоль границы
области (S) (фиг. 124).
Тройным (трёхкратным) инте-
гралом функции / (х, у, z), распространённым
на трёхмерную область (V), называется число,
определяемое следующим образом.
Область (V) произвольно разбивается
на элементарные части с объёмами Д
ДУ2.... ДУ„; внутри или на границе эле-
i Диаметром фигуры называется наибольшее
расстояние между двумя точками, находящимися на
её границе.
ментарной области с объёмом ДУ/ выби-
рается точка М/ (X/, у/, ?/), и вычисляется пре-
п
дел суммы 2 / ’Vi’ zi) vi ПРИ условии,
1 = 1
что наибольший из диаметров элементарных
областей стремится к нулю:
J J J / (х, у, z) dV= lim 21 (Xi, yt.Zi) ДУ/.
(V) i=l
ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
Вычисление двойного интеграла сводится
к последовательному вычислению двух опре-
делённых интегралов, причём способ вычис-
ления зависит от выбора системы координат.
Вычисление двойного интеграла в де-
картовых координатах. Вместо символа
JJ/(x,y)dS обычно употребляют символ
S
Jj Нх,у) dxdy.
(S)
Это объясняется тем, что способ вычис-
ления в декартовых координатах основан на
разбиении области интегрирования (S) на
элементарные площади прямыми, параллель-
ными оси ОХ и оси OY, при этом Д5=ДхДу
(фиг. 125).
Если А и В — точки контура области (S)
с наименьшим и наибольшим значениями х
(х = а и х = ft), а у = ух (х) и у= у2 (х) —
уравнения частей этого контура АтВ и
АпВ (фиг. 126), то
1 {x,y)dxdy dx J /(x,y)dy.
(S) a y, (x)
Первое (внутреннее) интегрирование про-
изводится при постоянном х.
Если С и D—точки контура области (S)
с наименьшим и наибольшим значениями у
(у = а и у = ₽), а х = xt (у) и х = х2 (у) —
уравнения частей этого контура CpD и CqD
(фиг. 127), то
₽ х, О’)
J J / (х,у) dx dy = J dy j / (x,y) dx.
<S) «. x, (y)
Первая из указанных формул применима,
если всякая прямая, параллельная оси ОХ
(за исключением, быть может, конечного
числа таких прямых), пересекает контур
области (S) не более, чем в двух точках;
вторая, если всякая прямая, параллельная
оси OY, пересекает контур области (S) не
более, чем в двух точках.
Если ни одно из указанных условий не
выполнено, то следует область (S) разбить
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
151
на две или несколько частей (фиг. 128) и
воспользоваться равенством
/ (x.y)dxdy =
(S)
= j" j / (х,у) dx dy + У / (х,у) dx dy.
(S.) (S.)
Фиг. 127
Пример. Вычислить J* Г (ха+у) dx dyt если область
(S)
(S) заключена между параболами у =« ха и х«*уа
(фиг. 129): __
1 Ух
JJ(x4-y) dx dy - J dx j (x’+y)dy=.
(S) О X*
33
140*
Фиг. 130
Вычисление двойного интеграла в поляр-
ных координатах. Элементарная площадь в
полярных координатах выражается фор-
мулой
Д$=^рс/рс/-р (фиг. 130).
Заменив х и у в подинтегральной функ-
ции по формулам
X = р COS ср, у = Р sin ср,
получаем:
/ (х>у) = / (р COS ср, Р sin Р) - F (р,<р)
и
tff(x,y)dxdy = ffF(p,cp)pdp<lcp.
(S) (S)
Если А и В—точки контура области (S)
с наименьшим и наибольшим значениями ср
('? = '?! и у = ср2), а р = ?! (ср) и р = р2 (?)—
уравнения частей АтВ и АпВ контура
(фиг. 131), то
<Pi р«(?)
Jf/7 (Р»?)р^рй<р = У d? j (р,«?) р d р.
(S) ¥> fi (fl
ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА
а) В декартовых координатах
fff / (.x,y,z) dV = | ff / (x,y,z) dx dy dz ==
(V) (V)
ч(х,у)
= ff dxdy f / (x, y, z) dz =
(S) z, (x,y)
t> y, (X) z, (x,y)
= J dx f dy f /(x,y,2)d2,
a y,'(x) z,(x,y)
где (S) — проекция области (V) на плоскость
OXY, 2 — 2t (x,y) и г = 2a (x, у) — уравнения
нижней и верхней частей поверхности, огра-
ничивающей область (S) (фиг. 132).
Фиг. 132
б) В цилиндрических координатах (стр. 187)
Ш / (х> 2) Ш F (Р> ? 2)Р dt?d? dz =
(V) (V)
= .l.|pdpd-p j F(p, <p, z)dz =
(S) Zi (p,<p)
?« Ri (?) z,(p,<p)
= J dy j pdp j F (p, cp, z)dz,
9i Pi(?) Zi <p,cp)
где (S) — проекция области (V) на плоскость
OXY, 2 = 21 (p, ср) и 2 = г2 (p, ср) — уравнения
нижней и верхней частей поверхности, огра-
ничивающей область (V), и
F (р, ср, z) = / (р cos ср, р sin ср, 2).
в) В сферических координатах (стр. 187)
Элементарный объём
Д V = г2 sin 0 Дер ДО Дг (фиг. 133)
jff Кх,у, z) dV =
(V)
= fjj F {г, <р, 0) г2 sin 0 dy d 0 dz =
(V)
<Р1 6«(?) Г, (6, <Р)
= J d ср j sinOdO j F (г, ср, 0) r2dr,
91 0i (?) П(0,9)
где F (г, ср, 0) =
= / (г Sin 0 COS ср, г sin 0 sin у, г cos 0).
152
МАТЕМАТИКА
Таблица 18
Приложения двойных интегралов
Общая формула В декартовых координатах В полярных координатах
Площадь плоской фигуры ИР (S) И dxrfy (S) ^"Jpdipdp (S)
Площадь поверхности s= f f-A1 * * J J COST (5) (S) (S)
Объём тела’ v4.bds (S) Hzdxd'' (S) JJzpd<p dp (S)
Момент инерции плоской фигуры относительно оси ОХ 7x“J.f>”dS (S) J y' dx dy <S) J J p1 $ins Cp d Cp d p (5)
Момент инерции плоской фигуры относительно полю- са О 7o=,fpds (S) j* j* (xa ly«) dx dy (S) j* p1 d <p dp (S)
Масса плоской фигуры с переменной плотностью 5 M= j* J<5 dS (S) £Pdxdj’ (S) У <5p d cp d p <S)
Координаты центра тяже- сти однородной плоской фигуры Lfxds Jp JJxdxdy (S) f J dx dy (S) J у dx dy (S) J.fdXdy (S) j" J p’ cos cp d <f d p (S) J J p dcpd p (S) j* p* sin cp d cp d p (S) j* p d cp dp (S)
1 В данном случае (S)—проекция поверхности на плоскость ОХУ , у—угол, образованный нормалью
к элементу поверхности с осью OZ (угол между элементом поверхности и плоскостью ОХУ).
а Имеется в виду объём тела, форма которого указана на фиг. 124.
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
Криволинейным интегралом
выражения Р(х, у) dx-J-Q (х,у) dy вдоль дуги
(О ^обозначение: J Р (х, у) dx + Q (х,у) dyj
называется число, получаемое следующим
образом (фиг. 134): если А (а, а) начальная,
а В (b, Р) конечная точка дуги (/), то, обоз-
начив а = х„, b = х„, а = у0, Р = Уп' делят
дугу (1) на п элементарных частей точками
Ml(x1,y1), M2(x2,ys),..., (Х„_
(нумерация производится так, что точка
Д4, следует за точкой если двигаться
по дуге от точки А к точке В).
Внутри или на границе каждой элемен-
тарной дуги Mi выбирают произ-
вольную точку Ni (Zi, ги), составляют сумму
S [Р(^,Г,;)ДХ; +Q(£/,^)Ay/],
i=l
где
A Xi = X; — X{_]
и
А Vi = У1 — Pi-i,
и находят предел, к которому стремится
эта сумма, когда длина наибольшей из эле-
ментарных дуг стремится к нулю:
J Р (х, у) dx -|- Q (х,у) dy =
(О
п
=lim S +
i = l
Если Р (х,у) и у (х, у)— проекции векто-
ра силы F (х, у), приложенного в точке
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
153
Приложения тройных интегралов
Таблица 19
Общая формула В декартовых координатах В цилиндрических координатах В сферических координатах
Объём тела ЧТИ (V) (V) У У У? df dp dz (У) УУУ r’sinO dtp d0 dr GO
Момент инерции тела относительно оси OZ (У) J J J (х2 * *+У2) dx dy dz yyyP=d?dpdz | (V) УУУ r‘sins * *9dtpd0 dr (V)
Момент инерции тела относительно полюса О (V) J J J(x«+y=+z!) dxdydz (V) УУУ(ра+г>)р<гсрйр dz J J r<sin9 d<? dO dr W
Масса тела с пере- менной плотностью S 4TT;v (V) У У У5 ах av (V) j* J Jfy d<? dp dz (V) <5r8slnQdtpdftdr (V)
Координаты центра тяжести однородно- го тела иь у =ЛХ) *с у Ш-» z - W - у У х dx dy dz (V) УУУ dxdydz (V) УПydxdv az (V) yyy^xdydz (V) yyy^xdydz OO yyy^n^z (V) /
(х, у), на координатные оси (фиг. 135), взя-
тые со знаком + или — в зависимости от
того, совпадает ли направление проекции с
направлением соответствующей координат-
ной оси или нет, то
Р (х, у) dx + Q (х,у) dy
(Ъ
даёт величину работы силы F при передви-
жении точки по дуге (Z) из положения А в
положение В.
Определение криволинейного интеграла
f Р (х, у, z) dx + Q (х, у, z) dy +
(D
+ R (х, у, z) dz
для дуги (Z) пространственной кривой со-
вершенно аналогично определению для дуги
плоской кривой (см. стр. 152).
Фиг. 136
Фиг. 135
Простейшие свойства криволинейного
интеграла
1. При изменении направления движения
по дуге интеграл изменяет знак (фиг. 136):
J P(x,y)dx + Q (x,y)dy =
(Г>
= — f Р (х, у) dx + Q (х,у) dy.
(О
МАТЕМАТИ КА
154
2. Если дуга (1) состоит
(/,),..., (/р), то
f = I + I + - +
(О ((,) (/.)
из дуг
(li).
(подинтегральное выражение одно и то же
для всех интегралов) (фиг. 137).
Вычисление криволинейного интеграла.
Если плоская дуга
В (Ъ, [5) — конечная
(1) пересекается всякой
прямой, параллельной
любой координатной
оси, не более чем в од-
ной точке, то её урав-
нение может быть раз-
решено как относи-
тельно X [х = X (у)],
так и относительно
У[У=У(Х)Ь
Если при этом
А (а, а) — начальная, а
точки дуги, то
J Р (х, у) dx + Q (х, у) dy =
(О
”. 3
= J Р [х, у(х)] dx + J Q [ х (у), у] dy.
а а
Если дуга (1) не удовлетворяет приве-
дённому выше условию, то её следует раз-
бить на несколько частей и применять ука-
занную формулу к каждой части в отдель-
ности.
Если уравнения дуги даны в параметри-
ческой форме х = х (1), у = у (1), т и Т —
значения параметра t, соответствующие точ-
кам А и В, то
f Р (х, у) dx + Q (х, у) dy =
О)
т
= Н₽[* *(О.у(О1 (0 +
*5
+ Q [х (Г), у (О] У
Аналогичным образом для пространствен-
ной кривой х = х(1), У = у (t)> z = z(t):
Jp (х, у, z) dx + Q(x, у, z) dy+ft (х, у, z) dz=
т
= У {Р 1^(0-У (0. z(l)]x'(O +
+ Q^(O.y(O>z(t)]y'(O +
+ Р [х(1),у(1), 2(1)1 2' (О 'fdt.
Пример. Вычислить I ydx — xdy, где (1)—окруж-
(!)
ность радиуса г с центром в начале координат (на-
правление обхода обратное ходу часовой стрелки).
Уравнение окружности х» г cost, у — г sin t
и
2 г.
f ydx — xdy — Г [г sin t (— г sin t) —
(О О
2 т:
— г cos t-r cos t] dt — — f r> dt = — 2 X r‘.
0
Связь между криволинейным и двойным
интегралами. Если (Z) — замкнутый контур,
обходимый в положительном направлении
(положительным направлением обхода замк-
нутого контура будем считать такое направ-
ление, при котором ограниченная контуром
область остаётся слева), (S) — область, огра-
ниченная контуром (Z) (фиг. 138), функции
Р (х, у) и Q (х, у) непрерывны вместе со свои-
ми частными производными в области (S), то
J Р (х, у) dx + Q (х, у) dy =
(О
f(T<)Q(x, у) дР(х,у)
= JJLT—~—ду— dxdy
(S)
(формула Грина).
Если область (S) не односвязная1 и её
граница состоит из нескольких контуров,
то под (1) в формуле Грина следует пони-
мать совокупность всех этих контуров, при-
чём направление обхода на каждом контуре
выбирается так, чтобы область (S) находи-
лась слева (фиг . 139).
Фиг. 138 Фиг. 139
Для того чтобы криволинейный интеграл
У p(x,y)dx+ Q(x,y)dy,
АВ
где функции Р (х, у) и Q (х, у) и их частные
производные непрерывны в области (S), имел
одно и то же значение для всех путей, ле-
жащих в односвязной области (S) и идущих
от точки А(х0,у0) к точке В (xlt ух), необ-
ходимо и достаточно, чтобы подинтеграль-
ное выражение Р (х, у) dx + Q(x,y) dy было
полным диференциалом, т. е. чтобы2
д Р (х, у) д Q (х, у)
ду — дх
В этом случае
f Р(х,у) dx + Q(x,y)dy =
(О
= и (Х1.У1) — и (х0, уо)»
где
dU (х, у) = Р (х, у) dx + Q (х, у) dy.
Независимость интеграла от пути инте-
грирования в области (S) равносильна ра-
венству нулю интеграла по всякому замкну-
тому контуру, лежащему в этой области.
Если подинтегральное выражение являет-
ся полным диференциалом, но внутри кон-
тура имеется особая точка, в которой на-
рушается непрерывность функций Р (х, у)
или Q(x,y) или их частных производных,
то интеграл по такому контуру может ока-
заться не равным нулю, но в этом случае
интеграл по всякому замкнутому контуру,
окружающему одно и то же число раз одну
и ту же особую точку, сохраняет постоян-
ное значение.
1 Конечная область (S) называется односвяз-
ной, если все точки, лежащие внутри любого замк-
нутого контура, проведённого в этой области, при-
надлежат области (S).
* Условие независимости криволинейного ин-
теграла по пространственному контуру от пути
интегрирования см. на стр. 155.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
155
Пример, Найти J — вдоль пути (I)»
(О
окружающего один раз начало координат (начало
координат — особая точка). Воспользовавшись пара-
метрическими уравнениями окружности х в г cos t,
у» г sin t, имеем
2 тс
(О О
При помощи криволинейного интеграла
можно вычислить площадь S области (S) по
формуле
S= — jx dy — ydx,
2 (О
где (/) —контур области (S).
ИНТЕГРАЛ ПО ПОВЕРХНОСТИ
Интегралом функции / (х, у, z) по обла-
сти (а), расположенной на некоторой поверх-
ности, называется число, определяемое сле-
дующим образом.
Область (а) разбивается произвольно на
элементарные области с площадями Даа,
Даа,..., Дав (фиг. 140), внутри или на
границе каждой элементарной области вы-
бирается точка Mi (Xi,yt,Zi), составляется
сумма
п
2 / (*/» Ук Да*
1=1
и находится предел, к которому стремится
эта сумма, когда наибольший из диаметров
элементарных областей стремится к нулю:
п
я/ (X, у, Z) da = lim 2 / (*<> Ук 2<) Да<-
6) i= 1
Если область (а) состоит из нескольких
частей (at), (a2),..., (ap), то
JJ / (х, у, z) da = / (x, у, z) da +
O) (®i)
+ JJ / (x> y> z) d a + ... + jj / (x, y, z) da.
(=,) Op)
Вычисление интеграла по поверхности.
Вычисление интеграла по поверхности сво-
дится к вычислению двойного интеграла при
помощи формулы
О) (8)
где (S) — проекция области (а) на плоскость
OXY (фиг. 141), z = z(x,y)— уравнение по-
верхности, на которой расположена область
(a), (л, z)— угол между нормалью к поверх-
ности и осью OZ, и, следовательно:
| cos (и, z)| =
=____ 1
/ рг(х,уур , Г dz (х, у)~Т ’
1+[~l)x“~J + [ dy------------
Связь интеграла по поверхности с криво-
линейным и тройным интегралами. Если
(а) — замкнутая поверхность, ограничиваю-
щая трёхмерную область (V), п — нормаль к
поверхности (а), направленная вне области
(V) (внешняя нормаль) (фиг. 142), то
Я
(V)
д Р(х, у, z) 0Q(x, у, z)
дх "Г ду
dJ?(x, у, z)
r dz
JJ [Г(х, у, z) cos(и, х) +
(°)
+ Q (х, у, z) cos (л, у) + R (х, у, z) cos (и,z)] da
(формула Остроградского).
Фиг. 143
Если (а) — область, лежащая на некото-
рой поверхности, ограниченная контуром (1),
и — нормаль к поверхности, направленная
так, что она образует острый угол с осью
OZ (фиг. 143), то
J Р (х, у, z) dx+Q (х, у, z) dy+R(x, у, z) dz=
(i)
BdR(x,y,z) OQ(x,y, z)“|
--------dy-----------di----Jcos <n’x>+
C)
~ dP(x, y, z) dR (x, y, z) 1
+ [-----dz----------dx----Jcos +
, pQ(x,y, z) dP(x, y,z) 1 , J j
+ L-----dx---------------- I cos (л, z)| da
(формула Стокса).
В случае, если область (а) многосвязна,
под (I) следует понимать совокупность кон-
туров, составляющих её границу.
Условия независимости криволинейного
интеграла по пространственной кривой от
пути интегрирования, получаемые из фор-
мулы Стокса, следующие:
dR _ dQ дР OR OQ~OP_
dy ~ dz ’ dz ~ dx ’ dx~ dy ’
при этих условиях подинтегральное выраже-
ние является полным диферепциалом неко-
торой функции U (х, у, г):
Р (х, у, г) dx -|- Q (х, у, г) dy +
+ R (х, у, z) dz = dU (х, y,z).
156
МАТЕМАТИКА
БЕСКОНЕЧНЫЕ РЯДЫ
ЧИСЛОВЫЕ РЯДЫ
Частной сум-мой Sn числового ряда
01 + Оа + + •••
называется сумма его первых п членов
Sn — ai + аг + + ап-
Если lim Sn существует и конечен, то ряд
п 00
называется сходящимся и указанный
предел называется суммой ряда
S = lim S„.
п 00
Если lim Sn не существует или беско-
n-f-0'J
нечен, то ряд называется расходящимся.
Отбрасывание любого конечного числа чле-
нов ряда (или изменение величин этих чле-
нов) не нарушает сходимости или расходи-
мости ряда.
Остатком сходящегося ряда назы-
вается разность между его суммой и част-
ной суммой
Rn = S — Sn — nn+i + оп+2 + ...
геометрическая прогрессия
Бесконечная геометрическая прогрессия
со знаменателем q
а + aq + ацг + ... + aqn + ...
сходится, если—1 <q<l и расходится,
если | q | > 1.
Сумма сходящейся бесконечной геомет-
рической прогрессии вычисляется по фор-
муле
НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА
Если ряд сходится, то предел его общего
члена равен нулю:
lim ап - 0.
п_>оо
Этот признак недостаточен. Так, напри-
мер, гармонический ряд
1,1 1
1+ 2 + 3 +•••+„+•••
расходится, хотя необходимый признак
выполнен, так как
ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ
И РАСХОДИМОСТИ ЗНАКОПОЛОЖИТЕЛЬНЫХ
рядов
а) Сравнение рядов. Пусть даны два знако-
положительных ряда:
°1 + й2 + • • • + йП + •••>
Ь1 + &2 + ••• + Ьп + •••
Если первый ряд сходится и то
второй ряд тоже сходится.
Если первый ряд расходится и Ь„ > ап,
то второй ряд тоже расходится.
„ ап
Если отношение ~j~ ограничено снизу и
°п
сверху (т. е. существуют такие положитель-
ные постоянные а и ₽, ЧТО a , то
оба ряда сходятся или расходятся одновре-
менно.
Пример 1. Ряд
расходится, так как его члены больше соответ-
ствующих членов гармонического ряда.
Пример 2. Ряд
сходится, так как его члены равны или меньше
соответствующих членов сходящейся геометрической
прогрессии
б) Признак Лобачевского. Если члены
ряда
оо
2/(п)
п= 1
монотонно убывают, то этот ряд сходится
или расходится одновременно с рядом
5 р^~т,
т=1
гДе Рт определяется из неравенств:
f (Рт + О < 2“т.
Можно также определить рт из равенства
если функция / (х) монотонна и определена
для любых значений х.
Пример.
Из уравнения
- 2~т ;
т
определяем рт «2*
и составляем ряд
оо 00 „
2 р-2"т = 2 2 2-
Л=1 П=1
Этот ряд является сходящейся геометрической про-
грессией и, следовательно, ряд
также сходится.
в) Признак Даламбера. Если существует
такая постоянная q<i, что, начиная с
некоторого п имеет место неравенство
< q < 1, то ряд сходится.
Если, начиная с некоторого п, выполне-
Ду, , 1
но неравенство *- > 1, то ряд расходится.
ап
БЕСКОНЕЧНЫЕ РЯДЫ
157
Особенно удобно пользоваться признаком
Даламбера, когда существует
lim ^±2 = к.
n-f-ОО вп
В этом случае ряд сходится, если к < 1,
и расходится, если к > 1; если же к = 1, то
ряд может сходиться или расходиться.
Пример. Ряд
12 п
-Я- + ят + ... Н-F •• • сходится.
3 о- Зп
Здесь:
п г Ь 1
“n= 3„: “n+1 = Зп+1
и
n-f.no ап 3
г) Признак Коши. Ряд сходится, если,
начиная с некоторого п,
у7 а„ < q < 1
и расходится, если уап > 1.
В частности, если существует
1- пг~ »
пт у ап = к,
п->-оо
то ряд сходится при к < 1 и расходится при
к > 1; в случае, когда к — 5, ряд может как
сходиться^ так и расходиться.
Пример. Ряд
1 , / 2 \2 . / 3 \3 / П \п
~з + (т) + (у) + ( 2НУ1) + -
сходится, так как
П/— 1
п ™ г “П = '2 < '•
д) Интегральный признак сходимости.
Общий член ап ряда aL + а2 + ... а„ + ...
является функцией своего номера п:
an=f(n).
Если определённая таким образом функ-
ция / (х) непрерывна и монотонна при всех
значениях х >-/ (а—любое число), то дан-
ный ряд сходится, если сходится интеграл
J Kx'fdx,
а.
и расходится, если этот интеграл расхо-
дится (стр. 14-1).
Пример. Ряд
сходится при р> 1 и расходится при р < 1, так
как функция f (х) = —- монотонна и непрерывна
хР
при х >1 (и даже при х > 0) и интеграл
оо А
( ~ - Пт С = Вт --------------------1- _ 1
J хР А-^оо J хР A-^colP”1 (p-i)AP-lj
сходится равен j при р > 1 и расходится
(и равен со) при р < 1.
При р 1 ряд тоже расходится (в этом случае
мы имеем гармонический ряд), так как
оо А
f dx .. (* dx . .
I —- « lim i -------- lim In A »» oo.
J x A-^x> J x A->oo
1 1
Таким образом наш ряд сходится при р > 1 и
расходится при р < I»
е) Признак Ермакова. Если прн х > а
(а — любое число) функция / (х) монотонна
и непрерывна, то ряд с общим членом
On = / (п)
сходится, если существует такая постоянная
q < 1, что при всяком х > а
?' (*)/[? (х)] . . .
/ (X) < 9 <
и расходится, если при всяком х > а
(х)/[?(х)]
/ (х) > ’
где ср (х) — произвольная диференцируемая
функция, удовлетворяющая условию <р (х) >х,
при х > а.
Если существует
то ряд сходится при К < 1 и расходится
при К > 1.
Признак Даламбера может быть получен
из признака Ермакова, если поло?кить ср (х)=<
= х + 1.
Пример. Приняв при исследовании сходимости
ряда
111 1
1 -2 + 3-4 + 5-6 + • • + (2л - 1) 2п + ’ ’ '
9(х) = ех , получаем:
f <Х) = Г2х~ П2у' ; = / "т ” \-у 1
(2X-1J2X \2ех~\)2ех
<?' (х) =» ех
" 11т = 11т = 0 !.
х-*оо IW х-^оо 2ех — 1
Следовательно, данный ряд сходится.
ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ
Достаточный признак сходимости знако-
чередующегося ряда
И1 — и, + U3— ц4 + ... + (— l)n+1 ип + ...
(здесь через ц1( ц2,... обозначены абсолют-
ные величины членов ряда) содержится в
следующей теореме (теорема Лейбни-
Ц а).
Если lim ц„=0 и, начиная с некоторо-
П->оо
го п (т. е. для всех п N), абсолютная
величина члена ряда изменяется монотон-
но:
ип > «п+1 > >
то знакочередующийся ряд сходится.
Если ряд удовлетворяет условиям теоре-
мы Лейбница, то абсолютная величина
остатка ряда при n > N не превосходит
абсолютной величины первого отброшенного
члена ряда:
I I < ап+1-
Например, ряд
1 1 1
1 — 2 + 3 — 4 + •••
сходится, так как оба условия, входящие в
признак Лейбница, выполнены. Подсчитав
сумму первых четырёх членов ряда, найдём
1117
S4 = 1 — у + 3— j = 12 = 0,58333...
158
МАТЕМАТИКА
Остаток ряда удовлетворяет неравенству
1Я«1 < 4 =0’2-
Следовательно, величина суммы ряда от-
личается от найденной нами величины S4 не
больше, чем на 0,2.
АБСОЛЮТНАЯ И УСЛОВНАЯ СХОДИМОСТЬ
Если ряд
+ + + +...,
составленный из абсолютных величин членов
данного ряда
а» +а3 + ... + «л + •••
сходится, то данный ряд тоже сходится и
называется абсолютно сходящимся
рядом.
Например, ряд
2,2 1
1 — 2» + З3 “' 43 + •”
сходится абсолютно, так как ряд, членами
которого являются абсолютные величины
членов этого ряда, сходится, как было уста-
новлено выше, с помощью интегрального
признака.
Может случиться, что знакопеременный
ряд сходится, тогда как ряд, составленный
из абсолютных величин его членов, расхо-
дится. Такой ряд называется неабсолют-
н о (или условно) сходящимся.
Например, ряд
1 1 1
1-2+у-4+-
сходится (по теореме Лейбница), в то время
как ряд, составленный из абсолютных вели-
чин его членов (гармонический ряд), расхо-
дится; следовательно, данный ряд является
условно сходящимся.
При исследовании сходимости знако-
переменного ряда иногда полезно составить
два вспомогательных знакопостоянных ряда:
один, составленный из одних положительных
членов данного ряда, другой— из одних от-
рицательных членов. Если оба упомянутых
ряда сходятся, то данный ряд сходится и
притом абсолютно; если один из ннх схо-
дится, а другой расходится, то данный ряд
расходится; если же оба составленных нами
ряда расходятся, то данный ряд либо схо-
дится (условно), либо расходится.
Пример 1. Ряд
1 ~ 2* + ~2! ~ 3* + "З! ~ 4" + 4~! ~
сходится абсолютно, так как ряды
1 + ~2! + *3*1 + 41 + "•
сходятся.
Пример 2. Ряд
1_1+ 2_1+А_1+±_
2 21 3 3! 4 + 41 *
расходится, так как ряд
1 + 4l+ 41+ 4; + -
сходится, в то время как ряд
расходится. * а *
Пример 3. Если для рядов
1 - 1 + 1 - 1 + ...
составить вспомогательные ряды из положитель-
ных и отрицательных членов, то мы легко уста-
невим, что обе пары этих рядов расходятся, в то
время как первый из данных рядов расходится
/Пт ап 0\, а второй сходится условно (по тео-
X П_>.00 '
реме Лейбница).
Свойства абсолютно и условно сходящих-
ся рядов. Переместительное свойство сложе-
ния, имеющее место для конечных сумм,
распространяется только на абсолютно схо-
дящиеся ряды: произвольная перестановка
членов абсолютно сходящегося ряда не может
ни нарушить сходимость этого ряда, ни из-
менить его сумму. В то же время для услов-
но сходящегося ряда имеет место следующее
предложение (теорема Римана): со-
ответствующей перестановкой членов услов-
но сходящегося ряда можно его сумму сде-
лать равной любому наперёд заданному
числу и даже превратить этот ряд в расхо-
дящийся.
Сочетательное свойство имеет место для
всякого сходящегося ряда.
ДЕЙСТВИЯ НАД РЯДАМИ
Суммой (разностью) рядов:
а1 + at + ••• + ал + •••»
61 + bs + ... + bn + ...
называется ряд:
(Л1 ± Ьг) + (аа ± 63) + ... + (ал± 6Л) -}-...
Если данные ряды сходятся, то их сумма
(разность) тоже является сходящимся рядом
и притом сумма этого ряда равна сумме (раз-
ности) сумм данных рядов; сумма (разность)
абсолютно сходящихся рядов есть тоже ряд
абсолютно сходящийся.
Примечание. Если данные ряды расходятся, то
их сумма (разность) может быть тем не менее схо-
дящимся (и даже абсолютно сходящимся) рядом:
если же один из данных рядов сходится, а другой
расходится, то их сумма (разность) есть всегда ряд
расходящийся.
Произведением рядов:
Дх + аг + ••• + ап + ...,
61 + bt + ... + Ьп +...,
называется ряд
С1 + + сп +•••
с общим членом
сл = й1Ьп + а2бл—1 + + o„bi^
Если каждый из двух данных рядов схо-
дится и при этом по крайней мере один из
них сходится абсолютно, то их произведение
является сходящимся рядом, сумма которо-
го равна произведению сумм данных рядов.
Если оба ряда сходятся абсолютно, то их
произведение — тоже абсолютно сходящийся
ряд.
БЕСКОНЕЧНЫЕ РЯДЫ
159
СУММЫ НЕКОТОРЫХ ЧИСЛОВЫХ РЯДОВ
1 1 1
+ з -~4 + = 1п2;
1 J_ 2 _ *
’ - з + 5 — 7 + ••• - 4 ;
111 д*
1 + 22 + 3’+ 42 + = 6 ’
111 да
’ +3«+ э>+ 7« + - = 8 ’
111 _ 21.
1 — 2« + 3’ 42 + ••• — J2 ’
111 _ 21
1 “ 32 + 5s ~ V + ••• - 32 ;
1111
1 + П + 2! + 3! + 4! + •'• = е’
1 111 _ 1 .
1 ~ П + 2! — 3! + 4! — •" “ е ’
1 —3! ~ 7! + ••• = sin 1;
1 1 1
’~2! +4!~ 6! + - = COS1,
РЯДЫ ФУНКЦИЙ
ОБЛАСТЬ СХОДИМОСТИ
Областью сходимости функцио-
нальное о ряда
/о M + /1W + ••• + fn(x) + ...
называется совокупность всех значений аргу-
мента х, при которых этот ряд сходится.
Пример. Область сходимости ряда
состоит из всех значений х, определяемых неравен-
ством х > 1 (стр. 157).
Суммой ряда функций называется
lim S„ (х) = S (х),
Л->ОО
где
$п (х) = /о (х) + /1 (х) 4- ... + fn (х).
Областью сходимости с тепенного
ряда
«о + <>1Х + а2х2 + ... + апхп + ...
всегда является интервал (интервал
сходимости) с центром в точке х = О,
причём во всех внутренних точках этого
интервала ряд сходится абсолютно; на кон-
цах интервала сходимости ряд может или
сходиться или расходиться. Половина
длины интервала сходимости называется
радиусом сходимости ряда. Радиус
сходимости г степенного ряда определяется
формулой
1 п.----
— = hm а„|
П->0О
(если этот предел существует или бесконе-
чен).
Если радиус сходимости равен нулю, то
ряд сходится только в точке х = 0; если
радиус сходимости бесконечен, то ряд схо-
дится при всех значениях аргумента
(— оо < х < оо).
Для степенного ряда более общего вида
д0 + аг (х — а) + at (х — а)2 + ... +
+ ап (х — а)” + ...
центром интервала сходимости является
точка х = а.
Можно, не прибегая к приведённой выше
формуле для радиуса сходимости (которая
к тому же не всегда применима), для опре-
деления интервала сходимости степенного
ряда непосредственно пользоваться призна-
ками сходимости знакоположительных ря-
дов, применяя эти признаки к ряду,состав-
ленному из абсолютных величин членов
исследуемого степенного ряда; достаточно
при этом использовать признак Коши или
Даламбера. При исследовании сходимости
на концах интервала признаки Коши и Да-
ламбера чаще всего не решают вопроса о
сходимости и здесь следует прибегать к дру-
гим признакам (интегральный, признак Лейб-
ница и т. п.).
Пример. Определить интервал сходимости ряда
х + 1 (х+р‘ (х+1)а
2-1 + 2а-2 2а*3 •"
Общий член ряда имеет вид:
_ (х+1)п
“п~ 2п п'
Применяя признак Даламбера к ряду, состав-
ленному из абсолютных величин членов данного
ряда, получаем:
„ (х+1)п+1 • 2«-п
Л—>00 I ип I (х + 1)" • 2n +1 (п +1)
I х+1 |
-----2— < 1.
Решая неравенство, определяем интервал сходи-
мости:
- 3 < х < 1.
При х = 1 получаем гармонический ряд
который расходится, а при х — — 3 — ряд
который сходится (условно) по теореме Лейбница.
Итак, ряд сходится, если — 3 < х < 1.
РАВНОМЕРНАЯ СХОДИМОСТЬ.
ИНТЕГРИРОВАНИЕ И ДИФЕРЕНЦИРОВАНИЕ
РЯДОВ
Ряд функций
/о (х) + /j (X) + ... + fir (X) + ...
называется равномерно сходящим-
ся в некоторой области, если, каково бы
ни было число а > 0, всегда можно найти
такое N (s), что при п > N (е) для всех зна-
чений х, принадлежащих рассматриваемой
области, имеет место неравенство
I Rn (х) I < е,
где
tfn(X) = /n+1(x)+fn+2to+
Если абсолютные величины членов дан-
ного функционального ряда не превосходят
в некоторой области величин соответствую-
щих членов сходящегося числового (поло-
160
МАТЕМАТИКА
жительного) ряда, то данный ряд сходится
в этой области равномерно (признак
Вейерштрассак Если ряд сходится
равномерно на некотором отрезке, то его
сумма S (х) непрерывна и этот ряд мож-
но на данном отрезке почленно интегриро-
вать, т. е. для всех значений х и а, при-
надлежащих рассматриваемому отрезку,
имеет место равенство
J S (x)dx = J ;0 (х) dx +
а а
+ J А (х) dx + ...+ J /„ (х) dx +...,
а а
причём сходимость ряда, стоящего в правой
части равенства, равномерна-
Если в некоторой области производные
членов данного функционального ряда непре-
рывны и ряд, составленный из этих произ-
водных, сходится равномерно, то сумма этого
последнего ряда равна производной от суммы
исходного ряда, т. е.
S' (х) = /0 (х) +/) (х) + ... + /„ (х) + ...
Степенной ряд сходится равномерно на
всяком отрезке, лежащем целиком внутри
интервала сходимости этого ряда.
При диференцировании и интегрировании
степенного ряда интервал сходимости не
изменяется.
РЯДЫ ТЭЙЛОРА И МАКЛОРЕНА
Ряд Тэйлора позволяет представить за-
данную функцию / (х) как сумму степенного
ряда
х —а
|M-fW + -jfl '(«> +
+-e4r1''(«>+...+fcra£/<">«+...
Эта формула справедлива, если оста-
точный член ряда
Rn (х) = /(х) —S„(x)
стремится к нулю при п->-оо.
Формулы для остаточного члена:
. X
Rn W = тг J (х -О" /(п+1) dt -
а
интегральная форма;
(X) = /(П+1) [а + о(х-«)];
(0 < 0 < 1) — форма Лагранжа;
Rn (х) = (1 - 0)« /<л+1> [fl +
п!
4-0(х —а)]; (0 < 0 <1) — ф о р м а Коши.
Ряд Маклорена получается из ряда Тэй-
лора при а = 0:
/(х) = /(0) + -^-г (0)+ (0)+ ..• +
+ /(л)(0)+..-
Формулы для остаточного члена:
1 х
Rn W = 7г! J ~ t)n /(П+1) <0 dt =
о
x"+l
(л + 1)!
/(Г1+1)(01 х) =
52 (1-02)«/(«+’> (02х)
(0<61 < 1;
О < 02 < 1).
Ряд Тэйлора для функции многих пере-
менных. Для функции двух переменных:
/(х + к,у + к) = / (х,у) +
1 df (х,у) ь 6/(х,у) ,
ТГ ~дГ~к + ~ду~к
д*1 (х,у}
дх* п дхду
кк -|-
д*1 (х.у)
ду*
к* + ...
+
или (в символической записи):
/(х + к,у + к) = f(x,y) +
, 1 / д , д \
+ 6? fej/<X’y) +
1/6 д
+ 2!^6х Л+ ду к)1(х’У> +
1/6 6 \п
+ - + ld[^h + lyk) f <Х’У) +-
Остаточный член ряда
1 /6 6 \п+1
Rn = (п + 1)! \ дх h + ду к) / <*+
+ did; у + Ьгк) (0 < 0Х < 1; 0 < 02 < 1).
В .общем случае (для функции п перемен-
ных)
/ (х + к,у + к,г Z,...) = / (х,у,г,...) +
^,1/6 6 6 V
+ 12 г! (бх h + ду к + 6zZ+ —jf(x,y,z,...).
Остаточный член
, . 1 / d 6
Rn(x)~ (и + 1)! \дхк + дук +
6 \п+1
+ ) /(х+01 ft, у + 02/с,г+631,...).
Оценка остаточного члена. При помощи
разложения функции в степенной ряд вычис-
ляются приближённые значения алгебраи-
ческих и трансцендентных функций. Ошибка,
совершаемая при замене суммы ряда его
частной суммой, равна остаточному члену
ряда. При такого рода вычислениях тре-
буется уметь решить следующие три основ-
ные задачи:
1. Оценить ошибку, зная число членов
частной суммы, принятой за приближённое
численное значение функции, т. е. оценить
1 Rn(х)I при данных значениях п и х.
2. Задавшись максимально допустимой
величиной ошибки, найти число членов част-
ной суммы, которую можно принять за
искомое численное значение функции, т. е.
БЕСКОНЕЧНЫЕ РЯДЫ
1G1
РАЗЛОЖЕНИЕ НЕКОТОРЫХ ФУНКЦИЙ В СТЕПЕННОЙ РЯД
Разложение в ряд Область сходимости ряда К заданной функции
(ач х)т^ат+ тат- >хЧ- . : . Ч- -ы..-.ат-п хп _ - |а( < х<ч-|а|
v х In a x2lnaa хп lnz? а а ' “ 14 ~1Г + 2Т“+ • + - пГ " + - • • —~ <1Х+ + ОО
v X Xя хп ех — 1 + - -4 и . . j .4- 1! 2! и! — “ <Х <оо
X х3 , t X 2п+1 SlnX = 'lT Зт+ • ••+(-!) "(2п“f)T + ’ ’ ’ — о^<Х<оо
уЗ yi у2п cos х j_ 5_+ .. + (-1)" т-т+. .. -оо<Х<оо
х3 2х5 17х7 , 62х9 tg х-х+-3—Ь-15'т- ~315+ 2 8351’’ ' ’ г. тс 2 <х '2^
х 1 ( X Xs 2х5 X7 1 ctg Х х~ 1 3~ ' "45 + 945 + 4'725 ? ’ f —г<х<+, кроме х = О
1-х» 1-3-х5 1-3-5-х’ 1-3-5. . ,(2n-l)x2n+1 arc sin х=х 1 2-З'^’а-Ч - 5 !2-4 - 6- 7 + ' ‘ - б. . ,(2;1)-(2/1-:1) + '' ‘ -1 <х<1
, X3 X5 , Z 1 чП X2rt+ 1 arc tgx=x- -3— (—5- . .-F(-Drt + - • • -КХС1
х х3 ^2п+1 Sh Х~ 1! + 3! ‘ ,+ (2п+1)! +"’ — оо <Х<оо
№ х4 х2" ch х= i । -2Т+—+ .. . + --- + ... ~ 00<Х<0О
хи х3 2х5 17х’ thx=x— --u_ --+.., 3 15 315 tT<X<~2~
.. 1 , х Xs , 2х‘ х’ С Х х + 3 45+945 4 725 —7t<x<r., кроме х=О
л х3 Д-3-ха 1-3-5-х’ ,, ,ч„ 1-3-5. . ,(2п—1)х2,1+1 .rs х х 2 дЧ 2-4-5 2-4-6-7+ •-+( > 2 4 6 . . . (2п)'2п+1) +‘” -14Х<1
х3 X5 Arthx^x+ 3- + -5 +...+^71-г + ... —1<х<1
у2 уЗ у>1 1п(1ч-х) = х 2~Ч-~3 - Г1 А--.. -1<х<1
1пх = 2(х+1 + '3- X-J1 у i f X-1V 1__ f х-1 х-г 1/ +~5 \ Х+1/ +' ’ * +2п+ц Х+1/ +’' х>0
— 1<х <1
, Х+ 1 In ----- = 2 X—1 1 1 , 1 , 1 + 4- +...Ч- о 1- • • х Зх3 5хй (2п + 1)х2п + 1 х<—1, х> 1
X ('sin х , х Xs Xs „ х2пЧ-1 J х dX 1-1! 3-3!+5-5! ••• + l ° (2н+ 1)(2п+1)!+ * * ‘ О — со <Х < со
X С „! х Xs х‘ „ х2п + 1 У dX 1 3-1!+5-2! ••+< *> (2п+Т)пГ +' •' 0 — оо<Х<хп
11 Том I
162
МАТЕМАТИКА
найти п из неравенства | Rn (х) | < 6, где х и
6 даны.
3. Определить, для каких значений аргу-
мента приближённая формула, полученная
заменой суммы ряда его частной суммой с
определённым числом членов, даёт ошибку,
не превышающую заданной величины, т. е.
найти х из неравенства |/?п(х)| < где п и
8 известны.
Пример 1. Какова величина допущенной ошиб-
ки, если положить
е “ 2 + '2'! + 4i + 4l ?
В разложении функции ех остаточный член в
форме Лагранжа имеет вид:
ХГ£-г 1 fly-
п = 4, а так как х = 1. то
и
|R4(l)l<-|f = 0,025.
Пример 2. Сколько нужно взять членов ряда
X , ха
,х
2!
точностью до 0,0001?
чтобы вычислить число е с
е9
Rn(1)~ (п+1)Й ’ " "
Следовательно, достаточно взять п, удовлетво-
3
ряющее неравенству < 0,0001 или (п-Ы)!>
> 30 000; наименьшее значение, удовлетворяю-
щее этому неравенству п—7 (8! « 40 320); итак,
с точностью до 0,0001
21 3!
Пример 3. При каких
иая формула
cos х *
4! 5i б! 7!’
значениях х приближён-
х’
2
даёт ошибку, не превышающую 0,001?
Здесь п = 3,
cos 9х
так как
| cos 6х | < 1,
то
I я. WI < .
Xе
Решив неравенство < 0,001, получаем:
1х| < 0,024 ~ 0,394 (радианов) «> 22° 33',
РЯДЫ ФУРЬЕ
РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ
Если функция / (х), определённая в интер-
вале (—тс,тс), удовлетворяет так называемым
условиям Дирихле, т. е. если она в
этом интервале:
а) равномерно ограничена (т. е. сущест-
вует такая постоянная М, что 1 / (х) I < М
во всех точках интервала);
б) имеет не более, чем конечное число
точек разрыва и притом только первого рода
(стр. 130);
в) имеет не более, чем конечное число
точек максимума и минимума,
то она может быть разложена в ряд Фурье,
т. е. тригонометрический ряд вида:
«о
/ (х) = -% + °i cos х + &1 sin х +
+н2 cos 2x+&3sin2x + ...
+ ап cos пх + Ьп sin их + ... =
оо
~ тг + S cOS пх + sin пх^’
2 П= 1
где числа а0, alt blt ..., а„, Ьп, ... (коэфи-
циенты Фурье) определяются по фор-
мулам:
ТС
ап = j / (х) cos пх dx (п = 0,1,2,...);
—тс
тс
bn = J j (х) sin пх dx (п=1,2, ...).
— ТС
Ряд Фурье можно также записать в фор-
ме:
оо
/(*) = Со + 2 Crtsin(nx + <?„) -
П=1
оо
= Со + S С« cos (пх + — т)’
И=1
где
с„= й2°; сл= /+ ь2-, tg<fn=~n.
В интервале (—тс,тс) сумма этого ряда
$(х) равна:
а) значению функции / (х) в каждой точ-
ке, где / (х) непрерывна;
б) среднему арифметическому предельных
значений / (х) слева и справа (стр. 129) во
всякой точке разрыва (фиг. 144), т. е.
. /(х — 0) + / (х + 0)
S (х)=-----------2-------- ’
где
/ (х — 0) = lim / (х — е)
е О
И
/(х + 0) = lim / (х-н) (е > 0).
• ->- о
Вне интервала (— л, л) сумма ряда пред-
ставляет собой периодическое (с перио-
дом 2л) продолжение определённой выше
функции S (х).
Если функция / (х) чётная, т. е.
/(—х) = /(х),
то
Ьп = О (п = 1,2,...)
и она разлагается в неполный ряд Фурье по
косинусам кратных дуг:
а0
~2 + flicos х+а2 cos 2х + ... + ап cos пх4-...,
где коэфициенты ап могут быть вычислены
по формулам:
ТС
ап — — J/(x)cosnxdx (п = 0,1,2,...).
о
БЕСКОНЕЧНЫЕ РЯДЫ
163
Если функция / (х) нечётная, т. с.
/(- х) = -/(х),
то
ап = 0 (72 = 0,1,2,...)
и она разлагается в неполный ряд Фурье
по синусам кратных дуг:
Ьг sinx + b., sin2x 4- ... + bn sinnx + ...,
где коэфициенты bn могут быть вычислены
по формулам:
2 f
bn = — I/(х) sin их dx (и =1,2,...).
о
Фиг. 144
Функция, заданная в интервале (0,л),
может быть продолжена в интервал (— л, 0)
либо как чётная функ-
ция (фиг. 145), либо как
нечётная (фиг. 146), по
нашему усмотрению;
если, следовательно,
она удовлетворяет ус-
ловиям Дирихле в ин-
тервале, на котором
она определена, то её
можно разложить, по
желанию, в неполный ряд Фурье по одним
синусам или по одним косинусам кратных
дуг.
В более общем случае, если функция / (х)
определена и удовлетворяет условиям Дирих-
и
2 ч п~-х
ал = ~ /(x)cos-y-dx (л = 0,1,2,...).
о
Если же функция / (х) нечётная, то
ап = 0 (л = 0, 1,2, ...)
и
I
2 Г л лх
Ь„ = у /(x)sin — dx (п=',,2,...).
о
СВОЙСТВА КОЭФИЦИЕНТОВ ФУРЬЕ
Если некоторая функция / (х) приближён-
но заменена на интервале (а, 6) функцией
4>(х), то средней квадратической
погрешностью такого приближения
называется число В, определяемое равен-
ством:
ь
52 = J[/(x)-T(x)pdx.
а
Фиг. 145 Фиг. 146
ле в интервале (—1,1), то её можно разло-
жить в ряд вида:
а0 лх лх
2 + «1 cos-p 4- bj, sin у +
2 л х 2 лх
+ а2 cos —у + &2 sin —у + ... +
пЛХ П~х
+ a„cos -у + &„sin -у- + ...,
где
I
1 (* , Пт.Х
ап = -у I / (х) cos -у dx (л = 0,1,2,...),
—I
i
1 С л^х
Ъп = -у i /(x)sin -у dx (л=1,2,...).
-I
Сумма такого ряда Фурье S(x) опреде-
ляется так же, как и в предыдущем частном
случае.
Если функция /(х) чётная, то
(fryO (п =1,2,...)
Коэфициенты Фурье функции / (х) обла-
дают следующим экстремальным свойством:
средняя квадратичная погрешность прибли-
жённого выражения функции / (х) при по-
мощи тригонометрического полинома л-го
порядка
-у + «J cos х 4- by sin х 4- а2 cos 2 х 4-
4- b2sin2x 4- ... 4- cosnx+&„sinnx
будет наименьшей, если коэфициенты такого
многочлена взять равными соответствующим
коэфициентам Фурье функции / (х).
Коэфициенты Фурье функции / (х) связа-
ны со средней квадратичной величиной (сред-
ним квадратичным отклонением от нуля)
этой функции:
оо тс
Л ** J
1 —тс
пли, соответственно, в общем случае
fc=i —I
Если функция / (х) удовлетворяет на
любом конечном интервале условиям Ди-
оо
рихле и интеграл J | / (х) | dx сходится
— оо
(см. стр. 144), то имеет место предельная
(при /-><») формула разложения функции
в ряд Фурье (интеграл Фурье):
оо
/ (х) = -у J cfs J / (f) cos s(t — х) dt.
о -jo
11*
164
МАТЕМАТИКА
РАЗЛОЖЕНИЕ НЕКОТОРЫХ ФУНКЦИЙ В РЯД ФУРЬЕ
Функция Разложение в ряд Область схо- димости ряда к заданной функции График суммы ряда
у=х т: 4 / COS Зх , COS 5х \ 2 : 3= ’I О х<к Vi ТЛ in &i 5и
У=я»Х ( sin х sin 2х sin Зх \ V1 I —г<х<п Y /?
у=х /sin x , sin 2x , sin 3x \ "'A 1- + -2-+-3- + --J 0<х<2тс У J У /У4>
7? 0 '>Tt t
у^а 4n ( . sin 3x sin 5x \ v^sm x+-3- + -5- + ..J 0<хО ——1 71 « Я К I» X -1 1—"• LZ
у=О при О«х<а И при а<Х<т; у=П при а<Х<тс—а —П ( cos a sin X4-—1— cos 3a sin 3x4- re \ 3 4- -1- cos 5a sin 5x4-. . . j 0« х<к кроме Х=а и х —а -1 -к, — * х о. я ?hz j ; 1 i Z 1—’
у=х2 n2 /cos x cos 2x cos 3x \ ‘3 ~41 1 23 +~3- •••/ —п<х<тс Y -1 AAA,
n Iff 51 45f Л
y=X(tr—X) na __ /cos 2x cos 4x cos 6x \ "6 \ Р-4 2’- + 3! +••• } 0<Х<к V
-v о r '/V 31’
У = Х(г-Х) 8 I . sin 3x sin 5x \ — ^SinxT 33 1 5, +...J 0<х<п * о / Z>r/~\ *
яХ_у ЗЯ
y=sin х 2 4 /cos 2x cos 4x cos 6x | к - tr \ 1 -3 + 3-5 + 5-7 +---j 0<х<п Y„ -и 0 ii ?я л
y=cos х 8 /sin 2x 2sin4x 3sin 6x \ it \ 1-3 + 3-5 1 5-7 +•••/ Y _ Г\ g \JAJz\jjr-
у~ех 1 , *2 . ’V / ,,ь cos kx—к sin kx z Sh^+ л- Shx J)fc 1 + fcJ fc=l —л<Х<те у V/Z^/X^y
-зтг-п-т \o я n за м
ДИФЕРЕНЦИЛЛЬНЫЕ УРАВНЕНИЯ
165
ДИФЕРЕНЦИЛЛЬНЫЕ УРАВНЕНИЯ
ОБЫКНОВЕННЫЕ ДИФЕРЕНЦИЛЛЬНЫЕ
УРАВНЕНИЯ
Обыкновенным дифере н ц и а л ь-
ным уравнением называется уравне-
ние, содержащее аргумент, искомую функ-
цию этого аргумента и её производные раз-
личных порядков:
Е(х,у,у(п)) = 0.
Наивысший порядок производной иско-
мой .функции в данном уравнении назы-
вается порядком этого уравнения.
Всякая функция, которая, будучи вместе
со своими производными соответствую-
щих порядков подставлена в диференциаль-
нос уравнение вместо искомой функции и её
производных, обращает уравнение в тожде-
ство (удовлетворяет уравнению), называется
решение м (интегралом) диферен-
циального уравнения.
Решение диференциального уравнения
может содержать произвольные постоянные.
Для определения этих произвольных по-
стоянных требуются дополнительные, так
называемые начальные, условия.
УРАВНЕНИЯ 1-ГО ПОРЯДКА
Теорема Коши. Если в некоторой области
плоскости ОХУ функция / (х, у) непрерывна
и удовлетворяет условию Липшица:
I / (*> У1) ~ / (*> Уз) I < A I у2 - у21
(А постоянно для данной области), то суще-
ствует, и притом только одна, непрерыв-
ная в рассматриваемой области функция
у = с?(х), являющаяся решением уравнения
у' =/(х, у) и удовлетворяющая начальному
условию
у = у0 при х = х0,
где (х0, у0) — произвольная точка данной
области.
Всякое решение, о котором идёт речь в
теореме Коши (при заданных .значениях х0
и у0), называется частным решением
диференциального уравнения.
Совокупность всех частных решений на-
зывается общим решением. Общее
решение уравнения 1-го порядка содержит
одну произвольную постоянную. Решение
уравнения, не содержащее произвольной
постоянной и не являющееся частным реше-
нием (и, следовательно, не получаемое из
общего решения ни при каких значениях
входящей в него произвольной постоянной),
называется особым1.
Г рафик решения диференциального уравне-
ния называется интегральной кривой
этого уравнения. Общее решение уравнения
1-го порядка изображается, следовательно,
однопараметрическим семейством интеграль-
ных кривых.
Диференциальное уравнение
У' = /(*>у)
задаёт угловой коэфициент касательной к
интегральной кривой, как функцию координат
1 Во всех точках кривой, изображающей особое
решение, нарушаются условия теоремы Коши.
точки касания. Совокупность точек, в кото-
рых определена функция / (х, у), и отрезков,
направленных ио касательным к интеграль-
ный! кривым, проходящим через эти точки,
образует так называемое поле направ-
лений данного диференциального урав-
нения.
Кривые / (х, у)= С называются изокли-
нами. Во всех точках каждой изоклины
касательные к проведённым через эти точки
интегральным кривым
параллельны между
собой. На фиг. 147 изо-
бражены интегральные
кривые (окружности
х2 -фу2 = С) и изоклины
(у = Сх) для уравнения
Уравнения в
Уравнение
М (х, у) dx + N (х, у) dy = О
в случае, если имеет место тождество
дМ(х,у) dN(x,y)
ду — дх ’
Фиг. 147
диференциалах.
называется уравнением в полных
(точных) д и ф е р е н ц и а л а х.
Общее решение такого уравнения опре-
деляется равенством
и (X, у) = С,
где
би(х,у)
~~дх----
т. е.
du (х, у) = М (х, у) dx -J- N (х, у) dy.
Функция и (х, у) определяется при этом
формулой
и (х, у) = J М (х, у) dx + у (у),
где ср (у) находится (при помощи интегриро-
вания) из уравнения
[ j' Л4 (х, у) dx + у (у)] = N (х, у).
дМ dN
Если условие не выполнено, то
можно найти такую функцию р-(х,у) (инте-
грирующий множитель), что урав-
нение Mdx + Ndy = 0 обратится в уравне-
ние в полных диференциалах после умноже-
ния на (л(х,у).
В качестве интегрирующего множителя
можно выбрать любое частное решение урав-
нения
д(цМ) d(p-N)
ду ~ дх
или
д In ц д In р. дМ dN
Ndx~ ~М~дГ= ду' дх‘
166
МАТЕМАТИКА
дМ _dN
ду дх
Если, в частности, выражение -------
зависит только от х, то при отыскании
интегрирующего множителя можно предпо-
ложить, что он тоже зависит только от х.
Пример. Решить уравнение (х> + у) dx— xdy •= О.
дМ 6N
ду дх_______2
N ' ~ х ;
=«р.(х), соЛ-авляем для отыскания р.
_х1^ = 2,
dx
Здесь
полагая р.
уравнение
откуда
После
умножения на и.= получаем урав-
нение в полных диференциалах
+ х‘) dx---Г Лу-О.
Его общее решение
Пример.
Выполнив подстановку, получим:
и'х + и = еи + ut
.. dx
е udu =» —,
х
— е~и — In х — In О,
t . С
и « — in in —,
X
~ - In In
X X
f . С
у — — х In In —.
X
Уравнения вида
, _ / «1*+ М+ СА
у ~ \ а3х + Ь3у + с3 )
приводятся к однородным, в случае если
Уравнения с разделяющимися перемен-
ными. Уравнение вида
У' = <? (х) Ф (У)
называется уравнением с разделяющи-
мися переменными.
Преобразовав его к виду (разделив пере-
менные):
dy
ФоТ “?<х)dx ~ °’
мы найдём общий интеграл1:
Пример. Найти частное решение уравнения
у' «« — У у sin xt
удовлетворяющее начальному условию:
у — -i- При X W О.
Разделив переменные, получим
dy
Bin xdx + —— = о
/у
и общий интеграл определяется равенством:
— cos х + 2 У~у = С;
из начального условия определяем С:
С - — cos 0+2 -1 = О
и искомое решение:
— cos х + 2 У у « О
ИЛИ
у -1_ C0S* х.
Однородные уравнения. Однородное
уравнен ие имеет вид:
Оно сводится к уравнению с разделяю-
щимися переменными подстановкой у = их
(тогда у' == и'х 4- и).
* Следует иметь в виду, что при умножении или
делении обеих частей диференциального уравнения
на выражение, содержащее искомую функцию,
могут быть приобретены или утеряны решения.
подстановкой
х = и + а, у = v + р,
где аир определяются из системы уравне-
ний:
aia 4- М + Ci = О,
а3а 4- &2Р 4* — о.
Если же
01 М =
Ой ^2 |
ТО, положив
Я1Х + ьгу = t,
получим уравнение с разделяющимися пере-
менными.
Линейные уравнения. Линейным ди-
ференциальным уравнением 1-го порядка
называется уравнение вида
У’ = Р (х) у 4- Q (х),
линейное относительно у и у'.
Его общее решение находится по фор-
муле
у _ ef Р (х) dx [ J q ^ху е— J Р (х) dx (fx-pc].
Пример.
у1 « у tg х + cos х.
у x=i tgxdx [j cos xe J tg xdx dx + C ] “
„ e-ln cos X [J cos xeln COS X dx + c] =
. 4- x + sin 2x + C
—----(J cos’xdx+c] =----------------—.
cos x cos x
Если известно одно частное решение ли-
нейного уравнения у = уг (х), то общее ре-
шение находится при помощи одной квад-
ратуры (одного интегрирования):
у — у, (х) 4- Се$ р (х) dx.
Если известны два линейно независи-
мых частных решения (стр. 169)
У = У1(х) и у = у2 (х),
то общее решение находится без квадратур:
У = У1 W 4-С [У» (х)-У1(х)].
ДИФЕРЕНЦИЛЛЬНЫЕ УРАВНЕНИЯ
167
Уравнения Бернулли. Уравнение вида
у' = Р (х) у + Q (х) уп (уравнение Вер-
нули и)
приводится к линейному с помощью под-
становки у1-" = /.
Уравнения Риккати. Общее решение
уравнения Риккати
у' = Р (х) у2 + Q (х) у + R (х)
не может быть в общем виде получено с по-
мощью квадратур.
Если известно одно частное решение
уравнения Риккати у = yt (х), то подстанов-
ка у = У1(х)+-1_ приводит к линейному
уравнению. Зная, кроме того, ещё одно ча-
стное решение у = уч (х) уравнения Рик-
кати, можно найти частное решение
z =-------!------упомянутого выше линей-
Уа(х) — Уг(х)
ного уравнения. Если, наконец, известны
три частных решения уравнения Риккати:
У = УЛх), у = у2(х) и у=у,(х), то его
общ?е решение определяется равенством
у — у2(х) _ уз (х) - - у2 (х) = с
Уравнения высших степеней. Степенью
уравнения
Г(х, у, у') = 0
алгебраического относительно у' называется
наибольший из показателей степеней у'
(предполагается, что все показатели степеней
у' целые и положительные).
Разрешив уравнение n-ой степени отно-
сительно у', получим, вообще говоря, п
уравнений вида
У' =//(х, у) (1 = 1,2,..., п).
Совокупность решений этих уравнений
определяет общее решение данного уравне-
ния п-ой степени.
Пример.
рируя, получают у == Сх и у = — . Общее решение
данного уравнения можно также записать в форме
(у-Сх) = 0.
Уравнения Клеро. Общее решение урав-
нения Клеро
у = ху' + ф(у')
имеет вид:
у = Сх + ф(С).
Особое решение этого уравнения опреде-
лястся в параметрической форме равенст-
вами:
( у = Сх+ ф(С);
I О = х + ф'(С).
Интегральная кривая, соответствующая
особому решению, является огибающей
(стр. 198) семейства прямых, определяемого
общим решением (фиг. 148).
Пример. Общее решение уравнения у = ху’ +
4-у'8 имеет вид: у — Сх + Са; исключая С из системы
у = Сх 4- С8; 0 = х + 2С, получаем особое решение в
явном виде:
Уравнения Лагранжа. Уравнение Клеро
является частным видом уравнения Ла-
гранжа:
У = Х?(У') + Ф(У').
Произведя замену у' = р и продиферен-
цировав затем полученное равенство по х,
приходим к системе уравнений:
у = х?(р) + ф(р);
dx х ср' (р) + ф' (р)
dp'~ р — <? (р)
Второе из этих уравнений [р~у (р) =£0]
является линейным н его общее решение
совместно с первым уравнением определяет
Решив это уравнение, найдём х = —ч(1пр-|-С)
и, следовательно, искомое общее решение опреде-
ляется в параметрической форме равенствами;
х <ln Р + с>-
у = 2рх + -А-,
или
1
X - Р+С);
у _ -L (1+ 2 In р + 2 С).
УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
Теорема Коши
Для того чтобы уравнение
У(п) = / (х,у, у',..., /"-’>)
имело единственное решение у = ср (х), не-
прерывное в окрестности точки х0 и удовле-
творяющее начальным условиям: у = у0, у'==
= Уо>..., у(п-1) = /"“‘’при х=х0, достаточ-
но, чтобы функция
f <Х’У’ У1... У«-х)
(где х, у, у! Уп—j—независимые между
собой аргументы) в некоторой окрестности
точки (х0, у0, Уо, ...,у^-1)), т. е. для всех
значений аргументов, удовлетворяющих си-
стеме неравенств:
х0 — h < х < х0+й, у0 — к < у < Уо+А,
уо А, < У2 < Уо+
У(о"-1) - А„-1 < Ул-х < У^"_1) + к^ ,
ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
169
Для понижения порядка уравнения, не
содержащего аргумента х,
полагают
dy
dx
d-у dp
dx2 = p dy
и т. л.
Пример.
dy n
dx = ₽:
У>
dy
dx’
"А
"dxy
d2y dp.
dx2 ~ P dy’
Линейные уравнения
Л иней н ы м диференциальным уравне-
нием называется уравнение вида
/п) (х) Ж <;., (:<)/"^2) -р... ф-
+ ап-1 (х) У' +«,, (х) у = / (х),
линейное относительно искомой функции и
её производных.
Если правая часть уравнения / (х)
тождественно равна нулю, уравнение назы-
вают однородным (или уравнением без
правой части).
Если функции уДх), уz (х), ..., уп (х) яв-
ляются частными решениями линейного одно-
родного уравнения и если эти функции
линейно независимы, то общее решение та-
кого уравнения имеет вид:
У = (х) + С.,у3 (х) -р ... + Спуп (х).
Функции У1(х), у2(х), ..., у,, (х) называют-
ся л и и е й и о - н е з а в и с и м ы м и, если
тождество «1У1 (х)-ра2у2 (х)-р...-р а„у„(х) = О,
где аг — постоянные, может иметь место
только при ах = а3 = ... = а,, = 0. Для этого
необходимо и достаточно, чтобы так назы-
ваемый определитель Вронского
(вронскиан)
У1(х) у2(х) ... у„(х)
у'(х) / (х) ... у„(х)
W = ................
у\п 1\х) уУ1 !)(х) ...у[п ° (х)
был отличен от нуля. Определитель Врон-
ского, составленный для п частных решений
линейного уравнения п-го порядка (если
коэфициенты «1(х), а„ (х), ..., н„ (х) этого
уравнения непрерывны), может обращаться
в нуль только тождественно.
Если У (х) — решение неоднородного ли-
нейного уравнения, а и (х) — общее решение
соответствующего однородного уравнения, то
функция и (х) рУ (х) является общим реше-
нием данного неоднородного уравнения. Если
Vi (х) и У2 (х) — решения двух линейных
уравнений с одной и той же левой частью и
с правыми частями (х) и /2 (х), то функ-
ция Ух(х) + Е3(х) является решением урав-
нения с той же левой частью и с правой
частью /2 (х) ф- /2 (х).
Линейные однородные уравнения с по-
стоянными коэфициентами. Для отыскания
общего решения линейного однородного
уравнения с постоянными коэфициентами
у(л) + й1у(л-1)+ ... у'+апу =0
(а1? а», ап — вещественные постоянные)
следует составить так называемое харак-
теристическое уравнение:
к'1 ф- ... +a„_j к ф- ап = О
и найти его корни, после чего п линейно-
независимых частных решений у±(х), у2 (х),
..., уп (х) уравнения находятся (в веществен-
ной форме) по следующим правилам:
1) каждому действительному корню к
кратности р соответствует р линейно-неза-
висимых частных решений:
еКХ, xe’iX, х2екх, хр~* екх-,
2) каждой паре взаимно сопряжённых
комплексных корней а + [Зг кратности q соот-
ветствует 2q линейно-независимых частных
решений:
cos [3 х, еах sin [Зх, хе*х cos [3 х,
хеах sin рх...х9"1 e“xcos рх, х9”1 еах sin Зх,
и общее решение выражается равенством
У - CjJ-j (х) + С2у2 (х) ф- .... ф- СпУ,г (х).
Пример I.
у" + 4 у = О.
Решая характеристическое уравнение ка4-4 = О,
находим к = 2i и общее решение;
у = С, cos 2x+Cs sin 2х.
Пример 2.
У'" — 4у" ч- 4у' = 0;
к3 — 4к‘4 4к = 0:
к. = °* к2-з = 2:
v = Ci+ е2х (Са + С3х).
Пример 3.
+ . — у" — у= 0;
fc"+fc“ - к- - 1 = 0;
к, = — 1; к2 = 1; k3 i — г; к& <, ~ — i;
У = с, е~х + С2ех + (С3+с4х) cos х +
+ (С, + С-.х) sin х.
Линейные неоднородные уравнения с по-
стоянными коэфициентами. Если найдено
какое-либо частное решение У (х) неоднород-
ного линейного уравнения
у(л) + й1У(«-1) + ... +ап__} y'pany=f(x),
а и (х)—общее решение соответствующего
однородного уравнения, то (см. выше)
у = и (х) ф- У (х)
— общее решение данного неоднородного
уравнения. Если, в частности
/ (х) ~ Р (х) еах cos Ьх
или
/ (х) = Р (х) еах sin Ьх,
где Р(х)— некоторый многочлен степени т,
то частное решение следует искать в виде
У (х) = хр еах [Qj (х) cos bxpQ., (х) sin bx\,
где Qj (х) и Q., (х)—многочлены степени т
с неопределёнными коэфициентами, р—крат-
ность корня характеристического уравнения,
равного а ф- Ы (если число а-у-Ы не являет-
ся корнем характеристического уравнения,
то р = 0).
170
МАТЕМАТИКА
Пример, Найти общее решение уравнения
- У , х
У + 4 ~ Х S ° 2 ’
а+Ы = ~
Здесь число
является однократным кор-
уравнения к' ч—— «= 0
нем характеристического
и, следовательно, частное решение уравнения сле-
дует искать в виде
У(х) = X рА,х + В,) sin -*- -?- (А.х + В,) COS yj.
Найдя отсюда У* и подставив в уравнение, по-
лучим:
[- 2А,х + (2 А, - Bs)] sin у- +
+ [2А,х + (2А, + В,)] cos * = х sin у.
Сравнивая соответствующие коэфициенты в обе-
их частях равенства, будем иметь:
- 2Да - 1; 2At — £я = 0; 2 At = 0, 2Д8 + е! = 0,
откуда
At = 0; Bt •= 1; Ая = — ; В2 = О
и
у (х) = х sin “ — ~2 х cos 2 ’
Общее решение однородного уравнения:
X X
и = С, COS -у + Са sin —
и, следовательно,
У “ С, eos у + С, sin у + х sin —
В более частных случаях можно пользо-
ваться следующими правилами:
1) Если / (х)—многочлен степени т:
К.х) = boxm + ... + 6т_! х+ Ьт
и ап #= О,
то частное решение уравнения следует искать
в виде многочлена той же степени (с неопре-
делёнными коэфициентами):
Y (х) = Лох”!+ В, хт-1 + ... + В,п_} х + Вт;
если же
° Л ~ ап— 1 = ••• = ап—р+1 = ап—р О’
то частное решение имеет вид:
Y(x) = хР(В0 хт-^В1хт-'+ ... +
+ Вт_} х+ Вт)_
2) Если / (х) = еах и а не является кор-
нем характеристического уравнения, то
частное решение имеет вид:
У(х)= Аеах,
где А — неопределённый коэфициент; если
же а — корень характеристического уравне-
ния кратности р, то
Y (х) = АхР еах.
3) Если / (х) = т cos bx + n sin bx и bi не
является корнем характеристического урав-
нения, то частное решение следует искать
в виде
Y (х) = М cos bx + N sin bx,
где M,N — неопределённые коэфициенты,
если же ± Ы — пара корней характеристи-
ческого уравнения кратности р, то
Y (х) = хр (М cos bx + N sin bx).
В случае правой части / (х) произволь-
ного вида общее решение неоднородного
уравнения находится методом вариации
произвольных постоянных в форме
у=Сх (х) уг (х)4-С2 (х)у2 (х)+... + Сл(х) у„(х),
где у, (х), у2 (х), ..., уп (х) — попрежнему ли-
нейно-независимые решения соответствую-
щего однородного уравнения и, следова-
тельно, у = С1у1(х) +С2у2 (х) + ... +С„у„(х)
при постоянных CL, С2 Сп—общее реше-
ние этого однородного уравнения, а функ-
ции С, (х), С2 (х),..., Сп (х) определяются сле-
дующей системой алгебраических уравнений
1-й степени относительно их производных:
с.' (x)yi(x)4-Ca (х)у3(х) 4-... 4-
+ Сп (X) Уп (•<) = °,
с; (х)у' (х)4-С> (x’yi (х) 4- ... 4-
+ Сп(х)Уп(х) = °-
С[ (х)у<п-2)(х)4-С', (х)у("-2)(х)4- ... 4-
+ С„(х)у<',-2)(х)==0.
с; (х)у<'!-1>(х)4-с; (х)/Г|>(х)-|- ... 4-
4- Сп (х)у<п”-г> (х) = /(х).
Решив эту систему, находим С, (х),
С2 (х)....Сп(х); при помощи интегрирова-
ния можно определить функции С^х),
С2(х), ...,Сп (х), причём каждая из этих
функций будет содержать произвольное по-
стоянное слагаемое.
Пример. Найти общее решение уравнения
е~х
у"+2у'+у~ —
Общее решение ищется в форме
у - С, (х) е~~х + Са (х) хе~х
(у — (~~x+Ctxe~~x — общее решение однородного
уравнения).
Для определения Сх (х) и Са(х) составляем си-
стему уравнений:
[ (х)е~х + с' (х)хе-*= 0;
। — с' (х) е~~х + с' (х) (е““х — хе~х) __ _е_*
I х
или
с' (х) + С' (х) х = О;
(х)+ < (х)-(1 - х) = 1-;
отсюда
С, (х) = - 1; С> (х) = у
И
Ci (х) «= — х + С,, С2 (х) — In х + Са.
Таким образом
У (Сг — х) + (Са + In х) хе^х-
Уравнение Эйлера. Линейное уравнение
с переменными коэфициентами вида:
(« х 4- ₽)" yW + а, (ах4-?)п-1 у('!_1)4-... +
+ап-х (“X4-P)yz + апу = / (х)
(уравнение Эйлера) приводится к
линейному уравнению с постоянными коэфи-
циентами подстановкой ох4-р = еУ
ДИФЕРЕНЦИЛЛЬНЫЕ УРАВНЕНИЯ
171
Уравнение Бесселя. Линейное уравнение
с переменными коэфициентами вида
х2у"+ху' + (х2 — Vs) у = О
называется уравнением Бесселя. Об-
щее решение его не может быть, в общем слу-
чае, выражено при помощи элементарных
функций.
Одним из частных решений уравнения
Бесселя при заданном \ является бесселева
функция 1-го рода порядка ч:
к\Г 0Ч-/С + 1)
(о функции Г (х) см. стр. 149).
Функция J_,(x) тоже является решением
уравнения Бесселя и, если \ не целое, то
функции (х) и J_v(x) линейно независимы
и общее решение уравнения Бесселя имеет
вид
У = СхЛ (x)+CaJ_y(x').
Если ч—п, где и—целое, то j_„(x) =
= (-1)"Л(х) и в этом случае общее реше-
ние определяется равенством
У — CiJn (х)4-С2Уп (х),
где Уп (х)—бесселева функция 2-го рода,
которая выражается через бесселевы функции
1-го рода при помощи формулы
Между бесселевыми функциями имеют
место следующие основные соотношения:
2
Л (X) (х)- У, (x)Jv_j (х) = — ;
2м ,
Л+1 (х) = — Л (х) —(х);
2\
У,+ 1 (х)= — Уу (X)- (х);
(х) = (х) - Л (х);
У;(х)= yv_j (х)--^- У, (х).
лое) являются элементарными. При помощи
приведённых выше формул они выражаются
через Jj (х) и J , (х), причём
2 “ 2
— sin х;
2 ПХ
J 1 (X) = ]/ — COSX.
~2 V пх
Функции Бесселя целых порядков при
помощи тех же формул могут быть выраже-
ны через J0(x), Ji(x), У0(х), Уг(х). Табли-
цы этих функций даны на стр. 81.
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Преобразование Лапласа
F(p) = J e~pxj(x)dx
о
ставит в соответствие функции /(х) функцию
F(p) параметра р.
В силу соотношений:
J е~рх f (x)dx = pF(p) — /(0);
О
J е-Рх /' (х) dx = p2F (p) — [pf (0)+/' (0)];
о
J e~pX (x) dx =
о
= p" F(p) - [ pn~' / (0) + pn~2 /' (0) + ... 4-
+ p/(n~2) (0)+/<"-1>(0)],
преобразование Лапласа переводит линей-
ное диференциальное уравнение с постоян-
ными коэфициентами
у('°(х) + а1у("-п(х) + у' (х) +
+ ап У (X) = / (X),
в котором искомая функция у(х) удовлетво-
ряет начальным условиям у(0) = у' (0)=...=
(п-1)
= у (0)=0(так называемое нормаль-
ное частное решение), в алгебраическое
уравнение
(рп + й! рп-1 + ... +a„_iP+ a„)Y (р)=Е(р),
где У (р)— результат преобразования Лап-
ласа над функцией у (х), т. е.
оо
У (р) = J е~рх у (х) dx.
о
Разрешая это уравнение относительно
У (р), имеем
pn+atpn '+ ...+an_ip+a„‘
Таким образом, теперь следует найти функ-
цию у(х), зная ее лапласово преобразова-
ние У (р), что при определённых условиях
выполняется однозначно. После того как
функция у(х) найдена, можно, прибавляя
к ней общее решение соответствующего одно-
родного уравнения, найти общее, а следова-
тельно, и любое частное решение данного
неоднородного уравнения.
Как видно из приведённой ниже таблицы,
если правая часть уравнения ; (х) имеет^ в
частности, вид
/ (х) = Р (х) еах sin bx
или
/ (х) = Р (х) еах cos Ьх,
где Р (х) — многочлен, то функция F (р), а
следовательно, и У (р) является правильной
рациональной дробью. У (р) можно предста-
вить в виде суммы простейших рациональных
дробей. Функции, лапласовы преобразования
172
МАТЕМАТИКА
которых имеют такой вид, могут быть най-
дены из прилагаемой таблицы:
Cl
С 2 к. Дх) Н(Р)
1 Л(х)+Л(х) К>(р)+К5(р)
2 С/(х) CF(p)
3 I'M рР(Р)-/(О)
4 4пХх) р” F(p)-[ Р,,~1/(0)+ + р',--2/-(0)+. ..+ +р/(«-2)(0)+7(п-1)(0)]
5 F(p+a)
6 1 р
7 хп 1
п ! р/1-1
8 е—ах р 4- а
9 хп * е-ах 1 _
п 1 <Р+а)"
10 sin ах а р*4-а3
11 cos ах ps±a2
12 а
р2—а2
13 ch ах Р _ р2—а2
14 X sin ах 2а Р
<.Р‘+а‘У
15 -Л-(sin ах—ах cos ах) а£
(р24-а‘Ч*
1 п хп sin ах 2п п !а Рп
(pa + oa)«+1
17 e~axsin Ьх ь _ Ср !-’п) а •’7> 2
18 е—axCos р-1-а Тр \~а)2 ~Ьй
Пример. Найти нормальное частное и общее ре-
шения уравнения
у"' 4* 2у" 4* у' 4* 2у ~ s in х.
Преобразование Лапласа приводит к алгебраи-
ческому уравнению:
<Р> + 2р2 + р + 2) У(р) = --Ь ,
откуда 1
У(р)“ (p*+1)(p’+2F4-7+2) = (Р^+О’Др+г)’
Разложив на сумму простейших дробей, по-
лучим
-1/5р + а/а + ‘/2„
у ~(F+ТУ- + —-р»ДТ-----------+ У-Г2
и, воспользовавшись приведённой таблицей, найдём
нормальное решение:
, . 1 х . ,2 1 .
у(х) “ — • ~2 Sin х 4- у ’ -о- (Sin X — X cos х) —
или
„ Ч ’ -2х 1 7
У W = 25 ' 2х ~ Г5 COS х + - sin х -
— ~ (2 cos х 4- sin х).
Общее решение соответствующего однородного
уравнения имеет еид:
ц = 4- Сй cos х +• С., s in х.
и, следовательно, общее решение данного уравне-
ния:
у = с\ + С2 cos х 4- С;> sin х —
— — (2 cos х 4- sin х).
При нахождении только общего решения урав-
нения вычисления значительно упрощаются, так
как достаточно, учитывая вид общего решения од-
нородного уравнения, иметь в виду только первую
из простых дробей в выражении для У(р).
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
С ПОСТОЯННЫМИ КОЭФИЦИЕНТАМИ
Однородная система 1-го порядка, состоя-
щая из п уравнений с неизвестными функ-
циями Ух(х), у2 (х), уп (х):
аи У1 4’ а12 У 2 4- У и 4“
4~ 411У1 + З12У2+ ~ 0;
а21}’1 +а22у2 + ... +х2пУп~,-
4~ ^21У1_Ь322УзН’ •** +р2/гУ/2 ”
а/п У1 + 7/22 У2 4" +аллУл Д'
4" Г'Л1 У14’г/г2Уи+ ••• 4* $пн У и “
в случае, если
О,
аП2 ••• апп
может быть разрешена относительно у; и при-
ведена к так называемому нормальному виду:
У1 + «ыУ1+«12У2+ ••• +ашУп = 0;
Уз + «21У1+«22У2 + + «2яУл = 0;
Уп + ®П1У 14~«/72У‘>~Ь ••• + аппУ11 — 0-
Хар актер и ст и ческим уравнением
такой системы называется уравнение:
«и + к 012 Ощ
«21 «»» + к ... а2п
= 0.
«Я1
«Л2 ••• «ЯП + к
Всякому действительному корню к ха-
рактеристического уравнения кратности т
соответствует система решений вида:
Vi = А, (х) е'£Х;
у2 = А2 (х) еКХ;
Уп = Ап(х\еКХ,
где А, (х), А2(х), Ап(х) — многочлены
степени не выше т—1. Все коэфициенты
этих многочленов могут быть выражены
через т из них. Для этого следует выраже-
ния для у1г у2, ...,уп, где Аг(х), А2(х),
А„(х) — многочлены степени т—1 с неопре-
ДИФЕРЕНЦИ АЛЬНЫЕ УРАВНЕНИЯ
173
делёнными коэфициентами, подставить в дан-
ную систему диференциальных уравнений.
Оставшиеся неопределёнными т коэфиписн-
тов принимаются за произвольные постоян-
ные.
Всякой комплексной паре а ± Ы корней
характеристического уравнения кратности
р соответствует система решений вида:
у, = еах [Рх (х) cos fex-f-Qj (х) sin ft.x];
у2 = еах [Р2 (х) cos ftx+Q3 (х) sin fex];
уп = еах\Рп (х) cos 6x+Q„ (х) sin fex],
где Рх(х), Р2(х), ...,Р„(х); Qx (х), Q3(x), ...,
Q„(X)— многочлены степени р— 1.
Коэфициенты этих многочленов тем же
способом, как и в предыдущем случае, могут
быть выражены через р произвольных по-
стоянных.
Сложив найденные таким образом для
каждой из неизвестных функций решения,
соответствующие различным корням харак-
теристического уравнения, мы получим об-
щее решение данной однородной системы
линейных диференциальных уравнений, Это
решение будет содержать п произвольных
постоянных.
Пример.
у\ - 2у, - 2у, + у3 = О;
y's + 2уг - 4уа - у, = 0;
у’ + Зу, — 8уа—2уа = О.
Решив характеристическое уравнение:
к —2 - 2 1
2
3
к — 4 — 1 = О,
- 8 к - 2
находим ку — 6, к„ = 1.
Корню fci — 6 соответствует система р сшений:
Подстановка этих решений в систему диферен-
циальных уравнений приводит к равенствам:
4 — 2 А3 + А3 = О.
2 А, + 2 А2 — А3 = 0;
3 Д, — 8 А3 + 4 А, = О,
откуда Аг = О, А3 = 2 А3; положив А3 = Clt имеем
Ах — О, А2 = А3 = 2 Ct.
Корню /с., з ~ 1 соответствуют решения:
У1 = (В,+ Di х) ех J
уя ~ (В2 + D3 х) ех >
у., — (В3 + D3 х) ех .
Для определения В^ и получим уравнения:
— О, — 2Da + D3 =0; Dt — В, — 2Ва+Вя = О;
2 Di — 3Da— D3 = 0; 2 Bi + Di - ЗВ.-Вз « 0;
3 Di— 8Da— Da = 0; 3 В,— 8 Ba+Da — B3= 0,
откуда
Di = 5 Cgj Da ~ CaJ D3 = 7 Ca;
Bi == 5 C3 —• 6 Ca; Ba = C8; B3 = 7 C3 - 11 C8,
и общее решение системы таково;
Vi = (5 С3 — G С2 -г 5 Са х) ех ;
У , = С,е6Л + (С3+Сах) ех ",
Уз = 2 С,еЙЛ + (7 С, - 11 Са + 7С,х) ех .
Если Fx(x), У2(х). ..., Y„(x) — какая-ли-
бо система частных решений неоднородной
системы:
У1 "Ь ДХ 1У1 + а12Уг •• • + а1пУп = /1 I*)»
Уг + а21У,1 + и22У» 7~ ... + Й2ЛУЛ= /а (х);
У„ + ал1У1+ йлаУа+ ... + аппУп =
а
Ух — Ух (^> Сх,..., Сл);
у2= у3(х,С1, ...,Спу,
Уп= уп{х, Сх,
—общее решение соответствующей! однородной
системы, то обшее решение данной неодно-
родной системы имеет вид;
Ух = У1 (x,Cx, ...,С„) 4- Г, (х),
у2 = у2 (x,Clt ...,С„)+ У2(х);
уп=- УгЛХ’Ск :-<Сп) + Г„(х).
Для отыскания общего решения неодно-
родной системы по методу вариации произ-
вольных постоянных следует в выражениях
для у,, у2, ...,ул, взятых из общего решения
соответствующей однородной системы, заме-
нить произвольные постоянные Сг, С2, ..., Сп
через неизвестные функции Сх (х), С2 (х), ...,
С„ (х). После такой замены подстановка
Ух,у2, ...,ул в данную неоднородную систему
диференциальных уравнений приводит к
алгебраической линейной системе уравнений
для Cj (х), С2(х), ..., Сп(х), при помощи ко-
торой можно определить все неизвестные
функции Сх (х), С2 (х)....С„(х) (в выраже-
ние для каждой из них войдёт при этом
одна произвольная постоянная).
Пример
у[ + 8 у, — з у, = 5
У2 + 18 у,— 1у3 = 12 е~х.
Общее решение соответствующей однородной
системы:
Ух « Ci6x -I- Са е“2 х;
у, = 3 С,ех + 2Сге- 2х.
Частное решение неоднородной системы ищем
в виде
Yi = А е~~х, Ув = А2 е~~х.
Подстановка в систему дает:
— Ai е~х + 8Ai е~ х — 3 А3е~х = 5e~xt
— А2 е~~х + 18 AjC-х — 7 Аяе~х =12 е~~х»
или
7Ai — ЗА2 = 5; 9Ai — 4А8 = 6,
откуда
Аг = 2, А2 = 3
и
у, = 2е~х, Уа= Зе~х.
Следовательно, искомое общее решение:
У1 = Ci сх + С2 + 2е-х;
у3 = ЗС, ех + 2С,е—2х + Зе^х.
Можно применить к решению той же системы
метод вариации произвольных постоянных.
Положив
У1 - с, (х) ех + Ct (х) е~ 2х,
у, =ЗС, (х) ех + 2 Cs (х) е-2*.
174
МАТЕМАТИКА
после подстановки в систему, получим, произведя
упрощения:
С' ех + С* е~~^х = 5е““х;
3 с' ех + 2с'г е~2х = 12 е~х,
откуда
с'-2е~2х, + -3сх
И __
С, ~ - е~ 2х + С„
С, = Зех + С„
Общее решение, таким обрвзом, имеет вид:
у, = (— е~~2х + С?) ех + (3 ех + С2) е~2х‘,
у, = 3 (— е~~2х + С,) ех + 2 (з ех + Сг) <г—2х,
или ________ _
у, = С, ех + Са е~~2х + 2е—х;
у, ЗС? ех + 2С, е~2х + Зе~х.
Всякая система диференциальных урав-
нений выше 1-го порядка может быть
приведена к системе 1-го порядка. Так, на-
пример, система
ап у, 4-1X12 У2 + Р11У: +₽12У2 + 711 У1 +
+713 У2 + rjii У1+®1з Уг — О,
а21 У1 + «22 Уз +Р21У1 +Р22У2 +Т21 У] +
+ ?22 Уз + 821У1+822Уз = О
равносильна системе:
У1 = и Г,
и, = у,;
Уз = и2;
«з = у2;
“и V1 + «12W2 + ₽11 у1 + ₽12 У2 + 711 “1 +
, + 712 «2 -И 811 У1+В12Уз = 0>
«21 У1 + «22^2 + ₽21 У1 + ₽ 22 У2 + 721 U1 +
+ 722 И2 + 821 У1 + 822 Уз = 0.
УРАВНЕНИЯ В ЧАСТНЫХ
ПРОИЗВОДНЫХ
ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Для отыскания общего решения линей-
ного однородного уравнения
dz dz
ХДХрХз......xn)fa +xe(xi>Xi,-., хп)^ +
4- ... 4- Хп(х1,х2,..., хп) — О
составляем систему обыкновенных диферен-
циальных уравнений:
</Х1 _ </Х_2 _ _ <^п
Xt Х2 хп
Если общее решение этой системы пред-
ставить в виде:
?i(х,, х2, ...»xn) = Cjj
?з (Xi, х2,..., хп) ~ С2;
fn— 1 (Xl> Х1> •••’ Хп) = С71—1,
то общий интеграл данного уравнения в
частных производных выразится равенством:
2= Ф(<Р1» ?2> •••> ?п-1)»
где Ф — произвольная функция.
В случае неоднородного уравнения
„ dz
xi (Х1, х2,...,xn, z) 4- ... +
, dz
~1~ Хп (х,, Х2, ..., Хц, Z) = Z (Xj, Х2, ...,Хи, z)
составляют систему:
dXi _ _ dx„ _ rf z
X, = •••= Xn~ Z •
Её общее решение имеет вид:
fi (Xi> х2, ...» xn, г) = Сх",
fdxx, х2, ...,х„, Z) = С2;
(Xi, Х2, ..., Xn, Z) — Сп,
и общий интеграл неоднородного уравнения
выражается неявно при помощи равенства
Ф<?1> ?2» ••»?«) = О,
где Ф — произвольная функция.
В частности общий интеграл уравнения
dz
= / (Х,У,2)
имеет вид:
? [х,у,2, С(у)] =0,
где С(у)—произвольная функция, а
<Р (x,y,z, С) = О
общее решение обыкновенного диференциаль-
ного уравнения
dz
в котором у рассматривается, как пара-
метр.
ЛИНЕЙНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
В случае двух независимых переменных
линейное уравнение второго порядка имеет
вид:
d2z dzz ^d‘-z dz ,
A dx2 + 2 B dx dy + C dy2 + B dx
dz „ „
4- £ + Fz = G (x, y),
где A,B,C,D,E,F могут зависеть от x
и у.
Интегральные кривые обыкновенного
диференциального уравнения
A dy2 — 2В dx dy+Cd& = О
или
dy _ В ± 7/В2 — АС
dx~ А
называются характеристиками дан-
ного уравнения в частных производных.
Если АС — В2 < 0, уравнение принад-
лежит к гиперболическому типу и
имеет два семейства действительных харак-
теристик.
Если АС — В2 = 0, оба семейства харак-
теристик совпадают и уравнение принад-
лежит к параболическому типу.
Если АС — В2 > 0, характеристики мни-
мые и уравнение принадлежит к эллипти-
ческому типу.
ДИФ ЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
175
Приведение к канонической форме. Урав-
нение гиперболического типа приводится к
каноническому виду:
d2z dz dz
—=7- + а -У b - = + cz = g ( х, у)
dx dy dx dy
при помощи замены
Х = <р(Х,у), у = ф(х, у),
где у (х, у) = const и ф (х,у) = const — урав-
нения характеристик.
Уравнение параболического типа можно
привести к виду:
o-z dz dz - —.
" г:= + 6 + cz = g (х, у)
дх2 дх ду
с помощью преобразования
х = <р(х,у), у = Ф(х,у),
где ф(х,у) = const—уравнение характери-
стик, а ^(х,у) — произвольная функция,
не выражающаяся через ф(х,у).
Уравнение эллиптического типа прини-
мает каноническую форму:
d2z
дх2
d2z dz . dz
4- и = Ь —
ду2 дх ду
g(x, у)
после замены
Х.= <?(Х, у), у = ф(х,у),
где <р (х, у) ± / ф (х, у) = const — уравнения
характеристик.
Задача Коши. Метод Римана. Требуется
найти решение однородного уравнения гипер-
болического типа:
d2z dz dz
дхду + а dx + b dy + cz==Q’
если вдоль некоторой кривой Г (не являю-
щейся характеристикой) известны значения
искомой функции z и одной из её частных
производных (задача Коши).
Для решения этой задачи следует найти
функцию Римана U (х, у; 5, т(), зави-
сящую от четырёх переменных х,у,$,у]и
определяемую следующими условиями:
1) как функция переменных Е и т], функ-
ция и должна удовлетворять так называе-
мому сопряжённому уравнению:
д2и д(аи) д (Ьи)
дт\ +с« = °;
2) при Е = х должно иметь место тожде-
ство ди
- а (х, т)) и
и при 1] = у аналогично
du
= Ь(Е,у)и;
3) и = 1 при £ = х, V] = у.
После того как функция Римана найдена,
решение задачи Коши даётся равенством:
(uz)P+ (uz)Q Г
z,„ =-------2~.... + J uz (а — & dE) 4-
1 f ! dz dz \
+ T J “ dr‘ ~ ТЕ d ') +
PQ
1 Г / du du \
+ ~2 J
PQ
Фиг. 149
Здесь E и — текущие координаты вдоль
кривой Г (фиг. 149), Р и Q — точки пересе-
чения с кривой Г пря-
мых, параллельных осям,
проведённых через точку
М(х,у). Значения г(Е,У
и одной из частных про-
изводных — или
дЕ di\
вдоль Г известны из усло-
вий, и, следовательно, дру-
гая частная производная тоже может быть
определена.
Пример 1. Телеграфное уравнение
после подстановки г1= е °9 -z
d9z d*z ( 1
— а ая — 4- Ьгх; | а* «= —,
dt9 дх9 у а0
принимает вид:
и после замены
х« у(х 4-аО, у « -- (х — ai)
приводится к канонической форме:
дх ду 4
Функция Римана и (х> у\ Z, т\) должна удов-
летворять условиям: — “ 0 при £ =» х> —- « 0 при
— у и и ( Xt у J х, у) = 1.
Функцию Римана ищем в виде
и = V (y^(i — х) (ц — у))-
Обозначив у (£ — х) G) — у) через X и подставив
(X) в диференциальное уравнение (которое совпа-
дает в данном случае с ему сопряжённым), получаем
для определения (X) уравнение Бесселя (стр. 171)
нулевого порядка:
9' W + 4- 9' (*) + 9 (*) - о,
А
и, следовательно, можно принять
и (х, у ’, Е, ч]) = J, (у^(5 — х) (ч) — у)).
Если начальные условия такоаы, что z = f (х) и
Г(х) при t = О (в плоскости х, у прямой t=0
соответствует биссектриса координатного угла и
вдоль неё £ то, подставив в формулу Римана
найденную функцию и, воспользовавшись началь-
ными условиями и возвратясь к переменным х и
найдём
П f(x + at)+fix-at)
- к* > * / Q
х bat
- -2L j
x- at
J, [ " /G-xr-a-f]
/(E - x)’ - a’t«
x+at
+ a J F © j° [т V J dt.
x—at
Пример 2. Уравнение свободных колебаний стру-
ны имеет вид:
d9z _ d9z
——- = а9 — .
dt3 дх9
Характеристиками этого уравнения являются
прямые:
х — at = const
и
X 4- af = const.
Положив
х = х — at, у » х + at.
175 МАТЕМАТИКА
придём к канонической форме:
дх ду
Общее решение этого уравнения (получаемое с
помощью квадратур): _ _
z = О, (х) + 0а (у),
И ли
Z == ог (х - at) + 62 (х + at),
г де О] и 02 — произвольные функции.
Решение, соответствующее начальным условиям
z = / (х), —= F (х) при t = 0, имеет вид (после воз-
вращения к переменным х и t):
х + at
, =. /Ч - «О + / (* + аО + Д. J р
х — at
Задача Дирихле. Метод Грина. Требуется
найти в некоторой области функцию, удо-
влетворяющую однородному уравнению
эллиптического типа:
д-z д-z dz dz
dx2 + + а дх +bd~ + cz = О
и принимающую на границе этой области
заданные значения (внутренняя за-
дача Дирихле).
Для решения задачи Дирихле следует
найти функцию Грина G (х, у; т,),
определяемую следующими условиями:
1) как функция 5 и т;, функция G должна
удовлетворять сопряжённому уравнению
дЮ d*G д (aG) д (bG)
+ ----dl-----^d:T+l:G^0’
всюду, кроме точки ij = х, -q = у;
на границе данной области (5 и г] —
текущие координаты на границе)
G (х, у; у = 0;
3) функция G (х, у; g, у In г [где г =
= V (5—х)2 + (т,— у]2 непрерывна в рас-
сматриваемой области вместе со своими
производными 1-го и 2-го порядков.
После того как функция Грина найдена,
решение задачи Дирихле выражается фор-
мулой
1 С д
*(£, У G (х, у; 5, yds,
г
где Г — контур, ограничивающий данную
область, ds — диференциал дуги на этом кон-
туре, п—направление внутренней нормали
к контуру.
Уравнение Лапласа. Решение задачи
Дирихле для круга и шара. Функции, удов-
летворяющие уравнению Лапласа
д*г дг2
dx2 + ду* = °
(на плоскости) или
d2u д*и д*и
дх2 + ду* + dz2 = 0
(в пространстве) называются гармони-
ческими.
Уравнение Лапласа совпадает с ему со-
пряжённым.
Функция, дающая решение задачи Ди-
рихле для круга (т. е. гармоническая внутри
круга и принимающая на окружности этого
круга заданные граничные значения) может
быть выражена при помощи и нтеграла
Пуассона:
2 т:
г (х. у) = 2^ J
о
где р и 6 — полярные координаты точки
(х, у), если полюс находится в центре дан-
ного круга (x = pcosO, y = psinO), R —
радиус этого круга, z (с) — заданная на ок-
ружности круга функция, определяющая
граничные значения функции z (х, у).
Формула Пуассона, определяющая значе-
ние гармонической функции внутри шара
через её граничные значения на сфере, имеет
вид:
и (М) = ~ f С и (Р) as,
(S)
где (S) — поверхность сферы, функция н(Р)
определяет заданные значения функции и на
поверхности сферы, р — расстояние точки М
от центра шара, R —радиус шара и г — рас-
стояние между точками М и Р.
Метод Фурье. Уравнение теплопровод-
ности. Во многих случаях удаётся найти
частные решения линейного однородного
диференциального уравнения в частных про-
изводных в виде произведения функций,
каждая из которых зависит только от одного
аргумента и является решением некоторого
обыкновенного диференциального уравнения.
Взяв линейную комбинацию полученных
такил! образом частных решений (являю-
щуюся также решением данного уравнения),
которая в результате предельного перехода
даёт некоторый ряд или интеграл, являю-
щийся решением уравнения1, можно опре-
делить из начальных условий остающиеся
неопределёнными величины и функции.
Метод Фурье можно применить, к отыска-
нию решения уравнения теплопроводности
(уравнение параболического типа):
du а о1 и
dt = а2 дх* ’
удовлетворяющего начальному условию:
и = / (х) при ( == 0.
Положив и = Т (() • X (х) и подставив в
V X"
данное уравнение, получаем: или
Т' X"
= — X2, %- = — X2, откуда
Т = е х‘а,/ ; X = А (X) cos X х + В (X) sin Хх,
и = е_х’а’‘« [А (X) cos Хх + В (X) sin X х].
Проинтегрировав по X, получим решение
уравнения теплопроводности в виде
и (х, Г) =
= J е~ [А (X) cos X х+ В (X) sin X х] dX.
— ОО
I Следует, конечно, проверить, приводит ли дей-
ствительно указанный предельный переход к решению
данного уравнения.
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
177
Начальному условию и = / (х) при t = О
можно удовлетворить, положив
оо
А (7) = 2^; J / (5) cos X? d',
—ОО
В (X) =
оо
/ (5) sin Ц
—оо
(см. интеграл Фурье, стр. 163) и, следова-
тельно, искомое решение имеет вид:
00 оо
и (х, t) = / (5) е- cos X (5-х) </л
—ОО —оо
или (стр. 147, формула 17)
00 (^Х)’
fl — 4 a2t
f (5) е d 5.
i a V tz t
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Расстоянием между двумя кривыми
у = у (х) и у = у (х) на отрезке а < х < а
называется наибольшее значение величины
I у (х) — у (х) I на этом отрезке; е-окресдно-
стью кривой у = у (х) называется совокуп-
ность кривых у = у (х), расстояния кото-
рых от кривой у = у (х) меньше е (фиг. 150).
ПРОСТЕЙШАЯ ЗАДАЧА
Дана функция F (х, у, у'), зависящая от
трёх аргументов х, у и у', которая, вместе
со своими частными производными до второго
порядка включительно по всем аргументам,
непрерывна при всех значениях х и у, при-
надлежащих некоторой области (S-) пло-
скости OXY, и при всех значениях аргу-
мента у'.
Требуется найти в области (S) дугу, сое-
диняющую точки А (а, Ь) и В (а, (3) такой
кривой у = у (х) [функция у (х) непрерывна
вместе со своей производной у' (х) на отрезке
а < х < а], которая даёт интегралу
I = j F (х, у, у') dx
а
наибольшее или наименьшее значение по
сравнению со всеми кривыми у = у (х)
некоторой е-окрестности кривой у = у (х)
(сильный экстремум)1.
Кривая у = у (х), дающая экстремум инте-
гралу /, должна удовлетворять уравне-
нию Эйлера
<1F _ d (dF\
ду dx ( ду') ~
или
d2F d’lF d2F dF
$y'‘ y dy ду’ У + dx dy' dy ~ °'
Уравнение Эйлера — обыкновенное дифе-
ренциальное уравнение 2-го порядка; его
общее решение у = у (х, Cj, С2) зависит от
двух произвольных постоянных, которые
должны быть определены так, чтобы кривая
проходила через точки А (и, Ь) и В (а, р).
Интегральные кривые уравнения Эйлера
называются экстремалями.
Для того чтобы
тремум интегралу
вдоль экстремали выполнялось условие
экстремаль давала экс-
/, необходимо, чтобы
Лежандра:
d2F
> 0
dy’
(в
или
случае минимума)
d2F
T7V <°
dy'
(в случае максимума).
Простейшие достаточные условия для
того, чтобы экстремаль давала минимум
(максимум) интегралу, следующие:
1)
d2F d2F / d2F V
dy’’ dy2 Idydy'l
для всех значений х и у, принадлежащих
некоторой е-окрестности экстремали и для
любых значений аргумента у'.
Пример 1, Среди всех дуг, имеющих концы в дан-
ных точках А (а, &) и В (а, 3), найти ту, которая при
вращении около оси ОХ образует поверхность с ми-
нимальной площадью.
Здесь
а
' = 2Ч yV"i+y”dX,
а 9
уравнение Эйлера имеет вид:
УУ- , у-а .
Его общее решение даёт семейство экстремалей:
. х —С.
1 Кривые у — у(х), о которых идёт речь, должны
удовлетворять тем же требованиям, что и кривая
у =» у (х), т. е. должны проходить через точки А н В
и функции у (х) вместе со своими производными
у' (х) должны быть непрерывны на отрезке
а < х < а.
Постоянные С, и С8 должны быть определены из то-
го условия, что кривая проходит через точки А (а. д)
и В (а, 3).
Пример 2. Определить траекторию, соединяющую
точку А с точкой В, двигаясь по которой под дей-
ствием силы тяжести, матеоиальная точка пройдёт
путь АВ в кратчайшее время (задача о брахи-
стохроне).
Принимая точку А за начало координат и обоз-
начая координаты точки В через (xt, УО» получаем:
ds _______
V “ dt = /2 gy ; ds =. V t + dx;
1 +У'
1Z2
12 Гом I
178
МАТЕМАТИКА
Составив и решив уравнение Эйлера, найдём урав-
нения искомой кривой:
х « Сг (и — sin и) + С8;
у == С, (1 — cos u).
Кривая проходит через начало координат и, сле-
довательно, Са = 0; постоянную Ci можно найти,
подставив в уравнения кривой координаты точки В.
Найденная кривая — циклоида.
ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
В более общем случае требуется найти
экстремум интеграла
Xl
/ = J F (х, у, у') dx,
х,
причём концы рассматриваемых дуг должны
находиться на заданных кривых: у = <р (х) и
у = ф (х) (х0 и Xj — абсциссы концов этой
дуги тоже подлежат определению).
В этом случае уравнение искомой дуги
у — у (х) должно, кроме уравнения Эйлера,
удовлетворять дополнительным условиям:
dF
F + (<(,'_ у') — = 0 при х = х.;
dF
F + (Ф' — /) jp = 0 пРи х = хи
(условия трансверсальности).
Условия трансверсальности устанавли-
вают зависимость между угловыми коэфи-
циентами касательных к экстремали и к
граничным кривым в точках х = х0 и х = хг.
В случае, если функция F имеет вид:
F (х, у, у') = А (х, у) К1+ у'а ,
эти условия требуют ортогональности экстре-
мали к этим кривым. Так, например, обстоит
дело в задачах о кратчайшем расстоянии
между двумя линиями, между точкой и
линией, где требуется дать минимум инте-
гралу Х1
J/1 + у'3 dx .
х„
Если один из концов дуги неподвижен,
то условие трансверсальности должно соб-
людаться только для другого конца.
ПРОСТРАНСТВЕННАЯ ЗАДАЧА
Требуется найти дугу пространственной
кривой у = у (х), z = z (х), соединяющую
точку А (а, Ь, с) с точкой В (а, р, 7) и даю-
щую экстремум интегралу
J = J F (х, у, У', 2, Z') dx.
а
Искомая кривая определяется решением
системы:
dF __ d / dF \
dy dx уду' у “ ’
dF __ d_ (dF\ _
dz dx ydz' у ~~
при начальных, условиях, следующих из
того, что кривая должна проходить через
точки А и В.
СЛУЧАЙ ПРОИЗВОДНЫХ ВЫСШИХ ПОРЯДКОВ
Если решается задача об экстремуме ин-
теграла
а
/ = j F (х, у, у', у".... у(,!)) dx,
а
то уравнение Эйлера принимает вид:
dF _ d /dF\ d2 /dF\
dy dx \dy'y ‘ dx2 Idy" у ~ +
dn I dF \
Это уравнение имеет порядок 2 и и его
общее решение у = у (х, Сх, С2, . . ., С2п) со-
держит 2 п произвольных постоянных." Про-
извольные постоянные определяются из того
условия, что в точках х = а и х = а заданы
значения искомой функции и её производных
до порядка п—1 включительно.
ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА
Среди функций у = у (х), для которых ин-
а
теграл К = J G (х, у, у') dx принимает за-
а
данное значение I и для которых у (а) b
и у (а) = р, требуется найти такую функцию
у = у (х), которая даёт экстремум интегралу
I = J F (х, у, у') dx.
а
Для решения изопериметрической задачи
следует искать обычный (безусловный) экс-
тремум интеграла
L = J(F + kG) dx,
а
где — неопределённая постоянная.
Проинтегрировав уравнение Эйлера для
интеграла L, найдём у = у (х, Ct, С„, X).
Постоянные Сх, С2 и X определяются из ус-
ловия К = I и из начальных условий.
УСЛОВНЫЙ ЭКСТРЕМУМ
Требуется найти кривую у = у (х), г—г (х),
соединяющую две данные точки А и В,
которая среди всех кривых, расположенных
на данной поверхности <р (х, у, z) — 0 и
удовлетворяющих тем же начальным усло-
виям, даёт экстремум интегралу
а
/ = J F (х, у, z, у', z') dx.
« >
Для решения этой задачи требуется со-
ставить функцию
Ф (х, у, z, у', z') = F + л (х)
и искать безусловный экстремум интеграла
J Ф dx.
а
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
179
Уравнения Эйлера дадут систему:
dF , dj>________ d /dF \
dy + 1 dy~dx\dy!/ = 0;
dF d<p______ d /dF\
dz + 1 dz dx (dz' ] = 0
с тремя неизвестными функциями: у (х),
Z (х) и X (х), которая совместно с соотноше-
нием ср (х, у, z) = 0 позволит определить эти
функции, причём решение будет содержать
две произвольные постоянные, определя-
емые из начальных условий.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА
ПЛОСКОСТИ
МЕТОД КООРДИНАТ НА ПЛОСКОСТИ
Между всеми точками плоскости с одной
стороны и парами чисел, взятых в опреде-
лённом порядке, с другой стороны, можно
установить взаимное соответствие при по-
мощи метода координат. Наиболее "употре-
бительны две координатные системы: п р я-
моугольная декартова и поляр-
н а я. Реже применяются косоугольная
и другие системы координат.
х
Фиг. 151 Фиг 152
Декартова прямоугольная система коор-
динат. Две взаимно-перпендикулярные пря-
мые ОХ и ОУ на плоскости (фиг. 151) назы-
ваются координатными осями (ось
ОХ — осью абсцисс, ось OY — о с ь ю
ординат), точка О пересечения осей — н а-
чалом координат. Если выбрать длину
некоторого отрезка за единицу масштаба и
положительное направление на оси ОХ—впра-
во от начала координат, а на оси ОУ— вверх,
то положение любой точки М на плоскости
может быть определено при помощи двух
чисел х и у, соответственно выражающих
расстояния от точки М до оси ординат и до
оси абсцисс в выбранном масштабе. Запись:
М (х, у).
Числа х и у называются координа-
тами (абсциссой и ординатой)
точки М и берутся с определённым знаков
(+) или (—), в зависимости от того, сов-
падают ли направления отрезков О А и ОВ
с положительным направлением на оси
ОХ и OY или не Совпадают.
На фиг. 152 дана схема распределения
знаков координат во всех четырёх к в a fl-
pa н т а х, на которые координатные оси делят
всю плоскость.
Преобразование прямоугольных коорди-
нат. Переход от одной прямоугольной си-
стемы координат к другой состоит из двух
преобразований:
1) преобразование параллельного пере-
носа осей (фиг. 153), при котором коорди-
наты х ( = О А) и у ( = AM) точки М в си-
стеме OXY связаны с координатами х' и у'
той же точки М в системе OX'Y' соотноше-
ниями:
х = х' + а;
у = у' + Ь,
где а и b—координаты нового начала коор-
динат О' в системе координат ОХУ;
2) преобразование поворота осей (фиг. 154),
при котором координаты х (=ОА) и у (=АМ)
в системе OXY связаны с координатами
х' ( = ОВ) и у' ( = ВМ) той же точки М
в системе OX'Y' соотношениями:
х = х' cos а — у' sin а;
У = х' sin а + у' COS а,
где а — угол между осью ОХ' и осью ОХ.
Поэтому в общем случае преобразования
координат (фиг. 155) имеют место соотно-
шения:
х = х' cos а — у' sin а + а;
у = х' sin а -|- у' cos а
Косоугольная система координат. Угол
между осями координат называется коор-
динатным углом. Если выбрать коорди-
натный угол о острым или тупым, то мы
получим так называемую косоугольную
систему координат (фиг. 156). За координаты
х и у точки М в этой системе принимаются
длины отрезков ОА и ОВ, отсекаемых на
осях прямыми, проходящими через точку М
и параллельными координатным осям.
Точка М с косоугольными координатами х
и у записывается, как и в прямоугольной
системе, в виде: М (х, у).
Полярная система координат. Полу-
прямая ОХ называется полярной осью,
12*
МАТЕМАТИКА
180
точка О на ней —полюсом (фиг. 157).
Если выбрать длину некоторого отрезка за
единицу масштаба, то положение любой
точки М на плоскости определяется двумя
числами: радиусом - вектором р = ОМ,
выражающим длину отрезка ОМ (в выбран-
ном масштабе), и полярным углом
МОХ (в радианной мере). При этом
полярный угол считается положительным,
если он отсчитывается от полярной оси в
направлении, обратном движению часовой
стрелки» и отрицательным — в направлении
движения часовой стрелки. Числа р и ср на-
зываются полярными координа-
там и точки М. Принято записывать1 точку
М с полярными координатами р и и в виде
М (?, ср).
Связь между декартовыми прямоуголь-
ными и полярными координатами. Если вы-
брать полярную систему координат таким
образом» чтобы её полюс совпал с началом
Фиг. 157
Фиг.
координат прямоугольной координатной
системы, а полярная ось совпала с положи-
тельной частью оси абсцисс (фиг. 158),
то между прямоугольными координатами
х ( = ОА) и у(—АМ) и полярными коорди-
натами р(=ОМ) и <?( = /. АОМ) точки М
имеют место следующие соотношения, даю-
щие возможность перехода от прямоугольной
системы координат к полярной и обратно:
х = р cos ср; у = р sin ср;
р = Гх2 + у2; ср = arc tg -- .
НЕКОТОРЫЕ ПРОСТЕЙШИЕ ЗАДАЧИ
НА ПЛОСКОСТИ
Расстояние между двумя точками. В
прямоугольной системе координат расстоя-
ние между двумя точками плоскости
М1(«1> У1) и Ма (х2, у2) (фиг. 159) определяется
по формуле __________________
d = У(х2— х,)г+ (у2— yj2.
Фиг. 160
В частном случае, когда одна из точек
(например, М2) совпадаете началом коорди-
нат (фиг. 160), имеем
<* = ]/" xi + У?
1 Можно условиться придавать координате р
также и отрицательные значения, считая точку
(—р. <₽) совпадающей е точкой (р, ? + п).
В косоугольной системе координат рас-
стояние между двумя точками Мг (xv у\) и
М2(х2, у2) (фиг. 161) определяется подфор-
муле
rf=/(x2_xI)2+(y2_yi)2_2 (x2-X1)(y3-y1)COSW,
где w — координатный угол.
В полярной системе координат расстоя-
ние между двумя точками М2 (рг, ср2) и
М2 (р2, у2) (фиг. 162) определяется по
формуле
</ У р^+ Рз —2 р1?2 008(^2—?!).
Деление отрезка прямой в данном отно-
шении. Прямоугольные координаты точки
Р (х, у), делящей расстояние между началь-
ной точкой М1(х1, У1)и конечной М2 (х„, у.,)
я М1А \
внутренним образом в отношении р-щ = К
(фиг. 163), определяются по формулам:
хх 4~ X х2 _ ух _|_ х у.
х = 14-х ; у = -урТ•
В частном случае, когда точка Р нахо-
дится посредине (X = 1), формулы деления
отрезка МХМ2 пополам принимают вид:
- _ Х1 + *2 -, _ У1 + Уз
х- 2 , У - 2
Для деления отрезка внешним образом
(точка деления Рх) применяются те же
формулы, но X принимается отрицательным.
Площадь треугольника. Площадь тре-
угольника, заданного своими вершинами:
A (хх, ух), В (х2, у2) и С (х3, Уз) (фиг. 164),
определяется по формуле
(Уз—Уз)+Х2( Уз—У1)+Х3 (У1~У2)
или посредством определителя
I
1
Х1 У1
*2 Уз
Х3 Уз
2 8
А
1
_1
• 2'
При этом положительным значениям S.
соответствует обход вершин треугольника А,
В и С в направлении движения против ча-
совой стрелки, а отрицательным — по часовой
стрелке.
АНАЛИТИЧЕСКАЯ геометрия
181
В частном случае, когда одна из
вершин (С) совпадает с началом координат
(фиг. 165), формула принимает вид:
<xi у* — х*
или
с = £ |Х1 У1
л 2 Х2 Уз
Площадь многоугольника. Площадь много-
угольника, заданного своими вершинами:
Лх (хп П), А2 (х2, у2), Д3 (х3, Уз)>- ..Мл (хп, уп),
определяется по формуле
S = 4 (*i — *г) (У1 + Уз) + (х2 — х3) (у2+у3)+
+ (х8-Х4) (у3+у4)+.. . + (Хл-Х1) (У„+У1) .
ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ
Уравнение F (х, у) = 0 или у = / (х),
:вязывающее две переменные х и у, яв-
ляется уравнением некоторой действи-
тельной или мнимой линии (геометрического
места точек) в декартовых координатах, ес-
ли декартовы координаты любой точки этой
линии удовлетворяют данному уравнению
(т. е. обращают его в тождество при под-
становке вместо х и у), а координаты всех
точек, не принадлежащих линии, не удов-
летворяют этому уравнению.
Порядком кривой называется степень
уравнения этой кривой (если это уравнение
алгебраическое).
Подобно этому уравнение F (р, <р) = 0 или
р= / (tp), связывающее две переменные р и <р,
геометрически представляет собой также
линию в полярных координатах.
ПРЯМАЯ ЛИНИЯ
В декартовой системе координат прямая
линия выражается аналитически уравнением,
линейным относительно координат х и у.
Различают следующие основные формы урав-
нения прямой.
Общее уравнение прямой:
Ах + By + С = О,
где коэфициенты А, В и С — постоянные
величины. При С = 0 прямая проходит через
начало координат, при В=0 прямая парал-
лельна оси OY, а при А = 0 — параллельна
оси ОХ (фиг. 166).
Уравнение прямой с угловым
к оэфи цие н том:
у=кх + Ь,
где угловой коэфициент к равен
тангенсу угла, образованного прямой с по-
ложительным направлением оси OX (&=tgc?),
а параметр ft, называемый также на чаль-
ной ординатой, есть отрезок, отсекаемый
прямой на оси OY, взятый со знаком (+), если
он расположен над осью ОХ, и со знаком (—)
в противном случае (фиг. 167). Уравнение
прямой с угловым коэфициентом может изо-
бражать любую прямую, за исключением
прямой, параллельной оси OY (к >=tg^ = оо).
Чтобы общее уравнение прямой, не парал-
лельной оси OY, привести к уравнению с
угловым коэфициентом, нужно его решить
относительно у:
А С
У~ В Х~ В
/ А С\
Г В :6 = — в)'
Уравнение прямой в отрезках,
отсекаемых на координатных осях:
а т b
где параметры а и Ь, взятые со знаком (+)
или (—), суть длины отрезков, отсекаемых
прямой на координатных осях (фиг. 168).
Если b — оо (прямая параллельна оси OY),
то уравнение прямой х = а; если а — оо (пря-
мая параллельна оси ОХ), то уравнение
прямой у = Ь.
Нормальное уравнение пря-
мой:
х cos а + у sin а — р = О,
где а—угол, образованный перпендикуляром,
опущенным из начала координат на прямую,
Фиг. 169
с положительным направлением оси ОХ, а
параметр р — ОР — длина этого перпендику-
ляра (фиг. 169).
Общее уравнение прямой Ах + By + С=0
может быть приведено к нормальному виду
путём умножения на нормирующий
МАТЕМАТИКА
182
1
множитель X = ± г > гДе знак
у А2 + В2
в правой части выбирается таким образом,
чтобы он был обратен знаку свободного
члена С.
Между коэфициентами А, В и С и пара-
метрами а и р имеют место соотношения:
А В
ИЛИ
cos а == ±
, sin а = ± —7 — ,
/ А2+В2
С
Р= * / А2 + ВГ
В полярной системе координат уравнение
прямой, не проходящей через полюс (фиг.
170), имеет вид:
Xi У1 1
х2 у2 1 = 0.
ха Уз 1
3. Угол 0 между двумя прямыми, задан-
ными уравнениями в общем виде:
А1х-|-В1у-|-С1 = 0 и А2х + В2у + С2=0,
определяется по формуле
tg 0 = А1Вз.~ A2Bi
АХА2+ВХВ2
Угол 0 отсчитывается от первой прямой
ко второй в направлении против
часовой стрелки (фиг. 174),
= Р
р COS (<р — а) ’
где р — длина перпендикуляра, опущенного
из полюса на прямую, а — угол между этим
перпендикуляром и полярной осью;<р=<в0—
уравнение луча, выходящего из полюса
и образующего с полярной осью угол
(фиг. 170).
То
движения
левыми
о
Фиг. 170
Ниже приводятся формулы, для решения
некоторых, наиболее часто встречающихся,
задач на прямую линию.
1. Уравнение прямой, проходящей через
данную точку Mx (хх, ух) в заданном направ-
лении (фиг. 171):
У — У1 = к (х — xi),
где /с —угловой коэфициент (/с = tg<p).
Если рассматривать угловой коэфициент к
как произвольный параметр, то это урав-
нение представляет собой уравнение пуч-
ка прямых, проходящих через точку
Mi (хх, ух), называемую центром пучка
(фиг. 172).
2. Уравнение прямой, проходящей через
точки Mi (хх, ух) и М2 (х2, у2)
коэфициентами:
у = kt х + bi и у = к2 х + Ь2,
то соответствующая формула принимает вид:
к з ki
Условие параллельности двух прямых:
Ах , t
В~„ ИЛИ к1 “
Условие перпендикулярности двух пря-
мых:
1
АХА3 + ВХВ2 = 0 или к2 =— .
4. Расстояние d= MtN от точки Мх (хх,ух)
до прямой, заданной нормальным уравне-
нием
2 —
X COS a + у sin а — р = О,
определяется по формуле
d = ± (хг cos а -|- ух sin а — р)
(в левую часть нормального уравнения пря-
мой надо подставить вместо текущих коор-
две данные
(фиг. 173):
У — У1
Уз~У>
х
х —хх
или
х2 Хх 1
У
У1
Уз
= 0.
Фиг. 175
Фиг. 174
Угловой
коэфициент в этом случае опре-
деляется по формуле
Х2 — Х1 '
Условие нахождения трёх точек Мг (хх, ух),
Mg (х2, у2) и Мя (х3, уз) на одной прямой:
Уз ~~ Ух _ х3 — Xi
Уз ~У1 Х2 _ Х1
динат координаты данной точки; если прямая
задана общим уравнением, то его следует
предварительно привести к нормальному
виду).
Для получения положительной величи-
ны d = MtN следует брать выражение для
d со знаком (+), если точка М± (хх, ух) и
начало координат расположены по разные
стороны от прямой (фиг. 175а), и со знаком
(—), если — по одну сторону (фиг. 1756).
АНАЛИТИЧЕСКАЯ геометрия
183
5. Координаты точки пересечения М0(х0,у0)
двух прямых
А1 х + В2 у + Сг = 0 и А2х + В2у С2—0
определяются путём совместного решения
этих уравнений по формулам:
I Ci I I Ci At I
|B2 C2| |C2 A2|
x° - I А, в; I ; y" - I Ax I ’
Ia2 b2| |a2 b2|
причём предположено, что
В случае, если
I А] Вг I q
IА2 В2|
а
li1 с21 *°<или £к0)’
то прямые параллельны.
Если же
I Ai I___[^1 Ci I__1^1 -Ail__ а
|А2 В21 “ |в2 С21 “ |С2 А21 “ и’
т. е. выполнены условия:
Ai _ _ Сj
Ag Bq С q *
то прямые сливаются друг с другом (имеют
бесчисленное множество общих точек).
б. Условие прохождения трёх прямых
Ai х В±у -f- Ci = 0» А2х •-)- В2у Са О,
А3х 4" В$у 4~ С3 == О
через одну точку:
Ах
А2
Ct
С2
С3
= 0.
7. Уравнение пучка прямых, проходящих
через точку пересечения двух данных пря-
мых
AjX -J- В1У 4* Ci =0 и А2х 4- В2у 4- С2 — 0,
имеет вид:
(А1Х 4- Biy 4- Сх) 4’ р(А2х 4- В2у 4- С2) = 0,
где множитель ji произволен. Изменяя мно-
житель р, можно получить любую прямую
пучка, не совпадающую со второй из данных
прямых.
ОКРУЖНОСТЬ
Уравнение окружности в декартовых коор-
динатах:
(х — а)2 4- (У — &)2 = /?2,
где R — радиус окружности, а а и b — коор-
динаты центра Oj (фиг. 176).
Если центр находится в начале координат,
уравнение окружности принимает вид:
х2 4- У2 = Rs
(в параметрической форме:
х = R cos t; у = R sin /).
Уравнение окружности радиуса R, про-
ходящей через начало координат с центром
на оси ОХ:
х2 4- у2 = 2Rx.
Уравнение окружности радиуса R, про-
ходящей через начало координат с центром
на оси OY:
х2 4- ya =2Ry.
Общее уравнение 2-й степени относитель-
но х и у:
Ах2 4- 2 Вху 4- Су2 4- 2 Ох 4- 2 Еу 4- В = 0
представляет собой уравнение окружности
при условии, что А = С и В = 0, т. е. когда
оно может быть приведено к виду:
х3 4- у2 + 2 D'x 4- 2 Е'у 4- В' = 0.
Фиг.
176
Фиг. 177
Радиус и координаты центра окружности
при этом определяются по формулам:
/?= VD'‘ 4- Е'* — В' , a— — D’, b — — Е'.
Если D'* 4- Е'* — В' > 0, то мы имеем дей-
ствительную окружность, если
£>'* Е'* —В' < 0 — мнимую окружность,
а если
D’‘ + Е'* 4- В' =0 — точку.
В полярных координатах уравнение ок-
ружности (фиг. 177) имеет вид:
р2 — 2 рр0 cos (ср — <?„) 4- Р» = В2>
где R — радиус окружности, а р0 и <р0 —
полярные координаты центра Ot.
Если окружность проходит через полюс
и центр лежит на полярной оси (фиг. 178),
Уравнение окруж-
ности, центр которой
совпадает с полюсом:
Р = /?.
Уравнение к а с а т е
^i(xi>yi) окружности,
то уравнение окружно-
сти принимает вид:
р = 2 R cos ср.
Фиг. 178
л ь н о й в точке
заданной общим
уравнением в декартовых координатах:
(х — а) (х, — а) 4- (у — Ь) (уг — b) = R1,'
а уравнение нормали в этой же точке:
у—Ь х —а
У! — b ~~ Xj — а’
В случае, когда центр окружности на-
ходится в начале координат, уравнение
касательной в точке А4Т (х15 ут) принимает
вид:
хх! 4- уу! = /?2,
а уравнение нормали в той же точке
У1Х — Х1у = 0.
184
МАТЕМАТИКА
ЭЛЛИПС
Эллипсом (фиг. 179) называется гео-
метрическое место точек М (х,у), сумма рас-
стояний которых от двух данных точек Fx и
F2, называемых
фокусами, есть
величина постоян-
ная:
rt + г2 = 2 а.
Если фокусы
эллипса находят-
ся на оси ОХ, а
начало координат
является середи-
ной отрезка F]F2,
то уравнение эл-
липса имеет вид:
х2 у2
= 1 (каноническое уравнение),
где а и b — полуоси эллипса.
Параметрические уравнения эллипса:
х = a cos t; у = b sin t.
Большая полуось эллипса а=ОА, ма-
лая полуось Ь = ОВ, полуфокальное
расстояние с = OFL; соотношение между
этими величинами:
&2 = а2—- с2.
с
Эксцентриситет эллипса е- —
/7
меньше единицы.
Радиусы-векторы точки эллипса с абсцис-
сой х вычисляются по формулам:
Г1 = а — е х; г2 = а + е х.
Директрисами эллипса называются
прямые, параллельные малой полуоси и от-
fl
стоящие от неё на расстоянии - в обе сто-
роны. Уравнения директрис:
Основное свойство директрис: отношение
радиуса-вектора любой точки эллипса к
расстоянию от этой точки до соответствующей
директрисы есть величина постоянная, рав-
ная эксцентриситету эллипса
Между двумя сопряжёнными диаметрами
эллипса, равными по длине соответственно
2 flt и 2 bi и образующими между собой угол у,
существуют следующие соотношения (т е о-
рема Аполлония):
-(- b‘ = а2 + b2; aibi sin ? = ab.
Оси эллипса являются взаимно сопряжён-
ными и взаимно перпендикулярными диа-
метрами (главные диаметры).
Фиг. 180 Фиг. 181
Уравнений касательной к эллипсу
в заданной на нём точке М (хх, yj:
i . УУ1 _ ,
а2 'г Ь2 ~ *’
Уравнение нормали в той же точке:
х —х, у —у,
&2Xi a2yi ~
Нормаль к эллипсу (фиг. 181) является
биссектрисой внутреннего угла, образован-
ного радиусами-векторами точки эллипса, а
касательная — биссектрисой соответствую-
щего внешнего угла.
Построение то-
чек эллипса по за-
данным его полу-
осям (фиг. 182). Вычерчи-
вают два круга с общим
центром в точке О радиу-
сами, равными полуосям эл-
липса а и Ь. Если провести
луч из центра О, пересекаю-
щий окружности в точках
А и В, и затем точку А спро-
ектировать на перпендику-
ляр ВС, опущенный из точ-
ки В на ось ОХ, то проек-
ция А (точка М) будет точ-
кой эллипса.
Фиг. 182
ГИПЕРБОЛА
Диаметром кривой, сопряжённым
данному семейству параллельных хорд, назы-
вается геометрическое место середин этих
хорд.
Диаметром эллипса является всякая
хорда, проходящая через центр эллипса; он
делится в центре пополам. Два диаметра
называются взаимно сопряжёнными
(фиг. 180), если каждый из них делит по-
полам хорды, параллельные другому.
Связь между угловыми коэфициентами
двух взаимно сопряжённых диаметров эл-
липса
й2
Гиперболой (фиг. 183) называется
геометрическое место точек М (х, у), разность
расстояний кото-
рых от двух дан-
ных точек Fi и F2,
называемых ф о-
кусами, есть ве-
личина постоян-
ная:
Г1 — г2 = ± 2 а.
Если фокусы Fi
и F2 находятся на
оси ОХ, а начало
координат является серединой отрезка FiF2,
го уравнение гиперболы имеет вид:
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
185
X2 у2
= 1 (каноническое уравнение),
где а и b — полуоси гиперболы.
Параметрические уравнения:
х — a ch t; у = b sh t.
Действительная полуось гиперболы
о = О А', мнимая полуось b = ОВ; и о л у-
фокальное расстояние с = OF,. Со-
отношение между этими величинами:
Ь2 = с2 — а2.
„ с
Эксцентриситет гипероолы е = —
больше единицы.
Радиусы-векторы точки гиперболы с
абсциссой х вычисляются по формулам:
rt= — а + ех ) для точек правой ветви гипер-
г2= а 4- ex J болы,
Директрисами гиперболы назы-
ваются прямые, параллельные мнимой оси
а
и отстоящие от неё па расстоянии - в обе
стороны. Уравнения директрис:
Основное свойство директрис: отношение
радиуса-вектора любой точки гиперболы к
расстоянию от этой точки до соответствую-
щей директрисы есть величина постоянная,
равная эксцентриситету гиперболы
Прямые у = ± - х (фиг. 184) являются
асимптотами гиперболы (стр. 196).
X2 у2
Гипербола -2—& = — 1 называется со-
... г- У~
пряженной гиперболе —^-2=1.
Сопряжённые гиперболы имеют общие
асимптоты; действительная ось одной из них
является мнимой осью другой, и наоборот.
Гипербола х2 — у2 = а2,у которой полу-
оси а и b равны между собой, называется
равноосной. Её асимптоты взаимно пер-
пендикулярны.
Если за оси координат принять асимптоты
равноосной гиперболы (фиг. 185), то её урав-
нение будет
а2
ХУ =± 2 •
Диаметрами гиперболы являются пря-
мые, проходящие через центр гиперболы
(фиг. 186). Связь между угловыми коэфи-
циентами двух взаимно сопряжён-
ных диаметров (т. е. таких, каждый из
которых делит пополам хорды, параллельные
другому) гиперболы:
Ь2
кк* = а2
Фиг. 186
Оси гиперболы являются взаимно сопряжён-
ными и взаимно перпендикулярными диа-
метрами (главные диаметры).
Уравнение касательной к гиперболе в
заданной на ней точке Мг (х,, ух):
ХХ1 _ УУ1 _
а2 Ь2 - *•
Уравнение нормали в той же точке:
+ Ы» =0
Ь2х, ~ а2у.
Касательная к гиперболе (фиг. 187) является
биссектрисой внутреннего угла, образован-
ного радиусами-век-
торами точки гипер-
болы, а нормаль —
биссектрисой соот-
ветствующего внеш-
него угла.
Построение то-
чек гиперболы по
заданным её полу-
осям (фиг. 188). Опре-
делив с по данным полу-
осям а и b и построив
на оси ОХ вершины А, В
ней ряд точек 1,2,3 ит. д.*; из фокуса F, радиуса-
ми А1, А2, АЗ и т. д. описывают дуги.
Точки С, D, Е пересечения этих дуг с дугами,
описанными из фокуса Fa радиусами В1, В2, ВЗ
и т. д., будут точками гиперболы.
ПАРАБОЛА
Параболой (фиг. 189) называется гео-
метрическое место
гочек М (х, у), равно-
удалённых от данной
точки F, называемой
фокусом, и данной
прямой, называемой ди-
ректрисой.
Если ось ОХ про-
ведена через фокус пер-
пендикулярно директ-
рисе, а начало коорди-
нат является серединой
отрезка оси ОХ между
фокусом и директрисой,
то уравнение параболы
имеет вид:
186
МАТЕМАТИКА
У2 = '2рх (каноническое уравнение),
где р — параметр параболы, равный рас-
стоянию между фокусом F и директрисой.
Вершина параболы, заданной уравнением
в канонической форме, совпадает с началом
координат. Эксцентриситет параболы
равен единице. В отличие от эллипса и гипер-
болы парабола не имеет центра.
Радиус-вектор точки параболы с абсцис-
сой х вычисляется по формуле
г= х + ?.
Уравнение директрисы параболы:
Р
х
Все диаметры параболы (фиг. 190) парал-
лельны оси параболы. Уравнение диаметра
параболы, сопряжённого параллельным хор-
дам с угловым коэфициентом к
Уравнение касательной к параболе в за-
данной на ней точке Мг (х1( yj:
УУ1 = Р + Xj).
Уравнение нормали в той же точке:
У1
У — Уг=—р (х —X,).
Касательная к параболе (фиг. 191) яв-
ляется биссектрисой внутреннего угла,
образованного радиусом-вектором точки
параболы и перпендикуляром, опущенным из
этой точки на директрису, а нормаль — бис-
сектрисой соответствующего внешнего угла.
Уравнение
у = ах2 + Ьх + с,
правая часть которого есть квадратичный
трёхчлен, является уравнением параболы
(фиг. 192) с осью, параллельной оси OY.
Параметр её р = . При а > 0 парабола об-
ращена вогнутостью вверх, при а < 0 — вниз.
Координаты вершины параболы
Ъ 4ас—Ь^
хо = — 2а ’ У» = ' 4 а •
Построение точек параболы. Даны:
ось симметрии параболы ОХ, вершина О и какая-
нибудь точка параболы Л1 (фиг. 193).
Разделив ординату ОЕ точки М и её абсциссу ЕМ
на одинаковое число равных частей, соединяют лу-
чами вершину Ос точками деления абсциссы, затем
в точках деления ординаты восставляют перпенди-
куляры, продолжая каждый из них до пересечения
с лучом соответствующего ему номера. Полученные
точки пересечения будут точками параболы.
Фиг. 192
ОБЩАЯ ТЕОРИЯ КРИВЫХ 2-го ПОРЯДКА
Общее уравнение кривой 2-го порядка:
Ах2 + 2 Вху + Су2 + 2 Dx +2:Еу + F = О
определяет эллипс (в частности окружность),
гиперболу, параболу или пару прямых (рас-
падающаяся кривая 2-го порядка).
Кривая, имеющая определённый центр
(центр симметрии), называется централь-
ной. Центральными кривыми 2-го порядка
являются эллипс, гипербола и пара пересе-
кающихся прямых.
Инварианты кривой 2-го порядка:
А В D
ВСЕ
D Е F
?1=АС~В2;
S = А + С.
Д =
Эти величины не изменяются при переносе
и повороте осей координат, т. е., если после
преобразования координат уравнение кривой
примет вид:
А'х'2 +2 В'х'у' + С'у'2 +2 D'x’ + 2 Е'у' +F'=0,
то величины Д, 6 и S, вычисленные для но-
вых значений коэфициентов, сохраняют
первоначальные значения.
Общие свойства кривых 2-го порядка.
Конус второго порядка, в частности пря-
мой круговой конус, при пересечении с
плоскостью образует на ней коническое
сечение. Если секущая плоскость не про-
ходит через вершину конуса, то сечение
будет гиперболой, параболой или эллипсом
в зависимости от того, пересечётся ли ко-
нус с плоскостью, параллельной данной
и проходящей через вершину, по двум
образующим, по одной образующей или в
одной точке. При пересечении конуса с
плоскостью, проходящей через его вершину,
получаются распадающиеся конические се-
чения (Д = 0, см. табл. 20). Параллельные
прямые получаются, если конус вырождает-
ся в цилиндр.
Геометрическим местом точек, отношение
расстояний которых до данной точки (фокуса)
и до данной прямой (директрисы) есть вели-
чина постоянная, равная е, является кривая
2-го порядка с эксцентриситетом, равным е,
а именно: эллипс, если е < 1, парабола,
если е= 1, и гипербола, если е > 1.
Схема приведения общего уравнения
кривой 2-го порядка к каноническому ви-
ду дана в табл. 20.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
187
Таблица 20
Приведение общего уравнения кривой второго порядка к каноническому виду
Централь- ные кривые 6^0 а>0 Д-/--0 Вид кривой Преобразование координат Каноническое уравнение кривой после преобразо- вания
Эллипс а) Д-ScO — действи- тельный б) Д«5>0 —мнимый 1) Перенос начала в центр кривой с координатами BE—CD BD-AE х“- й ’ У“= 0 • 2) Поворот осей на угол а, определяемый уравнением 2В tg 2«-^, причём знак sin 2а должен совпадать со знаком 2В. Угловой коэфициент но- вой оси х': С—А + У (С-АУ + 4В' ,;=- 2В А'х'*+С-у’+4- -0; 0 А+С + /(А-С)2+4В» 2 А+С-/(А-С)‘ + 4В2 2 ’ (Д' и С' являются корнями квадратного уравнения as—S a+6=0)
д=о Пара мнимых пря- мых, имеющих общую действительную точку
й<0 Д*0 Гипербола
д=о Пара пересекающих- ся прямых
Параболические кривые1 6=0 д^о Парабола 1) Поворот осей на угол а, определяемый уравне- нием А tg а— в, причём знак sin а должен быть обратен знаку А. 2) Перенос начала в верши- ну параболы, координаты которой х0 и у0 опреде- ляются из уравнений: о , AD+BE А ~ 1 1 —в 0 • Г А1 + В* „ BD-AE , AD + BE , 2--. ~ Х„ + у,+ Уа'+ь“ Уа'+в* +р=о у'* ^2рх'; AE-BD SV А* + В*
д=о Пара параллель- ных прямых, если D’—AF>0; сливаю- щихся, если D3—AF=* = 0; мнимых, если D2-AF<0 Поворот осей на угол а, оп- ределяемый уравнением tg я=- А В ’ причём знак sina должен быть обратен знаку А. Sy’1 +2yD + BE v’ + F-O V А» + В*
1 Имеется в виду, что ни один из старших коэфициентов (А, В, С) не равен нулю. Если два коэфициента
(А и В или В н С) равны нулю, то упрощение уравнения сводится к параллельному переносу осей; при
этом уравнение Cy! + 2Dx + 2Ey+E=0 преобразуется к виду (у—Уо)!-2р (х—х„) и Ах2 + 2Dx+2Ev+F=0 —
к виду (х—х0)!= 2р (у—у0).
ние полярной оси п
Лению от фокуса i
Полярное уравнение конического сечения.
Если полюс находится в фокусе, а направле-
фотивоположно направ-
к ближайшей вершине
(фиг. 194), то уравне-
ние конического сече-
ния в полярных коор-
динатах имеет вид:
= Р
? 1 — е cos <р '
где р (параметр кри-
вой)— отрезок прямой,
параллельной директри-
се, от фокуса до пересе-
чения с кривой; е—экс-
центриситет.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
В ПРОСТРАНСТВЕ
МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Положение точки М в прост-
ранстве (фиг. 195) чаще всего определяют:
1) абсциссой х = ОА, ординатой у = AN
и апликатой z = NM (прямоугольные
декартовы коор-
динаты);
2) радиусом-век-
тором р = ОМ; углом
<р = AON и углом
0= ^КОМ (сфери-
ческие или по-
лярные координа-
ты), причём: р > 0;
0< <р <2тс; 0 < 0 < тс.
3) радиусом-век-
тором г = ON; углом
ср = AON и апли-
катой z = NM (ци-
линдр иче ские
координаты), причём:
г > 0; 0 < ср < 2 л.
Декартовыми прямоугольными координа-
тами точки М являются числа х, у и г,
выражающие взятые в выбранном масштабе
188
МАТЕМАТИКА
в с определёнными знаками расстояния этой
точки до трёх взаимно перпендикулярных
координатных плоскостей или, иначе, проек-
ции радиуса-вектора р точки М на три
взаимно перпендикулярные оси. В зависи-
мости от выбора положительных направлений
на координатных осях различают правую
(фиг. 196а) и левую (фиг. 1966) координат-
ные системы.
Фиг. 196 Фиг. 197
В дальнейшем применяется правая коор-
динатная система.
Координатные плоскости делят простран-
ство на 8 октантов (фиг. 197). Знаки коор-
динат зависят от октанта, в котором нахо-
дится точка, и приведены в табл. 21.
Преобразование прямоугольных координат.
В случае параллельного переноса
осей координаты х, у и z точки М в си-
стеме OXYZ (фиг. 198а) связаны с координа-
тами х', у' и z' той же точки в системе
O'X'Y'Z' соотношениями:
х = х’ + а,
У = У' + Ь,
Z = Z' + с ,
где а, Ь, с—координаты нового начала
координат О' в системе OXYZ.
В случае поворота осей координаты
х, у, z точки М в системе OXYZ связаны с
координатами х', у', г' той же точки в си-
стеме O'X'Y'Z' (фиг. 1986) соотношениями:
х = х' cos 04 4- у' cos аа 4- z' cos о3;
у = х' cos + у' cos + z' cos ₽3;
z = х' cos h + У cos 4- z' cos ys,
где а2, 3i> 7i—углы, образованные осью OX',
a2, p„, 72—осью Y'O и a3, p3, 73 — осью OZ'
co старыми осями:
ОХ' OY' OZ'
ох “1 иа «8
OY Рх 3, За
OZ 7х 7. Та
Эти девять углов связаны соотношениями:
cos2 4- cos2 (4 4- cos2 7i = l,
cos2 a2 4- cos2 p2 4- cos2 72 = 1,
cos2 a3 + cos2 ₽3 4- cos2 73 = 1 ,
cos aj cos a24~ cos Pj cos p2+ cos 7j cos 72- 0,
cos a2 cos a3 + cos p2 cos p3 + cos 72 cos 73=0,
cos a3 cos 04 + cos p3 cos Pi + cos 73 cos 71=0.
Общее преобразование. При одно-
временном переносе начала координат в
точку О' (а, Ь, с) и повороте осей
х = х' cos <*1 4- У' cos a2 4- z' cos a3 + <1;
у = x' cos Pi 4- y' cos p2 -4 z' cos p3 4- b;
z= x' cos 7i 4- y' cos 72 4- z’ cos 73 4- c.
Переход от одной системы коор-
динат к д р у го й. Переход от прямоуголь-
ных координат к сферическим и обратно:
х = р sin 0 cos <р;
у = р Sin 0 sin у;
z = р cos 0;
р = Ух2 4- у2 4- z2 ;
/х24- У2.
tgO =----*----
. У
tg a = —
° Т х
Переход от прямоугольных координат к
цилиндрическим и обратно:
х = Г cos <р, у= Г sin ср, Z — Z,
г = / х2 4- У2> tg 4 = £ , z = z.
НЕКОТОРЫЕ ПРОСТЕЙШИЕ ЗАДАЧИ
В ПРОСТРАНСТВЕ
Расстояние между двумя точками. Рассто-
яние между точками М^х^ у1Г гг) и
М.> (х2, у2, z2) определяется по формуле
d = /(х2 — хх)2 4- (Уа — Ух)2+ (г2 — zi)2;
в частности, расстояние точки Mj (xlt y2,Zi)
от начала координат
d =У xl 4- у, 4- г;.
Деление отрезка прямой в данном отно-
шении. Координаты точки М (х, у, z), де-
лящей отрезок прямой М1М2, ограниченный
точками A4j(Xj, ylt zj и М2 (х2, у2, z2), в
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
189
MjAl
отношении мм" = (Фиг- 19®)’ опреде-
ляются по формулам:
— _ *i 4-х2 Vi + у2 - zi '4' z2
х- i + x > у = -т+х~ ; z= 1 + х •
Если точка М — середина отрезка МтМ^,
то:
- X; + Х2 - У1 + Уз - 2Х + Z3
х - 2 ; у — 2 ;z— 2
Направляющие косинусы прямой. Если
прямая проходит через точки М, (х,, у,, z,)
и M2 (х2, у2, z2) и образует с осями коор-
динат углы а, 0 и у (фиг. 200), то
xi xi „ У2 Уг
cos а = --т---- : cos 0 = ------;
а ’ а ’
22—2!
C0S 7 = ---j--,
где ___________________________________
d = /(х2 — Xi)2 + (у2 — угу + (z2 — Zi)3.
Направляющие косинусы прямой связаны
между собой соотношением
cos2 а -ф cos2 0 + cos2 f = 1.
Объём тетраэдра. Объём треугольной пи-
рамиды с вершинами А4Х (Xj, у,, Zj).
м2 (*2, Уз» 23), А43 (х3, Уз, Z3)nM4(x4,y4,Z4)
определяется по формуле
V = I
6
*1 — Х2 у, — у2
*1 —Х3 У1 —Уз
Х1 — Х4 У! — у4
?1 —Z2
21 — z3
21— 24
При этом объём V по этой формуле полу-
чается со знаком (-(-) или (—) в зависимости
от того, образуют ли векторы MiA42, МХМ3 и
М'М4 правую или левую связку.
ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
УРАВНЕНИЯ С ТРЕМЯ ПЕРЕМЕННЫМИ
Уравнение F (х, у, г) = 0 или г = / (х, у),
связывающее три переменные х, у, г, яв-
ляется уравнением некоторой поверхности
(действительной или мнимой), если рассмат-
ривать х, у и z как декартовы координаты
точек этой поверхности. При этом коорди-
наты любой точки поверхности удовлетво-
ряют данному уравнению, а координаты всех
точек, не принадлежащих поверхности, не
удовлетворяют этому уравнению.
Уравнение цилиндрической поверх-
ности с образующими, параллельными оси
ОХ, не содержит координаты х, т. е. имеет вид
F (у, z) = 0 (аналогично в отношении дру-
гих осей—ОУ и OZ).
На плоскости OYZ это же уравнение
F(y,z) = 0 изображает линию пересечения ци-
линдрической поверхности с данной коорди-
натной плоскостью.
Уравнение конической поверхности с
вершиной в начале координат имеет
вид: Г(х, у, г) = 0, где F— однородная
функция переменных х, у и г, т. е. удовле-
творяет условию:
F (tx, ty, tz) = tn F (x, у, z).
Уравнение поверхности враще-
ния плоской кривой z = j (х) (в плоскости
OXZ) вокруг оси OZ имеет вид:
2 = / (/Х2 + у2)
(аналогично в отношении вращения вокруг
оси ОХ).
Два уравнения:
Fx (х, у, z) = 0 и F2 (х, у, z) = 0,
заданные совместно, определяют некоторую
пространственную линию, а именно линию
пересечения поверх-
ностей, заданных
этими уравнениями.
Например, уравне-
ния:
X2 Л. у2 Z2 = а2
z = с, где с < а,
определяют окруж-
ность (пересечение
сферы с плоскостью).
В параметриче-
ской форме уравне-
ния пространствен-
ной кривой имеют
вид:
* = ?i (О; у = (О; z = ?з (/).
Пример. Прямая в плоскости OXZ, проходящая
через точку А (а, О, О) и образующая с осью ОХ
угол а такой, ито tg а , накладывается (без рас-
тяжения) на прямой круговой цилиндр радиуса а,
осью которого является ось OZ так, что алликаты
её точек не изменяются, а точка (а, О, О) остаётся
неподвижной (фиг. 201). Образованная таким обра-
зом на поверхности цилиндра линия (винтовая
линия) имеет уравнения:
х = a cos t; у = a sin t: z = bt,
где t —угол между осью ОХ и проекцией на пло-
скость ОХУ радиуса-вектора точки винтовой линии.
ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
В декартовой системе координат уравне-
ние плоскости — линейное относительно
координат х, у и z. Различают следующие
основные формы уравнения плоскости.
Общее уравнение плоскости:
Ах + By + Cz + D = 0.
При D = 0 плоскость проходит через на-
чало координат. При А = 0 (или В = 0, или
С = 0) плоскость параллельна оси ОХ (или
OY, или OZ). При А = В =0 (или А = С =0,
или В = С = 0) плоскость параллельна пло-
скости OXY (или OXZ, или OYZ).
Уравнение плоскости в отрез-
ках, отсекаемых на координатных
190
МАТЕМАТИКА
где а, Ь, с — взятые с соответствующим
знаком отрезки, отсекаемые плоскостью на
осях OX, OY и OZ (фиг. 202).
Если b = с = оо (плоскость параллельна
плрскости OYZ), то уравнение плоскости
х = а.
Если а = с = оо (плоскость параллельна
плоскости OXZ), то уравнение плоскости
У = Ь.
Если а = b = со (плоскость параллельна
плоскости OXY), то уравнение плоскости
г = с.
Нормальное уравнение плос-
кости
х cos а 4- у cos 3 + г cos 7 — р = 0,
где а, 3, 7 — углы, образованные перпенди-
куляром, опущенный из начала координат
на плоскость, с положительными направле-
ниями координатных осей, а р — длина этого
перпендикуляра (фиг. 203).
Чтобы общее уравнение плоскости при-
вести к нормальному виду, надо все члены
его умножить на нормирующий множитель
1
К = ± ,—,
/А24- В2 4- С2
причём знак X обратен знаку D.
Параметры р, cos a, cos 3, cos 7 вычисля-
ются по коэфипиентам общего уравнения с
помощью формул:
D
р = ± ",----- ;
н / А24-В2 + С2
А
cosa=±/А^+^RC2 ;
cos 3 = ± уАг+ S2 + сТ >
С
1 /А24-В24-С2
Ниже приводятся формулы для решения
некоторых задач.
1. Уравнение связки плоскостей, прохо-
дящей через данную точку Мо (х0, у0, z0):
А (х — ха) + В (у — у0) + С (z— z„) = 0.
2. Уравнение пучка плоскостей, прохо-
дящих через прямую, заданную системой
уравнений:
Ах + By + Cz + D =0,
А4х 4~ B4y 4- CiZ 4“ —0,
имеет вид:
(Ax 4- By 4- Cz 4- D) 4-
4- (A4x 4- Bty 4- Cxz 4- Di) = 0.
3. Уравнение плоскости, проходящей через
три данные точки: М4 (Xi,y4, zx), М2 (x.,,y,,z.,)
и М3 (х3, у„ z3):
X — Xj у — ух Z — Zj
х2 — *1 у2 - У1 Z, — г4
*3—Xi У3-У1 z3 — Z1
= 0.
4. Угол <р между двумя плоскостями, дан-
ными нормальными уравнениями:
х cos а 4-у cos р 4-z cos 7 —р =0,
х cos 04 4- у cos 3i 4- z cos 71 — px = 0,
определяется по формуле
cos 7) = cos a cos 04 + cos 3 cos 3i 4- cos 7 cos 7X.
Если уравнения даны в общем виде:
Ах + By 4- Сz 4- D =» 0;
Ахх + В4у 4- CjZ 4- Dx= 0,
то
АА, 4“ ВВ4 4“ СС1
cos = ± ------,
У А2 4- В2 4- с2 У А^+В’+С"
Условия параллельности двух плоскостей:
cos а = cos ах; cos 3 = cos 3i; cos 7 = cos (1
или
А _ В _ С
Ах В4 Сх
Условие перпендикулярности двух пло-
скостей:
cos а cos 04 4- cos 3 cos 3i 4- cos 7 cos 71 — 0
или
AAt 4- BBi 4- CCi = 0.
5. Чтобы найти расстояние от точки
Л4г (хх, у1( z4) до плоскости Ах 4- By 4- Cz 4-
4-0 = 0, надо привести уравнение плоскости
к нормальному виду и заменить в левой
части полученного уравнения текущие ко-
ординаты координатами данной точки; най-
денное число даст искомое расстояние d:
d = ± (х cos.а 4- у cos 3 4- z cos 7 — р).
При этом для получения положительной
величины d следует брать выражение для d
со знаком (4-), если точка М4 и начало ко-
ординат расположены по разные стороны от
плоскости (фиг. 204), и со знаком (—), если —
по одну сторону (фиг. 205).
6. Для отыскания координат точки пере-
сечения трёх плоскостей, заданных уравне-
ниями:
Ахх 4- В4у 4- CjZ 4- =0,
А2х 4- В2у 4- C2z -j- D2 =0,
А3х 4- В3у 4“ C3z 4“ П3 —0,
надо решить совместно данную систему урав-
нений.
7. Условия нахождения четырёх точек
Мг (х,, У1, z4), М2 (х2, у2, z2), М3 (х3, у3, z3)
и М4 (х4, у4, z4) в одной плоскости:
X1 — х 2
Х1 х3
Х1— х4
У 1— Уз
У 1— Уз
У 1-
Zi— Z,
Z1— z3
Zi— Z4
=0.
ПРЯМАЯ В ПРОСТРАНСТВЕ
Прямая в пространстве определяется как
пересечение двух плоскостей и задаётся
системой двух уравнений:
Ах + By 4- Cz 4- D = 0,
А4х 4- Bty 4- C4z 4- Dx = 0.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
191
При определении положения прямой пе-
ресечением плоскостей, проектирующих её
на координатные плоскости OXZ и OYZ,
её уравнения примут вид:
X = tnz 4- а;
у = nz + Ь,
где а и b — координаты точки пересечения её
с плоскостью ОХУ.
Нормальные уравнения прямой:
X —Х1 = У — Уг = Z— Zt
COS a cos з COS 7 ’
где Xj, yt, ?! — координаты одной из точек,
прямой, а а, р, 1 — углы прямой с осями
координат.
Канонические уравнения прямой:
х — Xj у — yt 2— ?!
т ~~ п ~ р '
где x1F ух, Zj — координаты одной из точек
прямой, а т, п, р — числа, пропорциональные
направляющим косинусам:
т : п : р = cos а : cos 3 : cos 7.
Для перехода от общих уравнений прямой
к каноническим уравнениям нужно подо-
брать Xj, yt и Zj так, чтобы они удовлетво-
ряли общим уравнениям, а числа т, п, р
определить по формулам:
Чтобы канонические уравнения прямой
привести к нормальному виду, надо знаме-
натели умножить на нормирующий
м п о ж ит е л ь:
/т- + п1 +~р2
и, следовательно:
т
COS а = ± -7=== •
У т2 + п2 + р~
Р
cos 7 - - ± -----— —
V т2 + п2 + р’
Знак нормирующего множителя определяет
направление прямой.
Параметрические уравнения
прямой:
х = х0 -|- mt; y = y0+nt; z = z0 + pt,
где t — параметр.
Некоторые частные случаи. Уравнения
прямой, параллельной плоскости ОХУ:
х — х, _ у —У! = z — ?!
т ~~ п О
или
X —*1 __ У — У1
т п
Z =Zi.
Уравнения прямой, параллельной оси ОХ:
х —Xi _ у —У1 _ Z — 2,
т ~ 0 _ О
ИЛИ f У ~~ У1’
I Z = ?!.
Уравнения оси ОХ:
х у z
т = 0 = О
(У = О,
ИЛИ 12= 0.
Формулы для решения основных задач
1. Уравнения прямой, проходящей через
точки АД (Xi, У1, zx) и М2 (х2, у2, г.,):
X — Х1 _ у — У1 = Z — ?!
Х2—Х1 У2-У1
2. Если прямые даны уравнениями:
Х-Х! У —У1 = z — 2д _
cosa ‘ cos 3 cos 7 ’
X — Х2 у — Уз _ z — z2
COS «1 ~ COS 31 — COS 71 ’
то угол между ними определяется формулой
COS ср = COS a COS a-! + COS 3 COS 3i + COS 7 COS 7j.
Если прямые даны уравнениями:
х — xt = у —У1 = Z — ?! _
т п Р ’
X — Х2 у — Уз __ z — 2а
шГ = Л1 •" Р1 '
то
тт, + лЛ1 + ppt______
с08? ± Vт2+п2+р2
Условия параллельности двух прямых:
COS a = COS 0Ci; cos 3 — cos 3i,’ cos 7 == cos 7j
или
tn n p
ГП1= p, •
Условие перпендикулярности двух пря-
мых:
cos a cos a] 4- cos 3 cos 3i + cos 7 cos 7i = 0
или
mmt 4- nn, 4- = 0.
3. Прямые, данные уравнениями:
X — xt _ у— Ух __ Z — zx _
m ~ n ~~ p ’
x-^x2 _ y^- y., _ z — z2
Wj Hj “ Pi
192
МАТЕМАТИКА
лежат в одной плоскости (к о м п л а н а р н ы),
если выполнено условие:
х2— Xi У2 — У1
т п
п,
Р
Pi
4. Если прямая и плоскость даны уравне-
ниями:
X — Хг = у —у, = z — гд _
т п р ’
Ах + By + Cz 4- D = О,
то угол 4 между ними определяется фор-
мулой
Ат + Вп +Ср
г У т‘ 4- и2 + рг У А24-В24-С2
Условие параллельности прямой и плос-
кости:
Ат + Вп 4- Ср = 0.
Условия перпендикулярности прямой и
плоскости:
А _ В С
т ~ п ~ р '
х — х, у — У1 z— ?i
5. Прямая —-------—= —-— лежит
в плоскости
Ах + By 4- Cz 4- D = 0,
если выполнены условия:
АХ! 4- By! 4- C?j 4- D = 0
(прямая и плоскость имеют общую точку)
и
Ат 4- Вп 4- Ср = 0
(прямая и плоскость параллельны).
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
2-го ПОРЯДКА
1. Эллипсоид (фиг. 206):
х2 у2 z2
й2 + (,2 + =*•
Если а = Ь, то
Фиг. 207
х2 4- у2 z2
—— +^а=1 — эллипсоид вращения
X2 Z3
(поверхность вращения эллипса — 1
вокруг оси OZ).
Если а = b =с, то х3+у- 4- z2 = а2—сфера
радиуса а.
2. Одпополостный гиперболоид
(фиг. 207):
X2 У2 Z2
й2 + (,2 ~ С- ~ '
Если а = Ь, то
х2 4- у2 z2
— 2------3 = ! — о д н о п о л о с т п ы и ги-
перболоид вращения
поверхность вращения гиперболы
X2 22 \
-2— =1 вокруг оси OZ I.
Фиг. 208 Фиг. 209
3. Двуполостный гиперболоид
(фиг. 208):
а2 + 62 с2 *'
х2 4- у2 z2
Если а = Ь, то —-----~ ~~ 1 — дву-
полостный гиперболоид вращения
^поверхность вращения гиперболы
X2 Z2 л \
=— 1 вокруг оси OZ I.
4. Конус 2-го порядка (фиг. 209):
х2 у2 ?а
а2 + й2 — с2 =0,
Его образующие являются асимптотами
гиперболоидов:
X2 у2 Z2
а2 + й2 с2 ± У
по отношению к этим гиперболоидам конус
называется асимптотическим.
5. Эллиптический параболоид
(фиг. 210):
Если p — q, тох2 4- у2 = 2pz—п араболо.ид
вращения (поверхность вращения парабо-
лы х2 = 2pz вокруг оси OZ).
6. Гиперболический парабо-
лоид (фиг. 211):
£-
Р
V3 .
7 = 2-
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
193
7. Цилиндры с образующими,
параллельными оси OZ:
X2 у2
— 4- =1 — эллиптический цилиндр
а2 о1
X2 у2
Гиперболический параболоид -—— = 2z
также имеет два семейства прямолинейных
Фиг. 215
(фиг. 212), в частности, при а = Ь — кру-
говой цилиндр;
х2 у2
—£2 = 1— гиперболический цилиндр
(фиг. 213);
образующих (фиг. 215,б, па чертеже показано
только одно семейство):
У2 = 2 рх -— параболический цилиндр
(фиг. 214).
Прямолинейные образующие поверхностей
2-го порядка. Прямолинейной обра-
зующей поверхности
называется прямая линия,
которая целиком находит-
ся на поверхности; тако-
вы, например, образую-
щие цилиндрической и ко-
нической поверхностей.
Фиг. 212
Фиг. 213
Из поверхностей 2-го порядка имеют
прямолинейные образующие (кроме цилинд-
ров и конуса) однополостный гиперболоид и
гиперболический параболоид.
Однополостный гиперболоид
X2 у2 Z2
а2 Ь2 с2 ~ 1
имеет два семейства прямолинейных образу-
ющих (фиг. 215,а, на чертеже показано
только одно семейство):
где и и о — произвольные параметры.
13 том I
где и и v — произвольные параметры.
Через каждую точку поверхности одно-
полостного гиперболоида или гиперболиче-
ского параболоида проходят по одной обра-
зующей из каждого семейства.
Круговые сечения. Если какое-либо се-
чение поверхности 2-го порядка плоскостью
есть круг, то все сечения плоскостями,
параллельными данной, тоже круговые.
Всякая поверхность 2-го порядка, являю-
щаяся поверхностью вращения (кроме сферы,
у которой все плоские сечения — круговые),
имеет одно семейство круговых сечений (об-
разуемое плоскостями, перпендикулярными
к оси вращения). В общем же случае эллип-
соид, гиперболоиды, эллиптический паробо-
лоид, эллиптический цилиндр и конус имеют
по два семейства круговых сечений. На
фиг. 216 показано одно из круговых сече-
ний эллипсоида.
ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ 2-ГО ПОРЯДКА
Вид поверхности 2-го порядка, заданной
общим уравнением:
x2+az.1y2 + о-j z’- + 2ог2ху 4-2a23.vz 4-
4- 2 auxz + 2 a14x + 2 аыу + 2 «3iz + a41 = 0,
194
МАТЕМАТИКА
определяется, как показано в табл. 22, зна- S = а1г + а2, + а23; Т = а32а33 4- а33ац +
ками величин ап «12 (здесь «13 «14 2ij aji>: 1«11 «12 «13 4* «Ц«22 «23 «31 «12»
А «21 «22 «23 «24 . ?, «21 «22 «28 являющихся инвариантами этого урав-
41 — О Cl Cl J1 <3 <3 ° И 'Я <3 « «33 «34 «43 «44 (центра/ ’ 1 «31 «32 «33 Исследование вид ъные поверхности) нения (эти величины не изменяются при преобразовании системы координат). Таблица 22 а поверхности 2-го порядка //. <5=0 (параболоиды, цилиндры и пары плоскостей)
S 5>0; Т>0 88 и Т не оба >0 т>о Т<0
Д<0 Эллипсоид Двуполостный гипербо- лоид д+о Эллиптиче- ский параболоид Гиперболический пара- болоид
д=о Цилиндрическая поверхность, направ- ляющей которой служит кривая 2-го порядка. В зависимости от вида этой кривой цилиндр будет эллиптическим (при Т>0), гиперболическим (при Т<0), параболическим (при Т=0) или поверх- ность распадается на две плоскости (дей- ствительные, миимые или сливающиеся).
Д>0 Мнимый эллип- соид ОднополостныЙ гипер- болоид
ДвзО Мнимый конус (с действитель- ной вершиной) Конус
ДИФЕРЕНЦИАЛ ЬНАЯ ГЕОМЕТРИЯ
ПЛОСКИЕ КРИВЫЕ
КАСАТЕЛЬНАЯ И НОРМАЛЬ
Уравнение плоской кривой обычно зада-
ют в одном из следующих видов:
а) в декартовых координатах:
явное
У = / (х);
неявное
F (х, у) = 0;
в параметрической форме х = х (t); у=у (t);
б) в полярных координатах:
явное
Р = / (ч>);
неявное
Г(р, ф) = 0.
Если не оговорено противное, то функции,
входящие в эти уравнения, вместе с их про-
изводными тех порядков, о которых будет
итти речь, предполагаются непрерывными.
ДИФЕРЕНЦИАЛ ДУГИ
Диференциал дуги плоской кривой выра-
жается при помощи одной из следующих
формул:
а) в декартовых координатах
ds= V dx2 + dy2
или
если кривая задана явным уравнением;
если уравнения кривой заданы в параметри-
ческой форме;
б) в полярных координатах
За положительное направление отсчёта
дуг принимается такое направление, в кото-
ром диференциал дуги положителен.
Касательной в точке М называется
предельное положение секущей MN (N —
произвольная точка кривой, фиг. 217), когда
нормалью называется перпенди-
куляр к касательной, проведённый через
точку касания.
Вид уравне- ния кривой Уравнение касательной Уравнение нормали
Неявный . , Явный « , • . Параметри- ческий . • dF к (Х'Х)+ дР У-у”4х (х-х) Y-у Х—х у' “ х' Х—х У—у dF ° dF дх ду Х-х y-y—d^ dx х'{Х-х-)+ + у(У-у) -0
Здесь X, Y — текущие координаты; х, у —
координаты точки на кривой, через которую
проведена касательная или нормаль.
Фиг. 217
Фиг. 218
Положительное направление на касатель-
ной совпадает с положительным направле-
нием на кривой в точке касания.
Направление касательной определяется
углом а между положительным направле-
нием оси ОХ (в декартовых координатах) и
положительным направлением касательной
или (в полярных координатах) углом ц
между радиусом-вектором ОМ = р и по-
ложительным направлением касательной
(фиг. 218).
диференциальная геометрия
195
Углы а и ц определяются по формулам:
dy dx dy
= 7х >с03л== ds ’ ™*=ds’
Р dp d ®
^ = ^-р; coSfi=d- ; sinp = p^ .
dtp
Углом между двумя кривыми называется
угол между касательными к этим кривым
в их общей точке.
Если кривые заданы
уравнениями:
У = /1 (х), у = /2 (х),
то угол <р между ними
в точке пересечения
М (х0, у„) определяется
по формуле
. /о(х0)-/'(х0)
tg ? = ——;-----5--- •
1 + А(х0) А (х0)
ТРИ
Фиг. 219
рестность точки X/, что во всех точках этой
окрестности слева от х, знак /"(х) один,
а справа противоположный, то точка х = х;.
является точкой перегиба; если указанные
знаки одинаковы, то точка х=хг- не является
точкой перегиба.
Другой, более простой способ исследова-
ния применим, если при х = X/ (х/ — корень
уравнения /" (х) = 0) существуют производ-
ные более высоких порядков функции / (х).
Если (х/) #= 0, то Xt — точка перегиба,
если (х,) = 0 и /1V (X;) =£ 0, то Xi — не
точка перегиба. Вообще если (X/) — пер-
вая из неравных нулю производных, то х;-
является точкой перегиба, если п нечётное,
и не является точкой перегиба, если п чётное.
Если уравнение кривой дано в неявном
виде Р (х, у) = 0, то координаты точки пере-
гиба должны удовлетворять системе урав-
нений:
В декартовой системе координат с каса-
тельной и нормалью связаны длины следую-
щих отрезков (фиг. 219):
У
МТ =
Оу
dx
(отрезок касательной);
Для кривой, заданной в параметрической
форме х = х (О, у = у (t), значения пара-
метра t, соответствующие точкам перегиба,
удовлетворяют уравнению:
MN =
(отрезок нормали);
dx dy
dt dt
РТ =
У
(1у
dx
(подкасательная);
(поднормаль).
d'2x d2y
dt2 dt2
= 0.
Если кривая дана уравнением в поляр-
ных координатах р = / (ср), то значения ар-
гумента ср, соответствующие точкам перегиба,
удовлетворяют уравнению
ВЫПУКЛОСТЬ И ВОГНУТОСТЬ;
ТОЧКИ ПЕРЕГИБА
Говорят, что в точке М кривая у = / (х)
обращена выпуклостью вниз (или
вогнутостью вверх), если в некоторой
окрестности этой точки касательная проходит
ниже кривой; если же касательная проходит
выше кривой, то кривая обращена выпу-
клостью вверх (фиг. 220).
Выпуклость направлена вверх во всякой
точке, где /" (х) < 0,
и вниз во всякой
точке, где 1" (х) > 0.
Фиг. 221
Точка, в которой касательная переходит
С одной стороны кривой на другую (фиг. 221),
называется точкой перегиба. В точке
перегиба /" (х)=0 (или /" (х) не существует).
Находить точки перегиба можно следую-
щим образом: решив уравнение /" (х) = 0,
следует исследовать знак /" (х) в окрестности
каждого корня X/. Если найдётся такая ок-
Пример 1.
Х,~~; /"'<'Х'У + 0;
обе точки являются точками перегиба.
Пример 2.
у = (х-1)‘; /"(х) = 12 (х- !);
*1,2= 1; Г"(1)“О; /1V(1)^O;
точек перегиба нет.
Пример 3,
1
1
значению ср = —— соответствует л.нимое р и точка
перегиба определяется полярным углом ср = — .
КРИВИЗНА КРИВОЙ
Кривизной /< кривой в точке М назы-
вается предел отношения угла между поло-
жительными направлениями касательных
МАТЕМАТИКА
196
в точках М
к длине дуги
К
и N (угол смежности)
MN, когда N-+М (фиг. 222):
Да da
~ lim ДТ = ds'
4s->0as as
кривой, проведённой в точке М в сторону
вогнутости кривой.
Координаты (X, Y) центра кривизны
кривой у = / (х) вычисляются по формулам:
между положительными на-
касательной в точке М и
где a — угол
правлениями
оси ОХ.
Радиусом кривизны R называется
величина, обратная кривизне: Z? = —. Кри-
К
вымч постоянной кривизны являются ок-
/ 1
ружность ( К — где а—радиус окружно-
Х = х — g—
dx2
Г==у +
d*y
dx*
(*)
сти^ и прямая (К = 0).
Формулы для вычисления кривизны
радиуса кривизны:
И
1
K = R
d2y
dx2
(для уравнения
в
явной форме);
F'xx
Fxy
Рх
f" f'
ху х
Руу
Ру о
Эволюта кривой — геометри ческое
место центров кривизны.
Если в формулах для определения коор-
динат центра кривизны рассматривать X и
Y, как текущие координаты точки на эво-
люте, то эти формулы дают параметрические
уравнения эволюты.
Пример. Найти уравнение эволюты параболы
у = Х«;
Здесь
и, исключив параметр х, найдём уравнение эволюты
в явном виде:
(для уравнения в неявной
dx
dt
(Рх
dt*
форме);
dy
dt
d‘y
dP
1
dy\21’/,
(для уравнений в параметрической форме);
(для уравнения в полярных координатах).
Фиг. 222
Фиг. 223
Точки кривой, в которых кривизна имеет
максимум или минимум, называются вер-
шинами кривой.
Кругом кривизны кривой в точ-
ке М называется предельное положение
круга, проведённого через точку М и две
другие точки кривой N и Р (фиг. 223),
когда N-+M и Р-+М.
Радиус круга кривизны равен радиусу
кривизны, а центр круга кривизны (центр
кривизны) расположен на нормали к
Эвольвента (инволюта) кривой —
такая кривая, для которой данная является
эволютой.
Нормаль МС эвольвенты Г3 является
касательной к эволюте (фиг. 224), длина
дуги CCi эволюты равна соответствующему
приращению радиуса кривизны эвольвенты
СС\ = MtCt — МС; поэтому эвольвенту Г2
называют также развёрткой кривой Гр
получающейся разматыванием натянутой
нити, намотанной на Г,. Каждая кривая
имеет бесчисленное множество эвольвент,
соответствующих различным первоначаль-
ным длинам нити (фиг. 225).
Если X = X (/), У — Y (t) — параметри-
ческие уравнения кривой, то формулы (*)
дают систему диференциальных уравнений,
решения которой x = x(t,C), y—y(t,C)
определяют семейство эвольвент.
АСИМПТОТЫ
Если расстояние до некоторой прямой от
точки, удаляющейся в бесконечность1 по
данной кривой, стремится к нулю, то эта
прямая называется асимптотой данной
> Хотя бы одна из координат этой точки стре-
МИТСЯ К
ДИФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
197
кривой. Асимптота может либо не пересе-
кать (фиг. 226, а), либо пересекать кривую
(фиг. 226, б).
Кривая у = / (х) имеет горизонтальную
асимптоту, если существует предел
lim / (х) = b или lim / (х) =
х->оо х->—оо
В этом случае у—Ь (или, соответственно,
у = р) — уравнение этой асимптоты.
Если lim/(x) = ±oo, прямая х=а —
вертикальная асимптота.
Фиг. 226
Для отыскания наклонной асимптоты
следует вычислить пределы
/ (х) / / (х)\
к — lim (или lim —— ]
х_>оо х \ х_>—оо х /
п
b = lim [/ (х) — /сх]
Х->00
/соответственно lim [/ (х) — fcx] \ .
1 х-^-оо )
Если пределы, определяющие величины
к и Ь, существуют, то прямая у — кх Ь—
асимптота данной кривой.
Для отыскания асимптоты кривой, за-
данной параметрически х = х(0, у = у(0,
следует найти такое значение t = т, чтобы
limx(/)=±oo или limy(/)=±°o;
если при этом
lim x(f)= ± оо, a lim у (t) = b,
то у = b — асимптота (горизонтальная).
Если
Если при этом не обращается в нуль
хотя бы одна из производных второго по-
рядка:
А = р'кх (*о,Уо); В »= F*y (хо,Уо);
С = Гуу(х0,у0),
то точка называется двойной.
Двойная точка является:
а) изолированной (т. е. в некоторой
её окрестности нет других точек данной
кривой), если Д = AC — EF > 0 (фиг. 227,а);
б) узловой, если Д < 0 (фиг. 227,6);
в) точкой возврата 1-го (фиг. 227, в)
или 2-го (фиг. 227, г) рода или точкой
самосоприкосновения (фиг, 227,6),
если Д = 0.
Если кривая алгебраическая1, то,
перейдя при помощи параллельного переноса
к системе координат 0XY, начало которой
находится в исследуемой особой точке,
получим уравнение кривой в форме
АХ2 + 2 BXY + CY* + R (X,Y) = О,
где многочлен R (X, Y) содержит только
члены порядка выше второго относительно
X и Y.
В этом случае АХ2 + 2 BXY + СУ2 = О
есть уравнение пары касательных в особой
точке, и, следовательно, эта точка будет
узловой, если имеются две действительные
касательные (т. е. АС—В2 < 0), изолиро-
ванной, если обе касательные мнимые (т. е.
АС — В2 > 0), и точкой возврата 1-го или
2-го рода или точкой самосоприкосновения,
если обе касательные совпадают (т. е. АС—
— В2 = 0). Если в особой точке обращаются
в нуль все частные производные второго
порядка функции F (х, у), по не обращается
в нуль хотя бы одна производная третьего
порядка, то такая точка называется трой-
ной, и т. д.
limy(/)=±oo, a limx(/) = a,
то х = а—асимптота (вертикальная).
Если limx(/)=±oo и limy(f)=±oo
и, кроме того, существуют пределы
у (О
fc=,im77A и & = Кт [у (/) — А'х (/)],
то прямая у = кх + b является асимптотой
данной кривой.
Пример.
х3 + 2 х1 + 6
у - " х> + 3 ’
= 1;
Й =
/х’ + 2 х3 + 6
\ ха + 3
b *= lim
х_^оо
асимптота имеет уравнение у = х+ 2.
ОСОБЫЕ ТОЧКИ
Особая точка кривой F (х, у) = 0 назы-
вается кратной (двойной, тройной
и т. д.), если её координаты х0, у0 удовле-
творяю! системе уравнений
р (*<» у<>)=0; Ех <хо> >’о) - °; F'y (*о, у») --= о.
Фиг. 227
У неалгебраических кривых, кроме пере-
численных особых (кратных) точек, могут
быть особенности другой природы, напри-
мер, точки прекращения (фиг. 227, е),
находящиеся на границе области существо-
вания функции у = / (х), определяющей
кривую, или в точках разрыва 1-го рода
(см. стр. 130) этой функции, угловые
точки (фиг. 227, ж), где левый и правый
пределы (см. стр. 129) производной /' (х)
существуют и различны, и некоторые дру-
гие.
* Т. е. F (х, у) — многочлен.
198
МАТЕМАТИКА
ОГИБАЮЩИЕ СЕМЕЙСТВА КРИВЫХ
Огибающей семейства плоских кривых
называется кривая (или совокупность не-
скольких кривых), которой касаются все
линии данного семейства, причём каждой
дуги этой кривой касается бесконечное
множество линий рассматриваемого семей-
ства.
Если зависящее от одного параметра
семейство кривых
F (х, у, а) = О
имеет огибающую, то параметрические урав-
нения последней определяются из системы
F(x, у,а) = 0; Ед(х, у,а) = 0.
Если из этой системы исключить пара-
метр а, то получим неявное уравнение
D (х, у) = 0.
Кривая D (х, у) = 0 (дискриминант-
ная кривая) наряду с огибающей, если
таковая имеется, может содержать также
геометрическое место особых точек, не яв-
ляющееся огибающей.
Пример 1. Дискриминантная кривая семейства
у — (х— а)’ (фиг. 228) у=О (ось ОХ) является геоме-
трическим местом точек перегиба и огибающей.
Пример 2. Дискриминантная кривая семейства
у’ = (х — «)8 (фиг. 229) у=О является геометриче-
ским местом точек возврата и огибающей.
Точка перегиба, совпадающая с центром
симметрии кривой
2&! — 9 abc
27 а!
График многочлена п-й степени (фиг. 233)
у = аохп + ajx"-1 + ... + a„_i х + a„.
Кривая пересекает ось ОХ не более л раз.
Если п нечётное, то эта функция или
совсем не имеет экстремумов, или имеет
Фиг. 232
чётное число (от 2 до п—1) экстремумов,
максимумы и минимумы чередуются; точек
перегиба — нечётное число (от 1 доп—2).
Если п чётное, то функция имеет нечётное
число экстремумов (от 1 до л—1), максиму-
мы и минимумы чередуются; точек переги-
ба—чётное число (от 0 до л — 2). Асимптот
и особых точек нет.
Равноосная гипербола, 1) у = (на
фиг. 234 сплошная линия для а>0 и пунк-
Фиг. 229
Фиг. 231
Фиг. 233
Фиг. 234
тирная для а<0). Асимптоты — оси коорди-
нат. Вершины гиперболы
Пример 3. Дискриминантная кривая семейства
у* — (х — а)8 (фиг. 23о) у=О есть геометрическое
место точек возврата и не является огибающей
Пример 4. Дискриминантная кривая семейства
строфоид
(а + х) (у — а)8 = х8 (а — х)
(фиг. 231) распадается на прямые х = о (геометри-
ческое место узловых точек) и х=с (огибающая).
НЕКОТОРЫЕ ПЛОСКИЕ КРИВЫЕ1
Кубическая парабола (фиг. 232):
у = ах3 + Ьхг + сх + d.
Точки пересечения с осью ОХ определя-
ются действительными корнями уравнения
у = 0; их может быть одна, две (в этом
случае в одной из точек происходит касание),
или три: Av А2, А3. Точка пересечения с
осью OY: В (0, rf)._Экстремумы
L’ и \ За ’ ____
. 2 Ь3 — 9 abc ± (бас— 2 &2) V— Д X
+ 27а2 ) ’
где Д = 3 ас — &!.
А, В, Аг, В, (±У\а\, ±Г|ат).
Экстремумов нет.
G«X “И Ь1
2)>* = а1гг»;(фиг-235)’
Фиг. 235
Асимптоты параллельны осям координат;
центр f — —V
вершины гиперболы
А в{-Ь±^Х а> ± '
\ flg fl2
1 См. (2) на стр. 266 и (59) на стр.267.
где D — а^-а^.
ДИФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
199
Полукубическая парабола (фиг. 236):
у^ах’1, (уравнения в параметрической
форме: х = t2, y = at3). Асимптот не имеет.
В начале координат—точка возврата
1-го рода.
Длина L кривой от начала до произволь-
ной точки М (х, у):
Ь = 2-^-2[(4 + 9а2х)’/>-8].
Фиг. 237
Фиг. 238
График степенной функции, а) у = ахп
(л > 1 и целое) — парабола л-го порядка
(фиг. 237, а и б).
При л чётном кривая симметрична отно-
сительно оси 0Y и имеет в начале коорди-
нат экстремум, при л нечётном симметрична
относительно начала координат, являющего-
ся точкой перегиба. Асимптот нет.
б)у=^п = ах (л—целое положительное)
(фиг. 238) — кривая гиперболического типа.
Асимптоты—координатные оси. Эстрему-
мов нет. При л нечётном кривая симме-
трична относительно начала координат, а
при л чётном—относительно оси 0Y.
а3
Локон Аньези (фиг. 239). у = --2_р—2 .
Асимптота—ось ОХ. Максимум А (0, а); ра-
диус кривизны в нём y • Точки перегиба
_ / а За\
В, С ± у— , -4* ). Площадь между криво»
и асимптотой те а2.
Н
Фиг. 240
Декартов лист (фиг. 240). х3 + у3 = 3аху
(уравнения в параметрической форме:
За/ За!2
х = 1 + t3 ’ у = 1 + Р '
где t = tg МОХ).
В начале координат—узловая точка с ка-
сательными — осями координат; радиус
. За
кривизны ветвей в нем —гт-- . Асимптота
/ 3 3 \
х + у + а = 0. Вершина A I а, -% a ). Пло-
щадь петлит,- а2; площадь между кривой и
3
асимптотой а2.
Циссоида (фиг. 241). Геометрическое место
точек М, для которых ОМ = PQ (Р— точка
производящего круга с диамет-
ром а).
х3
Уравнение: у2 = ;
в параметрической форме
at2 at3
х — > у j j2 (1 = tg МОХ)’
в полярных координатах
a sin2 ср
Р _ COS <р
В начале координат—точка возврата 1-го
рода. Асимптота х = а. Площадь между
кривой и асимптотой j'a2.
Строфоида (фиг. 242). Геометрическое
место точек М, и М., для которых РМ, =»
= РМ2 = ОР.
Фиг. 241 Фиг. 242
Уравнение:
в параметрической форме
I2 — 1 Р — 1
х = а р +”1 ’ y = at Р~+Т = tg М0ХУ’
в полярных координатах
cos 2 ср
Р — cos у
В начале координат—узловая точка (ка-
сательные у = + х). Асимптота х = а. Вер-
те а2
шина А( — а, 0). Площадь петли а2 — —у- ,
-а'
площадь между кривой и асимптотой а2+~4~.
Конхоида (фиг. 243). Геометрическое ме-
сто точек М, для которых ОМ = OP ± I,
причём для знака (4-) внешняя ветвь, для
знака (—) внутренняя.
Уравнение:
(х — а)2 (х2 + у2) — Рх2 = 0;
в параметрической форме
х = а + I cos ср, у — a tg <₽ + I sin у;
в полярных координатах
а
Р ~ cos у
200
МАТЕМАТИКА
Внешняя ветвь: асимптота х = I; вершина
А (а + I, 0); две точки перегиба В, С [х равен
наибольшему из корней уравнения х3—
— За2х + 2а(а2—Z2) = 0]. Площадь между
ветвью и асимптотой бесконечна.
Внутренняя ветвь: асимптота х = I; вер-
шина D (а—1,0); в начале координат —
двойная точка:
а) при I < а — изолированная точка
(фиг. 243,а). Точки перегиба Е и F (х равен
второму по величине положительному корню
уравнения х3 — 3 а2х + 2 а (а2 — Z2) = 0);
Фиг. 243
б) при /> а — узловая точка (фиг. 243, б).
,, з,—
Максимум и минимум при х = а—j/ al2.
Наклон касательных в начале координат:
± У1*^а2
tga=±---------.
I УР — а2
радиус кривизны ------- ;
в) при I =а— точка возврата (фиг. 243, в).
Улитка Паскаля (фиг. 244). ОМ = OP ± I.
Уравнение:
(х2 + у2 — ах)2 = /2(х2 + у2);
в параметрической форме
х = a cos2 у + Z cos у, у ~ a cos у siny-f-Z sin у;
в полярных координатах
р = a cos у + Z.
Вершины А, В (а+ 1,0). Четыре экстре-
мума, если а>1, и два, если a<^Z:
( — I ±У Z2 + 8 а2 \
С, D,E,F ^cos у =--
а) 1>?а 5}q<1 <2а
Фиг. 244
/ 2a2+Z2\
Точки перегиба G, НI cos у =— —— 1,
если a < Z < 2a. Начало координат — двой-
ная точка: изолированная при а < I, узловая
при а > I ( наклон касательных в ней
__/2 ____\
tga = ± —j, радиус кривизны У a2—Vs }
и точка возврата при а = Z (в последнем
случае кривая — к а р д и о и д а).
Площадь улитки
л а2
-2-+KZ2
(в случае фиг. 244,в площадь внутренней
петли при вычислении по этой формуле
считается дважды).
Кардиоида (фиг. 245). Частный случай
улитки Паскаля: ОМ = ОР ± а.
Уравнение:
(х2 + у2)2 — 2 ах (х2 + у2) = а2у2;
в параметрической форме
х = a cos у (1 + cos у), у = a sin у (1 + cos у);
в полярных координатах
р = а (1 + cosy).
Начало координат—точка возврата. Вер-
шина А (2 а, 0).
те
Максимум и минимум при у = ± — :
(3 з Уз \
С, D ^4 а, ± -д— a J .
Площадь те а2; длина 8 а.
Овал Кассини (фиг. 246).
Геометрическое место точек
М, для которых произведе-
ние расстояний от данных то-
чек Fy{c,0) и F2(—с, 0) (фо-
кусов) постоянно и равно а2.
Уравнение:
Фиг.
(х2 + у2)2 — 2 с2 (х2 — у2) ~ а* — с4;
в полярных координатах
р2 = с2 cos 2 у ± Ус* cos2 2 у + (а1 — с1).
а) а>с]/Л2 — выпуклый овал (фиг. 246, а)
Точки пересечения с осью ОХ:
А, С(± У а2 + с2 , 0);
в)а<с
Фиг. 246
точки пересечения с осью ОУ:
В, D(0, ± Уа2^7г).
Если а = сУ‘2 , то в точках В и D кри
визна равна нулю.
б) с < а < сУ^2 (фиг. 246>б).
ДИФЕРЕНЦИАЛЬНЛЯ ГЕОМЕТРИЯ
201
Точки пересечения с осями те же, что и
в случае а);
максимумы и минимумы:
В, О(0, + Уа^^с3);
( УТс*^а* а3\
Е, G, К, I -------2'с--- ’ ±2 с) '
Точки перегиба
Р, L, (т—п), Т )/”4 (m+n)
где _____
а1— с1 1 Га*-— с*
т= ’ п = У ~г~-
в) а < с—два овала (фиг. 246, в). Точки
пересечения с осью ОХ:
А,С( + Уй^+с2, 0) и Р, Q (Ус3—а3, 0);
максимумы и минимумы:
для укороченной Х< 1); ООг = 2ла;
максимумы
Ап А3, ... [(2 к -(- 1) л а, (1 + Х)а],
минимумы
ВО,ВХ,В2, ... [2 X л а, (1 — X) а].
Для удлинённой циклоиды—узловые точки
Dt,DltD2, ... [2Иа,а (1 -j/x2- /8 )],
где t0 — наименьший положительный корень
уравнения t = X sin t.
Фиг. 248
г) а = с—лемниската Бернулли (см. ниже).
Лемниската Бернулли (фиг. 247). Частный
случай овала Кассини при а — с.
Уравнение:
(х2 + у2)2 — 2 а3 (х2 — у2) = 0;
\ /
247
осью ОХ
в полярных координа-
тах . ,
И / г
р2 = 2 a3 cos 2 у. *
Начало координат к/
является точкой пере-
гиба И УЗЛОВОЙ ТОЧКОЙ фиг.
с касательными у=±х.
Точки пересечения кривой с
А,С(± а У2, 0); максимумы и минимумы
( а УЗ а \ л
Е, G, К,1{± — , ± 2 J ; ? = ± б
Площадь каждой петли а2.
Циклоида (фиг. 248). Траектория точки
окружности, катящейся без скольжения по
прямой.
Уравнение:
_________________ а — у
х +V у (2 а — у) = a arc cos —а~
(а — радиус окружности);
в параметрической форме:
x — a(t — sin t), y=a(l —cost),
где t = МС1В.
Точки возврата
О, Ог, Ог, ... (ОО± = ОгО2 = . . . = 2ла).
Вершины Alt А2, . . . [(2 А + J) л а, 2 а].
Длина одной ветви 8а, площадь между
ней и осью ОХ Зла2. Радиус кривизны
в вершинах 4а. Эволюта циклоиды — та-
кая же циклоида (отмечена пунктиром).
Удлинённая (фиг. 249, а) и укороченная
(фиг. 249, б) циклоиды («трохоиды»). Тра-
ектория точки, лежащей вне или внутри
окружности, которая катится без скольжения
по прямой линии.
Уравнения в параметрической форме:
X = a (t — X sin t), у = а (1 — X cos t),
где а — радиус окружности, t — МС1В,
\a-C-iM (для удлинённой циклоиды Х> 1,
Для укороченной циклоиды—точки пере-
гиба
Е,, Е2,... [a (arc cos X—~кУ 1 — X2), а (1 — X2)],
Площадь, заштрихованная на фиг. 249,
ла2 (2-j- X2). Радиус кривизны в точках
(1 + *)!
максимума а—--------,а в точках минимума
( 1 - X)2
а—------.
Эпициклоида (фиг. 250). Траектория точ-
ки М окружности, катящейся без скольжения
по другой окружности вне её.
Уравнения в параметрической форме:
А + а
х — (А + a) cos <р — a cos —-— у,
А + а
у = (А + a) sin — a sin —-— <р
(А—радиус неподвижного, а — подвижного
круга; ср = СОХ).
6)Л<1
Фиг. 249
При т = - = 1 — кардиоида.
а) При т целом кривая замкнута и со-
стоит из т одинаковых частей (фиг. 250,а);
точки возврата А1; А,, ..., А„г:
2 к г.
р=А, ? =-~-(А= 0, 1, . . ,,m —1) .
Вершины Blt В2, ... Вт:
2 л / Г
Р = А + а, ?=-(fc+2
202
МАТЕМАТИКА
б) При т дробном (рациональном)
(фиг. 250,6) кривая тоже замкнутая, но
самопересекающаяся.
Длина одной ветви
_ 8(А + а)
~ т ’
Кривая состоит из двух ветвей, симмет-
ричных относительно оси ОХ. Луч OR пере-
секает кривую в точках O,Alt А2..Ап...,
находящихся друг от друга на постоянном
расстоянии А( Ai+1 = 2 л а.
Длина дуги ОМ (М—любая точка спирали)
(? У?2 + 1 + Ar sh ?) .
Площадь сектора Mj ОМ2:
о (?а8-т?) •
_ а
Радиус кривизны в начале координат у .
а
Гиперболическая спираль (фиг.253): р=— .
Кривая состоит из двух ветвей, симметрия-
при т целом длина всей кривой 8(А + а).
Площадь сектора AjBjAjA (без сектора не-
подвижного круга)
/ ЗА + 2 а\
710 ( A ) •
4а (А+а)
Радиус кривизны в вершинах „ , ~г- .
i U ”f“ А
Гипоциклоида (фиг. 251). Траектория
точки окружности, катящейся без скольже-
ния по другой окружности внутри неё. При
любом т (т > 1) уравнение гипоциклоиды
получается из соответствующего уравнения
эпициклоиды заменой а на — а.
При т—2 кривая вырождается в диаметр
неподвижного круга.
Фиг. 253
Фиг. 251
пых относительно оси ОУ. Асимптота у = а.
Начало координат — асимптотическая точка.
Площадь сектора М10М2
а2/£_
2 \?1 ?2 / ’
Логарифмическая спираль (фиг. 254). Кри-
вая пересекает все лучи, выходящие из
полюса О, под одним и тем же углом а.
Уравнение в полярных координатах
Р = ае''^
( тс
( к — ctg а; если а = -g , то fc=0 и кривая-
окружность^. Начало координат — асимпто-
тическая точка. Длина дуги М1М,,
При т = 3 (фиг. 251,а)
х = а (2 cos? -J- cos2?), у=а (2sin? — sin2?).
Длина 16 а; площадь 2 it а2.
При т = 4 (фиг. 251,6) (астроида)
х = A cos3 ?, у = A sin3 ?;
(или х'1, + уг,г = А’^“). Длина 24а (или б А);
/ 3
площадь ба2 (или -g- А2
Архимедова спираль (фиг. 252). Траекто-
рия точки, движущейся с постоянной ско-
ростью и по лучу, вращающемуся около
полюса О с постоянной угловой скоростью со.
Уравнение в полярных координатах
р = а?,
aVT+k*
к
(Рз — Р1)-
Параболическая спираль (фиг. 255): р2=а?.
Полюс—точка прекращения.
Фиг. 256
где
а
р2 = Полюс—асимпто-
г ?
v
Жезл (фиг. 256):
тическая точка. Полярная ось — асимптота.
ДИФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
203
Показательная кривая (фиг. 257):
у = ах (а> 0).
При а = е — натуральная показательная
кривая у = ех. Функция у принимает только
положительные значения. Асимптота —
ось ОХ.
Логарифмическая кривая (фиг. 258):
y=log„x (а > °).
При а=е—натуральная логарифмическая
кривая у = Inx. Функция у существует толь-
ко при х>0. Асимптота—ось ОУ.
График функции у=е— (ах^ (фиг. 259). Кри-
вая симметрична относительно оси ОУ. Асим-
фиг. 259 Фиг. 260
птота—ось ОХ. Максимум в точке
точки перегиба В и С
наклоны касательных в них:
К этому виду относится кривая нор-
мального закона распределения
ошибок (кривая Гаусса):
у = 4= e~h‘x‘ (стр. 227).
Кривая затухающего колебания (фиг.
260):
у = Ае axsin(<»x + <p0).
Она заключена между кривыми у= ± Ае~ах>
которых касается в точках:
71 — <Ро
------,(— 1)кАе~ах
А|( А:
<о
Асимптота — ось ОХ.
Точки пересечения с осями координат:
В (О, A sin у0) и Сп °, о).
' к л — у0 + а\
Х=-------5---- •
Экстремумы Dlt D2, ...
Точки перегиба
/ /с л — у0—2 а
> ... I х
ш
, где
Величина
(где у{ и yi+I — ординаты двух соседних
экстремумов) называется логарифми-
ческим декрементом затухания.
Цепная линия (фиг. 261):
v = a ch у
а
Линия равновесия гибкой тяжёлой нера-
стяжимой нити, подвешенной в двух точках.
Кривая симметрична относительно оси ОУ.
х
Вершина А (0, а). Длина дуги AM a sh — ;
площадь О AMP a2 sh — .
Трактриса (фиг. 262):
а -------------------
х — a ar ch — — V а2 — у2
У
а + “Ка2—у2
У ~
Эвольвента цепной линии (развёртывание
начинается в вершине А).
Асимптота — ось ОХ. Точка возврата (с
вертикальной касательной) А (0, а). Кривая
Фиг. 261
Фиг. 262
симметрична относительно оси ОУ. Длина
а
дуги AM а In — .
Развёртка (эвольвента) окружности
(фиг. 263). Траектория конца натянутой нити,
разматывающейся с окружности (АВ=ВМ).
Уравнение в параметрической форме:
х = a cos у + а у sin у, у = a sin у — а у cos у
(а — радиус круга, у = МОХ).
Фиг. 264
Кривая имеет две ветви, симметричные
относительно оси ОХ. Точка возврата
А (а, 0). Длина дуги AM % а у2.
Квадратриса Динострата (фиг. 264):
у
X = У ctg - ;
в полярных координатах: р sin у=а у.
204
МАТЕМАТИКА
Асимптоты у=паг. (п — ± 1, ±2,...). Вер-
шина А (а,0).Все остальные точки, для кото-
рых х — а—точки перегиба.
ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
Кривая в пространстве может быть зада-
на как линия пересечения двух поверхностей
F(x, у, г) = 0; Ф(х, у, г) = 0,
либо в параметрической форме:
x = x(t); y = y(r); z = z(t).
В частности, если параметр t совпадает с
одной из текущих координат точки на кривой
(например t = х), то уравнения кривой при-
нимают вид:
у = у(х); 2=2(х).
Иногда удобно в качестве параметра вы-
брать длину s дуги кривой от некоторой
начальной точки А (соответствующей значе-
нию t = f0) до текущей точки М
тогда уравнения кривой имеют вид:
x = x(s); у = y(s); z = z (s).
Диференциал дуги кривой выражается
формулой
ds = V dx2 + dy2 + dz2.
Сопровождающий трёхгранник
В каждой точке Л4 пространственной
кривой, где хотя бы одна из производных
dx dy dz
dt ’ dt ’ dt не Равна нУлю> определяются
три взаимно перпендикулярные прямые и
три взаимно перпендикулярные плоскости,
каждая из которых проходит через две из
трёх упомянутых прямых. Эти прямые и
плоскости, образующие так называемый
сопровождающий трёхгранник
(фиг. 265), следующие:
1) касательная — определяется так
же, как и для плоской кривой (стр. 194);
2) нормальная плоскость, — пер-
пендикулярная к касательной. Прямые, ле-
жащие в этой пло-
скости и проходя-
щие через точку
Л4, называются
нормалями к
кривой;
Фиг. 265
Фиг. 266
3) соприкасающаяся плос-
ко с т ь—предельное положение плоскости,
проходящей через точку М и две другие
точки кривой N и Р, когда N-+M и Р-+М
(фиг. 266);
4) главная нормаль — та из норма-
лей, которая лежит в соприкасающейся
плоскости (линия пересечения нормальной
и соприкасающейся плоскостей);
5) бинормаль — нормаль, перпендику-
лярная к соприкасающейся плоскости;
6) спрямляющая плоскость —
проходящая через касательную и бинормаль.
Положительное направление на касатель-
ной устанавливается так же, как и для
плоской кривой (стр. 194), и определяется
единичным вектором t (стр. 208); на главной
нормали—идёт в сторону вогнутости кривой
и определяется единичным вектором я; на
бинормали определяется единичным вектором
Ь = t X п (стр. 209).
Если кривая задана в форме
F(x, у, 2) = 0; ф(х, y,Z) = O,
то касательная имеет уравнения:
X —х У —У Z-z
dF dF dF dF dF dF
ду dz dz дх дх ду
дФ дФ дФ дФ дФ дФ
ду dz dz дх дх ду
а нормальная плоскость
X — х У-у Z— 2
dF dF dF
дх ду dz = о,
dj> дФ дФ
дх dF dz
где х, у, z—координаты точки Л4, а X, У,
Z — текущие координаты на касательной
или, соответственно, на нормальной плоско-
сти.
Уравнения элементов сопровождающего
трёхгранника, когда кривая задана парамет-
рическими уравнениями, следующие:
касательная
Х-х У-у z-z
х' у' ~ z' ’’
нормальная плоскость
х'(Х — х) + у'(У — у) + z'(Z — 2) = 0;
соприкасающаяся плоскость
У'
У"
бинормаль
X —х
I у' 2'1
I у" 2" I
У —у
I 2' X' I
I 2" X" I
спрямляющая плоскость
Х-х Y-y Z — z = 0
х' у' 1 т Z' п
где 1 = y'z" — y"z',
т = z'x" — z"x'
п = х'у" — х"у';
главная нормаль
X— х У — у Z
| у' Z' I I 2' х' I I X' . У ; ’
I т п | j п /I | i т I
ДИФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
205
где х, у, z попрежнему координаты точ-
ки М, а X, Y, Z— текущие координаты.
В случае, когда за параметр принята
длина дуги s, уравнения главной нормали
и спрямляющей плоскости упрощаются:
Х~х Y — у Z — z
Х' = —тт,— — —р;— (главная нормаль);
Кручением Т (второй кривиз-
н о й) кривой в точке М называется предел,
к которому стремится отношение угла О
между положительными направлениями би-
нормалей (или, что то же, между соприка-
сающимися плоскостями) в точках М и N
к длине As дуги MN, когда
х"(Х — х) + y"(Y — у) + z"(Z — 2) = О
(спрямляющая плоскость).
9
т = ,im a“s •
КРИВИЗНА И КРУЧЕНИЕ
Кривизной К. кривой в точке М на-
зывается предел, к которому стремится отно-
шение угла В между положительными на-
правлениями касательных к кривой в точках
М и N(yron смежности) к длине Д s
дуги MN, когда
о
К - Нт д-
х' у' z'
х" у" Z"
т = -= -р2 —= _________________________
т Г (х'‘ + у'“ + 2'* )3 (х'* +У
Так как касательные в точках М и N,
вообще говоря, не пересекаются, то угол ®
измеряется, как угол между прямыми, про-
ходящими через произвольную точку про-
странства О параллельно этим касательным
(фиг. 267).
Фиг. 267
Фиг. 268
Радиусом кривизны р называется
с 1
величина, обратная кривизне р= .
Если кривая задана параметрическими
уравнениями, то _________
L +?'* + z'‘ Xх"* +y"‘+z"‘ ) ~(x'x" + y'y” + z' z")s
K=P= (Xz-+y,-+z,-)-/.
В частности, если параметром является ---------
длина дуги s, то ПОВЕРХНОСТИ
Для измерения угла 9 следует из произ-
вольной точки О провести прямые, парал-
лельные упомянутым бинормалям (фиг. 268).
Радиусом кручения т называется
величина, обратная кручению т = у Если
кривая задана параметрическими уравнени-
ями, то
х' у' z'
хв у" z"
__________
+ z'a )(х"а + у"’ + г"‘ (x'x"+y'y"+z'z"}z
Если параметром является длина дуги s,
то
X' у' Z'
X" у” z"
1 х'" у'" z"'
Т - т х"а + у"’ + 2"а
Пример. Для винтовой линии
Т= .— = (кручение постоянно).
Формулы Серре-Френе. Производные еди-
ничных векторов t, п и Ь по длине дуги s
выражаются через эти единичные векторы с
помощью радиуса кривизны р и радиуса
кручения т посредством формул:
dt п dn ± b_ db _ _ n
ds~ p ’ ds p т ’ ds т
Пример. Для винтовой линии (стр. 189)
х = a cos /; у — a sin f; z «=• bt,
приняв за начальную точку t = О, имеем
t
s — j* У аа + bs dt =t Уа*"+"ь* ,
О
откуда
S с
х “ а cos =.; у — a sin ---------•
У а2 + Ь* У а* 4- ь-
bs
Z~ /а2 + &> ’
К ~ — = jv (кривизна постоянна).
Неявная форма уравнения поверхности:
F (х, у, г) = 0.
Параметрическая форма уравнений:
х = х(и, у); у = у(и, и); z = z(u,v).
В частности, если в качестве параметров вы-
браны какие-либо две координаты (например,
х и у), то уравнение поверхности имеет вид:
2=2(х, у) (явная форма).
Всякая зависимость между параметрами
/ (и, и) = 0 или и = и (() и v = v (Z) вместе с
уравнениями поверхности определяет кри-
вую на поверхности; в частности, уравнения
и = const и и = const определяют на поверх-
ности два семейства так называемых к о-
о р д и н а т н ы х линий, соответствующих
данному выбору параметров.
206
МАТЕМАТИКА
Всякая пара значений и = и0; v = v0
определяет на поверхности некоторую точ-
ку М (u0, и„ — гауссовы координаты
этой точки); через точку М проходят две
координатные линии: и=и0 и v = v0 (фиг. 269).
КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ
Если в точке М (х, у, г) поверхности
F,(x,y, z) = 0 хотя бы одна из производных
рх(х, у, z). Fy (х, у, z); F'z (х, у, z) не обра-
щается в нуль, то касательные ко всем кри-
вым, лежащим на поверхности и проходящим
через точку М, лежат в одной плоскости,
называемой касательной плоско-
стью (фиг. 270). Перпендикуляр, проведён-
Фиг. 270
ный через точку М к касательной плоскости,
называется нормалью к поверхности.
Если гг и г2 — единичные векторы, опре-
деляющие положительные направления на
координатных линиях v = const и и — const
в точке М, то положительное направление
на нормали к поверхности определяется
единичным вектором:
I П х г21 •
Всякая плоскость, проходящая через
нормаль к поверхности, называется нор-
мальной плоскостью.
Если в некоторой точке на поверхности
Fx = Fy = Fz = 0, то касательные к различ-
ным кривым, лежащим на поверхности и
проходящим через точку М, не лежат в
одной плоскости и образуют коническую
поверхность.
ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА
Диференциал ds дуги, лежащей на по-
верхности, проходящей через точку M(u.y)1
(линейный элемент поверхности),
находится по формуле
ds2 = Edu2 + 2 F du dv + G du2,
где
E - \du J +\du) +{duj •
dx dx , dy dy , dz dz
p = —----—< — — •
du dv du dv du dv ’
dx.2 , (&У\* , (dz\2
dv I ’’’ ydr у "T" ) •
Эта формула называется первой квад-
ратичной формой поверхности; её коэ-
фициенты зависят только от положения точ-
ки М на поверхности.
Длина дуги линии и = и (Г); и = v (t),
лежащей на поверхности
t, -----------------------------
С,/ tduX1 du dv [dv\2
s=.n +2Fat dT+G[dt)
где t0 и tt — значения параметра t, соответ-
ствующие концам дуги.
Две различные поверхности, имеющие
одну и ту же первую квадратичную форму,
могут быть наложены одна на другую путём
изгибания (т. е. без изменения длин дуг
на поверхности).
Элементарная площадь, ограниченная
линиями и = а; и + du = а; v = ₽; v + dv=$
(фиг. 271), находится по формуле
ds= Veg — f2 du dv.
КРИВИЗНА
Две кривые, проходящие через точку М
на поверхности и имеющие в 'ней об-
щую соприкасающуюся плоскость, имеют
в этой точке одинаковую кривизну (в част-
ности одна из этих кривых может быть
1 и и v — гауссовы координаты точки М-
Уравнения касательной плоскости и нормали к поверхности
Вид уравнения поверхности Касательная плоскость Нормаль
Неявный dF ( \ VP ( \ дР - X—х + —- У —у + -т— дх \ ) ду \ л ) dz М = ° X—X Y—у Z—z dP = dF ' ° dF дх ду дг 1
Явный г_.2.^(Х-х) + ^(у-у) I 11 r 1 Cl-1 i ^1^4 i I? • N
Параметрический Х-х У—у Z—z дх ду дг ди ди ди дх ду дг dv dv dv -=o X - x dy dz du du dy dz dv dv Y-y dz du du dz dx dv dv Z — z dx dy du du dx dy dv dv
Примечание. Здесь х, у, z — координаты точки М, а X, Y, Z — текущие координаты.
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
207
плоской, т. е. целиком лежать в соприка-
сающейся плоскости).
Если р — радиус кривизны некоторой
кривой на поверхности в точке М, a R —
радиус кривизны в точке М кривой, полу-
ченной в сечении поверхности нормальной
Фиг. 271
плоскостью, проведённой через эту точку и
через касательную к данной кривой (нор-
мальное сечение), то р = R cos а, где
а—угол между положительными направле-
ниями главной нормали к данной кривой и
нормали к поверхности; R следует брать
положительным, если единичный вектор N
нормали к поверхности направлен в сторону
вогнутости нормального сечения, и отри-
цательным — в противном случае.
Нормальные сечения, проходящие через
точку М с наименьшим и наибольшим
радиусами кривизны, называются главны-
ми сечениями, а соответствующие радиу-
сы кривизны Ri и R2—г лавными радиу-
сами кривизны.
Плоскости главных сечений взаимно пер-
пендикулярны. Радиус кривизны любого
нормального сечения выражается через глав-
ные радиусы кривизны с помощью формулы
Эйлера:
1 cos2 а> sin3 <и
R- Ri + Ra ’
где и — угол между плоскостью рассматри-
ваемого нормального сечения и плоскостью
одного из главных сечений.
Если Rj и R3 в точке М одинакового
знака, то поверхность (в некоторой окрест-
ности точки М) расположена по одну сто-
рону от касательной плоскости и точка М
называется эллиптической (таковы,
между прочим, все точки эллипсоида). В
частности, если R1=R2, то точка М — кру-
то в а я.
Если Rx и R2 противоположных знаков,
то поверхность пересекается в точке М ка-
сательной плоскостью и точка М—гипер-
болическая (таковы, в частности, все
точки однополостного гиперболоида).
Если Rx = оо или R2= оо, то для одного
из главных сечений точка М является точкой
перегиба или это главное сечение—прямая.
Точка М в этом случае — параболиче-
ская (таковы все точки цилиндра).
1/1 1 \
Выражение Н = I I называется
средней кривизной поверхности в дан-
ной точке; выражение К = п п —полной
или гауссовой кривизной.
Линии кривизны и геодезические Линии.
Кривые на поверхности, имеющие в каждой
точке направление главных сечений, назы-
ваются линиями кривизны.
Кривые на поверхности, для которых в
каждой точке главная нормаль совпадает с
нормалью к поверхности, называются гео-
дезическими линиями.
Из всех дуг, лежащих на поверхности и
соединяющих две данные точки, наименьшую
длину имеет дуга геодезической линии.
Пример. Геодезическими линиями на поверхно-
сти круглого цилиндра являются винтовые линии»
на плоскости — прямые, на шаровой поверхности —
окружности больших кругов.
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
ВЕКТОРНАЯ АЛГЕБРА
Величины, которые характеризуются од-
ним положительным или отрицательным
числом, называются скалярными или
скалярами (длина, температура, масса,
работа и т. д.). Величины, для определения
которых необходимо знать размеры и их
направление в пространстве, называются
векторными или векторами (сила,
скорость, ускорение и т. д.). Геометрически
векторная величина изображается направ-
ленным отрезком АВ и обозначается АВ = а
(фиг. 272), Точка А называется началом
(точкой приложения), а В—концом вектора.
Длина вектора а обозначается через | а | или
а. Она называется также его модулем.
Прямая, по которой направлен вектор,
называется линией действия или
носителем вектора.
Различают следующие векторы:
1) свободные, которые могут быть
перенесены параллельно самим себе так,
чтобы начало вектора совпало с любой точ-
кой пространства (например, скорость по-
ступательного движения твёпдого тела);
2) скользящие, которые могут пере-
мещаться только вдоль линии своего дейст-
вия (например, сила в твёрдом теле);
3) неподвижны е—связанные с точкой
приложения (например, скорость движения
частицы жидкости в движущемся потоке).
Нуль-вектор (0) вектор, у которого
начало и конец совпадают; его длина равна
нулю, а направление
неопределённое.
Всё дальнейшее от-
носится к свободным
векторам и поэтому два
вектора считаются рав-
ными (а = ft), если рав-
ны их длины | а I = | ft| и
они одинаково направле-
ны; векторы с параллельными линиями дейст-
вия называются коллинеарными, при
этом, если их направления совпадают, они
называются также параллельными,
если не совпадают — антипар аллель-
ными. Векторы называются взаимно
противоположными, если они равны
по длине и антипараллельны: АВ = а,
А
Фиг. 2 72
208
МАТЕМАТИКА
BA = — а. Векторы, расположенные в одной
или в параллельных плоскостях, называют-
ся компланарными.
Ортом или единичным вектором
вектора а называется вектор, совпадающий
с ним по направлению и имеющий длину,
равную единице (обозначение: а0).
Орты положительных координатных осей
обозначаются через i, J, k.
Проекции вектора а на оси прямоуголь-
ной прямолинейной системы координат1
(фиг. 273) связаны с длиной вектора и его
направляющими косинусами соотношениями:
ах — \а I cos (а, х);
av — I а | cos (а, у);
линяющий начало А первого слагаемого
вектора а с концом С второго слагаемого Ь:
с = а + Ь.
Модуль вектора-суммы связан с модулями
векторов-слагаемых соотношением
с2 = а2 + &2 + 2 ab cos (а, Ь),
Понятие суммы векторов (геометрической
суммы) может быть обобщено и на случай
любого конечного числа слагаемых.
az — | a I cos (а, z).
Вектор вполне определён тремя скаляра-
ми—своими проекциями на оси координат.
Проекции ах, ау, аг называются также
координатами вектора в прямоугольной
системе OXYZ.
Если Xi.yi,?! — координаты начала век-
тора, а х2, у2, z2—координаты его конца,
ТО (1Х Х2 " X,, йу ~ У? У If ~ - %!•
f Длина вектора а и его направляющие
косинусы определяются через проекции век-
тора по формулам:
I я I = j/" а2 + Ду+ ;
cos (а, х) =
cos(а, у) =
___аУ
У а2х+а2 + а2
Сумма векторов а, b....е (фиг. 276)
есть вектор r= AR, представляющий собой
замыкающую ломаной ABC ...R, составлен-
ной из векторов-слагаемых
/* — а b -|- с 6,
Векторная сумма обладает следующими
двумя основными свойствами:
1) свойством переместительности
(коммутативности)
а + b — b + а;
2) свойством сочетательности (ас-
социативности)
(а + Ь) + с = а + (& + с). _
Разностью двух векторов а = АВ и
Ь — ВС (фиг. 277) называется вектор с‘ —
— АС, соединяющий начало А вектора а с
'' az
cos (а, z) = -у-—.
у ах+ау + аг
Вектор ОМ = г называется радиусом-
вектором точки М, если начало его сов-
падает с началом координат, а конец с
Фиг. 277
С
Фиг. 273 Фиг. 274
точкой М (х, у, z); при этом проекции
радиуса-вектора г (фиг. 274) совпадают с
координатами точки М:
гх = X; Гу = у; Гг = г.
Суммой двух векторов а=АВ и Ь=ВС
называется вектор с = АС (фиг. 275), сое-
1 Проекции положительны или отрицательны в
зависимости от того, совпадают ли их направления
с положительными направлениями соответствующих
координатных осей или нет.
концом С вектора — Ь, противополож-
ного вектору Ъ (ВС = ВС). Эта разность
является суммой векторов а и — &:
с = а — b = а + (— Ь).
Сумма и разность двух векторов а и &
(фиг. 278) могут быть получены, как два
вектора-диагонали параллелограма с и с',
построенного на векторах а и Ь.
Длины вектора-суммы и вектора-разности
двух векторов связаны с длинами составляю-
щих векторов неравенствами:
1а| — |&|<|а±&|<!а1 + 1&1.
Произведение скаляра т на вектор а
есть вектор, коллинеарный с а, имеющий
длину I т | • | а | и направление, совпадающее
с а при т > 0 и противоположное а при
т < 0.
Если вектор b коллинеарен вектору а,
то b = т а.
Если векторы а, b и с компланарны, то
один из них является линейной комбинаци-
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
209
ей двух других, т. е. с = та + nb (т и
п — скаляры).
Всякий вектор а выражается через свой
единичный вектор а° следующим образом:
а = | а 1 а°.
Выражение вектора а через орты коор-
динатных осей:
a = axi+ ayJ + a2k,
где ах, ау, а2 — проекции вектора на коор-
динатные оси.
Векторы axl, ayj, a2k называются с о-
ставляющими, или компонентами,
вектора а по координатным осям.
В частности, для радиуса-вектора г
точки М (х, у, z) (фиг. 279) имеем:
r= xi+yj + zk.
Основные свойства:
та = ат; тпа — rima; (т + л)а=та+па;
т(а + Ь)= та + mb.
Координаты вектора-суммы и вектора-
разиости двух векторов равны соответствен-
Фиг. 279
Фиг. 280
но сумме и разности координат составляю-
щих векторов, т. е. если с = а ± ft, то:
сх == ах i bx; су — ау by; с2 ®= и2 i b2.
Скалярное (внутреннее) произ-
ведение двух векторов а и b [обозначе-
ние: (а, Ь) или ab] есть величина скаляр-
ная, равная произведению длин векторов-
сомножителей на косинус угла между ними
или, иначе, равная произведению длины
одного из векторов-сомножителей на проек-
цию второго (фиг. 280) на направление
первого:
(a, b) = ab — | а 11 b | cos (a, й) =
= I а I пра Ь = | Ь | прь а.
Скалярное произведение двух векторов
обладает следующими свойствами:
1) аЬ = Ьа;
2) т • аЬ = та • Ь ~ а • mb;
3) а (Ь + с) = ab + ас.
Скалярные произведения координатных
ортов дают
//=//== 1; iJ=jk = ki=O.
Выражение скалярного произведения
двух векторов через координаты векторов-
сомножителей:
ab = ахЬх + ауЬу + а2Ь2.
Угол между векторами а и ft определяется
по формуле
ab
cos <а-= rsw “
a.ybx 4~ а.уЬу + azb2
Условие перпендикулярности двух век-
торов
ab = 0
или в координатах
ахЬх 4- ауЬу + а2Ь2 = 0.
Векторное (внешнее) произве-
дение двух векторов а и Ь (обозначение:
[a, ft] или а х ft) есть вектор с (фиг. 281) с
длиной, численно равной
площади параллелограма,
построенного на векторах-
сомножителях, и направ-
ленный перпендикулярно к
плоскости параллелограма
таким образом, чтобы век-
торы а, Ь и с образовали
правую связку, т. е. чтобы
кратчайший поворот от а
к ft, если смотреть с конца
вектора с, совершался против направления
движения часовой стрелки.
Длина векторного произведения связана
с длинами векторов-сомножителей равенст-
вом
I с | = 1а х ft| = | а | [ ft ( sin (a, ft).
При перестановке местами векторов-сомно-
жителей векторное произведение изменяет
знак на противоположный
ftxe=-axft.
Векторное произведение обладает свойст-
вами ассоциативности и дистрибутивности
m (а х Ь) =» та х ft = a х mb;
ax(ft + c) = axft + axc.
Векторные произведения координатных
ортов дают:
i х i ~J xj = kx ft = 0;
ixj^k; Jxk = i; kxi^j;
Jxi = ~k; kxj = — i; ixk = —J.
Выражение векторного произведения че.
рез координаты векторов-сомножителей
I J k
ах ау а2
bx bv Ь2
с = а х ft ==
__I а у а2 I _] а2 ах | I а % ау |
Сх~|А А|; Су=рг Ар С*“|А АГ
Площадь параллелограма, построенного
на векторах а и Ь, может быть вычислена
по формуле
5 = I а х ft | =
Условие коллинеарности двух векторов:
а X ft » О,
а в координатах:
i J k
ах ау а2
Ьх Ьу Ь2
210
МАТЕМАТИКА
или
Ох_
Ьх~ Ьу~ Ьг'
Смешанное (векторно-скаляр-
ное) произведение трёх векторов
а, Ь и с (фиг. 282) [обозначение: (а X Ь) с
или о&с] есть скаляр, численно равный
объёму параллелепипе-
да, построенного на ве-
кторах а, & и с, как на
рёбрах. Смешанное про-
изведение положитель-
но, если векторы а, b
и с образуют правую
Фиг. 282
связку, и отрицательно,
если они образуют левую связку.
Смешанное произведение трёх векторов
при перестановке двух сомножителей изме-
няет знак; при циклической (круговой)
перестановке всех трёх сомножителей не
изменяет знака:
Если за начало переменного вектора
г = r(t) выбрать некоторую неподвижную
точку О, то конец вектор-функции г = г (t)
опишет кривую в пространстве (фиг. 283),
называемую годографом вектора г.
Уравнение годографа в координатной
(параметрической) форме:
x = x(0; y = y(t); z=z(t),
где г = xi + yj + zft.
Производная вектор-функции a=a(t)
по скалярному аргументу t представляет
da (t)
собой новую вектор-функцию —щ—и опре-
деляется по формуле
da (t) a(t + &t) — a(t)
-<n- -X -—г,-— -
= a'x(t) i + a'y (t)J + a'z (t)k.
„ dr(t)
Производная радиуса-вектора =
abc bca = cab = — acb = Ьас == — cba.
Выражение
трёх векторов
сомножителей:
смешанного произведения
через координаты векторов-
= lim —дт— представляет собой вектор
(фиг. 284), касательный к годографу в со-
ответствующей точке.
abc =
dx ®Z
bx bv ьг
сх cv cz
По этой формуле производится вычисле-
ние объёма параллелепипеда, построенного
на векторах а, Ь, с.
Условие компланарности трёх векторов:
abc = 0
Фиг. 284
или в координатах:
ах
Ьх
С.г
ау az
by bz
Су CZ
Двойное векторное произ-
ведение трёх векторов [обозначение:
а х (& х с)] есть вектор, компланарный
векторам & и с; он может быть вычислен по
формуле
гт
Длина вектора зависит от выбора
параметра Z; если t есть длина дуги годо-
графа, отсчитываемой от некоторой началь-
ной точки годографа до точки М, то длина
dr
равна единице.
Основные правила диференцирования век-
тор-функции скалярного аргумента:
d _ da db de
1) at^ + b-^ = dF + dt~dt >
а X (& X с) = Ъ (ас) — с (ab).
2)
d (® a) d у da
~dt~ =dTa + !?dt '
ДИФЕрЕНЦИРОВАНИЕ
ВЕКТОР-ФУНКЦИИ
СКАЛЯРНОГО АРГУМЕНТА
где s==y(Z) — скалярная функция от t;
d (ab) da db
~d~r-di b+adt ;
3)
Если вектор а изменяется по длине и
направлению в зависимости от некоторого
скалярного аргумента /, то он называется
в е к т о р-ф у н к ц и е й скалярного аргу-
мента
а = а (/).
Вектор-функция a=a(t) может быть
определена, если заданы три скалярные
функции — её проекции на координатные
оси:
ax = ax(t); ay=atJ(t)-, az = az(t).
В этом случае выражение вектор-функции
в координатах будет
а = ах (t) i + ау (t)j + az (t) ft.
d da db
4) -lt(ay.b)^ x b + ax-^-,
d da d<t>
5) dt a [?(()] = jy •
Для единичного вектора и вообще для
вектора г постоянной длины имеет место
соотношение
dr
rdt =0'
которое показывает, что касательная к го-
дографу перпендикулярна к радиусу-векто-
ру; в этом случае годограф" представляет
собой кривую на поверхности сферы.
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
211
ТЕОРИЯ поля
Скалярная функция / (х, у, z), определён-
ная во всех точках пространства, может
рассматриваться, как функция точки P(x,y,z)
этого пространства [обозначение: / (Р)] и
определяет в пространстве некоторое ска-
лярное поле. Поверхности /(x,y,z) = с
(с = const) называются поверхностями
уровня данного скалярного поля (в слу-
чае функции двух переменных — функции
точки на плоскости — кривые / (х, у) = с —
л и н и и у р о в н я).
Через всякую точку М (х0, y0,z„) прохо-
дит поверхность уровня, для которой зна-
чение с определяется равенством
с = /(7И) = /(х0,у0, z0).
Производная функции / (х, у, z) в точке М
по всякому направлению (стр. 133), лежаще-
му в касательной плоскости к поверхности
уровня [по направлению касательной к ли-
нии уровня для функции /(х, у)], проходящей
через точку М, равна нулю. Наибольшее (по
абсолютной величине) значение имеет про-
изводная по направлению нормали к по-
верхности уровня.
Градиентом функции /(х, у, z) [обо-
значение: grad / (х, у, z)] в данной точке
М (х, у, г) называется вектор, направлен-
ный по нормали п к поверхностй уровня
[для функции /(х,у) к линии уровня], про-
ходящей через эту точку, в сторону воз-
растания функции, и по длине равный
производной данной функции по этому на-
правлению:
. df (х, у, z)
1 grad / (х, у, z)| = .
Таким образом, при помощи скалярного
поля функции / (х, у, z) определяется век-
торное поле градиента этой функции.
Если I — произвольное направление, вы-
д/
ходящее из точки М, то производная
равна проекции градиента на направление I:
df df
01 = dn cos С” л>=| grad f 1 cos (Z’ л) = grad£
В частности
dt dt df
Sradx/ = d£; SraM = dy ; =
Пример, Построить поле градиента функции
f (х,у ,z) № + № + z®.
Поверхности уровня этой функции х24-уаЧ- z3 «
= С — сферические поверхности с центром d начале
координат.
Далее
gradx/=2x, gradv/=2y, grad, /=2z
и _____
I grad У | = 2 /ха + у» + г! .
Таким образом, градиент в каждой точке на-
правлен по радиусу-вектору этой точки (нормально
к поверхности сферы ха 4- у3 + za = С) и по модулю
равен удвоенному радиусу-вектору.
Если дано'векторное поле A(x,y,z), то
в каждой точке (х, у, z) известны скалярные
функции Ах(х, у, z); А(/(х,у, z); Аг(х,у,г)—
проекции вектора А на координатные оси
(обратно: Ах, Ау, Аг определяют некоторое
векторное поле).
Дивергенцией вектора 4 (х; у; z)
(обозначение: div А) называется скаляр:
дАх (х, у, z) дАу(х, у, z) dA2(x,y,z)
dx ' dy dz
(для вектор-функции A(x, у), зависящей от
двух переменных,
dAx dA„\
div А = 4- 1 .
dx ' dy / ‘
Векторное поле А (х, у, z) определяет
скалярное поле дивергенции вектора А.
Вихрем вектора А (х, у, z) называется
такой вектор В (х, у, z) (обозначение: Z? =
= rot А или В = curl А), проекции которого
на координатные оси Вх, В;/, Bz выражают-
ся через проекции вектора А при помощи
равенств:
о _ d dAv _ О А? _ 0Az
х dy dz ’ a‘J~ dz dx ’
о __ — (>&x
z dx dy '
В случае вектор-функции A (x, у), зави-
ящей от двух аргументов:
п „ n „ dAv dAx
вл =Ву = 0, В, =-^-----и вихрь В —
= rotA направлен всегда по оси OZ; в этом
случае иногда удобно вихрь считать скаляром
О R ^Ау
в-вг= Тх _ .
Векторное поле А определяет, таким об-
разом, другое векторное поле rot А.
с
ИНТЕГРАЛЬНЫЕ СООТНОШЕНИЯ
Циркуляцией вектора А (х, у, z)
(циркуляцией векторного поля) по замкну-
тому пространственному контуру (С) назы-
вается криволинейный интеграл
f As ds,
(С)
где ds— диференциал дуги контура (С), а А,—
проекция вектора А на положительное на-
правление касательной к контуру (С).
Если ds — вектор, длина которого равна
диференциалу дуги контура (С) и который
направлен по касательной к контуру (С) в
положительную сторону (dx, dy, dz—проек-
ции вектора ds на координатные оси), то
Asds — Ads.
Циркуляция вектора А по контуру (С)
может быть записана в форме
J Ads или f A rdx + Aydy + A-dz
(С) (С)
[для плоского векторного поля А (х, у) цир-
куляция выражается при помощи криволи-
нейного интеграла
I' Asds — J Ads = f Axdx + Aydy].
(С) (С) (С)
Потоком вектора А (х, у, z) (потоком
векторного поля) через поверхность (S) на-
зывается интеграл но поверхности
CS) г 14*
212
МАТЕМАТИКА
где Ап — проекция вектора А на выбранное
на нормали к поверхности направление п.
Если d S вектор, длина которого числен-
но равна элементарной площади dS поверх-
ности и который направлен по нормали к
поверхности в положительную сторону, то
And's = Ad S и поток вектора через поверх-
ность можно записать в виде
(S)
ИЛИ £ПА*С°8(П,Х)+А^СО8(Л,у) 4-
4- Аг cos (и, z)] d S.
В случае, если вектор А (х,у) определяет
плоское поле, потоком поля через дугу (С)
называется криволинейный интеграл
[ Ands = \ A dn =
(С) (С)
_ [ [Ад. cos (п,х) + Ау cos (л, у)] ds —
(С)
== \Ajcdy-Aydx,
(С)
где dn —вектор, длина которого равна ds
и который направлен по нормали к контуру
в положительную сторону.
Формулы Стокса (для плоского
поля — формула Грина) и Остро-
градского связывают циркуляцию и
поток вектора с вихрем и дивергенцией:
J Asds = fj rotn A d S,
(C) (S)
где (С) — замкнутый контур, ограничиваю-
щий поверхность (S), а л — внешняя нормаль
к поверхности (формула Стокса);
И AndS = Ш div A du,
(S) (V)
где (S) — замкнутая поверхность, ограничи-
вающая область (V), а л—внешняя нормаль
к поверхности (S) (формула Остроградского).
Следующие векторные равенства связы-
вают скалярную функцию / с её градиентом
и вектор А с его вихрем:
fd S= JJJ grad fdw,
(S) (V)
Axd S — — rot Ade,
(S) (V)
где (S) — замкнутая поверхность^ (V) — объ-
ём, ею ограниченный.
Поле вектора А называется потен-
циальным, или безвихревым, если
вектор А является градиентом некоторой
функции f (х, у, Z), называемой потен-
циальной функцией: А = grad /; в
этом случае
d/ d/ df
Ах== дх'> Av “ ду : Аг = dz
и выражение
Axdx + Aydy + Azdz = df
является полным диференциалом; для этого
необходимо и достаточно, чтобы
л dAx п
ду dz - dz дх = и’
дА„ дАх
дх ду и’
т. е. чтобы вихрь поля rot А равнялся нулю
в каждой точке. В потенциальном поле цир-
куляция вектора по любому замкнутому
контуру (С) равна нулю:
J Asds = 0.
(С)
Поле вектора А называется с о л е нои-
да льны м, если в каждой точке поля
div А — 0,
т. е.
йАх , дАу dAz
дх + ду + дг
в этом случае поток вектора через любую
замкнутую поверхность равен нулю.
Если поле является одновременно потен-
циальным и соленоидальным, то div grad /=0
(/ — потенциальная функция) и потенциаль-
ная функция является гармонической,
т. е. удовлетворяет уравнению Лап-
ласа:
_ d2/ d2/ d2/ _
А t ~ dx2 "* dy2 dz2 ~
/ d2 d2 d2
= dx2 +d72 + d?2-°пеРат°Р Лап’
лас a
Для записи формул векторного анализа
удобно пользоваться оператором Га-
мильтона v (набла), где V — символиче-
ский вектор:
д , д . d
^ = dxi+ ду^ + dzk‘
Так, например,
gradf = V/; divA = VA,
rot А = у X A; w = Д.
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
Ряд с комплексными членами
ai + Ад + . . . 4- ап + • • (О
называется сходящимся, если сущест-
вует конечный предел1 его частной суммы
» Определение предела та же, что и в случае
действительных величин (стр. 128); в этом опреде-
лении следует лишь понятие абсолютной величины
заменить понятием модуля*
Sn = al4-a24-- . - + ап
при п -> оо.
Этот предел называется суммой ряда:
S = lim Sn.
П-* 00
Если
a« = an4-i?n (ап ирп—действительные числа),
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
213
то ряд (1) сходится тогда и только тогда,
когда сходятся ряды:
а1 + а2 + • • • + аП + • • • •
₽1 + ₽2 + • • - + •
Если сходится ряд
I | + | а21 + • • • + I ап I + • • • >
членами которого являются модули соответ-
ствующих членов ряда (1), то ряд (1) тоже
сходится и называется абсолютно схо-
дящимся рядом (стр. 158).
Правила действия над абсолютно сходя-
щимися рядами с действительными членами
распространяются и на тот случай, когда
члены ряда комплексные.
Областью сходимости степенного ряда
с0 -f- cxz -f- c2z2 4- ... 4- cnzn + • • •
является круг (круг сходимости)
| z | < р с центром в точке 2 = 0. Радиус
этого круга (радиус сходимости)
определяется по формуле
р = lim —!-----, (2)
п -* 00 Г| __
если этот предел существует.
Ряд сходится абсолютно во всякой точке
внутри круга сходимости и равномерно
(стр. 159) во всякой области, лежащей це-
ликом внутри круга сходимости.
Радиус сходимости ряда
со + ci (z —д) 4- (z — а)2 4- ... 4-
4- сп (z — а)п 4- . . .
определяется формулой (2), центр круга
сходимости находится в точке г — а.
ОСНОВНЫХ
ОПРЕДЕЛЕНИЕ
ТР АНСЦЕНДЕНТНЫХ ФУНКЦИЙ
Показательная и тригонометрические
функции определяются при помощи рядов,
сходящихся во всей плоскости комплекс-
ного аргумента z (см. стр. 161).
11 2! ' ’
• Z3 2®
Sinz«Z—-Ч-4 — . .
3! 5!
, 22 2^
COS Z = 1 — 4- — . . .
21^4!
Показательная функция связана с триго-
нометрическими функциями при помощи
формулы Эйлера:
е2* = cos z 4- I sin z.
Показательная функция—периодическая—
с периодом 2л/
ez + 2к~/ = (/< = о, ± 1, 4- 2, . . . ).
В частности:
е2Ы _ j,
"o’ + 2кп/
е2 = I;
Логарифмическая функция определяется
как обратная показательной: если
z = ew,
е(2к + !)«/__ р
т? i + 2kni
е2 = —i.
то
W = In z.
Логарифмическая функция многозначна:
In z = In I z | 4- I arg z 4- 2Лл/
(A = 0, ±1,±2,. . .),
где In | z | — действительное число.
Главные значения логарифма принято
определять условиями:
к = 0; — л < arg z л.
При любом основании а, по определению,
а1 = ег 1п а.
Соотношения между показательной, три-
гонометрическими и гиперболическими
функциями, а также между логарифмиче-
ской, обратными тригонометрическими и
обратными гиперболическими функциями
приведены на стр. 126 Эти соотношения
справедливы для любых комплексных зна-
чений аргумента.
ДИФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
КОМПЛЕКСНОГО АРГУМЕНТА
Производная функции iv = / (z)
lim / (z + Az) — / (z)
dz a? о Az
Здесь
существует, если выполнены условия
Кош и—Р и м а н а:
Он _ до_. ди _ _ди
дх ду’ду дх ’
где и и v—действительная и мнимая части
функции W, а х и у — действительная и
мнимая части аргумента z
(iv = и 4- lu, z = х 4- /у).
Пример-.
iv — ег — ех + О' — ех (cos у + / sin у);
и — ех cos у, V -ех sin у.
ди Y dv
— — ех cos у — —;
dx z dy *
ди _ , dv
— = — ex sin у — ——
dy ' dx
Условия Коши—Римана выполнены.
Формулы для диференцирования элемен-
тарных функций — те же, что и в случае
действительного аргумента.
Функция, диференцируемая во всех точ-
ках некоторой области, называется анали-
тической в этой области. Производная
любого порядка от аналитической функции
также является функцией аналитической.
Сумма степенного ряда является аналитиче-
ской функцией внутри круга сходимости.
Действительная часть и(х,у) и мнимая
часть и (х, у) функции, аналитической в не-
которой области, являются в этой области
гармоническими функциями (стр. 176 и 212).
Если существует такая окрестность точки
а (т. е. область, для которой эта точка яв-
ляется внутренней), в которой функция
/ (z) — аналитическая, то функция / (z) на-
зывается аналитической в точке а, а точка
а — правильной точкой функции /(z);
в противном случае точка а называется осо-
бой точкой функции / (z).
214
МАТЕМАТИКА
Точка z — оо (бесконечно удалён-
ная точка) называется правильной или
особой точкой функции / (z) в зависимости
от того, является ли точка z = О правильной
или особой для функции / . Окрест-
ностью точки z — со называется область,
лежащая вне круга достаточно большого
радиуса.
ВАЖНЕЙШИЕ СВОЙСТВА
АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Если функция / (z)— аналитическая в не-
которой области, то точки, в которых зна-
чение |/(z)| наибольшее (по сравнению со
значениями |/(z)i в остальных точках обла-
сти), находятся на границе этой области
(принцип максимума модуля).
Если функция / (z)— аналитическая для
любых конечных значений z (во всей пло-
____ скости) и существует Ta-
x'^X кая постоянная М, что
/ с'. -.а с ) всюду
( 1,- V J
---- | / (z) | < М,
Фиг. 285 т0 /(2)= const (теоре-
ма J1 и у в и л л я).
Если две функции / (z) и ?(z), аналити-
ческие в некоторой области G, имеют оди-
наковые значения в точках alt a2> . .,
an, . . . , причём lim an = а и точка a тоже
n->oo
находится в области Q (фиг. 285), то во всей
области G имеет место тождество / (z) (z)
(теорема единствен пост и).
ИНТЕГРИРОВАНИЕ ПО КОМПЛЕКСНОМУ
АРГУМЕНТУ
Криволинейным интегралом функции / (z)
по дуге С называется число, определяемое
следующим образом.
Дуга С произвольным образом разде-
ляется на элементарные дуги (фиг. 286) при
помощи точек, изображающих комплексные
числа z0, Zj, z2, . . . , z„ (z0 — начальная,
z.;—конечная точки данной дуги); на каж-
дой элементарной дуге с конечными точками
zk и гл+1 выбирается по одной точке ; со-
ставляется сумма
/ (^1) + / (W AZ3 -J- . . . -|- / (£,;) Azn,
где
tzi = Z1 — z0, Az2 = z3 — Zt, . . .,
Azn — zn 2,1— p
и вычисляется предел этой суммы при усло-
вии, что наибольшая из величин I AZ/J стре-
мится к нулю:
У /(z)dz= lim [/(Ci)Azi +
’ J max|Azfe[-> 0
(C)
+ /(C2)Az3+ . . .4-f (QAz,J,
Основные свойства криволинейного инте-
грала:
1. Если дуги С и С совпадают, но имеют
противоположные направления, то
У /(z)dz = — £ /(z)dz,
(С) (С)
2. Если дуга С состоит из дуг С, и С,, то
У / (z)dz^ [ /(z)dz+ j’ /(z)rfz.
(С) (С,) (С.)
3. Если I / (z) | < М во всех точках дуги
С, то
I f / (z) dz | < Ml,
1(C) I
где I — длина дуги С.
Если С — замкнутый кусочно-гладкий
контур (т. е. в каждой точке контура, за
исключением конечного числа угловых точек,
имеется определённая касательная) и если
функция / (z) — аналитическая как на кон-
туре С, так и в области G, ограниченной
этим контуром, то
У / (z) dz — о (теорема Кош и).
(С)
В случае, когда (фиг. 287) область G мно"
госвязна (стр. 154), под С следует пони"
Фиг. 286
Фиг. 287
мать совокупность контуров, образующих
границу этой области, причём на каждом
из этих контуров направление обхода вы-
бирается так, чтобы область G оставалась
слева (положительное направление обхода).
Из теоремы Коши следует, что если / (z)—
функция, аналитическая в односвязной об-
ласти G, а I — дуга, расположенная в этой
области и соединяющая точки z0 и z, то ин-
теграл
2
у /(z)dz= J /(z)rfz
(О г»
не зависит от
вида дуги I, Если
F' (z) = /(z),
то
У / (z) dz = F (z) — F(z0).
г»
Если функция / (г) — аналитическая на замк-
нутом контуре Сив области G, ограничен-
ной этим контуром, то значение / (z) в лю-
бой точке z области G выражается через
значения этой функции на контуре С при
помощи формулы Коши
= 1 f / (t)dt
2r.i J t — z ‘
(C)
В случае, когда область G многосвязна,
под С следует, как и выше, понимать сово-
купность контуров (фиг, 287), составляю?
щих границу области G,
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
215
РАЗЛОЖЕНИЕ АНАЛИТИЧЕСКОЙ
ФУНКЦИИ В СТЕПЕННОЙ РЯД
Если функция / (z) — аналитическая и
однозначная в окрестности точки а, то
в круге |z— а| < р с центром в точке а
имеет место разложение / (z) в р я д Т е й-
л о р а
/ (2) -- с0 4- Ci (z — а) 4- с. (z — а)2 4-
4- ... 4- cn(z — а)п+ . . .
Радиус р круга сходимости определяется
по формуле (2) (стр. 213) и равен расстоя-
либо по формулам
нию точки а до бли-
жайшей особой точки
функции / (г).
Коэфициенты ряда
Тейлора могут быть
вычислены либо так
же, как было указано
для функции действи-
тельного аргумента
(стр. 160):
, _ f(n) W
. . . , Сп — -j- 1 . . ,
' f /(t)dt
2r-‘ J (t—a)ni 1 ’
(С)
где С — любой контур, лежащий внутри
круга сходимости и окружающий точку а,
обходимый в положительном направлении
(т. е. в направлении против хода часовой
стрелки).
Если
I/ (2) | < М
в круге сходимости, то
где р—радиус сходимости.
Точка а называется нулём порядка т
функции / (г), если
со = Ct = . . . = cm_, = 0; ст ф 0.
Функция / (z), аналитическая в круговом
кольце (фиг. 288)
г < I z—a\ < R,
разлагается в этом кольце в рядЛорана:
/ (2) = с„ 4- с1 (z — а) + с3 (z — а)3 +...4-
+ cn(z-ay+. . . 4-~Ь- +
> ____________________________ /7 1
-|---“_____L_ , 4. _ .
(z—а)2 ' • ^(z — а)"
Коэфициенты ряда Лорана вычисляются
по формулам
сп= ' f
(1-й)п+1
(Г) (3)
Ьп=~~. ( /(ОО-иГ'й,
2nz J
(Г)
где Г — любой замкнутый контур, содержа-
щий окружность | z | = г и расположенный
в данном кольце.
Ряд
оо
л = О
называется п ра в и л ьн ой частью, а ряд
оо
2 Мг-<0"л
в+1
главной частью ряда Лорана.
Если а — изолированная особая
точка функции / (z) (т. е. если в некото-
рой окрестности точки а нет других особых
точек этой функции), то / (г) можно разло-
жить в ряд Лорана, сходящийся во всех
точках внутри некоторого круга с центром
в точке а, кроме самой точки а (разло-
жение функции в окрестности
изолированной особой точки).
Радиус этого круга равен расстоянию
точки а до ближайшей к ней особой точки
функции / (z), а коэфициенты ряда вычис-
ляются по формулам (3), где Г — любой зам-
кнутый контур, лежащий внутри круга схо-
димости и окружающий точку а.
В случае, когда точка а — правильная,1
= Ь2 = . . . = Ьп = . . . = 0
и ряд Лорана превращается в ряд Тейлора.
Разложение в ряд Лорана функции /(z),
аналитической при | z | > R, в окрестности
бесконечно удалённой точки имеет вид:
/ (2) = со + с12 + с2г2 4- ... 4- си2” 4- . • 4*
+- ~ + || + • • + + • • •
Коэфициенты этого ряда вычисляются по
формулам (3), где!1 — любой контур, содер-
жащий окружность | z | = R.
оо
Ряд с0 4- bnz~~ п называется при этом
П=1
оо
правильной ч а о т ь ю, а ряд У! cnzn—
п=1
главной частью разложения.
Бесконечно удалённая точка — правиль-
ная, если
Сх = с2 = . . . = с„ = . . . = 0.
ОСОБЫЕ ТОЧКИ
Изолированная особая точка z — а функ-
ции / (z) называется полюсом, если глав-
ная часть разложения / (z) в ряд Лорана
в окрестности этой точки содержит лишь
конечное число отличных от нуля членов;
в противном случае точка z = а называется
существенно особой точкой.
Разложение / (z) в ряд в окрестности
полюса имеет вид
оо
/ (2) = 2 сп (2 - а)п 4-
п=о 2 — а
гае ЬтуО.
МАТЕМАТИКА
Если m=l, полюс называется про-
сты м; если т > 1, полюс — кратны й;
число т — порядок полюса.
Разложение функции / (г), для которой
бесконечно удалённая точка является по-
люсом порядка т в окрестности этой точки,
имеет вид
оо
/ (2) “ Со 4- 2 bnZ~ п 4- сх2 4- c2z2 4-
л=1
4- . . . + cmzm,
где с,„ ¥= О,
Если точка z = a — полюс функции / (z),
то
lim j (z) = оо.
г -> а
Точка 2= а, являющаяся нулём порядка т
функции / (z), является в то же время по-
люсом порядка т функции ; если точка
г = а — полюс порядка т функции / (z), то
она является в то же время нулём порядка
т функции _1_ .
/ (z)
В сколь угодно малой окрестности суще-
ственно особой точки функция / (z) при-
нимает значения, сколь угодно близкие
к любому числу (теорема Вейер-
ш т р а с с а).
Если С — замкнутый контур, обходимый
в положительном направлении, а функция
/ (z) — аналитическая на контуре С и во
всех точках внутри этого контура, кроме
точки z — а, то значение
resa/ (z) = -L f / (z)dz
2w (С)
называется вычетом функции / (z) относи-
тельно особой точки а.
В частности, если С — любой замкнутый
контур, содержащий точку а, то
1 С dz = 1-
2ni J z — a
(C)
J f __dz__ = o (n = 2, 3, . . .).
2-.i 1 (г-а)"
(C)
Вообще, если в окрестности точки а
f(z) = S cn(z-a)"+ bn(z — a)-n,
п=О п=1
ТО
resa/ (z) = bx.
Для функции j (z), аналитической на
замкнутом контуре С и во всех точках
внутри этого контура, кроме точек а1г а.,, ...,
ай, величина
Д. С /(z)dz
2ni J
(С)
равна сумме вычетов функции / (z) относи-
тельно точек ах, й2> . . . , а* (основная
теорема теории вычетов).
Величина
1 Г /' (z)dz
2л/ J / (z)
(С)
называется логарифмическим выче-
том функции / (z) относительно контура С.
Если функция / (z) ие имеет на контуре
С ни нулей, пц особых точек, единствен-
ными особыми точками / (z) внутри С явля-
ются полюсы а,, а2, , . . , а^, порядки кото-
рых равны соответственно ах, . . . , а*, и
если нулями функции j (z) внутри С явля-
ются точки Ьг, Ьг, . . . Ьт, причём порядки
этих нулей равны соответственно рх, ••>
Нт- то
1 f t’ (z) dz = N_p
'2к1 J j (z)
(Q
где N = 4- ₽3 + . . . 4-
P — ai 4- «2 4- . . . 4- «/j.
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
Функция комплексного аргумента w=f (z),
где
z = х 4- iy и w = и 4- iv,
определяет две функции действительных
аргументов
а = и (х, у), (4)
v = v(x, у).
При помощи равенства w = / (z) каждой
точке z плоскости Оху (плоскости перемен-
ной z) соответствует определённая точка iv
плоскости Они (плоскости переменной w).
Если при этом функция / (z) непрерывна,
то совокупности точек Z, образующих об-
ласть g, соответствует (фиг. 289) совокуп-
Фиг. 289
ность точек w, образующих некоторую об-
ласть О (область g отображается на
область О).
В случае, когда не только каждой точке
области g соответствует определённая точка
области G, но и, обратно, каждой точке об-
ласти G соответствует единственная точка
области g, отображение называется взаим-
но- од н о з н а ч н ы м.
Когда точка z движется по линии у, со-
ответствующая точка в- описывает (фиг. 290)
Фиг. 290
некоторую линию Г: функция w =• / (z) осу-
ществляет отображение линии 7 плоскости
переменной z на линию Г плоскости пере-
менной w. Если при этом уравнение линии 7
(х, у) =0 (5)
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
217
или, в параметрической форме,
x = x(t), (6)
У = У (О,
то уравнение линии Г может быть полу-
чено исключением х и у из (4) и (5) или
(4) и (6).
Пример
ip - z“ ~ (х + iy)a = х9 — у9 + 2ixy.
Здесь
и « х1 — у’; v = 2ху.
Прямые х — с отображаются (фиг. 291) в параболы,
уравнения которых
v* — 4с® (и — с’)
или в параметрической ферме
и « са .. -у8, и «я 2су.
Прямые у = с отображаются в параболы
Vя - 4с9 (и + са)
или
и » х8 — са, v == 2сх.
Если при отображении, осуществляемом
при помощи аналитической функции 1У=/ (z),
точке z0 соответствует точка iv0, а линии 7
плоскости переменной z, проходящей через
точку z0, линия Г плоскости переменной
1V, то
arg/' (z0) = Ф —<f,
где <р и Ф — углы, образованные с положи-
тельными направлениями соответствующих
действительных осей касательными к ли-
ниям у и Г в точках z0 и iv0 (фиг. 292).
Величина | /' (z0) | является коэфициен-
том растяжения в точке z0, т. е. преде-
лом ккоторому стремится отношение расстоя-
Фиг. 293
ния|Дш0| между точками iv0 и iv0 + Aiv0
плоскости iv к расстоянию | Az0 | между со-
ответствующими точками z0 и z0 + Az0 пло-
скости z (фиг. 293), когда Az0 -* 0.
Во всякой точке z0, где /' (z0) ф 0, ото-
бражение, осуществляемое при помощи ана-
литической функции, является конформ-
н ы м, т. е. обладает двумя свойствами:
1. Если линии 71 и уз плоскости 2
(фиг. 294), проходящие через точку z0, отоб-
ражаются в линии Г1 и Г2 плоскости IV,
проходящие через соответствующую точку
iv0, то угол между касательными к 71 и 7,
в точке z0 равен углу между Г\ и Га в точке
(свойство консерватизма у г-
л о в).
2. Коэфициент растяжения в точке z0
одинаков во всех направлениях, т. е. не
зависит от направления (фиг. 295) вектора
Дс0 (свойство постоянства растя-
ж е и и й).
Фиг. 295
Если функция f = ?i(z) осуществляет
конформное и взаимно-однозначное отобра-
жение некоторой области g плоскости пере-
менной z па область S плоскости перемен-
ной /, а функция t = <₽2(iv) отображает кон-
формно и взаимно-однозначно область Q
плоскости переменной iv на ту же область
S, то, разрешив относительно w равенство
(W) = ?1 (z),
мы определим функцию iv = /(z), осущест-
вляющую конформное и взаимно-однознач-
ное отображение области g на область G.
Таким образом, если для каждой из не-
скольких данных областей известна функ-
ция, отображающая конформно и взаимно-
однозначно эту область на некоторую «стан-
дартную» область S, то можно вышеуказан-
ным способом найти функции, отображаю-
щие любую из этих областей на любую
другую. В качестве такой «стандартной»
области обычно берут (если речь идёт об
одпосвязных областях) круг с центром в на-
чале координат и радиусом, равным еди-
нице (единичный круг), или полу-
плоскость, ограниченную действительной
осью и расположенную выше этой оси
(верхняя полуплоскость).
218
МАТЕМАТИКА
ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ
Дробно-линейная функция
w = az+b
cz + d
в случае, когда ad — be =#= 0 (если
ad — be = 0, то w = const), осуществляет
взаимно-однозначное и конформное ото-
бражение всей плоскости переменной
Z на всю плоскость переменной w, при
этом точке z = оо соответствует точка
W = — и точке z—— — точка iv = оо. Значе-
с с
ния z, для которых iv = z, находятся из
уравнения
z = а*+ ь
cz + d
и определяют так называемые неподвиж-
ные точки дробно-линейного преобразо-
вания.
Так как
az + b _ а Ьс — ad 1
cz -р d с с ' cz + d ’
то в самом общем случае отображение, осу-
ществляемое при помощи дробно-линейной
функции, может быть по-
’’ ''7* лучено последовательным
I, / применением следующих
X ^-*1 простейших отображений
(для наглядности на чер-
-0!^-------»-/« тежах плоскости перемен-
фиг 286 пых z 11 w совмещены
так, что действительная
ось Ох совпадает с действительной осью
Он, а мнимая ось Оу с мнимой осью Оу).
1. iv = z + Ь.
Каждая точка z переносится в соответ-
ствующую точку iv (фиг. 296) при помощи
вектора, изображающего комплексное число
b (преобразование параллель-
ного переноса).
2. iv = e;''z.
Здесь
I W | = | z | и arg iv = arg z + а;
всякая точка z переходит в соответствую-
щую точку IV (фиг. 297) при помощи пово-
рота около начала координат на угол а
(преобразование поворота).
3. iv = rz (г — действительное, положи-
тельное число).
Фиг. 297
Здесь arg w =- arg z и | w |= г | z всякая
точка z перемещается (фиг. 298) в точку iv
по лучу, выходящему из начала координат
и проходящему через точку z, причём отно-
I iv
шение 2—= г одинаково для всех точек
(преобразование подобия сцент-
ром подобия в начале координат;
г — козфициент подобия).
4, )v—_L .
Z
Здесь I iv | = -I--- и arg iv — arg z.
I z |
Опишем изначала координат О (фиг. 299),
как из центра, окружность радиуса 7?. Выб-
рав внутри этой окружности какую-либо
точку А, проведём луч ОА и перпендикуляр
АТ к этому лучу; из точки Т пересечения
этого перпендикуляра с окружностью про-
ведём касательную ТВ к окружности, пере-
секающую в точке В луч ОА. Точки А и В
называются взаимно симметрич-
ными относительно данной окружности.
В частности, всякая точка, лежащая па ок-
ружности, симметрична сама себе, а центр
окружности симметричен бесконечно уда-
лённой точке. Если одна из точек А или В
определяется комплексным числом z, то
D2
другая соответствует числу , где z —
z
комплексное число, сопряжённое числу 2
(стр. 99). В частности точки z и А взаимно
Z
симметричны относительно окружности с
центром в нулевой точке и радиусом, рав-
ным единице (фиг. 300).
I 1
Точка iv -— — симметрична точке от-
носительно действительной оси (фиг. 300).
Таким образом, преобразование w =со-
стоит из двух симметричных преобразова-
ний: симметричного преобразования (и н в е р-
с и и) относительно окружности |z|=l и
симметричного преобразования относительно
действительной оси; при этом внутренность
единичного круга отображается конформно
и взаимно-однозначно на область, внешнюю
по отношению к этому кругу.
Лине й н а я фу н к ц ня w = az 4- b мо-
жет быть преобразована в общем случае
к виду
iv = re,a z + Ь,
где
a=relct (г = | а |, а = arg а),
и отображение, осуществляемое этой функ-
цией, состоит из преобразований поворота,
подобия и параллельного переноса.
Общее дробно-линейное преобразование
(в частности и линейное) обладает следую-
щими основными свойствами:
1. Всякая окружность (в том числе и
прямая, являющаяся окружностью с беско-
нечным радиусом) отображается в окруж-
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
219
ность или в прямую (круговое свой-
ство).
2. Пара точек, взаимно симметричных
относительно окружности, переходит в пару
точек, взаимно симметричных относительно
отображённой окружности (прямая, как и
выше, рассматривается как частный слу-
чай окружности).
Существует, и притом единственное,
дробно-линейное преобразование:
W — а.' Р' — т' __ Z — а 3 — 7
И' — 7' Р' — a' Z — 7 * Р — а
при помощи которого три данные точки а,
₽, 7 плоскости z переходят соответственно
в заданные точки а', Р', 7' плоскости w.
Фиг. 301
При этом область, внутренняя к окружно-
сти, проходящей через точки а, р, 7, ото-
бражается либо на область, внутреннюю
к окружности, проходящей через точки а',
Р', 7' (фиг. 301), либо на область, внешнюю
по отношению к этой окружности (фиг. 302),
в зависимости оттого, определяют ли точки
а, р, 7 то же направление на окружности,
что и точки а', Р',7', или противоположное.
Фиг. 302
Общий вид функции, отображающей еди-
ничный круг на самого себя (т. е. круг
|’z | < 1 на круг | w | < 1):
w = ei,f ,
1 — a Z
где а (| <х | < 1) —точка плоскости г, перехо-
дящая в точку w — 0, a 7 = arg^ при z—a.
dz
Если | а| > 1, то это преобразование отоб-
ражает внутренность единичного круга на
область, лежащую вне единичного круга.
Общий вид функции, отображающей
верхнюю полуплоскость плоскости z на
единичный круг плоскости iv:
w = е* ,
Z — a
где а (мнимая часть а положительна) — точка
плоскости z, переходящая bw = 0, и tp — L =
div
“ arg — в точке z = а.
dz
степенная функция
Производная степенной функции w = z”
(п > 1 и целое) обращается в нуль при
z = 0. В этой точке нарушается свойство
консерватизма углов. Если
z — re,!e; w = pe,e,
Фиг. 303
ТО
Р = Г’* 1,
О = П'-р.
Лучи 7 = const и окружности г = const пе-
реходят в лучи 0 = const и в окружности
р = const. В точке z — 0 все углы при отоб-
ражении увеличиваются в п раз. Ввиду
п
многозначности обратной функции z = V^w,
каждой точке w, кроме точек w — 0 и w — со
(эти точки называются точками раз-
ветвления), соответствует (фиг. 303) п
точек zlf г2, . . . ,zn.
Угол величины — с вершиной в нуле-
п
вой точке (0 < у < —1 отображается вза-
\ п /
Фиг. 304
имно-однозначно на верхнюю полуплос-
2-
кость (фиг. 304). Угол величины — с вер-
шиной в нулевой точке ^0 < ? < отоб-
ражается на всю плоскость iv с разре-
зом (фиг. 305) вдоль действительной поло-
жительной полуоси ^верхнему краю этого
разреза соответствует сторона угла ? = О,
2л \
а нижнему краю—сторона угла у = _ \ .
о
Фиг. 305
При помощи степенной функции можно
отобразить на верхнюю полуплоскость
(а, следовательно, и на единичный круг)
область, заключённую между дугами двух
пересекающихся под углом 7 в точках z—a
и z = & окружностей (в частности и круго-
вой сегмент, соответствующий случаю, когда
одна из окружностей — прямая). Для этого
220
математика
сначала при помощи дробно-линейной функ-
ции
t = г~а
z — b
данная область отображается на угол с вер-
шиной в нулевой точке плоскости t (фиг. 306),
затем при помощи поворота Т = е'“ t одна
сторона этого угла совмещается с положи-
тельной действительной полуосью и, нако-
нец, функция
w = Тп= I z~aVе‘па,
\ z—b J
где п = 21 , отображает этот угол на верх-
7
нюю полуплоскость (фиг. 307).
Фиг. 307
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ
ФУНКЦИИ
Если
w = ez (z = In iv) и z — x + iy, w = Pe*0,
TO
p = ex,
0 = y.
Прямые x — const переходят в окружности
p » const; прямые y=const — в лучи t)= const
(фиг. 308).
Всякой точке iv0, кроме точек развет-
вления w = 0 и w = 00, соответствует бес-
численное множество точек
z = z0 + 2А'л/ (к —0, ±1,±2, . . .).
Полоса 0 < у < л ширины л (фиг. 309)
отображается взаимно-однозиачно на верх-
нюю полуплоскость. Полосы шириной
2л(0 < <р<2л; 2л < <р < 4л; . . . ; — 2л < <р<0;
— 4л < <р < — 2л; . . .) отображаются на всю
плоскость w с разрезом вдоль действитель-
ной положительной полуоси (фиг. 310).
Область, заключённая между двумя ка-
сающимися друг друга (фиг. 311) в точке
z = г0 окружностями [в частности область
между окружностью и касательной к ней
(фиг. 312)], при помощи функции
2— гв
отображается на полосу; эта полоса при
помощи параллельного переноса, поворота
Фиг. 309
и преобразования подобия, т. е. при помощи
линейной функции
Т = at + b,
Фиг. 310
может быть отображена на полосу шириной
л, прилегающую к действительной оси,
эта последняя в свою очередь при помощи
функции w — ет —на верхнюю полупло-
скость.
Функция w = In z (z—ew) отображает кри-
волинейный прямоугольник (фиг. 313), ог-
раниченный верхними полуокружностями
|z| = l, |2| = г(г>1) и действительной
осью на прямолинейный прямоугольник со
Фиг. 313
Фиг 314
сторонами In г ил; последний можно отобра-
зить на верхнюю полуплоскость при помощи
функции, указанной на стр. 221.
Полуполоса х > О, 0 < у < л ширины л
(фиг. 314) отображается при помощи функ-
ции w = —е~ г на верхнюю половину еди-
ничного круга, а при помощи функции
на верхнюю полуплоскость
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
221
Функция iv—siiiz отображает полупо-
лосу
у> О, —<x<Z.
(фиг. 315) на верхнюю полуплоскость.
Функция w = tg z отображает полосу
— L. < х < — (фиг. 316) па единичный круг.
4 4
Фиг. 315
ОТОБРАЖЕНИЕ МНОГОУГОЛЬНИКА
НА ВЕРХНЮЮ ПОЛУПЛОСКОСТЬ
Функция, определяемая эллиптическим
интегралом
Z
и> = / (г) = Г___ ____dt... .......
J /(1 — /2)(1 — кН2)
о
(0< к < 1),
отображает верхнюю полуплоскость плоско-
сти z на прямоугольник (фиг. 317) в плоско-
Вершинам этого прямоугольника соот-
ветствуют точки ±1, ± 1 плоскости z. Функ-
ция z = s(w), обратная по отношению к функ-
ции w = / (z), осуществляющей это отобра-
жение (и отображающая, следовательно,
прямоугольник на верхнюю полуплоскость),
является эллиптической (двояко-
периодической) функцией. Эта функ-
ция имеет два периода: действительный 2о>х
и мнимый 2/о>2> т. е.
s (iv + 2то>! + 2п/ш2) = s (w)
(т, п = 0,± 1, ± 2, . . .).
Для того чтобы отобразить верхнюю по-
луплоскость на заданный прямоугольник,
нужно сначала подобрать такое значение
к, чтобы отношение o>j: <о2 было равно от-
ношению сторон данного прямоугольника;
функция w = / (z) отобразит при этом верх-
нюю полуплоскость на прямоугольник, по-
добный данному; после этого остаётся при
сти w с вершинами —
2»
где
и>1 = 2 f dt ,
J /(1 — /2)(1— кН2)
помощи подобного преобразования, парал-
лельного переноса и поворота, т. е. при по-
мощи линейной функции Т — ctw + с2, отоб-
разить полученный в плоскости и> прямо-
угольник на заданный.
Функция
и> = / (z) =
=J(t—Дх)®1-1 (t—д2)а,—*. .. (Г-д,,)1*-1 dt (7)
отображает верхнюю полуплоскость плоско-
сти1 z на n-угольник плоскости »(фиг. 318)
с внутренними углами
__________dt___________
/(t2— 1) О — *2<2)’
а, л, а2гс, . , . , апп
(а1 + а2 + • • + ап = п~ 2).
При этом вершинам многоугольника соот-
ветствуют точки дх, а2' • • • > ап действитель-
ной оси плоскости z. Длины сторон много-
угольника вычисляются по формулам (пред-
полагается, что дх < д2 < . . . < ап)-.
И1 И1 , I
2 ’ т+ /ш2
О,
'1= J « - аг)’*-1 (й2 - 0е*"1 (аз - О’*"1 • • • (ая- ~ * dt,
= J (t - ах)”1"1 (Г - д2)а“-’ (д8 - О”1'1 • • • (а« - t )n dt,
а»
f (t-fli)*1-1 («-Д2)я,_1 • • • 0-а«-1) ‘(««-tf" ’dt.
ап-1
222
МАТЕМАТИКА
Для того, чтобы отобразить верхнюю по-
луплоскость на заданный п-угольник со сто-
ронами d1( d2, . . . , dn, следует, выбрав
произвольно три из чисел ait например аг,
а2, а3, определить остальные из уравнений
/2 _ d2. /3 _ d2. .. 1п-2 _ rfn-2
li di li dt l1 di
При найденных таким образом значениях
di с помощью функции (7) верхняя полу-
плоскость отобразится на многоугольник,
подобный данному; после этого следует при
помощи линейной функции Т = и» + с» отоб-
разить полученный в плоскости w много-
угольник на заданный.
Отображение единичного круга на мно-
гоугольник с углами atn, а2п, . . ., осу-
ществляется при помощи функции
жающая функция w — f (z) определяется
единственным образом следующими усло-
виями:
/ (0) = 0, f (0) > 0
(второе условие обозначает, что arg/'(O)=O,
т. е. что направлению положительной дей-
ствительной полуоси в точке z — 0 соответ-
ствует такое же направление в точке и>=0).
Если функция, аналитическая на контуре
Г и в области G, им ограниченной, отобра-
жает взаимно-однозначно контур Г на кон-
тур Г' области G', то область G также
взаимно-однозначно отображается на область
G' (принцип соответствия границ).
Если при помощи аналитической функции
w = / (z) область G отображается на область
G' так, что часть у границы области G,
iv == ci J (t — е'^'У1 1 (f — г'¥з )’2 1 . . . (t — е Чп )1 dt,
о
где ef?1, е^г,. . . ,eil?n—точки окружности
единичного круга, соответствующие верши-
нам многоугольника.
ОБЩИЕ ПРИНЦИПЫ КОНФОРМНЫХ
ОТОБРАЖЕНИЙ
Всякая односвязная область, кроме всей
плоскости (включая бесконечно удалённую
точку) и плоскости с одной выключенной
точкой, может быть взаимно-однозначно и
конформно отображена на любую другую
область такого же типа (например на внут-
ренность единичного круга). Это отображе-
ние определяется единственным образом,
если потребовать, чтобы заданной точке и
заданному направлению в этой точке одной
области соответствовали заданные точка и
направление в этой точке другой области
(теорема единственности). Если,
например, отображаемая область в плоско-
сти z содержит нулевую точку, то отобра-
являющаяся дугой окружности или отрез-
ком прямой, отображается на дугу окруж-
ности или прямолинейный отрезок 7', вхо-
дящий в границу области G', то всякая
точка zs, симметричная точке z2 области G
относительно 7, перейдёт в точку н>2, сим-
метричную относительно 7' точке Wj, являю-
щейся отображением точки zx (фиг. 319),
т. е. если точки zx и z2— симметричны от-
носительно 7, то точки и’х = / (zx) и w2 =
= / (z2) симметричны относительно (п р и н-
ц и п симметрии).
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
ОСНОВНЫЕ ПОНЯТИЯ и ТЕОРЕМЫ
События А, В, . . . , N называются н е-
совместимыми, если может произойти
только одно из них.
События А, В, ... , N называются
единственно возможными, если по
крайней мере одно из них должно произойти.
Система несовместимых и единственно
возможных событий называется полной.
Два несовместимых и единственно воз-
можных события А и А называются про-
тивоположными, или дополните л ь-
н ым и.
Вероятностью события А [обозначе-
ние: Р(А)] называется отношение числа т
случаев, благоприятствующих этому собы-
тию, к числу всех несовместимых, равно-
возможных и единственно возможных слу-
чаев: Р(А)=~; например, вероятность
вынуть белый шар из урны, содержащей п
шаров, из которых т шаров белых, рав-
Вероятность достоверного события
равна единице, вероятность невозмож-
ного события равна нулю; в остальных
случаях вероятность положительна и меньше
единицы.
Если при п поставленных в одинаковых
условиях опытах некоторое событие А появи-
т
лось т раз, то отношение -- называется
частотой (статистической или эм-
пирической вероятностью) собы-
тия А:
т
. W(A) = -.
С вероятностью, сколь угодно близкой к
достоверности, можно утверждать, что при
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
223
достаточно большом числе опытов частота
события как угодно мало отличается от его
вероятности (закон больших чисел).
Обобщением закона больших чисел является
теорема Чебышева (стр. 226).
Вероятность того, что произойдёт одно
из несовместимых событий А,, А2.....Ап,
равна сумме вероятностей этих событий
(теорема сложения вероятно-
с т е й):
P(Ai или А, или . . . или A„)=P(Ai) +
+ Р(А2) + ...+Р(Ал).
В частности, сумма вероятностей двух
противоположных событий и вообще сумма
вероятностей событий, образующих полную
систему, равна единице.
Пример. В урне имеется 5 белых, 3 красных и
4 зелёных шара Какова вероятность вынуть цвет-
ной (не белый) шар?
Вероятность вынуть цветной шар равна
3 4 7
12+ 12 “ 12'
События называются независимыми,
если вероятность одного из них не зависит
от того, произошло или не произошло дру-
гое; в противном случае события зависимы
и условной вероятностью собы-
тия А называется вероятность этого событие,
найденная в предположении, что произошло
другое событие В. Обозначение условной
вероятности: Рв (А).
Вероятность наступления обоих событий
А и В равна произведению вероятности
одного из них на условную вероятность
другого в предположении, что произошло
первое (теорема умножения веро-
ятностей):
Р (А и В) = Р (А) РА (В) = Р (В) Рв (А).
В частности, если события А и В неза-
висимы, то Р (А и В) = Р (А) Р (В).
В более общем случае теорема умножения
вероятностей выражается при помощи равен-
ства
Р(АТ и А. и ... и А„) =
= Р (А,) РА1 (А2) • • Рд, д, ... Ап_} (А„),
где, например, Рд, да.д,^, (Ал) — веро-
ятность события Ая, в предположении, что
произошли события Aj, Д2,. . . , An_i.
шар в
белый
Пример 7. В урне имеется 5 белых, 3 красных
и 4 зелёных шара. Какова вероятность вынуть под-
ряд два белых шара?
Вероятность вынуть белый
5
равна вероятность вынуть
того как один белый шар уже
первый раз
шар, после
4
равна — и,
вынут,
следовательно, вероятность
5 4 5
белых шара равна ff " о а
вынуть подряд два
Пример 2. Работа механизма, в который входят
две одинаковые детали, нарушается, если при сбор-
ке обе поставленные детали больше номинала. У
сборщика имеется 10 деталей, из которых 3 больше
номинала и 7 меньше. Сборщик берёт наудачу две
детали. Какова вероятность того, что работа меха-
низма нарушится?
Вероятность того, что первая деталь больше
3
номинала Р (Ах) * — ; вероятность того, что вторая
деталь больше номинала при условии, что первая
деталь оказалась больше номинала Р А (Аа) — а-, и
3 2 1'
следовательно, Р (Л, и Л2)“ — • д- = )3-
Вероятность события А, зависящего от
событий В1; В2,...Вп, причём J3X, Bs,..., Вп—
система несовместимых и единственно воз-
можных событий и, следовательно, Р (Bj)+
+ Р (В.,) + Р (В„) = 1, вычисляется по
формуле
Р (А) = Р (Вг) РВ' (А) + Р (В,) РЕг (А) +
+ . . . + Р (В„) Рвп(А)
(формула полных вероятностей).
Если событие А может наступить при
появлении одного из несовместимых собы-
тий В1( В2, . .., Вп, то
Р(В,)Рв.(А)
РА pT(BjPBi (А) + Р (В,,,) РВп (А)
(ф орму л а Беп ес а).
Пример. В комнате стоят три одинаковых урны.
В первой 2 белых шара и 1 чёрный, во второй —
1 белый и 1 чёрный, а в третьей—1 белый и 2 чёр-
ных.
Вынимают из некоторой урны шар, который
оказывается белым (событие А). Какова вероятность
того, что шар вынут из первой (событие Вх), второй
(событие 7з3), третьей (событие В3) урны?
Так как урны одинаковы, то Р (Вг) = Р (£2) «
= р у •
Вероятность вынуть белый шар из первой, вто-
рой, третьей урны равна соответственно:
Рп (А) = 2, рв (а>=4, Рв =
xjj о ij 3 •• о
и по формуле Бейеса имеем
1 2
3 + 3 4
р а >> = 1 Г”к= 9 ’
'з ’ 3 + 3 ’ 2 + 3 ‘ 3
1 2
аналогично Р л (Ев) « х-, Рл (З3)= —.
z‘ о 9
Цепи Маркова. Если имеется совокуп-
ность событий Ап (к) (к = 1,2, . . . , т) и при
любом значении п события Ап(к) образуют
полную систему, причём событие A„+1(fc) за-
висит только от событий A.,(z) (/ = 1,2,..., т),
но не зависит от событий A„_j (/), Art_2(z)
и т. д., а условная вероятность a(fc,z) со-
бытия А , + 1 (к) в предположении, что прои-
зошло событие А„(/), не зависит от п, то
совокупность вероятностей рп (к) событий
Ап (к) называется цепью Маркова.
Для определения этих вероятностей сле-
дует решить систему уравнений в конечных
разностях (стр. 253):
Рп+1 (1) = « (1,1) Рп О) + а (1,2) рп (2) +
+ . . . +a(l,m)p„(m);
р„+1 (2) = а (2,1)р„ (1) + а (2,2)рл (2) +
+ . . . 4- а (2, т) рп (ту,
Рп+1 (т) ^а(т,1)рп(1) + а(т,2)р„ (2) +
+ . . . + а (т,т)рп(т).
В частности, если т = 2, то, обозначив
Аа (1) = Ал, Ап (2) = Ап\рп (1) = рп’,
224
МАТЕМАТИКА
а(1,1) = а; а(1,2) = b и, следовательно,
рп (2) = 1 - рп; а (2,1) = 1 - а-, а (2,2) =1-0,
получим для определения рп, в предположе-
нии, что pj дано, уравнение в конечных
разностях:
Pn+i = ар„ + b (1 — рп).
Если а = 1 и b = 0, то pn+i = рх при лю-
бом п. В остальных случаях уравнение
в конечных разностях имеет решение
+ ("‘ - Г=4+ъ)
которое при n-t-oo стремится к пределу, не
зависящему от рг:
lim p„+t= ----L— .
П-*СО I — й + и
Вероятность повторения события. Если в
некотором опыте вероятность появления
некоторого события равна р, то вероят-
ность того, что в п опытах это событие
произойдёт т раз, равна
С™рт(1 - р)п~т или
т\(п — т)\ Р u Р>
При тех же условиях вероятность появ-
ления события по крайней мере т раз
(т. е. т раз или более) равна
2
i=m
В частности, вероятность появления со-
бытия по крайней мере один раз равна
1 — (1 — р)’“; все п раз — рп.
Если в результате некоторого опыта про-
исходит одно из несовместимых событий Ах,
А2, .. . , А*, вероятности которых соответ-
ственно равны Рц ра, ..., pk, и
к
S pi = ь
1-1
то вероятность того, что в п опытах собы-
тие Aj произойдёт т1 раз, событие А2 —та
раз и т. д., событие А* — тк раз
fc \
2 fni=n |, равна
i=i /
(mt+ ma+ . ., + mfe)i
mJ mJ ... mJ
. nm* nm« nmA •
•Pi Рг • • • Рк >
в частности, вероятность того, что каждое
событие произойдёт по одному разу (т1 =
= т2 = ... = nth = 1) равна
ргр3 ...pk-
Пример 1. Вероятность попасть в цель равна
0,5. Какова вероятность того, что в результате 8
выстрелов произойдёт 4 попадания?
Р - с4 0,54 . (1 _ 0,5)8-4 _ ™ „ 0 2733.
о 2оо
Пример 2» Из урны, в которой имеются белые,
чёрные, красные и зелёные шары в одинаковом коли-
честве, вынимается шар.
Какова вероятность того, что после 10 испыта-
ний (после каждого испытания шар возвращается
в урну) окажется, что 4 раза был вынут белый,
3 раза чёрный, 2 раза красный и один раз зелёный
шар?
В этом случае
1
Р1 и р8 в =в р< =,
rrii » 4, тл =• 3, т9«» 2 , «=» 1
и
^Ч^^^'^Ш^^ 0-01222-
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Величина называется случайной, если
в результате некоторого опыта она может
принять то или другое значение.
Если случайная величина может прини-
мать отдельные значения х2, х2.Хп
она называется дискретной, если же
она может принимать все значения из не-
которого промежутка а < X < £ (или даже
все значения от—оо до + оо), то она на-
зывается непрерывной.
Распределение дискретной случай-
ной величины определяется вероятностями
Р (хх), Р (х2),... , Р (хп) значений хх, х2,..., х„
п
2 р (х/) =1
1—1
Это распределение может быть геометрически
изображено при помощи многоуголь-
ника распределения (фиг. 320).
Интегральной функцией рас-
пред е,л ен ия непрерывной случайной ве-
личины называется функция Р (х), равная
вероятности того, что случайная величина
примет любое значение X, меньшее, чем х:
F(x) = P(X<x).
Вероятность того, что значение, прини-
маемое случайной величиной, окажется в
промежутке между Х — а и Х=Ь, опреде-
ляется равенством
Р (а < X < b) - F (b) — F (а).
Для дискретной случайной величины
Г(хк)~ 2 р(х/)-
1
Диференциальным законом рас-
пределения (или п л о т н о с т ью веро-
ятности) непрерывной случайной вели-
чины называется функция ?(х), определяе-
мая равенством
?(х) = lim
A х-+0
Р(х<Х<х-|-Дх)
Д х
lim ^.+4х)-Г(х)
A Х-+0 ‘Х х
F' (х);
обратно:
X
F (х) = J <f (х) dx.
—00
При достаточно малом Д х имеет место
приближённое равенство:
Р (х < X < х + Д х) « <? (х) Д х,
ТЕОРИЯ ВЕРОЯТНОСТЕЙ и метод наименьших квадратов
225
Для всякого закона распределения
ОО
j <? (х) dx — 1.
—оо
Если построить кривую распределе-
ния у = (х), то вероятности Р (а < X < ₽)
и Р(Х <x) = F(x) изобразятся площадями,
указанными на фиг. 321. Вся площадь между
кривой распределения и осью ОХ равна
единице.
Распределение вероятностей пары слу-
чайных величин (X, Y) определяется функ-
цией плотности v (х> у), причём
оо оо
У J <Р(х> y)dxdy = 1-
—оо —оо
X у
Величина F (х, у) = J J ?(х> у) dxdy
—со —со
равна вероятности того, что X < х и У < у.
Если величины X и У независимы между
собой и если плотности их вероятностей
определяются соответственно функциями
<Р1 (х) И с2 (у), то <Р (х, у) = <рг (х)-?2 (у). Так,
например, если две независимые величины
подчинены закону Гаусса с одинаковыми
параметрами, то (стр. 227)
? (х> у)= е-Л ’ [(х-а)’+(у - о).
Значение случайной величины, имеющее
наибольшую вероятность (в случае дискрет-
ной величины) или наибольшую плотность
вероятности (в случае непрерывной величи-
ны), называется её модой.
п
Величина М(Х), равная 2 ? (х/) Х1 в
г = 1
случае дискретной случайной величины, и
оо
j х ср (х) dx в случае непрерывной слу-
—-00
чайной величины, называется математи-
ческим ожиданием этой величины.
Если вероятности того, что случайная
величина X меньше или больше числа jx,
равны между собой, то pi называется медиа-
ной, или срединным значением,
случайной величины X. Для непрерывной
случайной величины
р. со j
J <p(x)dx=J c?(x)dx==2-
—ОО р.
Если многоугольник распределения (для
дискретной величины) или кривая распре-
деления (для непрерывной величины) имеет
ось симметрии х = а, то центр симметрии
х = а является одновременно и математиче-
ским ожиданием и медианой.
Отклонением случайной величины X
от её медианы называется положительная
величина I X — ц |.
Если число е таково, что одинаково
вероятно — окажется ли отклонение случай-
ной величины от её медианы ббльшим или
меньшим, чем е, то это число называется
вероятным отклонением случайной
величины:
Р ( I X - [л 1 > е) =- Р ( | X - [а I < е).
15 том I
В случае непрерывной случайной вели-
чины
°? |Х±г 1
J <p(x)dx+ j c?(x)dx= J tp(x)dx=2-
—CO р-4-s p.—g
Средним арифметическим от-
клонением (X) величины X назы-
вается математическое ожидание отклонения
этой случайной величины X от её матема-
тического ожидания М (X):
Ех(Х) = М (| X - М (X) |).
В случае дискретной величины
п
Е!(Х)= 2 IX,-M(X)|P(XZ).
г=1
В случае непрерывной величины
оо
Ej(X)= J |х — М(Х) | <j>(x) dx.
—00
Аналогично корень квадратный из мате-
матического ожидания величины [X—М(X)]3
называется средним квадратиче-
ским отклонением Е2 (X) величи-
ны X. Для дискретных случайных величин:
Я2(Х)- |/ У. [xz -М(Х)рР(х4) ,
* i= 1
а для непрерывных случайных величин:
Е2(Х) = |Л У [х-М(Х)р?(х) dx.
Дисперсией случайной величины на-
зывается квадрат ее квадратического откло-
нения
D (X) = [Е2 (X)]3.
Если известно распределение вероятно-
стей пары случайных величин (X, У), опре-
деляемое функцией <р(х, у), то математиче-
ские ожидания каждой из этих величин
определяются формулами:
оо оо
М (X) = j j хср(х, у) dxdy;
—оо —оо
оо оо
М (У) = У У у<?(х, у) dxdy.
—со —оо
Аналогичным образом определяются и
другие вероятностные характеристики.
Теоремы о математических
ожиданиях и дисперсиях
1. М(С) = С (С — постоянная).
2. М (Х4-У) =М (X) -j-М (У); в частности,
М(С + Х) = С ф-М(Х).
3. Если X и У—независимы, то М(ХУ)=
=М (X) М (У); в частности М (СХ)=СМ (X).
В общем случае: М (ХУ) =М (X) М (У) +
+ Р(Х,У)Е2(Х)Е2(У), где R (Х,У)—коэфи-
циент корреляции (стр. 226).
4. М (аХ-Ь b) = аМ (X) + b (а и Ь—посто-
янные).
5. Если X изменяется от 0 до 2 л, то
М [sin (X а)] =М [cos (X 4- а)] = 0 (а — по-
стоянная).
226
МАТЕМАТИКА
6. D (С) = О (С — постоянная).
7. Если X и У независимы, то О (Х+У) =
=D (X) +D (У); в частности D (C-j-X)=D (X).
В общем случае D (Х+У) = D (X)+D (У) +
+ 2R(X, У)Е2(Х)Е2(У).
8. D(XY)^D(X)D (Y)+D (Х)[Л4(У)]2 +
-j- D (У) [Л4(Х)]4, в частности D(CX)=C2D (X).
9. D(aX + &) = Д2О(Х).
10. Если X изменяется в интервале от 0
до 2 г., то
D [sin(X + a)] =D [cos(X+ а)]=
Если в определениях вероятностных характери-
стик заменить вероятность частотой (статистической
вероятностью) случайной величины, то вместо этих
вероятностных характеристик мы получим ста-
тистические характеристики, а именно: статисти-
ческую моду вместо моды, статистическую медиану
вместо медианы, среднее арифметическое наблюдае-
мых значений вместо математического ожидания,
статистическое срединное значение вместо вероятного
отклонения, статистическое среднее арифметическое
отклонение вместо среднего арифметического откло-
нения, статистическое среднее квадратическое от-
клонение вместо среднего квадратического отклоне-
ния, статистическую дисперсию вместо дисперсии.
Обозначения для статистических характеристик
сохраняют обычно те же, что и для соответствую-
щих вероятностных характеристик.
11. Если математические ожидания вели-
чин Х1; Х2, • • Х„, . . . одинаковы:
М (XJ = М (Х2) = . . . = М (Х„) = . . . ,
а Дисперсии этих величин равномерно огра-
ничены:
D(X;) < C(i—1,2,. . . , п, . . непостоянная),
то с вероятностью, сколь угодно близкой к
достоверности, можно утверждать, что при
достаточно большом п среднее арифметиче-
ское величин Х„ Х2,. . . Х„ будет сколь
угодно мало отличаться от их математиче-
ского ожидания (теорема Чебышева).
Вероятностная зависимость между двумя
случайными величинами называется корре-
ляцией.
В частности, эта зависимость сводится к
функциональной зависимости, если значе-
ния, принимаемые одной случайной величи-
ной, позволяют с достове.рностыо вычислить
значения другой. Случайные величины не-
зависимы, если значения одной величины
не влияют на закон распределения другой.
Степень корреляционной зависимости
вычисляется с помощью коэфициента
корреляции
М{[Х-М(Х)] [У — Л4(У)]}-
R (Х’ У) = УЩхПЦу)
Если X и У независимы, то R (X, У)=0
(обратное утверждение несправедливо).
Если У зависит линейно от X :
У=аХ+Ь,
го /?(Х, У) = 1, если а>0, и R (X, У)= — 1,
если а<0, в общем случае 1 7? (X, У) | < 1 и
считают, что «прочность» корреляционной
зависимости тем больше, чем больше
| R (X, У)|.
Пример. Вычислить с помощью таблицы коэфи-
циент корреляции между облачностью, оцениваемой
по 10-балльной системе, и частотой попадания в
цель(рассматриваем вместо вероятности статисти-
ческую вероятность и вместо математического
ожидания и дисперсии соответствующие статисти-
ческие характеристики).
Дата наблю- дения Облачность Число
выстрелов попаданий
;wi 3 15 11
4/VI 0 22 18
7/VI 5 12 7
8/VI о 25 21
9/VI 16 14 10
Есл~и X — облачность, a Y — частота попаданий и
каждый день наблюдений рассматривать как от-
дельный опыт, то имеем:
xi 3 2 h)
И 0,73 0,82 0,58 0,84 0,71
wi 1 5 1 5 5~ 1 5 1 5
где жстатистическая вероятность пары значений
(Xj, Vi ). Далее: *
М (X) = 2 lvi xi “ М (У) = 2 У, = 0,7 4;
М ГХ - Л4(Х)] [У - М(У)] =
“ X wi (xi ~ 4) (Vi - 0,74) = - 0,18;
О (X) (х4 - 4)= = 11,6;
D (У) = 5} tvi (У, — 0,74)" = 0,0095
R (X ,
- 0,18____
V 11,6- 0,0095
0,54.
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Биномиальному закону подчиняется ве-
роятность того, что некоторое событие при
п испытаниях, в каждом из которых ве-
роятность события равна р (р — постоянно),
произойдёт х раз (х = 0, 1, 2, . . . , п):
Р(х) =С*рх (1 — р)п~х =
n! v
^хЦ'Г=^Р (1-р) х-
Параметры этого закона: р (0 < р < 1) и
п (п — целое и положительное).
Если параметр р достаточно мал, так
что величина а = пр тоже невелика, то би-
номиальный закон может быть приближённо
заменён законом Пуассона:
/7^ р
р (X) = -----
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ
ВЕЛИЧИН
Если между случайными величинами
X и У имеется функциональная зависи-
мость У =/(Х), причём функция / (х) моно-
тонна (и имеет непрерывную производную),
то, зная закон распределения <pt (х) величины
X, можно найти закон распределения для
величины У по формуле:
, . <Р1(Х)
(У) ~ | /' (х)| ’
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
227
где х выражается через у из уравнения
у = /(Х). В частности, если у = ах + Ь, то
! /у — b ,
Если известны функции 'эд (х) и Г?2(У),
являющиеся законами распределения двух
независимых случайных величин X иУ, .то
величина Z=X-|~r имеет закон распределе-
ния,- определяемый формулой
оо
<P»(z) = J <t1(x)<?i(z-x)dx.
—00
Закон равной вероятности. Закон равной
вероятности имеет место, например, при
ошибках в измерениях, производимых при
помощи отсчёта по ближайшей отметке па
шкале.
Если область возможных значений из-
меряемой величины X при этом заключена
между х = а —8 и х = а-|-о, то (р(х)=^
при а — о < х < а 4 В и (х) = 0 для всех
_ остальных значений х
' ] (фиг. 322).
Для этого закона:
|-----1 М(Х) = а;
Закон распределения величин, являю-
щихся суммой двух случайных величин,
каждая из которых подчинена закону равной
вероятности (причём параметры этого зако-
на а и В для обеих величин одинаковы),
выражается формулами (фиг. 323):
В — а + х
у(х) =---------при а — о < х < а-
В + а — х
о (х) = —------ при а < х < а + о;
у(х) = О для всех остальных значений х.
Здесь М (X) = a; D (X) = |о2.
Нормальный закон распределения. Нор-
мальный закон распределения или закон
Здесь М (X) = a- D (X) = ;
f<p(x)dx не выражается через элементарные
функции и приводится к интегралу вероят-
ностей Ф (/) (см. таблицы стр. 148) подста-
новкой V‘2h(x— a) = t. Так, например,
X X
( у (х) dx - -Ji-— i е -йа<х~а)- dx—
J У - J
a a
= Ф [/2/!(x-a)].
Эмпирическое определение параметров
закона Гаусса. Если случайная величина X,
вад которой было произведено п наблюде-
ний, давших результаты Xj, х3, . . . , х„, под-
чиняется закону Гаусса, причём параметры
этого закона (один или оба) неизвестны, то
для их определения считают эти параметры
случайными величинами и за величину этих
параметров принимают, обычно, либо их наи-
вероятнейшее значение (моду), либо мате-
матическое ожидание; в последнем случае
вычисляют также среднее квадратическое
отклонение искомого параметра, характе-
ризующее возможную погрешность.
Равноточные наблюдения.
1. Мера точности h известна, центр рас-
сеивания а неизвестен. (Например, в одних
и тех же условиях одним и тем же инстру-
ментом, мера точности которого установ-
лена ранее, произведено п измерений ве-
личины X; требуется найти наивероятней-
шее значение Х — а этой величины).
Мода (наивероятнейшее значение) иско-
мого центра рассеивания, совпадающая с
его математическим ожиданием, равна сред-
нему арифметическому полученных из на-
блюдений значений
~Ь • • • + хп
п ’
О a-S а
Фиг. 323
Фиг. 324
причем среднее квадратическое отклонение
величины а равно
1
h /2п ’
Результат обычно записывается в форме
^11-^+ • + Хд
__1
± hVzn
Гаусса (фиг. 324) имеет место для величины,
которая может быть представлена в виде
суммы «бесконечно большого» числа незави-
симых друг от друга случайных величин
(обосновывается при помощи предельной
теоремы Ляпунова):
?(х)=
у ~
Параметры закона: а (центр рассеивания)
н h (мера точности).
Пример. При стрельбе с мерой точности й = 0,04
отмечены абсциссы точек попаданиях/: 369,378,
315, 420, 385, 401, 372, 383 (в сантиметрах).
Найти центр рассеивания а.
Математическое ожидание (и наивероятнейшее
значение) величины а равно
369+378+315-Ь420-Ь385-Ь401+372-1-383
--------------------------------------- 377> 875>
о
Среднее квадратическое отклонение этой величи-
ны равно
hV2n 0,04^2-8
Следовательно, а = 377,875 + 6,25 см.
15*
МАТЕМАТИКА
228
2. Центр рассеивания а известен, мера
точности Л неизвестна (например, в одних
и тех же условиях при помощи одного и
того же инструмента произведено п измере-
ний величины X, истинное значение которой
X = а известно; требуется найти в данных
условиях меру точности инструмента).
Наивероятиейшее значение (мода) вели-
чины h равно ________________
h =
и- 1
2 2 (Л-ay
г— 1
Математические ожидания и средние
квадратические отклонения величин а и h
определяются формулами:
2 3 (х/ - ау
г=-1
Математическое ожидание М (Ji) и сред-
нее квадратическое отклонение Ea (ft) вели-
чины ft определяются формулами:
(таблицы функции Г, см. па стр. 149);
и
Л = М (Л) ± Е3 (Ji).
Пример» При стрельбе с центром рассеивания
а «а 375 отмечены абсциссы точек попадания:
369, 378, 315, 420, 385, 401, 372, 383.
Найти меру точности h.
Находим наивероятиейшее значение меры точ-
ности.
Имеем:
(X, - <ОВ - 36; (ха - а} ‘ = 9; (Х8 — л)а - 3 600;
(Х4 _ - 2 025; (ха - а)“ = 100; (х„ — а)' « 676;
(х7 — а)’ = 9; (х8 — аУ = 64
И - а)8 ~ 6 518.
Следовательно, наивероятнейшее значение вели-
чины Л равно
/-276^519 =°-0247-
Математическое ожидание величины h равно
1 Г (5)
V^5i9 ’г(4>) =0-0255’
среднее квадратическое отклонение этой величины
—Г._____V „ о.ооб!.
J/6 519 Г (4,5)
h = 0,0255 + 0,0061.
3. Оба параметра закона Гаусса а и h
неизвестны (например, в одних и тех же
условиях, при помощи одного и того же
инструмента произведено п измерений не-
которой величины X; требуется найти наи-
вероятнейшее значение X = а измеряемой
величины и меры точности инструмента).
В этом случае наивероятнейшие значения
величин а и й определяются равенствами:
п
2 xi
в==_1Г1__;
П
Пример. Известны абсциссы точек попадания
при стрельбе x.j
369, 378, 315, 420, 385, 401, 372, 383.
Требуется найти центр рассеивания а и меру
точности h.
Имеем у xj » 3 023 и наивероятнейшее значение
а, совпадающее с его математическим ожиданием,
равно
У23 «378.
Далее £ (.х^ — 378)*=» 6 453, среднее квадратиче-
ское отклонение величины а равно
а = 378 ± 12.
Наивероятнейшее значение h равно
К-27б7453 “ °’°233'
Математическое ожидание величины h равно
г(4,5)
г (4)
* 0,0241,
среднее квадратическое отклонение этой величины
_1Д.<4)±(5) УДОДУ „ 0,0061
Г (4) Кб 453
и, следовательно
h = 0,0241 ± 0,0061.
Неравноточные наблюдения.
Пусть произведено п наблюдений над величи-
ной X, в результате которых получены зна-
чения х1( х2, ,хп. Каждое наблюдение под-
чиняется закону распределения Гаусса, при-
чём неизвестный центр рассеивания а во
всех случаях одинаков, а меры точности
известны и различны: ftv ft,. . .. , Ли. В этом
случае наивероятнейшее значение а совпадает
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
229
с его математическим ожиданием и опреде-
ляется равенством
X xt
М[а)=1-^--------,
У ft?
I
i= 1
а среднее квадратическое отклонение при
этом вычисляется по формуле
Весами наблюдений называются вели-
чины g;, пропорциональные квадратам мер
точности: gi = Kh?. Наивероятнейшее зна-
чение величины а равно, таким образом
г= 1__
2^
t=i
т. е. так называемому среднему взве-
шенному из результатов наблюдений.
Распределение по отрезкам кривой Гаус-
са. На практике часто встречается распре-
деление по от р е з к а м кривой Гаусса.
Пусть, например, требуется установить рас-
пределение размеров только тех деталей,
которые находятся в пределах области до-
пусков. Если при этом центр области допу-
сков а совпадает с центром рассеивания
закона Гаусса, которому подчиняются раз-
меры всех деталей (в том числе и выходящих
за пределы области допусков; па чертеже
соответствующая кривая обозначена пунк-
Фиг. 325
Фиг. 326
тирной линией), а максимальная допустимая
величина отклонения размера детали от
величины а равна 6 (т. е. допускаются детали
с размерами от а — Ъ до а + В), то диферен-
циальный закон распределения определяется
функцией (фиг. 325)
<р(х) =
he - (.X - ay h‘
г _<5Л 1/2 _
V2 ( е 22 dz
О
при а— В < х < а + В
и 7(х) = 0 для остальных значений х.
Если случайная величина X является
геометрической суммой двух других случай-
ных величин у и z(x = Vy2+ z2), подчиняю-
щихся закону Гаусса с одними и теми же
параметрами (например, эксцентриситет зуб-
чатого колеса, вызванный двухмерным рас-
сеиванием), то кривая распределения
(фиг. 326) определяется формулой
<f(x) = 2ft2xe-'!’ х*,
где й — мера точности в законе Гаусса, и
предположено, что а = 0 (а — центр рассеи-
вания в законе Гаусса).
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Получаемый из закона Гаусса принцип
наименьших квадратов утверждает,
что:
1) наивероятнейшим значением случайной
величины, которое может быть получено из
ряда измерений одинаковой точности, яв-
ляется то, для которого сумма квадратов
ошибок наименьшая;
2) наивероятнойшим значением случайной
величины, которое может быть получено из
ряда измерений различной точности, являет-
ся то, для которого сумма произведений
квадратов ошибок на веса измерений наи-
меньшая.
Из принципа наименьших квадратов сле-
дует, что, в случае равноточных измерений,
наивероятиейшим значением измеряемой
величины является средняя арифметическая
из результатов измерений, а в случае не-
равноточных измерений — средняя взвешен-
ная.
Если из т измерений получены значе-
ния некоторых функций п случайных вели-
чин х2,. . . , хп, подчинённых нормаль-
ному закону распределения, т. е. если дана
так называемая система условных
у р а в н е н и й (обычно т > п и система не-
совместна):
/1 (Х1, Х2, . . . , Хп) =
/2 (-^1’ -^2» • • " » '’•к) “ а2>
1т Я2, . . . , “ ат*
то наивероятнейшие значения случайных
величия—те, для которых является наимень-
шей сумма произведений квадратов ошибок
на веса g, соответствующих измерений
т
R = 2 Si [/< хп) — а;]2.
г=1
В случае равноточных измерений gx = g2 =
— . . . = gn 1.
Для определения наивероятнеиших зна-
чений величин х1( х2, . . . , хп по способу
наименьших квадратов получаем, таким
образом, систему уравнений
Если функции линейны, то для
определения наивероятнейших значений
Xj, х2,. . . ,хп удобно пользоваться следую-
щей схемой.
Данные измерений дают линейную систе-
му условных уравнений:
ai xi + х2 4* Ci х3 + . .. + Zi хп + гО,
а2 xi 4- х2 + с2 х3 4- . .. 12 хп + г2= О,
ат xi 4- Ьт х2 4- Ст х34- • 4- х»4- г/п =- О,
230
МАТЕМАТИКА
а наивероятнейшие значения величин х/
определяются из так называемой системы
нормальных уравнений, которая,
в случае равноточных измерений, в обозна-
чениях Гаусса имеет кпд:
[аа] х, + [аЬ) х,, + [ос] х3 + ... +
+ [<?/] х,, + [аг] =- 0,
[&а] Xj + [66] х2 + [6с] х3 + . . . +
+ [bl] хп [6г] = О,
[/о] х, + [/6] х3 + [Zc] х, -}-... +
+ ПП хп + UH = О,
где
т т
м = ["*]= S й< й/
i=i ;=1
и т. д.
Чтобы получить первое нормальное урав-
нение, нужно обе части каждого из услов-
ных уравнений умножить на коэфициент
при Xj в этом уравнении и потом все урав-
нения сложить; чтобы получить второе нор-
мальное уравнение, нужно обе части каждого
условного уравнения умножить на коэфи-
циент при х2 в этом уравнении и потом все
уравнения сложить и т. д.
Средняя квадратическая ошибка ej вели-
чины Xj, найденной по методу наименьших
квадратов, определяется равенством:
[66] [бс]...[б/]
[6с] [сс]... [cZ]
[6/] [cZ] ...[ZZ
(т — л)
[аа] [a6]...[aZj [аг]
[аб] [66]. ..[6Z] [6г]
[аг] [ 6г] ... [Zr] [гг]
4=
аа] [об] ... [aZ]
об] [66] ... [6Z]
[«Z] [6Z] .. . [ZZ]
Аналогичным образом определяются сред-
ние квадратические ошибки е2, е3, . . . , е„
величин х2, х3, ... х„.
В случае, если система условных урав-
нений получена из неравноточных на-
блюдений с весами gj, g2........ gn, еле
дует предварительно умножить обе части
каждого условного уравнения на корень
квадратный из соответствующего веса;
в полученной, таким образом, новой систе-
ме условных уравнений с коэфициента-
ми aj= a,- Vgi, b\ = b: Vgt... , Ц = Z; Vgt,
ri = г,- 'Kg, веса следует считать одинако-
выми.
Таким образом, в этом случае система
нормальных уравнений имеет вид:
[a' a'] Xj + [a' 6'] х.. + [а' с'] х3 + . . . +
+ [а' 1']х„ + [а' г'] = О,
[b'a'] Xi + [b' 1>']х2 + (b'c'] х8 + . . . -f-
+ [Н']хя + [6'г'] = 0,
[/' а'\Xi + [/' 6'] х2 + [Z' с']х, + ... +
+ [I' хп + [I' г'] “ 0.
Если функции fi нелинейны, то, выбрав
в качестве первых приближений некоторые
значения х^0), х$,0), . . . , х<°\ заменяют
функции fi через линейные функции при
помощи приближённых равенств:
6 (xlt х2, . . ., х„) к fi (Xi<°>, х<°>,.. . , х^Ъ +
п я
г=1
и затем применяют способ наименьших
квадратов.
Определённые таким путём значения
х^\ х^\ • . . , х<П можно, если нужна боль-
шая точность, опять принять за исходные
приближения и снова применить указанный
приём.
ЭМПИРИЧЕСКИЕ ФОРМУЛЫ
В результате экспериментального иссле-
дования может быть получен ряд отдельных
значений функции у/, соответствующих зна-
чениям аргумента X/, или график, связываю-
щий значения х и у.
Аналитическое выражение функциональ-
ной зависимости между х и у, т. е. формула
у=/(х), которая составляется по этим
экспериментальным данным (таблице или
графику), называется эмпирической
формулой.
Составление эмпирической формулы яв-
ляется задачей неопределённой, так как
имеется бесчисленное множество функций
у=у(х), удовлетворяющих условиям задачи.
Так, например, если для значений хп х2,..,хл
аргумента х получены из опыта значения
Уи Ун • • >Уп функции у, то функциональ-
ная зависимость у = f (х) может быть найде-
на с помощью формулы Лагранжа (стр. 246),
причём этой зависимости будут в точности
удовлетворять все экспериментальные дан-
ные. Однако при большом п полученная
таким путём формула громоздка и не удобна
для пользования. В таком случае следует
выбрать более простую формулу, не требуя
при этом, чтобы экспериментальные данные
в точности ей удовлетворяли.
Задача составления эмпирической форму-
лы состоит, таким образом, в выборе типа
формулы, т. е. вида функциональной зависи-
мости между х и у, и в нахождении наилуч-
ших значений, входящих в формулу пара-
метров. После решения этой задачи следует
произвести проверку пригодности получен-
ной эмпирической формулы.
ВЫБОР ТИПА ЭМПИРИЧЕСКОЙ
ФОРМУЛЫ
Нельзя указать общего метода для выбора
наилучшего типа формулы, соответствующей
экспериментальным данным. Теоретические
соображения физического характера иногда
предопределяют тип формулы.
ЭМПИРИЧЕСКИЕ ФОРМУЛЫ
231
;J случаях периодического иЗхМенения
функции с периодом I обычно выбирают
формулу в виде
. 2- 2п /2 it \
у = asm-j х + &cos -у х —- A sin х + aj,
или в виде тригонометрического полинома
2 к г 2 к л
у = 2j ak cos ~— х + sin х-
К=1
В тех случаях, когда пет возможности
руководствоваться теоретическими соображе-
ниями для выбора типа формулы, экспери-
ментальные данные наносятся на чертёж при
помощи точек с координатами X; и у,. Если
построенный по этим точкам график окажется
прямой линией или близким к прямой,
то следует выбрать формулу в виде линейной
функции
у = а + Ьх.
Если же график окажется плавной кри-
вой линией, то следует его перестроить в
какой-либо функциональной сетке (логариф-
мической, полулогарифмической и т. д.), в
которой он может оказаться прямолинейным.
Ниже приводятся некоторые из формул, ко-
торые следует выбрать в таких случаях, с
указанием соответствующего преобразования
к линейному виду (анаморфоза):
1) у=ахп. Логарифмируя, имеем: 1g у =
= 1g а + п 1g х; положив lg х = X и Igy = У,
получим в логарифмической сетке линейную
функцию У = 1g а -г- пХ (фиг. 327);
2) у = аеЬх или у = abx. Логарифмируя,
имеем: 1g у = lg а + bx 1g е или 1g у = 1g а +
+ xlgfi; положив х = X и lgy=y, получим
в полулогарифмической сетке (фиг. 328)
линейные функции:
У — lga + b-Xlge или У = \ga + Х-lg Ь;
3) ут= а + —п (заданы т и п). Положив
gr — X и ут = У, получим линейную функ-
цию У = а+ЬХ.
В других случаях для удобства вычисле-
ния параметров эмпирической формулы
рекомендуется выбрать вид функции по воз-
можности линейным относительно парамет-
ров.
Фиг. 328
Основываясь на теореме исчисления ко-
нечных разностей (стр. 244) о том, что если
разности п-го порядка табличной функции
постоянны (при равноотстоящих значениях
аргумента), то функция представляет собой
многочлен n-й степени, весьма часто выбирают
эмпирическую формулу в виде многочлена
у = а + Ьх + сх2 + .. . + 1хп,
число членов которого определяется указан-
ной теоремой.
Так, например, если в таблице конечные
разности третьего порядка почти постоянны,
то соответствующую эмпирическую формулу
следует выбирать в виде многочлена третьей
степени
у ~ а + Ьх + сх2 + dx3.
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ПАРАМЕТРОВ
ЭМПИРИЧЕСКОЙ ФОРМУЛЫ
Для определения значений параметров
выбранного типа эмпирической формулы
применяют обычно три основных метода:
метод выбранных точек (графический метод),
метод средних и метод наименьших квадра-
тов.
МЕТОД ВЫБРАННЫХ ТОЧЕК
(ГРАФИЧЕСКИЙ МЕТОД)
Этот метод применяется в случае линей-
ности выбранной эмпирической формулы
(в равномерной или функциональной сетке)
и заключается в том, что экспериментальные
данные наносятся на чертёж при помощи
точек с координатами X/ и у, (в равномерной
сетке) или X,- = (хг) и yt = ф (у;) (в функ-
циональной сетке), после чего проводится
прямая таким образом, чтобы она проходила
возможно ближе к каждой из нанесённых
точек.
232
МАТЕМАТИКА
Уравнение этой прямой и даёт искомую
функциональную зависимость.
Этот метод весьма несовершенен и может
быть рекомендован только для отыскания
значений параметров с небольшой точностью.
Можно также рекомендовать предваритель-
но подсчитать координаты центра тяжести
данной системы экспериментальных точек
(X/;yi) по формулам х0 = - s xf, уа = ~ЪУ1
(п — число экспериментальных точек) и вы-
бирать искомую прямую среди тех, которые
проходят через точку (х0; у0).
Пример. Составить эмпирическую формулу по
следующим табличным данным:
х 5,0 12,5 16,9 22,6 35,1 40, 1 45,0
У 10,45 13,61 15,50 17,58 22,81 25,22 26.93
Наносим на чертёж точки, определяемые задан-
ной таблицей (фиг. 329). Так как построенные точ-
ки располагаются примерно на прямой линии, то
зависимость между х и у выбираем в виде линейной
функции
у = а + Ьх
и проводим прямую как можно ближе ко всем точ-
кам.
Для определения параметров а и 5 берём две
точки, лежащие на этой прямой: (10,0; 12,5)
и (28; 20), ‘обозначенные на фигуре звёздочками,
и, подставляя их координаты в уравнение, полу-
чим систему уравнений:
12,5 = а + 10 5;
20 = а + 28 Ь,
откуда а= 8,3 и 5=0,42 и, следовательно, искомая
эмпирическая формула будет
у = 8,3 + 0,42 х.
МЕТОД СРЕДНИХ
Метод средних применяется для опреде-
ления значений параметров таких эмпириче-
ских формул, которые линейны относительно
параметров или легко могут быть преобразо-
ваны к линейному относительно параметров
виду. Он основан на допущении, что наи-
более подходящей формулой будет та, для
которой алгебраическая сумма уклонений
(т. е. разностей между табличными значе-
ниями функции и значениями, полученными
из выбранной эмпирической формулы путём
подстановки в неё соответствующих значе-
ний аргументов X/) равна нулю.
Для нахождения по методу средних пара-
метров эмпирической формулы подставляем
в неё все пары экспериментальных табличных
значений X/ и у,. Полученные уравнения раз-
биваем на столько групп, сколько имеется
параметров, с таким расчётом, чтобы каждая
группа содержала по возможности одина-
ковое число уравнений.
Приравнивая нулю сумму уклонений в
каждой из групп (для чего складываем
между собой уравнения каждой группы),
получим систему уравнений, число которых
равно числу искомых параметров. Решая
эту систему уравнений, определяем значения
параметров эмпирической формулы.
Пример. Составить эмпирическую формулу по
данным, помещённым в первых двух столбцах при-
ведённой ниже таблицы:
X У Ду
0 0,957 0,012
0,1 0,969 0,007 -0,005
0,2 0,976 0,002 —0,005
0,3 0,978 —0,003 —0,005
0,4 0,975 —0,007 —0,004
0,5 0,968 —0,014 -0.007
0,6 0,954 —0,015 -0,001
0,7 0,939 —0,021 —0,006
0,8 0,918 —0,024 -0,003
0,9 0,894
Для выбора вида функциональной зависимости
в таблице подсчитаны конечные разности первого
и второго порядка. Так как вторые разности почти
постоянны, то выберем эмпирическую формулу
в виде
у = а + Ьх + сх8.
Подставляя в неё значения х$ и из нашей
таблицы, получим следующие соотношения:
0,957 — а 4-0 . &4-0-С \
0,969 = а 4- 0,1 b 4- 0,01 с I
0,976 = а 4-0,2 0 4-0,04 с f С1 >
0,978 = а 4- 0,3 0 4- 0,09 с I
0,975 = а 4 0,4 b 4- 0,16 с 1
0,968 = а 4- 0,5 b 4-0,25 с У (II)
0,954 = а 4- 0,6 b 4- 0,36 с >
0,939 == а 4- 0,7 b 4- 0,49 с 1
0,918 « а 4-0,8 b 4-0,64 с f (III)
0,894 = а 4- 0,9 b 4- 0,81 с >
Распределяя эти соотношения на три группы,
как указано выше, и складывая между собой урав-
нения каждой группы, получим систему нз трёх
уравнений для определения параметров a, b и с:
3,880 «= 4а 4- 0,6 b 4- 0,14 с;
2,897 == 3 а 4- 1,5 Ь 4- 0,77 с;
2,761 = За 4- 2,4 b 4- 1,94 с.
Решая эту систему, находим
а = 0,958; b = 0,130, с = — 0,2248
и, следовательно
у = 0,958 4- 0,130 х — 0,2248 ха.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Метод наименьших квадратов (стр. 229)
в применении к составлению эмпирических
формул основан на предположении, что экс-
периментально найденные значения аргу-
мента X/ точные и что наилучшей формулой
является та, для которой сумма квадратов
уклонений функции наименьшая. Заметим,
что так как квадраты уклонений положи-
тельны, то при этом и абсолютные значения
ПРИБЛИЖЁННЫЕ ВЫЧИСЛЕНИЯ
233
уклонений будут малы, т. е. кривая, изобра-
жающая эмпирическую формулу, пройдёт
весьма близко ко всем экспериментальным
точкам.
Для определения значений параметров
эмпирической формулы по методу наименьших
квадратов составляют сперва условные урав-
нения относительно п искомых параметров
аг, аг, аа, ... , ап, для чего в выбранную
эмпирическую формулу подставляют экспе-
риментально полученные значения аргу-
мента X/ и функции у;. Предполагая, что
искомые параметры входят линейным обра-
зом, получим систему т условных уравне-
ний (т > и), линейных относительно пара-
метров. Количество уравнений в этой си-
стеме равно числу экспериментальных точек.
Далее, при помощи системы условных
уравнений составляется система нормаль-
ных уравнений (стр. 230), из которой оп-
ределяются наилучшие значения парамет-
ров Я/.
Пример. Определить по методу наименьших квад-
ратов параметры эмпирической формулы квадратич-
ного вида у = а + Ьх -+- сх8 по следующим данным:
Табличные данные подставляем в формулу у =
= а + Ьх + сх* и получаем систему условных уравне-
ний:
3,1950 « а + 0-Ь + О-с:
3,2299 «= а + 0,1 b + 0,01 С;
3,2532 = а + 0,2 Ь + 0,04 с;
3,2611 = а + 0,3 Ь + 0,09 с;
3,2516 = а + 0,4 Ь + 0,16 с;
3,2282 == а + 0,5 д -+- 0,25 с;
3,180? = а + 0,6 Ь + 0,36 с;
3,1266 « а + 0,7 Ь + 0,49 с;
3,0594 = а + 0,8 Ъ + 0,64 с;
2,9759 = а + 0,9 b + 0,81 с.
Для получения из этой системы условных урав-
нений первого нормального уравнения складываем
их почленно (умножать в данном случае не нужно,
так как коэфициенты при а во всех уравнениях
равны единице); для получения второго нормального
уравнения умножаем обе части первого условного
уравнения на 0 (коэфициент при 5), второго — на
0,1, третьего — на 0,2 ит. д. и складываем их; ана-
логичным образом получаем и третье нормальное
уравнение. Решив полученную таким образом сис-
тему:
31,7616 = 10 а + 4,5 Ъ 4- 2,85 с;
14,0896 = 4,5 а + 2,85 b + 2,025 с;
8,82881 = 2,85 а + 2,025 Ь + 1,5330 с,
найдём параметры эмпирической формулы:
а = 3,1951; b = 0,44254; с «= — 0,76531,
н, следовательно, эмпирическая формула запишется
в виде
у = 3,1951 + 0,44254 х — 0,76531 Xs.
X 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8
У 3.1950 3,2299 3,2532 3,2611 3,2516 3,2232 3,1807 3,1266 3,0594 2,9759
ПРИБЛИЖЁННЫЕ ВЫЧИСЛЕНИЯ
ПРИБЛИЖЁННЫЕ ЧИСЛА
Различного рода измерения, лежащие
в основе почти любого технического расчёта,
неизбежно сопровождаются погрешностями
вследствие несовершенства способов измере-
ний и других причин. Поэтому исходные
числовые данные технических расчётов яв-
ляются не точными, а приближёнными, вер-
ными обычно до двух, трёх и реже боль-
шего числа знаков. Многие из точных чи-
сел, встречающихся в расчётах (я, е, корни,
тригонометрические величины, логарифмы
и т. д.), выражаются бесконечными десятич-
ными дробями; при вычислениях приходится
их обрывать на том или ином знаке и тем
самым превращать в приближённые числа.
Располагая приближёнными данными, вы-
числитель должен уметь правильно исполь-
зовать их и с наименьшей затратой труда
получить результаты с требуемой точностью.
Абсолютная величина разности между
точным значением величины х и её прибли-
жённым значением а называется абсолют-
ной погрешностью приближённого
числа: аа = | х— al; отношение абсолютной
погрешности а к модулю приближённого
числа а называется его относительной
погрешностью: da = —. Относитель-
la I
ную погрешность часто выражают в про-
центах.
Так как обычно величина погрешности
неизвестна, то на практике пользуются так
называемыми предельными погрешностями.
Предельной абсолютной по-
грешностью приближённого числа а на-
зывается число которого не превосходит
абсолютная погрешность аа-.
sa > аа-
Принято говорить, что а есть приближён-
ное значение х с точностью до е0.
Предельной относительной по-
грешностью 8Й называется отношение
предельной абсолютной погрешности к мо-
дулю приближённого числа а:
Например, если эа приближённое значение
числа я = 3,14159... принять число 3,14, то
абсолютная погрешность
а — 13,14159... —3,14 | = 0,00159... ,
а за предельную абсолютную погрешность
можно принять
е = 0,002.
Относительная погрешность
а = 0^00159^: = 0,000506...
3,14
а предельная относительная погрешность
= 0^02 = 0 00064 = 0,0б4°/о.
3,14
Числоа является приближением числа х с
п верными знаками, если предельная
абсолютная погрешность его не превосходит
234
МАТЕМАТИКА
единицы, или, как иногда уславливаются,
половины единицы разряда n-й цифры при-
ближённого числа. Приближённые числа
принято записывать, сохраняя только верные
знаки; так, например, если предельная абсо-
лютная погрешность числа 34 500 равна 50,
то его записывают в виде 345 • Ю3. При этом
способе записи легко оценить погрешность
приближённого числа по числу его верных
знаков. Например, для числа 2,72, являю-
щегося приближением числа е — 2,71828...
с тремя верными знаками, имеем:
е= ]е — 2,721 — 0,0017.. < 0,С02 = 2-10~3;
5= 2’А0 3== 0,74 • 10 3 = 0,074%.
2,72
Если приближённое число имеет п вер-
ных знаков, то его предельные погрешности
можно определить по формулам:
га < 1 • Ют - п + 1 ,
где ш—наивысшая степень 10, не превы-
шающая числа а,
2z
1
10п—1 ’
где Z—первая значащая (т. е. пер-
вая отличная от нуля) цифра числа а.
Пользуясь последней формулой, можно
составить таблицу для определения отно-
сительной погрешности приближённого числа
при сохранении в нём определённого числа
верных знаков.
Таблица 23
Определение относительной погрешности
в процентах при округлении чисел и сохранении п
верных знаков
(z — первая значащая цифра числа)
и Z 1 2 । 3 4 5
1 50 5,0 0,5 0.050 0,0050
2 25 2,5 0,25 0,025 0,0025
3 17 1,7 0,17 0,017 0,0017
4 12 1,2 0,12 0,01г 0,0012
к 10 1.0 0,1 0,010 0,0010
6 8,3 0,83 0,083 0,0083 0,00083
7 7.1 0,71 0,071 0,0071 0,00071
8 6.3 0,63 0,063 0,0063 0,00063
9 5,6 0.56 0,656 0,0056 0,00056
Велти приближённое число а имеет пре-
дельную относительную погрешность оа, то
число а его верных знаков можно опреде-
лить из неравенства
(1 + с)Зя < Ю1-",
где z—первая значащая цифра числа а,
ап — наибольшее целое число, удовлетво-
ряющее этому неравенству.
Здесь предполагается, что наличие п вер-
ных знаков обозначает, что абсолютная по-
грешность не превосходит единицы разряда
п-го знака.
При помощи последнего неравенства
можно составить таблицу для определения
количества верных знаков приближённого
числа по его предельной относительной по-
грешности.
Таблица 24
Определение количества верных знаков числа но его
предельной относительной погрешности S
(z — первая значащая цифра числа)
В случае, когда приближённое число со-
держит сомнительные или лишние знаки,
его округляют, т. е. отбрасывают эти
знаки, причём последнюю из оставшихся
цифр увеличивают па единицу, если первая
из отбрасываемых цифр равна или больше 5;
в случае, когда отбрасываемая часть со-
стоит из одной цифры 5, округление произ-
водится таким образом, чтобы последняя
сохраняемая цифра была чётной. Так, на-
пример, число я = 3,1415926... при округле-
нии принимает значения: 3,14; 3,142; 3,1416
п т. д.; число 2,725 при округлении пре-
вращается в 2,72, а число 83,55 в 83,6.
По этому правилу абсолютная погреш-
ность при округлении приближённых чисел
не превышает половины единицы разряда
последней цифры округлённого числа.
ПРАВИЛА ДЕЙСТВИЙ
НАД ПРИБЛИЖЁННЫМИ ЧИСЛАМИ
1. Предельная абсолютная погрешность
алгебраической суммы s приближённых чи-
сел а1( аа, а3, ... , ап равна сумме пре-
дельных абсолютных погрешностей г; сла-
гаемых:
f j = h + s2 + • • + ги-
2. Предельная относительная погреш-
ность алгебраической суммы определяется
по формуле
I я, I I «2; , I,
= I 7 Р1 + |'ST2 + ’ ’ ' + Is Iп’
где Й/— предельные относительные погреш-
ности слагаемых.
Примечание. Относительная погрешность суммы
положительных чисел заключена между наибольшей
и наименьшей из относительных погрешностей сла-
гаемых; относительная погрешность разности поло-
жительных чисел может оказаться очень большой
по сравнению с относительными погрешностями
уменьшаемого и вычитаемого, если последние очень
близкие между собой числа.
3. Предельная относительная погреш-
ность произведения или частного прибли-
жённых чисел а и & равна сумме предель-
ных относительных погрешностей сомножи-
телей1:
ЬаЬ = % -
Ъ
1 В формулировке всех правил, кроме первых
двух, предполагается, что относительные погреш-
ности величин, над которыми производятся действия,
столь малы, что их произведениями, а также и
степенями с показателями, большими единицы,
можно пренебречь.
ПРИ БЛИЖЁННЫЕ ВЫЧИСЛЕНИЯ
235
Это правило распространяется и на боль-
шее число сомножителей и делителей.
4. Предельная относительная погреш-
ность степени приближённого числа а равна
предельной относительной погрешности ос-
нования, умноженной на абсолютное значе-
ние показателя степени:
= I п | оа .
5. Предельная абсолютная погрешность
натурального логарифма некоторого числа
равна предельной относительной погрешно-
сти самого числа, а предельная абсолютная
погрешность десятичного логарифма равна
предельной относительной погрешности са-
мого числа, умноженной на логарифмиче-
ский модуль (М = 1g е):
®1п х ’ rjln х>
elgx = Mr4gx~°>0434 8lgx-
6. Предельная абсолютная погрешность
функции у = / (х) равна произведению аб-
солютного значения производной этой функ-
ции на предельную абсолютную погреш-
ность аргумента, т. е. имеет структуру,
аналогичную структуре диференциала функ-
ции
= I Г (х) I ея.
В частности:
I Н—1 I
вх„ — 1ПХ I ех ; esin х = | COS X | ех ;
£cos х = I Sin X I ех ;
etpx = —‘ e-v и т- Д-
tg * COS2X
7. Предельная относительная погреш-
ность функции у = / (х) равна абсолютному
значению произведения аргумента на про-
изводную логарифма функции (логарифми-
ческую производную), умноженному на пре-
дельную относительную погрешность аргу-
мента
В частности
Чжх = I х ctg х | Вх ; Scos х = | х tg х | Вх
и т. д.
8. Предельная абсолютная погрешность
функции нескольких аргументов и=/ (х, у,...)
определяется по формуле
idf I , I df I ,
е« = иг Н» + Lr ev + • • *
Idx [ J dy j
т. e. имеет структуру, аналогичную струк-
туре полного диференциала. Например, если
и = е ах cos by,
то
еи = 1 ае~ах cos by I 4- | be~ ах sin by |г„.
При помоши этих правил решаются так
называемые прямая и обратная задачи при-
ближённых вычислений: как оценить точ-
ность вычисленного значения функции при
заданных значениях аргументов и их пре-
дельных погрешностей (прямая задача)
и как определить, каковы должны быть
предельные погрешности аргументов, чтобы
предельная погрешность функции не превы-
шала заданной (обратная задача).
Если для вычисления функции прихо-
дится производить действия сложения и вы-
читания, то при решении прямой задачи
удобнее пользоваться абсолютными погреш-
ностями данных чисел; если же произво-
дятся действия умножения, деления, возве-
дения в степень и извлечения корня, то ре-
комендуется пользоваться относительными
погрешностями.
В общем случае целесообразно перехо-
дить от абсолютных погрешностей к отно-
сительным и обратно в зависимости от ха-
рактера производимых действий.
При вычислении по формулам, имеющим
вид дробей, у которых числитель и знаме-
натель являются произведениями несколь-
ких множителей, можно производить сокра-
щения числителя и знаменателя даже тогда,
когда точное сокращение невозможно, при
условии, что вводимые при этом новые от-
носительные погрешности меньше погрешно-
стей данных чисел.
Обратная задача часто бывает неопреде-
лённой. Поэтому приходится вводить доба-
вочные условия об искомых погрешностях;
так, например, в зависимости от характера
задачи можно принимать равными между
собой либо все искомые абсолютные погреш-
ности, либо все относительные погрешности.
Следует учесть также, что в случае пря-
мой задачи при вычислении погрешности
функции допускаются округления чисел при
условии увеличения искомой погреш-
ности, а при решении обратной задачи до-
пускаются округления чисел при условии
уменьшения искомых погрешностей.
Пример 7. Вычислить индикаторную мощность
N паровой машины в лошадиных силах по формуле
при следующих данных: среднее давление на пор-
шень Р "* 6,3 ке(см1, площадь поршня
4 4
ход поошня S «= 0,485 м и число оборотов в минуту
п = 120.
Составляем буквенное выражение предельной
относительной погрешности результата ( <5,, =» 0);
°"дг= 4р + + 6S = + 25а + ss;
так как
Щ5 1 , 0,2 1
° Р°“ 60 “ 120 ’ “ 300 ” 1 600 *
o,os = 1 . л _ о,5 ’•
= 25 500’ S ” 4 50 “ SO0 *
то
к __ 1 1 _2_ 1 75 + б 4- 36 -г 11?
N~ 120 + 1 500 ' 500 900 " 9 ООО ~
127 £
“ 9 000 < 75’
Подставив данные числовые значения, получим
6,3 • 3,14 • 28,4 - 28,4 *0,485 . 120
1 ” 30-75-4 *“
« 103 ЛС
и, следовательно
- 103,0 • 1 = 1,4 ЛС.
Л I 5
Пример 2. С какой точностью надо измерить
диаметр основания и высоту цилиндра, чтобы абсо-
лютная погрешность объёма не превышала 0,5
236
МАТЕМАТИКА
при диаметре основания d «=> 20 см и высоте h *
м 80 см?
ndsh
v ------ .
4 *
откуда Sv <= + 2Sd + £л .
Задача неопределённая (одно уравнение с тремя
неизвестными: бп,^и 6^), поэтому вводим допол-
нительные условия, предполагая, что погрешность
может быть сделана сколь угодно малой, а погреш-
ности и 0ft равны между собой (будем обозначать
их через <5), Тогда
= ч + 33.
Имеем
v „ 3’2 ' 2QE ‘ 00. 25 G00 см3 < 30 Ом3;
4
0,5 1
°v > 'ЗО ” 60 •
Если принять тс «=3,14, то .
По сравнению с величиной величина , даже
при трёх значащих цифрах числа тс, настолько мала,
что ею можно пренебречь. Получаем
5 180
и, следовательно
20 - > 0,1 см!
т. е. диаметр цилиндра должен быть измерен с точ-
ностью до 0,1 см, а высота — до 0,4 см.
чащих цифр, сколько их имеет приближённое дан-
ное с наименьшим числом значащих цифр.
Если первая цифра результата по крайней мере
вдвое больше первой цифры того из данных чисел,
которое имеет наименьшее количество значащих
цифр, то следует в полученном числе взять одной
значащей цифрой меньше.
3. При возведении в квадрат и в куб прибли-
жённых чисел в результате следует сохранять
столько значащих цифр, сколько их имеет возводи-
мое в степень число, кроме тех случаев, когда пер-
вая цифра степени по крайней мере вдвое больше
первой цифры основания; в этих случаях в резуль-
тате следует последнюю значащую цифру отбросить.
4. При извлечении квадратного и кубического
корня из приближённых чисел в результате следует
брать столько значащих цифр, сколько их имеет
подкоренное число.
При этом последняя цифра квадратного и осо-
бенно кубического корня более надёжна, чем по-
следняя цифра подкоренного числа.
5. При вычислении промежуточных результатов
следует брать одной цифрой больше, чем рекомен-
дуют предыдущие правила. В окончательном резуль-
тате зта «запасная» цифра отбрасывается.
6. Если некоторые приближённые данные имеют
больше десятичных знаков (при сложении и вычи-
тании) или больше значащих цифр (при умножении,
делении, возведении в степень и извлечении корня),
чем другие, то их предварительно следует округ-
лять, сохраняя только одну лишнюю цифру.
7. Если данные можно брать с произвольной
точностью, то для получения результата с циф-
рами следует брать данные с таким числом цифр,
которое даёт, согласно правилам 1 — 4, в результате
Л'4-l цифру.
8. При вычислении одночленного выражения
посредством логарифмов следует подсчитать число
значащих цифр в приближённом данном, имеющем
наименьшее число значащих цифр, и взять для
пользования таблицы логарифмов с числом десятич-
ных знаков на единицу бдльшим; в окончательном
результате последнюю значащую цифру надо от-
бросить.
ПРАВИЛА ПОДСЧЁТА ЦИФР
ПРИ ДЕЙСТВИЯХ
С ПРИБЛИЖЁННЫМИ ЧИСЛАМИ
БЕЗ ТОЧНОГО УЧЁТА ПОГРЕШНОСТЕЙ
В приведённых выше правилах оценки
погрешностей предполагается, что различ-
ные погрешности усиливают друг друга,
тогда как на практике, в случае массовых
вычислений, это бывает редко. Если отка-
заться от требования строгого определения
предельных погрешностей, то можно дать
другие, практически пригодные способы
оценки точности полученного результата,
называемые правилами подсчёта цифр. Поль-
зуясь ими, можно считать, что в среднем
полученные в результате приближённые
числа имеют все знаки верные., хотя в от-
дельных случаях возможна ошибка в не-
сколько единиц разряда последнего знака.
В качестве примера могут быть приведены сле-
дующие правила (по В. Брадису):
1. При сложении и вычитании приближённых
чисел в результате следует сохранять столько де-
сятичных знаков, сколько их имеется в прибли-
жённом данном с наименьшим числом десятичных
знаков.
2. При умножении и делении приближённых
чисел в результате следует сохранять столько зна-
ПРИБЛИЖЁННЫЕ ФОРМУЛЫ
В табл. 25 приводятся некоторые при-
ближённые формулы, для каждой из кото-
рых указано наибольшее значение абсолют-
ной величины х, при котором формула даёт
п верных десятичных знаков.
Таблица 25
Приближённые формулы
Формула п = 2 п = 3
(Н-х)’~1 + 2х 0,07 0,022 0,007
(1 + х)3»Ц-Зх 0,04 0,012 0,004
V 1 + Х и 1 + > /2 х з у/Г 14-х 0,19 0,062 0,020
0,20 0,065 0,021
1 ; <*1 —X 1-f-X 0,06 0,022 0,007
10х ~1+2,ЙОЗх 0,04 0,014 0,004
lg(14-x>«0,4343x 0,14 0,047 0,015
lg^«0,8686x 1—X 0,25 0,119 0,055
sin х«х 17°48' 8°15' 3°50'
cos х« 1 5°43' 1’48' 0°34'
COS х*1- —- tg х«х 33°43' 18’58' 1 0'40'
14 °8' 6°25' 3°2'
ПРИБЛИЖЁННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ
УРАВНЕНИЙ
ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ
Графические методы решения алгебраи-
ческих и трансцендентных уравнений при-
меняются в тех случаях, когда не требуется
большая точность.
Для отыскания графическим методом дей-
ствительных корней уравнения вида f (х) = О
следует построить график функции у = / (х)
и определить точки пересечения или, в слу-
чае кратных корней, точки касания его
ПРИБЛИЖЁННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИИ 237
с осью ОХ. Абсциссы этих точек являются
искомыми корнями уравнения /(х) = 0.
Пример. Решить графически уравнение
х3 + Зх8 — 2 = О.
Строим график функции у = х3 + 2ха — 2: абс-
циссы пересечения этого графика с осью ОХ яв-
ляются корнями уравнения
xt=>—2,73; х,— — 1; х3= 0,73
(фиг. 330; на чертеже масштаб на оси OY выбран
в шесть раз меньше, чем на оси ОХ).
Иногда бывает полезно разбить члены
уравнения / (х) = О на две группы, оставив
в левой части один или несколько членов
и перенеся остальные в правую часть. Тогда
уравнение примет вид Д(х) = /2 (х), после чего
следует вычертить два графика у — (х) и
у = /2(х) и найти точки пересечения по-
строенных графиков. Абсциссы этих точек
являются искомыми корнями уравнения
/(х)=0.
Если удастся выбрать функции (х) и
/2(х) так, что их графики строятся проще,
чем график функции / (х), то этот способ
выгоднее первого; его преимущества особенно
сказываются в тех случаях, когда одна из
функций, например /2 (х)— линейная и гра-
фическое решение уравнения сводится к на-
хождению точки пересечения кривой y=/i (х)
с прямой линией у =/2 (x)=fcx + b. При необ-
ходимости решать большое количество одно-
типных уравнений вида (х) = кх + Ь, отли-
чающихся только коэфициентами линейной
функции в правой части, целесообразно вы-
чертить один раз график функции у = (х)
на отдельном листе прозрачной бумаги, после
чего для решения какого-либо уравнения
данного типа остаётся построить в том же
масштабе прямую линию у = кх + Ь, нало-
жить на неё лист с вычерченной кривой
у = /1 (х) и определить абсциссы точек пере-
сечения. Для решений любого другого урав-
Фиг. 330
Фиг. 331
нения этого типа приходится строить только
новую прямую, соответствующую правой
части этого уравнения, каждый раз исполь-
зуя тот же лист с графиком функции
У = fi (х).
Пример. Решить графически квадратное уравне-
ние
ха + рх + q «= О.
Переписываем уравнение в виде
ха = — рх — q
и строим параболу у «= ха и прямую у =» — рх — q.
Абсциссы точек пересечения параболы с прямой
являются искомыми корнями. На фиг. 331 показано,
как графически решается уравнение Xs— 1,9 х —
— 4,6 == О. Его корни: х, = 3,3 и х,= - 1,4. На том
же чертеже видно, что уравнение Xй - 1,4х + 4 = 0
не имеет действительных корней, так как парабола
ха и прямая у ==» 1,4 X — 4 не пересекаются между
собой. Масштаб на оси ОУ выбран в четыре раза
меньше, чем на оси ОХ.
Аналогичный! образом решается кубическое
уравнение
х3 + рх | q --= О
и, вообще, трёхчленные уравнения вида
хп + рх + q == О.
На фиг. 332 дано графическое решение двух
кубических уравнений:
х3 — 7 х —- 6 = О н х: + 2,8 х — 7 = О.
Корни первого ’ уравнения: х, = — 2, х8 — — 1,
х3=3; второе уравнение имеет один действительный
корень Xi = 1,4. Масштаб на оси OY выбран в двад-
цать раз меньше, чем на оси ОХ.
Для графического решения системы двух
уравнений с двумя неизвестными:
/ (х, у) = 0;
? (х, у) = О,
строят кривые, соответствующие этим урав-
нениям, и определяют точки пересечения кри-
вых. Координаты каждой из точек пересече-
ния дают пару значений неизвестных х и у,
удовлетворяющих системе.
Пример. Решить систему уравнений:
X3 + 2у8 == 1;
бу8 + х2 — 2ху — 4.
Вычертив кривые, соответствующие этим уравне-
ниям (фиг. 333), мы видим, что они пересекаются
только в одной точке Р; следовательно, эта система
имеет только одно действительное решение.
Из чертежа находим:
X =» — 0,65; у “ 0,8.
МЕТОД ИТЕРАЦИИ
Для решения уравнения / (х) — 0 методом
итерации (повторения) перепишем урав-
нение в виде
х + / (х) — х = О
или
х = ? (х), где ср (х) = х - / (х).
Графическим или каким-либо иным спо-
собом находим начальное приближённое
значение корня х0 и подставляем его в пра-
вую часть уравнения х = ср (х) вместо х,
получим первое уточнённое значение корня
х<1> = ?(х0).
Аналогично подставляя в ср (х) вместо х
вычисленное значение х^'\ будем иметь вто-
рое уточнённое значение
Х<2> = ср(х<1)).
Повторяя этот процесс несколько раз,
получим:
х(3) = ?(х(2)),
Х<4)=с,(х(3)),
х^^~»).
Процесс итерации прекращается, как
только достигается требуемая точность, т. е.
когда абсолютная величина разности между
двумя соседними значениями корня стано-
вится меньше допускаемой погрешности.
23Я
МАТЕМАТИКА
Для того чтобы процесс итерации был
сходящимся, достаточно выполнение условия
|е>/(х)| < I в окрестности искомого корня.
Сходимость тем быстрее, чем меньше [ <pz (х) 1.
Так как функцию (х) можно выбрать по-
разному, то следует иметь в виду, что при
неудачном выборе с? (х) процесс итерации
может привести не к уменьшению, а к уве-
личению погрешности. Так, например, метод
итерации нельзя применить к уравнению
х = tg х, но если это уравнение преобразо-
вать к виду x = arctgx, то процесс итера-
ции станет сходящимся.
Пример. Найти действительный корень уравне-
ния
lg х — 2х + 7=0.
Для нахождения начального приближённого зна-
чения корня перепишем уравнение в форме
1g х = 2х - 7,
построим кривую у = 1g х и прямую у = 2х — 7
(фиг. 334) и определим абсциссу точки пересечения
х, = 3,8.
Преобразуем данное уравнение к виду
х = ~ (lg X + 7)
и подставим в правую часть вместо х значение
X, ==> 3,8, получим уточнённое значение корня
= -i- (1g 3,8 + 7) = 3,79.
Аналогичным образом вычисляем:
хГ) = 4 Се 3,79 + 7) = 3,7893;
х<’> “ % (lg3,7893 т 7) = 3,7893.
Если ограничиться приближённым значением
корня с пятью верными знаками, то на этом
вычисления можно прекратить, приняв № 3,7893.
Быстрая сходимость процесса итерации объяс-
няется тем, что в нашем случае величина [ф' (х) i
мала:
1 =' W 1 “ I 2х | “ 7,6 •
Метод итерации может быть применён и тогда,
когда уравнение задано в виде бесконечного ряда.
Так, например, если дано уравнение
х3 xJ х7 хв
3 + 10 - 42 + 2Тб ~
то, переписав его в виде
X = 0,4431 + *-
= 0,4431,
+ х? _ х‘ +
10 42 216 г
отбросив старшие члены, начиная с ха, и округлив
свободный член, положим
) = 0,44.
Подставляя значение 0,44 в правую часть урав-
нения вместо х, будем иметь:
х<‘> = 0,4431 + . (0144? м
3 10 42
~ 0,470.
Аналогично получим
Х<*> = о ,4431 + _ «Ь47> + (0^47)’ _
« 0,476 и т. д.
Для применения метода итерации к ре-
шению системы двух уравнений с двумя не-
известными:
/1(х,у) = 0;
/2 (х,у) —О,
переписываем их в виде:
х = (х, у);
У = (х, у).
Определив графически (или иным путём)
начальные приближённые значения корней
х0 и у0 и подставив их в уравнения, полу-
чим первое приближение:
х^ =?i(x0, Уо);
У(,) = ®2 Оо- Уо)-
Аналогично находим последующие при-
ближения:
ХС) _ ( х(‘>, /*’) ) х(,) = ?1(х« /">, I
у<3> = ?2(х<‘>, у<*>) ) у<’> = ( х<!>, уе)) /
и т. д.
Для сходимости процессов итерации до-
статочно выполнение условий
} d?i I + i I 1 и ) | +1I < I,
I дх j ! дх I I ду I I ду |
в окрестности точки (х0, у0), причём сходи-
мость будет тем быстрее, чем меньше будет
каждая из левых частей обоих неравенств.
Подобным образом применяется метод
итерации и к решению систем уравнений
с большим числом неизвестных.
ОТДЕЛЕНИЕ КОРНЕЙ УРАВНЕНИЯ
Отделение корней уравнения / (х)=0
состоит в определении двух чисел а и Ь, ме-
жду которыми находится только один дей-
ствительный корень уравнения. Если левая
часть уравнения / (х) представляет собой
непрерывную функцию и если уравнение
/ (х) = 0 имеет действительные корни, то,
придавая х различные последовательные чи-
словые значения и вычисляя соответствую-
щие значения функции /(х), можно опреде-
лить такую пару близких между собой зна-
чений а и b (а < &), при которых значения
функции будут иметь разные знаки:
/ (а) < О, а /(&) > О,
или наоборот. В этом случае между а и b
находится по крайней мере один действи-
тельный корень нашего уравнения. Продол-
жая вычислять значения функции для зна-
чений х, расположенных между а и Ь, мы
можем интервал (а, Ь) заменить меньшим
интервалом (а', Ь')> на концах которого / (х)
также имеет разные знаки, и так можно
продолжать до тех пор, пока этот интервал
нс станет меньше абсолютной погрешности,
с которой желательно определить корень
уравнения. Так, например, если дано урав-
нение х 1g х— 1,2 = 0, то для отделения
корня составляем таблицу значений х и со-
ответствующих им значений / (х)=х 1g х —1,2:
п
г-
4 -
X /(x)=xlgx—1.2
0 -1.2
0,2 —1,34
0,4 -1,36
0,6 —1,33
0,8 —1,28
1.0 -1.2
2,0 -0,6
3,0 4-0,23
4,0 + 1,21
Из этой таблицы заключаем, что так как
/(2) и /(3) разных знаков, то в интервале
(2,3) находится корень уравнения xlgx —
ПРИБЛИЖЁННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНХ1ЕНТНЫХ УРАВНЕНИЙ 239
— 1,2 = 0; уменьшая указанным способом
найденный интервал, можно было бы найти
значение этого корпя с любой точностью.
Указанный метод отделения корней не-
пригоден для отделения кратного корня
функции /(х), если кратность корня чётная
или в случае наличия чётного числа весьма
близких корней. Такой корень является
простым или кратным корнем нечётной
кратности производной /' (х) и его отделе-
ние может быть произведено при помощи
указанного выше способа, который следует
применить к /' (х). Следует, конечно, иметь
в виду, что не всякой корень функции /' (х)
является корнем функции / (х), поэтому не-
обходимо произвести проверку, подставляя
найденный корень в ((х).
МЕТОД ЛОЖНОГО ПОЛОЖЕНИЯ
Для приложения этого метода следует
предварительно произвести отделение иско-
мого корня уравнения / (х) = 0, т. е. уста-
новить интервал (а, &), на концах кото-
рого функция /(х) имеет разные знаки.
Дальнейшее уточнение значения корня можно
производить по формуле ложного положения.
/) - а_ rt_)-,(aL
Hb)-J(a)
или
х<‘> = b — —й> /Хб)
/(&)-/(а)
Найденное по этой формуле приближён-
ное значение корня является абсциссой
точки пересечения хорды MN, кривой у =
= / (х) с осью ОХ (фиг. 335) в то время как
точное значение корня — абсцисса точки пе-
ресечения дуги MNt с осью ОХ.
Полученное первое приближение корня
может быть опять уточнено путём повтор-
ного применения той же формулы для того
из меньших интсрвалов(я, х^) или (х^‘\&),
на концах которого / (х) имеет разные знаки:
х(!) = а_ ( *(1) - д) / (Д)
/( х(1>) — / (а)
ПЛИ
ХС) = b — ~ х<>)) /<6)
/(&)-/(х«) ’
Повторное применение метода ложного
положения геометрически означает прибли-
жение к корню при помощи хорд MNlr
MN„ и т. д.
Пример. Решить уравнение
х lg х — 1,2 = О.
Из приведённой на стр. 238 таблицы мы видели,
что корень этого уравнения находится между 2 и 3.
Поэтому, вычисляя первое приближённое значение
корня, получим
(3 -J) (-0,6)
0,23—(—0,6)
2,72.
Так как f (2,72) = — 0,017 и /(3) = 0,23 разных
знаков, то, применяя правило ложного положения
к интервалу (2,72; 3), получим следующее прибли-
жение:
х
(3 - 2,72) — (-0,017)
0,23 - (- и,01 7)
~ 2,74.
МЕТОД НЬЮТОНА
Для уточнения приближённого значения
корня х = а уравнения / (х) = 0 можно при-
менить фор м у л у Ньютона
х(‘) = а ... /(а)
/' (а) ’
которая геометрически означает, что дуга
кривой у = / (х) заменяется касательной МТ
(фиг. 336) и вместо точного значения корня
Фиг. 339
х (абсциссы точки пересечения кривой с осью
ОХ) принимается в качестве его приближён-
ного значения = а + h (абсцисса точки
пересечения касательной с осью ОХ), где по-
правка h = — .
Г (а)
Повторным применением метода Ньютона
можно уточнить полученное первое прибли-
жение корня:
/ОТ
/' (
х(,) = х(р —
у('О = _ К х(П °)
/'ОТ**) •
Геометрически это означает приближение
к корню при помощи касательных МТ, NS
и т. д.
Если кривая у=/(х) при пересечении
с осью ОХ почти горизонтальна, т. е. если
величина /' (х) близка к нулю или, если
вблизи точки пересечения кривой с осью
ОХ имеется точка перегиба, то метод Нью-
тона не следует применять. В этом случае
рекомендуется обратиться к методу ложного
положения или к другим методам.
Если в некотором интервале (а, Ъ), содер-
жащем корень уравнения / (х) = 0, величина
/' (х) знакопостоянна, то целесообразно од-
новременно производить вычисления как по
методу Ньютона, так и по методу ложного
240
МАТЕМАТИКА
положения; при этом один метод будет да-
вать приближённые значения корня с недо-
статком, а другой — с избытком, что позво-
лит судить о достигнутой точности.
Пример. Найти действительный корень уравне-
ния
х8 — 2х — 5 = О.
Начальное приближение х = 2 (фиг. 337) опре-
деляем графически.
Дальнейшее уточнение корня производим по
формуле Ньютона, которая даёт
Затем находим
Х<’> = 2,1 - = 2,1 - 0,0054 = 2.0046
.* (*>1)
2,0946 — ^£^ 2,0946 -
— 0,00004852 - 2,09455148.
Рассмотренный метод применим и для
получения приближённых значений корней
Фиг. 337
системы уравнений.
Например, если в си-
стеме:
/г(х, У) = 0; ;2 (х,
У) = о,
Фнг. 338
х(°>< /"> — начальные приближённые значе-
ния корней системы, то следующие их при-
ближения = х« -}- у(-1> ~ у<- >4- к<-')
мы получим, определяя //"' и из систе-
мы уравнений:
у'-1] к^+ [/,]„
ду о
= 0;
й(,)+
dx Jo
*(1>+
ду j
= О,
’д/1] Л<*>4-
дх 0
где индекс 0, поставленный у скобок, обо-
значает, что в функции и их производные
надо поставить вместо х и v значения х^0)
и у<°>.
Для получения более точных значений
корней следует повторить указанный приём
и найти последующие поправки:
/!<’), и т_
Пример. Решить систему уравнений:
fi (х, у) =• ха 4- ул — 1 = О,
Л (X, у) = х3 — у = 0.
Начальные приближения находим графически,
как координаты точек пересечения окружности с ку-
бической параболой (фиг. 338):
X1* ’ = 0,9; yk ' =0,5.
^Вычислив /1(0,9; 0,5) =• 0,06; /я (0,9; 0,5) = 0,23
составим систему уравнений для определения по-
правок и/ \ имеем:
1,08 h(1) + = - 0,06;
2,43 Л<‘> - Л(,) = - 0,23.
Решая её, находим поправки:
- — 0,07; = 0,06
и, следовательно, первые уточнённые корни будут
= Хо+ 1У) = 0,83; у, = у. + = 0,56.
Аналогично составляем новую систему поправоч-
ных уравнений:
l,66h(,)+ 1,12 fc(,) = - 0,0025;
2,067 _ - 0,0118,
из которой находим поправки
= - 0,0040 и iS') = - 0,0036,
а затем и вторые приближения:
(») Р)
хч ' = 0,8260; у4 ' «=» 0,5636.
Третье приближение обнаружит, что все знаки
второго приближения верные.
МЕТОД ЛОБАЧЕВСКОГО
Метод Лобачевского применяется к реше-
нию алгебраических уравнений и не тре-
бует предварительного отделения корней.
Он даёт возможность находить все кор-
ни алгебраического уравнения, включая
и комплексные. Основная идея метода Ло-
бачевского заключается в преобразовании
данного уравнения в другое, Для которого
корнями служат некоторые достаточно вы-
сокие степени корней данного уравнения.
При этом преобразовании абсолютные вели-
чины корней нового уравнения оказываются
настолько сильно отличающимися друг от
друга, что в соотношениях между коэфи-
циентами и корнями уравнения (стр. 105)
меньшими из корней можно пренебречь и,
таким образом, получить простые прибли-
жённые формулы для определения корней.
Преобразование данного алгебраического
уравнения п-ой степени
/(х) = лох" 4- a1xn~i 4- а2хп~2+-..+
+ ап_2ха 4- an—ix 4- ап = 0 (1)
в другое, корнями которого являются квад-
раты корней данного уравнения («к вадри-
роваиие корней уравнения»), про-
изводится путём умножения многочлена
/(х) па многочлен
(— 1)п / (— х) = aoxn — аре"-1 4-
4- flix"-2— ... 4- (— О" an ,
замены в полученном произведении х2 на у
и приравнивания этого произведения нулю;
при этом мы приходим к уравнению:
bayn + biyn~'1 4- b2yn~2 + ... 4-
4- Ь„-1 У + bn = °- <2>
Вычисление коэфициентов преобразован-
ного уравнения удобно производить по слет
дующей схеме:
ПРИБЛИЖЁННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ 94;
Ci а. а3 а, а5 ...
—а, а., —а3 а. —<+ ...
aj — al a'l — al al ~al
-r'2a0a., —23^.; +'2azai —2asa5 +2atae —...
—2(цз5 —203^7 4~...
4-2noae —^2д1о7 +2a2a8 —...
+2«„3S —2a1o„ +...
4-2aoalo —...
й0 bt b2 b3 bt Ь,л ...
Коэфициенты Ьъ, bu b„, ... получаются,
как суммы соответствующих столбцов. При
этом числа первой строки под первой чертой
являются квадратами расположенных над
ними коэфициеитов с чередующимисязнаками
(плюс для чисел, стоящих на нечётных мес-
тах, и минус—на чётных). Числа, находящие-
ся под этими квадратами, являются удвоен-
ными произведениями пар коэфициеитов.
симметрично расположенных относительно
коэфициеитов, стоящих над квадратами: зна-
ки этих удвоенных произведений чередуются
вдоль строки и вдоль столбца, причём знак
первого произведения в каждой строке бе-
рётся соответственно знакам множителей.
Это правило остаётся в силе и для по-
строения последующих уравнений. Если по-
добную операцию повторить с уравнением
(2), то мы получим новое уравнение:
cazn + CiZn~' + c2z"_* + ...4-
т С„_1 z 4- с,, = О, (3)
корни которого равны квадратам корней
уравнения (2) или четвёртым степеням кор-
ней уравнения (1). Дальнейшее квадрирова-
ние корней уравнения (3) приведёт к урав-
нению, корни которого равны восьмым сте-
пеням исходного уравнения, и т. д.
Квадрирование корней следует прекра-
тить, как только обнаруживается, что коэ-
фициенты нового уравнения равны, в преде-
лах нашей точности вычисления, квадратам
коэфициеитов предыдущего уравнения, т. е.
(если при вычислении пользуются логариф-
мами) когда логарифмы коэфициеитов нач-
нут удваиваться. Следует, впрочем, иметь
в виду, что некоторые коэфициенты могут
и не обнаружить Этого свойства при после-
довательных квадрированиях; это происхо-
дит тогда, когда исходное уравнение имеет
либо кратные, либо комплексные корни,
либо те и другие.
Случай 1-й. Все корни действительные
и разные. В этом случае в процессе квад-
рирования корней обязательно наступит мо-
мент, когда коэфициенты некоторого преоб-
разованного уравнения (хт — t)
Aotn + Aitn~l + A3tn~2 + ... +
+ An-i t + An = 0
окажутся почти равными квадратам коэфи-
циентов предыдущего уравнения, после чего
процесс квадрирования корней прекращаем.
Если расположить искомые корни в порядке
убывания (по модулю)
|Х11 > |х31 > |х3| > ... > |х„|,
то для определения их применяются фор-
мулы:
ytn — _Аз . . .т _ Ап
' Д3 > •’ ХП *
Пример. Решить уравнение [см. (90) на стр. 268]
1,23х5 - 2>52х4 - 16,1ха + 17,3х« 4- 29,4х - 1,34 =0.
Необходимые для решения этого уравнения вычи-
сления располагаем в виде таблицы (табл. 26), по-
Таблица 26
Схема вычислений для нахождения корней уравнения 1,23 х5—2,52 х4—16»! х’4-17,3 х2+29,4х— 1,34—О
Xs х* 1 1 X» X»
Данное уравнение 1,23 -2.52 -16,1 17,3 29,4 -1,34
1.513 —0.635*10 —3,961 +2.592.10* +0,872 +0,723 —2,993.10- -9,467 —0,063 +8,644-Ю2 +0.464 -1,796
2-я степень 1.513 —4,596.10 +4,187-Ю1 1 -l.253.lu’ 4-9,108-10’ ! —1,796
2,289 -2,112.10s + 1.267 + 1,753-10® —1,152 +0.028 -1,570.10» +0.763 * +8,296-10® —0,045 —3,226 •
4-я степень 2,289 -0,845-10’ +0,629-10’ —0,807.10» +8.251-10’ —3,226
5.240 —0./14-10® 4-0.2->8 +0,396-10*° —0,136 * —0,651-10*8 +0,104 • +6.803-10** —10.41
8-я степень 5,240 -0,426-10® +0,260-10*° -0,547-10*» +6,808.10” — 10,41
2,746-10 —1,815-101» 4-0,272 +6,76-10*° —0,47 —2,99.’-10а& 0,035 +4,635-10 «• —1,084.10’
16-я степень | 2,746-10 -1,543-101* +6.29-10” —2.957.10” । +4,635-10” —1,084.10’
7,541-10“ —2,381.10»» +0,035 +3,96.10” -0,01 —8,744.10” +2,148.10” —1,175.10*
32-я степень | 7,541.10- j —2,8.5.10“ | +•3,95.10” —8,711 «Ю4в ] + 2,148.10*’ -1,175-10®
16 1 ом I
242
МАТЕМАТИКА
строенной в соответствии с указанным правилом
(очень малые удвоенные произведения, которыми
можно пренебречь, заменены в таблице звёздочками).
Согласно приведённым выше формулам имеем:
за 2,34G-1088
=Tj4iTi(F ’ °ткуда 1X11 = 4,066;
„ 3,95-10”’ , „
Х” “ 2,346.-16“ ’ °ТКУЯа 'Хг,“ 2,9911
ss 8,744-ю*” , ,
*. = 3^5TlO«~’ °ТКУДа iXs' = b 5 '
83 2,148-10*’ o*i*w'4rrm !v I —
' 8,744- 10*” ’ » иТтхуДсХ |Л4|
88 1 1 75 • 104
*• _ , откуда 1х61 = 0,0445.
Для определения знаков корней подставляем в
исходное уравнение приближённые значения корней
4; ± 3; ± 2; ± 1; ± 0,04 и определяем, какое из
значений, положительное или отрицательное, лучше
удовлетворяет уравнению. Таким образом, находим
корни уравнения:
Xl = 4,066; х£ = - 2,091; ха = 1,959;
х4--- 1,0285; х5 =~ 0,0445.
Случай 2-Й. Все корни действительные, но
среди них имеются равные по модулю. В этом
случае в процессе квадрирования корней
уравнения обнаружится, что некоторые коэ-
фициенты преобразованного уравнения
Aot:1 + A1tn—1 + A2tn~2 + ... +
+ An_ft + An ~ о
станут почти равными квадратам коэфици-
снтов предыдущего уравнения, в то время
как остальные окажутся равными половине
квадратов соответствующих коэфициентов.
Так, например, если
ixj > )х2[ = ix3| > |х4 | > |хл|,
то коэфициент А2 окажется равным поло-
вине квадрата соответствующего коэфи-
циспта предыдущего уравнения.
Формулы для определения корней урав-
нения в этом случае:
„т _ 4-1 . гт _ ,.т
Х1 ~ — Ао ’ х2 ~ Х3 - 2Aj
А %
Пример. Решить уравнение
5х” + 2х” — 15х — 6 = 0.
Вычисления для решения этого уравнения приве-
дены в табл. 27, из которой видно, что коэфициент
Л. уравнения, полученного после четвёртого квадри-
рования, равен половине квадрата соответствующего
коэфициента предыдущего уравнения и, следова-
тельно, корни х, и хв равны между собой.
Применяя соответствующие формулы, получим:
it 1» 1,986.101*
Х‘ “ Х” ~ 2.1,52бЛщГ ’
откуда |х. | = | X, | = 1,731;
» = 2>822.’0>!
Х” 6,61 о -То*” ’
откуда | X, | = 0,3999.
Испытывая значения корней ± 1,7 и ±0,4, на-
ходим:
х, - 1,7; х, = — 1,7 их, — — 0,4.
Случай 3-й. Среди корней уравнения име-
ются комплексные. В случае наличия комп-
лексных корней оказывается, что сколько бы
мы ни продолжали процесс квадрирования
корней этого уравнения, не все удвоенные
произведения коэфициентов исчезнут.
Так, например, если среди корней урав-
нения имеется две пары комплексных кор-
ней:
х2,3 = !fi i и х5,б = i
причём
iXii > |хй| = |Х3| = П > |Х4| > |хв1 = |хв1 ==
= г2 > |х7| > ... > \хп1,
где Fi и г2—модули сопряжённых корней
(r^l^ vi ; r2=K tt22+vl ) ,
то действительные корни и модули комплекс-
ных корней определяются по формулам:
Таблица 27
Схема вычислений для нахождения корней уравнения: 5л*84-2л8—15л -6^0
ха X” X х«
Данное уравнение 5 2 -15 -6
25 — 4 -150 225 +24 -36
2-х степень 25 -1-54-10' +2,49-10” -36
6,25»1и- —2,3716-10* 4-1,2450 4-6,2091.10‘ —1,1008 —1.296.108
4-я степень 6,25-10' -1.1266-10* 4-5.C993.104 —1.296-103
3,9062*10е -1.269.10е 4-0,637 4-2,600.10® —0,029 -1.680-10”
8-я степень 5,9062-10” —0.632-108 + 2,571-10” —1,680*10“
1,526-Ю8» —3,994.10»» 4-2,008 4-6.GIO-id8 * —2.822- Нл®
16-я степень 1,526-10”” —1,986. 6,610-10“ -2,822-11)”’-
ПРИБЛИЖЁННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ 243
.2т
2
“ : х
т
7
Ад
А;-
И т. д.
X
т
8
Действительные части комплексных кор-
ней уравнения находятся из соотношений:
~~ — 2Ui + 2и2 + + х4 + х7 +...+ хп',
и0
2ui 2«а 1 , _|_ — _( 1- Г2 X, ! Ь *4
1 1
х, + ••• +
а мнимые из формул:
При наличии только одной пары ком-
плексных корней и ± in, т. е. когда только
один из коэфициентов изменяется при квад-
рировании беспорядочным образом, имеем
для определения действительной и мнимой
частей корня соотношения:
4- x2 + ... + xn_2 ;
l)= V ’ r- —ЙЮ
Пример. Решить уравнение
X’ — 2x* - 3№ + 4№ — 5x + 6 = 0.
Соответствующие вычисления даны в табл. 28.
Так как в коэфициентах последнего преобразованного
уравнения As и Ав наблюдаются отклонения от обыч-
ного правила, то мы заключаем о наличии двух пар
комплексных корней:
x?j 4 = иг ± iVi
хб 7 = а2 ± iva.
Таблица 28
Схема вычислений для нахождения корней уравнения: х’—2х“—Зх8+4ха—5х+6=0
X’ х« ХЬ Х‘ i Xs j X* j X» | X»
Данное уравнение 1 о -2 0 —3 4 -5 6
1 0 -4 4 0 —6 0 12 0 -10 9 0 20 0 -16 30 0 25 —48 -36
2-я степень 1 -4 -2 2 29 14 -23 —36
1 16 53 —4 -Н6 -112 -4G 8,41.10» —0,56 +0,92 -2,88 —1,96.10» — 13,34 + 1.44 5,29’10» 10.08 —1,296’10s
4-я степень 1 -20 7,8-10 -5,4.10 +5,89-10* -1,386-10» + 1,537-10» -1,296-10»
1 —4,00«10» + 1,55 + 6,084-103 —2,160 + 1,173 —0,2916’10» +9,1884 -5,5440 +0,3074 + 3,4692» 10* —1,4969 +2,3977 —0,5184 —1,9210-10» 4-1,8106 —0.1400 +2,3624’10» —3,5925 —1.680-10»
8-я степень 1 —2,44«10а +5,102 -10» +3,660.10» +3,852-10‘ —0,2504.10» —1,230. 10» , —1,680.10»
- 1 —5.9336. Ю)4 4-1,0204 + 2.6830-10» + 1.7661 +0,0770 -1,3396- 10» + 3,9306 —0,1222 —0,0025 + 1,4833- 10” +0,1833 -0,1255 -0,0032 —0.62Н). Юн -9,4759 + 1,2298 + 1,5129» 10»а —0,8413 -2,8224-10»»
16-я степень 1 —4,933’Ю4 +4,456’107 + 2,466-10’ + 1,533-10” —8,873.10” +0,6716-10»» —2,822.10”
1 —2,433.10» +0,000 + 1,9945- 101® +0,2433 4-0,(ХЮЗ -0,6081-101» 1,3693 —0.0088 +2,350» 10аа + 0.438 +0,006 * —7,873. Юаз +2,059 4-0,130 +0,4510-10»» -5,0079 -7,964-10»»
32-я степень 1 -2,344- И:» +2.238 -10^ +0.7524-10»» +2,794-10” -5.675- 10” —4,537 * 10а* -7,964-10”
1 —5.494 • 1Ы8 4-0,004 +5.009- 30” +0,035 * -0,5661-10» + 1,2502 * + 7.806.10*» 4-0,085 * —3,221-Ю47 -2,546 +0,001 + 2.077 «Ю49 —0,904 -6,343-10*»
64-я степень 1 -5,490-1 Г.” 5,044 • 10Е0 +6,841.10»’ +7,891.10” —5,766-Ю»7 + 1,173-1049 -6,343-10*»
1 —3, UK'. R 37 6 п-2,544 • Ю«» * —4,680’1076 + 7,960 + 6,227-Ю89 +0,001 -3,325-10” , 4-0,185 + 1,376’ 10’8 —0,731 —4,023.10”
128-Я степень 1 —3,014’1087 + 2,544- 10е» +3.280-10’° +6,228-Ю8» -3,140-10»» । 0,645.10». -4,023-10»»
1 —9,084’ 10” + 6,472.101 м —1»O76-1C||SJ +3,169 + 3,879’101’» —9,860’IO”» +0,008 +0,416.10»»» —0,253 —1.618.10»’’
256-я степень 1 |—9,084-107i 1+6,472.101” +2.093-10» + 3,8,79-10»’» —S.452-!(>»• + 0,163-19»»» — 1,618-10»’»
v2 = V rl-ul .
и
16*
244
МАТЕМАТИКА
Определяем сперва по приведённым выше форму-
лам действительные корни х,, х8 и х8:
25в 9,084-10"
X, =-------1
откуда IxJ = 1,9625;
sse __ 6,472- 10i8i
*• “ эГовТЛобг'
откуда ix3| s= 1,5379;
асе _ 9,852. Ю180
Xs ~ 3?879^10> ’
откуда |х8| — 1,1080.
Применение правила для определения знаков
корней даёт:
Xj = — 1,9625; ха = 1,5379 и х5 = 1,1080.
Для определения модулей комплексных корней
rt и имеем:
на _ 3,879- 1O1J’ /_ А4 \
Г* “ 6,4'72/10”=' А,) '
откуда г, = 1,2909;
>18 1,618-IO1" / А, \
Га ~ 9,852- 10”» А, ) ’
откуда га =» 1,0618.
Действительные части их и и8 комплексных кор-
ней находим из системы уравнений:
2uj + 2w8 - 1,9625 + 1,5379 + Ы08О =
2ux , 2us 1
(1,2909)’ + 7170618). 1,9625“ +
1 1 5 С “п-1 \
+ 1,5'379 + 1,1080 б' ап ) ’
решив которую, получим:
Uj = — 0,6445, a ua == 0,3028.
Мнимые части и va комплексных корней нахо-
дим по формулам:
Vi ~ j/ rj -uj » F (n + «О (П — uj = 1,1185;
1’2 = ]/ / — и, = /(г, + U,) (г, - и„) = 1,018;
и, следовательно
X, = - 0,6445 ± 1,11851;
3,4
X „ = 0,3028 + 1,0181.
6,7
Для определения знаков и проверки точ-
ности, с которой полученные по метопу
Лобачевского корни алгебраического урав-
нения удовлетворяют этому уравнению,
следует подставить найденные значения кор-
ней в уравнение. Для этой цели и вообще
для вычисления числового значения много-
члена
/(х) = <70х" + а]х'г~1-р а„хп~~'2 + ... 4-
+ «,1-1 х +
при значении аргумента х = х0 удобно поль-
зоваться так называемой схемой Хор-
пера. Выписываем коэфициенты многочлена
в одну строчку:
<?„ аг а.2 а3 ... а„;
первый коэфициент е0 умножаем на х0 и
складываем с коэфициентом alt для чего
подписываем аохо под iZj. Полученную сумму
доХо4-Д1 обозначаем через а и подписываем
под аохо и ах, число аг умножаем опять на х„ и
находим а = а х0 4- а.2.
Произведя дальнейшие вычисления по
этой схеме, образуем число а* == a'sx0 + а3
и т. д. до последнего ап~ ап_х х0 4- ап. Чи-
сло ап и есть искомое значение функции
/(х) при х = х0:
</= До-
запись вычислений по схеме Хорнера
производится следующим образом:
а0 fli а2 а3 ... ап_3 ап
(IoXq @iXq H^Xq ... ttn—2^0 —lxo
«i a, a, an_t j a'n = /(x0) |
Пример. Определить значение многочлена
/ (х) = Xs — 5,72х“ — 2,26ха + 7,36 при х = 1,27.
, I 1 О -5,72 -2,26 О 7,36
*>27 I 1,27 1,61 -5,22 -9,49 -12,05_________
1,27 -4,11 -7,48 -9,49 |—4,69 = /(1,27)1
ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ И ИНТЕРПОЛИРОВАНИЕ
КОНЕЧНЫЕ РАЗНОСТИ
Конечной разностью первого
порядка функции у = / (х) называется
величина Д/(х) =/(х 4-/1) — /(х), где h —
так называемый шаг разности.
Конечные разности первого порядка при-
нято также обозначать:
Д Уо = У1 — Уо! А Уг = Уе — Ух
и вообще
ДУ1 = Ti+i-^
где У1 = /(х4-Л)> У1 = /(х 4- ih).
Конечные разности конечных разностей
первого порядка называются конечными
разностями второго порядка и также
могут быть выражены через заданные зна-
чения функции:
Д2/(х) = Д /(х 4- ft) — А /О) =
= /(x + 2ft)-2/(x4-ft)4-/(x),
ИЛИ
А2У0 = А У1 — А у0 - у2 — 2ух + у0,
А2У1 = А у3 — А Ух = Уз — 2у2 4- у,
и вообще
Д2у,- = А у/+1 - А У| = yi+ г ~ 2yi+1 4- Vi
Аналогично определяются и выражаются
конечные разности высших порядков:
Д* /(х) == Дл~1/(х4-/|)-А'<-1/(х)-
=/(Х4-/1x4-(к - 1)/г]4-
T-^^/Ix 1 (fc-2)ft]- ... 4-
4- (- 1// (х).
Вычисление конечных разностей удобно
производить при помощи таблицы разностей
по следующей схеме:
ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ И ИНТЕРПОЛИРОВАНИЕ
245
у I Д’-’ ДЕу | Д’/ | Д’* у | Д6у
Х-4 У-4
д
-“4
х-з У-Я
3 Д’У-4
V Д*'-_ л
А 2 ' 0 у—3
4-V-2 43у-3 д«х_4
х-1 . j д*>-2 Д^-3
Д“ Д’у-з
хо V» Д4у_ q
дУо двУ-2
Х1 4%
4% 4*V-1
Х2 У2 43'’1 д%
^2
Х8 5 S 4%
Х4 *4
ОСНОВНЫЕ СВОЙСТВА КОНЕЧНЫХ РАЗНОСТЕЙ
1. Конечная разность алгебраической
суммы функций равна алгебраической сумме
разностей слагаемых функций:
Д [/(х) ± <р(х)] = Д /(х) ± Д -Дх).
2. Постоянный множитель может быть
вынесен за знак конечной разности:
ДС <f(x) = С Д <f (х).
3. Конечная разность постоянной вели-
чины равна нулю: Д С = 0.
4. Конечная разность периодической
функции равна пулю, если её период равен
шагу разности ft: Д у (х) = 0, если у (х4-й)=
= ?’(х).
5. Конечная разность произведения двух
функций определяется формулами:
Д [сс (х) ф (х)] = ? (х) Д ф (х) 4- ф (х 4- й) Д и (х),
ИЛИ
Д [<р(х) ф(х)1 =ф(х)Дср(х)+<р(х 4- й)Дф(х),
КОНЕЧНЫЕ РАЗНОСТИ НЕКОТОРЫХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. Степенная функция у = хп:
Д х” - (х +h)n —хп =nhxn~' 4-
‘ ’ Л2хп-2 + х + hn .
Д"гх” вычисляется с помощью разложения
по факториальным функциям.
2. Факториальная функция у = х^ =
= х(х — ft)(x— 2ft) ... [х — (п — l)ftj:
Дх<'”=.лЛх("-,) =
= nhx (х — ft) (х — 2/г) ... [х — (и — 2)ft];
дт х(/г) = и (И — 1) _.. (п _ т _t. ] )/гт yj.n-m') _
п(п — 1)(п — 2) ... (п-т 4- 1) ftm х
X X (X — ft) (X — 2ft) ... lx — (Я — /72 — l)ftl;
д.т x(.’i) ,
а при т > п 2.т х(п) = 0
(факториальная функция в разностном ис-
числении аналогична степенной функции
в диф.-ренциальном исчислении).
3. Показательная функция у = ах'.
Ддх = ax+h_ax^ ax{ah—\)-,
Атах = а': (ail — l)m.
4. Тригонометрические функции y-=sinx
и у — cos X:
Д sin X = 2 sin sin I X ф-
l ft \m [ ft 4- - \
Дcos x = I 2 sin -.£ I cos I x 4- m —2— i
РАЗЛОЖЕНИЕ В РЯД ПО ФАКТОРИАЛЬНЫМ
ФУНКЦИЯМ
Если функция у = /(х) непрерывна и ди-
ференцируема до (// 4- 1)-го порядка вклю-
чительно, то:
Д Vo
У = Уо + П/Г(х —хо) +
Д2у
+ Alfts’ (х — х0) (х — х„ — ft) 4- ... 4-
Д"Уо
+ ^(х —х0)... [х — х0 — (и — l)ft] +Rn,
где остаточный член
Rn = (х - х0).. .(х - х0 - nh)
(х„ < £ < х0 4- nh).
Если lim Rn = 0, то получаем разложение
n_.ee
/<х) в ряд по факториальным функциям.
Для многочлена n-й степени Дп+1уо = О
и разложение обрывается на (п4-1)-м члене.
Например, в случае степенной функции х"
при ft = 1 имеем:
Д 0п Д20’’1
хп= -j j- х 4- ~2Г х(х— 1) 4- ••• 4-
Д«0л
---Х(х - 1) ... (х —л 4- 1).
Коофицленты А (>”, i’O", Да0,,! и т. д. да-
ны в табл. 29.
Таблица 29
СВЯЗЬ МЕЖДУ КОНЕЧНЫМИ РАЗНОСТЯМИ
И ПРОИЗВОДНЫМИ
Формула Тейлора даёт выражение конеч-
ной разности первого порядка функции /(х)
ч.рез производные /'(х), /"(х) и т- д.;
246
МАТЕМАТИКА
A /(х) = /(х + Л) — /(х)= — /'(х) +
+ —-/" (х)+ ...+ f/^x) +
4- _+ * /(л+1) /г\
(п+1)Г
(х < 5 < X + й).
Для конечной разности порядка т имеем
формулу
Am /(х)= A™ hm /(т)(х) +
+ A^+1ftm+1 /(т+,)(х)+...+
+ А" й” /<п) (х) + А"+1 й'г+1 /(п+’>(5)
(х < I < х + mil),
где
Л г 1 (Дт(х-аУ )
ll'1 J И /х=а ‘
Таблица 30
Значения величин
(m+ 1) (т + 2) . . . i Агт « Нгт
торым можно пользоваться для последова-
тельного вычисления коэфициентов Агт.
В свою очередь производная вы-
ражается через конечные разности по фор-
муле
йт /(т\х)=В™ Дт/(х) +
+ В™+1 Дт+1/(х) +... + В^г Д"/(х) +
+ в"+1йп+1 /<пч »(о
(х < 5 < х + nh),
где
1 ( d"1 I
V/z- Kt —О ...(#—/+ i)Jz=0-
T а б л и Ц a 31
Значения величин
(-l)i-m (m+i) (m+2) . . . 1Вгт ~ D]n
Между числами , D’n, и £>^_j имеет
место соотношение D^1"1 = iD,n , ко-
торым можно пользоваться для последова-
тельного вычисления коэфициентов В^.
ИНТЕРПОЛИРОВАНИЕ
Если для ряда значений аргумента: х0,
Xj, х2, хп известны значения некоторой
функции: у0, уи у2, ...,у„, то можно построить
такую функцию у = /(х), которая принимала
бы указанные значения у, для заданных
значений аргумента х> Найденная функция
называется интерполирующей ф у н к-
цией, а самый процесс её нахождения —
интерполяцией или интерполи-
рованием; точки X, называются узлами
интерполяции. Если интерполирующая функ-
ция строится в виде многочлена, то интер-
поляция называется параболической.
Для периодических функций удобно выбрать
интерполирующую функцию в виде тригоно-
метрического многочлена; такая интерполя-
ция называется тригонометрической.
Интерполирующая функция позволяет
определить приближённые значения таблич-
ной функции для промежуточных значений
аргумента, не содержащихся в таблице. Это
также называется интерполяцией (в узком
смысле слова). Нахождение же значений
функций для значений аргумента, выходя-
щих за пределы заданной таблицы, назы-
вается экстраполяцией.
ИНТЕРПОЛЯЦИОННЫЕ ФОРМУЛЫ
Интерполяционная формула Лагранжа
_ <х ~ х0 (х ~ х0 •" <х — Хп)
У~ (Хо — Х1) (хп — х„) ... (х0 — х„)Уо +
(X — х0) (х — х2) (х — х,,)
(X, —Хо) (Xj — х2) ... (Xj - х„) У1 +
(X — Хо) (X — Хх) ... (х —х„_,)
(хп х0) (х„ х1)...(х„ хп—|) Уп
Формула Лагранжа на практике мало
применима вследствие её неудобства для
вычислений. Вместо неё обычно применяются
разностные интерполяционные формулы,
содержащие конечные разности функции.
Первая интерполяционная формула Нью-
тона (для равноотстоящих значений аргу-
мента xi+1 — х^ = Il = const):
х —х0
У = Уо + д Уо +
1213 4 5 6 7 8 1 9 10
2 6124
3 11 Iso
1 6'35
1 10
1
120
274
225
45
15
1
720 5 040 40 320 362 880
1 764 13 068 109 584 1 026 576
1 627 13 132 118 124 1172 700
735 6 769 67 284 723 680
175 1 960 22 449 269 325
21 322 4 536 63 273
1 28 546 9 450
1 36 870
1 45
1
~ 21й2 '
, (X —x0)(x-x0-ft)...[x-x0-(n-l)ft]
+--------------nW1--------------'У о-
Эта формула в сущности представляет
собой разложение многочлена степени п по
факториальным функциям.
Положив—° —и, получим другой вид
ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ И ИНТЕРПОЛИРОВАНИЕ 247
формулы:
а А и(и — 1)
У — Уо + j[ ДУо+ 2! Д2Ур4-.-- +
, u(u-l) ... (и—п+ 1) А„
+----------П\-----------д Уо-
Первая формула Ньютона называется
также формулой для «интерполирования
вперёд», так как содержит значения функ-
ции, находящиеся вправо от у0 («вперёд»
или вниз по столбцу) и не содержит значе-
ний, лежащих влево. Поэтому она употреб-
ляется для интерполирования значений око-
ло начала таблицы разностей и для экстра-
полирования немного назад (налево от у0).
Вторая формула Ньютона
у = Уо + у_1 +
, (X - х0) (X — х0 + ft) А „
+ ... ---------------Д3у_2 4- ... 4
, (х-х0)(х—x0+ft)...[x-x0+(n— l)ft] А„
+--------------------------------Д”у_„
или
и а(и 4 1)
у = v„ 4- Ду_1 + б; Д2У— 2 + 4-
. и(а 4 О (а 4- п — 1) 4„
+-----------m-------“— д У-п-
Здесь, как и в предыдущем случае, пред-
полагается, что х{ — Xj_j = ft = const и и =
= * • Эта формула называется также
формулой для «интерполирования назад»
(налево от у0 или вверх по столбцу). Она
служит для интерполирования значений
около конца таблицы разностей и для экс-
траполирования немного вперёд (направо
от у0).
Если значения аргумента хг даны через
неравные интервалы, то пользуются следу-
ющим видом формулы Ньютона (формула
Ньютона с разделёнными конеч-
ными разностями):
у = /(х) = /(х0) + (х — х„) /(Хх , х0) 4
+ (х — х„) (х — хх) / (х„, хх, х0) 4
4 (х - х0) (х — Хх) (х—х2)/(х„ х2, х1( х„)4...,
где символами /(Xj, х0), /(х2, хх, хс),
/(х3, х2, Хх> х0) и т. д. обозначены так на-
зываемые разделённые конечные раз-
ности:
первого
порядка
/(Xj, х„) =
/(Хх) — /(х0)
Хх — х„
второго порядка
/(х2, Хх, х0) “
/(х2, Хх) — /(Хх, х0)
Х2 — Хр
третьего порядка
/ (Хз, Х2, Хх, Х„) =
= /(Хз, х2, Х1) — /(Х-2, Хх, х0)
Хз Хр
и т.
Интерполяционная формула Стирлинга
о Аув4Ду_! и8 ,
У = У«4ТГ-----2--- + 2Т Д У—1 +
u(u3—1) Д3у 14Д3У~2 ,
3! 2
п2(п2-- О .. ,
4!
и3(а3-1) (п3-22)...[и3-(п-1Г] , 2„ .
+ (2п)! У-п
X —х0
В этой формуле положено и= —— и со-
держится 2п41 членов; интерполирующий
многочлен совпадает с данной функцией в
2п 4 1 точках:
и —— п,—(п—1),—(п— 2), .... -2,
— 1, 0, 1, 2, ..., (п —2), (n —1), п
или
X — Х„ — nil, х0 — (п — 1) ft,
х0 —(и —2)ft, ..., Хр — 2ft, Хр—ft, х0,
х„ 4 ft, Хр 4 2ft, ..., х0 4 (« — 2)h,
х0 4 (п— 1) h, х0 4 nh.
Интерполяционная формула Бесселя
/ 1 \
у = 4 Д Уо +
2 1!
и {и — 1) Д2У_14азУ<> +
4 2! ’ 2 ~
и (и — (и — 1)
4 ._Х--------------Д3у_j 4
и(и2-1) (а—2)Д4У_24 Д4У-1 , ,
4------.,----------,-------+••• +
и^и— -g-j И (W- - i2)
4 X
X (и — п) Д 2,1+1 у_;г.
1
При и = формула Бесселя называется
формулой «интерполирования на середину»,
так как она даёт величину функции для
значения аргумента, являющегося средним
арифметическим между х0 и Xj:
Уо 4 Ух 1 Д2У-1 + Д2Уо
у ..... 2.. +
4-li4y~2 + Д4у-1 _
128 ' 'ГГ ......
5 Д°У з 4 Д6У 2
+(_i)«L12^- • •<2”-1)Дад2пу-П4Д2*у-я+1
22п(2п)! 2
В формуле Бесселя также положено и —
х —х0
—-—-]—и содержится 2п42 члена; интерпопи-
МАТЕМАТИКА
рующий многочлен совпадает с данной функи
цисй в 2п 4- 2 точках:
и = —-п, — (п—1), ..., —1, 0, 1, ...
. . . , п —-1, п, п + 1
или
X = Хо — nh, Л'о — (п — l)h ...
... , x0 — h, х0, х„ + h, ..., х0 + (п — 1) Л,
х0 + nh, ха + (п + !)/г.
Формулы Стирлинга и Бессели обладают
почти одинаковой точностью, но формула
Бесселя даёт более точный результат при
интерполировании около середины интервала
(примерно от и = 0,25 до и = 0,75), а фор-
мула Стирлинга — около начала или около
конца интервала (примерно от и =—0,25 до
и <= 0,25).
В табл. 32 приводятся коэфициенты ин-
терполяционных формул Ньютона и Бесселя
для значений аргумента и от 0 до 1 через
0,01 п формулы Стирлинга для значений и
от 0 до 0,5 также через 0,01.
В табл. 32, в знаки слева соответствуют
значениям и от 0,00 до 0,50, знаки справа—
значениям и от 0,50 до 1,00.
ОСТАТОЧНЫЕ ЧЛЕНЫ ИНТЕРПОЛЯЦИОННЫХ
ФОРМУЛ
Если задана интерполируемая функция
/(х), то остаточный член /?„ интерполяцион-
ной формулы (т. е. разность между /(х) и
интерполяционным многочленом степени п)
выражается при помощи формул:
Интерпо-
ляционная
формула
Ньютона
II
Выражение остаточного члена
Лагранжа
1) 0
= f —хо) (х—)
Ньютона
I
= (n+Tj~! /”+1)(?)u(u—п)
hn 1
= (Н+Тм /"+1> (У u(u+l)....(u+n)
Стирлинга рп 21__________ Д2п+1) _
;<2п=(2п+1)! Г (5) u(u2-l)...(u2-n2)
^2n~j-2
1 Бесселя я2п+1 “° (tri+2)] (У « X
I x(u2 — 1)... (и2 — n2) (и — n + 1)
Здесь — некоторое промежуточное значение
между наименьшим и наибольшим из чисел
Хо, Х1, х2)...
ЛИНЕЙНОЕ ИНТЕРПОЛИРОВАНИЕ
При пользовании таблицами для вычи-
сления значений функций для промежуточ-
ных значений аргумента применяют обычно
линейное интерполирование, т е.
в качестве интерполирующей функции бе-
рётся линейная функция, совпадающая с
интерполируемой функцией при двух бли-
жайших (слева и справа) табличных значе-
ниях. Если, таким образом, х2<х<х2 и таб-
личные значения функции, соответствующие
значениям аргумента Xj и х2, обозначены со-
ответственно через уг и у„, то искомое зна-
чение функции (соответствующее аргументу
X) вычисляется но формуле
У = У1 + “д-- <Уз — У1)’
Пример. Найти мантиссу 1g 97 122. По табли-
цам (стр. 53) находим, что мантиссы lg97 120 и
lg 97 130 равны соответственно:
У! = 087 309 и у3 ~ 987 353;
имеем:
h = 10; ys - у, = 44; х- х, = 97 122 - 97 120 = 2
и
у = 987 309 + 0,2*44 * 987 309 + 9 = 987 313.
Если две соседние табличные разности
У2 — У1 и Уз~- У1 отличаются друг от друга
больше чем на 4 единицы последнего знака,
то следует вместо линейной интерполяции
применять интерполяционную формулу
с большим числом членов (интерполяция
квадратичная, кубичная и т. д.).
ТРИГОНОМЕТРИЧЕСКОЕ ИНТЕРПОЛИРОВАНИЕ
Для периодических функций периода 2 тс
применяется тригонометрическое интерполи-
рование по формуле Эрмита:
sin (х— Xi) sin (х — x2)...sin (х — хп)
sin (Хо — Xj)sin (Хо — x2)...sin(xo—Х„)
sin (х — х0) sin (х — х2) ... sin (х — х„)
' sin (хх— x0)sin (Xj— x2)...sin (Xi~~ xn) +
sin (X — Xo) ... sin (X — Xn_]) ...
4“ ••• 4“ 7 \ 7 \ УП'
sin(x„—x0)... sin (x„— x„_j) ...
ПОЛИНОМЫ ЧЕБЫШЕВА
В вопросах, связанных с теорией прибли-
жения функций, весьма важную роль играют
полиномы Чебышева:
Тп(х)= cos(n arc cos х) = х”+С', х'!-2(х2-1) +
+ С'п хп~4 (х2— 1)°- + • - •
Если полином Тп (х) расположить по убы-
вающим степеням х, то коэфициент при хп
окажется равным 2Л—1 (zi > 1), в частности:
То (х)= 1.
7\ (х)= х,
Т„ (х) = 2х2 — 1,
Т:1 (х) == 4х3 — Зх,
Т4 (х) 8х4 — 8х2 + 1,
7\ (х) = 16х3 — 20х“ + 5х.
Полиномы Чебышева различных степеней
связаны следующим рекуррентным соотно-
шением:
г.ч ч 2 = 2х т,г +1 (*) — тп
Полином Чебышева степени п обращается
в нуль в точках
(2m — 1) тс
х = cos-----------(m = 1,2, ... , п),
m тс
в точках же cos полином Тп (х) обра-
щается в + 1 или —1:
Тп (cos^J = (— l)m.
ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ И ИНТЕРПОЛИРОВАНИЕ
249
Коэфициенты интерполяционных формул
Таблица 32
а) Интерполирование по первой формуле Ньютона
п(«-1) u (и—1) (и—2) и (и—1)(и—2) (и—3) и(и-1) и (и—1) (и—2) и (и-1) (и-2) (и-3)
2 •— 24 2 о 24
0,00 —0,00000 4-0,0000 —0,0000 0,50 —0,12500 4-0,0625 —0,0391
0,01 00495 0033 0и24 0,51 12495 0621 0386
0,02 00980 0065 0048 0,52 12480 0616 0382
0,03 01455 0095 0071 0,53 12455 0610 и377
0,04 01920 0125 0093 0,54 12420 0604 0372
0,05 —0,02315 +9,0154 —0,0114 0,55 -0,12376 4-1,0598 -0,0366
0,06 02820 0182 0134 ,56 12320 0591 0361
0,07 3255 0209 G153 -.57 12255 058-1 0355
С. 08 (.3680 0235 0172 о,58 12180 0576 0349
v,09 04095 0261 0190 0,59 12095 <568 0342
0,10 —0,04500 4-0,0285 —0,0207 •,6и —0,12000 4-0, и660 —0,0366
0.11 04895 0308 0223 0,61 11895 0551 0329
0,12 05280 0331 0238 0,62 1178и 0542 0322
0,13 05655 0352 0253 0.63 11655 0532 0315
0,14 06020 0373 0267 и,64 11520 07522 0308
0,15 —0,06375 4-0,0393 —0,0280 и,65 —0,11075 4-0,'’о!2 —0,0301
0,16 06720 0412 0293 0,66 11220 О501 0293
0,17 07055 0430 0304 0,67 11055 0490 0285
0,18 07380 0448 0316 0,68 10880 0479 0278
0,19 07695 0464 0326 0,69 10695 0467 0270
0,20 —0,08000 4-0,0480 —0,0336 0,7о —0,10530 +0,0455 —0.0262
0,21 08295 0495 0345 0,71 10295 0443 0253
0,22 08580 0509 0354 0,72 10080 0430 0245
0,23 08855 0522 0362 0,73 09855 0417 0237
0.24 09120 0535 0369 0./4 09620 0404 0228
0,25 —0,09375 4-0,0547 —0.0376 0,75 —0,09375 4-0,0391 —0,0220
0,26 09520 0558 0382 0,76 09120 0377 0211
0,27 69855 0568 0388 0,77 08855 0363 0202
0,28 10080 0578 0393 0,78 08580 0349 0194
0,29 10295 <,587 С398 0,79 08295 0335 0185
0,30 —0,10500 +0,0595 —0,0402 0,80 —0,08000 4-0,0320 - 0.6176
0,31 10695 0602 6405 0,81 07695 0305 U167
0,32 10880 0609 0408 0,82 07380 0290 0158
0,33 11055 0615 0411 0,83 07055 0275 0149
0,34 11220 U621 0413 0,84 06720 0260 0140
0,35 -0,11375 +0,0626 —0,0415 0,85 —0.06375 4-0,0244 —0,0131
0,36 11520 сбЗО 0416 0,86 06020 0229 0122
и,37 11655 0633 0416 0,87 05655 0213 0113
0,38 11780 0636 0417 0,88 05280 0197 0104
0,39 11895 0638 041'3 0,89 04895 0181 0095
0,40 -0,12000 4-0.0640 —и.0416 0,90 —0,04500 4-.).0165 -0,0087
0,41 12095 и641 0415 0.91 04095 0149 и078
0.42 12180 0641 0414 0,92 03680 0132 0069
0,43 12255 0641 0412 О,иЗ 03255 0116 0060
0,44 12320 0641 0410 0,94 02820 010^ 0051
0,45 —0,12375 -Ь' ’,0639 —0,0408 0,v5 —0,02375 4-0,0083 —0,0043
0,46 12420 0638 0405 0,96 01920 0067 0034
v,47 12455 0635 0402 0,97 01455 0053 0025
0,48 12480 0632 0398 0,98 00980 осзз 0017
0,49 12495 3629 0395 0,99 00495 0017 0008
0,50 —0,12500 +0,0625 —0,0391 1,00 —0,00000 4-0,0000 -0,0000 1
250
МАТЕМАТИКА
б) Интерполирование
по формуле Стирлинга
Продолжение табл. 32
в) Интерполирование по формуле Бесселя
и иа 2 и (и«-1) 6 и» (иа-1) 24 и и (и-1) и(и-1) (и — (и + 1) и (и—1) (и—2) и
2 6 24
0,00 +0,00000 —0,0000 —0,0000 0,00 —0,0000— +0,0000— +0,0000+ 1,00
и,01 00005 0017 0000 0,01 00495 0008 0008 0,99
0,02 00020 0033 0000 0,02 00980 0016 0016 0,98
0,03 00045 0050 0000 0,03 01455 0023 0025 0,97
0,04 00080 0067 0001 0.04 01920 0029 0033 0,96
0,05 +0,00125 —0,0083 —0,0001 0,05 -0,02375— +0,0036— +0,0041 + 0,95
0,06 00180 0100* 0001 0,06 02820 0041 0048 0,94
0,07 00245 0116 0002 0,07 03255 0047 0056 0,93
0,08 00320 0133 0003 0,08 03680 0052 0064 0,92
0,09 00405 0149 0003 0,09 04095 0056 0071 0,91
0,10 +0,00500 -0,0165 —0,0004 о.Ю —0,04500— +0,0060— +0,0078+ 0,90
0,11 00605 0181 0005 0,11 04895 0064 0086 0,89
0,12 00720 0197 0006 0,12 05280 0067 0093 0,88
0,13 00845 0213 0007 0,13 05655 0070 0100 0,87
0,14 00980 0229 0008 0,14 06020 0072 0106 0,86
0,15 +0,01125 —0,0244 —0,0009 0,15 —0,06375— +0,0074— +0,0113+ 0,85
0,16 01280 0260 0010 0,16 06720 0076 0120 0,84
0,17 01445 0275 0012 0,17 07055 0078 0126 0,83
0,18 01620 0290 0013 0.18 07380 0079 0132 0,82
0,19 01805 0305 0014 0,19 07695 0080 0138 0,81
0,20 +0,02000 —0,0320 —0,0016 0,20 -0,08000— +0,0080— +0,0144+ 0,80
0,21 02205 0335 0018 0,21 08295 0080 0150 0,79
0.22 02420 0349 0019 0,22 08580 0080 0155 0,78
0,23 02645 0363 0021 0,23 08855 0080 0161 0,77
0,24 02880 0377 0023 0,24 09120 0079 0166 0,76
0,25 +0,03125 -0,0391 —0,0024 0,25 —0,09375— +0,0078— +0,0171 + 0,75
0,26 03380 0404 0026 0,26 09620 0077 0176 0,74
0,27 03645 0417 0028 0,27 09855 0076 0180 0,73
0,28 03920 0430 0030 0,28 10080 0074 0185 0,72
0,29 04205 0443 0032 0,29 10295 0072 0189 0,71
0,30 +0,04500 —0,0455 —0,0034 0,30 -0,10500— +0,0070— +0,0193+ 0,70
0,31 04805 0467 0036 0,31 10695 0068 0197 6,69
0,32 05120 0479 0038 0,32 10S80 0065 0201 0,63
0,33 05445 U490 0040 0,33 11055 0063 0205 0,67
0,34 05780 и501 0043 0,34 11220 0060 0208 0,66
0,35 +0,06125 -0,0512 —0,0045 0,35 -0.11375- +0,0057- +0,0211 + 0,65
0,36 06480 0522 0047 0,36 1152ь 0054 0214 0,64
0,37 06845 0532 0049 0,37 11655 0050 0217 о,бз
0,38 07220 0542 0051 0,38 11780 0047 0219 0,62
0,39 07605 0551 0054 0,39 11895 0044 0222 0,61
0,40 +0,08000 —0,0550 —0,0056 0,40 —0,12000— +0,0040— +0,0224 + 0,60
0,41 08405 0568 0058 0,41 12095 0036 0226 0,59
0,42 08820 0576 0060 0,42 12180 0032 0228 и,58
0,43 09245 11584 0063 0,43 12255 0029 0229 0,57
0,44 09680 0591 0063 0,44 12320 4025 0231 0,56
0,45 +0,10125 —0,0598 —и ,0067 0,45 —0,12375— +0,0021— +0,0232 + 0,55
0,46 10580 0604 0069 и,46 12420 0017 0233 0,54
0,47 11045 0610 0072 и, 47 12455 0012 0233 0,53
0,48 11520 0616 0074 и, 48 12480 0008 0234 0,52
0,49 12005 2621 0076 0,49 12495 0004 0234 0,51
0,50 +0,12500 -3,0625 —0,0073 0,50 —0,1250U— +0,0000— + 0,0234 + 0,5)
ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ И ИНТЕРПОЛИРОВАНИЕ
251
Полиномы Чебышева обладают свойством
ортогональности на отрезке (—1,1) с
весом V -4г .г а
1(1—х2) 2 , т. е.
1
(*) Гт(х) = 0(к^ т);
-1 Yi — x*
если же к = т, то имеем:
Г Т20(х)
J
dx — тс;
Лю
Yi —xs
dx — —
2
(к = 1,2,
Основное свойство полиномов Чебышева,
на котором основано решение многих задач в
теории приближения функций, состоит в том,
что из всех многочленов степени и, имеющих
коэфициент при хп, равный единице, полином
Тп (х) наименее уклоняется
от н у л я на отрезке (—1., 1), т. е. макси-
мальное значение величины | 7^-—j Тп (х) |
на отрезке (—1,1) меньше, чем максималь-
ное значение на этом же отрезке величины
IZ=>(x)|, где Р (х) — любой другой многочлен
степени и, у которого коэфициент при х'г ра-
вен единице.
Это максимальное значение величины
I 1 I 1
| Т (х) I равно -^т-1 .
Пример 7. Среди всех многочленов степени п, при-
нимающих в точке х0, лежащей вне отрезка (—1,1),
данное значение у0, наименее уклоняется от нуля
на отрезке (—1,1) многочлен
Метод итерации. Метод итерации показан
ниже в применении к первой формуле Нью-
тона, которой можно придать вид:
_ У -- У а _ и(и—1) Д2Уо
и- &у0 2! Ду0 “
и(и—1)(и —2) Д3у0
3! А у0 -
Для определения значения и принимаем
в качестве первого приближения
и, подставив значение и, в нашу формулу,
получим:
, _ У~У« и1 (ц1— О Д2Уо
ДУо 2! Ду0 -
_ u^tti — 1) (Hl —2) Д3у0
3! Ду0
Найденное значение и2 подставим в ту
же формулу и получим следующее прибли-
жённое значение и8:
У —У о и2(и2 — 1) Д2у0
Ду0 2! Ду0 ~
_ —1) (»2~ 2) Д3у0
31 Ду0
Аналогичным образом находим последу-
ющие приближения и4, и, и т. д. От най-
денного значения и можно перейти к иско-
мому значению аргумента х, пользуясь фор-
мулой х = х0 + uh.
Метод итерации может быть применён
также к формулам Стирлинга, Бесселя и др.
Метод обращения рядов. Расположим ин-
терполирующую функцию по возрастающим
степеням аргумента и:
у = а0 + atu + а2иг + ...,
тогда
____
Т fi ( X 0 )
Т п (х)«
Пример 2, Из всех тригонометрических многочле-
нов fl0+£iCos x+disin хч ... + am cos mx + bm sin mx
порядка m < n, принимающих в точке x() (*»< I x0 | < -)
данное значение y0, наименее уклоняется от нуля
на отрезке [— а, а] тригонометрический многочлен
степени л:
где коэфициенты сх, с2, cs и т. д. определя-
ются формулами:
ОБРАТНОЕ ИНТЕРПОЛИРОВАНИЕ
Определение значения аргумента, соот-
ветствующего данному значению функции,
находящемуся между двумя табличными
значениями, называется обратным ин-
терполированием. Ниже указаны два
основных метода для решения задачи обрат-
ного интерполирования: метод итерации и
метод обращения рядов.
Обратная интерполяционная
формула Лагранжа:
(У —У1) (У-Уз) (У —У«) ,
Х (Уо ~ У1)(Уо-Уг).-.(Ув-Уп) " +
, (У-Уо) (у —уа) (У —Уи) v ,
+ (У1 —Уо)(У1 —у2)—(У1 —Уп) 1 +
’ + (Уп~ Уо) (Уп — У1).~(У« — уя_») Х/г'
252
М'ТЕМАТИКА
ИНТЕГРИРОВАНИЕ ПО КОНЕЧНЫМ
РАЗНОСТЯМ
Неопределённым интегралом по конечным
разностям или неопределённой суммой функ-
ции /' (х) называется функция F (х) — v / (х),
удовлетворяющая условию A F (х) = / (х),
а определённым интегралом по конечным
разностям называется выражение
о < nh
v j (х) = F \а + (п + Г) /г] — F (а) =
= I (а) + f (а + h) + ... + f (а + nh).
Если io (х) есть периодическая функция
с периодом h, т. е. а (х + h) = а (х), то функ-
ция F (х) + (о (х) также является неопреде-
лённым интегралом функции / (х).
Основные свойства неопределённого инте-
грала по конечным разностям:
1) ХД/(х) = /(х);
2) v [? (х) ± ф (х)] = S? (х) ± Уф (х);
3) Хс'?(х) = сХ«(х);
4) S? (х) Дф (х) (х) ф (х) ~2ф (х+Л) Д-(х)
(формула неопределённого сумми-
рования по частя м).
Все указанные равенства справедливы с
точностью до периодической функции а> (х)
с периодом й.
НЕОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ
ПО КОНЕЧНЫМ РАЗНОСТЯМ ОТ НЕКОТОРЫХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. Факториальная функция:
х(п + 1)
=’(/ГП)“й +w<*>-
2. Многочлен. Неопределённый интеграл
от многочлена n-й степени есть многочлен
(/1 4- 1)-й степени; для его вычисления над-
лежит разложить подинтегральный много-
член по факториальным функциям.
Это относится и к степенной функции хл.
3. Показательная функция:
W—1 а-*
SаХ = "ah _ i" + а м-
4. Тригонометрические функции:
/ h\
cos lx — гН
2 sin х =---i--—2 + w (X).
2 sin 2"
ПРИМЕНЕНИЕ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ
ПО КОНЕЧНЫМ РАЗНОСТЯМ
К СУММИРОВАНИЮ РЯДОВ
Формула определённого интеграла по
конечным разностям
a +nh
У. j (х) = F [а + (п -г 1) Л] — F <--)
а
может быть использована для суммирования
некоторых рядов в случае, если общий член
ряда, рассматриваемый как функция номера,
может быть проинтегрирован. В качестве
примера вычислим сумму кубов натураль-
ного ряда чисел от 1 до п.
По формуле
п
Sx3= F(n+ 1) —F(0).
о
Разложение функции х3 по факториальным
функциям даёт:
Д303
х3 = Д 03х + -gj- х (х — 1) +
ДЗО3
+ -др- х (х — 1) (X - 2),
где числа ДО3, Д203, Д303 найдём в табл. 29
(стр. 245), тогда
х3 = х + Зх (х — 1) + х (х— 1) (х— 2).
Функция F (х) вычисляется посредством
формулы интегрирования факториальных
функций:
F (х) ='^х+3^х(х—1)+у]х(х—1)(х-2)=
х (х— 1)
= ----2--+х(х-1)(х-2) +
+ Z х (х — 1) (х — 2) (х — 3) =
и, следовательно, полагая х=п-|-1, получим:
", Г«(п + 1) 1г
“ |~~2—] •
В случае, если интегрирование по конеч-
ным разностям общего члена ряда затрудни-
тельно, можно ряд просуммировать прибли-
жённо, применив формулу Э й л epa-
AI а к л о р е н а, устанавливающую связь
между интегралом по конечным разностям и
определённым интегралом:
, а + nh
а + nh 1
У !№ = -/{ J t(x)dx + Atlf (a->nh)-
- / (a)] + A,h [f (a + nh) — j' (д)] +
+ AJF \Г" (a + nh)-j'" («)] +
+ A6ft5 ]/(5) (a + nh) — /(5) (a)] + • • I-
+ A2m - 2 ft2m “ 3 t/<2m ' 3> (a + лЛ) —
_ /(2m - 3) (a)] пд2т h2ni f(2m)
где a •: c, <a + nh и
L 1 _ J.
Щ — 2 ’ ~ 12 ’ V-
1 i
= 30240 ’ A>> 1 209 C00 ’ ‘
Пример. Вычислить сумму ряда
1_ 1 1
S = fop г JQ3-, (- 1Q5, + . . .
Здесь
оо
1 , dx 1
J --- 101; 2; /i = ОС ; j - iOl ;
10*
ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ И ИНТЕРПОЛИРОВАНИЕ
253
7(Ю1)= 1’f : г (101)= - А-,;
(101)--3±-; . . . ; J (ОО) = f (СО) =
= /"(00)= ... =0,
и, пс л’-зуясь формулой Эйлера-Маклорена, получим
6 = ТЛоТ + 2 • ЮР “ 3 -ЮР
- -15 ,41ор + • = 0,00499983335.
УРАВНЕНИЯ В КОНЕЧНЫХ РАЗНОСТЯХ
Общий вид уравнения в конечных
разностях следующий:
Ф [х, / (х), Д / (х), Д2 / (х),..Д” / (х)] = О,
где / (х) — неизвестная функция аргумента х.
Заменяя в нём конечные разности их вы-
ражениями через значения функции, по-
лучаем
F [х, / (х), / (x+ft), / (х +2/1)./ (х+лй)]=О,
или, положив / (х) = ух и /1 = 1 (общий слу-
чай сводится к этому подстановкой х -- hz):
р (X, ух, ух + 1 , Ух + 2 ’ • • • ’ УХ + п ) = °-
Если уравнение содержит ух, то его по-
рядок равен п. Если же в уравнении отсут-
ствуют ух, ух+])... yx+fc_i:
Р Ух + Л ’ Ух+к I Р Ух+к+2 ’ * • "Ух+П )
то порядок его определяется разностью п —к,
так как уравнение последнего вида сводится
к предыдущему подстановкой ух+к — zx :
р (X, zx, zx+, , zx+2 zx+n_k) = 0.
Общее решение уравнения п-го по-
рядка
Ух = <f [х, Ci (х), С2 (х),. .., Сп (х)],
обращающее в тождество это уравнение, со-
держит л произвольных периодических функ-
ций с периодом 1 (в частности постоянных).
Частное решение получается из общего,
если функции Сх (х),. . . , Сп (х)—определён-
ные .
При данной системе начальных значений
Уа’ Уа + Р Уд + 2 ’ • ' ‘ ’ Уа+п— 1
решение разностного уравнения заключается
в определении уа + т при любом целом т.
Уравнение
До (Х) УХ4П + Al Ух+п—1 + • • • +
-г An W Ух = / (х)
называется линейным разностным урав-
нением; если / (х) = 0, оно называется одно-
родным, в противном случае — неодно-
родным.
Если а0, аи . . ., а„ — постоянные, то урав-
нение
а« Ух+п + а1 Ух+п-1 + • • • + апУх — / (х)
называется линейным у р а в н е и и ем
с постоянными коэфициентами.
Общее решение линейного неоднород-
ного уравнения равно сумме ух -|- ух общего
решения соответствующего однородного урав-
нения и какого-нибудь частного решения
неоднородного уравнения.
Для отыскания общего решения однород-
ного уравнения с постоянными коэфициен-
тами
аоУх+п + «1Ух+,;-1 + - • • + апУх = О
составляется ха рактери сти ческое
уравнение
аогл + а^-1 j------+ ап = 0.
Каждому действительному корню г характе-
ристического уравнения кратности к соот-
ветствует к решений однородного уравнения
Г х, ХГх, . .., xfc-1 l'x-
Каждой паре р (cos 9 ± i sin 0) сопряжённых
комплексных корней характеристического
уравнения кратности к соответствует 2к ре-
шений однородного уравнения
A cos 0 х, p-v sin 0 х, х рх cos 0 х, х pxsin 0 х,...,
хк~1 рх cos 6 х, хк—1 p-v sin 6х.
Таким образом, решив характеристическое
уравнение, мы найдём п частных решений
однородного разностного уравнения У1 (х),
у, (х), . . . , уп (х), и общее решение этого
уравнения имеет вид:
Ух — С1У1 (х) + С2Уг (х) + . . . 4- С„у„ (х).
Частное решение неоднородного уравнения
находится путём подбора. При этом, если
правая часть есть многочлен т-й степени, то
его разлагают по факториальным функциям:
/ (х) = Аох(т) 4- At х(т-1) 4- . .. 4- Ащ
и ищут частное решение в виде многочлена
(если единица не является корнем харак-
теристического уравнения) той же степени:
Ух = Вох<т) 4- BtX*"'-” 4- • • • 4- Вт.
Подставляя этот многочлен в левую часть
уравнения и сравнивая коэфициенты при
факториальных функциях одинаковой сте-
пени в обеих частях равенства, можно оп-
ределить коэфициенты В;.
Если единица является корнем характе-
ристического уравнения кратности к, то
частное решение следует искать в виде много-
члена степени т-\-к.
Пример. Найти частное решение уравнения
2ухь4-5ух+3 +5yx+i -2ух =2
при начальных условиях уо = О, уг = 11, у8=» — 8, у3 = б
И ВЫЧИСЛИТЬ
Характеристическое уравнение имеет вид:
2М - 5г8 + 5г-2=2(г-1) (Г-Ь1) (г - »/а) (г-2)=О,
откуда Г!=1, г2= — 1, г8=»/8, г^2 и общее решение
соответствующего однородного уравнения выра-
жается равенством
с, + С, (- 1)х + С, + С.2* :
число 1 является однократным (простым) корнем ха-
рактеристического уравнения и частное решение
следует искать в виде
у! = В,х(!) + В, = Р„х -Г В,.
Подставив в данное уравнение, получаем
2 [В„ (х-4) + В,] - 5 [В„ (Х+3) + В,] +
+ 5 (В. (х+1) + В,] -2 (В„х + В,)=2,
откуда — 2ВС=2 и Во= —1, следовательно =—х 1 В,
254
МАТЕМАТИКА
(Bi—произвольно) и общее решение уравнения имеет
вид:
/ 1
у=С,+Са (-1)* + с3 м + С«2' - х
(Bi включено в С4).
Начальные условия дают:
yn==Cj -!-С2+С3-)-С4=О;
у,-С, - Са + 4; С2 + 2С. - 1 - 11;
Уз = С1 + С3 + + 4С4 2 =— 8;
у, =с, - с, + Lс., + ес, - з- e,
откуда Cj=C4 » 0; С2 =—8; С8 *= 8 и искомое частное
решение
/ 1 \х
УХ = ~ 8 <-1)х +8 Ь- 1 -X
И
З’юо = 2^7)0 “ 108-
ЧИСЛЕННЫЕ И ГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
ЧИСЛЕННОЕ ДИФЕРЕНЦИРОВАНИЕ
Если функция задана таблицей своих
значений, то её можно численно продиферен-
цировать, т. е. приближённо вычислить
значения её производной путём составления
для функции аналитического выражения по
какой-либо из интерполяционных формул и
последующего диференцирования получен-
ной интерполирующей функции. Выбор ин-
терполяционной формулы осуществляется в
зависимости от местонахождения точки, в
которой отыскивается значение производной
(в начале, в конце или в середине таблицы).
Из первой формулы Ньютона получаем:
1 Г 2и — 1
Г (х0 + ftu) = у А У„+ А'2УП +
Г (х,; + /ш) = 2, [А2,-! + U Д:-г ' + Д2т1+
би2 — 1 1
+ ]2 А4У-2 + • • .J ;
г(хо+йИ)= 1 ГА_2-г+д8^,+
Й“ L 2!
+ и Д4У_ 2 + . . . ;
При и = 0 эти формулы переходят в
следующие:
3u2—6и+2 4u3— 18u2+22u_ 6
+-----g---- А’у0+ 24~~-----Д Vo+---
1 Д’У-^+Д’у-г
6 2 ’+
/' (х„ + 1ш) = & Д2у„+(И—1)Д8УО +
6и2 — 18и + 11 дд ,
+-----12----- А Уо + • • J ;
1 Г 2и —3
(x0+hu) = /7з Д3Уо+—г~ Д4у0 + • ••
Эти формулы при и = 0 дают:
/' (х«) = S’ [^Д Уо —£ Д2Уо + з дзУо —
- г Д4Уо + • • •
Г (Хо) = S2 Д2у» “ Д8у° + li ^iy° ~
5 , 1
- 6 Д5Уо + • • • ;
1 Г. 3
Г(хо) = ^3 ДЗУо - 2 Д4Уо +
7 15 1
+ 4 д6Уо — 8 дв Уо + • • ;
Аналогичным образом из формулы Стир-
линга:
1 Д6у_2+ Д6У—з
+ 30 2
Г(Хо)=1
/'ЧХо)=1
Д2У-1 - Д4У-2+
Дэу 1 + Д3у 2 _
2
1 Д6у_2 + Д6У-з
"4 2 + '
Из других интерполяционных формул
можно получить выражения для производ-
ных подобным же путём.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
(МЕХАНИЧЕСКИЕ КВАДРАТУРЫ)
6
Если в определённом интеграле j / (х) dx
а
подинтегральная функция задана таблицей,
то её можно численно проинтегрировать, т. е.
приближённо вычислить значение опреде-
лённого интеграла путём интерполирования
подинтегральной функции по какой-либо из
интерполяционных формул с последующим
интегрированием полученной интерполирую-
щей функции в заданных пределах. Числен-
ное интегрирование определённого интеграла
называется иначе механической квад-
ратуре й.
ЧИСЛЕННЫЕ И ГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
255
Ниже приводятся некоторые наиболее
употребительные формулы механических
квадратур.
Формула прямоугольников
Р b — а
J f(x)dx як —п—(уо+ У1+у2 + • • + y„_i)
а
ИЛИ
р b — а
J / (х) dx х —— (уг + у2 + у3 + • . • + у,;),
а
где
Уо= / (-о)- У1= / (хо+ Й).
Уа= / (Х„+ 2Л), ...» У„ = / (Хо 4- nil),
Ь — а
причём х0 = а, хп — а + nh = b, h = —~ .
Те же обозначения приняты и в следующих
трёх формулах.
Формула трапеций
ь
J / (х) dx як
а
Ь —а
== ~2п~ (Уо + 2У1 + 2у24- . .. + 2yn_j + у„).
Формула парабол
р b — а
J / (х) dx к (у0 + 4yt + 2у24-4у3 +
+ 2у4 + .. . 4- 4у„_2 4- 2уп_, 4- уп),
где п — чётное.
Формула Котеса
? Ь — а
\f(x)dx= —
а
Уа + У1+ У2 +
+ - •• + Н"у«
где коэфициенты Нгп даны в табл. 33.
Формула Чебышева
6
J /(х) dx як
а
__ Ь — а Г “I
~п~ р(Х4) + /(Х2) 4- ... + /(Х„)| ,
а абсциссы х,- даны в табл. 34.
При п = 8 и при п > 9 формула Чебышева
неприменима (абсциссы мнимые).
Формула Гаусса
ь
j'/(x) dxx(b-a) [A1/(x1)4-
4-Аа/(Х2) 4-. • • + А„/(Х„)],
где Х,- = а4-(й — а)х,-, а коэфициенты А, и
абсциссы х, даны в табл. 35.
Сравнение формул механических квадратур
Точность каждой формулы механических
квадратур, как правило, тем больше, чем
больше п. Наименее точной является, во-
обще говоря, формула прямоугольников.
Формула трапеций получается в результате
линейной интерполяции подинтегральной
функции на каждом отрезке (xz, хл +1) и даёт
меньшую точность при том же п, чем фор-
мула парабол, получаемая при помощи квад-
ратичной интерполяции подинтегральной
функции на каждом отрезке (х,, xi+2)
с узлами интерполяции х,-, xi+1 , xi+2-
Формула Котеса является более обшей
формулой; формула трапеций получается при-
менением формулыКотеса при п — 1 к каждому
из отрезков (X/, xi+1 ); формула парабол
соответствует случаю п = 2.
Ещё более точной является формула Га-
усса; формула Гаусса даёт точный резуль-
тат, когда подинтегральная функция —много-
член степени не выше, чем 2п—1.
Если экспериментально вычисленные ор-
динаты у; содержат случайные ошибки, то
вызываемая этим ошибка в значении вычи-
сляемого интеграла—наименьшая при поль-
зовании формулой Чебышева. В этом пре-
имущество формулы Чебышева перед осталь-
ными формулами.
К
Пример. Вычислить I = J sin xdx (точное знп.-
0
чение 1 = 1).
а) По формуле трапеций. Положив
М“Ю, получим
~ = 0,1570706 . . . = 9“
п 20
и
7 = L . 0,1570796 . . . fsin 0° + 2 sin 9°-fr-2 sin 18°-h
4- ... + 2 sin 81° 4- sin 90°] = 0,997946.
б) П о формуле л а о а б о л. При п = 10:
2=1-. 0,1570796 . . . [Sin 0° +4 sin 9°+ 2 sin 18° +
+ 4 sin 27’ + . . . + 4 sin 72° + 2 sin 81° +
+ sin 90’1 = 1,000005.
в) П о ф 1 p я уле Чебышев а. Так как эта
формул*: более точная, чем предыдущие, то положив
п = 5.
9^,
МАТЕМАТИКА
Таблица 34
Абсциссы для формулы Чебышева
п Xt ха Х„ А. Х3 X. X, х8 х9
2 0,577350 -0,577350
3 0.707107 0 —0,707107
4 0,794654 0,187592 -0,187592 —0,794654
5 0,832498 0,374541 -0,374541 —0,832498
6 0,866247 0,422519 0,266635 -0,266635 —0,422519 —9,866247
7 0,883862 0,529657 0,323919 0 —0,323919 —0,529657 —0,883862
9 0,911589 0.6U1G19 0,523762 0,167906 и —0,167906 —0,528762 —0.601019 -„,911536
Абсциссы Xj и коэфициенты Aj формулы Гаусса
Таблица 35
п Абсциссы
Xi X, | х, X. X, X. х, | х„
1 2 3 4 5 6 7 8 0,5 0,211325 0,112702 0,069432 0,046910 0,033765 0,025446 0,019855 0,788675 0,5 0,330009 0,230765 0,169395 0,129234 0,101667 0,887298 0,669991 v,5 0,380690 0,297077 0,237234 0,930568 0,769235 0,619310 0,5 0,408283 0,953090 0.830605 0,702923 0,591717 0,966235 0,870766 0,762766 0,974554 0.898333 0,930145
Продолжение табл. 35
п Коэфициенты Aj
А, Аа А, А. А, Ав А -Ав
1 2 3 4 5 6 7 1 _1 2 5 18 0.173927 0,118463 0,085662 0,064742 _1 2 4 9 0,326073 0,23^314 0,180381 0,139853 _5 18 0,326073 0,284444 0,233957 0,190915 0,173927 0,239314 0,233957 0,208980 0,118463 0,180381 0,190915 0,085662 0,139853 0,064742 0,050614
8 0,050614 0,111191 0,156853 0,181342 0,181342 0,156853 0,111191
Пользуясь табл 34, имеем:
X, =— х6 - 0,832498; х„ - — х, = 0,374541; X, = 0.
Далее:
„ а + Ь Ъ — а
Xj = —2---* ~2— xi “ 45° + 45’ Xj
Х,=45’+45’х1 = 82°27',74;
Ха=45°+45’ха=6Г5Г,26;
Х3=45°+45’ха=45’;
Х.=45°+45’х1=28°08’,74;
Xs=45’+45°xs=7’32',26;
sin Х,= 0,99136;
sin Х,= 0,88176;
sin Х.= 0,70711:
sin Xt= 0,47171;
sin X,= 0,13117;
1
5
(sin X, + sin Xa+sinX„+sin X.+
+ sin X.) = 1,00000.
г) П о формуле Гаусса. Взяв п = 5, на-
ходим х,, ха, х3, х„ х, и A,, A„ А„ А„ As из табл. 35.
Далее Xj = а + (5 - a) Xj =90’ Xj , откуда
Xt =4’13'18*,87; X,= 20’46’7*,96; Х8=45°;
Х,=69’13'52*,03; Х, = 85’46'41”,13
И
‘ = 2 sin Х' + А‘ sin *" А‘ s!n х»+ A sin X. +
+ A; sin Х,) = 1,000000.
вычислены приближённо по любой из фор-
мул механических квадратур.
Разделив интервал (0,2 л) на 4г равных
частей, обозначив абсциссы точек деления
/ П л \
через х„, Хц х2, . . ., xir I хп= I и соот-
ветствующие им ординаты графика у = / (х)
через у0, у1г у2, .. yir (Уьг = Уо)> получим
приближённое представление функции / (х):
2г
/ (х) « ак cos kx + bK sin kx).
fc=l
Если для вычисления коэфициеитов поль-
зоваться формулой трапеций (стр. 255), то
будем иметь:
1
а«= 2г
Уп,
ГАРМОНИЧЕСКИЙ АНАЛИЗ
Периодическая функция / (х) с периодом 2л
может быть приближённо представлена в
виде тригонометрического полинома. Для
вычисления коэфициеитов этого полинома
следует воспользоваться формулами коэфи-
циентов Фурье (стр. 162), которые могут быть
4г
2г 2 Vn C0S kXn (fc = b2’ • • • > 2г- 1,:
п==1
4г
а2Г^ 2г
П = 1
ЧИСЛЕННЫЕ И ГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
257
4Т
= fr 2 y"sitl/,:x (Z< = 1,2> • • • >2г —О;
Л=1
0.
Вычисления удобно производить по сле-
дующей схеме:
У1Г У1 У4г- У2 1 ^4r— Уз -2 У 4Г—3 ' • • У2г-1 Узг • • У2г+1
Суммы ц0 «1 U3 •u2r-l “sr
Разности V1 a3 ' • v2r—l
«0 «1 «2 • • ur-i ur
и2г u2r-l U2r—2 * • ' ur+l
Суммы iVo H'r-i Wr
Разности IVo ivi IV» • <-l
Vi Vs •• ^r-1 vr
v2r- 1 V2r-2 v2r-3 • • "r+1
Суммы Z, z2 Z8 • zr-l Zr
Разности zi zi zi . • • zr-\
Коэфициенты определяются при этом по
формулам:
1 "Ч?
а° “ 2r Wn’’
л = 0
( п-0
wn cos кхп при к нечётном;
iv„ cos кхп при к чётном;
а2г= ™п,
zn sin кхп при к нечётном;
z'n sin кхп при к
чётном;
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
ОБЫКНОВЕННЫХ ДИФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
ДИФЕРЕНЦИЛЛЬНЫЕ УРАВНЕНИЯ
1-го ПОРЯДКА
Для отыскания приближённого частного
, dy
решения диференциального уравнения
= / (х, у), удовлетворяющего начальному
условию у = /0, при х = х0 могут быть при-
менены следующие методы.
Метод последовательных приближений.
Используя начальное условие, находим из
уравнения у' = /(х, у) выражение, для у
в виде:
х
У = Уо + j f (х> У) dx.
х„
За исходное приближённое значение у
принимаем уо, подставляем его в подинте-
гральную функцию вместо у, берём квад-
ратуру (точно или приближённо) и полу-
чаем первое приближение
X
У1 = Уо + J / (х, у0) dx.
Второе и последующие приближения на-
ходим аналогично, последовательно подстав-
ляя в подинтегральную функцию вместо у
вычисленные приближения: ух, у2, у3, ...
и т. д.
X
У2 = Уо + ,f /(X, У1) dx,
х0
X
Уз = Уо+ J / (х,Уз) dx,
*0
X
Уп = Уо+ J / (X, уп~! ) dx.
х„
Процесс последовательного приближения
обычно прекращают, как только абсолют-
ные значения разности между двумя сосед-
ними приближениями у„+1 и уя становится
меньше допускаемой ошибки.
Пример. Найти решение диференциального урав-
нения
удовлетворяющее начальным условиям: ха=0, у,—1.
Имеем:
х ,
Ух - 1 + J (х+1) dx= 1 + х + ;
о
X ,
у, = 1 + J (х +1 + х + у) dx =
О
= 1+ х + х’ + ~ ;
6
у3=1 + |(х+1 + х + х,+ - у dx —
О
уЗ yi
= 1 + X + ха + \ .
3 24
Этим приближением можно ограничиться; оно
даёт при х=0,1 у— 1,1103, а при х=0,2 у = 1,2427.
Если сравнить эти числа с соответствующими зна-
чениями точного решения, то окажется, что в пер-
вом из них все знаки верные, а во втором ошибка
достигает одной единицы последнего знака.
Применение рядов. Частное решение ди-
ференциального уравнения ищем в виде
бесконечного ряда Тейлора:
Уо , „ У о
У = Уо + ПТ (х — хй) + 2,- (х — х0)‘- + ...
В этом разложении х0 и у0 заданы на-
чальными условиями. Остаётся определить
17 Том I
258
МАТЕМАТИКА
начальные значения производных: у0,
у”, У." ,
Подставляя в диференциальное уравнение
и у0 вместо х и у, получим начальное
значение первой производной
Уо = / (Х0, Уо).
Для определения начальных значений
высших производных продиференцируем
наше уравнение по х:
у" = /х(х> у) +/у <х’
в полученном выражении положим: х=х„,
у = у0, у' = у0 и находим
у.' = /х (х„, Уо) + /у (х0> Уо) У» •
Аналогичным образом определяем началь-
ные значения остальных производных.
Иногда для нахождения коэфициентов
ряда применяется метод неопределённых
коэфициентов. В этом случае» обозначая
неизвестные коэфициенты разложения через
а0, а!» а2...» ап,пишем решение в виде:
у = а0 + 01 (х — х0) + аг (х — х„)2 + ...
Диференцируем по х:
у' = аг + 2 (х — х0) ...»
и подставляем эти разложения в уравнение;
в полученном тождестве сравниваем коэфи-
циенты при одинаковых степенях (х — х„)
в левой и правой частях тождества и при-
ходим к системе уравнений для определе-
ния коэфициентов а0, а1г а2,...
Метод отыскания решения диференциаль-
ных уравнений в виде бесконечного ряда
применим также к уравнениям высших по-
рядков и к системам диференциальных урав-
нений.
Пример. Найти частное решение уравнения
у" -j- J- у' 4- у == 0 при начальных условиях: у = Н
у' = 0 при х — 0.
Положив
у » а, 4- djX + дйха + ... 4- ап—2 хП~~<2 4-
+ ап_1 хп~1 + ап х“ + ...,
получаем
У’ = а> + 2 а, х + ... + (п — 2) ап_2 хп~3 +
+ (/1 — 1) а;|_! хп—-Ц-?(а.г +
у'* = 2 я» + ... + (л — 3) (п — 2) _2 Х« 4*
+ (п - 2) (п-1) ап_} хп~3+ (п- 1) пал х/г~3 + . . ..
Подстановка в уравнение дает:
+ («о + 2 а» 4- 2 а») 4" ... 4-
4- 1ап-2 + пап 4- (п- D па„ J хп~- 4- ... = о,
или
- 4- (я» 4- 1 о») 4- ••• 4*
4- (ал-2 + п’яп ) хп~~ 4- ... = О.
Отсюда
а» “ О;
а„ 4- 2’ а» = О;
а» 4- З1 а, = О;
аа 4- 4а а, — 0;
«п-2 + п‘ ап “ °-
Решая эту систему уравнений, получаем:
а, = а, = д5 = ... = 0;
°п-2 + а«
ап-------2a-4a ... п»
(п — чётное), и
/ № X4 Xе ч
? = “° 2" + 2a»4a 2".4’.6a +••)•
Для определения а, пользуемся начальными
условиями.
Положив х =» О и у = 1. находим д0 = I (условие
У’ = 0 при х = 0 выполняется при любом а0).
Искомое частное решение является функцией
Бесселя (стр, 171):
Ха X4 Xе
у = 1 —“ । — — -1.
л 2® 2а‘4а 2а*4а»63
Метод Эйлера — Коши. Переписав дифе-
ренциальное уравнение в виде
dy = ) (х, у) dx
и заменив диференциалы конечными разно-
стями, получим равенства:
д Уо = / (*о, Уо) д х0;
ДУ15= / (Xi.yJAxj;
дУо = / (х2, у2)Дх3;
Д Уп—1 / (хп—1> Уп —1) Хп—1 •
Из первого равенства определим у, по
формуле
У1 = У» + д Уо = Уо + / (Хо, Уо) Д Хо
и подставим во второе равенство. Аналогич-
ным образом из второго равенства опре-
делим у2:
Уз = У1 + Д У1 = У1 + / (Xi, ух) Дх3
и подставим в третье и т. д.
Способом Эйлера — Коши обычно поль-
зуются лишь для грубого приближения,
беря небольшое п.
Метод Рунге. Этот метод основан на при-
менении следующей основной формулы:
А Уп = | + 2 к™ + 2 к&> + к\п>),
где
fi == xi — xz_j — const,
/г(1П) = hf (x,„ yn),
Уп+^\
k^= к) (хл+ II,у.п + к^) .
Полагая п = 0 и имея заданные значения
х0 и Уо, находим А у0, после чего опреде-
ляем уг, соответствующее значению xt =
= Хо + h.
Имея хх и уп можно по этой же формуле
отыскать д Vj, а значит и у3, затем Ду., и
Уз и т. д.
Метод Адамса. Этот метод основан на
применении следующей формулы:
1 5
дУп — 'г: + 2 -v.-l + ]2 2 >
ЧИСЛЕННЫЕ И ГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
259
где
11л = ynh = t Уи) ll-
Если, кроме начального значения функции
У = Уа при х = х0, известны ещё два значе-
ния функции у2 и у2, соответствующие зна-
чениям аргумента х4 == х0 + h и х2 = x0+2ft,
то можно составить таблицу:
X У Ду 1) Д1) 4’’1
Хо Уо 4 У» По Д’!» д%.
Хх У1 4У> Тд Дт}х
X» Уз Та
Эта таблица может быть продолжена при
помощи основной формулы. В самом деле,
положив п = 2, находим по формуле А у2, а
значит и у3 (у,, = у., ф- А у„). Вычисляем т3
по формуле -1)з = / (х3, Уз) ft и конечные раз-
ности Дт]2 и Д-т(4 и, таким образом, допол-
ним правую часть таблицы одной косой
строчкой. Пользуясь последней, а также
основной формулой, определяем Ду3, а зна-
чит и у4, вычисляем т]4, Av)3 и А2 т;2 и, следо-
вательно, дополним таблицу ещё одной
косой строчкой. Аналогичным образом про-
должим построение таблицы и дальше.
Значения у4 и у,, необходимые для по-
строения начальных строк таблицы, можно
определить либо с помощью разложения у
в ряд, либо по способу последовательных
приближений, предложенному академиком
А. Н. Крыловым и основанному на двух
формулах:
д Уо = Ъ + дг0—Д2 т0,
1 5
дУ1 = ’ll + 2 Дт° 12 ^о-
В первом приближении принимаем:
д Уо = Ч>-
Зная у0 и вычислив по формуле т0 =
= 1(x0,y„)h, находим У1 (У1 = Уо + д Уо =
= Уо + 71о)- Теперь вычислим т]4, а с ним и
д'(о (A’lo = ’ll — ’о) и исправим значение Ду0,
полагая на этот раз
дУо — fto + "о д<о-
При помощи этого уточнённого значения
Д Уо исправим значения у4, тц и Дт,0 и нахо-
дим Д у4 по формуле
ДУ1 -= Т,1 + 2 д^°-
Теперь можно определить у, (у2 = у4 +
+ А у4), а также
Д’ Ат]х = г|2 т(1 и A-/jo “ А Д’о -
Остаётся проверить выполнение фор-
мул (*).
Часто Д2г0 оказывается настолько ма-
лым, что эти формулы верпы, хотя для
вычисления А у0 и А у, величина А2т0 не
принималась в расчёт. Если это нс так, то
переиычисляем А у0 и А у4 уже полностью
по формулам (*), заново вычисляем тг,, т]2,
Ат0, Ду11 и Дгг„ и опять проверяем выполне-
ние формул (*) и т. Д. Обычно этот процесс
быстро приводит к достаточно точным значе-
ниям у4 и уа.
Пример. Найти приближённое решение урав-
нения
при начальных условиях: х„ = о, у„ = 1.
Составим таблицу значений искомой функции
в промежутке от х -= О до X = 1 через 0,1 (т. е. по-
ложив h=O,l); определим сначала по методу Кры-
лова значения у, и ув.
х0у0
т,0 = а а • Л = 0;
х» + Уо
в первом приближении полагаем Ду0 = т;0 = О,
У, = Уо + 4Уо = 1
и
Xi-y. . 0,1-1
’ll = а а -Л = а 1а । ia 0,1 = 0,0099,
+ У, ’ ‘
откуда Д1)0 = т), — т0=О,ОО99.
Исправляем значение Ду0, полагая
4Уо = >1о +-| = 0 + -0,0009 = 0,005,
откуда
У1 = Уо + Ду» = 1,005
Х,у, . 0,1-1,005 „ ,
i;1-' i а 03’+ 1,005" ’ °’1 “ °099-
Л1 “г Ух
4"), = ’ll — 1)0 = 0,0099 — 0 = 0,0099
и
4У1 = ’ll + Дц, = 0,0099 - • 0,0099 = 0,015;
следовательно
Уа = У: + Ду, = 1,005 + 0,015 = 1,020.
Далее:
Аа “г У»
А-Г1 = 7ja — = 0,0189 — 0,0099 = 0,0090
и . ‘
Дат]0 « Д^ — Дт]а = 0,0090 — 0,0099 = — 0,0о09.
Проверим теперь выполнение формул (♦) для зна-
чений
У1 = 1,005 и уа « 1,020:
1 2
4У« “ 0 + ^--0,0099 - — -(-0,00091 = 0,005,
1 £
1 5
Ду1=О,ОО99+-- -0,0099 + “ 0,0009) = 0,0145.
Таким образом, первая формула выполнена
точно, а неточность второй столь мала, что скажется
только в пятой значащей цифре значения у.
Дальнейшие вычисления значений у по методу
Адамса даны в табл. 36.
Таблица 36
Решение уразнения у' =
х У 4У п -А.) Д,1
0,0 1,000 0,005 0 0,0099
0,1 1,005 0,0099 —0,0009
0,015 0,0090
0.2 1,020 0,023 0,0189 0,0077 —0,0013
0,3 1,013 0,030 0,0266 —0,0016
0,0061
0,4 1,073 0,0327 -0,0013
0,035 0,0048
0,5 1,103 0,039 0,0375 0,0036 —0,0012
0,6 1,147 0,042 0,0411 0.0026 -O.OOlu
0.7 1,189 0,045 0,0437 0,0019 -0,0007
0,8 1,234 0.0456 -0,0004
0,046 0,0015
0,9 1,280 0,048 0,0471
1,0 1,328
17*
260
МАТЕМАТИКА
СИСТЕМЫ ДИФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1-го ПОРЯДКА
Для отыскания приближённых частных
решений системы диференциальных урав-
нений:
dy dz
dx = A (х,у, z); rf- = /2 (x,y,z)
(где у и z—искомые функции аргумента х),
удовлетворяющих начальным условиям:
У = Уо, Z= ?о при X = х0,
укажем следующие методы.
Метод Эйлера—Коши. Переписав урав-
нения в виде:
dy = /1 (х, у, z) dx; dz = /2 (х, у, z) dx
и заменив диферепциалы конечными разно-
стями, получим равенства:
ДУо=/1 <хй, Уо, Z„) Дх0;
ДУ1 = /1(Х1> Ут» Z1) Дх,;
кУп— 1 ~ ti (хп—1 > Уп—1 ’ гп— 1 ) &хп— 1 ;
Дг0= /2(х0,у0,г0) Дх0;
Дг, = /2(х1( у1,г1)Дх1;
Д2п—I “ /2 (ХП— 1 ' Уп—1 ’ zn-l ) &хп— 1 •
При помощи выражений для Ду0 и Дг0
определяем у, и г, по формулам:
У1 = Уо + дУо = Уо + /1 <х0, у0, Zo) ДХо
и
Zj = z0 + Дг0 = z0 + /2 (х0, уо, г0) Дх0
и подставляем во вторую пару равенств.
Аналогичным образом во второй паре ра-
венств определяем у2 (у2 = yi + Ayj и
za (z2 = Zj + Azj) и подставляем в третью
пару и т. д.
Следует иметь в виду, что последователь-
ные вычисления значений у^ и z* произво-
дятся обязательно одновременно для обеих
искомых функций.
Метод Адамса. Этот метод основан на
применении основной формулы для случая
одного уравнения (стр. 258) и присоединении
к ней аналогичной формулы
1 -
Д2л = + 2 ^п— 1 + 12 ^п—2 ’
где
= zn h = /2 (хп, Ул» zn) h.
Начальный процесс протекает здесь
так же, как и в случае одного уравнения,
причём к формулам (*) (стр. 259) следует
присоединить две дополнительные формулы:
Дг0 = ^0 т у Д^о |2 Д2^«’>
1 5
Az, = Ci + ”2" Д^о + J2 Д2^о*
Как и в методе Эйлера—Коши.последова-
тельные вычисления значений у„ и z„ произ-
водятся обязательно одновременно для обеих
искомых функций.
Заметим, что для отыскания приближён-
ного решения диференциального уравнения
или системы уравнений выше 1-го порядка
можно заменить это уравнение или систему
системой уравнений 1-го порядка (стр. 174)
и применить любой из указанных выше
методов.
ГРАФИЧЕСКОЕ ДИФ2РЕНЦИР0ВАНИЕ
Если функция у = / (х) задана графиком
(фиг. 339), то её производная /'(х) мо-
жет быть найдена графически следующим
образом.
Отрезок [а, &], на котором задана функ-
ция у == f (х), делим на п частей настолько
малых,чтобы соответствующие участки кривой
по возможности мало отличались от прямо-
линейных отрезков. Части отрезка [а, &] ие-
Фиг. 339
обязательно должны быть равными: их сле-
дует брать меньшими там, где функция / (х)
изменяется быстрее. Из середины каждой
части отрезка mlt m2, т3, ... проводим пря-
мые Щ1М1( m2M2, т3М3.....перпендикуляр-
ные к оси ОХ,до пересечения с кривой в точ-
ках М2, М3, ..., в каждой из которых
проводим касательные. Затем, выбрав на
отрицательной части оси ОХ полюс Р на
расстоянии РО = X от начала координат,
проводим из него параллельно касательным
к кривой в точках Мп М2, М3,... прямые
Р/li, Рп3, Рп3,до пересечения с осью ОУ
в точках л1( л2, п3,... Из этих точек про-
водим параллельно оси ОХ прямые r^Ni,
n3N3, n3N3, ... до пересечения с соответст-
вующими ординатами (или их продолже-
ниями) пцМх, т2М2, т3М3>... в точках
N,, N~, Nз, ...
Ломаная или кривая является
приближённым графиком функции у= X/' (х);
при Х= 1 получим искомый график произ-
водной у =/' (х).
Если А 1, то мы строим точки Q3
Q3,... с ординатами, равными ординатам
точек IVi, N.lt N3..., разделённым на X. Кри-
вая, соединяющая точки Qx, Q2, Оз,...,
является графиком производной.
ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
Если дан график функции у - - / (х)
(фиг. 340), то значение определённого пнте-
ь
грала j" f (х) dx можно найти графически слг-
а
дующим образом. Площадь MNTP, величина
которой даёт величину определённого инте-
грала, разбиваем на входящие и выходящие
прямоугольники так, чтобы входящие и вы-
ходящие криволинейные (заштрихованные)
площади были приблизительно равны; тогда
искомую площадь можно заменить сум-
мой площадей прямоугольников PMNtQa,
QiNj NsQa и т. д.
ЧИСЛЕННЫЕ И ГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
261
Чтобы графически получить число, рав-
ное числу, измеряющему площадь первого
прямоугольника RMNiQt, отложим на оси
ОХ от начала координат отрезок OP = X, а по
оси О/ отрезок 0‘A^NyQi и из точки R про-
ведём прямую, параллельную РАг до пере-
сечения с QjNi в точке St. Длина отрезка
QjSj будет графически выражать площадь
прямоугольника RMNiQ1, делённую на X.
Затем таким же способом строим отрезок,
длина которого численно равна площади
второго прямоугольника. Для этого откла-
дываем на оси OY от начала координат от-
Фиг. 340
резок OA2=Q2N2 и из точки проводим
прямую, параллельную РА2, до пересечения
с прямой Q.,N2 в точке S2. Отрезок S[S2 даёт
площадь второго прямоугольника, делённую
на X, а отрезок Q2i’2 — сумму площадей пер-
вого и второго прямоугольников, делённую
на X, и т. д. При л = 1 длины отрезков
QjSj, S,S2 и т. д. численно равны площадям
прямоугольников PMiVxQn QXN tN2Q2 и т.д.,
а длина отрезка Q2S2 — сумме площадей
этих прямоугольников. Продолжая построе-
ние, придём к отрезку TS, который при
Х=1 даст графически величину интеграла
ь
J / (х) dx. Ломаная /?SjS2S3S будет (при Х=1)
а
представлять приближённо график функции
х
y = \l (х) dx.
а
ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
ОБЫКНОВЕННЫХ ДИФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ 1-го ПОРЯДКА
dy
Всякое уравнение = / (х, у) даёт зави-
симость между координатами точки (х, у)
и угловым коэфициепто.м касательной к ин-
тегральной кривой в этой точке.
Если дано начальное значение искомой
функции у = уо при х = х0, то из семейства
кривых, даваемых общим решением данного
уравнения, можно выделить определённую
кривую, проходящую через точку Мо (х0,у0).
Для приближённого построения этой кри-
вой разбиваем координатную плоскость пря-
мыми х = х0, х = х1; х = х2 и т. д., парал-
лельными оси 0Y, и от начала координат на
оси ОХ откладываем отрезок ОР = 1.
Определив из данного уравнения / (х0, у0),
откладываем на оси 0Y отрезок 0Аа =
= /(Хо. Уо) (фиг. 341).
Прямая РА0 параллельна касательной
к интегральной кривой в точке Мо, так как
сё угловой коэфициент равен / (х0, у0).
Из точки Мо проводим прямую M0Mi || РА0
до пересечения с прямой х = xt и измеряем
ординату у, точки Mt. Затем на оси ординат
откладываем отрезок 0At = / (хх, у-А и из
точки Mj проводим прямую PAt до
пересечения с прямой х==х2 в точке М2,
измеряем ординату у3 этой точки, отклады-
ваем по оси 0Y отрезок 0А2 = /(х2, у2)
и т. д.
Построенная ломаная Л10Л11Л42Л43Л14М5
представляет приближённо интегральную
кривую.
Графическое интегрирование системы двух
диференциальных уравнений 1-го порядка.
Пусть даны уравнения:
dy dz
(x,y,z)- = h (x,y,z).
Рассматривая x, как абсциссу, а у и z, как
ординаты, получаем две интегральные
Фиг. 341 Фиг. 342
кривые, соответствующие решению системы,
удовлетворяющему начальным условиям:
у = Уо и z = z0 при х = х0, т. е. кривые,
проходящие через точки Ма (х0,у0) и
Мо (х0, z0) (фиг. 342).
Проводим на плоскости ряд прямых
х = х0, х=х1( х = х2 и т. д., параллельных
оси 0Y, и от начала координат отклады-
ваем отрезок OP = 1.
Определив из системы уравнений вели-
чины /i(x0>y0,Zo) и /2 (х0, у0, z0), отклады-
ваем на оси 0Y отрезки ОА0 = /х (х0, у„> г0)
и 0В„ -f., (х„, уа, г0); тогда отрезки РА0 и
РВ0 будут соответственно параллельны каса-
тельным к интегральным кривым в точках
Мо и No.
Из этих точек проводим прямые
Mo-МхЦРАо и N0Mi || РВ0 До пересечения
с прямой х = х, в точках Mt и и изме-
ряем ординаты уг и этих точек.
Затем откладываем на оси 0Y отрезки
OAi = fiix^y^zO и OBi =/2(x1,y1,z1) и из
точек Mi и Nl проводим прямые MiM2 || РА1
и NLN2 II РВ, до пересечения с прямой х—х2
в точках М2 и N2; измеряем ординаты у2 и
za этих точек, откладываем на оси 0Y от-
резки OA2=f1(_xl,y..,z2) и 0В2=/2(х2,у2,г2)
и т. д.
Ломаные MjM.iMaMiM;... и N^NaN^...
будут представлять приближённо искомые
интегральные кривые.
262
МАТЕМАТИКА
В случае, когда z) = z
имеет вид:
dy rfz
dTx = z’ dx ^f
система
т.’е. равносильна уравнению
d2y
и построение упрощается: /х (х, у, г) совпадает
с ординатой z ломаной ..., которая
и является приближённой интегральной
кривой последнего уравнения.
О приближённом решении диферекциель-
ных уравнений в частных производных см.
(86) на стр. 268.
НОМОГРАФИЯ
ФУНКЦИОНАЛЬНАЯ ШКАЛА
Если на прямой выбрана начальная
точка, то функциональная шкала
функции / (х) строится следующим образом:
составляется таблица значений функции
/ (х) и значения функции в выбранном мас-
штабе откладываются на прямой от на-
чальной точки, причём положительные Т*"
значения / (х) откладываются в одну }
I
I
Фиксировав значение переменной z, по-
ложив, например, 2 1, мы можем построить
в декартовой системе координат кривую
F(x,y, 1) = О, которую мы снабдгш отмет-
кой 1; аналогичным образом строим кривые
F (х, у, 2) = 0, Е(х,у, 3)=0 ит. д., снаб-
жая каждую из них соответствующей от-
меткой, указывающей значение Z, которому
эта кривая соответствует.
После того как номограмма таким обра-
зом построена для отыскания, скажем,
Д5 I {5 г is з_________________
о i
Фиг. 343
f
I
I
I
сторону от начальной точки, а отри-
цательные в другую. Около каждой
точки построенной таким образом шка-
лы подписывается то значение аргумен-
та х, которому эта точка соответствует.
Пример /.Шкала функцииу=х1 (фиг. 343).
где в качестве единицы масштаба взят отре-
зок ОА, построена с помощью таблицы:
-3
8
х | 0 | 0,5| 1 | 1,3| 2 | 2,5| 3 | 3,5 | 4
у | 0 |о,25| 1 |2,25| 4 |б,2б| 9 | 12,25 | 16
Пример 2. Фиг. 344 изображает шкалу
функции у — 1g х (логарифмическая
шкала). Единицей масштаба служит отре-
зок АВ.
Удобно функциональную шкалу
функции / (х) строить при помощи урав-
нения у=Х/(.х), где х — отвлечённое
число, а X—единица масштаба, выра-
женная, например, в миллиметрах
(модуль шкалы).
Изменение начала шкалы отсчёта
Фиг. 345
J
••г, 5
равносильно переходу от уравнения
у = X / (х) к уравнению у = kf (х) + s.
Функциональная шкала линейной
функции называется равномерной
шкалой.
СЕТЧАТЫЕ НОМОГРАММЫ
Сетчатая номограмма, поз-
воляющая из уравнения F (х, у, z)=0
находить значения одной из перемен-
ных величин по данным значениям
двух других, строится следующим
образом.
В декартовой системе координат
ОХУ вычерчивается сетка, состоящая
.4 + 1
1-13,!?
Фиг. 344
из прямых, параллельных координатным
осям, причём прямые, параллельные оси ОУ,
помечаются соответствующими значениями
х, а прямые, параллельные оси ОХ — значе-
ниями у.
значения упри данных х=Хи z = Z, следует
итти по прямой х=Х до пересечения с кри-
вой, имеющей отметку Z, и в точке пересе-
чения прочесть соответствующее значение у.
Пример 1. Фиг. 345 изображает номограмму
для уравнения ху = z.
Пример 2. Фиг. 346 изображает номограмму для
вычисления давления ветра по формуле Р=0,12.р.и",
где Р—нормальное давление ветра в кг; В — пло-
щадка в мг; v — скорость в м/сек.
Иногда удобно строить сетчатые номо-
граммы в функциональных сетках,
т. е. при помощи функциональных шкал на
осях ОХ иОУ; при этом прямые, параллель-
ные координатным осям, имеют отметки, соот-
ветствующие этим функциональным шкалам.
На фиг. 327 (стр. 231) показана логариф-
мическая сетка (логарифмические шкалы
на обеих координатных осях), а на фиг. 328
(стр. 231) полулогарифмическая
сетка (логарифмическая шкала на оси OY
и равномерная — на оси ОХ).
НОМОГРАФИЯ
263
Пример. Уравнение ху — z после логарифмиро-
вания перейдёт в lg х + 1g у = 1g г и гиперболы
ху == const в логарифмической сетке перейдут в пря-
мые 1g х + 1g у — const (фиг. 347).
D
Фиг. 346
НОМОГРАММЫ С ПАРАЛЛЕЛЬНЫМИ
ШКАЛАМИ
Номограмма с тремя параллельными шка-
лами служит для расчётов по уравнению
вида /3 (z) =(х) +/, (у).
Построение номограммы происходит сле-
дующим образом. Проводятся две параллель-
точки пересечения
1 X 2 К
т
q—-------------д
---I ----J (
Фиг. 348
<ал вдоль линий,
ные прямые на расстоянии I одна от другой
(фиг. 348), причём величина I может быть
выбрана произвольно в соответствии
с требуемыми размерами номограммы.
Перпендикулярно к проведённым линиям
проводится прямая ОО,
которой с этими ли-
ниями определяют на-
чала шкал х и у. Фун-
KI иональныс шкалы
для х и у строятся по
уравнениям
+ S1 и v = Х2/2 (у) + s2.
Модули X, и Х2, опреде-
ляющие масштаб, и
параметры s, и s2, ха"
растеризующие сдвиг и
на которых они расположены, следует вы-
брать так, чтобы в пределах отведённого для
номограммы места уместились все те зна-
чения переменных х и у, для которых
с помощью номограммы будут производиться
подсчёты, и чтобы всё отведённое для номо-
граммы место было при этом использовано.
После того как величины /.2, s,, s2 подо-
браны, между шкалами величин х и у и
параллельно им на расстоянии т=—
1+т-
от шкалы х проводится шкала для вели*
чины г; уравнение этой шкалы
1^2 , , х . “Ь 52^1
-Х,+ х2 /з (*)+ х1 + х2
а начало отсчёта в точке её пересечения
с прямой ОО. Когда указанное построение
выполнено, прямую ОО можно стереть.
Для того, чтобы с помощью построенной
номограммы вычислить значение z при дан-
ных значениях х и у, следует соединить
прямой соответствующие этим значениям
точки шкал х и у и на пересечении этой
прямой со шкалой z прочесть искомое зна-
чение 2.
Пример. Момент инерции эллиптического сече-
ния с полуосями а и b относительно оси 2а опре-
деляется по формуле
4
Для того, чтобы привести это уравнение к виду
/»(/) = А (а)+ /, (6),
логарифмируем его:
1g 1 — lg -J- = lg a + 3 lg b .
и полагаем
А О) = lg 7 - lg Д-; a (a) = lg(a); Д (b) = 3 lg b.
Пусть требуется построить номограмму (фиг. 349>
так, чтобы уместить значения а от 1 до 10 и b — от
1 до 10; длина шкалы 125 мм, расстояние между
шкалами 140 мм.
Уравнения шкал для а и &:
и kj lg а + Si
v = Ха.З lg b 4- sa.
Для того, чтобы полностью использовать длину
шкал, нужно, чтобы значения а — 1 и & == 1 нахо-
дились на прямой ОО, т. е. соответствовали зна-
чениям и " О и v «в О, а значения а ~ 10 и b » 10
находились в конце соответствующих шкал, т. е.
соответствовали значениям:
и = 125 и v *= 125;
О = Хх 1g 1 + Si;
о = За X lg 1 + sa,
264
МАТЕМАТИКА
откуда st = 0; ss = О.
125 = X, 1g 10;
125 = 3 X, Ig 10,
125
откуда Xi « 125; *>=•—.
Далее вычисляем mi
I 140
—1—_ « io5 мл:
1+v 1+4
и строим шкалы по уравнениям:
и = 125 Ig а,
125
V - 3— 1g 6 = 125 Ig b,
125
-125 / ,ч
“ 31,25 ( Ig I - Ig =
= 31,25 (Ig I + 0,105),
а
eox.
<iooo
3000
№
S
s
s
i
J
Z.5
I
1,7
l,S
1,2
i -
A
Фиг. 349
Уравнение /4 (z) = /1 (x) + /2 (у) + /3 (/)
может быть заменено системой:
« = A W + А (У);
A (*)=* +A (().
Для определения значений z по данным
значениям х, у и t можно построить номо-
грамму с четырьмя параллельными шкалами
и одной немой шкалой.
С этой целью сначала строим номограмму
с тремя параллельными шкалами х, у, а. для
первого уравнения; параметры этих-функцио-
нальных шкал и их взаимное расположение
определяем в соответствии с размерами
номограммы и предела,ми изменения вели-
чин хну так, как это было указано выше,
но размечаем только шкалы х и у, а шкалу
а оставляем неразмеченной (немой). Далее
строим номограмму с тремя параллельными
шкалами a, t, z для второго уравнения, при-
чём шкалу а совмещаем со шкалой а, уже
построенной для первого уравнения номо-
граммы, параметры этой немой шкалы сохра-
няем прежние, подбираем параметры для
Фиг. 350
шкалы t и вычисляем параметры шкалы г и
её расстояние от шкалы а.
При пользовании такой
(фиг. 350) проводим прямую
шкал х и у, соответствую-
щие данным значениям этих
величин, и точку пересечения
этой прямой с немой шкалой
а соединяем прямой с точкой
шкалы (, соответствующей
данному значению t. Точка
пересечения этой последней
прямой со шкалой z позво-
лит прочесть искомое значе-
ние z.
Аналогичным образом строятся номо-
граммы с большим числом немых шкал.
Пример,. Максимальное касательное напряжение
<? (в “р) винтовой пружинь, с круговым попереч-
ным сечением выражается через растягивающее
усипие Р (в кг), действующее по оси витка, радиус
витка к (в мм) и диаметр проволоки d (в мм) при
помощи формулы
Q = 2? ™ .
-nd3
Требуется построить номограмму (фиг. 351) для
значений d от 2 до 10, J? от 10 до 50 яР от 5 до 503
(и, следовательно, как показывают вычисления, для
значений Q от 0,25 до 15 900).
н омограммой
через то’’ки
X a Y I l
-aw
12000
WO60
вооо
sooo
'5000
2000
ш
WQO
700
500
Ы)0
300
2С0
150
50
40
30
20
15
10
8
6
4
3
2 /
1
53
0,8
0/>
Фиг. 351
Логарифмируя, имеем:
ig Q - ig = ig р + >£ п - з ig а.
Для построения номограммы с немой шкалой
заменяем это уравнение системой:
а с= Ig Р + Ig R;
« = (ig Q — ig -^) + з ig a.
НОМОГРАФИЯ
26 5
Уравнение шкалы Р ищем в виде
= 1g P + s(.
Если необходимо иметь шкалу длиной SO лш, то
параметры Xi и st определяем из равенств:
О = Хг 1g 5 -I-
SO = \ 1g 500 + s,,
откуда 80 « Xj (1g 500 — 1g 5) = 2 Хг и XL = 40, =
= — 40 tg 5; следовательно, уравнение этой шкалы
u==40(lgP — Ig 5).
Аналогично для Р:
v = Ха 1g /? + .'а,
где Х2 и sa определяются из уравнений (длина шкалы
взята равной 84 мм):
О = Ха Ig 10 -h sa;
84 = X, Ig 50 + s2.
Вычисления приводят к следующему уравнению
этой шкалы:
ъ'= 120 (Ig Р- 1).
Взяв расстояние между шкалами Р и Р равным
80 мм, определим (стр. ^63 ) по формуле
расстояние немой шкалы а от шкалы Р: т == 20.
Модуль Ха шкалы а равен —= 30.
Zi + Х8
Далее переходим к построению номограммы
уравнения
«= (ig <? - 1g +3 Ig d.
Уравнение шкалы d имеет вид:
и' — Х^. 3 Ig d +
Длину этой шкалы выбираем, напсимер, в
168 мм (чтобы получить целое значение X ). Из
уравнений
0 » ЗХ' 1g 2 + s',
168 = 3 X/ Ig 10 + s'
определим
)/» 80; s'= - 3-80 Ig 2
и
и' » 240 (Ig d — ig 2).
Теперь можно, зная модули шкал а и d, найти
модуль Х8 шкалы Q из равенства
(шкалу а мы расположили здесь между шкалами
d и Q).
Разрешив это равенство относительно Х2, найдём
X' = 48,
следовательно, уравнение шкалы Q будет
V = 48 ( Ig Q - Ig + /, = 48 (Ig <? - Ig <?„),
где Qo подлежит определению.
Выбрав расстояние между шкалой Q и шкалой
d в 160 мм, найдём расстояние т' шкалы а от шка-
лы d:
т* — 100 мм,
следовательно, расстояние шкалы Q от немой шкалы
а равно 60 мм.
Начальную точку шкалы d можно выбрать
произвольно; выбрав её, можно следующим обра-
зом определить начальную точку шкалы Q : соеди-
ним, например, отметку 20 на шкале Р прямой
с отметкой 12 шкалы р. Точку А пересечения
этой прямой с немой шкалой а соединим, например,
с отметкой 10 шкалы d и продолжим эту линию
до пересечения со шкалой Q.
„ . Л 16РЯ
По формуле ’v = —~— находим, что в этой
точке, соответствующей значениям Р = 20, Р = 12,
d = 10, мы должны иметь Q = 1,2; это и есть, сле-
довательно, отметка этой точки.
Положив Qn = 1,2 в уравнении шкалы Q, полу-
чим уравнение этой шкалы: с' = 48 (Ig Q — Ig 1,2)r
цричём точка 1 ,2 на этой шкале — начальная.
Z - НО МСГ РАМ МА
Z -н о м о г р а м м а для уравнения
/ (-Л _ /1 (х)
/з u)
строится следующим образом.
Проводим две параллельные линии
(фиг. 35'2), выбрав расстояние d между ними
Фиг. 352
в соответствии с раздирами чертежа. Если
длины шкал х и у на этих линиях взяты
равными и /2 (величины 1Т и /2 выбираются
также в зависимости от желательных раз-
меров номограммы), то шкалы х и у имеют
уравнения:
и = о [/1 (X)— /1 (о,))]; V = >3[/3 (У) —/3(МЬ
где аа п Ьв — значения х и у, при которых
/, (х) и /, (у) принимают наименьшие значе-
ния, а модули и Х2 определяются равен-
ствами:
А________с_______? ________к
где а и b — значения х и у, при которых
соответственно /, (х) и f., (у) принимают наи-
большие значения. Направления шкал х и
у выбираются противоположными.
Далее, из начальных точек А и В, име-
ющих отметки х = с0 и у — Ьо, проводятся
прямые, перпендикулярные шкалам х и у,
и на них откладываются отрезки
АЛ “ + + q
И
X2tZ/2 (ЬА
вв'- ’
где q—расстояние по вертикали между на-
чалами шкал (т. е. точками А и В). Шкала
z строится на прямой А'В*. Выбрав какие-
либо значения х0 и у0 и подсчитав соответ-
ствующее значение z0, соединяем точки
с отметками х0 и у0 и в точке пересечения
А'В' с этой прямой ставим отметку 20. При-
няв эту точку за начальную, строим шкалу
z по уравнению
w _ S х [ __________/з (Zp) 1
w - Ч [>,2 + ХД, (г) Х2 + G/3(z0)j ’
266
МАТЕЛ1АТИКА
где
S = j/”[Xj/j (а0) 4- Х2/2 (б0) 4- <?р -|- (/а.
Положительные значения w откладыва-
ются от точки с отметкой г0 к шкале у, а
отрицательные — к шкале х.
Пример. Возвышение наружного рельса Н глав-
ного пути (в метрах) в зависимости от скорости по-
езда V (в км/ч) и радиуса закругления /? (в метрах)
определяется соотношением
0,012 У»
“ R
Требуется построить номограмму (фиг. 353) для
значений V от 60 до 100 и R от 500 до 2 500 (и,
следовательно, как показывают вычисления, для
значений Н от 0,017 до 0,24).
Переписав формулу в виде
R _ °,°12 У3
строим шкалы V и Н на параллельных прямых.,
а шкалу R — на наклонной.
Уравнение шкалы V:
и = X;-0,012 (Vя — 603)
Взяв длину этой шкалы ^==153,6 мм, имеем
153,6 153,6 2
1 ~ 0,012 (10;)= - 60г) 78,8 _
и, следовательно
и = 0,024 (Vй — 6О3).
Уравнение шкалы Н:
v - Х2 (К - 0,017).
Взяв длину этой шкалы ls— 156,1 мм, имеем
. 156,1 156,1
а= 0,24 -0,017 “ 0,223
и, следовательно
v = 700 (Н- 0,017).
Приняв расстояние rf между шкалами равным
150 мм, а расстояние q по вертикали между начала-
ми шкал 140 мм, получим:
АА' 2- 150-0,012-60’
= 2-0,012-602 + 700-0,017+ 140 == 4’4,
ЯВ'О 700-150.0,017
2-0,12-602 + 700-0,017 + 140 ’ ’
«-]/(2.0,0'12.604 700.0,01'7 + 140)5+150’-= 281,3.
Взяв У„ = 72, Но = 0,027, получим 7?„ ==
0012-722
» , ' — = 2304. Соединив отметку 72 шкалы
V с отметкой 0,027 шкалы Н, ставим в точке пере-
сечения этой прямой с прямой А'В' отметку 2301
и строим на А'В' шкалу R по уравнению
/ R __ 2304 ____\
281,3-2 ^-700 +~2Д- - 700^'2'^2304')
ИЛИ
-=281’3 (3-50+-7Г-0’868)-
ЛИТЕРАТУРА И ИСТОЧНИКИ
Общая справочная литература
1. Астафьев А. Ф. Инженерная справочная
книга. Т. I, изд. 16-е, Л.-М., ОНТИ, 1937.
540 с.
2. Бронштейн И. Н. и Семендяев К. А.
Справочник по математике М. — Л.. Гостехиз-
дат, 1948, 556 с.
3. Выгодский М. Я. Справочник по элемен-
тарной математике. Изд. 3-е, М, — Л., Гостех-
издат, 1948, 280 с.
4. Машиностроение. Энциклопедический справоч-
ник. Под ред. Е. А. Чудакова. Т. I, М.»
Машгиз, 1947, 456 с.
5. Справочное руководство по машиностроению.
Под ред. В. М. Майзел ь. Г. I, Математика.
Харьков. ГНТИ Украины. 1937, 764 с.
6. Технический справочник транспортника. 1. 1,
М.—Л., Гострансиздат. 1932.
1. Hfltte. Справочник для инженеров, техников
и студентов. Т. I, М. — Л., Госмашмет. 1936.
Математические таблицы
8. Брадис В. Четырёхзначные магматические
таблицы. М., Учпедгиз, 1948, 63 с.
9. Б р е м и к е р К. Таблицы логарифмов чисел и
тригонометрических функций с шестью десятич-
ными знаками. М., Редбюро ГУГСК НКВД,
1938.
10. Г л а з е н а п С. П. Математические и астроно-
мические таблицы. В двух частях. Л., Изд-во
Академии наук СССР, 1932, 240 с.
11. Петерс И. Шестизначные таблицы триго-
нометрических функций. М. Изд. 2-е. Изд-во
ГУГСК НКВД СССР, 1937, 294 с.
12. Рыжик И. М. Таблицы интегралов, сумм
рядов и произведений. Изд. 2-е, М. — Л., Гос-
техиздат 1948, 400 с.
13. Сегал Б. И. и Семендяев К. А. Пяти-
значные математические таблицы. М., Изд-во
Академии наук СССР. 1948.
14. Таблицы Барлоу — квадратов, кубов, корней
квадратных, корней кубичных и обратных вели-
чин целых чисел от 1 до 10 000, Изд. 2-е,
М.-Л., ОНТИ, 1936, 233 с.
15. Хохлов А. И. Карманные математические
таблицы (пятизначные). М. — Л., Гостехиздат,
1947.
16. Янке Е. и Эм де Ф. Таблицы функций с
Формулами и кривыми. М. — Л.. Гостехиздат,
1948, 420 с.
Арифметика, алгебра и элементарная геометрия
17. и ног ра дов С. П. Основания теории детер-
минантов. М. — Л., Гл. ред. общетех. лит-ры,
1935 103 с.
18. Киселёв А. П. Арифметика. М, Учпедгиз,
1948, 168 с.
19. К и с. е л ё в А. П, Алгебра. Ч. 1—2. М. Учпед-
гиз. 1947; ч. I, 112 с.; ч. 2. 232 с.
20 К и с е л ё в А. П. Геометрии. Ч. 1 (Планимет-
рия), ч. 2. (Стереометрия) М,. Учпедгиз. 1943.
21. КУрош А. Г. Курс высшей алгебры. М. —Л.,
Гостехиздат, 1946, 314 с.
22. М л о д з е е в с к и й Б, К, Основы высшей алгеб-
ры. М.—Л., Госиздат, 1922, 1 11 с.
23. Шапиро Г. М. Высшая алгебра. М., Учпед-
гиз, 1935, 317 с.
Тригонометрия (прямолинейная, гиперболическая
и сферическая)
24. Б е р м а н т А. Ф. и Л ю сте рни к Л. А.
Тригонометрия. Изд. 2-с., М., Учпедгиз, 1947.
192 с.
ЛИТЕРАТУРА И ИСТОЧНИКИ
267
25. Рыбкин Н. Прямолинейная тригонометрия.
Изд. 14-е, М., Учпедгиз. 1935, 104 с.
26. Степанов Н. Н. Сферическая тригономет-
рия. Изд. 2-е, М.-Л., Гостехиздат, 1948. 154 с.
27. Шмулевич П. К. Прямолинейная тригоно-
метрия. М.-Л., ОНТИ, 1937, 228 с.
28. Фишман Н. М. Комплексные числа, ряды и
гиперболические функции, М,—Л., ГТТИ, 1933,
104 с.
Математический анализ (диференциальное
исчисление, интегральное исчисление,
бесконечные ряды, диференциальные
уравнения)
29. БариН. К. Теория рядов. М.5 Учпедгиз,
1936, 139 с.
30. БермантА. Ф. Курс математического ана-
лиза для втузов. Ч. 1 — 2. Изд. 3-е, М.—Л.,
Гостехиздат, 1946,
31. Гурса Э. Курс математического анализа.
Т. 1. 2 и 3. Пер. с франц., изд. 3-е, М.—Л.,
ОНТИ. 1936.
32. Кошляков Н. С. Основные диференциаль-
ные уравнения математической физики. М.—Л.,
ГТТИ, 1933, 512 с.
33. Курант Р. иГильбертД. Методы мате-
матической физики. Т. 1 — 2. Пер. с нем., М.—Л.,
Гостехиздат, 1933 — 1945.
34. Серебренников М. Г. Гармонический
анализ. М.—Л., Гостехиздат. 1948.
35. Л опшиц А. М. Шаблоны для гармонического
анализа. М,—Л.» Гостехиздат, 1948, 30 л.
36. Лузин Н. Н. Диференциальное исчисление.
М., «Советская наука», 1946, 451 с.
37. Л у з и н Н. Н. Интегральное исчисление. М.»
«Советская наука». 1946, 379 с.
38. Л у р ь е А. Й. Операционное исчисление в
приложениях к задачам механики. М. — Л.,
ОНТИ, 1938, 222 с.
39. Немыцкий В. В.. С л у д с к а я М. И. и
Черкасов А. Курс математического анализа.
Т. 1 — 2, М.—Л., Гостехиздат, 1944.
40. Петровский И. Г. Лекции по теории обык-
новенных диференциальных уравнений. Изд.
2-е, М.—Л., Гостехиздат, 1947, 196 с.
41. Поссе К. и Привалов Й. Курс диферен-
циального исчисления. Изд. 5-е. М. — Л.,
ОНТИ, 1939, 355 с.
42. Поссе К. и Привалов И. Курс интеграль-
ного исчисления. М.—Л., ОНТИ, 1939. 480 с.
43. Стеклов В. А. Основные задачи математиче-
ской физики. Ч. 1. Пг, Изд. Российской Ака-
демии наук, 1922. 286 с.
44. Степанов В. В. Курс диференциальных
уравнений. Изд. 4-е, М. — Л., Гостехиздат,
1945. 406 с.
45. Привалов И. И. Ряды Фурье. М. — Л.,
ОНТИ, 1934. 164 с.
46. Смирнов В. И. Курс высшей математики,
Т. 1, 2, 3, М. —Л., Гостехиздат, т. 1 и 2, 1948;
т. 3, 1949.
47. Тимофеев А. Ф. Интегрирование функций.
М.—Л., Гостехиздат, 1948, 432 с.
48. Фихтенгольц Г. М. Курс деференциаль-
ного и интегрального исчисления. Т. I, II, III.
М.—Л., Гостехиздат, 1947—194 8—1949.
49. Фихтенгольц Г. М. Математика для инже-
неров. Изд. 3-е. М. —Л., ГТТИ ч. I, 1931; ч. 2,
вып. 1, 1932; ч. 2, вып. 2, 1933.
50. Фра Й Т. Элементарный курс диференциальных
уравнений. Пер. с англ. М. — Л., ГТТИ, 1933,
196 с.
51. Фра нк Ф. и Мизес Р. Диференциальные и
интегральные уравнения математической физи-
ки. Ч. 2, М.-Л.. ОНТИ, 1937. 998 с.
Вариационное исчисление
52. Егоров Д. Ф. Основания вариационного
исчисления. Пг., Госиздат, 1923, 77 с.
53. Лаврентьев М. А. и Люстерник Л. А.
Курс вариационного исчисления. М. — Л.,
ОНТИ. 1938, 192 с.
54. С м и р н о в В. И., Крылов В. И. и Кан-
тарович Л. В. Вариационное исчисление. Л.,
КУБУЧ, 1933, 203 с.
См. также [31] и [33].
Аналитическая геометрия
55. Бескин Н. М. Курс аналитической геомет-
рии для втузов. М, — Л., Гостехиздат, 194У,
500 с.
56. БюшгенсС. С. Аналитическая геометрия.
Ч. 1, М.—Л., Гостехиздат, 1946. 560 с.
57. Мусхелишвили Н. И, Курс аналитиче-
ской геометрии. Изд. 3-е, М.—Л.. Гостехиздат.
1947, 644 с.
58. П р и в а л о в И. И. Аналитическая геометрия.
Изд. 13-е, М,—Л., ОНТИ. 1942. 251 с.
Диференциальная геометрия
59. Графический справочник по математике. Атлас
кривых. Под ред. А. Ф. Берманта. М.—Л.,
ОНТИ. 1937.
СО. Е г о р о в Д. Ф. Диференциальная геометрия.
Госиздат, 1923. 288 с.
61. Рашевский П. К. Курс диференциальмой
геометрии. М.-Л., ОНТИ, 1938, 336 с.
62. Фиников С. П. Диференциальная геометрия,
М., Учпедгиз, 1936. 216 с.
См. также [2] н [55].
Векторное исчисление
63. Г о л ь д ф а й н И. А. Элементы векторного
исчисления. М.—Л., Гостехиздат. 1948, 176 с.
64. Дубнов Я- С. Основы векторного исчисления.
Ч. 1, изд. 3~е. М. — Л.. Гостехиздат, 1939а
330 с.
65. К о ч и н Н. Е. Векторное исчисление и начала
тензорного исчисления. Изд. 6-е. М. — Л.,
ГОНТИ, Ред. техн, теорет. лит., 1938, 456 с.
Теория функций комплексного переменного
66. Лаврентьев М. А. Конформные отображе-
ния. М.—Л., Гостехиздат, 1946, 160 с.
67. Маркушевич А. И. Элементы теории ана-
литических функций. М., Учпедгиз, 1944. 544 с.
68. Привалов И. И. Введение в теорию функ-
ций комплексного переменного, М.—Л., Гостех-
издат, 1945.
69. Днчевский С. А. Функции комплексного
переменного. М.—Л.,, ОНТИ, 1937. 198 с.
См. также [46].
Теория вероятностей и метод наименьших
квадратов
70. Бернштейн С. Н. Теория вероятностей.
Изд. 4-е, М.—Л., Гостехиздат, 1946, 556 с.
71. Г л и в е н к о В. И. Теория вероятностей. М.,
Учпедгиз, 1937.
72. Гнеденко Б. В. иХинчннА. Я. Элемен-
тарное введение в теорию вероятностей, М.—Л.,
Гостехиздат, 1946, 128 с.
73. Гончаров В. Л. Теория вероятностей. М.,
Оборонгиз, 1939, 428 с.
74. Иванов А. А. Теория сшибок и способ наи-
меньших квадратов Пг., Научное книгоизд-во.
1921, 56 с.
75. Романовский В. И. Основные задачи тео-
рии ошибок. М.—Л., Гостехиздат. 1947, 116 с.
76. Романовский В. И. Математическая ста-
тистик:!. М. —Л., ОНТИ, 1938, 528 с.
77. Фрай Т. Теория вероятностей для инженеров.
М.-Л., ГТТИ, 1934, 383 с.
См. также. 191).
Исчисление конечных разностей и интерполирование
78. Безикович я. С. Исчисление конечных
разностей. Л., Изд. Лен. гос. унив., 1939, 370 с.
79. ГельфондА. О. Исчисление конечных раз-
ностей. Ч. 1. М.—Л., ОНТИ. 1936.
80. Гончаров В. Л. Теория интерполирования
и поиближення функций. М. — Л., ОНТИ, 1934,
316 с.
81. Марков А. Исчисление конечных разностей.
Изд. 2-е, Одесса, «Mathesis», 1910, 274 с.
См. также [84], [85] и [90].
Приближенные вычисления, приближённое решение
алгебраических и трансцендентных уравнений,
численные и графические методы анализа,
эмпирические формулы
82. Безикович я. иФридман А. Прибли-
жённые вычисления. Изд. 2-е, Л., Гостехиздат,
1930. 188 с.
268
МАТЕМАТИКА
83. Брадис В. Арифметика приближённых вы-
числений. Изд. 2-е, М. — Л.» Госиздат, 1931,
231 с.
84. За идеи Г. Элементы прикладного анализа.
АХ.-Л., ГТТИ. 1932, 204 с.
85. КрыловА. Н. Лекции о приближённых вы-
числениях. Изд. 2-е, Л., Изд-во Академии наук
СССР, 1933, 543 с.
86. П а н о в Д. Ю. Справочник по численному
решению диференциальных уравнений в частных
производных. Изд. 3-е, М.—Л., Гостехиздат,
1949. 128 с.
87. Панов Д. Ю. Счётная линейка. Изд. 5-е,
М. -Л.. Гостехиздат, 1946, 127 с.
88. Рунге К. Графические методы математических
вычислений. Пер. с нем., М.—Л.. ГТТИ. 1932,
167 с.
89 Семендяев К. А. Эмпирические Формулы.
М. - Л., ГТТИ, 1933, 88 с.
90. Скарборо Д. Численные методы математи-
ческого анализа. Пер. с англ., М.-Л., ГТТИ,
1934. 440 с.
91. Уиттекер Э. и Робинсон Г. Математи-
ческая обработка результатов наблюдения. Пер.
с англ., М.-Л., ГГТИ, 1933, 36 1 с.
92. Ф р а н к М. Л. Элементарные приближённые
вычисления. М.-Л.» ГТТИ, 1932, 166 с.
См. также [49].
Номография
93. Гавра Д. А. Основы номографии. Л, КУБУЧ,
1934. 162 с.
94. Герсеванов Н. М. Основы номографии.
М.-Л., ГОНТИ, 1932, 90 с.
95. Глаголев Н. А. Теоретические основы номо-
графии. Изд. 2-е, М.—Л., ГТТИ, 1936, 252 с.
96. Мелентьев П. В. Номография. М. — Л.
ГТТИ, 1933, 248 с.
97. Мелентьев П. В. Построение номограмм,
Гостехиздат, 1930, 101 с.
98. Справочник по номографии. Под ред.
И. А. Г л а г о л е в а. М.-Л., ОНТИ. 1937,
276 с.
99. Франк М. Л. Номографический справочник
по математике, механике, физике и сопротив-
лению материалов. М.~Л., ГТТИ, 1933, 151 с.
См. также [49].
ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ Д. И. МЕНДЕЛЕЕВА
ПЕРИОДИЧЕСКИЙ ЗАКОН
Д. И. МЕНДЕЛЕЕВА
Периодический закон был открыт
Д. И. Менделеевым в 1869 г. Этот закон
Д. И. Менделеев сформулировал следую-
щим образом: «Свойства простых тел, а
также формы и свойства соединений эле-
ментов находятся в периодической зависи-
мости от величины атомных весов». Совре-
менная формулировка периодического за-
кона: все химические и большинство физи-
ческих свойств элементов представляют со-
бой периодическую функцию (прерывную)
от величины заряда атомного ядра.
Периодическая система элементов
Д. И. Менделеева
Открытый Д. И. Менделеевым периоди-
ческий закон позволяет расположить все
элементы в определённом порядке в таблице,
названной периодической системой элемен-
тов.
Все 92 элемента от водорода (Н) до урана
(U) распределены в девяти группах, от I
до VIII, за которой ещё следует нулевая
группа. Группы расположены вертикаль-
ными столбцами. Каждая из первых семи
распадается на две подгруппы а и Ь. Все
элементы, принадлежащие одной подгруппе,
обладают весьма близкими друг к другу
химическими свойствами. Горизонтальные
строки, по которым распределяются элемен-
ты, называются рядами. Общее число рядов
равно 10. Ряды объединяются в периоды.
Число периодов равно семи. Первые три
периода и 7-й содержат по одному ряду,
4-й, 5-й и 6-й—по два ряда. Число элемен-
тов, входящих в различные периоды, сле-
дующее:
I II III IV V VI VII
28 8 18 18 32 6
7-й период не закончен. Число элемен-
тов, входящих в период, показывает, через
сколько элементов повторяются их свой-
ства. Окончательно не установлено сущест-
вование в природе элементов 43, 61, 85 и 87.
Элементы 2-го и 3-го периодов Менделеев
назвал типическими. Типические элементы
часто объединяют с элементами чётной (Ь)
или нечётной (а) подгруппы в одну глав-
ную подгруппу, являющуюся более харак-
терной для данной группы; в таком случае
другая подгруппа называется побочной. Эле-
менты группы 1а называются щелочными ме-
таллами, группы Па — щелочно-земельными
металлами, группы II] — землями, группы
VII — галоидами, нулевой группы — инерт-
ными газами. Определённому горизонталь-
ному ряду и определённой вертикальной
подгруппе соответствует один элемент. Су-
ществует два исключения: 1) все девять
элементов, входящих в группу VIII, кото-
рая не делится на подгруппы; здесь в трёх
местах вместо одного элемента имеется три,
так называемые триады; 2) в 8-м ряду
в подгруппе 111а находится вместо одного
пятнадцать элементов (начиная с 57 La до
71 Ср), которые называются редкими зем-
лями, или лантанидами. Последние двенад-
цать элементов таблицы от Z=81 до Z=92
(Z — атомный номер — порядковое число
элемента, стоящее перед символом элемента
в периодической системе) радиоактивны.
Первые три элемента имеют также и по
устойчивой, т. е. нерадиоактивной, разно-
видности. Сюда относятся Т1 (Z = 81), Pb
(Z = 82) и Bi (Z = 83). Все разновидности
остальных семи известных элементов (Z=
=84, 86, 88, 89, 90, 91 и 92) радиоактивны.
В ряду от водорода до урана существует
всего 92 элемента. Пользуясь рентгенов-
скими лучами, можно определить номер
элемента. Сравнение атомных весов А с по-
рядковыми числами Z показывает, что для
небольших Z приблизительно, а иногда и
весьма точно порядковое число равно поло-
вине атомного веса, т. е. Z = ~^А. Чем боль-
ше Z и А, тем больше атомный вес прево-
сходит 2Z; для урана мы имеем А = 2,6 Z.
Наибольшая валентность элементов каж-
дой группы в их кислородных соединениях,
за немногими исключениями, равна номеру
группы, в которой стоит элемент. Типы
высших кислородных соединений приведены
внизу таблицы. Элементы I, II и III групп
почти исключительно металлы, которые или
совсем не образуют соединений с водоро-
дом или эти соединения малоустойчивы.
Металлоиды же, находящиеся в IV, V, VI
и VII группах, дают характерные водород-
Периодическая система элементов Д. И. Менделеева
Пе- РИС'ДЫ g Группы элементов
I а b II а b III а b IV а b V а b VI а b VII а Ь VIII 0
I 1 р 1 ‘ 5 1.0030 В одород Н- 4,ооз Г слий
I! 2 Li Литий ? я о (к . 4* 10.? В Бор 12.о? С Углерод 7 14,oosN Азот 816,еооО Кислород 919,со Г Фто;> Ме’° Неон
III Na22,” Натрий Магний 26. эт А1 Алюминий 28,с? Si Кремний 15зо,88Р Фосфор 16 с 32,С6бЬ Сера *7 35.457Ci Хлор А»-18 39,944 Аргон
IV 5 И-г 19 Cli М„-дь Г-т - л. 20 КельнИЙ 30 7„ Цинк SC 45.1?? Скандий a69,72Ga •Г аллий It 47л?2 „ „Титан б 2 72,боОе Германий V 50,9а3 Ванадий 3374,91AS Мышьяк СГ 52,24 X ром 3478.86Se Селен Мп.Л Мг; ганец 3579,91! Вг Бр> м ге.щ! Железо СО58? Кобальт Никель 35 ^Г83,7 Криптон
V С» 7 t D 8-3?7 КуВия7 107.580 Ag Серебре §Т 87,63® Стре нций ii2,4iCd Кадмий ¥ 88,? Иттрий 49 । 114,76*а Индий Zr 914° Цирконий 50 П8,7оЬП Олово Nd 92,9/ Ниобий 121.76Sb Сурьма МО 95.? Молибден 52 *т'л 127.611 е Теллур 43_ 53 I 126-92*» И од RuioiV Рутений Ш1102? Родий Pdio647° Палладий Хеки ,з Ксенон
VI 8 g CSiS259i Цезий 79 197,2 AU Зол ото On ( G £:ь‘ 137,36 Барий 8200,6iHg Ртуть . Lai38,927 Лантан 204.39Т1 Таллий Hfl78?2 Гафний 207,21РЬ Свинец Tai8o7838 Тантал 209,ooBi Висмут W18374 Вольфрам 84 гь (210)РО Полоний Re 186? Рений 85- OS 190? Осмий 1Г19377 Иридий Ptl95,? Платина Rn86222 Раден
VII 10 87- fe226J Радий АС(227)89 Актиний Th232,n Торий Ра2319’ Протактиний и238,0972 Уран
Высшие со- леобразую- щие окислы r2o RO и2о3 RO2 R2o5 RO8 R2O7 ro4
Высшие во- дородные соединения 1 rh4 rh8 RH2 RH
♦Л а н т а н иды
Се58 140.13 Церий Рг59 140,92 Празеодим Nd60 144,27 Неодим I1 Sm62 Eu63 150,43 152,0 Самарий Европий Gd64 156,9 Гадолиний Tb65 Dy68 Но67 Егез 159.2 162,46 164,91 167,2 Тербий Диспрозий Гольмий Эрбий Ти89 169.4 Тулий Yb70 Т’Ч 7 !zl Иттербий Ср7* 174.99 Кассиопей
270 химия
ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ Д. И. МЕНДЕЛЕЕВА
271
ныс соединения, типы которых приведены
внизу таблицы. Из приведённого ряда вид-
но, что валентность элементов но водороду
равна восьми минус номер группы. Таким
образом сумма валентностей по водороду и
кислороду равна 8. В каждую клетку пе-
риодической системы входит несколько раз-
новидностей данного элемента, называемых
изотопами, которые обладают одинаковыми
химическими свойствами, но разным атом-
ным весом. Так как практически вся масса
атома сконцентрирована в ядре (см. Строе-
ние атома, стр. 318), то очевидно, что эти
разновидности отличаются друг от друга
составом и строением ядра. Изотопы имеют
разные атомные веса, но одинаковые атом-
ные номера. Большинство элементов пред-
ставляет собой смесь изотопов постоянного
состава. Изотопы образуются и при радио-
активном распаде атомов (см. Строение
атома, стр. 318). Изотопы могут быть полу-
чены и при искусственном преобразовании
элементов (см. Строение атома, стр. 318).
Разновидности различных элементов, имею-
щие различные порядковые числа Z, но
одинаковые атомные веса, называются изо-
барами (см. Строение атома, стр. 318). По-
рядковый номер элемента Z соответствует
числу электронов в атоме пли же числу
элементарных положительных зарядов ядра
(см. Строение атома, стр. 318), Современ-
ное определение элемента гласит: химиче-
ский элемент есть вид атомов, обладающих
одинаковым ядерным зарядом, устойчивость
которого зависит от массы ядра.
Таблица 2
Изотопы
Массовое число—скруглённый до целого числа атом-
ный вес; в скобках отмечено буквой Е—естественный
изотоп; цифра после Е означает его процентное со-
держание; й-, р—изотоп получен искусственным путём
и радиоактивен.
Массовое число
Таблица 1
Международные атомные веса
Название элемента Порядковыи № Символ Атомный вес Наз- вание элемента | Порядковый № | | Символ Атомный вес
Азот . . . Актиний . Алюминий Аргон . . Барий . . Бериллий Бор . . . Бром . . . Ванадий . Висмут Водород . Вольфрам Гадолиний Галлий . . Гафний . . Гелий . . Германий Гольмий . Диспрозий Европий . Железо Золото . . Индий . . Иод . . . Иридий Иттербий Иттрий . . Кадмий Калий . . Кальций . Кассиопей Кислород Кобальт . Кремний . Криптон . Ксенон . . Лантан . . Литий . . Магний Марганец Медь . . . Молибден Мышьяк Натрий 7 89 13 18 56 4 5 35 23 83 1 74 64 31 72 2 32 67 66 63 26 79 49 53 77 70 39 48 19 20 71 8 27 14 36 54 57 3 12 25 29 42 33 11 N Ас А1 Аг Ва Be В Вг V Bi Н W Gd Ga Hf Не Ge Но Dy Eu Fe Au In J Ir Yb Cd К Ca Cp 0 Co Si Kr Xe La Li Mg Mn Cu Mo As Na 14,008 (227) 26,97 39,944 137,36 9,02 10,82 79,916 50,95 209,00 1,0080 183,92 156,9 69,72 178,6 4,003 72,60 164,94 162,46 152,0 55,85 19/,2 114,76 126,92 193,1 173,04 88,92 112.41 39,096 40,08 174,99 16.0000 58,94 28,06 83,7 131,3 138,92 6,940 24,32 54,93 63,54 95,95 74,91 22,997 Неодим Неон . . Никель Ниобий . Олово . . Осмий . . Палладий Платина . Полоний . Празеодим Протакти- ний . . . Радий . . Радон . . Рений . . Родий . . ртуть . . Рубидий . Рутений . Самарий . Свинец . . Солен . . . Сера . . . Серебро . Скандий . Стронций Сурьма . . Таллий . . Тантал Теллур Тербий . . Читан . Торий . . Тулий . . Углерод . Уран . . . [Фосфор 1 Фтор . . . 1 Хлор . . . Хром . . . Цезий . . Церий . . Цинк . . . Цирконий Эрбий. . . 60 10 28 41 50 76 46 78 84 59 91 88 86 75 45 80 44 62 82 34 16 47 2) 51 81 73 52 22 % 69 6 92 15 9 17 24 55 58 30 40 68 Nd Ne Ni Nb Sn Os Pd Pt Po Pr Pa Ra Rn Re Rh Hg Rb Ru Sm Pb Se S Ag Sc Sr Sb Tl Ta Те Tb Ti Th Tu C LJ P F Cl Cr Cs Ce Zn Zr Er 144,27 20,183 58,69 92,91 118,70 190,2 106,7 195,23 (210) 14о,92 231 226,05 222 186,31 102,91 200,61 85,48 101,7 150,43 207,21 78,96 32,066 107,88,0 45,10 87,63 121,76 204,39 180,88 127.61 159,2 47.90 232,12 169.4 12,010 238,07 30,98 19,00 35,457 52,01 132.91 140,13 65,38 91,22 167,2
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
23
24
25
26
27
28
29
30
31
И
Не
Li
Be
с
N
О
F
Ne j
Na!
Mg
Al
Si
P
S
Cl
Ar
К
Ca
Sc
Ti
V
Cr
Mn
Fe
Co
I
I Ni
Cu
Zn
Ga
32 Ge
33 As
1(E 99,98); 2(E 0,02); 3(и, p)
3(E ~ IO~S); 4(E 10G); 6(и, p)
6(E 7,5); 7(E 92,5); ."(и, p)
7(11, p); 9(E 10(1); 10 (и, p)
10(E IS,4); 11(E 81,6); 12 (и, p)
Щи, p); 11(и,р); 12(E 98,9); 13(E 1,1); 14(и, p)
13(и, p); 14(E99,62); 15(E 0.38); 16(и, p)
15(и, p); 16(E99, 76); 17(E 0.041); 18(E O.20);
19(и, p)
17(и, p); 18(и. p); 19(E 100); 2((и, p)
19(и, p); 2C(E 90,00); 21(E 0,27); 22(E 9,73);
23(и, p)
21(и, p); 22(и, p); 23(E 100); 24(и, p); 2Е(и, p)
23(и, p); 24(E 77,4); 25(E 11.5); 26(E 11,1);
27(n, p)
26 (и, p); 27(E 100); 2Ч(и, p); 2?<и, p)
27(и, p); 28(E 89,6); 2l(E 6,2); 30(E 4.2); 31
(и, p)
2?(и, p); 3l(ii. p); 3i(E 100); 32(и, p)
31(u, p); 32(E 95,1); 33(E 0,74); 34(E 4.2);
35 (и, p); 3i(E 0,016)
33(и, p); 34(и. p); 35(E 75,4); 3C(n, p); 37
(E 24.6); 38(и. p)
35(ii, p); 3C(E 0,3,17); 3,(и, p); 3'(E 0.06); 39
(и, p); 4((E 99,632); 41(n, p)
38(и, p), ЗЦЕ 93,3.); 4C(E 0,012); 41(E 6,1);
4‘.:(и. p); 42(11, p); 44 (и, p)
39(и, p); 4,‘( L-, 96,96); 41(и, p); 4‘2(R 0,64);
43 (E 0.15); 44(E 2.06); 45(11, p); 4f.(0.0033);
43(E 0.19); 49(u, p)
41(n, p); 42(и, p); 43(и. p); 44(и, p); 45
(E 100); 46(И,Р); «(u.p); 4t(u,p); 49(и, p)
4o(n, p); 4((E 7.95); 47(E 7,75); 48(E 73,45);
4‘(E 5.51); 5,(E 5.34)); 51(и, p)
47(и. p); 12(ii. p); 4:(и, p); 50(и, p); 51(E 100);
52(и, p)
49(и, p); 5((E 4,4;); 51(п, p); 52(E 83,75); 53
(E 9,43); 54 (E 2,30); 55( и. p)
51(n, p); 52(11, p); 54 (и, p); 55(E 100); 50(11, p)
53(n, p); 54(E 6,04); 55(и, p); 56(E 91,51); 57
(E 2.11); 58(E 0.25): 59(и, p)
55(и, p); 56(и, p); 57(ц. p); 58(11,p); C9(E 100);
6С(и, p)
57(п, Р); 58(E 67,4); 61'(E 26,7); 61(E 1.2); 62
(E 3,8); 63(11, p); fl4(E 0,88)
58(и, p); 6 (и, с); С1(и, p); 62(и, p); 63
(E 70,’.3); 04(и. p); K-.(E 29,87); С6(и, p)
63(n, p); 61(E 50,<•); 65(n, p); C6(E 27,3); 67
(E 3.9); 6S(E 17.4); о9(и. p); 7i(E 0,5)
64(и, p); 65(и, p); 60(11. p); 67(», p); 68(и, p);
69(EG1,2); 70(и, p); 71(E 38,8), <2(и. p):
74(и, p)
69(и, p); 7C(E 21.2); 71(и, p); 72(E 27,3); 73
(E 7.9); 74(E 37,1); 7Т(и. p); 76(E 6.5); 77
(и. p)
72(и. p); 73(11, p); 74(и, p); 75(E 100); 71(11, p);
78(n. p);
272
химия
Продолжение табл. 2
Продолжение табл. 2
Массовое число
Массовое число
34
35
36
37
38
39
40
43
44
45
46
47
48
49
50
Se
Вг
Кг
Rb
Sr
Y
Zr
Nb
Mo
Ru
Rh
Pd
Ag
Cd
In
Sn
Sb
Те
J
Xe
55 Cs
56 Ba
La
Ce
74(E 0,9); 75(и, p); 76(E 9.5); 77(E 8,3); 78
(E 24,0); 7‘(n, p); 80(E 48,0); 81(11, p);
82(E 9,3); 83(и, p);
78(и, p); 79(E 50, 6); 80(и, p); 81(E,
49,4); 82(и, p); 83(и, p); 84(и, p); 85(и,
p); 87(и, p)
78(E 0,35); 79(и, p); 8,(E 2,01); 81(и, p); 82
(E 11,53); 83(E 11,53); 83(и, p); 84(E 57,11)
82(и, p); 84(и, p); 85(E 72,S); 85(и,р); 86(и,р);
87(E27,2); 88(и, p); 89(и, p)
84(E 0,56); 85(и, p); 86(E 8,86); 87(E 7,02);
87(и, p); 88(E 82,56); 89(и. p); 9С(и, p); 91
(", P)
87 (и, p); 88 (и. p); 89 (E 100); 90 (и. p);
91(и, p); 89(я,р); 90(E 48); 91(E 11,5); 92(E
22); 93(и, p); 94(E 17); 95 (и, p); 96(E 1,5);
97 (ll, p);
92(и, p); 93(E 100); 94(и, p); 95(и, p)
91(n, p); 92(E 14,9); 93(и, p); 94(6 9,4); 95
(E 16,1); 96(E16,6); 97(E 9,65); 98(E 24,1);
99(и, p)
96(и, p); 99(и, p); 101(и, p)
95(и, p); 96(E 5,68); 98(E 2,22); 99(E 12,81);
100(E 12,70); 101(E16,98); 102(E 31,34); 104
(E 18,27); 105(и, p)
102(и, p); 103(E 100); 104(и, p); 105(и, p)
102(E 0.8); 104(E9,3); 105(E 22,6); 106(E27,2);
107(и, p); 108(E 26.8); 109 (и, p); 110(E 13,6);
111(и, p); 112(и. p)
102(и, p); 104(и, p); 105(и, p); 106(и, p); 107
(E 51,9); 108(и, p); 109(E 48,1); 110(и, p);
111(и, p); 112(и, p)
106(E 1,4); 107(и, p); 108(E 1,0); 109(и, p); 110
(E 12.8); lll(E 13,0); 112(E 24,2); 113(E 12,3);
114(E 28,0); 115(и, p); 116(E 7,3); 117(и, p)
110(и, p); 111 (и, p); 112 (и, p); 113(E 4,5);
114(и, p); 115(E 95.5); 116(и, p); 117 (и, p)
112(E21.1); 113(и, p); 114 (E 0,8); 115(E 0,4)
116 (E 15.5); 117 (E 9.1); 118(E 22,5); 119
(E 9,8); 120 (E 28,5); 122(E 5,5); 124(E 6,8);
125(и, p)
116(и, p); 118(и, p); 120(и, p); 121(E 56); 122
(и, p); 123(E 44); 124 (и, p); 127(и, p); 129
(и, p); 133(и, p)
120(Е<1); 121(и. p); 122(E 2, 9); 123(E 1,6); 124
(E 4,5); 125(E 6,0); 126(E 19,0); 127(и, p);
128(E 32,9); 129(и, p); 130(E33,l ); 131(и, p);
133(h, p); 135(и, p)
124(и, p); 126(И, p); 127(E 100); 12S(n, p); 130
(и. p); 131(и, p); 133(и, p); 135 (u.p); 137
(и. p)
124 (E 0,094); 126 (E 0,088); 127 (и, p); 128
(E 1,90); 129(E 26,23); 130(E 4,07); 131
(E21.17); 132(E 24,96); 133(и, p); 134(E 10,54);
135(и, p); 136(E 8.95); 137(и. p); 138(и, p);
139(и, p); 140(и, p)
133(E 100); 134(и, p); 138(и, p); 139(и, p); 140
(и. p)
130(E0.101); 132(E 0,097); 133(и,р); 134(E 2,42);
135(E 5,59); 136(E 7,81); 137(E 11.32); 138
(E 71,66); 139(11, p); 14С(и, p)
137(и, p); 13=(и. p); 139(E 100); I40(ll, p)
136(E<1); №(E<1); 139(n, p) ;140(E 89); 141
(и, p); 142(E 11); 143(и p);
Cg
59
60
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
86
88
89
90
91
92
Pr
Nd
Sm
Eu
Gd
Tb
Dy
Ho
Er
Ти
YB
Lu
Hf
Ta
W
Re
Os
Ir
Pt
Au
Hg
Pb
Bi
Ро
Rn
Ra
Ac
Th
Pa
V
140(и. p); 141(E 100); 142(и, p); 143(и , p)
141(и. p); 142(E 25,95); 143(E 13,0); 144(E 22,6);
145(E 9,2); 146(E 16,5); 147(и , p); 148(E6,8);
150(E 5,95); 151(и, p)
144(E 3); 147(E 17); 148(E 14); 149(E 15); 150
(E 5); 152(E 26); 154(E 20)
150(и. p); 151(E 45,1); 152(и, p); 153(E 50,2);
154(и, p)
152 (E 0,2); 154 (E 2,86); 155(E 15,61); 156
(E 20.59); 157(E 16,42); 158(1- 23,45); 159
(и. p); 160(E 20,87); 161(и, p)
159(E 100); 160(и, p)
158(E 0,1); 160(E 1,5); 161(E 22); 162(E 24); 163
(E 24); 164(E 28); 165(и, p)
164(h, p); 165(E 100); 166(и, p)
162(E 0,1); 164(E 1,5); 165(и, p); 166(E 32,9);
167(E 24.4); 163(E 26,9); 169(и, p); 170
(E 14,2); 171(и, p)
I69(E 100); 170(и, p)
168(E 0,06); 170(E 4,21); 171(E 14,26); 172
(E 21,49); 173(E 17.02); 174 (E 29,58); 175(и,
p); 176(E 13.38); 177(и, p)
17c(E 97,5); 176(E2,5); 176(и, p); 177(и, p)
174(E 0,18); 176(E 5,30); 177(E 18,47); 178
(E 27,13); 179(E 13,85); 18C(E35,14); 181(и,р)
180(и, p); 181(E 100); 182(и, p)
180(EO,2); 182(E 22,6); 183(E 17,3); 184(E30,l);
185(и, p); 186(E 29,8); 187(и, p)
184(и, p); 185(E 38,2); 186(и, p); 187(E61,8);
188(и, p)
184(E 0,018); 186(E 1,59); 187(E 1,64); 188
(E 13,3); |89(E 16.1); 190(E 26,4); 191(и, p);
192(E 41,0); 193(и, p)
191(E 38,5); 192(h, p); 193(E 61,5)
192(E 0,8); 194(E30,2); 195(E35,3); 196(E 26,6);
196(и. p); 197(и, р); 198(E 7,2); 199(и, p)
196(и, p); 197(E 100); 198(и, p); 199(и, p); 206
(и. p); 202(и, p)
196(E 0,15); 197(и, p); 198(E 10,1); 199(E 17,0):
200 (E 23,3); 201 (E 13,2); 202(E 29,6); 20E
(и, p); 204(E 6,7); 205(и, p)
200(и, p); 202(и. p); 203(E 29,1); 204(и, p);
205(E 70,9); 206(и, p); 207(E Ac C"); 208
(E ThC"); 210 (E RaC")
203(и, p); 204(E 1,5); 205(и, p); 206(E 23,6);
207(E 22,6); 208(E 52,3); 209 (и, p); 21C
(E RaD); 211(E AcB); 212(E ThB); 214
(E RaB)
207(и, p)'; 209(E 100); 210(E RaE); 2ll(E AcC);
212(E ThC); 2!4(E RaC);
210(и, p); 211(E AcC); 212(E ThC'); 214
...--------- 215 (E AcA); 216 (E ThA); 216
(E RaC');
(E RaA)
222(E 10u)
223(E AcX);
(E MsTh,)
227(E); 228(E____
227(E RaAc); 228(E RaTh); 230(E Jo); 231
(E Uy); 232(E 100); 233(и, p); 234(E Ox,)
231(E); 233(E); 234(E Uz); 234(E Ox,)
234(E 0,006); 235(E 0,71); 237(и, p); 238(E 99.2),
239(и, p)
224(E ThX); 226(E Ra);
MsThg)
НЕОРГАНИЧЕСКАЯ ХИМИЯ
Основные законы и понятия
Закон сохранения массы ве-
щества М. В. Ломоносова. Масса ве-
ществ, вступающих в реакцию, всегда равна
массе веществ, образовавшихся в резуль-
тате реакции.
Закон постоянства состава.
Откуда и каким бы путём ни было получено
данное химическое вещество, состав его
всегда остаётся одним и тем же. При обра-
зовании данного вещества элементы всегда
соединяются друг с другом в строго опре-
делённом весовом соотношении.
Закон кратных отношений. Ес-
ли два элемента образуют друг с другом
несколько химических соединений, то ве-
совые количества одного из элементос, при-
НЕОРГАНИЧЕСКАЯ ХИМИЯ
273
холящиеся в этих соединениях на одно и
то же количество другого, должны отно-
ситься между собой, как целые числа.
Закон паев (эквивалентов).
Элементы соединяются друг с другом в ве-
совых количествах, пропорциональных их
эквивалентам.
Атомный вес —число, показывающее,
зо сколько раз атом данного элемента тя-
желее 1/18 части веса атома кислорода.
Грамма том — число граммов, равное
атомному весу.
Молекулярный вес — сумма атом-
ных весов или, другими словами, относи-
тельная величина, показывающая, во сколь-
ко раз молекула данного вещества тяжелее
1/1в части веса атома кислорода.
Граммо л е ку л я рп ый вес (грам-
моль) — число граммов, равное молеку-
лярному весу.
Эквивалент — весовое количество
элемента, соединяющееся с 8 весовыми ча-
стями кислорода или заменяющее их в сое-
динениях. Атомный вес элемента всегда яв-
ляется величиной,кратной его эквиваленту.
Г раммэквива лент —число граммов,
равное эквивалентному весу.
Валентность — число, показываю-
щее, сколько атомов водорода (или другого
одновалентного элемента) может присоеди-
нить или заменить атом данного элемента.
Валентность — число, показываю-
щее, сколько эквивалентов содержится в
атомный вес
атомном весе. Соотношение ~
эквивалент
=валентности.
Валентность определяется числом элек-
тронов, которые атом отдаёт или принимает,
вступая в соединение. Поэтому можно го-
ворить о положительной (число электронов,
отданных атомом) и отрицательной (число
электронов, принятых атомом) валентности.
Валентность элемента в свободном со-
стоянии равна нулю.
Некоторые элементы обладают перемен-
ной валентностью. Для элементов главных
групп периодической системы максимальная
положительная валентность равна числу
электронов на внешней оболочке атома и
совпадает поэтому с номером группы, а
максимальная отрицательная валентность
равна числу электронов, которые могут
быть приняты атомом, и поэтому равна 8 ми-
нус номер группы.
Химическая символика. Атом
каждого элемента обозначается особым, ме-
ждународно принятым знаком. Обычно это
первая буква латинского названия элемен-
та, например, О — кислород (Oxygenium),
Н — водород (Hydrog: nium). Иногда символ
атома состоит из двух букв его латинского
названия, например, Си — медь (Cuprum).
Символ выражает и весовое количество эле-
мента, равное его атомному весу. Так, Н соот-
ветствует 1,0080 весовой части водорода; О—16
весовых частей кислорода. Сочетание сим-
волов элементов даст формулу одной моле-
кулы сложного вещества, выражая его ка-
чественный и кол йоге! вщщый состав. Так,
Н.,О — формула м.',.:с.;улы воды — показы-
вает, что молекула воды состоит из двух
18 Тим I
атомов водорода и одного атома кислорода;
формула серной кислоты H„SO4 показывает’,
что в молекулу серной кислоты входят два
атома водорода, один атом серы и четыре
атома кислорода; О3 —формула молекулы
кислорода—показывает, что она состоит из
двух атомов кислорода.
Химическое уравнение есть изо-
бражение химической реакции при помощи
формул молекул веществ, вступающих в ре-
акцию и образующихся в результате её.
Например, реакция образования воды из
элементов описывается уравнением 2Н2 4-
4-О2 = 2Н2О, показывающим, что две моле-
кулы водорода, соединяясь с одной молеку-
лой кислорода, дают две молекулы воды.
Стехиометрические расчёты.
Химические уравнения служат на практике
главным образом для расчётов, связанных
с реакцией. Например, чтобы рассчитать,
сколько кислорода понадобится для пол-
ного сжигания 1 г углерода, пишем уравне-
ние С+О2=СО2, из которого следует, что
для сжигания 12 г углерода требуется 32 г
кислорода; следовательно, для сжигания
32
1 г углерода нужно =2,66 г кислорода.
Электролиты •— вещества, дающие
в растворах ионы.
Ионы — атомы или группы атомов, об-
ладающие электрическим зарядом. Ионы,
несущие положительный заряд, называются
катионами; ионы, несущие отрицательный
заряд,—анионами. Ион изображается сим-
волом элемента, справа вверху которого
ставятся знаки зарядов по их числу. Так,
катион железа, обладающий двумя заря-
дами, изображается Fe++ или Fe”; ани-
он кислотного остатка серной кислоты
SO4 или SO/*.
Электролитическая диссоци-
ация (ионизация) — распад молекул элек-
тролита на ионы в водных растворах. Мо-
лекула, диссоциируя, образует катионы и
анионы, сумма зарядов которых равна ну-
лю. Диссоциация — обратимый процесс.
Уравнение диссоциации запишется для
сернокислого железа: FeSO, i Fe"-f-SO4 ;
для серной кислоты H2SO4 J 2Н--|-SO4 ;
для едкого кали KOHJK’ 4-ОН'.
Степень диссоциации (иониза-
ции)— отношение ч-исла молекул, распав-
шихся на ионы, к общему числу молекул.
Гидролиз — обратимая реакция об-
менного разложения между водой и солью.
Гидролизу подвергаются соли, образован-
ные: 1) сильной кислотой и слабым основа-
нием, например FeCl3 4- ЗН3О Т Fe(OH)3 4-
4- ЗНС1; 2) сильным основанием и слабой
кислотой, например NajSiO, 4- 2 FLO X
2NaOH 4-H2SiO3, 3) слабой кислотой п
слабым основанием, нанпимеэ СН..ССОМН4 4-
4- H2O^CH3COOH ь nh4oh.
О к iic лите л ьп о-в одета н овпте л ь-
н ы е реакц и и — иеакцпн, протекающие
с изменением валентности участвующих
в них атомон. Увеличение положителен
валентности или уменьшение отргщат.'льш:.!
валентности связано с потерей
274
химия
электронов. Этот процесс носит название
окисления. Увеличение отрицательной ва-
лентности или уменьшение положительной
валентности есть восстановление. Восста-
новление одного вещества всегда происхо-
дит за счёт окисления другого, например
2FeCl3 + SnCl2 = 2FeCl2 + SnCl4, В этой ре-
акции два иона железа Fe-", отнимая два
электрона у иона Sn”, переходят в 2Fe”.
Ион Sn”, потеряв два электрона, превра-
щается в ион Sn”“. Хлорное железо (FeCl3)
восстанавливается в хлористое (FeCl,), оки-
сляя двухлористое олово (SnCl2) в четырёх-
хлористое (SnCl4). В этом процессе FeCI3 —
окислитель, SnCl2—восстановитель.
Металлы
Элементы, относящиеся к металлам, об-
ладают, как правило, характерным блеском
в куске (раздробленные в порошок обычно
чёрные), ковкостью, высокой теплопровод-
ностью и электропроводностью. При обыч-
ной температуре все металлы, кроме ртути,
твёрдые. Окислы металлов (низшие) обла-
дают основными свойствами.
Первые три группы периодической си-
стемы, все побочные подгруппы и восьмая
группа заняты металлами. В пределах глав-
ных групп периодической системы метал-
лические свойства возрастают с увеличе-
нием порядкового номера (сверху вниз).
Металлоиды
Элементы, относимые к металлоидам, не
обладают блеском и ковкостью. Элек тро-
проводность и теплопроводность металло-
идов малы. Окислы металлоидов (высшие)
обладают кислотными свойствами. Типич-
ные металлоиды: галоиды, сера, фосфор.
Основные типы химических соединений
Окислы. Все элементы, кроме инерт-
ных газов, соединяются с кислородом. По-
лучающиеся при этом соединения называ-
ются окислами. Некоторые элементы обра-
зуют несколько окислов, например
FeO, Fe2O3; N„O, NO, NOa, N2O6.
Основания. Окислы металлов, соеди-
няясь с водой, образуют гидраты окислов,
называемые основаниями. Растворимые в
воде основания называются щелочами. В
растворах основания дают ионы металла,
заряженные положительно и отрицательно
заряженные ионы гидроксила ОН'.
Растворы различных оснований одинако-
вой концентрации вследствие различной
степени ионизации дают различную кон-
центрацию ионов ОН'. Чем больше степень
ионизации основания, тем выше концентра-
ция ионов ОН', тем сильнее основание.
Кислоты. Окислы металлоидов, сое-
динясь с водой, дают кислоты. Такие оки-
слы называются ангидридами соответствую-
щих кислот. В растворах кислоты образуют
положительно заряженные ионы (катионы)
Н‘ и отрицательные ионы (анионы) кислот-
ного остатка. Существуют также кислоты,
не имеющие ангидридов и не содержащие
в молекуле кислорода, по при ионизации
дающие также ноны Н", например, НС1,
НВг, H2S и т. п., так называемые бески-
слородные кислоты. Чем больше степень
ионизации кислоты (тем большую концен-
трацию ионов FF она создаёт), тем сильнее
кислота. Кислоты, при полной ионизации
дающие один ион Нф, носят название одно-
основных. Кислоты,при полной ионизации
дающие несколько ионов Н’, называются
многоосновнымп, например H2SO4, дающая
при полной ионизации два FF, — двухоснов-
ная кислота; Н3РО4— трёхосновная кис-
лота.
Амфотерные окислы. Некоторые
окислы, соединяясь с водой, дают гидраты
окислов, ионизирующиеся одновременно
в двух направлениях: как основание, давая
ионы ОН', и как кислота, давая ионы Н’.
Такие окислы называются амфотерными, на-
пример, 2Н‘ +ZnO2^ Zn (ОН)2 J Zn” -j- 2OH'.
Амфотерные гидраты окисей реагируют
и с кислотами и с основаниями, давая соли:
Zn (ОН)2 + 2НС1 = ZnCL, 4- 2Н3О;
Zn (ОН)2 + 2NaOH = Na2ZnO3 + 2Н„О.
Обычно, если металл образует несколько
окислов, то низшие обладают основными
свойствами, средние амфотерны, а высшие
обладают кислотными свойствами.
С о л и — продукт замещения ионов водо-
рода в кислоте ионами металлов или, что
то же, продукт замещения ионов гидроксила
в основании ионами кислотного остатка.
Средние соли — продукт полного за-
мещения ионов водорода в кислоте ионами
металлов. При ионизации средние соли дают
катионы металлов и анионы кислотного
остатка.
Кислые соли — продукт неполного
замещения ионов водорода в многоосновной
кислоте ионами металлов. При полной иони-
зации в растворах дают катионы металла,
катионы водорода и анионы кислотного
остатка, например KHSO4 — кислый серно-
кислый калий, NaH2PO4 — кислый фосфор-
нокислый натрий (однозамещённый).
Основные соли — продукт неполного
замещения гидроксильных анионов основа-
ния кислотными анионами. В растворах
основные соли дают катионы металла, анио-
ны гидроксила и анионы кислотного ос-
татка, например Bi(OH) (NO3)2 qt Bi” • +
+ OH' -J- 2N0'3.
Двойные соли — продукт замещения
катионов водорода в кислоте на катионы
двух металлов, например KAl(SO4)a.
Смешанные соли — продукт заме-
щения одним катионом металла катионов
водорода в двух кислотах, например CaOCl,
/ОС1
или Са<^^| — кальциевая соль соляной и
хлорноватой кислот.
ЭЛЕМЕНТЫ НУЛЕВОЙ ГРУППЫ
ПЕРИОДИЧЕСКОЙ СИСТЕМЫ ЭЛЕМЕНТОВ
(ИНЕРТНЫЕ ГАЗЫ)
В нулевой группе стоят газообразные
элементы: гелий Не2, неон NCj°, аргон
Afjg, криптон Kr|g, ксенон Xl^1 и радон
НЕОРГАНИЧЕСКАЯ ХИМИЯ
275
Rn^2, не образующие химических соедине-
ний, поэтому они названы инертными или
благородными газами. Молекулы инертных
газов состоят из одного атома. Инертные
газы содержатся в воздухе (около 1%).
Основную массу составляет аргон, осталь-
ные лишь в незначительных количествах.
Гелий, аргон и иногда неон встречаются
в газах минеральных источников. Гелий как
продукт радиоактивного распада встре-
чается в радиоактивных минералах. Все
инертные газы бесцветны и не обладают
запахом. Гелий применяется для наполне-
ния дирижаблей, газовых термометров и
для получения самых низких температур.
Неон и аргон используют для наполнения
световых трубок.
ЭЛЕМЕНТЫ ГЛАЗНОЙ ПОДГРУППЫ ПЕРВОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Водород н}
В природе в свободном виде встре-
чается в газах вулканических извержений.
В связанном состоянии очень распростра-
нен, являясь составной частью воды и всех
органических веществ.
Свойства. Водород—легкий газ без
цвета и запаха, со взрывом сгорает в ки-
слороде, образуя волу. 2Нз 4-О2 = 2Н„О.
Хранится в стальных баллонах под давле-
нием. Является энергичным восстановите-
лем, особенно в момент выделения в ре-
зультате какой-либо реакции. Атомы водо-
рода быстро соединяются в молекулы
с большим выделением тепла Н4-Н — Н2 +
4- 105 кк. Атомный водород применяется
для сварки тугоплавких металлов и спла-
вов. При помощи водородной горелки можно
получить температуры до 4000° С.
С кислородом водород даёт два соедине-
ния: воду Н2О и перекись водорода Н2О2.
Перекись водорода Н2О,. Чистая пере-
кись водорода представляет собой голубо-
ватую жидкость, легко распадающуюся на
воду и кислород, являясь поэтому сильным
окислителем. Попадая на кожу, вызывает
сильные ожоги. Перекись водорода приме-
няется как окислитель в ракетных двига-
телях. 3—1%-ные растворы Н,О2 применя-
ются в медицине как дезинфицирующее
средство.
Литий Lig
Серебристо-белый лёгкий мягкий металл.
В свободном виде в природе не встречается.
Встречается только в связанном виде в ми-
нералах. Легко окисляется, покрываясь на
воздухе плёнкой окисла Li„O. При незна-
чительном подогревании вспыхивает и сго-
рает в Li3O. С водой бурно реагирует, вы-
деляя водород и давая гидрат окисла LiOH,
представляющий собой сильную щёлочь.
Натрий Na^j
В природе встречается только в виде
соединений. Наиболее распространённые:
хлористый натрий (каменная соль), альбит
(алюмосиликат натрия), криолит Na3AlFe,
мирабилит Na,SO4-1СН2О, чилийская се-
литра NaNO3.
Свойства. Натрий — серебристо-белый
мягкий металл. На воздухе покрывается
плёнкой окисла Na2O. С водой бурно реа-
гирует, вспыхивая п выделяя водород
2Na + 2Н»О = 2NaOH 4- Н2. Хранят метал-
лический натрий погружёниььм в керосин
в железной посуде. Применяется Na для
приготовления перекиси, при органическом
синтезе, а также как сильный восстано-
витель.
Окись натрия Na„O образуется при мед-
ленном окислении натрия с недостатком
кислорода. Окись натрия бурно раство-
ряется в воде, давая гидрат окиси — силь-
ную щёлочь.
Перекись натрия Ка2О3 — светложёлтое
твёрдое вещество, образуется при горении
натрия на воздухе и в кислороде. Na»O2
сильный окислитель, обугливающий бумагу,
дерево. Из воздуха поглощает углекислоту,
выделяя кислород 2NaaO„ 4- 2СО2 =
= 2Na2CO3 4- О2, поэтому применяется для
очистки воздуха в закрытых помещениях
(подводные лодки и т. п.). Применяется
также как отбеливающее вещество. В воде
Na?O„ растворяется с сильным разогрева-
нием, образуя перекись водорода и едкую
щёлочь. Хранится в запаянных железных
банках.
Гидрат окиси катркя NaOH (едкий натр,
каустическая сода) — белое твёрдое веще-
ство. На воздухе расплывается, поглощая
влагу. Поглощает углекислоту. В воде
легко растворяется с сильным разогрева-
нием. Сильная щёлочь. Гидрат окиси нат-
рия применяется в мыловаренной и кра-
сочной промышленности, при производстве
искусственного волокна, при белении тка-
ни, при очистке нефтепродуктов, при про-
изводстве бумаги и во многих других от-
раслях промышленности.
Сода Na2CO3-10H2O— белое кристалли-
ческое, растворимое в воде вещество. Один
из главных продуктов основной химической
промышленности. Применяется в стеколь-
ной, мыловаренной и бумажной промышлен-
ности. Хранится в деревянных барабанах.
Безводный карбонат натрия Na2CO3 назы-
вается кальцинированной содой.
Бикарбонат натрия NaHCO3 — белое кри-
сталлическое вещество, растворимое в воде.
Соли натрия. Натрий образует боль-
шое число солей со всеми кислотами. Важ-
нейшие: поваренная соль NaCl; раствори-
мое стекло Na3SiO3; гипосульфит натрия
Na2S2O3; сульфит натрия Na2SO3; сульфид
натрия Na2S. Все—белые кристаллические
вещества, растворимые в воде.
Калий Kfg
В природе калий встречается только
в виде соединений: калиевый полевой шпат
KA!Si3Os, калиевая слюда KH2Al3Si8O12,
карналлит КС1-MgCl26H2O, сильвин КС1,
сильвинит KCl-NaCl.
Свойства. Серебристо-белый мягкий
металл. На воздухе покрывается плёнкой
18*
276
химия
окисла. С водой реагирует со взрывом
2К + 2Н2О = 2К0Н 4- Н2, поэтому, также
как и Na, хранится погружённым в керосин
в железной посуде
Гидрат окиси калия (едкий кали) КОН —
белое твёрдое вещество, расплывающееся
на воздухе, поглощающее углекислый газ.
Хранится в закрытой железной посуде.
Раствор гидрата окиси калия в воде—силь-
ная щёлочь. КОН дороже едкого натрия,
поэтому применяется реже. Основной по-
требитель — мыловаренная промышленность.
Соли калия применяются в сельском хо-
зяйстве как удобрения. Минералы сильвин
КС1, карналлит КС1 -MgCl2-6Н2О и др. не-
посредственно после грубого размола могут
j/потребляться как ценные калийные удо-
брения.
Нитрат калия KNO3 — белое кристалли-
ческое вещество. Применяется при произ-
водстве пороха и органических красителей.
Йодистый и бромистый калий KJ и
КВг — белые кристаллические вещества,
растворимые в воле.
Углекислый калий (поташ) К2СО3—белый
порошок, легко растворяющийся в воде.
Применяется в стекольной промышленности,
в сельском хозяйстве.
Рубидий Rbf®, Цезий Cs^3
Относятся к наиболее редко встречаю-
щимся металлам. Лишь небольшие количе-
ства их находятся в некоторых минералах
и минеральных водах. Эти металлы сами
загораются на воздухе. Их гидраты оки-
сей— самые сильные из известных щелочей.
ЭЛЕМЕНТЫ ПОБОЧНОЙ ПОДГРУППЫ ПЕРВОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Медь Ctjjg
В природе редко встречается в сво-
бодном состоянии. Чаще в виде своих сое-
динений: медный колчедан CuFeS2, медный
блеск CuS,CuCO3-Cu (ОН)2—малахит, Си2О—
красная медная руда.
Свойства. Медь представляет собой
металл характерного красноватого цвета,
хорошо проводит ток и тепло. При нагре-
вании на воздухе переходит в окислы:
Си,0 — закись меди и СиО — окись меди.
Соответственно образует два ряда солей:
соли одновалентной меди и двухвалентной
меди. Легко соединяется с галоидами, да-
вая соли. Медь широко применяется глав-
ным образом в визе сплавов с другими ме-
таллами (латунь, бронза и др.).
Сел:: меди. Сульфат меди CuSO4— белый
порошок, жадно притягивающий воду, пе-
реходя в CuSO4-5H,O— »4-.:nuii купорос —
синие кристаллы. Применяется в сельском
хозяйстве для борьб!,: с ь-редьтелямн, при
i роизводствс искусственного волокна. Хлор-
ная медь СиСП-211,0— зелёные кристаллы;
применяется в пиротехнике (зелёные раке-
ты). Все соли меди ядовиты.
Серебро Ag^°8
В природе встречается в самородном
состоянии, по основная масса серебра добы-
вается из руд. Важнейшие руды: серебря-
ный блеск Ag,S, роговое серебро AgCl.
В большем или меньшем количестве серебро
в качестве примеси находится в медных и
особенно свинцовых рудах.
Свойства. Мягкий тягучий металл,
лучше всех металлов проводит тепло и элек-
трический ток. В чистом виде не приме-
няется из-за мягкости. Применяются сплавы
с большим или меньшим количеством меди.
Серебро — одновалентный металл.
Азотнокислое серебро (ляпис) AgNO3 —
белые кристаллы. Применяется в медицине
для прижигания ран.
Хлористое серебро AgCl — белый, не рас-
творимый в воде порошок, постепенно тем-
неет па свету, разлагаясь с выделением
металлического серебра. Такими же свой-
ствами обладают бромистое AgBr и йоди-
стое серебро AgJ. Галоидные соли серебра
применяются в фотографии.
Золото Аи]д7
В природе встречается почти всегда
в самородном состоянии.
Свойства. Яркожёлтый блестящий
металл, очень ковкий. Ввиду мягкости
употребляется исключительно в сплавах
с серебром и медью. Химически малоактив-
ный металл. На воздухе даже при сильном
нагревании не изменяется. Из кислот золо-
то растворяется только в «царской водке»
(смесь 1 ч. HNO3 и 3 ч. НС1), превращаясь
в жёлтые игольчатые кристаллы золотохло-
ристоводородной кислоты Н[АиС14].
Существует два окисла золота: Au,О —
закись золота и Аи„О3 — окись золота, и
соответственно два ряда солей: соли одно-
валентного и соли трёхвалентного золота.
Все соединения золота легко разлагаются
при нагревании с выделением металличе-
ского золота.
ЭЛЕМЕНТЫ ГЛАВНОЙ ПОДГРУППЫ ВТОРОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Бериллий Be®
В природе мало распространён. Вхо-
дит в состав некоторых минералов, из ко-
торых наиболее распространён берилл
Be3A!2(SiO3)3. Некоторые разновидности
берилла, окрашенные примесями в различ-
ные цвета, являются драгоценными камнями
(изумруды, аквамарины).
Бериллий — твердый белый лёгкий ме-
талл. Применяется главным образом в не-
которых лёгких сплавах. Даст очень туго-
плавкий окисел. Металлические свойства
выражены слабо. Гидрат окиси амфотерен.
Магяий
В природе магний довод:,но распро-
странён. В пкнейшне минералы: магнезит
MgCO,, доломит .VigCO;-С;.СО,, с'.-прокисл ый
НЕОРГАНИЧЕСКАЯ ХИМИЯ
7
магний MgSO4 и хлористый магний ?«lgCl2,
входят в состав минералов кашшта и кар-
наллита, а также содержатся в морской
воде, сообщая ей горький вкус. Магний
входит в состав асбеста.
Сво йства. Магний — серебристо-белый
очень лёгкий металл. Применяется для при-
готовления различных лёгких сплавов. Из
них особенно ценен «электрон» (90% Mg,
остальное Al, Zn, Sn, Мп), применяемый
в авиационной и автомобильной промышлен-
ности. Магний на воздухе покрывается
тонкой плёнкой окисла, защищающей ме-
талл от дальнейшего окисления. При на-
гревании Mg вспыхивает ярким пламенем
(используется при фотографировании и в
осветительных ракетах) и сгорает в MgO.
Магний при нагревании медленно разлагает
воду с выделением Н2. В кислотах раство-
ряется легко с выделением водорода и об-
разованием соответствующей соли.
Гидрат окиси магния Mg(OH)„ — белый
порошок. Обладает основными свойствами,
представляя собой основание средней силы.
Сульфат магния или горькая соль
MgSO4-7H2O— белые кристаллы, раствори-
мые в воде.
Основной хлорид магния Mg(OH)Cl,
«цемент Сореля», применяется в качестве
вяжущего материала при изготовлении
мельничных жерновов, точильных камней.
Смесь цемента Сореля с древесными опил-
ками (ксилолит) употребляется для по-
крытия полов.
Кальций Са^о
В природе очень широко распростра-
нён в виде своих соединений, главным об-
разом карбоната кальция СаСО3 (мел, из-
вестняк, мрамор), а также в виде гипса
CaSO4-2H2O и фосфоритов Са3 (РО4)„.Кальций
входит в состав многочисленных силикатов.
Свойства. Кальций — ковкий твёр-
дый белый металл, на воздухе покрывается
плёнкой окисла, а при нагревании сгорает
ярким красноватым пламенем. Из горячей
воды довольно быстро вытесняет водород,
образуя гидрат окиси: Са-|-2Н2О=Са(ОН)2+
4-Н2. Кальций очень активный металл,
легко соединяющийся с галогенами, серой,
азотом, водородом. При нагревании восста-
навливает окислы почти всех металлов.
Металлический Са применяется в некоторых
сплавах со свинцом для изготовления под-
шипников.
Окись кальция (негашёная пли жжёная
известь) СаО—белое тугоплавкое вещество,
поглощающее воду с сильным разогрева-
нием, переходя при этом в гидрат окиси
кальция, или гашёную известь.
Гидрат окиси кальцпл (гашёная известь)
Са(ОН) 2 — белый порошок, обладает свой-
ствами довольно сильного основания. При-
меняется в строительной технике в смеси
с песком и водой—«известковый раствор»—
для связывания кирпичей. Г.нпёиая известь
входит в состав штукатурки.
В а ж н ей ш не со л п к а л ьц и л
Хлористый кальций СаСК — белое веще-
ство, жадно поглощ.лощее вру. Приме-
няется для высушивания многих оргаши.е-
ских жидкостей.
Сернокислый кальций C.aSO4-2H2O — бе-
лое вещество, при нагревании до )5о°С те-
ряет одну молекулу воды, переходя о
жжёный гипс, или алебастр. Алебастр, заме-
шанный на воде, даёт тесто, довольно быстро
затвердевающее, снова превращаясь в кри-
сталлогидрат. Безводный CaSO4 называется
ангидритом.
Азотнокислый! кальций Ca(NO3)2 — бес-
цветные кристаллы, растворимые в воде.
Кальциевая селитра является прекрасным
удобрением.
Белильная известь СаОС12 — белый по-
рошок, сильный окислитель, широко при-
меняется для дезинфекции и как дегазатор.
Стронций Sr®g
В природе мало распространён, встре-
чается в виде целестина SrSO4 и стронци-
анита SrCO3.
Свойства. Стронций — очень актив-
ный двухвалентный белый металл, быстро
разлагает воду и окисляется на воздухе,
легко соединяется непосредственно со мно-
гими элементами. Гидрат окиси стронция
Sr(OH)2—сильное основание. Соли строн-
ция применяются в пиротехнике, так как
они окрашивают пламя в красный цвет.
Барий BaJg7
В природе встречается в виде барита
BaSO4 и витерита ВаСО3 в сравнительно
больших количествах.
Свойства. Барий — очень активный
двухвалентный серебристо-белый металл,
быстро разлагает воду и окисляется на воз-
духе. Гидрат окиси бария Ва(ОН)2 — силь-
ное основание. Соли бария ядовиты.
Радий Ra||6
В природе довольно распространён, но
содержание его в рудах ничтожно. Самая
богатая радием ура.човая руда содержит
около 0,2 г радия на In, поэтому получить
его очень трудно и он дорог.
Свойства. Радий — серебристого цве-
та, довольно мягкий металл, разлагающий
воду при обыкновенной температуре; по хи-
мическим свойствам он похож па барий.
Радий относится к ряду радиоактивных
веществ, являясь промежуточным звеном рас-
пада урана (см. Радиоактивность, стр. 320).
Соли радия светятся в темноте. Испу-
скаемые ими лучи обладают способностью
вызывать многие химические реакции: вода
распадается на водород и кислород, аммиак—
на азот и водород и т. д. Многие вещества
начинают светиться, когда па них попа-
дают лучи радия. Луи радия разрушают
ткали организма, убивают бактерии.
ЭЛЕМЕНТЫ ПОБОЧНОЙ ПОДГРУППЫ ВТОРОЙ
ГРУППЫ ПЕРИОЦПЧЕСКОЙ СИСТЕМЫ
В а ж и е й щ и е о у а ы: цинковая обе.’ап-
ка (сернистый цинк) ZnS, галмей (карбонат
цинка) ZnCOs.
278
химия
Свойства. Синевато-белый двухва-
лентный металл, на воздухе покрывается
тонким слоем основного карбоната, что пре-
дохраняет его от дальнейшего окисления.
С водой не реагирует. Легк растворяется в
разведённых кислотах, давая соответствую-
щие соли и водород. Растворяется также в
щёлочах, образуя цинкаты и водород, так
как гидрат окиси цинка амфотерен.
Гидрат окиси цинка Zn(OH)2— белое не
растворимое в воде вещество растворимо
в кислотах Zn(OH)2 + 2НС1 = ZnCl2+2H»O
и в щёлочах Zn(OH)» + 2 NaOH = Na2ZnO2 +
+ 2Н,О. Амфотерный характер гидрата окиси
цинка выражен очень отчётливо. Растворы
сернокислого цинка и хлористого цинка
применяются для пропитки дерева во избе-
жание его гниения. Соли цинка ядовиты.
Кадмий Cd^g2
В природе встречается в рудах вместе
с цинком.
Свойства. Двухвалентный металл, по
внешнему виду напоминает цинк. На возду-
хе не окисляется, поэтому служит для кад-
мирования, покрытия других металлов с
целью предохранения от коррозии. Кадмий
применяется как компонент легкоплавких
сплавов. Гидрат окиси кадмия обладает в
отличие от цинка только основными свой-
ствами. Сернистый кадмий CdS применяется
как жёлтая краска.
Ртуть Mg2"1
В природе встречается изредка в са-
мородном состоянии в виде вкраплений в
горные породы, но главным образом в виде
сернистой ртути—HgS киновари яркокрас-
ного цвета, применяющейся как краска.
Свойства. Ртуть — единственный жид-
кий металл при обыкновенной температуре.
Из металлов данной подгруппы ртуть наи-
менее активна. На воздухе при обыкновен-
ной температуре не окисляется. Существуют
два окисла ртути: закись ртути Hg2O — чёр-
ного цвета и окись ртути HgO — красного
цвета. Оба окисла при нагревании разла-
гаются с выделением металлической ртути.
Гидраты окпслов ртути не существуют.
Металлическая ртуть применяется для
наполнения различных физических прибо-
ров: термометров, барометров и т. д. Много
ртути используется для приготовления гре-
мучей ртути — Hg(OCN)2, одного из важней-
ших детонаторов, которым наполняют раз-
ные запалы.
Амальгамы. Ртуть растворяет в себе мно-
гие металлы, образуя иногда жидкие, иног-
да твёрдые сплавы, называемые амальга-
мами. Амальгама натрия применяется как
восстановитель, амальгамы олова и сереб-
ра— для пломбирования зубов. Золото осо-
бенно легко даёт амальгамы. Поэтому ртуть
применяют для извлечения золота из поро-
ды. Пары ртути очень ядовиты даже в той
концентрации, которая создаётся при обык-
новенной температуре. Перевозят ртуть в
железных бутылях, так как железо не об-
разует амальгамы.
Соли ртути. Существует два ряда солей
ртути: соли одновалентной и двухвалентной
ртути. Каломель—хлорид одновалентной
ртути Hg2Cl2 — белое, не растворимое в воде
вещество применяемое в медицине. Суле-
ма-хлорид двухвалентной ртути HgCl.,—
белые кристаллы, растворимые в воде.
1%-ный водный раствор её применяется в
медицине как дезинфектор. Все соли ртути
сильно ядовиты.
ЭЛЕМЕНТЫ ГЛАВНОЙ ПОДГРУППЫ ТРЕТЬЕЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Бер В^1
В природе мало распространён. Встре-
чается в виде кислородных соединений:
борной кислоты Н3ВО3 и буры Na2B4O7.
Свойства. Бор — довольно инертный
трёхвалептный металлоид. С кислородом сое-
диняется только при высокой температуре,
давая борный ангидрид В2О3. В воде бор
не растворим, растворяется в щёлочах:
2 В + 2 КОН + 2 Н2О = 2КВО2 + ЗН2.
Борная кислота Н3ВО3 — белое кристал-
лическое вещество, растворимое в воде.
Кислота очень слабая.
Алюминий А12з
В природе алюминии встречается ча-
ще всех металлов, входя в состав глин,
нолевых шпатов, слюд и многих других
минералов. Важными рудами являются
крио лит AlF3-3 NaF и боксит А!2О3-2Н2О.
Свойства. Серебристо-белый трёхва-
лентный металл, легко прокатывается в
проволоку и тонкие листы. На воздухе по-
крывается тонким слоем окисла, который
предохраняет металл от дальнейшего окис-
ления. С водой алюминий не реагирует.
Разведённые серная и соляная кислоты рас-
творяют алюминий с образованием солей.
Холодная азотная кислота не действует на
алюминий. Щёлочи легко растворяют алю-
миний с образованием алюминатов.
Окись алюминия (глинозём) А1„О3 встре-
чается в природе в кристаллическом виде,
образуя корунд, по твёрдости уступающий
только алмазу. Кристаллы корунда, окра-
шенные в красный и синий цвета, — драго-
ценные камни: рубин и сапфир.
Гидрат окиси алюминия А1(0Н)3. Типич-
ный амфотерный гидрат окиси. Даёт два
ряда солей, растворяясь в кислотах и щё-
лочах. В последнем случае он даёт соли
метаалюминиевоп кислоты — НА1О2, назы-
ваемые алюминатами.
Хлористый алюминий А1С13. Безводный
хлористый алюминий представляет собой
белые кристаллы, дымящие во влажном воз-
духе вследствие гидролиза, приводящего к
образованию соляной кислоты. Хранится в
закрытых железных барабанах. Приме-
няется как катализатор при органических
синтезах.
Сернокислый алюминий A12(SO4)3-18 Н2О
белые кристаллы. Применяется для очист-
ки воды и в бумажном производстве.
НЕОРГАНИЧЕСКАЯ ХИМИЯ
279
Алюминиевые квасцы KA1(SO4)2 - 12Н2О
белые кристаллы. Применяются для дубле-
ния кож и как протрава при крашении
тканей.
Галлий Gag®, Индий In Таллий Tig®4
В природе встречаются крайне редко.
Свойства. В свободном состоянии все
три элемента представляют собой серебри-
сто-белые мягкие металлы. На воздухе они
довольно устойчивы, воду не разлагают, в
кислотах растворяются легко, а галлий
и индий растворяются также и в щёлочах.
Кроме максимальной валентности они могут
проявлять и более низкие степени положи-
тельной валентности. Для таллия, напри-
мер, характерны соединения, в которых он
одновалентен. Гидроокиси галлия и индия
амфотерны, а Т1(ОН)3 обладает только ос-
новными свойствами.
ЭЛЕМЕНТЫ ПОБОЧНОЙ ПОДГРУППЫ ТРЕТЬЕЙ
ГРУППЫ ЭЛЕМЕНТОВ ПЕРИОДИЧЕСКОЙ
СИСТЕМЫ
Скандий SCgj, Иттрий y|®
В природе скандий и иттрий встре-
чаются очень редко, входя вместе с целым
рядом других, сходных по химический свой-
ствам элементов в состав некоторых мине-
ралов, так называемых иттриевых земель.
Свойства свободных металлов скандия и ит-
трия изучены пока мало, так как получить
их в чистом виде очень трудно. В соедине-
ниях скандий и иттрий положительно трёх-
валентны. Окиси и гидраты окисей этих
металлов обладают свойствами оснований.
Соли скандия и иттрия бесцветны и боль-
шинство из них легко растворимо в воде.
Соединения скандия и иттрия практического
применения пока не нашли.
Редкие земли, или лантаниды
Название «редкие земли» объединяет
15 элементов (один из них ещё не открыт)
от порядкового номера 57 до номера 71:
лантан La^9, церий Се^°, празеодим Рг^1,
неодим Ndgg4, С1, самарий Sm^0» европий
Eug®2, гадолиний Gd^®7, тербий ТЬд®9, дис-
прозий Оудд2, гольмий HoJ®5, эрбий ЕГц|7,
туллий Тц’д9, иттербий Yb|g3 и Кассио-
пей Ср|7и.
В природе редкие земли распростра-
нены мало и обычно встречаются в смеси
друг с другом, а также с цирконием, гаф-
нием и торием. Вследствие большого сход-
ства этих элементов разделение их очень
сложно, поэтому лишь немногие из них (La,
Се, Рг и Nd) получены в чистом виде, а
некоторые вообще мало изучены. В свобод-
ном состоянии они представляют собой туго-
плавкие металлы. Воду они разлагают или
при обыкновенной температуре или при не-
большом нагревании. При этом образуются
водород и соответствующий гидрат окисла.
Легко растворяются в разбавленных кисло-
тах, образуя соответствующие соли. Все
лантаниды обнаруживают валентность + 3;
церий, празеодим и тербий, кроме того, мо-
гут быть четырёхвалентными, а самарий,
европий и иттербий — двухвалентными. Все
гидраты окисей лантанидов обладают явно
выраженными свойствами оснований.
Актиний Ас|27
Актиний встречается вместе с радием в
урановых рудах. Содержание актиния в
этих рудах ничтожно. В чистом виде акти-
ний не выделен. Актиний радиоактивен. В
соединениях актиний трёхвалентен. Соеди-
нения актиния пока почти не изучены.
ЭЛЕМЕНТЫ ГЛАВНОЙ ПОДГРУППЫ ЧЕТВЁРТОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Углерод Cg2
В природе углерод — один из самых
распространённых элементов; встречается
как в свободном, так и в связанном виде.
Свободный углерод встречается в виде двух
простых веществ—алмаза и графита. Иско-
паемый каменный уголь близок по своему
составу к чистому углероду. Соединения
углерода очень распространены в виде неф-
ти, солей угольной кислоты (главным обра-
зом кальциевых: известняк, мел, мрамор).
Воздух всегда содержит углекислый газ.
Растения и животные построены из веществ,
главной составной частью которых являет-
ся углерод. Для углерода известно громад-
ное количество соединений. Изучено не-
сколько сотен тысяч их, в то время как для
всех других элементов, вместе взятых, на-
считывается не более 25—30 тыс. соединений.
Соединения, содержащие углерод, водо-
род и другие элементы, рассматриваются в
специальном разделе химии «Органическая
химия».
Свойства. В свободном состоянии для
углерода известны три аллотропических
видоизменения — алмаз, графит и уголь
(аморфный углерод).
Алмаз—бесцветное кристаллическое веще-
ство, сильно преломляющее световые лучи.
Встречается в виде небольших кристаллов.
Алмаз — одно из самых твёрдых веществ
и поэтому находит широкое применение
для обработки различных твёрдых ма-
териалов, для резки стекла, для бурения
горных пород. Шлифованные алмазы— брил-
лианты. При нагревании без доступа воз-
духа алмаз переходит в графит.
Графит — тёмносерое кристаллическое,
мягкое вещество. На воздухе не горит
даже при сильном накаливании. Сгорает при
накаливании в чистом кислороде, превра-
щаясь в СО2. Графит в смеси с глиной идёт
для изготовления огнеупорных тиглей для
плавления металлов. В смеси с маслом или
водой применяется как смазочное вещество.
Угольный ангидрид СО2 и угольная ки-
слота Н2СО2. СО, — газ без цвета и запаха,
образующийся при горении различных, со-
держащих углерод веществ. СО2 выделяется
при дыхании животных. Под давлением СО,
80
химия
превращается в жидкость, хранящуюся в
стальных баллонах. При выливании из бал-
лона вследствие испарения отнимается так
много тепла, что СО., превращается в твёрдую
белую массу, которая, не плавясь, возго-
няется при—79' С. Твёрдый угольный анги-
дрид «сухой лёд» нашёл широкое применение
для охлаждения скоропортящихся продук-
тов, особенно при перевозках, а также в
других случаях, когда требуется низкая
температура. Угольный ангидрид раство-
ряется в воде, образуя очень слабую уголь-
ную кислоту Н2СО3. Кислота в свободном со-
стоянии не существует; при попытках вы-
делить её она разлагается на СО2 и Н2О.
Существует лишь в растворах небольшой
концентрации.
Соли угольной кислоты. Угольная кислота
как двухосновная даёт два ряда солей: сред-
ние (карбонаты) и кислые (бикарбонаты),
со слабыми основаниями даёт основные соли.
Карбонаты некоторых металлов (например
А1) полностью разлагаются водой. Все кар-
бонаты, кроме карбонатов щелочных метал-
лов, не растворимы в воде и разлагаются
при нагревании: СаСО3 = СаО + СО2.
Бикарбонаты при нагревании переходят
в карбонаты. Большинство бикарбонатов
значительно растворимо в воде.
Окись углерода СО. Газ без цвета и за-
паха, ядовит. С водой не реагирует. Окись
углерода горит на воздухе, образуя уголь-
ный ангидрид. На солнечном свету или в
присутствии катализаторов окись углерода
соединяется с хлором, образуя очень ядови-
тый газ фосген СОС12.
Сероуглерод CS2—бесцветная летучая жид-
кость, при долгом хранении желтеет и при-
обретает отвратительный запах. CS2 ядовит,
очень легко воспламеняется и поэтому тре-
бует большой осторожности при работе с
ним. Применяется для борьбы с вредителями
в сельском хозяйстве и при производстве
вискозы.
Синильная кислота (цианистоводородная)
HCN — бесцветная очень летучая жидкость,
обладает характерным запахом горького
миндаля. Один из самых сильных ядов.
Цианистый калий KCN—бесцветное кри-
сталлическое вещество. Ядовит так же силь-
но, как синильная кислота. На воздухе раз-
лагается углекислым газом: 2KCN + CO2-|-
+ Н„О = К2СО3 + 2 HCN. Обладает способ-
ностью растворять золото и серебро. При-
меняется для извлечения их из руд.
Кремний Sij8
В природе кремний — один из самых
распространённых элементов. Он составляет
около 28% доступной нашему исследованию
земной оболочки, входя в состав многих
минералов (силикатов — солей кремневой
кислоты), а также в виде кварца SiO2 (крем-
невого ангидрида).
Свойства. Кремний существует в
аморфном и кристаллическом состоянии. В
соединениях Si чстырёхвалентен. При обык-
новенной температуре он довольно инертен,
соединяясь непосредственно только с фто-
ром. При нагревании аморфный кремний
легко сгорает, образуя кремневый ангид-
рид. При нагревании соединяется с хлором,
образуя четырёххлористый кремний SiCl4—
бесцветную жидкость, разлагаемую водой с
образованием соляной и кремневой кислот
SiCl4 -р 3Н2О = H2SiO3 + 4НС1. Если испа-
рять SiCl4 во влажном воздухе, образуется
густой белый дым; поэтому SiCl4 применяют
как дымообразователь. В кислотах кремний
не растворяется, но легко реагирует со щё-
лочами: Si -р 2 КОН + Н2О = K2SiO3 + 2 Н2.
Иногда эта реакция употребляется для по-
лучения водорода. С углеродом Si даёт кар-
бид SiC (карборунд), по твёрдости прибли-
жающийся к алмазу. С металлами даёт
силициды (например Mg2Si).
Кремневый ангидрид SiO2. Кремневый
ангидрид (кремнезём, кварц), кислотный
окисел — наиболее характерное и устойчи-
вое соединение кремния. Природные разно-
видности SiO2 горный хрусталь, аметист,
дымчатый топаз, кремень. Кварц — основ-
ная составная часть песка. SiO2 не раство-
рим в воде, очень тугоплавок. Кислоты,
кроме плавиковой (HF), не действуют на
SiO2.
Кремневая кислота. Кремневому ангид-
риду соответствует очень слабая кремневая
кислота H2SiO3. Соли её называются сили-
катами. Кремневая кислота — белая твёрдая
полупрозрачная масса, пронизанная громад-
ным количеством пор и обладающая поэтому
большой поверхностью. Её под названием
силикагеля используют для поглощения раз-
личных газов и паров, а также для очист-
ки смазочных масел.
Кремневый ангидрид образует много раз-
личных кремневых кислот, отличающихся
соотношением SiO2 и воды в молекуле. Со-
став многих из них точно неизвестен; общее
название их — поликремневые кислоты.
Силикаты. Соли кремневых кислот очень
распространены в природе: полевые шпаты,
слюды, глина, асбест, тальк и многие дру-
гие. В воде растворимы только силикаты
щелочных металлов Na2SiO3 и K2SiO3, нося-
щие название растворимых стёкол. Так как
кремневая кислота очень слабая, то раство-
римое стекло вследствие гидролиза имеет
щелочную реакцию
Na2SiO3 + 2 Н2О £ 2 NaOH + H2SiO3.
Стекло. Сплавы смесей различных сили-
катов друг с другом пли с кремнезёмом
представляют собой аморфные прозрачные
твёрдые тела и называются стёклами. Обык-
новенное оконное стекло, которое идёт и на
изготовление основной массы стеклянной
посуды, представляет собой сплав силика-
тов кальция и натрия с кремнезёмом; его
приблизительная формула: Na2O-CaO-6 SiO2.
Примеси железа придают стеклу зелёную
окраску (бутылочное стекло). Цветные стёк-
ла готовят добавлением в расплавленную
массу стекла небольших количеств различ-
ных веществ: Сг2О3 — даёт зелёное стекло
МпО2 — лиловато-красное, СоО—синее, нич-
тожные количества металлического золота
окрашивают стекло в рубиново-красный цз :т
и т. д.
Кварцевое стекло, получаемое плавлением
при очень высокой температуре кварца, об-
ладает рядом ценных качеств: не задержи-
НЕОРГАНИЧЕСКАЯ ХИМИЯ
281
вает ультрафиолетовых лучей, прочнее обык-
новенного, обладает ничтожным коэфициен-
том расширения при нагревании.
Цемент—продукт, получаемый прокали-
ванием смеси глины с известняком. При
прокаливании образуются силикаты алюми-
ния и кальция. При замешивании цемента
с водой получается тестообразная, быстро
твердеющая даже под водой масса; смесь
цемента с водой и песком (цементный раст-
вор), а также смесь этого раствора с гравием,
щебнем (бетон) широко применяются в строи-
тельной технике.
Германий Ge^
Один из наиболее редких элементов; при-
менение его очень ограничено. На воздухе
не окисляется, воды не разлагает. Оба окис-
ла германия GeO и GeO2 имеют амфотерный
характер. Его соединения с галоидами раз-
лагаются водой, подобно SiCl4.
Олово Sn^
В природе встречается изредка в са-
мородном состоянии, чаще же в виде оло-
вянного камня SnO2.
Свойства. Олово существует в трёх
модификациях. Белое олово — серебристо-
белый мягкий металл, легко прокатывается
в тонкие листы — станиоль. Если изделия
из белого олова подвергаются длительному
действию низкой температуры, то па них
появляются серые пятна («оловянная чу-
ма»). Это объясняется переходом белого
олова в другую модификацию — серое
олово. Серое олово при нагревании снова
переходит в белое. При нагревании олова
выше 161°С оно переходит в .третью моди-
фикацию, которая отличается своей хруп-
костью: легко толчётся в порошок, разби-
вается, как стекло. При обыкновенной тем-
пературе олово на воздухе не окисляется,
применяется поэтому для покрытия метал-
лов, а также в виде сплавов: бронза, .баб-
биты и др. В расплавленном состоянии по-
степенно переходит на воздухе в SnO2. С
водой Sn не реагирует, растворяется в кон-
центрированной соляной кислоте с образо-
ванием SnCl2. Растворяется в щёлочах, лагая
станниты. Образует два окисла — SnO и
SnO2— и соответственно два ряда соедине-
ний — двух- и четырёхвалептного олова. SnO
и SnO2— амфотерные окислы, но у двухва-
лентного олова металлические свойства вы-
ражены сильнее, чем у четырёхвалентного.
Соли двухвалентного олова сравнительно
легко переходят в соли четырёхвалентнего
и являются постог.у восстановителями.
Cexiici; Р
В природе свинец встречается в виде
различных соединений. Наиболее важная
руда — свинцовый блеск PbS.
Свойства. Голубовато-серый тяжёлы i
мягкий металл, па воздухе покрывается
защитной плёнкой скисла. Вода па сгпьгц
не действует, но в присутствии вссдуа
свинец медленно разрушается ьодой. И;
кислот легче всего свинец растворяется
в азотной и уксусной (в присутствии кис-
лорода воздуха): Pb + 4HNO3 = Pb(NOs)24-
+ 2 NO2+2 Н?О. Свинец легко растворяется в
щёлочах с образованием плюмбитов — солей
Н.,РЬО2. Свинец широко применяется для
изготовления покрышек для кабеля, пластин
для аккумуляторов, для изготовления пу-
лемётных и шрапнельных пуль, дроби
и т. д. В своих соединениях свинец поло-
жительно двухвалентен. Имеются соедине-
ния четырёхвалентпого свинца, но они менее
устойчивы, чем у олова.
Все растворимые соединения свинца ядо-
виты. Свинец образует два простых окисла—
РЬО и РЬО2.
Окись свинца РЬО — жёлтый порошок,
после сильного прокаливания приобретаю-
щий красноватый цвет (глёт); применяется
для изготовления пластин в аккумуляторах.
Гидрат окиси свинца РЬ(ОН)2 — амфотер-
ное соединение, растворимо в щёлочах и
кислотах: РЬ(ОН), 4- 2 HNO3 = Pb(NO3)2 4-
4- 2Н2О; РЬ(ОН)2 4- 2NaOH = Na2PbO2 4-
4- 2 Н2О.
Уксуснокислый свинец (СН8СОО)2РЬ
(свинцовый сахар) — белое кристаллическое
вещество; применяется при крашении тка-
ней. Ядовит.
Основной карбонат свинца РЬ(ОН)„ -
• 2РЬСО3 — свинцовые белила; применяется
для изготовления белой масляной краски.
Двуокись свинца РЬО2—тёмнобурый поро-
шок, амфотерный окисел с преобладанием
кислотных свойств; ему соответствуют ерто-
и метасвипцовые кислоты: Н4РЬО4 и Н2РЬО3,
не существующие в свободном состоянии,
но образующие соли.
Сущ.к'РЬ3О4— яркокрасного цвета; при-
меняется при изгетовлепил масляной краски.
Представляет ссбсй соль двухвалентного
свинца и opioci .oiiiK'Boii кислоты РЬ2РЬО4.
ЭЛЕМЕНТЫ ПОБОЧНОЙ ПОДГРУППЫ
ЧЕТВЁРТОЙ ГРУППЫ ПЕРИОДИЧЕСКОЙ
СИСТЕМЫ ЭЛЕМЕНТОВ
Титан Tig|
В природе довольно распространён.
Получается обычно в виде сплава с желе-
зом— ферротитана — и применяется в метал-
лургии.
Свойства. Металл с максимальной по-
ложительной валентностью, равной 4. По
отношению к иоде и воздуху довольно
устойчив. Ti(OH)j — гидроокись титана ам-
фотерна.
Двуекись титана TiO2 —белый порошок,
не растворимый в воде. Служит для приго-
товления очень прочной мзеллной краски —
титановых белил.
Цирконий Гафний
В п р п р о д е оба металла мало распро-
странены и имеют ограниченное применение.
В свободном состоянии имеют вид типичных
металлов. При обыкновенной температуре
устойчивы по отношению к воде и воздуху.
В своих соединениях чстырёхзалентны.
282
химия
Торий Thgfl2
В природе торий встречается доволь-
но редко. Главным образом вместе с редки-
ми землями входит в состав минерала мона-
цита. По внешнему виду этот металл похож
на платину. Радиоактивен.
ЭЛЕМЕНТЫ ГЛАВНОЙ ПОДГРУППЫ пятой
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Азот N|4
В природе азот находится в свобод-
ном состоянии, составляя 78% воздуха.
В связанном состоянии встречается в виде
солей азотной кислоты. Входит в состав
молекулы животного и растительного белка.
Свойства. Бесцветный, не обладаю-
щий запахом газ. В химическом отношении
очень инертен. Только при очень высокой
температуре соединяется с кислородом и
водородом.
А.мми.тк NH3 — бесцветный газ с .харак-
терным резким запахом (запах нашатыр-
ного спирта). При охлаждении до темпера-
туры — 33,4°С аммиак сжижается. Жидкий
аммиак хранится в стальных баллонах под
давлением 6—7 ат. Аммиак горит в кисло-
роде, давая воду и азот: 4 NH3 4- ЗО2 =
= 6Н2О 4- 2 N2.
Аммиак легко растворяется в воде. Рас-
твор имеет шелочную реакцию. 5%-нып рас-
твор называется нашатырным спиртом. Ам-
миак реагирует с кислотами, образуя соли
аммония 2 NH3 4- HaSO4 = (NH1)2SO4. Группа
аммония NH4, имеющая один положительный
заряд, в соединениях аналогична катиону
металла. В свободном виде аммоний не су-
ществует.
Аммиак широко применяется в холодиль-
ном деле для производства азотной кислоты
и для получения аммонийных удобрений.
Сернокислый аммоний (NH4)2SO4 — белое
кристаллическое вещество, хорошо раство-
римое в воде. Применяется как удобрение,
входит в состав взрывчатого вещества аммо-
нала.
Хлористый аммоний (нашатырь) NH4C1 —
белое кристаллическое вещество, хорошо
растворимое в воде. Применяется в красиль-
ном деле, при паянии и лужении.
Окислы азота
Азотный ангидрид NaO6— твёрдое кри-
сталлическое вещество, растворяется в воде,
давая азотную кислоту. Многие органиче-
ские вещества при соприкосновении с ним
воспламеняются. Сильный окислитель.
Четыг.ёхсжись азота N..O4—при низкой
температуре слегка желтоватая жидкость.
При нагревании переходит в двуокись азота.
Двуокись азота NO2—бурый газ с харак-
терным запахом. Ядовит.
Азотистый ангидрид N2O,S — известен
только при низкой температуре в виде тём-
посивей жидкости; ему соответствует азоти-
стая кислота HNO2.
Окись азота NO — бесцветный газ, на
воздухе моментально буреет, переходя в
NO2.
Закись азота («веселящий газ») N2O —
бесцветный газ без запаха, вдыхание не-
больших количеств которого вызывает со-
стояние, подобное опьянению.
Азотная кислота HNO3 — бесцветная жид-
кость, дымящая на воздухе, так как её пары
сгущают влагу воздуха. Растворяется в воде
в любых отношениях. Обыкновенная про-
дажная азотная кислота (окрашенная обыч-
но двуокисью азота в желтоватый цвет)
известна под названием дымящей азотной
кислоты. Азотная кислота довольно легко
разлагается при хранении, особенно на све-
ту: 4 НГ<03 = 2 Н2О 4- 4NO2 4- О,. Чем кон-
центрированнее кислота п чем выше темпе-
ратура, тем легче идёт разложение. По
химическим свойствам азотная кислота пред-
ставляет собой одну из наиболее сильных
кислот. Азотная кислота — один из самых
сильных окислителей. Попав на кожу, вы-
зывает тяжёлые ожоги. Нагретые древесные
опилки загораются от капли азотной кисло-
ты. От азотной кислоты загораются многие
органические вещества, например скипидар.
Есе металлы, за исключением золота, плати-
ны и некоторых редких металлов, раство-
ряются в азотной кислоте. Хранят азотную
кислоту в стеклянных бутылях, помещённых
в плетёные корзины или деревянные ящики.
Переносить бутыли с азотной кислотой и
переливать кислоту нужно с крайней осто-
рожностью, следя, чтобы капли не попадали
на кожу или одежду, а также не могли
попасть па какие-нибудь легковоспламе-
няющиеся вещества.
Азотная кислота применяется в больших
масштабах при производстве удобрений, ор-
ганических красителей, серной кислоты,
взрывчатых веществ и во лиюгих других
отраслях промышленности.
Соли а з о т н о й кислоты (нитраты)
Азотнокислый натрий («чилийская селит-
ра») NaNO3— белое кристаллическое веще-
ство, хорошо растворимое в воде.
Нитрат калия KNOS—белое кристалличе-
ское вещество, растворимое в воде; приме-
няется для изготовления дымного пороха.
Азотнокислый кальций (кальциевая се-
литра) Ca(NO3)2 —белое кристаллическое
вещество, растворимое в воде; служит пре-
красным удобрением.
Фосфор Р|5
В природе фосфор довольно распростра-
нён в виде соединений. Е свободном состоя-
нии не встречается. Наиболее важные при-
родные соединения: фосфорит Са3(РО4)2;
апатит кроме Са3(РО4)2 содержит Саг., или
СаС12. Фосфор, как и азот, входит в состав
животного и растительного белка. Большое
количество фосфора содержится в костях
животных.
Свойства. Фосфор существует в не-
скольких аллотропических видоизменениях.
Белый фосфор. Твёрдое кристаллическое
бесцветное или слегка желтоватое вещество.
На воздухе окисляется и поэтому светится
в темноте; при очень слабом нагревании или
НЕОРГАНИЧЕСКАЯ ХИМИЯ
283
даже при трении белый фосфор вспыхивает
на воздухе. Хранят белый фосфор под водой,
чтобы предохранить его от окисления. С во-
дой не реагирует. Растворим в сероуглеро-
де. Белый фосфор — сильный яд.
Красный фосфор по своим свойствам рез-
ко отличается от белого: очень медленно
окисляется на воздухе, ле светится в тем-
ноте, не растворяется в сероуглероде и не-
ядовит. Красный фосфор применяется в спи-
чечной промышленности.
Фосфор—типичный металлоид, довольно
активный в свободном состоянии. Он соеди-
няется непосредственно с многими элемен-
тами.
Фосфорный ангидрид Р2О5, белый поро-
шок, жадно поглощающий воду. Поэтому па
воздухе расплывается, притягивая влагу и
переходя в метафосфорпую кислоту. Хра-
нится герметически закупоренным.
Фосфорные кислоты
В зависимости от температуры фосфорный
ангидрид может присоединять различное
количество воды, образуя три фосфорные
кислоты: P2OS + Н2О = 2 НРО3 — метафэс-
форная кислота, Р2О5 2 Н.,0 = Н4Р2О7 —
пирофосфорная кислота, Р2О5 +3 Н2О =
= 2 Н3РО4 — ортофосфорная кислота.
Метафосфорная кислота НРО3— твёрдое
бесцветное вещество, хорошо растворимое в
воде, ядовита.
Ортофосфорная кислота Н3РО4 — твёрдое
бесцветное вещество, хорошо растворимое
в воде, неядовита. Н3РО4— трёхосновная
кислота к образует три ряда солей (фосфа-
тов): средние Ма.-РО4, кислые однозамещён-
ные (первичные) Г^аН2РО4 и кислые двуза-
мещённые (вторичные) Na2HPO4.
Соли фосфорной кислоты
Соли фосфорной кислоты имеют большое
значение для сельского хозяйства как удоб-
рения.
Суперфосфат—смесь первичного фосфата
кальция Са(Н2РО4)2 с гипсом (CaSO4-2H2O)—
белый или серый порошок. Первичный фос-
фат кальция хорошо растворим в воде. Наи-
более распространённое фосфорное удобре-
ние.
Преципитат — серый порошок. Содержит
вторичный фосфат кальция СаНРО4, не рас-
творим в воде, по растворим в кислотах, на-
ходящихся в почвах. Применяется как удоб-
рение.
Аммсфосы — различные фосфат:,: аммо-
ния. Важнейшим 'является дп,аммофос:
(NH4)2HPO4. Аммофосы ценны как удобре-
ния тем, что кроме фосфора содержат азот.
Мышьяк Лез®
В природе мышьяк встречается глав-
ный: образом в виде соединенно.
Свойства. Мышьяк — тёмпоеерое ве-
щество с металлическим блеском, очень хру-
пок, довольно хорошо проводит ток г, тепло.
При нагревании возгоняется, не плавясь.
При накаливании па воздухе сгорает с ха-
рактерным чесночным запахом, образуя
мышьяковистый ангидрид As2O3 —белое кри-
сталлическое вещество, довольно плохо рас-
творимое в воде с образованием амфотер-
ной мышьяковистой кислоты H3AsO3, изве-
стной лишь в растворах.
С кислородом мышьяк образует ещё один
окисел, в котором он пятивалентен.
Мышьяковый ангидрид As2O5—белая стек-
ловидная масса. Мышьяковая кислота
H3AsO4 — белое твердое вещество, раствори-
мое в воде. Амфотерна, ио кислотные свой-
ства выражены сильнее, чем у H3AsO3. Все
соединения мышьяка ядовиты. Подобно азо-
ту, мышьяк образует соединения с водородом.
Мышьгасовистый водород AsH3 (арсин) —•
бесцветный газ с чесночным запахом; очень
ядовит. При нагревании разлагается с вы-
делением мышьяка.
Соли мышьяковой кислоты (арсенаты) и
соли мышьяковистой кислоты (арсениты)
применяются в сельском хозяйстве для борь-
бы с вредными насекомыми.
Сурьма Sbgj2
В природе сурьма встречается глав-
ным образом в виде сурьмяного блеска Sb2S3.
С в о п с т в а. В свободном состоянии Sb
представляет собой серебристо-белое твёрдое
вещество с металлическим блеском. Sb при-
меняется в сплавах. По химическим свой-
ствам сурьма похожа па мышьяк, по метал-
лические свойства у неё выражены сильнее.
С водородом образует сурьмянистый водо-
род SbH3— ядовитый газ. С кислородом об-
разует дна окисла, обнаруживая валент-
ность, равную 3 и 5.
Трёх- и пятисернистая сурьма Sb„S3 н
Sb2S5 — красные порошки—применяются как
наполнители и красители резины.
Висмут Bi|®9
В природе висмут встречается и в сво-
бодном виде и в виде соединений висмуто-
вой охры Bi2O3 и висмутового блеска Bi2S3.
Свойства. Блестящий красновато-бе-
лый металл. При обыкновенной температу-
ре па воздухе не окисляется. При накали-
вании даёт Bi2O3—окисел, обладающий
только основными свойствами.
Гидрат окиси висмута Bi(OH)3 — белый
порошок, не растворимый в воде. Предста-
вляет собой слабое основание.
Азотнокислый висмут Bi(NO,)3— белые
кристаллы, растворяющиеся в воде с обра-
зованием основной соли Bi(NO3)3 -г Н2О —
= Bi(OH)(NO3)2 4- HNO3.
ЭЛЕМЕНТЫ ПОБОЧНОЙ ПОДГРУППЫ ПЯТОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Ванадий V5!'
В природе ванадий довольно распро-
странён, но его соединения очень рассеяны и
не образуют значительных скоплений, по-
этому его считают редким элементом.
Свойства. Ванадий — серовато-белый
очень твердый лёгкий металл. На воздухе
не окисляется. Не реагирует с соляной к
284
серной кислотами. Растворяется в азотной
кислоте, «царской водке» и плавиковой кис-
лоте; с кислородом образует VO, V2Oa, VO2
и V2O5. Ванадиевый ангидрид V2O5 - твёр-
дое вещество оранжевого цвета, обладает
кислотным характером. Свободная ванадие-
вая кислота HVO3 не выделена, существуют
только её соли — ванадаты. Двуокись вана-
дия VO., амфотерна, а низшие окислы VO и
V2O3 проявляют только основные свойства.
" Ванадий применяется при производстве
особых сортов стали. Ванадиевая сталь, со-
держащая 0,1—0,3% ванадия, обладает цен-
ными механическими свойствами.
Ванадиевый ангидрид и ванадаты приме-
няются в химической промышленности в
качестве катализаторов при получении сер-
ной кислоты, заменяя платину.
Ниобий Nb^j, Тантал ТаЦ1
Ниобий и тантал встречаются в природе
значительно реже, чем ванадий. В свобод-
ном состоянии ниобий и тантал представляют
собой металлы серого цвета, тугоплавкие,
твёрдые. Эти металлы не растворимы во
всех кислотах даже в «царской водке». Ис-
ключением является плавиковая кислота, ко-
торая действует на металлические Nb и Та.
Растворы щёлочей на Nb и Та не действуют,
но их можно растворить в расплавленных
щёлочах с образованием солей, в которых
Nb и Та входят в состав аниона. Nb и Та
применяются для изготовления полюсов ка-
тодных ламп. Ниобий за последнее время
находит широкое применение при изгото-
влении специальных сталей. Стали, содержа-
щие Nb, применяются для изготовления
сварных конструкций, так как Nb резко
повышает прочность сварных швов. Та при-
меняется в сплаве с углеродом, обладающем
высокой твёрдостью, для изготовления нако-
нечников резцов и свёрл. Сплавы тантала
с другими металлами применяются для из-
готовления некоторых мелких изделий: ча-
совых пружин, свёрл, наконечников зубо-
врачебных инструментов и т. п. Для Nb и
Та наиболее типичны соединения, в которых
они пятивалентны. Соединения Nb и Та по-
ка не нашли технического применения.
Протактиний Ре^1
В природе мало распространён, встре-
чается в урановых рудах. Ра—тяжёлый ра-
диоактивный металл серебристо-белого цве-
та, не окисляющийся на воздухе. В химиче-
ском отношении протактиний ещё мало изу-
чен .
ЭЛЕМЕНТЫ ГЛАВКОЙ ПОДГРУППЫ ШЕСТОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Кпслсрсд Og'J
В природе кислород встречается чаще
всех элементов. В свободном состоянии он
входит в состав воздуха. В связанном виде
входит в состав воды, различных минералов
и горных пород. Общее количество кислоро-
да в наружной оболочке земного шара (воз-
дух, вода, земная кора) составляет около
50%.
Свойства. Кислород—газ без цвета
и запаха. При низкой температуре под вы-
соким давлением может быть превращён в
жидкость, которая хранится и перевозится
в стальных баллонах под давлением 150 ат.
Жидкий кислород в смеси с горючими мате-
риалами (угольный порошок, масло) обла-
дает сильными взрывчатыми свойствами.
Кислород соединяется со многими веще-
ствами с выделением тепла и света. Этот
процесс называется горением. Горение в
чистом кислороде происходит гораздо энер-
гичнее, чем на воздухе. Дыхание предста-
вляет собой процесс окисления, доставляю-
щий живым организмам необходимую энер-
гию.
Во всех соединениях кислород имеет ва-
лентность —2. Молекула кислорода состоит
из двух атомов.
Кислород применяют для получения вы-
соких температур, сжигая в нём, в специаль-
ных горелках, ацетилен или водород. Кис-
лород применяется также в химической
промышленности. Доменный процесс может
быть интенсифицирован, если вместо воздуха
будет подаваться смесь воздуха с кислоро-
дом.
Озон. Кислород в свободном состоянии
может существовать г> двух аллотропических
видоизменениях: в виде обыкновенного кис-
лорода О, и в виде озона, молекула кото-
рого состоит из 3 атомов кислорода. Озон
О3—бесцветный газ с характерным запахом.
При сильном охлаждении озон переходит в
синюю жидкость. Жидкий озон легко взры-
вает.
В химическом отношении озон является
более сильным окислителем, чем кислород.
Как сильный окислитель озон убивает бак-
терии и применяется поэтому для обеззара-
живания воды и воздуха.
Сера Sjg
В природе сера встречается как в
свободном состоянии, так и в виде различ-
ных соединений. Многие природные соеди-
нения серы с металлами (сульфиды метал-
лов) являются ценными рудами (например
свинцовый блеск PbS, медный блеск CnS,
цинковая обманка ZnS и др.). Большое рас-
пространение в природе имеют также соли
серной кислоты (сульфаты) CaSO4, MgSO4
11 ЯР-
С в о й с т н а. Сера существует в несколь-
ких аллотропических видоизменениях.
Природная сера представляет собой твёр-
дое жёлтое вещество, кристаллизующееся в
ромбической системе.
Черенковая сера состоит из таких же
кристаллов. Если расплавленную серу мед-
ленно охлаждать, то осаждаются жёлтые
кристаллы моноклинической серы, при даль-
нейшем охлаждении переходящие в ромби-
ческую серу.
Если расплавленную серу вылить в хо-
лодную воду, то опа превратится в мягкую
резиноподобную коричневую массу. Это
ьидопзменение носит название пластической
серы. Через несколько > асов пластическая
НЕОРГАНИЧЕСКАЯ ХИМИЯ
2 Я
сера светлеет, твердеет и переходит в ром-
би ескую.
По химическим свойствам сера предста-
вляет собой типичный металлоид. Опа соеди-
няется непосредственно со многими элемен-
тами. С металлами она образует сульфиды.
С кислородом даёт два окисла: SO2 — серни-
стый газ — ангидрид сернистой кислоты и
SO3 — серный ангидрид, которому соответ-
ствует серная кислота. С водородом сера
образует сероводород H2S. Таким образом,
для серы в её соединениях известны валент-
ности—2, 4-4 и 4-6.
Сероводород H2S — бесцветный газ с ха-
рактерным запахом тухлых яиц. Ядовит.
Сероводород горит на воздухе: 2 H2S 4-
4-30., — 2Н2О 4-2 SO,. Смесь сероводорода с
воздухом взрывоопасна. Сероводород обла-
дает очень сильными восстановительными
свойствами. В воде сероводород растворяет-
ся, образуя сероводородную воду, обладаю-
щую свойствами очень слабой кислоты. Соли
этой кислоты называются сульфидами.
Сернистый ангидрид (сернистый газ)
S03 — бесцветный газ с характерным запа-
хом горящей серы. S02 легко сжижается в
бесцветную жидкость, которая хранится и
перевозится в стальных баллонах, S02 при-
меняется для беления шерсти, шёлка и как
дезинфицирующее вещество. S02 раство-
ряется в воде, образуя сернистую кислоту
H2SO3.
Сернистая кислота H2SO3 —очень непроч-
ное соединение, может существовать только
в растворе. H2SO3 обладает восстановитель-
ными свойствами, окисляясь в H2SO4. Как
двухосновная кислота образует два ряда
солей: средние соли — сульфиты и кислые
соли — бисульфиты.
Бисульфит натрия NaHSO4— белое кри-
сталлическое вещество, хорошо растворимое
в воде.
Бисульфит кальция Ca(HSO3)2 — белое
кристаллическое вещество, растворимое в
воде.
Серный ангидрид S03 — кристаллическое
прозрачное вещество,жадно соединяющееся
с водой, давая серную кислоту S03 Н20=
= H,SO4. Эта реакция протекает с сильным
разогреванием. Попадая на кожу, S03 даёт
сильные ожоги.
Серная кислота H2SO4 — чистая серная
кислота «моногидрат» — представляет собой
маслянистую жидкость, при температуре
10,6° С затвердевающую в кристаллическую
массу. Продажная серная кислота, называе-
мая купоросным маслом, содержит 96,5%
Н.,30, и имеет уд. вес 1,84. Серная кислота
может растворять в себе значительные ко-
личества SO3, обпазуя так. называемые
олеугаы. Серная кислота жадно поглощает
воду, отнимая её даже у таких веществ,
как клетчатка. Этом объясняется обуглива-
ние бумаги, дерева и других веществ, если
на 1.их попадает серная кислота. Попадая
па кожу, вызывает тях C.i’iae ожоги. !(оп-
цегтрпроптпнач серная кислота нс дей-
ствует ia железо, ПОЭТОМУ 'ё МОЖ'Л
перевозить в железных цистернах. Не-
большое ксо.ичсст но серной кислоты хра-
нится и перевозится В СТеКЗЖЧИ,:;; бу
защищённых ст ударов пледе си и го,•си-
пами с соломой. При разбавлении серной
кислоты водой выделяется очень много тепла.
Серная кислота является одной из наиболее
сильных кислот. Серная кислота как двух-
основная кислота образует средние соли
(сульфаты) и кислые соли (бисульфаты).
Купоросы
Купоросы — сульфаты меди, железа,
цинка и некоторых других металлов, содер-
жащие кристаллизационную воду.
Медный купорос CuSO4-5H2O — синие кри-
сталлы, растворимые в воде.
Железный купорос FeSO4-7 Н2О —- светло-
зелёные кристаллы, растворимые в воде.
Квасцы алюминиевые KA1(SO4)2-12Н2О —
белые кристаллы, растворимые в воде.
Селен Sag®
В природе селей встречается главным
образом в качестве примеси вместе с сульфи-
дами Pb, Fe и др.
В свободном состоянии Se существует,
подобно сере, в нескольких аллотропических
видоизменениях. Ничтожная электропровод-
ность одного из них сильно увеличивается
при освещении. На этом основано примене-
ние селена в фотометрах и фотоэлементах.
По химическим свойствам селен является
типичным металлоидом и похож на серу.
Теллур Те^8
В природе теллур мало распростра-
нён. Свободный теллур известен в двух мо-
дификациях— аморфной и кристаллической.
Кристаллический Те светлосерого цвета, об-
ладает значительной электропроводностью и
теплопроводностью.
По химическим свойствам теллур —метал-
лоид, однако его металлоидные свойства
выражены не так интенсивно, как у серы и
селена.
ПОЛОНИЙ P0g4°
В природе полоний встречается в
урановых рудах. Полоний обладает очень
высокой радиоактивностью. Препараты, со-
держащие очень незначительное количество
полония, по своей активности превосходят
чистые препараты радия. С химической сто-
роны полоний почти не изучен.
ЭЛЕМЕНТЫ ПОБОЧНОЙ ПОДГРУППЫ ШЕСТОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Хром Ctof
В природе хром встречается главным
обэазом в виде хоомистого железняка
FeO.Cr.,O3.
Свойства. Хром представляет собой
твёрдый белый блестящий металл. Воздух
и вода при обыкновенной температуре не
действуют па хром. Сг иримеияется в ме-
таллов ром:лшлепкостц. Сталь, содержащая
I—:с% Сг, об падает высокой прочностью и
Т1 ёрлостью. Хрьмсгтые стали идут па изгото'.'-
ленг.с О.'опсОечиых 1щпт, орудийных стьо-
химия
лов, инструментов и различных машинных
частей. Нержавеющая сталь содержит около
52% Сг. Хром применяется также для по-
крытия других металлов с целью предохра-
нения их от коррозии (хромирование). С
кислородом хром образует три окисла: за-
кись хрома СгО, обладающую основными
свойствами, окись хрома Сг2О3—амфотер-
ное соединение и хромовый ангидрид СгО3—
типичный кислотный окисел.
Окись хрсма СгаО3 — зелёный порошок,
не растворимый в воде. Применяется для
изготовления клеевой и масляной краски
(;:е::ёпый крон).
Хромовые квасцы KCr(SO4)„ • 12 Н;О—
с пн'-фиолетовые кристаллы, растворимые в
годе. Применяются в качестве протравы при
крашении тканей и для хромового дубления
кож.
Хреновый ангидрид СгО3— тёмнокрасные
кристаллы, растворимые в воде с образова-
нием хромовой НаСгО4 и двухромовой
Н2Сг2О7 кислот. Сильный окислитель. Не-
которые органические вещества воспламе-
няются, если в них попадает СгО3.
Хроматы
Хроматы —соли хромовой кислоты, су-
ществующей только в растворах.
Хромат свинца РЬСгО4—не растворимое
в воде яркожёлтое вещество; применяется
при изготовлении масляной краски «жёлтый
крон».
Хромовокислые натрий и калий Na2CrO4
и К2СгО4 — жёлтые кристаллические веще-
ства, растворимые в воде.
Бихромат калия К2Сг2О,—крупные оран-
жевые кристаллы, растворимые в воде.
К2Сг,О7 сильный окислитель, применяющий-
ся при производстве многих органических
соединений, в кожевенной промышленности,
текстильной и др. Соли хромовых кислот
ядовиты.
Молибден Мо®|
В природе молибден встречается глав-
ным образом в виде MoS2 — молибденового
блеска.
Свойства. Серебристо-белый металл,
на воздухе устойчив при обыкновенной тем-
пературе и сгорает при накаливании в бе-
лый молибденовый ангидрид МоО3. Молиб-
ден применяется для изготовления спе-
циальных сортов стали. Молибденовые стали
отличаются большой твёрдостью, упруго-
стью и применяются для изготовления бро-
невых плит, ружейных и орудийных стволов
и т. п. В соединениях молибден обнаружи-
вает валентности +6, +5, -J-4, 4-3 и 4-2.
Наиболее устойчивы соединения шестива-
лентного молибдена. Соли молибденовой
кислоты Н„МоО4—молибдаты — часто имеют
очень сложный состав (комплексные соли).
Молибдат аммония (NH4)eMo,024-4 НаО—
белое кристаллическое вещество, раствори-
мое в г.оде.
Вольфрам W*®4
В п р п р о д е вольфрам встречается глав-
ным о б разом в виде солей вольфрамовой кисло-
ты H2WO4. Наиболее важные руды: вольфра-
мит—железная и марганцевая соли вольф-
рамовой кислоты, кристаллизующиеся вместе
с FeMn(WO4)2,n шеелит—вольфрамовокис-
лый кальций CaWO4.
Свойства. Вольфрам —тяжёлый белый
металл, самый тугоплавкий из всех метал-
лов. На воздухе окисляется только при
накаливании докрасна.
Вольфрам применяется в металлургии для
приготовления быстрорежущей инструмен-
тальной стали. Сталь, содержащая 18—22%
W, пе теряет твёрдости даже при накали-
вании докрасна. Вольфрам применяется
также для изготовления нитей в электро-
лампах. Нити из вольфрама выдерживают
нагревание до белого каления практически
не испаряясь.
Карбиды вольфрама WC и WaC — вещест-
ва, по твёрдости близкие к алмазу. Они
входят в состав «сверхтвёрдых» сплавов.
«Победит» состоит из карбидов W с добав-
кой 10% металлического кобальта.
Уран U^8
Свойства. Уран — тяжёлый белый ра-
диоактивный металл. Уже при слабом на-
гревании загорается на воздухе, давая сме-
шанный окисел U3O8, легко соединяется с
галогенами, серой, растворяется в разбав-
ленных кислотах с образованием солен че-
тырёхвалентного урана. Вытесняет водород
из тёплой воды. Уран образует большое
число соединений. Наиболее характерны
соединения шестивалентного урана. К ним
относятся соли урановой H2UO4 и диурано-
вой H2U2O7 кислот, а также соли уранила,
в которых роль металла играет двухвалент-
ный ион UO'', например UO2(NO3)2— азотно-
кислый уранил — жёлтое кристаллическое
вещество, растворимое в воде.
Уран в настоящее время приобрёл боль-
шое значение как источник энергии (см. Цеп-
ной распад урана, стр. 323).
ЭЛЕМЕНТЫ ГЛАВНОЙ ПОДГРУППЫ СЕДЬМОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ (ГАЛОГЕНЫ)
Фтор Fg®
В природе фтор встречается чаще
всего в виде плавикового шпата.
Свойства. Фтор—газ зеленовато-жел-
того цвета с характерным запахом. Ядовит.
В химическом отношении фтор типичный
металлоид. Чрезвычайно активен, непосред-
ственно соединяется со многими элементами;
с водородом соединяется со взрывом, обра-
зуя фтористый водород. Фтор очень сильный
окислитель.
Фтористый водород HF — бесцветный газ
с резким запахом, легко сжижается. На
воздухе он дымит, притягивая влагу. В
воде растворяется неограниченно. Раствор
HF в воде называется плавиковой
кислотой. Из всех галоидоводородных
кислот плавиковая кислота самая слабая.
Отличительным свойством HF является его
способность взаимодействовать с кремневым
ангидридом с образованием газообразного
фтористого кремния: SiO24-4HF=SiF44-2H2O.
НЕОРГАНИЧЕСКАЯ ХИМИЯ
287
Это свойство HF используют для нанесения
на стекло рисунков, надписей и приготовле-
ния матового стекла. Плавиковую кислоту
поэтому нельзя хранить в стеклянной посу-
де; её храпят в парафиновых бутылях пли
в стеклянных, покрытых слоем парафина.
Хлор С1^
В природе хлор встречается только в
связанном виде. Важнейшим природным
соединением хлора является поваренная
соль NaCi.
Свойства. Хлор — газ жёлто-зелёного
цвета с резким запахом; ядовит. Под дав-
лением около б ат сжижается. Хранится и
перевозится в жидком состоянии в стальных
баллонах.
Химически хлор очень активен, соеди-
няется со многими элементами, особенно
энергично с металлами, давая соли соляной
кислоты. С1„ обладает сильными окислитель-
ными свойствами. На этом основано приме-
нение хлора для стерилизации питьевой
воды. Хлор используется для приготовления
белильной извести, при производстве красок
и лекарственных веществ, в сельском хозяй-
стве для борьбы с полевыми вредителями и
во многих других отраслях промышленности
и народного хозяйства. С водородом хлор
соединяется особенно хорошо на солнечном
свету, образуя хлористый водород НС1. С
кислородом непосредственно не соединяется.
Кислородные соединения получаются кос-
венным путём; наиболее устойчивы соли
кислородных кислот хлора. Известны четы-
ре кислородные кислоты: хлорноватистая
НС1О (соли называются гипохлоритами),
хлористая НСЮ, (соли называются хлори-
тами), хлорноватая НСЮ3 (соли называются
хлоратами), хлорная НС1О4 (соли называют-
ся перхлоратами). Все кислородные соеди-
нения хлора — сильные окислители.
Хлористый водород и соляная кислота.
Хлористый водород—бесцветный газ с рез-
ким запахом, хорошо растворим в воде.
Раствор хлористого водорода в воде назы-
вается соляной кислотой. Насыщенный вод-
ный раствор НО при температуре 18°
содержит 48% НО. Продажная концентри-
рованная соляная кислота содержит около
38% НО и имеет d= 1,19. Такая кислота
дымит на воздухе вследствие выделения
НС1, который притягивает влагу из воздуха,
образуя туман. Соляная кислота является
одним из главных продуктов основной хи-
мической промышленности для получения
хлористых металлов, нашатыря, в кожевен-
ной промышленности, в пищевой и многих
других. Соляная кислота, входя в состав
желудочного сока животных, играет важную
роль в пищеварении. Соли соляной кислоты
называются хлоридами. Наиболее важные
из них описаны в разделах соответствующих
металлов.
Бром Вгз5
В природе бром встречается в виде
соединений с натрием, калием, магнием.
Обычно они встречаются вместе с соедине-
ниями хлора, но значительно менее рас-
пространены.
Свойства. Бром представляет собой
тяжёлую красно-бурую жидкость с резким
запахом. Попадая на кожу, вызывает тяжё-
лые ожоги. Жидкий бром легко испаряется,
образуя красно-бурые пары, вдыхание кото-
рых вызывает отравление.
По химическим свойствам бром — метал-
лоид менее активный, чем фтор и хлор. С
водородом бром образует бромистый водород
НВг, по свойствам похожий на НС1, но
значительно менее прочный. Из кислородных
кислот для брома известны только бромно-
ватистая НВгО и бромноватая НВгО3 кисло-
ты. Эти кислоты тоже менее устойчивы, чем
соответствующие им у хлора.
Иод
В природе под содержится в виде
соединений, главным образом в морской
воде и в буровых водах нефтяных скважин.
Иод накапливается в тканях морских водо-
рослей, которые и служат источником полу-
чения иода.
Свойства. Иод — твёрдое вещество,
образующее тёмносерые кристаллы со сла-
бым металлическим блеском. При нагрева-
нии эти кристаллы, не плавясь, переходят
в тёмпофполетовые пары с характерным за-
пахом. По химическим свойствам иод — ме-
таллоид, но значительно менее активен,
чем хлор и бром. С водородом иод образует
подпетый водород — непрочное соединение,
распадающееся на иод и водород. Из кисло-
родных кислот для иода известны йоднова-
тая HJO3 и иодная HJO4.
ЭЛЕМЕНТЫ ПОБОЧНОЙ ПОДГРУППЫ СЕДЬМОЙ
ГРУППЫ ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
ЭЛЕМЕНТОВ
Марганец Мп^
В природе соединения марганца до-
вольно распространены. Чаще всего он
встречается в виде кислородных соединений:
пиролюзита МгЮ2, гаусманита Мп3О4 и
браунита Мп2О3.
Свойства. Марганец представляет
собой твёрдый блестящий металл, похожий
по внешнему виду на железо. На воздухе
покрывается плёнкой окисла, задерживаю-
щей дальнейшее окисление. Марганец
растворяется в разбавленных кислотах с
образованием соответствующих солей с ка-
тионом двухвалентного марганца.
С кислородом образует пять окислов:
МпО, Мп2О3, МпО2, МпО3, Мп,О,. Окислы
двух- и трёхвалентного марганца имеют
основной характер, окисел четырёхвалент-
ного марганца амфотерен и высшие окислы
(шести- и семивалентного Мп) обладают
кислотными свойствами.
Двуокись марганца МпО, — коричневый
порошок, не растворимый в воде. Приме-
няется как окислитель.
Марганцовокислый калий (перманганат)
КМпО4—соль марганцевой кислоты—тёмно-
фиолетовое кристаллическое вещество, рас-
творимое в воде. Обладает сильными окисли-
тельными свойствами. Применяется как
дезинфицирующее вещество, а также как
окислитель в химической промышленности.
288
химия
Рений иЩ6
Очень редкий металл, мало исследован-
ный.
ЭЛЕМЕНТЫ ВОСЬМОЙ ГРУППЫ ПЕРИОДИЧЕ-
СКОЙ СИСТЕМЫ ЭЛЕМЕНТОВ
Железо Fe|®
В природе железо после алюминия —
наиболее распространённый металл. Встре-
чается только в виде соединений. Важней-
шими железными рудами являются: магнит-
ный железняк Fe3O4, красный железняк
Fe2O3, бурый железняк 2Fe2O3-H,O, шпа-
товый железняк FeCO3, железный колчедан,
или пирит, FeS2.
Свойства. Железо—серебристо-белый
блестящий металл. В сухом воздухе железо
не изменяется, но во влажном быстро ржа-
веет, покрываясь рыхлым бурым налётом
гидрата окиси железа, который не предо-
храняет металл от дальнейшего окисления.
При накаливании в воздухе железо сгорает,
образуя FesO4 (закись — окись железа). В
разбавленных кислотах железо легко рас-
творяется с образованием соответствующих
солей двухвалентного железа. Щёлочи не
действуют на железо. Fe образует два
окисла: закись железа FeO и окись железа
Fe2O3. Окислы обладают только основными
свойствами, давая два ряда солей двух-
валентного и трёхвалентного железа.
Ксбальт Со|®
В природе кобальт мало распростра-
нён, он встречается в виде кобальтового
шпата CoAs2 и кобальтового блеска CoAsS.
Свойства. Кобальт—твёрдый серова-
тый блестящий металл, обладающий магнит-
ными свойствами, устойчивый по отношению
к воде и воздуху, растворяется в разведён-
ных кислотах с образованием соответствую-
щих солей с двухвалентныгл катионом
кобальта. С кислородом образует два окисла
СоО и Со2О3, которые обладают основными
свойствами, давая соли. Соли трёхвалентного
кобальта неустойчивы и переходят в соли
двухвалентного. Соли двухвалентного ко-
бальта в безводном состоянии синего цвета,
в водных растворах и кристаллах, содержа-
щих воду,— красного или розового. Кобальт
входит в состав некоторых сплавов, сообщая
им большую твердость (победит, стеллит),
Никель
В природе никель встречается глав-
ным образом в виде соединений с мышьяком
и серой: купферникель NiAs, мышьяково-
никелевый блеск; NiAsS и др.
Свойства. Никель — белый твёрдый
хорошо полирующийся металл, обладающий
лигнитными свойствами, устойчивый по
отношению к воздуху и поле. Ni широко
применяется для покрытия других металлов,
а т.в сплавах с железом, медью, цин-
ком к, другими металлами. Нрнытака штейн
к стали н'Т1 даёт eii eeai ш-ю ууу рсуст'чш::-
еость и сонртняляемосп, керро:Напри-
мер, хромоникелевая сталь широко приме-
няется для производства артиллерийских
орудий, брони бронебойных снарядов, обо-
лочек для пуль и т. п.
Сплавы никеля с медью, содержащие
большой процент Ni, практически не под-
вергаются коррозии, применяются в хими-
ческой промышленности, в самолётострое-
нии, морском судостроении. Инвар-
сталь, содержащая 36% Ni, обладает
очень малым коэфициентом расширения и
идёт на изготовление измерительных при-
боров. Платинит—сталь, содержащая
0,15% С и 46% Ni, имеет такой же коэфи-
циент расширения, как стекло, и может
впаиваться в стекло. Применяется для из-
готовления электрических ламп. Н и х р о м—
сплав Ni с хромом и никелин—сплав
меди, никеля и цинка — обладают большим
электрическим сопротивлением и применя-
ются для изготовления реостатов и различ-
ных нагревательных электроприборов. С
кислородом Ni образует два окисла: закись
никеля NiO и окись никеля Ni3O3. Соли
никеля известны только с катионом двух-
валентного Ni”.
Сернскислый никель NiSO4-7 Н2О — изум-
рудно-зелёные кристаллы, растворимые в
воде. Растворы этой соли служат для на-
полнения никелировочных ванн.
Окись никеля Ni2O3—порошок; приме-
няется при изготовлении щёлочиич железо-
никелевых аккумуляторов.
Рутений Ruj®2
В природе рутений встречается вме-
сте с платиной как небольшая примесь.
Серебристо-белый твёрдый хрупкий и очень
тугоплавкий металл, устойчивый по отно-
шению к кислотам, при нагревании на воз-
духе окисляется, образуя сине-чёрную дву-
окись рутения RuO2. В своих соединениях
большей частью четырёхвалентен. Четырёх-
окись рутения RuO4 — жёлтые игольчатые
кристаллы, при нагревании взрывают, об-
разуя окись рутения и кислород.
Родий RII453
Встречается родий в платиновых рудах
и в некоторых золотых как небольшая
примесь.
Rh—белый ковкий металл, не раствори-
мый ь кислотах, в том числе и в «царской
водке». С кислородом даёт два окисла:
Rh,,O3 (серо-чёрное вещество, не раствори-
мое в кислотах, нрм нагревании выше 1101FC
распадается на металл и кислород) и дву-
окись RhO2.
Палладий Pd|p
Палладий встречается в платиновых
рулах как небольшая примесь. Он предста-
вляет собой серебг.псто-белый тугоплавкий
дгеталл, растворимый в «царской водке»,
азотной кислоте и горячей серной кислоте;
н'-л пошгухе при нагревании не изменяется.
Мете..1: тн’а'сш’й пг лладий способен но гло-
тать ьолород. 1 объем палладия при обык-
НЕОРГАНИЧЕСКАЯ ХИМИЯ
289
Свойства неорганических соединений
Таблица 3
Название Формула Молеку- лярный вес Уд. вес» Темпера- тура плавления °C Темпера- тура кипения °С(760) Внешний вид и свойства
Азот —закись «веселящий N, 28,016 Жидк. (—195.6°) 0,879 -210,1 -195.67 Газ бесцветный, без запаха
газ» NaO 44,02 Жидк. (—89,4°) 1,226 —90,7 —88,7 Газ бесцветный, ядовит
—окись NO 30,01 Жидк. (—151,8°) 1.27 -163,7 — 151,8 То же
—двуокись N.O.J 2NO. 92.02 Жидк. (0°)1,48 -10 21.2 Бурый газ, ядовит
Азотная кислота . . HNO, 63,102 1,53 -41,3 86(разл.) Бесцветная жидкость, вы- зывает ожоги
Алюминий Al 26,97 2,70 658 -20U0 Серебристо-белый металл
— окись AlgOj 101,94 3,96 2050 2980 Белый порошок
—хлористый A1C1, 133,35 2,41 190 (2,5 ат) 183 Бесцветный кристаллич., на вбздухе дымит и расплы- вается
Аммиак Аммоний азотнокис- NH, 17,032 Жидк. (0°)0.638 -77,7 -33,4 Бесцветный газ с характер- ным запахом; раздражает слизистую оболочку
лый —углекислый сред- NH.NO, 80,05 1,73 165 Разлаг. 200 Бесцветные кристаллы
ний (NH.), COa-HaO 114,1 — — Темпер, разл. 58 Белые кристаллы, возго- няется
—хлористый NH.C1 53,50 1,53 — Темп, воз- гон. 335 Бесцветные кристаллы, воз- гоняется
Аргон Ar 33,94 Жидк. (—183°)!, 38 3.6 -190 — 185,8 Бесцветный газ, без запаха
Барий Ba 137,36 658 1537 Серебристо-белый твёрдый
— едкий Ba(OH),. • 8H,0 315,5 1,66 Непо- стоянные (безв. плав, не разлаг.) Белый твёрдый, ядовит
—хлористый BaCI,-2H,0 244,4 3,10 (безводн.) 960 — Бесцветные кристаллы, ядо- вит
Бериллий Be 9,02 1,85 1280 Серебристо-белый твёрдый
Бор В 10.82 1.73 2300 — Бурый аморфный
Борная кислота . . . - HaBO 61,84 1,46 Разл. прн — Бесцветные кристаллы
Бор фтористый . . . BF3 67,82 2,31 —127 —101 Бесцветный газ
Бром Br, 159,832 3,14 —7,3 58,7 Тёмнобурая жидкость, вы- зывает ожоги
Ванадий V 50,95 5,7 1715 — Серебристо-белый твёрдый
Висмут Bi 209,0 9,80 271,0 — 1500 Красноватый твёрдый
Вода H,0 18,016 Твёрд, (0°) 0,9168 0 100 Бесцветная жидкость
—«тяжёлая» D,0 20,017 (4°):1,106 3.8 101.42 Бесцветная жидкость, ядо- вита
Водород Ha 2,016 Жидк. 0,070— (—252,81°) —259,18 —252,81 Бесцветный газ, без запаха
—перекись HaO2 34,016 Жидк. (0°)1,465 —0,89 (47 мм) 80,2 Бесцветная жидкость, вызы- вает ожоги
Вольфрам w 184.0 19.1 3370±50 Рассчита- но 4830 Белый твёрдый
Гелий He 4,003 Жидк. 0,122 —272 —268.8 Бесцветный газ, без запаха
Железо Fe 65,84 7,86 1530 2450 Серый твёрдый
—гидроокись .... Fe(OH)3 106,86 — — — Красно-бурый твёрдый аморфный
—закись —закись—окись (маг- FeO 71,84 5,7 1377 — Чёрный твёрдый
нетит) FesO. 231,52 5.16 1527 — То же
—окись (гематит) Fe,O. 159,68 5,1—5.2 1565 Красный аморфный
—хлористое Fed, 126,76 2,99 — Бесцветные кристаллы, рас- плываются на воздухе
—хлорное ...... FeCl, 162,22 2,80 302 — Тёмнокоричневые кристал- лы, расплываются на воз-
Золото ....... Au 197.2 19,3 1063 2677 Духе Жёлтый твёрдый
Иод J, 253,84 4.942 113,5 184,35 Чёрные, блестящие крис- таллы, возгоняются
1 Удельные веса жидкостей и твёрдых тел даны при температуре +20° С в г!см^, в отдельных случаях
при другой температуре, указанной в скобках; удельные веса паров (газов) даны в кг!м* прн нормальных
физических условиях (0° С, 760 мм рт. ст.).
19 Том I
290
химия
__________________________________________________________________________Продолжение табл. 3
Название Формула Молеку- лярный вес Уд. вес Темпера- тура плавление °C Темпера- тура кипения °С(760) Внешний вид и свойства
Кадмий Cd 112.41 8,64 321 770 Голубовато-белый твёрдый
Калий К 39,104 0,86 63,5 762,2 Серебристо-белый, вспыхи-
—азотистокислый KNO, 85,11 1,92 297,5 вает в воде Бесцветные кристаллы
— азотнокислый . . . KNO, 101,11 2,10 336 — Бесцветные кристаллы
— едкий кон 56,11 2,12 (Безвод- 1324 Белые кристаллы, вызывают
—хлористый (силь- вин) KCI 74,56 1,989 ный) 360,4 ~768 1415 ОЖОГИ Бесцветные кристаллы
—хлорноватокислый КСЮ, 122,56 2,344 370 Разл. То же
— цианистый .... KCN 65,11 1,56 623,5 — Бесцветные кристаллы, ядо-
Кальций Са 40,07 1.55 851 1240 вит Белый твёрдый
—едкий Са(ОН), 74,09 2,08 Разла- — Белый аморфный
—окись СаО 56.07 Кр. 2,24 3,2-3,4 гается при нагрева- нии 2572 Белый аморфный
—углеродистый (кар- бид) СаС, 64,07 2,22 2300 — Белые кристаллы (техи. серый) Белые кристаллы, расплы-
—хлористый СаС1, 110,99 2,15 774
—хлорноватистокис- лый Ca(OCl), ЗН.О 197,03 — — — ваются на воздухе Бесцветные кристаллы
—цианамид CaCN, 80,09 ^1190 Серый порошок
Кислород О, 32 (183°)-1,20 -218,8 -183 Бесцветный газ, без запаха
Кобальт Со 58,94 8,8 1490 30 мм’. Серый твёрдый
Кремний Si 28,06 2,35 '*'1414 '*-2375 2400 Серый кристаллический или
—карбид, карборунд SiC 40,06 3,12 коричневый аморфный Бесцветные кристаллы
— окись (ангидрид кремневой кислоты) SiO, 60,06 2,20 2590 Бесцветный аморфный
—окись, каарц . . . SiO, 60,06 2.65 1470 } 2590 Бесцветные кристаллы
— окись, кристобалит —хлористый .... SiO, 60,06 2,32 1710 То же
SiCl4 169,90 1,48 -68,7 57 Бесцветная жидкость, на
Литий Li 6,94 0,534 180 1336 воздухе дымит Серебристо-белый, вспыхи-
—азотнокислый . . . LiNO5 68.95 2,366 249 вает в воде Бесцветные кристаллы
Магний Мд 24,32 1,74 650 1120 Серебристо-белый твердый
—окись MuO 40,32 3,2-3,7 <2500 2800 Белый порошок
Марганец Mn 54,93 7,3 1191—1250 1900 Серый твёрдый
—двуокись (пере- кись) (пиролюзит) MnOa 86,93 5,03 Диссоц. Коричневый порошок
Медь Cu 63,54 8,93 выше 530° 1083 2360 Красноватый твёрдый
—азотнокислая, гид- рат Cu(NOa), 3H,O 241,63 2,05 — — Синие кристаллы
—сернокислая, гидрат CuSO, 5HaO 249,72 2,29 При 258° — То же
Молибден Mo 96,0 10,2 станов, безводн. 2500 ^3560 Серебристо-белый твёрдый
Мышьяк ...... As 74,96 5,72 817° (давл.) т. возгон. Серый кристаллический
—мышьяковистый ангидрид As2Os 197,92 3.86—4,0; Возгон. 620 Белый аморфный, ядовитый
—мышьяковый ангид- рид As2Ot 229.92 аморфн. 3-7 4,09 Разлаг. То же
Натрий Na 22,997 0,97 97,7 880 Серебристо-белый, вспыхи-
—бромистый NaBr-2HaO 133,95 2,18 Без- (Безвод.)’ 1395 вает в воде Бесцветные кристаллы
—едкий NaOH 40.01 води. 3,2 2,02—1,83 740 318 1388 Белый кристалл, вызывает
—кремнекислый . . NaaSiO.t 122,06 2.4 1088 ожоги Белый'кристаллический или
—сернистый, норм. Na,S-9H,O 240.21 (Безводн) аморфный Бесцветные кристаллы
—углекислый (кис- лый), первичн. . . NaHCOj 84,01 1.86 2,21 Разл. при Белые кристаллы
—углекислый втор, гидрат (сода) . , . NaaCO3*10HaO 286,16 1,5 нагрев. - Бесцветные кристаллы
неорганическая химия
291
Продолжение табл. 3
Название Формула Молеку- лярный вес Уд. вес Темпера- тура плавления °C Темпера- тура кипения СС (760) Внешний вид и свойства
Натрий—хлористый NaCl 58,46 2,17 800 1440 Бесцветные кристаллы
Ниобий Nb 93,5 8,56 1950 Серый твёрдый
Никель Ni 58,69 8.8 1455 (30 мм) Белый твёрдый
—азотнокислый гид- рат Ni(NO3), 6H,0 290,79 2,05 (ЗН3О)95 2340 Зелёные кристаллы
Олово Sn 118,70 Бел. 7,28 231.84 2275 Серебряно-белые кристаллы
—хлористое гидрат (оловянная соль) . SnCl,-2H,0 225,64 Сер. 5,7 2,70 Безводн. Безводн. Белые кристаллы
—хлорное SnCl4 260,54 2,28 241 —33 603,25 113,9 Бесцветная жидкость
Палладий Pd 106,7 11,5 1553 Серебряно-белый таёрдый
Платина Pt 195,23 21,4 1771 3800 То же
—хлорная Ptci, 337,04 (8Н,О)2.43 — — Красновато-коричневые
Радий Ra 225,97 700 кристаллы Серебряно-белый твёрдый
Ртуть . Hg 200,61 13,595 (0°) —38,89 357 Серебряно-белая жидкость
—окись HgO 216.6 11,2 —— — Красная или жёлтая
—сернистая (кино- варь) HgS 232,67 Кр. 8,09; Темп, воз- Красный кристаллический
—однохлористая (ка- ломель) Hg.Cl, 472,12 Чёрн. 7,67 7,15 гон. 586 (давл.) 1450 243 383,2 или чёрный аморфный Белый порошок
—двухлористая (су- лема) HgCla 271,52 5,42 275 301 Белые кристаллы
Свинец Pb 207,21 11,34 327 1540 Голубовато-серый твёрдый
—азотнокислый . . . Pb(NO3), 331,2 4,5 Разл. — Бесцветные кристаллы
—окись (свинцовый глёт) PbO 223,2 Жёлт. 9,5 начиная с 200° 880 1470 Жёлтый или красный поро-
— окись (сурик) . . . PbsO, 685,6 Кр. 9.3 9.07 Дисс. при — шок Красный порошок
—окись (ангидрид) . PbO, 239,2 (крист.) нагрев. Дисс. при Бурый порошок
—сернистый PbS 239,3 9,5 7,1 (кри- нагрев. 1110 Чёрные кристаллы
Сера ромбическая . s 32,07 ст. 7,5) 2,07 112,8 Жёлтые кристаллы
—моноклиническая . s 32,07 1,96 118,95 444,55 Светложёлтые кристаллы
—аморфная s 32,07 1,92 — Светложёлтый аморфный
—двуокись (серни- стый ангидрид) . . so, 64,07 Жидк. —72,7 -10.0 Бесцветный газ с характер-
—трёхокись (серный ангидрид) so, 80,07 (— 10°)! ,46 Жидк. (а) 16,8 44,6 ным запахом Белые кристаллы, на возду-
—хлористая S,C1, 135,06 1,92 <3):<1.97) 1.68 —80 133 хе дымят и расплываются Тёмножёлтая жидкость с
—серная кислота . . HaSO4 98,09 Жидк. 10,49 338 (дисс.) неприятным запахом Бесцветная жидкость, вызы-
—хлорист. сульфурил SO,Cl, 134,99 1,85 1,67 —54.1 69,1 вает ожоги Бесцветная жидкость,
—сернистый водород H,S 34,09 Жидк. —83 —60,2 дымит Бесцветный газ с неприят-
Серебро Аг 107.880 (-60,2°) 0.96 10,50 960,5 -^2000 ным запахом, ядовит Белый твёрдый
—азотнокислое . . . AgNO, 169,89 4,35 208,5 — Бесцветные кристаллы
Стронций Sr 87,63 2,60 797 1366 Серебряно-белый
—азотнокислый . . . Sr(NO3), 211,62 2,93 645 —. Бесцветные кристаллы
—хлористый гидрат . SrCl,-6H,O 266,62 1,96 (Безв.) 870 — То же
Сурьма Sb 121,76 6,69 630 1440 Серебряно-белый твёрдый
—трёхсернистая . . . SbBS8 339,8 4,12 548 Перег. без Оранжевый или красный
—пятисернистая . . SbaS3 404,0 разл. аморфный порошок Оранжевый аморфный
Тантал Ta 181,5 16,6 3030 Серый твёрдый
Титан Ti 47,90 4,50 -^1800 Серый твёрдый
—окись (рутил, ана- тас, брукит) .... TiO, 79,9 Рутил: 1560 Белый порошок
—четырёххлористый TiCl, 189.94 4,26, ана- тас! 3,84 1,76 -23 136,5 Бесцветная жидкость»
Торий Th 232,12 11,5 1842 дымит Тёмносерый твёрдый
—азотнокислый гид- рат Th(NO,), 4H,0 552,20 — — Бесцветные кристаллы
19*
292
химия
Продолжение табл. 3
Название Формула Молеку- лярный вес Уд- вес Темпера- тура плавления Темпера- тура кипения °С(760) Внешний вид н свойства
— окись Т11О, 264.1 9,87 3050 Белый порошок
Углерод с 12 3.51 (алмаз) 2.17—2,3 (графит) Бесцветный кристалличес- кий, серый кристаллический
— окись ........ —двуокись—угольный со 28 Жидк. (~Ь0°) 0,7923 (100 мм) -207 — 190 Бесцветный газ, без запаха, ядовит
ангидрид — сернистый серо- соа 44 Твёрдый (—79е) 1,53 (5.1 ат) -57 Темп, воз- гон. —78.5 Бесцветный газ
углерод CS, 76,14 (0°) 1.114 -107 7 Бесцветная жидкость, легко воспламеняется
— четырёххлористый —хлорокись, хлорис- тый карбонил, фос- СС1. 153,84 (0°) 1,632 -23.77 76.6 Бесцветная жидкость
ген СОС1а 98,92 (0°) 1.436 —126 8.2 Бесцветный газ, ядовит Серебристо-белый твёрдый
Уран и 238,14 18,7 ^,1690 —
—двуокись —трёх окись (ура но- 10. 270,2 10,75 2176 — Лёмнокоричневый или крас- ный твёрдый
вый ангидрид) . . ио9 286.2 6,0 — — Жёлто-коричневый или крас- ный твёрдый
— закись—окись . . и,08 842,6 8,2 — — Зелёный или чёрный твёрдый
—шестифтористый иг. 352.2 4.68 69,5 Возгон. 56 Светложёлтый кристаллич.
Фосфор р 31,02 1,83 44 280,5 Белые кристаллы, ядовит
—красный р 31.02 2.20 — — Красные кристаллы
Кислота фосфористая НаРО3 82,06 1,65 73.6 — Бесцветные кристаллы
—фосфорноватистая Н.РО, 66,06 1,49 17.4 Разл. при нагрев. То же
— метафосфорная . . (НРО,)Х 80,05х — — — Бесцветный аморфный
—ортофосфорная . . Н3РО. 98,06 1,88 Бел. 41,75 Бесцв. 37 — Белые кристаллы
—пирофосфорная . . —пятиокись(фосфор- Н4Р2О7 178,11 — (Крист.) 61 — Бесцветный стекловидный или кристаллический
ный ангидрид) . . —фосфористый в ОДО- P,OS 142,08 2,39 563 — Белый порошок, на воздухе расплывается
род (фосфин) . . . РН3 34,06 Жидкий -88° 0.74 -133 -87.4 Бесцветный газ, ядовит
Фтор F, 38 Жидкий (—188°) 1.11 Жидкий (19°) 0,987 —223 -188 Жёлто-зелёный газ, ядовит
Фтористый водород HF 20,01 —92,3 19,5 Бесцветная жидкость, вы- зывает ожогн
Хлор С1а 70,914 Жидкий 1,57 -100.5 -33,9 Жёлто-зелёный газ, ядовит
Хлористый водород НС1 36,47 Жидкий (-85) 1,185 -114 -85 Бесцветный газ, раздражает слизистую оболочку
Хром Сг 52,01 7.1 1765 ^2200 Белый твёрдый
— квасцы KCr(SO4)a 12Н„О 499.4 1,84 89 — Фиолетовые кристаллы
— окись Цианистый водород CrsO3 152.0 5,21 2140 — Зелёный порошок
<(синильная кислота) HCN 27.01 Жидкий 0,691 -13 26.5 Бесцветная жидкость, ядо- вита
Цинк Zn 65,38 7,14 419,44 907 Голубовато-белыекрнст аллы
—окись ZnO 81.38 аморфный 5,42 Кр. 5,78 — Темп. возгон. 1800 Белый порошок
—хлористый .... ZnCI2 136,29 2,92 365 730 Белые кристаллы
новенной температуре поглощает больше
300 объёмов водорода.
Для Pd наиболее характерны соединения,
в которых он двухвалентен. Соли, содержа-
щие катион Pd”, коричневого цвета, легко
растворимы в воде, расплываются на возду-
хе. Палладий образует различные комплекс-
ные соединения.
Осмий ОвЦ0
Осмий содержится в платиновых рудах
в виде не растворимого в «царской водке»
сплава с иридием—осмиридия.
Os — синевато-серый металл, очень твёр-
дый, хрупкий, очень тугоплавкий. При на-
гревании на воздухе легко окисляется,
образуя OsO4—бледножёлтое летучее веще-
ство с характерным запахом, которое легко
восстанавливается в OsO2— чёрный поро-
шок.
Os при нагревании реагирует с галои-
дами, давая смесь галоидопроизводных, в
которых Os бывает двух-, трёх- и четырёх-
валентен. Металлический Os находит при-
менение как катализатор.
НЕОРГАНИЧЕСКАЯ ХИМИЯ
293
Иридий 1г|®3
Иридий встречается вместе с платиной
и осмием. Небольшие количества иридия
встречаются вместе с золотом. Иридий —
серебристо-белый, очень твёрдый, хрупкий,
тугоплавкий металл. Он не растворяется в
«царской водке» и кислотах. На воздухе
тонкий порошок иридия при температуре
красного каления окисляется до 1гО2, кото-
рая при более высокой температуре вновь
разлагается с выделением металла. Иридий
образует многочисленные комплексные сое-
динения. Сплавы иридия с платиной твёрды
и очень устойчивы к химическим воздей-
ствиям. Из сплава, содержащего 90% Pt и
10% 1г, изготовлены международные этало-
ны метра и килограмма. Этот сплав приме-
няется также при изготовлении свечей для
автомобильных моторов.
Платина Pt^g5
В природе платина встречается в
самородном состоянии в виде крупинок, со-
держащих небольшие примеси рутения,
родия, палладия, осмия и иридия.
Свойства. Платина — белый блестя-
щий ковкий тяжёлый металл, в химическом
отношении очень инертный. Даже при очень
сильном нагревании на воздухе платина не
изменяется. Кислоты не действуют на пла-
тину. Её можно растворить только в «цар-
ской водке» (смесь 3 ч. соляной и 1 ч.
азотной кислот). При этом образуется ком-
плексное соединение Ha[PtCle]—платино-
хлористоводородная кислота, которая может
быть выделена из раствора в виде кристал-
лов Н2 [Pt С16]-6 Н2О коричневато-красного
цвета. Платинохлористоводородная кислота
является обычным продажным препаратом.
Платина образует большое число комплекс-
ных соединений. Применяется как катали-
затор, а также для изготовления многих
приборов (термопар, электродов и т. д.). В
химических лабораториях употребляют пла-
тиновую посуду: тигли, чашки и т. п.
Таблица 4
Удельный вес воды при разных температурах
в г/см3
t° с d Г С d t° С г с *
0 0,99987 14 0,99927 27 0,99654 40 0,99224
1 0.99993 15 0,99913 28 0,996’6 45 0,99024
2 0,99997 16 0,99897 29 0,99597 50 0,98807
3 0,99999 17 0,99880 30 0,99567 55 0.98573
4 1,00000 18 0,99862 31 O.V9537 60 0,98324
5 0,99999 19 0,99843 32 0,99505 65 0,98059
6 0,99997 20 0,99823 33 0,99473 70 0,97781
7 0,99993 21 0,99802 34 0,99440 75 0,97489
8 0,99988 22 0.99780 35 0,99406 80 0,97183
9 0,99981 23 0,99756 36 0,99371 85 0,96865
10 0,99973 24 0.99732 37 0.99336 90 0,96534
11 0.99963 25 0,99707 38 0,99299 95 0,96192
12 0,9995’2 26 0,99681 39 0,99262 100 0,95838
13 0,99940 !
Таблица 5
Удельные веса водных растворов соляной (НС1)>
азотиой (HNOa), серной (H8SO4) и уксусной (СН3СООН>
кислот при 20°С в зависимости от концентрации
(в весовых процентах) в г/см*
о/ /0 НС1 d HNO3 d H3SO4 d сн3соон d
1 1.0032 1.00364 1,0051 0,9996
2 1,0082 1,00909 1,0118 1,0012
3 1,01457 1,0184 1,0025
4 1,0181 1,02008 1,0250 1,0040
5 1,02563 1,0317 1.0055
6 1,0279 1,03122 1,0385 1,б069
7 1,0369 1,0453 1,0083
8 1,0376 1,0427 1,0522 1,0097
9 1,0485 1,0591 1,0111
10 1,0474 1,0543 1,0661 1,0125
11 1,0602 1,0731 1,0139
12 1,0574 1,0661 1,0802 1,0154
13 1,0721 1,0874 1,0168
14 1,0675 1,0781 1,0947 1,0182
15 1,0842 1,1020 1,0195
16 1,0776 1,0903 1,1094 1,0209
17 1,0964 1,1168 1,0223
18 1,0878 1,1026 1,1243 1,0236
19 1,1088 1,1318 1.0250
20 1,0980 1,1150 1,1394 1,0263
21 1,1213 1,1471 1,0276
22 1,1083 1,1276 1,1548 1,0288
23 1,1340 1,1626 1,0301
24 1,1187 1,1404 1,1704 1,0313
25 1,1469 1,1783 1,0326
26 1,1290 1,1534 1,1862 1,0338
27 1,1600 1,1942 1,0349
28 1,1392 1,1666 1,2023 1,0361
29 1,1733 1,2104 1,0372
30 1,1493 1,1800 1,2185 1,03.14
31 1,1867 1,2267 1,0395
32 1,1593 1,1934 1,2349 1,0406
33 1,2002 1,2432 1,0417
34 1,1691 1,2071 1,2515 1,0428
35 1,2140 1,2599 1,0438
36 1,1789 1,2205 1,2684 1,0449
37 1 1885 1,2270 1,2769 1,0459
38 1,2335 1,2855 1,0469
39 1,1980 1,2399 1,2941 1,0479
40 1,246 3 1,3028 0,0488
41 1,2527 1.3116 1,0498
42 1,2591 1,3205 1,0507
43 1,2655 1,3294 1,0516
44 1,2719 1,3384 1,0525
45 1,2783 1,3476 1,0534
46 1,2847 1,3569 1,0542
47 1,2911 1,3663 1,0551
48 1,2975 1,3758 1,0559
49 1,3040 1,3854 1,0567
50 1,3100 1,3951 1,0575
51 1,3160 1,4049 1,0582
52 1,3219 1,4148 1,0590
53 1,3278 1,4248 1,0597
54 1,3336 1,4350 1,0604
55 1,3393 1,4453 1.0611
56 1,3449 1,4557 1,0618
57 1,3505 1,4662 1,0624
58 1,3560 1,4768 1,0631
59 1,3614 1,4875 1,0637
60 1,3667 1,4983 1,0642
61 1,3719 1,5091 1,0648
62 1,3769 1,5200 1,0653
63 1,3818 1,5310 1,0658
64 1,3866 1,5421 1,0662
65 1,3913 1,5533 1,0666
66 1.3959 1,5646 1,0671
67 1,4004 1,5760 1,0675
68 1,4048 1,5874 1,0678
69 1,4091 1,5989 1,0682
70 1,4134 1,6105 1,0685
71 1,4176 1.6221 1,6687
72 1,4218 1,6338 1,0690
73 1,4258 1,6456 I 1,0693
294
химия
Продолжение табл. 5
о/ 1 /О НС1 d HNO3 d H.SO4 d CH8COOH d
74 1,4298 1,6574 1,0694
/5 1,4337 1,6692 1,0696
76 1,4375 1,6810 1,0698
/1 1,4413 1,6927 1,0699
1,4450 1,7043 1,0700
79 1,4486 1,7158 1.0700
80 1,4521 1,7272 1,0700
81 1,4555 1,7383 1,0699
82 1,4589 1,7491 1,0698
83 1,4622 1,7594 1,0696
«4 1,4655 1,7693 1,0693
85 1,4686 1,7786 1,0689
86 1,4716 1,7872 1,0685
87 1,4745 1.7951 1 ,l680
88 1,4773 1,8022 1,0675
89 1,480и 1,8087 1,0668
90 1,4826 1,8144 1,0661
91 1,4850 1,8195 1,0652
92 1,4873 1,8240 1,0643
93 1,4892 1,8279 1.0632
94 1,4912 1,8312 1,0619
95 1,4932 1,8337 1,0605
96 1,4952 1,8355 1,0588
91 1,4974 1.8364 1,0570
98 1,5008 1,8361 1,0549
99 1.5056 1,8342 1,0524
100 1.5129 1,8305 1,0498
Таблица б
Удельные веса водных растворов щёлочей едкого
кали (КОН), едкого натра (NaOH) и аммиака (NH.)
в зависимости от концентрации (в весовых
процентах) в г!см*
о/ /о КОН d NaOH d NHa d % KOH d NaOH d NH. a
0 0,9991 0,9991 26 1,2489 1,2879 0,9069
1 1,0083 1,0106 0,9948 27 1,2592 1,2988
2 1,0175 1,0219 0,9905 28 1,2696 1,3096 0,9010
3 1,0267 1,0332 29 1,2800 1,3204
4 1,0359 1,0444 0,9822 30 1,2905 1,3311 0,8u51
5 1,0452 1,0555 31 1.3011 1,3417
6 1,0544 1.0666 0,9742 32 1,3117 1,3522 0,8892
7 1,0637 1,0777 33 1,3224 1,3627
8 1,0730 1,0889 0,9665 34 1,3331 1,3732 0,8832
9 1,0824 1,1000 35 1,3440 1,3835
10 1.0918 1,1111 0,9591 36 1,3549 1,3937 0,8772
и 1,1013 1,1222 37 1,3659 1,4039
12 1.1108 1,1333 0,9519 38 1,3769 1,4140 0,8712
13 1,1203 1,1444 39 1,3879 1,4240
14 1,1299 1,1555 0,9450 40 1,3991 1,4339 0,8651
15 1,1396 1,1665 41 1.4103 1,4437
16 1,14„3 1,1776 0,9383 42 1.4215 1,4534
17 l,15uO 1,1887 43 1,4329 1,4630
18 1,1688 1,1998 0,9317 44 1,4443 1.4726
19 1,1786 1,2108 45 1,4558 1,4822
20 1.1884 1,2219 0,9253 46 1,4673 1,4918
21 1,1984 1,2330 47 1,4790 1,5013
22 1,2083 1,2440 0,9190 48 1,4907 1,5108
23 1,2184 1,2553 49 1,5025 1.5203
24 1,2285 1,2660 0,9129 50 1,5143 1.5297
25 1,2387 1,2770
ОРГАНИЧЕСКАЯ ХИМИЯ
Номенклатура органических соединений
Научная номенклатура органических
соединений разработана Женевским кон-
грессом в 1892 г. (преимущественно для
соединений с открытой цепью) и Римским
съездом химиков в 1938 г. (для циклических
соединений). В табл. 7 приводится краткая
сводка названий групп углеводородов по
женевской номенклатуре:
Таблица!
Названия групп и формулы углеводородов
Определение группы Общая формула Название группы по женевской номенклатуре Окончание наимено- ваний соединений данной группы Примеры
Насыщенные углеводороды от- крытого строения,или парафины . сп н2п+2 Алканы ан Метан
Ненасыщенные углеводороды от- крытого строения с одной двойной связью, или олефины Сп ^2л Алкены ен СН4 Бутен—2
Ненасыщенные углеводороды от- крытого строения с дв\мя двойны- ми связями, или диолефины .... сп н2п—2 Алкадиены После окончания ставится цифра, ука- зывающая номер углеродного атома, при котором распо- ложена двойная связь диен сн,-сн=сн-сн, Бутадиен
Ненасыщенные углеводороды с одной тройной связью, или ацети- леновые углеводороды Сп Hvn-2 Алкины то же ин сн.-сн-сн-сн. Этин
Н асыщенные моноциклические углеводороды, или нафтены .... Сп н2п Цикланы то же ан сн^сн Циклогексан
/ X сн, сн, 1 1 сн, сн, сн,
ОРГАНИЧЕСКАЯ ХИМИЯ
295
Наименования остальных органических
соединений производятся от соответствую-
щих углеводородов прибавлением характер-
ного окончания:
Определение соединения Окончание названия Примеры
Спирты .... Альдегиды . . . Кетоны .... Кислоты ... ол аль он овая к-та Метанол СНИОН Этаналь сн8<сно Пропанон СН8-СО‘СН3 Этановая кислота СН3.СООН
или прибавлением к названию углеводорода
наименования атома или группы атомов с
цифрой, указывающей номер углеродного
атома цепи, к которому присоединена
группа:
Определение соединения Примеры
Галоидопроизводные угле* водородов Нитропроизводные угле- водородов 2-хлорпропан СН8-СНС1-СНа Нитр ометан СН8—NO,
Наименования соединений с разветвлён-
ной цепью по женевской номенклатуре про-
изводятся от самой длинной цепи, включаю-
щей кратные связи и неуглеродные группы.
Наименования и местоположения боковых
цепей располагаются перед названием сое-
динения, отвечающего самой длинной цепи,
например 2—метилпропанол
СН3—СН—СН..ОН
I
сн3
или 1—хлор, 2—метилбутен—2
СН2С1—С=СН—СН3
I
сн3
Наряду с женевской номенклатурой до
сих пор ещё широко применяется рациональ-
ная номенклатура, а также тривиальные
названия органических соединений, так как
для некоторых классов соединений научная
номенклатура ещё недостаточно разработа-
на. В рациональной номенклатуре в основу
кладётся название группы атомов, харак-
терной для данного ряда соединений, и
перед ним помещаются наименования ради-
калов, соединённых с этой группой, напри-
мер названия аминов производятся прибав-
лением названий радикалов к слову амин
СН3. СН3\
СН3— NH,; > NH; СН3—N
сн/ СН3-СН8/
Метиламин. Диметиламин. Диметнлэтиламин.
Углеводороды
Углеводородами называются соединения,
состоящие только из углерода и водорода.
Алканы, или парафины
Гомологический ряд алканов.
Алканами, или парафинами, называются
углеводороды состава, выражаемого общей
формулой СиН2„+2 (п—целые числа, начи-
ная с 1). Алканы (табл. 8) являются предель-
ными углеводородами,так как углеводородов
с большим отношением водорода к углероду
нет.
Таблица 8
Названия и формулы первых представителей
ряда алканов
п Название алкана Фор- мула Структурная формула
н
1 Метан . . сн, н-с-н 1 н н н
2 Этан . . • с, н, н-с - с-н 1 1 н н н н н
3 Пропан с, н. н-с-с-с-н 1 1 1 н н н н н н н
4 Бутан . . с. н„ 1111 н-с-с-с - с-н 1111 н н н н н н н н н
5 Пентан . • с, н„ 1 1 1 1 1 Н-с- С— С— С—С—н 1 1 1 1 1 н н н н н
Название последующих, как и пятого,
производятся от греческих названий цифр.
Гомологическая разность ряда алканов—
СН2— называется метиленом.
Изомерия алканов. Начиная с
C4Hi3—бутана, каждая суммарная формула
охватывает несколько углеводородов, отли-
чающихся структурой. Углеводороды с не-
разветвлённой цепью называют нормальны-
ми, углеводороды с разветвлённой цепью —
изоугл еводородами.
Формуле С4Н1в отвечают два бутана:
СН3—СН2—СН2—СН3 нормальный бутан;
СН3—СН —СН3 изобутан илн
| 2-метилпропан,
СН3
Формуле СВН12 отвечают три пентана:
нормальный пентан и два изопентана
(2-метилбутан и 2, 2-диметилпропан).
Число изомеров очень быстро возрастает
с увеличением числа углеродных атомов в
алкане. Формуле С14НЗВ отвечает уже 1855
изомеров тетрадекана.
Изомеры отличаются по физическим и
химическим свойствам.
Физические свойства алканов.
В ряду нормальных алканов с увеличением
молекулярного веса температуры кипения
и плавления равномерно увеличиваются и
удельные веса (в нормальных физических
296
химия
условиях) возрастают, не превышая 0,9 г/см*
для самых тяжёлых. Температуры кипения
изопарафинов несколько меньше соответст-
вующих нормальных парафинов,а темпера-
туры плавления выше и тем выше, чем более
разветвлена цепь. При комнатной темпера-
туре и атмосферном давлении метан, этан,
пропан, н-бутан и изобутан — газы. Все
нормальные алканы от пентана до гекса-
декана — жидкости; остальные — твёрдые
тела. Газообразные алканы плохо раствори-
мы в воде, твёрдые совершенно нераство-
римы. Все алканы хорошо растворимы в раз-
личных органических растворителях (бен-
зол, эфир и др.).
Химические свойства алканов.
Алканы в отсутствии катализаторов отли-
чаются пониженной способностью к реакци-
ям. Высокие температуры вызывают различ-
ные реакции разложения и изомеризации,
широко используемые в нефтеперерабаты-
вающей промышленности для производства
бензина (термический крекинг) и сажи.
Сильные окислители и кислород при
низких температурах не действуют на ал-
каны. На этом основана защита металлов
от коррозии при помощи смазки. При по-
вышенных температурах они окисляют
алканы до органических кислот. При высо-
ких температурах кислород окисляет алканы
до СО2 и Н2О (горение). Смеси кислорода с
газообразными алканами в определённых
пределах взрываются при поджигании.
Галоиды (в особенности хлор) на свету
и при повышенных температурах медленно
галоидируют алканы с образованием га-
лоидопроизводных с„н2п+1х, С„Н2пХ2
и др. (X — галоид).
Крепкая серная кислота не действует на
алканы. Дымящая серная кислота при сла-
бом нагревании сульфирует алканы с обра-
зованием сульфокислот—Сп Н2 л+1 SO2OH.
Разбавленная азотная кислота при на-
гревании под повышенным давлением нитру-
ет алканы с образованием нитросоединений
C„H2n+1NO2.
Метан СН4 — газ без цвета и запаха,
плохо растворимый в воде и хорошо в орга-
нических растворителях. Горит почти не-
светяшимся голубоватым пламенем. tKun =
= 161,5°С, Глл= - 184°С; d=0,415 г/см3 при
— 165° С. Критическая температура метана —
1Г С; критическое давление 180 аги. Метан
входит главной составной частью в нефтяные
газы, рудничный газ и болотный газ; он
также содержится в светильном газе.
Этан С,Н6—газ без цвета и запаха, плохо
растворим в воде и хорошо в органических
растворителях. tKun = —93° С, tnjl = — 172° С;
d = 0,446 г/см3 при 0° С и 23,8 ат. Крити-
ческая температура этана +4° С; критиче-
ское давление 46 ат. Этан содержится в
нефтяных газах и в светильном газе, полу-
чаемом при сухой перегонке каменного угля.
н-гептан С7Н7в— бесцветная легколету-
чая жидкость, не растворимая в воде и хо-
рошо растворимая в органических раство-
рителях. tKun= 98° С; /пл = —97°С; d =
= 0,730 г!см3. Наряду с изооктаном гептан
избран для нормировки октановой шкалы
антидетонационных свойств бензинов. Окта-
новое число чистого гептана принято рав-
ным нулю.
Изооктан С8Н18 2,2 - д и м е т и л - 4 -
метилпентан — бесцветная жидкость.
Наряду с н-гептаном избран для норми-
ровки октановой антидетонационной шкалы.
Октановое число изооктана принято рав-
ным 100.
Триптан С7Н1в 2,2-д и м е т и л - 3 - м е-
тилбутан — бесцветная жидкость. Обла-
дает высокими антидетонационными свойст-
вами; в Америке положен в основу новой —
триптановой — антидетонационной шкалы.
Цикланы, или нафтены
Гомологический ряд цикланов.
Цикланами, или нафтенами, называются угле-
водороды циклического строения и состава,
выражаемого общей формулой С„Н2П, начи-
ная с и = 3.
Таблица 9
Названия и формулы первых представителей ряда
цикланов
п Название циклана Фор- мула Структурная формула
3 Циклопропан .... С, н. сн2
4 Циклсбутан С. н. СНа--СН3 СНа--СН, 1 1
5 Циклопентан .... с, н1о СНа-СН, CH.t Z \ сн, сн,
6 Циклогексан .... с. н18 \ сн.-сн, сн, / \ сн, сн, 1 1
сн8 сн, сна
Замещением водорода в кольце циклана
на углеводородные радикалы образуется
гомологический ряд данного циклана. На-
пример, С6Н1Х — СН3 — метилциклогексан,
СвНг1— С2Нб — этилциклогексан и др. яв-
ляются гомологами циклогексана.
Циклогексан и его гомологи называются
гидроароматическими, так как могут быть
получены гидрированием (присоединением
водорода) ароматических углеводородов.
Изомерия цикланов. Каждый из
основных цикланов имеет изомеры (углево-
дороды с одинаковой формулой, но различ-
ного строения), являющиеся одновременно
гомологами предыдущих цикланов. Напри-
мер, изомерами циклопентана являются
гомологи циклобутана и циклопропана:
сн,— сн2 /\~ 3
СН2—СН —СН3 СН2->Н-СН3
Метилциклобутан Диметилциклопропан
сн2
сн2 — 'сн — сн2 — сн3
Этилциклопропан
ОРГАНИЧЕСКАЯ ХИМИЯ
297
У цикланов наблюдаются также оптиче-
ская и цистрансизомерия.
Физические свойства цикла-
нов. По физическим свойствам цикланы
похожи на алканы. При комнатной темпе-
ратуре и атмосферном давлении циклопро-
пан и циклобутан — газы, а остальные цик-
ланы— бесцветные жидкости с удельным
весом меньше единицы, не растворимые
в воде, но хорошо растворимые в органи-
ческих растворителях.
Химические свойства цикла-
нов, за исключением циклопропана и цил-
лобутана, сходны с химическими свойствами
алканов. В отличие от алканов цикланы
окисляются с образованием двухосновных
кислот, подтверждающих циклическую
структуру нафтенов. Циклопропан и цикло-
бутан более способны к реакциям, легко
галоидируются и присоединяют галоидово-
дородные кислоты с разрывом кольца; при
высокой температуре изомеризуются в ал-
кены. Циклогексан и его гомологи при высо-
кой температуре и в присутствии мелкораз-
дробленного палладия или никеля (катали-
заторы) легко дегидрируются (отдают водо-
род) с образованием ароматических углево-
дородов.
Циклопентан С8Н10 — бесцветная легко-
летучая жидкость. tKun = 51 °C, tnjl = — 80° С;
</д°= 0,754 г', см3. Содержится в значитель-
ных количествах в нефтях СССР, в особен-
ности в бакинской.
Циклогексан CeHi2 — бесцветная легколе-
тучая жидкость. 1КИЯ = 81°С, tnA = 8° С;
<2д° = 0,778 г/см3. Содержится в значитель-
ных количествах в нефтях СССР, в особен-
ности в бакинской.
Алкены, или олефины
Гомологический ряд алкенов.
Алкенами, или олефинами, называются ацик-
лические углеводороды состава, выражае-
мого общей формулой С„Н2„ (начиная с л=2)
и имеющие одну двойную связь между дву-
мя соседними углеродными атомами.
Таблица 10
Названия и формулы первых представителей
ряда алкенов
И Название алкена Фор- мула Структурная формула
2 Этилен, или этен С2Н. н\г_г/н Н/с“е\Н
Н Н
3 Пропилен, или пропен сан. н\с = С— С-Н Н/ |
н
н н н
4 Бутилен, или бутен с,н, Н\с=с_с_с_н н/ [ j
- н н
Алкены являются непредельными сое-
динениями.
Изомерия алкенов вызывается как раз-
личным положением двойной связи, так и
различной структурой углеродного скелета.
Например, существует три бутена:
СН2=СН—СН2—СН3 СН3—СН=СН-СНа
бутен-1 бутен-2
сн2 = с — сн3
I
сн3
2-метил пропен-1
Цифра в конце названия указывает по-
ложение двойной связи. Алкены, или оле-
фины, являются изомерами цикланов.
Физические свойства алкенов.
По физическим свойствам алкены сходны
с алканами и цикланами. При комнатной
температуре и атмосферном давлении этен,
пропен и бутен—газы. Следующие за ними
алкены — жидкости и высшие — твёрдые
кристаллические тела. Удельные веса алке-
нов меньше единицы, но выше соответствую-
щих алканов. Алкены не растворимы в воде
и хорошо растворимы в органических раст-
ворителях. Теплоты образования алкенов
меньше соответствующих алканов.
Химические свойства алкенов.
Алкены, или олефины, очень реакционно-
способны. Реакционная способность их обус-
ловлена наличием двойной связи. Поэтому
для алкенов характерны реакции присоеди-
нения: галоидов (при обыкновенной темпе-
ратуре), водорода (при повышенной темпе-
ратуре и в присутствии катализаторов —
мелкораздробленного никеля, меди и др.),
кислот, воды (в присутствии катализатора)
и др. Алкены легко окисляются с разрывом
цепи по месту двойной связи и образованием
различных продуктов окисления. Под дей-
ствием серной кислоты и других веществ
алкены легко полимеризуются, т. е. моле-
кулы алкена соединяются друг с другом,
образуя молекулы более тяжёлого алкена.
Этилен, или этен, С2Н4 — бесцветный газ,
плохо растворяющийся в воде и хорошо
в органических растворителях. Горит на
воздухе светящимся пламенем. В смеси
с воздухом при поджигании взрывает; выше
350° С разлагается. tKun = — 102° С, 1„л —
= — 169° С; = 0,6095 г^см3 (жидк.). Эти-
лен содержится в светильном газе, продуктах
сухой перегонки различных органических
веществ и газах крекинга нефтяных про-
дуктов. Этилен является сырьём для полу-
чения синтетического этилового спирта, син-
тетического каучука, взрывчатых веществ
иприта, лекарственных веществ, пластмасс
растворителей и других важных материа-
лов. Этилен может заменять ацетилен в ав-
тогенной сварке. Этилен перевозится в сталь-
ных баллонах под давлением.
Изобутилен, или 2-метилпропен-1, С4Н8—
бесцветный газ. tKu„ = —6° С. Содержится
в газах крекинга нефтяных продуктов. Изо-
бутилен является сырьём для получения
изооктана, присадок к смазочным маслам и
заменителей каучука.
Алкадиены, или диолефины
Так называются ациклические углево-
дороды состава С„Н 2и—2 , содержащие две
298
химия
двойные связи. Важнейшими из них явля-
ются:
СН2 = СН — СН = СН2; СН2 = С — СН = СН2
дивинил или бутадиен-1,3 |
сн3
изопрен или 2-метилбу-
тадиен-1,3
полимеризацией которых получают синтети-
ческий каучук.
Дивинил — газ, конденсирующийся при
4-4° С. Изопрен — жидкость, кипящая при
34° С.
Алкины, или ацетиленовые
углеводороды
Общие положения. Алкинами на-
зываются ациклические углеводороды соста-
ва, выражаемого общей формулой С„Н2п _2
(начиная с п — 2) и имеющие одну тройную
связь между двумя соседними углеродными
атомами. Первым и важнейшим углеводоро-
дом этого ряда является ацетилен, или
этин, С2Н2 (со структурной формулой
Н — С г= С — Н), вторым — аллилен С3Н4,
или пропин (Н—С = С —СН3), и т. д.
Изомерия алкинов вызывается
различным расположением тройной связи
и различной структурой углеродного ске-
лета (см. Изомерия алкенов, стр. 297).
Физические свойства алкинов.
По физическим свойствам алкины сходны
с алканами, цикланами и алкенами. Удель-
ные веса алкинов несколько выше соответ-
ствующих алканов. Теплоты образования
алкинов меньше соответствующих алкенов.
Химические свойства алкинов.
Алкины ещё более реакционноспособны, чем
алкены, благодаря наличию тройной связи.
Для алкинов характерны реакции полиме-
ризации и присоединения по месту тройной
связи с переходом последней сначала в двой-
ную, а затем в одинарную связь. Алкины
легко присоединяют галоиды,водород (в при-
сутствии катализатора — солей окиси ртути)
и другие вещества.
Окисление алкинов сопровождается раз-
рывом тройной связи. Водород у углерод-
ного атома с тройной связью способен за-
мещаться на металл.
Ацетилен, или этин, С2Н2 — бесцветный
газ, немного легче воздуха, плохо раство-
римый в воде и хорошо во многих органи-
ческих растворителях. tK„„ = —84° С, tnJI =
= — 81° С. Горит коптящим пламенем. С воз-
духом образует взрывающиеся смеси в ши-
роком интервале концентраций (от 3 до
-^le ацетилена). Ацетилен легко взрывается
от детонации, в особенности в сжатом и
сжиженном состоянии. В атмосфере кисло-
рода ацетилен горит ослепительно-белым
пламенем, температура которого достигает
3000°. Главная масса ацетилена получается
действиеА! воды на карбид кальция: СаС2 4-
+ 2Н2О=Са(ОН)2 + С2Н2. Ацетилен является
сырьём для производства синтетического
каучука, уксусной кислоты, изоляторов,
растворителей и других материалов. Ацети-
лен перевозится в стальных баллонах в сжи-
женном состоянии.
Ароматические углеводороды
Гомологический ряд бензола.
Ряд углеводородов, содержащих в своих мо-
лекулах так называемое бензольное кольцо,
составляет гомологический ряд бензола.
Первым представителем этого ряда яв-
ляется бензол, имеющий по Кекуле струк-
туру:
СН
СН^СН
II I
СН сн
Замещением атомов водорода в бензоле
на углеводородные радикалы образуются
гомологи бензола. Например, СвН5 — СН3—
толуол, СаН5 — С2Н5 — этилбензол,
СвН5 — СН = СН2 — стирол и др.
Существуют, кроме того, двух-, трёх- и
более замещённые гомологи бензола (напри-
мер— см. ниже).
Изомерия углеводородов ряда
бензола. Изомерия однозамещённых го-
мологов бензола может вызываться лишь
изомерией бокового радикала. Изомерия
двух- и более замещённых гомологов, кроме
того, вызывается различным расположением
радикалов в кольце. Например, существует
три изомера ксилола:
СН3
СН3 СН3
Параксилол Метаксилол
Г СНз
ч /СНз
Ортоксилол
сокращённо обозначаемые латинскими бук-
вами р, т, о.
Физические свойства углево-
дородов ряда бензола. Первые пред-
ставители ряда бензола — бесцветные жид-
кости, следующие — твёрдые тела. Все
они обладают более или менее сильным спе-
цифическим запахом, не растворимы в воде,
но хорошо растворимы в различных органи-
ческих и неполярных неорганических рас-
творителях. Удельный вес их меньше еди-
ницы. Горят коптящим пламенем.
Химические свойства углево-
дородов ряда бензола. Для бензола
и его гомологов характерны реакции заме-
ОРГАНИЧЕСКАЯ ХИМИЯ
299
щения водородных атомов: галоидами (при
обыкновенных условиях), сульфогруппой —
SO2OH (при действии крепкой или дымя-
щей серной кислоты), нитрогруппой—NO2
(при действии крепкой азотной кислоты) и
др. Сильные окислители обычно окисляют
боковые цепи, не разрушая бензольного
кольца. Так, при окислении толуола обра-
зуется бензойная кислота. Бензол и его
гомологи в присутствии катализатора —
мелкораздробленного никеля или палладия—
присоединяют водород, образуя циклогексан
и его гомологи (реакция, обратная дегидри-
рованию цикланов).
Бензол СвН„ — бесцветная легкоподвиж-
ная и легколетучая жидкость. 1кив=80°С,
tnjl = 6° С; d%° = 0,879 г/см3. Не растворим
в воде. Горит коптящим пламенем. Бензол
находится в некоторых нефтях. Главная
масса его получается из каменноугольного
дёгтя—продукта сухой перегонки камен-
ного угля и продуктов пиролиза жидких
фракций нефти, получающихся нагреванием
нефти выше 600 — 700°. Бензол является
сырьём для производства большого числа
красителей, отравляющих веществ, лекарст-
венных веществ и других материалов. Бен-
зол широко применяется как растворитель.
Толуол СвН5 — СН3—бесцветная легко-
подвижная жидкость. /кип=111оС; t„4=—95°С;
= 0,867 г/см3. Находится в небольших
количествах в некоторых нефтях. Как и
бензол, добывается из каменноугольной
смолы и продукта гидролиза нефти.
Толуол является исходным материалом
для производства многих красителей и
взрывчатых веществ.
п-, м-, о-ксилолы — СаН4(СН3)2 — бес-
цветные легкоподвижные жидкости. Приме-
няются в качестве растворителя лаков и
каучука, а также как сырьё для производ-
ства некоторых красителей.
Стирол СаН5 — СН = СН2 — бесцветная
жидкость. tKun = 145° С; d%° = 0,907 г[см\
Получается каталитическим отщеплением во-
дорода от этилбензола. Служит сырьём для
получения электроизоляционных пластмасс
и вместе с бутадиеном является исходным
материалом для производства синтетическо-
го каучука—«Буна S».
Полициклические ароматические соедине-
ния. Углеводороды, содержащие в молекуле
несколько бензольных ядер, называются
полициклическими, или многоядерными, аро-
матическими соединениями. Те из них, у ко-
торых два или более бензольных ядра имеют
общие углеродные атомы, называются аро-
матическими соединениями с конденсирован-
ными бензольными ядрами. Примерами по-
лициклических ароматических соединений
являются дифенил, нафталин, тетралин,
декалин, антрацен, фенантрен, пинен и др.
Дифенил СаН6 • СвН6. Название соедине-
ния происходит от названия радикала СаН5—
фенил. Замещением водородных атомов на
углеводородные радикалы образуются гомо-
логи дифенила. Сам дифенил представляет
собой бесцветные кристаллы, плавящиеся
при 70° С; d%° — 1,16 г{см3. Небольшие ко-
личества его содержатся в каменноуголь-
ном дёгте. Производные дифенила (амины
и др.), легко получающиеся из одноядерных
ароматических соединений, служат исход-
ным материалом для синтеза ряда краси-
телей.
Нафталин Ci0Hs — является родоначаль-
ником гомологического ряда нафталина.
Нафталин при обыкновенных условиях —
твёрдое тело. Кристаллизуется в блестящих
листочках; плавится при 80° С; легко возго-
няется. Не растворим в воде, но хорошо
растворим в органических растворителях.
Обладает характерным запахом. Горит коп-
тящим пламенем. Нафталин получается из
каменноугольной смолы—продукта сухой
перегонки каменного угля и применяется
в качестве сырья для производства многих
красителей.
Тетралин С10Н12— бесцветная жидкость.
tKun = 205° С, = - 20° С; d‘° =0,971 г/см\
Получается гидрогенизацией нафталина в
присутствии катализатора и мелкораздроб-
ленного Ni под давлением. Применяется
в качестве растворителя лаков.
Декалин С10Н16 — бесцветная жидкость,
= 190° С; d^° = 0,89 г/см3. Получается
гидрогенизацией нафталина при избытке во-
дорода. Применяется, как и тетралин, в ка-
честве растворителя лаков.
Фенантрен С14Н10— кристаллизуется в
блестящих листочках с температурой пла-
вления 99° С. Находится в каменноугольном
дёгте.
Пинен С10Н16 — является представителем
терпенов— соединений с конденсированными
шестичленным и четырёхчленным кольцами.
Пинен — жидкость; является главной состав-
ной частью скипидаров. tKlln = 156° С; d^°=
= 0,858 ijcM3.
Галоидопроизводные углеводородов
Общие положения. Галоидопроиз-
водными углеводородов называются соеди-
нения, которые получаются замещением во-
дородных атомов в углеводородах на атомы
галоидов. Замещением одного атома полу-
чаются однозамещённые, двух — двухзаме-
щённые галоидопроизводные и т. д. Назва-
ния галоидопроизводных образуют или от
наименования радикалов, с которыми связан
галоид, или от углеводородов, от которых
могут быть произведены эти соединения
(женевская номенклатура). Например:
СН3С1
Хлористый метил,
или хлорметан
С2Н5Вг
Бромистый этил, или
бромэтан
С6Н5-С1
Хлористый фенил,
или хлорбензол
СН2С1..
Хлористый метилен,
или дихлорметан
СН2 = СНС1
Хлористый винил,
или хлорэтилен
СаН5-СН2С1
Хлористый бензоил
Изомерия галоидопроизвод-
ных углеводородов. Изомерия гало-
идопроизводных углеводородов может про-
исходить от изомерии углеводородного ра-
дикала и от различного положения атомов
300
хим ия
галоида. Например, двухзамещенный этан
имеет два изомера:
СН„С1 —СН2С1 СН3 —СНС12
Хлористый этилен, Хлористый этилиден,
или 1,2-дихлорэтан или 1,1-дихлорэтан
Физические свойства. Введение
галоида в углеводород увеличивает удель-
ный вес и повышает температуру кипения.
Бромзамещённые имеют температуры кипе-
ния выше соответствующих хлорзамещён-
ных, а иодзамещённые выше соответствую-
щих бромзамещённых. Газами при обыкно-
венных условиях являются хлорметан, хлор-
этан и бромэтан. Большинство галоидоза-
мещённых — бесцветные жидкости притор-
ного запаха. Из твёрдых галоидозамещён-
ных можно назвать трииодметан CHJ3 (йодо-
форм). Все галоидозамещённые не раство-
римы в воде, но растворимы в органических
растворителях и сами являются хорошими
растворителями. Удельные веса бромистых
и иодистых соединений больше единицы.
Некоторые из галоидозамещённых обладают
обезболивающими (анестезирующими) свой-
ствами; все более или менее ядовиты.
Химические свойства. Галоидо-
замещённые алканов обладают высокой ре-
акционноспособностью. Они легко обмени-
вают галоидные атомы на группы: ОН, NH2,
CN, NO2 и др. Галоидозамещённые алкенов
и ароматических углеводородов, в которых
галоид находится в бензольном кольце, зна-
чительно менее реакционноспособны. Все
галоидопроизводные реагируют с металлами
(например Na, Zn, Mg), образуя углеводо-
роды или металлоорганические соединения
и соответствующие соли.
При действии сильных щёлочей на гало-
идозамещённые алканы образуются алкены.
Хлорметан, хлористый метил СН3С1—газ,
не растворимый в воде и растворимый в ор-
ганических растворителях. tKun = ~ 24° С,
1ЛЛ = — 92° С; d = 0,952 г/см3.
Хлороформ и йодоформ CHCL и CHJ3 —
по женевской номенклатуре трихлорметан и
трииодметан. Первый является тяжёлой
жидкостью при обыкновенных условиях,
второй — твёрдым веществом жёлтого цвета.
Оба не растворяются в воде и не горят.
tKan СНС13 = 61° С, tnJ СНС13 = — 63° С;
lnjJCHJ3 = 119°С; </2°СНС13 = 1,488 г/с.и3;
(/2°CHJ3 = 4,008 г/см3. Хлороформ приме-
няется в медицине в смеси с эфиром как
средство наркоза. Получается хлороформ
действием белильной извести на спирт.
Йодоформ применяется в медицине как анти-
септик. Оба на свету разлагаются.
Четырёххлористый углерод, тетрахлорме-
тан, СС14—бесцветная жидкость. 1КЛП=77°С,
<пл= — 23° С; cf2°= 1,594 г/см3. Широко при-
меняется как растворитель, особенно цен-
ный тем, что не горит. Применяется для
тушения пожаров в тех случаях, когда дру-
гие средства, например вода, могли бы испор-
тить предметы.
Дихлорэтан, или 1,2-дихлорэтан, СН2С1—
— СН2С1 тяжёлая бесцветная жидкость.
tKan= 84° С, /,л = — 35° С; d%° = 1,261 г/см3.
.Несмотря на ядовитость, широко приме-
няется как растворитель благодаря дешевиз-
не. Получается действием хлора на этилен.
Хлорбензол С3Н5С1—бесцветная жидкость,
/ЛЛ„=132°С, Гил = — 45° С; d^°=l ,106 г/см3.
Применяется как растворитель.
Хлористый бензил С3Н5-СН2С1 — название
происходит от названия радикала бензил
СвН5-СН2—. Хлористый бензил — бесцветная
жидкость с резким, вызывающим слёзотече-
ние запахом. /КлЛ=179°С, ——39° С;
rf2°= 1,113 г/см3.
Спирты и фенолы
Общие положения. Спиртами, или
алкоголями, называются соединения, кото-
рые получаются замещением водородных
атомов в углеводородах на гидроксильные
группы. Спирты с гидроксильной группой
в бензольном кольце называются фенолами,
а с гидроксильной группой в боковой цепи—
ароматическими спиртами.
Спирты и фенолы с одной гидроксильной
группой называются одноатомными, напри-
мер этиловый спирт СН3-СН2ОН, фенол
СвН6ОН и др. Спирты и фенолы с двумя
гидроксильными группами называются двух-
атомными, например этиленгликоль СН2ОН—
СН2ОН, резорцин СвН4(ОН)2 и др. Спирты
и фенолы с тремя гидроксильными группами
называются трёхатомными, например гли-
церин СН2ОН — СНОН — СН2ОН, пирогал-
лол СвН3(ОН)3 и др.
Номенклатура спиртов и фено-
лов. Спирты, в которых гидроксил связан
с первичным углеродным атомом (—СН2ОН),
называются первичными, с вторичным угле-
родным атомом (—СНОН—) — вторичными
и с третичным углеродным атомом (—СОН—)—
третичными. I
Наименование спиртов производится либо
от радикала, с которым связан гидроксил,
либо прибавлением окончания «ол» к на-
званию углеводорода, отвечающего самой
длинной цепи в молекуле спирта (женев-
ская номенклатура). Например:
СН3
I
СН3ОН СН3 —СН—СН2ОН
Метиловый спирт, Первичный изобутиловый спирт,
или метанол или 2-метилпропанол-1
Одноатомный фенол, произведённый от
бензола, называется фенолом, от толуола—
крезолом.
Изомерия спиртов и фенолов
может быть вызвана изомерией углеродного
скелета и различным расположением гид-
роксильных групп. Например, известны че-
тыре изомера бутилового спирта:
СН3 —СН2 —СН2 —СН2ОН
Нормальный бутиловый спирт,
или бутанол-1
СН3 — СНОН — СН2 — сн3
Вторичный бутиловый спирт,
или бутанол-2
сн3 —сн—сн2он сн3
I I
сн3 сн3 —сон —сн3
Первичный ^зобутиловый Третичный изобутиловый
спирт, или 2-метилпропа- спирт, или 2-метилпропа-
нол-1 нол-2
ОРГАНИЧЕСКАЯ ХИМИЯ
301
Известны три изомера двухатомного фе-
нола:
ОН ОН
он V/ он 1 !|ОН X/ он 1^Х| X/
ОН
Пирокатехин Резорцин Гидрохинон
Физические свойства спиртов
и фенолов. При обычных условиях
спирты — либо жидкости, либо твёрдые ве-
щества (при большом молекулярном весе).
Фенолы—все твёрдые. Низшие спирты сме-
шиваются с водой во всех отношениях и
хорошо растворимы в органических раство-
рителях. С повышением молекулярного веса
растворимость спиртов в воде уменьшается.
Низшие фенолы плохо растворимы в воде,
а высшие совсем нерастворимы, но все хо-
рошо растворимы в органических раствори-
телях.
Температуры кипения спиртов и фенолов
выше соответствующих галоидопроизводных
и тем более соответствующих углеводоро-
дов. Многие спирты и в особенности фенолы
ядовиты, применяются как дезинфицирую-
щие средства.
Химические свойства спиртов
и фенолов. Фенолы имеют слабокислую
реакцию, поэтому сам фенол называют кар-
боловой кислотой. Фенолы реагируют с силь-
ными щёлочами как слабые кислоты с обра-
зованием соединений, называемых феноля-
тами. Как фенолы, так и спирты взаимодейст-
вуют с щелочными металлами с образова-
нием фенолятов и соответственно алкоголя-
тов, хотя спирты имеют нейтральную реак-
цию. Дегидратация спиртов (концентриро-
ванной серной кислотой или в присутствии
катализатора А12О3 при высокой темпера-
туре) приводит, в зависимости от условий,
либо к алкенам, либо к образованию про-
стых эфиров. Фенолы не дегидратируются.
Спирты, в отличие от углеводородов, легко
окисляются с образованием альдегидов (при
окислении первичных спиртов) и кетонов
(при окислении вторичных спиртов). Окис-
ление третичных спиртов сопровождается
разрывом углеродной цепи и образованием
кислот. Фенолы также легко окисляются.
При действии галоидангидридов кислот или
галоидоводородных кислот на спирты обра-
зуются галоидопроизводные углеводородов.
Фенолы значительно легче нитруются,
сульфируются, галоидируются и т. д., чем
соответствующие им ароматические углево-
дороды.
Метиловый спирт, метанол, карбинол, или
древесный спирт, СН3ОН — бесцветная лег-
коподвижная жидкость со спиртовым запа-
хом. /еи„=65° С, 1Пл= -—98°С; с^о=0,790г/сл<3.
Метиловый спирт очень ядовит; отравление
метанолом вызывает слепоту. Горит бледно-
синим пламенем. Смешивается с водой во
всех отношениях.
Метанол широко применяется как рас-
творитель лаков, смол и как сырьё для про-
изводства формалина, некоторых красителей,
отравляющих веществ. Метанол получается
при сухой перегонке дерева и синтетически
из СО и Н2 (водяной газ) в присутствии
катализаторов (ZnO, Си и др.) при темпера-
туре 300° С и давлении 150 — 600 ат.
Этиловый спирт, этанол, или винный
спирт, СН3—СН2ОН—бесцветная жидкость,
смешивающаяся с водой во всех отношениях.
<«ип=78° С, 1пл= —114,15° С; rf2°= 0,806 г/см3.
Горит бледноголубым пламенем. Находит
широкое применение в технике как раство-
ритель и сырьё для приготовления синте-
тического каучука, уксусной кислоты, эфира
и других веществ. Технический спирт дена-
турируется прибавлением ядовитых веществ
и какой-либо краски для распознания. Эти-
ловый спирт получают брожением сахари-
стых веществ и синтетически присоедине-
нием воды к этилену.
Изоамиловый спирт, или 2-метилбутанол-1,
(СНа)2 = СН — СН2 — СН2ОН — бесцветная
маслянистая жидкость. tKun= 131° С; d^0 =
= 0,810 г/см3. Изоамиловый спирт имеет не-
приятный запах; смешивается с водой во
всех отношениях. Сильно ядовит. Примесь
изоамилового спирта к этиловому придаёт
последнему характерный «сивушный» запах
и вкус.
Этиленгликоль, или этаиол-1,2, СН2ОН—
СН2ОН-бесцветная маслянистая жидкость,
сладковатая на вкус, очень гигроскопична.
tKan = 197° С, = —12°С; d2°=i,i09 г 1см3.
Смешивается с водой во всех отношениях.
Применяется как антифриза, т. е. для при-
готовления так называемых незамерзающих
растворов для радиаторов двигателей внут-
реннего сгорания.
Глицерин, или пропанол - 1,2,3, СН2ОН—
СНОН — СН2ОН — бесцветная, сиропооб-
разная жидкость сладкого вкуса. tKun =
= 290° С, tnj = 19° С; d2f = 1,260 г/сл3.
Смешивается с водой во всех отношениях.
Глицерин применяется как антифриза и
в больших количествах в качестве сырья
для производства нитроглицерина (нитро-
глицерин — сложный эфир глицерина и азот-
ной кислоты — является сильиовзрывчатым
веществом); кроме того глицерин широко
применяется в медицине, парфюмерной, кон-
дитерской и других промышленностях. Гли-
церин получается омылением жиров, кото-
рые являются сложными эфирами глицерина
и жирных кислот, а также синтетически
действием воды на пропилен (продукт кре-
кинга нефти) в присутствии катализаторов
и при высокой температуре.
Фенол, или карболовая кислота, СвН5ОН—
бесцветное твёрдое кристаллическое веще-
ство, краснеющее на воздухе вследствие
медленного окисления. tKun= 182° С, 1!1Л —
= 42,5° С; d = 1,058 г! см- (60°). Фенол обла-
дает характерным «карболовым» запахом,
ядовит. Выше 68° С смешивается с .водой во
всех отношениях; при обыкновенной темпе-
ратуре плохо растворяется в воде. Водный
раствор фенола применяется для дезинфек-
ции. Фенолом могут пропитываться шпалы
для предупреждения гниения. Фенол служит
сырьём для производства пластмасс, краси-
телей, взрывчатых веществ, бакелитовых
302
химия
лаков, лекарственных веществ и других
материалов. Фенол содержится в каменно-
угольной смоле — продукте сухой перегонки
каменного угля. Значительные количества
его готовят синтетически из бензола.
п-, м, о-крезолы СН3— СвН4 — ОН. Кре-
золы— твёрдые вещества, обладающие рез-
ким неприятным запахом. Водные растворы
крезолов обладают сильными дезинфици-
рующими свойствами. Раствор мыла и кре-
золов, применяющийся для дезинфекции
помещений, называется лизолом. Крезолами
пропитываются шпалы для предупреждения
гниения. Крезолы являются сырьём для
производства пластмасс типа бакелита, кра-
сителей и взрывчатых веществ.
Крезолы содержатся в каменноугольной
смоле — продукте сухой перегонки камен-
ного угля.
Нафтолы. Замещением водородных ато-
мов нафталина на гидроксильные группы
получаются нафтолы. Например:
ОН
/\А /\/Ч-он
i I I I I I
Ч/W ч/w
а-нафтол р-нафтол
По своим свойствам нафтолы похожи на
фенолы. Нафтолы служат сырьём для про-
изводства красителей.
Альдегиды и кетоны
Общие положения. Соединения, со-
держащие карбонильную группу (—С=о),
углеродный атом которой соединён с водород-
ными атомами или углеводородными ради-
калами, относятся к двум классам органи-
ческих соединений, называемых альдегидами
и кетонами. В альдегидах углеродный атом
карбонильной группы по крайней мере
одной своей валентностью соединён с ато-
мом водорода; в кетонах же этот атом
обеими валентностями соединён с двумя
углеводородными радикалами. Альдегиды
и кетоны могут быть трактованы и как
производные углеводородов, в которых два
водородных атома при одном и том же
углероде заменены атомом кислорода. Об-
щую формулу альдегида можно записать
так: R—С , кетона R—С—R, где R—угле-
ЧН
водородный радикал.
Номенклатура. Отдельные пред-
ставители альдегидов и кетонов могут
быть названы, исходя из принципа рацио-
нальной или женевской номенклатуры.
Иногда пользуются тривиальными назва-
ниями, применяя тривиальные названия
кислот того же углеродного скелета, в ко-
торые альдегиды превращаются при окисле-
нии. Кетоны называют, характеризуя оба
углеводородных радиката. В табл. 11 даны
формулы и различные наименования некото-
рых низших альдегидов и кетонов.
Физические свойства. При обык-
новенной температуре низшие альдегиды и
кетоны, за исключением муравьиного альде-
гида, являющегося газообразным вещест-
вом,— жидкости, высшие же являются
твёрдыми телами. Лишь первые представи-
тели альдегидов и кетонов растворимы
в воде и смешиваются с ней. Высшие аль-
дегиды и кетоны не растворимы в воде и
растворяются лишь в органических раство-
рителях.
Химические свойства. Альде-
гиды и кетоны легко окисляются. Альде-
гиды окисляются до соответствующих кис-
лот, кетоны окисляются до кислот с разры-
вом цепи, с образованием смеси кислот,
углеродные скелеты которых являются
осколками скелета исходного кетона. Аль-
дегиды и кетоны легко восстанавливаются,
образуя спирты, за счёт присоединения
водорода по месту двойной связи карбониль-
ной группы. Альдегиды и кетоны легко
взаимодействуют со спиртами, аммиаком,
гидроксиламином.
Муравьиный альдегид, формальдегид, или
метанал, СН2О—получается обычно окисле-
нием метилового спирта. Газ, сжижающийся
при—21°С, легко растворимый в воде,
обычно поступающий в продажу в виде
40%-ного раствора, называемого форма-
лином, является хорошим дезинфицирующим
веществом и средством консервирования
препаратов. Служит исходным сырьём
в производстве красящих веществ, пласти-
ческих масс и фармацевтических препаратов.
Газообразный формальдегид при обыкно-
венной температуре сам собой легко поли-
Таблица 11
Названия и формулы альдегидов и кетонов
Альдегиды Кетоны
формула строения наименование формула строения наименование
тривиальное женевское рациональное женевское
Н О
н-с=о Муравьиный Метанал сн,-с-сн, Диметил- Пропанон
н о
1 сн3-с=о Уксусный Этанал сн3-с-сн,-сн„ Метила тил- Бута нон
н о
сн3-сн„-с=о Пропионовый Пропанал СНз-С-СН,—сн„-снэ Метил пр опил Пентанон-2
ОРГАНИЧЕСКАЯ ХИМИЯ
303
меризуется; получающийся при этом твёр-
дый белый порошок носит название пара-
формальдегида. При действии на формалин
или формальдегид аммиака образуется
кристаллическое очень гигроскопическое
вещество состава (СН2)0 N4— гексаметилен-
тетрамин, употребляемое в медицине под
названием уротропина. Продукты конден-
сации формальдегида с фенолами образуют
пластическую массу, называемую бакелитом.
При конденсации формальдегида с казеином
получается пластмасса, называемая гала-
литом.
Уксусный альдегид, ацетальдегид, или
этанал, С2Н4О— легколетучая жидкость
с температурой кипения 20,2° С. Получается
окислением этилового спирта или по реакции
Куч“ерова действием воды на ацетилен
в присутствии солей окиси ртути как ката-
лизаторов. Окислением ацетальдегида по-
лучается уксусная кислота. При действии
на безводный альдегид одной капли кон-
центрированной серной кислоты он превра-
щается в тримерный паральдегид—жидкость
с температурой кипения 124°С (СН3СНО)3.
При более низких температурах из ацеталь-
дегида образуется другая полимерная
форма — метальдегид. Метальдегид — твёр-
дое вещество, нашедшее себе применение как
горючее под названием «твёрдый спирт».
Бензойный альдегид, или бензальдегид,
C6HS — СН= О — жидкость с температурой
кипения 179°С миндального запаха. Полу-
чается синтетически из фенилдихлорметана
или умеренным окислением толуола. Широко
употребляется в парфюмерии и в качестве
исходного продукта в синтезе красящих
веществ и других органических препаратов.
Фурфурол, или фурановый альдегид,
С4Н3О—СН=О бесцветная жидкость с темпе-
ратурой кипения 162'С, желтеющая при стоя-
нии, с запахом свежего ржаного хлеба.
Получается отнятием воды от сахаристых
веществ или действием серной кислоты на
отруби. Применяется в производстве пласт-
масс и в нефтяной промышленности для
селективной очистки масел.
Ацетон, или диметилкетон, CHSCOCH3 —
простейший кетон. Бесцветная жидкость со
специфическим запахом и температурой ки-
пения 56,1°С. Широко применяется в качестве
растворителя и в качестве исходного про-
дукта в целом ряде органических синтезов.
Ацетон получается в промышленных масшта-
бах сухой перегонкой кальциевой соли
уксусной кислоты или брожением сахари-
стых веществ под влиянием специфических
бактерий. Хлорацетоп СН3СОСН2С1 и бром-
ацетон СН3СОСН2Вг применяются в ка-
честве боевых отравляющих веществ слезо-
точивого действия.
Карбоновые кислоты
Органические соединения, в состав кото-
рых входит карбоксильная группа—С—ОН,
II
О
относятся к классам органических или кар-
боновых кислот. В зависимости от числа
карбоксильных групп карбоновые кислоты
делятся на одноосновные, содержащие одну
карбоксильную группу, и многоосновные,
содержащие больше чем одну карбоксиль-
ную группу.
Гомологические ряды, изоме-
рия. Карбоновые кислоты можно себе
представить как производные соответст-
вующих углеводородов, у которых одна или
несколько расположенных на концах угле-
родных цепей одновалентных метильных
групп заменены карбоксильными группами.
Каждому нормальному предельному углево-
дороду соответствует лишь одна однооснов-
ная карбоновая кислота с тем же числом
углеродных атомов и таким же углеродным
скелетом. Простейшая одноосновная карбо-
новая кислота муравьиная Н — СООН. Му-
равьиная кислота является родоначаль-
ником гомологического ряда предельных
одноосновных кислот эмпирического со-
става СпН2п+1О2. За муравьиной кислотой
следуют её гомологи: уксусная кислота
СН3СООН, пропионовая кислота СН3СН.,
СООН, масляная кислота СН3СН2СН2СООН
и т. д. Число изомерных карбоновых кислот,
соответствующих углеводородам изострое-
ния, зависит от строения этих углеводородов.
СН3
Так, из изобутана СН3—СН—СН3 можно
произвести только одну кислоту, изомерную
с нормальной масляной кислотой и назы-
ваемую изомасляной кислотой.
Номенклатура. Женевская номен-
клатура к карбоновым кислотам приме-
няется редко. В ряду карбоновых кислот,
а также их производных широко приме-
няются тривиальные названия. Эти названия
чаще всего связаны с наименованием либо
природных продуктов, из которых эти кис-
лоты были впервые выделены, либо исход-
ных продуктов, из которых они получа-
ются синтетически. Таковы, например,
широко применяемые названия: муравьиная,
уксусная, янтарная, винная, яблочная и т. д.
Физические свойства. Органи-
ческие кислоты являются в подавляющем
большинстве бесцветными веществами. Низ-
шие представители предельных одноосновных
кислот и некоторые непредельные однооснов-
ные кислоты являются жидкими при обыкно-
венной температуре веществами. Высшие пре-
дельные кислоты и большинство кислот выс-
шей основности являются твёрдыми, хорошо
кристаллизующимися телами. Низшие кис-
лоты обладают острым специфическим за-
пахом, в безводном состоянии весьма едки
и вызывают появление на коже пузырей.
В ряду одноосновных кислот низшие пред-
ставители смешиваются с водой во всех
отношениях. По мере удлинения углеводо-
родного радикала растворимость в воде
падает. Высшие предельные кислоты, как
например пальмитиновая и стеариновая,
в воде не растворяются. Двухосновные кис-
лоты показывают большую растворимость
в воде, чем соответствующие им по угле-
родному составу одноосновные кислоты.
Химические свойства. Карбоно-
вые кислоты являются слабыми кислотами.
Из их солей с различными металлами более
сильные минеральные кислоты вытесняют
304
химия
свободные карбоновые кислоты. Соли одно-
основных кислот со щелочными металлами
в водных растворах способны гидролизо-
ваться, что проявляется в слабой щёлоч-
ности этих водных растворов. Растворы
натриевых или калиевых солей однооснов-
ных кислот с высоким молекулярным весом,
как пальмитиновая,стеариновая или олеино-
вая, обладают способностью образовывать
стойкие эмульсии, вспениваться и широко
применяются под названием мыл. Много-
основные кислоты образуют соли, как ней-
тральные, так и кислые.
Производные карбоновых кислот. Хлоран-
гидриды карбоновых кислот. Хлорангидри-
дами карбоновых кислот называют соедине-
ния общей формулы /?—С , где R —
ЧС1
углеводородный радикал. Эти соединения
можно рассматривать как продукты заме-
щения гидроксила кислоты атомом хлора.
Например, хлорангидрид уксусной кислоты
будет иметь формулу: СН3СОС1. В присут-
ствии воды хлорангидриды гидролизуются
с образованием соответствующих кислот.
Амиды кислот — соединения общей фор-
/°
мулы R—С . Амиды кислот предста-
XNH2
вляют собой нейтральные вещества, не
склонные к реакциям солеобразования.
Амиды подвергаются гидролизу с образо-
ванием аммиака и соответствующей орга-
нической кислоты.
Ангидриды карбоновых кислот. Об-
щая формула строения этих соединений
О О
II II
R—С—О—С—R. Их можно рассматривать
как продукт отщепления воды от двух мо-
лекул кислоты.
Сложные эфиры карбоновых кислот—сое-
О
II
динения общей формулы R— С—О—R. Их
можно рассматривать как продукты отще-
пления одной молекулы воды от молекулы
карбоновой кислоты и молекулы спирта.
Сложные эфиры плохо растворимы в воде,
но хорошо растворимы в органических рас-
творителях. Подобно другим производным
кислот сложные эфиры подвергаются гидро-
лизу с образованием соответствующей кар-
боновой кислоты и спирта.
Нитрилы — соединения общей формулы
R—C = N. Нитрилы с небольшим молекуляр-
ным весом представляют собой жидкости.
Низшие нитрилы хорошо растворимы в воде.
При взаимодействии с водой гидролизуются
с образованием карбоновой кислоты и
аммиака; при обычной температуре гидролиз
идёт медленно.
Муравьиная кислота Н—СООН—жидкость
с температурой кипения 105°С. Обладает
крайне о.стрым запахом; смешивается с водой
во всех отношениях; 1,25%-ный раствор её
известен под названием муравьиного спирта.
Муравьиная кислота гораздо сильнее дру-
гих карбоновых кислот; по степени диссо-
циации она приближается к фосфорной
кислоте. Применяется как протрава при
крашении тканей, а также в качестве дезин-
фицирующего вещества в пищевой про-
мышленности.
Уксусная кислота СН3СООН. В безвод-
ном состоянии образует кристаллическую,
похожую на лёд массу, плавящуюся при
температуре 16,5°С и потому называемую
иногда «ледяной уксусной кислотой». Кипит
при температуре 118° С. Уксусная кислота
растворяется во всех отношениях в воде,
спирте, эфире. Она содержится (2 —3°/0)
в уксусе. Уксусная кислота широко при-
меняется в технике для приготовления
многих красящих вещества, фармацевтиче-
ских препаратов, ацетона, искусственного
волокна, пластических масс, белил и дру-
гих важных продуктов. Из производных
уксусной кислоты важное значение имеют:
а) ацетаты алюминия и железа, применяе-
мые при окраске тканей; б) уксусноэтило-
вый эфир, или этилацетат, СН3СООС»Н5 —
жидкость с ароматным запахом, с темпера-
турой кипения 77° С, применяется как рас-
творитель органических веществ; в) уксусно-
изоамиловый эфир СН3СООС6Нц—жидкость
с температурой кипения 65° С, обладает
своеобразным запахом («грушевая эссен-
ция»), широко применяется как раствори-
тель лаков и в частности целлулоида;
О
II
г) ангидрид уксусной кислоты СН3—С—
О
II
—О—С—СН3—жидкость с резким запахом,
с температурой кипения 139,6° С, приме-
няется для введения ацетильных групп
в другие соединения, например при полу-
чении ацетилцеллюлозы; д) амид уксусной
кислоты, или ацетамид, CH3CONH2—кристал-
лическое вещество с температурой плавле-
ния 82° С, растворимое в воде, является
исходным продуктом в ряде органических
синтезов.
Пальмитиновая кислота С15Н31—СООН —
твёрдое вещество с температурой плавле-
ния 62,6"; входит в состав растительных и
животных масел.
Стеариновая кислота С17Н35СООН—твёр-
дое тело с температурой плавления 69,3° С;
также входит в состав жиров; в смеси
с пальмитиновой кислотой представляет
собой так называемый стеарин.
Олеиновая кислота Сг,Н33—СООН — жид-
кость, застывающая при температуре 14° С;
входит в состав растительных жиров; со-
держит одну двойную связь и после гидри-
рования переходит в стеариновую кислоту.
Щавелевая кислота НООС—СООН—яв-
ляется двухосновной карбоновой кислотой.
Она представляет собой твёрдое вещество,
кристаллизующееся с двумя молекулами
воды (СООН)2-2 Н2О, хорошо растворима
в воде. Щавелевая кислота проявляет до-
вольно сильные кислотные свойства, ядо-
вита. Соли щавелевой кислоты называются
оксалатами.
Бензойная кислотаСвН5—СООН—кристал-
лическое вещество с температурой плавле-
ОРГАНИЧЕСКАЯ ХИМИЯ
305
ния 122,5° С. Первый представитель аромати-
ческих карбоновых кислот. Применяется для
изготовления фармацевтических препаратов
и красящих веществ.
Жиры. Растительные и животные жиры
представляют собой в основном смесь раз-
личных сложных эфиров, образованных
трёхатомным спиртом—глицерином и карбо-
новыми кислотами, среди которых преобла-
дают кислоты: стеариновая С13Н36СООН,
пальмитиновая С16Н31СООН, олеиновая
€i,HS3COOH. Эти сложные эфиры назы-
ваются глицеридами. Глицериды предель-
ных * кислот представляют собой твёрдые
вещества, а глицериды непредельных кис-
лот—жидкости; первые встречаются большей
частью в организме животных, вторые —
.в плодах растений. Все жиры легче воды,
в воде не растворимы, хорошо растворимы
в органических растворителях: бензине,
эфире, четырёххлористом углероде, дихлор-
этане, сероуглероде.
Мыл'а. Мылами называют соли высокомо-
лекулярных органических кислот. Твёрдые
мыла — натриевые соли жирных кислот,
жидкие мыла — калиевые соли жирных
кислот. Мыло можно получить, действуя на
жирную кислоту щёлочью или содой или
действуя щёлочью непосредственно на жир.
Воск. Воск состоит главным образом из
•сложных эфиров одноатомных спиртов с боль-
шим молекулярным весом и высокомолеку-
лярных жирных кислот.
Азотсодержащие производные
углеводородов, амины цепные и кольчатые
Амины можно рассматривать как про-
дукты замещения атомов водорода аммиака
NH3 углеводородными радикалами R. Пер-
вичные амины являются продуктами заме-
щения одного атома водорода аммиака и
имеют общую формулу RNH2. Вторичные
амины являются продуктами замещения
двух атомов водорода аммиака общей фор-
мулы NH. Третичные амины—продукты
R'
замещения всех трёх атомов водорода
аммиака и имеют общую формулу R— N.
Группа атомов NHa называется аминогруп-
пой. Если в молекуле содержится одна
аминогруппа, то амин называется одноатом-
ным. В молекулах многоатомных аминов
содержится несколько аминогрупп.
Физические свойства. Первые
представители аминов жирного ряда явля-
ются газами. Следующие за ними, равно,
как и первые ароматические амины,—жид-
кости и лишь высшие представители—твёрдые
тела. Низшие амины жирного ряда обла-
дают специфическим аммиакоподобным, но
более острым запахом. По мере увеличения
молекулярного веса уменьшается и лету-
честь аминов. Некоторые низшие амины
обладают селёдочным запахом.
Химические свойства. Химиче-
ская природа амина зависит от характера
20 Том I
соединённого с аминогруппой радикала и
от специфических особенностей аминогрупп.
Последние, являясь остатками аммиака,
сообщают содержащим их соединениям
основной характер, усиливаемый или осла-
бляемый соединёнными с аминоазотом ради-
калами. Так, например, метиламин CH3NH2
является более сильным основанием, чем
аммиак NH3, т. е. алкильные радикалы
усиливают основной характер аминогруппы.
Ароматические радикалы играют обратную
роль. Все амины с кислотами дают соли,
подобные солям аммония и носящие анало-
гичные названия, например метиламин,
присоединяя соляную кислоту, даёт хлори-
стый метиламмоний или хлористоводород-
ный метиламин CH3NH2-HC1. Соли аминов
представляют собой кристаллические, рас-
творимые в воде вещества. Из образовав-
шихся солей могут быть выделены свобод-
ные амины действием щёлочей. Амины можно
считать органическими основаниями.
Метиламин CH8NH2—бесцветный газ с за-
пахом аммиака, температура кипения—6° С.
Встречается при распаде некоторых при-
родных веществ, особенно белковых. Легко
растворим в воде, образуя раствор гидрата
окиси метиламмония, являющегося более
сильным основанием, чем гидрат окиси
аммония.
Анилин, или фениламин, CeH6NH2—жид-
кость с температурой кипения 184° С, со
специфическим запахом. Широко приме-
няется в качестве исходного продукта для
синтеза различных органических веществ,
иногда называемых поэтому анилиновыми.
Нафтиламии-альфа C10H7NH2— бесцвет-
ные, темнеющие на воздухе кристаллы с
температурой плавления 50° С. Обладают
весьма неприятным фенольным запахом.
Альфа-нафтиламин и различные его суль-
фокислоты применяются для производства
различных азокрасителей.
Нафтиламин-бета C10H,NH3—изомер пре-
дыдущего. Бесцветные кристаллы с темпе-
ратурой плавления 112° С. Применяется для
производства различных красителей.
Нитросоединеиия цепные и кольчатые
Нитросоединениями называются веше-
ства, содержащие нитрогруппу—N ,азот
которой непосредственно связан с углеро-
дом. Гомологический ряд нитросоединений
ряда метана начинается с нитрометана
СН3- NO2, бензола—с нитробензола С6Н5. NO2.
Названия нитросоединений как по старой,
так и по женевской номенклатуре про-
изводятся от углеводородов с приставкой
впереди слова «нитро».
Физические свойства. Низшие
гомологи нитросоединений парафинового
ряда — жидкости, не растворимые в воде,
смешивающиеся со спиртом и эфиром. Удель-
ные веса низших нитросоединений больше
единицы; при повышении молекулярного
веса удельный вес нитросоединений умень-
шается. Низшие гомологи нитросоединений
ароматического ряда — жидкости с высокой
306
химия
температурой кипения. Вообще полинитро-
соединения аромат-ических углеводородов
являются твёрдыми веществами. Обычно
ароматические нитросоединения окрашены
в жёлтый цвет. Они не растворимы в воде
и в водных кислотах или щёлочах и, сле-
довательно, являются нейтральными ве-
ществами.
Химические свойства. По мере увеличе-
ния числа нитрогрупп возрастает способ-
ность нитросоединений взрываться от удара
или детонации, некоторые из полинитро-
соединений широко применяются в военной
технике для начинки снарядов, бомб, мин
и т. п. В результате восстановления нитро-
соединений получаются амины.
Нитробензол CeH6NO2 — светложёлтая
жидкость, тяжелее воды, с резким запахом,
напоминающим запах горького миндаля.
Ядовит. Применяется в больших количест-
вах при производстве анилина; кроме того,
применяется в парфюмерии.
2, 4, 6-тринитротолуол (тротил, тол)
СН3С,Н2 (NO3)3—твёрдое вещество жёлтого
цвета, плавящееся при температуре 81,5°С.
Он является одним из наиболее важных
бризантных (дробящих) взрывчатых веществ
и применяется в значительном количестве
для снаряжения артиллерийских снарядов,
иин, подрывных шашек и т. п. Зажжённый
гротил горит коптящим пламенем не
взрываясь и вполне безопасен в обращении,
только от детонатора он сильно взрывает.
В смеси с нитратом аммония применяется
для подрывных работ под названием
«аммонал».
Трииитрофенол (пикриновая кислота)
CeH2(OH)(NO3)3 — светложёлтое кристалли-
ческое вещество с температурой плавления
122°С. Щелочные соли пикриновой кислоты
применяются в качестве взрывчатых веществ
под названием «мелинит».
Серосодержащие производные
Тиоспирты и тиофенолы. Тиоспирты и
тиофенолы характеризуются наличием в их
составе сульфогидрильной группы — SH.
Строение тиоспиртов и тиофенолов может
быть выражено общей формулой' R—SH
(где R— углеводородный радикал). Поэтому
их можно рассматривать как продукты за-
мещения водорода в сероводороде на угле-
водородный радикал. Тиоспирты и тиофенолы
называются меркаптанами. Для их полной
характеристики перед словом меркаптан
пишется название углеводородного радикала.
Так, например, соединение CH3SH назы-
вается метилмеркаптан, CH3CH2SH — этил-
меркаптан, CeH6SH —фенилмеркаптан.
Низшие меркаптаны кипят при более
низких температурах, чем соответствующие
им по углеродному скелету спирты. Они
обладают чрезвычайно неприятным запахом,
более сильным, чем запах сероводорода.
Меркаптаны как содержащие остаток
сероводорода — слабой кислоты — также
имеют слабокислые свойства. Это про-
является в том, что водород SH группы заме-
щается на металл при действии гидратов
окисей щелочных металлов, при действии
щёлочными металлами и при действии осно-
ваниями тяжёлых металлов. Эти соединения,
называемые меркаптидами, не растворяются
в воде.
Тиоэфиры, или сульфиды. При обработке
меркаптидов галоидопроизводными углеводо-
родов образуются тиоэфиры, или сульфиды,—
соединения общей формулы R—S—R. Их
можно рассматривать как производные серо-
водорода, у которых оба атома водорода
заменены углеводородными радикалами,
например CH,SCHs — диметилсульфид, СН3
CH2SCH2CHs —диэтилсульфид. Меркаптаны
и тиоэфиры содержатся в нефтях Второго
Баку и придают им специфический неприят-
ный запах.
Этилмеркаптаи C2H6SH—бесцветная жид-
кость с температурой кипения 37°С, весьма
неприятного запаха. Применяется для обна-
ружения пропусков в трубопроводах, в част-
ности при испытании газовых сетей. Приме-
шивается в небольших количествах к есте-
ственному метановому газу при применении
его для бытовых целей.
Й!'-дихлорэтилсульфид(иприт)С1СН2СН28.
3СН2С1—в неочищенном виде представ-
ляет собой тёмнобурую жидкость с запахом
горчиць?; лука или чеснока. Кипит при темпе-
ратуре 217°С, затвердевает при температуре
14°С, относится к числу стойких отравляю-
щих веществ, проникает через обувь и
платье и вызывает нарывы, болезненные
пузыри и ожоги.
Сульфокислоты — органические сульфо-
кислоты, называемые иногда сульфоновыми
кислотами. Характеризуются наличием в них
остатка серной кислоты, называемого суль-
О
II
фогруппой—S—ОН, и имеют общее строение
II
О
RSO3H. Наиболее интересны ароматические
сульфокислоты и их производные, получае-
мые непосредственным сульфированием аро-
матических углеводородов, аминов, фенолов
и тому подобных соединений. Ароматиче-
ские сульфокислоты—кристаллические веще-
ства, хорошо растворимые в воде. Подобно
серной кислоте, очень гигроскопичны. Они
являются сильными кислотами. С металла-
ми, основными окислами и основаниями
сульфокислоты образуют соли.
Бензолсульфокислота C4H5SO3H — белое
кристаллическое вещество, очень хорошо
растворимое в воде, обладает сильными
кислотными свойствами. Обычно выделяется
в виде натриевой соли CeH6SO3Na. Служит
исходным сырьём для получения фенола.
Сульфоновая кислота, аиилин-парасуль-
фокислота или парааминобензолсульфо-
кислота NH2CeH4SO3H — белые кристаллы,
хорошо растворимые в горячей воде, плохо
растворимые в холодной воде. Широко при-
меняется для производства азокрасителей.
Металлоорганические соединения
Общая характеристика. Соеди-
нения, в молекулах которых атом угле-
рода связан с атомом металла, называются
металлоорганическими, например CH3L i—
ОРГАНИЧЕСКАЯ ХИМИЯ
307
метиллитий, СаН.2пС2Н. — диэтилцинк,
с,н С2Н5
у Pb f — тетраэтилсвинец. Если
Сан/ ХС2Н6
с атомом металла связан ещё и неорганиче-
ский остаток, то такое соединение называют
смешанным металлоорганическим соедине-
нием, например CH3MgJ — иодистый метил-
магний. Металлоорганические соединения
представляют обширный класс соединений.
В настоящее время известны металлоорга-
нические соединения большинства металлов.
Многие металлоорганические соединения весь-
ма реакционноспособны, поэтому использу-
ются в лабораторной практике для синтеза
различных органических веществ.
Тетраэтилсвинец РЬ(С2Н6)4 — прозрач-
ная бесцветная жидкость с неприятным за-
пахом, пары которой весьма ядовиты. Он
не растворяется в воде, но растворим
в органических растворителях. Если поджечь
тетраэтилсвинец, то он горит на воздухе
большим пламенем с образованием желтовато-
белого дыма, состоящего из частиц окиси
свинца. Применяется как антидетонатор для
моторного топлива.
Производные углеводородов, содержащие
различные функциональные группы
Углеводы. Название «углеводы» является
устаревшим. Оно относится к тому времени,
когда считали, что в соединениях этого
типа углерод, водород и кислород на-
ходятся в тех же соотношениях, что и в гид-
ратах углерода, и, следовательно, соответ-
ствуют общей формуле С„(Н2О)т. Совре-
менное учение относит к классу углеводов
все соединения, имеющие характер сахаров
и близкие им по строению или характеру
вещества. Углеводы делятся на: а) моноса-
хариды, или простые сахара, например
виноградный сахар (глюкоза), фруктовый
сахар (фруктоза); б) сахароподобные поли-
сахариды, построенные из моносахаридов и
ещё довольно близкие им по растворимости,
вкусу и химическому характеру; среди них
тростниковый, солодовый и молочный сахар;
в) несахароподобные полисахариды, которые
являются продуктами конденсации простых
сахаров, но они уже не дают истинных вод-
ных растворов, а в лучшем случае образуют
коллоидные растворы. И в других отноше-
ниях они также значительно отличаются от
простых сахаров, например крахмал, клет-
чатка (целлюлоза).
Моносахариды. Моносахариды сущест-
вуют в виде двух форм, находящихся в рав-
новесии: окисной формы и формы оксиальде-
гидов (альдоз) или оксикетонов (кетоз) с от-
крытой цепью (см. ниже на примере глюкозы
и фруктозы). Моносахариды представляют со-
бой нейтральные вещества, легко раствори-
мые в воде и трудно—в спирте; в эфире они
совсем не растворяются. Все природные
моносахариды обладают оптической актив-
ностью (вращают плоскость поляризации
света). Моносахариды являются сильными
восстановителями. При окислении альдоз
слабым окислителем образуются оксикис-
лоты с тем же числом углеродных атомов,
под действием сильных окислителей обра-
зуются дикарбоновые кислоты. При окисле-
нии кетоз получаются две кислоты, в каждой
из которых содержится меньшее число
атомов углерода, чем в исходном веществе.
Моносахариды способны образовывать эфиры
и алкоголяты (сахараты).
Глюкоза, декстроза, или виноградный
сахар, СвН12О6 — представляет собой смесь
двух форм: оксиальдегида (а) и окисной (Ь),
находящихся в равновесии:
Н Н Н Н Н
I I I I I /Н .
н-с-с—с—с—с—с
I I I I I
он он он он он
(а)
н н н н н н
I I I I I /н
2"н— С—С—С—с— с—с.
I III хон.
он он он он
(Ь)
В твёрдом состоянии равновесие сильно
сдвинуто в сторону окисной формы (Ь).
В окисной форме не все гидроксилы (ОН)
равноценны. Один из них, связанный с ато-
мом углерода, при котором имеется «эфир-
ный кислород» (кислород, связанный со
вторым и последним атомами углерода),
отличен от других и называется глюко-
зидным гидроксилом. Глюкоза представляет
собой белое твёрдое кристаллическое веще-
ство, хорошо растворимое в воде и обла-
дающее сладким вкусом, несколько более
слабым, чем у обыкновенного сахара.
Содержится почти во всех тканях организ-
мов животных и растений, особенно много
в винограде и других сладких плодах.
Фруктоза СвН12Ов имеет одинаковую
бруттоформулу с глюкозой, но отличное
строение; так же, как и глюкоза, предста-
вляет собой равновесную смесь двух форм;
оксикетона (а) и окисной (Ь):
Н О Н Н Н Н
I II I I I I
н—С—С—С—С— с — с—н
I I I 1 I
он он он он он
(а)
н он н н н н
. I I I I I I
н—с—с—с-с —с—с —н .
* I III
он он он он
(Ь)
Фруктоза находится во многих сладких
плодах вместе с глюкозой. Смесь глюкозы
и фруктозы является главной составной
частью мёда. Фруктоза обладает более слад-
ким вкусом, чем обыкновенный свеклович-
ный сахар.
Полисахариды. Углеводы, из одной мо-
лекулы которых образуются при гидролизе
две, три и больше молекул моносахаридов.
20*
308
химия
называют соответственно дисахаридами,
трисахаридами и вообще полисахаридами.
Примером дисахарида является сахароза.
Сахароза, или тростниковый сахар,
С12-Н22ОИ является ангидридом глюкозы и
фруктозы. Строение её можно представить
следующей формулой:
НН Н Н Н
I I I I I
ОН н2с—с—с—с—с—с—о—
I I I
он он он
---о----
---------О----
н н
I I
— С — с —с —с—СН2ОН
I III
СН2ОН он он Н
сахароза
Как видно из этой формулы, остатки
моносахаридов (глюкозы и фруктозы) в мо-
и под действием ферментов подвергается
гидролизу, промежуточным продуктом кото-
рого является декстрин и конечным про-
дуктом— глюкоза. Крахмал содержится в
растениях: в клубнях картофеля 18—21%,
в зёрнах пшеницы до 64—65%, в зёрнах
риса 77%.
Клетчатка, целлюлоза (СвН10О6)Л, — вы-
сокомолекулярное вещество, основная со-
ставная часть древесины. Высоким содержа-
нием клетчатки отличаются волокна льна,
пеньки и особенно хлопка, состоящие почти
из чистой клетчатки.
Клетчатка имеет огромное техническое
значение. Она служит материалом для из-
готовления тканей, искусственного волокна,
бумаги. Гидролизом клетчатки получаются
сахаристые вещества, служащие хорошим
кормовым средством для скота; путём бро-
жения этих сахаристых веществ получают
спирт.
Часть молекулы клетчатки, представ-
ляющей собой нитевидную молекулу с мо-
лекулярным весом порядка 300 000—500000,
можно представить формулой
----О-----i |----- О-----1
СН2 (ОН)-СН-СН-СН (ОН) - СН-(ОН) СН СН2 (ОН)-СН-СН-СН (ОН)-СН (ОН)-СН-
I________О_________I I---------О -------1
лекуле сахарозы связаны, как в простых
эфирах, через кислород.
Подобные же эфирные связи между остат-
ками моносахаридов имеются и в других
полисахаридах.
При гидролизе эти связи разрываются
и образуют свободные моносахариды.
В молекуле сахарозы в образовании эфир-
ной связи участвуют глюкозидные гидрок-
силы. Поэтому сахароза не обладает вос-
становительной способностью.
При растворении в воде происходит ги-
дролиз сахарозы с образованием глюкозы
и фруктозы. Эта реакция называется инвер-
сией сахара.
Сахароза широко распространена в рас-
тительном мире—встречается в значитель-
ных количествах в сахарном тростнике (в
стеблях содержится 14 — 20°/о), в корнях
сахарной свеклы (16—20%) и во многих
других плодах и овощах.
Полисахариды, не обладающие
свойствами сахаров
Крахмал (С„Н10О6),— принадлежит к вы-
сокомолекулярным веществам. Молекуляр-
ный вес крахмала измеряется сотнями тысяч.
Крахмал представляет собой белое аморф-
ное вещество, не растворимое в холодной
воде; в горячей воде образуется коллоидный
раствор, так называемый крахмальный
клейстер.
С иодом крахмал даёт характерное синее
окрашивание. При нагревании с кислотами
Нитроклетчатка — смесь эфиров полной
этерификации [C0H7O2(ONO2)3]A, и неполных
эфиров различного состава, например
[С.Н,О4 (ONO2)L И [CeH8O8(ONOa)s]x, по-
лучаемая при обработке клетчатки смесью
азотной и серной кислот. Смесь, содержа-
щая наибольшее количество азота, назы-
вается пироксилином. Пироксилин является
бризантным взрывчатым веществом. Смесь
пироксилина и коллоксилина, представляю-
щего собой нитроклетчатку, с меньшим чем
у пироксилина содержанием азота, образует
бездымный порох. Коллоксилин идёт на
приготовление коллодия, целлулоида, нитро-
целлюлозных лаков, киноплёнки.
Ацетилцеллюлоза — эфир клетчатки н
уксусной кислоты — идёт на изготовление
лаков, искусственного волокна, киноплёнки.
Горит с трудом.
Оксикислоты, или спиртокислоты,-соеди-
нения со смешанными функциями, молекулы
которых содержат карбоксильную и гидро-
ксильную (окси-) группы, например
НО—С
хон
оксимуравьиная, или
угольная, кислота
но-сн3-с
чон
оксиуксусная, или
гликолевая, кислота
а-оксипропионовая, или
а молочная, -кислота
органическая химия
309
Известны также и двухосновные окси-
кислоты. Примером могут служить окспянт
тарная, или яблочная, кислота (а) и диокси-
янтарная, или винная, кислота (Ь):
НООС—СН2—СН (ОН)—СООН
(а)
НООС—СН(ОН)—СН(ОН)-СООН
(Ь)
Молочная кислота СН3СН (ОН) СООН —
густая сиропообразная жидкость, реагирует
и как кислота и как спирт. Существует
в двух пространственно-изомерных формах,
вращающих плоскость поляризации в раз-
ные стороны. Это свойство вызвано тем
обстоятельством, что в состав этой кислоты
входит асимметрический атом углерода, от-
меченный звёздочкой. Асимметрическим ато-
мом углерода называют атом, который соеди-
нён с четырьмя различными атомами или
группами атомов. Проекции моделей про-
странственнб-изомерных молочных кислот
приведены ниже:
СООН СООН
I I
Н—С—ОН НО—С—Н
I I
СН3 СНз
Вещества, имеющие одинаковый состав и
строение, но отличающиеся пространствен-
ным расположением атомов в молекуле, на-
зываются стереоизомерами, а самое явление—
стереоизомерией. Существует три молочные
кислоты: правовращающая молочная кис-
лота, левовращающая молочная кислота и
оптически-недеятельная кислота, предста-
вляющая собой смесь равных количеств
право- и левовращающих молочных кислот.
Вещества, подобные оптически-недеятельной
молочной кислоте, которые можно разделить
на оптические антиподы, называют рацеми-
ческими или рацематами. Рацемическая
молочная кислота образуется при молочно-
кислом брожении сахаристых веществ. Она
содержится в кислом молоке, квашеной ка-
пусте, силосованных кормах. Правовращаю-
щая молочная кислота содержится в мышеч-
ных тканях. Под действием специальных
бактерий путём брожения сахара может быть
получена левовращающая молочная кислота.
Винная кислота
НООССН (ОН)СН(ОН) СООН — со-
держит два асимметрических атома угле-
рода. В природе встречается правовраща-
ющая винная кислота. Она содержится
в плодах в свободном состоянии или в виде
солей «тартратов». Калиевая соль винной
кислоты—винный камень и винная кислота—
находят применение как протрава при кра-
шении тканей.
Лимонная кислота
СООН
I
НООС СНа — С—СН2 СООН — трёхосновная
ОН
оксикислота. Принадлежит к самым распро-
странённым кислотам, содержащимся в ра-
стениях. Много её содержится в незрелых
лимонах и листьях табака.
Угольная кислота. Угольную кислоту
Н2СО3 можно рассматривать как оксиму-
равьиную. К производным угольной кислоты
относятся фосген и мочевина.
Фосген С12С. О—хлорангидрид угольной
кислоты. Бесцветный газ с температурой ки-
пения + 8° С; поражает дыхательные органы
и обладает удушающим действием. Запах
фосгена напоминает запах гнилого сена.
Мочевина NH2CONH2 — амид угольной
кислоты. Твёрдое кристаллическое вещество
С температурой плавления 135°, хорошо рас-
творимо в воде. Является ценным удобре-
нием. Применяется для изготовления пла-
стических масс и химико-фармацевтических
препаратов.
Аминокислоты
Аминокислоты — соединения, содержащие
в своём составе и аминогруппы (NH2) и кар-
боксильные группы. Аминокислоты можно
трактовать как производные карбоновых
кислот, в которых атомы водорода при угле-
родном скелете замещены аминогруппами,
например, соответственно замещённые про-
изводные уксусной кислоты — аминоуксус-
ная кислота, называемая гликолем или
глицином, имеет строение NH2CH2COOH.
Аминокислоты являются бесцветными кри-
сталлическими веществами, обычно сладкого
вкуса. Почти все аминокислоты природного
происхождения являются оптически актив-
ными. Аминокислоты имеют исключительно
большое биологическое значение, так как
они входят в состав различных природных
белков, главной составной части протоплаз-
мы всех клеток. Присутствие аминогруппы
и карбоксила определяет двойственный ха-
рактер аминокислот. Они обладают как
основными, так и кислотными свойствами,
образуют со спиртами сложные эфиры, а
с основаниями — соли, как все кислоты, и
образуют соли с кислотами, так же как и
амины. Поэтому их нужно отнести к раз-
ряду амфотерных соединений.
Белки (протеины)
Всякий организм содержит белки. Белки
входят в состав протоплазмы всех клеток.
Белкй трудно получить в чистом виде, по-
этому их точный состав в большинстве слу-
чаев неизвестен. В состав белков входят
углерод, водород, кислород, азот, сера и
иногда фосфор. Белки нестойкие вещества.
При кипячении с водой и под действием
спирта они свёртываются. Все белки опти-
чески-деятельны. Конечным продуктом гид-
ролиза белков являются аминокислоты.
Белок не только является основой жизни,
но имеет и большое техническое примене-
ние. Белками являются шерсть, шёлк,
кожа, волос, рог.
Гетероциклические соединения
Гетероциклическими называются соеди-
нения, молекулы которых содержат замкну-
тую цепь атомов, состоящую не только из
атомов углерода, но и атомов других эле-
ментов. Гетероциклические соединения ши-
роко распространены в природе. Соедине-
310
химия
ния, состоящие из одного или нескольких
гетероциклических ядер, преимущественно
содержащих азот, содержащиеся в расте-
ниях и обладающие сильным физиологиче-
ским действием, получили название алко-
лоидов. К ним относятся: никотин из листьев
табака, кофеин из чая и кофе, теобромин из
бобов какао, кокаин из листьев кока, хинин
из коры хинного дерева, морфий — один из
главнейших алколоидов оиия и много дру-
гих. К важнейшим пятичленным гетеро-
циклам, в состав кольца которых входит
лишь один гетероатом, относятся:
Пиррол C4H4NH — бесцветная жидкость,
кипящая при температуре 130°С, очень легко
окисляется, содержится в каменноугольном
дёгте и в костяном масле, получаемом при
сухой перегонке костей. Зелёное красящее
вещество растений хлорофил и красное кра-
сящее вещество крови — гемоглобин содер-
жат пиррольные кольца.
Фуран С4Н4О — бесцветная жидкость,
кипящая при температуре 32° С, не раство-
римая в воде. Важнейшим производным
фурана является альдегид фурфурол (см.
Фурфурол, стр. 314).
Таблица 12
соединений
Структурные формулы некоторых важнейших циклических органических
сн нс^^н II 1 НС ^сн ^сн бензол (CSHS) СН нс^^с-он II 1 HC^^fH сн Фенол (CSHS ОН) СН HC^^-NH, II 1 НС сн сн Анилин (CsHsHHi) СН л 1 НС C-N 1 « । % ' НС СН Ч X/ СН Нитробензол (Cf н3Н0г)
сн нсх с-сн3 нс ^с-сн3 сн 0 ксилол !СН^С(н4Сн,) сн3 С нс^ *\н II 1 НС ^С-СН3 сн ле- ксилол )_ сн3 ^с НС сн II 1 НС сн 1 сн3 п - ксилол (СН3 CsHt СН3) Ух. Л нс с-с II 1 % нс сн о X/ СН бензальдезид (С/ Hs СНО)
Л /0Н нс с-с 4 СН^О х/ сн бензойная кислота /с(н6 свои) СН НС^ ^C-CH’CHj нс сн \/ сн Стирол (CeHsCH снг] on 1 NO.-С ^C-NO, ! II 1 2 НС сн 1 N0? Аикринобая кислота ОНО С,нг(Н0г)3] НН НН /С=С С — с С-С сн чс—/ хс—сх НН НН Дифенил fCsHs CSHSJ
сн сн / X / X нс с сн 1 И L нс ^сН сн сн Нафталин (С№ Hs) СН СН, /\/< НС С CHj НС (! сн2 ^сн сн^ Г^тралин (Clt Н/г) ^СН^ НгС СН СН2 нгс сн снг снг снг Декалин (C,g Ht)j CH CH CH /Х/Ч/х нс с с CH I II 1 1 - HC c C CH X/\ /х Д CH CH CH Антрацен (CieHg)
нс—сн нс=сн нс j; — < > нс—с' >—бн нс=сн Фенантрен (С,Й нгеу неси, сн, сн нгс ЧИн, XI/ сн Линен fC„ H,s] HgC CHj Н2с снг сн2 Циклогексан fCg Н/г) HC CH Il 11 HC CH s Гиофен fСд •$)
/СН нс II 1 НСХ н Пиридин fC3Hs Н) НО -сн II И НС сн NH Пиррол (Се Нг НН) нс сн II II НС сн Фуран (Се Не 0) HC CH n II 11 / HC C — c X / \H 0 H Фурфурол (CHO Ce •<, 0)
ОРГАНИЧЕСКАЯ ХИМИЯ
311
Свойства органических соединений
Таблица 13
Название Формула Молеку- лярный вес Уд. вес1 * Температура Внешний вид Характерные свойства
пла- вления °C кипе- ния |°С (760)
Акриловая кислота . СН, :СН-СООН 72,03 1,062 13 141 Бесцветная жидк ость Острый ки- слотный запах
Акролеин СН, : СН - СНО 56,03 0,841 52 То же Острый за- пах подгорев- шего жира, раздражает слизистую оболочку
Ализарин С„ О, Н« (ОН), 240,06 — 289 430 Коасные иглы Краска
Аллиловый спирт . . Амиловый спирт СН, : СН • СН, ОН 58.05 0,855 -129 97 Бесцветная жидкость
норм, первичный С, Н„ ОН 88,10 0,815 — 138 То же
Анилин С. Н, • NH, 93.06 1,022 —6 184 Бесцветная жидкость, буреет на воздухе Ядовит
Антрацен Ацетальдегид (см. Уксусный альдегид) Н1о 178,08 1,242 217 351 Бесцветные призмы с го- лубой флуо- ресценцией
Ацетамид СН, . СО • NH, 59.05 1,159 80 222 Бесцветные кристаллы Разлагается
Ацетон СН, • СО • СН, 58,05 0.792 —94 56 Бесцветная жидкость Хороший растворитёль
Ацетилен с, н, 26,02 — -81 -84 Бесцветный газ Взрывает от детонации
Бензальдегид .... С, Н, • СНО 106,05 1,046 —26 179 Бесцветная жидкость Запах мин- даля
Бензил хлористый С. Н, • СН, CI 126,52 1,103 -39 179 То же Слезоточивый
Бензойная кислота . С, Н3 - СООН 122,05 1.266 121 249 Белые пластинки Выше 100 °C возгоняется
Бензол Бензолсульфоновая С. Н, 78,05 0,879 6 80 Бесцветная ЖИДКОСТЬ Ядовит
кислота с. н, • so, н + н, о 176,13 — 44 136 Кристалл и- ческое тело
Бромбензол Бутадиен-1,3 (диви- С, Н, • Вг 156,96 1,495 -31 156 Жидкость Ядовит
нил) СН, : СН • СН : СН, 54,05 — — - 5 Бесцветный газ
н-Бутан Бутиловый спирт с< н„ 58,08 0,600° -135 1 То же
норм, первичный . Бутиловый спирт изо (см. Изобутиловый спирт) Бутиловый спирт с, н, он 74.08 0,804 -80 117 Бесцветная жидкость
вторичный Бутиловый спирт сн, сн, • снон -сн, 74,08 0,808 -89 100 То же
третичный Вииная кислота d (СН,), сон 74,08 0,789 25 83 —
(обыкн.) СООН •снон -снон • • СООН 150,05 1,760 170 — Прозрачные кристаллы
Винная кислота 1 . . СООН • снон • снон • . СООН 150,05 1,760 170 — То же
Виноградный сахар . С, Н„ 0. + Н, 0 498,11 1,56 82 __ » » Сладкий вкус
Гексан норм С. Н;, 86,11 0,660 -94 69 Бесцветная жидкость
Гептан норм с, н,« 100,13 0,730 — 91 98 То же
Гликоль сна он.сн2 он 62,05 1.109 -12 197 » » То же
Глицерин Глюкоза, или сахар сн,он•снон • сн, он ^2,06 1,260 19 290 Бесцветная вязкая жидкость » *
виноградный . . . с, н„ о, 180,10 1,544 146 — Белые кристаллы » »
Гремучая ртуть . . (С : NO), Hg (+ 1 Н, 0) 284,6 4.42 — — — Взрывает
Декалин Дивинил (см. Бута* длен-1,3) Сю Няа 138,14 0,877 -125 188 —
Дифенил с, н, • с. н. 154,08 1,16 70 255 Бесцветные кристаллы
1 Удельные веса жидкостей и твёрдых тел даны при +20°С в г/см8; для жидкостей, кипящих при тем»
етературе ниже4-2О°С, удельные веса даны при температурах кипения (760 мм рт. ст.).
312
химия
Продолжение табл. 13
Название Формула Молеку- лярный вес Уд. вес Температура Внешний вид Характерные свойства
пла- вления °C кипе- ния °C (760)
Дихлорбензол о . . . С, Н,С1, 146,95 1,328 -18 179 Бесцветная ЖИДКОСТЬ Ядовит
* м . . . С, Н,С1, 14,695 1,282 -24 173 То же
» п . . . С. Н,С1а 146,95 1,458 53 174 Бесцветные кристаллы »
Дихлорэтан • . • . СНа С1 - СН, С1 98,95 1,261 -35 84 Бесцветная жидкость Хороший растворитель, ядовит
Изоамиловый спирт (СН3)2: СН • СНа-СН2ОН 88,10 0.810 130 То же Ядовит
Изобутан с4н,„ 58,08 — ' — -10 Бесцветный газ
Изобутиловый спирт (СН„)а : СН • СН, ОН 74,08 0,800 —108 108 Бесцветная жидкость »
Изооктаи с, Н„ 114,14 __ __ То же
Индиго С„ На О4 (NH), 262,10 1,35 390—392 Возг. Синие кристаллы Краска
Изопропиловый
спирт (СН„), СНОН 60,06 0,789 -86 82 Бесцветная жидкость Ядовит
Йодоформ CHJ8 393,77 4,008 119 Возг. Жёлтые кристаллы Разлагается на свету
Иприт СН,С1—СН,—S—СН,— -СН, С1 126,97 — 14 217 Жидкость ОВ!
Камфара d С„ Н„ О 152,13 0,811 180 209 Бесцветная вязкая кристалличе- ская масса Возгоняется
Карболовая кислота (см. Фенол)
Кетен СН,:СО 42,02 — -151 -56 Бесцветный газ
Крахмал Крезол о » м » (С, Н„ О.)х СН, • С, н4 он СН, • С. н, он сн, • нс„он 162.09Х 108,06 108,06 108,06 1,046 1,035 1,031 30 4 37 190 201 200 Белое порош- кообр азное тело
Ксилол о с, Н4 (СН,), 106,08 0,863 -27 141 Бесцветная жидкость Ядовит
» м С. Н. (СН,), 106,08 0,862 -54 139 Бесцветная жидкость »
» п С, Н4(СН,)а 106,08 0,861 15 136 То же »
Лимонная кислота . С, Н4(0Н)(С00Н), + Н,0 210,08 1,542 153 Разл. Бесцветные кристаллы
Масляная кислота . СН, • СН,СН, • СООН 88,06 0,964 -8 162 Бесцветная жидкость Запах про- горклого масла
Меркаптан (-см. Этилмеркаптан)
Метам СН, 16,03 0,415 —184 —161,4 Бесцветный газ
Метиламин СН, NH, 31.05 0,696 Менее -79 —6 То же
Метил бромистый . . СН8 Вг 94,94 1,732 . 4,5 » » Ядовит
Метил иодистый • . СН, J 141,94 2,279 -66 43 Бесцветная жидкость »
Метилен хлористый . СН, С1, 84,94 1,336 —97 42 То же »
Метиловый спирт . . СН, ОН 32,03 0,790 -98 65 » » Ядовит, от- равление вызывает слепоту Растворитель
Метил хлористый . . СН, С1 50,48 0,952 -92 -24 » » Ядовит
Молочная кислота СН, СН ОН • СООН 90,05 1,240 18 122/15 мм Бесцветная кристалличе- ская масса
Мочевина NH, • СО . NH, 60.05 1,335 133 — Бесцветные кристаллы
Муравьиная кислота Муравьиный аль- НСООН 46,02 1,220 (-20*) 8 101 Бесцветная жидкость Резкий кис- лотный запах
дегид НСНО 30,02 0,815 -92 -21 Бесцветный газ
Нафталин С„ н, 128,06 1,145 80 218 Бесцветные блестящие листочки Летуч
Нафтила мин-а . . » . С1о Н, NH, 143.08 1,171 50 301 Бесцветные кристаллы Неприятны й запах
Нафтиламин-р . . . . С„ H.NH, 143.08 1,216 112 306 То же
Нитробензол . . . . Hs NOj 123,05 1,203 9 211 Жидкость слабожёлтого цвета Ядовит, запах миндаля
Нитроглицерин . . . С8 Нй (ONO3)a 227,06 1,596 13 257 Маслообраз- ная тяжёлая жидкость Взрывает, ядовит
ОРГАНИЧЕСКАЯ ХИМИЯ
313-
Продолжение табл. 13
Название Формула Молеку- лярный вес Уд. вес Темпе пла- вления °C эатура кип-е- ния °C (760) Внешний вид Характерные свойства
Нитрометан .... Олеиновая кислота . Пальмитиновая кис- лота Пентан норм .... Пикриновая кислота- 1, 2, 4, 6 Пинен Пиридин Пирогаллол-1,2,3 . . Пиррон Пропан Пропилен Пропиловый спирт . Сахар виноградный (см. Глюкоза) Сахар тростниковый (см. Тростниковый сахар) ....... Сахар фруктовый (см. Фруктовый са- хар) Сахарин (о-бензой- иой кислоты сульф- амид) Свин ец- тетр аэтил (см. Тетраэтил- свинец) Сероуглерод Скипидар (см. Пинен) Стеариновая кислота Стирол Сульфаниловая кис- лота Тетралин, или тетра- гидронафталин . . Тетраэтилсвинец . . Тиофен Толуол Триметиламин .... Триметилен Тринитротолуол (тро- тил)-2,4 ,6,1 ® ... Тринитротоу л (тротил)-2,3,4,1 р . Тринитротолуол (тротил)-2.4„5,1 у . ТринитрофенОл- S.4,6,1 Тринитрофенол- 2,3.6,1 Тростниковый сахар Уксусная кислота (ледяная уксусная кислота/ ..... Уксусноизоамиловый эфир СН3 NO, с„ н„соон C1S HS1 СООН с, н„ НО с. н, (NO,), С„ Н„ С, H N С. Н, (ОН), С, Н, : NH С3 Н, СН, • СН : СН, СН, • СН, СН, ОН С, В. О, : NH, CS, С,, Н„ СООН С, Н„ • СН : СН, NH, . С. Н, • SO, ОН + + 2Н, О С„ н„ РЬ (С, НО, С« Н, : S С. Н„ . СН, (СН,), : N С, Н. (NO,), С. Н, • СН, (NO,), С. Н, СН, (NO,), С, Н, • СН, (NO,), С, Н, • ОН (NO,), С. Н, . ОН С1, н„ о„ СН,СООН СН, СООС, нп 61,03 282,27 256,26 72,10 229,05 136,13 79,05 126,05 67,05 44,06 42,05 60,06 183,12 76,14 284.29 104,06 209,17 132,10 323,4 84,10 ь2,06 59,08 42,05 227,06 227,06 227,06 229,05 229,05 342,18 60,03 130,11 1,133 0,898 0,853 (62°С) 0,626 1,767 0,858 0.981 1,453 0,948 0,804 1,262 0,941 0,907 0,971 1,62 1,066 0,867 0,673 0,720 при -79е 1,588 1,049 0,874 -29 14 62 -131 122 —42 132 —190 -127 223 —112 69 288 Менее -20 -30 -ь5 Менее -75 81 112 104 96 117 ^160 17 102 233/15 мм 215/15 мм 36 156 116 293 131 -45 -50 97 46 232/ 15 мм 145 205-207 91 /19мм 84 111 Около -3 118 137-145 Бесцветная жидкость Бесцветная маслянистая жидкость Бесцветная кристалличе- ская масса Бесцветн ая жидкость Жёлтые листочки Бесцветная жидкость Жидкость Тёмнозелёные кристаллы Бесцветная жидкость, темнеет на воздухе Бесцветный газ То же Бесцветная жидкость Бесцветные кристаллы Бесцветная жидкость Бесцветная кристалличе- ская масса Бесцветная жидкость Бесцветные кристаллы Бесцветная жидкость То же » >> » » Бесцветный газ То же Бесцветные кристаллы Бесцветная жидкость То же Взрывает Запах скипидара Сладкий вкус Ядовит, само- воспламе- няется Разлагается при высокой температуре Ядовит Запах селё- дочного рас- сола Взрывает Сладкий вкус Резкий кис- лотный залах Разлагается
314
химия
Продолжение табл. 13
Название Формула Молеку- лярный вес Уд. вес Температура Внешний вид Характерные свойства
пла- вления °C кипе- ния °C (760)
УксусноэтиловыЙ эфир Уксусный альдегид . Уксусный ангидрид . Фенантрен Фенол, или карболо- вая кислота .... Формальдегид (см. Муравьиный аль- дегид) Фосген Фруктовый сахар • . Фуран ........ Фурфурол ..... Хингидрон Хинин ........ Хлорбензол .... Хлороформ Хлортолуол о . . . . » м . . . . » п . . . . Целлулоза Циклобутан ..... Циклогексан .... Циклопентан .... Четырёххлористый углерод . Щавелевая кислота . Этан Этиламин Этилен Этилмеркаптан . . . Этилен хлористый (см. Дихлорэтан) Этиловый спирт . . . Этил хлористый . . . с, н, о, с, н, сц. сно (СН, СО), о С,« н„ с, н,он СОС1, СН, ОН (СНОН), сосн, он С, Н, : О С, н, о • сно С, Н, О С, Н, (ОН), С„ Н„ O,N,( + 3 Н, О) С. Н,С1 СНС1, CI • с, н. • сн, С1 • с, н, . сн, CI • с, н, сн, (С, Н,„ О,) X С. н, С. н„ С, Н1О CCI. СООН СООН + 2 н, о с, н. С, Hs . NH, с, н, С, Н , SH с, н4 он С, Н- С1 88,06 44,03 102,05 178.08 94,05 98,92 180,10 68,03 96,03 218.08 324,21 112,50 119,39 126,52 126,52 126,52 162,08 • •X 56,06 84,10 70,08 153,84 126,05 30.05 45,06 28,03 62.12 46,05 64,50 0,901 0.783 1.082 1,063 приЮО® 1,058 при 60° 1,42 1,669 0,944 1,159 1,401 1,106 1,488 1,081 1,072 1,069 1,525 0,704 0,778 0.754 1,594 1,653 0,708 0,839 0,806 0,921 -83 -123 100 42,5 —118 95 -31 171 57 -45 -63 -34 -48 7 <—80 8 Менее —80 -23 189 безвод- ной -172 -81 —169 —114 -114,15 -139 77 20 140 340 182 8 32 162 Воз- гон. 132 61 159 162 162 12 81 51 77 Воз- гон. —93 11 — 102 37 78 13 Бесцветная жидкость То же • » Блестящие листочки Газ Бесцветные кристаллы Бесцветная жидкость . То же Тёмнозёленые иглы Бесцветиая жидкость То же » » » » То же Белый волоки. Бесцветный газ Бесцветная жидкость То же Бесцветная жидкость Бесцветные кристаллы Бесцветный газ То же » » Бесцветная жидкость То же » » Приятный фруктовый запах Резкий уду- шающий запах Медленно разлагается Выше 96°С возгоняется Ядовит ОВ! Сладкий вкус Запах свеже- го ржаного хлеба Ядовит » Сладковатый запах Ядовит » » Ядовит, хоро- ший раство- ритель Ядовита Неприятный запах Ядовит
Тиофен C4H4S — бесцветная жидкость,
кипящая при температуре 84°С, не раство-
римая в воде, содержится в небольших ко-
личествах в каменноугольном бензоле и в
нефтях Второго Баку.
Примером шестичленного гетероцикла,
содержащего один гетероатом, может слу-
жить пиридин C6H6N — бесцветная жид-
кость с температурой кипения 115° С, вхо-
дит вместе с гомологами в состав каменно-
угольной смолы. Является слабым основа-
нием, с водой смешивается во всех отноше-
ниях. Смесь пиридина и его гомологов,
называемая сырыми пиридиновыми основа-
ниями, применяется как растворитель, а
также для денатурации спирта.
ФИЗИЧЕСКАЯ ХИМИЯ
315
ФИЗИЧЕСКАЯ ХИМИЯ
АГРЕГАТНЫЕ СОСТОЯНИЯ
Идеальные газы
Идеальным газом называется газ> строго
подчиняющийся законам Бойля-Мариотта,
Шарля-Гей-Люссака (и Джоуля). Идеальный
газ — физическая абстракция. К идеальным
газам приближаются реальные газы при
низких давлениях и высоких температурах.
Уравнения состояния идеального газа —
уравнение Клапейрона. Уравнение состояния
даёт связь между давлением идеального га-
за Р, его объёмом v и температурой Т.
Для одной граммолекулы идеального газа
оно имеет вид:
Ру = RT,
где R— универсальная газовая постоянная,
одинаковая для всех газов;
Р— давление;
i> —объём одной граммолекулы;
Т —абсолютная температура.
Для п граммолекул идеального газа
m
PV = nRT, или PV= RT,
где m—масса газа в г;
М — молекулярный вес газа.
Последнее выражение используется для
определения молекулярного веса вещества
по известным значениям давления, объёма,
температуры и массы газа или пара веще-
ства.
Универсальная газовая постоянная. Уни-
версальная газовая постоянная R одинакова
для всех газов и имеет размерность энер-
гии, делённой на температуру. Численное
значение R приведено ниже.
R = 8,31 10’ эрг/моль°С. =
= 8,315 джоуль/моль'С =
= 1,986 кал /моль°С =
= 0,08206 литр атм./моль°С.
Реальные газы
Уклонения реальных газов от законов
идеальных газов. При увеличении давления
и уменьшении температуры реальные газы
уклоняются от законов идеальных газов,
так как при этом начинают заметно сказы-
ваться силы притяжения между молекулами.
Реальные газы в отличие от идеальных
сжижаются.
В уравнении Ван-дер-Ваальса учтены
поправки на силы притяжения между моле-
кулами и объём молекул. Для одной грам-
молекулы это уравнение имеет вид:
Р + - b) = RT,
где а — константа, характеризующая моле-
кулярное притяжение и измеряю-
щаяся в единицах давления, умно-
женных на единицу объёма в квад-
рате;
Ь—константа, равная учетверённому
собственному объёму молекул, со-
держащихся в одной граммолекуле
газа.
Это уравнение удовлетворительно харак-
теризует свойства реальных газов лишь при
невысоких давлениях. На фиг. 1 изобра-
Фиг.1 Кривые уравнения Ван-дер-Ваальса
(изотермы)
жены кривые уравнения Ван-дер-Ваальса
в координатах Р и о для разных темпера-
тур Т (изотермы). На фиг. 2 в тех же ко-
ординатах даны действительные кривые за-
висимости Р от v при разных Т для СОа.
316
химия
Уравнение качественно приложимо и к
жидкостям.
Уравнение Бертло. Уравнение состояния
реальных газов. Для одной граммолекулы
оно имеет вид:
(р + =
где а' — константа молекулярного притяже-
ния.
Уравнение Бертло учитывает темпера-
турный ход константы а Ван-дер-Ваальса.
Критическое состояние и связь критиче-
ских величин с константами Ван-дер-Ва-
альса. Д. И. Менделеев открыл, что для
каждого газа существует температура, выше
которой этот газ ни при каком давлении не
может быть сжижен. Эта температура на-
зывается критической и обозначается Тк.
В семействе изотерм реального газа она
отвечает изотерме с точкой перегиба, в ко-
торой кривая проходит горизонтально. Са-
ма точка и состояние вещества, отвечающее
этой точке, называются критическими.
Давление газа и удельный объём его в
этом состоянии также называются критиче-
скими и обозначаются соответственно Рк
и VK.
Между критическими величинами и кон-
стантами Ван-дер-Ваальса существуют сле-
дующие зависимости:
Тк ~ 27bR ’ Рк ~ 27b2 : Vk ~ЗЬ’
ИЛИ
R — -- Рк Vk а—ЗР 2 •
‘ к
b =
3 ’
а и b — константы Ван-дер-Ваальса.
Эти соотношения дают возможность по
экспериментально определяемым критиче-
ским величинам вычислять константы Ван-
дер-Ваальса.
Уравнение соответственных состояний.
Так называются уравнения, получающиеся
введением б уравнение состояний вместо
обычных давления, объёма и температуры
Р ,
приведенных величин давления z=h—, ооъ-
“ к
V Т
ёма о = и температуры о = •
• к 1 к
Приведённое уравнение Ван-дер-Ваальса
имеет вид:
3 \
к + (3 ? — 1) = 89.
Оно не содержит констант, зависящих
от природы вещества, и является поэтому
универсальным. Однако оно, как и исходное
уравнение, является приближённым, в осо-
бенности в области высоких давлений, и
совершенно непригодно для веществ, моле-
кулы которых содержат группы ОН, СООН,
СО и др.
Твёрдые тела
Кристаллическое и аморфное состояние
твёрдых тел. Твёрдые тела встречаются
в двух состояниях: кристаллическом и
аморфном. Кристаллическое состояние твёр-
дого тела характеризуется правильным рас-
положением молекул атомов или ионов
в пространстве (кристаллическая решётка),
существованием определённой температуры
плавления и скачкообразным изменением,
многих свойств при плавлении. Аморфное
состояние характеризуется хаотическим
расположением молекул, существованием,
температурного интервала размягчения и
непрерывного хотя и резкого изменения
всех физических свойств в интервале раз-
мягчения. Большинство веществ встречается
в обоих твёрдых состояниях. Однако есть
вещества, существующие только в кристал-
лическом или только в аморфном состоянии.
Кристаллические системы. Кристалло-
графией — наукой о геометрических формах
кристаллов и связи их (форм)с внутренней
структурой кристаллов — установлено су-
ществование 32 кристаллических классов
(Е. С. Фёдоров), которые сводятся к б кри-
сталлическим системам, отличающимся раз-
личной степенью симметрии:
1) правильная система
2) квадратная *
3) гексагональная »
4) ромбическая »
5) моноклиническая »
6) триклиническая »
Рентгенографическое и электронографи-
ческое исследование кристаллов. Современ-
ное исследование внутренней структуры
кристаллов основано на явлении дифракции
рентгеновских или электронных лучей про-
странственной кристаллической решёткой,
играющей роль дифракционной решётки.
Дифракционная картина либо фотографи-
руется, либо изучается при помощи иони-
зационной камеры. Анализ дифракционной
картины основан на соотношении русского
учёного Г. В. Вульфа
п X — 2d sin а,
где X — длина волны монохроматического
рентгеновского луча или длина фа-
зовой волны электронов;
а — угол между лучом и совокупностью
параллельных отражающих плоско-
стей кристаллической решётки, при
котором получается наиболее интен-
сивное отражение луча;
d— расстояние между параллельными
отражающими плоскостями кристал-
лической решётки;
п — целое число.
Если известны два значения а для одной
и той же X и одной и той же совокупности
параллельных плоскостей кристаллической
решётки, то d определяется решением си-
стемы двух уравнений с двумя неизвест-
ными:
X = 2d sin aj;
п2 X = 2d sin я2.
По найденным основным значениям d
устанавливается внутренняя структура кри-
сталла.
ФИЗИЧЕСКАЯ ХИМИЯ
317
В настоящее время пользуются тремя
методами рентгенографического исследова-
ния кристаллов.
В первом методе (наиболее старый) ис-
пользуется пучок неоднородных рентгенов-
ских лучей. Исследуемый кристалл нахо-
дится в покое.
Во втором методе используется монохро-
матический пучок рентгеновских лучей.
В этом методе либо кристалл вращается
вокруг одной оси, либо рентгеновский луч
вращается вокруг неподвижного кристалла.
В третьем методе используется также
монохроматический рентгеновский луч, но
вращающийся кристалл заменяется неподвиж-
ным кристаллическим порошком, в котором
практически осуществляются все возможные
расположения микрокристалла. Аналогич-
ные принципы положены в основу методов
электронографического анализа. Последний,
однако, в силу малой проницаемости элек-
тронных лучей в кристаллы нашёл широкое
применение для исследования поверхно-
стных слоёв и фолы.
Решётки металлов. Решётки металлов об-
разованы преимущественно положительными
нонами металла, между которыми свободно
движутся связывающие их электроны. На-
личие свободных электронов или так назы-
ваемого электронного газа определяет хо-
рошую электропроводность металлов я ряд
других специфических свойств. Металлы
кристаллизуются в кубической (Al, Си, Ag,
Au, Ni, f=Fe, a=Fe, Pb, Pt, V, Cr, W, Na,
K, Rb, Cs и др.) и гексогональной (Be, Mg,
Zn, Cd, Ti и др.) системах. Сплавы метал-
лов либо сохраняют решётку компонента,
преобладающего количественно, либо обра-
зуют свою отличную структуру.
Решётки неорганических соединений.
Большинство неорганических соединений,
солей, окислов и др. имеют ионные решётки
и переходные типы решёток от ионных к
молекулярным. Ионные решётки образованы
правильным чередованием положительных
и отрицательных ионов. Значительные элек-
трические силы, действующие между ио-
нами, обусловливают прочность кристаллов
с ионной решёткой. Этим же объясняются
высокие температуры плавления, ничтожная
упругость паров и ряд других свойств
неорганических соединений. Простые неор-
ганические соединения кристаллизуются
в кубической (NaCl, AgCl, ZnS, A1N и др.),
квадратной (TiO., и др.) и гексогональной
(ZnO, CdS и др.) системах. Сложные неор-
ганические соединения кристаллизуются
в менее симметричных системах — ромбиче-
ской, моноклинической и триклинической.
Решётки органических соединений. Для
органических соединений типичной является
молекулярная решётка, образованная из
правильных рядов определённым образом
ориентированных молекул. Связь между
молекулами осуществляется силами Ван-
дер-Ваальса. Этим обусловливаются сравни-
тельно небольшая прочность кристаллов
органических веществ, низкие температуры
плавления и большая летучесть их. Благо-
даря сложности строения молекул органи-
ческие соединения кристаллизуются чаще
в гексагональной, ромбической и монокли-
нической системах.
Полиморфизм. Полиморфизмом называет-
ся способность вещества существовать в двух
и более кристаллических формах (модифи-
кациях), отличающихся друг от друга кри-
сталлическими решётками, механическими,
физико-химическими и термодинамическими
свойствами. Каждая кристаллическая форма
устойчива в определённой области темпера-
тур и давлений. Вне этой области она не-
устойчива (метастабильна) и с большей или
меньшей скоростью превращается в другую
более устойчивую форму. Так, например,
ниже 910° С устойчиво a-железо (гексаго-
нальная система), выше 910° у-железо (ку-
бическая система). Закалка железа заклю-
чается в том, что у-железо при быстром
охлаждении сохраняется в неустойчивом
состоянии чрезвычайно долго благодаря
незначительной скорости превращения в
a-железо. Нагревание ускоряет это превра-
щение (отпуск металла). При температуре
910° С устойчивы обе модификации.
Полиморфизм простых веществ назы-
вается аллотропией.
Изоморфизм. Изоморфными называются
два или более вещества, кристаллизующиеся
при одинаковых условиях в одинаковых
кристаллических формах и способные до-
страивать решёт-
ку друг друга. ff
Такие вещества "g' 5
обычно сходны по | 4
химическому со-
ставу, например g1’
СаСО3, MgCO3, -V
МпСО3, ZnCO3 и ЧI
СоСО3 изоморфны *
и кристаллизу- “
ются в триклини- ~~*~'а6с
ческой системе. Фиг. Лэд тройной тепло-
Теплоёмкость ёмкости с температурой
твёрдых тел. Теп-
лоёмкость твёрдых тел в отличие от тепло-
ёмкости жидких и газообразных тел сильно
зависит от температуры, в особенности
в области низких температур. Фиг. 3 изо-
бражает типичные кривые Cv = f(T). В обла-
сти, близкой к абсолютному нулю, кривые
могут быть описаны уравнением
уз
Cv = 465 QS— ,
где Сj, — теплоёмкость твёрдого тела при
постоянном Объёме в г/мЬ г атом-
6 — характеристическая температура,
зависящая от природы тела.
При высоких температурах теплоёмкость
твёрдого тела при постоянном объёме Cv
асимптотически приближается к постоян-
ной величине. Теплоёмкость при постоян-
ном давлении Ср несколько выше и непре-
рывно растёт с увеличением температуры.
Атомные теплоёмкости простых веществ
в твёрдом состоянии при комнатной темпе-
ратуре и постоянном давлении приблизи-
тельно одинаковы и в среднем равны,
6,2 кал/град, Атомной теплоёмкостью назы-
318
химия
вается произведение удельной теплоёмко-
сти на атомный вес. Исключение из правила
составляют некоторые лёгкие элементы, для
которых в области комнатной температуры
ещё сильна зависимость от температуры
(см. Теплоёмкость твёрдых тел, стр. 317),
например алмаз (1,35), графит (1,92), крем-
ний (4,84). Молекулярная теплоёмкость
сложного вещества в твёрдом состоянии
равна сумме атомных теплоёмкостей элемен-
тов, содержащихся в нём:
Ср = п-6,2,
где Ср — молекулярная теплоёмкость твёр-
дого тела при постоянном давле-
нии;
п —число атомов, составляющих моле-
кулу твёрдого тела;
6,2 — атомная теплоёмкость твёрдого те-
ла при постоянном давлении.
Квантовая теория теплоёмкости. Кван-
товая теория теплоёмкости, накладываю-
щая условия квантования колебательной
энергии элементов кристаллической ре-
шётки, объясняет температурную зависи-
мость теплоёмкости твёрдых тел и даёт
ряд соотношений, хорошо совпадающих
с опытом. Наиболее важными являются фор-
мула Дебая и формула Эйнштейна для те-
плоёмкости простого твёрдого тела при по-
стоянном объёме:
о
Jim
fh w \2 екТ
=3/? ( кТ ) '
4 7 е^т — 1
где Л — постоянная Планка;
к—постоянная Больцмана;
ы — частота собственных колебаний
атомов;
е — основание натуральных логариф-
мов.
Недостатком формулы Эйнштейна является
то, что она предполагает существование
в твёрдом теле только одной частоты соб-
ственных колебаний, поэтому плохо оправ-
дывается и области низких температур.
Для перехода к теплоёмкости при посто-
янном давлении существуют эмпирические
формулы, из которых приведём формулу
CP=CV fl + 0,0214 Cv тТ \
\ ‘ Пл/
где Т„л — абсолютная температура плавле-
ния.
СТРОЕНИЕ АТОМА
Электрон
Электрон — носитель элементарного (наи-
меньшего наблюдаемого в свободном виде)
количества отрицательного электричества,
составная часть атомов вещества. Электроны
могут быть получены из любого вида- веще-
ства независимо от его 'физического и хи-
мического состояния. Законы электролиза
являются одним из важнейших оснований
для допущения атомной структуры элект-
ричества. Согласно законам Фарадея при
прохождении через электролиты одного и
того же количества электричества на элек-
тродах выделяется одно и то же число ато-
мов одновалентного вещества, вдвое мень-
шее количество атомов двухвалентного ве-
щества и т. д. Таким образом, электричество
связано с атомами вещества в виде дискрет-
ных порций, кратных заряду одновалентного
иона. Электроны в свободном виде испу-
скаются при радиоактивном распаде атомов,
из накалённых металлов, вырываются из
вещества под действием света (фотоэффект)
или сильного электрического поля и т. п.
Определение заряда электрона. Прямое
доказательство дискретности электрических
зарядов и первые точные определения вели-
чины заряда электрона путём нахождения
зарядов отдельных частиц были выполнены
Р. А. Милликеном и А. Ф. Иоффе. Опыты,
поставленные Милликеном, заключались
в следующем. Между двумя горизонталь-
ными металлическими пластинами, которые
могут быть заряжены, получают туман,
состоящий из мелких масляных капель. Он
освещается сбоку ярким светом и рассмат-
ривается в микроскоп, увеличение которого
так подобрано, что можно удобно следить
за отдельной каплей масла. Под действием
силы тяжести капли опускаются вниз. Если
осветить туман сбоку на короткое время
рентгеновскими лучами, то воздух между
пластинами ионизируется, и капельки ту-
мана получают электрические заряды. Если
теперь сообщить металлическим пластинам
электрическую разность потенциалов так,
чтобы электрическая сила действовала
в противоположном направлении, чем сила
тяжести, то капельки начинают двигаться
вверх. Если продолжительное время сле-
дить за одной и той же каплей, то её ско-
рость время от времени внезапно меняется,
что связано с изменением её заряда. Ско-
рость изменяется не непрерывно, а скач-
ками. Отсюда можно заключить, что и за-
ряд меняется скачками. Из этих опытов
легко вычислить величину наименьшего
(элементарного) заряда. Для заряда элек-
трона получается величина
е = 4,80 • 10~10 COSE =
=>1,60-2- 10-2OCOSM.
При помощи этой величины легко опре-
делить число атомов в грамматоме элемента
или число молекул в граммолекулярном
количестве вещества — авогадрово число N.
Один граммэквивалент любого электролита
несёт заряд Е=96 487 кулонов. Но так как
заряд одновалентного иона равен заряду
электрона е, то авогадрово число
96 487-0,1
1,60-2-Ю-20
6,023-1023 •
F
N = —
е
Отклонение электронов в электрическом
поле. Если электрическое поле направлено
перпендикулярно первоначальному пути
электрона, то траектория электронов изме-
ФИЗИЧЕСКАЯ ХИМИЯ
319
няется: они начинают описывать параболы
подобно снаряду под действием силы тяже-
сти. Величина отклонения электронов по
линии, перпендикулярной первоначальному
пути электронов, у определяется следую-
щим равенством:
где е — заряд;
zn0 — масса;
t>e— скорость электрона;
Е— напряжение электрического поля;
х — путь, проходимый электроном
в электрическом поле.
Отклонение электронов в магнитном поле.
Магнитное поле, силовые линии которого
направлены перпендикулярно направлению
движения электронов, вызывает появление
силы в направлении, перпендикулярном как
магнитному полю, так и направлению
электрона в каждый данный момент. По-
этому электрон в таком поле двигается по
^0^0 гг
кругу радиуса г = — , где Н—напря-
жение магнитного поля.
Удельный заряд электрона. Комбинируя
методы электрического и магнитного откло-
нений при параллельном направлении их
е
силовых линий, можно определить —--------
ш0
отношение заряда электрона к его массе
(удельный заряд электрона) и его ско-
рость иа:
е ______Ех2__ Ех2
mQ ~~2Н2уг2 * = ~2Нуг ‘
е
Измерения показали, что - одинаково
для всех электронов независимо от способа
их получения и соответствует 5,273-101’
CGSEa~1 •
Зависимость массы от скорости. Приве-
дённое значение удельного заряда относится
к электрону, скорость которого мала по
сравнению со скоростью света. Опыт пока-
зывает, что значение удельного заряда за-
висит от скорости электрона. По теории
относительности масса любого тела зависит
от скорости его движения. Эта зависимость
выражается формулой
где т — масса движущегося тела;
zn0—масса покоящегося тела;
v — скорость его движения;
с — скорость света.
Из формулы видно, что скорость света
является пределом поступательных скоро-
стей, так как при[7=с, т = оо, т. е. масса
тела при его скорости, равной скорости
света, становится бесконечно большой. При
очень больших скоростях удельный заряд
электрона вследствие возрастания его массы
падает.
Электромагнитная масса. Наличие у ма-
териальной частицы электрического заряда
приводит к увеличению её инерции, так
как работа внешней силы затрачивается при
движении такой частицы не только на при-
ращение её кинетической энергии, но и на
создание магнитного поля. Поэтому элек-
трон кроме «механической» должен обла-
дать и «электромагнитной» массой. «Элек-
тромагнитная масса» покоя электрона равна
2____е2
т»= 3 ~2~ ’
где с — скорость света;
е и г — заряд и радиус электрона.
Если считать, что электрон обладает
только электромагнитной массой, то можно
из предыдущего соотношения определить
его радиус:
2 е2
г=-о- -дгТа- = 1,87-10—13см.
3 тос2
Электрон-вольт. В атомной физике энер-
гию очень часто выражают в электрон-воль-
тах. Один электрон-вольт есть та энергия,
которую приобретает электрон, пробегая
ускоряющую разность потенциалов в 1 вольт;
1 eV = 1,602-10“12 эрг. Энергия в 1 eV, рас-
считанная на N = 6,023 • 1023 электронов,
равна: eV моль—1=9,б4 - 1011 эрг моль"1 =
= 2,305-104 кал-моль~'=23,05 ккал-моль~* .
Миллион электронов-вольт обозначается
MeV.
Положительные ноны
Метод парабол. Масса положительно за-
ряженных ионов может быть найдена из
определения отклонения положительных
ионов в электрическом и магнитном поле.
Из каждого вида атомов и молекул, спо-
собных обращаться в газ, можно получить
поток положительно заряженных частиц
(ионов). Для этого изучаемое вещество вво-
дится в виде летучего соединения под низ-
ким давлением в разрядную трубку АК
(фиг. 4), катод которой состоит из массив-
Фиг. 4/Установка для определения удельного
заряда положительных ионов
ного цилиндра с отверстием посредине.
Когда через трубку проходят электриче-
ские разряды, то газ частично ионизируется.
Образующиеся положительные ионы двига-
ются по направлению к катоду К, и не-
большая часть их проходит через особое
отверстие катода в виде тонкого (ион-
ного пучка). Электрическим полем (ме-
жду LL) и магнитным полем (магнит PQ)
320
химия
луч отклоняется и попадает на фотографи-
ческую пластинку R. Так как первоначаль-
ные скорости и0 отдельных положительных
частиц различны, то под влиянием электри-
ческого и магнитного полей в месте паде-
ния их на пластинку получается не резко
счерченная точка, а целая кривая, пред-
ставляющая для всех частиц с одинаковым
удельным зарядом параболу. Из получен-
ных таким образом парабол можно, зная
заряд частиц, рассчитать их массу.
Масс-спектограф. В дальнейшем этот ме-
тод был усовершенствован путём фокуси-
ровки пятна, происходящего от частиц оди-
наковой природы, т. е. имеющих одинако-
е .
вое —, но различные скорости в. Фоку-
сировка в масс-спектографе схематически
изображена на фиг. 5. Электрические и маг-
Ф и.. 5. Схема масс-спектографа
нптные поля в масс-спектографе располо-
жены не параллельно, как в методе пара-
бол, а перпендикулярно. Первое действует
между пластинками РГР2> тогда как сило-
вые линии магнитного поля, расположен-
ного внутри окружности О, перпендику-
лярны плоскости чертежа. Пучок ионов,
пройдя диафрагмы 8; и S2, отклоняется сна-
чала электрическим полем РгР% и частично,
как это показано на фигуре, расщепляется
вследствие различных первоначальных ско-
ростей ионов. Далее этот расщепленный
луч проходит магнитное поле М, которое
вновь собирает однородные частицы в одну
точку/7 независимо от их скорости. Если од-
новременно присутствуют частицы различ-
ной природы, различающиеся по удельному
заряду, то получается соответствующее ко-
личество фокусов, лежащих на кривой FG,
вдоль которых и располагается фотографи-
ческая пластинка. При помощи этого при-
бора можно очень точно определить массу
ионов. Оказалось, что масса положительных
ионов всегда равна массе отдельных атомов
пли групп атомов (радикалов).
Протон. Положительно заряженный ион
водорода Н+ получил название протона.
, е
Для Нт удельный заряд — = 9,579- 103
CGSMa—1. Масса протона в 1837,5 раза больше
массы электрона.
Изотопы, Вышеописанными методами
было показано, что атомы одного и того
же элемента могут обладать разными мас-
сами. Атомы, обладающие одинаковыми
химическими свойствами, но разными масса-
ми, получили название изотопов (см. таб-
лицу изотопов), так как все они попадают
в одну и ту же клетку периодической си-
стемы элементов, т. е. имеют один и тот
же порядковый номер.
Изотоп водорода—дейтерий. Изотоп водо-
рода был открыт спектроскопическим путём.
Этот изотоп получил особое название дей-
терия и особый символ D( = H2). Его масса
приблизительно в 2 раза больше массы
обычного водорода. Атомный вес тяжёлого
водорода (определённый по отношению х/1в
веса атома кислорода с атомным весом 16)
соответствует 2,01473.
Дейтон. Положительно заряженный ион
тяжёлого водорода называется дейтоном.
Тяжёлая вода D2O. Вода, в состав моле-
кулы которой входит тяжёлый водород —
дейтерий, называется тяжёлой водой. Физи-
ческие свойства тяжёлой воды сильно от-
личаются от свойства обычной воды, моле-
кулы которой состоят главным образом из
изотопа водорода с массовым числом 1.
Шкала атомных весов. Открытие изотопов
кислорода с атомным весом 16, 17 и 18,
которые в обычном кислороде содержатся в
отношениях 506 : 1 : 0,204, приводит к необ-
ходимости установления двух единиц атом-
ных весов. Прежняя химическая единица
равна 1/хв части веса среднего атома кисло-
рода (т. е. в основу кладётся естественная
смесь изотопов кислорода), новая единица—
физическая—равна 1/1в части атома изото-
па О18. Атомный вес кислорода по физиче-
ской шкале равен 16,0043. Для перехода от
одной шкалы к другой существует соотно-
шение Афаз = Ахим-1,00027.
Ради оактивн ость
Явления радиоактивности. Радиоактив-
ными веществами называются такие веще-
ства, которые без всякого предварительного
воздействия на них извне ионизируют воз-
дух вокруг себя и вследствие этого делают
его электропроводящим, действуют на фото-
графическую бумагу, завёрнутую в не
прозрачную для видимого света бумагу, и
вызывают свечение экранов, покрытых
такими веществами, как сернистый цинк.
Радиоактивные вещества испускают троя-
кого рода лучи: а, £ и у. Это излучение
сопровождается превращением элементов.
Природа а-лучей. а-лучи представляют
поток двукратно ионизированных атомов
гелия Не+ + , носящих название а-частиц.
а-частицы выбрасываются из атомов радио-
активных элементов с различной энергией.
Энергию а-частицы можно измерить непо-
средственно из отклонения пучка а-частиц
в магнитном поле. Двигаясь в воздухе,
а-частицы постепенно теряют свою скорость.
Каждая а-частица обладает определённой
дальностью пробега в воздухе, которая из-
меряется в сантиметрах при температуре
15° С и 1 ат. Дальность пробега обратно
пропорциональна квадратному корню из
атомного веса вещества, через которое про-
ходят а-частицы.
Природа р-лучей. (3-лучи представляют
собой поток электронов. [3-лучи выбрасы-
ваются из атомов с различными скоростями.
Природа у-лучей. у-лучи представляют
одну из форм лучистой энергии, спектр
ФИЗИЧЕСКАЯ ХИМИЯ
321
которых частью совпадает, частью же лежит
за спектром лучей Рентгена.
В результате выброса из атома а- или
{3-частицы происходит превращение одного
химического элемента в другой. Каждому
отдельному радиоактивному превращению
отвечает совершенно определённое, харак-
терное для него излучение или а или р;
7-излучение никогда не встречается само по
себе, а всегда сопровождается ₽- или (в ма-
лой интенсивности) «-излучением.
Скорость радиоактивного распада атомов.
Скорость
распада
радиоактивных атомов
элемента, а его масса на четыре единицы
меньше исходного; если распадающийся
элемент излучает р-частицу, то образуется
элемент, стоящий на одну группу вправо,
а его атомный вес остаётся таким же, как
у исходного.
Радиоактивные семейства. Все природные
радиоактивные элементы делятся на три
семейства: ряд тория, ряд урана и ряд
протактиния. На фиг. 6 приведены схемы
превращения в этих рядах. В кружочках
стоят наименования элементов: цифры около
кружочков
Th
М
33
ThX'ilS
33
S3
35
IW
S3
35
88
85
85
83
85
83
м
Фиг. 6. радиоактивные семейства
ThB
83
ПС
81
ты
Ы)
82
РЬ
82
сС
АсС
ИС
Лс
уравнению мономолекулярной
подчиняется
химической реакции
N = Noe"ftf,
где N—число атомов, не распавшихся к
моменту времени t;
No — исходное число атомов;
е_основание натуральных логариф-
мов;
к — константа распада.
Обратная величина к называется средней
продолжительностью жизни т = . Кон-
станта распада, или средняя продолжитель-
ность жизни элемента, всегда одинакова,
независимо от того, в каком соединении он
находится. Химическое вмешательство во
время распада также не оказывает на него
ни малейшего действия. Константа распада
не зависит от температуры (в пределах,
достигнутых в лабораториях).
Между константой распада и дальностью
пробега а-частиц R существует зависимость
1g/с = А + В IgR,
В — константы, меняющиеся при
от одного радиоактивного ряда
1 г радия.
означают порядковое число
элемента; вертикальная
стрелка соответствует вы-
бросу одной а-частицы,
горизонтальная— выбросу
электрона. Конечным про-
дуктом распада во всех
трёх семействах являются
изотопы свинца: Pb, RaQ
и AcD.
Единица радиоактив-
ности. Количество радио-
активных веществ можно
характеризовать массой,
выраженной в граммах или
миллиграммах; однако при-
нято выражать эту массу
в особых единицах, харак-
теризующих активность
данного элемента. Эти еди-
ницы называются кюри и
определяются следующим
образом: 1 кюри радона (ра-
диоэманации RaEm) равен
количеству радона, на-
ходящемуся в равновесии
количество радона при 0° С и
Г6 г.
Это
с
160ммимеет объём0,66дьи3 имассу 6,51 • 10
Так как кюри—единица большая, то поль-
зуются производными единицами: 1 милли-
кюри (10~3 кюри), 1 микрокюри (10~6 кю-
ри). Кюри любого радиоактивного элемента
есть такое его количество, при котором в
1 сек. распадается 3,7- 1О~10 атомов этого
элемента.
где А и
переходе
превращений к другому.
Закон смещения. Если распадающийся
элемент излучает а-частицу, то образуется
элемент, стоящий в периодической системе
на две группы влево от распадающегося
Строение ядра и искусственное
преобразование атомов
Заряд и масса ядра. На основании опы-
тов по изучению отклонения а-частиц при
прохождении их через тонкие металлические
фольги было найдено, что в центре
находится положительно заряженное
которое занимает очень небольшую
пространства атома (диаметр ядра
размеры порядка 10~12—КГ"13 см).
ядра атомов оказался равным порядковому
номеру элемента, если за единицу заряда
принять заряд электрона. Следовательно,
порядковый номер соответствует числу за-
рядов ядра. Так как атом в целом электро-
нейтрален, то, следовательно, вокруг ядра
располагаются электроны, число которых
должно быть равно числу зарядов ядра,
т. е. обшее число электронов в атоме равно
порядковому номеру элемента. Так как мас-
са электрона много меньше массы протона,
атома
ядро,
часть
имеет
Заряд
21 Том I
322
химия
то очевидно, что вся масса атома приходится
на его ядро. Массу ядра в относительных
единицах с достаточной степенью точности
можно принять равной атомному весу. Для
полной характеристики атома элемента
обычно пишут символ элемента, сверху—в
виде индекса массовое число, внизу—поряд-
ковый номер, например, Cg2 и т. п.
Нейтрон. В 1930 г. было открыто, что
при облучении а-частицами лития и особен-
но бериллия испускаются частицы, масса
которых очень близка к массе протона, но
без заряда. Эти частицы получили название
нейтронов. Масса нейтрона по физической
шкале равна 1,00897. Нейтрону можно при-
дать порядковый номер Z = 0.
Позитрон. При исследовании космических
лучей (лучи, поступающие из мировых про-
странств на землю) Д. В. Скобельциным
был открыт ещё один новый вид частиц,
получивших название позитрона. Позитроны
имеют положительный заряд, по величине
равный заряду электрона, и массу, равную
массе электрона. Позитроны имеют неболь-
шую продолжительность жизни. При встрече
с электроном позитрон легко вступает во
взаимодействие. Оба они уничтожаются и
образуются фотоны.
Строение ядра. По современным предста-
влениям ядро атома, как было доказано
Е. Н. Гапоном и Д. Д. Иваненко, построено
из протонов и нейтронов. Так как атом в
целом — электронейтральная система, то
очевидно, что число протонов в ядре равно
порядковому номеру элемента, а число ней-
тронов соответствует величине А—Z, где
А — массовое число элемента (округлённый
до целого числа атомный вес).
Закон эквивалентности массы и энергии.
Эйнштейном был найден закон, по которому
всякая масса обладает энергией или всякая
энергия обладает массой. Между энергией
Е и массой т имеется соотношение Е = тс2,
где с — скорость света.
Дефекты массы. Рассматривая точные
значения атомных весов изотопов элементов,
нетрудно заметить, что у лёгких элементов
атомная масса несколько больше ближайших
целых чисел, а у элементов со средним
атомным весом—несколько меньше. У самых
тяжёлых атомов атомные массы вновь ста-
новятся несколько больше целых чисел.
Разность между нецелой истинной атомной
массой М и целым массовым числом А назы-
вается дефектом массы А=М—А. Наиболее
устойчивыми являются элементы, для кото-
рых Д отрицательна.
Энергия связи частиц в ядре. Так как
число протонов и нейтронов в ядре всегда
известно, а также точно известны массы
протона и нейтрона, то всегда легко рассчи-
тать атомный вес элемента. Расчёт показы-
вает, что сумма масс протонов и нейтронов,
входящих в ядро, всегда больше, чем атом-
ный вес, определённый опытным путём. Это
объясняется тем, что при образовании устой-
чивого ядра происходит превращение части
массы в энергию излучения. Так, при обра-
зовании 1 грамматома гелия из протонов и
нейтронов выделяется энергия, равная
28 MeV на 1 грамматом. Рассчитанная таким
образом величина, делённая на число про-
тонов и нейтронов в ядре, характеризует
собой энергию связи частиц в ядре.
Искусственное преобразование атомных
ядер, а) О п ы ты Р е з е р фо р да. Подвергая
азот бомбардировке а-частицами, испускае-
мыми RaC, Резерфорд нашёл,что при удачном
столкновении а-частица захватывается ядром
азота. При этом выбрасывается протон, и
азот превращается в изотоп кислорода по
реакции: iN’4 + Не£-* Fg8 О”+Н’. Ава-
логичные реакции наблюдались с рядом
других элементов, например:
Fg9 + Не4^ Ne22 + Hj
Alj3 + Не4 Si89 + Н}
б) Циклотрон. Источником быстрых
частиц в опытах Резерфорда служили радио-
активные вещества. Помимо слабой интен-
сивности а-частиц,
испускаемых этими
веществами, они об-
ладают скоростями,
а следовательно, и
энергиями, лежащи-
ми в определённых
узких пределах. Ве-
сьма удобной уста-
новкой для получе-
ния быстрых частиц
искусственным путём
является циклотрон.
Принцип циклотрона
очень прост.Он пред-
ставляет собой мета-
лическую коробку в
Фиг. 7. Схема циклот-
рона
виде плоского полого цилиндра, разрезан-
ную пополам (дуанты D) (фиг.7). Коробка по-
мещается в поперечное магнитное поле S, N и
на обе половинки её накладывается сравни-
тельно небольшая разность потенциалов
(порядка 10000—20000 V) от высокочастот-
ного генератора. Если в разрезе между дуан-
тами находится положительный ион, и ле-
вый дуант А заряжен отрицательно, то ион
будет втянут в него и в магнитном поле
начнёт двигаться по кругу. Описав полуок-
ружность, ион вновь попадает в пространство
между дуантами. В это время правый дуант В
заряжается отрицательно. В результате, ион
испытывает новое ускорение и втягивается
в правый дуант. Дальше то же повторяется
в левом дуанте; вследствие этого, проходя
пространство между дуантами, он будет по-
лучать всякий раз новые добавочные импуль-
сы. Если разность потенциалов между дуан-
тами равна Vi, то при п оборотах ион приоб-
ретает энергию, эквивалентную ускоряюще-
му потенциалу V = 2nVj. При помощи
циклотронов возможно получение протонов,
а-частиц и дейтонов с энергиями в несколь-
ко десятков миллионов электронов-вольт.
Искусственные радиоактивные элементы.
Под действием ударов искусственно полу-
ченных быстрых протонов, а-частиц и дей-
тонов удалось осуществить большое число
реакций искусственного преобразования
элементов. Многие из вновь возникающих
изотопов оказываются радиоактивными, на-
пример, в результате обстрела алюминия
ФИЗИЧЕСКАЯ ХИМИЯ
323
а-частицпми получается радиоактивный фос-
фор, который затем в результате излучения
позитрона е превращается в устойчивый изо-
топ кремния. Схема ядерной реакции:
Al jg + Hej -* Pj5 Р(5 + Пд
Pfg-Si^+e.
nJ — нейтрон.
Деление тяжёлых ядер. Цепной распад
урана. Принципиально новый тип ядерных
реакций был открыт в 1939 г. Тяжёлые ядра
(уран, торий, протактиний) в результате
захвата нейтрона раскалываются приблизи-
тельно пополам с образованием двух новых
элементов с близкими массами, и эти вновь
возникшие ядра разлетаются с огромной
энергией. В результате распада урана об-
разуются изотопы элементов средней части
периодической системы от селена (Z — 32)
до лантана (Z = 56). Деление тория и прот-
актиния вызывается только быстрыми ней-
тронами. Деление урана может быть вызвано
как быстрыми, так и медленными (тепловы-
ми) нейтронами. Тепловые нейтроны вызы-
вают деление только изотопа урана с массо-
вым числом 235, но не урана с массо-
вым числом 238. Если скорость нейтрона
равна 25 eV, то они захватываются Ug88,
который превращается в неустойчивый изо-
топ урана с массой 239. Последний распа-
дается с выбросом электронов и превращается
в элементы с атомными номерами Z = 93 —
нептуний Np и Z = 94—плутоний Рп по
следующей реакции:
С^8 + nJ- U^9 - Np^9+ e'
Np^9 - Pu^9+’e.
Энергия, освобождаемая при делении ядра
урана, составляет около 200 MeV. В процессе
деления выбрасываются быстрые нейтроны,
которые теряют энергию путём неупругих
столкновений с ядрами урана. В случае изо-
топа урана с массой 235 под действием медлен-
ных нейтронов происходит цепной распад,
так как в результате исходного деления обра-
зуется не меньше чем два нейтрона, которые
в свою очередь вызывают распад. Число рас-
падающихся атомов лавинно нарастает, что
приводит к взрыву с выделением огромного
количества энергии. Образующиеся в резуль-
тате распада нейтроны могут вылетать за
пределы взятого объёма урана, и цепной
процесс остановится. Поэтому размер уст-
ройства, содержащего уран, должен быть
больше критического, т. е. такого, при кото-
ром количество освобождаемых при делении
нейтронов в точности равно их потере вслед-
ствие вылета и захватов, не сопровождаю-
щихся делением. Изотоп урана с массой 235
содержится в природном уране в количестве
0,71%. Поэтому для осуществления реакции
цепного взрыва необходимо уран обогатить
содержанием лёгкого изотопа, что дости-
гается с большим трудом рядом методов
(электромагнитное разделение, термодиффу-
зия и т. д.). Цепному распаду подвергается
и элемент с Z=94—плутоний. Плутоний
получают из обычного урана в так назы-
ваемых обогащённых котлах. В котлы по-
мещают блоки из металлического урана или
его окиси, в которые вставляют стержни
из графита. Под действием нейтронов на-
чинается распад урана. Для того чтобы
реакция поддерживалась автоматически,'
необходимы тепловые нейтроны, вызывающие
цепной распад Ц236. Замедлителем нейтронов
служит графит. Таким образом, за счёт
распада U235 поддерживается реакция пере-
вода U238 в Ри239. При этом в котлах выде-
ляется большое количество энергии, которая
может быть использована для мирных целей
(в паросиловых установках). Образовавший-
ся Рц отделяется от урана химическим
путём. Открытие цепного распада урана
открывает новые перспективы перед техни-
кой, так как человечество получило в свои
руки мощный источник энергии.
Строение атомов и спектры атомов
Модель атома Резерфорда-Бора. В центре
атома находится положительное ядро, число
зарядов которого равно порядковому номеру
элемента; вокруг ядра, подобно планетам,
движутся электроны, число которых тоже
равно порядковому номеру элемента. По
законам классической электродинамики
электрон, движущийся по круговой орбите,
должен излучать, т. е. терять, энергию и,
следовательно, в конце концов упасть на
ядро. Поэтому Бором были введены специ-
альные постулаты.
Теория Бора. Первый постулат Бора
гласит, что электрон не теряет энергии при
своём круговом движении, если он движется
по особым квантовым орбитам. Эти орбиты
должны удовлетворять условию:
Л
тиа = п 2%,
где т ио — масса и скорость движения
электрона;
а — радиус электронной орбиты;
h — универсальная постоянная
Планка;
п — главное квантовое число, кото-
рое может быть равно только-
целым числам: 1, 2, 3 ... и т. д.
Второй постулат Бора гласит, что когда
электрон в атоме перескакивает с более-
отдалённой орбиты на более близкую к ядру,
то потерянная атомом энергия переходит в.
один квант лучистой энергии, испускаемой,
атомом, т. е.
Е2 — Et = ft
где Е, и Е, — энергии электрона на высшей
и низшей орбите;
м— частота испускаемого света.
Вводя эти постулаты в классическую
электродинамику, легко определить радиус
электронной орбиты
/г2
а~ mn*'
скорость электрона
2 тс Ze3 1
v~ ft ’ n ’
21*
324
химия
полную энергию электрона Еп на орбите с
квантовым числом п:
77
/£2
2 а ’
частоты спектральных линий, испускаемых
атомом при переходе электрона с орбит с
энергиями Е.2 на орбиты с энергиями Ер.
2л!те4 /1 1 > _|
,= Z4 -3-Л;3 сек .
Теория оказалась хорошо применима к
атому водорода, объяснив линейчатый спектр
атомного водорода.
Недостатки теории Бора. Теория Бора
не смогла объяснить целый ряд наблюдаемых
фактов: дублетный характер линий в атом?
водорода, спектры атомов, содержащих
более чем один электрон.
Четыре квантовых числа. Для целей рас-
шифровки спектров и их классификации
пришлось ввести новые квантовые числа,
характеризующие положение электрона в
атоме. Электроны в атомах группируются
в слои. Каждый слой характеризуется глав-
ным квантовым числом п. Первый слой
имеет главное квантовое число п=1, второй
п = 2 и т. д. Слои делятся на уровни. Каж-
дый уровень характеризуется побочным
квантовым числом 2. Число I может быть
равным для каждого слоя 0, 1,2, ... и—1.
Число уровней в слое определяется числом
возможных значений I. Каждый уровень
разбивается на ряд подуровней, которые
характеризуются внутренним квантовым
числом j = I 4- з, где s — квантовое число,
характеризующее вращение электрона во-
г , 1 1
круг собственной оси и равное + 5- и —
^электрон может вращаться по часовой
стрелке—характеризуется квантовым числом
+ — и против часовой стрелки—характери-
1 \
зуется квантовым числом — )• Число под-
уровней, на которое распадается каждый
уровень, определяется числом возможных
значений /. Каждый подуровень в силовом
поле (электрическом или магнитном) рас-
щепляется ещё на ряд подуровней, которые
характеризуются магнитным квантовым чис-
лом т. Оно может принимать все отличаю-
щиеся на единицу значения, лежащие между
+ j и —
Символическое обозначение термов. Энер-
гия электрона в атоме (терм) зависит от
его положения, которое определяется че-
тырьмя квантовыми числами. Термы записы-
ваются так, что вначале пишут главное
квантовое число, затем букву, характери-
зующую побочное квантовое число (2 = 0
приписывают букву S; 2=2— букву р; 1 =
=3—букву <2; 2=4 —букву / и т. д.); снизу
в виде индекса записывают внутреннее кван-
товое число и сверху слева—в виде индекса
мультиплетность терма, т. е. число подуров-
ней, на которые расщепляется данный уро-
вень, определяемое числом возможны:-; зна-
чений j. Например, для одноэлектронного
1
атома при п = 2, 2=1, j = тсрм символи-
чески запишется: 22Р,^.
Правила отбора. Переходы электронов в
атомах с одного уровня на другой возможны
не все, а только те, которые удовлетворяют
определённым условиям: квантовое число п
может изменяться на любую величину;
квантовое число 2 всегда увеличивается или
уменьшается на единицу: Д2 = ±1; кван-
товое число / также уменьшается или уве-
личивается на единицу или не меняется:
Д/=±1 или 0. Переходы между другими
уровнями энергии не вполне исключаются,
но происходят гораздо реже, чем нормаль-
ные переходы.
Принцип Паули. Внутри атома не могут
существовать два электрона, у которых все
четыре квантовых числа — п, I, j, т — оди-
наковы, т. е. если какой-нибудь электрон
внутри атома имеет определённые значения
квантовых чисел па, la, ja, та, то характе-
ризованное ими состояние считается занятым
и не может быть занято никаким другим
электроном.
Принцип Паули и построение периодиче-
ской системы. Принцип Паули позволяет
определить, сколько электронов может быть
расположено в данном слое на данном уров-
не и на данном подуровне. Число электро-
нов с одинаковыми значениями п, I и /,
различающихся магнитным квантовым чис-
лом т, равно 2/4-1; число электронов с
одинаковыми квантовыми числами п и 2
[авно 2(2 2+1); число электронов с одинако-
вым квантовым числом п равно 2 и2. Поль-
зуясь спектроскопическими данными и прин-
ципом Паули, можно точно установить, как
распределяются электроны по слоям, уров-
ням и подуровням во всех атомах периоди-
ческой системы элементов, а также устано-
вить число элементов, входящих в каждый
период, и причину повторения химических
свойств элементов в группах.
Волновая теория. Теория Бора не смогла
объяснить необходимости введения новых
квантовых чисел, правил отбора; кроме того,
она оказалась бессильной в своих попытках
объяснить строение молекул. В 1924 г.
де-Бройль установил, что любая материаль-
ная частица обладает волновыми свойствами.
Всякая частица, обладающая массой т и
скоростью движения и, одновременно ведёт
себя как волна, длина которой X, частота ч
и скорость распространения и. Длина этой
, h
волны определяется соотношением л=
где h — универсальная постоянная Планка.
Волны, свойственные движущимся частицам,
называются волнами материи. Каждая части-
ца обладает и корпускулярной и волновой
природой, в одних явлениях проявляются
свойства частицы как корпускулы, в дру-
гих—как волновой процесс. Теория де-Ерой-
ля Сшла экспериментально подтверждена в
опытах с дифракцией! электронов.
ФИЗИЧЕСКАЯ ХИМИЯ
325
На базе теории де-Бройля была создана
математическая теория атома и молекулы,
так называемая квантовая, или волновая,
механика, которая объяснила большинство
найденных эмпирических закономерностей и
позволила предсказать целый ряд новых
явлений.
ТЕРМОХИМИЯ
Тепловой эффект реакции. Каждая хими-
ческая реакция сопровождается либо выде-
лением теплоты (экзотермическая реакция),
либо поглощением теплоты (эндотермическая
реакция). Тепловым эффектом реакции на-
зывается то количество теплоты, которое
выделяется или поглощается при превраще-
нии одного моля вещества. В технике расчёт
ведётся на 1 кг. Тепловой эффект реакции
зависит от условий (V, Р, Т), в которых
протекает реакция. В отличие от термоди-
намики, в термохимии теплота, выделяемая
системой, принимается положительной и
обозначается Q. Поэтому Q = — Q. Тепло-
вой эффект реакции при постоянном объёме
Qz, равен убыли внутренней энергии системы
U при превращении одного моля вещества
Qv = A Uv.
Тепловой эффект реакции при постоян-
ном давлении равен убыли энтальпии си-
стемы при превращении одного моля ве-
щества
Qp = -AHp.
Между Qv и Qp существует зависимость
Г/dm 1 _
Qp — Qv
. dU\
Для идеального газану) = 0, а РДУ
при превращении одного моля равно AnRT,
поэтому
Qp = Qv — Д nRT,
где Ди — изменение количества граммолей
газа при превращении одного моля
вещества.
Экспериментальное определение Qp зна-
чительно легче, чем Q^.
Для конденсированных систем РДУ ма-
ло, поэтому =
Теплота растворения. Растворение всегда
сопровождается выделением или поглоще-
нием теплоты. Различают интегральную,
диференциальную и полную теплоты раство-
рения. Интегральной теплотой растворения
называется то количество теплоты, которое
выделяется при растворении при постоянной
температуре одной граммолекулы вещества
в количестве растворителя, достаточном для
образования раствора определённой кон-
центрации. Диференциальной теплотой рас-
творения называется теплота, которая
выделяется при растворении при постоянной
температуре одной граммолекулы вещества
в большом количестве раствора определён-
ной концентрации так, чтобы введение одной
граммолекулы не вызвало заметного изме-
нения концентрации раствора. Теплоты рас-
творения важнейших веществ даны в табл. 18.
Полной теплотой растворения называется
интегральная теплота, получаемая при обра-
зовании насыщенного раствора.
Теплота разведения. Теплотой разведения
называется то количество теплоты, которое
выделяется при постоянной температуре при
прибавлении одной граммолекулы раствори-
теля к большому количеству раствора опре-
делённой концентрации.
Теплота нейтрализации. Тепловой эффект
нейтрализации (см. Тепловой эффект реак-
ции, стр. 325) граммэквивалента сильной кис-
лоты в разбавленном растворе граммэквива-
лентом сильного основания практически
одинаков для различных пар кислот и осно-
ваний и равен в среднем Qp = — ДН =»
= — 13,8 ккал. Равенство тепловых эффек-
тов нейтрализации объясняется теорией
электролитической диссоциации как резуль-
тат практически полной диссоциации силь-
ных кислот, сильных оснований и солей
сильных кислот и оснований в разбавленных
растворах. В результате реакция нейтрали-
зации сводится лишь к образованию воды
из ионов водорода и гидроксила. Например,,
нейтрализация соляной кислоты едким
натром:
Н+ + Cl" + Na+ + ОН"= Na+ + Cl"+ Н2О;
Qp — — АН — — 13,68 ккал,
или, сокращая в обеих частях равенства
одинаковые ионы:
н+ + ОН" — Н2О;
Qo = — АН = — 13,68 ккал.
Теплота нейтрализации слабой кислоты
сильным основанием или сильной кислоты
слабым основанием обычно меньше 13,8 ккал.
Закон постоянства сумм теплоты являет-
ся основным законом термохимии. Тепловой
эффект химической реакции при /=const за-
висит только от начального и конечного
состояния системы и не зависит от того,
каким путём система переходит от началь-
ного состояния к конечному.
Теплота образования соединений из эле-
ментов и теплота горения. Теплотой обра-
зования соединений из элементов называется
тепловой эффект образования его из простых
(элементарных) веществ, так как в термо-
химии понятие элемента совпадает с поня-
тием простого вещества. Например, реакция
образования NaCl из элементов записывается:
Na + у Cl2 -> NaCl;
её тепловой эффект:
Qp = — АН = 97,8 ккал.
Теплота образования простых веществ
принимается равной нулю. Полученные
опытным путём или путём вычисления теп-
лоты образования различных соединений
для стандартных условий — 25° С и 1 ат—
приведены в табл. 17. Пользуясь этой
таблицей, можно определить тепловые эффек-
ты реакций.
326
химия
Теплота образования соединений из эле-
ментов чаще всего определяется по теплотам
сгорания их, которые легко определяются
сжиганием вещества в калориметрической
бомбе.
Теплота сгорания важнейших соединении
дана в табл. 17 (стр. 347).
По теплоте сгорания может быть опре-
делена теплота реакции:
где SQi—сумма теплот сгорания веществ,
вступающих в реакцию;
— сумма теплот сгорания веществ,
образующихся в результате реак-
ции.
Зависимость теплового эффекта реакции
ojr температуры. Для реакции.
*iAi + ^sAa + v3A3 + ... =
= * Д 4- * А 4~ \ А 4~ .
1 > IV У ч
Зависимость теплового эффекта от темпе-
ратуры выражается следующей формулой:
_ _ г
Q = Qe+ | Z[vC]dT,
b
или
_ _ т
Q = QT,+ [ S[vC] dT,
т0
где
S [мС] = МХСJ 4- М2С2 + MjCз + ... -
— ч C —v c —» C ------...
1, а я as
>!, m2, .......m2> ^3 ... — стехиометриче-
ческие коэфи-
циенты,
a C1( C2, C3,.., С , Ct, С ...— молярные те-
плоёмкости ве-
ществ Aj, А3,
А3,.., А', Д',
А ... и т. д.,
<20 — тепловой эффект реакции при абсо-
лютном нуле;
qt — тепловой эффект реакции при абсо-
лютной температуре Та.
ПРИМЕНЕНИЕ ВТОРОГО ЗАКОНА
ТЕРМОДИНАМИКИ К ПЕРЕХОДУ
АГРЕГАТНЫХ СОСТОЯНИЙ
Уравнение Клаузиуса-Клапейрона выра-
жает зависимость между давлением, темпе-
ратурой системы Т и теплотой А превраще-
ния фаз индивидуального вещества:
dP
где X — теплота превращения одного моля
или одного грамма при постоянной
температуре Т и давлении Р, ко-
торое преодолевается при фазовом
переходе;
V’i — молярный, или удельный, объём
фазы, более устойчивой при низкой
температуре;
V2 — молярный, или удельный, объём
фазы, более устойчивой при высокой
температуре.
Это уравнение применимо к процессам
превращения фаз, например испарению,
плавлению, возгонке. Оно неудобно для
интегрирования, так как содержит много
переменных (X, Vt, V2, Р, Т), поэтому часто
пользуются приближённым уравнением
ДР
* = 7'(V2-V1)Ar,
где ДР и &Т — конечные изменения давле-
ния и температуры.
Испарение. Для случая испарения инди-
видуальной жидкости уравнение имеет вид:
t/P
X = Г (Vпар VЖ;;8к) (j']' 1
dP
-,f — изменение упругости пара жидкости
с температурой.
Интегрирование его ^прп предположении
РТ\
А = const, Vj« и V3 = р~ I Дает выра-
жение:
ig р= igc — ^-т,
пли
k
Р = Сг~ ~RT-t
и интегрирование в пределах от Tt до Т.г—
выражение:
X / 1 1 \
1g ^2— = 2,303 R\ Т, 1\)-
Это важное приближённое выражение
даёт возможность определять теплоту испа-
рения по двум значениям давления насы-
щающих паров и соответствующим им тем-
пературам, либо по известной теплоте испа-
рения и одному значению давления пара
находить давление пара при другой темпе-
ратуре. Более точное выражение получает-
ся, если при интегрировании учесть, что X
зависит от Т. Зависимость А от Т даётся
уравнением, аналогичным уравнению зави-
симости теплового эффекта реакции от тем-
пературы.
Упругость паров некоторых жидкостей
дана в табл. 1э и 16.
Кривые зависимости упругости пара
жидкостей от температуры. Типичные кри-
вые зависимости давления пара жидкостей
от абсолютной температуры Т изображены
на фиг. 8. Кривые обрываются в критиче-
х
ских точках. Уравнение Р = Се RT удов-
летворительно описывает эти кривые лишь
при температурах, далёких от критиче-
ской.
Плавление. Для случая плавления урав-
нение имеет вид:
, dP
X — Т (Ужи8к Vтд) ар,
ФИЗИЧЕСКАЯ ХИМИЯ
327
где X — теплота плавления;
Ужидк и Vme — молярные объёмы жидкой и
твёрдой фаз;
Р— внешнее давление.
В ряде случаев удобно применение при-
ближённой формулы:
ДР
Л ~ Т (Vжидк У те) ’
vme) АР
Последнее выражение даёт возможность
определить изменение температуры плавле-
ния чистого вещества ДГ, вызванное изме-
нением внешнего давления ДР.
4
5’
Крцт.Р'ЛЗО*
Крит P'tISam
6
4
2
40
О
, 6
4
2
30
• Те чка кипени" при 7 ат
• Критическая тт.ка
CS
3
о
4
Шесть постпян-
го
w
K.f't55*
К.р 730ат
КЛ’^374'
К.р217,5ап;.-
жооге-гш so оогмшш оогоо гооооо золоо
1—-
Фиг. 8. Кривые давления пара жидкостей
Из этого же выражения видно, что если
VжЛк < Vme при температуре плавления, то
с увеличением давления температура пла-
вления должна уменьшаться. Такие отноше-
ния наблюдаются у воды, висмута и чу-
гуна.
ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
И УСЛОВИЯ РАВНОВЕСИЯ
Определение. Функция состояния назы-
вается характеристической, если при помощи
этой функции и её производных разных
порядков все термодинамические свойства
системы могут быть выражены в явной фор-
ме. Характеристической функция состояния
может быть лишь при вполне определённых
независимых переменных.
Внутренняя энергия. Внутренняя энергия
U является характеристической функцией
при независимых переменных S и V. Не-
удобством при использовании этой функции
для выражения различных термодинамиче-
ских свойств системы является переменная
S — энтропия, так как последняя не может
быть измерена.
Энтальпия. Энтальпия, или теплосодер-
жание, Н является характеристической функ-
цией при независимых переменных S и Р.
Энтальпия, так же как внутренняя энергия,
неудобна для выражения термодинамических
свойств системы (см. Внутренняя энергия,
стр. 327). С внутренней энергией U энтальпия
связана соотношением
Н = и + PV.
Свободная энергия. Часть внутренней
энергии системы U, которая может быть
превращена в работу при постоянной темпе-
ратуре Т, называется свободной энергией F.
Она определяется уравнением
F = U — TS,
где S — энтропия системы.
Свободная энергия является характери-
стической функцией, когда работа системы
А состоит только из работы расширения:
dF = — PdV — SdT,
откуда
/0F\ /6F\
т. e. энтропия есть мера убыли свободной
энергии в системе с ростом температуры
при постоянном объёме системы, а давление
есть мера убыли свободной энергии с ростом
объёма при постоянной температуре.
Свободная энергия является характери-
стической функцией (см. Характеристиче-
ские функции,стр.327) при независимых пере-
менных V и Т. Так как обе переменные
легко измеримы, то свободная энергия яв-
ляется очень удобной функцией для выраже-
ния различных термодинамических свойств
системы через неё и её производные.
Свободная энергия при постоянном да-
влении (термодинамический потенциал). Сво-
бодной энергией при постоянном давлении
Ф называется та часть энтальпии Н систе-
мы, которая при постоянном давлении Р и
постоянной температуре Т может быть пре-
вращена в полезную работу А (без работы
расширения).
Эта часть определяется выражением
Ф=Н — Т8-,
S — энтропия системы.
Свободная энергия при постоянном.да-
влении является функцией состояния. Со
свободной энергией F она связана соотно-
шением
Ф = F+ PV.
Важным диференциальным уравнением
является
dd> = VdP — SdT,
328
химия
откуда следует, что
__s. (дф\ =V
\dTjp- d> \dPJT v'
т. е. энтропия является мерой убыли Ф —
системы с ростом температуры при постоян-
ном давлении, а объём является мерой при-
роста Ф с увеличением давления при по-
стоянной температуре.
Свободная энергия при постоянном да-
влении является характеристической функ-
цией при независимых переменных Р и Т,
что делает её особенно ценной, так как, во-
первых, Ри Т легко измеримы, а во-вторых,
большинство процессов происходит при по-
стоянном давлении
Условия равновесия. Общими условиями
равновесия системы являются:
при постоянных U и V
(dS)U: у < 0;
система находится в устойчивом равно-
весии, если её энтропия постоянна и ма-
ксимальна в данных условиях;
при постоянных V и Т
(dF)v> 0;
т. е. система находится в устойчивом равно-
весие если её свободная энергия постоянна
или минимальна в данных условиях.
При постоянных Р и Т
(йФ)Р)Т > 0.
Система находится в устойчивом равно-
весии., если её свободная энергия при по-
стоянном давлении постоянна и минималь-
на в данных условиях.
РАСТВОРЫ
Концентрация. Существуют различные
выражения концентрации данного вещества
в растворе.
Весовые концентрации. Весовой
концентрацией данного вещества в растворе
называется число его граммов, содержащих-
ся в единице веса или объёме раствора или
другого компонента. Единицы весовой кон-
центрации г/г, г/кг, г/мл, г/л.
Объёмные концентрации. Объём-
ной концентрацией данного вещества в рас-
творе называется число его миллилитров
или литров, содержащихся в единице объёма
раствора или второго компонента. Единицы
объёмной концентрации мл/л, л/л и др.
Нормальная концентрация.
Нормальной концентрацией, или нормально-
стью, раствора называется число граммэкви-
валентов вещества, содержащееся в 1 л
раствора.
Молярные концентрации. Мо-
лярной концентрацией данного вещества в
растворе называется число его молей, содер-
жащихся в единице веса или в единице объёма
раствора, или в одном моле смеси или в одном
моле другого компонента. Единицы моляр-
ной концентрации моль/кг, моль/л, моль/моль.
Безразмерные концентрации (г/г, мл/мл,
моль]моль) могут быть выражены в процен-
тах.
Наиболее часто в теории употребляется
концентрация, выраженная в молях данного
вещества, содержащихся в одном моле
смеси:
где Ni — концентрация, называемая моляр-
ной долей;
щ — число молей данного вещества в
смеси;
S п—число молей всех веществ в смеси.
Растворы газов в жидкостях
Растворимость газов в жидкостях. Рас-
творимость газов в жидкостях зависит от
природы газа, природы растворителя, пар-
циального давления газа и температуры
(см. Влияние температуры на растворимость
газов, стр. 328).
Растворимость газов часто характери-
зуют коэфициентами / и р.
Коэфициентом растворимости I называют
число объёмов газа при заданных условиях
(без приведения их к нормальным условиям),
растворившихся в одном объёме жидкости.
Коэфициентом абсорбции [3 называют
число объёмов газа, приведённых к нормаль-
ным условиям (0°; 1 ат), поглощённых одним
объёмом жидкости при парциальном давле-
нии газа в 1 ат.
Концентрацию растворённого газа в
жидкости выражают в граммах или милли-
граммах газа в 1 л растворителя или в
объёмах растворённого газа в 1 л раство-
рителя.
Закон Генри-Дальтона. Растворимость Ci
(весовая концентрация насыщенного раство-
ра) газа в жидкости при постоянной темпе-
ратуре прямо пропорциональна парциаль-
ному давлению Р,- этого газа в смеси над
жидкостью при условии, что газ не взаимо-
действует с растворителем:
Ct = kP,.
Закон Генри-Дальтона оправдывается,,
как это показано И. М. Сеченовым, лишь
при малых давлениях.
Влияние температуры на растворимость
газов. С повышением температуры раство-
римость всех газов уменьшается. На этом
основана термическая деаэрация питатель-
ной воды для паровых котлов. При кипя-
чении воды достигается практически полное
удаление растворённого воздуха.
Растворы твёрдых тел в жидкостях
Растворимость и влияние температуры
на неё. Растворимостью твёрдого тела в
жидкости называется весовая концентрация
насыщенного раствора. Она часто выражает-
ся в весовых процентах растворённого ве-
щества от веса раствора. Растворимость за-
висит от природы твёрдого тела, природы
растворителя, температуры и в меньшей
степени от давления.
С повышением температуры растворимость
некоторых (большинства) твёрдых тел уве-
личивается, а некоторых (меньшинства}
ФИЗИЧЕСКАЯ ХИМИЯ
329
уменьшается (фиг. 9). Кривые растворимости
обычно непрерывны, за исключением тех
случаев, когда наблюдаются переходы твёр-
дого вещества из одной формы в другую
(различные кристаллические формы, различ-
ные кристаллогидраты). Увеличение раство-
римости при повышении температуры на Г,
выраженное в процентах, называется темпе-
ратурным коэфициентом растворимости. Те-
ла, растворимость которых увеличивается
с повышением температуры, обычно раство-
ряются с поглощением тепла и, наоборот,
Фиг. 9. Зависимость растворимости веществ
от температуры
тела, растворимость которых уменьшается
с увеличением температуры, растворяются
с выделением тепла.
Растворимость Важнейших твёрдых тел
дана в табл. 18.
Заковы разбавленных растворов
Закон Рауля. Давление пара любого ве-
щества понижается, если в нём растворить
другое вещество. Относительное понижение
давления паров данного вещества численно
равно молярной доле второго вещества в
смеси
Р «i+Па
где Р° — давление паров чистого раствори-
теля;
Рг — давление паров растворителя над
раствором;
N2 — молярная доля второго компонен-
та;
Hj — число граммолекул первого вещест-
ва (растворителя) в смеси;
п2 — число граммолекул второго компо-
нента в смеси.
Этот закон может быть выражен иначе:
молекулярное понижение температуры за-
мерзания (см. Криоскопия, стр. 329) и моле-
кулярное повышение температуры кипения
(см. Эбулиоскопия, стр.329) являются величи-
нами постоянными для данного растворителя
и не зависят от природы растворённого
вещества.
Закон оправдывается лишь для разба-
вленных растворов.
Криоскопия- Температура замерзания
воды или другой жидкости понижается при
растворении в ней какого-либо вещества,
не вымерзающего вместе с растворителем.
Понижение температуры замерзания стано-
вится понятньш при рассмотрении фиг. 10,
изображающей кривые давления пара чисто-
го растворителя в жидком и твёрдом состоя-
нии АОЕ и кривую давления пара раство-
рителя над раствором DC, лежащую всегда
ниже кривой чистого растворителя. Точка
замерзания растворителя в растворе T#
лежит левее точки замерзания чистого рас-
творителя Tg
Для разбавленных растворов понижение
точки замерзания растворителя ДТА, про-
порционально молярной концентрации рас-
творённого вещества и не зависит от при-
роды последнего:
ДТ? = Кп2 = К ,
где п2 — молярная концентрация растворён-
ного вещества, выраженная в
.иоль/1000 г;
g—количество граммов вещества, рас-
творённого в 1 000 г растворителя;
М — молекулярный вес растворённого
вещества;
К— криоскопическая константа, назы-
ваемая молекулярным понижением
температуры замерзания; зависит
от природы растворителя (для во-
ды—1,856, бензола—5,146 ит.д.).
Эта формула широко используется для
определения молекулярных весов по пони-
жению температуры замерзания раствори-
теля: д
Метод определения молекулярных весов
по понижению температуры замерзания но-
сит название криоскопии.
Эбулиоскопия. Температура кипения воды
или другой жидкости повышается при рас-
Фиг. 10. Понижение давления
пара растворителя в растворах
нелетучего растворённого веще-
ства
творении в ней какого-либо нелетучего'
вещества, что ясно видно из фиг. 10, изобра-
жающей кривые давления паров чистого
растворителя АОЕ и давления паров раство-
рителя над раствором DC. Жидкость заки-
пает, когда давление паров становится рав-
ным внешнему давлению. Точка кипения
раствора Ts лежит правее точки кипения
чистого растворителя Ts
Для разбавленных растворов повышение
температуры кипения раствора ДТ4 пропор-
330
химия
•цпонально молярной концентрации раство-
рённого вещества и не зависит от природы
последнего:
АЛ = Епг = Е±,
где Е — эбулиоскопическая константа, назы-
ваемая молекулярным повышением
температуры кипения; зависит от
природы растворителя (для воды—
5,12, бензола—26,7 и т. д.).
Эта формула используется для определе-
ния молекулярных весов по повышению
температуры кипения раствора (эбулиоско-
пия):
М — Е ду; .
Эбулиоскопический метод определения
молекулярных весов более трудоёмкий по
сравнению с криоскопическим и поэтому
применяется реже.
Осмос. Осмосом называется явление само-
произвольного перехода растворителя через
полунепроницаемую перегородку из более
разбавленного раствора (или чистого раство-
рителя) в более концентрированный раствор.
Интенсивность осмоса характеризуется так
называемым осмотическим давлением. Мерой
осмотического давления является разность
внешних давлений на оба раствора, способ-
ная остановить осмос.
Закон осмотического давления. Законы
осмотического давления совпадают с зако-
нами идеальных газов.
v=CRT,
где п — осмотическое давление;
С = ” —разность молекулярных концентра-
V ций обоих растворов;
А’— универсальная газовая постоян-
ная;
Т— абсолютная температура.
Это уравнение оправдывается лишь для
разбавленных растворов.
Растворы электролитов. Водные растворы
электролитов обнаруживают ряд аномалий:
ДР, \Тg и &TS, определённые эксперимен-
тально, оказываются больше, чем вычислен-
ные по вышеприведённым формулам. Все эти
аномалии объясняются диссоциацией элект-
ролитов в водном растворе на ионы, т. е.
увеличением числа частичек по сравнению
с недиссоциирующим веществом. Для того
чтобы к разбавленным водным растворам
электролитов могли быть применены все
законы разбавленных растворов, в них
должен быть введён множитель I, показы-
вающий, во сколько раз возросло число
частиц в результате электролитической дис-
социации, например
я = CIRT;
i связано со степенью диссоциации а (доля
диссоциированных молекул):
7 = 1 + (v — 1) а;
v — число ионов, на которые диссоциирует
молекула.
Концентрированные растворы. Концентри-
рованные растворы не подчиняются законам
Рауля и др. Причины этого лежат в том,
что во всех вышеприведённых формулах не
учитываются силы взаимодействия между
молекулами. Достаточно разработанной тео-
рии концентрированных растворов до сих
пор нет.
Растворы жидкостей в жидкостях
Идеальные растворы. Идеальными раство-
рами называются растворы, строго подчи-
няющиеся закону Рауля (при любых кон-
центрациях). К идеальным растворам при-
ближаются смеси бензол—толуол, бензол
хлорбензол, метиловый и этиловый спирты
и др. Вообще, идеальные растворы образуют
вещества, близкие по своим химическим
свойствам. На диаграмме «состав—давле-
ние» Рдв и РВА кривые парциальных дав-
лений обоих компонентов и давления смеси
Рд Рв в случае идеального раствора изобра-
жаются прямыми (пунктирные кривые на
фиг. 11 и 12).
Отклонения реальных растворов жидко-
стей в жидкостях от законов идеальных
растворов. Подавляющее большинство реаль-
ных растворов более или менее сильно от-
клоняется от закона Рауля. Наблюдаются
отклонения двух типов: положительные
(фиг. 11) и отрицательные (фиг. 12). Пунк-
Фиг. И . Положительные Фиг. 12. Отрицательные
отклонения от закона отклонения от закона
Рауля Рауля
тирами на фигурах обозначены кривые, от-
вечающие идеальным растворам.
Положительные и отрицательные откло-
нения качественно можно объяснить разли-
чием энергий связи между однородными и
разнородными молекулами. Достаточно раз-
работанной теории реальных растворов пока
нет.
Жидкости, не растворимые друг в друге.
Примерами таких жидкостей являются ртуть
и вода, бензол и вода и т. д. Давление пара
каждого компонента в этом случае незави-
симо от природы другого компонента.
Жидкости, растворимые в любых отно-
шениях. Примерами жидкостей, раствори-
мых в любых отношениях, являются вода и
спирт, два любых углеводорода, хлороформ,
ацетон и др. Каждому составу такой жидкой
смеси при данной температуре отвечает пар
вполне определённого давления и состава,
причём состав пара, как правило, более или
менее сильно отличается от состава жидкости.
По характеру дестилляции и форме соот-
ветствующих ей кривых кипения растворы
жидкостей, смешивающихся во всех отно-
шениях, можно разбить на две группы:
ФИЗИЧЕСКАЯ ХИМИЯ
331
Фиг. 13. Диаграмма
«состав — температу-
ра» кипения смеси
двух взаимно раство-
римых жидкостей, не
имеющих постоянной
температуры кипе-
ния
а) растворы, не имеющие постоянной точки
кипения, и б) растворы с минимальной или
максимальной точкой кипения.
Растворы, не имеющие постоянной точки
кипения. В координатах «состав (N) — да-
вление (Р)» диаграмма состояния смеси двух
жидкостей, дающих та-
кой раствор при по-
стоянной температуре,
изображается двумя
кривыми—верхняя да-
ёт зависимость упру-
гости пара от со-
става жидкости, ниж-
няя—от состава пара.
В координатах «состав
(N) — температура (/)»
при постоянном давле-
нии диаграмма состоя-
ния изображена на
фиг. 13. Она также
имеет две ветви, обра-
щённые по сравнению с
кривыми давления:
верхняя—пара, ниж-
няя — жидкости. Так
отличается от состава
жидкости, находящейся с ним в равновесии,
то при перегонке жидкость будет обеднять-
ся тем компонентом, который преобладает
в паре. Изменение составов жидкости и пара
и рост температуры будут продолжаться до
полного испарения жидкости. Последние
порции жидкости будут состоять практически
из одного компонента — жидкости с более
высокой температурой кипения.
Закон Коновалова (первый). При равно-
весии бинарной жидкой смеси, не имеющей
как СОСТ
Фиг. 14. Диаграмма
«состав —температура»
кипения для бинарных
смесей с максимальной
точкой кипения
Фиг. 15. Диаграмма «со-
став-температура» ки-
пения для бинарных
смесей с минимальной
точкой кипения
постоянной точки кипения, легколетучего
компонента в паровой фазе содержится
больше, чем в ясидкой фазе.
Растворы с минимальней и максимальной
точкой кипения. Типичная кривая кипения
раствора с максимальной точкой кипения
изображена па фиг. 14; с минимальной точ-
кой кипения—на фиг. 15; общей особен-
ностью этих кривых является совпадение
составов жидкости и пара в экстремальных
точках (см. Закон второй Коновалова,
стр. 331). Геометрически это выражается в
совпадении в экстремальной точке касатель-
ных к кривым жидкости и пара.
Дестилляция раствора любого состава с
максимальной точкой кипения приводит к
составу т', отвечающему максимальной точ-
ке т. Смеси с этим составом кипят при по-
стоянной температуре б J3 изменения состава
и потому носят название постоянно кипящих
или азеотропных смесей. Примером такой
смеси является водный раствор соляной
кислоты (20% НС1), кипящей при 110° С.
Поэтому невозможно путём дестилляции по-
лучить концентрированный раствор соляной
кислоты.
Дестилляция раствора с минимальной точ-
кой кипения приводит к одному из чистых
компонентов в зависимости от того, каким
компонентом богаче исходный раствор по
сравнению с составом т', отвечающим мини-
мальной точке т. Примером такого раствора
является водный раствор этилового спирта.
Минимальную точку кипения 78,13° С имеет
раствор, содержащий 95,57% спирта.
Закол Коновалова (второй). В экстре-
мальных точках кривых давления пара
и температуры кипения бинарных смесей,
составы жидкой и парообразной фаз оди-
наковы.
ПРАВИЛО ФАЗ
Гомогенная система. Гомогенной, или одно-
родной системой, называется система, обла-
дающая одинаковыми физическими и хими-
ческими свойствами в любом участке её.
Примеры гомогенных систем: смесь газов,
истинный раствор и др. Гомогенная систе-
ма является однофазной (см. ниже Фазы
системы).
Гетерогенная система. Гетерогенной си-
стемой называется система, состоящая из
нескольких фаз (см. Фазы, стр. 331). Примеры
гетерогенных систем: насыщенный раствор
в присутствии кристаллов соли, вода в при-
сутствии пара и др.
Фазы системы. Фазой называется сово-
купность всех гомогенных частей системы,
обладающих одинаковыми составом и термо-
динамическими свойствами и находящихся
в одинаковом состоянии. Например, сово-
купность всех льдинок в воде при 0° С и
760 мм представляет одну фазу, несмотря
на пространственную разделённость кусоч-
ков льда.
Компоненты системы. Компонентами си-
стемы называются независимые составляю-
щие вещества её. Составляющими вещества-
ми системы называются вещества, которые
могут быть извлечены из системы и суще-
ствовать вне её. Число компонентов системы
равно числу веществ, составляющих систе-
му, минус число независимых реакций, мо-
гущих протекать между этими веществами
при данном состоянии системы. Обратимая
реакция считается одной реакцией. Напри-
мер, смесь газов СО, СО2 и О2 при комнат-
ной температуре является трёхкомпонентной
системой, а при высокой температуре, когда
уже заметно протекает реакция 2СО +
+ О2 52СО2, — двухкомпонентной.
Степень свободы системы. Степенью сво-
боды системы F называется число термоди-
намических переменных системы (P,T,Ct,
С2, С,... и т. д.), которые можно в определён-
ных пределах произвольно изменять, не
изменяя числа фаз системы. Состояние фаз
при этом, конечно, будет изменяться. Си-
332
химия
стема с Е=0 называется инвариантной,
система cF=l —моновариантной, система
с F = 2 — дивариантной и т. д.
Правило фаз даёт связь между числом
степеней свободы F, числом компонентов п
и числом фаз системы к-.
F=n+2 — k.
Однокомпонентные системы. Однокомпо-
нентная система вполне определяется двумя
переменными Р и Т. Поэтому состояние си-
стемы может быть изображено точкой на
координатной плоскости Р—Т.
Для однокомпонентных систем (п=1) пра-
вило фаз принимает вид:
Г = 3— к.
Однокомпонентная система при числе фаз
к — 3—инвариантна (F=0), т. е. система
существует только при вполне определённых
значениях Р и Т; при числе фаз к=2 —мо-
новариантна (F = 1); произвольно может из-
меняться одна из двух переменных, тогда
другая изменяется зависимо, например
Р = / (Т); при числе фаз к = 1 — диварпаптна
(F = 2); при этом обе переменные могут
произвольно изменяться. Таким образом,
максимальное число фаз однокомпонептной
системы, которые могут одновременно су-
ществовать, равно трём. Число всех фаз,
в которых может встречаться данная одно-
компонентная система, может быть и больше
трёх.
Диаграмма состояния воды. Фиг. 16
изображает диаграмму состояния воды в
области невысоких давлений. Точка О отве-
чает инвариантной трёхфазной системе лёд—
вода—пар, существующей только при Р =
= 4,579 мм и t = + 0,0076° С, и называется
тройной точкой. Изменение давления или
температуры приводит к исчезновению одной
фазы. Например, при нагревании исчезнет
лёд, при увеличении давления исчезнет пар.
Три кривые, исходящие из тройной точки,
соответствуют трём возможным моновариант-
ным двухфазным системам: АО— вода—пар,
ОВ — лёд—пар, ОС —вода —лёд. Каждая
кривая является графиком функции Р= / (Т)
или Т = / (Р). Изменение и давления и тем-
пературы приводит к исчезновению ещё
одной фазы. Например, при нагревании и
повышении давления в системе вода — пар
исчезает пар. Три поля, заключённых между
кривыми, соответствуют трём возможным
дивариантным однофазным системам: поле
АОВ— пар, поле АОС— вода, поле ВОС —
лёд.
При высоких давлениях лёд может суще-
ствовать в нескольких кристаллических
формах, каждая из которых имеет свою
область устойчивости.
Метастабильное состояние. Если осто-
рожно охлаждать чистую воду ниже 0° С, то
можно получить переохлаждённую жидкую
воду. Но достаточно встряхнуть её или бро-
сить кусочек льда (затравить), чтобы вызвать
мгновенное замерзание. Такое неустойчивое
состояние переохлаждённой воды называется
метастабильным. Оно наблюдается и у дру-
гих веществ и всегда характеризуется повы-
шенным давлением паров по сравнению с
устойчивым состоянием. На фиг. 16 ему
соответствует продолжение (пунктиром) кри-
вой О А' в область льда. Продолжения ОВ в
область воды не существует, так как пере-
греть лёд нельзя. Однако твёрдое вещество
может находиться в
метастабилыюм со-
стоянии (см. Поли-
морфизм, стр. 317).
Энантиотропия и
монотропия. У мно-
гих веществ встре-
чается две и более
твёрдые модифика-
ции (см. Полимор-
физм, стр.317). Явле-
ние энантиотропии
состоит в том, что
каждая твёрдая мо-
дификация имеет
свою определённую
область (температур
чивости. Для энантиотропии характерна
сбратимость превращений модификаций. На-
пример, энантиотропия наблюдается у олова.
Обычное белое олово (квадратная система)
устойчиво до 18° С. Ниже 18’С устойчива
ромбическая модификация олова, так назы-
ваемое серое олово, обладающее большим
удельным объёмом. Наблюдаемое иногда на
морозе явление «оловянной чумы» заклю-
чается в превращении не устойчивого на
морозе белого олова в устойчивое серое,
сопровождающееся разрушением оловянных
предметов.
Явление монотропии состоит в том, что
одна из модификаций не имеет своей области
устойчивости, т. е. всегда метастабильна.
Для монотропии характерна необратимость
превращения модификаций.
Двухкомпонентные системы. Двухкомпо-
нентная система вполне определяется тремя
переменными—давлением Р, температурой Т
и концентрацией одного из компонентов С.
Для изображения состояния двухкомпонент-
ной системы необходима пространственная
система координат —Р, Т, С. Для упроще-
ния одну переменную сохраняют постоян-
ной и.изображают изменение двух других
на координатной плоскости.
Для двухкомпонентной системы (п = 2)
правило фаз принимает вид:
F = 4- к.
Двухкомпонентная система может быть
при числе фаз к = 4—инвариантна (Р = 0);
система существует только при вполне опре-
делённых значениях Р, Т и С. Точка, изо-
бражающая состояние этой системы в про-
странственной системе координат, называет-
ся четверной; при числе фаз к = 3—моно-
вариантна (F = 1); произвольно может из-
меняться одна переменная; две другие пе-
ременные изменяются зависимо от первой,
например Р = / (Т) и С=ф(Т); при числе
фаз к — 2 — дивариантна (Р=2); произволь-
но могут изменяться две переменные; третья
изменяется зависимо от первых двух, на-
пример Р — / (С, Т); при числе фаз к = 1 —
тривариантна (F=3); все три переменные
могут произвольно изменяться.
ФИЗИЧЕСКАЯ ХИМИЯ
333
Сплавы двух металлов, не растворяющих-
ся в твёрдой фазе. Для изображения бинар-
ных сплавов пользуются обычно плоскостной
диаграммой «состав—температура» при по-
стоянном давлении. Типичная диаграмма
плавкости для сплавов двух металлов, не
растворяющихся в твёрдой фазе, дана на
фиг. 17.
Прибавление одного из компонентов по-
нижает температуру плавления другого.
Кривые плавле-
ния обоих метал-
лов встречаются
в точке С, называ-
емой эвтектичес-
койточкой (см. Э1 -
тектика, стр. 333).
Поле выше кри-
вых плавления
является обла-
стью расплавов;
поле ниже прямой
DE — областью
твёрдых сплавов.
Поля A'CD и
В'СЕ называются
Фиг. 17. Случаи простой
эвтектики
гетерогенными, так как система, попавшая
в одно из них, распадается на расплав
и твёрдую фазу, например система в точ-
ке Z распадается на расплав, характе-
ризующийся точкой Z2, и кристаллы чистого
вещества А. Система в точках А', В’ и С
инвариантна, в остальных точках кривой
плавления—моиовариантна и в поле распла-
ва— дивариантна. Примеры сплавов описан-
ного типа:
Cd + Bi, Sb -f- Pb, Cr + Mn.
Эвтектика. Эвтектикой называется твёр-
дая смесь (сплав) мелких кристаллов обоих
металлов состава Хо (фиг. 17), выделяющая-
ся из раствора в точке С. Эвтектика бинар-
ного сплава представляет собой две твёрдые
фазы. При затвердении расплава, более
богатого компонентом А по сравнению с со-
ставом эвтектики, образуется сплав, состоя-
щий из крупных кристаллов чистого метал-
ла А, сцементированных эвтектикой (поле
ADCXa на фиг. 17); для расплавов, более
богатых компонентом В, — кристаллы чисто-
го металла В, сцементированные эвтектикой
(поле ВЕСХ0),
Для сплава олово—свинец состав эвтек-
тики соответствует РЬ — 37%, Sn—63%.
Эвтектическая температура 181° С.
Благодаря низкой температуре плавления
эвтектика свинца и олова применяется в
качестве припоя. Состав эвтектики отвечает
(приблизительно) 2/з олова и */а свинца по
весу, поэтому сплав носит название трет-
ника.
Химические соединения в сплавах. Кон-
груэнтные и инконгруэнтные точки. Если
металлы, входящие в бинарный сплав, обра-
зуют химическое соединение, то в кривой
плавления появляются две новые ветви
(фиг. 18)—ОС' и DC", являющиеся кривыми
плавления этого химического соединения в
присутствии избытка одного или другого
металла. Точка D — точка плавления чистого
химического соединения—называется кон-
груэнтной точкой.
В некоторых случаях химическое соеди-
нение двух металлов устойчиво лишь в при-
сутствии избытка одного из металлов. В этом
случае кривая плавления состоит из трёх
ветвей (фиг. 19): ветвь А'С — кривая плав-
ления металла А, ветвь СЕ — химического
соединения АпВт и ветвь ЕВ’—металла В.
Точка Е — точка превращения твёрдых фаз—
Фиг.
18. Случай образования
химического соединения
называется инконгруэнтной точкой. Система
в конгруэнтной и инконгруэнтной течках
инвариантна.
Диаграмма сплава двух металлов может
иметь несколько конгруэнтных и инконгру-
энтных точек.
Диаграмма кристаллогидратов. Многие
соли образуют с водой непрочные молеку-
лярные соединения, называемые кристалло-
гидратами. Кривые растворимости (или плав-
Фиг.19. Случай образования
химического соединения с ин-
конгруэнтной точкой плавления
кости) кристаллогидратов (фиг. 20) похожи
на кривые плавления бинарных сплавов
металлов. Компонентами здесь являйся
соль и вода. Максимальные точки кривой
растворимости (О,, О2, Оа, О4 на фиг. 20)
определяют температуру плавления и состав
чистых кристаллогидратов. Точки CI , СП,
С111, CIV и Cv являются обычными эвтек-
тическими точками. Из них' CI носит назва-
ние криогидратной, а смесь льда и кристал-
334
химия
логидрата, соответствующая этой точке, —
криогидратной. Во всех точках С и D система
инвариатна.
Охладительные смеси. Значительное по-
нижение температуры плавления льда в при-
Фиг. 20. Диаграмма растворимости
кристаллогидратов хлорного железа
сутствии некоторых солей (см. Диаграмма
кристаллогидратов ) является причиной
использования смеси льда, воды и какой-
либо соли в качестве охладительной смеси.
Наиболее часто употребляется смесь льда,
воды и поваренной соли.
Сплавы двух металлов, частично раство-
ряющихся в твёрдой фазе. Типичные диа-
граммы плавкости даны на фиг. 21 и 22.
Фиг. 21. Диаграмма «гсостав—тем-
пература» плавления сплава двух
металлов, частично растворяю-
щихся в твёрдой фазе (случай 1)
Особенностью этих систем является наличие
двух областей гомогенных твёрдых раство-
ров. В то время как в расплаве металлы сме-
шиваются во всех отношениях, в твёрдых
фазах наблюдается прерывный ряд смешан-
ных кристаллов (твёрдых растворов). Точка
С на фиг. 21 является эвтектической, точ-
ка С на фиг. 22 точкой превращения. Си-
стемы в обеих точках инвариантны.
Трёхксмпонентные системы (см. Правило
фаз, стр. 331). Трёхкомпонентная система оп-
ределяется четырьмя переменными: давле-
нием Р, температурой Т и концентрациями
двух компонентов—например Сг и С2. По-
этому изучение трёхкомпонентных систем
представляет большие трудности.
Для трёхкомпопентной системы правило
фаз принимает вид:
F = 5— к.
Инвариантная трёхкомпонентная система
содержит пять фаз. Однофазная трёхкомпо-
нентная система имеет четыре степени сво-
боды.
Графическое изображение трёхкомпояент-
ных систем. Для графического изображения
трёх компонент-
ных систем поль-
зуются двумя ме-
тодами:
1) когда свой-
ства двух компо-
нентов сильно от-
л и ч а ю т с я от
свойств третьего,
используют обыч-
но прямоуголь-
ные координаты
в пространстве,
например, в слу-
чае растворов
двух солей от-
кладывают по
двум осям кон-
центрации солей
и по третьей—тем-
Фиг. 22. Диаграмма «со-
став — температура» пла-
вления сплава двух метал-
лов, частично растворяю-
щихся в твёрдой фазе (слу-
чай 2)
пературу;
2) когда свойства всех трёх компонентов
сходны, пользуются методом треугольника
(фиг. 23). Метод основан на свойстве равно-
стороннего треугольника: сумма перпенди-
куляров, опущенных из любой точки внутри
треугольника на стороны треугольника, по-
стоянна и равна высоте треугольника. Если
высоту треугольника принять за 1, то дли-
ны перпендикуляров, опущенных из какой-
либо точки, могут выражать молярные доли
трёх компонентов системы (Ра — NА; РЬ —
— NB и Pc — Nc), а сама точка будет изо-
бражать состав трёхкомпонентной системы.
Состав двухкомпонентной системы изобра-
Фиг. 23. Треугольная диаграмма
зится точкой на стороне треугольника, а вер-
шины треугольника будут отвечать чистым,
компонентам. В методе треугольника можно
вместо перпендикуляров брать отрезки на
одной из сторон треугольника,образующие-
ФИЗИЧЕСКАЯ ХИМИЯ
335
ся при проведении через данную точку ли-
ний, параллельных сторонам треугольника,
тогда (фиг. 22)
B-( = NA; Az = Nb и еу = Nc_
Пользуясь методом треугольника, можно
изобразить зависимость любого свойства
системы от состава. Для этого из точки
треугольника, изображающей состав, вос-
станавливают перпендикуляр, на котором
откладывают численное значение данного
свойства, например температуру плавления.
Совокупность окончаний перпендикуляров,
построенных для всех возможных составов,
даёт некоторую поверхность, которая и
является графическим изображением плав-
кости трёхкомпонентной системы. Для про-
стоты обычно пользуются проекцией этой
поверхности на плоскость треугольника.
Закон распределения. Для двухфазных
трёхкомпонентных систем, состоящих из
двух слоёв несмешивающихся жидкостей с
растворённым в них третьим веществом, уста-
новлен закон: если третье вещество имеет
один и тот же молекулярный вес в обоих
слоях, то при постоянной температуре и
достижении равновесия отношение концент-
раций третьего вещества в обоих слоях (Cj и
С2) постоянно и не. зависит от абсолютной
величины этих концентраций:
Сг
~р - = const при t — const.
2
Значительное изменение отношения с
изменением концентрации третьего вещества
указывает на ассоциацию его в одном из
растворителей.
ХИМИЧЕСКОЕ РАВНОВЕСИЕ
Закон действующих масс. При постоян-
ной температуре для обратимой реакции
Vl^l + + ^з^з + ... -<—t
ч-> A -f-v A -f-\ А -)-....
it а аза
в состоянии равновесия
C^-C'-C4’ ..
1 а а .. ,
— стехиометрические коэфициенты;
С,- — концентрации веществ;
К—константа равновесия, являющаяся
функцией температуры и давления
(при условии изменения числа моле-
кул в результате реакции). При
больших концентрациях константа
равновесия начинает зависеть от
концентрации, т. е. закон действую-
щих масс для реальных систем яв-
ляется приближённым.
Различные выражения константы равно-
весия и связь между ними. Концентрация
в законе действующих масс может быть вы-
ражена через молекулярно-объёмные едини-
цы Сг:
____1______а_____з
С'\ -с'^ C'v>
12___________3
через молярные доли Nf реагирующих ве-
ществ:
N -N -N ...
12 3
и для газовых реакций через парциальные
давления Pi:
Р^-Р^-Р^...
Кр= , : ~ ~ •
р \ ,р •‘г .р ’» ...
12 3
Между KCi KN и Кр существует следую-
щая связь:
;<c = kn-v-
ИЛИ
fRT
KN --- Кс I р ) ;
Кс = Kp(RTy~',
или
Кр = /<С(.?Т)Л
Кр = KN-P^‘,
пли
KN = к,р р~\
где
V-, ~ V. -|- V2 4. -,3 -р ... _
-Vj — ч2 —v3 —...;
V — объём системы;
Р—давление смеси газов;
Т — абсолютная температура;
R— универсальная газовая постоянная.
Если = 0, то
«с = KN = Не-
зависимость константы равновесия от
температуры. При постоянном объёме
d In Кс _ Qv .
dT " RT- ’
Кс— константа равновесия (см. Закон
действующих масс, стр. 335);
Qv—тепловой эффект реакции при по-
стоянном объёме.
Уравнение носит название уравнения
изохоры реакции. При постоянном давле-
нии
dlnKp CR, .
dT RT*’
Кр — константа равновесия, выраженная
через парциальные давления;
Qp — тепловой эффект реакции при по-
стоянном давлении.
Уравнение носит название уравнения
изобары реакции.
Оба уравнения могут быть проинтегри-
рованы, если известна зависимость Qv и Q„
от температуры. Для узкого интервала
температур можно считать Q постоянным;
тогда интегрирование в этом интервале
даёт:
1П К, Q ( 1_____1 \
Кг R \Тг Т2 ’
336
химия
или _
Уравнение даёт возможность определить
константу равновесия при данной темпера-
туре, если известны тепловой эффект реак-
ции и константа равновесия при другой
температуре, или определить тепловой эффект
реакции по двум значениям константы рав-
новесия при двух разных температурах.
Гомогенные и гетерогенные реакции.
Реакция называется гомогенной, если она
протекает в гомогенной, т. е. однофазной,
системе. Реакция называется гетерогенной,
если она протекает в гетерогенной системе,
т. е. если в ней участвует несколько фаз
(твёрдая, жидкая, газообразная). Для гете-
рогенных реакций закон действующих масс
(см. стр. 335) упрощается, так как концентра-
ции или парциальные давления паров ве-
ществ, имеющихся в твёрдой или жидкой
фазе, остаются постоянными в течение реак-
ции. Так, например, для гетерогенной реак-
ции термической диссоциации углекислого
кальция СаС03 Са0+С02.
Константа равновесия
_ ^СаО ‘ ^СО,
----—--------
*СаСО3
принимает вид Кр =РСО2’так как Рсасо,=
= const и РСаО = const при t = const. Кр в
случае гетерогенной реакции называется
упругостью диссоциации,
Константа равновесия реакции 2С +
+ О3Х^2СО + 94,5 ккал.
при 1000°С
Кр = 7.10- 17_
Константа равновесия реакции 2СО -f-
+ О2 2СО2 + 136 ккал. Константа равно-
весия Кр гомогенной реакции окисления
окиси углерода до углекислого газа (или
реакции диссоциации углекислого газа при
обратном чтении) равна:
а^Р ~ Р^р-Рр,
K/1 ~ (2+а) (1—a)2 P2COs ’
где а — степень диссоциации углекислого
газа;
Р — давление в системе;
вследствие малости а по сравнению с 1 до
температуры 1500° С
с<3Р
Кр "2 ' •
Значения а для Р = 1 ат при различных
температурах:
Увеличение давления смещает равновесие
в сторону образования СО2.
Константа равновесия реакции получения
водяного газа СО + Н2О СО2 + Н2. Реак-
ция гомогенная; константа равновесия реак-
ции
~ л0; • ж
для различных температур равна:
г с 250 600 700 830 900 1000
к р 0,15 0,32 0,56 0,90 1,25 1,62
Константа равновесия реакции СО2 -р
+ С 2СО— 41,22 ккал. Реакция гетеро-
генная; играет большую роль при горении
угля в топке и доменных процессах.
Константа равновесия реакции Кр равна:
_ со,___1 — а
'р р2~
'со
где а — доля СО.,, восстановившегося в СО;
Р — общее давление в системе.
Константа равновесия реакции FeO +
+ СО jit Fe 4- СО2 + 3,4 ккал. Реакция гете-
рогенная; играет большую роль в доменном
процессе; константа равновесия реакции
'со, Ссо,
так как = 0, давление не влияет на реак-
цию.
Химическое сродство. Реакции, протекаю-
щие между веществами, указывают на суще-
ствование сродства между этими веществами.
После неудачных попыток измерять сродство
скоростью реакции или тепловыА эффектом
реакции было показано, что мерой химиче-
ского сродства между веществами является
максимальная полезная работа, которую
может произвести реакция (полезной рабо-
той называется сумма всех работ, за исклю-
чением работы расширения).
Максимальная работа химической реак-
ции. Максимальная работа А химической
реакции Aj +v2 А2 + ... Хм А + м,Аа +...
при постоянной температуре Т равна
А = RTI In--------а ----------- — In Кс
у С' ’ ’С, ’• •••
/ р’>.р’« \
= RT / In--------1----Ц2-- — In Кр ’
I Р \-Р ’„••• )
\ 1 8 /
т° к 1000° w 1400° 1000° 1300° 1900° 2000° 2200° 2509® 3000°
« % 2.10~ 5 — 4 9,3.10 0,0146 0,110 0,546 1,04 1,84 5,0 15,6 48,6
ФИЗИЧЕСКАЯ ХИМИЯ
337
. где Кс — константа равновесия, выражен-
ная через молекулярно-объёмные
концентрации;
Кр — константа равновесия, выражен-
ная через парциальные давления;
С;—исходная концентрация вещества
Л;
Т —абсолютная температура;
R — универсальная газовая постоян-
ная;
—стехиометрический коэфициент ве-
щества А,;
Pi — парциальное давление паров ве-
щества А/.
Уравнение максимальной работы или
уравнение изотермы химической реакции
строго применимо лишь к веществам, пары
которых подчиняются законам идеальных
газов, и к разбавленным растворам.
Максимальная работа химической реак-
ции при постоянной температуре и постоян-
ном объёме равна убыли свободной энергии
системы А= — АР.
Максимальная полезная работа химиче-
ской реакции при постоянной температуре
и постоянном давлении равна убыли сво-
бодной энергии при постоянном давлении
(термодинамического потенциала) в системе
А= — Д Ф.
Если исходные концентрации или парци-
альные давления всех веществ равны еди-
нице, то уравнение максимальной работы
реакции принимает вид:
А = — AF= — RTlnKc;
А = ~ АФ =—RT \п Кр.
В этом случае А называется приведён-
ным, или нормальным сродством.
Тепловая теорема. На основании обоих
законов термодинамики и опытных фактов
о независимости термических свойств твёр-
дых кристаллических тел от температуры
при температурах, близких к абсолютному
нулю, сформулирована тепловая теорема,
по которой
/ dA\ =(_dQ\ =0
' dT )т=о \dT /т=о
Уравнение выражает совпадение каса-
тельных с кривыми теплового эффекта ре-
акции 7$ и максимальной работы химической
реакции А при абсолютном нуле и парал-
лельность их оси абсцисс (Г).
Уравнение максимальной работы для кон-
денсированных систем. На основании вто-
рого закона термодинамики и тепловой тео-
ремы уравнение максимальной работы для
конденсированных систем имеет вид:
А = — Т [ ,
J Т*
или, применяя^ формулу зависимости тепло-
вого эффекта Q от температуры:
т т
С dT С
А = Qo - т ) -fi- Ср) ат.
о о
Уравнение для Кр. Применение тепловой
теоремы к равновесиям в газовой фазе даёт
уравнение для константы равновесия К.р:
Qp, S'* Ср
1пКр=-^ + - R ° ШГ +
ат +
S v I,
где Qp — тепловой эффект реакции в паро-
образной среде при Т=0;
Ср0—часть теплоёмкости вещества, не
зависящая от температуры;
т
Ург=^ CP.dT’
где СРг — часть теплоёмкости вещества, за-
висящая от температуры;
I—химическая постоянная, являю-
щаяся константой интегрирова-
ния уравнения Клаузиуса—Кла-
пейрона для упругости пара
твёрдого тела;
2v + ••• ——v.,t? — •••
Приближённое уравнение для Кр:
ь р 4,575 Г
+ 2 1,75 1g Г + S (» С')>
где Qp — тепловой эффект реакции при ком-
натной температуре;
Sv — алгебраическая сумма произведе-
ний стехиометрических коэфици-
ентов в уравнении реакции на С'—
условные химические постоянные
реагирующих веществ.
Третий закон термодинамики. «Если эн-
тропию любого элемента в кристалличе-
ском состоянии принять при абсолютном
нуле за нуль, то энтропия любого чистого
кристаллического вещества при абсолютном
нуле температуры равна нулю, а энтропия
любого другого вещества больше нуля».
Под словами «любого другого вещества»
надо понимать смесь веществ, растворы, ве-
щества в аморфном состоянии. Закон позво-
ляет определять абсолютные значения эн-
тропий веществ.
Определение максимальной работы реак-
ции при помощи тепловых эффектов и эн-
тропий. Метод основан на выражении
А = Zi — Z2 = Hi — Н2 + Т (S2 — Sj) =
= -ДН + Г-AS,
или _
А = Qp + Т AS,
и требует знания лишь теплового эффекта
реакции при постоянном давлении Q„, аб-
солютной температуре Т и абсолютной эн-
тропии S веществ системы в исходном и ко-
нечном состояниях.
Стандартные свободные энергии. Стан-
дартной свободной энергией вещества при
постоянном давлении ДФ называется
22 том I
338
химия
максимальная работа образования моля дан-
ного вещества из простых веществ при 25° С
и 1 ат, взятая с обратным знаком. Стан-
'дартная свободная энергия простых ве-
! ществ принимается равной нулю. Стан-
| дартная свободная энергия важнейших сое-
динений дана в табл. 17.
Расчёты максимальных работ при помо-
щи таблиц стандартных свободных энергий.
Так как максимальная полезная работа си-
стемы при постоянном давлении равна убы-
ли свободной энергии — ДФ, то максималь-
ная работа реакции
+ ч2А2 + ... J А| +i<2 А2 + ...
при стандартных условиях (25°С, 1 ат)
равна
А = —Д Ф°= — (— vj Д Ф°А1 — ч2 Д Фда —
— ... + Vi А Ф •На АФ
* -А, Л. '
Для вычисления максимальной работы
при иных температурах пользуются уравне-
нием
т о
ДФ:Г = д ф°98 - т j --тс₽. ат +
298
Т
+ ^C°p-dT.
298
Индекс ° при ДФ и ДСр указывает, что эти
величины отнесены к стандартному давле-
нию — 1 ат.
Активность и летучесть. Большинство
уравнений физической химии (закон дей-
ствующих масс, изохора и изобара реакции
и др.) выведено и применимо строго лишь
к идеальным системам (идеальным газам,
сильно разбавленным растворам). Для того
чтобы эти уравнения были строго приме-
нимы и к реальным системам, в них вместо
концентрации вводят так называемую ак-
тивность а, а вместо парциальных давле-
ний— летучести/. Так, например, уравнение
А = - Д Ф° = - RT 1п 2..Z.?—-
является, точным для реальных систем.
Активность является функцией концен-
трации а = Л.С,
где j(— коэфициент активности, меньший
единицы и приближающийся к еди-
нице с уменьшением концентрации.
Летучесть является функцией давления
пара. Летучесть равна давлению пара, когда
пар является идеальным газом.
Активность и летучесть или их коэфи-
циеиты, соответствующие определённым кон-
центрациям и давлениям, находят рядом
методов и сводят в таблицы.
ЭЛЕКТРОХИМИЯ
Электролиз. Электролизом называется
выделение веществ на поверхности электро-
дов при прохождении тока через раствор
или расплав вещества. Отрицательный элект-
род называется катодом, положительный —
анодом.
Электролиты. Электролитами называются
вещества, растворы и расплавы которых
проводят электрический ток при одновре-
менном выделении веществ на поверхности
электродов.
Электролитами являются соли, кислоты
и основания. Проводимость электролитов
объясняется частичной или полной диссоци-
ацией их в растворах или расплавах на
ионы — электрически заряженные частички,
движение которых в электрическом поле
создаёт электрический ток в электролите.
Положительно заряженный ион называется
катионом, отрицательно заряженный—ани-
оном.
Законы Фарадея для электролиза. Пер-
вый закон: количество вещества т, выде-
лившегося при электролизе, пропорцио-
нально количеству электричества q, про-
шедшему через электролит:
т ^K.q = Kit,
где I — сила тока;
t — время;
К — константа, зависящая только от
природы вещества; носит название
электрохимического эквивалента
данного вещества; измеряется в
мг/кулон, например К меди =
= 0,3294 мг/кулон, К серебра =
= 1,118 мг/кулон и т. д.
Второй закон: один и тот же ток в одно
и то же время при прохождении через рас-
творы различных веществ выделяет на
электродах количества вещества, пропор-
циональные их химическим эквивалентам.
Следствием обоих законов Фарадея яв-
ляется пропорциональность электрохимиче-
ского эквивалента химическому эквивален-
ту Э вещества:
К= 1,036-1(Г5-Э = 1,036-10~5 А- ,
где А — атомный вес;
п— валентность.
Фарадей. Фарадеем называется электро-
химическая единица количества электриче-
ства, равная 96487 абс. кулонов. При прохожде-
нии через раствор или расплав электролита
одного фарадея электричества разлагается
или выделяется один химический эквива-
лент вещества. Свободный заряд одного
граммэквивалента иона равен фарадею ве-
щества. Фарадей обозначается буквой F.
Удельная, эквивалентная и молекулярная
электропроводность растворов. Удельной
электропроводностью х называется величина,
обратная удельному сопротивлению р:
Удельным сопротивлением называется
сопротивление столбика вещества длиной
в 1 см с поперечным сечением в 1 смг.
Зависимость х растворов некоторых элек-
тролитов от концентрации их дана на фиг. 24.
С возрастанием температуры удельная
электропроводность растворов электролитов
увеличивается.
ФИЗИЧЕСКАЯ ХИМИЯ
339
Эквивалентная электропроводность. Если
один эквивалент электролита содержится
в <р хм3 раствора, то произведение удельной
Фиг.24. Зависимость удельной элек*
тропроводности от концентрации
электролита
электропроводности на ф называется экви-
валентной электропроводностью :
или
1
так как <р= , где С —эквивалентная кон-
/ молях \
центрация I в ~сМ*~ I'
Зависимость % растворов некоторых
электролитов от С дана на фиг. 25.
Фиг.25. Зависимость эквивалентной
электропроводности от разведения
Молекулярная электропроводность. Если
1 моль электролита содержится в V см3 рас-
твора, то произведение удельной электро-
проводности на V называется молекулярной
электропроводностью Х,п:
Хт = У?..
Скорость движения ионов. Скоростью
движения иона называется скорость его
в воде при 18'' в электрическом поле, падение
потенциала в котором равно 1 в/см. Размер-
ность скорости иона — см-сек'1. Ско-
рости для катиона и аниона обозначают
буквами Uo и Vo.
Подвижность ионов. Подвижностью иона
(Д-— катиона, 1а — аниона) называется про-
изведение скорости его на фарадей F-.
lK — F-Un для катиона;
ia= F-Vo для аниона.
Эквивалентная электропроводность рас-
твора электролита при бесконечном разве-
дении равна сумме подвижностей обоих
ионов:
Хоо = 1К + 1а.
Сильные и слабые электролиты. Резкой
границы между сильными и слабыми элек-
тролитами нет. Сильными электролитами
называют электролиты, которые в растворах
при любых концентрациях полностью дис-
социированы на ионы, а потому обладают
большой электропроводностью. Эквивалент-
ная электропроводность X — сильных элек-
тролитов —подчиняется формуле
X = а — bVc,
где с —молярная концентрация раствора;
а и b — константы.
Слабыми электролитами называют элек-
тролиты, степень диссоциации которых
в 0,1 N растворах меньше 0,5. Диссоциация
слабых электролитов на ионы, в отличие
от сильных электролитов, подчиняется за-
кону действующих масс.
Гальванические элементы. Совокупность
твёрдых и жидких проводников, способная
давать электрический ток в замкнутой цепи
за счёт химических реакций, называется
гальваническим элементом. Примером галь-
ванического элемента является элемент
Даниэля, в котором в растворы CuSO4 и
ZnSO4, соединённые между собой, погружены
медный и цинковый стержни. Электриче-
ский ток, возникающий при замыкании мед-
ного и цинкового электродов, идёт за счёт
реакции
Zn + CuSO4~* ZnSO4 + Cu.
Аккумуляторы также являются гальва-
ническими элементами.
Нормальный элемент. Так называется
неполяризующийся ртутно-кадмиевый галь-
ванический элемент, принятый в качестве
нормального или стандартного для различ-
ных потенциометрических измерений за его
ничтожно малый температурный коэфициент
э. д. с. Положительным электродом является
ртуть, отрицательным — 12,5%-ная амальга-
ма кадмия. Ртуть покрыта пастой из Hg2SO4
и слоем кристаллов 3CdSO4-8H.2O. Амаль-
гама покрыта также 3CdSO4-8H2O. Сверху
в оба колена наливается насыщенный рас-
твор CdSO4. При работе элемента протекает
реакция Cd + Hg2SO4XCdSO4 + 2Hg.
Электродные потенциалы. При погруже-
нии металлического проводника в раствор,
содержащий ионы этого металла, между
22*
340
химия
раствором и металлом устанавливается раз-
ность потенциалов, или скачок потенциала,
который не совсем верно называют элек-
тродным потенциалом. Величина электрод-
ного потенциала зависит от - природы ве-
ществ, образующих электрод, от концен-
трации раствора и температуры.
Формула для электродных потенциалов:
где г—электродный потенциал при концен-
трации ионов металла в растворе,
равной С моль/л-
е0—электродный потенциал при С =
= 1 моль) л-,
п — валентность иона металла;
F —фарадей.
Более точное выражение для электрод-
ного потенциала получается при подста-
новке вместо концентрации активности иона
металла — а;
е„— — Ina.
nF
Для комнатных температур 2,3 —«
г
« 0,058, поэтому
0.05S
е=ео— —„— >g«-
Стандартные, или нормальные, потенци-
алы. Стандартным, или нормальным, элек-
тродным потенциалом называется скачок
потенциала, образующийся между металлом
и раствором ионов этого металла, концен-
трация (или точнее активность) которых
равна единице. Эти потенциалы отнесены
к нормальному водородному электродному
потенциалу, принятому за нуль. Стандарт-
ные, или нормальные, потенциалы важней-
ших электродов при 25° С даны в табл. 19.
Газовые электроды. Газовым электродом
называется электрод, образующийся в ре-
зультате адсорбции газа на поверхности
металла. Для поддержания постоянной сте-
пени насыщения металла газом через раствор
полуэлемента пропускаются непрерывной
струёй пузырьки газа. Водородный элек-
трод (см. ниже: стандартный водородный
электрод) широко применяется в потен-
циометрии.
Стандартный водородный электрод. Стан-
дартный, или нормальный, водородный элек-
трод (полуэлемент) получается при погру-
жении металлической пластины, насыщен-
ной водородом, при давлении 1 ат в раствор
кислоты с активностью водородных ионов,
равной единице. При температуре 25° С по-
тенциал стандартного водородного электрода
принят условно равным нулю. При точных
работах измерения производятся с разбав-
ленной кислотой, а затем данные экстрапо-
лируются до активности ионов водорода,
равной единице.
Каломельный электрод. Неудобство ра-
боты с нормальным водородным электродом
заставило избрать в качестве вторичного
стандартного электрода постоянный в своих
свойствах и легко воспроизводимый кало-
мельный электрод. Каломельный электрод
состоит из металлической ртути и насыщен-
ного раствора каломели—Hg2Cl2 в растворе
КС1. Если раствор КС1 1,0 N, каломельный
электрод называют нормальным: потенциал
его по условно нулевому водородному равен
0,2822 в. Если раствор КС1 0.1 W каломель-
ный электрод называют децинормальным;
потенциал его равен 0,3351 в.
•Измерение электродных потенциалов.
Электродные потенциалы экспериментально
определяются путём измерения э. д. с. галь-
ванического элемента, составленного из
измеряемого электрода и каломельного (или
нормального водородного).
Так как э. д. с. гальванического эле-
мента Е равна разности электродных потен-
циалов, то
еизм = екал i Е
(с каломельным электродом);
( + ) Е если е„зл > гкая; (—) Е если еИ!Ш < е„ал,
или
еизм = ± В
(с нормальным водородным электродом, так
как ен> = 0);
ецзл1 —скачок потенциала измеряемого элек-
трода;
екал — скачок потенциала каломельного элек-
трода.
Обратимые элементы. Обратимыми назы-
ваются элементы, которые обратимы по от-
ношению к направлению тока, т. е. если
через элемент пропускать ток в обратном
направлении, то в нём будут протекать ре-
акции, обратные тем, которые протекают
при работе элемента, и элемент восстанав-
ливается.
Примером обратимого элемента является
элемент Даниэля.
Концентрационные цепи. Так как вели-
чина электродного потенциала зависит от
концентрации ионов металла электрода
(см. выше: формула для электродных по-
тенциалов), то соединение двух одинаковых
полуэлементов, отличающихся лишь концен-
трацией ионов металла (Ci и С2), в раство-
рах образует гальванический элемент, на-
зываемый концентрационной цепью.
Э. д. с. концентрационной цепи Е равна:
или точнее
с учётом диффузионного потенциала
£ = Л *Т1п£-;
и + V nF <4
если подвижность катиона U больше,
или
U+V nF
если подвижность аниона V больше (валент-
ности катиона и аниона равны).
ФИЗИЧЕСКАЯ ХИМИЯ
341
Выражение концентрации водородных
ионов через pH. Помцмо весовой и ионной
концентрации водородных ионов для харак-
теристики кислотности среды широко упо-
требляется величина pH, которая пред
ставляет собой отрицательный десятичный
логарифм концентрации водородных ионов
Сн+:
PH = -lgCH+.
Пример: pH раствора, содержащего в литре
0,01 граммиона Н (Сн+=0,01), равно—1g 0,01= 2.
Кислотность, нейтральность и щёлоч-
ность среды. Так как чистая нейтральная
вода имеет pH — 7 (Сн+ =10— 7 молъ!л) ,
то принято нейтральным называть раствор
с pH = 7, кислыми — растворы с pH меньше
7 (Сн + >10—7 моль/л), щёлочными—раство-
ры с pH больше 7 (Сн + < 10*7 моль/л}.
Потенциометрическое определение кон-
центрации ионов. Формула для электрод-
ного потенциала
• = е0
0,058
п 'SC
даёт возможность определить концентрацию
иона С по потенциалу полуэлемента, обра-
зованного данным раствором и электродом,
концентрацию ионов которого хотят опре-
делить в этом растворе (см. Измерение эле-
ктродных потенциалов, стр. 340). Здесь е0—
стандартный, или нормальный, потенциал
данного электрода, п—валентность иона
металла.
Широко распространено потенциометри-
ческое определение концентрации водород-
ных ионов.
Химические цепи. Гальванические эле-
менты, в которых электрическая работа
производится за счёт энергии химической
реакции, называются химическими цепями.
Если в элементе протекает реакция
4- ^2-Аз 4" -|-^2^2 *•’’
то э. д. с. элемента Е определяется выра-
жением
RT t
Е = Е0- nF in
С'-.С'* ...
1 а________
с -с' .
1 я
или точнее
а'1 -а** ...
E = Eo- nFln-1;--;--------
а 1 -а • ...
1 а
где Cz — концентрация вещества А/;
а, — активность вещества А,;
V/ — стехиометрический коэфициент ве-
щества А,- в уравнении реакции;
Ео — э. д. с. химической цепи при кон-
центрациях (или точнее активно-
стях) всех веществ, равных единице.
Примером химической цепи является ши-
роко распространённый элемент Даниэля,
в котором при работе протекает реакция
Zn-|- Cu++ -> Zn++ + Cu:
p f _ RT in flcu++
эл. Даниэля ce £F aZn+ +
*e0-
2F ^-zn+ +
Диффузионный потенциал. Диффузион-
ным потенциалом называется скачок потен-
циала на границе двух растворов, возника-
ющий благодаря различию подвижностей
катиона и аниона. Диффузионный , потен-
циал Едифф для случая одинаковой валент-
ности катиона и аниона и одинаковой при-
роды обоих растворов,отличающихся только
концентрацией, равен
Р _ 4. u~v RT \ n--i-
Едифф - ± f^F 1п а2
± ,
U + V nF с2
(4-)если U > V и (—) если U < V;
Qj и а2— активности электролитов;
С2 и С2 — концентрации;
п — валентность ионов;
F — фарадей.
Диффузионный потенциал часто является
помехой при потенциометрических измере-
ниях, так как не может быть непосред-
ственно измерен. Устранение (вернее зна-
чительное снижение) диффузионного потен-
циала достигается введением между раство-
рами соединительного мостика из концен-
трированного раствора электролита, ноны
которого приблизительно одинаково по-
движны (например КС1, NH4NO3 и др.).
Поляризация и деполяризация. Возник-
новение при электролизе э.д.с., действующей
противоположно приложенной разности по-
тенциалов, носит название поляризации.
Поляризация объясняется двумя причинами,
действующими одновременно или порознь:
1) возникновением разности концентраций
электролита в анодном и катодном прост-
ранстве (концентрационная поляризация);
2) изменением природы электролитов и при-
роды поверхности электродов (химическая
поляризация). Поляризация наблюдается в
гальванических элементах. Сила тока 1 при
электролизе определяется выражением:
.__А У Епол
R ’
где ДУ — разность потенциалов, приложен-
ная к электродам;
ЕПол — э.д.с. поляризации;
R — внутреннее сопротивление раство-
ра электролита.
Уничтожение поляризации называется
деполяризацией. Концентрационная поляри-
зация значительно уменьшается интенсив-
ным перемешиванием и нагреванием электро-
литического раствора. Химическую поляри-
зацию уничтожают введением в систему
деполяризаторов — веществ, химически реа-
342
химия
тирующих с продуктами электролиза, вызы-
вающими поляризацию, например МпО2
в элементе Лекланше, К2Сг2О7 в элементе
Грене и др.
Напряжение разложения. Разложение
электролита при электролизе происходит,
если разность потенциалов, приложенная к
электродам, превышает некоторую величину
Ер, называемую напряжением разложения.
Напряжение разложения зависит от приро-
ды и концентрации электролита. Напряже-
ние разложения многих кислот и оснований
ss 1,7 в; напряжение разложения сульфатов и
нитратов — около 2,2 в.
Перенапряжение Перенапряжением назы-
вается разность между напряжением разло-
жения и э.д.с. поляризации.
КИНЕТИКА И КАТАЛИЗ
Скорость реакции. В качестве величины,
определяющей истинную скорость химиче-
ской реакции, принята отрицательная про-
изводная от концентрации С любого реаги-
рующего вещества по времени t при усло-
вии постоянства объёма:
Средняя скорость и за отрезок времени
А/ будет:
_ ДС С2 — С,
V Д< =“ t2-t! ’
где С2 — концентрация реагирующего веще-
ства в момент времени /3;
С2 — концентрация в момент времени/,.
Скорость необратимой химической реак-
ции v2 Aj 4- v2 А2 4- v3 А3 4- пропорцио-
нальна концентрациям реагирующих веществ
в данный момент времени и не зависит от
концентрации продуктов реакции:
_ d- A = кС'-С^-С^. . .
dt . .
Сумма Sv = v2 4- v2 4- v3 .. . называется
порядком реакции; если порядок реакции
равен единице, реакция (А->) называется
мономолекулярной, или первого порядка;
если Sv = 2, реакция (А4-В-» или 2А-»)
называется бимолекулярной, или второго
порядка, и т. д. Однако действительный
порядок реакции часто не совпадает с Sv,
так как сложная реакция протекает по ста-
диям и порядок реакции будет определять-
ся порядком наиболее медленной стадии.
Скорость необратимой мономолекулярной
реакции А-» . Если к моменту времени /
dC
концентрация А равна С, то — ^-= кС.
Интегрирование этого уравнения даёт
выражение для определения константы ско-
рости к необратимой мономолекулярной
реакции:
, 1 , Со _ 2,303 Со
к = ?1п с-- —1g ~с -
где Со—концентрация вещества А при
t = 0;
к — константа скорости мономолеку-
лярной реакции, имеет размер-
ность /~*.
В практических расчётах часто пользу-
ются выражениями:
— = /с (д — Х)
1 а
к = т 1п-----------
t а — х
2,303 а
t а — х
где а—количество вещества А в начальный
момент (/ =0);
х — количество вещества А, превратив-
шееся за время /.
Время полураспада—время превращения
половины количества вещества—определяет-
ся выражением:
_ 1п2 _0,6932
1Ч, = к " к
Скорость необратимой бимолекулярной
реакции А + В-> определяется диференци-
альным уравнением:
dC
dl — fc'C1C2,
где Ci — концентрация вещества А в момент
времени /;
С2 — концентрация вещества В в момент
времени t;
к' — константа скорости.
а — х „ Ь — х
у , Сг = у и
1 dx \
V dt ) и интегРиРование дают вы-
Подстановки (с2 =
dC
dt
ражение константы бимолекулярной реак-
ции:
|п=
К~ t a-ba(b-x)
— 2'303 _ b(a — х)
— / (a — b) а(Ь — х) ’
где а — количество молей А при / =0;
b — количество молей В при / = 0;
х — количество молей А или В, превра-
тившихся ко времени /.
Здесь к = -у , т. е. константа скорости
бимолекулярной реакции зависит от объёма,
а значит и начальной концентрации систе-
мы. Размерность
к' = [/“'С-1] = [t~lM~lL3 J.
Если а=Ь, то интегрирование приводит
выражению:
_ Г /_1_____!Л — 1 х
к ~ t — х а } t (а — х) а '
Скорость обратимой реакции. Скорость
обратимой реакции
viAi 4- v2A2 4- . . . v( А, 4- v2 А2 4- ...
определяется диференциальным уравнением
de > ' > '
-g7=fc1CI*C’"4-...-fc2C1’iC2’2...,
где Ct — концентрация вещества А/;
v/ — стехиометрический коэфициент ве-
щества А/;
к
ФИЗИЧЕСКАЯ ХИМИЯ
343
к1 — константа скорости прямой реак-
ции (->);
к2— константа скорости обратной реак-
ции («-).
Для мономолекулярной обратимой реак-
ции уравнение после подстановок (сг =
а — х b + х\
= —У— иС2=—у— 1 и интегрирования
принимает вид:
1 В
ki 4- к2 -= у In g-ZTY >
где
kta + к2Ь ____ а — kb
кi к2 1 4- к *
~ к
есть константа равновесия обрати-
мой реакции; она равна
fe» й ~ х оо
ki & 4- х оо
Влияние температуры на скорость реак-
ции. Повышение температуры увеличивает
скорость гомогенной реакции в 2 — 4 раза
на каждые 10°. Отношение —,— называет-
к<
ся температурным коэфициентом скорости
реакции (kt и kt+l0 — константы скорости
реакции при температурах t и t 4- 10).
Зависимость константы скорости реак-
ции К от температуры Т выражается урав-
нением
А 1
. 1 п к == р ' Т & *
или
к= Се RT ’
где А — энергия активации, представ-
ляющая собой сумму минималь-
ных энергий сталкивающихся
молекул, при которых они могут
вступать в реакцию, рассчитан-
ная на моль вещества;
В и С — константы, причём В — 1пС.
Исключение В из вышеприведённого
уравнения и переход к десятичным лога-
рифмам приводят к уравнению
. - А Ц
lgft2 2,303 7? \Т8 Т1у1’
которое даёт возможность- по известной
энергии активации и константе скорости
реакции при одной температуре находить
константу скорости реакции при другой
температуре или по константам скорости
реакции при двух температурах определять
энергию активации.
Катализ. Катализом называется явление
изменения скорости реакции при введении
в реагирующую систему постороннего ве-
щества, не изменяющегося в результате
реакции ни по составу, ни по количеству.
Такие вещества называются катализатора-
ми. Катализ может быть отрицательным
(катализатор замедляет или прекращает
реакцию) или положительным (катализатор
ускоряет реакцию). В первом приближении
скорость гомогенной реакции пропорцио-
нальна количеству катализатора. В случае
обратимой реакции катализатор одинаково
ускоряет (или замедляет) прямую и обратную
реакцию, не смещая тем самым положения
равновесия. Явление катализа чрезвычайно
распространено в органическом мире (дейст-
вие различных ферментов) и находит всё бо-
лее широкое применение в современной хими-
ческой промышленности, например, синтез
аммиака из водорода и азота (при 550° и
200 ат) в присутствии железа в качестве
катализатора; контактный способ получения
серной кислоты (катализаторы Pt, V2O5);
синтез метанола из СО и Н2 в присутствии
смеси окислов цинка и хрома; крекинг нефти
в присутствии алюмосиликатных катализа-
торов; гидрогенизация ароматических и де-
гидрогенизация нафтенов в присутствии ме-
таллов Pt, Ni, Pd.
ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
Молекулярное давление. Равнодействую-
щая молекулярных сил, действующих на
молекулу, находящуюся внутри жидкости,
равна нулю. Молекулы, находящиеся на по-
верхности жидкости, испытывают притяжение
лишь от молекул, расположенных под ними,
поэтому равнодействующая всех сил, дей-
ствующих на молекулу, уже не равна нулю.
Равнодействующая этих сил, направленная
нормально к поверхности и рассчитанная
на 1 см2 (т. е. взятая для всех молекул,
образующих 1 см2 поверхности жидкости),
называется молекулярным, или внутренним,
давлением и измеряется в динах/см2 или
кг!см2.
Поверхностное натяжение. Поверхност-
ным натяжением а называется та работа А,
которую надо затратить для того, чтобы
создать единицу площади новой поверхно-
д
сти S; а = ? эрг/см2. Поверхностное натя-
жение может быть определено и как сила,
действующая на единицу длины (1 см) линии,
ограничивающей поверхность жидкости. Эта
сила лежит в плоскости, касательной к по-
верхности в данной точке, и направлена по
нормали к ограничивающей поверхность ли-
нии. В этом случае поверхностное натяжение
выражается в динах/см. Абсолютная вели-
чина поверхностного натяжения не зависит
от выбранных единиц эрг/см2 или дин/см.
Поверхностная энергия. Поверхностный
слой обладает некоторым избытком энергии
по сравнению со слоем такой же толщины;
расположенным внутри жидкости. Этот из-
быток энергии поверхностного слоя назы-
вается поверхностной энергией.
Парахор. Парахором называется величи-
Ma*Z‘
на Р — — , где М — молекулярный веа
жидкости; а — её поверхностное натяжение;
d— её плотность. Парахор не зависит от
температуры и численно равен молекуляр-
ному объёму жидкости в условиях, когда
её поверхностное натяжение равно единице.
Парахор является аддитивной величиной,
т. е. величиной, численное значение кото-
344
химия
рой может быть сведено к сумме значений,
относящихся к составным частям соедине-
ний. Для расчёта значения парахора надо
сложить парахоры атомов и связей, входя-
щих в данную молекулу (табл. 14).
Таблица 14
Атомные и структурные парахоры Р
Атом р Атом р Структура р
Н 17.1 р .. 39,7 Связь С—С . 0
с 4,8 F . . 25.7 » с=с . 23,2
N 12,5 С1 . . 54,3 » с=с . 46,6
о 20,0 Вг . . 68,0 3-членное
О в сложных J . . 91,0 кольцо . . 16,7
эфирах . . 30,0 As . . 50,1 4-членное
S 48,2 Hg . 69. q кольцо . . 5-членное 11,6
кольцо . . 6-членное 8,5
кольцо , . 6,1
Растекание капли по поверхности твёр-
дого тела. Нанесённая капля жидкости,
растекаясь по твёрдой поверхности, образу-
ет при этом определённый краевой угол (0),
который может изменяться от 0 до 180°
(фиг. 26). На фигупе изображён случай,
6,з
3
Фиг. 26. Растекание капли жидкости
по поверхности твёрдого тела
когда жидкость 7 смачивает твёрдое те-
ло 3 в газовой фазе 2. На границах
каждой из двух фаз существует вполне
определённое поверхностное натяжение, ко-
торое может быть изображено векторами.
Вектор а12— поверхностное натяжение на
границе жидкость 7 — газ 2; а23—поверхно-
стное натяжение на границе твёрдое тело 3—
газ 2\ at8 — поверхностное натяжение на
границе жидкость 7 — твёрдое тело 3. Из
фигуры легко установить условие равнове-
сия капли. Очевидно, что изображённая
капля может существовать при условии, что
а28 —3 О18 “f* Cj2 COS 0,
или
Растекание происходит, когда 0 < 90° и
В > 0; растекания нет, когда 0>90° и В<0.
В пределах 0=90° до 0° имеются различные
градации смачивания, а в пределах от 0 =
= 90° до 0=180° различные градации несма-
чивания. Угол 90° является пограничным
углом этих двух свойств. Случай 6 = 0° со-
ответствует полному смачиванию, случай
О = 180° соответствует полному несмачива-
нию, жидкость в этом случае собирается в
шар, деформированный силой тяжести.
Капиллярное давление. Кривой поверх-
ностный слой жидкости является источни-
ком силы, направленной от выпуклой сто-
роны слоя к вогнутой стороне. Эта сила,
рассчитанная на единицу площади поверх-
ности, называется капиллярным давлением.
Капиллярное давление Р можно рассчитать
по формуле Лапласа, пригодной для случа-
ев, когда поверхность жидкости имеет лю-
бую форму, допускаемую физической при-
родой жидкого состояния. Эта формула
имеет вид:
где а— поверхностное натяжение;
/?! и Rt— два главных радиуса кривиз-
ны, которые имеют следующее
значение. В какой-нибудь точ-
ке М поверхности жидкости
(фиг. 27) нужно вообразить
нормаль MN и через эту нор-
маль провести две взаимно
перпендикулярные плоскости,
которые пересекут поверх-
ность жидкости по кривым
АМВ и CMD. Радиусы кри-
визны этих кривых в точке А4
и обозначаются через Rt и Р2.
Из формулы Лапласа для плоской по-
верхности получается, что Р = 0, а для
2 а
шаровой поверхности Р = , где R—ради-
ус шара. Капиллярное давление для вогну-
той поверхности
является отрица-
тельным (т. е. на-
правлено от жид-
кости вне её), а
для;гвыпуклой по-
верхности—поло-
жительным (т. е.
направлена
внутрь жидко-
сти). Это соответ-
ствует тому усло-
вию, что радиус
кривизны ^>0, когда он направлен к цент-
ру кривизны внутрь жидкости, и 7? < 0,
когда он лежит вне жидкости. В случае
жидкой поверхности, ограниченной твёрды-
ми стенками, при достаточно малых рас-
стояниях между ними (мениск в капилляре
или между двумя, расположенными близко
друг к другу твёрдыми поверхностями),
кривизна жидкой поверхности определяется
условиями смачивания, т. е. краевым уг-
лом 0. Для капиллярной трубки с круговым
сечением достаточно малого радиуса г ме-
ниск можно считать частью сферической
поверхности радиуса R, определяемого по
величине и по знаку выражением:
г
R = COS0 '
Фнг. 27. Определение глав-
ных радиусов кривизны
Капиллярное давление, соответствующее
такому мениску, составляет:
2 а 2 а
Р = = — —- COS0.
К г
В случае, если жидкость смачивает стен-
ки капилляра, капиллярное давление будет
отрицательным, и жидкость будет подни-
маться по капилляру на высоту
2 a cos 0
11 = rpg ’
9
ФИЗИЧЕСКАЯ ХИМИЯ
345
где р — плотность жидкости; g— ускорение
силы тяжести. В случае же несмачивания
наблюдается опускание жидкости в капил-
ляре по сравнению с нормальным уровнем
жидкости в широком сосуде.
Зависимость поверхностного натяжения
жидкости от температуры. Поверхностное
натяжение жидкостей падает с увеличением
температуры. Для чистых жидкостей зависи-
мость поверхностного натяжения от темпе-
ратуры линейная, т. е. at = а0 — ~t t, где
о/ — поверхностное натяжение при темпе-
ратуре t; а0—поверхностное натяжение при
0°; 7 — постоянная величина, характерная
для каждой данной жидкости.
Поверхностное натяжение растворов. При
растворении одних веществ в жидкости по-
верхностное натяжение на границе раздела
двух фаз падает, при растворении других
веществ поверхностное натяжение на гра-
нице двух фаз растёт.
Поверхностно-активные вещества. Веще-
ства, которые снижают поверхностное на-
тяжение на границе раздела двух фаз, на-
зываются поверхностно-активными. По от-
ношению к воде поверхностно-активными
веществами являются вещества, молекулы
которых содержат группы ОН, СООН, СО,
NH2, NO2 (т. е. из органических веществ
спирты, кислоты, альдегиды, кетоны, амины,
нитросоединения). Обычно молекулы этих
веществ полярны, т. е. обладают собствен-
ным дипольным моментом.
Поверхностно-инактивные вещества. Ве-
щества, которые повышают поверхностное
натяжение на границе раздела двух фаз,
называются поверхностно-инактивными. По
отношению к воде поверхностно-инактивны-
ми веществами являются некоторые электро-
литы, например хлористый натрий.
Поверхностная активность. Способность
вещества снижать поверхностное натяжение
характеризуется величиной поверхностной
d а
активности g = —(/с" > где^—концентрация
раствора. Поверхностная активность опре-
деляется как тангенс угла, образованного
касательной к кривой зависимости поверх-
ностного натяжения от концентрации раство-
ра н положительным направлением оси аб-
сцисс в точке, когда С = 0.
Правило Дюкло-Траубе. Способность по-
нижать поверхностное натяжение при оди-
наковых концентрациях возрастает в по-
стоянное число раз в геометрической про-
грессии при переходе от одного гомолога к
последующему. При обычной (комнатной)
температуре поверхностная активность воз-
растает в 3 — 3,5 раза при удлинении цепи
на одну СН2 группу.
Адсорбция из растворов. Концентрация
веществ, снижающих поверхностное натя-
жение жидкостей, в поверхностном слое
(толщиной в одну молекулу) больше, чем в
слое такой же толщины внутри объёма. Из-
быток концентрации вещесть'а на границе
раздела двух фаз, рассчитанный на единицу
площади, называется адсорбцией, обозна-
чается буквой Г и выражается обычно в
молях1см2.
Уравнение Гиббса. Гиббс строгим термо-
динамическим путём нашёл связь между
адсорбцией, температурой, поверхностным
натяжением и концентрацией растворённого
вещества. Уравнение Гиббса для адсорбции
из разбавленных растворов имеет вид:
1 „da
r = ~~RTC dC ’
где С — концентрация раствора;
а—поверхностное натяжение.
Теория адсорбции Лангмюра. Разрабо-
танная Лангмюром теория адсорбций при-
менима как для адсорбции газов твёрдыми
телами, так и для адсорбции из растворов.
Предполагая, что на поверхности имеется
п адсорбционных центров, к каждому из
которых может присоединяться одна моле-
кула газа, и что адсорбированные молеку-
лы не действуют друг на друга, т. е. силы,
действующие на молекулу газа у одного ад-
сорбционного центра, не зависят от того,
заняты соседние центры или нет, Лангмюр
для адсорбции газа Г получает следующее
уравнение:
Г=Г
‘ 1 °°Р + Ь ’
где — предельное значение адсорбции
на данной поверхности;
Р— давление газа;
b — численный коэфициент, зависящий
от природы газа и природы ад-
сорбента.
Из этой формулы следует, что при ма-
р
лых давлениях (Р - t т_ е г
пропорционально Р, при больших же давле-
ниях (Р > Ь) Г = = const, т. е. наступа-
ет насыщение, причём на поверхности обра-
зуется насыщенный слой адсорбированного
вещества толщиной в одну молекулу (на-
сыщенный мономолекулярный слой). В слу-
чае растворов формула Лангмюра принимает
вид:
где С — концентрация раствора;
а — численный коэфициент, зависящий
от природы растворённого вещест-
ва, растворителя и адсорбента.
Молекулы поверхностно-активных ве-
ществ, адсорбируясь на границе раздела
двух фаз, определённым образом ориенти-
руются так, что полярная группа обращается
в сторону той из фаз, с которой имеет
большее сродство. Так, например, при ад-
сорбции поверхностно-активных веществ на
границе вода—воздух или вода—бензол по-
лярные группы обращаются в сторону воды,
а неполярные группы в сторону воздуха или
бензола, так что, когда заканчивается про-
цесс адсорбции, на поверхности образуется
мономолекулярный слой из ориентирован-
ных молекул. Если полярную группу моле-
кулы изобразить кружком, а неполярную—
палочкой, то насыщенный мономолекуляр-
ный слой можно представить схемой, изо-
бражённой на фиг. 28.
346
химия
При исследовании адсорбции твёрдыми
пористыми адсорбентами или порошками
часто применяется эмпирическая формула,
не имеющая теоретического обоснования:
1
х = ЛС",
где х — количество вещества, адсорбиро-
ванного 1 г адсорбента;
С — концентрация раствора;
к и численные коэфициенты, завися-
п щие от природы раствора и ад-
сорбента; эти коэфициенты нахо-
дят на основании эксперименталь-
ных данных.
Формула эта выражается параболой; глав-
ный -------------- —"""
даёт
28. Ориентация мо-
поверхностно-ак-
Фиг.
лекул
тивных веществ на гра-
нице двух фаз по Ланг-
мюру
ВозЗу>
Bale
вается общий случай
её недостаток состоит в том, что она
непрерывное возрастание адсорбции с
концентрацией, не
указывая на суще-
ствование предела
адсорбции. Формула
даёт правильные ре-
зультаты только при
умеренных концент-
рациях.
Классификация
сорбционных процес-
сов. Сорбцией назы-
поглощения газа или
пара пористым телом. Сорбентом называется
твёрдое тело, поглощающее газ или пар.
Термин «сорбция» охватывает реальные
случаи поглощения газов и паров, обычно
слагающиеся из сочетания нескольких про-
цессов различной природы.
1. Абсорбция—сорбция газа за счёт его
проникновения (диффузии) в массу сорбента,
приводящая к образованию твёрдого раство-
ра. Термину «абсорбция» придаётся и более
широкий смысл как процессу поглощения
объёмом. Так, например, растворение газа
в жидкостях называется абсорбцией газа,
поглощение света веществами — абсорбцией
света.
2. Адсорбция — уплотнение газа на по-
верхности твёрдого тела. Термину «адсорб-
ция» придаётся и более широкий смысл как
поглощению вещества поверхностью. По-
этому адсорбцией называется и избыток кон-
центрации поверхностно-активных веществ
на границе раздела жидкость — газ и жид-
кость — жидкость.
3. Капиллярная конденсация — сорбция
пара за счёт его конденсации в порах сор-
бента. Это явление обусловлено понижением
упругости насыщенного пара в ультрапорах
(капиллярах) сорбента и является эффек-
том, создаваемым капиллярными силами.
4. Хемосорбция—химическое взаимодей-
ствие газа с твёрдым телом, связанное с об-
разованием новой фазы и происходящее либо
на поверхности тела, если продукты реак-
ции покрывают поверхность хемсорбента
плёнкой, не проницаемой для газа, т. е.
лишённой пор, либо распространяющееся на
всю массу хемсорбента. Сорбционные про-
цессы, наблюдающиеся на опыте, являются
сложными, так как обычно слагаются
Таблица 15
Давление насыщенного пара воды в мм рт. ст.
(мм Hg)
1° р Г р (° р г°| р
-15 1,436 14 11,987 43 64,80 72 254,6
-14 1,560 15 12,788 44 68,26 73 265,7
-13 1,691 16 13,634 45 71,88 74 277,2
-12 1,834 17 14,530 46 75,65 75 289,1
—И 1,987 18 15,477 47 79,60 76 301,4
-10 2,149 19 16,477 48 83,71 77 314,1
— 9 2,326 20 17,535 49 88,02 78 327,3
— 8 2,514 21 18,650 50 92,51 79 341,0
- 7 2,715 22 19,827 51 97,20 80 355,1
— 6 2,931 23 21,068 52 102,09 81 369,7
- 5 3,163 24 22.377 53 107,20 82 384,9
— 4 3,410 25 23,756 54 112,51 83 400,6
— 3 3.673 26 25,209 55 118,04 84 416,8
— 2 3,956 27 26,739 56 123,80 85 433,6
- 1 4,258 28 28.349 57 129,82 86 450,9
0 4,579 29 30,043 58 136,08 87 468,7
1 4.926 30 31,824 59 142,60 88 487,1
2 5,294 31 33,695 60 149,38 89 506,1
3 5,685 32 35,663 61 156,43 90 525,8
4 6,101 33 37,729 62 163,77 91 546,0
5 6,543 34 39,898 63 171,38 92 567,0
6 7,013 35 42,175 64 174,31 93 588,6
7 7,513 36 44,563 65 187,54 94 610,9
8 8,045 37 47,067 66 196,09 95 633,9
9 8,609 38 49,692 67 204,96 96 657,6
10 9,209 39 52,442 68 214,17 97 682,1
11. 9,844 40 55,324 69 223,73 98 707,3
12 10,518 41 58,34 70 233,7 99 733,2
13’ 11,231 42 61,50 71 243,9 100 ,760.0
Таблица 16
Давление насыщенного пара некоторых органических
веществ в мм рт. ст. (мм Hg)
н.-октан Р Циклогек- сан С.НХ1 Р ч о О Ной. 'хХ ч* X т х “X <ий. Хлоро- форм СНС13 Р
0 10 20 2,94 5,62 10,45 27,55 47,05 76,9 61 100,5 159,6
30 18,40 121,3 36,7 246,0
40 30,85 181,6 59,1 366,4
50 49.35 ' 269.2 92,6 2,4 526,0
60 77,55 385,0 139,5 5,7 739,6 (760 при 60,9°С)
70 117,9 540,8 202,4 10,6 1 019
80 174,8 741,3 (760 при 80,75°С) 289.7 18,0 1 403
90 253,4 992 404,6 29.2 1 880
100 353,6 1 304 557,2 45,7 2 430
110 481,9 1 687 69,2 3 100
120 646,4 (760 при 125,8°С) 2 140 96,6 3 890
130 859 2 695 144,5 4 860
140 ISO 1 114 1425 3 355 4 140 204,0 5 950 7 080
из нескольких одновременно протекающих
процессов различной физической природы.
Теплота сорбции. При сорбции обычно
происходит выделение тепла. Этот тепловой
эффект является энергетическим эквивален-
том работы, совершаемой сорбционными си-
лами. Обычно экспериментально определяют
выделение тепла, наблюдающееся при сорб-
ции определённого количества газа или
пара на сорбенте, тщательно освобождённом
от посторонних газов. Суммарное выделив-
шееся количество тепла Q, отвечающее уста-
новившемуся сорбционному равновесию, но-
сит название интегральной или полной
ФИЗИЧЕСКАЯ ХИМИЯ
347
Таблица 17
Теплоты плавления, испарения, горения, образования и стандартные свободные энергии некоторых
важнейших веществ в ккал'молъ
Вещество Формула Теплота плавления Теплота ис- парения Теплота горения Агрегатное состояние* Теплота образова- ния из эле- ментов (теплосо- держание) ДН° 298 Стандарт- ная сво- бодная энергия Д Ф° 298
т° к Т’ к X
Азот N, 63 -0,169 77 -1,336 г 0,000 0,000
Азотная кислота HNO, 226 -0,60 359,2 -7,2 — ж —41,66 —26,5
Аммиак NH, 195 -1,84 240 -5,56 — г —11,04 — 3,94
Анилин С„ н5 NH, 267,2 -1,95 257,2 -10,2 — ж 4-63,68 +35,40
Антрацен .... С„н„ 490,2 -6,9 — — 1684,7 т + 16,94 + 54,5
Ацетилен .... С, н, 191,7 -0,60 191,7 —5,74 311,1 г +54,23 +50,0
Ацетои сн,- со сн, 179,2 -1,14 329,2 -7,27 — ж —57,3 -35,1
Бензол с. н. 278,6 —2,350 352,8 -7,39 782 ж + 11,2 +29,06
Бутадиен, или дивинил .... сн,=сн-сн- =сн8 164,3 —1,908 268,6 —5,398 618,1 687,9 г +26,87
н-Бутан С. Н„ 134,87 -1,113 272,66 -5,351 т —29,81 -3,72
Вода н, о 273,16 —1,437 373,2 —10,571 — ж —68,32 —56,68
Водород .... 11, 11 —0,0282 18 —0,216 — г 0,000 0,000
н-Гексан . • • с, ни 178,6 —3,00 298,16 -7,41 1002,4 ж —47,56 —2
н-Гептан . . . С, н„ 182,52 —3,355 371,51 -7,66 1159,4 ж —53,63 —0,31
Г рафит с 3873 -И — — — т 0,000 0,000
Дифенил .... с, н, с,н, 344,2 -4,0 — — 1494,73 т +24,8 + 61,7
Едкий натр . . NaOH — — — — — т -102,7 -90,8
Изобутан . . . С, Н„ 113,74 —1,085 261,44 —5,089 686,3 г —31,45 -4,26
Изооктан . . . С, Н„ 165,79 -2,201 372,33 -7,41 — ж -61,98 0
Кислород . . . О, 54,5 -0,106 90 -1,629 — г 0,000 0,000
Ксилол мета . . С, Н, (СН,), 225,3 —2,760 298,16 —10,00 1089,4 ж -4.4 +27,4
Ксилол орто . . » 247,82 —3,250 298,16 -10,47 1090,4 ж —3,4 +29,2
Ксилол пара » 286,39 —4,09 298,16 —10,11 1089,9 ж —3,9 +28,3
Метан сн. 90,6 -0 224 114,2 —1,95 212,8 г —17,89 —12,11
Метиловый спирт сн, он 175,2 -0,76 337,7 —9,01 182,75 ж -57,03 -39,96
Мочевина .... NH, • СО • NH, —— — —— — — т —78,6 —47,3
Муравьиная кислота .... Н•СООН 281,2 —3,05 374,2 -5,52 62,8 ж —99,45 —85,2
Нафталин .... С„Н, 353,2 —4,57 491,2 1231,3 (20°) т + 18,03 +45,5
Окись кальция . СаО 2840 —28 — — — т -151,7 —26,39 -141,7
Окись углерода со 62 —0,1997 81,5 —1,444 67,61 г —32,78
Серная кислота н, so, 283 -2,55 599,2 -1.3 — ж —193,75 —177,60
Сернистый газ . so, 200 -1.9 263 -6,07 — г -70,94 —71,6
Серный ангидрид so, 290 —1,9 326 —10,3 — г —94,44 —87,0
Сероводород . . H,S 163 -0,4 212 —4,5 — г —4,8 —7,83
Толуол с,н, • сн, 178,18 —1,560 298,16 -9,115 935,5 ж +1,2 +25,6
Углекислый газ со, 217 -2,24 217 -6,0 — г —94,03 -94,24
Уксусная кисло- та сн,СООН 290,2 -2,70 391,7 -5,82 208,3 ж — 116,0 -94,5
Фенантрен • . . С./Н,, 371,4 -4,3 — 1674,9 т +26,74 +64,0
Фенол с,н, он 314,2 -2,77 455,3 —10,74 — т + 16,55 -11,00
Формальдегид . н . СНО — — — — 134,1 г —28,48 -27,1
Хлор С1, 107,7 -1,62 237 -4,4 — г 0,000 0,000
Хлористый водо- род HC1 159 -0,476 188 -3,86 г -22,03 —22,74
Хлористый нат- рий NaCl 1073 —7,22 1473 -43,5 — т —98,3 -91,8
Циклогексан . , C.Hlt 279,84 —0,627 298,16 -7,940 936,4 ж —37,68 +6,2
Циклопентан . . С.Н.. 179,69 —0,144 298,16 —6,983 783,3 ж —29,45 +4,6
Четырёххлори- стый углерод . СС1, 249 -0,67 196 -7,27 — г -25,6 —16,5
Этан С,Н, 89,87 -0,682 184,1 -3,325 372,8 г —20,24 —7,83
Этилен сан4 103,95 —0,800 169,40 —3,237 337,2 г + 12,56 + 16,36
Этиловый спирт СН, сн, он 159,2 -1,15 351,4 -10,19 337,06 ж -66,35 -42,20
* г — газ
ж—жидкость
т —твёрдое
348
химия
Таблица 18
Растворимость и теплота растворения неорганических соединений в воде
Название соединения Формула Растворимость Интегральная теплота раство- рения при оо разведении
t °C % (вес) Q ккад1молъ
Азота окись NO 20 а « 0,04706
Аммоний азотнокислый NH.NO, 20 63,9 81,52
Аммоний хлористый NH.C1 20 27,1 71'33
Барий едкий Ва(ОН), • 8Н,О 20 3,36 ♦♦ 237,7
Барий хлористый ВаС1, 2НаО 20 26,3 ** 207,69
Борная кислота Н.ВО, 21 4,9 «• 246,3
Вг,
Водорода перекись н,о, ОО ♦♦ 45,0
Железа гидроокись Fe (ОН), 18 * 4,8 - 10~9
Железа закись—окись (магнетит) FeaO. н. р.
Железа окись (гематит) Fe,O, н. р.
Железо хлористое . . . . FeCl, 2o 40,7 •» 99,83
Железо хлорное «... FeCla 20 47,9 ♦♦ 128,2
Иод J. 15 * 0,0276
Калий азотнокислый KN О, 20 24,1 110,19
Калий хлористый (сильвин) KC1 20 25,5 *• 99,95
Кальций едкий Ca(OH), 20 0,123 »» 238,9
Кальций хлористый CaCI, 20 42,7 208,8
Кислород o, 20 а = 0,03102 3,3
Кремния карбид (карборунд) SiC н. р.
Кремния окись (ангидрид кремневой кис-
лоты) SiO, н. р.
Кремния окись (кварц) SiO, н. р.
Марганца двуокись (перекись, пиролюзит) MnOe н. р.
Медь сернокислая CuSO. 5H,O 25 • 18,7 ♦♦ 194,8
Мышьяковистый ангидрид AsjOj 25 2,00 ** 149,0
Натрий бромистый ............. NaBr • 2H,O 20 47,5 • ♦ 86,212
Натрий сернистый NaaS 18 15,3 • » 105,3
Натрий углекислый (кислый) первичный . NaHCOs 20 8,76 ♦♦ 223,5
Натрий углекислый вторичный, гидрат
(сода) NaaCO, • ЮН.О 20 17,8 •» 276,37
Натрий хлористый NaCl 20 26,39 97,15
Ртуть однохлористая (каломель) Hg.Cl, 18 • 2,1 . 10-4
Ртуть двухлористая (сулема) HgCl, 20 6,2 53,47
Свинец азотнокислый Pb(NOa), 20 34,3 *» 100,7
Свинца окись (свинцовый глёт) PbO 20 » 1,7 • IO”2
Свинца окись (сурик) PbaO. н. р.
Свинца окись (ангидрид) PbO, оч. тр. р.
Сера ромбическая s н. р.
Серы двуокись (сернистый ангидрид) . . . so, 20 а ®= 39, as ♦♦ 77,91
Серы трёхокись so. ОО 139,0
Сернистый водород (сероводород) .... H,S 20 а «= 2,554 ♦ * 9,88
Серебро авотнокислое AgNO, 20 ьз ,3 ♦ * 24,68
Углерода окись CO 20 а = 0,02319 29,89
Углерода двуокись (угольный ангидрид) . CO. 20 а = 0,878 99,21
Углерод сернистый (сероуглерод) .... cs, • 0,179
Углерод четырёххлористый CCI. 20 0,080
Фосфористая кислота H.PO, оч. р. 229,0
Фосфорноватистая кислота HaPO, оч. р. ** 141
Фосфорная кислота мета (HPOS) x оч. р. * * 234,7
Фосфорная кислота орто HaPO. оч. р. ♦♦ 306,86
Фтористый водород Хлор HF Ci, 0 оо В 1 объёме • • 75,75 »» 5,3
Н,О раствор
4,6 об. С!а
Хрома окись Cr,Os н. р.
Цинка окись ZnO оч. тр. р.
Цинк хлористый ZuCla 20 78,6 115
Примечание, н. р. — не раст! зоримо.
оч. р. — очень растворимо.
оч. тр. р. — очень трудно растворимо.
а — коэфициент абсорбции — объём газг (приведенный к Ои давлению
760 мм) поглощенный 1 объемом жидкости при г, когда парциаль-
ная упругость газа равна 760 мм Hg
• Растворимость дана в граммах растворённого вещества в 100 г растворителя,
♦ t Дана интегральная теплота растворения 1 моля вещества в больших количествах (200,
400 лолеи) растворителя, мало отличающаяся от интегральной теплоты при оо разведении.
КОЛЛОИДНАЯ химия
349
теплоты сорбции. Её обычно относят к еди-
нице массы сорбента и выражают в калориях
Q
на грамм: q = ~m, где тп — масса сорбента.
Частная производная от интегральной теп-
лоты адсорбции q по величине сорбции Г
при постоянной температуре называется
диференциальной теплотой сорбции
/dQ\ I
ч* = (дг)ткал1моль-
В общем случае диференциальная тепло-
та сорбции зависит от величины сорбции и
температуры. Начальные теплоты адсорбции,
соответствующие адсорбции небольших пор-
ций газов, на освобождённом от газов
адсорбенте, сильно отличаются от теплот
адсорбции при поглощении последующих
сравнительно больших количеств. Опыт по-
казывает, что в то время как интегральная
теплота адсорбции чаще имеет значение
около 10000 кал, начальные теплоты дости-
гают значения 30000 — 40000 кал, а иногда
лежат ещё выше. Эти экспериментальные
факты имеют большое значение при теоре-
тическом рассмотрении адсорбционных про-
цессов.
Таблица 19
Нормальные, или стандартные, потенциалы при 25°С
(ряд напряжений)
Электрод Электродный процесс Eo в воль- тах
Li/Li + Li-*Li 4-е (электрон) +2,959
Rb/Rb + Rb—>Rb+ + e +2,926
к/к+ К—>К++е +2,9284
Sr/Sr+ + Sr—>Sr+ + + 2e +2,92
Ва/Ва+ + Ba—>Ba+ + + 2e + 2,90
Са/Са+ + Ca—»-Ca + + + 2e +2,76
Na/Na+ Na—*"Na+ 4-e +2,7185
Mg/Mg++ Mg->-Mg+ + + 2e +1.55
А1/А1 + + + Al—>Al++++3e + 1.33
Mn/Mn+ + Mn—>-Mn+ ++2e +1.1
Fe/Fe (ОН), Fe+2OH--*Fe(OH),+2e +0,86
Pt(H,)/OH~ Ч, H.+OH-—>-H,O+e +0,828
Zn/Zn++ Zn^Zn+ + -l-2e +0,762’
Pt(Fe+ + )/Fe(OH )„ Fe(OH),+
+OH-_,Fe(OH),+e +0.65
Продолжение табл. 19
Электрод Электродный процесс E в воль- тах
Ag/Ag (CN), Ag + 2CN ^Ag(CN), +el+0,5
Fe/Fe+ + Fe-*Fe + + + 2e 4-0,441
pt(Cr + +)/Cr+ + + Cr++—Xr+ + + + e 4-0,4
Cd/Cd + + Cd—>Cd+ + + 2e +0,401
T1/T1+ TI—»-Tl+ + e 4-0,33
Pb/PbSO, Pb+SO,——<-PbSO,+2e +0,31
Co/Co+ + Co—*Co+++2e +0,29
Ni/Ni + + Ni—>-Nl + + + 2e +0,231
Ag/Ag J Ag+j-—*AgJ + e +0,15
Sn/Sn + + Sn—»-Sn+ + + 2e +0,136
-p J- Pb/Pb Pb—>Pb + + + 2e +0,122
Pt(H,)/H + */,H,—>H++e 0,000
Ag/AgBr Ag+Br-—>AgBr+e -0,10
Pt(Cu + )/ Cu + + Cu+—>Cu + + + e -0,17
Ag/AgCl Ag+Cl~—*Agd+e -0,223
Hg/HgCl 2Hg + 2Cl-—>HgaClt4- 4-2e -0,270
Cu/Cu + + • Cu—>-Cu + + +2e —0,344
Cu/Cu+ Cu—•-Cu'^+e -0,51
Pt,(J-)/J, Pt(Fe+ + )/Fe+ + + 2J —>J,+ 2e Fe + +~+ Fe+ +++e -0,535 -0,74
Hg/Hg + Hg—*Hg +e -0,799
Ag/Ag + Ag—>-Ag++e -0,798
Hg/Hg+ + Hg—>Hg + +e -0,86
Pt(Br")/Br, Pt(Tl+)/Tl + + + 2Br —>Br, + 2e TI+ —>Tl++++2e -1,065 —1,2
Pt(Cl-)/Cl, 2C1 —>-Cl,+2e -1,359
Au—>-Au ++e -1,5
PbSO,/PbO, PbSO,+ 2H,O—>PbO,+ + 4H + + SO,~ + 2e -1.74
Pt(F-)/F, F——>4-F, + e -2.8
КОЛЛОИДНАЯ химия
Основная терминология и классификация
дисперсных систем
Основные особенности коллоидных систем.
Для изучения физических свойств веществ
и законов их превращения в результате хи-
мических реакций необходимо иметь вещества
в возможно чистом виде. Лучший метод полу-
чения веществ в чистом виде — перекристал-
лизация. Было обнаружено, что не все веще-
ства способны к кристаллизации, и так как
их трудно было идентифицировать, то их
мало изучали. Серьёзное внимание на эти
вещества обратили в шестидесятых годах
XIX в. Борщёв и Трем. Первый изученный
представитель этих.веществ был клей. По-
гречески клей называется «колла». Поэтому
Г рем всю группу такого типа веществ назвал
коллоидами в отличие от веществ, способ-
ных к кристаллизации, которые он назвал
кристаллоидами.
Трем нашёл, что все коллоиды не способны
к кристаллизации, обладают очень малым
осмотическим давлением, малой скоростью
350
химия
диффузии и не способны к диализу. Диали-
зом называется проникновение вещества
через ультрапористые мембраны (пергамент,
животный пузырь, плёнки из ацетилцеллю-
лозы или коллодия). Позднейшие опыты
показали, что одно и то же вещество в зави-
симости от выбранного растворителя ведёт
себя или как коллоид или как кристаллоид.
Например, поваренная соль вводе ведёт себя
как кристаллоид, а в бензольном растворе
показывает свойства коллоида; стеариново-
кислый натрий в воде является типичным
коллоидом, а в спиртовом растворе ведёт
себя как кристаллоид. Кроме того, было
‘установлено, что коллоидные частицы могут
иметь кристаллическое строение.
Дисперсионная среда. Растворитель в кол-
лоидной химии называется дисперсионной
средой.
Дисперсная фаза. Растворённое или тонко
диспергированное в растворителе вещество
называется дисперсной фазой.
Золи. Жидкие коллоидные растворы назы-
ваются золями. Для полной характеристики
такого раствора к слову «золь» часто добав-
ляется приставка, характеризующая природу
растворителя. Например, золи, в которых
растворителем является вода, называются
гидрозолями; если растворитель спирт, —
алкозолями; золи, в которых растворителем
является органическое вещество, называются
органозолями; если дисперсной средой яв-
ляется воздух, то такие системы называются
аэрозолями.
Гели. Часто коллоидные системы бывают
твёрдыми, студнеобразными, хотя дисперси-
онная среда их жидкая, как у золей. Такие
системы называются гелями. Для полной
характеристики гелей также ставится при-
ставка, характеризующая природу раствори-
теля. Если дисперсионной средой является
вода, то такие гели называются гидрогелями.
Коллоиды как дисперсные системы. Малое
осмотическое давление, малая скорость диф-
фузии, неспособность к диализу указывает
на то, что коллоидные частицы имеют раз-
меры большие, чем молекулы соответствую-
щих веществ, т. е. коллоидные частицы яв-
ляются агрегатами атомов или молекул.
Поэтому коллоиды относят к разряду дис-
персных систем.
Классификация дисперсных систем по сте-
пеням дисперсности. Если линейные размеры
частиц: 1) больше 0,1 ь, то они образуют
грубо дисперсные системы (суспензии и эмуль-
сии); 2) лежат в пределах от 0,1 р до Imp,
то они образуют коллоидные системы;3) мень-
ше .1 т pi образуют истинные растворы (моле-
кулярно или ионнодисперсные системы).
Суспензии. Суспензией называется грубая
взвесь твёрдых частиц в жидкой дисперсион-
ной среде.
Эмульсии. Эмульсией называется грубая
взвесь жидких частиц в жидкой дисперсион-
ной среде.
Необратимые коллоиды. Необратимыми
коллоидами называются такие коллоиды, ко-
торые, будучи выделенными из дисперсионной
среды, при соприкосновении с ней вновь само-
произвольно не переходят в коллоидное со-
стояние. Необратимые коллоиды делятся на
два подкласса. Необратимыми коллоидами
первого подкласса называются коллоиды, не
способные образовывать гели, например, кол-
лоидные металлы, коллоидные сульфиды
металлов. Необратимыми коллоидами второго
подкласса называются коллоиды, способные
образовывать гели, например, коллоидная
кремневая кислота, гидраты окиси железа,
алюминия и т. п. Все необратимые коллоиды
чувствительны к действию электролитов. При
добавлении электролитов они разрушаются
(см. Коагуляция, стр. 352).
Обратимые коллоиды. Обратимые колло-
иды— такие коллоиды, которые, будучи
выделены из дисперсионной среды, при со-
прикосновении с ней вновь переходят в кол-
лоидное состояние (состояние золя). Все
обратимые коллоиды делятся на два под-
класса: коллоиды типа желатины, набухаю-
щие в растворителе, но для образования золя
требующие некоторого повышения темпера-
туры, и коллоиды типа гуммиарабика, спо-
собные непосредственно переходить в колло-
идный раствор при простом соприкосновении
с дисперсионной средой. Все обратимые кол-
лоиды способны образовывать гели и мало
чувствительны к действию электролитов.
Лиофобные коллоиды. Лиофобными кол-
лоидами называются коллоиды, не способные
к сольватации. Сольватацией называется
уплотнение молекул чистого растворителя
вокруг частиц. В частном случае, когда раст-
ворителем является вода, явление носит наз-
вание гидратации. Не способные к гидрата-
ции коллоиды называются гидрофобными.
Типичными лиофобными коллоидами явля-
ются необратимые коллоиды первого под-
класса.
Лиофильные коллоиды. Лиофильными кол-
лоидами называются коллоиды, способные
к сольватации. В частном случае, когда
растворителем является вода, способные к
гидратации коллоиды называются гидро-
фильными. К типичным лиофильным коллои-
дам относятся все обратимые коллоиды.
Методы получения коллоидных систем
Дисперсионные методы
Дисперсионными методами называются все
методы, при которых массивные тела тем или
иным способом дробятся до размеров кол-
лоидных частиц.
Механические методы. Механический метод
состоит в прямом дроблении тел механиче-
скими приёмами. К механическим методам
относятся: 1) дробление в ступке и 2) дроб-
ление в коллоидных мельницах. В обоих
случаях получить высокодисперсные системы
не удаётся. При дроблении обязательным
является добавление веществ, которые адсор-
бируются на образующихся частицах и пре-
пятствуют их слипанию. Такие вещества
называются стабилизаторами.
Пептизация. Пептизацией называется
переведение осадка в золь под действием
небольших количеств электролита. Этим ме-
тодом в состояние золя можно перевести
только такие осадки, в которых ультрамик-
роны (коллоидные частицы) не потеряли
своей самостоятельности. Переход в золь
происходит потому, что каждая частица ад-
КОЛЛОИДНАЯ химия
351
сорбирует на своей поверхности ионы одного
и того же знака> вследствие этого между
ними возникают силы отталкивания, и они
равномерно распределяются по всему объёму
растворителя.
Конденсационные методы
Конденсационные методы заключаются в
том, что отдельные атомы или молекулы
заставляют объединяться вместе в агрегаты,
которые имеют коллоидные размеры.
Восстановление. Применяя неорганиче-
ские или органические восстановители, мож-
но получить из растворов солей многих
металлов в воде коллоидные растворы метал-
лов в воде. Например, действуя в щелочной
среде на раствор хлорного золота в воде
формалином, получают коллоидный- раствор
металлического золота яркокрасного .цвета.
Гидролиз. Гидролизом можно получить
коллоидные растворы гидратов окисей метал-
лов (образующих слабые основания) или не-
которых кислот — кремневой, оловянной.
Кристаллизация. Подбирая соответствую-
щим образом исходные соли и растворители,
можно добиться того, что рост кристаллов
нерастворимых веществ, образующихся в
результате обменного разложения, будет
прекращаться тогда, когда их размеры будут
лежать в пределах размеров коллоидных
частиц.
Электрические методы
Коллоидные растворы многих веществ
можно получать электрическим распылением.
Вещества, подлежащие распылению, погру-
жаются в растворитель, соединяются с источ-
ником тока — постоянного (метод Бредига)
или переменного высокой частоты и напря-
жения (метод Сведберга) — так, чтобы между
ними зажглась электрическая дуга. Тогда в
результате горения дуги происходит распы-
ление вещества с образованием коллоидного
раствора.
Оптические свойства коллоидов
Вид золей в проходящем свете. При рас-
сматривании коллоидных растворов в про-
ходящем свете как невооружённым глазом,
так и под микроскопом они окажутся совер-
шенно прозрачными и однородными. Предель-
ная разрешающая сила микроскопа 0,15 р,
размеры же коллоидных частиц лежат в пре-
делах от 0,1 у до 1 тр, поэтому видеть кол-
лоидные частицы под микроскопом нельзя.
Свет, проходя через коллоидный раствор,
частично им поглощается — абсорбируется.
Если коллоидный раствор поглощает в види-
мой части спектра свет всех длин волн в
одинаковой степени, то он кажется бесцвет-
ным. Когда же нацело абсорбируются лучи
только определённой длины волны, то золь
кажется окрашенным в цвет, дополнительный
поглощённому. У многих золей окраска зави-
сит от степени дисперсности. Высокодисперс-
ные золи окрашены в красный цвет, низко-
дисперсные— в фиолетовый.
Вид золей в отражённом свете. При рас-
сматривании золей в отражённом свете (т. е.
при рассматривании перпендикулярно падаю-
щему свету) заметно помутнение. Это явление
называется опалесценцией. При прохождении
пучка света через коллоидный раствор виден
его путь, если наблюдать перпёндикулярно
его ходу. Интенсивность рассеянного света
для частиц, размер которых лежит в преде-
лах 0,1 р—1 т р, определяется формулой:
где I — интенсивность рассеянного света;
V — объём частицы;
п — число частиц в единице объёма;
К — постоянная, зависящая от природы
света и коллоидного раствора;
X — длина волны света. Рассеянный свет
обычно частично поляризован.
Ультрамикроскоп. Для обнаруживания
присутствия коллоидных частиц случт
ультрамикроскоп. од
Принцип устрой- ------------.. ;
ства щелевого / )
ультрамикроско-
па показан на Ц ‘ '
фиг. 29. Парал- „„ „
дельный пучок фиг- 29' СрХ>паЛЬТра"ИК'
света А попадает
в кювеку С с коллоидным раствором.Объектив
D и окуляр микроскопа расположены пер-
пендикулярно падающему свету. Поэтому
поле зрения остаётся тёмным, й в окуляр
попадают только лучи, рассеянные коллоид-
ными частицами. В ультрамикроскоп видны
не сами коллоидные частицы в присущей им
геометрической форме, а светящиеся точки,
которые являются результатом дифракции
света (дифракционные ореолы). Ультрами-
кроскоп позволяет не увидеть коллоидные
частицы, а обнаружить их присутствие.
Молекулярно-кинетические свойства
коллоидов
Броуновское движение. Частицы, которце
обнаруживаются при помощи ультрамикро-
скопа, не находятся в состоянии покоя, а
совершают беспорядочное (хаотическое) дви-
жение подобно молекулам газа. Это движе-
ние было открыто броуном и получило
название броуновского движения. Броунов-
ское движение в коллоидных системах играет
большую роль, так как сообщает системам
кинетическую устойчивость, т. е. способность
противостоять действию силы тяжести. Так
как массы и плотности коллоидных частиц
велики, то дисперсная фаза должна была бы
оседать под действием силы тяжести. Однако
этого не наблюдается, так как в результате
броуновского движения частицы самопроиз-
вольно двигаются и против силы тяжести.
Электрические свойства коллоидов
В большинстве случаев дисперсная фаза
и дисперсионная среда в коллоидных систе-
мах несут электрические заряды, причём знак
заряда дисперсной фазы противоположен
знаку заряда дисперсионной среды.
Электрофорез». Если коллоидный раствор
поместить в электрическое поле, то частицы
дисперсной фазы, поскольку они несут заряд
определённого знака, начинают двигаться к
одному из полюсов, заряд которого противо-
352
химия
положен заряду частиц. Это движение дис-
персной фазы в электрическом поле назы-
вается электрофорезом. Коллоидные метал-
лы, сульфиды металлов, кремневая кислота,
глина обычно заряжены отрицательно; по-
этому в электрическом поле они двигаются
к аноду. Коллоидные окиси и гидроокиси
металлов обычно заряжены положительно и
в электрическом поле двигаются к катоду.
Электроосмос. Электроосмосом называется
движение дисперсионной среды в постоянном
электрическом поле. Дисперсионная среда
движется к тому электроду, заряд которого
противоположен знаку заряда дисперсионной
среды.
Причины возникновения заряда у колло-
идных частиц. Основной причиной возникно-
вения зарядов у коллоидных частиц является
адсорбция ионов. Каждая коллоидная части-
ца адсорбирует на своей поверхности ионы
одного и того же знака и приобретает заряд,
по знаку совпадающий со знаком заряда
адсорбированных ионов.Ионы противополож-
ного знака остаются в растворителе и придают
ему заряд. Кроме того, заряд может возник-
нуть в результате достройки кристалличе-
ской решётки коллоидных частиц ионами из
раствора или же в результате диссоциации
молекул, входящих в состав коллоидных
частиц, на их поверхности на ионы.
Мицелла. Мицеллой называется нейтраль-
ный комплекс молекул, образующих колло-
идную частицу с адсорбированными ионами
и ионами-спутниками (т. е. ионами противо-
положного знака, оставшимися в избытке в
растворителе). Вся остальная жидкость назы-
вается интермицеллярнбй жидкостью.
Фиг. 30. Распределение
потенциала у коллоид-
ной частнцы
Распределение потенциала у коллоидной
частицы. На фиг. 30, а в сильно увеличенном
виде представлена поверхность коллоидной
частицы К, на кото-
рой расположены
адсорбированные от-
рицательные ионы,
буквой 8 отмечена
толщина сольватно-
го слоя. Часть по-
ь ложительных ионов
попадает в этот соль-
ватный слой, а часть
диффузно распро-
страняется в глубь
жидкости. Число от-
рицательно заряжен-
ных ионов на поверх-
ности частицы равно
числу положитель-
ных ионов, частично
попадающих в сольватный слой, а частично
распространяющихся от сольватной оболочки
в глубь раствора. Распределение потенциала
V у коллоидной частицы в зависимости от рас-
стояния г показано на графике фиг' 30, Ь. Вся
разность потенциалов между коллоидной ча-
стицей и окружающей средой е называется
термодинамическим потенциалом. Разйость
потенциалов 5 между неподвижным слоем
жидкости, связанным с коллоидной частицей
толщиной 8 (сольватным слоем), и осталь-
ной — подвижной— частью жидкости назы-
вается электрокинетическим, или дзета-по-
тенциалом. Скорость движения коллоидных
частиц в электрическом поле, помимо напря-
жения электрического тока, вязкости и
диэлектрической постоянной среды, опреде-
ляется величиной ^-потенциала.
Чем больше С-потенциал коллоидных час-
тиц, тем больше между ними отталкивание.
Коагуляция коллоидных систем
Коагуляция. Процесс понижения степени
дисперсности коллоидных систем называется
коагуляцией.
Седиментация. Конечной стадией коагу-
ляции является процесс выпадения вещества
дисперсной фазы в осадок. Этот процесс
называется седиментацией.
Коагуляция лиофобных коллоидов
под действием электролитов
Коагуляцию лиофобных коллоидов можно
вызвать путём прибавления электролитов.
Ионы прибавляемого электролита снижают
величину электрокинетического потенциала,
благодаря этому уменьшаются силы отталки-
вания между коллоидными частицами, и они
получают возможность соединиться вместе
в более крупные агрегаты.
Порог концентрации. Наименьшее коли-
чество прибавленного электролита, которое
вызывает процесс коагуляции, называется
порогом концентрации.
Критический потенциал. Минимальный
электрокинетический потенциал коллоидных
частиц, при котором начинается процесс
коагуляции, называется критическим потен-
циалом.
Изоэлектрическая точка. Наименее устой-
чивой система будет тогда, когда электро-
кинетический потенциал становится равным
нулю. Это состояние коллоидной системы
называется изоэлектрической точкой.
Правило значности. Для того чтобы вы-
звать процесс коагуляции, ионов высшей
валентности требуется меньше, чем ионов
низшей валентности. Соотношение между
количествами ионов, вызывающими коагуля-
цию, редко соответствует их валентности.
Если концентрацию ионов калия (К’)> вызы-
вающую коагуляцию отрицательно заря-
женного коллоида, принять за единицу, то
оказывается, что ионов бария (Ва") потре-
буется в 20 раз меньше, а ионов алюми-
ния (Al’") в 1 000 раз меньше.
Явление неправильных рядов или зон коа-
гуляции. Явление это заключается в том,
что при коагуляции некоторых золей много-
валентными ионами при постепенном прили-
вании электролита наблюдается то коагу-
ляция, то переход вновь в высокодисперсное
состояние в результате адсорбции ионов,
противоположных по знаку заряда колло-
идной частицы в большом количестве, что
связано с изменением знака её заряда.
Явление привыкания заключается в том,
что если определённое количество электро-
лита прибавить сразу, то наступает коагу-
ляция, заканчивающаяся выпадением веще-
ства в осадок. Если то же самое количество'
электролита прибавлять постепенно, то вы-
падение вещества в осадок не наблюдается.
КОЛЛОИДНАЯ химия
353
Антагонизм ионов. Ионы в смеси обычно
понижают коагулирующую способность друг
друга.
Быстрая и медленная коагуляция. Если
к коллоидному раствору прибавлять неболь-
шие количества электролита так, что изо-
электрического состояния не достигается,
то в этом случае скорость коагуляции зави-
сит от концентрации прибавляемого электро-
лита: она растёт с увеличением концентрации
электролита. Это — область медленной коа-
гуляции, и только в этой области оказы-
вается справедливым правило значности и
наблюдаются явления неправильных рядов,
привыкания и антагонизма ионов. Если же
количество прибавляемого электролита пре-
восходит необходимое для достижения изо-
электрического состояния, то скорость коа-
гуляции перестаёт зависеть от концентрации
электролита. Это — область быстрой коагу-
ляции, при этом правило значности и пере-
численные выше явления не наблюдаются.
Коагуляция лиофильных золей
Золи лиофильных коллоидов мало чув-
ствительны к электролитам. Для коагуляции
золя лиофильного коллоида всегда требуется
больше электролита, чем для коагуляции
лиофобного золя. В результате коагуляции
золей лиофильных коллоидов образуются
гели или в виде хлопьевидного объёмистого
осадка или вся система застудневает, удер-
живая всю массу растворителя.
Грубая схема частицы лиофильного колло-
ида представлена на фиг. 31 буквой А. Если
Фиг. J1. Схема коагуляции
лиофильных золей
прибавлять электролит, то в первую очередь
снимается заряд и частицы переходят в со-
стояние без заряда, но с сохранением соль-
ватной оболочки В. Коагуляции при этом
не наблюдается, так как сольватная оболочка
препятствует соединению частиц. Большие
порции электролита разрушают сольватную
оболочку (жидкость расходуется на построе-
ние сольватных оболочек ионов), и частицы
переходят в состояние С, когда они лишены
и заряда и сольватной оболочки. При этом
наступает коагуляция. К коагуляции можно
притти и другим путём: сначала при помощи
какого-нибудь подходящего реактива унич-
тожить сольватную оболочку и перевести
частицу в состояние D. Коагуляции при
этом наблюдаться не будет, так как частицы
заряжены, но если теперь добавить электро-
лит, то частицы перейдут в состояние С, при
котором наступит коагуляция.
23 том I
Агрегативная устойчивость коллоидных
систем. Агрегативная устойчивость — это
устойчивость по отношению к процессу пони-
жения степени дисперсности. Агрегатив-
ная устойчивость лиофобных систем опреде-
ляется величиной электрокинетического по-
тенциала: чем выше электрокинетический
потенциал, тем более устойчива система.
Агрегативная устойчивость лиофильных си-
стем определяемся: электрокинетическим по-
тенциалом и сольватацией.
Вязкость лиофобных коллоидов
Зависимость вязкости от концентрации.
Формула Эйнштейна. Вязкость золей лио-
фобных коллоидов обычно мало отличается
от вязкости чистого растворителя. Это объ-
ясняется тем, что лиофоС
чивы только в области
малых концентраций.
Вязкость лиофобных
коллоидов изменяется
линейно с концентра-
цией. Зависимость вяз-
кости от концентрации
даётся формулой Эйн-
штейна:
1 + 2>5 у >
ые коллоиды устой-
фиг. 32. Зависи-
мость вязкости лио-
фобных 7 и лиофиль-
ных 2 золей от кон-
центрации
где т) — вязкость коллоидного раствора;
— вязкость дисперсионной среды;
Ф — суммарный объём дисперсной фазы;
V — объём раствора.
Зависимость вязкости золя лиофобного
коллоида о г его концентрации 8 изображена
на фиг. 32 кривой Z.
Зависимость вязкости лиофобных колло-
идов от степени дисперсности. Вязкость золя
лиофобного коллоида с увеличением степени
дисперсности обычно растёт.
Зависимость вязкости от времени. С тече-
нием времени вязкость золей лиофобных
коллоидов падает, так как со временем идёт
процесс коагуляции.
Зависимость вязкости от температуры.
Вязкость золей лиофобных коллоидов с по-
вышением температуры падает, так как па-
дает вязкость чистого растворителя.
Зависимость вязкости от присутствия
электролитов. Под действием электролитов
вязкость золей лиофобных коллоидов падает,
так как происходит процесс коагуляции, в
конечном итоге приводящий к выделению
вещества в осадок.
Вязкость лиофильных коллоидов
Зависимость вязкости от концентрации.
Вязкость лиофильных коллоидов растёт с
увеличением концентрации. Многие лиофиль-
ные коллоиды уже при небольших концен-
трациях переходят в состояние геля. Послед-
ние обладают очень высокой вязкостью.
Поэтому вязкость резко увеличивается с
концентрацией (фиг. 32, кривая 2).
Зависимость вязкости от времени. С тече-
нием времени вязкость золей лиофильных
коллоидов растёт, так как в растворе обра-
зуется определённая внутренняя структура,
354
химия
приводящая в конечном счёте к образованию
геля.
Зависимость вязкости от температуры.
С повышением температуры вязкость золей
лиофильных коллоидов падает, так как раз-
рушается внутренняя структура раствора и
уменьшается вязкость растворителя.
Зависимость вязкости от присутствия
электролитов. В одних случаях вязкость зо-
лей лиофильных коллоидов при небольших
концентрациях прибавляемого электролита
падает, а затем по мере увеличения концен-
трации электролита начинает резко расти.
Это объясняется тем, что малые концентрации
электролита разрушают внутреннюю струк-
туру раствора вследствие пептизации, а
затем при больших концентрациях электро-
лиза наступает коагуляция, и вязкость на-
чинает расти. В других случаях вязкость
при прибавлении электролита сразу начинает
расти.
Структурная вязкость. Золи многих лио-
фильных коллоидов имеют определённую
внутреннюю структуру. Для того чтобы за-
ставить такой золь течь, требуется прило-
жить определённую силу. Течение начинается
тогда, когда напряжение сдвига превзойдёт
некоторую определённую величину. Закон
Пуазейля, по которому скорость истечения
растёт с увеличением давления линейно, при
этом не выполняется; скорость истечений
растёт пропорционально давлению степени,
большей единицы. Коэфициент вязкости в
этомдйучае оказывается функцией градиента
скорости, причём с ростом градиента ско-
рости вязкость падает. Вязкость в этих слу-
чаях называется структурной.
Эмульсии
Условия образования устойчивых эмуль-
сий. Для образования устойчивой эмульсии
из двух взаимно нерастворимых жидкостей
необходимо присутствие третьего вещества,
так называемого стабилизатора или эмуль-
гатора. Эмульгатор всегда является поверх-
ностно-активным веществом. Адсорбируясь
на границе раздела двух фаз — частица
эмульсии/дисперсионная среда, эмульга-
тор тем самым снижает поверхностное на-
тяжение и, следовательно, уменьшает запас
свободной поверхностной энергии, делая тем
самым систему устойчивой. Однако не всегда
вещества, сильно снижающие поверхностное
натяжение, являются хорошими эмульгато-
рами. Вещество должно не только снижать
вследствие адсорбции поверхностное натя-
жение, но и образовавшаяся адсорбционная
плёнка вокруг капелек эмульсии должна об-
ладать высокой поверхностной прочностью
(сопротивлением на разрыв). Поэтому хоро-
шие эмульгаторы,обычно имеют коллоидную
* природу и способны к сольватации, при этом
они образуют наиболее прочные адсорбци-
' онные слои. Кроме того, на устойчивость
эмульсий значительное влияние оказывает
' заряд частиц эмульсии: чем он выше, тем
более устойчива эмульсия.
Коалесценция. Разрушение эмульсии, при-
водящее к расслаиванию, т. е. к отделению
обеих жидкостей, называется коалесценцией.
Самопроизвольное расслаивание эмульсии
называется автокоалесценцией.
Тип эмульсии, Дисперсионной .средой
в эмульсиях всегда является та жид-
кость, в которой хорошо растворимо поверх-
ностно-активное вещество. Например, если
поверхностно-активное вещество хорошо рас-
творимо в; воде, но плохо в масле, то обра-
зуется эмульсия типа масла в воде (М — В),
т. е. дисперсной фазой является масло, а
дисперсионной средой'—вода. Если же по-
верхностно-активное вещество хорошо рас-
творимо в масле, но плохо в воде, то обра-
зуется эмульсия воды в масле (В — М).
Методы разрушения эмульсии. Эмульсии
могут быть разрушены: а) центрифугирова-
нием; б) нагреванием; в) в результате дли-
тельного стояния; г) путём пропускания
постоянного тока в случае, если дисперсная
фаза несёт электрический заряд (электро-
форез); д) под действием переменного тока
высокой частоты и напряжения; е) под дей-
ствием поверхностно-активных веществ, об-
ладающих большей поверхностной активно-
стью, чем эмульгатор, поменьше* поверхност-
ной прочностью; ж) под действием поверхно-
стно-активных веществ, образующих другой
тип эмульсии, т. е. хорошо растворимых в ди-
сперсной фазе, при этом при определённой
концентрации добавленного вещества проис-
ходит разрушение эмульсии, а при больших
концентрациях — так называемая инверсия
фаз, т. е. образуется эмульсия, по типу об-
ратная той, которая была .вначале.
Гели и их свойства
Основные пути получения гелей. Сущест-
вует два основных пути получения гелей:
а) коагуляция золей лиофильных коллоидов:
так называемое желатинирование; б) погло-
щение сухим веществом растворителя с обра-
зованием геля; этот процесс носит название
набухания.
Желатинирование. Желатинированию лио-
фильных коллоидов способствуют: а) повы-
шение концентрации дисперсной фазы; б) по-
нижение температуры; в) время; г) электро-
литы, причём главную роль в этом процессе
играют анионы, которые могут быть распо-
ложены в определённый ряд (лиотропный
ряд), в котором каждый предшествующий
анион действует желатинирующим образом
сильнее, чем предыдущий: SO< > CeHjO^ >
> CeH8O" > СН3СОО' > С1' > СЮ' > NO' >
> Br' ?> J' > CNS'.
Набухание есть процесс поглощения су-
хим веществом, представляющим собой вы-
сушенный гель, растворителя, связанный с
увеличением объёма вещества.
Эластичные и неэластичные гели. Первые
при потере растворителя уменьшаются в
объёме до тех поргпока не получится совер-
шенно сухое вещество, способное при новом
действии на него растворителя набухать и
превращаться в первоначальный гель; по-
этому такие гели называются ещё набухаю-
щими. Неэластичные гели при потере жид-
кости уменьшаются в объёме до известной
величины, после чего потеря жидкости уже.
не сопровождается заметным изменением
объёма. Последующее погружение высохшего
геля в растворитель хотя и влечёт за собой
КОЛЛОИДНАЯ химия
355
проникновение этого последнего в капилляр-
ные пустоты, пронизывающие гель, но это
поглощение жидкости уже не связано с за-
метным изменением объёма геля; такие гели
называются ещё ненабухающими. Набухаю-
щие, или ‘•ластичные, гели способны погло-
щать жидкость только определённой при-
роды. Так, например, желатина набухает в
воде, но не набухает в спирте; резина набу-
хает в бензине, но не набухает в воде.
Предельно или ограниченно набухающие
гели поглощают растворитель только до опре-
делённого предела, причём количество по-
глощённой жидкости зависит от её при-
роды. Примером ограниченно набухаю-
щего геля являются резина, желатина и др.
Беспредельно или неограниченно набухаю-
щие гели поглощают постепенно всё большее
и большее количество растворителя и затем
переходят в состояние золя. Превращаясь
в золь, они могут иметь любую концентра-
цию. Примером является гуммиарабик, не-
которые белки, каучук.
Явления, сопровождающие набухание.
Суммарный объём вещества и растворителя
в результате набухания сокращается. В ре-
зультате набухания выделяется теплота
(теплота набухания). Набухающее тело ока-
зывает давление на встречаемые им препят-
ствия. Это давление называется давлением
набухания.
Факторы, влияющие на набухание. Давле-
ние на систему набухающее вещество — рас-
творитель способствует набуханию. Повыше-
ние температуры увеличивает скорость
набухания. Анионы по своему действию на
процесс набухания можно так же, как и в
случае желатинирования, расположить в ряд.
Но так как процесс набухания является
обратным желатинированию, то ряд надо рас-
положить в обратном порядке.
Структура гелей. Внутренняя структура
гелей очень сложна. В большинстве случаев
гели имеют сетчатое строение, т. е. отдель-
ные ультрамикроны соединяются вместе,
образуя нити, перепутанные между собой, и
в пространстве между этими нитями заклю-
чён растворитель, содержащий примеси,
сопутствующие гелю, а также не связанные
между собой мицеллы. По механическим свой-
ствам гели занимают промежуточное положе-
ние между жидкостями и твёрдыми телами.
Тиксотропия. Тиксотропией называется
свойство многих гелей после механического
перемешивания становиться жидкотекучими,
т. е. переходить в золи, а после выдержи-
вания в спокойном состоянии вновь затвер-
девать, восстанавливая упругие свойства
геля. Процесс этот вполне обратимый и может
быть повторен много раз. Тиксотропными
свойствами обладают: гидрат окиси железа,
содержащий количество электролита, недо-
статочное до полной коагуляции, гели окиси
алюминия, глины (бентониты), некоторые
белки.
Синерезис. Всякий гель с течением вре-
мени разрушается— стареет. Одним из про-
цессов, связанных со старением геля, яв-
ляется процесс сжатия геля с отделением
жидкой фазы, представляющей собой золь с
небольшой концентрацией дисперсной фазы.
Этот процесс называется синерезисом.
Таблица 20
Важнейшие константы по Р. Т. Барджу (1941 г.)
Константа Обозначение и величина
Число Авогадро . . Заряд электрона . . Удельный за ряд элек- трона Постоянная Планка. Масса электрона . . Масса атома водоро- да (Ht) Масса протона . . . Масса а-частицы . . Отношение массы атома водорода к массе электрона Отношение массы протона к массе электрона Энергия 1 абс. вольт- электрона в эргах Энергия в калориях на моль для 1 элект- рон-вольта на моле- кулу Постоянная закона смещения Вина . . Вторая радиацион- ная постоянная . . Постоянная закона Стефана-Больцмана Число Лошмидта . . Скорость света . . . Гравитационная по- стоянная Ускорение силы тя- жести (стандартное значение) То же на широте 45° Стандартная атмо- сфера 4б°-ная атмосфера . Литр ( = 1 000 мл. литр) Объём 1 моля иде- ального газа (0° С; 1А) Механический экви- валент теплоты . . Температура плавле- ния льда по абсо- лютной шкале . . . Газовая постоянная на 1 моль Отношение единиц физической и хими- ческой шкал .... Постоянная Фарадея (по химической шкале) Постоянная Фарадея (по физической шкале) Плотность ртути <0°; Ао) А=6,02-1Саз моль 1 е="4,80-10“"'CGSE- —20 «1,602-10 CGSM — = 1,759-10’ CGSMa~: = -=5.273.10” CGSE г Л-6.62.10"27 э сек m=9.106-10-28 г —24 M =1,6733.10 г н —24 М - 1,6724 НО г Р —24 М = 6.644.10 г а М —— = 1837.5 т М —Л- - 1836,5 гп Ео = 1.6О20.10—12э —1 23,052 ккал» моль А «0,28791 см* г рад Са=» 1,4384 см*град а=5,672.1о“5 э.сле"2 —4 —1 град сек п0=2,687-10 19см 3 С = 2,99776* 10’° см-сек~1 —Я о g=6.670*10 дин»см*»г _2 g0 «980,665 см*сек __9 g45 = 980,61 6 см* сек Ао«1.013246.10е дин-смГ2* —1 • ат А«в=1.013195.10е дин-см~~2- —1 • ат /==]ue().('j8 смъ = 22,4140 л • ат -молъ 1 Ju=4,1855 абс. дж, кал То=273,16° К } моль * = 1.9864 кал^град * моль 1 = -=8,2054 л - ат - моль * г=1,00027 Г=В6501 межд. кул. г. экв ' = = 96487 абс. кул. г. экв * = =9648.7 CGSM г. экв. Г=96514 абс. кул. г. экв * = =9651,4 CGSM г. экв —3 £)о = 13,595О г*см
23*
356
химия
ЛИТЕРАТУРА И ИСТОЧНИКИ
Бродский А. И. Физическая химия. Т. 1—2.
М.. Госхимиздат, Т. 1. Свойства материи. Хими-
ческая термодинамика. 6-е изд., 1948, 488 с.
Т. 2. Растворы, электрохимия, химическая
кинетика, фотохимия. 6-е изд., 1948, 491—998 с.
Глиика Н. Л. Общая химия. 4-е изд., М.—Л.,
Госхимиздат, 1948, 605 с.
ДумаискийА. В. Учение о коллоидах. 3-е,
изд., М.—Л., Гостехиздат, 1948, 416 с.
Липатов С. М. Физико-химия коллоидов. М.—
Л., Госхимиздат, 1948, 372 с.
Менделеев Д. И. Основы химии. Т. 1 — 2.
13-е изд., М-—Л., Госхимиздат, 1947. Т. 1,624 с.
Т. 2, 708 с.
Некрасов Б. В. Курс общей химии. 8-е изд.,
М.—Л., Госхимиздат, 1948, 1008 с.
Павлов Б. А. Курс органической химии. М.,
Госхимиздат, 1943, 501 с.
Песков Н. П. и Александрова-
Прейс Е. М. Курс коллоидной химии. 2-е
изд., М.—Л., Госхимиздат. 1948, 384 с.
Раковский А. В. Введение в физическую хи-
мию. М., ГОНТИ. Ред. Хим. лит-ры, 1938,
677 с.
Раковский А. В. Курс физической химии. М.,
Госхимиздат, 1939, 544 с.
С ем ат Г. Введение в атомную физику. Пер. с
англ. М., Гос. изд. иностр, лит-ры, 1948, 439 с.
Техническая энциклопедия. Справоч-
ник физических, химических и технологических
величин. Т. I—X. М., Советская энциклопедия,
1929-1936, 10 т.
Федулов И. Ф. Учебник физической химии.
2-е изд., М.—Л., Госхимиздат, 1946, 296 с.
Чичибабин А. Е. Основные начала органиче-
ской химии. Вып. 1—2, М.—Л., Госхимтехиздат,
1932.
ШорыгинП. И. Курс органической химии. М.
Л., Гос. иаучн.-техн. изд. хим. лит-ры, 1940,
563 с.
Шпольский Э. В. Атомная физика. М,—Л.,
Гостехиздат, 1944, 674 с.
МЕХА НИ КА
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Механика представляет собой учение об
общих законах движения физических тел.
Движение является неотъемлемым свойством
материи, и все происходящие в окружаю-
щем нас мире явления и процессы представ-
ляют собой различные формы движения ма-
терии.
Механика занимается изучением простей-
шей формы движения материи — так назы-
ваемого механического движения, т. е. из-
менения положения тела в пространстве
с течением времени.
В основе классической механики лежат
законы, изложенные в точном и закончен-
ном виде Ньютоном в его «Philosophiae natu-
ralis principia mathematica» в 1687 г.*. Эти
законы представляют собой обобщение тех
многочисленных фактов, относящихся
к области механики, которые постепенно
в течение многих веков накопило человече-
ство в результате непосредственных наблю-
дений, опыта и производственной деятель-
ности. Хотя возникшая в первой четверти
XX века теория относительности произвела
коренные принципиальные изменения и в об-
ласти физики, и в области механики, и от-
вергла законы классической механики, од-
нако классическая механика сохраняет своё
значение и в настоящее время. Это объяс-
няется тем, что, как показывают опыт и
вычисления, количественные расхождения
между выводами классической механики и
новой механики, основанной на теории от-
носительности, становятся существенными
лишь при изучении таких явлений, где на-
блюдаются движения с очень большими
скоростями, близкими к скорости света
(3- 10ь км/сек)-, при скоростях же, далёких
от скорости света, эти расхождения на-
столько незначительны, что ими вполне мож-
но пренебречь. Поэтому классическая меха-
ника и в настоящее время является той тео-
ретической базой, на которой строятся все
прикладные технические дисциплины и про-
изводятся все технические расчёты.
Механика делится обычно на три основ-
ных раздела — статику, кинематику и дина-
мику. Статика есть отдел механики, посвя-
щённый изучению условий равновесия ме-
ханических систем. Кинематика занимается
изучением движения механических систем
с геометрической точки зрения, независимо
от сил, действующих на эти системы. Пред-
метом динамики является установление и
изучение связи между движением механи-
ческих систем и действующими на них си-
лами.
При измерении величин пользуются двумя
общепринятыми системами единиц: или ф и-
зической системой (система CGS)
или технической системой еди-
ниц (система MKS). В физической системе
основными единицами являются: единица
длины — сантиметр (см), единица массы —
грамм-масса (г) и единица времени — се-
кунда (сек.). В технической системе основ-
ными единицами являются: единица длины—
метр (м), единица силы — килограмм (кг) и
единица времени — секунда (сек.). Все дру-
гие единицы, служащие для измерения раз-
личных величин, являются в обеих систе-
мах производными от трёх указанных ос-
новных единиц. В механике принята тех-
ническая система единиц.
СТАТИКА
СИЛЫ С ОБЩЕЙ ТОЧКОЙ ПРИЛОЖЕНИЯ
Сложение сил. Абсолютно твёрдым телом
называют такое тело, расстояния меж-
ду точками которого постоянны; следова-
тельно, форма и размеры такого тела оста-
ются неизменными. В твёрдом теле силу
можно переносить вдоль линии её действия,
т. е. сила, приложенная к твёрдому телу,
является скользящим вектором.
* Русский перевод этого сочинения сделан акад.
А. Н. Крыловым.
Две силы Р] и Р2, приложенные в одной
точке твёрдого тела, можно заменить при-
ложенной в той же точке равнодейст-
вующей силой R, равной по направ-
лению и величине диагонали параллело-
грама, построенного на силах Рх и Рг (фиг. 1)
(закон параллелограма сил).
Если несколько сил Plt Рг, Р3, Р4, Р3
(фиг. 2, а) приложены в одной точке твёр-
дого тела или если линии действия сил пе-
ресекаются в одной точке, то эти силы мож-
358
МЕХАНИКА
но привести к одной равнодействующей,
которая проходит через общую точку при-
ложения всех сил. Это можно сделать, скла-
дывая данные Силы последовательно по пра-
вилу параллелогоама или построением сило-
вого многоугольни-
уГ-------------ка (Фиг- ПРИ‘
р ' iLs-'"/' чём вектор, соеди-
У / няющий начало пер-
вой силы с концом
последней (замыкаю-
* щая сторона много-
фиг- 1 угольника), предста-
вляет собой равно-
действующую данных сил (правило силового
многоугольника). Последовательность, в ко-
торой складываются силы, не имеет при
этом никакого влияния на конечный резуль-
тат.
При аналитическом способе определения
равнодействующей силы выбирают прямо-
угольную систему координат с началом в об-
щей точке приложения всех данных сил и
проектируют эти силы на направления трёх
координатных осей.
Фиг. 26
Фиг. 2а
Проекции равнодействующей:
Rx = R cos а = SP, cos <Х; = S X/;
Ry = R cos р = S Р, cos = S Vi>
R2 = R cos -( = S Pt cos 7г = SZ;.
Величина равнодействующей определяет-
ся, как диагональ параллелепипеда:
R — v'rI + R* + R2X ,
а её углы с осями координат определяются
из равенств:
Rx
COS а == — х------------ ;
/r2 + R2 + R2
- ,п _ R,
CuS [5 == - ---------- ,
Vr2x + R2 + R2
D
COS 7 — ....... z v
|/ R2x + R2 + R;
Равновесие сил. Условие равнове-
сия сил с общей точкой приложения со-
стоит в том, чтобы их равнодействующая R
равнялась нулю, т. е. чтобы многоугольник
этих сил замыкался сам собой; аналитиче-
ски это условие выражается так:
S Xi = 0; Yi = 0; VZ; = 0
(сумма проекций всех сил на каждую из
координатных осей равна нулю).
Разложение силы. Задача разложения
данной силы Р по двум заданным направ-
лениям 7 и 2, лежащим с ней в одной плос-
кости, имеет единственное решение и ре-
шается построением параллелограма, сторо-
ны которого имеют заданные направления
7 и 2 и диагональю которого является дан-
ная сила Р (фиг. 3).
По трём направлениям 7, 2, 3, не лежа-
щим в одной плоскости, сила Р может быть
разложена единственным образом. Эту за-
дачу можно решить аналогично предыду-
щей— построением параллелепипеда, рёбра
которого имеют заданные направления и
диагональю которого является данная сила
Фиг. 4
Разложение силы Р по трём или более
заданным направлениям, лежащим с ней
в одной плоскости, или более чем по трём
заданным направлениям, не лежащим в од-
ной плоскости, является уже задачей не-
определённой.
ПАРАЛЛЕЛЬНЫЕ СИЛЫ
Сложение параллельных сил. Если линии
действия двух данных сил Pt и Р2, прило-
женных к твёрдому телу, параллельны, при-
чём эти силы направлены в одну сторону,
то такие две силы приводятся к одной рав-
нодействующей силе R, величина которой
равна арифметической сумме данных сил,
т. е. R = Р, + Ра (фиг. 5). Линия действия
силы R параллельна линиям действия дан-
ных сил и делит расстояние между ними на
части, обратно пропорциональные этим си-
АС Р —
лам, т. е. . Если силы PL и Р2 на-
правлены в разные стороны (антипарал-
лельны) и не равны по величине, то в этом
случае их равнодействующая равна по вели-
чине их разности и направлена в сторону
большей силы (фиг. б). Линия действия этой
равнодействующей делит расстояние АВ
р
в отношении —? внешним образом; следова-
СТАТИКА
359
тельно, предыдущая пропорция имеет место
и п этом случае, но точка С лежит вне от-
резка АВ, за большей силой. Из этой про-
порции получаем (в обоих случаях) следую-
щие равенства:
АС = СВ = АВ
К Рг R ’
откуда
АС = АВ и СВ = -1 АВ.
R R
Если две антипараллельные силы равны
по величине, т. е. = —Рг, то они образуют
пару сил. Такие две равные по величине
антипараллельные силы не могут быть при-
ведены к одной равнодействующей силе,
т. е., другими словами, пара сил не
имеет равнодействующей.
Легко решается и обратная задача: дан-
ную силу R разложить на две параллель-
ные ей составляющие силы, линии действия
которых должны проходить через две задан-
ные точки А и В. Так как линии действия
искомых составляющих сил известны, то
остаётся найти только их величину. По-
скольку точки А к В заданы, то расстоя-
ния АВ, АС и СВ будут известны (точка’С
есть точка пересечения линии действия силы
R с прямой АВ), а потому из вышеуказан-
ных пропорций находим
„ СВ „ п АС „
р = гг р и Р,= —. R.
1 АВ 2 АВ
Если к твёрдому телу приложены не-
сколько параллельных сил, направленных
в одну сторону, то последовательным сло-
жением эти силы приводятся к одной рав-
нодействующей силе, параллельной данным
силам, направленной в ту же сторону и
равной по величине их арифметической
сумме. Система параллельных сил, из кото-
рых одни направлены в одну сторону, а
другие — в противоположную сторону, при-
водится или к одной равнодействующей
силе, равной по величине алгебраической
сумме всех данных сил, или к одной паре
(в этом случае алгебраическая сумма всех
данных сил равна нулю), или находится
в равновесии, т. е. приводится к двум си-
лам, равным по величине и направленным
по одной прямой в противоположные
стороны.
Центр параллельных сил. Центром дан-
ной системы параллельных сил называется
такая точка, через которую проходит линия
равнодействующей этих сил и положение
которой зависит только от величины данных
параллельных сил и от точек их прило-
жения, но не зависит от их направления.
Следовательно, если фиксировать точки при-
ложения и величину данных параллельных
сил, а изменять только направление этих
сил, сохраняя, однако, их параллельность,
то равнодействующая этих сил, изменяя своё
направление, будет проходить через одну
и ту же точку — центр этих параллельных
сил. Если параллельные силы представляют
собой веса материальных частиц данного
тела, то центр таких параллельных сил на-
зывается центром тяжести этого тела.
Координаты центра параллельных сил С
определяются по формулам:
_i ^i_ yi 5
; Ус- ; z„- s-p
В этих формулах x,, yt, Zf обозначают
координаты точек приложения данных па-
раллельных сил, а величины Р/ этих сил
берутся в алгебраическом значении, т. е.
силы, направленные в одну сторону, счита-
ются положительными, а силы, направлен-
ные в противоположную сторону, — отрица-
тельными.
МОМЕНТЫ
Момент пары. Преобразование пар. Мо-
ментом данной пары называется вектор,
равный по величине произведению величины
одной из сил пары на плечо этой пары,
т. е. на расстояние между линиями дейст-
вия сил пары. Этот вектор направлен по
перпендикуляру к плоскости пары в ту сто-
рону, с которой наблюдатель, смотрящий с кон-
ца этого вектора на пару, видел бы обе силы па-
ры направленными против часовой стрелки от-
носительно сере- л
дины плеча этой ' - _
пары (фиг. 7). Что
касается точки у
приложения этого /у Sf
вектора (его на- —//
чала), то эта точ- /
ка может быть
выбрана произ- фиг- 7
вольно, т. е. мо-
мент пары есть вектор свободный.
Эффект действия пары на данное твёрдое тело
вполне определяется её вектором-моментом.
Отсюда следует: 1) если две пары имеют
равные векторы-моменты (т. е. равные по
величине, параллельные и направленные
в одну сторону), то эти пары эквива-
лентны, т. е. производят на данное твёр-
дое тело одинаковое действие и потому мо-
гут быть заменены одна другой; 2) не изме-
няя действия данной пары на тело, можно
производить всякие преобразования этой
пары, при которых её вектор-момент ос-
таётся неизменным. Поэтому данную пару
можно как угодно перемещать в её плоско-
сти; пару можно переносить в другую пло-
скость, параллельную плоскости этой пары;
величину сил и плеча данной пары можно
изменять, но так, чтобы величина её мо-
мента оставалась неизменной.
Сложение пар. Если к данному твёр-
дому телу приложена система пар, как
угодно расположенных в пространстве, то
эти пары всегда можно привести к одной
равнодействующей паре, момент которой ра-
вен геометрической сумме моментов данных
пар; следовательно, операция сложения пар
приводится к сложению по правилу много-
угольника их векторов-моментов. Если
(в частном случае) все данные пары лежат
в одной плоскости, и их моменты парал-
лельны, то в этом случае они скла-
дываются алгебраически, причём моменты,
направленные в одну сторону, считаются
положительными, а моменты, направленные
Збй
МЕХАНИКА
в противоположную сторону, — отрицатель-
ными. Если сумма векторов-моментов дан-
ных пар равна нулю, то такие пары урав-
новешиваются.
Момент силы относительно точки. Если
к телу приложена сила Р, изображаемая
вектором АВ, и дана какая-нибудь точка О
(фиг. 8), то момент этой силы относительно
точки О, подобно моменту пары, изобра-
жается в виде вектора. Этот вектор прило-
жен в точке О и направлен по перпендику-
ляру к плоскости треугольника ОАВ в т,у
сторону, чтобы наблюдатель, смотрящий
с конца этого вектора на этот треугольник,
видел силу Р направленной против часовой
стрелки относительно точки О. Величина
(модуль) этого вектора равна произведению
величины данной силы на её плечо относи-
тельно точки О, т. е. на длину h перпенди-
куляра, опущенного из точки О на линию
действия силы Р (на высоту треугольника
ОАВ), следовательно |mom0(p)| = Ph =
-- 2 площ. ОАВ.
Если к данному телу приложена система
сил Pit приводящаяся к одной равнодейст-
вующей силе R, то момент этой равнодейст-
вующей относительно любой точки О равен
геометрической сумме момен-
тов с и л Pi относительно той же точки
(теорема Вариньона), т. е.
тот0 (R) — £тот0 (Р{ ).
Если силы Pi лежат в одной плоскости,
то их моменты относительно какой-нибудь
точки, лежащей в той же плоскости, на-
правлены по одной прямой, и потому
в этом случае эти моменты складываются
алгебраически, причём моменты сил, на-
правленных относительно данной точки про-
тив часовой стрелки, считаются положитель-
ными, а моменты сил, направленных по ча-
совой стрелке, — отрицательными.
В случае пары сил геометрическая сумма
моментов сил этой пары относительно любой
точки О есть величина постоянная, равная
вектору-моменту этой пары, т. е.
т от (Pi — р) = тот0 (р) + тото (— Р).
Мсмент силы относительно оси. Кроме
момента силы относительно точки в меха-
нике приходится рассматривать также мо-
мент силы относительно оси; чтобы найти
момент силыР относительно данной оси г
(фиг. 8), нужно спроектировать эту силу
на плоскость, перпендикулярную к этой оси,
например на плоскость Оху, и величину р
полученной проекции умножить на длину h'
перпендикуляра, опущенного на линию этой
проекции из точки пересечения О оси z
с этой плоскостью, т. е.
тотг (Р) = h'p = 2 площ. ОаЬ.
При этом момент считается положитель-
ным, если для наблюдателя, смотрящего
с положительного конца данной
оси, проекция силы Р на плоскость, перпен-
дикулярную к этой оси, будет направлена
против часовой стрелки относительно точки
пересечения данной оси с этой плоскостью;,
в противном случае момент считается отри-
цательным; следовательно, момент силы от-
носительно оси есть скалярная алгебраиче-
ская величина. Если сила и данная ось ле-
жат в одной плоскости, то момент силы
относительно этой оси равен нулю, так как
в этом случае или р = 0 (сила парал-
лельна оси), или h' — 0 (линия действия
силы пересекает ось).
Аналитически моменты силы Р относи-
тельно координатных осей х, у, г определя-
ются по формулам:
тотх (Р) = yZ—zY; тоту (Р) = zX — xZ;
тотг (р) = xY — уХ,
где х, у, z обозначают координаты точки
приложения данной силы, а X, У, Z — про-
екции этой силы на координатные оси.
Для осевых моментов, так же как и для
моментов сил относительно точки, имеет ме-
сто теорема Вариньона, т. е.
momx(p) = 2 тот* ( Рг ).
Если обозначим угол вектора тото (р)
с положительным направлением оси z через
7 (фиг. 8), то проекция этого вектора на
ось z будет равна
| тот0 (р) |coS7 = 2 площ. ОАВ cos 7.
Но треугольник ОаЬ есть проекция треуголь-
ника ОАВ на плоскость хОу, перпендику-
лярную к оси z, а потому
2 площ. ОАВ cos 7 = 2 площ. ОаЬ =
= тотг (Р).
Следовательно,
| тото (р) | cos 7 = mom2 (р),
т. е. проекция вектора-момента силы отно-
сительно данной точки на какую-нибудь,
ось, проходящую через эту точку, равна мо-
менту этой силы относительно той же оси.
Если к данному твёрдому телу, которое
может вращаться вокруг неподвижной оси,
приложена система сил Р,, то для равнове-
сия такого тела необходимо, чтобы алге-
браическая сумма моментов сил Рг относи-
тельно оси вращения тела равнялась нулю.
Этим условием равновесия твёрдого тела,
могущего вращаться вокруг неподвижной оси,
часто пользуются в задачах статики, напри-
мер в задачах, относящихся к случаю рав-
новесия рычага.
СТАТИКА
36 i
ПЛОСКАЯ СИСТЕМА СИЛ
Приведение системы сил к данному
центру. Пользуясь возможностью переноса
точки приложения силы по линии действия
этой силы и правилом параллелограма, си-
стему сил, лежащих в одной плоскости,
можно привести к одной равнодействующей
силе или к одной паре сил.
Однако при изучении плоской системы
сил обычно пользуются другим методом, ко-
торый называется приведением систе-
мы сил к данному центру.
Нужно иметь в виду, что силу, как сколь-
зящий вектор, можно переносить только
вдоль линии её действия.
При параллельном переносе силы Р в
другую точку (в положение Рг), находя-
щуюся на расстоя-
нии d от линии дей-
ствия силы Р, полу-
чается добавочная
пара, момент которой
равен M=Pd (фиг.9).
Этой вспомогатель-
ной теоремой и поль-
зуются при применении метода приведения
системы сил к данному центру, который со-
стоит в следующем: выбирают произвольную
точку О, лежащую в плоскости данной си-
стемы сил и называемую центром при-
ведения, и переносят все силы парал-
лельно самим себе в эту точку, причём при
переносе каждой силы получается добавоч-
ная пара, момент которой равен моменту
этой силы относительно выбранного центра
приведения. Все перенесённые силы склады-
вают по правилу многоугольника и приво-
дят к одной силе R, называемой главным
вектором данной системы сил. Складывая
далее все добавочные пары, приводят их
к одной паре, момент которой Мо называется
главным моментом данной си-
стемы сил относительно центра О. При
этом:
R =
Rx = S Rv = S Yi и Ма = 2 тота (Pi) =
= S (х,Уг - у,Х,).
Условия равновесия плоской системы
сил. Если плоская система сил находится
в равновесии, то главный вектор этой си-
стемы и её главный момент будут равны
нулю; следовательно:
S = 0; S Yt = 0 и 2(хгУ; - у;Х;) = 0.
Эти три условия равновесия плоской си-
стемы сил можно выразить в другой форме,
приравнивая нулю сумму моментов всех сил
системы относительно каждой из трёх про-
извольно выбранных точек, не лежащих на
одной прямой.
Очень часто при решении задач статики,
когда из двух опорных реакций известно
направление только одной из них, удобно
пользоваться следующей теоремой: если три
непараллельные силы находятся в равновесии,
то линии этих сил пересекаются в одной
точке. Опорные реакции определяются в этом
случае из того соображения, что на основа-
нии указанной теоремы линия равнодейст-
вующей всех заданных сил и линии дейст-
вия двух опорных реакций должны пересе-
каться в одной точке и что многоугольник
этих трёх сил должен быть замкнутым.
Пример. На фиг. 10 изображена схема крана. Опор-
ная реакция Rq верхнего подшипника направлена
горизонтально; через точку О пересечения заданной
силы Q и опорной реакции Rq должна проходить
линия опорной реакции этим определяется на-
правление силы Ra- Величины и Rq определя-
ются затем из силового треугольника.
При аналитическом способе решения этой
задачи нужно написать три условия равно-
весия всех сил, приложенных к крану. На-
правляя координатную ось у по АВ, а ось
х —перпендикулярно к АВ, проектируя затем
все силы на эти оси и составляя сумму мо-
ментов всех сил относительно точки А, по-
лучают следующие три уравнения:
Хд-Рв = °; ya - Q = °; ,1^в -dQ= О,
где h = АВ, d— плечо силы Q относительно
точки А, а ХА и Y А обозначают проекции
силы RА. Из этих трёх уравнений опреде-
ляются все три неизвестные силы
Хд= Rs=df, Va=Q.
Величина реакции
Ra = / Л + У А-
Ив.
Фиг. 10
3 заданы. Опреде-
Если все силы, приложенные к телу
(включая и силы реакции связей), парал-
лельны, то проекция каждой силы на ось х,
перпендикулярную к этим силам, будет
равна нулю, а потому
в этом случае вместо
трёх условий равнове-
сия имеем следующие
два:
SF; = 0, Sx;Fi = 0.
В качестве второго
примера рассмотрим
следующую задачу.
Данная плоская си-
стема сил, которая при-
водится к одной равно-
действующей R, долж-
на уравновешиваться
тремя силами, линии
действия которых 7, 2,
лить величины этих сил (фиг. 11).
Для решения этой задачи выбирают центр
моментов в точке пересечения двух задан-
ных линий, например в точке пересечения
линий 2 и 3; величину силы Рг, направлен-
ной по линии 7, находят из уравнения мо-
ментов относительно этой точки: Rax= Р^;
следовательно, Pt = 1,1 R.
362
МЕХАНИКА
Аналогично из уравнений моментов от-
носительно точек пересечения прямой 7
с прямыми 2 и 3 находят силы Р2 и Ра:
Р2 = R и Ps = р R*.
Ь 2 &3
Решение возможно лишь в том случае,
когда три заданные прямые 7, 2 и 3 не пе-
ресекаются в одной точке.
СИСТЕМА СИЛ В ПРОСТРАНСТВЕ
Приведение системы сил к данному центру.
Для сложения сил Ph действующих на твёр-
дое тело и расположенных как угодно в прост-
ранстве, поступают подобно тому, как и при
сложении сил, лежащих в одной плоскости.
В общем случае система сил в пространстве
приводится к одной силе R, приложенной в
произвольно выбранной точке О, называемой
центром приведения, и к одной
паре с моментом М„.
Эта сила R называется главным век-
тором д а нн о й системы сил, а
вектор-момент М„ называется её главным
моментом относительно выбран-
ного центра приведения О.
При этом:
R = X Р[ и Мо = 2 тото ( Р, ).
Отсюда:
Rx = S Хг; Ry = v Yr, R2 = v zf;
Mox = '&momx(Pi ) = v (ytZi — ZiY;);
= 2 momv (Pj ) = 2 (z,Xz — x;Z,);
M03 = Smotn, (Pi ) = S (XiYi — y,X,).
Одну из сил пары, которая получается
в результате приведения данной системы сил
к какому-нибудь центру, всегда можно вы-
брать так, чтобы эта сила была приложена
в центре приведения. Тогда, сложив эту
силу с главным вектором, получают две скре-
щивающиеся силы. Следовательно, систе-
му сил в пространстве можно
всегда привести к двум скре-
щивающимся силам.
Условия равновесия. Для равновесия си-
стемы сил в пространстве необходимо и до-
статочно (так же как и для равновесия
плоской системы сил), чтобы главный век-
♦ В том случае, когда две из данных прямых,
например 2 и 3, параллельны, для определения Р\
нужно «оставить уравнение проекций на ось, пер.
пендикулярную к этим прямым.
тор этой системы и её главный момент от-
носительно произвольно выбранной точки
равнялись нулю или (в аналитической форме)
чтобы сумма проекций всех сил данной си-
стемы на каждую из трёх координатных
осей.равнялась нулю и чтобы сумма их мо-
ментов относительно каждой из этих осей
также равнялась нулю.
Следовательно, для системы сил в про-
странстве имеем шесть условий равновесия:
2Х( = 0; 2 Y{ = 0; S Z,-= 0;
S (y,-Z; — z,Yt) = 0; v (ZiXi — x^j) = 0;
^(XiYt-y.Xi) = 0.
Задачи статики, относящиеся к равнове-
сию твёрдого тела, находящегося под дей-
ствием пространственной системы £ил, ре-
шаются при помощи этих шести уравнений.
При помощи тех же шести уравнений мо-
жет быть решена и задача о разложении
какой-либо силы Р на составляющие, кото-
рые должны быть направлены по заданным
прямым линиям, ибо при изменении направ-
ления этих составляющих на противополож-
ное получим систему сил, для которой за-
данная сила Р является уравновешивающей.
Следовательно, все эти силы должны удо-
влетворять указанным выше шести условиям
равновесия. Так как линии действия иско-
мых составляющих заданы, то, имея шесть
уравнений, можно определить из них вели-
чину шести составляющих сил; следователь-
но, разложение данной силы по шести за-
данным в пространстве прямым линиям есть
задача статически определённая.
Задача становится невозможной, если за-
данные шесть прямых расположены так, что
можно провести прямую линию, пересекаю-
щую все эти шесть прямых и не пересекаю-
щую линии действия данной силы Р.
Для решения этой задачи можно выбрать
две оси, пересекающие четыре из шести за-
данных прямых, и составить уравнения мо-
ментов относительно этих осей. В получен-
ные два уравнения из шести неизвестных
сил войдут только две, которые из этих
уравнений и определяются.
Пример (фиг. 12). Горизонтальная плита ук-
реплена при помощи шести стержней и испытывает
действие сосредоточенной силы Р. Линия тт пересе-
кает стержни 1, 2, 3, 4 и 5 на конечном или беско-
нечно большом расстоянии; поэтому моменты сил
реакции этих стержней относительно оси тт равны
нулю, и из. уравнения моментов относительно этой
оси можно найти реакцию стержня <5. Затем из урав-
СТАТИКА
ЗбЗ
нения моментов относительно оси пп определяется
реакция стержня 5. Далее из уравнения моментов
относительно оси И находится реакция стержня
7 и т. д.
Рассмотренная задача имеет важное зна-
чение для случаев укрепления какого-нибудь
тела на тонких стержнях, которые могут
подвергаться только растягивающим или
сжимающим, но не изгибающим усилиям.
Чтобы задача была статически определён-
ной, таких стержней не должно быть более
шести.
ПРИНЦИП ВИРТУАЛЬНЫХ
ПЕРЕМЕЩЕНИЙ
Виртуальным (возможным) перемещением
механической системы называется всякое
бесконечно-малое перемещение этой системы,
допускаемое в данный момент наложенными
на систему связями. Если виртуальное пере-
мещение какой нибудь точки системы обозна-
чим через 3S, тб проекции этого вектора
на координатные оси будут равны Зх, Sy, Sz,
т. е. равны изменениям (вариациям) коорди-
нат этой точки.
Виртуальной работой силы Р называется
работа этой силы при виртуальном переме-
щении её точки приложения. Если обозна-
чим виртуальную работу через ЗА, то
8А = Р cos (Р, 6S)oS,
или (в аналитической форме)
ЗА = ХЗх + Уоу + Zbz.
Если данное твёрдое тело может вра-
щаться вокруг неподвижной оси г, то вир-
туальным перемещением для такого тела
является поворот на любой элементарный
угол Зср вокруг осн z. Виртуальная работа
силы Р, приложенной к этому телу, выра-
жается так:
ЗА = тотг(Р')Ъ<?.
В общем случае виртуальное перемещение
твёрдого тела можно разложить на два пе-
ремещения: 1) поступательное перемещение
8S0, равное перемещению какой-нибудь точки
О тела, и 2) поворот на элементарный угол
Зср вокруг некоторой оси, проходящей через
эту точку О. Сумма виртуальных работ сил
Pi, приложенных к этому телу, будет равна:
У. ЗА/ = R cos ф 8S0 + Mo cos 0 Зср,
где R — главный вектор данных сил Ру ф —
угол между/? и 3S0; Мо — главный момент
сил Pi относительно точки О и 0 — угол ме-
жду вектором Мо и осью вращения тела.
Если связи, наложенные на систему, та-
ковы, что сумма работ сил реакции этих
связей при всяком виртуальном переме-
щении системы равна нулю, то такие связи
называются идеальными.
Равновесие системы. Принцип виртуаль-
ных (возможных) перемещений состоит в
следующем: для того чтобы механическая
система оставалась в равновесии в данном
положении, необходимо и достаточно, чтобы
сумма работ всех действующих на неё сил
при всяком виртуальном перемещении си-
стемы равнялась нулю, т. е. чтобы при
всяком виртуальном перемещении системы
имело место равенство:
ZtXiSxi + Yflyi + Zfizi) = 0.
Это уравнение выражает в самом общем
виде необходимое и достаточное условие
равновесия любой механической системы.
В случае идеальных связей в это уравнение
силы реакции связей не входят, так как ра-
бота этих сил при всяком виртуальном пе-
ремещении системы равна нулю.
Принципом виртуальных перемещений
можно пользоваться для решения всякой
задачи статики. Согласно этому принципу
условие равновесия твёрдого тела выразится
уравнением
R созф35о + Мо cos 0 Bep =s 0.
Если тело сво-
бодно, т. е. не сте-
снено никакими
связями, то посту-
пательное и вра-
щательное пере-
мещения дтя та-
кого тела явля-
ются вполне про-
извольными. По-
этому, чтобы пре-
дыдущее уравне-
ние имело место
у
В
Фиг. 13
для всякого виртуального перемещения
тела, должны быть, очевидно, выполнены
условия:
R = 0 и Мо = О,
т. е. известные (см. выше) условия, которым
должны удовлетворять силы, приложенные
к твёрдому телу при равновесии.
Принципом виртуальных перемещений
часто пользуются для определения положе-
ния равновесия системы.
Пример (фиг. 13). При каком положении стер-
жень АВ =» I, несущий в точке В груз Q, будет на-
ходиться в равновесии, если пренебречь собственным
весом стержня и трением в точках А и С?
Будем определять положение стержня углом на-
клона а. Если начало координат возьмём в точке С,
то ордината точки В
УВ =» I sin а — d tg а.
Проекции силы Q на координатные оси равны:
Л = О и У « — Q.
Следовательно, виртуальная работа этой силы
равна
XSxB + = -<?%--« (/ cos « - fa.
Так как при равновесии эта работа должна быть
равна иулю, то
откуда
Геометрически положение равновесия стержня оп-
ределяется из того условия, что касательная в точке
В к траектории, которую описывает эта точка при
перемещении стержня, должна быть горизонтальной.
Равновесие называется устой-
чивым, если при достаточно малом откло-
364
МЕХАНИКА
нении механической системы от положения
равновесия и достаточно малых начальных
скоростях материальных точек этой системы
во всё время последующего движения си-
стема будет оставаться сколь угодно близ-
кой к положению равновесия (т. е. откло-
нения всех точек системы от положения
равновесия будут оставаться сколь угодно
малыми).
Пример. Неоднородный шар с эксцентрично
расположенным центром тяжести находится на го-
ризонтальной плоскости в устойчивом равновесии,
если центр тяжести лежит ниже геометрического
центра шара на одной вертикали с иим.
Равновесие называется неус-
тойчивым, если система, будучи выведена
из положения равновесия, при последующем
движении не будет оставаться сколь угодно
близкой к этому положению, как бы малы
ни были начальные скорости точек системы
и их начальные отклонения от положения
равновесия.
Пример. Неоднородный шар с эксцентрично
расположенным центром тяжести находится на гори-
зонтальной плоскости в неустойчивом равновесии,
если центр тяжести лежит выше геометрического
центра шара на одной с ним вертикали.
Равновесие называется без-
различным, если система, будучи выве-
дена из положения равновесия, остаётся и
в новом положении в состоянии равновесия.
Пример. Однородный шар, центр тяжести и
геометрический центр которого совпадают, нахо-
дится на горизонтальной плоскости в безразличном
равновесии.
Если система находится в потенциальном
силовом поле, то проекции на координатные
оси сил, действующих на систему, равны
в этом случае частным производным от по-
тенциальной энергии П по соответствующим
координатам, взятым с обратным знаком,
т. е.
v ЙП.,. <)П „ <)П .
Л;------— , х i — — — , Х/= — —
дх,- dyi dZi
Сумма виртуальных работ в этом случае
выражается так:
2 Xfix{ + Yfiyt + Zfizi =
S/дП» дП » , ffl. \
r dy, yi T dzt ')
Следовательно, согласно принципу вир-
туальных перемещений необходимым и до-
статочным условием равновесия системы,
находящейся в потенциальном силовом поле,
является равенство 8П = 0.
Чтобы судить о том, является ли равнове-
сие системы устойчивым или неустойчивым,
можно пользоваться следующим признаком
(признак Дирихле): если в положении рав-
новесия системы потенциальная энергия
имеет минимум, то равновесие является ус-
тойчивым.
В том случае, когда система находится
в поле силы тяжести, т. е. когда на неё дей-
ствуют только силы тяжести, потенциальная
энергия выражается так:
П = Mghe,
где М — масса всей системы, a hc — высота
центра тяжести системы, отсчитываемая от
некоторой горизонтальной плоскости (на-
пример, от поверхности земли). Следова-
тельно, в этом случае равновесие будет ус-
тойчивым при том положении системы, ко-
гда высота её центра тяжести имеет наимень-
шее из всех возможных значений. В том
положении, когда высота центра тяжести
системы имеет наибольшее значение, система
находится в неустойчивом равновесии. Если
hc = const, т. е. если центр тяжести системы
может перемещаться только в горизонталь-
ной плоскости, то равновесие является без-
различным.
ГРАФОСТАТИКА
Определение. Графическая ста-
тика, или графостатика, занимается графи-
ческим решением задач статики. Многие
задачи, не относящиеся непосредственно
к статике, например определение моментов
инерции, могут быть также весьма просто
решены методами графостатики.
Если дана система сил, как угодно рас-
положенных на плоскости, то для нахожде-
ния их равнодействующей графостатика даёт
простой метод, который основан на построе-
нии силового и верёвочного многоугольни-
ков.
Верёвочный многоугольник. Пусть дана
система сил Plt Р2, Р3, Pt (фиг. 14), рас-
положенных как угодно на плоскости; тре-
Фиг. 14
буется найти равнодействующую этой си-
стемы. Для этого строим в выбранном мас-
штабе силовой многоугольник abcde, стороны
которого равны по величине и направлению
заданным силам. Замыкающая сторона ае
этого многоугольника равна по величине и
направлению равнодействующей данной си-
стемы сил. Для нахождения линии действия
этой равнодействующей делают следующее
построение: берут произвольную точку О,
которая называется полюсом, и соединяют
её лучами 7, 2, 3, 4, 5 с началом и концом
каждой силы, имеющейся в многоугольнике
abcde. Затем из произвольной точки М про-
водят прямую 7' параллельно лучу Оа до
СТАТИКА
365
пересечения в точке А с линией действия
силы Pi; затем из точки А проводят вторую
прямую 2' параллельно лучу ОЬ до встречи
в точке В с линией действия силы Ра. Точ-
нотакже проводятся, далее, линии 3',4',5'.
Многоугольная линия MABCDN называется
верёвочным многоугольником,
или многоугольником Вариньона.
Продолжая крайние стороны Г и 5' верё-
вочного многоугольника до их пересечения,
находят точку К, через которую проходит
линия действия равнодействующей данной
системы сил; перенося в эту точку вектор
ае, определяющий величину и направление
искомой равнодействующей, получают пол-
ное решение задачи.
Применяя построение силового и верё-
вочного многоугольников, легко решить гра-
фически и обратную задачу о разложении
данной силы на две составляющие. Пусть
требуется данную силу R разложить на две
составляющие силы, направленные по задан-
ным прямым I и II, параллельным силе R
(фиг. 15). Для этого строят вектор ас, рав-
ный и параллельный силе R, и соединяют
точки а и с лучами 1 и 3 с произвольно вы-
бранным полюсом О. Затем проводят из
произвольной точки прямую Г, параллель-
ную лучу 1, которая пересечёт прямую I и
линию действия силы R в точках А и К; из
точки /< проводят прямую 3', параллельную
лучу 3, которая пересечёт прямую II в точ-
ке В. Если соединить точки А и В прямой
2' и провести из полюса О прямую, парал-
лельную АВ, то получим на силовом много-
угольнике луч 2. Если обозначить точку пе-
ресечения этого^ луча с вектором ас через
Ь, го векторы ab и Ьс представляют собой
искомые составляющие силы.
Этим способом можно графически найти
опорные реакции в случае балки, лежащей
на двух опорах А и В (фиг. 16). Для этого
нужно найти равнодействующую R задан-
ных параллельных сил Р1Г Р2 и Р3, прило-
женных к балке, и затем разложить эту
равнодействующую на две параллельные ей
силы, проходящие через опоры.
Эти составляющие силы определяют дав-
ления балки на опоры. Силы, равные им по
величине и противоположные по направле-
нию, представляют собой искомые реакции
опор Ra и Rb.
Если данная плоская система сил такова,
что многоугольник этих сил окажется замк-
нутым, то крайние (т. е. первый и послед-
ний) лучи на силовом многоугольнике сов-
падут, а соответствующие им стороны ве-
рёвочного многоугольника будут парал-
лельны; точка К пересечения этих сторон
окажется бесконечно удалённой, и, следова-
тельно, верёвочный многоугольник не будет
замыкаться.
В этом случае данная система сил не
имеет равнодействующей и приводится к паре
сил. Чтобы данная система сил находилась
в равновесии, необходимо (и достаточно),
чтобы совпадали не только крайние лучи на
силовом многоугольнике, но и соответст-
вующие им крайние стороны верёвочного
многоугольника, т. е. для равновесия пло-
ской системы сил необходимо и достаточно,
чтобы и силовой, и верёвочный многоуголь-
ники были замкнутыми.
При помаши замкнутого верёвочного мно-
гоугольника легко найти так называемый
изгибающий момент для какого-
нибудь сечения балки. Рассмотрим балку,
лежащую на двух опорах и нагружённую
параллельными силами Ри Р3 и Рг (фиг. 16),
которые уравновешиваются двумя вертикаль-
ными реакциями опор. Силовой и верёвоч-
ный многоугольники, построенные для этой
уравновешивающейся системы пяти сил,
являются замкнутыми (фиг. 16). Изгибающим
моментом Ма для какого-нибудь поперечного
сечения ss балки называется алгебраическая
сумма моментов всех сил (включая и опорную
реакцию), расположенных по одну сторону
от этого сечения (например, справа) отно-
сительно точки пересечения плоскости этого
сечения с осью балки. Если обозначим через
Н полюсное расстояние, т. е. расстояние по-
люса О от прямой, на которой расположены
силы в силовом многоугольнике, то можно
доказать, что Ms = Ну, где у—длина за-
ключающегося внутри замкнутого верёвоч-
ного многоугольника отрезка прямой, парал-
лельной приложенным к балке силам и
проходящей через точку пересечения пло-
скости рассматриваемого сечения с осью
балки. Полюсное расстояние Н из-
меряется в том же масштабе, в котором по-
строены данные силы Р, в силовом много-
угольнике, а величина у измеряется в мас-
штабе длин (в том масштабе, в котором изо-
бражена на чертеже длина балки). Отсюда
легко находится «опасное сечение»
балки, т. е. то сечение, для которого изги-
бающий момент имеет наибольшую величину
и для которого, следовательно, у = утах. На
фиг. 16 наибольшим является, очевидно,
366
МЕХАНИКА
изгибающий момент для сечения, проходя-
щего через точку приложения силы Р2.
Примечание. О других применениях верё-
вочного многоугольника см. ТСЖ, т. II, «Сопротив-
ление материалов».
Если для данной системы сил (например,
для сил Pt и Р2) построить силовой много-
угольник и затем два верёвочных многоуголь-
ника, соответствующих двум каким-нибудь
полюсам О и О', то точки пересечения соот-
ветствующих сторон обоих верёвочных мно-
гоугольников все лежат на одной прямой,
параллельной линии, соединяющей оба по-
люса О и О’ (фиг. 17). Этой теоремой поль-
зуются иногда для более простого, построе-
ния второго верёвочного многоугольника,
когда первый многоугольник построен; при
□том способе построения нет надобности про-
водить лучи из второго полюса.
ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ
ФЕРМЫ
Определение. Фермой называется кон-
струкция, состоящая из прямых стержней,
соединённых между со£)ой по концам шар-
нирными узлами и образующих геометриче-
ски неизменяемую систему. Если оси всех
стержней фермы и все действующие на неё
силы лежат в одной плоскости, то ферма
называется плоской. Если трения в шар-
нирах нет и все заданные силы приложены
только в узлах фермы, то это обеспечивает
наличие в стержнях плоской фермы только
сжимающих или растягивающих усилий.
Если все опорные реакции и усилия встерж-.
нях фермы могут быть определены при по-
мощи уравнений статики абсолютно твёр-
дого тела, то такая ферма называется ста-
тически определимой. В противном
случае . ферма называется статически
неопределимой.
Если с фермы нельзя снять ни одного
стержня без нарушения условия геометри-
ческой неизменяемости, то такая ферма на-
зывается фермой без лишних стержней.
В противном случае ферма носит название
фермы с лишними стержнями. Между числом
т стержней и числом п узлов фермы без
лишних стержней существует зависимость:
щ = 2п — 3. Если число неизвестных реак-
ций опор плоской фермы без лишних стерж-
ней не более трёх, то ферма является стати-
чески определимой. Ферма с лишними стер-
жнями является статически неопределимой.
При расчёте фермы прежде всего нужно
определить сжимающие или растягивающие
усилия, возникающие в стержнях фермы
при действии на ферму заданных сил (на-
грузок), приложенных в её узлах. Но прежде
чем определять эти усилия, нужно найти
реакции опор. Для этого нужно знать кон-
структивное оформление опоры. В плоских
фермах различают следующие виды опор:
а) Подвижной опорный шарнир
(опора на катках — см. на фиг. 18 опора
В—или качающаяся опорная колонка).
Опорная реакция проходит через ось
шарнира и перпендикулярна к направлению
его возможного перемещения; так как в этом
случае направление реакции известно, то
при определении реакции такой опоры нужно
найти только одну неизвестную величину —
величину этой реакции.
б) Неподвижный опорный шар-
нир (фиг. 18, опора А). Опорная реакция
проходит через ось шарнира; в этом случае
неизвестны ни величина, ни направление
реакции. При определении реакции такой
опоры имеем две неизвестные величины: го-
в) Н е п о д в и ж н ое закрепление
(например, заделанный в стену конец балки);
в этом случае силы реакции приводятся
к одной силе и к одной паре, а потому
имеем три неизвестные величины: горизон-
тальную и вертикальную составляющие этой
силы и момент пары.
Если число неизвестных опорных реак-
ций не более трёх, то в случае плоской
фермы эти реакции можно определить или
аналитически — при помощи трёх уравнений
равновесия, которым должны удовлетворять
все внешние силы, приложенные к ферме
(заданные силы и опорные реакции), или гра-
фически— построением замкнутых силового
и верёвочного многоугольников. После того
как опорные реакции найдены, переходят
к определению усилий в стержнях фермы.
Для решения этой задачи применяют обычно
аналитический или графический способ.
Аналитический способ определения усилий
в стержнях фермы (способ Риттера). Ферма
условно разрезается на две части и одна часть
фермы мысленно отбрасывается. Действие
отброшенной части фермы на оставшуюся за-
меняется силами, направленными вдоль пере-
резанных стержней. Первый разрез следует
делать так, чтобы при этом перерезались не
более чем три стержня, не имеющие общей
точки пересечения. Далее, для нахождения
усилий в трёх разрезанных стержнях состав-
ляют три уравнения, приравнивая нулю
суммы моментов всех сил, приложенных
к оставшейся части фермы относительно
трёх точек Риттера (точкой Риттера назы-
вается точка пересечения осей двух перере-
занных стержней); в каждое из этих урав-
СТАТИКА
367
нений войдёт только одна неизвестная сила,
которая из этого уравнения и определяется.
При составлении уравнений моментов
каждую из сил, заменяющих действие раз-
резанного стержня, следует направлять
вдоль этого стержня от узла фермы, что
соответствует случаю растяжения стержня.
Если в результате решения этих уравнений
числовая величина усилия окажется поло-
жительной, то стержень растянут; если же
эта величина окажется отрицательной, то
истинным направлением искомого усилия
будет направление, противоположное при-
нятому, т. е. стержень будет сжат.
Если из трёх разрезанных стержней два
параллельны, то точка пересечения осей
этих стержней является бесконечно удалён-
ной. В этом случае вместо трёх уравнении
моментов составляют два уравнения момен-
тов (относительно двух точек Риттера) и
уравнение проекций всех сил на ось, пер-
пендикулярную к этим параллельным стерж-
ням.
Пример (фиг. 19). Для определения усилий
S,, S, и в стержнях 7, 2, 3, не пересекающихся
в одной точке, перерезаем эти стержни и удаляем
правую часть фермы. Принимая во внимание, что
опорные реакции равны == -% Р и Pg = Р и
составляя уравнение моментов относительно точки
#ресечения О стержней 2 и 3 (для левой части
рмы), находим
4а~- Р - ЗаР - 2аР - аР - SJi = О,
откуда S, = 8 “ Р.
h
Аналогично определяются усилия Sa и S3.
Делая последовательно ряд других раз-
резов, можно найти этим способом усилия
во всех стержнях данной фермы.
.. Графический способ определения усилий
в- стержнях фермы (способ Кремоны). Выре-
зают какой-нибудь узел фермы, т. е. перере-
зают сходящиеся в'нём стержни, и заменяют
их силами, направленными вдоль этих стерж-
ней; затем рассматривают получившийся
после этого пучок сил^ приложенных к это-
му узлу и находящихся в равновесии. Так
как для равновесия пучка сил необходимо и
достаточно, чтобы многоугольник этих сил
замыкался, то, построив замкнутый много-
угольник всех сил, приложенных к выре-
занному узлу, можно найти величину иско-
мых усилий в перерезанных стержнях.
При этом при вырезании каждого узла
нужно следить за тем, чтобы в нём сходи-
лось не более двух стержней, усилия в ко-
торых ещё не найдены, так как в противном
случае построение замкнутого силового мно-
гоугольника не даёт возможности найти
неизвестные силы, приложенные к рассмат-
риваемому узлу.
Для определения по этому способу уси-
лий во всех стержнях фермы нужно по-
строить диаграмму Кремоны, для чего посту-
пают следующим образом. Ферма схемати-
чески чертится в выбранном масштабе
(фиг. 20). Затем одним из способов, графи-
ческим или аналитическим, определяются
опорные реакциии R2.
Далее обозначают цифрами 1, 2, 3, 4
внешние области, т. е. части плоскости, ог-
раниченные внешним контуром фермы и ли-
ниями заданных внешних сил и опорных
реакций, и цифрами 5, 6, 7, 8, 9— внутрен-
ние области, т. е. части плоскости, распо-
ложенные внутри фермы и ограниченные
только стержнями фермы. Затем строят
замкнутый многоугольник внешних сил,
причём строят эти внешние силы в том по-
рядке, в котором мы их встречаем при об-
ходе фермы по часовой стрелке (т. е.
в порядке: Р2, Plt 7?х, R2). В начале и в
конце каждой силы ставят те же цифры,
какими обозначены две смежные области,
для которых линия данной силы является
общей границей. После этого построение
диаграммы Кремоны начинают с того узла,
в котором сходится не более двух стержней,
т. е. в данном случае с левого опорного
узла. Через точку 4 на многоугольнике сил
проводят прямую, параллельную стержню
4—5, т. е. стержню, разграничивающему
/1ве смежные области 4 и 5, а через точку
3—прямую, параллельную стержню 5—3',
в пересечении этих прямых получают точку
5. Обходя построенный таким образом сило-
вой треугольник 3—4—5 в направлении
силы /?!, можно заметить, что усилие в стер-
жне 4—5 направлено к уз л у, следовательно
этот стержень сжат; усилие в стержне 5—3
направлено от узла, следовательно, этот
стержень растянут. Далее, переходя к верх-
нему левому узлу и построив для него та-
ким же способом силовой треугольник 4 —
5 — 6, определяют усилия в стержнях 5 — 6
и 4 — 6. Подобным же образом определяются
усилия и в остальных стержнях фермы.
Если на диаграмме Кремоны некоторые
стороны силовых многоугольников обраща-
ются в точки, то усилия в соответствующих
стержнях фермы равны нулю. Так, в рассма-
триваемо,м примере совпадают три точки —
б, 7, 8; следовательно, усилия в стержнях
б— 7 и 7 — 8 равны нулю (подробнее см.
«Статика сооружений»).
368
МЕХАНИКА
КИНЕМАТИКА
ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
Закон движения. Скорость. Ускорение.
Положение точки, движущейся прямоли-
нейно, в каждый данный момент вполне оп-
ределяется расстоянием s этой точки от не-
которой неподвижной точки О, произвольно
выбираемой на прямолинейной траектории
движущейся точки. Это переменное расстоя-
ние s, рассматриваемое как алгебраическая
величина (как абсцисса точки), является не-
которой однозначной и непрерывной функ-
цией времени, т. е. s = f(t).
Это уравнение называется у р а в н е-
нием или законом движения
точки. Если изобразим зависимость между
s и t графически, т,о получим некоторую
кривую, которая называется графиком
изображается прямой линией с углом наклона
а (фиг. 23), причём v =tg а = и s = vt.
В этом случае ускорение точки равняется
нулю. Движение точки называется равно-
мерно-ускоренным или равно-
мерно-замедленным, если ускорение
а является величиной постоянной, а именно:
движение называется равномерно-ускор. н-
ным, если ускорение положительно, и рав-
номерно замедленным, если оно отрица-
тельно. Для случая равномерно-перемен-
ного движения график скорости является
прямой линией с углом наклона (3
(фиг. 24).
Из фиг. 24 имеют:
а = tg ₽ = .
движения или кривой расстоя-
ний (фиг. 21). Величина скорости
точки определяется по формуле
V = S = /' (О-
dt
Отсюда следует, что величина скорости
численно равна тангенсу угла наклона ка-
сательной к графику движения (фиг. 21),
т. е. у — tg а. Направление скорости сов-
падает с направлением прямолинейной тра-
ектории точки. Ускорение точки в
прямолинейном движении равно производ-
ной от скорости по времени, т. е.
Если изобразить зависимость между и и t
графически, то получим некоторую кривую,
которая называется графиком скоро-
сти или кривой скоростей (фиг. 22).
Величина ускорения численно
равна тангенсу угла наклона касательной
к графику скорости, т. е. а = tg ₽ (фиг. 22).
Равномерное и равномерно-переменное
движение точки. При равномерном
движении точки, т. е. при движении
с постоянной скоростью, график движения
Отсюда
а ~ г о 4- atf
где у0 — начальная скорость, соответствую-
щая моменту t = 0.
Так как
то
ds = vdt = (у0 4- at) dt
и
s = j vdt = vot 4- 1 at2,
о
или
s = (2yo+at)^=^t-4
2 2
s = V~ V0 — v ~VO
2 ’ a 2a ’
При y0 = 0 получим
v = at и s= — t2,
2
или
s = v_ и y= Vlas.
2a
кинематика
369
При равномерно-переменном движении
график движения является параболой
(фиг. 25).
Если в общем случае прямолинейного
движения точки исключим из уравнений
S = / (/) и v = /' (0 время t, то получим за-
висимость между виз; графически эта за-
висимость выразится некоторой кривой
линией, изображённой на фиг. 26.
Рассматривая скорость и как функцию
переменного s, будем иметь
в = ?(з).
Основные задачи кинематики точки в
случае прямолинейного движения. В зависи-
мости от того, какие из четырёх величин —
S, и, a, t даны и какие требуется найти,
имеются следующие основные типы задач,
относящихся к прямолинейному движению
точки:
1. Дано v = / (0; найти s и а.
Решение: s = з0+ f vdt\ а = .
о dt
2. Дано v = / (s); найти а и t.
Решение:
s
t == С а = = dv ds _ v
J v' dt ds ' dt ds
s„
3. Дано a —J (f); найти s и v.
t t
Решение: v = w0+ J adt; s = s04- J vdt.
и о
4, Дапо a = / (s); найти v и t.
So »0
5. Дано a = / (t>); найти s и t.
V V
Г v
Решение: s=s0+ I - dv; t =
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ
Способы задания движения точки. Поло-
жение движущейся точки М в пространстве
может быть определено сё радиусом-
вектором г, который проводится из не-
которой произвольно выбранной неподвиж-
ной точки О (из начала координат, фиг. 27).
Если радиус-вектор является заданной
функцией времени, т. е. г = F (f), то движе-
ние точки будет вполне определено, так как
в каждый данный момент положение точки
в пространстве будет известно. В этом со-
стоит векторный способ задания движения
точки в кинематике.
Второй, так называемый естественный,
способ задания движения точки состоит в том,
что задаётся (является известной) траектория
точки и закон, или уравнение, движения
точки по этой траектории, т. е. уравнение
s = /(0.
В этом уравнении s обозначает длину
дуги траектории, причём началом этой дуги
является некоторая произвольно выбранная
на траектории неподвижная точка (напри-
мер, начальное положение Мв движущейся
точки), а концом — положение движущейся
точки в данный момент t (фиг. 27).
Третий (аналитический или координат-
ный) способ задания движения точки со-
стоит в том, что положение точки опреде-
ляется её декартовыми координатами х, у, z.
При движении точки эти координаты явля-
ются некоторыми однозначными и непрерыв-
ными функциями времени, т. с.
х = fl (О, У = (t), z~f3 (t).
Эти уравнения
движения точки в
Если точка дви-
жется в одной и
той же плоскости,
то эту плоскость
можно принять за
к о о р д и н атн ую
плоскость х О у и
для определения
движения точки
в этом случае до-
статочно двух
первых уравне-
ний.
называются уравнениями
декартовых координатах.
Фиг. 27
Чтобы найти траекторию точки в том слу-
чае, когда её движение задано уравнениями
в декартовых координатах, нужно из этих
уравнений исключить время t.
Пример. Найти траекторию точки, если её
движение задано уравнениями: х ~ a cos (kt), у =
= b sin (kt). Переписав данные уравнения в виде:
X у
~ = cos (kt) и -у = sin ОЮ» возведём их в квадрат
и сложим. Тогда
следовательно, траектория точки есть эллипс с полу-
осями а и Ь.
Скорость. Скорость криволиней-
ного движения точки определяется
как производная (векторная) от радиуса-
вектора этой точки по времени, т. е. у =
dr —
Вектор скорости v направлен по
касательной к траектории (фиг. 27). Вели-
чина скорости, так же как и в случае
прямолинейного движения, определяется по
формуле
v = = Г (О-
dt
В том случае, когда движение точки за-
дано аналитическим способом, скорость оп-
ределяется по её проекциям на координат-
ные оси, причём эти проекции равны про-
изводным от соответствующих координат
движущейся точки по времени, т. е.
~=/;ю; «у
dz .•
~ dt~t3^‘
24 Том 1
37 G
МЕХАНИКА
Величина скорости
Для определения направления скорости
нужно найти углы а, (3, у вектора V с коор-
динатными осями; эти углы определяются
по формулам:
cos а = Чу ; cos р= Чу ; cos т=
v v v
в
Ускорение. Ускорением точки
криволинейном движении назы-
вается производная (векторная) от вектора
скорости по времени, т. е. а = -JL. Проек-
ции ускорения на координатные оси равны
вторым производным от соответствующих
координат движущейся точки по времени,
т. е.
d-~ = Л (0; а
dt3 1 ’ -
d-y' == /2 (0;
dt2 '2V
а
dez
dt3
Величина ускорения
а = ]/" ах + ау + а?г *=
Углы at, pi, -ft вектора а с координат-
ными осями, определяющие его направление,
находятся по формулам:
cos а, = Чу ; cos Pi = Чу ; cos 71 = Ч?
а а а
Для определения ускорения точки в том
случае, когда её движение задано естествен-
ным способом, нужно вектор а разложить
на два составляющих ускорения: касатель-
ное (тангенциальное) ускорение at и нор-
мальное ускорение ап. Величины этих со-
ставляющих ускорений равны
а/ =
dw
dt
d-s_
dt3
an=
v3
P
где p—радиус кривизны траектории в той
её точке, с которой совпадает в данный мо-
мент движущаяся точка. Касательное уско-
рение at направлено по касательной к траек-
тории в ту же сторону, что и скорость о, при
ускоренном движении, и в сторону, проти-
воположную скорости, при замедленном дви-
жении. Нормальное ускорение ап направ-
лено всегда по нормали* к центру кривизны
траектории.
Величина ускорения а определяется в
этом случае по формуле
* В том случае, когда траектория точки не ле-
жит в одной плоскости, нормальное ускорение ап
направлено по главной нормали траектории.
Так как для прямой линии радиус кри-
визны р = оо, то в случае прямолинейного
движения точки ап = 0, и, следовательно,
в этом случае
а = at = .
r dt
Для окружности радиус кривизны р ра-
вен радиусу R этой окружности; следова-
тельно, в случае движения точки по окруж-
а2
ности ап = — ; в этом случае нормальное
ускорение ап называется также центро-
стремительным.
В общем случае, когда траектория точки
есть некоторая плоская кривая, заданная
уравнением у = <р (х), радиус кривизны
_ й + У'8)3/2
Р — у" '
где
У> ЧУ и „ = О
dx dx3
Если точка движется равномерно, то
v = const и at = 0, а потому а = ап = — .
Следовательно, в случае равномерного
криволинейного движения ускорение точки
а совпадает с нормальным ускорением а„.
Ускорение возникает в этом случае, оче-
видно, потому, что изменяется направление
вектора скорости.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
Понятие о сложном движении точки. Ес-
ли наблюдать движение точки относительно
некоторой системы координат (системы от-
счёта), которая сама движется относительно
другой неподвижной системы отсчёта, то та-
кое движение точки относительно подвижной
системы отсчёта называется относитель-
ным.
Движение подвижной системы отсчёта
относительно неподвижной называется п е-
реносным движением. То движение точки,
которое получается в результате сложения
относительного и переносного движений,
т. е. её движение относительно неподвиж-
ной системы отсчёта, называется абсолют-
ным.
Таким образом, движение точки относи-
тельно неподвижной системы отсчёта (абсо-
лютное движение) является в этом случае
сложным, поскольку его можно рассматри-
вать как результат сложения двух движе-
ний (относительного и переносного). На-
пример, если точка (тело) движется относи-
тельно движущегося вагона, то это движе-
ние будет относительным; движение вагона
будет называться переносным, а движение
точки (тела) относительно земли — абсолют-
ным.
Подвижной системой отсчёта здесь являет-
ся система координат, связанная с вагоном,
КИНЕМАТИКА
371
а неподвижной системой отсчёта — система
координат, связанная с землёй.
Сложение скоростей и ускорений. В со-
ответствии с этим приходится рассматри-
вать скорость и ускорение точки в каждом
из этих трёх движений, т. е. рассматривать
абсолютную скорость v и абсолютное уско-
рение а точки, относительную скорость иг и
относительное ускорение аг точки, а также
переносную скорость точки ve и сё пере-
носное ускорение ав. При этом под перенос-
ной скоростью точки понимают ту скорость,
которую имела бы в данный момент эта
точка, если бы она была неизменно соеди-
нена с системой подвижных осей, т. с., дру-
гими словами, переносной скоростью назы-
вается скорость той точки, неизменно сое-
динённой с системой подвижных осей, с ко-
торой совпадает в данный момент движу-
щаяся точка. То же определение относится
и к переносному ускорению точки.
Абсолютная скорость точки равна по ве-
личине и направлению диагонали паралле-
лограма, сторонами которого являются от-
носительная и переносная скорости этой
точки, или, что то же, абсолютная скорость
равна геометрической сумме относительной
и переносной скоростей, т. е.
V = vr + ve
(теорема сложения, или теорема параллело-
грама скоростей).
Та же теорема имеет место и для абсо-
лютного ускорения точки, но только в том
случае, когда переносное движение является
поступательным. Следовательно, если пере-
носное движение является поступательным,
то
а = аг + ае.
Если же переносное движение является
вращательным (если подвижная система от-
счёта вращается вокруг некоторой оси с уг-
ловой скоростью «), то в этом случае абсо-
равно геометриче-
ской сумме трёх
ускорений: отно-
сительного, пере-
носного и доба-
вочного, которое
называется уско-
рением Кориоли-
са, т. е.
лютное ускорение точки
а = ат 4- ае + ak
(теорема Корио-
лиса).
Для определения величины и направле-
ния добавочного ускорения ак можно пользо-
ваться следующим правилом: 1) через движу-
щуюся точку М проводят плоскость, перпен-
дикулярную к оси С переносного вращения;
2) проектируют па эту плоскость вектор от-
носительной скорости точки; 3) умножают
эту проекцию на удвоенную угловую ско-
рость переносного вращения и 4) получен-
ный после этого вектор поворачивают па
00° в направлении переносного вращения
(фиг. 28).
Таким образом, вектор добавочного уско-
рения а,,. лежит в плоскости, перпендику-
лярной к оси переносного вращения, и пер-
пендикулярен к относительной скорости
точки. Если обозначить через vr проекцию
относительной скорости иг на плоскость,
перпендикулярную к оси переносного вра-
щения, а угол вектора vr с этой осью обоз-
начить через 0 (фиг. 28), то р, = vr sin 6> а
потому
аА = 2ощг sin 6.
Если вектор vr перпендикулярен к оси
переносного вращения, то sin6= 1, и, сле-
довательно, в этом случае ajt = 2шрг.
Если же вектор vr параллелен этой оси,
то sin 0 = 0, и, следовательно, в этом слу-
чае аА = 0.
ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА
Поступательным движением
твёрдого тела называется такое дви-
жение, при котором всякая прямая, произ-
вольно взятйя в этом теле, перемещается
параллельно самой себе.
Примером такого движения может слу-
жить движение кузова вагона на прямоли-
нейном участке пути.
При поступательном движении все точки
тела описывают одинаковые траектории и
в каждый данный момент имеют равные и
параллельные скорости и ускорения.
Отсюда следует, что поступательное дви-
жение твёрдого тела вполне определяется
движением одной какой-нибудь его точки,
например движением центра тяжести тела.
Таким образом, изучение поступательного
движения твердого тела в кинематике сво-
дится к задаче кинематики точки.
ВРАЩЕНИЕ ТВЁРДОГО ТЕЛА ВОКРУГ
НЕПОДВИЖНОЙ оси
Закон вращения. Угловая скорость и уг-
ловое ускорение. Положение твёрдого тела,
вращающегося вокруг неподвижной оси,
определяется углом поворота у тела,
выражаемым в радианах и отсчитываемым от
некоторой неподвижной плоскости, прохо-
дящей через ось вращения тела. При вра-
щении тела этот угол является некоторой
однозначной и непрерывной функцией вре-
мени, т. е. <р = / (0.
Это уравнение называется уравнением
или законом вращательного дви-
жения тела вокруг данной неподвижной
оси. Производная от угла о по времени на-
зывается угловой скоростью тела; следова-
тельно, угловая скорость ш = = /'(0. Про-
изводная от угловой скорости по времени
называется угловым ускорением тела; следо-
du> d2<f
вательно, vrnoBoa ускорение е = -17-= =
J dt dt2
— Если ш = const, то вращение тела
называется рапномерным. Когда задано
24*
372
МЕХАНИКА
число п оборотов тела в минуту, его угло-
вая скорость определяется по формуле
хп 1
о> == - —- ,
30 сек
Если е = const, то вращение тела называет-
ся равномерно-переменным (равномерно-
ускоренным или равномерно-за-
медленным, в зависимости от того, будет
ли е > 0 или е < 0). При равномерно-пере-
менном вращении тела имеем следующие
формулы для угловой скорости
и угла поворота, аналогичные фор-
мулам для скорости и пройденного пути при
равномерно-переменном прямолинейном дви-
жении точки:
со = и>д -J- et; '.> = wot L е/2
ИЛИ
-4- « .
ср = t,
где <а„—начальная угловая скорость тела.
В кинематике твёрдого тела его угловая
скорость часто изображается в виде вектора.
Векторе) направляется по оси вращения
тела в ту сторону, чтобы наблюдатель, смот-
рящий вдоль этого вектора в направлении
от его конца к началу, видел вращение тела
происходящим против часовой стрелки (пра-
вило правого винта). Л1одуль (длина) век-
тора со равен (в выбранном масштабе) абсо-
лютной величине угловой скорости тела; что
касается начала вектора ш, то эта точка
может быть выбрана на оси вращения тела
произвольно; следовательно, вектор угловой
скорости, подобно силе, есть вектор сколь-
зящий.
При вращении тела вокруг неподвижной
оси каждая точка тела описывает окруж-
ность, центр которой лежит на оси враще-
ния тела и плоскость которой перпендику-
лярна к этой оси. Если обозначить радиус
этой окружности, равный расстоянию данной
точки от оси вращения, через R, то вели-
чина скорости этой точки равна v = R<o.
Касательное и нормальное ускорения
точки определяются по формулам:
at = } (R“) = R ~ = -Re;
dt dt dt
an = - = Rws.
" R
Следовательно, величина ускорения точки
равна ________
а = У а]+ ain = R /е2 +
Если со = const, то е = 0, а потому at = О
и а = а„ = RcP. В этом случае ускорение
с совпадает с нормальным (центростреми-
тельным) ускорением.
ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ
ТЕЛА
Плоско-параллельным движе-
нием твёрдого тела называется та-
кое движение, при котором расстояние каж-
дой точки тела от данной неподвижной пло-
скости остаётся постоянным.
При таком движении все точки тела опи-
сывают плоские траектории, расположенные
в плоскостях, параллельных данной непо-
движной плоскости. Кроме того, все точки
тела, лежащие на одной прямой, перпенди-
кулярной к данной неподвижной плоскости,
движутся по одинаковым траекториям с рав-
ными (по величине и направлению) в каж-
дый данный момент скоростями и ускоре-
ниями. Отсюда следует, что изучение пло-
ско-параллельного движения твёрдого тела
сводится к изучению движения точек, при-
надлежащих сечению этого тела плоскостью,
параллельной данной неподвижной плоско-
сти, т. е. к изучению движения некоторой
плоской фигуры, движущейся в своей пло-
скости. ____
Примером та-
кого движения те- S' / * 1
ла может служить / /сА-______'
качение вагонного /| /ъ'й
колеса по рельсу; *
расстояние каж- \ ' j
дой точки колеса /V) -Йм
от неподвижной f
вертикальной пло- фиг 29
скости, перпенди-
кулярной к оси колеса, остаётся неизмен-
ным .
Пусть данная плоская фигура (плоское
сечение данного тела) движется в плоско-
сти чертежа (фиг. 29). Движение этой пло-
ской фигуры в общем случае можно разло-
жить на два движения: 1) поступательное
со скоростью, равной скорости vA произ-
вольно выбранной точки А фигуры, и 2) вра-
щательное с некоторой угловой скоростью
а> вокруг этой точки А. Отсюда на основа-
нии теоремы сложения скоростей заключаем,
что скорость любой точки В фигуры равна
геометрической сумме скоростей этой точки
в каждом из этих двух движений, т. е.
vb = va + vba •
где иВА обозначает скорость точки В во
вращательном движении вокруг точки А,
причём
± АВ и vba~ABg).
Мгновенный центр вращения плоской фи-
гуры. Центроиды. Указанные два движения
приводятся к одному вращательному дви-
жению с той же угловой скоростью а> вокруг
некоторой вполне определённой для дан-
ного момента точки Р, скорость которой
в данный момент равна нулю, и которая
называется мгновенным центром
вращения фигуры или мгновенным
центром скоростей (фиг. 29).
Следовательно, в течение любого беско-
нечно-малого промежутка времени движение
плоской фигуры является вращением вокруг
мгновенного центра скоростей. А потому
v А = РА<я
и
ей = РВ<1>,
КИНЕМАТИКА
373
откуда
^4__ А4
"в ~ РВ ’
т. е. скорости точек плоской фигуры про-
порциональны расстояниям этих точек от
мгновенного центра вращения фигуры; кроме
того vA lPA и vb ± РВ; отсюда следует, что
мгновенный центр вращения фигуры лежит
в точке пересечения перпендикуляров, вос-
становленных из двух каких-нибудь точек
этой фигуры к скоростям этих точек.
Положение мгновенного центра вращения
Р фигуры не остаётся неизменным: каждому
моменту t соответствует своё определённое
положение точки
Y Р. Если построить
_—геометрическое
' место точек Р на
[ i неподвижной пло-
/ \ ‘ х'/ I й скости, то эта ли-
—I-----ния называется
1 । л j л неподвижной цен-
\ [ / троидой, или не-
X, I У подвижной поло-
!-- дней. Геомстриче-
Фиг 30 ское место мгно-
венных центров
вращения на плоскости самой движу-
щейся фигуры называется п о д в и ж-
н о й центроидой или подвижной
полодией. При движении фигуры свя-
занная с ней подвижная центроида переме-
щается так, что она катится без скольже-
ния по неподвижной центроиде. Следова-
тельно, всякое движение плоской фигуры,
движущейся в своей плоскости, можно пред-
ставить как качение без скольжения по-
движной центроиды по неподвижной (тео-
рема Пуансо).
Пример. Прямолинейный отрезок АВ = I дви-
жется в плоскости чертежа так, что его концы А и
В перемещаются соответственно по осям хну.
Найти центроиды (фиг. 30).
Точка Р пересечения перпендикуляров, восста-
новленных из точек А и В к скоростям этих точек,
есть мгновенный центр вращения отрезка АВ. Так
как ОР » АВ. то OP — I = const. Отсюда следует,
что геометрическое место точек Р на неподвижной
плоскости (неподвижная центроида) есть окруж-
ность, описанная из центра О радиусом, равным I.
Так как СР — */, ОР, то СР = = const, т. е. рас-
стояние точки Р от середины отрезка АВ остаётся
постоянным. Отсюда следует, что подвижная цент-
роида есть окружность, описанная из центра С ра-
диусом, равным -i-. При движении отрезка АВ эта
вторая окружность катится без скольжения по пер-
вой.
Мгновенный центр ускорений. Для опре-
деления ускорения какой-нибудь точки В
фигуры диференцируют по t равенство ив=
= vА + vba :
d»B = dvA , d~vBA t
dt dt dt
или
“в = aA + aBA>
где aBA обозначает ускорение точки В во
вращательном движении вокруг точки А.
Это ускорение можно разложить на к а с а-
тельное и нормальное (центро-
стремительное) ускорения, т. е.
авА ~ аВА + аВА’
а потому
“в = ~аА + ~аВА +^ВА-
Центростремительное ускорение на.
правлено по ВА и равно по величине АВы*.
Касательное ускорение а$А направлено по
перпендикуляру к АВ в сторону вращения
фигуры вокруг точки А, если е > 0, и в сто-
рону, противоположную вращению фигуры,
du>
если е < 0, где е = —
dt '
Величина этого касательного ускорения
равна АВ | с |. Отсюда следует, что
аВА = АВ
Направление ускорения аВА определяется
углом ос, который это ускорение образует
с направлением ВА; этот угол находится из
равенства
Точка Р фигуры, ускорение которой в дан-
ный момент равно нулю, называется мгно-
венным центром ускорений. Если
в предыдущем равенстве вместо точки А
взять точку Р, го ав = ар+ авр, но а р= О,
а потому йв= аВР , т. е. ускорение всякой
точки фигуры равно (по величине и направ-
лению) ускорению этой точки во вращатель-
ном движении вокруг мгновенного центра
ускорений. А потому
ав= РВ уРea-f- <д4,
а угол вектора ав с направлением ВР равен
а = arctg — .
О)2
Отсюда следует, что ускорения точек фи-
гуры пропорциональны расстояниям этих
точек от мгновенного центра ускорений и
что угол ос для всех точек фигуры имеет
в данный момент одно и то же значение.
Для определения положения мгновенного
центра ускорений имеем следующее правило:
1) находим ускорение аА какой-нибудь точ-
ки А фигуры; 2) поворачиваем полупрямую,
по которой направлен вектор аА, вокруг
точки А на угол
* I е|
ос = arctg —i.
в направлении вращения фигуры, если е > О,
и в направлении, противоположном враще-
нию фигуры, если s < 0; 3) на полученной
после этого поворота полупрямой отклады-
а .
ваем от точки А отрезок АР = —-
у е2-|- <о4
Тогда точка Р есть искомый мгновенный
центр ускорений.
374
МЕХАНИКА
Если е = 0, то мгновенный центр уско-
рений Р лежит на полупрямой, по которой
- ал
направлен; вектор а А и АР — ~ .
Л О)3
ВИНТОВОЕ ДВИЖЕНИЕ ТЕЛА
Если твёрдое тело вращается вокруг не-
подвижной оси z с угловой скоростью ш и
в то же время движется поступательно со
скоростью и, направленной вдоль этой оси,
то такое движение тела называет-
ся винтовым; ось z называется винто-
вой осью (фиг. 31).
Скорость всякой точки тела при винто-
вом движении равна геометрической сумме
скоростей этой точки в каждом из этих со-
ставляющих движений; то же относится и
к ускорению точки. Следовательно,
— _ — fl ц —
Р = и + ивр и а = - ^Gep.
При этом
аер ± и и vep=r<»,
°ер=
где е = , а г — расстояние данной точки
тела от винтовой оси. Отсюда следует, что
v = н2 -f- Г2<о2
и
a=V (ег+<°4)-
точки тела, например его центра тяжести
С, и 2) вращательное с некоторой угловой
скоростью ш вокруг мгновенной оси, про-
ходящей через эту точку С. Примером та-
кого движения тела может служить движение
артиллерийского снаряда.
В общем случае направление оси враще-
ния тела не остаётся неизменным: каждому
моменту t соответствует своё определённое
направление этой оси. Скорость всякой точки
тела равна геометрической сумме скоростей
этой точки в каждом из двух составляющих
движений, т. е.
у = ус + Увр,
причём
Рду = Лш,
где h — расстояние данной точки тела от
мгновенной оси вращения, проходящей че-
рез точку С.
СЛОЖЕНИЕ ДВИЖЕНИЙ ТВЁРДОГО ТЕЛА
Если тело участвует в двух движениях
(относительном и переносном), причём оба
эти движения являются поступательными,
то результирующее (абсолютное) движение
Если ~ ~ const, то траекторией точки
Фиг.
тела при его винтовом движении является
винтовая линия
2\
расположенная на поверх-
ности круглого цилин-
дра радиуса г. Ско-
рость и точки направ-
лена по касательной к
этой винтовой линии.
Винтовая линия пере-
секает все образующие
цилиндра под одним и
тем же углом у, причём
tg Y = . При развёрт-
ке цилиндра на плоско-
сти винтовая линия пре-
вращается в прямую.
Расстояние h, на кото-
тело вполь винтовой оси
тела будет также поступательным, ско-
рость которого равна геометрической сумме
скоростей составляющих движений.
Если оба составляющие движения (относи-
тельное и переносное) являются вращательны-
ми ДВИЖеНИЯМИ С уГЛОВЫМИ СКОРОСТЯМИ COj и
&>а вокруг параллельных осей и z2, причем
эти вращения направлены
в одну сторону (фиг. 32, а),
то в этом случае абсолют-
ное движение тела являет-
ся вращением вокруг мгно-
венной оси с угловой ско-
ростью й = fflj + ша (фиг.
32,6). Эта мгновенная ось
вращения С параллельна
данным осям zt и z2 и делит
fl
Фиг, 33
рое перемещается
при одном полном обороте вокруг этой оси,
называется шагом винтовой линии, причём
h = 2кг ctg у = .
со
расстояние между ними вну-
тренним образом на части,
обратно пропорциональ-
ные данным угловым скоростям, т. е.^ =
ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ
СВОБОДНОГО ТВЁРДОГО ТЕЛА
В общем случае движение свободного
твёрдого тела можно разложить на два дви-
жения: 1) поступательное со скоростью,
равной скорости произвольно выбранной
— —? . Если составляющие вращения вокруг
“1
параллельных осей направлены в разные
стороны, то абсолютная угловая скорость й
равна разности угловых скоростей этих со-
ставляющих вращений; мгновенная ось вра-
щения тела делит в этом случае расстояние
О, О3 в отношении внешним образом.
“л
ДИНАМИКА
375
Если векторы угловых скоростей шх и <о2
равны по величине, параллельны и направ-
лены в разные стороны, т. е. <ох = — ш3, то
они образуют пару угловых скоро-
стей (пару вращений); в этом случае аб-
солютное движение тела является посту-
пательным, скорость которого равна
(по величине и направлению) вектору-мо-
менту этой пары.
Если оси z1 и z2 переносного и относи-
тельного вращений пересекаются в непо-
движной точке О, то в этом случае абсолют-
ное движение тела является вращением во-
круг мгновенной оси, проходящей через эту
неподвижную точку. Абсолютная угловая
скорость вращения тела вокруг мгновенной
оси равна (по величине и направлению)
диагонали параллелограма, построенного на
относительной и переносной угловых скоро-
стях, т. е. ft = + шг (фиг. 33).
Из этих результатов следует, что угло-
вые скорости складываются так же, как
в статике складываются силы (параллельные
или сходящиеся).
ДИНАМИКА
ДИНАМИКА материальной точки
Диференциальные уравнения движения
точки. В основе классической динамики ле-
жат следующие законы—«аксиомы движе-
ния»—Галилея—Ньютона: 1) закон инерции;
2) закон зависимости между силой и ко-
личеством движения; 3) закон равенства
действия и противодействия и 4) закон не-
зависимости действия (закон сложения) сил.
Согласно второму закону
F = та,
где т— масса материальной точки; а—её
ускорение и F—действующая на эту точку
сила. В скалярной форме (т. е. в проекциях
на три координатные оси) этот закон выра-
жается следующими тремя уравнениями:
тах = FX т-=Х;
х х dt2
d^v
mav ~ Fv или т —± = V;
У У dt*
таг = Fz т^,= z-
dt2
Эти уравнения, называемые д и ф е р е н-
циальными уравнениями движе-
ния материальной точки, явля-
ются основными уравнениями динамики
точки. При помощи этих уравнений реша-
ются обе основные задачи динамики точки,
а именно:
Первая задача. Зная движение точки и её
массу, найти силу, действующую на эту
точку.
Вторая задача. Зная массу точки и дей-
ствующую на неё силу, найти движение этой
точки.
Если движение точки задано кинематиче-
скими уравнениями
x = /i(0, У = /2(О» *= /з(0,
то, диференцируя два раза по t эти уравне-
ния, находят проекции ускорения точки ах,
ау и а. на координатные оси; умножая эти
проекции на массу точки т, получают про-
екции действующей на точку силы и по этим
проекциям определяют величину и направ-
ление этой силы.
Если, наоборот, известны проекции дей-
ствующей силы X, Y, Z, а требуется найти
движение точки, т. е. найти её координаты
х, у, z как функции времени t, то решение
этой второй основной задачи динамики сво-
дится к интегрированию диференциальных
уравнений движения точки.
При интегрировании этих уравнений по-
являются произвольные постоянные С; (в об-
щем случае их будет шесть), значения кото-
рых определяются по начальным условиям
движения точки, т. е. по её начальному по-
ложению (по её координатам х0, у0, z0 в на-
чальный момент движения) и по её началь-
ной скорости г0, которая задаётся тремя её
проекциями vox, voy и на координатные
оси.
Масса. Когда материальная точка сво-
бодно падает по вертикали (в пустоте) под
действием только силы тяжести, то действу-
ющая сила Р есть вес материальной точки,
а ускорение a —g = 9,81 м[сек* — 981 см) сек.2.
Поэтому
Р = mg,
откуда
Эта формула позволяет определять массу
точки (т е л а) по её весу; таким образом,
определение массы тела сводится к его взве-
шиванию.
Свободное падение материальной точки
в пустоте. Так как в этом случае ускоре-
ние постоянно, то движение точки является
равномерно-ускоренным, а потому скорость
точки и прейдённый её путь определяются
по формулам
V = Vo + gt И s = vot + 1 gl2,
где v0—начальная скорость точки. Если
v0 = 0, то v = gt и s= ^gt2; исключив от-
сюда t, получим v = y^lgs. Если высота па-
дения точки равна Л, то её скорость при
падении на землю равна v = 7/2gft.
Если точка брошена (в пустоте) по вер-
тикали вверх с начальной скоростью vB, то
её движение будет равномерно-замедленным,
а потому в этом случае
v=v0 — gt, s=- vat — 1 gt2.
Время T, по истечении которого точка до-
стигает наибольшей высоты подъёма, опре-
деляется из того условия, что в момент
376
МЕХАНИКА
t = Т скорость точки равна нулю; следова-
тельно,
Т = -°
g
Наибольшая высота подъёма равна
2
Падение материальной точки в сопротив-
ляющейся среде. Материальная точка ве-
сом Р = mg свободно падает по вертикали
с высоты /г. Сила сопротивления воздуха
пропорциональна квадрату скорости точки,
т. е. величина этой силы равна kv2, где к—
коэфициент пропорциональности, зависящий
от плотности воздуха (для тела конечных
размеров этот коэфициент зависит также от
формы тела и от площади его наибольшего
поперечного сечения и определяется из
опыта).
Найти скорость точки при падении на
землю, если её начальная скорость и0 = 0.
Если примем начальное положение точки
за начало координат и направим ось z по
вертикали вниз, то диференциальное урав-
нение движения точки имеет вид
fit?
m- = me — kv2,
dt2
dz
или, принимая во внимание, что — =
m — = mg — kv2.
dt
Так как нам нужно найти зависимость ме-
жду скоростью и высотой падения, то из
этого уравнения нужно исключить время,
d. z
что можно сделать, заменяя dt через — ;
v
тогда
mv = mg — kv* t
dz
или
Если обозначим через с скорость точки,
при которой сила сопротивления воздуха
равна весу точки, то
кс2 = mg
и
/£ _ J
mg с2 ’
а потому предыдущее уравнение принимает
вид
p^ = gfi-O=-V‘;S-^
dz у c~J с1
или
.vdv..= L dz.
С2—Vs с2
Интеграл этого уравнения будет
In (с2— V2) — — z + С.
с2
Постоянная С определяется из того условия,
что в начальный момент (при z = 0) ско-
рость V,, = 0; следовательно, С = Inc2, а по-
тому
In _ 2? z,
с2 с2
откуда
с2 — v2 = с2е с~
Полагая здесь z = h, получим ответ задачи;
- ~h
если высота к велика, то член е с мал в
сравнении с единицей, и тогда с достаточной
точностью можно принять, что скорость прп
падении на землю будет равна с. Из полу-
ченной формулы для v следует, что
lim v — с.
z оо
Поэтому скорость с называют предель-
ной скоростью.
Криволинейное движение тяжёлой точки
в пустоте. Материальная точка М (напри-
мер, пуля) брощена с начальной скоростью
v0 под углом of к горизонту. Найти движе-
ние этой точки., пренебрегая силой сопроти-
вления воздуха.
Примем начальное положение точки за
начало координат О, ось у направим по вер-
тикали вверх, а горизонтальную ось х на-
правим так, чтобы вектор у0 лежал в плоско-
сти Оху; тогда угол вектора v0 с осью х бу-
дет равен а (фиг. 34).
Диференциальные уравнения движения
точки имеют вид:
m^Jo; m^=-mg,
dt2 dt2 L
ИЛИ
^ = 0; dvv = -g.
dt ’ dt
Интегрируя эти уравнения, находим
— Cjj vу — ‘ — gt -j- С«.
Первое из этих равенств показывает, чти
проекция скорости на ось х остаётся посто-
янной. Так как в начальный момент (при
t = 0)
Vox — Vo COS а И Vov — I’o sin a,
TO
Ct = v0 COS a и C2 == va sin a,
а потому
yx=y0COSa, Vy = Co sin a — gt,
WZ
ДИНАМИКА
377
или
dx dv
— = Уо c°s а> — = Уо Sin а — Pt.
dt dt
Интегрируя эти уравнения, находим
х — у0 cos а • t + С3;
У = v0 sin а • t— 1 gP + Ct.
2
Так как в начальный момент точка нахо-
дится в начале координат, то х0 = у0 = 0, а
потому С3 = С4 = 0 и, следовательно,
X = Уо COS а t; у = у0 sin а • t — 2- gt2.
Эти уравнения, выражающие координаты
точки в функциях времени, полностью оп-
ределяют движение точки. Если исключить
из этих уравнений время t, то уравнение
траектории точки будет
у = х tga — —-------(парабола).
2су cos2 a
Полагая у = 0, находят из этого уравне-
ния абсциссу точки А, в которой траекто-
рия пересекает ось х, т. е. так называемую
дальность полёта
х. = — sin 2 a.
g
Продолжительность полёта Т определяется
из уравнения
хЛ = у0 cos a • Т,
откуда
Т = sin а.
g
Наибольшая высота подъёма равна
у? sin2 a
/1 = Утях = — ~7i- •
< Шал — Ор
9
Фиг. 35
нутой пружины
О, — через \Ст,
Гармоническое колебание материальной
точки. Груз весом Р кг подвешен на верти-
кальной пружине, длина
которой в естественном
состоянии равна /0 (фиг.
35). Приняв за начало ко-
ординат О положение рав-
новесия груза, т. е. то по-
ложение, в котором вес
груза уравновешивается
силой реакции пружины,
ось у направим по вер-
тикали вверх. Если обоз-
начить удлинение пружи-
ны через X, а её статиче-
ское удлинение, т. е. рас-
стояние от конца нерастя-
до положения равновесия
то X = Хг„, — у.
По закону Гука сила натяжения пру-
жины пропорциональна её удлинению, т. е.
величина этой силы равна сЛ, где с — посто-
янный для данной пружины коэфициент про-
порциональности (жёсткость пружины). В по-
ложении равновесия имеем
C^cm — Pf
откуда
Р Р
С = г— И ^ст ~~ — •
^ст с
Диференцмальное уравнение движения
груза имеет вид
т — сЪ — Р,
Н 42
или, заменяя X через Хет — у,
d2v
тп = — су.
dt1
Вводя обозначение — = к2, приводят это
m
уравнение к виду
12У + = 0.
dt2
Общее решение этого уравнения имеет
вид
у = a sin (kt + a),
где a и a — произвольные постоянные; в этом
легко убедиться, подставляя это значение
у в предыдущее диференциальное уравнение,
которое в результате этой подстановки об-
ращается в тождество. Отсюда следует, что
движение груза есть гармоническое колеба-
ние около положения равновесия. Величина
а называется амплитудой колебания; аргу-
мент fct + а называется фазой колебания;
значение фазы при t = 0, т. е. величина а,
называется начальной фазой колебания. Ве-
личина к = yf “ есть частота колебания.
Период колебания равен
Если принять во внимание, что
Р Р
m — - и с= .— ,
g Асот
то __
7 = 2,^.
Скорость груза равна
и = = ак cos (kt + а),
dt
Если в начальный момент (при t — 0) у = уе
и и — v0, то
Уо = a sin а и v0 = ак cos a;
отсюда
Эти формулы определяют амплитуду и на-
чальную фазу колебания по начальным ус-
ловиям движения груза. Если и0 — 0, то
а = Уо, а = ~ и, следовательно, в этом слу-
чае
у = у0 sin (fct + = уо cos (kt).
378
МЕХАНИКА
Количество движения. Импульс силы.
Теорема о количестве движения. Количе-
ством движения материальной
точки называется векторная величина,
равная ти, где т—масса точки и v — её
скорость; направление вектора mv совпа-
дает с направлением скорости v. Согласно
второму закону динамики
та = F,
но
а = ,
dt
а потому
-l(mi>) = F, или d (mu') = Fdt.
Произведение F dt называется элемен-
тарным импульсом силы; направ-
ление элементарного импульса совпадает
с направлением силы F. Интегрируя преды-
дущее уравнение, получают
_ _ t
mv — той = j F dt.
о
Векторный интеграл, стоящий в правой
части этого равенства, называется импуль-
сом силы F за время t.
t _
Если ввести обозначение J F dt — S, то
_ о
mv — mv0 = S, т. е. изменение количества
движения материальной точки за данное
время равно импульсу приложенной к ней
силы за то же время (теорема о коли-
честве движения). В скалярной форме
(в проекциях на координатные оси) эта тео-
рема выражается следующими уравнениями:
t
mvx — invox = Sx = J X dt-, mvy — mvov =
о
t t
= SV=\ Ydt-, тог — mvoz = Ss = JZdt,
о о
t. e. изменение проекции количества движе-
ния материальной точки на данную непо-
движную ось равно проекции на ту же ось
импульса силы, приложенной к этой точке.
Если к точке приложено несколько сил,
то в правых частях предыдущих уравнений
нужно писать сумму" (геометрическую) им-
пульсов всех этих сил или сумму (алгебраи-
ческую) проекций этих импульсов на дан-
ную ось.
Если F= const, т. е. если сила сохра-
няет постоянную величину и постоянное
направление, то
mv — mv0 = F- t.
ДИНАМИКА СИСТЕМЫ
Количество движения системы. Если име-
ем не одну материальную точку, а механи-
ческую систему, т. е. совокупность мате-
риальных точек, в которой движение каж-
дой точки зависит от положения и движе-
ния остальных (например, абсолютно твёр-
дое тело), то количеством движения системы
называется сумма (геометрическая) коли-
честв движения всех материальных точек
этой системы. Следовательно, количество
движения системы
Q = 2 mv.
Отсюда проекции количества движения
системы на координатные оси:
Qx = s mvx-, Qv=^mvv; Qz = ^,mvz.
Все силы, действующие па материальные
точки данной механической системы, можно
разделить на две категории: силы внешние
и силы внутренние. Внутренними си-
лами называются силы взаимодействия
между материальными точками данной си-
стемы. Внешними с и л а м и называются
силы, с которыми действуют на данную си-
стему материальные точки или тела, не при-
надлежащие к этой системе. Так, например,
для движущегося паровоза, рассматривае-
мого как одна система, его вес, нормальная
реакция рельсов, трение между рельсами и
бандажами колёс, сопротивление воздуха —
все эти силы являются внешними; к внут-
ренним силам будут относиться давление
пара на стенки котла и на поршень, а так-
же силы трения, возникающие между от-
дельными частями паровоза. Поскольку
внутренние силы являются силами взаимо-
действия между материальными точками си-
стемы, эти силы согласно закону равенства
действия и противодействия всегда попарно
равны по величине и направлены по одной
прямой в противоположные стороны. Отсюда
следует, что сумма всех внутренних сил си-
стемы всегда равна нулю.
Из равенства Q = Ыпи следует
= 2т = S та.
dt dt
По второму закону динамики
та = Fe + Fj,
где Fe обозначает равнодействующую
всех внешних сил и F, — равно-
действующую всех внутренних
сил, приложенных к данной материальной
точке системы. Следовательно,
= £ р -р Fh но S Ft = О,
dt
а потому
= S ?е,
dt
т. е. производная по времени от количества
движения системы равна сумме всех внеш-
них сил или. что то же, равна главному
вектору внешних сил, действующих на эту
систему.
Этот результат представляет собой обоб-
щение второго закона динамики на систему.
В скалярной форме этот результат выра-
жается следующими уравнениями:
dQx__уу* aQy_____у у • dQz_у- 7
llt^ e’ Т(--ЪУе,
ДИНАМИКА
379
т. е. производная по времени от проекции
количества движения системы на данную
неподвижную ось равна сумме проекций на
ту же ось всех внешних сил, действующих на
эту систему.
Если У F„ = 0, то = 0 и, следовательно,
Q = const, т. е. если сумма внешних сил си-
стемы все время равна нулю, то количество
движения системы остаётся постоянным
(случай сохранения количества
движения систем ы). Аналогично, если
SX„ = О (если, например, все внешние силы
перпендикулярны к оси х), то Qx = const
(случай сохранения проекции количества
движения системы на данную ось).
Из равенства
(( Q __ v р
dt ~~ “ г
следует
dQ = S Fe dt,
откуда, после интегрирования,
t
Q - Qo = S f Fc dt = S Se,
b
t. e. изменение количества движения систе-
мы равно сумме (геометрической) импульсов
всех внешних сил, действующих на эту си-
стему (теорема о количестве дви-
жения системы). В скалярной форме
эта теорема выражается следующими урав-
нениями:
t
Qx-Qox = ^^edt = 2S„;
О
t
Qy — Q«v~ 2 f Yedt = SSfJ/;
6
t
Q.z Qoz — 2 J Ze dt — s Sez,
b
t. e. изменение проекции количества движе-
ния системы на данную неподвижную ось
равно сумме (алгебраической) проекций на
ту же ось импульсов всех внешних сил, дей-
ствующих на эту систему.
Центр масс системы. Теорема о движении
центра масс. Координаты центра тяжести С
системы (в частности, твёрдого тела) опре-
деляются по формулам (см. «Статика»):
хс = ХР ’ = SP ’ zc = ~р ’
где через Р обозначены веса материальных
точек системы (материальных частиц твёрдо-
го тела), а х, у, г—координаты этих точек.
Если заменить здесь Р через mg, то по со-
кращении на общий множитель g получим:
\тх %ту Xmz
хс = At ; Ус = ~м"! гс = ~м ’
где М = У)т—масса всей системы. Геометри-
ческая точка, координаты которой опреде-
ляются по этим формулам и положение ко-
торой зависит только от масс материальных
точек данной системы и от их положения
в данный момент, называется центром
масс системы. Если система находится
в поле силы тяжести, то центр масс этой
системы совпадает, очевидно, с её центром
тяжести. Из предыдущих равенств находят:
2mx = Mxr ; Smy = Мус ; £mz — Mzc ,
откуда
dx , dxt„ . dy
v m = M —£; 2 m -.~
" dt dt dt
dz dz,.
~S,m M —L
dt dt
dt
или
2 mi)x = Mvcx; 2 mvy — Mvcy; S mvz = MvC2,
или
Qx ~ Mucx, Qy “ tytvcy, Qz —
где ucx, vcy, о,:г обозначают проекции ско-
рости vc центра масс системы.
Из этих равенств, выражающих равенство
проекций на координатные оси двух век-
торов Q и М vc , вытекает равенство этих
векторов; следовательно, Q = Mvc, т. е.
количество движения системы равно (по ве-
личине и направлению) количеству движения
центра масс этой системы, если предпо-
ложить, что в этом центре сосредоточена
вся масса системы. Поэтому, например, ко-
личество движения колеса, катящегося по
рельсу, равно произведению массы колеса
на скорость его центра тяжести.
Если твёрдое тело вращается вокруг не-
подвижной оси, и если центр тяжести С
этого тела лежит на оси вращения, то ко-
личество движения тела будет равно пулю,
так как в этом случае vc = 0.
Из равенства Qx = Mvcx следует, что
dQx dvcx d*xc dQx
= M = M ------------— , но = 2 Xe,
dt dt dp at
а потому
M - Xc_ = s X
dt2
e
и аналогично
d2yr
M _= s Уе; м
dt* e
dt*
= V,Ze.
Эти уравнения называются д и ф е р е н-
циальными уравнениями дви-
жения центра масс системы.
Отсюда следует теорема о движении цен-
тра масс: центр масс (центр тяжести) си-
стемы движется так же, как материаль-
ная точка, масса которой равна массе всей
системы и к которой приложены все внешние
силы, действующие на эту систему. По-
этому, например, центр тяжести тела, бро-
шенного под углом к горизонту (в пустоте),
описывает всегда параболу.
Из этой теоремы следует: 1) внутренние
силы системы не влияют на движение её
центра масс; 2) при отсутствии внешних сил
центр масс системы или остаётся неподвиж-
ным, или движется прямолинейно и равно-
мерно. Поэтому, например, силы трения
между рельсами и ведущими колёсами паро-
воза являются теми внешними горизонталь-
ными силами, благодаря которым оказы-
380
МЕХАНИКА
кается возможным перемещение паровоза
в горизонтальном направлении; на абсо-
лютно гладких рельсах движение паровоза
было бы невозможно.
Момент количества движения. Наряду
с моментами сил в динамике приходится
рассматривать моменты количества движе-
ния, т. е. моменты вектора ту относительно
данной точки или данной оси, причём эти
моменты определяются аналогично моментам
силы.
Моментом количества движе-
ния относительно точки О называется век-
тор, имеющий начало в точке О и перпенди-
кулярный к' плоскости, в которой лежат
точка О и вектор mv. Модуль этого век-
тора равен произведению модуля вектора
mv на 'длину перпендикуляра, опущенного
из точки О на линию вектора ту, или, что
то же, модуль вектора тото (mv) равен
удвоенной площади треугольника, основа-
нием которого является вектор ту, а про-
тивоположная вершина совпадает с точкой О.
Проекция вектора тото (mv) па какую-
нибудь ось, проходящую через точку О,
равна моменту количества движения ти
относительно этой оси. Моменты количества
движения относительно координатных осей
х, у, z определяются по тем же формулам,
как и моменты силы, но в этих формулах
проекции силы X, Y, Z нужно заменить
проекциями mvx, mvy, mvz количества дви-
жения на координатные оси; следовательно:
тотх (mv) = у-mv2 — z-mvy =
/ dz dy\
-m\y dt~zdi)’
mom,j (mv)= z-mvx — x-mvz =
( dx dz\
= m г -у,— хуту ;
[al dt j ’
mom, (mv)= x-mvy — y-mvx =
( dy dx\
= m\x~dt-yJty
Диференцируя первое из этих равенств
по времени, получим:
d г —\ (dy dz , d2z
dt momx(mv) = m dt+y ^-
dz
~~ dt
Ho
dy
dt
-2—У
dt2
' d~z
y-dl2~z
d2z d2y
-dt2 = Z 11 m dt2 = Y’
m
потому
d . _.
momx(mv) = yZ — zY = momx
Аналогично
d
momv(mv) = zX — xZ = momy
d
momz (mv) = xY —yX = moma
(F).
(F)-,
(F).
Эти уравнения выражают теорему о мо-
менте количества движения: производная по
времени от момента количества движения
материальной точки относительно данной
неподвижной оси равна моменту действую-
щей на эту точку силы относительно той
же оси.
Так как моменты вектора ту относитель-
но осей х, у, z равны проекциям на эти
оси вектора тото (ти), то из предыдущих
трёх скалярных уравнений вытекает вектор-
ное равенство
тот0 (mv) = тото (F),
выражающее ту же теорему в векторной
форме, т. е. производная по времени от мо-
мента количества движения материальной
точки относительно данного неподвижного
центра равна моменту действующей на эту
точку силы относительно того же центра.
Если на материальную точку действуют
несколько сил, то на основании теоремы
Вариньона в правых частях предыдущих
уравнений нужно писать сумму (геометри-
ческую) моментов всех этих сил относи-
тельно данного центра или сумму (алгебраи-
ческую) их моментов относительно данной
оси. В случае системы материальных точек,
кинетическим моментом си-
стемы относительно данной точки или дан-
ной оси называется главный момент коли-
честв движения всех материальных точек
системы относительно этой точки или этой
оси. Следовательно, если обозначить кине-
тический момент системы относительно точки
О (начала координат) через Go, а кинети-
ческие. моменты системы относительно коор-
динатных осей через Ох, Gy, Gz, то
Go = Д тота (mv)', Gx— - тотх (mv)',
Gv = 3 тоту (mv);
G,~— X momz ( mv ).
Диференцируя первое из этих равенств
по времени, получим
= S £ тота(т7>),
но на основании предыдущей теоремы
тот0 (mv) = тото (Fe)+momo(Fi ),
а потому
= v тото ( ре ) + v тОто (Jp. ).
Так как внутренние силы системы попарно
равны по величине и направлены по одной
прямой в противоположные стороны, то
сумма их моментов относительно любой
точки (или любой оси) всегда равна нулю.
Следовательно,
^2o-=Smomo (Fe ),
dt 0
т. е. производная по времени от кинетиче-
ского момента системы относительно дан-
ного неподвижного центра равна главному
ДИНАМИКА
381
моменту внешних сил, действующих на си-
стему, относительно того же центра (тео-
рема о кинетическом моменте
систем ы).
Аналогично получают три скалярных
уравнения, выражающих ту же теорему
в скалярной форме:
^^тотх(Ре),^
= S тот,, (Fe ), = s тот- (Fe ),
т. е. производная по времени от кинетиче-
ского момента системы относительно данной
неподвижной оси равна главному моменту
внешних сил, действующих на систему,
относительно той же оси.
Если
£ тот0 (Ре ) = О,
то
dGp __ q
at
и, следовательно,
Go = const,
т. е. если главный момент внешних сил
относительно данного центра всё время
равен нулю, то кинетический момент си-
стемы относительно этого центра остаётся
постоянным (случай сохранения кинетиче-
ского момента системы). Аналогично: если
S тотг (Ёе ) = О,
то
G2=const,
т. е. если главный момент внешних сил
относительно данной оси всё время равен
нулю, то кинетический момент системы отно-
сительно этой оси остаётся постоянным.
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Работа. Если материальная точка М (х, у,
г), на которую действует сила F, проходит
элементарный путь ds, переместившись в по-
ложение М' (x+dx, у + dy, z-j-dz), то
работа силы F на этом пути (элементарная
работа) равна
SA = F cos ср ds,
где 9 — угол между направлением силы F
и направлением скорости о точки М, или
(в аналитической форме)
BA = X dx + У dy + Z dz,
где X, У, Z — проекции силы F на коорди-
натные оси.
Работа А на конечном пути при переме-
щении точки М из положения в поло-
жение М3 выражается криволинейным инте-
гралом, взятым вдоль траектории этой
точки, т. е.
(М,)
А — | F cos 9 ds =
(АГ,)
(Мв)
= f X dx + У dy + Z dz.
(MJ
Если точка М перемещается по прямой
линии и сила F направлена по этой пря-
мой, то 9 — 0 или 9 = 180°, а потому в этом
S
случае 6А = ± F ds и А =± J F ds; если
о _ _
F = const, то А = ± Fs. Если F I и, то
cos 9 = 0, а потому ЗА = 0.
Пусть точка М перемещается из поло-
жения Mi (хг, У1, zx) в положение М2 (х2,
у2, z2) под действием силы тяжести. Если
обозначить вес этой точки через Р, а ось z
направить по вертикали вверх, то Х=У =0
и Z = — Р, а потому
Za
БА — — Р dz и А = — j Р dz = Р (zx — z2),
т. е. работа силы тяжести равна произве-
дению веса материальной точки на разность
высот этой точки в начальном и конечном
положениях, причём эти высоты отсчиты-
ваются от произвольно выбранной горизон-
тальной плоскости. Отсюда следует, что
работа силы тяжести не зависит ни от длины,
ни от вида траектории, по которой переме-
щается точка из начального положения
в конечное.
В случае твёрдого тела конечных разме-
ров в полученной формуле для работы А
под и z2 нужно понимать координаты
центра тяжести тела.
Теорема кинетической энергии. К и н с-
тической энергией (ж ивой си-
лой) движущейся материальной
точки называется скалярная величина,
равная половине произведения массы этой
точки на квадрат её скорости, т. е. ве-
тлу2
личина ~2~ .
Чтобы установить зависимость между
изменением кинетической энергии мате-
риальной точки и работой действующей
на эту точку силы F, возьмём основное урав-
нение динамики, выражающее второй закон
Ньютона:
та == F.
Проектируя это векторное уравнение на
направление касательной к траектории точ-
ки, получим
mat = Ft,
НО
du
а* = л
(см. «Кинематика». Криволинейное движе-
ние. точки) и
Ft = F cos 9,
а потому
dv
т м — F cos 9.
Умножая обе части этого уравнения па ds
получим
dv
т Л ds = F cos ? rfs’
или
mvdv = F cos-pls — SA.
МЕХАНИКА
382
Интегрируя это уравнение, находим
, (М)
= j* Fcostfds>
(лад
или
ту2 гт‘о_ .
2 2
т. е. изменение кинетической энергии ма-
териальной точки равно работе силы, дей-
ствующей на эту точку (теорема кинетиче-
ской энергии).
Если на точку действуют несколько сил,
то в этом случае в правой части предыду-
щего уравнения нужно писать алгебраиче-
скую сумму работ всех этих сил на данном
пути.
Кинетической энергией системы матери-
Smy2
—2~, где
суммирование распространяется на все ма-
териальные точки системы; следовательно,
если обозначим кинетическую энергию си-
стемы через Т, то
Написав уравнение кинетической энергии
для каждой материальной точки системы и
сложив затем эти уравнения, получим
Т-Т0 = ЪА,
т. е. изменение кинетической энергии си-
стемы равно сумме работ всех сил, дейст-
вующих на эту систему, как внешних, так
и внутренних.
При стационарных (т. е. не изменяю-
щихся с течением времени) связях без тре-
ния силы реакции таких связей в уравне-
ние кинетической энергии не войдут, так
как работа этих сил равна нулю (например,
при движении материальной точки по
гладкой, неподвижной поверхности
работа нормальной реакции этой поверх-
ности равна нулю, так как эта реакция
перпендикулярна к направлению скорости
точки). В тех случаях, когда трением пре-
небречь нельзя, в правую часть уравнения
кинетической энергии войдёт работа сил
трения.
Пусть данная система представляет собой
абсолютно твёрдое тело. При поступательном
движении этого тела скорости всех его то-
чек равны, а потому в этом случае
где М — масса тела, а о — скорость любой
его точки, например центра тяжести. Если
твёрдое тело вращается вокруг оси z с угло-
вой скоростью со, то скорость v всякой его
точки равна гео, где г есть расстояние этой
точки от оси г, а потому в этом случае
но S тгг = J2 (момент инерции тепа относи-
О)2
тельпо оси z) и, следовательно, Т = J2~>
т. е. кинетическая энергия твёрдого тела,
вращающегося вокруг данной оси, равна поло-
вине произведения квадрата его угловой ско-
рости на момент инерции тела относительно
оси вращения.
В общем случае движение твёрдого тела
можно разложить на два движения: 1) по-
ступательное, скорость которого равна ско-
рости vc центра тяжести этого тела, и 2) вра-
щательное с угловой скоростью о> вокруг
некоторой оси, проходящей через центр тя-
жести С этого тела («Кинематика», стр. 374).
В этом случае кинетическая энергия твёр-
дого тела определяется по формуле
где первое слагаемое выражает кинетиче-
скую энергию тела в поступательном движе-
нии, а второе слагаемое — кинетическую
энергию тела во вращательном движении
(J обозначает момент инерции тела относи-
тельно оси вращения, проходящей через
центр тяжести тела).
Если данная система находится в потен-
циальном силовом поле, то проекции на
координатные оси сил, действующих на
материальные точки этой системы, равны
частным производным от потенциальной
энергии П по соответствующим координатам,
взятым с обратным знаком, т. е.
_дП дП dll
Хк = ~ дхк> Yk= ~ дук ’ Z«=“ dzK ’
Следовательно,
S6A = S (Хк dxK + YKdyK 4- ZKdzK) =
(К)
/дП дП
= “(к) дук аУ“+
, дП \
+ dzKdz“)=~dn’
откуда, интегрируя, находим
SA =* — (П2 - Щ) = Пх — Па,
т. е. работа сил потенциального поля при
перемещении системы из положения 1 в
положение II равна падению (уменьшению)
потенциальной энергии.
Если при некотором определённом поло-
жении системы, называемом «нулевым» по-
ложением, считать потенциальную энергию
равной нулю (Г1о = 0), то при перемеще-
нии системы из данного положения в нулевое
S А = II — По = П.
Отсюда следует, что величина потенциаль-
ной энергии при данном положении системы
представляет собой ту работу, которую совер-
шают силы поля при перемещении системы
из данного положения в нулевое.
В случае, например, упругого деформи-
рованного тела мы имеем поле сил упру-
гости. Потенциальная энергия упруго-де-
формированного тела равна работе, кото-
рую совершают силы упругости при пере-
ДИНАМИКА
383
ходе тела из данного деформированного
состояния в недеформированное. При есте-
ственном состоянии упругого тела, т. е.
когда оно не деформировано, потенциальная
энергия тела принимается равной нулю.
Закон сохранения механической энергии.
Применяя теорему кинетической энергии
к движению системы в потенциальном си-
ловом поле, поЛучим
Л-Т1 = 2А = П1-П!,
откуда
Т2 + И2 = Л + И,,
или
Т 4- П = const,
т. е. при движении системы в потенциаль-
ном силовом поле сумма кинетической и
потенциальной энергии остаётся постоянной
(закон сохране н*и я механиче-
ской энергии). Этот результат верен,
конечно, только в том случае, когда движе-
ние системы в данном потенциальном поле
происходит без притока энергии извне и без
потери энергии, происходящей вследствие
наличия различных вредных сопротивлений,
например, сил трения.
Примеры: 1. Система находится в поле силы
тяжести. В этом случае потенциальная энергия
П = Mgzc ,
где М — масса всей системы, а гс — высота центра
тяжести С системы, отсчитываемая от некоторой
горизонтальной плоскости (например, от поверх-
ности земли). Следовательно, в этом случае имеем
— + Mgz с = cons t.
2. Потенциальная энергия сжатой или растяну-
той пружины
где с —жёсткость пружины, а X—сжатие или удли-
нение пружины. Следовательно, при вертикальных
колебаниях груза, подвешенного на пружине (при
отсутствии сопротивлений), будем иметь
77W3 С . .
-3- +mgzc + —Xе == const.
ПРИНЦИП ДАЛАМБЕРА
Для каждой материальной точки Мк (к =
= 1, 2, ..., п) данной механической системы
согласно второму основному закону дина-
мики
= FK + NK
или
FK + NK — тк ак = О,
где FK—равнодействующая всех заданных
(активных) сил, приложенных к точке Мк,
a WK—равнодействующая сил реакции свя-
зей, приложенных к той же точке.
Векторная величина—тк ак называется
силой инерции материальной точки ТИ,£.
Следовательно, если обозначить силу инер-
ции через F*£>, то F^ = — тк ак, т. е. си-
ла инерции материальной точки равна по
величине произведению м.-.ссы зтой точки на
величину её ускорения и направлена проти-
воположно ускорению. Предыдущее уравне-
ние принимает вид
Fk + WK + F<$ = О,
откуда следует, что три силы FK, NK и
уравновешиваются. То же имеет место
и для всех остальных точек системы. Таким
образом, приходим к следующему резуль-
тату, который представляет собой пр-инцип
Даламбера: в каждый данный момент задан-
ные (активные) силы, действующие на си-
стему, силы реакции связей и силы инерции
уравновешиваются. Отсюда следует, что си-
стема заданных сил, сил реакции связей и
сил инерции удовлетворяет уравнениям ста-
тики твёрдого тела, т. е. сумма проекций
всех этих сил на любую ось и сумма их
моментов относительно любой точки или
любой оси в каждый данный момент равна
пулю. Проекции силы инерции материаль-
ной точки на координатные оси равны:
Х/гк = тах — т dt2 ’
d-y
У ин = — тау — — т ,
d2z
Zim = — та2 = —т .
Проекции силы инерции на естественные
оси (на касательную и главную нормаль
траектории точки) равны
dv
Pun ——mat— —т
И
mv2
F™=-man = - ~ -
Составляющие силы инерции по каса-
тельной и главной нормали называются
соответственно касательной и • нормальной
силами инерции материальной точки. В слу-
чае движения точки по окружности нормаль-
ная составляющая сила инерции, направ-
ленная по радиусу окружности от центра,
носит название центробежной силы.
Так как в этом случае скорость точки
v = гы и радиус кривизны траектории р=г,
то величины касательной и нормальной сил
инерции равны соответственно тг | е | и
йы
тгы-, где г—радиус окружности, а е= ,
Нужно иметь в виду, что в действитель-
ности сила инерции не приложена к дви-
жущейся материальной точке; в действитель-
ности на точку действуют только силы
F и N, которые и сообщают ей соответст-
вующее ускорение.
Применяя же принцип Даламбера, мы
прилагаем силы инерции к каждой мате-
риальной точке системы дополнительно
(условно), для того, чтобы привести си-
стему к состоянию равновесия и затем вос-
пользоваться уравнениями статики. Этот
приём часто оказывается весьма удобным
при решении динамических задач, в осо-
бенности в кинетостатике, т. е. в тех зада-
чах, где требуется найти реакции связей
при данном движении системы (так назы-
ваемые кинетические реакции).
Объединяя принцип Даламбера с прин-
ципом возможных перемещений (см. «Ста-
тика»), приходим к заключению, что в слу-
384
МЕХАНИКА
чае идеальных связей сумма элементарных
работ всех заданных (активных) сил, дей-
ствующих на систему, и сил инерции при
всяком виртуальном перемещении системы
равна нулю, т. е.
S 1(Хк+ 4«’) +
\к)
+ +Z<^) Sz,t] = О
или
й2хк\ ? 4.
тк 'lit- ) Sx,; +
, Л. ^2Ук\- 4-
+ ( У к — тк -^)йУк +
Это уравнение называется общим
уравнением динамики.
Пример. С вертикальной осью, укреплённой
в подпятнике А и подшипнике В, жёстко соединены
три горизонтальных стержня длиной г,, г8, г8> несу-
щие на концах грузы Mlt Мъ и Л18, веса которых
равны Pxt Ръ и Р3. Расстояние АВ — ft. Вся система
вращается с данной угловой скоростью ш = const.
Найти реакции в подпятнике А и подшипнике В,
пренебрегая трением и массой стержней (фиг. 36).
Так как ш = const, то е «» — 0, и следовательно,
касательные силы инерции грузов равны нулю. По-
этому приложим к этим грузам только центробежные
силы, равные
F1 ин = -g r'“‘: f2 ин =
= Y Га“!; Гз “» “7 г,ш‘-
Горизонтальную и вертикальную реакции в под-
пятнике А обозначим соответственно через Хд и
Уд, а горизонтальную реакцию в подшипнике В обо-
значим через Xq . Так как система сил Рх, P.it Р3,
сил реакции и центробежных сил согласно принципу
Даламбера находится в равновесии, то, проектируя
все эти силы на оси хи у и составляя сумму их мо-
ментов относительно точки А, получим следующие
три уравнения:
1) ХА + Хв + (Рц, + Р.г, - Р3г3) у = о;
2) Ya- Р, - Р3 - Р, = 0;
3) — hXB + P(rsy3P3 — rsv2P„ — плР,) "g- —
— P,r, — Psr, + P3r3 = 0.
Отсюда находим искомые реакции ХА
у А и Хв •
Для того чтобы значения этих реакций
совпадали со статическими, т. е. с теми зна-
чениями, которые соответствуют состоянию
равновесия данной системы (при ш = 0),
члены, содержащие <п2, в предыдущих урав-
нениях должны исчезать, т. е. должны быть
выполнены условия
PjTi + Р2г2 — Р3г3 = О
И
rsy3Ps — Г2у2Р. — г1у1Р1 = 0.
Принимая во внимание, что
= хп г2 = х2 и га = —х3,
где х12х2, х3 —абсциссы грузов М1г М2, М3,
этгг условия можно написать в виде
2 тх = 0 и 2 тху = 0.
Но
2 тх = Мхс и 2 тху = Jxv,
где М — общая масса всех грузов,
хс — абсцисса их центра тяжести и
Jxy — центробежный момент инерции.
Следовательно, чтобы кинетические реак-
ции совпадали со статическими, должны
быть выполнены условия хс = 0 и Jxy = 0,
т. е. центр тяжести вращающихся масс
должен лежать на оси вращения и центро-
бежный момент инерции Jxy этих масс дол-
жен равняться нулю. Если эти условия вы-
полнены, то говорят, что вращающиеся
массы динамически уравновешены.
ДИНАМИКА ТВЁРДОГО ТЕЛА
Вращение твёрдого тела вокруг непо-
движной оси. Пусть данное твёрдое тело
имеет две неподвижно закреплённые точки.
Неподвижную прямую,
проходящую через эти
две точки, примем за
ось z. Если к этому те-
лу приложена произ-
вольно заданная систе-
ма сил Flt F2, Р3,...(фиг.
37), то тело будет вра-
щаться вокруг непод-
вижной оси z. Обозна-
чим угловую скорость
тела через ш и найдём
его кинетический мо-
мент (т. е. главный мо-
мент количеств движе-
ния материальных ча-
стиц тела) относительно
оси вращения; принимая во внимание, что ве-
личина линейной скорости и всякой точки
тела равна гш, где г — расстояние этой
точки от оси Z, и что вектор ти лежит в
плоскости, перпендикулярной к оси z, будем
иметь
G, = 2 тот, (mv) = 2 т^г =
= 2 mr- <и = ш v mr2
или
= ЛШ>
где Jz = ^тг2 — момент инерции тела отно-
сительно оси z. Применяя теорему о кинети-
ческом моменте системы относительно оси 2,
получим
ДИНАМИКА
385
, ь*ш
Jz ~ Rtomz \F)‘,
d<p
так как ш = где ? — угол (в радианах),
определяющий положение вращающегося
тела, то предыдущее уравнение принимает
вид:
Л dP = S тотг (F)
или
Jz OF = Мг,
где
Мг = S тот, (F).
Это есть диференциальное уравнение вра-
щательного движения твёрдого тела вокруг
неподвижной оси. Это уравнение аналогично
основному уравнению динамики точки, вы-
ражающему второй закон Ньютона, но
только вместо массы в это уравнение входит
момент инерции тела, вместо линейного
ускорения— угловое ускорение тела и
вместо силы (или суммы сил) — сумма мо-
ментов приложенных к телу сил относи-
тельно оси вращения.
В диференциальное уравнение вращатель-
ного движения тела силы реакции закреп-
лённых точек не входят, так как моменты
этих сил относительно оси вращения равны
нулю. Проинтегрировав это уравнение, на-
ходят угол у, как функцию времени t, т. е.
находят закон вращательного движения, ко-
торое получает тело под действием прило-
женных к нему сил.
Если Мг = 0, то
d2'-f> dm
dF “ dt
и, следовательно, <n = const, т. е. тело вра-
щается равномерно. Если
Мг = const,
то
du> М2
di=J7 = const’
т. е. угловое ускорение е является постоян-
ным, и, следовательно, вращение тела в этом
случае будет равномерно-переменным.
Работа силы F, приложенной к вращаю-
щемуся твёрдому телу, при повороте тела
на элементарный угол d<p равна
1А = тотг (Ё) d-f,
а потому
S SA = S тот, (Ё) d<? =
ч>
= M2-d<p и S А = J M2drp.
Так как кинетическая энергия вращающе-
го2
гося тела равна _/г , то уравнение кине-
тической энергии для твёрдого тела, вра-
щающегося вокруг неподвижной оси г, при-
нимает вид
25 Том I
<Р
J Jz (“2 — “о) = J M;-d?.
Мощностью N называется работа, произ-
ведённая в единицу времени, т. е.
dA
N = dF
Мощность измеряется или в лошадиных си-
лах или в киловаттах, причём 1 л. с. =
= 75 кГм/сек и 1 кет = 102 кГм/сек.
В случае вращательного движения твёр-
дого тела
N =
или
dA dA dy
dt ~ dy dt
— M2‘<a,
N = M, эд кгм/сек,
где n — число оборотов тела в минуту.
Отсюда
N = 30775 пМ° л- с-
и
N
30-75 N N
М‘= — - = 716,2 - кГм.
Для определения реакций, возникающих
в закреплённых точках вращающегося твёр-
дого тела, можно воспользоваться принци-
пом Даламбера.
Если к каждой материальной частице
вращающегося тела приложим касательную
и нормальную силы инерции, то система
заданных сил FK, сил реакции закреплён-
ных точек и сил инерции будет удовлет-
ворять шести уравнениям статики, выра-
жающим условия равновесия сил, прило-
женных к твёрдому телу (три уравнения
проекций на координатные оси и три урав-
нения моментов относительно этих осей).
Возьмём начало координат О в одной из
закрепленных точек; расстояние между
этими точками обозначим через ft, ось г
направим по оси вращения тела; проекции
искомых реакций на координатные оси
обозначим через Rx, Rv, Rz, Rx, Ry, Rz.
В уравнение моментов относительно оси z
не войдут ни искомые реакции, ни центро-
бежные силы, так как моменты всех этих
сил относительно оси z равны нулю; это
уравнение совпадает с диференциальным
уравнением вращательного движения тела.
Из остальных пяти уравнений получают:
R* =— {S momv (f)+ +Jyzt];
Ry = -^ [L momx (Ё) — Jyz^ + J2l г ];
Rx = — — W“! — Myc e +
+ [S тот, (Ё) + JzxaA + Jyze];
Rt, = — SFy— Му<м- 4- Mxce —
- ~ [\momx (F)-Jy^- +
Rz + R'z = -
386
МЕХАНИКА
В этих формулах М — масса данного
тела, хс и ус — координаты его центра тя-
жести, a J vz и Jzx обозначают центробеж-
ные моменты инерции тела, т. е.
Jyz = S,myz
и
Jzx = -mzx.
Из этих формул видно, что динамические
реакции закреплённых точек будут сов-
падать со статическими (т. е. с реакциями,
соответствующими тому случаю, когда тело
под действием заданных сил Рк находится
в покое), если члены, содержащие ш2 и е,
в этих формулах исчезают, т, е. если
хс ~ Ус ~ ® и JyZ =Jzx — 0.
Если оси х, у, z, имеющие начало в
какой-нибудь точке данного тела, выбра-
ны так, что центробежные мо-
/'?><''. менты инерции Jyz, Jzx, Jxy
! Л \ \ равны нулю, то такие оси на-
\ W зываются главными о с я-
\ 1—ми инерции тела в
\| ft \ данной точке.
\ \ ) Главные оси инерции, имею-
\ 1 щие начало в центре тяжести
i тела, называются главны-
* ми центральными ос я-
Флг 38 м и инерции. Поэтому
приходим к заключению:
для того чтобы при вращении твёрдого тела
вокруг, неподвижной оси динамические реакции
закреплённых точек совпадали со статиче-
скими, необходимо и достаточно, чтобы ось
вращения тела являлась одной из главных
центральных осей инерции этого тела. Если
это условие выполнено, то говорят, что вра-
щающееся тело динамически уравновешено.
Физический маятник. Физическ им
(или сложным) маятником назы-
вается твёрдое тело, которое может вра-
щаться вокруг неподвижной горизонтальной
оси под действием только силы тяжести. Если
обозначить угол отклонения маятника от
положения равновесия (отсчитываемый в на-
правлении, противоположном движению ча-
совой стрелки) через ср, расстояние центра
тяжести С маятника от оси вращения О,
(перпендикулярной к плоскости чертежа) —
через s и вес маятника — через Р (фиг. 38),
то момент силы Р относительно оси враще-
ния равен
— Ps-sin ср = — Mgs-sin ср,
где М — масса маятника; диференциалытое
уравнение движения маятника имеет вид
(Рср
Тр = — W-sm
где J„ —момент инерции маятника относи-
тельно оси вращения. Но
Jo = Jc + М s’- = Mi‘c + Ms2 =
= м (,; + ?).
Здесь Jc — момент инерции маятника относи-
тельно оси, параллельной оси вращения и
проходящей через центр тяжести С (см.
«Моменты инерции», стр. 393), a ic— радиус
инерции относительно той же оси, а потому
диференциальное уравнение движения маят-
ника принимает вид
S ) dti= — gs-sm ср.
При малых колебаниях маятника
можно принять sin ср ср.
Тогда получим диференциальное уравне-
ние малых колебаний маятника
,d2cp
(<c + s) dP = ~W>
или
^ + ^=0.
где
/<2 = .
ic + s2
Это есть диференциальное уравнение
гармонических колебаний (см. «Динамика
материальной точки», стр. 377).
Интегрируя это уравнение в предполо-
жении, что начальный угол отклонения
маятника равен у0, а его начальная угловая
скорость равна нулю, получим
ср = <р0 cos (kt).
Период малых колебаний маятника
Эта формула является достаточно точной при
ср0 < 20°; в этом случае ошибка не превы-
шает 0,8%. При больших значениях угла
ср0 можно пользоваться более точной фор-
мулой:
Период малых колебаний простого или мате-
матического маятника (т. е. материальной
точки, подвешенной на нити длиной I)
определяется по формуле
Из сравнения этой формулы с вышеука-
занной следует, что период малых колеба-
ний физического маятника равен периоду
колебаний математического маятника, длина
которого
+J2 (’
I ~~ S s-^ S
Эта длина называется приведённой
длиной физического маятника. Есчи па
прямой ОС отложить от точки О отрезок
OL == I s + s ,
то точка L называется центром кача-
ний физического маятника.
УДАР
Основные положения. Явление удара
характерно тем, что скорость тела, подверга-
ющегося удару, а следовательно, и его ко-
ДИНАМИКА
387
личество движения за очень короткий про-
межуток времени изменяются на конечную
величину. Такое почти мгновенное конечное
изменение количества движения тела проис-
ходит потому, что развивающаяся при
ударе сила достигает весьма большой ве-
личины, так что её импульс, несмотря на
то, что сила действует на тело в течение
весьма малого времени, имеет конечную ве-
личину. Такая сила называется ударной
силой, а её импульс называется ударным
импульсом. Ударный импульс определяется
(по величине и направлению) изменением
количества движения тела, т. е.
S(yd) = тие — mvc,
где т — масса тела, a vc и ис — скорости
центра тяжести тела в начале и в конце
удара.
Фиг. 39
При разделении величины S(5"^ на время т
действия ударной силы получают сред-
нюю величину этой силы. Так как импульс
неударной силы (например, силы тяжести)
за время т весьма мал по сравнению
с Siyd\ то эффектом действия неударных
сил при явлении удара обычно можно пре-
небречь.
Прямой центральный удар двух тел.
Пусть два тела, массы которых равны т1 и
т2, движутся прямолинейно и поступательно
со скоростями Hi и у2 (фиг. 39). Если эти
тела сталкиваются, то наблюдают явле-
ние удара. В течение весьма малого про-
межутка времени т сек. тела будут касаться
друг друга в некоторой точке и будут давить
друг на друга. Сила этого давления является
ударной силой. Общая нормаль к поверх-
ностям этих тел в точке их касания назы-
вается линией удара. Если скорости и va
направлены по линии удара, то в этом слу-
чае удар называется прямым; если линия
удара проходит через центры тяжести Сг и С2
обоих тел, то удар называется централь-
ным. На фиг. 39 изображён случай прямого
центрального удара двух тел. Если обозна-
чим скорости тел после удара через н, и
п2, то в случае прямого центрального удара
эти скорости будут направлены по линии
удара. Величины этих скоростей опреде-
ляются по формулам:
т2
и, = У1 - (1 + к) (щ - р2);
т1
«2 = «г - (1 + к) mi + m2 (г2 - U1),
где к—так называемый коэфициент
восстановления, причём
. — и2
= ~ ’
т. е. коэфициент восстановления равен
отношению относительных скоростей тел
после и до удара, взятому с обратным
знаком.
В этих формулах скорости тел берутся
в алгебраическом значении, т. е. со знаком
плюс или минус, в зависимости от того, в
какую сторону по линии удара направлена
скорость тела.
Таблица 1
Ударяющиеся
тела
К
Величина коэфициента восстановления
(безразмерное число) зависит от материала
ударяющихся тел и определяется из опыта.
Полученные из опыта значения коэфициента
к для некоторых тел указаны в табл. 1.
Если к = 0, то
удар называется
н е у п р у г и м;
если к— 1, то удар
называется в п о л-
н е или совер-
шенно упру-
гим. Хотя для
реальных физиче-
ских тел к всегда
есть некоторая
правильная поло-
жительная дробь, но в некоторых случаях,
когда к невелико или близко к единице,
можно без существенной погрешности рас-
сматривать удар как неупругий или как
вполне упругий.
При к = 0 из предыдущих формул
находят
Дерего о гуттаперчу
Деревянные шары .
Стальные шары . .
Стеклянные шары .
Шары из слоновой
кости .............
0,26
0,50
0,56
0,94
0.89
mlvl + f^2P2
«1 - и2
/Hi 4* т
В этом случае тела после удара не отде-
ляются Друг от друга, а движутся вместе
с одинаковой скоростью.
Если к — 1. то
,2 т2
2m,
В случае прямого центрального удара тела,
о неподвижную поверхность нужно,-
очевидно, положить t>8 == и2 = 0, тогда
к = —““««! = — kvv-,
знак минус указывает на то, что скорость
тела после удара направлена противопо-
ложно его скорости до удара (тело, ударив-
шись о неподвижную поверхность, отска-
кивает от неё в противоположном направ-
лении).
Величина ударного импульса опреде-
ляется по изменению количества движения
одного из ударившихся тел, т. е.
= т2и2 — m2v., = т2 (н2 — t>,) =
= (!+^)7НГ+"-шТ ^-Уг)-
Полагая здесь /с = 0 или fc = l, можно
получить величину ударного импульса при
неупругом и при вполне упругом ударе.
При ударе двух тел происходит потеря
кинетической энергии, т. е. общая кинети-
ческая энергия Т обоих тел после удара
будет меньше их кинетической энергии Т„
в начале удара. Потерянная кинетическая
25*
МЕХАНИКА
388
энергия переходит в тепловую энергию;
известно, что при ударе тела нагреваются.
Величина потерянной при ударе кинети-
ческой энергии определяется по формуле
То-Т = (1-ЛО
или по формуле
То-Т = Ц.-А
Пусть скорость молота в начале удара равна »х.
Так как поковка и наковальня до удара непо-
движны, то vt = О, а поэтому
ma v
т
где т, — масса молота. Потерянную при ударе кине-
тическую энергию определяем по первой из ука-
занных выше формул
к [ mi ((7;-
И1)2
Г. - т = (I - Л*) V
2 (иц + ma\
' 2 J •
Если к = 0, то из последней формулы
получаем
т Т _ mi ц1)а , ("г—
' О 1 —
Эта энергия затрачивается на работу деформации
поковки, которая является в данном случае полез-
ной работой, а потому искомый к. п. д. будет
но
i о
ша
rrii + *
2
т. е. при неупругом ударе двух тел потерян-
ная кинетическая энергия равна кинетиче-
ской энергии этих тел, соответствующей их
потерянным скоростям (теорема Карно).
Если к ~ 1* то То — Т = 0 и Т=Т0, т. е.
при вполне упругом ударе кине-
тическая энергия не теряется.
Рассмотрим случай, когда к = 0 и р2=0,
т. е. случай неупругого удара, при котором
одно из ударяющихся тел до удара непо-
движно, В этом случае:
pt
g
и
ffl, -
P«
s
а потому
P 15
^'^рГ^рГ0’64 16 = 0'6*
Пример 2. При забивке свай боёк копра ве-
сом Р[=4 5О кг падает без начальной скорости с вы-
соты h = 2 м. Вследствие полученного удара свая
весом Ра « 50 кг углубляется в грунт на расстояние
S= 1 см. Найти среднюю величину силы сопротив-
ления грунта и к. п. д. копра, считая удар неупругим.
В начале удара скорость бойка равна
;
m, w, m, u,
r,)=-yi;r=-2 ' '
2
mi
_______________т
2 (/П1 + тг) m1imi 0
1
То.
больше
Если масса т1 значительно
массы Шч, то дробь — будет мала,
чина Т будет близка к То, т. е. потеря ки-
нетической энергии будет невелика; такой
случай имеет место, например, при забивке
свай или при вбивании гвоздя молотком.
Когда неподвижному телу (например, свае)
нужно сообщить посредством удара значи-
тельную скорость, масса этого тела должна
быть значительно меньше массы ударяющего
тела.
Если, наоборот, масса т2 значительно
т..
больше массы т1г то дробь — будет ве-
лика, а потому величина Т будет состав-
лять небольшую часть от Т0(если, напри-
и вели-
мер,
ГП2
= 10, то величина Т составляет
9% от
следоватепьно, значительная
начальной кинетическом энергии при
теряется; такой случай имеет место,
при ковке или штамповке ме-
часть
ударе
например,
талла.
Пример 1, Вес парового молота Р, =« 1 т, об-
щий вес сдковки и наковальни Рг=15т. Коэфи-
циенг восстановления /с=0,6. Найти к.п.д. молота.
v, = У 2 gh,
а скорость сваи
=» 0.
Так как удар считаем неупругим, то общая ско-
рость этих тел после удара равна
Кинетическая энергия
после удара равна
Т = 4- mt)--
2 2
Р| V,
2 2
ml Pl
2 (m, + m,)
Plh
2й(Л + Рг) ~ Pi + Pa *
Обозначая среднюю величину силы сопротивле-
ния грунта через Р и применяя теорему кинетической
энергии к движению сваи после удара, получим
откуда
Р}П
pl^ + (Pi + Pas“ps’
Р1Л
p-Pi + P. + ^r^r 500 +
450’.2- 100
500
= 81 500 кг.
Кинетическая энергия в начале удара равна
F
Pl
2 g
2
V1
= Pjft.
Оставшаяся после удара кинетическая энергия Т
расходуется на работу вбивания сваи, которая яв-
ляется в данном случае полезной работой; поэтому
искомый к. п. д. равен
_ ..„«SO = 09
Г. Р, + Р, 500 ’ '
Пример 3. Железнодорожный вагон весом
Рх «=з 25 т, движущийся со скоростью Vi>»12 км/час,
нагоняет другой вагон весом Ра=20 т, имеющий
скорость V, = 8 км1ччс. Найти скорости этих ваго-
нов после столкновения, если удар в буферах мож-
но считать вполне упругим.
Так как то искомые скорости находят по
формулам:
2 та ,
их = --------- (Vt — Va) =»
Ш1+ m,
“ рДр/Г — га) = 12 — ^*4 = 8,44 км1чаС;
ДИНАМИКА
389
2 тх z
U„ = V8--,--(Va — Vx)
8 8 т^т2 4 8 l'
- V,- p~lpt (».-»>)“ 8 + ^-4 = 12,44 км/час.
Удар двух тел, вращающихся вокруг не-
подвижных параллельных осей. Пусть два
тела вращаются вокруг осей (перпен-
дикулярных к плоскости чертежа) О2 и
О2 с угловыми скоростями шс1 и ш02 (фиг. 40).
Пусть в некоторый момент эти тела стал-
киваются, причём соприкосновение тел во
время удара происходит в некоторой точке А;
общая нормаль к поверхностям этих тел
в точке А является линией удара. В этом
случае применимы те же формулы, как и
в случае прямого центрального удара двух
тел; только в этих формулах скорости i>v
и2, ц, и и2 нужно заменить нормальными
составляющими (т. е. составляющими в на-
правлении линии удара) vln, и2п, и1П и и2П
скоростей тех точек данных тел, которые
совпадают с точкой А, а массы т1 и т2
следует заменить через mi и т2> причём
т. — и т‘г, = Ja ,
1 hi 2 2
где Jr и J2— моменты инерции данных тел
относительно осей вращения Ог и О2, a /1Х
и й2— расстояния линии удара от Ог и О2.
Эти величины т^ и т2 называются мас-
сами данных тел, приведёнными к точкам
В и С, т. е. к основаниям перпендикуляров
/г, и й3.
Следовательно,
т9
И1п=у1п— G + O————— (Pin
..... ... т t + т*
т'
^2/: — V2n (1 + к) —-1-— (1>2Л Vln)‘
т + та
Так как
Vln — kl ш01» ~ ШО2» «In = W1 11
Пал ш2,
то получаем формулы для угловых скоро-
стей «ц и ш2 вращающихся тел после удара:
, т> ( \
Ш1 = ШО1 (1 + К) —-—2--— ( <Яо1 Ь №О2 1 >
т + т \ П1 )
1 >
т1 / \
й>2 в %2 О “Ь —---------— I Ю02 L I .
ггу + т* ' 2 /
По тем же формулам, какие были даны для
случая прямого центрального удара двух
тел, делая в них указанную выше замену,
можно найти величину ударного импульса
и величину потерянной кинетической
энергии.
Действие ударной силы на твёрдое тело,
вращающееся вокруг неподвижной оси. Центр
удара. Пусть твёрдое тело вращается во-
круг неподвижной оси г с угловой скоро-
стью <ов и пусть на это тело действует в те-
чение весьма малого промежутка времени
т сек. ударная сила F, приложенная к телу
в некоторой точке (х, у, г). Ударный им-
пульс, приложенный к телу, будет равен:
= jFdt>
о
а его проекции на координатные оси равны:
Sl/d) = J X dt; S^d) = j У dt;
о о
S(yd) = J z dt>
О
где X,Y, Z — проекции на оси ударной
силы F.
Диференциальное уравнение вращатель-
ного движения тела имеет вид
. d(a \
Л dj = тот, (F) = xY — уХ,
где Jz — момент инерции тела относительно
оси вращения.
Отсюда, интегрируя, находим:
х т
Jz (ш — соо) = J хУ dt — § уХ dt.
о о
Так как перемещения точек тела за время
т сек. весьма малы, то ими можно пренебречь^
и, следовательно, координаты х иу точки при-
ложения ударной силы в течение этого вре-
мени можно считать постоянными, а потому
Jz (<» — “о) = х J У dt — у J X dt =
о о
= xS</d> - yS^ = тот,
откуда
Jz
т. е. изменение угловой
скорости тела под дей-
ствием приложенного к
нему ударного импульса
равно моменту этого
импульса относительно
оси вращения, разделён-
ному на момент инер-
ции тела относительно
той же оси.
Пусть данное тело вращается вокруг не-
подвижной оси О, перпендикулярной к плос-
кости чертежа (фиг. 41), и пусть эта плос-
кость является для тела плоскостью
симметрии. Предполагается, кроме того,
что подшипники, поддерживающие ось, на
которой закреплено данное вращающееся
тело, расположены симметрично от-
носительно точки О.
МЕХАНИКА
390
Если к этому телу приложен ударный
импульс, то для технической практики
весьма важным является вопрос: при ка-
ких условиях действие этого импульса не
будет передаваться на подшипники, т. е.
подшипники не будут испытывать удара?
В рассматриваемом случае симметричного
тела для осуществления этого требования
должны быть выполнены следующие условия:
1) ударный импульс должен лежать в плос-
кости симметрии тела; 2) направление этого
импульса должно быть перпендикулярно
к прямой ОС, т. е. к прямой, соединяющей
центр тяжести тела С с точкой О пересече-
ния оси вращения с плоскостью симметрии
тела; 3) расстояние липин удара (пинии
действия ударного импульса) от оси вращения
тела должно равняться , где Jo — мо-
мент инерции тела относительно оси вра-
щения; М — масса тела; s — расстояние
центра тяжести тела от оси вращения, т. е.
s = OC. Точка К, лежащая на прямой ОС
па расстоянии от О, равном ОК = ’ па'
зывается центром удара. Следова-
тельно, чтобы подшипники не испытывали
удара, линия действия ударного импульса
должна проходить через центр удара. Так
как Jo = Jc+ Ms'2, где Jc — момент инерции
тела относительно оси, проходящей через
его центр тяжести и параллельной оси вра-
щения О, то
Отсюда следует, что ОК > ОС.
ЦЕНТР ТЯЖЕСТИ И МОМЕНТЫ ИНЕРЦИИ
ОБЩИЕ ФОРМУЛЫ ДЛЯ КООРДИНАТ
ЦЕНТРА ТЯЖЕСТИ
Всякая система параллельных сил, при-
водящаяся к одной равнодействующей си-
ле, имеет свой центр, т. е. точку, через ко-
торую всегда проходит эта равнодейству-
ющая независимо от того, какое направление
будем давать этим параллельным силам, при
условии, что их величина и точки при-
ложения остаются неизменными. Центр
параллельных сил, представляющих собой
веса материальных частиц данного тела,
называется центром тяжести этого тела.
Для нахождения центра тяжести данное
тело делят на такие части конечных разме-
ров, чтобы положение их центров тяжести
было известно, или же на части бесконечно-
малые. В зависимости от этого координаты
центра тяжести выражаются через конечные
суммы или через интегралы.
Если тело имеет плоскость, ось или
центр симметрии, то его центр тяжести лежит
соответственно в этой плоскости, на этой
оси или в этом центре симметрии.
В общем случае координаты центра тя-
жести С определяются по формулам:
f хр dV
(V)____
м
Ус =
f у? dV
(К)____
м
zc
f z?dV
(V)____
М
Г хр dS
s ________
М ',Ус =
,f ур dS
s ____
М ' ’
где dS — элемент площади, а р попрежнему
обозначает плотность, т. е. в этом случае
величину массы, приходящейся на еди-
ницу площади; интегралы распростра-
няются на всю площадь S пластинки. Если
р = const, то
( xdS f ydS
(S) (S)
- § > Ус- §
х,
Эти формулы определяют координаты центра
тяжести плоской геометрической фигуры
(или центра тяжести площади). Интегралы,
стоящие в числителе этих формул, выражают
так называемые статические момен-
т ы данной плоской фигуры относительно
координатных осей Оу и Ох. Точно так же
интегралы J xdV и два аналогичных выра-
(Ю
жают статические моменты геометрического
тела относительно координатных плоскостей
yOz, zOx и хОу.
В случае тела одного измерения, т. е.
так называемой материальной линии (на-
пример, тонкого стержня или куска тонкой
проволоки, поперечными размерами которых
в сравнении с длиной можно пренебречь),
имеем:
f pxdl j ру dl | pz dl
где М — масса тела; р — плотность в данной
точке тела; dV — элемент объёма и х, у, z —
координаты этого элемента; интегралы рас-
пространяются на весь объём V данного
тела. Если тело однородно, то плот-
ность имеет одно и то же значение во всех
точках тела, т. е. р = const. В этом случае
М = рV, а потому (по сокращении на р)
fxdV ( уdV f zdV
(V)____ _ (V)__________ _ (V)___
у > Ус— у > ‘-С~ у
В случае тела двух измерений (например,
плоской тонкой пластинки, толщиной кото-
рой можно пренебречь)
где dl'— элементарная дуга данной линии;
М— масса этой линии, а р обозначает ли-
нейную плотность, т. е. величину массы,
приходящейся на единицу длины. Интегралы
берутся вдоль всей данной линии.
Если р = const (для однородной линии),
хс = 1 j* xdl; уе = 1 ydl;
(О (О
‘'’Тр"'1
(О
где I — есть длина данной линии.
ЦЕНТР ТЯЖЕСТИ И МОМЕНТЫ ИНЕРЦИИ
391
Для однородных поверхностей и тел вра-
щения положение центра тяжести, лежащего
на оси вращения, определяется следую-
щим образом: пусть ось х есть ось вра-
щения и пусть уравнение меридиональной
кривой имеет вид
У = /(х).
Тогда:
для поверхности вращения
X..
2 г. f
хс = -s \xydl,
X,
где
х3 ________
S - 2г уdl и dl--= j/"
для тела вращения
Хз
= Т xy-dx,
Xi
где
V = т. J y-dx.
ПОЛОЖЕНИЕ ЦЕНТРА ТЯЖЕСТИ
НЕКОТОРЫХ ОДНОРОДНЫХ ЛИНИЙ,
ФИГУР И ТЕЛ
Прямолинейный отрезок. Центр тяжести
находится на середине отрезка.
Периметр треугольника. Центр тяжести
находится в центре круга, вписанного
в треугольник, вершины которого лежат
в серединах сторон данного треугольника.
Расстояние центра тяжести от стороны тре-
угольника а равно
. _ hq b + с
а<1~ 2 ' а + b 4- с ’
где а, Ь, с — стороны данного треугольника
и. ha—высота, соответствующая стороне а.
Периметр параллелограма. Центр тя-
жести находится в точке пересечения
диагоналей.
Дуга круга радиуса R. Центр тяжести
находится на прямой, делящей пополам
центральный угол дуги, на расстоянии от
центра дуги, равном
R sin а
Хс = ------ .
с а
где а—половина центрального угла дуги
в радианах.
г
При « = (половина окружности)
хс = 0,6366 R.
It
При “ = "4 (четверть окружности)
хс= 0,9003 R.
it
При а = -g (шестая часть окружности)
Треугольник. Центр тяжести находится
в точке пересечения медиан:
1
хс = -j (%1 4- х2 4- х3);
Ус = | (У1 + + Уз);
1
zc = з (zt 4- z2 + z3),
где Xi,yi,zx; x,,y.>,z2; x3, у», z3 — коорди-
наты вершин треугольника.
Параллелограм. Центр тяжести находится
на пересечении диагоналей.
Трапеция. Центр тяжести G находится
в точке пересечения прямой EF с прямой,
соединяющей середины М и N параллель-
ных сторон АВ и CD (фиг. 42). Расстояния
tia и hb центра тяжести от этих сторон равны:
h а + ~b h 2а 4- b
= 3 ' ~а + b~’ 1>ь 3 ’ ~а~+1Г ’
где h—высота трапеции.
Четырёхугольник. Для нахождения центра
тяжести разбивают данный четырёхугольник
А- А3 А3 Ai одной диагональю на два тре-
угольника с центрами тяжести Сх и С2
(фиг. 43) и другой диагональю на два тре-
угольника с центрами тяжести С3 и С4.
Точка пересечения прямых СХС2 и С3С4
есть искомый центр тяжести С данного
четырёхугольника.
Правильный многоугольник. Центр тя-
жести находится в центре вписаннного или
описанного круга.
Круговой сектор (фиг. 44). Центр тяжести
лежит на оси симметрии, причём
2 R sin а
Хс =----л----~ .
с За
it
При а = (площадь полукруга)
хс = 0,4244 R.
It
При “ = 4 (площадь четверти круга)
хс = 0,9549 R.
хс = 0,6002 R.
392
МЕХАНИКА
При а = g (площадь шестой части круга)
хс = 0,6366 R.
Круговой сегмент. Центр тяжести лежит
на оси симметрии, причём
4 R sin3 а
Хс 3 2 а—sin 2 а ’
где хе — расстояние ц. т. от центра О дуги
сегмента и а — половина центрального угла
этой дуги в радианах.
Часть плоского круглого кольца (фиг. 45).
Центр тяжести лежит на оси симметрии,
причём
2 R3 — г3 sin а
Хс = 3 R^-^r3 ’ ~ •
Эллиптический сегмент (фиг. 46). Центры
тяжести симметричных сегментов AXBXD и
AJ3.JJ совпадают с центром тяжести кру-
гового сегмента ABD, отсекаемого хордой
эллипса от круга, диаметр которого равен
оси эллипса, перпендикулярной к этой
хорде.
Половина параболического сегмента
(фиг. 47)
3 3
хс> = а; УС1 = ~g ь Для фигуры О АВ;
3 3
*с, = jo а; ус= 4 ь для фигуры ODB.
Поверхность шарового пояса. Центр тя-
жести находится в середине высоты.
Фиг. 47
Боковая поверхность правильной пира-
миды или круглого конуса. Центр тяжести
находится на прямой, соединяющей вершину
с центром тяжести основания, на расстоянии
одной трети высоты (пирамиды или конуса)
от основания.
Боковая поверхность круглого усечённого
конуса. Если радиусы верхнего и нижнего
оснований равны г и R, а высота равна й,
то центр тяжести лежит на прямой, соеди-
няющей центры оснований, на расстоянии
от большего основания, равном
й R + 2г
Zc ~ 3 ’ R + г •
Призма или цилиндр с параллельными
Основаниями. Центр тяжести находится на
середине прямолинейного отрезка, соединяю-
щего центры тяжести оснований.
Цилиндрическая подкова (непараллельно
усечённый круглый полуцилиндр) (фиг. 48).
Центр тяжести лежит в плоскости симметрии,
причём
3
Ус= j6 тт;
3
= 3?) к *
Пирамида или конус. Центр тяжести на-
ходится на отрезке, соединяющем вершину
с центром тяжести основания , на расстоя-
нии 3/4 этого отрезка от вершины.
Параллельно усечённые пирамида или
конус. Центр тяжести лежит на отрезке,
соединяющем центры тяжести оснований;
расстояние центра тяжести от нижнего
основания равно
_ Л + 2~KSiSr+ 3S.
Zc~ 4 s1 + /s1s3 + s2
где S, и S2 — площади нижнего и верхнего
оснований и й— высота.
Шаровой сегмент. Расстояние центра тя-
жести, лежащего на оси симметрии, от осно-
вания сегмента равно
3 (2 г - й)2
Zc ~ 4 3 г • Й ’
где й — высота сегмента и г—его радиус.
Шаровой сектор. Расстояние центра тя-
жести, лежащего на оси симметрии, от
центра шара равно
гс = | (2 г - й),
где г — радиус шарового сектора и й—вы-
сота шарового сегмента.
Параболоид вращения. Расстояние центра
тяжести, лежащего на оси вращения,, от
основания параболоида равно
1
йс= з й,
где й — высота параболоида.
Октант трёхосного эллипсоида. Если оси
координат совпадают с осями эллипсоида, то
3 3 3
хс = g Ус ~ g й; zc = g- с,
где а, Ь, с — полуоси эллипсоида.
МОМЕНТЫ ИНЕРЦИИ
Полярным моментом инерции Jo тела от-
носительно точки (полюса) О называется
сумма произведений из массы dm каждой
элементарной частицы тела на квадрат рас-
стояния г этой частицы от точки О, т. е.
ЦЕНТР ТЯЖЕСТИ И МОМЕНТЫ ИНЕРЦИИ
393
Jo = f г2 dm = J г2 pdu,
(») (»)
где р—плотность в данной точке тела.
Интеграл распространяется на весь
объём v данного тела. Если О есть начало
координат, то
Г2 — X2 + у2 + Z2 и
Jo= f р(х2 + у2 + z2) dv.
(V)
Аналогично для момента инерции мате-
риальной плоской фигуры относительно
точки О, лежащей в плоскости этой фигуры,
имеем
Jo = f г2 dm = J г2 pds.
<S) (S)
Интеграл распространяется на всю площадь
S фигуры.
Осевым моментом инерции Ji
тела относительно данной оси I назы-
вается сумма произведений из массы dm
каждой частицы тела на квадрат расстояния
h этой частицы от оси I, т. е.
Ji = J h2 dm — J h2pdv.
(») (и)
Аналогично для момента инерции мате-
риальной плоской фигуры относительно
оси I, лежащей в плоскости этой фигуры,
имеем
Ji = f h2dm = J h2 p ds.
(S) (s)
Для однородных тел p = const, а потому
множитель p можно вынести за интеграл, и
задача сводится к вычислению интегралов:
J r2dv; J h2 dv; J r2 ds; j ft2 ds,
(») (v) (s) (s)
выражающих моменты инерции не физиче-
ских, а геометрических тел или плоских
фигур.
Моменты инерции тела относительно
координатных осей х, у, z определяются по
формулам:
Jx = f Р (У2 + z2) dv;
(”)
Jy = f Р (Z2 + X2) dv; Jz= f P (X2 + y2) du.
M (»)
Для моментов инерции плоской фигуры
относительно осей х и у, лежащих в плос-
кости этой фигуры,
Л= f РУ2 ds; Jy~- f рх2 ds.
(s) (s)
Между моментами инерции тела относи-
тельно начала координат О и относительно
трёх координатных осей существует очевид-
ная зависимость
Jo = 2 (Jx + Jу + Jz)-
В случае плоской фигуры Jo = J? (ось z
направлена перпендикулярно к плоскости
фигуры), а потому предыдущая зависимость
переходит в Jo = Jx ф Jy.
Между моментами инерции тела относи-
тельно двух параллельных осей / и ",
из которых первая проходит через центр
тяжести С тела и расстояние между кото-
рыми равно d, существует зависимость
Jr = Ji + Md2,
где М — масса данного тела.
Такая же зависимость имеет место между
полярными моментами инерции тела отно-
сительно центра тяжести С и относительно
любой точки О, т. е.
Jo = Jc + Md2,
где d — ОС. Пусть данное тело разделено
на две части, массы которых равны тг и
т2. Обозначив центры тяжести этих частей
через Cj и С2, а центр тяжести данного
тела через С, проведём три параллельные
оси через точки С1( С2 и С. Пусть момент
инерции данного тела относительно оси, про-
ходящей через С, равен J, а моменты инер-
ции его частей относительно осей, прохо-
дящих через и С2, равны Jt и J2. Тогда
т, т,
J = Ji+J-2+-m^rn;tIi’
где d — расстояние между параллельными
осями, проходящими через Ct и С.,.
Если момент инерции Jo тела относительно
точки О представить в виде Jo = Mi , то ве-
личина /0 называется радиусом инер
ции тела относительно точки О. Следова-
тельно, г0 = 'j/' J~ . Радиус инерции есть,
очевидно, расстояние от О такой точки, в
которой нужно сосредоточить всю массу
данного тела, чтобы момент инерции этой
сосредоточенной массы (материальной точки)
был равен Jo. Аналогично, если Ji = Mi2,
то ii называется радиусом инерции тела
относительно оси I; следовательно, Ц =
= i/А
V м ’
Центробежным моментом инерции
тела относительно двух координатных плос-
костей yOz и zOx называется сумма произ-
ведений из массы dm каждой частицы тела,
на координаты х и у этой частицы, т. е.
Jxy= f ху dm = f pxydv
(u) (y)
и аналогично
jyz = f yzdm= f pyzdv,
(r) (»)
Jzx= f zxdm= J pzxdv.
(») (®)
В случае плоской материальной фигуры
центробежный момент инерции относительно
двух координатных осей х и у, лежащих
в плоскости этой фигуры, равен
Jxy = f ху dm = f pxyds.
(s) (s)
Если p = const, to Jxy = p [ xydv и (для
(и)
плоской фигуры) Jxy=p f ху ds; интегралы
(S)
в правых частях этих равенств выражают
центробежные моменты инерции гсомстри-
394
МЕХАНИКА
ческого тела и геометрической плоской
фигуры.
Если обозначить координаты центра тя-
жести данного тела через хс, ус, zc
и провести через этот центр систему осей
х', у', г', параллельных данным осям х,
2, ТО
Jxy = Jx'y'^ ^ХсУс> J yz = Jy'z' +
+ Myczc; J2X = Jz,x. + Mzcxc,
где M — масса данного тела.
Осевой момент инерции тела J относи-
тельно какой-нибудь оси, проходящей через
начало прямоугольной системы координат и
образующей с координатными осями углы
а, 3, 7, определяется по формуле
J = Jx cos2 а + Jv cos2 р + J2 cos2 7 —
— 2 Jxv cos a cos 3 — 2 JV2 cos fi cos 7 —
— 2 J,A cos 7 cos a.
Аналогично для момента инерции плос-
кой фигуры относительно оси, лежащей в
плоскости этой фигуры и образующей с
осью х угол а:
J = JX COS2 а + Jy sin2 a — Jxv sin 2 a.
В каждой точке тела (или плоской фигуры)
можно построить такую прямоугольную си-
стему координат, для которой центробежные
моменты инерции равны нулю; оси такой
системы называются главными осями инер-
ции в данной точке тела, а моменты инер-
ции относительно этих главных осей назы-
ваются главными моментами инерции и
обычно обозначаются через А, В и С.
Момент инерции тела J относительно оси,
проходящей через начало координат и обра-
зующей углы а, 3,7 с главными осями инер-
ции, определяется по предыдущей формуле,
ь которой нужно положить:
Jx — A; Jy = В, Jg = С и
Jxy ~ Jyz — Jzx = 0;
а потому
J = A cos2 а + В cos2 р + С cos2 7,
й (в случае плоской фигуры)
J = A COS2 а 4- в sin2 а.
Если из произвольной точки данного тела,
принятой за начало координат О, проведём пу-
чок осей и вдоль каждой из этих осей отложим
от точки О отрезок, равный
1
v J ’
где J —
момент инерции тела относительно этой оси,
то геометрическим местом концов таких
отрезков является поверхность эллипсоида,
центр которого совпадает с точкой О и
уравнение которого имеет вид
Jx*2 + JvV2 + Jz*2 - 2 Jxy*y ~~
2 J угУ % 2 J 2X~* = 1 •
Этот эллипсоид называется эллипсои-
дом инерции; оси этого эллипсоида
совпадают с главными осями инерции тела
в точке О. Если оси координат, имеющие
начало в точке О, направим по главным
осям инерции тела в этой точке, то урав-
нение эллипсоида инерции упрощается, так
как в нем исчезают члены, содержащие
произведения двух координат; это уравне-
ние принимает вид
Ах2 + By2 4- Cz- = 1.
Если из трёх коэфициеитов А, В, С два
равны, то эллипсоид инерции является
эллипсоидом вращения. Если А = В= С, то
эллипсоид инерции превращается в шар.
Если эллипсоид инерции построен, то
момент инерции тела относительно любой
оси I, проходящей через центр О этого
эллипсоида, находится весьма просто: обоз-
начая через L точку пересечения оси I
с поверхностью эллипсоида инерции, будем,
очевидно, иметь
1
Ji = 6 U •
Эллипсоид инерции, центр которого сов-
падает с центром тяжести тела, называется
центральным эллипсоидом инерции, а
его оси называются главными цент-
ральными осями инерции тела.
Если тело имеет плоскость симметрии,
то одна из главных центральных осей инер-
ции тела перпендикулярна к этой плоскости,
а две другие лежат в этой плоскости. Если
тело имеет ось симметрии, то эта ось яв-
ляется одной из главных центральных осей
инерции тела, а две другие оси лежат в
плоскости, перпендикулярной к оси сим-
метрии.
МОМЕНТЫ ИНЕРЦИИ НЕКОТОРЫХ
ОДНОРОДНЫХ ЛИНИЙ, ФИГУР И ТЕЛ
В нижеследующих формулах р обозна-
чает плотность, т. е. массу, приходящуюся
на единицу объёма или на единицу площади
или на единицу длины, и М обозначает
массу данного тела (фигуры, линии).
Прямолинейный отрезок
АВ = I. Ось х проходит
через точку А и образует
с направлением АВ угол а.
с центральным
где h — расстояние точки
В от оси х.
Дуга круга радиуса г
углом 2 а (фиг. 49):
Jx = Р <2°- sin 2 а) =
г3
Jv = Р ~2 (2 a 4- sin 2 a) =
г2 { , sin 2<
= М I 1 Н-------------
Л \ 2 a
Jo = 2 par3 = Mr2.
Треугольник. G — центр тяжести тре-
угольника (фиг. 50)
&/г3 , Л2 &Л3
Л, “ Р 4 = М 2'; Л, = Р 36 =
/г2 bh3 Л2
= j'g; Jx =• Р -^2 = М q
ЦЕНТР ТЯЖЕСТИ И МОМЕНТЫ ИНЕРЦИИ
395
ФХ) s+f
--12” = М ~~6~г
Ь2 Ьа3 . а2
Ь1г , Л ( Ь1 т- 62)
36 '* 12
где а,Ь,с — стороны треугольника.
Момент инерции относительно любой оси,
проходящей через центр тяжести, равен
J = 12 ( dA + dB + dc)’
где dA, dB, dc — расстояния вершин тре-
угольника от этой оси.
Неправильный четырёхугольник ABCD
(фиг. 51)
ВО ( II’ + II’)
jbd-p—
ХФ м,.
~ РГ • PJP/h ” ”6’ (Л. Л Л* + Л2 )•
Параллелограм ABCD. Угол между диа-
гоналями АС и BD равен у.
BP (AC sin
Jbd = Р 48 '' =
М
- 24 (Лс sin г)~-
Ромб ABCD
t BD-АС3 М
Jbd = Р 48 ~ 24' АС2.
Прямоугольник (фиг. 52)
Ьа3 а2 Ь3а
Jx~ р~12 = М 12 ’ Jy= р 12 “
ab (Ь2 + ар а2 + Ь2
J» = Р 12 = М - —12 - .
Квадрат со стороной а. Момент инерции
относительно любой оси, проходящей через
центр тяжести О квадрата, равен
а4 а2 а* а2
J ~ Р 12 ~ м fl ; Jo = Р "б = м 6 .
Равнобедренная трапеция (фиг. 53). Точка
С — центр тяжести трапеции.
bh (b., -- ЬР)2
18 ~~
IC (а + 3 &) п2 а 4- 3 b
J 1 12 б а 4- b ’
, /;’ (3 а 4- b) h2 3 а 4- 6
Jx= р 12 = М 6 ’ ~а~+ Ь~
h а* — Ь4 а2 4- Ь2
Jy = Р 48 ’ ~ = М 24 :
, /г3 а2 4- 4 ab 4- Ь2
Jx^ ? 36 ' а + Ь =
h2 а24- 4о& 4- Ь2
= М 18 ‘ (стЯ- Ь)2^
Правильный многоугольник. Если а —сто-
рона, п — число сторон, г—радиус вписан-
ного, R—радиус описанного круга, то для
момента инерции относительно всякой оси,
проходящей через центр тяжести О много-
угольника, имеем
паг (12 г2 4- а2) 12 г2 4- а2
J= р 96 1=1 М 48 “
Круг. Момент инерции относительно лю-
бого диаметра
ттг4 vdi г2
J = P -4’=Р 64 =М Т ;
момент инерции относительно центра О
Круга
т.г1 r.d1 г2
Jo = Р = Р ЗУ = м 2 ’
где г — радиус круга nd — его диаметр.
Половина круга. Ось у направлена по
оси симметрии. Начало координат в центре
полукруга О.
396
МЕХАНИКА
, ЯГ4 , г3
Jx =* Jу *= P -g" = M 4 5
, *r* «4 r*
Jo — P 4 — M 2 •
Полярный момент инерции относительно
центра тяжести
Круглое плоское кольцо: внешний ра-
диус— R, внутренний радиус — г.
Момент инерции относительно любого
диаметра
J = ?----4— = м —-4— .
Момент инерции относительно центра О
Jo = 2J-
Круговой сектор радиуса г. Ось х на-,
правлена по оси симметрии; начало коорди-
нат — в центре О дуги сектора.
, г1 г2 / sin 2
Jx = Р § (2 а—sin 2 а) =М 4 (1—~у
Г4 г3 ( sin 2 а
Jy~P g (2а 4-Sin2a) = М 4 (1+~2Т~
Г4 гз
J о — Р 2 а = М *2 ,
где а—половина центрального угла Дуги
сектора (в радианах).
Полярный момент инерции относительно
центра тяжести
Г4 / 8 sin2a\
,/с= Р 2 а 9 ) =
Круговой сегмент радиуса г. Оси коор-
динат выбраны так же, как в предыдущем
случае
, г4 f 4 1 \
Jx = Р g- ( 2 а— 2 sin 2 аg sin 4а I =
Г2 / 2 sin2 а sin 2 а \
4 3 * 2 а — sin 2 а J ’
Г* ( 1 \
Jy = Р g (2а— Sin 4 а 1 —
Г2 / 2 sin2 а sin 2 а\
' = М T\J+ 2а —sin2a ) ’
, Г4 / 1 1 \
Jo = Р -2 I « — j sin 2а — 12 sln 4а I =
г2 / 2 sin2asin 2а\
== Ai "q | 1 “Ь 'о "о ' «/«"п ) »
2 у 3 2а — sin 2а/’
где а—половина центрального угла дуги
сегмента.
Площадь эллипса. Начало координат О—
в центре эллипса; оси х и у совпадают с
осями эллипса. Полуоси эллипса равны
а и Ь.
nab3 ,, b* па3 b а2
= Р — = М 4 ; Jy = р —у- = М 4 ;
nab ч а2 4- Ь2
Jo=p-4~ (а2 + b2) = М----4— .
Параболический сегмент (фиг. 54):
4 ай3 Ь2 , 4 а3 b
Jx = р ~15“ = М 5 ’ Jy^P ~Т~ =
За2 , 32а3 b 8а2
= М 7-; Jy, = р -105 =- М ~35 ;
1ба36 12а2
Прямая призма или прямой цилиндр с пло-
щадью основания s и высотой й. Начало
координат О — в центре тяжести призмы
(цилиндра); ось z перпендикулярна к осно-
ванию призмы (цилиндра). Если обозначим
моменты инерции площади поперечного
сечения призмы (цилиндра) плоскостью Оху
относительно осей г и х через J2 и J', то
Jx=ph(^Jx + j2s/i2J=7 {Jx + 12sh2J ;
Jz — ph J2 — s Jz •
Прямоугольный параллелепипед. Оси x,
у, z проходят через центр тяжести и парал-
лельны соответственно рёбрам параллеле-
пипеда а, Ь, с:
abc
Jx = p-i2(b2 + с2) =
б24-с2
= Jy=M
с2 4- а2
12 ’
Л==М
а2 4- Ь2
12
Куб. Оси координат выбраны так же,
как в предыдущем случае
а6 а2
Jx = Jy = Jz = Р g = м -g ,
где а — ребро куба.
Прямой круглый цилиндр. Радиус осно-
вания—г, высота — й; оси х, у, z выбраны
так же, как в случае прямой призмы:
лг4й г2
Jz= Р "У = Л1 2 ’
тсг2й „ 3 г2 4- й2
Jx = Jy = Р ПТ (3 г2 + Л2) = М-----------------J2----
Момент инерции относительно оси, обра-
зующей с осью z угол Ср,
ЦЕНТР ТЯЖЕСТИ И МОМЕНТЫ ИНЕРЦИИ
397
Ttr^h
Jt = р -j?- [3 г‘ (1 + cos2 ?) + й2 sin2 ?] =
М
= [3 г2 (1 + cos2 ?) + ft2 sin2 ср].
Боковая поверхность прямого круглого
цилиндра. Обозначения те же и оси х, у, z
выбраны так же, как в предыдущем случае
Jz = р 2 лг3й = Mr2-,
r.rh 6 г2 + й2
Jx = Jy=? -q (6 г2 + й2) = М------J2-- .
Полый круглый цилиндр. R и г — внеш-
ний и внутренний радиусы, й — высота; оси
х, у, z выбраны так же, как в предыдущем
случае:
лй
Jz = Р 2 <-Ri -~Г*) — М
r.h(R2-r2)
J* = Jy = Р------4----!R2 + г2+ з
R2 + г2
2
й2
3
1
R2+r? + о Л3
= М --------------
4
Пирамида или конус. Высота — Л; площадь
основания—s. Ось z совпадает с высотой и
проходит через центр тяжести основания;
ось х перпендикулярна к оси z и проходит
через центр тяжести пирамиды (конуса).
Если обозначить моменты инерции площади
основания относительно оси z и относи-
тельно оси х', параллельной оси х и про-
ходящей через центр тяжести основания,
через j'z и Jx,, то
, 1 , 3 М .
Л = 5?ЛЛ = 5 s Л !
рЛ , . ч 3 М . , ч
80’s (16Л-+^2)-
Если основание пирамиды — прямоугольник
со сторонами а и b и ось х параллельна
стороне а, то
abh а2 + b2
Jz = Р go (fl2 + = М 20 ’
abh) 3ft2\ 4й2 + 3й2
J* = р 60 (62 + 4 ) “ М 80 '
В случае круглого конуса, радиус осно-
вания которого равен г, имеют:
3
Jr= ? ю =Ю Мг'"’
ЛЙГ4
ЛГ2Й
Й2
4
Боковая поверхность круглого конуса.
Ось z совпадает с осью вращения конуса;
, кг3/ г2
Jz = р 2 = М 2 ’
где I — длина образующей конуса и г — ра-
диус его основания.
Усечённый круглый конус. Радиусы парал-
лельных оснований — /? и г, высота —Л,
образующая — /; ось z совпадает с осью
вращения;
лй R5 —г5 3 R5 — г6
= Р 10 ’ R — Г = 10М ’ R3 — г3 ‘
Для боковой поверхности усечённого круг-
лого конуса имеют
л/ R4 — г4 R2 + г2
Jz = Р 2 ‘ R — г “ М 2
Шар. Радиус — г; центр — О.
4 3
Jo = Р 5 "Г5 = g Mr2;
момент инерции относительно любого диа-
метра
R5 — гь
, 8 лг5 2
J = p-1F = 5 Mf2-
Полушар радиуса г. Если начало коор-
динат находится в центре полушара О и
ось z совпадает с осью симметрии, то
4 лг5
Jx~Jy = Jz — ? 15 =
2 3
= •5 Mr2; Jo= 5 Mr2.
Полый шар. R — внешний радиус, г —
внутренний радиус; момент инерции относи-
тельно любого диаметра
8 л 2
J — Р Т5 ~ ~5 М /рз _ гз •
Поверхность шара радиуса г. Относи-
тельно любого диаметра момент инерции
8лг4 2
>рт='з МгК
Шаровой сегмент. Высота— й; радиус
шара — г; ось z совпадает с осью симметрии
лй3
Jz = Р 30 (20 г2 — 15 гй + 3 й2) =
, й 20 г2 - 15гй+ 3й’
= м io'--------зТ^й-------•
Шаровой сектор. Радиус
сота шарового сегмента —й.
дает с осью симметрии;
, 2лг2й2
Jz=P 15
Параболоид вращения. Высота —
диус основания — г. Ось z совпадает
вращения. Начало координат — в
тяжести параболоида;
1 1
Jz = Q ”РЛг4 = 3 Мг2>
Jx — Jy ~ (3 Г2 + Й2) =
= i^M(3r2 + й2).
Эллипсоид. Оси координат совпадают с
осями эллипсоида. Если длины полуосей
эллипсоида равны а, b и с, то:
4 1
Jx = 15 ”Р аЬс (Ь2 + с2) = 5 М (62 + с2);
4 1
Jv = 15 кр аЬс <с2 + а2> = 5 м (с2 + а2);
шара — г; вы-
Ось z совпа-
(Зг—й) = М (3r—h).
й; ра-
с осью
центре
398
МЕХАНИКА
4
Jz = fg яр abc (а3 + й2) =
Jx=2S(R2S + 3J'z+2Jx).
= М (а2 + й2).
Кольцо. Пусть данное тело кольцеобраз-
ной формы представляет собой тело, полу-
чающееся вращением данной плоской зам-
кнутой фигуры вокруг оси г, лежащей в
плоскости этой фигуры (фиг. 55). Пусть
z эта фигура имеет ось
1 ----R —-у симметрии С, парал-
I лельную оси z. Г1ло-
------щадь фигуры—S; рас-
у. стояние между ося-
0 ' ~ ми z и £ равно R.
------Ось х иерпендику-
1 лярна к оси z и про-
' ходит через центр
Фиг. 55 тяжести С фигуры.
Если моменты инер-
ции площади фигуры относительно осей
Сих обозначить через и Jx , то для мо-
ментов инерции рассматриваемого тела вра-
щения относительно осей z и х имеем
Jz^2npR (R*S + 3j;\,
jr = wR (r*s ч- з j' + 2 jx) :
Объём V рассматриваемого тела вращения
равен (по теореме Гульдена) произведению
площади вращаемой фигуры на длину окруж-
ности, описываемой её центром тяжести,
т. с.
V = 2r.RS,
а потому масса этого тела
М = 2 лр RS.
Следовательно,
М .
J2 = -s (R2S + 3J.);
Если вращаемая фигура есть круг радиуса
г, то тело вращения называется тором.
В этом случае
л г4
’ 4~ ’
S = nr2; = J'x
а потому
J2 = 2 n2pRr2 R2 + г2
/ 3 \
= М I Д’ + 4 гг ;
Jx = r.2pRr2 [ R2 + J Г2
м
= 2
Если вращаемая фигура есть эллипс, причёл,
ось этого эллипса, совпадающая с осью х.
равна 2а, а его ось, совпадающая с осью
равна 2 й, то
, ~ab:: , ~a'J,b
S = лай, Jx = .j ; J- = -4
а потому
Jz = 2r^abR Ir3 + 4 a2 ) =
/ 3 \
= M ( R2 + 4- a2 I ;
/ 3 1 \
Jx = л2р abR I R2 + 4 a2 + ту й2 j
M/3 1 \
= -Ц R2 + 4 a2 + - Й2 ) .
ТРЕНИЕ
Сопротивление, возникающее при движе-
нии одного тела по поверхности другого, на-
зывается трением.
В зависимости от вида движения разли-
чают два рода трения: трение скольжения
(трение первого рода), возникающее, на-
пример, при движении поршня в цилиндре,
и трение качения (трение второго рода),
возникающее, например, при качении ко-
леса по рельсу.
Так как сила трения есть сила сопро-
тивления, то эта сила всегда направлена
в сторону, противоположную относи-
тельной скорости движущегося тела.
ТРЕНИЕ СКОЛЬЖЕНИЯ
Чтобы заставить данное тело скользить
под действием силы F по поверхности друго-
го тела (фиг. 56), нужно преодолеть силу
трения скольжения. Величина Т силы тре-
ния скольжения пропорциональна нормаль-
ному давлению одного тела на другое, т. е.
Т = <iN = pF (закон Кулона).
Коэфициент <1 называется коэ-
фициентом трения скольжения;
его величина зависит от материала трущихся
тел, от состояния трущихся поверхностей (ше-
роховатость, смазка,
температура и т. п.),
от скорости движе-
ния и от удельного
давления. Коэфици-
ент трения скольже-
ния имеет наиболь-
шее значение в на-
чале движения, т. е.
в тот момент, когда
тело выходит из со-
стояния покоя, и в
большинстве случаев
убывает по мере того, как увеличивается
относительная скорость тела. Коэфициент
трения скольжения есть число отвлечённое
(безразмерное).
Если трущиеся тела находятся в отно-
сительном покое, то в этом случае трение
называется статическим или трением в по-
ТРЕНИЕ
399
кое. Для величины Т силы 'статического
трения всегда
T<^cmN,
где ует— значение коэфициента трения
скольжения, соответствующее моменту нача-
ла движения, т. е. тому моменту, когда тело
выходит из состояния покоя.
Если сложить нормальную реакцию N и
силу трения Т (фиг. 56), то получим равно-
действующую силу R.
Эта сила R составляет с нормальной
реакцией угол <?, определяемый из урав-
нения
Т
Угол ср называется углом трения. В слу-
чае статического трения углом трения назы-
вается угол ср, соответствующий наиболь-
шему значению силы статического трения;
следовательно, в этом случае tg у = и.ст.
Геометрическое место прямых линий, про-
ведённых из точки А под углом ср к направ-
лению силы N, есть коническая поверхность,
называемая конусом трения.
Согласно многочисленным и весьма точ-
ным опытам проф. Н. П. Петрова и других
исследователей, при обильной жидкой смазке
трущихся поверхностей, коэфициент трения
|л пропорционален:
1) коэфициенту внутреннего трения (вяз-
кости) жидкой смазки;
2) скорости относительного движения
трущихся, поверхностей, и обратно пропор-
ционален:
а) толщине слоя смазки между трущимися
поверхностями;
б) удельному давлению, т. е. давлению,
приходящемуся на единицу площади тру-
щейся поверхности.
Коэфициент внутреннего трения жидкости
различен для разных жидкостей; для дан-
ной жидкой смазки он зависит от её темпе-
ратуры и с повышением температуры смазки
уменьшается.
При торможении железнодорожных вагонов
для определения коэфициента трения сколь-
жения между чугунными тормозными колод-
ками и стальными бандажами пользуются
формулой Вихерта:
1 + 0,0112 v
,± = 1 + 0,06 и
где и—скорость скольжения в км!час,
;л0 = 0,45 для сухих поверхностей;
— 0,25 для влажных поверхностей.
На основании экспериментальных данных
Научно-исследовательского института же-
лезнодорожного транспорта (ЦНИИ) для
того же коэфициента получена следую-
щая формула:
17
|J "(40+ v) -/Р ’
где v — скорость в км/час;
Р — давление в т на стандартную чугун-
ную тормозную колодку.
Величина коэфициента трения почти не
зависит от нагрева тормозных колодок; для
влажных колёс эта величина уменьшается
на 10—20°/о.
Таблица 2
Коэфициенты трения для некоторых тел при небольших давлениях (от 1 до 1,5 кг/см9)
Коэфициент трения скольжения Коэфициент трения скольжения
при движении для момента трогания с места
Трущиеся тела трущиеся поверхно- сти сухие 1 слабая смазка нормаль- ная смаз- ка поверхно- сти смоче- ны водой трущиеся поверхно- сти сухие слабая смазка нормаль- ная смаз- ка поверхно- сти смоче- ны водой
Металл по металлу
Бронза по бронзе 0,20 — __
v) » чугуну 0.21 — — — __ —- — —
» » железу — 0,16 — — —
Чугун по чугуну или бронзе . . — 0,15 0.31 0,16 __ —
Железо по чугуну или бронзе . 0.18 — — 0.19 — — —
Железо по железу 0.44 — —— 0,13 —
Сталь по стали — — — — 0,15 — — —
Различные тела
Чугун по дубу 0.49 0,19 0,22 — — 0.65
Железо по дубу Кожаный ремень по дубовому — — 0.08 0,26 — — 0,11 0.65
барабану 0.27 — — — 0,47 —
Кожаный ремень по чугуну . . Пеньковый канат по несбрабо- 0,56 — — 0,36 — 0.28 0,12 0.38
тайному дереву Пеньковый канат по полирован- — — . — — 0.50 — — —
нему дереву — — — — 0,33 —
Сталь по льду 0,014 — — —. 0,027 — —
Камни или кирпич по кирпичу — — — 0,50-0,73
Камни по железу - — — — 0.42—0,19 —
» в дереву —• — — — 0,46—0,60 — , — —
400
МЕХАНИКА
Таблица 3
Коэфициенты трения металлов в зависимости от
удельного давления по Ренни
Давление в кг/см9 Железо по железу Чугун по железу Сталь по чугуну Жёлтая медь по чугуну
Р 1А Р- р- I1-
8,79 0,140 0,174 0,166 0,157
13,08 0,250 0,275 0,300 0,225
15,75 0,271 0,292 0,333 0,219
18.28 0.285 0.321 0,340 0,214
20.95 0,297 0,329 0,344 0,211
23,62 0,312 0,333 0,347 0.215
26,22 0,350 0,351 0.351 0,206
27,42 0,376 0,363 0,353 0,205
31,50 0,395 0,365 0,354 0,203
34,10 0.403 0,366 0,356 0,221
36,77 0,409 0,366 0,357 0,223
39,37 * 0,367 0,358 0,233
42,18 0,367 0.359 0.234
44,58 0,367 0,367 0,235
47,25 0,376 U. 403 0,233
49,92 0.434 — * 0,234
55,12 — * 0,232
57,65 — — — 0,273
* При этом давлении трущиеся поверхности
сказались повреждёнными.
Таблица 4
Коэфициенты трения в зависимости от скорости
Железные бандажи по сухим желез- ным рельсам Стальные бан- дажи по стальным рельсам Чугунные тормозные колодки по стальным бандажам
скорость в км/час р- скорость в км/час р- скорость в км/час Р-
16,56 0,209 0,00 0,242 0,00 0,330
26,28 0,206 10,93 0,088 8,05 0,273
31,68 0,171 21,80 0,072 16,09 0,242
51,48 0,145 43,90 0,070 40,03 0,166
72,00 0,136 65,80 0,057 72,36 0,127
79,20 0,112 87.60 0,038 96,48 0,074
Таблица 5
Коэфициент трения для деревянных тормозных
колодок (при скорости от 1 до 20 м/сек и при
давлении от 0,60 до 10 кг/см9)
Материал . Бук Дуб Тополь Вяз Ива
Чугун . . . 0,29— 0,37 0,30— 0,34 0,35— 0,40 0,36— 0,37 0,46— 0,47
Железо . . 0,54 0,Si- О.40 0,65— 0,60 0,60— 0,49 0,63— 0,60
Значения коэфициентов трения скольже-
ния железнодорожных вагонов со стальными
бандажами по стальным рельсам в зависи-
мости от скорости приведены в табл. 6.
Таблица 6
Скорость в км/час 10 30 50 70 90
Коэфициент трения р. 0,10 0,07 0,06 0,05 0,04
Для определения коэфициента трения
скольжения железнодорожных вагонов поль-
зуются также формулой Боше:
_______Ио
1 + 0,03и ’
где v — скорость в м/сек-
;л0—коэфициент, равный 0,31 для очень
сухих рельсов, 0,22 для сухих рель-
сов и 0,14 для мокрых рельсов.
Кроме коэфициента трения скольжения
важное значение имеет коэфициент сцепле-
ния ф между колесом и рельсом. Коэфици-
ентом сцепления называется отношение наи-
большего возможного при отсутствии бок-
сования окружного усилия на колесе к нор-
мальному давлению колеса на рельс. Весьма
важная роль коэфициента сцепления при
расчётах объясняется тем, что значение этого
коэфициента лимитирует величину тяговой
силы.
На основании многочисленных исследо-
ваний для определения коэфициента сцеп-
ления при различных скоростях от нуля до
150 км/час предложены эмпирические фор-
мулы, например
1
а 4- 0,035р ’
где v — скорость в км1час, а величина а ко-
леблется в пределах от 3,8 до 4,7.
Как видно из этой формулы, коэфициент
сцепления уменьшается при увеличении ско-
рости.
ТРЕНИЕ ПРИ ДВИЖЕНИИ ТЕЛА
ПО НАКЛОННОЙ ПЛОСКОСТИ
Пусть тело весом Р кг движется равно-
мерно вверх по наклонной плоскости под
действием силы F, параллельной этой плос-
кости (фиг. 57); угол наклона плоскости
равен а. Величина силы F, необходимой
для равномерного поднятия тела по
наклонной плоскости,
определяется по фор-
муле f
Р = р sin <“ + ?)
cos ср ’ ------
где ср — угол трения, Фиг. 57
т. е. tg ср = (1.
Если а > ср, то при равномерном спуске
тела по наклонной плоскости
Р
Sin (ot — ср)
COS ср
Сила F является в этом случае для тела
тормозящей силой; при отсутствии этой силы
и при а > ср движение тела вниз по наклон-
ной плоскости было бы ускоренным.
Если а < ср, то в этом случае для равно-
мерного спуска тела по наклонной пло-
скости сила F должна иметь направление,
противоположное указанному на фиг. 57, и
F = P
sin (ср — а)
COS
ТРЕНИЕ
401
Если а -- -f, то F 0; следовательно,
в игом случае тело, предоставленное дейст-
вию только силы тяжести, будет спускаться
по наклонной плоскости равномерно (при
условии, что ему сообщена некоторая на-
чальная скорость).
Если тело, лежащее на наклонной плос-
кости и предоставленное действию только
сиды тяжести (F=0), находится в покое,
то это возможно только в том случае, когда
составляющая веса Р, параллельная на-
клонной плоскости, не превышает .максималь-
ного значения силы трения Т, т. е.
Р sin а< Ттах.
Ню
Т'тах Ргт W = 2™ Р COS а,
а потому
Р sin а ' [).em -Р cos а
пли
tg а 'л Уст ~~ ^8 ?ст
и, следовательно, а < zrm, т е. для того,
чтобы тело, лежащее на наклонной плоскости'-,
могло оставаться в покое, угол наклона пло-
скости не должен превышать угла статиче-
ского трения.
При поднятии тела по наклонной пло-
скости коэфициент полезного действия этой
плоскости, равный отношению работы силы
Р к работе силы F, определяется по формуле
sin a cos с
“ sin (а + е) '
ТРЕНИЕ КЛИНА И ВИНТА
Клин (фиг. 58). Если клип с углом
заострения 2а находится в равновесии, то,
пренебрегая трением п принимая N, = N,
имеют
Р =•= 2 N sin а.
При учете силы трения (коэфициент тре-
ния [J- == tg о, где о — угол трения) имеем:
а) при вбивании клина
sin (а 4- е)
Р - 2 N (sin а ;> cos а) 2 N - )Ч „ т - ;
б) при удерживании клина от выталки-
вания
sin (7. —
Р - 2 N (si п у. — ц cos а) == 2 .V --
cos у
Самозащемлеипе клипа происходит при
tg :< . р, т. е. при а ж 9.
Винте прямоугольной нарезкой (фиг. 59).
Введем следующие обозначения: вращающий
момент, приложенный к винту, равен М,
шаг винта — h, расстояние точек средней
винтовой линии от винтовой оси — г, угол
подъёма средней винтовой липни равен
ft
«- arctg.y^, угол трения—9, коэфициент
трения скольжения — у = tg 9, вертикальная
сила, направленная вдоль оси винта (на-
пример, вес поднимаемого груза), равна Q.
Тогда при равномерном поднятии груза
_М Q-r-tg (а + 9);
при равномерном опускании груза
М - Q-r-tg (а — ?);
при а<ср винт является самотормозящимся.
Коэфициент полезного действия винта при
подъёме груза равен
tga___
т‘ ‘ tg (.« + ?)
Винт с треугольной нарезкой (фиг. 60).
В случае винта с треугольной нарезкой,
сохраняя предыдущие обозначения, имеем
М = Q-r-tg (а±/),
где ____________
tg 9' = у' = у COS а У i + tg= а + tg2 р =
= у У1 + COS2 а tg2 р.
Если угол а невелик, то приближённо
можно принять cos a;:l и, следовательно,
У Г+tg2 ₽ =
пли
Так как у' > у, то в винтах с прямо-
угольной нарезкой трепне меньше, чем
в винтах с треугольной нарезкой; поэтому
первые применяются преимущественно в
подъёмных устройствах, а вторые — в скреп-
ляющих устройствах (болты).
ТРЕНИЕ ЦАПФ
Поддерживающая цилиндрическая цапфа.
Опорное давление Р перпендикулярно к осн
вала.
Общий момент сил трения относительно
осп вращения вала равен
АУ, - уР?,
где — радиус цапфы.
Мощность, расходуемая на преодоление
трения цапфы, равна
т.п
N =~ Мт/)ш ;>.Рр<» —- <i.P р эд ,
где о> — угловая скорость вала;
п — число оборотов в минуту.
Пятовая цапфа. Опорное давление Р на-
правлено вдоль осп вала. Трущейся поверх-
ностью является торец цапф’ы (круг). Общий
момент сил трения относительно осп враще-
ния вала для сплошной круговой пяты
равен
2
Mntp -- j уРр;
26 i им I
402
МЕХАНИКА
для кольцевой пяты
где р2 и pj — внешний и внутренний радиусы
опорного кольца.
Коэфициент трения р можно принять
равным: 1) для новых цапф — от 0,06 до
0,10, в среднем р = 0,08; 2) для хорошо при-
работавшихся цапф—от 0,02 до 0,06, в среднем
р=0,04.
ТРЕНИЕ ГИБКИХ ТЕЛ
Если гибкое тело (ремень или канат)
охватывает цилиндр (шкив или барабан) и
если обозначим через S, и S2 натяжения ве-
дущей и ведомой частей гибкого тела (фиг. 61),
то для тихоходных передач:
St < 52ерл;
S1-S2=P< (1 - е~И 81 =
= ( е^ - 1) 8.,.
Для быстроходных передач, учитывая
центробежные силы, можно пользоваться
более точными формулами:
Р<(1-е-Н
ИЛИ
V / и2 \
р<(ед»_1) (s3-9 yj ,
где Р = Sx—Sa — окружное усилие, переда-
ваемое гибким телом ци-
линдру;
е — основание натуральных ло-
гарифмов;
а—угол (в радианах) обхвата
гибким телом цилиндра;
р — коэфициент трения гиб-
кого тела о цилиндр
(табл. 7);
q— вес погонной единицы
длины гибкого тела (ремня,
каната);
v — линейная скорость гибкого
тела (ремня, каната);
g — ускорение силы тяжести;
еи''—см. табл. 8.
Знак равенства имеет место, если гибкое
тело скользит по цилиндру, знак неравен-
ства— при относительном покое.
Таблица 7
Коэфициенты трения
Кожаные ремни Пеньковые канаты Железные тор- мозные ленты
по деревян- ным шкивам по чугунным шкивам по железным барабанам по деревян- ным бараба- нам по чугунным колёсам
состояние ремня
сильно смазан слабо смазан сырой
р.=О,47 р.= 0,12 р.=0,28 [1=0,38 [1=0,23 [1=0,40 р.=О,18
и_а
Значения е
Таблица 8
а 2тс р
0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50
0,1 1,01 1,10 1,13 1,17 1,21 1,25 1,29 1,33 1,37
0,2 1,13 1,21 1,29 1,37 1,46 1,55 1,65 1,76 1,87
о’З 1,21 1,32 1,45 1,60 1,76 1,93 2,13 2,34 2,Ь/
0,4 1,29 1,46 1,65 1,87 2,12 2,41 2,73 3,10 3,51
0,5 1,37 1,60 1,87 2,19 2,57 3.00 3,51 4,11 4,81
0,6 1,46 1,76 2,13 2,57 з,ю 3,74 4,52 5,45 6,59
ОЛ 1,55 1,93 2,41 3,00 3,74 4,66 5,81 7,24 9,02
0,8 1’65 2,13 2,73 3,51 4,52 5,81 7,47 9,60 12,35
0j9 1,76 2,34 3,10 4,11 5,45 7,04 9,60 12,74 16,90
1.0 1’87 2,57 3,51 4,81 6,59 9,02 12,35 16,90 23,14
1.5 2,57 4,11 6,59 10,55 16,90 27,08 43,38 69,49 111,32
2^ о’51 6,59 12,35 23,14 43,38 81.31 152,40 285,68 535.19
2’5 4^81 23,14 50,75 111,32 244.15 535,49 1 174,5 2 575,9
3,0 6,59 16,90 43,38 111,32 285,68 . /33,14 1 881,5 4 828,5 12 391
3,5 9’02 27,08 81,31 244,15 733,14 2 19о,9 6 610,7 19 851 59 60S
4,0 12’,35 93,38 152,40 535,49 1 881.5 6 610,7 23 227 81 610 286 74'zi
ТРЕНИЕ
403
ТРЕНИЕ КАЧЕНИЯ
Пусть цилиндрический каток находится
в покое на горизонтальной плоскости под
действием вертикальной силы Р (например,
под действием собственного веса). Каток
получит деформацию и кривизна его кон-
тура на участке АВ несколько изменится
(фиг. 62). Опорная площадка АВ также по-
лучит деформацию: из плоской она стано-
вится цилиндрической.
Вследствие полной
симметрии все элемен-
тарные силы реакции q
опорной площадки при-
ведутся к одной равно-
действующей R, которая
пройдёт через
•катка О.
Как только к катку
будет приложена гори-
зонтальная сила F (фиг.
62), каток будет стре-
по плоскости,
участке АВ, препятст-
A в
Фиг. 62
центр
но вслед-
мяться скользить
ствие трения на
вующего скольжению, он будет поворачи-
ваться по часовой стрелке, причём элемеп-
тарные силы реакций q слева будут умень-
шаться, а справа увеличиваться.
При этих условиях равнодействующая
R не^пройдёт через центр О, и в результате
сила F должна будет преодолеть сопротив-
ление, называемое трением качения. Вели-
чина силы F, необходимая для преодоления
этого сопротивления, определяется из урав-
нения
Fr = IP
или
где г — радиус катка;
А — коэфициент трения качения, имею-
щий размерность линейной вели-
чины (длины).
Таблица 9
1 1 Трущиеся тела Коэфициент трения качения X в см
1 Дерево по дереву Мягкая сталь по мягкой стали . , ! Дерево по стали ! Шарик из закалённой ста- j ли по стали 0,05—0,06 0,005 0,03—0,04 0,001
Если горизонтальная сила F приложена
не в центре катка, а в его самой верхней
точке, то
Р-Хр
г ~ к 2г
При перемещении груза с помощью кат-
ков (фиг. 63) имеют
о 1.,(Р + 2р) + ГР
~ 2г
груза (вместе с доской);
катка;
где Р — вес
р — вес
л — коэфициент трения качения между
катком и горизонтальной плоско-
стью, по которой он катится;
X' —коэфициент трепия качения между
катком и доской, на которой лежит
груз.
Если вес катков мал по сравнению с ве-
сом груза, то им можно пренебречь, и тогда
„ 0 + И Р
р — —
а>иг' 63
/
Кроме вышеуказанной формулы Кулона
для определения силы F, необходимой для
преодоления трения качения (сопротивления
перекатыванию), в настоящее время приме-
няются и другие формулы, например:
з ,— з /------------
/ Р1 Р | / г
F~cy lr2 = с г г Р I ’
где Р — вертикальная нагрузка на катящий-
ся цилиндр;
г— его радиус;
Z—длина образующей и
с — коэфициент, зависящий от механи-
ческих свойств грунта.
Коэфициент общего сопротивления дви-
жению вагонов (включая силу сопротивле-
ния воздуха). Для железнодорожных ваго-
нов р можно принимать в зависимости от
ширины колеи (на прямолинейном участке
пути):
Ширина колеи Коэфициент р.
Нормальная .... 0.0025 4-0.6-10—
1 000 мм...... 0,0026 + 0.3-10—6«2
750 » .... 0,0027 г 0.2-10“6г =
600 » ..... 0,0028 । 0.2-10-ei;!
где г—скорость вагона в км'час.
литература и источники
Артоболевский И. И. Теория механизмов и
машин. М.—Л.. ГТТИ, 1940, 762 с.
Бухгольц Н. Н. Основной курс теоретической
механики. 5-е изд., ч. 1—2. М.—Л., Гостехиздат,
1945. Ч. 1. Кинематика, статика, динамика ма-
териальной частицы; 371 с. Ч. 2. Динамика си-
стемы частиц, 248 с.
Воронков И. М. Курс теоретической механики.
3-е изд. М.—Л., Гостехиздат, 1944, 436 с.
К и р п и ч е в В. Л. Основания графической стати-
ки. 6-е изд., М.—Л., ГТТИ, 1933, 227 с.
Левенсон Л. Б. Теория механизмов и машин.
Кинематика и динамика механизмов, м., Машгиз.
1948, 406 с.
ЛойцянскийЛ. Г. и Лурье А. И. Курс
теоретической механики. 3-е изд. Ч. 1 — 2. М.—
Л., Гостехиздат, 1940. Ч. I. Статика и кинема-
тика, 324 с. Ч. 2. Динамика, 468 с.
Некрасов А. И. Курс теоретической механики
3-е изд. М,—Л., Гостехиздат, 1945—1946. Т. I.
Статика и кинематика, 1945, 355 с. Т. 2. Дина-
мика, 1946, 456 с.
Николаи Е. Л. Теоретическая механика. Ч. 1 —
3. 1938—1939. Ч I. 1. Статика твёрдого тела,
2. Кинематика, 13-е изд. 1938, 258 с. Ч. II.
Динамика, 7-е изд. 1939, 284 с. Ч. III. 1. Урав*
нения Лагранжа. 2. Теория малых колебаний,
3. Теория гироскопов, 1939, ЗЮ с.
Суслов Г. К. Теоретическая механика. 3-е изд-
М —Л., Гостехиздат, 1946, 656 с.
26*
ГИДРОМЕХАНИКА
ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ .
УДЕЛЬНЫЙ ВЕС И ПЛОТНОСТЬ
ЖИДКОСТЕЙ
Жидкими телами, или просто жидкостя-
ми, называются тела, легко изменяющие
свою форму и не оказывающие заметного
сопротивления сдвигу. Все жидкости делят-
ся на капельные жидкости, характеризуе-
мые очень малой сжимаемостью, и газооб-
разные жидкости (газы), сжимаемость ко-
торых весьма велика.
Плотностью жидкости называется масса
жидкости, заключённая в единице объёма
М [ кГ-сек1
р ' V J м>
Удельным весом жидкости называется вес
единицы объёма жидкости:
Удельный вес и плотность связаны между
собой равенством
7- ?'g>
где g — ускорение силы тяжести.
Значения удельных весов некоторых жид-
костей в зависимости от температуры и не-
которых газов при 15°С и 750 мм рт. ст.,
а также воздуха в зависимости от темпера-
туры и давления приведены в табл. 1—5.
'Г а б л (1 ц а 1
Удельный вес жидкостей в зависимости
от температуры
Наименование жидкости i Темпера- тура в °C у в кГ)м3
Вода пресная 15 999
» морская 15 1 020
Ртуть 15 13 ЬЬ8
Касторовое масло .... 15 970
Керосин 15 790-820
Бензин 15 680—780
Бензол 0 900
Ацетон 20 790
Древесный спирт 0 800
А,-:Льголь 15 790
Глицерин безводный . . . Нефть 0 20 1 260 761—ьОО
Таблица 2
Удельный вес воды в зависимости
от температуры
Темпера- ! । тура в °С| 7 в Г!см3 Темпера- 1 тура в °Cj 7 в Г/сма Темпера- I тура в сс| 7 в Г/см3 Темпера- тура в °C 7 в Г/см3
0 0,99987 22 0,99780 44 0,99066 64 0,98113
2 0,99997 24 1 26 0,99732 46 0,98982 66 0,98005
4 1,00000 0,99681 48 0,98896 68 U,97894
6 0,99997 1 28 0,99626 50 0,98807 70 0,97781
8 0,99988 30 0,99567 52 0,98715 75 0,97489
(10 0,99973 32 0.99505 54 0,98621 80 0,97183
12 0,э9953 34 0,99440 56 0,98525 85 0,96865
14 0,99927 36 0,99371 58 0,98425 SO 0.S6534
16 0,99897 38 0,99299 да 0,98324 95 0,96192
18 0,99862 40 0.99224 62 0,98220 101 0.95338
20 0,99823 । 42 0.99147 1
Таблица 3
Удельный вес ртути в зависимости
от температуры
Темпера- тура к °C ; В Г/С.«> Темпера- тура в °C Y в Г1сма
-20 13,645 i + 50 13,472
-10 13,620 + 60 13,448
0 13 595 I -t- 70 13,4'24
I +10 13,570 | 4- 80 13,400
: л 2<' 13,546 + 90 13,376
13,522 4-100 13,351
4-4'' 13,497
Таблица 4
Удельный вес газов при 15u С и атмосферном
давлении 750 мм рт. ст.
Наименование В нГ'/Л!3 Наименование газа 7 в кПм3
Воздух Кислород . . . , Водород Гелий 1,209 1 ,312 0,0827 0,164 Углекислота . . Водяной пар Окись углерода 1,804 0,739 1,148
ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ
405
Таблица 5
Удельный вес сухого воздуха кГ/м3 в зависимости
от атмосферного давления и температуры
Таблица 8
Значения коэфициента объёмного расширения
нефтепродуктов по Казанкину (у^6 в кГ1м*)
Давление в мм рт. ст.
= Л}
< Q,
П>
720
730
7S0
0 5 1,225 1,203 1,242 1,220 1,259 1,230 1,276 1.253 1,293 1,270 1,310 1,286 1,327 1,303
10 1,182 1,198 1,214 1,231 1,247 1.264 1,280
15 1,161 1,17/ 1,193 1,209 1,226 1,242 1.258
20 1,141 1,157 1,173 1,153 1,189 1,205 1,220 1,236
25 1,122 1,138 1,169 1,184 1,200 1,216 1,195
30 1.104 1,119 1,134 1.149 1.165 1 .180
Часто удельный вес и плотность даются
в условных градусах (Боме, API и т. д.).
В табл. 6 приведены формулы для пересчёта
условных градусов в плотность и удельный
вес; в таблице п — условные градусы, изме-
ренные соответствующим ареометром.
Таблица 6
Формулы для определения удельного веса и
плотности по условным градусам
Наименование ареометров Нормаль- ная тем- пература в °C Т а Г/см3 или р в г/см3
Для жидкостей тяжелее воды ДЛЯ жидкостей легче воды
Боме (рациональный) 144,3 144.3
144,3— п 14 4,3 4- л
Боме Герлаха (или 146,78 146,78
новый) 17.5 146. 78—м 146,784-л
Боме голландский 12,5 144 144
(или старый) . . • 144—п 1444-/1
Боме американский . 15.56 145 140
145—л 200 1304-п 200
17,5
Баллинга
200—п 200+п
Бека 12.5 170 170
170—л 1704-п
Бригс-Фишера . . . 15,625 400 400
400—л 400+п
Стоппани 15,625 166 166
166-л 166 4-л 141,5
API (американский) 15,56
131,5-|-л 136,8
Картье 12,5
126,] 4-л
Для определения удельного веса и плот-
ности при данной температуре можно поль-
зоваться следующими формулами.
Для нефти и нефтяных продуктов:
* - 1+3, (t -15)’
где 3; —коэфициент объёмного расширения,
зависящий от плотности нефти, при
t = 15°С (табл. 7 и 8).
Таблица 7
Значение коэфициента объёмного расширения
нефтепродуктов по Менделееву (^1а в ггцмл)
71., 0,70 0,80 0,85 0,90 0,92
7 0,00082 0,00077 0,00072 0,00064 0.00060
Весовая плот-
ность при
ю* 3
700
7101720
740
. 700 7101720 740 760 780 800 О'.ОО 830
. _ 8,97|8.83 8,51 8.2017,90 7,5917,39'7.27
760 780
830
Для ртути:
_ _____7о__ __
1 + 6,0001815 +’
где '(о — удельный вес ртути при 0°С.
СЖИМАЕМОСТЬ КАПЕЛЬНЫХ
ЖИДКОСТЕЙ
Сжимаемость характеризуется коэфициеп-
I см П
том объёмного сжатия Зо , который
выражает относительное изменение объёма V
при увеличении давления р на 1 кГ1см2.
Коэфициент объёмного сжатия для ка-
пельных жидкостей весьма незначителен;
значения его для некоторых жидкостей при-
ведены в табл. 9.
Таблица 9
Значение коэфициента объёмного сжатия для
капельных жидкостей
Жидкость
Вода 0,0000525-г0,0000475«-—2— 20 UUU
Алкоголь 0,000077
Эфир 0,000110
Ртуть 0,000003
Бензин 0,000092
Глицерин 0.000025
Модуль упругости—величина, обратная
коэфициенту объёмного сжатия:
_1_Г—"
[сл,2_
В табл. 10 приведены значения модуля
упругости воды в зависимости от давления
и температуры.
Таблица 10
Значение модуля упругости воды = -д— кГ/сч2
t “С Давление р в кГ/см*
5 10 20 | 40 | 80
0 18 900 19 000 19 200 19 500 19 800
5 19 300 19 500 19 700 20 100 20 700
10 19 500 Ь 700 20 100 20 500 21 200
15 19 700 20 000 20 300 20 900 21 700
20 19 800 20 200 20 600 21 200 22 100
406
ГИДРОМЕХАНИКА
вязкость
Под вязкостью подразумевают свойство
жидкости, в силу которого при перемеще-
нии одного слоя жидкости по другому в ней
возникают силы внутреннего трения.
Сила внутреннего трения F по Ньютону
определяется уравнением
/ dv \
где <о —величина трущихся поверхно-
стей;
/ dv \
I “-г- — градиент относительной скорости
\ аУ/п перемещения одного слоя жид-
кости по другому в направлении,
нормальном к движущимся
слоям;
fi — некоторый коэфициент, завися-
щий от физических свойств жид-
кости,— коэфициент абсолютной
вязкости.
В системе CGS:
р. = [г-см (пуаз).
Коэфициент v, равный
называется кинематическим коэфициентом
вязкости.
В системе CGS--
ч = [см2/сек] (стокс).
В технике вязкость измеряют при помо-
щи особых приборов — вискозиметров и ха-
рактеризуют обычно относительными вели-
чинами по отношению к воде, например в
градусах Энглера, Сейболта и др. Для пере-
вода градусов Энглера Е в единицы кине-
матической вязкости можно пользоваться
формулой:
6,31
lO’-v = 7,31 Е---g- м2/сек
или / 1 \
( 1 I
10е у = Е-7,60 \ м2/сек.
В табл. 11 даны о сновные данные виско-
зиметров различных систем и переводные
формулы от условных единиц к кинемати-
ческому коэфициенту вязкости в см2/сек.
Вязкость изменяется в зависимости от
температуры и давления. Для воды кине-
матический коэфициент вязкости при раз-
личных температурах может быть определён
по формуле:
[Л _ 0,0178 см-
v = р — 1+0,0337 t+ 0,000221 t2 ’ сек ’
В табл. 12 даны значения коэфициен-
та р для воды.
Таблица 12
Коэфициент вязкости воды р. (в сантипуазах)
Темпера- тура в °C Р- Темпера- 1 тура в °с| р- Темпера- тура в °C Р- Темпера- ! тура в °Ci
и 1,7921 25 0,8937 50 0,5494 75 0,3799
5 1.5188 30 и,8007 55 0,5064 80 0,3565
10 1,3077 35 0,7225 60 0,4688 85 0,3355
15 1,1404 40 0,6560 65 0,4355 90 0,3165
20 1,0050 45 0,5988 70 U, 4061 95 0,2994
Основные данные вискозиметров различных систем
Таблица 11
Наименование условной единицы Условное обо- значение Страны, в ко- торых рас- пространены Объём испы- туемой жидко- сти, подлежа- щей измере- нию, в см* Выражение для ус- ловной единицы (Т — время истечения ис- пытуемой жидкости в сек,, Т — то же в воды, Тр —то же Константа прибора в сек. Формулы перевода условной единицы в кинематический коэфициент вязкости в см*1сек
рапсового масла)
Градусы Эн- °Е СССР, 200 Т при ГС Тв ==50-53 ,.0,0731.E_2^L Е.
глера Герман ия Те при f = 20°C
Секунды Эн- 'Е То же 200 'Е=Т при ГС 51 v=0 пО1435'Р.
глера
Секунды Сей- болта Уни- версаль 'S США 60 'S=T при t°F — »- и,0022 'S ъ
Секунды Сей- болта Фурол SF' То же 60 SF' = T при t°F — ,=0.022'(SF)-
Секунды Ред- R' Англия 50 R' = Тр = 555 1 72 и 0 026 *Г> ’
вуда Торге- ЮОр T при t°F
вог о 915 Тр при t=60°F
Секунды Ред- вуда Адми- ралти RA' США 50 RA' = T при 32°F О 4114 ,-0.0239-(RA)-^f?
Градусы "В Франция см* в час °В=число см3 в час — 48,5
Барбье ' °в
ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ
407
о w гоя ы so № ю ао зо Ш’С
Фиг. 1
На фиг. 1 показана кривая зависимости
кинематического коэфициента вязкости во-
ды и воздуха от температуры.
В капельных жидкостях кинематический
коэфициент вязкости уменьшается с повы-
шением темпера-
туры, в газах —
увеличивается.
В табл.13 при-
ведены значения
коэфициента вяз-
кости для некото-
рых жидкостей в
зависимости от
температуры.
Изменение коэ-
фпциента вязко-
сти нефтепродук-
тов с изменением
температуры определяется по формуле
lg1g(-»+0,08) = A+ft-lgT,
где ч — кинематическая вязкость в санти-
стоксах (мм21сек)-,
Т — абсолютная температура в °К;
Ап Ь — коэфициенты.
Для подсчёта вязкости по этой формуле
необходимо знать значение вязкости при
каких-либо двух температурах. На фиг. 2
приведён график, облегчающий производ-
ство подсчётов. Для получения вискограм-
мы через две известные точки проводят
прямую линию.
С увеличением давления вязкость капель-
ной жидкости возрастает, но значительно
меньше, чем от температуры,—в среднем на
1''soo — 1/soo своей величины при увеличении
давления на 1 кГ/см2.
Таблица 13
Абсолютная вязкость некоторых жидкостей
в зависимости от температуры
Вещество Температура в °C Вязкость в пуазах
Бензол Глицерин 100% • • • »> 86% . . . »> 42% . . . Касторовое масло . Метиловый спирт Ртуть ... Серная кислота 100% Толуол Углекислота .... Уксусная кислота . Этиловый спирт . . Масло льняное . • . 0 20 80 0 30 18 18 1,8 17,5 50 —98,7 0 20 —20 20 340 0 76,5 15 60 5 20 29 15 76,5 0 75 150 20 50 80 и,00972 0,00652 0,00329 121,0 6,29 0,971 0,043 51,8 12,25 1,22 0,1387 0,00821 0,00597 0,01855 0,01554 0,00921 0,484 0,00518 0,00623 0,00387 0,000925 0,000812 ' 0,000539 0,01410 0,00563 0,0177 0,00471 0,00166 0,516 0,182 0,082
Абсолютная вязкость газов может опре-
деляться по формуле
1 + — /—
_ 213 .f Т
N j £ V 273 ’
+ т
Фиг. 2
408
ГИДРОМЕХАНИКА
где u0 — вязкость при 0°С;
Т — абсолютная температура в °К;
С — постоянная.
В табл. 14 даны значения вязкости неко-
торых газов.
Таблица 14
Абсолютная вязкость некоторых газов при 0э С
где г1 и г.2—главные радиусы кривизны рас-
сматриваемого элемента поверх-
ности.
Дополнительное давление обусловливает
в свою очередь поднятие или опускание
уровня жидкости по отношению к нормаль-
ному уровню. Высота поднятия жидкости
в капилляре равна
Название газа
С ' 10- и,, в .сек/лР
I
Воздух ..........
Азот.............
Кислород ........
Углекислый газ . .
Окись углерода . .
Метан............
Водород .........
Гелий ...........
Аммиак ..........
Ацетилен.........
Хлор ............
В<дяной пар . . . .
Г20 1,755
107 1,703
138 1,262
150 1,402
102 1,687
198 1,657
83 0,85
80 1,88
626 0,96
198 1,02
531 1,29
673 0,87
где ?— угол соприкосновения жидкости со
стенкой;
d — диаметр капилляра;
7 —удельный вес жидкости.
В табл. 15 и 16 приведены величины коэ-
фицпента поверхностного натяжения воды
и других жидкостей при различных темпе-
ратурах.
1' а б л и ц а 15
Поверхностное натяжение воды при различных
температурах (во влажном воздухе и давлении
750 мм рт. ст.)
Темпе- I а I Темпе-
Ратура \дин/см | ратура
в °C ! ' в °C
а
дин! см
Темпе- 1 а
Ра\УРа 'дин/см
ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
И КАПИЛЛЯРНОСТЬ
Поверхностным натяжением называется
свойство жидкости сокращать свою свобод-
ную поверхность до наименьших размеров.
Силы поверхностного натяжения характери-
зуются коэфициентом поверхностного натя-
жения а, численно равным силе, с которой
действует по линии раздела на единице дли-
ны одна часть поверхностного слоя на дру-
гую. Коэфициент а определяется экспери-
ментально и в зависимости от температуры
изменяется следующим образом:
а = а0— Р* [кГ/Л(] или [дин/см],
где а0—коэфициент поверхностного натя-
жения при t = 0°С.
Поверхностное натяжение обусловливает
дополнительное давление
5
10
15
20
75.49
74,75
74,01
73,26
72,53
25
30
35
40
45
71,78
71,03
70.29
69.54
68,6
Таблица 16
Поверхностное натяжение жидкостей по отношению
к воздуху
Вещество Темпера- тура в °C а дин/см
Едкий натр 35% 20 99,7
Серная кислота 98,7% . . . 18 53,66
Соляная кислота 25% . . . 20 70,74
Бензол 17,5 29,16
Глицерин ............ 18 64,7
Керосин 20 23,96
Нефть 18 23,6
Олифа 20 32,0
Спирт этиловый* 35 2и,6
Эфир серный* , . 25,3 16,7
ГИДРОСТАТИКА
ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ,
ЕГО ИЗМЕРЕНИЕ И СВОЙСТВА
Если жидкость, находящуюся в покое,
рассечь некоторой плоскостью, выделить па
ней элементарную площадку ш и суммарное
давление на неё со стороны отброшенной
Р
части жидкости обозначить через Р, то — на-
<11
зывается средним гидростатическим давле-
нием (напряжением) жидкости—рср.
Если площадку ш уменьшать до нуля, то
предел, к которому стремится среднее гидро-
статическое Давление рср, называется
гидростатическим давлением (напряжением)
р в данной точке:
Гидростатическое давление измеряется,
в технических атмосферах и пьезах:
1 am = 1 KrfcM1 = 10 000 кГ)м*-,
1 пз = 1 стен/л/2 101,97 1:Г:м- =
= 0,010197 кГ!см\
1 По отношению к азоту.
ГИДРОСТАТИКА
409
Свойства гидростатического давления (на-
пряжения):
а) гидростатическое давление направ-
лено по внутренней нормали к площадке
действия;
б) гидростатическое давление в точке не
зависит от направления, в котором оно рас-
сматривается.
откуда
z + = const С, (4)
где g—ускорение силы тяжести.
Зная ординату какой-нибудь точки a—Za
и I пдростатпческое давление в пей — ра,
найдём постоянную
ДИФЕРЕНЦИЛЛЬНЫЕ УРАВНЕНИЯ
гидростатики Эйлера
Уравнение (4) тогда перейдёт в урав-
нение
др
дх
0р
оу
(1)
0р
dz
Разность между давлением в данной точ-
ке, если оно больше атмосферного, и атмо-
сферным давлением называется избыточным
давлением:
Р = Ра Рат-
где X, V, Z— проекции на оси координат
равнодействующей сил, дей-
ствующих на единицу массы
жидкости;
р — плотность жидкости.
Из уравнений (1) путём умножения их
соответственно на dx, dy, dz и сложения
получается основное уравнение гидроста-
тики:
dp = р (X-dx+Y-dy+Z-dz). (2)
Интеграл его даёт величину и распреде-
ление давления в каждом конкретном слу-
чае.
ПОВЕРХНОСТИ УРОВНЯ
Уравнение поверхности равного давления
или поверхности уровня получается из урав-
нения (2), если в нём положить dp = 0:
X-dx + Y-dy+Z-dz= 0. (3)
Левая часть этого уравнения представ-
ляет элементарную работу массовых сил на
возможном перемещении, т. е. в данном слу-
чае на направлении поверхности равного
давления.
Из уравнения (3) следует, что элемен-
тарная работа массовых сил вдоль поверх-
ности равного давление равна нулю.
Последнее же возможно лишь в том случае,
если суммарное ускорение массовых сил
перпендикулярно элементу поверхности рав-
ного давления.
РАВНОВЕСИЕ ЖИДКОСТИ,
НАХОДЯЩЕЙСЯ ПОД ДЕЙСТВИЕМ
СИЛЫ ТЯЖЕСТИ
Если оси координат взяты, как показано
на фиг. 3, то уравнение (2) принимает вид:
dp =-p-gdz =— ydz
или
d
( Р\
z 4- - =0,
k 7/
Разность между атмосферным давлением
и давлением в данной точке, если оно мень-
ше атмосферного, называется вакуумом:
Рвак = Рат Ра
Если Ze — вертикальная координата точ-
ки, то величина давления в ней из уравне-
ния (5) будет:
Рв = (Р«±7-Л), (6)
где h = (Z8 — Za) — глубина погружения
одной точки под другой.
Для избыточного давления
^«3= (Pall3±th).
Если ра = 0, т. е. точка взята на сво-
бодной поверхности, где р= рагп, то
ЗАКОН ПАСКАЛЯ
Уравнение (6) является математическим
выражением закона Паскаля: внешнее дав-
ление, оказываемое па поверхность жидко-
сти, передаётся без изменения всем частицам
жидкости.
р
Величины z и ~~ в уравнении (5) назы-
ваются соответственно геометрическим ц
пьезометрическим напорами.
р
Сумма z + = Н — величина постоян-
ная для всех точек покоящейся жидкости,
называется гидростатическим напором.
410
ГИДРОМЕХАНИКА
РАВНОВЕСИЕ ЖИДКОСТИ
В СООБЩАЮЩИХСЯ СОСУДАХ
1. Открытые сообщающиеся сосуды за-
полнены однородной жидкостью. В этом слу-
чае:
Zj = Z2,
т. е. жидкости расположены на одинаковом
уровне.
2. Один из сосудов закрыт (давление в
нём р0). Тогда:
Ро Ра „ ~
zi>
т. с. разность высот уровней в сосудах рав-
на разности пьезометрических высот.
3. Оба сосуда открыты и наполнены пе-
смешивающимися жидкостями с удельным
весом и -fj. При этом:
- J2.
2= 71
т. е. высоты жидкостей, отсчитываемые от
поверхности раздела, обратно пропорцио-
нальны удельным весам.
ОТНОСИТЕЛЬНЫЙ покой
жидкости
Относительный покой жидкости — покой
относительно движущихся сосудов, в кото-
рых эта жидкость находится. В этих слу-
чаях применяют принцип Даламбера и к
силам тяжести присоединяют силы инерции
переносного движения, т. е. движения со-
суда.
1. Сосуд с жидкостью вращается с неко-
торой угловой скоростью to. Пусть ось
z — ось вращения; начало координат на
свободной поверхности (фиг. 4), где р = р0,
Г = 0 И 2 — 0.
Интегрирование уравнения (2) даёт выра-
жение
Ш2-Г2
Р = Ро + 7 + 72- (7)
справедливое для всех точек рассматривае-
мой жидкости.
Уравнением поверхности уровня (dp= 0)
будет:
<о2
-z=-2j-r2+C, (8)
т. е. поверхностью уровня будет параболоид
вращения.
Для свободной поверхности
о,2
~ Zo = 2j r2’
где z0 — превышение точек свободной по-
верхности над плоскостью XOY.
Имея в виду последнее уравнение, можно
представить уравнение (7) в следующем
виде:
Р = Ро + 7 (2 — г<1) = Ро + 7
т. е. закон распределения давления в жид-
кости, находящейся во вращающемся сосуде,
тот же, что и bi покоящейся жидкости.
2. Сосуд с жидкостью движется с посту-
пательным ускорением а (железнодорожный
вагон-цистерна).
Если оси координат расположены так,
как показано на фиг. 5, то:
р — Ро + и [u-cos a-^+<(g — a-sin i) г]. (9)
Свободная
уравнением
— 2
поверхность определяется
a-cos а.
g — a -sin а
(Ю)
т. е. представляет собой плоскость, на-
клонённую к горизонту под углом 3, тан-
генс которого
O-COSa
tg * :: g — a-sin a ' )
ДАВЛЕНИЕ ЖИДКОСТИ НА ПЛОСКИЕ
СТЕНКИ
1. В силу первого свойства гидростати-
ческого давления равнодействующая сил да-
вления Р направлена нормально к стенке.
Фиг. 6
2. Сила давления жидкости на плоскую
стенку равна произведению смоченной пло-
щади этой стенки на величину гидростати-
ческого давления в центре тяжести этой
площади (фиг. 6):
Р = (Ро + 7-йч.т)“- (12)
ГИДРОСТАТИКА
411
Для избыточного давления формула бу-
дет иметь вид:
Риз У hg.m “> ОЗ)
где —глубина погружения центра тя-
жести смоченной площади стенки
под уровнем жидкости;
р0 — давление на свободной поверх-
ности жидкости;
ш — величина смоченной площади.
Из формулы (12) вытекает, что величина
силы давления жидкости на дно резервуара
зависит от рода жидкости, площади дна и
глубины погружения его центра тяжести
и не зависит от формы сосуда (гидростати-
ческий парадокс).
3. Точка приложения равнодействующей
сил давления называется центром давления.
Координаты центра избыточного давления
определяются уравнениями (оси взяты так,
как показано на фиг. б):
I ху IX
<14)
где 1ху — центробежный момент инерции
смоченной площади относительно
осей х и у;
1Х — момент инерции смоченной пло-
щади относительно оси, парал-
лельной оси хх и проходящей
через центр тяжести площади.
Для плоской стенки, симметричной от-
носительно оси оу, 1ху = 0 и х = 0, т. е.
центр давления лежит на оси симметрии.
Формулы для вычисления избыточного
давления и координат центра давления для
различных плоских фигур приведены в
табл. 17.
Расчёт давления жидкости на плоские
стенки с помощью эпюр давления. Формулы
(12) и (13) можно представить в следующем
виде:
Р
и> ~ Ро"^
В соответствии с этим эпюра полного
давления будет иметь вид трапеции, а
эпюра избыточного давления—форму тре-
угольника. Величина силы давления, при-
ходящейся на единицу длины стенки,
соответственно равна площади трапеции или
треугольника. Ордината центра давления
равна ординате центра тяжести площади
эпюры.
ДАВЛЕНИЕ ЖИДКОСТИ
НА КРИВОЛИНЕЙНЫЕ СТЕНКИ
В общем случае для определения силы
давления Р достаточно вычислить её проек-
ции на три оси координат. Величина силы Р
определяется как диагональ прямого парал-
лелепипеда, рёбра которого Рх, Ру, Pz
(фиг. 7):
Р = |/’р!Тр| +pf, (15)
Рх и Ру—горизонтальные составляющие
вектора давления на криволинейную поверх-
ность; они равны давлению жидкости на
проекции криволинейной поверхности на
вертикальные плоскости и направлены в
сторону стенки:
Рж = 7 Р„= ? J (16)
Рг — вертикальная составляющая вектора
давления жидкости на криволинейную по-
верхность, равная весу жидкости в объёме,
ограниченном рассматриваемой криволиней-
ной поверхностью и плоскостями YOZ и
ZOX:
P^^z-d^y. (17)
Здесь — проекции смоченной
площади на соответствующую координатную
плоскость.
рх
cos (Р, х) = -р-
cos (Р, у) =
р
cos (Р, г) = ~р^
Направление силы
Р определяется коси-
нусами направляющих
углов:
1
(18)
ПЛАВАНИЕ ТЕЛ
Тело, погруженное в жидкость, испыты-
вает давление, направленное снизу вверх,
равное весу жидкости, вытесненной телом
(закон Архимеда):
Р = 7 • V, (19)
где V — объём погруженной части тела;
7— удельный вес жидкости.
Задачи о плавании тел сводятся к опре-
делению: пловучести тела, погруженного
в жидкость, п способности плавающего тела
восстанавливать после крена своё пер-
воначальное положение (остойчивость тела).
Пловучесть тел. Если вес погруженной
части тела G < Р, то тело всплывает; при
G > Р тело тонет; при G — Р тело плавает.
Вес жидкости в погруженном объёме тела
называется водоизмещением. Пло-
скость сечения судна свободной поверхно-
стью жидкости называется плоскостью пла-
вания, а линия сечения — ватерлинией. Ось
плавания — вертикальная прямая, нормаль-
ная к плоскости плавания и проходящая
через центр тяжести тела. На оси плава-
ния расположены три характерные точки
(фиг. 8): 1) центр тяжести тела С; 2) центр
водоизмещения D — точка приложения ре-
зультирующей давления жидкости на тело;
3) метацентр М — точка пересечения оси
плавания с равнодействующей сил дав-
ления жидкости на плавающее тело при
крепе.
412
ГИДРОМЕХАНИКА
Таблица 17
Сила давления жидкости и координаты центра давления для различных плоских фигур
Cxt-Md Наименование фигуры Площадь фигуры Глубина погружения центра тя- жести [ц т Си ла давления ЖИДКОСТИ на фигуру Глубина погружения центра давления
-V - е» р г4-Ц Ijr »- b -* 1 luT ^•b — f L jL 7 L 1 Прямоу- ольник t)L L - +— 7 + -4 с +_L .7 + Зс 3 L 4- 2с
Прямоугольник bL L ') —7 bL2 4L
/у£ц1 \/y Квадрат fe« 4^7 4- 7 О’
^-8 \МЛ 4 V/J Равнобедренный треугольник 4 BL L 3 4tBL3
и® И’ Трапеция 4 l <-в+ь'> L 2d + В 3 ъ + в -^-yL’(2b + В) 1 3& + в 2 L' 2b+B~
Круг re r’ с+г т-7 Г’(Г + с) С + Г+4(г+С)
Полукруг 1 — rer« 4 Г ~ п 2 3 — гег
7 я j"c ЛХТ *r17 -2Л-Т Эллипс read а+с Y rea д(а + с) а+ с + — + 4 (а+с)
н- a l*i w?>* Xs—*- I Парабола * 4 «ь 4^- тЬaL' 1 4ь
ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
413
Для равновесия плавающего тела необхо-
димо, чтобы центр тяжести и центр водоиз-
мещения лежали на одной вертикали. Рас-
стояние от метацентра до центра тяжести
плавающего тела называется метацентриче-
ской высотой — т.
Расстояние между метацентром и центром
водоизмещения называется метацентриче-
ским радиусом р:
₽-Ц°-, <2о>
где /0 — момент инерции плоскости плава-
ния относительно продольной оси
плавания;
V — водоизмещение судна.
Остойчивость плавающих тел. Положение
судна остойчиво, если пара сил— вес судна
О и результирующая R сил, действующих
со стороны жидкости,—стремится уничто-
жить крен (фиг. 8). Из чертежа следует, что
для остойчивости плавающего тела необхо-
Фиг. 8
димо, чтобы расстояние 3 между центром
тяжести и центром водоизмещения было
менее длины метацентрического радиуса р.
гидродинамика идеальной жидкости
МЕТОДЫ ЛАГРАНЖА И ЭЙЛЕРА
Изучение движения жидкости можно про-
водить двумя различными методами. Можно,
начиная с некоторого начального момента,
проследить за движением отдельных частиц
жидкости, определив для них траекторию
движения; скорость и гидродинамическое
давление (метод Лагранжа).
Если а, Ь, с — координаты выбранной ча-
стицы в начальный момент, то координаты
у, у, 2 в произвольный момент времени t бу-
дут определяться но методу Лагранжа урав-
нениями
х = /1 (а, Ь, с, t)
У -= /2 (а, Ь, с, О
z = /3(н, Ь, с, t)
| (21)
По методу Эйлера в определённый момент
определяется движение всех частиц жидко-
сти данной области относительно выбранной
системы координат.
Уравнения (21), решённые относительно
а, Ь. с, выражают движение жидкости по
.методу Эйлера:
а - Гг (х, у, г, О ]
b =- F, (х, у, z, О S . 122)
с = F3 (х, у, z, t) '
В этих уравнениях х, у, z—координаты
неподвижной точки пространства, по кото-
рым определяется, какие частицы жидкости
проходят через эту неподвижную точку про-
странства с течением времени;
Метод Эйлера практически более удобен,
ибо даёт общую картину распределения ско-
рости и давления в любой точке простран-
ства, тогда как уравнения Лагранжа иссле-
дуют движение отдельных частиц жидко-
сти.
ДИФЕРЕНЦИЛЛЬНЫЕ УРАВНЕНИЯ
ДВИЖЕНИЯ ИДЕАЛЬНОЙ
НЕСЖИМАЕМОЙ ЖИДКОСТИ ЭЙЛЕРА
Уравнения Эйлера имеют вид:
X 1 — Р др _ дх dvx dt ' (23)
У 1 Р др _ ду dvv dt ' (24)
Z 1 р др dz ~ dv, dF (25)
1ЛП иначе:
1 X — - Р рр дх “ Ргл- = dt + V, dv, dx "
ж И/ dvx ~ду -Ь vz dy v dz
1 У др ду ж":/ dv,, ’ 'dt' dv,, ду- у. vz dv,, dx dv,, lz ’ . (26)
1 Z - — др dz dv, ~dt -1- V.X dvz d:; +
- Fl dv. ду' + v~- dv. ~dz
Вместе с уравнением неразрывности не-
сжимаемой жидкости
ди v dv,, . ди,
+ dv-+ ~dz “° <27>
эти уравнения дают полную систему урав-
нений с четырьмя неизвестными.
Интегрирование вышеуказанных диферен-
циальных уравнении представляет значи-
тельные трудности и выполнено лишь для
некоторых частных случаев.
414
ГИДРОМЕХАНИКА
ОСНОВНАЯ ТЕРМИНОЛОГИЯ
Установившееся движение — движение,
яри котором гидродинамические параметры
жидкости в каждой точке занятого ею про-
странства остаются неизменными с течением
времени, т. е.
В частном случае, когда движение жидко-
сти будет установившимся и плавно изме-
няющимся, система уравнений (30) примет
вид:
dw.
dvy
dt
dv, dp
Уравнения установившегося движения в
форме Эйлера имеют вид:
р
1
У — —
р
1
z ——
р
dx
д/ = о
ду
о
dz
(31)
,, 1 dp dv, dv,
Х~ 7 dx = Vx ~dx + иУ ~ду~ +
Расход—объём жидкости, протекающей
через поперечное сечение потока в единицу
времени:
Q = ш-v. (32)
__ дР _ J^v. I ,
Р dy Vx dx ' vv ду'
(28)
Расход равен произведению площади по-
перечного сечения ш на среднюю скорость
течения жидкости у.
Условие неразрывности в конечной форме
может быть представлено уравнением посто-
янства расхода
1 dp dv, dv,
Z~~ P dz = Vx ~dx + vv dy +
Q = const.
(33)
Осреднённая местная скорость. Уста-
новившееся движение в полном смысле дан-
ного выше определения встречается очень
редко. Часто имеет место движение, при
котором постоянен вектор так называемой
осреднёпной местной скорости, вычисляемый
по формуле
т
j >’i dt
7Р=°-^------ (29)
Таким образом осреднённая местная ско-
рость есть средняя скорость в данной точке,
определяемая за достаточный промежуток
времени Т.
Живое сечение — поверхность, прове-
дённая в пределах потока жидкости, нор-
мальная в каждой своей точке к осреднён-
ной местной скорости в этой точке; в част-
ном случае плавно изменяющегося движе-
ния — плоскость, проведённая в пределах
потока и нормальная к направлению дви-
жения.
Плавно изменяющееся движение — не-
равномерное движение, характеризующееся
плавностью изменений живых сечений и
направления потока, при которых живые
сечения практически можно считать пло-
скими.
Уравнения движения для этого случая в
форме Эйлера имеют вид (ось х совпадает
с направлением вектора скорости):
Линия тока —линия, в каждой точке
которой в данный момент вектор скорости
жидкости к ней касателен. В случае уста-
новившегося движения линия тока является
траекторией лежащих на ней частиц жидко-
сти.
Диференциальные уравнения линии тока:
dx
vx
dy dz
Vy — vz-
(34)
Поверхность тока — поверхность, в каж-
дой точке которой в данный момент вектор
скорости жидкости в ней касателен.
Элементарная трубка тока (струйка)—
часть жидкости, ограниченная линиями то-
ка, проведёнными через все точки любого
бесконечно малого простого замкнутого
контура, находящегося в области, занятой
жидкостью.
Плоскопараллельное движение (плоское
движение) — движение, при котором части-
цы жидкости движутся параллельно некото-
рой неподвижной плоскости со скоростями,
не зависящими от расстояния частиц до этой
плоскости.
Для движения в плоскости XOY урав-
нения Эйлера примут вид:
1 dp dvx dvx dvx \
X "" 7 dx = ~dT + L’x dx + vv
1 dp dvv dv,, dv„ k ’
ду-тг + Vx + )
уравнение неразрывности:
dp _ dvx )
у
л — р ’ dx ~ dt 1
_i dp 1
У — р ‘ ду ~ 0 I
1 др _
Z — р ' dz ~ 0 1
(30)
уравнение линии тока:
(36)
— = -- или vx-dy = Vy-dx. (37)
<H’r dvy
dx + ~dy = ’
ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
415
Функция тока, В плоскопараллельном
движении несжимаемой жидкости функция
ф (переменные Эйлера), связанная с состав-
ляющими скорости следующими зависимо-
стями:
называется функцией тока.
Абсолютная величина числового значения
этой функции в любой точке равна расходу
между линией тока, проходящей через эту
точку, и линией тока, с ф = 0.
Уравнения линий тока могут быть запи-
саны через функцию тока:
Оф ОФ
~^xdx+'bydy = 0’ <39>
или
или
с? ф = О,
ф = const.
ЗАКОН КОЛИЧЕСТВА
ДВИЖЕНИЯ
Имея в виду математическое выражение
закона количества движения
Фиг. 9
d
= ХР
в приложении к слу-
чаю установившегося
движения жидкого тела
(фиг. 9), можно запи-
сать:
Y / 2 2\
g (Ш2’у2 —
= Р1Ш1 — > (40)
где R' = — R — реакция стенок канала;
индексы 1 и 2 относятся соответственно к
сечениям I и II.
ЗАКОН ЖИВОЙ СИЛЫ
(уравнение энергии)
Математическое выражение закона живой
силы для жидкого тела имеет вид:
Xdx + Y-dy + Zdz — J- (dp - dt ) =
P \ dt j
u2
= d~Y. (41)
dp
Для установившегося движения = 0;
тогда
dp и2
X-dx + Y-dv + Z-dz—-'- = d-ту. (42)
P
Если объёмные силы, компоненты кото-
рых на оси координат х, у, г входят в это
уравнение, будут иметь потенциал, как это
в большинстве случаев имеет место в при-
роде, т. е.
X-
Х ~ ~ дх ’
дУ
ду ’
Z --
дУ
dz '
где U = I (х, у, z), то интеграл уравнения
(42) будет
Р и2
У + — + тт = const.
Р "
Для тяжёлой жидкости:
dU = g-dz, (Х=0, К = 0, Z = g)
и, следовательно,
2 2
л. 1 D ^2
21 + Y + =- 22 + Y + 2g = const- (43)
Последнее уравнение называется урав-
нением Даниила Бернулли и спра-
ведливо для элементарной струйки.
Интерпретация уравнения Бернулли. Для
всех точек элементарной струйки сумма трёх
р
высот — положения z, давления ~ и ско-
V2
ростного напора —есть величина посто-
янная.
Все члены уравнения Бернулли выража-
ют собой энергию, несомую единицей веса
жидкости, проходящей через сечения рас-
сматриваемой струйки.
Сумма всех членов уравнения выражает
суммарную, потенциальную и кинетическую
энергию, отнесённую к единице веса жидко-
сти.
ПОНЯТИЕ О ВИХРЕ
Вихревое движение — движение жидкости
с угловыми скоростями, не равными нулю.
По теории Коши—Гельмгольца, скорость
перемещения любой точки жидкой частицы
в общем виде слагается из трёх скоростей:
поступательной, деформационной и враща-
тельной:
до - , ,
ух(с) = vx + dx + (Q,jdz + O2dy) j +
+ (a>tJ dz — шг dy)
[dv,, Д ,
~^<1У+ (М* +еД*2) ] + (44)
+(w3dx — wxdz)
^dz+^dy+Qy dx) +
+ (шг dy — w,jdx) I
где: 1) ил, vy, vs — компоненты скорости
движения точки
А(х, у, z) (фиг. 3);
416
ГИДРОМЕХАНИКА
“) !'x(c)>i\(c)’t'j(c) - компоненты скорости
движения точки С [Сх
+ dx), (y+dy), (z+dz)]:
(45)
(46)
нения (50), будет безвихревым, или потен-
циальным.
Компоненты скоростей потенциального по-
тока должны удовлетворять не только усло-
виям (50), но и уравнению неразрывности,
следовательно, удовлетворять уравнению
Лапласа:
д-Ф д2Ф д-Ф
дх2 ду2 + dz2 ~ °’
или
Д Ф = 0.
(51)
Из последнего уравнения и сравнения
уравнении (38) и (50) следует, что для пло-
ского потока функция ф должна удовле-
творять уравнению
д2д
(52)
компоненты угловой скорости по осям
кш рдипат (компоненты вихря скорости и н:
просто компоненты вихря).
Полная угловая скорость вращения
ш = j/" co* + Шу + . (47)
Вектор угловой скорости в данной точке
.называется вихрем.
Удвоенная угловая скорость называется
ротором и обозначается rot и:
rot v — 2 ш.
(48)
ЦИРКУЛЯЦИЯ СКОРОСТИ.
эквипотенциальные поверхности.
ОСОБЕННОСТЬ БЕЗВИХРЕВОГО ПОТОКА
Циркуляцией скорости называется криво-
линейный интеграл, взятый по какому-либо
замкнутому контуру (фиг. 10):
Г = у) у-cos (г, dl) dl '=
i
= (vx-dx +- u,,-dy -I- v.-dz). (53)
потенциальное движение.
УРАВНЕНИЕ ЛАПЛАСА
Условием потенциального (безвихревого)
движения жидкости является равенство нулю
компонентов вихря:
= <|> у —- со - О,
пли, согласно формулам (46):
до. дои ।
Ov dz'
<4, онд !
дх ду
Оох до,
dz ' дх
Из условий (49) следует:
дФ (х, у, z}_
vx " — дх
= У.'I).
V V оу
дФ (х, у, 2)
Л ------------------
(49)
где функ пия пространства Ф (х, у, г) назы-
вается потенциалом скорости. Таким обра-
зом, движение жидкости, в котором имеется
потенциал скорости, т. е. соблюдены урав-
Циркуляция Г и ротор rot о связаны меж-
ду собой равенством:
Г = j (rot г) </А, (54)
где dF — элемент площади;
rot t> — ротор для оси, перпендикулярной
dF.
Интегрирование распространяется по всей
площади, ограниченной рассматриваемым
контуром.
Для потенциального движения:
в
f /ОФ дФ дФ \
Г = ] (jx dx + ду-аУ + dTdz)^
А
И
= J dФ = Фв-ФA' (55)
А
где А и В (фиг. 10) —начало и конец кон-
тура.
ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
417
Если потенциал скорости будет однознач-
ной функцией координат, то
Г~ФВ—ФА = 0,
т. е. циркуляция скорости будет равна
нулю.
Поверхности, выделенные в потоке жидко-
сти, так, что все их точки имеют одинако-
вые функции потенциала скорости, назы-
ваются поверхностями равного потенциала
(эквипотенциальные поверхности).
В безвихревом потоке жидкости линии
тока нормальны к поверхностям равного по-
тенциала.
УРАВНЕНИЯ ГРОМЕКИ—ЛЕМБА
Уравнения Громеки — Лемба являются
теми же уравнениями Эйлера, выраженными
через компоненты вихря:
X 1 _ д-^ |_ А 7 ,
Х р дх - dt + дх \ 2 ) +
+ 2(^ — 1^ <ог)
_ _1 dp dvy д_ /v*\
р ду dt ду 2 J 4 j
+ 2 (ух шг — t>№)
(56)
1 др dvz д fv2\
р dz = dt dz 2 )
+ 2 (vy <s>x — ох «0 J
Для установившегося потенциального
движения интеграл Лагранжа — Коши пере-
ходит в интеграл Бернулли—Эйлера:
р
U + — + -о- = const,
р z
справедливый, в отличие от интеграла Бер-
нулли (43), уже не для струйки, а для всех
точек жидкости.
ЭЛЕМЕНТАРНЫЕ СЛУЧАИ
ПОТЕНЦИАЛЬНОГО ДВИЖЕНИЯ
ЖИДКОСТИ
Плоскопараллельный поток — потенци-
альный поток, имеющий в бесконечности
скорость v, которую сохраняет по вели-
чине и направлению во всех точках про-
странства.
Если скорость v параллельна оси ОХ, то
Ф (x,y,z) = vx-x. (59)
Диференциальное уравнение линии тока
dx dy
vx = v„ ’
но = 0, тогда vx-dy =- 0.
Уравнение семейства линий тока будет
vx-y = с-у = const. (60)
Радиальный поток. Жидкость течёт из
одной точки (источника) по радиусам по всем
направлениям в бесконечность (фиг. 11). Если
Если объёмные силы имеют потенциал,
то уравнения Громеки—Лемба выглядят так:
д ( Р vz\ dvx ,
dxf -U +
+ 2 (ОгШу — Vywz)
<4 ,, p. vl\d4i ,
dy\—u~ p - 2 J~ dt +
+ 2 (ихш, — vz<»x)
(57)
dz\ . p 2 J dt
+ 2 (vv<»x — vx4>y)
расход Q отрицателен, то поток называется
стоком.
Скорость v на расстоянии г равна
ИНТЕГРАЛ ЛАГРАНЖА—КОШИ
Интеграл системы уравнений (57) для не-
установившегося безвихревого движения—
интеграл Лагранжа — Коши — имеет вид:
р , vi дФ
U+p + 2-dT = F^’ (58>
где Ф (х,у,г) — функция потенциала скоро-
стей;
F(О — некоторая произвольная
функция времени, имеющая
в каждый момент времени
вполне определённую вели-
чину, одинаковую для всех
точек движущейся жидкости.
Функция потенциала скорости
Г Q
Ф (x,y,z) = ± J д-dr =
О
= ± _£- =±4L
1 4пг г
где q = = const -«напряжение*, или эф-
фективность, источника (стока).
При плоском движении, когда источник
сосредоточен не вточке,а распределён вдоль
27 Том 1
418
ГИДРОМЕХАНИКА
прямой линии, скорость v на расстоянии г
где q = — эффективность источника, или
стока.
Функция потенциала скоростей
О
Ф (х,у) = ± — In г = ± j 1п г. (62)
Циркуляционный поток. Жидкость дви-
жется по концентрическим кругам вокруг
некоторой оси так, что всюду, кроме как
на самой оси, она свободна от вихрей
(фиг. 12).
Скорость v в точке А на расстоянии г от
вихря
Г
v = >
71 Т
где Г—циркуляция скорости вокруг оси.
Функция потенциала скоростей
Г / У\
Ф-2^атс^^)> <63>
Г
гдет^- = v • г — момент количества движения
жидкости для массы, равной
единице.
Функция потенциала скорости является
многозначной, ибо выражается обратной
круговой функцией.
МЕТОД НАЛОЖЕНИЯ (СУПЕРПОЗИЦИИ)
ЭЛЕМЕНТАРНЫХ потенциальных
потоков
Если п потенциальных потоков, соответ-
ственно с функциями потенциала скоростей
Фп Ф2, ...,Фп, суммировать геометрически,
то суммарный поток будет также потенциаль-
ным с некоторой функцией г^>тенциала ско-
ростей Ф = Фх + Ф2 + . .. + Фп, ибо
Vx = у л-1-l- Ул-2 4- •••4-Ухя
или
дФ, дФ„ дФп
Vr = + ~5— 4- ... 4- -л-” =
х дх ~ дх л- • • • -г
__ д + Фа + ••• 4- Фп)
~ дх ~ дх '
Аналогично:
д (Ф1Ч-Фг 4~ • •• 4-Фя) 6Ф
vv = by ~ ду ’
_ д <ф14- Ф-Л 4- Фп) _ дФ
Vl!~ dz dz ’
Таким образом,суммарное движение будет
удовлетворять уравнению неразрывности Ла-
гранжа:
Дф = кФ! ДФ2+ ...+ ДФ„ = 0. (64)
Ниже приводятся некоторые частные
случаи.
Источник и параллельный поток (фиг. 13).
Функция потенциала скоростей, результи-
рующего движения, равна
о
Ф (х, z) = и • х + -у-=2 (65)
г А 4
Жидкость, вытекающая из источника,
остаётся внутри некоторой поверхности.
Параллельный поток как бы обтекает
«полутело».
Если а — расстояние источника от перед-
ней точки тела, D - толщина тела в доста-
точно большом удалении от его края, то
для пространственного потока
для плоского потока
_ Я _ О
а “ v ~ 2 л*
где q — напряжение, или эффективность,
источника;
v — скорость невозмущённого парал-
лельного потока.
Эти соотношения определяют положение
и напряжение источника при заданных D
и V.
Пара источник — сток (источник н сток
равных напряжений) (фиг. 14). Функция
потенциала скоростей
q q
ф<^)= =
= -^===£-===7=^ — -----(66)
У(х + а)2 + z2 V (х — а)2 + z2
Если уменьшить расстояние 2 а до нуля
и одновременно увеличить расход Q так,,
чтобы
a-Q = М = const,
то как предельный случай получается так
называемый дублет, или диполь (фиг. 15).
Величина М называется моментом диполя.
В пространственном потоке:
/ М \
vx = \^4лг3) (3 со£2 1)’
М „ .
vv = — 4^73 -3sin <?-cos<p;
у = l/ Ух 4- Vy = V3 cos2 <р + 1;
Al
ф (X,y,z) =- 4~r COS <?. (67)
ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
419
В плоском потоке:
vx = — (2 cos» с? - 1);
М
vv “ “27г»2 sln <p‘cos <р:
М
Ф (х,у) = cos<p. (68)
Плоскопараллельный поток и пара ис-
точник— сток (фиг. 16). Граничная поверх-
ность подобна эллипсоиду вращения. Для
плоского потока
$
граничная линия соответ-
ственно подобна эллипсу.
Практически важный
случай: диполь и парал-
лельный поток (фиг. 17).
Граничная поверхность —
сфера, для плоского пото-
ка—окружность
Фиг. 15 Фиг. 16
Диаметр этой фигуры d и скорость у её
поверхности W:
для пространственного потока (шар)
2 то I . (69)
w = 1,5 v sin<? I
для плоского потока (круг)
w = 2 v sin <р
Обтекание бесконечного круглого ци-
линдра суммарным плоскопараллельным и
циркуляционным потоком (фиг. 18). При
движении плоскопараллельного потока сле-
ва направо, а циркуляционного—по часовой
стрелке суммирование скоростей для верх-
Фиг. 17
чей части цилиндра даёт увеличение, а для
тижней—уменьшение абсолютного значения
:корости. Следовательно (По уравнению Бер-
нулли), по сравнению с давлением в плоско-
параллельном потоке давление в верхней
части цилиндра будет падать, а в нижней
увеличиваться.
Результирующее давление будет направ-
лено вверх; по теории Жуковского, под-
держивающая сила на единицу длины равна
R = у Ги. (71)
ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ
Зависимость между потенциалом скорости
и функцией тока через компоненты скорости
их и иу согласно формулам (50) и (38) вы-
ражается так:
дФ дф 1
Vx ~ дх ~ ~ду I
дФ дф | " ^2)
vv “ ду = ~ ~дх I
Эти диференциальные уравнения явля-
ются уравнениями Коши—Римана.
Известно, что вещественная и мнимая
части каждой регулярной аналитической
функции (т. е. имеющей непрерывную про-
изводную) / (г), где z = х + i-у, удовлетворя-
ют уравнениям Коши — Римана, и наоборот,
если функции Ф(х,у) и ф(х,у) удовлетворяют
уравнениям Коши—Римана, то эти функции
можно рассматривать соответственно как
вещественную и мнимую части регулярной
аналитической функции комплексного пере-
менного. Таким образом, потенциал скорости
и функция тока плоского движения пред-
ставляют вещественную и мнимую части
некоторой функции / (z), называемой харак-
теристической функцией или комплексным
потенциалом:
/ (z) = Ф + i ф. (73)
Характеристическая функция имеет боль-
шое значение в изучении плоских потен-
циальных потоков, так как значительно
упрощает их исследование.
Производная от характеристической функ-
ции
dt (z) дФ оф
“55“ = ох + г' <74>
выражает вектор, сопряжённый с вектором
скорости. Эту производную называют поэто-
му комплексной скоростью.
Модуль комплексной скорости равен дей-
ствительной скорости:
(75)
ВИХРЕВЫЕ ЛИНИИ
И ТРУБКИ
Вихревая линия — линия, в каждой точке
которой в данный момент вектор угловой
скорости жидкости к ней касателен. Дифе-
ренциальные уравнения вихревой линии
аналогичны диференциальным уравнениям
линий тока:
dx dy dz
“л: “ “г/ = ’
Поверхность, образованная вихревыми
линиями, проходящими через какую-нибудь
заданную линию в жидкости, называется
вихревой поверхностью. Если заданная ли-
ния представляет замкнутый элементарный
контур, то проходящие через неё вихре-
вые линии образуют вихревую трубку.
Жидкость, заключённая внутри вихревой
трубки, называется вихревой нитью. Произ-
27*
420
ГИДРОМЕХАНИКА
ведение величины вихревой скорости в ка-
кой-нибудь точке вихря на площадь попереч-
ного сечения вихревой нити в этой точке
называется напряжением вихревой нити:
d/=2<nrf&. (76)
Теорема Стокса. Циркуляция скорости
по всякому замкнутому контуру, обращаю-
щемуся в точку, не выходя из жидкости,
равна удвоенной сумме напряжений всех
вихревых нитей, проходящих сквозь этот
контур:
Г = S2®d8 = 2ff «>.<В. (77)
(«)
Теорема Томсона. Если массовые силы
имеют потенциал и плотность жидкости
является функцией давления, то циркуля-
ция скорости по любому замкнутому конту-
ру во всё время движения является посто-
янной:
Ъ = 0. (78)
Теорема Лагранжа. Следствием теоремы
Томсона является теорема Лагранжа. Если
движение было в какой-нибудь момент по-
тенциальным, то оно будет потенциальным
во всё время движения.
ПРИНЦИП СОХРАНЕНИЯ
ВИХРЕЙ
Принцип сохранения вихрей (устойчи-
вость вихревой нити) определяется теоре-
мами Гельмгольца:
1) напряжение вихревой нити вдоль еб
длины одинаково;
2) если силы, действующие на жидкость,
имеют потенциал, то:
а) вихревая нить состоит всегда из одних
и тех же частиц жидкости, даже передви-
гаясь или меняя свою форму;
б) напряжение вихревой нити во всё время
движения остаётся постоянным.
ГИДРОДИНАМИКА РЕАЛЬНОЙ (ВЯЗКОЙ) ЖИДКОСТИ
реальная жидкость
В отличие от идеальной реальная жид-
кость обладает свойством вязкости—оказы-
вать сопротивление растягивающим и каса-
тельным усилиям.
Для учёта всех сил, влияющих па форми-
рование движения вязкой жидкости, необхо-
димо вводить в рассмотрение некоторую до-
бавочную силу на поверхности раздела в
виде сё нормальной и касательной состав-
ляющих.
По гипотезе Ньютона, касательные на-
пряжения т от действия сил вязкости рав-
ны:
где ц—коэфициент вязкости;
dv
. — градиент скорости по нормали к
ап перемещающимся слоям, или
zx. = Ъх = Р (5 + £) j > (8°)
(dvv . буД
zyz ~ =• Р дг ду ) )
т. е. касательные напряжения по двум взаим-
но перпендикулярным плоскостям в любой
точке равны друг другу.
Добавочные нормальные напряжения от
действия сил вязкости будут растягиваю-
щими:
бух дУу
Рхх — 2р ~дх ’ “ 2 д ,
= <81)
Благодаря влиянию сил вязкости гидро-
динамическое давление в реальной жидко-
сти будет зависеть от направления рассмат-
риваемой площадки. За гидродинамическое
давление в точке в гидродинамике вязкой
жидкости принимают среднее арифметическое
гидродинамических давлений по трём взаим-
но перпендикулярным направлениям:
Рх+Ру+Рг
р =----3------f (82)
величина которого не зависит от направле-
ния.
КОМПОНЕНТЫ СИЛ ВЯЗКОСТИ
В ФУНКЦИИ КОМПОНЕНТОВ СКОРОСТИ
Компоненты сил вязкости, действующие
на элементарный параллелепипед, равны
сумме проекций поверхностных сил на оси
координат и могут быть выражены в функ-
ции компонентов скоростей:
/d2vx d2v-.
X^W+6F
Y„
7 _ /б2Уг б2Уг
~ k 6x? ' dy2
62у v\
-----dxdydz
dz2 J 7
/d2vv d2vv d2vv\ .
= U __________________) dx dy dz
r \ dx2 dy2 dz2 /
d2v,\
---) dx dy dz
dz2 /
, (83)
Если по аналогии с компонентами вихря
ввести понятие о компонентах «вторых вих-
рей» («вихрей от вихрей»), равных:
1 |
Cjf ~ ~2 \~бу ~dz ) |
1 [ д«>х _ dtDz\ <
еу~2\д1 дх '
1 /дшу дм Л
ег ~ 2 \дх ~ бу/
(84)
ГИДРОДИНАМИКА РЕАЛЬНОЙ (ВЯЗКОЙ) ЖИДКОСТИ
421
то уравнения (83) примут вид:
Хл = - 4 р е , dx dy dz ч
Уе = — 4 р. sy dx dy dz > . (85)
Ze = — 4 p s2 dx dy dz J
УРАВНЕНИЯ НАВЬЕ—СТОКСА
Вводя в уравнения Эйлера выведенные
для идеальной жидкости компоненты сил
вязкости, легко перейти к диференциаль-
ным уравнениям движения реальной жид-
кости:
V 1 dp _dvx _
A I1 p У p p dx3 1 P /daa„ dx dt d2vx d2vx\ dy- dz2 / dp du у dy dt 4 (86)
T z p p < dx2 1 P /d2az dx2 r dy2 dz2 J dp dvz dz= dt~ d2az ! d2az\ + dy3" "dz2 )
Эти уравнения впервые были выведены
Навье и Стоксом и являются основными урав-
нениями динамики вязкой жидкости. С по-
мощью оператора Лапласа уравнения (86)
приводятся к виду:
X- 1 dp dx dv x -i j
1 dp do v ।
У — F dy (87)
7 2 dp da.
z< — dz — У • Л Vy 1 dt " 1
где ч — кинематический коэфициент вязко-
сти жидкости.
Если воспользоваться выражением компо-
нентов сил вязкости через компоненты вто-
рых вихрей, то у равнения (87) перейдут в
v 1 dp dvx
X — . _L = — + 4v-sr
P dx dt
1 dp dv v
p dy = 77 +4^ (. (88)
z-l.dp dv, 1 = — +4v-e, !
P dz dt )
Ниже приведены уравнения Навье—Сток-
са и уравнение неразрывности в цилиндри-
ческих и сферических координатах.
В цилиндрических координатах г, <р, z:
dvr dv,
dT + U' dr
a dvr daz
Р dr <dra
р dr
1 d2v. d2a. 1 dv.
+ ...J -1- —- 4. - —-
гя dp2 dz1 r dr
_ 2 dv? _ a_A
r2 d<?
dv,. da.. v.. dv.. dv..
.—-4- Dr dt т i „X. dr r t ... +
vrv.. , 1 dp ox
prdp +д 7,? +
1 d2a d2a 1 da
”1 •> r2 9 , dtp3 dza + 7 dr
2 dur MY
r2 d p r2 /
da, dvz , v<d dv z dv.
— + i j -1- _X — 4- y, _ =
dt r dr r 0^ dz
1 dp , /d2az 1 d^z
Cl dz ' \ dr2 1 „Л r- d tp3 1
d2u, 1 daX
dz2 r drу >
da. I dv„ dv z V
77 + _ ..A 4. . r dp di ; 4 r - = 0
. (89)
I
В сферических координатах г, ®, 0:
)
dvr dvr Va dvr v.„ dvr
____ ..i. у .. „£ ।_L-__L । ____?
dt r dr r dQ r sinO d-p
2 I 2 1 dp Г о2 a.
_J Y r — id~r + 'Л —- 1 dr'2. L +
1 d2a. 1 4. ' 4 r2 d()2 r2sin20 ctg 0 dvr r2 d0 _ 2 da? 2a, O'-v, 2 dp2 n r 2 da9 72 ~d0 " 2 ctg d vr dr 0 1 +
r2 sin 0 dtp r2 r- -
<4 t di 1 dv0 ur * dr ae da0 r dQ
.j. 1 rsiny daa d-p ‘ r -2tct r go
— -- 1 dp pr dO Г О2 L dr2 +
2 d_ J + r>- dO2 1 + r2 sin20 duJ 4 2 dp2 r dae dr
ctgO r2 da0 2cosO da.? dO r2 sin20" ~dp +
J dvr d0 r3 ] sin2 0 J
dt r 0уо a Vr -J +- dr r dO +
• (90)
+ % ^tp rsinO dtp + ‘7 +
Vn V ctgO 1 dp
. — 4. J prsin-6 d?
R2 1 32a,„
+ L dr2 -- —+ r2 dO2 T
422
ГИДРОМЕХАНИКА
1
d2v^ i 2 dv^ ctg 0 du?
г2 sin2 0 df2 г dr г2 дб
2 диг 2 cos 9 dt>9
г2 sin 0 df г2 sin20 df"
-_л1;
г2 sin2 О J
М J # <4 1 <Чр_
dr r dd r-sinO df
2^.4. Pp ctgQ_0
(90)
Простейшие случаи интегрирования урав-
нений Навье-Стокса. Уравнения Навье- Сток-
са вместе с уравнением неразрывности (27)
дают систему четырёх диференциальных
уравнений с четырьмя неизвестными: vx, vt/,
vz и р, которая ввиду математической слож-
ности разрешена лишь для некоторых част-
ных случаев.
Ниже приведено несколько таких част-
ных случаев интегрирования этой системы
уравнений, причём в каждом из них предпо-
лагается существование потенциала U для
массовых сил.
Движение потенциальное. По-
следние члены уравнений Навье—Стокса
равны нулю:
• Д vx = ч-di vv = v-Д va — 0.
В результате получается известный ин-
теграл Лагранжа—Коши:
р v2 d v
у + ?+ 2= <91>
Движение потенциальное
установившееся. В данном случае
=0, и интеграл получает вид:
р V2
U + — + тг = const (92)
Р
— интеграл Бернулли — Эйлера.
Движение установившееся.
Интегрирование в этом случае уравнений по
длине струйки приводит к интегралу Бер-
нулли, справедливому для струйки реальной
жидкости:
р V2
U + ~ +• 2 + = const, (93)
где h„ — работа сил вязкости, потерянная
единицей массы жидкости.
Для плавно изменяющегося потока по-
следнее уравнение примет вид:
п сп
и + Г- + -тг~ + dw= const, (94)
Р *
J и3 d ш
где а——а------—поправочный коэфициент,
1Г-ш
ср
учитывающий неравномерность распределе-
ния скоростей в поперечном сечении потока—
коэфициент Кориолиса.
Для ламинарного режима а = 2, для тур-
булентного а= 1,04.
ОДНОРАЗМЕРНОЕ НЕУСТАНОВИВШЕЕСЯ
И УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ
Во многих задачах гидравлики предста-
вляется возможным, когда поперечные раз-
меры потока по сравнению с его длиной
весьма малы, рассматривать движение не
как сумму движений элементарных струек,
а как движение одной конечных размеров
струи.
Уравнение такого движения, называе-
мого одноразмерным, можно представить
как функцию лишь двух переменных: вре-
мени t и расстояния I.
В общей форме уравнение одноразмер-
ного неустановившегося движения имеет вид:
dz , 1 dp . d I vcp\ \dv
~di + ^--dT + dr 1 2g” / ’oT +
+ («,= 0, (95)
где iw — член, учитывающий потери энергии
на сопротивление и не являющийся непре-
рывной функцией от длины.
Для капельной жидкости 7 = const, и
уравнение (95) примет вид:
d
dl
. 1
+ 'g йТ + /«==0-
(96)
Если движение будет установившимся,
член = 0 выпадет из всех вышеприведен-
ных уравнений.
ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ
КРИТЕРИЙ РЕЙНОЛЬДСА
При движении жидкости возможны два
характерных режима: 1) жидкость движет-
ся без пульсации скоростей, приводящей
К перемешиванию движущегося потока;
2) жидкость движется с пульсацией ско-
ростей — происходит перемешивание частиц
движущегося потока жидкости.
Первый режим называется ламинарным;
второй— турбулентным.
Режим движения определяется критерием
Рейнольдса:
Re = V~^, . (97)
где v — средняя скорость движения жидко-
сти;
d—диаметр трубопровода;
v — кинематическая вязкость жидкости.
При Re < 2 300 — режим ламинарный; при
Re > 2 300— режим турбулентный.
ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ
423
Число Re, при котором ламинарный ре-
жим переходит в турбулентный, называется
критическим числом Рейнольдса—Rerp.
ReKp, строго говоря, не является посто-
янным,—оно зависит от начальных возмуще-
ний на входном участке трубы. По Шил-
леру Л. и Белоконь Н. И., минимальное
значение ReKP=l 160, а максимальное ReKp=
= 60 000.
КРИТЕРИЙ ПОДОБИЯ
Два потока называются подобными, если
они удовлетворяют условиям:
геометрического подобия, т. е.
li — а1 ' ^2»
где аг— коэфициент пропорциональности;
и 12 — линейные размеры потоков;
кинематического подобия, т. е.
между перемещениями двух потоков должно
существовать соотношение:
_ dXj dy-j dzr
а~ dx2 = dy2 ~ dz2 ’
кроме того, отношения времени прохожде-
ния соответствующих участков двумя части-
цами должны быть повсюду равны: at = у;
динамического подобия, когда:
Г . • /. V»• / 2 _ .
—у—- = ——= Re (параметр Рейнольдса);
2 2
У1 v2
ут = -—т- = Fr (параметр Фруда).
S1’1! 62’12
Одновременное выполнение этих двух ус-
ловий не всегда возможно, ибо первое тре-
бует соблюдения и • I — const, а второе
а2
-у = const.
Если преобладает влияние вязкости, не-
обходимо соблюдение условий Рейнольдса;
в случае большего влияния сил тяжести
необходимо выполнение условий Фруда.
ЛАМИНАРНЫЙ РЕЖИМ
Характеристика ламинарного режима. Кри-
вая распределения скоростей в ламинарном
потоке — парабола
где i — «гидравлический уклон» -—потеря
напора на единицу длины трубопро-
вода;
р. — абсолютная вязкость.
Максимальная скорость при г=0 (на оси
потока)
имак = "J?/ ГО-
Формула (98), выраженная через импК1.,
принимает вид:
<100)
Расход через трубу
Q 2 ^макс» (101)
Средняя скорость потока:
Q -г d2
v£P = - = 0,5 - имаке = i. (10?)
Из последней формулы можно определить
потерю напора на единицу длины трубопро-
вода (формула Пуазейля):
. 128 ;i Q
l~327-d2 ’ или 1 ~~ yd* ' <103>
Таким образом, потеря напора на еди-
ницу длины при ламинарном режиме про-
порциональна первой степени средней ско-
рости.
Формулу (103) можно привести к виду:
_ 64» J г2 64 l_ v2
~ v-d ' d ‘2g = Re' d'2g-
„ 64
Безразмерную величину называют
коэфпциентом гидравлического сопротивле-
ния X.
Таким образом:
. , 1 г2
ft = ^7-2g’ <!04>
где I — длина трубопровода.
Опытные данные подтверждают все при-
ведённые теоретические уравнения.
Линии вихрей ламинарного потока.
Ламинарное движение является вихревым:
= 47 (го —г2>; = °; = °-
Компоненты вихря равны:
1 va_d vy\
2 уд у д z )
1 (д vx д иг\
> = ~2 у d~ ~dT) =
= - т- z = — az
4р.
1 1>у д ух\ _
Шг 2 \ д х д у J
I{
= 4— у = ау
4 р1 '
(105)
Следовательно
ш = “х + <°у + = 4’7 г
Уравнение вихревых линий
dy _ dz
“?/ ~ “z
согласно формулам (105) примет вид:
у • dy + z • dz = 0.
После интегрирования
у2 + z2 = г2, (107)
424
ГИДРОМЕХАНИКА
т. е. «вихревые линии» суть концентриче-
ские окружности с центром на оси трубы.
Ламинарный поток в некруглых трубах.
Все формулы, приведённые для движе-
ния жидкости с круглых трубах, имеют
место и для случая движения жидкости по
некруглым трубам с той лишь разницей, что
расчёт ведётся не по диаметру d, а по гидра-
влическому радиусу /?, равному
где
Значение / берётся из табл. 18.
(ИЗ)
СО
R = /- , (108)
где «о — площадь живого сечения;
X — смоченный периметр,
или по эквивалентному диаметру dj = 4 R.
Для круглой трубы:
Таблица 18
Значение коэфициента f в формуле (1 К)
• 2.5 2,2 2,09 1,83 1,40 1.12 0,93 0.5 0
а 1 1,25 1.5 2 3 4 5 10
При а
о) л d2 а
R = 77 = 47 d = ~4
(109)
Ь;
4 vb
Re = ——
и формулы для li,Re и л соответственно при-
96
= Re • (И4)
.Ниже приведены формулы для некоторых
видов поперечного сечения труб (гх и г3 —
радиусы наружной и внутренней труб).
Концентрические труб ы:
Г1 — Г.2 ~ 2v(r1 — г3)
= “2~; Re —------------------
.____I_____t>2
/г = л 2(?;--г;у -2g
_ 32 _____________________1
~ / r“ - r?.\
vl r21 + r22+ - - - \
111 к
Трубы прямоугольного сече-
ния (2a и 2b— стороны прямоугольника,
причём b <а):
а-Ь 4 abv 1
/?=(7Т&): Re='(a~+b)\ I
, . Ца + b) v* 64 • а \ b (112)
1 “ Л -lab ~ '2 g • '-Re'-f\b) ]
Начальный участок. Все вышеприведён-
ные формулы справедливы для развив-
шегося ламинарного движения. Как пока-
зывает опыт, распределение скоростей при
входе в трубу не подчиняется параболиче-
скому закону. Жидкость вступает в трубу
приблизительно с одинаковой скоростью по
всему поперечному сечению, исключая весьма
тонкий слой, непосредственно прилегающий
к стенке трубы. Постепенно, по мере удале-
ния от входа, скорость осевых слоёв растёт,
а пограничный слой, расширяясь, вызывает
уменьшение скорости в наружных слоях
жидкости.
На некотором расстоянии 1нач устанавли-
вается развившееся ламинарное движение.
Характер изменения распределения скорости
в поперечном сечении по длине начального
участка иллюстрируется табл. 19, где пока-
зано изменение коэфициента Кориолиса а.
Длина начального участка равна:
по Буссинеску /нач = 0,065 d-Re '|
по Шиллеру 1нач = 0,02875 d-Re (
Коэфициент X для различных сечений
начального участка по Шиллеру равен:
(116)
Значения А приведены в табл. 20.
Таблица 19
Значение коэфициента а для различных сечений начального участка ламинарного потока
d-Re
0 2.5 5 7,5 10 12,5 15 17,5 20 25 28 75 30 40 | 65
а по Буссинеску
1 1 465 1,66 1,775 1,805 1,840 1,860 - - 1,915 | — 1,935 1,94 2
а
по Шиллеру
1 | 1,405 1,552 1,642 1,716 1 779 1,82 1,866 1,906 1,964 2 -
ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ
425
Таблица 20
Значение коэфициента А в формуле X = —
х-10* d-Re 2,5 5 7,5 10 12,5 15 17,5 20 22,5 25 28.75
А 122 105 96,66 88 82,4 79,16 76,41 74,375 72,77 71,5 69,56
ТУРБУЛЕНТНЫЙ РЕЖИМ
Осреднённая скорость. В отличие от
ламинарного режима, в котором наблюдается
постоянство скорости в рассматриваемой
точке потока, турбулентный режим харак-
терен быстрыми знакопеременными измене-
ниями (пульсацией) местной скорости около
некоторого её осреднённого значения.
Осреднённая местная скорость—средняя
скорость в данной точке (она направлена
по Оси трубы), определяемая за достаточно
большой промежуток времени Т как
т
С vi
v — I у dt,
о
(117)
где и, — вектор мгновенной скорости в дан-
ной точке потока.
Касательное напряжение. Если для пло-
ского турбулентного потока ось х напра-
вить параллельно осреднённой скорости vx,
то суммарное касательное напряжение будет
равно:
где I— параметр Прандтля, называемый дли-
ной пути перемешивания.
Исследования Кармана привели к сле-
дующей формуле для I:
/dvx d*vx\
I = ktdf-W)' (П9)
где к — опытный коэфициент.
Если длина пути перемешивания I — О,
то уравнение (118) даёт:
т. е. в ламинарном потоке касательные на-
пряжения пропорциональны вязкости и пер-
вой степени скорости.
В случае турбулентного режима второй
член уравнения (118) значительно больше пер-
вого и вязкостным напряжением можно пре-
небречь:
(120)
т. е. в турбулентном потоке касательное на-
пряжение пропорционально плотности и
и квадрату скорости.
Пограничный слой. Условия движения
турбулентного потока у твёрдых стенок
имеют своеобразные особенности. В отличие
от центральной части потока здесь возмож-
ность перемешивания жидкости исключает-
ся, так как наличие твёрдой границы
исключает появление поперечных движений;
длина пути перемешивания у стенки стре-
мится к нулю. В связи с этим в непосред-
ственной близости к стенкам образуется
весьма тонкий ламинарный так называемый
пограничный слой.
Толщина ламинарного пограничного слоя
равна:
v d
S - 11,6— = 32,8——у- , (120 а)
“г ReVk
где ч — кинематическая вязкость жидкости;
х — коэфициент гидравлического сопро-
тивления;
их—скорость среза у стенки.
Закон распределения скоростей. Турбу-
лентный поток вследствие перемешивания
частиц жидкости отличается большой равно-
мерностью распределения скоростей, причём
с увеличением степени турбулентности от-
ношение средней скорости по сечению к
максимальной скорости приближается к еди-
нице.
v
На фиг. 20 приведена кривая =
‘'max
= / (lg/?e) по результатам опытов Стантона,
Панелля и Никурадзе. Закон распределения
скорости по сечению трубопровода опре-
деляется формулой Кармана:
(121)
где = f/ ~ — скорость среза у стенки
(т0 — напряжение на стенке). Опыты Нику-
радзе хорошо подтверждают теоретическую
формулу Кармана.
Прандтль, пренебрегая изменением т, даёт
более простую зависимость:
°маке и 1 г
= К1,1 55^7 •
(122)
Последнее уравнение также подтвер-
ждается опытами Никурадзе, причём здесь
величина К должна быть принята равной
0,40.
Закон распределения скоростей в тур-
булентном потоке может быть также выражен
с помощью формулы
где п—функция числа Re (табл. 21).
(123)
426
ГИДРОМЕХАНИКА
Таблица 21
Значение коэфициента п в формуле (123)
/?е 4-10» 8-10» 43.10’ 396-10» 1536-10» 3240.10s
п 6 6,6 7 8,5 9.8 10.0
Значения —-- для турбулентного потока
и макс
в зависимости от числа Re приведены в
табл. 22.
Таблица 22
Значения-----в зависимости от числа Рейнольдса
ъ
макс
Ре 4-10» 43-10s 200-10а 700-10» 3 240-10»
п 6 l 8 9 10
ср V max 0.792 0,817 0,837 0.848 0.886
Шероховатость труб. На практике обыч-
но приходится иметь дело с трубами,
У гидравлически гладких труб толщина
ламинарного пограничного слоя о>е. Если
3 < е, трубы гидравлически шероховатые.
Само понятие «гладкая» труба относи-
тельно: с увеличением числа Re толщина
ламинарного пограничного слоя уменьшает-
ся и труба, будучи вначале «гладкой», на-
чинает вести себя как «шероховатая».
Абсолютная шероховатость труб е при-
ведена в табл. 23.
Таблица 23
Абсолютная шероховатость труб
Трубы е в мм
Чистые цельнотянутые трубы из латуни, меди и свинца Новые цельнотянутые стальные трубы Стальные трубы с незначительной коррозией Новые чугунные трубы Асбоцементные трубы Старые стальные трубы 0.01 0.05—0.15 0,2—0,3 0,3 0,3—0,8 0.5—2.0
Эквивалентное соотношение высоты вы-
ступов песчаной (ех) и полусферической (е2)
е,
шероховатости — = 1,4.
внутренняя поверхность которых не гладкая,
а шероховатая. Во время эксплоатации
трубы меняют свою шероховатость от по-
явления ржавчины, различных осадков
и т. п.
Шероховатость определяется высотой е
выступов и относительным расстоянием их
друг от друга.
Различают шероховатость неравномерную
(фиг. 21, а) и равномерную (фиг. 21,6). В
равномерную шероховатость входят также
так называемая волнистость (фиг. 21,с)
и полусферическая шероховатость (Бе-
локонь Н. И.) — плотное распределение
полусферических частиц.
Относительной шероховатостью называют
е
отношение s = — .
ч>
Определение потерь в турбулентном по-
токе. Вследствие беспорядочности турбу-
лентного движения потери энергии в нём
b МШШМШМЪ
Фиг. 21
при прочих равных условиях превышают
потери энергии в случае ламинарного режи-
ма. Коэфициент гидравлического сопротив-
ления в формуле Дарси—Вейсбаха в общем
ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ
427
случае не является лишь функцией числа Re,
как это имело место в ламинарном потоке.
Для турбулентного потока
X = / (Re, в),
где е—относительная шероховатость.
Для гладких труб, по Карману — Нику-
радзе, X зависит только от числа Рей-
нольдса и определяется из уравнения
1
-0,8+21§(7?е/л), (124)
или в менее точном, но более удобном виде:
X = 0,0032 + 0,221 • /?е~0’237. (125)
Формула (125) справедлива для 105 <
< Re < 108.
Для гладких труб предложен также ряд
эмпирических зависимостей Л от Re. Все
они могут быть представлены в виде:
/ = А + В Re~rn, (126)
где А, В и т—постоянные (табл. 24).
Таблица 24
Значение коэфициентов А, В и т в формуле (126)
Автор А 1 г, j Примечания
Блазиус • . , Омбек . . • . Якоб . . . . Лис Шиллер-Гер- ман Лоренц . , . Никурадзе . Рихтер . . • 0 0 0 0,0072 0,0054 0,0076 0,0032 0,0070 0,316 0,242 0,327 0,6104 0,396 0,899 0,221 0,596 0,25 0,224 0,254 0,35 0,30 0,394 0,237 0,35 Вода и воздух Воздух Вода и воздух Вода и воздух Вода » Вода и воздух
Для шероховатых труб X = / (Re, е). Тип
шероховатости в значительной степени влия-
ет на X.
Коэфициенты гидравлического сопротив-
ления труб с равномерной песчаной шеро-
ховатостью, на основании очень тщательных
опытов Никурадзе, приведены на фиг. 22.
Из этой фигуры следует, что всю область
чисел Re можно разделить на три зоны.
Фиг. 22. Зависимость коэфициента трения от шеро-
ховатости и числа Рейнольдса по опытам
Никурадзе
В первой зоне при малых числах Re
X = f (Re) и не зависит от шероховатости —
труба гладкая. Эта зона охватывает область
ламинарного режима и часть турбулентной
области, тем большую, чем меньше относи-
тельная шероховатость.
Во второй зоне X = f (Re, в):
-L_2!g^ = /(ig^y (127)
где ___
;
?
v*e
для 0,55 <lg — 0,85
— 2 lg— = 1,18 + 1,13 lg ; (128)
для 0,85 <lg — < 1,15
21g J =2,14; (129)
v*e
для 1,15 1 g — < 1,83
21g J = 2,81- 0,588 lg . (130)
В третьей зоне X = / (e) — квадратичный
закон сопротивления; сопротивление не за-
висит от числа Re и пропорционально квад-
рату скорости:
i-2lgrf-l.T4. <131)
Эмпирические зависимости для третьей
зоны имеют вид:
X = А • е~х, (132)
где А и х — постоянные (табл. 25).
Таблица 25
Значения коэфициентов Лихв формуле (132)
Автор А X
Якимов 0,15 0,333
Шифринсон 0,093 0,25
Часто применяют следующие критерии,
разграничивающие отдельные зоны: при
трубы гладкие; при Re3 >
382,4
> -у———квадратичным закон сопротивле-
V X В
ния (третья зона).
Если X определять по формуле Блазиуса,
то
59,5
/?С1 = .
Если X определять по формуле Никурадзе
(131), то
665,4 — 764,8 1g е
По Белоконь Н. И., для в < 1/б0
Re3 18,6 | ^2 lg -^ + 1,74'j .
В последнее время для определения X
Колебруком и Уайтом была предложена
формула:
1 / В 2,51 \
Ю- = -2<7Т4+/т£)- <133>
428
ГИДРОМЕХАНИКА
Если пренебречь первым слагаемым в
скобках, то формула (133) переходит в фор-
мулу (124); если пренебречь вторым слагае-
мым, то формула (133) переходит в фор-
мулу (131).
Для стальных труб формула (133) даёт
лучшее согласование с опытными данными,
чем формулы Никурадзе.
Чугунные трубопроводы, бывшие в упот-
реблении, рассчитывают по формуле
О2
i = 0,00148 -^зз , (134)
где i — гидравлический уклон;
Q — расход воды в м3/сек;
d—в м,
или, если трубы малых диаметров (< 100 мм),
по формуле:
и = 85 7?0,63- i0-54. (135)
где и—скорость в м/сек;
R — гидравлический радиус в м.
Для бетонных и железобетонных труб
у2
i = 0,0009 ; (136)
где v — в MjceK, (1 — в л.
Для деревянных труб
у!,8
/ = 0,000885 -Г47 , (137)
d ’
где и—в м/сек, d — в м.
Потеря напора в пеньковых и прорези-
ненных рукавах по Ясюковичу (Q—в л/мин,
d — в мм);
Q1’9
1 = 1 000 К ~^2-5; (138)
для пеньковых рукавов /<=5,0, прорезинен-
ных — К = 3,0, резиновых — К = 2,0;
или:
у2
i = К ; (139)
для пеньковых рукавов К = 0,00213, про-
резиненных — К = 0,0009, резиновых — К =
= 0,00084 (у — в м/сек, d — в м).
Коэфициент гидравлического сопротив-
ления прорезиненных шлангов, армиро-
ванных внутри проволокой, Хщ по Черпики-
ну В. И. равен:
/ 1632 X
(139а)
где Л — вычисляется по формулам (126) или
(132);
S — высота выступов проволочной спи-
рали над внутренней поверхностью
шланга;
I — шаг проволочной спирали.
РАСЧЁТ ТРУБОПРОВОДНЫХ СИСТЕМ
КОРОТКИЕ ТРУБОПРОВОДЫ
Если суммарные потери в трубопроводе
на местные сопротивления и сопротивление
по длине сопоставимы между собой, то такой
трубопровод называется коротким.
Расход, устанавливающийся в коротком
трубопроводе:
Q = p<oV2gH', (140)
где ш — площадь поперечного сечения трубо-
провода;
;л — коэфициент расхода;
при истечении в атмосферу
1
1 + se + х
при истечении под уровень жидкости
5
7/ — напор;
/ — длина трубопровода диаметром d;
S; — сумма коэфициентов местных сопро-
тивлений;
X—коэфициент гидравлического сопро-
тивления.
Ниже приведено несколько типов корот-
ких трубопроводов.
Сифон. Максимальная высота сифона
(фиг 23), по । которой перетекание жчдко-
Фиг. 23
фиг. 24
сти становится невозможным из-за давления
в струе ниже давления паров жидкости,
. __ Pa-Рц _ ЬАс+ d
hMaKe ~ н ТГ+Т ’ ° °
где Lac— длина участка АС;
L — длина сифонной трубы АВ;
d—диаметр сифонной трубы;
ра — давление на поверхность жидко-
сти;
ру — упругость паров жидкости.
Величина вакуума при скорости перете-
кания v равна
о2
= 2~g + Л + hn, (142)
где 1гп — потеря напора на пути трубо-
провода до точки С.
РАСЧЁТ ТРУБОПРОВОДНЫХ СИСТЕМ
429
Самотёчная труба (фиг. 24). Необходи-
мый диаметр трубы для поддержания за-
данного расхода определяется по уравне-
нию (140).
Дюкер (провод) — труба, проложенная под
выемкой.
Расчёт дюкера сводится к определению
его диаметра, обеспечивающего данный рас-
ход, по тому же уравнению (140).
Всасывающая труба (фиг. 24). Задача
сводится к определению геометрической вы-
соты всасывания
2
1 + Xy + S^27’ (143)
где Не — вакуум у насоса;
иве—скорость всасывания.
ДЛИННЫЕ ТРУБОПРОВОДЫ
Если потери напора в трубопроводе на
местные сопротивления незначительны по
сравнению с потерями по длине, то такой
трубопровод считают длинным. В практи-
ческих расчётах выбираемый напор преду-
сматривает определённый запас на местные
сопротивления (обычно 2-1-5%).
Если считать движение на участках тру-
бопровода одного диаметра равномерным, то
для каждого из них
Q = KVT, (144)
где К = <о R — расходная характеристи-
ка, или модуль расхода;
Q — расход;
Н—потеря напора в трубо-
проводе длиной L;
С — коэфициент Шези, С =
_ i/О.
~ Г I ’
R — гидравлический радиус.
Таблица 26
Значения скоростных и расходных характеристик
по формуле Маннинга (173)
1 Диаметр II « 1 чистые Трубы —а= «9о
в дм в мм S в м/сек К в л/сек К‘ I 000
1 ооо К‘
1,5 40 4,424 5,308 0,028 35,50
2 50 5,175 9,624 0,092 10,80
3 75 6,423 28,37 0,805 1,242
4 100 7,771 61,11 3,734 0,269
5 125 9,030 110,8 12,28 0,0813
6 150 10,186 180,2 32,46 0,0309
7 175 11,342 271,8 73,86 0,0134
8 200 12,353 388,0 150,6 0,0056
9 225 13,359 531,2 282.2 0,0035
10 250 14,332 703,5 494,9 0,0023
12 300 16,248 1 144 1 309 0,00076
14 350 17,934 1 726 2 978 0,00034
16 400 19,643 2 464 6 070 0,00016
18 450 21,207 3 373 11 380 0,00009
20 500 22,756 4 467 19 950 0,00005
24 600 25,717 7 264 52 750 0,0000189
28 700 28,535 10 960 120 100 0.0000083
30 750 29,808 13 170 173 400 0,0000058
32 800 31,172 15 640 244 700 0,0000041
36 900 33,664 21 420 753 600 0,0000022
40 1 000 36,120 28 360 801 500 0,0000012
Продолжение табл. 26
Диаметр Нормальные трубы— 2- =8(1
в дм В мм S в м/сек К в л!сек X’ 1 000 1 000 к-
1,5 2 3 4 5 6 7 8 9 10 12 14 16 18 20 24 28 30 32 36 40 40 50 75 100 125 150 175 200 225 250 300 • 350 400 450 500 600 700 750 800 900 1 000 3,713 4,550 5,646 6,823 7,930 8,954 9,938 10,859 11,744 12,605 14,224 15,766 17,240 18,542 20,003 22,574 25,019 26,205 27,369 29,591 31.750 4,666 8,460 24,94 53,72 97,40 158,4 238,9 341,0 467,0 618,5 1 006 1 517 2 166 2 965 3 927 6 386 9 632 И 580 13 750 18 830 24 93.. 0,022 0,072 0,622 2,886 9,487 25,09 57,08 116,4 218,1 382,5 1 011 2 301 4 691 8 792 15 410 40 780 Л 780 134 100 189 ЮС 354 500 621 700 45.93 13,97 1,607 0,353 0,105 0,040и 0,0175 0.0086 0,0046 0,0026 0,00098 0,00041 0,00021 0,00011 0,00006 0,0000246 0,0000108 0,0000075] 0,00uu053l 0,0000023' 0.0000016
Диаметр 1 Грязные Трубы в=7(.
5 6. № 1 00 с
в дм В мм в м/сек в лtсек ГооТ к!
1.5 40 3,219 4,083 0,017 59,99
2 50 3,981 7,403 0,055 18,25
3 75 4,941 21,83 0,476 2,099
4 100 5.973 47,01 2,209 0,455
5 125 6,945 85,23 7,264 0,138
6 150 7,834 138,6 19,21 0,0526
7 175 8,695 209.0 43,70 0,0224
8 200 9,501 298,5 89,03 0,0112
9 225 10,276 408,6 167,0 0,0060
10 250 11,029 541,2 292,8 0,0034
12 300 12,445 880 774,4 0,0013
14 350 13,796 1 327 1 762 0,00057
16 400 15,085 1 8ь5 3 592 0,0002
18 450 16,314 2 594 6 731 0,00015
20 500 17,501 3 436 11 810 0,00008
24 600 19,744 5 587 31 220 0,0000392
28 700 21,883 8 428 71 040 0,0000141
30 750 22,932 10 130 102 600 0,о000097
32 800 23,938 12 030 144 800 0,0000069
36 900 25,882 16 470 271 400 0,0000037
40 1000 27,780 21 820 476 000 0.0000021
Для водопроводных труб различного
диаметра составлены таблицы значений
К и №, вычисленных в соответствии с од-
ной из формул для коэфициента Шези С.
В табл. 26 даны значения К по формуле
Маннинга, а также значения скоростной
характеристики S = R.
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
ТРУБОПРОВОДОВ
Последовательным соединением назы-
вается такое соединение, при котором расход
жидкости на всём протяжении трубопрово-
да остаётся постоянным, сам же трубопровод
состоит из отдельных участков различных
длин и диаметров.
430
ГИДРОМЕХАНИКА
При последовательном соединении трубо-
проводов
H = (145)
Расчёт последовательного соединения
труб различного диаметра значительно упро-
щается, если он ведётся по диаметру экви-
валентного трубопровода. Эквивалентный
трубопровод — это фиктивный трубопровод
равной длины с данным и таким постоянным
диаметром D, который обусловливает равен-
ство потерь напора в действительном и экви-
валентном трубопроводах.
При условии, что Z. не зависит от диа-
метра трубы, эквивалентный диаметр
(146)
где L — длина трубопровода;
I — длина участков равного диаметра D.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
ТРУБОПРОВОДОВ
Параллельным соединением называется
такое соединение, при котором потери напо-
Фиг. 25
ра в любом трубопроводе, соединяющем точ-
ки А и В (фиг. 25), равны
Я = Нд - «в •
Расход через любой трубопровод
= (147)
Система п таких уравнений и уравнение
баланса расхода
Q — Qi + 0.2 + • • • + Qn
позволяют определить (п + 1) неизвестных,
которыми чаще всего бывают напор Н и п
расходов в каждой линии.
УВЕЛИЧЕНИЕ ПРОИЗВОДИТЕЛЬНОСТИ
ТРУБОПРОВОДОВ. ЛЮПИНГИ
Для увеличения производительности тру-
бопровода можно: а) увеличить число
насосных станций; б) поставить люпинги;
в) повысить напор действующих станций;
г) уменьшить подогревом вязкость перека-
чиваемой жидкости.
При увеличении числа насосных станций
новый расход
I
Q = п2~т Qo, (148)
где Qo — прежний расход;
п — число участков, на которое разде-
лён трубопровод;
т — показатель степени при числе Рей-
В
нольдса в формуле А = .
Если поставлена одна станция, т. е.
п = 2, режим турбулентный и по Блазиусу
0,3164
X = —тт- (т = »/4), то расход:
Re '4
____________1_
Q = 2 2-0,25 Qo = 1,485 Qo.
Вставка люпинга (подключение парал-
лельной трубы) уменьшает потери в трубо-
проводе, что позволяет увеличить её про-
изводительность.
Длина люпинга X, определяющего новый
расход Q:
Х=9 1 — 1 /, (149)
где I — длина трубопровода;
ср — коэфициент, равный:
а) при диаметре люпинга, равном диа-
метру трубопровода,
<Р -----1-----; (150)
1—
q2—т
б) при диаметре люпинга и диаметре
трубопровода d2
5—т
“112—т
2—т
— 1
(151)
Новый расход Q, определяемый увели-
ченным напором ft, находят из уравнения
= <152>
Чо \J‘o/
На практике увеличение производитель-
ности достигается комбинированием этих
трёх способов в зависимости от экономи-
ческих соображений.
ЗАВИСИМОСТЬ ПОТЕРИ НАПОРА
ОТ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ
РАСХОДА
Непрерывный расход в пути. При расчёте
водопроводных систем часто представляется
возможным приближённо принимать, что
расход по пути убывает непрерывно на еди-
ницу длины трубопровода (фиг. 26).
РАСЧЁТ ТРУБОПРОВОДНЫХ СИСТЕМ
431
Потеря напора на участке длиной S в
этом случае
Qo- (Qo-« • Я3
Hs~ 3
(153)
3. Пункт 1 питается из резервуара А,
пункт II—из резервуаров А и В (фиг. 30),
Этот случай соответствует условию
где Qo —расход в точке А;
q—расход на единицу длины трубо-
провода.
Путевой расход. В частном случае, когда
расход в конце трубы равен нулю, длина
трубы S = I и Qo = ql, формула (153) при-
нимает вид:
QqI
(154)
77,
(Q + д)*, ,
к? 11 + к22
„ - 4)а/«
^2 — „2
(158)
где q — часть расхода Q, получаемая пунк-
том II из резервуара А.
Расход в этом случае называется путе-
вым — Q,,
Фиг. 26
Из формул (144) и (154) видно, что при
непрерывной раздаче потерянный напор в 3
раза меньше, чем при постоянном расходе.
Транзитный расход. Если S = /, Qo> ql,
то Q„ — ql = Qo -- Q„ = QT называется тран-
зитным расходом.
Потеря напора в этом случае
(Qn + QT)3-Q3
нав= SK^q ‘ (155)
4.
ют с я
Пункты 1 и II п резервуар Б пита-
из резервуара А (фиг. 31).
Фиг. 30 Фиг. 31
Условие такого режима может быть вы-
ражено равенством
ЗАДАЧА О ДВУХ РЕЗЕРВУАРАХ
Если (фиг. 27) А и Б—питающие резер-
вуары, I и II — расходные пункты, то режим
питания может быть одним из нижеследую-
щих.
Hi
(Q1 + Q3+Q5 )2
к?
Фиг. 27
(Q2 + Qe )2 Qs 1®
'+ “ST.
--= Нг. (159)
ЗАДАЧА О ТРЁХ РЕЗЕРВУАРАХ
Если три резервуара расположены так,
как это показано на фиг. 32, и величины
77х, Т/2, 7/;.; /х, /2, Z3; d,, d2, <Z3; Нд явля-
ются заданными, то при определении пока-
1. Пункт 1 питается из резервуара А,
пункт II— из резервуара Б. Такой режим
требует равенства пьезометрических высот
йх и й2 в обоих пунктах. Последнее воз-
можно при условии (фиг. 28)
Qi li Q2 is
Hl ~~is2 = ^2 ~гг-2~ (156)
К3
2. Оба пункта питаются из резервуара А
(фиг. 29), что возможно при h^H^, т. е.
должно быть соблюдено равенство
„ [(Q1+Q3)2
/11—1------о---
L к22
q% la
11 + ~~к'г
= н2.
(157)
зания пьезометра в точке А и расходов Qx,
Q2 и Q3 возможны три случая.
1. Резервуар II является питаемым.
Пьезометрическая линия показана на
432
ГИДРОМЕХАНИКА
фиг. 33. Аналитически этот случай выра-
жается следующей системой уравнений:
Фиг. 33
h Q2!
Hi-(Il +HA)~ ~~г
1-2 ' Q2
й + Мд = W2 +
Is • Q3
h + HA = H3 + —-~2
A3
2. Если h при решении системы уравне-
ний (160) получит мнимое значение, то ре-
зервуар II — не питаемый, а питающий.
Пьезометрическая линия дана на фиг. 34;
при этом Qi + Qa = Q3 и НА + h < Н2.
3. Если при решении системы уравне-
ний (160) будет иметь место равенство
НА + h = то резервуар II будет запас-
ным, и на участке /2 движения воды не
Фиг. 34 Фиг. 35
будет. Пьезометрическая линия соответст-
венно будет иметь вид, представленный на
фиг. 35.
МЕСТНЫЕ СОПРОТИВЛЕНИЯ
ОБЩИЕ ПОНЯТИЯ
Наряду с потерей напора по длине во
всяком трубопроводе имеют место так назы-
ваемые местные потери напора, обусловли-
ваемые местными сопротивлениями (задвиж-
ки, тройники, краны, клапаны и т. д.), где
скорость меняется по величине или по на-
правлению.
Падение напора, вызываемое местным
сопротивлением, определяется формулой
Таблица 27
Коэфициент сопротивления при внезапном сужении
v2
(161)
где i — коэфициент ме-
стного сопроти-
вления.
Ниже приведены зна-
чения коэфициеитов $
Таблица 23
Коэфициент сопротивления диафрагмы (фиг. 37)
ю| S 0,1 0.2 0,3 0.4 0,5 0,6 0,7 0,8 0,9
£ 225,9 47,8 17,5 7,8 3,8 1,8 0.8 0.3 0,06
для наиболее типичных видов местных
сопротивлений.
Внезапное сужение или расширение. Со-
гласно теореме Борда:
, — г'з)2
/! ~ 2g
(162)
где Vi и у2 — скорости в сечениях 7—7 и
2—2 (фиг. 36).
Уравнения (161) и (162) дают для этого
случая:
(163)
Опытные данные для внезапного сужения
труб приведены в табл. 27, для диафрагм —
в табл. 28.
Вход в трубу и выход из неё.
а) Цилиндрическая труба отходит под
углом а:
t-gx = 0,505 + 0,303 • sin а + 0,226 sin2 я.
6) Труба отходит перпендикулярно:
кромки входа острые: tsx = 0,50;
кромки входа плавные: Zgx = 0,1 4- 0,04.
Колена и закругления в трубах.
а) Колено без закругления (фиг. 38).
МЕСТНЫЕ СОПРОТИВЛЕНИЯ
Для труб малого диаметра:
б О
; = 0,946 sin’ ту + 2,05 sin1
Значение S для различных углов 0 при-
ведены в табл. 29.
Таблица 29
Коэфициент сопротивления колен
без закругления
в” 20 40 60 80 90 1ои 120 140
е 0,046 0,139 0,364 0,740 0,985 1,26 1,861 2,431
Для труб большого диаметра:
; = 6,76-(б°)2’17-10-5;
б) Колено с закруглением (фиг. 39):
1) для круглой трубы
Г /</\3,5Ле°
5= 0,131+0,163^) 90°:
Фиг. 39
2) для прямоугольной трубы с размером &
в плоскости закругления
0,124 + 3,104
Для труб большого диаметра
б°
? — 0,25 QQO •
Тройники. Величина потерь будет опре-
деляться характером ответвления и соотно-
шением расходов в основном трубопроводе
Q и в ответвлении (фиг. 40).
£а— коэфициент сопротивления для от-
ветвлений, отнесённый к скоростному
напору в магистрали;
— коэфициент сопротивления для маги-
страли.
Фиг. 40
Дроссельные клапаны и пробковый кран
(табл. 30).
Задвижки и вентили. Для различных вен-
тилей значения коэфициента сопротивления
приведены в табл, 31.
Зависимость коэфициента сопротивления
задвижки в круглой трубе от отношения
высоты поднятия к диаметру трубы дана в
табл. 32.
Клапаны. Значения коэфициентов сопро-
тивления для клапанов приведены в табл. 33.
Решётки. Для вертикальных решёток
(фиг. 41 — 43)
Таблица 30
Коэфициент сопротивления шиберных и пробковых кранов
Углы от- крытия а 5° | 10е 15е 20е 25® 30“ 35е 40° 45° 50’ 55° 60е 65’ 82,5®
Шиберный кран . . . , 0,24 0,52 0,9 1,54 2,51 3,91 6,22 10,8 18,7 32,6 58,8 118 256 —
Пробковый кран . . . . 0,05 0,29 0,75 1,56 3,10 5,47 9,68 17,3 31,2 52,6 106 206 486 ОО
Таблица 31
Значения коэфициентов
сопротивления вентилей при
полном открытии
Вентиль Е
Косва .... Прямоточный Нормальный Рей 1,85—1,40 0,44—0,8 2,9 1,96
28 Том I
Таблиц:: 32
Коэфициент сопротивления задвижек в зависимости
h
от степени открытия - -
h/D 13/72 7/36 5/24 1/4 1/3 3/8 5/12 11/24 1/2 7/12 2/3 1
Малые трубы (£><0,5 м) . . . 43 35 28 17 7,9 5,5 4,о 2.9 2,0 1,1 0,57 0,05
Большие трубы (£>>0,5 м) . . . 41 35 31 23 12 8,6 6,3 4,6 3.3 1,5 0.77 0,06
434
ГИДРОМЕХАНИКА
Таблица 33
Значения коэфициентов сопротивления 6
клапанов
где р — некоторый коэфициент, значения
которого в зависимости от типа решёток
приведены в табл. 34 (фиг. 42).
Таблица 34
Коэфициент ₽ для решёток различных
типов
Тип клапана
Тарельчатый кла- пан без нижнего на- правления ш л Г.
Тарельчатый кла-
пан с нижним на-
правлением
Конусный клапан с
плоской нижней по-
верхностью
Конусный клапан с
конусной поверхно-
стью
Шаровой клапан с
конусной опорной
поверхностью
Значения ксэфициентсв
0,55 + 4(5 — 0,1 d) : d I
(3 = 0,16 <-0,15 ।
Тип сечения стержней ре- шётки а Ъ с а е / Ч
2,42 1,83 1,67 1,035 0,92 0,76 1.79
£= а + [3 Id’ : (п d - is) ft
i— число рёбер;
s — ширина ребра
а = (0,8-г 1,6) [0,55 + [
-1- 4 (й — 0,1 d) : d[
в зависимости ст степени J
стеснения рёбрами пло- ।
щади прохода от 0,87 '
до 0,8 го
₽ - 1.7 ~ 1,75
2,6-0,8 (d : Л) +
+ 0.14 (d : ft)»
10 Ь = d
i = 0.6 + 0.15 (d : h)
2,7 — 0,8 (d : h) +
+ 0.14 (d : Л)*
4 < d : ft < 10
Если характер обтекания решётки анало-
гичен обтеканию решётки с квадратным се-
чением стержней (фиг. 43), то коэфициент
сопротивления В определяется формулой
где коэфициент сжатия г берётся в зависи-
мости от х = — по табл. 35.
Фи! . Ч .
Переходные расширяющиеся конусы
(фиг 44). Коэфициент сопротивления, отне-
сённый к выходной скорости, равен
где К зависит от угла 6 и берётся по
табл. 36.
Таблица 35
(О.
Коэфициент сжатия решёток е в зависимости от-----------
1 0.0 0,1 0,2 0,3 0,4 0.5 0,6 0,7 0,8 0,9 1.0
1 11 0,611 0,612 0,616 0,622 0,633 0,644 0,662 0,687 0,722 0,781 1,000
Фиг. 44
МЕСТНЫЕ СОПРОТИВЛЕНИЯ
435
Таблица 36
Коэфициенты сопротивления переходных
расширяющихся конусов
6° К е° к е° к в° к
5 0,13 30 0.71 60 1.12 100 1.J06
10 0,17 40 0.90 70 1,]3 120 1,06
15 0.26 45 0,98 80 1.10 1,и4
20 0,41 50 1,03 90 l,v7 160 1,02
где 1а — длина трубопровода, эквивалентная
местным сопротивлениям.
Эквивалентные длины наиболее часто
встречающихся местных сопротивлений при-
ведены в табл. 37.
Таблица 37
Эквивалентные длины некоторых местных
сопротивлений
Наименование местного
сопротивления
Значение
I
d~
Обратный клапан. В табл. 36а приведены
значения коэфициента сопротивления вса-
сывающих коробок с обратным клапаном.
Таблица 36а
Коэфициенты сопротивления всасывающих
коробок с обратным клапаном
а в м 0,04 0,07 0,10 0,15 0,20 0,30 0,50 0,75
6 12 8,5 7 6 5.2 3.7 2,5 1,6
Вход жидкости из резервуара в трубу
с острыми краями ................. .
То же, если труба вдаётся внутрь
резервуара ....................._
То же при округлённых краях входн'.й
трубы ..........................
Колена (отводы) с большим радиусом
закругления ....................
То же с радиусом от 2 до S диаметров
1 о же с радиусом закругления, равным
1 диаметру ................
Угольник станд->;->тный * J .* ’ ’
20
1и
Ничтожно
»
10
20
30
Если всасывающая коробка не снабжена
обратным клапаном, то ; определяется по
формуле:
/ш \я
? = /0,675 4- 1,575) - ) , (164)
у^с/
Тройники
»
»
»>
30
40
50
60
где <о — площадь поперечного сечения трубы;
<°с — сумма площадей отверстий сетки.
При пользовании справочными данными
необходимо иметь в виду, что коэфициенты
даны применительно к скоростному напору
теле местного сопротивления.
Задвижка открытая ................
Сальниковый компенсатор...........
П-образный компенсатор при уголь-
никах ...........................
То же при коленах с радиусе,закруг-
ления, равным 1 диаметру ........
То же при коленах с радиусом ст 2 до
8 диаметров . ....................
Лирообразный компенсатор
Фильтр односетчатый для тёмных неф-
тепродуктов, незагрязнённый . • . .
эквивалентная длина местных
сопротивлений
11
10
120
80
40
100
100
Фильтр односетчатый для светлых
нефтепродуктов, незагрязнённый . . 75
Обратный клапан ................., 75
Из равенства потерь напора на местные
сопротивления по формуле Вейсбаха и по-
терь по длине по уравнению Дарси
(у2 . у2
i d2g“?2’g
! следует
j (165)
। Величина /, представляющая собой длину
j трубопровода, эквивалентную по гидравличе-
; скому сопротивлению местному сопротивле-
j нию, называется эквивалентной длиной мест-
। ного сопротивления.
' Длина I, эквивалентная п местным со-
i противлениям, будет равна
1п= (166)
i г- 1
Таким образом, если трубопровод диа-
метра d с геометрической длиной L имеет
местные сопротивления, то его можно рас-
I считывать по формуле Дарси, но не по
действительной длине, а по приведённой
I длине, равной
Т = L + lB. (167)
ПРИНЦИП наложения потерь
Сущность этого принципа заключается в
том, что полная потеря напора равняется
арифметической сумме потерь, вызванных
каждым сопротивлением в отдельности.
Слагаемые полного гидравлического со-
противления для потока сжимаемой или
несжимаемой жидкости по Н. И. Бело-
конь [3]
s = s1 + s11 + sln + sIV + sv =
= 4Hp ~ , (168)
где и, и — удельный объём (и) и весовая
скорость потока (и) ь- руково-
дящем сечении ( /А у.
v — v = . (168а)
7а’
п = и4=_£_. (1686)
>А
G — весовой секундный расход;
— приведённый коэфициент со-
противления:
ЪПР = + 5" + 51П +
+ 51V + 5V, (168в)
28*
436
ГИДРОМЕХАНИКА
I- V rl—V
s —слагаемые полного сопротив-
ления и приведённого коэфи-
циента сопротивления (см.
табл. 37а).
МЕСТНЫЕ СОПРОТИВЛЕНИЯ
ПРИ ЛАМИНАРНОМ РЕЖИМЕ
Все вышеприведённые значения коэфи-
циентов $ справедливы только для турбу-
лентных потоков жидкости, для которых ?
не зависит от числа Re. Коэфициенты ?
местных сопротивлений в ламинарном пото-
ке, наоборот, являются функциями числа Re.
Эквивалентные длины местных сопротивле-
ний ламинарных потоков могут быть найдены
по диаграмме (фиг. 45).
Для того чтобы определить эквивалентную
длину местного сопротивления фитинга, не
помещённого на диаграмме, необходимо взять
соответствующую длину для турбулентного
режима и через полученную точку провести
ломаную линию, параллельную кривым,
имеющимся на диаграмме.
I
Фиг. 45
Таблица 37а
Слагаемые полного сопротивления и приведённого коэфициента сопротивления
Группа сопротивлений Слагаемые полного сопро- тивления системы (по участкам) Слагаемые приведённого коэфи- циента сопротивления системы
Местные сопротивления, определя- емые по наименьшим сечениям (/ . ) . min < I V 1 • Burnax\ ® "Iv 2g /< X га « сч^Е 3 Р1 р 'м ! 1 II 1
Сопротивления трения II V4 ( vcp u*)l /М* \ s 2j 2g (4//, 2
Сопротивления от изменения высоты центра тяжести потока (геометрическая разность высот) in V / Aft\ s =2u\vcp'l £Ш=
Сопротивления от изменения удель- ного объёма жидкости ( uj’ и vj — удель- ные объёмы жидкости на выходе и входе участка J 2 ?V -SsF0’"-’0' AJ V и*
разниить граничных динамических на- дпоров (конечного и начального) v VC1"'’). <ras)i ® = 2g 2g eV = ~ (”“*>» * в VU*
РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
437
РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
ФОРМУЛА ШЕЗИ
Равномерное движение жидкости в от-
крытом русле возможно только при соблю-
дении следующих условий:
1) постоянства расхода (Q = const);
2) постоянства площади поперечного се-
чения (<о = const);
3) постоянства гидравлического уклона i
(в данном случае i = sina—уклон дна);
4) постоянства степени шероховатости
смоченной поверхности по длине русла;
5) отсутствия местных сопротивлений.
Расчётное уравнение равномерного дви-
жения турбулентного потока жидкости
Q = a> С V"Ri или Q = Ко VT, (169)
где Kq = & С VR ~ модуль расхода — рас-
ход в русле заданного
живого сечения при гид-
равлическом уклоне, рав-
8g ном единице;
С — J/ у — коэфициент Шези— раз-
мерный множитель, учи-
тывающий влияние ше-
роховатости стенок рус-
ла, размеров и формы
живого сечения на вели-
чину средней скорости
потока;
7? — гидравлический радиус;
X — коэфициент гидравличе-
ского сопротивления;
g — ускорение силы тяжести.
ЭМПИРИЧЕСКИЕ ФОРМУЛЫ ДЛЯ
ОПРЕДЕЛЕНИЯ КОЭФИЦИЕНТА ШЕЗИ
а) Формула Базена (гидравлический ра-
диус-7? в л): 87
, (170)
где 7—коэфициент шероховатости (табл. 38).
Таблица 38
Коэфициент шероховатости у различных стенок
Род стенки
Коэфици- '
ент шеро- I
ховатости!
Очень гладкие стенки (строганые дос-
ки, гладкая цементная штукатурка
; и т. д.)...........................
, Гладкие стенки (нсстрсганые доски,
! тесовая и кирпичная кладка, бетон-
I ные и чугунные трубы, весьма хоро-
| шая бетонировка и др.).............
Негладкие стенки (хорошая бутовая
кладка, посредственная бетонировка)
Промежуточная категория (грубая бу-
товая кладка, весьма грубая бетони-
ровка по скале, замощение булыж-
никами, стенки в плотных землистых
грунтах, притом весьма хор/ шо со-
। держимых, стенки, чисто высеченные
Земляные стенки в обычном состоянии
' (сюда же мощёные, но несколько за-
росшие стенки, и т. п.) .............
Земляные русла, оказывающие сильное
сопротивление при плохом содержа-
нии, значительных водорослях, ска-
листом с валунами или круннсгалеч-
ном дне и пр.......................
0,06
0,16
0,46
0,85
1,30
1,75*
1 Это значение не является предельно наибольшим.
В табл. 39 приведены значения коэфици-
циента С, подсчитанные по формуле Базена.
Таблица 39
Коэфициент С по формуле Базена
? в 0,06 0,16 0,46 0,85 1,30 1,75
0,05 68,5 50,7 28,5 18,1 12,8 9,9
0,06 69,8 52,6 30,2 19,4 13,8 10,7
0,07 70,9 54,2 31,7 20,6 14.7 11,4
0,08 71,8 55,6 33,1 21,7 15,5 12,1
0,09 72,5 56,7 34,4 22,7 16,3 12,7
0,10 73,1 57,7 35,5 23.6 17,0 13,3
0,11 73,6 58,7 36,5 24,4 17,7 13,9
0,12 74,1 59,5 37,4 25,2 18,3 14,4
0,13 74,6 60,2 38,2 25,9 18,9 14,9
0,14 75,0 60,9 39,0 26,7 19,4 15,3
0.15 75,3 61,5 39,7 27,2 19,9 15.8
0,16 75,6 62,1 40,5 27,8 20,4 16,2
0,17 75,9 62,7 41,2 28,4 20,9 16,6
0,18 76,2 63,2 41,8 29,0 21,4 17,0
0,19 76,5 63,6 42,4 29,5 21,8 17,3
0,20 70.7 64.1 42,9 30,0 22,3 17,7
0,21 76,9 64.5 43,5 30,5 22,7 18,1
0,22 77,1 64,9 44,0 30,9 23,1 18,4
0,23 77,3 65,2 44,4 31,4 23,4 18,7
0,24 77,5 65,5 44.8 31,8 23.8 19,0
0 ,25 77.6 65,9 45,3 32,2 24 2 19,3
0,26 77,8 66,2 45,7 32,6 24,5 19,6
0,27 78,0 66,5 46,1 33,0 24,8 19,9
0,28 78,1 66,8 46,5 33,4 25,2 20,2
0,29 78,3 67,0 46,9 33,7 25,5 20.5
0,30 78.4 67,3 47,3 34,1 25,8 20,7
0,31 78,5 67,6 47,6 34,3 26,1 21,0
0,32 78,6 67,8 47,9 34,7 26,4 21,2
0,33 78,8 68,2 48,2 35,1 26.7 21.5
0,34 78.9 68,3 48,5 35,4 26,9 21,7
0,35 79,0 68,4 48,8 35,7 27,2 22,0
0,36 79,1 68,6 49,2 36,0 27,5 22,2
0,37 79,2 68,8 49,5 36,3 27,7 22,4
0,38 79,2 69,0 49,8 36,6 28,0 22,7
0,39 79,3 69.2 50.1 36,8 28,2 22,9
0,40 79,4 69,4 50,4 37,1 28,5 23,1
0,41 79,5 69,6 50,6 37,4 28,7 23.3
it, 42 79,6 69.7 50,9 37,6 28,9 23,5
0,43 79,7 69,9 51,1 37,9 29,2 23,7
0,44 79.7 70,1 51,4 38,1 29,4 23,9
0,45 79.8 70,2 51,6 38,4 29,6 24,1
0,46 79,9 /0,4 51,8 38,6 29,8 24,3
0,47 80,0 70,5 52,0 38,8 30,0 24,5
0,48 80.0 70,6 52,3 39,1 30,2 24,7
0,49 80,1 70,8 52,5 39.3 30,4 24,8
0,50 80.2 70,9 52,7 39,5 30,6 25,0
0.55 80.4 71,5 53,7 40,5 31,6 25,9
0,60 80.7 72,1 54.6 41,4 32.5 26,7
0,65 80,9 72,6 55,4 42,3 33,3 27,4
0,70 81.1 73,0 56,1 43,1 34,1 28,1
0,75 81,3 73,4 56.8 43,9 34,8 28.8
0,80 81,5 73,8 57,4 41,6 35,5 29.4
0,85 81.7 74,1 58.0 45,2 36,1 30,0
0,90 81,8 74,4 58.6 45.9 36,7 30,6
0.95 81,9 74,7 59,1 46.5 37,3 31,1
1,00 32,0 75,0 59.6 47,0 37,8 31,6
1,10 82,2 75.4 60.5 48,0 38,8 32,6
1,20 82,4 75,9 61,3 48,9 39,7 33,5
1,30 82,6 76,3 62.0 49,8 40.6 34,3
1,40 82,8 76,6 62,6 50,6 41,4 35,1 35,8
1.50 82,9 76,9 63.2 51,3 42,2
1,60 «3.0 77,2 63,8 52,0 42,9 36.5
1,70 83 1 77.5 64,3 52.6 43,6 37.1
1,80 8.4 9 77,7 64.8 53,2 44,2 37,7
1,90 83.3 77,9 6.5,2 53,8 44,8 38.3
2,00 83,4 78,1 65,6 54,3 45.3 38,9
2,20 83.6 78,5 66.4 55 3 46,4 39,9
2,40 83,7 78,8 67.1 56,2 47,3 40,8
2,60 83.8 79,1 67.7 57,0 48,1 41,7
2,30 83,9 79,4 68,2 57,7 48.9 42 5
3,00 84,0 79,6 68,7 58.3 49,7 43,3
3,20 84.1 79,8 69,2 58.9 50,4 44,0
3,40 84,2 80,0 69,6 59.5 51,0 44,6
3,60 84,3 80,2 70,0 60,1 51,6 45.2
3,80 84.4 80,4 70,4 60,6 52,2 45,8
4, U0 84,4 80,5 70,7 61,0 52.7 46.4
4,50 84,6 80,9 71.5 62,1 53,9 47,6
5.00 84,7 81.2 72,1 63,0 55,0 43,8
5.5J 84,8 81,4 72,7 63,8 56.0 49,8
6, ио 84,9 81,6 73,2 64,6 56,8 50,7
438
ГИДРОМЕХАНИКА
б) Формула Гангилье-Куттера:
п 1 , 0,00155
23+„~+—г~
с =________________
/ 0,00155 \
(171)
где п — коэфициент шероховатости (табп. 40);
i — уклон дна;
R — гидравлический радиус в м.
Таблица 40
Значения п и---- (по Гапгилье-Куттеру)
Род стенки п 1 п
Строганые доски. Глад- кая цементная штук; турка 0,010 100
Цементная штукатурка с примесью одной трети песка 0,011 90,9
Н естрм'аные дсски, хоро- шо пригнанные 0,012 83,3
Бутовая кладка с сбли- ц вкей тёсаным камнем. Т щательная бет< ниревка с железнением. Хорошая кирпичная облицевка . . . 0,013 76,9
Бетонированные каналы в хороших условиях 0,014 71.4
Каменная кладка с полу- чистой тёской. Кирпичная кладка 0,015 66,7
Бутовая кладка без сбли- цовки. Бетон среднего ка- чества 0,017 58,8
Мощение булыжником. Плотные грунты в естест- венном состоянии. Каналы в скале 0,020 50
Скалистые грунты при посредственной сбрзбстке скалы. Лёссовые и гравели- стые грунты 0,0225 41,4
Н еукр еплённые земляные русла в обычном их состо- янии 0,025 4U
Неукреплённые земляные русла, плохо содержимые (заросли) или оказывающие значительное сопротивление течению (камни и Т. п.) . . 0,030 33,3
Неукреплённые земляные русла с неправильным про- филем, с большим к* личе- ством водорослей, камней и т. п 0,035 28,6
Неукреплённые земляные русла, нах<дящиеся в ис- ключительно плохих усло- виях 0,040 25,0
При значениях i' 0,С005 следует пользо-
ваться сокращённой формулой:
23 п
i + VR
В табл. 41 даны значения коэфициента С
по Гаитипьс-Куттеру (R г м).
в) Формула Маннинга:
с - ‘ r‘!‘,
п
где п — коэфициент шероховатости; значе-
ния его те же, что и в формуле Ган-
гильс-Куттсра.
(172)
(173)
Таблица 41
Коэфициент С по формуле Гангилье-Куттера
Уклон
0,000025^0,00005о[о,0001|о,0002^0,0004^0,ОО1|о,01
0,010 0,05 38 44 51 54 55 57 58
0,10 49 56 61 65 68 70 71
6,20 КЗ 70 74 77 78 79 80
0,30 72 77 81 84 85 86 88
0,50 83 86 88 90 91 91 91
1 ДА) 100 100 100 100 100 100 100
2,00 115 111 109 107 106 105 105
3.00 124 117 113 111 110 109 108
5.00 134 123 118 115 113 112 111
15,00 151 135 125 121 118 117 116
0,013 0,05 28 31 35 38 40 41 42
0,10 36 41 44 47 49 50 51
0,20 46 50 53 56 58 59 59
0,30 53 57 60 63 64 64 65
0,50 62 65 67 69 69 70 70
1,00 77 77 77 77 77 77 77
2.00 90 87 85 84 83 82 82
3,1)0 99 94 89 88 87 86 85
5.00 108 100 93 91 90 89 88
15,00 125 114 102 98 96 94 92
0,017 0,05 19 2-> 24 26 28 29 29
0,10 25 29 32 34 35 36 36
0,20 34 37 39 41 42 42 43
0,30 40 43 45 46 47 47 48
0,50 47 49 50 51 51 52 52
1,00 58 58 58 58 58 53 58
2.00 71 69 67 66 65 64 64
З.оо 78 74 71 70 69 68 68
5. ОС 87 79 75 73 72 71 70
15,00 105 90 83 79 77 76 75
0,020 0,05 15 18 20 21 23 23 24
0,10 21 23 25 28 29 29 30
0,23 28 30 32 34 35 36 36
о.зс 33 35 37 38 39 40 40
0.5С 40 41 42 43 43 44 44
1.00 50 50 50 50 50 ко 50
2,00 61 59 57 56 56 55 55
3,00 69 64 61 59 59 58 58
5,0!] 76 70 66 63 62 61 61
15,00 94 81 74 70 68 67 66
0,025 0,05 12 13 15 16 17 18 18
0,10 17 18 19 20 21 22 22
0,20 22 23 24 25 26 27 27
0.30 26 28 29 30 30 31 31
0,50 31 32 33 34 34 35 35
1,00 40 40 40 40 40 40 40
2,00 50 48 47 46 45 45 45
3.00 56 53 51 49 48 48 47
5,00 64 59 54 53 52 51 50
15,00 81 71 63 59 57 56 55
0,030 0,05 10 11 12 13 13 14 14
0,10 13 14 15 16 17 18 18
0,20 18 19 19 20 21 22 22
0,30 21 22 23 24 24 25 25
0,50 25 26 27 27 28 29 29
1,00 33 33 33 33 33 33 33
2,00 42 41 40 40 39 38 38
3.00 48 45 43 42 42 41 41
5.00 56 51 47 45 44 43 43
15,00 72 62 55 52 51 49 48
0,035 0.05 8 9 9 10 10 11 11
0.10 И 12 12 13 13 14 14
0,20 15 16 16 17 17 18 18
0,30 18 19 19 20 20 21 21
0,50 22 23 23 23 24 24 24
1.00 29 29 29 29 29 29 •'9
2,00 36 35 34 34 33 33 33
3.00 42 40 38 37 36 36 36
5.00 49 45 43 42 41 40 39
15,00 65 56 51 47 45 44 43
0,040 0,05 6 7 7 8 8 у, 9
0.10 9 10 11 11 12 12 12
0.20 13 14 14 15 15 16 16
0,30 15 16 17 18 18 18 18
0,50 19 19 20 20 21 21 21
1,00 25 25 25 25 25 25 25
2,06 32 31 31 30 31) 29 29
3,00 37 35 34 33 3J 32 32
5.00 44 •11 39 3S ,37 36 35
15,0с 59 46 43 42 41 40
РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ 43g
В табл. 42 даны значения коэфициента С
по Маннингу.
Таблица 42
Коэфициент С по формуле Маннинга
X. п R в 0,010 0,013 0,017 0,020 0,025 0,030
0.10 68,1 52,4 ЗЭ.5 34,0 27,2 22,7
и, 12 70,2 54,1 40,7 35,1 28.1 23,4
0.15 72,8 56,1 42,2 36,4 29,1 24,2
0,20 76,5 58,9 44,4 38,2 30,6 25,5
0,30 81,8 63.0 47,4 40.9 32.7 27,3
0,40 85,8 66,1 49,8 42,9 34,3 28,6
0,60 91,8 70,7 53,2 45,9 36,7 30,6
е,,80 96,4 74,2 55,9 48,2 38,6 32,1
1,00 100,0 77,0 58,0 50,0 40,0 33,3
1,20 103,1 79,4 59,8 51,5 41,2 34,4
1,40 105,7 81,4 61,3 52,7 42,3 35,2
1,60 108.1 83,2 62,6 54,0 43,2 36,0
1,80 110,1 84,8 63,9 55,1 44,1 36,7
2,00 112,0 86,2 65,0 56,0 44,8 37,3
•2,50 116,5 89.7 67,6 58.2 46,6 38.8
3,00 120,0 92,4 69,6 60,0 48,0 40,0
3.50 123,2 94,9 71,5 61,6 49,3 41,1
4,и0 126,0 97,0 73,1 63,0 50,4 42,0
5,U0 131,0 100,8 76,0 65,5 52,4 43,7
КАНАЛЫ ГИДРАВЛИЧЕСКИ
НАИВЫГОДНЕЙШЕГО СЕЧЕНИЯ
Гидравлически наивыгоднейшим назы-
вается такое сечение канала, которое при
той же площади способно пропустить наи-
больший расход.
Из формулы Шези (169) следует, что
расход Q будет максимальным при R =
01
= у = max, т. с. гидравлически наивыгод-
нейшее сечение должно иметь минимальный
смоченный периметр.
Из всех равновеликих фигур наименьший
периметр имеет круг, который и будет яв-
ляться наивыгоднейшим сечением. Из ос-
тальных видов профилей наивыгоднейшими
будут те, которые возможно ближе прибли-
жаются по своему очертанию к полукругу:
для вертикальных стенок —• полуквадрат,
для наклонных — половина правильного
шестиугольника. При углах откоса р<60°
(практически встречаются наиболее часто)
наивыгодпейшим профилем будет трапеция.
При этом наивыгоднейшее соотношение между
шириной b и глубиной h определяется
равенством
6 = 2 й(Х1 +тп2 — т), (176)
где т = ctg 3—коэфициент крутизны откоса.
ГИДРАВЛИЧЕСКИЙ РАСЧЁТ КАНАЛОВ
В практике наиболее распространены ка-
налы трапецеидальной формы, которые вклю-
или приближённо:
при R < 1,0 м
чают в себя как частные случаи каналы
треугольного (при 6=0) и прямоугольного
(при т = 0) сечений.
при R > 1,0 м у ж 1,3 У п .
Для этих каналов (фиг. 47):
Формула предложена для гидравлических
радиусов, лежащих в пределах 0,l<R<J3,0 м,
и степени шероховатости п = 0,011-; 0,040.
На фиг. 46 даны значения коэфициента С
по Павловскому.
Фиг. 47
440
ГИДРОМЕХАНИКА
площадь живого сечения
«> = (& + mh) hi
смоченный периметр
X = Ь + 2 h УГ+йГ2 Ь (177)
гидравлический радиус
(b + mh)h
b + 2hVl+ma
1-я задача. Дано: i, b, h и т = ctg Р;
определить Q.
Из формул (177) находим о>, X, 7? и по
формуле Шези определяем Q.
2-я задача. Дано: Q, b, h и т; опре-
делить i:
1 ~ С2/? W2 ’
где 7? и ы определены по формулам (177).
3-я задача. Дано: Q, i и т; определить
h и Ь.
Задача имеет бесчисленное множество
решений. Исходя из технических соображе-
Ь
ний, задаются величиной х = . Тогда
где
_ VjT (х + т)’/з________
(х + 2 УТ^ЙУ )’/•
Для нахождения глубины потока в за-
данном русле, когда известны ширина по
дну b и крутизна откоса т, пользуются ме-
тодом Бахметева. Этот метод основан на том,
что у подобных русел ^у которых углы р и
отношения одинаковы I модули расхода
К относятся между собой, как некоторая
степень глубин:
Х2 /ЙДР /Х2\а ZW
нли ’
где К -= ыС У7?;
х — гидравлический показатель русла.
Бахметев допускает, что соотношение
(179) может быть распространено не только
на подобные русла, но и на данное русло
при разных глубинах его наполнения.
Для последнего случая равенство (179)
неточное; поэтому при вычислении х не сле-
дует брать величин hz и й2, сильно разня-
щихся между собой.
ДОПУСКАЕМЫЕ СКОРОСТИ
Верхний предел допускаемых скоростей
ограничивается способностью материала сте-
нок противостоять размыву, нижний—выпа-
дением взвешенных в жидкости частиц.
Для определения минимальной скоро-
сти omin (предохраняющей от заиления)
пользуются обычно следующими эмпириче-
скими формулами:
ymin = a • Л0’64! (180)
%in=a'^. (181)
В приведённых формулах:
й— глубина наполнения канала в м\
R — гидравлический радиус в м;
а, а' — некоторые коэфициенты, значения
которых приведены в табл. 42 а.
Формула Гончарова:
0,0535 I
Р=~1Г~\
ymln \4/
о0Й°'2/ V
й°>2
ут1п
(182)
где р — весовое содержание фракций
нанссов крупнее 0,005 мм в
промиллях;
v0MiceK — скорость, при которой проис-
ходит осаждение наносов дан-
ной крупности при глубине
потока ft = 1 м;
ymin — минимальная скорость.
В табл. 43 даны значения ymin, вычислен-
ные по формуле Гончарова.
В табл. 44 приведены допускаемые сред-
ние скорости в каналах («Стандарты, нормы
и технические условия проектирования гид-
ротехнических сооружений гидростанций»,
сборник № 1, 1939).
КАНАЛЫ, НЕ МЕНЯЮЩИЕ СВОЕЙ
СКОРОСТИ ПРИ ИЗМЕНЕНИИ ГЛУБИНЫ
НАПОЛНЕНИЯ
Для получения неизменной скорости при
различной глубине наполнения (предупреж-
дает заиление и размывание) канал должен
иметь профиль, при котором гидравлический
радиус не зависит от величины й. Уравнение
кривой откоса такого канала (фиг. 48) имеет
вид:
Z - /?1п
х + Ух2 - 7?2
а + Уа2- 7?2'
(183)
РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
441
Практически ввиду отсутствия данных о
величине коэфициента Шези С для такого
профиля каналу придают форму, изображён-
ную на фиг. 49.
Таблица 42а
Коэфициенты а и а'
Характеристика наносов а а'
Крупные песчано-илистые наносы 0,6 -0,71 0,65—0,77
Средние песчано-илистые наносы 0,54—0,57 0,58—0,64
Мелкие наносы 0,39—0,41 0,41-0,45
Очень мелкие наносы . . . 0,34—0,37 0,37—0,41
Таблица 43
Значения минимальных скоростей
(по Гончарову)
При весовом содержании
Состав взвешен- фракций наносов крупнее
К * 0,005 мм в промиллях
ных наносов
ЕС Л
О) >- Q.S 0,1 0,5 1.0 2,5 5,0 7,5 10
□ ю
Значения v , м1сек min
0,25—0,05 мм 0,30 0,22 0,28 0,32 0,3910,45 0,49 0,52
25% 0,60 0,28 0,37 0,43 0,520.60 0,66 0,70
0,05—0,005 мм 1,00 0,34 0,45 0,52 0.64 0,75 0,82 0,87
75% 1,50 0,39 0,54 0,62 0,76 0,89 0,97 1,04
2,00 0,44 0,60 0,7и 0,86 1.01 1,10 1,18
2,50 0,48 0,66 0,77 0,94 1.11 1,22 1,30
3,00 0.51 0,71 0,83 1,02 1,20 1,32 1,41
0,30 0,28 0,37 0,42 0,50 0,58 0,64 0,68
0,25—0,05 мм 0,60 0,36 0,48 0,55 0.67 0,78 0,85 0,91
75% 1,00 0,43 0.59 0.68 0,83 0,97 1,06 1,13
0,05—0,005 ММ 1,50 0,51 0,69 0,80 0,98 1,15 1,26 1,35
25% 2,00 0,57 0,78 0,91 1,11 1,31 1,43 1,53
2.50 0,61 0,86 0,99 1 22 1,44 1,57 1,69
3,00 0,66 0,92 1,07 1,32 1.55 1,70 1,82
0,30 1 0,39 0,51 0,58 0,70 J.81 0,88 0,94
1,0—0,25 мм 0,60 0,50 0,67 0,76 0,93 1,08 1,18 1,26
25% 1,00 0,60 0,82 0,94 1,15 1.34 1.47 1,57
0,25—0,05 мм 1,50 0.70 0,96 1,11 1,36 1,59 1,75 1,87
75% 2,00 0,78^1,08 1,26 1,54 1,80 1,98 2,12
2,50 0,851.19 1,38 1,69 1,99 2,18 2,33
3,00|0,924,28 1,49 1,83 2,15 2,36 2,53
0,30 0,57 0,73 0,84 1,00 1,16 1.27 1,35
1,0—0.25 мм 0,60 0,72 0,96 1,10 1,34 1,56 1,70 1,82
75% 1,00 0,87 1,18 1,36 1,66 1,93 2,12 2,27
0,25—0,05 мм 1,50 1,01 1,39 1,61 1,96 2,30 2,52 2,70
25% 2,00 1,13 1.56 1,81 2,12 2,60 2,86 3,06
2,50 1,23 1.71 1,99 2,44 2,87 3,15 3,37
3,00 1,32 1,85 2.15 2,64 3,10 3,41 3,65
Таблица 44
Допускаемые средние скорости в каналах
Материал стенок каналов Допускаемые сред- ние скорости в м1 сек
при средней глу- бине потока
0,4 м !1,0 л 2,0 м З.«и более
Малоплотные глины и су- глинки 0,33 0,40 0,46 0,51
Среднеплотные глины и суглинки 0,70 0,85 0,95 1,1
Плотные глины и суглинки 1,0 1,2 1,4 1.5
Очень плотные глины и суглинки 1.4 1.7 1.9 2,1
Лёссовые грунты средней плотности в условиях закон- чившихся просадок 0,6 0,7 0.8 0,85
Дёрн свежий плашмя . . 0,6 0,8 0,9 1
» » в стенку . . 1.5 1,8 2,0 2,2
Свежие хворостяные по- крытия и хворостяные креп- ления 1.8 2.2 2.5 2.7
Одиночная мостовая из булыжника размером около 20 см 2,5-2,9 3,0-3.5 3,54,0 3,8 4,3
Двойная мостовая из бу- лыжника размером около 20 см 3,1-3,6 3,7-4,3 4,3-5,6 4,6-5,4
Габионы до 4,2 до 5,0 ДО 5,7 до 6,2
Кладка из кирпича на це- ментном растворе 1.6 2.0 2,3 2.5
Бутовая кладка из слабых пород на цементном ра- створе 2,9 3,5 4.0 4,4
То же из средних пород . 5.8 7.0 8.1 8,7
Кладка из клинкера на цементном растворе .... 7.1 8,5 9,8 11
Деревянные лотки .... до 25
СОСТАВНЫЕ ПРОФИЛИ
Составными профилями называются такие-
(фиг. 49), которые состоят из нескольких
частей, различающихся своими гидравличе-
Фиг. 49
скими характеристиками. Вследствие этого
расчёт каналов составных профилей ведут
по частям:
Q = i>i «>! + й2 + v3 со8, (184)
ИЛИ
Q V Rri С2 <у2 Vr2i + С3 взг VRZL
со, со2 со8
г Де /?j = у \ Rq ~ -г j /?3 = у •
ла
442
ГИДРОМЕХАНИКА
ЕСТЕСТВЕННЫЕ РУСЛА
Ввиду трудности определения коэфици-
ента Шези С для естественных русел, коэ-
фициепты шероховатости которых зависят
от разнообразия конкретных случаев, вели-
чину средней скорости у принято рассчиты-
вать по одной из следующих формул:
а) Величина средней скорости определяет-
ся в зависимости от средней глубины hcp =
=д , где <о— площадь поперечного сечения
русла;
В—ширина русла у поверхности воды в м.
hcp < 1,5 м; v= 30,7 hcp Vi
1,5 < hcp <6 м; v = 34 VJ* Vi
hcp > 6 m; v = (50,2+ VT
°) г = 8,05 /?°>58.,0-3 (м/сек),
. (185)
(186)
где R ~ гидравлический радиус в м;
i—уклон свободной поверхности воды
в русле.
УСТОЙЧИВЫЕ ПРОФИЛИ КАНАЛОВ
Для параболического профиля
2
<о=2 haB.
Скорость в устойчивом русле равна:
•<.»)
где А - некоторый коэфициент (при R <3 м
и v < 3 м/сек A ss 0,6).
Расход в устойчивом русле:
Q = 0,5у,,(1 +0,8 AVha)haB. (190)
ТЕЧЕНИЕ В ТРУБАХ
С НЕЗАПОЛНЕННЫМ СЕЧЕНИЕМ
Расчётная формула
Q = К' Vi = АК VT, (191)
где А — коэфициент, зависящий от степени
заполнения трубы а = ц (фиг. 51, 52). По
При пропуске воды с большой скоростью
по размываемым естественным балкам и
склонам русло приобретает чаше всего ги-
перболическую или параболическую форму
(фиг. 50).
Фиг. 51
Фиг. 52
аналогии с формулой расхода скорость у
определяется равенством
v = BW Vi, (192)
где W = С Vr —модуль скорости при
сплошном заполнении тру-
бы;
В — коэфициент, зависящий от
степени заполнения трубы
Максимальная ордината размыва
(187)
где ___
sin2 3
— скорость начала раз-
мыва (эрозии);
vg — допускаемая ско-
рость при угле зало-
жения откоса;
? — угол естественного
откоса грунта в воде;
р — переменный угол за-
ложения откоса ка-
нала.
Живое сечение устойчивого русла опре-
деляется равенством:
te - (188)
Фиг. 53 Фиг. 54
Величины А и В для круглых и ово-
идальных труб берутся в зависимости 01 а
по графикам (фиг. 53 и 54).
Значения К и W для тех же груз при-
ведены в табл. 45 и 46.
водосливы
443
ДВИЖЕНИЕ В ОТКРЫТЫХ КАНАЛАХ
ПРИ ЛАМИНАРНОМ РЕЖИМЕ
Таблица 45
Значения К и VV в зависимости от диаметра
для круглых труб
12,86 0,75 11 270 25,52 1,2 30660 35,07
16,12 0,8 13 490 26,81 1,3 49090 37,04
19,09 0,9 18 310 28,94 1,4 60100 39,05
21,70 1,0 24 350 30,99 1,5 72470 41,02
24,27 1,1 31 480 33,09
Таблица 46
Значения К и V/ в зависимости от Н и b для
овоидальных труб
а) Расход жидкости в зависимости от
профиля сечения может быть выражен для
широкого потока на плоскости (глубина
потока h весьма мала по сравнению с ши-
риной) по следующей формуле:
1 h3
Q=3gl~, (193)
* ?
° со
С -с
0,45
0,60
0,75
0,9
1 05
1,20
1,35
1 523
3 314
6 119
10 000
15 210
21 550
29 930
14,43
18,03
21,31
24,19
27,03
29,34
32,17
I
1,0 42 690 34,43
1,1 51 430 37,00
1,2 64 390 38,92
1,3 78 580 40,12
1,4 92 190 42,68
1,5 115 800 44,81
где Q — расход жидкости;
i — уклон;
ч — кинематическая вязкость жидкости;
g—ускорение силы тяжести.
б) для прямоугольного сечения расход
жидкости может быть подсчитан (по Чарно-
му И. А.) по следующей формуле:
i b3 h3
<2 = 0,2672^.^4-^, (194)
где b — ширина потока.
Остальные обозначения те же, что и в
формуле (193).
ВОДОСЛИВЫ
КЛАССИФИКАЦИЯ ВОДОСЛИВОВ
Водосливом называется преграда на пу-
ти потока жидкости, через которую послед-
няя переливается.
Различают три группы водосливов по
форме порога:
1) водослив с тонкой стенкой: струя
жидкости, прикоснувшись к ребру порога,
переливается, не смачивая его; на фиг. 55
Фиг. 55. Водослив
с тонкой вертикаль-
ной стенкой (венти-
лируемый; давление
под струёй р равно
атмосферному)
Фиг. 56. Водослив
с тонкой наклонной
стенкой (вентилиру-
емый; давление под
струёй р равно атмо-
сферному)
Фиг. 60. Водослив
с широким порогом
затопленный
Фиг. 59. Водослив с
широким порогом не-
затопленный
Фиг. 57. Водослив
практического прямо-
угольного профиля
(вентилируемый; да-
вление под струей р
равно атмосферному)
Фиг. 58. Во-
дослив прак-
тического
криволиней-
ного профиля
и 56 показаны вертикальный и наклонный
(а =/= 90°) водосливы с тонкой стенкой;
2) водосливы практических профилей:
прямоугольный профиль (фиг. 57), криво-
линейный профиль (фиг. 58);
Фиг. 61. Водослив
прямоугольный
Фиг. 62. Ьидислив
треугольный
По конструкции водосливы могут разли-
чаться формой порога, сливного отверстия и
ребра.
3) водосливы с широким порогом (фиг. 59
и 60) — 8 > (2 4- 3) Н. Движение переливаю-
щейся жидкости приобретает характер
параллельно-струйного течения.
По форме сливного отверстия различают
водосливы прямоугольные (фиг. 61), тре-
угольные (фиг. 62) и т. Д.
444 ГИДРОМЕХАНИКА
По форме ребра в плане и его располо-
жению различают водосливы прямые (фиг. 63
и 64), косые (фиг. 65) и т. д.
Фиг. 63. Водослив
прямой с горизон-
тальным сжатием
Фиг. 64. Водослив
прямой без горизон-
тального сжатия
Фиг. 71. Водсслив
практического про-
фи л я—зато пленный
Фиг. 65. Водослив
косой с горизонталь-
ным сжатием
Фиг. 66, Водослив
с тонкой вертикаль-
ной стенкой и с от-
жатой струёй; давле-
ние под струёй мень-
ше атмосферного
Фиг. 72. Водослив практического профиля—
затопленный
а) водосливы с горизонтальным сжатием
(фиг. 63 и 65);
б) водосливы без горизонтального сжатия
(фиг. 64).
Фиг. 67. Водослив
с тонкой вертикаль-
ной стенкой с зато-
пленной снизу струёй
Фиг. 68. Водослив
с тонкой вертикаль-
ной стенкой и с при-
липшей струёй
По характеру сливной струи и по виду
сопряжения струи с нижним бьефом разли-
чают:
1) водосливы незатопленные:
а) вентилируемые (фиг. 55—57), б) с от-
жатой струёй (фиг*. 66), в) с затопленной
струёй снизу (фиг. 67), г) с прилипшей
струёй (фиг. 68), д) с отогнанным прыжком
(фиг. 69);
Фиг. 69. Водослив
с тонкой вертикаль-
ной стенкой и с ото-
гнанным прыжком
Фиг 70. Водослив
с тонкой вертикаль-
ной стенкой — затоп-
ленный
РАСХОД ЖИДКОСТИ
ЧЕРЕЗ ВОДОСЛИВ
Для определения расхода жидкости через
водосливы всех типов служит общая расчёт-
ная формула
Q =mbV2g \Н + , (195)
где Ь — ширина порога водослива;
Н — статический напор;
/>„ — скорость подхода жидкости к греб-
ню водослива;
а0 — коэфициент Кориолиса;
т — коэфициент расхода жидкости через
водослив.
Коэфициент расхода жидкости т, зави-
сящий от целого ряда факторов (типа водо-
слива, формы стенки, водосливного отвер-
стия, сливной струи и т. п.), определяется
опытным путём.
По Павловскому, коэфициент расхода т
выражается следующим равенством:
т =-- тг ау ан . а„ . аг ,
где тг—приведённый коэфициент расхо-
да при ау-ан-а„-ае = 1;
ау — коэфициент, зависящий от формы
гребня;
ан—коэфициент, зависящий от вели-
чины напора Н;
ап — коэфициент, зависящий от харак-
тера сопряжения струи с нижним
бьефом (коэфициент затопления);
2) водосливы затопленные (фиг. 70, 71
и 72).
Различают водосливы и по степени боко-
вого сжатия струи:
е / aov<> \
ае = 1 — I Н + у— I — коэфициент, за-
висящий от сжатия струи (табл.
47).
водосливы
445
Таблица 47
Значения коэфициента £ для определения з£
г=О,2 е=О,14 2=0,08
Таким образом, окончательно формула
расхода принимает вид:
_ ( МУ'*
Q = тгу2 2-ауаи-®я*о, -b\H + yj- I. (196)
। я1 Иг । ,
Расчётные данные для определения коэ-
фициента расхода т наиболее часто встре-
чающихся типов водосливов приведены в
табл. 48 — 50.
В табл. 50 Нпр—проектный напор плотин
и Но= Н + у^- .
Таблица 48
Расчётные формулы для коэфициента расхода водосливов с тонкой стенкой
Тип водослива № фи- гуры Формула коэфициента расхода т
Незатопленный прямоугольный водослив с вертикальной стенкой и с горизонтальным сжатием, 1; ^2 м Н С,Об до 0,6 М Н 1,13 м Pi (высота гребня водослива над дном верхнего бьефа) 55 61 63 „ Ъ При малых значениях , 0.0027 0,033 \ / 0,405 + —— ‘ < \ X " ’Я 1 \ J или при больших значениях ~ D т . |-о,405 + ^_0(03(*Ю_*)]Х
Незатопленный прямоугольный водослив с вертикальной тонкой стенкой без горизон- тального сжатия Н 1 ,13 м Pi Ь — В < 2 м Н ^1,24 М 55 64 /л л „ . О,0О27\ Г / Н \ 2 1 т =/0,405+ н j i+0,55/H + HpJ
Затопленный прямоугольный водослив с вер- тикальной тонкой стенкой без горизонтально- го сжатия 61 64 70 D70 1,05 т = 1,05 m ^1 + 0,2 z
Незатопленный прямоугольный водослив с наклонной тонкой стенкой без горизонталь- ного сжатия 56 64 m0 = Km, где К « 0,925 при a = 45° К = 0,958 при a = 71,5° К = 1,045 при a == 108,5° К - 1 ,115 при a = 135и
Незатопленный треугольный водослив с гонкой стенкой с углом 2 а == 90° Расчётные формулы даны применит ельно к уравнению Q 15 И н н + 2g ) 1 56 62 По опытам Томсона: 9 5 Q = 1,4 Н“’ , где Н = 0,05 ч- 0,25 м По опытам Барра в среднем: ’.5 Q = 1,39 Н , где Н - 0,075 4- 0,25 м По опытам Кинга: 2 47 Q » 1,343 Н 9 , где Н = 0,05 4- 0,55 м
446
ГИДРОМЕХАНИКА
Таблица 49
Расчетные данные для определения коэфициента расхода водосливов некоторых практических профилей
Наименование коэфициента Незатопленный водослив практического профиля Затопленный водослив практи- ческого профиля
прямоуголь- ный ппямоуголь- ный с закруг- лённым вход- ным ребром криволинейный высокий профиль прямоуг оль- ный прямоуголь- ный с закруг- лённым вход- ным ребром Криволинейный
-fib
dp л 1 3^1 < 11 I/Pl '-г х А
Приведённый коэ- фициент расхода т? 0,42 0,42 0,49 0,42 0,42 0,49
Коэфициент фор- мы g 1 1 + ТГ п0 1 1 1+-А Г7в 1
Коэфициент пол- ноты капора 0,7 + 0,185 — О 2,7 + 0,185 “ О 0,785 + 0,25 ^2- п пр Для ^2--0,1+0,8; /7 пр 0,88+0,12 •»/ ~2— V нпр иля Н°- > 0,8 н пр 0,7 + 0,185 ф 0,785 + 0,25 -S*. Г1 пр для -^2- -0,1 +0,8; п пр 0,88 + 0,12 Л/ ~ Г пр для —°- >0,8 П пр
Коэфициент затоп- ления G п 1 1 1 /2 Р Н» 0 0,45 0,6 0,7 С,8 0,9 1
3 п 1 С, 05 С,92 0,87 2,78 0,62 0
Коэфициент сжа- тия а 8 b, \ '2g J , S с ( „ “« 1’б\
Таблица 50
Расчётные данные для определения коэфициента расхода водоспивоа с широким порогом
Наименование коэфициента Незатопленный водослив с широ- ким порогом Затопленный водослив с широким порогом
порог без закруг- лённого входного ребра порог с закруг- лением входного ребра порог без закруглён- ного входного ребра порог с закруг- лением входного ребра
и
Л - — | - _ _ Т f 1«£ - • . 'JSt
Приведённый коэфициент расхода т (-.32 0,32
Коэфициент формы 1,00 1,09 1,00 1,09
Коэфициент полноты напора сн 1 - 1 1
Коэфициент затопления 1 1 ае | до н/р-7 9,8 0,87 0,9 0,94 0,98 0,У.9
a tl.OO л 1 9,929 0,815|0, 739|0,598|0,36|( ,<‘82
Коэфициент сжатия « .-¥(в+^) Г £ / я» '--ХМ
водосливы
447
СОПРЯЖЕНИЕ СТРУИ С НИЖНИМ
БЬЕФОМ
Удельная энергия потока выражается
трёхчленом уравнения Бернулли (94).
Если за плоскость сравнения принять
плоскость, проходящую через наинизшую
точку живого сечения водослива, то величина
а иг а О2
h+T- =Л + 2^-2=Э (197)
энергией сечения.
Один и тот же
расход, протекая с
различной скоростью
через сечение данной
формы (в зависимо-
сти от гидравличе-
ских условий), булет
создавать различную
глубину потока. При
этом будет меняться
как общая величина
удельной энергии се-
чения, так и соотно-
шение между потен-
циальной Эп и кинетической энергиями:
аО2
9=h + 2gW2 “ -Ь Эк
(198)
(199)
На фиг. 73 дан график зависимости Э =
= / (й). Глубина, соответствующая мини-
мальной величине удельной энергии сечения,
называется критической глубиной hKp.
Глубина потока й, при которой 3 = 3min,
определяется из уравнения
d Э a Q2B
dh g аг- ’
d со
где В = — ширина потока.
При h>hKp поток называется спокойным,
при й < hKp — бурным, при й=йкр—крити-
ческое состояние потока.
Явление, характеризующееся внезапным
резким увеличением глубины потоь'’. с рез-
Фиг. 74
ким переходом от больших скоростей тече-
ния к меньшим, называется гидравлическим
прыжком.
В зависимости от условий, в которых
происходит прыжок, он может принимать
различный вид. На фиг. 74, 75 и 75а показа-
Фиг. 75
пы совершенный прыжок, прыжок-волна и
поверхностный прыжок. Глубины в сечениях
до прыжка и за прыжком й' и й' назы-
ваются сопряжёнными глубинами (фиг. 74).
Разность й" — й' = а есть высота прыжка.
Сопряжённые глубины связаны равенством
так называемых прыжковых функций:
+ Йц.т “1 = (-00>
где йц т и й т—глубины погружения цент-
ров тяжести рассматриваемых сечений.
ВИДЫ СОПРЯЖЕНИЙ СТРУИ с нижним
бьефом
Профиль водослива сопрягается с дном
нижнего бьефа плавной кривой. Наименьшее
сечение переливающейся струи будет у
флютбета (сжатое сечение). Глубина йс в
этом сечении всегда меньше критической.
Характер сопряжения струи определяется
состоянием потока в нижнем бьефе—величи-
ной его бытовой глубины hg:
1) hg < hKp — сопряжение произойдёт в
виде плавной кривой подпора;
2) hg > hKp — возникает гидравлический
прыжок.
В зависимости от соотношения между
глубинами прыжок будет возникать при:
а) й(}= hc —в сжатом сечении;
б) hg < hc — за сжатым сечением, где
глубина hg = hc —так называемый отогнан-
ный прыжок;
в) hg > hc — прыжок «упрётся» в плоти-
ну— надвинутый прыжок.
Если при этом й0->/7р,, то водослив
будет затопленным.
Профиль водослива сопрягается с дн< м
нижнего бьефа вертикальным уступом
(фиг. 76) Если состояние потока в нпжг.^м
Фиг. 76
бьефе спокойное, сопряжение произойдёт в
виде гидравлического прыжка:
а) при hg — hc — совершенный прыжок,
б) при hg > hc — свободный или затоп-
ленный поверхностный прыжок.
Состояние перехода от совершенного
прыжка к свободному поверхностному пазы-
448
ГИДРОМЕХАНИКА
вается первым критическим режимом прыж-
ка. Состояние перехода от свободного
поверхностного прыжка к затопленному
называется вторым критическим режимом
прыжка. Возникновение сопряжения в фор-
ме отогнанного прыжка весьма нежелатель-
но, так как гашение прыжка вызывает раз-
мыв русла нижнего бьефа. Ввиду не-
устойчивости критического сопряжения при
изменении расхода (прыжок начинается не-
посредственно в сжатом сечении) всегда
стараются получить надвинутый прыжок,
который даёт наиболее благоприятный по-
верхностный режим потока (максимальные
скорости у поверхности).
Таблица 52
ЗАТОПЛЕННЫЕ ВОДОСЛИВЫ
Водослив называется затопленным, если
гребень его погружен под уровень нижнего
бьефа. Расположение гребня ниже уровня
нижнего бьефа—необходимое, но недостаточ-
ное условие затопления водослива, ибо в
случае отогнанного прыжка водослив всё же
не будет затоплен.
Условиями затоплениядляводосливов раз-
личных профилей будут:
а) водослив с широким порогом (фиг. 59
и 60)
2 ( wl \
(Йе-Нр.) > 3 |Н+ 2у ); (201)
б) водослив практического профиля
{фиг. 71)
( Z \
где tj- )
\ПР‘ 'о
(табл. 51);
зависит от профиля водослива
Таблица 51
для
«о $
л / Z \ 2j?
Зиачеиия \ — \ в зависимости от ———2—
1/7 1 П
\ Л/о Р‘
в) водослив с тонкой стенкой (фиг. 70)
Z
Нр.
(203)
табл. 52.
по Бахметеву, берётся из
БЕЗВАКУУМНЫЕ
ВОДОСЛИВЫ
В практике гидротехнических сооружений
из всех практических профилей водосливов
наибольшее распространение получили кри-
волинейные профили. Криволинейные про-
фили подразделяются на две группы—ваку-
умные и безвакуумные.
Если между поверхностью профиля водо-
слива и переливающейся через него струёй
будет свободное пространство, то в этом
пространстве образуется вакуум. Такой
профиль водослива называется вакуумным.
Наличие вакуума делает струю неустойчи-
вой и вызывает вибрацию и разрушение
плотины. Вследствие этого обычно предпо-
читают безвакуумный профиль — профиль,
совпадающий с нижним очертанием свобод-
ной струи. Безвакуумный профиль делает
минимальным сжатие струи и обеспечивает
наибольшую пропускную способность.
В основу построения безвакуумных про-
филей положено уравнение движения центра
тяжести струи как свободно падающего тела
с заданной начальной скоростью на гребне,
которое даёт координаты нижней и верхней
поверхностей струи и координаты криволи-
нейного профиля, несколько врезающегося
в нижнюю поверхность струи для более на-
дёжного примыкания последней. В табл. 53
даны координаты профиля и струи для двух
типов плотин (фиг. 77 и 78).
Для плавного сопряжения нижней части
профиля с дном нижнего бьефа предложено
выполнять переход по дуге круга, радиус
которого берётся в зависимости от напора
жидкости Н и высоты стенки водослива Р
(табл. 54).
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
449
Таблица 53
Координаты для построения профиля водослива
Форма I Форма Ц
У У
X очертания струи очертания струи
X х - и 2 я । а /трен- 1 ло- жное- X X - “ к :Х i 3 х э O-S 3 f- I i 6 <У о о Q.CI h . . X
? ч о X X о о CQ С X X г> х CQ X CQ ь S* ч о х х о о са с х X Ь i> х са X са ь
0,0 0, 125 -0,831 0,126 0,043 -0,781 0,043
0,1 0,036 —0,803 0,036 0,010 -0,756 0,010
0,2 0,007 -0,772 0,007 0,000 -0,724 0,000
0,3 0,000 —0,740 0,000 0,005 —0,689 0,005
0,4 0,007 -0,702 0,007 0,023 -0,648 0,023
0,6 0,060 —0,620 0,063 0,090 -0,552 0,090
0,8 0,142 -0,511 0,153 0,189 —0,435 0,193
1,0 и, 257 —0,380 0 ,267 0,321 -0,293 0,333
1,2 0,397 —0,219 0,410 0,480 —0,120 0,500
1,4 0,565 —0,030 0,590 0,665 -0,075 0,700
1,7 0,870 0,305 0,920 0,992 0,438 1,05
2,0 1,22 0,693 1,31 1,377 0,860 1,47
2,5 1,96 1,50 2,10 2,14 1,71 2,34
3,0 2,82 2,50 3,11 3,06 2,76 3,39
3,5 3,82 3,66 4,26 4,08 4,00 4,61
» 4,0 4,93 5,00 5,61 5,24 5,42 6,04
4,5 6,22 6,54 7,15 6,58 7,07 7,61
Примечание, кого» напора Но== 1 величинах напора ножить на На. Координаты даны для «лол- (в любых мерах); при других следует все числа таблицы ум-
Таблица 54
Значение сопрягающих радиусов г для плотин
(размеры в м)
РАСЧЁТ ОТВЕРСТИЙ МАЛЫХ МОСТОВ
И БЕЗНАПОРНЫХ ТРУБ
Отверстия малых мостов и безнапорных
труб обычно служат для пропуска весенних
и сливных вод через насыпи железных,
шоссейных и грунтовых дорог. Напор перед
этими отверстиями создаётся стеснением
поперечного сечения потока устоями и бы-
ками. Расчёт отверстий малых мостов и
безнапорных труб является частным случаем
водослива с широким порогом, в котором
подпор создаётся без возвышения порога
водослива над дном водостока. При расчёте
следует различать случаи затопленного и
незатопленного водослива.
Для незатопленного водослива ширина b
отверстия малого моста или безнапорной
трубы определяется по формуле
«О
й = (204)
где р—коэфициент расхода.
По Павловскому, р = г (коэфициент сжа-
тия) и выбирается по табл. 69.
Для затопленного водослива с широким
порогом
& = <205>
После определения ширины производят
проверочный расчёт на величину создавае-
мого подпора Z.
При незатопленном водосливе
I 1 I а°р<>
~ \ К 1 I ~
(206)
где v0—скорость подхода;
hn — глубина на пороге;
1234 5'6 7 89
10 3,0 4,2 5,4 6,5 7,5 8,5 9,6 10,6 11,6
20 4,0 6,0 7,8 8,9 10,0 11,0 12,2 13,3 14,3
30 4,5 7,5 9,7 11,0 12,4 13,5 14,7 15,8 16,8
40 4,7 8,4 11,0 13,0 14,5 15,8 17,0 18,и 19,0
50 4,8 8,8 12,2 14,5 16,5 18,0 19,2 20,3 21,3
60 4,9 8,9 13,0 15,5 18,0 20,0 21,2 22,2 23,2
?—коэфициент скорости, величину ко-
торого Павловский рекоме'ндует
брать равной 0,95.
При затопленном водосливе
a v0
z-^2-g-~2T :(? = 0’95>- <207'
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
ОСНОВНОЕ УРАВНЕНИЕ
При неравномерном движении глубина
потока ft, а следовательно, и поверхностный
уклон I зависят от длины пути потока s,
т. е. h=f(s). Свободная поверхность пото-
ка принимает форму «кривой подпора», если
с изменением з происходит увеличение ft,
и «кривой спада», если ft уменьшается.
Для призматического, медленно изменяю-
щегося русла (канала) любого очертания
общее диференциальное уравнение нерав-
номерного движения имеет вид:
dz __d^(<J_3\ ,dh
ds ~ds\2g) "г ds’
dz
где -~т~ •— изменение положения уровня по-
тока по длине русла—пьезомет-
рический уклон /;
d ( и*\
ds 2V ) — изменение скоростного напора
\zg/ («скоростной уклон»);
dh
-ту— потеря напора на гидравличе-
ские сопротивления; гидравли-
ческий уклон—I.
Если неравномерный поток рассматри-
вать состоящим из бесконечно большого
числа элементарных участков длиной ds
С равномерным движением, то, по Шеэи,
dh
ds = сЧ? '
29 Томl
450
ГИДРОМЕХАНИКА
Если уклон дна русла i0 на всём протя-
жении рассматриваемого участка потока
одинаков, то
dz . dh
ds = '° ds '
При этих условиях основное уравнение
упрощается:
dh d / о2\ о2
'о“ ds~ ds\2f’)‘C2R'
При постоянстве расхода Q = const и
площади поперечного сечения потока ш:
d [v*\ v2 /dt» dt» dh\
ds \2g J ~ gw3 \ ds dh' ds )'
Так как для призматических русел
dt» dt» . _
Т- = 0; V,-= В (фиг. 79),
ds ’ dh dh '
dh
ds
, __Qi_
« t»2C2R
& B~
~ g ‘ “3
Если расход на участках равномерного
и неравномерного движения одинаков, то
в случае широкого неглубокого русла
ш = B-h, R ~ A, a Q=Bhova= C0Bh0Vh„i
(у0, ha и Со — нормальные скорость, глубина
и коэфициент Шези на участке равномерно-
го движения). Тогда при С = Со
Фиг. 79
dh
ds
Д1>я широкого неглубокого русла пара-
болического очертания
2 2
и> = ~зВ11, R~~jh> t»^BR,
и следовательно
dh 'о (ft4 — ft*)
При допущении по Бахметеву приемле-
мости показательного закона (Ко: К)2 =
«= (ft0 : h)x, где х—гидравлический показа-
тель русла
ftr~~ftp
ds ~ 1° с2 10 В ‘
ЛЛ-----------AS
g 7 0
Критическая глубийа. В
когда знаменатель уравнений
«Уль, Не-
прерывности функции
h = / (s).
тех случаях,
обращается в
т. е. происходит разрыв не-
Глубина, при которой происходит раз-
рыв функции h = / (s), называется крити-
ческой глубиной — hK. Выше (199) было ука-
зано, что критическая глубина, определяе-
мая заданным расходом Q и формой русла,
характеризуется наименьшей удельной энер-
гией сечения. Значения критических глубин
для русел различных очертаний указаны
в табл. 55.
Таблица 55
Значение критических глубин hK для различных
очертаний русел
Очертания русла h к Примечание
Прямоугольное Параболическое Полукруглое . , Треугольное . . Трапецеидальное (симметричное) -х. + Я 1 W “ > м •= § 3 1 Й 1 * 4- оо е । я _ । в 2 - > - оо 1 е 1 <а а—коэфициент Кориолиса; m-=ctg3—коэфи- циент откоса «к —т- пк (см. фиг. 47)
Критический уклон. Критическим укло-
ном hK называется уклон дна канала, при
котором для заданного расхода Q нормаль-
ная глубина h0 равна критической глубине
hK, т. е.
g
= “тг •
а-Ск
Так как 1К = / (С«) > то критический
уклон зависит от шероховатости русла, воз-
растая с её увеличением. В табл. 56 приве-
дены значения критического уклона в зави-
симости от гидравлического радиуса и ше-
роховатости русла.
Таблица 56
Зависимость критического уклона от величины гид-
равлического радиуса и шероховатости русла
0,06 0,0017 0,0015 0,0014 0,0013 0,0013 0,0012 0,0012 0,0012
0,16 0,0026 0,0022 0,0018 0,0016 0,0014 0,0013 0,0013 0,0013
0,46 0,0070 0,0048 0,0032 0,0024 0,0020 0,0017 0,0015 0,0014
0,85 — 0,0098 0,0057 0,0038 0,0029 0,0022 0,0019 0,0017
1,30 _ _ 0,0094 0,0059 0,0041 0,0029 0,0023 0,0019
1,75 — — — 0,0083 0,0056 0,0037 0,0028 0,0023
Основное уравнение неравномерного дви-
жения, выраженное через hK, имеет вид;
dh . hx— hx
— = iB------------------.
ds hx— h*
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
451
КРИВЫЕ СВОБОДНОЙ ПОВЕРХНОСТИ
В зависимости от расположения нормаль-
ной й0 и критической линии глубин могут
иметь место три рода кривых свободной
поверхности в открытом русле, причём раз-
ные величины глубин потока могут созда-
вать различные случаи неравномерного дви-
жения:
I. Нормальная глубина больше критиче-
ской (й0 > hK):
</й
а) й > й0 или h > йк; > 0.
Глубины растут по течению (кривая под-
пора) — фиг. 80.
</й
б) й < й0, но й > hK\ < 0.
Фи1 . 80 Фиг. 81
Глубины уменьшаются по течению (кри-
вая спада) —фиг. 81.
</й
с) й < й0; й < йж; > 0.
Глубины возрастают по течению и могут
достичь линии критических глубин; здесь
следует ожидать образования прыжка —
фиг. 82.
Фиг. 82
Фиг. 83
II. Нормальная глубина меньше крити-
ческой (й0 < hK):
dh
а) Й < Йо или Й < йк; > 0.
Глубины возрастают в направлении тече-
ния— фиг. 83.
dh
6) h> й0, но й <й„; <0.
Глубины убывают по течению—фиг. 84.
dh
С) Й > Йо и Й > Й„; > 0.
Глубины возрастают по течению, но так
как нормальная глубина ниже порога, а
порог выше критической глубины, — обра-
зуется гидравлический прыжок — фиг. 85.
III, Нормальная глубина равна крити-
ческой (й0 = йк), в этом случае имеем
dh _
ds ~ 1о’
Фиг. 84
откуда следует, что линия поверхности
жидкости имеет постоянный уклон, т. е.
это прямая линия. Эта прямая наклонена
к линии, параллельной дну потока, под тем
же углом, под которым
дно наклонено к гори-
зонту, т. е. линия по-
верхности жидкости го-
ризонтальна — фиг. 86
и 87.
Таким образом, ка-
налы критического ук-
лона сопрягаются с
уровнем нижнего бьефа
без прыжка.
В каналах (руслах) с
дном или с обратным уклоном дна равно-
мерное движение невозможно.
В таких каналах возможны только два
вида кривых свободной поверхности пото-
ка: 1) кривая спада — фиг. 81 и 2) кривая
подпора для малых глубин, не превышаю-
щих критической йк, — фиг. 82.
Фиг. 85
Построение кривых спада и подпора. По-
строение кривых спада и подпора, т. е.
установление зависимости между глубиной
й и расстоянием s от некоторой исходной
точки для широкого, неглубокого русла,
Фиг. 86
приближающегося к прямоугольному, про-
изводится по формуле:
(s2 — Si) = (т]2 — ъ) —
/ С2 i \
/ . ио 'о | г,
Фиг. 87
Й
где 7] = т—; индексы 1 и 2 относятся к се-
но
чениям, находящимся на расстояниях и
s3 от исходного пункта.
Значения функций ф(т;) приведены g
табл. 57. fj < 1 соответствует кривым спада,
т; > 1—кривым подпора. Кривые свободной
поверхности удобнее строить, задаваясь глу-
бинами й, т. е. г;, и отыскивать соответствую-
щие им значения s2— Sj.
28*
452
ГИДРОМЕХАНИКА
Значения ф (т) Таблица 57
1 Ф (’;) ф (’i) ф (и) 1 ф (’l) ф (1)
0,00 0,01 0,15 0.20 0.25 0,30 0,35 0,40 0.45 0,50 0.51 0,52 0,53 0,54 и. 55 0,50 0.57 0,58 0,59 0,60 0,61 0,62 0,63 0.64 0,65 0,66 0,67 0,68 0,69 0,70 0.71 0,72 0.73 0,74 0,75 0,76 0,77 0.78 0,79 0,80 0,81 0,82 0,83 0,84 0,85 —0,’6046 -0,5946 -0.4545 -0.4012 -0,3536 -0,3025 -0.2508 -0.1980 -0,1438 -0.0878 -0.0763 -0,0647 —0,0530 -0,0412 —0,0293 —0,0172 —0.0050 0,0074 0,0199 0,0325 0,0454 0,0584 0.0716 0,0851 0,0987 0,1127 0,1268 0,1413 0,1560 0,1711 0,1864 0,2022 0.2184 0.2350 0,2520 0,2696 0,2877 0,3064 0.3258 0.3459 0.3668 0.3886 0,4114 0,4353 0,4605 0.860 0,870 0,880 0.890 0,900 0,902 0.904 0,906' 0,908 0.910 0,912 0.914 0,916 0.918 0.920 0,922 0,924 0,926 0,928 0.930 0.932 0,934 0,936 0.938 0,940 0.942 0,944 0,946 0,948 0,950 0,952 0,954 0,956 0,958 0,960 0,962 0.964 0,966 0.968 0.970 0,971 0,972 0.^73 0,974 <0975 0,4872 0,5156 0,5459 0.5785 0,6138 0,6213 0.6289 0.6366 0,6445 0.6525 ^,6607 0.6691 0,6776 0.6864 0.6953 0,7045 0,7138 0,7234 0.7332 0,7433 0,7537 0.7643 0,7753 0,7866 0,7982 0,8102 0.8226 0,8354 0,8487 0,8624 0,8767 0.8916 0.9071 0.9233 0.9402 0,9580 0,9767 0.9965 1.0174 1,0396 1,0512 1.0632 1,0757 1,0886 1,1020 0,976 0,977 0,978 0,979 0,980 0,981 0,982 0,983 0,984 0,985 0,986 0,987 0,988 0.989 ь,990 0.991 0.992 0.993 0.994 0,995 0,996 0,997 0,998 0,999 1,000 1,0000 1.0010 1,0020 1,0030 1,0040 1,0050 1,0060 1,0070 1,0081 1,0091 1.0101 1.0111 1,0121 1,0132 ' 1.0142 1,0152 1,0163 1.0173 1.0183 1,0194 1,1160 1,1305 1.1457 1,1615 1,1781 1.1955 1,2139 1.2333 1,2538 1,2757 1,2990 1,3241 1,3511 1,3804 1.4125 1,4480 1,4876 1,5324 1,5841 1.6452 1,7200 1,8162 1,9517 2,1831 2,1834 1,9523 1.8172 1,7213 1,6469 1.5861 1,5348 1.4902 1.4510 1,4159 1,3841 1,3551 1,3284 1,3087 1,2807 1,2592 1,2390 1.2199 1,2019 1,0204 1,0215 1.0225 1,0235 1,0246 1.0256 1,0267 1,0277 1,0288 1,0299 1,0309 1,0331 1,0352 1,0373 1,0395 1,0417 1.0438 1.0460 1,0482 1,0504 1,0526 1,0549 1,0571 1.0593 1,0616 1,0638 1,0661 1,0684 1,0707 1.0730 1,0753 1,0776 1,0799 1,0823 1,0846 1,0870 1.0893 1,0917 1,0941 1,0965 1,0939 1,1013 1,1038 1,1062 1,1848 1.1686 1.1531 1,1383 1,1241 1,1105 1,0974 1,0848 1.0727 1,0610 1.0497 1,0282 1.0080 0.9890 0,9709 0.9539 0,9376 0,9221 0,9073 0,8931 0.8795 0.8665 0.8539 0.8418 0.8301 0,8188 0,8079 0,7973 0,7871 0.7772 0,7675 0.7581 0,7490 0,7401 0.7315 0,7231 0,7149 0,7069 0,6990 0,6914 0.6839 0,6766 0,6695 0.6625 1,1086 1,1111 1,1173 1,1236 1,1299 1,1364 1.1429 1,1494 1,1561 1,1628 1.1696 1.4765 1,1905 1.2048 1,2195 1.2346 1.2500 1.2658 1,2821 1,2987 1,3158 1,3333 1,3514 1,3699 . 1,3889 1.4085 1,4286 1.4706 1,5152 1,5625 1.6129 1,6667 1,8182 1,9231 1,9608 2,0000 2,2222 2.5000 2,8571 3.3333 4,0000 5.0000 6,6667 10.0000 0,6556 0,6489 0.6327 0,6173 0,6025 0,5884 0.5749 0,5619 0.5494 0,5374 0.5258 0.5146 0.4932 0.4733 0,4544 0,4367 0,4198 0,4039 0,3886 0,3741 0,3603 0,3470 0,3343 0,3221 0,3104 0,2991 0.2883 0,2677 0.2486 0,2306 0,2138 0.1980 0,1625 0,1435 0,1376 0,1318 0,1052 0,0821 0,0623 0,0455 0,0314 0,0201 0,0113 0,0059
Построение кривых свободной поверхно- сти потоков в широких неглубоких руслах, приближающихся к параболическому очер- танию, производится по формулам Толк- митта. Кривые подпора (т( > 1): 4°- (s3 — s,) = F (r]2) — F (rji). ,!О Значения функций F(т) приведены в табл. 58. Кривые спада < 1): S1) = (T|3 — Тц) — / Cq * io \ — 1 g—) [F (т|2) — F (ru)]. Значения функции F (г,) приведены в табл. 59. Таблица 58 Значения F (т) для кривых подпора
7) F (О Р(т,) F (>,). F (Tj)
1.00 1,005 1,01 1.015 1.02 1.025 1,03 1,035 1,04 1,045 1,05 1,06 1,07 1,08 1,09 1,10 1.11 1,12 1,13 1.14 1,15 —CV -0.102 0,074 0.179 0,254 0,‘313 0,*362 0,403 0,440 0,473 0,502 0,554 0,599 0,635 0,675 0,708 0,738 0,766 0,793 0,-818 0.842 1,16 1.17 1,18 1.19 1,20 1.21 1,22 1.23 1,24 1.25 1,26 1.27 1,28 1.29 1,30 1,31 1,32 1.33 1.34 1,35 1.36 0.865 0,887 0.908 0.928 0,948 0,967 0,985 1,003 1,021 1,038 1,055 1,071 1,087 1,103 1,119 1,134 1,149 1,164 1,178 1,193 1,207 1,37 1,38 1,39 1.40 1.41 1,42 1,43 1,44 1,45 1,46 1.47 1,48 1,49 1,50 1,55 1,60 1,65 1.70 1,75 1.80 1,85 1,221 1,235 1,249 1,262 1,276 1,289 1,302 1,315 1.328 1,341 1.354 1,367 1.379 1,392 1,453 1.513 1,571 1,628 1.685 1,740 1,795 1,90 1,95 2,00 2,1 2,2 2.3 2.4 2,5 2.6 2.7 2,8 2.9 3.0 3.5 4.0 4,5 5,0 6,0 8,0 10,0 1,850 1,904 1,957 2,053 2,168 2.272 2.376 2,478 2,584 2,683 2,785 2,886 2,988 1 3,492 3,995 4,496 4,997 5,998 7,999 ю.ооо
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
453
Таблица 39
Значения F Ы для кривых спада
F 01) 5 БЫ ! 7, F (,) 1 Ti F О,)
1,000 ОО 0.925 1,185 0,80 0,887 0.65 0,676
0,995 1.889 0,920 1,166 0,79 0,870 0,64 0.664
0,990 1,714 0,915 1,149 0,78 0,854 0,63 0.652
0,985 1,610 0,910 1,133 0,77 0,838 0,62 0,640
0,980 1,536 0,905 1,117 0,76 0,823 0,61 0,628
0,975 1,479 0,90 1,103 0,75 0,808 0,60 0,617
0,970 1,431 0,89 1,075 0,74 0,794 0,55 0,561
0,905 1,391 0,88 1,049 0,73 0,780 0,50 0.506
0,960 1,355 0,87 1,025 0,72 0,766 0,45 0,454
0,955 1,324 0,86 1,002 0,71 0,732 0,40 0,402
0,950 1,296 0,85 0,980 0,70 0,739 0,35 0,351
0,945 1,270 0,84 0,960 0,69 0,726 0,30 0,300
0,940 1,246 0,83 0,940 0,68 0,713 0,20 0,200
0,935 1,224 0,82 0,922 0,67 0,701 0,10 0,100
0,930 1,204 0,81 0,904 0,66 0,688 0 0
Кривые свободной поверхности потоков
в искусственных призматических руслах
небольшой ширины и относительно большой
глубины, по очертанию отличающихся от
прямоугольного и параболического, строят-
ся по формуле Бахметева:
/0
У («2 — S1) = (Т)а — Т]1) —
_°(1-/)[/> (Г2)_ Б (^)],
где /—безразмерный параметр, введённый
Павловским,
. _ аС^'р В
1 = g -х ’
х—смоченный периметр канала (русла).
Значения функции Б (т,) приведены в
табл. 60 и 61.
Таблица 60
Значения Б (,;) по Бахметеву
, Канал с прямым уклоном 10>О при х=3,5
’l Б (П) ’I 1 БЫ ’l БЫ
0 0 0,77 0,860 0,980 1,642 1,20 0,341 1,49 0,166
0,05 0,050 0,78 0,877 0,985 1,726 1.21 0,330 1.50 0,163
0,10 0,100 0,79 0,895 0,990 1,844 1.22 0,320 1,55 0,148
0,15 0,151 0,80 0,913 0,995 2,043 1,23 о.зю 1,60 0,135
0,20 0,200 0,81 0,932 1,000 ОО 1,24 0,301 1,65 0,124
0,25 0.25СР 0,82 0,952 1,005 1,329 1.25 0,292 1.70 0,114
0.30 0,301 0,83 0,972 1,010 1,138 1,26 0,284 1.75 0J65
0,35 0,352 0,84 0,993 1,015 1,022 1,27 0,276 1,80 0,097
0,40 0,404 0,85 1,016 1,020 0,94. 1,28 0,269 1,85 0,696
0,45 и, 456 0,86 1,039 1,025 0,871 1,29 0,262 1,90 0,064
0,50 0,510 0,87 1,064 1,030 0,827 1,30 0,255 1,95 0,079
0,55 0,566 0,88 1,091 1,035 0.785 1,31 О,24>- 2.0 0,074
0,60 0.625 0,89 1,120 1,040 0,748 1,32 0,242 2,1 0,065
0,61 0.637 0,90 1,151 1,045 0,716 1,33 0,236 2,2 0,057
U, 62 0,649 0,905 1,168 1,05 0,688 1,34 0,231 2,3 0,051
0,63 0,661 0,910 1,185 1,06 0,639 1,35 0,22 2,4 0,046
0,64 0,674 0,915 1,204 1.07 0,599 1 ,.36 0,219 2,5 0.041
0,65 U. 687 0,920 1,223 1,08 0,564 1,37 0,214 2,6 0,037
U,66 0,700 0,925 1,243, 1,09 0,534 1,38 0,209 2,7 0,034
0,67 0,713 0,930 1,265 1,10 0,507 1,39 0.205 2,8 0,031
0,68 0,726 0,935 1,288 1,11 0,483 1,40 0,20( 2,9 0,628
0,69 0,740 0,940 1,313 1,12 0,461 1.41 0,196 3,0 0,026
0,70 0,754 0,945 1.339 1.13 0,442 1,42 0.192 3.5 0,018
0,71 0,768 0,950 1,368 1,14 0,424 1,43 0,188 4,0 0,012
0,72 0,782 0,955 1,400 1,15 0,407 1,44 0,184 4.5 0,009
0,73 0,797 0,960 1,436 1.16 0,391 1,45 0,180 5,0 0,007
0,74 0,812 0,965 1,476 1,17 0,377 1,46 0,176 6,0 0,004
0,75 0,828 0,970 1,522 1,18 0,364 1,47 0,173 8,0 0,002
0,76 0,844 0,975 1,576 1.19 0,352 1,48 0,169 10,0 0,001 1
Таблица 61
Значения Б Ы по Бахметеву
Канал с прямым уклоном и>0 х=4,0
п БЫ БЫ । БЫ 1, Б Ы B(’i)
0 0 0,77 0,838 0,980 1,537 1,20 0,252 1,49 0,111
0,05 0.050 0,78 0,85- 0,985 1,611 1,21 0,243 1,50 0,109
0,10 0,160 0,79 0,871 0,990 1.7Р 1,22 0,235 1,55 0,097
0,15 0,150 0.80 0,887 0,995 1,889 1,2с 0,227 1,6С 0,087
0,20 0,200 0,81 0,904 1,000 оо 1,24 0,219 1,65 0,079
0,25 0,250 0,82 0,922 1,005 1,107 1,25 0,212 1,7и 0,072
0,3( 0,300 0,83 0,940 1 ,010 0,930 1.26 0,205 1,75 0,066
0,35 0,351 0,84 0,960 1.015 0,836 1,27 0,199 1,80 0.060
0,40 0,402 0,85 0,98( 1.020 0,7«: 1.28 0,193 1 85 0,055
0,45 0,454 0,86 1,002 1,025 0,712 1.29 0,187 1 ,90 0,650
0,50 0,507 0,87 1,025 1.030 0,668 1.30 0.182 1,95 0,046
0,55 0,561 0,88 1,049 1,035 0,632 1,31 0,176 2.00 0,043
0,66 0,617 0.89 1,075 1,040 0,600 1,32 0,171 2,10 0,b37
0,61 0,628 0,90 1,103 1,045 0,572 1,33 0,167 2,20 0,032
0,62 0,640 0,905 1,118 1,05 0,548 1,34 0,162 2,30 0,0279
0,63 0,652 0,910 1,134 1,06 0,506 1,35 0,157 2t40 0,0245
0,64 0,664 0,915 1,150 1,07 0,471 1,36 0,153 2 „50 0,0216
0,65 0,678 0,920 1,167 1,08 0,441 1,37 0,149 2,60 0,0192
0,66 0,688 0,925 1,185 1,09 0,415 1,38 0,145 2,70 0,0171
0.67 0,700 0,930 1,204 1,10 0,392 1.39 0.142 2,80 0,0153
0.68 0,713 0,935 1,225 1.11 0,372 1,40 0.138 2,90 0,0137
0,69 0,726 0,940 1,247 1,12 0,354 1.41 0,135 3.00 0,0123
0,70 0,739 0,945 1.271 1,13 0,337 1,42 0,131 3.50 0.0077
0,71 0,752 0,950 1,297 1.14 0,322 1,43 0.128 4,00 0,0052
0,72 0,766 0,955 1,325 1.15 0,308 1,44 0,125 4.50 0,0037
0,73 0,78b 0,960 1,356 1,16 0,295 1,45 0,122 э.ОО 0,0027
0.74 0,794 0,965 1,391 1.17 0,282 1,46 0,119 6,00 0,0015
0,75 0.808 0,970 1,431 1.18 >,272 ,47 0,116 8,00 0.0007
0,76 0,823 0,975 1,479 1.19 0,262 1.48 0.113 10,00 0,0003
Порядок построения кривых подпора и
спада по Бахметеву следующий: вычис-
ляются h0 и hK\ в зависимости от их соот-
ношения устанавливается тип кривой сво-
бодной поверхности (I, II, III); вычисляют-
ся: гидравлический показатель русла х (179),
С + С»
коэфициент Шези С = ширина рус-
Bt+ ва
ла по верху В =------- и смоченный пери-
метр х = -индексы 1 и 2 соответствуют
сечениям с заданной или вычисленной глу-
бинами ht и йг; задавшись произвольными
величинами /г, определяют по уравнению
Бахметева, положения живых сечений
и s2 с заданными глубинами, после чего
строят кривые подпора или спада.
Ь равнение Павловского:
где
- (I -”/) [И СЧ) - П (х,)],
1 Й2-Й1
а Й0‘х2—7.,
к
х —относительный модуль расхода;
К° остальные обозначения прежние.
Значения функции П (х) приведены а
табл. 62.
454
ГИДРОМЕХАНИКА
Таблица 62
Значения П (х) по Павловскому
X П(х) X П (X) X П(х) X П(Х) X П(х)
0,00 0 0,77 1,020 0,980 2.297 1,20 1,199 1,49 0,813
0,05 0.051 0,78 1,045 0.985 2,442 1,21 1,177 1,50 0,805
0,10 0,100 0,79 1,071 0,990 3,646 1.22 1,156 1,55 0,767
0,15 0,151 0,80 1,098 0.995 З.ООС 1.23 1,136 1,60 0,733
0,20 0,203 0,81 1,127 1,000 оо 1,24 1,117 1,65 0.703
0,25 0,255 0,82 1,156 1,005 2,997 1,25 1,098 1,70 0,675
0,30 0,30£ 0,83 1,188 1.010 2,652 1,26 1,081 1,75 0,650
0,35 0,365 0.84 1,221 1,015 2,450 1.27 1,065 1,80 0,626
0,40 0,424 0,85 1,256 1,020 2,307 1,28 1,049 1,85 0,605
0.45 0,485 0,86 1,293 1,025 2,197 1,29 1,033 1,90 0,585
0,50 0.549 0.87 1,333 1.030 2,107 1,30 1,018 1,95 0,566
0,55 c,6is 0,88 1,375 1,035 2,031 1,31 1,004 2,0 0,549
0,60 0,693 0,89 1,421 1,040 1,966 1,32 0,990 2.1 0,518
0,61 0,709 0,90 1,472 1,045 1,908 1,33 0,977 2,2 0,490
0,62 0,725 0,905 1,499 1.05 1,857 1.34 0,964 2,3 0,466
0,63 0,741 0,910 1,527 1,06 1,768 1.35 0,952 2.4 0,444
0,64 0,758 0,915 1,557 1,07 1,692 1,36 0,940 2,5 0,424
0,65 0,775 0,920 1,589 1,08 1,621 1,37 0,928 2,6 0,405
0,66 0,792 0 925 1,622 1,09 1.572 1,38 0,917 2,7 0,389
0,67 0,810 0,930 1,658 1,10 1,522 1,39 0,906 2,8 0,374
0.68 0,829 0,935 1,696 1.11 1,477 1,40 0,896 2,9 0,360
0,69 0,848 0.940 1,738 1.12 1,436 1.41 0.886 3,0 0,346
0,70 0,867 0,945 1,782 1.13 1,398 1,42 0.876 3,5 0,294|
0,71 0,887 0,950 1,831 1,14 1,362 1,43 0,866 4,0 0,2551
0,72 0,907 0,955 1,885 1,15 1,321 1,44 0,856 4,5 0,226
0,73 0,9281 0,960 1,945 1,16 1,301 1,45 0,847 5,0 0,203
0 74 0,950 0.965 2,012 1.17 1,273 1,46 0,838 6.0 0,168
0,75 0,972 0,970 2,092 1,18 1,247 1.47 0,829 8,0 0,126
0,76 0.096 0,975 2,184 1,19 1,222 1,48 0,821 10,0 0,100
Преимущество метода Павловского со-
стоит в возможности строить кривые свобод-
ной поверхности для призматических русел
любой правильной формы, пользуясь только
одной таблицей, в то время как, по Бахме-
теву, необходимо подыскать нужную из
ряда таблиц.
Кривые свободной поверхности потоков
в горизонтальных руслах строятся при по-
мощи формулы:
(8г-81) = фо(и-фо(и,
“к
где hK — критическая глубина;
h— глубина потока;
1к — критический уклон;
Значения функции %(;) для гидравличе-
ского показателя русла х = 3,5 приведены
в табл. 63.
Построение кривых свободной поверхно-
сти потоков в непризматических руслах
производится по приближённому методу
среднего уклона трения—фиг. 88.
“в
2g + he
в Эс —- Эв.
Значения ф. (Е) по Павловскому
(Для горизонтального русла i.=O при х=3,5)
Таблица 63
Е Фо (£) Е Ф. (Е) Е Ф. (У Е Фо (У Е Ф. (У
0 0 0,78 —0,7074 0.990 —0,77/6 1,22 —0,6762 1,55 0,047
0,05 —0,0500 0,79 -0,7131 0,995 —0,7777 1,23 -0.6659 1,60 0,243
0,10 -0,1000 0,80 —0.7186 1,000 -0,7778 1,24 -0,6550 1.65 0.466
0,15 —0,1500 0,81 —0.7339 1,005 —0,7777 1,25 -0,6434 1.70 O,72j
0,20 -0.1998 0,82 —0.7290 1,010 —0,7776 1,26 —0,6313 1,75 1,007
0,25 —0,2496 0,83 —0.7339 1,015 -0,7774 1,27 —0,6185 1,80 1,330
0.30 —0.2990 0,84 —0,7386 1,020 —0,7771 1,28 -0,6051 1,85 1,690
0,35 —0,3480 0.85 —0,7430 1,025 —0,7767 1,29 -0,5911 1,90 2,092
0,40 —0,3964 0,86 —0.7472 1,030 -0.7762 1,30 -0,5764 1,95 2,537
0.45 —0,4439 0,87 —0,7512 1,035 -0,7756 1,31 -0,5610 2,0 3.028
0,50 —0,4902 0,88 —0,7550 1,040 —0,7749 1,32 —0.5449 2,1 4,163
0.55 —0,5349 0,89 —0.7585 1,045 —0.7741 1,33 -0,5281 2,2 5,521
0.60 —0,5777 0,90 -0,7617 1,05 -0,7732 1,34 —0,5106 2,3 7,131
0,61 —0,5860 0,905 —0,7632 1,06 -0.7711 1,35 —0,4924 2,4 9,02
0.62 —0.5941 0,910 - 0.7646 1,07 -0,7687 1.36 -0,4734 2.5 11,23
0,63 —0.6022 0,915 —0,7660 1,08 —0.7658 1,37 —0,4537 2,6 13,77
0,64 -0,6102 0,920 —0,7673 1,09 —0,7325 1,38 —0,4332 2 7 16,70
0,65 -0,6180 0.925 —0,7685 1,10 —0,7588 1,39 -0,4120 2,8 20.06
0,66 —0,6257 0,930 -0,7697 1.11 —0.7546 1,40 -0,390 2,9 23,87
0,67 -0.6333 0.935 —0,7708 1,12 —0.7499 1,41 -0.367 3,0 28,18
0,68 —0,6408 0,940 —0,7718 1,13 —0,7448 1,42 —0,343 3,5 58.89
0,69 —0,6482 0.945 —0,7727 1.14 —0.7393 1,43 —и,319 4.0 109,8
0,70 —0,6554 0,950 —0,7736 1,15 —0.7332 1,44 -0.293 4.5 188,8
0,71 —0.6624 0,955 —0,7745 1,16 —0.7266 1.45 -0,267 5,0 305.6
0,72 —0,6693 0,960 -0,7751 1,17 —0,7196 1,46 —0,240 6,0 699.4
0,73 —0,6761 0.965 —0,7757 1,18 —0,7120 1.47 -0,212 7.0 1405
0,74 —0,6827 0,970 —0,7762 1,19 —0.7039 1,48 —0.183 8,0 2566
0,75 -0,6891 0.975 —0,7767 1,20 -0,6952 1,49 —0,153 9.0 4365
0,76 -0,6954 0,980 —0,7771 1,21 —0,6860 1,50 —0,122 10.0 7017
0.77 —0,7015 0 985 -0,7774
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
455
где /0—уклон дна канала (русла);
ve и vc — скорости в сечениях потока, рас-
положенных на расстоянии /
друг от друга;
hs и hc — глубины потоков в тех же сече-
ниях;
I/ — средний уклон трения;
</ ~ C2R >
причём
,, _ vc t r _ £e_±_£c _ ffa+ Rc .
™ 2 , i*» — 2 ** i\ — >
Эв и Эс — удельные энергии в сечениях
В и С.
Процесс построения кривых свободной
поверхности потоков сводится к нахождению
I при известных he, hc и вычисленных ве-
личинах if, Эс и Эд.
К естественным речным руслам приведён-
ные выше методы построения кривых сво-
бодной поверхности потоков необходимо
применять весьма осторожно, так как они
не являются призматическими, уклон дна и
расход их непостоянны, а шероховатость
русла различна не только на разных участ-
ках, но и в разных местах одного и того
Таблица 64
Значение /
(для кривых подпора)
Z Ь? '(-0 * Z <) 1 Z О Z
0,010 0,0067 0,235 1,2148 0.460 1,6032 0,685 1,9077 0,905 2,1742
U,015 0,1452 0,240 1,2254 0,465 1,6106 0,690 1,9140 0 .910 2,1800
0.020 0,2444 0,245 1,2358 0,470 1,6179 0,695 1,9203 0,915 2,1858
0,02b 0,3222 0,250 1,2461 0,475 1.6252 0,700 1,9266 0,920 2,1916
0,030 0,3863 0,25Ь 1,2563 0,480 1,6324 0,705 1,9329 0,925 2,1974
0,035 0,4411 0,260 1,2664 0,485 1.6396 0,710 1,9392 0,930 2,2032
0,040 0,4889 0,265 1,2763 0,490 1,6463 0,715 1,9455 0,935 2,2090
0,045 0,Ь31б 0,270 1,2861 0,495 1,6540 0,720 1,9517 0,940 2,2148
0,050 0.5701 0,275 1,2958 0.500 1.6611 0,725 1,9597 0,945 2.2206
0,055 0,6053 0.280 1,3054 0,505 1,6682 0,730 1,9641 0,950 2,2264
0,060 0,6376 0.285 1,3149 0,510 1,6753 0,735 1,9703 и,955 2,2322
0,065 0,6677 0,290 1,3243 0,515 1,6823 0,740 1,9765 0,960 2,2380
0.Q70 0,6958 0,295 1,3336 0,520 1,6893 0,745 1,9827 0,965 2,2438
0,0/Ь 0,7222 0,300 1,3428 0,525 1.6963 0,750 1.9888 0,970 2,2496
0,080 0,7482 0,305 1,3519 0,530 1,7032 0,755 1,9949 0,975 2,2554
0,085 0,7708 0,310 1,3610 0,535 1.7101 0,760 2.0010 0,980 2.2611
0,090 0,7933 0,315 1,3700 • 0,540 1,7170 0,765 2,0071 0,985 2,2668
0,0У5 0,8148 0,320 1,3189 0,545 1,7239 0,770 2,0132 0,990 2,2725
0,100 0.8353 0,325 1,3877 0,550 1,7308 0,775 2,0193 0,995 2,2782
0,105 0,8550 0,330 1.3964 0,555 1,7376 0,780 2,0254 1,000 2,2839
0,110 0,8739 0,335 1,4050 0,560 1,7444 0,785 2,0315 1,100 2,3971
0,115 0,8922 0,340 1,4136 0,565 1,7512 0,790 2,0375 1,200 2,5083
0,120 0,9098 0,345 1,4221 1,570 1.7579 0,795 2,0435 1,300 2,6179
0,125 0,9269 0,350 1,4306 0,575 1.7647 0,800 2.0495 1,400 2,7264
0,130 0,9434 0,355 1,4390 0,580 1.7714 0,805 2,0555 1,500 2.8337
0,135 0,9595 0,360 1.4473 0,585 1,7781 0,810 2.0615 1,600 2.9401
0,140 0,9/51 0,365 1,4556 0,590 1,7848 0,815 2,0675 1,700 3,0458
0,145 0,9903 0,370 1,4638 0,595 1,7914 0,820 2,0735 1,800 3,1508
0,150 1,и051 0,375 1,4720 0,600 1.7980 0,825 2,0795 1,900 3,2553
0,155 1,0195 0,380 1,4801 0,605 1,8046 0,830 2,0855 2.000 3,3594
0,160 0,165 1,0335 1,0473 0,385 0,390 1,4882 1,4962 0,610 0,615 1,8112 1,8178 0.835 0,840 2,0915 2,0975 2,100 2,200 3,4631 3,5664
0,170 0,175 0,180 1,0608 1,0740 1,0869 0,395 0,400 0,405 1,5041 1,5119 1,5197 0,620 0,625 0,630 1,8243 1,8308 1,8373 0.845 0,850 0,855 2,1035 2,1095 2,1154 2.300 2,400 2,500 3,6694 3,7720 3,8745
0,185 0,190 0,195 о,200 0,205 1,0995 1,1119 1,1241 1.1361 1,1479 0,410 0,415 0,420 0,425 0,430 1,5275 1,5353 1,5430 1,5507 1,5583 0,635 0,640 0,645 0,650 0,655 1,8438 1,8503 1,8567 1,8631 1,8695 0,860 0,865 0,870 0,875 0,880 2.1213 2,1272 2,1331 2,1390 2,1449 2,600 2.700 2.800 2,900 3.000 3.9768 4,0789 4,1808 4,2826 4.3845
0.210 0,215 0,220 1,1595 0.435 1,5659 О,С60 1,8759 0,885 2.1508 3,500 4,8911
1,1821 0.440 0,445 1,5734 1.5809 0,665 0,670 1,8823 1,8887 0,890 0,895 2,1567 2.1625 4,000 4.500 5,3958 5,8993
0,230 1,1931 1,2040 0,450 0,455 1.5884 1.5958 0,675 0,680 1,8951 1,9j14 0,900 2,1683 5,000 6,4018
ГИДРОМЕХАНИКА
456
же сечения. В этих условиях (см. фиг. 89)
расчёт часто ведётся по формуле
in /х,\
I z\
Значения функции / приведены в
\"о j
табл. 64.
Остальные обозначения прежние.
Этот метод особенно удобен при построе-
нии кривых подпора в широких неглубоких
но которому может быть построена кривая
подпора.
Здесь:
hi h, i'a
Фиг. 89
руслах со слабым
уклоном (равнин-
ные реки).
Из приведен-
ных ранее формул
наилучшпе ре-
зультаты даёт
формула Бахме-
тева.
где
3v
= Wn ’
а — коэфициент Кориолиса — 1,54;
ч — кинематическая вязкость жидкости.
ГИДРАВЛИЧЕСКИЙ ПРЫЖОК
При построении кривых спада и Подпора
необходимо избегать чрезмерно больших рас-
стояний (s2— s,) между рассматриваемыми
сечениями, так как приближённость при-
ведённых методов может привести к серьёз-
ным ошибкам.
Высота прыжка h2 — ftj в руслах прямо-
угольного очертания определяется разностью
глубин потока в канале (русле) до прыжка
ht и после прыжка h2, hi и h2 связаны между
собой уравнениями:
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
ЖИДКОСТИ ПРИ ЛАМИНАРНОМ
РЕЖИМЕ
Этот случай был исследован Е. 3. Раби-
новичем, получившим основное уравнение
неравномерного движения при ламинарном
режиме (для призматических русел) в виде:
Рюо^о
dh _ , 1 ₽„«> R
",--10.-----------,
ds . в
1 —-------
“3-вк
где индексы «О» относятся к равномерному
движению, а индексы «к» соответствуют
критической глубине.
При выводе данного уравнения принят
линейный закон гидравлических сопротив-
лений, характеризуемых коэфициентом (3—
так называемым коэфициентом «формы сече-
ния», определяемым, в каждом отдельном слу-
чае, в зависимости от формы поперечного се-
чения потока.
Интегрирование этого уравнения для
случая призматического русла весьма боль-
шой ширины по сравнению с глубиной,
когда влиянием боковых стенок можно пре-
небречь (случай, аналогичный рассмотрен-
ному Брессом для турбулентного режима),
приводит к уравнению:
т]г + 1
(s2 — si) = (Ti2 ~ ’ll) F 1п Гц + 1
тц— 1
где hK—критическая глубина вютока.
Таким образом, высота прыжка, тем боль-
ше, чем глубина потока до прыжка меньше
критической глубины.
В руслах любого
высоты прыжка (ft2 -
дить по графику
прыжковой функ-
ции (200) фиг. 90.
Для этого вычи-
сляют значение
прыжковой функ-
ции 0 при разных
глубинах русла.
Так как значения
прыжковой функ-
ции для сопря-
жённых глубин
одинаковы, то,
зная одну из глу-
бин и, проводя
очертания определение
-hi) удобнее произво-
горнзонталь н у Ю Фиг. 90
прямую через точ-
ку с координа-
той hi до пересечения с другой ветвью
кривой 0, находят /г2. Из фиг. 90 следует,
что минимумы удельной энергии сечения Э
и прыжковой функции 0 поступают при
h=hK.
Длина русла L, на протяжении которо-,
го происходит переход от первой взаимной
глубины hi ко второй /г2, называется дли-
ной прыжка —фиг. 91. Длина прыжка опре-
деляет протяжение усиленного крепления
русла, размеры водобойных колодцев, сте-
нок и т. д.
Длина прыжка L в прямоугольных ка-
налах, по Павловскому, равна
1 tJ —1
+ _1_е/г01п-Ц-,
’ll-!
L = 2,5 [1,9 ;2 - U hK,
где
t _ К с = /!?
?1 ~ hK’ hK
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ
457
По Бахметеву, L зависит от Х= ,
На фиг. 92 приведена кривая зависимо-
L
сти -----т~ как от к (верхняя строка), так
и от (нижняя строка). В трапецеидаль-
ных каналах длина прыжка меньше, чем в
прямоугольных:
где В, и В2 — ширина трапецеидального
русла по верху в сечениях
до и после прыжка.
ческих профилей с плавными кри-
волинейными очертаниями; <р=0,90
при истечении из-под щитов;
b — ширина водослива.
Определение длины отгона прыжка
сводится к нахождению такой длины х, при
которой толщина струи hc возрастает до
глубины h„ —фиг. 94, взаимной с бытовой
глубиной (уровень нижнего бьефа) hs при
высоте прыжка — he. В этом случае,
зная hs (считая 1гб — 1г2), находят глуби-
ну he (считая йв=й,); длину отгона прыж-
ка х вычисляют по формулам, приведённым
выше.
ВОДОБОЙНЫЕ КОЛОДЦЫ И СТЕНКИ
Чтобы предупредить размыв русла пото-
ком, движущимся с большими скоростями
на протяжении длины отгона прыжка, не
Фиг. 95
Потеря удельной энергии потока Э при
образовании гидравлического прыжка рав-
на:
„ _ Й!)3
Глубина потока в сжатом сечении струи,
ниспадающей с водослива, hc-—фиг. 93,
определяется из энергетического уравнения
сопряжения бьефов:
‘ Т° = hc + 2^™% ’
где т0= А +н + г;
—коэфициент скорости; у =г= 0,95 при
истечении через водосливы практи-
допускают его отгона, затопляя прыжок в
водобойных колодцах (фиг. 95), или пре-
граждая поток водобойной стенкой (фиг. 96).
Для вычисления глубины водобойного
колодца а вычисляют hc, определяют взаим-
ную глубину /г2, считая /гх = hc>
откуда
а > h2 — h5.
Фиг. 96
При этом значении а прыжок будет за-
топлен.
Высота водобойной стенки а находится
из условия
а + Нс > /г2,
где Нс — толщина слоя воды, переливаю-
щейся через водобойную стенку.
Длина колодца или расстояние до стен-
ки L для предотвращения выхода части
вальца из колодца или за водобойную стен-
ку (фиг. 97) равна
Lo I ~Г Lf
458
ГИДРОМЕХАНИКА
где / — длина абсциссы струи, ниспадающей
с водослива
' £ — длина прыжка.
Длина ступеней перепадов (фиг. 98)
назначается из условия, чтобы в пределах
каждой ступени происходило максимальное
гашение кинетической энергии потока,
т. е. чтобы глубина потока вблизи конца
каждой ступени была равна hK.
Гидравлический расчёт перепадов коло-
дезного типа (фиг. 99) заключается в рас-
Фиг. 98
Фиг. 99
чёте высоты водобойных стенок и длин
колодцев.
УДАР жидкости
ТЕОРЕМА ЭЙЛЕРА
Основной теоремой, служащей для иссле-
дования действия жидкой струи на различ-
ные препятствия, является теорема Эйлера.
Производная по времени вектора Q ко-
личества движения некоторой системы ма-
териальных точек равняется главному
вектору всех внешних сил, действующих на
систему (фиг. 100):
dt = R»acc + Rno. • <208>
где RMacc—главный вектор внешних массо-
вых сил;
Rnae — главный вектор внешних по-
верхностных сил;
М — масса жидкости, протекающей
через живое сечение в единицу
времени.
В том случае, когда имеет место удар
жидкости о подвижную поверхность, урав-
нение (208) примет вид:
(Qp + Qr)
d dt = RMaec + Rnoe ' (2°9)
где Q„— вектор количества движения струи
__ в переносном движении;
Qr— вектор количества движения струи
в относительном движении.
Имея в виду, что
dQr — _ _ _
dt ~ ^nvn R^ro vro + X Qr , (210)
где Мп и Мг0— секундные массы жидкости
______ __ в относительном движении;
и vn — относительные скорости
жидкости;
X Qr— векторное произведение
вектора переносной угло-
вой скорости £ie и вектора
количества движения струи
в относительном движе-
нии Qr;
уравнение (209) преобразуется в
Mro vro vn + Rмасс + R пав =
— dQe ---------
-Tt^+QeXQr, (211)
В частном случае, когда переносное
движение поступательное и равномерное,
т. е. £2е=0 и = 0, уравнение (211) будет
выглядеть так:
R^ro vro Mrl vrl 4- RMacc 4- Rnoe — 0. (212)
Теорема Эйлера позволяет ‘определить
силу реакции плоскости RT , равную, по
принципу «действие равно противодействию»,
силе, с которой жидкость действует на
плоскость.
Ниже для ряда частных случаев приве-
дены формулы, определяющие силу реакции
УДАР жидкости
459
поверхности RT ; для упрощения предпола-
гается, что трение отсутствует и жидкость
невесома.
УДАР ЖИДКОСТИ О НЕПОДВИЖНУЮ
ПЛОСКОСТЬ
а) Плоскость перпендикулярна оси струи
(фиг. 101):
RT = . (213)
Фиг. 101
Действительная величина RT = ©рш v2„t где,
по Вейсбаху, ср = 0,92 — 0,96; р— плотность
жидкости; <и — поперечное сечение струи.
б) Плоскость образует с осью струи угол а
(фиг. 102):
RT = Mva sin а = рш tij sin а.
УДАР ЖИДКОСТИ О НЕПОДВИЖНУЮ
КРИВОЛИНЕЙНУЮ ПОВЕРХНОСТЬ
а) Поверхность имеет ось симметрии,
совпадающую с осью струи (фиг. 103):
RT = М v0 (1-f-cOS a) =p<i> (1-l-coSa); (214)
при а = 0, RT = 2 шр г, — максимум;
при а = 180°, RT = 0.
Фш. 102
Фиг. 103
б) Поверхность произвольной формы
(фиг. 104). Давление жидкости в этом случае
определяется двумя скрещивающимися си-
лами, приводящими к динамическому винту.
Фиг. 104
Если поток плоский, силы давления при.
водятся или к паре или к силе.
Теорема Эйлера определяет только глав-
ный вектор реакции:
Rx = м у0 (1 + cos a); Ry ~ М г0 sin а;
-ь =2 cosL. (215)
УДАР ЖИДКОСТИ О ДВИЖУЩУЮСЯ
ПОВЕРХНОСТЬ
Если поверхность движется равномерно
и прямолинейно со скоростью ve, то вели-
чина силы реакции поверхности RT будет:
а) для схемы на фиг. 105 )
RT = ро> (у0— vey J
б) для схемы на фиг. 106 J
RT = рш (у0 — wg)s sin а I
в) для схемы на фиг. 107 J
(216)
Фиг. 10b
Фиг. 105
Rx = Mro (v„ cos a, — y, cos a2) )
Rv = Mn (p0 sinat — tij sin a2) /’ >
= p-<o-vn.
ГИДРАВЛИЧЕСКИЙ УДАР
В ТРУБОПРОВОДАХ
Явление гидравлического удара в трубо-
проводах, наблюдающееся при всяком рез-
ком изменении расхода в нём (быстрое
закрытие задвижки и т. п.), проявляется в
ряде чередующихся волн повышенного и
пониженного давления. Повышение давления
при гидравлическом ударе обусловлено за-
тратой кинетической энергии потока жид-
кости на деформацию трубопровода и сжатие
жидкости, упругостью которой в этом случае
пренебрегать нельзя.
Скорость распространения ударной волны
определяется формулой Жуковского
(218)
где А" —модуль упругости жидкости;
р — плотность жидкости;
Е— модуль упругости материала стенок
трубы;
е—толщина стенок трубы;
D —внутренний диаметр трубы.
460
ГИДРОМЕХАНИКА
Если считать материал стенок абсолютно
неупругим (Е = оо), то выражение
представляет формулу для скорости звука в
жидкости.
К
Значения величины и Ь для воды и
наиболее часто встречающихся материалов
труб приведены в табл. 65.
Таблица 65
К
Значения — и Е для воды и наиболее часто
Е
встречающихся материалов труб
График зависимости скорости С от отно-
К D
шения £ • — (фиг. 108) показывает, что
скорость распространения упругих возму-
щений в трубопроводе по сравнению с
С м/сек
обычными скоростями в гидравлике весьма
велика, на что в значительной мере оказы-
вает влияние упругость стеноктрубопровода.
Скорость распространения ударной вол-
ны в воде:
9 900
С = ---у--- —м/сек,
у 48,3 +а ~
(219)
где а = 0,5 для стали и железа;
а = 1 для чугуна и меди;
а = 5 для свинца.
Величина ударного давления Др = р — ра
будет зависеть от продолжительности за-
крытия задвижки / и длины трубопровода L:
2L
1) t < (прямой удар).
Др = рС (va-v), (220)
где и0 и v — скорости течения в трубопро-
воде до и после закрытия задвижки.
В частном случае при и = 0 (полное за-
крытие задвижки)
Др = рСг„ (221)
(формула Жуковского).
Л. С. Лейбензон, учитывая неравномер-
ность распределения скоростей по сечению
трубы, предложил формулу
Др = рСго^И-1) > (221')
одинаково пригодную как для турбулент-
ного, так и для ламинарного режима.
Коэфициент V] в этой формуле учитывает
неравномерность распределения скоростей и
имеет следующие значения:
для ламинарного режима *] = 3"»
для турбулентного режима:
а) в гладких трубах — т; яа 0,015,
б) в обыкновенных трубах—т; ~ 0,035.
По Парному И. А., при и = 0 величина
ударного давления меняется в зависимости
от потери на трение в трубопроводе hr. На
фиг. 109 и ПО показано нарастание ударно-
го давления в зависимости от величины а =
= Ар
рО/
На графиках охвачен интервал времени
Ct
0 <х ~2L < 2-
2L
2) t > -q (непрямой удар).
Ввиду того что отражённая волна разря-
жения пробежит до задвижки за время г0=
2L
= •£- , величину давления, найденного по
вышеприведённым формулам, следует умень-
шить на величину избыточного давления,
имевшего место в момент t0.
2L
Если t >> -g- , то упругим процессом
вообще можно пренебречь.
К мерам,предохраняющим трубопроводы
от гидравлического удара, относятся:
а) медленное закрытие задвижки; если
задано допустимое повышение напора hg
(обычно 20%), то время закрытия задвижки
.. L ' v<> /77,
g (hg Но) V
где Нв—первоначальный напор;
б) устройство воздушных колпаков;
в) устройство предохранительных клапа-
нов.
ИСТЕЧЕНИЕ НЕСЖИМАЕМЫХ ЖИДКОСТЕЙ ПРИ ПОСТОЯННОМ УРОВНЕ
461
ИСТЕЧЕНИЕ НЕСЖИМАЕМЫХ ЖИДКОСТЕЙ ПРИ ПОСТОЯННОМ УРОВНЕ
КОЭФИЦИЕНТЫ СЖАТИЯ, СКОРОСТИ
И РАСХОДА
Вследствие сжатия, которое испытывает
струя вытекающей несжимаемой жидкости,
можно представить, что истечение происхо-
дит не через отверстие площадью ш (фиг.111),
а через сечение шс (сечение струи). Отно-
О)с
шение е = — называется коэфициентом сжа-
тия. Так как при истечении жидкость пре-
одолевает ряд гидравлических сопротивле-
ний и, кроме того, имеет место неравно-
мерное распределение скоростей по сечению
трубы, то действительная скорость истече-
ния у меньше теоретической ит ;
где а—коэфициент Кориолиса;
5 — коэфициент сопротивления.
Коэфициент учитывающий уменьшение
скорости истечения, называется коэфициен-
том скорости.
Формула расхода при истечении:
(222)
Q = гсрш у = [лю v,
Q
где и гср = ст— — коэфициент расхода.
Ут
Фиг. 111 Фиг. 1 12
СЖАТИЕ ПОЛНОЕ И НЕПОЛНОЕ,
СОВЕРШЕННОЕ И НЕСОВЕРШЕННОЕ
Сжатие струи будет совершенным, если
истечение происходит из отверстия а в дне
сосуда,в котором (фиг. 1*1'2) Г>3т и /1>3н.
Сжатие будет неполным, если одна или
несколько сторон отверстия имеют напра-
вляющие стенки. В угловом отверстии струя
сжата лишь с двух сторон, в среднем— b
с'трёх сторон.
В отверстиях ей/ струя сжата с одной
стороны, в отверстии d— с двух сторон.
В зависимости от характера сжатия коэ-
фициент сжатия е принимает различные
численные значения.
ИСТЕЧЕНИЕ ИЗ МАЛЫХ ОТВЕРСТИЙ
В ТОНКОЙ СТЕНКЕ
Малыми отверстиями называются отвер-
стия, вертикальный размер которых мал по
сравнению с напором жидкости. Если и
Р2 (фиг. 111)—соответственно давления на
свободной поверхности жидкости и на вы-
ходе из отверстия, Н — глубина погружения
центра тяжести отверстия, yj — скорость
жидкости в сосуде, 7 — удельный вес жид-
кости, то скорость истечения
Частные случаи:
1) скоростью Bj можно пренебречь (раз-
меры отверстия малы по сравнению с попе-
речным сечением сосуда):
2) у, незначительно, Р, = Р2:
в = у У 2gH. (225)
Величина расхода Q в общем случае
равна:
На величину коэфициента скорости
главным образом влияет коэфициент Корио-
лиса а, а потому с достаточной точностью
можно в этом случае принимать ср = 1 : У а.
При совершенном сжатии коэфициент
расхода ц для малых круглых и квадрат-
ных отверстий может быть принят равным
(л = 0,625.
Для несовершенного сжатия:
для круглых отверстий 1
~ (14* У) > I
для прямоугольных отверстий <’• (2271
!Ло = (1 + ^2)’ I
где коэфициенты )
О) 1
У =-= 0,0456 (14,8 Ш1 —?),
k ю ' j (228)
= 0,076 ( 9 “i-l) I
(ш — площадь отверстия; юх—площадь со-
суда).
Значения у и (с», вычисленные по фор-
мулам (228), приведены в табл. 66.
Таблица 66
Значения коэфициентов ki и ка
0,05 0,01 0,15 0,20 0,25 0,30 0,35 0,40
0,007 0,014 0,023 0,034 0,045 0,059 0,075 0,092
ка . . 0,009 0,019 0,030 0,042 0,056 0,071 0 ,088 0,107
Продолжение табл. 66
0,45 0,50 0,55 0,60 0,70 0,80 0,90 1,00
кх . . fc# . > 0,112 0,128 0,134 0,152 0,161 0,178 0,189 0,208 0,260 0,278 0,351 0,365 0,471 0,473 0,631 0,608
462
ГИДРОМЕХАНИКА
В случае неполного сжатия коэфициент
расхода р. может быть определён по формуле
, ( п
И = И ( 1 + к р
(229)
где р— коэфициент расхода при полном
сжатии;
п — длина периметра, испытывающего
сжатие;
Р—полный периметр отверстия;
к — некоторый коэфициент, величина
которого берётся в зависимости от
формы отверстия; для круга к =
= 0,128, квадрата к =0,152, прямо-
угольника к = 0,157 (отношение высо-
ты к ширине 1 : 2).
Все приведённые выше значения коэфи-
циентов расхода относятся к случаю турбу-
лентного режима.
При истечении вязких жидкостей через
отверстия в тонкой стенке коэфициент рас-
хода (л зависит от числа Re. Значения р. =
= j (Re) представлены на фиг. 113.
А
Траектория струи. Уравнение траектории
центра сечения струи, вытекающей из отвер-
стия в наклонной стенке (фиг. 114)
у = х tg 0 + 2 • (23°)
2v ср cos2 О
ИСТЕЧЕНИЕ ИЗ БОЛЬШИХ ОТВЕРСТИЙ
В ТОНКОЙ СТЕНКЕ
У больших отверстий отношение верти-
кального размера к напору значительно.
В общем случае (отверстие произвольной
формы) расход Q определяется уравнением
(фиг. 115)
jy
QsJ 7 6 dh.
н„,
(232)
Интеграл уравнения (232) можно предста'
вить также в виде
/ 1 \
Q=^r2gH0(l +——2 • (233)
\ о to Hq/
I,
где 1 = J by2dy— момент инерции площади
7,
отверстия относительно горизонтальной
оси, проходящей через центр тяжести.
Оиг. 115
Для прямоугольного отверстия шириной
b =const
Q= ^6/2 g (Н^-Н?),
0 f ^0*1 1
или, пренебрегая скоростью подхода,
Q = |_pb/2g (н’/«_н’/з). (235)
Для вертикальной стенки (0 = 0, cos 0= 1)
gx2
2гср‘
(231)
Выражая Н1 и Нг через глубину погруже-
ния центра тяжести отверстия — Но, вместо
последнего уравнения получим:
г______ ( аг \
Q = рсо У 2gH0 ^1 — 96 Н2 ) , (236)
где а— высота отверстия.
Анализ последней формулы показывает,
что для отверстий, у которых а или d < Но,
можно пользоваться формулами, приведён-
ными для малых отверстий (с точностью
до 1%).
Значения коэфициента расхода р в этом
случае берутся для прямоугольных отвер-
стий по табл. 67, а для квадратных — по
табл. 68.
ИСТЕЧЕНИЕ НЕСЖИМАЕМЫХ ЖИДКОСТЕЙ ПРИ ПОСТОЯННОМ УРОВНЕ
463
Таблица 67
Значения коэфициента |х для прямоугольных
отверстий в зависимости от их размеров и глубины
погружения
Ширина отверстия в м
1 Е ад b - 0,20 1 b - 0,60
Q.X ® О я £ Е X © высота отверстия в м
1 а 4; а 0,01 0,02 0,03 0,05 0,10 0,20 0,02 0,20*
0,10 0,667 0,655 0,637 0,630 0,611 0,592 0,639 0,602
0,20 0,655 0,649 0,634 0,631 0,615 0,598 0,635 0,605
0,30 0,650 0,645 0,632 0,630 0,616 0,600 0,633 0,607
0,40 0,646 0,642 0,631 0,629 0,617 0,602 0,631 0,607
0,50 0,643 0,640 0,631 0,628 0,617 0,663 0,630 0,607
0,70 0,638 0,637 0,629 0,627 0,616 0,604 0,628 0,607
0,80 0,635 0,635 0,628 0,626 0,616 0,605 0,628 0,606
0,90 0,632 0,634 0,627 0,625 0,615 0,605 0,627 0,606
1,00 0,629 0,632 0,627 0,625 0,615 0,605 0,626 0,605
1,50 0,617 0,620 0,621 0,619 0,611 0,602 0,623 0,602
2,00 0,613 0,613 0,613 0,613 0,607 0,601 0,620 0,602
3,00 0,60b 0,608 0,607 0,606 0,603 0,601 0,615 0,601
Таблица 68
Значения коэфициента расхода р. при истечении из
квадратных отверстий в зависимости от величины
напора и ширины отверстия
Напор в центре от- верстия в м Ширина квадратного отверстия в м
0,01 0,02 0,03 0,06 0,12 0,18
0,20 0,648 0,624 0,617 0,605 0,598
0,30 0,636 0,619 0,613 0,605 0,601 0,599
0,50 0,628 0,618 0,610 0,605 0,602 0,601
1,00 0,620 0,610 0,607 0,605 0,604 0,603
1,50 0,618 0,609 0,606 0,604 0,603 0,602
2,00 0,614 0,608 0,605 0,604 0,603 0,602
3,00 0,611 0,606 0,604 0,603 0,602 0,601
6,00 0,605 0,603 0,602 0,602 0,601 0,600
15,00 0,601 0,601 0,600 0,600 0,599 0,599
30,00 0,598 0,598 0,598 0,598 0,598 0,598
Для практических расчётов Павловский
рекомендует брать следующие значения коэ-
фициента расхода р.:
1. Отверстия средних размеров
со сжатием струи со всех сто-
рон при отсутствии направля-
ющих стенок ................ 0,65
2. Отверстия больших размеров
с несовершенным, не всесто-
ронним сжатием................. 0,70
3. Донные отверстия со значи-
тельным влиянием бокового
сжатия ........................0,65—0,70
4. Донные отверстия с умерен-
ным влиянием бокового сжа-
тия ...........................0,70—0,75
5. Донные отверстия с плавными
боковыми подходами............. 0,80—0,85.
6. Исключительные случаи весь-
ма плавных подходов воды к
отверстию со всех сторон . , 0,90
В табл. 69 и 70 даны значения коэфи-
циента расхода для искусственных сооруже-
ний в дорожном полотне по нормам МПС.
Таблица 69
Значения коэфициента расхода в зависимости от
типа опор малых мостов и труб
Тип моста или трубы р
Мосты с конусами и трубы неза- висимо от их очертания, с расхо- дящимися откосными крыльями . . 0,90
Мосгы без конусов и трубы неза- висимо от их очертания, без расхо- дящихся откосных крыльев, а так- же трубы, срезанные в плоскости Откоса насыпи 0,80
Трубы с выпущенными из тела насыпи концами, а также арочные мосты с затопленными пятами . . 0,75
Таблица 70
Значения коэфициента расхода для мостов разных
отверстий при коэфициеите скорости •» 0,95
Отверстия в м Коэфициент сжатия s Коэфициент расхода рЛ
4 0,80 0,80
6 0,85 0,80
10 0,90 0 85
20 0,95 0,90
200 1,0и 0,95
ИСТЕЧЕНИЕ ЧЕРЕЗ ЗАТОПЛЕННОЕ
И ПОЛУЗАТОПЛЕННОЕ ОТВЕРСТИЯ
В случае истечения через затопленное
отверстие (истечение под уровень) формулы
и коэфициенты одинаковы е таковыми при
истечении в атмо-
сферу.
Рассматривая рас-
ход через полуза-
топленное отверстие
(фиг. 116) как сумму
расходов—расхода Q
через незатопленную
часть высотой (a—t)
и расхода Q через
затопленную часть
высотой t, получают
известную формулу:
Q = (Л b rrg[ j ( 2a/1- Н?)+« У Z ] , (237)
где b — ширина отверстия.
ИСТЕЧЕНИЕ ЧЕРЕЗ НАСАДКИ
Насадками называются короткие трубки
[£<(3^-4) </] разнообразных форм и раз-
меров, через которые происходит истечение.
Коноидальные насадки (фиг.117)по форме
выходящей струи имеют наибольшие коэфи-
циенты расхода значения которых в зави-
симости от величины напора приведены в
табл. 71.
* Значения в этой графе соответствуют от-
верстию в доске толщиной 5 см.
1 Коэфициент расхода р. показан с округлением
до О,О5.
464
ГИДРОМЕХАНИКА
Таблица 7!
Значения коэфициентов расхода и скорости для
коноидальных насадок
Напор Н в м 0,02 0,05 3,5 17 103
И == ¥ 0,959 0,967 0,975 0,994 0,994
Цилиндрические насадки Борда и Вентури
(фиг. 118). При L < (3-1-4) d коэфициент
сжатия в = 1, р = '?. Коэфициент скорости ср
в этих насадках несколько меньше, чем в
Фиг. 118
Фиг 117
других, вследствие потери напора на расти-
ренне струи в насадке. В табл. 72 приведены
значения коэфициентов е, ср и р.
Таблица 72
Значение коэфициентов скорости, сжатия и расхода
насадок Вентури и Борда
Тип насадки
Вентури............... •
Борда:
с толстой стенкой . . •
с тонкой стенкой . . • •
0,82
0,82
0,71
1,0 0,82
1,0 0,82
1,0 0,71
Влияние угла наклона оси насадки Вен-
тури на величину коэфициента расхода р
может быть выражено данными, приведён-
ными в табл. 73.
Таблица 73
Зависимость коэфициента расхода от угла,
образуемого осью иасадки Вентури с нормалью
к поверхности резервуара
1 0“ 10° 20” 30° 40° 50° 60° |
1* 0,815 0,799 0,782 0,764 0,747 0,731 0,712 | 1
Напор, при котором в сжатом сечении
насадки давление равно давлению паров
жидкости при данной температуре, назы-
вается критическим напором. Напор более
критического делает истечение аналогичным
истечению через отверстие в тонкой
(струя не касается стенок насадки):
н = —. hy
КР 1 —в ~2^Г’
стенке
(238)
где упругость паров в метрах столба
жидкости.
Конические насадки (фиг. 119). Кониче-
ские насадки различают сходящиеся и рас-
ходящиеся. В сходящихся конических на-
садках с увеличением угла конусности коэ-
фициент сжатия в падает, а коэфициент
скорости tp растёт. Максимальный коэфи-
циент расхода ц соответствует углу конус-
ности 13°23'.
В табл. 74 приведены средние значения
коэфициентов скорости и расхода для кони-
ческих сходящихся насадок.
Таблица 74
Значения коэфициентов расхода, скорости и сжатия
для конических сходящихся насадок
Углы 0 0° 2° 3° 4° 5° 6° 8° 10°
Коэфици- ент расхо- да р. ... 0,829 0,873 0,892 0,909 0,920 0,925 0 931 0,937
Коэфици- ент ско- рости ср 0,829 0,873 0,892 0,909 0,920 0,925 0,933 0,949
Коэфици- ент сжа- тия г . . 1,00 1,00 1,00 1,00 1,00 1,00 0,998 0,987
Продолжение табл. 74
Углы 0 12° 13°23' 16° 25° 30° 35° 45°
Коэфици- ент расхо- да [х ... 0,942 0,946 0,938 0,908 0,896 0,883 0,857
Коэфици- ент ско- рости & 0,955 0,963 0,969 0,974 0,975 0,977 0,983
Коэфици- ент сжа- тия е . . . 0,986 0,982 0,968 0,932 0,919 0,904 0,857
В расходящихся конических насадках
коэфициент расхода имеет меньшую величину
по сравнению с насадками, упомянутыми
выше. Для насадок длиной I < 10 см коэфи-
циент расхода* (линейные размеры в м)-.
для острых входных кромок
и = 0,184 п
для закруглённых входных кромок (239)
!* = 0,287 nV/;
Коэфициент п, зависящий от угла конус-
ности, берётся по табл. 75.
Таблица 75
Значения коэфициента п в формулах (239)
Угол 6 | 1° ! 2° 3" 4° 5°
Коэфициент п| 8,18 8,83 9,53 10,2 10,63
Сочетания сходящихся и расходящихся
насадков наиболее выгодны в отношении воз-
ИСТЕЧЕНИЕ НЕСЖИМАЕМЫХ ЖИДКОСТЕЙ ПРИ ПЕРЕМЕННОМ УРОВНЕ
465
Гидравлические характеристики отверстий
Таблица 76
Род отверстия Коэфициент скорости Коэфициент j расхода р. Скоростной напор Х)ъ j 2? Но Работоспо- собность струи Q 7 н0 Коэфициент сопротивле- ния £ Примечание
Круглое отверстие в тонкой стенке Цилиндрическая наружная насадка (Вентури) 0,97 0,82 0,62 0,82 и,95 Но 0,67 Н 0,59 А 0,55 А 0,06 0,5 А = у т У 2g • Н30'2
Коническая сходящаяся насадка при угле конусности 13°40* ..... 0,96 0,96 0,93 Н„ 0,88 А с 0,09 { 1 < 1 -Hq/2 Ас < А
Коническая расходящаяся насадка 0,48 0,48 0,23 Нв 0,11 А р 3,3 Ар = 7 У 2? • нЗ/2 А > А
Насадки коноидальные (по форме струи) 0,93 0,98 0,96 Н„ 0,94 А с 0,04 Р А < А с
Внутренний цилиндр (насадка Бор- да) 0,71 0,71 0,5 0,36 А 1
В табл. 77 приведены значения коэфи-
циентов расхода р в зависимости от диа-
метра спрыска для брандспойтов, подобным
изображённому на фиг. 121.
Таблица 77
мощности увеличения коэфициента расхода м-
(фиг., 120).
Фиг. 120
Зависимость коэфициентов расхода и скорости от
диаметра спрыска
d с ВММ 19 22 25 30 32 35
Р- “ ¥ 0,983 0,982 0,980 0,976 0,971 0,959
В табл. 76 даны гидравлические характери-
стики отверстий с насадками и без них.
НАКОНЕЧНИКИ ПОЖАРНЫХ РУКАВОВ
Пожарный рукав кончается брандспой-
том, состоящим из ствола, конической на-
Фиг. 121. Насадок пожарный
садки и спрыска (цилиндрическая трубка,
обеспечивающая параллельность выходящих
струй).
Теоретическая горизонтальная дальность
полёта струи при наклоне наконечника к
горизонту под углом 9 определяется из
уравнения траектории (230) при у — 0:
v ! • sin 2 0 .
х = ------------ >
g
* max = у (при 6 =45°). (240)
Высота боя пожарных струй равна
Л = <241>
где Не — полный напор в начале ствола;
0,00025
п = d + (10 d)s ’
d — диаметр спрыска в м.
ИСТЕЧЕНИЕ НЕСЖИМАЕМЫХ ЖИДКОСТЕЙ ПРИ ПЕРЕМЕННОМ УРОВНЕ
ИСТЕЧЕНИЕ ПРИ ПЕРЕМЕННОМ УРОВНЕ
ПОД ПЕРЕМЕННЫЙ УРОВЕНЬ
В общем случае при переменных площа-
дях поперечных сечений резервуаров «>, и ш,
(фиг. 122) время понижения горизонта жид-
кости от первоначальной разности уровней Н
в резервуарах до разности h равно
н
t = — 1_( Hl ' (242)
рсо У2 g Jwi+w2 Уft
В частном случае призматических резер-
вуаров (фиг. 123) (coj — const; оа — const):
2 со, • со2 (ГН — V^h)
t — —-------—--------i__ - . (243)
(®i + ®а) Р® У 2 g
Фиг. 122
30 Том I
466
ГИДРОМЕХАНИКА
Время выравнивания уровней
2а>1 а>2 Ун
(й1+ й,) рй У2 g
(244)
где /—площадь поперечного сечения пат-
рубка.
Значения коэфициента расхода р в зави-
симости от кинематического коэфициента
вязкости приведены в табл. 78 (по Лейбен-
зону Л. С.).
Таблица 78
Горизонт выравнивания
Й! Н
У = «1 + «2 ‘
Ориентировочные значения коэфициента расхода
р. в зависимости от кинематического коэфициента
вязкости
v в см* 1 сек 0,01 — 0,1 | 0,69 | 5,5
0,61 | 0,34 | 0,24
б) Истечение через трубопровод (по Яб-
(245)
лонскому В. С.):
ВРЕМЯ ОПОРОЖНЕНИЯ РЕЗЕРВУАРОВ
Для тех случаев истечения, когда изме-
нение скорости совершается весьма медленно
и представляется возможным рассматривать
движение как установившееся, справедливы
следующие формулы:
Основное уравнение (фиг. 124)
Если Я = / (z) = const (призматический
резервуар), то
ИСТЕЧЕНИЕ ИЗ ЖЕЛ.-ДОР. ЦИСТЕРН
а) Истечение через короткий
Р. - Р2.
патрубок
Фиг. 125
Время опорожнения (фиг. 125)
i 3 н/ |/og ’
(248)
где L — длина цистерны;
D —диаметр цистерны;
/г0 — дополнительный напор;
Ei и Fj — полные эллиптические интегралы.
Значения функции <р0, стоящей в фигур-
/ь
ных скобках, в зависимости от д даны в
табл. 79.
Таблица 79
~ Ло
Значение функции <рв в зависимости от --
th D 0 0,5 1 2 3 5
•Ро 1 0,6 0,5 0,38 0,31 0,24
в) По Парному И. А., истечение вязких
нефтепродуктов из жел.-дор. цистерн может
протекать при двух режимах движения в
трубопроводе — турбулентном в начале и
ламинарном в конце.
Время истечения при турбулентном ре-
жиме
л LD г_____________
tr ~ 2р/ V2g + D ~
- Vt^+^p]. (250)
Время истечения при ламинарном режиме
32 ч/ОД Л0 + 2кр
— 1п —к---------• (251)
Полное время истечения Т — tT 4- Ц
Здесь zKp— высота нефтепродукта в цистер-
не, отвечающая переходу турбу-
лентного режима в ламинарный
2кр^ ~ h° (252)
I —приведённая длина сливного тру-
бопровода с диаметром d;
ч — кинематическая вязкость нефте-
продукта;
и. — коэфициент расхода;
ReKp = 2 300.
Если истечение совершается только при
турбулентном режиме, то zp„ — 0, если
только при ламинарном, zKp= D.
ВНЕШНЕЕ ОБТЕКАНИЕ ТЕЛ
467
ВНЕШНЕЕ ОБТЕКАНИЕ ТЕЛ
ОПРЕДЕЛЕНИЯ
В общем случае сопротивление обтекае-
мого тела складывается из:
а) сопротивления трения;
б) сопротивления формы (давления), обу-
словливаемого возмущающим действием вяз-
кости на спектр линий тока (происходит от-
рывание пограничного слоя);
в) сопротивления деформации, представ-
ляющего собой ту энергию деформации,
которая преобразуется в теплоту вдали от
тела. В отличие от сопротивления трения
сопротивление деформации имеет место при
очень небольших скоростях и размерах тела
или для очень вязких жидкостей (при/?е<<1);
г) волнового сопротивления (если тело
движется на границе двух жидкостей), об-
условливающего потерю энергии на волно-
образование.
Сопротивление, которое оказывает жид-
кость движущемуся телу, таким образом,
зависит от формы и положения тела, от раз-
меров его, от скорости движения и рода
жидкости.
Таблица $0
Коэфициенты сопротивления различных тел
а) Пространственное обтекание
ОБЩИЙ ЗАКОН СОПРОТИВЛЕНИЯ
Когда одновременно действуют силы
инерции, вязкости, тяжести и имеет место
сжимаемость, закон сопротивления выра-
жается в виде
р и'
W = / (Re, Fr, Ma) F
(253)
где W — сопротивление равномерно движу-
щегося тела;
F—проекция тела па плоскость, пер-
пендикулярную направлению тече-
ния;
р — плотность жидкости:
v — скорость движения тела относитель-
но невозмущённой жидкости;
f (Re, Fr, Ma) ~ с — коэфициент сопроти-
вления;
Re — критерий (параметр) Рейнольдса;
Fr — критерий (параметр) Фруда;
v
Ма— — ; Ма — критерий Маха;
со
с0— скорость звука в не-
возмущённой жидкости.
V
При — 1 сжимаемостью можно прене-
св
бречь.
Тогда
с = / (Re, Fr).
Круговой Цилиндр,
продуваемый парал-
лельно образующей
Кру, . И ЦИЛИНДР,
продуваемый пер-
пендикулярно обра-
зующей
— = 8,8 • 101
V
0,91
0,85
0,87
0,99
0,63
0,68
0,74
0,82
0,98
1,20
Теоретическое определение с = / (Re, Fr)
при современном состоянии теории не пред-
ставляется возможным.
В табл. 80 приведены коэфициенты
сопротивления различных тел.
Полушар (без ог-
раничивающей плос-
кости)
Выпуклый
Вогнутый
0,84
1,33
30*
468
ГИДРОМЕХАНИКА
Продолжение табл. 80
Продолжение табл. 80
Конус (с плос-
костью основания)
j-e— Q —sj
Решётчатая ферма
(а> — сумма площа-
дей отдельных
стержней)
Угловое отвер-
стие 60°
Угловое отвер-
стие 30°
От 1,5
ДО 1,7
б) Плоско-параллельное течение
Круговой ЦИЛИНДР
для — < 0,2
С
(F — I • d)
8 гс v___
(= " vd~'
2,0—ln —
Проволока
0,3
до 0,4
1,2
Около 1,1
Пластинка с
краями, закруг-
лёнными по дуге
окружности
— = 0,0333
г
— - = 5 - 10“
~ = 2 . 10"
Клинообразная
пластинка
0,0417
. 0,025
0,53
0,46
'Профили раз-
личной толщины:
2 - 0,и55
0,125
е,197
10"
0,193
0,096
0,080
С
F = bd
Профилированная vd о 1пз I
проволока ~ о • io u,d
до 10* I до 0,4
Профилированная
стальная труба
(каплеобразный
профиль)
— > прибл. 5*10*
v
0,2
0,1
На фиг. 126 приведены коэфициенты соп-
ротивления с в зависимости от числа Re для
цилиндра (7), пластинки (2), сплюснутого эл-
липсоида (5), шара ('7) и удлинённого эллипсо-
ида (5).
Фиг. 126
Если полное сопротивление состоит в
основном из сопротивления трения, то для
гладких пластинок, параллельных направле-
нию потока:
а) при Re < 5 - 105 (ламинарный ничный слой) 1,327* С = V"Re ’ погра- (264)
б) при Re > 5 . 10е (турбулентный ничный слой) 0,072* с = 5>— 5 у Re погра- (255)
в) при 5 • 105 < Re < 5 • 10е
0,074 1 700* с~ 5_— (256)
у Re Re
Если полное сопротивление—в основном
сопротивление деформации, коэфициент со-
* В формуле (253) в этом случае F — площадь
пластинки.
ДВИЖЕНИЕ ГРУНТОВЫХ ВОД
469
противления с пропорционален первой сте-
пени скорости, т. е.
а а
с== vl = Re’
(257)
где а — постоянный коэфициент;
I — какая-либо характерная длина тела.
В случае волнового сопротивления фор-
мулу (253) применяют в виде
PV 2
W = с • /2 • i (258)
где I — длина тела.
Коэфициент с = / (Fr).
Для глубокой боды ( t > -^
V2 gL
с = a gj- + b cos , (259)
где а и b — постоянные, зависящие от формы
тела;
L — длина, на которой образуются
волны.
gL 2п+1
При ==-------g--- с имеет минимум,
gL
при 7>2 = п— максимум; п — целое число.
Для мелкой воды (t < I) скорость волн
lz = Kgt (260)
и не зависит от длины волны (t — глубина
воды).
При v х gt наблюдается сильно выра-
женный максимум сопротивления; при
v > Vgt сопротивление несколько меньше,
чем при той же скорости на глубокой воде.
ДВИЖЕНИЕ ТЕЛ В ВОСХОДЯЩЕМ
ПОТОКЕ ЖИДКОСТИ
Все нижеприведённые формулы даны для
случая обтекания шара диаметром d с
удельным весом потоком жидкости в трубе
диаметром D или в межтрубном пространстве
труб диаметром и Е>2.
Под критической скоростью восходящего
потока понимают такую скорость течения,
при которой тело остаётся взвешенным в
жидкости и не падает.
Число Re в случае обтекания шара выра-
жается через диаметр шара d и скорость
потока жидкости v.
1. Формула Стокса (ламинарный режим;
Re < 2):
18ч f 1 J ’
ч—кинематическая вязкость, ат — удель-
ный вес жидкости.
Границы применения формулы:
а) движение внутри трубы
D < 2 300’;
б) движение в затрубном пространстве
d 2
Dt— < 2 300 '
2. Формула Риттингера (турбулентный
режим; Re > 300):
= <262>
где к = j/";
—коэфициент формы, определяемый
из опыта.
Прн Re > Ю 000 коэфициент ср « 0,5.
3. Формула Аллена (промежуточный ре»
жим; 2 < Re < 300):
(263)
ДВИЖЕНИЕ ГРУНТОВЫХ ВОД
ОПРЕДЕЛЕНИЯ
Грунтовыми содами называются воды,
насыщающие пористые пласты, подстилае-
мые водонепроницаемым пластом.
Движение грунтовых вод является част-
ным случаем фильтрации — движения одно-
родной жидкости в пористой среде.
Рассматривая движение грунтовых вод,
под термином «грунтовая вода» подразуме-
вают воду, которая заполняет все поры
грунта и способна передвигаться под дей-
ствием сил тяжести («гравитационная вода»).
Движение грунтовых вод может быть на-
порным (артезианские колодцы) и безнапор-
ным (фильтрация через тело плотины и т. д.).
Если W — объём грунта, w — объём содер-
жащихся в нём частиц, 2 — площадь сечения
выделенного объёма грунта и а — площадь,
занимаемая сечениями частиц грунта, то
IV — w
т = —— называется коэфициентом по-
S — и
розности, а п — —о— — коэфициентом по-
ристости.
ОСНОВНОЙ ЗАКОН ФИЛЬТРАЦИИ
На основе тщательно проведённых много"
численных опытов Дарси установил основ-
ной закон фильтрации, который выражается
уравнением:
d!I
Q = Ke>I = — Ка>
или 1, (261)
z/U !
470
ГИДРОМЕХАНИКА
гдг К—коэфициент фильтрации, зависящий
от свойств пористой среды и свойств
жидкости; имеет размерность ско-
рости;
Q — расход;
и — скорость фильтрации;
г dH
1 =——гидравлический градиент;
Н — потеря напора на пути филь-
трации L;
— площадь поперечного сечення по-
тока.
Если ввести понятие о коэфициенте про-
ницаемости Кп, который связан с коэфи-
циентом фильтрации соотношением
К _ (265)
7 “ Р
(р. — абсолютная вязкость жидкости), то за-
кон Дарси можно представить в виде
„ _ кп dP (266)
v- у" • 4L-
Размерность коэфициента проницаемости
- (с^).
Единица проницаемости:
-ggj \ 105 сл/2 « 10-8 cmz = 1 Дарси.
С введением понятия о Кп коэфици-
ент пропорциональности в формуле Дарси
оказывается расщеплённым на две констан-
ты:— Кп и fi, одна из которых зависит толь-
ко от свойств пористой среды, другая—толь-
ко от свойств жидкости.
Критерии существования закона Дарси.
При больших скоростях фильтрации закон
Дарси может нарушаться вследствие: а) влия-
ния сил инерции, которыми пренебрегают
при выводе закона Дарси; б) появления тур-
булентности.
По Павловскому, фильтрационный поток
в однородном грунте переходит из ламинар-
ного в турбулентный при
1
Re«P = (0,75 т + 0,"23У ' V ’ (2б7>
кде d — диаметр зёрен грунта;
ч»—кинематическая вязкость жидкости.
Для воды ReiP »7-?9.
Для неоднородных грунтов, по Щелка-
чёву В. Н.
10
Re‘.p = m2,3 М
ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
ГРУНТОВОГО ПОТОКА
Невозможность учесть движение жидкости
в каждой из отдельных пор заставляет ввести
понятие фиктивной жидкости, сплошь за-
полняющей каждую точку пространства вне
зависимости от того, чем занята эта точка
в действительности: частицей грунта или
воды.
При замене движения действительной
жидкости фиктивной должны быть удовле-
творены следующие основные условия:
1) произведение скорости фильтрации на
величину элементарной площадки должно
равняться действительному расходу фильт-
рующейся через эту площадку жидкости;
2) плотность фиктивной жидкости долж-
на быть равна плотности действительной
жидкости.
Пренебрегая силами трения внутри самой
жидкости, которые будут незначительны по
сравнению с силами сопротивления грунтово-
го скелета, рассматриваемыми в этом случае
как силы объёмные, можно применить к
грунтовому потоку уравнения движения
идеальной жидкости (уравнения Эйлера).
Если внести компоненты сил сопротивле-
ния грунтового скелета
х'кГр °х' y, = ~T^?Vy’
2 = - р
в уравнения Эйлера наряду с компонентами
силы тяжести, то уравнения (26) приводятся
к уравнениям движения грунтовых вод
Н. Е. Жуковского:
dy*- ди*
+ p* dx + vv “dy +
V_
dvx
dt
, dvx A
+ Vz dz p
di/j, dvy
to + °У dy +
do,,
dt
dvy
'г dz =
dv~
, dp
Kn "y + dy
•jvz dvz dvz
~dt+Vx to + vyfy +
.(268)
Пренебрегая
виду, что
силами инерции и
)
имея в
d_ (РЛ dr p_ \dH j
dx J dx\ t J to I
d /j) \ _ d ^p _ \ dH f , (269)
dy \ t J = dy v t ~ 2 J dy j
I
можно уравнения H. E. Жуковского пред-
ставить в виде:
„ _ • 7 dH_ 1
Vx ~ “рГ ’ dx
Кп - у dH
°У=~~ ' ду
„ _ V 7 dHJ
— • dZ j
Система этих уравнений представляет
закон Дарси в обобщённом виде.
Из уравнений (270) следует, что
Н = / (х, у, Z). (271)
Последняя функция носит название на-
порной функции.
ДВИЖЕНИЕ ГРУНТОВЫХ ВОД
471
Обозначив —— уН = Ф, можно систему
уравнений (270) записать иначе:
ОФ)
Vx^~di |
оф ;
vy “ ~ ьу г <272)
дФ I
Vz —dz 1
. К„
Функция Ф = Ф (х, у, z) = —Д уН есть
Р
потенциал скоростей. Таким образом дви-
жение грунтовых вод в пределах закона
Дарси является потенциальным. Следова-
тельно, задача о движении грунтовых вод
сводится к решению уравнения Лапласа:
д2Ф д2Ф д2Ф
дх2 + ду2 + dz2 = О’
(273)
Для грунтовых вод границами области
движения могут быть (фиг. 127):
Фиг. 127
а) непроницаемая граница ВС; скорость
фильтрации в любой точке направлена по
касательной, т. е.
если известно уравнение граничной кривой
F (х, у, z) — 0, то кинематическое условие
(269) может быть выражено производной:
dF dF dF
v* дх +v* ду + Vz dz = 0;
(275)
б) границы водоёмов АВ и DC; из-за мало-
сти скоростей фильтрации можно полагать
распределение давления по гидростатиче-
скому закону
” = Y+(W-z), (276)
где ра— давление на свободной поверхности
водоёма; Н— отметка этой поверхности, от-
несённая к горизонтальной координатной
плоскости;
в) граница выклинивания ED; грунтовые
воды примыкают к атмосферно?лу воздуху и
давление таким образом можно считать по-
стоянным;
г) свободная поверхность АЕ; пренебре-
гая явлением капиллярности, можно считать
давление постоянным и приблизительно рав-
ным атмосферному, Так как форма свободной
поверхности неизвестна, то условие постоян-
ства давления является недостаточным.
Для установившегося движения в первом
приближении дополнительным условием мож-
но считать равенство нулю нормальной
составляющей скорости фильтрации.
Нахождение потенциальной функции
Ф (х, у, z), удовлетворяющей уравнению
Лапласа и конкретным граничным условиям,
в общем случае трёхразмерной задачи,
представляет известные трудности; значи-
тельно проще решение задач установивше-
гося движения плоского потока.
ПЛОСКОЕ УСТАНОВИВШЕЕСЯ
ДВИЖЕНИЕ ГРУНТОВОГО ПОТОКА
В ряде инженерных задач (в случае иден-
тичности движения потока по его ширине)
представляется возможным свести задачу к
изучению двухразмерного движения в одной
плоскости.
Для плоского потока справедливы урав-
нения (51) и (52):
д2Ф д2Ф ]
дх2 + ду2 ~ О I
а2Ф д^> 1 ’ (277>
дх2 + ду2 = 0 J
где в общем виде функция потенциала ско-
ростей Ф в зависимости от расположения
потока будет выражаться:
а) при вертикальном расположении пло-
ского потока
К
Ф = 2JL у н =
р
«п
р
- (у + ; (278)
б) при горизонтальном расположении
плоского потока
ф = — тН = р. (279)
U г
Для плоского плавно изменяющегося
грунтового потока со свободной поверх-
ностью при горизонтальном подстилающем
слое, учитывая, что компоненты скорости
могут быть выражены по формулам
Кп dh Кп dh
t)„ = — v— т, vv — — ------’ лГ, 7, (280)
х ц дх 1 У ду ‘ х '
условие неразрывности может быть записано
так:
д 2h2 d2h2 2 та dh
~д& + fyF = T . Kn ' dt ' (281)
dh
При установившемся движении gj- = 0, и
последнее уравнение примет вид:
d2h2 d2h2
5^+a/r = °. <282)
т.е. функция потенциала скорости Ф в дант
ном случае заменяется величиной ft2,
472
ГИДРОМЕХАНИКА
ФИКТИВНЫЙ ГРУНТ
Фиктивный грунт — грунт, все частицы
которого имеют одинаковый диаметр de и
скорость фильтрации через который равна
скорости фильтрации через естественный
грунт. Диаметр частиц такого грунта на-
зывается эффективным диаметром.
Эффективный диаметр может быть найден
следующими способами.
1. Способ Кинга. Определяется суммарная
поверхность всех частиц в 1 см3 грунта,
которая затем делится на число частиц и
результат приравнивается поверхности час-
тицы с эффективным диаметром:
+ = У1- • > <283)
где
х- „ 2 6(1 —т) V1 Agt-
- 100 2j di ’
Д gi — доля каждой фракции в процентах по
весу в 1 см3;
di — средний диаметр частиц данной фрак-
ции;
tii — число частиц данной фракции.
2. Способ Газена. За эффективный диаметр
принимается диаметр отверстия такого сита,
через которое просеивается 10% по весу
испытуемого грунта.
3. Способ Крюгера—Цункера. Даётся по-
верхность частиц фиктивного грунта, все
частицы которого при той же порозности
имеют одинаковый эффективный диаметр de-
6(1—т) v1 A gj _ 6 (1 —m)
100 Zj di ~ de
откуда
где di— средний диаметр фракции (/).
4. Способ Козени. Эффективный диаметр
определяется по формуле
г=п
i=2
Здесь:
11/1 2 , 1 \
где dt и di — крайние диаметры данной
фракции;
di—верхний крайний диаметр
фракции с диаметром .менее
0,0025 мм;
A.gj — доля веса (в %) грунта,
падающая на эту фракцию
В случае отсутствия малых фракций формула
г-n Д g-
<255Хзаменяется формулой = 2 * в ко"
е г»1 *
торой d[ вычисляется таким же образом.
5. Способ Замарина. Эффективный диа-
метр определяется следующим образом:
1 i==rt d
а Хл-in-i-t-L. (286)
1=1 а1
Здесь А1( А2, А3 . . . представляют собой
угловые коэфициенты (относительно оси d)
последовательных прямых отрезков, из
которых в действительности состоит весо-
вая кривая.
Если весовая кривая начинается от ну-
ля, то:
, г=п я 3
12ArlnV-4 т
(Zei=i di 2
d
Величина de, вычисленная по способу За-
марина, больше, чем по Козени, но меньше,
чем по Крюгеру.
ОПРЕДЕЛЕНИЕ КОЭФИЦИЕНТА
ФИЛЬТРАЦИИ
Ниже приведены эмпирические формулы
для определения коэфициента фильтрации К,
полученные для фильтрации через песок.
Во всех формулах: de—в см, р— в пуа-
зах, К—в смIсек, t—в °C.
1. Формула Газена:
d2
К = с, (287)
I*
где с =0,8 для очень плотных песков;
с = 1,55 для песков средней порозности;
с = 2,0 для песков, составленных из
округлённых частиц почти одинако-
вого диаметра;
de определяется по способу Газена.
Для воды:
К = 75 cd2 t, (288)
где т = 0,7+0,031 — температурный коэфи-
циент.
2. Формула Слихтера:
К = 10,22 А , (289)
ра
1 — т
где а = - -п„ - .
Для воды при 10° С: р = 0,01333 и
d2
К = 766 -А .
а
3. Формула Крюгера—Цункера:
d2
К = 0,5 —- ; (290)
ра
(I-™)2
где = = т-------;
de определяется по способу Крюгера — Цун-
кера.
Для воды при 18° С:
d2
К = 46,3 ‘ . (291ф
ДВИЖЕНИЕ ГРУНТОВЫХ ВОД
473
Для температуры t величину К надо ум-
ножить на fi при 18° С и разделить на и при
температуре t.
Формула пригодна при de <0,2 см.
4. Формула Козеии:
X = 8,2 — , (292)
fia
de определяется по способу Козеии.
Для воды при 18° С:
,2
К = 780 —L .
a
Переход к другим температурам анало-
гичен указанному в п. 3.
5. Формула Замарина для воды 18°С
d2
К = 800 — , (293)
где a = 1,275—1,5 т, причём эффектив-
ный диаметр следует определить по спо-
собу Замарина.
Для других жидкостей:
d* (1,275— 1,5 ту
К = 8,4 —*---------------
а определяется по Козени.
Формула Терцаги (для глин и суглинков):
(—0,15)" + -Ар--
где т = 0,70 -f- 0,031 — температурный коэфи-
циент;
да
е = — отношение объёма грунта к
объёму, занимаемому зёрнами грунта;
Т| = ТГббббб — эмпирический коэфициент;
de определяется по способу Газена.
При плавно изменяющемся движении
грунтового потока гидравлический градиент
для всего живого сечения будет величиной
постоянной ;'следовательно, местные скорости
во всех точках живого сечения в однородном
грунте будут одинаковы:
v= — К ту = const. (295)
U Д/
Вследствие этого при плавно изменяю-
щемся движении скорость фильтрации в
живом сечении будет равна местной скорости
любой из точек живого сечения.
Формула (295) лежит в основе расчётов
илавно изменяющегося движения грунтовых
вод.
ПРИТОК воды К КОЛОДЦАМ
При движении к колодцу плоского ра-
диального потока артезианских вод в гори-
зонтальном пласте небольшой толщины
(фиг. 128) количество воды, притекающей
внутрь колодца, равно:
2яКН (HR-Ha)
Q=----------£------> (295а)
!n —
' о
где г0 — радиус колодца (скважины);
Нй—напор в колодце, равный высоте
столба воды в нём;
HR —напор воды на расстоянии R от ко-
лодца, где HR практически не из-
меняется (R—радиус влияния).
Фиг. 128
Распределение напора воды в пласте в
зависимости от расстояния от колодца г
определяется из уравнения:
Q г
ft== 27сКН1п'гГ +Н°*
Распределение скоростей в подтекающей
воде
Приток к колодцу безнапорных вод из
горизонтального водоносного слоя (фиг. 129)
Н2-й£
Q = п К---.
Понижение уровня воды (депрессиониая
кривая) в этом случае
Q г 9
й2=.^1П-- + Л£
Если с помощью колодца не получают
воду, а наоборот, сбрасывают её в водонос-
ный слой, то в последних двух формулах
знаки у Н и /г0 необходимо переменить на
обратные.
474
ГИДРОМЕХАНИКА
Если артезианская скважина питается
из реки или канала или вода отводится с
заболоченной местности с помощью дренаж-
ной трубы, то контуром питания будет пря-
мая линия. В этих случаях можно пользо-
ваться формулой (295), положив в ней 7?=2Z,
где I — расстояние от колодца до реки или
от дренажной трубы до поверхности грунта.
При питании колодца безнапорными во-
дами, поступающими из реки, дно которой
служит продолжением горизонтального под-
стилающего слоя, можно пользоваться фор-
мулой для расчёта притока безнапорных
вод, также положив в ней /? —21.
ФИЛЬТРАЦИЯ ЧЕРЕЗ ТЕЛО ПЕРЕМЫЧКИ
Выбрав оси координат ОХ и Oh так, как
это показано на фиг. 130, уравнение (282)
можно представить в. виде:
Отсюда (при х = L, h = Н) уравнение
кривой депрессии будет:
иг /,2
h*=h2 +-------—?-х. (296)
Единичный расход притекающей воды
0Л _ К О/га
9 = дх 2 дх ’
или согласно (296)
К(Н-~ h2)
7 2L
(297)
Внося значение q в уравнение (296), фор-
мулу кривой депрессии можно также предста-
вить в следующем виде:
, „ , •> 2 ох
h2 ~ ло = • (298)
ВОДОСБОРНАЯ ГАЛЛЕРЕЯ
Формула (298) позволяет определить при-
ток грунтовых вод к водосборной галлерее.
Если горизонт воды в галлерее ha
(фиг. 131) и ось h помещена по середине се-
чения галлереи, ширина которой 2 Ь, то,
Фиг. 131
имея ввиду, что по формуле преобразования
координат h = h' и х' = х + Ь, формулу (298)
можно написать в следующем виде:
(й')= - йо = ; (299)
здесь q— односторонний приток к галлерее,
откуда при х' = L и hf = Н
К (№ - h2)
9 - 2(L — b)
(300)
где Н — естественный уровень грунтовых вод
над горизонтальным водонепрони-
цаемым слоем.
АЭРО- И ГАЗОДИНАМИКА
УРАВНЕНИЯ СОСТОЯНИЯ
Состояние газа определяется тремя его
параметрами: давлением р, объёмом V и
абсолютной температурой Т.
Уравнение, связывающее эти три опреде-
ляющие параметра, называется уравнением
состояния.
Для идеального газа таким уравнением
является уравнение Клапейрона:
pV = GRT, (301)
где G— количество газа в кГ;
кГ-м
R — газовая постоянная в - ;
V — объём газа в м3.
V
Так как удельный объём v = q , то
pv = RT. (302)
Для реальных газов и паров нет универ-
сальной теоретической формулы. Ниже при-
ведены наиболее употребительные эмпириче-
ские уравнения состояния реального газа:
1) р (v — b) = RT (уравнение Бернулли—
Дюпре); (303)
/ а \
2) ( Р + у2) (у — 6) = RT (уравнение Ван-
дер-Ваальса); (304)
(v — b) = RT (уравне-
ние Клаузиуса), (305)
3) р+ T(v + с)2
где а, Ь, с, R — коэфициенты, различные для
различных газов и в общем
случае непостоянные.
Для некоторых газов в табл. 81 приве-
дены значения величин а и & в уравнении
Ван-дер-Ваальса.
АЭРО- И ГАЗОДИНАМИКА
475
Таблица 81
Значение коэфициентов а и & в уравнении
воздуха и fm—средняя температура столба
воздуха между этими точками, то, пренебре-
гая влажностью воздуха, можно пользо-
ваться формулой
ft2 _ft1 = (18,4+0,067 tm) Ig (309)
ОСНОВНЫЕ УРАВНЕНИЯ СТАТИКИ
ТЯЖЁЛОГО ГАЗА
Стандартная атмосфера. В воздухоплава-
нии п авиации принята так называемая
стандартная атмосфера, дающая определён-
ный закон изменения основных метеороло-
гических элементов с высотой.
Исходные данные стандартной атмосферы:
р„ = 10 332 кГ/м2; t0 = 15° С (Т„ = 288° К);
_ кГ • сек2
7о = 1,226 кГ/м3; Ро= 0,125-------.
Падение температуры до высоты 11 000м
6,5° на каждые 1 000 м.
Давление и плотность атмосферы до вы-
соты 11 000 м вычисляются по формулам:
Распределение давления в тяжёлом газе
определяется законом:
dz
(306)
т. е. падение давления по вертикали при
равновесии тяжёлого газа равно удельному
весу с обратным знаком.
Полагая известной зависимость между р
и 7 в виде
где р0 и 70 — значения давления и удельного
веса при z = 0,
т—показатель политропы,
уравнение (ЗС6) можно записать в виде:
1
. т 1
I Io
откуда при т + 1
= —z; (307)
при т = 1 (изотермический случай)
~ In Р = - г; (308)
1о ко
или иначе:
при т = 1 z
Р = Рое Rr<>
при т =f= 1, т
Барометрическая формула. Барометриче-
ское (свободное) давление воздуха над
уровнем моря в среднем равно 760 мм рт. ст.
и может колебаться в зависимости от
метеорологических условии в пределах ± 5%.
Если й2— —разность высот двух точек
в км, рг и р! — соответствующие давления
р / ft \5,256
рв = — "44300")
р / ft \4,256
р„ ~ 44 300 J
(310)
(311)
Выше 11 000 м отношение соответствую-
щих давлений и плотностей определяется
формулой:
_ /(L- ч 000\
р р \ 6 340 /
-(312)
Значения стандартной атмосферы для вы-
сот до 15 000 м приведены в табл. 82.
Таблица 82
Стандартная атмосфера
св О “у S m о р Ро р В мм рт. ст. ! ,wljK a L Р/Р»
0 1,0000 760,0 +15,0 1,2250 1,0000
1 000 0,8870 674,1 8.5 1,1120 0,9074
1 200 0,8656 657,9 + 7,2 1,0903 0,8897
1 400 0,8448 642, + 5,9 1,0690 0,8723
1 500 0,8345 634,2 + 5,3 1,0584 (1,8637
1 600 0,3243 626,4 + 4,6 L,0480 0,8551
1 800 0,8042 611,2 4- 3,3 1,0272 0,8382
2 000 0,7845 596,2 4- 2.0 1,0068 0,8216
2 200 0,7652 5/1,6 4- 0,7 0,9363 0,8052
,2 -+> 0,1463 567,2 - 0,6 0,9670 0,7891
2 500 0,7370 560,1 — 1.3 0,9572 0,7811
2 600 0,7278 553,1 — 1.9 0,9'475 0,7732
2 8о(: 0,7097 539,3 - 3,2 0,9283 0,7575
3 000 0,6918 525,8 — 4,5 0,9094 0,7420
3 500 0,6490 493,2 - 7,8 0,8634 0,7046
4 000 0,6082 462,3 —11,0 0,8193 0,6686
4 500 0,5696 432,9 —14,3 0,7770 0,6340
5 COG 0,5036 405,1 -17,5 (',7363 0,6008
5 50') 0,4983 373,7 —20.3 0,6972 0,5689
6 000 0,4655 353,8 —24,0 0,6593 0,5384
6 500 0,4344 330,2 —27.3 j, 6240 0,5091
7 000 0,4051 307,3 (1, 5'896 0,4820
7 500 0,3773 286,8 -33,8 (1,5567 0,4542
8 000 0,3512 266,9 — 37 0,5252 0,4285
9 000 0,3032 —43,5 0,4661 0,3806
10 000 0,2606 193,2 —59.6 0,4127 0,3667
И 000 0,2229 169.4 —56,5 0,3636 0,2967
12 000 0,1903 144.6 -56,5 0,3104 0,2533
13 000 0,1627 123,7 -56,5 0,2653 0.2165
14 000 0,1389 105,6 —56.5 0,2266 0,1849
15 000 0,1186 90,1 -56,5 0,1935 0.1579
ГИДРОМЕХАНИКА
476
УРАВНЕНИЯ ДВИЖЕНИЯ ГАЗОВ
ПО ТРУБАМ
Основные уравнения. При движении газа
по трубам помимо гидравлических явлений
будут иметь место и тепловые изменения со-
стояния газа. Для того чтобы учесть в
уравнении Бернулли тепловую энергию, не-
обходимо знать уравнение физического
состояния газа, т. е. должна быть известна
функция р = / (7).
Если пренебречь поправками на усредне-
ние, что допустимо сделать для большинства
практических случаев, то движение газа на
элементарно малом участке трубы dx с плавно
изменяющимся сечением будет определяться
следующими четырьмя уравнениями.
I. Уравнение движения:
/с2 \ dp J rfx са
d ('2g) + 7 +dh+l D 2~g= °’
II. Уравнение расхода:
cF
Qs-t-c-F = — .
III. Уравнение теплового баланса:
/с2 \
dq = di + Ad ( 9^ 1 + -44Й.
IV. Уравнение состояния:
р (vb) = RT,
J
где с—скорость газа;
—весовой расход;
i — энтальпия.
Уравнения III и IV определяют зависи-
мость
P = / (?)•
Общие уравнения движения газа по
трубе постоянного кругового сечения с пря-
молинейной осью. Так как сечение трубы
постоянно, т. е. dF — 0, и ось трубы прямо-
линейна, т. е. геометрический напор может
быть выражен через длину трубы h = sin a • х
(ос угол наклона трубы к горизонту), то на
основании уравнений (313)
\
. on с2+ 8 sin a
1 de _____
с dx (а *)2 — с2
(314)
где а * = у g — скорость распростра-
нения звука в газе (критическая скорость).
Интегрируя уравнение (314), получим:
(а*)*—с* de
х-~х0= 1 ’ V
J YD + 8 sin a
(315)
Уравнение состояния, физического про-
цесса и сплошности (7 с = const) позволяют
выразить к и а * через скорость с.
Изотермическое движение. В этом слу-
чае k = const, ибо в общем случае устано-
вившегося движения газа по трубе постоян-
ного сечения X зависит только от темпера-
туры.
Критическая скорость:
V^gRT VIrt
~ У g dt - 1-bt ==c~rrbs
Qg
F’
где s =
Тогда интеграл уравнения (315)
даёт х как функцию с:
2/7 (* *о) ~ 2 1п
В
sin a
— arctg
Dg
с* + 2 у sin a
Cq + 2 sin a
arctg
ca
р4 2 sin a
C
c
Sin a
C
c — bs
‘ с0 — bs +Cilnce— bs ’ (31б)
где А, В, Си Ci — постоянные, зависящие
от параметров, определяющих движение газа:
(ьч* — 2 sin a
~ Dg Га 1(
ЬЧ2 +2 -f sin a)
A =
Dg
2 у gRT bs sin a
B=—----:---------
£>g \а ’
&2S2 + 2 Y sin a J
______gRTbs
L ~ Dg ’
ЬЧ2 4-2-v sin a
/ Dg
gRT ( ЬЧ2 — 2 —- sin a
C
Dg .
sin a
2
Для горизонтального трубопровода (а=0)
уравнение (316) упростится:
* . . , с gRT / с
2D ~ хо> =- 1п ctt + ~(bs)2 tln са~
bs bs c—bs\
c — bsc0 — bs ln c0 — bs)'
Изохорическое движение. Уравнение фи-
зического процесса будет:
du = 0, и = const или 7 = const.
Уравнение сплошности даёт de = 0.
скорость по трубе постоянна.
Для интервала температур (—40)—(+i20)°C
X можно считать постоянным.
Интеграл уравнения (315) даёт:
“° + (х- ХО) sin a+ ^^0) 0. (318)
t. e.
АЭРО- И ГАЗОДИНАМИКА
477
Если за уравнение состояния принять
уравнение Бернулли—Дюпре, то для dq имеет
место равенство:
/ v — b \
dq = ( + Av I dp + A sin а • dx.
Принимая теплоёмкость cv = const, для го-
ризонтального трубопровода
q = ( + Аи\ (.Р — Ро) (319)
dp а2 ( к с2 \
Y +sin а; dx +
X. С2
(/с — 1) с2 р- 2gdx
(1 — Т Ь) (с2 — а2)~ ’
Изобарическое движение. Для случаев,
когда можно считать, что dp = 0, т. е. р —
, л с2
~ Y Ь) 0 2~g
(1 — qb) (с2— а11) +
= const, а * = j/" g = 0, уравнение (314)
примет вид:
de _ / Л. g sina\
с dx----Ы) + с2 ) '
sin а
с2 — а
dx,
Для горизонтальных (а = 0), коротких
трубопроводов последнее уравнение даёт:
1 de _к_
с dx 2D ’
Интегрируя, получим:
л х
~ 2D ,
с—сое
(320)
т. е. скорость газа быстро убывает.
Уравнение количества тепла даёт
/ р \ / с2
dq — Iе» + Ар \ dv + A d ( Qg
При cv = const
с2__с2
+ А . (321)
Движение при полной тепловой изоляции
трубопровода от внешнего пространства.
Для данного случая будет иметь место сле-
дующая система уравнений:
с2 de у
g с р А др
dp q di_ dj
q ' A dq q
sin a dx;
где а2 = gkRT 1 + ppp
I г\ 1
к — показатель адиабаты.
Уравнение теплового баланса для этого
случая
/, с2 \
rf 1 + А ту + Ах sin а = О
\ 6 j
или
с2
I А 2~„ + Ах sin а = -р А -|-
2g
+ Ахв sin а = АВ *
позволяет выразить а2 как функцию с:
(fc — 1) кс2
а* ~ 2(ck—bs) (с—&s)f2gB* —
— с2 — 2 gx sin а].
de
Заменив а2 в уравнении для — согласно
последнему равенству и интегрируя его для
случая горизонтального трубопровода, по-
лучим:
2 _______А_________
2D (х — х„) - ic (сок — bs)
______А_________В ск — bs
к (ск — bs) к 1п сйк -^~bs
(322)
где
c2 de dp
g c ’ q
л c~
~ Id ^dx — sma • dx;
^ + ^ = 0.
e q
Решая систему относительно диференци-
dc dq dp
алов — , — , — (принимая, что состояние
A=2\2k-l+g &2 S2 В *
1 В =— Г (/с 1 +8 - -1) кг о Л b2s2
1 с==-2- 1 ь - 1) к 1 -V5-7,— В * V2S‘
газа определяется уравнением Бернулли —
Дюпре), будем иметь:
ПРАКТИЧЕСКИЕ ФОРМУЛЫ
ДЛЯ ДВИЖЕНИЯ ГАЗОВ ПО ТРУБАМ
[1 с2
(k — qb) к рт —
i 1 7 D 2g
(1 — у&) (с2 — а2) **
Формула Мейера для ламинарного ре-
жима. Весовой расход газа или пара равен
r.dtp1Am Г
° “1287Г(Т + т) R0Tl I P1 ~~
sin а
с2—а2
dx;
(323)
478
ГИДРОМЕХАНИКА
где т — показатель политропы;
Д — отношение удельного веса газа к
удельному весу воздуха при одина-
ковых температурах и давлениях;
Ro — газовая постоянная воздуха;
7\ — температура газа в начале трубо-
провода.
Формулы Веймаута для турбулентного ре-
жима. Весовой расход
;,-Р1-Д- т
F I (1+ т)
(324)
где
С ~ 87009407 /?0 =6’64
в технической системе единиц.
Для изотермического потока (гл = 1)
G = 4,69 • а1’ JL22_ . (325)
При скорости движения газов, близкой к
скорости звука, весовой расход
1/ g • 11 Р1 - т- Л.
' 8 • 0,009407 RqT,-
Для случая турбулентного изотермиче-
ского потока при незначительном перепаде
давления вдоль газопровода Р1—Р2 формула
(326) принимает простой вид:
G = 6,64 <Г!‘ ]/'-РЦ , (327)
г IT j
Pi + Pi
где р = •—Q---— среднее абсолютное дав-
ление в газопроводе;
Н — Pi— р2 — разность давлений в на-
чале и конце трубопровода.
Формула (327) применима, если величина
(.Pi — Pi) составляет не более 10% величины
среднего давления Р в газопроводе.
Формула Кристиановича С. А., Тре-
бина Ф. А., Черникина В. И. (изотермиче-
ский режим)
л ZV 1 Г к I
с“4 v Ivd1 +
Px + Pa/J ' ITj.
(328)
где R — газовая постоянная;
X—коэфициент гидравлического сопро-
тивления;
к — коэфициент, учитывающий отклоне-
ние газа от закона Клапейрона:
р = 1+кр RT-
ДВИЖЕНИЕ СМЕСИ ЖИДКОСТИ И ГАЗА
ПО ТРУБАМ
Удельный вес смеси и уравнение её
состояния. Если на 1 кг жидкости прихо-
дится т; кг газа, то удельный вес смеси О
равен
6 =----1 1 ? • <329>
-------1-----
Ужидк Чгаза
Уравнение состояния газового компонента
в общем случае политропического процесса
определяется уравнением политропы:
'газа уР1] Чгаза
(330)
Из уравнений (329) и (330) следует:
О =
"(жидк
*1
7 газа
(331)
где "(газа и Pi ~ удельный вес газа и давле-
ние в начале газопровода.
Движение смеси по горизонтальному тру-
бопроводу при изотермическом режиме.
Этот случай наиболее часто отвечает дей-
ствительным условиям, ибо большая теплоём-
кость жидкого компонента и большой коэ-
фициент теплопередачи обусловливают не-
изменную температуру газа, близкую к
температуре жидкости.
Весовой расход
—— f Pl Ч- П
к2 gd6 (1 -|- ГЧ32Ч
64 к ’
где
Чжидк ’ПРх
а = 7'
газа
__ Чжидк *1 RоЛ *
~д ’
х
k = g-—коэфициент сопротивления, опре-
деляемый из опытов.
АЭРО- И ГАЗОДИНАМИКА
479
Приближённая формула для случая дви-
жения смеси жидкости и газа по гори-
зонтальному трубопроводу при политропи-
ческом процессе. Весовой расход
(3=1/"rS-gdb (1+т]) т A pl
Г (1+т)
Для изотермического процесса
(1 + 7]) А 9
128А riZ7'i/?0 (Pi ~P2>’
(334)
или, упрощая,
где
С = 7Й 1/" —А ~ 0,051.
16 У 29,27
Движение смеси жидкости и газа ио
вертикальной трубе при изотермическом
режиме (эрлифт). Весовой расход
r 1/Ag-d6 (!+/]) b(p^e2W—pf)A
°= И(33e)
где
1 + •»] 1газа (1 + т,) А
ь = V Pl = TiRaTi
О = с.т/'.^О+Тр12(^-Р1)( (335)
г К 7} 11 i
Формула не учитывает эффекта проскаль-
зывания газового компонента смеси относи-
тельно увлекаемой им жидкости.
ЛИТЕРАТУРА И ИСТОЧНИКИ
t Александров В. Л. Техническая гидро-
механика, М.—Л., ГТИ, 1946, 431 с.
2. Бахметьев Б. А. Гидравлика открытых
русел, 1934 г.
3. Б е л о к о н ь Н. И. Транспортное машино-
строение. № 10, 1937 г.
4. Гидравлика. Под ред. И. И. Агроскина. М.—Л.,
Госэнергоиздат, 1944, 332 с.
5. ГурвичД.Л. и Френкель Н. 3. Гидрав-
лика, изд. 2. М.— Л., Госэнергоиздат, 1940,
355 с.
6. Е в р е и н о в В. Н. Гидравлика, изд. 4, Л.—М.,
Речиздат, 1947, 740 с.
7. Жуковский Н. Е. Полное собрание сочине-
ний, М. 1937.
8. К о ч и н Н, Е- и Р о з е Н. В. Теоретическая
гидромеханика, ч. I и II, М.— Л., Гостехиздат,
1948, 150с.
9. Лейбензон Л. С. и др. Гидравлика,
М.-Л.-Н., ГНТИ, 1934 г. 369 с.
10. Маккавеев В. М. и Коновалов И. М.
Гидравлика. Л.—М., Речиздат, 1940, 642 с.
И. Малышко В. М. Гидравлика и основы гид-
ромеханики. Л., 1940, 301 с.
12. Павловский Н.Е. Гидравлический справоч-
ник. М., 1937.
13. Сборник физических констант. М,—Л.» ОНТИ,
1937, 658 с.
14. Страхович К. И.Прикладная газодинамика,
М.—Л., ОНТИ, 1937, 300 с.
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
&
МАГНИТНОЕ ПОЛЕ
Магнитным полем называется физическое
пространство, состояние и свойства которого
неразрывно связаны с движением электри-
ческих зарядов. За направление магнитного
поля в рассматриваемой точке пространства
принимают направление, в котором уста-
навливается свободно подвешенная магнит-
ная стрелка.
Магнитная индукция (В) характеризует
величину и направление магнитного поля и
может быть определена:
а) по механической силе, с которой маг-
нитное поле действует на движущиеся в нём
электрические заряды;
с той точкой поля, где опреде-
ляется индукция;
К — коэфициент пропорциональности,
зависящий от физических свойств
среды, в которой образуется маг-
нитное поле, и от выбора единиц
измерения магнитной индукции,
тока и длины.
В рационализированной практической си-
стеме единиц «вольт—ампер—сантиметр—се-
кунда» за единицу магнитной индукции при-
вебер
вольт-секунду
нимают ------------——
с.ч2
в-с
сма
Фиг. 1. Направление силовых линий от
прямолинейного проводника с током
б) по э. д. с., наводимой в проводнике,
движущемся в магнитном поле.
Индукция магнитного поля зависит от
физических свойств среды, от величины и
расположения электрических токов, создаю-
щих магнитное поле. Опыт показывает, что
в однородной среде вокруг прямолинейного
проводника с током образуется круговое
магнитное поле, направление которого опре-
деляется правилом буравчика (фиг. 1).
По закону Био и Савара, магнитная ин-
дукция в любой точке поля однородной
среды определяется:
Idl
dB = К -yr sin а, (1)
где Idl — элемент тока;
г — расстояние от элемента тока до той
точки поля, где определяется маг-
нитная индукция;
а — угол между элементом тока и лу-
чом, соединяющим элемент тока
см® ’ РавнУю Ю8 абсолютных электромаг-
нитних единиц магнитной индукции.
Абсолютная электромагнитная единица
магнитной индукции называется гаусс (гс);
вб
j = 108
СМ
В этой системе единиц закон Био и Са-
вара выражается формулой
„ Idl
dB = .a- sin 7.. (2)
Магнитная индукция, подсчитанная по
этой формуле, а также но формулам, при-
вб
водимым ниже, выражается в —.
Формула (2) применима для однородной
среды.
Здесь
ц=цои, (3)
где [л — магнитная проницаемость данной
среды;
— относительная магнитная прони-
цаемость среды (находится экспери-
ментально); для вакуума jxr=l;
fx0—магнитная проницаемость вакуума:
я я гя
1,256-10“8 0,4ге Ю-8— . (4)
Все физические тела в отношении магнит-
ной проницаемости могут быть разделены на
две группы: слабомагнитные тела и сильно-
магнитные тела. Относительная магнитная
проницаемость первых весьма близка к еди-
нице; при этом тела, у которых ;j.r < 1, на-
МАГНИТНОЕ ПОЛЕ
481
зываются диамагнитными, а те, у
которых p.r > 1, — парамагнитными.
К сильномагнитным телам относятся те,
магнитная проницаемость которых значи-
тельно превосходит единицу. Эти тела носят
название ферромагнитн ы х, так как
к ним принадлежат сталь, кобальт и никель,
а также некоторые сплавы.
Величина магнитной индукции
(В) определяется в зависимости от величи-
ны и распределения тока.
а) От прямолинейного бесконечно длин-
ного проводника (фиг. 2):
В « \ dB ~ -j- I sin а --2- ; (5)
из фиг. 2 видно, что
I = a ctg а; а г sin а;
поэтому
о
(б)
7С
Фиг. 2. Магнитная индукция от прямо-
линейного проводника
б) От прямолинейного проводника конеч-
ной длины:
С „ р0* f1 <и .
в = J j уг sin а =
тс—аа
(sin + sinp2>> <7)
где а—расстояние точки А, в которой опре-
деляется индукция, от проводника
с юком;
Р1и₽.л— углы, образуемые перпендикуляром
к проводнику с током из точки А,
в которой определяемся индукция, и
лучами, соединяющими концы про-
водников с точкой А.
в) Вдоль центральной оси кругового тока,
т. е. проводника, имеющего форму окруж-
ности (витка) (фиг. 3):
2 чй
B = = | sin Р =
о
_Ро7
~2Т?
sin3 р,.
(8)
где 7?—радиус витка;
3 — угол между осью и лучом, соеди-
няющим точку, в которой опреде-
ляется индукция, с витком;
все dB" на фиг. 3 в результате геометри-
ческого сложения равняются нулю.
г) В центре кругового тока (витка) вели-
чина индукции получается как частный слу-
чай индукции вдоль центральной оси, пола-
гая 3 = 90°:
В = . (9)
Фиг. 3. Магнитная индукция
от витка с током
д) Вдоль центральной оси цилиндрической
катушки (фиг. 4):
1
n f С I™ sin3 3
J J 17 ~а dx
о
Iw
— Ро 2Т (c°spx —cos Р2), (10)
где w— число витков катушки;
а—радиус витка в см;
I—длина катушки в см;
Pi и р2 — углы между центральной осью ка-
тушки и лучами, соединяющими
точку, в которой определяется ин-
дукция, с конечными витками ка-
тушки, указанными на фиг. 4.
В случае бесконечно длинной катушки
магнитная индукция в середине катушки
будет Iw
(11)
так как р1=0°,
Р2 = 90°.
На краю беско-
нечно длинной
катушки магнит-
ная индукция бу-
дет равна
/IV
В ~ Ро 21 • (12)
Фиг. 4. Магнитная индукция
Для ОДНОГО от катушки с током
края катушки
Р^О’, р2 = 90°.
Для другого края катушки
Р2 = 90°, р3 = 180°.
В середине катушки конечной длины
Lz
2
cos Рх = — cos р2 = —....... - .
у < + аа
31 Том I
482
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Магнитная индукция в середине катушки
конечной длины
B = i>.0________
(13)
Напряжённость магнитного
поля (Н) представляет отношение магнит-
ной индукции к магнитной проницаемости
среды в данной точке:
Н = А. (14)
у
Напряжённость есть вектор, совпадающий
в однородной среде с вектором В.
Единица напряжённости магнитного поля'
в практической'рационализированной систе-
а
ме единиц имеет размерность -- ;
см
а
1 — — 1,256 эрстед (э);
а а
1 э = 0,795 — = 0,8 — ,
с м см
где эрстед — единица напряжённости маг-
нитного поля в абсолютной электромагнит-
ной системе
В
Н = — э, (15)
если В выражено в гс.
Магнитный поток (Ф) представ-
ляет сумму произведений магнитной индук-
ции В на элементы площадок dS, на кото-
рые может быть разбита заданная поверх-
ность:
Ф = J В dS = J В dS cos- (В, dS).
s s
секундах. 1
В абсолютной
Магнитный поток измеряется в вольт-
в-с называется вебером.
электромагнитной системе
единиц магнитный
поток измеряется в
максвеллах:
1 66=10® мкс.
Фиг 5. Петля гистерезиса
Ферромагнетизм.
Магнитная проницае-
мость слабомагнит-
ных тел может счи-
таться величиной noJ
стоянной. Магнитная
проницаемость фер-
ромагнитных мате-
риалов меняется с
изменением индук-
ции и даже для од-
ного и того же значения индукции может
быть различна в зависимости от предыду-
щего магнитного состояния. Для характери-
стики ферромагнитных материалов обычно
пользуются основной кривой намагни-
чения, которая представляет зависи-
мость В = /i (Н), полученную для ненамаг-
ниченного предварительно материала.
Имея основную кривую намагничения ОА
(фиг. 5), можно легко найти зависимость
;л = /г (В) и у — /а (И). Исследование зави-
симости р = /а (Н) показывает, что по мере
увеличения напряжённости магнитного поля
магнитная проницаемость сначала возра-
стает, а затем начинает уменьшаться,
стремясь в пределе при Н = оо к единице.
Состояние, при котором дальнейшее увеличе-
ние напряжённости магнитного поля не повы-
шает значительно значение магнитной индук-
ции, называется магнитным насы-
щением.
Гистерезис. Весьма важной характери-
стикой ферромагнитных тел является зави-
симость В — f (И) при циклическом изме-
нении напряжённости магнитного поля от
+ Нтах До равной по абсолютной величине
и противоположной по знаку Hmin=—Hmax
и затем снова до + Нтах (фиг. 5). График
этой зависимости показывает запаздывание
изменения магнитной индукции от измене-
ния напряжённости магнитного поля. Это
явление носит название магнитного гис-
терезиса, а график изменения В=^г (Н)—
петли гистерезиса. При напря-
жённости поля Н = 0 магнитная индук-
ция имеет определённое значение В = Вг и
называется остаточной индукцией.
Для доведения индукции до нуля необхо-
димо создать напряжённость магнитного
поля Н = Нс, называемую коэрцитив-
ной силой.
Магнитные свойства ферромагнитных ма-
териалов. Совершенно чистое электролити-
ческое железо, свободное от всяких при-
месей, при температуре до 80° С обладает
высокими магнитными качествами. Примеси
в железе изменяют магнитные свойства.
Примеси, которые не образуют химических
соединений с железом, занимают лишний
объём, вследствие чего магнитные свойства
снижаются. Если примеси образуют с желе-
зом химические соединения, к тому же рас-
творяются в железе, то это приводит к рез-
ким изменениям магнитных свойств железа.
Сталь, содержащая более 0,9% углерода,
при быстром охлаждении приобретает боль-
шую магнитную стойкость: трудно намагни-
чивается и трудно размагничивается. При-
меси к стали марганца ухудшают магнит-
ные свойства снижая остаточный магнетизм
и увеличивая коэрцитивную силу Присут-
ствие в стали примесей кремния (в преде-
лах 4— 5%) значительно увеличивает маг-
нитную проницаемость и снижает коэпцитив-
ную силу, При длительных нагревах стали
отмечается явление старения, в резуль-
тате которого для достижения той же самой
магнитной индукции требуется большая на-
магничивающая сила, при этом весьма сильно
увеличивается коэрцитивная сила. Примеси
кремния к стали в значительной мере устра-
няют явление старения. В сплаве железа
с никелем удаётся путём соответственного
подбора соотношения железа и никеля (хотя
никель и обладает более низкими магнит-
ными свойствами, чем сталь) получить мате-
риал с необычайно высокими магнитными
качествами. Сплав из 21,5% железа и 78,5%
никеля, называемый пермалоем, обла-
дает относительной магнитной проницае-
мостью |лг = 90 000.
Для большей устойчивости магнитных
свойств в практике применяется пермалой'
МАГНИТНОЕ ПОЛЕ
483
с содержанием 50% железа и 50% никеля,
но в этом случае значение магнитной про-
ницаемости снижается до 12 000. Пермалой
применяется главным образом в технике
слабых токов, где мы имеем дело со сла-
быми магнитными полями. Для изготовления
постоянных магнитов применяются специаль-
ные стали с примесью кобальта хрома,
вольфрама и никеля, которые при большой
остаточной индукции обеспечивают большую
коэрцитивную силу.
На фиг. б приведены кривые намагничи-
вания для материалов, применяемых в ма-
шиностроении и аппаратостроении.
Расчёт магнитной цепи. Линейный интег-
рал напряжённости магнитного поля по
замкнутой силовой линии равняется намаг-
Фиг. б. Кривые намагничения некоторых
материалов
ничпвающей силе (произведению тока на
число витков):
(fi Hdl = + Н2/2 +
+ W3ZS + ••• —
Имея в виду, что
В Ф
Н = — ,
Н '.>s
(16)
получим:
_£/i_ + + ф
1*1 1*2 S2 1*3 S3
соответственно величина магнитного потока
составляет:
- wI
Hi Si р2 S2
wl
Нз S3
/?л<
(17)
Si
Соотношение это дало основание по ана-
логии с электрической целый называть произ-
ведение тока на число витков магнито-
движущей силой, выражение У —
магнитным сопротивлением, а всё выраже-
ние (17) — законом Ома для магнитной цепи.
Непосредственное использование формулы
Ома для магнитной цепи при расчётах не-
возможно, так как входящая в формулу
магнитная проницаемость ц изменяется в за-
висимости от магнитной индукции, следова-
тельно, и от магнитного потока.
В тех случаях, когда необходимо произ-
вести расчёт магнитной цепи по заданному
магнитному потоку, поступают следующим
образом. Вычерчиваем среднюю индукцион-
ную линию и отмечаем участки /, вдоль ко-
торых магнитная индукция имеет одно и
то же значение. По заданному магнитному
потоку вычисляем магнитную индукцию
на отдельных участках магнитной цепи
Ф
В— . Затем по кривым намагничения
для данного сорта материала находим для
каждого значения магнитной индукции
напряжённость магнитного поля. Напряжён-
ность магнитного поля в воздухе опреде-
ляется по формуле
Нвозд = В >
если В выражено в гс.
Умножая найденные значения Н на длины
соответствующих участков средней силовой
линии, определяем потребное число ампер-
витков для каждого участка магнитной цепи
(HI). Складывая значения потребных ампер-
витков по отдельным участкам, получаем
потребную намагничивающую силу wl для
образования в заданной магнитной цепи по-
тока Ф.
В тех случаях, когда требуется подсчи-
тать магнитный поток при заданных ампер-
витках, определяют потребные ампер-витки
при нескольких значениях магнитного потока;
построив на основании расчётов кривую
® = /(wi), можно найти тот магнитный
поток, который получается при заданных
ампер-витках.
Электромагнитная индукция. Во всяком
контуре, когда меняется пронизывающий его
магнитный поток, наводится э. д. с. индукции
независимо от того, какими причинами это
изменение магнитного потока вызывается.
Величина наведённой э. д. с. по закону
Фарадея—Максвелла определяется для одного
витка:
ЙФ
е=--й? (18)
или когда контур состоит из w витков
4Ф
(19)
Произведение числа витков на магнитный
поток называется магнитным поток о-
сце плением.
Знак минус в формулах (18) и (19) объяс-
няется тем, что индуктированная э.д.с.
стремится воспрепятствовать производимому
изменению магнитного потока.
При движении прямолинейного провод-
ника перпендикулярно силовым линиям маг-
нитного поля в проводнике возникает также
э. д. с. индукции, определяемая по формуле
е Blv в, (20)
„ вб
где В выражается в ;
31*
484
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
/—длина проводника в см (активная
длина, т. е. длина, находящаяся
в магнитном поле);
v — скорость движения проводника отно-
си
сительно поля, выражаемая в — - .
При движении проводника под углом к
магнитному полю э. д. с. подсчитывается по
формуле
е = B-l'V sin (В, v). (21)
Самоиндукция — явление наведения э. д. с.
в контуре, когда изменяется магнитный
поток за счёт изменения тока в самом кон-
туре. Э. д. с. самоиндукции определяется по
формулам (18) и (19). Когда магнитная цепь не
содержит ферромагнитных материалов или не
насыщена (,u = const), магнитный поток и ток
являются величинами прямо пропорциональ-
ными, и потому э. д. с. самоиндукции может
быть выражена так:
di Ф di di
e = -wdrdt^w -TTt^~L dt’ <22>
где L — коэфициент самоиндукции, или ин-
дуктивность.
Коэфициент самоиндукции, или индуктив-
ность, равен числу потокосцеплении, созда-
ваемых единицей тока
Ф
L = W — . (23)
Индуктивность в практической системе
единиц измеряется генри (гн). Индуктив-
ность цепи или катушки равна 1 гн, когда
при равномерном изменении тока на 1 а
в 1 сек. в ней наводится э. д. с., равная
1 в; 1 гн равен 109 абсолютных электромаг-
нитных единиц (сантиметров).
Коэфициенты самоиндукции в частных
случаях (при постоянном значении магнитной
проницаемости среды).
а) Прямолинейный провод длиной I, ра-
диус круглого сечения г, относительная
магнитная проницаемость материала цг, обрат-
ный провод земля:
при постоянном токе
L0 = 2Z (in у—1 ; (24)
при переменном токе низкой частоты
L = Lo’~t^48~ (j —TSO(25)
при этом полагаем
к = цг
где S — сечение провода, 7 — удельная про-
водимость материала провода,
если к > 2, то __
при переменном токе высокой частоты
Z.=L0-^. (26)
б) Два параллельных прямолинейных
провода круглого сечения радиуса г при
расстоянии между осями проводов d
для постоянного тока
io = 4Z (in у + > (24)
и если [ir = 1 и I > d, то
L0 = 4/(ln . (25)
Для переменного тока, полагая к =
= -|U>S, имеем:
L = 4( fin 4—4 + дЬ (26)
\ г 1 J
причём для низкой частоты
А — -г- — (1 +- — к2 •
А 4 96 180 к '
для высокой частоты
А — 1’- л/ А ;
4 У к
для очень высокой частоты А = 0.
в) Цилиндрическая катушка с равномерно
навитой обмоткой из w витков: радиус ци-
линдра R, длина I, толщина обмотки мала
по сравнению с i.
Для длинной катушки
(2nl?iv)a Г 8R R2 /?4"|
I 1 3 т.1ф 2I2 4 Z1
; (27)
для коротких катушек
L=2 Tcjf^iv2
2(1 + 32/?2
I2
64 R2
Z1
’ 1024 У?4 )
768 RlJ ‘
In
8R
I
(28)
г) Три параллельных прямолинейных про-
вода длиной I круглого сечения радиуса г
при произвольном расположении проводов
на расстоянии dKM друг от друга. Индук-
тивность первого провода будет
Lj = I ( 2 In + 0,5 (Л • (29)
Индуктивность других двух проводов L,, и
L3 получается путём круговой перестановки
индексов при d.
Взаимная индукция — явление наведения
э. д. с. в контуре, когда изменяется магнит-
ный поток, за счёт изменения тока в другом
контуре. Э. д. с. взаимной индукции подсчи-
тывается по формулам (18) и (19). Для цепей
без ферромагнитных материалов э. д. с.
взаимной индукции подсчитывается по фор-
муле, тождественной с формулой (20):
di
e--Mdi’
где М— коэфициент взаимной индукции, или
взаимоиндуктивность.
Коэфициент взаимной индукции изме-
ряется в генри.
Коэфициенты взаимной индукции различ-
ных контуров при постоянной магнитной
проницаемости среды определяются следую-
щими формулами.
МАГНИТНОЕ ПОЛЕ
485
а) Два круглых витка радиусов и /?2,
плоскости которых параллельны п центры
расположены на расстоянии d на прямой,
перпендикулярной к их плоскостям.
Полагая - RA — С, имеем:
I
f I3
= i Lidl = дж.
b
(36)
в /?, с
। 3d8 + с2 _ 3 d2 с3 - _
16 7?, 32
Плотность энергии электромагнитного
поля представляет энергию, сосредоточенную
в единице объёма. В том случае, когда маг-
нитная проницаемость постоянна, что для
ферромагнитных материалов справедливо
лишь при малых насыщениях, плотность
энергии магнитного поля будет
Более простая, но менее точная формула:
dW
dV
HdB =
НВ дж
2 см3 '
(37)
в
М = 4 г/?! In .... .. — 2) . (31)
1 \ У й2+ с2 J '
б) Два параллельных провода круглого
сечения длиной / на расстоянии d друг от
друга: __ _
l+VP+d3
d
_^+d2 d\ 32)
I I J
при I > d
/ 21 \
M = 2/^ln y"~ И- (33)
в) Для двух двухпроводных линий (1—2)
(3—4) длиной I прямые провода 1 и 3, об-
ратные провода 2 и 4:
М = 2 1 1п
dl-4 ' d2-3
dl-3 • '*2-4
(34)
где d —расстояние между осями проводов
соответствующих индексов.
Если линии расположить так, чтобы пло-
скость проводов одной линии была перпен-
дикулярна и проходила через середину плос-
кости проводов другой линии, то коэфициент
взаимной индукции М = 0. Для уменьшения
взаимной индуктивности линий провода ли-
нии перекрещивают через определённые рас-
стояния. Такое перекрещивание проводов
называют транспозицией.
Энергия магнитного поля (IV), В магнит-
ном поле содержится энергия, которая с
большей или меньшей плотностью распреде-
ляется по всему пространству, занимаемому
магнитным полем. Энергия магнитного поля
получается за счёт той электрической работы,
которая совершается электрическим током
во время создания магнитного поля;
t ф
IV — j( — eL) idt = j- id® дж. (35)
о о
При постоянном значении магнитной про-
ницаемости р = const энергия магнитного
поля может быть выражена через индуктив-
ность цепи:
t
W = | (-cL)idt =
b
Потери на гистерезис или потери на пе-
ремагничивание пропорциональны площади,
ограниченной петлёй гистерезиса. Поглощае-
мая на перемагничивание энергия выделяется
в виде тепла. На основании исследования
большого количества образцов разных сортов
ферромагнитных материалов получена сле-
дующая эмпирическая формула для подсчёта
потерь мощности, обусловленной явлением
гистерезиса:
Р = V/, (38)
где Р — мощность в вт;
Вт — максимальная магнитная индук-
ция в гс;
f—число циклов перемагничивания в
1 сек.;
V — объём перемагничиваемого тела в см3;
•г; — коэфициент, зависящий от материала
(табл. 1).
Таблица 1
Значения коэфициентов i) для различных сортов
ферромагнитных материалов
Материалы ч
Электролитическое отож- жённое железо Динамная сталь Динамная листовая сталь . Кровельная сталь Кровельная сталь отожжён- ная Трансформаторная сталь Чугун 0,00078.10—’ 0,00054.10—7 0,00134-0,0015.10-’ 0,004.1U-’ 0,002.10—7 0,00064-0,00075.10-7 0,013.10—7
Формула (88) даёт хорошие результаты
для магнитных индукций от 1 000 до 12 000 гс.
Для больших магнитных индукций более
точные значения потерь на гистерезис полу-
чаются ко формуле
р _ j _L. . _|_
1 ~ I° юо ю coo
+ b 100 у 10000/ J кг ' (39)
где все величины те же, что и в формуле
(38). Потери мощности на гистерезис полу-
чаются по этой формуле для 1 кг перемагни-
чиваемого железа. Значения коэфициентов
а и Ь даны в табл. 2.
486
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Таблица 2
Значения коэфициеитов а и b
Материалы Коэфи- циенты Толщина листов в мм
1 0,5 0,35
0 б ы кн о в е нн а я ди- на мная сталь . . а 0,9 0,9 0,9
b 3,5 3,5 3,8
Высоколегирован- ная сталь . . . . а 0,4 0,3
ь — 2,6 2.1
Формулы для подсчёта потерь на гисте-
резис пригодны лишь для симметричных
циклов намагничивания.
Токи Фуко. Если в переменном магнитном
поле находятся проводящие тела, то в них
под действием индуктированных э. д. с. воз-
никают переменные электрические токи, на-
зываемые токами Фуко. Тепло, выделяемое
по закону Джоуля —Ленца в проводящих
телах, называется потерями на токи
Фуко.
В цилиндрическом стержне с диаметром
d (в мм), ось которого параллельна направле-
нию магнитного потока, потери мощности
на токи Фуко равны при индукции В (в гс),
равномерно распределённой по сечению:
Р/=27 (40)
Потери на токи Фуко в листах с толщи-
ной d:
4 1 ..
Принимая удельное сопротивление стали
р = 10~5 ом-см и синусоидальную форму
э. д. с., для которой коэфициент формы
к = 1,11, потери на токи Фуко получим:
а) для круглых проволок
Pf = 0,62 /243ВД V- 10-13 вт;
б) для листов
= 1,64!Ч‘В'т V-10”13 вт,
где / — частота переменного тока в гц;
d — толщина (диаметр) проводника в мм;
Вщ — максимальная магнитная индук-
ция в гс;
V — объём стали в см3.
Механические силы в магнитном поле мо-
гут быть сведены к внутренним силам маг-
нитного поля, а именно: к силам натяжения
вдоль линий поля и к силам давления, пер-
пендикулярным к его направлению. Значение
этих сил, отнесённых к единице поверхности,
равно энергии, отнесённой к единице объёма:
Р
S
Для проводов с током I, расположенных
в магнитном поле, механические силы сле-
дует вычислять из элементарных сил, дейст-
вующих на отдельные элементы контура.
Обозначая элемент контура через dl, силу'
тока в нём I, магнитную индукцию поля—В
и угол, составленный элементом dl с вектором
В, через а, имеем для элементарной силы
dP = IB sin adl. (41)
Если поле однородно, для прямолинейного
проводника имеем:
Р = Bil sin (В, I ). (42)
Направление силы определяется по пра-
вилу левой руки.
Подъёмная сила подковообразного электро-
магнита определяется по формуле
„ В2 дж
р = 2S 277 "см ’
(43)
где 8 — поверхность одного полюса подково-
образного магнита в см2*.
Взаимодействие проводников с током.
Аналитическое определение силы взаимо-
действия двух проводников с током может
быть сделано только для простейших случаев,
когда проводники расположены симметрично
относительно друг друга и когда магнитная
индукция, создаваемая проводником с током,
может быть определена в любой точке поля.
Механическая сила взаимодействия между
двумя параллельными проводниками опреде-
ляется фи. /лой
F = 2,94 /J, “•IQ-8 кГ, (44)
где /1 и 13—токи, протекающие по провод-
никам, выраженные в а;
а — расстояние между прово-
дами в СМ;
I — длина проводов в см.
Направление силы взаимодействия зависит
от направления токов. Проводники с токами
одного направления притягиваются, а с раз-
ным направлением токов — отталкиваются.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Современная теория строения материи,
объясняющая большинство электрических и
магнитных явлений, считает, что всякий
атом вещества состоит из ядра, содержащего
положительный заряд, и из электронов —
отрицательно заряженных частиц, вращаю-
щихся вокруг ядра по замкнутым орбитам.
В нейтральном состоянии противополож-
ные заряды составных частей атома равны
между собой, и их электрические поля вне
атома, действуя в противоположные сторо-
ны, уравновешивают друг друга и никакого
действия не производят. Если тело имеет
избыток электронов, то оно оказывается
заряженным отрицательным зарядом; если
тело имеет недостаток электронов, то оно
оказывается заряженным положительным за-
рядом. Вокруг заряженного тела существует
электрическое поле избыточного заряда. По-
мимо протонов и электронов в ядрах ато-
* Для одного полюса вдвое меньше.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
487
мов существуют ещё частицы, называемые
нейтронами.
Электрон представляет собой атом отри-
цательного заряда, материальную частицу
наименьшего возможного отрицательного за-
ряда, обладающего массой.
Простейшим ядром является ядро ато-
ма водорода, называемое протоном, имею-
щее положительный заряд, равный по вели-
чине заряду электрона.
Заряд электрона на основании
ряда исследований последних лет можно
считать равным 0,159-!0—20 к, или 4,77-1О~10
абсолютных электростатических единиц.
Масса электрона атома водорода
в ! 848 раз меньше самого атома и равна
9,02- 10“26 г. Электрон атома водорода вра-
щается по замкнутой орбите вокруг ядра
атома. Радиус орбиты приблизительно равен
0,53 • 10~8 см. Число электронов, вращаю-
щихся вокруг ядра атома данного элемента,
определяет его порядковый номер в Менде-
леевской системе элементов.
Электрическое поле — особое состояние
пространства, обусловленное присутствием
в нём электрических зарядов. Электрическое
поле с неподвижными зарядами называется
эле к трос т атичес к им полем.
Закон Кулона. Электрическое поле какого^
нибудь заряда может быть обнаружено по
силе, с которой это поле действует на дру-
гой заряд. Согласно опытному закону, от-
крытому Кулоном, два заряда и q3, нахо-
дящихся в однородной среде и отстоящих
друг от друга на расстоянии г, действуют
друг на друга с силой, пропорциональной
произведению этих зарядов и обратно про-
порциональной квадрату расстояния между
ними:
• <45>
Коэфициент ег характеризует качество
среды, в которой происходит взаимодействие
зарядов, и называется относительным
диэлектрическим коэфициентом
среды или относительной диэлектриче-
ской проницаемостью.
Для изотропной среды, отличной от ва-
куума, закон Кулона в рационализирован-
ной практической системе единиц выражается
в следующем виде:
где е—диэлектрическая проницаемость
среды:
F к
е==с»-ег^-<46’а)
е° -= 8,86-10 14 -= 4тс . 9 . ]Оц —
есть диэлектрическая проницаемость вакуума
(для вакуума е,. = 1).
Напряжённость электрического поля Е
характеризует его механические действия и
численно равна силе, с которой поле дейст-
вовало бы на единицу положительного элек-
тричества, помещённого в данную точку:
_ F 1 q3 в
Е “ 4 ~гг 20 ' 7*“ Ем • <47>
Напряжённость электрического поля от
нескольких зарядов равна геометрической
сумме напряжённостей полей от каждого за-
ряда в отдельности:
Е = + Ё2 + Е3 + ... + Еп. (48)
Электрическое напряжение. Внесённые в
электрическое поле заряды под действием
сил со стороны поля перемещаются, при этом
поле совершает работу. Предел отношения
работы, которую совершали бы силы поля
при перемещении заряда из одной точки в
другую, к величине заряда, когда он стре-
мится к нулю, называется электриче-
ским напряжением между этими точ-
ками и обозначается символом U.
В практической системе электрических
единиц за единицу электрического напря-
жения принимается 1 в. Разность потенциа-
лов между двумя точками равна 1 в, когда
для переноса 1 к электричества из одной
точки в другую требуется затратить 1 дж
работы.
Потенциал электрического поля в какой-
либо точке представляет отношение работы,
которая была бы произведена силами поля
при перенесении какого-либо заряда за пре-
делы поля, к переносимому заряду, когда
последний стремится к нулю. Потенциал, как
и напряжение по ля,являются скалярными ве-
личинами и измеряются в вольтах. Для одно-
родного электростатического поля
= и = Ed, (49)
где и '£в — потенциалы электрического
поля;
U—электрическое напряжение;
Е — напряжённость электриче-
ского поля;
d — расстояние между заряжен-
ными пластинами.
Поляризация диэлектриков. Хотя диэлек-
трики и не проводят электричества, тем не
менее они испытывают те или иные измене-
ния под действием электрического поля.
Под действием электрического поля в диэлек-
трике выявляются определённым образом на-
правленные диполи1 и каждый из них
создаёт собственное электрическое поле.
Поля полюсов диполя накладываются на
поле свободных зарядов, и таким образом
создаётся то поле, которое имеется в дейст-
вительности в пространстве, заполненном
диэлектриком. Электрическое поле, создавае-
мое диполями, пропорционально напря-
жённости внешнего электрического поля.
Электрическое смещение (индукция) поля
диэлектрика численно равно
D = г0Ё + хЁ = Е(е0+х), (50)
к
где D — электрическое смещение в ;
* Диполь — два равных, но противоположных по
знаку заряда, находящихся на весьма малом рассто-
янии друг от друга.
488
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
е0 — диэлектрическая проницаемость ва-
F
куума в -м ;
Е — напряжённость внешнего электри-
в
ческого поля в — ;
СМ
х—коэфициент поляризации диэлект-
F
рика в — .
Отношение электрической индукции к на-
пряжённости поля
О
г0 + 7. = г = ег г0,
(51)
равное сумме диэлектрического коэфициента
вакуума и коэфициента поляризации, назы-
вается диэлектрическим коэфи-
циентом среды, а отношение диэлек-
трического коэфициента среды к диэлектри-
а объёмная плотность энергии
W ED — -^~дж, (53)
где Е — напряжённость электрического поля
в
в см ’
к
D — электрическое смещение ~2 ;
V — объём в cms.
Механические (пондеромоторные) силы в
электрическом поле. Образование электри-
ческого поля в какой-либо среде связано с
определённым видоизменением физического
состояния среды с накоплением в ней энер-
гии и с появлением внутренних сил. Сила
натяжения, которую испытывает среда в
направлении поля на единицу площади,
равна
ческому коэфициенту вакуума ег
е
Ео
относительным диэлектрическим ко-
эфициентом среды.
Значения диэлектрических коэфициентов
для различных материалов приведены в
табл. 3.
Таким образом, энергия, сосредоточенная
в единице объёма электрического поля, чис-
ленно равна силе натяжения и давления на
единицу площади.
Таблица 3
Характеристики изоляционных материалов (диэлектриков) при температуре t = 20“C и давлении 760 мм рт. ст.
Удельный Относи- тельный Электри- Теплопровод- Объёмное
диэлек- ческая несть
Материалы вес трический прочность ч дж л см сек °C сопротивле-
г/см2 коэфи- циент кв/мм* ние р ом* см
Асфальт естественный 1,1-1,3 2,7 13— 16 10»*
Бакелит (гетинакс) круглый 1.2—1,3 3,8-5 10— 15 0,0017 Ю* х — ic,*s
Бакелит (гетинакс) листовой 1,3—1,4 4,5-6 10— 20 0,0017 1011 — 101*
Бумага кабельная сухая 0,8 2,3—3,5 6- 9 1,0013 1013—101*
Бумага кабельная, пропитанная маслом , 3,4-3,7 10- 25 — 1016
Воздух при давлении 760 мм рт. ст. . . 0,00 !21 1 3— 4 0,006 —
Дуб парафинированный 0,76 4,5—5 4- 7 —- 1013
Берёза сухая 0,64 2 —3 3— 5 — 101“
Бук в сухом виде 0,73 3 -3,5 5- 6 — 1011
Лакированная ткань 1,10—1,35 3,5—5 32— 45 0,0025 1012-1013
Масло трансформаторное . . 0,85—0,89 2 -2,5 5- 18 0,002 1032—101»
Миканит 2,2 4,6—6 15- 20 0,001 101*
Мрамор 2,7 8,3 2- 3 0,03 10’ —ю8
Парафин 0,85—0,92 2 —2,2 15- 30 0,002 101б
Прессшпан сухой и,9 —1,3 2,5-4 8— Ю 0.0017 10е —101»
Прессшпан, пропитанный маслом — 4 -5 12— 17 — 1013—10»3
Резина листовая 1,3—1,8 3,5 10— 15 0,001 1013—101-
Слюда мусковит . . • . • 2,8 6 -7,5 120—200 0,0036 101*—1016
Слюда флогопит .... 2.8 4 -6 80—150 0,0036 ] 013-101*
Стекло 2,5 5,5-10 10— 40 0,011 1011—101®
Фарфор 2.4—2,7 4.5—6,5 6- 10 0,01 101*—101®
Фибра 1,2—1,4 3 -5 4— 11 0,011 10*°
Шифер 2,7—2,9 6 -7,5 1,5— 3 0,02 Ю’ —101»
Целлулоид 1,45 4 -16 10— 15 — 2.101°
Эбонит 1,15-1,3 2 —3,5 8— 10 0,0018 1017
Энергия электрического поля для про-
стейшего случая однородного поля, образую-
щегося между двумя параллельными пла-
стинками, равна
W = у EDV дж, (52)
♦ Данные этого столбца следует считать ориен-
тировочными, так как электрическая прочность за-
висит от толщины испытуемого образца.
Электрическая ёмкость численно
равна отношению заряда уединённого про-
водника к его потенциалу:
О
С = — = const.
В практической системе единиц ёмкость
измеряется в фарадах. Одна фарада (F)—
это ёмкость такого уединённого проводника.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
489
у которого при потенциале его в 1 в соби-
рается заряд, равный 1 к.
Так как фарада представляет собой очень
большую ёмкость (ёмкость земного шара
равна 0,7-10~3 F), то ёмкость принято из-
мерять в микрофарадах:
1 мкф = 10-6 F,
или в микромпкрофарадах:
1 мкмкф = 10~12 F.
В абсолютной электростатической системе
единиц ёмкость измеряют в сантиметрах:
1 F = 9-Ю11 см.
Конденсатором называют устройство,
предназначенное для накопления электри-
ческих зарядов и электрической энергии в
их полях. Энергия, накопленная в электри-
ческом поле конденсатора
Конденсатор представляет устройство из
двух проводников, называемых обкладками
конденсатора, разделённых диэлектриком.
Ёмкость конденсатора характеризует его
способность воспринимать больший или мень-
ший заряд и зависит от геометрической фор-
мы и размеров обкладок, а также от при-
роды разделяющего их диэлектрика.
Ёмкость различных уединённых прово-
дящих тел (в фарадах) приводится ниже;
при этом считают, что противоположный
по знаку заряд распределён на бесконечно
удалённой поверхности, охватывающей дан-
ное тело и имеющей потенциал, равный
нулю:
а) шар радиусом R в среде с диэлектри-
ческим коэфициентом е:
С = 4 та/? ; (56)
б) тонкий диск радиусом /?:
С = 8е/?; (57)
в) круговой цилиндр (круглый провод-
ник) радиусом 7? и длиной I при I > /?:
С=-~-« (58)
1п
Ёмкость конденсаторов (в фарадах):
а) плоский конденсатор, расстояние
между обкладками которого d и поверхность
каждой из которых S:
=5
с—у; (59)
б) плоский конденсатор, между обклад-
ками которого имеются параллельные слои
различных диэлектриков, с диэлектрическим
коэфициентом ех, г2, г3, ..., и толщиной </х,
d3, ..., dn:
(б0)
-i е2 ез е п
в) два параллельных диска радиусом /?г
толщиной b на расстоянии d друг от друга
при R > b и R > d:
г Г 16тг(/> + d)R ,
С d 4- sR 1 4- In н
4~ dl
+ ~d 1п т] > <0 61>
г) цилиндрический конденсатор длиной I,
радиусы внешней и внутренней обкладок
которого А\ и /?2:
д) два параллельных цилиндра радиусов
Ri " R2, длиной /, расположенных один вне
другого при расстоянии d между осями:
ч- ] ’ ' '
1п 27?^ I - (А? + /?Р + Аа]
где______________________________________
А* = ]/> - 2 (А2 + А2) + (/?2 - Z?f72
при d > 2?! и d > А»
2 та/
Ё ^2" ! (64)
111 7?Га2
е) бесконечно большая плоскость и ци-
линдр радиусом R и длиной I, ось которого
параллельна плоскости и находится на рас-
стоянии d от неё:
2 та/
С .------(65)
In p+Td2+ /?а\
при I > d > R
2т.г1
С = - ~2Ч • (66)
in R-
Последовательное соединение конденса-
торов. Если электрические поля последова-
тельно соединённых конденсаторов не влияют
друг на друга, то все конденсаторы имеют
один и тот же заряд:
</ = с1и1 = C2t/2 = CSU3 = ... Сп ип.
Эквивалентная ёмкость группы последо-
вательно включённых конденсаторов равна
1 Л I .. L.U +
к=п
-Д <ет>
Эквивалентная ёмкость при последова*
тельном соединении конденсаторов умень*
Параллельное включение конденсаторов.
При параллельном включении конденсаторов
полный заряд всей группы равен сумме за-
рядов отдельных конденсаторов:
9 = ?i + + <7з + ••• + Qn — 2
k=l
490
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Эквивалентная ёмкость группы парал-
лельно включённых конденсаторов равна
, = Сг -(- Са -(- Са -|- ... -(-
к=п
+ Сп=^ Ck- (69)
Л=1
Эквивалентная ёмкость при параллельном
включении конденсаторов увеличивается.
Воздействие электрических полей на ди-
электрики. Опыт показывает, что после сооб-
щение! заряда конденсатору с неоднородным
диэлектриком разность потенциалов на его
обкладках убывает, стремясь к некоторому
пределу. После разряда конденсатора на его
обкладках вновь появляется разность потен-
циалов, стремящаяся также к некоторому
пределу. Заряд, вызывающий эту разность
потенциалов, носит название остаточ-
ного заряда ив однородных диэлектри-
ках не наблюдается.
Явление остаточного заряда объясняют
диэлектрической вязкостью, которая
заключается в том, что для установления
смещения, соответствующего данной напря-
жённости электрического поля, необходимо
некоторое время. Диэлектрическая вязкость
влечёт за собой уменьшение ёмкости конден-
саторов в высокочастотных полях. В связи
с диэлектрической вязкостью наблюдается
явление нагревания диэлектрика в высоко-
частотных полях.
Пробой диэлектрика. Деформация электри-
ческого смещения в диэлектриках может
возрастать лишь до известного предела, при
переходе за который происходит разряд и
диэлектрик разрушается — пробивается.
Электрическая прочность изолирующих ма-
териалов характеризуется пробив н ы м
градиентом напряжения, соответствую-
щим предельной величине смещения.
ПОСТОЯННЫЙ ток
Ток и плотность тока. Процесс переме-
щения электрических зарядов носит название
электрического тока. Величина тока опреде-
ляется соотношением
где dq— количество электричества, протек-
шее за время dt через поперечное
сечение проводника или диэлек-
трика.
Ток, приходящийся на единицу площади
поперечного сечения проводника, называют
плотностью тока:
Ток, не изменяющийся во времени, назы-
вают постоянным током; обозна-
чается он буквой J в отличие от изменяю-
щегося тока, который обозначается буквой I.
Электрические токи измеряются в ампе-
рах. Один международный ампер есть вели-
чина неизменяющегося тока, который, про-
ходя через водный раствор азотнокислого
серебра, выделяет в 1 сек. 1,11800 мг серебра.
Первый закон Кирхгофа. В силу непре-
рывности электрического тока ток, проходя-
щий через замкнутую поверхность, равен
нулю. В соответствии с этим первый закон
Кирхгофа в применении к разветвлённым
цепям можно сформулировать следующим
образом: алгебраическая сумма токов, схо-
дящихся в точке разветвления, равна нулю,
или сумма притекающих токов равна сумме
утекающих.
Электродвижущая сила, напряжение, раз-
ность потенциалов. Всякую причину, вызы-
вающую электрический ток или могущую его
вызвать, называют электродвижущей
сило й (э. д. с.).
Э. д. с., действующую на некотором
участке внешней цепи, называют электри-
ческим напряжением или просто
напряжением.
В том случае, когда электрическое напря-
жение имеет потенциал, напряжение на кон-
цах участка есть разность потенциа-
лов на его концах. Э. д. с., напряжение и
разность потенциалов в практической системе
единиц измеряются в вольтах.
Закон Ома определяет ток в замкнутой
проводящей неразветвлённой цепи, когда
в ней действует источник энергии с э. д. с.:
е
1 = ^-, (72)
где 1 — ток в а;
е—э. д. с. источника энергии;
R — сопротивление всей замкнутой цепи:
внешнее (нагрузки) и внутреннее
(источника тока).
Для отдельных участков замкнутой цепи
U
t = Г • (73)
где U—напряжение на концах участка;
г—сопротивление участка.
Эта формула применима в том случае,
когда в участке отсутствует э. д. с.
Электрическое сопротивление или просто
сопротивление зависит от природы ве-
щества проводника, его геометрических раз-
меров и формы и может быть выражено при-
ближённой формулой
I
г —
Г dl
Р S’’
где dl — элемент длины;
S—поперечное сечение проводника;
р—коэфициент, зависящий от природы
вещества проводника и называемый
удельным сопротивлением.
Если сечение проводника по всей длине
однородно и одинаково, то
г = р -j- (74)
ПОСТОЯННЫЙ ток
491
Величина, обратная удельному сопротив-
лению, называется удельной прово-
I
димостью 7 = —, и тогда
r==V- (75)
Удельное сопротивление и удельную про-
водимость можно отнести к различным еди-
ницам длины и площади поперечного сечения
проводника. Обычно удельную проводимость
относят к длине проводника в 1 м и пло-
щади поперечного сечения в 1 мм2.
Сопротивление измеряется в омах. Один
международный ом есть сопротивление (при
неизменяющемся токе и при температуре
тающего льда) ртутного столба длиной
106,300 ем, имеющего одинаковое по всей
длине сечение и массу 14,4521 г (сечение
такого столба соответствует 1 мм2). Единицу
проводимости, равную проводимости провод-
ника, сопротивление которого равно 1 ом,
называют сименсом.
Температурный коэфициент представляет
изменение сопротивления в 1 ом при нагре-
вании его на ГС. Сопротивление металлов с
увеличением температуры увеличивается,
поэтому значение температурного коэфи-
циента металлов положительное. Сопротив-
ление угля (металлических земель) электро-
литов с повышением температуры умень-
шается, поэтому значение температурного
коэфициента для них отрицательное. Уве-
личение или уменьшение сопротивления
при нагревании проводников, с достаточной
степенью точности в интервале температур от
0 до 150° С, может быть выражено
= [1 +«<tK -'«)]> (76)
где RtK—сопротивление при конечной тем-
пературе tK;
Rtll—сопротивление при начальной тем-
пературе tH-,
а — температурный коэфициент.
Увеличение сопротивления проводника
наблюдается и от действия магнитного поля.
Особо резко это проявляется у висмута:
при увеличении поля от 0 до Н— 16 000 э
сопротивление висмута увеличивается
на 75%. Этим свойством висмута пользуются
для измерения сильных магнитных полей.
Свет также влияет на сопротивление про-
водника, что особенно сильно проявляется
у селена. Чем сильнее освещён селен, тем
меньше становится его сопротивление. Это
свойство селена в последнее время очень
широко используется для устройства всякого
рода световых реле. При длительном действии
света селен перестаёт реагировать на изме-
нение освещённости.
Всякие примеси к металлам увеличивают
их удельное сопротивление, точно так же и
сплавы имеют большее удельное сопротив-
ление, чем удельное сопротивление отдель-
ных составных частей. Объясняется это тем,
что в этом случае в проводнике больше
неоднородностей и неправильностей в распо-
ложении атомов, вследствие чего длина и
время свободного пробега атомов меньше,
чем в соответствующих чистых однородных
металлах. Неоднородность от примесей
в металлах и сплавах понижает значение
температурного коэфициента, поэтому в та-
ких проводниках температура оказывает
значительно меньшее влияние на изменение
сопротивления.
Последовательным соединением источни-
ков электрической энергии и приёмников
называется такое соединение , при котором
конец одного соединяется с началом другого
и т. д. При последовательном соединении
ток во всех участках цепи имеет одно и
то же значение. При последовательном соеди-
нении источников энергии результирующая
э. д. с.
Л=п
е = ei + г? + е3 + ... + еп= У ек. (77)
Л=1
Таблица 4
Проводимости, удельные сопротивления, температурные коэфициенты, удельные веса, теплоёмкости
и теплопроводности чистых металлов и некоторых сплавов
Материалы Удельная проводи- мость при 20°С сименс Удельное сопротив- ление при 2О°С ом •мм9 Среднее зна- чение темпе- ратурного коэфициен та для темпе- ратур от 0 до 100° С Удельный вес кг дм9 Теплоём- кость кал Теплопро- водность при 20°C кал
СС см'л °C сек
см м
Серебро 62,11.10* 0,0161 0,00400 10,4 0,056 0,01
Медь . 59,52.10* 0,0168 0,00445 8,9 0,094 0,92
Золото ••••. 43,19-10* 0,0237 0,00377 19,1 0,032 0,70
Алюминий 35,97 10* 0,0278 0,00423 2,65 0,214 0,42
Молибден 21,01.10* 0,0476 0,00435 10,2
Вольфрам 16,34 10* 0,0612 0,00464 18,7 0,037 0,38
Цинк 16,13*10* 0,0620 0,00390 7,0 0,093 0,265
Платина 11,55.10* 0,0966 0,00247 21,3 0,028 0,166
Железо 10,89.10* 0,0918 0,00625 7,9 0,119 0,14
Кобальт 9,17 10* 0,109 0 00658 8,9 0,103
Никель 7,25.104 0,138 0,00621 8,8 0,11 0,14
Олово . 6,99 10* 0.143 0,00440 7,2 0,055 0,157
Свинец 4,52.10* 0,221 0,00411 11.4 0,03 0,083
Ртуть . . 1,055 10* 0,948 0,00024 13,6 0,033 __
Висмут 0,72.10* 1,39 0,00364 9,8 0,031 0.019
Уголь ретортный 0,138*10* 7,25 0,0003 1,88
Латунь (50—15) 10* 0,02—0,06 0,002 8,5 0,9 0,26
Манганин 3.10* 0,33 0,000006 8,5 0,181 0,10
Никелин 2,38 10* 0,42 0,0003 8,8 —
Константан 2,04.10* 0,49 0,00004 8,9 0,10 0,054
Нейзильбер (2,2—2)-10* 0,45—0,50 0,0004 8,5
Нихром ..... (1,6-0,9). ИО* 0,94—1,1 0,00015—0,9004 — — —
492
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
При последовательном соединении приём-
ников энергии полное сопротивление
к=п
R = П + r2 + rs + ... + гп = гК. (78)
к—1
Параллельным соединением источников
электрической энергии или приёмников на-
зывается такое соединение, при котором на-
чала всех источников энергии или соответ-
ственно приёмников соединяются вместе,
точно так же как и концы. При параллель-
ном соединении на концах каждой из ветвей
действует одно и то же напряжение. При
параллельном соединении источников энергии
ток в неразветвлённой части I равен сумме
токов в разветвлениях:
к=п
/к. (79)
К=1
При параллельном соединении приёмни-
ков энергии полная (эквивалентная) прово-
димость равна сумме проводимостей отдель-
ных ветвей:
к = п
, 1 V 1
+ , (80)
fn гк
или
Sj = Si + "2 + 2з + ••• + Sn = 2 ^к’ (81)
К=1
1
где g = —- и называется проводимостью.
Сопротивление проводников различных
геометрических форм (в омах):
а) сопротивление слоя жидкости с удель-
ной проводимостью f между двумя металли-
ческими параллельными пластинами одина-
ковой площади S, находящимися на расстоя-
нии d друг от друга:
. (82)
б) сопротивление среды с удельной про-
водимостью '( между двумя одинакового ра-
диуса R параллельными цилиндрами, длиной
I, расстоянием между осями цилиндров d:
r=^l ln 4 • (83)
Следующие формулы дают величину пере-
ходного сопротивления заземляющих элект-
родов для случая неограниченной среды с
удельной проводимостью -р
а) шар радиуса /?:
'=4^ ; (84)
б) полушар радиуса R:
'= УД-Д ’ (85)
в) круглая тонкая пластина радиуса R:
r=8-;R ;
г) цилиндр, радиус основания которого
R, а длина I:
г=,р In J- ; (87)
2 л;/ R ’ '
д) прямоугольная пластина co сторонами
а и па, причём п> 1:
Г «-----In А , (88)
VА 1+п— д
где
8 п
А =(1 + п)2 — — .
Закон Джоуля—Ленца: количество тепла
в малых калориях, выделяемого постоянным
током в однородном проводнике, пропорцио-
нально квадрату силы тока в амперах, со-
противлению проводника в омах и времени,
в течение которого проходит ток по провод-
нику, в секундах:
Q = 0,24/2RZ; (89)
0,24—механический эквивалент тепла, чис-
ленно равный количеству тепла, выделяе-
мому' 1 дж электрической энергии.
Работа электрического тока, поглощаемая
в проводнике:
W = Uq = Ult. (90)
За единицу работы электрического тока в
практической системе единиц принимается
1 дж = 10’ эрг (ватт-секунда). На практике
пользуются более крупными единицами элек-
трической работы: 1 гектоватт-час (гвт-ч),
1киловатт-час (квт-ч),1 мегаватт-час (мгвт-ч).
Мощность электрического тока равна ко-
личеству энергии, поглощаемой в единицу
времени. Единицей мощности в практической
системе единиц служит ватт (вольт-ампер).
На практике пользуются более крупными
единицами электрической мощности: 1 гек-
товатт (гвт), 1 киловатт (кет), 1 мегаватт
(мгвт);
1 Л С — 7.36 вт = 0,736 квт\
1 кет = 1,36 ЛС.
Второй закон Кирхгофа устанавливает
связь между э. д. с. и падением напряже-
ния в замкнутых контурах разветвлённых
цепей. В замкнутом контуре алгебраическая
сумма э. д. с. равна алгебраической сумме
падения напряжения во всех сопротивлениях,
входящих в этот контур.
Определение токов в разветвлённых цепях,
а) М е т о д уравнений Кирхгофа. Пер-
вый и второй законы Кирхгофа вполне точно
и однозначно разрешают вопрос об опреде-
лении токов в любых сложных разветвлён-
ных цепях. Для определения токов во всех
участках цепи произвольно намечают направ-
ления токов и составляют ряд уравнений,
применяя первый закон Кирхгофа для отдель-
ных точек разветвления и второй закон Кирх-
гофа для отдельных контуров. Если сложная
цепь имеет п ветвей между а узлами,- то опреде-
лению подлежат п неизвестных токов. По
первому закону Кирхгофа составляется а — 1
уравнений, так как для последнего узла урав-
нение получается как следствие предыдущих
уравнений. Остальные п—а + 1 уравнений
составляются по второму закону Кирхгофа.
ПОСТОЯННЫЙ ток
493
При составлении уравнений следует обращать
внимание на то, чтобы получаемые уравне-
ния не были зависимы друг от друга, т. е.
чтобы какое-либо из них не являлось след-
ствием других. Для этого необходимо, чтобы
в каждый новый контур, для которого со-
ставляется уравнение, входила хотя бы одна
новая ветвь, ещё не входившая ни в один
из ранее рассматривавшихся контуров. Если
при решении составленных уравнений для
тока в какой-либо ветви получится отрица-
тельный знак, то это указывает на то, что
ток в этой ветви имеет направление, обратное
произвольно принятому при составлении
уравнений.
б) Метод наложения (супер-
позиции). В том случае, когда в сложной
разветвлённой цепи действует несколько
э. д. с., ток в любой ветви слагается из тех
токов, которые получились бы в этой ветви,
если бы в системе каждая э. д. с. действо-
вала в отдельности. Каждая э.д. с. в отдель-
ности создаёт во всех ветвях свою слагающую
тока; алгебраическая сумма слагающих тока
от каждой э. д. с. даёг величину тока при
одновременном действии всех э.д. с. При
определении слагающих токов от каждого*
источника энергии необходимо считать вклю-
чёнными все внутренние сопротивления всех
источников тока, даже тех, э. д. с. которых
принимаются не действующими при опреде-
лении данной слагающей тока. Метод супер-
позиции применим лишь в тех случаях, когда
все э. д. с. и сопротивления не изменяются
при изменении тока.
в) Метод холостого хода и ко-
роткого замыкания даёт возможность
весьма просто и быстро определить ток в
одной из ветвей сложной разветвлённой цепи
без одновременного определения токов во
всех ветвях. По этому методу вея заданная
сложная разветвлённая цепь, за исключе-
нием исследуемой ветви, рассматривается
как один источник тока, зажимами которого
являются те точки, которыми исследуемая
ветвь присоединяется к сложной разветвлён-
ной цепи. Для определения тока в какой-либо
ветви поступают следующим образом: считают
ветвь, в которой необходимо определить ток,
разомкнутой (холостой ход) и определяют
для этого случая разность потенциалов на
концах разомкнутой цепи Uo, после этого
считают, что в ветвь, в которой определяется
ток, включён источник энергии с э. д. с.,
равной Uo. Величина тока определяется
/ =
R3 + 7? ’
где I — ток в заданной ветви;
Uo — разность потенциалов на концах ра-
зомкнутой ветви под действием источ-
ника тока;
Rs—сопротивление всей сложной цепи
между точками, к которым присоеди-
нена ветвь с интересующим нас током,
включая и внутреннее сопротивление
всех источников энергии;
R — сопротивление ветви, в которой опре-
деляется ток.
В том случае, когда в сложной цепи дей-
ствует несколько источников энергии, ток в
заданной ветви определяется по методу
холостого хода и короткого замыкания от
каждого источника энергии в отдельности.
Ток при одновременном действии всех источ-
ников энергии получается как алгебраиче-
ская сумма токов, которые получились бы,
если бы каждая э. д. с. действовала в от-
дельности при наличии внутренних сопротив-
лений других источников энергии, но при
отсутствии их э. д. с.
г) Метод транс фигурации элек-
трических цепей. При определении
токов и напряжений в сложных цепях можно
внести в вычисления значительные упроще-
ния, если путём последовательных преобра-
зований (трансфигураций) упростить цепь
без изменения распределения токов в других
частях цепи. Примером такого преобразова-
ния (трансфигурации) может служить замена
двух параллельно включённых сопротивле-
ний и R., одним эквивалентным по фор-
муле
+ Ra
Ещё большее упрощение сложных развет-
влённых цепей может быть достигнуто, если
отдельные замкнутые контуры (треуголь-
ники), в которых нет источников энергии,
заменять эквивалентными разомкнутыми
схемами в виде трёхконечной звезды или
наоборот. Отдельные сопротивления эквива-
лентной звезды (фиг. 7) через заданные со-
противления схемы треугольника опреде-
ляются следующим образом:
Rsi'Ri^
/?10= Л'ГГ+ Rzs+~Rn ’ (91}
р ________^12^^23____
А20"' /?12+ ^23 + #31
(92)
(93)
р __ Rn'Ra_______
А30- R1Z + ^23 +/?31 ’
Фиг. 7. Трансфигурация схемы звезды в схему
треугольника, и наоборот
т. е. сопротивление луча звезды равно про-
изведению сопротивлений соответственно
прилегающих сторон треугольника, делённому
на сумму сопротивлений всех трёх сторон
треугольника. Для частного случая, когда
сопротивления отдельных ветвей схемы треу-
гольника между собой равны; 7?12~7?23 = R31,
сопротивления эквивалентной звезды Д1о =
= 7?ао=7?з0 также между собой будут равны:
494
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Г) /? *
Rio = /?20 = -^30= ' или = -у >
т. е. сопротивления луча эквивалентной
звезды равны одной трети сопротивления
ветви треугольника. Отдельные сопротивле-
ния эквивалентного треугольника через за-
данные сопротивления схемы звезды удобнее
определять, пользуясь значениями проводи-
мостей. Для схемы фиг. 7
<94)
(95)
(96)
т. е. проводимость стороны треугольника
равна произведению проводимостей лучей
звезды, примыкающих к тем же точкам, де-
лённому на сумму проводимостей всех лучей
звезды. Для частного случая, когда сопро-
тивления лучей звезды равны, Ri0=R20=
«= R30 и gio = gao = gso> проводимости сторон
треугольника g15, g2S и g31 между собой также
будут равны:
gia = , или gazs = А ,
т. е. проводимость ветви эквивалентного тре-
угольника равна одной трети проводимости
луча звезды.
Электролиз; законы Фарадея. Явление
разложения химических сложных веществ
при прохождении через них электрического
тока на составные части называется элект-
ролизом, а растворы, в которых это явле-
ние имеет место, называются электроли-
тами. При прохождении электрического
тока постоянного направления через электро-
лит происходит распадение электролита на
составные части, которые называются ио-
нами. Продукт электролиза, отлагающийся
на положительном электроде — аноде, на-
зывают анионом, а отлагающийся на
отрицательном электроде — катоде назы-
вается катионом. Законы Фарадея гласят:
первый закон — весовое количество вещества,
Нормальные потенциалы в в
1.1 к Na Zn Fe Cd Ni Pb H Cu Ag Hg CI
—3,02 —2,92 -2,71 —0,76 —0,43 —0,40 —0,22 -0,12 0 +0,34 4-0,80 +0,86 +1.35
разложенного при прохождении тока, а сле-
довательно, и весовые количества выделив-
шихся на электродах ионов, пропорциональ-
ны количеству электричества, протекшему
через электролит; второй закон— при одном
и том же количестве электричества, про-
шедшем через различные электролиту, весо-
вые количества выделившихся ионов пропор-
циональны их химическим эквивалентам.
Оба закона могут быть выражены одним
равенством
М = С 4 it' (97)
где М — весовое количество выделившегося
вещества;
А — атомный вес вещества;
п— валентность вещества;
i — ток;
t — время.
Если М выражено в г, i — в то
С = 0,00001036 и 4 = 96 500 к.
Весовое количество вещества, выделяемое
при прохождении через электролит 1 к элек-
тричества, называется электрохимиче-
ским эквивалентом этого вещества.
В 1837 г. русский учёный академик
Борис Семёнович Якоби применил электро-
лиз для получения рельефных отпечатков
(гальванопластика). В предисловии к своей
книге Якоби писал «Гальванопластика при-
надлежит исключительно России. Здесь она
открыта, здесь и развивалась». Русское тех-
ническое общество, празднуя в 1888 г. пяти-
десятилетие гальванопластики, так оценило
это изобретение: «В истории образованности
открытие гальванопластики должно быть
приравнено по своему значению к открытию
книгопечатания».
Гальваническим элементом называется
источник электрической энергии, в кото-
ром происходит преобразование химической
энергии в электрическую. Гальванические
элементы состоят из разнородных элек-
тродов, погружённых в один электролит
или отдельно в два разных электролита,
отделённых друг от друга пористой перего-
родкой. Между каждым электродом и элек-
тролитом возникает электролитиче-
ская разность потенциалов, ко-
торая объясняется давлением растворения,
под действием которого положительные ионы
металла переходят в электролит, сообщая
электролиту положительный потенциал по
отношению к электроду. Для определения
разности потенциалов пользуются шкалой
нормальных потенциалов (табл. 5). Эта шка-
ла даёт разность потенциалов между элек-
тродом данного металла, опущенного в
нормальный раствор его соли, и платино-
вым электродом, опущенным в такой же
раствор.
таблица 5 Для элемента Даниеля,
состоящего из цинкового
электрода, погружённого
в раствор цинкового купо-
роса, и медного электро-
да, погружённого в раст-
вор медного купороса, раз-
ность потенциалов соглас-
но таблице нормальных потенциалов будет
(7=0,34— (0,76) = 1,1 в.
Аккумулятором называется вторичный
элемент, в котором во время зарядки элек-
трическая энергия превращается в химиче-
скую, а затем накопленная химическая энер-
гия превращается во время разрядки обрат-
но в энергию электрическую. Самыми рас-
пространёнными аккумуляторами являются
свинцовые и щелочные. z
Свинцовый аккумулятор состоит из двоя-
кого рода пластин, погружённых в раствор
серной кислоты: положительные пластины,
постоянный ток
495-
на которых находится пористая активная
масса, состоящая из двуокиси свинца (РЬО2),
тёмнокоричневого цвета, и отрицательные
пластины с губчатым (пористым) металличе-
ским свинцом на поверхности. По мере раз-
рядки состав обеих пластин переходит в
сернокислый свинец. При зарядке химиче-
ская реакция в аккумуляторе протекает в
обратном направлении.
Химические реакции в свинцовом акку-
муляторе при зарядке и разрядке могут
быть представлены одним уравнением:
разрядка
РЬО, + 2 H2SO4 + Pb = 2 PbSO4 + 2 Н2О.
ч------------------------
зарядка
Плотность электролита по мере разрядки
снижается. Э. д. с. свинцового аккумуля-
тора порядка 2 — 2,2 в. При повышении
температуры э. д. с. увеличивается на
0,04% на 1°С. Напряжение аккумулятора в
конце разряда не следует доводить ниже
1,85 в, а в конце заряда—не выше 2,7 в.
Большая разница напряжений при заряде
и разряде объясняется изменением э. д. с.
аккумулятора вследствие изменения концен-
трации электролита в порах пластин и уве-
личением внутреннего сопротивления акку-
мулятора. Максимальный разрядный ток
аккумулятора зависит от поверхности пла-
стин.
Количество электричества, которое мож-
но взять от аккумулятора, называют ём-
костью аккумулятора:
t
Q = $idt. (98)
о
Ёмкость аккумулятора измеряется в а м-
пер-часах. Ёмкость аккумулятора изме-
няется в зависимости от величины разряд-
ного тока и температуры. С увеличением
разрядного тока ёмкость уменьшается, так
как образующийся на внешней поверхности
сернокислый свинец закрывает поры актив-
ной массы и тем самым исключает участие
в химической реакции более глубоких слоёв
активной массы. При понижении темпера-
туры ёмкость аккумулятора уменьшается.
Отношение количества электричества, полу-
ченного при разряде, к количеству элек-
тричества, затраченного при заряде, назы-
вается коэфициентом отдачи. Коэфи-
циент отдачи для свинцовых аккумуляторов
колеблется от 0,91 до 0,96.
Коэфици ент полезного дей-
ствия аккумулятора равен отноше-
нию электрической энергии, полученной при
разряде, к количеству электрической энер-
гии, затраченной при заряде, который ко-
леблется в пределах от 0,75 до 0,85.
Щелочной аккумулятор состоит из желез-
ной никелированной решётки, в промежут-
ках которой находятся карманы (пакеты)
из тонкой стали. В эти карманы заклады-
вается активная масса, которая для поло-
жительных пластин состоит из окиси никеля
с некоторой примесью графита, а для отри-
цательных пластин — из смеси окиси железа
и окиси ртути. В качестве электролита чаще
всего используется еДкое кали (щёлочь).
Химическая реакция при зарядке и разряд-
ке представляется следующим уравнением:
разрядка
Fe + 2Ni(OH)s = Fe(OH)2 + 2Ni(OH)2. (99)
зарядка
Напряжение аккумулятора в конце раз-
ряда не следует доводить меньше 1,15 в, на-
пряжение в конце заряда— 1,8 в.
Коэфициент полезного действия аккуму-
лятора колеблется в пределах 0,55 — 0,60.
Преимущества щелочных аккумуляторов
заключаются в том, что при их работе не
происходит вредных выделений. Щелочные
аккумуляторы достаточно прочны, не боятся
сотрясений и выдерживают разряд больши-
ми токами.
Контактное электричество. При соприкос-
новении двух разнородных металлов меж-
ду ними устанавливается разность потен-
циалов, которая не зависит ни от формы,
ни от размеров соприкасающихся провод-
ников. Эта разность потенциалов носит
название контактной разности по-
тенциалов. Её возникновение объясняется
перемещением электронов из одного металла
в другой ввиду различной плотности свобод-
ных электронов(число электронов в единице
объёма) в различных металлах. Свободные
электроны диффундируют из одного металла
в другой, в результате чего определённое
количество электронов перейдёт из одного
металла в другой. Металлы и другие твёр-
дые проводники, не разлагающиеся под дей-
ствием проходящего по ним электрического
тока на химически составные части, могут
быть расположены в ряд Вольта, который
обладает тем свойством, что всякое тело при
соприкосновении с любым из тел, стоящих в
этом ряду дальше, электризуется положи-
тельно, а при соприкосновении с предшеству-
ющими телами электризуется отрицательно.
Ряд Вольта: + Al, Zn, Sn, Cd, Pb, Bi,
нейзильбер, латунь, Hg. Fe, сталь, Cu, Ag,
Au, уголь, Ur, Те, Pt, Pl
Проводники, располагающиеся в ряд
Вольта, обладают следующим важным свой-
ством. Разность потенциалов, возникающая
при соприкосновении двух разнородных
проводников, равна сумме разностей потен-
циалов, возникающих при соприкосновении
попарно всех проводников, помещённых в-
ряд Вольта между двумя крайними провод-
никами. Если между крайними проводни-
ками М и N помещены проводники А и В,
то
UM-UN = (UM-UA) + (UA -UB) +
+ (UB-UN). (100)
Отсюда следует, что на концах цепи, со-
ставленной из нескольких металлов, но
имеюшей одинаковые металлы по концам,
разность потенциалов равна нулю, если все
звенья цепи имеют одну температуру.
Термоэлектричество. В замкнутой цепи,
состоящей из двух разнородных металлов,
появляется электрический ток, если места
стыка разнородных металлов будут иметь
разные температуры. Э. д. с., вызывающая
этот ток, называется термоэлектрон
496
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
движущей силой. Цепь, составленная
из двух разнородных металлов, называется
термопарой. Соединение разнородных
металлов между собой может быть произ-
ведено нажатием, скруткой, сваркой или
при помощи спая. В цепи, состоящей из
однородного металла, при любом распреде-
лении температур термоэлектродвижущей
силы не возникает. В цепи, состоящей из
разнородных металлов, термоэлектродвижу-
щей силы не возникает, если все места спаев
находятся в условиях одинаковой темпера-
туры. Величина термоэлектродвижущей
силы зависит от металлов, образующих тер-
мопару, от температуры мест соединения и
не зависит от длины звеньев, от способа их
соединения и от распределения температуры
по длине звена. Природа появления термо-
электродвижущей силы та же, что и приро-
да появления контактной разности потен-
циалов, и объясняется различной плотностью
свободных электронов в металлах. В термо-
паре имеет место непосредственное преобра-
зование тепловой энергии в электрическую
без промежуточного тела, какими являются
вода и водяной пар. Однако коэфициент
полезного действия этого преобразования
весьма низок (1—3%) и экономически оно
не оправдывается. Многочисленные попытки
создать термопару с высоким коэфициентом
полезного действия к положительным резуль-
татам пока не привели. При небольшой
разности температур спаев величина термо-
электродвижущей силы определяется по
закону
e = a(t1-fs), (101)
где а—коэфициент, характеризующий
металлы термопары;
ц — ta — разность температур спаев.
Все металлы могут быть расположены в
нижеприводимый термоэлектрический
ряд таким образом, что термоэлектрический
ток, возникающий в замкнутой цепи, состав-
ленной из двух металлов этого ряда, имеет
направление через более нагретое соедине-
ние от металла, стоящего ближе к началу
ряда, к металлу, стоящему ближе к концу:
— Na, К, Bi, Ni, Со, Pd, Hg, Pt, Au, Cu,
Sn, Al, Pb, Zn, Ag, Cd, Fe, Sb +.
Термоэлектродвижущие силы используют
для измерения температур. Спай помещают
в то место, температуру которого требуется
замерить, а два других конца присоеди-
няют медными проводами к гальванометру.
Для сравнительно низких температур (—50 —
4- + 500°С) весьма подходящей является тер-
мопара константан — медь, дающая около
40-10-6в/°С, или константан—железо, даю-
щая около 55 • 10—6 в/°С. Для измерения
температур до 1 600°С применяют термопару,
состоящую из 90% платины и 10% родия,
дающую около 10-10—6 в/°С. Градуировку
термопар производят по точкам кипения и
плавления определённых элементов. Термо-
пару или термоэлемент иногда применяют
для измерения весьма малых значений элек-
трического тока.
Электрический ток в вакууме. В идеаль-
ном вакууме отсутствует какое-либо весомое
вещество. Однако в вакууме возможно про-
хождение электрического тока, которое
происходит за счёт тех электронов, которые
выделяются металлическими электродами.
Свободные электроны в металле обладают
„ 1 2
кинетической энергией, равной -% т0 Vq .
Они удерживаются в металле силами поля.
В некоторых случаях кинетическая энергия
свободного электрона становится больше,
чем так называемая работа выхода, и элек-
трон вылетает из металла. Эмиссия (вылет)
электронов при обыкновенных температурах,
называемая холодной эмиссией, ничтожно
мала. Значительно большая эмиссия элек-
тронов металлами получается при так назы-
ваемой термоэлектронной эмис-
сии, когда металл накалён. С повышением
температуры металла скорость электронов
увеличивается, электроны приобретают боль-
шую кинетическую энергию, достаточную
для преодоления работы выхода, и эмиссия
электронов начинается при сравнительно
слабых электрических полях. Принцип
термоэлектронной эмиссии используется в
электронных лампах.
Фотоэлектричество. Фотоэлектрическое
явление происходит при поглощении атома-
ми вещества лучистой энергии и состоит в
том, что поток световой энергии вырывает
из металла электроны. Выведение электрона
из данного металла начинается лишь с опре-
делённой частоты световых волн /0, назы-
ваемой порогом фотоэффекта. Порог фото-
эффекта зависит от вещества освещаемого
тела. Порог в видимой части спектра имеют
щелочные металлы (литий, натрий, калий,
рубидий). Скорость, приобретаемая электро-
нами при фотоэффекте, зависит лишь от дли-
ны световых волн, но не от интенсивности ос-
вещения. От интенсивности освещения зави-
сит число электронов, отрываемых от атомов
в единицу времени. Фотоэффект может проис-
ходить и на поверхности тела (поверхно-
стный, или внешний эффект), и внутри него
(объёмный, или внутренний, эффект). При-
боры, в которых происходит преобразование
лучистой энергии в электрическую, назы-
ваются фотоэлементами.
Изобретателем фотоэлемента является ве-
ликий русский физик Александр Григорье-
вич Столетов (1839—1896 гг.), который пи-
сал: «Система цинк — серебро—воздух при
условии освещения серебра активными луча-
ми временно обращается в настоящий галь-
ванический элемент, в котором роль жидко-
сти играет газовая среда».
В представленном на фиг. 8 вакуумном
фотоэлементе с внешним фотоэффектом све-
товой поток падает на металлическую пла-
стинку А и вырывает из неё электроны.
Если электрон имеет достаточную кинетиче-
скую энергию, он доходит до пластинки В
и в случае замкнутой цепи по гальваноме-
тру пройдёт ток. К. п. д. такого фотоэле-
мента весьма мал. Если между пластинками
фотоэлемента создать электрическое поле
(фиг. 9), чтобы оно подхватывало все отры-
ваемые светом от пластинки электроны и
отводило их к пластинке В, то мы получим
ток насыщения I, который будет пропор-
ционален величине светового потока Ё, па-
ПЕРЕМЕННЫЙ ТОК
497
дающего на поверхность освещаемой пла-
стинки:
I = kF;
к зависит от материала, способа приготов-
ления, формы пластинки и от спектрального
состава падающего света.
При объёмном фотоэффекте, который осо-
бенно сильно проявляется у селена, лучи-
стая энергия, особенно красный и жёлтый
цвет, проникая в тело
вещества, отделяет
электроны от атомов,
в силу чего увеличи-
Фиг. 3. Фотоэлемент
Фит. 9. Схема фотоэлемента
вается число свободных электронов и тем
самым увеличивается электропроводность
селена. Современные фотоэлементы выпол-
няются в виде стеклянных баллонов, в ко-
торых светочувствительный слой наносится
на внутренней поверхности баллона. Свет
падает через неприкрытую часть (окошко)
баллона. Другим электродом служит поме-
щённое внутри баллона кольцо, имеющее,
так же как и светочувствительный слой,
вывод из баллона.
В цезиевых фотоэлементах светочувстви-
тельный слой состоит из слоя окиси се-
ребра, на который наносится слой окиси
металлического цезия. Для увеличения
светочувствительности баллон заполняется
инертным газом (аргоном или неоном),
который вследствие ионизации электро-
нами, выходящими из светочувствитель-
ного слоя, даёт дополнительное число сво-
бодных электронов. В таких фотоэлементах
токи насыщения пропорциональны светово-
му потоку и дают в случае вакуумных фо-
тоэлементов 10—80 мка на 1 лм, а в случае
наполнения газом —до 500 мка на 1 лм.
Электропроводность газов. Газы являют-
ся диэлектриками, но при известных усло-
виях через газы может устанавливаться
непрерывное перемещение электрических
зарядов (электрический ток); электрическая
проводимость газов может быть достигнута
за счёт ионизаторов. В качестве иони-
затора может быть поток электронов, испу-
скаемый накалённым телом, высокая темпе-
ратура, ультрафиолетовые, рентгеновские и
космические лучи. В некоторых случаях
газы получают электропроводность под дей-
ствием сильных электрических полей. Под
действием электрического поля имеющиеся
в газе ионы перемещаются: положительные
по направлению поля, отрицательные в об-
ратном направлении. Дойдя до электродов,
ионы превращаются в нейтральные молеку-
лы. Для того чтобы ток в газовой среде
постоянно существовал, необходимо непре-
рывное образование новых ионов, осущест-
вляемое ионизаторами.
ПЕРЕМЕННЫЙ ТОК
Переменным током в широком смысле это-
го слова называется ток, который изменяет
свою величину в зависимости от времени.
В электротехнике обыкновенно приходится
иметь дело с периодическими переменными
токами, т. е. токами, которые через опреде-
лённые промежутки времени изменяют своё
направление и величину.
Периодом переменного тока назы-
вается время Т, в течение которого ток или
э. д. с. совершает полный цикл своего из-
менения.
Ч астотой переменного тока называет-
ся число периодов в единицу времени. Ча-
стота измеряется в герцах. Частота рав-
на 1 гц, когда в 1 сек. совершается один
период:
;=у-;/Т=1. (102)
Частота переменного тока зависит от
числа оборотов п и числа пар полюсов р
генератора, вырабатывающего переменную
э. д. с.:
рп
/ = <103>
где п—число оборотов в 1 мин.
Угловая частота переменного тока ш
равна
а 2 ’
ш = у = у 2 тс /. (104)
В качестве стандартной частоты в СССР
установлена частота в 50 гц. Соответствую-
щая этой частоте угловая частота
ш= 2 л • 50 = 314 сек-1.
Переменный ток, изменяющийся по зако-
ну синуса, называется переменным синусои-
дально изменяющимся током (гармониче-
ским). Значение переменного тока или э. д. с.
для каждого значения времени называется
мгновенным значением и обозначается соот-
ветственно i или е. Наибольшее значение
переменного тока или э, д, с., которое пере-
менный ток принимает в течение одного
периода (один раз положительное, другой
раз отрицательное), называется а м п л и т у-
дойили максимальным значением и
обозначается Ет и
i — 1т 8’П ы t;
е = Ет sin ai t.
Изображение переменных токов. Перемен-
ные токи, напряжения и э. д. с., изменяю-
щиеся по закону синуса, могут быть изоб-
ражены графически: а) в прямоугольных
осях координат, откладывая по осн абсцисс
углы, а по оси ординат — значения перемен-
ных величин; такие диаграммы называются
л и в е й н ы м и или волновыми; б) в поляр-
ных координатах в виде вектора, равного
в определённом масштабе амплитуде этой
32 Г ом I
498
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
величины, который воображается вращаю-
щимся против часовой стрелки с равномер-
ной угловой скоростью, равной угловой
частоте около некоторого центра, так, что
угол, который составляется этим вектором,
равен фазовому углу а = ш t. Такие диаграм-
мы называются векторными.
Действующее, или эффектив-
ное, значение переменного тока равно
значению такого постоянного тока, который,
проходя через то же сопротивление, что
и переменный ток, выделяет за одно и то
же время такое же количество тепла. Дей-
ствующее, или эффективное, значение тока
и э. д. с. 1 и Е любой формы
(Ю5)
Для синусоидального переменного тока
1 = = 0,707 lmi
Е = = 0,707 Ет. (106)
Ср ед нее зн а чени е тока и э. д, с.
за целый период равно нулю. Среднее зна-
чение тока и э. д, с. за полупериод
г
2
2 С .
icp — у* । idt*,
о
L.
2
£Cp=^Jedt. (107)
О
Для переменного синусоидально изменяю-
щегося тока
1ср = 0,637 /м; Еср = 0,637 Ет. (108)
Поверхностный эффект. Постоянный ток
равномерно распределяется по всему сече-
нию проводника, т. е. плотность тока в
любом сечении проводника имеет одно и то
же значение.В противоположность этому при
переменном токе плотность тока в разных
сечениях проводника неодинакова. Это
происходит оттого, что образующееся вокруг
проводника переменное магнитное поле на-
водит в отдельных нитях (разделённым на
которые можно себе представить проводник)
неодинаковые з. д. с. самоиндукции.
Нити, которые находятся в центре сече-
ния проводника, сцепляются с большим
магнитным потоком, а нити, лежащие на
поверхности проводника, — с меньшим. В
силу этого э. д. с. самоиндукции в цен-
тральных нитях проводника больше, а на
поверхности меньше. Поэтому плотность
тока в центре проводника меньше, а ближе
к поверхности проводника больше. В резуль-
тате этого потери на нагревание в провод-
нике при переменном токе ббльшие, нежели
в том же самом проводнике при постоян-
ном токе. Это явление вытеснения тока на
поверхность проводника носит название
поверхностного эффекта. Поверх-
ностный эффект особенно резко проявляется
в проводах большого сечения и при высокой
частоте.
Активное сопротивление. При явлении
поверхностного эффекта происходит как бы
увеличение сопротивления. Отношение по-
терь на нагревание в проводнике к квадра-
ту эффективного тока называют активным
сопротивлением:
Активное сопротивление больше сопро-
тивления^ при постоянном токе, которое
учитывается по формуле
Rnotm = f j
Для цилиндрических проводников при
невысоких частотах
R к4 /2 d4
-----= 1 -j----------Д.;
Rnocm 48p2-io18
(109)
при больших частотах
(по)
RnoCm 2 V р-10» ”
где R— активное сопротивление;
Rnocm — сопротивление постоянному току;
/ — частота переменного тока;
d — диаметр провода в см-,
р удельное сопротивление, отнесён-
ное к 1 см длины и 1 см* попереч-
ного сечения (для меди ₽ =
= 175.10-8):
ptr — магнитная проницаемость.
Отношения активного сопротивления к
сопротивлению при постоянном токе для
медных проводов, в зависимости от произ-
ведения частоты на квадрат диаметра про-
вода указаны в табл. б.
Таблица б
R /d’ R fd* R
Rnocm Rnocm Rnocm
180 1,0258 ^80 1,4920 2 >00 2,(430
320 1,0805 I 280 1,677s 2 8-sO 2,3937
5С0 1,1747 1620 1,8628 5 120 3,0956
720 1.3180 — — 8 000 .3,7940 |
Явление поверхностного эффекта имеет
место и в проводниках машин и трансфор-
маторов.
Увеличение активного сопротивления з
машинах и трансформаторах гораздо боль-
ше, чем в отдельных проводниках, вслед-
ствие того, что неравномерность распределе-
ния тока по сечению проводника вызывается
не только потоком данного проводника, но
и магнитными потоками соседних провод-
ников.
ПЕРЕМЕННЫЙ ТОК
499
Цепь с активным сопротивлением. При
прохождении переменного тока через актив-
ное сопротивление или, как иногда говорят,
через сопротивление, имеют место следую-
щие основные соотношения.
1. Ток совпадает по фазе с приложенным
к цепи напряжением (фиг. 10), где представ-
Фиг. 10. Схема, векторная и линейная диаграммы
цепи с активным сопротивлением
линейная и векторная диаграммы тока
лены
и напряжения. Если напряжение изменяет-
ся по закону
и — Um sin ш t,
то ток изменяется по закону
i = Im sin ш t.
2. В каждый отдельный момент времени
ток равен напряжению, делённому на со-
противление цепи R
fa Um .
i*= -r ; i = sin u> t.
3. Максимальное значение тока равно
максимальному напряжению, делённому на
сопротивление
/ - —
'т~ R •
4. Эффективное значение тока I равно эф-
фективному напряжению U, делённому на
сопротивление
5. Мощность переменного тока равна
произведению действующих значений тока
и напряжения:
Р = VI, или Р = PR.
Цепь с индуктивностью L. Когда электри-
ческий ток проходит по катушке с индук-
тивностью и сопротивлением, то в катушке
образуется магнитное силовое поле. Если
ток в катушке будет изменяться по времени,
то меняющийся магнитный поток будет на-
водить в катушке э. д. с. самоиндукции.
Величина э. д. с. самоиндукции равна
d Ф
eL = - w jT в'
Если магнитный поток будет изменяться
по закону синуса
Ф = Фт sin ш t,
то величина э. д. с. самоиндукции в каж-
дый отдельный момент времени будет опре-
деляться равенством:
d Ф
eL ~ w = — w Фт <о cos <о t —
= u> Фт ш sin (co t — 90°),
t. e. 3. д. с. самоиндукции отстаёт от наво-
дящего её магнитного потока на угол
90°. Векторная и линейная диаграммы для
этого случая представлены на фиг. 11.
Максимальное значение э. д. с. самоин-
дукции будет
ELm = w фт“>-
Так как
ш = 2 л/,
то
ELm = 2TC/5 * * B’ фт-
Эффективное значение э. д. с. самоиндук-
ции
ELm 2к
el = 7Т = уТФт 4,44 fw Фп” (11
Другое выражение величины э. д. с. са-
моиндукции может быть получено следую-
щим образом:
Если ток изменяется по закону синуса:
I = Im sin ш t,
то
di
eL = —L — LIm <o cos <o t =
= L/m<»sin(u/— 90°),
t. e. в. д. с. самоиндукции отстаёт от
тока на угол 90°.
г/ wL
—— а——
фиг. 11. Схема, векторная и линейная диаграммы
цепи с индуктивностью
Величина максимальной э. д. с. самоин-
дукции будет
ELm~ L1m “•
Эффективное значение з. д. с. самоиндук-
ции
= LI ф.
Если катушка имеет сопротивление
R — 0, то подведённое напряжение покры-
вает э. д. с. самоиндукции:
32*
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
500
U = (/L = -eL;
UL = — [Llm «о sin (ш t — 90°)] =
= Llm<o&in(u> t +90°),
т. e. ток в индуктивной катушке
отстаёт от приложенного напря-
жения на угол 90° (фиг. 11).
Величинатока в индуктивной
катушке
/ = Т^= хГ ’
где Lo> = Xl—реактивное сопротивление
индуктивности,или реактанс индуктивности.
Реактивное сопротивление индуктивно-
сти измеряется в омах, если индуктивность
L подставить в генри.
ш — угловая частота переменного тока.
Мощность, затрачиваемая в
индуктивной катушке, равна н у-
л ю, так как при возрастании тока от ну-
ля до /т в катушке запасается энергия,
а при уменьшении тока от 1т до нуля та-
кое же количество энергии возвращается
обратно.
Энергия, запасаемая в катушке в виде
энергии электромагнитного поля, равна
и о
=> \Lidi =L—^. (112)
и
Цепь с ёмкостью'С. Если конденсатор с
ёмкостью С присоединён к источнику тока
с напряжением U, то на обкладках конден-
сатора собираются электрические заряды
(конденсатор заряжается).
Количество электричества, запасаемое в
конденсаторе
Q = CU.
Если конденсатор приключён к источнику
тока с переменным напряжением
и = Um sin ш t,
то с изменением напряжения изменяется и
количество электричества, запасаемое в кон-
денсаторе
dQ = Cdu.
Поэтому при включении конденсатора па
переменное синусоидально изменяющееся
напряжение в проводах всё время будет
иметь место перетекание зарядов, а следо-
вательно, и тока:
dQ du
i = = C — CUmii> cos ш t —
=CUm ш sin (w t -f- 90 ).
Таким образом, ток в цепи конден-
сатора опережает приложенное
к цепи напряжение на угол 90°.
Векторная и линейная диаграммы для этого
случая представлены на фиг. 12.
Максимальное значение тока в цепи кон-
денсатора
/т»СУт»,
или
, Um Um
= ~Г = х;,
где шС “ Хс называется реактансом
ёмкости и измеряется в омах. Ёмкость
в выражении реактанса ёмкости подстав-
ляется в фарадах.
ис о и
Фиг. 12. Схема? векторная и линейная диаграммы
цепи с ёмкостью
Для эффективного значения тока
1 ~ 1 ~ Хс •
шС
Мощность, затрачиваемая в цепи ёмко-
сти, равна нулю, так как за время увели-
чения напряжения от нуля до Um конден-
сатор потребляет от источника точка энер-
гию (заряжается), а за время уменьшения
напряжения от Um до нуля конденсатор
разряжается и отдаёт энергию обратно
источнику тока. Энергия, запасаемая кон-
денсатором при заряде, равна
uidt = С ~2~
(ИЗ)
Последовательное соединение активного
сопротивления и индуктивности. В индук-
тивных катушках сопротивление каждого
витка составляет часть всего сопротивле-
ния. Индуктированная во всей катушке
э. д. с. составляется из э. д. с. отдельных
витков. Поэтому схематически индуктивную
катушку можно представить двумя сопро-
тивлениями—активным и реактивным, вклю-
чёнными последовательно.
При прохождении через катушку пере-
менного синусоидально изменяющегося тока
приложенное к катушке напряжение в каж-
дый момент времени разбивается на два
слагающих:
di
U = tR -J- L dj .
Слагающая iR = Ua совпадает по фазе с
током, так как представляет падение напря-
жения в активном сопротивлении.
ПЕРЕМЕННЫЙ ТОК
501
Слагающая
di
Ьч7= LI <O^U,
dt L
опережает ток па угол 90°, так как пред-
ставляет компенсирующую э. д. с. самоин-
дукции. Поэтому полное подведён-
ное напряжение будет равно геоме-
трической сумме падений напряжений:
U = йа + UL *,
или
U =]/ + U2 = У (IR)2 +(IXL )2
= /|Л/?2 + Х2
Полное, или кажущееся, сопро-
тивление цепи
Z = y= J/V + X2.
Т о к в индуктивной катушке не совпа-
дает по фазе с напряжением, а Отстаёт на
угол ?:
R XL
Z r Z
Волновая и векторная диаграммы и схе-
ма соединений индуктивной катушки при-
ведены на фиг. 13.
Фиг. 13. Схема, векторная и линейная диаграммы
последовательной цепи с активным сопротивлением
и индуктивностью
Мощность, затрачиваемая в индуктив-
ной катушке
P = U /cos?= PR.
Активным током называется сла-
гающая тока, которая совпадает по фазе с
напряжением:
1а = I cos <р.
Реактивным током называется сла-
гающая тока, которая отстаёт по фазе от
напряжения на угол 90°:
• Следует иметь в виду, что мгновенные значения
синусоидальных величин складываются алгебраи-
чески, а максимальные и эффективные значения
этих величин, поскольку они являются вращающи-
мися векторами (см. выше),— геометрически.
ir— ts)n<p.
Величина, обратная полному сопротив-
лению, называется полной проводи-
мостью и измеряется в сименсах:
Исходя из понятий активной и реактив-
ной слагающих тока, в технике переменных
токов вводят понятия активной и реактив-
ной проводимости:
U R R
1а — I cos о = =г U -gi — Ug.
R
Величина g?. — Ы называется активной
п р о в о д и м о с т I. ю:
U X, X,
I. I sin ш = — = U —— = Ub.
r Г Z 7 Z»
X,
Величина называется и н д у к-
22 Ь
тивной проводимостью.
Хс
Величина = Ьс называется емкост-
ной проводимостью. Величина
X __
------i=bL — bc — b называется реак-
тивной проводимостью.
Последовательное соединение активного
сопротивления и конденсатора. В цепи, со-
стоящей из последовательного соединения
активного сопротивления и ёмкости, пол-
ное подведённое напряжение в каждый мо-
мент времени распадается на две составля-
ющие:
U = Ua + Uc = IR + у J idt.
Составляющая Ua представляет падение
напряжения в активном сопротивлении и
совпадает по фазе с током.
Составляющая Ue представляет компен-
сирующую напряжения на зажимах конден-
сатора и отстаёт от тока на угол 90°.
Полное падение напряжения
будет равно геометрической сумме падений
напряжения на отдельных участках:
U = Ua + ис,
или ______________
U = УU2 + U2 = у (IRY + ихсу =
= / У R2+ X2.
Полное, или кажущееся, сопротивление
цепи
z = 7 = ]A2 + xc2.
Схема соединений, волновая и векторная
диаграммы приведены на фиг. 14.
Вектор тока опережает напряжение
на угол о:
R . ~ХС
cos <р = 7 ; sin = —2~ •
Знак минус перед Хс условимся ставить
везде для того, чтобы отличать активно-
индуктивную цепь от активно-ёмкостной.
Отрицательное значение sin <р характе-
ризует опережение током напряжения, по-
502
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
яожительное значение sin у — отставание
тока от напряжения.
Мощность в цепи равна произведе-
нию эффективных значений тока, напряже-
ния и коэфициента мощности cos <р:
P = U1 cos <f> = PR.
Фиг. 14. Схема, векторная и линейная диаграммы
последовательной цепи с активным сопротивлением
и ёмкостью
Последовательное соединение активного
сопротивления, индуктивной катушки и кон-
денсатора. В цепи с последовательным сое-
динением активного сопротивления, индук-
тивной катушки и конденсатора приложен-
ное напряжение распадается на три состав-
ляющих:
U = iR + L 'У idt — Uа 4- + U с>
где iR— падение напряжения в активном
сопротивлении;
di
L~z— компенсирующая э. д. с. самоин-
а дукции;
р-l idt — компенсирующая напряжение на
u J конденсаторе.
Полное подведённое напряжение равно
геометрической сумме отдельных падений
напряжения:
U = Ua + UL + Uc.
Схема и векторная диаграмма рассматри-
ваемой цепи представлены на фиг. 15, из
которой следует, что
= =
= 1 ]/> + (Х£-Хс)2.
Ток в цепи будет:
Вектор тока по отношению к вектору
напряжения может: а) отставать, когда
XL > Хс', б) опережать, когда XL < Хс\
в) совпадать по фазе с напряжением, когда
XL = Хс.
Угол сдвига фаз между током и напря-
жением зависит от составляющих цепь со-
противлений:
Значение sin о может быть положитель-
ным и отрицательным в зависимости от
величин XL и X с.
Резонанс напряжений. В цепи, состоящей
из активного сопротивления, индуктивности
и ёмкости, векторы падений напряжения
в индуктивности и ёмкости направлены в
разные стороны и могут частично или пол-
ностью компенсировать друг друга. Особен-
но характерно такое состояние, когда имеет
место полная компенсация, т. е.
IX L = IX
или
XL = Хс ,Х =0.
Явление, когда сопротивление индуктив-
ности равно сопротивлению ёмкости, назы-
вается резонансом напряжений.
Фиг. 15. Схема и векторная диаграмма последова-
тельной цепи активного сопротивления, индуктивно’
сти и ёмкости
Частота, при которой в данной цепи
наступает резонанс, называется резонанс-
ной частотой:
ш = 2-f = Й14)
При резонансе напряжений реакции
ёмкости и индуктивности взаимно компен-
сируются; поэтому величина тока зависит
только от величины сопротивления:
U U
Z = R; 1 R = maX'
Значение тока при резонансе напряжений
достигает максимальной величины, несмотря
на весьма большие значения сопротивлений
X, и Хс
При резонансе напряжение на зажимал
ёмкости и индуктивности может очень сильнс
повыситься (если R мало), так как ток i
момент резонанса получает наибольше(
значение.
Угол сдвига фаз между током и напря-
жением в момент резонанса равен нулю
ПЕРЕМЕННЫЙ ТОК
503
cos<? = 1. Поэтому мощность, потребляе-
мая в цепи:
P=UI coscp= Ш.
Реактивный ток в момент резо-
нанса равен нулю.
В радиотехнике явление резонанса искус-
ственно создаётся за счёт переменной индук-
тивности или же за счёт изменения ёмкости.
Для определения длины волны, на кото-
рую настроен приёмник, пользуются следую-
щими соотношениями:
ш=2п'=й?:
/=^ = 2теУТС ' (П5)
Длина волны определяется по ско-
рости распространения энергии электромаг-
нитных волн, равной скорости света:
V3 = 300 000 км/сек.
Длина волны
Х= = 2 те V, VLC. (116)
I
Резонанс токов имеет место при парал-
лельном соединении приёмников электриче-
ской энергии, когда в ряде цепей имеется
реактивная проводимость индуктивности, а
в других—реактивная проводимость ёмкости.
Резонанс токов характеризуется тем, что
общий ток цепи совпадает по фазе с напря-
жением. Это навтупает тогда, когда реак-
тивный ток индуктивных цепей равен по
величине реактивному току ёмкостных цепей:
S 1Г = 0.
В момент резонанса токов алгебраическая
сумма реактивных проводимостейравнанулю:
S&= 0.
Резонанс токов используется в настоящее
время очень широко для целей улучшения
коэфициента мощности фабрично-заводских
установок. Это достигается за счёт парал-
лельного присоединения к электродвигателям
конденсаторов определённой ёмкости.
При резонансе токов имеют место следую-
щие соотношения:
а) угол сдвига фаз между полным током1
и напряжением равен нулю, cosy = 1;
б) полный ток в момент резонанса токов
получает минимальное значение при отсут-
ствии активного сопротивления в* цепи
ёмкости;
в) активная мощность в цепи равна про-
изведению эффективных значений неразвет-
влённого тока и напряжения:
Р = UI.
Символический метод даёт возможность в
весьма простой форме устанавливать соотно-
шения между напряжениями и токами в
случае их синусоидального изменения, при-
меняя законы Ома и Кирхгофа в том же
виде, как и для постоянного тока. Мгновен-
ные значения изменяющейся в зависимости
от времени по закону синуса величины опре-
деляются через проекции на определённую
1 Током по разветвления.
ось соответствующего вектора, вращающегося
с равномерной угловой скоростью ш около
центра, составляющего с начальной линией
угол a = o>t. Такой вращающийся вектор
может быть представлен в трёх видах:
А — а + /&;
А= А?т‘;
A — A (cos ш t + j sin ш t),
где А —модуль вектора, равный УЪ‘+Ь*;
j= —1—мнимая величина;
е— основание натуральных логарифмов;
—угол поворота вектора.
Закон Ома. Если неразветвлённая цепь
состоит из ряда последовательно соединён-
ных сопротивлений
А = G + />1 = е1 К
Zt = rt+jxt=Zt е^‘;
если в цепи действует несколько э. д. с.
Ё1 = Е\ 4- }Е\=Ег е1**,
Et ~ Е'2 + jE’2=Et е'Ч
то ток в цепи по величине и фазе опреде-
лится как отношение суммы комплексных
значений э. д. с. к сумме комплексных зна-
чений сопротивлений:
I = Ё* ^2^ + 1 (^1+ ^2> (117)
Zi 4-Za (Tj 4- га) 4- j (Xj 4- хг)
Первый закон Кирхгофа. Если к узлу
тока подходят токи I — 4- jl\\ / j = l'2 4-
4- jl2, а уходит ток 1, то сумма компле-
ксных значений токов и /2равна 1:
/ = /14-/а = (/1 +/2)+/ 1 + ^2)’
в каждой точке цепи алгебраическая сумма
всех действительных и всех мнимых состав-
ляющих токов равна нулю.
Второй закон Кирхгофа. В замкнутом
контуре сумма комплексных значений э. д. с.
равна сумме комплексных значений падений
напряжений в отдельных участках цепи:
SE = vjz.
На основании второго закона Кирхгофа
сложная цепь, состоящая из нескольких
параллельных ветвей, может быть заменена
одним эквивалентным сопротивлением:
1_ L+J. 4.I4-...4. 1
z-z1 + zs+z,+ 2;-
Для случая двух параллельных ветвей
7—
Zi 4- Z2-
Определение мощности по комплексным
значениям тока и напряжения. Пусть ком-
плексное выражение тока есть <
1 = I' 4- jl" =
и пусть
/=/'— /7" =
I и называются взаимно сопряжёнными
комплексными числами.
504
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Образуем новое комплексное число
Pi = U Л
которое назовём комплексной мощностью.
Если
U = UeJa,
то
Pt = UIeJ = UIeJ,f — W cos <? 4-
+ jUI sin'f = Pa + jPr’ (48)
т. e. действительная часть Р? равна актив-
ной мощности Ра (или Р), мнимая часть Pi
равна реактивной мощности Рг (или Q), а
модуль Pi равен
|р| =Pi = ui = S,
т. е. равен так называемой кажущейся мощ-
ности.
Нахождение распределения токов в слож-
ных цепях переменного тока символическим
методом. Законы Ома и Кирхгофа для цепей
переменного тока в символической форме
составляются так же, как п для цепей по-
стоянного тока. Поэтому для нахождения
распределения токов в сложных цепях
переменного тока могут быть применены те
же методы и способы, которыми пользуются
в цепях постоянного тока, т. е. уравнения
Кирхгофа, метод суперпозиции, метод холо-
стого хода и короткого замыкания, метод
трансфигурацпи, изложенные ранее.
Многофазные системы. Многофазной си-
стемой переменного тока называется такая
система, в которой действуют несколько
э. д. с. одинаковой частоты, но сдвинуты
по фазам на определённые углы.
Симметричной многофазной называется
такая система, в которой во всех фазах
действуют э.'д. с. одной и той же величины,
причём э. д. с. сдвинуты относительно друг
друга на одинаковые углы.
Из всех многофазных систем наибольшее
распространение получила система трёхфаз-
ного тока, предложенная Доливо-Доброволь-
ским, т. е. такая система, когда в цепи
действуют три э. д. с., сдвинутые друг от
друга на угол 120°:
е1 = Ет sin и> t;
е, = Ет sin (ш t — 120°):
es = Em sin(<«f — 240°).
Соединение в звезду. Соединением трёх-
фазной системы в звезду (фиг. 16) называется
такое соединение, когда три «одноимённые»
точки трёх обмоток соединяются в одну
общую точку, а от трёх других точек элек-
трическая энергия отводится к потребителю.
Общая точка трёх обмоток называется
нулевой или нейтральной точкой; провод,
отходящий от этой точки, называется нуле-
вым или нейтральным проводом. Ток нуле-
вого провода /0 равен геометрической сумме
линейных токов. Линейное напряжение при
соединении в звезду равно геометрической
разности двух фазовых напряжений.
При соединении в звезду симметричной
системы линейное или междуфазовое напря-
жение в VlT раз больше фазового напря-
жения. Линейный ток при соединении в
звезду равен фазовому току.
При симметричной нагрузке, соединённой
в звезду, г в пулевом провод" п->-!еп п'."но.
Сумма токов в трёх проводах линии при
симметричной нагрузке равна нулю:
<i + 'а + ,-s = Im sin ш t 4- lm sin (ш t — 120°)4-
+ 7m sin (<о t — 240°) = 0.
Соединение треугольником. Схемой соеди-
нения треугольником называется такая
схема, когда попарно соединяются между
собой разноимённые концы разных фаз
(фиг. 17).
В случае симметричной трёхфазной си-
стемы, соединённой треугольником, имеют
место следующие соотношения:
а) линейный ток в 'КЗ раз больше фазо-
вого тока: _
7л = Уз
б) линейное напряжение равно фазовому
напряжению:
Ел U,fi
Фиг. П. Схема соединения в треугольник
в) сумма трёх линейных токов в каждый
отдельный момент времени равна нулю:
11л -|- 12л 4~ * 3 л = 0.
Мощность симметричной трёхфазной си-
стемы. Мощность трёхфазной системы равна
сумме мощностей в отдельных фазах:
Р1 = 41 II C0S Pi = 42 h COS ?2i
Рз = 43 /3cos<r8;
Р = Р1 + Рз+ Рз
При симметричной системе
4i — 43 = Us', /1 = /2—7з> ?i — ?2 = »
ПЕРЕМЕННЫЙ ТОК
505
Поэтому мощность симметричной трёхфаз-
ной системы
Р = /о5 COSS', (И9)
где <? — угол сдвига фаз между фазовым
током и фазовым напряжением.
Так как для звезды
ил = Узиф,
а для треугольника
I л = Кз 1Ф,
то мощность трёхфазной симметричной си-
стемы для схемы звезды и для схемы тре-
угольника будет выражаться одной форму-
лой:
Р = Узил /л cos ср. (120)
Смешанные соединения. Иногда встреча-
ются схемы, в которых потребитель соединён
в треугольник, а генератор в звезду (или
наоборот) (фиг. 18). Такие схемы соединения
называют смешанными. Трансфигурируя
схему треугольник в эквивалентную звезду,
можно свести смешанную систему к схеме
звезды. Правила трансфигурации схемы звез-
Фиг. 18. Соединение генератора звездой и нагрузки
треугольником
ды в эквивалентную схему треугольника (и
наоборот) рассмотрены были ранее.
Разложение несимметричной трёхфазной
системы на две симметричные. Любая не-
симметричная трёхфазная система, сумма
векторов которой равна нулю, может быть
разложена на две симметричные трёхфазные
системы, имеющие разные амплитуды. При
этом одна система имеет тот же порядок
следования фаз во времени, что и несиммет-
ричная система, и называется системой
прямой последовательности.
Другая система имеет обратный порядок
следования фаз во времени и называется
системой обратной последователь-
ности.
Степень несимметрии системы
определяется отношением величин векторов
обратной и прямой последовательности. Для
источников энергии степень несимметрии по
стандарту не должна превышать 5%. Опре-
деление всех величин, характеризующих
трёхфазную цепь, когда действует несимме-
тричная система напряжений, сводится к
определению величин от двух симметричных
систем, и окончательное решение получает-
ся путём наложения результатов, полученных
в отдельности для каждой из составляющих
симметричных систем. Пусть дана несимме-
тричная система векторов Ё1г Ё2 и Ё3, сум-
ма которых ра'вна нулю. Величина векторов
прямой и обрат-ной последовательности
определяется:
ЗЁ„р = Е1+Ё3?120° +Е3 е~'120“; (121)
ЗЕойр= Ё,+ Ё2 e-j 120° + Ёз Ё 120°, (122)
где Ёпр — первый вектор прямой последова-
тельности;
Ёобр — первый вектор обратной последо-
вательности.
Определение векторов прямой и обратной
последовательности удобно производить
графически (фиг. 19). Для этой цели задан-
Фиг. 19. Нахождение симметричных составляющих
прямой и обратной последовательности
ную несимметричную систему векторов
строят в виде замкнутого треугольника АВС.
Взяв какую-либо сторону этого треугольника
за основание, например ВС, поворачивают
около точек В и С векторы ВА и СА на
120° в ту и другую стороны. Тогда век-
тор ED будет представлять утроенный век-
тор прямой последовательности, а вектор
FG— утроенный вектор обратной последова-
тельности. Угол сдвига между векторами
прямой и обратной последовательности опре-
деляется ‘углом между векторами ED и FG.
Разложение несимметричной трёхфазной
системы на три симметричные. Любая не-
симметричная трёхфазная система, сумма
векторов которой не равна нулю, может
быть разложена на три симметричные систе-
мы: нулевой, прямой и обратной последова-
тельности. В то время как системы прямой
и обратной последовательности каждая в
отдельности представляется тремя равными
между собой векторами, сдвинутыми на
угол 120°, система нулевой последователь-
ности представляет три равных вектора по
величине и совпадающих по фазе. Величина
вектора нулевой последовательности Ео опре-
деляется из условия
3 Ёп = Ё( -f- Ёг 4- Ё3. (123)
Определение вектора нулевой последова-
тельности проще всего производить графи-
чески. Для ятзго проводят три вектора не-
симметричной системы, сумма векторов ко-
торой не равна нулю, из общей точки О
(фиг. 20):
= ОС; Ё„ = О А; Ё3= ОВ.
Искомый вектор Ёо по величине и фазе
равен вектору, соединяющему точку О с
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
«
506
центром тяжести (точкой 170) треугольни-
ка АВС (центр тяжести треугольника АВС
отстоит от вершины С на расстоянии 2/3
длины медианы CD).
Определение векторов прямой и обратной
последовательности в этом случае произво-
дится следующим гра-
фическим построением.
Три вектора несиммет-
ричной системы, сумма
векторов которой не
равна нулю, строят из
Фиг. 20. Нахождение
вектора нулевой после-
довательности
Фиг. 21. Нахождение
векторов рямой и
обратной последова-
гельности
общей точки О (фиг. 21). Соединяя концы
двух векторов, например точки С и В, стро-
ят на линии СВ, как на основании, равно-
сторонние треугольники СМВ и CNB по
одну и другую стороны линии СВ. Соединив
точку М с концом третьего вектора точ-
кой А, получают вектор МА, численно
равный утроенному значению вектора прямой
последовательности. Соединив точку N с кон-
цом третьего вектора точкой А, получают
вектор NA, численно равный утроенному
значению вектора обратной последователь-
ности. Подобным же образом могут быть
получены векторы прямой и обратной после-
довательности для других фаз, если повто-
рить те же построения, взяв за основание
равностороннего треугольника отрезки АС
и ВА.
Несинусоидальные переменные токи. Ряд
Фурье. В большинстве случаев практики
форма кривых периодически изменяющихся
э. д. с. н токов в той или иной.степени от-
личается от синусоидальной формы. Причи-
ной этого являются как конструктивные
особенности генераторов переменного тока,
так и то обстоятельство, что параметры
цепи R, L и С лишь в редких случаях оста-
ются неизменными в течение периода.
Расчёт цепей переменного тока в случае
отступления э. д. с. от синусоидальной фор-
мы производится на основании теоремы
Фурье. Согласно теореме Фурье любая
периодическая функция, имеющая на конеч-
ном интервале конечное число точек разрыва
непрерывности первого рода, может быть
представлена в виде бесконечного ряда гар-
монических функций, период каждой из
которых в целое число раз меньше периода
данной функции:
/ (ш () = До + А4 sin (ш t + ?i) +
+ А2 sin (2 ш t + <р2) + А3 sin (3 ш t + <р3) +
4- . . . + As. sin (А ш i + <?/,),
где Ао—постоянная составляющая;
At— амплитуда основной гармоники;
Ак , А2, А3— амплитуды высших гармоник.
Разложение кривых на высшие гармоники
по способу Рунге. В технике сильных токов
приходится иметь дело большей частью с
такими э. д. с. и токами, которые симме-
тричны относительно оси t. В этом случае в
качестве составляющих гармоник входят
только нечётные гармоники синуса и коси-
нуса. Разложение таких кривых рассматри-
вается ниже.
Периодическая функция, подлежащая раз-
ложению в пяд Фурье, может быть задана в
виде графика (осциллограммы). В этих слу-
чаях коэфициенты ряда вычисляют при-
ближённым методом. Наиболее простым
методом приближённых вычислений является
метод Рунге. По этому способу для нахо-
ждения первых одиннадцати гармоник поло-
вина периода разлагаемой кривой (фиг. 22)
Фиг. 22. Несинусоидальная кривая
делится на двенадцать равных частей. Орди-
наты, измеренные по масштабу, пишу гея в
Сумма ординат, стоящих друг под дру-
гом, будет: S4, S2, Ss, S4, S6, Se.
Разность от вычитания нижних ординат
из верхних будет d4, d2, d3, d4, d6, de.
Кроме того, вычисляют следующие зна-
чения:
П — Sj + S3 —S6;
гг — Se;
ах — а3 — ал.
Значения S, d, rt, г2, е4 вставляют в
табл. 7. Помножив значения s, d, rv r2, e
на синус угла, указанного в той же гори-
зонтальной строчке, определяют суммы
i2, is, ^4 и т. д. до Ц12, а затем ампли-
туды отдельных гармоник синусоид и коси-
нусоид.
Для проверки разложения рекомендуются
следующие правила:
Bi + Вя -f- В5 + В, + В9 -f- В1г = 0;
А[ — А3т А( — А, + А3 — Ап — у„
ПЕРЕМЕННЫЙ ТОК
507
Таблица 7
Амплитуды А в
Для гармоник 1 и И 3 и 9 5 и 7 1 и И 3 и 9 5 и 7
а sin а
15 30 45 60 75 90 0,259 0,5 0,707 0,866 0,966 1 1 W 1 1 “ |и |и|о> 111^11 ^11111 | 1 w 1 i 1 р 1 у 1«1 1 ч 1 ч" 1 : 1 -°-15 i 111 if1 111^11 -d3
Сумма . . 2» 2. -л 2? 2д х. Х1.
Значение амп- литуд s,+s. А ~ А • (5 А= — л.... А’ в СО ©h -I'h я,-—g— 2n-2ia В,- g
Когда кривая симметрична относительно
оси абсцисс и точки перехода через нуль,
все разности dlt d2, ds, dit d,t обращаются
в нуль. Поэтому правая часть таблицы Рунге
для определения амплитуд косинусоид от-
сутствует.
Существуют и другие способы разложе-
ния, которые подробно рассматриваются в
специальных электротехнических справоч-
никах и в курсах электротехники.
Характеристики форм несинусоидальных
кривых. При оценке форм несинусоидальных
кривых в электротехнике принято пользо-
ваться коэфициентами.
а) К оэфици ентом формы, или
формфактором, называют отношение
эффективного значения к среднему зна-
чению, взятому за время одного положи-
тельного полупериода:
К/ = Д; Kf~-p. (124)
‘-ср ‘cP
Для синусоидально изменяющихся вели-
чин Kt = 1,11.
б) Коэфициентом амплитуды
называют отношение максимального значе-
ния к эффективному значению:
Ka-'-f- <125>
Для синусоидально изменяющихся вели-
чин Ка = 1,41.
в) Коэфициентом искажения
называют отношение эффективного значения
первой (основной) синусоиды к эффективному
значению несинусоидально изменяющейся
величины:
ка = kd= £-, (126)
*-*О f0
где Ео и 10—эффективные значения несину-
соидальной кривой.
Для синусоидально изменяющихся вели-
чин Кл = 1. !
Форма кривой считается практически
синусоидальной, если ни одна из её ординат
не отличается от соответствующей ординаты
основной гармоники более чем на 5% от ам-
плитуды.
Измерение несинусоидальных токов, Пере-
менный ток несинусоидалыюй формы изме-
ряется его эффективным значением, равным
такому эквивалентному постоянному току,
который, проходя по тому же активному
сопротивлению, что и переменный, выделяет
в единицу времени такое же количество
тепла, как и переменный ток.
Действующее значение переменного не-
синусоидального тока равно
/ = V 12} + ll+ 12т + + ‘2К • (127)
Аналогично этому выражается и дей-
ствующее значение э. д. с. и напряжения:
£= l/fi2 4- £2 + £2 + _ _ . ^2 . (128)
Мощность переменного тока несинусои-
дальной формы равна сумме мощностей от-
дельных составляющих гармоник:
Р = иг cos«?! 4-U3/3cos?34-...4-
4-O&/jC0S?t. (129)
Высшие гармоники в трёхфазных систе-
мах. В трёхфазной системе, соединённой в
звезду, междуфазовое напряжение не со-
держит высших гармоник, кратных трём.
Поэтому при симметричной трёхфазной си-
стеме
Если трёхфазная система, соединённая в
звезду, имеет нейтральный провод, то при
равномерной нагрузке всех трёх фаз в слу-
чае несинусоидальных токов в нейтральном
проводе ток не равен нулю, а равен тройной
сумме токов высших гармоник порядка,
кратного трём:
io = 3 [43msin (Зш t + а3) +
4- iotn sin (9 u> t -f- a9) -f-. ..]. (130)
При параллельной работе нескольких
генераторов на трёхфазную сеть с нулевым
проводом нулевая точка только одного
генератора присоединяется к нулевому
проводу, так как в противном случае
в проводе, соединяющем нулевые точки
генераторов, даже при ненагруженной
508
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
сети, могут получиться большие токи выс-
ших гармоник, кратных трём. В трёхфазных
системах, соединённых треугольником, при
несинусоидальных э. д. с., наводимых в от-
дельных фазах, сумма э. д. с., действующих
в замкнутом контуре треугольника, не равна
нулю, а равна тройной сумме э. д. с. выс-
ших гармоник порядка, кратного трём:
ei + е2 + ез = 3 [E3m sin (3 <о t -J- рз) 4-
+ Esm sin (9<о t 4- Po) 4- . .]• (131)
Поэтому в трёхфазном генераторе, соеди-
нённом в треугольник, даже при разомкнутой
внешней цепи, ток в обмотке не равен нулю.
При схеме соединения в треугольник в ли-
нейных токах отсутствуют гармоники, крат-
ные трём, поэтому при равномерной на-
грузке
> -й=.
" V з
Форма кривых тока и напряжения фазо-
вых величин отличается от формы кривых
тока и напряжения линейных величин.
Неустановившиеся процессы в электриче-
ских цепях. Процесс установления тока.
Если параметры, определяющие режим уста-
новившегося в цепи тока, изменяются, то
переход к новому режиму происходит не
мгновенно, а спустя какой-то промежуток
времени, так как энергия электрических и
магнитных полей цепи должна получить
изменение, на что требуется время.
Во время неустановившегося процесса на
ток установившегося процесса iy наклады-
вается так называемый свободный ток iCe.
Неустановившиеся процессы в цепях с со-
средоточенными постоянными R, L, С для
различных цепей подчиняются следующим
законам.
Разряд конденсатора с ёмкостью С на
активное сопротивление г:
= — £ J iee <И = ice
ИЛИ I 1 Г .
ice r + c icedt^ 0.
Из этого уравнения вытекает закон из-
менения свободного тока и напряжения на
обкладках конденсатора:
U —- —-
ice-~fe rc‘, Uc = Uce гс, (132)
где Uc— напряжение на обкладках конден-
сатора при t = 0.
Ток в цепи R fi L при прекращении дей-
ствия внешней (приложенной) э. д. с. удо-
влетворяет уравнению:
откуда
ica - Т (133)
где ! — ток в цепи при (=0, т. е. в момент
прекращения действия э. д. с.
Разряд конденсатора с ёмкостью С в цепи
с г и L удовлетворяет уравнению:
ПСа + L %" 4- £ j ice = 0,
ИЛИ d2 ice r dice 1 . n
dt2 + L dt + LC lcs = u-
Решение этого уравнения даёт закон из-
менения тока в цепи:
ice^ АеХ1' + A2e»f,
где Х1>2—корни характеристического урав-
нения:
X -- — 4-1/^ -L
1.2 2L± V 4L2~ LC~
= — a |/\2 —-ц-,'’
Ai и A2 — постоянные интегрирования.
Обозначив Uc—напряжение на обкладках
конденсатора при t = 0, рассмотрим следую-
щие случаи.
г’ 1
1) jp > ру; Xn Ха — действительные
корни. Закон изменения тока будет
— е к LCr (134)
В этом случае будет разряд, при кото-
ром ток возрастает от нуля до максимума
и затем убывает, асимптотически прибли-
жаясь к нулю.
г2 1
2) 4~£~2 ~ LC’ Х*’ Xi—равные корни. За-
кон изменения тока
ice- у -te-ai. (135)
Это даст апериодический разряд—ток воз-
растает от нуля до максимума и затем убы-
вает, асимптотически приближаясь к нулю.
г2 1
3) д-р < Хт, Х2 —мнимые корни.
1 г2
Если обозначить величину р — 0,2
( > 0),
то
Х| 2 = — а i /
Закон изменения тока и напряжения на
обкладках конденсатора будет
(са = ^т e~at sin<0,; О3®)
u== е~ “18in (ш 1+ф)* (137)
где
2 ш L «V
ф — arctg -у— •= arctg -.
ПЕРЕМЕННЫЙ ТОК
509
Разряд в этом случае получается зату-
хающий колебательный, характе-
ризуемый следующими величинами.
Коэфициент затухания
2у. (138)
Частота колебаний
<» 1 -./1 г1 2 3 4
LC~4L*' (139)
Период колебания
Декремент затухания, т. е. от-
ношение двух следующих друг за другом
амплитуд одного знака,
Д = (141)
Логарифмический декремент
затухания
В = 1пД=,0Т; (142)
при г — 0 получается колебательный незату-
хающий разряд, так как энергия при колеба-
нии не расходуется.
Включение цепи R и L под постоянное
напряжение U:
ir. + Ldt’
откуда
U ( -т '\
1 = 7^1—е L у (143)
т. е. ток возрастает от нуля, асимптоти-
чески приближаясь к току установившегося
режима, равного —.
Включение цепи г и С под постоянное
напряжение:
U = ir + J idt,
откуда
U -L
‘ = I» + ice = 7 е га (144)
т. е. ток убывает от начальной величины,-
„ U
равной 7, асимптотически приближаясь к
нулю.
Включение цепи г, L и С под постоянное
напряжение:
di , 1 Г
u + L^t + s^idt = u,
откуда
i e iy ‘с,-
Если напряжение на зажимах конденса-
тора при t — 0 будет 1Л, то решение будет
аналогично случаю разряда конденсатора на
сопротивление и индуктивность (разобран-
ного ранее), только вместо Uc надо подста-
вить значение U + Uc.
Включение цепи г и L под переменное
напряжение:
r di
rl + i- df ~ Um sln (“1 + W’
откуда
i ^iv + ica~ sin (a> 1+Ф — v) —
U ~т‘
---“Sin(^ — y)e L (145)
Ток устанавливается мгновенно, если
ф— ср = 0 или it, так как при этом ток уста-
новившегося режима в момент включения
при t = 0 равен нулю. Наибольшее значение
тока неустановившегося режима будет иметь
место при ф = 0 или it. Это значение будет:
_ 2_ L+ нН
Im Ll + sincp е Lm' 2/J <21т. (146)
Включение цепи г и С под переменное
напряжение:
rl + g J idt = Um sin (<o t + Ф),
откуда
i = iy + ici = sin (co t + ф — ?)—
ij I __ L.
2~77Cc°s (Ф —?)« rc- (147)
Наибольшее значение тока в момент
71
включения при t = 0 будет при ф=* Это
1т
COS
значение будет
Т.
е. может значитель-
но превзойти 1т. Максимальное напряжение
на обкладках конденсатора будет (при ма-
1
лом значении ^), если ср» но н тогда
оно не превысит двойного напряжения при
установившемся режиме.
ЛИТЕРАТУРА И ИСТОЧНИКИ
1. Бабикова М. А. Техника высоких напряже-
ний. Л., Госэнергоиздат, 1947, 312 стр.
2. Китаев Е. В. и Г р е в ц е в Н.Ф. Курс
общей электротехники. Изд. 2-е М., Оборон-
гиз, 1942, 694 стр.
3. Круг' К. А. Основы электротехники. В двух
томах, б-е изд. М.—Л. Госэнергоиздат, 1946.
4, М и т к е в и ч В. Ф. Физические основы электро-
техники. 3-е изд. Л,, Кубуч, 1933, 459 стр.
5. Попов В. С. Электротехнические измерения н
приборы. М., Госэнергоиздат, 1947, 363 стр.
6. СЭТ. Справочная книга для электротехников.
Под общей редакцией М. А. Шателена, В. Ф,
Миткевича и В. А. Голвинского. 6 т. л., Кубуч,
1928-1935.
7. Энергоснабжение железнодорожных узлов (ИТС).
Под редакцией М. А. Петрова, Трансжелдор-
издат, 1939, 726 стр.
Т Е П Л О
ОБЩИЕ ТЕПЛОВЫЕ СВОЙСТВА ТЕЛ
КИНЕТИЧЕСКАЯ ТЕОРИЯ МАТЕРИИ
Молекулярно-кинетические представления
встречаются уже в древности (Демокрит,
Левкипп —V в. до нашей эры). В XVII сто-
летии основные представления развиваются
П. Гассенди. В XVIII в. Д. Вернулли и
М. В. Ломоносов дают уже количественные
оценки явлениям. Во многих работах
М. В. Ломоносова, и особенно в «Размышле-
ниях о причине теплоты и холода* (1745 —
1746), разрабатываются основные положения
зарождающейся кинетической теории мате-
рии. В дальнейшем кинетическая теория
материи развивается в работах Р. Клаузи-
уса (1822—1888), Дж. К. Максвелла (1831—
1879), Л. Больцмана (1844—1906).
Кинетическая теория материи исходит»из
представлений о молекулярном строении ма-
терии, исследует их с точки зрения законов
механики статистики, теории вероятности.
Наиболее разработанной является кинети-
ческая теория газов; экспериментальные ис-
следования последних лет позволили изме-
рить размеры атомов, изучить их траекто-
рии.
Основные положения кинетической
теории газов
По отношению к идеальному газу при-
нимают следующие допущения:
1. Молекулы газа находятся друг от
друга на таких расстояниях, что сравни-
тельно с ними можно пренебречь собствен-
ным объёмом молекул и считать их точками,
обладающими определённой массой (мате-
риальные точки).
2. Между молекулами нет сил притяже-
ния и отталкивания, они ведут себя, как
абсолютно упругие шары в пустоте.
3. Скорости молекул по абсолютной ве-
личине могут быть самыми разнообразными,
теоретически от 0 до оо; каждому состоянию
газа, отвечающему определённой темпера-
туре, соответствует постоянная средняя
скорость молекул.
Если скоростью с, обладают пг молекул,
скоростью с2—п.2 молекул, . . скоростью
ск — пк молекул, причём Hi-f- п.г 4- . +пк=
В главе используются некоторые материялы
автора, напечатанное в т. I Энциклопедического
справочника «Машиностроение». Машгиз, 1947.
— N, то средняя арифметическая скорость
молекул
00
f cdN
S niCi о
a~ N ~ N '
ибо в обычных условиях л, можно считать
бесконечно малым по отношению к N.
Средняя квадратичная скорость Й нахо-
дится из выражения (табл. 1)
S П/С?
00
[ c2dN
О
Таблица 1
Средние квадратичные скорости молекул газов
в м!сек при абсолютных температурах Тqqc
Газ 100° 273,2° 1273,2° Газ 100° 273,2° 1273,2°
н, N, о3 1112 298 279 1838 493 461 3968 1064 996 С1„ СО, Hg (пары) 187 31J 390 180 669
Основное уравнение кинетической теории
Кинетическая теория отождествляет дав-
ление (упругость) газа р с действием на
единицу площади силы, секундный импульс
которой равен сумме импульсов, создавае-
мых за тот же промежуток времени разроз-
ненными по времени ударами молекул,
F
р = — ’
F-t = S/т,
где F — сила, действующая на площадь а;
t = Л
и—продолжительность воздействия си-
лы / при ударе молекулы о поверх-
ность.
Основное уравнение кинетической теории
pv — -j- Nm О.2,
где v — объём газа; ,
m — масса молекулы.
ОБЩИЕ ТЕПЛОВЫЕ СВОЙСТВА ТЕЛ
511
Следствия из основного уравнения
кинетической теории
1. На основании предпосылки о постоян-
стве средней скорости молекул при неиз-
менной температуре из основного уравнения
получаем
pv = const
—связь между объёмом и давлением газа в
условиях неизменности температуры.
2. Сопоставление условий pv — -g- NmQ2,
pv — const и уравнения состояния pv = RT
(с отнесением этих уравнений к молю) даёт
1 2
T=3^Nm22= 3^./,
Nm Й2
где / = —2— — внутренняя кинетическая
энергия газа, определяющая Т.
3. Для идеального газа внутренняя энер-
гия не зависит от объёма.
4. При данной температуре для двух га-
зов будем иметь !г=1]2, откуда
1 । >
тепловое и механическое равновесие как
следствие отсутствия изменения средних
кинетических энергий молекул
даёт, что при одинаковых температуре и
давлении Nj = N2—равенство чисел молекул
разных газов в равных объёмах при одина-
ковых р и Т.
Число столкновений молекул и средний
свободный пробег
Столкновения молекул, при которых они
ведут себя, как упругие шары, делают тра-
екторию молекулы ломаной, зигзагообраз-
ной линией. Прямолинейные отрезки пути
от столкновения до столкновения — свобод-
ные пробеги; длина их весьма разнообразна,
но средняя величина их для некоторой тем-
пературы и давления, определяемая по боль-
шому числу молекул, постоянна.
При движении молекул по всем направ-
лениям
ш_____1__ 1 _ 1 m
i= УТ ’ n^ а2 ~~ /2 ' р тс а2
где I — средний свободный пробег;
<а — средняя скорость молекул;
•V—число столкновений в единицу
времени;
Nj — число молекул в единице объёма;
m nd— масса и диаметр молекул;
p=N1-m—плотность газа.
Число столкновений в единицу времени
одной молекулы
а .—
у = — у 2
Полное число столкновений всех молекул
? = VT-TtiPw-Nj (см. табл. 2).
Таблица 2
Молекулярные данные для некоторых газов f40|
Газ Диаметр молекулы в см Скорость в см 1 сек Средний свободный пробег в см Число столкнове- нийв!сек. в 1 см3
л ри 0“ и 1 im
Н, 2,17.10—8 183 800 17,8-1С—6 10 330-106
О, 2,71 «1С—8 46 100 10,2-10—8 4 520-106
N, 2,95-10—8 49 300 9,5-10—8 5 190-10»
СО 2,74-10—8 49 300 9.5-10—6 5 190.10е
NO 2,59-10—8 47 700 9,4-10—6 5 070.106
СО, 2,90-10—8 39 300 6,5-10—8 6 050.1Св
N„O 3,33-10—8 39 300 6,5-10—6 6 050-106
SO, — 32 600 4,7-lu—6 6 940*10»
Н,0 2,27-10—8 01 500 7,2.U-6 8 540-1J6
Закон распределения скоростей
По Максвеллу, закон распределения ско-
ростей молекул может быть определён из
тех же предпосылок, какие применяются
в статистике для подсчёта ошибки опыта.
По Гауссу, функция вероятности ошибки
здесь v — число ошибок;
х —величина ошибок;
а и h — постоянные величины.
Число молекул, обладающих скоростями
между с и с + de, пропорционально числу
молекул N, объёму dv и функции вероят-
ности
dN = | (с + de)» — "-с3] • Nae~h*ci
4 4
здесь-3 тс (c+dc)3—з тс-с» — 4it'C2dc— dv —
объём, равный разности объёмов концентри-
ческих сфер, описанных радиусами с + de
и с; dN — число молекул со скоростями в
пределах с и с + de, концы векторов кото-
рых попадают в указанный объём.
Л3
Исследование уравнения даёт, что а= —q~
тс '*
1
и Л2 = —j-, где а— скорость, которой обла-
дает в данных условиях наибольшее число
молекул, так называемая наиболее вероят-
ная скорость молекул; откуда
если
4с3 -£г
V Ndc а3 (/'тс ’
dN
то у • de = ~-----доля общего числа моле-
кул, приходящаяся на молекулы со скоро-
стями между с и с 4- de (см. фиг. 1, кри-
512
ТЕПЛОТА
вую распределения скоростей по Максвеллу
и табл. 3).
Таблица 3
Распределение молекул по скорости [40]
1 dN
N de
Пределы
скоростей
оо
Число молекул N , скорости которых
Ср
превышают значение с0, будет
0,0223
0,0867
0,4394
0,8132
0,8312
0,81-13
0,5359
0,1654
м,0025
0,1-0,2
0,2—0,3
3,0—3,
тс2
2kT.dc =
1
-у тс2
где х2 =--------
кТ
2 Ттс<> I'-m-NiCu
х" — кТ ~ ~ k-Nvf
Е
RT ’
причём Е— кинетическая энергия моля, от-
Соотношения между скоростями
средней арифметической, средней
квадратичной и наиболее вероятной
вечающая скорости молекул са.
Интегрирование по частям даёт
Средняя арифметическая скорость
оо 2N
N = -т-=-
X»
00
J cdN
о
(О =------
N
для
НИЯ
1,128 а.
ных
Средняя квадратичная скорость
J c-dN оо
оа = 2-------—. —1= . ( с^е “2 -de =
N а3у г. J
О
3
2 “2’
Й = 1,2247 а.
Таким образом, а < со < £1.
3 2
Из условия Й2 = а2 имеем а2 = -д- £22;
делая подстановку Й3 из уравнения
1
pv = у
отнесённого к молю, получаем
2/н>3 ,/ R \ Т 2кТ
А'уп N± j иг m
R
где к — щ -—константа Больцмана.
Выражение для числа молекул, облада-
ющих скоростями между с и с + de (закон
распределения), имеет вид:
-I» - х2
е х -dx+x„-e I ;
о '
решения необходимы табличные значе-
Ха
2 f -х« .
интеграла —— I е dx для различ-
у тс J
о
2 Е
химии при xj > пре-
достаточной степенью при-
В физической
вышающем 30, с
ближения принимают
00 2N _ 2 / 1 1,3
i/V е I + 2х„ 4х2 8х®
Если рассматривать распределение ско-
ростей в двух измерениях вместо трёх, по-
лучается простое выражение. Закон распре-
деления, получаемый так, даёт численные
результаты, не сильно отличные от резуль-
татов трёхмерного распределения, и его
иногда используют для расчётных целей.
Если молекулы имеют компоненты ско-
рости между и и u + du и г и v-j-dv, и2+е2=
—с2, то общее число молекул со скоростями
между с и c+dc будет
-c-dc = -N--e RT -dE,
a2 RT
2кТ 1 Е
где а3 =-у > тс2=щ-~ , R=kNt, причём
Е—кинетическая энергия моля.
Число молекул, энергия моля которых
превышает заданную величину Е,
Е
Ns == W • е R ‘ .
Т.ЩйЕ 'ЕПЛОВЫЕ СВОЙСТВА ТЕЛ
513
ЕДИНИЦЫ ТЕПЛОТЫ И ТЕМПЕРАТУРА
Однозначная функция состояния тела—
температура,—широко используется как па-
раметр этого состояния.
Элементарное представление о температу-
ре базируется на повседневном опыте и ощу-
щениях различной нагретости тел; под тем-
пературой понимают степень нагретости тела;
точное представление даётся термодинами-
ческой шкалой.
По кинетической теории газов темпера-
тура определяется внутренней кинетической
энергией (J) газа Т — j (см. кинети-
ческую теорию материи).
Для определения температуры использу-
ются приборы, шкалы которых нанос;;гея,
исходя из изменения под влиянием темпе-
ратуры некоторых физических величин и
свойств тел.
Подробнее смотри: ТСЖ, т. I, «Единицы
теплоты», стр. 610 и т. II, «Измерения тем-
пературы».
ТЕПЛОЁМКОСТЬ
Под теплоёмкостью понимают отношепг:
количества теплоты, поглощённого системой
в каком-либо процессе, к соответствующему
повышению температуры.
Истинная теплоёмкость — тепло-
ёмкость системы, определяемая при условии,
что изменение температуры исчезающе мало
с ~ dt ’
где dQ — сообщённая теплота;
dt — исчезающе малое повышение темпе-
ратуры (для установления требует-
ся указание характера процесса,
температуры, давления, при кото-
рых определяется истинная тепло-
ёмкость).
Средняя теплоёмкость — тепло-
ёмкость системы, определяемая при условии
повышения температуры на конечную вели-
чину
где Q — сообщённая теплота;
t1 и t2—начальная и конечная темпера-
туры.
Для установления средней теплоёмкости
необходимо указание характера процесса,
начальной и конечной температур, давления.
удельная теплоёмкость^истим-
ккал ккал X
най г кг-град или сРедняя с- ~
теплоёмкость единицы массы вещества.
Атомная теплоёмкость — тепло-
ёмкость грамматома химического элемента,
равная удельной теплоёмкости, умноженной
на атомный вес.
Мольная теплоёмкост ь—теплоём-
кость моля вещества, равная удельной тепло-
33 Том j
ёмкости, умноженной на молекулярный вес,—
ккал \
истинная ис, средняя вс,„ -------;— .
l r г m кг-медь-граи I
Объёмная теплоёмкость — тепло-
ёмкость единицы объёма газа с, равная"с =
= с у, где f— удельный вес газа при тех
условиях, для которых известно значение
с и вычисляется с.
Чаще в теплотехнических расчётах нахо-
дят с по выражению
С == С‘7о°с,76С' = с'Чгг= %2,3~ ’
где с или р.с берётся при т?х условиях, для
которых находится с;
У
7о° с, 760 — 'н— 22,1 удельный вес при
нормальных (0°С, 760 мм рт. ст.) условиях.
Разница представлений в следующем: в
первом случае объёмная теплоёмкость опре-
деляется по отношению к массе газа, заклю-
чающейся в единице объёма при тех усло-
виях, для которых нужно найти ~с (масса
переменна, зависит отр и t); во втором —
объёмную теплоёмкость условно относят к
постоянной массе газа, заключающейся в
единице объёма при 0°С и 760 мм рт. ст.
„ — ккал
В первом случае размерность с — ~м^~град ’
ккал
во втором — — - V
‘ hM3-2pad
Изохорная теплоёмкость — те-
плоёмкость системы, определённая при ус-
ловии неизменности объёма, может быть
истинной или средней, притом удельной,
мольной, объёмной; обозначения: cv,
т> Iх m-
Изобарная теплоёмкость систе-
мы, определённая прн постоянном давлении,
может быть истинной пли средней, притом
удельной, мольной, объёмной; обозначения:
ср ’ ср , ср ’ ср, аг’ Iх ср, т’ ср, т-
Для идеального газа теплоёмкости зави-
сят только от температур:-.;, реальные газы
обнаруживают зависимость ст давления или
объёма.
При атмосферном давлении в пределах от
О до 1СЗ°С расхождения экспериментальных
данных дают: воздух—1%, Н» и N,—!.5%,
0,-1,75%, NH3 —2,5%, СО2—4,1%; Г!,О —
8,0%, для более высоких температур рас-
хождения выше.
Теплоёмкости газов для состояний, не
находящихся вблизи от условий конденса-
ции, растут с повышением темпсратупы,
влияние дазлення при более высоких темпе-
ратурах делает?;; -’е:и.:зе; изобарные тепло-
ёмкости ;;аютс'> Функциями t и р, изохор-
ные—функциям:; t я v (см. табл. 4).
В техничес.щх расчётах часто исходят
из предпосыл.л..- е?о мольные теплоёмкости
двухатомных гезог, одинаковы при равных
температур 'х и д ; злениях; уже трёхатом-
ные газы подчиняются этому правилу.
514
ТЕПЛОТА
Таблица 4
сп ------г Для воздуха
Р кг*г рад
При р—1 ат и различных температурах t°C
t -И —50 -25 25 50 75 160 150 200 250
Ср 0,2.385 0,23911 0,239-1 0,2099 0, 2'105 0,2410 0,2415 0,2419 0,2124 1 0,24.34 0,2443 0,2453
При t — 0° С и различных давлениях
Р 1 20 60 100 140 130 220
0,2105 0,2492 0,2655 6,2833 0,2985 0,3093 0,3183
При t=^230° С и различных давлениях
21 СО 100 140 180 220
ср 0,2453 0,2463 0,2500 0,2536 0,2566 0,2506 0,2622
По Лаптеву и Шреберу, истинные мольные
теплоёмкости двухатомных газов
мсг, = 4,914 +0,00106 t =
ккал
= 4,625 + 0,00106 Т ----------т- ;
’ ’ моль-град ’
р ср = 6,904 + 0,00106 t =
= 6,615 + 0,00106 Т ^---аЛ~~ -
т моль-град >
для СО2
р cv = 7,805 + 0,00378 t =
= 6,774 + 0,00378 Т ККаЛ—-~
г моль-град ’
рср = 9,795 + 0,00378 t =
= 8,764 + 0,00378 Т -х--™--*- ;
моль-град ’
для Н2О — при тех состояниях, в которых
он находится в дымовых газах и воздухе
(сильно перегрет, давления меньше атмо-
сферного)
Р cv = 7,488 + 0,00232 t =
= 6,855 + 0,00232 Т - 1
моль-град '
рСр = 9,478 + 0,00232 t =
= 8,845+ 0,00232 Т
ккал
моль-град
При линейных зависимостях истинных
теплоёмкостей от t°C пересчёт этих зависи-
мостей в функции Та6с даёт
ккал
pc^pa + pbt = pa' + lJbT-^:^ ;
c=a + bt-a' + bT ,
где а' = а — 273
_ _ — _ ккал
c=*a+bt = a' + ЬТН~^^ ,
— р а — р h _
где а = -Q2 4" , b ; а — а — 273 b .
При линейных зависимостях
pc — pa + pbt, с = а + bt, с = а + bt
—выражения средних теплоёмкостей в интер-
вале от t° С до Г С (Т[а6с до Т°абс) будут:
ti р Ь
pCm = Р а + у, (t« + >1) = U Ст =
«1 z г,
и д ,
= р а' + (Т2 + Тг),
t. b 7"’
ст = а+ Оз + 6) = ст —
t, Т,
Ь
= а'-Р 2 (Т3 + 7\);
!• - b -*
Ст = а + x-(t2 + ti) = ст =
t, 2 т,
— а' + 2 (Т2 + Т,),
где ра, a, a, pb, b, b—коэфициенты из вы-
ражений истинных теплоёмкостей.
Теоретические расчёты, основанные на
данных спектроскопического исследования,
относящиеся к 1933— 1936 гг., дали новые
значения теплоёмкостей. Для Н2О при тем-
пературах, бблыппх 1900°С, новые значения
оказываются меньшими, чем по данным
более раннего периода; при более низких
температурах, наоборот, новые значения
ОБЩИЕ ТЕПЛОВЫЕ СВОЙСТВА ТЕЛ
515
больше старых. Для СО2 новые значения
превышают старые значения. Для двухатом-
ных газов исследования показали, что обыч-
ное допущение о равенстве мольных тепло-
ёмкостей их не оправдывается; при доста-
точно высоких температурах (2000 — 2500°С)
мольные теплоёмкости для различных двух-
атомных газов отличаются друг от друга
на 6%). В работе М. А. Хайлова см.
обзор и анализ данных о теплоёмкостях;
теплоёмкости, опубликованные в работах
Юсти и Шмидта, признаются более точ-
ными по сравнению с теплоёмкостями, по-
лученными ранее калориметрическими ме-
тодами.
Табл. 5 и б дают истинные и средние
теплоёмкости при постоянном давлении по
Юсти. Табл. 7 даёт средние теплоёмкости
при постоянном объёме по Шмидту. Табл. 8
и 9 дают уравнения для теплоёмкостей по
Юсти и Шмидту. М. А. Хайлов для облег-
чения технических расчётов предлагает
упрощённые уравнения, выражающие тепло-
ёмкости линейными функциями темпера-
туры; эти уравнения дают теплоёмкость
с точностью до 1% по отношению к таблич-
ным данным (см. табл. 10 и 11).
В табл. II1 даются для СО2, N2, О2,
Н2О, воздуха сухого, воздуха влажного
(d = 10 г/кг) средние объёмные теплоёмкости
при постоянном давлении от 0°С до t°C,
разработанные ВТИ [35], как нормы для
теплового расчёта котельных агрегатов.
Данные о теплоёмкостях газов при вы-
соких давлениях приведены в работе И. Год-
нева и А. Свердлина [12].
Таблица 5
Истинные мольные теплоёмкости при постоянном
давлении и. с в ---------г- (по данным Юсти)
г р МОЛЬ.град
Газы Н. N, о, со н,о со. Воздух
гс
0 6,86 6,96 6,99 6,96 7,98 8,61 6,94
100 6,96 6,98 7.13 7.00 8,10 9,69 6.99
200 6,99 7,05 7,37 7,09 8,32 10,47 7,10
300 7,01 7,16 7,61 7.23 8,56 11,23 7,24
400 7,03 7,31 7,84 7,40 8,84 11,79 7,40
.500 7,06 7,47 8,02 7,57 9,12 12,25 7,57
600 7,12 7,63 8,18 7,75 9,41 12,63 7,72
700 7,20 7,78 8,31 7,90 9,72 12,94 7,87
800 7,28 7,91 8,41 8,03 10,02 13,20 7,99
90и 7,38 8,03 8,50 8,15 10,30 13,41 8,10
1000 7,49 8,14 8,60 8,24 10,58 13,60 8,21
1100 7,59 8,24 8,66 8,33 10,84 13,74 8,29
1200 7,69 8,32 8,73 8,41 11,08 13.87 8,37
1300 7,80 8,38 8,79 8.47 11,31 13,98 8,43
1400 7.89 8,44 8,85 8,53 11.52 14,07 8,49
1500 7,98 8,49 8,90 8,57 11,71 14.15 8,54
1600 8,08 8,54 8,96 8,62 11,88 14,22 8,59
1700 8,16 8,59 9,01 8,66 12,04 14,28 8,64
1800 8,24 8,63 9,08 8,69 12.19 14,33 8,68
1900 8,32 8,66 9,14 8,72 12,33 14,38 8,72
2000 8,38 8,70 9,19 8,75 12.45 14,42 8,77
2100 8,45 8,73 9,24 8,78 12.57 14,46 8,80
2200 8,51 8,76 9,29 8,81 12.68 14,49 8,83
2300 8,57 8,78 9,34 8,83 12,78 14,52 8,86
2450 8,62 8,80 9,39 8.85 12.87 14,54 8,89
2500 8,68 8,83 9,43 8.87 12,95 14,57 8,92
2600 8,73 8,84 9,47 8.89 13,02 14,59 8,94
2700 8,78 8,86 9,51 8,90 13,08 14,61 8,96
2800 8,83 8,88 9,55 8,91 13,14 14,63 8,98
2900 8,88 8,89 9,59 8,92 13,18 14,64 9, ОС»
3000 8,93 8,90 9.62 8,93 13,23 14,66 9,02
Таблица б
Средние мольные теплоемкости от 0°С до (°C
t
при постоянном давлении и.сп I „----ККал—.
г>"1 \а молы град
О
(по данным Юсти)
Газы н, N, О2 СО Н2О со. Воздух
гс
100 6,92 6,97 7,05 6,97 8,03 9,17 6,96
200 6,95 7,00 7,15 7,00 8.12 9,65 7,01
300 6,97 7,04 7.26 7,06 8,22 10,06 7,06
400 6,98 7,09 7,38 7,12 8,34 10,40 7,13
500 6,99 7,15 7.49 7,19 8,47 10,75 7,20
600 7,01 7,21 7,59 7,27 8,60 11,03 7,27
700 7,03 7,27 7,68 7,34 8,74 11,28 7,34
800 7,06 7,35 7.77 7,43 8.89 11,50 7.42
900 7,09 7,42 7,85 7,50 9,04 11,70 7,49
1000 7,12 7,49 7,92 7,57 9,18 11,88 7,56
1100 7,15 7,56 7,98 7,64 9,32 12,05 7,62
1200 7,20 7,62 8,04 7,70 9,45 12,19 7,68
1300 7,24 7,67 8,11 7,76 9,58 12,32 7,73
1400 7,28 7,73 8.16 7,81 9,72 12,45 7,78
1500 7,32 7,78 8,20 7,85 9,84 12,56 7,84
1600 7,36 7.82 8,24 7,90 9,96 12,66 7,88
1700 7,40 7,86 8,28 7,94 10.09 12,75 7,92
1800 7,45 7,91 8,33 7,98 10,20 12,84 7,96
1900 7,49 7,94 8,38 8,02 10,30 12,92 7,99
2000 7,53 7,98 8.42 8,05 10,41 12,99 8,03
2100 7,57 8,01 8,45 8.09 10,52 13,06 8,06
2200 7,62 8,05 8,48 8,12 10,61 13,13 8,08
2300 7,66 8,08 8,52 8,15 10,71 13,19 8,12
2400 7,70 8,10 8,56 8,18 10,79 13,24 8,14
2500 7,74 8,14 8,59 8,21 10,87 13,30 8.18
2600 7,78 8,17 8,63 8,24 10,96 13,34 8,20
2700 7,81 8,19 8,65 8,26 11,03 13,39 8.23
2800 7,85 8,22 8,68 8,28 11,11 13,43 8,25
2900 7,89 8,24 8,72 8,30 11,18 13/8 8,27
3000 7,92 8,26 8,76 8,32 11,23 13,52 8,29
Таблица 7
Средние мольные теплоемкости от 0%,*- до Т°
абс
Т
। к кал
при постоянном объеме u.cw m Q --------г
‘ » m I в молы град
О
____________(по данным Шмидта)
Газы Т°абс н. N, о. со Н8О со. сн4 Воздух
273 4,792 4,959 4,91 4,960 5,926 5,400 6,012 4.930
300 4,798 4,960 4,93 4,961 5,935 5,530 6,051 4,935
350 4,818 4,963 4,97 4,965 5,951 5,770 6,160
400 4,838 4,966 5,008 4.969 5.973 6,010 6,314 4,957
500 4,869 4,980 5,063 4,990 6,033 6,480 6,734 4,979
600 4.891 5,007 5,147 5.027 6,113 6.91С 7,236 5,018
700 4,913 5,047 5,239 5,077 6,210 7,290 7.797 5,068
800 4,932 5.097 5.333 5,137 6,318 7,670 8.356 5.101
900 4,953 5,154 5,427 5,202 6,433 7,990 8,929 5,191
1000 4,977 5,215 5,513 5,269 6.551 8,270 9,467 5,257
1100 5.006 5,272 5,592 5,338 6.681J 8,500 9,980 5,318
1200 5,034 5,33-1 5,667 5,403 6,815 8,770 10,50 5,382
1300 5,068 5,392 5,736 5,467 6,949 9,000 10.99 5,442
1400 5,102 5,452 5,801 5,526 7,081 9,180 11,50 5,502
1500 5,144 5,512 5,863 5,586 7,210 9,360 — 5,562
1600 5,182 5,568 5.917 5,639 7,338 9,510 — 5,618
170.J' 5,224 5,621 5,966 5,690 7,464 9,660 —— 5,669
1800 5,266 5,671 6,010 5,740 7,585 9,800 — 5.717
1900 5,308 5,717 6,059 5,786 7,704 9,940 — 5,764
2000 5,350 5.763 6,090 5,831 7.820 10,05 — 5,806
2100 5,392 5,804 6,140 5,872 7,930 10,16 — 5,848
2200 5,434 5,840 6,176 5,911 8.030 10,26 — 5.884
2300 5,474 5,880 6,211? 5,947 8.140 1о,зб — 5,922
2400 5,513 5,912 6,241 5,982 8,246 10,45 — 5,954
2500 5,554 5,944 6.274 6,014 8,340 10,53 — 5,986
2600 5.591 5,977 6,30J 6,047 8.430 10,61 — 6,017
2700 5,629 6,008 6,32^ 6.978 8.510 10,68 — 6.047
2800 5,673 6,040 6.353 6,107 8,610 10.75 — 6,074
2900 5,705 6,067 6.379 6.13-1 8,690 10.81 —. 6,104
3000 5,743 6.095 6,434 6.158 8.770 10,86 — 6,131
33*
516
ТЕПЛОТА
Таблица 8
Средние мольные теплоемкости от 0°С
ДО 1°С при p=const
(по данным Юсти)
Газы Эмпирические уравнения / I ккал \ 1 р,т в моль-град J
Воздух Для температур от /==100'” до t Р-С m | = 6,919 4- 0,374-10"2Ч + 0 4-0,3150- 10—6-Г Для температур от t— 900е до /=2000° С t р-ср,т | = 6,848 4- 0,815- 10~3.£- 0 -0,1120- IO”6-f3
О» Для температур от £=100° до f=1000°C t |ic m | = 6,931 + 1,21 J- 10-3-t- 0 —0,222- IO-6-/’ Для температур от 1 — 1000° до t~3000°С VcPtm 1=7,242+0,768. 10~3-i- 0 -0,09-10-®-ia
N, Для температур от 1=100° до t”1000°C t pepm | =6,939 + 0,279- 10“s-z + 0 + 0,287-10—®-H Для температур от 1 = 1000° до £=3000°С t V-cp rn | =6,773 + 0,S28-10-3-/— 0 -0,1 10Z - ic—®-r
н, Для температур от t=100° до 1 = 500°С t p.cp_m I =6.881 + 0,425-IQ-3./— 0 —0,416 -10"®-H Для температур от 1=500° до 1 = 1500'С t №ррп | =6.925+0,963-10-3-/+ 0 4-0,133.10~'<Р Для температур от i=150CO до £ = ЗСОЗ''С t VCpsm 1 =6.561 + 0.559- i0~3 -1— 0 -0,035- 10—®.(>
СО Для юмператур от *=100° до £=1000°С 1 ^ср,т \ = 6,894 + 0,49-10-®./+ 0 + 0,205-10—с-/а Для температур от г=1000*' до £ = ЗСС0еС £ VcpfTn | -6,8524-0,833.10~3.£- и —0,115-ИГ”6-/2
Продолжение табл. 8
соа Для темг+paiyp от 1=100° до /=1000°С t "ср,т ! =8,703 + 4,86- 10-s-Z- -1,683-10~3-Г Для температур от £=1000° до f-3000’C £ Р+р>т | =10,3+l,89-10-3-t- 0 -0,275- 10—s-t‘
нао Для температур ст £=100г до £=1300°С t | =7,897 U,08-10~s-t + + 0,178-10-®-Г Для температур от £=1000'’ до £ = 3000°С 1 ?ср>т |=7 513+1,863-Ю-3-/- и — 0, 209- 1Q—®-/3
Таблица 9 Средние мольные теплоемкости газов от 0° абс. до Т° абс. при p = const (по данным Шмидта)
Газы Эмпирические уравнения / Т \ 1 „„ [ к кал | 1 ni I В - | 1 Р,"‘ моль-грей ]
В оз дух Для температур от Т = 300° до Т=900° абс. Т Рср:т | =6,927 — 0,1730-10~ 3-Т + + 0,5-10-®-Т* Для температур от Т— 700° до Т=3000° абс. Т V*p,m i =6,52 + 0, 831-10-3-Т- 0 —0,1003.10—6 -Т3
О3 Для температур от 7' = 30С1° до 7’ = 900° абс. Т р.су>;п j = 6,761 + 0,4090-IO-3-7 + + 0,35- IO-S-7S Для температур от 7=903" до 7=3066" абе. 7 рср>т | =, 0,658 = 0,9720-10—3 • Т— —0, 1320- io—6-Т=
i i । Na I Для температур от Т = 300° до Т=900° абс. 'Г '•^р.т | “6.09S-0,344-10_3-Т+ + 0,556-10-а-7- Для тегдлерат-’р от 7 =900сдо Т--> 2003' абс. Т ?-cp,in I - 6,427 4- 0,874.10-3.Т- 0 - 0. 111 • 1О~
ОБЩИЕ ТЕПЛОВЫЕ СВОЙСТВА ТЕЛ
517
1 1 на Для температур от 7=300° до 7=1600° абс. Т V-Cp.m | “6,774+0,124 • 1О~3. Т + е + 0,071*10— ‘-Т‘ Для температур от 7=1600° до 7=3000° абс. 7 v-cp,m j = 6,424 + 0,496-10“3*7'- 1) -0, 021 - 10-в - Т"
j i 1 со Для температур от 7=300° до 7 = 1000° абс. Т >>СР1,П | = 6,989—0,325-10-3 - Т + 0 + 0,606*10—6-Та Для температур от 7=1 000' до 7=3000° абс. Т 9-Сртп | = 6,455+ 0,916 • Ю-3* Т— 0 -0, 118*10“6*Та
соа Для температур от 7 = 300° до 7=1300° абс. 7 ^ср,т I = 5,835+6,1*10“3-7'~ — 1,67 • 10“ е-Т“ Для температур от 7=1300° до 7=3000° абс. Т vcp,m | =8,018 4-2,795- 10“3*7'- 0 —0,395•10-6 Та
нао Для температур от 7=300° до 7-=1200°абс. 7 V-Cp,m | = 7( 857 + 0/017 • 1 О'-*'• 7 + 0 + 0,642-10“6- Т‘‘ Для температур от 7= 1 200° до 7 = 3000° абс. 7 V-Cp,m =6 948 ; 1,748-10“3-7'— и -0, 16-10 "' -7'а
Таблица 10
Средние мольные теплоёмкости газов от 0° абс
до Т 0 абс при p=const.
(по данным Юсти с точностью до 1%)
Газы Эмпирические уравнения / I к кал | 1 Р-Сп т в — — - 1 \ (J 1
Воздух Для температур от г —1 03“ до 2=1600“ С i V-Cp,m j = 6,92 + 0,61-I0“3-l и Для температур от 1=1600° до +-=3000°С t v-cP,m 1 = 7,41 + 0,3-10-3-t
Продолжение табл. 9
О8 Для температур от ( = 100° до ( = 1300° С t Р-ср,т | =, 7,02+0,86.10~3.( 0 Для температур от (=1300° до (=3000°С t V-Cpjn | = 7,64 + 0,38*10—3.( , ’ 0
N„ Для температур от t=100° до {=1600° С t P-cpfTn | = 6,89 + 0,6-10-3*f 0 Для температур от { = 1600° до {«3000° С t ^сргт | = 7,33 + 0, 32.10”3.( 0
Н3 Для температур от (=100° до (=1100° С ( Рср)ТП | = 6,9 + 0,21-10-3-( 6 Для температур от ( = 700° до ( = 3’000° С t №р>тп | = 6,75 + 0, 39-10—3.( 0
СО Для температур от (=100° до (--*-• 1600° С ( рСр'Ш | = 6,91+0,63-10-3-! Для температур от ( = 1600° до ( = 3000° С ( Vcp,m ! = 7, 42 + 0, 31 • 10“3 -1 и
со, ! Для температур от (=100° до ( = 800° С ( V-Cp,m | “ 8, 95 + 3,32 -10“3-1 0 Для температур от (-800° до (--=1700" С ( =.10,51 |-l,33*10-s.t Для температур ст (=1700° до ( = 3000° С ( Р-срш[ =11,79 + 0,59*10—3-( и
Н,0 Для температур от (=100° до ( = 2000° С ( Рср1ГП | = 7,85 1-1,31-10—3 .( 0 Для температур от (=1900° до (=3000° ( VCp m j = 8,70+0,86*1O~8., 1
518
ТЕПЛОТА
Таблица 11
Средние мольные теплоёмкости газов от О°абс. до Т абс. при p=const (По данным Шмидта с точностью до 1%)
Газы Эмпирические уравнения / Т \ 1 1 к кал 1 1 ^ср,т в моль-град j
Воздух о8 Для (емператур от Т = 300° до Т=2000° абс. Т ^ср,т J =6,708+0,543-1О-3-Т Для температур от 7=2000° до 7=3000° абс. 7 | = 7,08+0, 35.10~3-7 и Для температур от 7 = 300° до 7=1700° абс. 7 \у-ср т | =6.728 + 0,736.10'3-7 0 Для температур от 7=1700° до Т = 3000° абс. 7 | = 7,40+0,34.Ю“3.7 0
N, Для температур от 7= 300е до 7 = 2200° абс. 7 | = 6,74 + 0,5.10“8.7 0 Для температур от 7=2200° до -3000° 7 абс. 7 Р-Ср,т | = 7,05 + 0, 35* 10""3 *7 0
н. Для температур от 7=300° до 7 = 3000° абс. 7 ^Ср,т I = 0,68 + 0, 34 10“э • 7 0
СО Для температур от 7 = 300° до 7 = 2200° абс. 7 Р-Ср>т | = 6,72 + 0,55-Ю"3.7 0 Для температур от 7=1800° до 7 = 3000° абс 7 Р-ср>т | = 7,07 +0,37 • 10”'3. Т 0
со2 Для температур от 7^=300° до 7 = 1000° абс. 7 vcp,m =6,495 + 3,85.1О-3.Т () Для температур от 7 = 1000° до 7=2100°абс. 7 ^ср,т 1 “ 8,655 + !,7-10-3.7 0 Для температур от 7 = 1900° до 7=3000°абс. 7 I ^Ср,т =10'285 + 0 S8'10”3'7 1 ’ °
Продолжение табл. 11
HSO Для температур от 7 = 300° до 7=1300° абс. 7 Р-Ср,т | =7,535 + 1,02.10'3.7 0 Для температур от 7=1300° до 7=3000° абс. 7 p-cpjZn |=7,585+1,08. IO”3-7 0
сн. Для температур от 7 = 300° до 7 = 600° абс. 7 p.cpfW | « 7,01 + 3,3-10"3-7 0 Для температур от 7=600° до 7=1400° абс. 7 р.срт | = 6,06 + 5,З.Ю~3-7 0
Таблица И1
Средние объбмиые теплоемкости при постоянном
давлении воздуха и газов от 0“С до (°C
в ккал/нм3 сР1П1 j по данным ВТИ [35]
t СО, N, О2 н.о Воздух сухой Воздух | влажный 1 а=10 г 1кг
0 0,3805 0.3088 0,3116 0,3569 0,3093 0,3150
100 0,4092 0,3096 0,3145 0,3596 0,3106 0,3163
200 0,4290 0,3106 0,3190 0,3635 0,3123 0 3181’
30а 0.4469 0,3122 0,3240 0,3684 0,3147 0 3206
400 0,4628 0,3146 0.3291 0,3739 0,3175 0,3235
500 0.4769 0,3173 0,3339 0,3796 0,3207 0 3268
600 0,4895 0,3203 0,3385 0,3856 0,3241 0 3303
700 0,5008 0,3235 0,3426 0,3920 0.3275 0*3338
800 0,5110 0.3266 0,3464 0.3985 0,3307 0 3371
900 0.5204 0,3297 0,3498 0,4050 0,3338 0 3403
1000 0,5288 0,3325 0,3529 0,4115 0,3367 0 3433
1100 0,5363 0.3354 0,3548 0,4180 0,3396 0 3463
1200 0,5433 0,3380 0,3581 0.4244 0,3422 0 3490
1300 0,5495 0,3406 0,3608 0,4306 0,3448 0 3517
1400 0,5553 0.3430 0,3631 0,4367 0,3472 0 3542
1500 0,5606 0,3453 0,3653 0,4425 0,3494 0 3565
1600 0,5655 0,3473 0,3673 0,4482 0,3515 0 3587
1700 0,5701 0,3493 0,3693 0,4537 0,3534 0 3607
1800 0,5744 0,3511 0,3712 0,4590 0,3552 0 3625
1900 0.5783 0,3529 0,3730 0,4640 0,3570 0’3644
2000 0,5820 0,3545 0.3747 0,4689 0,3586 0,3661
2100 0,5855 0,3560 0,3764 0,4736 0,3602 0,3678
2200 0,5887 0,3574 0,3781 0,4780 0,3616 0,3693
2300 0,5919 0,3588 0,3796 0.4822 0,3631 0,3708
2400 0,5947 0,3601 0,3810 0,4864 0,3644 0,3722
2500 0,5974 0,3613 и,3825 0,4903 0,3657 0,3735
В табл. 12, 13, 14, 15 и 16 даны теплоём-
кости жидких и твёрдых тел.
100
Средняя теплоёмкость воды ст в интер-
0
вале 0—100°С приблизительно равна тепло-
ёмкости при 15°С — с1Я.
По Политцер, при t = — 35°С теплоём-
кость ртути с = 0,0350 ; как
среднее из разных наблюдений: при t == 0°С
с = 0,03333, при t — 100 С с = 0,03262, при
ОБЩИЕ ТЕПЛОВЫЕ СВОЙСТВА ТЕЛ
519
t = 200°С с = 0,03189, т, е. теплоёмкость
ртути убывает с повышением температуры;
по Курбатову, минимум с между 200—250°С,
по Barnes,— между 100—150°С; с — 0,03336—
—0,0000061 (в пределах от 0 до 250°С),
Таблица 12
Теплоёмкость воды [45]
1 Rowland Griffiths Callendar- Barnes Jager- Stelnwehr
10°С 1,0019 1,0021 5°С—1,0029
11 1,0014 1,0016 10 —1,0013
12 1,0010 1,0011 15 -1,0000
13 1,0007 1,0006 1,0007 20 —1,9990
14 1,0003 1,0003 1,0003 25 -0,9983
15 1,0000 1,0000 1,0000 30 —0,9979
16 0,9996 0,9997 0,9997 35 —0,9978
17 0,9993 0,9994 0,9994 40 -0,9981
18 0,9990 0.9991 0.9990 45 -0,9987
19 0,9986 0,9988 0,9988
20 0,9983 0,9985 0,9985 50—0,9996
21 0,9981 0,9^82 0,9983 ——
22 0,9979 0,99/9 0,9980 —
23 0,9976 0,9976 0,9977 —
24 0,9974 0,9973 0,9975 •—
25 0,9972 0,9970 0,9974 —
Триме ч а н и з. По Reg Tault, с == 1
4- 0,000041 + 0,0000009 ta, однако позднейшие
исследования даюг ми нимум с при температу-
рах от 20 до 40~С: так, значения с, по Callen-
dar и Barnes, для температур от 0 до 60° дают
С=О, 9982 + 0,0000045 1—40)2 (минимум около
40° С). Теплоемкость зодь при температурах ниже
нуля (по Tommasini-Cardanl до— 10° С, по Маг-
tineti до 6“ С) увел> тчивается с понижением
температуры на 1“ С приблизительно на 0,0005.
Таблица 13
Средняя удельная теплоёмкость сжиженных газов
[28]
Жидкость Пределы в 3 абс. ккал | кг*г рад |
Аммиак 200—220 1,08
Углекислый газ (при 63 п?;) 223—263 0,465—0,539
Окись углерода 67—83 0,0615
Хлор 68 0,229
Водород 15-21 1.75—2,33
Азот 64-76 0,475
Окись азота 115—117 0,580
Кислород ...... . „ . . 57—73 0,398
Сернистый ангидрид .... 273 0,317
вязкость
Внутреннее трение в реальных жидко-
стях- вязкость— является отличием реальной
жидкости от идеальной. Под влиянием вяз-
кости происходит видоизменение профиля
скоростей потока жидкости, набегающего
на поверхность.
1
По кинетической теории газов ;+= у р• со•/,
где со—средняя скорость молекул; I—свобод-
фиг. 2
ный пробег; так как I обратно пропорцио-
нально р, то по кинетической теории р.
идеального газа не зависит от плотности, а
следовательно, и давления, что частично—
при средних давлениях — подтверждается
опытом.
Фиг. з
Основные формулы и данные, относящие-
ся к определению вязкости жидкости и газов,
сил внутреннего трения, коэфициентов кине-
матической вязкости, см. ТСЖ, т. I, раздел
«Г идромеханика».
Коэфициент вязкости перегретого водя-
ного пара, по данным Д. Тимрот, приведён
на фиг. 2 [44].
Таблица 14
Средняя теплоёмкость ст воды между 0° и /°C до Дитеричи
20 40 60 80 100 | 120 140 160 180 200 220 240 260 280 300
Ст~ 1,0010 0,9973 0,9976 0,9985 1,оиоо| 1,0020 1,0046 1,0077 1,0113 1,0155 1,0203 1,0256 1,0315 1,0380 1,0449
ст -0,9983-0,005184.^ + 0,006912
520
ТЕПЛОТА
Таблица 15»
Истинная удельная теплоёмкость твёрдых тел выпажена в —1^яал______
кг-град
°C РЬ Zn Al Ag Au Cu Ni Fe Co SiO,
0 0,0359 0,0878 0,2220 0,0573 0,0317 0,1008 0,1095 0,1055 0,0912
100 U,0336 0,0965 0,2297 0,0583 0,0320 0,1014 0,1200 ОД168 0^0993 0,2372
200 U,U313 0,1052 0,2374 0,0594 0,0322 0,1020 0,1305 0,1282 0,1073 0,2416
300 0,0290 0,1139 0,2451 0,0605 0,0325 0,1026 0,1400 0,1396 0'1154 0,2460
400 0,0266 0,1226 0,2529 0,0616 0,0328 0,1032 0,1294 0’1509 0Д235 0,2504
500 0,0259 0,1173 0,2606 0,0627 0,0330 0,1038 0,1294 0,1623 0,1316 O’2548
600 0,0252 0,1141 0,2683 0,0638 0,0333 0,1045 0,1294 0Д737 0,1396 0’2592
700 0,0246 0,1109 0,2523 0.0649 0,0335 0,1051 0,1295 0,1850 0,1477 0,2636
800 0,0239 0,1076 0,2571 0,0660 0,0333 0,1057 0,1295 0,1592 0,1558 0,2680
900 0,0233 0,1044 0,2619 0,0671 0,0341 ОДО63 0,1295 0,1592 0,1639 0,2724
1000 0,0226 0,1012 0,2667 0,0687 0,0343 0,1069 0,1295 0,1448 0^2768
1100 — — —- 0,0694 0,0329 0,1128 0,1296 0,1448 0,1424 0.2812
1200 — — — 0,0750 0,0346 0,1159 0,1296 0,1448 0,1454 0,2856
1300 — — — 0,0807 0,0364 0,1291 0,1296 0,1449 0,1483 0,2900
1400 — —— — — —— 0,1296 0,1449 0,1512 0,2944
1500 — — — —— — — 0,1338 0,2142 0,1472 0,2988
1600 — — — — 0,1501 0,1472 —
♦ По Smithsonian Tables.
Таблица 16
Средняя удельная теплоёмкость в'к^.гра^ твёрдых и капельно-жидких тел между 0 и 160° [46J
Азот (жидкий) Алюминий . , . . 0,430 . 0,22 Дерево (сосна) . Древесный уголь 0,65 0,20 Марганец Медь . . . . . . . 0,12 . . . . 0,094 Сурьма 0.05
Свинец . 0,031
Аммиак .... .1,00 Железо и сталь . 0,115 Машинное масло 0,40 Стекло ..... . 0,20
Анилин .... . 0,49 Зола 0,20 Мраморный из- Серная кислота . 0,33
Базальт .... . 0,20 Золото 0,031 вестняк . ... 0,21 Серебро .... . 0,056
Бензол ..... . 0,44 Каменный уголь 0,31 Никель . . . . 0,11 Сера .0,18
Бетон ..... . 0,21 Керосин 0,50 Нафталин . . . . 0,31 Скипидар . . . 0,42
Висмут . 0,030 Константан . . . 0,098 Олово . . ... 0,056 Тантал . . _ . . O.O36
Вольфрам . , . . 0,034 Кирпич 0,22 Оливковое масло 0,40 Уксусная кислота 0*. 51
Гипс . 0,20 Кислород жидки? 0,347 Платина . . . . 0,032 Хлороформ . . . 0,23
Глицерин . , . . 0,58 Кокс 0,20 Песчаник . . . . 0,22 Цинк 0,094
Гранит . 0,20 Латунь ...... 0,092 Первичная смола 0, 5 Шлаки 0,18
Графит . 0,20 Лед . 0,50 Ртуть . . . . . . 0,035 Эфир 0,54
Дерево (дуб) . . 0,57 Магний 0,25 Спирт . . . . . . 0,58
Коэфициент кинематической вязкости у в
„, кг-секг
мг)сек и плотность воздуха р в —— при
различном барометрическом давлении и тем-
пературе см. фиг. 3 [22].
/110 ‘кгсек/м2
го оо so sol из too iso гго’С
Фиг. 4
Работы Всесоюзного теплотехнического
института (ВТИ) по вязкости водяного пара
представлены в табл. 17 и 18; они опира-
ются на определение вязкости методом
капилляра (по вопросу несовпадения данных
по методу капилляра и методу Лавачека
смотри [ 44]).
Вязкость смесей находят по формуле
Манна
или
± = , f_2 ,
И Hi 14 + ’ ‘ ”
где ц, р-1, р.2 . . . — динамические вязкости
смеси и составляющих компонентов; v, vx,
v2. . .—кинематические вязкости их; g1( g2...
и гх, г2. . .—доли компонентов смеси по ве-
су и объёму. Вязкости воды, водяного пара.
ОБЩИЕ ТЕПЛОВЫЕ СВОЙСТВА ГЕЛ
Таблица 17
Динамическая вязкость вод иного пара и воды
а» 1ОС кг сек/м* {7]
газов по правилам № 169 по измерению
расхода жидкостей газов и пара при помощи
сопел и диафрагм (Главное управление мер
и весов [39]) берутся из фиг. 4, 5, 6.
Вязкость жидкостей обычно определяется
100
1,23
110
120
130
140
1,30
1,34
1,38
28,8
25,9
23,5
21,6
:20,1
28,9
26,0
23,6
21,7
20,2
29,0
26,1
23,7
21,8
20,3
29,1
26.2
23,3
21,9
29,3 29,6
26,4 26,7
24,0
22,1
20,6
24,3
22,4
20,8
30,0
27,0
24,6
22,7
21,1
39.4 31,0
27,5 27,8
25,1 25,3
23,1 23,4
21,5 21,8
ц Ьр
отношением , где р. и р.' — коэфи-
Р i • р
циенты вязкости испытуемой жидкости и
воды; р и р' — плотности их; t и t' — время
истечения одинаковых объёмов жидкости и
воды при одинаковых условиях через одну
и ту же испытательную трубку (вискози-
метр). Абсолютная величина р. находится
пересчётом, так как значения р/ известны.
Свойства газов см. табл. 20.
150
160
170
180
190
1,42
1.47
1,51
1.54
1.58
18,8
17,6
16.6
15,7
И,9
18,9
17,7
16,7
15,8
14,9
19,0
17,8
16,7
15,8
15.0
19.2
18,0
16,9
15,9
15,1
19,4
18,1
17,0
16,0
15,1
19,5
18,3
17,2
16,2
15,3
19,8
18,5
17,3
16,3
15,4
20,1 20,4
18,8 19,1
17,6 17,9
16,5 16,8
15,6 15,8
200
210
220
230
240
1.62 !И,1
1,66
1,69
1,73
1,77
13,4
1.82
1.82
1,82
14,1
13.4
12,8
12,2
11,7
14,2
13,5
12,9
12,3
11,8
13,6
12,9
12,3
11,8
14,3
13,7
13,0
12,4
11,9
14,5
13,8
13,1
12.5
12.0
14,6
13,9
13,2
12,6
12,1
14,8 14,9
14,0 14,2
13,313.5
12,7 12.9
12,2 12,3
250
260
270
280
290
1,81
1.85
1,89
1.93
1,97
1,84
1,87
1,91
1,95
1,99
2.03
2.00
1.99
2,00
2,02
11.3
10,8
10.41
|1о,о
2,13 I 9,?
11,3
10,9
0,4
11,4
ЮЛ
10,5
10,1
9.7
11,5
11,0
10,6
10,2
9.8
11,6
11,1
10,7
10,3
10,0
11,711,8
11,2 11,3
10,8 10.9
10,4 10,5
10,1 10,2
300
310
320
330
340
2,00
2,04
2,08
2.12
2,16
2.03
2,07
2.11
2,14
2.06
2,09
2,13
2,17
2,21
2,13 2,27
2,24
2,23
2,24
2,27
2,15
2,17
2,20
2.24
2,41
2,35
2,33
2,34
9.2
8,4
7.9
9.6
9,3
9,0
8,6
9,7
9.4
9,1
8,7
8,3
9,9
9,6
9,3
9,0
8,6
350
360
370
380
390
2,20
2,24
2,28
2,32
2,36
2,22
2,26
2,30
2,34
2,38
2,25
2,29
2.33
2,37
2,41
2,28
2.32
2,36
2,40
2,44
2.31
2,35
2,39
2,43
2,47
2,36
2,39
2,42
2,46
2,50
2,54
2,55
2,58
2,61
400
410
420
430
440
2,40
2,44
2,48
2,53
2,57
2,42
2,47
2,51
2,55
2,59
2.45
2,49
2,53
2,58
2,62
2,48
2,52
2,56
2,60
2,64
2,51
2,55
2,59
2.63
2,67
2,54
2.58
2,62
2.66
2,70
2,64
2,67
2,71
2,75
2,79
7.5
7.8
7,4
2,34
2,78
2,77
5.4
3,4
8,2
7,7
7.2
6,6
5.7
450
460
470
480
490
2,61
2,65
2,70
2,75
2,79
2,63
2,67
2,71
2,76
2,81
2,66
2.70
2,75
2.80
2,84
2,68
2,73
2,78
2,82
2,87
2,71
2,75
2,80
2,85
2,89
2.74
2,78
2.33
2,87
2,83
2,87
2,91
2,96
3,00
2,79
2,81
2,84
2,88
2,91
2,94
2,93
3,02
3,06
3.10
3,2
3,1
3,0
3,0
3,1
4,6
3.9
3,7
3.5
3,4
3.1
3,1
3,4
3,4
3.2
3.2
3,3
3,4
500 2,84 2.86.2,89 2,92 2,94 2.97 3,05 3,14 3,3 3,4
510 2,89 2,91 2,94 2,96 2,99 3,02 3,10 3,19 3,3 3,4
520 2.94 2,96 2,99 3,01 3.04 3,07 3,15 3,24 3.4 3,5
530 2,99 3,01 3,04 3.06 3,09 3,12 3.20 3,28 3,4 3,5
540 3.04 3,06 3,09 3.11 3.15 3,17 3,25 3,33 3,4 3,6
550 3,09 3,12 3,14 3.16 3.20 3,23 3,30 3.38 3,5 3,6
Фиг. О
Физические константы воды между 0 и
200°С при давлении насыщения (между 0 и
100° при давлении 1 кг, см2) см. табл. 21.
В пределах небольших давлений р. жидко-
стей меняется с давлением линейно. Влияние
высоких давлений см. [5].
Качественное поведение исследованных
жидкостей, исключая воду, под воздействием
высоких давлений одинаково, количествен-
ное изменение вязкости весьма различно.
Вязкость увеличивается с повышением
давления, темп нарастания вязкости растёт
с повышением давления: для первых двух-
трёх тысяч кг/см2 соотношение между дав-
лением и вязкостью почти линейное; выше
3 000 кг/см2 вязкость растёт или в геометри-
ческой прогрессии или ещё быстрее, тогда
как давление растёт лишь в арифметической
прогрессии.
За исключением воды и ртути наимень-
шее влияние давления на вязкость у ме-
тилового спирта (при увеличении дав-
ления до 12 000 иг) см' вязкость увеличи-
вается лишь в 10 раз), у эйгенола —
наибольшее (при увеличении давления до
12 000 KcjCM2 вязкость растёт в 107 раз).
По Гайду, смазочные масла при давлениях
до 1 500 кг/см2 увеличивают вязкость более
чем в 15 раз. Герш и Шор обнаруживают уве-
личение вязкости смазочных масел в сотни
раз при повышении давления до 4 000 кг 1см2.
Цифровые измерения вязкости Бриджмен
даёт в сводке, где приведены логарифмы
относительной вязкости при различных тем-
пературе я давлении; вязкость исследуемой
жидкости при атмосферном давлении и ЗО‘С
принимается за единицу (табл. 10).
522
ТЕПЛОТА
Табл is и а 18
Кинематическая вязкость водяного пара и воды v»ioc м2/сен [7]
ГС р кг 1см*
1 | 20 40 | 60 | 80 I 100 | 150 | 200 | 250 | 300
100 20.9 0,295 0,295 0,297 0,293 0,299 0,301 0.304 0.308 0,313
по 22,2 0,267 0,268 0,269 0,269 0,271 0,273 0,276 0,280 0,283
120 23,4 0,244 0,245 0,246 0,247 0,248 0,251 0,254 0,258 0,260
130 24,7 0,225 0,227 0,228 0,229 0,230 0,233 0,236 0,240 0,242
140 26,1 0,213 0,214 0,215 0,216 0,217 0,219 0,221 0,225 0,227
150 27,6 0,201 0,202 0,204 0,205 0,206 0,207 0,208 0,212 0,215
160 29,1 0,190 0,191 0,192 0,194 0,195 0,196 0,198 0,200 0,202
170 30,6 0,182 0.182 0,182 0,134 0.185 0,186 0,187 0,189 0,191
180 32,1 0,174 0,174 0,174 0,175 0,176 0,177 0,178 0,180 0,181
190 33,6 0,167 0,167 0,167 0,168 0,163 0,169 0,171 0,172 0,172
200 35,2 0,160 0,160 0,161 0,161 0,162 0.163 0,163 0,165 0,165
210 36,8 о,ги 0,154 0,155 0,156 0,156 0,157 0,157 0,158 0,159
220 38,4 1,зб й 149 0,150 0,150 0,151 0,151 0,152 0,152 0,154
230 40,0 1,92 -,145 0,145 0,145 0,146 0,147 0,147 0,147 0,149
240 41,7 1,98 j 9,1 11 0.141 0,141 0,142 0.143 0,143 0,143 0,144
250 43,5 2,05 1,01 0,138 0,133 0,139 0,139 0,139 0,139 0,140
260 45,4 2,14 1,04 U, 135 0,136 0,136 0,136 0,136 0,136 0,136
270 47,2 2.24 1,07 6.1 0,133 0,133 0,133 0,133 0,133 0,133
280 49,1 2,34 1.11 ч, /23 0,131 0,131 0,131 0,131 0,131 0,131
290 51,0 2.44 1,16 0,748 0 129 0,129 0,129 0,130 0,13 0,13
300 52,9 2.55 1,22 0,778 0,563 | 0.128 0,128 0,121 0,13 0.13
310 54,8 2,65 1.27 0,812 0,584 ‘j 1'16 0,123 0,128 0,13 0,13
320 56,8 2,76 1,32 0,848 0,608 и,464 0,127 0,127 0,13 0,13
330 58,9 2,86 1,38 0,886 0,635 0,486 0,127 0,127 0,13 0,13
340 61,0 2,93 1,44 0,926 0,664 0,511 0.127 0,126 0 12 0,13
350 63,2 3,07 1,50 0,967 0,693 0,537 0,303 0,123 0,12 0,12
360 65.4 3,19 1,53 1,01 0,730 0,563 0,3217 0.1 >5 0,12 0,12
370 67,6 3.31 1,62 1,05 0,765 0,590 0,352 U, Ли 0,12 0,12
380 (59,8 3,42 1,68 1,09 0,798 0,618 0,375 0,240 0,14 0,12
390 72,1 3,54 1,74 1,14 0,832 0,647 0,397 0,262 0,16 0.13
400 74,4 3,66 1,80 1,18 0,865 0,675 0,418 0,283 0,19 0,14
410 76,8 3,79 1,86 1,22 0,899 0,704 0,410 0,308 0,21 0,16
420 79,3 3,92 1,93 1,27 0,^34 0,732 0,462 0,322 0,23 0,19
430 81,9 4,05 2,00 1,31 0.968 0,761 0,483 0.341 0,25 0,20
440 84,4 4,17 2,07 1,36 1,00 0,790 0,505 0,359 0,27 0,22
450 87,0 4,30 2.13 1,40 1,04 0,319 0,526 0,377 0,29 0.23
460 89, Z 4,43 2,20 1,45 1,07 0,849 0,548 0,395 0,30 0,24
470 92,5 4,57 2,27 1,50 1,11 0,880 0,570 0,413 0,31 0,25
480 95,4 4,72 2,35 1,55 1,15 0,911 0,593 0,431 0,33 0,26
490 98,3 4,87 2,42 1,60 1,19 0,943 0,615 0,448 0,35 0,28
500 101,3 5,02 2,50 1,66 1,23 0,976 0,638 0,466 0,37 0,29
510 104,4 5,18 2,58 1.71 1,27 1,01 0,662 0,435 0,38 0,30
520 107,6 5,34 2,66 1,76 1,31 1,04 0,686 0,504 0,40 0,32
530 110,8 5.50 2,74 1.82 1,36 1,03 0,710 0,522 0,41 0.33
540 114,0 5,67 2,83 1,87 1,40 1.П 0,735 0,541 0.42 0.35
550 117,3 5,85 2,91 1,93 1,45 1.15 0.759 0,551 0,44 0.36
ОБЩИЕ ТЕПЛОВЫЕ СВОЙСТВА ТЕЛ
523
Таблица 19
Вязкость жидкостей по Бриджмеиу [5i
Вещее Т В О Давление в кг/см2 Р-зо в пуазах
1 | ioa 4ХК SOOO 12 ОиО
Метиловый спирт ig-^ Р-о ( зо- 1 75° и.иОО 9.769 0,16'/ 9,933 J.471 0,208 0,751. 0,448 0,998 0,655 0.00520
Р-ао 1.702 1,714 1,832 2,004 2,203 -
Этиловый спирт 1g — Р-о 30ь 75е 0,000 9.657 0,200 9,873 0,61/ 0,289 1,023 0,634 1.390 0,919 0,01003
Р-ао P-?S 2,203 2,123 2,128 2,449 2,958 —
Пропиловый спирт норм. Ig -t- Р-о 30е 75° 0,000 9.598 0,283 9,880 J.836 0,36^ 1,402 0,827 1,915 1,223 0,01779
Р-30^ Р-7Й 2.523 2.529 2,938 3,753 4,920 -
Пентан норм. 1g — Р-0 зу- 75° U,ООО 9,811 0,315 0,163 -,1,847 и.676 1,360 1,119 1,846 1,493 0,00226
Р-80 Р-75 1.545 1,419 1,483 1.742 2,254 -
Гексан норм. 1 Р‘ Р-« ' 30е 75е 0,000 9,803 0,332 0,171 0,914 0,701 1,514 1,198 1.646 0,00296
Р-ЗО Р-75 1,574 1,449 1,633 2,070 — -
Октан норм. 1g — Р-0 [ 30е 75° и, ООО 9,810 0,327 0,153 1,088 0,763 1,363 - 0,м6483
P-3U Р-75 1,549 1,493 2,113 - -
Глицерин 1g — Р-0 J у 175‘ 0,000 8,810 0,260 9,023 0,936 9,529 1,741 1,091 и, 628 3.8
PSO Р-75 15,49 17,26 25,53 44,36 — -
Хлороформ ig Ji_ Р-0 f 30° 1750 0,900 9,858 0,211 J.094 _ ,660 0,480 о,914 - 0,00519
р-30 Р-75 1,387 1 ,309 1,514 - - -
Сероуглерод jaJL “ Р-о ' 30е t 750 0,000 9,875 0,160 .,<51 и, 509 0,372 и, 840 0,671 1,189 0,946 8.00352
Р-80 P-JS 1,334 1,285 1.37! 1,476 1.750 -
Эфир ig Ji- p-0 ' 30° [ 75С 0,000 9,878 О,32ч 0,149 0.792 и,6Л 1.261 0,986 1.670 1,311 0,00212
Р-эо Р-75 1,324 1,495 1,552 1.884 2,286 —
Толуол !gJJ Но ' 30° t 750 0,000 9,796 0.274 0,065 0.897 0,597 1,69г? 1.186 1,832 0,00523
Р-80 Р-75 1.600 1,618 1.995 3,258 - —
524
ТЕПЛОТА
Продолжение табл . 19
Вещество Давление в кг}см* pso 1 в пуазах
1 1000 4000 8000 12 000
Эйгенол lgJt р0 f 30° ( 75’ 0.000 9,429 0,541 9,810 2,273 (3000) 0,805 2,343 — -
Изо Р-7 а 3.724 5,333 -9,33 — - -
Петролейный эфир lg-^ Ро f 30° 75° 0.00 0,3<7 0,93 0,56 1,59 1,06 2,18 1,49 -
Рз?_ р7И — — 2,34 3,39 4,90 -
Керосин 1g ~ Р« f 30° 1 75° 0,00 0,46 1.71 0,91 1,88 2,80
Pan Р?5 - — 4,3 — -
Таблица 20
Свойства газов [39]
Наименование газа Формула газа Вес единицы объёма 7 при Динамическая вязкость р.Ю® кг-сек мг при ГС
0° и 760 лил рт. ст. 20°С и 1кг/см8 -30 0 + 50 + 100 4- 200 4- 300
Воздух 1,293 1,165 1,59 1,77 2,04 2,27 2,65 3,03
Кислород оа 1,429 1,288 1.77 1,94 2,22 2,51 3,06
Азот . Na 1,250 1,126 1,55 1,70 1,94 2,17 2,57
Водород .... Н, 0,0899 0,0809 0,82 0,89 0,99 1,09 1,26 1,42
Хлор С1а 3,220 2,900 1,16 1,28 1Ли 1,72 —
Окись углерод СО 1,250 1,126 1,58 1,76 2,04 —
Углекислый > лэ со. 1,977 1,783 1,30 1,44 1,66 1,89 2,32
Сернистый гзз so. 2,927 2,639 1,04 1,19 1,43 1.66 2,11
Сероводород ......... HaS 1,539 1,387 1,07 1,20 1,42 1,64 —
Аммиак NHa 0,771 0,695 0,85 0,94 1,15 1.34 __
Метан СН, 0,717 •-,646 0,95 1,05 1,22 1,40 __
Ацетилен ........... с,н, 1,171 1 ,и56 — 0,98
Этилен . C2H4 1,260 1,137 0,85 0,97 1,15 1,31 1,61 1,86
Эган . C.Hfi 1,350 1,223 0,79 0,88 1,02 — —
Водяной пар HaO 1,257* 1,133 — — — — — —
* 'Т олько расчётная величина
Таблица 21
Физические константы воды между О и 200°С при давлении насыщения
(между 0 и 100° при давлении 1 кгсм2) [13]
Темпера- тура Давление Удель- ный вес Удельная теплоёмкость Теплопро- водность Динами- ческая вязкость Кинемати- ческая вязкость Темпера- туропро- водность Критерий Прандтля
t Р 7 ср X р-10в у. 10е д-10< Рг
°C Кг]СМ2 кг 1м9 ккал кг'град ккал м-час-град кг •сек -И3 м2/сек м8/час
0 1 1000 1,009 0,480 182,5 179 4.8 13,3
10 1 1000 1,002 0,494 133,0 130 5,0 9,49
20 1 998 0,999 0,510 102,0 100 5,1 7,06
З^ 1 996 0,998 0,525 81,7 80,5 5,3 5,51
/и | 1 992 0,998 0,539 66,6 65,9 5,4 4,37
1 1 988 0,999 0,552 56,0 55,6 5.6 3,59
60 1 983 0,999 0,565 48,0 47,9 5,7 3,00
1 978 1,001 0,574 41,4 41,5 5.9 2,54
80 1 972 1,002 0,581 36,3 36,6 6,0 2,20
> 1 965 1,005 0,585 32,1 32,6 6,1 1,93
100 1,03 958 1,007 0,587 28,8 29,5 6.2 1,72
120 2,02 943 1,015 0,590 23,5 24,4 6,4 1,37
140 3,68 926 1,025 0,588 20,0 21,2 6,5 1,17
160 6,30 908 1,040 0,585 17,5 18,9 6,7 1,02
180 10,20 887 1,057 0,579 15,7 17,4 6,9 0,91
200 15,85 865 1,078 0.572 14,3 16,2 7,1 0,82 1
ОБЩИЕ ТЕПЛОВЫЕ СВОЙСТВА ТЕЛ
525
Изменения вязкости ртути относительно
невелики.
Вязкость ртути см. табл. 22.
Таблица 22
Вязкость ртути под давлением |5]
Давление в кг 1см* Абсолютная вязкость
зз°с 75°С
1 0.01516 0,01340
2 000 0,01585 0,01400
4 С00 0,01663 0,01463
6 000 0,01742 0,01528
8 000 0,01822 0,01593
10 000 0,01912 0,01674
12 000 0,02007 0,01759
Таблица 23
Относительная вязкость воды [5]
Давление в кг {см* Относительная вязкость
0°С 10.3°С 30°С 75°С
1 1,000 0,779 0,488 0,222
500 0,938 0,775 0,500 0,230
1 000 0,921 0,743 0,514 0,239
1 500 0,932 0,745 0.530 0.247
2 000 0,957 0,754 0,550 0,258
3 000 1,024 0,791 0,599 0,278
4 000 1,111 0,842 0,658 0,302
5000 1,218 0,903 0,740 0,333
6 000 1,347 0,931 0,730 0,367
7 000 ... 1,064 0,854 0,404
8 000 ... 1,152 0,923 0,445
9 000 0,986 0,494
10 000 Затвердела 1,058
11000 1,126 ...
По Гаузеру, вязкость воды при темпера-
туре ниже 30° с увеличением давления до
400 кг/см* понижается, выше 30°С—увеличи-
вается.
Бриджмен при t = 0°С и давлении
1 000 кг/см* находит минимум; при 30 и 75°С
установлено увеличение вязкости на всём
интервале увеличения давления.
Относительную вязкость воды см. в
табл. 23.
П О В Е Р X И О СТ Н О Е и л т я и: Е К И Е
Молекулы жидкости на границе между
жидкостью и другой средой (воздухом, па-
ром этой жидкости, стенками сосуда) обра-
зуют поверхностный слой. Внутри жидкости
молекула испытывает со стороны окружаю-
щих ее молекул воздействие, одинаковое во
всех направлениях; в поверхностном слое
воздействия на молекулы го стороны жидко-
сти и другой граничащей среды неодина-
ковы, равнодействующая всех сил направ-
лена по нормали к поверхности пограничного
слоя и зависит от свойств не только жидко-
сти, но и другой среды. Молекулы слоя
обладают большей потенциальной и свобод-
ной анергией, нежели молекулы внутри
жидкости. Естественное стремление системы
перейти к состоянию,отвечающему минимуму
свободной энергии (по второму началу термо-
динамики), удовлетворяется выходом моле-
кул пз поверхностного во внутренние слои
жидкости, что вызывает тенденцию сокра-
щения слоя и создаёт в нём поверхностное
натяжение.
Коэфициент поверхностного натяжения а
определяется либо как касательная к по-
верхности сила, отнесённая к 1 см линии
раздела поверхности, либо как свободная
энергия квадратного сантиметра поверх-
ностного слоя (азрг1см2-дн-см1см^—дн1см).
Стандартная жидкость для определения
поверхностного натяжения—вода (на грани-
це с воздухом), для пей при 18°Са = 72,5—
74,0, в среднем 73,1 дн1см.
Поверхностное натяжение воды является
наибольшим (табл. 24).
Повышение температуры снижает а.
При критической температуре а на гра-
нице с насыщенным паром жидкости равно
нулю. Поверхностное натяжение слоя ока-
зывает на жидкость нормальное к её по-
верхности давление (см. стр. 343).
Таблица 24
Псгслхнсстяое катях:ен’'е о- -жидкостей |40|
Вещество р и s ш в | Вещество р а в дн {см
Вода . . . Бензол . . Толуол . * cs, .... СС1, . . . СНС1, . . един, . сн.он . с.н„он . (СаН5)аО . СН,СОСН, сн.соон Не ... 18 20 20 20 20 20 0 20 20 20 16,8 20 —270,7 73,1 28,8 23,2 33,5 25,7 26 45.4 23,02 22,3 16.5 23.4 23,5 0.354 Не ... на ... н> . . . N, ... оа . • • Аг ... С1а ... Вг, . . . СО . . . со, . . NHS . . SO, . . ъО* . • —269,3 —258,5 —253 —195,9 -182,7 —186,1 — 72 + 13 —190 + 15,2 - 29 — 25 4- 2L 0,098 2.86 1,91 8,3 13 11 33.6 44.1 11 1,8 41,8 33,3 30
ТЕРМИЧЕСКИЕ КОЭФИЦИЕНТЫ
В случае однородного тела состояние его
определяется давлением р, удельным объё-
мом и и температурой Z.При наличии внут-
реннего равновесия эти параметры могут быть
связаны функциональной зависимостью —
так называемым уравнением состояния
F (р> V, Z) = 0; если F(p,v,t) известно, то
каждый из трёх параметров может рассмат-
цпваться как функция двух других незави-
симых, п для определения состояния доста-
точно двух параметров:
р = / (/, V) н аР == at +
ldv\ /dv\ .
a = Z1(t,p) и dt +
Idt \ /dt\ .
I = /3 (P> у) и dt = > dp + dy,
входящие сюда частные производные связаны
соотношением
/др \ ldt\ fdv\
’ \ди)Р' \bp;t
= — 1.
526
ТЕПЛОТА
Эти производные, давая изменение одного
из параметров в функции другого при неиз-
менности третьего, имеют значение для оцен-
ки физических свойств тела:
/др \
Hr j —расширяемость тела под влия-
\ f /р
нием изменения температуры при неизменном
давлении;
/др\
I j-I — сжимаемость тела пол влиянием
изменения давления при неизменности тем-
пературы;
я,
1 /др\
— дГ) — коэфициент давления;
! Рг-Р1
. ---——средний коэфициент дав-
но *2 Ч
(др I
Н,- I —упругость тела под влиянием
'и / V
температуры при неизменности объёма.
В термодинамике рассматриваются функ-
ции состояния:
1 (ди \
a=~t> \дТ —термодинамический коэфи-
циент расширения;
ления;
коэфициенты а, р, а—функции состояния
п отличны от величин а0, р0, а0; так, для
идеального газа уравнение состояния
р.у /?*Т
и
а = 1^Л
v \дТ у р Т ’
/р Г
тогда как
— L И - L " —
“0= ve\dT -р v0 'р ~ve'T~
т 1 _д_
:Т„'Т 273 ’
1 / ди\
р=—— \др) —термодинамический коэ-
фпцпент сжатия;
1 , др \
0= Т ( лТ ) — термодинамическим коэфи-
где у0 при То = 273 (табл. 25).
Для идеального газа
1
а0 = Зо = 273 •
Таблица 25
циент давления.
В технических расчётах и эксперименталь-
ной физике часто пользуются величинами:
1 [dv
ал “ Д \dt
1 «2 —
% = — • у-— f ' ~ средний коэфициент
— коэфициент расширения;
р
расширения;
₽0 = ~ v0 [др).
—коэфициент
1 «1 — «2
Ре = Г - D _ D ‘ — средний
ио Рг Pi
сжатия;
коэфициент
сжатия;
Термические коэфициенты газов при 1 am [40]
Газ ст •
Не 0,0036582 0,0036606
н, 0,0036588 0,0036621
N2 0,0036733 0,0036746
воздуха (при 1 м Hg) 0,0036728 0,0036744
Для твёрдых тел имеют значение коэфи-
циенты линейного («0 () и поверхностного
(»o,s) расширения (табл. 26).
Для изотр опных и квазиизотропных твёр-
дых тел приближённо а0 = 3а0 t а0л=2а0,/.
Таблица 26
Линейное расширение твёрдых тел между 0° и t° в мм; отнесено к 1 м длины при 0° [46]
Твёрдое тело Э до—190° 0 до 100° и до 200° 0 до 300° 0 до 400° 1' до 500° 0 до 600° 0 до 700°
Алюминий ......... j . —3,43 2,38 4,94 7,68 10,60 13,70 16,67
Берлинский фарфор. ..... - о „32 0,30 0,66 1,03 1,41 1,82 2,24 2,63
Бронза ... —2,84 1,75 3,58 5,50 7,51 9,61 —
Золото -2,49 1.42 —
Йенское стекло 16Ш ..... —1,12 0,81 1,67 2,60 3,59 4,63 —
Го же 59Щ . ......... —0,82 0,59 1,20 1,83 2,47 3,12 __ —
» » 1565Ш ......... —— 0,345 0,72 1,12 1,56 2,02 —
Константан . ........ . —2,26 1,52 3,12 4,81 6,57 8,41 —
Латунь ..... —3,11 1,84 3,85 6.03 8,39 __ __ —
Литое железо . . . . -1,67 1,20 2,51 3,92 5,44 7,06 8,79 10,63
Литая сталь . ......... —1.64 1.17 2,45 3,83 5,31 6,91 8,60 10,40
Магний —4,01 2,59 5,39 8,36 11,53 14,88 — —
Машинный чугун -1,61 1,04 2,19 3,45 4,82 6,31 7,91 —
Медв красная -2,66 1,65 3,38 5,18 7,07 9,04 11,09 —
Никель . -1,89 4,34 5,91 7,56 9,27 11,05
Олово ............. -4,24 2,67 —
Палладий -1,93 1,19 2,42 3,70 5,02 6,38 7,79 9,24
Платина -1,51 0,90 1,83 2,78 3,76 4,77 5,80 6,86
Платинз-иридий 80:2с% . . . -1,43 0,83 1,70 9 =.<’ 3,51 4,45 5,43 6,43
Сварочное железо. ...... —1,68 1,22 2.53 3,93 5,43 7,02 8,71 10,49
Свинец . . ...... -5,12 2,92 __ —
Стекло кварцевое ....... 0,0 С, 05 0,12 6,19 0,25 0,31 0,36 0.40
Серебро ........ .... -3,21 1,97 4.00 6,08 8,23 10,43 12,69 15.14
Цинк -1,85 1,65 —
Чугун высокого качества . . —1,59 1,04 2,21 3,49 4,9|; 6,44 8,09 9.87
ТЕРМОДИНАМИКА.
527
Средний коэфициент линейного расшире-
ния от 0 до 100°С имеет значения порядка
10 5, например [40]:
__________% 1________
20° 7,07-10—‘
А10_юо°... 2,28.10-5
Fe0—100° Cl -10-0
f__________
рь17—1ои°* • *2,93 !0
Ag0 —ЮО0"-1’98,10
W0_lcn°...0,45. IO'8
Pt16—250°-• .°'92’10 ~J
У анизотропных тел порядок величины
тот же, но зависит от направления главных
осей, так
Zn20’C || ч - 5,74-SO-5,
Zn20oC 1 az= 1,26-10—s.
Таблица 27
Объёмное расширение 1000 a при комнатной
температуре (20°) {46j
Алкоголь . . 1,10
Бензол . . . 1,25 Репейное масло
Вода .... 0,18 Ртуть .... 0.181
Глицерин . . 0,50 Серная кислота 0,55
Керосин . . 1,0—0,92 Скипидар . . . 1,00
Оливковое Эфир 1 .60
масло . . . 0,72
Всестороннее давление на твёрдое тело
уменьшает его линейные размеры и объём.
В случае аморфных и кристаллических тел
кубической системы р/ одинаковы во всех на-
правлениях 8 — 3 р/: у аморфных тел 8 поряд-
ка от 2 до 3-10"6, у кристаллических — от
0,5 до 3*10~6 (давление в кг/см2); в случаях
кристаллов других систем линейное сжатие
различно в различных направлениях, что
даёт различные соотношения между (3/
й р.
Сжимаемость жидкостей мала и близка к
сжимаемости твёрдых тел. По Бриджмену,
исследованные им жидкости грубо распада-
ются на три класса: в первый входит гли-
церин, во второй —вода, С(.Н5С1 и С6Н5Вг,
в третий — все остальные. Под давлением
12 000 кг/см'' при комнатной телшературе
глицерин теряет 13,4% своего первона-
чального объёма, вещества второго клас-
са - около 2С%, третьего — около 30%
(табл, 29).
Таблица 28
Линейная усадка некоторых металлов [46]
(относительное уменьшение линейных размеров отли-
того предмета при его затвердевании и охлаждении)
Бронза.........1 :63
Висмут.........1 : 265
Колокольный
металл.........1 : 65
Латунь ... ... 1 : 65
Литая сталь . . . 1 : 64
Олово .........1 : 128
Ковкий чугун . . 1 • 72
Пудлинговая сталь 1 : 72
Пушечный
металл.........1 : 134
Полосовое желе-
зо прокатное . 1 :55
Свинец..........1 : 92
Стальное литьё . 1 : 50
Цинк литой . . . 1 : €2
Чугун ...........1 : 96
ПХ1 вес. ч. меди
12,5 вес. ». олова 1:К4
Примечание. В сталепрокатных ма-
стерских принимают усадку равной в сред-
нем 12 мм на 1 пог. м.
Таблица 29
Относительный объем жидкостей па
Бриджмену (5J
ТЕРМОДИНАМИКА
ОСНОВНЫЕ ЗАКОНЫ ТЕРМОДИНАМИКИ
Первое начало. Основные законы термо-
динамики принято называть началами. В
классической термодинамике рассматрива-
ются только два начала. Первое начало-
частное выражение принципа превращения
и сохранения энергии, развившееся как
результат установления эквивалентности
теплоты и работы. В своих капитальных
работах об атомно-молекулярном учении
(1745— 1748 гг.), вылившихся по существу
в механическую теорию теплоты, М. В.Ломо-
носов даёт закон, являющийся начальным
этапом становления первого начала. Теоре-
тические и экспериментальные работы
Р. Майера (1842), Джоуля (1842—1850),
Гельмгольца (1847), являясь последующими
этапами развития первого начала, приводят
к широкому признанию его н 1850— 1860 гг.
Ф. Энгельс подчёркивает значение пер-
вого начала как учения именно о превра-
щении энергии, которая рассматривается им
как реальная сущность, качественно и ко-
личественно определяющая движение при
переходе его от одной формы к другой.
Новым и ценным является, следователь-
но, превращение форм движения, так как
утверждение количественного постоянства
движения высказано уже Декартом.
Часто встречающаяся формулировка пер-
вого начала «невозможно осуществить пер-
петуум мобиле (дословно «вечно движущее-
ся»)» есть утверждение невозможности
осуществления машины, увеличивающей ко-
личество энергии в изолированной системе.
Формулировка, не вскрывающая глубокого
значения первого начала, возникла истори-
чески в связи с попытками создания «веч-
ного двигателя», т. е. двигателя, который
производил бы работу из ничего.
Аналитическое выражение первого нача-
ла, служащее для решения конкретных тех-
нических задач, даётся так называемым ос-
новным уравнением теплоты.
Согласно закону, в любом процессе со-
общённая системе теплота Q равна прира-
щению внутренней энергии системы U,
528
ТЕПЛОТА
сложенному с работой, которую произвела
система IV:
Q = ДУ + И/,
где величины Q, ДО, IV выражены в одних
и тех же единицах.
Работу принимают положительной, если
она совершается системой, т. е. система от-
даёт работу; наоборот, если работа совер-
шается над системой, т. е. воспринимается
системой, — работа
отрицательна.
Примеры. Набо-
та расширения си-
стемы с увеличением
её объёма па dV и
преодолением внеш-
него давления р
dW = pdV;
X
работа п е р е н
электрического
ряда de между
а
о с
за-
дву-
мя точками с разностью потенциалов Е
dW = Ede;
работа сокращения поверхности жидкости
на величину dS при поверхностном натяже-
нии а
dV/ — — а dS.
2
Общий вид выражения работы l’/= J ydx
1
зависит от вида функции у — Р (х), т. е.
при переходе системы от состояния 7 к
состоянию 2 работа определяется не только
начальным и конечным состояниями, по и
формой пути перехода системы.
Работа процесса 1 — а — 2 (фиг. 7) есть
площадь т1а2пт, работа процесса 7—Ь—2—
площадь m1b '2nnv, вторая значительно мень-
ше, хотя у обоих процессов исходное и ко-
нечное состояния одинаковы.
В технической термодинамике уравнению
первого начала придают следующий вид:
/ в»2
dQ = dU -f- AG Id + dh
+ Ad LA,
где Q [ккал]— теплота, сообщаемая те-
лу или отнимаемая от
него, обычно называемая
теплотой процесса;
U [ккал] — внутренняя энергия тела;
Цкгм]—работа, совершаемая те-
лом или воспринимаемая
Большое распространение имеют процес-
сы, в которых давление на поверхность тела
имеет всюду одинаковую величину. В этом
случае равномерного поля давлений и когда
исключены массовые силы и поверхностные
силы, вызывающие перемещение центра тя-
жести тела и вращение последнего относи-
тельно первого, работа
dL = pdV,
где dV— изменение объёма.
Практически этим охватываются процес-
сы расширения и сжатия, протекающие внут-
ри замкнутой оболочки, допускающей изме-
нение объёма, распространяясь на газы и
пары, в известных пределах—на капельные
жидкости, а на твёрдые тела лишь при все-
стороннем равномерном сжатии или растя-
жении их.
Случай неравномерного поля давлений
практически охватывает теченье газов и
жидкостей в закрытых неподвижных или
подвижных каналах (например турбины).
Здесь работа
L = Lc + L3 ,
где Lc — работа, совершаемая подвижными
стенками канала; LB — работа вытеснения
жидкости, необходимая для создания тече-
ния её по каналу; Lc определяется условия-
ми перемещения стенок подвижного канала;
dLP = d (pV), L3 = [p2V2 — рjVi),
где V — объёмный расход жидкости за еди-
ницу времени.
Уравнения первого начала принимают
вид:
а) равномерное поле давлений:
dQ = dU + ApdV;
v3
Q = (U2 - UH 4- A J pdV ккал-
V,
/ V \
Относя уравнения к 1 кг (у = м3/кг\,
имеем
dii ~ du + Apdu;
^(u.-uJ + A^pdv
им, так называемая ра-
бота процесса;
G[кг]— вес тела;
б) неравномерное поле давлений — тече-
ние сплошной среды по каналу:
dQ = dU + Ad (pV) +
+ AG ( + dh \ + AdLc
: 2 g
А =
и Gh [кглг] — кинетическая и потенци-
альная энергии тела.
1 Г ккал]
777= *--! — термический эквивалент
4z/ J /.гм, । г
единицы работы.
< ккал.
J
* Вышеприведенная формулировка уравнения
первого начала термодинамики дальнейшие
следствия этого уравнения, получившие распро-
странение ь технической термодинамике, базируют-
ся на условном определении работы процесса (L).
В более общих выражениях первого начала термо-
динамики строго различаются процессы возникно-
вения и распределения термодинамической работы,
в связи с чем исключается необходимость введе-
ния условных определений -заботы и общи? выра-
жения первого начала термодинамики формулиру-
ются наиболее престо (ред.).
Уравнения отнесены к стационарному по-
току жидкостей, когда через любое сечение
канала в равные отрезки времени проходят
одинаковые массы; G и V — весовой и объ-
ёмный расходы за единицу гзремени.
Относя уравнения к 1 кг
(v =
V л3
G
ТЕРМОДИНАМИКА
529
ккал/кг.
В уравнениях первого начала dU— пол-
ный диференциал функции состояния U
(внутренняя энергия); dQ и dL — неполные
дифеэенциалы; Q и L — функции процессов.
Через функцию состояния — энтальпию
(см. термодинамические функции) i = и 4-
+ Ара ккал!кг, уравнения первого начала
выражаются:
а) равномерное поле давлений:
dq = di — Avdp\
Рг
q = (it — J’i) — A J vdp
Pi
б) неравномерное поле давлений — тече-
ние сплошной среды по каналу:
2 2
+
2 g
Q — ( G — G) + А
ккал/кг.
+ (ht — /*i) + А1С
Второе начало. Промышленный перево-
рот, вызванный развитием паровой машины,
требовал в начале XIX столетия научного
определения возможной экономичности теп-
лового двигателя. Второе начало в перво-
начальной формулировке, данной С. Карно
(1824), явилось научным ответом на эту
проблему. Последующие работы над вторым
началом (Р. Клаузиус — 1850, В. Томсон —
1852, Л. Больцман — 1900, М. Смолухов-
ский—1915) дали новые формулировки и
показали несравнимо большее значение это-
го закона; постепенно осуществилось пере-
растание второго начала из прикладного
закона теплотехники в один из основных
законов естествознания с глубоким фило-
софским содержанием. Аналитическая обра-
ботка второго начала, данная Клаузиусом,
путём формальной экстраполяции её приве-
ла к ложному идеалистическому толкованию
закона, к учению о так называемой «тепло-
вой смерти» вселенной. Ложность этого
толкования вскрыта Ф. Энгельсом, доказав-
шим фидеистичность сделанных выводов и
противопоставившего им учение диалекти-
ческого материализма о развитии природы.
Широкие обобщения второго начала,
строящиеся на формальной экстраполяции
его, отрицаемые категорически материали-
стической философией, ограничиваются уже
статистической физикой (Больцман, Смолу-
ховский). Классическая аксиоматика второ-
го начала не раз критически пересматрива-
лась (Каратеодори, Т. Эренфест — Афанась-
ева, Н. Н. Шиллер).
34 Том I
Вместе с тем имеются утверждения о том,
что понимание термодинамики как науки,
построенной на двух равно-фундаментальных
принципах, ошибочно.
Существуют мнения [3] о возможности
разграничения второго начала на два прин-
ципа: принцип существования энтропии
(функции, введённой Клаузиусом! и принцип
возрастания её, причём принцип существо-
вания энтропии признаётся следствием пер-
вого начала и имеет столь же широкое
распространение; наоборот, принцип возра-
стания энтропии рассматривается как ста-
тистический, и применение его ограничи-
вается обоснованиями, принятыми при ста-
новлении принципа. Классические обосно-
вания второго начала, как обобщающего оба
приведённые принципа, признаются в этом
случае идущими дальше, чем это допустимо
в строгом соответствии с исходными пред-
посылками.
Карно создал представление об идеаль-
ной машине, выполняющей некоторый кру-
говой процесс (см. ниже, стр. 539), кото-
рый принято называть циклом Карно.
В отношении идеальной машины доказы-
вается, что: 1) коэфициент полезного дей-
ствия цикла Карно не зависит от природы
рабочего тела; 2) при данных температурах
двух тепловых источников не существует
цикла тепловой машины более выгодного,
чем цикл Карно, с теми же температурами
теплоотдатчика и теплоприёмника.
Помимо этого второе начало получило ряд
других формулировок: постулат Клаузиуса—
теплота не может переходить сама собой от
более холодного тела к более тёплому; прин-
цип Планка—невозможно построить периоди-
чески действующую машину, всё действие
которой сводилось бы к поднятию некото-
рого груза и соответствующему охлаждению
теплового резервуара; принцип Каратео-
дори—сколь угодно близко произвольно выб-
ранному данному состоянию системы име-
ются такие её состояния, из которых
система не может быть переведена в данное
состояние адиабатным процессом; невозмож-
ность перпетуум мобиле второго рода, что
понимается как невозможность машины,
способной превращать в работу всю теплоту,
полученную ею от теплового источника и др.
Аналитически принцип Карно выражается
к. п. д. его цикла
Т2
- 1 — Т1 >
где Tj — абсолютная температура теплоот-
датчика (верхнего теплового источ-
ника);
Т2— абсолютная температура тепло-
приёмника (холодильника).
При аналитической обработке второго
начала Р. Клаузиусом (1851) введена функция
состояния системы—энтропия S.
Диференциал энтропии связан с приведён-
ной теплотой, т. е. отношением исчезающе
малого количества теплоты, сообщаемого
в процессе системе, к абсолютной темпера-
туре теплоисточника, соотношением
„ dQ
dS > ккал) град-,
530
ТЕПЛОТА
знак равенства отвечает обратимому про-
цессу> знак > —необратимому. Из выраже-
dQ
ния dS =~т , где dS—полный диференциал,
1 1
a dQ— неполный, следует, что уг=ш(Г)
(функция Карно) является интегрирующим
множителем для dQ.
Для конечного процесса, соответствую-
щего переходу системы из состояния 1 в со-
стояние 2, приращение энтропии S2 — S, >
2
f dO , а
> I -ф- ккал/град, что указывает на мень-
1
2
шее значение J в случае необратимого
1
процесса сравнительно с обратимым, так как
левая часть выражения как функция состоя-
ния сохраняет своё значение.
Для замкнутых круговых процессов
, Г dQ
(циклов) интеграл Клаузиуса ф ~у< 0, знак
равенства—для обратимых циклов, знак<—
для необратимых.
ОБЩИЕ СООТНОШЕНИЯ МЕЖДУ
ПАРАМЕТРАМИ р, v, и, i, s И СВЯЗЬ
ЭТИХ ПАРАМЕТРОВ С ср И cv
1. Независимые переменные
Гис.
dq — cvdT 4- АТ
дГ м /др\
ds — Су A f jyp 1
du=cvdT+ АТ
Л
dv ккал/кг;
________ккал_
vdv кг - граб •
— Ар dv ккал/кг.
2. Независимые переменные
Г и р:
( dv \
dq=cpdT — АТ ( ур 1 dp ккал/кг-,
dT
ds —-Ср -j. А
ккал
/р кг-град ’
di — CpdT+ Av — ATHy j dp ккал/кг.
L V 'pj
3. Независимые переменные
p и v:
/дТ\ /дТ\
= cp j dv + cv dp ккал I кг-
Cp (dT_\
T \ dv]
\ Ip
ккал
dP кг-град ’
ds =
du =
cp
— Ap
dp
do +
' ккал/ кг.
J
4. Теплоёмкости:
/ dp \ / dv \ ккал
ср — Ср= AT I дТ I I у?.- | кг.град ;
\ /г» X /р г
(др )т - Al (д^д-
1д±>\=АТ(д1р\
(дн
ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ,
УРАВНЕНИЯ МАКСВЕЛЛА
И КЛАУЗИУСА—КЛАПЕЙРОНА
Функции состояния системы, позволяю-
щие при определённом выборе независимых
переменных через свои производные (разных
порядков) наиболее просто и в явном виде
выражать термодинамические свойства си-
стемы, называются характеристическими.
Уравнение первого начала dq—du+Apdv
и второго dq — Tds исключением dq дают
зависимость Tds = du -f- Apdv, содержащую
пять переменных величин; р, о, Т, и, s.
Принимая две из них за независимые пере-
менные, необходимо иметь для определения
остальных трёх величин три уравнения,
тогда как в распоряжении имеются лишь
два: уравнение Tds=du + Apdv и уравнение
состояния / (р, и , Т)=0. Недостающее усло-
вие и даётся характеристической функцией;
если последняя известна, то через её част-
ные производные выражаются термодинами-
ческие свойства системы.
Внутренняя энергия — функция
состояния системы, выражающая величину
запаса энергии, который может быть вы-
делен системой в виде теплоты и работы;
производимой системой,—является при неза-
висимых переменных v и s характеристи-
ческой:
du = Tds — Apdv, откуда вытекает, что:
/ди\ „ д2ц ' д2и
Т = (дТJ ’ dT = ^2 -ds + dsdv - dv-,
1 (ди\ 1 Г д2 и [д2и\
Р~~ а(ЦМ dP=~A [dcds ds + (дТ2 )dv •
Энтальпия — функция состояния си-
стемы i=u+Apv—при независимых перемен-
ных р и s является характеристической:
di — Tds + Avdp;
отсюда следует, что
„ /di\ „ d2i
T==[ds) >dT = d^dP + [d^l ds’
1 (di\ IFW, d*i /
V~A (dp)/ dv^ A [(dpsJ/P+dpds 'dsJ ’
[di \
l = u + p{dp);
Свободная энергия — функция со-
стояния системы F—u—Ts—при независимых
переменных Гис является характеристи-
ческой:
dF = — Apdv — sdT,
ГАЗЫ
531
откуда
(dF\ (d3F\ d3F
а’=~~\дт)т/> ds==~~[dT3) dT"~"fffdu dv‘
dp = ~A
_ L(^X
p~~ A[dv}r ’
1 nd*F\ d*F
i \dv2)Tdv+ dvdTdT
P=U+T Р/
Термодинамический потенциал
при постоянном д а в л е и и и (изобар-
ный потенциал) — Ф = и — Ts -f- Apv = F +
+ Apv = i — Ts— при независимых перемен-
ных T и р служит характеристической
функцией:
дФ = Avdp — sdT,
откуда
/дФ \ д2Ф /д2Ф\
s = ~ (дТ ) : ds~ ~ дТ др dp ~ (дТ3 I dT’
\ /р г \ /р
1 /дФ\ 1Г/д3Ф\ д2Ф
v = А [др )т ' dv=А. [(dp2")т dp+dpdT
Уравнения Максвелла
/дТ\ /др\ /дТ\ /ди\
Ido / — Ids I ’ (др / ~ А Ids’/ ’
\ i S \ / v \ *iS /р
fds\ _ /др\ \
do L — А(дТ1 ’ — (др L ~А (df •
< i• \ IV \ 1 \ /р
Уравнение Клаузиуса—Клапейрона
дР_ =
дТ AT (o’—о')’
где Уф—скрытая теплота перехода одной
фазы в другую (плавления, парообразова-
ния, сублимации); и' и о"—удельные объёмы
фаз (см. «Водяной пар», стр. 546).
ГАЗЫ
ИДЕАЛЬНЫЕ ГАЗЫ
Основные законы
При переходе данной массы газа из од-
ного состояния в другое при условии неиз-
менности температуры объём, занимаемый
газом, и давление его связаны соотношением
Pi £1
Pi ’
или
Plfl = Рг fa-
закон, формулированный Бойлем в 1662 г.
и независимо от него Мариоттом в 1676 г.
Соотношение между объёмом, занимаемым
газом, и температурой при переходе данной
массы газа из одного состояния в другое
при условии сохранения неизменным давле-
ния его имеет вид:
= (1 + 0,003661 G);
Vi = vB (1 + 0,003661 Z2),
откуда
1 +__L2—
*+273,15
V1 1J-—
1+273,15
и
Ve Т g
fl =л
закон сформулирован Гей-Люссаком (1802).
Коэфициент расширения “о—27O5 =0,003661
одинаков для всех газов; v„, vlt t>2—объёмы
при 0° С; Zj С, и Т2—абсолютные
температуры.
Газы, строго подчиняющиеся законам
Бойля-Мариотта и Гей-Люссака, называют
идеальными. Реальные газы уклоняются от
этих закономерностей; эти отклонения тем
меньше, чем меньше давление газа и чем
выше его температура.
Для любого состояния идеального газа
параметры его отвечают условию
или
ро = RT,
являющемуся уравнением состояния
идеального газа (уравнение Клапей-
рона), отнесённым к 1 кг газа,
1кгм I
кг ’ град —для данного газа кон-
станта — газовая постоянная;
/ м3 \
v —— ) — удельный объём газа.
\ КС 1
Умножением ро = RT на G кг получают
уравнение состояния идеального газа, отне-
сённое к произвольному количеству газа
p-V = GRT,
где V = о-G (м3).
Значения R приведены в табл. 30.
Если (л — молекулярный вес газа, то при-
няв G = р., получают уравнение состояния
для 1 моля газа
pV^ivR) Т = 848Т,
где = ор, м31моль — объём моля;
кгм
= 848 мль-г^д ~ газовая постоянная;
отнесённая к молю газа, так называемая
универсальная газовая постоянная, одинако-
вая для всех газов (следствие закона
Авогадро).
Следствием закона Авогадро, согласно
которому одинаковые объёмы различных
34*
ТЕПЛОТА
532
газов содержат при одинаковых р и Т оди-
наковые числа молекул, является
Ъ = th . .
Ь - ,'>2 ’ fi - ’-’•а ’
Wl = f2Р2 = ,
т. е. что в равных условиях давлений и
температур объёмы молей различных газов
одинаковы.
Число молекул в граммолекуле, число
Авогадро, N — б ,064-102S; объём моля идеаль-
ного газа при 0° С и 760 мм рт. ст. V 0 =
= 22,416 мя[моль; объём моля при 15° С и
давлении 1 кг[см? V 15 ~ 24,4 м3/моль.
Удельный вес газа в произвольном со-
ц.
стоянии т = , где Уа — объём моля в тех
условиях, для которых ищут Y.
Удельный вес при 0° С и 760 мм рт. ст.
_____У____!-»
~ 22,416 ~ 22,4
(в обычных расчётах принимают У(1) 0 =»
= 22,4; в обоих случаях полагают, что газ
подчиняется закону Авогадро; отклонения
см. в табл. 30).
Газовые смеси
Давление
вующих друг
парциальных
химически не дейст-
газов равно сумме
(закон Дальтона)
смеси
на друга
давлений
i—n
п = У,
где pi — парциальное давление z’-ro компо-
нента, т.е. то давление, которое оказывал бы
этот компонент, если бы остальные компо-
ненты были удалены из объёма, занимаемого
смесью, а его температура оставалась рав-
ной температуре смеси.
Смеси химически не действующих друг
на друга газов подчиняются основным за-
конам в той же мере, как и их составля-
ющие. Уравнение состояния pV ~ GRr> Т;
здесь р, V, G, Rm,T— параметры смеси;
для смеси из п составляющих
i=n
v= 2 vi>
f=l
где V/—приведённый объём i-ro компо-
нента, т. е. объём, который занимал бы
z-й компонент, если бы при температуре
смеси он имел давление смеси р, а не своё
парциальное
1=п
G = X Gt,
Z=1
где С?/[кг] — вес z’-ro компонента.
Газовая постоянная смеси газов
i=n i=n
где Ri — газовая постоянная z-ro ком-
понента,
848
gt — весовая доля z-ro компонента;
PiV = G;RjT — уравнение состояния z-ro ком-
понента смеси;
pVi == GiRjT—уравнение состояния z-ro ком-
понента, соответствующее при-
ведённому состоянию его;
Свойства газов (18]
Таблица 30
Газ Формула Молекулярный вес в р- Газовая по- стоянная /? в кем/кг-град Нормальный удельный вес в кг 1м* Точка кипения в °C Точка плавле- ния в °C Критические параметры £ а Л= —- при О° С [
вычисл. измер. 1 'к в °C 1 шу Я(1 5 м сэ X Теплоёмк( Ср при 0° ккал кг . град
Азот .... N3 28,016 30.25 1,2498 1,2505 —195,81 —210,02 -147,1 33,5 0,311 0,249 1.40
Аммиак . . NHa 17,031 49,8 0,7593 0,7714 — 33,4 - 77,7 —132,4 111,5 0,235 0,492 1.32
Аргон . . . Аг 39,944 21,2 1,7819 1,7839 — 185,9 — 189,3 —122.4 48,0 0,531 0,125 1,67
Ацетилен . CSH. 26,04 32,5 1,1617 1,1709 — 83,6 — 81 35,7 61,6 0,231 0.392 1,23
Водород . . н3 2,0156 420,5 0,08992 0,08987 -252,78 —259,20 —239,9 12,8 0,0310 3,400 1,41
Воздух . . . 28,9(5 29,27 1.2922 1,2928 —194,0 -140,7 37,2 0,31 0,239 1,40
Гелий . . . Дифторди- Не 4,002 211,9 0,1786 0,1785 —268,9 -267,9 2,26 0,069 1,250 1,66
хлорметан CF.C1. 120,92 7,01 5,394 5,083 — 30,0 — 155 111,5 39,6 0,555 —- 1,14
Кислород . О, 32,0000 26,5 1,4276 1,42895 —182,97 —218,83 -118,8 49,7 0,430 0,218 1,40
Метан . . . Окись угле- СН. 15,04 52,8 0,7152 0,7168 —161,7 — 182,5 - 82,5 45.7 0,162 0,520 1,30
рода . . . со 28,01 30,25 1,2496 1,2500 -191,5 —205 —140,2 34,5 0,301 0,251 1,40
Пропан . . Пропилен , Сернистый С3Н. С3Н„ 44,09 42,08 19.25 20.15 1,967 1.877 2,019 1,915 — 42,6 — 47,0 —189,9 —135,2 96,8 92,0 42,0 45,3 0,226 1,14
ангидрид so. 64,06 13,23 2,8581 2,9263 — 10,0 — 75,3 757,3 77,8 0,524 0,151 1,40
Углекислота Фтор .... со. F, 44.01 38,000 19,25 22,3 1.9633 1,695 1,9768 1,695 — 78,48 —188 — 56 —220 31,0 — 101 73 0,46 0,197 1,31
Хлор . , . С1а 70,914 11,95 3,16 3,22 — 35,0 —103 -144 76 0,573 0,120 1,34
-Этан .... с.н. 30,07 28,2 1,341 1,356 — 88,6 —183.9 35 49 0,21 0,398 1,22
Этилен . . . С.Н. 28,05 30,23 1,251 1,2605 —103,5 —169,4 9,5 50,7 0.216 0,350 1,24
Примечание. Вычисленные значения получены делением р. на 22,416; расхождения вычисленным и измеренным значениями объясняются отклонениями от идеальных законов. между
ГАЗЫ
533
Весовой состав смеси определяется весо-
выми долями; весовая доля i-ro компонента
Объёмный состав смеси определяется
объёмными долями; объёмная доля i-ro ком-
понента
Здесь V, — приведённый объём i-ro ком-
понента.
Формулы пересчёта из весового состава
в объёмный и обратно:
Удельный вес смеси при произвольных
р и Т
t—n
G 1 V
Ут = у — i=n 2-1 Г‘ ti'
V & - = 1
Li 11
1=1
Удельный вес смеси при 0°С и 760 мм
рт. ст.
__ Рт
Ут, о — 22,4 ’
где рт — средний, кажущийся молекулярный
вес смеси (кажущийся потому, что это вели-
чина чисто расчётная, упрощающая подсчёты,
не связанная с химическим представлением
о молекулярном весе):
1=п
Рт = i—n jLj гЯЧ-
Парциальные давления
Ri
Pi — Si п~ -р = ггр-
Теплоёмкости смесей могут нахо-
диться по теплоёмкостям компонентов смеси
либо по весовому составу её, либо по
объёмному.
При заданных весовых теплоёмкостях
кал
Сг.с....с»’•••’с» и весоиых Долях
компонентов gt, g„, ..., g/,..., gn весовая
теплоёмкость смеси
ккал
кг-град
При заданных объёмных теплоёмкостях
_ _ __ ккал
С1, с2,..„ а,-.., И объёмном
составе смеси rlf г2, r-t, ...» гп объёмная
теплоёмкость смеси
1 = п
--- V4 “Г ккал 1
= 2j ri [ил/3.град J *
При заданных мольных теплоёмкостях
ккал
р.! сх, Мг С2,..., М; а, ..., ?пСп ~^ъ.град и
объёмном составе rlt г2, ...» Г/, ...» гп моль-
ная теплоёмкость смеси
i=n
fi (Pi Ci)
ккал
моль-град
При переменных теплоёмкостях [с=/ (1)]
расчёты получаются громоздкими, более
просто исходить из мольных теплоёмкостей
и объёмного состава с последующим в случае
необходимости пересчётом на весовые и объ-
ёмные теплоёмкости:
_ Ст) Ккал
Ст^ Рт [кг-град] ’
-- (^т Ст) Ккал
- 22,4 нм3-град ’
Давление и температура газов после
смешения
Смешение при V=const. Химически
не действующие друг на друга газы до сме-
шения имеют объёмы Vlt V2, Vп, веса
Gx, О2,..., Gn, при давлениях рх,р2,..., ра
и температурах ix, t2,..., объём смеси
1=п
V = 2 vi-
i=l
Температура смеси
'=« r. ,
2 P‘ (W CV, 1)q
7 = --------------- ,
V plYl / \T
-р1 (,Pi CVi ,)0
1=1
или
i=n
t =‘~~—-----------------
/=1 1
Давление после смешения
i—n
T V
P — V X Gi Ri “
Z=1
L V P‘ vj
V Li rt ' •
/=i
Предпосылкой получения приведённых
уравнений служит равенство внутренней
энергии системы до и после смешения» вы-
текающее по первому началу из условия
отсутствия теплообмена с окружающей сре-
дой и неизменности объёма до и после сме-
534
ТЕПЛОТА
шения, т. е. из условия отсутствия внешней
работы.
Смешение потоков газов. Потоки газов
имеют расходы в единицу времени по весу
Gj. G2, Gn, по объёму Vx, V2, ...» V„, их
давления и температуры р1г р2,. . р„; tlt
t2, . ., t„; давление р после смешения не
должно превышать давления того потока, у
которого оно было наименьшим. Отсутствие
при смешении теплообмена с окружающей
средой и отдачи внешней работы приводит
поставленную задачу к условию (по уравне-
нию первого начала для движущихся сред),
что энтальпия системы остаётся неизменной.
Температура после смешения
S Pl Vi (1ЧСР, z)r <
T = 1=1_____________
i=-n
SPi Vj , .r
Ti cp, ^0
/-1
или
1=1
SPi Vj < „
Tt (w cp,0o
Объёмный расход смеси в единицу вре-
мени при температуре Т и давлении р
1=п
V Р " Ti
Z-l
Если мольные теплоёмкости и давление
газов во всех потоках одинаковы, то
i—n
S Vi t~n
Т = ^Г— и v= S v‘-
V Yi 1=1
2j Ti
Соотношения между параметрами p, v, T,
u, i,; s и связь этих параметров с ср и cv
для газов, подчиняющихся уравнению
ро = RT.
Вводя в уравнения, приведённые на
стр. 528, выражения соответственных частных
производных, полученные из уравнения
состояния идеального газа, связывающего
р, о, Т, имеем:
1. Независимые переменные
Г и у:
dq = cvdT + Ар do [ккал/кг];
dT do
ds — cv -p + AR у
ккал
кг-град
du = cvdT [ккал/кг];
[ди\ ! др \
(ro)T-AT[dT-)v-AP = °>
что устанавливает независимость внутренней
энергии от объёма, т. е. и = / (Т) для газа,
подчиняющегося уравнению ро = RT.
2. Независимые переменные
Тир:
dq = cpdT — Avdp [ккал/кг];
dT dp
ds=cp T —AR ?
ккал
кг-гр ад
di = cpdT [ккал/кг];
что устанавливает независимость энтальпии
газа от давления, т. е. / = А(Т).
3. Независимые переменные
р и у:
С с
dq = R-pdo-f-j^ vdp [ккал[кг];
dv dp Г ккал
ds = Ср v +cv ~ кг-град •
4. Теплоёмкости:
Разность теплоёмкостей Ср — cv =» AR;
умножением на р получаем
1 Г ккал 1
= A (pR) = • 848 = 1,985 2 J ,
что устанавливает постоянство разности
мольных теплоёмкостей для различных газов
и равенство этой разности универсальной
газовой постоянной, выраженной в тепловых
единицах.
/дср\
—- = 0 — независимость со от давления;
\др /т
(дс \
•^1 = 0—независимость cv от объёма.
Отношение Пуассона, показатель адиабаты
с AR
к=-р—= 1+ —— ; к = / (О при повышении
Ср Ср
температуры убывает как следствие увеличе-
ния теплоёмкости Ср. Для двухатомных газов
при температурах, близких к 0° С, при-
нимают к = 1,4, для газов многоатомных
к меньше.
Интегрирование приведённых уравнений
может вестись либо в предположении, что
с — / (t) (часто эта функция принимает-
ся линейной), либо в предположении постоян-
ства теплоёмкости; последнее предположение
принимают, во-первых, при малых интерва-
лах температур, когда изменениями теплоём-
кости можно практически пренебречь, во-
вторых, в тех случаях, когда изменение
теплоёмкости учитывается тем, что в расчёт
вводят значение средней теплоёмкости в рас-
сматриваемом интервале.
Интегрирование при постоянных теплоём-
костях.
г>,
1. q = Ср(Т2 — TJ + A J pdv;
Vi
Т2 У,
«2 — «1 = cv >п + ar 1п — ;
1 1 vi
ui — u1 = Ср (Т2 — Тг).
ГАЗЫ
535
Pi
2. q = cp (T, -TJ-A^ vdp-,
Pl
2 А г> 1
s2Si = c„ In — AR In — ;
K * i hj
h — ii —Л).
^2 P3
3. q = J pdv+^^ vdp'’
V, P,
. У2_ . Pi
s2 Sj Cp In 4- Cp In •
Cl Pi
При переменных теплоёмкостях результат
будет зависеть от вида функции с = / (t).
При линейных функциях ср = av + ЬТ и
ср= ар + ЬТ, где ар — аР = AR, имеем:
1. q = av (Т2 — 7\) +
4- 4 (т2-т2)4- a J pdv,
Те v9
st — sl=av\n T^ + b(Ti-T1) + AR\n £ ;
u2 — Ui = (Tt — Ti) 4- у (r^ •
2. q = ap (Ts — T,) +
+ A(t22-t2)-aJ udp-
Pl
S8 —$! = (Zpln + b (T2 — TJ — AR In ~ ;
ii-h = ap(Ti-Tl) + ~ (Tl-Tl).
3. s2 — Si = ap In у 4- b (T2 —Л)4-а, ln^ .
H Cl Pi
Приведённые уравнения отнесены к 1 кг
газа; умножение обеих частей уравнений нар.
относит их к 1 молю, умножение на G кг
даёт уравнения для произвольного коли-
чества газа.
ЧАСТНЫЕ ВИДЫ ПРОЦЕССОВ
Изохорный процесс (фиг. 8 и 9) опреде-
ляется условием и = const, du = 0; соот-
р Я
ношения параметров: у = у = const; для
перехода из состояния 7 в 2 (2'):
Уравнение первого ’ начала
вид:
dqv = du = Ср dt-,
t,
qv n2 их = J Cp dt “
= kJ'(Hf2~'i) = I
[ C», m ]0‘ -fi~ [c»t m
принимает
Если c„
дано как
/ (О
(линейная
функция).
Работа процесса l = J pdu равна нулю
в,
(du «= 0); теплота, сообщаемая газу, идёт на
увеличение его внутренней энергии, отвод
теплоты осуществим за счёт уменьшения
внутренней энергии тела.
В диаграмме р — и процесс протекает по
прямой, параллельной оси ординат: 7 — 2 —
подвод теплоты (р2 > р2, Т2 > 7\); 7 — 2' —
отвод.
В диаграмме Т—s:
dsv — cp ? ;
С* dT г 1т* in т*
(S2 —Sx)p= I Ср у = [Ся>т]т, • 1П у ,
Г,
изохоры—логарифмики; 7 — 2—подвод те-
плоты (dsv > 0); 7—2'—отвод теплоты от
тела (ds„ < 0). Площадь под изохорой в диа-
грамме Т— s выражает (с учётом масштабов)
теплоту процесса qv, равно как изменение
внутренней энергии.
Изобарный процесс (фиг. 10, 11) опре-
деляется условием р = const, dp = 0; coot-
у R
ношения параметров = const, для пе-
О1 *^1
рехода из состояния 7 в 2 (2') = т >
М2 1 2
7—2—расширение; 7 — 2' — сжатие; T2>Ti>
Т'2 < Тх-
Уравнение первого начала принимает вид:
9р=н2-ц14-Ар(У2-У1)=<2-/1= х Если Ср
г 1 ** г дано как
= JcPdf = lcP,mJ (^-^)= }/(0(ли-
i, t, | нейная
t, у. t ^функция).
= lCP’m Jo JcP,m]0
536
ТЕПЛОТА
Qp — Ср —
7\
т
~ [ ср, т ] Tj • (^2 ~ 7\)-
Если ср
дано как
/1 (Т).
Работа процесса:
lp = Р (е2 — = R (Т2 — Тг) [кгм/кг];
Lp = p(V2-V1) = GR(Ts-T]) [кал].
В диаграмме р—и процесс протекает по
прямой, параллельной оси абсцисс, площадь
под кривой процесса выражает работу;
а—1 — 2 — b—а (с учётом масштабов)—работа
процесса расширения, положительна (dv>0).
В диаграмме Т — s изобары—логариф-
микп более пологие, нежели изохоры.
Плошади под кривыми процессов 7—2
и 7—2' (т. е. площади пг—7—2—п—пг и пг—
7—2' — п'— пг) выражают (с учётом масшта-
бов) количества теплоты qp, 1_2> qp, 1_2> и
равные им изменения энтальпии Aij_2 и
площади под изохорами, проведён-
ными в пределах изменения температур
в рассматриваемом процессе, т. е. площади
п—2—3—к—п и т—1—3'~к'~т, дают измене-
ния внутренней энергии Aut_2 и Ди1-2'1 Ра*
бота процесса (в тепловых единицах А1р) на
диаграмме определяется разностью площадей,
выражающих теплоту процесса qp и изме-
нение внутренней энергии. Знаки опреде-
ляются так: теплота процесса qp > 0 при
увеличении энтропии в процессе (s2 > sx),
Ди и Ai положительны при увеличении тем-
пературы (Т2 > Тх), работа положительна
при l>2 > Uj.
Изотермический процесс (фиг. 12, 13)
определяется условием Т = const, dT — 0;
соотношения параметров p-v — const; при
переходе из состояния 7 в 2 (2'):
р2 р2, иг
Pi ’ Pi v2.
Уравнение первого начала принимает вид
dqT= AdlT
(для газа, подчиняющегося уравнению
pv = RT при dT = 0, du = с„ • dT = 0 и
di = Cp-dT — 0); работа процесса
Г,
pdv = 2,303/ht»! 1g =
= 2,303 PiVi Ig -1 [кгм/кг],
Г2
где р1У1 = RT;
LT = 2,303pjVj lg-2=2,303pjVj Ig^1 [/сглг],
v i P?.
где р2Уг = GRT.
Теплота процесса qT = AlT , t)T — ALT .
В диаграмме p—v изотермы — равнобокие
гиперболы (7—2—расширение, v2>v1; 7—2'—
сжатие, v2, < ух); площади а —7 — 2— b — а
и а— 7— 2' — Ь'—а выражают 1Т, ,_2 ( > 0),
ZT, 1-2' (< °)-
В диаграмме Т—s площади пг—1—2—п—пг
и пг •— 7 — 2' — п' — пг выражают теплоту
процесса
qT> 1—2 ( > 0, так как ds > 0)
и Чт, г-2 ( < °>
так как ds <0) и
равные им рабо-
ты, выраженные
в тепловых еди-
ницах.
Для построе-
ния изотермы в
диаграмме р— v
(фиг. 14) из на-
чального состоя-
ния 7 проводят
параллельно осям
прямые 7 — А и 7 — В;
их пересекают лучами из начала коорди-
нат (о—пг, o—m-i, о—пг2,...) под про-
извольными углами. Проводя через точки
пересечения лучей с прямыми 7—А и 7 — В
линии, параллельные осям, получаем точки
пересечения 2, 3, . . ., принадлежащие изо-
терме: p1vl = р2и2 = ... = const.
Адиабатный процесс (фиг. 15, 16) опре-
деляется условием отсутствия теплообмена
с окружающей средой как в элементарном,
так и в конечном процессах dqA — О и
qA= 0. Уравнение первого начала прини-
мает вид:
du = — AdlA;
it
и2— u1 = cv>mj -(ts— П) = — AIa.
t,
Сущность процесса заключается в полу-
чении работы за счёт уменьшения внутрен-
ней энергии газа; наоборот, при сжатии
затрачиваемая работа идёт па повышение
внутренней энергии.
Соотношения параметров (ср и cv приняты
пост оянными):
ГАЗЫ
537
It . If , 1
p-v = const;
T • vk~' = const;
Тг-и^-^Т, yfc-1;
2 (
ft—1
T p k =const; i---------Tl_.
fc~1 'irl
Plk Pi k
Работа процесса:
Co
кгм/кг.
Приведённые соотношения параметров в
адиабатном процессе имеют место при усло-
вии, что теплоёмкости ср и сг, не зависят от
температуры. У реальных газов они пере-
менны, переменно и к. Уравнение адиабаты
при переменных теплоёмкостях см. ниже,
2-й столб. Обычно расчёты ведут по приведён-
ным соотношениям, но показатель к прини-
мают равным среднему арифметическому зна-
чению его между значениями при предельных
температурах процесса. Для двухатомных
газов при температурах, близких к 0°С,
принимают к = 1,4.
В диаграмме р—v адиабата (puk = const)
протекает круче изотермы (к > 1); 7—2—
расширение; 7—2'— сжатие; а—7—2—Ь—а
выражает работу расширения 1А ( > 0, так
как dv > 0); а— 7—2'—b'—а—работу сжатия
/д ( < 0, так как dv < 0).
В диаграмме Т — s адиабата — прямая,
параллельная оси ординат, ds = O (так как
dqA = 0 и dq А = Т-ds, где Т =А 0); 7 — 2 —
расширение (Т2<Т1); 7—2'—сжатие (Т2- >Т1).
Проведением изохор (7—3 и 7—3') в пре-
делах изменения температур в процессе по-
лучают площади m — 7 — 3 — п — тп и
тп—7 — 3' — п' — тп, выражающие измене-
ние внутренней энергии (Auj_2 и Ди1_2,) и
равные им, но обратные по знаку работы
в тепловых единицах [А1а и
При расширении
ДП1_2 < 0, А1а > 0;
при сжатии
Да1-2' > 0, А1а < 0.
Построение адиабаты в координатах р—v
по одной заданной точке адиабаты (состоя-
ние 7) дано на фиг. 17.
Под произвольным углом а к оси абсцисс
проводят из начала координат луч ОА, под
углом В к оси ординат—луч ОВ; угол (3
определяют из уравнения:
(1 + tg а)к = 1 + tg р.
Проектируя точку 7 на ось ординат, по-
лучают точку С; опуская из точки 7
перпендикуляр на ось абсцисс и продолжая
его до пересечения с лучом ОА, находят
точку D. Из точек С и D проводят под углом
45° наклонные Сс и Dd к ординате и абс-
циссе, из с проводят горизонталь, из d—
вертикаль, пересечение которых даёт точку
2 адиабаты; для получения точки 3 анало-
гично используется точка 2 и т. д.
Построение требует весьма тщательного
выполнения, так как допущенная ошибка
при дальнейшем построении увеличивается.
При линейной зависимости теплоёмкостей
от температуры cv = av -f- ЬТ, ср = ар + ЬТ
уравнение адиабаты
аР JL т
pvav -е °v — const.
Политропный процесс—процесс, удовле-
творяющий уравнению pi>"=const, где под п
подразумевают произвольное, но для дан-
ного процесса постоянное число. Для идеаль-
ного газа с постоянными теплоёмкостями
ср и cv политропный процесс характеризуется
тем, что распределение теплоты между
внутренней энергией и работой посто-
янно на всём протекании процесса; в этом
случае, сохраняя этот признак постоян-
ства распределения теплоты, уравнение
pvn = const обобщает процессы р = const
(п=0), Т — const (и = 1), dq = 0 и <; = 0
(п = к), v = const (п = оо ).
Если Ср и cv рассматриваются как функции
температуры, то определяющим признаком
является лишь вид уравнения.
Для подсчёта теплоты процесса помимо
уравнения первого начала dq = du + Adl,
q =-= u« — tir + Al используется уравнение
политропы dq = c-dT. Теплоёмкость поли-
тропного процесса
AR п — к
с — cv + ]_ п = cv п_. ]
может принимать любые положительные и
отрицательные значения в зависимости от
выбора п при данном к, чем определяется
зависимость теплоёмкости не только от при-
роды тела, но и от процесса, в котором,
подводится теплота; теплота процесса
т т
cdT = Cm (Т2- Ту.
1\ Тг
ТЕПЛОТА
'538
Соотношения параметров те же, что и для
адиабаты, но с заменой к на п:
р-ип = const;
Т -vn~l = const;
_ fi~1
Т-р п = const.
Работа процесса
равно тангенсу угла наклона прямой. Таким
образом для нахождения п необходим перенос
процесса по точкам из р—v координат в
координаты Ig р — 1g у и нахождение tga
(фиг. 21).
При расчётах важно влияние погрешно-
сти в определении показателя п [18]. При
1 Г /» 1
1^! 1-М =
L \t,2/
л-1 1
1
= п—1 (P1W1 ~/Мг) [кгм/кг].
Фиг. 18
вычислении давлений и температур через
показатель п относительная погрешность в
определении их будет превышать относи-
тельную погрешность в определении п при-
мерно в 2 — 3 раза.
При вычислении работы относительная
погрешность того же порядка, что и отно-
сительная погрешность определения п.
Особенно велика
может быть относи-
Показатель политропы п определяет её
протекание; характерные случаи даны на
фиг. 18.
Методы определения показа-
теля политропы по данной кривой
процесса в координатах р—и.
I. Предполагая, что процесс 1—2 удов-
летворяет уравнению рг и"=р2и2> имеем
тельная погрешность
при вычислении те-
плоты процесса, ког-
да показатель по-
литропы близок к
показателю адиаба-
ты; в этом случае
она может превы-
шать погрешность п
во много раз.
Фиг. 21
Приращение энтропии ds =
dT ккал.
с Т кг*град
Tt
I Т
s2 — s!~cm In —характер протекания
I ч
Т,
процесса в диаграмме Т — s определяется
значением и; протекание процессов при п=
= оо, п == 0, п = 1, п = к дано выше, при
рассмотрении процессов v = const, p=const,
значения р и и можно брать прямо из диа-
граммы без учёта масштабов (фиг. 19).
II. Для политропы /—2
Pi
f- vdp
р, площ. а'— 7— 2—Ь'— а'
п = v, = плот, а — 7— 2—Ь — а ’
J pdv
Фиг. 22
т. е. определение требует планиметрирова-
ния указанных площадей (фиг. 19).
III. Показатель п политропы для точки 7
процесса равен частному от деления и на а
у
(фиг. 20), т. е. п = —, где а — подкаса-
тельная.
IV. Из уравнения pva — const следует,
что Ig р + п Ig v = const, т. е. в координатах
Ig р, 1g и политропа—прямая, а значение п
T=const, d(?=0 и q =^0, которые могут рас-
сматриваться как частные случаи политропы.
Пример. На фиг. 22 1 — 2 — политропа при
\<п<к, процесс расширения. Площадь под кривой
процесса m—1—2—n—m определяет теплоту его, q>Q
(так как ds>0); площадь т — 1 — 3— n'—m (площадь
под изохорой 7—3) — изменение внутренней энергии
Див процессе 1—2. Здесь Д и<0 (так как Та<Тг).
На основании уравнения q—(ua — uO+Af, учитывая
знаки, имеем: площадь п'—3—7 — 2—п—п’ выражает
работу А1>0 (процесс расширения).
По кривой процесса 1 — 2 показатель п опреде-
ляется как отношение приращений энтропии в изо-
ГАЗЫ
539
термических процессах между изобарами крайних
точек процесса и изохорами тех же точек, т. е.
S. — S. X
п= ----? = —.
Ss—Sa У
Циклы. В термодинамике цикл— замкну-
тый круговой процесс, в результате которого
тело, выйдя из своего исходного состояния,
возвращается к нему. Процессы, представ-
ляющие отдельные участки цикла, осуще-
ствляются квазистатически, т. е. они могут
быть отождествлены с непрерывным рядом
следующих друг за другом равновесных
состояний тела, сколь угодно близких между
собой. При этих условиях как отдельные
элементы цикла, так и цикл в целом обра-
тимы.
Последовательное повторение цикла про-
извольно большое число раз приводит к не-
Фиг. 23
прерывному действию машины, осуществля-
ющей цикл. Вследствие цикличности про-
цесса габариты машины определяются пре-
дельными изменениями объёма рабочего тела
при выполнении одного цикла. Осуществле-
ние цикла требует наличия тепловых источ-
ников, играющих роль теплоотдатчиков и
теплоприёмников; экономика цикла машины
двигателя определяется термодинамическим
к. п. д.
~ 1 2 Q1 ’
где 2 Qi — количества теплоты, получаемые
от теплоотдатчиков;
2Qa — количества теплоты, отдаваемые
теплоприёмникам.
Работа цикла
А 7. = 2 Qi 2 Q2.
Цикл Карно. Протекание цикла для
газа, подчиняющегося уравнению pv~RT,
дано на фиг. 23.
Цикл составляется двумя изотермами:
7—2—изотерма расширения, 3—4— изотерма
сжатия, и двумя адиабатами: 2—3—адиабата
расширения, 4—7 — адиабата сжатия. Осу-
ществление цикла требует теплоотдатчика
при температуре Г1( совпадающей с темпера-
турой газа по изотерме 7—2, и теплоприём-
ника с температурой Т„, совпадающей с тем-
пературой изотермы 3—4.
Соотношения параметров на отдельных
участках:
по изотерме 7—2
по адиабате 2 — 3
Tj___(
Т2 I 0».
Л-1 . Л-1
\ П- / ’
по изотерме 3— 4
Т = Т2,- = — ;
2 «4 Рз’
по адиабате 4 — 1
_ , Л-1 , л-1
—1 _ f Д _ (Р1 \ л
Т 2 Vi / \Р4 )
Термодинамический к. п. д.
не зависит от природы рабочего тела и опре-
Т
деляется лишь отношением — абсолют-
ных температур теплоприёмника Т2 и тепло-
отдатчика Tj.
Работа цикла
А1 — =
= AftTjQ— f^ln— [ккал/кг];
I = RT\ (1— In [кгм/кг]
\ 1 1 1 Vi
на диаграмме р — v определяется площадью
замкнутого контура цикла 7—2 — 3—4—7.
В координатах Т — s (фиг. 24) цикл
представлен прямоугольником 7—2—3—4—7,
qt—площадью т—7—2—п—т, q2—площадью
т—4—3—п—т, А1—площадью 7—2—3—4—J;
Qi — Тг (s3 — Si), I I — (s2 Si)>
AZ — (T1 — T2) (s2 Si).
Характери-
стики других
циклов. Фиг.
25 и 26 схемати-
чески представл я-
ют цикл, образо-
ванный: двумя
изохорами, с—z
с подводом тепло-
ты qir b — а с от-
Фиг. 26
расширения, а — с —
нятием теплоты q„
и двумя адиабата-
ми, z—Ь— адиабатой
адиабатой сжатия.
Теоретическая машина, осуществляющая
этот цикл, принимается идеальной абстрак-
цией, к которой могут приближаться дей-
ствительные двигатели внутреннего сгорания
низкого сжатия. Цикл в старой литературе
без достаточных оснований называли циклом
Отто, что должно быть рассматриваемо как
условность.
Соотношения параметров на отдельных
участках:
540
ТЕПЛОТА
по адиабате сжатия а — с
по изобаре с—z
Тл_
т -f> Рг — Рс>
1 с
до адиабате z— b
Т Л-1 „ сл
Ть ~ р^-1’ pb ~ рл;
по изохоре b — а
где е—степень сжатия;
р — степень предварительного расшире-
ния.
Термодинамический к. п. д.
_ 1 Р*-1
?i — ср (Тz • Тс)>
q2 = с„(Тъ~ Та),
по изохоре b — а
Т_ь _ Р ь _,.
— —— л«
а Ра
va
где е = — — степень сжатия
Р-
Х= —-—степень повышения давления
Рс
Термодинамический к. п. д. т](=1——
(при выводе теплоёмкость с„ принята посто-
янной для всего цикла), qr=cv (Тг — Тс);
Чъ=сЛТЬ-Та)-, А1 = с„ (Тг-Тс-Т1, + Та).
На диаграмме Т—s: qt представлено пло-
щадью m — c—z—n — m, q2 — площадью
m—а—b—п—m, А1—площадью а—с—z—b—а.
Фиг. 27 и 28 представляют схематически
цикл, образованный: изобарой с — z с под-
водом теплоты qlt
изохорой b — а с
отнятием теплоты
q„ и двумя адиа-
батами, а —с —
ад иа ба то й сжа-
тия, z— b— ади-
абатой расшире-
ния.
Цикл обычно
Фиг. 28 называют циклом
Дизеля, что не
вполне точно, ибо теоретические циклы,
выдвинутые Р. Дизелем, не совпадают с
рассматриваемым.
Таким образом, цикл, данный на фиг. 27
и 28, вошёл в термодинамику не как теоре-
тический цикл, выдвинутый Р. Дизелем, а
как более поздняя термодинамическая аб-
стракция, развившаяся из анализа рабочего
процесса уже осуществлённого компрессор-
ного двигателя Дизеля.
Соотношения параметров:
по адиабате а — с
А1 = ср (Т2 - Тс) - со (Ть - Та).
На диаграмме Т — s q± представлено пло-
щадью m — c—z—n — m, q> — площадью
m—а—b—п—m, Al—площадью а—с—z—b—a.
Фиг. 29 и 30 схематически представ-
ляют цикл, образованный процессами: а—с—
— адиабата сжатия, с — z' — изохора с под-
водом теплоты ккал/кг, z' — z—изобара
с подводом теплоты qt ккал/кг, z—b—ади-
абата расширения, b — а—изохора с отводом
тепла q2 ккал/кг.
Теоретическая машина, осуществляющая
этот цикл, принимается идеальной абстрак-
цией, к которой могут приближаться дейст-
вительные двигатели внутреннего сгорания
высокого сжатия с бескомпрессорной подачей
топлива (бескомпрессорные дизели).
Рассматриваемый цикл часто называют
циклом Сабатэ, что не является достаточно
обоснованным. Термодинамическая идея
этого цикла является просто теоретическим
отображением тех изменений в процессе
сгорания, которые произошли при переходе
в двигателях внутреннего сгорания от ком-
прессорной подачи топлива к бескомпрессор-
ной.
Соотношения параметров:
по адиабате а — с
т~
1 а
Л-1
— С, ,
Pc =sk .
Ра ’
ГАЗЫ
541
по изохоре с — z'
то
ио изобаре z' — z
Tz
'fi = Р, Рг==
по адиабате z — b
Tb~' р*-1’ ръ
по изохоре Ь — а
Tf__ 8_
Л =
91 = С, (Тг— Тс)-,
9 2 = ср(Т/~ Та)-,
О - с
г^1— к
Термодинамический к. п. д.
X-pft — 1
т _ 1 _ _________1,
,г [(X—1)+U(O—1)]
Ч\ — с» (Т/— Тс), qt = ср (Т2 Тг )’
^г~Ср(Ть— Та), А1=ст(Тг'— тс— Ть 4- Та) 4-
+ ср(Тг — Тг') (при выводе теплоёмкости
принимаются постоянными).
Выражение к. п. д. разбираемого цикла
является обобщающим по отношению к двум
предыдущим циклам; действительно, при
р= 1 приведённое выражение примет значе-
ние
1
= 1 — 7й=т >
Если (фиг. 32) в цикле с подводом тепло-
-
гы по изобаре — = е, то
и с
f=**-* и д1 = ср(Тг-Тс)= cp.Tc(^-i\
‘а * г \* с )
9з = (Ту Та) = Ср‘Та (~г- 1 \
V а /
Термодинамический коэфициент полез-
ного действия
т, е. уже известный к. п. д. цикла низкого
сжатия; при Х = 1 выражение будет иметь
вид: k 1
pw — 1
” 1 к ek-1 (р — 1) ’
т. е. это будет термодинамический к. п. д.
цикла высокого сжатия с подводом теплоты
по изобаре.
На диаграмме Т—
—s дг представлено
так как из сравнения адиабат а — с и г — /
Ту Тг
вытекает, что
1 а ‘с
Предложенные циклы принимаются аб-
стракцией, к которой приближаются двига-
площадью m — с —
—z'—n’—m, qt—пло-
щадью n'—Z' — Z —
п—п', b2— площадью
т— а — Ь~ п— т.
Циклы фиг. 31,
32 образованы
сжатием по адиа-
Фиг. зз
бате а—с, подводом теплоты по изохоре
с—z (фиг. 31) или по изобаре с—г(фиг. 32),
расширением по адиабате z—/ и отводом
теплоты по изобаре / — а (фиг. 31 и 32).
Если в цикле с подводом теплоты по
изохоре (фиг. 31)
_ Е/_ g
Сс ’ vc
тели внутреннего сгорания с продолженным
процессом расширения, как то: газовые
турбины, реактивные двигатели, двигатели
с непосредственным воздействием давления
газов на столб воды (например насосы типа
Гемфри).
Приведённые циклы обычно называют
циклами Гемфри, хотя цикл, даваемый
фиг. 32, называют также циклом Брайтона.
Идеальный компрессор (фиг. 33) — ком-
прессор без вредного пространства; рассмо-
542
ТЕПЛОТА
трение потерь действительной машины (тре-
ние, гидродинамические и другие потери)
исключено: всасывание, наполнение рабочей
полости (а—&); сжатие по изотерме Ь — с
или по политропе & — с', или по адиабате
Ь—с"; выталкивание, удаление сжатого газа
с—d (или с'—d, или с" — d).
Площадь под кривой процесса сжатия
(т — & — с — е — т или т — & — с' — е'— т,
или т — b — с’ — е"—т) выражает абсо-
лютную работу процесса сжатия за один
цикл (работа, затраченная в компрессоре
только на одно сжатие газа)
с
— j pdv}
ь
площадь, ограниченная контуром цикла (а—
—b—c-—d—a или а—Ь— с'—d—a, или а—Ь—
— с" — d — а), выражает работу компрессора
за один цикл (т. е. сумму работ всасывания,
сжатия и выталкивания) — /; соотношение
между этими работами: / = п-1сж.
Из фиг. 33 следует, что работа цикла
при изотермическом сжатии будет меньше.
Значения показателя и:
а) по изотерме п — 1;
б) для двухатомных газов при небольших
пределах сжатия по адиабате п = к =1,4;
в) по политропе 1 < п < к, порядка
1,18— 1,2.
Значение п лимитируется возможностью
отвода теплоты к воде, охлаждающей стен-
ки цилиндра (условиями теплопередачи).
Работа цикла на 1 кг сжимаемого газа
в зависимости от показателя л будет
л=1, 1изотр = 2,303 pb-vb 1g ~ =
= 2,303 RTb Ig кгм!кг-,
Pc
п
bl о литр—и | Ръ'^ъ
п
~“1
Л — к, 1адиаб “
k
- k- 1
RTb
k
k—\ Рь vb
RTb
На диаграмме T — s (фиг. 34) процессы
сжатия представлены изотермой &—с, поли-
тропой Ь— с', адиабатой Ь— с".
Для анализа условий работы компрессора
по диаграмме Т — s используется уравнение
первого начала в форме dq = di— Avdp или
2
q =(i2—fx)+Aj—vdp, удобной для опре-
1
2
деления работы цикла Al=A ^—vdp, и урав-
1
нения
dq = du + Apdv и q=(ui — uj +
2
+ A J pdv
1
для нахождения работы процесса сжатия
2
J pdv.
1
Применение их приводит к заключениям: для
изотермического сжатия (du = 0, di = 0)
работа процесса сжатия в тепловых едини-
цах А1СЖ, равная работе цикла (л=1) Altl3omp,
представлена площадью т — Ь— с— т"—т;
для политропического сжатия работа процес-
са А1еж „„литр — площадью m — & — с'—Ь'—
— р'—т- работа цикла А1пмитр — площадью
т—Ь—с'—с — т’— т; для адиабатического
сжатия (dq = 0, q = 0) работа процесса сжа-
тия А1СЖ, адиаб представлена площадью т —
— с" — Ь" — р"--т; работа цикла AlaSuaS —
площадью т—с"—с—т"—т.
Во всех случаях на диаграмме Т — s
теплота (q), отводимая в воду, охлаждающую
стенки цилиндра компрессора, представлена
площадью под кривой процесса сжатия (для
изотермы—т—Ь—с—т"—т, для политропы—
т—Ь—с'—т'—т, для адиабаты q=0);
для изотермы
_ _ 2,303 рь _
Я — А^сж. изотр А^изотр 427 Рь ^61g р?
2,303 ~ , рь
427 RTb 1g Рс;
для политропы
п_______________________к »
q = c(Tc- Ть)—с„ —1 (Тс - Ть).
Площадь под изобарой, проходящей в гра-
ницах изменения температур в процессе
(для политропы — под сс', для адиабаты —
под сс"), даёт приращение энтальпии газа
при сжатии. Площади под изохорами, огра-
ниченными теми же температурами (для
политропы — под Ь' с’л для адиабаты —под
Ь" с"), дают изменения внутренней энергии.
Стремление снизить работу цикла и зна-
чительное повышение температуры при поли-
тропном сжатии (а изотермическое
практически не достигается) вызывают пере-
ход к многоступенчатому сжатию в компрес-
соре с промежуточным охлаждением газа
при переходе из одной ступени в последую-
щую.
глзы
543
Многоступенчатый идеальный компрессор
(фиг. 35, 36). На фиг. 35 работа первой
ступени lf ст представлена площадью а— Ь—
—c—d—a, второй ступени /ц>(.т — площадью
d — b'— с' — d' — d; если
у=
V Ръ Рь Рь
где щ,—давление начала сжатия 1-й сту-
пени, pi- — давление
конца сжатия z-и
ступени (Z — число
ступеней), т. е. во
всех ступенях отно-
шение давления кон-
ца сжатия к давле-
нию начала его де-
лается одинаковым,
J//’*
равным у и тем-
пературы начала
Фиг. 35 сжатия (т. е. в точ-
ках Ь, Ь', Ь", ...) во
всех ступенях одинаковы (Ть ), то при оди-
наковом п во всех ступенях работа каждой
ступени:
ll,cm ~ ZI1, cm ZIII, т—=
п /
= RTb — У п J кгм!кг.
После каждой ступени газ, нагревшийся
за счёт политропного сжатия с повышением
давления в у раз до температуры Тс =
п-1
— Тъ'У П ’ поступает в холодильник, где
его температура снижается до первоначаль-
ной Тй; процесс охлаждения осуществляется
при неизменном давлении, что вызывает
уменьшение объёма, пропорциональное паде-
, .. vt>' 1,ь~
нию абсолютной температуры — = --=...=
»с »с-
Ть
= уг; при этих условиях работа компрес-
1 с
сора:
На диаграмме Т—s площадью под кривой
b — с—Ь' представлена работа первой сту-
пени, под кривой Ь' — с'— Ь" — второй, ...;
k b — с — b' — к'— к = к' ~ Ь' — с' — Ь" —
— к" — к' = ...;
площадью под кривой b — с — теплота,
отдаваемая газом в охлаждающую воду пер-
вой ступени, под кривой Ь'—с'—то же второй
ступени; к — b — с — иг — к = к' — Ь’ — с’ —
т' — к' —
Ql.cm — ?П, ст~С (Тс— ть) =
П — к
= (тс~ тъ) ккал/кг-,
площадью под изобарой Ь'—с — теплота,
отдаваемая газом в охлаждающую воду пер-
вого промежуточного холодильника ср(Тс—
— Ть) ккал!кг-, под изобарой Ь" — с’—то же
второго промежуточного холодильника;
m—c—b'—k'—m^m' — с'— Ьг— к" — щ'—...
РЕАЛЬНЫЕ ГАЗЫ
Отклонения от закона Бойля-Мариотта
Для идеального газа pv = const, т. е.
в диаграмме pv—р это будут прямые, парал-
лельные оси р; каждая прямая, согласно
уравнению состояния pv = RT, отвечает
определённой температуре. Табл. 31 даёт,
по опытам Амага, значения pv для O2,N2,
СО2, Н2 при 0°С при изменении давления
от "1 до 2 500 ат.
Таблица 31
Значение pv для некоторых газов при О°С
по опытам Амага [40]
Давление в ат pv кислорода pv азота pv угле- кислоты pv водорода
1 1,0000 1.0000 1,0000 1,0000
100 0,9265 0,9910 0,202 1,0690
200 0,9140 1,0390 0,385 1,1380
500 1,1570 1,3900 0,891 1,3565
1 000 1,7360 2,0700 1,656 1,7250
2 500 3,3238 3,9200 — 2.6950
Только поведение гелия при 0°С и изме-
нении р от 1 до 850 ат близко к поведению
идеального газа, однако отклонения наблю-
даются и здесь. При
0°С только водород,
гелий, неон не об-
наруживают мини-
мума произведения
pv с изменением р;
другие газы при бо-
лее низких давле-
ниях сжимаются
сильнее, а при бо-
лее высоких давле-
ниях слабее, нежели
идеальные газы.
Фиг. 37 даёт ха-
рактер измене ния
произведений pv для
воздуха. Пунктир-
ная кривая на диаграмме проведена через ми-
нимумы значений pv при разных температу-
рах. Верхняя ветвь этой кривой пересекает
ось ординат в точке а,определяющей темпера-
туру Бойля для газа (для воздуха 54°С),
при которой строго соблюдается закон pv=
= const, и изотерма, начинающаяся в этой
точке, на некотором протяжении будет пря-
мой, параллельной оси абсцисс; изотермы,
начинающиеся выше точки а, не проходят
через минимум.
544
ТЕПЛОТА
Отклонения от закона Гей-Люссака
Для идеального газа в уравнениях v =
= г0(1 4-at) и р=ро(1+«О коэфициент
теплового расширения и термический коэ-
фициент давления совпадают и не зависят
ни от t пи от р; у реальных газов эти
коэфициенты близки, но не равны между
собой и зависят от р и t (см. «Общие тепло-
вые свойства тел» стр. 526).
Уравнение состояния
Уравнение состояния реального газа
можно дать так:
где S называют коэфициентом сжимаемости,
причём для данного газа $ = / (р, Т).
Два состояния газа, подчиняющиеся это-
му уравнению, будут связаны соотношением
Фиг. 38, 39, 40, 41 дают коэфициенты
сжимаемости £ воздуха, азота, водорода,
аммиака, метана [10J.
Отклонения от основных законов идеаль-
ного газа и возможность сжижения реаль-
ных газов обнаруживают чрезвычайно слож-
ную природу реального газа. Классической
попыткой охватить уравнением состояния
свойства реального газа является уравнение
Ван-дер-Ваальса (отнесено к молю газа):
(p+^(.t>~b)=RT. (1)
Здесь b называют кообъёмом; если эффек-
тивный радиус молекул г, N— число Аво-
гадро, то Ь = к-з nraN, и по Ван-дер-
Ваальсу к = 4 при шарообразной форме мо-
лекулы; при форме, отличной от шара, к при-
мет другое значение.
ГАЗЫ
545
Теоретически при любом давлении газ не
может занимать объёма, меньшего Ь. Таким
образом b служит поправкой к уравнению
pv = RT, связанной с собственным объ-
ёмом молекул.
а
Вторая поправка —2 к этому же уравне-
нию учитывает внутреннее давление газа,
являющееся следствием взаимного притяже-
ния молекул. Уравнение Ван-дер-Ваальса
является уравнением кривой 4-го порядка;
оно является кубическим уравнением отно-
сительно и и, как таковое, имеет для изотерм
при данном р или три действительных корня
или два мнимых и один действительный.
Для изотерм выше критической изобара
пересекает изотерму только один раз (дейст-
вительный корень, два других мнимые); изо-
термы ниже критической должны пересе-
каться изобарами 3 раза (три вещественных
корня, см. фиг. 42), наименьший объём (точ-
ка а) отвечает жидкости, наибольший—объём
сухого насыщенного пара (точка Ь), средний
(точкас)— нереализуемое, лабильное состоя-
ние.
Участки изотерм ат и Ьп полуустойчи-
вые метастабильные состояния перегретой
воды и переохлаждённого пара, участок
тп—состояния неустойчивые, лабильные.
Прямая а—Ь, отвечающая устойчивому
равновесию жидкости с её паром, по правилу
Максвелла определяется равенством площа-
дей а — т — с и с—п—Ь, ибо работа изотер-
мического цикла а—т—с—n—b—а должна
быть равна нулю.
При v = b р =оо, т. е. асимптота кривой
Ван-дер-Ваальса параллельна оси р и отстоит
от неё на величину &; когда у=оо, то р=0,
т. е. вторая асимптота ось v; для опреде-
ления пересечения изотермами оси v следует
принять р = 0, что даёт
• v — b v2
откуда __________
а ± Vа2~ 4ab RT
Точка пересечения будет действительной,
а
если аа>4а&7?Т, и при ^<4^^ изотермы
перейдут в область отрицательных давлений
(для этилового спирта осуществлены до
(—17) ат, для воды и этилового эфира — до
а
(—36 ат). При кривая касается оси
абсцисс. Максимумы и минимумы на изо?
35 Том I
термах Ван-дер-Ваальса находятся из усло-
/бр\
вия I ) =0, что даёт
av — 2ab
Р=-------
(2)
этим уравнением определится кривая, про-
ходящая через максимумы и минимумы, а
максимум её, т. е. критическая точка, опре-
деляется условием
6аЬ — 2av Q
(3)
Совместное решение уравнений (1), (2),
(3) с отнесением их к критической точке
позволяет связать параметры критического
состояния с константами a, b, R и обратно:
у*= 3 6;
а
Рк = 27Т2'
Т А а .
1Ь"" 2Т'b'R’
Ptt-
~8pk>
d_8 p^
R-3- ~T k
Критические параметры и константы а и bt
вычисленные по ним, приведены в табл. 32
и 33.
Таблица 32
Термические свойства газов [40]
Газ ‘к «°C Рк в ат в г }см* t кипения при 1 ат в °C t плавле- ния в °C
Рк vk
Не —267,8 2,26 0,066 3,184 —268,88 —272,2
Н, —239,9 12,8 0,031 3,28 —252,74 —259,1
Ne —228,7 27,8 о ,048 —245,9 —248,7
N, -147,1 33,5 0,311 3,42 —195,8 —209.9
СО —139 34,6 0,311 3,54 —191,47 -204,99
Аг -122,4 48,0 0,509 3,28 —185,7 —189,2
о. -118,8 50,8 0,4299 3,346 —182,95 —218,4
NO — 96 64 — —150,2 -167
СН. — 82,9 45,0 0,162 3,46 —161,4 —183,0
Кг — 62,5 54,3 — —151,7 —169
с,н4 + 9,5 52,4 0,22 -103,9 —169,4
Хе 4* 16,6 58,2 1,155 3,62 —109,1 —140,0
СО, + 31,35 73,0 0,449 3,49 — 78,5 - 56,4
NaO + 36,5 71,2 0,454 3,65 —
с,нв + 34,5 50,0 — 89,2 -172,1
С,Н. 4* 35,9 61,6 — — 83,9 — 81,8
с,н. + 95,6 45 — - 47,7
с,н, + 102,0 48,5 — — 44 —189,9
С1, + 144 76,1 0,573 3,63 __
NH, + 132,4 115,8 0,236 - 33,4 — 77,9
NO, + 153,2 Юо 0,524 + 22,0 - 10
СН,ОН +240,0 78,50 0,2722 4,559
с.н. + 288,5 47,89 0,3045 3,755 —
С,Н,ОН +243,3 62,96 0,2755 4,115 —
HtO +374 217,5 4,458
Воздух —140,7 38,4 0,35 — -192,0
—194,4
Таблица 33
Значения постоянных а и b в уравнении Ваи-дер-
Ваальса, вычисленные из критических данных
Вещества Тк Рк в ат Ъ а
Н,О 647 217,5 30,55 4,47.10е
C.HeF 559,6 44,62 128,5 19,98.10“
СН,СОСН, 505,8 52,2 99,4 13,92.10“
ci, 419,0 93,5 46,0 5,84.10“
со. 304,1 73,0 42,75 3,609-10’
Аг 155,6 52,9 30,2 1,303.10’
о» 154,2 50,8 31,18 1,332-10’
N, 126,0 33,5 39,6 1,345.10“
н, 33,18 12,80 26,70 0,244.10’
Не 5.16 2,26 23,42 0,03253.10е
546
ТЕПЛОТА
Приведённые параметры; соответственные
состояния
Если за единицу объёма вещества при-
нять объём в критическом состоянии, за
единицу давления—критическое давление,
за градус индивидуальной температурной
шкалы—критическую температуру, то v,p, Т
некоторого состояния будут выражены доля-
ми критических величин
v Р Т ч.
— = ср: — = z, = Я.
" Р.4 Тк
Параметры у, л, Я называют приведён-
ными объёмом, давлением, температурой.
Два вещества, определяемые одинаковыми
значениями приведённых параметров, нахо-
дятся в соответственных состояниях, они
одинаково отклоняются от своих критиче-
ских состояний.
Приведённое уравнение состояния Ван-
дер-Ваальса, общее для всех веществ в газо-
образном, парообразном и жидком состоя-
ниях, получается из обычного уравнения
Ван-дер-Ваальса, если в нём обычные пара-
метры и константы выразить через приведён-
ные
(3 ?- 1) = 8*>.
Уравнения Ван-дер-Ваальса хорошо отра-
жают в ряде случаев качественную сторону
изменений состояний реального газа, но не
дают достаточно точной количественной
оценки их для технических расчётов.
ВОДЯНОЙ ПАР
УРАВНЕНИЯ СОСТОЯНИЯ; ПАРАМЕТРЫ
В приводимых ниже обозначениях ин-
декс (') отнесён к состоянию жидкости при
температуре кипения, отвечающей давле-
нию р, а индекс (") — к состоянию сухого
насыщенного пара.
о', и" [дг3/кг]—удельные объёмы жидкости
и сухого насыщенного пара; х —степень
сухости (паросодержапие), количество сухо-
го пара в единице (1 кг) влажного пара;
vx [м3/кг] —удельный объём влажного пара;
q [ккал/кг]—теплота жидкости; г [ккал/кг]—
теплота парообразования (скрытая); и', I',
s' и и", i", s"—внутренняя энергия [ккал/кг],
энтальпия [ккал/кг], энтропия [ккал/кг-град]
жидкости при температуре кипения, отве-
чающей данному давлению р и сухого на-
сыщенного пара; р[к/мл/кг] — внутренняя
теплота парообразования
р = и" — и';
ф[ккял/«г]— внешняя теплота парообразо-
вания
ф = Ар (и* — у');
г = р + ф;
[ккал/кг]— полная теплота пара сухого
насыщенного, Л — q + г.
Насыщенный пар находится в равновесии
с жидкой фазой. Давление его —функция
температуры и кривизны поверхности раз-
дела между паром и жидкой фазой, а для
растворов ещё и функция концентрации
растворённого вещества.
Уравнение Клаузиуса-Клапейрона (см.
стр. 531) для процесса парообразования
принимает вид
др г
дТ7 = AT' (v"—v~y
при пользовании уравнением в узких пре-
, др
делах температур обычно производную
Ар
приолиженно заменяют отношением &
При достаточном удалении от критиче-
ского состояния возможно пренебречь объ-
емом жидкости, что даёт
др г
дТ' = АТ'и"’
если при тех же условиях допустить, что
пар подчиняется уравнению
p-v" = RT',
то
др г
~ = d (In р) = дТ.
Считая для узких пределов темпераtур г
не зависящей от температуры, имеем
. р2 г / 1 1 \
Pi AR VP, Т2 J
Аналогичные допущения делаются по от-
ношению к уравнению Клаузиуса-Клапейро-
на и для процесса перехода из твёрд :о
состояния в пар—сублимации.
Более правильное решение о зависимости
давления насыщенных паров жидкостей
(твёрдых веществ) от температуры требует
учёта функциональной зависимости от тем-
пературы для скрытой теплоты парообразо-
вания (сублимации).
Насыщенный пар, не содержащий капелек
жидкости во взвешенном состоянии, назы-
вают сухим насыщенным; содержащий ка-
пельки жидкости—влажным. Влажность
пара характеризуется степенью сухости
(паросо держанием).
Для влажного п’ара:
объел! влажного пара [лР/кг]
их = v"-x+ v' (1 — х),
vx « v"-x, tx~ ^';x;
полная теплота влажного пара
= q + rx;
энтальпия влажного пара
ix = i' + rx;
внутренняя энергия влажного пара
их = и' -I- р х;
энтропия влажного пара
г
sx ==$'-)- *х,
ВОДЯНОЙ ПАР
547
где Т'—температура кипения (по абсолют-
ной шкале).
Пар, температура которого выше темпера-
туры насыщенного пара, обладающего тем же
давлением, называют перегретым (ненасы-
щенным). Для перегретого пара предложено
много уравнений состояния.
Уравнение Тумлирца-Линде (1899 —
1905 гг.)
RT
и=> — — 0,016
Р
часто приводится в литературе, но не может
использоваться как расчётное, так как по-
правка к объёму в сравнении с идеальным
газом принята постоянной, не зависящей
пи от давления, ни от температуры.
Современные уравнения весьма сложны.
В таблицах перегретого пара по Коху
для вычисления объёма применена формула
где
кгм
R= 47,06 кг.грар,
А = 0,9172 лР/кг;
В= 1,3088-Ю-4 м2/кг-(м2/кг)2-,
с = 4,379-10’ м3/кг-(м21кг)2.
В теории состояния реального вещества
имеет значение учение об ассоциации моле-
кул (иногда называемой кажущейся); ассо-
циация понимается не о химическом смысле,
а лишь как объединение нескольких молекул
в один агломерат, получающий только не-
которые свойства большой молекулы; так,
предполагается, что при ассоциации молекул
не происходит перегруппировка атомов в
одиночных, составляющих молекулах, и ин-
дивидуальные свойства каждой из них
в основном сохраняются. Однако структура
сложной молекулы всё же может лишать
составляющие молекулы некоторых степеней
свободы. Ассоциация уменьшает число само-
стоятельных частиц, составляющих газ,
и снижает давление газа на стенки сосуда.
Уравнение состояния ассоциирующего газа
может быть получено из рассмотрения газа
как смеси, составленной компонентами с
одиночными, двойными, тройными и т. д.
молекулами. Сторонники учения считают,
что правильным учётом ассоциации можно
дать уравнения состояния, полностью отобра-
жающие природу реального газа.
Учение начало развиваться с 90-х годов
прошлого столетия. М. П. Вукаловичем и
И. И. Новиковым [8], [9] получены с учётом
ассоциации расчётные уравнения для опре-
деления термодинамических параметров
водяного пара, послужившие для составле-
ния паровых таблиц.
Уравнение состояния для водяного пара
имеет вид
P»=RT В(П^],
где
А ~ RT "* ТГгТгГ, — й;
т 2
Г,/тл______bCR_ ( к \
„ 3 +2тг [ Зпг.-Лт, ] "*
Т 2 I Т----2-- I
/ CR______\г/ 36 \
I j. 3 + 2m, 1 + у I •
Константы /?, a, b, С, К, т2, т3 имеют
следующие значения:
R = 47,053 а = 63,2 М*/кг-
кг-град
b = 0,0009 м2)кг-, К = 21,5; т2 = 1,968;
т3 = 2,957; С= 405 000.
Подстановка значений приводит уравне-
ние к такому виду:
Р - и = 47,053 Т— -
V
W 390,08 _
63,2 + 2 ,468
^100/
9,35107
Т \2,468~
— 0,04235 Т ) + -
/ и
Теплота перегрева
тп
9п = О» — i")P = J cpdT [ккал/кг]-,
т’
приращение энтропии в процессе
тп
(sn S") р = j"
Т'
перегрева
ккал
кг-град
в приведённых выражениях подстрочный
индекс п определяет состояние пере-
гретого пара; Т' — абсолютная темпера-
тура насыщенного пара того же давления.
Изменение внутренней энергии в процессе
перегрева
ип — и" — (in — i") — Ар (vn — а") [ккал/кг].
Теплоёмкость перегретого пара>
функция давления и температуры, ана-
литически выражается сложными зависи-
мостями, и проще использование табличных
данных или графиков (см. табл. 34, 35) фиг.
43 [7].
Полная теплота перегретого пара вклю-
чает в себя теплоту жидкости q, теплоту
парообразования г и теплоту перегрева qn,
т. е.
= 9 + г + 9л-
Энтальпия жидкости Г связана с тепло-
той жидкости соотношением
i' = 9 + Apv„,
35*
548
ТЕПЛОТА
где о „—объём жидкости при 0°С (зависи-
мостью объёма жидкости при 0°С от давле-
ния пренебрегают). Для состояний пара,
достаточно удалённых от критического со-
стояния, возможно пренебречь разностью
(/'— q); такое допущение приводит к при-
ближённым соотношениям:
/' = q,
lx = ^х>
i" s X,
Фиг. 43
Работы конференций по паровым таб-
лицам (Лондон —1929, Берлин — 1930, Нью-
Йорк—1934) дали скелетные таблицы (см.
табл. 36, 37, 38); этим определены наиболее
вероятные значения основных величин и
возможные отклонения их.
Приводимые ниже паровые табл. 39, 40,
41 взяты из работы М. П. Вукалович «Термо-
динамические свойства водяного пара», из-
данной в 1946 г. Таблицы согласованы с
нормами и допусками последней Третьей
международной конференции по пару; до
этого были распространены таблицы Кно-
блауха, Райша, Хаузена и Коха (1932) [23],
Бирюкова (1938) (о них смотри у М. П. Ву-
калович), а в 1937 г. были выпущены таб-
лицы Коха.
Диаграмма Т— s (фиг. 44). В диа-
грамме Т — s для пара наносятся нижняя
Фиг. 44
пограничная кривая а — b—к, определяю-
щая состояния жидкости при температурах
кипения (состояния влажного пара при х=0),
и верхняя пограничная кривая к — с, на ко-
торой располагаются точки, характеризую-
щие состояния сухого насыщенного пара
(х = I). Обе кривые смыкаются в точке к,
выражающей критическое состояние. Между
пограничными кривыми располагаются точ-
ки, определяющие состояния влажного пара
правее верхней пограничной кривой—состоя-
ния перегретого пара, левее нижней погра-
ничной кривой — состояния жидкости.
Приращения энтропии для состояний жид-
кости, находящейся в равновесии с насыщен,
ным паром, т. е. для точек на нижней погра.
яичной кривой, определяют по уравнению
Т'
здесь с' — теплоёмкость процесса, идущего
по нижней пограничной кривой; Т„ = 273°
абс.; Т'— температура кипения (насыщенного
пара); энтропию начального состояния, от-
вечающего условию равновесия при Т=273°
абс., обычно принимают равной нулю, тогда
273
вдали от критического состояния с' не отли-
чается ощутимо от обычной теплоёмкости
жидкости, не сильно зависящей от темпера-
туры; при приближении к критическому со-
стоянию с' сильно растёт, обращаясь в этом
состоянии в бесконечность. Этим опреде-
ляется характер нижней пограничной кри-
вой. Изобаро-изотермическому превраще-
нию 1 кг жидкости в сухой пар (процесс
b — с) соответствует приращение энтропии
г
s" — s' = j.;- , что позволяет, имея нижнюю
пограничную кривую, построить верхнюю
к — с (состояния сухого пара х = 1).
Изобары в области перегрева.(например,
с — d) определяются уравнением
Г'
где Т' — температура насыщенного пара;
Тп—температура перегретого пара.
В области жидкости изобары протекают
несколько! положе нижней пограничной кри-
вой, почти совпадая с последней; это объяс-
няется малым изменением теплоёмкости жид-
кости в зависимости от условий подвода
теплоты к ней и возможностью с большей
точностью принимать ср равным с'. Прира-
щение энтропии
г
Sx s' = Sm s' = x
определяет переход жидкости в изобаро-
изотермическом процессе b—m в состояние
влажного пара со степенью сухости х, что
позволяет находить по диаграмме значение х
делением отрезка b — m на Ь — с:
bm
x=-bE’
отсюда для построения на диаграмме кри-
вых с постоянной степенью сухости (x=const)
Ист ин ная теплоемкость перегретого водяного пара при постоянном давлении в ккал/кг °C [7] Табл и ц а 34
16? 186 20J 220 240 260 280 300 320 340 360 380 400 420 440 460 480 500 520 54С
1 0,487 0,480 0,474
5
SG
29
30
40
50
60
70
80
90
100
ио
120
130
140
150
160
170
180
190
260
210
220
230
240
250
260
270
280
290
300
0,471 | 0,470 0,471 0,473 0,474 0,477 0,479 0,481 0,483 0,486 0,489 0,492 0,495 0,498 0,501 0,505 0,507 0,511 и,514
0,537 0,52. 0,50S .500 J,497 0,495 0,494 0,493 0,494 0.495 0,496 0,498 0,499 0,502 0,50-1 0,506 0,508 0,511 0,514 0,516
(J,6l3 0,569 •0 546 И. 531 0,523 9,517 0,513 0,510 0,509 0,508 0,508 0,509 0,510 0,511 0,512 0,514 0,516 0,519 0,520
0,682 о,G2: | 1,591 J.570 0,555 0,546 0,539 0,534 0,530 0,528 0,527 0,526 0.524 0,526 0,527 0;528 0,528
0,765 e,68( | ),633 0,605 0,586 0,572 0,562 0,554 0,548 0,544 0,541 0,539 0,537 0,536 0,536 0,537
0,819 0,724 0 й.7 0.633 0,610 0,592 0,579 0,570 0,562 0,556 0,552 0,549 0,547 0,547 j, 546
0,854 и,757 0,693 . ,652 0,626 0,607 0,593 0,582 0,574 3,568 0,563 0,559 0,556 0.554
1,036 0 ,873 <>.765 ' .699 0,664 0,637 0,617 0,602 0,591 0,582 0,576 0,571 0,567 0,564
G.706 0,670 0,645 0,625 0,610 0,598 0,589 0,582 0,576 0,572
1,230 1,965 (’,836 0,754 0,707 0,674 0,649 0,630 0,616 0,604 0,594 0,587 0,582
0,746 0,706 0,674 0,650 0,632 0,618 0,607 0,599 0,592
1,333 1,952 0,896 0,794 0,740 0,702 0,673 0,651 0,634 0,621 0,610 0,601
0,846 0,779 0,732 0,696 0,670 0,650 J,634 0,622 0,612
1,406 1,073 0,905 0,822 0,763 0,721 0,691 0,667 0,649 0,634 0,622
0,869 0,798 0,749 0,712 0,685 0,665 0,647 0,631
2,143 1,352 1,063 0,923 0,837 0,778 0,735 0,704 0,679 0,660 0,644
0,984 0,878 o.tos 0,760 0,723 0,695 0,673 0,656
1,861 1,237 1,055 0,925 0,843 0,785 0,744 0,712 0,687 0,668
1,137 0,977 0,882 0,814 0,766 0,730 0,702 0,679
3,23 1,029 1,231 1,034 0,921 0,843 0,783 0,749 0,717 0,692
1.341 1,095 0,965 0,874 0,812 0,767 0,732 0,705
2,241 1,476 1.168 1,015 0,908 0,837 0,787 0,748 0,719
1,620 1,280 1,055 0,942 0,863 0,807 0,768 0,733
1,360 1,109 0,984 0,893 0,829 0,785 0,747
1.451 1,168 1,022 0,922 0,851 0,803 0,762
1,234 1,067 0,953 0,875 0,823 0,777
1,305 1,113 0,978 0,899 0,844 0,793
1,163 1,020 0,925 0,864 0,809
1,216 1,059 0,954 0,885 0,826
1,272 1,096 0,979 0,905 0,844
1,122 1,007 0,927 0,861
1,150 1,030 0,947 0,880
-> по данным автора [7]
По опытным данным <
ВОДЯНОЙ ПАР
550
ТЕПЛОТА
ю
св
а
s
ч
©
<в
Истинная теплоемкость перегретою водяного пара при постоянном объеме cv в ккал!кг °C [7]
300
ВОДЯНОЙ ПАР
551
Таблица 36
Свойства кипящей воды и насыщенного пара
Температура в °C Давление в'кг/'-м- Допуск -Jr Удельный объём Энтальпия (теплосодержание)
ж и цко- сти в с si2 !г допуск пара в см3/г допуск ± жидкости ккал 1кг допуск пара ккал<кг допуск ±
0 0,006228 0,000006 1,00021 0,00005 206.310 210 0 0 597,3 0,7
10 0,012513 0,000010 1,00035 0,00010 106,410 110 10,04 0,01 601,6 0,7
20 0,023829 0,000020 1,00184 0,00010 57,824 58 20,03 0,62 605,9 0,6
.30 0,043254 0,000030 1,00442 0,00010 32.922 33 з^.ео 0.02 610,2 0,5
40 0,075204 0.000038 1,00789 0,00010 19,543 19 39,98 0,02 614,5 0,5
50 0,12578 0,00006 1,0121 0,0002 12.045 12 49,95 0,03 618,9 0,5
G0 0,20312 0,00010 1,0171 0.0002 7678.3 7.7 59, Л 0,03 623,1 0,5
70 0,31775 0,00016 1,0228 0,0002 5046,3 5,0 69.93 0,03 627,3 0,5
80 0,48292 0,00024 1,0290 0,0002 3409,2 3.4 79,95 0,04 631.4 0,5
9» 0,71491 О.ООиЗб 1,0359 0,0002 2361,5 2,4 89.98 0,05 635,3 0,5
100 1,03323 0 1,0435 0,0002 1673,2 1,7 100,04 0,05 639,1 0.5
110 1,4609 0,001. 1,0515 0,0(04 1210,1 1.2 110,12 0,06 642,7 0,5
120 2,0245 0,0013 1,0603 и,0004 891.65 0,89 120,25 0.06 Р46.2 0,5
130 2,7544 0,0016 1,0697 0,0004 668,21 0,67 130,42 0,07 649,6 0.5
140 3,6848 0,0021 1.0798 0,0004 508,53 0,51 140,64 0.07 652,7 0,6
15!) 4,8535 0,0032 1.0906 0,0004 392,46 0,39 150,92 0,08 655,7 0.7
100 6,3023 J.0042 1,1021 0,5.004 306.76 и.31 161,26 0,08 658,5 0.8
г: о 8,0764 О,0053 1,1144 0,0004 242,55 0,24 171,68 0,09 661.0 0.8
133 10,225 0,007 1,1275 0,0004 193,80 0,19 182,18 0,09 663.3 0,9
;.оо 12,800 0,008 1,1415 0,0004 156,32 0,16 192,78 0.10 665,2 0,9
200 15,857 0,008 1,1565 0,0004 127,18 0,13 203.49 0,10 666,8 0.9
210 19,456 0,008 1,1726 0,0004 104,24 0,10 214,32 0.11 668,0 0,9
22!) 23,659 0,009 1,1900 0,0004 86,070 0,086 225,29 0,11 669,0 0.9
1*30 28,531 0,010 1,2087 0,0004 71,483 0,071 236,41 0,12 669,4 0.9
240 34,140 0,012 1,2291 0,0004 59,684 0,060 247,72 0,12 669,4 0.9
250 10.560 0,013 1,2512 0,0004 50,061 0,050 259,23 0,13 668,9 0.9
220 47,866 0,015 1,2755 0,0004 42,149 0,042 270,97 0.18 667,8 О.9
, 270 56,137 0,017 1,3023 0.0004 35,593 0,035 282,98 0,19 666.0 0,9
280 65,457 0,020 1,3321 0,00(14 30,122 0,030 295,30 0,20 663,6 0.9
КО 75,917 0,022 1,3655 0,0005 25,522 0,030 307,99 0,20 660.4 0,9
300 87,611 0,024 1,4036 0,0005 21,625 0,035 320,98 0,30 656,1 1,о
410 100,64 0,03 1,4475 0,0005 18,300 0,035 334,63 0,40 650,8 1,2
320 115,12 0,03 1,4992 0.0005 15,438 0,035 349,00 0,50 644,2 1,4
330 131,18 0,04 1,5619 0,0005 12,952 0,035 364,23 0,60 636,0 1.6
340 148,93 0,04 1,6408 0,0005 10,764 0,035 380,69 0,70 625,6 1,8
250 168.63 0,04 1,7463 0,0006 8,802 0,035 398,9 0,8 611,9 2.0
360 190,42 j,05 1,9066 0,0040 6,963 0,040 420,8 0,8 592,9 2,0
370 214,68 0,05 2,231 0,021 4,997 0,100 452,3 1.5 559,3 3.0
371 217,26 0.10 2,297 0,026 4,761 0,100 457,2 1.5 553,8 3,5
372 219,88 0,11 2,381 0,034 4,493 0,110 462,9 2,2 547,1 4,0
373 222 53 0,11 2,502 0,^53 4,182 0,120 471,0 3,5 538,9 4,5
374 225,22 0,11 2.79 0,15 3,648 0,120 488,0 5.0 523.3 5,0
552
ТЕПЛОТА
Удельный объем воды и перегретого водяного пара в см3/г
* . Тем п е р а т У р а в °C .
я к ЕС* 0 | 50 1 100 1 150 200 259 300 350 400 | 450 500 550
1 0,00016 с.00005 1,01210 0,00020 I 1730 1-1 1975 2 2216 о 2454 2 2691 3 2928 3 3164 3 3400 3 3636 4 3872 4 !
5 10 0,9999 0,0002 0,9997 0,0002 1,0119 0,0002 1,0117 0,0002 1,0432 0,0002 1,0431 0,0002 1,0906 0,0002 1,0902 0.0002 433,8 0,4 210.4 0,2 484,1 0,5 237,6 0,2 533,2 0,5 263,3 0,3 581,6 0,6 288,2 0,3 629,6 0,6 312,7 0,3 677,4 0,7 337,0 0,3 725,0 ^7 0.4 772.5 0,8 385,1
25 0,9989 0,0002 1,0110 0,0002 1,0422 0,0002 1,0893 0,0002 1,1556 0,0603 89,0 0,1 101,1 0,1 112,1 0,1 122.6 0,1 132,7 0,1 142.7 0,1 152,6
50 75 100 125 150 200 250 300 350 400 0,9977 0,0002 0,9965 0,0002 0,9952 0,0002 0,9940 0,0002 0,9929 0,0002 1,0099 0,0002 1,0088 0,0002 1,0077 0,0002 1,и067 0,0002 1,0056 0,0002 1,0409 0,0002 1,0397 0,0002 1,0385 0,0002 1,0372 0,0002 1,0360 0,0002 1,0877 0,0002 1,0861 0,0002 1,0845 0,0002 1,082% 0,0002 1,0814 0,0002 1,1532 0,0003 1,1508 0,0003 1,2495 0,0004 1,2452 0,0004 46,41 0,07 27,48 0,05 53,12 0,08 33.22 0,07 59,05 0,09 37,78 0,08 64,60 0,09 41,83 0,08 69,92 0,10 45,62 0,09 75,10 0,12 49,25 ' ,16
1,1485 0,0003 1,1462 0,0003 1,1439 0,0003 1,2410 0,0004 1,2369 0,0004 1,2330 0.0004 1,3979 0,0007 1,3877 0,0007 1,3782 0,0007 23,03 0,05 16,66 0,03 11,93 0,02 27,05 0,05 20,53 0,04 16,10 0,03 30,41 0,06 23,52 0.05 18,90 0,04 33,45 0,07 26,14 0.05 21,25 0,04 36,32 0,07 28,55 о‘о6 23,36 0,05
v.wua i.uikto 0,0002 0,0002 0,9882 1,0015 0,0002 0,0002 0,9859 0,9996 0,0002 0,0002 0,9837 0,9975 0,0002 0,0002 0,9814 0,9956 0,0002 0,0002 1,033/ 0,0002 1,0314 0,0002 1,0291 0,0002 1,0269 0,0002 1,0247 0,0002 давлением 1. Удельн кдых двух 1,0784 0,0002 1.0755 0,0002 1,0726 0,0002 1,0698 0,0002 1,0670 0,0002 1,1395 0,0003 1,1353 0,0003 1,1312 0,0003 1,1272 0,0003 1,1234 0,0003 1,2255 0,000.( 1,2184 0,0004 1,2117 0,0004 1,2054 0,0004 1,1994 0,0004 1,3612 0,0007 1,3462 0,0007 1,3327 0,0007 1,3207 0,0007 1,3097 0,0007 1.071 0,002 1,604 0,002 1,557 0,002 1,521 0,002 10,31 0,02 6,366 0,013 3,02 0,01 13,05 0,03 9,45 0,02 6,98 0,02 15,11 0,03 11,39 0,02 8,90 0,02 16,87 и, 03 12,96 0,03 10,35 0,02
Примечания. ’1,000027 см3/г. 2. В таблице из ка> ый объём жидкости при 4 чисел верхнее выражает перегретый пар °C и при давлении р = 1 ата принят равным установленную величину, а нижнее допуск (±).
Энтальпия (теплосодержание) воды и перегрето го водяного
Таблица 38
в ккал/кг
Давл. в кг /см3 Температура в °C
“ 1 50 100 | 150 | 200 250 300 350 | 400 | 450 | 500 j 550
1 0,023 49,97 639,2 663,2 686,5 710,1 734.0 758,0 782.4 807,2 832,3 857,8
0,005 0,03 0,5 0,5 0.6 0,6 1,2 1,2 1.2 1,2 1.2 2,0
5 0,120 50,05 100,11 150.92 681,9 706,7 731,5 756,1 780.8 805,9 831,3 856,9
0,005 0,03 0,05 0,08 1.0 1.0 1,2 1,2 1.2 1,2 1,2 2,0
10 0,240 50,15 100,20 151,00 675,1 702,1 728,0 753,5 778,9 804,5 830,1 855,9
0,005 0,03 0,05 0,08 1.0 1.1 1.2 1.2 1,2 1,2 1,2 2,0
25 0,599 50,45 100,46 151,21 687,8 718,0 746,3 773,3 800,0 826,5 852,6
0,005 0,03 0,05 0,08 0.1 1,1 1.2 1.2 1,2 1,2 1.2 2,0
50 1,20 50,96 100,90 151,58 203,8 698.4 732,9 763,1 791,6 819.9 347,3
0,01 0,03 0,03 0,08 0,1 0.1 1.2 1,2 1.2 1,2 1.2 2,0
75 1,79 51,46 101,34 151,95 204,1 259,2 672,6 717,6 752.1 783,2 813,1 841,8
0,01 0,03 0,05 0,08 0,1 0,1 1,2 1.2 1.2 1,2 1.2 2, ’
100 2,39 51,96 101,78 152,32 204,3 259,2 д_' >, ;> 699,5 740.0 774,5 8oG,G з 3'3,1
0,01 0,03 0,05 0,08 0,1 0,1 . Л 1.2 1 >3 ‘1,3 1.3 2,0
125 2,98 52,46 102,22 152,69 204,6 259,3 319,;* 676,7 726.9 765,2 799,1 83с ,3
0,01 0,03 0,05 0,08 0,1 0.1 0,3 1,2 1.3 1,3 1.3 °
150 3,57 52,93 102,65 153,06 204 8 259,3 319,3 646,8 712.1 755,3 791,8 82-5, 1
0,01 0,03 0,05 0,08 0,1 0,1 |',3 1,5 1.3 1,3 1.3 •
200 4,74 53,96 103,57 153,82 205,2 259,4 313,4 оуЗ , 1 676.5 733, 1 776,0 812.ll
0,01 0,03 0,05 0,08 0,1 0,1 0,3 и,8 2.0 2,и 2.0 2 5
250 5,90 54,96 104,46 154,57 205,8 259,5 317,6 387,6 622,5 707,5 758,8 798,9
0,01 0,03 0,05 0,08 0,2 0,2 0,3 0,8 2,5 2,5 2,5 3,0
300 7,05 55,96 105,35 155,33 206,2 259.7 317,0 384,0 524.5 677,5 739,7
0,01 0,03 0,05 0.08 0,3 0,3 0,3 0,8 3.0 2,5 2.5
Перегретый пар
под давлением^. .. ж______ж.
чание. Из каждых двух чисел верхнее выражает установленную величину, а нижнее
Вода
Приме
допуск (±).
ВОДЯНОЙ ПАР
Сухой насыщенный пар (по температурам) [7]
Таблица 39
t' Т' р т' 4 т* i' i" г S' S*
0 273,16 0,006228 0,0010002 206,3 0,004846 0 597,2 597,2 0 2,1863 2,1736 2 1613
2 275,16 0,007193 0,0010001 180,0 0,005557 2,01 598,0 596.0 0,0073
4 277,16 0,008289 0,0010000 157,3 0,006358 4,02 599,0 595,0 0,0146
в 279,16 0,009530 0,0010001 137,8 0,00725? 6,03 599,8 593,8 0,0218 2 * 14KQ
8 281,16 0,010932 0,0010002 121,0 0,008267 8,04 600,7 592,7 0.0290 2’1370 2 1953
10 283.16 0,012513 0.0010004 106,4 0,009396 10,04 601,6 591,6 0,0361
12 285.16 0.014291 0,0010006 93,85 0,01066 12,04 602,5 590,5 0,0431 2*1138 9 1П9А
14 287.16 0,016289 0,0010008 82,91 0,01206 14,04 603,4 589,4 0,0501
16 289,16 0,018527 D.0U10012 73,39 0,01363 16,04 604,3 588,3 0,0571 9*0915
18 291,16 0,02103 0,0010015 65,10 0,01536 18,04 605,1 587,1 О’0639 2'0804
20 293,16 0,02383 0,0010018 57,84 0,01729 20,03 606,0 586,0 0,0708 2'0697
22 295,16 0,02694 0,0010023 51,49 0,01942 22,03 606,9 584,9 0,0776 2,0592 2,0488 2.0386
24 297,16 0,03041 0,0010028 45,94 0,02177 24,02 607,8 583,8 0,0843
26 299,16 0,03426 0.0UU033 41,04 0,02437 26,01 608,6 582,6 0,0910
28 301,16 0,03853 0,0010039 36,73 0,02723 28,01 609.5 581,5 0,0976 2,0286 2.0187
30 303,16 0,04325 0,0010044 32,93 0,03036 30,00 610,4 580,4 0,1042
32 305,16 0,04847 0,0010051 29,58 0.03380 32,00 611.3 579.3 0.1108 2.0091
34 307,16 0.^5423 0,0010058 26,61 0,03758 33,99 612,1 578,1 0.1173 1 9994
36 309,16 0,06057 0,0010065 23,97 0,04171 35,99 613,0 577,0 0,1238 1,9901
38 311,16 0,06755 0,0010072 21,63 0,04622 37,98 613,9 575,9 0,1302 1,9810
40 313,16 0,07520 0,0010079 19,55 0,05114 39,98 614,7 574,7 9,1366 1,9718
42 315,16 0,08360 0,0010087 17,70 0,05650 41,97 615,6 573,6 0,1429 1.9699
44 317,16 0,09279 0,0010095 16,04 0,06233 43,97 616,4 572,4 0Д493 1,9541
46 319,16 0,19284 0,0010103 14,56 0,06867 45,96 617,2 571,2 0,1555 1 9455
48 321,16 0,11382 0,001011'2 13,24 0,07553 47,95 618,1 570,1 0,1617 1'9371
50 323,16 0,12578 0,0010121 12,05 0,08298 49,95 619.0 569,0 0,1679 1,9287
55 328,16 0,16051 0,0010145 9,584 0,1043 54,94 621.0 566,1 0,1833 1,9о8 \
60 333,16 0,2031 0,0010171 7,682 0,1302 59,94 623,2 563,3 0'1а84 1,8891
65 338,16 0,2550 0,0010199 6,206 0,1611 64,93 625,2 560,3 0,2133 1.8702
70 343,16 0,3177 0,0010228 5,049 0,1981 69,93 627,3 557,4 0,2280 1,8522
75 348,16 0,3931 0,0010258 4,136 0,2418 74,94 629,3 554.4 0,2425 1,8349
80 353,16 0,4829 0,0010290 3.410 0,2933 79,95 631.3 551,3 0,2567 1,8178
85 358,16 0,5894 0,0010323 2,830 0,3534 84,96 633.2 548.2 0,2708 1 8015
90 363,16 0,7149 0,0010359 2,361 0,4235 89,98 635,1 545,1 0,2848 1,7858
95 368,16 0,8619 0,0010396 1,981 0,5045 95,01 637,0 542,0 и, 2985 1,7708
100 373,16 1,0332 0,0010435 1,673 0,5977 100,04 638.9 538,9 0,3121 1,7561
105 378,16 1,2318 0,0010474 1,419 0,7045 105,08 640.7 535,6 0,3255 1,7419
по 383,16 1,4609 0,0010515 1,210 0,8265 110,12 642,5 532,4 0,3387 1,7282
115 388,16 1,7239 0,0010558 1,036 0,9650 115,18 644,3 529,1 0,3519 1,7150
120 393,16 2,0245 0,0510603 0,8914 1,122 120,3 646.0 525,7 0,3647 1,7с18
125 398,16 2,3666 0,0010650 0,7701 1,299 125,3 647,7 522,4 0,3775 1,6895
130 403,16 2,7544 0,0010697 0,6680 1.496 130,4 649,4 518,9 0,3901 1,6772
135 408,16 3.192 0,0010746 0,5817 1,719 135,5 650,8 515,3 0,4026
140 413,16 3,685 0,0010798 0.5084 1,967 140,6 652,5 511,6 О,415и 1,6539
145 418,16 4,237 0,0010850 0,4459 2,243 145,8 654,0 508,2 0,4272 1,6428
150 423,16 4,854 0,0010906 0,3924 2,548 150,9 655,5 504,6 U, 4395 1,6320
155 428,16 5,540 0,0010963 0,3464 2,88; 156,1 656,9 500,8 0,4516 1,6214
160 433,16 6.302 0,0011021 0,3068 3,260 161.3 658,3 497,0 0,4637 1,6112
165 438,16 7,146 0,0011082 0,2724 3,671 166,5 659.6 493,1 0,4756 1,6012
170 443,16 8,076 0,0011144 0,2426 4,122 171,7 660,9 489,2 0,4874
175 448,16 9,101 0,0011210 U,2166 4,617 176,9 662,1 485.2 0,4991 1,5813
180 453,16 10,225 0,0011275 0,1939 5,157 182,2 663.2 481,0 0,5107 1,5721
185 458,16 11,456 0,0011345 0,1739 5.749 187,5 664.3 476,8 0,5222 1,5629
190 463.16 12.800 0.0011415 0,1564 6.392 192.8 665,3 472,5 0,5336
195 468,16 14.265 0,0011490 0,1410 7,094 198,1 666,2 468,1 0,5449 1,5448
200 473,16 15,857 0,0011565 0,1273 7,857 203.5 667,0 463,5 0,5562 1 ,<535.8
210 483.16 19.456 0,0011726 0,1043 9,535 214.3 668,3 454,0 0,5788 1,5184
220 493,16 23,659 0,0011900 О.О8Ы4 11.61 225,3 669,2 443,9 0,6010 1,5012
230 503,16 28,531 0,0012088 0,07153 13,98 236.4 669,7 433,3 0,6229 1,4811-
240 513,16 34,140 0,0017291 O.U597O 16,75 247.7 669,6 421,9 0,6448 1,4669
250 523,16 40.56 0,0012512 0,050(16 19,98 259,2 669,0 409.8 0,6667 1,4499
260 533,16 47,87 0,0012755 0,04213 23,74 271.0 667,8 396,8 0,6886 1,4327
270 543,16 56.14 0,0013023 0,03,.>57 28,11 283,0 (565.9 382,9 0,7103 1,4153
280 553,16 65,46 ОЛЮ 13321 0,03010 33.22 295.3 863,5 368,2 0,7321 1,397-<
290 563.16 75.92 0,0013655 0,02532 39,18 308,0 660,2 352.2 0,7542 1,3797
300 573.16 87.61 0,(!и1 ЮЗо 0,02161 46,24 321,0 656,1 335,1 0,7767
310 583,16 100,64 0,001448 0,01380 :>4,64 334,6 650.8 0,7994 1,3115
320 593,16 115,13 0,001499 0,01544 64,79 349. U 644,2 295,2 0,8229 1,3206
330 603,16 131,18 0,001562 0,01295 77,20 364,2 636,0 271,8 0,8476 1.2982
340 613,16 148,96 0,001641 0,01076 92.90 380,7 625,6 244,9 0,8734 1,2728
350 623,16 168,63 0,001747 0,008803 113.6 398,9 611,9 213,0 0,9915 1.2431
355 628,16 179,24 0,001814 0,00787 127.0 409,5 193,7 0,9173 1,2263
360 633,16 190,42 0,601907 0,006963 143,6 420.9 592,8 171,9 0,9353 1,2072
365 638,16 202,21 0.00203 0,00606 165,0 431,2 579,8 145,4 0 Л-553 1,1833
370 643,16 214,68 0,00223 0,00500 200 452,3 559,3 107,0 0,9842 1,1506
374 647,16 225,2 0,00279 0.ОС355 274 488 523 ОО 1.04 1,09
Параметры критического состояния
374.2 -С
22.»,5 кг[см*
0,00307 м3 [кг
Температура..........♦ » ....... . .
Давление . , ........................
Объем .............
554
ТЕПЛОТА
I а б л и и а 40
Сухой насыщенный пар (по даслениям) |7|
• —
р Г V* с" 7' Г г' г
0,010 6,698 0.0010001 131,7 „ 0,0075,15 с,73 600,1 593 4 0 0243 2 1447
0,015 12,737 0,9010007 89,64 6,01116 12,78 602.8 59ь’о 0 0457 2'1096
0,020 17,204 0,0010013 68,27 0,01455 17.24 604,8 587'6 0 0619 2’о817
0,023 20,776 0.001062U 55,28 0,01809 20,80 606,4 53516 0 0735 2*0655
0,030 23,772 0,0010027 46,53 0.02149 23,79 607.7 583’о 0 0836 2 0499
0,035 26,359 0,0019034 40,23 0,02486 26,37 6U8.8 582*4 0'0923 2.0366
0,040 28,641 0,0010041 35,46 0,02820 28,65 609.8 581 *1 0 0O9S 2’ 253
и, и4й 30,69 и,0010047 31,73 0,03152 30,69 610.7 580'о 1)’1065 2,0153
0,050 (52,b<j 0,00100.53 28,73 0,03481 32,55 611,5 578 ’ 9 0 1126 2,0064
0,000 35,82 0,0010064 24.19 0,04131 3.5,81 612,9 577*1 0 1232 1 9908
0,070 38,66 0,0010071 20.92 0,04780 38,64 614,1 575'5 0 1324 1 :?779
0,080 41,16 0,0013084 IS,4л 0,05421 41,14 574 1 0 14J2 1.966'
0,090 43,41 0,0011093 16.51 0,66; '5л 43.38 616,2 0,1474 1 9554
0,10 4b,4о 0,0016101 14,95 0,06088 45,41 617,0 571 6 0 1538 i,4478
0,12 49, ьб 0,0010116 12,6л 0,07931 49.01 618,5 569 5 0,1650 1,9326
0.14 Ь2,18 0.0010130 10,89 Од-9171 52.13 619.9 567*8 0,1747 1 9197
0,10 54,94 0,0016144 9,612 0.Ю40 54,08 621,1 566’2 0 1831 1, Ч()81
0,18 о /, L\. 1 0,0010157 8,6(5 0,1162 57.36 622,1 564*7 1 8993
0,20 а9,67 0,0010178 7,79.5 0,1283 59.61 623.1 563 ’ 5 0 1974 1,8903
0,22 61,74 0,0010181 7,123 0,14;.3 61,67 623.9 562'2 0,2036 1.8826
0,24 63,60 0,9010191 6,568 0,1523 63,53 624,1 561 1 0,2093 1,8753
0,26 65,44 0.0010201 6,694 0.1641 65,37 625,4 0,2146 1’8685
0,23 67,11 0,0.40211 5.684 0,1759 67,04 626,1 559' i 0 2195 1,8624
0,30 68,68 0,0ilO22i 5,328 0,1877 68,61 626,8 558 0,2241 1 8567
0,40 75,42 0,0010201 4,069 0.2458 75.36 629,5 554 ’ 1 0 2437 1.8331
0,50 80,86 0,0иЮ29б 3,301 0,3929 80,81 631,6 О’2592 1 815-
0,60 85,45 0,0010326 2.783 0,3531 35,41 633,4 548'о 0’2721 1,8001
0,70 80,45 u.OOli 3)5 2,41)9 0.4152 89.43 634,9 545’5 0,2832 1.7874
0,80 92,69 0,0619381 2,125 0,470.) 92,99 636,2 543*2 0,2930 1,7767
0,90 96,18 0,0010405 1,964 0.5253 96,10 637.4 541'2 0 ЗОЮ 1,7673
1,0 99,09 0,0()1а423 1,725 0,5797 99,12 638,5 539 4 0’3096 1.7587
1,5 110,79 0,0019521 1.180 0,8472 По,92 642,8 53 Г 9 0,34.8 1, 726 ,
2,0 119,62 0.001U599 0,9016 1,10г. 119,87 645,8 525,9 0.3638 1 7029
2,5 126,79 0,0019666 0,7316 1,367 127,2 648.3 521 ! 0,3820 1,6851
3,0 132,88 0,0010/25 0,6166 1.632 133,4 650,3 516 9 0,3973 Гб703
3.5 138,19 0,0010780 0,5335 1.371 138,8 651.9 513 1 0,4106 1 ’(1579
4,0 142,92 0.0U1U828 0,47и6 2,125 143,6 653,4 509'8 0,4221 1 6-174
4,5 147.20 0,0010875 0,4213 2,374 148,0 654,7 506 7 0,4326 1,6380
5,0 151,11 0,0010918 0,3816 2,621 152,1 6.55,8 503 7 0,4422 1,6297
6,0 158,08 0,0010999 0,3213 3,112 159,3 657,8 498 5 0,4591 1,6151
7,0 164,17 0,0011072 0,2778 З.боо 165,6 659,4 493,8 0,4737 1.6029
8,0 169,61 0,0011140 0,2448 4.035 171,3 660,8 489 5 0,4865 1,5922
9,0 174,53 0,0011203 0,2189 4,568 176,4 662,0 0,4980 1.5827
10,0 1 / У, (_К 0,0011262 0,1981 5,049 181,2 663,0 481,8 О'5085 1,5749
12,5 188,92 0,0011399 0,1600 6,249 191,6 665,1 473,5 0,5311 1,5559
15,0 19/,36 0,0011.524 0.1343 7.446 200,6 666,6 466 0 0,5503 1,5406
17,5 204,76 О.О011641 0,1157 8.645 208.6 667,7 459,1 0,5570 1,5275
20,0 211,33 0,0011/Ь1 0.1016 9,346 215.8 668,5 452 7 0,5820 1,5160
22,5 217,39 0,0011354 0,09049 11,05 222,4 069.0 446.6 0,5953 1,505'J
25,0 222,90 0,0011952 0,08157 12,26 228,5 669,4 410 9 0,6074 1 -;062
27,5 228,00 0,0012149 0,07420 13,43 234,1 669,6 435'5 0,6185 11874
50 232,76 0,0012142 0,06802 14,79 239.5 669,7 430,2 0,6290 1,4793
35 241,42 0,0012320 0,05822 17,18 249,4 669.5 420Д 0,6479 1.4645
40 249,13 0,0012493 0,05078 19,69 258,2 669,0 410.8 0.6649 1.4513
45 256,23 0,0012651 0,04495 22,25 266,5 668,2 401,7 0,(803 1,4392
50 262,70 0,0012828 0,64021 24,85 274,2 667,3 393,1 0,6914 1.4280
55 268,69 0,0012989 0.03636 27,50 281,4 666,2 384,8 0,7075 1,4176
60 274,29 0,0013150 0,03311) 30.21 288,4 665,0 376,6 0,7196 1,4078
65 279,54 ь,00133о7 0,03033 32,97 294.8 663,6 368,8 0,7311 1,3986
70 284,48 0,0013467 0.02795 35,78 300,9 662,1 361.2 0,7420 1,389/
75 289,17 0,0013625 0,02587 38,66 307,0 660,5 353,5 0,7524 1,3813
80 293,62 0,0013786 0,02401 41.69 312,6 658.9 346.3 0,7623 1,3731
- S5 297,86 0,0013951 0.02241 44.62 318.2 657,0 338,8 0,7718 1.3654
90 331,92 0,001412 0.02096 47,71 323,6 655,1 331,5 0.7810 1.357/»
95 305,80 0,001428 0,01961 50,91 328.8 653,2 324,4 0,7893 1.351/1
100 309,53 0,001445 0,0184.5 54.21 334,0 651,1 317.1 0,7983 1,3421
ПО 316,58 о,001480 0,01637 61.08 344,0 646,7 302,7 U,8147 1.3279
120 323,15 0,001518 0,01462 68,42 353.9 641,9 288,0 0,8306 1,3133
130 329,30 0,001558 0,01312 7'6,23 363,0 636,6 273.6 0,8458 1.299*
140 3,35,09 0,001599 0,01181 84,68 372,4 631,0 258,6 0,8606 1,2 758
150 340,56 0.001646 0,01065 93,90 381,7 624,9 243,2 0,8749 1,2713
160 345,74 0,001699 0,00961ч 104,0 390,8 618,3 227,5 0,8892 1,2561
170 350,66 0,001756 0,0л8630 115.2 400,3 610,8 210,5 0,9035 1,2411
180 355,35 0,001821 0,007809 128,0 410,2 602,5 192,3 0,9186 1,2251
ISO 359.82 0,001902 0,006994 143,4 420,4 593,2 172,8 0,9347 1,2081
200 364,08 0,00201 0,00620 161,2 431,5 582,3 150,8 0,9514 1.1883
210 368,16 0,00214 0,00539 185.7 444.7 568.1 123,4 0,9714 1,1636
220 372,1 0,00239 0,00419 223 463.4 547 84 1,002 1,131
222 372,8 0,00248 0,00425 235 469 541 72 1,009 1.100
224 373,6 0.00261 0,00391 254 478 532 54 1,022 1,10
ВОДЯНОЙ ПАР
Вода и перегретый пар [1]
Таблица 41
— 0 01 ama 0,03 ama 0 ,05 ama 0, 10 ama
t' = =6,698 =2.3,772 V = 32,55 i =45,45
1 V* = 131,7 = ’6,53 v" =28,73 V ’ = 14,95
i" -600,1 i” =607,7 i" =011,5 Z '=617,0
s" = 2,1147 s" =2,0499 s" = 2,0064 s ' = 1,9478
V ' 1 s У ' 1 s » ; i | s У i ' 1 s
0 0,0010002 0,0 0,0000 и,0010002 0,0 0,0000 0,0010002 0,0 0,0009 0,0010002 0.0 0,0000
10 133,2 602,2 2,1507 0,0010003 10,0 0,0361 0,0010003 10,0 0,0361 0,0010003 10,0 0,0361
20 137,9 606,7 2,1662 1 0,0010018 20,0 0,0708 0,0010018 20,0 0,0708 0,0010018 20,0 0,0708
30 142,6 611,2 2,1812 47.50 611,0 2,0595 0,0010041 30.0 0,1042 0,0010044 30,0 0,1042
40 147,3 615 7 2,1957 49,08 615,5 2,0741 29,42 615,4 2,0175 0,0010075 40,0 0,1365
50 152,0 620 1 2,2093 50,65 620,0 2,0832 30,36 619,9 2,0316 15,16 619,6 1,9546
60 156,8 62Л 6 2,2235 52,22 624,5 2,1019 31,31 621, ; 2,0453 15,64 624,1 1,9685
70 161,5 629,1 2,2368 53,79 629,0 2,1152 32,25 629,0 2,0587 16.11 628,7 1,9818
80 166,2 633,6 2,2497 55,36 633,6 2,1281 33,19 633,5 2,0716 16,58 633,3 1,9948
90 170,9 638,1 2,2622 56,93 638,1 2,1407 34,14 633,0 2,0342 17,06 637.8 2,0075
100 175,6 642,6 2,2744 58,51 642,6 2,1529 35,08 642,5 2,0964 17,53 642,3 2,0198
110 180,3 647 1 2,2863 60,07 647,1 2,1648 36,02 647,0 2,1084 18,00 646,8 2,0317
120 185,0 '*51,6 2,2979 61,64 651,6 2,1765 36,96 651,5 2,1209 18,47 651,3 2,0434
130 189,7 656,2 2,3092 63,21 655,1 2,1879 37,91 656,1 2,1314 13,94 655,9 2,0548
140 194,4 660,7 2.3203 Cl,7-5 6 .'.i,7 2,1990 38.83 660,6 2,1425 19,42 660,4 2.0S59
199,1 665,2 2,3312 66,35 665,2 2,2099 39,79 665,2 2,1534 19,39 6G5,'j 2,0768
1С.0 203,8 669,8 2,3418 67,92 669,8 2,2205 40,73 669,8 2,1641 20,36 669,5 2,0875
208,5 674,4 2,3522 69,49 674,4 2,2309 41,68 674,3 2,1745 20,83 674,1 2,0979
213,2 678,9 2,3624 71,06 678,9 2,2411 42,62 678,9 2,1847 21,30 678,7 2,1081
190 218,0 633,5 2,3724 72,63 683,5 2,2511 43,56 683,4 2,1947 21,77 683,3 2,1181
200 222,} 688,1 2,3822 74,20 683,1 2,2609 44,50 688,1 2,2045 22,24 687,9 2,1279
210 227,4 692,7 2,3918 75,77 692,7 2,2706 45,44 692,7 2,2141 22,72 692,5 2,1375
22!} 232,1 697.3 2,4013 77,34 697.3 2,2800 46,39 697,3 2,2236 23,19 697,1 2,1470
203 235,8 701.9 2,4106 78,91 701,9 2,2893 47,33 701.9 2,2329 23,66 701,7 2,1563
240 241.5 705,6 2,4197 80.43 706,6 2,2984 48,27 706,5 2,2420 24,13 706.4 2,1655
250 246,2 711,2 2,4286 82,05 711,2 2.3071 49,21 711,2 2,2510 24,60 711,1 2,1745
2 G9 250,9 715.9 2,4375 83,62 715,9 2,3163 50,15 715,9 2,2599 25,07 715,7 2,1833
279 255,6 720.6 2,4462 85,19 720,6 2,3250 51,09 720,6 2,2686 25,54 720,4 2,1920
21'0 260,3 725,3 2,4547 86,76 725,3 2,3335 52,04 725,3 2,2771 26,02 725,1 2,2006
200 255 Л 729,9 2,4632 88,33 729,9 2,341..) 52,93 729,9 2,2856 26,49 729,8 2,2091
300 209,7 734,5 2,4715 39,90 734,6 2,3502 53,92 734,6 2,2939 26,96 734,5 2,2174
31 и 274,4 739,3 2,4797 91,46 739,3 2,358-1 54,86 739,3 2,3021 27,43 739.2 2,2256
320 279,1 744,1 2,4878 93,03 744,1 2,3605 55,80 744,1 2,3102 -7,90 743,9 2,2337
330 283,8 748,9 2,4957 94,60 748,9 2,3745 56,74 748,9 2,3181 28,37 743.7 2,2417
040 288,6 753,7 2,5036 06,17 753.0 2,3821 57, G) 753,0 2,3260 28,84 653.5 2,2496
359 293,3 753,5 2,5113 07,7-1 758, о 2,3901 58,63 753,4 2,3338 29.31 753,3 2,2574
.-.so 298,0 763,3 2,5190 19,31 763,3 2,3977 59,57 763,3 2,3415 29,78 763,1 2,2650
370 Зи2,7 768,1 2.5266 100,9 763,1 2,4031 60,51 768,1 2,3491 36,25 763,0 2,2726
3S0 307,4 7/3,0 2,5311 102,5 773,0 2,4100 61,46 773,0 2,3566 30,72 772,8 2,2801
320 312,1 777,9 2,5415 104,0 7/7,8 2,4203 62,40 777,8 2,364!; 31,19 777,7 2,2376
480 316,8 782,8 2,5483 105,6 782,7 2,4276 63,33 782,7 2,3713 31,67 782,6 2,2949
410 321,5 787.7 2,5569 107,2 787,7 2,43-19 64,27 787,7 2,3786 32,14 787,5 2,3021
420 326,2 792,6 2,5632 118,7 792,6 2,4421 65,21 792,6 2,3658 32,61 792,5 2,3093
430 330,9 797,6 2,5703 110,3 797,6 2,449j 66,15 79/,6 2,3929 33,08 797,4 2,3164
а а 335,6 802,6 2,5773 111.9 802,6 2,4562 67,09 802,6 2,4000 33,55 802,4 2,3235
:50 340,3 807,6 2,5843 113,4 807,6 2,4633 68,03 807,6 2,4070 34,02 807,4 2,3305
430 345,0 812,6 2,5912 115,0 812,6 2.4702 68,93 812,6 2,4139 34,49 812,4 2,3375
470 349,7 817,6 2,5981 116,6 817,6 2,4770 69,92 817,6 2,4207 34.96 817,5 2,3143
480 354,4 322,7 2,604y 118,1 822,7 2,4838 70,86 822,7 2,4275 35,43 822,6 2,3511
490 359,1 827,8 2,6116 119,7 827,8 2,49® 71,80 827,8 2.4342 35,90 827,7 2,3573
500 363,8 832,9 2,6182 121,3 832,9 2,4972 72,74 832,9 2,4409 36,38 832,8 2,3645
510 368,5 838,0 2,6248 122,8 838,0 2,5038 73,68 838,0 2,4475 36,85 837,9 2,3711
520 373,2 843,2 2,6314 124,4 843,2 2,5103 74,62 843,2 2,4540 37,32 343,1 2,3776
530 377,9 848,4 2,6379 126,0 848,4 2.5163 75,56 848,4 2,4605 37,79 848,3 2,3841
540 382,6 853,6 2,6444 127,6 853,6 2,5233 76,51 853,6 2,4670 38,26 853,5 2,3906
550 387,3 858,8 2,6503 129,1 858,8 2.5297 77.45 858.8 2,4731 38,73 858,7 2,3970
556
ТЕПЛОТА
Продолжение табл. 41
0,20 ата 0 , 40 ата 0,5 0 ата 1,0 ата
Г =•59.67 Г = 75,42 Г =80.86 t = 99,09
t v" -7,795 V* -4,069 V* =3,301 V '' = 1,725
г" —623,1 Г =629,5 i" =631,6 =638,5
е = 1,89оЗ S* = 1,8334 s" = 1,8150 s ' = 1,7587
S и 1 i 1 s V 1 i i s V 1 1 1
0 0.0010002 0,0 и,0000 0.0010002 0,0 0,000b 0,001и002 0,0 0,0000 0,0010002 0,0 о.оооо
10 0,0010003 10,0 0,0361 0,0010003 10.0 0.0361 0,0010003 10,0 0,0361 0,0ol00u3 10,1 0,0361
20 0,0010018 20,0 0,0708 0,0010018 20,0 0,0708 0,0010018 20,0 0,0708 0,0010018 20,1 0,0708
30 0,0010044 30,0 0,1042 0,0010044 30,0 и,1042 0.0010044 30,0 и,1042 U.0010044 30,0 0,1042
40 0.0010079 40,0 0,1365 0,0010079 40.0 и,1365 0,0010079 40,0 0,1365 0,0010079 40,0 0,1365
50 0.0010121 50,0 0,1679 0,0010121 50.0 0,1680 0,0010121 50,0 U.1680 0,0010121 50,0 0.1680
60 7.797 623,7 1,8908 0,0010171 59,9 0.1984 0,0010171 59,9 и,1984 0,0010170 60.0 0,1984
70 8,038 628,4 1,9046 0,0010228 69,9 0,2280 0,0010228 69,9 0,2280 4,0010227 69,9 0,228u
80 8,277 (>33,0 1,9178 4,123 632,0 1,8398 0,0010290 80,0 0,2567 0.0010289 80,0 0,2567
90 8,515 637,6 1,9306 4,245 636,8 1,8532 3,390 636,4 1,8278 0,0010359 90,0 и,2848
100 8,752 642,1 1,9429 4.365 641,5 1,8658 3,487 641,2 1,8407 1.730 639,1 1,7599
по 8,989 646,7 1,9549 4,485 (46,0 1,878.) 3,583 645,ь 1,8530 1.781 6'44,2 1.773b
120 9,226 651,2 1,9667 4,604 650,6 1,8898 3,679 65u, 5 1,8648 1,830 649,1 1,7861
130 9,463 655,7 1,9781 4.723 655,2 1.9013 3,775 655,0 1,8764 1,878 653,9 1,7979
140 9.699 660,3 1.9892 4,842 659,8 1,9125 3,870 659,6 1,8876 1,926 658.6 1,8093
150 9,935 664,9 2.0001 4,961 664,4 1,9235 3,95-5 664,3 1,8986 1,975 603,2 1,8204
160 10,17 669,4 2,0108 5,079 669,0 1,9342 4,069 668,8 1,9094 2,023 667,8 1,8312
170 10,40 674,0 2,0213 5,198 673,6 1,9447 4,155 673,4 1,9199 2,071 672,4 1.8418
180 10,64 678,6 2,0315 5.317 678,2 1,9550 4.250 678,0 1,9302 2,119 677,1 1.8522
190 10,88 683,2 2,0415 5.435 682,8 1.9650 4,345 682,6 1,9402 2,166 681,8 1.8624
200 11,11 687.8 2,0513 5,553 687,4 1,9748 4,440 687.3 1,9501 2,214 686,5 1,8724
210 11,35 692,4 2,0610 5,672 692.0 1,9845 4,535 691,9 1,9598 2.262 691,2 1,8822
220 11.58 697,0 2,0705 5,790 696,6 1,9940 4,629 696,5 1,9693 2,310 695,9 1,8918
230 11,82 701,7 2,0798 5,908 701,3 2,0иЗЗ 4,724 701,2 1,9786 2,357 700,7 1,9013
240 12,06 706,3 2,0890 6,026 705,9 2,0125 4,819 705,9 1,9878 2,405 705,4 1,9106
250 12.29 711,0 2,0980 6,145 710,6 2,0215 4,913 710,5 1,9968 2,452 710,2 1,9197
260 12,53 715,7 2,1068 6,263 715.3 2,0304 5,005 715,2 2,0057 2.500 714,9 1.9287
270 12,76 720,3 2,1155 6,382 720,0 2,0391 5,1=2 719,9 2,014-1 2,547 719,6 1,.376
280 13,00 725,0 2.1241 6,500 724.7 2.0477 5.197 724,6 2,0230 2,595 724.3 1.9а61
230 13,24 729,8 2,1326 6,618 729.4 2,0562 5,292 729.4 2,0315 2,642 729,1 1,955с
300 13,47 734,5 2,1410 6,736 734,2 2,0645 5,38/ 734,1 2,0398 2,690 733,8 1,9635
310 13,71 739,1 2,1492 6,854 739,0 2,0727 5.482 739, и 2,0480 2,737 738,6 1,971»
320 13.94 743.9 2,1573 6.971 743,8 2,0808 5,577 /43,7 2,0561 2,784 743,4 1,98.к>
330 14,17 748,7 2,1653 7,089 748,6 2,0888 5,672 748,5 2,0641 2,832 7-18.2 1,9881
310 14,40 753,5 2,1731 7,20/ 753,4 2,0967 5,767 753,3 2,0720 2,880 753,0 1,9961
350 14,64 758,3 2,1809 7,323 758,2 2,1и45 5,861 758,1 2,0793 2,927 757,8 2,0039
360 14,87 763,1 2,1886 7.413 703,0 2,1122 5,955 763,0 2.0375 2,975 762.6 2,0110
370 15,11 767,9 2,1962 7,501 767,9 2,1198 6,050 /67.8 2,0951 3,022 76/ ,3 2, .392
380 15,34 772,8 2,2037 7,679 772,'7 2,1273 6,144 772,7 2,1026 3,068 772,4 2,0263
390 15,58 777,7 2,2111 7,798 777.6 2,1347 6,239 777,6 2,1100 3,115 777,3 2,03/3
400 15,82 782,6 2,2185 7,916 782,5 2,1421 6,333 782,5 2,1173 3.163 782,3 2,0417
410 16,05 787,5 2,2257 8,033 787,4 2,1493 6,427 787,4 2,1246 3,210 787,2 2,049-
420 16,29 792,4 2,2329 8.151 792,4 2,1565 6,521 792,3 2,1318 3,25/ 792,2 2,0562
430 16,52 797,4 2,2400 8,269 797,3 2,1636 6,61 797.3 2,1389 3,3oj 797,1 2,0633
440 16,76 802,4 2,2470 8,387 802.3 2,170/ 6,710 802.3 2,1460 3,352 302,1 2,0703
450 16 99 807,4 2,2541 8,505 807,3 2,1778 6,804 807,3 2,1530 3.399 807,1 2.0773
460 17 23 812,4 2,2610 8,623 812,4 2,1847 6,898 812,3 2,1599 3.446 812,2 2,0819
470 17,46 817.5 2,2679 8,74'3 817,4 2,1915 6.992 817,4 2,1668 3.493 817.2 2,0910
480 17,70 822,5 2,2747 8.858 822,5 2,1983 7,087 822,5 2,1736 3,54.1 822,3 2,0977
490 17,93 827,6 2/’814 8,976 827,6 2,205и 7,181 827,6 2,1803 3,587 827,4 2.1044
500 18,17 832 7 2,2880 9,093 832,7 2,2117 7,275 832.7 2,1870 3,635 832,5 2.1110
510 18 41 837 9 2,2946 9,211 *37.8 2,2183 7,370 837,8 2,1936 3,682 837.7 2.1175
520 18,64 843,1 2 3012 9,329 843,0 2,2249 7,464 843.5 2,2001 3,72у 842.8 2,1240
530 18.83 848 3 2.3077 9,447 848,2 2.2314 7.558 848,2 2,2066 3,777 848,0 2,1304
540 19,11 853,5 2,3142 9,564 853,4 2,2378 7,652 853,4 2,2131 3,824 853,2 2,1368
550 19 34 858 7 2,3206 9.682 858,7 2.2412 7.746 858,7 2,2195 3,871 858,3 2,1431
ВОДЯНОЙ П4Р
557
Продолжение табл. 41
2,С ama 4, ) ama 6,0 ama 8,0 ama
Л =119,62 t = 142,92 t «= 158,08 t -169,61
t =0.9016 v" =0.4706 v*— 0,3213 V' —0,2448
i '« =645,8 «653.4 i*= 657,8 i" -660,8
s"«« 1,7029 1,6474 s' = 1.6151 s" = 1.5922
V 1 < 1 5 V 1 i 1 S г I i I S r | i | s
0 0,0010001 0,0 0,0000 0,0010000 0,1 0,0000 0,0009999 0,1 0,0000 0,00009998 0,2 0,0000
10 0,0010003 10,1 0,0361 0,0010002 10,1 0,0361 0,0010001 10,2 0,0361 0,0010000 10,2 0,0361
20 0,0010018 20,1 0,0708 0,0010017 20-l 0,0708 0,0010016 20,2 0,0708 0,0010015 20,2 0,0708
.30 0,0010043 30,0 0,1042 0,0010042 30.1 0,1042 0,0010041 30,1 0,1042 0,0010040 30,2 0,1041
40 0,0010078 40,0 0,1365 0,0010077 40-1 0,1365 0,0010077 40,1 0,1365 0,0010076 40,2 0,1365
50 0,0010120 50,0 0,1680 0,0010119 s°.° 0,1679 0,0010118 50,1 0,1679 0,0010118 50,1 0,1679
60 0,0010170 60,0 0,1984 0,0010169 60>° 0,1983 0,0010168 60,1 0,1983 0,0010167 60,1 0,1983
70 0,0010227 70,0 0,2280 0,0010226 70,0 0,2279 0,0010225 70,1 o,2279 0,0010224 70,1 0,2278
80 0,0010289 80,0 0,2567 0.0010288 80-° 0,2566 0,0010287 80,1 0,2566 0,0010286 80,1 0,2566
90 0,0010358 90,0 0,2848 0,0010357 в°>° 0,2847 0,0010356 90,1 0,2847 0,0010355 90,1 0,2846
100 0,0010435 100,1 0,3121 0,0010433 100,1 0,3120 0,0010432 100,1 0,3120 0,0010431 100,2 0,3119
по 0.0010515 110,1 0.3387 0,0010514 0,3386 0,0010513 110,2 0,3386 0.U010512 110,2 0,3386
120 0,9027 646,1 1,7033 0,0010602 120.3 0,3646 O.OOlubOl 120,3 0,3646 j,ooiu6oe 120,3 0,3646
130 0,9291 651,6 1,7169 0,0010697 130,5 0,3901 0,0010696 130,5 0,3900 0.0010695 130,5 0,3900
140 0,9545 656,7 1,7294 0,0010798 140,7 0,4150 0.0010797 140,7 0,4150 0,u010795 140,7 0,4149
150 0,9795 661,6 1,7412 0,4806 657,7 1,6575 | 0,0010906 150,9 0,4395 G,0010904 151,0 0,4394
160 1,003 666,4 1,7525 0,4940 663,3 1,6704 0,3232 659,1 1,6178 I 0,1011020 161.3 0.4636
170 1,028 671,2 1,7634 0,5070 668,5 1,6823 0,3326 664,9 1,6316 0,2450 661,1 1,5926
180 1,052 675,9 1,7740 0,5197 873,5 1,6935 0,3416 670,4 1.6439 0,2524 667,2 1,6067
190 1,077 680,6 1,7843 0,5323 678,4 1,7042 0,3504 675,7 1,6553 U.2594 672,9 1,6191
200 1,101 685,3 1,7944 0,5448 683,2 1,7146 0,3591 680,8 1,6662 0,2662 678,4 1,6307
210 1,125 690,0 1,8043 0,5573 688,0 1,7247 0,3677 685,8 1,6768 0,2729 683,7 1,6417
220 1,149 694,8 1,8140 0,5697 692,8 1,7346 0.3763 690.8 1,6871 0,2795 688,9 1,6523
230 1,173 699,6 1,8235 0,5821 697,7 1,7444 0,3848 695,8 1,6971 0,2860 694,0 1,6626
240 1,197 704,4 1,8329 0,5944 702,5 1,7540 0,3932 700,8 1.7069 0.2925 699,1 1,6726
250 1,221 709,2 1,8422 Q.6067 707,4 1,7634 0,4016 705,8 1,7165 0,2990 704,2 1,6824
260 1,245 714,0 1,8513 0,6190 712,4 1,7727 0,401,9 710,7 1,7259 0,3054 709,3 1,6920
270 1,269 718,8 1,8602 0,6312 717,3 1,7818 0,4181 715,7 1,7351 0,3117 714,4 1,7014
280 1,293 623,6 1,8689 0,6433 722,2 1,7907 0,4264 720,7 1,7441 0,3180 719,4 1,7106
290 1,317 728,5 1,8775 0,6555 727,2 1.7994 0,4346 725,7 1,7529 0,3242 724,4 1,7196
300 1,341 733,4 1,8860 0,6676 732,1 1,8080 0,4428 730,7 1,7616 0,3305 729,4 1,7284
310 1,365 738,2 1,8944 0,6796 737,0 1.8165 0,4509 735,7 1.7702 0.3367 734,4 1,7370 .
320 1,390 743,0 1,9027 0,6917 741,9 1,8249 0,4591 740,7 1,7787 0,3429 739,4 1,7455
330 1,413 747,9 1,9109 0,7037 746,8 1.8331 0,4672 745,7 1,7870 0,3490 744,5 1,7539
340 1,437 752,8 1,9190 0,7158 751,8 1.8412 0,4753 750,7 1,7952 0,3552 749,6 1,7622
350 1,461 757,7 1,9269 0,7278 756.7 1,8492 0,4834 755,7 1,8033 0,3613 754,7 1,7704
360 1,485 762,6 1,9347 0,7398 761,6 1.8571 0,4915 760,7 1,8113 0,3674 759,8 1.7785
370 1,509 767,5 1,9424 0,7518 766,6 1,8649 0,4996 765,7 1.8191 0,3735 764,8 1,7864
380 1,532 772,4 1,9500 0,7637 771,5 1,8726 o,5077 770,7 1,8268 0,3796 769,8 1,7942
390 1,556 777,3 1,9575 0 7756 776,5 1,8802 0,5157 775,7 1,8344 0,3857 774,8 1,8019
400 1,579 782,2 1,9649 0,7875 781,4 1,8876 0,5237 780,7 1.8419 0,3918 779,9 1,8095
410 1,602 787.2 1,9722 0,7995 786,4 1,8949 0,5318 785,7 1,8493 0,3978 785,o 1.8169
420 1,626 792,1 1,9794 0,8114 791,4 1,9021 0,5398 790,7 1,8566 0,4039 790,1 1,8242
430 1,650 797,1 1,9865 0,8233 796,4 1,9093 0,5478 795,7 1,8638 0,4099 795,1 1,8315
440 1,673 802,1 1,9936 0,8352 801,5 1,9164 0,5558 800,8 1,8710 0 4159 800,1 1,8387
450 1,697 807,1 2,0006 0,8471 806,5 1,9234 0,5637 805,9 1.8781 0 4219 805,2 1,8458
460 1,721 812,1 2,0075 0,8590 811,6 1,9304 0,5717 811,0 1,8851 0,4280 810,3 1,8528
470 1,744 817,1 2,0143 0,8709 816,6 1,9373 0,5797 816,1 1,8920 0,4340 815,4 1,8597
480 1,768 822,2 2,0210 0,8828 821,7 1,9441 0,5876 821,2 1,8988 0,4400 820,5 1,8665
490 1,792 827,3 2,0277 0,8947 826,8 1,9508 0,5956 826,3 1,9055 0,4460 825,7 1,8732
500 1,815 832,4 2,0343 0,9066 831,9 1 9574 0,6036 831,4 1,9122 0,4519 йЗ.,,9 1,8799
510 1,839 837,5 2,0408 0,9185 836,9 1,9640 0,6115 836,5 1,9188 0,4579 836,0 1,8865
520 1,864 842,6 2,0473 0,9304 842,0 1,9705 0,6194 841,6 1,9253 0,4639 841,1 1,8931
530 1.888 847,7 2,0537 0,9423 847,2 1,9769 0,6273 846,7 1,9318 0,4699 846,2 1,8996
540 1,911 852,9 0.0601 0,9542 852,3 1,9833 0,6352 851,8 1,9383 0,4759 851,4 1,9061
550 1,935 858,1 2,0665 0,9660 857,6 1,9896 0,6431 857,0 1,9447 0,4819 856,6 1.9126 1
558
ТЕПЛОТА
Продолжени е табл. 41
10,0 ата 12,5 ата 15,0 ата 17,5 ата
t t V” i" S* = 179, Л «=0,1981 =663.0 = 1,5740 t V в iT и~ а ' - СТ 00 Сл СЛ 1—• оэ От о - сл »-* о со СО С № 7 V i S а и а а i Г"* о со Сл О >“* 4а. - W - я / = 204,76 ^=0,1157 i"=667,7 $' = 1,5275
V 1 < S V 1 4 S V 1 4 s V 1 4 J
0 0,0009997 0,2 0,0000 0,0009996 0,3 0,0000 0,0009994 0,4 0,0000 0,0009993 0,4 и.0000
10 0,0009999 10,3 0,0361 0,0009998 10,3 0,0361 0,0009997 10,4 0,0361 0,0009995 10,4 0,0361
20 0,0010014 20,3 0,0707 0,0010013 20,3 0,0707 0,0010012 20,4 0,0707 0,0010011 20,4 0,070'.
30 0,0010040 30,2 0,1041 0,0010038 30,3 0,1041 0,0010037 30,3 0,1041 0,0010036 30,4 0,1041
• 40 0,0010075 40,2 0,1364 0,0010074 40,2 0,1364 0,0010073 40,3 0,1364 0,0010071 40,3 0,1364
50 0,0010117 50,2 0,1678 0,0010115 50,2 0,1678 0,0010115 50,2 0,1678 0,0000113 50,3 0,1678
60 0,0010166 60,1 0,1982 0,0010165 60,2 0,1982 0,0010164 60,2 0,1982 0,0010163 60,3 0,1982
70 0,0010223 70,1 U,2278 0,0010222 79,2 0,2278 0,0010221 70,2 0,2277 0,0010220 70.3 0,2277
80 0,0010285 80,1 0,2565 6,0010284 80,2 0,2565 0,0010283 80,2 0,2564 0,0010282 80,3 0,2564
90 0,0010354 90,1 0.2846 0,0010353 90,2 0,2845 и,0010352 90,2 0,2845 0,0010350 90,3 0,2844
100 0.001043U 100,2 0,3119 и,0010429 100,2 U,3118 0,0010427 100,3 0,3118 0,0010426 К0,3 0,3117
110 0,0010511 110,3 0,3385 0,0010510 110,3 0,3385 0,0010508 110,4 0,3384 0,0010507 110,4 0,3383
120 0.0010599 120,4 0,3645 0,0010597 120,4 0,3645 0,0010596 120,5 0,3644 0,0010595 120,5 0,3644
130 0,0015694 130,6 0,3900 0,0010692 130,6 0,3899 0,0010691 130,6 0,3898 0.00106S9 130,7 0,3898
140 0,0010794 140,7 0,4149 0,0010793 140,8 0,4148 0,0010791 140,8 0,4148 0.0010790 140,9 0,4147
150 0,0010902 151,0 0,4394 0,0010901 151,0 0,4393 0,0010899 151,1 0,4392 0,0010898 151,1 0,4391
160 0.0011018 161,3 0,4635 0,0011016 161,3 0,4635 0,0011015 161,4 0,4634 0,0011013 161,4 0,4633
170 0,0011142 171,7 0,4873 0,0011140 171,7 0,4872 0,0011109 171,8 0,4871 0,0011137 171,8 0,4870
180 0,1987 663,6 1,5755 | 0,0011273182,2 0,5106 0,0011271 182,2 0,5105 0,0011269 182,3 0,5103
190 0,2046 669,8 1,5864 * 0,1604 665,5 1,5572 | 0,0011413 192,8 0,5335 0,0011411 192,8 0,5334
200 0,2103 675,6 1,6015 0,1654 672,0 1,5711 ’ 0,1352 668,2 1,5440 | 0,0011563 203,5 0,5561
210 0,2159 681,2 1.6139 0,1702 678,1 1,5836 0,1395 675,0 1,5581 0,1175 671,0 1,5348
220 0,2214 686,7 1,6241 0,1748 683,9 1,5953 0,1436 681,2 1,5705 0,1212 677,8 1,5485
230 0,2268 692,1 1,6349 0,1793 689,5 1,6064 0,1475 687,0 1,5822 0,1247 634,0 1,5609
240 0,2321 697,4 1,6454 0,1837 695,0 1,6171 0,1513 692,6 1,5934 0,1281 689,9 1,5725
250 0,2374 702,6 1,6556 0,1881 700,4 1,6275 0,1550 698,1 1,6041 0,1314 695,6 1,5835
260 0,2426 707,7 1,6654 0,1924 705,7 1,6376 0,1587 703,5 1,6144 0,1347 701,2 1,5942
270 0,2477 712,8 1,6749 0,1967 710,9 1,6474 0,1624 708,8 1,6244 U,1379 706,7 1,6045
280 0,2529 717,8 1,6841 0,2010 716,0 1,6569 0,1660 714,1 1,6342 0,1411 712,2 1,6145
290 0,2580 722,9 1,6931 0,2052 721,1 1,6662 0,1696 719,4 1,6437 0,1442 717,6 1,6242
300 0,2630 728,0 1,7020 0.20сЗ 726,3 1,6753 0,1731 724,7 1,6529 0,1473 722,9 1.6331
810 0,2681 733,1 1,7108 0,2133 731,5 1,6842 0,1766 729,9 1,6620 0,1504 723,2 1,6431.
320 0,2731 728,3 1,7195 0,2173 736,7 1,6930 0,1800 735,1 1,6710 0,1534 733,6 1,6521 ;1
330 0,2780 743,4 1,7280 0,2212 741,9 1,7616 0,1833 740,4 1,6798 0,1563 739,9 1,6610 :
340 0,2829 748,5 1,7364 0,2252 747,0 1,7101 0,1867 745,7 1,6884 0,1592 744,3 1,6697 ?
350 0,2879 753,6 1,7447 0,2292 752,2 1,7184 0,1901 751,0 1,6969 0,1623 749,7 1,6783
360 0,3929 758,7 1,7528 0,2332 757,4 1,7266 0,1936 756,3 1,7052 0,1652 755,0 I,G867 ;
370 0,2979 763,8 1,7608 0,2373 762,6 1,7347 0,1970 761,3 1,7134 0,1631 760,3 1,6949
380 0,3028 768,9 1,7687 0,2413 767,8 1,7427 0,2003 766,7 1,7215 0,1710 765,6 1,7030
390 0,3077 774,0 1,7764 0,2453 772,9 1,7506 0,2036 771,9 1,7294 0,1739 770,9 1,7110
400 0,3126 779,1 1,7840 0,2492 778,1 1.7583 0,2070 777,1 1,7372 0,1768 776,2 1,7189
410 0,3174 784,2 1,7915 0,2531 783,2 1,7659 0,2103 782,3 1,7448 0,1796 781,4 1,7267
420 0,3223 789,3 1,7989 0,2371 788,3 1,7733 0,2136 737,5 1,7523 0,1825 786,6 1,7343
430 0,3272 794,3 1,8062 0.261U 793,5 1,7806 0,2169 792,7 1,7597 0,1853 791,8 1,7413
440 0,3320 799,4 1,8134 v.2649 798,6 1,7879 0,2201 797,9 1,7670 0,1882 797,0 1,7492
450 0,3369 804,6 1,8205 0,2688 803,8 1,7951 0,2234 803,0 1,7742 0,1910 802,2 1,7565
460 0,3417 809,7 1,8275 0,2727 808,9 1,8022 0,2267 803,1 1,7813 0,1938 507,4 1,7636
470 0,3465 814,8 1,8345 0,2766 814,0 1.3091 0,2299 813,3 1,7883 0,1966 812,6 1,7706
480 0,3513 819,0 1,8414 0,2804 819,2 1,8160 0,2332 818,5 1,7952 0,1995 817,8 1,7776
490 0,3561 825,1 1,8482 0,2842 824,5 1,8228 0,2365 323,8 1,8021 0,2023 S23.0 1,7845
500 0,3609 830,3 1,8549 0,2881 829,7 1,8296 0,2397 829,0 1,8089 0,2050 823,3 1,7913
510 0,3658 835,5 1,8616 0,292.. 834,9 1,8363 0,2430 834,2 1,8156 0,2078 833,6 1,7980
520 0,3706 840,7 1,8682 0,2959 840,1 1,8429 0,2462 839,4 1,8223 0,2136 833,9 1,8047
580 0,3754 845,9 1,8747 0,2998 845,4 1,8495 0.24Л 844,7 1,8289 0,21134 844,2 1,8113
540 0,3802 851,1 1,8811 0,3037 850,7 1,8560 0,2526 850,0 1,8354 0,2162 849,5 1,8179
550 0,3851 856,2 1,8875 0,3076 856, и 1,8625 0,2559 855,4 1,8419 0,2191 854,8 1,8245
ВОДЯНОЙ ПАР
559
Продолжение табл. 41
с.та 2о ama 3ii ama 35 ama
t = 211,38 t = 222,90 t == 232,76 i =241,42
t е" = 0,1016 v" = 0,08157 v" = 0,1'6802 V* -0,05822
i* = 668,5 669,4 ?* = 669,7 i* =669,5
s" = 1,5160 sv — 1 ,<9i-2 5 = 1 ,1793 s'=1,4645
г I i I s V 7 | S “ 1 i I s s"
0 0,0009992 0,5 0,0000 O,UG(!9989 0,6 0,0000' 0,6009987 0,7 0,0000 U,0009984 0.3 0,0000
10 0,0009994 10,5 0,0360 0,0069992 !0,6 0,0360 0,^009990 10,7 0,0360 0,0009987 10.8 0,0853
20 0,0010010 20,5 . 0707 0/ >010007 20,6 0,0706 0,0010605 20,7 0,0706 0,001ibC3 20,8 0,07u6
30 0,0010035 30,4 0,1041 0,0010033 30,5 0,1040 0,0010(31 30,6 0,1040 0,0010029 30,7 1,1040
40 0,0010070 40,4 0,1364 0,0010068 40,5 0,1363 0.0010066 40,6 0,1362 О.иОЮОб! 40,7 0,1362
50 0,0010112 50,4 .,1677 UjCOlullO 50,4 0,1677 0,(010108 50,6 0,1670 0,01,10106 5o,7 V.167.1
60 0,0010161 60,3 0,1981 0,0010159 60,4 0,1980 0,0010157 60,5 0,1980 0,0010155 60,6 0,1979
70 0,0010218 70,3 0,2276 0,0010216 70,4 0,2275 0,0010213 70,5 0,2275 0,0010211 70,6 0,2274
80 0,0010280 80,3 0,2563 0,0010278 80,4 0,2562 о,0016275 80,5 0,2561 0,6010273 80,6 0,2561
GO 0,001С349 90,3 0,2844 0,001o347 90,4 6,2843 0,0010344 90,5 0,2842 0,0016.342 90,6 0,2841
100 0,0010425 160,4 0,3117 0,6010422 100,5 0,3116 0,0010419 100,5 0,3115 0,0010417 100,6 0,3114
ио 0,0010306 И0,4 0,3383 0,0010503 110,5 <1,3382 6,0010501 110,6 0,3381 0.0010498 110,7 0,3380
120 0,0010593 120,5 0,3643 0,0016591 120,6 0,3642 0,001(588 120,7 u.3641 0,0010535 120,8 0,3640
130 0,001и688 130,7 6,3897 0,0010685 150,8 0,3896 0,0010682 130,9 0,3896 0,0010679 131,0 0,3894
140 0,001078ч 140,9 0,4146 9,9010785 141,0 0,4145 0,0010782 141,1 0,4144 0,0015779 141,1 0,4143
150 0,0010890 151,1 и,4391 0,0610893 151,2 0,4390 0,0010390 151,3 0,4388 6,0010886 151,4 0.438,-
гео 0,0011011 161,4 0,4632 161,5 0,4630 0,0011001 161,6 0,4629 0,0011001 161,6 0,4627
170 0,0011135 171,8 0,4869 0,0011131 171,9 C/1867 0,0011127 171,9 0,4865 0,0011124 172,0 0.4,893
180 0,0011267 182,3 0,5102 0,0011263 182,3 0,5100 0,0011259 182,4 0,5098 0,0011255 182,5 0,3096
190 0,0011409 192,9 1 ,5333 146 i 192,0 0/330 c .ooii 193,0 0,5221 u.oU113b5 193,и 3,5326
-ОЙ 0 ,0011561 203,5 0,5560 0,0011536 203,6 0,5558 0,0011552 2u3,6 0,5556 0,0011547 203,7 1,555,
| 0,0011726 214,3 0,575.4 0,0011720 214,4 0,5785 0,0011715 214,4 0,5782 0,0011710 214,4 0,5780
0,1043 674,6 1,5284 |_0,l!01W99_ 225,3 6.6609 U.0011892 225,3 g.6006 0,0011886 225,4 0.60U4
0,1077 681,2 1,5411 i.,, 08361 674,5 1,5065 1 |>,(\И2086 236,4 0,622/ 0,0012079 236,4 0,6224
240 0,1108 687,3 1э5534 0.08643 681,5 1.5205 0,06987 675,1 1,4905 0,0012290 247,7 и,6448
50 и,1138 693,2 1,5649 0,08906 687,9 1,532j 0,07230 082,1 1.5042 0,06019 676,2 1,4781
260 0,1168 698,9 1,5760 0,09158 694,1 1,5447 0,0745) 688,9 1.5171 0,06233 693.8 1,4922
270 0,1197 70.,5 1,5367 .,,'19403 700,2 1,5559 0,07678 695,5 1,5292 0,0o437 690,9 1,5053
280 0,1225 710,2 1,5970 0.1.95 h. 706,2 1.5668 0.U7889 761 9 '/Si'S 0,96630 697,7 1,5176
290 .,1253 713,8 1,6669 0,09813 712,1 1,5773 0.08094 708,1 1-5519 6,06817 704,2 1,5293
300 0,1281 721,3 1,6166 0,1010 717,8 1.5575 0,0829! 714,1 1,5625 0,66993 710,5 l,54u5
310 0,1308 726,8 1,6261 0,1023 723,4 1,5974 C,0o489 720,0 1.5727 0,07173 716,6 1,5512
320 0,1331 732,3 1,6354 0.1055 729,u 1,6070 u,v868o 725,9 1.5826 0,07344 122,6 1,5615
330 0,136. 737,8 1,6445 i., Ю77 734,7 1,6163 0,08869 , :|,7 1,5923 0,07511 728,6 1,5715
340 0,138!; /13,2 1,6561 0,1098 740,3 1,6251 U .09055 737,5 1,6018 0,07675 <34,6 1,5313
350 0,1412 748,5 1,6621 0,1120 '45.0 1,6343 0,09239 743.3 1,6110 0,07837 740,5 1,5». 6
360 0,1438 /53,8 1,6706 GJ 14! 751.4 1.6436 vi. (^4 21 749,0 1.6199 0,6-7997 7Р,3 l,5b'3
370 0,Ибэ 759,1 1,6739 0,1162 756,8 l,u516 0,09601 754,6 l,o287 0,08156 132,J 1,6088
380 0,1491 764,5 1,6871 0,1183 762,3 1,6600 0,09780 760,1 1.6373 0,08314 757,7 1,6176
390 0,1516 769,8 1,6952 0,1204 767,7 1.66S2 0,09958 765,6 1.6457 0.08470 763,3 1,6264
409 0,1542 775,1 1,7031 0,1223 773,1 1,0763 0,1013 771,1 1,6539 0,06624 768,9 1,6346
410 0,1567 780,4 1.7109 6,1243 773,4 I,63‘,i2 0,1031 776,5 1.6619 0,U5/7g 774,5 1,6428
420 0,1592 185,6 1,7186 0,1266 7J3.8 l ,692g 0,1048 781,9 1,6698 0,08:127 (60,0 l,650o
430 0,1617 790,9 1,7261 0,1287 789,2 1,6996 j,1006 787,4 1,6776 0,09078 785,5 1,6587
440 0,1642 796,1 1,7335 0,1308 794,5 1.7071 0,1084 792.8 1,6853 0,09228 791,0 1,6665
450 0,1667 801,3 1,7408 9,1328 799,8 1,7145 u.UUl 798,1 1,6928 0,09377 796.5 1,6741
460 0,1692 806,6 1,7480 0,1317 805,1 1,7218 0.ШЗ 803.5 1,7002 0.09525 802,0 1,6816
470 (‘,1717 811,9 1,7551 0,1367 810,4 1,7299 0,1134 808,9 1,7074 0,09673 807,4 1.6SS9
480 0,1741 817,2 1,7621 0,138I 815,7 1,7361 0.1151 811,3 1,7145 0,09820 812,9 1,69,1
490 0,1765 822,4 1,7690 C,14o6 821,0 1,7431 0,1168 819,7 1,7216 0,UW66 818,4 1.7C52
500 0,1790 827,7 1,7758 0,142u 826,4 1,7500 0,1185 025,1 1,7286 0,1:11 823,8 1,71:3
510 0,1815 833,0 1,7826 0,1446 831,8 1,7569 0,1201 830,4 1,7355 и,1025 829,2 1,7173
520 0,1840 838,3 1.7394 0,1466 837,1 1.7637 0,1218 835.8 1.7424 0,1039 834,6 1,7243
539 0,1864 843,6 1,7961 0/1486 842,5 1,7704 0,1235 841,2 1,7492 0,1654 840,6 1,7312
540 0,0883 848,9 1,8027 0,1505 847,8 1,7771 0,1252 846,7 1,7560 0,1069 845,5 1,7380
550 и,ЫЗ 854,2 1,8093 1,1527 853.1 1,7837 0.1269 852.1 1,7627 0,1083 850,9 1.7448
560
ТЕПЛОТА
Продолжение т абл. 41
f 40 ama 45 ama 50 ama 60 ama
t t -249,18 v*«0,05078 1*4=669,0 s*« 1,4513 t S*« = 256,23 -0,04495 = 668,2 = 1,4392 t = v" = s*«= 262,7 «0,04024 667,3 1,4280 t V i sA 274,29 '-0,03310 ’-665,0 -1,4078
V i s i 1 s V I * 1 s V i » s
0 0,0009982 l.o 0,0001 0,0009979 1.1 J,0001 0,0009977 1,2 0,0001 0,0009972 1,4 0,0001 0,0359 0 0704
10 0,0009985 10,9 0,0360 0,0009983 11.1 0,0359 0,0009981 11,2 0,0359 0,0009976 11.4
20 30 40 0,0010001 20,9 0,0705 0.0009998 21,0 0,0705 0,0009997 21,1 0,0705 0,0009992 21,3
0,0010027 30,9 0,1039 0,0010024 31,0 0,1039 0,0010022 31,1 0,1039 0,0010018 31,3 ОД038
0.0010062 40,8 0,1362 0,0010060 40,9 0,1361 0,0010057 41,0 0,1361 0,0010053 41,2 0,1360
50 60 0.0010103 50,8 0,1675 0,0010101 50,9 0,1674 0,0010099 51,0 0,1674 0,0010095 51 2 or1672
0,0010152 60,7 0,1978 0,0010150 60,8 0,Ь78 0,0010148 60,9 0,1977 0,0010144 61 1 0,1976 0,2270
80 90 0,0010208 70,7 0,2273 0,0010206 70,8 0,2272 0,0010204 70,9 0,2271 0,0010199 71,1
0,0010271 80.7 0,2560 0.0010269 80,8 0,2559 J,0010266 80,9 0,2558 0,0010262 81,1 0 2556
0,0010339 90,7 0,284J 0,0010337 90,8 0,2839 0,0010334 90,9 0,2838 0,0010329 91,1 0,2836
100 0,0010414 100,7 0,3113 0.0010412 100,8 0,3112 0,0010409 100,9 0.3111 0,u010404 101,1 0.3109
0,0010495 110,8 0,3379 0,0010493 110,9 0,3378 0,0010499 lll.u 0,3377 0,0010485 111,1 0,3375
0,0010582 120,9 0,3639 J,0010580 121,0 0,3638 0,0010577 121,1 0.3637 0,0010572 121,2 0,3635
0,0010676 131,0 0,3893 0,0010673 131,1 0,3892 0,0010670 131,2 0,3891 0,0010665 131,3 0.3889
150 160 0,0010776 141,2 0,4142 0,0010773 141,3 0,4141 0,0010770 141,4 0,4140 0,0010764 141.5 0,4137
0,0010883 151,4 0,4386 0,0010880 151,5 0,4384 0,0010677 151,6 0,4383 0.0010870 151,7 0,4381
170 0.001099/ 161,7 0,4625 0,0010994 161,8 0,4624 0,00109,4) 161,8 0.1622 0.0010984 162.0 0.4619
1Я0 0,0011120 172,1 0,4861 0,0011116 172,1 0,4859 0,0011113 172.2 0,4857 0,0011105 172.3 0,4854
190 0,0011251 182,5 0,5094 0,0011247 182,1 0,5092 0.0011243 182,6 J,5090 0,0011235 182,8 0,5086
200 210 0,0011391 193,1 0.5324 0,0011387 193,1 0,5322 0,0011382 193,2 0,5320 0,0011374 193,3 0,5316
0,0011542 203,7 0,5551 0,0011537 203,8 0,5549 0,0011532 203,8 0.5547 0,0011522 203,9 0.5543
220 0,0011704 214,5 0,5777 0,0011699 214,5 0,5775 0,0011694 214,6 0,5773 0,0011683 214,6 0,5768
930 0,0011880 225,4 0,6001 0,0011874 225,4 0,5999 0,0011868 225,5 0,5996 0,0011857 225,5 0,5991
0,0012072 236,4 0,6222 0,0012065 236,5 0,6220 0,0012058 236,5 0.6217 0.0012U45 236,5 0,6212
240 [ 0,0012282 247,7 O,6445_ 0,0012274 247,8 0.6442 0012266 247,8 0,6439 0,0012251 247,8 0,6433
250 0,u5096 669,8 1,4527| 0,0012504 259,2 0,6664 0,0012495 259,2 0,6661 0,0012478 259,2 270,9 0,6655 0,6878
260 b,05302 678,1 1,4686 0,04567 671,0 1,4456 | 0,0012751 271,0 0,6885 0,0012729
270 0,05495 685,8 1,4828 0,04757 680,0 1,4616 0,04156 674,0 l,440g| 0,0013014 283,0 0,7100
280 0,05679 693,0 1,4960 о,04935 688,0 1,4760 0,04330 682,6 1,4566 0,03405 670,5 1,4187
290 0,05854 699,9 1,5084 0.05102 695,4 1,4893 0.04493 690,7 1,471. 0,03563 680,2 1,4359
300 0,06022 706,6 1,5202 0,05260 702,5 1,5018 0,04646 698,4 1,4844 0,03711 689,0 1,4513
310 0,06183 713,1 1,5315 0,05411 ,709,3 1,5137 0,04790 705,5 1,4968 0.03848 697,3 1,4656
320 0,06338 719,4 1,5424 0,05556 715.9 1,5250 0,04927 712,3 1,5087 0,03v76 705a- 1.4788
330 0,06489 725,6 1,5529 0,05695 722,3 1,5358 О.ОЬиЬЭ 719,0 1,5200 0,04097 712,4 1,4912
340 J,06636 731,7 1,5630 0,05830 728,6 1,5462 0.05186 725,6 1,5307 0,04213 719,5 1,5028
350 0,06782 737,7 1,5727 0,05963 734,8 1,5562 0,05310 732,0 1.5410 0,04324 726,3 1,5139
360 0,06927 743,6 1,5821 0,06095 740,9 1,5659 0.05432 738,3 1,5510 0,04432 732,9 1,5245
370 0,07070 749,4 1,5912 0,06226 747,0 1,5753 0,05552 744,5 1,5607 0.04538 739,4 1,5347
380 0,07212 755,3 1,6001 0,06356 753,0 1,5845 0,05671 750,6 1,5701 0.04642 745,8 1,5445
390 0,07352 761,1 1,6088 0,06484 758,9 1,5935 0,05788 756,6 1,5792 0,04744 752,1 1,554»
400 0,07490 766,8 1,6174 0,06610 764,7 1,6022 0,05904 762,6 1,5881 0.U4845 758,3 1,5632
410 0,07627 772,5 1,6258 0,06734 770,5 1,6107 0,06018 768,5 1,5967 0,04944 764,4 1,5721
420 0,07763 778,1 1,6340 0,06856 776,2 1,6190 0,06130 774,3 1.6052 0.05042 770,4 1,6808
430 0,07897 783,7 1,6420 0,06977 781,9 1,6272 0,06241 780,0 1,6135 0,05138 776,3 1,5894
440 0,08030 789,3 1,6499 0,07098 787,6 1,6352 0,06352 785,8 1,6216 0,05233 782,2 1,5978
450 0,08162 794,9 1,6577 0,07218 793,2 1,6430 0,06462 791,5 1,6295 0,05327 788,0 1,606м
460 0,08293 800,4 1,6653 0,07337 708,8 1,6506 0,06571 797,2 1,6373 0.05420 793,8 1.6140
470 0,08424 805,9 1,6727 0,07455 804,4 1,6581 0,06679 802,9 1,6449 0,05512 799,7 1,6218
480 0,08554 811,4 1,6800 0,07572 810,0 1,6655 0,06786 808,6 1,6524 0,65604 805,5 1.6294
490 0,08684 816,9 1,6872 0,07688 815,6 1,6728 0,06893 814,2 1,6598 0,05695 811,2 1,6369
500 0,08813 822,4 1,6943 0,07804 821,1 1,6801 0,06999 819,8 1.6671 0,05785 816,9 1,6444
510 0,08941 827,9 1,7014 0,07920 826,6 1,6873 0,07104 825,3 1,6743 0,05874 822,6 1,6518
520 0,09069 833,4 1,7085 0,08035 832,1 1,6944 и,07208 83», 9 1,6815 0,05963 828,3 1,6591
530 0,09196 838,9 1,7155 0,08149 837,7 1,7014 0,07312 836,5 1,6886 0,06050 834,0 1,6663
540 0,09323 844,4 1,7224 0,08262 843,2 1,7084 0,07415 842,0 1,6957 0.06138 839,6 1,6734
550 0.09449 849,8 1,7292 0,08375 848,6 1,7153 0,07519 847,6 1,7028 0,06226 845,3 1,6804
ВОДЯНОЙ ПАР
561
Продолжение табл. 41
70 ата 80 ата 90 ата 100 ата
t 284,48 t = 293,62 t - 301,92 t = 309,53
t v"~ S"=: 9,02795 66°, 1 1,3897 li Ji Ц Со 1 0,02404 658,9 ,3731 Г= s*=» =0,02096 655.1 5,3576 0,01845 .651,1 =1,3424
V ’ 1 5S 1 [ 9 г | S V 1 i
0 0,0004967 1.7 0,0001 0,0009962 1,9 (<,0001 0,0009^57 2,2 0,0001 0.0009952 2,4 0,0001
10 0,0009972 11,6 0,0358 0,0009757 11,9 0.0358 0,0009962 12,1 0,0358 0,0009958 12,3 0,0358
20 0,0009988 21,6 0,0704 0,0009983 21,8 0,0703 0,0009979 22,0 0,0702 0,0009975 22,2 0,0702
30 0,0010014 31,5 0,1037 0.0010009 31.7 0,1036 0,0010005 31,9 0,1036 0,0010001 32,1 0,1035
40 0,0010049 41,4 0,1359 0.0010045 41.6 0,1359 0.001J04U 41,8 0,1357 0,0010036 42,1 0,1356
50 0,0010090 51,4 0,1671 О.ООЖЗб 51.6 0,1670 0,0010082 51,8 0,1663 0,0010077 52,0 0,1667
60 0,0010139 61,3 0,1974 0,0610135 61,5 0,1973 0.0010130 61,7 0,1971 0,0010126 61,9 0,1970
70 0,0010195 71,3 0,2268 0,0010190 71,5 0,2267 0,0010186 71,7 0,2265 0.0010181 71,8 0,2264
80 0,0010257 81,2 0,2555 ^,0010252 81,4 0,2553 0,0010248 81,6 0,2551 0,0010243 81,8 0,2550
90 0,0010325 91,2 0,2834 0,0010320 91,4 0,2832 0,0010315 Ы.6 0,2831 и,0010311 91,8 0 ,2829
100 0,0010399 101,3 0,3107 0,0010394 101,4 0,3105 0,0010389 101,6 0.3103 0,0010384 101,8 0,3101
НО 0,0010489 111,3 0,3373 0,0010475 111,5 0.3371 0,0010470 111,7 0,3359 0,0010464 111,8 0,3367
120 0,0010556 121,4 0,3633 0,0010561 121,6 0,3631 0.0010556 121,7 0,3628 0,0010550 121.9 0,3626
130 0,0010659 131,5 0,3887 и,0010653 131,7 0,3384 0,0010648 131.8 0,3382 0,0010642 132,0 0,3880
140 0,0010758 141,7 и.4135 0,0010752 141,8 0,4133 0,0010746 142,0 0,4130 0,0010740 142,1 0,4128
150 0,0010864 151,9 0,4373 0,0010858 152,0 0,4376 0,0010851 152,2 0.4373 0,0010845 152,3 0,4371
160 О.СО1С977 162,1 0,4617 0,0010970 162,2 0,4614 0,0010963 162,4 0,4611 0,0010957 162,5 0,4608
170 0,0011093 172,4 0,4851 0,001091 172,6 0,4848 0.0011083 172,7 0,4844 0,0011076 172,8 0,4841
180 0,0011226 18%9 0,5082 0,01111219 183,0 0,5079 0,0011211 183,1 0.5075 0,0011203 183,2 0,5072
190 0,0011365 193,4 0,5312 0,0011356 193,5 0,5308 0,0011348 193,6 0,5305 0,0011339 193,7 0,5301
200 0,0011513 204,0 0,5539 0,0011504 204,1 0.5535 0,0011494 204,2 0,5532 0,0011485 204.3 0,5527
210 0,0011673 214,/ 0.5764 0,0011662 214.8 0,5759 0,0011652 214,9 0,5755 0,0011642 215,0 0,5751
220 0,0011845 225,6 0,5986 0,0011833 225,7 0,5982 0,0011822 225,7 0,5977 0,0011810 225,8 0,5973
230 0,0012032 236,6 0,6206 0,0012019 236,6 0,6202 0,0012006 236,7 0,6196 0,0011993 236,7 0,6192
240 0,0012236 247.8 0,6428 0,0012221 247.8 0,6423 0,0012206 247,9 0,6417 0,0012192 247,9 0,6412
250 0,0012460 259,2 0,6649 0,0012443 259,2 0,6643 0,0012425 259,3 0,6638 0,0012409 259,3 0,6632
230 0,0012709 270,9 0,6871 0,0012639 270,9 0,6864 0,0012669 270,9 0,6358 0,0012650 270,9 0,6852
270 0,0012939 282,9 0,7092 0,0012965 232,9 0,7085 0,0012942 282,7 0,7078 0,0012919 282,7 0,7071
280 0,0013308 295,2 0,7317 0,0013279 295,1 0,7308 0,0013250 295,0 0,7300 0,0013222 294,9 0,7293
290 0,02381 668,2 1,4и11| 0,0013640 307,9 0,7538 0.0013604 307,7 0,7523 0,0013569 307,5 0,7520
300 0,^3029 678,6 2,4196 0,02503 666,6 1,3871 1 п,0014024 320,9 0,7762 0,0013979 320,7 0,7751
310 0,03163 688,1 1,4361 0,02635 677.8 1,4067 0,02213 665,9 1,3765 0,01851 651,7 1,3435
320 0,03287 696,9 1,4510 0,02757 687,9 1,4239 0,02336 677,6 1,3968 0,01988 665,9 1,3685
330 0,03403 705,1 1,4646 0,02870 697,1 1,4393 0,02448 688.2 1,4145 0,02105 678,2 1,3891
340 0,03512 712,8 1,4772 0,02976 705,6 1.4533 0,02553 697,9 1,4302 0.02210 689,0 1,4070
350 0,03615 720,1 1,4891 0,03076 713,6 1,4663 0,02652 706,8 1,4445 0,02307 698,8 1,4230
339 0.С37М 727,2 1,5005 0,03171 721,2 1,4785 0,02745 715,0 1.4577 0,02397 707,8 1,4374
370 0,03810 734,1 1,5114 0,03261 728,5 1,4900 0,02832 722,7 1,4700 0,02481 716,2 1,4506 ।
380 0,03903 740,8 1,5218 , 0,1'3348 735,6 1,50^9 0.02914 730,1 1,4815 0.02561 724,2 1,4629
390 0,03994 747.3 1,5317 0,03433 742,5 1,5113 0,02993 737,3 1,4923 и,02637 731,9 1,4744
400 0.04084 753,7 1,5413 0,03515 749,2 1,5213 0,03070 744,3 1,5027 0,02710 739.3 1,4853
410 0,04173 760,0 1.5506 0,03595 755,7 1,5310 0,и3145 751,1 1,5128 0,02781 746,5 1,4958
420 0,04260 766,3 1,5596 0,03671 762,1 1,Б4и4 0,03218 757,8 1,5226 0,02850 753,5 1,5060
430 0,04346 772,5 1,5684 0,03752 763,5 1,5495 0,03289 704,4 1.5321 0,02917 760,3 1,5159
440 0,04430 778.6 1,5770 0,03824 774,8 1,5584 0,03359 770,9 1,5413 0,02982 767,0 1,5255
450 0,04513 784.6 1,5854 0,03903 781,0 1,5671 0,03428 777,3 1,5502 0.03046 773,6 1,5348
460 0,04596 790,5 1,5936 0,03977 787,1 1,5755 0,03496 783,6 1,5589 0,03109 780,1 1,5438
470 0,04678 796,4 1,6016 0,04050 793,2 1,5837 Од 3563 789,9 1,5674 0,03171 786,5 1,5525
480 0,04759 802,3 1,6095 0,04122 799,2 1,5917 0,03629 796,1 1,5757 0,03232 792,8 1,5609
490 0,04839 808,2 1,6172 0,04194 805,2 1,5196 0,03691 802,2 1,5833 0,03292 799,1 1.5691
500 0,04918 814,1 ],6248 0,04265 811,2 1,6073 0,03758 808,2 1.5917 0,03352 805.3 1.5772
510 0,04996 819,9 1,6323 0,04335 817,1 1,6149 0,03821 814,3 1,5994 0,03411 811,5 1,5851
й20 0,05073 825,7 1,6396 0,04405 823,0 1,6224 о.03384 820,3 1.6069 0,03469 817,7 1,5928
5зо 0,05150 831,4 1,6463 0,04474 828,9 1,6298 0,039-17 826,3 1,6143 0,03526 823,8 1,6004
540 0,05227 837,2 1.6540 0,04542 834,8 1,6370 0,04009 832,4 1,6217 0,03583 829,9 1,6079
550 0,05303 843,0 1,6611 0,04610 840,6 1,6441 0,04070 838,4 1,6299 0,03636 836,0 1,6153
36 Том I
562
теплота
Продолжение табл. 41-
t 120 ama 140 ama 160 ama 180 ama
t' =323,15 v*=0,01464 t*=641,9 $*=1,3138 U и U II *4 <0 335,09 =0,01181 =631,0 1,2858 t = r= s" = 345,74 0,009616 618,3 1,2564 / = 355,35 ^*=0,007809 i*=602.5 $* = 1,2251
V 1 1 1 s V 1 ' S V < $ r 1 < 1 s
0 0,0009943 2,9 0,0002 0,0009933 3,3 0,0002 0,0009924 3,8 0 0002 0,0009914 4,3 0,0002
10 0,0009949 12,7 0,0357 0,0009940 13,2 0,0357 0,0009932 13,6 0,0356 0,0009922 14,1 0,0356
20 0,0009966 22,7 0,0701 0,0009958 23,1 0,07u0 0,0009950 23,5 0 0699 0,0009941 24,0 0,0698
30 0,0009993 32,6 0,1034 0,0009985 33,0 0,1032 0,0009976 33,4 0,1031 0,0009968 33,8 0,1030
40 0,0010028 42,5 0,1355 0,0010019 42,9 0,1352 0,0010011 43,3 0,1351 0,0010003 43,7 0,1350
50 0,0010069 52,4 0,1665 0,0010061 52,8 0,1663 0,0010052 53.2 0,1661 0,0010044 53,6 0,1659
60 0,0010117 62,3 0,1967 0,0010109 62,7 0,1965 0,0010100 63,1 0,1962 0.0010092 63,5 0,1959
70 0,0010172 72,2 0,2261 0,0010164 72,6 0,2258 0,0010155 73,0 0,2256 0,0010146 73,4 0,2253
80 0,0010234 82,2 0.2547 0,0010225 82,5 0,2544 0,0010216 82,9 0,2541 0,0010207 83,3 0,2533
SO 0,0010301 92,1 0,2825 0,0010292 92,5 0,2822 0,0010283 92.9 0,2819 0,0010274 93,2 0,2816
100 0,0010375 102,1 0,3097 0,0010365 102,5 0,3094 0.0010356 102,9 0,3090 0,0010347 103,2 0,3087
по 0,0010454 112,2 0,3363 0,0010444 112,5 0,3359 0,0010434 112.9 0,3356 0,0010425 113,2 0,3352
120 0,0010540 122,2 0,3623 0,0010529 122,6 0,3619 0,0010519 122,9 0,3615 0,0010508 123,2 0,3611
130 0,0010631 132,3 0,3876 0,0010620 132,6 0,3872 0,0010609 133,0 U.3868 0.0010598 133,3 0,3863
140 0,0010728 142,4 0,4124 0,0010717 142,8 0,4119 0,0010705 143,1 0,4115 0,0010694 143,3 0,4110
150 0,0010832 152,6 0,4366 0,0010820 152,9 0,4361 0,0010308 153,2 0,4357 0,0010796 153.5 0,4352
160 0,0010943 162,8 0,4603 0,0010930 163,1 0,4598 0,0010„17 163,4 0,4593 0,0010905 163.6 0,4588
170 0,0011062 173,1 0,4836 0,0011047 173,3 0,4830 0,0011033 173,6 0,4825 0,0011020 173,9 0,4819
180 0,0011188 183,5 0,5066 0,0011172 183,7 0,5060 0,0011157 183,9 0,5054 0*0011143 IM,2 0,5048
190 0,0011322 193,9 0,5294 0,0011306 194,1 0,5288 0,0011289 194,3 0,5281 0,0011273 194/6 0,5275
500 0,0011466 204,5 0,5520 0,0011448 204,7 0,5513 0,0011430 204,9 0,5506 0,0ull412 205,1 0,5499
210 0,0011621 215,1 0,5743 0,0011601 215,3 0,5735 0,0011582 215,5 0,5727 0,0011562 215,6 0,5720
220 0,0011/88 225,9 0,5964 0,0011766 226,1 0,5955 0,0011744 226,2 0,5946 0,0011722 226,3 0,5933
230 0,0011968 236,8 0,6183 0,0011943 237,0 0,6174 0,0011919 237,0 0,6164 0,0011895 237,2 0,6155
0,0012163 248, и 0,6402 0,0012136 248,0 0,6392 0,0012108 248,1 0,6382 0,0012084 243,2 0,6372
250 0,0012377 259,3 0,6621 0,0012346 259,3 0,6610 0.0012314 259,3 0,6599 0,0012284 259,4 0,6588
260 0,0012613 270,8 0,6839 0,0012576 270,8 0,6827 0,0012541 270,7 0,6816 0,0012506 270,7 0.M04
0,0012875 282,6 0,7057 0,0011832 282.5 0,7044 0,0012791 282,4 0,7033 0,0012751 282,3 9,7020
280 0,0013169 294,6 0,7278 0,0013118 294,5 0,7263 0,0013070 294,4 0,7250 0,0013023 294,2 0.7236
290 0,0013505 307,1 0,7501 0,0013443 306,9 0,7484 0,0013335 306,6 0,7468 0,0013329 306,4 0.7453
300 0,0013897 320,1 0,7729 0,0013820 319,5 0,7709 0,0013746 319,1 0,7690 0,0013678 318,7 0,7673
310 0,001436 333,8 0,7966 0,001426 332,9 0,7942 0,001417 332,2 0,7919 0,001408 331,6 0,7898
320 0,001495 348,6 0,8222 0,001481 347,5 0,8189 0,001468 346,4 0,8159 0,001457 345,5 0,8133
330 0,001552 363,3 0.8457 0,001533 361,7 0,8416 0,001517 360,6 0,8381
340 0,01679 668,9 1,3592 0,01253 642,6 1.3050 | 0,001621 379,2 0,8705 0,001596 376,9 0.865!
1 0.(001713 396.3 0.89/0
350 0,01780 681,3 1,3797 0,01374 660,1 1,3336 0,01632 63,U, 8 1,2767
360 0,01870 692,5 1,3976 0,01471 674,2 1,3561 0,01154 651,6 1,3106 0,00862 620,1 1,2533
370 0,01952 702,7 1,4135 0,01558 686,7 1,3758 0,01252 663,0 1,3365 0,00991 645,5 1,2935
380 0,02028 712,1 1,4279 0,01637 698,0 1,3932 0,01332 681,8 1,3581 0,01082 663,7 1,3218
3S0 0,02099 720.9 1,4411 0,01708 708,2 1,4088 0,01404 694,2 1,3769 0,01161 678,7 1,3446
400 0,02168 729,2 1,4534 0,01774 717,7 1,4230 0,01471 705,3 1,3934 0,0123! 691,5 1,3640
410 0,02234 737,1 1,4650 0,01837 726,6 1,4361 0.01533 715,4 1,4083 0,01293 7G3,0 1,3309
420 0,02296 744,7 1,4761 0,01896 735,1 1,4483 0,01591 724,8 1,4219 0,01349 713,6 1,3961
430 0,02357 752,1 1,4867 0,01953 743,2 1,4598 0,01646 733,6 1‘4345 0,01402 723,5 1,4100
440 0,02415 759,3 1,4969 0,02008 751,0 1,4708 0,01699 742,0 1,4463 0,01453 732,7 1,4230
450 0,02472 766,3 1,5067 0,02061 758,5 1,4813 0,01750 750,1 1,4576 0,01503 741.5 1,4352
460 0,02528 773,2 1,5162 0,02112 765,8 1,4914 0,01798 758,0 1,4684 0,01550 750,0 1,4463
470 0,02583 780,0 1,5254 0,02'62 773,0 1,5011 0,01844 765,7 1,4788 0,01595 758,2 1,45/8
480 0,02637 786,7 1,5343 0,02211 780,1 1,5105 0,01889 773,2 1,4888 0,01638 766,1 1,4654
490 0,02690 793,3 1,54*9 0,02259 787,1 1,5196 0,01933 780,5 1,4984 0,01679 773,8 1,4785
500 0,02742 799,8 1,5513 0,02306 793,9 1,5284 0,01976 787,7 1,5077 0,01720 781,3 1,4882
510 0,02793 806,2 1,5595 0,02352 800,6 1,5370 0.02018 794,8 1,5167 0,01759 788,7 1,4976
520 0,02843 812,5 1.5675 0,02397 807,2 1,5454 0.02059 801,8 1,5254 0,01797 796,0 1,50'37
530 0,02893 818,8 1,5754 0,02441 813,7 1,5536 0,02100 808.6 1,5338 0,01835 803,2 1,5155
540 0,02942 825,1 1,5832 0,02485 820,1 1,5616 0,02140 815,3 1,5420 0,01872 810,2 1,5242
550 0,02990 831,4 1,5909 0,02529 826,5 1,5694 0,02180 821,9 1,5500 0,01908 817,0 1,5325
ВОДЯНОЙ ПАР
563
Продолжение табл. 41
200 ата 220 ата 240 ата 260 ата
t Г V* 8* ним V-* СП О СО • оо- ь-* Ю О Л» 00- О- 00 СО О О Q3 to ос Г Vя $' II II II II ►— СЯ О СО со X В -° i н- о о 1 ъ i S V i S
•и 1 < 1 S у 1 i 1 S
0 0,0009905 4,7 0,0003 0,0009896 5,2 0,0003 0,0009887 5,7 0,0003 0,0009877 6,1 0,0003
10 0,0009914 14,6 0,0355 0,0009905 15,0 0,0355 0,0009897 15,5 0,0355 0,0009888 15.9 0,0354
20 0,0009933 24,4 0,0697 000009924 24,8 0,0696 0,0009916 25,3 0,0695 0,0009908 25,7 0,0695
30 0,00-9960 34,3 0,1028 0,0009952 34,7 0,1026 0,0009944 35,1 0,1025 0,0009933 35,5 0,1024
40 0,0009995 44,1 0,1347 0,0009986 44,5 0,1345 0,0009978 44,9 0,1354 ^,0009970 45,3 0.1342
50 0,0010030 54,0 0.1657 0,0010027 54,4 0,1655 0,0010019 54,8 0,1653 0,0010011 55,2 0,1651
60 0,0010083 63,8 0,1958 0,0010075 64,2 0,1955 0,0010067 64,6 0,1953 0,0010058 65,0 0,1951
70 0,0010137 73,7 0,2251 0,0010129 74,1 0,2248 0,0010121 75,5 0,2245 0,0010112 74,9 0,2243
80 0,0010198 83,7 0,2536 0,0010190 84,0 0,2533 0,0010181 84,4 0,2530 0,00101/2 84,8 0,2527
90 0,0010265 93,6 0,2813 0,0010256 94,0 0,2811 0,0010247 94,3 0,2807 0,0010238 94,7 0,2804
100 0,0010337 103,6 0,3084 0,0010328 103,9 0,3081 0,0010318 104,3 0,3077 0,0010309 104,6 0,3074
по 0,0010415 113,6 0,3348 0,0010405 113,9 0,3345 0,иСЮ395 114,3 0,3341 0,0010386 114,6 0,3337
120 0,0010498 123,6 0,3607 0,0010488 123,9 0,3603 0,0010478 124,3 0,3599 0,0010468 124,6 0,3595
130 0,001-588 133,7 0,3859 0,0610577 133,9 0,3855 0,0010567 134,3 0,3851 L,0010556 134,6 0,3847
140 0,0010082 143,7 0,4106 0,0010671 144,С 0.4101 0,0010661 144,3 3,4097 0,0010649 144,6 0,4093
150 0,0010784 153,8 0,4347 0,0010772 154,1 е.4342 0,0010760 154,4 0,4338 0,0010749 154,7 0,4333
160 0,0010892 163,9 0,4583 С.00К879 164,2 0,4578 0,0010865 164,5 0,4573 0,0010854 164,8 0,4568
170 0,0011006 174,1 0,4814 0,0010992 174,4 0,4809 0,0010979 174,7 0,4804 и,0010966 175,0 0,4799
180 0,0011128 184,4 0,5042 0,0011113 184,7 0,5037 0,0011099 184,£ 0,5031 0,0611085 185,2 0,5026
190 0,0011257 194,8 0,5268 0,0011242 195,0 0,5262 0,0011226 195,2 0,5256 0,0011211 195.5 0,5250
200 0,0011395 205,3 0,5492 0,001137^ 205,4 0,5485 0,0011362 205,6 0,5477 0,0011345 205,8 0,5472
210 0.0011543 215,8 0,5712 0,0011524 216,0 0,5705 0,0011506 216,1 0,5698 0,0011488 216,3 0,5690
220 и,0011701 226,5 -,593и 0,0011680 226,6 0,5922 0,0011660 226,7 0,5914 0,0011640 226,9 0,5906
230 0,0011871 237,3 0,6147 0,0011848 237,4 0,6138 0,0011826 237,5 0,6129 0,0011804 237,6 0,6121
240 (.,0012055 248,2 0,6363 0,0012029 248,3 0.6353 0,0012005 248,4 0,6343 0,0011980 248,5 0,6334
250 0,0012254 259,4 0,6578 0,0012225 259,4 0,6567 0,0012198 25а, 5 0,6557 0,0012170 259,5 0.6547
260 0,0012472 270,7 0,6792 0,0012439 270,7 0,6781 0,0012408 270,7 0,6769 0,0012376 270,7 0,6758
270 0,0012712 282,2 0,7007 0,0012674 282,2 L.6994 0,0012638 282.1 0,6982 0,0012602 282,1 0,6970
280 0,0012977 294,0 0,7222 0,0012933 293,9 0,7208 0,0012891 293,8 0,7195 0,0012850 293,7 0,7181
290 0,0013274 306,1 0,7437 0,0613222 305,8 0,7422 0,0013172 305,7 0,7408 0,0013125 305,5 0,7393
300 0,0013612 318,4 0,7655 0,0013549 318,0 0,7638 0,0013439 317,8 0,7622 0,0013433 317,5 0,7605
310 0,001400 331,1 0,7878 0,001392 330,8 0,7859 0,001385 330,4 0,7840 0,001378 330,0 0,7821
320 0,001446 344,7 0,8109 0,001436 344,2 0,8087 0,Ои1427 343,6 0,8065 0,001418 343,0 0,8043
330 0,001502 359,2 0,8351 0,001489 358,3 0,8324 9,001477 357,4 0,8298 0.001466 356,6 0,8273
340 0,001573 375,0 0,8611 0,001554 373,5 0,8575 -2,001538 372,2 0.8544 0,001523 371,1 0,8513
350 0,001671 393,1 0,8904 0,001641 390,6 0,8852 0,001617 388.5 0,8808 0,001596 386,8 0,8768
360 0.001841 416,9 0,928( '-,001768 411,j 0,9179 0.0Л722 407,3 0,91о8 0,001688 404,5 0,9055
370 O.UO746 610,2 1,2316 0 ,002085 443,6 9,0689 0,001914 432,2 0,9498 0,001834 426,0 0,9392
380 0,1)0870 640,0 1,2777 0,00662 606,7 1,2215 0,00370 526,0 1,0942 0,00230 457,2 0,9869
390 0,00953 660,3 1,3090 0,0077. 636,5 1,2668 0,0е,603 606,0 1,2155 0,00424 556,2 1,1372
400 0,01033 676,1 1,3330 0,00862 657,5 1,2981 0,00708 635,8 1,2600 0,00566 608,1 1,2148
410 0,01098 689,5 1,3527 6,00931 674.3 1,3236 0,00785 657,7 1,2923 0,00656 637,2 1,2577
420 0,01156 701,5 1,3701 0,00993 6/38,6 1,3445 0,00851 675,0 1,3175 0,00728 658,1 1,2881
430 0,01209 712,4 1,3858 0,01047 700,8 1,3622 0,00908 689,2 1,3378 0,00789 775,1 1,3125
440 0,01258 722,6 1,4001 0,01097 711,8 1,3778 0,0095; 701,7 1,3554 0,00841 689,5 1,3328
450 0,01306 732,2 1,4134 0,01143 722,3 1,3922 0,01006 712.0 1,3712 0,00889 701,2 1,3503
460 0,01352 741,3 1,4259 0,01186 732,3 1,4058 0,01049 722,8 1,3360 0,00933 712,8 1,3663
470 0,01395 750,1 1,4378 0,01227 741,8 1,4186 0,01089 733,С 1,3997 9,00974 723,7 1,3811
480 0,01436 758,6 1,4491 0,01267 750,9 1,4306 0,01128 742,7 1,4125 0,01011 734,1 1,3948
490 0,01475 766,8 1,4598 0,01305 /59,6 1,4419 0,01165 751,1 1,4245 и,01046 744,0 1,4076
500 0,01513 774,7 1,4700 0,01341 767,9 1,4527 0,01209 760,8 1,4358 0,01079 753,4 1,4197
510 0,01550 782,4 1,4798 0,01376 776,0 1,4630 У,01234 769,4 1,4466 0,01111 762,4 1,4311
520 0,01587 790,0 1.4893 0,01411 783,9 1,4729 0,01267 777,7 1,4570 0,01143 771,1 1,4419
530 0,01622 797,4 1,4985 0,01445 791,6 1,4824 0,01299 785,7 1,4670 0,01174 779,5 1,4522
540 0,01656 804,6 1,5074 0,01479 799,1 1,4916 0,01332 793,5 1.4766 0,01205 787,7 1,4622
550 0,01690 811,1 1.5161 0,01512 806.5 1,5005 и,01363 801,1 1,4859 0,01236 795,7 1,4719
36*
564
ТЕПЛОТА
Продолжение табл. 41
t 280 ата 300 ата
v i S V г S
0 0,0009868 6,6 0,0003 0,0009859 7,1 0,0003 10 0,0009880 16,4 0,0354 0,0009871 16,8 0,0354 20 0,0009900 26,2 0,0694 0,0009892 26,6 0,0693 30 0,0009928 36,0 0,1022 0,0009920 36,4 0,1021 40 0,0009962 45,8 0,1340 0,0009954 46,2 0,1338 50 0,0010003 55,6 0,1649 0,0009995 56,0 0,1647 60 0,0010050 65,4 0,1949 0,0010042 65,8 0,1947 70 0,0010104 75,3 0,2241 0,0010096 75,7 0,2238 80 0,0010164 85,2 0,2525 0,0010154 85,5 0,2522 90 0,0010229 95,1 0,2802 0,0010220 95,4 0,2799 100 0,0010300 105,0 0,3072 0,0010291 105,4 0,3068 110 0,0010376 115,0 0,3334 0,0010367 115,3 0,3330 120 0,0010458 124,9 0,3591 0,0010448 125,3 5,3587 130 0,0010546 134,9 0,3842 0,0010535 135,2 0,3838 140 0,0010639 144,9 0,4088 0,0010628 145,2 0,4084 150 0,0010737 155,0 0,4329 0,0010726 155,3 0,4324 160 0,0010842 165,1 0,4564 0,0010830 165,4 0,4559 170 0,0010953 175,2 0,4794 0,0010940 175,5 0,4789 180 0,0011071 185,5 0,5020 0,0011057 185,7 0,5015 190 0,0011196 195,7 0,5244 0,0011181 '195,9 0,5239 200 0,0011328 206,0 0,5466 0,0011312 206,2 0,5459 210 0,0011470 216,5 0,5683 0,0011452 216,6 0,5676 220 0,0011621 227,0 0,5898 0,0011602 227,1 0,5890 230 0,0011782 237,7 0,6112 0,0011761 237,8 0,6103 240 0,0011956 248,6 0,6324 0,0011933 248,6 0,6315 250 0,0012144 259,6 0,6537 0.0012118 259,6 0,6526 260 0,0012347 270,7 0,6747 0,0012317 270,7 0,6736 270 0.0012568 282,0 0,6957 0,0012534 282,0 0,6945 280 0,0012811 293,6 0,7167 0,0012773 293,5 0,7154 290 0,0013080 305,4 0,7378 0,0013и36 305,2 0,7364 300 0,0013380 317,3 0,7589 0,о013328 317,0 0,7574 310 0,001372 329,6 0,7803 0,001366 329,2 0,7786 320 0,001410 342,4 0,8022 0,001403 342,0 0,8002 330 0,001455 355,9 0,8249 0,001446 355,3 0,8225 340 0,001510 370,0 0,8484 0,001497 369,1 0,8456 350 0,001577 385,3 0,8729 0,001558 383,9 0,8694 360 0,001659 402,2 0,9006 0,0(11635 400,2 0,8958 370 0,001779 421,6 0,9310 0.00174 418,4 0,9240 380 0,00202 446,4 0,9692 0,00190 440,2 0,9577 390 0,и0284 490,5 1,0360 0,0и226 470,2 1,0034 400 0,00427 571,5 1,1571 0,00302 524,5 1,0847 410 0,00537 613,0 1,2182 0,00429 582,2 1,1698 420 0,00618 639,0 1,2560 0,00518 616,8 1,2201 430 0,00684 659,3 1,2852 0.00589 641,5 1,2555 440 0.00738 676,0 1,3086 0,00648 660,8 1.2827 450 0,00785 689,6 1,3283 0,00696 676,у 1,3056 460 0,00830 702,3 1,3462 0,00741 691,3 1,3259 470 0,00870 714,2 1,3625 0,00782 704,4 1,3439 480 0,(0907 725,4 1,3774 0,00820 716,4 1,3600 490 0,00942 735,9 1,3911 0,00855 727,5 1,3747 500 0,00975 745,8 1,4039 0,00888 737,9 1.3883 510 0,01007 755,3 1.4159 0,00918 747,9 1,4010 520 0,01038 764,4 1,4273 0,00947 757,5 1,4130 530 0,01068 773,2 1,4381 0,00976 766,7 1,4243 540 0,01098 781,7 1,4985 0,01005 775,6 1,4351 550 0,01127 790,0 1,4585 0,01034 784,2 1,4455
отрезки изобаро-изотермических процессов
b — с должны быть поделены в одинаковом
отношении, и через полученные точки прой-
дёт кривая х = const.
На диаграмме с учётом масштабов пло-
щадь под кривой процесса а — b даёт теплоту
жидкости q', подводимую к жидкости в ус-
ловиях равновесия её с насыщенным паром
для достижения жидкостью температуры ки-
пения Т' (t'), отвечающей заданному давле-
нию р; площадь под изобаро-изотермой b—с
даёт теплоту парообразования (скрытую) —г;
площадь же под участком изобаро-изотермы
b~ m — теплоту парообразования влажного
пара г - х. Площадь под изобарой с — d даёт
теплоту перегрева
Тп
Qn ~ f CpdT.
Т'
На диаграмме Т — s могут быть нанесены
также процессы у = const. В. Шюле заме-
няет нанесение изохор комбинированной
диаграммой Т — v — s, представляющей сов-
мещение диаграмм Т — s и Г —у [47].
Схема диаграммы i — s для водяного па-
ра приведена на фиг. 45.
На диаграмме нанесены нижняя а—Ь—к
и верхняя к — с — Cj пограничные кривые.
Обычно принимают для начального со-
стояния (t = 0°С) жидкости, находящейся
в равновесии с насыщенным паром, энталь-
пию i, = 0 и энтропию s = 0. Построение
кривых ведётся по точкам, значения I' s', i" s*
берутся из таблиц для пара. Кривые а —
— Ь — к и к — с— Cj сходятся в критическом
Фиг. 45
состоянии (точка fc); кривая а—b—к идёт
из начала координат; максимальная ордината
правой пограничной кривой отвечает макси-
муму значения энтальпии сухого насыщен-
ного пара. В области насыщения между По-
граничными кривыми изобары и изотермы
совпадают (процессы b — с), здесь они пред-
ставлены пучком расходящихся прямых.
В области перегрева изобары круто подни-
маются вверх, имея логарифмический харак-
тер; изотермы круто меняют направления
и представлены пологими кривыми, идущими
ВОДЯНОЙ ПАР
565
в сторону возрастания энтропии. Степень
сухости х определяется отношением отрез-
ков b — т и b — с, х — ; кривые x=const
строятся так же, как и в диаграмме Т — s.
Энтальпия заданного состояния прочиты-
вается по оси ординат; если b, с, d — состоя-
ния жидкости, сухого пара, перегретого пара
при заданном давлении р, то значения i",
in найдутся проектированием этих точек на
ось ординат, причём Г — i' = г, in — i" = qn.
Соотношение i = и + Ари позволяет для всех
случаев находить внутреннюю энергию как
u—i — Apv, так, например, и" = Г— Ари".
На диаграмме i—s в области перегрева
обычно наносят семейство процессов y=const.
Эти кривые протекают круче изобар, сохра-
няя тот же характер. Точка в области пере-
гретого пара определяет его удельный объём,
оцениваемый по значениям изохор, между
которыми находится рассматриваемая точка;
для определения объёмов влажного пара
используется выражение их № v" • х; для со-
стояния влажного пара, заданного давле-
нием р и степенью сухости х, находят по
точке на верхней пограничной кривой для
данного давления и" объём сухого пара,
а по нему vx » v" • х.
ОСНОВНЫЕ^ ПРОЦЕССЫ
Изобарный процесс (р = const). В области
насыщения процесс при р = const является
одновременно процессом изотермическим
(t = t' — температура насыщенного пара дан-
ного давления). Если у1( хп у2, х2— удель-
ные объёмы и степени сухости начального
и конечного состояний, то
о, = v" • хх + (1 —Xi) v';
y2 = v’ • x2 + (1 — x2) y';
для случаев не очень большой влажности
у2 = у" • хх;
у2= у' • Х2;
Vi = *1.
У2 Х2 1
количество теплоты, подводимое в процессе,
qp = Х2 — Xi = /2 — jj [кал/кг];
работа процесса
Ip — Р (у2 — Vi) [кгм/кг].
Если в процессе сообщения теплоты ко-
нечное состояние является перегретым паром,
то для определения этого состояния необ-
ходимо •'знать либо у2, либо t2; тогда уравне-
ние состояния / (р, у, t) = 0 позволит найти
третий недостающий параметр или он может
быть найден по диаграммам i —s, Т — и — S,
Т — s; теплота процесса и работа его нахо-
дятся так же, как и в области насыщения.
Изотермический процесс t — const (Т =
= const). В области перегретого пара (в об-
ласти насыщенного см. процесс р = const)
для нахождения параметров конечного со-
стояния может быть использовано уравнение
состояния перегретого пара / (р, у, t) = О
или они определяются по диаграммам. Теп-
лота процесса qT = Т (s2 — s,) [ккал/кг];
приращение энтропии легче всего опреде-
ляется из диаграмм i — s или Т — s; измене-
ние внутренней энергии
Ди = и2 — Uj = (z2 — Ap2vt) — (h— ApjyJ;
работа процесса
1
1 ~ А (Ут ~ & и) [кгм/кг].
Изохорный процесс (о = const). В области
насыщения условие у2 = у, даёт
V, Xt + у' (1 — xj = у' . Х2 + Уд (1 — х2),
где удельные объёмы жидкости у' и сухого
пара у* с подстрочным индексом 1 берутся
по давлению начальному (pj), а с индек-
сом 2 — по конечному (р2); при не очень
большой влажности, пренебрегая объёмом
влаги, получаем более простое соотношение
г’. хг « у'. х2.
Из приведённых выражений находится сте-
пень сухости конечного состояния. В случае,
когда конечным состоянием является пере-
гретый пар, параметры его могут находиться
по уравнению состояния перегретого пара
или из диаграмм. Работа процесса равна
нулю (у2 = v1 — у). Теплота процесса нахо-
дится по разности внутренних энергий
9» = — “1 = (G — Ар2у) — (ii — Appj) =
= i2 — i, + A (pj — p2) у [ккал/кг].
Адиабатный процесс (dq = 0, q = 0). Об-
ратимый адиабатный процесс (так как dq =
= Т ds, Т Ф 0, ds == 0) определяется усло-
вием s2 = s1( которое и может быть исполь-
зовано для определения параметров конеч-
ного состояния; аналитическое решение
задачи нахождения конечных параметров
сложно, наоборот, решение по энтропийным
диаграммам (г— s и Т — s), где адиабаты
изображаются прямыми, параллельными оси
ординат, весьма просто; адиабаты расширения
из начального состояния идут по вертикали
вниз, адиабаты сжатия — вверх; конечное со-
стояние определяется пересечением адиабаты
с кривой, характеризующей заданный пара-
метр конечного состояния (например изобары
конечного давления р2). Работа процесса
находится по разности внутренних энергий
начального и конечного состояний.
ц, — и*
I = = 427 (Ц1 _ Иа) =
= 427 (i! — z2) — (p^i — p2v2) [кгм/кг].
Цейнером предложены приближённые урав-
нения: при перегретом паре ру1’333 = const
уравнение применимо для процесса, пол-
ностью идущего в области перегрева; если
расширение, начавшееся в области перегрева,
переходит в область насыщения, то приме-
нимость уравнения ру1,333 = const ограни-
чивается моментом, когда пар, расширяясь,
достигнет верхней пограничной кривой, для
которой можно принять уравнение pv 2,
где р [кг/с-и2], у [м3/кг]. Дальнейшее рас-
ширение, начинающееся от состояния сухого
пара, по Цейнеру, подчиняется уравнению
ру1,135 = const. Для влажного пара с началь?
566
ТЕПЛОТА
ной степенью сухости х в пределах от 0,1
до 0,7 адиабатное расширение идёт по урав-
нению ру1-035 + °»1 х = const. По Каллен-
деру, для перегретого пара действительно
Р
до критического давления уравнение —
ТТ
= const; для малых и средних давлений ис-
ро
пользуется также формула ? = const. Ре-
шение вопросов, связанных с адиабатными
процессами, по приведённым приближённым
уравнениям следует заменять в тех случаях,
когда это возможно, решением по тепловым
диаграммам; не следует приведённые пока-
затели степеней в уравнениях адиабат пони-
• С о
мать как отношение теплоемкостей
КРУГОВЫЕ ПРОЦЕССЫ (ЦИКЛЫ)
Цикл Карно. Фиг. 46 и 47 дают характер
протекания цикла Карно для насыщенного
пара. Подвод qL [ккал/кг] теплоты по изо-
терме Тх— (&—1) для насыщенного пара
является одновременно процессом парообра-
зования, идущим по изобаре рх; отнятие
теплоты д2 [ккал/кг] по изотерме Г2 для
насыщенного пара одновременно является
изобарным сжатием 2 — а при давлении р2,
сопровождающимся значительным увлажне-
нием пара
I 9s I = G — la = г (х2 — ха);
1—2 и а — Ь — адиабаты расширения и сжа-
тия.
На диаграмме Т — s qr представлено пло-
щадью с — b — 1 — d — с, q2 — площадью с —
— а — 2— d—с; работа 1 кг пара в тепло-
вых единицах А1 = </х — д2 представле-
на на диаграмме Т — s площадью а—Ъ —
—1—2 —а.
На диаграмме р — v площадь а—b—1—
—2 — а даёт работу / [кгм/кг]. Термодина-
мическии к. п. д. цикла т^ = 1— — =1—
41 1 1
Если предположить при протекании цикла
Карно переход его в область перегрева (точ-
ки 7 и 2 расположатся за верхней погранич-
ной кривой), то подвод теплоты по изотерме
за верхней пограничной кривой уже не будет
совпадать с изобарным процессом, а будет
сопровождаться падением давления; наобо-
рот, изотермическое отнятие теплоты (сжатие
по изотерме Т2), начавшееся за верхней по-
граничной кривой, будет протекать с повы-
шением давления до прихода в состояние
сухого насыщенного пара. Таким образом,
переход цикла Карно в область перегрева,
/ ТЛ
не изменяя его к. п. д. Iти = 1 — , при-
водит к пароперегревателю и холодильнику,
работающим не при р = const, как в обычных
установках, а при t = const, что усложняет
их конструкцию.
Цикл Рэнкина — Клаузиуса. На фиг. 48
и 49 дан круговой процесс Рэнкина — Клау-
зиуса, состоящий из участка нижней погра-
ничной кривой а—Ь, изобары b — 1, адиа-
баты 1— 2 и изобары 2 — а. Установка, реа-
лизующая этот круговой процесс, должна бы
включать элементы: насос-подогреватель для
повышения давления воды от р2 до рх с одно-
временным увеличением объёма её от в2 до
v' и повышением температуры от t до t(
(для осуществления процесса а — Ь, идущего
по нижней пограничной кривой), котёл-испа-
ритель (процесс b — тп), перегреватель при
постоянном давлении (процесс m—7), рас-
ширительная машина, поршневая или тур-
бина (процесс 7—2) и конденсатор (процесс
2 — а). В действительных установках пита-
тельный насос не выполняет роли подогре-
вателя воды по нижней пограничной кривой,
сжатие в нём может рассматриваться адиа-
батным (а — ох). Однако для жидкости адиа-
батное сжатие не даёт сколько-нибудь ощу-
тительного повышения температуры. Таким
образом, по выходе из насоса нагнетаемая
вода имеет температуру, практически равную
исходной (в точке at t x t', причём как ре-
зультат адиабатного сжатия A t «0,1—0,7°С);
последующий по выходе из насоса подогрев
воды до t в точке b осуществляется или
в экономайзере или в котле (участок изобары
аг — Ь). Круговой процесс, отвечающий этим
условиям, определяется контуром а — ах —
—Ь — m—1—2 — а. Разница в затрате работы
на насос-подогреватель и питательный насос
(в котором практически адиабатное сжатие
может расцениваться как изотермическое без
изменения объёма) весьма мала, ощутима
может быть только при высоких давлениях,
близких к критическому состоянию.
Исходя из этих соображений, циклом иде-
альной паровой установки принимают кру-
говой процесс Рэнкина — Клаузиуса. В диа-
грамме I— s цикл Рэнкина — Клаузиуса дан
на фиг. 50. По диаграмме Т — s затрачивае-
мое количество теплоты qx и /х—ia выра-
жается площадью с — а — b — m — 1 — г — с;
теплота, отдаваемая в конденсаторе, q2— i2 —
— ia ~ z2 — t2 (t2 = f — температура насы-
ВОДЯНОЙ ПАР
567
щепного пара по давлению р2), представлена
площадью е—2 — а — с — е. Работа, совер-
шаемая 1 кг пара, выраженная в тепловых
единицах, А1 — цг — q2 = — 12 ккал/кг (пло-
щадь а — b—т — 7—2— а). Термодинами-
ческий к. п. д.
Диаграмма i — s позволяет проще всего найти
характеристики цикла.
ДРОССЕЛИРОВАНИЕ ГАЗОВ И ПАРОВ
Дросселирование газов и паров происхо-
дит при прохождении потока через местное
сопротивление (дроссель) в трубопроводе.
При отсутствии теплообмена с окружающей
средой и при условии пренебрежения раз-
ностью кинетических и потенциальных энер-
гий перед и за дросселем процесс удовле-
творяет требованию ir = i>. Данное утвер-
ждение становится очевидным из рассмотре-
ния уравнения первого начала для случая
течения по каналу, выраженному через
функцию энтальпия (см. стр. 527 первое
начало).
При принятых допущениях дросселиро-
вание рассматривается как необратимый
процесс, удовлетворяющий условию = Z2,
что позволяет по диаграмме i — s просто
решать задачу нахождения параметров газа
или пара в его конечном состоянии. Для
решения задачи по диаграмме /—s из на-
чального состояния 7 проводится изоэн-
тальпа до пересечения её с кривой, характе-
ризующей на диаграмме известный параметр
конечного состояния. Точка пересечения
даст состояние 2 и позволит прочитать по
диаграмме остальные параметры этого со-
стояния. Процессы дросселирования—не-
обратимые процессы, так как они могут
итти только в сторону падения давления
(p2<Pi), и всегда характеризуются возраста-
нием энтропии. Возрастание энтропии в этом
случае — свидетельство необратимости про-
цесса, а не подвода теплоты, так как тепло-
обмен со средой исключён из рассмотрения,
(это оговорено выше). Аналитическое реше-
ние задачи сложнее, но и оно может исхо-
дить из условия i'i = i2. Дросселирование га-
за или пара приводит к падению давления,
температуры (последнее лишь обычно) и
увеличению удельного объёма. Для пара,
в зависимости от исходного состояния перед
дросселированием, результат последнего мо-
жет вызывать либо увеличение, либо умень-
шение сухости пара.
В процессе дросселирования d/=»0, что
даёт в этом случае
(см. уравнение для di в независимых пере-
менных Тир стр. 530).
Для газа, подчиняющегося уравнению
состояния Pv = RT, числитель АТ ) —
\oi !р
— Av = 0, т. е. в этом случае = 0 и,
V>P)i
следовательно, дросселирование идеального
газа осуществляется без изменения его тем-
пературы.
Для реального газа возможны случаи:
1. АТ (д—\ - Av > 0,
т. е.
> ° И ^<0 < ° (так как < 0)
—это так называемый положительный дрос-
сель-эффект, дающий понижение темпера-
туры при дросселировании.
2. АТ — Av < 0,
(от/
\ /р
т. е.
< 0 и dT(Vl > 0
дР h
(так как dp^ всегда отрицательно), — это
так называемый отрицательный дроссель-
эффект, дающий повышение температуры
при дросселировании.
3.
т. е.
| — Ау = 0,
р
= 0 и dT'(j) = 0,
—в этих состояниях реальный газ ведёт себя
аналогично идеальному. Эти состояния на-
зывают точками инверсии, в них дроссель-
эффект меняет знак.
Предположение, что реальный газ подчи-
няется приведённому уравнению состояния
Ван-дер-Ваальса, даёт, что для точек инвер-
сии приведённый объём и приведённая тем-
пература будут
3
3± /9 — rcz
Т/ = Т 1^9 — ГС/ — ~ ГС/,
где тс/— приведённое давление в точке ин-
версии.
Исследование этих выражений показы-
вает, что
1. При тс/ > 9, со/ и т/ мнимы» т. е^ при
этих значениях давления точки инверсии
не имеются.
2. При тс/ == 9 имеется одна точка инвер-
сии с <о/ = 1 и Т/ -3.
3. При тс/ < 9, ш/ и т/ имеют по два зна-
чения» т. е. для каждого давления будет две
точки инверсии.
568
ТЕПЛОТА
ТЕЧЕНИЕ ГАЗОВ И ПАРОВ ПО ТРУБАМ, ИСТЕЧЕНИЕ ИЗ РЕЗЕРВУАРОВ
ИСХОДНЫЕ УРАВНЕНИЯ
Исходными уравнениями для анализа яв-
лений течения газов и паров служат
1. dq = dl +A(d~+dh\ +Adlc
— уравнение первого начала термодинамики
для течения сплошной среды по каналу (см.
первое начало термодинамики стр. 527).
2. Для случая установившегося течения,
когда в единицу времени через любое сече-
ние трубы проходит неизменное по времени
постоянное весовое количество среды, урав-
нение непрерывности будет
/л = fsw2 = /JV = const или dv = df + dW t
Vi V 2 v v f w
где /, /ц /2 — сечения трубы в лг2; w, w,, u>2—
скорости в м/сек; v, vlt v2 —удельные объёмы
в м2/кг.
3. Связь между объёмом, давлением и
скоростью
— vdp = d^~ .
2g
При рассмотрении обычных случаев тече-
ния по трубам принимают его адиабатным
(dq = (f), пренебрегают изменением внешней
потенциальной энергии потока за счёт обыч-
но малых перемещений по высоте центра
тяжести его (dh =0) и полагают работу
dlc равной нулю, считая стенки канала не-
подвижными. В этих условиях уравнение
первого начала принимает вид:
Ad w_L = — dl.
2g
СООТНОШЕНИЯ МЕЖДУ ПАРАМЕТРАМИ
ДВИЖУЩЕЙСЯ СРЕДЫ И СЕЧЕНИЕМ
ТРУБЫ
(1 \
v = —— const | ;
7 /
W2 ,V1
/1w1=/2wa, — Л = v (Рг — p2), т. e. уве-
личение скорости может иметь место лишь
при падении давления и уменьшении сече-
ний трубы в направлении движения жидко-
сти.
2. Упругие жидкости (газы и пары). Т е-
чение при малых изменениях дав-
ления. Принимают соотношения для ка-
пельных жидкостей, т. е. пренебрегают из-
менением удельного объёма (веса), и считают
V = — = const.
7
“'г wi
Приближённый подсчёт ~ — с
2g 2g
заменой точного значения этой разности
(___vdp приближённым значением v-bp
р
(фиг. 51) приводит в предположении адиабат-
ности расширения к относительной ошибке
8 =
v-Лр \ Jp р j 2k р
где к — показатель адиабаты.
Задаваясь значениями 8, к, р, определяют
падение давления Др, в пределах которого
подсчёт по приближённой формуле допустим.
Течение при больших измене-
ниях давления. Из уравнения непре-
рывности для упругой жидкости
/а — /1
Wj у2
w, у.
Фиг. 51
Таким образом, ввиду переменности удель-
ного объёма вопрос, будет ли сечение 2, взя-
тое в направлении движения потока, больше
или меньше исходного сечения 7, решается
в зависимости от того, будет ли отношение
больше или меньше единицы.
»2Ух
Дальнейшее исследование вопроса опи-
рается на анализ уравнения непрерывности
<!1= — — , которое в сочетании с усло-
/ у w
вием адиабатности течения = — к Е- и
dv v
dw^
уравнением-^-— =—vdp приводится к виду:
df _ gkpv — w2 dp
f ' k-w2 ’ p
Скорость звука в среде с давлением р
и удельным объёмом у подсчитывается по
выражению ws = V gkpv ; поэтому в приве-
дённой выше формуле (I) gkpv равно квад-
рату скорости звука, = gkpv.
Течение с ускорением
w2 > Wi> — = — vdp,
т. е.
dp < 0 и < 0
Р
Из уравнения (I) в этих условиях следу-
ет, что знак у определится тем, будет ли
gkpv больше или меньше iv2; при gkpv > w2,
что равносильно условию ws > ы, т. е, когда
течение по трубе осуществляется со скоро-
стью, меньшей скорости звука, ^-<0; таким
ТЕЧЕНИЕ ГАЗОВ И ПАРОВ ПО ТРУБАМ
569
образом, в этом случае ускорение потока до-
стигается за счёт уменьшения сечения тру-
бь» в направлении движения потока. Скоро-
Наиболее общей задачей, охватывающей
различные условия течения, является задача
сти iv, меньшие скорости звука, называют
подкритическими. При gkpv < w2, что рав-
о течении по трубе переменного
наличием в ней минимального
носильно условию ws < w, т. е. когда тече-
ние по трубе совершается со скоростью,
большей скорости звука, > 0; таким об-
Интегрируя
div2
уравнение -t~-
сечения с
сечения /т.
= — vdp в
разом, при скоростях течения, превышаю-
щих скорость звука, ускорение потока до-
стижимо при увеличении сечений трубы в на-
правлении движения потока; скорости по-
тока, превышающие скорость звука, назы-
вают надкритическими. Движение потока
с ускорением, начавшееся с подкритической
скоростью, может перейти в некоторых ус-
ловиях в движение со скоростями надкрити-
ческими, пройдя через значение скорости
потока _____
wk = V gkpv = ws,
предположении, что поток находится в адиа-
батных условиях (уравнение pvK = const),
обозначая величины, относящиеся к началь-
ному сечению трубы, индексом 0, относя-
щиеся к минимальному сечению, — индексом
т, получаем скорость потока в минималь-
ном сечении
™т
j/4w^+2g JL povo
К — 1
л-i-
1—/Pm\ 1
\Ро)
MjceK.
где wk—критическая скорость; при этом по
уравнению (I) у = 0, — сечение трубы, в ко-
тором достигается критическая скорость,
будет минимальным. Изменения р, f, IV да-
ются схемой фиг. 52.
Условие для достижения скоростью кри-
тического значения
к
В _ Рт,к _ "'о 2 У'1
к Ро \Л4-1 в>20 к 4-1/
где ivs 0 — скорость звука в среде с пара-
метрами р0 и va в начальном сечении
Подкрцти- Надкрити-
Напрабление движения
потока.
Фиг. 52
Надкрити-
ческая
область
Подкрити-
ческая
область,
Направление движения
потопа
Фиг. 63
о = У gkPova-
Критическая скорость в минимальном се-
чении
wm, к = т = / £кРт, kvm,k =
к—\
gkpnv^k ft
Степень сужения трубы при получении в
минимальном сечении /т> к критической ско-
рости
Течение с замедлением
iv2 < IV1, — = — vdp,
т. е. мы должны иметь dp > 0 и -В > 0.
Р
Уравнение (I) даёт: если iv2 > gkpv, т. е.
iv > tv* = iv5 (течение в надкритической об-
ласти), то < 0, — замедление потока до-
1т, к ТУр vm, к _
/о »т, к ' ve
1
' ~й~+ 1
к—1 wo 2 \2(к~
Л+1 в>20 *4-1/
Расход газа через сужающуюся трубу
стигается при уменьшении сечений трубы в
направлении движения потока; наоборот,
при iv2 < gkpv, т. е. iv < (в подкри-
тической области),^ >0—замедление по-
тока вызывается увеличением сечений трубы.
Переход из надкритической области в под-
критическую может осуществиться в неко-
торых условиях в наименьшем сечении fm,
где по уравнению (I) = 0 npn_iv^-iv*^ivA.
(фиг. 53).
Расход газа через сужающуюся трубу
при достижении в сечении /т к критической
скорости ivm к
п f т, к ' й’т, к
ик------ ----
vm, к
— f т,к‘
JH-1
ь_ 1 IV? о
L2-^-+-(ке/сек),
/< +1 IV2 /с +1 )
570
ТЕПЛОТА
ИСТЕЧЕНИЕ ГАЗОВ И ПАРОВ
ИЗ РЕЗЕРВУАРОВ НЕОГРАНИЧЕННОЙ
И ОГРАНИЧЕННОЙ ЁМКОСТЕЙ
Все случаи истечения из ёмкостей, вну-
три которых, несмотря на истечение из них,
не меняются параметры пара или газа, рас-
сматриваются как случаи истечения из ре-
зервуара неограниченной ёмкости. Эти ус-
ловия внутри резервуара могут достигаться
путём той или иной компенсации расхода,
например непрерывным парообразованием,
идущим в котле.
Истечение, вызывающее изменение пара-
метров среды внутри резервуара, именуется
ниже истечением из резервуара ограничен-
ной ёмкости.
Истечение из резервуара неограниченной
ёмкости
Возможно предположить отсутствие теп-
лообмена между истекающей средой и стен-
ками, образующими короткий выходной ка-
нал, насадку, через которую осуществляется
истечение.
Исходными уравнениями для определения
скорости служат (см. выше течение газов и
паров):
= О)
A^ = -dZ. (2)
2g
Уравнение (1) в сочетании с условием адиа-
батности истечения pwA = const и принятием
начальной скорости TVj = 0 и выходной ско-
рости iv2 = iv даёт
fc-r ’
. (3)
где подстрочным индексом 1 отмечены со-
стояния внутри резервуара, а индексом 2—
состояния среды, в которую происходит ис-
течение.
Уравнение 2 даёт
= V^A (к ~ h)’ (4)
Секундный расход, определяемый из ус-
ловия G = находится по формуле
Vi
/ г - *+11
G=/k 2g йМ [(£)*-(£) к (5)
где / [л2] — выходное сечение насадки.
Исследование приводит к двум случаям:
Истечение в подкритической области
Определяется условием
рА<р=£?<1,
Pi
где — давление среды, в которую проис-
ходит истечение;
Pi—давление среды, из которой проис-
ходит истечение;
Р —отношение этих давлений;
Рй— критическое отношение давлений:
3»
Для двухатомных газов
» перегретого пара .
» сухого насыщ. пара
» влажного насыщен,
пара с начальной сте-
пенью сухости х . . .
Л=-1,035+0,1х
1.4
1,3
1,135
0,528
0,546
0,577
приближённое выражение для ₽*:
з
^=1,2555—0,65]^ к (формула В. М. Таре-
ева).
В рассматриваемом случае (РА < р < 1)
применимы для расчёта формулы (3) и (5);
при одинаковых исходных условиях (pt wx)
по мере уменьшения р и приближения его
значения к Рй w и Q растут;
при р = P* достигаются:
w= wft=j/r2g^2__p,p1 (7)
— критическая скорость истечения и
1
— максимальный расход.
Для максимального расхода В. М. Тареев
даёт приближённую формулу
Коэфициенты в формулах (7) и (8) в за-
висимости от к принимают следующие значе-
ния:
к
У2* TF1
Для двух- атомныхгазов 1,4 3,38 2,145
Для пере- гретого пара 1,3 3,33 2,09
Для сухого насыщенного пара 1,135 3,23 1,99
Значение р* может быть использовано
в двух направлениях:
ТЕЧЕНИЕ ГАЗОВ И ПАРОВ ПО ТРУБАМ
571
во-первых, если задано давление внутри
резервуара рг и ставится вопрос, при каких
давлениях окружающей среды условия исте-
чения будут подкритическими, то из усло-
вия ₽ — ₽* имеем
=₽fe и p2ifc =
\P1/k
это значение р2 к определит максимальное
значение давления окружающей среды, ог-
раничивающее подкритические условия, т. е.
возможные пределы р2
Рг, к < Рг < Р15
во-вторых, если задано давление среды,
в которую происходит истечение р2, и ста-
вится вопрос о пределах plt то из I —) =?k
\P1'k
имеем
это значение pt определит его верхний пре-
дел для подкритических условий истечения,
т. е. возможные пределы
Ps < Pi< •
Pfe
В случае истечения при небольшой раз-
ности давлений, определяемой условием
0,9 < & < 1, можно пренебречь изменением
Pi
удельного объёма, что приводит к формулам
» = /2g« (Pi-p^ = [м/сек];
G = / У 2g &-~Рг1 =
= / — [кг/сек].
Истечение в надкритической области
Определяется условием
О <₽=£»< р*.
Pi
При истечении через простую насадку в
выходном сечении устанавливаются крити-
ческая скорость — см. формулу (7) и мак-
симальный секундный расход — см. фор-
мулу (8). Давление в выходном сечении пре-
вышает давление окружающей среды и оп-
ределяется из условия
= ₽*,
\Pi/
т. е.
Pbk — Plfikf
выходная скорость в
по уравнению
2g
этом случае находится
Рг, к
j -- vdp
Рх
= 0, как начальная скорость, отвечаю-
щая движению внутри резервуара), т. е. в
насадке совершается расширение лишь в пре-
делах от р, до р2 к, дальнейшее падение
давления в струе (от р2 до р2) происхо-
дит уже по выходе из насадки, не исполь-
зуется для превращения потенциальной
/ р. \
энергии j J—vdp I в кинетическую энергию
\ Рг, к /
струи, а затрачивается на потери при вы-
ходе.
Использование всей потенциальной энер-
гии, отвечающей полному расширению газа
от pj до р2, осуществляется в насадке Ла-
валя, в которой за наименьшим сечением
насадки идёт расширяющаяся часть, создаю-
щая условия для превращения потепциаль-
ной энергии I ( — vdp в кинетическую.
\ Рг, к /
Выходная скорость из насадки Лаваля пре-
вышает критическую и при расчётном ре-
жиме находится из уравнения (3) по отно-
шению давлений для полного перепада
Pi
давлений (р2—давление окружающей среды,
Pt—давление в резервуаре).
Секундный расход подсчитывается по
уравнению (8), где, однако, / = /min—наи-
меньшее сечение насадки, а не выходное;
по выходной скорости (w > на основа-
нии сплошности потока расход может быть
найден из выражения Gmax = , где /2
[№], w [м/сек], у2[л<2/кг] отнесены к выход-
ному сечению.
Определение скорости истече-
ния по разности энтальпиии по
диаграмме i — s. При пользовании фор-
мулой (4)
w = 1/^ (G - 12) = 91,53
г А
энтальпия i\ берётся по состоянию в резер-
вуаре; энтальпия (2 отвечает состоянию газа
или пара в том сечении насадки, для кото-
рого ищется скорость.
Если определяется скорость выхода из
насадки, то 12 отвечает состоянию в выход-
ном сечении (устье) насадки.
При истечении в подкритической области,
когда < £? < 1, при простой насадке в
Pi
устье её устанавливается давление окружаю-
щей среды р2; оно и определяет конец рас-
ширения и расчётное в формуле (4).
При истечении в надкритической обла-
сти, когда 0 <. Р? < P>k, при простой насадке
Pi
в устье её достигается лишь давление р2 ь—
= Рй P2>k > Pv и именно оно (p2,ft)
определяет конец расширения в насадке и
расчётное i2 для нахождения выходной ско-
рости, которая в этих условиях равна кри-
тической
W = wk = 91,53 / G—f2'.
При истечении в надкритической области
через насадку Лаваля давление Р»,^=^‘Р>
572
ТЕПЛОТА
создается в наименьшем сечении насадки;
здесь скорость достигает критического зна-
чения W/j и определяется по энтальпии /2,
отвечающей расширению до р2 к f
w* = 91>53]AI-i_f2;
в выходном сечении (устье расширяющейся
части), давление будет равно р2, и оно опре-
делит конец расширения, расчётное значе-
ние i2 и выходную скорость w > Д'/. (w =
Фиг. 54
= 91,53У71 — i2). Фиг.5Ф даёт схему опре-
деления расчётных i2 и 12 по диаграмме i—s
для пара.
Истечение из резервуара ограниченной
ёмкости
В общем случае рассматривают задачу
об истечении из резервуара, в котором за
время истечения параметры начального со-
стояния р0, vQ, То меняются, приобретая те-
кущие значения Pt, К/, Тр предполагают,
что изменения состояния внутри резервуара
подчинены условию р0 и™ = pfv™ (v0,vi —
удельные объёмы); при m = 1 — внутри ре-
зервуара изотермическое расширение, интен-
сивный подвод теплоты к массе газообраз-
ной среды резервуара; при m = к — отсут-
ствие теплообмена.
Ёмкость самого резервуара и выходное
сечение переменны во времени: Ve и V/—
начальный объём резервуара и его текущее
значение в л:3; /0 и ft — выходное сечение
начальное и его текущее значение в -и2.
Основное диференциальное уравнение,
описывающее условия истечения из резер-
вуара ограниченной, переменной ёмкости
через переменное выходное сечение
р2— давление среды, в которую происходит
истечение; t — время в сек.
Истечение из резервуара ограниченной
постоянной ёмкости Vo через постоянное
сечение F
Истечение в надкритической
области. В этом случае
₽*> Pl > £ ;
РЛ
0<^ <
Ро
Ф Фщах
Уравнение (9) принимает вид:
1 _ д
J. (Pi\2m 2 . (рЛ в
m \р0) [Ро/
= - Мтах
у о
Время, потребное для понижения давле-
ния в резервуаре от начального рв до дав-
ления Pi > —
t= 2 • v° X
Н-Фтах-*7
Vpovo
сек.;
то же, но до давления р: к*=-±
*•’ п R,
Г k
При изменении параметров внутри резер-
вуара по закону ppi: = pova (m = 1) время
на истечение для понижения давления до
t = 2>303 . Ер J_ . ig (М
^•Фтах' FVPo^o W
Истечение в подкритической
области. В этом случае
Ь < < 1, Pi <
Ро
Ра
Из уравнения (9) находим
1___з
!р,\2т 2
i_ 2% .Ы
ТЕЧЕНИЕ ГАЗОВ И ПАРОВ ПО ТРУБАМ
573
и время, необходимое для понижения давле-
ний до Pi
Здесь ф определяется уравнением (10).
В общем случае
i 1
I m+1
(n \ 2т ,
— I * Ф
Pl)
. /2?) находится графиче-
а \Р‘ /
ски, при некоторых частных значениях т—
аналитически [48].
При 0,9 < 21 < 1, т. е. при истечении под
Ро„
влиянием малой разности давлении, с неко-
торыми допущениями и в предположении,
подкритической области 10 <21 < дав-
• Ро
ление в резервуаре /?0 понижается до pi,
причём < 2» < 1 или pt < 2? , р — 21\
Pl ?k РА/
находим путём суммирования времени на ис-
течение в надкритической области при по-
нижении давления в резервуаре до -Р~
Pk
с временем для понижения давления в под-
критнческой области от pi к до pi .
Истечение из резервуара ограниченной,
переменной по времени ёмкости через
переменное по времени выходное сечение
а) При истечении из резервуара постоянной
ограниченной ёмкости (V„) через переменное
по времени сечение / фактором, определяю-
щим падение давления в резервуаре, слу-
жит произведение f-dt— «время—сечение»
[сек-м2]; для определения понижения давле-
ния от р0 до pi должен быть определён
t»
J fdt из уравнения (9)
(12)
что изменение параметров в резервуаре под-
чинено условию pivi = pov0 (m = 1), время
для понижения давления до р, (р2 < Pi < ра)
2,303 X
рР V 2gp„v„
для полного выравнивания давления в ре-
зервуаре с давлением окружающей среды,
т. е. при pi = р2,
14-1/1—2*
t = 2’303v° ig ' ._?> .
Р-Р У2gpeva 1 _ р/1 -2*
Время на истечение,
критической области и
начавшееся в над-
заканчивающееся в
Правая часть последнего уравнения от-
личается от таковой в уравнениях для на-
хождения времени, потребного на истечение
в изложенных выше задачах при F = const,
лишь отсутствием в ней постоянного мно-
жителя 2. , Исходя из этого, следует, что
все найденные выше выражения для опре-
деления времени истечения t будут пригод-
t,
ны для нахождения время — сечение \l-dt,
i.
если в правую часть уравнений не вводить
множитель А.
F
при нахождении j f-dt обла-
сти истечения должны учитываться согласно
указаниям, данным выше. Закон изменения
сечения по времени / = ?(/) может быть за-
дан или аналитически, или, как это бывает
чаще, графически—кривой изменения сече-
ния по времени, площадь под которой даёт
время — сечение.
574
ТЕПЛОТА
Сочетание закона / = у (О и формул для
it
§f-dt, вытекающих из уравнения (9), даёт
ii
решение вопроса о нахождении времени, не-
обходимого для искомого понижения давле-
ния в резервуаре и обратно.
б) При истечении из резервуара ограни-
ченной переменной по времени ёмкости че-
рез переменное по времени сечение факто-
ром, определяющим понижение давления в
резервуаре, служит уже 1^.. Решение ди-
ференциального уравнения (9) относительно
1^1, нахождение [ и использование этого
V/ Vi
параметра как расчётного обычно заменяют
приближённым решением, разбивая процесс
на ряд элементов, внутри которых ёмкость
резервуара принимают неизменной.
М. И. Жуковский рассматривает задачу
нестационарного течения газа, относя её
к случаям опорожнения и наполнения резер-
вуаров конечных объёмов в предположении
отсутствия ударных явлений [17].
ТЕПЛОПЕРЕДАЧА
Теплопередача—обусловленная разностью
температур передача теплоты от одного тела
к другому или от одних частей тела к дру-
гим частям того же тела. Рассматривают
теплопередачи: кондуктивную (кондукцию,
теплопроводность), конвективную (конвек-
цию), радиационную (теплопередачу излуче-
нием, лучистую теплопередачу). Действи-
тельные процессы теплопередачи обычно
сложны, в них все виды теплопередачи со-
путствуют друг другу; расчёт таких слож-
ных процессов упрощается путём изучения
отдельных видов теплопередачи, отвлекаясь
от других. Задачи теплопередачи могут
охватывать области, где каждая точка ха-
рактеризуется определённой температурой,
остающейся неизменной во времени (стацио-
нарное температурное поле), и области, где
каждая точка имеет температуру, меняю-
щуюся по времени (нестационарное темпера-
турное поле): в первом случае — установив-
шаяся (стационарная) теплопередача, во
втором — неустановившаяся (нестационар-
ная).
КОНДУКТИВНАЯ ТЕПЛОПЕРЕДАЧА
(КОНДУКЦИЯ, ТЕПЛОПРОВОДНОСТЬ)
Теплопередача, осуществляемая путём
передачи энергии элементарными частицами
вещества (электронами, атомами, молеку-
лами), представляет собой результат микро-
процессов обмена энергии между элементар-
ными частицами, вступающими в соприкосно-
вение друг с другом. В наиболее чистом
виде кондуктивная теплопередача происхо-
дит в твёрдых телах, в жидкостях и газах
реже и только в тонких слоях.
По гипотезе Фурье основное уравнение
теплопроводности
dQ = — A dF • dz;
здесь dQ— количество теплоты [ккал], пере-
даваемое за элемент времени dz [час] через
элемент изотермической поверхности dF[Ma] в
dt
направлении нормали к ней;— [град/м]=
= grad — температурный градиент, вектор-
ная величина,равная производной от темпера-
туры но нормали к изотермической поверх-
ности в данной точке её и направлен-
ная в сторону возрастания температуры;
Г ккал ]
* м гппп.ипг ~ коэфициенттеплопровод-
ности, количественная характеристика спо-
собности тел к осуществлению кондуктивной
теплопередачи, численно равная количеству
теплоты, передаваемому за 1 час через 1 л:3
изотермической поверхности (удельному теп-
ловому потоку) при grad t = 1. Если эле-
мент dFr не совпадает с изотермической по-
верхностью и нормаль s к dFx образует с нор-
малью п к изотермической поверхности
угол ?, то
dQ = — ' дп ‘ cos У ' ' dz =
= -х-
при постоянном А
Q - — А С С dt . dPt d z;
J J ds
о (F.)
dt
при стационарном температурном поле
не зависит от времени
dF1 = -A.t ^dFi-
(Л)
Влияние температуры на А
С ростом температуры А чистых металлов
обычно убывает (исключение алюминий), для
них отношение А к коэфициенту электропро-
водности приблизительно постоянно (закон
Видемана — Франца) и пропорционально аб-
солютной температуре (закон Лоренца); при-
сутствие посторонних примесей может сильно
менять А.
У теплоизоляционных материалов с повы-
шением температуры А обычно растёт (роль
радиации поверхностей твёрдых составляю-
щих теплоизолятора через внутренние воз-
душные прослойки).
Коэфициент теплопроводности жидкостей
лежит в пределах:
ТЕПЛОПЕРЕДАЧ А
575
от X =0,08 до X =0,6
У многих жидкостей с повышением тем-
пературы X убывает— см. фиг.55, где даются
значения X некоторых жидкостей; на фиг.55
кривая 1 даёт X глицерина, 2— метилового
спирта, 3 — этилового спирта, 4—ацетона,
5—сероуглерода, 6 — толуола, 7 — пентана,
8—этилбромида, 9— четырёххлористого угле-
рода, 70 — воды. У воды до 180°С X растёт,
при дальнейшем повышении — убывает;
между 0 и 80°С
на 11—15%. По кинетической теории, пока
длина свободного пробега молекул мала по
сравнению с толщиной газового слоя, X не
зависит от давления. При весьма малых
давлениях (значительно увеличена длина
свободного пробега) влияние давления тем
сильнее, чем меньше толщина слоя. На X па-
ров влияние t и р велико.
Таблица 43
Коэфициент теплопроводности металлов
Х = 0,447 (1 + 0,003 7)
ккал
м-час-град
Для газов значения X лежат в пределах
0,005 — 0,15
ккал
м-час-град ’
У газов с повышением температуры X уве-
личивается. Для смеси газов коэфициент
теплопроводности может быть определён пу-
тём опыта, закон аддитивности здесь непри-
меним.
Влияние давления на X
При увеличении давления от 1 до 2 000 ат
отмечено у многих жидкостей повышение X
ккал
час-м-град
Металлы и сплавы Темпера- тура в °C X
Чистые металлы
Висмут 18 7,0
» . . . . 100 5.8
ВольЛрам ... 20 138
Золото . . 18 252
» 100 253
Кадмий 18 80
» ........... 100 77,8
Магний 0—100 137
Платина 18 60
» 100 62,4
Ртуть 0 5,4
» 50 6,9
Сурьма . . 0 15,8
л • 100 14,5
Сплавы
Константан (60 Си, ДО N1) 18 19,5
Константан (60 Си, 40 NI) 100 23,1
Манганин (84 Си, 4 Ni, 1 18 19,1
12 Мп) 1 100 22.6
Сплавы никеля
70 Ni, 28 Си, 2 Ге . . . . 2и 30
62 Ni, 12 Сг, 26 ге .... 20 11,6
Никелевое серебро .... 0 25,2
То же 100 32
Платиноид 18 21,6
Подшипниковый металл
(белый) 20 20,4
Таблица 42
Влияние температуры иа коэфициент теплопроводности металлов и сплавов
ККиЛ
час - м-град
(По данным «Международных справочных таблиц») |28] X в
Металлы и сплавы Температура t в СС Точка плавле- ния в °C
0 1и0 200 ЗОЭ 400 500 600
Алюминий 174 177 197 234 274 319 364 649
Латунь (90—1 О) 88 101 115 128 143 155 168 1 050
» (70-30) 91 9-1 95 98 100 103 104 940
» (67-33) 86 92 97 104 110 116 130 940
» (60—40) 91 103 118 131 145 160 172 894
Медь (чистая) 337 331 327 322 315 311 307 1 080
Никель . . . 50,6 50,3 49,2 48,9 47,8 47,5 46,2 1 4.')0
Олово 54 51 46 — —« — — 231
Свинец 29,8 29,5 28,3 27,4 — м 34b
Серебро 364 358 353 348 344 339 334 960
Сталь (мягкая) 54 49 45 40 36 31 27 1 ьзо 2 900
Тантал (при 18°) 47 —- — — —• — —-
Цинк 97 92 88 84,5 80 — —« 419
I Чугун 43 42 30 34 48 67 82 1 200
I Чугун с высоким содержа- * нием кремния 45 - — — — — — 1 26j
ТЕПЛОТА
Таблица 44
Удельный вес, коэфициент теплопроводности,
теплоемкость и коэфициент температуропроводности
различных материалов [32, 28]
1 Наименование материала кг t С 1 1 1 [ ’ м- час•град 1 1 ккал ! с кг‘град а-103 — час
Изо пяциопные, строительные и другие материалы Альфоль Асбест листовой Асбест волокно . Асбестовый кар- тон Асбестовый ши- Фер Асбест Асфальт Бетон Бумага Рата хлопчато- бумажная . . . Войлок волося- ной (поперёк волокон) . . . То же шерстяной Газовый уголь . Гипс Глина огнеупор- ная Гравий . . .... Графит искусст- венный То же порошко- образный (40 отверстий на линейный см) . Дерево (поперёк волокон): клён ель Дерево—дуб х волокнам . . . Дерево—дуб =во- локнам .... Дерево—сосна х волокнам . , , Дерево — сосна « волокнам . , . /древесные стружки .... Доломит Древесный уголь кусковой . . . 1'емля сухая . . » влажная . Зола древесная . Зонолиг Известняк (15,3% НаО по объему) Каменный уголь Картон гофриро- ванный .... Картон для пере- городок, изоля- ционного типа 5-артон для пере- городок, плот- ная папка . . . 20 770 470 1 920 1 800 1 800 47о 470 700 700 580 580 530 580 580 580 580 580 2 110 2 300 80 272 331; 1 650 1 845 1 840 720 450 800 80 и 448 448 из 2 880 J 190 1 240 1 500 1 700 209 1 50 1 400 237 690 50 30 50 20 0 60 -200 0 -200 0 0 50 100 150 200 250 300 400 20 20 30 33 30 0—КО 450 20 0 40 50 60 20 20 20 20 30 50 80 80 0—100 100 24 29 21 30 О,', 40 о. к О.С95 0,64 .7,13 0,17 0, 72 0.134 0.134 0.2 0,13 0,141 0.135 0.174 0,1.9 0,132 0,185 0.192 0.60 1,10 0,112 9.030 0,031 0.045 0,25° 0,89 0.31 120 0.155 0,16 0,093 0,1/8 0,312 0,092 .,22 0.03 1.5 0,064 0,076 0,119 0,565 ),С61 ।), 08 - 0,8 0,16 0.055 0,342 0,06 ~ /—Г— с> I ДО- ] | | I I | | | | | ( | | | | й1 1 I I 1 1 1 | | 1 II Ч | | J I I I I | "'Г I I | СО 1 I I С"> и? со 1 Оч 1 1 1 1 1 1 1 1 1 1 1 1 । । 1 й.5 1 1 1 1 । । О 1 1 1 I " I I I 1 1 1 Is. 1 1 1 1 1 1 1 О -< О —' — О О
Продолжение табл. 44
На и Ален ование материала кг ^7? t °C ; , ккал 'ts с г» U ?3 ккал с — кг•град й-103 М-~ час
Кварц кристал- лический: х оси .... 2 500— 6, 0,2 12,0
= оси .... 2 800 2 500— 0 И. 9. 7
Кирпич изоляци- онный 2 800 55и 100 12
Кирпич строи- тельный .... 800— 20 0,20—
Кирпич карбо- рундовый . . . 1 500 1 000 0,25 9,7 0,162 6, а
Кладка строи- тельного кир- пича 20 0,6
Кирпич шамото- вый (обжиг 1330°) 500 0,9о
— 800 0,92 в*
— 1 100 0,94
— 3)00 0, -j)
То же (обжиг 1410°) 800 1, >3
— 1 100 1, иб
То же (обжиг 14 00 е) 500 1, 1
— 800 1, rs
— 1 1!)0 1, 21
Клинкер 1 400 30 9, 137
Кожа подошвен- ная 1 00л 0, и 137
Кокс порошко- образный . . . 449 190 164 0,29 0,126
Копоть ламповая 190 40 0,027
Лава — 0.73
Лёд 920 0 1. 95 .
Линолеум .... 1 180 20 0, 16
Магнезия 85% в порошке .... 216 too 0, 58
Мел 2 U00 50 о, Зо 3,21 1.91
Минеральная шерсть ..... 200 50 0.035 6,22 0,795
Мрамор 2 700 90 1, 12 0.21 1,98
Накипь котель- ная 65 1.1 3—
Окись магния (п рессованная) 800 20 2. 0, '115
Опилки ..... 2оО 20 1 i 061} .
Парафин ..... 92и 20 о, 23
Пемза — 21—66 0 21
Песчаник .... 2 250 4и 1.
Песок сухой . . 1 500 20 о. У. 0,19 9,85
» влажный . 1 650 20 0, 07 и, 50 1,77
Портланд-цемент 1 9о0 90 о, 26 0,27 0,506
Пробковая плас- тина 199 30 /36 0,45 0,42
Пробка гранули- рованная . . . 45 20 и 033
Сахарный песок 1 600 0 0,50 0,30 1,0
Сера моноклини- ческая ..... 100 0,1 34-
То же ромбиче- ская 21 о, 145 24
То же строитель- ная . ' 247 25 0,37
Слюда (поперёк слоёв) 50 0,50
Слюда 290 —. 0.5 0.21 82,0
Сланец 2 800 100 1, 28 —
Снег 560 — и, 40 0,50 1,43
Совелит . ... 450 100 0,08
Стекло 2 500 20 0.64 0,16 1,6
Стекло боро-си- ликатного типа 2 230 30—75 0, 95
Стекло оконное — — 0,^ —
Стекло натрово- известковое 0,91 0,45-
Стеклянная вата 200 0 0,65 0,032 0.16 1.0
ТЕПЛОПЕРЕДАЧА
577
Продолжение табл. 44
Наименование материала кг t “С ккал 1 м-час*град ккал С - кг•град « 1 U г о <□
Торфоплиты . . Углекислый маг- 220 50 0.055 - —
ний ....... 3 040 21 0,06 —
Фарфор Фибровый картон / 2 400 95 0,89 0,26 1.43
j 2 400 1 055 Ц69
изоляционный 237 21 0,042 ——
Фибра красная . 1 290 20 0,4 — ——
Холст — 30 0,075 — —
Целлулоид . , . 1400 30 0,18 —— —
Целотекс .... 215 20 0,04 —
Шерсть мине- j 160 30 0,0335 — —
ральная .... ( 315 30 0,036 — —
То же животная 110 30 0,031 — —
Шлак доменный Шлаковая — 24—127 0,095 — —•
шерсть Шлакобетон в 192 30 0,033 — —
куске 2 150 0,80 0,21 1,78
Шлаковая вата . Штукатурка ис- 250 100 0,06 —
кусственная . . 2110 21 0,64 — —
Эбонит Эмаль силикат- — — 0,15 — —
ная Металлы 610 0,75— 1.1
Бронза 8 000 20 55,0 0,091 75,0
Латунь 8 000 0 73.5 0,090 02,0
Никель 8 600 20 50,0 О.н 53,0
Олово 7 230 0 55,0 0,054 141
Свинец 11 400 20 30,0 0,031 85
Сталь 7 900 20 39,0 0,11 45.0
Цинк 7 000 20 95,0 0,094 145,0
Чугун 7 220 20 5 0,12 62,5
Таблица 45
Коэфициенты теплопроводности изоляционных
материалов при низких температурах
[281
. ккал
X в----------
час- м*град
в частных производных (независимые пере-
менные— время г и три пространственные
координаты, зависимая переменная — темпе-
ратура t)
dt
здесь а= [м2/час] — коэфициенттемпера-
7 СР
туропроводности, характеризующий быстро-
ту выравнивания температур различных то-
чек поля.
Для значения а, принимая размерность
см2!сек вместо м2!час, имеем
а[м2/час] = a [cjw2/cck]-2,778,
V2i — оператор Лапласа или диференциаль-
ный параметр 2-го порядка от t.
Уравнение в развёрнутом виде:
1) в декартовых координатах
dt _ [дН d*t d4\
dt “ Ддх2 + d/ + dz2];
2) в цилиндрических координатах
dt / d2t . 1 dt .
-г^--2-+7- +
1 d2t d4 \
+ /а~ j >
3) в сферических координатах
dt [dH , 2 dt., 1 d2t
dz= a \dr2 ' r dr ' г2 d^2 '
cos ф dt 1 d2t\
r2sinip ' dtp r2 sin2 ф ' d'f2r
где ср — долгота;
ф — полярное расстояние (дополнитель-
ный угол к широте).
Материал Объёмный вес в кг/м9 Температура в °C
0 -45,5 -73,3 -129 -184
Асбест .... То же .... Хлопок . . . Шёлк .... 700 465 80 100 0,20 0,1330 0.0484 0,0432 0,196 0,1280 0.0450 0,0381 0,194 0,1220 0,0411 0,0350 0,186 0.1072 0,0350 0,0292 0,149 0,0812 0,0295 0,0231
Диференциальное уравнение
теплопроводности
Предполагая, что: 1) поле температур
нестационарно и заполнено однородным те-
лом; 2) тело изотропно; 3) коэфициент тепло-
проводности л, удельный вес f и удельная
теплоёмкость с не зависят от давления и
температуры; 4) в теле не происходит изме-
нений агрегатного состояния, получаем урав-
нение теплопроводности в виде линейного
диференциального уравнения 2-го порядка
37 Том I
Кондукция (теплопроводность)
в стационарном температурном поле
Температура в любой точке не претер-
певает изменений по времени. Диференциаль-
ное уравнение теплопроводности
\721 = 0 ^так как = 0 и а 0 j.
Плоская стенка (одномерное стацио-
нарное температурное поле, t=/(x), изотер-
мические поверхности поля — плоскости,
параллельные боковым поверхностям стен-
ки). Стенка ограничена двумя изотерми-
ческими плоскостями с температурами tw ,
и tw 2 (tw j > tw 2); практически стенка долж-
на иметь ширину и высоту (направление осей
у и z), достаточно большие по отношению
к её толщине £ (направление оси х), чтобы
можно было считаться с изменением тем-
пературы в стенке лишь в направлении
оси х.
Температура в стенке (фиг. 50) t = / (х) —
прямая
grad t = ,
ха —Xi
578
ТЕПЛОТА
Таблица 46
Коэфициеиты теплопроводности изоляционных материалов при средних температурах
[28|
х ккал
X в -------т~
час*м*град
Материал Объёмный вес в кг/м* Температура в °C
38 93 149 204 316 427
Асбест Обожжённая инфузорная земля для покрытия тру- 577 0,130 0,145 0.164 0,175 0,180 0,186 0,194
бопроводов ... Изоляционный состав (рых- 200 0.064 0.063 0,077 0,085 0.092 0,109 0.127
ЛЫЙ) 400 0,060 0,068 0,075 0.07Э 0.082 — ——
Хлопок 80 0.048 0,052 0,058 — —
Шёлковая нить 146 0,039 0,045 0,050 — — — —
Шёлк 100 0,037 0,042 0,050 —— ——
Шерсть 136 0,033 0,04и 0,049 — —
Пробковый порошок .... 160 0,031 0,039 0,048 — —•
Инфузорная земля (рыхлая) 350 0.052 0,058 0.067 0,070 0.075 0,079 -
Таблица 47
Коэфициеиты теплопроводности изоляционных материалов при высоких температурах [28]
. ккал
X в----------------------------------------------
час*м*град
Материал До какой темпера- туры в °C Средняя температура в °C
38 93 149 204 260 316 371 427 j 482 538
Слоёный асбестовый войлок (около 40 слоёв на 25 мм) То же (около 20 слоёв на 25 мм) 370 260 0,049 2.067 0,055 0,075 0,06 0.082 0,065 0,090 0,071 0,097 -- — - -
Волнистый асбест (4 склад-
ки на 25 мм) 150 J. 075 0,086 0,103 __ — —
85%-ная магнезия Диатомит с асбестом и 315 0,058 0,061 0,064 0,069 — — — — — —
связующим материалом . 870 0,067 0,070 0,073 0,075 0,079 0,082 0,090 0,097 —
Диатомитовый кирпич . . . 870 0,080 0,083 0,086 0,090 0,094 0,097 0,103 0,109 ——
1 100 0.189 0,194 0,198 0.204 0,208 0,213 0,223 0,235 0,262 —
Диатомит порошкообраз- ный (объёмный вес 1 370 0.191 0,195 0,201 0,207 0,213 0,221 0,231 0,243 0,273 о, зоз
290 кг/м’) 0,058 0,062 0,066 0,071 0,076 0,080 0,091 0,101 __ —
Горный лён (rock wool) . . — 0,045 ©.050 0,058 0,066 0,075 0,085 — — —
< = ^,1--—s <w,2(x —*1).
Количество теплоты, передаваемое через
етенку иа участке поверхности F
Фиг. 56
Плоская многослойная стенка,
состоящая из п плотно прилегающих друг к
другу слоёв, с коэфициентами теплопровод-
ности и толщинами Хх и Sj, Х2 и .........
Х„ и 8„. Наружные плоскости стенки имеют
температуры tw j и tw п+1; температуры
в плоскостях стыка смежных слоёв
tiv,2> tw,3f..., tw,n', в i-м слое
, . .. / ^.z+i — fiv,i \ _
(grad t)i = — —------— —
\ л/+1 *1 j
__ ^w,i+X .
распределение температуры в i-м слое, —
ti = / (х) — прямая;
xw,i < х < 1 ’
Q = X F [ккал/час],
о
где X коэфициент теплопроводности в
ккал!м-град-час, F В м2, & в м.
Распределение температур в стенке t =
= / (х) — ломаная линия, проходящая через
температуры twA, tw>2,..., tw^n+).
ТЕПЛОПЕРЕДАЧА
579
Количество теплоты, передаваемое через
стенку на участке поверхности Г[л2]
(фиг. 57)
Q — t = п g. ^Ow.i
j) [ккал/час];
1 — 1 Таблица 48
Коэфициенты теплопроводности жидкостей X в
---------------—^-^-[281 *
час- м-грао
Жидкость Темпера- тура в СС 1
Уксусная кислота
100%-ная 0 0.183
50 0,127
То же 50%-ная 0 0,271
80 0.384
Ацетон 0 0,158
100 0,137
Аммиак 26%-ный ...... 0 0,360
80 0,474
Амилацетат 0 0,119
50 0,075
Амиловый спирт 0 0,128
100 0,124
Анилин 0 0.156
100 0,153
Бутиловый алкоголь (и) . 0 0.145
100 0,133
То же (iso) 0 0,145
80 0,133
Этиленгликоль 0 0,230
Этилацетат 12 0,1255
45 0.106
Сероуглерод 0 0,145
80 0,144
Четырёххлористый углерод 10 0.104
70 0,86
Касторовое масло 4 0.154
Хлорбензол 12 0,1185
Хлороформ 9-15 0.104
Цимол (р) . 30 0,117
60 0,118
Йодистый этил 0 0,0955
80 0,0925
0 0,243
Глицерин 100%-ный .... 50 0,250
0 0,335
То же 50%-ный 50 0,405
Гептан ... Ок. 4 0,1215
Гексан (п) 30 0,119
60 0,118
Хлористоводородная кис»
лота 30%-ная 20 0.363
60 0,420
Изопропиловый алкоголь . 30 0,137
60 0,135
Этиловый спирт 100%-ный 0 0,160
80 0,150
То же 90%-ный 0 0.137
80 0,250
Этиловый спирт 80%-ный . 0 0,16-1
» » 80%-ный . 80 0,275
» » 70%-ный , 0 0.185
80 0,29*
» » 60%-ный , 0 0,216
80 0,323
» » 50%-ный . 0 0,252
80 0.364
» » 40%-ный . 0 0,300
80 0.415
Морская вода 0% твёрдых —20 0.447
веществ
80 0,590
То же 1% твёрдых веществ -20 0,433 0,575
80
То же 2% твёрдых веществ -20 0,430
80 0,566
То же 3% твёрдых веществ -20 0,427
80 0,564
То же 3,5% твёрдых ве-
ществ —20 0,425
80 0,562
Рассол 25%-ный CaClj . . . —20 0,405
80 0,544
Продолжение табл. 48
Жидкость Темпера- тура в °C X
Рассол 25%-ный NaCl . • . —20 0.334
80 0,476
» 30%-ный 0 0,345
80 0,458
» 20%-ный 0 0,385
80 0,498
« 10%-ньгй 0 0.434
80 0,547
Бромистый этил 0 0,106
80 0,0978
Этиловый эфир 0 0,1190
80 0,1155
Оливковое масло 39 0,150
Терпентинное масло .... 39 0,109
Пентан (п) 0 0,119
80 0,110
Нефтяной эфир 0 0,113
80 0,109
Керосин 20 0,130
80 0,1185
Ртуть 100 7.2
Серная кислота 111%-ная 20 0,147
60 0,274
» » 98%-ная 20 0,231
60 0.243
» » 60%-ная 20 0,140
60 и, 161
Метиловый спирт 0 0,194
80 0,175
То же 40%-ный 10 и,28
80 0,31
Нефтяное масло Ок. 15 0,12
Пропиловый алкоголь (iso) 0 0,1325
80 0,13о
Октан 30 0,130
60 0,127
Касторовое масло 39 0,155
Толуол ........... 0 0,142
100 0,1215
Вазелин 20 0,188
0 0,124
Ксилол 40 0,143
о, Г м2-град-час ]
Г‘ = Т7 I ---------j-сопротивление кон-
дукции r-го слоя.
Фиг. 57
При стационарном температурном поле
количества теплоты, проходящие через каж-
дый слой Qi, равны между собой и равны
* Допускается линейная интерполяция величи-
ны по температуре. Оба приведённые в таблице
значения температуры представляют вместе с тем
для приводимых данных рекомендуемые пределы.
Составы приведены в процентах по весу.
37*
580
ТЕПЛОТА
Таблица 49
Тепловые параметры различных жидкостей [33]
Наименование жидкости кг t °C Q | м •час*град 1 ккал с т кг-град a’10s час
Аммиак Бензин Бензол Глицерин Керосин Крекинг-мазут . . . (Грозненского за- вода) Мазут А Нефтяное масло Смола . 617 665 900 900 900 1 260 "750 890 1 200 20 -32 О 50 5 30 60 20 30 75 80 27 47 32 65 200 80 0.49 0.48 0.125 0,095 0,12 0.137 0,130 0,25 0,129 0.120 0,12 0,117 0,115 0.102 0,099 0,089 0,12 1,13 1,10 0,43 0,44 0,40 0.58 0.56 0,58 0.703 0,656 0,323 0,24 0.30 0.342 2,85 0,173
Коэфициент теплопроводности воды
X ----[71
м*час>град
г с X нас. г» Р в см3
100 200 300 400
0 0,474 0,477 0,480 0,484 0,488
10 0.494 0,498 0.502 0,507 0.512
20 0,515 0,519 0,523 0,528 0,533
30 0,531 0,535 0,540 0,545 0,550
40 0,545 0,549 0.554 0,559 0,564
50 0,557 0,561 0,565 0,570 0,575
60 0,567 0,571 0,578 0,580 0,585
70 0,574 0,578 0,583 0,588 0,593
80 0.580 0,584 0,589 0,594 0,599
90 0,585 0,589 0,594 0,599 0,604
100 0,587 0,593 0,598 0,603 0,608
по 0,589 0,595 0,600 0.605 0,612
120 0.590 0,596 0.602 0,608 0,614
130 0,590 0,596 0,602 0,609 0,614
140 0,589 0.596 0.602 0.608 0,615
150 0,588 0,596 0,601 0,608 0,615
160 0,587 0.593 0,599 0,606 0,613
170 0,584 0,591 0,597 0,603 0,611
180 0,580 0,587 0.593 0,600 0,609
190 0,576 0,583 0,589 0,597 0,606
200 0,570 0,578 0,584 0,593 0,602
210 0,563 0,572 0,580 0,587 0.597
220 0,555 0,564 0,572 0,582 0,591
230 0,548 0,556 0,565 0,574 0,583
240 0,540 0,547 0,557 0,567 0,577
250 0,531 0,537 0,547 0,557 0,567
260 0.520 0,526 0,536 0,547 0,558
270 0,507 0,514 0,526 0,537 0.549
280 0,494 0.500 0,512 0,526 0,538
2,90 0,480 0.484 0,497 0,513 0,527
300 0,464 0,466 0,482 0,499 0,513
310 0,446 W— 0.464 0,482 0,499
320 0,425 0,444 0,463 0,482
330 0,402 0,420 0,443 0.466
340 0,376 ММ 0,392 0,422 0,447
350 0,344 0,359 0,395 0,425
360 0,306 0,314 0.364 0,401
370 0,252 — — 0,326 О‘,376
Таблица 50
Круглая цилиндрическая стен-
ка (труба). Стенка, стационарное темпе-
ратурное поле которой характеризуется
изотермическими поверхностями круговых
цилиндров, имеющих общую ось, состоит из п
слоёв; внутренняя изотермическая поверх-
ность радиуса гг имеет температуру tw ь
внешняя поверхность радиуса гп+1 — tw п +1.
коэфициеиты теплопроводности слоёв Х1( Х2...,
Хл; на участке длины L утечки теплоты в на-
правлении к торцам трубы не учитываются,
поле температур одномерно, — t = / (г).
На участке длины L [л] (фиг. 58) трубы
количество теплоты, передаваемое в час
" 1 dz4-l
,-1^’1П
-tw.n+i ) 1ккал/час],
где I — порядковый номер слоя (на фиг. 58).
Количества теплоты Q; на участке длины
Цм) трубы, передаваемые отдельными слоя-
ми, при стационарном температурном поле
равны между собой и равны Q.
количеству теплоты, проходящему через всю
стенку Q,
& = \ • F <ц,’'+-12 [ ккал[час\,
Q< — ] л fu'.f+l)’
— In—L±L-
2XZ di
Qi = Q-
ТЕПЛОПЕРЕДАЧА
581
Таблица 51
Коэфициент теплопроводности водяного пара [7]
rc Хнас. в P кг/см‘
1 20 40 60 80 Юо|15О 200 250 300
100 150 200 250 300 350 400 450 500 550 208 285 370 475 605' 910 208 244 284 326 368 416 467 548 652 774 395 408 436 490 565 668 790 475 440 456 508 584 685 802 500 482 538 605 702 815 517 560 622 715 828 570 586 640 728 830 780 670 680 750 850 850 783 805 880 1 250 930 867 904 1 200 1 000 970
Таблица 52
Значения динамической н кинематической
вязкости воды и водяного пара на кривой
насыщения [7]
Тем- пера- тура t9 C Давление насыще- ния Ps в кг/см* Вода Пар
Динамическая вязкость Р-КЛ кг-сек/и* Кинематиче- ская вязкость р.« 10е м*/сек Динамическая вязкость р.«10® кг’сек/м* Кинематическая | вязкость ; |х -103 м*1сек
150 4,8 18,9 0,202 1,50 5,70
160 6,3 17,7 0,191 1,55 4,67
170 8,1 16,6 0,181 1,61 3,83
180 10,2 15,6 0,173 1,67 3,18
190 12,8 14,8 0,166 1,72 2,64
200 15,9 14,1 0.160 1,77 2,21
210 19,5 13,4 0,154 1,82 1,86
220 23,7 12,8 0,149 1,87 1,58
230 28,5 12,2 0,145 1,92 1,35
240 34,1 11.7 0,141 1,98 1,16
260 40,6 11,2 0,137 2,03 0,997
260 47,9 10,8 0,135 2,09 0,864
270 56,1 10,4 0,133 2,15 0,750
280 65,5 10,0 0,131 2,22 0.654
290 75,9 9,6 0,129 2,28 0,571
300 87,6 9.3 0,128 2,35 0,499
310 100,6 9,0 0,128 2,42 0,435
320 115,1 8,7 0,128 2,50 0,379
330 131,2 8,3 0,127 2,59 0,329
340 149,0 7,9 0.127 2,70 0,284
350 168.6 7,4 0,127 2,84 0,245
360 190,4 6,8 0,127 3,03 0,207
370 214,7 5,8 0,127 3,36 0,163
Количество теплоты, передаваемое 1 пог. м
трубы
Q
1
——In—<+1
2 А,- di
[ккал/м.час].
Количество теплоты, передаваемое 1 л2 по-
верхности трубы, считая по внутреннему диа-
* Q
метру, Q то же, но по наружному
q я“п+1-
Температура tw>/+1 на стыке i-ro и (/-{-1)-го
слоёв
1 <* */4.1
1 = ~~ '<>' ‘In —Tj— • Q’
* 2 кА/ di
а также
z= i
W+l = *.v,l - 2^r ln -T1 'q-
i=a
Температура внутри i-го слоя t[ = j (d),
где d( < d < dl+i,
\v,iln + *iv,/+l *n —r
t. 4“<
Для однослойной трубы
Q = “1 ~d^-HtWl\ — tWl2)-
2T ln X~
Таблица 53
Физические параметры Р=1 для сухого воздуха при А [33] смй L J
Г С кг ккал с р кг-град ю*х । М‘Час* град ю*. а- час 1 . _. кг •сек 1°V м, - « О Рг
— 180 -150 -100 - 50 — 20 0 10 20 30 40 50 60 70 80 90 100 120 140 160 180 200 250 300 350 400 500 600 800 1 000 1 200 1 400 1 600 1800 3,685 2,817 1,984 1,534 1,365 1,252 1., 206 1,164 1,127 1,092 1,056 1,025 0,996 0,968 0,942 0,916 0,870 0.827 0,789 0,755 0,723 0,653 0,596 0,549 0,508 0,450 0;400 0,325 0,268 0,238 0,204 0.182 0,165 0,250 0,248 0,244 0,242 0,241 0,241 U,241 0,242 0,242 U, 242 0,243 0,243 0,243 0,244 0,244 0,244 0,245 0.245 0,246 0.247 0,247 0,249 0,250 0,252 0,253 0,256 0,260 0,266 0,272 0,278 0,284 0,291 0.297 0,65 1,00 1,39 1,75 1,94 2,04 2,11 2.W 2,22 2,28 2,35 2,41 2,46 2,52 2,58 2,64 2,75 2,86 2,96 3,07 3,18 3,42 3,69 3,93 4,17 4,64 5,00 ь,75 6.5.5 7,27 8,00 8,70 9,40 0,705 1,45 2,88 4,73 5,94 6,75 7,24 7,66 8,14 8,65 9,14 9,65 10,18 10,65 11,25 11,80 12,90 14,10 15,25 16,50 17.80 21,2 24,8 28,4 32,4 40,0 49,1 68,0 89,9 113,0 1-38.0 165,0 192.0 0,66 0.89 1,20 1,49 1,66 1,75 1,81 1.86 1,91 1,96 2,00 2,05 2,08 2,14 2,20 2,22 2.32 2,40 2,46 2,55 2.64 2,85 3,03 3,21 3,36 3,69 4,00 4,54 5,05 5,50 5.89 6,28 6,68 1,76 3,10 5,94 9,54 11,93 13,70 14,70 15,70 16,61 17,60 18,60 19,60 20,45 21,70 22,90 23.78 26,20 28,45 30,60 33,17 35,82 42.8 49,9 57,5 64,9 80,4 98,1 137.0 185,0 232,5 282,5 338,0 396,0 0,900 0,770 0,742 0,726 0.724 0,723 0,722 0,722 0,722 0,722 0,722 0.722 0,722 0,722 0.722 0,722 0,722 0,722 0,722 0,722 0,722 0.722 0,722 0.722 0,722 0,722 0,723 0,725 0.727 0,730 0,736 0,740 0,744
582
ТЕПЛОТА
Таблица 54*
Коэфициент теплопроводности газов и паров [28]
х ккал
X в-----------------------
м-час-град
1° С X X. 10». а С
Ацетон ....... 0 0,00782**
46 0,0101
ЮС 0,0134
184 0,0200
Ацетилен . • . • . -75 0,0094
С и,0149
50 0,0193
100 0,0238
Воздух (от — 191
до 212°С) ... . 0,0192 125
Аммиак (от—60 до
100»С) 0,0173 8,85
Бензол . 0 0,00709
46 0,0100
100 0,0140
184 0,0207
212 0,0240
Углекислый газ
(от 78 до 500° С) . 0,0118 5,5
Сероуглерод . . . 0 0,00550
8 0,00575
Окись углерода
(от -191 до 7,6° С) 0,0185 156
Четырёххлори-
стый углерод . . . . 46 0,00565
100 0,00695
184 0,0088
Хлор 0,0С63
Хлороформ . . . . 0 0,00525
46 0,00637
100 0,00800
184 0,0107
Циклогексан . . . 102 0,0141
Этан —70 0,00990
-34 0,0125
0 0,0155
100 0,0275
Этилацетат . . . . 46 0,6097
100 0,0131
184 0,0194
Этиловый спирт . 8 0,0107
20 0,0121
100 0,0168
Хлористый этил . 0 0,0075
100 0,0130
184 0,01*3
213 0,0267
Этиловый вфир . . 0 0,0104
46 0,0135
100 0,0177
184 и,0255
212 0,0283
Этилен ....... -71 0,009i)0
-50 0,6104
0 0,0141
50 0,0182
100 0,0226
Гексан (п) 0 0,0089
20 0,0098
Гексилен 0 0,0083
100 0,0143
Водород (от — 191
до 100°С) 0,136 94
Водород—углекис-
лый газ:
0% н 0,0122
17,01% Н, 0,021ь
36,98% Н 0.0373
♦ В таблице помещены значения X и Хо при 0е,
постоянная я в формуле X=*Xtt+ai и константа с
Sutherland в формуле:
2734-с
где Т—в° абс. и t— в °C.
♦♦ Главным образом по «Международным спра-
вочным таблицам», по установившейся традиции
значения коэфициента теплопроводности газов и
паров приведены с тремя значащими цифрами, ио
следует иметь в виду, что точность табличных дан-
ных порядка 10%.
Продолжение табл. 54
(» с X х. 10». а е
60,86% Н 83,45% Н, 100,00% На . . . . Водород-азот: 0% Н 15,9% Н 39,0% На 67,4% Н, 65,2% Н3 79,5% Н, 80,3% Н, 100,0% Н, Водород—закись азота: 0% Н, 7,5% Н, 20,9% Н, 38,6% Н 59,9% Н 81,2% Н, 100,0% н, Ртуть Метан (от — 180 до 10°С) Метиловый спирт То же Хлористый мети- лен Метилацетат . . . Бромистый метил Хлористый метил Йодистый метил . Азот (от — 192 до 100е С) Закись азота (от -70 до 100° С) . Окись азота (от—70 до 100°С) . Двуокись азота (55° С) Кислород (от—191 до 100» С) Пентан (и) . . . . Пентан (iso) , . . Сернистый ангид- рид Водяной пар . . . 200 0 100 0 46 100 213 0 20 и 100 0 46 100 184 213 0 46 100 0 20 0 46 46 100 0,0294 0,0114 0,0176 0,00528 0,00668 0,0086 0,0129 0,0081 0,0092 0.00495 0,0084 0,00725 0,0099 0,0127 0,0178 0,0203 0,0с372 0,0047 0,0061 0,0100 0,0111 О,Оо99 0,0131 0,0155 0,0188 0,0622 0,101 0,150 0,0198 0,0289 0,0457 0,0530 0,0700 0,0910 0,0925 0,146 0,0137 0,0173 0,0250 0,0386 0,0613 0,0980 0,146 0,0253 0,0195 0,0118 0,0179 0,0343 0,0200 0,0067 10,7 1,58 114 195 144
Температура стенки трубы
^н<,1 I*1 + ^ш,2 'п
U
где dt < d < d2.
Шаровая стенка (полый шар).
Стационарное, одномерное, t=/(r) темпера-
турное поле определяется изотермическими
поверхностями сфер, концентричных между
собой. Стенка состоит из п концентричных
слоёв, плотно прилегающих друг к другу,
радиусы их (внутренний), г2..., г,1+1
(внешний); коэфициенты теплопроводности
Xv Х2,... Х„, температуры поверхности сфер
ТЕПЛОПЕРЕДАЧА
583
Количество теплоты, проходящее в 1 час
через шаровую стенку (фиг. 53)
п _ 4 те (tw t
— 1=п
Vi 1 / 1________t \
2j h ri+i )
1=1
Количества теплоты, проходящие в 1 час
через каждый слой Qit равны между собой
и равны Q:
“М tw,/— iw,t+^ _ п
Qi = ~ / 1 1 у " Q'
х/ \ ri+i )
Фиг. 59
Температура на стыке Z-ro и (/ 4- 1)-го
слоёв
Qz 1 / 1 1 \
/ _____/ ____. — /-----------)
‘нм4-1 lw,i 4к к/ Г/ ’
а также
i
t -t _ Q .V 1 Р м
4+1 'w.i 4я- 2итд?;-7^7У
Температура внутри /-го слоя па поверх-
ности сферы радиуса г (Г[ < г < г,+ 1), /< =
она зависит от перемещения конечных масс
носителя энергии. Различают конвекцию
естественную (свободную) и вынужденную;
в первой перемещение масс жидкости есть
следствие неравенства удельных весов
жидкости в различных точках её за счёт
неравенства в них температур; во второй—
перемещение масс жидкости определяется
какими-нибудь внешними побудителями, на-
пример, напором вентилятора, циркуляцион-
ного насоса.
Особое значение имеет конвекция при
омывании жидкой средой поверхности твёр-
дого тела—теплоотдача (теплопереход).
Теплоотдача (Т -> Ж) с элемента поверх-
ности твёрдого тела (стенки) за
элемент времени dz [час], при разности тем-
ператур tw—tf (tw— температура поверх-
ности элемента стенки, tf—жидкости; пред-
положено tw > tf, если tf > tw, берут раз-
ность tf — tw — теплоотдача Ж-*Т):
dQ = a(tw — tf) dFd т [ккал];
здесь a
ккал
м^-граб-час
—коэфициент
тепло-
отдачи, численно равный количеству тепло-
ты, отдаваемому(или воспринимаемому)еди-
ницей поверхности стенки в единицу времени
при разности температур поверхности стенки
и жидкости в Г.
При стационарном температурном поле
и температуре tw на всей поверхности F
стенки
[ккал
час
Коэфициент теплоотдачи функция ряда
переменных
а — / (W, tw, tff~K,p, р, Ср, /1, /2,...),
где iv—скорость,
tf — температура жидкости,
X—коэфициент теплопроводности,
р. — коэфициент вязкости,
р — плотность,
ср — теплоёмкость,— параметры, отно-
сящиеся к жидкости;
tw— температура стенки;
llt L, ... — геометрические размеры, опреде-
ляющие условия движения.
Явление теплоотдачи в общем виде опи-
сывается системой диференциальных урав-
нений:
1. Уравнения движения вязкой жидкости:
КОНВЕКТИВНАЯ ТЕПЛОПЕРЕДАЧА
(КОНВЕКЦИЯ)
Общие уравнения
Конвективная теплопередача осущест-
вляется путём переноса энергии перемещаю-
щимися в пространстве частями жидкости
(капельной или газа). Теплообмен, достигае-
мый конвективной теплопередачей, является
следствием переноса энергии перемещаю-
щимися конечными массами жидкости, сопут-
ствуемого обязательно кондукнией, т. е.
переносом энергии элементарными частицами
носителя при их соприкосновении (контакте);
здесь кондукция осуществляется в условиях,
совершенно отличных, чем в твёрдых телах,
dwx
P'dT-
divv _
?~dz---
dwz _
P
где
dz
dp / 1
dx + "з
dp I 1 d6\
— dy + и \ + 3 dy)
dp [ 1 d0\
~dz + 1Ч у jd,
8 = ;
dx dy dz
d2wx d2iv„ d2wx
dwx dwx dwx dwx dwx
~d^~ dz +w*~dx' + wy-dy-' + wz dz 1
584
ТЕПЛОТА
dwv dwz
X/2wv, \/2wz, —г—составляются анало-
UT
гично.
2, Уравнение сплошности сжимаемой
жидкости при неустановившемся режиме
, /ЁЕе . dwv , dw2 \
д~ "* р [ дх + ду + dz ) +
dp д? до
+ w*dx+wyd'y + Wzdz~Q'
при установившемся движении = 0; для
движения несжимаемой жидкости
dp = ?? _ д? _Лр л
дъ дх ду dz
3. Уравнение конвективного переноса те-
плоты Фурье — Кирхгофа (уравнение тепло-
проводности в движущейся среде); стацио-
нарное температурное поле
dt dt dt ,’d2t , дЧ ,
Wjc dx + wydy + w* dz ~ a (. dx2 dy2 + dz2) ’
к
где a = [м2/час]— коэфициент темпера-
icp
туропроводности жидкости.
4. Уравнение теплообмена при конвектив-
ном переносе теплоты на границе раздела
потока жидкости и твёрдого тела
, dt
dn — а Gf ^wf-
Аналитическое решение этих уравнений
с учётом всех условий однозначности (опре-
деляющих частные случаи) удаётся лишь по
отношению к некоторым задачам и достигает-
ся на основе ряда упрощающих допущений,
что снижает возможность практического при-
менения его.
Теория подобия позволяет, не интегрируя
этих диференциальных уравнений, устано-
вить некоторые характеристические, безраз-
мерные величины—критерии подобия, сохра-
няющие своё значение для целого класса
(группы) подобных явлений; та же теория
констатирует для класса подобных явлений
обязательность функциональной зависимости
между найденными критериями, но устано-
вить вид её она не в состоянии. Согласно
атому для подобных явлений, описываемых
приведёнными уравнениями, должны суще-
ствовать зависимости между критериями:
при учёте влияний как естественной, так
и вынужденной конвекции
Nu = f(pe, Gr, Рг, 4-,
\ *0*0
при вынужденной конвекции
№ = /i
I
Re, Рг, -г,
*0
£1
1о
при естественной конвекции
! I li
Nu = /J Gr, Рг, -г-,
\ !0 10
для газов с вынужденной конвекцией
для газов с естественной конвекцией
; а = — [мЧчас] — коэфи-
Iер
Nu^fJor, -Г, -J1,
\ ‘О ‘0 /
где
критерии Рейнольдса Re = — ;
wl
критерии Пекле Ре=—;
критерий Прандтля Рг = —;
g.B.ft.p
критерий Грасгофа Gr ——--------;
al
критерии Нуссельта Nu=~.
Здесь »[м-/сек] — коэфициент кинематической
Р
вязкости, v = —
р
циент температуропроводности; >[ккал/м-
град-час] — коэфициент теплопроводности;
а [ккал/м2-град'час]— коэфициент теплоот-
дачи; W [м/сек] — скорость; g [м/сек2] —уско-
рение силы тяжести; 3 [ 1 /град] —коэфициент
объёмного расширения; & [град]—избыточная
температура; I [м] — характерный линейный
размер, для труб обычно диаметр.
Критерии Re и Gr выводятся из уравне-
ний движения, характеризуют подобие сил:
первый—сил внутреннего трения (вязкости),
второй—земного тяготения (подъёмную си-
лу). Критерий Ре находится из уравнения
Фурье—Кирхгофа, определяет подобие явле-
ний в отношении теплопроводности в дви-
жущихся средах. Критерий Nu даёт условия
подобия в пограничном слое. Критерий Рг
Ре v
находится как отношение ттт “ • ценен
Д с и
тем, что отражает физические свойства, при-
роду движущейся среды.
al X
Так как Nu = —, то о = у Nu, т. е.
знание критерия Нуссельта даёт возможность
определить коэфициент теплоотдачи.
Вид этих функциональных зависимостей
для явлений, входящих в класс подобных,
находится экспериментально.
При пользовании для нахождения а экспе-
риментальными формулами нужно обращать
внимание на пределы применимости форму-
лы, определяемые диапазоном изменения кри-
териев, охваченным при осуществлении
опыта; необоснованный выход за пределы
может привести к крупным ошибкам в ра-
счётах.
При пользовании расчётными форму-
лами, выраженными в критериях подобия,
температуру, по которой берутся вводимые
в формулу физические параметры, так назы-
ваемую определяющую температуру, следует
брать согласно приводимым указаниям к
ТЕПЛОПЕРЕДАЧА
585
формуле (при помощи подстрочного индекса)
ибо выбор этой определяющей температуры
у различных экспериментаторов не согла-
сован.
Теплоотдача в вынужденном потоке
жидкости (вынужденная конвекция)
1. Теплоотдача в прямой трубе. Турбу-
лентное движение.
Формула Нуссельта*
/ I \—0,05
Nu.;,= 0,0344 Ре%79 - ^1
строго применима для стабилизированного,
турбулентного потока газов и перегретых
паров, протекающих по прямой трубе и испы-
тывающих подогрев от стенки, при темпера-
туре газов не выше 600° С, при Рет= 1000—
7000; подстрочный индекс т—указание на
выбор определяющей температуры tm =
— tw и у — температуры стенки и
жидкости; I [л] — длина трубы; d [л] — диа-
метр.
Возможно экстраполирование формулы на
ббльшие значения Рет.
Формула Крауссольда
„ „ /1 \—0,054
Nuf = 0,032 Re°f-8 Pr’f I-j-j ;
индекс / — указание на определяющую тем-
пературу; tf — температура жидкости.
Формула применима как для капельных
жидкостей, так и для газов, для стабили-
зированного, турбулентного потока, при
Ref > 10 000 и при 0,7 < Рг/ < 10 000.
По Крауссольду, при нагревании жидкости
показатель у критерия Ргу т = 0,37, при
охлаждении т = 0,33; по М. В. Кирпичёву,
целесообразно принять тп = 0,35 в обоих
случаях.
I
При = 1004-400 приближённая форму-
ла Крауссольда
Nuf = 0,024 Re°f’8- Pr™.
Формулы Нуссельта и Крауссольда приме-
нимы не только для случая продольного
протекания потока жидкости (капельной или
упругой) внутри круглой трубы, но и для
прямого канала произвольного постоянного
сечения F; при расчёте вместо d вводят экви-
4F
валентный диаметр daKe = -ц-, где F—попе-
речное сечение канала; U — активный пери-
метр сечения, являющийся проекцией на
плоскость, нормальную к осп канала, по-
верхности его, участвующей в теплоот-
даче.
* Nusselt W., Mitt, Forschungsarbeit, 89. 1,
1910. .
Значения эквивалентного диаметра
Эквива-
лентный
диаметр
d
I
1. Круглая труба Q............... а
b
2. Прямоугольник | | а:
. _ 2аЬ
а) теплообмен через все стороны . . ---
а 4- b
б) теплообмен через,две противоле-
жащие стороны (а) ................ 2Ь
в) теплообмен через одну сторо-
ну (а) 4Ь
3. Квадрат || а ............ а
4. Кольцевое сечение:
а) теплообмен через внутреннюю и
внешнюю поверхности........... D—d
б) теплообмен только через Внеш-
D’ — d1
нюю поверхность.............. ———
в) теплообмен только через внут-
D’ — d*
рентою поверхность........... ........
М. А. Михеев считает наиболее точной
следующий вид формулы:
N17 = 0,023 Ре°’8 Рг°’4,
где определяющей температурой принимается
среднелогарифмическая температура жидко-
сти tf, а определяющим размером—диаметр
трубы d. Формула применима для всех ка-
пельных и упругих жидкостей при
Ref> 1-104, Prf = Q,7 4- 2500 и при темпе-
ратуре стенки ниже температуры кипения
жидкости. Формула применима и для труб
и каналов любого сечения при внутреннем
протекании жидкости, а также при внешнем
продольном омывании. Однако для продоль-
ного движения жидкости по кольцевому
зазору формула пригодна только для случая
теплообмена по внешней (большой) поверх-
ности.
Для случая теплообмена с внутренней
поверхностью кольцевого зазора М. А. Ми-
хеев предлагает пользоваться формулой
[33]
d. 0,45
NUf = 0,023 ~
ReQf’s Pr°f’4
где d2— наружный диаметр внутренней тру-
бы;
di — внутренний диаметр внешней трубы.
Обе последние формулы применимы при
с
Формула
NUf = 0,023 /?г°-8Рг°-4
в развёрнутом виде может быть представле-
на так:
где
?°’6.с0’4
В = 0,023 (36OO)0’4 -1—
(1-7 ‘ ’
586
ТЕПЛОТА
Гл] Г кг] г [ ккал “|
причем w j, 7 d [м], X
с [ ::кал 1 .
р I кг-град]
0,14
= 2,02
Значения В для воздуха
Вынужденный поток при лами-
нарном движении. Формула Краус-
соль да
/ f \ _Q 5
Nuf = 15,0 Ре0,23 I-J-)
при нагревании жидкости,
п*ч/ I \-°,5
Nuf= 11,5 Ре0,231-j-1
при охлаждении жидкости.
Обе формулы относятся к опытам с верти-
кально расположенной трубой и подводом
жидкости снизу. Для других условий распо-
ложения трубы и подвода жидкости расчёт
следует вести по формуле, дающей среднее
значение коэфициента теплоотдачи
о 9ч / I \-°-5
Nuf= 13,2* Рг°’23 •
Формула Ватцингера — Джонсона [22] для
ламинарной и переходной области (Rd—
= 1 350 — 4 600)
Nu# = 0,255 Gr0’25* Ре0,07- Рг°’37,
где определяющая температура
= tf — 0,54(?z — tw).
При ламинарном режиме движений в тру-
бах и каналах лучшее совпадение с опыт-
ными данными даёт формула Зидера и Тейта
[33].
Формула применима как при нагревании,
так и охлаждении жидкости; даёт среднее по
длине а при горизонтальном положении
трубы; при вертикальном положении трубы
формула не учитывает направления движения
жидкости.
,, / tZy/./pz\o,i4
W=1.86P^-Pry»(T) =
= 2,02 Gz*'* ру”’14.
\V-wJ
В развёрнутом виде формула принимает
следующий вид:
В этих формулах
_ Gen
Gz = — критерий Гретца;
iv — скорость жидкости в м/сек;
G — весовой расход жидкости в
кг/чдс;
d —диаметр трубы, принимаемый за
определяющий размер;
— температура омываемой поверх-
ности;
tf—средняя арифметическая темпе-
ратура жидкости, принятая опре-
деляющей;
и — коэфициент вязкости жидкости
соответственно по tf и tw.
Для применения формулы к каналам
вместо d вводится d3Ke.
2. Теплоотдача в изогнутых трубах (коле-
на, переходы, спирали). По опытам Иешке
[32], при турбулентном режиме движения
с воздухом до Re = 150 000
Num = ^0,039+0,069 Ре0’70 ,
где d — диаметр трубы; Р— радиус закруг-
ления.
Соотношение между теплоотдачей в изо-
гнутой трубе с теплоотдачей в прямой трубе
Иешке даёт формулой
Nu изогнут = I 1 +1 >77 j NliПрим-
S. Теплоотдача одиночной трубы, смы-
ваемой поперечным потоком жидкости. По
опытам Гильперта, со свободным неза-
вихренным потоком воздуха, направленным
нормально к трубе и получающим подогрев
от неё (скорость воздуха от 2 до 30 м/сек
при диаметрах трубы или цилиндра от 0,099
до 155 мм), теплоотдача определяется фор-
мулой
Nttf = c-Re’f,
где с и п выбираются из таблицы:
Rey с п
1-10"—5-10» 0,590 0,47
5*10’— 5-10* 0,197 0,60
5*10* и выше 0,023 0,80
Данные Гильперта дают наинизшее зна-
чение коэфициента теплоотдачи, характери-
зуют его значение в незавихренном потоке
воздуха (при нормальной турбулентности).
Влияние турбулентности учитывается
коэфициентом х
NUf = сРе”*х,
где х берут по таблице (см. стр. 587).
Приведённые соотношения даны для слу-
чая угла атаки (угол, составленный направ-
лением потока и осью трубы), равного 90°;
при угле атаки ф, отличном от 90°,
ТЕПЛОПЕРЕДАЧА
5§7
Таблица значений х
Автор экспери-
мента
Условия эксперимента
ЫО»—5.10s 0,652 0,47
5*1О“—5.10* 0,218 0,60
5» 10* и выше 0,0254 0,80
Гильперт .... 1,0
Эйгенсон .... 1,0
Кузнецов .... 1,0
Михеев ..... 1,08
Форнем и Рейер 1,18
Свободная струя по выхо-
де из сопла ...........
Всасывающая труба с
плавным входом . . . .
Всасывающая труба с
плавным входом . . . .
Замкнутая труба с успо-
коительной решёткой .
Замкнутая труба, после
вентилятора, с успокои-
тельной решёткой . . .
Замкнутая труба, после
вентилятора, без успо-
коительной решётки . .
Мак-Интайр . . 1,50
Угол атаки V
Фиг. 60
е = "Ф
где s, по данным Синельникова и Чащихина
[19], дан кривой I, по данным Форнема [33] —
кривой 2 (фиг. 60).
По Ульзамеру [33], обобщённая зависи-
мость для капельных жидкостей и газов
Nuf = с-R"- Р^'31,
где сип берутся из таблицы (корректи-
рованной по данным Гильперта и Эйген-
сона):
4. Теплоотдача пучков труб в поперечном
потоке воздуха. По работам Н. В. Кузнецова
во Всесоюзном теплотехническом институте,
теплоотдача от пучка труб к воздуху :при
поперечном обтекании пучка при коридорном
и шахматном расположениях труб опреде-
ляется соотношением
Num = c-Re^n.
При вычислении критериев коэфициент
теплопроводности X и коэфициент вязкости р.
отнесены к средней температуре tm погра-
ничного слоя, плотность р отнесена к той
температуре, к которой относится скорость
и>, берущаяся по самому узкому сечению в
пучке.
Константы сип берутся из табл. 55 и
56 по шагу Si между трубами вдоль ряда и
шагу s2 между рядами вдоль направления
потока воздуха и диаметру труб d.
Случай теплоотдачи [27], когда поток
направлен к пучку не под углом атаки 90°,
а под некоторым острым углом ф, учиты-
вается соотношением
Num =Nu(eoyo>,
где «> берётся из таблицы:
90 80 70 60 50 40 30 20 10
Ш = 1 1 0,98 0.94 0.88 0,78 0,67 0.52 0,42
В переработке Д. А. Литвинова для омы-
вания пучка труб поперечным потоком воз-
духа или дымовых газов опытные данные
Таблица 55
Значения сип для коридорных пучков [22]
Ряды в пучке d- От 1,2 до 1,5 От 1,5 до 2,0 От 2.0 ДО 2,5 От 2,5 до 3,0 От 3.0 ДО 4,0 п
Sa с с с с с
Для первого ряда .... Для каждого из осталь- От 1,2 0.182 0,188 0,195 0.200 0,205 0,60
ных рядов до 1.5 0.178 0.172 0,169 0,164 0,161 0,65
Для первого ряда .... Для каждого из осталь- От 1,5 0.177 0,182 0.188 0,190 0,192 0,60
ных рядов до 2,0 0,173 0,170 0.168 0,165 0,102 0,65
Для первого ряда .... Для каждого из осталь- От 2.0 0,175 0,176 0,179 0.183 0,190 0.60
ных рядов до 2,5 0,169 0,168 0,167 0,166 0,164 0,65
Для первого ряда .... Для каждого из осталь- От 2,5 0,178 0,183 0,187 0,198 0,200 0.60
ных рядов до 3,0 0,165 0,167 0,170 0,168 0,164 0.65
Для первого ряда .... Для каждого из осталь- От 3,0 0,180 0,192 0,207 0.217 0,225 0.60
ных рядов до 4,0 0.161 0.165 0/71 0,170 0,169 0,05
588
ТЕПЛОТА
Таблица 66
Значения сип для шахматных пучков [22]
Ряды в пучке S1 От 1,1 до 1,3 От 1,3 ДО 1,6 От 1,6 до 1,9 От 1,9 до 2.5 От 2,5 ДО 3,0 От 3,0 до 5,0 п
d с с С С с с
Среднее для первых че- тырёх рядов Среднее для каждого из От 1,1 1,3 0,220 0,205 0,218 0,230 0,240 — 0.62
остальных рядов . . . До 0,315 0,300 0.220 0,340 0,350 0,60
Среднее для первых че- тырёх рядов Среднее для каждого из От 1,3 1,6 0,205 0,207 0,215 0,225 0,230 — 0,62
остальных рядов . . . До 0,292 0.295 0,300 0,315 0,335 — 0,60
Среднее для первых че- тырёх рядов Среднее для каждого из От 1,6 2,0 0,202 0,206 0,212 0,218 0,224 — 0,62
остальных рядов . . . ДО 0,275 0,285 0,295 0,305 0,315 0,60
Среднее для первых че- тырёх рядов . . . . Среднее для каждого из От 2,0 3,0 0,200 0,205 0.208 0,213 0,218 — 0,62
остальных рядов . . . До 0,260 0.270 0,280 0,290 0,300 0,60
Среднее для первых че- тырёх рядов Среднее для каждого из От 3,0 0,200 0,204 0,206 0,208 0,214 — 0,62
4,0
остальных рядов . . . До 0,250 0,265 0,275 0,285 0,205 — 0,60
Среднее для первых че- тырёх рядов Среднее для каждого из От 4.0 5,0 — — — — — 0,214 0,62
остальных рядов . . . До — — — — — 0,290 0,60
Антуфьева [1] и Кузнецова [25] даются
формулой
№r = C.em Re",
где определяющий размер диаметр трубок—
d-, определяющая температура /у — средняя
температура газового потока, а скорость от-
несена к самому узкому сечению в пучке
(ряде).
Значения С, гт, п см. в табл. 57.
Таблица 57
Ряды Коридор- ное рас- поло- жение Шахмат- ное рас- положе- ние С
п е7П п ет
1 0,60 0,15 0,60 0.15 при -~= 1,2+3 а
2 0,65 0,138 0,60 0,20 c=i+o.i-2i- d
3 0,65 0,138 0,60 0,255 при -*-->.3 d
4 0,65 0,138 0,60 0,255 С=1 >3==const
Xi — расстояние между центрами труб в
ряде;
х2 — расстояние между осевыми линиями
двух смежных рядов.
Приведённые значения коэфициентов при-
менимы только для круглых труб при:
X,
-/-=1,2-5,
= 1,2 —
5,
d
Яе/= 5-103 — 7-Ю4.
В развёрнутом виде формула будет:
(щ* **
при п = 0,6 а = С-гтЕх ;
„ ~ / W у \ 0,65
при и = 0,65 * = СгтЕ^-^\ ,
где w — м/сек, -j — кг/м3, d — м, g — м/сек3,
X ккал кг-сек .
м-час-град ’ I1 — м3 ’
значения
X
Е1= (М£)°’6°
И
Е =______*____
2 (Р--£)0’65
для газов см. в табл. 58.
Таблица 58
Г JC 0 50 100 200 300 500 1000
14,7 15,7 16,4 17,9 19,2 21,4 25,0
Е, 25,0 27,0 28,2 30,4 32,1 35.6 40,9
Приведённые формулы дают среднее а для
трубки любого ряда (так как для рядов выше
четвёртого значения п и ет уже не меняют-
ся).
Средний коэфициент теплоотдачи апуч для
всего пучка будет л
_ аг^*°+---+ атРщ
°Пт~ Fl4-Fa+ ... + Fm ’
ТЕПЛОПЕРЕДАЧА
589
где яц а2,...,ат— коэфициенты теплоотдачи
по рядам; Ft, F.,,..., Fm — поверхности на-
грева всех трубок соответственного ряда.
Для поперечного обтекания пучка труб
капельными жидкостями достоверных фор-
мул не имеется, ориентировочно использует-
ся [33]
NUf = C-e'mRenfPrQ'3.
Коэфициенты см. в табл. 59.
Таблица 59
Коридорн. Шахматы.
Ряды п ‘т п sm С
1 0,60 0,17 0,60 0Д7 При—,2-5-3
2 0,65 0.155 0,60 0,225 c=i+o,iJL а
3 0.65 0.155 0,60 0,287 1‘Ри-^->3
4 0,65 0,155 0,60 0,287 С=> 1,3
Примечал для круглых труб и е. Коэфициенты применимы в случае
Xi <г = 1.2-т- 5; - 1.24-5 d Re. - J 5.105—7-10*
5. Теплоотдача плоских вертикальных
плит в вынужденном потоке воздуха. Форму-
ла Н. А. Скнаря [22]
Nuw = 0,044./?е°-77-
Определяющим линейным размером при-
нята длина плиты /0; определяющей темпе-
ратурой—температура стенки tw. Формула
даётся для значений 7?етоот 5-10е до 1,7-10е.
ТЕПЛООТДАЧА В СВОБОДНОМ ПОТОКЕ
ЖИДКОСТИ (ЕСТЕСТВЕННАЯ
КОНВЕКЦИЯ)
1. Теплоотдача вертикальных труб [50].
Приводимые ниже формулы Эйгенсона дают
возможность по критерию Нуссельта опре-
делить локальное значение коэфициента
теплоотдачи ах для любой высоты х и среднее
значение его а по высоте от х = 0 до х = Н.
Формулы справедливы для двухатомных газов
(Рг — 0,72) для расчёта теплоотдачи верти-
кальных проволок, труб, и плит, имеющих
по поверхности равномерную температуру.
Индекс х означает, что при рассмотрении
локального значения коэфициента за опре-
деляющий размер при нахождении крите-
риев принято расстояние х от низа трубы
или плиты.
Индекс Н указывает, что при рассмотре-
нии среднего значения коэфициента тепло-
отдачи на участке трубы или плиты вы-
сотой Н за определяющий размер принята
высота Н.
Индекс d указывает на определяющий
размер, диаметр для выяснения пределов
применимости формулы для труб и прово-
лок.
Индекс т указывает на определяющую
температуру.
. _ tw+tf
tm— 2 '
Плиты и трубы при Grmd > 10‘:
1) для Grmx < 10э — ламинарная область
движения:
= 0,36 Gr^‘x;
NumH^0,48Gr-^H.
2) для 10е < Grmx < 1,7.1010—переходная
область:
= 1,37.10~4.Gr°’x3;
= 51,5+7,26-10-^Gr°£3;
3) для Grmx > 1,7-1010:
N«mr= 0,148 Gr'^»;
NumH = 0,148 Gr^-127,6.
Трубы при Grmd < 10е.
Для Grmx> 1,7-1010
П p о в о л о ч к и:
V Grmd < 0,14 (при ламинарном течении):
= 0,45;
2) Grmd > 0,14:
Numd = В- Gr'^.
Значения величины В берутся из табли-
цы:
^rmd=K 10—1 j 10»,’ 10* 10’ 10а 10* 10в
В™ 1.93 0,934 0,545 0,349 0,245 0,184 0,156
6гт<1~ 10’ 10’ 10е 10“ 101« 10“
в=> 0,148 0,148 0,148 0,148 0,148 0,148
2. Теплоотдача горизонтальных наклон-
ных труб [22]. Для приближённых расчётов
горизонтальных труб в воздухе применима
формула Гриффитса-Дэвиса, среднее значе-
ние а
_ 4______
а—А |/ tu>—tf,
где tw и tf—температуры поверхности тру-
бы и воздуЖа; формула применима для
At > 15° С при d > 5 мм- А берётся из таб-
лицы:
d в мм — 5 10 50 100 200 500 1000
А- 4,85 3,53 1,94 1,80 1,73 1,73 1,73
590
ТЕПЛОТА
Для наклонных труб применяется форму-
ла Коха
а = D-Д/0,24,
1. Для проволок:
при (Gr-Pr)m = 10~4 4- 10~3
а = 0,5 ?—
где D берётся из табл. 60.
Таблица 60
Значения постоянной D в формуле Коха
Наклон к горизонту в градусах
О 15 30 45 60 75 90
при (Gr • Рг)т = 10~3 4- 5 • 102
« = 1,18(pg • Ргт)?
v'• \ Р /
где р— коэфициент объёмного рас-
2,6 2,5
2,2 2,1
2,0 1,94
1,94 1,89
1,89 1,87
1,88 1,87
1,92
1,80
1,78
1,78
1,78
1,61
1,61
1,61
1,61
По М. А, Михееву [33], при естественной
конвекции теплоотдача для горизонтальных
и вертикальных проволок, труб, плит и ита-
ров охватывается критериальным выраже-
нием
Num^C(Gr-Pr}nm,
где С берутся в зависимости от (Gr-Pr)m
по следующей таблице.
Значения Сип
(,Ог-Рг)т С п (Gr * Рг) т С п
1-10 —4-1.Ю-3 1-10 -3-5-10+ 2 0,50 1,18 0 1/8 5-10»—2.107 2-10’—Ы0*а 0,54 0,135 1/4, 1/34
Условия, определяемые в таблице стро-
кой первой, отвечают плёночному режиму
движения; строкой второй — ламинарному
режиму движения; строкой третьей — интен-
сивному ламинарному и локонообразному
режимам движений; строкой четвёртой —
вихревому режиму движения.
При вычислении критериев за определяю-
щий геометрический размер принимается для
труб и шаров их диаметр, для плит верти-
кальных— их высота, для плит горизон-
тальных—меньшая сторона плит.
Определяющей температурой берётся
средняя температура пограничного слоя
1
tm = 2 где ~ температура стен-
ки и tf—температура среды (жидкости) на
большом удалении от стенки (вне зоны,
охваченной процессом).
При определении из приведённого кри-
териального уравнения коэфициента теплоот-
дачи а для горизонтальной плиты получен-
ное расчётное значение а, если теплоотдаю-
щая поверхность плиты обращена кверху,
должно быть увеличено на 30%; наоборот,
если теплоотдающая поверхность обращена
книзу, а должно быть уменьшено на 30%.
Могут быть использованы частные фор-
мулы, вытекающие из приведённого выше
критериального уравнения.
ширения в
1 .
°C ’
g — ускорение силы тяжести в
м/сек'2-,
&t=tw—tf— температурный напор в °C;
I и Кмм)—определяющий линейный раз-
мер в м и мм-,
U8(pgPrm)*/»^- .
Значения Aj для воздуха и воды даны в
табл. 61 и 62.
2. Для труб, сфер и вертикальных плит:
при (Gr-Pr)m = 5-102 4. .2.10’
a = 0,54(pgPrm)IO-^
= 5,62А^Т(-^) ,
при Gr-Prm >2-10’
a=0,135(pgPrm)1/> —• ДГ’Л« АгДГ‘\
m
где
A2= 0,54(PgPrm)*/«4v- .
\ Ia
m
A3 = 0,135 (pgPrm)*/*- ^ ;
г(7Г
для воздуха и воды А, и А» см. табл. 61 и
62.
Т а б л и ц а 62
Значения Аг, Д8 и А3 для воды
0 20 40 60 80 100 150 200
9,64
75,3
130,0
13,2 13,9
119,0 128,0
228,0 254,0
14,4
137,0
276,0
ТЕПЛОПЕРЕДАЧА
591
Теплоотдача плит
При вертикальном расположении плит
условия теплоотдачи аналогичны условиям
теплоотдачи вертикальных труб (см. выше).
Приближённый расчёт плит при Н = 1 м:
оГ= 3,0 + 0,08 Д t (формула Нуссельта, при
Д( < 15° С);
а~= 3,45-Д(0,13 (формула В. С. Жуковского,
при 85 < Д( < 150°С);
а ’ |/ Тг~~н']/ 760’
где Н [м]— высота плиты; Ь — барометри-
ческое давление в мм ртутного столба (фор-
мула Шмидта и Бекмана).
Для горизонтальной плиты, обращённой
теплоотдающей поверхностью вверх,
— 4/--------
а = 2,8уД( (формула Хенки);
— 4/--------
а = 2,15 у At (формула Гриффитса-Дэвиса).
Формулы В. С. Жуковского:
Д/ < 15°С h = 2,2 ДГ0’25;
15 < Д/ < 90° С 7= 2,95 Д(°>27;
90 < Д» < 180° СЧ= 4,2-Д(°'19 .
Для горизонтальной плиты, обращённой
теплоотдающей поверхностью вниз,
а — 1,13Д(°’25 (формула Гриффитса-Дэвиса)
/ 30\
а = 120- Хда 1 Д/
где Хш — коэфициент теплопроводности воз-
духа (формула В. С. Жуковского).
Теплоотдача при конденсации
г [ ккал/кг] — теплота парообразова-
ния.
Локальное значение коэфициента
ккал I
а иа Р^стоянии х
X 4/--д--
“ = 3 г 4х-Д ( ’
где
Д ( —• (да,
. , .. ккал4
р. лГ -час4-°C3
г--(2-Х3
; среднее значение
— ккал I
коэфициента теплоотдачи а I ^.град.час
для всей стенки высотой Н
_ 4 у д
а = 0,943 1/ —.
V H-At
Параметр А выбирают по средней темпе-
ратуре слоя плёнки
1
tm — Us -J- tw).
Формула применима не только для верти-
кальной стенки, но и для вертикальных
труб, если, как это и бывает всегда на
практике, толщина плёнки невелика по срав-
нению с радиусом кривизны трубы.
Если угол наклона стенки к горизонту [3,
ТО _ _
~ а 90 ‘ yf sin р.
Для горизонтальной трубы
7= 0,7241/ А.._,
Г d • Д t
= 0,766 |/ —
аверт У
При осаждении конденсата на холодной
поверхности в виде сплошной плёнки кон-
денсацию называют плёночной, при осажде-
нии конденсата на поверхности в виде
отдельных капель—капельной.
По теории плёночной конденсации Нус-
сельта, для плоской вертикальной стенки
толщина плёнки конденсата & на расстоянии
х от верхнего конца плиты
1У4Х • tw) X
Г V г
где 6 [лс] — толщина плёнки;
, г ккал 1
Х 'м-град-час ~ коэФиииент теплопро-
L z J водности конденсата;
кг-члс]
pt —2— — коэфициент
L J конденсата;
вязкости
ts — температура насыщен-
ного пара;
— температура стенки;
х[.и] — расстояние от верха
плиты;
7 [кг/л<3] —удельный вес конден-
сата;
По С. С. Кутателадзе, при конденсации
пара связь между критериями подобия уста-
навливается зависимостью ф = / (9), в кото-
рой ф и 9 через критерии подобия
— — Н — ч — gH3
Nii = n‘j, Pr = — , Ga = - (критерии
Галлилея), К — с . д* (критерий, введённый
Кутателадзе) выражаются так:
. _ _______________— /_______1’гп__\
ф “ (бап-РГп)'* 1* ~ ’ у -Ч2т - Ст /
._______Кт__________r / Рт'Кп \
= (Oam-PrmY^~ At-l0\c4m-y2m ) ’
где (о — характерный линейный размер, т. е.
для горизонтальной трубы диаметр d, а для
вертикальной трубы её высота Н.
Результаты обработки опытных данных
привели Кутателадзе и Шренцеля к следую-
щим зависимостям:
при 8 > = 128 • IO"5
ф = ЫЗ-й'Ч или Num = 1,13 ^Оап-РГщ-Кт,
592
ТЕПЛОТА
при в < Ькр = 128 • 10 5
ф = 0,16 + 41,960,
или
Nun = 0,16(Gam.PrJ‘/s +41,9 Кт.
Теплоотдача при кипении жидкости
Опытные данные Якоба, Фритца и Лин-
ке, относящиеся к условиям парообразова-
ния, когда вода полностью покрывает по-
верхность нагрева и водяное пространство
над поверхностью нагрева достаточно велико
для свободного подъёма образующихся пу-
зырьков пара, дают следующие зависимости
для критериев:
для 103 < Grm-Prm < 2-10’
Num = 0,555 (Огот-Ргя,)*/';
для 2-10’ <GrmPrm < ЫО»
Num= 0,129 (Grm-Prm)'l>,
причём определяющей температурой прини-
мается средняя между температурой стенки
и температурой насыщенного пара, а физи-
ческие параметры, входящие в критерии,
берутся для воды.
ТЕПЛОПЕРЕДАЧА КОНДУКЦИЕЙ
И КОНВЕКЦИЕЙ
Распространённой технической задачей
является теплопередача от одной жидкой
(газообразной) среды через твёрдую стенку
к другой жидкой (газообразной) среде, т. е.
механизм теплопередачи охватывает и кон-
векцию и кондукцию.
Фиг. 61
Плоская стенка (фиг. 61). Плоская
многослойная (п слоёв) стенка, тем-
пературное поле в ней определяется теми же
условиями, что и в случае задачи о кондук-
ции теплоты. Поверхность А — В омывается
подвижной средой с температурой d при
коэфициенте теплоотдачи поверхность
С — D — средой с температурой t2 при коэ-
финпенте теплоотдачи а2. Количество тепло-
ты, передаваемое через поверхность F м3
коэфициент теплопередачи
1 Г_ккал 1
—___________________________. \мг-гпад-час ’’
± + y^+_L L J
«1 I Xj ~ a2
{= 1
термическое сопротивление теплопередаче
г—п
1 __1_ , V 21 a. JL Гл<2 -град-час!
k c<i ^—1 X,- ' аг ккал I
i=i
составляется из следующих величин:
1
— — сопротивление теплоотдаче от ле-
“1
вой среды к стенке;
i=n
V SZ
у — сумма сопротивлении кондукции в
i= 1
отдельных слоях;
1
— — сопротивление теплоотдаче от стен-
оз
ки к правой подвижной среде;
Q Г ккал 1
У = 9 ~TfTVJc- — Удельный тепло-
вой поток.
Соотношения между температурами:
Для однослойной стенки
9 ( 1 , 8 \
1 =«i-ax = г2+9^а + х
^2 = <2+а7=/1-9(а7 + г)-
Круглая цилиндрическая стенка (труба).
В круглой цилиндрической многослойной
стенке (трубе) поле температур определяется
условиями, совпадающими с таковыми в за-
даче о кондукции. Внутренняя поверхность
омывается подвижной средой с температурой
Ц при коэфициенте теплоотдачи alt внеш-
няя— с температурой t2 при а2-
Количество теплоты, передаваемое через
участок трубы длиной L [м]
Q = kmp-’K-L(t1 — 12)\ккал1час]-,
коэфициент теплопередачи трубы
1
лтр— j=n •
1 , У J., di + 1 , 1
“1^1 Д—I2X; П а2 dn+i
i— i
1
т— — сопротивление теплопередаче в трубе»
Kfnp
ТЕПЛОПЕРЕДАЧА
593
Часовой тепловой поток, отнесённый к
1 пог. м трубы,
Q , Г ккал I
9 “ L = —*«)[л».час]'
Температура на стыке z-ro и Ц + 1)-го
слоёв
изведение часового количества жидкости,
протекающей через теплообменник, на теп-
лоёмкость её.
При переменных температурах в расчёт
теплопередачи Ж — Т — Ж вводят средний
температурный напор:
= t
1
T7
J А/
п
/ 1 1 d2 ,
+ 2T1lndl+ -
In _£i+L^ =
di /
— In ^г+2'j + ...
4-i di+i}
1 \
a2 9ni-l '
^n+i
~d~n
Температуры внутренней и наружной по-
верхностен
9 _L _
Z1V, 1 = 6 — V ’ ;
_ 9 1
lw, n+1 — <2 + T. a2 dn (. г
Труба однослойная (п = 1);
_£ _1 _
1 — f 1 — T. ’
<7 1
'ip,2= Z2 + T’aT-d; •
Распределение температур в слое см. вы-
ше кондукцию.
Средний температурный напор. При рас-
чёте теплообменных устройств (теплопереда-
ча Ж — Т — Ж) различают относительное
направление жидкостей, омывающих поверх-
I
ности твёрдой стенки: прямоток — na-
il
раллельное движение жидкостей в одном па-
I
правлении; противоток — параллельное
II
движение жидкостей в прямо противополож-
ном направлении; перекрёстный ток I—t -* —
п
движение жидкостей в перекрёстном напра-
влении; возможны сложные комбинирован-
ные схемы движения жидкостей.
При теплопередаче Ж —Т —Ж темпера-
туры жидкостей, участвующих в теплообме-
не, остаются неизменными в случаях, когда
осуществляющийся теплообмен вызывает
изменение агрегатного состояния (парообра-
зование, конденсацию), в прочих случаях
температура горячей tx и температура холод-
ной жидкостей меняются. Схемы харак-
тера изменения температур при прямо- и
противотоке показаны на фиг. 62; на схемах
индекс (') означает вход, (") —выход жид-
кости; —разность температур горячей и
холодной жидкостей со стороны входа (на-
чальная разность температур); — разность
температур со стороны выхода (конечная
разность температур).
Водяной эквивалент жидкости W —
= G-C
ккал
час-град
подсчитывается как про-
38 том I
&! —
1ПЙ
I--3
= = »!•? (’»2
значения
см. табл. 63.
А
9 -~ ^2
, А),
1П 1 + A t2 1п
где tj и t2 — начальные температуры внеш-
него и внутреннего потоков;
A Ij и A t„ — перепады температур потоков.
Таблица 63
А ___ vm “&Г
0,0025 0,167 <>,10 0,391 0.50 0,722
0,005 0,138 0,12 0,415 0,55 0,753
0,01 0,215 0,14 0,438 0,60 0,783
0,02 0,251 0,16 0,458 0.65 0,812
0,03 0,276 0,18 0,478 0,70 0,841
0,04 0,298 0,20 0,497 0,75 0,869
0,05 0,317 0,25 0,542 0,80 0.897
0,06 0,336 0,30 0,581 0,85 0,924
0,07 0,350 0,35 0,620 0.90 0,950
0,08 0,364 0,40 0,655 0,95 0,975
0,09 0,378 0,45 0,690 1,00 1,000
& m ‘"а,
0а
Сложные схемы см. [22].
594
ТЕПЛОТА
Для приближённого учёта потерь во
внешнюю среду М. А. Михеев [33] рекомен-
дует в расчёты вводить вместо водяных эк-
вивалентов W = Gc исправленные значе-
ния их:
где р—потери тепла в процентах по отно-
шению к общему количеству переда-
ваемого тепла (знак минус для го-
рячей, а знак плюс для холодной
жидкости).
Н. И, Белоконь предлагает [2] рассмат-
ривать сложные схемы как задачу о тепло-
передаче в U-образном элементе с различным
индексом противоточности (р) (фиг. 62).
Условные обозначения (фиг. 62):
Ч и 1—температуры входа и выхода
внешнего потока;
t2 и t2 — температуры входа и выхода
внутреннего потока;
Ди Д (,— разности температур внеш-
него Д f, и внутреннего Д/9
потоков (абсолютные вели-
чины);
и W. — —-Ка.л—,, водяные эквива-
час град
ленты внешнего IV j и внут-
реннего W, потоков;
W
~ — соотношение водяных экви-
"I валентов потоков;
1, с ккал ч
лг---------- — водяной эквивалент поверх-
час • град ности теплопередачи U-об-
разного элемента, равный
сумме водяных эквивалентов
его противоточной kFapom и
прямоточной кРпрям частей:
kF “ (кР)прям 4* (кР)ярот‘,
р — индекс противоточности:
п —= kFnpom .
kF ’
Д/ — характеристическая разность
температур рабочего процесса
U-образного элемента:
Д/ = /(Д^ + Д^-ДрД^ДГ,;
Wm— приведённый водяной экви-
валент потоков:
i <1 । 1 Y 4р.
Wm "
Средняя арифметическая разность темпера-
тур потоков:
_ *1+4 _ (2 + *2
= 2 2
Характеристические разности температур
потоков ($] —наибольшая, 9П — наимень-
шая):
8П = йа, т — 2 Д
Расчётная средняя разность температур про-
цесса теплопередачи:
(причём 9, > 9П > 0, 9т > 0).
Критерий выбора схемы теплопередачи:
Тепловой баланс теплопередачи:
Q = k-F 9„, = Д G = IV 2 Д t2 =
и
0 _ 2 ( G — G ) Гикал I
W L 4. 1 < 1 /_£ час J
• W, + IV, + Wm • ct4 2 Wm)
Стержни и рёбра (фиг. 63). Стержни, ци-
линдрические тела с произвольным попе-
речным сечением F[m2] и периметром сече-
ния U [м] имеют в одном (начальном) торце
избыточную температуру (разность темпе-
ратуры стержня и окружающей среды),
поддерживаемую неизменной тепловым пото-
ком Q [ккал/час], проходящим через это
сечение; распространяясь кондукцией по
стержню, поток расходуется на теплоот-
дачу окружающей среде боковой поверх-
ностью и вторым торцом его; 9 — переменная
по длине стержня избыточная температура.
Поле температур стационарное, за изотер-
мические поверхности в теле стержня при-
нимаются плоскости, нормальные к оси
стержня.
Стержень бесконечной длины
(Де=оо). Температура стержня на расстоя-
нии х от торца с температурой й.
9x=l = 0 (температура стержня снизилась
до уровня температуры окружающей среды).
Тепловой поток, поступающий в стер-
жень
Q = 91j/al7kF [ккал/час];
ТЕПЛОПЕРЕДАЧА
595
ккал
м2-град-час
—коэфициент теплоотдачи
боковой поверхности стер-
жня;
. ккал |
л м-гпа/Вчпс ~~ коэфициент теплопровод-
L г J ности стержня.
Стержень конечной длины (Д л).
Температура стержня в сечении, отстоящем
от торца с температурой на расстоянии х,
(1-B)-e~m(L~x)+(l+B)e+m(L-x)
2 {ch (mL) + В sh (mL)}
Температура конца стержня
„ _________________________
'x-L ch (mL) + В sh (mL) ’
Тепловой поток, поступающий в стержень
через торец с температурой Я,
, „ sh (mL) + В ch (mL)
Q = X Fm
fa U ai
В формулах: т = ъ/ • В = —; а. —
f К г К-т
коэфициент теплоотдачи торца в конце
стержня;
gmL__g-mL
ch (mL) =----2----> sh(mL)= ---------~~
гиперболические функции.
Стержень конечной длины L, но
не учитывается теплоотдача конечного торца
его («£ = 0)
е-т (L - х) t + т (L — х)
9 = 01 2 ch (mL) ’
О .
ch (mL) ’
q = X-F.m-hj-th ()nL),
sh (mL)
где
охлаждающего воздуха 15 — 18° С даёт для
коэфициента теплоотдачи
— '8(1 +0.0075 ],
где Тт— средняя арифметическая из абсо-
лютных температур ребра и воздуха; Vm —
скорость воздуха в км/час.
По Паю [37], в расчёте охлаждения воз-
духом цилиндров быстроходных двигателей
внутреннего сгорания коэфициент теплоот-
дачи при обдуве оребрённого цилиндра
свободным потоком воздуха, параллельным
плоскости рёбер, выражается уравнением
а = 1,18(1 +0,0075 Т^).^ -V°’73;
здесь а, Тт, Ут—те же, что в формуле
Стантона; —к. п. д. (эффективность) реб-
ра, определяемый как отношение тепла, дей-
ствительно отдаваемого ребром (Q), к теплу,
которое ребро могло бы отдать (Qo), если
бы разность температур ребра и воздуха по
всей высоте ребра была постоянной (0о)
равной разности этих температур в корне,
ребра.
Для нахождения Пай даёт
Q _ th ah'
ah' :
здесь a = > Л' = Л + y >
причём 6 — толщина ребра;
h — высота его;
Qo — тепло, которое могло быть отда-
но в единицу времени с единицы
длины ребра при постоянной
разности температур (0О) ребра
и воздуха,
Qa = 2a%.h'.
Значения а и ah' для двух типов рёбер
нормальной (встречающейся в практике) фор-
мы и для специальных медных рёбер при-
ведены ниже, в таблице:
Материал ребра Высота ребра Л в м Толщина ребра д в м Теплопро- водность X |/ 2 « h' в м ah' к. п. д. r,f
Алюминий 0,025 0,0023 180 22,8 0,0261 0,595 0,90
Сталь 0,016 0,0008 39.6 83 0,0164 1,36 0,65
Медь 0.0254 0,00051 328 36,4 0,0256 0,93 0,79
При весьма коротких стер-
жнях, малой длине L
ch(mL)=l; th (mL)~mL;
Q = Va-H-L;
приведённые формулы стержней применимы
для расчёта плоских рёбер, расположенных
на плоской плите (стенке).
Стантон на основе опытов с медными
расположенными вокруг деревянного ци-
линдра диаметром 114 мм рёбрами (расстоя-
ние между рёбрами 8 мм, толщина их
0,55 мм, наружный диаметр 146 мм), при
температуре рёбер 30—150° С и температуре
Величина а принята одинаковой для всех
ккал
рёбер, равной 108 '^T4ltc.ef)a^ > что соответ-
ствует скорости свободного потока, обте-
кающего поверхность, в 145 км/час.
РАДИАЦИОННАЯ ТЕПЛОПЕРЕДАЧА
(ТЕПЛОПЕРЕДАЧА ИЗЛУЧЕНИЕМ)
Радиационная теплопередача осущест-
вляется путём переноса энергии электро-
магнитными волнами, имеющими квантовую
природу и подчиняющимися законам термо-
596
ТЕПЛОТА
динамики. Лучи, испускаемые излучающим
телом, отличаясь длинами волн (X) и часто-
тами (N), имеют общую природу и предста-
вляют собой,электромагнитные волны. Деле-
ние их на световые лучи, тепловые, химиче-
ские и другие условно (табл. 64).
Таблица 64
Классификация электромагнитных колебаний
Наименование волн Длина волн
Космические и гамма-лучи . Х-0,1 до 10 А
Лучи Рентгена Ультрафиолетовые лучи (химические лучи) .... Видимые (световые) лучи . Инфракрасные (тепловые) лучи Электромагнитные волны . 10-200А 200Д—0,4 мк* ** 0,4—0.76 мк 0,76—400 мк 0,4 мм—х км
пазоне от X до X ф- dX; соотношение
А ф- R ф- D = 1 имеет смысл по отношению
к интегральному (полному) излучению, охва-
тывающему волны всех длин.
Если £) = 0, тело непроницаемо для излу-
чения и А + R = Г, если D — 1, среда пропу-
скает излучение полностью, она диатер-
мична.
Лучеиспускательную способность тела для
интервала длин волн от X до X ф- dX, т. е. ко-
личество энергии монохроматического излу-
чения с единицы поверхности в единицу
времени Ех
ккал ]
Ь определяют из выраже-
ния Ех = А ' А
сивность излучения.
ккал
м3-час
— интен-
Излучение абсолютно чёрного тела
В однородной и изотропной среде лучи
распространяются прямолинейно; достигая
поверхности среды, они частично отража-
ются, частично проникают во вторую среду,
Где частично поглощаются, частично же про-
ходят её насквозь.
Отражение (преломление) называют пра-
вильным, если падающий и отражённый (пре-
ломлённый) лучи лежат в одной плоскости
с нормалью к поверхности раздела двух сред,
а поверхности, дающие такое отражение (пре-
ломление), называют абсолютно ровными.
Отражение (преломление) называют диф-
фузным, если падающие лучи, отражаясь
(преломляясь), расщепляются и идут во все-
возможных направлениях; такое отражение
дают шероховатые поверхности.
Гладкую поверхность, полностью отража-
ющую все падающие на неё лучи, называют
зеркальной; шероховатую поверхность, пол-
ностью и равномерно отражающую все падаю-
щие лучи, называют белой (абсолютно);
шероховатую поверхность, полностью про-
пускающую все падающие на неё лучи, назы-
вают абсолютно чёрной; тело, полностью
поглощающее все падающие на него лучи,
называют абсолютно чёрным.
A +R +D = 1,
где А — коэфициент поглощения, поглоща-
тельная способность тела, доля излучения,
поглощаемая телом; R—коэфициент отраже-
ния, отражательная способность тела, доля
излучения, отражаемая телом; D — коэфи-
циент проницаемости, пропускная способ-
ность, доля излучения, проникающая сквозь
тело.
Для абсолютно чёрного тела А= 1, для
абсолютно белой поверхности R = 1.
Приведённые коэфициенты (способности)
зависят не только от природы тела, но и от
вида лучей (длины волны X), поэтому соотно-
шение Ах -|- Rx ф- Dx = 1 даёт указания на
свойства тела по отношению к монохромати-
ческому пучку, у которого длина волн в диа-
Интенсивность излучения любого тела
А = / (Т, X). Закон Планка (1902 г.) устана-
вливает вид функции / для абсолютно чёр-
ного тела (индекс s — указание па абсолют-
но чёрное тело).
с, • Х~в ккал '
Jx,s~~~c, м3-час >
где Т — °абс.; X— в м;
Ci=3,17-10 ——— ; с2-=1,43-10 2м. град.
(фиг. 64).
Абсолютно чёрное тело испускает лучи
всех длин волн от X = 0 до X = оо при всех
Фиг. 64
температурах, отличных от абсолютного
нуля; при данной температуре интенсивность
излучения его больше интенсивности излу-
чения любого другого реального тела в тех
же условиях.
При малых значениях Х-Т по закону
излучения Вина
*А—единица измерения длины волны, ангстрем,
— 7
равная 10 мм.
** мк—микрон, равный 10“3 мм.
при ехг> 100 ошибка по формуле > 1%.
ТЕПЛОПЕРЕДАЧА
597
При больших Х-T применим закон Рэлея-
Джинса
Закон смещения Вина устанавливает связь
между длиной волны Хш, отвечающей макси-
мальному значению интенсивности излуче-
ния, и температурой. При повышении тем-
пературы в диаграмме У = A s’ х = мак'
симумы изотерм функции J, s ~ f (X, Т)
смещаются в сторону уменьшения X (см.
фиг. 64):
Хт.Т = 2,9 мм °К.
Закон Стефана — Больцмана, установлен-
ный Стефаном (1879) экспериментально,
Больцманом (1884) теоретически, дает ин-
тегральную, полную лучеиспускательную
способность абсолютно чёрного тела:
Х=оо
Г* . / Т \4Гк кал!
J A,s'd Х ~ ss‘Ti=cs • ^100/ [лРадс] ’
».=о
где с, или cs— коэфициент излучения.
, „ я Г ккал 1
= 4,96-10 ^2.4ac(°a6c.)4j:
м--час-
Излучение серых тел
Излучение серого тела характеризуется,
как и излучение абсолютно чёрного тела,
волнами всех длин, от X =0 до Х= со. Спектр
излучения и здесь непрерывен; однако в срав-
нении с чёрным телом интенсивность излу-
чения серого тела для каждой длины волны
понижена при всех температурах; если Jx —
интенсивность излучения серого тела, то
— г, где s < 1—степень черноты серого
A.s
тела, не зависящая ни от длины волны, ни
от температуры.
К серым телам применим закон Стефана —
Больцмана:
X « оо
J ,/х -dX = 3.74 =
X == О
/Т\*Г ккал 1
~ с ' \ЮОу [ л2 • час ] ’
где а и с — коэфициенты излучения, с = а • 108,
ккал
C=CS -е---------/°абс~\« <СМ- табл- б5)-
м2 час (лоо“)
Большинство технических твёрдых тел
достаточно близко подходит под понятие
серого тела; коэфициент излучения их зави-
сит не только от природы тела, но и от состо-
яния поверхности. Отклонение от закона (за-
висимость с от температуры) учитывается
обычно ссылкой на интервал температур,
для которого найдено значение с.
Таблица G 5
Степень черноты полного нормального излучения
различных поверхностей [28]
Поверхность “С 2
А. Металлы и их окислы
Алюминий
Тщательно полирован-
ная пластина, чистого
металла 98,3% . . . .
Полированная пластина
Шероховатая пластина
Окисленный при 600° С
Кровельный материал,
крытый алюминием
Поверхности, обрабо-
танные алюминием,
при нагреве до 600° С:
медь.................
сталь ...........
Вольфрам
Нить, бывшая в упо-
треблении ...........
Нить.................
Железо и сталь
Металлические поверх-
ности (или с очень тон-
ким слоем окисла)
Железо электролитное,
тщательно полирован-
ное .................
Железо полированное .
То же свежеобработан-
ное наждаком ....
Чугун полированный
Железо сварочное, тща-
тельно полированное
Чугун свежеобточенный
Стальное литьё полиро-
ванное ..............
Сталь листовая шлифо-
ванная ..............
Железо листовое глад-
кое .................
Чугун обточенный . . .
Окисленные поверхности
Железная пластина,
травленая и потом
докрасна заржавевшая
То же, но совершенно
заржавевшая..........
Сталь листовая прока-
танная ..............
Железо окислённое . .
Чугун, окисленный при
600° С.............
Сталь, окисленная при
600° С...............
Железо электролитное,
окислённое, гладкое .
Окись железа ........
Железо литое необра-
ботанное ............
Сталь листовая со зна-
чительным шерохова-
тым слоем окиси . . .
Сталь листовая с плот-
ным блестящим слоем
окиси ...............
Пластина литая гладкая
То же шероховатая . .
Чугун шероховатый,
сильно окисленный
Железо сварочное, окис-
лённое, тусклое , . .
Пластина стальная ше-
роховатая ...........
Сплавы стальные высо-
котемпературные (см.
«Сплавы никеля»)
225—575 0,039—0,057
23 0,040
26 0,055
200—6С0 0,11—0,19
13 0,216
200—600 0,18—0,19
200—600 0,52-0,57
25-3300 0,032—0.35
3300 0,39
175-225 0,052—0,074
425—1020 0,144—0,377
20 0,242
200 0,21
40-250 0,28
22 0,435
770—1040 0,52-0,56
940—1100 0,52—0,61
900-1040 0,55-0,60
830—990 ' 0,60—0,70
20 0,612
20 0,685
20 0,057
100 0,736
200—600 0,64—0,78
2 600-600 0,79
125-525 0,78—0,32
500—1200 0,85—U,89
925—1115 0,87—0,95
25 0.80
25 0,82
23 0,80
23 0,82
40—250 0,95
20—360 0,94
40-370 0,94-0,97
598
ТЕПЛОТА
Продолжение табл. 65
Продолжение табл. 65
Поверхность -с ‘п Поверхность °C •п
Расплавленный металл Чугун расплавленный . Сталь мягкая расплав- ленная Золото Чистое, тщательно по- лированное ...... Латунь Тщательно полирован- ная, состав по весу: 73,2% Си; 26,7% Zn; . 62,4% Си; 36,8%Zn;0,4% Pb; 0,3%AI; 82,9% Си; 17,0% Zn Прокатанная в твёрдом состоянии,полирован- ная, но притом: а) направление поли- ровки заметно . . . б) со слегка нарушен- ной полировкой . . в) со следами оставше- гося от полировки стеарина Полированная Пластина прокатанная: а) с естественной по- верхностью б) тёртая грубым наж- даком Пластина тусклая . . . Окислённая при нагре- ве до 600° С Медь Тщательно полирован- ная, электролитная . Торговая шлифованная, полированная,но с ос- тавшимися ямками . . Шабренная до блеска, но не зеркальная . . Полированная Пластина, предвари- тельно нагретая до 600° С Окись меди Пластина, продолжи- тельно нагревавшаяся, покрытая толстым слоем окиси Расплавленная .... Молибденовая нить . . Никель Нанесённый гальвано- пластическим спосо- бом на полированное железо и затем поли- рованный Технически чистый (98,9% Ni по весу + 8 Мп), полированный Никелированное трав- ленное железо, непо- лированное Проволока Пластина, окислённая при нагреве до 600° С Окись никеля Сплавы никеля Ni—Си, окисленный при 600° С Сг—Ni (по весу 18—32% Ni, 55-68% Си, 20% Zn), окислённыйсерый 1300—1400 1600—1800 225- 625 245-355 255-375 275 20 23 24 40-315 22 22 50—350 200—600 80 20 22 115 200—600 800—1100 25 1075-1275 725—2600 23 225—375 20 185—1000 200—600 650—1255 200—600 20 0,29-0,29 0,28-0,28 0,018—0,035 0.028—0,031 0,0388—0,037 0,030 0,038 0,043 0,053 0.096 0,06 0,20 0,22 0,61-0,59 0,013 0,030 0,072 (’>,023 0,57—0,57 0,66—0,54 0,78 0,16-0,13 0.096-0.292 0.045 0,07—0.037 0,11 0,096—0,186 0,37—0,48 0,59—0,86 0,41—0,46 0,262 Сплав со сталью (8%Ni, 18% Сг), слегка сереб- ристый, шероховатый, коричневый после на- гревания ....... То же после 24-часового нагрева при 525° С Сплав (20% Ni, 25% Сг), бурый загрязнённый, окислённый от време- ни Сплав (60% Ni, 12% Сг), гладкий, чёрный, с прочной окисной обо- лочкой от времени . . Олово, блестящее лужё- ное листовое железо . Платина Чистая полированная пластина Лента Нить Проволока Ртуть, очень чистая . . Свинец Чистый (99,96%), не окислённый Серый, окислённый . . Окислённый при 200° С Серебро Полированное, чистое . Полированное Сталь см. Железо Танталовая нить .... Хром см. в «Сплавах никеля» никельхромо- вую сталь Цинк Продажный (99,1%), по- лированный Окислённый при нагре- ве до 4ОО° С Оцинкованное листовое железо а) очень блестящее . б) герое, окисленное Б. Огнеупорные, стро и другие Асоестовый каргон . . . Асбестовая бумага . . . Бумага тонкая Наклеенная на лужё- ную железную пласти- ну Наклеенная на шерохо- ватую железную плас- тину Наклеенная на лакиро- ванную чёрным плас- тину Вода Гипс, слой толщиной 0,5 мм на гладкой или зачернённой пластине Дуб строганый Кварц плавленый, ше- роховатый Кирпич Красный шероховатый, но без больших неров- ностей Динасовый глазурован- ный, шероховатый , , 215-490 215-525 215-525 270-560 25 225—625 925—1115 25-1230 225-1375 0—100 125—225 24 200 225-625 38-370 1325-2525 225-325 400 28 24 лтсльные, материалы 24 40—370 19 19 19 0—100 20 20 20 20 1100 0,44—0,36 0,62-0,73 0,90—0,97 0.89-0,82 0,043—0,064 0.054—0,104 0,112—0,17 0,036—0,192 0,073—0,182 0,09—0,12 0,057-0,075 0,281 0,63 0,0198—0,0324 0,0221—0,0312 0.193—0,31 0,045—0,053 0,11 0,228 0,276 «расилъиые 0,96 0,93-0,945 0,921 0,929 0,944 0,95-0,963 0,903 U, 895 0,932 0,93 0.85
ТЕПЛОПЕРЕДАЧА
599
Продолжение табл. 65
Поверхность "С ‘п
Динасовый неглазуро- ванный шероховатый . Шамотный глазурован- ный Краски, лаки Белоснежный эмалевый лак на шероховатой железной пластине . . Чёрный блестящий лак, распылённый по желе- эу Чёрный блестящий шел- лак на лужёном ли- стовом железе .... Чёрно-матовый шеллак Чёрный лак Матовый чёрный лак . . Белый лак Масляные краски, 16 различных красок всех цветов Алюминиевые краски и лаки 10% А1, 22% лака по шероховатой или глад- кой поверхности . . . 20% А1, 27% лака по гладкой или шерохо- ватой поверхности . . Другие алюминиевые краски разной давно- сти и с переменным со- держанием А1 .... Алюминиевый лак по шероховатой пластине Алюминиевая краска после нагрева до 325° С Масло смазочное, слоем по полированному никелю Чистая полированная поверхность Слой масла 0,025 мм , То же 0,05 мм ’» » 0,125 * » » оо « Масло льняное на алюминиевой фольге Алюминиевая фольга (без масла) То же с 1 слоем масла * » » 2 слоями » Мрамор сероватый, по- лированный Огнеупоры, 40 различ- ных материалов . . . слабые излучатели . хорошие излучатели Резина Твёрдая, лощёная плас- тина Мягкая, серая, шерохо- ватая (рафинирован- ная) Серпентин (минерал) полированный .... Стекло гладкое Толь ........... 1000 1100 23 25 21 75—145 40- 95 4J— 95 40— 95 100 100 100 100 20 150—315 20 20 2U 20 20 100 100 100 22 600—1000 23 24 23 22 21 0,80 0,75 0.906 Д875 0.821 0,91 0.80—0,95 0.86—0,98 0,80—0,95 0,92-0,96 0,52 0.3 0,27—0,67 0,39 0,35 0,045 0,27 0,46 0,72 0.82 0,087- 0.561 0,574 0.931 (0,65—0,75 ( 0,75 J0,80—0,85 10,85-0,90 0,945 0.859 0,900 С. 937 0,91
* Хотя это значение слишком велико, оно при-
водится для сравнения с данным для слоёв масла
на алюминиевой фольге. Для полированного алю-
миния рекомендуется принимать 0,04.
Продолжение табл. 65
Поверхность °C ‘п
Углерод Очищенный уголь (0,9% золы) 125—625 0,81-0,79
Угольная нить ..... 1040—1405 0,526
Свечная копоть 95—270 0.952
Обмазка нэ жидкого стекла с ламповой са- жей 100—185 0,959—0,947
То же 125-225 0,957-0,952
Го же тонкий слой на железной пластине . . 20 0,927
То же толстая оболочка 20 0,967
Ламповая сажа 0,075 мм и толще 40—370 0,945
Фарфор глазурованный 22 0,924
Штукатурка шерохова- тая известковая , , . 10—88 0,91
Эмаль белая, приллав- ленная к железу . . . 19 0,897
По закону Кирхгофа при одинаковой
температуре соотношение между лучеиспус-
кательной Е и поглощательной А способ-
ностями данного и абсолютно чёрного тела
Е _ _ / T \4
А~ А, ~ Cs * ^100)
Этот закон утверждает независимость отно-
шения лучеиспускательной способности к по-
глощательной от природы тела.
Теплообмен излучением между твёрдыми
телами
Энергия излучения dQx , испускаемого
площадкой dF на площадку dF', внутри-
элементарного телесного угла dSl
d • dF • cos у • d й =
=Jx * ^x ‘ cos ? • dF • d Q — излучение диф-
фузное.
Фиг. 65
О
зависит только от Т и X; dQx считается
пропорциональным лучеиспускательной спо-
собности = Д • d X, пространственному
углу d й и видимой из точки В величине
излучающей поверхности cos и • dF (фиг. 65).
Пространственный угол
dF'
dSl — = sin • d d X,
где угол ср—полюсное расстояние, равен раз-
ности между 90° и географической широтой;
угол X — географическая долгота.
dQx = Д • dk • dF • cos 9 • sin ? • d <p • dX.
600
ТЕПЛОТА
Полусферическое излучение, излучение
в полупространство
2‘ 2г
Qx = J . . dF sin ? • COS 9 d у j dX =
b 0
= r. • E, • dF.
Нормальное излучение, т. e. излучение
в направлении нормали к dF (? = 0), отне-
сённое к единице пространственного угла,
Qx, п = Е, • dF.
Теплообмен излучением между поверхностями
твёрдых тел, разделённых непоглощающей
средой. Расчётная формула
<? = 4-9 -F [(^-(Жуф- *'>
где Q — результативный расход теплоты
в ккал/час;
F — площадь одной из поверхностей
в л2 с соответственным частному
случаю подстрочным индексом 1
или 2;
ф — угловой коэфициент, учитывающий
средний угол, под которым одна
поверхность видит другую;
F—приведённая степень черноты, яв-
ляющаяся функцией от индивиду-
альных степеней черноты поверх-
ностей (табл. 66).
,, , , „ к кал
Коэфициент 4,9 В'----/°flfaA4 ’’
л2час 100-
Защита от излучения экранами
Экран—.обычно металлический лист, уста-
новленный между двумя стенками, участ-
вующими в теплообмене излучением, их
температуры 7\ и Т2; 1\ > Т2; расстояние
между стенками достаточно мало по отно-
шению к размерам стенок, чтобы можно было
пренебречь потерями от рассеивания энергии
в боковых направлениях. Температура на
обеих поверхностях экрана Тд. При решении
предполагается," что температура экрана
с момента установки его начинает расти до
некоторого значения Тд, далее она остаётся
неизменной, а следовательно, экран пере-
стаёт аккумулировать теплоту и должен
далее всю воспринятую от поверхности I
теплоту передать поверхности //.
Первый случай. Коэфициенты излу-
чения стенки 7, стенки 2 и экрана равны
между собой
== fа == Сэ.
Приведённые коэфициенты излучения
будут
С1—Уэ~сэ—>-2=С1 —2 = ———j—
С cs
Количество теплоты, отдаваемое единицей
поверхности в единицу времени при отсут-
ствии экрана.
1 V) Г ккал 1
?0=2_2 IV00/ \100/ / [^"чосР
с О
то же при наличии экрана и при установив-
шемся режиме температур:
Таблица 66
Множители в формуле лучеиспускания между твёрдыми телами
I Случай Конфигурация поверхно- стей, между которыми про- исходит теплообмен лучеиспусканием Поверх- ность F Угловой коэ- фициент ф Приведённая степень черноты е' Примечание
1 Бесконечные параллель- ные пластины Любая 1 1 «1 6* 1. Если в формуле употреб- ляется площадь Fx, то поверх- ностьвнутреннеготелане долж- на иметь отрицательной кривиз-
2 Малое тело, заключённое внутри полностью охватыва- ющего его большого тела (индекс 1 относится к вну- треннему телу) 1 £1 ны, В случае же наличия тако- вой надо, определяя Fx, мыс- ленно перекрыть все углубле- ниявповерхности плоскостями, которым присвоить степень
3 4 ’1ело, заключённое внутри полностью охватывающего его большого тела величины одного с ним порядка(ин- декс 1 относится к внутрен- нему телу) Промежуточный случай между 2 и 3 (не поддаётся точному учёту за исключе- нием тел особой формы) F1 F1 1 1 1 1+J-1 £i еа черноты, повышенную (более близкую к единице)сравнитель- но с в прямой зависимости от глубины вогнутостей. 2. Первая форма получается, если принимать отражение пол- ностью рассеянным, вторая же получается при идеально зер- кальном отражении. Истинное значение ближе к первой фор-
5 Концентрические шары или бесконечные цилиндры, особый вид случая 4 (ин- дексы 1 относятся к внут- ренним телам, 2—к объемлю- щим) Pi 1 ИЛИ 1 l + 2-i £j е3 (см. примечание 2) ме, чем ко второй. Болеесложныеслучаисм. 128]
ТЕПЛОПЕРЕДАЧА
60 i
_i_ i____f/л? /ЬП‘
-4^2-2 ' 2 _£Ц100/ \100/( ’
с cs
(100 j ~2 | (100/ 100) ( ’
т. е. установка одного экрана снижает тепло-
передачу в 2 раза. Если qn — теплопередача
при п поставленных друг за другом экранах,
то
1
qn ~ п + 1 ’ q0-
Второй случай. сг = с2 — с; с3 с.
Приведённые, коэфициенты излучения:
1 1
С1—>2“ 2 _ £’ С1—>-?==1 1 ) =сэ->2;
с с с3 с3
?1——>2 ~
_ 1 1 [ !Тг у IT» V)
~ 2 ' 1_ £ __1_ | \iooj уоо/ / ’
с сэ cs
(Т \4 If /7\ \« /Т ' 4 1
10°/ ”2 j V100/ \100/ / ’
1 / /Ll VI
9о ~ ^—11 V00/ \,ио/ / ’
с cs
2 1
_ _ 1 с «г
91 - - ----------_ . д„.
С + cs cs
Излучение газов
Газы обладают селективной поглощатель-
ной способностью, а следовательно, и селек-
тивной испускательнойспособностыо;у твёр-
дых тел поглощение происходит в тонком
поверхностном слое, у газов за счёт большей
прозрачности для тепловых лучей следует
учитывать объёмное поглощение.
Поглощательная способность А^ по отно-
шению к волнам длиной от X до X-j-d X для газа
сложная функция от X; она зависит не
только от свойств среды (газа), но и от
формы и размера газового тела.
В объёме газового тела в зависимости от
давления содержится различное число мо-
лекул, поэтому поглощение газовым объёмом
луча, проникающего на глубину s (завися-
щую от формы и размера), будет зависеть
не только от глубины проникновения, но и
от давления газа; так как обычно приходится
иметь дело с газовыми объёмами, заполнен-
ными смесями газов, то, говоря о поглощении
каким-либо компонентом смеси, считают Ах
Р
зависящим от произведения s • jy , где р —
парциальное давление компонента; Р — дав-
ление смеси газов.
Энергия излучения, испускаемого газо-
вым телом,
X + ДХ р + Лх
Q = A -Р J
X
подсчёт по этой формуле должен быть про-
изведён для каждой полосы поглощения;
суммирование всех этих величин даст пол-
ное излучение газового тела.
Газы с симметричным строением молекул
(водород, кислород, азот и др.) не обнару-
живают полос поглощения» достаточных для
учёта их при встречающихся в технике тем-
пературах; окись углерода, углеводороды,
водяной пар, углекислота, сернистый ангид-
рид, аммиак, хлористый водород имеют по-
лосы поглощения, достаточно развитые.
По Шаку [47], лучеиспускание углекис-
лоты и водяного пара в топочных газах
учитывается следующими формулами.
Для углекислоты:
О С Г / 1 — е”16с\
9 Е 43Г5 р ~ к1'} Г “ ) +
. /> г 1—е~80с Г ккал!
(*2 кг) kt J j
Здесь с — p-S (формула действительна при
С>0,01); р—парциальное давление СО2 (в ат);
s—толщина в м лучеиспускающего слоя то-
почных газов над лучевоспринимаюшей по-
верхностью F в м2.
Величины к выражают лучеиспускание от-
дельных полос поглощения бесконечно тол-
стого слоя углекислоты (берутся из табл. 67).
Таблица В7
Уменьшенное лучеиспускание бесконечно толстого
слоя углекислоты [47]
Лучеиспускание
<3 о.
полоса 1 полоса 2 полоса 3
О. Ф , ккал fct в—- , ккал к9 в— , ккал к, В—.
ф ° Н са м* •час лр.час Л!8, час
200 0,004.10’ 0,07.10» 0,23-10»
300 0,05 .10» 0,24.10’ 0,36.10я
400 0,15 -10я 0,52.10’ 0,50.10s
500 0,24 • 1G8 0,95.10» 0,65-10»
600 0,96 .10’ 1,6 -10» 0,79-10»
700 1,9 -IO3 2,4 -10» 0,90-1U8
800 3,2 .10’ 3,3 .10’ 1,1 -Ю8
930 4,8 -10» 4,3 НО® 1,3 .10®
1000 6,8 .10’ 5,5 .10s 1,4 -103
1100 9,3 .10’ 6,8 .10’ 1,6 -.10’
1200 12,3 .10» 8,2 .10» 1,9 -К.»
1300 15,6 .10’ 9,7 .Ьа 2,1 -103
1400 19,2 . 103 11,2 -10» 2,4 ♦ 108
1500 23 .10’ 12,9 .10’ 2,7 .10*
1600 28 .10а 14,6 .10» 3,0 • i()3
1700 33 .10’ 16,6 .10° 3,4 .10s
1800 38 -10» 18,7 .10® 3,8 -103
1900 44 .10в 21,0 -10“ 4,2 -IO3
2000 51 ИО3 24 .10’ 4,5 .10s
к берётся по температуре газа; к' — по тем-
пературе лучевоспринимаюшей поверхности;
ккал
— коэфициент излучения
’7°К\4
A,2-4ac(ioo)
лучевоспринимающей поверхности; козфи-
цпенты 9 — поправочные, зависят отс и фор-
602
ТЕПЛОТА
мы газового тела; для округлённых корот-
ких форм (куб, шар) у = 0,7—0,8, для пло-
ских, вытянутых форм = 1,1 — 1,0; первые
значения соответствуют малым с, вторые —
большим; при с > 0,5 все значения ? равны 1;
у, должно быть ближе к 1, чем <рх; практи-
чески разница между и срэ в большинстве
случаев незначительна; при с < 0,01 и при
СО, < 2°/0 применяется формула
4 F 4,95[y1 ’ 16с Г
/ р-1 800 с\
+ 0,7ya(fra-V)(l ---) +
4-0,45<р, (fc,-fc,'> (1И, СД)]|
\ 80с /]1ма-час
Коэфициент ?2 принимают равным ?а.
Для водяного пара:
+ <?,(№,-№/) Х-»
0 66 , ...
*х 1-"бТ<1-е )-
0,34 ( -5с _ е-27 О')
22с
(j______g— 46е \ ]
1—— --------- >ккал/чае,
45с /I
значения ? оцениваются так же, как и для
углекислоты; лучеиспускания отдельных по-
лос водяного пара W,, Wa, W, берутся из
таблицы по температуре газа; Wj , W'2 >
IV3— то же, но по температуре лучевоспри-
нимаюшей поверхности (табл. 68).
Таблица 68
Лучеиспускание бесконечно толстого слоя
водяного пара
Температура в СС Лучеиспускание
полоса 7 2,24-3,27 р. ,, ккал VV Ц В - м**час полоса 2 4,8-8,5 |а ... ккад W, в — м**час полоса 9 12—25 р. ккал W, в— м**час
2оО Зое 400 5и0 60о 700 ъоо 900 100b Ибо 1200 1300 1400 1500 1600 1700 1800 1900 2 JOG 0,02.10» 0,25.10» 0,85.10» 2,5 .к» 5,0 .108 9,4 .10» 15,3 .10» 23,<5 .10» 33,8 .10» 46.10* 61.lv» 78.10» 97.10» 117.10’ 138.10» 161.103 185 • 10» 211.10» 230.10» 0,96.10* 2,2 .10» 3,9 .20» 6,1 -10» 9,0 .10» 12,2 .10» 15,8 НО» 19,6 .10» 23,3 . к» 27,2 .10» 31,ч .10» 35,6 .10» 40,1 .10* 44,6 «10» 49,4 .10» 51,4 .10» 59,5 .10» 64,9 .10» 71 .10’ 7 .10» 0,9 .10» 1.2 .10» 1,4 .10» 1,7 .10’ 2,0 .10» 2,35-10» 2,7 .1и» 3,0 .10’ 3,4 .10» 3,7 .10’ 4,1 .10» 4,5 .10» 4,9 .10» 5,3 .10» 5,8 .10» 6,2 .10» 6,7 .10’ 7,1 .10’
В работах Шака для пользования приве-
дёнными формулами даются графики,облег-
чающие расчёты. Другие методы расчёта
излучения несветяшимися газами см. [22],
[24], [28], [47].
Для углекислоты и водяного пара име-
ются теперь более надёжные данные, полу-
ченные путём непосредственного измерения
общей энергии излучения газа.
Они показывают, что излучение углекис-
лоты пропорционально 7'3,6, а излучение во-
дяного пара Т3. Однако для решения тех-
нических задач расчётным формулам условно
придают вид, согласный с законом Стефана—
Больцмана, внося соответственные поправки.
Фиг. 67
Окончательная расчётная формула лучистого
тёплообмена [33] между газом и оболочкой
*0. W = eu. • G eg ~
— A /ЛгА*] ккал
\10бу ]л<2-час ’
где — степень черноты газа, функция тем-
пературы газа и произведения из
парциального давления газа р и
длины пути луча I; е? — / (Т^, pl)
берётся по фиг. 66 для углекислоты
и по фиг. 67 для водяного пара.
ТЕПЛОПЕРЕДАЧА
603
Значение еНво> взятое по фиг, 67, умно-
жают на коэфициент (3, взятый по фиг. 68.
Если углекислота и водяной пар содержатся
одновременно, то eg находят по выражению
= есо, + ? • ен2о __ ДгА'’
где Д— поправка на частичное взаимопо-
глощение энергии, излучённой
углекислотой и водяным паром.
Дея невелико, порядка 2 — 4°/0, учиты-
вается при очень точных расчётах, берётся
по фиг. 69.
Если степень черноты твёрдой поверхно-
сти (оболочки, обнимающей газ) ew, то эф-
фективная степень черноты её в присутст-
вии газа будет приближённо (при =
= 0,8- 1,0) e^ = 0,5(ew+l).
А?= ACOj -|- АНлО — AAg — поглощатель.
ная способность газа, берётся по темпера-
туре оболочки tw С, причём
Асо, = гсо, • I — берется по фиг.66
ПО t о/ f
Ан 0 = J3 ен,о — берётся по из фиг. 67
и 68,
AAg = Asg —берётся по фиг. 69.
Таблица 69
Средняя длина пути луча для газовых тел
различной формы [33]
Формы газового тела 1
Сфера диаметром 4 о,бо а
Куб со стороной а . . . , . ...... 0,60 а
Цилиндр диаметром d, бесконечно ДЛИННЫЙ о,9о а
Цилиндр высотой d, излучение на боковую поверхность о.бо а
То же, излучение на центр основания 0.77 d
Цилиндр h—оо, основание—полукруг радиусом г, излучение на плоскую боковую поверхность 1.26 г
Плоско-параллельный слой бесконеч- ных размеров толщиной <5 1,8 3
Пучок труб диаметром d, с расстоя- нием между поверхностями труб х и при расположении труб: а) по треугольнику x=d . 2,8 х
б) по треугольнику x*=2d 3,8 х
в) по квадрату x—d 3,5 х
Для средних значений фактора pl табл. 69
даёт значение I в зависимости от формы га-
зового тела.
ЛИТЕРАТУРА И ИСТОЧНИКИ
1. Антуфьев В, М., Казаченко Л. С.
Теплоотдача и сопротивление конвективных по-
верхностей нагрева. М .—Л,, ОНТИ, 1938, 25-2 с.
2. БелоконьН, И . Теплопередача при лере*
мелных температурах. В кн. «Труды Московского
нефтяного института им. И. М. Губкина».
Вип. 2, 1940 г. и сб. «Транспортное машино-
строение» № 9 и 10, 1937 г.
3. Белоконь Н. И. Развитие учения об основ-
ных принципах термодинамики. В кн. «Труды
Московского нефтяного института им. И. М.
Губкина». Вып . 5, М.—Л., 1947, с. 290 — 370.
4 Брандт А. А. Основание термодинамики.
’ АЛ . — Л-, 1926, 255 с.
5 Бои дж мен П.В. Физика высоких давле-
ний . М.-Л.» ОНТИ, 1935, 402 с.
6 , Б ы к о в Н, А. Термодинамика, М - — Л .. 1928.
с.
7 By к а л ови ч М.П, Термодинамические свой-
ства водяного пара . Госэнергоиздат, 1946,88 с.
8. Вукалович М. П. и Новиков И. И.
«Доклады Академии наук СССР», 1939, № 8,
767 — 72 .
9. Вукалович М . П . и Н о в и к о в И . И.
Теплоёмкости реальных газов. Изв. ОТН АН
СССР № 6, 1939, с. 111-28.
10. Ге рш С. Я. Глубокое охлаждение. 2-е изд.
М., «Советская наука». 1947, 363 с.
11. Гиншельвуд Ч. Н. Термодинамика. Пе-
рев.. М.— Л., 1933, 174 с.
12. Годнее И. и Свердлин А. О теплоёмко-
стях газов при высоких давлениях. «Химстрой»,
1934, т. VI. № 1, с. 8 — 14.
13. ГреберГ. и ЭркС. Основы учения о теп-
лообмене. Перев. с нем., М.-Л., 1936.
14. ГреберГ. Введение в теорию теплопередачи .
2-е изд ., перев . с нем .. М . — Л.. Госэнергоиз-
дат, 1933, 263 с.
15. ГуггенгеймЭ. А. Современная термодина-
мика. изложенная по методу У. Гиббса. Перев.,
М.-Л.. 1941, 188 с.
16. ГухманА. А. Физические основы теплопе-
редачи. М.—Л.. Энергоиздат. 1934, 315 с.
17. Жуковский М. Й. Истечение газа из резер-
вуара конечного объёма. Вкн. «Теплопереда-
ча и аэрогидродинамика». М., Машгиз, 1947,
с. 3-28 (ЦКТИ, кн. 28).
18. Жуковский В. С. Техническая термоди-
намика, М.-Л.. 1940, 336 с.
19. Журнал технической физики, т. II. Вып. 9 —
10. 1932.
20. H(vpnan технической физики, т. VIII, вып.
13—14, 1938 .
21. Иноземцев Н. В. Течение и истечение га-
зов и паров. Изд. МАИ, М., 1938.
22. К и р п и ч ё в М. В. Михеев Н.А., Э й-
генсон Л. С, Теплопередача, М.-Л., Гос-
энергоиздат, 1940, 292 с.
23. Кн об л ау х О. Таблицы и диаграммы для
водяного пара, вычисленные на основе удель-
604
ТЕПЛОТА
ной теплоёмкости. М.—Л., Госэнергоиздат,
1943. 40 с.
24 . Котельные установки под ред. Кирпичёва М.В.,
Ромма Э. И.. Усенко Т. Т,, т. I. М.—Л., Гос-
энергоиздат, 1941—46, 2 т.
25. Кузнецов Н. В. и Локшин В, А. Теп-
лоотдача конвекцией в пучках труб, омывание
поперечным потоком газов. «Тепло и сила»,
1937, № 10, с. 19-26.
26. Кутателадзе С. С. Теплопередача при
изменении агрегатного состояния. Л., Машгиз,
1939, 136 с.
27 . Л о к ш и н В. А. Отчёты Всесоюзного теплотех-
нического института за 1939 г.
28. Мак-Адамс. Теплопередача. Перев. с
англ., М.-Л., ОНТИ, 1936, 439 с.
29. М ачинский В. Д. Теплопередача в строи-
тельстве. М.—Л., Госстройиздат, 1039, 344 с.
30. Майер Р. Закон сохранения и превращения
энергии. ГТТИ, М.-Л., 1933, 309 с.
31. Менш ут К и н В. Н. Труды М. В. Ломоносо-
ва по физике и химии. Изд-во АН СССР, М.—
Л., 1936, 537 с.
32. Меркель Ф. Основы теплопередачи, Перев.
с нем., М. — Л., ГИЗ, 1929, 344 с.
33. Михеев М. А. Основы теплопередачи. М.—
Л., Госэнергоиздат. 1947, 415 с.
34. Мл о дзеевс кий А. Б. Термодинамика, М.,
Учпедгиз, 1948, 184 с.
35. Нормы теплового расчёта котельных агрегатов.
«Известия ВТИ» № 6, 1946, с. 22—29.
36. О р л и н А. С. Двухтактные быстроходные дви-
гатели. М., Машгиз, 1947, 184 с.
37. П а й В. Р. Двигатели внутреннего сгорания,
Т. II, М., Оборонгиз. 1940,260 с.
38. П о л я к Т. Л. Теория лучистого теплообмена.
ЭНИН АН СССР, 1938.
39. Правила № 169 по измерению расхода жидко-
стей, газов и пара. Главное управление мер и
весов, Каталогиздат, М,—Л., 1938.
40. Раковский А. В. Введение в физическую
химию, М., ГОНТИ, 1932, 677 с.
41. Сборник статей под ред. А. К. Тимирязева,
Л.-М., ОНТИ, 1937, 220 с.
42. Сушков В. В. Техническая термодинамика.
М.-Л., 1946, 312 с.
43. Тен-Бош. Теплопередача. Перев. с нем., М —
Л., Нефтяное изд-во. 1930, 495 с.
44. Т и м р о т Д. Л. Определение вязкости пара и
воды при высоких температурах и давлениях.
Изв. ВТИ, 1940, № 3, с. 16-23.
45. Хвольсон О. Д. Курс физики, т. III, ГИЗ,
1923.
46. «Хютте». Справочник, т. I, М,—Л., 1936.
47. Ш а к А. Теплопередача в промышленных уста-
новках. Перев. с нем. М.—Л., Энергоиздат,
1933, 380 с.
48. ШюлеВ. Техническая термодинамика, т. II,
перев. с нем., М.—Л., 1938.
49. Энгельс Ф. Диалектика природы. М.,
Госполитиздат, 1948, 331 с.
50. Э й г е н с о н Л. С. Доклады АН СССР,
т. XXVI, № 5, 1940.
ЕДИНИЦЫ ИЗМЕРЕНИЙ
^ШВНЕЮНЖИИМИЯМНМИ^
&
ЕДИНИЦЫ ИЗМЕРЕНИЙ, ПРИНЯТЫЕ В СССР
Величина Единица Отношение к : главной единице Сокращённое обозначение Определение главных единиц
иностран- ным ; шрифтом русским шрифтом
Масса Длина I. Метричес! Килограмм Тонна Центнер Грамм Дециграмм Миллиграмм Метр Километр Дециметр Сантиметр Миллиметр Микрон Миллимикрон Ангстрем <ие ме 1 10» 102 10-3 КН КК» 1 103 10-! 10"2 10-8 10-‘ 10*» 10-1» )Ы (по kg t q g dg mg m km dm cm mm Iх mpi °A OCT вне E кг m Ц г дг мг м км дм см мм мк ммк °А 859) Килограмм есть единица массы, определяемая про- тотипом!. Международным прототипом килограмма Первой генеральной кон- ференцией по мерам и ве- сам в 1889 г. признана платино-иридиевая гиря, имеющая обозначение «К», которая хранится в Меж- дународном бюро мер и ве- сов в Севре (Франция) Для СССР за основной эталон килограмма при- нята платино-иридиевая копия международного прототипа килограмма, имеющая обозначение «12» и хранящаяся во Всесоюз- ном институте метрологии в Ленинграде Метр есть единица дли- ны, определяемая прото- типом. Международным прототипом метра Первой генеральной конференцией по мерам и весам в 1889 г. признана нарезная плати- но-иридиевая мера, имею- щая обозначение «М», ко- торая хранится в Между- народном бюро мер и ве- сов Для СССР за основной эталон метра принята пла- тино-иридиевая копия международного прототи- па метра, имеющая обо- значение «28» и храня- щаяся во Всесоюзном ин- ституте метрологии в Ле- ни н г раде
1 Прототипами называются международные и национальные эталоны метра и килограмма, изго-
товленные в Международном бюро мер и весов.
606
ЕДИНИЦЫ ИЗМЕРЕНИЙ
Продолжение
Величина Единица Отношение к главной единице Сокращённое обозначение Определение главных сдинии
иностран- ным шрифтом русским шрифтом
Площадь (поверх- ность) Объём Ёмкость (вмести- мость) А Сила Работа и*энергия Давление Б. Сила Работа и энергия Мощность Квадратный метр Г ектар Ар Квадратный де- циметр Квадратный сан- тиметр Квадратный мил- лиметр Кубический метр Кубический деци- метр Кубический сан- тиметр Кубический мил- лиметр Литр Килолитр Гектолитр Декалитр Децилитр Сантилитр Миллилитр II. Механические . Единицы систем Дина Эрг Бар Единица системы Килограмм (си- ла) Грамм (сила) Килограмм-метр Килограмм-метр в секунду *' »» Ml V 1 104 103 10- 2 10-1 10-« 1 10-3 10-» 10-’ 1 103 103 10 10-1 10'2 10-2 единиц >i CGS 1 1 1 MKS ( 1 10s 1 1 т2 ha а dm2 ст2 тт! щ3 dm3 ст3 тт! 1 kl hl dkl dl cl ml ы (no (сант dn e b метр, kG G kGm kGm sec м‘ (кв. м) га а дм- (кв. дм) см'- (кв. см) им1 (кв. мм) м:> (куй м) дМ3 (куб. дм) см'3 (куб. см) мм'3 (куб мм) л кл гл дкл дл сл мл ОСТ ВК»С б иметр, грам дн эрг б килограмм-с кГ Г кГм кГм сек Квадратный метр есть площадь квадрата, сторо- на которого имеет длину, равную 1 м Кубический метр есть объём куба, ребро которо- го имеет длину, равную 1 м Литр есть объём 1 кг во- ды при наибольшей её плотности и при нормаль- ной! атмосферном давле- нии; 1 л== 1,000028 дм'3 J52 и 6053) м, секунда) Сила, сообщающая мас- се в 1 г ускорение в 1 см в секунду на секунду Работа, производимая силой в 1 Он при переме- щении точки её приложе- ния на 1 см по направле- нию этой силы Давление, которое испы- тывает плоская поверх- новть в 1 cM‘i под дейст- вием силы в 1 дн ила, секунда) Килограмм (сила) есть сила, сообщающая массе в 1 кг ускорение 9,80665 м в секунду на секунду Работа, производимая силой в 1 кг при переме- щении точки её приложе- ния на 1 м по направле- нию этой силы Мощность, при которой в течение I сек. равномер- но производится работа, равная 1 кгм
ЕДИНИЦЫ ИЗМЕРЕНИЙ
607-
Продолжение
Величина Единица Отношение к главной единице Сокращённое обозначение Определение главных единиц
иностран- ным ’ шрифтов 1 русским шрифтом
Механическое напряжение (давление) II Электрическое сопротивление Сила тока Электрическое напряжение (электродвижу- щая сила) Электрическая мощность Работа электри- ческого тока Количество элек- тричества Электрическая ёмкость Индуктивность Килограмм на квадратный метр Килограмм на квадратный сан- тиметр (техни- ческая атмо- сфера) I. Международны е Международный ом Мегом Микроом Международный ампер Миллиампер Микроампер Между нар одный вольт Киловольт Милливольт Микровольт Международный ватт Киловатт Г ектоватт Международная ватт-секунда Ватт-час Международный кулон или ам- пер-секунда Международная фарада Микрофарада Международный генри Миллигенри 1 10‘ элект 1 10’ 10“ 1 ю-3 10-’ 1 103 10-’ 10-’ 1 103 10» 1 36-10» 1 1 10-’ 1 I0-8 kg т» kg ст» рическ й Мй р.2 А mA (лА V kV mV v-v w kW hW Ws Wh c F pF H mH кг м* кг см* ие единицы ом мгом МКОМ а ма мка в кв мв мкв вт кет гвт вт-с вт-ч к Ф гн Килограмм на квадрат- ный метр есть давление, которое испытывает пло- ская поверхность в 1 л<а под действием равномерно распределённой нагрузки в 1 кг (по ОСТ 515) Международный ом есть сопротивление ртутного столба длиной в 106,300 см, имеющего сечение, одина- ковое по всей длине, и массу в 144,521 г при тем- пературе тающего льда Международный ампер есть сила неизменяющегося электрического тока, ко- торый отлагает 0,00111800 г серебра в 1 сек., проходя через водный раствор азотнокислого серебра Международный вольт есть электрическое напря- жение или электродвижу- щая сила, которые в про- воднике, имеющем сопро- тивление в 1 ом, произво- дят ток силой в 1 а Международный ватт есть мощность неизменяю- щегося электрического jo- ка силой в 1 а при напря- жении в 1 в Международная ватт-се- кунда есть работа, совер- шаемая электрическим то- ком в течение 1 сек. при мощности тока в 1 вт Кулон есть количество электричества, протекаю- щее через поперечное се- чение проводника в тече- ние 1 сек. при токе в 1 а Фарада есть ёмкость кон- денсатора, заряжаемого до напряжения в 1 в одним кулоном электричества Г енри есть индуктив- ность электрической цепи, в которой индуктируется электродвижущая сила в 1 в при равномерном изме- нении тока в этой цепи со скоростью 1 а в 1 сек.
608
ЕДИНИЦЫ ИЗМЕРЕНИЙ
( ОСТ ,
IV. Тепловые единицы I г10[Ц{с
Величина Единица Сокращённые обозначения Определения
латинскими буквами русскими буквами
Температура Градус (между- народный) ®с °C Одна сотая температурного проме- жутка между точками 0° и 100° между- народной температурной шкалы, уста- навливаемой согласно положению о ней, принятому VII генеральной кон- ференцией по мерам и весам в 1927 г.
Теплота Килоджоуль kJ кжд Единица энергии в абсолютной си- стеме единиц MTS (ОСТ 6053), равная 1010 эргам
Джоуль J дж Одна тысячная килоджоуля (107 эр- гов)
Мегаджоуль MJ мгдж Одна тысяча килоджоулей (1013 эр- гов)
Килокалория (большая кало- рия) kcal ккал 4,182 килоджоуля. Килокалория практически (с точностью до 0,02%) равна количеству теплоты, потребному для нагревания массы воды в один килограмм от 19,5° до 20,5°С при нормальном атмосферном давлении (приложение)
Калория (ма- лая калория) cal кал Одна тысячная калории (4,1821)
1. По ОСТ 349 за нормальную температу-
ру должна приниматься температура 4-20°С.
Двадцатиградусная калория отвечает нагре-
ву от 19,5 до 20,5°С.
2. Килокалория, установленная междуна-
родной конференцией по таблицам пара в
Лондоне в 1929 г., подтверждённая междуна-
родной энергетической конференцией в Бер-
лине в 1930 г. и условно называемая элект-
рической, определяется как 1/8в0 междуна-
родного киловатт-часа. Она составляет
1,0013 килокалории, установленной ОСТ
В КС 6259.
Килокалория (19,5 —20,5°С) = 4,182 kJ =
1
= 426,4 kGm = ] kWh (международного).
Килокалория электрическая = 4,1875 kj =
1
«= 427 kGm = ggg kWh (международного).
OCT
3. По 6954 международная темпера-
турная шкала, принятая VIII генеральной
конференцией по мерам и весам в 1933 г., яв-
ляется практическим осуществлением термо-
динамической стоградусной температурной
шкалы, у которой температура плавления
льда и температура кипения воды при нор-
мальном атмосферном давлении обозначены
соответственно через 0° и 100°.
Международная температурная шкала ос-
новывается на системе постоянных точно
воспроизводимых температур равновесия
(постоянных точек), которым присвоены чис-
ловые значения. Для определения промежу-
точных температур служат интерполяцион-
ные приборы, градуированные по этим по-
стоянным точкам.
Основные постоянные точки международной
температурной шкалы
а) — 182,97° — температура равновесия
между жидким и газообразным кислородом
при нормальном атмосферном давлении (точка
кипения кислорода)
1р = «то»+ 0,0126 (р —760) —
— 0,0000065 (р_ 760)2;
б) 0,000° — температура равновесия между
льдом и насыщенной воздухом водой при
нормальном атмосферном давлении (точка
плавления льда);
в) 100,000° — температура равновесия меж-
ду жидкой водой и её паром при нормаль-
ном атмосферном давлении (точка кипения
воды)
tp = I,в0 4- 0,0367 (р-760)-
— 0,000023 (р — 760)2;
г) 444,60° — температура равновесия меж-
ду жидкой серой и её паром при нормаль-
ном атмосферном давлении (точка кипения
серы)
tp = 17во 4- 0,0909 (р -760)-
— 0,000048 (р —760)2;
д) 950,5°—температура равновесия между
твёрдым и жидким серебром при нормаль-
ном атмосферном давлении (точка затверде-
вания серебра);
е) 1063,0° — температура равновесия меж-
ду твёрдым и жидким золотом при нормаль-
ном атмосферном давлении (точка затверде-
вания золота).
ЕДИНИЦЫ ИЗМЕРЕНИЙ
609
Британская (англо-американская) система мер
Меры длины
1 миля (mile)=1760 ярдам=5 280 футам 1
1 ярд (jard)=3 футам=36 дюймам“360 линиям 1
1 фут (foot)=12 дюймам (inch) 1
1
Меры поверхности
1 квадратная миля (640 акров) (acre)
1 акр=10 кв. цепям=4 840 кв. ярдам - 1
=43 560 кв. футам j
Иногда применяются:
цепь (chain)=22 ярдам
фэсом (fathom)=2 ярдам=3 пядям (span)
ладонь (hand)=4 дюймам=288 пунктам
мил (mil) =0,001 дюйма
Меры объёма
кубический ярд=27 куб. футам
кубический фут=1 728 куб. дюймам
Меры сыпучих тел
1 америк. бушель (U. S. bushel)= 1,2445 куб. фута =2150,42 куб. дюйма
1 бушель=4 пекам (реск)=32 квартам (quart)=64 пинтам (pint)
1 англ, бушель (British Imperial bushel) = l,2837 куб. фута=2218,19 куб. дюйма
М е р ы жидкостей
1 бочка (tun)=2 пайпам (pipe) или буттам (butt)=4 баррелям (barrel)= 126 галлонам (gallon)
1 галлон=4 квартам=8 пинтам=32 джиллам (gill)
Меры веса (торговые)
1 большая или длинная тонна (gross or long ton)=2 240 фунтам
1 малая и короткая тонна (net or short ton)=2 000 фунтам
1 центнер (hundred—weight)=QQ-6onbtuoii тонны=4 квартерам (quarter)=8 стонам (stone)=
= 112 фунтам
1 фунт (pound)=16 унциям (ounce)=7 000 гранам (grain)
1 унция=16 драхмам (drachm)=437,5 грана
Меры веса («тройские» и аптекарские)
1 тройский фунт (troy pound)=12 тройским унциям=240 весовым пенни (penny—weight) =
=5 760 гранам
1 аптекарский фунт=12 унциям=96 драхмам=288 скрупулам (scrupl)=5760 гранам
Вес грана торгового, тройского и аптекарского одинаков
Вес фунта и унции тройских и аптекарских также одинаков
Единица давления
1 фунт на кв. дюйм=144 фунтам на кв. фут=0,063 атмосферы=2,042 дюйма ртутного
столба (62°F*)=27,7 дюйма водяного столба (62° F)
1 атмосфера=30 дюймам ртутного столба (62° F) = 14,7 фунта на кв. дюйм
1 дюйм ртутного столба (62° F)= 13,58 дюйма водяного столба=0,491 фунта на кв. дюйм
» 62' F-16'J, "С.
39 том 1
610
ЕДИНИЦЫ ИЗМЕРЕНИЙ
ПЕРЕВОДНЫЕ ТАБЛИЦЫ
Таблица 1. Дробные доли дюйма в десятичные доли дюйма
1/2 . .0,5 3/32 . . •0,09375 3/64 . . .0,46875 35/64 . . .0,546875
1/4 . .0,25 5/32 . . .0,15625 5/64 . . .0,78125 37/64 . . .0,578125
3/4 . .0,75 7/32 . . .0,21875 7/64 . . .0,09375 39/64 . , .0,609375
1/8 . . .0,125 9/32 . . .0,28125 9/64 . . .0,40625 41/64 . . .0,640625
3/8 . . .0,375 11/32 . . .0,34375 11/64 . . .0,171875 43/64 . * .0,671875
5/8 . . .0,625 13/32 . . .0,40625 13/64 . . .0,203125 45/64 . . .0,703125
7/8 . . .0,875 15/32 . . .0,46875 15/64 . . .0,234375 47/64 . . .0,734375
1/16 . . .0,0625 17/32 . . .0,53125 17/64 . . .0,265625 49/64 . . .0,765625
3/16 . . .0,1875 19/32 . . .0,59375 19/64 . . .0,296875 51/64 • . .0,796875
5/16 . . .0,3125 21/32 . . .0,65625 ' 21/64 . . .0,328125 53/64 . . .0,828125
7/16 . . .0,4375 23/32 . . .0,71875 23/64 . . .0,359375 55/64 . . .0,859375 1
9/16 . . .0,5625 25/32 . . .0,78125 25/64 . . .0,390625 57/64 . . .0,890625
11/16 . . .0,6875 27/32. . .0,84375 27/64 . . .0,421875 59/64 . . .0,921875
13/16 • . .0,8125 29/32. . .0,90625 29 64 . . .0,453125 61/64 . . .0,953125
15/16 . . .0,9375 31/32 • . .0,96875 31/64 . . .0,484375 63/64 . . .0,984375
1/32 . . .0,03125 1/64 . . .0,015625 33/64. . .0,515625
Таблица 2. Десятые доли дюйма и дюймы в миллиметры
Дюймы | 0" 1 0,1" 0,2" о,3" I 0,4" 1 0,5’ 0,6" 0,7" I 0,8’ | 0,9"
м и л л и м е т р ы
0* 2,54 5,08 7,62 10,16 12,70 15,24 17,78 20,32 22,86
1* 25,4 27,94 30,48 33,02 35,56 38,10 40,64 43,18 45,72 48,26
2" 50,8 53,34 55,88 58,42 60,96 63,50 66,04 68,58 71,12 73,66
у 76,2 78,74 81,28 83,82 86,36 88,90 91,44 93,98 96,52 99,06
4’ 101,6 104,14 106,68 109,22 117,76 114,30 116,84 119,38 121,92 124,46
5" 127,0 129,54 132,08 134,62 137,16 139,70 142,24 114,78 147,32 149,86
6* 152,4 154,94 157,48 160,02 162,56 165,10 167,64 170,18 172,72 175,26
7" 177,8 180,34 182,88 185,42 187,96 190,50 193,04 195,58 198,12 200,66
8" 203,2 205,74 208,28 210,82 213,36 215,90 218,44 220,98 223,52 226,06
У 228,6 231,14 233,68 236,22 238,76 241,30 243,84 246,38 248,92 251,46
Таблица 3. Тысячные и сотые доли дюйма в миллиметры
Дюймы 0 1 0,001" 0,002" | 0,003" | 0,004" 0,005’ 0,006" 0,007* | 0,008" 0,009’
м ИЛЛИ метр ы
0,00" 0,0254 0,058 0,0762 0,1016 0,1270 0,1524 0,1778 0,2032 0,2286
0,01" 0,2540 0,2794 0,3048 0,3302 0,3556 0,3810 0,4064 0,4318 0,4572 0,4826
0,02" 0,5080 0,5334 0,5588 0,5842 0,6096 0,6350 0,6604 0,6858 0,7112 0,7366
0,03" 0,7620 0,7874 0,8128 0,8382 0,8636 0,8890 0,9144 0,9398 0,9652 0,9906
0,04" 1,0160 1,0414 1,0668 1,0922 1,1176 1,1430 1,1684 1,1938 1,2192 1,2446
0,05" 1,2700 1,2954 1,3208 1,3462 1,3716 1,3970 1,4224 1,4478 1,4732 1,4986
0,06* 1,5240 1,5494 1,5748 1,6002 1,6256 1,6510 1,6764 1,7018 1,7272 1,7526
0,07" 1,7780 1,8034 1,8288 1,8542 1,8796 1,9050 1,9304 1,9558 1,9812 2,0066
0,08" 2,0320 2,0574 2,0828 2,1082 2,1336 2,1590 2,1844 2,2098 2,2352 2,2606
0,09" 2,2860 2,3114 2,3368 2,3622 2,3876 2,4130 2,4384 2,4638 2,4852 2,5146
ЕДИНИЦЫ ИЗМЕРЕНИЙ
611
Таблица 4. Футы и дюймы в миллиметры
1 фут=304,799 73 мм
е Дюйм 0' 1' 2' 3* 4' 5’ 6’ 7" 8" 9’ 10’ 11’ 12’
0 0 0 25,4 51 76 102 127 152 178 203 229 254 279 305 1 12 305 330 356 381 406 432 457 483 508 533 559 584 610 ? 24 610 635 660 686 711 737 762 787 813 838 864 889 914 О 36 914 940 965 991 1 016 1 041 1 067 1 092 1 118 1 143 1 168 1 194 1 219 4 48 1 219 1 245 1 270 1 295 1 321 1 346 1 372 1 397 1 422 1 448 1 473 1 499 1 524 к 60 1 524 1 549 1 575 1 600 1 626 1 651 1 676 1 702 1 727 1 753 1 778 1 803 1 829 К 72 1 829 1 854 1 880 1 905 1 930 1 956 1 981 2007 2 032 2057 2083 2108 2 134 7 84 2 134 2 159 2184 2210 2235 2261 2 286 2311 2 337 2362 2 388 2413 2 438 я 96 2 438 2 464 2 489 2 515 2 540 2 565 2 591 2616 2 642 2 667 2 692 2 718 2 743 9 108 2 743 2 769 2 794 2 819 2 845 2 870 2 896 2 921 2 946 2 972 2 997 3 023 3 048 in 120 3048 3073 3099 3124 3 150 3 175 3 200 3226 3251 3 277 3302 3327 3353 11 132 3 353 3 378 3 404 3 429 3 454 3 480 3 505 3 531 3556 3 581 3607 3 632 3 658 12 144 3658 3683 3708 3734 3759 3785 3810 3835 3 861 3886 3912 3937 3962 П 156 3962 3988 4013 4 039 4064 4089 4 115 4 140 4 166 4 191 4216 4242 4267 14 168 4267 4293 4318 4343 4369 4394 4 420 4445 4470 4496 4521 4547 4572 15 180 4572 4597 4623 4648 4674 4699 4724 4750 4775 4801 4826 4851 4877 1S 102 4877 4902 4928 4953 4978 5004 5 029 5 055 5 080 5 106 5 131 5156 5 182 17 204 5182 5207 5232 5 258 5283 5309 5 334 5359 5 385 5410 5 436 5461 5486 1Я 216 5 486 5 512 5 537 5 563 5 588 5 613 5 639 5 664 5 690 5 715 5 740 5 766 5 791 19 228 5 791 5817 5 842 5 867 5 893 5 918 5 944 5 969 5 994 6 020 6 045 6 071 6096 20 240 6 096 6121 6 147 6 172 6198 6 223 6 248 6 274 6 299 6 325 6 350 6 375 6 401 21 252 6401 6 426 6 452 6 477 6 502 6 528 6 558 6 579 6 604 6 629 6 655 6 680 6 706 22 264 6 706 6 731 6 756 6 782 6 807 6 833 6 858 6 883 6 909 6 934 6 960 6 985 7 010 23 276 7010 7036 7 061 7087 7 112 7 137 7 163 7 188 7 214 7 239 7264 7 290 7315 24 288 7 315 7 341 7 366 7 391 7417 7 442 7 467 7 493 7 518 7 545 7 569 7 594 7 620 ->5 300 7 620 7 645 7 671 7 696 7 722 7 747 7 772 7 798 7 823 7 849 7 874 7 899 7 925 26 312 7 925 7 950 7 975 8 001 8026 8 052 8 077 8102 8 128 8 153 8179 8 204 8 230 27 324 8 230 8 255 8 280 8 306 8 332 8 357 8 382 8 408 8 433 8 458 8 484 8 509 8 534 28 336 8 534 8 559 8 585 8 610 8 636 8 661 8 686 8 712 8 737 8 763 8 788 8 814 8 839 29 348 8 839 8 864 8 890 8 915 8 941 8 966 8 991 9017 9 042 9 068 9 093 9118 9144 30 360 9144 9169 9 195 9 220 9 246 9 271 9 296 9 322 9 347 9 373 9 398 9 423 9 449 31 372 9 449 9 474 9 500 9 525 9 551 9576 9 601 9 627 9 652 9 677 9 703 9 728 9 753 32 384 9 754 9 779 9 804 9 830 9 855 9 881 9 906 9 931 9 957 9 982 10 008 10 033 10 058 33 396 10058 10083 10109 10134 10160 10 185 10210 10236 10261 10287 10312 10337 10363 34 408 10363 10388 10414 10439 10465 10490 10515 10541 10566 10592 10617 10642 10668 35 420 10668 10693 10719 10744 10770 10795 10 820 10846 10871 10897 10922 10947 10973 36 432 10 973 10 998 11 024 11 049 И 075 11 100 11 125 11 151 11 176 И 202 11 227 11 252 11 278 37 444 11 278 11 303 11 328 11 354 11 379 11 405 11 430 11 455 11 481 11 506 11 532 11 557 582 38 456 11 582 11 607 11 633 11 658 11 684 11 709 11 734 11 760 11 785 11 811 11 836 И 861 1 887 39 468 11 887 11 912 И 938 11 963 11 989 12 014 12 039 12065 12 090 12 116 12 141 12 166 12 192 40 480 12192 12217 12 243 12268 12294 12319 12 344 12370 12395 12421 12446 12471 12497 41 492 12497 12 522 12 548 12 573 12 598 12 624 12 649 12 675 12 700 12 725 12 751 12 776 12 802 42 504 12 802 12 827 12 852 12 878 12 903 12 929 12 954 12 979 13 005 13 030 13056 13 081 13 106 43 516 13106 13 132 13157 13 183 13208 13233 13 259 13284 13310 13335 13360 13386 134 1 44 528 13411 13437 13462 13487 13513 13538 13 564 13589 13614 13640 13665 13691 13716 45 540 13716 13 741 13 767 13 792 13818 13 843 13 868 13 894 13919 13945 13 970 13 995 14 021 46 552 14021 14046 14072 14097 14 122 14 148 14 173 14 199 14224 14249 14275 14300 14326 47 564 14326 14351 14376 14402 14427 14453 14 478 14503 14529 14554 145^0 14 605 14 630 48 576 14630 14 656 14681 14 707 14732 14757 14783 14808 14834 14859 14884 14 910 14 935 49 588 14935 14961 14986 15011 15037 15062 15088 15 113 15 138 15 164 15 189 15 215 15240 50 600 15240 15265 15291 15316 15342 15367 15 392 15418 15443 15469 15494 15519 15545 51 612 15 545 15 570 15 596 15 621 15 646 15 672 15 697 15 723 15 748 15 773 15 799 15 824 5 850 52 624 15 850 15 875 15 900 15 926 15 951 15 977 16 002 16 027 16 053 16 078 16 104 16 129 16154 53 636 16154 16180 16205 16231 16256 16281 16 307 16332 16358 16383 16408 16434 16459 54 648 16459 16485 16510 16535 16561 16586 16 612 16637 16662 16688 16 713 16 739 16764
39*
612
ЕДИНИЦЫ ИЗМЕРЕНИЙ
Таблица 5. !/1в доли дюйма и
Дюймы 0 1/8 8 / /16 5 / /18 3/в 71.
0 0,000 1,588 3,175 4,763 6,350 7,938 9,525 11,113
1 25,400 26,988 28,575 30,163 31,750 33,338 34,925 36,513
2 50,800 52,388 53,975 55,563 57,150 58,738 60,325 61,913
3 76,200 77,788 79,375 80,963 82,550 84,138 85,725 87,313
4 101,600 103,188 104,775 106,363 107,950 109,538 111,125 112,713
5 127,000 128,588 130,175 131,763 133,350 134,938 136,525 138,113
6 152,400 153,988 155,575 157,163 158,750 160,338 161,925 163,513
7 177,800 179,388 180,975 182,563 184,150 185,738 187,325 188,913
8 203,200 204,788 206,375 207,963 209,550 211,138 212,725 214,313
9 228,600 230,188 231,775 233,363 234,950 236,538 238,125 239,713
10 254,400 255,588 257,175 258,763 260,350 261,938 263,525 265,113
11 279,400 280,988 282,575 284,163 285,750 287,338 288,925 290,513
12 304,800 306,388 307,975 309,563 311,150 312,738 314,325 315,913
13 330,200 331,788 333,375 334,963 336,550 338,138 339,725 341; 313
14 355,600 357,188 358,775 360,363 361,950 363,538 365,125 366,713
15 381,ООО 382,588 384,175 385,763 387,350 388,938 390,525 392,113
16 406,400 407,988 409,575 411,163 413,750 414,338 415,925 417,513
17 431,800 433,388 434,975 436,563 438,150 439,738 441,325 442,913
18 457,200 458,788 460,375 461,963 463,550 465,138 466,725 468,313
19 482,600 484,188 485,775 487,363 488,950 490,538 492,125 493,713
20 508,000 509,588 511,175 512,763 514,350 515,938 517,525 519,113
21 533,400 534,988 536,575 538,163 539,750 541,338 542,925 544,513
22 558,800 560,388 561,975 563,563 565,150 566,738 568,325 569,913
23 584,200 585,788 587,375 588,963 590,550 592,138 593,725 595,313
24 609,600 611,188 612,775 614,363 615,950 617,538 619,125 620'713
25 635,000 636,588 638,175 639,763 641,350 642,938 644,525 646,113
26 660,400 661,988 663,575 665,163 666,750 668,338 669,925 671,513
27 685,800 687,388 688,975 690,563 692,150 693,738 695,325 696,913
28 711,200 712,788 714,375 715,963 717,550 719,138 720,725 722,313
29 736,600 738,188 739,775 741,363 742,950 744,538 746,125 747,713
30 762,000 763,588 765,175 766,763 768,350 769,938 771,525 773,113
31 787,400 788,988 790,575 792,163 793,750 795,338 796,925 798,513
32 812,800 814,388 815,975 817,563 819,150 820,738 822,325 823,913
33 838,200 839,788 841,375 842,963 844,550 846,138 847,725 849,313
34 863,600 865,188 866,775 868,363 869,950 871,538 873,125 874,713
35 889,000 890,588 892,175 893,763 895,350 896,938 898,525 900,113
36 914,400 915,988 917,575 919,163 920,750 922,338 923,925 925,513
37 939,800 941,388 942,975 944,563 946,150 947,738 949,325 950,913
38 965,200 966,788 968,375 969,963 971,550 973,138 974,725 976,313
39 990,600 992,188 993,775 995,363 996,950 998,538 1 000,125 1 001,71
40 1 016,00 1 017,59 1 019,18 1 020,76 1 022,35 1 023,94 1 025,53 1 027,11
41 1 041,40 1 042,99 1 044,58 1 046,16 1 047,75 1 049,34 1 050,93 1 052,51
42 1 066,80 1 068,39 1 069,98 1 071,56 1 073,15 1 074,74 1 076,33 1 077,91
43 1 092,20 1 093,79 1 095,38 1 096,96 1 098,55 1 100,14 1 101,73 1 103,31
44 1 117,60 1 119,19 1 120,78 1 122,36 1 123,95 1 125,54 1 127,13 1 128,71
45 1 143,00 1 144,59 1 146,18 1 147,76 1 149,35 1 150,94 1 152,53 1 154,11
46 1 168,40 1 169,99 1 171,58 1 173,16 1 174,75 1 176,34 1 177,93 1 179,51
47 1 193,80 1 195,39 1 196,98 1 198,56 1 200,15 1 201,74 1 203,33 1 204,91
48 1 219,20 1 220,79 1 222,38 1 223,96 1 225,55 1 227,14 1 228,73 1 230,31
49 1 244,60 1 246,19 1 247,78 1 249,36 1 250,95 1 252,54 1 254,13 1 255,71
50 1 270,00 1 271,59 1 273,18 1 274,76 1 276,33 1 277,94 1279,33 1 281,11
51 1 295,4 1 297,0 1 298,6 1 300,2 1 301,7 1 303,3 1 304,9 1 306,5
52 1 320,8 1 322,4 1 324,0 1 325,6 1 327,1 1 328,7 1 330,3 1 331,9
53 1 346*2 1 347,8 1 349,4 1 35!,0 1 352,5 1 354,1 1 355,7 1 357,3
54 1 371,6 1 373,2 1 374,8 1 376.4 1 377,9 1 379,5 1 381,1 1 382,7
55 1 397,0 1 398,6 1 400,2 1 401,8 1 403,3 1 404,9 1 406,5 1 408,1
56 1 422,4 1 424,0 1 425,6 1 427,2 1 428,7 1 430,3 1 431,9 1 433,5
57 1 447,8 1 449,4 1 451,0 1 452,6 1 454,1 1 455,7 1 457,3 1 458,9
58 1 473,2 1 474,8 1 476,4 1 478,0 1 479,5 1 481,1 1 482,7 1 484,3
59 1 498,6 1 500,2 1 501,8 1 503,4 1 504,9 1 506,5 1 508,1 1 509,7
60 1 524,0 1 525,6 1 527,2 1 528,8 1 530,3 1 531,9 1 533,5 1 535,1 1,
ЕДИНИЦЫ ИЗМЕРЕНИЙ
613
дюймы в миллиметры
1/2 */ie 6/s “/1, */< 13/ /18 7s 1Б / /18 Дюймы
12,700 14,288 15,875 17,463 19,050 20,638 22,225 23,813 0
38,100 39,688 41,275 42,863 44,450 46,038 47,625 49,213 1
63,500 65,088 66,675 68,263 69,850 71,438 73,025 74,613 2
88,900 90,488 92,075 93,663 95,250 96,838 98,425 100,013 3
114,300 115,888 117,475 119,063 120,650 122,238 123,825 125,413 4
139,700 141,288 142,875 144,463 146,050 147,638 149,225 150,813 5
165,100 166,688 168,275 169,863 171,450 173,038 174,625 176,213 6
190,500 192,088 193,675 195,263 196,850 198,438 200,025 201,613 7
215,900 217,488 219,075 220,663 222,250 223,838 225,425 227,013 8
241,300 242,888 244,475 246,063 247,650 249,238 250,825 252,413 9
266,700 268,288 269,875 271,463 273,050 274,638 276,225 277,813 10
292,100 293,688 295,275 296,863 298,450 300,038 301,625 303,213 11
317,500 319,088 320,675 322,263 323,850 325,438 327,025 328,613 12
342,900 344,488 346,075 347,663 349,250 350,838 352,425 354,013 13
368,300 369,888 371,475 373,063 374,650 376,238 377,825 379,413 14
393,700 395,288 396,875 398,463 400,050 401,638 403,225 404,813 15
419,100 420,688 422,275 423,863 425,450 427,038 428,625 430,213 16
444,500 446,088 447,675 449,263 450,850 452,438 454,025 455,613 17
469,900 471,488 473,075 474,663 476,250 477,838 479,425 481,013 18
495,300 496,888 498,475 500,063 501,650 503,238 504,825 506,413 19
520,700 522,288 523,875 525,463 527,050 528,638 530,225 531,813 20
546,100 547,688 549,275 550,863 552,450 554,038 555,625 557,213 21
571,500 573,088 574,675 576,263 577,850 579,438 581,025 582,613 22
596,900 598,488 600,075 601,663 603,250 604,838 606,425 608,013 23
622,300 623,888 625,475 627,063 628,650 630,238 631,825 633,413 24
647,700 649,288 650,875 652,463 654,050 655,638 657,225 658,813 25
673,100 674,688 676,275 677,863 679,450 681,038 682,625 684,213 26
698,500 700,088 701,675 703,263 704,850 706,438 708,025 709,613 27
723,900 725,488 727,075 728,663 730,250 731,838 733,425 735,013 28
749,300 750,888 752,475 754,063 755,650 757,238 758,825 760,413 29
774,700 776,288 777,875 779,463 781,050 782,638 784,225 785,813 30
800,100 801,688 803,275 804,863 806,450 808,038 809,625 811,213 31
825,500 827,088 828,675 830,263 831,850 833,438 835,025 836,613 32
850,900 852,488 854,075 855,663 857,250 858,838 860,425 862,013 33
876,300 877,888 879,475 881,063 882,650 884,238 885,825 887,413 34
901,700 903,288 904,875 906,463 908,050 909,638 911,225 912,813 35
927,100 928,688 930,275 931,863 933,450 935,038 936,625 938,213 36
952,500 954,088 955,675 957,263 958,850 960,438 962,025 963,613 37
977,900 979,488 981,075 982,663 984,250 985,838 987,425 989,013 38
1 003,300 1 004,89 1 006,48 1 008,06 1 009,65 1 011,24 1 012,825 1 014,41 39
1 028,70 1 030,29 1 031,88 1 033,46 1 035,05 1 036,64 1 038,23 1 039,81 40
1 054,10 1 055,69 1 057,28 1 058,86 1 060,45 1 062,04 1 063,63 1 065,21 41
1 079,50 1 081,09 1 082,68 1 084,26 1 085,85 1 087,44 1 089,03 1 090,61 42
1 104,90 1 106,49 1 108,08 1 109,66 1 111,25 1 112,84 1 114,43 1 116,01 43
1 130,30 1 131,89 1 133,48 1 135,06 1 136,65 1 138,24 1 139,83 1 141,41 44
1155,70 1 157,29 1 158,88 1 160,46 1 162,05 1 163,64 1 165,23 1 166,81 45
1 181,10 1 182,69 1 184,28 1 185,86 1 187,45 1 189,04 1 190,63 1 192,21 46
1 206,50 1 208,09 1 209,68 1 211,26 1 212,85 1 214,44 1 216,03 1 217,61 47
1 231,90 1 233,49 1 235,08 1 236,66 1 238,25 1 239,84 1 241,43 1 243,01 48
1 257,30 1 258,89 1 260,48 1 262,06 1 263,65 1 265,24 1 266,83 1 268,41 49
1 282,70 1 284,29 1 285,88 1 287,46 1 289,05 1 290,64 1 292,23 1 293,81 50
1 308,1 1 309,7 1 311,3 1 312,9 1 314,4 1 316,0 1 317,6 1 319,2 51
1 333,5 1 335,1 1 336,7 1 338,3 1 339,8 1 341,4 1 343,0 1 344,6 52
1 358,9 1 360,5 1 362,1 1 363,7 1 365,2 1 366,8 1 368,4 1 370,0 53
1 384,3 1 385,9 1 387,5 1 389,1 1 390,6 1 392,2 1 393,8 1 395,4 54
1 409,7 1 411,3 1 412,9 1 414,5 1 416,0 1 417,6 1 419,2 1 420,8 55
1 435,1 1 436,7 1 438,3 1 439,9 1 441,4 1 443,0 1 444,6 1 446,2 56
1 460,5 1 462,1 1 463,7 1 465,3 1 466,8 1 468,4 1 470,0 1 471,6 57
1 485,9 1487,5 1 489,1 1 490,7 1 492,2 1 493,8 1 495,4 1 497,0 58
1 511,3 1 512,9 1 514,5 1 516,1 1 517,6 1 519,2 1 520,8 1 522,4 59
1 536,7 1 538,3 1 539,9 1 541,5 1 543,0 1 544,6 1 546,2 1 547,8 60
614
ЕДИНИЦЫ ИЗМЕРЕНИЙ
Таблица 6. Английские фунты lbs в килограммы
Англ, фунты Кило- граммы Центнеры англ. cwt. Центнеры амер. cwt. Англ, фунты Кило- граммы Центнеры англ. cwt. Центнеры амер. cwt. . 3 5g а >» Кило- граммы Центнеры £нгл. cwt. Центнеры амер. cwt. Англ, фунты Кило- граммы Центнеры англ. cwt. Центнеры амер. cwt.
1 0,453 0,008928 0,01 2 0,906 0,017856 0,02 3 1,359 0,026784 0,03 4 1,812 0,035712 0,04 5 2,265 0,044640 0,05 б 2,718 0,053568 0,06 7 3,171 0,062496 0,07 8 3,624 0,071424 0,08 9 4,077 0,080352 0,09 10 4,536 0,0893 0,10 И 4,989 0,0982 ,11 12 5,442 0,1071 0,12 13 5,895 0,1161 0,13 14 6,348 0,1250 0,14 15 6,801 0,1339 0,15 16 7,254 0,1428 0,16 17 7,707 0,1518 0,17 18 8,160 0,1607 0,18 19 8,613 0,1696 0,19 20 9,066 0,1786 0,20 21 9,519 0,187 5 0,21 22 9,972 0,1964 0,22 23 10,425 0,2054 0,23 24 10,878 0,2143 0,24 25 11,340. 0,2232 0,25 26 11,78 0,2321 0,26 27 12,23 0,2411 0,27 28 12,69 0,2500 0,28 29 13,14 0,2589 0,29 80 13,59 0,2678 0,30 31 14,04 0,2767 0,31 32 14,50 0,2856 0,32 33 14,95 0,2946 0,33 34 15,40 0,3035 0,34 За 15,85 0,3124 0,35 36 16,31 0,3213 0,36 37 16,76 0,3302 0,37 33 17,21 0,3392 0,38 39 17,67 0,3481 0,39 40 18,14 0,3571 0,40 41 18,57 0,3660 0,41 42 19,03 0,3749 0,42 43 19,48 0,3839 0,43 44 19,93 0,3928 0,44 45 20,38 0,4017 0,45 46 20,83 0,4106 0,46 47 21,28 0,4196 0,47 48 21,74 0,4285 0,48 49 22,20 0,4374 0,49 50 22,68 0,4464 0,50 51 23,10 0,4553 0,51 52 23,55 0,4642 0,52 53 24,01 0,4732 0,53 54 24,46 0,4821 0,54 ай 24,91 0,4910 0,55 56 25,37 0,4999 0,56 57 25,82 0,5089 0,57 58 26,28 0,5178 0,58 59 26,73 0,5267 0,59 «0 27,18 0,5356 0,60 61 27,61 0,5445 0,61 62 28,09 0,5535 0,62 63 28,53 0,5624 0,63 64 28,99 0,5713 0,64 «5 29,45 0,5802 0,65 66 29,90 0,5892 0,66 67 30,35 0,5981 0,67 68 30,81 и,6071 0,68 69 31,26 0,6159 0,69 70 31,71 0,6249 0,70 71 32,17 0,633» 0,71 72 32,62 0,6428 0,72 73 33,07 0,6516 0,73 74 33,52 0,6606 0,74 75 33,98 0,6696 0,75 76 34,43 0,6784 0,76 77 34,88 0,6875 0,77 78 35,34 0,6964 0,78 79 35,79 0,7053 0,79 80 36,28 0,7142 0,80 81 36,69 0,7231 0,81 82 37,15 0,7320 0,82 83 37,60 0,7410 0,83 84 38,05 0,7499 0,84 85 38,50 0,7588 0,85 86 38,96 0,7678 0,86 87 3s,41 0,77и7 0,87 88 39,86 0,7856 0,38 89 40,32 0,7946 0,89 90 40,77 0,8035 0,90 91 41,22 0,8124 0,91 92 41,68 0,8213 0,92 93 42,13 0,8303 0,93 94 42,45 0,8392 0,94 95 43,03 0,8481 0,95 96 43,49 0,8570 0,93 97 43,94 0,8660 0,97 98 44,39 0,8749 0,98 99 44,85 0,8839 0,99 100 45,36 0,8928 1,00
Таблица 7. Фунты на кв. дюйм («psi») в килограммы на кв. сантиметр
Фунты на кв. дюйм 0 1 1 1 2 3 4 1 5 1 6 1 7 8 9
килограммы на кв. сантиметр
0 0,0703 0,1406 0,2109 0,2812 0,3515 0,4218 0,4921 0,5625 0,6328
10 0,7031 0,7734 0,8437 0,9140 0,9843 1,0546 1,1249 1,1952 1,2655 1,3358
20 1,4062 1,4765 1,5468 1,6171 1,6874 1,7577 1,8280 1,8983 1,9686 2,0389
30 2,1092 2,1795 2,2498 2,3202 2,3905 2,4608 2,5311 2,6014 2,6717 2,7420
40 2,8123 2,8826 2,9529 3,0232 3,0935 3,1639 3,2342 3,3045 3,3748 3,4451
50 3,5154 3,5857 3,6560 3,7263 3,7966 3,8669 3,9372 4,0075 4,0779 4,1482
60 4,2185 4,2888 4,3591 4,4294 4,4997 4,5700 4,6403 4,7106 4,7809 4,8512
70 4,9216 4,9919 5,0622 5,1325 5,2028 5,2731 5,3434 5,4137 5,4840 5,5543
80 5,6246 5,6949 5,7652 5,8356 5,9059 5,9762 6,0465 6,1168 6,1871 6,2574
90 6,3277 6,3980 6,4683 6,5386 6,6089 6,6793 6,7496 6,8199 6,8902 6,9605
100 7,0308 7,1011 7,1714 7,2417 7,3120 7,3823 7,4526 7,5229 7,5933 7,6636
В№
W5SE
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
взяивжяштая^'
При пользовании настоящим указателем
следует иметь в виду, что каждое название
упоминается, как правило, один раз и не
повторяется в перестановке слов.
В указателе упоминается сперва основное
слово (за редкими исключениями), а потом
его определение, например: «Газы идеаль-
ные» и т. п.
В большинстве случаев, когда формула,
определение, уравнение, способ, метод и пр.
носят название того или другого учёного, то
в указателе приводится лишь фамилия учё-
ного (без сопровождающего термина), напри-
мер: Чебышев П. Л., а не «Чебышева П. Л.
уравнение» и не «Уравнение Чебышева П. Л.».
А
Абсорбция 346
Авогадро 531, 544
Автокоалесценция 354
Адамс 258
Адъюнкта 101
Адсорбция 345, 346
Азот 282
Аккумулятор 494
— свинцовый 494
— щёлочный 495
Активность 338
Актиний 279
Алгебра 91
— векторная 207
Алкадиены 297
Алканы 295
Алкены 297
Алкины 298
Алкоголь 300
Алмаз 279
Альдегиды 302
Алюминий 278
Амальгама 278
Амиды кислот 304
Амины 305
Аммиак 282
Аммонал 306
Аммоний 282
Аммофосы 283
Ампер-час 495
Амплитуда 497
Анализ гармонический 256
Ангидрид угольный 279
Ангидрит 277
Анилин — паросульфокис-
лоты 306
Анион 274, 319, 494
Анод 494
Антуфьев В. М. 587
Аньези 199
Аргон 274
Аргумент комплексного
числа 100
— в градусах 79
— в дуговых единицах 79
Арифметика 91
Арсенаты 283
Арсениты 283
Арсин 283
Архимед 411
Асимптота 185, 196
Ассоциативность 91
Атмосфера стандартная 475
Афанасьева Т. 529
Ацетилен 298
Ацетон 303
Ацетил-целлюлоза 308
Аэродинамика 474
Б
Вазен 437
Барий 277
Барометрическая формула
475
Вахметев Б. А. 440, 453
Безу 97
Белки 309
Белоконь Н. И. 426, 427,
435, 594
Бензил хлористый 300
Бензол 299
Вензолсульфокислота 306
Бериллий 274
Бернулли 167, 201, 415,
417, 445, 510
Бертло 316
Бессель 171, 247, 250
Бесселевы функции 70
Бесконечно-большая 129
— малая 129
Бикарбонат натрия 275
Бикарбонат кальция 285
Вином Ньютона 101
Бинормаль 204
Биссектриса 108, НО
Бисульфит натрия 285
Вихромат калия 286
Блазиус 427
Больцман Л. 318, 510, 512,
529, 597
Бойль 531, 543
Вор 278
Бора 323
Борда 432
Ворщёв 349
Бочка 90
Брайтон 541
Браунит 287
Бриджмен 525, 527
Бройль 324
Бром 287
В
Вакуум 409, 448
Ван-дер-Ваальс 315, 316,
474, 475, 544, 545, 546
Валентность 269, 271, 273
Ванадий 283
Варипьона- многоугольник
365
Ватерлиния 411
Вебер 480, 482
Вейерштрасс 160, 216
Веймаут 478
Вектор 207, 208, 210
— главный 361, 362, 363
— единичный 208
— компланарный 208
— момент 359
— неподвижный 207
— пулевой 207
616
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Вектор свободный 207, 359
— скользящий 207, 357
— скорости 369
— угловой скорости 372
— ускорения 370
— функция скалярного ар-
гумента 210
Вектора циркуляция 211
— носитель 207
Векторы коллинеарные 207
Величина абсолютная 95
— бесконечно-большая 129
— — малая 129
— дискретная 224
— непрерывная 224
— случайная 224
Величины комплексные 95,
129
— обратные 15
— постоянные 82
Вероятность 222, 223, 224
Вероятностей умножение
223
Вершина кривой 196
— угла 108
Вес атомный 273
— газов 405
— жидкости 404
— молекулярный 273
— удельный 289, 293, 294
Вещества поверхностно-ак-
тивные 345
---инактивные 345
Видеман 574
Вискозиметры 406
Вискограмма 407
Висмут 283
Вихерт 399
Вихрь 415, 416, 420
Вогнутость кривой 195
Вода гравитационная 469
— грунтовая 469
— и перегретый пар (по
Вукаловичу М. Н.) 555
— кипящая (свойства) 551
— тяжёлая 320
— (физические константы)
521, 524
Водоизмещение 411
Водород 275
Водосливы 443
Волновая теория 324
Вольта ряд 495
Вольт-секунда 480, 482
Вольфрам 286
Воск 305
Восстановление 351
Вронскиан 169
Вронского определитель 169
Вукалович М. П. 547,
548
Вульф Г. В. 316
Выпуклость кривой 195
Выражение алгебраическое
95
Высота НО, 113
— метацентрическая 413
Вычет функции 216
Вязкость динамическая во-
дяного пара и воды 521
— жидкостей и газов 406,
' 407, 408, 525
Вязкость кинематическая
водяного пара и воды 522
— лиофильных коллоидов
353
— лиофобных коллоидов
353
— ртути 525
— структурная 354
Г
Газ веселящий 282
Газодинамика 474
Газы благородные 275
— движение по трубам 476
— идеальные 315, 531
— инертные 274
— реальные 315, 531, 543
— (свойства) 524, 532, 545
Газен 472
Гайд 521
Галлерея водосборная 474
Галилей 591
Галлий 279
Галоиды 269
Гамильтон 212
Гамма-функция 149
Гангилье 438
Гайон Е. Н. 322
Гармоники высшие 506
Гаусс 227, 228, 229, 255,
256, 480, 511
Гаусманит 287
Гафний 281
Гей-Люссак 531
Гели 350, 354, 355
Гелий 274
Гельмгольц 415, 527
Г емфри 541
Генри 328, 484
Геометрия аналитическая
179
— диференциальная 194
Германий 281
Гиббс 345
Гидрат окислов 274
Гидродинамика идеальной
жидкости 413
— реальной (вязкой) жид-
кости 420
Гидролиз 273, 351
Гидростатика 408
Гильперт 586
Гипербола 86, 184, 198
Гиперболоид 192
Гипотенуза 109
Гипоциклоида 202
Гистерезис 482
Глинозём 278
Глицерин 301
Глубина критическая 447,
450
— сопряжённая 447
Глюкоза 307
Годнев И. 515
Гончаров 440, 441
Градиент пробивной 490
Г радус 108
— условный 405
Градусы вязкости 406
Грамматом 273
Граммоль (граммолекуляр-
ный вес) 273
Граммэквивалент 273
График движения 368
— прыжковой функции 456
— скоростей 368
Графит 279
Грин 154, 176, 212
Грифите 589, 591
Громека 417
Грунт фиктивный 472
Гюльден 147
Гук 377
Д
Давление гидростатическое
408
— избыточное 409, 410
— капиллярное 344
— молекулярное 343
— на криволинейные стен-
ки 411
— парциальное 532
— на плоские стенки 410
— струи 415
Да ламбер 156, 159, 383
Дальтон 532
Дарси 435, 469, 470
Движение абсолютное 370
— Броуновское 351
— винтовое 374
— вихревое 415
— в канале 439
— в открытых руслах 449
— грунтовых вод 469
— изобарическое 477
— изотермическое 476
— изохорическое 476
— ламинарное 423
— неравномерное 449, 456
— относительное 370
— переносное 370
— плавно изменяющееся
414
— плоско-параллельное
372, 414
— поступательное 371, 375
— потенциальное 416, 422
— равномерно замедленное
368
--- ускоренное 368
— сложное 370, 371
— установившееся 414, 422,
471
Дебай 318
Девис 589, 591
Дейтерий 320
Дейтон 320
Декалин 299
Декарт 527
Декартов лист 199
Декремент затухания 203,
509
Декстроза 307
Деление тяжёлых ядер 323
Делимость чисел 91
Детерминанты 101
Демокрит 510
Деполяризация 341
Дефекты массы 322
Джоуль 527
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
617
Диагональ 109
Диаграмма линейная или
волновая 497
— векторная 497
— Кремоны 367
— кристаллогидратов 333
— состояния воды 332
Дивинил 298
Диаметр 113
— кривой 184
Дивергенция вектора 211
Дизель 540
Диметилкетон 303
Дина 606
Динамика 357, 375
Динострат 203
Диолефины 297
Диполь 418, 487
Диссоциация электролити-
ческая 273
Дистрибутивность 91
Дирихле 162, 176
Дифенил 299
Диференциал прямой 132,
134
— дуги 194
Диференцирование (прави-
ла) 131, 144
Дихлорэтан 300
Длина эквивалентная 435
Доливо-Добровольский 504
Дополнение алгебраическое
101
Дроби 92, 93, 97
Дросселирование газов и
паров 567
Дублет 418
Дуга 77, 113
Дюкер 429
Е
Единица мнимая 99
Единицы измерений 605
— радиоактивности 321
Ёмкость электрическая 488,
489
— конденсаторов 489
— аккумулятора 495
Ермаков В. П. 157
Ж
Железо 288
Жезл 202
Жидкость газообразная 404
— капельная 404, 405, 568
— реальная 420
— упругая 568
Жиры 305
Жуковский В. С. 591
— М. И. 574
— Н. Е. 459, 460, 470
3
Закон больших чисел 223
— вращения 471
— движения точки 368
Закон действующих масс
335
Закон живой силы 415
— количества движения 415
— Коновалова 331
— кратных отношений 272
— Ляпунова 227
— паев (эквивалентов) 273
— постоянства сумм тепло-
ты 325
— постоянства состава 272
— равной вероятности 227
— распределения 226, 227,
335
— — скоростей 425
— Рауля 329, 330
— смещения 321
— сопротивления 467
— сохранения механиче-
ской энергии 383
---массы вещества
М. В. Ломоносова 272
— фильтрации 469
— эквивалентности массы
и энергии 322
Замарин 472, 473
Заряд остаточный 490
— электрона 487, 494
Звезды схема 493, 494
Земли 269, 279
Золи 350
Золото 276
И
Иваненко Д. Д. 322
Известь 277
Излучение (теплопередача)
595
— абсолютно чёрного тела
596
— газов 601
— различных поверхностей,
степень черноты 597
— серых тел 597
Измерение углов 108, ИЗ
Изобары 271
Изоклины 165
Изоморфизм 317
Изооктан 296
Изотопы 271, 320
Импульс силы 378
Индий 279
Индукция взаимная 484
— магнитная 480
— остаточная 482
— электромагнитная 483
Инволюта 196
— сходимости 159
Интервал 128
Интеграл криволинейный
152
— неопределённый 135
— определённый 143
— по поверхности 155
Интегралы (основная таб-
лица) 135
— двойные 150
— кратные 150, 152
— несобственные 144
— тройные 151
— Эйлеровы 149
— эллиптические 149
Интегрирование (правила)
136
—алгебраических иррацио-
нальностей 137
— гиперболических функ-
ций 141
— рациональных дробей
136
--- функций 136
— трансцендентных функ-
ций 141
— тригонометрических
функций 139
— численное 254
Интерполирование 246
— (формулы) 246, 247, 248
— (коэфициеиты) 249, 250
— линейное 248
— обратное 251
— тригонометрическое 248
Иод 287
Ионы 273, 319, 339, 494
Иоффе А. Ф. 318
Иприт 306
Иридий 293
Истечение газов и паров
568, 570
— из больших отверстий
462
---жел.-дор. цистерн
466
---малых отверстий 461
--- резервуаров 568
------- неограниченной
ёмкости 570
-------ограниченной ём-
кости 572, 573
— несжимаемых жидкостей
при переменном уровне
465
-------при постоянном
уровне 461
— через затопленное и по-
лузатопленное отверстие
463
— через насадки 463
Исчисление вариационное
177
— диференциальное 127
— интегральное 135
— операционное 171
Итерация 237, 251
Иттрий 279
К
Кадка 90
Кадмий 278
Калий 275
Калий циа-нистый 280
Калория 608
Каллендер 566
Каналы 439, 440, 442
Кальций 277
Капиллярность жидкостей
408
Каратеодори 529
Карбонаты 280
Карбинол 301
Кардан 104
Кардиоида 200
618
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Карно 529, 539, 566
Касательная 113, 194
Кассини 200, 201,
Катализ 343
Катет 109
Катион 274, 494
Катод 494
Квадрат 112
Квадратиса 203
Квадратуры механиче-
ские 254
Квадраты чисел 15
Квантовая теория тепло-
ёмкости 318
Кетоны 302
Киловатт 607
Килограмм 605
Кинг 472
Кинематика 357, 368
Кинетика 342
Кипения температура 289
Кирпичёв М. В. 585
Кирхгоф 584, 599
Кирхгофа второй закон
492 , 503
— первый закон 490,
503
— метод уравнений 492
Кислород 284
Кислотность среды 341
Кислота бензойная 304
— винная 309
— карболовая 301
— кремневая 280
— лимонная 309
— молочная 309
— муравьиная 304
— олеиновая 304
— пальмитиновая 304
— пикриновая 306
— сернистая 285
— синильная 280
— соляная 286
— стеариновая 304
— сульфоновая 306
— угольная 279, 309,
— уксусная 304
— щавелевая 304
Кислоты 274
— бескислородные 274
— карбоновые 303
Клапейрон 326, 530, 546
Клаузиус 326, 510, 529,
530, 546, 566
Клеро 167
Клетчатка 308
Клин 88
Коагуляция 352, 353
Коалесценция 354
Кобальт 288
Козсни 472 , 473
Колебания электромагнит-
ные 596
Коллебрук 427
Коллоиды 349
Количество движения 378
Колодец водобойный 457
— (приток воды) 473
Кольцо круговое 85
Комбинаторика 100
Коммутативность 91
Компоненты системы 331
Компрессор идеальный
541, 543
Конвекция 583
— вынужденная 585
— естественная 589
Конденсатор 489
Конденсация капилляр-
ная 346
Коидукция 574, 577
Коновалов 331
Консерватизм углов 217
Конус 89, 116, 117, 192
Конус трения 399
Конхоида 199
Координаты (определе-
ния) 179, ISO, 187
— центра тяжести 146
Корреляция 226
Корень уравнения 103
Кориолис 422, 424, 456
Корни (радикалы) 15, 98
Косинус 60
Котангенс 60
Ко те с 255
Кох 547, 548, 590
Коши 157, 159, 165, 167,
175, 213, 214,415, 417, 421
Коэфициент 95
— абсолютной вязкости 406
— амплитуды 507
— восстановления 486
— вязкости кинемати-
ческий 406
----воды 406
— гидравлического со-
противления 423, 425,
428
— диэлектрической среды
488
• — затухания 509
— искажения 507
— корреляции 226
— объёмного расшире-
ния 405
— отдачи 495
— относительный диэлек-
трический 487
•— поверхностного натя-
жения 408
— полезного действия ак-
кумулятора 495
— пропорциональности 94
— расхода 428, 444, 445,
446
— самоиндукции 484
— сжатия 405, 461
— скорости 461
•— сопротивления 432
----в трубах 432
----задвижек 433
---- клапанов 434
— — конусов 435
— — крапов 433
— — приведённый 436
----различных тел 467
— температурный 491
— теплопроводности 574
— — водяного пара 581
— — газов 582
----жидкостей 579, 580
----различных мате-
риалов 576, 577, 578
Коэфициент теплопровод-
ности металлов 575
Коэфициент трения различ-
ных тел 399, 400, 402,
403
--- скольжения 398
— фильтрации 472
— формы 507
— — сечения 456
— шероховатости 437, 438
Крахмал 308
Крезолы 302
Кремний 280
Кремона 367
Кривая логарифмиче-
ская 203
— подпора 449, 451
— расстояний 368
— свободной поверхности
451, 452, 453, 454
— скоростей 368
— спада 449, 451
Кривизна кривой 195, 205
— поверхности 206, 207
Кривые 2-го порядка 186,
187, 192
— плоские 194, 198
Криптон 274
Криоскопия 329
Кристаллизация 351
Критерий Рейнольдса 422
— подобия 423, 467
Круг 15, 84, 113
— кривизны 196
— сходимости 213
Кручение кривой 205
Крылов А. Н. 259, 357
Ксенон 274
Кузнецов Н. В. 587, 588
Кулон 403
Курбатов 519
Куб 87, 115
Кубы чисел 15
Купоросы 285
Кутателадзе С. С. 591
Кюри 321
Л
Лагранж 131, 134, 167,
246, 251, 413, 417, 418
Лантаниды 269, 279
Лаплас 171, 176, 212, 344
416, 577
Левкипп 510
Лежандр 177
Лейбензоп Л. С. 460
Лейбниц 157
Лемб 417
Лемниската 201
Летучесть 338
•— вихревая 419
Линия ломаная 108
— геодезическая 207
— кривизны 207
— тока 414
— цепная 203
Липшиц 165
Литвинов Д. А. 586
Литий 275
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
619
Лиувилль 214
Лобачевский Н. И. 156, 240
Логарифма характери-
стика 107
Логарифмы 107
Логарифмирование 107
Логарифмы десятичные 35
— натуральные 15, 107
Локон Аньези 199
Ломоносов М. В. 272,
511, 527
Лониталь 129, 132
Лоран <215
Лоренц 574
Лучеиспускание слоя
углекислоты 601
— — водяного пара 602
Лучи а 320
— 0 320
— т 320
— Рентгена 321
Ляпунов А. М. 227
М
Магний 276
Магнит постоянный 483
Маклорен 160, 252
Максвелл 482, 510, 511,
512, 531
Максимум 132
Маннинг 429 , 438, 439
Мантисса 107
Марганец 287
Марков А. А. 223
Мариотт 531
Масса 375
— электрона 487
— электромагнитная 319
Масс-спектограф 320
Математика 91
Математическое ожидание
величины 225
Машина идеальная 529
Маятник физический 386
Медиана 110, 225, 226
Медь 276
Менделеев Д. И. 269, 316
Металлоиды 269, 274
Металлы 274
— щелочные 269
— щелочно-земельные 269
Метан 296
Метанол 301
Метацентр 411
Метод выбранных точек 231
— ложного положения 239
— наложения 493
— наименьших квадра-
тов 229, 232
— неопределённых коэфи-
циентов 97
— обращения рядов 251
— парабол 319
— последовательных при-
ближений 257 ’
• — символический 503
— средних 232
— трансфигурации элек-
трических цепей 493
— холостого хода и ко-
роткого замыкания 493
Механика 357
Минимум 132
Минор 101
Минута 108
Михеев М. А, 585, 590
Милликен Р. А. 318
Мицелла 352
Многогранник 115
Многоугольник 84, 109,
112, 113
— Вариньона 36э
— верёвочный 364
— распределения 224
— силовой 358
Многочлен 96
Множитель интегрирую-
щий 165
Мода 225, 226
Модуль числа 95
— комплексного числа 100
— упругости 405
Молекула 273, 316
Молибден 286
Момент изгибающий 365
— главный 361, 362, 363
— инерции 146, 147, 392,
394, 395, 396, 397
--- осевой 393
--- полярный 393
— пары 359
— кинетический 380
— количества движения 380
— силы 360
— системы кинетический
380
— статический 146
— центробежный 393
Моменты инерции неко-
торых однородных линий
фигур и тел 394
Моносахариды 307
Монотропия 332
Мочевина 309
Мощность 385
— электрического тока 492
Мыла 305
Мышьяк 283
Н
Навье 421
Наложение потоков 418
Напор геометрический 409
— гидростатический 409
— пьезометрический 409
Напряжение источника 417
-— разложения 342
— электрическое 487, 490
Напряжённость магнит-
ного поля 482
— электрического поля 487
Насыщение магнитное 482
Насадка 463
Натр едкий 275
Натрий 275
Натяжение 408, 525
— поверхностное 343,
345, 408
Нафталин 299
Нафтены 296
Нафтолы 302
Начало термодинамики
второе 529
--- первое 527
Н-гептан 296
Нейтральность среды 341
Нейтрон 322
Неон 274
Непрерывность функций
130
Неравенство 106, 107
Никель 288
Никурадзе 425
Ниобий 284
Нитрилы 304
Нитробензол 306
Нитроклетчатка 308
Нитросоединения 306
Нить вихревая 419
Нихром 288
Новиков И. И. 547
Номограмма 262, 263, 265
Номография 262
Нормаль 194, 204
Носитель вектора 207
Ньютон 101, 239, 246, 249,
255, 357, 381, 385, 420
Нуль-вектор 207
Нуссельт 591
О
Обелиск 87
Объём жидкостей 527
Объём тела вращения 146
Область существования
функции 128
— сходимости 159
Обтекание тел 467
Овал Кассини 200, 201
• Одночлен 95, 96
Озон 284
Окислы 274
Окись углерода 280
Окрестность точки 128
Окружность 15, 113
Оксалаты 304
Олефины 297
Олово 281
Ом 483, 490, 491, 500, 503,
Оператор Гамильтона 212
Определитель 101, 169
Орт 208
Ортоцентр ПО
Осмос 330
Основания 274
Ось абсцисс 179
— действительная 99
— мнимая 99
Осмий 292
Октанта 188
Остойчивость плавающего
тела 413
Остроградский М. В. 137,
155, 212
Отделение корней урав-
нения 238
Отверстие (гидравлические
характеристики) 465
Отношение 94
Отображения конформ-
ные 216
Отрезок 108, 128
620
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
п
Павловский Н. Е. 439, 444,
453, 463, 470
Палладий 288
Пар водяной 546
— сухой насыщенный 553,
554
Пара сил 359
Парабола 85, 198, 199
Параболоид 90, 192
Парадокс гидростатиче-
ский 411
Пара источник—сток 418
Параллелограм 84, 112
Параллелепипед 87, 115
Параминобензолсульфо-
кислоты 306
Парафины 295
Парахор 343
Паскаль 200, 409
Паули 324
Пептизация 350
Перекись водорода 275
Переместительность 91
Перемещение виртуаль-
ное 410
Пе ремычки (фильтрация) 474
Перестановки 100
Периметр 109
Периодическая система эле-
ментов Менделеева 269
Периодический закон Мен-
делеева 269
Период переменного тока
497
Периодичность тригоно-
метрических функций 119
Перестановка 100
Пермаллой 482
Петля гистерезиса 482
Петров Н. П. 399
Пинен 299
Пирамида 115
Пиридин 314
Пиррол 310
Пифагор 111
Плавание тел 413
Плавления температуры
289
Планиметрия 108
Планк 318, 529, 596
Платина 293
Пловучесть тел 412
Плоскость 114, 189, 204
206
Плотность вероятности 224
— жидкостей 404
— тока 490
— энергии электромагнит-
ного поля 485
Площадь криволинейного
сектора 145
— криволинейной трапе-
ции 145
— поверхности вращения
145
Победит 288
Поверхность 116, 145
— тока 414
— уровня 211, 409
— эквипотенциальная 417
Погрешность 163, 233
Подвижность ионов 339
Подкова 88
Позитрон 322
Покой жидкости 410
Поле магнитное 480
— направлений 165
— потенциальное или без-
вихревое 212
— скалярное 211
— соленоидальное 212
— электрическое 487
— электростатическое 487
Полиморфизм 317
Полиномы 128, 248
Полисахариды 308
Полодия 373
Полоний 285
Полуинтервал 128
Полусегмент 128
Полюс 180, 215
Поляризация 341
— диэлектриков 487
Порог концентрации 352
Порядок кривой 181
Последовательность нуле-
вая 505
— прямая 505
— обратная 505
Постоянная произвольная
135
— универсальная газовая
315, 474, 531
Постоянство растяжений
217
Поташ 276
Потенциал диффузионный
341
— критический 352
— скорости 417
— термодинамический 327,
532
— электрического поля 487
— электродный 339
Потенцирование 107
Потери на гистерезис 485
— на токи Фуко 486
Поток бурный 447
— вектора 211
— магнитный 482
— параллельный 418
— плоско-параллельный
417
— радиальный 417
— спокойный 447
— циркуляционный 418
Потокосцепление магнитное
483
Пояс шаровой 89
Правило буравчика 480
— значности 352
— отбора 324
— параллелограма 358
— фаз 331, 332
Предел интеграла 143
— функций 128, 129
Прецепитат 283
Призма 87, 115
Признаки равенства тре-
угольников НО
— подобия треугольников
ПО
Принцип сохранения ви-
хрей 420
Пробой диэлектрика 490
Проводимость активная 501
— ёмкостная 501
— индуктивная 501
— полная 501
— реактивная 501
— удельная 491
Прогрессия 94, 95, 156
Производная функции 130
Производные высших по-
рядков 131
— определённого интегра-
ла 144
— частные 133
Проницаемость магнитная
480
— относительная диэлек-
трине екая 487
Пропанол 301
Пропорция 94
Протактиний 284
Протеины 309
Протон 320, 487
Профиль русел составной
441
— устойчивый 442
Проценты 93
Процесс адиабатный 536, 565
— изобарный 535, 565
— изотермический 536, 565
— изохорный 535, 566
— круговой 539, 566
— политропный 537
Прямая в пространстве 190
Прямые 108, 114
Прямоугольник 84, 112
Птоломей 111
Пуассон 176, 226
Прыжок — волна 447
— гидравлический 447, 456
— поверхностный 447
— совершенный 447
Р
Работа 363, 381
— электрического поля 492
Равновесие безразличное 364
— жидкостей 403, 410
— неустойчивое 364
— плавающих тел 413
— сил 358
— системы 363
Радиана 76, 117
Радий 277
Радикалы 98
Радиоактивность 320
Радиус-вектор 369
Радиус метацентрический
413
— кривизны 196, 205
— кручения 205
— окружности 113
— сходимости 159, 213
Радон 274
Развёртка кривой 196
— окружности 203
Разложение силы 358
Размещение 100
Разность конечная 224
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
621
Разность контактная 495 '
— потенциалов 490, 494
Разряд периодический 509
Распад урана цепной 323
Распределительность 91
Растворы 328
Расчёт гидравлический ка-
налов 439
Расчёты стехиометриче-
ские 273
Расширение внезапное 432
— линейное 526
— объёмное 527
Расход жидкости 414
— непрерывный 430
— путевой 431
— транзитный 431
Рауль 329, 330
Реакция гомогенная 336
— гетерогенная 336
— окислительно-восста-
новительные 273
Редкие земли 279
Режим второй критиче-
ский 448
— ламинарный 423
— первый критический
448
— турбулентный 425
Резервуары (время опорож-
нения) 466
Резонанс напряжений 502
— токов 502
Рейнольдса критерий 422
— параметр 423
Рений 288
Решение треугольников
123, 124
Решётки 317
Рикка ти 167
Риман 158, 175, 213
Родий 288
Розерфорд 322, 323
Ролль 131
Ромб 84, 112
Ротор 416
Ртуть 278
Рубидий 276
Рунге 258, 506
Русло естественное 442
Рутений 288
Ряды бесконечные 156
— (действия) 158
— знакочередующиеся 157
— Маклорена 160
— Тейлора 160
— термоэлектрический 496
— функций 159
— Фурье 162, 506
— числовые 95, 156
С
Сабатэ 540
Савар 480, 510
Самоиндукция 484
Саррюс 102
Сахар виноградный 307
— тростниковый 308
Сахароза 308
Свердлин А. 515
Свинец 281
Связи идеальные 363
Сегмент 77, 85, 89
— круга 113
— шаровой 117
Седиментация 352
Сектор 85, 89
— круга 113
— шаровой 117
Секунда 108
Селитра 282
Семейства радиоактивные
321
Сера 284
Серебро 276
Сероводород 285
Сероуглерод 280
Серп 85
Серре 205
Сечение живое 414
Сжимаемость капельных
жидкостей 405
Сила внешняя 378
— внутреннего трения 406
— внутренняя 378
— давления жидкости 412
— живая 381, 415
— коэрцитивная 482
— магнитодвижущая 483
— подъёмная подково-
образного электромаг-
нита 486
— термоэлсктродвижу-
шая 495
Силикаты 280
Символика химическая 273
Сименс 491
Синельников 587
Синерезис 355
Синусоида 86
Система гомогенная 331
— гетерогенная 331
— многофазная 504
Системы двухкомпонент-
ные 332
— коллоидные 349
— кристаллические 316
— однокомпонентные 332
— трёхкомпонентные 334
Сифон 428
Скаляры 207
Скандий 279
Скнарь Н. А. 589
Скобельцин Д. В. 322
Скорость комплексная 419
— осреднённая местная 414
— предельная 376
— угловая 371, 372
Слихтер 472
Сложение вероятностей 223
— параллельпьлх сил 358
Слой шаровой 117
Смеси газовые 532, 533,
534
— охладительные 334
Смесь жидкости и газа
(движение по трубам) 478
Смолуховский М. 529
Сода 275
Соединение в звезду 504
— параллельное (трубо-
проводов) 430
Соединение последователь-
ное 491
— последовательное (тру-
бопроводов) 429
— смешанное 505
— треугольником 504
Соединения 100
— гетероциклические 309
— конденсаторов 489
— параллельные 492
Соли 274
Сопротивление активное 498
— местное 432
— полное 501
— проводников 492
— удельное 490
— электрическое 490
Состояние метастабиль-
ное 467
Сосуды сообщающиеся 410
Сочетания 100
Сочетательность 91
Спираль Архимеда 202
— гиперболическая 202
— логарифмическая 202
— параболическая 202
Спирты 300, 301
Среда дисперсионная 350
Сродство химическое 336
Стантон 482, 531
Статика 357
Стекло 280
Стенка водосбойная 457
Степень 15, 98
— диссоциации 273
Стереометрия 114
Стирлинг 129, 247 , 250
Стирол 299
Стокс 155 , 212, 420 , 421
Столетов А. Г. 496
Стрелка дуги 77, 113
Стронций 277
Строфоида 199
Струйка 414
Сфера 117
Сходимость 158
Сужение внезапное 432
Сулема 278
Сульфиды 306
Сульфокислоты 306
Суперпозиция 418
Суперфосфат 283
Сурик 281
Сурьма 283
Суспензии 350
Т
Таллий 279
Тантал 284
Тареев В. М. 570
Тейлор 132, 160, 215, 257
Теллур 285
Тело абсолютно твёрдое 357
— вращения 146
— диамагнитное 481
— парамагнитное 481
— ферромагнитное 481
Теорема единственности 214
— о конечном приращении
131
622
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Теорема основная алгебры
96
— тепловая 337
Теплоёмкость (определение)
513
— газов 532, 533
Теплоёмкости жидкости 519
— истинные 515
— перегретого водяного па-
ра 549
— истинные при постоян-
ном давлении 515
— квантовая теория 318
— средние 513, 515, 516,
518
— твёрдых тел 317, 520
Теплообмен излучением ме-
жду твёрдыми телами 599,
600
Теплоотдача 585, 586, 587,
589,
— плит 591
— при кипении жидкостей
592
----конденсации 591
— труб 585, 586, 587, 589
Теплопередача излучением
595
— конвективная 583
— кондуктивная 574
— радиационная 595
Теплопроводность 574
Теплота горения 325
— нейтрализации 325
— сорбции 346
— разведения 325
— растворения 325
Термоэлектричество 495
Тетралин 299
Тетрахлорметан 300
Тетраэдр 115
Тиксотропия 355
Тимрот Д. Л. 519
Тиоспирты 306
Тиофен 314
Тиофенолы 306
Тиоэфиры 306
Титан 281
Тождество 95
Ток активный 501
— переменный 497, 506
— постоянный 490
— реактивный 501
Тор 89
Торий 282
Точки особые 197, 215
— изоэлектрическая 352
— перегиба 195
Трактриса 203
Траектория струй 462
Трансверсальность 178
Транспозиция 485
Трапеция 84, 112, 145
Требин Ф. А. 478
Трение 398, 399, 400. 401,
402, 403
Т реугольник 83,109,110,111
Трёхгранник сопровождаю-
щий 204
Триады 269
Тригонометрия сфериче-
ская 127
Триптан 296
Трохоида 201
Труба всасывающая 429
— самотёчная 429
Трубка вихревая 419
Трубопровод длинный 429
— короткий 428
эквивалентный 430
Трубы концентрические 424
— незаполненные (расчёт)
442
— прямоугольные 424
У
Углеводороды 295
Углеводы 307
Углерод 279
Угол 108, 109, 113, 114
— поворота 371, 372
— полярный 180
— смежности 196
— трения 399
Удар гидравлический
в трубопроводах 459
— жидкости 458, 459
— неупругий 387
— прямой 387
— совершенно упругий 387
— упругий 387
— - центральный 387
Уклон гидравлический 423
— критический 450
Улитка Паскаля 200
Ульзамер 587
Ультрамикроскоп 351
Универсальная газовая по-
стоянная 315, 474
Уравнение гидростатики
Эйлера 409
— движения грунтовых вод
470
— двучленное 104
— состояния газов 474
— состояния идеального
газа 315, 531
— статики тяжёлых газов
475
— трёхчленное 104
— химическое 273
Уравнения (алгебраиче-
ские) 95, 103
— диференциальные 165
---Бесселя 171
---в полных диферен-
циалах 165
— — в частных производ-
ных 174
---высших порядков 167
---высших степеней 167
---допускающие пони-
жение порядка 168
— квадратные 103
— — Клеро 167
— — Лагранжа 167
— — линейные 166, 169
— ----- второго порядка
174
------- неоднородные 169
--- — однородные 169
---однородные 166
* Уравнения диференциаль-
ные 1-го порядка 165
— — Риккати 167
(системы) 105
— — с разделяющими пе-
ременными 166
-----теплопроводности 176
----- Эйлера 170
Уран 286
Усадка линейная 527
Ускорение 368, 370, 371,
372
Устойчивость агрегатив-
ная 488
Участок начальный труб 424
Ф
Фаза дисперсная 350
Фа рада 488
Фарадей 338, 494
Фёдоров Е. С. 316
Фенантрен 299
Фенолы 300, 301
Ферма 366
Ферромагнетизм 482
Фокусы эллипса 184
Формфактор 507
Формула барометрическая
475
Формулы эмпирические 230
Фосген 309
Фосфор 282
Фотоэлектричество 496
Фотоэлемент 496
Фотоэффект 496
Френе 205
Фруда параметр 423
Фруктоза 307
Фтор 286
Фуко токи 486
Функции Бесселя 81
— гиперболические 79, 125,
126
— комплексного перемен-
ного 212
— многих переменных 132
— обратные тригономе-
трические 122
— показательные 79
— трансцендентные 213
— тригонометрические 54,
117, 126
Функция алгебраическая
128
— аналитическая 213, 214,
215
— возрастающая 132
— иррациональная 128
— многозначная 128
— монотонная 132
— напорная 470
— независимой переменной
128
— неявная 128
— одной переменной 127
— первообразная 135
— рациональная 128
— степенная 219
— тока 415
— трансцендентная 128
— убывающая 132
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
623
Функция характеристиче-
ская (в гидромеханике)
419
Элементарная 128
— явная 128
Фуран 310
Фурфурол 303
Фурье 162, 176, 506, 574,
584
X
Хайлов М. А. 515
Характеристика логариф-
ма 107
Хемосорбция 346
Хлор 287
Хлорбензол 300
Хлорметан 300
Хлороформ 300
Хорда 77, 113
Христиановнч С. А, 478
Хром 285
Хроматы 286
Ц
Цезий 276
Целлулоза 308
Цемент 281
Центр водоизмещения 411
— давления 411
— кривизны 196
— мгновенный 372, 373
— окружности 113
— параллельных сил 359
— приведения 361, 362
— тяжести 146, 147, 359,
390, 391, 392
— удара 390
Цепи Маркова 223
— химические 341
Цепь магнитная 483
Цикл Брайтона 541
— Гемфри 541
— Дизеля 540
— Карно 529, 539, 566
— Отто 539
1— Ренкина—Клаузиуса
566
— Сабатэ 540
— термодинамический 539
Цикланы 296
Циклогексан 297
Циклоида 201
Циклопентан 297
Циклотрон 322
Цинк 277
Цирконий 281
Цилиндр 88, 116, 193
Циркуляция вектора 211
— скорости 416
Циссоида 199
Цистерна железнодорож-
ная (истечение нефтепро-
дуктов) 466
Ч
Чан 90
Чарпый И. А. 443, 460, 466
Частные производные 133
Частота переменного тока
497
— резонансная 502
— события 222
Чащихин 587
Чебышев П. Л. 139, 223,
248 , 251, 255 , 256
Черникин В. И. 428, 478
Четырёхугольник 83, 111
Числа 91, 99
Ш
Шак 601, 602
Шар 89
Шарнир опорный 366
Шези 437
Шероховатость труб 426
Шиллер Н. 529
Шкала атомных весов 320
Шкала функциональная 262
Шмидт 515, 591
Шор 521
Щ
Щелкачев В. Н. 470
Щёлочность среды 341
Щёлочь 274
Э
Эбулиоскопия 329
Эвольвента 196
Эволюта 196
Эвтектика 333
Эйгенсон Л. С. 587
Эйлер Л. П. 139, 170, 177,
178, 179, 213, 252, 258,
260, 413, 417, 458
Эйнштейн 318, 353
Эквивалент 273
— механический тепла 492
— электрохимический 494
Экстремаль 177
Экстремум 132, 134,177, 178
Электричество контактное
495
Электрод 340
Электролиз 338, 494
Электролиты 273, 338, 339,
494
Электрон 318, 487
Электрон-вольт 319
Электроосмос 352
Электропроводность газов
497
— молекулярная 339
— эквивалентная 339
Электрофорез 351
Электрохимия 338
Элементы гальванические
339, 494
— нормальные 339
— обратимые 340
— типические 269
Эллипс 86, 184
Эллипсоид 90, 192
— инерции 394
Эмиссия термоэлектрон-
ная 496
Эмульсии 354
Энантиотропия 332
Энгельс 527, 529
Энергия внутренняя 327,
530
— кинетическая 381, 383
— магнитного поля 485
— свободная 327, 337, 530
— сечения 447
— электрического поля 488
Энтальпия 327, 530
Эпициклоида 201
Эренфест 529
Эрстед 482
Этан 296
Этанол 301
Этилен 297
Этиленгликоль 301
Этилмеркаптан 306
Этин 298
Эффект поверхностный 498
— реакции тепловой 325
Ю
Юсти 515
Я
Яблонский В. С. 466
Явление неправильных ря-
дов 352
— привыкания 352
Ядро 271, 321
— атома 487
Якоб 592
Якоби Б, С. 494
Ясюкевич 428
Техн, редактор Д. М. Юдзоп
Художник Б. В. Шварц
Отпечатано с матриц
Бумага 7Ох 1081 19х/а бумажных—
53,43 печатного листа. Уч-изд. 32 л.
ЖДИЗ 76521. Зак. тип. 1387.
Т 01792. Тираж 5 000 экз.
1-я тип. Трансжелдориздата МПС.