Прикладная теория пластичности и ползучести - Малинин Н.Н.

Автор: Малинин Н.Н.

Теги: механика деформируемых тел упругость деформация физика сопротивление материалов издательство машиностроение теория пластичности

Год: 1975

Похожие

Прикладная механика сплошных сред. Том 2. Механика разрушения деформируемого тела

Нелинейное деформирование тел

Теория и задачи механики сплошных сред

Механика деформируемого твердого тела

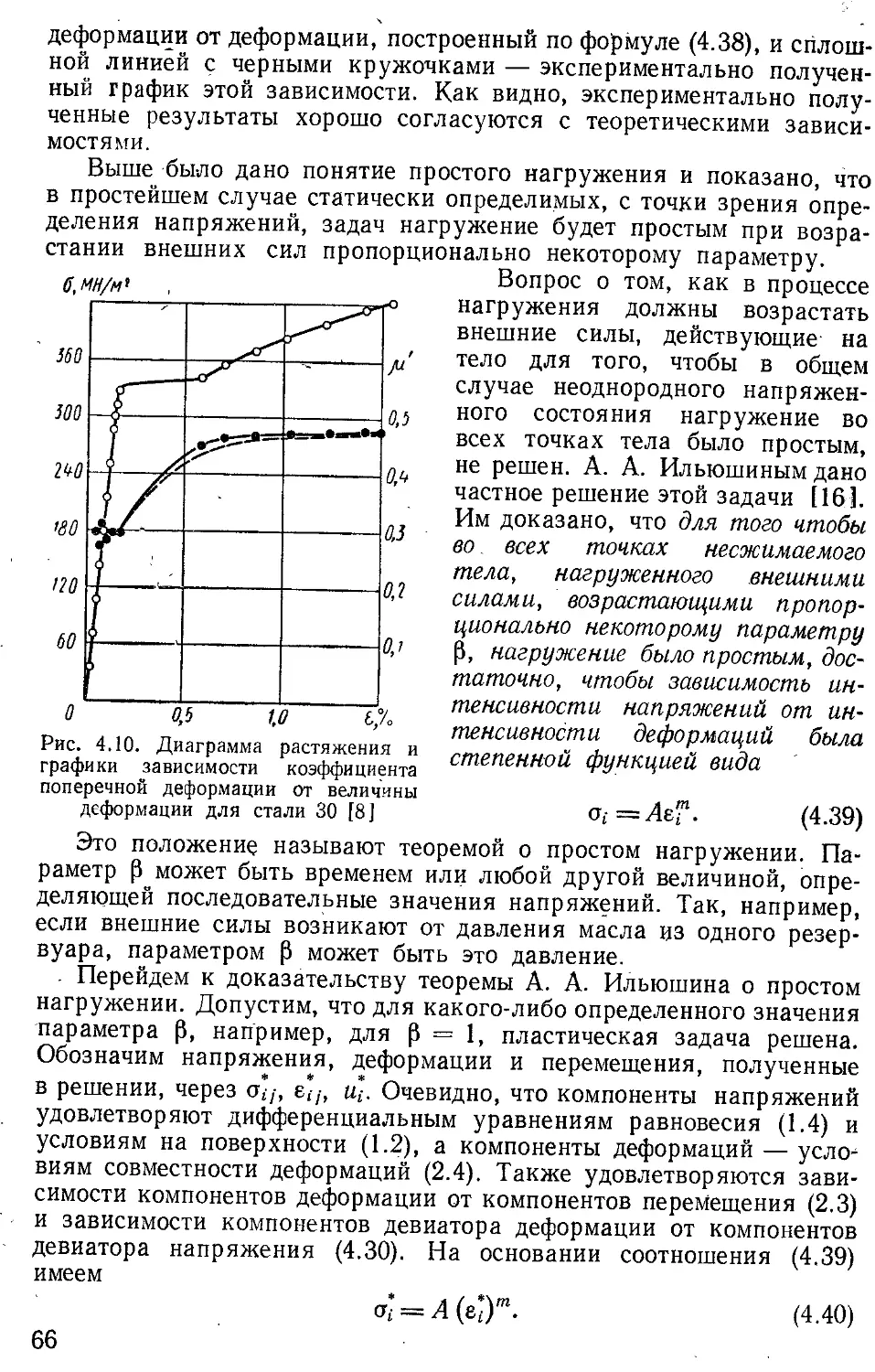
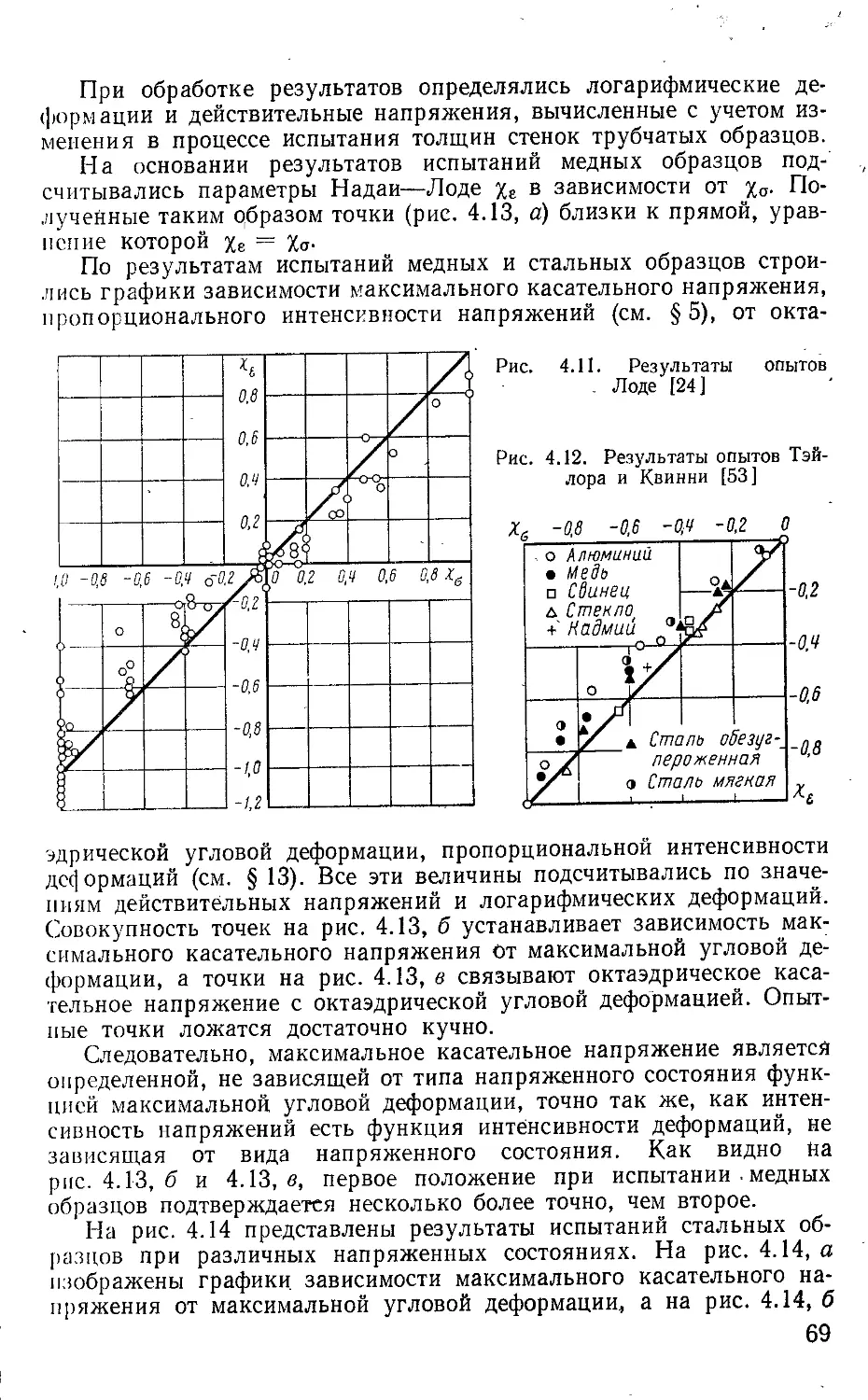
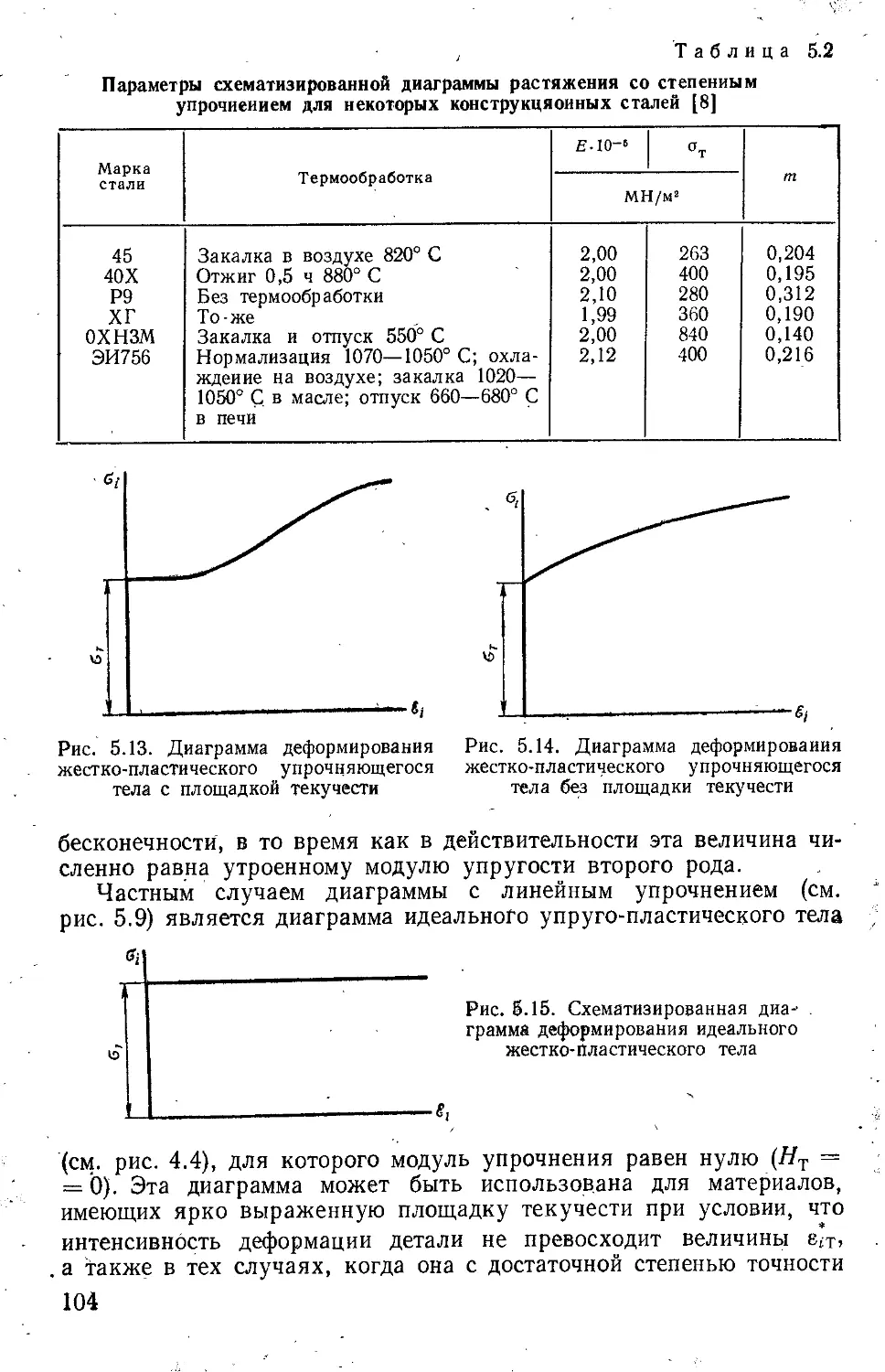
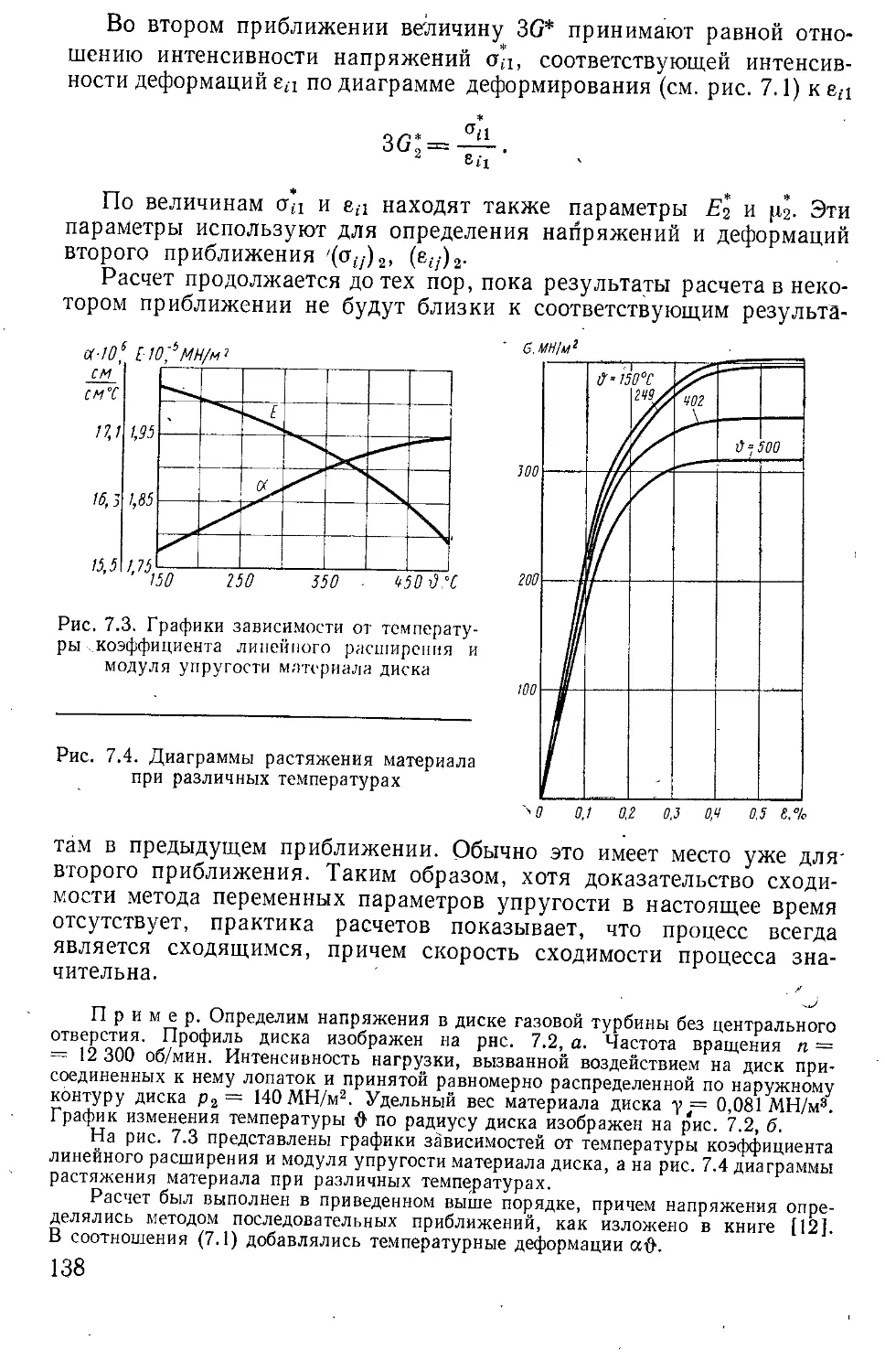
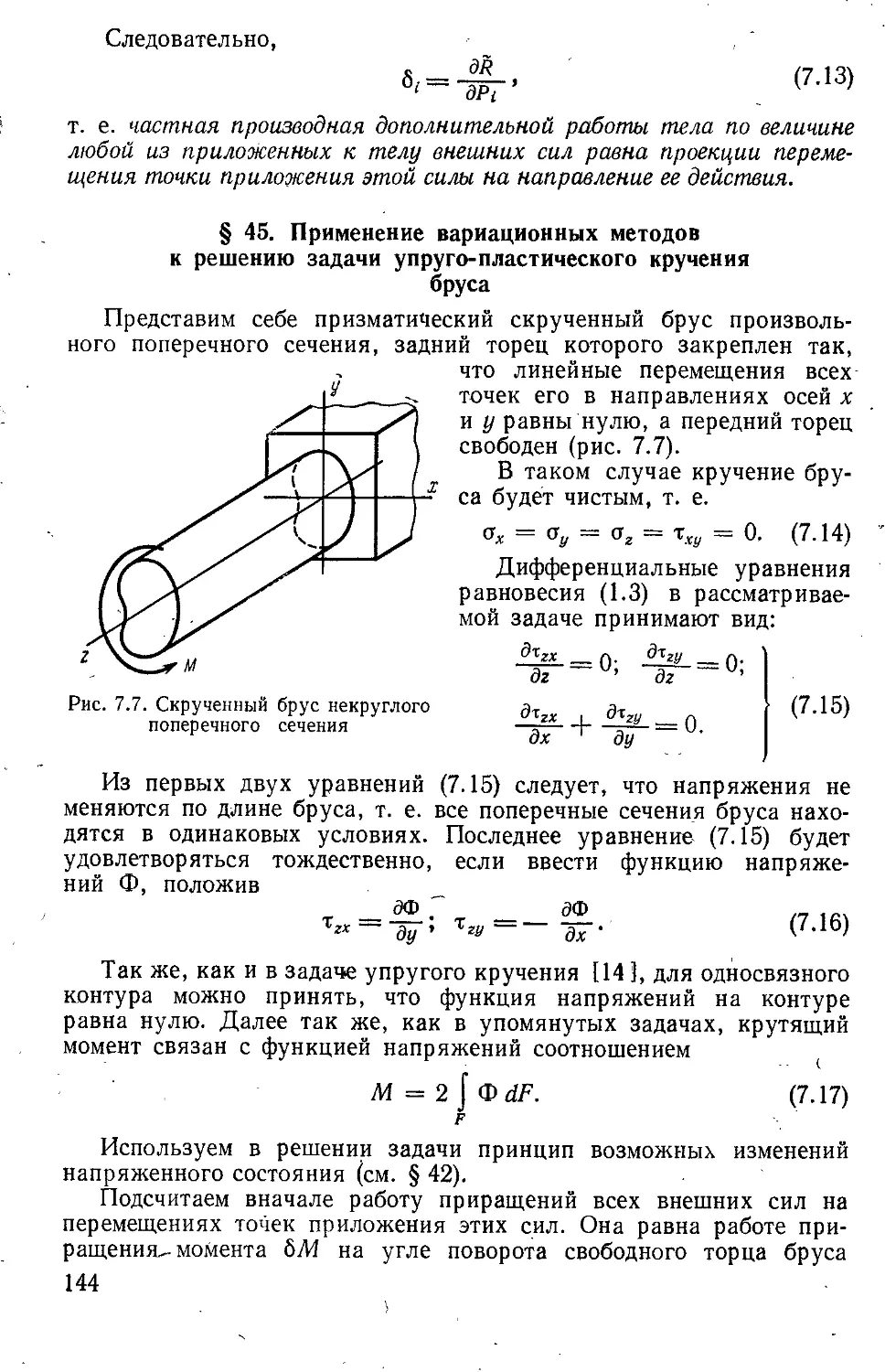
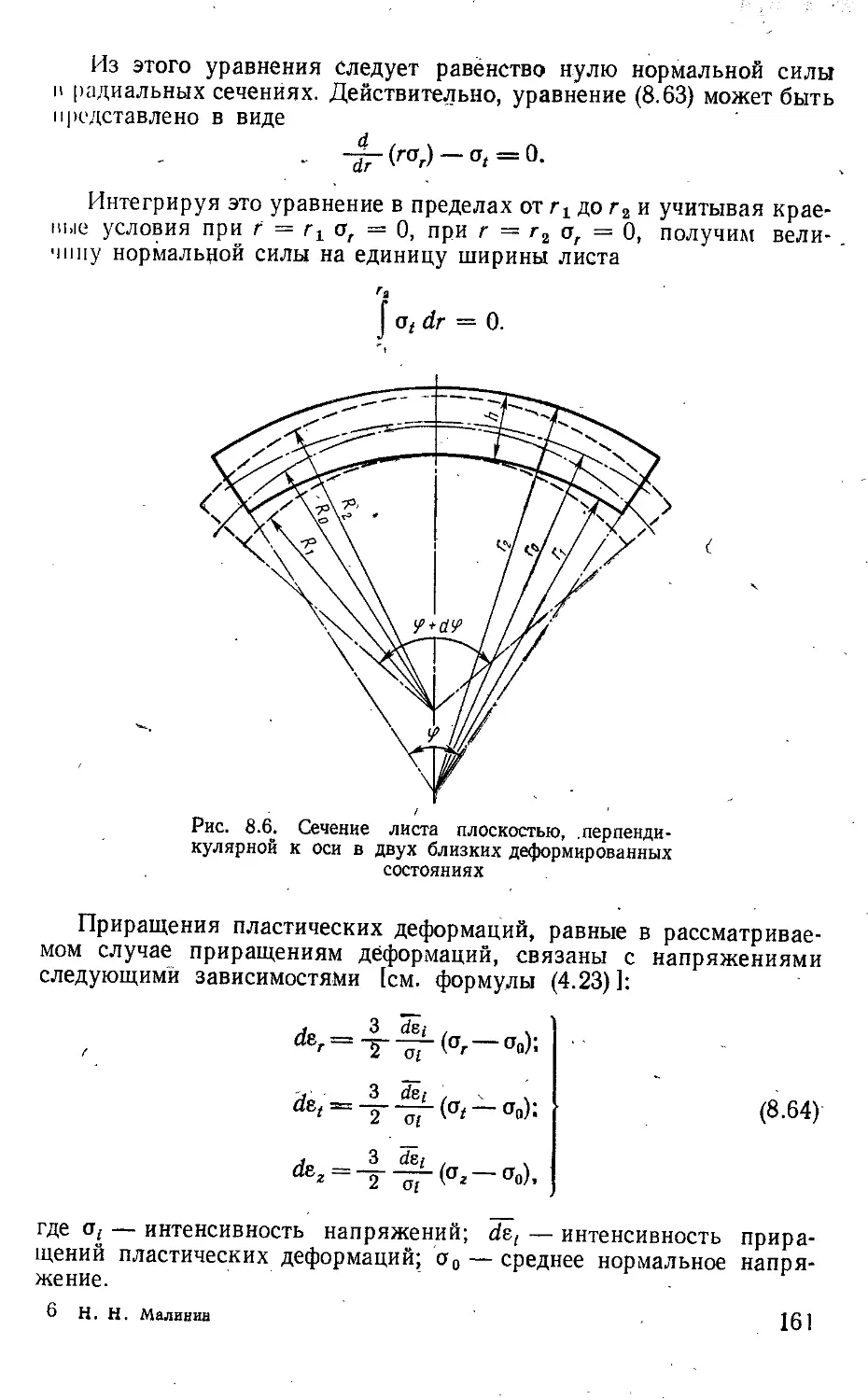
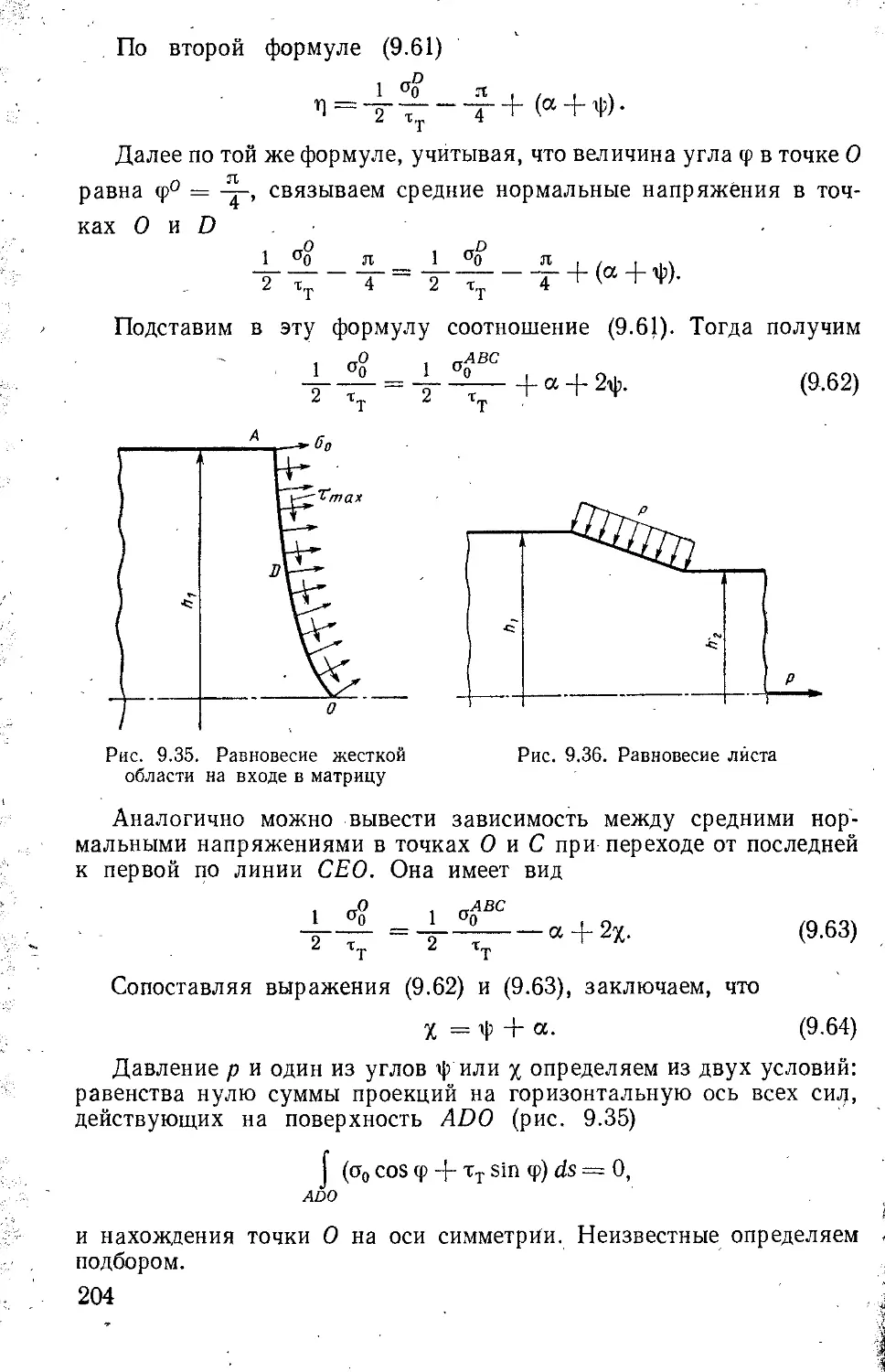
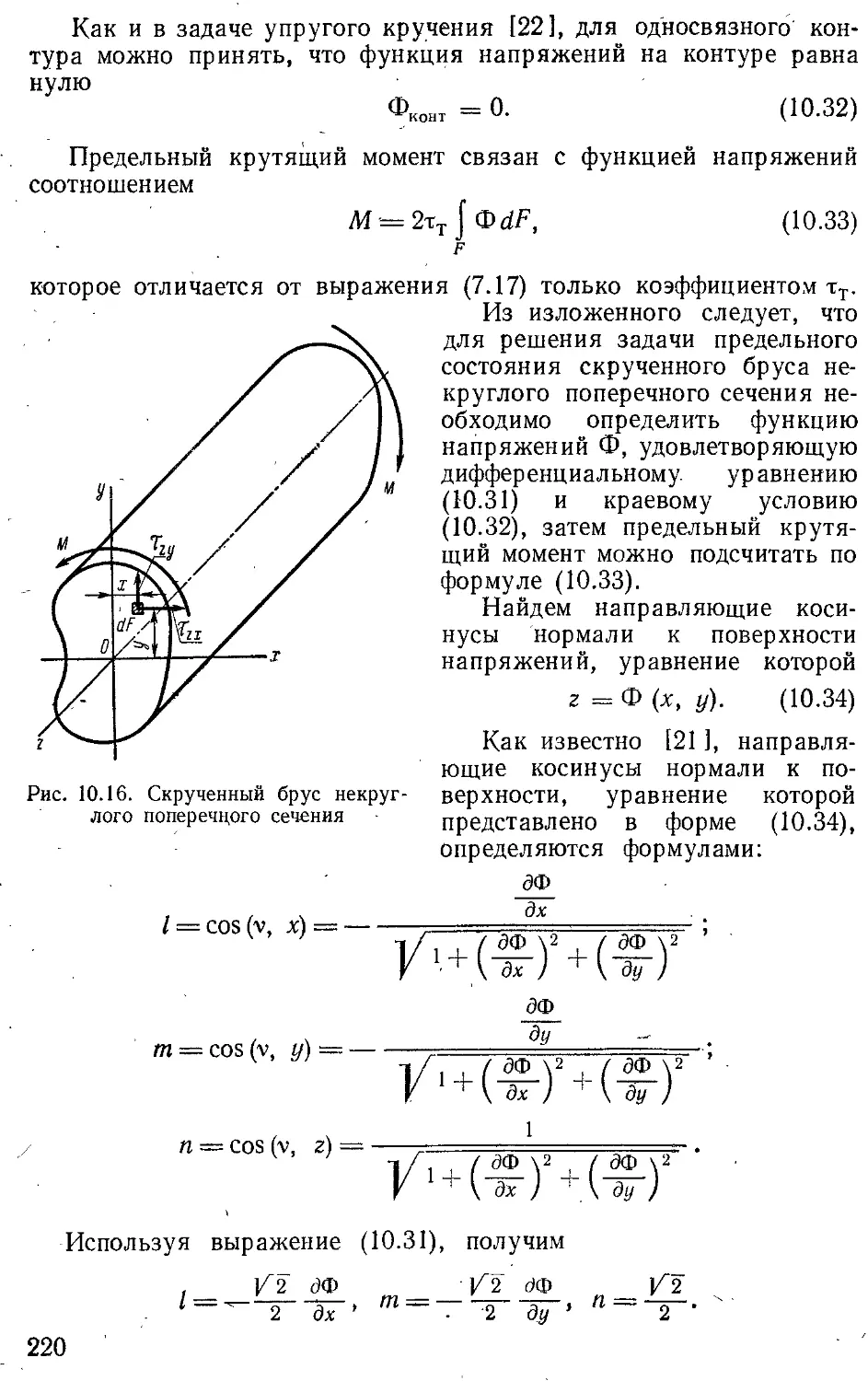
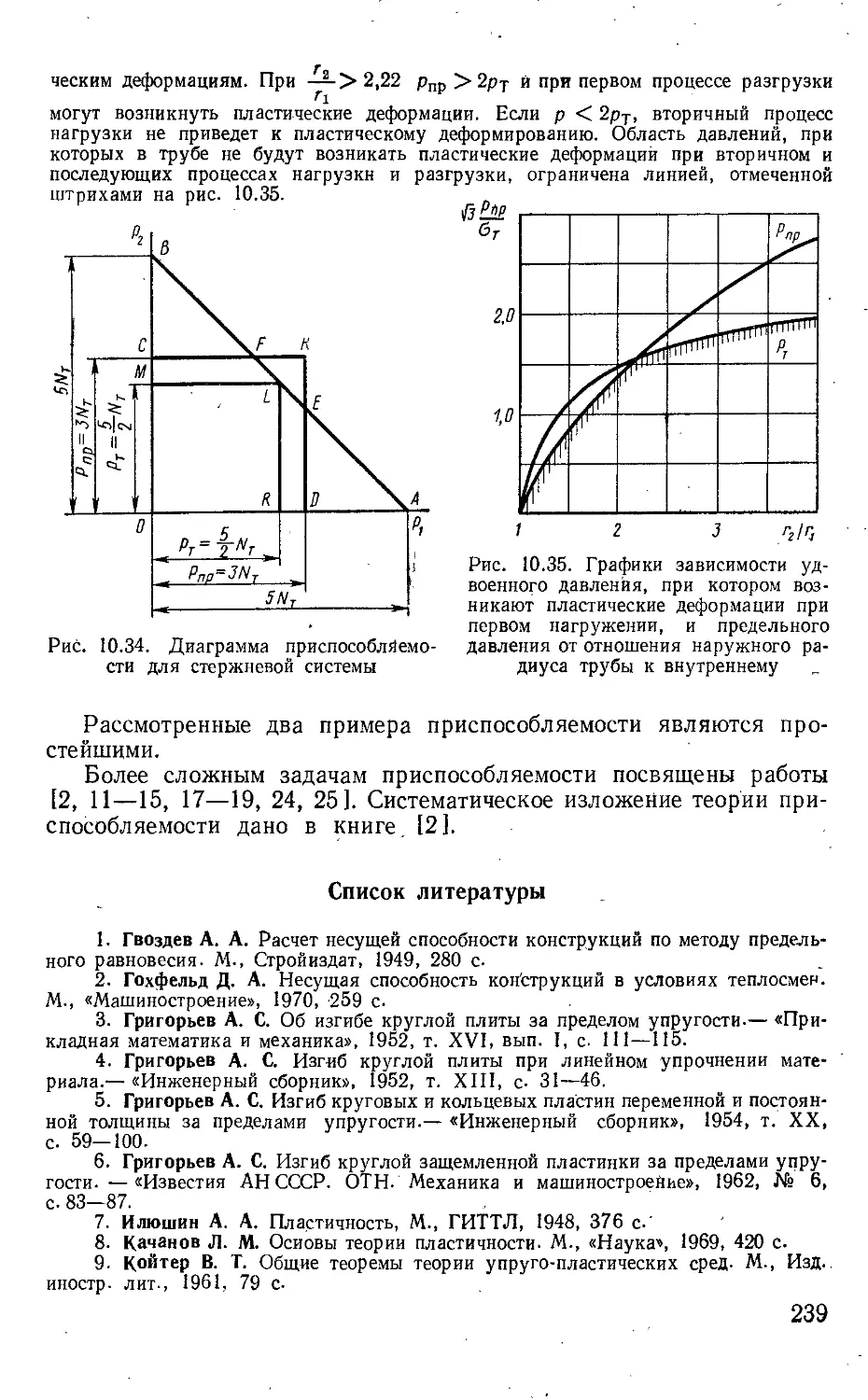
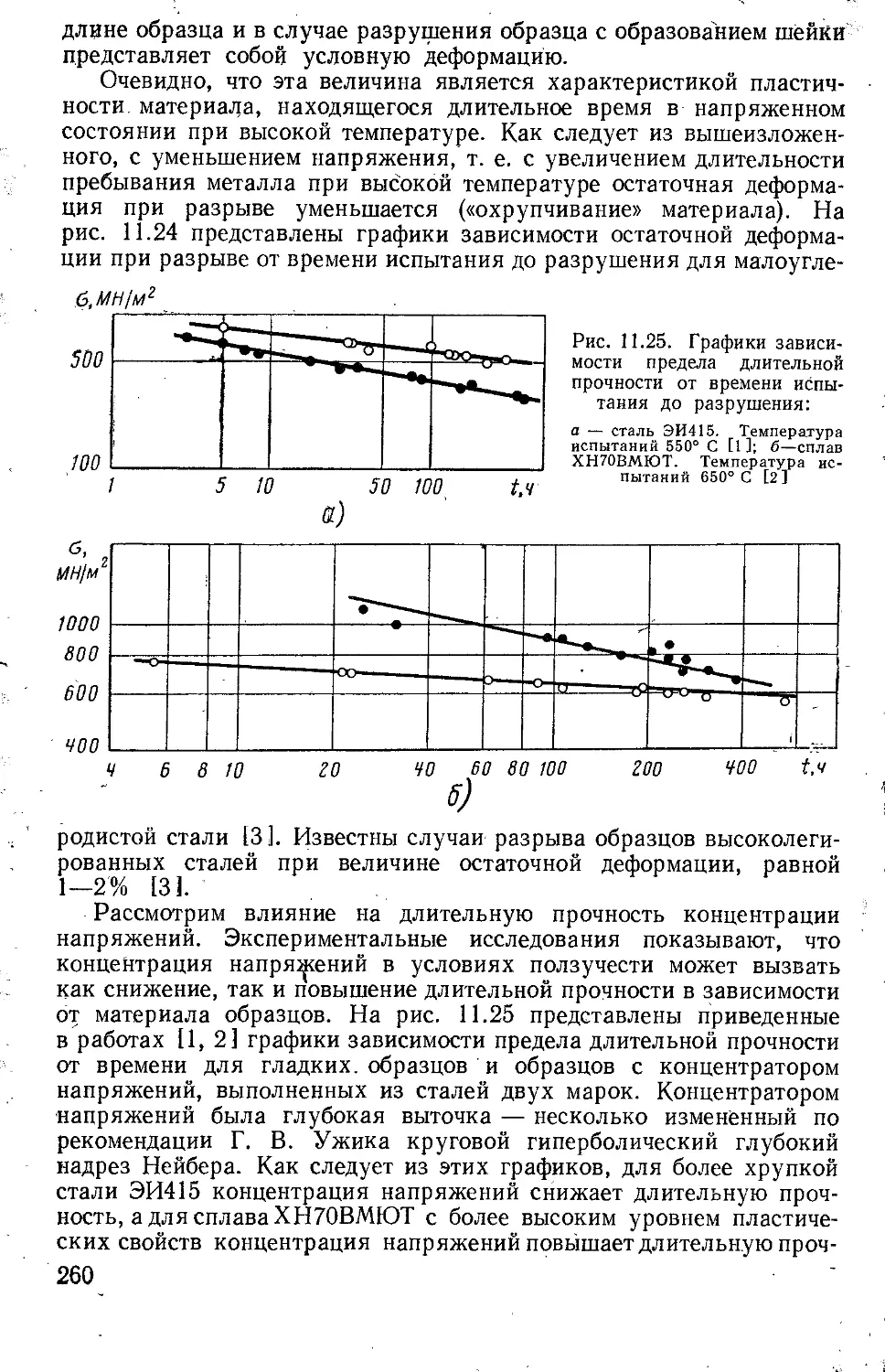
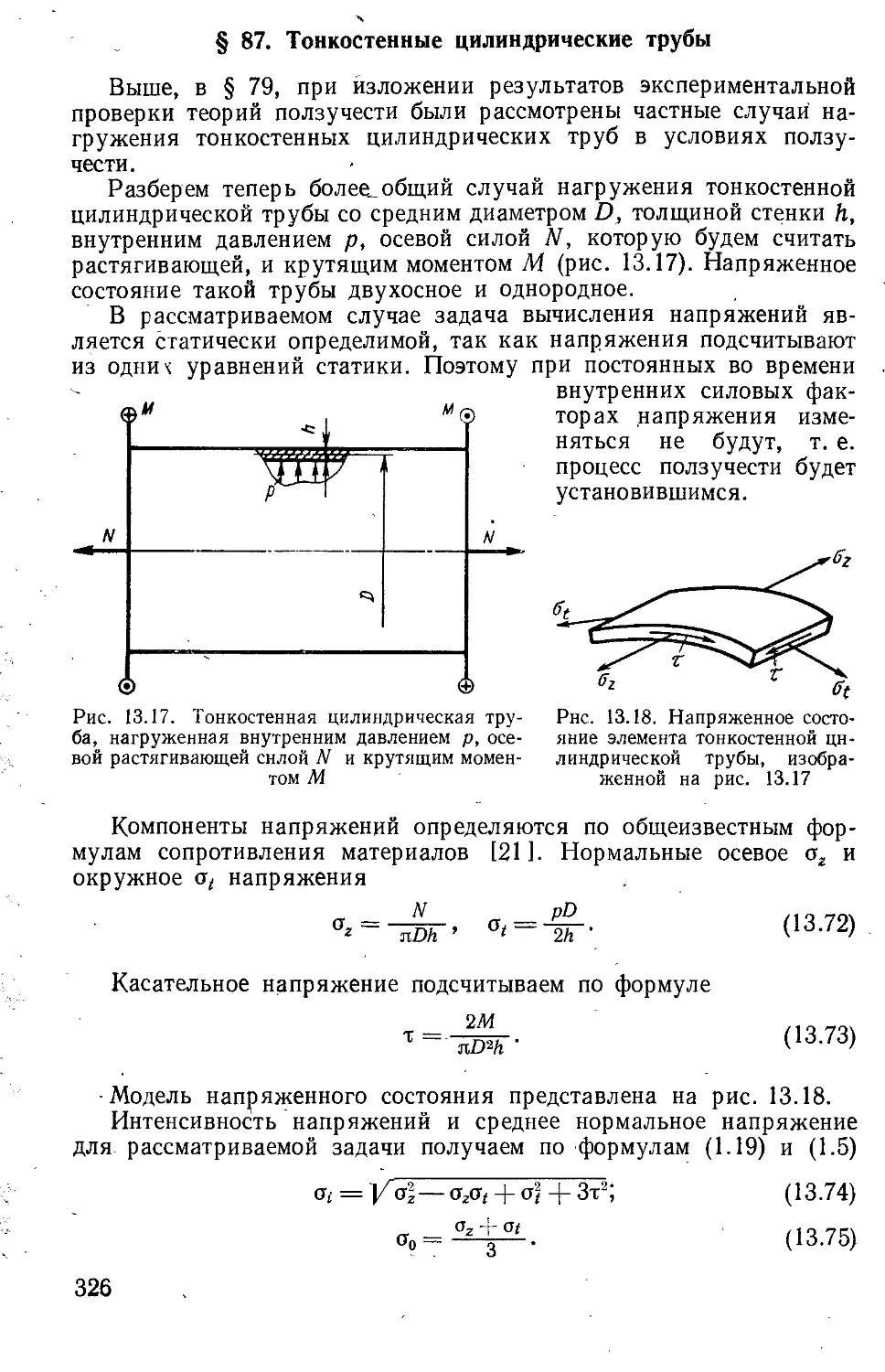
Текст

Н.Н.МАЛИ НИН
ПРИКЛАДНАЯ
ТЕОРИЯ
ПЛАСТИЧНОСТИ
И ПОЛЗУЧЕСТИ
от/щсно Министерством высшего и среднего специального
о<чпмшания СССР в качестве учебника дм студентов
niiioi трошпельных специальностей высших учебных заведений
БИБЛИОТЕКА
М81ТВМИПИГП
МАШИНОСТРОЕНИЕ. 1075

УДК 539.374 | 539.376:621@75)
Малииин Н. Н.
Прикладная теория пластичности и ползу-
ползучести. Учебник для студентов вузов. Изд. 2-е,
перераб. и доп. М., «Машиностроение», 1975,
проф. л. м. Кач
Редактор канд. техн. наук В. Л. Дав
Издательство «Машиностроение», 1975 г.

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Книга написана на основе лекций, читаемых автором для сту-
студентов специальности «Динамика и прочность машин» в Московском
высшем техническом училище им. Н. Э. Баумана в соответствий
с программой курса «Прикладная теория пластичности и ползу- -
чести».
Второе издание книги полностью переработано. В нем в отличие
от первого издания более подробно изложены общие вопросы теории
пластичности,, а также рассмотрены теория пластичности с анизо-"
тройным упрочнением, условие пластичности и теория пластичности
для анизотропных материалов, напряженное состояние в шейке
образца при растяжении, новые методы построения действительной
диаграммы деформирования, большие деформации и пластическая
устойчивость цилиндрических и сферических оболочек, численные
методы решения краевых задач плоской деформации и примеры при-
применения их, теория ползучести с анизотропным упрочнением, кратко-
кратковременная ползучесть, использование критерия Треска—Сен-Венана
в решении задач установившейся ползучести, методы решения задач
неустановившейся ползучести и примеры их применения, определе-
определение времени разрушения в условиях ползучести, вязкоупругость.
В связи с тем, что механические свойства материалов при одно-
одноосном растяжении и сжатии, а также расчеты стержней и стержневых
систем за пределами упругости находят все более полное отражение
в общеинженерных курсах сопротивления материалов, они исклю-
исключены из второго издания.

ВВЕДЕНИЕ
Стремление к уменьшению массы машин при улучшении их ка-
качества вызывает необходимость использования в процессе проекти-
проектирования наиболее совершенных методов расчета, в которых по воз-
возможности полно отражены действительные условия работы кон-
конструкции и механические свойства материалов.
При проектировании легких и экономичных машин часто при-
приходится рассматривать деформацию деталей за пределами упругости.
Это позволяет выявить дополнительные прочностные ресурсы кон-
конструкции. Так, например, в распространенном в машиностроении
методе расчета по допускаемым напряжениям за предельное состоя-
состояние конструкции принимают такое, при котором эквивалентное на-
напряжение в наиболее напряженной точке детали, изготовленной из
пластичного материала, достигает величины предела текучести по-
последнего. Коэффициент запаса детали по этому методу вычисляют
как отношение предела текучести к максимальному эквивалентному
напряжению. Однако очевидно, что в случае неоднородного напря-
напряженного состояния возникновение пластических деформаций в одной
наиболее напряженной точке еще не означает наступления предель-
предельного состояния конструкции в целом. После наступления текучести
в локальной зоне деталь еще может сопротивляться увеличению
внешних сил до тех пор, пока пластические деформации не охватят
значительного объема ее.
Для деталей из пластичного материала предельное состояние
должно определяться величинами тех перемещений, при которых на-
нарушаются условия нормальной эксплуатации, или же нагрузками,
при которых конструкция перестает сопротивляться воздействию
внешних сил (массовая текучесть) или разрушается.
4

Для деталей, выполненных из сравнительно хрупких матерчз"
лов, за предельное состояние следует принимать такое, при котором,
наступает разрушение.
Нагрузки, соответствующие предельному состоянию, называют,
предельными.
При расчете по предельному состоянию вначале определяют ве-
величину предельной нагрузки, после чего коэффициент запаса вы-
вычисляют как отношение этой нагрузки к действительной. Данный;
метод расчета позволяет создать более экономичные конструкции,
чем метод допускаемых напряжений, поскольку в нем в основу по-
положены величины предельных нагрузок, при которых исчерпывается
несущая способность деталей.
Ввиду того, что предельное состояние наступает После образова-
образования в детали пластических деформаций, для вычисления предельных
нагрузок требуется умение производить расчеты за пределами упру-
упругости.
В технологических процессах производства некоторых элементов
конструкций предусмотрены специальные операции, позволяющие
путем пластического деформирования повысить несущую способ-,
ность деталей в пределах упругости. Например, винтовые цилиндри-
цилиндрические пружины растяжения, сжатия и кручения после навивки и
термообработки выдерживаются в деформированном за пределы упру-
упругости состоянии определенное время. Такую операцию длительного-
деформирования пружин за пределами упругости в производствен-
производственной практике называют заневоливаннем.
Толстостенные трубы, нагружаемые в эксплуатации внутренним
давлением, после изготовления подвергают воздействию внутреннего
давления, вызывающего пластические деформации, В результате
этого в^трубе создается благоприятное поле остаточных напряжений,
снижающих рабочие напряжения в эксплуатационных условиях.
Такую технологическую операцию называют автоскреплением ил»
автофретированием. В результате автоскрепления рабочее давление
в трубе может быть повышено.
Аналогично автоскреплению толстостенных труб делались по-
попытки повысить несущую способность турбинных дисков путем пред-
предварительного пластического деформирования их (раскручивание
дисков). Для этого диски до эксплуатации на специальных стендах
приводились во вращение с такими скоростями, при которых в них
возникали пластические деформации.
Очевидно, что для установления наиболее эффективных условий
пластического деформирования, правильного назначения размеров
5

определения остаточных напряжений, необходимых для
расчета па прочность предварительно пластически деформированных
деталей, нужно уметь выполнять расчеты за пределами упругости.
Технологические процессы обработки металлов давлением (про-
(прокатка, ковка, штамповка, волочение, прессование, навивка пружин)
основаны на способности металла пластически деформироваться.
Расчеты таких процессов необходимы для правильного выбора мощ-
мощности прокатных станов, ковочных машин, штампов, волочильных
станов, прессов, автоматов для навивки пружин и т. п. Во многих
случаях они позволяют точно устанавливать размеры заготовок, вы-
выяснять оптимальные условия деформирования, обеспечивающие из-
изготовление изделий высокого качества, и оценивать прочность заго-
заготовок в процессе деформирования их.
Так, например, при холодной гибке листового металла в V-образ-
ных штампах для того чтобы получить изделие заданной формы и
размеров, следует правильно назначить радиус закругления пуан-
пуансона, расстояние между опорами, а также предусмотреть размеры
поперечного сечения заготовки, поскольку при гибке они сильно
изменяются.
В случае волочения тонкостенных труб через матрицы необхо-
необходимо правильно выбрать толщину стейки трубы, чтобы после из-
изменения ее диаметра в результате волочения получить нужную тол-
толщину стенки.
При правке или рихтовании возникают остаточные напряжения,
которые могут привести к короблению деталей вследствие перерас-
перераспределения во времени остаточных напряжений. Наличие остаточ-
остаточных напряжений в двутавровой балке, выпрямленной в плоскости
наименьшей жесткости, иногда приводит к боковому выпучиванию
балки при изгибе ее в плоскости наибольшей жесткости. Поэтому
¦ в расчетах" правки или рихтовки необходимо определять усилия,
нужные для пластического деформирования деталей, а также вы-
вычислять остаточные напряжения, возникающие в результате этой
технологической операции.
Из изложенного очевидно, что при исследовании процессов обра-
обработки металлов давлением также необходимо владеть расчетами за
пределами упругости.
Так как при обработке металлов давлением деформации обычно
значительны, технологические расчеты производятся, как правило,
в предположении больших деформаций.
При длительном нагружении деталей машин, эксплуатация ко-
которых протекает при повышенных температурах, возникают необра-
6

шмме деформации, в результате чего напряжения могут изменяться
ни ирсмени. Это явление изменения во времени деформаций и на-
напряжений, возникших при нагружении, называют ползучестью,
И практике известно много случаев, когда за счет ползучести
/мформации деталей достигали таких величин, при которых наруша-
нарушались условия нормальной эксплуатации агрегатов. Так, например,
in ледствие ползучести диска и лопаток газовой турбины перекры-
ii.i.niKi» зазорыГпредусмотренные между лопатками и корпусом, что
и пршюдило к поломке лопаток.
:ia счет уменьшения во времени напряжений наступает постепен-
постепенное ослабление плотности соединения деталей, скрепленных при
помощи упругого натяга. Плотность болтового соединения фланцев
паропровода или фланцев корпуса паровой турбины, работающих
при высоких температурах, с течением времени уменьшается, что
может привести к «пропариванию фланцев». Плотность посадки диска
п,ч нал в условиях его работы при повышенной температуре также
ослабевает. Падение созданного при посадке контактного давления
и,| поверхности соприкосновения диска с валом приводит к наруше-
нарушению плотного контакта между диском и валом (к так называемому
¦¦г\оду» диска).
Коли разрушение детали происходит по истечении значительного
промежутка времени после нагружения,.то напряжения и деформа-
деформации и этот момент могут сильно отличаться от значений их при на-
i ружении. Поэтому при анализе разрушения необходимо учитывать
перераспределение напряжений за счет ползучести материала. Рас-
Расчеты деталей машин на ползучесть тесно связаны с расчетами за
пределами упругости.
Из изложенного следует, что расчеты за пределами упругости
имеют большое значение в машиностроении. Они основаны на теориях
пластичности и ползучести. Последние являются отделами"механики
деформируемых тел.
В теории пластичности ставится задача определения напряжений
п перемещений в деформируемом теле за пределами упругости. При
лом предполагается, что деформации не зависят от времени. В тео-
теории ползучести изучается влияние времени на величины деформаций,
и напряжений.
Первые работы по теории пластичности были вкполнены в семи-
семидесятых годах прошлого века Сен-Венаном и Леви, которым при-
принадлежит создание одного из вариантов теории пластичности, а также
получение основных уравнений задачи плоской деформации.
В 1909 г. была опубликована работа Хара и Кармана. В ней
сделана попытка вывода основных уравнений теорий пластичности
7

из некоторого вариационного принципа. В статье Мизеса A913 r.v
система уравнений Сен-Венана — Леви дополнена иным условием
пластичности, которое несколько раньше было получено Хубером.
В двадцатых годах этого века начинается интенсивное развитие
теории пластичности.
Генки, Прандтлем и Мизесом были получены основные уравне-
уравнения различных вариантов теории пластичности и решения задачи
плоской деформации. В ряде работ опубликованы результаты экс-
экспериментальной проверки различных гипотез и приведены решения
задач теории пластичности. •
Первые работы по техническим теориям ползучести с применением
к расчетам деталей машин были опубликованы в тридцатых годах
Удквистом, Бейли и Содербергом. С тех пор теория ползучести ин-
интенсивно развивается.
Большой вклад в теории пластичности и пЬлзучести был сделан
советскими учеными, которым принадлежит анализ и развитие теорий,
экспериментальная проверка их, решения задач по различным
теориям, разработка приближенных методов решения задач и вне-
внедрение расчетов за пределами упругости и на ползучесть в технику.

РАЗДЕЛ I. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ
ГЛАВА I
ТЕОРИЯ НАПРЯЖЕНИЙ
§ 1. Напряженное состояние в точке тела
Поскольку теории напряжений и деформаций подробно изучаются
п курсах сопротивления материалов и теории упругости, в этой и
последующих главах ряд положений приводится без вывода и только
некоторые дополнительные сведения, необходимые для дальнейшего
изложения теории пластичности, рассмотрены подробно.
Из курса сопротивления материалов [7 3 известно, что девять
компонентов напряжения
п трех взаимно перпендикулярных площадках,' проходящих через
рассматриваемую точку тела (рис. 1.1), полностью определяют на-
напряженное состояние в этой точке, т. е., располагая их значениями,
можно найти напряжение в любой площадке ABC, проходящей
через рассматриваемую точку.
Проекции Xv, Fv-, Zv на оси координат х, у, z полного напря-
напряжения pv (рис. 1.2) в некоторой наклонной площадке определяются
по формулам
Xv = aj + тухт + хгхп
где I, m, n — направляющие косинусы нормали v к площадке.
После вычисления проекций полного напряжения Xv, Yv, Zv
уже нетрудно определить полное, нормальное и касательное напря-
напряжения в этой площадке по формулам
Yvm + Zvn;
tv =

Приведенные выше девять компонентов напряжения образуют
тензор напряжения
*ху
Согласно закону парности касательных напряжений в двух вза-
взаимно перпендикулярных площадках составляющие касательных на-
напряжений, перпендикулярные к линии пересечения этих площадок,
равны между собой и направлены либо к линии пересечения этих
б Т
р
площадок, либо от нее, т. е. хух — хху; хгу = xyz; ххг
= хгх. Таким
образом, компоненты тензора напряжения, расположенные сим-
симметрично относительно главной диагонали (диагонали, проходящей
через нормальные напряжения ох, ау, аг), равны между собой.
г'
Рис. 1.1. Напряжения в трех взаимно
перпендикулярных гранях элементар-
элементарного тетраэдра
Рис. 1.2. Напряжения в наклонной
грани элементарного тетраэдра
Обычно для изображения напряженного состояния в точке тела
в окрестности последней выделяют элемент объема в виде прямо-
прямоугольного параллелепипеда, три ребра которого принимаются за
оси-координат (рис. 1.3). По граням выделенного элемента изобра-
изображают составляющие напряжения в соответствующих плоскостях.
При этом предполагается, что длины ребер параллелепипеда равны
нулю, т. е. параллелепипед как бы представляет собой точку.
В дальнейшем при рассмотрении общих вопросов теории пластич-
пластичности и ползучести будут использованы тензорные обозначения, ко-
которые позволяют записывать ряд формул в более компактном виде.
При использовании тензорной символики декартовы коорди-
координаты х, у, z обозначают через хх, х2, х3 или в общем виде хп где ин-
индекс i принимает значения 1, 2, 3.
Нормальные напряжения обозначают а1Х, сг22, а33, а касатель-
касательные сг12, а23, а31,. Общий компонент записывают в виде аи (i, / =
— 1, 2, 3). Отдельные компоненты получают из общего компонента
заменой букв i и / цифрами 1, 2 и 3.
10

В дальнейшем под Оц будем понимать также совокупность всех
чсилти компонентов напряжения, т. е. тензор напряжения.
Обозначим через п( составляющие единичного вектора нормали
к площадке, равные направляющим косинусам нормали.
Тогда формулы A.1) можно пред-
iчаиить в виде
з
Сокращенная запись суммирования
11 к-тоит в том, что знак суммы опускает-
опускается и но всякому дважды повторяюще-
повторяющемуся в одночлене индексу проводится
суммирование по значениям 1, 2, 3.
Н таком случае предыдущая формула
принимает вид . г
Xvj = оц
A.2)
Рис. 1.3. Модель напряженного
состояния
Повторяющийся индекс (в рассматриваемом случае i) называют
немым, или подставным, а неповторяющийся (/) свободным.
§ 2. Дифференциальные уравнения равновесия
Выделим из тела бесконечно малый элемент в форме параллеле-
параллелепипеда, грани которого параллельны координатным осям (рис. 1.4).
Ребра параллелепипеда обозначим через dx, dy и dz. Воздействие на
параллелепипед отброшенной части тела заменим силами. На рис. 1.4
изображены только силы на видимых гранях. На невидимых гранях
~(TZy didy) аг
tzxdxdy^GZIaidg)dz
Рис. 1.4. Элементарный параллелепипед в равновесном
состоянии
11

силы будут те же,' что и,на параллельных им видимых гранях без
соответствующих приращений. Проекции на оси х, у, z силы,.при-
силы,.приходящейся на единицу объема (объемной силы), обозначим через X,
Y, Z. Уравнения равновесия элементарного параллелепипеда имеют
вид
дох j_ дхух _i_ дтгх^
дх
дх
ду
ду
_ у _
дг
A.3)
Таким образом, три уравнения равновесия A.3) связывают шесть
независимых компонентов напряжения ах, ау, ог, хху, хуг, хгх.
В сокращенной записи уравнения A.3) имеют вид
\-Х,=0. A.4)
§ 3. Разложение тензора .напряжения
Общий случай напряженного состояния (рис. 1.5, а) может быть
представлен в виде суммы двух напряженных состояний (рис. 1.5, б, в).
f
\
у
\
у
Тг
У
у
/
h
та/
/
—*-
1 X
Рис. 1.5. Разложение тензора напряжений на шаровой тензор и девиатор
Тензор напряжения первого напряженного состояния (рис. 1.5, б)
называют шаровым тензором
а0 О О
О 0. ап
где
A.5)
а второго напряженного состояния (рис. 1.5, в) — девиатором напря-
напряжения
S« Syx $zx
с с с
ъху ъу bzy
12

•су •;-;
,и - у,у — ст0; s^ = т^; I A.6)
Очевидно, что компоненты девиатора:
sx — ох ст0; sXy
sy = a
s2 = a
Представленное на рис. 1.5 разложение общего случая напря-
напряженного состояния на два равносильно разложению тензора на шаро-
ной тензор и девиатбр напряжения:
Та — Т01> + Dg.
Из формул A.6) и A.5) следует, что
sx + su + sz = О, - A.7)
т. е. во втором напряженном состоянии сумма нормальных напря-
напряжений в координатных плоскостях равна нулю.
В пределах упругости объемная деформация прямо пропорцио-
пропорциональна сумме нормальных напряжений [7]. Ниже будет установлено,
что это положение может быть распространено и за пределы упру-
упругости. Следовательно, во втором напряженном состоянии (рис. 1.5, в)
изменение объема равно нулю и искажается форма элемента.
Очевидно, что в первом напряженном состоянии (рис. 1.5, б) форма
элемента не изменяется, а изменяется его' объем.
Как показывают опыты, при всесторонних равных растяжениях
пли сжатиях пластические деформации не возникают. Образование
их связано с искажением формы элемента. Поэтому произведенное
разложение общего случая напряженного состояния на два физи-
физически оправдано. Девиатор .напряжений характеризует, насколько
заданное напряженное состояние отличается (уклоняется) от всесто-
всестороннего равного растяжения или сжатия с главными напряжениями,
равными среднему арифметическому нормальных напряжений ис-
исходного напряженного состояния.
Введем величину, называемую символом Кронекера (дельта-
символом). Она определяется следующими соотношениями:
„ • _ II, если i = /;
'; J0, если i Ф }.
Тогда, используя тензорные обозначения и записи суммирова-
суммирования (см. § 1), компоненты девиатора напряжений можно представить
в виде
su = аП — бг/°о. A-8)
где
§ 4. Главные площадки и главные напряжения
¦ В каждой точке тела существуют, по крайней мере, три взаимно'
перпендикулярные' площадки, в которых касательные напряжения
равны нулю. Эти площадки называют главными, а нормальные
13

напряжения в них — главными нормальными напряжениями или
главными напряжениями.
Главные напряжения являются корнями кубического уравнения
а3 - I, (Та) а2 - /2 (Та) а - /3 (Т„) = 0,
.A.10)
где
h (Та) =
(Та) = —охоу — оуог
аг;
&x tyx ^гх
°У %zy
A.11)
Используя тензорные обозначения и записи суммирования, рас-
рассмотренные в § 1, представим формулы A.11) в виде
(Ta) =
}lf
A.12)
Можно доказать [5], что все три корня кубического уравне-
уравнения A.8) вещественны.
В дальнейшем в большинстве случаев будем придерживаться
следующих обозначений для главных напряжений: а1 > а2 > а3.
Таким образом, через ах обозначено наибольшее, а через сг3 наи-
наименьшее из главных напряжений в алгебраическом смысле (с уче-
учетом знака).
Поскольку главные напряжения не могут зависеть- от выбора
осей координат, коэффициенты кубического уравнения также не из-
изменяются при повороте осей координат, т. е. являются инвариантами.
Их называют соответственно первым [/1(Т'<Т)]) вторым [72 (Та)] и
третьим [73 (Та) ] инвариантами тензора напряжений.
Из формул A.11) следует, что выражения инвариантов тензора
напряжений через главные напряжения имеют вид:
/х (Та) = at + сг2 + сг3;
^2 (Та) — —о1аа — о2а3 — Озо1'>
/з (Та) = ota2a3.
Очевидно, что формулы A.11) позволяют определить инвари-
инварианты шарового тензора и девиатора напряжений. Для этого необ-
необходимо подставить в них компоненты шарового тензора A.5) и де-
девиатора напряжений A.6). Определим второй и третий инварианты
девиатора напряжений. [Первый инвариант девиатора напряжений
согласно формуле A.7) равен нулю]. Для этого подставим в фор-
14

мулы A.11) компоненты девиатора напряжений A.6), используя при
пом соотношение A.5). Тогда получим:
1г Фо) = — sxSy — SySz — szsx + sly + 4* + sf * = -§- ГК ~ °v? +
+ (oy - вг? + (a, - a,J + 6 {%% + t\z +
A.13)
°x °yx °zx
Sxy sy szy
Ox — O0 Xyx
ozol
= -ff [2 (ol + a3y + al — 3 (af a, + а^аг + ala^ -j- a^a| + a^af +
12а,а^аг + 9a, {x\y - 2x2yz + тЬ) + 9a, (т|„ + tJ2 - 2tL) +
+ 9аг(— 2т^ + %% + tL) + 54тхЛгт„]. A.14)
В сокращенной тензорной записи согласно формулам A.12)
Л (°а) = "у s//s//!
§ 5. Интенсивность напряжений
Интенсивностью напряжений называют величину, пропорцио-
пропорциональную квадратному корню из второго инварианта девиатора на-
напряжений. В зависимости от принятого коэффициента пропорцио-
пропорциональности различают понятия интенсивности нормальных напря-
напряжений или просто интенсивности напряжений
A.15)
at*=y 3/2 (Д,)
и интенсивности касательных напряжений
A.16)
A.17)
Сопоставляя выражения A.16) и A.17), заключаем, что
A.18)
Подставляя в выражение A.16) соотношение A.13), получим
°i = -щ У (а* — а и? + К — °*У + (Ъ —
6
A.19)
В сокращенных обозначениях согласно формулам A.16) и A.15)
имеем
2 sHsii'
A.20)
.15

Зависимость интенсивности напряжений от главных напряже-
напряжений имеет вид
1 -.гт- -тй-7-7- -' ¦ '- _а1J. A.21)
Для частного случая одноосного растяжения (ах = а, а2 = а3 =
= 0) из формулы A.21) имеем
в, = о. A.22)
Таким образом, коэффициент пропорциональности ]/3 в фор-
формуле A.16) был выбран для того, чтобы в простейшем случае одно-
одноосного растяжения интенсивность напряжений совпадала с величи-
величиной наибольшего главного напряжения.
В случае чистого сдвига (ах = т, а2 — 0, о3 = —т) из форму-
4 лы A.21) имеем
. A.23)
Из зависимостей A.16) и A.21) следует также, что интенсивность
касательных напряжений Т совпадает с величиной наибольшего
касательного напряжения при чистом сдвиге:
Т = х.
Рассмотрим различные интерпретации понятия интенсивности
напряжений.
Выберем декартову систему координат ах, а2, а3 (рис. 1.6). На-
Напряженное состояние в некоторой точке тела характеризуется век-
вектором ОР, компоненты которого ах, а2, а3:
OP = oxix + a2i2 + osis,
где ilt i2, i3 — единичные векторы осей координат alt o2, o3.
Поскольку
ai — ао + su о2 = а0 + s2, cr3 — ао + S3>
где su s2, s3 — главные напряжения девиатора sijt имеем
~ОР = 'Щ + Щ.
В этом выражении
Ш? = а0 GХ + Т2 + Т3);
OQ = s1i1 + s2i2 + s3i3.
Так как
Si + s2 + s3 = 0, A.24)
вектор OQ лежит в. плоскости, проходящей через начало координат
и равнонаклоненной к осям главных напряжений, уравнение ко-
которой
о1 + о2 + о3 = 0.
Эту плоскость называют девиаторной, так как любой вектор, ле-
лежащий в ней, характеризует девиатор какого-то напряженного со-
16

стояния. Проекции осей аи а2, а3 на девиаторную плоскость обр-
чначим соответственно через l'2'З' (рис. .1.7). Очевидно, что они
составляют между собой углы 120°. Вектор OR, проекции которого
па оси координат одинаковы, направлен по нормали v (рис. 1.6)
к девиаторной плоскости. Направляющие косинусы этой нормали
1 т 1
равны —рг, а единичный вектор ее п = —^ (tx -f- i2 -f- i3),
уз уз
Рис. 1.6. Изображение напряженного состоя- Рис. 1.7. Проекции осей о^, о?2 и ай
пия в пространстве главных напряжений на девиаторную плоскость и диаг-
диаграмма Марциняка ?цля напряжений
п поэтому
Модуль вектора 0Q:
Возводя равенство A.24) в квадрат, получим
(sx + s2 + s3J = О,
откуда
sf + s| + si = — 2 (sis2 + s2s3 + S3S1).
Следовательно, согласно формуле A.13)
I (D)~
,_ \OQ\--
_
и поэтому
A.25)
Надаи [3] показал, что интенсивность напряжений пропорцио-
пропорциональна так называемому октаэдриче.скому касательному напря-
напряжению, т. е. касательному напряжению^ площадке, равнонаклонен-
иой к трем глс 1м5РИВ!ТГ«я^яртеяШ!ВДЖой площадке.
17

Величина последнего [5 3
1 -.г;
В. В. Новожилов [4] установил, что интенсивность напряжений
пропорциональна квадратному корню из среднего значения квадра-
квадратов касательных напряжений в точке тела. Для того чтобы пояснить
это положение, опишем вокруг точки тела сферу радиуса г. Нор-
Нормаль v к произвольной площадке пересекает поверхность сферы
в некоторой точке. Выделим в ее окрестности элемент dQ поверх-
поверхности сферы. Касательное напряжение в этой площадке обозначим tv.
Произведение \ dQ является элементарной касательной силой по
площадке dQ. С целью исключения знака касательного напряжения
рассмотрим вместо величины xvdQ выражение TydQ,. Определим
среднее значение квадратов касательных напряжений т§ следующим
образом:
т2 = lira 4- f 'rldQ. A.26)
Эта величина зависит от формы выделенного элемента и от его
ориентации по отношению к главным осям тензора напряжений. Вы-
Выбор сферы объясняется тем, что только на сфере (ввиду ее полной
симметрии) будет в равной мере представлено все множество площа-
площадок, проходящих через точку.
В результате вычисления интеграла в соотношении A.26) можно
установить [4 3, что
т2 - -jg-
— o2f + (<х2 — стзJ + (а3 — onJ].
Сопоставляя это выражение с соотношением A.21), заключаем,
что сформулированное выше положение доказано.
С. Д. Пономаревым [5 ] показано, что интенсивность напряже-
напряжений пропорциональна квадратному корню из минимального средне-
среднеквадратичного уклонения главных напряжений заданного напря-
напряженного состояния а1У а2, о3, от напряжений а некоторого равно-
равноосного напряженного состояния. Обозначим эту величину через А:
Л = т (К — аJ + (а» — аJ + (°з — аJ]- A-27)
Определим напряжение а равноосного напряженного состояния
таким образом, чтобы рассматриваемое уклонение Д имело мини-
минимальное значение. Такое равноосное напряженное состояние будем
называть «ближайшим» к заданному.
Для определения напряжений «ближайшего» к заданному равно-
равноосного напряженного состояния приравняем нулю производную вы-
выражения A.25) по а:
-^ = --| № — а) + (о, —о) + (о,-*)] - 0.
18

откуда
Поскольку вторая производная выражения A.27) по а положи-
положительна, найденное значение о = о0 соответствует минимуму выра-
выражения A.27).
Подстановка найденного значения а в выражение A.27) приводит
к следующей величине минимального среднеквадратичного укло-
уклонения:
Лшт = J- (К — **? + (о, ~ °зJ + (о3~ОгП A.28)
Сопоставляя выражения A.28) и A.21), заключаем, что интенсив-
интенсивность напряжений пропорциональна квадратному корню из мини-
минимального среднеквадратичного уклонения.
В работе В. М. Макушина [2] отмечено, что интенсивность на-
напряжений пропорциональна квадратному корню из суммы площадей
трех окружностей, ограничивающих круговую диаграмму.
§ 6. Геометрическое изображение напряженного
состояния
Геометрическим образом напряженного состояния в точке тела
может служить так называемый эллипсоид напряжений. Полуосями
его являются главные напряжения а1г о2 и а3 (рис. 1.8). Поверх-.
пость эллипсоида представляет собой геометрическое место концов
векторов полных напряжений в различных площадках,, проходя-
проходящих через рассматриваемую точку. Из эллипсоида напряжений сле-
следует экстремальность главных напряжений, т. е. одно из главных
напряжений является наибольшим, а другое наименьшим из всех
нормальных напряжений в площадках, проходящих через рас-
рассматриваемую точку.
В частном случае всестороннего равного растяжения или сжатия
(рис. 1.5, б) эллипсоид напряжений превращается в шар. Отсюда
и название тензора напряжений для такого напряженного состоя-
состояния — шаровой тензор.
Эллипсоид напряжений является пространственным геометри-
геометрическим образом напряженного состояния. В отличие от него круго-
круговая диаграмма напряжений, или диаграмма Мора, представляет со-
собой плоский геометрический образ напряженного состояния.
Круговая диаграмма напряжений состоит из трех полуокруж-
полуокружностей, диаметрами которых являются разности главных напряже-
напряжений (рис. 1.9). Координаты точек, лежащих в заштрихованной области
между полуокружностями, представляют собой нормальное и каса-
касательное напряжения в произвольно ориентированных площадках,
а координаты точек на полуокружностях /, // и /// (рис. 1.9) равны
нормальному и касательному напряжениям в связках площадок /,
//, /// (рис. 1.10), проходящих через главные оси 1,2 и 3. Из кру-
круговой диаграммы напряжений, так же как и из эллипсоида напря-
19

жений, следует экстремальность главных напряжений. Из круговой
диаграммы напряжений устанавливаем также, что экстремальные
значения касательных напряжений в сериях площадок, проходящих
через главные оси /, 2, 3, равны соответственно:
т„ =
—08
0J —02
A.29)
Рис. 1.8. Эллипсоид напряжений
Рис. 1.9. Круговая диаграмма напря-
напряжений
Эти экстремальные значения касательных напряжений называют
главными, касательными, напряжениями. Площадки, в которых воз-
возникают главные касательные напряжения, делят пополам прямые
углы между главными площадками. Поскольку ранее было принято,
что Ст] ;з> 02 ^ ст3, наибольшее касательное напряжение
0— 03
т — т — ¦
A.30)
Рис. 1.10. Нлощадки, параллельные главным осям
В случае равноосного растяжения или сжатия (см. рис. 1.5, б)
все три полуокружности круговой диаграммы стягиваются в точку
(рис. 1.11). Это означает, что для такого напряженного состояния во
всех площадках, проходящих через исходную точку, касательные
напряжения равны нулю, т. е. все площадки являются главными.
Как будет установлено ниже, образование пластических деформа-
деформаций связано с возникновением сдвигов и, следовательно, с наличием
20' ,

касательных напряжений. Поэтому естественно, что, как отмена-
лось выше, при равноосном растяжении или сжатии пластические
дефортции не возникают.
Рассмотрим параметр, характеризующий с точностью до равно-
равноосного растяжения или сжатия вид напряженного состояния. Он
связан с главными напряжениями следующей, зависимостью:
„. " 0 2 " ^3 1 ^2 ^1 *^3 /1 О 1 \
Ха-^БГ^Г Ci-O, • (L31)
Этот параметр был впервые введен в экспериментальной работе
Лоде [1], выполненной под руководством Надаи, и поэтому его на-
называют параметром Надаи—Лоде для %
напряжений. Из формулы A.31) сле-
следует, что при наложении на напряжен-
напряженное состояние равноосного растяжения
или сжатия параметр Надаи—Лоде не
изменяется. ч
Согласно формуле A.31) для одно-
одноосного растяжения (аг ф О, ст2 = о3 ~
б
'= и) 1а — —*> Для одноосного ежа- \
тия (аг = ст3 = 0, о3 ф 0) %а = 1,
для чистого сдвига (стх = —о3, ст2 =
= 0) Хо = 0. Круговые диаграммы на- рис ,„ диаграмма
зывают подобными, если параметры напряжений для трехосного
Надаи — Лоде одинаковы. . равного растяжения
§ 7> Тригонометрическая форма представления
главных напряжений
Кубическое уравнение
х3 + ах2 + Ьх + с = 0
с помощью подстановки
¦ а
3
можно привести к виду, не содержащему члена с у2,
У3 + РУ + Я = 0. A.32)
Как известно [6], если
Т ~^~ ИГ ^ '
то кубическое уравнение A.32) имеет вещественные корни. Решение
кубического уравнения в тригонометрической форме имеет вид [61
-4F^, A.33)
¦ о
где k = 0, 1, 2; '
>(р = — -2-. A.34)
\ 21

В соответствии с изложенным кубическое уравнение для определе-
определения главных напряжений A.10) при помощи подстановки
0
h
приводится к кубическому уравнению для определения главных на-
напряжений девиатора напряжений
s3 — /2 (Do) s - /3 (Da) = 0, A.35)
где величины /2 (Da) и IS{DO) определяются формулами A.11) и
A.12).
Согласно формулам A.33) и A.34) решение кубического уравне-
уравнения A.35) в тригонометрической форме имеет вид
+ -§-&i), (I-36)
s = ¦
cos
причем
cos 3^а==
A.37)
(Do)
Используя выражение A.16) и полагая в формуле A.36) последо-
последовательно k = 0, 2, 1, преобразуем выражения A.36) и A.37) к виду
— -§¦ aicos ^;
= -3- °icos
s3 = -j ot cos
COS Jl|)a —
+ -3-л
+ -3- л
A.38)
A.39)
Угол % будем называть углом вида напряженного состояния.
Если обозначить угол между направлением вектора OQ и осью /'
(рис. 1.7) через % и учесть, что косинусы углов между осями аъ ст2,
о3 и /', 2', 3' соответственно равны 1/ -^-, то формулы A.38) следуют
из рис. 1.7.
Выразим теперь через угол вида напряженного состояния вели-
величины главных касательных напряжений. Для этого, используя соот-
соотношения A.6) и A.38), преобразуем выражения A.29). Тогда получим:
A.40)
22
°2
1
а1— а8
2
Oi—ст2
2
— стз
2
«1
h
s
— S3
2
— s?
2
2 — % а< „¦
1/3
]/з "ш va 3 /'
а< "¦ { 2 \
,_ лп 1 гра 1 g я 1.

Если считать етг
ливы неравенства
sin 1|э„ > 0; s
Следовательно.,
Гг ^ °з, то согласно формуле A.40) справед-
Из этих трех неравенств устанавливаем пределы изменения угла
вида напряженного состояния:
Поэтому согласно формуле A.40) пределы изменения величины
х = т2 от -у- (при % = 0 и % = -у^ до -^- (при г|)а = -^-\ т. е.
Таким образом, пределы из-
мснения отношения
весьма
невелики. Среднее значение отно-
отношения составляет 0
2 +
=.1,87;
оно отличается от крайних зна-
значений У~3 и 2 примерно на 7%.
С достаточной степенью точ-
точности можно принять
Рис. 1.12. Звезда Пелчинского для
напряжений
= 0,933 К-
A.41)
Это выражение устанавливает приближенную зависимость интен-
интенсивности напряжений от главных напряжений. Она линейная, и по-
поэтому расчеты за пределами упругости с использованием ее проще
расчетов, в основу которых положена нелинейная зависимость A.21).
Неудобство использования соотношения A.41) заключается в том,
что обычно заранее неизвестно, какое главное напряжение является
наибольшим, а какое наименьшим.
Формулы A.38) и A.40) могут быть графически интерпретиро-
интерпретированы с помощью построения, изображенного на рис. 1.12, которое
называют звездой Пелчинского для напряжений [10]. Это построе-
построение очевидно из чертежа и пояснения не требуются.
Рассмотрим еще одно геометрическое построение.
Отложим на девиаторной плоскости (см. рис. 1.7) в направлении
осей Г, 2' и 3' главные напряжения.' Тогда, используя соотноше-
соотношения A.38), легко доказать, что замыкающая ломаной линии, отрезки
23

которой равны главным напряжениям, является интенсивностью
напряжений, а угол наклона ее к оси /' углом вида напряженного
состояния. Это построение называют диаграммой Марциняка [9].
Выразим параметр Надаи —Лоде через угол вида напряженного
состояния. Для этого преобразуем выражение A.31), используя соот-
соотношения A.6) и A.38). Тогда получим
Xa = -K3ctg (г|>а + -1я). A.42)
Как было отмечено выше, для одноосного растяжения %а = —1 и,
следовательно, % = 0, для одноосного сжатия %а = 1 % — -у,
для чистого сдвига %а = 0, % =
Список литературы
1. Лоде В. Влияние среднего главного напряжения на текучесть металлов. —
В кн.: Теория пластичности. М. Изд. иностр. лит.,. 1948, с. 168—205.
2. Макушин В. М. Об одном из условий пластичности. — «Вестник машино-
машиностроения», 1955, № 9, с. 6—8.
3. Надаи А. Пластичность .и разрушение твердых тел. М., Изд. иностр. лит.,
1954, 647 с.
4. Новожилов В. В. О физическом смысле инвариантов напряжения, использу-
используемых в теории пластичности. — «Прикладная математика и механика», 1952, т. XVI,
в. 5, с. 617—619.
5. Расчеты на прочность в машиностроении. Т. 1, М., Машгиз, 1956, 884 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К- Лихарев и др.
6. Смирнов В. И. Курс высшей математики. Т. II. М., Физматгиз, 1958, 628 с.
7. Ф.еодосьев В. И. Сопротивление материалов. М., «Наука», 1974, 559 с.
8. Филоненко-Бородич М. М. Теория упругости. М., Физматгиз, 1959, 364 с.
9. Marciniak Z. Mechanika procesow tioczenia blach, Paristwowe wydawnictwa
naukowo— techniczne, 1961, 271 s.
10. Pelczyriski T. V/piyw stanu napecia na przejScie materialu w stan plastyczny.—
«Przeglad mechaniczny», 1951. z 6, s. 175—179, z 7, s. 204—208.

ГЛАВА II
ТЕОРИЯ ДЕФОРМАЦИЙ
§ 8. Деформированное состояние в точке тела
Предположим, что некоторая точка М (рис. 2.1) тела в резуль-
результате его деформации перемещается в положение Мг. Обозначим
проекции перемещения точки М на оси координат через их, иу и иг.
В случае, когда компоненты деформаций малы по сравнению с еди-
единицей, а углы поворота [2] малы настолько, что квадратами и про-
произведениями их по сравнению с компонентами деформации можно
пренебречь, последние связаны с компонентами перемещения линей-
линейными зависимостями: у
Уху
Ууг
Угх
гх-
дщ
ду
= -
= -
— -
дих
ду
диц
дг
диг
дих
дх
+
- +
диу
дх
диг
ду
дих
dz
du;
dz
~ 1
*
B.1)
ц
Рис. 2.1. Перемещение точки тела в ре-
результате деформации
В дальнейшем, если не будет оговорено, будем считать,
что компоненты деформаций малы по сравнению с единицей,
а компоненты перемещения малы по сравнению с основными
размерами тела.
В курсах теории упругости [5] доказывается, что при повороте
прямоугольных осей координат компоненты деформации изменяются
так же, как компоненты напряжения. Сопоставление соответствую-
соответствующих формул для компонентов деформации и напряжения показывает,
что первые можно получить из вторцх заменой компонентов напря-
напряжения стих компонентами деформации е и -|- с соответствую-
соответствующими индексами.
25

Шесть компонентов деформации е*, гу, ег, -Щ-> -^f- -Щ- обра-
образуют тензор деформации:
B.2)
При использовании тензорной символики (см. § 1) общий ком-
компонент тензора деформации имеет вид еG- (г, / = 1, 2, 3), причем
е,
Ъу_
2
Угх
2
Уху
2
Ууг
2
Угх
2
Ууг
2
е,, =
622 —
езз — ег> 81г 2~
Ууг
2
8з1 —
Yz*
Зависимости компонентов деформации от компонентов переме-
перемещения B.1) в сокращенной тензорной записи имеют вид
дщ
дщ \
B-3)
§ 9. Условия совместности деформаций
Из зависимостей B.1) следует, что шесть компонентов деформа-
деформации выражаются через частные производные от трех компонентов
перемещения по координатам х, у и г. Следовательно, они не являются
независимыми функциями этих координат. Между ними должны
существовать зависимости, которые называют условиями совмест-
совместности деформаций.
Поясним высказанное положение. Представим себе деформируе-
деформируемое тело как бы состоящим из элементарных параллелепипедов. Если
теперь каждый параллелепипед подвергнуть произвольной деформа-
деформации так, что компоненты деформации не будут между собой связаны,
а затем попытаться сложить деформированные элементы, то это,
вообще говоря, окажется невозможным. Между некоторыми эле-
элементами образуются зазоры, для других элементов не окажется
места, и деформированные элементы в этом случае будет невозможно
объединить в непрерывное тело.
Для того чтобы получить условия совместности деформаций,
необходимо из уравнений B.1) исключить компоненты перемеще-
перемещения их, иу и uz. Опуская преобразования, приводимые в курсах
теории упругости [5], имеем:
B-4)
26
д2ухУ
дхду
дудг
дЧх
дЧу .
дг*
дЧг
1 д2?У .
1 дх* '
| d4z .
дгдх

дудг
2
дх
дх
ду
ду
ху
Г
дг дх
дхду
—
ду
дх
ду
ду*у \ •
дг ) '
= —(-
дг \
дг
B.4)
Эти соотношения представляют собой условия совместности
деформаций. В сокращенной тензорной записи они имеют вид
дх,
+
дх. дхк
d4ik
dXj
дх. дх
§ 10. Разложение тензора деформаций
Аналогично общему случаю напряженного состояния общий слу-
случай деформированного состояния, характеризуемый тензором дефор-
деформаций Те B.2), можно представить в виде суммы двух деформиро-
деформированных состояний.
Первое деформированное состояние характеризуется шаровым
тензором
е0 0 0
где
а второе девиатором
е 0
.0 0 е0
_ *х + гу + е.
B.5)
ХУ
Dxy °zx
6 6
причем
вх ?
, — с»* on
ег=ег-
= Ъг_
2
__ Jzx_
2 '
B.6)
В сокращенной тензорной записи компоненты девиатора дефор-
деформаций можно записать в виде
где
е0 — -д- — -д-
Таким образом,
De.
27

Из формулы B.6) заключаем, что
е* + е, + ег = 0, B.7).
т. е. во втором деформированном состоянии изменение объема равно
нулю.
Таким образом, в первом деформированном состоянии изменяется
объем (форма не изменяется), а во втором — форма (изменение объ-
объема равно нулю), в то время как в исходном деформированном со-
состоянии изменяется как объем, так и форма.
Произведенное разделение деформированного состояния имеет
определенный физический смысл, поскольку возникновение пласти-
пластических деформаций в материале связано с образованием сдвигов и,
следовательно, с изменением формы элементарного объема. При
всесторонних равных растяжениях или сжатиях пластические де-
деформации не возникают.
Девиатор деформаций показывает, насколько исследуемое де-
деформированное состояние уклоняется от всестороннего равного рас-
растяжения с главными линейными деформациями", равными среднему
арифметическому линейных деформаций исходного деформирован-
деформированного состояния.
§11. Главные оси и главные деформации
В каждой точке деформированного тела существуют три взаимно
перпендикулярные оси, для которых компоненты угловой дефор-
деформации равны нулю и, следовательно, угол между этими осями при
деформации не изменяется. Эти оси называют главными осями де-
деформации я обозначают цифрами 1,2,3. Линейные деформации в на-
направлении этих осей называют главными линейными деформациями
и обозначают: е1( е2, е3.
Главные линейные деформации являются корнями кубического
уравнения
е3 - /i (Те) е2 - /2 (Те) г - /, (Тв) = 0. B.8)
Таким же путем, как и для уравнений A.10), можно доказать [3],
что все три корня уравнения B.8) вещественны.
Поскольку главные деформации не могут зависеть от выбора осей
координат, то коэффициенты кубического уравнения также не из-
изменяются при повороте осей координат, т. е. являются инвариан-
инвариантами. Их называют соответственно первым, вторым и третьим инвари-
инвариантами тензора деформаций и определяют следующим образом:
гх + гу + ег;
2 2 2
— pf я Р — я я [ УхУ | У«г' | Угх
ьхьу Ь1/Ьг ь^ьх~Т д ' 4 ^ 4
28

Уху
Уху
Ууг
Угх
Ууг
«). B.9)
Очевидно, что выражения инвариантов тензора деформаций через
главные деформации имеют вид:
е3;
' 2 (•'е) == —
B.10)
Получим теперь второй и третий инварианты девиатора дефор-
деформаций. [Первый инвариант девиатора деформаций согласно фор-
формуле B.7) равен нулю]. Для этого подставим в формулы B.9) ком-
компоненты девиатора деформаций B.6), используя при этом соотноше-
соотношение B.5). Тогда получим
ехеу — еуег — е?х -f
е\г
-е\х =
\2 г / \2 | / Ч2 . 3 / 2
_____ р I _1__ /р ., р 1 _1_ (Р -I¦ . i Р I ..I— ..., .. . I Л1
с ьу) "г (,ьг/ ьг; ~г \ьг ьх) ~т~ п \ухУ
B.
¦ 3(е | е^
9
+ 4 е
-г ъУ D
ly
-2YL)
B-12)
Выражения для инвариантов тензоров и девиаторов деформации
в сокращенной тензорной записи можно получить аналогично фор-
формулам A.12) и A.15) в теории напряжений.
§ 12. Интенсивность деформаций
По аналогии с интенсивностью напряжений (см. § 5) uнmeнcuв^
ностью деформаций называют величину, пропорциональную квадрат-
квадратному корню из второго инварианта девиатора деформаций. В за-
зависимости от принятого коэффициента пропорциональности разли-
29

чают понятия интенсивности линейных деформаций или просто ин-
интенсивности деформаций
B.13)
и интенсивности утадовых деформаций
B.14)
Сопоставляя выражения B.13) и B.14), заключаем, что
е<=7Г <2Л5)
Подставим в формулу B.13) соотношение B.11). Тогда получим
в< = -х- V{ex—еуJ+(е* —8zJ+(ez ~ е*J+4- fr«r+^г+v») •
B.16)
Аналогично формуле A.20) можно получить сокращенную запись
интенсивности деформаций
e«e»- {2Л7)
Зависимость интенсивности деформаций от главных линейных
деформаций имеет вид
в, = YV>i —e.)a + (e» —e^ + fo-ei)*- B.18)
Для частного случая одноосного растяжения изотропного мате-
материала (гх = б, е2 = б3 = —в~ 8° j по формуле B.18) получаем
et == е — е0. B.19)
Для случая чистого сдвига H3OfponHoro материала (ех = еу =
= ег = 0, у^ = у, yV2 = y« = 0) из формулы B.16) имеем
в, = fg- B.20)
Из формул B.15) и B.20) следует, что интенсивность угловых де-
деформаций Г совпадает с величиной наибольшей угловой деформации
при чистом сдвиге
• Аналогично формуле B.16) интенсивность пластических дефор-
деформаций определяется выражением
+4^g2 + (Y^J+(YL7i B.21)
30

или в сокращенной тензорной записи
e? =
B.22)
Так же, как и в теории напряжений (см. § 5), можно доказать [3 ],
что интенсивность деформаций пропорциональна квадратному корню
па минимального среднеквадратичного уклонения рассматриваемого
деформированного состояния от ближайшего к нему всестороннего
равного растяжения или сжатия.
Можно также доказать [3], что средняя линейная деформация
равна линейной деформации в направлении, составляющем равные
углы с тремя главными осями, а интенсивность деформаций пропор-
пропорциональна максимальной угловой деформации между этим направ-
направлением и направлением, перпендикулярным к нему:
Эту величину называют октаэдрической угловой деформацией.
§ 13. Геометрическое изображение деформированного
состояния
Продолжая развивать аналогию между деформированным и на-
напряженным состояниями (см. § 8), можно заключить, что геометри-
чееким образом деформированного состояния в точке тела в про-
пространстве является эллипсоид
деформации, а на плоскости —
круговая диаграмма деформа-
деформаций (рис. 2.2).
В последнем случае по оси
абсцисс откладывают линейные
деформации, а по оси орди-
ординат — половины угловых де-
деформаций. Координаты точек,
лежащих на полуокружностях
/, //, ///, равны линейным
деформациям и половинам угло-
Рис. 2.2. Круговая диаграмма деформаций
вых деформаций по направлениям, лежащим в главных плоскостях
23, 31 и 12 соответственно.
Любая из точек, лежащих внутри области, ограниченной тремя
окружностями диаграммы, своими координатами определяет ли-
линейную и половину угловой деформации в направлениях, не лежа-
лежащих в главных плоскостях.
Из круговой диаграммы следует, что одна из главных линейных
деформаций является наибольшей, а другая — наименьшей из всех
линейных деформаций в окрестности исследуемой точки. Далее на
основании круговой диаграммы можно также заключить, что наи-
наибольшие угловые деформации Имеют место для направлений, лежа-
. 31

щих в главных плоскостях ,и составляющих угол 45° с главными
.осями.
Эти наибольшие угловые деформации, называемые главными угло-
угловыми деформациями, равны разности главных линейных дефор.
маций:
= е2 — 83, Y2 = ех — е3
= вх — е2
B.23).
По аналогии с соответствующей величиной для напряжений A.31)
параметр Надаи — Лоде для деформаций имеет вид
= 2
е3
1
B.24)
он характеризует вид деформированного состояния с точностью до
равноосного растяжения или сжатия.
Согласно формуле B.24) для одноосного растяжения (е2 = е3)
Xs = — 1, для одноосного сжатия {в1 = е2) %е = 1, для чистого
сдвига (ех = —е3, е2 = 0) %е = 0.
Сопоставляя эти величины параметров Надаи—Лоде по деформа-
деформациям с соответствующими величинами параметров Надаи—Лоде по
напряжениям, полученным в § 6, заключаем, что они одинаковы,
т. е. круговые диаграммы напряжений и деформаций для этих на-
напряженных состояний подобны.
§ 14. Тригонометрическая форма представления
главных деформаций
По аналогии с теорией напряжений главные компоненты девиа-
тора деформаций могут быть представлены в виде
е1 = е(. cos ijv,
где угол вида деформированного состояния if>8 определяется формулой
cos 3-фе = —3 з е • B.26)
Величины главных угловых деформаций можно выразить через
угол, вида деформированного состояния при помощи следующих за-
зависимостей:
Yx = КЗ е, sin фе;
72= —
-f it).
B.27)
32

Пределы изменения угла вида деформированного состояния
такие же, как и пределы изменения угла вида напряженного со-
состояния (см. § 7), т. е.
3
Поэтому пределы изменения величины утзх = у2 от -у 8г (при ife = О
и ¦Фв =ir) Д° У^г1 (ПРИ $е =1г)> т- е-
Рис. 2.3. Звезда Пелчинского для дефор-
деформаций
Рис. 2.4. Диаграмма Марциняка для
деформаций
Взяв среднее значение этого отношения, получаем
-г (х +
= -г (х + уъ) V-»» = °'622 (8i -
(Я.28)
Это значение отличается от крайних примерно на 7%.
Выразим теперь "параметр Надаи—Лоде через угол вида дефор-
деформированного состояния. Для этого преобразуем выражение B.24),
используя соотношения B.6) и B.25)., Тогда получим
, ' B.29)
что по форме совпадает с выражением A.42).
Поскольку для одноосного растяжения, одноосного сжатия и чи-
чистого сдвига параметры Надаи—Лоде по напряжениям и деформа-
деформациям совпадают, величины % и ipe для этих напряженных состояний
также совпадают, т. е. для одноосного растяжения if>e = 0, для одно-
одноосного сжатия ^e = ~5-> Для чистого сдвига tye — -c--
4 О О
Формулы B.25) и B.27) могут быть графически интерпретированы
при помощи построения, называемого звездой Пелчинского для де-
деформаций (рис. 2.3), которое аналогично построению на рис. 1.12 [71.
Оно очевидно из чертежа, и пояснений не требуется.
' 2 н. Н. Малинин 33

Диаграмма Марциняка для деформаций в предположении, что
сумма линейных деформаций равна нулю (объем тела при деформа-
деформации не изменяется — тело несжимаемо), изображена на рис. 2.4 [61.
Это построение может быть доказано при помощи формул B.25).
§ 15. Приращения деформаций
Предположим, что в течение бесконечно малого промежутка вре-
времени dt компоненты перемещения некоторой точки тела ut возрастают
на
йщ = v, dt, B.30)
где oi — компоненты скорости перемещения точки.
Вычислим по формулам B.1) бесконечно малые приращения ком-
компонентов деформации de{/. Тогда получим
B.31)
Эти величины образуют тензор бесконечно малых приращений
деформаций de{l- или
' de:
dex
B,32)
•г -г }
Аналогично тому, как это было сделано для деформаций, теперь
можно определить интенсивность приращений деформаций
TeЧ
Ч- V
(de*
B,33)
или интенсивность приращений пластических деформаций
- depx)
pJ
В сокращенной тензорной записи
deaden; Тер = |/\
B.34)
B.35)
Интенсивность приращений деформаций de,t не равняется прира-
щению интенсивности delt чем и объясняется введение черточки в обо-
обозначение для' интенсивности приращения деформаций.
34 ...

Как и раньше, можно построить круговую диаграмму для при-
приращений деформаций, а также определить параметр Надаи—Лоде
Компоненты приращения деформаций можно выразить через угол
н)а приращения деформаций ij>de и дать графическую интерпрета-
интерпретацию в виде диаграммы Мора, звезды Пелчинского или диаграммы
Млрциняка для приращений деформаций. -
В формулах B.31) приращения компонентов деформаций вычис-
вычисляют по отношению к текущему
(мгновенному) состоянию. В част-
частном случае одноосного однородного
растяжения стержня приращение осе-
ной деформации
А
de =
—
где / — текущая длина стержня; dl —
бесконечно малое ее изменение. Сум-
Суммирование приводит к так называемой
логарифмической деформации:
i
dl , I . /„4-Д/
80
20
/
/
so
во е,%
стержня до
B.37)
деформации;
о го.
Рис. 2.5. График зависимости
логарифмической деформации от
деформации
А/ -г- удлинение, е =
где /0 — длина
-; обычная деформация стержня.
'о
На рис. 2.5 представлен график зависимости B.37), из которого
следует, что при е < 20% различие между-логарифмической и обыч-
обычной деформациями незначительно. При е = 20% оно составляет 10%.
Поскольку значение обычной деформации, при которой обра-
образуется шейка, как правило, не превышает 10—15%, до образования
шейки логарифмическую деформацию приближенно можно считать
равной обычной.
В общем случае интегралы I d&tj можно вычислить, если изве-
известен путь деформирования, т. е. если известны компоненты прира-
приращений деформаций в функции некоторого параметра, характеризую-
характеризующего процесс деформирования. Если главные оси деформации при
деформировании не вращаются, то эти интегралы равны логарифми-
логарифмическим деформациям.
§ 16. Скорости деформаций
Подставив выражения B.30) в соотношения B.31), приходим к за-
заключению, что компоненты бесконечно малых приращений дефор-
деформаций имеют общий множитель dt. Разделив их, на этот множитель,
35

получим компоненты скоростей деформаций |г/, связанные с компо-
компонентами скорости перемещения vt соотношениями
~ i~ \~aiT ~т "аи Г B.38)
Эти величины образуют тензор скоростей деформаций gw или
Пху
Пху
2
1г
B.39)
По аналогии с интенсивностями деформаций и приращений де-
деформаций можно определить интенсивность скоростей деформаций
^=Ч- V& - у 2+{1у - ы 2+(|г - ^2+4- №*+^
или в сокращенной тензорной записи
B,40)
Если |0 = 0, то
Далее, так же как и раньше, можно построить круговую диа-
диаграмму для скоростей деформаций, определить параметр Надаи—
Лоде
:==2
B.42)
выразить компоненты девиатора скоростей деформаций через угол
вида скоростей деформаций гр| и дать графическую интерпретацию
в виде диаграммы Мора, звезды Пелчинского или диаграммы Мар-
циняка для скоростей деформаций.
Список литературы
1. Надаи А. Пластичность и разрушение твердых тел. М., Изд. иностр. лит.,
1954, 647 с.
2. Новожилов В. В. Теория упругости. М., Судпромгиз, 1958, 370 с.
3. Расчеты на прочность в машиностроении. Т. 1, М., Машгиз, 1956, 884 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К. К. Лихарев и др.
4. Феодосьев В. И. Сопротивление материалов. М., «Наука», 1974, 559 с.
5. Филоненко-Бородич М. М. Теория упругости. М., Физматгиз, 1959, 364 с.
6. Marciniak Z. Mechanika procesow tloczenia blach, Paiistwowe wydawnictwa
naukowo — techniczne, 1961, 271 s.
- 7. Pelczyiiski T. Wplyw stanu napiecia na przejscie materialu w stan plastyczny,
«Przeglad mechaniczny», 1951, z 6, s. 175—179, z 7, s. 204—208.

ГЛАВА HI
ЗАВИСИМОСТИ МЕЖДУ ДЕФОРМАЦИЯМИ
И НАПРЯЖЕНИЯМИ В ПРЕДЕЛАХ УПРУГОСТИ
И УСЛОВИЯ ВОЗНИКНОВЕНИЯ ПЛАСТИЧЕСКИХ
ДЕФОРМАЦИЙ
§ 17. Зависимости между деформациями
и напряжениями для упругого изотропного тела
Из курса сопротивления материалов известно, что в пределах
упругости зависимости компонентов деформации от компонентов на-
напряжения для изотропного тела имеют вид:
в* = 4" (о, — [х К + <хг)];
-?- [ау — (г (ог + ах)];
Уху
v
Уда
C.1)
где Е и G — модели упругости первого и второго рода, |» — коэф-
коэффициент поперечной деформации. Между этими величинами суще-
существует следующая связь:
<3-2>
Объемная деформация А, равная при малых деформациях сумме
линейных деформаций, пропорциональна сумме нормальных напря-
напряжений [15]
A = 3eo = e,-fei, + ez = 15rK + a, + CT,) = -^, C.3)
где К — объемный модуль упругости
Если принять (г = 0,3, то согласно формуле C.4) К = 0,84?.
В сокращенной тензорной записи соотношения C.1) имеют вид
C-5)
Как известно из курса теории упругости [10], для изотропного
упругого тела компоненты деформации могут быть представлены
37

в виде частных производных от удельной потенциальной энергии
деформации U по компонентам напряжения:
_ дЦ __' ди _ ди
г*~~Ш7' е"~~Щ~' 8г~-"а57;
ди ди
ulzx
или в сокращенной тензорной записи, с учетом закона парности ка-
касательных напряжений,
а компоненты напряжений, в свою очередь, могут быть представлены
в виде частных производных от удельной потенциальной энергии
деформации по компонентам деформации
1 / dU , dU
_
Установим зависимости между компонентами девиатора напря-
напряжений и компонентами девиатора деформаций в пределах упругости,
используя соотношения (З.б), C.3) и C.4):
~
ст0) —
Таким образом, в пределах упругости компоненты девиатора на-
напряжений пропорциональны компонентам девиатора деформаций,
причем коэффициентом пропорциональности является удвоенная ве-
величина модуля сдвига.
Выясним связь между интенсивностями напряжений и дефор-
деформаций в пределах упругости. Для этого подставим в формулу B.17)
выражения C.8). Тогда, используя зависимость A.20), получим
at = 3Gsi C,9)
или на основании соотношений A.18) и B.15),
Т = G Г,
Следовательно, в пределах упругости интенсивность напряжений
прямо пропорциональна интенсивности деформаций.
§ 18. Условия начала пластичности для изотропного тела
Зависимости C.1) можно вывести на основе закона Гука для
одноосного напряженного состояния [15]. Последний верен только
в начальной стадии нагружения. Поэтому уравнения C.1) справед-
справедливы тоже только в начальной стадии нагружения до образования
пластических деформаций. Условия возникновения пластических
38

деформаций — условия начала пластичности рассматриваются
II курсе «Сопротивление материалов» в разделе, посвященном гипо-
гипотезам прочности. Ниже эти вопросы будут изложены несколько
и иной форме.
Поскольку в начальной стадии нагружения справедлив закон
Гука, возникновение пластических деформаций однозначно опре-
определяется напряжениями. Следовательно, условие начала пластич-
пластичности может быть представлено в виде
/т(ст,у) = О. C.10)
В это уравнение входят также механические характеристики мате-
материала, определяющие возникновение пластических деформаций при
простейших напряженных состояниях, например, пределы теку-
текучести материала при одноосных растяжении и сжатии.
Для геометрической интерпретации условия начала пластичности
представим себе шестимерное пространство компонентов напряже-
напряжений, каждая точка которого (изображающая точка) представляет
собой некоторое напряженное состояние. Тензор напряжений в этом
пространстве условимся изображать вектором а(/-, составляющие ко-
которого равны компонентам тензора напряжений стG (рис. 3.1). Тогда
равнение C.10) является уравнением гиперповерхности начала пла-.
Личности 2jt-
Когда изображающая точка лежит внутри этой поверхности
(точка В на рис. 3.1), материал деформирован упруго, а когда она
лежит на ней (точка А на рис. 3.1) — возникают пластические де-
деформации. В трехмерном пространстве главных напряжений условие
начала пластичности является уравнением поверхности начала пла-
пластичности.
Для изотропного тела значения функции /т (а-/) не должны из-
изменяться при повороте системы осей координат, т. е. условие пла-
пластичности может быть записано в виде" функции инвариантов тен-
тензора напряжений ¦ ¦
. fr U, (Та), h(To), /,G\,)] = 0.
Как отмечалось выше (см. § 3), при всесторонних равных растя-
растяжениях или сжатиях пластические деформации не возникают. По-
Поэтому можно принять, что условие пластичности может быть пред-
представлено в виде функции второго и третьего инвариантов девиатора
напряжений (так как первый инвариант девиатора напряжений ра-
равен нулю)
/Т U2 (Da), /з (Da) 1 = 0. C.11)
В системе координат <тх, ст2> стз (рис. 1.7) уравнение C.11) описы-
описывает цилиндр, образующие которого перпендикулярны к девиатор-
ной плоскости, так как среднее нормальное напряжение не входит
в уравнение C.11). Поэтому достаточно рассмотреть след этого ци-
цилиндра на девиаторной плоскости. Эта кривая С (рис. 3.2) должна
обладать следующими свойствами: 1) не проходить через начало
координат, так как пластические деформации возникают лишь при
39

значительных напряжениях; 2) луч из начала координат должен пере-
пересекать кривую С только 1 раз (иначе существовало бы два подобных
напряженных состояния, удовлетворяющих условию начала пластич-
пластичности, что невозможно); 3) кривая должна быть симметрична
относительно осей /', 2', 3', так как они равноправны вследствие
изотропности тела; 4) кривая должна быть симметрична относи-
относительно прямых, перпендикулярных к осям /', 2', 3', поскольку
предполагается, что механические свойства материала при растяже-
растяжении и сжатии одинаковы и эффект Баушингера не учитывается.
Рис. 3.1. Поверхность начала плас-
пластичности в шестимерном простран-
пространстве напряжений
J'
Рис. 3.2. След пересечения поверх-
поверхности начала пластичности в си-
системе координат а1( а2, ст3 с
торной плоскостью
На основании изложенного заключаем, что кривая С состоит из
12 одинаковых дуг, как это изображено на рис. 3.2. В дальнейшем
(см. § 22) будет показано, что она должна быть выпуклой. В таком
случае очевидно, что кривая заключена между двумя правильными
шестиугольниками ACEGIK и BDFHJL (рис. 3.3), проходящими
через точки на осях /', 2' и 3' с координатами у -у aT) где стт — пре-
предел текучести материала при растяжении или сжатии. Это следует
из того, что косинусы углов между осями стх и /', ст2 и 2', аа и 3'
равны 1/ -у, а точки на осях 1, 2, 3, изображающие одноосные на-
напряженные состояния, при которых возникают пластические дефор-
деформации, имеют координаты стт.
Уравнения граней шестигранных призм, пересечение которых
с девиаторной плоскостью дает указанные выше шестиугольники
ACEGIK и BDFHJL, имеют вид соответственно
| а1 — (Т21 = (Тт; | ст2 — ст31 = стт; | а3 — стх | = стт C.12)
2
— сто|= —стт; |а2 —
2 2
стт; \а3—СТ0 | = -д- От. C.13)
40

Проведем окружность радиуса Т/-*-стт, описанную вокруг шести- *
угольника ACEGIK и вписанную в шестиугольник BDFHJL. Урав-
пие цилиндра, пересечение которого сдевиаторной плоскостью дает
эту окружность, имеет вид
(cti — ст2J + (ст2 — ст3J + (ст3 — ctiJ = 2стт. C.14)
На основании уравнений C.12) условие начала пластичности
можно представить в виде
C.15)
max
— ст2
ст2 — ст
3|>
или, если обозначать главные
напряжения, учитывая неравен-
неравенство стх ^ ст2 ^ ст3, то тогда их
можно объединить в одно
CTl_a3 = aT. C.16)
Впервые такое условие было,
получено на основании эксперимен-
экспериментальною исследования истечения
металлЛ через отверстия, про-
проведенного французским инженером
Треска в 1868 г. В этих испыта-
испытаниях было установлено, что в со-
состоянии текучести наибольшее ка-
касательное напряжение во всех точ-
точках среды постоянно и равно пре-
пределу текучести материала при чис-
чистом сдвиге. Сен-Венан дал матема-
математическую формулировку этого условия для плоской задачи. Усло-
Условие C.15) называют условием начала пластичности наибольшего
касательного напряжения или условием пластичности Треска — Сен-
Венана. В курсе сопротивления материалов оно известно как теория
прочности наибольших касательных напряжений.
Недостатком рассмотренного условия пластичности является,
как это следует из формулы C.16), неучет влияния промежуточного
главного напряжения ст2 на -возникновение пластических дефор-
деформаций.
На основании уравнений C.13) условие начала пластичности
можно представить в виде
2
Рис. 3.3. Следы пересечения поверхно-
поверхностей начала пластичности в системе
координат стх, а2> а3 с девиаторной
плоскостью
max {|ai — ст
о
— стп . Сто — ст„ =¦
- СТт
C.17)
Это условие было предложено вначале А. Ю. Ишлинским [6],
затем Хиллом [20], Д. Д. Ивлевым [4] и наконец Хейзорнсвей-
том [18]. Его называют условием наибольшего приведенного напря-
напряжения. Под приведенными напряжениями понимают компоненты де-
виатора напряжений.
* 41

Условие C.14) было предложено вначале Максвеллом [91, а по-
потом Хубером [211 на основе рассмотрения потенциальной энергии
деформации формы тела.
Затем Мизес [8] предложил приближенно заменить шестигран-
шестигранную призму Треска — Сен-Венана круговым цилиндром [уравнение
C.14)]. Мизес считал условие C.16) точным, а C.14) приближенным.
Однако произведенная в дальнейшем экспериментальная проверка
условий начала пластичности показала, что условие C.14) лучше
согласуется с результатами опытов, чем-условие C.16).
В курсе сопротивления материалов условие C.14) обычно
выводится путем рассмотрения потенциальной энергии измене-
изменения формы и называется энергетическим условием начала пла-
пластичности. Иногда его называют условием начала пластичности
Хубера—Мизеса.
Согласно уравнению A.21) условие C.14) может быть представ-
представлено в виде
а{ = <тт, . C.J8)
т. е. пластические деформации возникают тогда, когда интенсив-
интенсивность напряжений достигает величины предела текучести материала
при растяжении.
Учитывая установленное в § 7 приближенное выражение для
интенсивности напряжений A.41), заключаем, что условия наиболь-
наибольшего касательного напряжения и энергетическое незначительно от-
отличаются друг от друга.
Разберем теперь перечисленные выше условия начала пластич-
пластичности для частного случая плоского напряженного состояния (ст3 =*=
= 0). Условие наибольшего касательного напряжения C.15) при-
принимает вид
C.19)
Эти выражения в системе координат аи а2 являются уравнениями
шести прямых ас, gi, се, ik, eg, ka, отсекающих на осях коорДинат
отрезки, равные в определенном масштабе пределу текучести мате-
материала стт и образующие шестиугольник acegik (рис. 3.4).
Условие наибольшего приведенного напряжения C.17) выра-
выражается в форме
C.20)
Эти соотношения в системе осей координат стх, ст2 являются урав-
уравнениями шести прямых lb, fh, df, jl, bd и hj, образующих шести^
угольник bdfhjl (рис. 3.4).
42
при стгст
при ata
при ata
2 >0
2 >0
»<о
и
и
1 (
1<М :
ICT2|
Т1 С
> | <Ь
>\а1
Ч 1 =
1 1 ai I
1 ICT2
ат.
ПрИ G^G,
при ст^
при (Тхо
2 S 0 |
2 S0|
¦2 >о
^2| :
1 CTi 1;
>|<Т2|
>Hll
i?|<4
I 2a!
|2а2
1 CTi
— а21
— ai\
+ ot\
= 2ат;
= 2ат;
= 2ат.

Полагая в энергетическом условии пластичности C.14) сг3 = О,
получаем
о\ — СТ1СТ2 + а1 = (Тт, C.21)
г. с. уравнение эллипса, описанного вокруг шестиугольника acegik
п вписанного в шестиугольник bdfhjl (рис. 3.4).
6,16,
1.2
0,6
0.4
' 0.2
— ''
ч
• Л
Я
о°°#
7
>
/
J
Рмс. 3.4. Графики условия -начала пла-
пластичности наибольших касательных на-
напряжений, наибольших приведенных
напряжений и «энергетического» условия
нпчала пластичности для плоского на-
напряженного состояния в системе коор-
координат Ох а2,
к
О 0,2 0,4 0,5 0,8 бг
-0,7
-0,4
-0,6
а,
Т,
Рис. 3.6. Результаты испытаний сталь-
пых труб, проведенных Рошем и Эй-
хингером [14]
0.2 0.1 0.6
КО 1.2 б,/б,
А
/у
К*
//
J
Рис. 3.5. Результаты испытаний сталь-
стальных (о),< медных (#) и никелевых (Д)
труб, проведенных Лоде [7]
0,2 0,4 0,6 0,8 б,
-0,1
/у
А
/,
г
А
-0,6
-0.6
Рис. 3.7. Результаты испытаний труб
из меди. (о), алюминия {%), мягкой
стали (а) и обезуглероженной мягкой
стали (Д), проведенных Тейлором и
Квинни [26]
Из рис. 3.4 следует, для каких напряженных состояний расхо-
расхождение между рассмотренными выше условиями пластичности наи-
наибольшее и для каких наименьшее. В частности, соотношения между
пределами текучести для чистого сдвига (стх = —ста == т, о3 = 0)
43

и растяжения (ах = а, а2 = ст3 = 0) по условию наибольшего ка-
касательного напряжения
по условию наибольшего приведенного напряжения
2_
а по энергетическому условию пластичности
12
1.0
0,8
0,6
ОН
0.2
\
\
с
о
/
/
/
Уз '
G,/6r
1,2
10
0.8
0,6
0,4
0,2
О
' О
о\
1
и
/
/
0 0,2 ОМ 0.6 0.8 1.0 1,2б2/бт 0 0,2 ОН 0,6 0.8 1.0 1,2 б2\бт
Рис. 3.8. Результаты испытаний труб Рис. 3.9. Результаты испытаний труб
из хромоникелевои стали, проведенных
А. М. Жуковым [2]
из стали ЭИ415, проведенных
А. М. Жуковым [3]
Экспериментальная проверка условий возникновения пластиче-
пластических деформаций производилась путем испытания тонкостенных тру-
трубок при совместном нагружении их растягивающей силой Р и вну-
внутренним давлением р, растягивающей силой Р и крутящим момен-
моментом М, крутящим моментом М и внутренним давлением р. Во всех
этих случаях напряженное состояние тонкостенных трубок при-
приближенно можно считать однородным и плоским.
Ниже приведены результаты некоторых экспериментальных ис-
исследований, часть из которых проводилась для экспериментальной
проверки условий пластичности, а часть для проверки основных ги-
гипотез теорий пластичности, причем попутно проверялись и условия
пластичности. К последним испытаниям мы еще вернемся в следующей
главе.
На рис. 3.5 представлены результаты испытаний, проведенных
Лоде [7]. Испытанию подвергались тонкостенные стальные, медные
и никелевые трубы. Они нагружались растягивающей силой и вну-
внутренним давлением. На рис. 3.6 изображены результаты испыта-
испытаний, проделанных Рошем и Эйхингером [14]. Они испытывали тон-
44

костенные стальные трубы при совместном растяжении и кручении.
Такие же испытания тонкостенных стальных, медных и алюминиевых
труб были проведены Тейлором и Квинни [26]. Результаты их лзоб-
ражены на рис. 3.7. На рис. 3.8 и 3.9 приведены результаты опытов
Л. М. Жукова [2, 3]. Им были испытаны тонкостенные трубы из
хромоникелевой стали и стали ЭИ415 при совместном нагружении
растягивающей силой и внутренним давлением.
На рис. 3.5—3.9 в координатах -^- и -^- представлены графики
ат т
условий пластичности наибольшего касательного напряжения C.19),
наибольшего приведенного напряжения C.20) и «энергетического
условия» C.21).
Из этих графиков следует, что результаты экспериментальных
исследований лучше согласуются с энергетическим условием, не-
нежели с двумя другими.
§ 19. Условие начала пластичности
для анизотропного тела
Анизотропными материалами называют такие материалы, свойства которых
в разных направлениях различны. Металлы состоят из большого числа микроскопи-
микроскопических кристаллов, связанных в зерна. Кристалл анизотропен; Поскольку кри-
кристаллы в зернах и сами зерна ориентированы друг относительно друга самым раз-
различным образом, индивидуальные особенности каждого кристалла не проявляются
и часто поликристаллические металлы можно рассматривать как изотропные тела.
Однако в результате пластической обработки (ковка, прокатка) поликристалличе-
поликристаллические металлы могут стать анизотропными материалами, у которых механические
свойства зависят от направления. Иногда такую анизотропию называют деформа-
деформационной в отличие от начальной анизотропии кристалла. В то же время она является
начальной по отношению к анизотропии, возникшей при последующем деформирова-
деформировании. Одной из причин анизотропии, возникающей в результате пластического де-
деформирования, является появление текстуры, т. е. системы закономерно ориенти-
ориентированных кристаллитов.
В общем случае анизотропного материала Мизесом было предложено следующее
условие [23]:
4sslaCTj,Tw + 4Л2223аг/тг/г + 4Awnoyr
~т ^A^^oz%yz т 4^3331^^* ~т "A^^xy^yz ~\~ vAi33i%yzxzx -f- оА3112т:гхтху = 1,
которое иногда называют квадратичным условием' пластичности. Число различных
постоянных А им в этом уравнении равно 21.
В сокращенной тензордой записи это уравнение имеет вид
Aijkflipki = 1.
Как известно, тело, у которого имеется три взаимно перпендикулярных пло-
плоскости симметрии по отношению к механическим свойствам, называют ортотропным.
Примером такого тела является листовой материал.
Если оси х, у и г для такого тела совместить с осями симметрии (для листового
материала это будут направление прокатки и два направления, перпендикулярные
к нему), то из соображений симметрии следует отбросить все слагаемые, содержащие
касательные напряжения в первой степени и произведения различных касательных
45

напряжений, так как они могут изменять свой знак при изменении направления.
Тогда для ортотропного материала получим
у + A3333al у
+ lAm&jJy + 2А^33ауог + 2A3sllazax = 1. ' C.22)
В этом случае число постоянных уменьшилось до 9.
Примем, как это было сделано Мизесом [23], что при всестороннем равном
растяжении или сжатии в анизотропном материале так же, как и в изотропном
(см. § 18), пластические деформации не возникают. Это позволяет получить добавоч-
добавочные соотношения между постоянными Л^. Их можно установить из условия неиз-
неизменности соотношения C.22) при подстановке в него вместо компонентов тензора
напряжения
xzx компонентов тензора напряжения ох-\-р,
тгх, отли-
отличающегося от перрого на шаровой тензор с компонентами р. Приравнивая нулю
слагаемые при первой и второй степенях р, получим
2^1111 + 2Л1122 + 2Л3311 = 0;
^л.2222 ~> 1122 "¦ 2234 =" '
2>4 —|— 2>4 ~\~ 2у4 —~ 0 * /Q OQ\
•111 4" -222 4" Л3333 4"
Из первых трех соотношений C.23) легко установить
ОЛ . _ А I А А . 1
*ЛШ2 ЛП11 Т Л2222 Л3333> ч
^~ 2Л " ¦== Л - Ч~ Л — Л ' I ^3 24^
од — л i л л
Z/i3311 ~" Л3333 Т Л1111 Л2222- >
•>
Как легко убедиться, эти выражения удовлетворяют четвертому соотноше-
соотношению C.23).
Подставим теперь соотношения C.24) в условие пластичности C.22). Тогда
после, преобразований имеем: ' ^ '
i Но (ох - оиУ + Fo (ау — агJ 4- Go (аг — oxf +
где
«о- 2
F0 = — (Л2222 4" АВ
1
i);
— ~2~ (^3333 4" ^1111 ^2222/!
No = 2Л1212; Lo = 2Л2в23; Мо = 2Л3131.
В таком виде условие пластичности было предложено Хиллом [19]. Постоян-
Постоянные в условии C.25) можно определить, применяя его для частных случаев одно-
одноосных растяжений в направлении осей х, у, г и сдвигов между этими осями. Тогда
получим
Но 4- Go = —о—; Но + F 0 = —т—;
F о + G» = ¦
2r
хуТ
2т!
zxl
C.26)
46

откуда следует, что
1
4т
i
°1т
¦ 1
1
°1т
1
1 4т
1
1
4т
1
C.27)
Подставим выражения C.27) и C.26) в условие пластичности C.25). Тогда
получим иную форму этого условия
C.28)
Найдем теперь величину предела текучести avx в случае одноосного растяжения
образца, ось которого v лежит в плоскости ху и составляет угол а с осью х. В слу-
ч;и- листового материала это будет соответствовать образцу, вырезанному из листа,
причем угол между направлением образца и направлением проката равен а.
В этом случае
s2
ах — avT c°s2
= °vt sin2 a; az = 0;
— avT sin a cos a; %
yz
— %zx = 0.
Подставляя эти компоненты напряжений в условие пластичности C.25), по-
получим
avT = [Fо sin2 a + Go cos2 a + Ho +
+ BNo — Fo — Go — Шo) sin2 a cos2 a ]
C.29)
Исследование этого выражения приводит к заключению, что экстремумы имеют
место для направлений х н у, & также для направления, определяемого углом a
C.30)
Если No > Go + 2Ho и No > Fo + 2Яо, то предел текучести имеет максималь-
максимальные неравные значения в направлениях х и,у и минимальное значение в направле-
направлении под углом а к оси х. Если No < Go + 2#o и No < Fo + 2Я0, то предел теку-
текучести имеет минимальные неравные значения в направлениях х и у и максимальное
значение в направлении под углом а к оси х. Если No находится между Go + 2Яо
и Fo + 2//о, действительных значений для а не существует и предел текучести имеет .
максимум в направлении х и миниму,м в направлении у при Fo > Go и, наоборот,
при Fo < Go.
На рис. 3.10 представлена данное в рабрте [13] сопоставление графиков зави-
зависимости условного предела текучести от угла наклона оси образца к направлению
прокатки (ось х), построенных по формуле C.29), с результатами экспериментов,
47

изображенных точками. Как следует из этого чертежа, экспериментальные данные
хорошо согласуются с теоретическими.
Приведем результаты экспериментальной проверки рассмотренного условия
текучести [1J. Испытанию подвергались тонкостенные трубы из стали 45. Они на-
нагружались растягивающей силой и внутренним давлением. Пределы текучести
в продольном и окружном направлениях равны соответственно ох? = 335 МН/м2,
тн
300
200
i
шо
t
1—,
M
...
5__l
мн/ч
300
200
100
О
\
V
/
/
0
22,5
VS
615
100 200
Gt. мн/мг
300
Рис. 3.11. Результаты испытаний труб
из стали 45 [1]
Рис. 3-Ю. Графики зависимости услов-
условного предела текучести от угла наклона
оси образца к направлению прокатки
[13]:
/ — сталь 0XI8H9T; 2 — латунь Л62; 3 —
сталь 08кп; 4 — алюмиииевомагниевый
сплав АМГ6М; 5 — алюминий АМцАМ
atT = 311 МН/ма. На рис. 3.11 изображен график зависимости ох от сгг, построен-
построенный по формуле C.28). Точками представлены результаты экспериментов. И в этом
случае эксперимент подтверждает теорию.
Список литературы
1. Бастуй В. Н., Черняк Н. И. О применимости некоторых условий пластичности
для анизотропной стали. — «Прикладная механика», 1966, т. II, в. 1, с. 92—98.
2. Жуков А. М. Пластические свойства и разрушение стали при двухосном
напряженном состоянии. — «Инженерный сборник», 1954. т. XX, с. 37—48.
3. Жуков А. М. Сложное нагружение и теория пластичности изотропных ме-
металлов. — «Известия АН СССР, ОТН», 1955, № 8, с. 81—92.
4. Ивлев Д. Д. К построению теории идеальной пластичности. — «Прикладная
математика и механика», 1958. т. XXII, в. 6, с. 850—855.
5. Илюшин А. А., Ленский В. С. Сопротивление материалов. М., Физматгиз,
1959, 371 с.
6. И шли некий А. Ю. Гипотеза прочности формоизменения. — «Учебные записки
МГУ. Механика», 1940, вып. XLVI, с. 117—124.
7. Лоде В. Влияние среднего главного напряжения на текучесть металлов. —
В кн.: Теория пластичности. М., Изд. иностр. лит., 1948, с. 168—205.
8. Мизес Р. Механика твердых тел в пластически деформированном состоянии.
— В кн.: Теория пластичности. М., Изд. иностр. лит., 1948, с. 57—69.
48

9. Надаи А. Пластичность и разрушение твердых тел. М., Изд. иностр. лиг
Т. I, 1954, 647 с. Т. II, 1969, 863 с.
10. Папкович П. Ф. Теория упругости. М., Оборонгиз, 1939, 640 с.
11. Расчеты на прочность в машиностроении. Т. I, М., Машгиз, 1956, 884 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К. Лихарев и др.
12. Работиов Ю. Н. Сопротивление материалов, М., Физматгиз, 1962, 455 с.
13. Реиие И. П., Шевелев В. В., Яковлев С. П. Об оценке анизотропии механиче-
механических свойств листовых материалов. — В кн.: Технология машиностроения. Вып. 1.
Исследования в области пластических деформаций и обработки металлов давлением.
Тула, Приокское книжное издательство, 1967, с. 100—108.
14. Рош М., Эйхиигер А. Опыты, связанные с выяснением вопроса об опасности
разрушения. — В кн.: Теория пластичности. М., Изд. иностр. лит., 1948, с. 157—
167.
15. Феодосьев В. И. Сопротивление материалов. М., «Наука», 1974, 559 с.
16. филоненко-Бородич М. М. Теория упругости. М., Физматгиз, 1959, 364 с.
17. Филоиеико-Бородич М. М. Механические теории прочности. М., Изд. МГУ,
1961, 91 с.
18. Хейзорнсвейт Р. М. Дипазон изменения условий текучести для устойчивых
мдеальио-пластических тел. — «Механика. Периодический сборник переводов ино-
иностранных статей», 1961, вып. 5, с. 129—141.
19. Хилл Р. Математическая теория пластичности. М., ГИТТЛ, 1956, 407 с.
20. Hill R., Wills H. H. On the state of stress in a plastic—rigid body at the yield
point, «The philosophical magazine», Seventh series, 1951, Vol. 42, No 331, p. 868—875.
21. Huber M. T. Wiasciwa praca odksztaicenia jako miara wytfzenia materialu-
Pisma, т. II, Warszawa, Panstwowe wydawnictwo naukowe, 1956, s. 3—20.
22. Marln J. Mechanical behaviour of engineering materials, Prentice — Hall,
19G2, 502 p.
23. MIses R. Mechanik der plastischenFormanderungvon Kristallen.—«Zeitschrift
fiir angewandte Mathematik und Mechanik», 1928, Band 8, Heft 3, s. 161—185.
24. Pelczynski T. Zagadnienia wytfzenia materialow. Rys historyczny.—«Obrobka
plastyczna», 1962, No 1, s. 9—49.
25. Reuss E. Vereinfachte Berechnung der plastischen Formaenderungsgeschwindig-
kciten bei Voraussetzund derSchubspannungsfliessbedingung.—«Zeitschrift fur angewan-
angewandte Mathematik und Mechanik», 1933, Band 13, Heft 5, s. 356—360.
26. Taylor G. J. Quinney H. The plastic distortion of metals. — «Philosophical tran-
transactions of the Royal Society», 1931, Ser A, 230, p. 323—362.

РАЗДЕЛ II. ПЛАСТИЧНОСТЬ
ГЛАВА IV
ТЕОРИИ ПЛАСТИЧНОСТИ
§ 20. Поверхность пластичности
В случае одноосного растяжения или сжатия пластические де-
деформации возникают, когда напряжение достигает величины пре-
предела текучести материала (точка А на диаграмме растяжения на
рис. 4. 1, а). В теории пластичности понятия пределов текучести,
пропорциональности и упругости не различаются.
Если напряжение меньше предела текучести (точка В на диа-
диаграмме растяжения на рис. 4.1, а), материал деформирован упруго,
а если больше (точка С на рис. 4.1, а) — упруго-пластически.
Для неодноосного напряженного состояния пределы применимо-
применимости закона Гука для элемента тела определяются условием начала
пластичности, которое было рассмотрено в § 18.
При дальнейшем деформировании упрочняющегося материала
предел текучести его увеличивается. При нагружении до точки,С
(рис. 4.1, а) предел текучести увеличивается до ас. Теперь при на-
нагружении в пределах от 0 до ос соблюдается закон Гука. При уве-
увеличении напряжения сверх ас материал деформируется упруго-пла-
упруго-пластически. Напряжение ос является текущим пределом текучести,
разграничивающим упругую разгрузку и нагружение, сопровожда-
сопровождающееся дальнейшей пластической деформацией.
Для разграничения упругого и пластического деформирования
упрочняющегося материала в общем случае напряженного состоя-
состояния введем условие пластичности
ЛЫ=0, ' D-1)
которое обычно принимают совпадающим по виду с условием начала
пластичности C.10). Существенное отличие между ними заключается
в том, что в условие C.10), как отмечалось выше, входят постоянные
для материала механические характеристики, например, пределы
текучести при одноосных растяжениях или сжатиях, а в условие D.1)
должна входить еще и некоторая мера упрочнения. В качестве меры
упрочнения q обычно принимают или работу пластической дефор-
деформации
\ D.2)
50

или так называемый параметр Удквиста
i?. D.3)
Интегралы берутся по пути деформирования. В первом случае пред-
предполагают, что упрочнение материала определяется только работой
пластической деформации, т. е. работой, затраченной на необрати-
необратимую деформацию. Во втором считают, что мера упрочнения должна
отражать накопленную пластическую деформацию. В дальнейшем
(см. § 23) будет показано, что для изотропных материалов использо-
использование двух рассмотренных мер упрочнения в случае условия пластич-
пластичности Хубера—Мизеса приводит к одинаковым результатам.
Рис. 4.1. Диаграмма растяжения (а). Поверхности начала пластичности
VT и пластичности V (б)
Уравнение D.1) является уравнением гиперповерхности пластич-
пластичности 2 (рис. 4.1, б) в шестимерном пространстве компонентов тен-
тензора напряжения, которая для рассматриваемого состояния элемента
среды разделяет области упругого и пластического деформирования.
Так же, как и поверхность начала пластичности ?т, она может быть
изображена в трехмерном пространстве главных напряжений.
Размеры, форма и положение поверхности пластичности зависят
не только от конечного деформированного состояния, но и от всей
истории деформирования. В § 22 будет доказано, что поверхность
пластичности является выпуклой. Если компоненты тензора напря-
напряжений аС]- получают приращения da[f, то это догружение может при-
привести либо к упругой разгрузке, если вектор Ив^ направлен внутрь
поверхности нагружения, либо к нагружению^при котором разви-
развиваются пластические деформации, если вектор йвц направлен наружу
поверхности нагружения, либо к так называемому нейтральному
нагружению, если вектор Шц лежит в касательной плоскости к по-
поверхности нагружения, при этом материал деформируется
упруго.
51

§ 21. Постулат Друкера
Рассмотрим вначале одноосное растяжение. Диаграмма растя^
жени я материала представлена на рис. 4.2, а. Допустим, что обра-
образец, нагруженный вначале до напряжения 0 (точка С), разгружен
затем до напряжения 0° (точка D). Это состояние образца будем
принимать за исходное. Представим себе теперь нагружение образца
до напряжения о -\- do (точка Н) и последующую разгрузку до на-
напряжения 0° (точка Dx). Затраченная при этом невосполнимая работа
на единицу объема образца в определенном масштабе равна сумме
площадей параллелограмма ССгЬхЬ и криволинейного треуголь-
треугольника CHCi. Следовательно,
@ — 0°) deP > 0, dodep > 0, D.4)
где dep — приращение пластической деформации при переходе от
точки С к точке Н, т. е. при увеличении напряжения на do.
в
Рис. 4.2. К формулировке постулата Друкера при одноосном (а) и не-
неодноосном напряженном состоянии (б)
Из условия D.4) следует, что
da . п
Когда это условие нарушается, на диаграмме растяжения по-
появляется ниспадающий участок. Последний, как известно, обусло-
обусловлен возникновением шейки на образце, в результате чего деформи-
деформированное состояние становится неоднородным по объему образца.
Поэтому второе условие D.4) можно рассматривать как критерий
устойчивости деформирования за пределами упругости. При этом
под 0 понимают условные напряжения, а под е обычные (нелога-
(нелогарифмические) деформации.
Перейдем теперь к общему случаю напряженного состояния.
Представим себе нагружение по некоторому пути ОС (рис. 4.2, б)
до точки С, лежащей на поверхности пластичности 2, которой соот-
52

ветствует напряженное состояние а^ и последующее разгружение
до точки D, лежащей внутри поверхности пластичности (в частном
случае она может лежать и на ней), которой соответствует исходное
напряженное состояние 0?/. Таким образом, при переходе от точки С
к точке D имеют место только упругие деформации. Рассмотрим на-
гружение от точки D до точки С по некоторому пути, последующее
догружение до точки Я, которому соответствует изменение тензора
напряжений на datj, вызывающее соответствующее изменение упру-
упругой dsetj и пластической de^ деформаций и последующую' разгрузку
до точки D по какому-либо иному пути.
Согласно постулату Друкера, работа добавочных напряжений
на вызванных ими приращениях деформаций за цикл нагружения и
разгрузки положительна, т. е.
— о°ц) dept, + dot, йгрц > 0. D.5)
В это выражение не включена работа добавочных напряжений на
упругих деформациях, так как для замкнутого пути деформирования,
вследствие обратимости упругих деформаций, она равна нулю..
Если положить 0?/ = Оц, то тогда из выражения D.5) получаем
dotidt%i>0. D.6)
Если а°/ Ф ац, то величина ац — а\, может быть сделана сколько
угодно больше йо1:: Следовательно, из соотношения D.5) имеем
(ои— а°И)йгрГ1>0. D.7)
Условие D.6) по аналогии со вторым условием D.4) можно рас-
рассматривать как критерий устойчивости деформирования за преде-
пределами упругости в общем случае напряженного состояния.
Из выражения D.7) замечаем, что
at, dep, >> а°ц dep,. ,
Это соотношение является математической формулировкой прин-
принципа максимума работы пластической деформации, согласно кото-
которому: при любом заданном значении компонентов приращения пла-
пластической деформации^ приращение работы пластической деформа-
деформации oi.defj имеет максимальное значение для действительного напря-
напряженного состояния по сравнению со всеми возможными напряженными
состояниями, удовлетворяющими условию f (о1:) < 0.
§ 22. Ассоциированный закон течения
Компоненты приращения пластической деформации являются
функциями компонентов напряжения. Поэтому приращение работы
пластической деформации a^de^ также в конечном счете является
функцией компонентов напряжения. Однако они не являются не-
независимыми, так как удовлетворяют условию пластичности D.1).
Поэтому условие относительного максимума функции приращения
53
i

пластической работы o[fdeP{ по способу множителей Лагранжа за-
запишем в виде
д 1 . в
где dk — множитель Лагранжа, откуда следует, что
D.8)
т. е. функция / (аф — пластический потенциал.
Соотношение D.8) является математическим выражением так
называемого ассоциированного (с условием пластичности) закона
течения.
Рис. 4.3. К выводу ассоциированного закона течения
Поясним полученный результат геометрически. Из соотношения
D.7) следует, что скалярное произведение векторов ас! — а°ц и йгрц
(рис. 4.3) положительно, т. е. угол между ними острый. Так как
точка D может быть взята по обе стороны от вектора otj
(рис. 4.3, а), то поверхность пластичности выпукла, а вектор прира-
приращения пластической деформации def/ направлен по нормали к по-
поверхности пластичности. Только при выполнении этих двух условий
угол между векторами оС] — а?/ и de?/будет острым. Если вектор d&%
не перпендикулярен поверхности пластичности (штриховая линия
на рис. 4.3, а), всегда найдется вектор Oi/ — а°ц, . составляющий
с ним тупой угол.
Если бы поверхность пластичности была невыпукла (рис. 4.3, б),
то тогда независимо от направления вектора dsf,- всегда можно по-
подобрать точку D так, чтобы угол между векторами ait °
был тупой.
54
о°ц и

Поскольку направляющие косинусы нормали к поверхности про-
пропорциональны частным производным от уравнения поверхности по.
координатам, приходим к соотношению D.8).
Выше отмечалось, что функция / совпадает по виду с функцией /т
и в нее так же, как и в функцию /т, не входит первый инвариант
тензора напряжений или, что то же, величина о0 = ~j-- В таком слу-
случае можно доказать, что в результате пластических деформаций из-
изменение объема равно нулю.
def, = 3deo = O, D.9)'
т. е. тензор приращения пластической деформации является девиа-
тором.
Действительно, из соотношений A.9) и A.10) заключаем, что
поэтому
а/
_ df . / l .
Следовательно, согласно формуле D.8) компоненты приращения
пластической деформации могут быть представлены в виде
D.10)
Умножим обе части этого равенства на б(/. Тогда получим
т. е. приходим к соотношению D.9).
Определим величину dk. Поскольку тензор приращения пласти-
пластической деформации совпадает с девиатором, подставим компоненты
приращений пластических деформаций по формуле D.8) в выражение^
для интенсивности приращений пластических деформаций B.35).
В результате получим
2 DП)
dot,-
Из этой формулы следует, что dk > 0. Поэтому согласно соотно-
соотношениям D.6) и D.8) получаем при нагружении
Jg-dotl>0, /(aty) = 0, dk>0. D.12)
При разгрузке очевидно, что
Л = 0. D.13)
55

При переходе из пластического состояния в упругое вектор ц
проходит через плоскость, касательную к поверхности пластичности,
т. е. имеет место равенство
laCj = O, f(Gtj)~O, dA = O, D.14)
при этом конец вектора напряжения движется по поверхности пла-
пластичности. Такой тип нагружения называют нейтральным. Для него
законы пластичности и упругости должны совпадать, т. е. при ней-
нейтральном нагружении возникают только упругие деформации, что
является условием непрерывности.
6i
Рис. 4.4. Диаграмма деформирования иде-
идеального упруго-пластического материала
Рис. 4.5. К определению пластиче-
пластического течения на ребре поверхности
пластичности
Для материала, не имеющего упрочнения (идеально пластичного
материала), диаграмма деформирования которого представлена на
рис. 4.4, поверхность пластичности все время совпадает с поверх-
поверхностью начала пластичности. Тогда нейтральное нагружение является
основным типом нагружения, сопровождающимся приращением пла-
пластических деформаций. Таким образом, при нагружении
а при разгрузке
доц
D.15)
D.16)
Если поверхность пластичности гладкая (регулярная), т. е. ка-
касательная плоскость к ней непрерывно поворачивается, то тогда
в каждой точке определена и нормаль к поверхности пластичности.
В случае сингулярной поверхности пластичности, имеющей ребра
или вершины, это уже несправедливо. Примерами сингулярных по-
поверхностей пластичности, имеющих ребра, являются шестигранные
призмы Треска—Сен-Венана или Ишлинского—Хилла—Ивлева—
Хейзорнсвейта. Как будет показано далее, использование этих усло-
56

iihi'i в ряде случаев позволяет значительно упростить решения задач.
Тогда соотношение D.8) необходимо дополнить так, чтобы определить
пластическое течение на ребрах.
Можно доказать, что пластическое течение на ребре является
линейной комбинацией течений на поверхностях, пересечением ко-
которых является ребро. Допустим, что ребро образовано пересечением
днух поверхностей пластичности (рис. 4.5), уравнения которых
/i (pt{) = 0 И /2 (О,;) = 0.
Тогда для точек ребра усло-
условие относительного максимума
функции приращения пласти-'
ческой работы ацйъЧ, имеет вид
(а„ de?t, -
= 0,
откуда следует
D.17)
Течение на ребре развивает?
ся по направлению, лежащему
внутри угла, образованного
нормалями к двум смежным
граням (рис. 4.5).
Рис. 4.6. К определению пластического
течения на ребре шестигранной призмы
Треска—Сен-Венана
В качестве примера рассмотрим течение для точек на ребре шестигранной призмы
Треска—Сен-Венана в случае отсутствия упрочнения. След призмы на девиаторной
плоскости — правильный шестиугольник ACEGIK. (рис. 4.6).
Возьмем точку С, образованную пересечением линий АС и СЕ. Уравнение
соответствующих граней призмы (следами которых являются линии АС и СЕ) имеет
вид
к — ai — <*з — ат = 0,
h = аа — аз — аТ = 0.
Для первой грани согласно формуле D.8) имеем
причем
а для второй
причем
def:de$:dB§ = 0: 1 : —1,
def = dX2.
Для угловой точки, согласно формуле D.17),
57

§ 23. Теория течения
В зависимости от принятого закона изменения размеров и формы
поверхности пластичности, который и является законом упрочне-
упрочнения, можно получить различные теории пластичности.
Если в процессе нагружения поверхность пластичности равно-
равномерно (изотропно) расширяется (рис. 4.7), упрочнение называют
изотропным. В этом случае эффект Баушингера не описывается, по-
поскольку при прямом (ОА]) и обратном @А2) нагружении пласти-
пластические деформации возникают при напряженных состояниях одной
и той же интенсивности.
Такую теорию пластичности называют теорией течения с изо-
изотропным упрочнением или просто теорией течения.
Примем, что
Hatj) = 4- sijSii - [Ф {q)f = 0, D.18)
где q — мера упрочнения, опреде-
определяемая формулой D.3) — параметр
Удквиста. Тогда, используя соотно-
соотношения A.20), устанавливаем
Рис. 4.7. Равномерное (изотропное)
расширение поверхности пластич- откуда следует, что
ности в процессе нагружения , * ч
0, = Ф(|^). D.19)
Выбор условия пластичности в виде соотношения D.18) равно-
равносилен гипотезе о том, что интенсивность напряжений является
функцией параметра Удквиста, не зависящей от типа напряженного
состояния. Условие D.18) или D.19) по аналогии с условием начала
пластичности Хубера—Мизеса (см. § 18) может быть названо усло-
условием пластичности Хубера—Мизеса.
Рассмотрим определение функции Ф поддиаграмме растяжения
материала.
Для одноосного растяжения ох = оу = 0, az = 0, хху — %уг =
dep def
= tzx — 0, d&px = dsy = 4- = 5- (так как йгрх = йгру, а йгрх +
+ deP = 0). Поэтому по формулам A.19) и B.34) имеем
и, следовательно,
J def = j dep = е".
Таким образом, в случае одноосного растяжения из формулы D.19)
получаем
a = Ф (е").
Следовательно, для определения функции Ф по диаграмме растя-
растяжения материала необходимо построить график зависимости напря-
58

щения от пластической деформации: Рассмотрим построение этого
графика. Возьмем некоторую точку А на диаграмме растяжения
материала (рис. 4.8) и проведем через нее линию АВ, параллельную
первоначальной прямой нагружения. Из точки В пересечения этой
линии с осью абсцисс восстановим пер-
перпендикуляр до пересечения в точке С с
горизонтальной лднией, проведенной че-
через точку А. Абсцисса точки С равна
пластической деформации, а ордината —
соответствующему ей напряжению. По-
Поэтому кривая КС является графиком за-
1Исимости интенсивности напряжений от
параметра Удквиста.
При использовании соотношения D.18)
поверхностью пластичности в трехмер-
трехмерном пространстве главных напряжений
является круговой цилиндр (цилиндр Ху-
бер а—-Мизеса). В процессе, нагружения
радиус цилиндра непрерывно увеличи-
увеличивается. Величина его согласно выраже- Рис- 4-8. Определение функ-
ИЙЮ D.19) зависит от истории деформи- ции Ф (ер) по диаграмме рас-
рОВания. Следами цилиндров на девиа- тяжения материала
ТОрНой плоскости являются окружности
радиусов [/ "з"°г (рис. 4.9, а). Наименьший радиус равен I/ -g-aT.
При отсутствии упрочнения поверхность пластичности совпадает
С поверхностью начала пластичности и следом ее на девиаторнрй
Плоскости является окружность радиуса 1/ -^- от (рис. 4.9,-б).
Используя соотношение D.18), имеем
dsij
5)
Рис. 4.9. Следы цилиндров Хубера—Мизеса на девиаторной плоскости
при наличии (а) И' отсутствии (б) упрочнения
59

и согласно формуле D.10) получаем
Таким образом, при использовании условия пластичности D.18)
df _ df __„
и согласно соотнешениям D.11) и A.20)
а по формуле D.8) получаем
3 ~Щ 3 Зё?
Из формулы D.20) следует, что компоненты тензора приращений
пластических деформаций пропорциональны компонентам девиатора
напряжений.
Если в качестве меры упрочнения принять пластическую работу [формула D.2)],
то рассматриваемая теория не изменится. Действительно, используя разложение
тензора напряжений на шаровой тензор и девиатор (см. § 3), имеем
J ач йг"ц = J (ви + дио0) </ = J зч dsf, + J бч «tefyoo =
Очевидно, что второе слагаемое в этом выражении равно нулю, поскольку тензор
пластических деформаций является девиатором. Таким образом, используя соотно-
соотношения D.20) и A.20), получаем
Если принять, что интенсивность напряжений является функцией работы пла-
пластической деформации
°< = <Р (J
то согласно формуле D.21)
откуда следует соотношение D.19). Таким образом, гипотеза о том, что интенсив-
интенсивность напряжений является функцией работы пластической деформации, равно-
равносильна гипотезе, утверждающей, что она зависит от параметра Удквиста.
Приращения компонентов упругих деформаций согласно фор-
формуле C.5)
60

Добавляя их к компонентам приращений пластических деформа-
деформаций по формулам D.20), получаем компоненты приращений полных
деформаций
3 ^
¦2-—
-Vo).
D.22)
В координатной форме уравнения D.20) имеют вид
j
dex = -g- [dox — \i (daу -f~ do.
D.23)
Эти соотношения являются основными уравнениями теории те-
течения. Для случая плоской деформации они были предложены Пранд-
тлем в 1924 г. [52] и для общего случая Рёйссом в 1930 г. [351. По-
Поэтому их иногда называют уравнения Прандтля—Рёйсса. В работах
Прандтля и Рёйсса предполагалось, что материал не имеет упрочне-
упрочнения. Упрочнение было принято во внимание Удквистом [40 ].
Если приращения пластических деформаций велики по сравне-
сравнению с приращениями упругих деформаций и последними по сравне-
сравнению с первыми можно пренебречь, уравнения D.20) и D.22) совпа-
совпадают и принимают вид
d*4 = 4" it (°Ч — 8Иао)-
Поделив обе части на dt и учитывая, что
где i^ — интенсивность скоростей деформаций, определяемая фор-
формулой B.40), получаем зависимости компонентов скоростей дефор-
деформаций от компонентов девиатора напряжений
JL
D.24)
. Эти уравнения для частного случая плоской деформации были
впервые предложены Сен-Венаном [37], [38], а для общего случая
Леви [23] в 1871 г. и независимо от него значительно позднее
(в 1913 г.) Мизесом [27]. Поэтому их иногда называют уравнениями
Сен-Венана—Леви—Мизеса.
61

§ 24. Теория малых упруго-пластических деформаций
Вначале рассмотрим понятие простого нагружения. Простым
называют такое нагружение, при котором компоненты девиатора
напряжений возрастают пропорционально некоторому параметру.
В противном случае нагружение называют сложным. Иногда 121 ]
простым называют такое нагружение, при котором компоненты тен-
тензора напряжений возрастают пропорционально некоторому пара-
параметру. Очевидно, что при использовании второй формулировки
первая выполняется.
В случае однородного напряженного состояния нагружение тела
будет простым при возрастании внешних сил пропорционально од-
одному общему для всех сил параметру. Это объясняется тем, что при
однородном напряженном состоянии, возможном только в случае
отсутствия массовых сил, деформированное состояние тоже будет од-
однородным. Тогда дифференциальные уравнения равновесия A.3) и
условия совместности деформаций B.4) выполняются тождественно.
Поэтому напряженное состояние определяется только граничными
условиями, т. е. только поверхностными силами. При возрастании
их пропорционально некоторому параметру напряжения, а следо-
следовательно, и компоненты девиатора напряжений во всех точках тела
будут возрастать пропорционально тому же параметру и нагружение
тела будет простым.
Рассмотрим случай простого нагружения. Пусть компоненты де-
девиатора напряжений возрастают пропорционально некоторому па-
параметру р:
где звездочкой отмечены некоторые постоянные значения компонен-
компонентов девиатора напряжений, например, компоненты девиатора на-
напряжений в конце нагружения. В последнем случае О «S р ^ Г.
Из зависимостей D.20) имеем
Проинтегрируем это уравнение. Тогда получим, что в конце на-
нагружения .
*
ef. D.25)
Подставим полученные выражения в соотношение для интенсив-
интенсивности пластических деформаций B.22). После преобразований с ис-
использованием зависимости A.20) устанавливаем
,• — J OBi,
D.26)
откуда следует
62 "

Таким образом, в случае простого нагружения интенсивность
приращения пластических деформаций dsf равна приращению ин-
интенсивности пластических деформаций def. Соотношение D.25)
с помощью выражения D.26) приводим к виду (звездочка опущена)
е«/=4- 4г s«=4 4г (°ч -v°)- ^4-27)
Добавляя к компонентам тензора (девиатора) пластической де-
деформации D.27) компоненты девиатора упругих деформаций по
формуле C.8), используя при этом соотношение C.9), получаем
Подставим полученное выражение для компонентов девиатора
полных деформаций в формулу B.17). Тогда имеем
e, = e? + ef, ' D.29)
т. е. интенсивности полных, упругих и пластических деформаций
обладают теми же аддитивными свойствами, что и сами деформации.
Следовательно, из выражения D.28) получаем
или
В координатной форме эти уравнения имеют вид
D.32)'.
В теории малых упруго-пластических деформаций принимается,
что зависимость средней линейной деформации от среднего нормаль-
нормального напряжения такая же, как в пределах упругости C.3). Следо-
Следовательно, в результате пластических деформаций изменения объема
не происходит. Обычно изменение объема сравнительно невелико
и поэтому им можно пренебречь. Тогда на основании соотношения
C.3) можно положить
е0 = 0. D.33)
В таком случае 'принято говорить, что материал несжимаем,,
а условие D.33) представляет собой условие несжимаемости.
Зависимость интенсивности напряжений от интенсивности де-
деформаций может быть определена по результатам испытаний на
"растяжение. Проведение-последних, как правило, проще, чем испы-
испытаний при иных типах нагружения.
63

График зависимости интенсивности напряжений от интенсивности
деформаций будем называть диаграммой деформирования материала.
Выражения для интенсивностей напряжений и деформаций при
одноосном напряженном состоянии были получены в § 5 и 12 [фор-
[формулы A.22) и B.19)]. Они имеют вид
oi = о, D.34)
&i = е — е%. D.35)
Учитывая, что при одноосном растяжении сго = -|-, и используя
соотношения C.3) и C.4), получим
е,- = е—Ц^-а. D.36)
При помощи формул D.34) и D.36) можно по диаграмме растя-
растяжения материала подсчитать величины ос, eh определяющие диа-
диаграмму деформирования.
В работе [34] описаны графо-аналитические и графические ме-
методы построения диаграмм деформирования по диаграммам растя-
растяжения. Если принять условие несжимаемости материала D.33),
что равносильно допущению о том, что \i = 0,5, то тогда, как сле-
следует из соотношений D.34) и D.36), диаграмма деформирования
совпадает с диаграммой растяжения. Если не использовать этого
предположения, различие между диаграммами незначительно.
В следующей главе будет рассмотрено построение действитель-
действительных диаграмм деформирования.
Гипотеза о существовании диаграммы деформирования (гипотеза
«единой кривой»), не зависящей от типа напряженного состояния,
была выдвинута Людвиком [25 3.
Таким образом, в частном случае так называемого простого на-
нагружения появляется возможность использования зависимостей
между деформациями и напряжениями в конце процесса нагружения.
Теории, в которых такие зависимости устанавливаются, называют
деформационными. Уравнения D.30)—D.32) являются основными
уравнениями простейшего варианта деформационных теорий — тео-
теории малых упруго-пластических деформаций.
Впервые основные уравнения этой теории при условии отсут-
отсутствия упрочнения были получены Генки [4]. Упрочнение в теории
малых упруго-пластических деформаций было рассмотрено в работе
Шмидта [43]. Зависимости компонентов деформаций от компонентов
напряжений в форме D.32) были установлены А. А. Ильюшиным [16 3.
Ему же принадлежат анализ и развитие этой теории пластичности.
Из соотношений D.32) следует пропорциональность компонен-
компонентов девиаторов напряжений и деформации
¦ Угх
е< — во _ , , _ 2
Ох — 00 - %гх
64

или
— a0 a3 — a0
Из последних равенств можно получить условие пропорциональ-
пропорциональности главных угловых деформаций (см. § 13) и главных касательных
напряжений (см. § 6)
*i т2 т8 '
а также условие равенства параметров Надаи—Лоде по напряжениям
(§ 6) и деформациям (§ 13)
Ъ, = Хв- D.37)
Напомним, что в § 13 было установлено равенство этих параме-
параметров для трех простейших напряженных состояний: одноосных
растяжения и сжатия и чистого сдвига.
Рассмотрим теперь величину коэффициента поперечной дефор-
деформации за пределами упругости.
Как известно, для определенного материала при определенной
температуре испытания отношение поперечной деформации к про-
продольной при одноосном растяжении в пределах упругости является
постоянной величиной. Абсолютную величину этого отношения на-
ihiiiiiioT коэффициентом поперечной деформации или коэффициентом
Пуассона. Теория малых упруго-пластических деформаций позво-
позволяет установить эту величину и за пределами упругости. Будем на-
называть ее также коэффициентом поперечной деформации и обозна-
обозначать [л/.
Для одноосного растяжения (ах = ау = О, ст2 = о, хху = хуг =
г« = 0, ст0 = -j-J имеем
е0— з
и согласно выражению C.3)
О I (*
откуда, используя соотношение C.4), определяем
1 1—2ц a
ц =
2 2Е е
D,38)
Поскольку при увеличении деформации ——» 0, из уравнения
D.38) следует, что в этом случае ц' —> 0,5.
На рис. 4.10 сопоставлены теоретические и экспериментальные
величины коэффициентов поперечной деформации, полученные
А. М. Жуковым [8]. Сплошной линией с'белыми кружочками изо-
изображена диаграмма растяжения материалов, штриховой линией по-
показан теоретический график зависимости коэффициента поперечной
3 И. И. Малииии 65

б,МН/м1
деформации от деформации, построенный по формуле D.38), и сплош-
сплошной линией с черными кружочками — экспериментально получен-
полученный график этой зависимости. Как видно, экспериментально полу-
полученные результаты хорошо согласуются с теоретическими зависи-
зависимостями.
Выше было дано понятие простого нагружения и показано, что
в простейшем случае статически определимых, с точки зрения опре-
определения напряжений, задач нагружение будет простым при возра-
возрастании внешних сил пропорционально некоторому параметру.
Вопрос о том, как в процессе
нагружения должны возрастать
внешние силы, действующие на
тело для того, чтобы в общем
случае неоднородного напряжен-
напряженного состояния нагружение во
всех точках тела было простым,
не решен. А. А. Ильюшиным дано
частное решение этой задачи [16.1.
Им доказано, что для того чтобы
во всех точках несжимаемого
тела, нагруженного внешними
силами, возрастающими пропор-
пропорционально некоторому параметру
Р, нагружение было простым, дос-
достаточно, чтобы зависимость ин-
интенсивности напряжений от ин-
интенсивности деформаций была
560
500
>S0
no
60
i /-
V
1
0,5
а."
0,3
0,1
0,1
о
0,5
1.0
Рис 4.10. Диаграмма растяжения и степенной функцией вида
графики зависимости коэффициента ^s ^
поперечной деформации от величины т
деформации для стали 30 [8] <х,-=Ле^ . D.39)
Это положение называют теоремой о простом нагружении. Па-
Параметр р может быть временем или любой другой величиной, опре-
определяющей последовательные значения напряжений. Так, например,
если внешние силы возникают от давления масла из одного резер-
резервуара, параметром р может быть это давление.
Перейдем к доказательству теоремы А. А. Ильюшина о простом
нагружении. Допустим, что для какого-либо определенного значения
параметра р, например, для Р = 1, пластическая задача решена.
Обозначим напряжения, деформации и перемещения, полученные
в решении, через о*,-, е*,-, щ. Очевидно, что компоненты напряжений
удовлетворяют дифференциальным уравнениям равновесия A.4) и
условиям на поверхности A.2), а компоненты деформаций — усло-
условиям совместности деформаций B.4). Также удовлетворяются зави-
зависимости компонентов деформации от компонентов перемещения B.3)
и зависимости компонентов девиатора деформации от компонентов
девиатора напряжения D.30). На основании соотношения D.39)
имеем
в* = А(еТ- D.40)
66

Попытаемся найти решение той же пластической задачи для
отличного от единицы, в виде
<т//=Ро?/, D.41)
ut = vui, D.42)
где v — некоторая функция р.
На основании соотношений B.3) и D.42) заключаем, что
ef/ = ve7/. " D.43)
Очевидно, что если выбранные ранее компоненты напряжений о*]
деформаций е*/ и перемещений и* удовлетворяют уравнениям A.4),
A.2), B.4) и D.30), то компоненты напряжений, перемещений и де-
деформаций, определяемые формулами D.41)—D.43), также удовлет-
удовлетворяют этим уравнениям. На основании соотношений D.39)—D.41)
и D.43) заключаем
_ i
v = p« * , D.44)
При выполнении этого условия формулы D.41)—D.43) пред-
представляют собой решение упруго-пластической задачи. Если не ис-
использовать предположение о том, что тело является несжимаемым,
то из соотношения C.3) будет следовать зависимость между v и р,
противоречащая условию D.44). Как следует из вышеизложенного,
соблюдение зависимости D.39) является условием достаточным, но
не необходимым для обеспечения простого нагружения.
Простое нагружение имеет место в некоторых других частных
случаях при возрастании внешних сил пропорционально одному
общему для всех сил параметру, если зависимость интенсивности
напряжений от интенсивности деформаций отлична от зависимости
D.39) [16]. При отсутствии упрочнения в случае нагружения тела
силами, возрастающими пропорционально общему параметру, эле-
элементы тела могут испытывать сложное нагружение [16].
Д. Д. -Ивлевым [15] было показано, что если зависимость ин-
интенсивности напряжений от интенсивности деформации имеет вид
полинома, то для осуществления простого нагружения тела необ-
необходимо приложение внешних сил, изменяющихся непропорционально
одному общему для всех сил параметру. В таком случае, как уста-
установлено в этой работе, простое нагружение тела вообще практически
неосуществимо. Л. И. Седов пришел к заключению [36], что в общем
случае нагружения при больших деформациях тел простое нагруже-
кие также неосуществимо. ' N
Однако, учитывая, что выражение D.39) с достаточной степенью
точности аппроксимирует зависимость интенсивности напряжений от
интенсивности деформаций в области пластических деформаций,
приближенно можно считать, что нагружение тела будет простым,
если внешние силы возрастают пропорционально одному общему
для всех сил параметру.
б* 67

§ 25. Экспериментальная проверка теории течения
и малых упруго-пластических деформаций
Рассмотрим вначале результаты экспериментальных исследова-
исследований, по которым может быть проверена теория малых упруго-пла-
упруго-пластических деформаций. В таких исследованиях основное внимание
уделялось проверке равенства параметров Надаи:—Лоде по напря-
напряжениям и деформациям, а также проверке существования единой
диаграммы деформирования.
Опыты Лоде [24]. Опыты были проведены по инициативе
Надаи. Испытаниям подвергались тонкостенные стальные, медные
и никелевые трубы. Они нагружались продольной растягивающей
силой и внутренним давлением, что позволило осуществить различ-
различные двухосные напряженные состояния. Нагружение являлось
сложным.
По результатам испытаний определяли параметры Надаи—Лоде
%е в зависимости от Хо- На рис. 4.11 представлены экспериментально
полученные точки. Как следует из этого рисунка, они скучиваются
вблизи прямой, уравнение которой %s = %а, хотя при %а = —1
все же заметно значительное отклонение ряда точек от этой прямой.
Последнее, по-видимому, объясняется недостаточной точностью по-
построения диаграммы растяжения материала [16].
Таким сбразом, опыты Лоде в основном подтверждают равенство
параметров Иадаи—Лоде.
Опыты Тейлора и К в и н н и [53]. Испытаниям на
совместное растяжение и кручение подвергались стальные, медные,
алюминиевые, свинцовые, кадмиевые и стеклянные трубы. Послед-
Последние испытывались при повышенной температуре. В процессе испыта-
испытания отношение растягивающей силы к крутящему моменту не было
постоянным. Таким образом, нагружение в этих опытах являлось
сложным.
На основании испытаний подсчитывались параметры Надаи—
Лоде Хе в зависимости от Хо- Экспериментально полученные точки
(рис. 4.12) близки к прямой, уравнение которой %г = %а. Для кад-
кадмия и свинца согласование результатов теории и эксперимента ока-
оказалось лучшим, чем для алюминия, меди и стали. Для стекла эк:
спериментально полученные точки также близки к прямой.
Таким образом, опыты Тейлора и Квинни с еще большей степенью
точности, чем опыты Лоде, подтверждают равенство параметров
Надаи—Лоде.
Опыты Дэвиса [6], [7]. Испытаниям подвергались мед-
медные и стальные трубы. Они нагружались продольной растягивающей
силой и внутренним давлением. В результате такого нагружения
были созданы различные типы двухосных напряженных состояний.
В течение каждого испытания отношение величины растягивающей
силы к внутреннему давлению оставалось постоянным. Сле-
Следовательно, в каждом испытании имело место простое на-
нагружение. Почти во всех испытаниях образцы доводились до раз-
разрушения.
68

При обработке результатов определялись логарифмические де-
деформации и действительные напряжения, вычисленные с учетом из-
изменения в процессе испытания толщин стенок трубчатых образцов.
На основании результатов испытаний медных образцов под-
считывались параметры Надаи—Лоде %? в зависимости от %а. По-
Полученные таким рбразом точки (рис. 4.13, а) близки к прямой, урав-
уравнение КОТОрОЙ Хе = 1а-
По результатам испытаний медных и стальных образцов строи-
строились графики зависимости максимального касательного напряжения,
пропорционального интенсивности напряжений (см. §5), от окта-
Рис. 4.11. Результаты опытов
^ Лоде [24]
Рис. 4.12. Результаты опытов Тэй-
лора и Квинни [53]
ч
0.8
0.6
о.ч
0,2
,о -0,8 -о,б -о,ч оО.гЯ
V
L
V
L
о
о°
р
/
/
V
—
-о.ч
-0.6
-0,8
-1,0
-!?
А
/
Гио
/
О
л
о
а о.г о,ч 0,6 о,8 х6
-0,8 -0,6 -Q-V -0,2 О
о Алюминий
• Медь
п Свинец
д Стекпо1
+ Кадмии
Сталь обезуг-_
лероженная
а Сталь мягкая
эдрической угловой деформации, пропорциональной интенсивности
деформаций (см. § 13). Все эти величины подсчитывались по значе-
значениям действительных напряжений и логарифмических деформаций.
Совокупность точек на рис. 4.13, б устанавливает зависимость мак-
максимального касательного напряжения от максимальной угловой де-
деформации, а точки на рис. 4.13, в связывают октаэдрическое каса-
касательное напряжение с октаэдрической угловой деформацией. Опыт-
Опытные точки ложатся достаточно кучно.
Следовательно, максимальное касательное напряжение является
определенной, не зависящей от типа напряженного состояния функ-
функцией максимальной угловой деформации, точно так же, как интен-
интенсивность напряжений есть функция интенсивности деформаций, не
зависящая от вида напряженного состояния. Как видно на
рис. 4.13, б и 4.13,6, первое положение при испытании . медных
образцов подтверждается несколько более точно, чем второе.
На рис. 4.14 представлены результаты испытаний стальных об-
образцов при различных напряженных состояниях. На рис. 4.14, а
изображены графики зависимости максимального касательного на-
напряжения от максимальной угловой деформации, а на рис. 4.14, б
69

по
100
80
'60
. 20
-0^-0,6-0,^
Z
с
А
• °
>
/
/
/•¦
лкг
-0,8
-0,6
-OJt
0,2
Щ2
-Ofi
-0,6
-0,8
z
/о
/
О
* О
0,2 0,40,60,8Je
«)
а
Ж
OS
%
3
л
up
/
f
D
4 О
О AV
X"
•/
о
с
L °
1
о
о
OV
-
о
о
л ¦ с
¦ *
О 0
а Уц.
v Уг
Ў уг
« & 12 16 20
Го,
МИ/мг
6)
24" 25 J2 36
12 16 20 24- 28
60
20
• о*
О"
о- л
о
V
I
о
О «°,
л.
V
!
О
О
• а»
г
3 Л ^
о а
_ ° V
о
о
т
о
О [
¦
т
А °
• v" °'
О
D
о
1/lL
¦
•
/
1 д
'-
12
О
16
if-
28
16
JZ
2й г*
8 72
В)
Рис. 4.13. Результаты опытов Дэвиса. Испытания медных образцов [6]:
а —-проверка равенства параметров Надаи —Лоде; б — выявление связи максимального ка-
касательного напряжения с максимальной угловой деформацией; в — выявление связи окта-
эдрического касательного напряжения с октаэдрической угловой деформацией

графики зависимости октаэдрического касательного напряж1* ия от
октаэдрической угловой деформации, построенные по результатам
испытания труб на растяжение. В рассматриваемом случае в отличие
от испытаний медных труб разброс точек для зависимости макси-
0,10 0,20 0,30 OfiO 0,50 0,60 0,70 0,80 0,90 1,00 1,110 1,l2uj(mat
0,00 0,10 0,20 0,30 OfiO 0,50 0,60 0,70 0,80 0,90
МН/н>
400
350
300
250
200
НО
100
50
f
•— pQ-
рд#н0
0
u? .
^——
. ¦
г—"
о- о'6
д- ел
Т-«7й
v-20i
.
г
0
п
2
10
ij
0
в
, . . , , , , , ,
О 0,10 0,20 0,30 0,40 0,50 ,0,60 0,70 0,80 0,90 0,100 0,1H 0,120 /0
0,00 0,10 0,20 0,30 0,10 0,50 0,60 0,70 0,80 0,90
Ь)
Рие. 4.14. Результаты опытов Дэвиса. Испытания стальных образцов [7]:
а — выявление связи максимального касательного напряжения с максимальной
угловой деформацией; б— выявление связи октаэдрического касательного напря-
напряжения с ок'таэдрической угловой деформацией
мального касательного напряжения от максимальной угловой де-
деформации несколько больший, чем для зависимости октаэдрического
касательного напряжения от октаэдрической угловой деформации.
В более поздних опытах Дэвиса [47 ] тонкостенные стальные трубы
подвергались воздействию внутреннего давления, растяжения и
кручения. При этом направления главных осей в течение всего про-
71

цесса деформирования сохранились постоянными. В результате ис-
испытаний установлено, что интенсивность напряжений с достаточ-
достаточной степенью точности является "функцией интенсивности деформа-
деформаций, не зависящей от типа напряженного состояния.
На основании изложенного выше заключаем, что опыты Дэвиса
хорошо согласуются с теорией малых упруго-пластических дефор-
деформаций.
Опыты А. М. Жукова [10], [12], [13]. В работе [10J
описаны испытания хромоникелевых стальных труб при нагружении
их растягивающей силой и внутренним давлением. Большинство
ё- мн/м2 испытаний проводилось в услови-
" : ях простого нагружения, так что
заданное отношение главных нап-
напряжений сохранялось до момента
разрушения. Однако в некоторых
испытаниях это отношение в опре-
определенных интервалах нагружения
преднамеренно нарушалось. Этим
создавалось сложное нагружение.
На рис. 4.15 в координатах е,,
а{ представлены результаты ис-
испытаний образцов при различных
величинах отношения осевого на-
напряжения к окружному. Из рисун-
рисунка следует, что диаграмма дефор-
деформирования материала не зависит
от типа напряженного состояния.
В статье [12] описаны испытания трубчатых образцов из стали
ЭИ415 при нагружении их растягивающей силой и внутренним да-
давлением.
Восемь образцов были испытаны в условиях простого, а три —
в условиях сложного нагружения. Сложное нагружение состояло
в том, что отношение главных напряжений при испытаниях изме-
изменялось. При этом, однако,-ни одно из главных напряжений не убы-
убывало и направления главных осей сохранялись постоянными. Ре-
Результаты опытов (рис. 4.16, а) показывают, что как при простом
нагружении, так и при указанном выше сложном нагружении диа-
диаграмма деформирования не зависит от типа напряженного состояния.
На рис. 4.16, б точки, полученные экспериментально, предста-
представлены в координатах %а, %s. Они располагаются вблизи прямой,
уравнение которой Хе = Х<т> причем указанное выше сложное на-
нагружение заметным образом не удаляет точки от этой прямой.
В работе [13] приведены результаты испытаний трубчатых об-
образцов из стали ЗОХНЗА при нагружении их растягивающей силой
и внутренним давлением. Образцы испытывались как при простом,
так и при сложном нагружении. На рис. 4.17, а экспериментально
полученные точки представлены в координата-х %а, хе. Как следует
из рисунка, точки располагаются вблизи прямой, уравнение которой
Хе = %а- Результаты опытов (рис. 4.17, б) свидетельствуют также
72
750
500
250 5
О 1 2 3 4 eL,%
Рис. 4.15. Результаты опытов А.М.Жу-
А.М.Жукова. Испытания образцов хромонике-
левой стали [10]

о том, что как при простом, так и при сложном нагружении диаграмма
деформирования не зависит от типа напряженного состояния.
На основании изложенного заключаем, что теория малых упруго-
пластических деформаций хорошо согласуется с опытами А. М. Жу-
Жукова при простом нагружении и достаточно хорошо при сложном
800
600
ЧОП
900
1
г
5,
t «
Д 0
о 0,5
с
(
з 0,25
> 0,75
-1,
1
,
0
-0,8-0,6-0,4-0,
/
/
/
Ofi
Ц
o]
у
-Ofi
-0,6
-0,8
-1,0
tf a
•
•
0
д
D
A
A
n О
2 Ofi 0,
oo 0
0 ®
0,5 +¦
«гл Й
0,75
A
6 0,8 XS
,25
>•>
7,6W
19Ц
I
82
15
6)
<toa -
200
Рис. 4.16. Результаты опытов
А. М. Жукова. Испытания
образцов стали ЭИ415 [12]:
а — проверка существования
единой диаграммы деформирова-
деформироваб
др др
ния; б — равенства параметров
Надаи — Лоде
нагружении, близком к простому. Это же заключение имеет место
и при рассмотрении приведенных выше результатов других иссле-
исследователей.
Перейдем к рассмотрению экспериментальной проверки теории
течемия.
Опыты А. М. Жукова и Ю. Н. Работнова [9].
Испытаниям на растяжение и кручение подвергались тонкостенные
трубчатые образцы из стали 25. Образцы вначале растягивались,
а затем закручивались, причем в процессе кручения напряжение от
растяжения оставалось постоянным.
На рис. 4.18 изображены диаграммы предварительного растя-
растяжения (конец каждой кривой соответствовал началу догр.узки кру-
73

Xe
§1-0,55-0,495
9 1-0,94 e 1-0,95
• 0,5-1,225 + 1-1,78
а О Д1-1,91-2,1
о 0,5-0,45
•0,5 V<
О 1j,15-1,08
-1
Рис. 4.17. Результаты опытов
А. М. Жукова. Испытания
образцов стали 30ХНЗА[13]:
а — проверка равенства пара-
параметров Надаи—Лоде; б — ftpo-
верка существования единой
диаграммы деформирования
woo
о-0,5
0,495 ©- 1-1,16-1,0&
®-1-0,95
225 ®-1-1,28
-1-1,91-1,1
о- ехэ
- /
D- /

тящим моментом), а на рис. 4.19 — догрузки. В начальный момент
догрузки имеется небольшой линейный участок. Коэффициенты про-
пропорциональности, соответствующие этому участку, для первых трех
кривых 5-10* МН/ма, а для четвертой 4,5• 104 МН/м2. Величины
модулей упругости первого и второго рода Е ^2,15-Ю5 МН/м2,
G-8-104MH/m».
б, МН/м
Рис. 4.18. Диаграммы предварительного растяжения
в опытах А. М. Жукова и Ю. Н. Работнова [9]
По теории малых упруго-лластических деформаций согласно
формулам D.32) модуль сдвига в начальный момент догрузки дол-
должен быть равен одной трети секущего модуля, а по теории течения
согласно формулам D.23) — модулю сдвига в пределах упругости.
г,МН/мг
25
О
Рис. 4.19. Диаграммы догрузки в опытах А. М. Жукова
и Ю. Н. Работнова [9]. Кривые с кружочками получены
экспериментально, тонкие линии — по теории малых
упруго-пластических деформаций, штриховые — по теории
течения
На рис. 4.21 тонкими линиями нанесены начальные участки догрузки
по теории малых упруго-пластических деформаций, а штриховыми
линиями — по теории течения. Как следует из сопоставления этих
кривых е экспериментальными, ни теория малых упруго-пластиче-
упруго-пластических деформаций, ни теория течения не согласуются с данными опы-
75

тов. К такому же результату привели испытания тонкостенных труб
из стали 20, проведенные А. М. Жуковым по такой же методике,
как и в предыдущих испытаниях [11].
Опыты Ш. Н. К а ц а и Л. М. К а ч а н о в а [22 ]. Испы-
тывались тонкостенные трубчатые образцы из отожженной стали 20,
которые вначале нагружались внутренним давлением так, чтобы
в них возникли пластические деформации, а затем к ним приклады-
прикладывался крутящий момент (рис. 4.20). Как следует из результатов ис-
испытаний, модуль сдвига в процессе догрузки равен модулю сдвига
в пределах упругости независимо от степени пластической деформа-
деформации, что согласуется с теорией течения. По теории малых упруго-
пластических деформаций модуль сдвига при догрузке сильно за-
р,МН/м? 0
10
м.нм
10
2,5 Ад/Я, %
ДО
Рис. 4.20. График зависимости давления р от окружной деформации —=—,
где D — средний диаметр трубки (кружочки) и графики зависимости крутя-
крутящего момента М от угла закручивания <р при догрузке в опытах Ш. Н. Каца
и Л. М. Качанова [22]
висит от величины накопленной пластической деформации. Таким
образом, результаты рассмотренных испытаний при сложном на-
гружении хорошо согласуются с теорией течения и противоречат
теории малых упруго-пластических деформаций.
Опыты Моррисона и Шепферда [28]. Испыты-
вались тонкостенные стальные и силуминовые трубки по следующей
программе: 1 этап — продольное растяжение; растягивающая сила
увеличивается ступенями; 2 этап — крутящий момент увеличивается
ступенями, растягивающая сила убывает; 3 этап — растягивающая
сила увеличивается ступенями, крутящий момент убывает; 4 этап —
крутящий момент увеличивается ступенями, растягивающая сила
убывает.
Из результатов испытаний (рис. 4.21, 4.22) следует, что теория
течения в основном лучше согласуется с результатами опытов, чем
теория малых упруго-пластических деформаций.
На основании изложенного выше можно сделать следующее за-
заключение. При простом нагружении теория течения совпадает с тео-
теорией малых упруго-пластических деформаций. В этом случае экс-
экспериментальные данные хорошо согласуются с теорией пластич-
пластичности. Сложное нагружение экспериментально изучено недостаточно.
76.,

Т.МН/м2
17,5
02 0
46,5
310
/
п
1
/
/
/
/
/
1
2-й этап
Г, МН1м2
0,2 0,4 0,6 0.8 1,0 1,2 ?,У'1О
II/У
3-й этап
о
Т,МН/мг
171
VJb
140
124
10S
'ДО
77,^
02,0
А
/4
i
Ч-и этап
а)
О 2
Т, мн/мг
202
186
171
155
140
з ej-w3 o i
#
8
\
//*
^"
r
'<>
4-u -
/
man
к-"
2 3 4 ?,У-!03
В)
1'нс. 4.21. Графики зависимости касательного и нормального напряжений от угловой
и линейной деформаций для стальных труб в опытах Моррисона и Шепферда [28].
Сплошные линии—экспериментальные кривые, штриховые — по теории течения,
штрих-пунктирные — по теории малых упруго-пластических деформаций; а — пер-
первый образец; б — второй образец

Несмотря на это, однако, можно заметить, что результаты экспери-
экспериментального изучения сложного нагружения лучше согласуются с тео-
теорией течения, чем с теорией малых упруго-пластических деформаций.
Во всех опытах, результаты которых изложены выше, испыта-
испытаниям подвергались тонкостенные трубчатые образцы при совмест-
Г, МЩм2
о
б,МЩмг
и
If
iff
IN
Is.
к
V
f
1
/л
/ж
/
г-и .
/">
man
&J-W О
в.МЩм2
6 SJ-/O3
ЧВ.5
-г
в aw1
Рис. 4.22. Графики зависимости касательного и нормального напряже-
напряжений от угловой и линейной деформаций во втором и третьем этапах
нагружения для двух силуминовых труб в опытах Моррисона и Шеп-
ферда [28]. Обозначения те же, что и на рис. 4.21
ном нагружении их внутренним давлением, растягивающей силой
и крутящим моментом. При таком нагружении в образцах возникали
двухосные напряженные состояния.
§ 26. Разгрузка. Остаточные напряжения
и деформации
Согласно закону разгрузки при одноосном растяжении умень-
уменьшение напряжений при разгрузке аРазг прямо пропорционально
уменьшению деформаций еРазг, причем коэффициент пропорциональ-
пропорциональности тот же, что и в начальной стадии нагружения.
78

Выше (см. § 24) отмечалось, что интенсивность деформаций мо-
может быть представлена в виде суммы интенсивностей упругих и пла-
пластических деформаций. Поэтому диаграмма деформирования мате-
материала имеет такой же вид, что и диаграмма растяжения не только
при нагружении, но и при разгрузке. Следовательно, диаграмма раз-
разгрузки на графике е,, at является прямой (ВС), параллельной
начальной прямой нагружения (ОА)
(рис. 4.23).
Уменьшение интенсивности напряже-
напряжений при разгрузке прямо пропорционально
снижению интенсивности ^ деформаций,
причем коэффициент пропорциональности
тот же, что и в пределах упругости. Таким
образом, математическая формулировка
закона разгрузки имеет вид
afa3r =
разг
D.45)
Допустим, что в результате нагруже-
нагружения тела массовыми X/ и поверхностны-
поверхностными Xyj силами за пределы упругости в нем
возникли напряжения Оц и деформации
Рис. 4.23. Диаграмма дефор-
деформирования при нагружении
и разгрузке
Предположим далее, что нагруженное
тело разгружается. Объемные и" поверх-
постные силы уменьшаются до значений X/, Xvj, а напряжения
и деформации уменьшаются на величины of®31", е?'зг до значений
остаточных напряжений и деформаций а0", е°/т. Таким образом,
„разг
D.46)
Очевидно, что компоненты деформаций е?/ и е°" удовлетворяют
условиям совместности деформаций B.4).
Компоненты напряжений atj удовлетворяют дифференциальным
уравнениям равновесия A.4) и условиям на поверхности A.2) с мас-
массовыми силами X/ и поверхностными силами Xvi. Компоненты на-
„ ОСТ
пряжении Gij удовлетворяют тем же уравнениям с массовыми си-
силами Х) и поверхностными силами X*Vf. Поэтому и компоненты на-
напряжений aPif3r удовлетворяют дифференциальным уравнениям рав-
равновесия A.4) и условиям на поверхности A.2) с массовыми силами
X/ — Xj и поверхностными силами Xvl — X*v/, а компоненты де-
деформаций е?/зг удовлетворяют условиям совместности деформаций
B.4). '
Учитывая, что при разгрузке уменьшение интенсивности напря-
напряжений прямо пропорционально уменьшению интенсивности дефор-
деформаций, заключаем, что напряжения и деформации разгрузки следует
определять путем решения задачи теории упругости для внешних
79

сил, равных разностям силлри погружении, и сил, остающихся после
разгрузки. В случае полной разгрузки последние равны нулю и задача
теории упругости решается для внешних сил, нагружающих тело.
Остаточные напряжения и деформации согласно формулам D.46)
определяются как разности напряжений и деформаций, возникаю-
возникающих при нагружении, и уменьшений напряжений и деформаций при
разгрузке (разгрузочных напряжений и деформаций).
Изложенное выше справедливо в предположении, что в процессе
разгрузки материал вновь не выходит за пределы упругости. В книге
[29] рассмотрена разгрузка с учетом перехода материала в процессе
разгрузки за пределы упругости.
Вопросы образования остаточных напряжений, влияния их на
прочность, а также методы определения остаточных напряжений
в стержнях, пластинах, толстостенных трубах и дисках освещены
в книге [3].
§ 27. Теория пластичности изотропного материала
с анизотропным упрочнением
Как уже отмечалось в предыдущем параграфе, если считать, что в процессе
нагружения поверхность пластичности равномерно (изотропно) расширяется, то
в этом случае невозможно описать анизотропию, возникающую в процессе деформа-
деформации, так называемую деформационную анизотропию, простейшим проявлением кото-
которой является эффект Баушингера.
Для отражения деформационной анизотропии можно предположить, например,
что в процессе нагружения поверхность начала пластичности испытывает только
жесткое смещение (рис. 4.24).
В таком случае упрочнение называют трансляционным. Очевидно, что тогда
эффект Баушингера будет описан, поскольку при прямом @Ах) и обратном @А2)
нагружениях (рис. 4.24) за счет смещения поверхности пластичности пластические
деформации возникают при напряженных состояниях различной интенсивности.
Приняв условие пластичности Хубера—Мизеса, имеем
f Ы = 4" С'/ - р'/) Сч ~р'/) -4 = °- D-47)
В этом уравнении pt-/— координаты центра поверхности пластичности, изме-
изменяющиеся при пластической деформации и образующие девиатор. Этот девиатор
называют девиатором добавочного напряжения, а девиатор si/—рг/—девиатором ак-
активного напряжения. Таким образом, условие D.47) можно получить из выраже-
выражения D.18) подстановкой в него вместо компонентов девиатора полного напряжения
компонентов девиатора активного напряжения и заменой Ф (q) на О"т.
Используя ассоциированный закон течения D.8) и условие D.47), получаем
компоненты приращения пластической деформации
def, = 3dk(slJ-pil). D.48)
Следом поверхности пластичности, соответствующей условию пластичности
D.47) на девиаторной плоскости в трехмерном пространстве главных напряжений,
является окружность радиуса I/ -^- а смещающаяся в процессе нагружения
(рис. 4.25). Очевидно, что для определенности необходимо ввести допущение о сме-
смещении центра поверхности пластичности, т. е. о законе изменения девиатора рц.
80

А. Ю. Ишлинский в 1954 г. [19] предложил простейшую зависимость
Р17=</. D-49)
где с—постоянная для определенного материала. Согласно этой зависимости сме-
смещение центра поверхности имеет место в направлении деформирования. Подставим
что выражение в условие пластичности D.47). Тогда получим
Ы = "Г (su - <*?/) (sh - </) -4 = о-
D.50)
К такой же теории пластичности пришел
и 1955 г. Прагер [31]. Он проиллюстриро-
н,1л ее на простой кинематической модели.
11оэтому иногда эту теорию называют также
теорией кинематического упрочнения.
I'не. 4.24. Жесткое смещение поверхности Рис. 4.25. Жесткое смещение следа
пластичности в процессе нагружения цилиндра Хубера—Мизеса на деви-
аторной плоскости в процессе на-
нагружения
В простейшем случае одноосного растяжения—сжатия
а 2
ах = аУ = °> аг = а> ЪХУ=хУг= tzx— ®> Sx = Sy~ 3" ' Sz = ~3~ °'
„Р _ рр
ех — ъу ~
— vp — „р —
~ Ууг ~ Угх ~
п из уравнения D.50) имеем
Последнее уравнение преобразуем к виду
D.51)
причем знак плюс соответствует растяжению, знак минус—сжатию. Если учесть,
что
то тогда получаем уравнение диаграммы растяжения материала с линейным упроч-
упрочнением (рис. 4.26)
а = ат + Ет (8 - 8Т),
п котором модуль упрочнения -
З
'T
81

и, следовательно,
с =-
D.52)
1—•
Таким образом, приняв условие пластичности в форме D.47), получаем диа-
диаграмму растяжения материала с линейным упрочнением без площадки текучести.
Параметр с в формуле D.50) связан с модулем упрочнения Ет и модулем упругости Е
отношением D.52). В случае построения диаграммы растяжения в координатах ер, а
Рис. 4.27. Диаграмма растяжения с ли-
линейным упрочнением в координатах ер,
а и текущие пределы текучести при
растяжении и последующем сжатии
Рис. 4.26. Диаграмма растяжения с
линейным упрочнением в координата)/
8, а
(рис. 4.27) модулем упрочнения яв-
3
ляется величина — с.
Из уравнения D.51) следует, что
после растяжения образца первона-
первоначально изотропного материала до вели-
величины пластической деформации ер пре-
предел текучести его в направлении
растяжения увеличился на -^ сер. Если же после такого растяжения- разгрузить
образец, а затем сжать его, то тогда предел текучести уменьшится, причем, как сле-
следует из формулы D.51), сумма абсолютных значений этих новых пределов текучести
при растяжении и сжатии равна удвоенному пределу текучести недеформированного
материала (рис. 4.27)
В таком случае эффект Баушингера принято называть идеальным.
Установим теперь, насколько- изменились пределы текучести в направлениях,
перпендикулярных направлению растяжения. Иными словами, найдем предел теку-
текучести образца, растянутого до величины пластической деформации ер в направле-
направлении, перпендикулярном оси последнего.
Для этого необходимо в соотношении D.50) положить
ах = а, ау = аг .= 0, %ху = %уг = хгх = 0,
2 а
(поскольку образец растягивается в направлении оси х),
~Р вр Л_ „р _ 9р -,р ,,р ,,р п
ех — гу — 2 ' &г~г ' Уху~ Чух — Угх ~ °
(ввиду того что до растяжения в направлении оси х образец растягивался в напра-
направлении оси г).
82

Тогда получим
откуда
4а2 + бсеРа + 9 {сеР)г — 4а2т = О
и, следовательно,
—Зсе" ± 1ЛЦ. _27(cepJ
L__ ^ -^ D.53)
причем знак плюс соответствует растяжению, а знак минус — сжатию.
Обозначим превышение нового предела текучести в направлении растяжения
по формуле D.53) над первоначальным ат через а
. 3 „
ат
Тогда
Зсер = 2ат(а—1)
и из формулы D.53) устанавливаем
D.54)
"т
. Эта формула и является решением поставленной задачи. Например, принимай
а— 1,20, получаем по формуле D.54) = 0,885 в случае растяжения и =
= —1,085 в случае сжатия. Таким образом, в результате растяжения материала
до величины напряжения, на 20% большего предела текучести ат, предел текучести
его при растяжении в направлении, перпендикулярном первоначальному растяже-
растяжению, уменьшается на 11,5%, а при сжатии в том же направлении увеличивается
па 8,5%.
Как показала экспериментальная проверка [14], рассмотренная теория пластич~
ности с трансляционным упрочнением лишь качественно описывает явление дефор-
деформационной анизотропии.
Для лучшего количественного согласования результатов теории и экспери-
эксперимента целесообразно комбинировать расширение и жесткое смещение поверхности
пластичности (изотропное и трансляционное упрочнение). \
Вариант такой теории был предложен Ю. И. Кадашевичем и В. В. Новожило-
Новожиловым в 1957 г. [20]. Ими принято условие пластичности в виде
f (<Ч/) = -§- (si, - рч) (si, - рч) - [Ф (</)Р = 0, D.55)
и следующая зависимость координат центра поверхности пластичности от пластиче-
пластической деформации
где р,- = I/ -д- pijPij — интенсивность добавочных напряжений.
Компоненты приращения пластической деформации по-прежнему определяются
формулой {4.48).
В частном случае Ф (q) — ат = const и g (pf) = с— const. Эта теория совпа-
совпадает с теорией Ишлинского—Прагера.
83

Из выражения D.55) заключаем, что следом поверхности пластичности на де-
виаторной плоскости в трехмерном пространстве главных напряжений является
окружность, расширяющаяся и смещающаяся в процессе нагружения (рис. 4.28).
Решение по теории Кадашевича—Новожилова рассмотренной выше задачи опре-
определения предела текучести в направлении, перпендикулярном направлению предвари-
предварительного растяжения до величины пластической деформации ер, очевидно, приведет
к уравнению, которое может быть получено из уравнения D.53) заменой ат на Ф (ер)
и с на g (ер), поскольку в рассматриваемом случае функции Ф (q) и g (рг) в конечном
счете являются функциями ер:
D.57)
Таким образом, для подсчета предела текучести необходимо располагать функ-
функциями Ф (ер) и g (sp). Они могут быть определены на основе испытаний материала
на растяжение с разгрузкой в различных точках диаграммы растяжения при напря-
Рис. 4.28. Одновременное равномерное
расширение и жесткое смещение следа
поверхности Хубера Мизеса
Рис. 4.29. Диаграмма растяжения в ко-
ординатах еР, а и текущие пределы те-
кучести при растяжении и последую-
щем сжатии .
жениях ор и пластических деформациях ер и последующего испытания материала
на сжатие до появления пластических деформаций при напряжениях сгсж (рис. 4.29).
Аналогично тому, как ранее была получена формула D.51), в рассматриваемом
случае можно получить
Решая эти уравнения относительно Ф (ер) и g (ep), имеем
ф (8р) = qP~q^ , g (8p) = -р
*
Зер
D.58)
Последние формулы позволяют на основании результатов указанных выше
испытаний определить функции Ф (ер) и g (ep).
Рассмотренная теория не справедлива прн циклических нагружениях. Дей-
Действительно, при циклическом деформировании по замкнутой траектории (в начале
84

и конце цикла гр{. = 0) согласно приведенным выше уравнениям материал не приоб-
приобретает анизотропии, в то время как экспериментальные исследования показывают
возникновение анизотропии и при циклических нагружениях.
На это обстоятельство было обращено внимание Р. А. Арутюняном и А. А. Ва-
куленко [1, 2], которые предложили использовать то же условие пластичности D.55),
что и в теории Кадашевича—Новожилова, а зависимость координат центра поверх-
поверхности пластичности от пластической деформации D.56) заменить следующей;
dp{, = A (a,.) def'.
Это соотношение используют не только для исследования циклического дефор-
деформирования. Предполагают, что оно лучше отражает историю нагружения, чем выра-
выражение D.56).
Дальнейшее развитие теорий пластичности, отражающих деформационную ани-
анизотропию, дано в работах [5, 26, 44, 45, 50, 51] и др.
§ 28. Теория пластичности ортотропного материала
с изотропным упрочнением
Ниже изложена теория пластичности ортотропного материала без учета дефор-
деформационной анизотропии (изотропное упрочнение), предложенная Хиллом [41].
Эга теория широко используется для расчета конструкций из прокатаниых листовых
материалов, в которых одна из осей симметрии (ось х) совпадает с направлением
прокатки. Ось г перпендикулярна листу (см. § 19).
По этой теории условие пластичности имеет вид
2/ {oi j) = Н(ах- oyf + F{oy- <yzf +G{o2- oxf +
+ Wx\y + 2Lxyz + 2Mx\x -1 = 0, D.59)
где H, F, G, N, L, M — параметры, характеризующие текущее состояние анизо-
анизотропии.
Для начала пластичности оно совпадает с условием начала пластических дефор-
деформаций, предложенным Мизесом и Хиллом, рассмотренным в § 19 [уравнение C.25)].
В этом случае указанные выше параметры равны соответствующим величинам с ин-
индексом 0 (см. § 19).
Применяя условие пластичности D.59) последовательно для частных случаев
трех одноосных растяжений в направлении осей х, у, г и трех сдвигов между этими
осями, так же как в § 19 [см. формулы C.27)], получим
1
°1
ol
D,60)
где ах
%ху, хуг,
)
х у г х уг а — ординаты диаграмм растяжений и сдвигов (текущие
пределы текучести) в различных направлениях.
Ввиду того что упрочнение предполагается изотропным, поверхность пластич-
пластичности в процессе деформации расширяется равномерно и напряжения при растяже-
растяжении образцов, вырезанных в различных направлениях (текущие пределы текучести),
растут строго пропорционально по мере того, как материал упрочняется.
85

Поэтому
и согласно формулам D.60) и C.27) параметры анизотропии Н, . . ., М умень-
уменьшаются пропорционально
я--р~» •••» М = ~р"> D.61)
где величины Но, • • -, Ма определяются формулами C.27).
В соответствии со сказанным в § 20, параметр h является функцией или работы
пластической деформации или параметра Удквиста. В отличие от изотропного тела
в рассматриваемом случае в зависимости от прииятой гипотезы получаются различ-
различные варианты теории пластичности. Хиллом [41] было принято, что параметр h
является функцией работы пластической деформации. Такой вариант теории пла-
пластичности называют теорией энергетического упрочнения. Он используется в даль-
дальнейшем. Второй вариант, в котором принято, что величина h является функцией
параметра Удквиста, развит в статьях Дьяконица [48] и Чэкрэбэрти [46]. Его назы-
называют теорией деформационного упрочнения.
Введем, следуя Хиллу [41], понятие эквивалентного напряжения
+ °о
D.62)
(Д7 ?, М \
Но = Fo = Go = = ¦ = —^2. j величниа
эквивалентного напряжения аЭкВ совпадает с интенсивностью напряжений 07.
Используя соотношения D.61) и D.59), преобразуем выражение D.62) к виду
= у
2 (Яо + F0 + Go)
h,
D.63)
т. е. эквивалентное напряжение пропорционально h и является функцией работы
пластической деформации.
Зависимости приращений пластических деформаций от приращений напряже-
напряжений согласно ассоциированному закону течения D.8) и с использованием соотноше-
соотношений D.59) и D.61) имеют вид
К = -
["о (°, - °у) + GQ (ОХ - Ог)];
86

Найдем из выражений D.64) величины ах — ау, ау — аг, а2 — ах, тху, хуг,
" dk
¦ &_ H0F0 + G0H0 + F0G0 '
dl HoFo + GoHo + FoGo '
. _
' yz~
2dX ~T7~' %zx~ 2dk
Подставим эти величины в выражение D.62). После преобразований устанавли-
устанавливаем
аэкв ~ Л, (H0F0 + G0H0 + F0G0)
X /3
{"о Со К - Go dePf + F0 (G0deP- Ho ds')* +
Введем понятие эквивалентного приращения деформации
¦ ЛР !v
X ]/-|- (Яо + Fo + Go) |я0 (Fo d8P - Go de^J + Fo (God8P - Я
+ Go (Яо deP - Fo dejJ + ^- (Яо^о + GQH0 + FQGof x
Для изотропного материала f Яо = Fo = Go = —яр- = —^- = —Д- 1 - величина
эршивалентиого приращения деформации совпадает с интенсивностью приращений
деформаций.
Из выражения D.65), используя соотношения D.63) и D.66), устанавливаем
dX-a3-Bde«KB. D.67)
Покажем теперь, что величина dX равна приращению работы пластической
деформации
d4p = o{j deff. D.68)
87

Для этого подставим в выражение D.68) компоненты пластических деформаций
по формулам D.8). Тогда получим
:aiidb-5Z—- D.69)
Как следует из выражения D.59), выражение 2/(а,';) + 1 является однородной
функцией переменных О(/ второй степени. Поэтому на основании теоремы Эйлера
об однородных функциях
ац -щ- № (ац) + I] = 2 [2/ (о,/) + 1],
откуда, используя соотношение D.59), имеем
и поэтому из соотношения D.69) устанавливаем
dA" = dk.
Таким образом, из соотношений D.70) и D.67) заключаем, что
D.70)
D.71)
Если принять, как это было сделано ранее, что h, а значит, и эквивалентное
напряжение являются функциями работы пластической деформации, то тогда из соот-
соотношения D.71) можно показать (см. § 23), что эквивалентное напряжение является
функцией интеграла от эквивалентного приращения пластических деформаций
График этой функции называют диаграммой деформирования материала. Ниже
будет рассмотрено построение диаграммы деформирования по диаграмме растяжения.
-- Зависимости приращений пластических деформаций от напряжений D.64)
могут быть преобразованы с использованием соотношений D.67) и D.63) к такой же
форме, как и в случае изотропного материала:
<кв
2 (Но + F0 + Go) о-экв
3 *экв
\ х у) ' 0 \ х z)li
у 2 (Яо ¦
Go)
^-2Щ
Go
— [О0(а2-с
vp —
3/V0
Я„ + Fo + Go
3L0
Яо + fo
ЗМС
Яо + Fo + Go
v;
аьэкв
D.72)
88

Используем формулы D.62) и D'.72) для грех частных случаев одноосных
растяжений в направлениях осей симметрии х, у и г.
1) Одноосное растяжение в направлении оси х:
°х Ф 0; оу = ог = 0; хху = хуг = тад = 0; аЭкв = go*;
Щт =-?¦•> D-73)
2 (Я* + RxRy + R'y)
2) Одноосное растяжение в направлении оси г/:
ау Ф °; °г = с* = °; ta:i/ = V = тгл: = 0; аЭкв
D74)
.-у:
D.76)
D.77)
3) Одноосное растяжение в направлении оси г:
at. (\. * — п — П* т — т — т — О* п
2 =f= v, L/д; —¦ Uy — v, t%y tyz • ь%х \Jt иЭкВ
tfef
V= I/ -s— v"* ^ w . D.79)
Hi соотношений D.74), D.77) и D.79) следует, что
а2 + Ра + V2 = 3.
Формулы D.73)—D.79) позволяют по диаграмме растяжения в одном из трех"
м.шраилепий симметрии (х, у или z) и трем пределам текучести в этих направлениях
iinci'piiiiTii диаграммы растяжения в двух других.
Аналогично могут быть построены диаграммы растяжения образца, вырезан-
iini о им лисга в направлении под некоторым углом к оси х по диаграмме растяжения
it направлении х или у, трем пределам текучести при растяжении в направлениях
iiirfi v, // и z — ахт, оут, 0"гт и пределу текучести при чистом сдвиге ххут или пре-
лс-лу к'кучести при растяжении в направлении под некоторым углом к оси х.
Величину предела текучести при растяжении в направлении, перпендикулярном
илщпме листа, определить невозможно. Определение предела текучести при сжатии
him же направлении, равного'пределу текучести при растяжении, согласно допу-
1,1411110 о гом, что механические характеристики материала при растяжении и сжатии
•щпакопы, связано с трудностями. Поэтому предел текучести при растяжении
направлении, перпендикулярном толщине листа, обычно определяют с помощью
iMi'pemiii поперечных деформаций при растяжении образцов, оси которых совпа-
совпадают с направлениями х или у.
89

Действительно, на основании формул D.72J получаем при растяжении вдоль
оси х (ох фО, ау—аг— 0, хху — хУг = rzx = 0)
dep
и, следовательно,
Rx="j^f~ • D-80)
Таким образом, измерение поперечной деформации в направлении оси у при
растяжении вдоль оси х позволяет определить величину Rx.
Из формул C.27), используя соотношения D.75) и D.80), устанавливаем
1 _ 1 , 1-2ЦЯ»
Последняя формула дает возможность по двум пределам текучести в направ-
направлениях х а у и величине \iyx, устанавливаемой на основании измерений продольных
и поперечных деформаций, определить предел текучести в направлении, перпенди-
перпендикулярном листу.
Список литературы
1. Арутюнян Р. А. О циклическом нагружении упруго-пластической среды. —
«Известия АН СССР. Механика и машиностроение», 1964, № 4, с. 89—91.
2. Арутюнян Р. А., Вакулеико А. А. О многократном цагружении упруго-
пластической среды. — «Известия АН СССР. Механика», 1965, № 4, 6. 53—61.
3. Биргер И. А. Остаточные напряжения, М., Мащгиз, 1963, 232 с.
4. Геики Г. К теории пластических деформаций и вызываемых ими в материале
остаточных напряжений. — В кн.: Теория пластичности. М., Изд. иностр. лит.,
1948, с. 114—135.
| 5. Данилов В. Л. К формулировке закона деформационного упрочнения. —
«Известия Академии наук СССР. Механика твердого тела», 1971, № 6, с. 146—150.
6. Дэвнс Е. Рост напряжений с изменением деформаций и зависимость «напря-
«напряжения—деформации» в пластической области для меди при сложном напряженном
состоянии. — В кн.: Теория пластичности. М., Изд. иностр. лит., 1948, е. 336—363.
f 7. Дэвис Е. Текучесть и разрушение стали со средним содержанием углерода
при сложном напряженном состоянии. — В кн.: Теория пластичности. М., Изд.
иностр. лит., 1948, с. 364—374.
8. Жуков А. М. О коэффициенте Пуассона в пластической области. — «Изве-
«Известия АН СССР. Отд. техн. наук», 1954, № 12, с. 86—91.
9. Жуков А. М., Работнов Ю. Н. Исследование пластических деформаций стали
при сложном нагружении. — «Инженерный сборник», 1954, т. XVIII, с. 105—112.
10. Жуков А. М. Пластические свойства и разрушение стали при двухосном
напряженном состоянии. — «Инженерный сборник», 1954, т. XX, с. 37—48.
11. Жуков А. М. Пластические деформации стали при сложном нагружеиии. —¦¦
«Известия АН СССР. Отд. техн. наук», 1954, № 11, с. 53—61.
12. Жуков А. М. Сложное нагружение и теория пластичности изотропных ме-
металлов. — «Известия АН СССР. Отд. техн. наук», 1955, № 8, с. 81—92.
13. Жуков А. М. О пластических деформациях изотропного металла при слож-
сложном нагружении. — «Известия АН СССР. Отд. техн. наук», 1956, № 12, с. 72—87.
14. Жуков А- М. Деформационная анизотропия и ползучесть малоуглеродистой
' стали при нормальной температуре. — «Инженерный журнал», 1961, т. 1, вып. 4,
с. 150—153.
90

15. Ивлев Д. Д. К теории простого деформирования пластических тел. — «При-
«Прикладная математика и механика», 1955, т. XIX в. 6, с. 734—735.
16. Ильюшин А. А. Пластичность. М., ГИТТЛ, 1948, 376 с.
17. Ильюшии А. А., Ленский В. С. Сопротивление материалов. М., Физмат,
гиз, 1959, 371 с.
18. Ильюшин А. А. Пластичность. М., Изд-во АН СССР, 1963, 271 с.
19. Ишлииский А. Ю. Общая теория пластичное» с линейным упрочнением. —
«Украинский математический журнал», 1954, т. 6, № 3,-с. 314—324.
20. Кадашевич Ю. И., Новожилов В. В. Теория пластичности, учитывающая
остаточные микронапряжения. — «Прикладная математика и механика», 1958,
т. XXII, в. 1, с. 78—89.
21. Качанов Л. М. Основы теории пластичности. М., «Наука», 1969, 420 с.
22- Кац Ш. Н., Качанов Л. М. О пластической деформации при сложном'
нагружении. — «Известия АН СССР. Отд. техн. наук», 1957 № 11, с. 172—173.
23. Леви М. К вопросу об общих уравнениях внутренних движений, возникаю-
возникающих в твердых пластических телах за пределами упругости. — В кн.: Теория пла-
пластичности. М., Изд. иностр. лит., 1948, с. 20—23.
24. Лоде В. Влияние среднего главного напряжения на текучесть метал-
металлов. — В кн.: Теория пластичности. М., Изд. иностр. лит. 1948, с. 168—205.
25. Людвик П. Основы технологической механики. — В кн.: Расчеты на проч-
прочность. Вып. 15, М., «Машиностроение», 1971, с. 132—166.
26. Мансуров Р. М. О пластическом нагружении первоначально изотропных
сред с деформационной анизотропией. — В кн.: Упругость и неупругость. Вып. 2,
Изд-во Московского университета, М., 1971, с. 137—145.
27. Мизес Р. Механика твердых тел в пластически-деформированном состои-
нии. — В кн.: Теория пластичности. М., Изд. иностр. лит., 1948, с. 57—69.
28. Моррисон Д., Шепферд В. Опытное исследование соотношений между на-
напряжениями и деформациями за пределом упругости. — «Механика. Сборник сокра^
щенных переводов иностранной периодической литературы», 1952, в. 1., с. 107—
134.
29. Москвитин В. В. Пластичность при переменных нагружениях. М., Изд-во
Московского университета, 1965, 263 с.
30. Над аи А. Пластичность и разрушение твердых тел. М., Изд. иностр. лит.,
т. I, 1954, 647 с, т. II, 1969, 863 с.
31. Прагер А., Ходок Ф. Г. Теория идеально пластических тел. М., Изд. иностр.
лит. 1956, 398 с.
32. Работиов К). Н. Сопротивление материалов. М., Физматгиз, 1962, 455 с.
33. Работнов Ю. Н. Ползучесть, элементов конструкций. М., «Наука», 1966,
752 с. ¦'
34. Расчеты на прочность в машиностроении. Т. П., М., Машгиз, 1958, 974 с. .
Авт.: С. Д. Пономарев, В. Л. Бидерман, К. К- Лихарев и др.
35. Рейсе Э. Учет упругой деформации в теории пластичности. — В кн.: Тео-
Теория пластичности. М., Изд. иностр. лит., 1948, с. 206—222.
36. Седов Л. И. О понятиях простого нагружения и возможных путях де-
деформирования.— «Прикладная математика и механика», 1959, т. XXIII, в. 2,
с. 400—402.
37. Сеи-Венаи Б. Об установлении „уравнений внутренних движений, возни-
возникающих в твердых пластических телах за пределами упругости. — В кн.: Теория
пластичности. М., Изд. иностр. лит., 1948, с. 11—19.
38. Сен-Веиан Б. Дифференциальные уравнения внутренних движений, воз-
возникающих в твердых пластических телах, и граничные условия для этих тел. Неко-
Некоторые приложения. — В кн.: Теория пластичности. М., Изд. иностр. лит., 1948,
с. 24—33. -„
39. Смирнов В. И. Курс высшей математики. Т. I. M., Физматгиз, 1958, 478 с.
40. Удквист Ф. Упрочнение стали и ей подобных материалов.— В кн.: Теория
пластичности. М., Изд. иностр. лит., 1948, с. 283—290.
41. Хилл Р. Математическая теория пластичности. М., ГИТТЛ, 1956, 407 р.
42. Шевелев В. В., Яковлев С. П. Анизотропия листовых материалов и ее влия-
влияние на вытяжку. М., «Машиностроение», 1972, 135 с.
91

43. Шмидт Р. О зависимости между напряжениями и деформациями в области
упрочнения. — В кн.: Теория пластичности. М., Изд. иностр. лит., 1948, с. 231—
256.
44. Backhaus G. Zur Fliefigzenze bei allgemeiner Verfestigung.— «Zeitschrifl fur
angewandte Mathematik und Mechanik», 1968, Band 48, Heft 2, S. 99—108.
45. Baltov A., Sawczuk A. A rule of anisotropic hardening.—«Acta mechanica»,
1965, No 1, p. 81—92.
46. Chakrabarty J. A hypothesis of strain—hardening in anisotropic plasticity.—
«International journal of mechanical sciences», 1970, Vol. 12, No 2, p. 169—176.
47. Davis E. A. Combined tension-torsion test with fixed principal directions.—
«Journal of applied mechanics», 1955, Vol. 22, No 3, p. 411—417.
48. Diaconija U. Sur la theorie de la plasticite des corps orthotropes consoli-
dables, «Comptes Rendus», 1969, t269 Serie A, p. 802—804.
49. Johnson W., Mellor P. B. Plasticity for mechanical engineers, D. Van Nostrand
Company, LTD, 1962, 412 p.
50. Mroz Z. On the description of anisotropic workhardening.—«Journal of the
mechanics and physics of solids», 1967, Vol. 15, p. 163—175.
51. Mr6z Z. An attemp to describe the behavior of metals under cyclic loads
using a moregeneral workhardening model.—«Acta mechanica», 1969, No 7, p. 199—212.
52. Prandtl L. Spannungsverteilung in plastischen Korpern.— «Proceedings of
1-st International congress of applied mechanics», Delft, 1924, s. 43—54.
53. Taylor G., J., Quinney H., The plastic distortion of metals.—«Philosophical
transactions of the Royal Society», 1931, Ser. A, 230, p. 323—362.
54. Teoria plastycznosci, Warszawa Paristwowe wydawnictw.o naukowe, 1965,
399 s. Aut.: Z. Marciniak, Z. Mroz, W. Olszak i inni.

ГЛАВА V
ДЕЙСТВИТЕЛЬНЫЕ ДИАГРАММЫ ДЕФОРМИРОВАНИЯ
МАТЕРИАЛА
§ 29. Действительная диаграмма растяжения
Как следует из изложенного выше (см. §§ 23 и 24), для расче-
расчетов за пределами упругости необходимо располагать диаграммами
деформирования материала. В случае больших деформаций нужно
иметь действительные диаграммы деформирования, которые строят
по действительным диаграммам растяжения. Рассмотрим вначале
построение последних.
Экспериментальные исследования механических свойств мате-
материала при одноосном растяжении обычно обрабатывает в виде гра-
графиков зависимости напряжения от деформации. При этом силу Р,
растягивающую образец, относят к первоначальной площади попе-
поперечного сечения Fo, а удлинение образца А/—к первоначальной
расчетной длине образца /:
о=-р-; е=7—, E.1)
т. е. не учитывают изменение площади поперечного сечения образца
и предполагают равномерное деформирование образца по его длине.
Поэтому график зависимости напряжения от деформации (рис. 5.1),
построенный с использованием формул E.1), называют условной
диаграммой растяжения. Иногда его называют просто диаграммой
растяжения.
В действительности площадь поперечного сечения образца не-
непрерывно уменьшается, а при некоторой величине деформации на-
нарушается равномерное по его длине деформирование. Чем больше
величина деформации, тем в большей степени действительные на-
напряжения и деформации отличаются от условных. Поэтому для
решения технологических задач, характеризующихся большими де-
деформациями, необходимо располагать действительной диаграммой
растяжения материала.
Для построения действительной (истинной) диаграммы растя-
растяжения до образования шейки необходимо растягивающую силу отно-
относить к действительной площади поперечного сечения образца F:

Измерение действительных размеров поперенного сечения образца,
в процессе испытания его на растяжение производить неудобно.
Действительная площадь поперечного сечения F может быть легко
связана с первоначальной площадью поперечного сечения Fo, если
приближенно принять, что объем элемента образца Fo dz при его де-
деформации остается постоянным. Поскольку длина dz этого элемента
образца после деформации равна dz (I -f~ e), а площадь попереч-
поперечного сечения равна F, то согласно принятому допущению
Fo dz = Fdz A + е),
откуда
E.3)
Рис. 5.1. Условная диаграмма растяжения
Подставляя эту величину в
формулу E.2), получаем зави-
зависимость действительного напря-
напряжения от условного
ад = аA+е). E.4)
Выше (см. § 15) отмечалось,
что при величине обычной
деформации меньше 20% раз-
различие между логарифмической деформацией и обычной незна-
незначительно. Поскольку шейка образуется при обычной деформации
10—15%", то до этого момента логарифмическую деформацию при-
приближенно можно считать равной обычной. Поэтому до образования
шейки действительная диаграмма растяжения отличается от услов-
условной только по оси ординат и располагается выше ее.
Определим теперь на действительной диаграмме растяжения
материала точку, соответствующую пределу прочности материала.
Из выражения E.4) имеем \
а =¦
1+e •
Дифференцируя это выражение по е, получаем
da 1 daR ая
dz
1 +е dz
A
Полагая, что шейка возникает при условном напряжении, рав-
равном временному сопротивлению ав, имеем
da „
при а= ав —гг- = О
de
и поэтому
— "д
1+8
Согласно формуле E.4) устанавливаем
94

Таким образом, при условном напряжении, равном пределу
прочности, тангенс угла наклона касательной к действительной
диаграмме растяжения численно равен условному пределу прочно-
прочности материала (см. рис. 5.2).
Из последнего соотношения, используя понятие логарифмиче- г
ской деформации B.37) и выражение E.4), получаем
1 = ' rfg« = 1
E.5)
Следовательно, начало образования шейки соответствует на дей-
действительной диаграмме растяжения в координатах е, ад точке, для
которой величина подкасательной % равна единице (рис. 5.2).
Рнс. 5.2. К определению на действительной диа-
диаграмме растяжения точки, соответствующей образо-
образованию шейки
После образования шейки напряженное состояние образца ста-
становится неоднородным и неодноосным, и в этом случае можно по-
построить только действительную диаграмму деформирования.
Изложенный метод построения действительной диаграммы растя-
растяжения справедлив как для изотропных, так и для анизотропных
материалов.
§ 30. Напряженное состояние в шейке
До образования шейки действительную диаграмму деформирова-
деформирования можно принять совпадающей с действительной диаграммой
растяжения, поскольку последнюю строят в предположении несжи-
несжимаемости материала.
После образования шейки построение действительной диаграммы
деформирования должно быть основано на анализе напряженного
состояния в шейке.
Изложим предложенное Н. Н. ДавиДенковым и Н. И. Спири-
Спиридоновой [2] приближенное решение задачи о напряженном состоя-
состоянии точек, лежащих в наименьшем поперечном сечении шейки в об-
образце из изотропного материала.
95

Это решение основано на следующих трех допущениях: 1) ма-
материал несжимаем; 2) логарифмические окружная и радиальная
деформации в точках наименьшего поперечного сечения шейки равны
между собой и постоянны; 3) кривизна траектории одного из глав-
главных напряжений в некоторой точке наименьшего поперечного се-
сечения шейки на расстоянии г от оси (рис. 5.3) может быть предста-
представлена в виде
-Н-т^г- <5-6>
где гх — радиус наименьшего поперечного сечения шейки; R —
радиус кривизны контура шейки в точке наименьшего поперечного
сечения.
Из первых двух допущений следует, что логарифмическая осе-
осевая деформация в точках наименьшего поперечного сечения шейки
равна удвоенной логарифмической ра-
радиальной деформации и постоянна в
этом сечении
гг = — 2гг = const
и согласно формуле B.18) интенсив-
интенсивность логарифмических деформаций
равна логарифмической осевой деформа-
деформации и также постоянна в точках наи-
наименьшего поперечного сечения шейки
е,- = е,= const.
E.7)
На основании выражений B.37), E.7)
Рис. 5.3. К определению напря- и E.3) имеем t
жений в наименьшем попереч- г
ном сечении шейки — . Fn /г п.
- е. = 1п-г- E-8) ¦:
Из равенства логарифмических окружной и радиальной дефор-
деформаций следует равенство окружного и радиального напряжения ;
at = аг и согласно формуле A.21) величина интенсивности напря-
напряжений
а, = аг — аг E.9) .
Поскольку интенсивность логарифмических деформаций по-
постоянна в наименьшем поперечном сечении шейки, интенсивность
напряжений также постоянна в этом сечении.
Для определения напряжений в наименьшем поперечном сече- '
нии шейки используем одно из дифференциальных уравнений
равновесия в цилиндрической системе координат
да г
о> —at
дг
= 0.
E.10)
96

Рассмотрим в меридиональной плоскости траекторию главногб
напряжения аг (рис. 5.3).
Обозначим угол наклона касательной к ней с осью г через а.
Тогда согласно известным из сопротивления материалов [13] фор-
формулам для напряжений в площадке, перепендикулярнои к одной
из главных площадок, нормаль к которой составляет угол а с глав-
главном осью 1, получаем
sih2«.
Считая угол а достаточно малым, так что cos 2а *=» 1, sin 2а я»
<=» 2а, имеем
о, = о-,; аг = о* = On". \
, . , . f E.11)
тг, = (а! — а2) а = (аг — а,) а.)
Из первого уравнения E.10), используя выражение E.9) и E.11)
и учитывая, что для наименьшего поперечного сечения шейки а = О,
получаем
dr ' ' dz
Замечая, что
dot 1
dz ~Т'
и поэтому, используя соотношение E.6), имеем
dor oir
dr ~ rxR '
Проинтегрируем это уравнение, учитывая/ что интенсивность,
напряжений постоянна. Тогда получим
Постоянную интегрирования С определяем из условия аг = 0
при г — rv
В результате получаем
и, следовательно,
ii^) ¦ EЛ2)
А II. II. Малинии - 97

Из формулы E.9) устанавливаем
E.13)
Для определения интенсивности напряжений свяжем растяги-
растягивающую силу с осевыми напряжениями
V
.ш
700
¦600,
500
300
200
100
'гср
•'к
30 20 10 0 10 20г,мм
Рис. 5.4. Эпюры осевых, ради-
радиальных (окружных) напряжений
в минимальном сечении шейки
круглого образца из стали 30
для величины логарифмической
деформации е = 0,68. Началь-
Начальный диаметр образца do=6 мм,
наименьший диаметр шейки
d = 4,4 мм," радиус кривизны
контура шейки в точке наи-
наименьшего сечения R = 4,8 мм
Рис. 5.5. Рентгеновский снимок
шейки алюминиевого круглого
образца непосредственно перед
разрушением [9]
Подставим в это выражение соотношение E.13). После преобра-
преобразований имеем
E.14)
Формулы E.12)—E.14) определяют напряженное состояние в точ-
точках наименьшего поперечного сечения шейки.
На рис. 5.4 изображены эпюры осевых, радиальных (окружных)
напряжений в минимальном сечении шейки круглого образца из
стали 30. Из эпюр следует, что напряжения максимальны в централь-
центральной точке. Рентгеновский снимок (рис. 5.5) показывает, что разру-
разрушение образца, по-видимому, началось в центральной точке наи-
наименьшего сечения.
Формулы E.8) и E.14) позволяют построить действительную
диаграмму деформирования в координатах интенсивность логариф-
логарифмических деформаций — интенсивность напряжений. Для этого
необходимо в процессе испытания производить измерение минималь-
минимального диаметра шейки и радиуса кривизны ее контура в точках наи-
наименьшего поперечного сечения шейки. Поскольку проведение таких
замеров в процессе испытания образца на растяжение связано с боль-
большой затратой труда, для приближенного построения действительной
98

лпаграммы деформирования можно произвести замеры после разру-
разрушения образца (сжав две его половинки при помощи струбцинки).
! in да по формуле E.8) определяем интенсивность логарифмических
пластических деформаций ef в момент разрушения, а по формуле
(.'> М) интенсивность напряжений в момент разрушения. Соединив
i.iк 11м образом установленную конечную точку с точкой, соответ-
I-жующей началу образований шейки, плавной кривой или прямой,
i юл учим приближенную действительную диаграмму деформирова-
и mi.
Па рис. 5.6 приведена действительная диаграмма деформирова-
деформирования стали 30, построенная до образования шейки по формуле E.4),
а после образования ее по форму-
формулам E.8) и E.14). Штриховой ли-
NiiiM'i на том же чертеже представ-
представлена диаграмма растяжения, полу-
полученная без учета изменения на-
напряженного состояния в шейке.
I; лом случае действительные на-
напряжения определяются формулой
Р
Как следует из рис. 5.6, учет
п(менения напряженного состоя- ?00
пня в шейке существенно умень-
уменьшает величины действительных
напряжений.
800
600
if 00
inn
МН/
/
1
м
-—-
^—*
20 W 60 80 г;/.
Рис. 5.6. Действительная диаграмма
растяжения стали 30
Брнджменом [1 ] дано решение задачи в той же постановке с ис-
по.'и/юванием тех же первых двух допущений. Отличие этого реше-
решения от изложенного выше состоит в различии принятых законов
и 1М1Ч1сния кривизны траектории главных напряжений в точках
наименьшего поперечного сечения шейки. В работе [7] также при-
ih'U'iio решение рассмотренной выше задачи, но без использования
|реп>его допущения. Сопоставление полученных решений показы-
паег, что различие результатов невелико. В работах [1] и [2] вто-
второе допущение подтверждено экспериментально. В книге [1 ] и статье
110 I рассмотрено определение напряжений в наименьшем поперечном
еечеппн шейки растянутого плоского образца. В работе [4] получено
нinnоо решение задачи о напряженном и деформированном состоя-
образца в начальный период образования шейки.
§ 31. Схематизация диаграмм деформирования
Для упрощения расчетов за пределами упругости условные или
leiieтигельные диаграммы деформирования, так же как и диаграммы
раешжения [14], могут быть схематизированы, т. е. заменены кри-
iii.iм 11 пли прямыми линиями, имеющими достаточно простое мате-
маш'кгкое выражение и в то же время хорошо совпадающими с экс-
экспериментально полученными диаграммами. Таким образом, можно
99

представить себе диаграмму деформирования с площадкой текуче-
текучести и линейным упрочнением (рис. 5.7), с площадкой текучести и
степенным упрочнением (рис. 5.8).
Для первой диаграммы
при 0 sg ег sg elT ot = 3Ge;;
при е(Т sg: ег sg: е;т oi = аж
при е{
— е*т),
E.15)
E.16)
E.17)
Рис. 5.7. Схематизированная диаграмма
деформирования с площадкой текучести
и линейным упрбчнением
Рис. 5.8. Схематизированная диаграмма
деформирования с площадкой текучести
и степенным упрочнением
а для второй первые две строчки сохраняются, но
* / е,-
ПрИ 6(- ^ 6;т CTj = (Тт
где е(Т — интенсивность деформаций, при которой в материале воз-
возникают пластические деформации; е*т — интенсивность деформа-
деформаций, при которой на диаграмме деформирования кончается площадка
текучести и начинается область упрочнения; Нт — модуль упрочне-
упрочнения, показатель степени m изменяется от 0 до 1.
При помощи формул D.34) и D.36) легко показать, что эти вели-
величины связаны с соответствующими им в случае одноосного растяже-
растяжения 6Т, 8Т и ?т (модуль упрочнения при растяжении) зависимостями
2 ,. . ч * * 1 — 2ц
ЕТ
'-2ц Ет '
3 Е
Как уже отмечалось, если принять условие несжимаемости D.33)
или, что то же, fx = 0,5, получим 3G =?,_etT = ет, е}т = ет, [Нт =
= Ет, т. е. диаграмма деформирования совпадает с диаграммой
растяжения.
Если площадка текучести отсутствует, то следует положить ет =
= ет. Диаграммы деформирования с линейным и степенным упроч-
упрочнением для этого случая изображены на рис. 5.9. и 5.10.
100

В табл. 5.1 приведены основные параметры схематизированных
диаграмм растяжения с линейным упрочнением для некоторых ма-
материалов [12]. Величины ат и Ет получены путем обработки услов-
условных диаграмм растяжения материала по методу наименьших квадра-
квадратов до величины деформации, равной 5ет.
В табл. 5.2 приведены вели-
величины схематизированных пределов
текучести и показателей степени
m для некоторых сталей [8].
Рис. 5.9. Схематизированная дна- Рис. 5.10. Схематизированная диа-
диаграмма деформирования с линейным грамма деформирования со. степенным
упрочнением упрочнением
Иногда для упрощения расчетов зависимость интенсивности
напряжений от интенсивности деформаций не только в области упроч-
упрочнения, но и во всем интервале изменения деформаций аппроксими-
аппроксимируют степенной функцией
-Ае?,
E.18)
Рис. 5.11. Схематизированная диаграм-
диаграмма деформирования со степенным упроч-
упрочнением без упругого участка
Рис. 5.12. Схематизация диаграмма
деформирования диаграммой без упроч-
упрочнения
причем показатель степени щ изменяется от 0 до 1. Такая схемати-
чпрованная диаграмма деформирования изображена на рис. 5.11.
Такая схематизация диаграммы деформирования грубо искажает
жепериментально полученную диаграмму при малых деформациях.
Действительно, при 0 < m < 1 производная от интенсивности на-
напряжений по интенсивности деформации в начале координат равна
101

Таблица 5.1
Параметры схематизированной диаграммы растяжения с линейным упрочнением
для некоторых конструкционных сталей и сплавов [12]
Материал
Сталь 40Х
Сталь 40ХНМ
Сталь ЗОХГС
Сталь 18Х2Н4МА
Сталь Я1Т
Термообработка
Отжиг
Закалка, отпуск 500° С-
Закалка, отпуск 600° С
Закалка, отпуск 560° С
Закалка 330° С
Закалка, отпуск 500° С
Закалка, отпуск 600° С
Закалка, отпуск 525° С
Закалка 950° С, закалка 850° С, отпуск
150° С
Закалка 1050° С
МН/м'
700
1 200
1 000
1 100
1 600
1 200
1 000
1 150
1 320
620
б, %
25
6
9
10
8
8
12
9
10
49
Е-10-»
МН/м2
2^05
2,08
2,10
2,00
1,95
2,05
2,05
1,94
1,92
1,88
400
1 100
780
, 940
720
1 040
800
770
500
188
апц
1,07
1,04
1,1
1,055
1,34
1,07
1,095
1,28
1,37
1,17
Ет
Е
0,069
0,022
0,028
0,0285
0,224
0,035
0,018
0,0545
0,311
0,117

рэдакени; табл. 5.1
О
C
Материал
Сталь ЭИ257
Сталь ЭИ503
Сталь 15Х18Н12С4ТЮ
Сталь ЭИ659
Сплав В95
Сплав В95Т
Сплав ВТ1
Сплав Д16
Сплаэ Д16Т
Сплав АК4
Термообработка
—
'—
Закалка 950° С
Нормализация, отпуск 500° С
Закалка + искусственное старение
Закалка + искусственное старение
Отжиг 700° С
Закалка + естественное старение
Закалка + естественное старение
Закалка + искусственное старение
МН/м2
300
1 050
800
1 300
640
600
600
520
530
380
б, %
30
15
33
11
7
6
15
13
8
15
Е ¦ 10-*
°пц
МН/м!
1,70
2,00
1,80
1,94
0,717
0,7
1,17
0,746
0,72
0,724
160
600
220
520
550
•ч
460
330
305
340
195
°т
°пц
1,28
1,33
1,38
1,385
1,07
1,21
1,3
1,045
1,1
1,14
ЕТ
Е
0,131
0,104
0,327
0,226
0,0285
0,0353
0,079
0,0625
0,0445
0,126

Таблица 5.2
Параметры схематизированной диаграммы растяжения со степенным
упрочнением для некоторых конструкцяоиных сталей [8]
Марка
стали
45
40Х
Р9
ХГ
охнзм
ЭИ756
Термообработка
Закалка в воздухе 820° С
Отжиг 0,5 ч 880° С
Без термообработки
То-же
Закалка и отпуск 550° С
Нормализация 1070—1050° С; охла-
охлаждение на воздухе; закалка 1020—
1050° С в масле; отпуск 660—680° С
в печи
ЕЛО
стт
МН/м2
2,00
2,00
2,10
1,99
2,00
2,12
263
400
280
360
840
400
т
0,204
0,195
0,312
0,190
0,140
0,216
Рис. 5.13. Диаграмма деформирования
жестко-пластического упрочняющегося
тела с площадкой текучести
Рис. 5.14. Диаграмма деформирования
жестко-пластического упрочняющегося
тела без площадки текучести
бесконечности, в то время как в действительности эта величина чи-
численно равна утроенному модулю упругости второго рода.
Частным случаем диаграммы с линейным упрочнением (см.
рис. 5.9) является диаграмма идеального упруго-пластического тела
Рис. 6.15. Схематизированная диа-
диаграмма деформирования идеального
жестко-пластического тела
(см. рис. 4.4), для которого модуль упрочнения равен нулю (НТ =
= 0). Эта диаграмма может быть использована для материалов,
имеющих ярко выраженную площадку текучести при условии, что
интенсивность деформации детали не превосходит величины еп,
, а также в тех случаях, когда она с достаточной степенью точности
104

аппроксимирует действительйую диаграмму деформирования, на-
например, как это представлено на рис. 5.12.
При больших величинах интенсивностей деформаций величиной
упругой деформации по сравнению с пластической можно пренебречь,
пли, что равносильно, принять модуль упругости равным бесконеч-
бесконечности. Тогда получаем диаграмму деформирования, приведенную на
рис. 5.13. Ее называют диаграммой жестко-пластического упрочняю-
упрочняющегося тела с площадкой текучести.
В случае отсутствия площадки текучести (рис. 5.14) за уравнения
ее можно принять следующие выражения:
о{ = от + АеТ,
или
о, = Л(В + е,)и. E.19)'
При отсутствии упрочнения указанную диаграмму называют
диаграммой деформирования идеального жестко-пластического тела
(рис. 5.15).
Список литературы
1. Бриджмен П. Исследование болыцих пластических деформаций и разрыва
М., Изд. иностр. лит., 1955, 444 с.
2. Давиденков Н. Н., Спиридонова Н. И. Анализ напряженного состояния
II шейке растянутого образца. — «Заводская лаборатория», 1945, т. XI, №6,
с. 583—593.
3." Дэвис Е. Текучесть и разрушение стали со средним содержанием углерода
при сложном напряженном состоянии. — В кн.: Теория пластичности. М., Изд.
иностр. лит., 1948, с. 364—374.
4. Жуков А. М. К вопросу возникновения щейки в образце при растяжении. —
«Инженерный сборник», 1949, т. V, вып. 2, с. 34—51.
5. Лихарев К- К- Сопоставление характеристик материалов при одноосных
растяжении и сжатии. — В кн.: Расчеты иа прочность в машиностроении. Сб. 89,
М., Машгиз, 1955, с. 168—196.
6. Лихарев К. К. К методике построения действительных характеристик мате-
рннлов при одноосном растяжении и сжатии. — «Заводская лаборатория», 1957,
т. XXIII, № 12, с. 1472—1477.
7. Малииии Н. Н.., Петросян Ж. Л. Напряжения в наименьшем сечении шейки
растянутого круглого образца. — «Известия высших учебных заведений. Машино-
Машиностроение», 1967, № 6L с. 34—39.
8. Махонина Т. М. Экспериментальное исследование прессовых посадок. —
В кн.: Расчеты на прочность. Вып. 11, М., Машгиз, 1965, с. 385—395.
9. Надаи А. Пластичность и разрушение твердых тел- М., Изд. иностр. лит.,
1954, 647 с.
10. Петросян Ж- Л. Напряжения в наименьшем сечении шейки растянутого
плоского образца. — «Известия высших учебных заведений. Машиностроение»,
1967, № 7, с. 54—58. '
11. Расчеты на прочность в машиностроении. Т. I. M., Машгиз, 1956, 884 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К- Лихарев и др.
12. Сервисен С. В., Когаев В. П., Шнейдерович Р. М. Несущая способность н
расчеты деталей машин на прочность. М., Машгиз, 1963, 451 с.
13. Феодосьев В. И. Сопротивление материалов. М., «Наука», 1974, 559 с.
14. Johnson W., Mellor Р. В. Plasticity for mechanical engineers, D. Van N
rand company 1962, 412 p.

ГЛАВА VI
РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПО ТЕОРИИ
МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
§ 32. Упруго-пластическое состояние толстостенной
трубы, нагруженной внутренним давлением
и осевой силой при отсутствии упрочнения
Допустим, что толстостенная труба, внутренний радиус которой гъ
а наружный г2, нагружена внутренним давлением р и осевой силой N
(рис. 6.1). Примем, что материал трубы несжимаем (е0 = 0, \х = 0,5)
и не имеет упрочнения, т. е. диаграмма деформирования такая же,
как на рис. 4.4. Ниже (см. § 46) будет сопоставлено это решение
с точным, выполненным с учетом сжимаемости материала, а также
рассмотрен учет упрочнения (§ 33).
Для бесконечно дли шой трубы из условия симметрии очевидно,
что поперечные сечения ее при деформации остаются плоскими и
перпендикулярными к оси, т. е. осевая деформация трубы не изме-
изменяется по радиусу и длине
82 = Const. F.1)
Для трубы конечных размеров постоянство осевой деформации
может быть обеспечено приложением на торцах нормальных сил,
распределенных по определенному -закону, симметрично относи-
относительно оси трубы. Равнодействующая этих сил ./V определяется ве-
величиной осевой деформации. В сечениях, достаточно удаленных от
торцов, закон распределения по сечению внутренних нормальных
сил не зависит от того, как внешние нормальные силы распределены
по торцам. Последнее обстоятельство дает возможность для сечений
трубы конечной длины, достаточно удаленных от ее торцов, считать
условие F.1) справедливым.
Допустим, что постоянная в соотношении FЛ) равна нулю, т. е.
е2 = 0. F.2)
Ниже будет установлено, когда это условие справедливо.
В пределах упругости для толстостенной трубы наиболее опас-
опасными точками являются точки на внутренней поверхности [28].
В них первоначально возникают пластические деформации и, сле-
следовательно, пластическая область примыкает к внутренней поверх-
поверхности трубы. Из условия симметрии нагружения относительно оси
трубы следует, что пластическая область в поперечном сечении трубы
представляет собой кольцо. Обозначим радиус границы, разделяю-
разделяющей упругую и пластическую области, через гт (рис. 6.1). Очевидно,
106

что эта величина характеризует степень распространения пласти-
пластических деформаций в сечении трубы. Вследствие осевой симметрии
нагружения в упруго-пластическом состоянии напряжения, дефор-~
мации и перемещения являются функциями только радиуса г. По
этой же причине касательные напряжения в окружном и радиальном
сечениях отсутствуют и, следовательно, эти сечения, а также
поперечное сечение трубы являются главными. Напряжения в
них: радиальное оп окружное at и осевое ог — главные напря-
напряжения.
Радиальное и окружное напряжения в упругой области опреде-
определяем по формулам [281:
^) i (*) F-3)
ог=^=ат(А-^); „,= .i=oT (Л+-*-)•
2
Коэффициент -у= атв формулах F.3) введен перед скобками для
удобства последующих выкладок. Он влияет только на величины по-
постоянных интегрирования.
Рис. 6.1. Схема нагружения толстостенной трубы
В пределах упругости осевая деформация гг связана с осевым аг,
радиальным ог, окружным at напряжениями соотношением
— J_ г л
гг— Е
На основании равенства F.2) получаем зависимость осевого на-
напряжения от окружного и радиального
= -s- {ог + а,).
F.4)
Для определения напряжений в пластической области исполь-
используем дифференциальное уравнение равновесия элемента трубы [28]
dr
.
ar
= 0
F.5)
и поскольку упрочнение отсутствует, условие пластичности C.18).
107

Зависимости компонентов деформаций от .компонентов напря-
напряжений в решаемой задаче согласно соотношениям D.32) имеют вид:
3 е»
— ^
Т Г
F.6)
В рассматриваемом случае в соответствии с соотношениями A.21)
и A.5)
— стгJ-Нст2—огу, F.7)
F.8)
Используя условие F.2), из третьей формулы F.6) получаем
аг = ст0
и согласно выражению F.8)
а, = а„ =
F.9)
Подставляя эту величину в выражение для интенсивности на-
напряжений F.7), имеем
o{= + ^-(ot-br). F.10)
Знак плюс в этой формуле взят потому, что для трубы, нагружен-
нагруженной только внутренним давлением, величина, стоящая в скобках,
положительна. -
Согласно условию пластичности C.18)
* f л/~К~
F.П)
поэтому дифференциальное уравнение равновесия F.5) принимает
вид
d,Of 2 O'y
dr I/-*" r
Интегрируя это уравнение, получим
(Б Л 2)
где Сх — постоянная интегрирования.
108

По формулам F.11), F.9) и F.12) имеем
2 Л г . „ , ., F13)
F.14)
Для определения постоянных А, В и С и неизвестного радиуса
границы, разделяющей упругую и пластическую, области гт, исполь-
используем краевые "условия:
1) при г = г1 аг = —р;
2) при г = гг ог — 0;
3) при г = гт арг = о";
4) при г = гт а? = а?,
где индексами р ие отмечены напряжения соответственно в пласти-
пластической и упругой областях.
Из первого краевого условия, используя выражение F.12), имеем
ъ-^+ь—Ч-к- <бл5>.
Из второго краевого условия с помощью соотношений F.3)
устанавливаем, что
А ^=0. F.16)
'2
Третье и четвертое краевые условия при помощи соотношений
F.13), F.12) и F.3) дают.
С1 = А 2~; F-1')
гт
С1+Г=Л+-§-. .. F.18)
гт
Решая уравнения F.16)—F.18) относительно А, В, С, получаем
Подставим величину постоянной Сх в соотношение F.15). Тогда
выводим уравнение, связывающее" радиус границы, отделяющей
упругую область от пластической, и приложенное давление
" ' ' Г Г2 \
-3L__^ + l); F.20)
/3 у'" r\- ,2 j
109

это уравнение решается численно или графически. Решение значи-
значительно облегчается, если уравнение представить в виде
РО2 + 2 In -Ь- - 1 = 2 ln-^L - КЗ -?- .
Подставляя величины постоянных по выражениям F.19) в соот-
соотношения F.3), F.4), F.12)—F.14), получаем формулы для напря-
напряжений:
в упругой области
т
ot = -?=.[
и в пластической области
_ ат
F.21)
F.22)
Перейдем к рассмотрению радиальных перемещений.
Радиальная ег и окружная et деформации связаны с радиальным
перемещением и и радиусом г соотношениями
в =-^-; е< = —, F-23)
г dr ' г ' v '
откуда
« = etr. F.24)
Из условия несжимаемости D.33) и выражений F.2), F.23) мо-
может быть получено дифференциальное уравнение для радиального
перемещения, справедливое как в упругой, так и в пластической
областях. Поэтому зависимость радиального перемещения от радиуса
может быть установлена по формуле F.24) с использованием закона
Гука и величин напряжений в упругой области. Тогда получим
F.25)
Подставляя в это выражение напряжения по формулам F.21),
выводим зависимость радиального перемещения от радиуса, спра-
справедливую как в упругой, так и в пластической областях
U~
4
F.26)
ПО

Найдем теперь величину нормальной силы в поперечном сечении
трубы. Последняя связана с осевыми напряжениями соотношением
= 2n \
azrdr.
F.27)
Подставим в это выражение осевое напряжение по формулам F.21)
и F.22). Тогда получим
h(-±X rdr.
Используя соотношение F.20), имеем
N = рш\. F.28)
Очевидно, что такая осевая сила возника-
возникает в толстостенной трубе с днищами, нагру-
нагруженной внутренним давлением. Таким об-
образом, осевая деформация равна нулю, если
горны трубы не могут смещаться в осевом
направлении или если для трубы из несжима-
несжимаемого материала' величина осевой силы оп-
определяется ' формулой F.28). Последнее,
например, имеет место для трубы, у которой
осевая сила возникает только за счет дав-
давления на днище.
Определим теперь величину предельного
давления, т. е. такого давления, при кото-
котором исчерпывается несущая способность
трубы (пластическая область распростра-
распространяется на
Полагая в
лучаем
все сечение трубы гт = г2).
формуле F.20)
2 . г,
= -т=-От 1П—•
= г3, по-
F.29)
Рис. 6.2. Эпюры напря-
напряжений в толстостенной
трубе
In-
Величины напряжений в предельном состоянии определяем по
формулам F.22), полагая в них гт = г2:
2 .... г )
F.30)
111

На рис. 6.2 представлены эпюры окружных, радиальных и осе-
осевых напряжений, построенных по формулам F.21) и F.22) для трубы
с отношением — = 2 при различных отношениях — . На этом же
чертеже приведены эпюры напряжений в предельном состоянии
— = — = 2, построенные по формулам F.30). Как следует из
рис. 6.2, характер распределения окружных напряжений в предель-
предельном состоянии радикально отличен от распределения их в пределах
упругости. Наибольшее окружное напряжение возникает в точках
наружной поверхности. Это согласуется с опытами Бриджмена [5],
который экспериментально установил, что разрушение стальных
толстостенных труб, нагруженных внутренним давлением, начи-
начинается с наружной поверхности.
§ 33. Упруго-пластическое состояние толстостенной
трубы, нагруженной внутренним давлением
и осевой силой при линейном упрочнении
Допустим, что диаграмма деформирования материала трубы может быть схема-
схематизирована в виде диаграммы без площадки текучести с линейным упрочнением
(рис. 5.11).
Так же, как и в предыдущем параграфе, примем, что материал трубы лесжимаем
(8о = 0) и что осевая деформация трубы равна нулю (ег = 0). Тогда напряжения
в упругой области определяются по-прежнему по формулам F.3) и F.4) и соотноше-
ния F.9) и F.10) остаются справедливыми.
Определим напряжения в пластической области.
Дифференциальное уравнение равновесия F.5) с использованием соотноше-
соотношения F.10) приводим к виду
При отсутствии площадки текучести (е*т = 8г-т) для несжимаемого материала
(Нт = /?т) из формулы E.33) имеем при 8/ ^ е/т
oi = tarT + ETeh F.32)
Er
где % — 1 ^ параметр упрочнения.
Подставляя выражение F.32) в уравнение F.31), получаем
*1=_1./^1-ь32-\ F.33)
dr jA§ V г ' г . /
Определим закон изменения интенсивности деформаций. Из условия несжи-
несжимаемости D.33) и выражений F.2), F.23) получаем дифференциальное уравнение
для радиального перемещения, справедливое как в упругой, так и в пластической
областях
du _и .
кг "" ~Т ~
Интеграл его имеет вид
. «=^, F.34)
где С2 — постоянная интегрирования.
112

Согласно формулам F.23) имеем
Ям.
Из выражения B.18), используя соотношения F.2) и F.35), получим
2 С2
Подставим выражение F.36) в уравнение F.33). Тогда
__L_ / к 2
~]Лз Ч +
В результате интегрирования этого соотношения устанавливаем
F.35)
F.36)
]дс Са — постоянная интегрирования.
Из соотношений F.10), F.32), F.36), F.37) и F.9) имеем
Е7С2
¦Сг + к $
F.37)
F.38)
F.39)
Краевые условия имеют такой же вид, как и в предыдущем параграфе.
Из первого краевого условия, используя выражение F.37), имеем
Л In — h Сх —
те р
s s = ' s— —— •
3aTrf 2 O-т
Из второго краевого условия с помощью формулы F.3) получаем
F.40)
F.41)
Третье и четвертое краевые условия с использованием соотношений F.37), F.38)
и F.3) дают
*г_л
+ Сг + Х=Л +Л-.
4
F.42)
F.43)
Решаем уравнения F.41)—F.43) относительно А, В и С, учитывая, что при
/• == гт е;=ет и, следовательно, согласно формуле F.36)
4""^*
Тогда
4.
F.44)
113

По ;ставим величины Сг и С2 в соотношение F.40). Тогда получим уравнение»
связывающее радиус границы, разделяющей упругую и пластическую области,
и приложенное давление, аналогично уравнению F.20)
F.45)
Так же, как и уравнение F.20), это уравнение может быть решено численно
или графически.
Подставляя величинЪг постоянных Сг и С2 по формулам F.44) в соотношения
F.37)—F.39), получим выражения для напряжений в пластической области:
F.46)
Если в этих соотношениях положим Я = 1 (Ej= 0), то получим формулы F.22),
выведенные в предыдущем параграфе при отсутствии упрочнения. Подставляя вели-
величины постоянных А и В по формулам F.44) в соотношения F.3) и F.4)t получим урав-
уравнения для напряжений в упругой области такие же, как и в предыдущем параграфе
[см. формулы F.21)]. Далее, подставляя величину постоянной С2 по формуле F.44)
в уравнение радиальных перемещений F.34), приходим к заключению, что так же,
как и в предыдущем параграфе, радиальное перемещение как в упругой, так и в пла-
пластической областях определяется по формуле F.26).
Таким образом, упрочнение не влияет на законы распределения напряжений
в упругой области и радиальных перемещений в упругой и пластической
областях.
Определим теперь величину нормальной силы в поперечном сечении трубы.
Подставляя в формулу F.27) осевое напряжение по формулам F.46) и F.21), имеем
откуда, используя выражение F.40), получаем соотношение F.28). Таким образом,
как и в предыдущем параграфе, заключаем, что осевая деформация трубы равна
нулю, если торцы трубы не могут смещаться в осевом направлении или если для
трубы из несжимаемого материала величина осевой силы определяется формулой
F.28), что, например, имеет место для трубы, у которой осевая сила возникает только
за счет давления на днища.
Большие деформации толстостенной трубы по теории упруго-
пластических деформаций рассмотрены в работах [4, 14, 20, 25, 32].
Различным методам упрочнения толстостенных цилиндров и расче-
расчетам их на динамическую нагрузку посвящена книга [12]. Решение
задачи об упруго-пластическом состоянии толстостенной сферы,
114

нагруженной внутренним и внешним давлениями, изложено в кни-
книгах [11, 24].
Обобщение решения этой задачи на случай больших деформаций
дано в статьях [2, 14].
§ 34. Автоскрепление толстостенных труб
В практике производства толстостенных труб иногда повышают
их несущую способность в пределах упругости путем нагружения
труб внутренним давлением, при котором в трубе возникают пласти-
пластические деформации (автоскрепление или автофретирование) [26 ],
112]. Автоскрепление производится либо в упруго-пластической
стадии нагружения, когда в трубе существуют упругая и пластиче-
пластическая области, либо в пластической стадии, когда упругая область
исчезает и интенсивность напряжений от,- во всех точках трубы выше
предела текучести стт.
Существуют два способа автоскрепления.
Рис. 6.3. Схемы двух способов автоскрепления:
а — с продольным растяжением; б, в — без продольного растяжения
Первый способ; Автоскрепление с продольным растяжением.
Трубу закрывают пробками (рис. 6.3, а), за счет давления на которйе
возникает растягивающая сила
N = рпг\.
Второй способ. Автоскрепление без продольного растяжения.
В этом случае пробки, несущие обтюрирующие замки, не ввинчи-
иаются в трубу, а соединяются между собой посредством одного
центрального стержня (рис. 6.3, б) или нескольких нецентральных
стержней (рис. 6.3, в). При таком способе автоскрепления сила,
растягивающая трубу, равна нулю.
Рассмотрим пример расчета автоскрепленной трубы. Предположим, что труба
имеет внутренний-диаметр 2гг = 67 мм, наружный диаметр 2г2 = 187 мм. Диа"-
грамма растяжения материала трубы может быть схематизирована в виде диаграммы
растяжения с линейным упрочнением, без площадки текучести (рис. 5.П). Основ-
Основные параметры диаграммы растяжения Е = 2 - 10s МН/м2; Ет = 6850 МН/м2; ат=
— 476 МН/м3. Автоскрепление производится с продольным растяжением, при упруго-
пластическом нагружении.
115

Зависимость давления автоскрепления от радиуса границы упругой и пластиче-
пластической областей устанавливается формулой F.45).
На рис. 6.4 представлен график этой зависимости. Пластические деформации
в трубе возникают при рт = О,5О30Т= 240 МН/м2. Упругая область исчезает при
р = р'т = 1,28ат = 610 МН/м2.
Если труба не была предварительно автоскреплена, то давление, при котором
в ней возникают пластические деформации, является давлением рт- Рабочее давле-
Р
1,0
0,8
0,6
У
/
—--
111—1
'1,0 1,2 1,4- 1,6 1,8 2,0 12 2,4- 2,6 П-
Рис. 6.4. К примеру расчета автоскрепления
трубы. График зависимости давления авто-
автоскрепления от радиуса границы, разделяю-
разделяющей упругую и пластическую области
Рис. 6.5. К примеру расчета автоскрепления
трубы. Эпюры напряжений, возникающих
при автоскреплении, снимающихся при раз-
разгрузке, остаточных, номинальных и действи-
действительных напряжений
ние для нее не должно превышать этой вели-
величины. Если труба предварительно подверга-
подвергалась автоскреплению, то давление, при кото-
котором возникают пластические деформации, по-
повышается. Оно равно давлению автоскреп-
автоскрепления. Последнее для трубы заданных раз-
размеров из определенного материала зависит от
выбора радиуса границы упругой и пласти-
пластической областей. Эта величина должна быть
установлена из наблюдений за эксплуатацией
автоскрепленных труб. Так, например, пола-
гая в рассматриваемом примере — = 0,7 и
-i- = 1,954, по формуле F.45) получаем р =
= 1,1о"т=524 МН/м2. Следовательно, путем автоскрепления удается повысить
предельное давление с р = 240 МН/м2 до р = 524 МН/м2.
На рис. 6.5 представлены эпюры радиальных, окружных и осевых напряжений,
возникающих при автоскреплении I—- = 1,954 ) , а также снимающихся при раз-
разгрузке, остаточных и номинальных напряжений при величине внутреннего давле-
давления р = 403 МН/м2. На том же рисунке представлены эпюры действительных на-
напряжений, являющихся суммой остаточных напряжений, возникающих в резуль-
результате автоскрепления, и номинальных напряжений.
116

ТУТ
р
§ 35. Упруго-пластическое состояние диска
постоянной толщины, нагруженного внутренним
давлением при отсутствии упрочнения
Представим себе неподвижный диск постоянной толщины, вну-
внутренний радиус которого гъ а наружный г2, нагруженный внутрен-
внутренним давлением р (рис. 6.6). Дбпустим, что материал диска не имеет
упрочнения.
Используем те же допущения, что и в расчетах дисков в пределах
упругости [15]. Согласно первому допущению принимаем равномер-
равномерное распределение напряжений по нормали к срединной плоскости
дисков. Согласно второму допу-
допущению предполагаем, что в плос-
плоскостях, параллельных срединной
плоскости, напряжения отсутст-
отсутствуют. На основании первого допу-
допущения, учитывая, цто, нагружение
дисков осесимметрично, заключа-
заключаем, что напряжения, деформации
и перемещения являются функ-
функциями только радиуса. Из второго
допущения следует, что напря-
напряженное состояние во всех точках
диска является двухосным, или
ПЛОСКИМ.
Используя условие осевой сим-
симметрии и допущение об отсутствии
напряжений в плоскостях, параллельных срединной плоскости,
заключаем, что касательные напряжения в радиальном и окружном
сечениях отсутствуют. Следовательно, эти сечения являются глав-
главными, а напряжения в них— окружное о> и радиальное ог— глав-
главными напряжениями.
В пределах упругости наиболее опасными точками диска являются
точки внутренней поверхности. В них первоначально возникают
пластические деформации и, следовательно, так же как и в случае
толстостенной трубы, пластическая область примыкает к внутрен-
внутреннему контуру диска.
Радиальное и окружное напряжения в упругой области rT «s;
•^ г .^ г2 по-прежнему определяются формулами F.3).
Напряжения в пластической области должны удовлетворять
дифференциальному уравнению равновесия элемента диска, которое
имеет такой же вид, как и в случае толстостенной трубы [уравне-
[уравнение F.5)], и поскольку упрочнение отсутствует, также условию
пластичности C.18). Последнее вследствие'того, что в рассматри-
рассматриваемой задаче аг = 0, принимает вид
Рис. 6.6. Диск постоянной толщины,
нагруженный внутренним давлением
2 2 ~ 2
Ог OrOt -f- Ot = (ТТ.
F.47)
Принято говорить, что задача определения напряжений в пласти-
пластической области является статически определимой. Эта статическая
117

определимость условна, так как напряжения определяются не только
из одного уравнения статики, но также и из условия пластичности.
Однако заметим, что в отличие от задачи расчета толстостенной трубы,
в случае отсутствия упрочнения напряжения в диске находят без
использования теории упруго-пластических деформаций.
На основании рассмотренной в § 7 тригонометрической формы
представления главных напряжений радиальное и окружное напря-
напряжения в пластической области можно выразить через функцию
трч= ip (г) следующим образом:
2
F.48)
При этом условие F.47) удовлетворяется тождественно.
Подставим напряжения по формулам F.48) в дифференциальное
уравнение равновесия F.5). Тогда после преобразований получим
дифференциальное уравнение для функции ip:
Интегрируя это уравнение, имеем
^ = ехр (УЦ) sin (ip g-), F.50)
где Сх — постоянная интегрирования.
Уравнения F.48) и F.50) устанавливают связь напряжений
с радиусом через функцию ip.
Для определения постоянных А, В и С и радиуса гт используем
краевые условия:
1) при г = гх ог = —Pi,
2) при г = гг ог = 0;
3) при г = Гт Or = о%
4) при г = Гт of = о%
где индексами е и р отмечены напряжения в упругой и пластической
областях соответственно.
Из первого краевого условия, используя выражение F.48),
имеем
COSip].= п > F.51)
т
где ip! — значение функции ip на внутреннем контуре диска.
Выражение F.51) позволяет определить эту величину.
Постоянную Сг можно выразить через грх. Для этого необходимо
подставить в выражение F.50) г = гх. Тогда получ-им
= r\ ехр (УЦх) sin (m ?-
118

н, следовательно, формула F.50), связывающая радиус с функ-
функцией гр, принимает вид ,
F.52)
sta(*~r)
Согласно второму краевому условию, используя соотноше-
соотношение F.3), получаем
А 4- = 0. F.53)
Обозначим величину функции г|з на границе, отделяющей упру-
упругую область от пластической, где г = гт, через трт. Из третьего
и четвертого краевых условий, используя это обозначение и соотно-
соотношения F.48) и F.3), устанавливаем
л В
F.54)
F.55)
причем согласно формуле F.52) имеем
,2 Sinflb,— Чг"
Решая уравнения F.54) относительно А я В, получим
Подставив эти выражения в соотношение F.53); найдем
--=-). F.56)
F.57)
Перемножим теперь соотношения F.55) и F.57). Тогда получим
Sin I t|3l =-
cos I гсх —
F.58)
Уравнение F.58) является трансцендентным уравнением отно-
относительно ij)T. После определения г);т радиус гт может быть подсчитан
по формуле F.57).
Используем соотношения F.56) и F.53) и преобразуем уравне-
уравнения F.3) для определения напряжений в упругой области к виду
F.59)
119

, Определим величину радиального перемещения в предположе-
предположении, что материал несжимаем (е0 = 0, ц = 0,5). В упругой области,
используя соотношения F.24) и F.59), имеем
Bev = ^ (a,-?)-2g-<*»(*--?-) (l+3-З-)- F-60)
Для определения радиального перемещения в'пластической обла-
области запишем зависимости окружной и радиальной деформации от
напряжений. В рассматриваемом случае плоского напряженного
состояния
и по формулам D.32) получаем для несжимаемого материала (е„ = 0)
Используя эти зависимости, а также соотношения F.23), F.48)
и F.49), выводим дифференциальное уравнение для радиального
перемещения в пластической области
, sin (г|)—?-)
»»(*—г)
Интеграл этого уравнения имеет вид
„ р L * \ ° /J /с ci\
и — С2 ь . ¦ g=-, 6.61)
где С2 — постоянная интегрирования. Для определения ее исПоль-
зуем условие равенства радиальных перемещений на границе упру-
упругой и пластической областей. Приравнивая радиальные перемеще-
перемещения при г = гу, 1|з = \J)T по формулам F.60) и F.61) используя при
этом соотношение F.57), имеем
Подставим эту величину в уравнение F.60). Тогда получим
уравнение для радиального перемещения в пластической области
^f^/ >Я F.62)
Г sin^^-—)
120
/
l/
Г

Найдем величину предельного давления, при котором упругая
область исчезает и несущая способность диска исчерпывается.
В этом случае гт = г2 и из формулы F.57) имеем i|>T = -у-. Тогда
соотношение F.58) принимает вид
F.63)
Из последней формулы по заданному отношению — опреде-
определяем tylt после чего по формуле F.51) подсчитываем предельное
давление.
Формула F.51) дает воз-
возможность заключить,, что вели-ч
чина наибольшего давления
имеет место при
давление
Рпр. шах == ",
Величине -фх
формуле F.63)
-^- = 2,963.
я. Это
= я согласно
соответствует
Рис. 6.7. Эпюры окружных и радиальных
напряжений
Таким образом, если отно-
отношение наружного радиуса к
внутреннему превышает эту
неличину, никакое внутреннее
давление не может привести к
исчерпанию несущей способности диска. В этом случае часть его
всегда остается упругой.
Пример 1. Определим напряжения в диске — = 2, нагруженном внутрен-
ним давлением р — O,60j.
Из формулы F.51) устанавливаем, чтогЬ, = 2,117; затем, решая трансцендентное
уравнение F.58), получаем г|)т = 1,873. После этого по формуле F.57) находим
— = 0,625. Далее, задаваясь различными значениями г|) от \pt до г^т по формулам
F.48) подсчитываем напряжения в пластической области. С помощью соотноше-
соотношения F.52) устанавливаем величины радиусов для выбранных значений f. Таким
образом определяем зависимость напряжений от безразмерного радиуса. Напряже-
Напряжения в упругой области подсчитываем по формулам F.59). На рис. 6.7 представлены
эпюры напряжений.
Для диаграммы деформирования материала с линейным упрочне-
упрочнением исследование проведено Г. С. Шапиро [29 ], который показал, что
замкнутое решение поставленной задачи возможно, если использовать
приближенные выражения для интенсивноетей напряжений и дефор-
деформаций. Это решение положено в основу расчета развальцовки кон-
концов котельных труб в работе [6].
121

В статье [13] рассмотрено пластическое состояние диска перемен-
переменной толщины при степенном законе упрочнения. Принято, что тол-
толщина диска является степенной функцией радиуса. Полученные
результаты могут быть использованы и для диска постоянной тол-
толщины. Решение задачи о пластическом или упруго-пластическом
состоянии диска постоянной толщины можно значительно упростить,
если использовать выражения напряжений через тригонометриче-
тригонометрические функции некоторого угла, как это было сделано выше [17].
Это решение использовано в работе [18] для расчета прессовых
посадок дисков за пределами упругости.
Задача, изложенная в этом параграфе, является задачей плоского
напряженного состояния (ог = 0) в отличие от задачи упруго-пла-
упруго-пластического состояния толстостенной трубы (§ 32), которая была
задачей плоского деформированного состояния (ег = 0). Как изве-
известно, в пределах упругости решения этих задач отличаются только
упругими постоянными. Сопоставление решений, изложенных в этом
параграфе и в § 32, показывает, что за пределами упругости они
резко различаются, причем задача плоского деформированного
состояния проще, чем задача плоского напряженного состояния.
§ 36. Упруго-пластическое состояние бесконечной
пластины с отверстием, растянутой осесимметрично
относительно центра отверстия
Полученные в предыдущем параграфе формулы могут быть
использованы для расчета бесконечной пластины, ослабленной кру-
круговым отверстием при нагружении ее осесимметрично относительно
центра отверстия. Этот случай был исследован Г. Ю. Джанелидзе [10].
Им было разобрано два варианта нагружения пластины: 1) дав-
давлением на контуре отверстия; 2) растягивающими силами на контуре
пластины (на бесконечности), осесимметричными относительно цен-
центра отверстия.
Ограничимся рассмотрением второго случая (рис. 6.8), который
представляет интерес с точки зрения исследования концентрации
напряжений за пределами, упругости.
Радиальное напряжение на контуре отверстия равно нулю и
поэтому из соотношения F.51) получаем
fc = -f- F.64)
Поскольку радиальное напряжение на бесконечности равно
интенсивности растягивающей нагрузки р, вместо соотношения F.53)
имеем
• 2 0Т-
Сопоставляя это соотношение с первым выражением F.56),
устанавливаем
JL. F.65)
122

Так как косинус не может быть больше единицы, из формулы F.65)
заключаем, что несущая способность пластины исчерпывается при
Радиус границы, разделяющей упругую и пластическую области,
устанавливаем из выражения F.55) с использованием соотноше-
соотношения F.64).
Напряжения в пластической области подсчитываем по фор-
формулам F.48), а в упругой — согласно уравнениям F.3).
Для случая диаграммы растяжения со степенным упрочнением
Рассматриваемая задача решена в работах [13, 17].
Р/бг',0
I'iic. 6.8. Схема нагружения бесконеч-
бесконечной пластины осесимметрично относи-
|глыю центра отверстия силами, при-
приложенными на контуре пластины (на
бесконечности)
5 г/г,
Рис. 6.9. Эпюры напряжений в бесконеч-
бесконечной пластине с отверстием, растянутой
осесимметрично относительно центра от-
отверстия силами, приложенными на бес-
бесконечности
Пример 2. Определим напряжения, возникающие в бесконечной пластине
г отверстием, растянутой осесимметрично относительно центра отверстия силами,
приложенными на бесконечности. Примем следующие отношения интенсивности
распределенной нагрузки к величине предела текучести материала: -i—=0,5;0,8;
(),!); 1,0. Первая величина соответствует началу образования пластических дефор-
деформаций, а последняя—исчерпанию несущей способности пластины. Расчеты произво-
производились так, как было изложено выше. На рис. 6.9 изображены эпюры напряжений.
Как следует из эпюр, при развитии пластических деформаций происходит выравни-
папие напряжений.
Для оценки концентрации напряжений отметим, что при отсутствии отверстия
напряженное состояние пластины является однородным. Во всех точках пластины
окружное и радиальное напряжения равны интенсивности распределенной нагрузки.
(;.||сдовательно, этой же величине равна и интенсивность напряжений.
В пределах упругости окружное напряжение в точках контура отверстия
и 2 раза больше интенсивности растягивающей нагрузки, и, следовательно, теорети-
теоретический коэффициент концентрации напряжений равен двум. За пределами упругости
при отсутствии упрочнения интенсивность напряжений во всех точках пластической
области равна пределу текучести материала. Поэтому, если определить теоретиче-
теоретический коэффициент концентрации напряжений как отношение эквивалентных напря-
напряжений, то величины его для принятых отношений -—- равны обратным значениям
0Т
них отношений: 2; 1,25; 1,11; 1,00. Если же теоретический коэффициент концен-
123

трации напряжений определять как отношение наибольших главных напряжений,
то, как следует из рис. 6,9, величины его равны 2,00; 1,25-1,147= 1,43; 1,11-1,152 =
= 1,28; 1,00-1,170= 1,17. Таким образом, независимо от определения эффектив-
эффективного коэффициента концентрации, величина его уменьшается с развитием пластиче-
пластических деформаций.
§ 37. Упруго-пластическое состояние вращающегося
равномерно нагретого диска постоянной толщины
Рассмотрим равномерно нагретый, вращающийся с постоянной
угловой скоростью со диск постоянной толщины. Допустим, что
материал диска не имеет упрочнения.
Основные замечания о характере напряженного состояния,
приведенные в предыдущем параграфе, справедливы и в рассматри-
рассматриваемой задаче. Так же как и раньше, наиболее опасными точками
диска в пределах упругости являются либо центральная точка в слу-
случае диска без отверстия, либо для диска с отверстием точки вну-
внутреннего контура. Поэтому пластическая область либо включает
в себя центр диска, либо примыкает к внутреннему контуру его.
Напряжения в упругой области определяются формулами [15]:
- В
8
-4- В 1+3|х
"Г ~рг — —8
F.66)
где А и В — постоянные интегрирования; у — вес единицы объема
материала диска; g— гравитационное ускорение.
Для определения напряжений в пластической области может быть
использовано дифференциальное уравнение движения элемента диска
постоянной толщины [15]
и условие пластичности, которое имеет такой же вид, как и урав-
уравнение F.47). чВ отличие от задачи, рассмотренной в этом параграфе,
определение напряжений значительно осложняется из-за последнего
слагаемого в уравнении F.67). В этом случае возможно численное
решение задачи. Для этого, так же, как и раньше, удобно использо-
использовать тригонометрическую форму представления главных напряже-
напряжений F.48). Таким путем в более общем^случае диска переменной тол-
толщины и наличия упрочнения задача была решена В. В. Соколов-
Соколовским [24].
Для упрощения решения задачи используем условие пластич-
пластичности Треска—Сен-Венана, которое в рассматриваемом случае
ot > 07 > 0 имеет вид
у
at = стт. F.68)
124 ,

Проинтегрируем уравнение F.67), используя собтношение F.68).
Тогда получим
4« (б-69)
r T 3g ' г '
где С — постоянная интегрирования. .
Разберем вначале решение для диска без отверстия. Для опре-
определения постоянных Л, В, Си радиуса гт используем краевые
условия:
1) при г = 0 or = at;
2) при г = г2 аг — 0;
3) при г = гт а"г = а%
4) при г = rj of = aet.
Из первого краевого условия, используя уравнение F.69), полу-
получаем
С = 0. F.70)
Из второго краевого условия при помощи соотношений F.66)'
устанавливаем
3 -j- |л уа>гг% р.
•. В
8
F.71)
Наконец, из третьего и четвертого краевых условий на основании
выражений F.66), F.68) и F.69) имеем
rl
F.72)
Решим уравнения F.72) относительно А и В. Тогда получим
V—+ сгт;
12
F.73)
Подставляя эти величины в соотношение F.71), устанавливаем
значение угловой скорости, при котором радиус границы, разделяю-
разделяющей упругую и пластическую области, равен гт:
@ =
3 C + ц) ,J - 2 A + 3(i) ^«. + A +f3|i) 4
F,74)
125

Используя выражения F.73) и F.70), преобразуем формулы для
напряжений F.66) и F.69). В результате получим в упругой области
1 +
1+Зц
24 g
1 + Зц усо2
~24 g~
и в пластической области
-vco2/-2
V a* = ai
F.75)
F.76)
Предельную угловую скорость вра-
вращения, при которой пластическая об-
область заполняет весь диск и несущая
способность диска полностью исчерпы-
исчерпывается, получаем из выражения F.74),
полагая в нем гт = г2
F.77)
На рис. 6.10 представлены эпюры
Рис. 6.10. Эпюры напряжений напряжений, во вращающемся равно-
^^^ нагретом диске постоянной тол-
толщины без центрального отверстия.
При этом принято, что —- = 0,5.
Согласно формуле F.74) для этой величины отношения имеем
VCD2/"! OCC
-!—-^ = 2,65.
во вращающемся равномерно
нагретом диске постоянной тол-
толщины без центрального отвер-
отверстия
Рассмотрим теперь решение для диска с центральным отверстием.
Для определения постоянных А, В и С в уравнениях F.66) и F.69)
используем краевые условия:
1) при г = гг а, = 0;
2) при г = г2 аг = 0;
3) при г = гт о? = ае/,
4) при г = rT a? = от?.
В результате таким же путем, как и в предыдущем случае, полу-
получаем величину угловой скорости, при которой радиус границы,
разделяющей упругую и пластическую области, равен гт:
(О
-V
3 C + И) $т - A + Зц) 4B/1 - 4) - 4г? (r2 + 4) '
F.78)
126

Формулы для напряжений в упругой области
— 3
3fx
24g [(
Зц) 2rT
F.79)
и в пластической области
?¦)-?• ('-!)'
от, = огт
F.80)
Предельную угловую скорость вращения устанавливаем из
выражения F.78), полагая в нем гт = г2
F.81)
Принимая в этой формуле г1 = 0, приходим к соотноше-
соотношению F.77).
Расчет за пределами упругости вращающихся неравномерно
нагретых дисков по полученным экспериментально (не схематизиро-
схематизированным) диаграммам растяжения материала приближенным методом
переменных параметров упругости, разработанным И. А. Биргером,
будет изложен ниже в § 41.
В книге [30] задача расчета вращающегося неравномерно нагре-
нагретого диска переменной толщины решена в деформациях.
Исследованию пластического и упруго-пластического состояния
дисков на основе схематизированных диаграмм с использованием
условия Треска—Сен-Венана посвящен ряд работ.
В работе [8] исследовано упруго-пластическое состояние вращаю-
вращающихся дисков переменной толщины. В основу расчета положена
диаграмма растяжения материала без упрочнения.
В статье [19] рассматриваются пластическое и упруго-пласти-
упруго-пластическое состояние неравномерно нагретого диска переменной тол-
толщины. Предполагается, что диаграмма растяжения материала диска
не имеет упрочнения.
В статье [21 ] изучается упруго-пластическое состояние вра-
вращающегося равномерно нагретого диска. Принимается, что диа-
диаграмма растяжения материала может быть схематизирована в виде
дна! раммы с линейным упрочнением.
127

§r 38. Понятие об автоскреплении дисков
Автоскреплением (автофретированием) дисксв называют процесс
повышения несущей способности их путем пластического деформи-
деформирования перед эксплуатацией. Автоскрепление заключается в том,
что диски на специальных стендах приводятся во вращение с та-
такими угловыми скоростями, при которых в них возникают пласти-
пластические деформации. Поскольку при вращении равномерно нагре-
нагретого диска наиболее напряженными точками являются точки вну-
внутреннего контура, пластические деформации начинают развиваться
с внутренней расточки. С повышением числа оборотов пластическая
область, примыкающая к внутреннему контуру, увеличивается.
&t дейст
q) ¦ Рис. 6.11. Эпюры напряжений в автоскрепленном диске
В результате постепенного снижения числа оборотов и остановки
диска, деформированного так, что в нем возникла некоторая пласти-
пластическая область, диск полностью разгружается и в нем возникают
остаточные напряжения. Радиальные остаточные напряжения будут
сжимающими во всех точках, а окружные — сжимающими в области,
примыкающей к внутренней расточке, и растягивающими в осталь-
остальной части Диска.
На рис. 6.11, а изображен профиль диска, а на рис. 6.11. б —
примерные эпюры остаточных напряжений в диске. Остаточные
напряжения накладываются на номинальные, возникающие вслед-
вследствие вращения (рис. 6.11,' в), в результате чего в наиболее напря-
напряженных точках на внутренней расточке окружные напряжения могут
быть значительно уменьшены.
На рис. 6.11, г представлены .примерные эпюры действительных
напряжений в автоскрепленном диске, полученные сложением эпюр
остаточных напряжений (рис. 6.11, б) и напряжений, возникающих
вследствие вращения (рис. 6.11, в). Как следует из эпюр, изобра-
изображенных на рис. 6.11, автоскрепление может значительно снизить
напряженность диска. Поэтому автоскрепление дисков позволяет
использовать менее качественные и, следовательно, более дешевые
марки сталей.
Расчеты автоскрепления турбинных дисков описаны в статье [1 ].
128

§ 39. Большие деформации цилиндрических
и сферических оболочек, нагруженных
внутренним давлением
Представим себе тонкостенную цилиндрическую оболочку с дни-
днищами начального радиуса г0 и с начальной толщиной стенки h0,
нагруженную внутренним давлением р (рис. 6.12, а).
Определим величины напряжений и деформаций, не предпола-
предполагая, как обычно, последние малыми. При этом пренебрежем упру-
упругими деформациями по сравнению с пластическими, т. е. положим
Рис. 6.12. Цилиндрическая (а) и сферическая (б) оболочки, нагруженные внутренним
давлением
в основу расчета диаграмму деформирования жестко-пластического
упрочняющегося тела (см. рис. 5.16). В таком случае материал
можно считать несжимаемым (е0 = 0).
Окружное и осевое напряжения в цилиндрической оболочке
с днищами, нагруженной внутренним давлением, будут
JpjT_
Г
F.82)
где г и ft — средний радиус и толщина стенки оболочки в деформи-
деформированном состоянии. Радиальное напряжение для тонкостенной обо-
оболочки может быть приближенно принято равным нулю
аг = 0.
F.83)
Из формул F.82) следует, что процесс нагружения не только
при малых, но и при больших деформациях является простым.
Поэтому для несжимаемого материала можно применить основные
зависимости теории малых упруго-пластических деформаций и при
больших деформациях, используя при этом логарифмические дефор-
деформации.
5 Н. Н. Малинии 129

Логарифмические окружная, осевая и радиальная деформации
будут
1 Г , I
= 1п—, ег=1п-т-
F.84)
Согласно формулам D.32), A.5) и F.83) компоненты логарифми-
логарифмической деформации зависят от компонент напряжений:
F.85)
где et — интенсивность логарифмических деформаций, связанная
с компонентами логарифмических деформаций зависимостью B.18);
ос — интенсивность напряжений. В рассматриваемом случае со-
согласно формулам A.21), F.82) и F.83)
VI
F
F.86)'
Используя соотношения F.82) и F.86), преобразуем выраже-
выражения F.86) к виду
1
2 - _ 2 - 2 , г 2 , Л
е, = 0.
F.87)
Из последнего выражения следует, что при нагружении только
внутренним давлением в осевом направлении оболочка не удли-
удлиняется.
Формулы F.86) и F.87) позволяют по известной диаграмме
деформирования установить зависимость между давлением р и сред-
средним радиусом оболочки г или толщиной стенки h. Если зависи-
зависимость О[ от &i определяется формулой E.19), то, подставляя в нее
выражения F.86) и F.87), имеем
Установим пределы устойчивого деформирования оболочки. Как
ив § 31, приходим к заключению, что деформация оболочки устой-
устойчива при условии, что dp > 0. '
При
dp = 0 F.88)
-130

ночи икает местное утонение стенки — потеря устойчивости перво-
первоначальной формы равновесия. Подставляя в формулу F.88) р, по
формуле F.86) получаем
h dot . a dh O(h dr ~
II/III
dr
Используя соотношения F.87), имеем
F.89)
Д- 0,577
Л-0,677
Рис. 6.13. К определению неустойчивости растяну-
растянутого образца (г = 1), цилиндрической (г = 0,577)
и сферической (г = 0,667) оболочек
Слева в этом выражении — величина, обратная подкасатель-
ной к на диаграмме деформирования в координатах et, ot (рис. 6.13).
Таким образом,
^ = 0,577.
При растяжении X — 1 (см. § 29). Следовательно, при деформи-
деформировании цилиндрической оболочки с днищами внутренним давле-
давлением потеря устойчивости первоначальной формы равновесия воз-
возникает при меньших величинах интенсивности деформаций, чем
при растяжении.
Если зависимость а,- от е, определяется формулой E.19), то,
используя выражения F.89) и F.87), можно получить величины —,
'о
при которых возникает потеря устойчивости первоначальной формы
равновесия оболочки
'VI I т
131

Таблица 6.1
Величины радиусов при потере устойчивости оболочек
Материал
Медь мягкая
Медь средней твердости
Латунь средней твердости
Нержавеющая сталь
в
0,01633
0,1143
0,1274
0,01633
т
0,3
0,3
0,48
0,5
Безразмерный радиус
оболочек -Z—
Го
цилиндриче-
цилиндрической
1,15
1,05
1,14
1,27
сферической
1,10
1,04
1,10
1,17
В табл. 6.1 приведены величины — для некоторых материалов,
постоянные которых, по данным работы [34 ], приведены в той же
таблице.
Для сферической оболочки (рис. 6.12, б), нагруженной внутрен-
внутренним давлением, окружное и меридиональное напряжения
Логарифмические окружная et, меридиональная ет и радиаль-
радиальная ег деформации
Так же как ni случае цилиндрической оболочки, легко получить
___??_.
в, — 2 In — = — In -г-,
г0 «о
F.90)
F.91)
Эти формулы позволяют по диаграмме деформирования устано-
установить зависимость между давлением р и средним радиусом оболочки г
или толщиной стенки h. Принимая справедливой формулу E.19),
получаем
2^( 1п- Д
Потеря устойчивости возникает при
Jdai 3
132

или
К = 0,667,
т. i\ при несколько большем значении интенсивности деформаций,
чом для цилиндрической оболочки.
В случае использования формулы E.19) величина —- при потере
устойчивости определяется формулой
В табл. 6.1 приведены также подсчитанные по этой формуле зна-
значения —.
Решение задачи об устойчивости Двухосного пластического рас-
растяжения ортотропных листов и цилиндрических оболочек дано
к работе [16].
Список литературы
1. Адлер М. В., Карпин Е. Б. Автофретироваиие турбинных дисков. —«Тепло-
—«Теплоэнергетика», 1955, №7, с. 15—19.
2. Бахшиян Ф. А. Конечные перемещения в полом шаре, подверженном
внутреннему давлению. — «Прикладная математика и механика», 1948, т. XII,
в. 2, с. 137—140.
3. Биргер И. А. Круглые пластинки и оболочки вращения. М., Оборонгиз,
1961, 368 с.
4. Бочарова С. А. Напряженное состояние трубы, находящейся под действием
равномерного вдутреннего давления и продольной силы при больших пластических
деформациях. — В кн.: Расчеты иа прочность. [Сборник статей], вып. 9,- М., Маш-
гиз, 1963, с. 196—218.
5. Бриджмен П. В. Физика высоких давлений, М., ОНТИ, 1935; 402 ;С.
6. Глаголев Н. И. О приближенном расчете развальцовки концов котельных
труб. — «Инженерный сборник», 1956, Т. XXIII, с. 111—120.
7. Гоффмаи О., Закс Г. Введение в теорию пластичности для инженеров. М.,
Машгиз,' 1957, 279 с.
8. Гохфельд Д. А. Упруго-пластическое состояние дисков переменной тол-
толщины. — В кн.: Расчет и конструирование машин. [Сборник статей], вып. 1, М.,
Машгиз, 1954, с. 37—53.
9. Дэвис Е. Текучесть и разрушение стали со средним содержанием углерода
при сложном напряженном* состоянии. — В ки.: Теория пластичности. [Сборник
статей], М., Изд. иностр. лит., 1948, с. 364—374.
10. Джанелидзе Г. К). Концентрация напряжений на краю кругового отверстия
в равномерно напряженном тюле при пластической деформации. — «Труды Ленин-
Ленинградского политехнического института», 1947, № 3, с. 111—117.
11. Ильюшин А. А. Пластичность. М., ГИТТЛ, 1948, 376 с.
12. Ильюшии А. А., Огибалов П. М. Упруго-пластические деформации полых
цилиндров. М., Изд-во МГУ, 1960, 227 с.
13. Костюк А. Г. О равновесии кольцевой пластинки при степенном законе
упрочнения. — «Прикладная математика и механика», 1950, т. XIV, вып. 3, с. 319—
320.
14. Ломакин В. А. Большие деформации трубы и полого шара. — «Инженер-
«Инженерный сборник», 1955, т. XXI, с. 61—73.
15. Малинин Н. Н. Прочность турбомашии. М., Машгиз, 1962, 291 с.
16. Малинин Н. Н. Устойчивость двухосного пластического растяжения ани-
анизотропных листов и цилиндрических оболочек. — «Известия Академии наук СССР.
Механика твердого тела», 1971, № 2, с. 115—118. <
133

17. Махонина Т. М. Упруго-пластическое состояние шайбы при степенном
упрочнении. — В кн.: Расчеты на прочность. [Сборник статей], вып. 5, М., Машгиз,
1960, с. 212—225.
18. Махонина Т. М. Расчет прессовых посадок шайб за пределами упругости
при степенном упрочнении материала. — В кн.: Расчеты на прочность. [Сборник
статей], вып. 6, М., Машгиз, 1960, с. 97—106.
19. Микеладзе М. Ш. Упруго-пластические деформации в быстровращающихся
дисках переменной толщины. — «Инженерный сборник», 1953, т. XV, с. 21—34.
20. Надаи А. Пластичность и разрушение твердых тел, М., Изд. иностр. лит.,
т. I, 1954, 647 с, т. II, 1969, 863 с.
21. Работнов Ю. Н. Упруго-пластическое состояние вращающегося диска
при наличии упрочнения. — «Известия АН СССР. Отд. техн. наук. Механика и ма-
машиностроение», 1959, № 5, с. 154—156.
22. Расчеты на прочность в машиностроении. М., Машгиз, т. II, 1958, 974 с;
т. III, 1959, 1118 с. Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К- Лихарев и др.
23. Серенсен С. В., Кргаев В. П., Шнейдерович Р. М. Несущая способность
и расчеты деталей машин на прочность. М., Машгиз, 1963, 451 с.
24. Соколовский В. В. Теория пластичности. М., «Высшая школа», 1969, 608 с.
25. Соколов С. Н. Определение разрушающих давлений в трубах. — В кн.
Расчеты на прочность. [Сборник статей], вып. 2, М., Машгиз, 1958, с. 189—212.
26. Смирнов-Аляев Г. А. Теория автоскрепления цилиндров М Оборонгиз
1940, 286 с.
27. Томсен Э., Янг Ч., Кобаяши Ш. Механика пластических деформаций при
обработке металлов. М., «Машиностроение», 1969, 503 с.
28. Феодосьев В. И. Сопротивление материалов. М., «Наука», 1974, 559 с.
29. Шапиро Г. С. Об интегрировании в квадратурах уравнений плоской одно-
одномерной задачи теории пластичности с учетом упрочнения материала — «Прикладная
математика и механика», 1949, т. XIII, вып. 6, с. 659—662.
30. Шнейдерович Р. М. Прочность при статическом и повторно-статическом
нагружениях. М., «Машиностроение», 1968, 343 с.
31. Johnson W., Mellor P. В. Plasticity for mechanical engineers, D. Van Nostrand
Company, 1962, 412 p.
32. 'Mac Gregor С W., Coffin L. F., Fisher J. С The plastic flow of thick-walled
tubes with large strains. — «Journal of applied physics», 1947,Vol. 9, No 3, p. 291—297.
33. Marciniak Z. OdksztaJcenia graniczne przy tJoczeniu blach, Wydawnictwa
naukowo— techniczne, 1971, 232 s.
34. Mellor. P. B. Stretch forming under fluid pressure.^-«Journal of the mecha-
mechanics and physics of solids», 1956, Vol. 5, p. 41—56.
35. Philips A. Introduction to plasticity, The Ronald press company, 1956, 230 s.
36- Stodola A. Dampf und Gasturbinen, Julius Springer, 1924, 1109 s. . ч

ГЛАВА VII
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
ПО ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ
ДЕФОРМАЦИЙ
§ 40. Метод переменных параметров упругости
Как следует из приведенных выше решений некоторых упруго-
шшстических задач, основными уравнениями расчетов за пределами
упругости по теории малых упруго-пластических деформаций яв-
.'ннотся: дифференциальные уравнения равновесия A.3), условия
п,-| поверхности A.1), условия совместности деформаций B.4) и зави-
зависимости между деформациями и напряжениями D.32) и C.3).
Компоненты напряжений должны удовлетворять дифференциаль-
дифференциальным уравнениям равновесия и условиям на поверхности тела, если
па ней или на части ее заданы напряжения. Условия на поверхности
юсно связаны с дифференциальными уравнениями равновесия. Их
необходимо рассматривать совместно. Уравнения равновесия не могут
иметь определенного решения, пока не даны условия на поверхности.
1:сли дифференциальные уравнения и условия на поверхности удов-
удовлетворены, то это свидетельствует о том, что все элементы тела как
ннутри него, так и у поверхности находятся в равновесии. Следо-
нательно, обеспечено и равновесие тела в целом.
Условия совместности деформаций выражают отсутствие разры-
разрывов и непрерывность деформации тела. В ряде случаев условие
совместности деформаций заменяется кинематической гипотезой,
как например, гипотезой плоских сечений в расчете балок, или гипо-
гипотезой прямолинейности нормалей в расчете пластин.
Если на всей или части поверхности тела заданы перемещения,
то тогда компоненты перемещений должны удовлетворять этим
условиям.
Решение упруго-пластических задач, как правило, сопряжено
со значительными трудностями. Многие задачи расчетов за пределами
упругости до сих пор не имеют решения. Поэтому в теории пластич-
пластичности еще в большей степени, чем в теории упругости, имеют зна-
значение приближенные методы решения. Наиболее распространенными
из них являются вариационные методы, а также методы, в которых
упруго-пластическая задача сводится к последовательности упругих
чадач в результате применения процесса последовательных прибли-
приближений. Последние методы могут быть названы методами упругих
решений.
135

Впервые один из вариантов такого метода был предложен
А. А. Ильюшиным [5 ]. В дальнейшем эти идеи были развиты в рабо-
работах И. А. Биргера [1—4]. Ниже изложен так называемый метод
переменных параметров упругости, разработанный И. А. Бирге-
ром [2]. В основе этого метода лежит представление зависимостей
деформаций от напряжений по теории упруго-пластических дефор-
деформаций в форме обобщенного закона Гука, в котором параметры
упругости зависят от напряженного состояния в точке и поэтому
различны для различных точек тела.
Используя соотношения D.32) и C.3), преобразуем зависимо-
зависимости D.32) к виду
= pfK— H-* К
G.1)
где Е *, G *, ц *
гости;
так называемые переменные параметры упру-
01
Е* =
fi =
3? е,-
1—2ц
3?
1 +
1 — 2ц at
3? ei
G.2)
Как следует из формул G.2), связь между «переменными пара-
параметрами упругости» имеет тот же вид, что и для упругих постоян-
постоянных Е, G и ц>, а именно:
F*
2A+ц*) •
Для несжимаемого тела," у которого \i — -^-, по формулам G.2)
,*
_
т. е. «переменный модуль упругости» совпадает с секущим модулем,
а переменный коэффициент поперечной деформации равен половине.
Для решения упруго-пластической задачи по методу переменных
параметров упругости используют процесс последовательных при-
приближений [2]. В исходном (нулевом) приближении принимают,
что переменные параметры упругости равны параметрам упругости
и решают, упругую задачу, в результате чего определяют напряжения
и деформации нулевого приближения (оцH, (еиH. По этим величи-
136

нам в каждой точке тела при помощи формулы A.19) и B.16) под-
подсчитывают интенсивности напряжений и деформаций в нулевом
приближении а1Ъ и е10.
В координатах е,, а? (рис. 7.1) напряженное и деформированное
состояние некоторой точки тела изображается точкой О, лежащей
па луче, тангенс угла наклона которого пропорционален вели-
величине 3G. В первом приближении вносится поправка для вели-
величины 3G. Она принимается равной отношению интенсивности на-
напряжений <х*о, соответствующей
интенсивности деформаций е(-о по
диаграмме деформирования (рис.
7.1) к eL0:
3Gf =¦
Sio
«,¦
Рис. 7.1. Диаграмма деформирования
15
10
0
1
/
-
150250 350'#,'
6)
Рис. 7.2. Профиль диска (а) и гра-
график изменения температуры по ра-
радиусу (б)
По величинам сг*0 и ei0 определяют также параметры Е[ и цг
Параметры Ё[, G\ и ц\ будут различными в различных точках
тела.^ Таким образом, возникает задача определения напряжений
в «неоднородном» теле, параметры упругости в различных точках
которого различны. Далее решают эту задачу и определяют напря-
напряжения и деформации {рц)\, {ъц)\, являющиеся первым приближе-
приближением. По этим величинам в каждой точке тела при помощи
формул A.19) и B.16) подсчитывают интенсивности напряжений
и деформаций в первом приближении а?1, еа.
В координатах ег, at (рис. 7.1) напряженное и деформированное
состояния некоторой точки тела изображаются точкой 1, лежащей
на луче, тангенс угла наклона которого пропорционален вели-
величине 3Gi.
137

Во втором приближении величину 3G* принимают равной отно-
отношению интенсивности напряжений а а, соответствующей интенсив-
интенсивности деформаций гц по диаграмме деформирования (см. рис. 7.1) кец
По величинам о*ц и е,ц находят также параметры El и ц1. Эти
параметры используют для определения напряжений и деформаций
второго приближения '(сг(/J, (е,/J-
Расчет продолжается до тех пор, пока результаты расчета в неко-
некотором приближении не будут близки к соответствующим результа-
см
см'С
16,3
15,5 1,75
1,95
1,85
—
—
и.
X
,
N
в. Ш1иг
100
150
150
550
Рис. 7.3. Графики зависимости от температу-
температуры коэффициента линейного расширения и
модуля упругости материала диска
Рис. 7.4. Диаграммы растяжения материала
при различных температурах
100
/,
/
/
1
у,
чог
-hi .
, L,
0
о,1 о.г о.з о,ч 05 е.%
там в предыдущем приближении. Обычно это имеет место уже для-
второго приближения. Таким образом, хотя доказательство сходи-
сходимости метода переменных параметров упругости в настоящее время
отсутствует, практика расчетов показывает, что процесс всегда
является сходящимся, причем скорость сходимости процесса зна-
значительна. ' ,
~j
Пример. Определим напряжения в диске газовой турбины без центрального
отверстия. Профиль диска изображен на рнс. 7.2, а. Частота вращения я =
= 12 300 об/мин. Интенсивность нагрузки, вызванной воздействием на диск при-
присоединенных к нему лопаток и принятой равномерно распределенной по наружному
контуру диска р2 — НОМН/м2. Удельный вес материала диска у= 0,081 МН/м3.
График изменения температуры О по радиусу диска изображен на рис. 7.2, б.
На рис. 7.3 представлены графики зависимостей от температуры коэффициента
линейного расширения и модуля упругости материала диска, а на рис. 7.4 диаграммы
растяжения материала при различных температурах.
Расчет был выполнен в приведенном выше порядке, причем напряжения опре-
определялись методом последовательных приближений, как изложено в книге [12].
В соотношения G.1) добавлялись температурные деформации aft.
138

На рис. 7.5 изображены эпюры напряжений в нулевом, первом и втором при-
приближениях. Как следует из приведенных эпюр, различие между вторым и первым
приближениями незначительно, что позволяет ограничиться двумя приближениями.
В последующих параграфах будут рассмотрены некоторые общие
энергетические теоремы теории упруго-пластических деформаций
II разобраны приближенные вариационные методы решения упруго-
пластических задач на основе этой теории. Эти энергетические тео-
теоремы предложены Л. М. Качановым [6, 8].
Рис. 7.5. Эпюры напряжений. Штрих-пунктирные линии — нулевое прибли-
приближение, штриховые линии — первое приближение, сплошные линии — второе
приближение
§ 41. Принцип минимума полной энергии
Допустим, что тело, находящееся в равновесии, занимает
объем V, ограниченный поверхностью S. В дальнейшем исполь-
используются тензорные обозначения. Предположим, что на части поверх-
поверхности заданы поверхностные силы Xvi, а на части поверхности —
перемещения ut. Сообщим точкам тела бесконечно малые переме-
перемещения би?, совместимые с краевыми условиями, которые примем
за возможные. Согласно принципу возможных перемещений для
деформируемого тела необходимым и достаточным условием равно-
равновесия является равенство работ внешних и внутренних сил на воз-
возможных перемещениях
\ Х,6щ dV+\ Xvibut dS= I ои8ви dV,
G.3)
139

Второй интеграл фактически берется только по той части поверх-
поверхности, на которой заданы поверхностные силы, так как на другой
части, где заданы перемещения, вариации их равны нулю.
Преобразуем подынтегральное выражение в правой части ра-
равенства G.3.), используя разложения тензоров напряжений и дефор-
деформаций на шаровой тензор и девиатор (см. § 3 и § 10). Тогда получим
аи8ги = (sG + бGа0) (8еи + 8и8в0) = s(/6eG + 8иа08еи +
о8и8го = sf/6e0- + ао8еа + siFe0 + Зао8ео
ео,
так как
8и8еи = 8eiu 8i,su = su, 8ц8и = 3.
Очевидно, что второе и третье
слагаемые в этом выражении равны
нулю. Используя далее соотноше-
соотношения D.30), C.3), B.17), получаем
9 л1 ¦
= y -j: ец8еи + За0бе0 =
Г Т
где
G.4)
G.5)
Рис. 7.6. Диаграмма деформирова-
деформирования материала
Очевидно, что
дП
т. е. функция компонентов деформации П (гц) является потенциа-
потенциалом деформации.
Первое слагаемое в формуле G.5) представляет собой удельную
потенциальную энергию изменения объема, а второе удельную энер-
энергию изменения формы. Второе слагаемое в некотором масштабе"
равно площади, ограниченной диаграммой деформирования мате-
материала. На рис. 7.6 эта площадь заштрихована вертикальными ли-
линиями.
Обозначим работу внешних сил на возможных перемещениях —
два интеграла в левой части выражения G.3) через 8А. Тогда из
соотношений G.3) и G.4) имеем
\ 8ПйУ
или
140
8(П — А) = 0,

где
— потенциал деформации всего тела.
Величину в круглых скобках называют полной энергией системы
нагрузки — тело
Э = П — А. • G.6)
Таким образом,
85 - 0.
Определение второй вариации полной энергии системы показы-
показывает, что знак ее положителен [7].
Следовательно, действительная форма равновесия тела отли-
отличается от всех возможных форм тем, что для нее полная энергия
принимает минимальное значение.
§ 42. Принцип возможных изменений
напряженного состояния
Предположим, так же, как и в предыдущем параграфе, что тело,
находящееся в равновесии, занимает объем V, ограниченный поверх-
поверхностью S. Допустим, что на части поверхности заданы поверхно-
поверхностные силы Xh а на части поверхности — перемещения и{. Сопоста-
Сопоставим действительные напряженные состояния в различных точках
тела, характеризуемые компонентами напряжений ас1, со всеми
близкими напряженными состояниями, характеризуемыми компо-.
пентаминапряжений at]- + Sa(/, удовлетворяющими дифференциаль-
дифференциальным уравнениям равновесия и условиям на поверхности. Используя
сокращенные тензорные записи последних A.4) и A.2), имеем для
статически возможного напряженного состояния
(о и + 8ои)п, = Xvj + 8Xvj,
для действительного напряженного состояния
да..
atint = Xv/.
Вычитая из первого уравнения третье, а из второго четвертое,
получим
141

т. е. вариации напряжений 6а(/- и внешних сил 8Xj,Xb ч/ образуют
уравновешенную систему. Поэтому по принципу возможных пере-
перемещений для деформируемого тела, принимая за возможные пере-
перемещения действительные, имеем
+ ( 8Xvlut dS = j 6ot,Btl dV. G.7)
S V
Преобразуем подынтегральное выражение в правой части этого
равенства так же, как это было сделано в предыдущем параграфе.
Тогда получим
6<7г/8г/ = (8su + 8и8а0) {ец + 8г/е0) =
-f Ss(/6(/s0 + б(/баобг/е0 =
V
s 3 8< i о ж г1 1 я ( 3
= 6S// " -^ S<7 + 3e06ffo = -J7 ~2 8 {
—- О0о = &iOG{ + -щ баб = о^, G.8)
где
R = Sc+ JBcdat. G.9)
Очевидно, что
Функцию компонентов напряжения 7? называют дополнительной
работой. Соотношения G.10) аналогичны известным в теории упру-
упругости формулам Кастилиано. В пределах упругости частные произ-
производные берутся от удельной потенциальной энергии деформа-
деформации [141.
Первое слагаемое в формуле G.9) представляет собой удельную
потенциальную энергию изменения объема, а второе в некотором
масштабе равно площади, заштрихованной на рис. 7.6 горизонталь-
горизонтальными линиями.
Назовем дополнительной работой для всего тела выражение
R = f R dV.
v
Тогда, используя соотношение G.8), преобразуем равенство G.7)
к виду
f &Xtu, dV + f exv/u, dS = 8R. G.11)
V S
Уравнение G.11) является математической формулировкой так
называемого принципа возможных изменений напряженного состоя-
состояния тела, согласно которому сумма работ приращений всех внеш-
142

них сил на перемещениях точек приложения этих сил равна прира-
приращению дополнительной работы всего тела.
В пределах упругости дополнительная работа равна потенциалу
деформации или удельной потенциальной энергии и, следовательно,
сумма работ приращений всех внешних сил на перемещениях точек
приложения этих сил равна приращению потенциальной энергии
тела [14].
§ 43. Принцип минимума дополнительной работы
Рассмотрим такой частный случай нагружения тела, когда объем-
объемные силы равны нулю, на части поверхности заданы поверхностные
силы и, следовательно, вариации их равны нулю
8Xvi = О,
а на другой части поверхности равны нулю перемещения
ис = 0.
Тогда из формулы G.11) следует
8R = 0. G.12)
Как показано в работе [7], вторая вариация дополнительной
работы положительна.
Таким образом, в указанном частном случае из принципа возмож-
возможных изменений напряженного состояния тела получен принцип
минимума дополнительной работы, согласно которому из всех стати-
статически возможных напряженных состояний только для истинного
напряженного состояния дополнительная работа для всего тела
принимает минимальное значение.
§ 44. Теорема Кастилиано
В теории упругости теорема Кастилиано формулируется следую-
следующим образом [14]: частная производная от потенциальной энергии
деформации тела, взятая по величине любой из приложенных к телу
внешних сил, равна проекции перемещения точки приложения этой
силы на направление ее действия.
Рассмотрим обобщение этой теоремы на случай нелинейных
зависимостей между напряжениями и деформациями. Обозначим
через Pt сосредоточенные силы, приложенные к телу, через а,, р,-,
Y/ — направляющие косинусы линий действия этих сил, а через uxi,
uyh uzi — проекции перемещения точек приложения сосредоточен-
сосредоточенных сил Р[ соответственно на оси х, у и г.
Из вариационного уравнения G.11), полагая, что одна из сил
получает бесконечно малое приращение 8Pit устанавливаем
(их1щ + и„,р, + uziy{) 8P( = 8R.
Выражение в круглых скобках равно проекции перемещения
точки приложения силы Pt на направление линии действия силы б(-.
143

Следовательно,
OR
G.13)
т. е. частная производная дополнительной работы тела по величине
любой из приложенных к телу внешних сил равна проекции переме-
перемещения точки приложения этой силы на направление ее действия.
§ 45. Применение вариационных методов
к решению задачи упруго-пластического кручения
бруса
Представим себе призматический скрученный брус произволь-
произвольного поперечного сечения, задний торец которого закреплен так,
что линейные перемещения всех
точек его в направлениях осей х
и у равны нулю, а передний торец
свободен (рис. 7.7).
В таком случае кручение бру-
бруса будет чистым, т. е.
ах = ау = аг = хху = 0. G.14)
Дифференциальные уравнения
равновесия A.3) в рассматривае-
рассматриваемой задаче принимают вид:
дх,
Рис. 7.7. Скрученный брус некруглого
поперечного сечения
дг
дх
¦ = 0;
G.15)
Из первых двух уравнений G.15) следует, что напряжения не
меняются по длине бруса, т. е. все поперечные сечения бруса нахо-
находятся в одинаковых условиях. Последнее уравнение G.15) будет
удовлетворяться тождественно, если ввести функцию напряже-
напряжений Ф, положив _
ду '
дх
Так же, как и в задаче упругого кручения [14 3, для односвязного
контура можно принять, что функция напряжений на контуре
равна нулю. Далее так же, как в упомянутых задачах, крутящий
момент связан с функцией напряжений соотношением
М = 2 J Ф dF.
G.17)
Используем в решении задачи принцип возможных изменений
напряженного состояния (см. § 42).
Подсчитаем вначале работу приращений всех внешних сил на
перемещениях точек приложения этих сил. Она равна работе при-
приращения^ момента ЬМ на угле поворота свободного торца бруса
144

Ф = 8/, где -в — относительный угол закручивания бруса; I —
длина бруса.
f 8XvlutdS = 6М6/
или, используя соотношение G.17),
J 8Xviu( dS = 26/6 J Ф dF. G.18)
Подсчитаем теперь дополнительную работу для всего бруса.
Поскольку распределение напряжений во всех сечениях одно и та же,
R = J R dV = / J RdF.
Так как в случае чистого сдвига
где
то согласно формуле G.9)
т
R = \ у d x
ii, следовательно,
v
^JjdT. G.19)
Подставляя выражения G.18) и G.19) в основное уравнение
принципа возможных изменений напряженного состояния G.11),
получим
8/ = 0, . , G.20)
где
/=j \\ydx— 20Ф W. G.21)
Вариационное уравнение G.20) может быть решено методом
Ритца, при этом- функция Ф выбирается в виде
Ф=ЁС,Ф,, G.22)
все функции Ф; = Ф; (х, у) обращаются в нуль на контуре. Коэф-
Коэффициенты Ct определяются из условий равенства нулю вариаций
интеграла G.21), которые имеют вид
зет-0' - ' <7-23>
Вследствие нелинейности диаграммы сдвига условия G.23)
приводят к нелинейной системе алгебраических уравнений для
145

определения коэффициентов Ch составление и решение котором
даже при небольших п связано со значительными трудностями
В связи с этим воспользуемся методом последовательных при
ближений аналогично изложенному в § 40.
Связь между касательным напряжением т и угловой деформа-
цией у представим в виде
т = Gky, G.24)
где Gk — переменный параметр упругости,
определяемый формулой (см. рис. 7.8)
т
7
V
1
—--
Ч-\
G.25)
На основании соотношений G.24) и
G.25) имеем
^ G.26)
ч
Выражение G.21) принимает вид
Рис. 7.8. Диаграмма сдвига
В таком случае нелинейная система уравнений для коэффициен-
коэффициентов С; приводится к последовательности линейных систем.
Список литературы
1. Биргер И. А. Некоторые общие методы решения задач теории пластич
ногти. — «Прикладная математика и механика», 1951, т. XV, вып. 6, с. 765—770.
2- Биргер И. А. Круглые пластинки и оболочки вращения. М., Оборонги i,
1961, 368 с.
3. Биргер И. А. Теория пластического течения при неизотермическом нагру
жении.—«Известия АН СССР. Механика и машиностроение», 1964, № 1, с. 193—190
4. Биргер И. А. Расчет конструкций с учетом пластичности и ползучести. --
«Известия АН СССР. Механика», 1965, № 2, с. 113—119.
5- Ильюшин А. А. Пластичность. М., ОГИЗ, ГИТТЛ, 1948, 376 с.
1 6. Качанов Л. М. Механика пластических сред. ОГИЗ, ГИТТЛ, 1948, 215 с.
7. Качаиов Л. М. Основы теории пластичности. М., «Наука», 1969, 420 с.
8. Качанов Л. М. О вариационных методах' решения задач теории пластич-
пластичности. — «Прикладная математика и механика», 1959, т. XXXIII, в. 3, с. 616—617.
9. Качаиов Л. М. Пример решения вариационным методом задачи упруго-
пластического кручения. ¦— В кн.: Исследования по упругости и пластичности.
Сборник I. Изд-во Ленинградского университета, 1961, с. 157—161.
10. Лейбензон Л. С. Курс теории упругости. М., ОГИЗ, ГИТТЛ, 1947, 464 с.
11. Лурье А. И. Обобщение теоремы Кастилиано. — «Труды Ленинградского
политехнического института им. М. И. Калинина», 1946, № I, с. 9—15.
12. Малинии Н. Н. Прочность турбомашип. М., Машгиз, 1962, 291 с.
13. Надаи А. Пластичность и разрушение твердых тел. Т. 2, М., «Мир», 1969,
863 с.
14. Папкович П. Ф. Теория упругости. М., Оборонгиз, 1939, 640 с.
15. Расчеты на прочность в машиностроении. Т. 1, М., Машгиз, 1956, с. 884
Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К- Лихарев и др.
16. Смирнов В. И. Курс высшей математики. Т. 2. М., Физматгиз, 1958, 628 <.-
17. Филоненко-Бородич М. М. Теория упругости. М., Физматгиз, 1959, 364 с.
18. Lin Т. Н. Theory of inelastic structures, John Wiley and Sons, Inc, 1908,
454 p.
146

ГЛАВА VIII
РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ ПО ТЕОРИИ ТЕЧЕНИЯ
§ 46. Совместное растяжение и кручение
тонкостенной трубки
Рассмотрим совместное растяжение и кручение тонкостенной
Трубки (рис. 8.1). Обозначим средний диаметр трубки через D,
Тилщину стенки h, растягивающую силу N, крутящий момент М.
Задача вычисления напряже-
напряжений является статически опреде-
определимой. Нормальное а и касатель-
касательное т напряжения как в пределах,
Тик и за пределами упругости
Подсчитываем по формулам
Ш
— N
°~ nDh ' Т
Для упрощения выкладок в
дальнейшем будет считать, что
МИТориал несжимаем (е0 = 0) и Рис- 8Л. Растянутая и скрученная
диаграмма деформирования его не тонкостенная трубка
имеет упрочнения (см. рис. 4.4).
В рассматриваемом случае ах = ау = 0; аг = а; хху = %уг = 0;
'#» = т; 8г = е; ех — гу = ^- = ^- (так как материал не-
несжимаем и, следовательно, 8^ + ^ + 8^ = 0), y.v^ = Ууг = 0. 7г* = 7-
Поэтому интенсивности напряжений и приращений пластических
Деформаций согласно формулам A.19) и B.34) будут
\>1 •= у и -\- ОТ ,
Поскольку диаграмма растяжения не имеет упрочнения,
ot = 1/02 + Зт2= (хт.
Из соотношений D.23) имеем
л da , Щ
dx
C.1)
(8.2)
(8.3)
(8r4)
147

Введем безразмерные напряжения и деформации
а
s = —=
6 __ _
"т
V
__У_ _
и преобразуем соотношения (8.3) и (8.4) к виду
1;
q* + s2
Продифференцируем соотношение (8.6). Тогда получим
q dq + s ds = 0.
(8.5)
(8.6
(8.7)
(8.8)
Умножим первое из уравнений (8.7) на q, а второе на s и сложим
полученные выражения. Используя соотношения (8.6) и (8.8), находим
стт
Подставим эту величину в первое уравнение (8.7). Учитывая
соотношение (8.6), имеем
или
(8.10)
Преобразуем теперь второе уравнение (8.7) при помощи соотно-
соотношений (8.9) и (8.6). Тогда получим
(8.11)
С помощью подстановок
q= sinv; w=tg-j
уравнение (8.10) может быть приведено к виду
Таким же образом может быть преобразовано уравнение (8.11).
Следовательно, зависимости напряжений от деформаций по тео-
эии течения определяются интегралами уравнений (8.10), (8.11)
«ш (8.12). Путь деформирования в этих уравнениях отражается
dy dS,
троизводными -^- или -р-.
148

I Уравнение (8.12) является дифференциальным уравнением Рик-
К1ти. При произвольной функции -?¦ оно не приводится к квадра^
Турам.
Изучим некоторые частные случаи нагружения. Начнем с рас-
рассмотрения ступенчатого нагружения. Допустим, что сначала трубка
Только растягивается, а потом только закручивается. Тогда на пер-
|ой ступени нагружения
dX = 0
II из уравнения (8.10) имеем
Обозначим величину q при ? == 5i через qx и проинтегрируем
tro уравнение в пределах от ^ до \. Тогда получим
X = Х1бхр [2A — li)], (8.13)
Hi следовательно,
Хг—г^. (8.15)
Из формулы (8.14) следует, что
На второй ступени нагружения, когда трубка только закру-
закручивается,
d\ = О
И из уравнения (8.11) имеем
Интагрируя и выполняя преобразования, подобные тем, которые
были сделаны при рассмотрении первой ступени нагружения,
получаем
У= l^exp 12 (х — Xi) I, (8-17)
где
F=|±f; (8.18)
149

a sx — значение величины s при % — %v Из формулы (8.18) следует,
что
5 (82°)
Перейдем теперь к разбору линейного нагружения, т. е. такого
нагружения, когда % является линейной функцией |.
Примем для упрощения выкладок простейшую линейную функцию
1 = §•
Тогда уравнение (8.12) приводится к виду
<%, 2
Проинтегрируем это уравнение. После преобразований получаем
где
Z==i+W~^f.;. (8.22)
1 + w + /2 v 7
Z
а Шд — значение величины w при | = gx. Из формулы (8.22) имеем
A + ^5J1 + ^ (8>24)
^ ^
Таким образом, получены формулы, устанавливающие зависи-
зависимость напряжений от деформаций как при ступенчатом, так и при
линейном нагружениях по теории течения.
Интересно сопоставить приведенное решение этой задачи по тео-
теории течения с решением по теории малых упруго-пластических
деформаций. В случае использования последней из соотношений D.32)
получаем зависимости напряжений от деформаций
где интенсивность деформаций
е, = —L- К^е2 + Т2 (8.26)
Используя обозначения (8.5), преобразуем выражения (8.25)
{ форме
а~ г , g- =; .s= , х ¦¦-. (8.27)
1/ t2 J 2 I/ S2 12
50

Эти соотношения представляют собой зависимости безразмерных
иниряжений от безразмерных деформаций по теории малых упруго-
пластических деформаций. Как следует из формул (8.27), напря-
напряжения определяются конечными значениями деформаций и не зави-
зависит от пути нагружения.
На рис. 8.2 представлены результаты вычисления безразмерных
напряжений как по теории малых упруго-пластических деформаций,
так и по теории течения при двух ступенчатых нагружениях (сна-
X
2,00
К 00
0
021kB
S = 0,975
(q= 0,333)
[s-0,9i+3 j
0,707
1 = 0,909 fq = 0,707
<,=0,W7 [5 = 0,707/
/q=0,707
У 5 = 0,707
X
;, oo
^ ,
LOL'O
2,00
r
(?
a
('.
,
0,909
0,707)
0,707
= 0,975
O,9k3\
0,5331
Рис. 8.2. К сопоставлению теории течения с теорией
малых упруго-пластических деформаций на примере
совместного растяжения и кручения тонкостенной
трубки
чала растяжение, потом кручение и сначала кручение, потом растя-
растяжение) и одном линейном (% = ?) нагружении. Пути нагружения
в координатах g, % показаны на рис. 8.2 стрелками. Величины без-
безразмерных напряжений приведены у точек А, В, С и D, причем
в скобки заключены безразмерные напряжения, подсчитанные по
теории малых упруго-пластических деформаций.
Рассмотрим эти результаты более подробно. Вначале создаем
линейное нагружение тонкостенной трубки до наступления текуче-
текучести (линия ОА), которое происходит в пределах упругости. Поэтому
независимо от принятой теории пластичности по формулам (8.27)
для точки А (% — \ = 0,707) получаем q = s = 0,707. Затем трубку
растягиваем до \ = 2 (точка В). Для точки В величины деформа-
деформаций ? = 2ДХЮ; х = 0,707. По теории течения напряжения в точке В
вычисляем по формулам (8.16), (8.15), (8.13) и (8.6). При этом ?х =
= 0,707; I = 2,000; q1 => 0,707. По теории малых упруго-пласти-
упруго-пластических деформаций напряжения q и s вычисляем по формулам (8.27).
151

После этого трубку скручиваем до % = 2 (точка С). По теории
течения напряжения в точке С вычисляем по формулам (8.20), (8.19),
(8.17) и (8.6). При этом Xi = 0,707; % = 2,00; sx = 0,224. По теории
малых упруго-пластических деформаций напряжения подсчиты-
подсчитываем по формулам (8.27). При этом величины деформаций \ — % —
= 2,00.
Аналогично можно рассмотреть ступенчатый путь нагруже-
нагружения ADC и линейное нагружение,ЛС
Как следует из данных, приведенных на рис. 8.2, в зависимости
от пути нагружения напряжения в конечной точке С по теории
течения получаются различными, а по теории упруго-пластических
деформаций одинаковыми, отличными от напряжений, установлен-
установленных по теории течения. В случае линейного пути нагружения напря-
напряжения в конечной точке С как по теории течения, так и по теории
малых упруго-пластических деформаций одинаковы. Такой же ре-
результат имеет место и в общем случае линейного нагружения [5].
§ 47. Упруго-пластическое состояние
толстостенной трубы, нагруженной равномерным
внутренним давлением и осевой силой
Выше (см. § 32) была решена задача об упруго-пластическом
состоянии толстостенной трубы, нагруженной внутренним давлением
и осевой силой по теории упруго-пластических деформаций. Рассмо-
Рассмотрим теперь решение этой задачи по теории течения. Постановка
задачи такая же, как и в § 32. Отличие будет заключаться только
в том, что в изложенном ниже решении материал трубы не будем
считать несжимаемым (ц = 0,5), поскольку это не упрощает решения
задачи.
В решении, задачи по теории течения удобно принять, что напря-
напряжения в трубе являются функциями двух переменных: радиуса г
и радиуса границы, разделяющей упругую и пластическую обла-
области гт. Дифференциальное уравнение равновесия элемента трубы
F.5) имеет вид
^- + ?^. = 0. ^ (8.28)
Выражения для напряжений на основании соотношений A.6)
и C.3) могут быть представлены в форме
or = sr + о0 = sr + 3/Се0;
at ~ st + ао = st + 3/Се0;
аг = sz + а0 = — (sr + st) + 3/Ce0- .
(8.29)
Подставляя эти зависимости в формулу (8.28), получаем иную
форму дифференциального уравнения равновесия:
dsr | sr — st . ~„ де0 п /0 оп.
~дГ^ } ^3^-^ = 0. (8.30)
152

I Перейдем к выводу условия совместности деформаций. Исполь-
|уя выражения B.5), F.2) и F.23), поручаем величину средней линей-
линейной деформации
Введем-вспомогательную переменную
Эти две величины примем за основные неизвестные,
Из соотношений (8.31) и (8.32) следует, что
ди з . . . ч
и 3 (8>33)
е, = ^ = 4(ео-а); )
ы = 1-г(е0 —а). (8.34)
I Продифференцировав выражение (8.34) по г и сопоставив его
С первым из соотношений (8.33), получим условие ¦ совместности
i Деформаций в виде
де0 да. п а. ,й 0P.v
-к-2 з~ ^ *—• (о.оо)
or or г ч
Рассмотрим вначале напряжения и деформации в упругой обла-
области (гт ^ г ^ гг). Компоненты ^девиатора напряжений связаны
С компонентами девиатора деформаций зависимостями C.8), из кото-
которых следует, что
s, = 2Ger; st = 2Get. (8.36)
В соответствии с выражениями B.6) и (8.33) компоненты девиа-
девиатора деформаций
ег = -у (е0 + За); et = \ (е0 — За);
Поэтому компоненты девиатора напряжений
sr = G (г0 + За);
(8.37)
8,-0 (е„ - За). ) (8>38)
Уравнение равновесия (8.30) после использования зависимо-
зависимостей (8,38) принимает вид
153

4s
Подставляя в это уравнение выражение для -4s- из форму-
формулы (8.35), получаем
Решение выведенного уравнения имеет вид
« = ¦?-, (8.39)
где А — функция гт.
Подставим выражение (8.39) в уравнение (8.35). Тогда получим
dso _ q
дг '
откуда следует, что
е0 = В, (8.40)
где В — функция гт.
Согласно формулам (8.29), (8.38), (8.39), (8.40) получим выра-
выражения для напряжений:
(8.4Г)
;
аг =. (—2G + 3/0 -6.
Величины А и В определяются из краевых условий:
при г = г2 оГ = 0;
при г = гт ст,- = стт.
Из первого краевого условия имеем
(G + 3/0 В + ~^- = 0. . (8.42)
Из второго краевого условия, используя соотношения F.7)
и (8.41), устанавливаем
//r>D\2 I ^ ((/.Л) Т /О /io\
(СШ) -) JZ = -д-. @.43)
Решая уравнения (8.15) и (8.16) относительно А и В, получаем
п*г2 г>*
3G ' Л _|_ ЧЛ"' F.44)
_ _ • (8.45)
154

Следовательно, согласно формулам (8.41) и (8.44) формулы для
напряжений в упругой области принимают вид
З/С — 2G
3/C + G
(8.46)
Выражение для радиального перемещения и в упругой области
получаем при помощи соотношений (8.34), (8,39), (8.40) и (8.44)
(8.47)
Перейдем теперь к рассмотрению напряжений и деформаций
в пластической области (rx «S г ^ гт). Согласно теории течения
(см. § 23) приращения деформаций связаны с приращениями напря-
напряжений и напряжениями следующими соотношениями:
1
der = -g- [dor — ц (dat -f- doz)\ + dk (or — a0);
1
det = -gr [dot — ц {daz + dar
z — fx (dar + dat)]
(a, — a0);
стг—oro),
где обозначено
Преобразуем первые две зависимости. Для этого вычтем из
левых и правых частей уравнений по
, 1 —2ц. ,
"е = —тг^-сЦ
Тогда, учитывая соотношения B.6), A.6), A.5) и C.2), получим
j, dsr
Ж
(8.48)
Выражения (8.48) определяют приращения компонентов девиа-
тора деформации der и deu возникшие за счет приращения компонен-
155

тов девиатора напряжений dsr и dst. Заметим, что при этом радиус гт
границы, разделяющей упругую и пластическую области, являясь
характеристикой степени пластической деформации трубы, изме-
изменяется на величину drr. Поэтому из формул (8.48) следует, что
дег
17т-
det
дгт
1 dSf
~2(Г~дгт~
1 dst
2G drr
dX
+ a?f
, дХ_
' drT
8t.
(8.49)
Исключим из уравнений (8.49) величину -^—. Из второго урав-
уравнения (8.49) устанавливаем
dX _ J_ det_ 1_ _1_ dst
дгт st drT 20 st дгт'
Подставив эту величину в первую формулу (8.49), получим
-s'-fe)=°- (8-5°)
Поскольку диаграмма растяжения материала не имеет упрочне-
упрочнения, компоненты напряжений должны удовлетворять условию пла-
пластичности C.14), которое с помощью соотношений A.6) и A.5) может
быть представлено в форме
Решая это уравнение относительна st, получаем
—s.
(8.51)
В последней формуле берется положительное значение корня.
Это объясняется тем, что в упругой области и на границе упругой
и пластической областей
2s, +sr > 0.
Действительно, как следует из формул A.6), C.3), (8.46), (8.40)
и (8.44), в упругой области
G + 3/C
= рГ
3G
G+3/C
4 >о.
Подставим выражение (8.51) в уравнения (8.30) и (8.50), исполь-
используя зависимости (8.29). Тогда, в совокупности с выражением (8.35),
156

получим следующую систему уравнений для определения трех неиз-
1ЮСТИЫХ е0, а и sr:
де0 да 2а
Tr W Г"'
dst
dsr 30 ( 4 2
де0 _
_3s,+ ]/-i-a2T-3s?
r^ У 3 т г
2?
4 2 О2 о I/4 2 О2\д80
-g-стт —3sr — 3s, [/ -3-ffT—3s'jF~
gg
= 0.
(8.52)
Получить решение этой системы в замкнутом виде невозможно.
Она может быть решена только численными, методами. При ее реше-
решении должны быть использованы условия равенства радиального
напряжения на внутренней поверхности трубы, давлению с обратным
знаком и условие непрерывности радиальных и окружных напряже-
напряжений на границе упругой и пластической областей. После определения
величин е0, а и sr по формулам (8.51) и (8.29) подсчитывают компо-
компоненты напряжения, а по формуле (8.34) радиальное перемещение.
Сопоставим на примере толстостенной трубы при — = 2 и — =
= 1,5 для материала, у которого \i = 0,3; iAJ^ =0,003, расчеты,
выполненные по теории течения и теории упруго-пластических де-
деформаций без допущения о несжимаемости материала [20].
Как следует из сопоставления эпюр (рис. 8.3) и графиков (рис. 8.4)
различие в результатах по теории течения и теории упруго-пласти-
упруго-пластических деформаций ничтожно.
Докажем, что если принять материал трубы несжимаемым (\i =
= 0,5; К = °°', е0 = 0), то решения задач по теории течения и теории
упруго;пластических деформаций совпадают.
Уравнение совместности деформаций (8.35) в этом случае прини-
принимает вид
и, следовательно,
Это уравнение аналогично выражению для функции а, получен-,
ному для упругой области. Поэтому радиальное перемещение в трубе
из несжимаемого материала как в упругой, так и в пластической обла-
областях описывается уравнением (8.47) при /С = оо, т. е.
и =
2Qr '
(8.53)
157

где согласно формуле (8.45) для /С = оо
ат 4
(8.54)
IA г/г,
-1,2?
0,4
/
>
1,0
1,5 г/г
а) . б)
Рис. 8.3. Эпюры напряжений в толстостенной трубе
( — = 2 ), нагруженной внутренним давлением по тео-
теории течения (линия /), по теории малых упруго-пла-
упруго-пластических деформаций (линия 2), в предположении
несжимаемости материала (линия 3) [10]:
а — радиальных; б — окружных; в — осевых
г, о
0,5
/
1/
1
3
-г
1,1
Рис. 8.4. Графики зависимостей давле-
давления от радиального перемещения точек
наружной поверхности трубы для
толстостенной трубы ( — = 2 ), нагру-
женнои внутренним давлением по
теории течения (линия /), теории ма-
малых упруго-пластических деформаций
(линия 2), в предположении несжи-
несжимаемости материала (линия 3) [10]
.1,0
2,0
ТШмг
-17"
Из соотношений (8.53) и (8.54) окончательно получим
Зу/т
(8-55)
Далее зависимости (8.37) и (8.34) дают для несжимаемого мате-
материала (е0 = 0) «-
er = —et = -у ос; и — %~ аг' (8,56)
158

I ккжольку радиальное перемещение и > 0, то а < 0 и поэтому
е, > О, ег < 0. (8.57)
Соотношения (8.56) и (8.57) справедливы как в упругой, так и
и пластической областях.
На основании выражений (8.36), (8.56) и (8.57) заключаем, что
Л..ИЯ упругой области
sr = —st, (8.58)
причем
st > 0, sr < 0. (8.59)
Из соотношений A.6), A.5) и (8.46) следует, что
s, = 0
и поэтому в упругой области
st : sr : sz = 1 : — 1 : 0. (8.60)
Докажем, что это же соотношение выполняется и в пластической
области. Для этого рассмотрим точку А, лежащую на границе, раз-
разделяющей упругую и пластическую области. В этой точке справед-
справедливы соотношения (8.57) и (8.58). Увеличим внутреннее давление
на dp. Тогда радиус границы упругой и пластической областей уве-
увеличится на drr и точка А попадет в пластическую область. Из фор-
формулы (8.58) следует, что величины приращений напряжений в этой
точке
dsr = 2G der — 2G dksr;
ds/= 2Gde, — 2G dlst.
Поскольку соотношения (8.57) справедливы не только в упругой,
но и в пластической областях, то из формулы (8.58) имеем
dsr = — dst,
т. е. при увеличении давления соотношения (8.58) и (8.59) сохра-
сохраняются. Поэтому эти выражения, а следовательно, и соотношение
(8.60) справедливы не только в упругой, но и в пластической области.
На основании доказанного заключаем, что для трубы из несжи-
несжимаемого материала нагружение будет простым и, следовательно,
решения задачи по теории течения и по теории упруго-пластических
деформаций будут совпадать.
Как следует из сопоставления кривых 3 с кривыми 1 я 2 (см.
рис. 8.3 и 8.4), допущение о несжимаемости материала дает очень
небольшую погрешность в определении радиальных и окружных
напряжений и значительную погрешность при подсчете осевых
напряжений и радиальных перемещений. Как указано в книге [10],
кривая 2 на рис. 8.3 может быть получена из кривой 3 умножением
ординат ее на 2ц, а кривая 2 на рис. 8.4 может быть получена из кри-
кривой 3 умножением абсцисс ее на 2 A — ц), причем под \i понимают
величину коэффициента поперечной деформации в пределах упру-
159

гости. Таким образом, решение задачи, выполненное в предполо-
предположении несжимаемости, может быть-уточнено, если в выражении для
осевых напряжений и радиальных перемещений ввести корректи-
корректирующие множители, равные соответственно 2ц и 2 A — ц).
§ 48. Изгиб листа
Рассмотрим чистый изгиб листа при наличии больших деформа-
деформаций (рис. 8.5). Примем, что деформация листа в направлении, пер-
перпендикулярном плоскостям изгиба,
ег = 0. (8.62)
, Допустим, что упрочнение отсутствует, а упругими деформа-
деформациями по сравнению с пластическими можно пренебречь. Это равно-
равносильно использованию в решении диаграммы жестко-пластического
м тела (см. рис. 5.17).
Г * / Jt li При чистом изгибе вследст-
I Ух I Г" вие симметрии нагружения
,. лист изгибается ло дуге окруж-
окружности. Сопоставим лист в двух
близких друг к другу дефор-
деформированных состояниях (рис.
8.6). Допустим, что при пере-
переходе из первого состояния
(сплошные линии) во второе
(штриховые линии) деформации
и перемещения можно считать
малыми. Для определенности
примем, что при изгибе среднее
сечение листа не поворачивает-
Рис. 8.5. Лист в условиях чистого изгиба Ся и нижняя точка этого сече-
сечения неподвижна.
Назовем поверхность, разделяющую область листа, растянутую
в окружном направлении, от области, сжатой в этом направлении,
граничной. Обозначим внутренний и наружный радиусы листа в пер-
первом состоянии через гх и г2, а радиус граничной поверхности г0.
Далее обозначим через Rlt R2 и Ro радиусы окружностей, в которые
переходят точки окружностей радиусов гъ г2 и г0.
Из симметрии деформации следует, что радиальные и окружные
сечения листа, находящегося в деформированном состоянии, и напря-
напряжения в них (окружное at и радиальное ог) являются главными.
Дифференциальное уравнение равновесия элемента, вырезан-
вырезанного из листа, находящегося в деформированном состоянии, двумя
главными сечениями, имеет такой же вид, как н в задаче расчета тол-
толстостенных труб (см. § 33)
IF
ar — at
= 0.
(8.63)
160

Из этого уравнения следует равенство нулю нормальной силы
и радиальных сечениях. Действительно, уравнение (8.63) может быть
представлено в виде
Интегрируя это уравнение в пределах от гг до г2 и учитывая крае-
иые условия при г = гх аг = 0, при г = г2 аг = О, получим вели-
величину нормальной силы на единицу ширины листа
'я
jatdr = 0.
Рис. 8.6. Сечение листа плоскостью, .перпенди-
.перпендикулярной к оси в двух близких деформированных
состояниях
Приращения пластических деформаций, равные в рассматривае-
рассматриваемом случае приращениям деформаций, связаны с напряжениями
следующими зависимостями [см. формулы D.23I:
(8.64)
где Oi — интенсивность напряжений; d&t — интенсивность прира-
приращений пластических деформаций; а0 — среднее нормальное напря-
напряжение.
6 Н. Н. Малинин 161

В рассматриваемом случае в соответствии с соотношениями A.21)
и A.5)
J±?*. (8.66)
На основании выражения (8.62) заключаем, что
de2 = 0.
Поэтому из третьей формулы (8.64) имеем
Следовательно, согласно выражению (8.66)
ог
(8.67)
Подставляя эту величину в выражение для интенсивности напря-
напряжений (8.65), получим
i/T
°i=±1j-<pl — or), (8.68)
причем знак плюс соответствует области, растянутой в окружном
направлении, а знак минус для сжатой.
При отсутствии упрочнения напряжения должны удовлетворять
условию пластичности C.18), и, следовательно, согласно фор-
формуле (8.68)
а, —а — + -Л^а-г. (8.69)
Преобразуем дифференциальное уравнение (8.63), используя соот-
соотношение (8.69). Тогда получим
4г^= + -т= —, (8-70)
dr — |^з г к
причем по-прежнему знак плюс относится к области, растянутой
в окружном направлении, а знак минус к области сжатой.
Проинтегрируем уравнение (8.70). В результате устанавливаем:
при гх ^ г ^ г0
при г0 ^ г «S>2
- + С2. (8.72)
Краевые условия имеют вид:
при г = гх аг = 0, при г = г2 ст, = 0, при г = г0 агСЖ = алраст.
Последнее краевое условие отражает непрерывность радиального
напряжения на границе сжатой и растянутой в окружном направле-
направлении областей.
162

Из первого и второго краевого условия получаем
d = С2 = 0.
Поэтому согласно соотношениям (8.71), (8.72) и (8.69) формулы
для напряжений принимают вид:
при гх ^ г «S>0
ог = -^от\п±-; а|=я_-^„тA + 1„^-); (8.73)
при Го^Г^Га
Н1^ ( ^) (8.74)
Используя третье краевое условие, получим формулу для радиуса
граничного слоя
Го - V~rJl. (8.75)
Подсчитаем величину изгибающего момента на единицу ширины
листа. Для удобства вычислений запишем моменты внутренних сил
относительно центра кривизны
^2
М — j atr dr.
Используя выражения (8.73) и (8.74), представим это соотношение
в виде
После преобразований получим
^^-^^1 (8.76)
где h — г2 — гх — высота листа в деформированном состоянии.
В дальнейшем будет показано, что в процессе деформации высота
листа не изменяется, т. е. h = h0.
Формулы (8.67), (8.73) и (8.74) позволяют подсчитать нормальную
силу и изгибающий момент в поперечном сечении листа. Они связаны
с осевым напряжением соотношениями
ф
2 Гг
Nz = J J azr da. dr;
2
Ф
Mz =11 azrz cos a da dr.
2
163

Подставляя в эти соотношения осевые напряжения, по формулам
(8.67), (8.73) и (8.74) легко убедиться, что нормальная сила равна
нулю,- а изгибающий момент отличен от нуля.
Таким образом, для выполнения условия цилиндрического изгиба
на торцах листа должны быть приложены моменты. При отсутствии
их деформированная поверхность листа является поверхностью двоя-
двоякой кривизны.
Перейдем к рассмотрению деформаций и перемещений. Прира-
Приращение окружной деформации при переходе из первого состояния
во второе (рис. 8.6) в некоторой точке на радиусе г
' ГЦ) '
откуда
R=irkr-' <877>
ф
Поскольку в точках граничного слоя приращение окружной
деформации равно нулю, по формуле (8.77) имеем
(8J8)
Т
Запишем условие несжимаемости материала для слоя с внутрен-
внутренним радиусом г0 и наружным радиусом г с учетом того, что осевая
деформация равна нулю:
Подставим в это условие соотношения (8.77) и (8.78). Тогда после
преобразований, учитывая, что согласно условию (8.62) для несжи-
несжимаемого материала приращения окружной и радиальной деформации
равны, имеем
^ (?) (8.79)
Изменение высоты листа определяем по формуле
г, . ->
dh = J (der) dr.
г,
Подставляя в это соотношение выражение (8.79), получим
dh = О,
т. е. толщина листа при изгибе не изменяется.
Заметим, что при учете упрочнения толщина листа при изгибе
изменяется [17].
Из формулы (8.76) следует, что поскольку толщина листа в про-
процессе его изгиба не изменяется, изгибающий момент на единицу
ширины листа при отсутствии упрочнения также постоянен.
164

Формулы (8.73)—(8.75) позволяют определить напряжения для
заданного внутреннего радиуса листа rv При этом, так как толщина
.миста в процессе изгиба постоянна, наружный радиус листа г2 =
Установим зависимость между внутренним радиусом кривизны
п деформацией на внутреннем волокне. Для этого используем условие
постоянства объема листа, которое при равенстве осевой деформации
пулю сводится к условию постоянства площади сечения листа, пер-
перпендикулярного оси z (рис. 8.5
п 8.6). Запишем это условие
я (Г2 — Гх) -?— = /0Л0, (8.80)
где ф — центральный угол для
изогнутого листа; 10 — ширина
листа до изгиба.
Из соотношения (8.80), учи-
учитывая, что толщина листа при
изгибе не изменяется и, сле-
следовательно,
'rt-n = h0, (8.81)
получим
0,75
0,5
(ПгФо
0,25
0
\
1
А
\
\
-/
2.0 1.5 1.0 0,5 0 0,5 1,0 О
Рис. 8.7. Эпюры изменения напряжений
по толщине листа для величины логариф-
логарифмической деформации в точках внутренней
поверхности, равной 40%
"о— 2 2 . . '
Окружная деформация в точках внутренней поверхности
'о 'о
Используя формулу (8.82), получим
1
— 1.
Логарифмическая окружная деформация в этих точках
1
1)= 1п ¦
1 +
2гх
Из этого выражения устанавливаем, что
2 1-
exp
(8.83)
Задаваясь величиной логарифмической деформации в точках
внутренней поверхности, по формуле (8.83) вычисляем внутренний
радиус листа rv Наружный радиус определяем из соотношения (8.81),
а радиус граничной поверхности по формуле (8.75). Напряжения
подсчитываем по формулам (8.73) и (8.74).
165

На рис. 8.7 изображены эпюры изменения напряжений по толщине
листа для логарифмической деформации в точках внутренней поверх-
поверхности, равной 40%. .
С учетом упрочнения материала по теории течения эта задача
решена в работе [173, а по теории упруго-пластических деформаций
в статье [8 3. Большие деформации при пластическом изгибе полосы
по теории течения без учета упрочнения рассмотрены в статье [6 3,
а с учетом упрочнения в работе [7]. Пластический изгиб листа и по-
полосы из ортотропного материала при больших деформациях исследо-
исследован в статьях [18], [19 3.
§ 49. Деформирование цилиндрических труб
в конических матрицах
Представим себе, что тонкостенная труба протягивается или
проталкивается осевой силой через матрицу, так что радиус ее или
увеличивается или уменьшается. В зависимости от схемы нагруже-
Рис. 8.8. Схемы волочения, обжатия, протяжки и раздачи
ния будем называть эти операции волочением, обжатием, протяж-
протяжкой и раздачей.
На рис. 8.8, а и 8.8, б при приложении сил слева изображены
соответственно схемы волочения и протяжки, а при приложении
сил справа — обжатия и раздачи.
Так же, как и в предыдущей задаче, примем, что материал идеаль-
идеально жестко-пластический. Диаграмма растяжения такого материала
изображена на рис. 5.17. Допустим, что матрица имеет коническую
форму и является жесткой. Пренебрежем изгибающими моментами,
возникающими при деформации трубы, т. е. будем решать задачу
на основе безмоментной теории оболочек вращения. Решение постав-
поставленной задачи дано в работе [9].
Деформация трубы является осесимметричной. Поэтому напря-
напряжения, деформации и толщина стенки зависят только от радиуса.
При безмоментном осесимметричном нагружении оболочки вра-
вращения напряженное состояние всех точек оболочки плоское, а мери-
меридиональное ат и окружное at напряжения — главные напря-
напряжения.
166:

Уравнения равновесия элемента, вырезанного главными сече-
сечениями из осесимметрично нагруженной безмоментной оболочки вра-
вращения, имеют вид:
-J- (amrh) — ath + -^- = 0; (8.84)
От , О( pv
Рт Pi Я '
где рт — радиус кривизны меридионального сечения; р^ — радиус
кривизны сечения оболочки конической поверхностью, перпендику-
перпендикулярной дуге меридиана; г — радиус окружности в .сечении плос-
плоскостью, перпендикулярной оси оболочки; h—толщина стенки;
/>„, — интенсивность распределенной нагрузки в направлении мери-
меридиана; pv — интенсивность распределенной нагрузки в направлении
нормали; а — угол между касательной к меридиану и осью оболочки.
Для конической матрицы
cos a
и из уравнения (8.85), полагая pv = p, получаем формулу, связы-
связывающую давление между матрицей и оболочкой и окружное напря-
напряжение
(8.86)
Учитывая, что
Рт = /Р.
где f — коэффициент трения, и используя соотношение (8.86), пре-
преобразуем уравнение (8.85) к виду
r_dom , г dh п , ^ Un A tQ Q74
dr
где
k = 1 +fctg о.
В рассматриваемой задаче приращения деформаций в окружном
направлении det и в направлении нормали к оболочке dev связаны
с приращением радиуса и толщины соотношениями
Поэтому уравнение (8.87) может быть записано в следующей
форме:
r^r + -^-om + am-kot = 0. (8.89)
167

Для жестко-пластического тела приращения деформаций связаны
с напряжениями соотношениями D.20). В рассматриваемом случае
плоского напряженного состояния
»—
Тогда из уравнений D.20) следует
(8.90)
где
at - V<&— omat + a] , (8.91)
— интенсивность напряжений; det — интенсивность приращений
пластических деформаций.
Из выражений (8.90) имеем
, Поэтому уравнение (8.89) принимает вид
Компоненты напряжения ат и ст^ должны также удовлетворять
условию пластичности. В рассматриваемом случае согласно форму-
формулам C.18) и (8.91) имеем
Qm — °mOt + о] = а%. v
Для того чтобы удовлетворить этому условию, как и в § 35, вве-
введем функцию if, через которую напряжения выражаются следующим
образом: .
CTm = 171fCTTc0St; at^YfaTC0S{^ г)* (8>94)
Установим пределы изменения этой величины для различных
схем нагружения (рис. 8.8) исходя из знаков меридионального и ок-
окружного напряжений.
3 11'
В случае волочения <зт > 0; at < 0; -^ я < ip ^ —g- я; для об
5 3
жатия ап < 0; at < 0; -g- я «s if^ -^- я; при протяжке ат > 0;
ст^ > 0; 2- ^; я|? < -j-; для раздачи ат < 0; at > 0; -2- sg if
168

Подставляя напряжения по формулам (8.94) в уравнение (8.93),
выводим дифференциальное уравнение
dr
г
2 tg2
Проинтегрируем это уравнение. Тогда получим
- = ехр
ч (8.95)
(8.96)
где г{ — радиус окружности в
сечении оболочки плоскостью,-
псфпендикулярной ее оси на
входе в матрицу, af — значе-
значение функции я|) при г — Г{. По-
Последняя величина определяется
из граничного условия при г =
•- гх о, = аг%, где ofi — мери-
меридиональное напряжение на
входе в матрицу. Следователь-
Следовательно, согласно первой формуле
(8.94)
C0Sti = -T--r-
-6tl6r,
0,8
0.6
ом
0.2
о
/
у
//
\
У/
V
/
к
л/л,
'.16
иг
1.08
1,04
1.00
1.0 . 0.9 0.8 ОЛ 0,6 Пг,
Уравнение (8.96) устанавли- Рис 8.9. Эпюры меридиональных (кри-
вает зависимость функции ib от вая. ^ и ОКРУЖНЫХ (кривая 2) напряже-
^J — т HHHj а также эпюра толщины стенки (кри-
безразмерного радиуса —. вая 3) для случая волочения трубы без
ri противоиатяжения^(а = 14°, / = 0,1)
Перейдем к определению
толщины стенки. Из соотношений (8.88) и (8.92), (8.94) и (8.95)
имеем
dh tg_
h l/ч" _L I
Интегрируя это уравнение, получаем
-ф
(8.97)
Выведенное уравнение связывает изменение толщины с функ-
функцией я(>.
Интегралы (8.96) и (8.97) выражаются через элементарные функ-
функции. Однако проще вычислять эти интегралы численно.
169

Напряжения в зависимости от величины -ф определяем по форму-
формулам (8.94).
На рис. 8.9 представлены эпюры изменения меридиональных
и окружных напряжений, а также эпюра изменения толщины стенки,
построенные по формулам (8.94)—(8.97) для случая волочения без
противонатяжения. Как следует из эпюры, окружное напряжение
обращается в ноль при — = 0,5. Это значение радиуса является
наименьшим из всех возможных радиусов окружности в сечении
оболочки плоскостью, перпендикулярной ее оси при выходе из мат-
матриц. Оно характеризует наиболее возможную в рассматриваемом
случае степень обжатия трубы.
В работе [1 ] приведено решение этой задачи для жесткоупроч-
няющегося. материала. При этом использован критерий Хубера—
Мизеса. В статье [2] дано решение этой же задачи с использованием
критерия Треска—Сен-Венана. В статье [3 ] исследовано волочение
тонкостенных ортотропных труб через коническую матрицу.
Список литературы
1. Бубнова Л. В., Малинин Н. Н. Напряжения и деформации при формоиз-
формоизменении тонкостенных труб. — «Известия высших учебных заведений. Машино-
Машиностроение», 1965, № 10, с. 199—203.
2. Бубнова Л. В. Расчет формоизменения тонкостенных труб. — «Известия
высших учебных заведений. Машиностроение», 1965, № 11, с. 139—142.
3. Геогджаев В. О. Волочение тонкостенных анизотропных труб сквозь кони-
коническую матрицу. — «Прикладная механика», 1968, т. IV, в. 2, с. 79—83.
4. Гоффман О., Закс Г. Введение в теорию пластичности для инженеров,
М., Машгиз, 1957, 279 с.
5. .Качанов Л. М. Основы теории пластичности. М., «Наука», 1969, 420 с.
6. Малииин Н. Н. Большие деформации полосы при пластическом изгибе. —
«Известия АН СССР. Механика», 1965, № 2, с. 120—123.
7. Малинин Н. Н., Ширшов А. А. Исследование больших деформаций при
пластическом изгибе полосы с учетом упрочнения. — «Известия высших учебных
заведений. Машиностроение», 1965, № 2, с. 165—172.
8. Малинин Н. Н., Ширшов А. А. Пластический изгиб листа при больших
деформациях. — «Известия высших учебных заведений. Машиностроение», 1965,
№ 8, с. 187—192.
9. Малинин' Н. Н. Волочение труб через конические матрицы. — «Известия
АН СССР. Механика», 1965, № 5, с. 122—124.
10. Прагер В., Ходж Ф. Г. Теория идеально-пластических тел. М., Изд.
иностр. лит., .1956, 398 с.
11. Расчеты на прочность в машиностроении. Т. I, M., Машгиз, 1956, 884 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К- Лихарев и др.
12. Смирнов-Аляев Г. А. Механические основы пластической обработки ме-
металлов. М.—Л., «Машиностроение», 1968, 271 с.
13. Сторожев М. В., Попов Е. А. Теория обработки металлов давлением. М.,
«Машиностроение», 1971, 424 с.
14. Томсен Э., Яиг Ч.-, Кобаяши Ш. Механика пластических деформаций при
обработке металлов. М., «Машиностроение», 1969, 503 с.
15. Унксов Е. П. Инженерная теория пластичности. М., Машгиз, 1959, 328 с.
16. Хилл Р. Математическая теория пластичности. М., ГИТТЛ, 1956, 407 с.
17. Ширшов А. А. Исследование пластического изгиба листа с учетом упроч-
упрочнения. — «Известия высших учебных заведений. Машиностроение», 1965, № 7,
с. 168—174.
170

18. Ширшов А. А. Пластический изгиб листа из анизотропного материала при
больших деформациях. — «Известия высших учебных заведений. Машиностроение»,
1969, № 10, с. 148—152.
19. Щиршов А. А. Пластический изгиб' полосы из анизотропного материала
при больших деформациях. — «Известия высших учебных заведений. Машинострое-
Машиностроение», 1970, W» 2, с. 172—177.
20. Hodge P. С, White G. N. A qualitative comparison of flow and deformation
theories of plasticity — «Journal of applied mechanics», 1950, Vol. 17, No 2, p. 180—
184.
21. Johnson W., Mel lor P. B. Plasticity for mechanical engineers, D. Van Nostrand
Company LTD, 1962 412 p.
22. Marciniak Z. Mecnanika procesow tioczenia blach, Paristwowe wydawnictwo
naukowo-techniczne, 1961, 271 s.
23. Szczepinski W., Wste,p do analizy procesow obrobki plastycznej, Parist-
Paristwowe wydawnictwo naukowe, 1967, 319 s.
24. Theoria plastycznosti, Paristwowe wydawnictwo naukowe, 1965, 399 s. Aut.:
Z. Marciniak, Z. Mroz, W. Olszak i inni.

ГЛАВА IX
ПЛОСКАЯ ДЕФОРМАЦИЯ
§ 50. Основные уравнения
Представим себе, что тело, размеры которого в направлении оси г
значительны, нагружено уравновешенной системой сил, приложен-
приложенных к боковой поверхности и не изменяющихся по длине тела
(рис. 9.1). В таком случае напряжения, перемещения и деформации
не зависят от координаты г. Сечения- тела, перпендикулярные оси г,
при его деформации не искривляются. Они могут перемещаться по-
поступательно как жееткие плоскости вдоль оси г. Примем, что эти
перемещения равны нулю •
иг = 0. (9.1>
Поскольку сечения, перпендикулярные оси г, не искривляются,
касательные напряжения в этих сечениях равны нулю, т. е.
т» = тад = 0 (9.2)
и, следовательно, эти сечения являются главными.
Рассматриваемую деформацию тела называют плоской.
Предположим, что тело несжимаемо. Используем схему идеального
жестко-пластического тела, диаграмма деформирования которого
изображена на рис. 5.17.
Решение упруго-пластических задач плоской деформации связано
со значительными трудностями. Простейшая упруго-пластическая
задача плоской деформации — задача расчета Толстостенной трубы,
нагруженной внутренним Давлением и осевой силой, была рассмо-
рассмотрена в § 32 и 47.
Решение жестко-пластических задач плоской деформации имеет
большое практическое значение для исследования технологических
операций, таких как прокатка, волочение, прессование, а также для
определения предельных нагрузок при 'указанном выше нагруже-
нии тел.
При использовании диаграммы деформирования, изображенной
на рис. 5.17, в теле наряду с пластическими областями (ot — от)
возможно возникновение жестких областей (сг,- <сгт).
Из соотношений B.1) и (9.1) следует, что в рассматриваемом слу-
случае
ег = 0. (9.3)
172

Поэтому как по теории упруго-пластических деформаций [см.
формулы D.27) ], так и по теории течения [см. формулы D.24) ]
для несжимаемого тела имеем oz — о0 и, следовательно, согласно
формуле A.5)
Ох+Оу
(9.4)
Подставляя эту величину в условие пластичности C.18) и исполь-
нуя соотношения A.19), (9.2) и (9.4), получаем
(9.5)
где тт = —г— — предел текучести при чистом сдвиге.
Два первых дифференциаль-
дифференциальных уравнения равновесия A.3)
при отсутствии объемных сил
с использованием соотношений
(9.2) приводятся к виду
дох _j_ дтху _п.
дх
<Эт
¦ХУ
дх
ду
даи
ду
(9.6)
Рис. 9.1. Нагружение тела в условиях
плоской деформации
Третье дифференциальное
уравнение равновесия A.3)
удовлетворяется тождественно.
Если на границе тела за-
заданы напряжения, то три
уравнения (9.5) и (9.6) по-
позволяют определить компоненты напряжения независимо от де-
деформаций (если использовать теорию упруго-пластических де-
деформаций) или скоростей деформаций (если использовать теорию
течения). Такие задачи называют статически определимыми. Стати-
Статическая определимость напряжений является в некоторой степени
условной, поскольку для определения напряжений к уравнениям
равновесия необходимо присоединить условие пластичности.
После определения компонентов напряжений могут быть найдены
деформации или скорости деформаций. В дальнейшем, как это обычно
принято [81, будем говорить об определении скоростей деформаций
равновесия или скоростей перемещений.
Использование понятий скоростей деформаций и скоростей пере-
перемещений не означает учета фактора времени в развитии пластиче-
пластических деформаций. Это просто удобная запись, позволяющая избе-
избежать использования понятий приращений деформаций в случае
применения теории течения.
173

Из соотношений D.24), B.38), D.33) и (9.3) выводим два диффе-
дифференциальных уравнения относительно скоростей перемещения vx
dvu
dvx
~w
dvy
dvx
dvy
~~ду
= 0.
(9.7)
Первое из этих уравнений является условием лропорциональности
девиаторов скорости деформации и напряжения и условием совпаде-
совпадения направлений главных скоростей деформации и напряжений,
а второе условием несжимаемости тела.
Рис. 9.2. Исходные и главные площадки в условиях плоской деформации
Интегрируя уравнения (9.7), можно определить скорости пере-
перемещений.
Если на всей или на части границы тела заданы не напряжения,
а скорости перемещения, то задача определения напряжений не
является статически определимой. В этом случае напряжения и ско-
скорости перемещения определяют путем совместного решения уравне-
уравнений (9.5)—(9.7).
Рассмотрим некоторые особенности напряженного состояния,
возникающего в случае плоской деформации тела при ег = 0.
Как отмечалось выше, сечение тела плоскостью, перпендикуляр-
перпендикулярной оси z, является главной площадкой. Поэтому в рассматривае-
рассматриваемой задаче положение одной главной площадки известно. В таком
случае положение двух других главных площадок, параллельных
оси z, определяется формулой [19]
2a =
(9.8)
где а — угол между главной осью 1 и осью х (рис. 9.2).
174

Выражения для главных напряжений имеют вид
2я- ±
(9.9)
причем, учитывая соотношение (9.4), заключаем, что знак плюс в этой
формуле определяет наибольшее alt а знак минус — наименьшее сг3
главные напряжения.
Из формулы (9.-9) следует, что наибольшее касательное напря-
напряжение
*ГПЯУ
(9.10)
Таким образом, согласно соотношениям
(9.9), (9.4) и (9.10)
= °"о. 0*8 = 0*0 — ттах- (9.11)
Следовательно, напряженное состояние
п условиях плоской деформации можно
рассматривать как результат наложения
всестороннего равного растяжения с на-
напряжением а0 на чистый сдвиг с каса-
касательным напряжением ттах (рис. 9.3).
Рис. 9.3. Напряженное со-
состояние в условиях плоской
деформации
§ 51. Линии скольжения
Площадки действия максимальных касательных напряжений,
проходящие через ось z, делят пополам углы между главными пло-
площадками, в которых возникают наибольшее ох и наименьшее а8
главные напряжения. Назовем линиями скольжения — линии, касаю-.
щиеся всеми своими точками площадок максимальных касательных
напряжений. Очевидно, что имеются два ортогональных семейства
линий скольжения, лежащих в плоскости ху. Понятие линий сколь-
скольжения не связано только с задачей плоской деформации. Примером
линий скольжения являются линии Чернова, которые можно наблю-
наблюдать на поверхности плоского полированного образца при его растя-
растяжении за пределами упругости. Линии Чернова наклонены под уг-
углом 45°чк оси образца, так как в площадках под углом 45° к оси воз-
возникают наибольшие касательные напряжения.
Обозначим два взаимно-ортогональных семейства линий сколь-
скольжения через а и b (рис. 9.4). Если угол наклона касательной к одной
из линий скольжения семейства а в некоторой точке равен ф, то тогда
угол наклона касательной к линии скольжения семейства b в той же
точке равен ф + -у (рис. 9.4).
Дифференциальные уравнения семейств линий скольжения а
и b имеют соответственно вид:_
¦?
(9.12)
.1*5

Поскольку напряженное состояние в условиях плоской деформа-
деформации можно рассматривать как наложение всестороннего равного
растяжения с главными напряжениями сг0 на чистый сдвиг с каса-
касательным напряжением тюах, бесконечно малый элемент, выделенный
линиями скольжения, испытывает одинаковое растяжение в на-
направлении линий скольжения (рис. 9.5).
Выразим компоненты напряжений ох, ау, хху в некоторой точке
через тригонометрические функции угла ср наклона касательной к ли-
линии скольжения, проходящей через эту точку.
Рис. 9.4. Линии скольжения
Рис. 9.5. Напряженное состоя-
состояние элемента, выделенного ли-
линиями скольжения
Для этого вначале вспомним зависимости компонентов напряже-
напряжений в площадках, проходящих через ось г, от главных напряжений ох
и 03 U9]:
Qi — Оз
2
sin 2a,
(9.13)
где a — угол наклона к оси х нормали к площадке, в которой возни-
возникает главное нгпряжение стх (рис. 9.6).
Так как
о3 + аг,
то по формуле (9.4)
176

Далее из соотношений (9.10) и (9.5) заключаем
(9.15)
Поскольку площадки действия максимальных касательных на-
напряжений делят пополам углы между главными площадками
(рис. 9.6), то
Ф = «+,-^. (9.16)
Рис. 9.6. Напряжения в различных площадках в условиях плоской
деформации
Преобразуем формулы (9.13), используя соотношения (9.14)—
(9.16). Тогда получим
о у = 0О — тт sin 2ф;
1ху = — тт cos 2ф.
(9.17)
Подставив эти соотношения в условие пластичности (9*5), можно
убедиться, что последнее тождественно удовлетворяется.
Таким образом, для определения напряжений ох, оу и хху по
формулам (9.17) необходимо знать две величины 0О и <р.
Внося соотношения (9.17) в уравнен-ия равновесия (9.6), получаем
систему двух нелинейных дифференциальных уравнений в частных
производных первого порядка для функций сг0 и Ф
(9.18)
Поскольку в этой системе частные производные только в первой
степени, ее называют квазилинейной.
177

Докажем, что система уравнений (9.18) является гиперболиче-
гиперболической [15]. Для этого возьмем в плоскости х и у некоторую кривую,
вдоль которой будем считать функции 0О и ф известными. Тогда
дх
Зф
W
= -т- dx + -д2- aw
(9.19)
Уравнения (9.18) и (9.19) являются системой четырех линейных
алгебраических уравнений относительно частных производных -д-2-,
~Г~' ~д ' Г~ ' Решение этой системы может быть пред-
представлено в форме определителей. Частные производные определяются
единственным образом всегда, кроме случая, когда вдоль рассматри-
рассматриваемой линии определитель системы равен нулю. Такие линии назы-
называют характеристиками системы дифференциальных уравнений [15].
Уравнения" характеристик имеют вид:
1 0 2тт cos 2ф 2тт sin 2ф
О 1 2тт sin 2ф —2тт cos 2ф
dx dy О О
О 0 dx dy
= 0,
Раскрывая определитель, получаем квадратное уравнение отно-
относительно —т-
(9.20)
Корни этого уравнения
~&x~
Как известно [15], если: ' . •
1) два корня уравнения действительны и различны, систему урав-
уравнений называют гиперболической;
2) два корня уравнения одинаковы — параболической,
3) оба корня уравнения комплексные — эллиптической.
Таким образом, система уравнений (9.18) является гиперболи-
гиперболической и, как следует из сопоставления уравнений (9.12) и (9.20),
характеристики совпадают с линиями скольжения.
Если координатные оси sa и sb в каждой точке будут направлены
по касательным к линиям скольжения (рис. 9.7), то, полагая в диф-
дифференциальных уравнениях (9.18) ф = 0, получаем
~
(о0 + 2ттф) = 0;
178

Можно показать, что эти уравнения являются дифференциальными
уравнениями равновесия элемента, вырезанного линиями скольже-
скольжения. Интегрируя их, получаем
(9.21)
где I и т) — постоянные вдоль линий скольжения соответственно а
и Ь величины. При переходе от одной линии скольжения а (или Ъ)
к другой параметр | (или т))
изменяется.
Решая уравнения (9.21) отно-
относительно 0О и ф, устанавливаем
= 4-(? —Л)-
(9.22)
Последние уравнения позво-
позволяют по известным величинам |
п т) определить о0 и ф, а затем
при помощи формул (9.17) ком-
компоненты напряжения.
Рис. 9.7. Система координат sa, Sb, оси
которой направлены по касательным
к линиям скольжения
§ 52. Линеаризация основной системы
дифференциальных уравнений
Основная система дифференциальных уравнений (9.18) может быть линеаризо-
иппа. Для этого примем за неизвестные функции параметры \ и т). Подставим выра-
выражения (9.22) в уравнения (9.18). Тогда получим
ду ду
ду ""*¦ ду
дх дх
ду
Умножим вначале второе уравнение на tg <p и сложим с первым, а затем умно-
умножим второе уравнение на —ctg <p и сложим с первым. После преобразований уста-
устанавливаем
дх
3
ду
|2L
дх
ду
(9.23)
Таким образом получена система однородных квазилинейных дифференциаль-
дифференциальных уравнений, коэффициенты которой являются функциями только | и т).
Такая система путем обращения переменных может быть приведена к линейной
системе [15]. Поэтому ее называют приводимой.
Для доказательства заметим, что
х = х (?, т)), у = у (I, т)).
179

Дифференцируя эти выражения сначала по х, а потом по у, устанавливаем:
(9.24)
Полученную сумму уравнений можно рассматривать как систему четырех алге-
дх дх ду ду
браических уравнении относительно частных производных -is*-, -s—> ~а% > ~^~ •
Решая ее, получаем
дх _ 1 дц дх 1 j?|_
dl Д ду ' дц ~5~ ду
1 =
л
и —
л
и —
1
1 =
дх
dx_
dl
ду
dl
dy
3|
§
dl
ду
dl
дх
dl
ду
¦+2L
dx
+ дц
, dy
+ дц
'ду
^ дц
дц
Зг\,
~дуУ
дц.
дх '
дц
ду '
ду
_}_дц
Д дх '
1 31
где
дц
^1^1_ д% дЦ
дх ду ~д~у дх
(9.25)
(9.26)
— определитель системы алгебраических уравнений (9.24), который называют яко-
якобианом преобразования системы дифференциальных уравнений (9.23).
Внося частные производные (9.25) в дифференциальные уравнения (9.23), полу-
получаем следующую линейную систему дифференциальных уравнений:
$-о;
(9.27)
Эту систему линейных дифференциальных уравнений с переменными коэффи-
коэффициентами называют канонической. В каждом из уравнений содержатся производные
только по одному аргументу.
Система дифференциальных уравнений (9.27) не эквивалентна системе (9.23),
так как при выводе ее было произведено сокращение иа якобиан Д и, следовательно, -
потеряны решения, обращающие якобиан в нуль.
Найдем эти решения. Из уравнений (9.23) следует
ду
дц_
дх
dl
= — ctg ф
3%
Ж
Подставляя эти величины в выражение (9.26), получим
2 _а|_ _5tj___- 2 dj дц
sin 2ф дх дх ~ sin 2ф ду ду '
Д = -
Следовательно, якобиан обращается в нуль в трех случаях: 1) | = const; ц =
= const; 2) | = const; 3) ц = const. В первом случае имеет место так называемое
равномерное поле напряжений, а в двух других простые поля. Эти поля напряжений
будут рассмотрены ниже.
Решение системы линейных дифференциальных уравнений (9.27) проще, чем
решение системы квазилинейных дифференциальных уравнений (9.18). В этом заклю-
заключается практическое значение линеаризации этой системы. Решение линейной системы-
дифференциальных уравнений (9.27) разработано в книгах [8, 17, 32].
180

В дальнейшем будут рассмотрены иные методы решения задач плоской дефор-
м;щии, основанные на переходе от дифференциальных уравнений к конечно разност-
разностным соотношениям и на некоторых свойствах линий скольжения.
Независимо от используемых методов для решения задач необходимо распо-
члгать величинами а0 и ф на поверхности тела. Определение-их рассмотрено в сле-
слечу ющем параграфе. .
§ 53. Граничные условия для напряжений
Предположим, что линия С (рис. 9.8) — линия пересечения по-
г.ерхности тела с плоскостью ху. Обозначим угол наклона нормали v
к пей с осью я через ф. Будем считать нормальное crv и касательное xvt
напряжения на поверхности известными. Установим условия, кото-
которым должны удовлетворять на поверхности величины о0 и ф.
1'ис. 9.8. Напряженное состояние эле-
мента у поверхности тела
Рис. 9.9. Напряженное состояние элемен-
та у граничной плоскости, свободной от
напряжений
Нормальное и касательное напряжения на поверхности связаны
с напряжениями в площадках, перпендикулярных осям х и у, сле-
следующими соотношениями [19]:
~ %ХУ C0S
Подставим в эти зависимости выражения (9.17). Тогда после пре-
преобразований получим
°v — ао + тт sin 2 (ф — ф);
Tv< = Тт COS 2 (ф — R|)),
откуда
ao===crv — ттз1п2(ф—tjj); "I
,1 V . 1.1 (9-28)
ф = ф ± -л- arccos —— + to, v '
^ тт i
где ft — целое число.
181

В случае отсутствия на поверхности касательных напряжений
т?< = 0:
1
= av ± тт.
(929)
Если поверхность тела является плоскостью, свободной от напря-
напряжений (рис. 9.9), то
я
ф=±— + kn;
а0 = ± тт; сГд. = ± 2тт.
(9.30)
Зная величины сг0 и ф на поверхности тела, по формулам (9.21)
можно определить значения g и т) в точках поверхности.
§ 54. Свойства линий скольжения
Рассмотрим некоторые основные свойства линий скольжения.
Они были исследованы Генки и сформулированы им в виде несколь-
нескольких теорем. Рассмотрим только первую теорему Генки и следствия
из нее.
Первая теорема Генки. При переходе от одной
линии скольжения к другой (рис. 9.10) одного семейства (например, Ь)
вдоль линии скольжения другого семейства (а) изменения величин о0
и ф не зависят от того, по какой линии скольжения другого семейства
совершается переход.
Обозначим значения % и ц для линий скольжения alt а2, Ьх и Ь2
соответственно через |х, |2, ц1 и тJ. Тогда для точек Аа, А12, А22,
• А21 (рис. 9.10) согласно формулам (9.22) получаем:
аоп = тт (ii + /Hi); ао12 = % (ii + Л г);
0022 = тт (?г +, Л г); ао21 = ^т (?2 + Ц&,
Фп = -у (ii — Л1); Ф12 = — (?i — Лг);
Фаз = ~ Aа — Лг) 5 Фа1 = "J" (?2 ~ Л1) •
Из этих равенств имеем:
"он — 0012 = т-т Oil — Л a)?
^021 — сто22 = тт (Л1 — Лг)!
Фп— Ф12 = — "о" (Л1 — Ла);
1 , .
21 ф?2 = 9" (Л1 Л2).
182

т. е.
Ф11 — Ф12 = Ф21 — Ф22.
что и требовалось доказать. Второе из полученных соотношений
можно геометрически интерпретировать следующим образом: угол
пересечения касательных к двум линиям скольжения одного семейства
с точках пересечения этих линий линиями скольжения второго семей-
семейства не зависит от выбора последних.
Из доказанной теоремы следует, что если некоторый отрезок линии
скольжения одного семейства (например, Ь) между двумя линиями
скольжения другого семейства (например, а) является прямым
ь, , / /
Рис. 9.10. К доказательству первой теоремы
Генки ч
Рис.'9.11. Прямолинейные от-
резки в семействе линии сколь-
скольжения b
(рис. 9.11), то все соответствующие отрезки линий этого семейства,
отсекаемые линиями скольжения другого семейства, прямые. Это
следует из того, что изменение угла наклона касательной к двум
точкам прямой ,линии равно нулю.
Прямые отрезки линий скольжения одного семейства (например, Ь),
отсекаемые линиями скольжения другого семейства (например, а),
имеют одинаковую длину (рис. 9.11).
Для того чтобы это доказать, вспомним, что геометрическое место
центров кривизны кривой — так называемая эволюта кривой яв-
является огибающей семейства нормалей к кривой, а огибающей семей-
семейства линий называется линия, которая во всех своих точках касается
различных линий семейства. Сама кривая по отношению к эволюте
называется эвольвентой.
Очевидно, что линии скольжения аг и а2 (рис. 9.11) имеют одну
и ту же эволюту. Поскольку исходная кривая может быть получена
путем разматывания нити с эволюты, при вычерчивании кривых аг
183

и а2 длины нитей будут различаться на прямолинейный " отрезок
линии скольжения Ь, заключенный между линиями скольжения аг
и а%.
В работах [20, 21 ] приведён ряд других интересных свойств линий
скольжения.
§ 55. Простые поля напряжений
Поле напряжений, в котором одно семейство линий скольжений
(например, Ь) состоит из прямых линий (рис. 9.11), называют про-
простым. Вдоль прямой величина ф постоянна. Поскольку вдоль ее
параметр ц также постоянен, то из второй формулы (9.21) следует,
что величина сг0 вдоль прямой постоянна, а из формулы (9.17) заклю-
заключаем, что компоненты напряжений вдоль прямой тоже постоянны.
Рис. 9.12. Центрированное поле Рис. 9.13. Линии скольжения в
линий скольжения _ равномерном поле
Заметим, что на основании первой формулы (9.21) можно сказать,
что параметр ? постоянен вдоль прямой линии скольжения Ь, а так
как он постоянен вдоль линий скольжения а, то этот параметр -По-
-Постоянен во всей рассматриваемой области.
Важным частным случаем простого поля напряжений является
центрированное поле линий скольжения, образованное пучком пря-
прямых и концентрическими окружностями (рис. 9.12). Нормальные
напряжения в радиальных и окружных площадках равны вели-
величине <т0, и согласно второй формуле (9.21)
сг0 = 2тт (ф + г)),
т. е. они являются линейными функциями угла наклона прямых.
Поэтому центр О является особой точкой.
Если в некоторой области прямолинейны оба семейства линий
скольжения, то в этой области постоянны параметры ? и т) и напря-
напряжения распределены равномерно. Такое поле напряжений (рис. 9.13)
называют равномерным.
Докажем, что в области, соседней'с областью равномерного поля
напряжений, поле напряжений всегда является простым.
184

Пусть в области А (рис. 9.14) поле напряжений равномерное,
г. с. в этой области линиями скольжения является сетка взаимно
перпендикулярных прямых. Обозначим значения параметров | и т)
¦миг семейств линий скольжения а и b соответственно через |0 и тH.
/Допустим, что прямая L является границей области А. Поскольку
<га прямая принадлежит также и соседней с областью А области В
и является линией скольжения в ней, на основании следствия из пер-
nnii теоремы Генки заключаем, что в области В одно семейство линий
скольжения (например, Ь) состоит из прямых линий. Поэтому поле
в
Ч-
т
1
Ы
г
4
а
Гнс. 9.14. Линии скольжения в равно-
равномерном (область А) и простом (область В)
полях напряжений
Рис. 9.15. Линии скольжения в двух
равномерных полях напряжений (облас-
(области Л и С), соединенных центрированным
полем (область В) .
напряжений в области В является простым. Значение параметра j
для семейства линий скольжения а в области В, очевидно, такое же,
как и в области Л, т. е. ? = |0.
На рис. 9.15 в качестве примера изображено поле линий сколь-
скольжения, состоящее из двух равномерных полей напряжений, соеди-
соединенных центрированным полем линий скольжения.
§^56. Поля скоростей
Выше (см. § 60) отмечалось, что после определения напряжений
скорости перемещений могут быть найдены путем интегрирования
дифференциальных уравнений (9.7). Преобразуем эти системы .урав-
.уравнений. Для этого,подставим соотношения (9.17) в уравнения (9.7).
Тогда получим
(9.31)
dvx . dvy
дх ' ду
Если напряжения определены и угол ф известен, то система урав-
уравнений (9.30) для скоростей леремещений vx и vy является линейной.
Поступая так же, как и в случае уравнений (9.18), можно доказать,
что система уравнений (9.30) тоже является гиперболической, а ее
характеристики совпадают с линиями скольжения.
185

Обозначим проекции вектора скорости на направления коорди-
координатных осей sa и sb через va и vb (рис. 9.16).
Очевидно, что
vx = va cos ф — vb sin ф; vy = va sin ф + vb cos ф.
Подставим эти соотношения в уравнения (9.31). При этом учтем,
что
и, следовательно,
х = х (sa, sb); у = у (sa, sb)
J-( \~JL( \J!L4.±( \JL-
dsa\ ) дх\ ) dsa "•" ду \ ) dsa '
Рис. 9.16. Разложение вектора скоро-
скорости перемещения по направлениям,
параллельным осям х и 'у, и по направ-
направлениям, касательным к линиям сколь-
скольжения
-81Пф^( )+СО8ф|г( ) = 4г
После преобразований получим
Складывая и вычитая эти выражения, устанавливаем
?¦+<¦¦?-»¦
Таким образом, вдоль лийии скольжения a
(9.32)
186

а вдоль линии скольжения b
dvb + va
= 0.
(9.33)
Эти уравнения были получены Гейрингер. Из них следует, что
тменение полной скорости вдоль линий скольжения равно нулю,
i. с. относительная скорость течения вдоль линии скольжения равна
ш/лю (рис. 9.17).
Перейдем к рассмотрению полей скоростей, соответствующих
простым полям напряжений. В простых полях напряжений линии
скольжения одного семейства прямые (см. рис. 9.11). Следовательно,
согласно формуле (9.32) со-
составляющая скорости, на-
направленная по прямой линии
скольжения, постоянна.
В случае центрирован-
центрированного поля (см. рис. 9.12),
если радиальные прямые
принять за линии скольже-
скольжения Ь, то тогда вдоль них
скорость перемещения vb
постоянна, т. е. скорость vb
является функцией только
<1'. Примем, что
vb = г|/ (ф), (9.34)
где г|5 (ф) — некоторая функция ф. Тогда, как следует из формулы
31)
Рис. 9.17. К выводу уравнений Гейрингер
(),
». = *(Ф) + Х«, .(9.35)
''Де X (г) — функция г.
Очевидно, что в частном случае равномерного поля напряжений
(рис. 9.13) скорости перемещений в направлении линий скольжения
ндоль этих линий не изменяются.
§ 57. Линии разрыва
В ряде случаев решения задач плоской деформации невозможно
построить без разрывов в величинах напряжений (скоростей переме-
перемещений) или их производных. В первом случае разрывы называют
сильными, во втором слабыми. Простейшим, известным из курса
сопротивления материалов, примером разрыва в величине напряже-
напряжения является разрыв нормального напряжения в предельном состоя-
пни изогнутой балки. При переходе через нейтральную плоскость
оно изменяется скачком от —f—стт до —сгт.
Рассмотрим вначале разрывы в напряжениях. Пусть La — линия
разрыва в напряжениях (рис. 9.18). Нормальные at и a-v и касатель-
касательное xvt напряжения на гранях элемента, одна из сторон которого
перпендикулярна линии разрыва, с разных сторон этой линии будем
отличать знаками + и —.Из условия равновесия элемента следует,
что at = о^, %$t = т^ и разрыв возможен только для напря-
187

жения at. Условие пластичности (9.5), справедливое по обе стороны
от линии разрыва La, в рассматриваемом случае имеет вид
— tfvJ + 44, = 2t
tT,
откуда
В этой формуле напряжения at по обе стороны от линии разрыва
определяются двумя знаками. Следовательно, скачок в величине
напряжения at
" '- — tit. (9.36>
х.
'Рис. 9.18. Нормальные и касательные Рис. 9.19. Изменение составляющей ско-
напряжения по обе стороны от линии рости в направлении линии разрыва
разрыва напряжений скоростей в ее окрестности
Скачок в величине среднего нбрмального напряжения
равен
Напомним, что касательное напряжение на линий скольжения
максимально и по формулам (9.5) и (9.10)
поэтому согласно формуле (9.36) линия разрыва в напряжениях
не может совпадать с линией скольжения или с огибающей линий
скольжения. - '
Линию разрыва можно рассматривать как след бесконечно тон-
тонкого слоя (предельное положение упругой области), разделяющего
две пластические области. Это следует из того, что нормальное ov
и касательное гч, напряжения в тонком слое в окрестности линии
188

разрыва почти не изменяются, а нормальное напряжение at по тол-
толщине слоя изменяется очень резко, и поэтому условие пластичности
it тонком слое не может выполняться. Учитывая, что в рассматривае-
рассматриваемой теории используется схема жестко-пластического тела, в котором
\пругими деформациями по сравнению с пластическими пренебре-
i аем, заключаем, что линия разрыва напряжений в процессе дефор-
деформации не-изменяет длины.
Рассмотрим теперь разрывы в скоростях перемещений. Предпо-
Предположим, что линия Lv (рис. 9.19) является линией разрыва в скоростях
перемещений. Очевидно, что разрыв может быть только в составляю-
щей скорости vt, касательной к линии разрыва Lo, так как разрыв
11 составляющей vv, нормальной к линии разрыва, означает появле-
и не трещины в материале.
Линию разрыва в скоростях перемещений можно представить
как предельное положение слоя, в котором составляющая скорости vt
резко изменяется по толщине слоя, а нормальная постоянна.
Зависимости скоростей деформаций от скоростей перемещений
согласно формулам B.38) в рассматриваемом, случае имеют вид
? dvv 6 __ dvt _ dvv . dvt -
Sv — -fa-1 6* — -gf > 4vt - -Qf -Г -fo~ •
Из этих соотношений следует, что с уменьшением толщины слоя б
(рис. 9.19) скорость деформации сдвига будет непрерывно возра-
возрастать, а остальные компоненты скоростей деформации почти не из-
изменяются.
Зависимости скоростей деформаций от напряжений при отсут-
отсутствии упрочнения (а( = <тт) в соответствии с формулами D.24)
имеют вид:
I» 3 ffv — g0 . \t 3 at —g0 ,
n~ 2 "7"* ir~ 2 ~^r~•
(9.37)
где согласно формуле B.40) для случая плоской деформации несжи-
несжимаемого материала (?г = 0, ^ = —%) интенсивность скоростей
деформаций
1
Из последней формулы следует, что с уменьшением толщины слоя б
интенсивность скоростей деформаций непрерывно возрастает за счет
возрастания скорости угловой деформации. Поэтому на основании
формул (9.37) заключаем, что с уменьшением толщины слоя б напря-
напряжения <7V и ot стремятся к <т0, a xvt к тт, что характерно для площа-
площадок, совпадающих с линиями скольжения и перпендикулярных им.
Поэтому линия разрыва скоростей перемещений совпадает с линией
скольжения или с огибающей линий скольжения,
189

Из уравнений Гейрингер (9.32) и (9.33), учитывая непрерывность
нормальной к линии разрыва скорости перемещения vv,' заключаем,
что скачок в величине скорости перемещения направленной по каса-
касательной к линии разрыва vt, постоянен вдоль линии разрыва:
dlv,] = 0.
§ 58. Толстостенная труба, нагруженная
внутренним давлением
Упруго-пластическое состояние толстостенной трубы, нагруженной
внутренним давлением и осевой ciyioft при отсутствии упрочнения,
было рассмотрено в § 32 и 47. В конце § 32 была установлена величина
предельного давления и выведены формулы для напряжений в пре-
Рис. 9.20. Направление линий скольже- Рис. 9.21. К выводу уравнений линий
ния в толстостенной трубе, нагруженной скольжения в толстостенной трубе, наг-
внутренним давлением руженной внутренним давлением
дельном состоянии. Получим теперь эти формулы, используя теорию
линий скольжения. Поскольку окружное и радиальное напряже-
напряжения являются главными напряжениями, линии скольжения пересе-
пересекают радиальную линию (рис. 9.20) под углами -j- и
Из рис. 9.21 для бесконечно малого элемента имеем
dr = ±г
причем знак + относится к линии скольжения Ь, а знак — к линии
скольжения а.
Интегрируя это соотношение, получаем уравнение двух семейств
линий скольжения
г = А ехр (±г|>), ' (9.39)
которые являются логарифмическими спиралями (рис. 9.22).
В рассматриваемой задаче согласно формуле (9.4)
^±±. (9.40)
190

Из соотношений (9.21), (9,40), (9.38) и (9.39) получаем
Согласно формуле (9.5) имеем
ar = 2tf.
(9.41)
(9.42)
Из уравнений (9.41) и (9.42) устанавливаем величину радиального
напряжения
(9.43)
Параметр ц постоянен для опре-
определенной линии скольжения. Посколь-
Поскольку напряжения зависят только от ра"-
диуса, заключаем, что этот параметр
один и тот же для всех линий сколь-
скольжения. Величину его найдем из оче-
очевидного 'краевого условия при г = г1
®г Рпр •
В результате получаем
2тт
Подставляя эту величину в урав-
уравнение (9.43), устанавливаем
tfr = -PnP + 2TTln-L. (9.44)
Рис. 9.22. Линии скольжения
при нагружении толстостенной
трубы внутренним давлением
Величину предельного давления рпр находим из второго краевого
условия при г — гг, аг = 0, откуда выводим соотношение F.29).
Поэтому выражение (9.44) преобразуется к первой формуле F.30),
а согласно выражениям (9.42)'и (9.40) получаем две вторые форму-
формулы F.30). Таким образом, получены формулы для напряжений, сов-
совпадающие с формулами, выведенными при рассмотрении предельного
состояния толстостенной трубы.
§ 59. Вдавливание плоского штампа
Предположим, что в жестко-пластическое тело, ограниченное
плоскостью, вдавливается абсолютно жесткий штамп с плоским осно-
основанием (рис. 9.23). Обозначим силу, приходящуюся на единицу длины
штампа в направлении, перпендикулярном чертежу (в направлении
оси г), через Р, а скорость движения штампа v. Пренебрежем силами
трения по поверхности контакта.
Рассмотрим вначале решение этой задачи, данное Прандтлем [13].
Очевидно, что пластические области начинают образовываться в точ-
точках А и В сразу же после приложения нагрузки к штампу. Однако
191

жесткость тела между двумя местными пластическими областями'
в окрестностях точек А и В вначале исключает вдавливание штампа.
Последнее будет появляться только после того, как нагрузка на
штамп достигнет значения, необходимого для создания развитой
пластической области вдоль всего основания штампа.
После того как произойдет вдавливание, материал, выдавленный
штампом, образует по сторонам последнего возвышения. Таким обра-
образом, при развитом пластическом течении необходимо удовлетворять
краевым условиям на деформированной поверхности. Ограничимся
f А
щ
У
с
р
и.
0
В F
w
Рис. 9.23. Линии скольжения в жестко-пластическом
теле, ограниченном плоскостью, при вдавливании в
него абсолютно жесткого штампа с плоским основа-
основанием (решение Прандтля)
рассмотрением только начального пластического течения. В этом
случае в решении задачи могут удовлетворяться граничные условия
на недеформированной поверхности. ¦
Начнем построение поля напряжений со свободной поверхности
слева от штампа. Некоторый ее участок АЕ должен быть пластиче-
пластическим, чтобы возникла возможность образования выступа над по-
поверхностью. Поскольку поверхность свободна от нагрузок, то
ву = 0; хху = 0
из формулы (9.5) для точек этой поверхности получаем
ах = -2хт. (9.45)
Знак минус взят потому, что в направлении АЕ возникает сжатие.
Поскольку касательные напряжения на свободной поверх-
поверхности АЕ равны нулю, линии скольжения пересекают эту поверх-
поверхность под углами 45 и 135°. Так как ох, следовательно, и сг0, а также ф
постоянны вдоль линии АЕ, то согласно формулам (9.21) вдоль этой
линии параметры ? и т) не изменяются. Поэтому под линией АЕ
поле напряжений равномерное.
Согласно формулам (9.21), (9.4) и (9.45) вдоль линий скольжения а
(рис. 9.23) параметр
' 1 Л
6 о !*•
(9.46)
192

Если бы концевая точка Е пластического участка свободной
поверхности была' известна, то тогда было бы определено равномер-
равномерное поле напряжений под линией АЕ. Оно представляло бы собой
равнобедренный прямоугольный треугольник ADE.
Так как линия скольжения AD прямая, то, следовательно, семей-
семейство линии скольжения Ь справа от AD — прямые. Учитывая сим-
симметрию задачи, заключаем, что под штампом поле напряжений ABC
равномерное и, следовательно, давление под штампом постоянно.
Два равномерных поля напряжений соединены между собой цен-
центрированным полем ADC. Следовательно, линия скольжения а
и поле AED является прямой, затем в поле ADC переходит в дугу
окружности, которая, в свою очередь, в поле ABC — в прямую/
Отсюда следует, что длина пластического участка свободной поверх-
поверхности равна ширине штампа
АЕ = АВ = с.
Вдоль линий скольжения а параметр 1 постоянен. В области ABC
линии скольжения а наклонены к оси х под углом
Ф = -?*-. (9-47)
Поэтому из формул (9.21) и (9.46) заключаем
' Т"т7 + ~Т~ 4 Г' .
откуда
ао=—(я+1)тт. .. (9.48)
Подставляя выражения (9.47) и (9.48) в формулы (9.17), имеем
<г, = — ятт; ои = — (я + 2)тт.
Поскольку напряжения ау вдоль линии АВ не изменяются, сила,
вдавливающая штамп,
р = | Оу | с = (я + 2) хтс. (9.49)
Установим распределение скоростей. Очевидно, что треуголь-
треугольник ABC движется со скоростью штампа v вниз как жесткое целое.
Вдоль линии АС касательная .составляющая скорости разрывна,
а нормальная равна " ^ . Вдоль линии CD касательная составляю-
составляющая скорости разрывна, а нормальная равна нулю. В центрирован-
ном поле скорость в направлении линии скольжения а равна:—^—>
;i вдоль линии скольжения Ь равна нулю. Область ADE скользит
как твердое тело в направлении DE со скоростью -^-~—.
Рассмотрим решение, данное Хиллом [21 ]. Хилл показал,- что
решение Прандтля не является единственным, и предложил поле
скольжения, изображенное на рис. 9.24. Оно состоит из двух равно-
равномерных полей напряжений АОС и AED, соединенных центрирован-
I Н. Н. Малинин ¦ 193

ным полем ACD (рис. 9.24). В этом случае длина пластического
участка свободной поверхности равна половине ширины штампа-^-.
Напряжения в равномерных полях напряжений и центрированном
поле те же, что и в соответствующих полях решения Прандтля.
Поэтому сила, приложенная к штампу, также определяется форму-
формулой (9.53).
Поле скоростей иное, чем в предыдущем решении. Треуголь-
Треугольник АОС скользит как твердое тело вдоль ОС со скоростью ]/~2у.
Скорость на АС непрерывна.
В центрированном поле ско-
скорость в направлении линии
скольжения а равна j/~2u, a
вдоль линии скольжения b
равна нулю. Треугольник ADE
движется в направлении DE
со скоростью y~2v.
В книге Прагера и Ходжа
[12] показано, что можно цр-
строить решение, являющееся
комбинацией решений Прандтля
и Хилла.
Из рассмотренной задачи
следует, что при использовании
схемы идеального жестко-пластического тела возможна неодно-
неоднозначность решений. Поэтому при построении полей линий сколь-
скольжения и полей скоростей следует привлекать экспериментальные
данные.
§ 60. Численные методы решения краевых задач
В расчетах плоской деформации тел обычно приходится решать
три основные краевые задачи, которые рассмотрены ниже.
1. Начальная характеристическая за-
задача (задача Римана). Допустим, что на отрезках линий
скольжения О А и ОВ (рис. 9.25) величины сг0 и ф известны. Естест-
Естественно, что они удовлетворяют дифференциальным уравнениям равно-
равновесия элемента и поэтому связаны соотношениями (9.21).
Как будет показано ниже, в этом случае можно определить вели-
величины сг0 и ф в криволинейном четырехугольнике ОАСВ, ограничен-
ограниченном четырьмя линиями скольжения.
Для решения задачи разобьем отрезки линий скол жения ОА
и ОВ на малые части точками /, 0; 2,0; . , . .; т, 0; . . . .; 0,1; 0,2; . . .
. . .; 0, п; . . . . По первой теореме Генки величины сг0 и ф в точке т,
п определяются по формулам
Рис. 9.24. Линии скольжения в жестко-
пластическом теле, ограниченном плоско-
плоскостью при вдавливании в него абсолютно
жесткого штампа с плоским основанием
(решение Хилла)
¦^Om, n — °Om, О Т~ °0O, п °0O, С
Фт, п = Фт, О + ФО, л ~ Фо, О-
(9.50)
194

Для определения координат точки т, n по координатам точек
т — 1, п и т, п — 1 и углам ф в этих трех точках воспользуемся
дифференциальными уравнениями линий скольжения (9.12). Предста-
Представим их в разностной форме, полагая, что угол наклона хорд, заменяю-
заменяющих малые дуги, равен среднему значению углов наклона в крайних
точках. Тогда получим
(9.51)
Ут, п. Ут-1, п = (хт,п хт-1, п) tg -у (фт, „ + фт-1. п)\
Ут, п. Ут, га-1 ~ \хт. п. хт-1, п)
Таким образом, шаг за ша-
шагом, начиная с точки 1,1 опре-
определяются координаты точек и
величины а0 и ф в них и, следо-
следовательно, строится решение за-
задачи Римана в криволинейном
четырехугольнике О АС В.
Если отрезок линии сколь-
скольжения ОВ (или О А) стянут в
точку (рис. 9.26) и в точке О
сходятся все линии скольже-
скольжения семейства а (или Ь), имеет
место вырожденный случай на-
характеристической
(фт, п ~~Ь Фт, n-l)-
чальной
задачи.
Тогда
особой и
разрывна
точка О является
величина сг„ в ней
Рис. 9.25. К решению.начальной харак-
характеристической задачи (задачи Римана)
В этом случае известно сг0 и ф на О А и изменение угла ф в точке О,
т. е. угол АОС. Для решения задачи отрезок линии скольжения О А
делим на малые части и, проведя через точку 1,0 линию скольже-
скольжения Ьг, исключаем из рассмотрения особую точку О. Угол АОС
также делим на малые части и проводим начальные участки линий
скольжения 0,1,0,2 . . . ., On. Таким образом определяем величины ф
в точках линии скольжения Ьг. По величинам o0i,o и ф/, о для
точки 1,0 линии О А, используя вторую формулу (9.21), определяем
параметр т) для линии Ь±
а
01,0
(9.52)
Далее по той же формуле определяем величины сг0 в различных
точках линии Ь1
во>,п = 2тт (гь + фЛ „).
Таким образом, вырожденный случай задачи Римана сводится
к основному. Определение напряжений в криволинейном четырех-
четырехугольнике l,0DCA производится, как было изложено выше.
195

2. Задача о начальных значениях (за-
(задача К о ш и). Предположим, что на гладкой линии АВ
(рис. 9.27), не совпадающей с линией скольжения и пересекаемой
каждой линией скольжения только 1 раз, заданы величины а0 и ф,
непрерывные вместе с первыми и вторыми производными. Тогда,
как будет показано ниже, можно определить величины сг0 и ф, а зна-
чит и напряжения, в криволинейном треугольнике АСВ, сторонами
которого является линия АВ и две линии скольжения АС и ВС
семейств а и Ь\ проходящие точки А я В.
У
.С/
Рис. 9.26. К решению начальной
характеристической задачи (задачи
Римана) в вырожденном случае
Рис. 9.27. К решению задачи о началь-
начальных значениях (задачи Коши)
Для решения задачи разобьем дугу Л В на малые части точками
0,0; 1,1; .... m, m ... (рис. 9.27). Проведем через точки т, т
и т + 1, т + 1 две линии скольжения семейств а и Ъ и обозначим
"точку пересечения их т, m+ч 1. Из условия постоянства параме-
параметров | и ц [см. формулы (9.21)] на линиях скольжения а и Ь
имеем
гп _L
тт, «1+1 — 2
Фот+1, m+V
(9.53)
Из этих двух уравнений определяются величины oQm<m+i
И <Pm,m+l-
При написании формул (9.53) не предполагалось, что точки т,
т, т -f•• 1, т + 1 и т, т + 1 расположены близко одна к другой.
Однако это предположение существенно для определения координат
точки т, т + 1, которые подсчитывают по формулам, аналогичным
формул-ам (9.51). Таким образом определяют величины сг0 и ф в точ-
точках, которые являются вершинами криволинейных треугольников,
примыкающих к линии АВ. В дальнейшем для построения решения
в криволинейном треугольнике ABC решают начальную характе-
характеристическую задачу.
196

Аналогично тому, как было построено решение задачи Коши
для определения напряжений, можно было бы построить решение
этой задачи для определения скоростей перемещений.
Как отмечалось выше, постановка задачи допускает существо-
существование наряду с пластическими ббластями и жестких областей. Дока-
Докажем, что границей между жесткими и пластическими областями
является линия скольжения или огибающая линий скольжения.
Примем, что жесткая область неподвижна, что всегда можно до-
добиться наложением жест-
жесткого ' смещения.
Допустим вначале, что
на границе скорости vv и
vt непрерывны. В таком
случае они равны нулю,
и если граница нигде не
совпадает с линией сколь-
скольжения, то для определений
скоростей в пластической
области имеем задачу
Коши. Поскольку уравне-
уравнения для скоростей явля-
являются однородными, то
при нулевых граничных
условиях во всех точках
пластической области ско-
скорости равны нулю, что
противоречит исходному
положению. Если же граница совпадает с линией скольжения, то
равенство нулю скоростей в ее точках не ведет к нулевым скоростям
в пластической области.
Если же на границе возникает разрыв в скорости, то, как было
доказано в § 57, она совпадает с линией скольжения или с огибаю-
огибающей линий скольжения.
Таким образом, доказано, что граница между жесткими и пла-
пластическими областями является линией скольжения или' огибаю-
огибающей линий скольжения.
3. Смешанная задача. Предположим, что на отрезке
линии скольжения ОА (рис. 9.28) величины а0 и ф, удовлетворяю-
удовлетворяющие уравнениям равновесия, известны, а на линии ОВ, не совпадаю-
совпадающей с линией скольжения, задан угол ф. Это справедливо, например,
если линия ОВ является следом поверхности тела, свободной от тре-
трения. Тогда линии скольжения пересекают линию ОВ во всех точках
под углом 45°.
Как будет показано ниже, в рассматриваемом случае можно
определить величины сг0 и ф в криволинейном треугольнике ОАВ,
ограниченном линиями скольжения ОА и АВ и линией ОВ.
Будем предполагать, что угол ф в точке 0 на линии скольжения
О А и линии ОВ один и тот же. Случай неравенства углов рассмотрен
ниже.
/ 197
Рис. 9,28. К решению смешанной задачи

Для решения задачи разобьем отрезок линии скольжения ОА
на малые части точками 1,0; 2,0; . . ., т, 0. Проведем из точки 1,0
перпендикуляр к линии скольжения ОА до пересечения в точке С'
с линией ОВ. Поскольку на последней значения ф известны, уста-
устанавливаем эту величину для точки С. По величинам ф в точках 1,0
и С' находим среднее значение угла ф и из точки 1,0 проводим пря-
прямую линию, перпендикулярную прямой, наклоненной к оси х под
средним значением угла для точек 1,0 и С. Таким образом опреде-
определяем точку С". Повторяя подобные построения до тех пор, пока раз-
различие между последовательными положениями точки С не станет
малым, определяем точку /,/. Величину а0 в этой точке определяем
так же, как в вырожденном случае начальной характеристической за-
задачи. Вначале по формуле (9.53)
определяем параметр т) для линии
скольжения семейства Ь, прохо-
проходящей через точки 1,0 и /,/. За-
Затем, используя соотношение (9.21),
вычисляем величину 0О в точке 1,1
Ooi.i— 2тт(г|14-ф/,/).
Величины а0 и ф в точках 2,1;
3,1; ... вычисляем так же, как
в решении начальной характе-
1 1 ристической задачи. Определение
Рис. 9.29. К рассмотрению общего слу- положения точки 2,2 и величины
чая смешанной задачи О() в Heg производится таким же
образом, как для точки 1,1. Та-
Таким образом, шаг за шагом, начиная с точки /,/, определяются сг0
и ф, следовательно, строится решение смешанной задачи в криво-
криволинейном треугольнике ОАВ.
Если углы ф в точке О на линиях ОВ и ОА не равны между собой
например, если первый больше второго (рис. 9.29), то тогда область
АОВ разбивается на две АОАг и АХОВ, так чтобы угол ф в точке О
на линиях ОВ и ОА^ был один и тот же. Для первой области имеем
вырожденный случай начальной характеристической задачи, а для
второй смешанную задачу.
§ 61. Сжатие слоя между жесткими
шероховатыми плитами
Представим себе слой толщиной 2/i, шириной 21, сжатый между
двумя жесткими шероховатыми плитами силой Р (рис. 9.30).
Допустим, что плиты настолько шероховаты, что интенсивность
сил трения на плоскостях контакта равна максимально возможному
напряжению трения, а именно пределу текучести при сдвиге ттах =
= тТ.
Примем, что к торцу слоя примыкает жесткая область АфАг,
ограниченная прямыми линиями АгВ и А2В ¦ Поскольку, как отме-
отмечалось выше, граница между жесткой и пластической областями
198

является линией скольжения, линии АгВ и А2В — линии скольже-
скольжения. Вследствие прямолинейности их напряжения в точках этих
линий не изменяются. Так как на срединной плоскости OG из усло-
условия симметрии касательные напряжения отсутствуют, линии А ХВ
У
Рис. 9.30. К решению задачи сжатия слоя между жесткими шероховатыми плитами
и А2В должны быть наклонены к оси OG под углом -^-. На гранях
Ахв и А2В касательные напряжения распределены равномерно и
равны тт. Из условия равновесия жесткой области АХВА (рис. 9.31)
заключаем, что равномерно распределенные в этих гранях нормаль-
нормальные напряжения равны той же величине
а0 = —тт. Примем, что к жесткой области
АхВАг примыкают центрированные поля ли-
линий скольжения АХВС и А2ВС2. Параметры I
и г] для линий скольжения А 2ВСХ (а) и
АХВС2 (Ь) согласно формулам (9.21) соответ-.
ственно равны
е 1 . я 1 я
Располагая этими величинами, по тем же
формулам (9,21) можно определить значения
а0 в точках линий скольжения ВСХ и ВС2-
Ттах
Рис. 9.31. Равновесие
жесткой области, при-
„ _ / я \ жесткой области, npi
В частности, в точке С1[^ =—J , а следова- мыкающей к торцу
тельно, и во всех точках линии Л^ по первой
формуле (9.21), учитывая приведенную выше величину
получаем
Этой же величине равно напряжение ау в точках линии АгС{.
Следовательно, сила на единицу длины в направлении, перпендику-
перпендикулярном чертежу, действующая на площадь контакта AiCt
Зная величины ст0 и ф в точках линий скольжения ВС{ и ВС2,
приходим к начальной характеристической задаче, решение которой
позволяет определить напряженное состояние в области CXBCJ).
199

В области CXDEX имеем смешанную'задачу, так как вдоль СХЕЪ
задан угол ср = -S-, поскольку на линии контакта касательные на-
пряжения приняты максимальными, и, следовательно, площадки
скольжения совпадают с границей слоя. Решение смешанной задачи
позволяет определить напряжение оу в точках линии С1Е1. Интегри-
Интегрирование этой функции дает силу Р2 на единицу длины в направлении,
перпендикулярном чертежу, действующую на площадь контакта СХЕЪ
Р, =» f a,,dx.
В результате решения смешанной задачи определяются вели*
чины о0 и.ср в Точках линий скольжения DEX и DE2 и, следовательно,
снова приходим к началь-
\рп ной характеристической
задаче, решение которой
позволяет определить на-
напряженное состояние в
области DE1FE2 и, т. д.
Поскольку на вертикаль-
вертикальной плоскости симметрии
слоя касательные напря-
напряжения отсутствуют, что
противоречит условию по-
постоянства касательного
напряжения на плоскости контакта, к вертикальной плоскости сим-
симметрии должна примыкать жесткая область, ограниченная линией
контакта и линией скольжения HXG, приходящей в точку G. Рас-
Распределение давления на участке НХ1Г неопределенно. Сила на
единицу длины слоя в направлении, перпендикулярном чертежу,
приходящаяся на этот участок, может быть подсчитана из условия
равновесия области HXIXG (рис. 9.32)
Рис. 9.32. Равновесие жесткой области, при-
примыкающей к вертикальной плоскости симметрии
= \ (rTcos <р-\-\ао\ sin <p)ds.
HQ
Сила, сжимающая весь слой,
Р =
Рп).
Изложенное решение справедливо при условии, что точка D не
попадает по другую сторону оси симметрии 11г. Это справедливо
при-?-В> 3,64 [8]. Для меньших значений этого'отношения реше-
решение „задачи изложено в книге [17].
В случае очень тонкого слоя, когда / значительно больше h,
решение задачи дано Прандтлем. Оно может быть представлено
200

в замкнутом виде. При выборе начала координат в середине левого
торца слоя выражения для напряжений в виде
X
(9.54)
удовлетворяют дифференциальным уравнениям равновесия (9.6) и
условию пластичности (9.5). В этом легко убедиться, подставив вы-
выражения (9.54) в соотношения (9.6) и (9.5). Однако, как следует из
уравнении (9.54), ах и хху не обращаются в ноль на торцах при х — О и
х = 21 и напряжение ххи не обращается в ноль на вертикальной
плоскости симметрии. Таким образом, вблизи торцов и в средней
части слоя решение Прандтля неудовлетворительно.
Краевое условие на левом торце можно удовлетворить интег-
интегрально в смысле принципа Сен-Венана исходя из условия отсутствия
нормальной силы на левом торце
lxdy = 0, (9.55)
—h
что дает возможность определить постоянную Ci. Подставляя первое
выражение (9.54) при х = 0 в условие (9.55), после преобразований
получим
и, следовательно, согласно второй формуле (9.54) имеем следующий
линейный закон изменения давления на контактной поверхности
Сила, действующая на слой,
Подставим в эту формулу уравнение (9.56). Тогда устанавливаем
Можно показать [8], что в рассматриваемой задаче линии сколь-
скольжения представляют собой семейства циклоид с радиусом произво-
производящего круга h. Прямые у == ±h являются огибающими этих се-
семейств циклоид.
201

Выражения для скоростей перемещений в виде
(9.58)
где v — скорость движения плит, удовлетворяют уравнениям (9.7).
Постоянная С2 может быть найдена из условия равенства потока
материала через сечение х = О количеству, выдавливаемому на
длине 2/ при сближении плит
Подставляя в это соотношение скорость vx при х — О, получим
Сг~и(~2 А")'
Выше предполагалось, что на поверхности контакта интенсив-
интенсивность сил трения равна максимальному касательному напряжению —
пределу текучести при сдвиге тшах = тт. Случай, в котором интен-
интенсивность сил трения постоянна, но меньше этой величины, изучен
В. В. Соколовским [17].
§ 62. Волочение листа
Установившимся процессом деформирования тела называют
такой процесс, в котором напряжения и скорости перемещения
в любой фиксированной точке тела не изменяются во времени. В про-
противном случае процесс деформирования называют неустановившимся.
Рассмотрим установившийся процесс волочения через жесткую
матрицу листа, начальная толщина которого hx (рис. 9.33). Для
упрощения решения задачи трением на плоскостях контакта листа
и матрицы пренебрежем. Обозначим конечную толщину листа h2,
а скорости на входе в матрицу и выходе из нее vt и v2 соответственно.
Из условия несжимаемости материала имеем
Допустим, что давление на контактной поверхности АВ (рис. 9.33)
распределено равномерно. Величину его обозначим через р. В та-
ком% случае, к линии АВ примыкает равномерное поле напряже-
напряжений* ABC. Присоединяем к нему два центрированных поля ACD
и ВСЕ с неизвестными пока центральными углами г|з и %.
Из условия равновесия области ABC ¦ (рис. 9.34) определяем
среднее нормальное напряжение в этой области
Оовс = — (Р — тт). (9.59)
202

Располагая этой величиной, а также величиной угла <р в точке С
по формуле (9.21) устанавливаем параметры 1 и т] для линий BCD
и АСЕ соответственно
(9.60)
Рис. 9.33. К решению задачи волоче-
волочения листа
Во
Рис. 9.34. Равновесие области
равномерного напряженного со-
состояния
После этого по тем же формулам (9.21) можно определить значе-
значения о0 в точках линий скольжения CD и СЕ, которые являются
окружностями радиусов соответственно АС и ВС. Таким образом
приходим к начальной характеристической задаче. Численное ре-
решение ее изложенным выше методом позволяет определить напря-
напряженное состояние в области CDOE.
Для того чтобы установить зависимость между неизвестными
углами г|з и %, выразим среднее нормальное напряжение в точке О
через величину его в точке С, продвигаясь от точки С к точке О
вначале по линии CDO, а затем по линии СЕО.
Учитывая, что величина ф в точке D
по первой формуле (9.21), используя первую формулу (9.60), имеем
, _о - . павс
1 ТТ 4 ^ Тт 4
откуда
2 т^
1 °0
(9.61)
Определим теперь параметр ц для линии скольжения ADO.
203

По второй формуле (9.61)
1 ао я
Далее по той же формуле, учитывая, что величина угла ср в точке О
равна ф° = -г-, связываем средние нормальные напряжения в точ-
точках О и D . ¦ - .
2 %„
JL= ' ^ я [ (а | г|з).
Подставим в эту формулу соотношение (9.61). Тогда получим
1 п° 1 аАВС
(9.62)
Рис. 9.35. Равновесие жесткой
области на входе в матрицу
Рис. 9.36. Равновесие листа
Аналогично можно вывести зависимость между средними нор-
нормальными напряжениями в точках О и С при переходе от последней
к первой по линии СЕО. Она имеет вид
ЛВС
V
Сопоставляя выражения (9.62) и (9.63), заключаем, что
% = г|> + а. (9.64)
Давление р и один из углов г|з'или % определяем из двух условий:
равенства нулю суммы проекций на горизонтальную ось всех сил,
действующих на поверхность ADO (рис. 9.35)
j (a0 cos ф + тт sin Ф) ^s — 0.
ADO
и нахождения точки О на оси симметрии. Неизвестные определяем
подбором.
204

v После определения давления р усилие волочения Р на единицу
длины в направлении, перпендикулярном чертежу, подсчитываем
по формуле
Р = р (ftj. - ft,), (9.65)
которая следует из условия равновесия листа (рис. 9.36).
Максимальное обжатие -*—г—- соответствует г|> = 0, когда че-
четырехугольник CDOE стягивается в точку (рис. 9.33). В этом слу-
случае (рис. 9.37) отпадает необходимость численного решения началь-
начальной характеристической задачи. Согласно формуле (9.64)
1 =«
Рис. 9.37. К решению частного случая Рис. 9.38. Равновесие жесткой области
задачи волочения листа. на выходе из матрицы
и, следовательно, линия ВО наклонена к горизонтальной оси под
углом-j • Величины hu h2 и а связаны между собой. Действи-
Действительно, как следует из рис. 9.37,
К — К
4 sin a '
откуда
1
А =
hx 1 + 2 sin а '
Среднее нормальное напряжение в точках линии ВО находим
по второй формуле (9.21), используя соотношения (9.59) и вторую
формулу (9.60)
1
„во
л
"Т
11
ос.
откуда
а?0 = — р4-тт(Г+2а). ,'(9.66).
Из условия равновесия жесткой области, изображенной на
рис. 9.38, получаем
205

Подставим в это выражение соотношение (9.66). Тогда, исполь-
используя формулу (9.65), после преобразования имеем
_ 4A+и) sin и h
h
^~ 1+2 sin a TT^- '
Величина 2ттй2 равна предельной нагрузке при растяжении
листа постоянной толщины h2. Поэтому волочение возможно при
условии, что
Р < 2xTh2
или
<
откуда следует, что а< 42° 27'.
Другие примеры применения теории плоской деформации для
исследования технологических процессов обработки металлов при-
приведены в книгах [1, 4, 12, 16, 17, 21—23, 26—28, 32].
Определение предельных нагрузок при помощи линий скольже-
скольжения изложено в книгах [8, 17, 31 ].
Решение задач плоской деформации для анизотропных тел дано
в работах [14, 24], а для неоднородных тел в трудах [3, 5, 9, 11].
Теория плоского напряженного состояния разработана в мень-
меньшей степени, чем теория плоского деформированного состояния.
Изложение теории плоского напряженного состояния и решение
ряда задач по этой теории содержится в книгах [8, 17].
Список литературы
1. Бровман М. Я. Применение теории пластичности в прокатке. М., «Метал-
«Металлургия», 1965, 249 с.
2. Генки Г. О некоторых статически определимых случаях равновесия в пла:
стических телах.— В кн.: Теория пластичности, М., Изд. иностр. лит., 1948, с.
80—101.
3. Григорьев О. Д. Некоторые задачи теории пластичности неоднородных тел.
«Труды Новосибирского института инженеров водного транспорта». Вып. 48, Н.,
1969, 207 с.
4. Джонсон В.) Кудо X. Механика процессов вдавливания металлов. М., «Ме-
«Металлургия», 1965, 174 с.
5. Друянов Б. А. Численное решение задачи о вдавливании гладкого штампа
в пластически неоднородную полуплоскость.— «Известия Академии наук СССР.
Механика и машиностроение», 1961, № 3, с. 163—166.
6. Друянов Б. А. О применении жестко пластического анализа к некоторым
технологическим задачам.— «Известия Академии наук СССР. Механика твердого
тела», 1971, № 3, с 179—183.
7. Ильюшин А. А. Пластичность. М., ГИТТЛ, 1948, 376 с.
8. Качанов Л. М. Основы теории пластичности. М., «Наука», 1969, 420 с.
9. Кузнецов А. И. Плоская деформация неоднородных пластических тел.—
«Вестник Ленинградского университета», 1958, № 13, с. 112—131.
, 10. Надаи А. Пластичность и разрушение твердых тел. М., Изд. иностр. лит.,
1954, 647 с.
11. Ольшак В.. Рыхлевский Я-> Урбановский В. Теория пластичности неодно-
неоднородных тел. М., «Мир», 1964, 156 с-
206

12. Прагер В.» Ходж Ф. Г. Теория идеально пластических тел. М., Изд. иностр.
лит., 1956, 398 с.
13. Прандтль Л. О твердости пластических материалов и сопротивлении реза-
резанию.— В кн.: Теория пластичности. М., Изд. иностр. лит., 1948, с. 70—79.
14. Саркисян М. С. К теории плоской деформации пластически анизотропных
тел.—«Прикладная математика и механика», 1960, т. 24, № 6, с. 1136—1139.
15. Смирнов В. И. Курс высшей математики, том IV. М., Физматгиз, 1958, 812 с.
16. Смирнов В. С. Теория прокатки. М., «Металлургия». 1967, 460 с.
17. Соколовский В. В. Теория пластичности. М., «Высшая школа», 1969, 608 с
18. Томсен Э.,.Янг Ч.. Крбаяши Ш. Механика пластических деформаций при
обработке металлов. М., «Машиностроение», 1969, 503 с.
19- Феодосьев В. И. Сопротивление материалов. М., «Наука», 1974, 559 с.
20- Фрейденталь А.. Гейрингер X. Математические теории неупругой сплошной
среды. М., Физматгиз, 1962, 432 с
21- Хилл Р. Математическая теория пластичности. М., ГИТТЛ, 1956, 407 с.
22. Целиков А. И. Основы теории прокатки. М., «Металлургия», 1965, 247 с
23. Целиков А. И., Грншков А. И. Теория прокатки. М., «Металлургия», 1970,
358 с
24. Шевелев В. В.,-Яковлев С. П. Анизотропия листовых материалов и ее влия-
влияние на вытяжку. М., «Машиностроение», 1972, 135 с.
25. Dietrich L., Miastkowski J., Szczepinski W. Nos'nosc graniczna elementow
konstrukcji, Panstwowe wydawnictwo naukowe, 1970, 271 s.
26. Ford H. Advanced mechanics of materials, Longmans, 1963, 672 p.
27. Johnson W., Mellor P. B. Plasticity for mechanical engineers, D. Van Nost-
rand Company LTD, 1962, 412 p.
28. Johnson W. Sowerby R.. Haddow J. B. Plane-strain slip-line fields. Theory
and bibliography, London, Edward Arnold, 1970, 176 p.
29. Spencer G. С An introduction to plasticity, Chapman and Hall LTD, 1968,
118 p.
30. Szczepinski W. Wst§p do analizy procesow obrobki plastycznej, Panstwowe
wydawnictwo naukowe, 1967, 319 s.
31. Szczepinski W. Projektowanie elementow masz'yn metoda, nosnosci granicznej,
Panstwowe wydawnictwo naukowe, 1968, 129 s.
32. Teoria plastyczno'sci,Panstwowe wydawnictwo naukowe, 1967, 399 s. Aut:
Z. Marciniak, Z. Mroz, W. Olszakj inni.

ГЛАВА X
ПРЕДЕЛЬНОЕ СОСТОЯНИЕ
§ 63. Статическая и кинематическая теоремы
Как было показано выше, решение пластических задач в пред-
предположении, что материал идеальный жестко пластический (диа-
(диаграмма деформирования изображена на рис. 5.17), имеет большое
практическое значение для определения предельных нагрузок кон-
конструкций, а также вычисления усилий деформирования в различ-
различных технологических операциях. Однако даже при ограничении
условием плоской деформации (см. предыдущую главу) решение
в ряде случаев связано с большими трудностями. Эти трудности
возрастают при переходе'к общему случаю деформирования.
Поэтому большое значение имеют методы приближенной оценки
нагрузок, соответствующих предельному состоянию по схеме идеаль-
идеального жестко-пластического тела.
Ниже изложены статическая и кинематическая теоремы, позво-
позволяющие дать двустороннюю оценку предельных нагрузок, приве-
приведены примеры применения их, а также дано полное решение неко-
некоторых задач предельного состряния.
Назовем статически возможным состоянием тела такое состоя-
состояние, для которого удовлетворены условия на поверхности для напря-
напряжений и уравнения равновесия в каждой точке тела, а точки, изобра^"
жающие напряженное состояние в пространстве,напряжений аи для
различных точек тела, лежат или внутри поверхности начала пла-
пластичности, или на ней. Обозначим эти точки М*, а соответствующие
им тензоры напряжений в*с/ (рис. 10.1). Таким.образом, эти напря-
напряженные состояния удовлетворяют условию
Изображающие точки для действительного состояния тела обозна-
обозначим М, а соответствующие им тензоры напряжений а,,.
Статическая теорема. Нагрузка, соответствующая
статически возможному состоянию, меньше, чем предельная нагрузка.
Для простоты доказательства допустим, что объемные силы от-^
сутствуют. Применим принцип возможных перемещений для дей-
действительного и статически возможного состояний, приняв за воз-
возможные перемещения, пропорциональные скоростям v,- и ?//
208

действительного состряния. Тогда получим для действительного
состояния. -
' ubjdV A0.1)
A0.2Х
и для статически возможного состояния
где Xvi и Xvt — проекции на оси координат интенсивности распре-
распределенной нагрузки на поверхности.
Вычтем из соотношения A0.1)
выражение A0.2). Тогда получим
Как отмечалось в § 21,
fa— al,)dspt}>0
и, следовательно (рис. 10.1),
поэтому
Рис. 10.1. К доказательству статиче-
статической теоремы
A0.3)
т. е. мощность поверхностной нагрузки, отвечающей статически
возможному напряженному состоянию на действительных скоростях
перемещений всегда меньше мощности действительной поверхностной
нагрузки на тех же скоростях.
Если внешние силы являются сосредоточенными, то согласно
формуле A0.3) имеем
(Ю.4)
В случае одной силы получаем
Р* < Р,
что и требовалось доказать.
Статическая теорема устанавливает приближение для предель-
предельной нагрузки снизу. Рассматривая различные статически возмож-
возможные состояния, можно подсчитать различные нагрузки, меньшие
предельной. Наибольшая из них будет ближе всего к предельной
нагрузке. .
Метод определения предельной нагрузки путем рассмотрения
статически возможных состояний называют статическим.
209

Назовем кинематически возможным состоянием тела такое состоя-
состояние, для которого удовлетворены условия на поверхности для пере-
перемещений и условия совместности деформаций в каждой точке тела.
Уравнения равновесия могут быть не удовлетворены. Очевидно,
что точки, изображающие напряженные состояния в точках тела,
находящегося в кинематически возможном состоянии, лежат на
поверхности начала пластичности, так как иначе согласно схеме
идеального жестко-пластического тела деформирование невозможно.
Обозначим эти точки М**, а тен-
тензоры напряжений, соответствую-
соответствующие им, aYj (рис. 10.2).
Кинематическая тео-
теорема. Нагрузка, соответст-
соответствующая кинематически возможному
состоянию, больше, чем предель-
предельная нагрузка.
Полагая, так же как и в до-
доказательстве предыдущей теоремы,
объемные силы равными нулю,
применим принцип возможных пе-
перемещений для действительного
состояния. За возможные переме-
перемещения примем перемещения, про-
пропорциональные скоростям v7 и
\7j кинематически возможного
состояния. Тогда получим
\xviv7dS=\a4t7jdV.
s v
Преобразуем это равенство:
J Xviv7 dS = J aYfcY, dV - J (си, - a,,) t7j dV.
S V V
Поскольку, как отмечалось выше (рис. 10.2),
имеем
:viv7dS. A0.5)
Интеграл слева представляет собой мощность внутренних сил
в кинематически возможном состоянии тела. Очевидно, что можно
так подобрать величины поверхностных нагрузок Х^, что их мощ-
мощность на кинематически возможных скоростях будет равна мощ-
мощности внутренних сил
YilYidV. A0.6)
Рис. 10.2. К доказательству кинемати
ческой теоремы
210

Следовательно, согласно выражению A0.5) имеем
4ttHdS, A0.7)
т. е. мощность поверхностной нагрузки, отвечающей кинематически
возможному состоянию на кинематически возможных скоростях,
перемещений, всегда больше мощности действительной поверхностной
нагрузки на тех же скоростях.
Если внешние силы являются сосредоточенными, то по формуле
A0.7)
S pTvT > S ptvT.
В случае одной силы
Р**>Р, A0.8)
где согласно выражению A0.6)
Р = ^ J ач1ч dV,
v
что и требовалось доказать.
В отличие от статической теоремы кинематическая теорема уста-
устанавливает приближение для предельной нагрузки сверху. Рассма-
Рассматривая различные кинематически возможные состояния, можно
определить различные нагрузки, большие предельной. Наименьшая
из них будет наиболее близка к предельной нагрузке.
Метод определения предельной нагрузки путем рассмотрения
кинематически возможных состояний называют кинематическим.
Таким образом, статическая и кинематическая теоремы дают
возможность установить двустороннюю (снизу и сверху) оценку
предельной нагрузки. /
Для того чтобы статически возможное состояние было действи-
действительным, необходимо, чтобы оно было одновременно кинематически
нозможным и наоборот. Если предельные нагрузки, определенные
статическим и кинематическим методом, совпадают, то это означает,
что полученная предельная нагрузка является действительной, а
выполненное решение полным.
§ 64. Примеры применения статической
и кинематической теорем
Пример 1. Балка, заделанная одним концом, оперта другим и нагружена
равномерно распределенной нагрузкой интенсивности q (рис. 10.3, а). Балка I раз
ггатически неопределима.
Как известно из курса сопротивления материалов [23], если диаграмма растя-
растяжения материала не имеет упрочнения, несущая способность статически определи-
определимых балок и рам исчерпывается тогда, когда в опасном сечении балки возникает
пластический шарнир.
211

Если сечение имеет одну ось симметрии в плоскости действия изгибающего
момента, а диаграммы растяжения и сжатия материала совпадают, величина пре-
предельного изгибающего момента в пластическом шарнире
М„р = СГТ (SXp + Sjccjk),
где S'jcp и S^chc,— абсолютные значения статических моментов растянутой и сжатой
частей сечения (площади которых одинаковы) относительно нейтральной линии.
Для статически неопределимых балок Образование, одного пластического шар-
шарнира еще не приводит к исчерпанию несущей способности. Для этого в случае балки,
изображенной на- рис. 10.3, а, необходимо образование одного пластического шар-
шарнира в заделанном сечении А и второго — где-то в пролете балки АВ.
9
1
1
2
Рис. 10.3. Статически неопределимая балка (а); эквивалентная системач(б)
Изменяя реакцию Rg (рис. 10.3, б), можно рассмотреть все статически возмож-
возможные состояния балки.
Изгибающий момент в-сечении с координатой г
72
M = Rqz —
Максимальное значение момента при
q&_
2
A0.9)
Из условия, что величина этого момента не превышает предельного, /
(Ю.10) ,
Наибольшее значение момента в заделке
имеем
2
Из того же условия, что величина этого момента не превышает предельного
Л*наиб sg Мпр,
I
A0.11)
На рис. 10.4 область, в которой выполняются неравенства A0.10) и A0.11), ¦
заштрихована. Согласно статической теореме предельная нагрузка больше всех ;
нагрузок, определяемых точками заштрихованной области, т. е. определяется точ- (
кой К пересечения линий ОК и LK (рис. 10.4). Абсцисса ее I
Яд =2(^2"
¦ = 4,82
A0.12>*
212

Этому значению /?д соответствует величина предельной нагрузки
¦ п и р. "^иР.
A0.13)
Из соотношений A0.9), A0.12) и A0.13) получаем г = 0,414/, что близко к рас-
расстоянию сечения В до сечения, в котором изгибающий момент в пределах упругости
максимален @,375/).
Определим теперь интенсивность предельной нагрузки кинематическим мето-
методом. На рис. 10.5 штриховой линией показано кинематически возможное состояние
системы.
Если угол поворота стержня ВС обозначить 6, то тогда угол поворота стержня АС
г
|>;и)сп
/¦
-. Работа равномерно распределенной нагрузки
<?пр (/ - г) -L 9 _i_ (/ - г) + ?пРг
Эту работу можно было бы сразу подсчитать как произведение интенсивности
раиномерно распределенной нагрузки на площадь треугольника АСгВ (рис. 10.5).
К
Рис. 10.4. Графики зависимости q, от Rb
Рис. 10.5. Механизм исчерпания несущей способ-
способности
I 'лбота предельных моментов равна Afnp8
ческой теоремы
2Afnp
. На основании кинемати-
= МпрВ + 2МП
0z
и куда получаем
2МПР
1 + г
г) '
A0.14)
Таким образом, предельная интенсивность нагрузки зависит от координаты пла-
• шческого шарнира г.
(Согласно кинематической теореме действительной предельной нагрузкой будет
• щшмальная из всех нагрузок, определяемых формулой A0.14). Для вычисления
• е приравняем нулю первую производную от qnp по г. Тогда получим квадратное
\ р.пшение
г2 _|_ 2/г — Р = 0,
г ш.-я которое, устанавливаем, что г = (]А2" — 1) / = 0,414/.
(пределение знака второй производной показывает, что при этом значении г
¦ Г1, пкция A0.14) имеет минимум. Подстановка найденной величины г- в выражение
i In. 11) приводит к-соотношению A0.13). Таким образом, предельные нагрузки, опре-
|'еиные статическим и кинематическим методом, совпадают. Следовательно, прове-
и иное решение является полным.
213

Пример 2. Прямоугольная портальная рама, выполненная из стержней
постоянного поперечного сечения, нагружена горизонтальной силой Р и вертикаль-
вертикальной силой 2Р (рис. 10.6). Рама 3 раза статически неопределима. Решим задачу кине-
кинематическим методом.
Поскольку рама не нагружена распределенной нагрузкой на каждом из четырех
участков рамы 12, 23, 34, 45, поперечная сила постоянна и изгибающий момент изме-~
няется по линейному закону. Поэтому пластические шарниры могут образоваться
только в сечениях 1—5.
Поскольку рама 3 раза статически неопределима, она становится геометрически
изменяемой при возникновении четырех пластических шарниров. В некоторых слу-
случаях возможно исчерпание несущей способности и при меньшем числе пластических
2Р
грпр и
3 \ч
Рис. 10.6. Прямоугольная порталь- Рис. 10.7. Механизм бокового смещения
ная рама
шарниров. Из кинематической теоремы следует, что действительной предельной
нагрузкой будет наименьшая из предельных нагрузок, определенных для этих
вариантов.
Допустим, что пластические шарниры возникают в сечениях 1, 2, 4 и 5.
Очевидно, что в этом случае возможным перемещением рамы в предельном со-
состоянии будет поворот стержней 12 и 45 на некоторый угол 0 (рис. 10.7). Перемеще-
Перемещение стержня 234 в вертикальном направлении является величиной второго порядка
малости по сравнению с перемещением есо в горизонтальном направлении. Такой
механизм исчерпания несущей способности будем называть механизмом бокового
смещения.
Определим теперь, исходя из этого механизма, величину предельной силы.
Работа горизонтальной силы Рпр равна 1,5Рпр/в, работа вертикальной силы 2Рпр —
нулю, а четырех предельных моментов — 4УИпр9. На основании кинематической
теоремы
- 1,5Рпр/9 = 4Мпр0.
откуда следует, что
я /и
A0.15)
Допустим теперь, что пластические.шарниры образовались в сечениях 2, 3 и 4.
Кинематически возможное состояние в таком случае изображено штриховой линией
на рис. 10.8. Такой механизм исчерпания несущей способности будем называть ба-
балочным механизмом.
Определим величину предельной силы. Работа вертикальной силы 2Рпр равна
2Рпр/0, работа горизонтальной силы — нулю; работа четырех предельных момен-
моментов — 4Л1пр0. Согласно кинематической теореме
2Р Ю = 4Мпр0,
откуда имеем
A0.16)
214

Допустим теперь, что пластические шарниры образовались в сечениях 1, 3,
4 и 5. На рис. 10.9 штриховой линией показано кинематически возможное состояние.
Этот механизм исчерпания несущей способности будем называть комбинированным
механизмом.
Определим для него величину предельной нагрузки. Работа горизонтальной
силы равна Рпр-1,5/6, вертикальной — 2РпрЮ; работа шести предельных момен-
моментов — бУИпр8. На ' -°- "
получаем
1а основании кинематической теоремы
1,5Рпр/е+ 2/>пр/9 =
_ '¦* ¦'"пр _ , 71
— 7 / —
М-
пр
I
A0.17)
Ш/Л
Рис. 10.8. Балочный механизм
~М^
Рис. 10.9. Комбинированный механизм
Значение предельной нагрузки в этом механизме исчерпания несущей способ-
способности оказалось наименьшим из полученных выше величин. Следовательно, фор-
формула A0.17) определяет действительную предельную нагрузку и реализоваться бу-
будет именно этот механизм исчерпания несущей способности.
При других соотношениях между нагрузками, приложенными к раме, и дли-
длинами стержней действительным механизмом исчерпания несущей способности может
оказаться не комбинированный, а балочный механизм, как для рамы, изображенной
1,51
1
Рис. 10.10. Статически неопределимая рама
с частичным (балочным) механизмом исчер-
пания несущей способности
Рис. 10.11. Статически неопредели-
мая балка с частичным механизмом
исчерпания несущей способности
па рис. 10.10. Такой механизм называют еще частичным механизмом исчерпания не-
несущей способности. Отличие его от комбинированного механизма или механизма
бокового смещения заключается в том, что он возникает при числе пластических
шарниров, меньшем, чем п + 1 для п раз статически неопределимой системы. При
чтом механизме в предельном состоянии рама не является статически определимой.
Такое исчерпание несущей способности часто возникает в балках, например, в балке,
изображенной на рис. 10.11.
Возможны случаи, когда предельная нагрузка для двух различных механизмов
исчерпания несущей способности оказывается одинаковой и является действительной
215

предельной нагрузкой. Тогда говорят об избыточном исчерпании несущей способ-
способности, как например, для рамы, изображенной на рис. 10.12. Для этой рамы, как
легко определить изложенными выше методами, предельные нагрузки, соответствую-
соответствующие механизму бокового смещения и комбинированному механизму, равны между
собой. Величина их Рпр = 2 —-НЁ-. Предельная нагрузка, соответствующая балоч-
балочному механизму, больше: Рпр ~ 4 —jS-. Поэтому кинематически возможное состоя-
состояние получается наложением кинематически возможных состояний для механизма
бокового смещения и комбинированного. На рис. 10.13 оно изображено штриховой
2Р
I
Рис. 10.12. Статически неопределимая
рама с избыточным механизмом исчер-
исчерпания несущей способности
Рис. 10.13. Избыточный механизм исчер-
исчерпания несущей способности рамы
линией. .Механизм, возникающий после образования пяти пластических шарниров,
имеет две степени свободы. Уравнение работ в таком случае может быть получено
сложением таковых для механизма бокового смещения и комбинированного меха-
механизма.
Предельная нагрузка не зависит от величины остаточных напря-
напряжений, которые могут возникнуть в ненагруженной конструкции
в результате сварки ее элементов, неточности монтажа, осадки опор
или предварительного н,агружения. Это объясняется тем, что пре-
предельная нагрузка определяется из уравнений статики, в которые
самоуравновешенные силы не входят. ' .
ПримерЗ. Плита высотой h с отверстием диаметра d растянута в условиях
плоской деформации (ez = 0) силой, величина которой на единицу длины в направ-
направлении, перпендикулярном1 чертежу, Р, (рис. 10.14).
¦ ~,_ ¦ м
Примем за статически возможное состояние такое, при котором в заштрихован-
ной части плиты напряжения равны нулю, а в верхней и нижней полосках высо-
„ h—d , -
три —-—
Из условия пластичности (9.5) имеем
ах = const.
о-х=2тт. A0.18)
Уравнение равновесия приводит к следующей величине предельной нагрузки,
определенной статическим методом:
Р* = 2тт (h - d). A0.19)
Найдем предельную нагрузку кинематическим методом. Выберем за кинемати-
кинематически возможное такое состояние, в котором пластическая область сосредоточена
"в наиболее ослабленном месте в окрестности отверстия. Тогда поле линий скольже-
скольжения состоит из логарифмических спиралей, примыкающих к контуру отверстия,
216 '

и сетки прямых линий (равномерного поля) у прямолинейных границ плиты
(рис. 10.14). Эти поля смыкаются в точке С, расстояние которой от центра отвер-
отверстия гс. Поля скоростей и напряжений в пластических областях ABC и CDE могут
быть легко определены. При этом их мощность положительна а^%" > 0, т. е. поля
напряжений и скоростей согласованы. ,
Различные кинематически возможные состояния и соответствующие им нагрузки
будут зависеть от положения точки С. Нагрузка для некоторого кинематически воз-
возможного состояния
ft
Т
= 2 J otdr + 2 J axdr,
A0.20)
где at — окружные напряжения в области
ABC; ах — напряжения в области CDE.
Напряжения в области А ВС, как
указывалось выше (см. §59), определяем
по формулам (9.44) и (9..42) при рпр = 0,
т. е.
0 = 2т 1п
—j- , а, = 2т ( 1 + In—т ). -Рис. 10.14. Плита с отверстием, растя-
d \ , d I нутая силой Р, МН/м
A0.21)
Напряжение в области CDE подсчитываем по формуле A0.18). Подставляя соот-
соотношения A0.21) и A0.18) в выражение A0.20), получаем
Р** = 2тт (A -d)
с
J In Ц- dr.
Второе слагаемое в этом выражении положительно и увеличивается с увеличе-
увеличением гс. Поэтому наименьшее значение Р** при гс~ —
Pmin = 2тт {h — d). - A0.22)
Сопоставляя формулы A0.19) и A0.22), заключаем, что нагрузки, соответствую-
соответствующие статически и кинематически возможному состояниям, совпадают, т. е. эти фор-
формулы определяют действительную предельную нагрузку и приведенное решение
является полным.
Пример 4. Плита высотой h, ослабленная односторонним узким глубоким
вырезом, изогнута в условиях плоской деформации (ez = 0) моментом, величина
которого на единицу длины в направлении, перпендикулярном чертежу, М МН-м/м
(рис. 10.15). *
Примем за статически возможное состояние такое, при котором в части плиты
ниже разреза хху =0, <3у = 0, | ох | = const, причем абсолютное значение напря-
напряжения ах определяется формулой A0.18).
Тогда, как и в случае чистого изгиба плиты, имеем следующую' величину пре-
предельного изгибающего момента, определенного статическим методом:
М* = I сг.. I ~ = 2т_ 4- = ¦
A0.23)
Для нахождения предельного изгибающего момента кинематическим методом
выберем за кинематически возможное состояние такое, при котором пластическая
область сосредоточена в наиболее ослабленном месте в окрестности выреза. Тогда
поле линий скольжения в растянутой области состоит из двух равномерных полей,
217

соединенных центрированным полем, а в сжатой из равномерного поля, как изобра-
изображено на рис. 10.15. По этим полям напряжений могут быть легко определены поля
скоростей.
Для определения напряжений в равномерном поле OCAD заметим, что в пло-
плоскости разреза ах = 0, %ху — 0 и, как следует из условия пластичности (9.5),
поэтому
Величина ф в точках разреза ф = -j-я. Следовательно, согласно первой форг
муле (9.23) для линии скольжения а
6-4-+-U
Располагая этой величиной и учиты-
вая, что для точек О А ф =-т-, по пер-
первой формуле (9.21) определяем сг0 в этих
я
4
откуда
Рис. 10.15. Плита, ослабленная одно- % тт ^п ~*~ ')
сторонним узким глубоким вырезом, и следовательно
изогнута моментом М, МН-м/м ' '
ах + ау = 2тт (я + *>• (Ю.24)
Поскольку в точках ОА по условию симметрии касательные напряжения хху
отсутствуют, из условия пластичности (9.5) имеем для этих точек
°Х-ад= 2ХТ A0-25)
Решая уравнения A0.24) и A0.25), получаем нормальное напряжение ах в точ-
точках О А
ах = тт (я + 2). A0.26)
В точках равномерного поля ОАВ, примыкающего к свободной поверхности
плиты, нормальные оу и касательные тху напряжения равны нулю и поэтому абсо-
абсолютная величина напряжения ах определяется формулой A0.18).
Располагая теперь величинами напряжений ах во всех точках АОК, запишем
условие равенства нулю нормальной силы в сечении, следом которого является
линия АОК
тт (я + 2) (а — Ь) — 2тт6 = 0,
откуда
Ь = -
A0.27)
Величина предельного изгибающего момента, найденного кинематическим
методом,
Подставляя в это соотношение величину Ь, по формуле A0.27) получаем
М** = ^Ь2- WJ2 = 0,720гта2. A0.28)
218

Действительное значение изгибающего момента лежит в интервале между вели-
величинами, определенными статическим [формула A0.23)] и кинематическим [фор--
мула A0.28)] методами.
Приведенное решение справедливо при условии, что глубина надреза больше,
чем размер АС, т. е. при условии, что
h — а> а — Ь,
откуда, используя соотношение A0.27), приходим к следующему условию справед-
справедливости приведенного решения:
о
h — a> р—г а = 0,280а.
Ряд других примеров определения предельных нагрузок для
элементов конструкций статическим и кинематическим методами
приведен в книгах [8, 11, 17, 24, 28, 31].
Использование статической и кинематической теорем для реше-
решения технологических задач дано в книгах [8, 26, 29].
§ 65. Предельное состояние скрученного стержня
произвольного поперечного сечения
Рассмотрим определение предельного крутящего момента в слу^
чае чистого кручения стержня произвольного' поперечного сечения.
Как будет показано ниже, рассматриваемая задача статически
определима и поэтому полученное решение является полным.
Напомним (см. § 47), что при чистом кручении стержня в попе-
поперечных сечениях его возникают только касательные напряжения
(рис. 10.16), одинаковым образом распределенные во всех попереч-
поперечных сечениях, т. е.
ох = оу = аг = 0, хху = 0.
В предельном состоянии компоненты касательного напряжения
в поперечных сечениях стержня т2Л: и хгу должны удовлетворять
условию пластичности /
т2 =tL Л-xly =т2т. A0.29)
Так же, как и в § 47, для того чтобы удовлетворить третье урав-
уравнение равновесия G.15), введем функцию напряжений, положив
x i X X
Отличие от функции напряжений, введенной в § 47, заключается
голько в коэффициенте тт. Он рведен для упрощения последующих
формул. Размерность функции напряжений в этом параграфе —
метр.
В таком случае условие A0.29) принимает вид
219

Как и в задаче упругого кручения [22], для односвязного кон-
контура можно принять, что функция напряжений на контуре равна
нулю
Фк
= 0.
A0.32)
Предельный крутящий момент связан с функцией напряжений
соотношением
\ A0.33)
которое отличается от выражения G.17) только коэффициентом тт.
Из изложенного следует, что
для решения задачи предельного
состояния скрученного бруса не-
некруглого поперечного сечения не-
необходимо определить функцию
напряжений Ф, удовлетворяющую
дифференциальному. уравнению
A0.31) и краевому условию
A0.32), затем предельный крутя-
крутящий момент можно подсчитать по
формуле A0.33).
Найдем направляющие коси-
косинусы нормали к поверхности
напряжений, уравнение которой
г = Ф (х, у). A0.34)
Как известно [21 ], направля-
направляющие косинусы нормали к по-
поверхности, уравнение которой
представлено в форме A0.34),
определяются формулами:
дФ
~~дх~
Рис. 10.16. Скрученный брус некруг-
некруглого поперечного сечения
/ = COS (v, х) =
[ = cos (v, у) = —
дФ
ду
п = cos (v, г) —
Используя выражение A0.31), получим
. _ V~2 дФ_ __ ¦ V2 дФ
П — ¦
220

Таким образом, поверхность функции напряжений представляет
собой поверхность с постоянным и равным 45° углом наклона нор-
нормали к оси z. Такую поверхность называют поверхностью постоян-
постоянного уклона или постоянного ската.
Величина угла наклона нормали к оси z определяется коэффи-
коэффициентом в формулах A0.30). Если, как это было сделано выше, этот
коэффициент принять равным тт, угол получается равным 45°.
Представим себе, что на пластинку, имеющую форму попереч-
поперечного сечения скрученного стержня, находящуюся в горизонтальном
положении, насыпан сухой мелкий песок. Образуется, холм, есте-
естественный откос которого дает представление о функции напряже-
напряжений Ф. На рис. 10.17 представлены фотографии песчаных насыпей
па пластинках, имеющих форму круга, эллипса, прямоугольника,
кнадрата и равностороннего треугольника, круга с полукруглой
выточкой и круга с прямоугольной выточкой.
Аналогия с песчаной насыпью при _ пластическом кручении
стержней была установлена Надаи [10]. На случай многосвязных
областей она была распространена Садовским ПО].
Аналогия с песчаной насыпью дает возможность эксперимен-
|.'1льно. исследовать пластическое кручение бруса произвольного
поперечного сечения и определять величину предельного крутящего
момента. Последний на основании соотношения A0.33) пропорциона-
пропорционален объему песчаной насыпи на горизонтально расположенной пла-
и инке, имеющей форму поперечного сечения скрученного бруса.
Подсчитаем предельный крутящий момент для некоторых попе-
поперечных сечений.
Круглее сечение диаметра d (рис. 10.18). Поверхностью функции
напряжений является конус, построенный на поперечном сечении с высотой, равной
ппловине диаметра поперечного сечения.
Согласно выражению A0.33) предельный крутящий момент равен удвоенному
ши.ему этого конуса, умноженному на величину предела текучести материала при
питом сдвиге
_ 1 jwP d _ nd?
МПР — ^т -g- -j~ — — тт ~W~ '
¦но совпадает с формулой, известной из курса сопротивления материалов [16].
Прямоугольное сечение со сторонами b и h (h^- b) (рис. 10.19).
И рассматриваемом случае поверхностью функции напряжений является «крыша»,
iи«• iроенная на прямоугольнике с высотой, равной—. Объем, ограниченный этой
б2
пришей», включает обием треугольной призмы STLKVU с площадью основания ¦—
и пысотой h — b и объем правильной четырехугольной пирамидыт сложенной из двух
¦ •Шмаковых половин ADSKV и BCTLU; площадь квадрата основания этой пира-
,, " Ъ
щды о , а высота—;-.
" _
Предельный крутящий момент Мпр равен удвоенному объему, ограниченному
крышей» [см. формулу A0.33)], умноженному на величину предела текучести мате-
I'li.uia при чистом сдвиге
M =:
пр
221

"• •". '?лт.лг*«зе
•f -
Л «^ ft "+: %
Рис. 10.17. Песчаные насыпи на плас-
пластинках:
а — круглой) б — эллиптической; в —
прямоугольной; г — квадратной, 'д — в
форме правильного треугольника; е —
круглой с полукруглой выточкой; ж —
круглой с прямоугольной выточкой

ч куда окончательно
Мп = тт -g- Cft — b). A0.35)
На основании соотношений A0.30) и вида поверхности функции напряжений
включаем, что в предельном состоянии в областях сечения APD и BWC (рис. 10.20)
v.ii-ательные напряжения параллельны оси *, а в областях APWB и DPWC — оси у.
Рис. 10.18. Поверхность
функции напряжений для
круглого сечения
Рис. 10.19. Поверхность функции напря-
напряжений для прямоугольного сечения
Ноличины касательных напряжений равны пределу текучести материала при чистом
гдниге. Линии АР, DP, PW, WB и WC, вдоль которых направления касательных
напряжений терпят разрыв, называют линиями разрыва. Как отмечалось выше
(см. § 57), они являются предельным положением упругих областей.
У
lu
1 1 \°
\\\
|И
ttt
ttt
1 1 1
%
b
X
В
Рис. 10.20. Направление ка-
касательных напряжений и ли-
линии разрыва (АР, PD, PW,
WB, WC) при пластическом в
кручении бруса прямоуголь-
прямоугольного поперечного сечения
Рис. 10.21. Направление ка-
касательных напряжений и ли-
линии разрыва (АС и BD) при
пластическом кручении бру-
бруса квадратного поперечного
сечения
Для квадратного сечения (рис. 10.21) линиями разрыва являются диагонали
киадрата.
Для тонкой полосы h > b пренебрегая в формуле A0.35) величиной Ъ по сравне-
сравнению с Zh, получаем
62ft
A0.36)
Сечение в виде равностороннего треугольника со
«•¦юроной а (рис. 10.22). Поверхностью функции напряжений является поверхность
223

трехгранной пирамиды высотой —^— а, где а — сторона треугольника. Площадь F
основания этой пирамиды равна площади равностороннего треугольника
. x 1 /3
= тг- п —X—
Таким образом, на основании соотношения A0.33) предельный крутящий момент
1Гв = -«т-5- <10-37)
М -2,' *?
пр Т 3 4
Рис. 10.22. Поверхность функции на- Рис. 10.23. Деформированная мембрана И
пряжений для сечения в виде равно- поверхность постоянного ската ;
стороннего треугольника
Решение задачи упруго-пластического кручейия стержня некр^г*
лого поперечного сечения, даже если диаграмма сдвига не имЙт
упрочнения, предствляет значительные математические, трудности,
В этом случае кручение может быть-экспериментально иссЛедовз%
при помощи аналогии с песчаной насыпью в сочетании с мембранной
аналогией. v ".
Для экспериментального изучения упруго-пластического круче-
кручения бруса некруглого поперечного сечения вначале изготовляют
жесткую поверхность постоянного ската. Она может быть получеАа
по форме песчаной насыпи. Основание этой поверхности затягивают
мембраной. Последнюю нагружают равномерно распределенным
давлением. При некоторой величине давления части мембраны при-
придут в соприкосновение с жесткой поверхностью постоянного ската
(рис. 10.23). Под частями мембраны, касающимися жесткой поверх-
поверхности постоянного ската, расположена пластическая область сече-
сечения, а под поверхностью свободно деформированной мембраны—¦
упругая.
Поверхность мембраны, прогибы которой ограничены жесткой
поверхностью постоянного ската, является поверхностью функций
напряжений при упруго-пластическом кручении бруса. Объем, огра-
ограниченный ею, пропорционален крутящему моменту, а уклон по-
поверхности мембраны касательному напряжению. На этом принципе
основаны специальные приборы для экспериментального изучений*
упруго-пластического кручения бруса.
224

;Kf|a put, 10.24 представлено полученное экспериментально раз-
ёЩЩ пластической области при кручении бруса квадратного попе-
рё^ййэго сечения. Пластическая область возникает сначала в сере-
середине, сторон квадрата, где в пределах упругости касательные
й'4&|>яжения являются наибольшими (рис. 10.24, а). С увеличе-
увеличением крутящего момента пластические области увеличиваются
(фШл 10.24, б). При достаточно большом крутящем моменте упругая
оМасть практически вырождается в линии разрыва (рис. 10.24, в)
Рис. 10.24. Развитие пластических областей при кручении бруса квадратного
поперечного сечения. (Упругая область — темная, пластические — светлые)
§ 66. Основные уравнения задачи предельного
состояния круглых и кольцевых пластин
Из курса сопротивления материалов известно, что несущая спо-
способность балки исчерпывается (балка становится геометрически
изменяемой) при наличии в ней упругой области. Решение задачи
об упруго-пластическом состоянии пластин связано со значительными
трудностями даже в простейшем случае осесимметричного нагруже-
пия из материала, диаграмма деформирования которого не имеет
упрочнения. Этот вопрос исследован в работах [3—7, 20] и др.
Изучение упруго-пластического изгиба круглых и кольцевых
осесимметрично нагруженных пластин позволило установить, что
и отличие от изгиба балок несущая способность пластин в большин-
большинстве случаев исчерпывается при отсутствии упругой области, т. е.
когда во всех точках пластин интенсивность напряжений достигает
пелйчины предела текучести материала.
Как следует из изложенного ниже, в решении задачи определе-
определения предельных нагрузок для круглых и кольцевых осесимметрично
нагруженных пластин используются как уравнения равновесия,
так и гипотеза о характере деформации пластины (гипотеза прямо-
прямолинейных нормалей), заменяющая условия совместности деформа-
деформаций. Поэтому полученное решение будет полным.
При рассмотрении чисто пластического изгиба круглых и кольце-
Ш.1Х осесимметрично нагруженных пластин примем, что срединная
плоскость их не растягивается, и используем те же допущения, что
N Н. Н. Малинин 225

и при расчетах пластин в пределах упругости, а именно: 1) точки,
расположенные на некоторой прямой, перпендикулярной к сре-
срединной плоскости пластины, после ее деформации также лежат на
прямой, перпендикулярной деформированной срединной поверх-
поверхности (гипотеза Кирхгофа), 2) нормальные напряжения в плоско-
плоскостях, параллельных срединной плоскости, отсутствуют. Как и при
расчетах пластин в пределах упругости, будем пренебрегать каса-
касательными напряжениями в окружных сечениях и плоскостях, па-
параллельных срединной плоскости. Используя второе допущение,
заключаем, что напряженное состояние во всех точках пластин яв-
является двухосным.
Дифференциальное уравнение равновесия элемента пластины
имеет вид [23 ]
jL(M,r)-Mt= — Qr, _ A0.38)
FAe Mr и Mt — интенсивности изгибающих моментов соответственно
в окружном и радиальном сечениях; Q — интенсивность поперечной
силы в окружном сечении.
Интенсивности изгибающих моментов Мг и Mt связаны с нормаль-
нормальными напряжениями в окружном н радиальном сечениях аг и at соот-
соотношениями [23] .
< 2 ~г~
Мг= j arzdz; Mt = j otzdz, A0.39)
h ft
где. 2 — расстояние от некоторой точки пластины до срединной
плоскости; h — толщина пластины.
Зависимости скоростей радиальной Ъ,г и окружной %t деформаций
от скорости х угла поворота О нормали к срединной плоскости пла-
пластины определяются формулами
% = z-§-; % = z-j-t - . A0.40)
которые легко получить дифференцированием по времени зависимо-
зависимостей деформаций от угла поворота [23].
Из последних выражений следует, что отношение этих скоростей
деформаций
является функцией только радиуса г.
Зависимости компонентов скоростей деформаций от компонен-
компонентов напряжений по теории течения для жестко-пластического ма-
материала (е0 = 0) согласно формулам D.24) имеют вид:
^ = 41г^-ст«); ^ = т!г^-сто), (Ю.42)
где at —. интенсивность напряжений; ?, — интенсивность деформа-
деформаций; а0 — среднее нормальное напряжение.
226

В рассматриваемом случае (аг = 0) согласно формулам A.21)
и A.5)
<; A0.43)
A0.44)
OyOV
Поскольку принимается, что диаграмма деформирования не
имеет упрочнения ot = aT и, следовательно,
: — orot + O( = aT. A0.45)
Из выражений A0.41), A0.42) и A0.44) следует, что
,__ 2аг — Of
откуда
A0.46)
A0.47)
Рис. 10.25. Эпюры окружных и радиальных напряжений
по высоте для пластины, находящейся в предельном
состоянии
На основании соотношений A0.45) и A0.47), учитывая, что г\
является функцией только радиуса, заключаем, что напряжения
являются функцией только радиуса и, следовательно, в пределах
h . h
изменения г: j^^z^O и O^z^-пт- напряжения по высоте
пластины не изменяется. Эпюры напряжений по высоте пластины
имеют вид "двух прямоугольников (рис. 10.25). Отличие от эпюры
напряжений в сечении пластического шарнира балки только в том,
что величины напряжений не равны пределу текучести материала.
Учитывая последнее из "формул A0.39), устанавливаем, что
М =-о,4г; Mt = ot~. A0.48)
Выражая напряжения через интенсивности изгибающих моментов
и подставляя их в соотношение A0.45), получаем
A0.49)
где
A0.50)
227

следует из формулы A0.50), величина Мт определяется
толькб пределом текучести материала и толщиной пластины h,
и для рассматриваемой пластины — постоянная величина.
Уравнения A0.38) и A0.49) являются основными уравнениями
для исследования несущей способности пластин.
Краевые условия имеют вид:
1) для круглой пластины в центральной точке Мг = М(;
2) для пластины, нагруженной по контуру равномерно распре-
распределенным моментом интенсивности m на контуре Мг = ±/и;
3) для пластины со свободным или опертым контуром Мг = 0;
4) для пластины -с заделанным контуром Ф = 0; % = 0 и, как
следует из соотношений A0.40), A0.42), A0.44) и A0.48), аг = 2о,
и Mr = 2Mt.
§ 67. Примеры определения предельных нагрузок
для круглых и кольцевых пластин
Для удобства интегрирования основных уравнений целесообразно,
как и в § 35, ввести функцию if, через которую интенсивности изги-
изгибающих моментов выражаются' следующим образом:
—J-) . A0.51)
cos
В таком случае соотношение A0.49) удовлетворяется тожде-
тождественно.
Подставим интенсивности изгибающих моментов по формулам
A0.51) в дифференциальное уравнение равновесия A0.38).
Тогда после преобразований получим
2 Мт °
Полученное уравнение интегрируется в замкнутой форме, если
Q — 0 (чистый изгиб) и если
Q = 7~f A0.53)
где а~— постоянная.
Это справедливо при нагружении пластины сосредоточенной си-
силой в центре, а также при нагружении пластины силой, равномерно
распределенной по окружности, концентричной контуру. В других
случаях интегрирование этого уравнения может быть проведено
численными методами.
Рассмотрим вначале интегрирование уравнения A0.52) при Q = 0.
В этом случае
dr sin г|з di|)
— ~ ~Т. лГТ*
Sin ( 1|> тг- ]
228

Выведенное уравнение совпадает с уравнением, полученным
в § 35. Интеграл его имеет вид
-^-=exp(K3i|,)sin(i|>— -2-), A0.54)
где С — постоянная интегрирования.
Рассмотрим примеры использования полученного интеграла для
определения предельных нагрузок.
Пример 1. Круглая пластина радиуса г2 нагружена на контуре равно-
равномерно распределенным моментом /ипр (рис. 10.26).
I
/ \
( Y//////////////y/////////////, I
. If, J
'«пр
Рис. 10.26. Круглая пластина нагру- Рис. 10.27. Кольцевая пластина
жена на контуре равномерно распре- нагружена на внутреннем кон-
деленным моментом туре равномерно распределенным
моментом
В рассматриваемом случае Q = 0. Краевые условия имеют вид:
при г = 0 Мг = Mt;
при г — г2 Мг= тпр.
Из первого краевого условия, используя соотношения A0.51) и A0.54), полу-
получаем
и, следовательно, для всех значений г ф = -^-. Учитывая это, из второго краевого
условия устанавливаем
Пример- 2. Кольцевая пластина радиусов г1 и г2 нагружена на внутреннем
контуре равномерно распределенным моментом тпр (рис. 10.27).
Как и в предыдущем случае, Q = 0. Краевые условия имеют вид:
при /•=/-! Мг= тпр;
при г — г2 Мг = 0.
Из второго краевого условия, используя соотношения A0.51) и A0.54), а также
учитывая, что на наружном контуре интенсивность изгибающего момента Mt отри-
отрицательна, получаем значение функции г|) на наружном контуре — г|>2 и величину
постоянной С:
^ ¦ ^(АрL A0.55)
229

Из первого краевого условия, используя соотношения A0.51), A0.54) и A0.55),
устанавливаем
I =-yrexpH^-iя)]sin (*-
тпр = -~- Мт cos -фх- A0.57)
где t|3x — значение функции ф на внутреннем контуре при г — rt.
Из уравнения A0.56) по заданному отношению — может быть определена
величина фх, после чего по формуле A0.57) подсчитана предельная интенсивность
момента.
Формула A0.57) дает возможность заключить, что наибольшая предельная интен-
интенсивность момента возникает при t|3t = 2я
2
"%ip шах — у-- Л1Т«
Величине ф1 = 2я согласно формуле A0.56) соответствует
Таким образом, если отношение наружного радиуса к внутреннему превышает
величину — = 2,963, никакая интенсивность не в состоянии привести к исчерпанию
ri
несущей способности пластины. Часть ее всегда остается упругой. Напомним, что
аналогичный результат был получен в § 37 прн рассмотрении несущей способности
диска постоянной толщины, нагруженного внутренним давлением.'
Разберем теперь интегрирование уравнения A0.52) при выпол-
выполнении соотношения A0.53). Тогда получим
dr sin фйф /irv го.
A0/. 58)
где
6 = ijL JL-. A0.59)
2 My v '
Интеграл этого дифференциального уравнения определяется вы-
выражением
ln-pj- = l/3ij) + In [6 — sin (ф ^-jl —
A0.60)
где С — постоянная интегрирования. ч
Последний интеграл берется различно в зависимости от вели-
величины Ь по сравнению с единицей.
Разберем пример использования полученного интеграла для.
определения предельной нагрузки в одном частном случае.
230

Пример 3. Круглая пластина оперта по контуру и нагружена сосредоточен-
сосредоточенной силой Рпр, приложенной в центре пластины (рис. ,10.28).
В этом случае
и, следовательно, согласно соотношениям A0.53) и A0.59)
Краеиые условия имеют вид:
при г = 0 Mr = Mt; при ' = г, Мг = 0.
Рис. 10.28. Круглая пластина оперта по
контуру н нагружена в центральной точке
сосредоточенной силой
Рпр
У////////////Л -с:
2гг
Из этих условий устанавливаем значения функции ф в центральной точке и
при
на контуре:
г = 0
-^; (Ю.62)
при г
Проинтегрируем теперь уравнение A0.58), используя соотношение A0.63).
Тогда получим
1п —= Г siav"y . A0.64)
я
Из выражения A0.62) следует, что интеграл
A0.65)
я
б
расходится. Поскольку пределы интегрирования конечны, подынтегральная функ-
функция при некотором значении аргумента должна обращаться в бесконечность.
Из соотношенвй A0.58), A0.62) и A0.63) заключаем, что
Ь — sin ( ф ?г- J ^ 0.
аемом интервале изменен!
ф р- J равно „ , устанавливаем, что
Поскольку в рассматриваемом интервале изменения -g-^Ф ^ -g- наибольшее
устанавливаем что 6^—^—.
231

Для того чтобы подынтегральная функция в выражении A0.65) обращалась
в бесконечность, необходимо выполнение равенства
b = -
A0.66)
Тогда подынтегральная функция будет обращаться в бесконечность при я|з = ¦
Выполняя интегрирование в выражении A0.60) для Ь ?
A0.05) для полученной величины b расходится.
Сопоставляя формулы A0.61) и A0 66), получаем
Рпр = 2пМт.
1 заключаем, что интеграл
A0.67)
§ 68. Использование условия пластичности
Треска—Сен-Венана в исследованиях
несущей способности круглых пластин
Использование условия пластичности Треска—Сен-Венана
позволяет значительно упростить определение предельных нагру-
нагрузок для круглых пластин. Как было отмечено в § 18 в случае пло-
_2го
2гг
Рнс. 10.29. График зависимости
между интенснвностями окруж-
окружного и радиального моментов по
условию пластичности Хубера—
Мнзеса (эллипс) и условию пла-
пластичности Треска—Сен-Венана
(шестиугольник)
Рис., 10.30. Круглая пластина радиуса
г2 оперта по контуру и нагружена рав-
равномерно распределенной по контуру
радиуса г0 нагрузкой
ского напряженного состояния замена
условия пластичности Хубер'а—Мизеса
условием пластичности Треска—Сен-
Венана равносильна замене эллипса в
координатах главных напряжений впи-
вписанным в него шестиугольником (см.
рис. 3.4). В координатах интенсивно-
стей изгибающих моментов такая замена
равносильна замене эллипса [уравне-
[уравнение A0.49)] вписанным в него шестиугольником (рис. 10.29). По-
Поэтому при использовании условия пластичности Треска—Сен-Венана
в зависимости от соотношений между интенсивностями изгибаю-
изгибающих моментов условие пластичности записывается по-разному.
Рассмотрим на двух примерах использование условия пластич-
пластичности Треска—Сен-Венана для определения предельных нагрузок
круглых пластин.
Пример 4. Круглая пластина радиуса г2 оперта по контуру и нагружена
равномерно распределенной по кругу радиуса га нагрузкой интенсивности рпо
(рис. 10.30).
В рассматриваемом случае уравнения для, поперечных сил записываются сле-
следующим образом:
232

при 0 ^ г ^ го
Q=_p^. A068)
при Го ^ г ^ гг
Q= °pf°, A0.69)
Краевые условия имеют вид:
при г = О Мг = /И^;
при г = го (/Wr)x = (МлJ;
при г = г2 Мг = О,
где индексами «1» и «2» обозначены первый (О^г^го) и второй (г о sg: г ^ >)
участки.
Из первого краевого условия заключаем, что центральной точке пластины соот-
соответствует точка с на рис. 10.29. В окрестности ее возможны пластические состояния,
изображаемые точками, лежащими на прямых са или се.
Докажем, что в рассматриваемом случае будет пластическое состояние са.
Для этого представим дифференциальное уравнение A0.38) в виде
dM,
г —^- + Mr — Mt + Qr=0. A0.70)
Для пластического состояния се Мг = Л4Т и поэтому г = 0. Далее, как
следует из рис. 10.29, для пластического состояния се Мг — М( > 0. Поскольку
Q > 0, то нз дифференциального уравнения A0.70) следует, что г <0. Это про-
противоречит полученному ранее результату. Следовательно, пластическое состоя-
состояние се невозможно.
Допустим, что возникает пластическое состояние са. В этом случае
Mt=MT, A0.71)
и из уравнения A0.38), используя соотношения A0.68), A0.69) и A0.71), получаем
дифференциальные уравнения при 0 ^ г ^ го
-J— (Мгг) = МТ~
при го
--
Интегралы этих уравнений имеют вид:
при 0 ^ г ^ го
Мг = Мт — i2El_ + -^i-; A0.72)
r<> «S r ^ r2
Mr = Mj — 1 . A0.73)
Из первого краевого условия, используя соотношение A0.75), устанавливаем
Сх = 0. A0.74)
Из второго краевого условия получаем
С3 = -^р-. A0.75)
¦ 233

Используя третье краевое условие, находим предельную интенсивность равно-
равномерно распределенной нагрузки
A0.76)
В случае равномерного распределения нагрузки по всей пластине (го = л>)
из уравнения A0.76) имеем
о - 6 Мт
Г2
В результате решения этой задачи на основе условия пластичности Хубера—
Мизеса при помощи численного интегрирования дифференциального уравнения
получаем [20]
Рпр = 6,5-^.
/У/////////////
У/////////////,
\2гг
Рпр
Р
Рис. 10,31. Круглая пластина заделана по
контуру и нагружена равномерно распре-
распределенной нагрузкой
Для того чтобы из уравнения A0.76) получить величину, предельной силы для
пластины, нагруженной сосредоточенной силой в центре, представим это уравнение
в виде
Положим, что при г0 ->• 0
Рпр. Тогда
Рпр = 2яМт,
т. е. получен такой же результат, как й в решении этой задачи на основе условия
пластичности Хубера—Мизеса (см. пример 3).
Пример 5. Круглая пластина заделана по контуру и нагружена равномерно
распределенной нагрузкой (рис. 10.31).
В рассматриваемом случае пластину можно разбить на две области. В первой
@ ^ г .g г0) возникает пластическое состояние са, а во второй (го ^ г ^ г2) пласти-
пластическое состояние ак. Интенсивность поперечной силы как в первой7так~и во второй
области определяется формулой A0.63), а интенсивность радиального момента в пер-
первой области — соотношениями A0.72) и A0.74). Раднус границы областей опреде-
определяем из условия
при г — га Мг — 0.
Используя соотношения A0.72) и A0.74), получаем
Рпр
A0.77)
A0.78)
Дифференциальное уравнение для интенсивности радиального момента во вто-
второй области получаем из соотношения A0.70), используя уравнение для интенсив-
интенсивности поперечГной силы A0.68) и учитывая, что уравнение прямой ak
Mt~Mr= Мт.
В результате устанавливаем
dMr _ Mi pnpr
dr ~ r 2 '
234

Интеграл этого уравнения имеет вид
Мг = Mj In —
Постоянную Сй определяем из соотношения A0.77)
Г = МТЫ- BsgL + Cj. A0.79)
Подставим эту величину постоянной в уравнение A0.79). Тогда получим
р (г2 ~ г%\
Мг=тИт1п- -^-Ц 01, A0.80)
В рассматриваемом случае в заделанном сечении не может быть выполнено усло-
условие Мг = 2М(, так как согласно прямой ak интенсивности изгибающих моментов Мг
и Mt имеют разные знаки. В заделанном сечении образуется круговой пластический
шарнир. Поэтому при г = г2 Мг = —Mj.
Из этого соотношения, используя уравнение A0.80) и выражение A0.78), полу-
получаем трансцендентное уравнение для радиуса границы двух областей
5+2 In -^- — 3(-^- =0.
ra \ r0 )
Корень этого уравнения
-^- = 0,730.
Подставляя эту величину в формулу A0.78), находим величину предельной
интенсивности нагрузки
D из Мт
§ 69. Понятие о приспособляемости
При повторных нагружениях конструкции за пределами упру-
focth возможны следующие три случая деформирования какого-
либо из ее элементов: 1) знакопеременная пластическая деформация;
2) нарастание с каждым циклом постоянной по знаку пластической
деформации; 3) прекращение после одного или нескольких первых
циклов роста пластической деформации и переход конструкции
к чисто упругому поведению.
В первом случае результатом повторных нагружений может
быть разрушение усталостного характера (малоцикловая усталость).
Неограниченный рост односторонней деформации (второй случай)
может привести к нарушению условий эксплуатации конструкции
или к исчерпанию пластических свойств материала и разрушению.
Что касается возможности перехода к чисто упругому поведению
в третьем случае, то она связана с возникновением в системе неко-
тброго распределения остаточных напряжений в результате пласти-
пластического деформирования на первых этапах нагружения. Если эта
возможность реализуется, то говорят, что конструкция приспосо-
приспособилась к повторным нагружениям данного типа.
235

Таким образом, возникает задача об определении максимальных
интервалов изменения приложенных внешних воздействий, при ко-
которых приспособляемость конструкции еще возможна. При этом
последовательность нагружения по условию задачи может быть про-
произвольной или заданной.
При анализе условий приспособляемости обычно используется диа-
диаграмма идеального упруго-пластического тела (см. рис. АЛ.). Рассмот-
Рассмотрим два примера, иллюстрирующих явление приспособляемости.
Пример 1. Допустим, что конструкция состоит из стального стержня и
медной трубки, связанных с параллельными жесткими плитами, к которым прило-
приложены две равные противоположно направленные силы Р (рис. 10.32). Будем обозна-
Рис. 10.32. Стержневая система (к примеру исследо-
исследования приспособляемости)
Рис. 10.33. Диаграммы растя-
растяжения материалов стержней
1
1
р
1
1
р
/
// .
/ / чЬ
// "
// ?
If
II
Чз
чать величины, относящиеся к стальному стержню, индексом «с», а к медной трубке —
индексом «м». Примем, что Fc = F, Fa = 3F. Диаграммы растяжения материалов
стержней изображены на рис. 10.33. Примем, что Ес = 2Е; Ем = Е; атс = От,
2
a атм = -Q- ат- Будем считать, что диаграммы сжатия совпадают с диаграммами растя-
ження.
Решив рассматриваемую статически-неопределимую задачу в пределах упру-
упругости, получим
NC = ~P, Nu=-j-P. A0.81)
Обозначим через NTC и /VTM величины внутренних сил в стержнях, при кото-
которых напряжения в стержнях достигают предела текучести. Очевидно, что
= oTF = NT;
A0.82)
Сопоставляя выражения A0.81) к A0.82), устанавливаем значение силы Р = Рт,
при превышении которой в системе возникнут пластические деформации (в стальном
стержне)
Рт = 4" *т.
236

Предельную нагрузку найдем, подставляя величины A0.82)'в уравнение равно-
равновесия
Nc+Nu = -P. A0.83)
Тогда получим
Рпр = 3NT. A0.84)
Допустим теперь, что система вначале нагружается силой Рх, величина кото-
которой находится в интервале Рт -g Р1 ^ Рпр, а затем разгружается.
Тогда при нагружении
Nc = NT ¦ A0.85)
и, как это следует из уравнения равновесия A0.83),
Л'м = Pi ~ JVT. . A0-86)
Уменьшение нормальных усилий при разгрузке, согласно закону разгрузки,
определяем по формулам A0.81)
дгразгр 2_ ууразгр _ JL р -
'vc — 5 *' м — 5 '*
Остаточные усилия после полной разгрузки
Предположим далее, что после разгрузки система нагружается некоторой си-
силой Р2, направление которой противоположно направлению силы Pv т. е. сила Р2
сжимает стержень и трубку. (Под Рх и Р2 подразумеваем абсолютные значения соот-
соответствующих сил).
Если при вторичном нагружении пластические деформации не образуются,
то внутренние силы, возникающие за счет нагружения силой Р2, по-прежнему выра-
выражаются формулами A0.81). Суммарные силы (с учетом остаточных)
A0.87)
Сопоставляя выражения A0.87) и A0.82), заключаем, что пластические дефор-
деформации при сжатии возникают вначале в стальном стержне. Для определения зна-
значения силы Р2, при которой напряжения в этом стержне достигнут предела теку-
текучести (при сжатии), необходимо приравнять первое выражение A0.87) к усилию
текучести — Nj. Тогда получим
откуда
Р1+ Р2 == 5NT. A0.88)
При соблюдении условия A0.88) повторные нагружения (растяжение силой Pv
затем сжатие силой Р2) не будут приводить к пластическому деформированию.
Результат становится более отчетливым, если A0.88) переписать в виде
Pl+Pt=2PJ.
237

Отсюда ясно, что знакопеременное пластическое течение при повторных нагру-
жениях не возникает, если изменение силы не превышает удвоенного значения силы,
при котором в наиболее напряженном (стальном) стержне возникают пластические
деформации.
Кроме того, на величины нагрузок Рх и Р2 должно быть наложено еще одно
ограничение — они не должны достигать предельного значения A0.84), прн кото-
котором несущая способность системы исчерпывается.
Полученные результаты можно проиллюстрировать с помощью графического
построения (рис. 10.34). Здесь прямая АВ, отсекающая на координатных осях от-
отрезки, равные 5Nj, построена по уравнению приспособляющих нагрузок A0.88).
Нанесем на том же чертеже две горизонтальные СК. н ML и две вертикальные пря-
прямые DK и RL, отсекающие на осях координат отрезки Рт = 2,5NT и Рпр = ZNj.
Тогда получим несколько характерных областей нагружения. Каждая точка на пло-
плоскости Р1; Р3 характеризует цикл нагружения (сначала растяжение силой Plt
а потом сжатие силой Р2 или наоборот). Если точка лежит в области [0RLM, то тогда
Pt < Р"х и Р2 < Рт. Поэтому при таком цикле пластические деформации не возни-
возникают. Если точка лежит в областях MCFL или LEDR, то тогда Р2 > Рт или Рх >
> Pj, но Р1 + Р2 < бЛ'т. Следовательно, в этом случае пластические деформации^
возникнут при первом нагружеиии, а затем система приспособится. Если точка,
изображающая цикл, лежит в области FKE, то тогда Р1 -\- Р2 > бЛ'т и поэтому при
таком цикле возникают знакопеременные пластические деформации в стальном
стержне. Наконец, если точка, изображающая цикл, лежит вне или на границе
квадрата ODKC, то Рх ^ Рпр или Р2 ^ Рпр. Поэтому в этом случае уже при первом
нагружении исчерпывается несущая способность конструкции и, следовательно,
область вне квадрата ODKC, включая и его границу, является областью неосуществи-
неосуществимых циклов.
Пример 2. Рассмотрим толстостенную трубу, нагруженную внутренним
давлением (см. рис. 6.1). Величина внутреннего давления рт, пРи котором в трубе
возникают пластические деформации (на внутренней поверхности), может быть уста-
установлена по формуле F.20), если подставить в нее rj = гх:
(ИШ)
Предельное давление, при котором исчерпывается несущая способность трубы
(пластическая область распространяется на все сечение ее гт = г2) определяется
формулой F.29).
После нагружения трубы давлением р (рт < р < рПр) и разгрузки в ней возни-
возникают остаточные напряжения. Вычисление их было разобрано в § 34.
Разгрузка будет упругой, если в наиболее напряженных точках внутренней
поверхности трубы интенсивность остаточных напряжений меныце предела теку-
текучести материала а°ст ^ ат. Если интенсивность остаточных напряжений равна
пределу текучести материала, то при повторном нагружении для образования пла-
пластических деформаций необходимо вначале приложить давление рт, которое при-
приведет к снижению интенсивности напряжений- в точках внутренней поверхности
до нуля, а затем для образования пластических деформаций в точках этой поверх-
поверхности (при интенсивности напряжений, равной пределу текучести материала) уве-
увеличить это давление до 2рт.
Таким образом, при повторном нагруженни пластические деформации не воз-
возникнут, если давление будет меньше 2рт. Для того чтобы несущая способность трубы
не была исчерпана, давление должно быть меньше предельного.
На рис. 10.35 представлены графики зависимости от отношения радиусов ——
величин 2 УЪ — и j/-^2E-._Пересечение этих графиков имеет место,при — = 2,22.
Таким образом, при— < 2,22 рпр < 2рт и при р < рпр первый процесс
разгрузки и все последующие процессы нагрузки и разгрузки не приводят к пласти-
238

ческим деформациям. При -2->2,22 рпр > 2рт й при первом процессе разгрузки
могут возникнуть пластические деформации. Если р < 2рт, вторичный процесс
нагрузки не приведет к пластическому деформированию. Область давлений, при
которых в трубе не будут возникать пластические деформации при вторичном и
последующих процессах нагрузки и разгрузки, ограничена линией, отмеченной
штрихами на рис. 10.35.
\
с
1
к
м
II
0
б
\.
Ч
¦ / L
R
Pnp=JNT
\
Е
В \
I
л
ггттттттт
тгтгттгп
2,0
1,0
' 2 J />//;
Рис. 10.35. Графики зависимости уд-
удвоенного давления, при котором воз-
возникают пластические деформации при
первом нагружении, и предельного
Рис. 10.34. Диаграмма приспособляемо- давления от отношения наружного ра-
сти для стержневой системы
диуса трубы к внутреннему
Рассмотренные два примера приспособляемости являются про-
простейшими.
Более сложным задачам приспособляемости посвящены работы
12, 11—15, 17—19, 24, 25]. Систематическое изложение теории при-
приспособляемости дано в книге. [2].
Список литературы
1. Гвоздев А. А. Расчет несущей способности конструкций по методу предель-
предельного равновесия. М., Стройиздат, 1949, 280 с
2. Гохфельд Д. А. Несущая способность кон'струкций в условиях теплосмен.
М., «Машиностроение», 1970, 259 с
3. Григорьев А. С. Об изгибе круглой плиты за пределом упругости.— «При-
«Прикладная математика и механика», 1952, т. XVI, вып. I, с. 111—115.
4. Григорьев А. С. Изгиб круглой плиты при линейном упрочнении мате-
материала.—«Инженерный сборник», 1952, т. XIII, с- 31—46.
5. Григорьев А. С. Изгиб круговых и кольцевых пластин переменной и постоян-
постоянной толщины за пределами упругости.— «Инженерный сборник», 1954, т. XX,
с. 59—100.
6. Григорьев А. С. Изгиб круглой защемленной пластинки за пределами упру-
упругости. — «Известия АН СССР. ОТН. Механика и машиностроение», 1962, № 6,
с 83-87.
7. Илюшин А. А. Пластичность, М., ГИТТЛ, 1948, 376 с.'
8. Качалов Л. М. Основы теории пластичности. М., «Наука1», 1969, 420 с.
9. Койтер В. Т. Общие теоремы теории упруго-пластических сред. М., Изд.
иностр. лит-, 1961, 79 с
239

10. Надаи А. Пластичность и разрушение твердых тел. М., Изд. иностр. лит-,
1954, 647 с.
11. Нил Б. Г. Расчет конструкций с учетом пластических свойств материалов.
М-, Госстройиздат, 1961, 315 с.
12. Прагер В., Ходж Ф. Г. Теория идеально-пластических тел: Изд. иностр.
лит., 1956, 398 с
13. Прагер В. Проблемы теории пластичности. М., Физматгиз, 1958, 136 с-
14. Прагер В. Расчет конструкций за пределом упругости при циклических
температурных воздействиях.— «Механика. Сборники переводов и обзоров ино-
иностранной, периодической литературы», 1957, № з, с. 104—111.
15. Прагер В. Приспособляемость в упруго-пластической среде, подвергнутой
циклам нагрузки и температуры.— «Механика. Периодический сборник переводов
иностранных статей», 1958, № 5, с. 121—125.
16. Работков Ю. Н. Сопротивление материалов. М., Физматгиз, 1962, 455 с.
17. Ржаницын А. Р. Расчет сооружений с учетом пластических свойств мате-
материала. М., Госстройиздат, 1954, 287 с.
18. Розбиблюм В. И. О приспособляемости неравномерно нагретых упруго-
пластических тел.— «Известия АН СССР. ОТН», 1957, № 7, с. 136—1-38.
19. Розенблюм В. И. К теории приспособляемости упруго-пластических тел.—
«Известия АН СССР. ОТН», 1958, № 6, с 47—53.
20; Соколовский В. В. Теория пластичности. М., «Высшая школа», 1969, 608 с
21. Смирнов В. И. Курс высшей математики. Т. 2. М., Физматгиз, 1958, 628 с.
22. Филоненко-Бородич М. М. Теория упругости. М., Физматгиз, 1959; 364 с.
23. Феодосьев В. И. Сопротивление материалов. М-, «Наука» 1974, 559 с.
24. Ходж Ф. Г. Расчет конструкций с учетом пластических деформаций. М.,
Машгиз, 1963, 308 с
25. Ходж Ф. Г. Приспособляемость упруго-пластических конструкций.—
В кн.: Остаточные напряжения в металлах и металлических конструкциях. М.,
Изд. иностр. лит., 1957, с. 186—213.
26. Avitzur В. Metal forming processes and analysis, Me. Graw—Hill book com-
company, 1968, 500 p.
27. Calladine С R. Engineering plasticity, Pergamo^ press, 1969, 318 p.
28. Dietrich L., Miastkowski J., Szczepinski W. Nosnosc graniczna elementow
konstrukeji, Panstwowe wydawnictwo naukowe, 1970, 271 s.
29. Johnson W. Mellor P. B. Plasticity for mechanical engineers, D. Van Nost-
rand Company LTD, 1962, 412 p.
30. Spencer G. S., Introduction to plasticity, Chapman and Hall, 1968, 118 p.
31. Szczepinski W. Projektowanie elementow maszyn metoda nos'nosci gianicznej,
Panstwowe wydawnictwo naukowe, 1968, 129 s.
32. Teoria plastyczriosci, Panstwowe wydawnictwo naukowe, 1965, 399 s. Aut.:
Z. Marciniak, Z. Mroz, W. Olszak i inni.

РАЗДЕЛ III. ПОЛЗУЧЕСТЬ.
ГЛАВА XI
ОСНОВНЫЕ РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНОГО
ИЗУЧЕНИЯ ПОЛЗУЧЕСТИ ПРИ ОДНООСНОМ РАСТЯЖЕНИИ
§ 70. Ползучесть и релаксация напряжений
Напряжения и деформации, возникшие при нагружении деталей,
изменяются во времени, даже если нагрузки остаются постоянными.
Это явление называют ползучестью материала. Одну сторону этого
явления — изменение во времени деформаций — называют собственно
ползучестью или последействием, а другую ¦— изменение во времени
напряжений — релаксацией.
Последействие может быть упругим и пластическим. При упругом
последействии деформации, возникшие во времени, после разгрузки
уменьшаются и с течением времени совсем исчезают, при пласти-
пластическом они в основном необратимые и после разгрузки уменьшаются
во времени медленно и в незначительной степени.
На рис. 11.1 графически изображены процессы упругого
(рис. 11.1, а) и пластического (рис. 11.1, б) последействия в случае
постоянного во времени напряжения, меньшего предела пропор-
пропорциональности материала при температуре испытания.
Деформация, возникшая при нагружении (ОА), равная -^, с те-
течением времени увеличивается (кривая АВ). При разгрузке умень-
уменьшение деформации (ВС) так же, как и в случае кратковременного
испытания на растяжение, равно упругой деформации -^-. В даль-
дальнейшем после разгрузки деформации уменьшаются (кривая CD).
Это явление называют обратным последействием или обратной пол-
ползучестью. Ниже оно будет рассмотрено более подробно.
В случае упругого последействия возникшие во времени дефор-
деформации исчезают полностью (рис. 11.1, а), а в случае пластического
процесс уменьшения деформаций с течением времени затухает
(рис. 11.1,6).
В дальнейшем будем рассматривать пластическое последействие,
которое для краткости назовем просто последействием или собственно
ползучестью. Ползучесть возникает как при нагружении детали за
пределы упругости, так и при нагружении в пределах упругости.
Экспериментальные исследования показали (рис. 11.2), что
охлаждение образца без его разгрузки не сказывается на ходе про-
процесса ползучести в целом. После нагрева образца ползучесть возоб-
241

новляется с той же скоростью, как и перед охлаждением. Охлажде-
Охлаждение, сопровождаемое разгрузкой, отражается на кривой ползучести.
В этом случае после нагрева и нагрузки на кривой ползучести обра-
образуется горб, соответствующий проявлению первой стадии ползу-
ползучести, о которой будет сказано ниже.
о N
5)
Рис. 11.1. Графики, иллюстрирующие явления упругого (а) и пластического (б)
последействия
Таким образом, в случае кратковременных перерывов в подаче
тока к нагревательным печам разгружать образцы нецелесообразно.
Имеющиеся в литературе сведения отображают влияние на ход
процесса ползучести кратковременных A0—30 мин) охлаждений [3].
Однако известны испытания с длительным охлаждением [26], ко-
которые татоке 'не оказали влияния на процесс ползучести (рис. 11.3).
0,30
0,28
0,26
0,24
WOO 1100 1200 1300 t,4
a) <
Рис. 11.2. Участки кривых ползучести, полученные при испытании образцов стали
ЭИ454 при температуре 550° С и напряжении 90 МН/м2 [22 ]:
а — охлаждение в точке А без разгрузки; б — охлаждение в точке А с рззгрузкой
Рассмотрим более подробно явление релаксации при постоян-
постоянной деформации.
Предположим, что образец нагружен растягивающей силой, ко-
которая вызвала напряжение, меньшее предела пропорциональности
материала при данной температуре, и испытание поставлено таким
образом, что полная деформация образца в течение времени не
изменяется.
242
2000
t,4

Полная деформация, остающаяся вовремени постоянной, является
суммой упругой деформации ге и деформации, образовавшейся
в процессе ползучести ес, т. е.
8 = 8е -f &C-
Рис. 11.3. Кривая ползучести, полученная
при испытании образцов хромоникелемо-
либденовой стали при температуре 400° С
и напряжении 77,5 АШ/м2 с охлаждением
без разгрузки [26]. Продолжительность
охлаждения: в точке А —118 ч; В—53 ч;
С — 54 ч; D — 93 ч; Е — 120 ч,
0,0006
0,000?
Г
BE
. о-о
О 2000 ?000 6000 Ь,ч
Деформация ползучести в" возрастает во времени, а следовательно,
упругая деформация ге уменьшается. Таким образом, в течение вре-
времени составляющие полной деформации перераспределяются.
На основании закона Гука
8е =
а
Т
Поскольку полная деформация во времени не изменяется и равна
начальному значению е @) и, кроме того, в начальный момент вре-
времени справедлив закон Гука, имеем
где а @) — напряжение в начальный момент времени.
Тогда получим
A1.1)
Дифференцируя это соотношение по времени, устанавливаем
Е dt ~ dt ~ S "
A1.2)
Из выражения A1.1) заключаем, что за счёт увеличения дефор-
деформации ползучести напряжение будет непрерывно уменьшаться,
однако деформация ползучести при релаксации не может увеличи-
ваться* беспредельно. Если представить себе, что деформация пол-
ползучести достигла величины деформации, возникшей при нагруже-
нии е @), то напряжение в стержне становится равным нулю (стер-
(стержень разгружается).
В процессе ползучести деформация растет до такой величины,
при которой образец разрушается. В процессе релаксации деформа-
деформация ползучести не превосходит величины деформации, образовав-
образовавшейся при нагружении.
При экспериментальном изучении релаксации в случае растя-
растяжения начальную растягивающую нагрузку (а следовательно, и на-
243

пряжение) понижают с течением времени так, чтобы длина образца,
определенная начальной нагрузкой, сохранялась постоянной.
На основании испытаний строят график зависимости напряжения
от времени, который называют кривой релаксации (рис. 11.4).
Для стальных и чугунных деталей явление ползучести суще-
существенно при повышенных температурах (ориентировочно более
300° С) и чем она выше, тем интенсивнее протекает этот процесс. ¦
При небольших температурах изменение во времени деформаций и
напряжений, возникших в результате нагружения, незначительно
и им можно пренебречь.
Однако для ряда материалов, как например, для металлов с низ-
низкой температурой плавления (свинец, алюминий, дуралюмин и др.),
а также для высокополимер-
высокополимерных материалов (резина, кау-
каучук, пластмассы и др.) явле-
явление ползучести весьма заметно
и при комнатной температуре.
Таким образом, вопрос о
необходимости расчета детали
на ползучесть должен решать-
решаться в зависимости от материала,
температуры нагрева и сте-
0 * пени напряженности детали.
Рис. 11.4. Кривая релаксации Обычно ползучесть учиты-
учитывается при расчете и конструи-
конструировании деталей машин, находящихся в процессе эксплуатации
¦длительное время в нагретом состоянии. В таких условиях работают,
например, элементы конструкций паровых и газовых турбин, реак-
реактивных двигателей, ядерных реакторов, паровых котлов, узлы обо-
оборудования нефтяной промышленности, детали химических аппара-
аппаратов и тепловых приборов.
Особенностью расчетов на ползучесть является учет фактора
времени, который в обычных расчетах на статическую нагрузку во
внимание не принимается.
Расчеты деталей на ползучесть в основном базируются на ре-
результатах экспериментального изучения ползучести материала при
одноосном растяжении нагрузкой, постоянной во времени.
§ 71. Кривые ползучести
При нагружении образца деформация его возрастает от нуля
до некоторой величины. Деформация, возникшая при нагружении,
может быть либо упругой, либо упруго-пластической в зависимости
от величины напряжения, при котором производится испытание.
В течение времени деформация образца увеличивается.
Обычно результаты экспериментального изучения ползучести
обрабатывают в виде графиков (рис. 11.5), представляющих зави-
зависимость от времени деформаций при постоянных напряжениях и
температуре. Эти графики называют кривыми ползучести.
244

Вид кривых ползучести зависит от напряжения и температуры,
при которых испытывался образец. При нагружении нагретого
образца деформация весьма быстро возрастает от нуля до некоторой
величины (отрезок О А на рис. 11.6). Если напряжение не превосхо-
превосходит предела пропорциональности материала образца, то эта часть
деформации является упругой, в противном случае эта деформация*
состоит из упругой и пластической (остаточной) деформации.
После прекращения роста нагрузки, полная деформация нагре-
нагретого образца будет постепенно увеличиваться во времени по закону,
изображенному линией ABCD. Ординаты этой линии представляют
собой величины деформаций е для определенного значения времени.
ec 10
Лердая
Вторая
Третья
Рис.
стали
Кривые ползучести
ЭИ756 при температуре
600° С [2]
Рис. 11.6. Кривая ползучести
Они складываются из деформации, возникшей при нагружении,
и деформации . ползучести.
Иногда на графике изображается зависимость от времени только
одной деформации ползучести ес, тогда ось абсцисс графика располо-
расположена так, как это показано штриховой линией на рис. 11.6.
Тангенс угла наклона касательной к линии ABCD с осью абсцисс
выражает в масштабе скорость деформации |, равную скорости
деформации ползучести Ъ?
__
dt
dt
A1.3)
Процесс ползучести можно разделить на три стадии.
В первой стадии (участок АВ) скорость деформации ползучести
постепенно уменьшается. Бейли [26] объяснил это уменьшение ско-
скорости взаимодействием механического упрочнения и термического
разупрочнения. В первой стадии преобладает механическое упроч-
упрочнение, связанное с ростом деформации ползучести.
Во второй стадии (участок ВС) устанавливается равновесие
между механическим упрочнением и термическим разупрочнением
и процесс ползучести протекает с минимальной постоянной во вре-
2 45

мени скоростью |min, которая зависит от напряжения и темпера-
температуры. При определенной температуре она будет функцией напряже-
напряжения
gmin = Q <<Г).
Наиболее экспериментально проверенной является степенная
зависимость минимальной скорости деформации ползучести от
напряжения
Smln = Q (<Т) = АО* A1.4)
и закон гиперболического синуса
&iin = Q(<r) = csh-Jf-. A1.5)
Величины k, n, с и d в формулах A1.4) и A1.5) дли каждого
материала зависят от температуры.
В дальнейшем будет использоваться формула A1.4), поскольку
она, как показано ниже, достаточно хорошо согласуется с данными
опытов и удобна для использования в расчетах. Зависимость A1.5)
несколько лучше подтверждается экспериментальными данными,
чем выражение A1.4), но ее использование для расчетных целей
более сложно, и численные значения коэффициентев\; и d, входя-
входящих в формулу A1.5), менее изучены, чем значения коэффициентов k
и п в зависимости A1.4).
Логарифмируя соотношение A1.4), получаем
lglmin = lg'A +n\gO. A1.6)
Из выражения A1.6) следует справедливость линейной зави-
зависимости между логарифмами минимальной скорости деформации
ползучести и напряжения. Как следует из рис. 11.7, эксперимен-
экспериментально полученные точки подтверждают эту зависимость [21 ].
Располагая серией кривых ползучести при определенной тем-
температуре и различных напряжениях, можно установить величины
коэффициента k и показателя степени п.
Для этого вначале необходимо подсчитать минимальные скорости
деформации ползучести при различных напряжениях и полученные
результаты изобразить в виде точек в логарифмических координа-
координатах lg gmin. lg о (рис. 11.8). Затем следует провести прямую, аппро-
аппроксимирующую результаты опытов, и выбрать на этой прямой две
какие-либо точки / и 2 с координатами соответственно lg ^ш ь
lg ffi и lg gmin 2, lg a2. Согласно формуле A1.6) имеем
lg Imin 1 = lg k + tl lg CD
lg grain 2 = lg k + П lg ff2,
246

откуда следует
п — ¦
. 5min2
18 То
femlnl
A1.7)
"A1.8)
= lg ?min 1 — «
lg & = lg imin 2 —
В табл. 11.1 приведены величины k и п для некоторых материалов
при определенных температурах.
б,МН/мг
600
500
400
300
Рис. 11.7. Графики зависимостей напря-
напряжения от минимальной скорости деформа-
деформации ползучести для хромомолибденовой
стали марки 60Х16М2А [21]
Рис. 11.8. К определению показателя сте-
степени п и коэффициента k
zoo
100
15
50
25
10
5-Ю'8 10-
Зависимость величины k от температуры может быть представ-
представлена в виде [4}
Ш^ A1.9)
где кг — постоянная для материала; Т — абсолютная температура;
R — газовая постоянная; АЯ„ — энергия активации ползучести.
Под последней понимается величина энергии элемента тела, пре-
превышение которой приводит к смещению элемента и вследствие этого
к деформации.
В третьей стадии ползучести (участок CD на рис. 11.6) скорость
деформации непрерывно возрастает, пока не наступает разрушение
образца (точка D).
Ранее предполагалось, что увеличение скорости деформации пол-
ползучести в третьей стадии вызвано повышением напряжения, которое,
в свою очередь, обусловлено уменьшением площади поперечного
сечения образца за счет его растяжения с последующим развитием
247

Таблица 11.1
Основные характеристики ползучести некоторых материалов
, Материал
Углеродистая
сталь
Хромомолибдено-
вая сталь ЗОХМ
Хромомолибдено -
вая сталь
60X16М2А
X ромом олибдено-
вая сталь ЭИ10
Хромоникеле-
вольфрамовая
сталь ХНВМ12
Химический
состав, %
0,15 С;
0,50 Мп;
0,23 Si;
0,032 S;
0,025 Р
0,60 С;
0,46 Si;
'0,28Мп;
16,9 Сг;
0,22 Ni;
2,00 Mo;
0,013 S-
0,030 Р
0,28 С;
0,24 Si;
0,58 Mn;
1,55 Cr;
0,38 Mo;
0,16 Va;
0,12 Ni
0,48 C;
0,68 Si;
0,47 Mn;
0,012 P;
2,24 W;
13,6 Cr;
14,5 Ni;
0,54 Mo
Термическая
обработка
Отжиг 844° С
Отжиг в тече-
течение 1 ч при
600° С
Закалка в
воздухе с тем-
температуры
1050° С; от-
отпуск при тем-
температуре
800—820° С
Закалка
900° С (масло)
отпуск 650° С
Закалка
1100° С, охла-
охлаждающая сре-
среда — воздух
Темпера-
Температура ис-
испытания,
°С
427
538
593
649
500
500
550
575
600
450
500
550
500
600
700
' ft,.'
/ м2 \л/
' 6,32- Ю-21
1,43-10-"
3,10-10»
9,04-10"»
2,46-10'
8,19-Ю-12
2,31 -Ю-11
9,80-Ю1
3,03-10""
9,63-Ю5
3,38-10-"
9,34-10-"
8,57-Ю-25
3,34-10-28
2,46-Ю-15
п
6,24
3,04
3,18
3,03
5,33
1,82
2,12
2,02
2,59
2,99
1,83
2,06
7,76
10,3
5,21
248

Продолжение табл. 11.1
Материал
Хромоникеле-
вольфрамовая
сталь
45Х14Н14В2М
Хромоникеле-
вольфрамовая
сталь ЭИ122
Хромомарганцо-
вованадиевая
сталь СХМВ18
Медь
Химический
состав, %
0,45 С;
0,60 Si;
0,76 Мп;
13,9 Сг;
13,8 Ni;
1,75 W;
0,4 Mo;
0,008 S;
0,024 Р
0,52 С;
2,05 Si;
0,77 Мп;
16,4 Сг;
13,9 Ni;
2,55 W;
0,88 Ti;
0,012 S;
0,04 Р
0,46 С;
1,15 Si;
14,9 Мп;
2,25 W;
0,042 Р;
13,9 Сг
Термическая
обработка
Закалка
1175° С, ста-
стабилизация при
750° С в тече-
течение 5 ч.
_
Закалка
1100° С, охла-
охлаждающая сре-
среда — воздух
Темпера-
Температура ис-
испытания,
°С
600
650
700
550
650
600
700
165
235
к,
2,00-10-1»
1,71-10-9
1,24-10-8
5,12-10-13
2,50-10-13
2,24-Ю6
2,39-Ю8
3,65-10-1»
5,63-10-9
п
3,00
2,93
2,90
2,63
3,63
9,15
6,84
1,60
2,16
шейки. Это положение подтверждалось опытами Эндрейда [25],
изучившим ползучесть образцов из чистых металлов, при постоянном
напряжении и постоянной нагрузке. В опытах Эндрейда постоянство
напряжения в процессе деформации достигалось при помощи исполь-
использования грузов специального очертания, погружающихся в воду
по мере удлинения стержня (рис. 11.9).
На основании таких исследований Эндрейд установил, что если
опыт ведется при строго постоянном напряжении, то третья стадия
отсутствует, а при испытаниях при постоянной нагрузке третья
стадия имеет место.
Однако позднее было показано, что третья стадия не всегда соот-
соответствует образованию и развитию шейки.
В настоящее время установлено, что в случае отсутствия шейки
увеличение скорости деформации ползучести в третьей стадии объяс-
249

няется образованием местных трещин внутри образца, которые
развиваются в материале в течение времени под влиянием напряже-
напряжений и температуры и ослабляют образец. По своему эффекту это
явление эквивалентно уменьшению площади поперечного сечения
образца. Причины образования указанных трещин и механизм их
развития должны быть подвергнуты дальнейшему эксперименталь-
экспериментальному изучению. • ¦ . .
С увеличением напряжения и температуры скорости деформации
ползучести возрастают, а продолжительность второй стадии умень-
уменьшается.
Процесс ползучести зависит от так называемой сходственной
или гомологической температуры, равной отношению абсолютной
Рис. 11.9. Схема испытания образцов при постоян-
постоянном напряжении в опытах Эндрейда [25]
Рис. 11.10. Диаграмма гомологических
температур
woo
1500 if,°C
500
WOO
1500 Т°К
температуры, при которой производилось испытание; к абсолютной
температуре плавления металла Т/Тпл.
Если взять два металла с различными абсолютными темпера-
температурами плавления Тпл г и Тпл 2, то процесс ползучести для них бу-
будет во многом сходен, если абсолютные температуры испытаний Ti
и Т2 удовлетворяют следующему отношению:
Т2
т
1 пл
т. е. если гомологические температуры в обоих испытаниях одина-
одинаковы. Так, например, температура плавления свинца 327° С, в то
время как температура плавления стали 1500° С. Процесс ползу-
ползучести свинца при температуре 27° С во многом качественно сходен
с процессом ползучести стали при температуре 614° С, так как
27 -f 273 _ 614 + 273
327 + 273 ~~ 1500 + 273 '
Поэтому многие экспериментаторы для установления основных
закономерностей ползучести металлов при повышенных температу-
температурах изучали ползучесть путем испытания свинцовых образцов при
комнатной температуре, что практически гораздо проще.
250 :

На рис. 11.10 представлена диаграмма гомологических темпера-
температур. По верхней горизонтали отложена температура по шкале
Цельсия, по нижней — абсолютная температура, а по вертикальной
оси — гомологическая температура в процентах. Начало координат
соединено прямыми линиями с точками на верхней горизонтали,
отражающими температуры плавления металлов по шкале Цельсия.
При помощи такой диаграммы можно определить температуры для
различных металлов по шкалам Цельсия и Кельвина, соответствую-
соответствующие определенной гомологической температуре. Так, например, из
диаграммы на рис. 11.10 следует, что гомологической температуре
50% соответствуют температуры 27° С C00 К) для свинца и 614° С
(887 К) для стали.
Для исследования напряженного и деформированного состояний
деталей в условиях ползучести наибольший интерес представляют
первая и вторая стадии, так как эксплуатация деталей обычно про-
протекает в интервалах времени, соответствующих . этим стадиям.
Исследование,третьей стадии существенно в связи с анализом раз-
разрушения деталей.
На основании исследования кривых ползучести были предло-
предложены различные уравнения, отражающие первую и вторую стадии
этих кривых. Различные зависимости деформации ползучести е°
от времени и напряжения при определенной температуре можно
разбить на две группы.
В основу первой группы формул положена гипотеза о том, что v
кривые ползучести в координатах t, гс при различных напряжениях
и одной и той же температуре геометрически подобны. Это означает,
что они могут быть получены из одной кривой умножением ординат
ее на некоторую величину, являющуюся функцией напряжения.
Следовательно, зависимость деформации ползучести от напряжения
и времени записывается в виде произведения двух функций, из ко-
которых одна Q является функцией напряжения и температуры, а
другая Q — функцией времени и температуры:
г° = QQ. A1.10)
Во второй группе формул принимается, что деформация ползу-
ползучести может быть представлена в виде
где Qi и Q2 — функции напряжения и температуры, а I — моно-
монотонно и быстро убывающая функция времени.
Таким образом, при малых значениях времени вторым слагае-
слагаемым выражения A1.11) по сравнению с первым можно пренебречь,
и тогда процесс ползучести описывается первым слагаемым (первая
стадия ползучести). Как следует из структуры первого слагаемого,
кривые ползучести в первой стадии геометрически подобны.
При больших значениях времени можно пренебречь первым сла-
слагаемым, и тогда процесс ползучести описывается вторым слагаемым
уравнения, из рассмотрения которого следует, что зависимость де-
деформации ползучести от времени во второй стадии линейная, функ-
251

ция Q2 представляет собой минимальную скорость деформации пол-
ползучести.
Различные рекомендации относительно вида функций Q, Qb
Qj и f приведены в литературе [14].
При Qt = Q2 = Q из зависимости A1.11) следует формула A1.10),
которая, таким образом, является частным случаем более общей фор-
формулы A1.11).
К виду A1.11) приводится уравнение, предложенное Эндрейдом
в одной из первых работ по исследованию ползучести [25]. Им была
экспериментально установлена зависимость длины образца от вре-
времени в общем случае больших деформаций
где /0 — начальная длина образца, р и k — для определенного ма-
материала функции напряжения и температуры.
Следовательно, величина логарифмической деформации пол-
ползучести
A1.12)
0
а скорость ее
Таким образом, по Эндрейду ползучесть может рассматриваться
как наложение двух видов течения: Р-течения, происходящего
с убывающей скоростью, и ^-течения, скорость которого постоянна.
В случае малых деформаций из уравнения A1.12) получаем
что совпадает с уравнением A1.11).
-Очевидно, что зависимость A1.11) является более гибкой и по-
позволяет точнее описать кривые ползучести, чем зависимость A1.10).
Однако, как будет показано ниже^ и соотношение A1.10) дает до-
достаточную для практики степень точности. Вместе с тем оно проще,
чем выражение A1.11), и поэтому более удобно в расчетах. В даль-
дальнейшем будем дридерживаться формулы A1.10), полагая при этом,
что функция Q является степенной функцией напряжения.
Таким образом, приходим к следующей зависимости деформа-
деформации ползучести от напряжения и времени:
е< = a"Q. A1.13)
Функцию времени Q не будем аппроксимировать аналитическими
зависимостями, так как выполнение расчетов на ползучесть, как
будет показано далее, возможно и без такой аппроксимации.
252

Выражение A1.13) обычно хорошо подтверждается результатами
опытов. Поскольку при t = О гс = 0, то при t = О Q = 0.
Дифференцируя соотношение A1.13), получаем
Iе = о»В,
где
A1.14)
A1.15)
Величину показателя степени п в уравнении A1.13) определяют
на основе вычисления минимальных скоростей деформации ползу-
ползучести при различных напряжениях, как это было указано выше.
tc 10
7,5
5,0
И
о t
Рнс. 11.11. Графики функций Q и В
1—-—
-
0 20 ?0 60 80 г,ч
Рис. 11.12. Кривые ползучести стали
45Х14Н14В2М при 800° С [10]
Затем по кривой ползучести можно определить функцию Q.
Для этого согласно формуле A1.13) необходимо ординаты кривой
ползучести, полученной путем испытания образца при определен-
определенном напряжении, разделить на величину этого напряжения в п-й
степени.
Если кривые ползучести подобны и зависимость A1.13) справед-
справедлива, то из всех кривых при различных напряжениях и определен-
определенной температуре должен получиться один и тот же график функции Q.
По разбросу точек можно оценить точность предположения о по-,
юбии кривых ползучести и судить о справедливости формулы A1.13).
Функция В может быть найдена после определения функции Q
графическим или численным дифференцированием. На рис. 11.11
представлен примерный вид графиков функций Q и В.
Как отмечалось выше, во второй стадии процесс ползучести про-
протекает с постоянной скоростью. Поэтому на основании соотноше-
соотношений A1.4) и A1.14) заключаем, что во второй стадии ползучести
В = k
и, следовательно, согласно формуле A1.15)
Q = а + Ы,
ае а — отрезок, отсекаемый продолжением линейного участка
(рафика зависимости Q от t на оси ординат (рис. 11.11).*
263

На рис. 11.12 изображены кривые ползучести стали 45Х14Н14В2М
при температуре 800° С и различных напряжениях [10].
На рис. 11.13 в логарифмических координатах представлен гра-
график зависимости напряжения от минимальной скорости деформа-
деформации ползучести. В рассматриваемом случае п — 4. На рис. -11.14
изображен график функции Q, полученный путем обработки кривых
ползучести, представленных на рис. 11.12, с использованием полу-
полученной величины показателя степени п. Ординаты точек на рис. 11.4
в соответствии с формулой A1.13) равны отношению деформации пол-,
зучести для фиксированного момента времени при определенном
напряжении к величине этого напряжения в п-я степени.
60
SO t.4
Рис. 11.13. График зависимости нап-
напряжения от минимальной скорости де-
деформации ползучести для стали
45ХНН14В2М при температуре 800° С
Рис. 11.14. График функции Q для ста-
стали 45Х14Н14В2М при температуре 800° С;
Из рис. 11.14 следует, что разброс точек сравнительно невелик,^
и это позволяет считать предположение о подобии кривых ползу-'
чести справедливым, а зависимость A1.13) достаточно точной.
Функция времени и температуры Q может быть аналогично
формуле A1.9) представлена в виде
h, (П.16|
где пг — функция только времени, остальные обозначения приве-]
дены в пояснении к формуле A1.9). ,,•
Рассмотренные кривые ползучести являются основой расчетов!
на ползучесть. Для сопоставления сопротивлению ползучести раз|
личных материалов введена условная характеристика — так назы-1
ваемый предел ползучести. ' |
Пределом ползучести стпл называют напряжение, при которой
деформация ползучести за заданный промежуток времени достигает'
величины, установленной техническими условиями. \
Из этого определения следует, что для данного материала предел
ползучести зависит от температуры и времени испытания, а также
от принятой величины деформации ползучести. Заданный промет
жуток времени обычно принимают равным сроку службы детали;
Деформацию ползучести выбирают исходя из условий нормальной
эксплуатации детали за срок ее службы.
254 ' #

Если приближенно принять скорость деформации ползучести
постоянной, то величина деформации ползучести
ве = &!„/; ¦ A1.17)
из этого соотношения по принятой
величине деформации ползучести
за определенный промежуток вре-
времени можно установить минималь-
минимальную скорость ее.
В таком случае возможно и
иное определение предела ползу-
ползучести сгпл, которое часто исполь-
используют в практике: пределом ползу-
ползучести называют напряжение, при
котором скорость деформации
ползучести равна определенной
величине, установленной техниче-
техническими условиями. Величина пре-
предела ползучести в таком опреде-
определении зависит от температуры и
принятой величины скорости де-
деформации ползучести.
Ввиду того что погрешность формулы A1.17) тем больше, чем
меньше время, второе определение предела ползучести обычно
используют для деталей, работающих длительный срок. Например
Cgs
Рис. 11.15. Семейство кривых ползу-
ползучести
l-gimin
А
i
Рис. 11.17. График зависимости на-_
пряжения от минимальной скорости
деформации ползучести
для сталей стационарных паровых
Рис. 11.16. График зависимости туобин поелел ползучести обычно
напряжения от деформации ползу- ТУРОИН предел ползучести ооычно
чести для фиксированного значения определяется как напряжение, при
времени котором минимальная скорость де-
деформации ползучести равна 10~7
или 10~81/ч. Для сталей авиационных газовых турбин при определении
предела ползучести часто исходят из величины деформации ползучести
0,1% за время 300—500 ч. Величина предела ползучести устанавли-
устанавливается путем обработки семейства кривых ползучести (рис. 11.15).
255

Рассмотрим вначале определение предела ползучести на основе
выбранной величины деформации ползучести ес за определенный
промежуток времени /. Для этого на чертеже семейства кривых
ползучести при различных напряжениях проведем вертикаль на
расстоянии t от оси ординат (рис. 11.15), и установив зависимость
напряжения от деформации ползучести для выбранного значения
времени t, построим график (рис. 11.16). По этому графику и нахо-
находят величину предела ползуче- $ мн/м?
сти как ординату точки, абсцисса
которой ес. Для определения пре-
предела ползучести по избранной ми-
100
во
60
чо
550
600
», "С
60
20
\
\
ъ.
>
0
±50
500
Рис. 11.18. Графики зависимости от Рис. 11.19. Графики зависимости от
температуры предела ползучести, опре- температуры предела ползучести,
деленного по величине деформации определенного по минимальной ско-
ползучести за 100 000 ч для жаропроч- рости деформации ползучести для
ной стали ЭИ123 [20]
хромомолибденовой стали 35ХМ [20 ]
нимальной скорости деформации ползучести |min при помощи кри-
кривых ползучести (см. рис. 11.15) устанавливают вначале значения
ее при различных напряжениях. Затем в логарифмических коорди-
координатах строят график (рис. 11.17), который, как отмечалось выше,
является линейным. По этому графику и находят величину предела
ползучести.
На рис. 11.18 изображены графики зависимости от температуры
предела ползучести, определенного по величинам деформации пол-
ползучести за 100 000 ч для хромоникелевольфрамовой стали ЭИ123,
а на рис. 11.19 — графики зависимости от температуры предела
ползучести, подсчитанного по величине минимальной скорости де-
деформации ползучести для стали 35ХМ [20].
§ 72. Длительная прочность
Как отмечалось выше, разрушение образца, находящегося в усло-
условиях ползучести, может происходить как с образованием шейки
(вязкое разрушение), так и без него (хрупкое разрушение). В первом
случае разрушение имеет внутризеренный (транскристаллический)
256

характер. Во втором случае разрушение имеет межзеренный (интер-
(интеркристаллический) характер. При этом наблюдаются многочисленные
трещины внутри материала.
Первый тип разрушения характерен для поликристаллических
металлов при относительно невысоких температурах и относительно
больших скоростях деформации, а также для металлических моно-
монокристаллов. Второй тип разрушения обычно наблюдается в поли-
поликристаллических металлах при относительно высоких температурах
и относительно малых скоростях деформации. Иногда встречается
разрушение смешанного типа, промежуточное между описанными
выше, частично транскристаллическое, а частично интеркристалли-
интеркристаллическое, причем последнее возникает в области, примыкающей к по-
поверхности образца. Этот тип разрушения встречается в поликристал-
поликристаллических металлах при температурах, промежуточных по отноше-
отношению к температурам первого и второго типов разрушения. Такой
смешанный тип разрушения обычно не сопровождается образованием
шейки. Таким образом, с повышением температуры вязкое разру-
разрушение сменяется хрупким.
Установлено, что с увеличением длительности пребывания ме-
металла в нагретом состоянии за счет постепенного ослабления гра-
границ зерен наблюдается переход от вязкого разрушения к хрупкому.
Это явление называют охрупчиванием материала.
В свете изложенного становится ясным ошибочность утвержде-
утверждения, что в условиях ползучести на концентрацию напряжений
можно не обращать внимания, поскольку пики напряжений в усло-
условиях ползучести якобы сглаживаются. В действительности, в рассма-
рассматриваемом случае при хрупком разрушении, оно начинается, как
правило, в окрестности концентраторов напряжений. Поэтому изуче-
изучение концентрации напряжений в условиях ползучести имеет большое
практическое значение.
Прочность материала, находящегося длительное время в напря-
напряженном состоянии при высокой температуре, оценивается так назы-
называемым пределом длительной прочности. Пределом длительной проч-
прочности сгдл называют отношение нагрузки, при которой происходит
разрушение растянутого образца через определенный промежуток
времени, к первоначальной площади его поперечного сечения.
Таким образом, предел длительной прочности для рассматривае-
рассматриваемого материала зависит от температуры испытания и отрезка времени
до момента разрушения. Последний выбирают равным сроку службы
детали. В зависимости от условий эксплуатации деталей представ-
представляют интерес пределы длительной прочности, определенные на базе
от 100 до 100 000 ч. Очевидно, что с увеличением температуры и
заданного промежутка времени до разрушения величина предела
длительной прочности снижается.
При исследовании длительной прочности материала испытывают
несколько одинаковых образцов при различных напряжениях и уста-
устанавливают время, необходимое для разрушения каждого образца.
По результатам испытаний строят график зависимости предела дли-
длительной прочности от времени испытания до разрушения и по нему
9 Н. Н. Малинир 257

определяют предел длительной прочности для заданного промежутка
времени испытания до разрушения.
В логарифмических координатах график зависимости предела
длительной прочности от времени имеет вид ломаной линии, состоя-
состоящей из двух прямых (рис. 11.20). Точка перелома графика обычно
соответствует переходу от транскристаллического к интеркристал-
интеркристаллическому разрушению. На рис. 11.20 крестиками изображены ре-
результаты испытаний образцов, разрушившихся транскристалли-
чески, а кружочками — результаты опытов, завершившихся интер-
°дл
б.МН/М2
300
гоо
100
,10
—а .
—о
—
-°-о-
—о—
—
-----<
Ч,
дО0,°С-
бЭО'с-
^тоо
°с
о igt
Рис. 11.20. График зависимости преде-
предела длительной прочности от времени
испытания до разрушения
25
100 250 500 1000 2500 t.v
Рис. 11.21. Графики зависимости предела
длительной прочности от времени испыта-
испытания до разрушения для стали ЭИ69 [12]
кристаллическим разрушением. Очевидно, что в определенных ин-
интервалах времени и напряжений точки перегиба на рассматриваемом
графике может и не быть.
Поскольку в логарифмических координатах график зависимости
предела длительной прочности от времени является линейным, за-
зависимость времени до разрушения от предела длительной прочности
является степенной
t = Aa~m,
A1.18)
где Лит — для определенного материала зависят от температуры
и характера разрушения транскристаллического или интеркристал-
интеркристаллического.
На рис. 11.21 в логарифмических координатах изображены гра-
графики зависимости предела длительной прочности от времени испы-
испытания до разрушения при различных температурах [12].
Формула A1.18) устанавливает зависимость предела длитель-
длительной прочности от времени разрушения для некоторого материала при
определенной температуре. Для того чтобы отразить влияние на
длительную прочность температуры, установить так называемые
температурно-временные зависимости длительной' прочности, были
предложены различные температурно-временные параметры П, яв-
являющиеся функциями предела длительной прочности. Это означает,
что результаты испытаний на длительную прочность при различных
температурах можно представить в виде одного графика зависимости
предела длительной прочности от температурно-временного пара-
параметра П.
258

Параметр Ларсона—Миллера [30] имеет вид
Пг = Т (с + lg t),
A1.19)
где Т — абсолютная температура; lg t — десятичный логарифм вре-
времени, измеряемого в ч; с — постоянная материала.
Параметр Мэнсона—Хафер-
Мэнсона—Хаферда [27] определяется формулой
[t-
:ta
A1.20)
где Та и ta — постоянные ма-
материала.
С помощью параметра Мэн-
Мэнсона—Хаферда, содержащего
две постоянных, можно лучше
отразить экспериментальные
результаты, чем с помощью па-
параметра Ларсона—Миллера, в
который включена только одна
постоянная.
На рис. 11.22 изображена
зависимость предела длитель-
длительной прочности от параметра
Ларсона—Миллера для нержа-
нержавеющей стали [30 ], а на
в, МН/М2
628
314
157
та
S4
63
>
ч
\
S,
\
ч
ч
Рис. 11.22. График зависимости предела
длительной прочности от температурно-
временного параметра Ларсона—Милле-
Ларсона—Миллера [30]: • — кратковременные испыта-
испытания; о — 649° С; ? — 740° С; Д —
760° С; V— 815° С; О— 871° С; X —
970° С
д.%
60
SO
10
30
го
\
*——.
540° С
1111 —
35 40 45 50 55 60 В5 10 75 Пг
О ZOO 400 600 800 t.4
Рис. 11.24 График зависимости ос-
остаточной деформации при разрыве
от времени испытания до разру-
разрушения для малоуглеродистой
стали [3 ]
Рис. 11.23. График зависимости
предела длительной прочности от рис. 11.23 —ОТ параметра Мэн-
температурно-временнбго парамет- Г ХяЛрпля ттггя jtrvx мяппк
ра Мэнсона—Хаферда [27]: СОна—Лаферда ДЛЯ двух марок
сп л о „ нимоника [27].
/ !— ннмоник 80А; 2 — нимоник 90; тт-
• < зооо ч; + > зооо ч Как следует из этих рисунков,
для рассматриваемых материалов
эксперименты подтвердили как температурно-временной параметр
Ларсона—Миллера, так и параметр Мэнсона—Хаферда.
Одновременно с экспериментальным определением предела дли-
длительной прочности материала иногда устанавливают и величину
остаточной деформации образца при разрыве. Она определяется как
отношение остаточного удлинения при разрыве к первоначальной
259

длине образца и в случае разрушения образца с образованием шейки
представляет собой условную деформацию.
Очевидно, что эта величина является характеристикой пластич-
пластичности, материала, находящегося длительное время в напряженном
состоянии при высокой температуре. Как следует из вышеизложен-
вышеизложенного, с уменьшением напряжения, т. е. с увеличением длительности
пребывания металла при высокой температуре остаточная деформа-
деформация при разрыве уменьшается («охрупчивание» материала). На
рис. 11.24 представлены графики зависимости остаточной деформа-
деформации при разрыве от времени испытания до разрушения для малоугле-
6.МН/М2
500 —
100
ИН/м'
1000
800
600
400
?—I
5 10
й)
50 WO
t.4
Рис. 11.25. Графики зависи-
зависимости предела длительной
прочности от времени испы-
испытания до разрушения:
а — сталь ЭИ415. Температура
испытаний 550° С [1 ]; б—сплав
ХН70ВМЮТ. Температура ис-
испытаний 650° С [2]
—"О-
¦—«
¦.к
'
¦со—
—¦¦—,
*¦—
о—
-о-
v ¦—гР
1—
о
6 в 10
го
40 60
5)
80 100
гоо
?00
t.4
родистой стали [3]. Известны случаи разрыва образцов высоколеги-
высоколегированных сталей при величине остаточной деформации, равной
1—2% [31.
Рассмотрим влияние на длительную прочность концентрации
напряжений. Экспериментальные исследования показывают, что
концентрация напряжений в условиях ползучести может вызвать
как снижение, так и повышение длительной прочности в зависимости
от материала образцов. На рис. 11.25 представлены приведенные
в работах [1, 2] графики зависимости предела длительной прочности
от времени для гладких, образцов и образцов с концентратором
напряжений, выполненных из сталей двух марок. Концентратором
напряжений была глубокая выточка — несколько измененный по
рекомендации Г. В. Ужика круговой гиперболический глубокий
надрез Нейбера. Как следует из этих графиков, для более хрупкой
стали ЭИ415 концентрация напряжений снижает длительную проч-
прочность, а для сплава ХН70ВМЮТ с более высоким уровнем пластиче-
пластических свойств концентрация напряжений повышает длительную проч-
260 • "

ность. Однако прямая длительной прочности образцов с концентра-
концентратором напряжений для сплава ХН70ВМЮТ, хотя и расположена выше
прямой длительной прочности гладких образцов, но наклонена к ней.
Следовательно, можно ожидать пересечения этих прямых и снижения
длительной прочности при испытаниях большей продолжительности.
Объяснение различного влия-
влияния концентрации напряжений на
длительную прочность в зависимо-
зависимости от материала образцов можно
дать на основе анализа напряжен-
напряженного состояния в окрестности кон-
концентратора в условиях ползучес-
ползучести [2]. На рис. 11.26 изображен
примерный вид эпюр осевых аг,
окружных at и радиальных аг на-
напряжений в наименьшем попереч-
поперечном сечении образца. Напряжен-
Напряженное состояние точек в окрест-
окрестности концентратора — трехосное
растяжение. У материалов с низ-
низкими пластическими свойствами
(например, сталь ЭИ415) эпюры
осевых и окружных напряжений
имеют резкий подъем от средней ча-
части к периферии. Пики напряже-
напряжений с течением времени сохраня-
сохраняются, что приводит к снижению
прочности надрезанных образцов
по сравнению с гладкими. У мате-
материалов с более высоким уровнем
пластических свойств пики нап-
Рис. 11.26. Эпюры осевых (/), окруж-
окружных B) и радиальных C) напряжений
в наименьшем поперечном сечении об-
образца с глубокой выточкой в началь-
начальный момент времени (сплошные линии)
и после перераспределения напряже-
напряжений в течение некоторого промежутка
времени (штриховые линии)
ряжений меньше и с течением времени они. уменьшаются. Трехосное
растяжение в окрестности надреза затрудняет развитие деформаций
ползучести и поэтому длительная прочность образцов с концентра-
концентратором может быть выше, чем гладких.
б
1
1
п
+ *
tpa3p
0
Рис. 11.27. Нестационарный режим напряженности и нагрева, заканчиваю-
заканчивающийся разрушением
261

Рассмотрим длительную прочность материала при нестационар-
нестационарной напряженности и нестационарном нагреве в случае одноосного
напряженного состояния. Представим себе, что растянутый образец
вначале испытывается при напряжении сгх и температуре ¦&! в течение
времени t\, затем при напряжении а2 и температуре $г в течение
Рис. 11.28. Графики зависимости предела длительной
прочности от времени испытания до разрушения при раз-
различных температурах
w
времени t\ и т.д. (рис. 11.27). Процесс испытания заканчивается
разрушением при напряжении ok, которое имело место в течение
времени С при температуре Ьк. Общее время до разрушения
4>азр == 2шЛ '•
Обозначим через ty разр, t2 разр)
• —> ttpaap, 4 разр значения вре-
времени, необходимые для разруше-
разрушения при напряжениях аъ а2, . . .
. . ., О(, . . ., ak. Эти величины
определяются по кривым длитель-
длительной прочности материала при раз-
различных температурах 1&1, Ь2, . . .
. . .,®i ^(рис. 11.28). Назо-
Рис. 11.29. Графики непрерывного из-
изменения напряжения и температуры во
времени
вем отношения
1 разр '2 разр
разр
повреждениями на первом, втором и т. д.
ti разр'
режимах.
Экспериментальные исследования длительной прочности при
нестационарных напряженности и нагреве позволили устано-
262

вить, что сумма повреждении для данного материала равна
единице
I. A1.21)
Ч разр
Это положение называют условием линейного суммирования
повреждений.
При непрерывном изменении напряжений (рис. 11.29) формула
A1.21) принимает вид
'ра_зр
~- = 1, A1.22)
'разр
где /разр — время до разрушения, а /разр — время, необходимое
р ру р р
для разрушения при некотором напряжении а. Эта величина яв-
является функцией времени. Она может- быть определена по графику
изменения напряжения во времени (рис. 11.29) и кривым длительной
прочности материала при различных температурах (рис. 11.28).
§ 73. Определение коэффициента запаса
Рассмотрим определение коэффициента запаса при длительном
нагружении в случае одноосного напряженного состояния. Допустим,
что напряжение в детали в течение времени t постоянно и равно о
(рис. 11.30). Тогда, располагая графиком зависимости предела дли-
длительной прочности от времени испытания до разрушения, можно
определить коэффициент запаса по времени (коэффициент запаса
по долговечности или запас долговечности), а также коэффициент
запаса по напряжениям (коэффициент запаса по прочности или
запас прочности).
Коэффициент запаса по времени равен отношению времени раз-
разрушения при напряжении о — /разр к времени t
^ A1.23)
Коэффициент запаса по напряжениям равен отношению нaпpяжe^
ния при разрушении для времени t — сгразр к напряжению о:
A1.24)
" а
Поскольку согласно формуле A1.18)
I — -^^разр» разр — **^ »
имеем
263

Представим себе теперь некоторый режим нестационарной на-
напряженности и нестационарного нагрева. Предположим, что в тече-
течение времени tlt t%, . . ., th . . ., tk при температурах Ь1г ®2, . . .
. . ., Ф,-, . . ., ФА имеют место напряжения alt а2, . . ., а(-, . . ., ak
(рис. 11.31). Определим коэффициенты запаса по времени nt и по
напряжению па для этого режима. б
igt
\о
ts
о t
Рис. 11.30. К определению коэффициента Рис. 11.31. Нестационарный режим
вапаса по времени и напряжениям при напряженности и нагрева
напряжении, постоянном во времени
Для определения коэффициента запаса по времени допустим, что
отрезки.времени tlt t2, . . ., tit . . ., tk увеличены в одинаковое
количество раз, так что в конце нового (растянутого по оси абсцисс)
режима происходит разрушение (рис. 11.27). Очевидно, что величина,
указывающая, во сколько раз
нужно увеличить отрезки времени
tu t2, . . ., tt, . . ., tk для того,
чтобы в конце режима произошло
разрушение, является коэффици-
коэффициентом запаса по времени:
U =
ntt
k,
k
t{ =
Рис. 11.32. Нестационарный режим
напряженности и нагрева, заканчи-
заканчивающийся разрушением (напряжения
по сравнению с заданными увеличены
в по раз)
Подставляя соотношения A1.25)
в выражение A1.21), выводим
формулу для определения коэф-
коэффициента запаса по времени
(И.26)
Для определения коэффициента запаса по напряжениям пред-
представим себе, что напряжения аъ а2, . . ., а,-, . . ., ak увеличены
в одинаковое количество раз «а, где па — коэффициент запаса по
264

напряжениям, так что в конце нового (растянутого по оси ординат)
режима происходит разрушение (рис. 11.32).
Тогда в выражении A1.21) согласно формуле A1.18)
( 7)
где О[ разр — величина напряжения, необходимая для разрушения
через время t(. Ее находят по кривым длительной прочности мате-
материала при различных температурах (см. рис. 11.28). Подставляя
выражения A1.27) в формулу A1.21), получаем трансцендентное
уравнение для определения коэффициента запаса по напряжению
A1.28)
(=1
Это уравнение решается численно. В частном случае постоянной
температуры формула A1.28) значительно упрощается, так как
тогда т1 = тг = tnt = • ¦ •= mk = m, и из уравнений A1.28) по-
получаем
A1.29)
07
. °7разр
Аналогично можно рассмотреть определение коэффициентов за-
запаса в случае непрерывного изменения во времени напряжения и
температуры (рис. 11.29).
Список литературы j
1. Бойков В. Н. Влияние концентратора на напряженное состояние и длитель-
длительную прочность.— «Известия высших учебных заведений. Машиностроение», № 6,
1964, с. 42—50.
2. Бойков В. Н. Прочность надрезанных образцов при длительном нагруже-
иии.— «Известия высших учебных заведений. Машиностроение», № 6, 1966, с. 25^-
29-
3. Борздыка А. М. Методы горячих механических испытаний металлов. М.,
Металлургиздат, 1955, 352 с.
4. Гарофало Ф. Законы ползучести и длительной прочности металлов. М.,
«Металлургия», 1968, 304 с.
5. Ильюшин А. А., Ленский В. С. Сопротивление материалов. М., Физматгиз,
1959, 371 с
6. Кочанов Л. М. Теория ползучести. М., Физматгиз, 1960, 455 с.
7. Кеннеди А. Д. Ползучесть и усталость в металлах. М., «Металлургия»,
1965, 312 с
8. Малииин Н. Н." Основы расчетов на ползучесть. М., Машгиз, 1948, 120 с.
9. Малинин Н. Н. Прочность турбомашин,'М., Машгиз, 4962, 291 с.
Ю. Марковец М. П. Расчет деталей на прочность с учетом ползучести.— «Тех-
«Техника воздушного флота», 1944, № 10, с. 17—19.
265

11. Надаи А. Пластичность и разрушение твердых тел. Т. I., M., Изд. иностр.
лит., 1954, 647 с, т II, М., «Мир», 1969, 863 с-
12- Никитина Л. П. Прочность стали типа ЭИ69 при повышенных температу-
температурах.— В кн.: Исследование жаропрочной стали типа ЭИ69. Книга 6. М., Машгиз,
1947, с 131—156.
13. Работнов Ю. Н. Сопротивление материалов. М., Физматгиз, 1962, 455 с-
14- Работнов Ю. Н. Ползучесть элементов конструкций. М., «Наука», 1966,
752 с
15. Расчеты на прочность в машиностроении. Т. II. М-, Машгиз, 1958, 974 с-
Авт.: С Д. Пономарев, В. Л. Бидерман, К- К- Лихарев и др-
16. Розенберг В. М. Ползучесть металлов. М., «Металлургия», 1967, № 276 с.
17. Сазонова Н. Д. Испытание жаропрочных материалов на ползучесть и
Длительную прочность. М., «Машиностроение», 1965, 265 с-
18. Салли А. Ползучесть металлов и жаропрочные сплавы. М., Обороигиз,
1953, 291 с
19. Сервисен С. В., Когаев В. П.. Шнейдерович Р. М. Несущая способность и
расчеты деталей машин на прочность- М., Машгиз, 1963, 451 с.
20. Сичиков М. Ф. Металлы в турбостроении. М-, Машгиз, 1954, 320 с.
21. Смирнов В. И., Никитина Л. П. Прочность при высоких температурах
высоколегированной хромомолибденовой стали марки 60Х16М2А.— «Советское
котлотурбостроение», 1945, № 4, с- 9—12.
22. Солоноуц М. И.! Терешкович А. С. Некоторые вопросы методики испытания
на ползучесть — В кн.: Релаксация и ползучесть металлов. Книга 45. М., Машгнз,
1952, с- 163—172. '
23. Станюкович А. В. Хрупкость и пластичность жаропрочных материалов-
М., «Металлургия», 1967, 199 с-
24. Теория ползучести и длительной прочности металлов. М., Металлургиздат.
1959, 488 с- Авт.: И. А. Одинг, В. С. Иванова, В. В. Бурдукский, В. Н. Геминов.
25. AndradeE. N. CiOn the viscous flow in metals, and allied phenomena.—«Pro-
phenomena.—«Proceedings of the Royal society», Ser A, Vol. 84, No A 567, 1910, p. 1—12.
26. Bailey R. W. The utilization of creep test data in engineering design.—«The
Institution of mechanical engineers. Proceedings», Vol. 131, 1935, p. 131—269.
27. Betteridge W. The extrapolation of the stress—rupture properties of the ni-
monic alloys.—«Journal of the Institute of metals», 1958, vol. 86, No 5, p. 232—237.
28. Finnie I.. Heller W. R. Creep of engineering materials, Me Graw-Hill Book
Company Inc., 1959, 341 p.
29- Jaoul B. Etude de la plasticlte e't application aux metaux, Dunod, 1965, 600 p.
30. Larson R. R., Miller J. A time — temperature relationship for rupture and
creep stresses.—«Transactions oftheASME», 1952, Vol. 74, No 5, p. 765—775.
31. Lubahn J. D.i Felgar R. P. Plasticity and creep of metals, John Wiley and
Sons, 1961, 608 p.
32. Marin J. Mechanical behavior of engineering mate ials, Prentice—Hall.
Inc., 1962, 502 p.

ГЛАВА XII
ТЕХНИЧЕСКИЕ ТЕОРИИ ПОЛЗУЧЕСТИ
§ 74. Основные понятия
В предыдущей главе для одноосного растяжения были рассмо-
рассмотрены процессы изменения во времени деформаций при постоянном
напряжении (последействие или собственно ползучесть) и напряже-
напряжений при постоянной деформации (релаксации).
В общем случае ползучести изменение деформаций сопровождается
изменением напряжений. Для установления зависимостей между
деформациями, напряжениями, скоростями их изменения и временем
предварительно необходимо максимально ограничить число перемен-
переменных и высказать предположение о том, между какими из них суще-
существует функциональная зависимость.
Это предположение и носит название технической теории пол-
ползучести. В настоящее время существуют три технические теории
ползучести: старения, течения и упрочнения. Эти названия в зна-
значительной мере являются условными.
Обычно технические теории ползучести формулируются для
простейшего случая одноосного напряженного состояния [26]. Ниже
будет рассмотрена формулировка их в общем случае неодноосного
напряженного состояния. Поскольку деформации ползучести яв-
являются в основном необратимыми, для случая неодноосного напря-
напряженного состояния постулируется применимость основных гипотез
теории пластичности. Аналогично ассоциированному закону тече-
течения (см. § 22) примем существование потенциала скоростей деформа-
деформации ползучести или потенциала ползучести /, т. е. допустим, что
компоненты скоростей деформаций ползучести определяются фор-
формулой
Подставив компоненты скоростей деформаций ползучести по фор-
формуле A2.1) в выражение для интенсивности скоростей деформаций
B.41), как и в § 22, получим
X=l/X_JL_. A2.2)
Л/ д/ , д/
V doij doij
267

Уравнение *
/ = 0 A2.3)
представляет собой уравнение гиперповерхности в пространстве
компонентов тензора напряжений аг/-, к которой ортогональны век-
векторы скоростей деформаций ползучести. Эту гиперповерхность
будем называть гиперповерхностью ползучести.
Функция / аналогична соответствующей функции в теории пла-
пластичности. ~~
Примем материал изотропным и будем считать, что изменения
объема в процессе ползучести не происходит, т. е.
<ч; = 0 A2.4)
или
i?j = 0. A2.5)
Вначале допустим, что упрочнение является изотропным, т. е.
поверхность ползучести в процессе деформации изменяется подоб-
подобным образом (изотропно). Далее будет изложена теория ползучести
с анизотропным упрочнением.
Для случая изотропного упрочнения первоначально изотропного
несжимаемого материала функция / зависит от второго и третьего
инвариантов девиатора напряжений. Так же как и при изложении
теорий пластичности в гл. IV, включим в функцию / только второй
инвариант девиатора напряжений, что равносильно в теории пла-
пластичности использованию критерия Хубера—Мизеса. Тогда, как
и в § 23
дац ~ dsij —°ЬЧ
и поэтому согласно формулам A2.2) и A.20)
Следовательно, зависимости компонентов скоростей деформаций
ползучести от компонентов девиатора напряжений принимают вид
iif==! ~2—а~г \aii — 6г/(То). A2-6)
Полагая, что при начальном нагружении и в процессе ползучести
мгновенные пластические деформации не возникают и добавляя к со-
соотношениям A2.6) скорости упругих деформаций, полученные путем
дифференцирования по времени соотношений C.5) при ц = 0,5 (ма-
(материал несжимаем), имеем
где
268
точкой
обозначена
производная
3
2
по
11 , .
ас ( Ч
времени.

В работах {27—29] рассмотрены различные варианты построе-
построения потенциала ползучести, в результате чего достигнута возмож-
возможность описания ползучести анизотропных материалов, различно
сопротивляющихся растяжению и сжатию, с учетом деформационной
анизотропии.
В одной из изложенных ниже теорий ползучести — теории ста-
старения используется гипотеза о существовании потенциала деформа-
деформаций ползучести, т. е. как и в теории малых упруго-пластических
деформаций, принимается, что
Полагая, что в случае изотропного упрочнения первоначально
изотропного несжимаемого материала в функцию /х включен только
второй инвариант девиатора напряжений, как при выводе уравне-
уравнений A2.7), получаем зависимости компонентов деформаций от ком-
компонентов напряжений
гЧ = ~2G (°<1 ~ 6»<т«) + Т ~оГ (°И~5И0о) =
= <aV)
В теории пластичности в функцию /, кроме второго инварианта
девиатора напряжений, входил еще параметр Удквиста.
В теории ползучести функция / зависит от некоторой меры ско-
скоростей деформаций ползучести, за которую обычно принимают
интенсивность скоростей деформаций ползучести. Кроме этого, функ-
функция f может зависеть еще от ряда переменных. Ими могут быть пара-
параметр Удквиста, время и другие величины. Bf теориях течения и
упрочнения, кроме интенсивности скоростей деформаций ползучести,
в потенциал ползучести обычно включается одна из этих величин:
в теории течения время, а в теории упрочнения параметр Удквиста.
В теории старения в потенциал ползучести fx включается интенсив-
интенсивность деформаций ползучести и время. Ю. Н. Работнов [24 Ь указал
на возможность включения в потенциал ползучести f нескольких
переменных, которые он назвал структурными параметрами.
Изменение некоторого &-го структурного параметра описывается
следующим кинетическим уравнением:
dqk^ak~d7ci + bkdoi+ckdt-\-fkdT, A2.10)
где ak, bk, ck, fk — некоторые функции от J del, at, t и Т, а также
qlt . . ., qk, . . ., qn, если число структурных параметров п.
В зависимости от того, какие из них включены в потенциал
ползучести / или fu получаем ту или иную теорию ползучести.
При использовании ассоциированного закона течения A2.1)
необходимо иметь в виду, что при заданных структурных параметрах
269

это уравнение определяет положение нормали к поверхности пол-
ползучести при данном напряженном состоянии. Поэтому при дифферен-
дифференцировании согласно формуле A2.1) структурные параметры остаются
неизменными.
§ 75. Теория старения
Допустим, что потенциал ползучести /г зависит от второго инва-
инварианта девиатора напряжений, интенсивности деформаций и вре-
времени. Уравнение поверхности потенциала ползучести имеет вид
откуда, используя соотношение A.20), имеем
<*, =<Di(e,, f). A2.11)
Уравнения A2.9) и A2.11) определяют зависимости компонентов
деформаций ползучести от компонентов напряжений по теории
старения.
Из соотношений A2.9) и A2.11) следует, что определение напря-
напряжений и деформаций для некоторого значения времени по теории
старения эквивалентно решению задачи по теории малых упруго-
пластических деформации для известной диаграммы деформирования.
В частном случае одноосного растяжения
О; = о, г1 = е
и из зависимости A2.11) получаем
а =Ф1(е, f). A2.12)
Теория старения обычно формулируется для одноосного растя-
растяжения в виде A2.12), т. е. предполагается, что при заданной тем-
температуре между деформацией, напряжением и временем существует
определенная зависимость.
Эта теория была предложена Содербергом [44]. Обобщение и
анализ ее были даны Ю. Н. Работновым [22 ].
Высказанное предположение равносильно допущению о суще-
существовании при определенной температуре поверхности в координатах
е, а, /.
Рассекая поверхность плоскостями, перпендикулярными осям а,
е и t, получаем соответственно кривые ползучести при постоянном
напряжении (рис. 12.1), кривые релаксации напряжений при по-
постоянной деформации (рис. 12.2), графики зависимости напряжения
от деформации для определенных значений времени A2.3). Последние
называют изохронными кривыми ползучести.
Для построения изохронных кривых ползучести для определен-
определенного значения времени t необходимо на кривых ползучести для
различных значений напряжений (рис. 12.1) провести вертикальную
прямую на расстоянии t от оси ординат. Точки пересечения этой
прямой с кривыми ползучести определяют величины напряжений
270

для определенных значений деформаций. Полученные результаты
легко перевести в координаты е, а (рис. 12.3).
Если при расчете какой-либо детали на ползучесть необходимо
определить напряжения и деформации для заданного значения
времени, то следует провести расчет на прочность и жесткость этой
детали, используя изохронную кривую ползучести для принятого
значения времени.
6г>5,
Рис. 12.1. Сечения поверхности в коор-
координатах е, о, t плоскостями, перпенди-
перпендикулярными оси а, — кривые ползу-
ползучести
Рис. 12.2. Сечения поверхности в ко-
координатах е, a, t плоскостями, перпен-
перпендикулярными оси е, — кривые релак-
релаксации
Такая общая трактовка теории старения была предложена
Ю. Н. Работновым [22].
Если изохронные кривые ползучести подобны, т. е. могут быть
получены из одной кривой умножением ее ординат на некоторую
б,МН/мг
Рис. 12.3. Сечение поверх-
поверхности в координатах 8, a, t
плоскостями, перпендику-
перпендикулярными оси t,— изохрон-
изохронные кривые ползучести
Рис. 12.4. Изохронные кривые ползучести для
хромистой стали [22]
величину, являющуюся функцией времени, то расчеты значительно
упрощаются. В этом случае зависимость напряжения от деформации
и времени может быть представлена в виде произведения двух функ-
27i

ций, из которых одна ф (е) является функцией только деформаций,
а другая -ф (t) — функцией только времени -
а = ф(е)ар@- A2.13)
Если принять, что -ф @) = 1, то функция ф (е) описывает диа-
диаграмму растяжения материала.
Подобие кривых ползучести в координатах t, ec еще не означает
подобия изохронных кривых ползучести в координатах е, о. Второе
подобие является следствием первого только в том случае, если можно
пренебречь упругими деформация-
деформациями по сравнению с деформациями
ползучести.
На рис. 12.4 представлены гра-
графики зависимости напряжения от
деформации для различных зна-
значений времени и график функции
Ф (е) для хромистой стали [22].
Хорошее согласование с ре-
результатами эксперимента дает
следующее аналитическое пред-
представление функции:
*(*) = 1—г, A2.14)
TV/ I 1 _jfl V '
о t
Рис. 12.5. К построению кривой ре-
релаксации по кривым ползучести по
теории старения
где а и Ь — коэффициенты для рассматриваемого материала, зави-
зависящие от температуры. В случае постоянной деформации это уравне-
уравнение описывает релаксацию напряжений.
Приведем метод построения кривой релаксации по серии кривых
ползучести на основе этой теории. Предположим, что кривые пол-
ползучести при различных напряжениях известны. Допустим, что не-
необходимо построить кривую релаксации при начальном напряже-
напряжении а @). В таком случае надо на кривых ползучести для различных
значений напряжения (рис. 12.5) провести горизонтальную прямую
на расстоянии е @) =
(р
от оси абсцисс. Точки пересечения этой
прямой с графиками зависимости деформации от времени определяют
величины напряжений для определенных значений времени. Полу-
Полученные результаты легко перенести в координаты t, о и построить
кривую релаксации (см. рис. 11.4).
Рассмотрим теперь различные аналитические зависимости дефор-
деформации ползучести от напряжения и времени. Они являются обобще-
обобщением уравнений кривых ползучести A1.10) и A1.11) на случай на-
напряжений, изменяющихся во времени, и имеют вид
ес = QQ A2.15)
или
A2.16)
здесь Q, Qi и Q2 — функции напряжения и температуры, a Q и
функции времени и температуры.
272 ' .

Если Q — степенная функция напряжения, то тогда
г" = апп A2.17)
и в общем случае неодноосного напряженного состояния формула
A2.11) принимает вид
или
e?=G?Q. A2.19)
Выведем уравнение семейства кривых релаксации по теории ста-
старения в варианте A2.17). Для этого подставим выражение A2.17)
в уравнение A1.1). Тогда получим уравнение семейства кривых
релаксации в неявном виде по теории старения в формулировке
A2.17)
EQcn +а = <т@). A2.20.)
Теория старения не может описать ступенчатое нагружение,
так как согласно этой теории в момент изменения напряжения де-
деформация ползучести должна иметь разрыв, что, очевидно, невоз-
невозможно.
§ 76. Теория течения
Допустим теперь, что потенциал ползучести / зависит от второго
инварианта девиатора напряжений, интенсивности скоростей де-
деформаций ползучести и времени. Уравнение поверхности потенциала
ползучести имеет вид
откуда, используя соотношение A.20), имеем
ot = Фа Ш, t). A2.21)
Уравнения A2.6) и A2.21) определяют зависимости компонентов
скоростей деформаций ползучести от компонентов напряжений по
теории течения.
В случае одноосного растяжения
а = о; g = Г,
и4 из зависимости A2.21) имеем
<х = Ф,@е, t). A2.22)
Теория течения обычно формулируется для одноосного растяже-
растяжения в виде уравнения A2.22), т. е. предполагается, что при заданной
температуре между напряжением, скоростью деформации ползучести
и временем существует определенная зависимость.
273

Эта теория была предложена Давенпортом [341. Она получила
довольно большое распространение в связи с работами Л. М. Кача-
нова [7].
Рассмотрим метод построения кривой релаксации при одноосном
растяжении по серии кривых ползучести на основе этой теории.
Предположим, что кривые ползучести для различных величин напря-
напряжений известны (рис. 12.6). Проведем на расстоянии ^ ' от оси
абсцисс горизонтальную прямую. Разобъем промежуток времени,
за который надо исследовать процесс релаксации, на ряд неболь-
небольших интервалов Д^, которые
могут быть равны или не
равны между собой. Полага-
Полагаем, что за небольшой проме-
промежуток времени At1, считая
от начального момента, про-
процесс нарастания деформации
ползучести протекает при по-
постоянном напряжении а @),
тогда увеличение деформа-
деформации ползучести за проме-
промежуток времени At1 выра-
выражается отрезком А В (рис.
12.6). Эту величину плас-
пластической деформации обоз-
обозначим г°А.
Учитывая, что полная
деформация е во времени
не меняется и равна на-
начальному значению е @) =
ст@) • /11 1\
= —-~- , можно из уравнения A1.1) определить величину упругой
деформации для значения времени t{ = At1
0! g@) с
Рис. 12.6. К построению кривой релаксации
по кривым ползучести по теориям упрочне-
упрочнения и течения
Величина —¦ в выбранном масштабе выражается отрезком АС.
Во второй промежуток времени At2 можно приближенно считать,
что процесс нарастания деформации протекает при постоянном на
пряжении av Согласно теории течения скорость деформации пол-
ползучести является функцией напряжения и времени, а от величины
деформации ползучести она не зависит. Поэтому начальная скорость
деформации ползучести во втором промежутке времени At2 опреде-
определяется тангенсом угла наклона касательной в точке D к кривой пол-
ползучести при напряжении ах (рис. 12.6). Через D обозначена точка
пересечения вертикальной линии, проведенной из точки А, с кривой
ползучести при напряжении ах.
274

Следовательно, во втором промежутке времени Л/а деформация
ползучести нарастает по закону, изображенному линией АЕЪ пред-
представляющей часть кривой ползучести при напряжении <хь передви-
передвинутой параллельно самой себе из точки D в точку А и взятой до пере-
пересечения в точке ?хс вертикальной линией, отстоящей от оси ординат
на расстоянии t2 = А^ -f At2.
Увеличение деформации ползучести за время At2 выражается
отрезком EiF, а полная деформация ползучести e?l для значения
времени t2 = Atx -f At2 — отрезком Efi.
Теперь из уравнения A1.1) находим величину упругой деформа-
деформации для значения времени t2:
а2 _ о@) с
Эта величина выражается отрезком ЕХН. Продолжая подобные
построения, получим кривую O?Vi- Расстояния от этой кривой до
оси абсцисс равны величинам деформации ползучести для соответ-
соответствующего значения времени, а расстояния до линии О-^СН — вели-
величинам упругой деформации.
Умножением упругой деформации на модуль упругости первого
рода можно получить напряжения для соответствующих значений
времени. Таким образом строится кривая релаксации.
Неудобство изложенного метода построения кривой релаксации
заключается в том, что для использования его необходимо распола-
располагать большим количеством кривых ползучести. Чтобы избежать
этого, целесообразно предварительно связать скорость деформации,
ползучести, деформацию ползучести и напряжение определенной
аналитической зависимостью, на основе которой и вывести уравне-
уравнение кривой релаксации.
Наиболее распространенной аналитической зависимостью ско-
скорости деформации ползучести от напряжения и времени является
зависимость вида
Iе = опВ, A2.23)
где п — коэффициент для определенного материала, зависящий от
температуры; В — для определенного материала функция времени
и температуры.
Зависимость A2.23) можно рассматривать как обобщение фор-
формулы A1.14) на случай напряжений, изменяющихся во времени.
Если использовать соотношение A2.23), то тогда в общем случае
неодноосного напряженного состояния выражение A2.21) прини-
принимает вид
,в )
или
Ь = <т?В. A2.24)
Это соотношение является необходимым дополнением к уравне-
уравнениям A2.6) и A2.7).
275

, Учитывая, что теория течения в варианте A2.24) наиболее широки
использована в расчетах на ползучесть Л. М. Качановым [7], в даль-
дальнейшем будем называть ее теорией течения Л. М. Качанова.
Проинтегрируем уравнение A2.23), полагая а = const, исполь-
используя соотношение A-1.15) и учитывая, что при t = 0 гс¦ = 0. Тогда
получим уравнение семейства кривых ползучести в виде A1.13).
Следовательно, по теории течения Л. М. Качанова кривые пол-
ползучести являются геометрически подобными.
Получим уравнение семейства кривых релаксации по теории
течения Л. М. Качанова.
Рис. 12.7. К построению кривых ползучести при сту-
ступенчатом нагружении по теориям упрочнения и течения
Из соотношений A1.2) и A2.23) имеем
¦Щг-^-EBdt.
а
Проинтегрируем это уравнение. Если учесть, что при t = О
а = а @) и использовать выражение A1.15), то после преобразова-
преобразований получим
а = а @) [1 + (п — 1) Еоп-Щ Q Г~К A2.25)
Уравнение A2.25) является уравнением семейства кривых ре-
релаксации по теории течения Л. М. Качанова.
Рассмотрим описание ползучести при ступенчатом нагружении
по теории течения. Этот вопрос решается аналогично тому, как
это было сделано при построении кривой релаксации. Представим
себе, что образец испытывается на ползучесть в течение времени tx
при напряжении аъ а затем напряжение мгновенно увеличивается
до величины а2 (рис. 12.7). За время t1 деформация ползучести воз-
возрастает до величины есА, равной в выбранном масштабе отрезку АВ.
276

Точка Л является точкой пересечения вертикальной линии, прове-
проведенной на~*расстоянии t{ от оси ординат, с кривой ползучести при
напряжении ах. Согласно теории течения после возрастания напря-
напряжения от аг до сг2 скорость деформации ползучести определяется
углом наклона касательной в точке С к кривой ползучести при на-
напряжении av Точка С является точкой пересечения вертикальной
линии, проведенной через точку А, с кривой ползучести при напря-
напряжении а2. При t > tx деформация ползучести нарастает по закону,
изображенному линией ADX, представляющей собой часть кривой
ползучести при напряжении а2, передвинутой параллельно самой
себе из точки С в точку А.
§ 77. Теория упрочнения
Предположим, что потенциал скоростей деформаций ползучести
зависит от второго инварианта девиатора напряжений, интенсив-
интенсивности скоростей деформаций ползучести и параметра Удквиста.
Уравнение поверхности потенциала имеет вид
откуда, используя соотношение A.20), имеем
A2.26)
Уравнения A2.6) и A2.26) определяют зависимости компонентов
скоростей деформации от компонентов напряжения по теории упроч-
упрочнения.
В случае одноосного растяжения
и из зависимости A2.26) имеем
а = Ф3 (Iе, е<). A2.27)
Теория упрочнения так же, как и две предыдущие технические
теории ползучести, обычно формулируется для одноосного растяже-.
ния в виде уравнения A2.27), т. е. предполагается, что при заданной
температуре между напряжением, деформацией ползучести и ско-
скоростью деформации ползучести существует определенная зависи-
зависимость.
Эта теория была предложена Людвиком [10], Надаи [15] и Да-
венпортом [34]. Дальнейшее развитие теории упрочнения при-
принадлежит Ю. Н. Работнову [24].
Метод построения кривой релаксации по серии кривых ползу-
ползучести аналогичен рассмотренному выше способу построения кривой
релаксации на основе теории течения. Различие заключается лишь
в том, что согласно теории упрочнения скорость деформации пол-
ползучести является функцией напряжения и деформации ползучести
и от времени не зависит. Поэтому начальная скорость деформации
ползучести во втором промежутке времени At2 определяется тан-
277

генсом угла наклона касательной в точке L к кривой ползучести при
напряжении ах (см. рис. 12.6). Точка L является точкой пересечения
горизонтальной линии, проведенной из точки А, с кривой ползу-
ползучести при напряжении av
Следовательно, согласно теории упрочнения во втором промежутке
времени At2 пластическая деформация нарастает по закону, изобра-
изображенному линией АЕ2, представляющей собой участок кривой пол-
ползучести при напряжении оъ передвинутой параллельно самой себе
из точки L в точку А и взятой до пересечения в точке Е% с вертикаль-
вертикальной линией^ отстоящей от оси ординат на расстоянии t2 = Д^ -f
-f, At2. Продолжая подобные построения, получим кривую 0Е212:
Ввиду того, что скорость дефор-
деформации ползучести для некоторого
значения времени по теории упроч-
упрочнения меньше, чем по теории тече-
течения, кривая релаксации, построенная
на ее основе, располагается всегда
выше кривой релаксации, построен-
построенной по теории течения.
Аналитическая зависимость меж-
между скоростью деформации ползуче-
ползучести, деформацией ползучести и на-
напряжением обычно представляется
в виде
= / (а),
A2.28)
Рис. 12.8. Графики зависимости
напряжения от деформации ползуче-
ползучести при постоянной скорости ее
¦jc причем предполагается, что /@)=0.
Для функции напряжения / (а) бы-
ли предложены следующие выра-
выражения:
/ (а) = aav; A2.29)
- l);
A2.30)
A2.31)
где а, р, v, а и Ь— коэффициенты, для определенного материала,
зависящие от температуры. Очевидно, что выражение A2.31) не-
несправедливо при малых напряжениях и при 0 = 0, так как / @) ф 0.
С. А. Шестериковым [32J установлено необходимое условие,
которому должна удовлетворять функция / (а).
Как показывают экспериментальные данные, с ростом нагрузки
величина накопленной деформации ползучести растет быстрее, чем
по линейному закону, т. е.
I. A2.32)
Это означает, что линии, по которым поверхность в координатах
вс, Iе, о пересекается плоскостями, перпендикулярными оси 1е,
278

и которые представляют собой графики зависимости напряжения
от деформации ползучести при постоянной скорости деформации,
являются выпуклыми (рис. 12.8).
Продифференцируем дважды выражение A2.28) по ст. Тогда
получим
Е«р (Р -1) и*-2 (^) + ?СР (ес)Р-2 |?-=Г (о).
Исключая из этих двух выражений -д—, имеем
*гс(сф-1&е =*М P~l [/'«DI-
[/'«DIPS (V) Г (О)
PS (V) да2 — Г (О) р дст) •
На основании неравенства A2.32) заключаем, что
Легко показать, что выражение A2.29) удовлетворяет этому
неравенству при v > р, а соотношение A2.31) — всегда. Функция
A2.30) не удовлетворяет неравенству A2.33) при малых значениях ст.
Поскольку, как отмечалось выше, для выражения A2.31) / @) ф 0,
из трех функций / (ст) наилучшей следует признать функцию A2.29)
при v > р.
Если использовать выражения A2.28) и A2.29), то тогда в общем
случае неодноосного напряженного состояния соотношение A2.26)
принимает вид
4
Оно является необходимым дополнением к уравнениям A2.6)
и A2.7).
Получим уравнение кривых ползучести, используя выражения
A2.28) и A2.29). Учитывая формулу A1.3), имеем
(е')Э dec = aav dt. A2.35)
Проинтегрируем это уравнение. При этом учтем, что напряжение
постоянно, а при t — 0 гс — 0. Тогда получим уравнение кривыхпол-
зучести
1 V 1
1)] Р+1 ар+х /p+I • A2.36)
Полученное уравнение кривой ползучести является частным слу-
случаем уравнения A1.13). Согласно ему кривые ползучести геометри-
геометрически подобны. Поскольку в степенной зависимости деформации
ползучести от напряжения A1.13) показатель степени больше еди-
единицы, заключаем, что v >• р + 1. Из условия С. А. Шестерикова
A2.33) следует только, что v > р.
279

Теперь, исходя из зависимостей A2.28) и A2.29), получим урав-
уравнение кривых релаксации. Преобразуем уравнение A2.35), исполь-
используя соотношения A1.1) и A1.2). В результате устанавливаем
—[а @) — а]3 -^- =
Проинтегрируем полученную зависимость, используя начальное
условие при t — 0 а = а @). Тогда имеем
0@)
Уравнение A2.37) является уравнением семейства кривых ре-
релаксации в неявном виде. В общем случае произвольных величин (J
и v интеграл A2.37) определяется численно.
Рассмотрим описание ползучести при ступенчатом нагружении
по теории упрочнения. Отличие от аналогичного исследования по
теории течения заключается только в том, что по теории упрочнения
после возрастания напряжения от величины ах до а2 скорость де-
деформации ползучести определяется углом наклона касательной
в точке G к кривой ползучести при напряжении а2 (рис. 12.7).
Точка G является точкой пересечения горизонтальной линии, про-
проведенной через точку А, с кривой ползучести при напряжении сг2.
При t > tx деформация ползучести нарастает по закону, изобра-
изображаемому линией AD2, представляющей собой часть кривой ползу-
ползучести при напряжении a2j передвинутой параллельно самой себе
из точки G в точку А.
Как уже отмечалось в предыдущем параграфе, Ю. Н. Работно-
вым [24] была предложена более общая теория, согласно которой
в потенциал ползучести, кроме интенсивности скоростей деформаций
ползучести, может быть включено несколько параметров, которые
названы структурными. Кинетическое уравнение A2.10) для к-го
структурного параметра приведено в предыдущем параграфе. Если
за структурный параметр принять параметр Удквиста, получим из-
изложенную выше теорию упрочнения.
Рассмотрим частный случай одного структурного параметра,
когда за него принята работа внутренних сил на перемещениях,
возникших в результате ползучести материала. В случае одноосного
напряженного состояния
q = J a d&c. A2.38)
Тогда метод построения кривой релаксации по серии кривых пол--
зучести аналогичен рассмотренному выше способу построения кри-
кривой релаксации на основе теории упрочнения. Различие заключается,
лишь в том, что согласно рассматриваемой теории скорость дефор-
деформации ползучести определяется точкой К (см. рис. 12.6), ордината
которой ед благодаря введенному структурному параметру A2.38).
при a = const определяется из условия
а@)есА=
280

Следовательно, согласно рассматриваемой теории во втором про-
промежутке времени At2 деформация ползучести нарастает по закону,
изображаемому линией АЕ3, представляющей собой участок кривой
ползучести при напряжении аъ взятый от точки К до пересечения
в точке Е3 с вертикальной линией, отстоящей от оси ординат на рас-
расстоянии t2 — Att +At2. Продолжая подобные построения, полу-
получаем кривую 0Е313.
Ввиду того что скорость деформации ползучести для некоторого
значения времени по рассматриваемой теории меньше, чем по теории
упрочнения, процесс релаксации по этой теории идет медленнее,
чем по теории упрочнения.
Получим уравнение кривой релаксации по рассматриваемой тео-
теории с помощью аналитических формулировок A2.28) и A2.29) тео-
теории упрочнения, используя вместо деформации структурный пара-
параметр A2.38).
Для того чтобы в частном случае постоянного напряжения
а = const, q = огс
выражение
g(\o decf = сих*»
совпало с соотношениями A2.28) и A2.29), необходимо положить
Тогда, используя выражение A1.3), получим
(J a decf dec =
Подставим соотношение A1.2) в это уравнение и введем пределы
интегрирования от а @) до а. В результате имеем
-- •¦? Мг-
откуда после разделения переменных и интегрирования с использо-
использованием начального условия при t = 0 а = а @) получаем
°/.0)га2@)— аЦЫа
Это уравнение и является уравнением семейства кривых релакса-
релаксации в неявном виде. Интеграл A2.39) в общем случае произвольных
величин р и v определяется численно.
Построение кривой ползучести при ступенчатом нагружении
производится аналогично тому, как это было сделано по теории
упрочнения. Отличие заключается в том, что согласно рассматри-
рассматриваемой теории после возрастания напряжения от аг до сг2 (см.
рис. 12.7) скорость деформации ползучести определяется углом
281

наклона касательной в точке Е к кривой ползучести при напряже-
напряжении сг2. Координата точки определяется из условия
oiecA = а2есЕ.
При t > tt деформация ползучести нарастает по закону, изобра-
изображаемому линией AD3, представляющей собой часть кривой ползу-
ползучести при напряжении а2, взятой от точки Е. Ввиду того что скорость
деформации ползучести при t — tx по рассматриваемой теории
больше, чем по теории упрочнения, кривая ползучести по ней рас-
расположится выше кривой ползучести по теории упрочнения.
Рассмотрим возможность отражения разупрочнения при помощи
теории структурных параметров. Для простоты примем один струк-
структурный параметр, зависящий от деформации ползучести и времени,
кинетическое уравнение для которого в случае одноосного напряжен-
напряженного состояния согласно формуле A2.10) имеет вид
dq = dec — cdt.
Коэффициент при dt взят отрицательным, поскольку он характе-
характеризует скорость разупрочнения. Абсолютная величина его должна
увеличиваться с увеличением степени упрочнения. Примем простей-
простейшую линейную зависимость ее от параметра q. Тогда
dq = dec — Kqdt, A2.40)
где Я, — коэффициент для рассматриваемого материала, зависящий
от температуры.
Зависимость между скоростью деформации ползучести, напря-
напряжением и структурным параметром q примем в форме A2.28), A2.29),
т. е.
A2.41)
Допустим, что в течение времени tt образец был нагрет до тем-
температуры ¦& и нагружен так, что в нем возникло постоянное во вре-
времени напряжение а. Затем он был разгружен и в течение времени
t2—tx находился при той же температуре ¦&, после чего образец был
нагружен вновь до первоначального напряжения а. Выясним, как
повлияла разгрузка на процесс ползучести образца.
Располагая кривой ползучести, можно определить параметр q
в момент времени tv Для этого представим выражение A2.40) в виде
Интеграл этого линейного неоднородного дифференциального
уравнения, как известно, имеет вид
q = exp (-It) \с +1 exp (It) ^- ЛJ .
282

Выполняя интегрирование по частям, устанавливаем
t
q = exp (—%t) [С + exp (kt) ec — К j exp (kt) ec dt].
Используем начальное условие при t = 0, ес = О, q = 0. Тогда
получим С — 0 и окончательно
= 6е — A, exp (—М) j exp (М) ec dt.
Эта формула позволяет определить значение qt для момента вре-
времени ti, при котором величина деформации ползучести равна е[:
V
qx = &{ — к ехр (—ktj J exp (kt) &° dt.
о
Далее при t > tx напряжение равно нулю и, следовательно,
согласно выражению A2.41) скорость деформации ползучести равна
нулю. Эта теория не описывает явления обратной ползучести. По-
Поэтому из соотношения A2.40) имеем
dq = —kq dt.
Интегрируя это уравнение и используя начальное условие при
t = tlt q = qt, получаем v
q = qx exp [—A, (t — tt) ].
При помощи этого уравнения можно определить величину q для
значения времени t2
q2 = qvexp [—A, (t2 — tx) 1.
Очевидно, что величина q2 <3 qx уменьшается с увеличением t2
и, следовательно, согласно формуле A2.41) скорость деформации
ползучести после вторичного нагружения до напряжения а тем
больше, чем больше время выдержки образца в ненагруженном
состоянии при температуре ¦& (разупрочнение материала). Интегри-
Интегрирование выражения A2.41) позволяет получить уравнение кривой
ползучести после вторичного нагружения.
§ 78. Теория ползучести с анизотропным упрочнением
В изложенных выше теориях ползучести предполагалось, что упрочнение яв-
является изотропным. Экспериментальные исследования ползучести при сложном
нагружении указывают на существенно анизотропный характер упрочнения в усло-
условиях ползучести. Учет деформационной анизотропии может быть произведен путем
разделения тензора напряжений на тензоры активных и добавочных напряжений
(см. § 27).
На возможность построения такой теории было указано Генкв [2] и Д. Д. Ивле-
вым [4]. В работах И. 3. Паллея [20], [21] дана неизотермическая теория цикличе-
циклического нагружения, учитывающая эффект анизотропного упрочнения материалов.
' Ниже изложена теория ползучести с анизотропным упрочнением, разработан-
разработанная Г. М. Хажинским [14,31,41].
283

Примем, что тензор напряжения 0(/- может быть представлен в виде суммы двух
тензоров: активного а(/- и добавочного Xi/ напряжений
ач = аи+ xij- A2.42)
Допустим, что девиаторы полных s^, активных pi/ и добавочных рц напряже-
напряжений могут быть, представлены в аналогичном виде
sij=Vtj+ptj A2.43)
и что для одноосного напряженного состояния два главных напряжения тензоров
активных и добавочных напряжений равны нулю.
Далее примем потенциал скоростей деформаций ползучести в такой же форме,
как в § 27, когда предполагалось, что в процессе нагружения поверхность пластич-
пластичности испытывает только жесткое смещение (трансляционное упрочнение). Тогда
получим
= 0. A2.44)
Согласно определению потенциала скоростей деформаций ползучести компо-
компоненты скоростей деформаций ползучести даны формулой A2.1). Потенциал не за-
зависит от среднего нормального напряжения. Направление вектора скорости дефор- .
мации, которое согласно формуле A2.1) нормально к поверхности потенциала,
не изменяется при смещении ее как жесткого целого. Поэтому
Ч да if dfyij '"
Подставим эту величину в выражение для интенсивности скоростей деформаций
ползучести B.41). Тогда, используя соотношение A.20), получим
И, следовательно,
«/-т1?Р'/- A2-45)
Из соотношения A2.44), используя выражение A.20), заключаем, что при опре-
определенной температуре интенсивность активных напряжений является функцией
интенсивности скоростей деформаций. Примем, что интенсивность скоростей дефор-
деформаций ползучести является произведением двух функций
14 = GQ, A2.46)
одна из которых G — G ($) есть функция температуры, а вторая <? = Q (а,) — функ-
функция интенсивности активного напряжения.
Функция G обычно принимают в форме, которая была рассмотрена в § 71.
A2.47)
где G1 — постоянная для материала; АНп — энергия активации ползучести; R —
газовая постоянная; Т — абсолютная температура.
Функция интенсивности активного напряжения может быть принята в одной
из_форм, о которых говорилось ранее: степенная зависимость
Q (at) = <
закон гиперболического синуса
384

экспоненциальная зависимость
Q(a,i) =exp-y-. ' A2.48)
Использование экспоненциальной зависимости позволяет значительно упро-
упростить расчеты. Очевидно, что она несправедлива при малых активных напряжениях,
так как согласно формуле A2.48) Q @) Ц= 0.
Допустим, что приращение компонентов девиатора добавочного напряжения
зависит от компонентов приращения деформации ползучести, а также приращения
времени и может быть представлено в форме
dpt. = -|-Л dectj - DQ (Xl) -?У- dt, A2.49)
где А и D — функции температуры, которые могут быть представлены в форме
A2-47)
&НГ — энергия активации возврата (разупрочнения); Q (%f) — функция интенсив-
интенсивности добавочных напряжений, такая же как Q (а,) — функция интенсивности
активных напряжений. Для уточнения теории, особенно при напряжениях выше
предела пропорциональности, можно принять, что величина А является функцией
не только температуры, но также и интенсивности напряжений о,- [14]. При записи
соотношения A2.49) использована идея Бейли [33] о том, что в. процессе ползучести
механическое упрочнение (первое слагаемое) взаимодействует с термическим разу-
разупрочнением (второе слагаемое с отрицательным знаком) подобно тому, как это было
сделано в теории структурных параметров (см. § 77).
Переходя к частному случаю одноосного напряженного состояния, при кото-
2
ром g? = |gc|; о. = |о| = |а + х1;«* = |а|; X; = 1x1; Р = "з" х И ИСПОЛЬЗУЯ эксп°-
ненциальную зависимость A2.48), получаем из соотношений A2.45)—A2.49)
r |07xl ; A2.50)
d% = A d&c — D sign % ехр -^ dt, A2.51)
где символом sign (a — х)> sign X обозначены знаки величин а -— % и % соответ-
соответственно.
Рассмотрим вначале ползучесть при постоянном напряжении. Есла до началь-
начального момента времени ползучесть отсутствовала и напряжение бьио меньше, чем
предел пропорциональности материала при температуре испытания, то добавочное
напряжение в начальный момент времени равно нулю и активное напряжение равно
приложенному. В дальнейшем происходит увеличение во времени добавочного на-
напряжения и уменьшение активного.
Получим уравнение кривых ползучести при постоянном напряжении, исполь-
используя выражения A2.50) и A2.51) и учитывая, что в рассматриваемом случае
sign (а — х) " +1 и sign I = -f 1. Продифференцируем соотношение A2.50) по вре-
времени, учитывая, что напряжение во времени не изменяется. Тогда получим
285

Подставляя в это выражение соотношение A2.51), используя еще раз уравне-
уравнение A2.50), получаем после преобразований
ill 4- а2 (?? — d2 = 0 A2.52)
dt -г " \s )
где
Интеграл уравнения A2.52) имеет вид
ус d
s =•
а 1 — р ехр (— 2
где
A2.55)
a ?с @) — скорость деформации ползучести в начальный момент времени. Эту ве-
величину определяем по формуле A2.50) при % = 0
Г@) = Оехр-|-. " A2.56)
Из соотношения A2.54) следует, что минимальное значение скорости деформа-
деформации ползучести при t -* оо
Интегрируя уравнение A2.54) и учитывая, что при /=0 &с = 0, получаем
уравнение кривой, ползучести
'a v '
которое является частным случаем уравнения A1.11).
Получим теперь уравнение кривой релаксации напряжений. Используя выра-
выражение A1.2) и учитывая, что в рассматриваемом случае sign (а — Х) = ~И и
i = +l> преобразуем уравнения A2.50) и A2.51) к виду:
A2.59)
Продифференцируем соотношение A2.59) по времени
d2a _ GE о —х (da d%
Подставим в полученный результат выражение A2.60). После преобразований
с использованием формулы A2.56) выводим дифференциальное уравнение для на-
напряжения а:
286

где
DGE
Это уравнение при помощи подстановки
("зг) ={/
может быть приведено к линейному дифференциальиому уравнению
Для интегрирования уравнения A2.61) необходимо знать в начальный момент
da
времени не только напряжение о @), ио и его производную —г-
Последняя
t = о
может быть получена из соотношения A2.59) с учетом того, что при t = 0 % = 0
da\ пп а @)
—гг = — GE ехр —\~- .
dt \ (=0 Ъ
В результате интегрирования уравнения A2.61) и использования начальных
условий получим уравнение кривых релаксации
о@)
f d° A2.62)
где
[ 1=1Й]^[±^*] A2.63)
Поскольку в основу вывода уравнения A2.62) положена формула A2.48), невер-
неверная при малых значениях напряжения, это уравнение дает погрешность при малых
величинах напряжения.
Рассмотрим теперь ползучесть при ступенчатом нагружении. Представим, что
вначале образец испытывается на ползучесть в течение времени t1 при напряже-
напряжении alt а затем напряжение мгновенно увеличивается до величины о2. Очевидно, что
как при напряжении а1г так и при напряжении а2 ползучесть описывается уравне-
уравнением A2.58).
Различие состоит только в величинах напряжений, по которым определяются
параметры d и |" @). Вычисление этих величии при а1 [формулы A2.53) и A2.56)],
а также подсчет d при о2 [формула A2.53)] очевидны. Начальная скорость дефор-
деформации ползучести после мгновенного изменения напряжения с о1 до о2 вычисляется
по формуле A2.50) при sign | a2 — % | = +1
A2.64)
Для вычисления добавочного напряжения %i при t = tlt возникшего в резуль-
результате процесса ползучести при напряжении alt обратимся к уравнениям A2.50)
и A2.51). Из этих уравнений при sign (а1 — %) = +1, sign % — -f 1 и a = их полу-
получаем дифференциальное уравнение для определения %
287

После интегрирования этого уравнения с использованием Подстановки
= exp
X
получим
f X\ d 1 Oj \ l+pexp(—2dat) .,„ ...
exp г-) = —n exP r- I • , —*4—s-7-rf • A2.65)
\ b ) aG r V 6 / 1 — p exp (—2 dat) v '
Для вычисления по этой формуле величины %i необходимо вместо t подста-
подставить tlt а параметры d, р и gc @) определить по величине напряжения at.
Выведем теперь уравнение кривой обратной ползучести. В этом случае может
быть рассмотрен процесс ступенчатого нагружения при мгновенном уменьшении
напряжения от а до 0. В рассматриваемом случае sign (а — %) = —I, sign % = +1
и уравнения A2.50) и A2.51) принимают вид
Iе = — Gexp-?-; A2.66)
-|-. A2.67)
Проинтегрируем уравнение A2.67),
учитывая, что при t = tx % = %v Тогда
получим
t
Рис. 12.9. К построению кривой обрат-
обратной ползучести по теории ползучести
с анизотропным упрочнением
-p
(--f)-
A2.68)
Величина добавочного напряжения %i> возникшего в результате ползучести
при напряжении а1 в течение времени tlt определяется так, как было указано при
рассмотрении процесса ступенчатого нагружения.
Подставим выражение A2.68) в уравнение A2.66). Используя соотношение
A1.3), получим
dec
dt
AG+D
(<-'i) + exp(—Й,
A2.69)
Интегрируя это уравнение и используя начальное условие при / = tl ect= г\,
получаем
*%с .. „с _ „с ^__ ____ __ __ 1— I 1 .// . + \ луп _Af_ i
-Ж+ТГ
A2.70)
Формула A2.70) позволяет определить уменьшение деформации ползучести
е° = ef — гс после разгрузки.
§ 79. Экспериментальная проверка и анализ теорий
ползучести
Наиболее простым способом экспериментальной проверки раз-
различных теорий ползучести является сопоставление эксперименталь-
экспериментальной кривой релаксации при постоянной деформации с теоретиче-
теоретическими, построенными по различным теориям ползучести.
288

На рис. 12.10—12.12 сопоставлены теоретические кривые релакса-
релаксации напряжений с экспериментальными, полученными в опытах
Дэвиса [35] (рис. 12.10), Джонсона [38] (рис. 12.11), а также в опы-
опытах Ю. Н. Работнова, В. И. Даниловской и Г. М. Ивановой [3]
(рис. 12.12).
6, МН/м
80
100
50
VIHJm2
¦——
-
600 800 t,A
Рис. 12.10. Сопоставление эксперимен-
экспериментальной (сплошная линия) и теоретиче-
теоретических кривых релаксации для меди при
температуре 165° С и начальном на-
напряжении а @) = 94,9 МН/м2. Штри-
Штриховая линия по теории старения в фор-
формулировке A2.15), штрихпунктирная
линия по теории течения Л. М. Кача-
нова [26 ]
О
Z0000 40000 60000 80000 t.MUH
Рис. 12.11. Сопоставление эксперимен-
экспериментальной (сплошная линия) и теоретиче-
теоретических кривых релаксации для хромомолиб-
деновой стали при температуре 525° С и •
начальном напряжении а @) = 146 МН/м2.
Штриховая линия — по теории старения.
в варианте A2.15), штрихпунктирная
, линия по теории течения Л. М. Кача-
нова [26 ]
4,Mh
250
200
150
100
V ^>-—
.?f'fi«om
Г " ]
6@) = jfy jmm/m г ''
r 1
"-—
о
10
30
'Ю
t.4
Рис. 12.12. Сопоставление экспериментальных кривых релакса-
релаксации для хромомолибденовой стали ЗОХМ при температуре 500° С
и различных начальных напряжениях (сплошные линии) с теоре-
теоретическими, построенными по теории упрочнения в варианте
A2.28), A2.29) (штриховые линии) [3] •
Как следует из рис. 12.10 и 12.1,1, экспериментальная кривая
релаксации располагается между теоретическими кривыми по гипо-
гипотезам старения и течения. Теория упрочнения хорошо подтверждается
экспериментально (рис. 12.12).
Ю Н. Н. Мал
289

Результаты экспериментального исследования ' ползучести при
ступенчатом нагружении (рис. 12.13, 12.14) показывают, что они
лучше согласуются с данными, полученными по теории ползучести
0,05
Рис. 12.13. Сопоставление экспери-
экспериментальной (сплошная линия) и тео-
теоретических кривых ползучести . при
ступенчатом нагружении для образцов
сплава ХН77ТЮР при температуре
700° С. Штриховая линия по теории
ползучести с анизотропным упрочне-
упрочнением, штрихпунктирная по теории
упрочнения [1]
i
25
t.4
с анизотропным упрочнением, чем по теории упрочнения. На рис.
12.13 представлены результаты испытания двух образцов, описанные
в работе [1 ]. Один из образцов (а) 10 ч деформировался при напряже-
напряжении о = 400 МН/м2, а затем 40 ч при напряжении а = 300 МН/м2,
ю
6 = 310 МН/м2
=' "¦
IS/
10
70
t.4
Рис. 12.14. Сопоставление экспериментальной (сплошная линия) и теоре-
теоретических кривых ползучести при ступенчатом нагружении для образцов из
алюминиевого сплава Д16АТ при температуре 150 С. Штриховая линия по
теории ползучести с анизотропным "упрочнением, штрихпунктирная по теории
упрочнения [41]
290

а другой (b) испытывался в обратном порядке: вначале в течение
40 ч при напряжении а = 300 МН/м2, а затем 10 ч при напряжении
а = 400 МН/м2. Как следует из кривых ползучести, деформация
второго образца оказывается несколько больше, чем первого. Это
описывается теорией ползучести с анизотропным упрочнением,
а теория упрочнения дает качественно обратный результат.
На рис. 12.14 представлены результаты испытаний, проведенных
В. С. Наместниковым [19]. При напряжениях выше предела про-
пропорциональности (рис. 12.14, а) теория упрочнения приводит к завы-
завышенным деформациям после догрузки по сравнению с экспериментом,
а при напряжениях ниже предела пропорциональности (рис.
12.14, б) — наоборот. Как указывалось выше, при ступенчатом на-
Рис. 12.15. Сопоставление экспери-
экспериментальных (сплошные линии) и тео-
теоретических (штриховые линии) кри-
кривых обратной ползучести для сплава
ХН77ТЮР при температуре 700° С [1]
?,025
МИ
¦*ooik
_ _1
20
t.v
гружении в случае увеличения напряжения теория течения дает кри-
кривую ползучести, расположенную ниже кривой по теории упрочне-
упрочнения, т. е. еще хуже согласуется с опытом, чем теория упрочнения,
а теория старения вообще не отражает ступенчатого нагружения.
Поэтому сопоставление экспериментальных данных с результатами,
полученными по теориям течения и старения, не производилось.
Результаты экспериментального исследования обратной ползу-
ползучести (рис. 12.15 и рис. 12.16) показывают, что они хорошо согла-
согласуются с данными, полученными по теории ползучести с анизотроп-
анизотропным упрочнением. Как уже упоминалось выше, теории ползучести
с изотропным упрочнениёк обратной ползучести не отражают.
На рис. 12.15 представлены результаты опытов, описанных в работе
[1 ], а на рис. 12.16 — данные обширного экспериментального иссле-
исследования, проведенного Джонсоном [37].
Из изложенного выше можно заключить, что лучше всего отра-
отражает все стороны явления ползучести как качественно, так и коли-
количественно теория ползучести с анизотропным упрочнением. В част-
частности, она, в отличие от других теорий, описывает явление обратной
ползучести.
Теория упрочнения хорошо согласуется с экспериментальным
исследованием релаксации напряжений и лучше, чем теория тече-
течения, описывает ползучесть при ступенчатом нагружении. Возможно,
как это было предложено Ю. Н. Работновым, совершенствование
этой теории путем введения структурных параметров, отличных от
деформации ползучести.
291

Недостатком теории течения, как и теории старения, является
то, что в основные уравнения этих теорий время включено явным
образом, вследствие чего эти уравнения неинвариантны относительно
изменения начала отсчета времени.Однако при плавно изменяющихся
нагрузках теории течения и старения хорошо согласуются с резуль-
результатами опытов.
Теория старения предполагает наличие функциональной связи
между деформацией, напряжением и временем. В действительности
это невозможно, так как наличие такой связи означало бы, что
C^ 01
Op, I o
0,008
0008
0,004
о
.—¦
109
_—«¦—
гг^П —
-• ' '
93
Of, in
0,008
оооц
0
124
"^Tof
¦—'
a)
— и ¦—'
—i —
.- -'
—i "^
—
— "—
-.. i '—
0,004
Er,°/c
1
§3_
—g'—
m "
•
6)
*—
/^93
/^
109
I
I24y
___ —
_--—
— — —
— — — —
.
8)
о - го
40 60
г)
Рис. 12.16. Сопоставление экспериментальных (сплошные линии) и теоретических
(штриховые линии) кривых обратной ползучести для малоуглеродистой стали при
температуре 455° С после предварительной ползучести [41]:
а — после выхода во вторую стадию; б «~ 145 ч; в — 20 ч; г — 2 ч
величина деформации е в момент времени t не зависит от процесса
нагружения, т. е. от величин напряжений в моменты времени, пред-
предшествующие моменту t, что противоречит опыту.
Как указывалось выше, расчеты на ползучесть по теории ста-
старения Ю. Н. Работнова эквивалентны расчетам на прочность и жест-
жесткость при нелинейных зависимостях между напряжениями и дефор-
деформациями, заданных графически. Поэтому многочисленные' решения
подобных задач могут быть использованы в этом случае и для расче-
расчетов на ползучесть. В расчетах на ползучесть по теории старения
Ю. Н. Работнова возможно непосредственное использование серии
экспериментально полученных кривых ползучести, без аппроксима-
аппроксимации их аналитическими зависимостями, что повышает точность
расчетов, /
292

Рассмотрим теперь экспериментальные исследования ползучести
при неодноосном напряженном состоянии. В большинстве случаев
они проводились путем испытания тонкостенных трубчатых образ-
образцов, нагруженных постоянными во времени внутренним давлением,
растягивающей силой и крутящим моментом. При таком нагружении
задача определения напряжений в образце является статически опре-
II 11
-
Ёг- -
0 20 ifO 50 80 t,v
2t
Рис. 12.17. Графики зависимости от времени величин
(сплошная ¦ линия) и —— (штриховая линия) [17]
OS
делимой и при постоянных во времени внешних силах напряжения
во времени изменяться не будут. В этом случае результаты испытаний
не позволяют оценить теорию ползучести. Они только дают возмож-
возможность проверить гипотезы о су-
существовании потенциала скоро-
скоростей деформации ползучести.
На рис. 12.17 представлены ре-
результаты испытаний на ползучесть
трубчатых образцов, нагруженных
постоянными во времени растяги-
растягивающей силой и крутящим момен-
моментом, проведенных В. С. Наместни-
ковым [17]. Напряженное состоя-
состояние при таком нагружении изо-
изображено на рис. 12.18.
Согласно формулам A2.7) для рассматриваемого напряженного
состояния, с учетом того, что напряжения во времени не изменяются,
скорости линейной деформации в направлении нормального напря-
напряжения и угловой деформации
= -^-а; т) =
гг ' '
Рис. 12.18. Напряженное состояние
при совместном растяжении и круче-
кручении трубчатого образца
откуда
.Hi
2 а
ту
293

Как следует из рис. 12.17, экспериментальные данные хорошо
согласуются с теоретическими.
Очень интересны результаты экспериментального исследования
ползучести при неодноосном напряженном состоянии в случае
изменяющихся во времени нагрузок. При таких испытаниях про-
проверяется не только гипотеза о существовании потенциала ползучести,
но также и теория ползучести.
V
Рис. 12.19. Сопоставление эксперимен-
экспериментальной (сплошная линия) и теорети-
теоретических кривых ползучести при знако-
знакопеременном прямом (кривые 1) и об-
обратном (кривые 2) кручении образцов
из сплава Д16Т при температуре
150° С и напряжении т = 140 МН/м2.
Штриховая линия по теории ползуче-
ползучести с анизотропным упрочнением,
штрихпунктирная по теории упрочне-
упрочнения [41 ]
10
го jo
чо
t.4
На рис. 12.19 представлены теоретические данные и результаты
испытаний на ползучесть трубчатых образцов, проведенных В. С. На-
местниковым [18] по следующей программе. Вначале образец де-
деформировался в течение пятидесяти часов при постоянном во времени
?с-10'
20
10
/у
1
f-ю1
1-2,5
а)
/у
.у"
t,4 0
12,5
В)
Рис. 12.20. Сопоставление экспериментальной (сплошная линия)
и теоретических кривых ползучести трубчатых образцов из мало-
малоуглеродистой стали при температуре 450° С. Штриховые линии по
теории ползучести с анизотропным упрочнением, штрихпунктирные
по теории упрочнения [41 ]
крутящем моменте, создающем постоянное касательное напряже-
напряжение, затем разгружался и вновь нагружался таким же по величине,
но обратным по направлению, постоянным во времени крутящим
моментом и вновь испытывался в течение 50 ч. Абсолютная величина
деформации сдвига при обратном кручении больше, чем при прямом.
Следовательно, предварительное кручение, по знаку обратное после-
294

дующему, разупрочняет материал, что является проявлением де-
деформационной анизотропии.
На рис. 12.20 приведены результаты экспериментального иссле-
исследования ползучести при сложном нагружении, проведенного Джон-
Джонсоном [39 ], и теоретические данные. Тонкостенные трубки из алюми-
алюминиевого и магниевого сплавов, а также углеродистой стали вначале
растягивались в течение 25 ч (ст = 112 МН/м2), а затем в течение
такого же времени растягивались и скручивались (а = 112 МН/м2,
г = 18,6 МН/м2). Из графиков следует, что теория ползучести
с анизотропным упрочнением значительно лучше описывает пол-
ползучесть при сложном нагружении, чем теория упрочнения.
§ 80. Особенности кратковременной ползучести
Кратковременной ползучестью называют процесс ползучести,
протекающий в течение секунд и минут при высоких напряжениях
и температурах. Поэтому при рассмотрении кратковременной пол-
ползучести в простейшем случае одноосного растяжения снимем введен-
введенное выше ограничение об отсутствии мгновенных пластических де-
деформаций. Тогда скорость деформации может быть представлена
в виде суммы скоростей упругой деформации |е, мгновенной пласти-
пластической деформации \р и деформации ползучести |с
I = Iе +1" +1". A2.71)
Экспериментальные исследования кратковременной ползучести
различных материалов при одноосном растяжении позволили уста-
установить, что в определенном диапазоне температур и напряжений
первая стадия на кривых ползучести отсутствует и начальные участки
кривых ползучести являются прямыми. Этот диапазон температур и
напряжений может быть представлен на диаграмме в координатах
температура ¦&, напряжение а (рис. 12.21). Линия АВ на этой диа-
диаграмме представляет график зависимости предела прочности мате-
материала от температуры, и выше этой линии нагружение без мгновен-
мгновенного разрушения невозможно. Линия CD отделяет область (слева
от нее), в которой ползучесть практически не наблюдается. Остав-
Оставшаяся область BCD, в которой ползучесть существенна, может быть
разделена на две. При меньших напряжениях и температурах (об-
(область FECD) существует первая стадия ползучести, при больших
(область BEF) ползучесть протекает без первой стадии.
Для установления зависимости деформации от напряжения при
одноосном растяжении подставим в формулу A2.71) зависимости
скоростей деформаций от напряжений. Тогда получим
i О2-72)
где Е—модуль упругости; S (сг) — функция напряжения, отража-
отражающая мгновенную пластическую деформацию; Q (а) — постоянная
во времени скорость деформации ползучести, точкой обозначена
производная по времени. Величина х, равная единице или нулю
295

вводится в уравнение A2.72)' для того, чтобы это уравнение отра-
отражало процессы нагружения в пределах упругости, за пределами
упругости, а также процесс разгрузки. Если а > 0 и а больше лю-
любого из достигнутых ранее значений а, то х = 1. В противном слу-
случае х = 0. Например, на рис. 12.22 изображен график изменения
во времени напряжения. На участках О А и CD х = 1, а на участках
АВ и ВС х = 0.
Интегрирование уравнения A2.72) по времени дает величину
деформации
е = ¦
и5 (ст)
A2.73)
Рис. 12.21. Области ползучести с на-
начальной стадией (FECD) и без нее
(BEF)
0 t
Рис. 12.22. График зависимости напряже-
напряжения от времени
в виде суммы упругой деформации -^-, мгновенной пластической
деформации х S (а) и деформации ползучести ес
ес = \ Q (a) dt.
A2.74)
Функция Q (а) может быть выбрана в виде степенной функции A1.4).
Из формулы A2.73) следует, что при высоких температурах
ползучесть может оказать влияние на диаграмму растяжения мате-
материала. Деформации ползучести зависят, как это следует из формулы
A2.74), от закона изменения во времени напряжений. Когда явле-
явление ползучести существенно, диаграмма растяжения уже не является
характеристикой материала.
Получим теперь на основе соотношения A2.72) уравнения диа-
диаграмм растяжения материала при постоянных скоростях деформа-
деформации и напряжения. Деформации будем предполагать малыми. Рас-
Рассмотрим вначале случай постоянной скорости деформации (при испы-
испытании образца на растяжение с постоянной скоростью движения
захвата испытательной машины). В этом случае ? = const и из урав-
уравнения A2.72), учитывая, что х = 1, имеем
dt
¦ + S' (a)
296

Из этой формулы следует, что при некоторой величине напряже-
напряжения скорость изменения его обращается в нуль и в дальнейшем обра-
образец растягивается при постоянном напряжении.
Интегрируя уравнение A2.75) и умножая полученную величину
времени на постоянную скорость деформации, выводим уравнение
диаграммы растяжения
Рис. 12.23. Диаграмма мгновенного
растяжения (кривая 1) титанового
сплава ВТ5-1 при температуре
600° С [25 ] и диаграммы растяже-
растяжения при постоянных скоростях
деформации: |= 1,67- \0~* 1/с (кри-
(кривая 2); I = 16,7-10 1/с (кривая 3)
и постоянных скоростях напряже-
напряжения а = 7,5 МН/м2с (кривая 4) и
а= 75МН/м2с (кривая 5) [13]
l-QW
da.
A2.76)
200
100
1
/
/
/
л
1/
'А
J
г
„—•¦
О 0,25 0,50 0,75 1,00 1.Z5 1,50 1,75 ?,%
Рассмотрим теперь случай постоянной скорости изменения на-
напряжения (для малых деформаций при испытании образца на растя-
растяжение с постоянной скоростью изменения растягивающей силы).
Тогда о = const и а = at.
Подставляя последнюю величину в формулу A2.72) и интегри-
интегрируя полученный результат по времени, учитывая, что х = 1, имеем
t
z = -^--\-S{a)-\-\Q(at)dt. A2.77)
Если использовать степенную зависимость A1.4), то тогда получим
На рис. 12.23 представлены диаграммы мгновенного растяжения
и диаграммы растяжения при постоянных скоростях изменения
деформации и напряжения титанового сплава ИЗ]. Этот рисунок
подтверждает значительное влияние на диаграмму растяжения ско-
скоростей изменения деформаций или напряжений.
В работе [13] рассмотрено построение действительной диаграммы
растяжения материалов при больших деформациях с учетом кратко-
кратковременной ползучести, а в статьях [6, 8] описаны результаты экспе-
экспериментального изучения кратковременной ползучести и растяжения
при постоянных скоростях деформации и условного напряжения
в случае больших деформаций.
297

§ 81. Неустановившаяся и установившаяся ползучесть
Неустановившейся ползучестью называют процесс ползучести,
протекающий при изменяющихся во времени напряжениях. Если
напряжения во времени постоянны, то этот процесс называют уста-
установившейся ползучестью.
Установившаяся ползучесть существует в случае статически опре-
определимых задач при постоянных во времени внешних силах. Это
объясняется тем, что в таких задачах напряжения определяются
только уравнениями статики, а поскольку внешние силы постоянны,
напряжения также во времени не изменяются. Например, в образце,
растянутом постоянной во времени силой при малых деформациях,
когда можно пренебречь изменением площади поперечного сечения,
напряжения во времени не изменяются. В тонкостенной трубке,
нагруженной внутренним давлением, растягивающей силой и кру-
крутящим моментом, при постоянных нагрузках и малых деформациях
напряжения также во времени не изменяются.
В статически неопределимых задачах для вычисления напряжений
необходимо добавочно рассматривать деформации, которые изме-
изменяются во времени за счет ползучести материала. Поэтому в таких
задачах даже при постоянных во времени внешних силах и малых
деформациях изменение деформаций всегда связано с изменением
напряжений и перераспределением их по объему детали. Если
при решении этих задач приближенно предположить, что напряже-
напряжения во времени постоянны, то получающиеся величины напряжений
и закон распределения их отличны от таковых в начальный момент
времени, когда деформаций за счет ползучести еще не было.
Но процесс изменения напряжений во времени остается невыяс-
невыясненным.
В действительности, как показали исследования неустановив-
неустановившейся ползучести, напряжения непрерывно изменяются во времени,
все более и более приближаясь к величинам, полученным в решении
задачи установившейся ползучести. Таким образом, распределение
напряжений при установившейся ползучести является как бы пре-
предельным. После некоторого промежутка времени распределение
напряжений близко к установившемуся.
В решении задач неустановившейся ползучести условиям совмест-
совместности деформаций должны удовлетворять компоненты полных де-
деформаций.
В решении задач установившейся ползучести упругими деформа-
деформациями по сравнению с деформациями ползучести можно пренебречь
(это справедливо для достаточно больших значений времени). Тогда
условиям совместности деформаций должны удовлетворять компо-
компоненты деформаций ползучести.
Для того чтобы наглядно проиллюстрировать установившуюся
и неустановившуюся ползучесть, рассмотрим упругое и чисто пла-
пластическое состояния, а также состояния установившейся и неуста-
неустановившейся ползучести для системы трех стержней АВ, АС и AD
одинаковой длины /, одинаковой площади поперечного сечения F
298

и из одинакового материала, нагруженных постоянной во времени
силой Р (рис. 12.24).
Основными уравнениями для рассматриваемой задачи является
уравнение равновесия, которое может быть представлено в виде
аг +а2 = s, A2.79)
где ох и а2 — напряжения соответственно в первом (АВ и AD)
р
и втором (АС) стержнях, s = -p-, а также условие совместности
деформаций
е2 = 2ъх. A2.80) .
Решая задачу в пределах
упругости, устанавливаем ве-
величины напряжений в стерж-
стержнях
При чисто пластическом
состоянии системы (если упроч-
упрочнение отсутствует) напряжения
в стержнях одинаковы и из
уравнения A2.79) имеем
о? = aS = ^-.
Рис. 12.24. Статически-неопределимая
стержневая система
Для определения напряжений в условиях установившейся пол-
ползучести используем степенную зависимость деформации ползучести
от напряжения A1.13). Подставляя величины деформации ползу-
ползучести по этой формуле в условие совместности деформаций A2.80),
имеем
Ю» = 2 (<гЭ«. A2.81)
Решим уравнения A2.79) и A2.81). Тогда
1+2"
s; o2 = -
S.
A2.82)
1+2"
Из соотношений A2.82) при п — 1 получаем величины напря-
напряжений в пределах упругости, а при п = оо значения напряжений
в чисто пластическом состоянии.
Между полученными выше решениями существует следующая
связь:
о\ = a°l+k(a[~ ст°);
а\ = а° + k (a'2 — о°),
299

где
О" 1
Решим теперь задачу неустановившейся ползучести, используя
теорию течения в формулировке Л. М. Качанова и предполагая, что
напряжения в стержнях меньше предела пропорциональности ма-
материала при данной температуре. В соответствии с этим величина
скорости полной деформации согласно формуле A2.23)
?=1« + Г=4--ЗГ+оПВ- A2.83)
Продифференцируем по времени условие совместности деформа-
деформаций A2.80). Тогда получим
U = 4i- A2.84)
Подставляя в это уравнение выражения для скоростей полных
деформаций, согласно формуле A2.83) устанавливаем
4 -таг + а*в = -г чг + 2а"в- <12-85>
Из уравнения равновесия A2.78) имеем
а1 = s — а2
и, следовательно, поскольку сила Р и величина s постоянны во вре-
времени, получаем
da± da2
~dT Ш~' '
подставим эти величины в уравнение A2.85). Тогда после преобра-
преобразований выводим дифференциальное уравнение дли аа:
' dt. A2.86)
2(S-°2)"-°2
Введем безразмерное напряжение о*2 и безразмерное время Г:
Тогда уравнение A2.86) принимает вид
dal
2 (I-el)" ~ (el)"
Проинтегрируем это уравнение, учитывая, что в начальный мо-
момент времени
300

Тогда получим
t* =
2A—?)" — ?"
A2.87)
р
= 0,667 до установивше-
установивше0,650
где С — переменная интегрирования.
На рис. 12.25 представлен график зависимости A2.87) при п = 2,
из которого следует, что с течением времени напряжения изменяются
от начального упругого состояния (а^)' 0667
гося (а*2)" =0,586, причем состояние
установившейся ползучести практиче-
практически реализуется весьма быстро.
Таким образом, поскольку расчеты
с допущением установившейся ползу-
ползучести значительно проще, чем без него,
можно, если срок службы детали до-
достаточно велик, использовать предполо-
предположение установившейся ползучести.
Однако в тех случаях, когда необ-
необходимо исследовать изменение и пере-
перераспределение напряжений во време-
времени, как например, в задаче о релак-
релаксации контактного давления в диске,
посаженном на вал с натягом, предпо-
предположение установившейся ползучести не
может быть принято.
Зависимости компонентов скоростей
деформации ползучести от компонентов
напряжений в условиях установив-
установившейся ползучести можно получить из соотношений A2.7), полагая
скорости изменения напряжений равными нулю,
hi = lh = -jr -37" (ff'7 ~ SiPo).
Интегрируя эти уравнения по времени, принимая во внимание,
что напряжение во времени постоянны, получаем
A2.88)
Такие же соотношения следуют из зависимостей A2.9), если пре-
пренебречь упругими деформациями по сравнению с деформациями пол-
ползучести.
Зависимость интенсивности деформаций ползучести от напряже-
напряжения может быть принята такой же, как и в теории старения [фор-
[формула A2.19)], т. е.
A2.89)
301
0.500
рис зависимости
безразмерного напряжения а* от
безразмерного времени t*

Она следует также из степенной зависимости интенсивности ско-
скоростей деформаций ползучести от интенсивности напряжений A2.24),
принятой в теории течения Л. М. Качанова, в случае постоянных
во времени напряжений.
Таким образом, при установившейся ползучести вывод зависи-
зависимостей компонентов деформаций ползучести от компонентов напря- •
жений не связан с использованием теорий ползучести.
Поскольку в решениях задач установившейся ползучести усло-
условиям совместности деформаций должны удовлетворять компоненты
деформаций ползучести, определяемые формулами A2.88), эти реше-
решения эквивалентны расчетам при нелинейных зависимостях между
напряжениями и деформациями. В частности, при использовании
зависимости A2.89) они эквивалентны решениям чисто пластических
задач со степенным упрочнением.
§ 82. Длительная прочность при неодноосном
напряженном состоянии
Для расчета на прочность при длительном нагружении в усло-
условиях ползучести необходимо располагать теорией прочности, с по-
помощью которой можно определить эквивалентное напряжение. Тогда
коэффициент запаса для определенного интервала времени вычис-
вычисляют как отношение предела длительной прочности для этого зна-
значения времени к эквивалентному напряжению.
Попытка использования известных теорий прочности для кратко-
кратковременного нагружения привела к неудовлетворительным резуль-
результатам. Поэтому были предложены эмпирические критерии прочности.
Наиболее экспериментально проверенной является формула для экви-
эквивалентного напряжения, предложенная И. И. Труниным [30].
Эта формула имеет вид
"экв = 4' [ff< + -t(°i + \°i I)] а1'2ц, A2-90)
где
4 = г^ • A2.91)
°i + -у (ох + I ох |)
Рассмотрим случаи одноосного растяжения (ctj = а; о2 — а3 — 0),
одноосного сжатия (аг = а2 = 0; а3 = —а) и чистого сдвига (at =т;
а2 = 0; а3 = —т).
По формулам A2.91) и A2.90), используя соотношение A.19),
имеем:
для одноосного растяжения
для одноосного сжатия
.Т1 = —1; стэкв=-^-; A2.92)
302

для чистого сдвига
/3
•та.
A2.93)
Применим теперь соотношения A2.92) и A2.93) для случая раз-
разрушения, т. е. положим в них аэкв = адл. ?; а = ад
й
т =
где
сж, тдл — пределы длительной прочности при растя-
растяТ
^ р ^ д р
жении, сжатии и чистом сдвиге. Тогда получим
а —
или
а =
°дл. р
180
140
100
W
1
_
^——•-
=•—
-а
-•
_
>
100
1000
t,4
700
500
300
1
1
ц
я 31
X
--
1
¦-
4-
i
10
100
t.4
¦ Рис. 12.26, Графики зависимости от времени разрушающих эквивалентных напряже-
напряжений. Черными кружочками изображены результаты испытания образцов при одноос-
одноосном растяжении; светлыми кружочками — тонкостенных трубок, нагруженных вну-
внутренним давлением; крестиками — тонкостенных трубок при кручении и черными
треугольничками — тонкостенных трубок при совместном растяжении и круче-
кручении [30]:
о г- сталь 20, температура 500° С, б — сплав ЭИ 437Б, температура 700° С
Таким образом, величина а, зависящая для определенного мате-
материала от температуры и времени испытания до разрушения, может
быть определена по результатам испытания на длительную проч-
прочность при двух напряженных состояниях.
Формула A2.90) построена таким образом, что эквивалентное на-
напряжение при всестороннем равном растяжении (at = a2 = a3 = ст)
не равно нулю, в то время как эта величина для всестороннего
равного сжатия (а1 = а2 = а3 — —а) обращается в ноль, что, ве-
вероятно, должно согласоваться с данными опытов.
1 На рис. 12.26 представлены графики зависимости от времени
разрушающих эквивалентных напряжений при различных напря-
напряженных состояниях. Как следует из этих графиков, формула A2.90)
хорошо подтверждается опытами.
303

Список литературы
I. Высокотемпературная ползучесть сплава ЭИ437Б при различных режимах
нагружения.— «Известия высших учебных заведений. Машиностроение», 1969, № 9,
с. 77—81. Авт.: В. Н. Бойков, Ю. И. Бойцов, Н. Н. Малинин, Г. М. Хажинский.
2. Геики Г. Новая теория пластичности, упрочнения, ползучести и опыты над
неупругими материалами. В кн.: Теория пластичности. [Сборник статей]. М., Изд.
иностр. лит., 1948, с. 427—446.
3. Даниловская В. И., Иванова Г. М., Работиов Ю. Н. Ползучесть и релак-
релаксация хромомолибденовой стали.— «Известия АН СССР, Отд. техн. наук», 1955,'
№ 5, с. 102—109.
4. Ивлев Д. Д. К теории неустановившейся ползучести. В кн.: Проблемы
механики сплошной среды. [Сборник статей]. М., Изд. АН СССР, 1961, с. 157—160.
5. Ильюшин А. А., Леиский В. С. Сопротивление материалов. М., Физматгиз,
1959, 371 с.
6. Исследование растяжения сплава Д16 при повышенных температурах. —
«Известия высших учебных заведений. Машиностроение». 1971, № 6, с. 21—24.
Авт.: В. Н. Бойков, Ю. И. Бойцов, Э. С. Лазаренко, Н. Н. Малинин.
7. Качанов Л. М. Теория ползучести^ М., Физматгиз, 1960, 455 с.
8. Кратковременная ползучесть Д16 при больших деформациях.— «Известия
высших учебных заведений. Машиностроение», 1971, № 4, с. 34—37. Авт.: В. Н. Бой-
Бойков, Ю. И. Бойцов, Э. С. Лазаренко, Н. Н. Малинин.
9. Кулешова 3. Г. Проверка гипотезы упрочнения путем анализа экспери-
экспериментальных исследований ползучести.— «Известия высших учебных заведений.
Машиностроение», 1959, № 12, с. 69—76.
10. Людвик П. Элементы технологической механики.— В кн.: Расчеты на
прочность. [Сборник статей]. Вып. 15, М., «Машиностроение», 1971, с. 132—166.
II. Малииин Н. Н. Основы расчетов на ползучесть. М., Машгиз, 1948, 120 с.
12. Малинин Н. Н. Обзор отечественных работ по расчетам деталей машин на
ползучесть. В кн.: Расчеты на прочность. [Сборник статей]. Вып. 11. М., Машино-
Машиностроение, 1965,' с. 229—278.
13. Малииин Н. Н. Действительные диаграммы растяжения при высоких тем-
температурах.— «Известия высших учебных заведений. Машиностроение», 1968, № 1,
с.-41—46.
14. Малинии Н. Н., Хажинский Г. М. К построению теории ползучести с анизо-
анизотропным упрочнением.— «Известия АН СССР. Механика твердого тела», 1969, № 3,
с. 148—152.
15. На дай А. Влияние времени на ползучесть.— В кн.: Теория пластичности..
[Сборник статей]. М., Изд. иностр. лит., 1948, с. 405—426.
16. Надаи А. Пластичность и разрушение твердых тел. Т. I, M., изд. иностр.
лит., 1954, 647 С; т. II, М., «Мир», 1969, 863 с.
17. Наместников В. С. О ползучести при, постоянных нагрузках в условиях
сложного напряженного состояния.— «Известия АН СССР, Отд. техн. наук», 1957,
№ 4, с. 141—146.
18. Наместников В. С. Прямое и обратное кручение в условиях ползучести.—
«Журнал прикладной механики и технической физики», 1960, № 3, с. 121.—122.
19. Наместников В. С. О ползучести алюминиевого сплава при переменных
нагрузках.— «Журнал прикладной механики и технической физики», 1964, № 2,
с. 99—105.
20. Паллей И. 3. Приложение теории остаточных микронапряжений к неизо-
неизотермическому деформированию.— «Известия АН СССР. Механика», 1965, № 2,
110—113.
21. Паллей И. 3. К построению неатермической теории циклических нагруже-
ний.— «Инженерный журнал. Механика твердого тела», 1968, № 1, 130—134.
22. Работиов Ю. Н. Расчет деталей машин на ползучесть.— «Известия АН
СССР. Отд. техн. наук», 1948, № 6, с. 789—800.
23. Работиов Ю. Н. Сопротивление материалов. М., Физматгиз, 1962, 455 с.
24. Работиов Ю. Н. Ползучесть элементов конструкций. М., «Наука», 1966
752 с.
25. Работиов Ю. Н., Милейко С. Т. Кратковременная ползучесть, М., «Наука»,
1970, 222 с.
304

26. Расчеты на прочность в машиностроении. Т. II, М., Машгиз, 1958, 974 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К- Лихарев и др.
27. Сосиии О. В. К анизотропной ползучести материалов.— «Журнал приклад-
прикладной механики и технической физики», 1966, № 4, с. 160—163.
28. Соснии О. В. Анизотропная ползучесть упрочняющихся материалов.— «Ин-
«Инженерный журнал. Механика твердого тела», 1968, № 4, с. 143—146.
29. Сосиин О. В. К вопросу о существовании потенциала ползучести.— «Изве-
«Известия АН СССР. Механика твердого тела», 1971, № 5, с. 85—89.
30. Труиии И. И. Критерии прочности в условиях ползучести при сложном
напряженном состоянии.— «Прикладная механика», 1965, том I-, вып. 7, с. 77—83.
31. Хажинский Г. М. Основные уравнения неизотермического деформирова-
деформирования.— «Известия высших учебных заведений. Машиностроение», 1969, № 8, с. 30-!-
35.
32. Шестериков С. А. Об одном условии для законов ползучести, «Известия
АН СССР. Отд. техн. наук. Механика и машиностроение», 1959, № 1, с. 131.
33. Bailey R. W. The utilization of creep test data in engineering design.— «The
Institution of mechanical engineers. Proceedings», 1935, Vol. 131, p. 131—269.
34. Davenport С. С Correlation of creep and relaxation properties of copper.— «Jo-
«Journal of applied mechanics», 1938, Vol. 5, No 2, p. A—55-=-A—60.
35. Davis E. A. Creep and relaxation of oxygen—free copper.— «Journal of applied
mechanics», 1943, Vol. 10, No 2, p. A—101-r-A—105.
36. Finnie 1., Heller W. R., Creep of engineering materials, Me. Graw—Hill
Book Company, Inc., 1959, 341 p.
37. Johnson A. E. The creep recovery of 0,17 per cent carbon steel.—«The Institu-
Institution of Mechanical Engineers. Journal and Proceedings», 1941, Vol. 145, No 5, p. 210—
220.
38. Johnson A. E. Creep and relaxation of metals at high temperatures.— «Engi-
«Engineering», 1949, Vol. 168, No 4362, p. 237—239.
39. Johnson A. E., Henderson J., Mathur V. Creep under changing complex stress
system.—«Engineer», 1958, Vol. 206, No 5350, p. 209—216; No 5351, p. 251—257,
No 5352, p. 287—291.
• 40. Lubahn J. D., Felgar R. P. Plasticity and creep of metals, John Wiley and
Sons, Inc., 1961, 608 p.
41. Malinin N. N., Khadjinsky G. M., Theory of creep with the anisotropic har-
hardening.— «International journal of mechanical sciences», 1972, Vol. 14, No 4,
p. 235—246.
42. Malinin N. N. Tensile creep and some reference to metal processing.—«Archi-
processing.—«Archives of Mechanics. Archiwum mechaniki stosowanej», 1972, Vol. 24, issue 3L p. 439—448.
43. Odqvist F. K- G. Mathematical theory of creep and creep rupture, Clarendon
Press, 1966, 170 p.
44. Soderberg C. R. The interpretation of creep tests for machine design.—
«Transactions of the ASME», 1936, Vol. 58, No 8, p. 733—743.

ГЛАВА XIII
РЕШЕНИЯ НЕКОТОРЫХ ЗАДАЧ УСТАНОВИВШЕЙСЯ
ПОЛЗУЧЕСТИ
§ 83. Чистый изгиб бруса
Рассмотрим чистый изгиб бруса, поперечное сечение которого
име^ет две оси симметрии х и у, причем одна из них (ось у) лежит
в плоскости изгиба (рис. 13.1). Если механические свойства мате-
материала в условиях ползучести при растяжении и сжатии одинаковы,
ось симметрии х является нейтральной.
При чистом изгибе бруса поперечное сечение его остается пло-
плоским. Поэтому деформация является линейной функцией расстоя-
расстояния у от нейтральной оси х. Поскольку, как указывалось в § 81,
при установившейся ползучести условиям совместности деформации
должны удовлетворять компоненты деформации ползучести, имеем
гс =укс, A3.1)
где хс — кривизна оси бруса, образовавшаяся за счет ползучести
материала.
Из выражений A1.13) и A3.1) получаем
1
\уУГ~ у. A3.2)
Форма уравнения A3.2) обусловлена изменением знака напряже-
напряжения а при изменении знака координаты у.
Составим выражение изгибающего момента
М = I ay dF.
F
Подставляя в него соотношение A3.2), имеем
1
\\V\ n dF.
Назовем интеграл в выражении A3.3) обобщенным моментом инер-
инерции поперечного сечения относительно оси х и обозначим его
lyf^dF. A3.4)
306

Из соотношения A3.3), воспользовавшись выражением A3.4),
представим кривизну изогнутой оси балки, возникшую в результате
ползучести материала, в виде
Q. A3.5)
Из выражений A3.2) и A3.5) получаем формулу для нормального
напряжения в поперечном сечении бруса
1
а =
М\у
Jnx
-У-
A3.6)
Рис. 13.1. Брус, поперечное сечение которого имеет две оси симметрии
Для бруса прямоугольного поперечного сечения шириной Ь и высотой h из фор-
формулы A3.4) устанавливаем
п+1
Г 2+
Jnx = 26 J у п
dy.
Выполняя интегрирование, имеем
где
а, =
2/1+1
~7~
2п + 1 #
A3.7)
A3.8)
2 "
Для бруса круглого полого сечения с наружным диаметром D и внутренним
диаметром d по формуле A3.4)
п+1
п+1
Положим в первом и втором интегралах соответственно
г. - JL- r.^Jy I
Тогда получим
Jnx =
D "
2 "
Зп+1
1 V D
A3.9)
307

где
1
о
При помощи подстановки
g2 = u; dt, = ~-u 2 du;
этот интеграл может быть приведен к виду
1
1 1
Поскольку бэта-функция или эйлеров интеграл первого рода определяется
равенством [17] \
имеем
/ = ——
2 "\ 2п 2 У
Бэта-функция двух аргументов ри ^ связана с гамма-функцией или эйлеровым
интегралом второго рода этих аргументов соотношением [17]
Следовательно,
1
,
2 „ / In -f I , 3
~2~п ^"Т
Последнее выражение при помощи известных в теории специальных функций
формул [17]
Г (s + 1) = sT (s);
Г (s) Г (s + i-) = 21-25 \Гп Г Bs),
4-)-^ 'D-)-
а также соотношений
Vn
приводится к виду
-
2"п
. Зп+1 г / 2п + 1 \ '
308

Поэтому согласно формуле A3.9) имеем
3n+l I
/ И \ п I
. A3.10)
Зп+1 Г 3"+П
~ г-D) " •
где
2Cn+l)
A3.11)
Для сплошного круглого бруса диаметром D имеем
3/1+1
Jnx = atD~7!~. A3.12)
Аналогично для бруса, поперечное сечение которого представляет собой тонко-
тонкостенное кольцо со средним диаметром D и толщиной стенки б, по формуле A3.4)
получим
" б, A3.13)
где
A3.14)
На рис. 13.2 представлены графики зависимостей этих коэффициентов от пока-
показателя степени п.
Максимальное нормальное напряжение можно получить по фор-
формуле A3.6), полагая у =-~- (h — высота поперечного сечения).
Тогда имеем
<W=t^. A3.15)
где WnX — обобщенный момент сопротивления изгибу поперечного
сечения
Wnx = 2^-^-. A3.16)
Для прямоугольного поперечного сечения
Г- = ТBЙЛУМ2- A3Л7)
Для круглого полого сечения
^ =.2» atD»[l-(-§-) " j. A3.18)
309

Для круглого сплошного сечения
Для тонкостенного кольца
На рис. 13.3 представлены графики зависимостей
A3.19)
A3.20)
ОТТ"'
построенные по формулам A3.6)—A3.8). Эти графики характеризуют
вид эпюр распределения напряжений в прямоугольном поперечном
0.2
речном сечении изогнутого бруса в уело
виях установившейся ползучести при раз-
различных значениях показателя степени п
О.ОдО,0Ч0.3\
I 3 5 7 9 И п
Рис. 13.2. Графики зависимостей
коэффициентов <х1у а2 и а3 от пока-
показателя степени п
сечении бруса в случае раз-
различных величин показателя
степени п при установившейся
ПОЛЗучестИ. Из Графиков На Рис 13.3. Эпюры безразмерных нормаль-
рис. 13.3 заключаем, ЧТО мак- ных напряжений в прямоугольном попе
симальное нормальное напря-
напряжение при ползучести меньше,
чем максимальное нормальное
напряжение в начальный момент времени. Далее из этих графи-
графиков следует, что чем выше показатель степени п, тем значительнее
уменьшается наибольшее нормальное напряжение и нормальные
напряжения выравниваются по сечению.
Как отмечалось в § 81, расчеты на установившуюся ползучесть
эквивалентны расчетам на прочность и жесткость при нелинейных
зависимостях между напряжениями и деформациями. Поэтому для
решения задачи установившейся ползучести изогнутого бруса может
быть использован один из вариационных методов. Рассмотрим при-
применение принципа минимума дополнительной работы для исследова-
исследования установившейся ползучести равномерно нагретого бруса прямо-
прямоугольного поперечного сечения при чистом изгибе.
Поскольку в условиях ползучести изменение объема равно нулю,
а напряженное состояние при чистом изгибе является одноосным,
310

то в формуле G.9) можно положить К = оо, ос = о, е* = г\ = гс.
Тогда получим
а
R = \ ес da.
Используя степенную зависимость деформации ползучести от на-
напряжения A1.13), имеем
Дополнительная работа для всего бруса
v
Так как брус находится в условиях чистого изгиба и равномерно
нагрет, имеем
A3-21)
где Ь и h — ширина и высота поперечного сечения; / — длина бруса.
Допустим, как это было предложено Л. М. Качановым [2], что
распределение напряжений в поперечном сечении бруса при уста-
установившейся ползучести может быть представлено в виде (см. также
§81)
а = а0 + * (о' — а0), A3.22)
где а' —напряжения в пределах упругости; ст° — напряжения в пре-
предельном (чисто пластическом) состоянии.
Поскольку для прямоугольного сечения
0 4М _ , \2Му
имеем
A3,23)
Подставляя эту величину в формулу A3.21), получаем
А
22п+3Мп+1Ш
R== (п + 1) h?
A3.24)
Согласно принципу минимума дополнительной работы из всех
статически возможных напряженных состояний дополнительная ра-
работа для всего тела R принимает минимальное значение только
311

для истинного напряженного состояния. Поэтому для такого со-
состояния
dR
dk
0.
Подставим в это выражение соотношение A3.24). Тогда получим
h
0,8
0,6
0,4
0,1
\
\
\
— —
— 1 -
— —
г- ч
10 П 14 16 П
Рис. 13.4. График зависимости коэффи-
коэффициента k от локазателя степени п
Рис. 13.5. Эпюры безразмерных нормальных
напряжений в прямоугольном поперечном се-
сечении изогнутого бруса в условиях устано-
установившейся ползучести для различных значений
показателя степени п. Сплошные линии —
эпюры, построенные . по точной формуле
A3.6). Штриховые линии — эпюры, построен-
построенные по приближенной формуле A3.23)
1,0
0,5
0,5
h/2
Выполняя интегрирование, выводим уравнение, из которого опре-
определяем коэффициент k в зависимости от показателя степени п
1+ (я+ !)*¦'
A3.25)
, Как следует из формулы A3.25), при п = 1 k = 1, при п = оо
k = 0, чего.на основании выражения A3.22) и следовало ожидать.
На рис. 13.4 представлен график зависимости k от п, построенный
по формуле A3.25). Сопоставление эпюр (рис. 13.5) показывает не-
незначительное их различие.
§ 84. Поперечный изгиб бруса
. Предположим, что поперечное сечение бруса имеет две оси сим-
симметрии, одна из которых лежит в плоскости изгиба.
В случае поперечного изгиба бруса в поперечном сечении его
возникают касательные напряжения и при деформации бруса оно
312

не остается плоским, как в случае чистого изгиба. Однако для бруса
сплошного поперечного сечения влиянием касательных напряжений
при поперечном изгибе можно пренебречь и приближенно принять,
что поперечное сечение бруса при его деформации остается плоским,
как и в случае чистого изгиба. Тогда выведенные в предыдущем
параграфе формулы для напряжений и кривизны остаются прибли-
приближенно справедливыми. Они являются точными для частного случая
постоянной по длине бруса поперечной силы [21].
В отличие от чистого изгиба при поперечном изгибе изгибающий
момент и кривизна не остаются постоянными по длине балки. Основ-
Основной задачей в случае поперечного изгиба бруса является определе-
определение прогибов. При малых прогибах для определения их можно
воспользоваться известной приближенной зависимостью кривизны
изогнутой балки от прогиба [21 ]. На основании этой зависимости
кривизна изогнутой балки хс и прогиб Vе, возникшие за счет пол-
ползучести материала, связаны соотношением
dz2
Подставляя в это соотношение кривизну по формуле A3.5),
устанавливаем, что
' Q. A3.26)
Интегрирование" последнего уравнения дает возможность полу-
получить величину прогиба, возникшего за счет ползучести материала
балки.
Анализируя приведенное выше решение задачи о ползучести
изогнутой балки, можно заключить, что оно полностью эквивалентно
решению задачи об изгибе балки из материала; у которого диаграммы
растяжения — сжатия могут быть аппроксимированы степенной
функцией. Поэтому определение прогибов, возникших за счет
ползучести в рассматриваемом случае, может быть произведено
и при помощи интеграла Мора для определения перемещения брусьев,
выполненных из материала, не подчиняющегося закону Гука [151:
vc = J kcMi dz, A3.27)
где хс — кривизна изогнутой оси балки, возникшая за счет ползу-
ползучести материала; М — изгибающий момент в текущем сечении от
единичной нагрузки, приложенной в направлении искомого переме-
перемещения в той точке, перемещение которой определяется; интегрирова-
интегрирование проводится по длине бруса.
Подставив соотношение A3.5) в выражение A3.27), получим
xf
= J (-?-)" MiQ dz. A3,28)
Рассмотрим примеры определения линейных и угловых перемеще-
перемещений в балках в условиях установившейся ползучести.
313

Пример 1. Определим зависимость от времени максимального прогиба, воз-
возникшего в результате ползучести консольной балки, заделанной одним концом и
нагруженной на другом силой Р (рис. 13.6).
В рассматриваемом случае изгибающий момент в текущем сечении от заданной
нагрузки
Л* = Рг,
а изгибающий момент в текущем сечении от единичной силы, приложенной на сво-
свободном конце
Мг = г.
Подставляя эти выражения изгибающих моментов в формулу A3.28), после
преобразований получим величину максимального прогиба, образовавшегося за счет
ползучести материала балки
Пример 2. Определим зависимость от времени максимального прогиба,
возникшего в результате ползучести материала равномерно нагретой балки на двух
опорах, нагруженной равномерно распределенной нагрузкой интенсивности q, МН/м
(рис. 13.7).
г Р
Рис. 13.6. Консольная балка
Рис. 13.7. Двухопорная балка
Изгибающий момент в текущем сечении от заданной нагрузки
.. ql qz*
а изгибающий момент в текущем сечении от единичной силы, приложенной в сере-
середине пролета,
Подставляя эти выражения изгибающих моментов в формулу A3.28), уста-
устанавливаем
Полагая
получаем
где
314
ymax —
A3.29)

При помощи подстановки 1 — ? = у, dt,— —dy, преобразуем этот интеграл.
Тогда имеем
\{\-y'iTdy-11~Vj. A3.30)
0 0 0
Используя подстановку у% = z, 2ydy = dz, приводим первый интеграл к виду
Согласно соотношениям A3.29) и A3.30) окончательно получим
с U [Г (я+1I» ' ) cf42n+2Q
"max \ Г[2(л+1)] 2(n+\)j 23n+2Jn '
пх
Пример 3. Определим зависимость от времени угла поворота сечения над
опорой, возникшего в результате ползучести материала равномерно нагретой балки,
одни конец которой заделан, а другой оперт, нагруженной моментом т над опорой
(рис. 13.8)
Рис. 13.8. Статически неопредели- Рис. 13.9. Эквивалентная система
мая балка для статически неопределимой бал-
балки, изображенной на рис. 13.8
Рассматриваемая балка статически неопределима. Вначале найдем реакцию
опоры В (рис. 13.9). Для этого составим условие равенства нулю прогиба в сечении В
в эквивалентной системе (рис. 13.9). Изгибающий момент в текущем сечении экви-
эквивалентной балки от заданной нагрузки
М = т — Хг, A3.31)
а изгибающий момент в текущем сечении от единичной силы, приложенной в сече-
иии В,
Mt = z.
Подставим эти выражения изгибающих моментов в формулу A3.28) и прирав-
приравняем полученный результат нулю. Тогда получим
Хг\п
г dz = 0.
К'-4)"
о
Выполняя интегрирование по частям, устанавливаем
A — a)"+i (ап + а + 1) — 1 = 0, A3.32)
где
а = -^-. A3.33)
Уравнение A3.32) может быть решено графически или численно, после чего
по формуле A3.33) определяем реакцию опоры В — X. "
После вычисления реакции X определяем угол поворота сечения В. Для этого
используем формулу A3.28). Поскольку изгибающий момент в текущем сечении
315

эквивалентной балки от заданной нагрузки определяется формулой A3.31), а изги-
изгибающий момент в текущем сечении от единичного момеАта, приложенного в сече-
сечении В
Mj=l,
то по формуле A3.28) получаем
"пх О
Выполняя интегрирование, имеем .
По полученной формуле после определения реакции опоры В может быть
вычислен угол поворота сечения В для любого момента времени.
§ 85. Кручение бруса кольцевого
поперечного сечения
При кручении бруса, поперечное сечение которого представляет
собой круговое кольцо с наружным диаметром D и внутренним
диаметром d, поперечные сечения бруса остаются плоскими, а ра-
радиусы прямолинейными. Поэтому в условиях установившейся пол-
ползучести угловая деформация ус, возникшая в результате ползучести
материала в точке поперечного сечения на расстоянии г от центра,
определяется формулой
. ус =г9с, A3.34)
где 8е — относительный угол закручивания, образовавшийся за счет
ползучести материала бруса.
< Интенсивности напряжений и деформаций ползучести для чи-
чистого сдвига согласно формулам A.19) и B.16)
7з' A3>35)
Подставляя зависимости A3.35) в формулу A2.89), получаем
Yc = 3~t"Q. A3.36)
Сопоставляя выражения A3.36) и A3.34), устанавливаем закон
распределения касательных напряжений в поперечном сечении
316

Обратимся к определению относительного угла закручивания,
возникающего за счет ползучести материала. Для этого составим
выражение крутящего момента
D_
2
M=2n\xr*dr. A3.38)
Подставляя в этот интеграл касательное напряжение т, по фор-
формуле A3.37) получим
-L 4
" dr. A3.39)
Выражение
D_
2
2^
Jnp = 2я j r n dr A3.40)
назовем обобщенным полярным моментом инерции кольцевого попе-
поперечного сечения.
После интегрирования получим
Зп+1
Х 2 »
Для бруса круглого поперечного сечения величину обобщенного
полярного момента инерции можно получить по формуле A3.41),
полагая в ней d = 0. Тогда имеем
Зп+1
^^—D^.' A3.42)
2 "
Из соотношения A3.39), с учетом выражения A3.40), находим
величину относительного угла закручивания, возникшего за счет
ползучести материала бруса
6* = (JL.)n3~T~Q. A3.43)
Если подставим выражение A3.43) в зависимость A3.37), то по-
получим формулу для определения касательных напряжений
j_
т = 4^- A3.44)
Jnp
317

D
Величина наибольшего касательного напряжения при г =~
по формуле A3.44)
*mav "¦—
м
где Wnp — обобщенный момент сопротивления кручению
пр 4 Зп + 1
Для бруса круглого сечения
г
0,8-
/0
V
V
ISt
Уп=6
0,2
0,6
0,8 Л.
в/г
Рис. 13.10. Эпюры безразмерных каса-
касательных напряжений в поперечном сече-
сечении скрученного круглого бруса в усло-
условиях установившейся ползучести для раз-
различных значений показателя степени п
3"+'
A3.45)
A3.46)
W — —
пр~~ 4 Ъп + 1
D3. A3.47)
На рис. 13.10 представлены
графики зависимости отноше-
ния -WWZ от -щ для
круглого поперечного сечения,
построенные по формулам
A3.44) и A3.42). Эти графики
-характеризуют вид эпюр рас-
распределения напряжений в по-
поперечном сечении при устано-
установившейся ползучести. Из гра-
графиков на рис. 13.10 следует,
что с увеличением показателя
степени п наибольшее касатель-
касательное напряжение уменьшается и
распределение касательных на-
напряжений по сечению стано-
становится все более и более равно-
равномерным.
§ 86. Кручение бруса некруглого
поперечного сечения
Рассмотрим чистое кручение бруса, поперечное сечение которого
ограничено односвязным контуром (рис. 13.11).
При чистом кручении бруса выполняются равенства G.14), т. е.
напряженное состояние всех точек бруса является чистым сдвигом.
Дифференциальные уравнения равновесия в рассматриваемой
задаче такие же, как и в задаче, изложенной в § 45 [уравнение G.15) ].
С помощью соотношений G.16) введем функцию напряжений Ф, ко-
которая для односвязного контура обращается в ноль на контуре.
Крутящий момент связан с функцией напряжений Ф соотноше-
соотношением G.17).
318

Зависимости компонентов перемещения исх и ису точек попереч-
поперечного сечения, возникших в результате ползучести материала от от-
относительного угла закручивания за счет ползучести 8е имеют та-
такой же вид, как и в пределах упругости [22]:
ux = — Qcyz\ uy = Qcxz. A3.48)
Перемещение в направлении оси г—uz, связанное с искажением
плоскости поперечного сечения в случае бруса некруглого попереч-
поперечного сечения, не равно нулю.
Зависимости угловых дефор- v ^^ \\м
маций ползучести от компонен-
компонентов перемещения, возникающего
за счет ползучести материала,
согласно формулам B.1) имеют вид
ди\
dui
1гх — я, Т я, .
дг
дх
_
Рис. 13.11. Скрученный брус некруг-
некруглого поперечного сечения
дг ^ ду '
Подставляя в эти выражения соотношения A3.48), устанавливаем
*-<*+¦?.
A3.49)
Продифференцируем первое из этих уравнений по у, а второе
по х и из первого результата вычтем второй. Тогда получим условие
совместности деформаций ползучести
dyl
ду
дх
29е = 0.
A3.50)
Зависимости компонентов деформаций ползучести от напряжений
согласно формулам A2.88)
8> « 8/
= 3 —- %гх\ угу = 3 —'
A3.51)
Подставим эти зависимости в условие совместности деформаций
A3.50), используя соотношение A2.89). Тогда получим
A3-52)
Отметим, что для рассматриваемой задачи интенсивность напря-
напряжений получаем из формулы A.19), полагая в ней все компоненты
напряжений, кроме хгх и тгу, равными нулю
Щ^Т^)- A3.53)
319

¦ Подставим эту величину в уравнение A3.52). Используя выра-1-
жения компонентов напряжений через функцию напряжений G.16),
получаем дифференциальное уравнение для функции напряжений Ф
в случае установившейся ползучести бруса некруглого поперечного
сечения
д
дх
п-1
2П 2
п-1
2 дФ
29е
п+1
3 2 "й
= 0. A3.54)
Если это уравнение при использовании граничного условия
для функции напряжений на контуре (для односвязного контура
фкбнт =0) будет решено, то затем при помощи формул G.16) и
G.17) можно связать касательные напряжения и крутящий момент
и определить зависимость относительного угла за-
закручивания от крутящего момента.
'У Решение уравнения A3.54) связано с больши-
большими трудностями. Оно может быть легко решено
для поперечного сечения в форме тонкой полосы
(рис. 13.12). В этом случае (к % Ь) можно прибли-
приближенно принять
хгх =0
и, следовательно, на основании соотношений G.16)
45L = o.
Рис. 13 12. По- Тогда дифференциальное уравнение A3.54) при-
перечное сече- НИМает ВИД
ние скрученного
бруса в форме
вытянутого пря-
__а_Г|_аФ_ п-1 дФЛ 29е
дх \_ \ дх .дх \~ ?+1
моугольника
й
Проинтегрируем это уравнение, учитывая, что при х = 0, т2„ =
-W44
= 0 -^— = 0. В результате получим
дх
дФ
дх
Интегрируя еще раз, имеем
Ф = С—
где С — постоянная интегрирования. '
320
п+1

Последнюю можно получить из условия равенства нулю функ-
функции напряжений на контуре, а именно
при х — Ъ Ф = 0.
Из этого условия находим
\3 2 Q.
и, следовательно,
A3.55)
Q
Выражение для крутящего момента G.17) в рассматриваемой
задаче принимает вид
ь
M = %h\®dx.
о
Подставляя в него функцию напряжений по формуле A3.55),
после интегрирования и преобразований получим
^)n34LQ A3.56)
где жесткость при кручении
~^~. A3.57)
Касательное напряжение определяем по второй формуле G.16),
используя соотношения A3.55) и A3.56). После преобразований
получим
тжу = 2»-?г\х\» х. V A3-58)
Величину максимального ^касательного напряжения получаем,
подставляя в эту формулу х = Ь. Тогда имеем
м
^ A3.59)
где момент сопротивления кручению
^ A3.60)
Полученными результатами можно воспользоваться и для рас-
расчета бруса, поперечное сечение которого представляет собой тонкс -
стенный открытый профиль в форме изогнутой полосы с постоянной
И Н. Н. Маливин 321

толщиной стенки (рис. 13.13) или состоящий из т отдельных полос
(рис. 13.14).
В первом случае в выведенные выше формулы следует вместо 26
подставить толщину стенки профиля б, а вместо 2h — длину сред-
средней линии /.
Во втором случае для получения расчетных формул можно при-
приближенно считать, что отдельные полосы, составляющие профиль,
поворачиваются на один и тот же угол.
Обозначим крутящий момент, воспринимаемый некоторой поло-
полосой, через М1г а жесткость ее J'nkl.
.- (-r ..,*?
Рнс. 13.14. Поперечное сечение скрученного
бруса в форме тонкостенного открытого про-
профиля, состоящего из отдельных полос
Рис. 13.13. Поперечное
сеченне скрученного
бруса в форме тонко-
тонкостенного незамкнутого
профиля со стенкой по-
постоянной толщины
Согласно формуле A3.57)
2n+l
/„... =^Л-т-/..б71^
т'А
A3.61)
где lt и б; — длина и ширина f-ой полосы соответственно.
Приравнивая относительный угол закручивания профиля отно-
относительному углу закручивания t-ой полосы, по формуле A3.55) по-
получим
rt-i-l
Jnkt
Q,
откуда
'nfe
A3.62)
Просуммируем крутящие моменты на всех m полосах и прирав-
приравняем полученную сумму моменту,М. Тогда, принимая во внимание
соотношение A3.62), получим
322

откуда на основании соотношения A3.61) имеем
. A3.63)
Таким образом, в рассматриваемом случае, относительный угол
закручивания, возникающий за счет ползучести материала, находим
по формуле A3.56). Жесткость Jnk в этой формуле определяется
выражением A3.63).
Наибольшее касательное напряжение можно вычислить по фор-
формуле A3.59), причем согласно соотношению A3.58) момент сопро-
сопротивления кручению
Несколько особый случай представляет собой брус, поперечное
сечение которого—тонкостенный замкнутый профиль (рис. 13.15).
Задача кручения такого бруса статически определима с точки зре-
зрения вычисления напряжений, и поэтому при постоянном во времени
крутящем моменте напряжени-я во времени изменяться не будут.
Таким образом, в рассматриваемом случае процесс ползучести яв-
является установившимся.
Как известно [21 ], касательное напряжение при кручении бруса,
поперечное сечение которого представляет собой тонкостенный
замкнутый профиль, определяют по формуле
* = -Щ-> A3-64)
где б — толщина стенки; f — площадь, ограниченная средней ли-,
нией тонкостенного сечения.
Рассмотрим определение относительного угла закручивания
бруса. За основу примем условие однозначности осевого смещения
uz = 0. A3.65)
Используя соотношение A3.49), получаем
дис дис
dCd + ^d cd
~~
Преобразуем это выражение, используя формулы A3.51), A2.89)
и A3.53), а также замечая, что dx = ds cos a; dy = ds sin а, где
ds — длина элемента дуги средней линии контура, а а — угол между
касательной к контуру и осью (рис. 13.16). Тогда получим
ducz = 3 2 т"~ п (%гх cos а +"% sin а) ds + 0е (у coS а — х sin a) ds,
где
ъ = Ут&с + ъ1у A3.66)
— полное касательное напряжение. *
323

Как следует из рис. 13.16
хгх cos а + тгу sin а = т,
—у cos а + х sin а == г,
где г — длина перпендикуляра, опущенного из начала координат
на направление касательного напряжения. Следовательно,
Рис. 13.15. Поперечное сече-
сечение скрученного бруса в фор-
форме тонкостенного замкнутого
профиля
Рнс. 13.16. К выводу формулы для
угла закручивания бруса, попереч-
поперечное сечение которого имеет форму
тонкостенного замкнутого профиля
Поскольку
rds = 2df,
где df -—площадь элемента, поштрихованного на рис. 13.16, имеем
duz = 3 2 t"Q ds — 29е df.
Подставим это выражение в формулу A3.65). Используя фор-
формулу A3.64), заключаем, что выражение для относительного угла
закручивания за счет ползучести материала может быть приведено
к виду A3.56), где жесткость при кручении определяется формулой
Jb = 2 » —L г~
A3.67)
ds
б"
В более сложных случаях для решения задач кручения некруг-
некруглых брусьев может быть использовано выведенное в § 45 вариацион-
вариационное уравнение кручения бруса некруглого сечения при нелинейных
зависимостях между напряжениями и деформациями G.20).
324

Угловая деформация ползучести связана с касательным напря-
напряжением соотношением A3.36), что позволяет представить уравнение
G.20) в виде
6/ = 0, A3.68)
где
Используя уравнения A3.66) и G.16), имеем
Р f _2±L n+i
I j 3 2
7
П+1
Вариационное уравнение A3.68) может быть решено методом
Ритца. При этом функция Ф выбирается в виде
Ф = ЕС,Ф,. A3.70)
Все функции Ф( для односвязного контура обращаются в ноль да
контуре. Коэффициенты Ct определяются из условий равенства нулю
вариации интеграла A3.68)
В. Д. Вылекжаниным [1] дана верхняя и нижняя оценка жест-
жесткости при кручении стержня произвольного поперечного сечения.
Им установлено, что
где
Зи+1
1nF
(Зп+1)
2л
Я
п+1
2п
— обобщенный полярный момент инерции стержня круглого попе-
поперечного сечения, площадь которого F равна площади заданного
стержня:
периметр поперечного сечения.
325

§ 87. Тонкостенные цилиндрические трубы
Выше, в § 79, при изложении результатов экспериментальной
проверки теорий ползучести были рассмотрены частные случаи на-
нагружения тонкостенных цилиндрических труб в условиях ползу-
ползучести.
Разберем теперь более^общий случай нагружения тонкостенной
цилиндрической трубы со средним диаметром D, толщиной стенки h,
внутренним давлением р, осевой силой N, которую будем считать
растягивающей, и крутящим моментом М (рис. 13.17). Напряженное
состояние такой трубы двухосное и однородное.
В рассматриваемом случае задача вычисления напряжений яв-
является статически определимой, так как напряжения подсчитывают
из орднч уравнений статики. Поэтому при постоянных во времени
внутренних силовых фак-
МО торах напряжения изме-
изменяться не будут, т. е.
процесс ползучести будет
установившимся.
Рис. 13.17. Тонкостенная цилиндрическая тру-
труба, нагруженная внутренним давлением р, осе-
осевой растягивающей силой N и крутящим момен-
моментом М
Рнс. 13.18. Напряженное состо-
состояние элемента тонкостенной ци-
цилиндрической трубы, изобра-
изображенной на рис. 13.17
Компоненты напряжений определяются по общеизвестным фор-
формулам сопротивления материалов [21]. Нормальные осевое аг и
окружное at напряжения
„ _ N „ _ PD
- nDh ' "'— 2h \
Касательное напряжение подсчитываем по формуле
2М
% =
A3.72)
A3.73)
¦Модель напряженного состояния представлена на рис. 13.18.
Интенсивность напряжений и среднее нормальное напряжение
для рассматриваемой задачи получаем по формулам A.19) и A.5)
A3.74)
= Y°l—aifJt + °1 +
-at
326

Зависимость компонентов деформаций ползучести от компонен-
компонентов напряжений устанавливаем по формулам A2.88), используя соот-
соотношения A2.89), A3.74) и A3.75). В результате получаем
Bа, —
гсг = -i- (or; — a(o2 + о; + Зт ) 2 Bог — a() й;
л-1
у = 3(of — огаг + oi + Зт2) 2 tQ.
A3.76)
Располагая величинами деформаций ползучести, можно опреде- '
лить перемещения, образовавшиеся в результате ползучести мате-
материала.
Удлинение трубы длиной I:
Приращение среднего диаметра можно определить из зависимости
ADC = ectD.
Угол закручивания трубы при условии, что крутящий момент
не меняется по длине
Если тонкостенная труба, имеющая днища, подвергается воз-
воздействию только внутреннего давления р и крутящего момента М,
то
и согласно формулам A3.72)
°' — 2 *
Сопоставляя это выражение со второй формулой A3.76), заклю-
заключаем, что в этом случае деформации в осевом направлении отсут-
отсутствуют.
В работе [18] дано решение задачи установившейся ползучести
тонкостенной трубы, нагруженной внутренним давлением, изгибаю-
изгибающим и крутящим моментами и осевой силой.
§ 88. Толстостенные трубы
Рассмотрим толстостенную трубу с днищами, нагруженную вну-
внутренним давлением р и осевой силой N (см. рис.,6.1).
Обозначим внутренний радиус трубы через rlt а наружный ра-
радиус г2.
327

Примем, что осевая деформация ползучести трубы
г2 = 0. A3.77)
Как будет показано далее, так же, как и в расчете толстостен-
толстостенных труб за пределами упругости (см. § 32), это справедливо в том
случае, когда осевая сила возникает только за счет давления на
днища.
На основании зависимостей, приведенных в § 32, в рассматри-
рассматриваемом случае установившейся ползучести окружная щ и радиаль-
радиальная гс, деформации ползучести в некоторой точке трубы на расстоя-
расстоянии г от ее центра могут быть выражены через радиальное смеще-
смещение и° в этой точке, возникающее за счет ползучести материала,
следующим образом:
е?=4' e' = "lF- A3-78)
Условие несжимаемости материала имеет вид
е? + е? + е^ = 0. A3.79)
Подставляя выражения A3.77) и A3.78) в соотношение A3.79),
получаем
дис ис
дг ~~ г *
Интегрируя это уравнение по радиусу, можно установить закон
изменения по радиусу радиального перемещения, возникшего за счет
ползучести материала трубы
и? *=¦%-, A3.80)
где С — некоторая функция времени.
Подставим теперь выражение A3.80) в соотношения A3.78).
Тогда
с С с С /1 о о 1 \
Ъ=-р?\ *' = — 7Г- A3.81)
Интенсивность деформаций ползучести в рассматриваемой задаче,
согласно формулам B.18) и A3.77), запишем следующим образом:
у 4- efe, + (ecr)\ A3.82)
Подставляя в уравнение A3.82) выражения A3.81), имеем
8(=-^--^-. A3.83)
328

Зависимости компонентов напряжений от компонентов деформа*
ций ползучести для рассматриваемой задачи, согласно формулам
A2.88), определяются соотношениями:
at — 00 =
2oj с.
3e?
20/ zc.
2а, с
A3.84)
Из формул A3.84), учитывая выражение A3.77), получаем
2ст,- с
A3.85)
Преобразуем теперь выражения A3.85) при помощи соотноше-
соотношений A2.89), A3.83) и A3.81).
Тогда получим
п+1
п+1
а,—аг = -
2 "
A3.86)
Подставляя первое соотношение A3.86) в дифференциальное
уравнение равновесия элемента трубы F.5), имеем
dor
п+1
п 1
"+1 •
п
Проинтегрируем это уравнение по радиусу, тогда
п+1 _1_
A3.87)
Используя краевые условия:
при г = Г! аг=—р, при г =гг сгг = 0, из соотношения A3.87)
329

получаем
п+1
± i
± ± i 1
P = ^Gf) Ы —П— A3-89)
Из выражения A3.89) следует, что .
п гп
2 2
n+1 1
. я - n
Подставим соотношения A3.90) в уравнение A3.88). Тогда, ис-
используя выражение A3.89), получим формулу для радиального на-
напряжения
~
гхп
Формулы для окружного и осевого напряжений выводим из вы-
выражений A3.86), используя соотношения A3.90) и A3.88):
A3.93)
На рис. 13,19 представлены эпюры напряжений в толстостенной
трубе, подверженной воздействию внутреннего давления. При этом
принято, что отношение внутреннего радиуса трубы к наружному
— = 0,5, а величина показателя степени п — 3. Эпюры окружных
напряжений при установившейся ползучести и в пределах упруго-
упругости различны. При установившейся ползучести наибольшее окруж-
окружное напряжение возникает в точках наружного контура, а не
в точках внутреннего контура, как в пределах упругости.
330

Определим радиальное перемещение, возникающее за счет пол-
ползучести материала трубы. Из формулы A3.90) имеем
.22
• 2n"
п
Рп
2_\n
, n
Q.
Подставляя это соотношение в уравнение A3.80), получаем
п+1
IIе = ¦
2пп
РП
-2 2
Г2Т\
2 \п
ri- —ri
Q.
A3.94)
Докажем теперь, что осевая дефор-
деформация трубы равна нулю в том случае,
когда продольна'я сила возникает только
за счет давления на днища.
Подставляя в формулу F.97) соотно-
соотношение A3.93), после интегрирования и
преобразований получаем выражение
F.28), что и подтверждает сказанное.
В работах [19, 20] даны решения
задач установившейся ползучести тол-
толстостенной ¦ трубы, нагруженной внут-
внутренним давлением и изгибающим момен-
моментом, а также внутренним давлением и
крутящим моментом.
§ 89. Вращающиеся диски
Как уже отмечалось в § 81, решение
р'р ' р
1,5
0,6
0.5
\
\^
\
ч
/
1— "
у
6l
*
0.5
0,6 0,7 Ofi 0,9 r/r2
Рис. 13.19. Эпюры напряже-
напряжений в толстостенной трубе,
нагруженной внутренним
давлением при установившей-
установившейся ползучести (сплошные
линии) и в пределах упру-
упругости (штриховые линии)
задач установившейся ползучести экви
валентно исследованию пластического со-
состояния при заданной зависимости интен-
интенсивности напряжений от интенсивности де-
деформаций,. Поэтому расчет диска на уста-
установившуюся полвучесть может быть выпол-
выполнен, например, методом переменных параметров упругости (см. §40).
Ниже изложено решение задачи установившейся ползучести вра-
вращающегося с постоянной угловой скоростью со равномерно нагре-
нагретого диска переменной толщины при использовании степенной зави-
зависимости интенсивности деформации ползучести от интенсивности
напряжения A2.89). В решении использован метод последователь-
последовательных приближений.
Дифференциальное уравнение движения элемента диска пере-
переменной толщины имеет вид [8]
331
где у — удельный вес материала диска.

Проинтегрируем его в пределах от г{ до г, учитывая, что на вну-
внутреннем контуре при г =гх аг = —рх. Тогда получим
arrh + ptfjix — J athdr + Ф =0, A3.95)
где
Г
A3.96)
Отметим, что при г = гх
Ф = 0. A3.97)
Интеграл в формуле A3.96) представляет собой момент инерции
части радиального сечения диска относительно его оси.
Полагая в уравнении A3.95) г = гг и учитывая, что на внеш-
внешнем контуре при г — г2 ог = р2, получаем
р2/-2Л2 + pjrjhi — J athdr + Ф2 = 0, A3.98)
»ч
Где Ф2 — значение функции Ф на внешнем контуре.
Из уравнения A3.35) имеем
J ath dr - ф\. A3.99)
Перейдем к рассмотрению деформации. Как и в предыдущем
параграфе, окружная и радиальная деформации ползучести в не-
некоторой точке диска на расстоянии г от центра могут быть выра-
выражены через радиальное смещение ис в этой точке, возникающее за
счет ползучести материала, соотношениями A3.78).
Исключая из выражений A3.78) радиальное перемещение и0, по-
получим условие совместности деформаций в виде
дес
г-о+ + е° — е°=О. A3.100)
Зависимости компонентов деформаций ползучести от компонентов
напряжения определяются формулами A2.88). Преобразуя эти урав-
уравнения для рассматриваемого частного случая плоского напряжен-
напряженного состояния (о2 =ч=.0), получаем
8?=-|-B0, — or), er = ^Bor — ot), A3.101)
где
Y — otar + al A3.103)
332

Из выражения A3.102), используя соотношения A2.89) и (-13.103),
получаем i
п—\
Х = о?~1а=(<х? — atar-\- a2) 2 Q. A3.104)
Подставляя зависимости A3.101) в уравнение A3.100), имеем
г 4г 1% Bа, — а,)] + Зх (а, - а,) = 0.
Поделим каждый член этого равенства на х B°t — аЛ). Тогда
получим
д
дл 3 !-В A3.105)
%Bot—or)
г 2 —
где
A3.106)
Интегрируя уравнение A3.105), устанавливаем, что
In [Х Bа, - а,)] - 1п С = -3 J 1=| -^
и, следорательно,
-3 JyErfr '
г, /
где С — некоторая функция времени.
Подставляя в это выражение соотношение A3.104) и используя
обозначение A3.106), имеем
fl—1 /Г \
откуда
где
j
)
1 —
n—i
B-P)J
A3.107)
A3.108)
Для диска без отверстия в центральной точке при г = 0 а, = аг
Поэтому согласно выражению A3.106) в центральной точке при г = 0
Р = 1. В связи с этим для центральной точки подынтегральная
функция в интеграле, входящем в выражение A3.108), обращается
333

в неопределенность. Можно показать после раскрытия неопределен-
неопределенности, что она равна нулю, т. е.
lim-н—? =0.
Далее из соотношения A3.108) следует, что в диске без отвер-
отверстия для центральной точки при г = 0 г\ = 1.
Для определения функции времени С" в формуле A3.107) под-
подставим окружное напряжение по формуле A3.107) в уравнение A3.98).
После преобразований получим
hr\ dr
и, следовательно, на основании соотношения A3.107)
/it] dr
Подставляя выражение A3.109) в интегральное уравнение равно-
равновесия A3.99), получаем
^t^^ ldr-o\ A3.110)
J /IT]
Выясним, что дают формулы A3.109) и A3.110) в центральной
точке диска без отверстия. Полагая в формуле A3.109) гг — 0 и
г == 0, используя соотношение A3.108), имеем
аA = ±Щ1т^_ A3.111)
kx\ dr
Подставляя в формулу A3.110) г = 0 и /¦? = 0, раскрывая не-
неопределенность и используя соотношение A3.108), получаем
/Ц A3.112)
I I I j /it) dr
0
334

Сопоставляя выражения A3.111) и A3.112), заключаем, что
в центральной точке диска без отверстия <jtl = ari; это, как оче-
очевидно, и должно иметь место.
Уравнения A3.109) и A3.110) являются основными уравнениями
расчета диска при установившейся ползучести. По ним определяются
напряжения. После этого может быть подсчитано радиальное пере-
перемещение, возникшее за счет ползучести материала диска. Из первой
формулы A3.78) имеем
Подставим в это соотношение окружную деформацию ползу-
ползучести по формуле A3.101), используя при этом выражение A3.104).
Тогда получим
^B o2rJ Bot — or)ttr. A3.113)
Уравнения A3.109) и A3.110) будем решать по метрду последова-
последовательных приближений. В исходном нулевом приближении примем,
что напряжения распределяются таким же образом, как и в пре-
пределах упругости; такой выбор нулевого приближения обеспечивает
достаточно быструю сходимость процесса.
После подсчета напряжений в нулевом приближении из соотно-
соотношения A3.106) определим величину р\ Затем по формуле A3.108)
подсчитаем функцию ц. После этого с помощью выражений A3.109)
и A3.110) вычислим окружное и радиальное напряжения в первом
приближении.
В дисках без центрального отверстия очень часто на большей
части радиуса (от центра до обода) окружное и радиальное напряже-
напряжения почти постоянны и равны между собой. В таком случае расчет
значительно упрощается, поскольку на указанном участке в первом
приближении можно допустить, что величины {J и ц равны единице.
Напряжения во втором и последующих приближениях подсчиты-
подсчитывают так же, как и в первом приближении, причем за исходные при-
принимают напряжения предыдущего приближения. Как следует из
многочисленных расчетов, второе приближение дает очень хорошую
степень точности. В случае грубых, ориентировочных подсчетов
можно ограничиться даже первым приближением.
Пример. Определить напряжения и зависимость от времени радиального
перемещения на наружной поверхности обода для диска газовой турбины, профиль
которого изображен на рис. 13.20, а. Частота вращения п = 7200 об/мин. Интен-
Интенсивность равномерно распределенной по наружной поверхности обода нагрузки
р2 = 173 МН/м2. Давление на внутренней расточке равно нулю. Температура
равномерного нагрева диска 600° С. Материал диска—сталь 45Х14Н14В2М. Удель-
Удельный вес у = 0,0785 МН/м3. Среднее значение коэффициента линейного расширения
в интервале температур 20—600° С аср = 18-10~6 1/°С. Модуль упругости при тем-
температуре 600° С Е = 1,40 • 105 МН/м2. На рис. 13.21 изображен ориентировочный
график функции Q для стали 45Х14Н14В2М при 600° С. Величина показателя
степени для этой стали при указанной температуре п = 3,00.
Вначале методом, изложенным в книге [8], определяем напряжения в нулевом
приближении (ст/)о и (о>)о (в пределах упругости). При этом коэффициент поперечной
деформации принимаем равным 0,5. Эти величины приведены в табл. 13.1. Затем
335

из соотношения A3.106) устанавливаем величину р\ после чего по формуле A3.108)
подсчитываем функцию т). Эту функцию умножаем на толщину диска и потом вычис-
г
ляем интеграл | tn\ dr. Произведенные подсчеты позволили по формулам A3.109)
и A3.110) определить напряжения в первом приближении. Вычисление напряжений
во втором приближении производим в таком же порядке, как и в первом прибли-
а)
150 200 250 6t>(>rMrf/M2
Рис. 13.20. Эпюры напряжений в диске газовой турбины в нулевом (штрих-
пунктирные линии), первом (штриховые линии) и втором (сплошные линии)
приближениях
жении, с тем отличием, что величину Р определяем по напряжениям первого при-
приближения. Результаты подсчетов сведены в табл. 13.2.
Из эпюр (рис. 13.20, б) следует, что напряжения второго приближения незна-
незначительно отличаются от соответствующих величин первого приближения.
336

Таблица 13.1
К расчету диска газовой турбины на ползучесть.
Подготовка расчета
г, см
5
7
9,5
11
14
18
22
26
28,5
29,5
30
h, см
8
8
6,4
4,4
3,7
3,1
2,5
1,9
2,0
2,6
3,0
г
J hr' dr, см4
rs
0,0
581,3
1 918
2 732
4 588
8 062
12 520
17 570
20 830
22 770
24 010
Ф, Н
0
26 440
87 250
124 300
208 700
366 800
569 500
799 200
947 500
1 036 000
1 092 000
(ст/)о
(Мо
МН/мв
341,0 .
254,4
223,1
242,2
246,0
249,3
257,8
275,3
253,9
218,9
214,7
0,0
78,34
135,6
199,9
226,7
242,4
260,5
290,9
246,1
178,4
172,8
После вычисления напряжений определяем перемещения. Установим зависи-
зависимость от времени радиального перемещения в точках наружного контура. Для этого
находим из табл. 13.2 напряжения на наружном контуре диска во втором прибли-
приближении. Они равны: (сг<2)ц = 276 МН/м2; (стГ2)ц= 173 МН/м2. Подставляя эти вели-
величины в формулу A3.113) и учитывая, что п~ 3,00 и г = гг = 30 см, получаем
величину радиального перемещения, образовавшегося за счет ползучести мате-
материала, в зависимости от времени
<4= 0,03332- 1013Q.
Полное радиальное перемещение складывается из радиального упругого пере-
перемещения, возникающего в начальный момент времени в результате вращения и™
и нагрева и*, и радиального перемещения, образующегося за счет ползучести мате-
материала диска.
Величина и™ определяется формулой
^=4[(°(.)о-и»,.)о], A3-114>
где (а<2)о и (о>2)о — окружное и радиальное напряжения в точках наружного кон-
контура в пределах упругости. Как следует из табл. 13.1 (Ot2)o = 215 МН/м2, (сгГг)о =
= 173 МН/м2. Подставляя их в формулу A3.104) и учитывая, что модуль упругости
Е = 1,40 -105 МН/м2, получаем и% = 0,0275 см.
Величина
4 = «с
-о.)'
A3.115)
где О — температура нагрева диска; #н — начальная температура ненапряженного
диска, которую примем равной 20° С. По формуле A3.115), учитывая, что аср =
= 18 -10 6 1/°С, получаем «* = 0,313 см. Полное радиальное перемещение точек
наружного контура в начальный момент времени определяем путем сложения ра-
радиальных перемещений, возникших в результате вращения и нагрева диска
и2 @) = и® + tq = 0,341 см
337

зучесть
ч
о
Б
X
3
турби
о
ска га:
к
К расчету
в
1
<а-
X
о
J
J
иэ 'Uy
U
„U
J J
¦> a-s r°o
¦ip a-1J b"
иэ/1 .-^-1^
1 i d-i
,) j («d + d-i)
1-й
sd
d
ИЭ 'J
иближе
ft
с
9i
О
CO
cu
о см
ocoooco^cMcooicoco
^^ QQ f О ih« ^* ^^ CQ t*4^ <^^ IjO O^
—'CMCMCMCMCOCMCM—<
сл^сосо^тсосо — coo
CMCNCMCMCMCNCMCMCNCMCM
gCD^COCOg^^-^O,
О O^ CO O3 *-* О 00 lO 00 ^Э ^~-
O 00 Ol ^? O^ ^~- 00 Ol "^* О CO
COCO^CO<M<M СЧ
0,7937
0,7760
0,7499
0,7387
0,7194
0,7101
0,7151
0,7258
0,7268
0,7231
0,7209
0,5000
0,4672
0,4216
0,4031 ,
0,3723
0,3581
0,3657
0,3823
0,3840
0,3781
0,3747
000
6218
4469
4055
3727
3581
3657
3822
3840
3804
3773 '
-oooooooooo
OfNlO NO COOCON
ooooo^-oooo
0,1000
0,05843
0,02963
0,01353
0,005196
0,001497
—0,005055
0,001041
0,005288
0,005443
000
331
060
006
001
000
9999
9997
000
006
007
(М____-,О0-< — —
00000
09480
3698
6810
8492
9454
022
115
9397
6644
6477
OOOOOO--OOO
0,000
0,3079
0,6081
0,8252
0,9215
0,9723
1,011
1,056
0,9694
0,8151
0,8048
in 1О1Л.
ion m—« ^c оо см cooo'mo
—¦—'—'CM CM CM <M CO
s
иближе
ft
с
cu
о
$
m
oco — o>o — cococMcMco
— CMCMCMCMCOCMCM —
cocoot^-*ooco —cnco
CMCMCMCNCMCMCMCMCMCMCM
ОСМ1П — OOOO^COO —
О ^ t*4* 00 ^* —« ^^ CD O) CM CO
in ^^ со ^э со ^^ —«см ^^ со со
COCO^COCMCM —— —<—«CM
0,7937
0,7642
0,7324
0,7290
0,7119
0,7133
0,7244
0,7505
0,7596
0,7547
0,7442
0,5000
0,4463
0,3928
0,3874
0,3607
0,3629
0,3801
0,4227
0,4382
0,4299
0,4121
000
6186
,4348
3901
3606
3628
3795
,4183
4382
,4351
4302
-oooooooooo
,0000
,4803
,8328
,9414
020
,014
,9690
,8715
,8250
,8322
,8436
tt_il C'i t'i t,_,J ¦*—Щ r~* L,_,J t'i t,_,J t'i t'i
0,1000
0,06014
0,03387
0,01445
0,003103
x—0,002074
—0,005445
—0,01078
—0,001615
0,006414
0,008693
ооооост>ст>стэсоо—'-*
см — —< — oooo — —«—<
00000
07426
2764
6579
9113
073
225
,486
,090
,5878
4189
OOOOO — —' — — OO
0,0000
0,2725
0,5257
0,8111
0,9546
1,036
1,107
1,219
1,044
0,7667
0,6472
_4_h--hCN<NCS)C4CO
338

Складывая теперь эту величину с найденным выше пластическим радиальным
перемещением, окончательно получим зависимость от времени полного радиального
перемещения точек наружного контура,
- ~ и2 = 0,341 + 0,333- 1013Q.
На рис. 13.22 представлен построенный по этой формуле график зависимости «2
от времени.
Как следует из этого графика, за время, равное 500 ч, радиальное перемещение
возрастает примерно на одну четверть величины радиального перемещения в на-
начальный момент времг-нч.
о
Рис. 13.21. Ориентировочный график
функции п для стали 45Х14Н14В2Мпри
температуре 600° С
Рнс. 13.22. График зависимости от време -
ни радиального перемещения в точках
наружного контура, диска
§ 90. Использование критерия Треска—Сен-Венана
Из предыдущего параграфа следует, что решение задачи уста-
установившейся ползучести при плоском напряженном состоянии (вра-
(вращающийся диск) сложнее, чем при плоской деформации (толстостен-
(толстостенная труба). Для осесимметричных задач плоского напряженного
состояния возможно упрощение решений за счет использования кри-
критерия Треска — Сен-Венана. Этот вопрос был исследован В. И. Ро-
зенблюмом [16]. Ю. В. Немировским [12] для решения таких задач
применен критерий максимального приведенного напряжения.
В случае использования критерия Треска — Сен-Венана потен-
потенциал деформаций ползучести может быть представлен в виде
fx = а, _ аз _ ф (eJ) =0, A3.116)
причем
Используя ассоциированный закон течения A2.8) и соотноше-
соотношение A3.116), получаем
El = А, Е2 = U, 8з = — Л. ^lo.II//
Поскольку в случае одноосного растяжения зависимость дефор-
деформации ползучести от напряжения определяется формулой A1.13),
получаем X = (а1 — а3)п Q и, следовательно,
К — о3)"п, е| = 0, г1 = - (о, — 03)"
A3.118)
339

Последние соотношения могут быть использованы для расчета
вращающихся дисков.
В случае равномерно нагретого диска с отверстием, когда erf = at,
ст2 = ог, о3 = 0 согласно соотношению A3.118) имеем
et = o?Q; er = 0; ег = — о"п.
Вспоминая зависимости A3.78), получаем
^ A3.119)
Использование дифференциального уравнения движения диска
и краевых условий для радиальных напряжений совместно с соот-
е ношением A3.119) позволяет опре-
определить радиальное и окружное на-
напряжения.
' Если диск не имеет отверстия,
{ то тогда в окрестности централь-
центральной точки (круг радиуса rt) ot = аг,
что соответствует ребру с призмы
Треска—Сен-Венана (рис. 13.23).
Ребро с является пересечением пло-
плоскостей ас и се.
Для точек плоскости ас ot =ot;
о2 = о,; ст3 = О
и согласно формулам A3.118)
Рис. 13.23. Графическое изображе- Et = OtQ; ег = 0; ег = —Щ
ние условия Треска—Сен-Венана
Для точек плоскости се о
а2 =ot; a3 = 0 и по тем же соотношениям A3.118)
= ог;
Как отмечалось в § 22 [см. формулу D.17)], течение на ребре
получается комбинацией течений справа и слева от ребра, т. е.
на ребре с
Полагая Xt + k2 —l и учитывая, что ot = or, получаем в точ-
точках ребра с
ect = Лю?О; е^ = (!— li)o"Q; ec2=—o^ A3.120)
причем 0 «^ кх =^ 1.
. Таким образом, если диск без отверстия, возможны две области
0^г<Г! и rx s^ r ^ г2. В первой справедливы соотношения
A3.120), а во второй A3.119).
Подробное изложение решений задач установившейся ползучести
дисков на основе этих соотношений приведено в работах [3, 23,
29—31 ].
340

В качестве примера рассмотрим растяжение бесконечной пла-
пластины с отверстием силами, приложенными на бесконечности о'сесим-
метрично относительно центра отверстия в условиях плоского на-
напряженного состояния (см. рис. 6.8). В этом случае
Oi =.ст,; а2 = ог; а3 = О,
причем радиальное перемещение ис является функцией только вре-
времени и от радиуса не зависит.
Из выражения A3.119) устанавливаем закон изменения по ра-
радиусу окружного напряжения
?Г- A3Л21)
Дифференциальное уравнение равновесия элемента пластины
имеет такой же вид, как и дифференциальное уравнение равновесия
элемента трубы F.5). Оно может быть представлено в форме
Подставим в это уравнение соотношение A3.121). Тогда получим
Интегрируя это уравнение, имеем
иСУТг--7Г+ —
' г
Используем краевое условие
при г — гх аг — 0.
Тогда устанавливаем
и, следовательно,
<13-122)
Как следует из формул A3.121) и A3.122), при увеличении ра-
радиуса окружное напряжение уменьшается, а радиальное возрастает.
Однако радиальное напряжение не может быть больше окружного,
так как это означало бы равенство нулю радиального переме-
перемещения.
341

Найдем радиус окружности г*, в точках которой радиальное
и окружное напряжения равны между собой. Приравнивая соотно-
соотношения A3.121) и A3.122), получаем
— «"~l rt.
A3.123)
При г <: г* законы изменения окружного и радиального напря-
напряжений определяются формулами A3.121), A3.122). При г ?> г* они
равны между собой и, как это следует из краевого условия, при
г —* оо ог —» р,
при г г> г*
о, -стг =/?. A3.124)
Приравнивая окружное напряжение при г = г* величине /7,
получаем
/_|Ljn =p(r*)T A3.125)
и, следовательно,
ыс =p"r*Q. A3.126)
ч
———
-—_
5 7
Рис. 13.24. График зависимости от пока-
показателя степени п коэффициента концентра-
концентрации напряжений в бесконечной пластине
с отверстием, растянутой силами, прило-
приложенными на бесконечности симметрично
относительно центра отверстия, в усло-
условиях плоского напряженного состояния
Используя соотношения A3.125) и A3.123), преобразуем фор-
формулы для напряжений A3.121) и A3.122) к окончательному виду
A3.127)
A3.128)
Из формулы A3.128) следует, что наибольшее окружное напря-
напряжение возникает в точках внутреннего контура при г = гх и коэф-
коэффициент концентрации напряжений
k = п
п'х
A3.129)
На рис. 13.24 предста'влен график зависимости его от показа-
показателя степени п.
342

При п = 1
1
in-i =e==2,78.
Как известно, в пределах упругости величина его равна двум.
Таким образом, в этом случае погрешность рассмотренного решения
составляет 36%, т. е. весьма значительна.
Эта задача применительно к пластическому и упруго-пластиче-
упруго-пластическому деформированию с использованием критериев Хубера—Мизеса
и Треска—Сен-Венана была решена в работах [4, 11].
Список литературы
1. Вылекжанин В. Д. Неравенства для жесткого кручения призматического
стержня при установившейся ползучести.— «Известия АН СССР. Механика твер-
твердого тела», 1972, № 5, с. 191—195.
2. Качанов Л. М. Приближенное решение задач установившейся ползучести.—
«Известия АН СССР. Отд. техн. наук. Механика и машиностроение», 1959, № 3,
с. 84—95. '
3. Качанов Л. М. Теория ползучести. М., Физматгиз, 1960, 455 с.
4. Костюк А. Г. О равновесии кольцевой пластинки при степенном' законе
упрочнения. — «Прикладная математика и механика», 1950, т. XIV, вып. 3, с.
319—320.
5. Малинин Н. Н. Основы расчетов на ползучесть. М., Машгиз, 1948, 120 с.
6. Малинин Н. Н. Расчет на ползучесть вращающихся неравномерно нагре-
нагретых дисков переменной толщины.—В кн.: Вопросы прочности материалов и кон-
конструкций. М., Изд-во АН СССР, 1959, с. 268—286.
7. Малинин Н. Н. Закономерности ползучести металлов и расчеты ма ползу-
ползучесть деталей машин.— «Вестник машиностроения», 1959, № 1, с. 6—14.
8. Малинин Н. Н. Прочность турбомашин. М., Машгиз, 1962, 291 с.
9. Малинин Н. Н. Обзор отечественных работ по расчетам деталей машин
на ползучесть.— В кн.: Расчеты на прочность. [Сборник статей], вып. II, М., «Ма-
«Машиностроение», 1965, с. 229—278.
10. Малинин Н. Н. Ползучесть элементов машин. Обзор.— В кн.: Расчеты
на прочность. [Сборник статей]. Вып. 14, М., «Машиностроение», 1969, с, 217—267.
11. Махонина Т. М. Упруго-пластическое состояние шайбы при степенном
упрочнении материала.— В кн.: Расчеты на прочность. [Сборник статей]. Вып. 5.
М., Машгиз, 1960, с. 97—106.
12. Немировский Ю. В. Об уравнениях ползучести, основанных на критерии
максимального приведенного напряжения.— «Известия АН СССР. Механика и
машиностроение», 1964, № 3, с. 117—122.
13. Работиов Ю. Н. Ползучесть элементов конструкций. М., «Наука», 1966,
752 с.
14. Расчеты конструкций на тепловые воздействия. М., «Машиностроение»,
1969, 599 с. Авт.: В. Л. Бажанов, И. И. Гольденблат, Н. А. Николаенко, А. М. Си-
нюков.
15. Расчеты на прочность в машиностроении. Т. II. М., Машгиз, 1958, 974 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К. К- Лихачев и др.
16. Розенблюм В. И. О приближенных уравнениях ползучести.— «Известия
АН СССР. Отд. техн. наук. Механика и машиностроение», 1959, № 5, с. 157—160.
17. Смирнов В. И. Курс высшей математики. Т. 3, ч. 2, М., Физматгиз-, 1958,
674 с.
18. Стасенко И. В. Установившаяся ползучесть тонкостенной трубы в общем
случае действия сил.— «Известия высших учебных заведений. Машиностроение»,
1973, № 7, с. 21— 25.
343

19. Стасенко И. В. Установившаяся ползучесть толстостенной трубы при дей-
действии внутреннего давления и изгибающего момента.— «Известия высших учетных
заведений. Машиностроение», 1973, № 8, с. 18—22.
20. Стасенко И. В. Установившаяся ползучесть толстостенной трубы.— «Изве-
«Известия высших учебных заведений. Машиностроение», 1974, № 2, с. 14—17.
21. Феодосьев В. И. Сопротивление материалов. М., «Наука», 1974, 559 с.
22. Филоненко-Бородин М. М. Теория упругости. М., Физматгиз, 1959, 364 с.
23. Creep tests of rotating disks at elevated temperature and comparison with
theory, «Journal of applied mechanics», 1954, Uol. 21, No 3, p. 225—235. Aut.:
A. M. Wahl, Q. O. Sankey, M. J. Manjoine, E. Shoemaker.
24. Finnie I., Heller W. R. Creep of engineering materials, Me. Graw—Hill Book
Company, Inc. 1959, 341 p.
25. Hult J. Creep in egineering structures, Blaisdell Publishing Company, 1966,
115 p.
26. Lubahn J. D., Felgar R. P. Plasticity and creep of metals, John Wiley and
Sons, Inc., 1961, 608 p.
27. Odqvist F. K- G., Hult J., Kriechfestigkeit metallisher Werkstoffe, Spring-
Springier—Verlag, 1962, 303 s.
28. Odqvist F. K- G. Mathematical theory of creep and creep rupture, Clarendon
Press, 1966, 170 p.
29. Wahl A. M. Analysis of creep in rotating disks based on the Tresca criterion
and associated flow rule.—«Journal of applied mechanics», 1956, Vol. 23, No 2, P- 231—
238.
30. Wahl A. M. Stress distributions in rotating disks subjected to creep at elevated
temperature. —«Journal of applied mechanics», 1957, Vol. 24, No 2, p. 299—305.
31. Wahl A. M. Futher studies of stress distribution in rotating disks and cylin-
cylinders under elevated temperature creep conditions.—«Journal of applied mechanics»,
1958, Vol.25, No2, p. 243—250.

ГЛАВА XIV
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НЕУСТАНОВИВШЕЙСЯ
ПОЛЗУЧЕСТИ
§ 91. Теория старения
В решениях задач неустановившейся ползучести в отличие от
задач установившейся ползучести учитывается изменение напряже-
напряжений во времени. Последнее позволяет решать задачи при перемен-
переменных во времени нагрузках, что недопустимо в предположении уста-
Рис. 14.1. Эпюры окружных на-
напряжений для различных значений
времени (сплошные линии) и в пре-
пределах упругости (штриховая линия)
в равномерно нагретом до темпера-
температуры 575° С диске постоянной тол-
толщины с отверстием из стали РЗ [14]
196
98
/
/
г /
/
/
200 ч
^50ч
~~10ч
1
1
1
/
1
1
/
/
10
50
392
новившейся ползучести. Перед тем
как решать задачу неустановив-
неустановившейся ползучести, необходимо вы-
выбрать теорию ползучести. Рас-
Рассмотрим вначале применение тео-
теории старения в решениях задач
неустановившейся ползучести. Как
уже указывалось в § 75, опре- ;* '° 6 г'см
деление напряжений и деформаций для некоторого значения времени
по теории старения эквивалентно решению задачи по теории малых
упруго-пластических деформаций для известной диаграммы дефор-
деформирования. Этой диаграммой является изохронная кривая ползу-
ползучести. Для установления кинетики напряженного и деформирован-
деформированного состояния необходимо произвести ряд однотипных расчетов пс
различным изохронным кривым деформирования. В случае постоян-
постоянных во времени внешних силах напряженное состояние с течением
времени стабилизируется, приближаясь к состоянию установившейся
ползучести.
На рис. 14.1 представлены полученные расчетом эпюры окруж-
окружных напряжений для различных значений времени в равномерно
нагретом вращающемся диске постоянной толщины с отверстием [ 14 ].
345

Как следует из этих эпюр, напряжения почти полностью перерас-
перераспределяются за первые десять часов.
В литературе [8—12] приведены методы расчетов многих эле-
элементов машиностроительных конструкций по теории старения.
§ 92. Теория течения
Рассмотрим применение теории течения в расчетах на неустано-
неустановившуюся ползучесть на примере простейшей задачи чистого из-
изгиба бруса прямоугольного' поперечного сечения (рис. 14.2). По-
Рис. 14.2. Брус прямоугольного поперечного сечения в усло-
условиях чистого изгиба
скольку при чистом изгибе бруса поперечное сечение его остается
плоским, деформация е в точках на расстоянии у от нейтральной
оси связана с кривизной х соотношением
е = ух.
Дифференцируя его по времени, получим скорость деформации
I =ух, A4.1)
dy.
где х. =¦
dt
скорость изменения кривизны.
Выражение для скорости деформации в частном случае одноос-
одноосного напряженного состояния (oi = а, а0 = -?-) по теории тече-
течения согласно формулам A2.7) и A2.24) имеет вид
Сопоставляя выражения A4.1) и A4.2), имеем
A4.2)
A4.3)
Зависимость изгибающего момента М от нормальных напряже-
напряжений а в рассматриваемой задаче определяется формулой
А
2
М = 2?>J oydy. A4.4)
о
Таким образом, для определения двух функций х = х (t) и
о = о (у, t) получены два уравнения A4.3) и A4.4). Решение их
346

связано с большими трудностями. В более сложных задачах эти
трудности возрастают. Поэтому в расчетах на неустановившуюся
ползучесть большое значение имеют приближенные методы. Ниже
будет изложен установленный Л. М. Качановым [3, .4] вариацион-
вариационный принцип минимума дополнительной мощности, а затем рас-
рассмотрены основанные на нем приближенные методы решения задач,
разработанные также Л. М. Качановым [3, 4].
А. А. Ильюшиным и И. И. Поспеловым [2, 13] разработан метод
последовательных приближений в решении задач неустановившейся
ползучести по теории течения. В этом методе нелинейная задача
неустановившейся ползучести по теории течения сводится к после-
последовательности задач линейной теории вязкоупругости с нестацио-
нестационарными (фиктивными) внешними силами.
§ 93. Принцип минимума дополнительной мощности
В § 42 был установлен принцип возможных изменений напряжен-
напряженного состояния, который записывается в виде равенства G.7). Пере-,
ходя в нем от перемещений и деформаций к их скоростям, имеем
J 8XiVidV + J 8XvivtdS = J botjllsdV. A4.5)
V S V
Скорости деформаций по теории течения определяются формулой
A2.7). Первое слагаемое в этой формуле представляет собой скорость
упругой деформации.
Компоненты упругой деформации связаны с удельной потенциаль-
потенциальной энергией деформации U соотношением C.7). Последняя может
быть представлена в виде
Формулы C.7) и A4.6) могут быть получены из соотношений (ty
и G.10). Для этого следует использовать зависимости между интен-
сивностями напряжений и деформаций в пределах упругости а(. =
= 3Ge(..
Таким образом, скорости упругой деформации
Аналогично тем же соотношениям G.9) и G.10), учитывая, что
в условиях ползучести изменение объема равно нулю (ц = 0,5;
К == оо), можно получить скорость деформации ползучести
?с дА
347

где функция напряжений и времени
Uoi . A4.9)
называется дополнительным рассеянием.
В случае степенной зависимости интенсивности скоростей дефор-
деформаций от интенсивности напряжений A2.24) выражение A4.9) при-
принимает вид
Л _ °"+lB A4.10)
rt+1 *
Складывая соотношения A4.7) и A4.8), получаем скорости пол-
полной деформации
Функцию
W:=^r + A A4Л2)
назовем дополнительной мощностью деформации. Тогда
dW
и соотношение A4.5) принимает вид
J bXfli dV+j 8Xviv{ dS = 8W, A4.14)
V S
где
A4.15)
— дополнительная мощность деформации всего тела.
Рассмотрим три задачи неустановившейся ползучести для случая
отсутствия объемных сил 8Х( = 0.
1. Основная задача. На всей поверхности тела заданы
напряжения. Тогда &Xvi = 0.
2. Релаксационная задача. На всей поверхности
тела заданы постоянные во времени смещения. Тогда скорости их
Vi = 0.
3. Смешанная задача. На части поверхности тела St
заданы напряжения, а на другой ее части S2 постоянные во времени
смещения. Тогда на St 8Xvi =0, на S2 vt —0.
Этими тремя случаями не исчерпываются все возможные задачи
неустановившейся ползучести.
348

Однако для них соотношение A4.14) принимает особенно про-
простой вид
8W =0. A4.16)
Можно доказать, что вторая вариация дополнительной мощности
деформации положительна [4]. '
Таким образом, для указанных частных случаев получаем прин-
принцип минимума дополнительной мощности деформации, согласно ко-
которому из всех статически возможных напряженных состояний
только для истинного напряженного состояния дополнительная мощ-
мощность деформации всего тела принимает минимальное значение.
§ 94. Приближенные методы решения задач
неустановившейся ползучести
Рассмотрим приближенные методы решения основной и релак-
релаксационной задач неустановившейся ползучести.
В случае основной задачи приближенное решение записывают
в форме
°ц = о'ц + X \о"ц — о'ч), A4.17)
где a'tf — напряжения в пределах упругости, o'lj — напряжения,
вычисленные в предположении установившейся ползучести, % =
= % @ — функция времени.
Допустим, как обычно, что в начальный момент времени пласти-
пластические деформации отсутствуют и что с течением времени распреде-
распределение напряжений стремится к установившемуся. В таком случае
значения функции % для нулевого значения времени и для бесконеч-
бесконечности % @) = 0, % (оо) = 1.
Если использовать выражение A4.17), то тогда из формул A4.15),
A4.12), A4.6) и A4.10) очевидно, что дополнительная мощность
деформации всего тела является функцией параметра х- Условие
минимума этой функции имеет вид
Из этого условия может быть найдена функция х = 1 @- После
этого при помощи формул A4.17) могут быть подсчитаны напря-
напряжения, а затем на основании соотношений A2.7) скорости деформаций.
В случае релаксационной задачи неустановившейся ползучести
лриближенное решение записывают в форме
оч =va'ih A4.19)
где v = v (t) — функция времени.
Поскольку, как было принято ранее, в начальный момент вре-
иени пластические деформации отсутствуют и с течением времени
спряжения стремятся к нулю, v @) =, v (oo) = 0.
349

В рассматриваемой задаче дополнительная мощность деформации
всего тела является функцией параметра v и поэ-гому условие ми-
минимума этой функции имеет вид
4?- = 0- A4.20)
Из этого условия определяется функция v = v (t). После этого
при помощи формулы A4.19) могут быть подсчитаны напряжения.
Рассмотрим решение основной задачи для чистого изгиба бруса
прямоугольного поперечного сечения (рис. 14.2). Напряженное со-
состояние во всех точках бруса одноосное (oi =a;a0 =-^-j и согласно
формулам A4.6) и A4.10) получаем
и 2Е
и, следовательно,
<*L-_Z_j?l_ /142П
dt ~ E dt ' (l^U
Л-gf-. 04.22,
Подставляя соотношения A4.21) и A4.22) в формулу A4.12),
получаем
w E dt ^ п + 1 A*.гб)
Примем нормальное напряжение а в форме A4.17)
о =0' + %(а"— о'). A4.24)
, В рассматриваемой задаче напряжение в пределах упругости
a' = ^f, A4.25)
а напряжение в условиях установившейся ползучести а" опреде-
определяется формулой A3.6). Подставляя выражения A4.25) и A3.6)
в формулу A4.24) и используя формулы A3.7) и A3.8), получаем
о = стшах @) (С + %Y), A4.26)
где
,m Mh
<W @) = -277
¦—= максимальное напряжение в начальный момент времени;
1='-Щ-\ У = Щ±&-г-1. A4,27)
350

Подставим теперь уравнение A4.26) в соотношение A4.23). Тогда
получим
W = %gL ft + %Y) Y -g- + °™ffi B (C + »y. (H.28)
Преобразуем условие A4.18), учитывая соотношения A4.15),
A4.28), а также то, что в рассматриваемой задаче
Тогда получим
1
о
После преобразований, принимая во внимание, что
^<« = 1&
9п (я + 2)
и
и обозначая
олучаем
^_+_2l?a«-@)Bd^-^. A4.29)
Введем безразмерное время
**= 9"w(!-|)a2) №i@)Q- A4.30)
Тогда выражение A4.29) примет вид
Интегрируя с учетом того, что при ^ = 0, /* = 0, х = 0. полу-
получаем
Это уравнение устанавливает зависимость безразмерного времени
5т параметра %. С помощью уравнения A4.31) может быть вычислена
зеличина % для любого значения времени, после чего по фор-
луле A4.24) можно определить напряжения, а по формуле A4.3)
жорость изменения кривизны.
351

На рис. 14.3 представлен график функции % = %(t*), где п = 3,
а на рис. 14.4 эпюры безразмерных напряжений в поперечном сече-
сечении для различных значений безразмерного времени.
0,8
0.6
0,4
0,2
/
/
/
. ¦ '
0 15 50 75 100 125 t*
Рис. 14.3. График функции % = % (P)
Разберем теперь решение релаксационной задачи для кручения
бруса круглого поперечного сечения. В этом случае напряженное
состояние во всех точках бруса — чистый сдвиг (at = У^Зт, о0 = 0)
и согласно формулам A4.6) и A4.10) имеем
- б — -- -,t*'O //__!!_
2G
0,8
0,6
О.Н
0,2
V
V
V
25
50
WO
и, следовательно,
dU т дт
я+1
Л =
. A4.33)
о
0.2
0,4
0.6
0,8
Подставляя соотноше-
соотношения A4.32) и A4.33) в
формулу A4.12), полу-
получаем
Рис. 14.4. Эпюры безразмерных напряжений в
поперечном сечении изогнутой балки для раз-
различных значений безразмерного времени t*
(сплошные линии) и в условиях установиршейся
ползучести (штриховая линия)
п+1
2
G dt
A4.34)
Примем касательное напряжение в форме A4.19)
т =vt\
A4.35)
где v — искомая функция времени: v = v (t), а т' — касательное
напряжение в пределах упругости. Последнее может быть представ-
представлено в виде
@)Р,
352

где
Р
и, следовательно,
Т = *тах @) PV- A4.36)
Подставим уравнение A4.36) в соотношение A4.34). Тогда по-
получим
A4.37)
Преобразуем условие A4.20), учитывая соотношения A4.15) и
A4.37), а также то, что в рассматриваемой задаче
Тогда получим
dv J [ G * v dt ' я + 1
Выполнив интегрирование и дифференцирование, приходим к сле-
следующему дифференциальному уравнению
я+1
Проинтегрируем последнее уравнение, введя безразмерное время
я+1
/' = (п— 1) Gx?l2 @) З^^Й. A4.38)
Тогда получим
Следовательно, согласно формуле A4.36)
Подставим эту величину касательного напряжения в выражение
для крутящего момента
2 '
| ^|р2ф. A4.40)
о о
Учитывая, что
н. Н. Малинин 353

крутйщий момент при t = О, получим закон изменения во вре-
времени крутящего момента
n. A4.42)
Рассматриваемая задача может быть решена точно в замкнутом
виде. Интересно сопоставить приведенное выше приближенное реше-
решение задачи, основанное на принципе минимума дополнительной
мощности, с точным.
JL
0,75
0,50
0,25
— —
***
Рис. 14.5. Графики изменения
во времени безразмерного кру-
крутящего момента по точному
(сплошная линия) и приближен-
приближенному (штриховая линия) реше-
решениям
О 25 50 75 ' 100 125 150 t
Разберем точное решение. Угловая деформация в некоторой точке
поперечного сечения на радиусе г связана с относительным углом
закручивания бруса 6 соотношением
Y =/-6
и, следовательно, при постоянном во времени относительном угле
закручивания угловая деформация во всех точках поперечного сече-
сечения постоянна, а скорость ее
ч\ =0. A4.43)
Согласно формулам A2.7) и A2.24) по теории течения, учитывая
К имеем
я+1
2
в,
откуда на основании выражения A4.43)
dx
= —G3 2 Bdt.
Проинтегрируем это уравнение, введя безразмерное время по
формуле A4.38). Учитывая, что при t =0 т = т @) = тшах @) р,
получаем закон изменения во времени касательного напряжения
в текущей точке поперечного сечения с безразмерной координатой р
-\\l-n
354

Подставляя это выражение в формулу A4.40) и используя соот-
соотношение A4.41), устанавливаем закон изменения во времени крутя-
крутящего момента
М = 4М @) J р3 A + ^Р")'"" dP- A4.44)
о
На рис. 14.5 представлены графики изменения во времени крутя-
крутящих моментов по точному A4.44) и приближенному A4.42) решениям
для п = 5. Как следует из рис. 14.5, различие между ними невелико.
§ 95. Теория упрочнений
Решение задач неустановившейся ползучести по теории упроч-
упрочнения связано со значительно большими трудностями, чем по дру-
другим теориям. Эффективным методом расчета с использованием элек-
электронных вычислительных машин является предложенный Ю. Н. Ра-
ботновым [15] метод расчета шагами во времени. Проиллюстрируем
этот метод на примере расчета стержневой системы, рассмотренной
в § 81 (см. рис. 12.26). Примем аналитическую формулировку теории
упрочнения A2.28) и A2.29). Задача решается на основе уравнения
равновесия A2.79), условия совместности деформаций A2.80) и зави-
зависимостей между скоростями деформаций ползучести, деформациями
ползучести и напряжениями, записанными для первого и второго
стержней.
Разобьем интервал времени, за который необходимо исследовать
процессы изменения во времени напряжений и деформаций на ряд
небольших интервалов А^, которые могут быть равны лли неравны
между собой. Допустим, что в момент времени tK напряжения и де-
деформации известны. Выведем уравнения, которые позволят по этим
величинам определить напряжения и деформации в момент вре-
времени 4+i = к + Д4-
Для этого момента времени уравнение равновесия A2.79) прини-
принимает вид
<*i,ft+i + o?.,k+i =s. A4.45)
Преобразуем условие совместности деформации A2.80), разделив
в нем полную деформацию на упругую и деформацию ползучести
и записав его для момента времени tk+1:
=, 2 (^*±Ъ + ej, ,+1). A4.46)
При помощи зависимостей A2.28) и A2.29) свяжем деформации
ползучести в моменты времени tkArl и th для первого и второго стерж-
стержней. При этом учтем, что
355

Тогда получим
82, k+1 = 82,
« (82.
СХ2,
Четыре уравнения A4.45)—A4.47) позволяют определить четыре
неизвестных: два напряжения и две деформации ползучести для мо-
момента времени tk+1 по значениям их для момента времени tk.
Уравнения A4.47) неудобны для использования в начальный мо-
момент времени, когда деформация ползучести равна нулю, поскольку
эта величина в правой части уравнений возводится в отрицательную
Рис. 14.6. График изменения
во времени безразмерного на-"
пряжения во втором стержне
для стержневой системы, пред-
представленной на рис. 12.26
t.4
степень. Для этого случая зависимости, между деформациями пол-
. зучести в моменты времени ^+i и 4 могут быть представлены
в иной форме.
Интегрируя выражение A2.28) в пределах изменения t от tk
до 4+i. используя соотношение A2.29), получаем
Полагая в течение малого промежутка времени Atk — tk+1 — tk
напряжение постоянным а = ak, получаем для первого и второго
стержней
(ef. *+1)p+1 = (ef. kf+l + а ф + 1) а?. k Atk; \
(eb+i)P+1 = (еЬ)Э+1 + аф + 1)а|. kAtk. J ^ ]
Эти уравнения несколько сложнее.уравнений A4.47), однако они
, могут быть использованы и для начального момента времени.
На рис. 14.6 изображен график изменения во времени безраз-
безразмерного напряжения во втором стержне
в предположении, что материал стержней сталь ЗОХМ, температура
ft =500° С. Постоянные в уравнениях A2.28) и A2.29) для этого
материала при указанной температуре [5]:
р = 0,630; v = 6,63;
а = 1,00-101 (m2/MH)v 1/ч.
356

Из графика следует, что так же, как и в случае решения задачи
по теории течение (см. §81), напряжения быстро изменяются от на-
начального упругого состояния до установившегося. Величина безраз-
безразмерного напряжения в условиях установившейся ползучести при
п = утгр" = 4>07> согласно формуле A2.82), (а*)" =0,543.
Список литературы
1. Биргер И. А. Расчет конструкций с учетом пластичности и ползучести.—
«Известия АН СССР. Механика», 1965, № 2, с. 113—119.
2. Ильюшин А. А., Поспелов И. И. О методе последовательных приближений
в задаче о неустановившейся ползучести. — «Инженерный Журнал», 1964, т. IV,
вып. 4, с. 697—704.
3. Качаиов Л. М. К теории неустановившейся ползучести.— «Прикладная
математика и механика», 1949, т. XIII, вып. 4, с. 381—390.
4. Качанов Л. М. Теория ползучести. М., Физматгиз, I960, с. 455.
5. Кулешова 3. Г. Проверка гипотезы упрочнения путем анализа экспери-
экспериментальных исследований • ползучести.— «Известия высших учебных заведений.
Машиностроение», 1959, № 12, с. 69—76.
6. Куратов П. С, Розеиблюм В. И. Об интегрировании уравнений неустано- .
вившейся ползучести твердых тел.— «Прикладная математика и механика», 1960,
т. XXIV, вып. I, с. 146—148.
7. Малииин Н. Н. Основы расчетов на ползучесть. М., Машгиз, 1948, 120 с.
8. Малинии Н. Н. Некоторые одномерные задачи неустановившейся ползу-
ползучести.— «Инженерный сборник», т. X, Изд-во АН-СССР, 1951, с. 17—34.
9. Малинин Н. Н. Обзор отечественных работ по расчета деталей машин на
ползучесть. В кн.: Расчеты на прочность. [Сборник статей]. Вып. II, М., «Машино-
«Машиностроение», 1965, с. 229—278.
10. Малииин Н. Н. Ползучесть элементов машин. Обзор. В кн.: Расчеты на
прочность. [Сборник статей]. Вып. 14. «Машиностроение», 1969, с. 217—267.
11. Подгорный А. Н. Ползучесть толстостенного цилиндра конечной длины.—
В кн.: Тепловые напряжения в элементах конструкций. Вып. 5, Киев «Наукова
думка», 1965, с. 260—269.
12. Подгорный А. Н. Толстостенный цилиндр конечной длины в условиях
ползучести.— В кн.: Тепловые напряжения в элементах конструкций. Вып.-11.
Киев, «Наукова думка», 1971, с. 155—159.
13. Поспелов И. И. Метод последовательных приближений в задаче о неуста-
неустановившейся ползучести и нелинейной упругости.— «Ученые записки ЦАГИ», 1970,
т. 1, № 2, с. 94—100.
14. Рабинович В. П. Прочность турбинных дисков. М., «Машиностроение»,
1966, 151 с.
15. Работнов Ю. Н. Ползучесть элементов конструкций. М., «Наука», 1966,
752 с.
16. Расчеты на прочность в машиностроении. Т. II. М., Машгиз, 1958, 974 с.
Авт.: С. Д. Пономарев, В. Л. Бидерман, К- К. Лихарев и др.
17. Шестериков С. А. Об одном вариационном принципе в теории ползучести.—
«Известия АН СССР. Отд. техн. иаук», 1957, № 2, с. 122—123.
18. Шестериков С. А. Расчет дисков на релаксацию.— «Журнал прикладной
механики и технической физики», 1960, № 1, с. 117—120.
19. Finnie I., Heller W. R. Creep of engineering materials, Me Graw—Hill Book
Company Inc, New-York, Toronto, London, 1959, 341 p.
20. Hult J. Creep in engineering structures, Blaisdell Publishing Company, Wal-
tham, Massachusetts, Tordnto, London, 1966, 115 p.
21. Lubahn J. D., Felgar R. P. Plasticity and creep of metals, John Wiley and
Sons, Inc. New-York, London, 1961, 608 p. .
22. Odqvist F. K- G., Hult J. Kriechfestigkei-t metallischer Werkstoffe, Springer—
Verlag, Berlin, Gottingen, Heidelberg, 1962, 303 s.
23. Odqvist F. K. G. Mathematical theory of creep and creep rupture, Oxford,
At the Clarendon Press, 1966, 170 p.

ГЛАВА XV
ОПРЕДЕЛЕНИЕ ВРЕМЕНИ РАЗРУШЕНИЯ
§ 96. Растяжение стержня
Выше в § 73 было рассмотрено определение коэффициента запаса
в случае одноосного растяжения как при стационарном, так и при
нестационарном режимах нагружения и нагрева. В § 82 приведена
величина эквивалентного напряжения для оценки длительной проч-
прочности при неодноосном напряженном состоянии. В простейшем слу-
случае стационарных режимов нагружения и нагрева оценка прочности
производилась путем сопоставления эквивалентного напряжения
с пределом длительной прочности. Возможен иной путь Исследования
длительной прочности: определение времени разрушения элемента
конструкции. При этом следует рассмотреть различные типы разру-
разрушений: вязкое при больших деформациях, хрупкое при малых,
а также смешанное.
Изложим вначале решение задачи определения времени вязкого
разрушения растянутого стержня. Это решение было дано Хоффом
[24]. Обозначим изменяющиеся во времени площадь поперечного
сечения стержня и его длину через F и / соответственно. Значения
их в начальный момент времени Fo и /0.
Из условия несжимаемости материала имеем
Fl = Folo. ¦. A5.1)
Напряжение в поперечном сечении стержня
р
° = -г
или с использованием соотношения A5.1)
а = -?--/-. A5.2)
го h
Ввиду того что вязкое разрушение возникает при больших дефор-
деформациях, пренебрежем упругими деформациями по сравнению с де-
деформациями ползучести, которые будем оценивать логарифмиче-
логарифмическими деформациями (см. § 15).
358

Скорость логарифмической деформации ползучести
dkc
dt
dl
dt
A5.3)
Допустим, что зависимость скорости логарифмической деформа-
деформации ползучести от напряжения является степенной, так же, как
и при малых деформациях [см. формулу A1.4)]
|с = kan.
Подставим в это выражение соотношения A5.2) и A5.3). Тогда
получим
dl feog .
/n+l- tn at-
100
50
—s
i—v
"V-
"-—,
/о2
10*
t.4
Рис. 15.1. Сопоставление графика зависимости A5.5) с результатами опытов [7]
Проинтегрируем полученное уравнение, используя условие при
t=0l=l0.
Тогда после преобразований с учетом соотношения A5.1) имеем
—
-j- = -р- == A — tika^t)n . A5.4)
Назовем временем вязкого разрушения время, для которого
площадь поперечного сечения стержня обращается в нуль или для
которого длина стержня стремится к бесконечности. Из выражения
A5.4) получаем время вязкого разрушения
tl = -l—. , A5.5)
На рис. 15.1 представлен график этой зависимости и даны точки,
полученные в опытах Ш. Н. Каца [7]. Экспериментальные данные
хорошо согласуются с теоретическими.
Однако изложенная выше концепция имеет ограниченное приме-
применение, так как она не отражает хрупкие разрушения, происходящие
при малых деформациях. В частности, согласно рассмотренной схеме,
в случае ползучести скрученного стержня невозможно разрушение,
так как при кручении не происходит изменения размеров стержня.
359

Л. М. Качановым 15, 7} была предложена теория хрупкого и
вязко-хрупкого разрушений элементов конструкций. Процесс раз-
разрушения рассматрирается как процесс возникновения и развития
трещин в условиях ползучести. При этом принимается, что процесс
развития трещин не влияет на деформацию ползучести.
Введем понятие сплошности ip, которое характеризует развитие
трещин (пбврежденность материала). В начальный момент времени
при отсутствии поврежденности ip = 1. С течением времени сплош-
сплошность ip убывает. Допустим, что в момент хрупкого разрушения
Ч> = 0.
Примем следующую зависимость сплошности от максимального
главного напряжения:
где Ант — постоянные для материала при определенной темпера-
температуре. Отношение ^jp можно рассматривать как некоторое действи-
действительное (эффективное) напряжение.
Определим время хрупкого разрушения растянутого стержня.
В этом случае, пренебрегая изменением площади поперечного сече-..
ния, имеем
__ р — р —
°W — -f - 77 — ао
и из формулы A5.6) получаем
= — Aofdt.
Проинтегрируем это уравнение, используя условие
при t = 0 ip = 1. A5.7)
Тогда получим
Время хрупкого разрушения ?р получим, полагая в этом уравне-
уравнении ip = 0
Установим теперь время вязко-хрупкого разрушения растянутого
стержня. При этом учтем измен"ение площади поперечного сечения
в процессе ползучести материала.
Тогда согласно формулам A5.4) и A5.5)
„ __?._„ Л L
ишах — р — и0 ' ,в
Подставим эту величину в формулу A5.6). Тогда получим диффе-
дифференциальное уравнение для функции ip
—
> = — Aof A —-Y " dt.
360

Проинтегрируем его, принимая во внимание условие A5.7). После
преобразований с использованием соотношения A5.8) имеем
-» i*
A5.9)
Полагая в этом уравнении \р = 0, получим время вязко-хруп-
вязко-хрупкого разрушения tp:
L = tl И- 1
/X
-ОТ р
A5.10)
В логарифмических координа-
координатах lg /p, lg oro (рис. 15.2) уравне-
уравнения A5.5) и A5.8) описывают пря-
прямые АВ и CD. Учитывая, что пря-
прямая CD, соответствующая хруп-
хрупкому разрушению, наклонена под „.
большим углом к оси абсцисс, чем
прямая АВ для вязкого разруше-
разрушения, заключаем, что п >> т. Урав-
Уравнение A5.10) в тех же координатах
является уравнением кривой ли-
линии GH, асимптотически прибли-
приближающейся к прямой CD. Ординату
точки G пересечения этой кривой
с прямой АВ можно определить, приравнивая выражения A5.5)
и A5.10). После преобразований с использованием соотношений
A5.5) и A5.8) получаем
Рис. 15.2. Графики зависимостей'
A5.5) - АВ, A5.8) — CD и A5.10) —
GH
(ОТ+ 1) А Лп-т
Г (т+\)А I
L (n-m)k J
A5.11)
При больших напряжениях разрушение является вязким, и время
разрушения подсчитывают по формуле A5.5).
§ 97. Кручение, круглого стержня
Как уже указывалось в предыдущем параграфе, при кручении
стержня вязкое разрушение невозможно, так как в этом случае
размеры стержня не изменяются. Приведем полученное Л. М. Кача-
новым [5] решение задачи определения времени хрупкого разру-
разрушения круглого стержня при кручении.
Хрупкое разрушение начинается в момент времен» tp в наиболее
напряженных точках при г = -»-. Этот промежуток времени назы-
называют стадией скрытого разрушения. Возникшее разрушение с тече-
течением времени распространяется и в момент времени tp происходит
полное разрушение. Промежуток tp — tp называют стадией распро-
распространения разрушения.
361

Определим время начала разрушения tp. В случае чистого сдвига
стшах = т. Подставляя в формулу A5.6) величину касательного на-
напряжения по формулам A3.44) и A3.42), получаем
Cn +
л2я •?-
== — А
Проинтегрируем это уравнение, используя условие A5.7). Тогда
получим
п2л
^. A5.12)
В момент начала разрушения при
D „
г —-nty =0.
Из этого условия получим время на-
начала разрушения
(т+\)А
\)М
A5.13)
«2я
№
Рис. 15.3. Несущее ядро Сплошность в момент начала разру-
радиуса г* в поперечном Шения ib* в зависимости от радиуса по-
сечении ^ругло^ скручен- ^ ф A12)
сечении
скручен-
лучаем ^ формуле A5.12)
-тгГС A5.14)
После начала разрушения в точках, наиболее удаленных от
D
центра при г ~ -^ , оно распространяется к центру и в некоторый
момент t захватывает область, ограниченную окружностями радиусов
г* и -j- (рис. 15.3). Радиус г* несущего ядра является функцией
времени.
В несущем ядре 0 ^ г sg r* сплошность i]>>>0, а на границе
его (окружность радиуса г*), которая в рассматриваемом случае
является фронтом разрушения, т|з = 0. Поскольку это равенство
выполняется в любой момент времени, имеем при г — г*
362
V dt )r=r* \ dt "^ дг* dt )r=r* '

откуда
dr* V dt Jr^r" -A5.15)
dt (dty \
\d*)
Для вычисления производных, стоящих в числителе и знамена-
знаменателе этой формулы, получим вначале выражение для т|з.
После возникновения области разрушения касательное напряже-
напряжение в некоторой точке поперечного сечения на радиусе г определяем
по формулам A3.44) и A3.42) путем подстановки в них вместо ра-
радиуса сечения -*- радиуса несущего ядра г*. Тогда получим
г \т
Подставим эту величину т в формулу A5.6). Тогда получим
Из уравнения A5.16) следует, что
*]" A5.17)
Проинтегрируем уравнение A5.16), учитывая, что при t — tp
tp = tp*.
Тогда получим
t
р
Продифференцируем это соотношение по радиусу г. В результате
имеем
J
Ь
A5,18)
Величину (я|5*)т-^— устанавливаем при помощи формулы A5.14)
J v 2;
363

Подставим эту величину в формулу A5.18) и затем положим г = г*.
Тогда получим
т „ fCre+ \)МЛт
2я«
(Г*) »
A5.19)
Подставим теперь выражения A5.17) и A5.19) в формулу A5.15).
Тогда получим
dr*
dt
„ _3от—-+1
— (/¦*) "
2 . f
A5.20)
" dt
Обозначим
(/-*)
Тогда уравнение A5.20) приводится к виду
dR Зге+i
A5.21)
A5.22)
Перепишем уравнение A5.22) в форме
'р dt
и полученный результат продифференцируем по времени. Тогда
имеем
или
dR Зге + 1 R
dt
= О
и, следовательно,
A5'23)
Проинтегрируем полученное дифференциальное уравнение
364

й, следовательно,
Я^^^^Т^- A5.24)
Интегрируя еще раз, имеем
Ъп
Rto+i^-Cjt+Ct. ' A5.25)
Постоянные Сг и С2 определяем из условий, которые следуют
из выражений A5.21) и A5.22):
D „ /D\3m+r
^/р л* =4 *=(т
при ^=;р 1Г = ^-(-2-
р
3m+f
Используя эти условия и соотношения A5.24) и A5.25), получаем
„ Зя
р
D \3m
A5.26)
Время полного хрупкого разрушения ?р определяется из условия
равенства нулю радиуса г* и, следовательно, согласно формуле
A5.21) из условия равенства нулю величины 7?, Полагая в формуле
A5.25) R = 0 и используя соотношения A5.26), устанавливаем
A5'27)
Поскольку величина п обычно значительно больше единицы,
в рассматриваемом случае стадия распространения разрушения по
времени значительно меньше стадии скрытого разрушения.
§ 98. Тонкостенные трубы
Ниже изложены полученные Л. М. Качановым [5, 7] решения
задач определения времени вязкого, хрупкого и вязко-хрупкого
разрушения тонкостенных труб. Вначале разберем определение
времени вязкого разрушения.
Рассмотрим тонкостенную трубу с днищами, нагруженную внут-
внутренним давлением р. Обозначим изменяющиеся во времени толщину
и средний диаметр трубы соответственно через h и D. Значения их
в начальный момент времени h0 и Do.
Из условия несжимаемости материала имеем
Dh =О0/г0. A5.28)
365

Окружное и осевое напряжения в тонкостенной трубе с днищами,
нагруженной внутренним давлением,
Радиальное напряжение в тонкостенной трубе, нагруженной
внутренним давлением, может быть приближенно принято равным
нулю аг = 0. Величину интенсивности напряжений определяем
по формуле A.21)
Как и в § 96, учитывая, что вязкое разрушение возникает при
больших деформациях, пренебрежем упругими деформациями по
сравнению с деформациями ползучести, которые будем оценивать
логарифмическими деформациями.
Зависимости скоростей логарифмических деформаций от напря-
напряжений примем в форме A2.6), A2.24), учитывая, что для больших
значений времени В = k:
A5.31)
T
Поскольку для рассматриваемого напряженного состояния
ot 4- Or ty
получаем, используя соотношения A5.28) — A5.31),
я+1
п+l га+1
5~
L = о.
В рассматриваемой задаче логарифмическая окружная деформа-
мация
а скорость ее
366

Приравнивая выражения A5.32) и A5.33), получаем дифферен-
дифференциальное уравнение для среднего диаметра трубы
л+1
) d
Проинтегрируем это уравнение, используя условие при t = О
D =D0.
Тогда после преобразований с использованием соотношения A5.28)
имеем _
"D--17-(^у) ' A5-34)
где
«-¦SET <15-35»
— время вязкого разрушения, для которого толщина стенки
трубы обращается в ноль, а диаметр стремится к бесконечности;
л+1
— скорость логарифмической деформации в начальный момент
времени.
Сопоставляя выражение A5.34) для тонкостенной цилиндричес-
цилиндрической трубы с соответствующими ему соотношениями A5.4) и A5.5)
для растянутого стержня, приходим к выводу, что для первого слу-
случая показатель степени вдвое меньше, чем для второго. Учитывая,
что постоянная п обычно значительно больше единицы, заключаем,
что для тонкостенной трубы- «последний» период деформирования,
в котором происходит резкое уменьшение толщины стенки трубы,
еще меньше, чем «последний» период деформирования для растяну-
растянутого стержня, когда происходит резкое уменьшение площади попе-
поперечного сечения. Это объясняется тем, что в тонкостенной трубе на-
напряжение растет не только за счет уменьшения толщины стенки, но
также и вследствие увеличения диаметра трубы. Для растянутого
стержня «последний» период деформирования тем меньше, чем больше
показатель степени п.
Перейдем теперь к определению времени хрупкого разрушения
трубы. В этом случае можно пренебречь изменением размеров трубы
в процессе ползучести. Тогда максимальное главное напряжение
°тах равняется окружному напряжению в начальный момент вре-
времени а(„
сттах = ст,0=в-. A5.37)
Из формулы A5.6) получаем
367

Интегрируя это уравнение с учетом условия A5.7), имеем
Полагая в этом уравнении \р = 0, устанавливаем время хрупкого
разрушения трубы
txp = ! -. A5.38)
Выведем теперь формулу для времени вязко-хрупкого разруше-
разрушения трубы. При этом учтем изменение толщины стенки в процессе
ползучести материала. Тогда согласно формулам A5.29), A5.34) и
A5.37) получаем
Подставляя эту величину в .формулу A5.6), устанавливаем
Проинтегрируем полученное уравнение, принимая во внимание
условие A5.7). После преобразований с использованием соотношения
A5.38) получаем выражение A5.9). Полагая в нем т|з = 0, находим
время вязко-хрупкого разрушения тонкостенной трубы в,форме*
A5.10), такой же, как и для растянутого стержня. Однако следует
помнить, что величины t\ и ^ определяются иначе, чем в случае
растянутого стержня.
Как и для растянутого стержня, формула A5.10) имеет смысл
при /р <С ?р. Из этого неравенства, используя соотношения A5.10),
A5.35); A5.38) и A5.32), заключаем, что формула A5.10) справед-
справедлива при окружных напряжениях в начальный момент времени,
меньших величины
Л
'<• I п-
1з^
k (n — m)
При окружных напряжениях, больших этой величины, разру-
разрушение является вязким и время разрушения определяется формулой
A5.35).
В работах [1,3—12, 20,21,23, 26 ] решены задачи определения .
времени разрушения различных элементов конструкций. В рабо-
работах [2, 13—19, 22, 23] рассмотрен несколько иной подход к опреде-
определению времени разрушения.
V
Список литературы
1. Григорьев А. С. О времени вязкого разрушения и критическом времени
в условиях ползучести.— «Инженерный журнал. Механика твердого тела», 1968,
№ 4, с. 147—148.
36S

2. Ильюшин А. А. Об одной теории длительной прочности «Инженерный
журнал. Механика твердого тела», 1967, № 3, с. 21—35.
3. Кац Ш. Н. Ползучесть и разрушение труб под действием внутреннего
давления.— «Известия АН СССР. Отд. техн. наук», 1957, № 10, с. 86—89- "
4. Кац Ш. Н. О разрушении в условиях ползучести при сложном напряжен-
напряженном состоянии.— «Известия АН СССР. Механика и машиностроение», i960, № 4,
с. 160—162.
5. Качанов Л. М. О времени разрушения в условиях ползучести.— «Изве-
«Известия АН СССР. Отд. техн. наук», 1958, № 8, с. 26—31.
6. Качанов Л. М. О времени разрушения в условиях ползучести.— «Изве-
«Известия АН СССР, Механика и машиностроение», 1960, № 5, с. 88—92.
7. Качаиов Л. М. Теория ползучести1. М., Физматгиз, 1960, 455 с.
8. Качанов Л. М. Время разрушения в условиях ползучести. В кн.: Про-
Проблемы механики сплошной среды. К. семидесятилетию академика Н. И. Мусхелн-
швили. М., Изд-во АН СССР, 1961, с. 186—200.
9. Качаиов Л. М. Некоторые вопросы разрушения в условиях ползучести.—
В кн.: Ползучесть и длительная прочность. Труды Всесоюзного совещания по теории
расчетов на ползучесть и длительную прочность, Новосибирск, Изд-во СО АН СССР,
1963, с. 3—14.
10. Качанов Л. М. К вопросу о разрушениях в условиях ползучести. В кн.:
ЛГУ им. А. А. Жданова. Исследования по упругости и пластичности. Сборник 6,
Л., Изд. Ленинградского университета, 1967, с. 18—24.
11. Качаиов Л. М. Хрупкие разрушения в условиях ползучести при цикличе-
циклическом нагружении. В кн.: Проблемы механики твердого деформируемого тела. К ше-
шестидесятилетию академика В. В. Новожилова. М., «Судостроение», 1970, с. 197—204.
12. Качанов Л. М. Разрушения в условиях ползучести при сложном нагруже-
нагружении.— «Известия АН СССР. Механика твердого тела», 1972, № 5, с. 11—15.
13. Милейко С. Т. Оценка долговечности в условиях ползучести.— «Инженер-
«Инженерный журнал. Механика твердого тела», 1968, № 5, с. 82—87.
14. Наместников В. С. О времени разрушения при ползучести.— «Журнал
прикладной механики и технической физики», 1961, № 1, с. 137—139.
15. Немировский Ю. В. О времени эксплуатации и разрушения конструкций
в условиях ползучести.— «Прикладная механика», 1970, том VI, вып. 3, с. 47—54.
16. Работиов' Ю. Н. О механизме длительного разрушения. В кн.: Вопросы
прочности материалов и конструкций. AL, Изд-во АН СССР, 1959, с. 5—7.
17. Работиов Ю. Н. О разрушении вследствие ползучести.— «Журнал при-
прикладной механики и технической физики», 1963, № 2, с. 113—123.
18. Работнов Ю. Н. Ползучесть элементов конструкций. М., «Наука», 1966,
752 с.
19. Работиов Ю. Н. Влияние концентрации напряжений на длительную проч-
прочность.— «Инженерный журнал. МТТ», 1967, № 3, с. 36—41.
20. Розеиблюм В. И. Время до разрушения вращающегося диска в условиях
ползучести.— «Прикладная математика и механика», 1957, т. XXI, вып. 3, с. 440—
444.
21. Розеиблюм В. И. Влияние пластических деформаций на время разрушения
при ползучести.— В кн.: Ползучесть и длительная прочность. Труды Всесоюзного
совещания по теории расчетов на ползучесть и длительную прочность. Новосибирск,
Изд-во СО АН СССР, 1963, с. 63—69.
22. Хажииский Г. М. О теории ползучести и длительной прочности метал-
металлов.— «Известия АН СССР. Механика твердого тела», 1971, № 6, с. 29—36.
23. Хжановски М. Влияние перераспределения напряжений на время хрун-
когсг разрушения в условиях ползучести.— «Известия высших учебных заведений.
Машиностроение», 1971, № 11, с. 13—21.
24. Hoff H. J. The neckling and the rupture of rods, subjected to constant tensile
loads.—«Journal of applied mechanics», 1953, Vol. 20, No 1, p. 105—108.
25. Odqvist F. K- G. Mathematical theory of creep and creep rupture, Oxford, At
the Clarendon Press, 1966, 170 p.
26. Piechnik S., Chrzanowcki M., Time of total creep rupture of a beam under
combined tension and bending.—«International journal of solids structures», 1970.
Vol. 6, p. 453—477.
13 H. H. Малинин

ГЛАВА XVI
ВЯЗКОУПРУГОСТЬ
§ 99. Механические модели деформируемого тела
Явление ползучести может быть описано также при помощи ме-
механических моделей тел и наследственных теорий ползучести, ко-
которые можно рассматривать как обобщение механических моделей.
Наследственные теории ползучести нашли применение в расчетах
элементов конструкций из полимерных материалов и бетонов,
а также в описании ползучести грунтов и горных пород. Имеются
отдельные попытки использования наследственных теорий (в нели-
нелинейных вариантах) в расчетах конструкций из металлов.
Рассмотрим вначале два основных элемента механических моде-
моделей тел: упругий и вязкий.
Конструктивно упругий элемент можно представить себе в виде
пружины (рис. 16.1). Удлинение ее 8У пропорционально приложен-
приложенной силе Р
бу =^Р, ^ A6.1)
где kx — коэффициент пропорциональности.
Вязкий элемент может быть изображен в виде цилиндра, запол-
заполненного жидкостью, внутри которого перемещается поршень так,
что жидкость вытекает через зазор между цилиндром и поршнем
(рис. 16.2). Скорость перемещения бв поршня относительно цилиндра
пропорциональна приложенной силе Р:
%- = /гаР, A6,2)
где 62 — коэффициент пропорциональности.
Если соединить упругий и вязкий элементы последовательно
(рис. 16.3), то изменение расстояния между точками приложения
сил Р будет равно сумме удлинения пружины бу и перемещения
поршня относительно цилиндра бв:
б = бу + 6В; •
дифференцируя это соотношение по времени и используя выражения
A6.1) и A6.2), имеем
dt 1 dt i 8 *
370

Переходя от перемещения б и силы Р к деформации г и напря-
напряжению а и заменяя коэффициенты kx и k2 на -р и —¦ соответственно,
где Е — модуль упругости, ц — коэффициент вязкости, получаем
dt
1 da
E dt
A6.3)
Последнее уравнение описывает так называемое.вязко-упругое
тело Максвелла, а модель, изображенная на рис. 16.3, называют
моделью вязко-упругого тела Максвелла, или элементом Максвелла.
Рис. 16.1. Упругий
элемент
Рис. 16.2. Вязкий
элемент
Рис. 16.3. Модель тела
Максвелла — последова-
последовательное соединение упру-
упругого и вязкого элементов
Рассмотрим некоторые свойства этого тела. Как следует из урав-
уравнения A6.3), при постоянном во времени напряжении деформация
растет с постоянной скоростью, пропорциональной напряжению,
т. е. материал течет подобно вязкой жидкости, что не подтверждается
экспериментальными исследованиями конструкционных материалов.
При постоянной деформации из уравнения A6.3) следует, что
E dt ' r\
Интегрируя это уравнение и используя начальное условие при
t =0 о — о @), получим
= а@)ехр (—¦?),
где величина
A6.4)
371

представляет собой время, за которое начальное напряжение а @)
уменьшается в е = 2,718 раз. Эту величину называют временем
релаксации. Согласно полученной зависимости напряжение умень-
уменьшается во времени по экспоненциальному закону, стремясь к нулю
(рис. 16.4).
' Соединим теперь упругий и вязкий элементы параллельно
(рис. 16.5). Тогда очевидно, что сила Р, воспринимаемая соединением
элементов, равна сумме сил Ру и Рв, действующих1 на упругий и вяз-
вязкий элементы
Используя выражения A6.1) и A6.2), получаем
k2 dt
Переходя от силы Р и перемещения б
напряжению а и деформации г и заме-
Рис. 16.4. Кривая релаксации напря-
напряжений в теле Максвелла
Рис. 16.5. Модель тела
Фойгта — параллельное
соединение упругого и
вязкого элементов
няя так же, как и раньше, коэффициенты kx и &s
юответственно, получаем
о = Ее-
1
на т
х\
dt
A6.5)
Это уравнение описывает так называемое вязко-упругое тело Фойгта,
i модель, изображенную на рис. 16.5, называют моделью вязко-упру-
вязко-упругого тела Фойгта или элементом Фойгта.
Интегрируя уравнение A6.5) при постоянном напряжении и
учитывая, что в начальный момент времени деформация равна нулю,
юлучаем
e—f [l_e*p(-f *)]. . A6.6)
Из уравнения A6.6) заключаем, что деформация растет по экспо-
генциальному закону, стремясь к величине -g- (рис. 16.6).
372

Как следует из уравнения A6.5), при постоянной деформации
напряжение постоянно, т. е. это уравнение не отражает релаксации
напряжении, что является его недостатком.
Как следует из изложенного, модели Максвелла и Фойгта только
качественно отражают некоторые стороны сложных процессов де-
деформирования материалов во времени.
Рассмотрим более сложную модель, состоящую из упругого эле.
мента /, последовательно соединенного с двумя параллельно соеди*
ненными упругим элементом 2 и вязким i
элементом 3 (рис. 16.7).- \t>
В этом случае изменение расстояния '
между точками приложения сил Р будет
О ' t
Рис. 16.6. Кривая последействия в теле
Фойгта
Рис. 16.7. Модель тела Кельвина
равно сумме удлинения пружины / - 8Х и удлинения пружины
в 7язком Элементе %»**"****>¦ П°рШНЯ ™°™ьно, цилиндра
Дифференцируя это соотношение по времени, получаем
It = ~Ж + -& • A6.7)
^ .Зависимости между перемещениями б? и б2 и силами, действую-
действующими на модель, - Р, на пружину 2 - Ру и поршень 3 - Рв
причем
О, =^Р; 62 =*2Ру; '^.= k3PB, A6.8)
Р=Ру + Рв. A6.9)
Подставим соотношения A6.8) в выражение A6.7), используя
при этом равенство A6.9). Тогда получим
373

откуда
dP . fe,(*i + *i) p_ 1 db kB .
Переходя от перемещения б и силы Р к деформации е и напря-
напряжению а и заменяя коэффициенты k{ и ks соответственно на р— и
1,1
•р-, a ks на —, получаем
¦^ + аа = ?(-^- + Р8), A6,10)
где
a = _EL±?L. p=?i.. ? = ? A6.11)
Уравнение A6. ГО) описывает вязко-упругое тело Кельвина,
а модель, изображенная на рис. 16.7, называется моделью вязко-
упругого тела Кельвина.
В частном случае очень быстрого приложения нагрузки, когда
производные по времени от напряжений и деформаций достаточно
велики и вторыми слагаемыми в правой и левой частях равенства
A6.10) по сравнению с первыми можно пренебречь, получаем
da г- d&
и, следовательно,
а = Еъ.
Таким образом, величина Е представляет собой мгновенный мо-
модуль упругости. В другом частном случае очень медленного прило-
приложения нагрузки, когда производные по времени от напряжений и
деформаций малы и ими по сравнению со вторыми слагаемыми в пра-
правой и левой частях выражения A6.10) можно пренебречь, получаем
Следовательно, величину -—¦ можно назвать длительным мо-
модулем упругости.
Из соотношений A6.11) заключаем, что —^ <3 1 и поэтому дли-
длительный модуль упругости меньше мгновенного.
Вначале решим уравнение A6.10) относительно деформации.
При этом предположим, что в начальный момент времени t = 0
деформации являются упругими, а модуль упругости равен мгноЕен-
'ному модулю Е. Тогда после преобразований получим
if,' 1
е =-L a + (a — fi) [ a (?) exp [— $(t— Q]d?\. A6,12)
374

В случае постоянного напряжения а = const (процесс ползу-
ползучести или последействия) получаем уравнение кривой ползучести
A6.13)
Из этой формулы следует, что ордината асимптоты кривой
ползучести в выбранном масштабе равна деформации, подсчитан-
подсчитанной по напряжению а при помощи tp
длительного модуля упругости -2- -^ Л
(рис. 16.8).
Если процесс ползучести при по-
постоянном напряжении а протекает
в течение времени ^ (рис. 16.8),
а затем напряжение мгновенно умень-
уменьшается до нуля, то деформация мгно-
мгновенно уменьшится на величину упру-
упругой деформации -?-, а последующий
процесс изменения деформации (обрат-
Рис. 16.8. Кривая ползучести до и после
разгрузки (обратной ползучести)
Рис. 16.9. Модель тела из
четырех элементов
ная ползучесть или обратное последействие) будет определяться
формулой A6.12)
8 =
A6.14)
Из полученного уравнения. следует, что при неограниченном
увеличении времени деформация г стремится к нулю, т. е. вся де-
деформация ползучести является обратимой и последействие в теле
Кельвина упругое.
Решим теперь уравнение A6.10) относительно а. Предположим,
что в начальный момент времени / = 0 деформации являются упру-
375

гими, а модуль упругости равен мгновенному модулю. После пре-
преобразований получим
o = eL- (a-P) J г(?)ехр [-а(*-?)] d?. A6.15)
В случае постоянной деформации г = const (процесс релаксации)
лз этого уравнения получаем уравнение кривой релаксации
— ехр(— а/)]}. A6.16)
Как следует из изложенного, модель тела Кельвина в отличие
от моделей тел Максвелла и Фойгта отражает обе стороны явления
ползучести — собственно ползучесть или последействие и релакса-
релаксацию напряжений, а также явление обратной ползучести. Однако
экспериментальные исследования ползучести большинства мате-
материалов не согласуются количественно с результатами, полученными
на основе модели тела Кельвина.
Возможно построение более сложных моделей тел, состоящих
из четырех (рис. 16.9) или большего числа упругих и вязких эле-
элементов.
Однако использование сложных многоэлементных моделей при-
приводит к громоздким математическим выражениям и, все-таки, не
позволяет удовлетворительно описать деформирование реальных
материалов во времени.
Можно обобщить уравнения A6.10), добавив в правой и левой
частях равенства производные более высокого порядка, что приведет
к следующему выражению:
, da . . dna , , , de . , , dne
A6.17)
Это равносильно построению многоэлементных моделей.
§ 100. Линейная теория наследственности
Простейшей линейной теорией, в основе которой лежит принцип
наложения (суперпозиции) деформаций, является линейная тео-
теория наследственности, предложенная Больцманом.
Допустим, что в момент времени ? (отсчет времени ведется от на<-
чала нагружения), в течение малого промежутка dt,, напряжение
в растянутом стержне равно a (?). Это напряжение вызвало неко-
некоторую деформацию, которая впоследствии изменяется во времени.
Пркмем, что в момент времени t > ? эта деформация пропорциональна
напряжению a (?), длительности воздействия d? и некоторой убы-
убывающей функции отрезка времени t — ?, которую обозначим Н (t—?)",
и обратно пропорциональна модулю упругости Е. Функция Н (t—?)
должна быть убывающей функцией времени t, так как с течением
времени материал «забывает» воздействие напряжения а. Зависи-
376

мость функции Н от разности двух аргументов / — ? свидетель-
свидетельствует о том, что эта функция не изменяется при изменении начала
отсчета времени — инвариантна по отношению к началу отсчета
времени.
Для описания деформирования стареющих материалов, механи-
механические свойства которых изменяются во времени, как например,
бетонов, функция Н должна быть функцией t и ? по отдельности..
Согласно принципу суперпозиции величина деформации в мо-
момент времени t, возникшей за счет напряжений, действовавших до
момента времени t, равна
Напряжение в момент времени / вызывает упругую деформацию
-?-. Следовательно, полная деформация в момент времени t склады-
складывается из этой деформации и деформации, возникшей за счет напря-
жений, действовавших до момента времени t,
1
A6.18)
Уравнение A6.18) позволяет по заданному закону изменения
напряжений во времени определить закон изменения деформации и,
в частности, описать явление ползучести (последействия) при по-
постоянном напряжении. В этом случае о = о @) = const и из урав-
уравнения A6.18) получаем
8=^М + ГЯ(/—?)rf? . A6.19)
L oJ J
При помощи последнего уравнения может быть построена кривая
ползучести при постоянном напряжении, если известно ядро инте-
интегрального уравнения A6.18). Последнее может быть найдено из
известной кривой ползучести. Для этого продифференцируем выра-
выражение A6.19). Тогда получим
где
X = t-L A6.20)
откуда
Таким образом, ядро интегрального уравнения A6.18) опреде-
определяется законом изменения скорости деформации во времени.
377

Простейшим ядром интегрального уравнения A6.18) является
затухающая показательная функция
H(t — ?) = Се-°«-*>. A6.21)
Подставляя ее в выражение A6.18), получим
A6.22)
Продифференцируем это уравнение по t. Тогда имеем
t
+CaJCe-('-C)(?)d? A6.23)
Исключая из уравнений A6.22) и A6.23) интеграл, устанавливаем
da , ,~ . . ,-, / de , \
— + (C + a)o^E(-lf + ae).
Сопоставляя полученный результат с уравнением A6.10), за-
заключаем, что они совпадают, причем
a = С + а; Р = а.
Таким образом, выбор ядра в виде функции A6.21) равносилен
использованию модели вязко-упругого тела Кельвина.
Если а = 0 и ядро выбираем в виде постоянной величины, полу-
получаем тело Максвелла [см. уравнение A6.3)].
Ядро интегрального уравнения A6.18) может быть выбрано
в виде суммы затухающих показательных функций
Я(/ —?)==? C/e-V'-E). A6.24)
i=\
Можно показать, что в таком случае интегральное уравнение
A6.18) эквивалентно линейному дифференциальному уравнению п-го
порядка A6.17).
Больцманом было предложено ядро интегрального уравнения
в виде
? A6.25)
?) = _?_..
Ядро Больцмана A6.25) имеет сильную особенность в том смысле,
что в начальный момент времени скорость деформации бесконечно
велика и интеграл от него расходится. Этот недостаток может быть
устранен выбором ядра в виде, предложенном Дюффингом
H{t—Q = —, A6.26)
где 0 < а < 1.
378

В таком случае из выражения A6.18) получаем уравнение кривой
ползучести при постоянном напряжении
В работах [4, 10, 14] приведены иные типы ядер. Ю. Н. Работ-
новым [12,13] введено ядро вида
где Г A + а) — гамма функция, и разработана теория так назы-
называемого Эа оператора, ядро которого является резольвентой ядра
A6.27).
Из формулы A6.19) следует, что предел деформации при стремле-
стремлении времени к бесконечности
Таким образом, величина
Е
+ J Н (х) dt
о
1 +
о
может быть названа длительным модулем упругости.
Рассмотрим явление обратной ползучести. Допустим, что после
ползучести стержня при постоянном напряжении а @) в течение
времени tx стержень разгружается. Мгновенное уменьшение дефор-
деформации при разгрузке по закону разгрузки (закону Гука) равно -^р>
Дальнейшее уменьшение деформации устанавливаем согласно фор-
формуле A6.19)
]
Lo о J
A6.28).
V
Разность интегралов в квадратных скобках равна поштрихован-
ной на рис. 16.10 разности площадей, которая, очевидно, уменьшается
с увеличением времени t и стремится к нулю при стремлении вре-
времени t к бесконечности. Таким образом, как и в случае тела Кель-
Кельвина, последействие является упругим (см. рис. 16.8).
379

Уравнение A6.18) относительно функции а является линейным
интегральным уравнением Вольтерра второго рода. Функция Я (t—?)
представляет ядро этого уравнения (^-переменная интегрирования,
изменяющаяся от 0 до t).
Н. X. Арутюняном [2] развит вариант этой теории, отражающий
ползучесть и старение бетона. В этом случае
= т-1'
+с <<.
A6.29)
где ?i — возраст материала:
С (t, ?) — так называемая
мера ползучести.
Соотношение A6.29) яв-
является линейным интеграль-
интегральным уравнением Вольтерра
для функции а с ядром
Рис. 16.10. График функции Н (?)
Как показывают экспе-
экспериментальные исследования,
теория линейной наследст-
¦^ венности Н. X. Арутюняна
хорошо подтверждается опы-
опытами при напряжениях, мень-
меньших половины временного
сопротивления бетона [21.
§ 101. Применение преобразования Лапласа
Как известно [6], преобразование Лапласа.определяется следую-
следующим действием над функцией / (t):
A6.30)
Полученную в результате преобразования функцию /* (к) назы-
называют изображением функции/ (t), которая, в свою очередь, является
оригиналом изображения^
Оригинал может быть найден по изображению с помощью фор-
формулы [6]
Мв2ЯГ 1 f(*)e"<a,. A6.31)
Интегрирование ведется по любой прямой, параллельной мнимой
оси плоскости X, расположенной вправо от всех особых точек функ-
функции /* (X). Результат не зависит от выбора числа у.
380

Применим преобразование Лапласа к уравнению A6.18). Тогда
получим
е* = -i- (a* + Ф*), A6.32)
где Ф* = Ф* (X) — изображение функции
Оно определяется формулой
Ф* = 7е-«Л f H(t — ?)a(g#.
6 6
Функцию Ф @ называют сверткой двух функций Н (t) и a (/).
В операционном исчислении доказывается следующая теорема о
свертках [6J:
Ф* =Н*о*. A6.33)
Подставляя это соотношение в формулу A6.32), получим
в* =-?A+//•),
откуда
°* <1634>
Положим
1
и, следовательно,
Тогда выражение A6.34) принимает вид
a* = е (е* — V*), . A6.36)
где -
W* = R*&* A6.37)
согласно теореме о свертке является изображением свертки
функций R (t) и е @. Из формул "A6.33), A6.34), A6.35) и A6.37)
следует, что
ф* = EW*. A6.38)
Переходя в выражении A6.36) от изображений к оригиналам,
получаем
о=Е\? — [R(t — i) е(?)AЦ, A6.39)
381

где функция разности двух переменных R (t — Q — резольвента
интегрального уравнения A6.18).
Уравнение A6.39) позволяет по заданному закону изменения
деформаций определять закон изменения напряжений и, в частности,
описать явление релаксации при постоянной деформации. В этом
частном случае е (t) = е @) = const и из уравнения A6.39) имеем
. A6.40)
При помощи последнего уравнения может быть построена кри-
кривая релаксации напряжений при постоянной деформации, если из-
известна резольвента интегрального уравнения A6.18). Последняя
определяется по изображению /?* с помощью формулы A6.31), ко-
которое, в свою очередь, определяется формулой A6.35).
Переход от изображения к оригиналу по формуле A6,31) обычно
связан с преодолением значительных трудностей математического
характера.
§ 102. Принцип Вольтерра
В случае неодноосного напряженного состояния разложим тен-
тензоры напряжений и деформаций на шаровые тензоры и девиаторы.
Выразим компоненты девиатора деформаций через компоненты де-
виатора напряжений, используя те же рассуждения, что и при под-
подсчете деформации в простейшем случае одноосного напряженного
состояния (§ 100). Тогда получим
]. 06.41)
Поскольку обычно при всесторонних равных растяжениях и
сжатиях механические свойства материалов практически не зави-
зависят от времени, можно принять, что средняя линейная деформация
е0 и среднее нормальное напряжение а0 связаны законом Гука C.3).
Таким образом, для решения задач линейной теории наследствен-
наследственности имеем следующую систему уравнений: дефференциальные
уравнения равновесия A.4), условия на поверхности A.2), зависи-
зависимости компонентов деформаций от компонентов перемещений B.3)
и зависимости компонентов деформаций от компонентов напряжений
A6.41) и C.3).
Эта система уравнений отличается от системы уравнений линей-
линейной теории упругости только уравнением A6.41). Поскольку свой-
свойства материала, определяющие операторы по времени в уравнении
A6.41), для однородных тел не зависят от координат, временные и
пространственные операции переставимы и при решении задач можно
произвольно выбирать порядок выполнения операций. Если вна-
вначале выполнить все операции по координатам, полагая операторы
382

по времени постоянными и используя граничные условия для теку-
текущего момента времени, получим решение упругой задачи, в котором
упругие постоянные заменены реологическими операторами. Та-
Таким обр.ч.чом, для получения решения задачи линейной теории на-
наследственности следует в решении задачи линейной теории упругости
заменить упругие постоянные соответствующими им операторами.
Этот принцип называют принципом Вольтерра. Из него следует,
что все результаты теории упругости, не зависящие от упругих по-
постоянных, справедливы и в условиях линейной наследственнности.
Очевидно, что при формулировке принципа Вольтерра существенно,
чтобы граничные условия не изменялись в процессе деформации.
Ограничение, связанное с предположением об однородности тела,
может быть снято при помощи преобразования Лапласа. Применим
его для рассмотренной выше системы уравнений линейной теории
наследственности.
Тогда получим
A6.42
'Ж '
При преобразовании уравнения A6.41) была использована фор-
формула A6.32).
Уравнения A6.42) представляют собой систему уравнений ли-
линейной теории упругости для изображений. Таким образом, для по-
получения решений задачи линейной теории наследственности нужно
решить задачу линейной теории упругости и от полученных величин
изображений а?/ и щ перейти к оригиналам ац и щ.
В качестве примера рассмотрим нагружение толстостенной трубы
с днищами внутренним давлением р. Внутренний и наружный ра-
радиусы трубы соответственно rt и г2.
Напряжения в пределах упругости определяются формулами [20]:
о, =
П —
A6.43)
383

Поскольку в рассматриваемом случае напряжения не зависят от
упругих постоянных, формулы A6.43) справедливы и в условиях
линейной наследственности. Для определения радиального переме-
перемещения используем уравнение A6.41).
и = etr = (et + e0) r = eor + ¦— \at — a0 -f
L о
До , ¦ p< — До
3K ^ 2G r
Подставим в это выражение величины окружного напряжения
по формуле A6.43) и среднего нормального напряжения а0) которое
согласно формулам A6.43)
0O= —
Тогда после преобразований, используя соотношение C.4), по-
получим
F Л'1' .2ч !— 2И + A +й)тг 1 + (Я(/— l)dt, . A6.44)
Последняя формула позволяет подсчитать радиальное переме-
перемещение для произвольной точки трубы на радиусе г в любой момент
времени /, если известно ядро интегрального уравнения Я (t —?).
§ 103. Нелинейные теории наследственности
Стремление наиболее полно отразить процессы деформирования
различных материалов во времени вызвало разработку нелинейных
вариантов теории наследственности.
Чтобы описать деформирование бетона при напряжениях, пре-
превышающих половину временного сопротивления, Н. X. Арутюня-
ном предложена теория нелинейной наследственности [2], отражаю-
отражающая явления ползучести и старения материала. По этой теории
-*- A6-45)
Для описания процессов деформирования металлов Ю. Н. Работ-
нов [13] предложил обобщить линейную теорию наследственности
и представил основное уравнение, связывающее деформацию, напря-
напряжение и время в виде
<р(е) = а+ [//(* —?)о(?Ы?. . A6.46)
о
381

В уравнении A6.46) функция ф (s) является функцией только
деформации. Она описывает диаграмму растяжения материала (при
t = 0). Эта теория получила название теории пластической наслед-
наследственности. Автор ее предлагает следующее выражение для ядра:
Иной вариант теории нелинейной наследственности предложен
М. И. Розовским [16—18]. Согласно ему
Еще Вольтерра предложил нелинейную теорию наследственности^
в форме
?е = |Я1(/— ?)
о
0 0 0
Можно показать, что из последней зависимости как частный
случай вытекают уравнения нелинейной теории наследственности
Ю. Н. Работнова и М. И. Розовского [15].
Список литературы
1. Алфрей Т. Механические свойства высокополимеров. М., Изд. иностр. лит,
1952, 619 с.
2. Арутюнян Н. X. Некоторые вопросы теории ползучести. М., ГИТТЛ,
1952, 323 с.
3. Бленд Д. Теория линейной вязко-упругости. М., «Мир», 1965, 199 с.
4. Бронский А. П. Явление последействия в твердом теле.— «Прикладная
математика и механика», 1941, т. V, в. I, с. 31—56.
5. Бугаков И. И. Ползучесть полимерных материалов. Теория и приложения. ,
М., «Наука», 1973, 287 с.
6. Диткин В. А., Прудников А. П. Операционное исчисление. М., «Высшая
школа», 1966, 405 с.
7- Ильюшии А. А., Победря Б. Е. Основы математической теории термовязко-
упругости. М., «Наука», 1970, 280 с.
8. Ишлинский А. Ю. Уравнения деформирования не вполне упругих и вязко-
пластических тел.— «Известия АН СССР. Отд. техн. наук», 1945, № 1—2, с. 34—45.
9. Ишлинский А. Ю. Пространственное деформирование не вполне упругих
и вязко-пластических тел.— «Известия АН СССР. Отд. техн. наук», 1945, № 3,
с. 250—260.
10. Москвитии В. В. Сопротивление вязко-упругих материалов. М., «Наука»,
1972, 327 с.
11. Надаи А. Пластичность и разрушение твердых тел. М., Изд. иностр. лит,
г. I, 1954, 647 с, т. II, 1969, 863 с.
385

12. Работнов Ю. Н. Равновесие упругой среды с последействием.— «Приклад-
«Прикладная математика и механика», 1948, т. XII; в. I, с. 53—62.
13. Работнов Ю. Н. Ползучесть элементов конструкций. М., «Наука», 1966,
752 с.
14. Ржаницын А. Р. Некоторые вопросы механики систем, деформирующихся
во времени. М., ГИТТЛ, 1949, 252 с.
15. Ржаницын А. Р. Теория ползучести. М., Госстрой из дат, 1968, 416 с.
16. Розовский М. И. Ползучесть и длительное разрушение материалов,— «Жур-
«Журнал технической физики», 1951, т. XXI, вып. II, с. 1311—1318.
17. Розовский М. И. О некоторых особенностях упруго-пластических сред.—
«Известия АН СССР. Механика и машиностроение», 1961, № 2, с. 30—36.
18. Розовский М. И. Механика упруго-наследственных сред. В кн.: Итоги
науки. Упругость и пластичность, 1965. М., ВИНИТИ, 1967, с. 165—250.
19. Смирнов В. И. Курс высшей математики, т. IV. М., Фнзматгиз, 1958, 812 с.
20. Феодосьев В. И. Сопротивление материалов. М., «Наука», 1974, 559 с.
21 Freudenthal A. M. The inelastic behavior of engineering materials and stru-
structures, John Wiley and Sons, Inc., 1950, 587 p.
22. Nowacki W. Teoria pelzania, Arkady, 1963, 170 s.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
виях установившейся ползучести 321,
Автоскреплеиие 5, 115
дисков 128 — Эпюры напряже-
напряжений 128
толстостенных труб 115 — Расчет
115 —Способы 115
Автофретирование — см. Автоскреп-
Автоскрепление
Аналогия с песчаной насыпью 221—224
с песчаной насыпью в сочетании
с мембраной 224
Анизотропия деформационная 45, 80—
85
начальная 45—48, 85—90
Ассоциированный закон течения —
53-54
Брус кольцевого сечения — Каса-
Касательные напряжения 317—318
— Кручение 316—318
— Относительный угол закручива-
закручивания—317
Брус — Кручение (релаксационная
задача) 352
— Поперечный изгиб 312—316
— Упруго-пластическое кручение
144—146
— Чистое кручение 144
— Чистый изгиб 306—312, 346, 350
Брус некруглого поперечного сечения—
Вариационное уравнение упруго-
пластического кручения 145
— Жесткость при установившейся пол-
ползучести 321—323
— Касательное напряжение в усло-
усло— Крученне при установившейся пол-
ползучести 318—325
— Относительный угол закручивания
в условиях установившейся ползу-
ползучести 320, 324
В
Вдавливание штампа — Линии сколь-
скольжения 192, 194
— Поле напряжений 192, 193, 194
— Поле скоростей 194
— Решение Прандтля 191
— Решение Хилла 193
— Сила 193, 194
Волочение — Усилие 205 — Условие
возможности волочения 206 — Уста-
Установившийся процесс 202
листа 202
труб 166
Время вязкого разрушения растяну-
растянутого стержня 358, 359
вязкого разрушения тонкостен-
тонкостенных труб 365—367
вязко-хрупкого разрушения тон-
тонкостенной трубы 368
начала разрушения скрученного
стержня 362
разрушения 358
релаксации 372
хрупкого разрушения круглого
стержня при кручении 361
хрупкого разрушения растяну-
растянутого стержня 360
хрупкого разрушения тонкостен-
тонкостенной трубы 367—368
Вязкоупругость 370—385
387

Гиперповерхность ползучести 268
Гипотеза единой кривой 64
Кирхгофа 226
о существовании потенциала де-
деформации ползучести 269
о существовании потенциала ско-
скоростей деформации ползучести 293 —
Экспериментальная проверка 293
о характере деформации пласти-
пластины 225
прямолинейных нормалей 225
Граничная поверхность — см. По-
Поверхность граничная
Граничные условия — 181—182
Д
/'Давление предельное 111, 191, 121, 225
Девиатор — Компоненты 13
деформаций 29 — Главные ком-
компоненты 32 — Инварианты 29
—— напряжений 13
Дельта — символ — см. Символ Кро-
некера
Деформация — Главные оси 28
— Дополнительная мощность 348
— Интенсивность деформаций 29—31
— Интенсивность приращений 34
~— Компоненты 37
— Потенциальная энергия 38
— Скорость — см. Скорости дефор-
деформаций
— Скорость по теории течения 347
— Угол вида приращений 35
— Условия совместности 135
— Эквивалентное приращение 87
— Эллипсоид 31
Деформация во вращающемся диске
332
в упругом теле 37
главная — Тригонометрическая
форма представления 32—35
главная линейная 28, 32
главная угловая 32^
логарифмическая 35, 252
объемная 13, 37
октаэдрическая угловая 31
пластическая 13, 21, 42, 50 —
Компоненты 25 — Принцип макси-
максимума работы 53 — Тензор прираще-
приращения 55
пластическая накопленная 51
плоская — Краевые задачи 194—
198 — Линии разрыва 187 — Поля
напряжений 184 — Поля скоростей
187 — Понятие 172—Скорости пере-
перемещений 174
ползучести 243 — Гипотезы о су-
388
ществовании потенциала скоростей
293 — Зависимость от напряжения
и времени 272—273, 275 — Скорость
245
полная 243
поперечная
при кратковременной ползуче-
ползучести 295
при кручении бруса 146
средняя линейная 31
труб толстостенных 328
труб тонкостенных 327
упругая 244
упруго-пластическая 50, 244
Деформированное состояние в точке
тела 25—26 — Геометрическое изобра-
" жение 31—32
Диаграмма деформирования — Схема-
Схематизация 99
без упрочнения 101
действительная 93, 95
жестко-пластического тела 104
идеального жестко-пластического
тела 104
материала 56, 64, 88
с линейным упрочнением 101
со степенным .упрочнением 101
со степенным упрочнением без
упругого участка 101
с площадкой текучести и линей-
линейным упрочнением 100
с площадкой текучести и сте-
степенным упрочнением 100
Диаграмма Марциняка для деформаций
33, 34 х
Марциняка для напряжений 17
мгновенного растяжения 297
Мора 19, 35
напряжений круговая 19, 20 —
, Условие подобия 21
приспособляемости стержневой
системы 239
растяжения 93
растяжения действительная 93
растяжения условная 93
растяжения материала с линей-
линейным упрочнением 82
Дополнительная мощность деформа-
деформации — см. Мощность деформации
дополнительная
Дополнительное рассеяние 348
¦ ¦ Диск вращающийся в условиях ползу-
ползучести — Деформации 332
— Напряжения 333
— Основные уравнения расчета 334
— Пример расчета 335—339
— Радиальное смещение 332
Диск газовой турбины — Расчет на
ползучесть 335—339
¦ Диск постоянной толщины, нагружен-
нагруженный внутренним давлением

— Допущения 117
— Напряжения в пл;1стической об-
области 117, 118
— Напряжения » упругой области
117, 119
— Предельное даиленщ" 121
— Уравнение равновесия элемента 117
— Ураннепия радиального перемеще-
перемещения в упругой и пластической обла-
областях 120
— Упруго-пластическое состояние
117-122
Диск постоянной толщины, равномер-
равномерно нагретый, вращающийся
— Краевые условия 125, 126
— Напряжения в пластической обла-
области 126, 127
— Напряжения в упругой области
124, 12G, 127
— Опасные точки 124
— Предельная угловая скорость 126,
127
— Упруго-пластическое состояние
124-127
— Уравнение движения элемента ди-
диска 124
Ж
Жесткость при кручении бруса 321, 323
Зависимость Ишлинского 81
Задача Коши 196—197
начальная характеристическая
194— Вырожденный случай 195, 198
неустановившейся ползучести
основная 348
неустановившейся ползучести ре-
релаксационная 348
неустановившейся ползучести
смешанная 348
о начальных значениях 196—197
Римана — см. Задача начальная
характеристическая
смешанная 197—198 — Общий
случай 198
Закон гиперболического синуса 246,
284
Гука 243
парности касательных напряже-
напряжений 10
— разгрузки 78
течения ассоциированный 53—54
упрочнения 58
Запас долговечности 263, 264
прочности 263, 265
Звезда Пелчииского для деформаций 33
для напряжений 23
И
Изгиб — Момент сопротивления изги-
изгибу 309
пластины 225
поперечный бруса 312—316 —
Перемещения при установившейся
ползучести 313, 314, 315, 316
чистый бруса 306—312, 346, 350
Изгиб листа чистый 160—165 — Вну-
Внутренний радиус
— Граничная поверхность 160
— Деформация и перемещения 164—
165
— Изгибающий момент 163
— Краевые условия 162
— Напряжения 163
— Наружный радиус 165
— Нормальная сила 163
— Уравнение равновесия 160
Инварианты тензора деформаций
девиатора 27
шарового 27
Инварианты тензора напряжений 14
девиатора 14
шарового 14
Интенсивность скоростей деформа-
деформаций 36
приращений деформаций 34
Интенсивность деформаций 29—31, 38
линейных 30
пластических 30
угловых 30
Интенсивность напряжений 15, 18, 19,
24, 38
¦ нормальных 15
касательных 16
К
Кинематическая теорема—см. Теорема
кинематическая
Кольцо тонкостенное в условиях уста-
установившейся ползучести — Момент
сопротивления изгибу 310 — Момент
сопротивления кручению 315
Компоненты деформаций 25, 26, 37 —
Упругое изотропное тело 37
напряжений 9—10
—— перемещений 25
приращения деформаций 34
скорости деформации 36
Концентрация напряжений — Влия-
Влияние на длительную прочность 260
Коэффициент запаса по времени 263,
264
389

запаса по долговечности 263, 264
запаса по напряжениям 263, 265
—— запаса по прочности 263, 265
—— поперечной деформации 37, 65 —
Зависимость от деформации 66
—— Пуассона — см. Коэффициент
поперечной деформации
Кривизна оси балки при чистом изгибе
бруса 307
Кривые ползучести 242, 243, 244 —
Подобие 254, 276 — Уравнение 375
обратной ползучести 286
ползучести изохронные 270, 345
Кривые релаксации 244, 270, 276,
277, 280, 281
теоретические 289
экспериментальные 289
Критерий прочности эмпирический 302
Треска — Сен-Венана —Примене-
—Применение 339—343
устойчивости деформирования за
пределами упругости 52, 53
Кривая диаграмма 19, 35
Кручение бруса в условиях установив-
установившейся ползучести кольцевого сече-
сечения 316—318
круглого сечення 318—325
Кручение бруса упруго-пластическое—
Вариационное уравнение 145 —
Применение вариационных методов
144—146
чистое 144
Кручение стержня пластическое 219—
224 — Предельный крутящий мо-
момент 220
круглого сечения 221
прямоугольного сечення 221, 223
сечення в виде равностороннего
треугольника 223—224
Л
Линии разрыва скоростей перемеще-
перемещений 189
напряжений 188
Линии скольжения — Дифференциаль-
Дифференциальные уравнения семейства 175
— Определение 175 — Свойства 182 —
Теорема Генки 182
в простом поле напряжений 185
в равномерном поле напряжений
184, 185
в центрированном поле напря-
напряжений 184
Линии Чернова 175
Лист — Чистый изгиб 160—65
М
Материал анизотропный 45 — Усло-
Условие пластичности 45
390
Мера упрочнения 58
Метод допускаемых напряжений 5
определения нагрузки кинемати-
кинематический 211
определения нагрузки статиче-
статический 209
переменных параметров упруго-
упругости — Описание 136—138 — Пере- '
менные параметры упругости 136 —
Процесс последовательных прибли-
приближений 136
расчета шагами во времени 355
упругих решений — Понятие 135
Методы вариационные — Применение
135—146, ЗЮ
Механизм бокового смещения 214
балочный 215
комбинированный 215
Модель вязко-упругого тела Кельвина
373
Максвелла 371
Фойгта 372
Модели деформируемого тела 370
Модуль упругости второго рода 37
длительный 374, 379
мгновенный 374
объемный 37
первого рода 37
Момент предельный крутящий —Круг-
—Круглое сечение 221 — Прямоугольное
сечение 221—223 — Сечение в виде
равностороннего треугольника
сопротивления изгибу в условиях
установившейся ползучести — Круг-
Круглое сеченне 309, 310 — Прямоуголь-
Прямоугольное сечение 309 — Тонкостенное
кольцо 310
Моменты инерции обобщенные 306 —
Круглое сечение 309
- Прямоугольное сечение 307
Мощность деформации дополнитель-
дополнительная 348
поверхностной нагрузки 209, 211
Н
Нагрев нестационарный 262
Нагружение длительное 302 — Эмпири-
Эмпирические критерии прочности 302
нейтральное 51, 56 — Условие
непрерывности 56
простое 62 — Теорема 66
Нагрузки переменные 345
Нагрузки предельные 208 — Кинема-
Кинематический метод определения 211 —
Статический метод определения 209—
Оценка 211
кольцевых пластин — Примеры
определения 228—232
круглых пластин — Использова-

ние условия пластичности Треска—
Сен-Венана 232—235 — Примеры
определения 229, 231—232
Напряжения — Интенсивность 15—
18, 19, 24, 38
— Компоненты 9—10
— Концентрация 260
Напряжения главные касательные 20,
22
—— действительные 94, 99, 360
нестационарные 262
нормальные 9, 10
полные 9
приведенные 41
условные 94
эквивалентные 86, 302
Напряжения главные 14 — Средне-
квадратическое уклонение 18
— Тригонометрическая форма пред-
представления 21—23
— Экстремальность 19, 20
Напряжения касательные 9 — Обо-
Обозначение 10
— Экстремальность 20
октаэдрнческое 17
при крученнн бруса кольцевого
сечения в условиях установившейся
ползучести 317—318
при кручении бруса некруглого
сечения в условиях установившейся
ползучести 321, 323
Напряженное состояние — Геометри-
Геометрический образ 19
равноосное 18
в пространстве главных напряже-
напряжений — Изображение 17
в точке тела 9 — Компоненты
напряжения 10 — Модель 11 —
Разложение 13 — Тензор напряже-
напряжения 10 — Тензорное обозначение 11
Несущая способность — Избыточное
исчерпание 216
пластин 225
труб 111
Неустановившаяся ползучесть — см.
Ползучесть неустановившаяся
Обжатие труб 166
Оболочки, нагруженные внутренним
давлением сферические 129, 132 —
Напряжения 132 — Потеря устой-
устойчивости 132 — Схема нагружения
129
цилиндрические 129 — Деформа-
Деформации 129—131 — Напряжения 129—
131 • Потеря устойчивости 131 —
Схеми нагружения 129
Ортотрошюе тело — см. Тело орто-
троппог
Охрупчивинис материала 257
П
Параметр Ларсона — Миллера 259
Мэнсона Хаферда 259
Надаи — Лоде-21, 32, 33, 35, 65
структурный 280, 281, 282
температурно-временнбй 258
Удквиста 86, 51, 280
Перемещения — Компоненты 25
в балках линейные при устано-
установившейся ползучести 314
в балках угловые при установив-
установившейся ползучести 315—316
в балках при установившейся
ползучести — Примеры определе-
определения 313—316
радиальные в трубах При уста-
установившейся ползучести 331
радиальные в дисках при устано-
установившейся ползучести 335
Пластина бесконечная с отверстием —
Варианты нагружения 122
— Напряжения в пластической обла-
области 118, 123
— Напряжения в упругой области
111, 123
— Несущая способность 123
— Упруго-пластическое состояние
122—123
Пластины круглые и кольцевые —
Изгиб 225
— Интенсивности изгибающих момен-
моментов 227
— Краевые условия 228
— Несущая способность 225
— Предельные нагрузки 225
— Примеры определения предельных
нагрузок 228—232
— Уравнения равновесия 226
Пластичность — Поверхность начала
пластичности 40
— Поверхность пластичности 50
— Проверка условий пластичности 44
— Условие начала пластичности 39
— Условие пластичности 50
— Энергетическое условие начала
пластичности (условие Хубера —
Мизеса) 42
Плита с глубоким вырезом 218 —
Предельно-изгибающий момент 218
с отверстием — Предельная на-
нагрузка 217
Плоскость девиаторная 16, 17
Площадки главные 13
октаэдрнческие 17
Поверхность граничная 160
начала пластичности 40
пластичности 51
пластичности регулярная 56
пластичности сингулярная 56
391

Ползучесть 6, 241, 244 — Гипотезы
о существовании потенциала скоро-
скоростей деформации 293
— Деформации 245
— Закон гиперболического синуса 246
— Кривые 241, 244
— Логарифмическая деформация 252
— Основные характеристики 248
— Особенность расчетов 244
— Релаксация 241, 242, 243
— Скорость логарифмической дефор-
деформации 252, 264
— Собственно ползучесть — см. Пос-
Последействие
— Стадии 245—246
Ползучесть кратковременная 295 —
Деформации 296 — Эксперименталь-
Экспериментальное исследование 295
обратная 241 — Эксперименталь-
Экспериментальное исследование 288
Ползучесть неустановившаяся 298—
302, 345 — Методы решения задач
300—301, 345—357
— Основная задача 348, 350
— Релаксационная задача 348, 352
— Смешанная задача 348
Ползучесть установившаяся 298—
302, 306—343 — Вращающиеся ди-
диски 331—339
— Поперечный изгиб бруса 318—316
— Применение критерия Треска—
Сен-Венана 339—343
— Решение задач 306—343
— Трубы толстостенные 33?—^331
— Трубы тонкостенные цилиндриче-
цилиндрические 326—327
— Чистый изгиб бруса 306—312
Ползучесть установившаяся в стати-
статически неопределимых задачах 298,
299
в статически определимых зада-
задачах 298
Поля напряжений простые №4, 185
равномерные 184
Поля скоростей 185, 187
Последействие 241
обратное 241
пластическое 241 — График 242
упругое 241, ЗТб — График 242
Постулат Друкера 52, 53
Потенциал деформации 140
пластический 54
—— ползучести 267, 270
Предел длительной прочности 257
— Зависимость от времени 258
Предел ползучести 254, 255 — Опре-
Определение 256
Предел прочности материала .94
- условный 95
392
Предел текучести текущий 50
Предельные нагрузки 4
Предельное состояние 208
Преобразование Лапласа -г- Примене-
Применение 380
Призма Треска — Сен-Венана 56
Принцип возможных изменений напря-
напряженного состояния тела 141—143 —
Дополнительная работа 142
Вольтерра 383 — Применение 383
максимума дополнительной ра^
боты 143
максимума работы пластической
деформации 53
минимума дополнительной мощ-
мощности 347
минимума дополнительной рабо-
работы 310
минимума полной энергии 139—
141 — Потенциал деформации 140
Приспособляемость 235 — Диаграмма
239 —Примеры 236—239
Условия 236
Протяжка труб 166
Прочность — Предел 94
— Условный предел 95
Прочность длительная — Влияние кон-
концентрации напряжений 260
— Исследование 257, 262
— Коэффициент запаса 263
— Предел 257
— Эмпирические критерии 302
Прочность длительная при неодноос-
неодноосном напряженном состоянии 302—
303
при нестационарном нагреве 262
при нестационарном напряжении
262
Процесс деформирования неустановив-
неустановившийся 202
установившийся 202
Пружины — Заневоливание 5
Разгрузка — Диаграмма 79
— Деформации 79
— Закон 78, 79
— Напряжения 79
Раздача трубы 166
Разрушение — Время 358 — Стадия
распространения 361
вязкое 256, 257, 358
смешанное 358
хрупкое 256, 257, 358
Разупрочнение термическое 285
-Растяжение мгновенное — Диаграмма
297
трехосное 261

Растяжение и' кручение совместное
тонкостенной трубки — Зависимости
напряжений от деформаций 148, 160
Рассеяние дополнительное 348
Релаксация 241, 242 — Время 372 —
Кривые 244, 289
Сечения главные 172
круглые — Момент сопротивле-
сопротивления изгибу в условиях установившей-
установившейся ползучести 309, 310
прямоугольные — Момент сопро-
сопротивления изгибу в условиях уста-
установившейся ползучести 309
Сжатие слоя между жесткими плитами
198—202 — Решение Прандтля дли
тонкого слоя 200—201
— Сила 200, 201
— Скорости перемещения 202
— Схема 199
Скорости деформаций 35 — Графиче-
Графическая интерпретация 36
— Интенсивность 36
— Компоненты 36
— Компоненты девиатора 36
— Параметр Надан — Лоде 36
—Тензор 36
— Угол вида 36
Скорость угловая предельная 127
Символ Кронекера 13
Состояние действительное 209
деформированное однородное 62
кинематически возможное 210
предельное 4 — Коэффициент "за-
"запаса 4 — Расчет деталей 4
статически возможное 209
Сплошность 360, 362
Старение — см. Теория старения
Статическая теорема — см. Теорема
статическая
Стержневая система — Расчет на пол-
ползучесть 355
Схематизация диаграмм деформиро-
деформирования 99
Тело изотропное — Зависимость меж-
между деформациями и напряжениями
в пределах упругости 37
— Зависимость между компонентами
девиаторов напряжений и деформа-
деформаций в пределах упругости 38
— Условия начала пластичности 38—
39
— Условия пластичности 50
Тело ортотропное 45 — Условие на-
начала пластичности 46
- Условие пластичности 85
Температура гомогологическая 360 —
Диаграмма 250, 251
Температура сходственная — см. Тем-
Температура гомогологическая
Тензор бесконечно малых приращений
деформации 34
приращения пластической дефор-
мации 55
скорости деформации
Тензор деформаций 26 — Инварианты
28, 29 — Разложение 27—28
давиатор 27
шаровой 27
Тензор напряжения 10, И — Разло-
Разложение 12
дввиатор 12
шаровой 12
Теорема Генки 182
Кастилиано 143—144
кинематическая 210 — Доказа-
Доказательство 210—211—Применение
214—216
о простом нагружении 66
статическая 208 — Доказатель-
Доказательство 208—209 — Применение 211—
213
Теории деформационные 64
Теория малых упруг о-пластических де-
деформаций — Диаграмма деформиро-
деформирования материалов 64
- Методы решения задач 106—133,
135—146
- Упрочнение 64
- Уравнения 63
- Условие несжимаемости 63
- Экспериментальная проверка 68—
77
Теория наследственности линейная 376
нелинейная 384—385
пластическая 385
Теория пластичности — Задача 7
изотропного материала 80—86
ортотропного материала 85—90
с анизотропным упрочнением 80
с трансляционным упрочнением
83
Теория ползучести — Задача 7 —
Экспериментальная проверка и ана-
анализ 288—295
наследственная 370
с анизотропным упрочнением
283—288
—— старения 267, 269, 2?0—2?3
техническая 267
течения 267, 269, 273—277
упрочнения 267, 269, 277—283
393

Теория старения 345—346 — Экспери-
Экспериментальная проверка 289
Теория течения — Решение задач 147—
170
— Совместное растяжение и кручение
тонкостенной трубки 147—152
— Экспериментальная проверка 68—
78
Теория течения ползучести 273—277
Теория течения с изотропным упроч-
упрочнением — Основное уравнение 61
— Уравнение Прандтля — Рейсса 61
— Уравнения Сен-Венана — Леви —
Мизеса 61
Теория упрочнения — Решение задач
355
— Экспериментальная проверка 291
Течение пластическое на ребре 57
Труба толстостенная — Упруго-пла-
Упруго-пластическое состояние 106—112
Труба толстостенная нагруженная вну-
внутренним давлением и осевой силой —
Деформации, ПО, 155, 158, 328
— Напряжения ПО, 114, 152, 154,
155, 328, 329, 330
— Напряжения в предельном состоя-
состоянии 111
— Осевая сила 111
— Предельное давление 111
— Решение задачи по теории течения
152
— Эпюры напряжений 111
— Радиальное перемещение 112, 331
— Нормальнзя сила 114
Труба тонкостенная — Время вязкого
разрушения 365—367
— -Время вязко-хрупкого разруше-
разрушения 368
— Время хрупкого разрушения 367—
368
— Деформирование в конических ма-
матрицах 166—170
— Изменение толщины стенки 169
— Совместное растяжение и круче-
нне 147—152
Угол вида деформированного состоя-
состояния 32 — Пределы изменения 33
напряженного состояния 22, 24 —
Пределы изменения 23
приращения деформаций 35
скоростей деформаций 36
Угол закручивания' бруса относитель-
относительный в условиях установившейся
394
ползучести) некруглого сечения 320,
324
кольцевого сечення 317
Угол закручивания труб тонкостен-
тонкостенных цилиндрических в условиях уста-
установившейся ползучести 327
Упрочнение — Закон 58 — Мера 50, 58
анизотропное 283, 288
изотропное 85
трансляционное 80
Уравнение Гейрннгер 187
гиперповерхности 51
линейной теории наследствен-
наследственности 383
линий скольжения 190
поверхности потенциала ползу-
ползучести 270
Прандтля — Рейсса 61
равновесия элемента 117
Сен-Венана — Леви — Мнзеса 61
Условие линейного суммирования по-
повреждений 263
Условие начала пластичности 39, 50 —
Графики 43 — Испытания 44
изотропного тела 41
квадратичное — см. Материал
анизотропный
' наибольшего касательного напря-
напряжения 41, 42
наибольшего приведенного напря-
напряжения 41, 42
ортотропного тела 46
Треска—Сен-Венана 41, 232
Хубера — Мизеса 42, 58
энергетическое 41—43
Условие несжимаемости 63
пропорциональности угловых де-
деформаций и касательных напряже-
напряжений 65
совместности деформаций 26—27
Условия граничные для напряжений
181—182
Ф
Формулы Кастилиано 142
Чистый изгиб бруса в условиях уста-
установившейся ползучести 306—312
— Кривизна оси 307
— Напряжение нормальное 307
— Напряжение нормальное макси-
максимальное 309

ш э
Шаровой тензор 19 Экстремальность напряжений 19, 20
Шейка 94 Элемент механически» моделей тел —
— Напряженное состояние в наимень- Схемы 371
шем поперечном сечении 98 вязкий 370, 371
— Эпюры напряжений 98 упругий 370, 371
Штамп — см. Вдавливание штампа Эллипсоид деформаций 31
напряжений 19, 20 — Поверх-
Поверхность 19
ц
Энергия деформации потенциальная 38
Цилиндр Хубера—Мизеса 59 Эффект Баушингера 40, 82

ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 3
Введение *. 4
Раздел I. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ
Глава I. Теория напряжений 9
§-1. Напряженное состояние в точке тела 9
¦ § 2. Дифференциальные уравнения равновесия 11
§ 3. Разложение тензора напряжения 12
§ 4. Главные площадки и главные напряжения 13
§ 5. Интенсивность напряжений 15
§ 6. Геометрическое изображение напряженного состояния 19
§ 7. Тригонометрическая форма представления главных напряжений 21
Список литературы 24
Глава II. Теория деформаций 25
§ 8. Деформированное состояние в точке тела 25
§ 9. Условия совместности деформаций 26
§ 10. Разложение тензора деформаций 27
§ 11; Главные оси и главные деформации 28
§ 12. Интенсивность деформаций 29
§ 13. Геометрическое изображение деформированного состояния .... 31
§ 14. Тригонометрическая форма представления главных деформаций 32
§ 15. Приращения деформаций 34
§ 16. Скорости деформаций 35
Список литературы 36
Глава III. Зависимости между деформациями и напряжениями в пределах
упругости и условия возникновения пластических деформаций 37
§ 17. Зависимости между деформациями и напряжениями для упругого
изотропного тела 37
§ 18. Условия начала пластичности для изотропного тела 38
§ 19.' Условие начала пластичности для анизотропного тела 45
Список литературы 48
Раздел II. ПЛАСТИЧНОСТЬ
Глава IV. Теории пластичности 50
§ 20. Поверхность пластичности 50
396

§ 21. Постулат Друкера „ 52
§ 22. Ассоциированный закон течения 53
§ 23. Теория течения .....' 58
§ 24. Теория малых упруго-пластическнх деформаций 62
§ 25. Экспериментальная проверка теории течения и малых упруго-
пластических деформаций 68
§ 26. Разгрузка. Остаточные напряжения и деформации 78
§ 27. Теория пластичности изотропного материала с анизотропным
упрочнением " 80
§ 28. Теория пластичности ортотропного материала с изотропным упроч-
упрочнением --. 85
Список литературы 90
Глава V. Действительные диаграммы деформирования материала 93
§ 29. Действительная диаграмма растяжения 93
§ 30. Напряженное состояние в шейке 95
§ 31. Схематизация диаграмм деформирования 99
Список литературы 105
Глава VI. Решение некоторых задач по теории малых упруго-пластических
деформаций 106
§ 32. Упруго-пластическое состояние толстостенной трубы, нагруженной
внутренним давлением и осевой силой при отсутствии упрочнения .... 106
§ 33. Упруго-пластическое состояние толстостенной трубы, нагружен-
нагруженной внутренним давлением и осевой силой при линейном упрочнении 112
§ 34. Автоскрепление толстостенных труб 115
§ 35. Упруго-пластическое состояние диска постоянной толщины, на-
нагруженного внутренним давлением при отсутствии упрочнения 117
. § 36. Упруго-пластическое состояние бесконечной пластины с отвер-
отверстием, растянутой осесимметрично относительно центра отверстия . ... 122
§ 37. Упруго-пластическое состояние вращающегося равномерно на-
нагретого диска постоянной толщины 124
§ 38. Понятие об автоскреплении дисков 128
§39. Большие деформации цилиндрических и сферических оболочек,
нагруженных внутренним давлением 129
Список литературы 133
Глава VII. Приближенные методы решения задач по теории малых упруго-
пластических деформаций 135
§ 40. Метод переменных параметров упругости 135
§ 41. Принцип минимума полной энергии 139
§ 42. Принцип возможных изменений напряженного состояния .... 141
§ 43. Принцип минимума дополнительной работы 143
§ 44. Теорема Кастилиаио 143
§ 45. Применение вариационных принципов к решению задачи упруго-
пластического кручения бруса 144
Список литературы 145
Глава VIII. Решение некоторых задач по теории течения 147
§ 46. Совместное растяжение и кручение тонкостенной трубки 147
§ 47. Упруго-пластическое состояние толстостенной трубы, нагружен-
нагруженной равномерным внутренним давлением и осевой силой 152
§ 48. Изгиб листа 160
§ 49. Деформирование'цилиндрических труб в конических матрицах 166
Список литературы 170
397

Глава IX. Плоская деформация 172
§ 50. Основные уравнения 172
§ Ы. Линии скольжения 175
§ 52. Линеаризация основной системы дифференциальных уравнений 179
§ 53. Граничные условия для напряжений 181
§ 54. Свойства линий скольжения , 182
§ 55. Простые поля напряжений 184
§ 56. Поля скоростей 185
§ 57. Линии разрыва 187
§ 58. Толстостенная труба, нагруженная внутренним давлением .... 190
§ 59. Вдавливание плоского штампа 191
§60. Численные методы решения краевых задач ¦ 194
§ 61. Сжатие слоя между жесткими шероховатыми плитами 198
§ 62. Волочение листа 202
Список литературы " 206
Глава X. Предельное состояние 208
§ 63. Статическая и кинематическая теоремы 208
§ 64. Примеры применения статической и кинематической теорем 211
§ 65. Предельное состояние скрученного стержня произвольного попе-
поперечного сечения 219
§ 66. Основные уравнения задачи предельного состояния круглых и коль-
кольцевых пластин 225
§ 67. Примеры определения предельных нагрузок для круглых и коль-
кольцевых пластин 228
§ 68. Использование условия пластичности Треска—Сен-Венана в ис-
исследованиях несущей способности круглых пластин , 232
§ 69. Понятие о приспособляемости 235
Список литературы ¦ . 239
Раздел XI. ПОЛЗУЧЕСТЬ
Глава XI. Основные результаты экспериментального изучения ползучести
при одноосном растяжении 241
§ 70. Ползучесть и релаксация напряжений 241
§ 71. Кривые ползучести 244
§ 72. Длительная прочность 256
§ 73. Определение коэффициента запаса 263
Список литературы 265
Глава XII. Технические теории ползучести 267
§ 74. Основные понятия 267
§ 75. Теория старения 270
§ 76. Теория течения 273
§ 77. Теория упрочнения 277
§ 78. Теория ползучести с анизотропным упрочнением 283
§ 79. Экспериментальная проверка и анализ теорий ползучести 288
§ 80. Особенности кратковременной ползучести 295
§ 81. Неустановившаяся и установившаяся ползучесть 298
§ 82. Длительная прочность при неодноосном напряженном состоянии 302
Список литературы 304
Глава XIII. Решения некоторых задач установившейся ползучести 306
§ 83. Чистый изгиб бруса ,. . . 306
§ 84. Поперечный изгиб бруса 312
§ 85. Кручение бруса кольцевого поперечного сечения 316
§ 86. Кручение бруса некруглого поперечного сечения 318
§ 87. Тонкостенные цилиндрические трубы 326
398

§ 88. Толстостенные трубы 327
§ 89. Вращающиеся диски 331
§ 90. Использование критерия Треска—Сен-Венана 339
Список литературы 343
Глава XIV. Методы решения задач неустановившейся ползучести 345
§ 91. Теория старения 345
§ 92. Теория течения 346
§ 93. Принцип минимума дополнительной мощности 347
§ 94. Приближенные методы решения задач неустановившейся ползу-
ползучести 349
§ 95. Теория упрочнения 355
Список литературы 357
Глава XV. Определение времени разрушения 358
§ 96. Растяжение стержня 358
§ 97. Кручение круглого стержни 361
§ 98. Тонкостенные трубы 365
Список литературы 368
Глаза XVI. Вязкоупругость 370
§ 99. Механические модели деформируемого тела 370
§ 100. Линейная теория наследственности 376
§ 101. Применение преобразования Лапласа 380
§102. Принцип Вольтерра 382
§ 103. Нелинейные теории наследственности 384
Список литературы 385
Предметный указатель 387

Николай Николаевич Малинии
ПРИКЛАДНАЯ ТЕОРИЯ
ПЛАСТИЧНОСТИ
И .ПОЛЗУЧЕСТИ
Редактор издательства Т. С. Грачева
Технический редактор Л. А. Макарова
Корректор О, В. Мишина
Художник Ё. Г. Шубенцов
Сдано в набор 24/Х 1974 г. Подписано к печати 4/IV 1975 р.
Т-05196 Формат 60X90/16. Бумага типографская № 3
Усл. печ. л. 25,0. Уч.-изд. л. 29,75
Тираж 18 000 экз. Заказ 1332
Цена 1 р. 20 к.
Издательство «Машиностроение», 107885, Москва,
Б-78, 1-й Басманный, д. 3
Ленинградская типография JVs 6 Союзполиграфпрома
при Государственном комитете Совета Министров, СССР
по делам издательств, полиграфии и книжной торговли
193144, Ленинград, С-144, ул. Монсеенко, 10