Theory and Problems
of
Continuum Mechanics
by
George E. Mase,
Ph. D., Professor of Mechanics
Michigan State University
Schaum's Outline Series
MCGRAW-HILL BOOK COMPANY
New York, St. Louis, San Francisco, London, Sydney,
Toronto, Mexico, and Panama 1970

ДжМейз
Теория и задачи
механики
сплошных сред
Перевод с английского
Е. И. Свешниковой
Под редакцией
М. Э. Эглит
ИЗДАТЕЛЬСТВО «МИР» МОСКВА 1974

УДК 532+539.3+539.4
В книге очень сжато излагаются общие принципы механики
сплошной среды и описываются наиболее употребительные матема-
математические модели сплошных сред. Изложение сопровождается тща-
тщательно подобранными задачами общим числом около пятисот; при-
примерно две трети из них приводятся с решениями. Это позволяет ис-
использовать книгу как своеобразный сборник задач по курсу механи-
механики сплошной среды.
Книга написана ясно и четко. Высокие методические достоин-
достоинства позволяют использовать ее как учебное пособие для техни-
технических вузов и университетов по курсу механики сплошной среды.
Она интересна широкому кругу математиков-прикладников, меха-
механиков и инженеров, работающих в области механики сплошной
среды.
Редакция литературы по математическим наукам
© Перевод на русский язык, «Мир», 1974
„ 20305—043 .„ 7.
М 041 @1)- 74 43~74

Предисловие
редактора перевода
В последние годы практика все чаще требует от инженеров и
исследователей в области механики умения строить новые модели
сплошных среде усложненными свойствами, ставить и решать задачи
о поведении таких сред. В связи с этим все более важным становит-
становится глубокое понимание не только частных конкретных закономернос-
закономерностей, но — в первую очередь — самого смысла основных концепций
и законов механики континуума. Именно поэтому механика сплош-
сплошной среды из набора отдельных специальных дисциплин (теория уп-
упругости, гидромеханика, теория пластичности и т. д.) превращается
в единую науку. Это обстоятельство находит отражение и в учебной
литературе; один из примеров — предлагаемая вниманию читателя
книга Дж. Мейза.
Книга представляет собой своеобразное сочетание краткого
учебника по курсу механики сплошной среды и справочника по
этой дисциплине. В ее девяти главах очень сжато вводятся основные
понятия и излагаются общие принципы механики континуума, а
также описываются наиболее употребительные математические мо-
модели сплошных сред. Более половины объема занимают задачи, ко-
которые отчасти дополняют основной текст (в решения задач вынесены
доказательства многих важных результатов), а отчасти являются
обычными упражнениями. Таким образом, книгу можно исполь-
использовать и как задачник (снабженный пояснительным текстом).
Отбор и расположение материала в основном соответствуют тому,
что должно входить в обязательный курс механики сплошных сред
для студентов университетов и технических вузов. Однако некото-
некоторые важные разделы полностью остаются за рамками изложения.
Так, вообще не рассматриваются условия на поверхностях силь-
сильного разрыва, взаимодействие сплошных сред с электромагнитным
полем, подобие и моделирование механических явлений.
Предельную краткость авторского изложения можно считать
достоинством книги: основные идеи и факты даются в легко обо-
обозримом, не загроможденном подробностями тексте. В то же время
эта краткость приводит к тому, что многие существенные детали ока-
оказываются упущенными и некоторые вопросы освещаются недоста-
недостаточно. Поэтому при работе с книгой неизбежно обращение к допол-
дополнительным источникам. Исходя из этого, мы снабдили настоящее
издание списком литературы (в оригинале он отсутствует), охваты-
охватывающим основные учебники на русском языке, в которых читатель
может найти более полные сведения по интересующим его вопросам.

6	ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В первую очередь можно рекомендовать весьма обстоятельный
двухтомный учебник Л. И. Седова, отвечающий современному
состоянию механики и новым направлениям в этой науке.
При переводе были исправлены замеченные опечатки и мелкие
неточности текста; как правило, это не оговаривалось специально.
Пользуюсь случаем выразить свою благодарность автору, лю-
любезно представившему список замеченных в книге опечаток и крат-
краткое предисловие к русскому изданию.
М. Э, Эглит

Предисловие
Механика сплошной среды играет важную роль в современной
технике благодаря тому, что она рассматривает основные понятия и
принципы. В современные программы начального обучения инжене-
инженеров и научных работников прочно входит ряд курсов, в которых
используются понятие сплошной среды и основанные на нем теории,
причем число таких курсов продолжает расти. Программы по меха-
механике и смежным дисциплинам на следующем этапе обучения преду-
предусматривают существенное углубление в этот предмет.
Настоящая книга представляет собой попытку помочь студентам
средних и старших курсов усвоить основы теории сплошной среды.
Каждая ее глава включает решенные задачи, что даег возможность
читателю отточить свое мастерство в решении задач, относящихся к
механикр континуума и ее приложениям.
Последовательность изложения материала и достаточно непре-
непрерывное его развитие позволяют использовать книгу как учебник по
вводному курсу механики сплошной среды. В то же время она может
оказаться весьма полезной в качестве дополнительного справочника
по дисциплинам, базирующимся на методах теории континуума:
курсы сопротивления материалов, гидромеханики, теории упругос-
упругости, теории пластичности и, теории вязкоупругости тесно связаны с
содержанием книги и могут быть построены на ее основе.
По всей книге важные уравнения и фундаментальные соотноше-
соотношения представлены как в индексной (тензорной), так и в классиче-
классической символической (векторной) записи. Это дает возможность
студентам сравнить эквивалентные выражения и привыкнуть к
обозначениям обоих видов. Используются только декартовы тен-
тензоры, поскольку книга задумана как введение в предмет и посколь-
поскольку существо многих теорий может быть описано с помощью таких
тензоров.
Книга по сути дела состоит из двух частей: в первых пяти главах
излагаются общие основы механики сплошной среды, а в последних
четырех — некоторые конкретные ее приложения. За начальной гла-
главой, посвященной математическому аппарату, следуют главы, относя-
относящиеся к общим вопросам, а именно анализу напряженного состояния,
теории деформаций, понятиям движения и течения, а также
основным законам механики сплошной среды. Приложения, рас-
рассматриваемые в последних четырех главах, относятся к теории упру-
упругости, гидромеханике, теории пластичности и теории вязкоупру-
вязкоупругости. В конце каждой главы приводится набор решенных задач и

g	К РУССКОМУ ИЗДАНИЮ
упражнений, служащих для иллюстрации и закрепления идей, при-
приведенных в основном тексте.
Автор пользуется случаем выразить свою признательность всем,
оказавшим ему помощь. Особую благодарность он приносит своим
коллегам — профессорам У. Брэдли, Л. Малверну, Д. Иену,
Дж. Фоссу и Г. Лапалму, прочитавшим различные главы и указав-
указавшим, как улучшить изложение, профессору Д. Монтгомери за его
поддержку и помощь во всех отношениях, д-ру Ричарду Хартунгу
из Исследовательской лаборатории компании «Локхид» (Пало-Аль-
то, Калифорния), ознакомившемуся с первоначальным вариантом
рукописи и внесшему много полезных предложений, а также про-
профессору М. Стиппсу из Иллинойсского университета за ценные
замечания и предложения.
Джордж Э. Мейз
Университет штата Мичиган
К русскому изданию
Механика сплошной среды, будучи фундаментальной наукой,
служит хорошей основой для последующего изучения теории уп-
упругости, пластичности, вязкоупругости и гидромеханики. Поэтому
для студентов важно, чтобы основные концепции и исходные
принципы теории сплошной среды были изложены ясно и аккуратно.
С такой целью и написана эта книга. Автор надеется, что она
поможет читателям понять основы предмета и явится стимулом
к дальнейшему изучению этой важной области механики.
Дж. Мейэ
4 марта 1974
Ист Лансинг, Мичиган

Глава 1
Математические основы
1.1.	Тензоры и механика сплошной среды
Механика сплошной среды имеет дело с физическими величинами,
которые не зависят от выбора системы координат, применяемой для
их описания. Однако очень часто эти физические величины наиболее
удобно изучать в некоторой надлежащим образом выбранной систе-
системе координат. Математически такие величины представляются
тензорами.
Тензор как математический объект существует независимо от
системы координат. В то же время в каждой системе координат его
можно задать некоторой совокупностью величин, называемых ком-
компонентами тензора. Если компоненты тензора заданы в одной си-
системе координат, то они определены и в любой другой системе, ибо
определение тензора включает закон преобразования его компонент.
Точные определения различных видов тензоров будут даваться да-
далее в тех местах, где они впервые появятся в изложении.
Физические законы механики сплошной среды выражаются тен-
тензорными уравнениями. Вследствие линейности и однородности тен-
тензорных преобразований тензорные уравнения, верные в одной си-
системе координат, верны и в любой другой. Такая инвариантность
тензорных соотношений относительно преобразований координат
является одной из основных причин того, что тензорное исчисление
весьма полезно в изучении механики сплошной среды.
1.2.	Тензоры. Декартовы тензоры. Ранг тензора
Если имеют дело с любым преобразованием одной произвольной
системы криволинейных координат в другую, то тензоры называют
Ьбычными тензорами; если же ограничиваются преобразованиями
однородных систем координат, то тензоры называют декартовыми.
Так как большая часть механики сплошной среды может быть изу-
изучена при помощи декартовых тензоров, в этой книге термин «тен-
«тензор» будет означать «декартов тензор», если особо не оговаривается,
что рассматривается более общий случай.
Тензоры можно классифицировать по рангу, или порядку, в
соответствии с частным видом законов преобразования, которым
они подчиняются. Та же классификация отражается и в числе ком-
компонент тензора в и-мерном пространстве. В трехмерном евкли-
евклидовом пространстве, таком как обычное физическое пространство,

10	ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
число компонент тензора равно 3^, где N—порядок тензора.
Тензор нулевого ранга задается в любой системе координат в про-
пространстве любого числа измерений одной компонентой; такие тензо-
тензоры называются скалярами и выражают физические величины,
характеризующиеся только численным значением. Тензоры первого
ранга имеют три координатные компоненты в трехмерном простран-
пространстве, называются векторами и представляют величины, которые
характеризуются как численным значением, так и направлением.
Тензоры второго ранга называются диадиками и описывают неко-
некоторые характеристики, важные в механике сплошной среды. При
математическом изучении механики сплошной среды также опреде-
определяются и часто используются тензоры более высокого ранга, в
частности третьего и четвертого (триадики а тетрадики).
1.3. Векторы и скаляры
Некоторые физические величины, такие, как сила и скорость,
характеризующиеся и численным значением, и направлением, мож-
можно изображать в трехмерном пространстве направленными отрезка-
отрезками, которые подчиняются закону сложения по правилу параллело-
параллелограмма. 1акиенагпдавленные охреаки _являются геометрическими
представлениями тензороалервого ранга «называются векторами.
а.
\
Рис. 1.1.
Графически вектор — просто соответствующим образом направ-
направленная стрелка, имеющая длину, пропорциональную величине
(модулю) вектора. Векторы равны, если они одинаково направлены
и имеют _равные длины. Единичным вектором называется вектор,
у которого длина равна единице. Нулевой вектор имеет нулевую
длину и неопределенное направление. Отрицательным по отноше-
отношению к данному называется" вектор с тем же модулем, но противо-
противоположно направленный.
Такие физические величины, как, например, масса и энергия,
которые характеризуются только величиной, относятся к тензорам
нулевого ранга, т. е. к скалярам.
В символической, или гиббссвой, системе обозначений векторы
изображаются жирными прямыми буквами, например a, b и т. д.
Скаляры обозначаются светлыми курсивными буквами, например
a, b и т. д. Единичные векторы, кроме того, отмечают крышечкой
над жирной прямой буквой. На рис. 1.1 показаны произвольные
векторы а и Ь, единичный вектор е и два равных вектора с и d.

1.4. ВЕКТОРНОЕ СЛОЖЕНИЕ. УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
11
Абсолютную величину произвольного вектора а обозначают
просто а или, чтобы подчеркнуть векторную природу объекта, ис-
используют символ |а|.
1.4. Векторное сложение. Умножение вектора на скаляр
Сложение векторов подчиняется правилу параллелограмма, со-
согласно которому сумма двух векторов изображается диагональю
параллелограмма, смежными сторонами которого являются слагае-
слагаемые векторы, отложенные из одной точки. Этот закон сложения
эквивалентен правилу треугольника, по которому суммой двух век-
-Ь	Ь
торов является вектор, идущий из начала первого вектора в конец
Bjogorcb—если суммируемые векторы построены таким образом,
что начало второго совпадает с концом первого. Графическое по-
построение, соответствующее сложению векторов а и b по правилу
параллелограмма, показано на рис. 1.2, а. Алгебраически операция
сложения выражается векторным равенством
a + b = b + a=c.	A.1)
Вычитание вектора выполняется путем прибавления отрицательно-
отрицательного вектора, как сделано, например, на рис. 1.2, б, где использо-
использовано правило треугольника. Таким образом,
a-b = -b + a = d.	A.2)
Рис. 1.2, в иллюстрирует свойство коммутативности и ассоциатив-
ассоциативности операций сложения и вычитания векторов в соответствии с
равенствами
= a -f- (b -f- g) = п.	A-<j)
Умножение вектора на скаляр в общем случае дает новый век-
вектор, имеющий то же направление, что и исходный, но другую дли-
длину. Исключение составляет умножение на нуль, которое дает в
результате нулевой вектор, и умножение на единицу, которое
не меняет вектора. При умножении вектора b на скаляр т в зависи-
зависимости от численного значения т возможен один из трех случаев,
представленных на рис. 1.3.

12
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
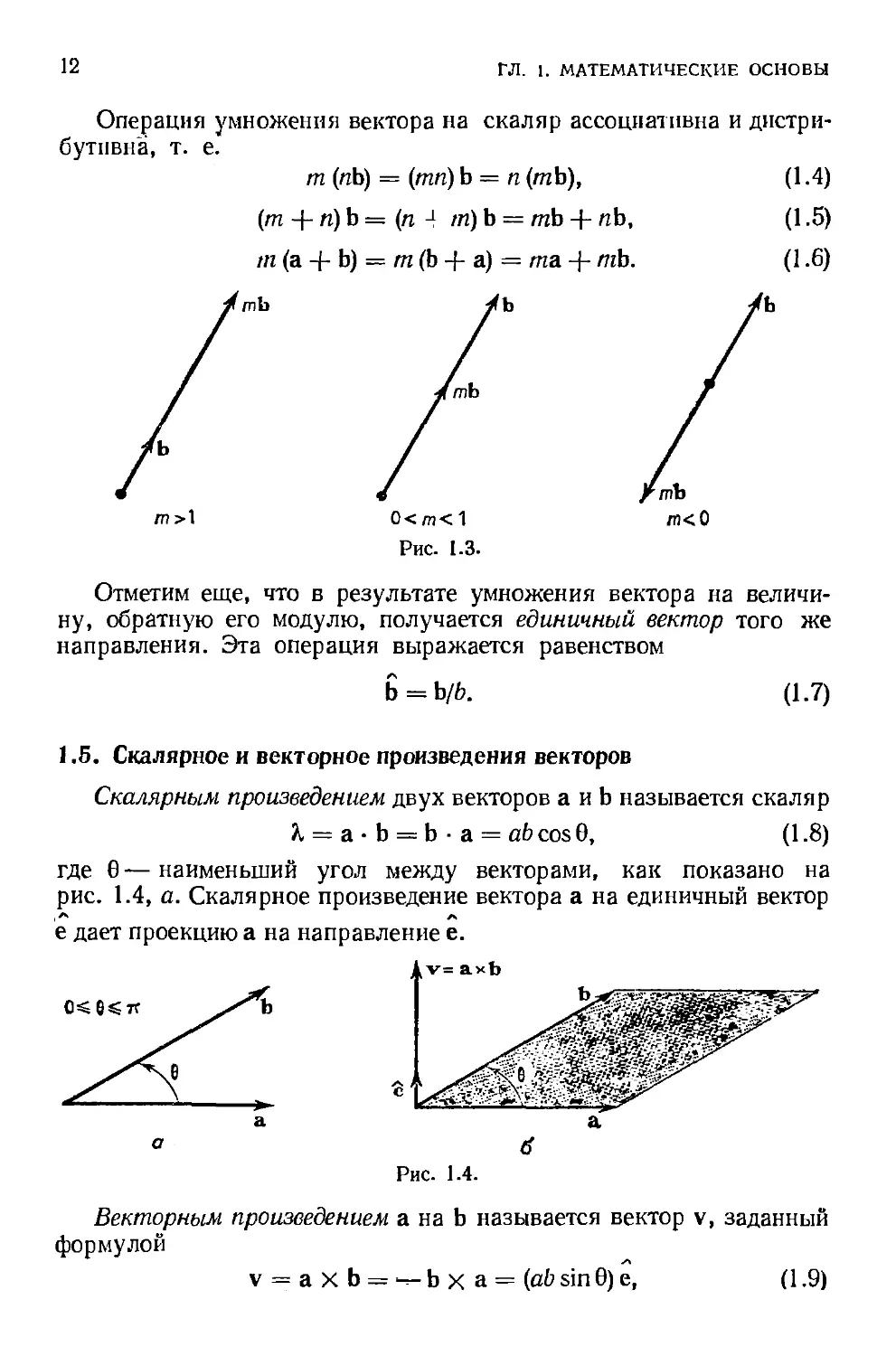
Операция умножения вектора на скаляр ассоциативна и дистри-
дистрибутивна, т. е.
т (пЬ) = (тп) Ъ = п (тЪ),	A.4)
(т + п)b = (п л т)Ъ = тЪ + пЪ,	A.5)
т (а + Ь) = т (Ъ -f- а) = та + тЪ.	A.6)
Рис. 1.3.
Отметим еще, что в результате умножения вектора на величи-
величину, обратную его модулю, получается единичный вектор того же
направления. Эта операция выражается равенством
b = Ъ/b.
A.7)
1.5. Скалярное и векторное произведения векторов
Скалярным произведением двух векторов а и b называется скаляр
Я = а- b = b ¦ a = a6cos9,	A.8)
где 6—наименьший угол между векторами, как показано на
рис. 1.4, а. Скалярное произведение вектора а на единичный вектор
е дает проекцию а на направление е.
Рис. 1.4.
Векторным произведением а на b называется вектор v, заданный
формулой
v = а X b = — b x a = (ab sin 6) е,	A.9)

1.6. ДИАДЫ И ДИАДИКИ	13
где б ¦— угол между векторами а и Ь, меньший чем 180°, а е — еди-
единичный вектор, перпендикулярный к их плоскости и направленный
так, что поворот по правилу правой руки вокруг е на угол 6 перево-
переводит а в Ь. Модуль v равен площади параллелограмма со смежными
сторонами а и Ь, затененного на рис. 1.4, б. Векторное произведение
некоммутативно.
Смешанным произведением называется скалярное произведение
двух векторов, один из которых сам является векторным произведе-
произведением:
а- (Ь х с) = (ах b) -c = a-b x с = Я,.	A.10)
Из этой формулы видно, что скалярное и векторное умножение
здесь можно менять местами. Так как векторное умножение долж-
должно выполняться первым, скобки не нужны и, как показано, их
можно опустить. Это произведение иногда записывают как labc].
Величина А, смешанного произведения равна объему параллеле-
параллелепипеда с ребрами а, Ь, с.
JJfioUHoe_eetsrnop_HQ^ произведение — это ^векторное произведение
двух^ векторов, один из которых сам является векторным произве-
произведением. Для представления векторного произведения а на b x с
часто бывает полезно следующее тождество:
а X (Ь х с) = (а • с) b — (а • Ь) с = w.	A.11)
Из формулы A.11) видно, что w лежит в плоскости векторов b и с.
1.6. Диады и диадики
Диадой называется неопределенное произведение двух_ векторов
а и Ь, которое по определению"Задаётся написанием векторов один
за другим, например ab. Неопределенное произведение в общем слу-
случае некоммутативно, т. e._ab Ф Ьа. ДиадикомР_ называется тензор
второго ранга; он всегда может быть представление виде суммы ко-
конечного числа диад:
+ ••• +awbw.	A.12)
Однако это представление неединственно. В символических обозна-
обозначениях тензоры второго ранга (диадики) изображаются заглавными
жирными буквами, как это сделано выше.
^_с^и_Е.даждой_ддаде.фср_м.улы__(Ы2) первый и второй сомножи-
сомножители поменять местами, _ то полученный тензор называется сопря-
сопряженным исходному и записывается так:
Dc - Ь1Й1 + Ь2аа + ... +bwaw.	A.13)
Если каждую диаду в сумме D в формуле A.12) заменить скалярным
произведением соответствующих векторов, то получится скаляр,

14	ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
называемый скаляром диадикаХ) и. записываемый &виде
DJ = a1.b1 + aa.b,+ ••• + а„ • Ь„!	A.14)
Если каждую диаду в сумме D в формуле A.12) заменить векторным
произведением составляющих ее векторов, то результат будет на-
называться вектором диадика D и записываться так:
Dc = a,xb,+a2xb2+ •¦• +awxbr	(J.15)
Можно показать, что D,, Ds и D^ не зависят от выбора представле-
представления A.12).
Неопределенное произведение векторов обладает свойством
дистрибутивности:
a(b + c)= ab + ac,	A.16)
(a+b)c = ac + bc,	A.17)
(a + b)(c+d) = ac + ad + bc + bd,	A.18)
и если К и ц, — скаляры, то
(К + ц) ab = ХаЪ + цаЪ,	A.19)
(Я,а)Ь = а(АЬ) = Я,аЬ.	A.20)
Если v — любой вектор, /го скалярные произведения v ¦ D и
D • v тоже являются векторами, которые определяются соответст-
соответственно формулами
v.D = (va1)b1 + (v-a2)b2+ ••• + (v • &N) bN = u, A.21)
D ¦ v = ax (bx - v) + a2 (b2 • v) + • • • + aN <frN • v) = w. A.22)
Дв_а_диадика D и Е равны тогда и только тогда, когда для любого
вектора v
v • D = v • Е или D ¦ v = Е • v.	A.23)
Единичный-диадик I — это такой диадик, который представляется
в виде
I = е^ + ee2 + е3е3,	A.24)
л * л
где еь е2, е3 — векторы любого ортонормированного базиса в трех-
трехмерном евклидовом пространстве (см. § 1.7). Единичный диадик I
характеризуется следующим свойством:
|.v = vl = v	A.25)
для всех векторов v.

16 ДИАДЫ II ДИАД-1КИ
15
Векторные произведения v x D и D x v являются диадиками,
которые определяются соответственно формулами
VXD = (vxa1)b1 + (vXa2)b2+ ••• +(vXa,)bw=F, A.26)
Dxv = a,(b1xv) + a2(b2xv)+ • • - + aN (bN xv) = C. A.27)
Скалярное произведение двух диад ab и cd по определению есть
диада вида
ab • cd = (b • с) ad.	A.28)
Пользуясь формулой A.28), легко усмотреть, что скалярное произ-
произведение любых двух диадиков D и Е тоже является диадиком:
D • Е = fob, + a2b2 + • • • + а„Ь„). (сА + c2d2 + • •• + с^) =
= (bx • Cj) a^ + (b2 • c2) a2d2 + • • • + (bN • cN) aN&N = G.
A.29)
Диадики D и Е называются взаимно обратными, если
E-D=D-E=I.	A.30)
Для обратных диадиков часто используются обозначения Е = D~'
и D = Е.
Дважды скалярное, смешанное и дважды векторное произведения
диад ab и cd по аналогии можно определить следующим образом:
ab: cd = (a • с) (Ь • d) = К
ab >< cd = (а х с) (Ь • d) = h
ab x cd = (а • с) (b x d) = g
ab x cd = (а х с) (b x d) = uw
Пользуясь этими формулами, легко получить дважды скалярное
и векторное произведения тензоров второго ранга. Некоторые
авторы двойное скалярное произведение диад определяют так:
ab •• cd = (b- с) (а • d) = Я, (скаляр).	A.35)
Диадик D называют самосопряженным или симметричным, если
D = DC,	A.36)
и антисимметричным, если
D = — Dc.	A.37)
Каждый диадик можно представить в виде суммы симметричного и
антисимметричного диадиков, причем это представление единст-
единственно. Действительно, для любого диадика D можно написать
D = V» (D + Dc) + V« (D — Dc) = G + H,	A.38)
(скаляр),
(вектор),
(вектор),
(диада).
A.31)
A.32)
A.33)
A.34)

16
где
и
ГЛ 1 МАТЕМАТИЧЕСКИЕ ОСНОВЫ
Gc - V, (Do + (Dc)c) = V, (De + D) = G (симметричный) A.39)
= х/г (D —
(Dc)c) = V2 (Dc — D) = — H (антисимметричный).
A.40)
Для того чтобы установить единственность такого разложения,
предположим, что существует другое разложение D = G* -f H*;
тогда
G* + H* = G + H.	A.41)
Равенство, сопряженное этому, будет
G* —H* = G —H.	A.42)
Почленное сложение и вычитание A.41) и A.42) приводит соот-
соответственно к требуемым равенствам G* = G и Н* = Н.
1.7. Системы координат. Базисные векторы.
Триэдр единичных векторов
Относительно выбранной системы координат вектор можно зада-
задавать его компонентами в этой системе. Выбор системы координат
произволен, но в некоторых си-
ситуациях бывает выгоднее пользо-
пользоваться специальной системой. За-
Задать систему осей координат —
это значит задать единицы изме-
измерения длин векторов и указать
направления осей в пространстве,
чтобы можно было определить ори-
ориентацию векторов.
Общеизвестную ортогональную
декартову систему координат Охуг
обычно представляют взаимно пер-
перпендикулярными осями, показан-
показанными на рис. 1.5. Любой вектор
v в такой системе можно задать в
виде линейной комбинации трех
произвольных некомпланарных векторов, которые называются ба-
базисными векторами. Через базисные векторы а, Ь, с и соответст-
соответствующим образом выбранные скалярные коэффициенты К, ^, v век-
вектор v выражается так:
v = ta + ^b+vc.	A.43)
Рис. 1.5.

1.7 СИСТЕМЫ КООРДИНАТ
17
Базисные векторы по определению линейно независимы, т. е. урав-
уравнение
?ia
= О
A.44)
удовлетворяется только при К = \i = v = 0. Говорят, что совокуп-
совокупность базисных векторов для данной системы координат образует
базис этой системы.
В ортогональной декартовой
системе в качестве базиса обыч-
обычно берут набор единичных век-
торов i, j, k, направленных вдоль
осей координат, как показано
на рис. 1.5. Эти базисные векто-
векторы образуют правый триэдр еди-
единичных векторов, для которых
i х j = k, j x k = i,
kxi=j A.45)
= jj = k k=l,
]' = ]"• k = k- i = 0. A.46)
Рис. 1.6
Такой набор базисных векторов часто называют ортонормированным
базисом.
Вектор v, изображенный на рис. 1.6 стрелкой, можно представить
в виде линейной комбинации единичных векторов Г, f, к:
v = vx
vzk,
A.47)
в которой декартовы компоненты
vx = v • 1 = v cos a, vy = v • j = v cos p, vz = v • k = v cos у
являются проекциями v на оси координат. Согласно формуле
A.7), единичный вектор направления v дается выражением
е0 = v/v = (cosoc) i + (cosP) j + (cosy) k.
A.48)
Вектор v произволен, следовательно, для любого единичного век-
вектора его направляющие косинусы являются его декартовыми компо-
компонентами.
В декартовых компонентах скалярное произведение векторов а
и b записывается в форме
а • b = (axi + ay\ + агк) ¦ (bj + bj + b2k) = axbx + ayby + a A. A.49)

18
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
Для тех же двух векторов векторное произведение а х b имеет
вид
а х b = (aybz — агЬу) \ + (агЬх - ахЬг) 1 + (а А — ЙЛ) •<¦ A.50)
о	6
Рис. 1.7.
а — цилиндрическая система координат; б — сферическая система координат.
Последнее выражение часто записывают в виде определителя
j
а х Ь =
ах ау аг
К Ьу Ъг
A.51)
с элементами которого оперируют, как с обычными числами.
Смешанное произведение векторов тоже можно представить че-
через компоненты в виде определителя
ах ау аг
[abc] =
К ьу ьг
A.52)
Диада ab через декартовы компоненты выражается так:
ab = (а х\ + ау\+ агк) (bj + by] + b?) =
i + ciybyj j + aybA k +
a,b? \ + агЬу& j + ajb$k.	A.53)

1.8. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ФУНКЦИИ. ДИАДИКИ	19
Из-за того, что выражение A.53) состоит из девяти членов, оно
называется девятичленной формой диады ab. Любой тензор второго
ранга можно записать в девятичленной форме. Девятичленная форма
единичного диадика представляется через единичные векторы i, j,
к следующим образом:
l = T?+jf+kk.	A.54)
Кроме уже рассмотренной ортогональной декартовой системы,
в дальнейшем широко используются системы криволинейных коор-
координат, такие, как цилиндрическая G?, 6, г) и сферическая (г, 6, ф),
изображенные на рис. 1.7. С этими системами связаны триэдры едн-
л	/\	л	л л	л
ничных базисных векторов (е«, ее, ег) и (ел, ее, еф), показанные на
рисунке. Однако в этих случаях базисные векторы не имеют постоян-
постоянных направлений и поэтому, вообще говоря, являются функциями
точки.
1.8. Линейные векторные функции.
Диадики как линейные векторные операторы
Говорят, что вектор а является функцией другого вектора Ь,
если а определен, как только задан Ь. Это функциональное соот-
соотношение выражается формулой
a = f(b).	A.55)
Функция f называется линейной, если для любых векторов b и с
и любого скаляра К имеют место равенства
f (Ь + с) = f (b) + f (с),	A.56)
М(Ъ).	A.57)
При использовании декартовых компонент вектора b равен-
равенство A.55) принимает форму
а = ЦЬх\ + Ьу) + Ь2к);	A.58)
в случае линейности f это можно переписать так:
a = bj(i) + bJQ) + bJ(k).	A.59)
л	л	/\
Пусть в формуле A.59) f (i) = u, f (j) = v, f (k) = w, так что
a = u (I • b) + v (j • b) + w (k • b) = (ui + vj + wk) - b. A.60)
Видно, что а представляет собой скалярное произведение диаднка
на вектор, т. е.
a = D-b,	A.61)
/\	л	л
где D = ui + vj + wk. Это показывает, что любая линейная век-
векторная функция f может быть выражена произведением диадика на

20	ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
вектор. В формуле A.61) диадик D служит линейным векторным опе-
оператором, который, действуя на векторный аргумент Ь, переводит
его в вектор-функцию а.
1.9. Индексные обозначения. Интервал изменения
индексов и соглашение о суммировании
Компоненты тензора любого ранга и сам тензор можно наглядно
и кратко представить с помощью индексных обозначений. Эти обо-
обозначения состоят в том, что к характерной, или основной, букве,
представляющей интересующую нас тензорную величину, добав-
добавляются верхние или нижние буквенные индексы. Типичными при-
примерами, иллюстрирующими употребление индексов, являются тен-
тензорные символы
ait V, TlhFi, elik, RPQ.
По правилам индексных обозначений буквенный индекс может
встречаться в каждом члене один или два раза.Если индекс употреб-
употреблен один раз, то подразумевается, что он принимает значения
1, 2, ..., N, где N— заданное положительное целое число, которое
определяет размерность индекса, т. е. интервал его изменения. Не-
Неповторяющиеся индексы называются свободными. Тензорный ранг
данного члена равен числу свободных индексов в этом члене. Пра-
Правильно написанные тензорные соотношения имеют одинаковые
свободные индексы в каждом члене.
Если индекс употреблен дважды, то подразумевается, что этот
индекс принимает все значения из своего интервала изменения и
члены, соответствующие каждому значению индекса из этого на-
набора, суммируются. В этом так называемом соглашении о суммиро-
суммировании повторяющиеся индексы часто называют немыми, так как их
замена на любые другие буквы, не использованные в качестве сво-
свободных индексов, не меняет значения члена, в который они входят.
Вообще говоря, в правильно написанном выражении ни один индекс
не встречается более двух раз. Если для желаемого представления
какой-либо величины совершенно необходимо использовать не-
некоторый индекс более чем дважды, соглашение о суммировании
употреблять не следует.
По числу и расположению свободных индексов непосредственно
можно судить о тензорном характере величины, выраженной в ин-
индексных обозначениях. Тензоры первого ранга (векторы) обознача-
обозначаются основными буквами с одним свободным индексом. Так, любой
вектор а изображается символом с единственным верхним или ниж-
нижним индексом, т. е. в одной из двух форм
а(, а1.

1.9. ИНДЕКСНЫЕ ОБОЗНАЧЕНИЯ	21
В следующих выражениях, имеющих только один свободный индекс,
тоже можно узнать тензоры первого ранга:
аф-1г Fikk, Rp.qp, e.tjkUjVk.
Тензоры второго ранга обозначаются символами с двумя свободны-
свободными индексами. Так, произвольный тензор второго ранга D будет
записываться в одной из трех возможных форм
D", Di1 или D[h DCj.
В смешанной форме точка указывает, что / — второй индекс. Тен-
Тензорные величины второго ранга могут выглядеть по-разному,
например
Логически продолжая вышеуказанную схему, тензор третьего
ранга записывают символом с тремя свободными индексами. А сим-
символ, который не имеет связанного с ним индекса, такой, как, напри-
например, К изображает скаляр, или тензор нулевого ранга.
В обычном физическом пространстве базис состоит из трех не-
некомпланарных векторов, и любой вектор в этом пространстве пол-
полностью задается своими тремя компонентами. Поэтому индексы у
величин at, представляющих вектор а в физическом трехмерном про-
пространстве, принимают значения 1, 2, 3. Согласно этому, подразуме-
подразумевают, что символ а,- представляет сразу три компоненты аг, а2, а3.
Таким образом, иногда символ at можно толковать как i-ю компо-
компоненту вектора, а в других случаях — как сам вектор. В трехмерном
пространстве, где оба индекса i, j меняются от 1 до 3, символ Ац
представляет девять компонент тензора второго ранга А. Часто тен-
тензор Аи задают подробно, записывая все девять его компонент в виде
квадратной таблицы, заключенной в большие скобки:
(1 2 з\
An Лм АгЛ.	A.62)
1 2 3/
Таким же образом компоненты тензора первого ранга (вектора)
в трехмерном пространстве можно наглядно изобразить упорядо-
упорядоченными строкой или столбцом из компонент в виде
о* = (fli. о2. о3) или а,- = а2 I.	A.63)
W
В общем случае в Af-мерном пространстве тензор /г-го ранга будет
иметь Л'" компонент.

22	ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
Удобство индексных обозначений для записи систем равенств
в компактной форме мы проиллюстрируем двумя следующими ти-
типичными примерами. В трехмерном пространстве уравнение в ин-
индексной записи
A.64)
представляет в развернутой форме три уравнения:
*i = Сц?! + с12г2 + с13га,
х2 = с21гг + с22г2 + с23г3,	A.65)
Х3 ==	Ч	\
Если / и / принимают значения 1 и 2, то равенство в индексной записи
Ац = BipCjqDpq	A.66)
в развернутой форме дает четыре соотношения:
¦<4п = BnCnDn + BnC12D12 -f- B12CnD2l -\- Bl2C12D22,
Al2 = BnC21Dn -\- BllC22Dl2 -f B12C21D21 + B12C22D22, ^ 1.67)
A21 = B21CnDn -\- B21C12D12 + Bi2CnD21 -f- B22Cl2D22,
Если же i, / = 1, 2, 3, то формула A.66) даст девять соотношений,
каждое из которых имеет девять членов в правой части.
1.10. Соглашение о суммировании в символических обозначениях
Соглашением о суммировании часто пользуются в связи с пред-
представлением векторов и тензоров в символических обозначениях
через базисные векторы, снабженные индексами. Так, если декар-
декартовы оси и единичные векторы базиса, изображенные на рис. 1.5,
переобозначить, как показано на рис. 1.8, то произвольный век-
вектор v можно записать в виде
v = V& + v2e2 + v3e3,	A.68)
где vlt v2, v3 — декартовы компоненты вектора v. Применяя к
этому равенству соглашение о суммировании, его можно переписать
в сокращенной форме:
v=»ft,	A.69)
где i — индекс суммирования. Здесь обозначения по существу
символические и в то же время использовано соглашение о суммирова-
суммировании. При таком сочетании обозначений не действует правило сво-
свободных индексов, принятое в чисто индексном обозначении тензор-
тензорных величин.

1.11. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. ОБЩЕЕ ПОНЯТИЕ ТЕНЗОРА
23
Тензосы второго ранга то-
тоже могут быть представлены
суммированием по базисным
векторам, снабженным индек-
индексами. Так, диаду ab, задан-
заданную в девятичленнсш форме
A.53), можно записать в виде
ab = (й,е() (Ьуву) = ар^^.
A.70)
В этом выражении важно со-
сохранять порядок написания
базисных векторов. Подоб-
Подобным же образом девятичлен-
ная форма любого тензора
второго ранга D может быть
представлена в компактных
обозначениях так:
A.71)
Рис 1.8.
1.11. Преобразование координат. Общее понятие тензора
Пусть х1 — произвольная система координат х1, х2, х3 в трех-
трехмерном евклидовом пространстве и б1 — любая другая система
координат б1, б2, б3 в том же пространстве. Здесь цифры, написан-
написанные сверху, являются индексами, а не показателями степени, сте-
степени х можно записывать при пом'ощи скобок, например так: (хJ
или (хK.
Итак, цифры (или буквы), написанные сверху, как только что
было указано, служат индексами. Формулы преобразования коорди-
координат
6' = 6'(x\ х2, а-3)	A.72)
определяют для любой точки (х1, х2, х3) системы хг новый набор ее
координат (б1, б2, б3) в системе б1. Относительно функций б1, свя-
связывающих две совокупности переменных величин (координат),
предполагается, что они однозначные, непрерывные и дифференциру-
дифференцируемые. Определитель
J
дх1
дв2
дх1
дх2 дх3
дх2 дх3
A.73)
дх1
дх2 дх3

24	ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
или в компактной форме
J =
A.74)
называется якобианом преобразования. Если якобиан не обращается
в нуль, то уравнения A-72) можно локально единственным образом
разрешить относительно х1:
*' = *'¦ (б1, е2, G3).	A.75)
Системы координат х и б', использованные при написании A.72)
и A.75),— самые общие: они могут быть любыми криволинейными
или декартовыми.
Из A.72) найдем компоненты дифференциала аЪ1:
й# = ^г&хК	A.76)
дх1
Это равенство определяет класс тензоров, называемых контра-
вариантными векторами. В общем случае величины Ъ1, связанные с
точкой Р, представляют компоненты контравариантного тензора
первого ранга, если при преобразовании координат эти величины
преобразуются tio закону
fe'< = -^-fe/,	A.77)
дх>	v
причем частные производные вычислены в точке Р. В A.77) Ь' яв-
являются компонентами тензора в системе координат х/, а Ь1— его
компонентами в системе 6'. В общей теории тензоров для обозначения
контравариантных тензоров используют верхние индексы. Это де-
делается по той причине, что для координаты обозначение х1 пред-
предпочтительнее, чем а;,; однако нужно заметить, что тензорный харак-
характер имеют только дифференциалы dx, но не сами координаты.
Естественнее обобщение правила A.77) приводит к определению
контравариантного тензора второго ранга, компоненты которого
подчиняются правилу преобразования
B'li-^^Brs-	a-78)
Контравариантные тензоры третьего, четвертого и более высокого
порядков определяются аналогичным образом.
Слово «контравариантньиЬ использовано выше, чтобы отличить
эти тензоры от тензоров другого типа, называемых ковариантными.
В общей теории для изображения ковариантных тензоров исполь-
используются нижние индексы. Типичный ковариантный вектор образу-
образуют частные производные от скалярной функции по координатам.

1.12. МЕТРИЧЕСКИЙ ТЕНЗОР. ДЕКАРТОВЫ ТЕНЗОРЫ	25
Действительно, если <р = <р (х\ х2, х3) — такая функция, то
д& — дх1 д& "	{i- '
В общем случае величины bt называются компонентами ковариантно-
го тензора первого ранга, если они преобразуются по правилу
Здесь bi являются ковариантными компонентами вектора в системе
6', aft; — компонентами в системе х*. Кодариантные тензоры вто-
второго ранга подчиняются закону преобразования
о' дхТ dxs г,	/, on
B	B	(L8I)
Ковариантные тензоры более высокого порядка и смешанные тен-
тензоры, например
гр'г	двг дх" дх? rptn	n qo\
определяются очевидным образом.
1.12. Метрический тензор. Декартовы тензоры
Пусть хг представляют систему ортогональных декартовых ко-
координат в евклидовом трехмерном пространстве, а в1 — любую
другую систему ортогональных прямолинейных или криволиней-
криволинейных координат (например, цилиндрических или сферических) в том
же самом пространстве. Вектор х, имеющий декартовы компоненты
х', называется радиусом-вектором произвольной точки Р (х1, хг, хэ)
в декартовой системе. Квадрат дифференциала расстояния между
близкими точками Р (х) и Q (х + rfx) дается формулой
(dsJ = dxfdxf.	A.83)
Из преобразования координат
х1 = х1 (е\ е2, е3)	0.84)
получим связь между их дифференциалами:
dx' = ^dep.	A.85)
Тогда выражение A.83) перейдет в следующее:
|L Jg	e",	(i .86)
где тензор второго ранга gpq — (djcVcW) (dxl/dQg) называется мет-
метрическим или фундаментальным тензором пространства. Если 6'

26
ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
образуют тоже ортогональную декартову систему, скажем х1, то
дх'р дх"
0-87)
где 6PQ — дельта Кронекера (см. § 1.13), т. е. bpq = 0, если р ф q,
и бр<? = 1, если р = q.
Система координат, для которой квадрат бесконечно малого
элемента длины всюду имеет вид A.83), называется системой од-
однородных координат. Преобразования, переводящие одну систему
однородных координат в другую, являются ортогональными, и
если ограничиться только ортогональными преобразованиями, то
тензоры, определенные таким образом, называются декартовыми
тензорами. В частности, это верно для законов преобразования ор-
ортогональных декартовых систем координат с общим началом. Для
декартовых тензоров нет различия между контравариантными и
ковариантными компонентами, и поэтому в выражениях, представ-
представляющих декартовы тензоры, принято пользоваться исключительно
нижними индексами. Как будет показано далее, в законах преобра-
преобразования, определяющих декартовы тензоры, частные производ-
производные в общих тензорных определениях A.80) и A.81) заменяются кон-
константами.
1.13. Законы преобразования декартовых тензоров.
Дельта Кронекера. Условия ортогональности
Пусть Охгх^к& и Ох[х2Хз — две ортогональные декартовы
системы координат с общим началом в произвольной точке О
(рис. 1.9). Можно считать, что система со штрихами получена из
системы без штрихов поворотом осей около начала координат или
отражением осей относительно одной из координатных плоскостей,
или, может быть, комбинацией того и другого. Если символом ац
обозначен косинус угла между ?-й осью системы со штрихами и /-й
осью системы без штрихов, т. е. ац = cos (х,-, х7), то ориентацию
какой-либо оси каждой системы относительно другой системы
удобно'задавать таблицей
х\
х\
х'з
Xl
ап
«21
«31
*2
«12
«22
«32
*3
«13
«23
«аз

1.13. ЗАКОНЫ ПРЕОБРАЗОВАНИЯ ДЕКАРТОВЫХ ТЕНЗОРОВ
27
или же тензором преобразования
(«11 «12 «1з\
«21 «22 «23 I •
«31 «32 «зз/
Из такого определения ац следует, что единичный вектор е! оси х[
в соответствии с формулой A.48) и соглашением о суммировании
представляется выражением
A.88)
Ясно, что, обобщая это ра-
равенство, любой базисный век-
вектор можно записать в виде
Ъ^ър/. A.89)
Произвольный вектор v,
изображенный на рис. 1.9,
можно выразить через его
компоненты в системе без
штрихов:
v=o,-e) A.90)
и в системе со штрихами:
i	A.91)
рис. ь9.
Заменяя е» в сумме A.91) эквивалентным выражением A.89), по-
получаем
'	A.92)
Сравнивая формулы A.92) и A.90), обнаруживаем, что компоненты
вектора в исходной и преобразованнол системах связаны соотноше-
соотношением
vi = a,,v'i-	A.93)
Это равенство дает закон преобразования декартовых тензоров пер-
первого ранга. Как видно, он является частным случаем общих законов
преобразования тензоров первого ранга, которые были представле-
представлены формулами A.80) и A.77). Меняя ролями в предыдущих рассужде-
рассуждениях базисные векторы со штрихами и без штрихов, получаем со-
соотношение, обратное A.93):
»; = flyD/.	A.94)

28	ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
Нужно заметить, что в формуле A.93) у а-ч- свободным был второй
индекс, а в выражении A.94) свободный индекс является первым.
Выбрав надлежащим образом немые индексы и объединив A.93)
и A.94), можно написать
A.95)
Так как вектор v является произвольным, то это уравнение долж-
должно сводиться к тождеству Vj = v,. Поэтому коэффициент ацаш,
значение которого зависит от индексов / и k, должен равняться либо
1, либо 0 в зависимости от того, одинаковые или различные числен-
численные значения принимают / и k. Для представления величин такого
типа, как а^а^, можно пользоваться дельтой Кронекера, которая
определяется следующим образом:
если i = j,
.'.	A.96)
если i Ф /.	у '
С помощью дельты Кронекера условия, которым должны удовле-
удовлетворять коэффициенты уравнения A.95), можно записать следую-
следующим образом:
QtjQoi — fyjt.	A-97)
В развернутом виде соотношение A.97) состоитлз девяти равенств,
которые называются"«/сугш«ялы ортогональности, или ортонормиро-
еанностп. Это условий, наложенные на направляющие косинусы
ац.ГН6 соотношения A.93) и A.94) можно скомбинировать иначе
и получить равенство vi = йцащу^ что дает другую форму усло-
условий ортогональности:
= 6,-ft.	A.98)
Линейные преобразования типа A.93) или A.94), коэффициенты
которых удовлетворяют условиям ортогональности A.97) или A.98),
называются ортогональными преобразованиями. Поворот осей ко-
координат и отражение их относительно какой-либо координатной
плоскости являются ортогональными преобразованиями.
Дельту Кронекера иногда называют оператором замены, пото-
потому что она дает, например, следующие преобразования:
6,,-Ь, = 6,А + 6,А + 6i3b3 = bt	A.99)
или
bjFik = e,yF,ft + 62/2* + S3jF3k = Flk.	A.100)
В_силу этого свойства^ ясно,лхо.дельта Кронекера является аналогом
в индексных обозначениях единичного тензора второго ранга I,
определенного формулой A.54).

i.ia. умножение тензоров	29
В соответствии с правилом преобразования векторов A.94)
диада utVj в системе координат со штрихами имеет компоненты
и'р'. = (ЩрЧр) (a;qvq) = aipCijqUpVr	A.101)
Естественным обобщением формулы A.101) будет правило преобра-
преобразования любого декартова тензора второго ранга
.	A.102)
Используя условия ортогональности, легко найдем соотношение,
обратное A.102) и дающее правило перехода от компонент в си-
системе со штрихами к компонентам в системе без штрихов. Оно вы-
выражается формулой
Тц = apladfpq.	A.103)
Законы преобразования декартовых тензоров первого и второго
рангов обобщаются для декартовых тензоров ранга N:
T'uk.. =aipaIQahm...TMm	A.104)
1.14. Сложение декартовых тензоров. Умножение на скаляр
Декартовы тензоры одинакового ранга можно складывать (или
вычитать)"покомпонентно согласно следующему правилу:
Aiik. .±Bilk. =Tl7fc....	A.105)
Сумма тензоров есть тензор того же ранга, что и слагаемые. Заметим,
что одинаковые индексы расположенн в одной и-той -же последова-
последовательности в каждом члене.
Умножен не. всех_к.омпонент тензора на данный скаляр дает новый
тензор TorojKe ранга^При умножении на скаляр~Х типичные примеры
записи произведения в индексной и в символической форме имеют
вид
b{ = %alt или b = ?ia,	A.106)
Вц^КАс,; или В = ЯА.	A.107)
1.15. Умножение тензоров
Вне111ним_произве§?Нием двух тензоров произвольного ранга на-
называется новый тензор, у_которого компоненты образованы умно-
жением каждой^компоненты одного тензора на^ каждую компоненту
другого7 Ранг_ полученного^ тещора равен сумме рангов сомножи-
сомножителей. Типичными примерами внешних произведений являются
следующие выражения:
а)	afl, = Ttfi в) DijTkm = Ф,т;
б)	viFik = aiik; r)

30	ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
Как видно из этих примеров, внешние произведения получаются
простым написанием перемножаемых тензоров друг за другом.
(Заметим, что именно эта операция образует из двух векторов ди-
аду.)
Свертыванием тензора по двум свободным индексам называется
такая операция, когда два индекса обозначаются одной и той же
буквой, вследствие чего они становятся индексами суммирования.
В результате свертывания получается снова тензор (свертка), по-
порядок которого на две единицы меньше, чем у исходного. Приведем
несколько типичных примеров сверток.
а) Свертки тензора Тц и диады ucVj-.
Тц = Тп + 7^22 + Т33,
б)	Свертки тензора Ецак:
EijCLj = О,-,
Eijui = С/,
Eiflk = dk.
в)	Свертки тензора EijFkm'
t*ij* im === *~l]mi	fccjrkk == *ijj
tijt ki == Hjk>	Hi]*1 jm == ^limi
t-ii^km ==z A*m>	t^ij'kj == Ait-
Внутренним произведением двух тензоров называется резуль-
результат операции свертывания, примененной к внешнему произведению
данных тензоров, причем совпадающие индексы должны фигуриро-
фигурировать по одному в каждом из сомножителей. Для справок приведем
некоторые часто используемые в механике сплошной среды произ-
произведения тензоров, записанные в индексных и в символических обо-
обозначениях.
Внешнее	Внутреннее произведение
произведение	индексные символические
обозначения обозначения
й,-Ьу	<xibl	a • b
ОцЬ- jk	(lit, ik = /д,	а • t = I
afiji = h,	E • a = h
EijFkm	EijFjm = Gim	E • F = G
p .p,	P F 	 R.	F . F ¦	 ^F\2
Иногда пользуются свертками тензоров четвертого и более
высокого рангов по нескольким парам индексов. Вот два таких

1.16. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ТЕНЗОР ЛЕВИ-ЧИЬИТЫ	31
примера:
EF
]Fkm свертывается в EijFq или Е: F;
EijEkmEpq свертывается в ЕцЕ1тЕт или (ЕK.
1.16. Векторное произведение. Тензор Леви-Чивиты. Бивектор
Чтобы записать векторное произведение а X b в индексных обо-
обозначениях, удобно ввести тензор третьего ранга е^-, известный как
тензор Леви-Чивиты (альтернирующий тензор). Этот часто ис-
используемый тензор определяется следующим образом:
1, если значения индексов t, /, k образуют четную
перестановку из 1, 2, 3;
— 1, если значения индексов i, /, k образуют нечетную
перестановку из 1, 2, 3;
О, если значения ?, /, k не образуют перестановки
из 1, 2, 3, т. е. если два или все три индекса
принимают одинаковые значения
С помощью этого тензора векторное произведение а X b = с пред-
представляется в индексной записи так:
eiika1bh=cl.	A.108)
Так же можно представить и смешанное произведение а X b • с =
= К:
X =»= BtikOfiiC/,.	A.109)
Это же смешанное произведение формулой A.52) задано в виде опре-
определителя, поэтому не удивительно, что тензор Леви-Чивиты часто
используют и для выражения величины определителя третьего по-
порядка.
Заслуживает внимания то обстоятельство, что el/ft подчиняется
правилу преобразования декартовых тензоров третьего ранга толь-
только в случае таких преобразований, у которых det ац = 1 (например,
при повороте осей). Если же преобразование таково, что det ai, —
= —1 (например, преобразование отражения относительно одной
из координатных плоскостей, в результате чего правая система
координат превращается в левую), то формулу преобразования
Eijk следует писать со знаком минус. Такие тензоры называются
псевдотензорами.
Объект, определяемый равенством
Vi = eilkTlk,	A.110)
называется бивектором произвольного декартова тензора второго
ранга Ti, и является аналогом в индексных обозначениях вектора
Т„ диадика Т, который был определен формулой A.15).

32	ГЛ 1 МАТЕМАТИЧЕСКИЕ ОСНОВЫ
1.17. Матрицы Матричные представления декартовых тензоров
Прямоугольная таблица элементов, заключенная в квадратные
скобки и подчиняющаяся определенным правилам обращения с ней,
называется матрицей. (М X Л^-матрицей называется матрица,
которая имеет М (горизонтальных) строк и N (вертикальных) столб-
столбцов элементов. В символе Ас,-, которым изображают любой элемент
матрицы, первый индекс означает номер строки, а второй — номер
столбца, на пересечении которых находится данный элемент. Сама
матрица обозначается символом своего типового элемента в квад-
квадратных скобках или той же заглавной рукописной буквой, что и
элементы матрицы. Например, (М х ^-матрица А, или [At,-],
задается таблицей
1 2 • • • Л/
1 2 • • • ЛГ
А = [А-,] =
_ Ami
A.111)
Если М — N, то матрица называется квадратной матрицей
порядка N. Если М = 1, то получается A X Л/)-матрица; она обо-
обозначается [аи] и называется матрицей-строкой. Соответственно
(М х 1)-матрица обозначается [йы ] и называется матрицей-столб-
матрицей-столбцом. Матрица, у которой все элементы равны нулю, называется
нулевой. Квадратная матрица, у которой все элементы, стоящие вне
главной диагонали, равны нулю, называется диагональной матри-
матрицей. Если все диагональные элементы (от Ап до Ann) такой ма-
матрицы равны единице, то матрица называется единичной. (N X М)-
матрица АТ, полученная путем перемены местами строк_и~столёцов
(М х ЛО-матрицы А, называется^ транспонированной матрицей
или транспозицией А.
Матрицы, имеющие одинаковое число строк и столбцов, можно
складывать (или вычитать) поэлементно. Умножение матрицы [Ац]
на скаляр X дает матрицу [?lA/1. Произведение двух матриц А$?
определено только в том случае, когда число столбцов в первом
множителей равно числу строк во втором множителе 38. Произве-
Произведением (М X Р)-матрицы на (Р X Л^-матрицу будет (М х Af)-
матрица. Умножение матриц обычно обозначается простым написа-
написанием их символов один за другим, например
AS9 = G, или \Ац\ [Blk] = [C,fc].	A.112)
Операция умножения матриц, вообще говоря, некоммутативна;
ASS Ф 38А.
Квадратная матрица А называется вырожденной, если ее оп-
определитель | Aij | равен нулю. Алгебраическим_^рпоАнением A\j

1.17 МАТРИЦЫ	33
элемента Ах, квадратной матрицы А называется величина
A^J-iy+'Mi,-,	A.113)
где Mij — минор элемента Ац, т. е. определитель квадратной мат-
матрицы, остающейся после вычеркивания строки и столбца, на пере-
пересечении которых находится элемент Д7. Если каждый элемент мат-
матрицы А заменить его алгебраическим дополнением, а затем поменять
местами строки и столбцы, то полученная таким образом матрица
называется присоединенной (или взаимной) к матрице А. Для любой
невырожденной квадратной матрицы А = 1А,-1 существует един-
единственная обратная матрица А~~х, которая по определению равна
присоединенной к А матрице, деленной на определитель матрицы А,
т. е.
Из определения обратной матрицы A.114) следует, что
А~ХА=АА~1^3,	A.115)
где  — единичная матрица, у которой по главной диагонали стоят
единицы, а остальные элементы равны нулю. Она называется также
тождественной матрицей, так как обладает свойством
UA^AU^A.	A.116)
Совершенно ясно, что 7 является матричным представлением дельты
Кронекера 6i} и единичного диадика I. Матрица А, для которой АТ =
¦= А~~ , называется ортогональной. Для ортогональной матрицы А
имеет место следующее равенство:
ТТ = Я.	A.117)
Так как в трехмерном пространстве можно любой тензор второго
ранга выразить в девятичленной форме A.53), а компоненты его
записать в виде квадратной таблицы A.62), оказывается крайне
полезным представлять тензоры второго ранга (диадики) квадрат-
квадратными матрицами третьего порядка. Тензор первого ранга (вектор)
можно записать либо в виде строки, т. е. A X 3)-матрицы, либо в
виде столбца, т. е. C X 1)-матрицы. Хотя каждый декартов тензор,
ранг которого не выше двух (диадик, вектор, скаляр), можно пред-
представить матрицей, не каждая матрица представляет тензор.
Если обе матрицы третьего порядка в произведении А!Ш = С
представляют тензоры второго ранга в трехмерном пространстве,
то операция умножения матриц эквивалентна внутреннему произ-
произведению тензоров и в индексной записи выглядит так:
2 Дж. Мейз

34
ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
здесь индексы i, j, k принимают значения 1, 2, 3. Расшифровка фор-
формулы A.118) дает правило умножения матриц по принципу «строка
на столбец»: элементы /-й строки первой из перемножаемых матриц
умножаются поочередно на элементы ft-го столбца второй матрицы,
эти произведения суммируются и дают элемент, стоящий на пересе-
пересечении i-й строки и й-го столбца результирующей матрицы. Некоторые
произведения такого рода, часто встречающиеся в механике сплош-
сплошной среды, приведены здесь для справок и сравнения,
а) Скалярное произведение векторов:
а • b = b • а = К, [aij] [bn] = [К],	,л , igx
щЬ{ = bfii = X, [alf air a3]
i:H
+ с
a3b3].
б) Скалярное произведение вектора на тензор второго ранга:
а • Е = Ь,	а% = Я,
арц = bh [аи] [Ец] =» [Ьи],
г, а2, с3]
Е»
'31 С32
в) Скалярное произведение тензора на вектор
Е ¦ а = с, Ли = с,
Eiflj = с,-,
A.121)
F F
¦С12 ?-1з
tf 22 С.23
-32
-33
 Г «1 1 pl^ll + Й2^13 + Оз^1з1
N °2 I ^ I Gl^21 ~^~ Й2^22 + Й3?23 |
J L °3 J L 01^31 + «2^32 + Й3?"ззЛ
1.18. Симметрия диадиков, матриц и тензоров
Согласно определению A.36) (или A.37)), диадик D называется
симметричным (или антисимметричным), если он равен (или противо-
противоположен по знаку) сопряженному с ним диадику Dc. Подобно этому
тензор второго ранга Dij симметричен, если
D,,= Dlt,	A.122)
и антисимметричен, или кососимметричен, если
D,i=—Djt.	A.123)
Поэтому аналогично A.38) D,;- можно разложить на два слагаемых:
ОИ = V, (Dt, + Da) + V2 (A/ - Dfi),	A.124)

1.19. ГЛАВНЫЕ ЗНАЧЕНИЯ И ГЛАВНЫЕ НАПРАВЛЕНИЯ
35
или (в сокращенной записи)
Dt = Dvn
D
m,
A.125)
где индексами в круглых скобках обозначена симметричная часть
Dt}, а индексами в квадратных скобках — антисимметричная часть.
Изменение порядка индексов у тензора второго ранга эквива-
эквивалентно перемене местами строк и столбцов в соответствующей ему
матрице; следовательно, квадратная матрица А симметрична, если
она равна своей транспозиции А7. Таким образом, симметричная
матрица А третьего порядка имеет только шесть независимых ком-
компонент и записывается в виде
А =^г =
га
13
23
Аз
A.126)
Антисимметричная матрица равна своей транспозиции с обратным
знаком. Поэтому антисимметричная матрица 38 третьего порядка
и, следовательно, содержит
Она выглядит так:
В.
имеет нули по главной диагонали
только три независимые компоненты.
О
-42
О
¦^23
в
О
23
A.127)
Свойства симметрии можно распространить на тензоры более
высокого порядка (выше второго). В общем случае произвольный
тензор называется симметричным относительно пары индексов,
если значение каждой его компоненты не меняется при обмене
местами этих индексов. Тензор антисимметричен по паре индек-
индексов, если замена их друг на друга ведет к изменению знака, но не
абсолютной величины компоненты. Вот примеры свойств симметрии
у тензоров более высокого ранга:
а)	Rtjkm = Rtkim	(симметричен по ft и /).
б)	Ei/ft = — ел/1	(антисимметричен по ft и i),
в)	Gijkm = Gjtkm = Gilmk = Gjimk	(симметричен по i и j, k и т),
r) Piyft = pJfc/- = pfc/,- = Рдо	(симметричен по всем индексам).
1.19. Главные значения и главные
тензоров второго ранга
направления симметричных
В дальнейшем будут рассматриваться только симметричные тен-
тензоры с действительными компонентами. Это несколько проще в ма-
математическом отношении, а так как тензоры, важные для механики
2*

36	ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
сплошной среды, обычно симметричны, то мы не многим жертвуем,
принимая такое ограничение.
Для каждого симметричного тензора Тц, заданного в некоторой
точке пространства, и для каждого направления в этой точке (ха-
(характеризуемого единичным вектором nt) существует вектор, опре-
определяемый внутренним произведением
A.128)
Здесь Tij можно рассматривать как линейный векторный оператор,
который ставит в соответствие направлению я, вектор vL. Если на-
направление таково, что вектор vL параллелен щ, то указанное внут-
внутреннее произведение выражается скаляром, умноженным на я(-.
В этом случае
bn,	A.129)
и направление щ называется главным направлением или главной
осью тензора Ttj. С помощью тождества я,- = ЬцЩ соотношению
A.129) можно придать форму
(Тц — %Ьц)к] = О, _	A.130)
которая представляет систему трех уравнений для четырех неиз-
неизвестных nt и %, соответствующих каждому главному направлению.
В развернутой записи система, которую следует разрешить, имеет
вид
(Тц — ^)п1 + Т12п2 + Т1зп3 = О,
Т,1п1 + (Т„ — Х)па + Ткря = 0,	A.131)
Тлпу + Т32п2 + (Г33 — X) п3 = 0.
Заметим прежде всего, что при любом к существует тривиальное
решение щ = 0, однако нашей целью является получение нетриви-
нетривиального решения. Кроме того, вследствие однородности системы
A.131), не теряя общности, можно ограничиться только решениями,
для которых «;«, = 1. Начиная с этого момента мы будем требовать,
чтобы это условие выполнялось.
Для того чтобы система A.130), или, что то же самое, система
A.131), имела нетривиальное решение, определитель из коэффи-
коэффициентов должен быть равен нулю, т. е.
|Г*У —Му| = 0.	A.132)
В развернутом виде это кубическое уравнение относительно X:
К3 — 1Д2 + ПД — Шт = 0,	A.133)
которое называется характеристическим уравнением тензора Тц,
а его скалярные коэффициенты
1Т = Тц = tr Tij (след матрицы [Тц\),	A.134)

].2О. СТЕПЕНИ ТЕНЗОРОВ ВТОРОГО РАНГА	37
т = /г (-' &¦¦» /у — * //¦• lih	(I.loo)
Шт = |7\7|=detT,/	A.136)
называются соответственно первым, вторым и третьим инварианта-
инвариантами тензора Тц. Три корня кубического уравнения A.133), обозна-
обозначенные ЯA), ХB), Яр), называются главными значениями тензора Tij.
У симметричного тензора с действительными компонентами главные
значения действительны; если все они различны, то три главных
направления взаимно ортогональны. В главных осях таблица из
компонент тензора приводится к диагональной форме:
Т = |0
A.137)
Если ХA) = ?iB), то диагональный вид тензора не зависит от выбора
осей, соответствующих \1} и ХB), и нужно установить только глав-
главную ось, соответствующую ХC). Если все главные значения равны,
то любое направление является главным. Если главные значения
упорядочены, то принято обозначать их через ХA), Х(ц), Х(ш) и
располагать в порядке убывания: X(i, > Я.(Ц) > \щ).
Преобразование от системы Ох^х^х^ к системе главных осей
Ox\xlxl дается элементами таблицы
*
*3
«11
«21
«31
хг
«12 =
«22 =
«32 =
/4°
л?1
^3
«13 == ^3
«23 = tt3
«зз == ^з
где я" — направляющие косинусы /'-го главного направления.
1.20. Степени тензоров второго ранга.
Соотношение Гамильтона — Кэли
Непосредственным матричным умножением квадрат тензора Тц
получается как внутреннее произведение ТигТщ, куб — как про-
произведение TikTkmTmj и т. д. Таким образом, если Тц представлен
в диагональной форме A.137), то о-я степень этого тензора (и соот-

38	ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ветствующей матрицы) дается формулой
I» О О
(Т)п = | О Я(% 0 |, или Э =г
0 Х
О к
О О
. A.138)
Сравнение A.138) и A.137) показывает, что тензор Тц и все его це-
целые степени имеют одни и те же главные оси.
Все главные значения удовлетворяют уравнению A.133), а
матрица^" имеет диагональный вид A.138), поэтому сам тензор Т
будет удовлетворять уравнению A.133). Таким образом,
+ Пт^ __ 1Цтзг = О,	A.139)
где  — единичная матрица. Это соотношение называется соотно-
соотношением Гамильтона — Кэли. Умножим каждый член этого соот-
соотношения A.139) на $~ пе правилу перемножения матриц и придем к
равенству
у* = lrsrs — Цту2 + Шт^.	A.140)
Исключая У3 из A.140) и A.139), будем иметь
JT4 = A»_ цт) у* + (Шт — ITIIT) ST + ITIIIT7. A.141)
Продолжая эту процедуру, можно получить все целые положитель-
положительные степени У в виде линейных комбинаций S3, У и 7.
1.21. Тензорные поля. Дифференцирование тензоров
Тензорное поле ставит в соответствие каждой точке простран-
пространства и каждому моменту времени (х, t) тензор Т (х, t), где радиус-
вектор х меняется в заданной области пространства, a t — в задан-
заданном интервале времени. Тензорное поле называется непрерывным
(или дифференцируемым), если компоненты Т (х, t) являются не-
непрерывными (или дифференцируемыми) функциями х и t. Если ком-
компоненты тензора зависят только от х, то тензорное поле называется
стационарным.
В ортогональной декартовой системе координат, где радиус-
вектор любой точки имеет вид
x = xfit,	A.142)
поля тензоров различного ранга можно записать в индексных и
символических обозначениях, например
а) скалярное поле <p = (p(*i( 0t или Ф = Ф(Х> О» AЛ43)

122 КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ТЕОРЕМА СТОКСА	39
б)	векторное поле vt = vc (x, t), или v = v (x, t), A.144)
в)	поле тензора второго ранга Тц = Тц (х, I),
или Т = Т(х, t). A.145)
Дифференцирование компонент тензора по координате xt обо-
обозначается дифференциальным оператором d/dxL, или сокращенно в
индексной записи д[г что указывает на то, что это тензорный опера-
оператор первого ранга. В символических обозначениях для записи этой
операции употребляется общеизвестный символ V (набла), который
расшифровывается так:
Частное дифференцирование по переменной х,- иногда изображают
нижним индексом после запятой, как показано в следующих
примерах:
Эти примеры показывают, что при дифференцировании оператор dt
приводит к тензору на один порядок выше исходного, если i остается
свободным индексом (случаи «а» и «в»), и к тензору на один порядок
ниже исходного, если i становится индексом суммирования (случай
Здесь для справки приведены некоторые важные дифференциаль-
дифференциальные операторы, часто употребляемые в механике континуума:
grad ф = Уф = -^- ef, или д$ = ф>(,	A.147)
divv=V v,	или dpt = Vc,i,	A.148)
rotv=Vxv,	или ?ijkdjVk ~ eClkVk,h A.149)
у2ф=У-Уф,	или (Энф = ф.к.	A.150)
1.22. Криволинейные интегралы. Теорема Стокса
Пусть в данной области пространства в каждой точке кусочно
гладкой кривой С, изображенной на рис. 1.10, определена вектор-
функция F = F (х). Если dx — элементарный вектор касательной

40	ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
к кривой в произвольной точке Р, то интеграл
JF-dx= J F-rfx,
с	*А
A.151)
взятый вдоль кривой от Л до В, называют криволинейным интегра-
интегралом от функции F по контуру С. В индексных обозначениях интеграл
A.151) имеет вид
(Х1)В
J^s J FtdXl.	A.152)
С	(xl)A
Теорема Стокса утверждает, что криволинейный интеграл
от функции F вдоль замкнутой стягивающейся в точку кривой С
Рис. 1.10.
Рис 1.11.
(рис. 1.11) можно представить в виде интеграла по любой двусторон-
двусторонней поверхности S, границей которой служит контур С, т. е.
-dx = Jn-(V X T\dSt
A.153)
где n — единичный вектор нормали на положительной *) стороне
S, a dS — элемент поверхности, показанный на рисунке. Формулу
A.153) можно записать и в индексных обозначениях:
A.Г54)
!) Выбор положительной стороны S однозначно определяется направлением
обхода контура С по правилу правого винта.— Прим. перев.

ЗАДАЧИ С РЕШЕНИЯМИ
1.23. Теорема Гаусса — Остроградского
Теорема Гаусса — Остроградского (теорема о дивергенции) дает
преобразование интеграла по объему в интеграл по поверхности.
В обычной формулировке теорема утверждает, что для векторного
поля v = v (х)
^ fn •
S
vdS,
A.155)
где п -^единичный вектор внешней нормали к поверхности S, огра-
ограничивающей объем V, внутри которого определен вектор v. В ин-
индексных обозначениях формула A.155) принимает вид
vudV =
A.156)
Теорема Гаусса — Остроградского в форме A.156) может быть
обобщена на поля тензоров любого ранга. Так, для произвольного
тензорного поля Tijk... теорема утверждает, что
J Tqk... .pdV = \ Tijk. ¦ .rtpdS.
v	s
A.167)
ЗАДАЧИ С РЕШЕНИЯМИ
Алгебра векторов и диадиков (§ 1.1—1.8)
1.1. В ортогональной декартовой системе координат (рис. 1.12)
определить: а) единичный вектор, параллельный вектору v = 2i +
+ 3j — 6k; б) единичный век-
вектор прямой, соединяющей точ-
точки Р{\, 0, 3)и <2@, 2, 1).
a) |v| = о =
= YW+WTVIW= 7,
б) Вектор, идущий из Р в Q, есть
u=@— l)f+B — 0)j+(l — 3)k =
Л	Л	/N
= — i + 2j— 2k,
I u | = V{~ I)* + BJ + (- 2)« = 3.
Таким образом,
Рис. 1.12.
или
u = — V3i + 2/3j — 2/3k направлен от Р к Q
u = V^i — 2/г1 + s/3k направлен от Q « P.

42
ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
1.2. Доказать, что вектор v = di + Ь\ + ск перпендикулярен
плоскости, заданной уравнением ах -f- by + cz = К (рис. 1.13).
ПуСТЬ Р (XI, У у, Zy) И Q (Xi, yz, Zn) —
две любые точки этой плоскости. Тогда
пХ\ -\- Ьу\ -\- CZl = к И 0X2 -Г" 6j/2 "Г" сг2 ==
= Я, а вектор, соединяющий эти точки,
есть u = (xs — хх) i + №*— УЛ+ («2 —
— zt) k. Проекция вектора v на направ-
ление и равна
U ¦ V
Рис. 1.13.
+ (г2_Zl)k] . |fl?+ 6?+ ск] =
— Ьуу — сгу) =	— = 0.
Так как и — любой вектор, лежащий в плоскости, вектор v перпендикулярен этой
плоскости.
*\	Л	Л
1.3.	Пусть г = xi + УЪ + zk — вектор,, идущий из начала в
^Ч	Л	/N
произвольную точку Р (х, у, г), a d = а\ + b\ + ck — некоторый
постоянный вектор. Показать, что (г — d) • г = 0 есть уравнение
сферы.
Раскрывая скалярное произведение, будем иметь
(r-d) • r = [(*-a)f+ {y-bU + (г- с) к] • [хЛ + у)+гк] =
= х2 + «/2 + г2 — ах — by— сг = 0.
Добавляя <Р/4 = (а2 + />2 + с2)/4 к правой и левой частям этого уравнения,
получаем
(х - аУ2J +{у- 6/2J + (г _ с/2)г = (d/2)s>,
т. е. уравнение сферы с центром в точке d/2 и радиусом d/2.
1.4.	Доказать что [а • b X c]r = (а • г) b X с + (Ь • г) сХа +
+ (с • г)а X Ь.
Рассмотрим произведение а X [(Ь X с) X г]. Раскроем векторное произведе-
произведение в скобках
а X [(Ь X с) X г] = а X [(Ь • г) с — (с ¦ г) Ь] = — (Ь • г) с X а — (с • г) а X Ь,
С другой стороны, полагая Ь X с = v, напишем
а X [(Ь X с) X г] = а X (v X г) = (а • г) Ь X с — (а • Ь х с) г.
Таким образом,
— (Ь ¦ г) с х а— (с • г) а X Ь = (а • г) Ь X с — (а • b x с)г
и, следовательно,
(а • Ь X с) г = (а • г) Ь X с + (Ь ¦ г) с X а + (с ¦ г) а X Ь.
Это тождество полезно, когда перемещение твердого тела определяется через пере-
перемещения трех произвольных его точек.

ЗАДАЧИ С РЕШЕНИЯМИ
43
1.5. Показать, что а • b X с = 0, если векторы a, b и с линейно
зависши. Проверить линейную зависимость (или независимость)
следующей тройки векторов:
и = зГ+ j — 2k,
Л	/S	/N
v=4i — j— k,
w=.i — 2j + k.
Векторы а, Ь и с линейно зависимы, если существуют коистаиты К, fx и v, ие
все равные нулю и такие, что Ха + цЬ + vc = 0. Это векторное уравнение дает
в компонентах три скалярных
%ах -f- \ibx -f- \сх = О,
Ха^ + yby + vcff = 0,
%аг + ц6г + ^сг = 0.
Эта система имеет ненулевое решение для "к, \i и v только в том случае, когда
детерминант из коэффициентов обращается в нуль
Uy Uy Uy = 0.
аг Ьг сг
а это эквивалентно равенству а ¦ Ь X с = 0. Для предложенной тройки векторов
u, v, w
3 1 —2
4—1—1
I —2 1
= 0.
Следовательно, эти векторы u, v, w линейно зависимы. В самом деле, v = u +
+ w.
1.6.	Показать, что любой тензор второго ранга, заданный в виде
суммы ./V диад, можно свести к сумме трех членов, если использовать
/N	Л	Л
базисные векторы elf e2, е3 в качестве: а) первых сомножителей,
б) вторых сомножителей в диадах.
Пусть D = aibi + a2b2 + ... a^b^ = а*Ь( (i — 1, 2, .... N).
а) Запишем все первые сомножители диад а* через базисные векторы: а,- =
= auei + a2it2 + a3ie3 = aj{e,; тогда D = a.,e/b,- = e/ (a.^bj) = eye/, где / =
= 1, 2, 3.
б) Аналогично, представляя fy в виде fy = 6.fe/, получаем D = а^б^е/ =
= (bjfltfa = g/e/, где / = 1, 2, 3.
1.7.	Показать, что для произвольных диадика D и вектора v
справедливо равенство D ¦ v = v • Dc.
Пусть D = aibi + a2b2 + . . + a^b^. Тогда
D • v = ад (b, • v) + a2 (b2 - v) + ¦ • ¦ + aN (bN ¦ v) =
¦= (v ¦ bj ai + (v • b2) a2 + • • ¦ -f- (v • Ьд,) aN =v ¦ Dc.

44	ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
1.8. Доказать, что (Dc ¦ D)? = Dc • D.
Согласно A.71), D = Dye,-e/ bDc= D/дее/. Поэтому
Dc • D = D^e.e,- • Dpqepeg = D,tDpg (e,- . ep)
и
А	А	АЛ
(Dc ¦ D)c = ОцВря (e,- - ep) e,ej = Dpqtq (ep • e,) <нПц = ?>р,е,ер ¦ О^е^ = De • D.
1.9. Показать, что (D X v)c = —v X Dc.
(DX v)/J = (b1Xv)a1+(bIX v)a2+ ••• + (bN X v) aN =
= — (v x bj) ax — (v x b2) a2 — • • • — (v X b^) aw =¦
= — v X Dc.
1.10.	Пусть D = al \ -\- b]\-\- ckk, а г— радиус-вектор, г=
^Ч	/^	Л
= xi + #j + zk. Показать, что уравнение г • D • г = 1 представ-
представляет эллипсоид ах2 -\- by2 -f сг2 = 1.
г-О.г=(л:Т+</Г+гк) •(aTT+bjj'+ckk) • (х? + f/1 + гк) =
=¦ (л"+ И + гк) • (ах\ + Ьу\ + сгк) = ах2 + 6«/2 + сга = i.
1.11.	Для тензоров D = з11 + 2j j—lk + 5кк и F = 41к +
/ч Л	^^ ^ч	*ч А
+ 6j j ¦— 3kj 4- кк вычислить и сравнить двойные, скалярные про-
произведения D : F и D • • F.
По определению ab : cd = (а • с) • (Ь • d), следовательно, D : F = 12 + 5=
= 17. Аналогично ab- -cd = (b • с) (а • d) и, следовательно, D ¦ ¦ F = 12 +
+ 3 + 5 = 20.
1.12.	Определить диадики G = D-FhH=F-D, если D и
F — тензоры, указанные в задаче 1.11.
Воспользуемся правилом умножения диад ab • cd = (b ¦ с) ad. Тогда
G= Ci i + 2j j —j k + Ekk) • Di k-f 6j J —
= 12ik+ 12jT+ 3j"f— ?k— i5kf+5kk.
Подобным же образом
Н=.DГк + б] j — Зк^ + кк) • C?T+2j j—1
*ь *ь	АЛ	АА	АЛ	АА
= 20i к + 12j j — 6J к — 6к J + 8к к.
1.13. Исходя из девятичленной формы записи тензора второго
ранга D, показать, что его можно представить в виде D = (D • i)i 4-
+ (D • j)j + (D • k) k; показать также, что
i . D • i = Dxx, I ¦ D ¦ j = Dxy и т. д.

ЗАДАЧИ С РЕШЕНИЯМИ
45
Напишем D в девятичленной форме и перегруппируем члены
D = (Dxx f+ Dyx ] + Dzx к) f+ (Dxy ?+ D
yy
к)
2f+ d3k = (D ¦ Г) i+ (D • j)]+ (D ¦ kfk.
Следовательно,
Г. d, = f. (D ¦ T) = f • (D
"} . dt =1 • (D • ?) = Dyx,
x? + DffJ+ D« k)
j • d2= j • (D ¦ j) =
Dxx,
yy и т. д.
1.14. Показать, что для антисимметричного тензора второго
ранга А и любого вектора b выполняется формула 2Ь • А = Ао х Ь.
Из задачи 1.6,а имеем А = e\ci + е2с2 + е3с3; вследствие антисимметрии
тензора А можно написать 2А = (А — Ас), или
2А = (е1с1
е3с3 — c^j — с2ег — с3е3) =
еасг — с2е2 + е3с3 — с3е3).
Поэтому
2Ь-А=[(Ь
—(b
b-eJCg — (Ь ¦ Сг)ег] +
+ [(Ь- е3)с3—(Ь- с3)е3]=
= [(е,Хс,)ХЬ + (ег X сг) X Ь + (е3 X с3) X Ь] = (Ао X Ь).
1.15. Пусть D = б]Г + 3?f + 4kk и u = 2i + k, v = 5j. Пока-
Показать непосредственным вычислением, что D • (u X v) = (Dx и) • v.
Так ка« и X v = B?+ к) X 5^ = 10к — 5?, то
D • (и X v) = F??+ 3Tf+ 4кк) ¦ (— 5?+ Юк) = — Зо7 + 40к.
С другой стороны,
(Dxu)-v=Cil-6ij-6ik+8kj) -5] =-30i
1.16. Рассматривая диадик
D = 317 — 4? j + 2J i +J j +kk
как линейный векторный опе-
оператор, найти вектор г', кото-
который получается при действии
оператора D на вектор
г =41 + 2j+ 5k (рис. 1.14).
г' = D ¦ г = 12?+ 8j— 81 + 2J +
= 4?+ 10)Г+5к.
Рис. 1.14.

46
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
1.17. Определить диадик D, который служит линейным вектор-
векторным оператором для вектор-функции а = f (b) = b + b X г, где
г = xl -}- у] + zk, a b ¦— некоторый постоянный вектор.
При помощи формул A.59) и A.60) построим векторы
f Л1
u = f fi) =Л+1 X г =? — г] + у\,
v = f (?) =1 + ?Х г =. г?+1-*к,
w = f (к) =к + кх г = — «/? ?
Тогда
a = D.b=(bx+byz^b2y)l+ (—bxz + by + Ьгх) j + Фху — byx + Ьг) к.
Для проверки можно получить тот же результат, непосредственно раскрывая век-
тор-фуикцию:
а = Ь + Ь х г = Ъх i + Ьу f+ Ьгк + (Ъуг-Ьгу)\ + (Ь2х-Ьхг) \ + (bxy-byx)k.
1.18. Выразить единичные векторы еф, ее, ег через i, j, k и пока-
зать, что этот триэдр составляет правую систему, т. е. что е X ее =
Непосредственным проектировани-
проектированием (рис. 1.15) найдем
/^	^	/N
е^ = (cos ф cos 6) i + (cos ф sin 6) j —
— (sin ф) к,
ee = (— sin
(cos e) Ti
er = (sin ф cos 6) i -f (sin q> sin 6)
Рис. i.i5.
отсюда
i	j	k
cos ф cos 6 cos ф sin 6 — sin ф
— sin 6	cos 6	0
= (sin ф cos 6) f+ (sin ф sin 6) j + [(cos2 6 + sin2 G) cos ф] k = e,.
1.19. Разложить тензор D = 3iT -f 4?k + 6\l + 7\f+ 10kf+
¦\- 2kj на симметричную и антисимметричную части.

ЗАДАЧИ С РЕШЕНИЯМИ	47
Пусть D = Е + F, где Е = Ес и F = —Fc. Тогда
Е - V, (D+ Dc) = V, (бГГ+ 4 Гк + 4 к Г+ 6 \l + 6f f+ M Г Г+
+ 10 k"i + 101 к + 2Vj + 2 j к) =
F = V2 (D — Dc) = V2 D? к — 4 kf+ 6 j?— 6?Г+ 10kf—
— 10 i к + 2k j — 2 j k) =
= — 3?Г— з1к + з]Г— Jk+ЗкТ + к^— Fc.
1.20. Векторы а1, а2, а3 образуют взаимный базис для базисных
векторов ах, а2, а3 (не обязательно единичных), если а^ • а3 = йу.
Найти необходимые соотношения для построения взаимного базиса
и выполнить эти вычисления для следующих базисных векторов:
Согласно определению, ai ¦ а1 — i, aa • а1 = 0, а3~- а1 = 0. Следовательно,
а1 перпендикулярен векторам ая и а3 и поэтому параллелен аг X а3, т. е. а1 =
= I. (аг X ая). Так как ai ¦ а1 = 1, то at • Я-ая X а3 = 1 и Я = i/(ai ¦ а2 X а3) =
= l/[aia2a3). Таким образом, мы нашли общее правило получения взаимного
базиса:
1 _ аг X а3	а _ а3 X at	3 _ at X а2
[**1<*2а3]	laia2a3]	[a^a2a^J
Для указанных базисных векторов bi, b2, b3 имеем Ilk = Ы ¦ Ьг X b3 = 12
и, следовательно,
Ы = (ЬгХЬ3)/12 = A—k)/4.
Ь2 = (bg X Ь,)/12 = — Г/3 + j/4 + k/12,
Ы = (bj X Ь„)/12 = 2 Г/3 — |/2 + 5k/6.
Индексные обозначения — декартовы тензоры
(§ 1.9 — 1.16)
1.21. В трехмерном пространстве расшифровать следующие тен-
тензорные символы (тензоры декартовы): Аи, By/, Ri,-, atTij, atbjSij.
Ац представляет одну сумму: Ац = Аи + Ац + Л33;
Вц, представляет три суммы:
1)	при i = 1 Вш + В1Ш + В133,
2)	при i *= 2 В211 + б222 + Bias.
3)	при I = 3 В311 + Взм + В333;
/?,7 представляет девять компонент: 7?и, /?и, /?13, /?ia, Я22, /?ая. /?81,

48	ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
представляет три суммы:
1)	при / = 1 о,Ги + ааТп + a3Tsl,
2)	при / = 2 0,7-^ + axTw + аяГм,
3)	при / «= 3 atTM + a2Ti3 + a3T33;
jii представляет сумму девяти членов. Первое суммирование по i дает
= aibjSij + aibjSzi + a3biSsj. Затем каждое из этих трех слагаемых сум-
суммируем по /:
aibjSij = a1blSn + aibaSia + o163S13 + a26i5ai + аф^ш +
+ aJ}3S23 + ^Ai + a3b 2S32 + a363S33.
1.22.	В трехмерном пространстве вычислить следующие вы-
выражения, содержащие дельту Кронекера бц: а) 6И, б) бубц,
в) бу6гйб7-*, г) буб/Л, д) буЛ».
а)	бй = бп + б22 + б33 = 3.
б)	61;б,;- = б^б^- + 68/-6s/ + 6»/6s/ = 3-
в)	&ifiikujk = 6iAfc6/fe + 62/62ft6/fe + 6s/8sk6jk = 3.
г)	fij/6/й = б^б^ +
Д) бг/Лй ¦= ^i/Aft
1.23.	Для тензора Леви-Чивиты еуА непосредственным рас-
расписыванием по индексам показать, что: а) е^Еед =» 6, б)
= 0.
а) Просуммируем сначала по ii
Затем суммируем по /, записывая только отличные от нуля члены:
Наконец, суммируем по k, опять оставляя только ненулевые члены:
Eyfce/и/ = emeSi2 + Е132еиз + емзе321 + егз1е123 + е31ге331 + езие132 =
= A) A) + (- О (- О + (~ О (- 1) + A) (О + (П A) +
+ (-1) (-•) = 6-
б) Суммируем по /, потом по k:
e,itsa3as + e^Ogflx + е,-32а3аг.
Из этого выражения получим:
при i =. i ефп/ak = с2аз — °зл2 = О,
при i = 2 гцкп/аи =» я^з — °зй1 = °.
при ? = 3 Ефарь. = 0^2 — OjOi = 0.
Заметим, что eyfca;Cfc является индексной формой записи векторного произведения
вектора а самого на себя и, следовательно, а X а = 0.
1.24. Определить компоненту /2 данных ниже векторов: а) ft =»
= EijkTjk, б) /? = Ctjbj — Cj,ibj, В) Bif;.
— Т13 + Т31.

ЗАДАЧИ С РЕШЕНИЯМИ	49
б) ft ~ С2,161 + С2,262 + С2,363 — С1,261 "~ С2,262 ~~ С3,263 =¦
= (С2 , — С, 2) fct + (С2 з — С3-2) 63-
В) f2 = В21
1.25. Написать в развернутой форме и по возможности упрос-
упростить выражение D^x,-, если: а) Д;- = Dj,-, б) Dit = —D,,-.
Имеем
+ О^Хо
Поэтому
а)	D{/XiXf = Dn (xO* + DM (x2J + D33 (x3)» + 2О1Лх2 + 2D23x2x3 + 20,3X^3;
б)	DijXiXj = 0, так как Dn = — Du, D12 = — D21 и т. д.
1.26. Показать, что гц^крд = ОгроЛ—б(98^р: а) при t = 1,
/ = q = 2, р — 3 и б) при i = q — 1, / «= р = 2. (В задаче 1.59
будет доказано, что это тождество справедливо при любом выборе
индексов.)
а) Положим i = I, / => 2, р = 3, <7 = 2 и заметим, что ft — индекс суммирова-
суммирования и, следовательно, пробегает значения 1, 2, 3. Тогда
б) Пусть i=l, / = 2, р = 2, q=\. Тогда e,/fteftp9 = ецзвза! = — 1 и
1.27.	Показать, что тензор Bik = е^а/ антисимметричен.
В соответствии с определением et-.fe перемена местами двух индексов ведет к
изменению знака, так что
Bik = *ifkai = - (ЧцаИ = - (Bki> "= - Bkf
1.28.	Пусть задан антисимметричный декартов тензор В,;- и
вектор bc = 1/t SijkBjk- Показать, что Bpq = fc
Умножим данный вектор иа Epgi и воспользуемся тождеством, доказанным в
задаче i.26:
-= Х/» Qpfiqk ~ V9/) Bik = V, (Bpq - Bqp) =.
1.29. Непосредственным вычислением найти компоненты метри-
метрического тензора в сферической системе координат, изображенной на
рис. 1.7,6.
Формулу A.87) запишем ввиде#рв= (дх[/двр) (дх{/двч). Нумерацию коорди-
координат примем такую, как показано на рис. i.16 (г = Qi, ф = 6а, 6 = 68). Тогда

50
jtj = Ql sin 62 cos 63,
Следовательно,
„ dx-i
ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
: 6t sin 62 sin 63, *3 = 61 cos 62,
дх,
дХа
дх3
= sin 62 sin б,
¦ = cos 62,
ее,
•	= 6Х cos 62 sin 63,
•	= — в1 sin 62,
-	— — 6t sin 6„ sin 6?,
-	= Q1 sin 62 cos 63,
= 0.
Отсюда найдем
= sin2 ег cos2 e3 +
1 C6,
+ sin2 e2 sin2 e3 + cos2 e2 = i,
Рис. 1.16.
dxi dxt
ej cos2 e2 sin2 e3 + ti\ sin2 e2 = ef.
= ej sin2 e2 sin= e3 + e^ sin2 ег cos2 e3 = e? sin» e,.
Кроме того, gpq = 0 для р ф q. Например,
(sin 62 cos 63) (Bi cos % cos 63)+
+ (sin e2 sin e3) (Bi cos e2 sin e3) — (cos e2) (et sin ег) = о.
Таким образом, в сферических координатах
/ j_\2 	 / jO \2 I /D
или
(ds)* = (drJ + /
'¦ + (et sin eaJ (de3J,
+ (r sin фJ (dGJ.
1.30. Показать, что длина линейного элемента ds, соответствующе-
соответствующего приращению криволинейной координаты dBit равна ds = VglidQl
(не суммировать!). Применить
полученный результат к сфери-
сферической системе координат (за-
(задача 1.29).
Запишем формулу (i .86) в виде
(ds)* = gpq dQpdQq. Тогда для линейно-
линейного элемента (d6i, 0, 0) получим выраже-
выражение (dsJ = gu (dBjJ и ds = YgTi deb
Аналогично для @, dBa, 0) получим
ds = У g22 dBa^a для @, 0, d63) полу-
получим ds==Vg^3dQ3. В сферической	Рис. 1.17.

ЗАДАЧИ С РЕШЕНИЯМИ
51
системе координат (рис.	1.17) имеем следующие выражения!
1)	для (dBlt 0. 0) ds = det = dr,
2)	для @, de2, 0) ds = 6^Э2 = rdcp;
3)	для @, 0, de3)	ds = et sin e2d63 = r sin (pd6.
1.31. Пусть P12— угол между линейными элементами (d0lf 0, 0)
и @, dG2, 0). Показать, что cos P12 = 8п
Пусть dsj = l^gudBi — длина линейного элемента (d6i, 0, 0), a d
•= V&sd^s — Длина линейного элемента @, йбг, 0). Тогда квадрат длины
линейного элемента (d6lP d%, 0) можно вычислить так: (rfsK = 2 cos Pdd
+ (rfs,)* + (dsa)a. С другой стороны,
(ds)* =
Отсюда, пользуясь результатом задачи 1.30, получаем
cos p12
gla -
ds, ds.
1.32. Оси декартовой системы координат О^л^з получены
поворотом системы Ox1xaxs на угол 0 вокруг оси х3. Определить
коэффициенты преобразования ау указанных осей и найти компонен-
Л	Л	^ч
ты вектора v = Uje, -J- ^2e2 +
По определению (см. § 1.13) fly = cos (я,-, х). Углы между соответствующими
осями указаны на рис. 1.18, что позволяет найти таблицу направляющих коси-
косинусов:
~' I
в системе со штрихами,
найти
x'i
cose
— sinB
0
sine
cos 6
0
*з
0
0
1
Таким образом, тензор преобразования
имеет вид
cos 6 sin e
А = I — sin e cos 6
Рис. 1.18.
По правилу преобразования векторов A.94) получаем
Vf — пх/Vj = v1 cos e + и2 sin 0,
V2 == aiivi == — fI sin 6 -f- f2 cos 6,
vs = a3/ti/ = va.
о
о

52
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
1.33. В приведенной таблице частично заданы направляющие
косинусы углов л;ежду осями двух декартовых ортогональных си-
систем координат. Определить элементы нижнего ряда таблицы так,
чтобы система 0х\х^ъ была правой.
х'\
х'2
х'з
3/
/5
0
Хг
-%
0
0
1
Первая строка таблицы дает единичный вектор е,' оси х\ в виде е', = 3/6е1—
— */6 е2. Точно так жее2 = е3. Для правой системы должно быть выполнено
равенство ej = ej X е2, или е3 = C/6 et — */6 ег) X е3 = — 3/6 е2 — */5 е,- Та-
Таким образом мы получим третью строку таблицы:
*з
	 3/
0
1.34. Пусть углы между направлениями осей координат системы
со штрихами и системы без штрихов даны в следующей таблице;
х'з
хг
135°
90°
45°
60°
45°
60°
120°
45°
120°
Определить коэффициен-ы преобразования ац и показать, что
выполнены условия ортогональности.
Коэффициенты Оу являются направляющими косинусами и могут быть сразу
вычислены в соответствии с данной таблицей углов. Таким образом,
(— 1//2 1/2 - 1/2
О	1//2 1//2
1/1^2 1/2 — i/2
Условия ортогональности a{-aik = 6-k требуют, чтобы выполнялись следующие
условия:
1)	при / = k= 1 должно быть яцоц + ацпц + 0^0^= 1; левая часть,
очевидно, представляет собой сумму квадратов элементов первого столбца;
2)	при / = 2, k = 3 должно быть выполнено равенство а-^а^ + о2г°гз +
+ а32а33 = 0, левая часть которого является суммой произведений соответствую-
соответствующих элементов второго и третьего столбцов;
3)	сумма произведений соответствующих элементов любых двух столбцов

ЗАДАЧИ С РЕШЕНИЯМИ	53
должна быть равна нулю; сумма квадратов элементов любого столбца должна быть
равна единице.
Есл.ч условие ортогональности записано в форме fl^afc(- = 6-k, то вместо столб-
столбцов перемножаются строки.
Указанное выше решение удовлетворяет всем этим требованиям.
1.35. Показать, что сумма Я-Лу + цВу представляет компонен-
компоненты тензора второго ранга, если известно, что Лу и В,-,- — тензоры
второго ранга.
Согласно формуле AЛ03) и условию задачи Acj = %1%А'рд иВ(;.= aplaqiB'pq,
Отсюда
%Ац + цВ,у = К (apiaqlA'j + ц {apiaqjBpq) = ap[aql &А'„ + цВр9),
а это значит, что указанная сумма преобразуется как декартов тензор второго ран-
ранга.
1.36.	Показать, что (Pijk + Pjm + Pjik) xtx}xh =
Так как все индексы являются немыми и, следовательно, порядок написания
переменных xi не играет роли, все слагаемые эквивалентны друг другу. Это легко
показать, введя другие немые индексы. Так, заменив i, j, k во втором и третьем
членах на р, q, r, получим
PllkXlXjXk + PqrpXpXqXr + PqprXpXqXr.
Теперь вернемся в тех же членах к прежним индексам суммирования i, j, k и по-
получим сумму
pijkxixixk + Pi/kXkXiXj + PljkXjXiXk = ?>PijkXiXjXk.
1.37.	Пусть Bij — антисимметричный и Л„- — симметричный
тензоры. Показать, что Афц = 0.
Так как Ац = Ajt и Btf = —В^, то АЦВЦ = —А^В.:, или А^Вц + А^В^ =
= АцВц + ApqBpq = 0. Поскольку все индексы являются немыми, ApqBpQ =
= АцВц, и поэтому 2AijBij = 0, или AljBlj = 0.
1.38.	Показать, что квадратичная форма Diixixl не изменится,
если вместо тензора Dl7- взять его симметричную часть D^.
Разложим ?>,-¦ на симметричную и антисимметричную части:
°Ч = D(H) + °ЦЦ = Ч* (°Ц + Dld + Ч* (°1/ - °л>-
Тогда
DpqXqxp) =
1.39. Используя индексные обозначения, доказать векторные
тождества
1) а X (Ь X с) = (а • с)Ь—(а • Ь)с, 2) а X b • а = 0.
1) Пусть v = Ь X с. Тогда и,- = Eyfe6/Cfe, и если а X v = w, то
wp = EpqiaQEijkbick =
= (йр;й9й — SpAe<j/) a4bick =	(см ¦ задачу 1.26)
= aqbpcq — aqbqcp = (aqcq) bp =¦ (aqbq) cp.

54
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
В символических обозначениях это выражение имеет вид
w = а X (Ь X с) = (а ¦ с) Ь — (а ¦ Ь) с.
2) Пусть а X b = v, т. е. v{ = e,-/fea/fcft, и если Я = v • а, то Я = e,-/-/s
Но 8,-;-ft антисимметричен по индексам i и /, в то время как произведение
симметрично по этим индексам. Следовательно, ег,йо,-а/6й обращается в нуль, что
можно показать, непосредственно расписывая это выражение по индексам:
Я = ъ
= (ез21°заг + e23i02a3) fct + • ¦ • =
= (— O2O3 -J" а2аз) bl "t" @) ^2 "t" @) 63 = 0.
1.40. Показать, что определитель
[ft /г-t
det Ait =
"
'12 -3
22 -3
*88
можно записать в виде
По формулам A.52) и (i. 109) смешанное произведение [аЬс] можно представить
Я = а • b X с = [abc] = e(/.fcai6/cfc =
Если теперь положить о,- = Ац, 6,- = A2i и С/ = А31, то будем иметь
,-. Показать, что a =—-
Этот же результат можно получить и непосредственным разложением определите-
определителя по строке. Определитель можно также записать в виде е^ъ^И/г^АЗ» очевидно,
эти два выражения эквивалентны.
1.41. Вектор vt задан в базисе а, Ь, с своими компонентами t),=
= aa,- + Pbj +'
Мы имеем
tix = aat + P&i + Ycii
По правилу Крамера
a =-

ЗАДАЧИ С РЕШЕНИЯМИ	55
и, пользуясь формулами A.52) и (i.109), можно написать
а = -
Подобным же образом находим
Матрицы и матричные методы (§1.17—1.20)
1.42. Для векторов а = 3i -(- 4k, b = 2j — 6k и диадика D ==
= 3i i -f- 2i k — 4j j — 5kj путем перемножения матриц вычислить
произведения а • D, D • b и а • D • b.
Пусть а • D = v ; тогда
гЗ 0 2-j
[«1. иг, v3] = [3, 0, 4] 0 — 4 0 = [9, - 20, 6].
Lo — 5 oJ
Пусть D • b = w; тогда
lw3J L0 —5 OJ 1 — 6 J I—
Пусть a-D-b=v-b = ^; тогда
[Ц
Г °1
= [9,-20,6] 2 =[-76],
1.43. Найти главные направления и главные значения декартова
тензора Т второго порядка, который представлен матрицей
3 —1
[Ти]= -1 3 0|.
О О
°1
?¦
Для определения главных значений Я, согласно AЛ32), имеем уравнение
3-Я — 1 О
— i 3-Я 0 = A —Я)[C —ЯJ—1] = 0,
О	0 i—%
Это кубическое уравнение
Я3 — 7Я2 + i4A,— 8 = (Я — 1) (I — 2) (Я— 4) = О,
корни которого Я(]. = li^2« = 2, ЯC> = 4.
Пусть теперь л'-1* — компоненты единичного вектора главного направления,
соответствующего ЯA) = 1. Тогда два первых уравнения системы A.131) дают

бб
ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
2л*,1' — nty = 0 и — п',1' 4- 2nB!) = 0, откуда я',1' = nty = 0, а из условия щщ=
= i получим «з'' = ±i.
Для КB) = 2 система уравнений A.131) дает nf> — яB2) = °. —п'2' + 42) =
0 и — п^2) = 0. Таким образом, я^2' = 0, а п(,2) = пB2) = ± 1/} 2", так как n,nj =¦
= 1.
Для кC — 4 из системы A.I3I) получаем —пC) — пB3) = 0, —я(,3) —
— 43) — 0 и Зп^3' = 0. Таким образом,
2
0 и п(,3' = — лB3) =
Ориентация главных осей xt относительно исходной системы Х{ определяется
направляющими косинусами, которые даны в следующей таблице:
*
х\
х\
±
Ч
0
IIY2
1/1^2
I
.1.
*2
0
1/Г2
1/1^2
± i
0
0
Отсюда видно, что матрица тензора преобразования такова:
О	О
± UV~2 ± 1/V
±
1.44. Показать, что главные оси тензора, определенные в задаче
1.43, образуют правую систему ортогональных осей.
Для ортогональности требуется выполнение условий atjaik = б^. Так как
при определении о,-, уже были использованы соотношения гцщ = \, условия орто-
ортогональности для/ = k выполнены автоматически. Умножив элементы любой строки
(столбца) на соответственные элементы любой другой строки (столбца) и
сложив эти произведения, убедимся,
что для решения, полученного в за-
задаче 1.43, условия ортогональности
выполнены и для / Ф k.
Чтобы система к тому же была
правой, необходимо, чтобы пB) X
X пC) = пA)- Таким образом,
е2 е3
i/l^ 0
i/V 0
Рис. 1.19.	=A/2+1/2)е3=«ез.
Наличие знаков ± у величин а,-у. в задаче i.43 указывает на то, что существуют две
системы главных осей х1 и xt . Как показывает рис. 1.19, главные направления х\
образуют правую систему, а х^ — левую.

ЗАДАЧИ С РЕШЕНИЯМИ
57
1.45. Показать, что матрица тензора Тц задачи 1.43 может
быть приведена к диагональной (главной) форме преобразованием
(или в матричной записи ЗГ* — <А?ГАТ).
PV/H 1//2
L—1/у
3
— 1
о
—1
3
о
¦О 1//2 — \lVr\
I
"О i//2	— 1/J/2T Г1 О
0	1/^2 l/j/2 =|0 2
1	О	О J 1_0 О
1.46. Доказать, что если все три	главных значения
ЯB),
\з) симметричного тензора второго ранга различны, то главные
направления взаимно ортогональны.
Доказательство проведем для направлений, соответствующих ЛB)
Для каждого из них выполняется соотношение A.129), так что Т?
и Я
C).
= ^C) п
/3'-
Умножим первое из этих равенств на nf\ а второе на г
= Tw"; ' и
Так как тензор Ту симметричен, можно поменять местами немые индексы i и /'
в левой части второго уравнения и затем второе уравнение вычесть из первого.
Получим
!2Ф
Поскольку ЯB) Ф \з)> их разность отлична от руля. Следовательно, n^nf^ =
= 0, а это и есть условие ортогональности данных двух направлений.
1.47. Вычислить главные значения тензора (ТJ задачи 1.43
и убедиться, что его главные оси совпадают с главными осями
тензора Т.
io
г 3 -1 O-jr 3 -1 01 г 10
L0 OiJLo OiJLO
Характеристическое уравнение для этой матрицы таково:
— 6 0
— 6 iO —X 0 = A—Я)[(Ю—ЯJ—36] = (i—Л)(Я —4)(Я—i6) = 0,
0	0 1-Я
откуда Я(,. = i, ЯB) = 4, ЯC. = i6. Подставляя эти значения в A.131) и учиты-
учитывая условие П{П{ = \, получаем
ДЛЯ Я/1, = 1
'Ч^
или
;0, 41}=±

58
ГЛ. I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
= 4
для
- 6n<2> + 6nB2' = 0
- 342> = О
для Я(з> = i6
или
или
- 1543) = О
Видно, что главные направления Т и (ТJ одни и те же.
1.48. Воспользовавшись тем, что тензор (ТJ и симметричный
тензор Т имеют одни и те же главные направления, найти тензор
Y% если
/5—1	—Г
Т=(—1 4	О
\ — 1 0	4>
Прежде всего мы будем искать главные значения и главные направления тен-
тензора Т. Действуя так же, как в задаче i.43, найдем диагональную форму Т:
C 0	0\
О 4	0 j ,
0 0	6/
причем матрица преобразования имеет вид
0
_-2//б муъ
Итак, ясно что
i/уъ]
Тогда, зная матрицу [а,-,-], вернемся к первоначальным осям при помощи преоб-
преобразования У Т = Ас }^Т*А, что можно записать в матричной форме так'
0 — 2//б"
1//2
_1//3 - 1/У2
/3 0
0 2
0 О
1//3 1//3
0 1//2 — 1//2
.— 2/У~6 1//6 1/УЪ .

ЗАДАЧИ С РЕШЕНИЯМИ	59
2 + 4 /2-2
/2 — 2 /2 + /6 + I
=
L/2 —2 /2 — /6+1
[5,4i4 —0,586 —0,5
— 0,586 4,863 —0,С
— 0,586 — 0,035 4,?
Декартовы тензоры и операции над ними (§ 1.21 — 1.23)
1.49. Для функции К = At/XiXj, где Ац—постоянные, по-
показать, что дк/дх{ = (Ац + Aji) Xj и d^K/dxfiXj = Ац + Л,-,-.
Упростить эти производные в случае Ац = Ац.
дХ	dxi	dxi	dxi ,	дХ
Рассмотрим —— = Ац —— х, + Ацхс —— . Так как -— = 01к, то —— =
дхк	дхк i	дхк	дхк	дхк
= AkX/-\- AikXi = (Akj + Лл) Xj. Дифференцируя второй раз, получаем
= (Ai + V -§ = ^*Р + V- Ес^ л„ = ап, то-^
1.50.	Пользуясь индексными обозначениями, доказать вектор-
векторные тождества: а) V X Уф = 0, б) V • V X а = 0.
а) Согласно A.147), Уф записывается в виде <р(-, тогда v = V X Уф имеет
компоненты и,- = zi/kd^ k = е^ф fc/-. Но ei;-fe антисимметричен по индексам / и
ft, тогда как фй/. симметричен по этим индексам, следовательно произведение
е(-^ф ft. обращается в нуль. К тому же результату можно прийти, вычисляя
отдельно каждую компоненту v; например
Vl = 8123ф12з + Е132Ф,32 = (Ф.23 — Ф.32) = °-
6)V-VXa = >. = {Biikakij)tt = BljkakJt = 0, так как akij = akji и e,/fe =
= -»,**¦
1.51.	Найти производную функции К = (х^2 + 2^д;2 — (х3)г по
направлению, заданному единичным вектором п = 2/7 ех — 8/7 е2 —
/ч	Л	/\	л	Л
— в/7е3, или п = Bех — Зе2 — 6е3)/7.
Искомая производная вычисляется по формуле дХ/дп = VX • п = X 1щ.
Таким образом,
|	-j	B^) -5- + B*3) _ = -f- (_ д^ + 2
1.52. Пусть Ац — декартов тензор второго ранга. Показать,
что его производная по хь, т. е. Atj,k, является декартовым тензором
третьего ранга.

60
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
Если Х[ и х\ — декартовы системы координат, то xt = а^х- и дх(/дх', = а-(.
Тогда будем иметь
дхт
а это и есть правило преобразования декартова тензора третьего ранга.
1.53. Пусть г2 = xtXi и / (г) —l произвольная функция г. По-
Показать, что: a) V(/ (г)) = f\r) xlr и б) V2 (/ (г)) = /"(г) + 2/7г,
где штрихом обозначено дифференцирование по г.
а) Вектор V/ имеет компоненты/,, причем/ i=^J—-J— ,атак как -^- =
л	• or dxt	dxj
i	™ -^ = ^ . Следовательно, h = -^ ^- = /' Л- .
1.54. Воспользовавшись теоремой Гаусса — Остроградскогс,
показать, что J x,-ny-dS = Кб,/, где nydS — элемент поверхности S,
s	ограничивающе?! объем V
(рис. 1.20), xL — радиус-век-
радиус-вектор элемента tijdS и nL —
внешняя нормаль этого эле-
элемента.
По формуле A.157)
4V:
1.55. Пусть даны вектор
b=V х v и скалярная функ-
функция координат К = К (xt); по-
показать, что
Рис. 1.20.
По условию b = V X v, т. е. bi = e,/ftDfc ,. Тогда
J et/7,
(CM- A.157))
так как
= 0.

ЗАДАЧИ С РЕШЕНИЯМИ
Смешанные задачи
1.56. Для произвольных векторов а и b показать, что
61
Поменяем местами скалярное и векторное умножение в первом члене. Тогда
К = а ¦ b X (а X Ь) + (а • Ь) (а • Ь) =
= а • [(Ь • Ь) а — (Ь • а) Ь] + (а • Ь) (а ¦ Ь) =
= (а ¦ а) (Ь • Ь) — (Ь • а) (а ¦ Ь) + (а • Ь) (а • b) = {abf,
так как второй и третий члены взаимно уничтожаются.
1.57. Пусть и = охи и v = со х v; показать, что
~- (и х v) = со X (и X v).
а)	В символических обозначениях:
d	_-	_	—
dt
= (v • ю) u — (v • u) о) + (u • v) к» — (u ; ai) v =•
= (v • ю) u — (u • w) v = w X (u X v).
б)	В индексных-обозначениях:
d
Пусть —jT- (u x v) = w; тогда
d
и vk = ekmna>mvn, то
а так как щ =
Пользуясь результатом задачи 1.59, а, получаем
wi = F,me/n — е,„е/т -^ ь1ть1п
= Ффтп — 6гЛт) uF>nfln
что в индексной форме представляет величину ю X (u X v).
1.58. Доказать тождество
Рассмотрим определитель Ац
det Л==
тр
Аи Al2 А13
чза Лзз

62
ГЛ I. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
Перестановка строк или столбцов ведет к изменению знака определителя, например
•^21 2 3	2 1 Ai3
А Л А «*— А	Л	а	_ __ лат А
г\\\ *»12 ^*13 	 **22 ¦'•21 **2Я ~~" uct *1*
31	32	8
Если строки менять местами произвольное число раз, то
пт\ "тЧ лт3
Ап\ Ап2 Кг
= <W det A'
а если менять местами столбцы, то
А\р AXq Au
Зп "\п 3s
Следовательно, для произвольной последовательности перестановок строк и столб-
столбцов получим
у, Amq AmS
Arp Arq Ars
Если положить At, = б//, то det A = 1; тождество доказано.
1.59. Воспользовавшись результатами задачи 1.58, доказать,
что:
fl) &pqs&snr = QpnOqr OprQqm б) &pqs?sqr == 	 *&pr.
В тождестве, доказанном в задаче 1.58, разложим определитель по первой
строке:
а) Положив т— s, получим
,-зе„др:
б) В полученном в «а» соотношении положим п равным q\ тогда
б_ с*. ¦== о о ^— о о ^* о —^ Зо ^^ ~— 2о_ .
pqsbsqr qp fq qq tp pr	рг	рт
1.60. Тензор второго ранга В косооимметричен, т. е. В = —Вь.
Показать, что Ъ„ X а = 2а • В.
Запишем В в виде В = tnei + Ьгеа + Ь3е3 (см. задачу 1.6). Тогда
Вц = bj X в! + b2 X еа + b8 X eg

ЗАДАЧИ С РЕШЕНИЯМИ	63
И
В„ X а = (bj х ех) X а + фг X е2) X а + (Ь3 X е3) X а =
= (а • bt) ti — (а ¦ ех) bt + (а ¦ Ь2) е2 — (а • е2) Ь2 + (а • Ь3) е3 — (а • е3)Ь3=
Л	л	л	л	л	л
= а • (bi et + b2e2 + b3e3) — a • (e^ -\- eab2 + e3b3) =
^= a • В — a • Bjp = 2a • В.
1.61. Воспользовавшись соотношением Гамильтона — Кэли,
найти (ВL для тензора
В =
Проверить результат непосредственным возведением в квадрат
(ВJ.
Характеристическое уравнение для тензора В имеет вид
-Я О — 1
соотношением
1
0
— 1
0 -
3
0 -
-1\
0 •
-2
О 3-Я О
_1 о — 2-Я
=— (К3 — 2№— 6Я. + 9) =
По теореме Гамильтона— Кэли тензор удовлетворяет своему собственному харак-
характеристическому уравнению. Следовательно, (ВK — 2 (ВJ — 6В + 91 = 0. Умно-
Умножив это равенство на В, получим (ВL = 2 (ВK + 6 (ВJ — 9В, или (В)* = 10 (ВJ +
+ ЗВ — 181. Отсюда найдем
B 0 К / 3 0—3\ /18 0 0\ /5 0 7\
0 9 01 + 1 0 9 Oj—I 0 18 0 1 = I 0 81 Oj,
1 0 5/ \—3 0—6/ \0 0 18/ \7 0 26/
Проверим этот результат, непосредственно умножая тензор (ВJ самого на себя
/2 О К /2 0 1\ /5 0 7\
(ВL= 0 9о)|0 9о) = 1о81 Oj.
М 0 5/\1 0 5/ \7 0 26/
1.62. Доказать, что: а) Аи, б) АцАц, в) 8;;-*.е*.урЛ,р являются
инвариантами относительно преобразования координат A.103),
т. е. что Аи — Аи, и т. д.
а) Согласно A.103), Ац = apiaqjA'pq; следовательно,
AU =* apiaqlA'pq = дрдА'рЧ = А'рР = A'if
б)	АЧАЦ = ЧрР^А'рр^щА'тп = &pm^qnA'pqA'mn = A'pqA'pq = A\jA'ir
в)	etlk4lpAip = eijk4lpamianpA'mn =• fiifiip —dipdjj) amfinpA'mn =
= Фтп — дтп&ц) А'тп = Fm/6,,,— &mndjj) A'mn = *mjk4
1.63. Показать, что бивектор произвольного тензора Тц за-
заT	TS	T
р р	р ц
висит только от T[i[\, однако произведение Ti/Sij тензора Tij на
симметричьый тензор Si, от Т^^ не зависит.

64	ГЛ. 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
По определению A.1 ГО) бивектор тензора Т.. имеет компоненты vi = zljkTk,
или Vi = ei/k{Tuk) + Tim) = BtlkTljky так как zijkT{jk) = 0 (El./fe антисиммет-
антисимметричен по I и k, a T(/ft) симметричен по индексам / и ?)¦
Указанное произведение можно записать в виде T^S^ — T^,.Sr+ ^шА;-
Здесь Ty^Sjj = 0 и, следовательно, T^S^ = 7"(J/)S(/-
1.64.	Показать, что D : E равно D-E, если Е — симметрич-
симметричный тензор второго ранга.
Запишем тензоры в виде D = ?>(/е,е/ и Е = Ердеред. Согласно A.31),
D : Е = DifEpq (е,- • е„) (е/ - eff). В силу A.35) имеем
D Е = Dl7?w (е/ ¦ ер) ¦ (et ¦ ев) - D,y Eqp{t; ¦ ел) (е,- ¦ е9),
так как ?р? = Eqp. Если теперь в последнем выражении поменять местами
немые индексы р и q, то получим D • Е = ?\;.?рG (е/ • ев) (е; ¦ ер).
1.65.	Пользуясь индексными обозначениями, доказать вектор-
векторное тождество V X (а х Ь) = (Ь • V) а — b (V • а) + а (V • Ь) —
— (а ¦ V)b.
Пусть V X (а X b) = v; тогда vp = zpqizijkdgajbk, или
vp = ePgiei,k (aih),q = tpqfink (°/. Д + albk.q> =
А это означает, что v = (b ¦ V) а — b (V- а) + а (V ¦ b) — (а • V) b.
1.66. При помощи теоремы Гаусса — Остроградского показать,
п X (а X х) dS = 2аV, где V — объем, заключенный внутри
s
поверхности S, n — внешняя нормаль, х — радиус-вектор любой
точки объема V, а — произвольный постоянный вектор.
В индексных обозначениях данный интеграл по поверхности имеет компоненты
' eqpinpeljkaixkdS- По формуле A.157) он переводится в интеграл по объему
j(eqpieljkajxk) р йУ- Учитывая, что а — постоянный вектор, последнее выраже-
выражение можно преобразовать следующим образом:
J EgPi^ikaixk,pdV = $ (ввДц - 8gk8pj) axkpdV = J (agXpp - арХд р) dV =
J (q«6pp ~ aP
1.67. Показать, что преобразование отражения осей координат
(рис. 1.21) является ортогональным.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
65
Из чертежа видно, что матрица преоб-
преобразования такова:
1 0 От
0 — 1 0 .
О О U
Условия ортогональности <2/.aift = Sk или
о-.-аи = б,-*,, очевидно, выполнены. В мат-
ричной форме это можно проверить, поль-
пользуясь формулой A.117):
II 0 Oirl OO-i rl 0 От
0—1 00—1 0 = 0 1 0 .
О 0 iJlo 0 lJ Lo 0 1J
1.68. Показать, что (I X v) ¦ D = v X D.
= i(uJ/k-u2]) + j(-l>xk
Рис. 1.21.
к (cxj - fyij =
= (v x iI + (v X1) Г+ (v Xk) к = v - I
Отсюда следует, что (IXv)-D=vXI-D=vXD.
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
л л л	л л
1.69.	Показать, что векторы u=i+] — к и v=l — j взаимно перпенди-
кулярньи Найти такой вектор w, чтобы u, v, w образовали правый триэдр.
Ответ: w = (— 1/К'б) (Г+ ?+ 2к).
1.70.	Найти матрицу преобразования, связывающего тройку векторов ц, v,
w задачи 1.69 и орты осей координат.
[
—
О
— 1//6 -2//б_
1.71.	Используу индексные обозначения, доказать, что:
а) V • х = 3, 3) V X х = 0, в) а • V х = а, где х — радиус-вектор, а а — не-
некоторый постоянный вектор.
1.72.	Найги главные значения симметричной части тензора
5 —1
1 —6—6
v_3 —18 Ь
Ответ: лA) = — 15,
3 Дж. Мейз
= 5, Ха=10.

66
ГЛ 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ
1.73. Для симметричного тензора
T,j=h 7 4
\0 4 7/
определить главные значения и направления главных осей.
Ответ: Я.A) = 2, Я.B) = 7, ?iC) = 12,
*
*
*
хз
- 3/E /2)
4/5
3/E Y%
Ч
1//2
0
\lV~2
х3
- 4/E } 2)
-3/5
4/E » 2)
1.74.	Дан произвольный вектор v и любой единичный вектор е. Показать, что
v можно разложить на две компоненты — параллельную и перпендикулярную
вектору е, т. е. что v = (v • е) е + е X (v x е).
1.75.	Пусть v-v = O, \?Xv=v/u\Xvi= — v. Показать, что V2v = v.
1.76.	Провести проверку решения задачи 1.48, показав непосредственным
перемножением, что } Т } Т = Т.
1.77.	Извлечь корень квадратный из тензора
,3 2 Ov
В = 2 3 O
\0 0 9/
Ответ:
1.78.	Воспользовавшись решением задачи 1.40, т. е. равенством det A =
= eijk^ 4^2j^3k' показать, что det (АВ) = det A det В.
1.79.	Удостовериться в том, что: а) 63ри/> = "з. б) 63И/? = Ajb< B) &ijeijk ~
= 0, г) ei2ey-3^,7 = лгз-
1.80.	Преобразование, связывающее системы координ?г Ох^х^с^ и
задано таблицей
*;
ч
н
ч
3/E \ 2)
4/5
-3/E} 2)
Ч
0
л Y2
х3
4/E \ 2)
-3/5
-4/E^2)

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ	67
а)	Показать, что выполнены условия ортогональности я,-;-йд, = 6y.ft и
б)	Определить в системе со штрихами координаты точки, имеющей радиус-
вектор х = 2ei — е3.
в)	Как выглядит в системе со штрихами уравнение плоскости xi — *2 + Здг3 =
= 1?
Ответ: б) B/E/2), 11/5, — 2/E j/2)), в) Vix\ — х2 — 2/2*? = 1.
1.81. Показать, что объем V, заключенный внутри поверхности S, можно
I f
задать выражением ^=-^-J v(x • х) • п"^> гДе х — радиус-вектор, а п —
" s
единичный вектор внешней нормали к поверхности.
Указание: записать V в виде V = -E~i(xixc),j njdS и использовать формулу
A.157).	S

Глава 2
Анализ напряженного состояния
2.1. Понятие сплошной среды
Хотя молекулярная природа строения материи точно установ-
установлена, во многих исследованиях поведения материалов важно по-
поведение не отдельных молекул, а лишь материала как целого.
В этих случаях при объяснении наблюдаемых макроскопических
процессов не учитывают молекулярную структуру вещества, а
предполагают, что оно непрерывно распределено по всему зани-
занимаемому им объему и целиком заполняет этот объем. Такая концеп-
концепция сплошности вещества является основным постулатом ме-
механики сплошной среды (континуума). В пределах ограничений,
при которых гипотеза сплошности оправдана, эта концепция обес-
обеспечивает основу для единого изучения поведения твердых тел,
жидкостей и газов.
Принятие гипотезы сплошности как основы для математического
описания поведения материалов означает, что поля величин, таких,
как напряжения и переме-
перемещения, выражаются кусоч-
кусочно непрерывными функци-
функциями координат и времени.
• 2.2. Однородность.
Изотропия. Массовая
плотность
Однородным называется
материал, имеющий едина-
2 ковые свойства во всех точ-
точках. Материал будет изо-
изотропным по отношению к
некоторому свойству, если
это свойство в точке ока-
Рис 2.1.	зывается одинаковым по
вгем направлениям. Ма-
Материал является анизотропным по отношению к тем свойствам,
которые зависят от направления в точке.
Понятие плотности вводится для окрестности точки сплошной
среды как отношение массы с ^объему. Обозначим массу малого

2.4, ПРИНЦИП НАПРЯЖЕНИЯ КОШИ. ВЕКТОР НАПРЯЖЕНИЯ	69
элемента объема AV (рис. 2.1) через AM. Средняя плотность мате-
материала внутри Д V равна-
Pep — ду •	B.1)
Плотность в некоторой точке Р элемента объема Д V в соответствии
с понятием сплошной среды задается пределом
Массовая плотность р является скалярной величиной.
2.3.	Массовые силы. Поверхностные силы
Силы — это векторные величины, которые интуитивно лучше
всего представляются такими понятиями, как давление или тяга.
Те силы, которые действуют на все элементы объема сплошной сре-
среды, называются массовыми силами. Примером тгГКтпс-сил могут слу-
служить силы гравитации и инерции. Эти силы мы будем обозначать
через bt (сила, отнесенная к единице массы) или р, (сила, отнесен-
отнесенная к единице объема). Между собой они связаны включающим
плотность соотношением
P^i = Pi, Или рЬ = Р-	B-й)
Те силы, которые действуют на элемент поверхности, будь то
часть граничной или любой внутренней поверхности, называются
поверхностными силами. Они обозначаются через ft (сила, отне-
отнесенная к единице площади). Силы контактного взаимодействия
между телами относятся к типу поверхностных сил.
2.4.	Принцип напряжения Кош и. Вектор напряжения
На рис. 2.2 изображена область R пространства, занятая ма-
материальным континуумом, на который действуют поверхностные
силы fi и массовые силы bt. Из-за того, что действие сил переда-
передается от одной части среды другой, материал внутри произвольно-
произвольного объема V, ограниченного поверхностью S, взаимодействует
с материалом вне этого объема. Возьмем щ в качестве единичного
вектора внешней нормали в точке Р к малой площадке AS поверх-
поверхности S и обозначим через Д/^ результирующую силу, действую-
действующую через площадь; AS на материал внутри V со стороны внешней
среды. Ясно, что элементарная сила Afi зависит от выбора AS и от
щ. Следует также заме"г^ть, что распределение силы на AS не обя-
обязательно однородно. В самом деле, в общем случае это распределение
эквивалентно одной силе ч моменту, приложенным в точке Р и
представленным на рис. 2.2 векторами Af{ и АМ

70
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Средняя сила, отнесенная к единице площади площадки AS,
задается величиной AfL/AS. Принцип напряжения Коши утвер-
утверждает, что это отношение АД/AS стремится к определенному пре-
пределу dfJdS, когда AS стягивается в точку Р, в то время как момент
силы A/i относительно точки Р в пределе стремится к нулю. Ре-
Результирующий вектор dfJdS (сила, отнесенная к единице площади)
называется вектором напряжения
(рис. 2.3). Если бы момент в
Рис. 2.2.
Рис 2.3.
точке Р при предельном переходе не обращался в нуль, то в этой
точке был бы также определен вектор момента (пары) напряжений,
изображенный на рис. 2.3 стрелкой с двойным острием. Один из раз-
разделов теории упругости изучает такие поверхностные пары, но
в этой книге они не рассматриваются.
Вектор напряжения определяется следующим образом:
— "-, или t ' = lim -т-=- = -т^-.
t\n) = lira
AS->0
Д-S
dS
Обозначение_4п)_(или^(п)) используется для того, чтобы подчеркнуть
тот факт, что вектор напряжения_в_данной точке Р сплошной среды,
очевидно, зависит 6т~орйентацйи выбранного элемента поверхности
AS, которая задается единичным вектором нормали nL (или п).
Если взять любой иначе ориентированный элемент поверхности с
другой единичной нормалью, то связанный с ним вектор напряжения
в точке Р тоже будет другим. Вектор напряжения, выражающий
действие через площадку AS в точке Р материала, расположенного
внутри V, на внешнюю среду, есть вектор —#а>. Тогда по закону
Ньютона о равенстве действия и протиро-действия
— ?(п) = й~П\ или — t(n> = t<~n>.	B.5)
Вектор' напряжения иногда называют вектором натяжения.

2.5. НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ. ТЕНЗОР НАПРЯЖЕНИЙ
71
2.5. Напряженное состояние в точке. Тензор напряжений
Принцип напряжения Коши ставит в соответствие в произволь-
произвольной точке Р сплошной среды каждому единичному BjKTopy нормали
tii, определяющему ориентацию бесконечно малого элемента по-
поверхности, содержащего точку Р, вектор напряжения 4"' (рис. 2.3).
Совокупность всех возможных пар таких векторов /}п) и nt в точке
Рис. 2.4.
Р определяет напряженное состояние в этой точке. К счастью, для
того чтобы полностью описать напряженное состояние в данной точ-
точке, нет необходимости указывать все пары векторов напряжения и
нормали. Это можно сделать, задавая векторы напряжения на трех
взаимно перпендикулярных площадках в точке Р.
Для определения напряженного состояния в точке выберем
плоскости, перпендикулярные осям координат, и будем обозначать
векторы нормали и наьояжения так, как это сделано на рис. 2.4.
Для удобства три отдельные схемы рис. 2.4 часто заменяют
одним схематическим изображением, приведенным на рис. 2.5.
Каждый из трех векторов напряжения на площадках, параллель-
параллельных координатным плоскостям, согласно A.69), можно выразить
через их декартовы компоненты:

12
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
е3 =
/fi
+ ,?) е2 + /&> e3 = /&
tu) = /(es) ^ + /?¦) е2 + #•> е3 = /<;
Девять компонент векторов напряжений
B.6)
tfi^Oi,	B.7)
являются компонентами декартова тензора второго ранга *), так
называемого тензора напряжений. Этот тензор напряжений мы
Рис. 2.5.	Рис. 2.6.
обозначим через Е, так что развернутые (покомпонентное и мат-
матричное) его представления будут иметь следующий вид:
13\
021 °22 °23 1 > ИЛИ ["'(Л =
ГСТП 012 013
I C21 °2 ^23
L°3i °32 °зз
B.8)
Напряжения, определяемые компонентами тензора напряжений
в декартовой системе координат, и координатные плоскости изобра-
изображены на рис. 2.6. Компоненты <гш ам, а33, соответствующие перпен-
перпендикулярным к указаннымТтлощадкам сияамгназ-ываются нормальны-
нормальными напряжениями. компоненты ои, о13,а21,0?3. o31, а32, действующие
в касательных плоскостях, называются касательными напряжени-
напряжениями (или напряжениями сдвига). Компонента напряжения положи-
тельнаГёСЛй на гьлощадке, внешняя нормаль к которой совпадает с
положительным направлением одной из осей координат, сила дей-
действует вдоль положительного направления эгой оси. Компонентаац
задает силу, действующую в направлении /-й оси координат на пло-
площадку с внешней нормалью, параллельной i-й оси координат. Все
компоненты напряжений, изображенные га рис. 2.6, положительны.
1) Это обстоятельство можно доказать с помощью формулы B.12); см. так-
также задачу 2.11.— Прим. ред.

2.6. СВЯЗЬ МЕЖДУ ТЕНЗОРОМ НАПРЯЖЕНИЙ И ВЕКТОРОМ НАПРЯЖЕНИЯ
73
¦(.«О
Рис. 2.7.
2.6. Связь между тензором напряжений
и вектором напряжения
Связь между тензором напряжений о,-,- в точке Р и вектором
напряжения ^п) на произвольно сриентированной площадке в той
же то"чке~можно установить из условия равновесия сил, или уравне-
уравнения количества .движения
для элементарного матери-
материального тетраэдра с верши-
вершиной в точке Р. Возьмем ос-
основание тетраэдра перпен-
перпендикулярным к л,-, а три -<Г
боковые грани перпенди-
перпендикулярными к осям коор-
координат, как показано на
'рис. 2.7. Пусть dS — пло-
площадь основания ABC; то-
тогда площади боковых гра-
граней как площади проекций
основания на координат-
координатные плоскости будут рав-
равны dSy = dStiy для грани СРВ, dS% = dSn2 для грани АРС и
dS3 = dSn3 для грани ВРА, или
dS, = dS(n- е,) = dS cos (n, e<) = dSnt.	B.2)
На рисунке показаны векторы средних значений напряжений— /J(ey>
на боковых гранях и ?*(п> на основании, а также средней массовой
силы Ъ\ (включая силы инерции, если они имеются), действующих
на тетраэдр. Для равновесия тетраэдра под действием этих сил
необходимо, чтобы выполнялось равенство
t] (")dS — t*^dSl — t*&dS2 — t*&dSs + pb]dV = 0. B.10)
Если теперь линейные размеры тетраэдра будут пропорционально
уменьшаться, то массовые силы, малость которых на порядок выше,
будут стремиться к нулю быстрее поверхностных сил. В то же время
векторы средних напряжений стремятся к характерным значениям,
которые присущи указанным направлениям в точке Р. Таким пре-
предельным переходом с учетом B.9) равенство B. Ю) приводится к виду
Л	А*	Л	/S	/S
После сокращения на общий множитель dS и использования тож-
тождества /J.e/> = Op соотношение B.11) будет выглядеть так:
/<") = от,, или t("> = n • 2.	B.12)

74	Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Соотношение B.12) часто представляют в матричной записи
[ф] = Inik] [с*/],
которую можно развернуть следующим образом:
Т23
B.13)
B.14)
Матричное равенство B.14) эквивалентно уравнениям в компонен-
компонентах
п3ази
«3^32,
«3^33-
B.15,
2.7. Равновесие сил и моментов.
Симметрия тензора напряжений
Для равновесия произвольного объема V сплошной среды под
действием системы поверхностных сил ?[."> и массовых сил Ь,- (вклю-
(включая силы инерции, если они
существуют), изображенных
на рис. 2.8, требуется, чтобы
результирующие сила и мо-
момент, действующие на этот
объем, были равны нулю.
Суммирование поверхност-
поверхностных и массовых сил приво-
приводит к интегральному соотно-
соотношению
= 0,
или
Рис. 2.8.
B.16)
' t<">dS + J p bdV = 0.
Заменяя здесь t\"i через ацп, и переходя от интеграла по поверх-
поверхности к интегралу по объему при помощи теоремы Гаусса — Остро-
Остроградского A.157), приводим уравнение B.16) к виду
j + pbt) dV = 0,
или
J (V • S + pb) dV = 0. B.17)

2.8. ЗАКОНЫ ПРЕОБРАЗОВАНИЯ НАПРЯЖЕНИЙ	75
Поскольку объем V произволен, подынтегральное выражение в
формуле B.17) должно обратиться в нуль, так что
Ojij + pb{ = 0, или V • 2 + pb = 0.	B.18)
Эти уравнения называются уравнениями равновесия.
При отсутствии распределенных моментов (поверхностных и
массовых пар) для равновесия моментов относительно начала отсче-
отсчета требуется, чтобы
J eyfc*,j?>dS + f ещярЬьЫ = 0,
s	V
или	B.19)
Jx x t<">dS + fxx pbdF=O,
S	V
где xt — радиус-вектор элемента поверхности или объема. Снова
совершив подстановку Лп'=0/,п/, применив теорему Гаусса —Остро-
—Остроградского и использовав результат, полученный в B.18), объеди-
объединим интегралы в B.19) и придем к уравнению
0, или JsodV = 0.	B.20)
V	V
В силу произвольности объема V из B.20) следует, что
ец*о> = 0, или 2о=0.	B.21)
Формула B.21) содержит в себе равенства о12 = с21, о23 =о32,
13	ЗИ
aiL = afi,	B.22)
которые показывают, что тензор напряжений симметричен. Учиты-
Учитывая B.22), уравнения равновесия B.18) часто пишут в виде
оц.1 + 9b i = 0,	B.23)
что в развернутой форме выглядит так:
<2-24>
2.8. Законы преобразования напряжений
Пусть в точке Р две ортогональные декартовы системы коорди-
координат Рх1х2х3 и РХ1Х2Х3 (рис. 2.9) связаны одна с другой таблицей на-
направляющих косинусов

76
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Xl
*2
*3
Xl
«11
«21
«31
Хч,
«12
«22
«зг
*3
«13
«23
«33
или — что эквивалентно — ли-
	 бо матрицей преобразования
[at,], либо тензором преобразо-
преобразования
Рис. 2.9.
А = atfifi,. B.25)
Согласно правилу A.93) преобразования декартовых тензоров
первого ранга, компоненты вектора напряжения ^п), отнесенные к
осям системы без штрихов, связаны с компонентами ^(п) в системе
со штрихами формулой
ф) =
или
t'<"> = А • t<n>.
B.26)
Подобным же образом по правилу преобразования A.102) для де-
декартовых тензоров второго ранга компоненты тензора напряжений
в двух системах связаны соотношением г)
или
2' = А • 2 • Ас
B.27)
В матричной форме преобразование вектора напряжения запи-
записывается в виде
B.28)
B.29)
m = [«. ^
а преобразование тензора напряжений — в виде
[о],] = [dip] [aPQ] [а„1\.
В развернутой записи произведений матриц формулы B.28) и B.29)
соответственно выглядят так:
B.30)
«21
«31
«12
«22
«32
«13
«23
«33
— л —
1
ф
х) Смотри задачу 2.11.—Прим. ред

>9. ПОВЕРХНОСТИ НАПРЯЖЕНИЙ КОШИ
77
Cl 1
021
«И
G2l
«31
012
022
«12
«22
fl32
Cl3
023
«13
«23
«33
«II «21 ^31
Й12 «22 «32
«13 «23 «33
. B.31)
2.9. Поверхности напряжений Коши
Пусть в точке Р сплошной среды тензор напряжений имеет
компоненты oijt отнесенные к направлениям, параллельным мест-
местным декартовым осям Р^С^
(	У
р
(рис. 2.10). Уравнение
°iy?i& = ± ^z (k — постоянная)
B.32)
представляет геометрически по-
подобные поверхности второго по-
порядка (квадрики), имеющие об-
общий центр в точке Р. Выбор зна-
знака плюс или минус обеспечивает
то, что поверхности будут дей-
действительные.
Рассмотрим вектор напряже-
ния /|п) на площадке с единичной
нормалью nt. Радиус-вектор г,
идущий в направлении п к про-
произвольной точке поверхности B.32), имеет компоненты ?, = гщ.
В точке Р нормальная составляющая oNni вектора напряжения <<.">
имеет величину
aN = *<">«, = t<"> • n = оцщщ.	B.33)
Геометрическое место точек o^r2 = const = ±&2, т. е. поверхность
* = ± к\	B.34)
Рис. 2.10.
называется поверхностью напряжений Коши (или квадрикой Коши).
Из этого определения следует, что величина 0,v нормальной компо-
компоненты напряжения на площадке dS, перпендикулярной радиусу-век-
радиусу-вектору г в точке Р, обратно пропорциональна квадрату расстоя-
расстояния вдоль г от точки Р до поверхности напряжений Коши, т. е.

78
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
0W = ± k2fr2. Кроме того, можно показать, что вектор напряже-
ния t{"\ действующий на такой площадке dS, параллелен нормали
к плоскости, касательной к поверхности напряжений Коши в точ-
точке, радиус-вектор которой есть г.
2.10. Главные напряжения. Инварианты тензора напряжений.
Эллипсоид напряжений
В точке Р, где компоненты тензора напряжений равны Оц,
соотношение B.12) йп) = апп, ставит в соответствие каждому
направлению nt вектор напря-
жения t{"]. Направления, для
которых йп) и п, коллинеарны
(рис. 2.11), называются главны-
главными направлениями (или главны-
главными осями) тензора напряжений.
Для главного направления име-
имеет место равенство
или
= an,
B.35)
Рис. 2.11.
где а — величина вектора на-
напряжения — называется главным
напряжением. Подставляя B.35) в B.12) и используя тождества
щ = Ьип, и 0,/ = Оц, приходим к уравнениям
= 0,
или
B — I a) ¦ п = 0.
B.36)
Три уравнения B.36) содержат четыре неизвестных, а именно три
направляющих косинуса пс и величину главного напряжения 0.
Для того чтобы система B.36), кроме п,- = 0, имела еще и не-
нетривиальное решение, детерминант из коэффициентов | с,-,- — 8иа |
должен обращаться в нуль, т. е.
Tie	О,
— bijO | = 0, ИЛИ
an — a
Jl3
¦ — а а.
23
= 0, B.37)
что после раскрытия определителя приводит к кубическому урав-
уравнению относительно 0
— llh = 0,
B.38)
где

2.10. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ИНВАРИАНТЫ ТЕНЗОРА НАПРЯЖЕНИЙ	79
B 39)
Hs = '/2 (ацап — ot/оц),	B.40)
HIS = |a,7| = detS	B.41)
называются соответственно первым, вторым и третьим инварианта-
инвариантами тензора напряжений.
Три корня уравнения B.38) a(i), о{2), о13) являются значениями
трех главных напряжений. Каждому главному напряжению aih)
соответствует главная ось, для которой направляющие косинусы
п\к) находятся как решения уравнений
а„ - а{к1бц) nf = 0, или B - с(й) I) • п<*> = 0 (k = 1, 2, 3). B.42)
Здесь верхние или нижние буквы, заключенные в скобки, являются
просто индексами и не участвуют ни в каком процессе суммирования.
Например, развернутая форма B.42) для второй главной оси такова:
f
= 0,
0.
B.43)
+ (<rJ3 — crB)) nf
Так как тензор напряжений симметричен и его элементы — дей-
действительные числа, главные напряжения тоже принимают действи-
действительные значения.
Матрица [ои], отнесенная к главным осям, имеет вид
[ос/] =
Гс„, 0 0
0 а{2) 0
0 0 op,
ИЛИ [Olf] =
а, 0
0 (Гц
0 0 аш
0
0
B.44)
Во второй форме в качестве индексов использованы римские цифры
для того, чтобы показать, что главные напряжения упорядочены,
т. е. ci >сц >сш. Вслед-
Вследствие того что главные оси
тензора напряжений сов-
совпадают с главными осями
поверхности напряжений
Коши, значения главных
напряжений включают как
максимальное, так и мини-
минимальное значения компо-
компонент нормального напря-
напряжения в точке.
В пространстве главных
напряжений, т. е. в про-
пространстве, где оси коорди-	Рис. 2.12.

W	Гл 2 АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
нат совпадают с главными осями тензора напряжений, а
единицами измерения координат служат величины (ti ', t? , h ),
как показано на рис. 2.12, произвольный вектор напряжения *,п)
в соответствии с формулой B.12) имеет компоненты
/(") = а0)пъ if = crB,n2, ф = аC,«3.	B.45)
Но поскольку (пхJ + (п2J + {пзу = 1 для каждого единичного
вектора п,-, то вектор *'п) в пространстве главных напряжений
удовлетворяет уравнению
¦ +
= 1.
B.46)
Это уравнение эллипсоида, известного под названием эллипсоида
напряжений Ламе.
2.11. Максимальное и минимальное касательное напряжение
Разложим вектор напряжения /'п) на ортогональные компонен-
компоненты _ нормальную и касательную к элементу поверхности dS, на
котором он действует. Ве-
Величину нормальной ком-
компоненты можно определить
по формуле B.33), а квад-
квадрат величины касательной'
компоненты (напряжения
сдвига) получается как раз-
разность
так, что
равны
Эта операция продемонст-
продемонстрирована на рис. 2.13, где
оси координат выбраны по
главным осям тензора на-
напряжений и главные на-
Pl:c- 2ЛЗ"	пряжения упорядочены
>crii >сгш. Из B.12) следует, что компоненты rln)
If = аипг,
= amti3,
B.48)

2.11. МАКСИМАЛЬНОЕ И МИНИМАЛЬНО? КАСАТЕЛЬНОЕ НАПРЯЖЕНА Р1
а из B.33) получается величина нормальной компоненты
eN = охп\ + апп\ + ошп1	B.49)
Подставляя B.48) и B.49) в формулу B.47), вычислим квадрат ве-
величины касательного напряжения как функцию направляющих ко-
косинусов я,-:
а! = о\п\ + о2пп\ -f ашп! — (схп] + ounl + ощп1J. B.50)
Максимальное и минимальное значения os можно получить
из B.50) методом множителей Лагранжа. Процедура состоит в
построении функции
F = o%~ U.n,,	B.51)
где скаляр Я называется множителем Лагранжа. Равенство B.51)
представляет функцию направляющих косинусов п,, так что усло-
условие экстремума (максимума или минимума) величины F имеет вид
dFldtij = 0. Приравнивая нулю эти частные производные, приходим
к уравнениям:
пу [а\ — 2ст, (crinf + aunl -f ашп1) + Ц = 0,	B.52а)
п2 [of, — 2о„ (cr,n? + annl + атп1) + X] = 0,	B.526)
"з [ofii — 2огц| {am! + or,,n| + ffmn?) + M = 0,	B.52в)
которые вместе с условием я,п? = 1 можно разрешить относительно
X и направляющих косинусов nlt n2, ns, соответствующих площадкам
экстремальных значений касательного напряжения.
Вот одно из решений системы B.52) и соответствующее ему
касательное напряжение, найденное по формуле B.50):
я1 = ±1, п2 = 0, п3=0, as = 0.	B.53а)
П1 == 0, п, = ± 1, п3 = 0, ffS = 0.	B.536)
пг = 0, п2 = 0, я3 = ± 1, os = 0.	B.53в)
Величины касательного напряжения в B.53), очевидно, являются
минимальными. Кроме того, так как B.53) указывает на то, что
эти величины обращаются в нуль на главных площадках, то направ-
направления, полученные в B.53), совпадают с главными осями тензора
напряжений.
Другие решения системы B.52) имеют вид:
/4 = 0,	п2 = ±1/|/2, п3 = ±1/К2, cts=(cth —стш)/2;
B.54а)
п, = ± 1/|/2, п, = 0,	п3 = ± 1/К2, as = (a,,, - о,)/2;
B.546)
п, = ±1/Г2, п3 = 0,	as = (a,-au)/2.
B.54в)

82	Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Формулы B.546) дают максимальное значение касательного напря-
напряжения, равное полуразности наибольшего и наименьшего главных
напряжений. Таким образом, из B.546) следует, что максималь-
максимальная компонента касательного напряжения действует в плоскости,
которая делит пополам прямой угол между направлениями макси-
максимального и минимального главных напряжений.
2.12. Круги Мора для напряжения
Удобное двумерное графическое представление трехмерного
напряженного состояния в точке дают известные круги Мора.
Для того чтобы разъяснить это понятие, снова возьмем в качестве
осей координат главные оси
тензора напряжений в точке
Р, как показано на рис. 2.14.
Предполагается, что все глав-
главные напряжения различны и
упорядочены, так что
ctiXthXtih. B.55)
При таких условиях вектор
напряжения 4"' имеет нор-
нормальную и касательную ком-
компоненты, величины которых
удовлетворяют соотношениям
Рис. 2.14.
oN =
2
+ &s =
+ ац/zf + опт!,
2 2
ti
22
+ c\\n2 +
B.56)
B.57)
Комбинируя эти два равенства с тождеством nini = 1 и разрешая
относительно направляющих косинусов nit получаем
~ ац) (ал; ~ ащ) + (asJ
КJ =
B.58a)
(п2J =
B.586)
(aHI—
B.58b)
На этих равенствах основывается построение кругов Мора на
плоскости напряжений, где ось aN является осью абсцисс, а ось as —
осью ординат (рис. 2.15).
Так как из B.55) следует, что Oj ~ a» > 0 и аг — аш > О,
а величина (пхJ неотрицательна, то числитель в правой части B.58а)

2.Г2. КРУГИ МОРА ДЛЯ НАПРЯЖЕНИЯ
83
удовлетворяет соотношению
(о> — ои) (aN —
(crsJ > 0,
которое в плоскости напряжений (aN, as) представляет точки,
лежащие вне круга
[oN - (сг„ + стш)/2]2 + (osJ = Цаи - аш)/2]а
и на его границе. На рис. 2.15 этот круг обозначен буквой
B.59)
очки,
B.60)
Рис. 2.15.
Точно так же из B.55) следует, что сгц — ощ >0иоц — а\ <
< 0; кроме того, величина (п2J неотрицательна. Тогда в формуле
B.586) числитель в правой части удовлетворяет неравенству
К — om)(aN — cti) + (<JsJ < 0,	B.61)
которое представляет точки внутри круга
[on - (ат + o{)l2f + (asJ - [(aIU - a,)/2]2,	B.62)
обозначенного на рис. 2.15 буквой С2, и на его границе. Наконец,
из B.55) видно, что ощ — аг < 0 иош — аи < 0, а величина (п3J
неотрицательна, поэтому из формулы B.58в) следует неравенство
(aw — сп) (ад, — он) + (asJ > 0,	B.63)
которое представляет точки вне круга
[aN - (a, + a,,) /2]2 + (asJ = [(a, - а„)/2]2,	B.64)
обозначенного на рис. 2.15 буквой С3, и на его границе.
Каждая «точка напряжения» (пара величин aN и as) на плос-
кости напряжений (aN, as) соответствует вектору напряжения /{"',
а напряженное состояние в точке Р, описанное формулами B.58),
можно представить на рис. 2.15 затененной областью, ограничен-
ограниченной кругами Мора для напряжения. Это построение подтвержда-
подтверждает, что максимальное напряжение сдвига равно (ог—ощ)/2, как

84
Гл 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНЬЯ
было установлено анали ически в §2.11. Вследствие того что знак
напряжения сдвига не имеет принципиального значения, часто изо-
изображают только верхнюю половину симметричной диаграммы.
Связь между диаграммой напряжений Мора и физическим напря-
напряженным состоянием может быть установлена при помощи рис. 2.16,
ош
Рис. 2.16.
на котором изображен первый октант сферы с центром в точке Р
сплошной среды. Нормаль л, к сферической поверхности ABC
в произвольной точке Q одновременно является нормалью к элемен-
элементу поверхности dS в точке Р. Из-за симметрии тензора напряжения
и из-за того, что на рис. 2.16 использованы главные оси тензора на-
напряжений, напряженное состояние в точке Р полностью характе-
характеризуется совокупностью тех положений, которые может занимать
точка Q на поверхности ABC. На рисунке круговые дуги KD, GE
и FH указывают такие положения Q, где один направляющий коси-
косинус из п, имеет постоянную величину, а именно
nj = costp на KD, n2 = cosfi на GE, n3= cos 6 на FH,
а на граничных дугах ВС, СА и АВ
пг = cos л/2 = 0 на ВС, я2 = cos л/2 = 0 на С А,
п3 = cos л/2 = 0 на АВ.
В соответствии с первым из этих равенств и уравнением B.58а)
векторы напряжения для точек Q, лежащих на ВС, будут иметь

2.13. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
85
компоненты, определяемые точками напряжения на круге Сг
(рис. 2.15). Подобным же образом СА на рис. 2.16 соответствует
кругу Сг на рис. 2.15, а АВ — кругу Са.
Компоненты вектора напряжения aN и as для произвольного по-
положения Q можно определить при помощи построения, выполнен-
выполненного на рис. 2.17. Так, положение точки е на С3 можно получить,
проводя радиусы из центра С3 под углом 2р. Заметим, что углы в
Рис. 2.17.
физическом пространстве (рис. 2.16) при переходе в пространство
напряжений (рис. 2.17) удваиваются (дуга АВ на рис. 2.16 содержит
90°, а соответствующие точки напряжения О\ и огц отстоят друг
от друга на круге С3 на 180°). Аналогичным образом на рис. 2.17
получены точки g, h и / и соответствующие пары соединены круго-
круговыми дугами, имеющими центры на оси Он. Точка пересечения кру-
круговых дуг ge и hf дает компоненты стлг и as вектора напряжения t("]
на площадке с нормалью п,- в точке Q на рис. 2.16.
2.13. Плоское напряженное состояние
В том случае, когда одно и только одно из главных напряжений
равно нулю, говорят, что существует плоское напряженное состоя-
состояние. Такая ситуация возникает в свободной от нагрузки точке на
свободной поверхности, ограничивающей тело. Если главные
напряжения упорядочены, то расположение кругов Мора будет иметь
один из видов, представленных на рис. 2.18.
Если главные напряжения неупорядочены и в качестве направ-
направления нулевого главного напряжения взято направление xs, то
плоское напряженное состояние имеет только компоненты в пло-
плоскостях, параллельных плоскости х^. При произвольном выборе
ориентации ортогональных осей х, и хг в этом случае матрица

86
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
напряжений имеет вид
(Гц сг12 0"|
СТ12 °22 О I •
О	0 Oj
B.65)
Поверхность напряжения для плоского напряженного состояния
является цилиндром, основание которого лежит в плоскости ххх2
и описывается уравнением
оих2\ + 2а12х1х2 + G,2*1 = ± №.	B.66)
В элементарных курсах сопротивления материалов плоское
напряженное состояние часто представляют одним кругом Мора.
oI=0
Рис. 2.18.
Как показывает рис. 2.18, такое представление всегда неполно,
так как для полной характеристики напряженного состояния нуж-
нужны все три круга. В частности, если этот единственный круг окажет-
окажется одним из внутренних кругов на рис. 2.18, то величина максималь-
максимального касательного напряжения в точке не будет определена. Диа-
Диаграмма в виде одного круга Мора может, однако, указать точки
напряжения для всех тех площадок в точке Р, которые содержат
ось нулевого главного напряжения. Если оси координат выбраны
в соответствии с представлением напряжений, данным формулой
Рис. 2. It».

2.14. ДЕВИАТОР И ШАРОВОЙ ТЕНЗОР НАПРЯЖЕНИЙ	87
B.65), то для таких площадок уравнение единственного круга Мора
для плоских напряжений будет
\oN — (оп + ст22)/2]2 + (osJ = [(an — сг22)/2]2 + КгJ. B.67)
На рис. 2.19 представлены характерные точки этого круга. Он
имеет центр С в точке о,\ = (ои + а22)/2, и радиус его, согласно
уравнению B.67), равен R = Vl(ou—ог22)/2]2 + (а12J. Точка А
на окружности представляет напряженное состояние на элементе
поверхности с нормалью пг (правой боковой грани прямоугольного
параллелепипеда, изображенного на рис. 2.19). Точка В на окруж-
окружности представляет напряженное состояние на верхней грани па-
параллелепипеда с нормалью я2. Точки главных напряжений О\ и стц
так и помечены этими буквами на диаграмме, а точки Е и D на
окружности являются точками максимального значения касатель-
касательного напряжения.
2. И. Девиатор и шаровой тензор напряжений
Очень часто бывает полезно разложить тензор напряжений ait
на два тензора, один из которых (шаровой тензор или тензор гид-
гидростатических напряжений) имеет вид
(ом 0 0 \
2,м = см\ = 0 ам О I,	B.68)
V 0 0 ам)
где ам = —р = okk/3 —среднее значение нормального напряже-
напряжения, а второй (девиатор напряжений) — вид
(Оц~ом о12	al3 \ (sn s12 s13\
cr21 cr22 — oM o23 I = s21 s22 s23 I • B.69)
CT3i	°32 ^зз — oM' \s31 s32 s33/
Это разложение описывается формулами
оц = бцакк/З + sih или S = ом I + SD.	B.70)
Главные оси девиатора s,;- совпадают с главными осями тензора
О;у. Таким образом, главные значения девиатора напряжений равны
S(fc) = от (^) — ом-	B.71)
Характеристическое уравнение для девиатора напряжений так же,
как и характеристическое уравнение B.38) для тензора напряжений,
представляет собой кубическое уравнение вида
B.72)

88
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Легко показать, что первый инвариант девиатора напряжений
ISd тождественно равен нулю, что и объясняет его отсутствие в
уравнении B.72).
(К)
ЗАДАЧИ С РЕШЕНИЯМИ
Напряженное состояние в точке. Вектор напряжения.
Тензор напряжений (§ 2.1—2.6)
2.1. Векторы напряжений /|п) и /f-"*' в точке Р действуют со-
соответственно на элементы поверхности л,-AS и n'&S*. Показать,
что компонента /[-п) в на-
направлении tii равна компо-
нснте /,-"*' в направлении пс
(рис. 2.20).
Требуется показать, что
В силу B.12) *["*) щ =
'/, а в силу B.22) а// =
Рис. 2.20.	= о-.л так что
°ЦП/Щ = (рищ) п* = fjn)n*-
2.2. Тензор напряжений в точке Р задан так:
у _
Определить вектор напряжения в точке Р на площадке с единичным
вектором нормали п = 2/3е1 — 2/3е2 + x/3e3.
Из B.12) имеем t(n) = п ¦ S. Умножение лучше всего выполнить в матричной
форме B.13):
..	Г 7 0-2-
[<<п), 4П). 4ПI = Г2/з. -2/з. V,]
_Г_14
~| 3	3 ' 3
Гакнм образом, t(n) = 4ei — Ш/Зеа.
2_ —10 —4
3	"~~
Г 7 0-2-,
0 5 0
L—2 0 d
, 4 1
+~3"J "

ЗАДАЧИ С РЕШЕНИЯМИ	89
2.3. Для вектора напряжения задачи 2.2 определить:	а) ком-
поненту, перпендикулярную площадке; б) модуль #п);	в) угол
между t'in) и п.
а)	<f»> • п = D - »/л) ¦ («/а - »/л + V3e3) = «/,.
б)	| 4"' | = Г 16 + «*>/„ да 5,2.
в)	Так как <}"> • л= | *J-n) \ cos в. то cos 6 *=: D4/„): 5,2 ж 0,94 и 6 *= 20°.
Г\	У\	гч
2.4.	Даны векторы напряжения Йе°, f'ei) и йе>) , действую-
действующие на три координатные площадки. Показать, что сумма квадратов
модулей этих векторов не зависит от ориентации координатных пло-
плоскостей.
Пусть S — указанная сумма. Тогда
5 = /?•>?¦> + tf'hf^ + fatf'K
а из B.7) следует, что S = аиаи + a2ja2i + a3ia3i = ада/,-—инвариант.
2.5.	Напряженное состояние в некоторой точке задано тен-
тензором напряжений
а ао Ьа,
= | аа а са
{ba ca a
где а, Ь, с — константы, а а — некоторое значение напряжения.
Определить константы а, Ь и с так, чтобы вектор напряжения на
октаэдрической площадке (см. задачу 2.22.— Перее.) с единичной
нормалью n = A/V 3) ei + A/КЗ) еа + A /|/ 3) е3 был равен нулю.
Для данных тензора напряжений и вектора нормали величина ^п) = оцп,-
должна быть равна нулю. Запишем это в матричной форме:
[а ао ?о1П/|/з1 П)
аа а со 1/^3 = 0
Ьа са 0JLI//3J |_0
откуда а -f- с — — 1,
Решая эти уравнения, получим а = Ь = с= —1/2- Итак, решение дается тензо-
тензором
/а —о/2 —а/2,
aij = I — а/2 а — а/2
V— а/2 — а/2 с
2.6. В точке Р задан тензор напряжений
7 —5 On
2=|—5 -3 1
О 1 2У

90
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Рис. 2.21.
[3/7. в/7, 2/7]
Определить вектор напряжения на
площадке, проходящей через точку
Р параллельно плоскости ЛВС, изо-
изображенной на рис. 2.21.
Плоскость ABC определяется уравне-
уравнением 3xi + 6*2 + 2лг3 = 12, а вектор еди-
единичной нормали к ней (см. задачу 1.2)—урав-
1.2)—уравнением j
По формуле B.14) вектор напряжения мож-
можно определить умножением матриц
7-5 0]
-5 3 1 =V7[-9, 5, 10].
. 0 1 2i
Таким образом, t<n) = —9/, ei + Б/7 е2 + ш/7 е3.
2.7. Напряженное состояние в любой точке сплошной среды
в декартовой системе координат задано тензором
5x1
0
Определить вектор напряжения в точке Р B, 1, к 3) на площадке,
касательной в этой точке к цилиндрической поверхности х\ + х| =
= 4.
Компоненты напряжения в точке Р
принимают значения
F5	0
5 0 2/3
0 2/3 0
Единичный вектор нормали в точке Р
определяется вектором grad ф = уф =
= у (х\ + л;| — 4). Таким образам,
Уф = 2х2е2 + 2х3е3
и, следовательно, в точке Р	Рис. 2.22.
Тогда единичный вектор нормали в точке Р есть п = -#• + -я- е3 (это легко ви-
видеть и из рис. 2.22). Наконец, вектор напряжения на площадке, перпендикулярной

ЗАДАЧИ С РЕШЕНИЯМИ
к п в точке Р, равен
В1
или
6 5 О
5 0 2/3
.0 2/3 О
t<"> = ?,/2
ГО"
1/2
Ь'з/2.
=
¦5/2"
3
/з.
¦ Зе,
Уравнения равновесия (§ 2.7)
2.8.	Какой вид должны иметь компоненты массовой силы,
если при распределении напряжений, указанном в задаче 2.7, всюду
выполнены уравнения равновесия B.24)?
Подставим в уравнения B.24) значения, непосредственно вычисленные по
заданному в задаче 2.7 тензору напряж ний 2:
Зх2 + 10х2 + 0 + рЬг = 0,
0 + 0 + 2 + р62 = 0,
0 + 0 + 0 + р63 = 0.
Эти уравнения удовлетворяются при 6i = — 13хг/р, 6г = —2/р, Ь3 = 0.
2.9.	Вывести уравнение B.20) из уравнения B.19).
Начнем с уравнения B.19):
( eljkXjpbkdV = 0.
(
Подставим ^"' = о/ел/ в янтеграл по поверхности и преобразуем результат
к интегралу по объему по формуле A.157):
]	^ {eilkxppdp dV,
s	v
Выполним в этом интеграле по объему дифференцирование и объединим результат
с другим интегралом по объему, входящим в формулу B.19):
*1 (apk,P + Pbk)] dV = O
Но вследствие уравнений равновесия а . + рб^ = 0, а лс- = б/р, и поэтому
интеграл по объему приводится к виду B.20): Je?/fca/ftdV = 0.
V
Преобразования тензора напряжений (§ 2.8)
2.10.	Напряженное состояние в некоторой точке задано в де-
декартовой системе координат Охгх2хя тензором
2—2	0>
2 = | — 2 J/2	0
0 0 —

92
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Определить тензор напряжений 2' для повернутых осей
которые связаны с осями без штрихов тензором преобразования
О
1/1/2
_ 1/1/2
Формула B.27) дает закон преобразования напряжений в виде о^,—
или 2' = А • 2
риц [а[.у] = |
О
К/1 =
Ас. Детальные вычисления лучше провести умножением мат-
I [°?/]> согласно формуле B.29). Таким образом,
1/У2
1/2
1/2
1//2
-1/2
-1/2.
2
— 2
0
— 2
0
0
0
— \Г2
0
1/У2
1/|/2
1//2 -1|^2"|
1/2 1/2
- 1/2 - 1/2 J
[00	21
0 l—j/2 —1
2 -1 l+l^J
2.11. Показать, что закон преобразования напряжений можно
получить, воспользовавшись выражением B.33) aN = а^псп, для
величины нормального напряжения на произвольной площадке,
имеющей единичный вектор нормали nt.
Так как aN — тензор нулевого порядка, в любой системе осей координат (со
штрихами или без штрихов) он записывается одинаково:
но, согласно A.94), л,- = одл/, и поэтому
°ijninj = ai,aipnPaign9 = С
где в последнем члене использованы новые индексы суммирования. Таким образом,
а поскольку направления осей без
штрихов произвольны,
2.12. В системе осей без
штрихов (рис. 2.23) тензор на-
пряжений дан в виде
Рис. 2-23.

ЗАДАЧИ С РЕШЕНИЯМИ
93
Определить тензор напряжений в осях со штрихами, направления
которых указаны на рисунке.
Прежде всего необходимо полностью определить матрицу преобразования
А. Ось *| составляет одинаковые углы с осями Х[, поэтому первая строка таблицы
преобразования, а также с33 известны:
Х2
х'з
1/у1
ч
ч
i/Кз
1/1/2
Недостающие элементы таблицы преобразования можно определить из условия
ортогональности (щащ — в/*. Читателю предоставляется в качестве упражнения
показать, что
Следовател ьно,
" 1/1А3 l/yij
— 2УЪ 1/yTi
0 — 1/1/2
т'1/3 т/1/3
— 2т/1/б т/У"б
0 —т/1/2
" 1//3
1/1^
-2/1/6 1/1/6
- 0 — I//
1/>^3-1Гт 0 0"
1//6 11 0 т 0
1/}А2_11_0 0 т.
Т//3"
¦чуъ
т/1/2-
~иУз —
1/1^3 1
-1/Уз 1
муТ
1/1'б
2 1/К2.
1/J/1
2//б
гуъ i
1//6
l/V^
0
1//2
1Уг
0
- 1/V
1/^2
т
0
.0
2
0
т
0
Полученный результат не покажется удивительным, если рассмотреть круги Мора
для напряженного состояния с тремя равными значениями главных напряжений.
Поверхность напряжения Коши (§ 2.9)
2.13. Найти поверхности напряжения Коши в точке Р для сле-
следующих состояний напряжения:
а)	всестороннее равномерное растяжение (сжатие)
°п = °22 = °зз — а» СТ12 = ffi3 = °гз = 0;
б)	одноосное растяжение (сжатие)
аи = о, а22 = а33 = а12 = а13 = а23 = 0;
в)	простой сдвиг
а1а = огг1 = т, ап = а22 = о33 = ст13 = а23 = 0;

94
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
г) плоское напряженное состояние
tfn = СТ22 = а, CTi2 = о.а — т, Одз = а31 = а23 = 0.
Согласно B.32), уравнение поверхности напряжений в символической записи
таково: ? ¦ 2 ¦ ? = ±й2. Используя матричную форму, получаем следующие
результаты.
а)
[о О 0"|
О а О
О 0 а]
Отсюда видно, что поверхность напряжений для всестороннего равномерного рас-
растяжения является сферой t% + ?| + ?3 =
о
б) Кг, Е«. Ed
I С,
bs
=oCf=±A*.
Поверхность напряжений для одноосного растяжения представляет собой две
плоскости, перпендикулярные линии действия напряжения.
в)
Ed

т
.0
т
0
0
0'
0
0_
ГЧ
LJ
== ±
Поверхность напряжений для простого сдвига есть гиперболический
с образующей, параллельной оси ?
цилиндр
г) К*
= ± »¦
Для плоского напряженного состояния поверхность напряжения представляет
собой цилиндрическую поверхность с образующей, параллельной оси нулевого
напряжения, и направляющей в виде кривой второго порядка.
2.14. Показать, что для напряженного состояния, заданного
тензором
Га 0
о ъ о
0
поверхность напряжения (квадрика) Коши будет эллипсоидом (эл-
(эллипсоидом напряжения), если a, b и с имеют одинаковые знаки.
Уравнение поверхности напряжений имеет вид
о ь olu21 = .
о о JLeJ
Это эллипсоид
1.
be
ос
¦+¦

ЗАДАЧИ С РЕШЕНИЯМИ
95
Главные напряжения (§ 2.10—2.11)
2.15. Тензор напряжений в точке Р в декартовых осях Охгхгхй
имеет компоненты
/3 1 Г
Определить главные напряжения и главные оси тензора напряжений,
с которыми будет связана система осей координат 0х\х1хз.
Согласно B.37), главные напряжения а определяются из уравнения
Л а 'К 1
= 0,
2* ~
или в развернутом виде
Главные напряжения являются корнями этого уравнения аA) = —2, аB) = 1,
аC) = 4. Пусть ось х[ совпадает с осью главного напряжения а(,., и пусть п?'1 —
направляющие косинусы этой оси. Тогда, согласно B.42),
Отсюда п\1) = 0, «У = —п§\ а так как щщ = 1, то (л?'J = V2. Поэтому
„О) = о, л»' = ЩГ% 41} = - 1Г/2.
Пусть точно так же ось х2 соответствует главному напряжению аB). Тогда,
согласно B.42),
гак что nf =
Пусть, наконец, х"г соответствует аC). Тогда, согласно B.42),
что л<3) = —2/VW, гф = —1/) 6, л^3> = — 1/^6!

96
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
2.16. Показать, что тензор преобразования, состоящий из
направляющих косинусов, определенных в задаче 2.15, приводит
первоначальный тензор напряжения к диагональному виду, т. е.
оси к] являются главными.
Согласно B.29), [а^] = [с,р] [apq\ [aqj\, что для нашей задачи сразу дает
— 1/J/2
I//3 — 1/|
О —/2
0
.— 1//2 -
— 4/ УЪ — 4/УЪ
3 1 1
1 0 2
1 2 О
О	1/) — 2УК 6
1/^2 — 1/^3 — 1/| 6
- 1/|2 — l/i 3 — 1/| 6
1/КЗ —
— 1//6
— 2 О О
О 1 О
0 0 4
2.17. Определить главные напряжения и главные оси тензора
напряжений
Согласно B.37),
т — а
х
х
х — а
х
X
т — а
= 0,
или (т — а) [-
аC) =
2то + а2] + 2т2а = [Зт — о] а3 = 0. Отсюда стA) = 0, аB) = 0,
стC) = Зт в силу уравнений B.42)
и, следовательно, пу* = fij' = л™ = 1/^3.
Для a.j. = аB =0 уравнения B.42) сводятся к виду
пх + «г + л3 = 0,
"i + л2 + л3 ¦= 0,
ni + лг + пз == 0;
вместе с щщ = 1 этого недостаточно для однозначного определения первой и вто-
второй главных осей. Таким образом, любая пара взаимно перпендикулярных осей,
перпендикулярных направлению nf\ может служить главными осями. Рассмот-
Рассмотрим, например, оси, определенные в задаче 2.12 матрицей преобразования
1/J/3 1//3 1/УЪ'
— 2/1/6 ЩИ 1/^6
0 — 1/1 2 1/»Л2.

ЗАДАЧИ С РЕШЕНИЯМИ
97
По закону преобразования B.29) матрица главных напряжений [а'{] имеет вид
Г i/»l
L о
[/Зх VA3i
О О
О О
[	1//3
— 2/Ve 1//6 1//6
- 1/У2 l//2
0 1/J/3
0 JL
3~|Гт т т"|
6 ттт
2_|b t tJ
1//3 —2/6 О
-1//2
\1\Г2
-2/J/6
1//6
1//б
О I ГЗт О О
-1/^2= О О О
1/V2 ] [о О О
2.18. Показать, что оси Ох\х'2хл (где лгг, *3 и *з лежат в одной и
той же вертикальной плоскости, а х\, xt и дс2 — в одной горизонталь-
горизонтальной плоскости) тоже явля-
являются главными осями тен-
тензора напряжений задачи
2.17.
Ясно, что некоторые элемен-
элементы матрицы преобразования [ац],
связывающей две системы осей,
известны:
О
ОГС СО!
_1//3 1//3 1//3
это хорошо видно на рис. 2.24.
Остальные четыре элемента
определяются из условий ортого-
ортогональности uijuik — б/;» так что
Рис.2.24.
ч,\ = - \iY
-1//2
0
¦]
Поступая как и прежде, находим
1//2	0
К/1 = - 1//6 - 1//6 /2//3
]
0
0
)АЗт
о 0 ~| Г
0 0
/Зт ГЗт J L
- 1//2
1/|/2
О
Т Т X
Т X X
% X X
-1//6
- 1/VA6
/2//3
— 1/
^2
1/^2
0
1//3"
1//3
1/V1
=
-1/Гб
-1/Кб
1//3.
0 0
0 0
0 0
1
2.19. Показать, что главные напряжения a{k) и компоненты на-
напряжения сгG- в произвольной системе координат, получающейся
из главных осей преобразованием с коэффициентами ас„ связаны со-
соотношением
4 Дж. Мейз
p=i

88	Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
По правилу преобразования напряжения B.27) а,-/ = apiaqja , но так как
о* — главные напряжения, в правой части этого равенства остаются только три
3
члена с р = q. Значит, правую часть можно записать в виде ац = 2 apiapiap'
p=i
2.20. Доказать, что oitaikakj — инвариант тензора напряжений.
По правилу преобразования компонент тензора B.27)
a'iPika'kj = a{pajqapqairaksl:Jrsakmajnamn =
•= (aipair) (VV (aksakm) °pgarsamn =
= 6pr6qn6smapqarsamn =
= arqaqmarm = cifik
2.21. Непосредственным вычислением найти инварианты I?t
II?, Ills тензора напряжений
/ 6—3 0\
ст17 = (— 3 6 О].
\ 0 0 8/
Найти главные -напряжения для этого напряженного состояния и
показать, что диагональная форма приводит к тем же самым зна-
значениям инвариантов.
Согласно B.39)
ls = ait = 6 + 6 + 8 = 20.
Согласно B.40)
a22a33 + °"ззап —
= 36+48 + 48 — 9= 123.
Согласно B.41)
1"я = I °ц I = 6 D8) + 3 (- 24) = 216.
Величины главных напряжений тензора Оу равны aj = 9, an = 8, Ощ = 3. Ин-
Инварианты, подсчитанные через главные значения напряжений, равны
IIj. = ajo-,, + anant + amaI = 72 + 24 + 27 = 123.
HIj, = ojpnoin = G2) 3 = 216.
2.22. Октаэдрической называется площадка, которая составляет
равные углы с главными направлениями напряжений (рис. 2.25).
Показать, что касательное напряжение на этой площадке, так

ЗАДАЧИ С РЕШЕНИЯМИ
9Э
называемое октаэдрическое касательное напряжение, вычисляется
по формуле
= V, V{oi —
, V{oi — cti,) + (ап — стшJ
Нормаль к октаэдрической площадке s главных осях дается выражением
Тогда, согласно B.12), вектор напряжения на такой площадке равен
аше3е3) =
апе2 + оше3),
а его нормальная компонента будет
а„
Следовательно, для касательной
компоненты имеем
= V, C (а?
= Vs {(of - 2а,а„ + of,) + (of, - 2о„оп, + of„) + (о?„ - 2olual + а\))
V. =
= V.
- а,,M' + (о„ - ош)« + (о,п - о,)».
2.23. В некоторой точке задан тензор напряжений
(Ь 0 0\
— 12 1/
Определить максимальное касательное напряжение в этой точке
и показать, что оно действует в плоскости, которая делит пополам
угол между площадками максимального и минимального нормаль-
нормальных напряжений.
Используя формулу B.38), читатель убедится в том, что главные напряже-
напряжения равны с, = 10. ап = 5, аП1 = —15. Из B.546) найдем величину максималь-
максимального касательного напряжения as = (ош — Oj)/2 = — 12,5. Главные оси Ох{х2х3
4*

100
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
связаны с осями Ох1х2х3 максимального касательного напряжения приведенной
ниже таблицей преобразования и расположены так, как показано на рис. 2.26.
Ч
х'ъ
А
1/J 2
0
-1/^2
«2
0
]
0
4
MY 2
0
1/К2
Тензор напряжения, отнесен-
отнесенРис. 2.26.
//2 0
0 1
1//2 0
l/y/2"
0
1/V2-
Р
Lo
0
5
0
ныи к осям со штрихами, та
0
0
— 15_
/^2
0
J/>2
0
1
0
-1/V2"
0
1//2 _
Рис. 2.27.
Эти результаты можно дополнительно пояснить, указав напряжения, дейст-
действующие в данной точке на элементарные кубики, грани которых перпендикуляр-
перпендикулярны осям координат (рис. 2.27).
Круги Мора (§ 2.12—2.13) .
2.24. Построить круги Мора для напряженного состояния.,
описанного в задаче 2.23. Отметить важнейшие точки. Установить
связь между системой осей координат Ох^х^ (соответствующей

ЗАДАЧИ С РЕШЕНИЯМИ
101
компонентам аи) и главными осями ОХ1Х2Х3 и нанести на диаграмму
Мора точки, характеризующие напряженное состояние на коорди-
координатных плоскостях системы Ох^Хз-
Оа=5 ог=10
Рис. 2.28.
На верхней половине симметричной диаграммы кругов Мора (рис. 2.28) ука-
указана точка Р максимального касательного напряжения и отмечены главные на-
напряжения. Таблица направляющих косинусов для преобразования координат
ч
0
~3/,
V.
4
~ 1
0
0
4
0
Зи
приводит к схеме взаимного располо-
расположения осей координат, показанной на
рис. 2.29. Оси Х\ и х*2 совпадают. Оси
хг и х3 лежат в плоскости х\х^, как по-
показано на рисунке. По указанным углам а = 36,8° и fl = 53,2° находим положе-
положение точки А (— 6, 12), характеризующей напряжение на площадке, перпендику-
перпендикулярной оси хг, и точки В A, 12), дающей напряженное состояние иа площадке,
перпендикулярной оси х3. Точка С E, 0) представляет напряженное состояние
на площадке, перпендикулярной оси xi.
2.25. Напряженное состояние в некоторой точке в системе
координат OXiXjjXg задано компонентами
/—5 0
0 —6—12
0—12 Ь
Определить аналитически компоненты вектора напряжения на
площадке с единичной нормалью п = 2/3е1 + 1/8е2 + 2/3е3. Про-
Проверить результаты с помощью диаграммы Мора для этой задачи.

102
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Воспользовавшись B.13) и свойством симметрии тензора напряжений, по-
получим вектор напряжения на площадке с нормалью п в виде произведения матриц
0
0
О —6 —12
0—12 1
- 10/з
— 10
Таким образом, с(п) = —10е,/3 — Юег — 10е3/3, а из B.33) получаем Од, =
= t(n) ¦ п = — 70/9. Тогда из B.47) следует, что as = 70,7/9.
СТщ=-15
Рис. 2.30.
Для данного тензора atf главные напряжения равны а, = 10, ап=—5,
аш = — 15, а главные оси связаны с осями Ох^ХйХ^ преобразованием, определя-
определяемым следующей таблицей:
*
х\
х\
*
хз
Ч
0
1
0
ч
0
/б
ч
0

ЗАДАЧИ С РЕШЕНИЯМИ
103
Таким образом, в главных осях nj =
главных осях ni = aijtij, или
[о-3/8 ч„-\ г2/3п гч
10 0	¦/, = V:
О V. 3/6J L2/3J 1%
В соответствии с этим углы, изображенные на рис. 2.16, имеют величины 6 = Р =
= arc cos 2/3 да 48,2° и <j> = arc cos V3 cs 70,5°, а диаграмма кругов Мора, со-
соответствующая рис. 2.17, для данного случая построена на рис. 2.30.
2.26. Построить круги Мора для трех случаев плоского напря-
напряженного состояния, соответствующих напряжениям, действую-
действующим на элементарный куб, ребра которого параллельны осям ко-
а	С
Рис. 2.31.
ординат, как показано на рис. 2.31. Определить максимальное
касательное напряжение в каждом случае.
Круги Мора изображены на рис. 2.32.
Шаровой тензор и девиатор напряжений (§ 2.14)
2.27, Разложить тензор напряжений
4
9 —2
0 —2 3,

104
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
на шаровую часть и девиатор и показать, что первый инвариант
девиатора равен нулю.
Мы имеем ам = akk/3 = A2 + 9 + 3)/3
причем s# = 4 + 1 — 6=0.
2.28. Показать, что девиатор напряжений эквивалентен супер-
суперпозиции пяти состояний простого сдвига.	'
Существует разложение
fsu s1a s13^
S21 S22
^31 «32
0-S3:
0 0 s33,
где два последних тензора, очевидно, эквивалентны состояниям простого сдвига
по аналогии со случаями «а» и «б» задачи 2.26. Заметим также, что — su — s33 =
= S22, ПОСКОЛЬКУ S« = 0.
2.29.	Определить главные значения девиатора напряжений для
/ 10—6 О'
о(/ =1—6 10 0
\ 0 0 1
Девиатор напряжений для а,-/ имеет вид
3 —6
6 3 0
0 0 —в)
а его главные значения можно найти, приравняв нулю определитель
3_s —6 0
— 6 3 — s 0 = (— 6 — s) (s + 3) (s — 9) = 0.
0 0 —6 —s
Таким образом, Sj = 9, slx = —3, Sjjj = —6. Тот же результат получится, если
сначала вычислить главные значения тензора напряжений ету, а затем восполь-
воспользоваться формулой B.71). Для тензора оу, как может убедиться сам читатель,
главные значения равны аг = 16. аи — 4, аш = 1, откуда sl = 16 — 7=9,
sn = 4 — 7=— 3, sIU = 1 — 7= — 6.
2.30.	Показать, что второй инвариант девиатора напряжений
выражается через главные значения девиатора следующим обра-

ЗАДАЧИ С РЕШЕНИЯМИ	105
зом: IISd = (siSn + SnSiii + sniSi), или (что то же самое)
Характеристическое уравнение для девиатора напряжений, записанное через
главные значения девиатора, получается приравниванием нулю определителя
[—s О	О
О sn— s О
О 0 snI — s
(s, — s) (sn —s) (sn, — s) = 0 =
i r J
Отсюда в соответствии с B.72) имеем IIS = (s{su + snsin + s,,,!,). Так как
sr + SH + sni = 0, то
llxD = V, [2slSll + 2slAlI + 28,,,*, - (s, + s,, + s,,,J] = - V, D + 4i + sm)-
Смешанные задачи
2.31.	Доказать, что любой симметричный тензор, например
тензор напряжений ст,/, при переходе к любой другой системе пре-
преобразуется также в симметричный тензор а^-.
По формуле B.27) а'<;. = щрщ,ррЧ = ЩцЩр'Зцр = а^.
2.32.	Главные напряжения в точке Р таковы, что 2оп = ог +
+ Оц1. Определить единичный вектор нормали nt к площадке, на
которой aN = оц и os = (oi — аш)/4.
Согласно B.33), Од, = и^ + п^ (аг + стП1)/2 + nlam = (а, + аП1)/2, и,
так как п^ + и| + и| = 1, из совместного решения этих двух уравнений
можно получить rti = rt3- Далее, из B.47)
aj = п\а\ + п\ (а, + аи1)Щ + л§о?п - (а, + аш)Щ = (а, - ашJ/16.
Подставляя в это уравнение п3 = rti и я| — 1 = — п\ — rtj = — 2/ip а затем раз-
разрешая его относительно rti, находим направляющие косинусы rti = 1/B \Г2),
я» = V3/2, ns = 1/B У 2). Читателю предлагается использовать эти результаты
для тензора напряжений
4 0 0'
2.33. Показать, что разложить тензор напряжений о,-/ на шаро-
шаровую часть и девиатор можно только единственным образом.
Предположим, что существуют два разложения Оц = 6,/Х + *у = 6,/Х* +
+ s*;., для которых sn = 0 и s*,- = 0. Тогда оц = Зк= ЗХ* и, следовательно, % =
= Х*\ а из MS,-/ + si/ — №щ + stj следует, что %¦ = sjy.

106	Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
2.34. Доказать, что если 2—симметричный тензор с дей-
действительными компонентами, то главные напряжения тоже дей-
действительны.
При действительных значениях компонент напряжения инварианты тензора
напряжений действительны и, следовательно, все коэффициенты уравнения B.38)—
действительные величины. По теории таких уравнений хотя бы один корень
(главное значение) должен быть действительным. Обозначим его через о,^ и рас-
рассмотрим совокупность осей со штрихами х[, причем направление х3 соответствует
аC). Относительно таких осей характеристическое уравнение имеет вид
= 0,
или (аC) — а) [(а'и — а) (а'22 — а) — (а',2) ] = 0. Так как дискриминант квадра-
квадратичной формы, стоящей в квадратных скобках, положителен:
D = (а',, + а22J -4 [а'иа22 - (а'12J] = (а'п - а22J + 4 <р\2у > 0,
то и остальные корни должны быть действительными.
2.35. Используя метод множителей Лагранжа, показать, что
экстремальные (максимальное и минимальное) значения нормаль-
нормального напряжения on совпадают с главными напряжениями.
Из B.33) Од, = Оцщп;, причем щщ = 1. По аналогии с B.51) построим функ-
функцию Н = Од, — Кщщ, для которой дЩдщ = 0. Тогда
дН
CT'll
с
Г21
0
-а
а,'2
а22~
0
-а
аC)
0
0
а
= apjnj + а1рщ — 2Uipn{ = 2 (opl — Щр) пс = 0,
а это эквивалентно уравнению B.36) для определения главных напряжений.
2.36. Предположим, что компоненты напряжения о,-, получены
из симметричного тензорного поля ц>ц при помощи соотношения
aU ~ eipqeimn4>qn,pm- ПокаЗЭТЬ, ЧТО При ОТСУТСТВИИ МЭССОВЫХ СИЛ
удовлетворяются уравнения равновесия B.23).
Пользуясь результатами задачи 1.58, найдем компоненты напряжения
%¦ = «|/ (№„„ - <?ЯР,яр) + ЪШ + Vip.pi - fpp.il ~ %-i.pp.
или в развернутой записи
all = ФзЗ,22 + Ф22.33'	a12 = a21 = — ЧРЗЗ.21'
СТ22 = фп зз + ФзЗ.П-	а23 = °зг = — Фц,23-
азз= Фгг.и + Фц.221	ач — а1з= — Фгглз*

ЗАДАЧИ С РЕШЕНИЯМИ	107
Подставляя эти значения в уравнение Оц ^ = 0, получаем
а11.1 + а12.2 + а13.3 = ФзЗ.221 + Ф22.331 ~ ФЗЗ,212 ~ Ф22.133 = °»
а21,1 + а22.2 + а23.3 = ~ ФзЗ.211 + Ф] 1,332 + ФзЗ,1]2 ~ Фи,233 = °>
а31.1 + а32,2 + аЗЗ.З = — Ф22.131 "~ Фп.232 + "P22.1I3 + Фц.223 = °-
2.37. Показать, что, как утверждается в § 2.9, нормаль к по-
поверхности напряжений Коши в точке с радиусом-вектором г парал-
лельна вектору напряжения *<"'.
Пусть поверхность напряжений задана уравнением ф = oyj/g/ ± fe2 — 0.
Нормаль к ней в любой точке определяется как уф, или д<р/д?/ = ф,-. Следова-
Следовательно, ф о = Oifiip^j + Oijtj&jp = 2ор&1- Но так как ?j = ги,-, последнее выра-
жение превращается в 2ор/гл; или 2r (apirii) = 2^п).
2.38. Тензор напряжений в точке Р, отнесенный к осям
имеет вид
15—10 0'
Пусть новые оси 0*1X2X3 получены поворотом около начала
отсчета, т. е. преобразованием с матрицей
[fliy-]
Г'/. о -4/в
= О 1 0
1% о »/B
Определить вектор напряжения на каждой из координатных площа-
площадок системы со штрихами путем проектирования вектора напряже-
напряжения в первоначальных осях на направления осей со штрихами.
Определить таким образом сг,/. Проверить результат, используя
формулу преобразования B.27).
Из B.6) и тождества t'1 = ац B.7) следует, что векторы напряжения на
координатных площадках в системе без штрихов равны
t<«'> = 15е, — 10Ле2, t««>» = — 10е, + 5е2, t^ =- 20^3,
что соответствует строкам тензора напряжений. Проектируя эти векторы на оси
*^	/\	s\
системы со штрихами, при помощи соотношения B.12) t(n) = mt(ei) -f- n2t(e!> +
-f- n3t(et> получаем
t(ei) = »/. A5e, - l(te2) - •/. B0e3) = 9e\ - 6e2 - ?
после преобразования единичных базисных векторов это равенство принимает вид
V 1 = 9 C/ье, + V 3) _бе 2 - 16 (- «Де, + */ъе? = 91е,/5 - 6е2 - 12е3/5.

108
Аналогично
и
так что
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
5е'2—
Л'
t(e3)
atr.
— 12е j/5 —
— 6 5 —8
-»/, -8
С другой стороны, по формуле B.27)
15 —10
- 10	5
^ = 1 0 1 0
9 -6
— 10 5
12 —8
-16
о
12
0
в/ь о V,
2.39. Показать, что второй инвариант девиатора напряжений
D связан с октаэдрическим касательным напряжением соот-
соотношением аокт = у —*
Из задачи 2.22 аокт . V, /(а, -оиГ+(ои -о,п)« + (аш -а,)».
но
-f- Sl o-ц
+ sn и т. д.; поэтому
V,
и - *ш>" + («ш -
Атак как Sj
= V, V2 D+ sn + «fii) -2 («,«„ + «,,«,„ + sins,)-
sn + snl =¦ 0, то и (s: + su + «1ПJ = 0, или
si + sii + sin = — 2 (sisii + SH SHI + shi si)-
Отсюда
аокт = Vs K—
= /— a/s»s
аокт = Vs K—etsisn+susm+smsj) = /— /s»sD-
2.40. Напряженное состояние во всех точках тела задано тен-
тензором напряжений
/ 0 Сха О
otj = I Сх3 0 — Схг
\ 0 — CXl О
где С— произвольная постоянная, а) Показать, что если массо-
массовые силы равны нулю, то уравнения равновесия удовлетворяются.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
J09
б)	Вычислить вектор напряжения в точке Р D, — 4, 7) на плоско-
плоскости 2*! + 2хг — х3 = — 7 и на сфере (л,J + (*2J + (-*эJ = (9J-
в)	Определить главные напряжения, максимальное касательное
напряжение и главные значения
девиатора напряжений в точке Р.
г)	Построить круги Мора для на-
напряженного состояния в точке Р.
а)	Подставляя непосредственно в
B.24) компоненты ац, убеждаемся в том,
что уравнения равновесия удовлетворяют-
удовлетворяются тождественно.
б)	Из задачи 1.2 следует, что единич-
единичный вектор нормали к плоскости 2*i -f-
+ 2дг2 — хз = — 7 определяется выраже-
выражением п i= 2/3ei + 2/3е2 — V3e3. Тогда, согласно формуле B.12), вектор напряже-
напряжения на этой площадке в точке Р равен
j(n> _ B/gej _}- 2/3еа — 1/3е3) ¦ ^Ce^j, + 7Се2е1 — 4Се2е3 — 4Се3е2) =
= С A4/3е2 + 14/3е, — 8/3е3 + V3e2) = V3C A4^ + 18е — 8е3).
рис- 2.33.
Нормаль к сфере х№ = (9J в точке Р определяется выражением п,- = ф t, где
s^	/ч	s\	/\
«f = x,Xj — 81; следовательно, п =. */eei — %е2 + 7/8ез. Вектор напряжения
в точке Я, согласно B.14), в матричной записи имеет вид
Г О 1С О "I
'? 1 =1%, - %. 7/в] 7С 0 _ 4С = [-
L 0 —4С О J
28С/9, О, 16С/9].
= а(а2 — 65) = О,
в)	В силу B.37) для главных напряжений а имеем уравнение
— а 7 О
7 —а —4
О —4 —а
откуда CTj = ^65, ап = 0, а1п = — |^65. Величина максимального касательного
напряжения по формуле B.546) равна as =¦ (аш — а:)/2 = ±| 65. Так как сред-
среднее нормальное напряжение вточке Р равно ам = (аг + ап + а1П)/3 = 0, глав-
главные значения девиатора напряжений те же, что и у тензора напряжений.
г)	Круги Мора изображены на рис. 2.33.
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
2.41. В точке Р дай тензор напряжений
14 7 —;
7 21 О
- 7 0 35>

110
Гл. 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ
Определить вектор напряжения
о точке Р на площадке, парал-
параллельной плоскости: a) BG3,
б) BGFC в элементарном парал-
параллелепипеде, изображенном на
рис. 2.34.
Ответ:
a) t'n)
б) 1(">
1 lei +
	 -	+ !4е2 + 12
^r	F~	2.42. Определить нормаль-
X)	ную и касательную компоненты
напряжения на плоскости BGFC
задачи 2.41.
Ответ: oN =. 63/5, as = 37,7/5.
2.43.	Главные напряжения в точке Р таковы: а1 =¦ 12, ап =¦ 3. аП1 =—6.
Определить вектор напряжения и его нормальную компоненту на октаэдрической
площадке в точке Р.
Ответ: t(n) = A2ei + Зе — 6e)/]/3", о„ = 3.
2.44.	Определить величины главных напряжений для тензоров
(О 1 1\	/2 1 1\
1 0 1 I и б) at/ = I 1 2 1
110/	\1 1
и показать, что главные оси этих тензоров совпадают.
Ответ: а) а, =. 2, at] = аш = — 1; б) а, = 4, а
2.45. Разложить тензор напряжений
3—10
и
1.
на шаровую часть и девиатор и найти главные значения девиатора напряжений.
Ответ: s, = 31, su — 8. sm = —39.
2.46.	Показать, что нормальная компонента вектора напряжения на окта-
эдрической площадке равна одной трети первого инварианта тензора напряжений.
2.47.	В некоторой точке задан тензор напряжений
¦0 1 2'
причем величина а22 не указана. Определить а23 так, чтобы вектор напряжения
на некоторой площадке в этой точке обращался в нуль. Найти единичную нормаль
к этой свободной от напряжения площадке.
Ответ: а22 = 1, п = (ei — 2^ + е3)/\г6-

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ	111
2.48. Построить круги Мора и определить максимальное касательное на-
напряжение для следующих напряженных состояний:
Ответ:
а) с
a) as
Г
= т;б)
т
т
0
as
о/
= Зт/2.
б) а?/
Г
Jo-
\о
0
— т
0
0
О
— 2т
2.49.	Используя результат задачи 1.58 и закон B.27) преобразования напря-
напряжений, показать, что произведение ?iji&pqmaipai<Pkm является инвариантом-
2.50.	Поле напряжении в сплошной среде задано тензором
0
Определить: а) распределение массовых сил, если уравнения равновесия удов-
удовлетворены повсюду; б) величины главных напряжений в точке Р (а, 0, 2}га);
в) максимальное касательное напряжение в точке Р; г) главные значения девиато-
ра напряжений в точке Р.
Ответ: a) b3 = — 4х3; б) а, —а, 8а; в) ±4,5е; г) — Па/3, — 5а/3, 16с/3.

Глава 3
Деформации
3.1.	Частицы и точки
В кинематике сплошной среды смь!сл слова «точка» должен
быть строго уяснен, так как оно может относиться либо к «точке»
пространства, либо к «точке» сплошной среды. Во избежание недо-
недоразумений слово «точка» будет использоваться исключительно для
обозначения места в неподвижном пространстве. Слово «частица»
будет означать малый элемент объема (или «материальную точку»)
сплошной среды. Короче говоря, точка есть место в пространстве,
а частица — малая часть материального континуума.
3.2.	Конфигурация сплошной среды.
Деформация и течение
В любой момент времени / объем V сплошной среды, ограничен-
ограниченный поверхностью S, занимает некоторую область R физического
пространства. Если в определенной системе координат указано со-
соответствие частиц некоторого объема сплошной среды и точек про-
пространства, которые они занимают в момент времени t, то говорят,
что в этот момент времени указана конфигурация сплошной среды.
Термин деформация относится к изменению формы континуума
от некоторой начальной (недеформированной) конфигурации до
последующей (деформированной) конфигурации. При изучении де-
деформации учитываются только начальная и конечная конфигурации;
промежуточным состояниям, или частной последовательности кон-
конфигураций, по которым происходит деформация, внимания не уде-
уделяется. В противоположность этому термин течение используется
для обозначения непрерывного состояния движения континуума.
В самом деле, изучение истории конфигурации является неотъем-
неотъемлемой частью исследования течения, для которого задано перемен-
переменное во времени поле скоростей.
3.3. Радиус-вектор. Вектор перемещения
На рис. 3.1 изображены недеформированная конфигурация ма-
материального континуума в момент / = 0 и деформированная кон-
конфигурация того же самого континуума в более поздний момент
времени t = t. В проводимом нами исследовании целесообразно

3.3. РАДИУС-ВЕКТОР ВЕКТОР ПЕРЕМЕЩЕНИЯ	113
отнести начальную и конечную конфигурации к различным осям
координат, как это сделано на рисунке.
Тогда в начальном состоянии характерная частица среды за-
занимает точку Ро пространства и имеет радиус-вектор
X = ХЛ + Х2% + Х313 = Хк\к	C.1)
относительно ортогональных декартовых координат ОХ1Х2Х3.
Здесь в качестве индексов суммирования использованы заглавные
буквы; они будут появляться также в некоторых равенствах и в
дальнейшем, но их использование в качестве индексов суммирования
ограничено этим параграфом. В остальной части книги заглавные
буквы служат только различительными верхними или нижними
индексами. Здесь они применяются для того, чтобы особо подчерк-
подчеркнуть связь некоторых выражений с системой координат про-
пространства начального состояния (Xlt Хг, Х3), которые называ-
называются материальными координатами. В деформированном состоя-
состоянии частица, которая сначала была в точке Ро, займет положение Р
и будет иметь относительно ортогональных декартовых координат
охгх2хъ радиус-вектор
х = хгех + х2е2 + *3е3 = *А-	C-2)
Здесь в качестве нижних индексов использованы строчные буквы,
чтобы указать на связь с координатами (хи х2, х3), которые дают
текущее положение частицы и часто называются пространственными
координатами.
Относительная ориентация материальных осей 0ХгХ2Х3 и
пространственных осей oxix^ca характеризуется направляющими
косинусами ot/гк и aKk, которые определяются скалярными произ-
произведениями единичных векторов
eft • 1л = Ik • eft = akK = aKk.	C.3)

114	Гл. 3. ДЕФОРМАП vH
Суммирование по индексам в этих выражениях не подразумевается,
так как h и К — различные индексы. Ввиду того что дельта Кроне-
кера определяется равенствами 1К ¦ \Р = 8КР и ek • ер = 8kp,
условия ортогональности пространственных и материальных осей
принимают вид
ак№кР = ал^арк = Skp, аКрамр = арКарм = &км. C.4)
Вектор и, соединяющий точки Ро и Р на рис. 3.1 (соответственно
начальное и конечное положения частицы), называется вектором
перемещения. Этот вектор можно записать в виде
u = ukek	C.5)
или же в виде
C.6)
где компоненты U^ и uk связаны через направляющие косинусы
аик- Согласно A.89), единичный вектор еА выражается через мате-
материальные базисные векторы 1^ следующим образом:
C.7)
Подставляя C 7) в C.5), получаем
u = uk (awIK) = UKlK = U,	C.8)
откуда
Uк = akKuk.	C.9)
Так как направляющие косинусы — величины постоянные, компо-
компоненты вектора перемещения, как видно нз C.9), подчиняются прави-
правилу преобразования декартовых тензоров первого ранга, что и сле-
следовало ожидать.
Вектор b на рис. 3.1 служит для определения положения на-
начала координат о относительно точки О; очевидно,
u = b + x — X.	C.10)
В механике сплошной среды очень часто существует возможность
совместить системы координат OXiX2X3 и оххх^хъ\ тогда b = о,
а C.10) принимает вид
и = х—X.	C.11)
В декартовых компонентах это равенство в общем случае выглядит
так:
Однако для совмещенных осей триэдры единичных базисных векто-
векторов обеих систем одни и те же, а это ведет к тому, что направляющие
косинусы aw превращаются в дельты Кронекера. Вследствие этого

3.4. ЛАГРАНЖЕВО И ЭЙЛЕРОВО ОПИСАНИЯ ДВИЖЕНИЯ	115
C.12) упрощается и сводится к равенству
uk=xk-Xk,	C.13)
где в качестве нижних индексов используются только строчные
буквы. В остальной части книги, если специально не оговорено
противное, материальные и пространственные оси предполагаются
совмещенными, и поэтому для индексов будут применяться только
строчные буквы.
«3.4. Лагранжево и эйлерово описания движения
Если в некотором объеме сплошной среды происходит деформа-
деформация (или течение), то его частицы двигаются вдоль различных
путей в пространстве. Это движение можно описать уравнениями
вида
xt = xt (Х„ Х2, Х3, t) = xt (X, 9, или х = х (X, t), C.14)
которые дают положение хх в текущий момент частицы, занимавшей
в момент t=0 точку (Xi, X2, Х3)- Таким образом, C.14) можно тол-
толковать как установление соответствия между точками начальной
конфигурации и их положением в текущем состояния. Предполага-
Предполагается, что такое соответствие взаимно однозначно и непрерывно с
непрерывными частными производными любого порядка, который
потребуется. Такой способ описания движения или деформации,
выраженный формулой C.14), называется лагранжевым.
С другой стороны, если движение или деформация задаются урав-
уравнениями вида
X, = Х,(хь *2, х3, /) = Х,(х, t), или Х = Х(х, t), C.15)
в которых независимыми переменными являются координаты xt и
время t, способ описания называется эйлеровым. Это описание можно
рассматривать как такое, которое позволяет проследить к началь-
начальному положению частицу, которая теперь занимает положение
(xlt x2, xa). Если C.15) дает непрерывное взаимно однозначное со-
соответствие с непрерывными частными производными, как было до-
допущено для C.14), то эти два соответствия представлены единствен-
единственной парой взаимно обратных функций. Необходимым и достаточным
условием существования обратной функции является отличие от
нуля якобиана
Например, лагранжево описание движения уравнениями
*i = Xi + X2(e*-l),
xt = Xl(e-*—l) + Xt,	C.17)
хз —

116
Гл. 3. ДЕФОРМАЦИИ
имеет взаимно обратную эйлерову формулировку
v	— <i + *2 (е' — 1)
Х2 =
(ЗЛ8)
Х3 — xs.
3.5. Градиенты деформации. Градиенты перемещения
Дифференцирование C.14) частным образом по X/ приводит
к тензору dxJdXj, который называется материальным градиентом
деформации. В символических обозначениях dxLldX, представляется
тензором второго ранга
C.19)
дх
дх
дх
е
з>
где Vy =
1 =
— Л У vl I ЛУ ЧТ ду
ил j	ил 2	ил з
-е,- (материальные и пространственные оси
предполагаются совмещенными). Матричная форма F служит для
дальнейшего уяснения этого тензорного свойства оператора Vx>
когда он выступает в качестве второго сомножителя в диаде. Та-
Таким образом,
е а.] =
C.20)
dxJdX, д
= I дх^/дХг дх^дХ2 дхг/дХ3 I = [dxJdX,].
yjdx^dXx dxg/dX2 dxg/dX3^
Частное дифференцирование C.15) по xt приводит к тензору
dXJdXj, который называется пространственным градиентом де-
деформации. Этот тензор представляется диаднком
имеющим матричную форму
е3>
C.21)
лц>
JX =
I д	д д 1
I дхх '	дхя ' дх3 \~
)Xjdxy	dXi/dx2 дХг/дх3
Wz/dx!	дХ21дх2 dXjdx3
_dXs/dx1	дХ3/дхг
]
C.22)

3.6. ТЕНЗОРЫ ДЕФОРМАЦИЙ. ТЕНЗОРЫ КОНЕЧНЫХ ДЕФОРМАЦИЙ
117
Материальный и пространственный тензоры деформации связаны
правилом частного дифференцирования
dxi дХ,- _ 6Xt dxj
dxk
dXk
= 6,
ik-
C.23)
Частное дифференцирование Еектора перемещения ut по коор-
координатам приводит либо к материальному градиенту перемещения
duJdXj, либо к пространственному градиенту перемещения dujdxj.
При помощи формулы C.13), которая представляет ut через разность
координат, эти тензоры выражаются через градиенты деформации в
лагранжевых (материальных) переменных
дщ _ дх, б_^ или JsuVx = F_|	C.24)
дХ/ ~ dXj ""•
и в эйлеровых (пространственных) переменных
или К = uV
дщ
dxj
dxf
C.25)
Как обычно, матричные формы J и К имеют соответственно вид
"«Г
& =
дХ3
[дщ/дХ,. диг/дХ2
ди^дХх ди2/дХ2 duJdX3 \=[ди,/дХ,]-
ди3/дХх дщ/дХ2 ddX]
C.26)
Ж =
Г д д д 1 _
I дХ1 ' дх2 • дхэ\~
dujdx3
[dujdx! dujdx
ди2/дхг
dd
ди3/дх3
= \dujdxj[.
C.27)
3.6. Тензоры деформаций. Тензоры конечных деформаций
На рис. 3.2 начальная (недеформированная) и конечная (де-
(деформированная) конфигурации отнесены к совмещенным ортого-
ортогональным декартовым осям координат ОХ^^Хъ и 0XxX2xb. Сосед-
Соседние частицы, которые находились в точках Ро и Qo до деформации,
перемещаются соответственно в точки Р и Q деформированной кон-
конфигурации.

118
Гл. 3. ДЕФОРМАЦИИ
Квадрат бесконечно малого расстояния между Ро и Qo есть
(dXf = d\-d\ = dXtdXt = ^dX^X,.	C.28)
Согласно C.15), дифференциал расстояния dXit очевидно, равен
dXt
OXj
dxh или
= H-dx,
<3.29)
*з.*з
Рис. 3-2.
так что квадрат длины (dXJ в формуле C,28) можно написать в
виде
(dXJ =
или
= dx • С •
где тензор второго ранга
dXk
или С = tt. Н.
C.30)
C.31)
~ч ~ dxt dxt '
называется тензором деформаций Коши.
В деформированной конфигурации квадрат бесконечно малого
расстояния между Р и Q равен
(dxJ = dx ¦ dx= dxldxl = Sijdxjdx/.	C.32)
В силу C.14) этот дифференциал расстояния имеет вид
djc, =
или dx = F • dX,
C.33)
так что квадрат длины (dxJ в формуле C.32) может быть записан
следующим образом:
(dxf =
f = -Zjg- -^г dXtdXt =
, или (dxf = tfX • G . dX,
C.34)

3.6. ТЕНЗОРЫ ДЕФОРМАЦИЙ. ТЕНЗОРЫ КОНЕЧНЫХ ДЕФОРМАЦИЙ	119
где тензор второго ранга
или G =
называется тензором деформаций Грина.
Разность (dxJ — (dXJ для двух соседних частиц сплошной
среды используется как мера деформации некоторой окрестности
этих частиц между начальным и конечным состояниями. Если эта
разность тождественно равна нулю для всех соседних частиц, то
говорят, что имеет место абсолютно жесткое перемещение (пере-
(перемещение сплошной среды как абсолютно твердого тела). Используя
C.34) и C.28), эту разность можно представить в виде
- б«) или Lg = -Т(F< • F -
(dxJ - (dXf = (-|g~gg- - и/) dXfiX, = 2LlidXldXh
или
(dxJ — (dXJ = dX ¦ (Fc • F — I) • dX = dX • 2LC • dX, C.36)
где тензор второго ранга
называется лагранжевым тензором конечных деформаций (или тен-
тензором конечных деформаций Грина).
Используя C.32) и C.30), ту же самую разность можно предста-
еить в виде
(dxJ - (dXf = (б(/ - -^ ^-) dXldx, = 2Eiidxidxh
или
(dxJ — (dXf = dx-(l — HcH)-dx = d\- 2EA ¦ dx, C.38)
где тензор второго ранга
) • или Еа = 4"(| ~ Не" Н)> C'39)
называется эйлеровым тензором конечных деформаций (или тензо-
тензором конечных деформаций Альманси).
Особенно полезна такая форма i лагранжева и эйлерова тензо-
тензоров конечных деформаций, когда эти тензоры представлены в виде
функций градиентов перемещения. Тогда, если dxJdXj из C.24)
подставить в C.37), то после некоторых простых алгебраических
преобразований лагранжев тензор конечных деформаций примет вид
;	1 / дщ дщ duk duk \
Ll' " Т [~дХГ + dXi + ~Sx~ ~дХГ) • или
и-4-<л-1+*-л C-401

120	Гл. 3. ДЕФОРМАЦИИ
Таким же образом, если dXJdXj из C.25) подставить в C.39), в
результате получим эйлеров тензор конечных деформаций в виде
\ I дщ . дщ еик дик \
[Г + -Щ-—ШГ~^Г)' или
Матричные представления тензоров C.40) и C.41) можно напи-
написать, непосредственно используя формулы C.26) и C.27) соответ-
соответственно.
3.7. Теория малых деформаций.
Тензоры бесконечно малых деформаций
Так называемая теория малых деформаций в механике сплошных
сред имеет своим основным условием требование малости градиентов
перемещения по сравнению с единицей. Основной мерой деформации
служит разность (dxJ — (dX)*, которую можно выразить через
градиенты перемещения, подставляя C.40) и C.41) в C.36) и C.38)
соответственно. Если градиенты перемещения малы, то тензоры
конечных деформаций в C.36) и C.38) сводятся к тензорам беско-
бесконечно малых деформаций, а результирующие соотношения пред-
представляют малые деформации.
Если все компоненты градиента перемещения ди{/дХ/ малы
по сравнению с единицей, то произведения в формуле C.40) прене-
пренебрежимо малы и их можно опустить. В результате получим ла-
гранжев тензор бесконечно малых деформаций, который имеет вид
'" = ~Т (-Щ- + ~wt) • или L = -Т ("Vx + Vx") = 4"(J + J<>-
C.42)
Аналогично если dujdxj ^ 1, то в C.41) произведением можно
пренебречь и мы придем к эйлерову тензору бесконечно малых де-
деформаций, который по определению равен
«/=4-(¦??¦+-§?¦)• или E=4-(uVx+vxu) = 4-(K+Ki).
C.43)
Если как градиент перемещения, так и само перемещение малы,
то разница между материальными и пространственными координа-
координатами частицы среды очень мала. Поэтому компоненты материаль-
материального градиента duJdX; и компоненты пространственного градиента
duL/dXj почти равны и эйлеров и лагранжев тензоры бесконечно ма-
малых деформаций можно принять равными. Таким образом,' если и
перемещения, и их градиенты достаточно малы, то
hi = «i/, или L = Е.	C.44)

3.8. ОТНОСИТЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ.
121
3.8. Относительное перемещение.
Тензор линейного поворота. Вектор поворота
На рис. 3.3 перемещения двух соседних частиц изображены век-
векторами н'Ро) и h{Qo) (см. также рис. 3.2). Вектор
dut = нР — и\р'\ или du = u(Qo) — u(Po),	C.45)
называется вектором относительного перемещения частицы, рас-
расположенной первоначально в точке Qo, относительно частицы, за-
занимавшей положение Ро. Предположим, что для поля перемещений
выполнены условия непрерывности; тогда w,-Qo) можно разло-
разложить в ряд Тейлора в окрест-
окрестности точки Ро. Пренебрегая в
этом разложении членами более
высокого порядка, для вектора
относительного перемещения по-
получаем
du = (uVx)p0 • dX.
или
C.46)
Здесь скобки у частных произ-
производных поставлены, чтобы под-
подчеркнуть, что производные вы-
вычислены в точке Ро. Эти про-	рис. з.з.
изводные на самом деле явля-
являются компонентами материального градиента перемещения. Ра-
Равенство C.46) представляет лагранжеву форму вектора относи-
относительного перемещения.
Полезно также определить вектор относительного перемещения,
приходящийся на единицу длины рассматриваемого отрезка, dut/dX,
где dX — модуль бесконечно малого вектора расстояния dXt.
Согласно этому, если vt — единичный вектор направления dXit
так что dXt = vtdX, то
dut	дщ dXj	дщ	„	da	„ *; , ~
	i_ == 	:	L_ ^	* v»	ИЛИ	 = UV v • V = J • V
ол	dXj dX	dX/ '	d\
C.47)
Так как материальный градиент перемещения dutldXj можно
единственным образом разложить на симметричную и антисиммет-
антисимметричную части, то вектор относительного перемещения dut можно
записать в виде
или
= [-1-
~(uVx - Vxu)] • dX.
C.48)

122	Гл 3. ДЕФОРМАЦИИ
В первом члене в квадратных скобках формулы C.48) можно
узнать лагранжев тензор линейной деформации 1ц. Второй член
называется лагранжевым тензором линейного поворота и обознача-
обозначается
(§)	w = ^("Vx-Vxu). C.49)
Если тензор деформации ltj тождественно равен нулю в окрестности
точки Ро, то относительное перемещение окрестности этой точки
будет бесконечно малым поворотом абсолютно твердого тела. Этот
бесконечно малый поворот можно представить лагранжевым векто-
вектором линейного поворота
u>i= lUe-ijkWkj, или w = V2Vx X и;	C.50)
тогда соответствующее относительное перемещение запишется так:
dut = EijkWjdXk, или du = w х dX.	C.51)
Рассуждения, проведенные при лагранжевом описании вектора
относительного перемещения, тензора линейного поворота и век-
вектора линейного поворота, полностью можно повторить для эйле-
эйлеровых аналогов тех же величин. Так, при эйлеровом подходе имеем
для вектора относительного перемещения
dut = -^r dxh или du = К • dx,	C.52)
а для вектора относительного перемеи^ния, приходящегося на
единицу длины,
dui дщ dx\ дщ	du	„ " ., ~ .„ -„.
—г1- = "И" —г- — -д-5- Ц/> или тг— = UVX • U = К • I*. C.53)
dx dxj dx dxj r/>	dx	^	^ v '
Разложение эйлерова градиента перемещения dujdx, дает
, Г 1 / дщ |^ duj \ . 1 / дщ duj \ 1 ,
' L 2 \ dxj ~~*~ dxi ) 2 \ dxj dxi ]\ '"'
или	C.54)
du
= [-1- (uVx + Vxu) + -i- (uVx - Vxu)
dx.
Первый член в квадратных скобках в C.54) является эйлеровым
тензором линейной деформации е(/-. Второй член есть эйлеров
тензор линейного поворота
4-иг--И)> или
Формула C.55) определяет эйлеров вектор линейного поворота
«i = VaEf/ftWft/, или ш = V2Vx X и;	C.56)
тогда относительное перемещение выражается следующим образом:
dut = ec/kdijdx^ или du = to X dx.	C.57)

J.9. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ТЕНЗОРОВ ЛИНЕЙНЫХ ДЕФОРМАЦИЙ
123
3.9. Геометрический смысл тензоров линейных деформаций
В теории малых деформаций лагранжев тензор конечных дефор-
деформаций Ьц в формуле C.36) можно заменить лагранжевым тензором
линейных деформаций lijt и тогда эта формула примет вид
(dxf — (dXf = (dx — dX) (dx + dX) = 2lijdXl4Xh
или	C.58)
{dxf — {dXf = (dx — dX) (dx + dX) = dX • 2L • dX.
Для малых деформаций dx ^ dX, поэтому последнее равенство
можно представить еще и так:
dx — dX	dX{ dXj ,	dx — dX
= ^ -T~= 'W или
dX
или
= v- L- v. C.59)
Левая часть C.59) характеризует изменение длины бесконечно
малого элемента, приходящееся на единицу первоначальной дли-
длины, и называется коэффициентом
относительного удлинения линей-
линейного элемента, первоначально
имевшего направляющие косину-
косинусы dXJdX.
Применим формулу C.59) к
бесконечно малому линейному
элементу Ро Qo, расположенному
относительно местных осей в точке
Ротак, как показано на рис. 3.4, и
получим коэффициент относитель-
относительного удлинения этого элемента.
Так как в этом случае Ро Qo распо-
расположен вдоль оси Х%,
Рис. 3.4.
и поэтому в силу C.59)
dx — dX
dX
— too —
ди2
C.60)
Итак, оказывается, что коэффициент относительного удлинения
элемента, первоначально расположенного вдоль направления Xv
равен компоненте /22. Точно так же для элементов, первоначально
лежащих вдоль осей Хх и Х3, по формуле C.59) коэффициенты от-
относительных удлинений равны /и и 133 соответственно. Таким обра-
образом, диагональные члены тензора линейных деформаций вообще
представляют собой коэффициенты относительного удлинения вдоль
осей координат.

124
Гл. 3. ДЕФОРМАЦИИ
Физическая интерпретация недиагональных членов ltl осно-
основывается на рассмотрении линейных элементов, которые перво-
первоначально лежат вдоль двух осей координат. На рис. 3.5 линейные
Рис. 3.5.
элементы P0Q0 и Р0М0, взятые первоначально на осях Х2 и Х3,
после деформации превращаются соответственно в линейные эле-
элементы PQ и РМ в локальной системе координат с осями, параллель-
параллельными исходным, и началом в точке Р. Первоначально прямой угол
между линейными элементами превращается в угол 0. По формуле
C.46) в предположении теории малых деформаций в первом при-
приближении единичный вектор, идущий из точки Р в точку Q, равен
По =
ди3
~дХ7
а единичный вектор, идущий из Р в М, равен
пя =
Ж
Поэтому
дХя
или, пренебрегая членами более высокого порядка малости,
cos 0 =
^**2
ди2 , ди3
¦+¦
дХ.
= 2/о9.
C.61)
C.62)
C.63)
C.64)
Кроме того, если рассмотреть изменение прямого угла между
этими элементами ум = зх/2 — 0 и вспомнить,, что в линейной тео-
теории Угз мало, то можно написать
¦уаз «=» sin -уаз = sjn ("/2 — 6) = cos 0 = 2ln.	C.65)

3.10. КОЭФФИЦИЕНТ ДЛИНЫ. ИНТЕРПРЕТАЦИЯ КОНЕЧНЫХ ДЕФОРМАЦИЙ 125
Следовательно, недиагональные члены тензора линейных деформаций
представляют собой половины изменения углов между двумя пер-
первоначально ортогональными линейными элементами. Такие ком-
компоненты деформации называются деформациями сдвига, а из-за
множителя 2 в C.65) эти компоненты "тензора деформаций равны
половине обычных «технических» деформаций сдвига.
Рассуждения, в основном аналогичные тем, которые только
что были проведены для выяснения смысла компонент /,-/, могут
быть проведены и для эйлерова тензора линейных деформаций e,tj.
Основное различие заключено в выборе линейных элементов, ко-
которые при эйлеровом подходе должны быть направлены вдоль осей
координат после деформации. Диагональные члены являются ко-
коэффициентами относительного удлинения, а недиагональные —
деформациями сдвига. Для таких деформаций, для которых верно
предположение /,-, = el7-, разницы между эйлеровым и лагран-
жевым подходами нет.
ЗЛО. Коэффициент длины.
Интерпргтация конечных деформаций
Важной мерой деформации бесконечно малого линейного эле-
элемента является отношение dx/dX, известное под названием коэф-
коэффициента длины. Эту величину можно определить как для точки
Ро в недеформированном состоянии, так и для точки Р в деформи-
деформированном состоянии. Так, в силу C.34) квадрат коэффициента
длины в точке Ро для линейного элемента, взятого вдоль единичного
вектора m = dX/dX, дается формулой
/ dx У .2 ^ dXi dXj	A2 " /-, " /о им
-ту- = Л „ = Gt; —т^- —rrf , или Л „ =m • G • m- C.66)
\ dX ]p0	(m)	4 dX dX '	(m)	v	'
Аналогично в силу C.30) обратная величина квадрата коэффи-
коэффициента длины для линейного элемента в точке Р, взятого вдоль
•ч
единичного вектора.n = dxldx, дается формулой
/ dX V	1 п dx( dxi	1 Л	" ,„ „.
-j— = —5~ = Сц—г-~г-, или -г-= п • С • п. C.67)
\ dx /p j?	; dx dx '	%\	v '
(n)	(n)
Для элемента, первоначально расположенного вдоль местной
оси Xz (рис. 3.4), m ^ е2, и поэтому dXJdX = dX3ldX = 0,
dX^jdX — 1, так что C.66) для такого элемента дает
Л2Л = G22 = 1 + 2L22.	C.68)
(е2)
2	2
Такие же результаты получаются для Л ~ и Л ~ .
'	(в|)	(е,)

126	Гл. 3. ДЕФОРМАЦИИ
Для элемента, параллельного оси лг2 после деформации, формула
C.67) дает
1/12г =1— 2?22	C.69)
и аналогичные выражения для 1/Я2~ и 1А2„ . В общем случае
(е.)	(es)	•	}
Л Л не равно К ~ , так как элемент, расположенный до деформации
(е2)	(е2)
вдоль оси Х2, не обязательно будет после деформации направлен
вдоль оси х2.
Понятие коэффициента длины дает основу для интерпретации
тензоров конечных деформаций. Так, изменение длины, приходя-
приходящееся на единицу первоначальной длины (относительнее удлине-
удлинение), определяется отношением
?'-**-'•	<3-70>
а для элемента PoQo> расположенного вдоль оси Х2 (рис. 3.4), оно
составляет
LB) = Лг — 1 = V\ +2L22 — 1.	C.71)
Этот результат можно также получить непосредственно из
C.36). В теории малых деформаций формула C 71) сводится к
C.60). Относительные удлинения L(i, и Lpj выражаются подоб-
подобными равенствами через Ln и L33 соответственно.
Изменение угла между двумя малыми линейными элементами,
изображенными на рис. 3.5, характеризуется величиной ум =
= зх/2—0 и выражается через Л Л и Л Л следующим образом:
C-72)
Если деформации малы, то C.72) сводится к C.65).
3.11. Тензоры коэффициентов длины. Тензор поворота
[ В тензорном исчислении существует так называемое поляр-
полярное разложение произвольного неособого тензора второго ранга.
Оно состоит в том, что такой тензор можно представить произ-
произведением симметричного положительного (с положительными глав-
главными компонентами) тензора второго ранга на тензор второго ранга
с ортогональной матрицей х). Если такое представление применить
к градиенту деформации F, то в результате получится
Ftj = -§?- = RikSk,- = TutRk,, или F = R S = T R, C.73)
') Смотри, например: Седов Л. И., Введение в механику сплошной среды,
гл. 1, § 4, Физматгиз, М.. 1962.— Прим. перев.

3.12. СВОЙСТВА ПРЕОБРАЗОВАНИЙ ТЕНЗОРОВ ДЕФОРМАЦИЙ
127
где R — ортогональный тензор поворота, a S и Т — положитель-
положительные симметричные тензоры, которые называются правым и левым
тензорами коэффициентов длины соответственно.
Интерпретацию C.73) легко получить, воспользовавшись со-
соотношением C.33) dxt = (dxJdXj) dXj. Подставляя сюда ска-
скалярные произведения, взятые из формулы C.73), получаем
dXi = RtkSkjdXj = TikRkjdXh или dx = R S • rfX = T • R • dX.
C.74)
При помощи этих выражений превращение элемента dXt в dx(
(рис. 3.2) можно физически интерпретировать двояко. Согласно пер-
первой форме записи правой части C.74), это преобразование состоит
из растяжения (S) и затем поворота с последующим переносом как
твердого тела в точку Р. При второй форме записи сначала проис-
происходит параллельный перенос как твердого тела в точку Р, затем
поворот и, наконец, растяжение (Т). Параллельный перенос не ме-
меняет, конечно, компонент вектора относительно декартовых осей
Xt и xt.
3.12. Свойства преобразований тензоров деформаций
Все тензоры деформаций Llt, Ец, 1ц и е„, определенные со-
соответственно формулами C.37), C.39), C.42) и C.43), являются де-
декартовыми тензорами второго ранга. В соответствии с этим для со-
Рлс. 3.6
вокупности повернутых осей Х\, имеющих матрицу преобразования
[bLj\ относительно совокупности локальных осей без штрихов Xt
в точке Ро (рис. 3.6, а), компоненты 1ц и 1ц выражаются форму-
формулами
Ill =
hq,
или
или
•ве.
L = В • L .
C.75)
C.76)

128
Гл. 3 ДЕФОРМАЦИИ
Точно так же для повернутых осей Хс, имеющих матрицу преоб-
преобразования [ац ] относительно осей без штрихов (рис. 3.6, б), компо-
компоненты Etj и e,'ij имеют вид
Ец = CLijfliqEvth или Еа = А • Ел • Ас,	C.77)
e'ij = aipa/qepq, или Е' = А • Е • Ас.	C.78)
По аналогии с поверхностью напряжений, описанной в § 2.9,
можно ввести лагранжеву и эйлерову поверхности линейных дефор-
деформаций (квадрики деформаций) относительно локальных декартовых
Рис. 3.7.
координат т)(- и ?,- в точках Ро и Р соответственно (рис. 3.7). Так,
уравнение лагранжевой поверхности деформаций имеет вид
/уть-т]/ = ± Л2, или г\ ¦ L ¦ г\ = ± Л2,	C.79)
а уравнение эйлеровой поверхности деформаций — вид
= ± g2, или ? • Е • Е = ± gs.	C.80)
или
Существуют два следующих важных свойства лагранжевой
{эйлеровой} поверхности линейных деформаций.
1.	Коэффициент удлинения вдоль некоторого луча, отнесенный
к начальной {конечной} длине линейного элемента, обратно про-
пропорционален квадрату расстояния от центра поверхности деформа-
деформаций Ро {Р} до точки на этой поверхности.
2.	Относительное перемещение соседней частицы, расположенной
в точке Qo [Q)i параллельно нормали к поверхности деформаций
в точке ее пересечения с линией P0Q0 {PQ}.
Следующим шагом в изучении природы локальных деформаций
в окрестности точки Ро является определение эллипсоида деформаций
в этой точке. Для этого возьмем в недеформированной среде матери-
материальный объем, ограниченный поверхностью в виде бесконечно малой

3.13. ГЛАВНЫЕ ДЕФОРМАЦИИ. ИНВАРИАНТЫ ДЕФОРМАЦИЙ	129
сферы радиуса R. Уравнение этой поверхности в материальных
координатах в соответствии с формулой C.28) будет
{dXf = SifdXtdX, = /?2, или (dXf = dX ¦ I • dX = R\ C.81)
После деформации уравнение поверхности того же самого мате-
материального объема при использовании формулы C.30) оказывается
таким:
(dXf = CtjdXjdXj = R2, или (dXf = dx-C-dx= R2, C.82)
и определяет эллипсоид, известный как материальный эллипсоид
деформаций. Сферический в недеформированном состоянии объем
сплошной среды превращается при деформации в эллипсоид с цен-
центром в точке Ро. Подобным же образом заключаем, что бесконечно
малый сферический объем в точке Р деформированной среды в не-
недеформированном начальном состоянии был эллипсоидальным. Урав-
Уравнения этих поверхностей в локальных координатах получаются
при помощи формулы C.32) для сферы в виде
(dxf = bijdXjdXj = г2, или (dxf = dx . I • dx = г2, C.83)
и при помощи формулы C.34) для эллипсоида в виде
(dxJ = GtjdXidXj = г2, или (dxf = dX ¦ G . dX = г2. C.84)
Эллипсоид C.84) называется пространственным эллипсоидом де-
деформаций. Такие эллипсоиды, как описаны здесь, часто называются
эллипсоидами деформации Коши.
3.13. Главные деформации. Инварианты деформации.
Кубическое расширение
Лагранжев и эйлеров тензоры линейных деформаций являются
симметричными декартовыми тензорами второго ранга, и поэтому
определение их главных направлений (главных осей) и главных
значений (главных деформаций) ведется стандартным методом,
изложенным в § 1.19. С физической точки зрения главное направ-
ление тензора деформаций — этп тякое. л.пя кптпрпгп пририт^ццп
"элемента в данной точке не меняется при чистой деформации.
Главное значение деформации есть просто приходящееся на единицу
длины относительное перемещение (коэффициент^ ртносительног о
удлинения) вдоль главного направления.
—Д-лтгтгагранжева-тензора- деформаций 1ц вектор относительного
перемещения на единицу длины дан формулой C.47), которую можно
представить еще и так:
^	h или -gL^L + W).;. C.85)
б Дж. Мейз

'30	Гл. 3. ДЕФОРМАЦИИ
Обозначим через /i"' величины duJdX для линейного элемента в
направлении единичного вектора пс. Для чистой деформации (№,-/зз
=5 0) из C.85) следует
if = /,/П/, или I™ = L . п.	C.86)
Если направление лг главное, а / — соответствующее главное зна-
значение тензора 11п то
if = in, = /6,-уП/, или 1(п) = /п = /I • п.	C.87)
Приравнивая правые части C.86) и C.87), приходим к соотношению
(/,/ — б,//) п, = 0, или (L — I/) • п = 0,	C.88)
которое вместе с условием щщ = 1 на единичные векторы щ дает
необходимые уравнения для определения главного значения де-
деформации / и направляющих косинусов щ соответствующего глав-
главного направления. Нетривиальные решения системы C.88) сущест-
существуют тогда и только тогда, когда определитель из коэффициентов
обращается в нуль, т. е.
11ц — М 1=0. или IL — I/1 = 0,	C.89)
что после раскрытия определителя приводит к характеристическому
уравнению для тензора /,-,-. Это кубическое уравнение
I3 — kl' + UJ — UU. = 0,	C.90)
где
IL = iH = tr L, IIL = V, (luh, - U/ta), IHl = I Ui | = det L C.91)
— соответственно первый, второй и третий лагранжевы инварианты
деформации. Корни уравнения C.90) являются главными значениями
деформации и обозначаются /(i,, /B) и /C).
Первый инвариант лагранжева тензора деформаций является
суммой главных деформаций
II = Ui = /(i) + 'B) + /(з,	C.92)
и имеет важный физический смысл. Чтобы обнаружить это, рассмо-
рассмотрим элементарный прямоугольный параллелепипед, ребра которого
параллельны главным направлениям деформации (рис. 3.8). Изме-
Изменение объема на единицу первоначального объема этого элемента
называется коэффициентом кубического расширения и по определе-
определению равно
п _ AV0 _ dXi (I + /(.,) dX2 A + ZB)) ЧХ3 A + /C)) - dX.dX.dX,
В теории малых деформаций это соотношение в первом приближении
дает интересующую нас сумму
Il.	13.94)

3.14. ШАРОВОЙ ТЕНЗОР И ДЕВИАТОР ДЕФОРМАЦИЙ
131
Что касается эйлерова тензора деформаций еи- и соответству-
ющего вектора относительного перемещения е'п), главные направ-
направления и главные деформации е(и, еB), еC) определяются точно
Рис. 3.8.
так же, как их лагранжевы аналоги. Эйлеровы инварианты дефор-
деформации выражаются через главные деформации следующим образом:
Ie = e(i, + еB) + еC),
Пе = 6A,6B) + 6BNC) + eC)F(I),	C.95)
IIIe = 6A,6B,6,3).
Для кубического расширения в эйлеровом описании при малых
деформациях получается
AV/V = D = е(„ + еB, + еC,.	C.96)
3.14. Шаровой тензор и девиатор деформаций
Лагранжев и эйлеров тензоры линейных деформаций можно
разложить на шаровые тензоры и девиаторы тем же самым способом,
как в гл. 2 было выполнено разложение тензора напряжений.
Если компоненты лагранжева и эйлерова девиаторов обозначить
через йц и ес,- соответственно, то нужные выражения имеют вид
1ц = dij + fy/иА или L = LD + I (tr L)/3, C.97)
и
ei/= еу + буеик/3, или Е = ED +1 (tr E)/3. C 98)
Первые инварианты dit и ett девиаторов деформаций тождественно
равны нулю. Поэтому девиаторы описывают деформацию сдвига,
для которой кубическое расширение равно нулю,
5*

132	Гл. 3. ДЕФОРМАЦИИ
3.15. Плоская деформация. Круги Мора для деформации
Когда одна и только одна из главных деформаций в точке сплош-"
ной среды равна нулю, говорят, что в этой точке существует со-
состояние плоской деформации. Если в эйлеровом описании (лагран-
жево описание проводится точно по той же схеме) за ось х3 принять
направление нулевой главной деформации, то плоская деформация
происходит в плоскостях, параллельных плоскости х^х^, и харак-
характеризуется тензором линейных деформаций
/еп е12 0\
.	C.99)
0 0 0/
Если хг и х2 — тоже главные направления, то тензор деформаций
принимает вид
/еA) 0 0\
е„= 0 е 0 .	C.100)
V о о о/
Во многих книгах по сопротивлению материалов и теории
упругости плоской деформацией называют состояние с плоским
полем коэффициентов длины (тензоров Коши или Грина), когда
это поле одно и то же во всех плоскостях, перпендикулярных к на-
направлению нулевого главного удлинения. Для плоской деформации,
перпендикулярной к оси х3, вектор перемещения является функцией
только хг и х2. Соответствующие компоненты перемещения для этого
случая обозначим так:
"l =  (*ь *г), "в=М*1, *г), «з = С;	C.101)
здесь С — постоянная, которую обычно считают равной нулю. Под-
Подстановка этих значений в формулу C.43), определяющую ес[, дает
тензор плоских деформаций того же вида, что C.99).
Графически состояние плоской деформации в точке описывается
кругами Мора для деформации точно таким же способом, что при-
приведен в гл. 2 для кругов Мора для напряжения. При этом тензор
деформаций часто представляют в виде
I	C.102)
V.YmI-
Здесь Yi; (ПРИ i Ф /) — компоненты так называемых «технических»
деформаций сдвига, которые равны удвоенным тензорным компонен-
компонентам деформаций сдвига.
При экспериментальном исследовании, включающем измере-
измерение деформаций в тех точках поверхности тела, где деформиро-

3.16. УРАВНЕНИЯ СОВМЕСТНОСТИ ДЛЯ ЛИНЕЙНЫХ ДЕФОРМАЦИЙ
133
ванное состояние можно счи-
считать локально плоским, три
нормальных удлинения изме-
измеряются посредством «розетки
деформаций» (т. е. набора ра-
диально расположенных дат-
датчиков, измеряющих деформа-
деформации в точке по разным направ-
направлениям), а диаграмма кругов
Мора строится по этим удли-
удлинениям. По аналогии с кру-
кругами Мора для плоских на-
напряжений типичная диаграм-
диаграмма для плоской деформации
приведена на рис. 3.9. Глав-
Главные удлинения помечены теми
же буквами на диаграмме, а величинам максимальных деформаций
сдвига соответствуют точки D и Е.
3.16. Уравнения совместности для линейных деформаций
Если компоненты деформации е,а заданы в явном виде как функ-
функции координат, то шесть независимых уравнений C.43)
1
можно рассматривать как систему шести уравнений в частных
производных для определения трех компонент перемещения «,-.
Система переопределена и в общем случае не имеет решения при
произвольном выборе компонент деформации el7-. Значит, чтобы
существовали однозначные и непрерывные компоненты перемеще-
перемещения uL, на компоненты деформаций должны быть наложены не-
некоторые условия. Необходимые и достаточные условия для суще-
существования такого поля перемещений выражаются уравнениями
е'7 |	^?|	\t	IHL- = о C 103)
dxi/dxm	dxtdxj дх,-дхт дх{дхк	'	\ • )
Всего в C.103) содержится восемьдесят одно уравнение, но только
шесть из них различны. Эти шесть уравнений, записанные в раз-
развернутой и символической форме, выглядят так:
C.104)

134
Гл. 3. ДЕФОРМАЦИИ
дхгдх2
или
Vx X Е х Vx = 0.
Уравнения совместности можно написать и для компонент
лагранжева тензора линейных деформаций вследствие очевидной
аналогии с эйлеровой интерпретацией, приведенной выше. Для
плоской деформации, происходящей в плоскостях, параллельных
г, шесть уравнений C.104) сводятся к одному:
где Е определяется формулой C.99).
ЗАДАЧИ С РЕШЕНИЯМИ
Перемещение и деформация (§3.1—3.5)
3.1.	Относительно совмещенных материальных осей Xt и про-
пространственных осей xt задано поле перемещений сплошной среды
хх — Х1г хг = Х2 + АХ3, х3 — Х3 + АХг, где А — константа.
Определить компоненты вектора перемещения в материальной и
пространственной форме (в лагранжевых и эйлеровых переменных).
Компоненты перемещения в материальной форме находим непосредственно
из C.13): и, =¦ xi — Xi = 0, и2 = лс2 — Х2 ==, АХз, и3 = xs — Хз =• АХг. Раз-
Разрешая относительно X;, получаем Х\ =¦ xi, Xa «• (^2 — Ахз)/(\ — А2), Хз =
=(лсз — Ах2)/A — Л2), а пространственные компоненты вектора и будут равны
и, = 0, и2 = А (хз — Л*2)/A — А2). и3=,А (х2 — АхзI{\ — А2).
Из полученных результатов видно, что первоначально прямая линия в мате-
материальной частице, представленная уравнениями Xi =. 0, Х2 + Хз = 1/A + А),
займет после деформации положение xi = 0, х2 + хз = 1. А материальная линия
X, = 0, Х2 = Хз станет после деформации xi = 0, х2 = хз- (Истолковать механи-
механический смысл этих результатов.)
3.2.	Для поля перемещений задачи 3.1 определить смещен-
смещенное положение материальных частиц, которые первоначально со-
составляли: а) круге границей А'1 + Хз »=¦ 1/A —А2) в плоскости
Хх = 0 ; б) бесконечно малый куб, ребра которого лежат на осях
координат и имеют длину dXt = dX. Нарисовать смещенные кон-
конфигурации для «а» и «б», если А = x/g,

ЗАДАЧИ С РЕШЕНИЯМИ
135
а) Замена координат Х2 = (х2 — Ах3I{\ — А2) и Хя = (х3 — Axs)/(\ — Л2)
переводит круг в область, ограниченную эллипсом A-|-Л2)*2—4j4x2x;s +
+ A + Л2) лс| = A — Л2). При Л = 1/2 уравнение эллипса Ъх\ — 8дс2*з + 5л| =»
i= 3; в главных осях xi (образующих углы 45° с х,-, i =¦ 2, 3) оно принимает вид
9*з2 =¦ 3. На рис. 3.10 показано геометрическое место смещенных точек.
1*3
Рис. 3.11.
б) Из задачи 3.1 перемещения ребер кубика находятся без труда. На ребре
Xi = Xi, X2 = Хз = 0 компоненты перемещения и, = и2 = из = 0. На ребре
Xi = 0 = Х2. Хз = Хз мы имеем и, = из => 0, и2 = ЛХз, и частицы перемеща-
перемещаются в направлении Ха пропорционально их расстоянию от начала коор-
координат. Для ребра Xi = Хз = 0, Х2 = Х2. ut = и2 = 0, и3 = АХ2. Начальное и
смещенное положения куба показаны на рис. 3.11.
3.3.	Относительно совмещенных материальных и пространст-
венных осей задан вектор перемещения u = iX]Cx + Х2Х??г +
+ Х^зед. Определить смещенное положение частицы, первона-
первоначально находившейся в точке A, 0, 2).
Радиус-вектор начального положения частицы равен X = et + 2e3. Ее сме-
смещение составляет и => 4е: + 4е3, и, поскольку х = X + и, радиус-вектор конеч-
иого положения будет х = 5е, + 6е3.
3.4.	В ортогональной декартовой материальной системе ко-
координат Х[ задано поле перемещений U1 = —ЛХ2Х3, U2 = ЛХ1Х3,
U3 — 0, где А — константа. Определить компоненты перемещения в
цилиндрической пространственной системе координат *,-, если обе
системы имеют общее начало.
В силу геометрии задачи (рис. 3.12) тензор преобразования осей арК = ер • 1Л
имеет вид
а к = 1 — sin xa cos хг

136
Гл. 3. ДЕФОРМАЦИИ
Рис. 3.12-
а из обращенной записи формулы C.9)
ир = a.pKUK. Так как декартовы и ци-
цилиндрические координаты связаны со-
соотношениями X — xi cos х2, Х2 =¦
= хг sin ха, Ха = хз, формула C.9)
дает
их = (— eos хг) ЛХ2Х3 + (sin x2) X
X АХгХ3 •= (— cos x2) Ах3хх X
X sin x2 + (sin x2) Ах3хк cos лс2=0,
и2 = (sin лс2) ЛХ2Х3 + (cos xz) x
X ЛХ^з = (sin2 *2)
+(cos2 лс2) Лх^з
u3 = 0.
Это смещения в круглом стержне при
кручении.
3.5. Деформация задана в лагранжевой форме: хг = Хг +
+ Х3 (е2 — 1), х2 = Х2 + Xs (е2 — е-2), х3 = е2Х3, где е — кон-
константа. Доказать, что якобиан J отличен от нуля, и найти эйлеровы
уравнения, описывающие эту деформацию.
Из C.16)
е2—1
е'-е-2
= в2 ф 0.
„—2„
Обращенные уравнения будут таковы:
X1=»x1 + Jc3(e-E—1), Х„
3.6. Дано поле перемещений и = Х^з^ + AiX2e2 +
Определить независимо материальный градиент деформации F
и материальный градиент перемещения J и удостовериться в пра-
правильности формулы C.24) J =• F — I.
По данному вектору перемещения и находим J:
О
Так как х = и +
Xl = Хх A + Х|). ^2
дим F:
О 2Х X
поле перемещений можно также описывать соотношениями
A + Х^), х3 = Х3 A + Х|). из которых легко нахо-
2Х2Х8

ЗАДАЧИ С РЕШЕНИЯМИ	137
Непосредственной подстановкой полученных тензоров F и J в C.24) убеждаемся,
что равенство выполнено.
3.7.	Некоторый объем сплошной среды совершает перемещение
и = (ЗХ2 — 4Х3) е, + BXj — Х3) е2 + DХ2 — Хх) е3. Определить
смещенное положение вектора, соединяющего частицы А A,0, 3)
и В C, 6, 6), считая, что материальные и пространственные оси
совпадают.
Согласно C.13), пространственные координаты прн таком перемещении равны
я, = X, + ЗХ2 — 4Х3, х2 = 2Х1 + Х2 — Х3, х3 = —X, + 4Х2 + Х3. Таким
образом, в смещенном положении частица А имеет координаты xi = —11, лса =¦
= — 1, х3 = 2, а частица В — координаты х1 = — 3, хг = 6, лс3 = 27. В смещенном
•ч	Л	^ч
положении вектор, соединяющий точки Л и В, имеет вид V = 8ei + 7е2 -)- 25е3-
3.8.	Для поля перемещений задачи 3.7 определить смещенное
положение радиуса-вектора частицы С B, 6, 3), который паралле-
параллелен вектору, соединяющему частицы А и В. Показать, что эти два
вектора остаются параллельными и после деформации.
Теми же операциями, что и в задаче 3.7, получим радиус-вектор точки С после
деформации: U = 8е! + 7е2 + 25е3. Ясно, что он параллелен вектору V. Это при-
пример так называемой однородной деформации.
3.9.	В общей формулировке деформация называется однородной,
если она задана полем перемещений вида ui = АцХ,-, где Ац —
константы или, быть может, функции времени. Доказать, что при
такой деформации: а) плоские сечения остаются плоскими, б) пря-
прямые линии остаются прямыми.
а)	Из C.13)
xi = Хг + ui = Xf + AtiX/ *= F;/ + Atl) X/.
Согласно C.16), обращенные соотношения X; = F,/+ Вф xi существуют, если
детерминант 16,,- + Л,/| не обращается в нуль. Если предположить это, то уравне-
уравнение материальной плоскости Р;Х,- + а = 0 перейдет в Pi F,7 + Вф Xj + а = 0,
что можно записать в виде стандартного уравнения плоскости kjXj + а. = 0,
где коэффициенты к; = р;- F1;- + Вф.
б)	Прямую линию можно рассматривать как пересечение двух плоскостей.
В деформированном состоянии, как доказано, плоскости остаются плоскостями и,
следовательно, линия пересечения двух плоскостей остается прямой.
3.10.	Бесконечно малой однородной деформацией называется
такая деформация, для которой коэффициенты Ац в формуле ut =*
= AuXj настолько малы, что их произведениями можно пренебречь
по сравнению с самими коэффициентами. Доказать, что полную де-
деформацию, полученную в результате двух последовательных бес-
бесконечно малых однородных деформаций, можно рассматривать как
сумму двух отдельных деформаций и порядок, в котором про-
происходят перемещения, не влияет на конечную конфигурацию.
Пусть xi = Fj/ + Аф Xj и хс = F,7 + Bij) Xj определяют последователь-
последовательные бесконечно малые перемещения. Тогда х\ = F,у + Вф F/fc + Ajk) X& =

138
Гл 3. ДЕФОРМАЦИИ
¦= F,7d + Bik + Aik + ВцАц;) Xk- Пренебрегая произведениями
лыми высшего порядка, получаем xi = F^ + В,* + Л,д.) Xk ¦= (fij
что представляет бесконечно малую однородную деформацию
u't = x't- Xi *= CikXk = (Bik + Alk) Xk = (Alk + Blk) Xk = щ
как ма-
маТензоры деформаций (§ 3.6—3.9)
3.11. Некоторый объем сплошной среды испытывает деформацию
*! = Хи хг = Хг + АХ3, Хз = Х3 + АХ2, где А — константа.
Вычислить тензор деформаций Грина G и использовать его для
определения лагранжева тензора конечных деформаций Lc.
Из C.35) имеем G
формуле C.20):
а*.
dXj
1
0
0
0
1
А
0
А
1
Fc • F, причем F в матричной форме определяется по
так что [Gt.] =
Таким образом, из C.37)
Рис. 3.13.
3.12. В случае поля перемещений
2 задачи 3.11 вычислить квадрат длины
(dxJ сторон О А и ОВ и диагонали ОС
малого прямоугольника, изображен-
изображенного на рис. 3.13, после деформа-
деформации.
Воспользовавшись тензором G, определенным в задаче 3.11, по формуле C.34)
найдем квадрат длины диагонали в матричной форме:
0	0
(dx)" = [0, dX2, dX3]
1 + А'
Г °
dX2
ldX3
2Л
Э 2Л 1 + Л2.
= A + Л2) (dX2J + 4AdX2 dXa + A + Л2) i
Подобным же образом для ОА имеем (dxJ = A + Л2) (dX2J и для ОВ имеем
(dxf = A + Л2) (dX3J.
3.13. Вычислить изменение квадрата длины линейного элемента
задачи 3.12 и сверить результат с полученным по формуле C.36),
воспользовавшись тензором деформаций Lc, найденным в задаче
3.11.
Непосредственно по результатам задачи 3.12 найдем изменения
а) для ОС: (dxJ — (dXJ = A + Ла) (dX\ + i

ЗАДАЧИ С РЕШЕНИЯМИ
139
б) для OB:
— (dXJ = A -f A*) dX\ — dX\ = АЧХ\,
в) для ОА: (dx)z — (dXJ = A + Л2) dX% — dX\ =
Из уравнения C.36) для ОС имеем
¦¦ АЧХ%
-{dXr=[0, dX2, dX3]
[
0
0
0
0
ла
2Л
0 "
2Л
А2
- о
dX
dX
= Л2 (d
Изменения ОЛ и ОВ можно установить тем же путем.
3.14. Для поля перемещений задачи 3.11 вычислить матери-
материальный градиент смещения J и использовать этот тензор для опре-
определения лагранжева тензора конечных деформаций Lc. Сравнить
с результатами задачи 3.11.
В силу условий задачи 3.11 компоненты вектора перемещения равны
иг => АХ3, us ¦= ЛХ2, так что
0,
что совпадает с результатами задачи 3.11.
3.15. Дано поле перемещений дгх= Хх + АХ2, лг2 = Х2 +
х3 = Х3 + АХЪ где Л — константа. Вычислить лагранжев тензор
линейной деформации L и эйлеров тензор линейной деформации Е.
Сравнить L и Е в случае, когда константа А очень мала.
Из C.42)
'О Л 0\ /0 0 Л\ /0 А А\
Путем обращения получим формулы для перемещений
вх = А (А2хх + *2- Лх3)/A + ЛЗ), и2 = Л (- Л^! + A
us = Л (*! - Лх2 + Л^3)/A + Л3),
Л3),

140
Гл. 3. ДЕФОРМАЦИИ
откуда по формуле C.43) найдем
А2
2Е = (К + Ю) =
Если константа А очень мала, то членами с Л2 и более высокими степенями А
можно пренебречь. В результате Е сводится к L.
3.16. Поле перемещений задано формулой и = Х?Х2ех+
+ (Х2 — Хз) е2 + ХгХ3е3. Определить вектор относительного пе-
перемещения du в направлении оси —Х2 в точке Р A, 2, —1). Опре-
Определить относительные перемещения uQ. —иР для точек Q1(l, 1,
- 1), <?2 A, 3/2, -1), <?з A. 7/41 -1) и Qt A, 1Б/8, - 1) и сравнить
их направления с направлением du.
Для данного и градиент перемещения J в матричной форме выглядит так:
Xai	0 "
{duildXj] = \ 0	1 -2Х3
[2XJ
0
0
2Х2Х3
У*
так что по формуле C.46) относительное перемещение в точке Р в направлении
—Л2 равно
Г4 1 01 Г 01 Г-11
[йщ\ =0 12 -1 = _1.
L 0 — 4 4 J L Oj L 4j
Далее непосредственным вычислением из выражения для и найдем ир — 2ei +
Л	Л	Л	Л	Л	Л	Л
+ е2 — 4ез и u^ = et — е3. Тогда и^ — ир = —et — е2 + Зе3. Подобным же
образом и^ — иР = (— в! — е2 + 3,5е3)/2, и^ — ир = (— ег — е2 + 3,75 е3)/4,
U(jt — Up=(—в! — е2 + 3,875 е3)/8. Ясно, что, когда Q/ приближается к Р,
направление относительного смещения двух частиц стремится к предельному
направлению du.
3.17. Для поля перемещений задачи 3.16 определить относи-
относительное перемещение единичного вектора, идущего из точки
РA,2,-1)вточку QD,2, 3).
Единичный вектор в направлении из Р в Q есть v c= Зе^б + 4ез/5, так что
по формуле C.47), используя матрицу J, вычисленную в задаче 3.16, получаем
4 1 О! Г»/в"| Г»/,"!
0 1 2 0 = 8/о
0-4 4 J L4/BJ Lie/6J

ЗАДАЧИ С РЕШЕНИЯМИ
141
3.18. Для поля перемещений а — (х1—л;3Jе1 + (х2 + х3J е2—
— х^хг е3 при ограничениях, принятых в теории малых деформаций
(L = Е), определить тензор линейной деформации, тензор линей-
линейного поворота и вектор поворота в точке Р @, 2, — 1).
В данном случае градиент перемещения имеет матричную форму
О
[дис/дх,] =	О
L —" "^2
и в точке Р принимает вид
Разложим эту матрицу на симметричную и антисимметричную составляющие:
2 0—2
0 2 1
2
0
— 2
0
2
0
— 2
2
0
+ К7] =
— 2 1
ГО 0 0
¦001
L о — 1 о
Тогда, как показывает формула C.56), вектор со,- имеет компоненты <ol = — 1,
соа = cos = 0.
3.19. Для поля перемещений задачи 3.18 найти изменение дли-
длины, приходящееся на единицу начальной длины (относительное
удлинение), в направлении v = (8ех — е2 + 4е3)/9 в точке
Р @, 2, - 1).
Пользуясь формулой C.59) и тензором деформаций в точке Р, вычисленным
в задаче 3.18, получаем относительное удлинение в точке Рв направлении v как
произведение матриц
= ["/.. -х/в, 4/fl]
8/8
=-6/,
81"
3.20. Доказать, что в теории малых деформаций изменение
прямого угла между двумя ортогональными единичными векторами
v и )и недеформированной конфигурации дается формулой
Vvn = v • 2L ¦ |и.
При предположении малости градиентов перемещения единичные векторы
направлений, полученных при деформации из v и |Л, в силу C.47) имеют соответ-
ственно вид v+J- v и ц + J ¦ и- (Читателю предлагается проверить этим мето-
методом правильность соотношений C.61) и C.62).) Запишем J ¦ v в эквивалентной фор-
форме v ¦ Jc и перемножим скалярно полученные при деформации векторы. Тогда

142
Гл. 3. ДЕФОРМАЦИИ
(как и в C.63)) получим cos 6 = sin (я/2 — 6) = sin yvtl = vv(X или Yv)x =
+ v ¦ Jc] • [ji + J ¦ ц] = v ¦ |i + v - (J + Jc) • ц + v • Jc • J • fT Здесь в
случае малых градиентов перемещения Jc • J имеет более высокий поря-
порядок малости, чем другие члены. Кроме того, v _]_ц и, следовательно, v ¦ fi =¦ 0.
Таким образом, используя C.42), окончательно получаем yVm = v - 2L • ц.
3.21.	Используя результаты задачи 3.20, найти изменение пря-
прямого угла между векторами v = (8ej — е2 + 4е3)/9 и ц = Dех +
+ 4е2 — 7е3)/9 в точке Р @, 2, — 1) для поля перемещений задачи
3.18.
Так как в теории малых деформаций L =¦ Е, компоненты тензоров деформаций
в,-/ =¦ /// и, следовательно, в точке Р
Г 4 0 — 41 Г 4/9"
Vvn = Р/.. - V.. 4/в] 0 4 2 ' •/. =318/81.
L- 4 2 Oj L-7/b_
Коэффициенты длины и поворот (§ 3.10—3.11)
3.22.	Для деформации сдвига хг = Хг, х2¦= Х2 + АХ3, х3 =
= Х3 + АХ2 задачи 3.11 показать, что коэффициент длины Л -
(т)
линейного элемента, параллельного оси
Хх, равен единице (относительное удли-
удлинение равно нулю). Найти Л - для
диагональных направлений ОС aDB бес-
бесконечно малого квадрата OBCD (рис.3.14)
и сравнить результаты с непосредствен-
непосредственно вычисленными по полю перемеще-
перемещений.
По формуле C.66), пользуясь матрицей О,
найденной в задаче 3.11, получим квадрат коэф-
Рис. 3.14.
фициента длины для направления m = et:
Г1 °
Al =[1. 0. 0] 0 1 + Л2
L 0 2/1
л	уч л
Для направления m
0
2/1
(еа + ез)/^2 вдоль ОС аналогично находим
Л2Л =[0, 1//2, 1//2]
(Ш)
1 0
0 1 +А2
0 2А
0
Ч.А
0 '
I//2
= A + А)*.
Согласно соотношениям, определяющим перемещения, положение точки С после
деформации таково: х^ = 0, х2 = dL+ AdL, x3 = dL + AdL. Таким образом,

ЗАДАЧИ С РЕШЕНИЯМИ
143
(dxf = 2 A + Af (dLJ, а так как dX = \/r2dL, квадрат коэффициента длины
(dx/dXJ равен A+ ЛJ, как и было подсчитано по формуле C.66).
Точно так же для направления DB т = (— е2 + е3)/|^2 и, следовательно,
А\ = A - АJ.
11П)
3.23. Коэффициенты длины Л~ и к*, равны только в том
(Ш)	(П) V
случае, когда направление, характеризуемое вектором п, получено
при деформации из направления вектора т. Для поля перемещений
задачи 3.22 вычислить &, если п = (е2 + е3)/]Л2, и показать, что
(п)
оно совпадает сЛл, вычисленным в задаче 3.22 для диагонали ОС.
(т)
Обращая соотношения задачи 3.22 для перемещений, получаем
Хг = хи Х2 = (хг — Ах3)/( 1 — Л2), Х3 = (дг3 - Ах2)/A - А2),
откуда можно найти тензор деформации Коши С Затем, используя C.67), вычис-
вычисляем
(n)
I	0	0
0 A + Л2)/A — Л2J — 2Л/A—Л2J
.0 — 2Л/A— Л2J A + Лг)/A — Л2J.
0 '
1//2
= A — ЛJ/A— Л2J.
Таким образом, к\ = A — ЛгJ/A — ЛJ = A + ЛJ, что совпадает с Л2„ ,
(п)	<т)
вычисленным для ОС. Диагональный элемент ОС не меняет своего направления
при данной деформации сдвига.
3.24. Используя полярное разложение градиента деформации
F при деформации сдвига хх — Хи х2 = Х2 + АХ3, х3 — Х3 +
+ АХ2, определить правый тензор коэффициентов длины S и тензор
поворота R. Показать, что главные значения тензора S являются
коэффициентами длины диагоналей ОС vtDB задачи 3.22.
При полярном разложении F тензор коэффициентов длины S = \ G; по фор-
формуле C.73) имеем R = FS~'. Согласно C.35), G = Fc • F, или в нашем случае
1
0
0
0
1 + Л2
2Л
0
2Л
1 +Л2,
Главные оси тензора G получаются поворотом на 45° вокруг оси Х2, а сам тензор
в главных осях имеет вид
[1	0	0
0A — ЛJ	0
0	0 A -f А)

144
Гл. 3. ДЕФОРМАЦИИ
поэтому
1
0
0
1
0
—
0
А
1
о ¦
0
+ А
Г1 0	0-1
Lo О A(OC)J
В системе координат X,- это разложение записывается в виде
1
0
.0
0
I
0
0"
0
1
1 0 01
О I А .
О A J
В этом примере градиент деформации F сам является тензором коэффициентов
длины S, а тензор поворота R = 1. Это результат совпадения главных осей тен-
тензоров LG и ЕА для данной деформации сдвига.
3.25. Бесконечно малый поворот твердого тела задан форму-
формулами нх = — СХ2 + ВХ3, ыя = CXt — АХ3, и3 = — ВХг + АХ2,
где А, В, С — очень малые константы. Доказать, что растяжение
отсутствует (S = I), если пренебречь членами, содержащими квад-
квадраты и произведения констант.
Для заданного поля перемещений
+ С2 + Вг —АВ	—АС
—	АВ 1 + А2 + С2 —ВС
—	АС	—ВС 1 + Л2 + Вг_
Пренебрегая малыми высшего порядка, получаем
1
0
_0
0
1
0
0"
0
1_
Преобразования тензоров деформации
и главные деформации (§ 3.12—3.14)
3.26. Доказать, что для деформации сдвига хх — Хх, х2 = Ха +
+ У^Х3, х3 = Х3 + У^2Х2 главные направления тензоров Lo
и Ед совпадают, как было упомянуто в задаче 3.24.
Согласно C.37),
0 0 0 "
0 1 /2
.0 \Г2 1 .
Этот тензор в главных осях, определяемых матрицей преобразования

0
0 —
о
0 1
1/^2 ,
1/1 2 |

ЗАДАЧИ С РЕШЕНИЯМИ
приводится к виду
J45
[о о
о '->
о о
Аналогично, согласно C.39),
0 0 0 1
о т/г — 1.
и преобразованием с той же самой матрицей [а,-/1 этот тензор приводится к диа-
диагональному виду
ГО О
О —1—12
0	0	—
0 1
0 Г
l+VA2j
Проверка этих вычислений предоставляется читателю.
3.27. Используя определение C.37), доказать, что при пре-
преобразованиях координат xt = bHXj и Х\ = ЬцХ, лагранжев тен-
тензор конечных деформаций Ьц преобразуется как декартов тензор
второго ранга.
По формуле C.37) L,-/ =¦ — I—	-ггг — ^Чп, что при указанном преоб-
2 \ dXi oX.f	J
разовании координат дает
дХ'»> д(Ь^ дХ'п дх,\ _
дХ? дХ-п дХ, дх; )
дХ'т
dx'q
дХ'п
дх'п
(так как bpkbqk = 6рв)
-^J-j.(?..?--c)l-wi-
3.28. Некоторое поле однородной деформации приводит к тен-
тензору конечных деформаций
[1 3—2"
3 1 -2
— 2—2 6_
Определить главные деформации и направления главных осей.

146
Гл. 3. ДЕФОРМАЦИИ
Мы имеем дело с симметричным декартовым тензором второго порядка по-
поэтому главные деформации являются корнями уравнения
1—L 3 —2
3 1 — L —2
_2 —2 6— L
— 2, LB) = 2, LC) = 8.
Матрица преобразования к главным на-
I//2 -1//2 О
1//3 1//3 I//3
Отсюда L(I)
правлениям имеет вид
3.29. Для однородной деформации xt = УЗХ^ х2 — 2Х2, х3 —
= ^ЗХз — Х2 определить материальный эллипсоид деформаций,
получающийся при деформации сферической поверхности Х2\ + Х\ -\-
+ Хз = 1. Показать, что уравнение этого эллипсоида имеет вид
?? l% l%
Используя C.82), или, что то же самое, обращая данные формулы для переме-
перемещений и подставляя результат в уравнение сферы X,Xi =¦ 1, получим уравнение
материального эллипсоида деформации х\ + х\ + х\ + х2хз =¦ 3. Это уравнение
приводится к каноническому виду в главных осях х2у/3 + х|/6 + х|/2 = 1 пре-
преобразованием с матрицей
0	0 "
[fl?/]= 0 I//2 1//2
Lo — 1//2 1//2.
Из соотношений теории деформаций найдем тензор деформации S =
(вычисления подобны тем, которые были проведены в задаче 3.24):
[Si/1 =
Преобразованием с матрицей
Уз
2)/2
2 \' 2
/3 + 3
2/2
Lc
| = I 0 /3/2 -
этот тензор приводится к главным осям (диагональной форме)
/3 0 0
0 /6 0
0 0 /2_

ЗАДАЧИ С РЕШЕНИЯМИ
147
где главные значения коэффициентов длины равны Л,2,, = 3, Л:
6,Л?3)
Заметим также, что эти главные коэффициенты длины можно вычислить непосред-
непосредственно по формуле C.66), используя приведенную выше матрицу Г
3.30. Для деформации, заданной в задаче 3.29, определить
пространственный эллипсоид деформации и показать, что его урав-
уравнение Л?0Х? + ^Xl + A^Xl = 1.
1 получена н результате деформации эллипсоида
Согласно C.84), сфера .вд =
G ¦ X =. 1, или

0
-0 -
0
5
-У
о -
-УЗ
3 3
= 1 получ
\_х
= ЗЛ-f +
— 2 УЗХгХ3 = 1.
Это уравнение эллипсоида приводится к каноническому виду (в главных осях)
6Л| -f- 2Л| = 1 преобразованием с матрицей
10	0
0 УЗ/2 72
0 -Vi ^3/2.
3.31. Непосредственным разложением проверить, что второй,
инвариант Hl тензора деформаций можно представить в виде
'и
I
21
'
22
fal 1ъ
loo L
'З
23
'31 '33
Вычисление данных детерминантов приводит к выражению
Hit ill \ 1 I	//2 I /2 I /2 \
L — 'и'гг "Г 'аг'зз + 'зз'и — ui2 "г" 'гз "Г 'з^-
С другой стороны, вторая формула C.91) в развернутой записи дает то же самое:
HL = Vi [(»u + 'а + U If, - Ci/i/ + h,hj + 'з/з/I =
= Vi Wu + '22 + U (»u + '22 + 'si) - Cu'u + W11 + Uu +
~г 'м'21 Н~ 'гг'гг "Ь 'гз'гз Т 'з1'з1 4~ 'зг'за "г 'зз'зз)! ==
= /ц'га 4~ 'гг'зз 4~ 'зз'и — Cl2"
3.32. Однородная конечная деформация характеризуется соот-
соотношениями ui — AijXi, где Ац—константы. Найти выражение
для относительного изменения объема (изменения, приходящегося
на единицу начального объема). Доказать, что при очень малых Ait
оно сводится к кубическому расширению.
Рассмотрим прямоугольный параллелепипед с начальными размерами dXv
dX-i, dXs вдоль осей координат. При данной деформации xt = (Ац + б,у) X/.
Согласно C.33), этот начальный объем dVo превращается в скошенный паралле-
параллелепипед с ребрами длины dxt = (At (n) + б,- (п)) dX(rV), n = 1, 2. 3. В силу формулы
A.109) этот деформированный элемент имеет объем
dV = elIk (Лп + в„) {Ар + б/2) {А

148	Гл. 3. ДЕФОРМАЦИИ
Тогда
dV dVB + AV . , AV
Если Ац очень малы и их степенями выше первой можно пренебречь, то
= Ai + Аа + А*-
В линейной теории коэффициент кубического расширения равен 1ц ш, дщ/дХ[,
что в случае щ = АцХ) дает /,-,- ¦= Ли + Лщ + Лзз-
3.33. Линейная (малая) деформация задана соотношениями
и\ — 4^i — х2 + Зх3, «2 = xi + 7х2, иа = — Зхг + 4х2 + 4х3. Най-
Найти для такой деформации главные деформации (удлинения) е(п)
и главные значения девиатора деформаций е(П).
Так как гц является симметричной частью градиента перемещения
для данного случая
D 0 0^
0 7
0 2
или в главных осях
0
4 0
0 Ъ)
Итак, 8/tfc/3 =¦ 5; находим девиатор деформаций
(—10 (
0 2 2
0 2-1.
который в главных осях имеет вид
Заметим, что е(т) = е(т) — ekk/3.
Плоская деформация и уравнения совместности (§ 3.15—3.16)
3.34. Сорокапятиградусной розеткой деформаций измерены про-
продольные деформации вдоль осей, изображенных на рис. 3.15. В точке
Р найдены ец = 5 ¦ 10~4, ем = 4 • 10~\ е22 =7 ' 1СГ. Определить
деформацию сдвига е12 в этой точке.

ЗАДАЧИ С РЕШЕНИЯМИ
149
Воспользуемся формулой C.59). Учитывая, что v = (е[ + е2)//2 — еди-
единичный вектор направления Хр составляем уравнение для е12:
[1//2,
[5 ¦ 10~4 81а О
е12 7 ¦ Ю-4 О
О	0 0
1//2
= 4-10"
Отсюда
12 • 10
~4
= 4 ¦ 10 , или е12 = — 2 • 10"
3.35. Построить круги Мора для случая плоской деформации
и определить максимальную
деформацию сдвига. Прове-
Проверить результат аналитиче-
аналитически.
Рис. 3.15.
Для данного состояния деформации, отнесенного к осям Х[, точки В (е^ = 5,
еаз = /3) и D расположены на концах диаметра наибольшего из внутренних кру-
кругов (рис. 3.16). Для плоской деформации величина главного напряжения еA) = О,
поэтому другие круги Мора выглядят так, как показано на рисунке.
Поворотом на угол 30° (рис. 3.17) вокруг оси х1 (что эквивалентно углу 60°
на диаграмме Мора) приведем тензор деформации к главным осям с главными зна-
значениями е(-:
F
Еще одним поворотом на 45° (рис.3.18) вокруг оси х*ъ (на 90° на диаграмме кру-
кругов Мора) придем к системе координат х\, в которой тензор деформаций имеет ком-
компоненты 8,-у, представленные матрицей
1
0
0
0
/3/2
-V,
0 "
V.
/3/2.

0
.0
0
5
/з
0 '
СО1
3

0
_0
0
/3/2
Va
о -
— '/г
/3/2 _
=
0
0
.0
0
6
0
0"
0
2_
1//2
-1//2
0
1//2
1//2
0
о"
0
1
"О
0
0
0
6
0
°1
0
2
//2
1//2
0
-I//2
1/1^2
0
о"
0
1
Г3
0
3
3
0
0
0
2

150
Гл. 3. ДЕФОРМАЦИИ
Рис. 3.17.
Рис. 3.18.
Здесь первые две строки описывают деформированное состояние в точке F
(рис. 3.16). Заметим, что поворот на —45° около х3 соответствовал бы точке Е
на рис. 3.16.
3.36. Деформированное состояние сплошной среды задано
тензором
гч =
Удовлетворяются ли уравнения совместности?
Непосредственной подстановкой в C.104) убеждаемся, что все уравнения удов-
удовлетворяются тождественно. Читателю предлагается проделать эту проверку де-
детально.
xl
xl
xxx3
xl
5
Смешанные задачи
3.37. Вывести индексную форму лагранжева тензора конечных
деформаций LG C.40), воспользовавшись его определением C.37).
В силу формулы C.24) имеем dxJdXj = Ьц + дщ IdXj. Тогда, пользуясь
C.37), можно получить
duk duk
дХ[ ~*~ dXt
дщ
дщ
dXt
duk duk
dXt dX;
3.38. Дано поле перемещений xt — Xt — CX2 + BX3, x% —
= CXi + X2 — AXS, xa = — BXX +AX2 + X3. Показать, что эти
перемещения соответствуют повороту абсолютно твердого тела,
если константы А, В, С очень малы. Определить вектор поворота
w для бесконечно малого поворота твердого тела.

ЗАДАЧИ С РЕШЕНИЯМИ
151
1 1/
Для данного поля перемещений
1 —С
С 1
к— В А
и, согласно C.37),
- ¦ " "- —АС \
— ВС .
Л2 + В2/
Если пренебречь произведениями малых констант, то этот тензор деформаций ра-
равен нулю, а перемещение сводится к повороту абсолютно твердого тела. По фор-
формуле C.50) вектор поворота равен
, I& + C* — АВ
=-о-[ —АВ А* + С*
\ —АС —ВС
е2
w = —	Я1ЯУ1	д/дХ2	д/дХ3	=М* +Ве* + Се*-
ВХ3 СХг — ЛХ3 — ВХЛ + АХ2
3.39.	Поворот абсолютно твердого тела описывается полем
перемещений их = 0,02Х8, щ = —0,03Х3, ы8 = — 0,02Х1 + 0,03Х2.
Определить перемещение точки Q C, 0,1, 4) относительно точки
РC>0>4)-
Поле перемещений для точек Q и Р дает Uq = 0,08е! — 0,12е2 — 0,057ез
и Up = 0,08е, — 0,12е2 — 0,06е3. Отсюда rfu = u^ — up = О.ООЗе^. Тот же
результат получим, пользуясь формулой C.51), где w = 0,03ei + 0,02e2:
0,03 0,02 0 =0,003е3.
0 0,1 0
3.40.	Для плоской деформации, происходящей в плоскостях,
параллельных х2х3, определить выражение для относительного
удлинения ей и деформации сдвига е^з, если оси со штрихами и без
штрихов расположены так, как показано на рис. 3.19.
Рис. 3.19-
Рис 3.20.

152	Гл. 3. ДЕФОРМАЦИИ
Из формулы C.59)
ГО О 01Г О I
22 = [О, cos 6, sin 6] 0 егг е23 cos 6 =
|_0 егз 833J Lsin G I
= е22 cos2 6 + 2е23 sin 6 cos 6 + е38 sin2 6 =
2 ' 2
Аналогично, используя C.65) и результат задачи 3.20, находим
ГО 0 0]Г 0 I
е23 = [0, cos 6, sin 6] I 0 е22 е23 I — sin 6 =»
L° еаз ?зз] L cos 6 J
= — е2г sin 6 cos 6 + 823 cos2 6 — е23 sin2 6 + е33 sin 6 cos 6 =¦
= e23 cos 26 —e22 ~ езз sin 20
3.41. Для однородной деформации дан тензор малых деформаций
0,01 — 0,005
Ы =
— 0,005 0,02
0 0,01
0 "I
0,01 •
— о.оз J
[1//2, -1/^2,0]
Каково изменение прямого угла ADC на грани элементарного
тетраэдра ОАВС (рис. 3.20), если ОА = ОВ = ОС, а точка D —
середина ребра АВ?
Единичные векторы v и ц, выходящие из точки D, можно записать в виде v =
с= (ei — е2)/^2 и ц =• Bе3 — е2 — е,)/}/6. Тогда, используя результат задачи
3.20, получаем
" 0,02 —0,01 0 ~| Г	1/|Аб I
— 0,01 0,04 0,02 I _1/|Аб = — 0,01//3\
0 0,02 — 0,06_|L 2//6J
3.42. В некоторой точке тензор деформаций имеет вид
/ 5—1 —Г
Щ = [ — 1 4 0
\-1 0
т. е. в главных осях
/6	0
еу=[0	4 0
\0	0 3,
Вычислить инварианты для каждого из этих тензоров и показать,
что они совпадают.

ЗАДАЧИ С РЕШЕНИЯМИ
153
Применяя формулу C.95) и результат задачи 3.31, находим IE
13, 1Е, = 6 + 4 + 3 =. 13. Подобным же образом НЕ = 19 + 19 + 16 = 54,
ПЕ. = 24+ 18+ 12 = 54. Наконец, 1ПЕ = 5 ¦ 16 — 4 — 4 =, 72, ШЕ.
6-4 ¦ 3 = 72- Читатель может проверить эти вычисления.
3.43. Для поля перемещений xl — X1+ АХ3, х2 = Х2 — АХ3,
х3 = Х3 — AX-l + АХ2 определить тензор конечных деформаций
LG. Показать, что если константа А очень мала, то перемещение
представляет поворот абсолютно твердого тела.
Из условия задачи следует, что ых =. АХз, иг = — АХз, т = — АХХ + АХ2\
тогда по формуле C.40)
/0 0 Л \ /0
0
<-А
Л2
2LG =
0 —А
А 0
-Л2
Л2
0 2Л
Если А мало, то Л2 можно пренебречь и LG
равен w = Ле1 + Ае2-
/ А
-Л2
\ 0
'¦ 0. Вектор поворота, согласно (З.БО),
3.44. Показать, что поле перемещений их = Ахх + Зх2, иъ *=
= Зхг — Вх2, и3 = 5 дает состояние плоской деформации. Найти
связь между Л и В, при которой деформация будет изохорической
(отсутствует объемное расширение).
По полю перемещений и формуле C.43) найдем
ГА 3 01
3 -В 0 ,
Lo о oj
что соответствует форме C.99) для плоской деформации. Согласно C.96), коэффи-
коэффициент объемного расширения равен D = ец = А — В. Он обращается в нуль, если
А = В.
3.45. Так называемая дельта-розет-
дельта-розетка для измерения продольных поверх-
поверхностных деформаций имеет форму рав-
равностороннего треугольника и измеряет
относительные удлинения еЦ) еп, 6ц в
направлениях, показанных на рис. 3.21.
Пусть ец = а, еп = fe, еп = с; опреде-
определить е12 и е22 в той же точке.
В случае L = Е формула C.59) для направления х\ дает
Рис. 3.21-
Р/
Га е12 0"
, 0] е12 е22 0
10 0 0
*/2
jT/2
0
¦b, или 2 >1"е1г + Зе22 = 46 — а.

154	Гл. 3. ДЕФОРМАЦИИ
Для направления х, так же получаем
а в12 О
О | ^3~/2 I = с, или — 2 /Зе12 + Зе22 = 4с — а.
[™Ь
[-V2, /3/2, 0]
0 0 0
Решая эту систему уравнений относительно е12 и е22, находим е12 = F — с)//3 и
е22 =. (— а + 26 + 2с)/3.
3.46. Вывести формулу C.72), выражающую изменение угла
между координатными направлениями Х2 и Х3 в случае конечной
деформации. Доказать, что если градиенты перемещений малы, то
эта формула сводится к C.65).
Пусть Y23 =¦ я/2 — 6 — интересующее нас изменение угла (рис. 3.5). Тогда
sin Y23 =¦ cos (я/2 — 6) = па ¦ п3, или в силу C.33) и C.34)
dxa	dx4	dX., ¦ Fe • F ¦ dX3
Sin Y24 = i.i1 • 1 j 1 = —,	—.	.
\dx2\ Idx31 Yd\2 ¦ G • dX2 Vd\3 ¦ G ¦ dX3
Разделим числитель и знаменатель этого выражения на | dX2 | и | d\3 |. Учитывая
C.35) и C.66), получаем
У е2 ¦ G • е2 У е3 • G ¦ е3	?j (Г3)
Далее, в силу C.37) имеем е2 • G • е3 = е2 • BLG + 1) ¦ е3 = е2 ¦ 2LG . е3 +
е2 - 1 • е3 = 2L23, так как е2 • е3 = 0. Согласно C.68), Л„ =¦ /l + 2L22
и т. д.; следовательно,
sin Y2g = —	=
1 (duk!dX^
У1
Если дщ/dXj < 1, это равенство сводится к следующему виду: sin y23
+ ди3/дХ2 =. 2/2з.
3.47. Для перемещения простого сдвига хг = Хи х2 = Х2, х3 =
= Х3 + 2X2/j/l3 определить направление линейного элемента в
плоскости Х2Х3, для которого относительное удлинение равно нулю.
Л	Л	Л
Пусть m = m2e2 + тзез — единичный вектор нормали в направлении нуле-
нулевого удлинения. Тогда из C.66), учитывая, что Л2Л =¦ 1, получаем
(т)
i
[0, m2, m3]
2//3"

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
155
или 7m2, + 4>A3m2m3 + 3m| = 3. Кроме того. т\-\- mf = I. Решая совместно
эти два уравнения, находим m2 = ±V3/2, ms = Ф'/2 или тг =. О, тз =¦ ±1.
Таким образом, нулевое удлинение имеют элемент, расположенный вдоль оси Х3,
и элемент, идущий под углом 60° к оси Х3.
Читателю предлагается пронерить этот результат, воспользовавшись соот-
соотношением m ¦ 2L0 • m <= 0, которое получается из C.36).
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
3.48.	Для перемещения сдвига задачи 3.47 найти уравнение эллипса, в кото-
который переходит при деформации круг Х\-\- Х| = 1.
Ответ: х\ + 9а;| =. 3.
3.49.	Определить угол сдвига Угз для деформации задачи 3.47"(рис. 3.22).
Ответ: у23 = arcsin B/1^7).
3.50.	Дано поле перемещений хх = X, + 2Х3, х2 = Х2 — 2Х3, х3 = Х3 —
— 2Xt + 2Х2. Найти лагранжев и эйлеров тензоры конечных деформаций Lo
и Ел.
Ответ: LG =
3.51. Найти диагональную форму обоих тен-
тензоров задачи 3.50.
Ответ:
Рис. 3.22.
3.52.	Для поля перемещений задачи 3.50 найти градиент деформации F и,
воспользовавшись полярным разложением F, определить тензор поворота R и
правый тензор коэффициентов длины S.
Ответ:
, / 2 1 2\	/ 2 — 1 0\	/ I 0 2>
R = -5- 1 2 —2 Ь S= _i 2 0 , F= 0 1 -2
\—2 2 1/	\ 0 0 3/	\—2 2
3.53.	Доказать, что первый инвариант тензора Lc можно представить через
главные значения коэффициентов длины следующим образом:
2- - О + (Л2Л - 1) + (Л2Л - 1)]/2,
(е,)	(е2)	(еа)
Указание: воспользоваться соотношением C.68).
3.54. В некоторой точке задан тензор деформаций
1 — 3 Y2

156
Гл. 3. ДЕФОРМАЦИИ
Л Л	Л	Л .
Определить относительное удлинение в направлении v = ех/2 — ег/2 + <У К 2
и изменение угла между направлениями v и |х «= —
Ответ: е,« = 6, vv,. = 0.
ea/2
3.55. Как выглядит в главных осях тензор ву задачи 3.54? Учесть, что на-
направления v и jx, указанные в этой задаче, являются главными (следовательно,
V,,., =• 0).
Ответ:
3.56.	Построить круги Мора для деформированного состояния задачи 3.54
и найти величину максимальной деформации сдвига. Проверить результат анали-
аналитически.
Ответ: Ymax = 4.
3.57.	Вычислить все три инварианта тензора еу задачи 3.54 и тензора е.п зада-
задачи 3.55 и сравнить результаты.
Ответ: I,
6, ПЕ=. —4, ШЕ= —24.
3.58. Для тензора еу задачи 3.54 определить девиатор ец и вычислить его
главные значения.
/_1 _ з У 2 \	/4 0 0\
Ответ: в// = |—3 — 1 —/2"). е^. = |0 0 0 1.
3.59. Дано поле перемещений «t
иг =
делить тензор 8у и проверить, удовлетворяются ли условия совместности.
Ответ:
е?=1,5- Ю-4
Г г
-I 4v v
— *i«a- Опре-
Опре; да.
— хг/2
Vs 2-КГ4
Рис. 3.23.
3.60. Для дельта розетки деформаций
найдены относительные удлинения, величи-
величины которых указаны на рис. 3.23. Опреде-
Определить е12 и е22 в этой точке.
Ответ: ем = МО, е,2 =. — 0,2885 • КГ.
3.61. Для поля перемещений хг= Хг-\- АХ3, х2 = Х2, х3 = Х3 — AXt
вычислить изменение объема и показать, что оно равно нулю, если константа
А очень мала.

Глава 4
Движение и течение
4.1. Движение. Течение. Материальная производная
Термины движение и течение используются при описании мгно-
мгновенного или непрерывного изменения конфигурации сплошной
среды. Иногда словом течение называют движение, приводящее к
остаточной деформации, как, например, в теории пластичности.
Однако при изучении жидкостей это слово означает непрерывное
движение. Как было указано в C.14) и C.15), движение некото-
некоторого объема сплошной среды можно выразить либо в материаль-
материальных координатах (лагранжево представление):
xl = xl(Xl, Х2, Х3, 0 = Jf|(X, 0, или х = х(Х, 0, D.1)
либо, разрешая эти уравнения, в пространственных координатах
(эйлерово представление):
Xt = XlOcuxi,x*t) = XlQL,f), или X = X(х, 0. D.2)
Для существования обратных функций D.2) необходимо и доста-
достаточно, чтобы якобиан
J-=\dxt/dX,\	D.3)
был отличен от нуля. С физической точки зрения лагранжев спо-
способ описания фиксирует внимание на индивидуальных частицах кон-
континуума, в то время как при эйлеровом подходе интересуются
определенной областью пространства, занятой сплошной средой.
Так как D.1) и D.2) взаимно, обратны, любое физическое свой-
свойство континуума, приписанное индивидуальной частице (в лаг-
ранжевом, или материальном, описании), может также быть выра-
выражено для определенного места в пространстве, занятого этой час-
частицей (в эйлеровом, или пространственном, описании). Например,
если в материальных переменных дана плотность р
0. илир = р(Х, 0,	D.4)
то пространственное представление ее получается заменой X в
этом соотношении функцией из D.2). Таким образом, в простран-
пространственных координатах плотность равна
р = р (X, (х, 0, 0 = Р* (*е 0, «ли р = р (X (х, 0, 0 = р* (х, t),
D-5)

158	Гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
где символ р* использован для того, чтобы подчеркнуть, что вид
функции в эйлеровом представлении не обязательно тот же, что в
лагранжевом.
Скорость изменения со временем любого свойства в индивиду-
индивидуальных частицах движущейся среды называется материальной
(или индивидуальной) производной по времени от этой величины.
Материальную производную (также называемую субстанциональной
или полной производной) можно представить себе как скорость из-
изменения рассматриваемой величины со временем, которая была бы
измерена наблюдателем, движущимся вместе с индивидуальной
частицей. Мгновенное положение частицы xt само является свой-
свойством этой частицы. Материальная производная по времени от
положения частицы есть ее мгновенная скорость. Поэтому, принимая
символ dldt или точку над буквой для обозначения операции мате-
материального дифференцирования (в некоторых книгах используют
символ D/Dt), получаем определение вектора скорости:
vt = dxjdt = xt, или v = dxjdt = х.	D.6)
Вообще, если Р,-;-... — любое скалярное, векторное или тензорное
свойство континуума, которое можно описать локальной функцией
координат, и если в лагранжевом представлении
/V. = /V.(X, t),	D.7)
то индивидуальная производная по времени от этой величины имеет
вид
dP,, dPi; (X, О
dt
Правую часть D.8) иногда записывают в форме [dP,;-... (X, f)/dt]x,
чтобы подчеркнуть, что координаты X считаются постоянными,
т. е. что при вычислении производной имеют дело с одними и те-
теми же частицами. Если некоторое свойство задано функцией Р,/...
в пространственных переменных
Рц... = Рц...(х. 0.	D-9)
то вычисление .материальной производной приводит к выражению
dPij... (*» 0 _ dPii... (*¦ 0 , дРЦ... (х, 0 dxk
dt — dt "i d7k	1Г~' (q'w>
где второй член в правой части появляется из-за того, что инди-
индивидуальные частицы меняют свое местоположение в пространстве.
Первый член в правой части D.10) характеризует скорость из-
изменения данного свойства в фиксированной точке пространства и
соответственно называется локальной (или местной) скоростью из-
изменения. Этот член иногда записывают в виде [дЛ/... (х, O^^Ix.
чтобы подчеркнуть, что х считается постоянным при этом дифферен-

4.2. СКОРОСТЬ УСКОРЕНИЕ. МГНОВЕННОЕ ПОЛЕ СКОРОСТЕЙ	159
цировании. Второй член в правой части равенства D.10) называется
конвективной скоростью изменения, так как он выражает вклад,
обусловленный движением частиц в переменном поле данного свой-
свойства.
Принимая во внимание D.6), для индивидуальной производной
можно написать
что сразу наводит на мысль ввести оператор материального диф-
дифференцирования по времени
который используется при вычислении индивидуальных производ-
производных от величин, записанных в пространственных координатах.
4.2. Скорость. Ускорение. Мгновенное поле скоростей
Определение поля скоростей дано формулой D.6) в виде vt =
= dxjdt (или v = dx/df)- Другое определение того же вектора
можно получить из C.11), согласно которому xt = ut + X,- (или х =
= и + X). Тогда скорость можно определить так:
_ dxt _ d(u[ + Xt) _ du(
< ~ dt	dt	dt '
или	D.13)
_ _dx_ __ d (u + X) _ du
dt ~ dt ~ dt •
так как Х не зависит от времени. Если в D.13) перемещение выра-
выражено в лагранжевых переменных ut = и^ (X, f), то
du,(X, 0 ди.(Х, о
^s^=-V- = -Lir—•
или	D.14)
¦ du (X, t) __ ди (X, о
u ~ dt ~ dt
Если, с другой стороны, перемещение задано в эйлеровой форме
щ = и,- (х, t), то
du. (х, 0 ди. (х, 0	ди.(\, t)
4г4г	ir
или	D.-1 Б)
v(x, 0-i(x. /)^-^A = -^|A + v(x, 0-Vxu(x, 0.
Этой формулой скорость задается в неявном виде, так как она
входит и как множитель во второй член правой части. Говорят, что

160	Гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
функция
о, = i»f(x, /), или v = v(x, t),	D.16)
гфедставляет-titMg скоростей—
Материальная производная от скорости по времени есть ускоре-
ускорение. Если скорость задана в лагранжевой форме D.14), то
dv (X. t) dvt (X, о
или	D.17)
a v	s
a = v-	It	s	dt	•
Если же скорость выражена в эйлеровой форме D.15), то
dv (х, о dv (х, t)	dv (х,
или	D.18)
, .. dv (x, 0 dv (x, Q ¦ , ,, t-, , ,4
a(x, 0 =	dt^	^- + v(x- O'Vxv(x, *).
4.3.	Траектории. Линии тока. Установившееся движение
Траектория — это линия, по которой следует частица в процес-
процессе ее движения или течения. Линией тока для поля скоростей
в некоторый момент времени называется кривая, касательная к
которой в любой точке совпадает по направлению со скоростью
в этой точке. Движение континуума называется установившимся
(или стационарным), если поле скорости не зависит от времени,
так что dvjdt = 0. Для установившегося движения линии тока
и траектории совпадают.
4.4.	Скорость деформации. Завихренность.
Приращения деформации
Пространственный градиент мгновенного поля скорости дает
тензор градиента скорости dvjdxj (или Уц). Этот тензор можно раз-
разложить на симметричную и антисимметричную части следующим
образом:
ИЛИ
Y = V, (vVx + Vxv) + V» (Wx - Vxv) = D + V. D.19)
Симметричный тензор
g) или D = Va(Wx + Vxv), D.20)

4 4. СКОРОСТЬ ДЕФОРМАЦИИ. ЗАВИХРЕННОСТЬ	161
называется тензором скоростей деформации. Антисимметричный
тензор
или V = V,(vV»-Vxv), D.21)
называется тензором завихренности, или вихря.
Легко показать, что тензор скоростей деформации представ-
представляет собой материальную производную по времени от эйлерова
тензора линейных деформаций 1). Так, если в выражении
_^/__J	d ( ди{ duf \
dt ~~ 2 dt \ dxj ~^ dxi )'
или	D.22)
поменять местами операции дифференцирования по координатам
и времени, т. е. заменить-^-j-^-j на-^—i-^-J, то указанное
равенство примет вид
d^ij	I / dii(	dvj \ ¦-.
dt	2 \ dxj	dxi j ''"'
или	D.23)
dt ~ T ^V x ' x ~ '
Таким же образом можно показать, что тензор вихря равен мате-
материальной производной по времени от эйлерова тензора линейного
поворота. Этот результат выражается формулой
*Ну _ 1 / foj dvj \ _ v
~ST ~ T \~dx~i дхТ/ ~ Vlh
или	D.24)
-f- = 4-(Wx-Vxv)=V.
Довольно интересную интерпретацию можно придать равенству
D.23), если переписать его в форме
deij = Dijdt, или dE = Ddt.	D.25)
Левая часть D.25) представляет собой компоненты тензора,
которые широко используются в теории пластичности (см. гл. 8)
и которые мы будем называть приращениями деформации.
х) Это утверждение верно только в том случае, когда гц бесконечно малы
(см. задачу 4.40). О связи между тензором скоростей деформации и производ-
производными по времени от тензоров конечных деформаций см., например: Седов Л. И.,
Введение в механику сплошной среды, гл. II, §6, 7, Физматгиз, М., 1962.— Прим.
ред.
В Дж. Мейэ

162
Гл, 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
4.5. Физическая интерпретация тензоров скоростей
деформации и завихренности
На рис. 4.1 скорости соседних частиц, находящихся в точках
Р и Q движущегося объема сплошной среды, обозначены соответ-
соответственно v( и vl + dvL. Таким
образом, скорость частицы Q
относительно точки Р равна
dv, =
-dxh
или
дх,
dv = vVx • dx,
D.26)
где частные производные вычис-
вычислены в точке Р. Это выражение
можно записать через D,.- и
Vif:
dv = (D + V) . dx. D.27)
Рис. 4.1.
dvt = (Dij + Vtj) dxu или
Если тензор скоростей деформации тождественно равен нулю (Dlf зз
= 0), то
dvt = VijdXf, или dv = V • dx,	D.28)
и движение в окрестности точки- Р будет вращением абсолютно
твердого тела. По этой причине поле скоростей называют «без-
«безвращательным» (безвихревым), если тензор завихренности обращается
в нуль во всех его точках.
Ассоциированный с тензором завихренности вектор определя-
определяется соотношением
или
= Vx X v,
D.29)
и называется вектором завихренности. Символическая форма запи-
записи D.29) показывает, что вектор завихренности получается дей-
действием оператора ротор (rot или curl) на поле скоростей. Вектор,
равный половине вектора д,
гл	1	I
или
-i-q = -i-Vx X v, D.30)
называется вектором вихря скорости. При вращении абсолютно
твердого тела, как получено в D*28), относительная скорость час-
частицы, соседней с Я и находящейся от нее на расстоянии dxit дается
формулой
dvi—eijiSijdxkt или dv = Q X dx.	D.31)

4.6. МАТЕРИАЛЬНЫЕ ПРОИЗВОДНЫЕ ОТ ЭЛЕМЕНТА ОБЬЕМА	163
Компоненты тензора скоростей деформации имеют следующий фи-
физический смысл. Диагональные элементы D,, —это скорости от-
относительного удлинения отрезков, расположенных вдоль осей коор-
координат. Так, для чистой деформации из D.27) следует, что
dvL = Dtjdxj, или d\ = D • dx,	D.32)
а так как скорость изменения длины линейного элемента dxit при-
приходящаяся на единицу мгновенной длины, есть
^) = T = D'"'-S- = Dl^' или drv) = D-v, D.33)
то скорость удлинения в направлении единичного вектора v? равна
d = d!v)v, = DijVjVi, или d = v • D • v.	D.34)
Если v( — направление какой-либо оси координат, например е2,
то, согласно D.34),
d = D22, или d = е2 • D • е2 = D22.	D.35)
Недиагональные элементы ?>,, характеризуют скорости сдвига и
являются мерой скорости изменения прямых углов между направ-
направлениями отрезков, расположенных вдоль осей координат (см. зада-
задачу 4.18).
Вследствие того что DLj является симметричным тензором вто-
второго ранга, для него существуют такие понятия, как главные
оси, главные значения, инварианты, поверхность скоростей де-
деформации и девиатор скоростей деформации. Кроме того, для
компонент тензора скоростей деформации можно написать уравне-
уравнения совместности, аналогичные уравнениям, полученным в гл. 3
для тензора линейных деформаций.
4.6. Материальные производные по времени от элемента
объема, элемента поверхности и линейного элемента
В результате движения из некоторого начального состояния
в момент t = 0 к рассматриваемому в момент t состоянию частицы
сплошной среды, которые вначале занимали элементарный объем
dV0, займут элементарный объем dV. Если начальный элемент объема
взят в виде прямоугольного параллелепипеда (рис. 4.2), то, согласно
A.10),
dV0 = dX^i X dX2e2 • dX,e3 = dXxdX2dX3.	D.36)
При движении этот параллелепипет перемещается и искажается,
но нз-за непрерывности движения не разрушается. Действительно,
6*

164
Гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
вследствие связи C.33) dxt = {dxJdXD dXj между материальными
и пространственными линейными элементами, «жидкий отрезок»,
который раньше был dXu теперь образует бесконечно малый ли-
линейный отрезок dx? = {dx-JdX^) dXx. Аналогично dX2 переходит в
dx?] = {дхс/дХ2) dX2, a dX3 превращается в dx?] = {дх^дХ3) dX3.
Поэтому бесконечно малый элемент объема dV представляет собой
скошенный параллелепипед
с ребрами dxf\ dx?\ dx?\
Величина его объема вычис-
вычисляется как смешанное произ-
произведение
dV = dx0) x dxB) ¦ dx0) =
= e^dxlVxfdx?. D.37)
Очевидно, этот объем равен
¦ дх[ dxj
dV = еф
дХ3
X
X
, = /dV0, D-38)
где J = | dxJdXj \ — якоби-
якобиан, определенный формулой
D.3).
Теперь, используя D.38), можно получить материальную про-
производную от dV по времени:
Рис. 4.2.
dt
¦{JdVo)
dt
dV0,
D.39)
поскольку dV0 от времени не зависит, так что —п- (dV0) => 0. Мож-
Можно показать (см. задачу 4.28), что материальная производная от
якобиана J равна
dJ т dv,-	-, ,„ у>	DЛ0)
ИЛИ J —
и, следовательно, D.39) принимает вид
dV, или -п- (dV) —
D.41)
Бесконечно малый элемент поверхности, имеющий в начальном
состоянии площадь dS°, можно задать (вместе с его ориентацией)
при помощи единичного вектора его нормали nt выражением dS0'^.
При движении среды частицы, вначале составлявшие площадку
dS°nit в рассматриваемом состоянии заполняют элемент площади

4.7. МАТЕРИАЛЬНЫЕ ПРОИЗВОДНЫЕ ОТ ИНТЕГРАЛА ПО ОБЪЕМУ	165
dSn\, или dS(. Можно показать, что
dSt=J-jb-dXh или dS = Jd\-XVx,	D.42)
откуда находим материальную производную элемента площади:
тг т - т
Материальную производную от квадрата длины бесконечно ма-
малого линейного элемента dxL можно вычислить аналогичным об-
образом:
4- <d*2>=4- <** ***'>=2 т- ^'- D-44)
Но так как d*? = {dxJdX,) dXh мы имеем
D.45)
и тогда D.44) примет вид
или	D.46)
Vxv • dx.
Выражение в правой части в индексной форме D.46) симмет-
симметрично по индексам ( и k, и, следовательно, можно написать
А*. D-47)
либо, принимая во внимание D.20),
~~- {dx2) = 2Dtjdx,dxj, или ~
{dx2) = 2Dtjdx,dxj, или ~ (dx2) = 2dx • D . dx. D.48)
4.7. Материальные производные по времени от интеграла
по объему, интеграла по поверхности
и линейного интеграла
Не все свойства континуума можно задать для индивидуальной
частицы функцией ее координат так, как это сделано в D.7) и D.9);
некоторые свойства определяются интегралами по конечной части
континуума. Пусть, например, какое-либо скалярное, векторное

166	Гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
или тензорное свойство представлено интегралом по объему
Pt,:..(t) =J Pi/..-(х. t)dV,	D.49)
v
Где у — объем, который рассматриваемая часть сплошной среды
занимает в момент t. Материальная производная от Р,,-... (t) равна
а так как интегрирование идет по определенной части континуума
(т. е. индивидуализированной системе масс), операции дифферен-
дифференцирования и интегрирования можно менять местами. Таким об-
образом,
-i- f #/... (х, 0 dV = f 4" К-... (х, О dV].	D.51)
После выполнения дифференцирования с учетом D.41) приходим
к следующему равенству:
(х, 0^ = j[i%l± + ^..<x. „_?_]*, D.52)
Оператор индивидуальной производной определен формулой D.12)
как dldt = д/dt + vpd/dxp. Тогда равенству D.52) можно при-
придать вид
1.53)
По теореме Гаусса—Остроградского A.157) преобразуем второй
член в правой части D.53) в интеграл по поверхности; получим
~ J Р'и... (х, Q dV = f aP'7-af' ° dV + f Vp [Py... (x, 01 dSp. D.54)
i/	V	s
Это соотношение утверждает, что скорость изменения некоторой
величины Pi/.., (t) в части сплошной среды, занимающей в данный
момент объем V, равна сумме изменений этой величины во всех
точках внутри V плюс поток величины Р*,-.. (х, t) через поверх-
поверхность S, ограничивающую V.
Процедура определения материальных производных от интегра-
интеграла по поверхности и линейного интеграла в общем та же, что только
что проделанная для интеграла по объему. Так, для любого тензор-
тензорного свойства сплошной среды, которое выражается интегралом

ЗАДАЧИ С РЕШЕНИЯМИ	167
по поверхности
Qi/...@ = jQ*;...(x, QdSp,	D.55)
где S — поверхность, занятая в момент t рассматриваемой частью
континуума, имеем, как и прежде,
S	S
Отсюда, учитывая D.43), получаем правило дифференцирования
интеграла по поверхности:
[«Ц?! ?й Ц^;^] ,4.57,
[	Ц
s	s
Для величин, выраженных линейным интегралом типа
&/... (О = J/&... (х, /)^р,	D.58)
с
J
с
материальная производная равна
-i- f Лу... (х, 0dxp = f -^ IRl-... (x, /)d*p].	D.59)
с	с
Проводя указанное дифференцирование в правой части D.59) и учи-
учитывая при этом D.45), находим материальную производную линей-
линейного интеграла:
4г №/¦¦¦ W1 = J ' 1*'"-?' ^ dxp + l^lRl. (*, 0]dxg. D.60)
ЗАДАЧИ С РЕШЕНИЯМИ
Материальные производные. Скорость.
Ускорение (§ 4.1—4.3)
4.1. Дано пространственное (эйлерово) описание движения кон-
континуума Хх = Ххе1 + Х3 (е' — 1), х2 = Х3 {ё — ег-*) + Х2, х3 =
= Х3. Доказать, что якобиан J для такого движения отличен от
нуля, и найти материальное (лагранжево) представление этого
движения, обращая уравнения для перемещений.

168
Гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
Согласно D.3), якобиан равен
ё-\
ё-е~'
1
ё.
Обращая уравнения движения, получаем Хг =«= х^е *-\-х3(е '—I), Хг =»
р ур	у	г ^е *-\-х3(е ') г
х2— х3 (е* — е~'), Х3 = х3. Заметим, что нри обоих способах описания х,- =
X при < = 0.
= е' (Х3 +
)/
4.2. Дан закон движения континуума хх = Xlt
Х)/2 + ' (Х Х)/2	<* + Х/2
Х3)/2
е-'
(Х2 -
Х3)/2 -
C
- Х3)/2.
33 (з 3)
Определить компоненты скорости в эйлеровой и лагранжевой форме.
Из второго и третьего уравнений получаем Х2 -\- Х3 = ё~* (хг + л:3) и Х2 —
—	Х3 = е (х2—^з)- Разрешая их, находим обращенные уравнения Х1=х1,
Xz = е-' (х2 + х3)/2 + et(x2— X3)J2, Х3 = е~' (х4 + х3)/2 -е' (л:2 - х3)/2. Тогда
компоненты перемещения щ = х,- — Xi можно записать либо в лагранжевой фор-
форме: Ui = 0, и2 = е' (Х4 + Х3)/2 + е~' (Х2 — Х3)/2 - X2, ks = ё (Х.г + Х3)/2 —
—	e~f (Xz — Х3)/2 — Х3, либо в эйлеровой форме: их = 0, и4 = х2 — е~* (х2 +
+ х3I2 - е' (х4 - *8)/2, «з = *з - е~' (^ + *з)/2 + е' (х2 — *3)/2.
Согласно D.14), г,- =дщ1дг = dxildt, и компоненты скорости в лагранже-
вом представлении будут равны yt = 0, в2 = е' (Х2 + АГ3)/2 — е~* (Xt — Х3), 2,
vs = е' (Х2 + Х3)/2 + е~' (Х2 — Х3)/2. С учетом соотношений А2 + Х3 =
= е~' (х2 + х3) и Ха — Х3 = е' (л:2 — ха), эти выражения для компонент сводят-
сводятся Kt, = 0, v% = x3, v3 = x2. С другой стороны, если движение задано в эйле-
эйлеровых переменных, то из формулы D.15) находим
dujdt = v2 = е~{ (хг + *3)/2 - е' (х2 — л:3)/2 + v2 B - е~' - е')/2 +
- х3)/2 + г2 (— е~* + е*)/2 +
Разрешая эти уравнения относительно в3 и ч3, получаем, как и прежде, v2 = лг3,
v3 = х2.
4.3. Дано поле скоростей их = лга/A + ^
v3 = 3x3/(l + ^). Найти компоненты ускорения.
Пользуясь формулой D.18), находим
dvxidt = fll = —
dv2ldt = а2 = -
dv3ldt = а3 = - Злг3/A + 0а + 9xs/(I +
ог = 2лг2/A +/),
+ О2.
= 6*3/A + О2-
4.4. Проинтегрировать выражения для скорости, данные в зада-
задаче 4.3, и получить уравнения для перемещений хс = хс (X, f) (за-
(закон движения); по ним найти компоненты ускорения в лагранже-
лагранжевой форме.

ЗАДАЧИ С РЕШЕНИЯМИ	169
По определению D.13) ui = dxjdt = xil(\ + /); разделяем переменные
dxi/xi — dtf (I + t) и интегрируем: )п xi = )п A + /) + In С, где С — постоян-
постоянная интегрирования. Так как х\ = Х\ при / = 0, то С = Ад, и, следовательно,
xi = Х\ A + 0- Точно так же находим х2 — Х2 A + О2 и х3 = Х3 A + /K.
Затем, используя D.14) и D.17), получаем Vi = Xi, иг = 2Хг A + /), v3 =
= ЗХ3 A + О2 и fli = 0, а2 = 2Х2, а3 = 6Х3 A + /}.
4.5. Задан закон движения сплошной среды xt ~ А +
+ (e~m/A) sin Я (А + at), х2 = —5 — (e~Bh/X) cos X (Л + of), л:3 =
= Х3. Показать, что траектории — окружности, а величина ско-
скорости постоянна. Определить также связь между Хх и Х2 и кон-
константами А и В.
Перепишем закон движения в виде х1—А = (е A) sin Я (А -\- со/), х2 +
-\- В = (— е~в>7Я) cos Я (Л + со/). Возведя эти равенства в квадрат и сложив ре-
результаты, исключим /и получим траектории—окружности (х,—АJ + (х2 +
+ ВJ = е~2ВК/№. По формуле D.6) найдем скорости иг = сое~вя- cos Я (А + со/),
yz = (oe~BK sin Я(Л + со/), иэ = 0, следовательно, у2 = i>f + v\ + v\ = a2e~2Bh.
Наконец, xt = Xt- при / = 0, откуда Xj =» А + (ё~Бк1%) sin ЯЛ, Ха = — В —
4.6. Поле скоростей задано вектором v = x2tet + x2t2e2 +
t^3. Определить скорость и ускорение частицы, находящей-
находящейся в момент t= 1 в точке Р A, 3, 2).
л	л	л
Прямой подстановкой найдем Vp = ех + 3e2 + 2eg. Пользуясь векторной фор-
формой формулы D.18), получим поле ускорений
а = х\ в!
или
л	Л	л
Таким образом, ар = Ъех + 9е2 -1* 6е3.
4.7. Для поля скоростей задачи 4.3 найти линии тока и траекто-
траектории и доказать, что они совпадают.
Касательная к линии тока в каждой точке направлена по вектору скорости.
Следовательно, для бесконечно малого вектора dx касательной к линии тока мож-
можно написать v X dx = 0 и получить таким образом дифференциальные уравнения
линий тока dxi/vi = dxilv^ = dx3/vs. Для указанного течения эти уравнения
имеют вид dx1/x1=dx2l%X2 = dx3l3xs. Интегрируя их с учетом начальных условий
Xi = Xi при / = 0, находим уравнения линий тока: (xi/X\J = WX2, (я/XiK =
= x3/Xa, (WX2K = (*3/X3J.
Интегрирование выражений для скорости dxjldt = Vi было выполнено в за-
задаче 4.4 и дало закон движения х\ = Xi A + /), xi = Х2 A + Z)z. *з = -^з A +
+ О3- Исключая из этих уравнений время t, получаем траектории, которые в точ-
точности совпадают с найденными выше линиями тока.

170	Гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
4.8. В электромагнитном континууме напряженность магнит-
магнитного поля равна Я. = ё~ 1г, где га = *? + х\ + х\ и А — констан-
константа, и движение задано' полем скоростей vt = Bx^xJ, v2 — Bx\t2,
vs = Вх3хг. Определить скорость изменения напряженности маг-
магнитного поля для частицы, расположенной в момент t = 1 в точке
Р B, -1,2).
Так как d(r~l)ldxt = —Х[/г3, формула D.11) дает
К = — Аё~м1т — ё~м (Bx\x&t + Вх3^ + В
Таким образом, в точке Р в момент t = 1
А	В)/9.
4.9. Дано поле скоростей г»х = 4х3 — Зх2, v2 = 3xlt v8 — —4^.
Определить компоненты ускорения в точках Р {Ь, 0, 0) и Q @, 4Ь,
ЗЬ) и обратить внимание на то, что поле скоростей соответствует
вращению абсолютно твердого тела с угловой скоростью, равной 5,
Л	Л	S*
вокруг оси, направленной вдоль вектора е = Dе2 + Зе3)/5.
По формуле D.18) а, = — 25х!, а2 = — 9лга + \2х&, а3 = 12х2 — 16х3. Тог-
да в точке Р ф, 0, 0) а = — 256ej и ускорение имеет только осестремительную
компоненту, а в точке Q @, 46, 3fe), расположенной на оси вращения, а =
Л	Л	АЛЛ
= 0. Можно заметить, что v = «Xx= De3 -f- Зе3) X (*ie! + *aes
/ч	Л	Л	^ч
= Dл:3 — 3jcs) ej + З^е,, — 4*1е3 и, следовательно, ю = 5е.
Скорости деформации, завихренность (§ 4.4—4.5)
4.10. Некоторое течение задано полем скоростей vt = 0, v2 =
= А (ххл:2 — хз) e~Bt, v3 = А (х\ — х^ ё~в\ где А и В — констан-
константы. Найтн градиент скорости dvjdxf для этого движения и вы-
вычислить тензор скоростей деформации D и тензор завихренности
V в точке Я A, 0, 3) в момент t — 0.
Согласно D.19),
@ 0 0 \
х2 Xi — 2х3 I Ae~Bt.
— х3	2хг —Xj)
Этот тензор можно вычислить в точке Р в момент t = 0, а его составные части
подсчитать соответственно по формулам D.20) и D.21):
/0	0 0 \
= 0	А —6Л =
\— ЗА	0 —А)
/0	0 — 1,5Л\ /0 0
10	А — ЗЛ) + ( 0 0
\— 1.5Л	— ЗЛ --Л/ \—1.5Л ЗЛ

ЗАДАЧИ С PFUIEttMMH	171
4.11. Для движения хх = Хи х2 — Х2 + Хх (е-2' — 1), х3 =
= Х3 + Хх (е-3' — 1) вычислить тензор скоростей деформации
D и тензор завихренности V. Сравнить компоненты D с detl/dt —
скоростями изменения компонент эйлерова тензора малых дефор-
деформаций Е.
В данном случае компоненты перемещения равны и\ = 0, иг = х\ (е~21 — 1),
иа = xi (e~3i — 1), и по D.14) компоненты скорости будут t>i = 0, fa = —2*ie~2',
vs=—3*ie~3'. Разложение градиента скорости dvi/dxj дает dvjdxj = ?>,/ +
-f- Vi,; т. е.
О 0 0\
— 2е~2' 0 0| =
Зе~3' О О/
0
-e~2t
0
0
-Зе-3'/2\ ,
0 +
о ) У
( о
— e~2i
W3e~3'/2
е-21
0
0
Зе
0
0
Аналогично получаем разложение градиента перемещения дщ/дх/ = е(/- + со,-/,
т. е.
О 0 0\
Сравнивая D с dE/dt, видим, что
О	0
.2 0	0
Читателю предоставляется самому показать, что dutij/dt =
4.12.	Вихревой линией называется такая линия, касательная
к которой в каждой точке движущейся среды направлена по век-
вектору вихря Q = 11.1(\. Доказать, что уравнения вихревых линий
имеют вид dxl/ql = dx2/q2 — dx3/q3.
Пусть dx — бесконечно малый вектор в направлении q. Тогда q X dx^O,
или
(q2dxs — q3dx2) в! + (^з^ — д^х3) е2 + (qidx2 — q^dx^ e8a0,
откуда получаем уравнение вихревой линии dxjqi = dxzlqi = dx^lqz.
4.13.	Доказать, что для поля скоростей v = (Ах3 —Вл:2)е, +
+ {Bxi—Сх3) е2 + (Сх2 — Ах1)ея вихревые линии являются пря-
прямыми. Написать их уравнения.

172	Гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
По определению D.29) q = ^х X v = 2 (Се1 + Лег + Bes), а, согласно
результату задачи 4.12, дифференциальные уравнения вихревых линий будут
Adx3 = Bdxs, Bdxi = Cdx3, Cdx2 — Adxi. Интегрируя их, найдем уравнения
вихревых линий в конечной форме х8 = Вхг!А + /Ci, xi = CxsfB + Кг, Х2 —
== Axi/C + /С3, где /С/ — постоянные интегрирования.
4.14. Доказать, что поле скоростей задачи 4.13 представляет
вращение абсолютно твердого тела, так как для него D = 0.
Вычислим градиент скорости dvildx;. Он оказывается антисимметричным
тензором, а это значит, что
/0 ~В А \
dvi/dxf*=\ В 0 —С =Vf,
\—А СО/
и А/ = 0.
4.15. Для вращения абсолютно твердого тела со скоростью
v = Зя^! — 4д;де2 + D*2 — Зх^ед определить вектор вихря ско-
скорости fi и показать, что v = fi x x.
По определению D.30) 2Q = q или Q =¦ 4ei + Зег. Этот вектор направлен
вдоль оси вращения. Можно проверить, что
Dе, + Зе2) X foe, + хае2 + х3е^ = Зх^ — 4^3е2 + Dх2 — Зхг) е8 = v.
4.16. Дано стационарное поле скоростей v = (*? — *1л|)е14-
+ (х2х2-\-х2) е2. Найти скорости относительно точки Я A, I, 3)
частиц в точках Qx A, 0, 3), Q2 (I, 3/4, 3), Q3 A,7/8, 3), отнесен-
отнесенные к расстоянию от этих точек до точки Р, и показать, что их
величины стремятся к относительной скорости, определенной фор-
формулой D.26).
Непосредственное вычисление дает vp — Vq = —ei + 2е2, 4 (vp — Vq ) =
= —7ei/4 + 2ez и 8 (vp — VqJ = —I5ei/8 + 2ez. Матрица градиента скорости
имеет вид
[о„2	 2
ах1 Х2
2x^2 х\
О
[5и//бх/]=| 2x1xi x\+.\ О
О	0.
и в точке Р A, 1,3) градиент скорости в отрицательном направлении оси xs равен
Г2-2 ОТГ 01 Г 2]
^ = 2 2 0 —1 = —2 .
*•' L0 о о J L oJ I oj
/ч	/ч
Таким образом, (dv/dx)^ = —2ei + 2ег, и это величина, к которой стремятся от-
носшч;льные скорости Vp — Vq , отнесенные к расстоянию до точки Р.

ЗАД4ЧИ С РЕШЕНИЯМИ
173
4.17. Для стационарного поля скоростей v = Злг?лг2е] +
х*е + х^хЫз определить скорость удлинения материаль-
4ез)/5.
ного отрезка в точке Р A, 1, 1) в направлении v =Cех
В нашем'случае градиент скорости равен
0 4x2xs
ХпХо Х\Х^з
и его симметричная часть в точке Р принимает значения
о
J
Г 6 1,5 0,5"|
[Dt]p= 1,5 4 1,5 .
L0,5 1,5 2 J
По формуле D.34) для направления v = Cei — 4еа)/5 получаем
Г 6 1,5 0,51 Г 3/» 1
d = \sU, 0, -*/5] 1,5 4 1.5	0 =74/25.
Lo,5 1,5 2 J L —4'J
4.18.	Для движения, предложенного в задаче 4.17, определить
в точке Р скорость изменения угла между ортогональными направ-
направлениями v = (Зе, —4е3)/5 и ц, = Dех + Зе3)/5.
Пользуясь результатами задачи 3.20, скорость сдвига y^v можно найти по
формуле Yn v = (* • 2D ¦ v, или в матричной форме
Г12 3 ИГ 3/в I
iW = [4As. °. 31ь\ 3 8 8 0 = 89/25.
L 1 3 4|L-4/,J
4.19.	Дано стационарное поле скорости их = 2х3, v2 = 2х3,
v3 = 0. Найти главные направления и главные значения тензора
скоростей деформации.
В данном случае
[0	0	2"] ГО	0	П ГО 0	П
0	0	2=0	0	1+ 0 0	1
о	о	oj Ь	I	oj L—1—1	oj
и главные значения К тензора
— К 0
0	—К 1
1	I —
находятся из уравнения
1
=0=>—
откуда
+ YX ьп = о, яш = -/2.

174
Гл. 4. ДВИЖЕНИЕ II ТЕЧЕНИЕ
Преобразование тензора к главным осям дается матрицей
"-V, -V,
1/У2 — 1/У2 О
1/К2 1
0
и приводит тензор скоростей деформации к виду
'Г2 0 0 1
0 0 0,
. 0 0-/2J
4.20. Определить максимальную скорость сдвига
движения, заданного в задаче 4.19.
для
По аналогии с нахождением главных де-
деформаций сдвига в гл. 3 найдем максималь-
максимальную скорость сдвига *Ymax= (^j — *-ш)/2 =
Этот же результат получится, если за-
заметить, что указанное движение представля-
представляет собой простой сдвиг, параллельный плос-
кости xixn в направлении вектора v = (ei +
-f- Ы/У 2 (рис. 4.3). Поэтому, как и прежде,
[0, 0, 1]
Рис. 4.3.
о о inn ,
0	0 1 Ь,'
1	1 О J L О
Следует также заметить, что максимальная скорость удлинения для данного
движения имеет место в направлении n = (ei + ег + J 2eg)/2, как было найдено
в задаче 4.19. Таким образом,
Г° °
Чг, V2, 1л2/2] 0 0
Li I
v, ¦
V,
L1 /2
Материальные производные от объемов, площадей,
интегралов и т. д. (§ 4.6—4.7)
4.21. Вычислить вторую материальную производную по време-
времени от скалярного произведения двух линейных элементов, т. е.
найти d* (dx") Idt*.
По формуле D.45)— ' =* ~ь ' ¦ dx^, но равенство D.48) показывает, что
dt
dt
. Поэтому
d= (dx^
" dXkdxi + D4dXi

ЗАДАЧИ С РЕШЕНИЯМИ	175
После простой операции по переименованию индексов суммирования полечим
4.22. Найти материальную производную —п-] PidS, от потока
at s
некоторой векторной величины pt через поверхность S.
По формуле D.57)
4.23. Доказать, что формулу для производной от потока, полу-
полученную в задаче 4.22, в символических обозначениях можно запи-
записать следующим образом:
-±- Jp • ndS = Д-J- + v(V • р) + V х (р X v)] • ndS.
Переписывая непосредственно в символических обозначениях результат
задачи 4.22, получаем
-i- Г р • nrfS = П -^Н_ + р (v . v) - (р • V) v | • SdS =
• v) - (р • V) v]
V) р + р (V • v) - (р • V) v] • ndS.
s
Теперь (см. задачу 1.65) воспользуемся векторным тождеством
V X (р X v) =¦ р (V • v) — v (V • р) + (v ¦ V) р — (р • V) v;
тогда
-A- fp-ndS= f[-J-+v(Vp)+VX(pXv)j.ndS.
4.24. Представить теорему Рейнольдса о переносе, выраженную
формулами D.53) и D.54), в символических обозначениях.
Пусть Р* (х, 0 —любая тензорная функция эйлеровых координат и времени.
Тогда D.53) записывается так:
dV.

176	гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
По теореме Гаусса — Остроградского этому выражению придадим вид, соответ-
соответствующий D.54):
4.25.	Если функция Р* (х, t) в задаче 4.24 есть скалярная вели-
величина, равная 1, то интеграл в левой части есть просто мгновенный
объем некоторой части континуума. Найти материальную произ-
производную от этого объема.
Используя векторную форму равенства D.53) в том виде, в котором она при.
ведена в задаче 4.24, получаем 	\ dV — \ у • vdV. Здесь у • \dV пред-
ставляет скорость изменения dV, и поэтому у ¦ v называют скоростью кубического
расширения. Это соотношение можно также установить непосредственным диф-
дифференцированием D.38); см. задачу 4.43.
Смешанные задачи
4.26.	Используя определение вектора завихренности D.29)
q = rot v, доказать, что <?, = eiikVki и что 2Vti = ъцкЯк-
Представим выражение для q D.29) в виде суммы qt = Zijifikj = ъЦк ("[А,/] +
+ V(k д). А так как г-/^к ^ = 0 (см., например, задачу 1.50), то щ = f-i\kv[k,\\ я
= z{jkVkj. Отсюда окончательно получим
е/г, Qi = eirsEijkVki = F,/6sA — бгА/) Vkj = 2Vsr
4.27.	Доказать, что ускорение а можно записать в виде
Согласно D.18), <ц — —~- + Vk "' ¦ Отсюда получаем
dvi . o ,. , 1 д (vkVk) dvt	1 д (vkvk)
Читатель может сам убедиться в том, что это индексная форма доказываемого
равенства.
4.28. Доказать, что d {\nJ)/dt = div v.
Запишем dxildXp в виде xt р, так что J = ePQRX[ px2 qX^ r и J будет пред-
представлено суммой трех определителей:
J = ep(j? (х1.рх2,С1хЗЯ + xl,Px2,QK3,R + xI.Px2.QX3.r}' Далее' xl,P = vl,SxS,P
и т. д., поэтому
J = ePQR (V\,SXS,PX2,QK3.R + xl,Pv2,SxS,QXS.R + x\.Px2,QV3,SXS.fi>-

ЗАДАЧИ С РЕШЕНИЯМИ	177
Из девяти определителей третьего порядка, получающихся при суммировании
этого выражеиия по S, только три отличны от нуля. Таким образом, 'J = и, ,./ +
+ v22J -\- vS3J =vssJ, или J = J(V-v) и, следовательно, d (In J)ldt = div v.
4.29.	Доказать, что при установившемся движении среды
(dvjdt = 0) линии тока и траектории совпадают.
Как было показано в задаче 4.7, линии тока в данный момент времени t яв-
являются решениями дифференциальных уравнений dxi/vi = dxz/v2 = dxjv^,
а траектории — решениями дифференциальных уравнений dxildt = vi (x, t).
Если t>,- = vi (x), то уравнения траекторий принимают вид dt = dxjvi =
= dxilv-г. = dx3/v3 и, следовательно, совпадают с уравнениями лпний тока.
4.30.	Для стационарного поля скоростей их = х2\Х2 + х\, v2 =
= —х3\ — Xi-xJi v3 = 0 найти главные значения тензора скоростей
деформации D в произвольной точке Р (xlt x2, х3).
По формуле D.19) dvi/dx/ = Dy + Vij, или
0^
о	о о/ \ о	о
0	2(х\ + 4 ^
0	0
Главные значения d^. являются решениями уравнения
2Xlx2-d —x\+x\ 0
»_ д;2 _|_ j^2 __ 2х*Хп 	 d О
О	0	— d
= 0 = - d [-
Отсюда dA) = 0, dB) = — (*? + ^Ф» ^<з) = -^l + xl- ^™ значен«я можно
упорядочить по мере их убывания d} = х\ + -^2. ^ц *= 0. ^ш = — ix\ + -^f)-
4.31. Доказать равенство D.43), вычислив материальную про-
производную от площади dSc, записанной в виде векторного произве-
произведения dS, = e^dxf'djd3'.
Используя формулу C.33), получим dSi = Eijii(dxjJdX^dX'2(
dxt ._	dxt dxj dxk ,v Av 1AV Av
O/l!	'к ОЛ! ОЛ2 OXS
Таким образом,
dXi dxi	dXi

178	Гл. 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ
и, учитывая результат задачи 4.28, находим
dVq
дхр
4.32. Используя результаты задач 4.27 и 4.23, доказать, что
материальная скорость изменения потока завихренности, т. е. про-
производная -тг f q • n dS, равна потоку вектора rot от ускорения а.
s
Применим операцию rot к выражению ускорения, полученному в задаче 4.27,
д\
Vx Vx	+ VX(X) + Vx
и учтем при этом, что q = V X v и VxV (уг/2) = 0; тогда V X а = dq/dt +
+ V X (q X v) = dq/dt +. q (V • v) — (q • V) v. Если в формулу задачи 4.23 вмес-
вместо р подставить q, то получим требуемый результат
d С л	Г Г da	1 « Г
— J q ¦ ndS = J y-jj- + q (V ¦ v) - (q • V) vj ¦ nd5 =^ (V X a) ¦ ndS.
s	s	's
4.33. Доказать, что для вектора завихренности q имеет место
равенство -^- [ qtdV = f [eilkak + qjvi — qtv,] dS,.
I'	S
Тождество задачи 4.32 V X a =» dq'dt + V X (q X v) можно переписать в
индексной форме dqi/dt = e,{]kakJ — eisp(epmrqmvr) s; тогда
dV.
V	V
Воспользовавшись теоремой Гаусса — Остроградского A.167), получим
dv ~ 1 *4kukdSi ~ | (e"«e»- ~ W»JiQmVr) dS
V	S	S
s
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
4.34. Дан закон движения среды xt — Х^ -\- Xs (е' — 1), х2 = Хл + Х3 (е'—
— е ), х3 = Ха. Показать, что J Ф 0, и найти компоненты скорости.
Ответ! г\ == (Xj + Хв) е*, v2 = Х9 (е' + е~*), о8 = 0, или иг ¦= лгх — ха,

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ	179
4.35.	Поле скоростей задано в переменных Лагранжа v^ = — Х2е=', а2 =
= —Х8, v3 = 2t. Найти компоненты ускорения в эйлеровой форме.
Ответ: ах — ё~1 (х2 + tx3 — t3), a2 = 0, а3 — 2.
4.36.	Доказать, что поле скоростей Щ — вдоЬ/Хд + Ъ, где be и c-t —постоян-
—постоянные векторы, представляет вращение абсолютно твердого тела, и определить век-
вектор вихря скорости Rj для этого движения.
Ответ: 2ft,- = qt = bix^ f- — bi = 26/.
4.37.	Доказать, что для течения ut-= #j/(l + t) линии тока и траектории
совпадают.
4.38.	Напряженность электрического поля в области, занятой движущейся
жидкостью, равна К — (A cos 3>t)/r, где г2 = х\ + х\ и А — константа. Скорость
жидкости задана своими компонентами vt = х\хг -\- х\, v2 = — х\ — х-^х\, v3 = 0.
Найти dh/dt в точке Р (хи х„, х3).
Ответ: dkldt = (— ЗЛ sin Щ'г.
4.39.	Доказать, что для поля скоростей их = х\хг + х\, v2 =¦ — д^ — х^
vs = 0 линии тока будут окружностями.
4.40.	Дан закон движения сплошной среды х± = Хи хг = е' (Х2 + Х3)/2 -|-
+ e-'(Xs —Xs)/2, xs = e1(Xu + Xs)/2— е~* (Х2 — Х3),'2. Доказать, что йц =
= dzqldt при < = 0. Сравнить эти же тензоры при f = 0.5.
4.41.	По данному полю скоростей vx «= xtxt + je^, v2 = — (jtj + х-^Щ, va = 0
найти главные оси и главные значения тензора D в точке РA, 2, 3).
(бо о\	/з/jTo l/VTo о>
0 0 0 I; ai(.= 0	0	1
0 0—Б/	\1/|Лб — 3/ТТО 0У
4.42.	Для поля скоростей задачи 4.41 определить скорость удлинения мате-
л	л	л	л
риального отрезка в направлении v =± (е!—2е2+ 2е3)/3 в точке РA, 2, 3). Ка-
Какова максимальная скорость сдвига в точке Pi
Ответ: d<v)= — 24/9, Ymax== 5.
4.43.	Доказать, что d (dxi!dXj)/dt = и,- kxk -r и, используя это равенство,
получить формулу D.41) непосредственно из D.38).
4.44.	Доказать тождество \l2epqr (vsvrs)Q = Qpvqq + vQQp q — QQvpq, где
Vi — скорость, а И,—вектор вихря скорости. Показать также, что vl-Ujt =
DD2QA
4 45. Доказать, что материальная производная от суммарной завихренности
вычисляется по формуле
— J qcdV = j lel7ftcft + qjVi] dSj,
J

Глава 5
Основные законы механики
сплошной среды
5.1. Сохранение массы. Уравнение неразрывности
Всякий материальный континуум обладает свойством, называе-
называемым массой. Суммарная масса некоторой части сплошной среды,
занимающей в момент t объем пространства V, выражается инте-
интегралом
m = Jp(x, t)dV,	E.1)
v
где р (х, i) — непрерывная функция координат, называемая плот-
плотностью. Закон сохранения массы утверждает, что масса выделенной
части среды остается постоянной и, следовательно, материальная
производная от E.1) равна нулю. Если в формуле D.52) положить
P*ij... (х, 0 = р (х, t), то получим выражение для скорости измене-
изменения массы т
4J([l ^ = 0. ,5.2,
V
Поскольку это равенство верно для произвольного объема V, подин-
тегральное выражение само должно обращаться в нуль, т. е.
^	0, или -^ + p(v.v) = 0.	E.3)
Это уравнение называется уравнением неразрывности (или непре-
непрерывности). Раскрывая оператор материальной производной, его
можно написать в другой равнозначной форме
-|^ + (р^).*=0 или -g^+V.(pv) = 0.	E.4)
В несжимаемой среде плотность массы каждой частицы не за-
зависит от времени, т. е. dp/dt = 0, и уравнение E.3) принимает вид
Vk.k = 0, или divv=0.	E.5)
Поле скорости v (x, /) в несжимаемой среде можно /юэтому пред-
представить выражением
Vi = eijkSk.j, или v = V х s,	E.6)
где функция s (x, t) называется векторным потенциалом \.
Уравнение неразрывности можно записывать а лагранжевой,
или материальной, форме. Для сохранения массы требуется, чтобы

5.2. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
181
выполнялось уравнение
Jpo(X,
, f)dV.
E.7)
Здесь оба интеграла взяты по одним и тем же частицам, т. е. V —
это объем, который теперь занимает среда, заполнявшая в момент
t = 0 объем IV Используя D.1) и D.38), интеграл в правой части
E.7) можно преобразовать следующим образом:
f р0 (X, 0) dV0 = \ р (х (X, t), t) JdV0 = f p (X, 0 JdV0. E.8)
Соотношение E.8) должно иметь силу для произвольно выбран-
выбранного объема Vo, и поэтому
Ро = Р^ •	E.9)
Это означает, что произведение р/ не зависит от времени, так как
объем V произволен, т. е. что
d ' " -0.	E.10)
Уравнение E.10) является лагранжевой дифференциальной фор-
формой уравнения неразрывности.
5.2. Теорема об изменении количества движения.
Уравнения движения. Уравнения равновесия
. На рис. 5.1 изображен движущийся объем сплошной среды V
в момент I. На него действуют массовые силы с плотностью распре-
распределения &,. На каждом бес-
бесконечно малом элементе dS
поверхности, ограничиваю-
ограничивающей рассматриваемый объ-
объем, действует вектор на-
напряжения *р. Во всей об-
области, занятой средой,
определено поле скоростей
vt = dui Idt. Общее коли-
количество движения системы
масс, заполняющих объем
V, определяется интегра-
интегралом
VjdV.	(Б. 11)
Рис. 5.1.
Основываясь на втором законе Ньютона, теорема об измене-
изменении количества движения утверждает, что скорость изменения со

182	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ MFWHHKII СПЛОШНОЙ ГРЕДЫ
временем количества движения некоторой части континуума равна
результирующей сил, действующих на рассматриваемую область *).
Если внутренние силы, действующие между частицами данного
объема (рис. 5.1), подчиняются третьему закону Ньютона о дейст-
действии и противодействии, то теорема об изменении количества движе-
движения для этой системы масс выражается уравнением
V
или	E.12)
J t^rfS -f j рЫУ = -J- f pvriV.
После подстановки ^п) = -СцЩ в первый интеграл и преобра-
преобразования интеграла по поверхности в интеграл по объему (согласно
теореме Гаусса — Остроградского) это уравнение примет вид
V	V
или	E.13)
Распишем материальную производную правой части E.13) и вос-
воспользуемся уравнением неразрывности в форме E.10). Это даст
Подстановка этого выражения в правую часть E.13) и объединение
членов приводят к интегральной форме теоремы об изменении ко-
количества движения:
или	E.15)
\ (VK • S + pb — pv) dV = 0.
x) Теоремы об изменении количества движения и об изменении момента ко-
количества движения (см. стр. 183) фактически уже были использованы в гл. 2.~
Прим. перев.

j.4. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ	183
Так как объем V произволен, само подинтегральное выражение
E.15) должно обращаться в нуль. Полученные таким образом урав-
уравнения
= Р^. или Vx • S + pb = pv	E.16)
называются уравнениями движения.
Для важного случая равновесия, когда отсутствуют ускорения,
' из E.16) сразу получаются уравнения
O/t. i + pb,- = 0, или Vx • 2 + pb = 0.	E,17)
Они называются уравнениями равновесия и широко используются
в механике твердого тела.
5.3. Теорема об изменении момента количества движения
Будем предполагать, что момент количества движения для
сплошной среды равен моменту вектора количества движения от-
относительно какой-либо точки. Так, для части континуума, изоб-
изображенной на рис. 5.1, полный момент количества движения отно-
относительно начала координат по определению равен интегралу
Nt (*) = \ Ъ/kXjpVkdV, или N = \ (х X pv) dV, E.-18)
V	V
где к, — радиус-вектор элемента объема dV. Теорема об изменении
момента количества движения утверждает, что скорость измене-
изменения момента количества движения произвольно выбранной части
континуума относительно любой точки равна главному моменту
(относительно той же точки) массовых и поверхностных сил, дей-
действующих на рассматриваемую область среды (более общая форму-
формулировка этой теоремы дана в задаче 5.35). Для объема V сплош-
сплошной среды можно написать уравнение момента количества движе-
движения в интегральной форме:
J eijkXjtpdS + J eijkxjPbkdV = -4-J e.^-
S	V	V
или	(Б. 19)
J (x X tA) dS + f (x X pb) dV = -J- f (x x pv) dV.
S	V	V
Уравнение E.19) справедливо для таких сред, в которых силы вза-
взаимодействия частиц равны по величине, коллинеарны и противопо-
противоположны по направлению, а распределенные моменты отсутствуют.
Уравнение момента количества движения не всегда представляет
собой новое дифференциальное уравнение. Если в E.19) подставить
4П) = ОркПр и предположить симметрию тензора напряжений,
то уравнение будет удовлетворено тождественно при учете только

184	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
соотношения E.16). Если же симметрия тензора напряжений не
предполагается заранее, то она получается как прямое следствие
уравнения E.19), которое после подстановки tl"* = вркпр сводит-
сводится к виду
f ziikajkdV = О,	или fSadV-O. E.20)
V	v
В силу произвольности объема	V это ведет к равенствам
eijkOjk = 0,	или 2„ = 0, E.21)
откуда видно, что ajk = akj.
5.4. Сохранение энергии. Первый закон термодинамики.
Уравнение энергии
Если изучаются только механические величины, то закон со-
сохранения механической энергии для объема сплошной среды можно
вывести непосредственно из уравнения движения E.16). Чтобы
сделать это, нужно сначала E.16) скалярно умножить на вектор
скорости vt, а затем результат проинтегрировать по объему V.
Таким образом,
J pupidV = J ирщМ + \ pvfrdV.	E.22)
V	V	V
Интеграл
v	v	v
представляет скорость изменения со временем кинетической энер-
энергии К объема V сплошной среды. Заметим, что vpji,-, = (vflj^j —
— Vi рп и, согласно D.19), Vij = Dit + Уи-\ если еще учесть, что
ViPa = 0, то уравнение E.22) можно записать в виде
•§- + J ВцОцпУ = f (ры),, dV + f pvfitdV.	E.24)
V	V	V
Наконец, преобразуя (по теореме Гаусса — Остроградского) первый
интеграл в правой части E.24) в интеграл по поверхности и исполь-
используя тождество ^n) = o^tij, получаем уравнение механической
энергии для сплошной среды
4г + (' DlfsltdV - f v$dS + J pbfrdV.	E.25)
V	S	V
Оно устанавливает связь между скоростью изменения полной
механической энергии континуума, стоящей слева, и мощностью

54 СОХРАНЕНИЕ ЭНЕРГИИ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ	185
(работой за единицу времени) поверхностных и массовых сил,
которая стоит в правой части уравнения. Интеграл в левой части
называется скоростью изменения внутренней механической энер-
энергии (эта величина со знаком минус называется также работой
внутренних поверхностных сил в единицу времени). Тогда E.25)
можно записать короче:
dt + dt - dt '
где —8P!dt и б Wldt — соответственно мощность внутренних и внеш-
внешних сил, а символ б указывает, что соответствующее приращение
в общем случае не является точным дифференциалом какой-либо
функции.
Если, кроме механической, следует учитывать и другие виды
энергии, то закон сохранения энергии должен использоваться
в самой общей своей форме. В такой форме этот закон утверждает,
что скорость изменения со временем кинетической плюс внутренней
энергии равна сумме механической работы внешних сил, совершае-
совершаемой в единицу времени, и притока прочих видов энергии за единицу
времени. Приток энергии может включать в себя тепловую, хими-
химическую, электромагнитную энергию и т. д. В дальнейшем будем
рассматривать только механическую и тепловую энергии, а уравне-
уравнением энергии будет знаменитый первый закон термодинамики.
Для термомеханического континуума скорость изменения внут-
внутренней энергии U обычно представляют интегралом
v
где и называют удельной внутренней энергией. (Символ и для удель-
удельной внутренней энергии столь прочно установился в литературе,
что и мы будем пользоваться им в уравнении энергии этой главы;
вероятность же того, что он будет спутан с символом абсолютной
величины вектора перемещения и,, очень мала.) Пусть вектор сс
характеризует поток тепла через единицу площади в единицу
времени за счет теплопроводности, и пусть г — постоянная тепло-
теплового излучения на единицу массы в единицу времени. Тогда скорость
притока тепла к среде выражается суммой
j	E.28)
S	V
Закон изменения энергии термомеханического континуума запи-
записывается уравнением

186	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
или (при представлении всех величин интегралами)
V
= f fi*VtdS + j pvfodV + J pzdV — j" ctntdS. E.30)
S	V —	V	S
Преобразуя здесь интегралы по поверхности в интегралы по объему
(теорема Гаусса — Остроградского) и снова используя произ-
произвольность объема V, приходим к локальной форме уравнения энер-
энергии:
& С+z
-J- D- +и)-т р^
( )
или	E.31)
TT + T = 7W.-7v-t + l" + ' + '-'-1-
Внутри произвольного малого элемента объема, для которого
справедливо локальное уравнение энергии E.31), должно также
быть выполнено и уравнение количества движения E.16). Возьмем
скалярное произведение уравнения E.16) и вектора скорости:
pvcVi = v?Ojij +pvibl, проделаем с ним некоторые простые пре-
преобразования, а затем вычтем его из E.31). В результате получим
более короткую, но крайне полезною форму записи локального
уравнения энергии
—^*л + *-	E.32)
Это уравнение утверждает, что скорость изменения внутренней
энергии равна сумме 'мощности напряжений плюс приток тепла
к среде.
5.5. Уравнения состояния. Энтропия.
Второй закон термодинамики
Задать состояние термодинамической системы (в нашем случае
континуума) это значит полностью охарактеризовать систему. Это
описание в общем случав определяется несколькими термодинами-
термодинамическими и кинематическими величинами, которые называются па-
параметрами состояния. Если параметры состояния изменяются со
временем, то происходит термодинамический процесс. Параметры
состояния, используемые для характеристики данной системы,
обычно не все независимы: между ними существуют функциональ-
функциональные связи, которые выражаются так называемыми уравнениями
состояния. Любой параметр состояния, который можно предста-
представить однозначной функцией других параметров состояния, назы-
называется функцией состояния.

5.6. НЕРАВЕНСТВО КЛАУЗПУСА - ДЮГЕМА. ДИССИПАТИВНАЯ ФУНКЦИЯ	187
Как было установлено в предыдущем параграфе, первый закон
термодинамихи постулирует взаимный переход механической и
тепловой энергии одной в другую. Соотношение, выражающее
переход тепла и работы в кинетическую и внутреннюю энергии во
время термодинамического процесса, заключено в уравнении энер-
энергии. Однако первый закон оставляет без ответа вопрос, является
ли этот переход обратимым или необратимым. Все реальные про-
процессы необратимы, но обратимые процессы представляют очень
полезную идеализацию, так как во многих ситуациях диссипацию
энергии можно считать пренебрежимо малой. Основной критерий
необратимости содержится во втором законе термодинамики,
который устанавливает некоторые ограничения на производство
энтропии.
Второй закон термодинамики постулирует существование двух
различных функции состояния — абсолютной температуры Т и
энтропии S, свойства которых будут указаны ниже. Абсолютная
температура Т — положительная величина, которая является функ-
функцией только эмпирической температуры 8. Считаем, что энтропия
обладает свойством аддитивности, т. е. что полная энтропия системы
равна сумме энтропии ее частей. В механике сплошной среды вво-
вводят удельную энтропию (на единицу массы), или плотность энтро-
энтропии s, так что полная энтропия S равна интегралу ? psdV. Энтропия
v
системы может меняться либо из-за взаимодействия с окружаю-
окружающей средой, либо за счет изменений, которые происходят внутри
самой системы; поэтому можно написать
ds - dsie) + ds®,	E.33)
где ds — приращение удельной энтропии, ds — приращение,
вызванное взаимодействием с внешней средой, a ds{i)— внутрен-
внутреннее изменение. Приращение ds"'> никогда не бывает отрицатель-
отрицательным. Оно равно нулю при обратимых процессах и положительно при
необратимых. Таким образом,
ds® > 0 (при необратимых процессах),	E.34)
ds® = 0 (при обратимых процессах).	E.35)
Если при обратимом процессе обозначить приток тепла на единицу
массы системы через dq^, то изменение ds{e) выразится формулой
dsie) = dq{R)/T (при обратимых процессах).	E.36)
5.6. Неравенство Клаузиуса — Дюгема.
Диссипативная функция
Согласно второму закону термодинамики, скорость изменения
полной энтропии S сплошной среды, занимающей объем V, никогда
не может быть меньше, чем сумма притока энтропии через границу

188	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
объема и энтропии, производимой внутри объема внешними источ-
источниками. Математически этот закон изменения энтропии выражается
в интегральной форме в виде неравенства Клаузиуса — Дюгема
-±- J psdV > J pedV _ j -2p- dS,	E.37)
V	V	S
где е — мощность локальных внешних источников энтропии, отне-
отнесенная к единице массы. Равенство в формуле E.37) осуществля-
осуществляется для обратимых процессов; неравенство относится к процессам
необратимым.
Неравенство Клаузиуса — Дюгема верно при произвольном
выборе объема V, так что, преобразуя в формуле E.37) интеграл по
поверхности в интеграл по объему, прежним методом приходим
к локальной форме соотношения для скорости внутреннего произ-
производства энтропии у; отнесенной к единице массы:
»
Это неравенство должно удовлетворяться при каждом процессе
и при любом выборе параметров состояния. По этой причине оно
играет важную роль, накладывая известные ограничения на так
называемые определяющие уравнения, которые будут обсуждать-
обсуждаться в следующем параграфе.
В механике сплошной среды часто предполагают (основываясь
на статистической механике необратимых процессов), что тензор
напряжений можно разложить на две части:
<$,	E.39)
где о1ср — тензор консервативных напряжений, a ojf** — тензор
диссипативных напряжений. При этом предположении уравнение
энергии E.32) можно переписать с учетом D.25) в виде
<&«, + -$l-	<5-40>
В этом уравнении A/р) о^ъц представляет собой скорость дисси-
диссипации энергии в единице массы напряжениями г), a dqldt — ско-
скорость притока тепла к среде на единицу массы. Если в среде проис-
х) Так поступают, например, при изучении движения вязкой жидкости, ког-
когда напряжения представляют в виде суммы давления и вязких напряжений.
В теории пластичности, наоборот, раскладывают деформации на «обратимые»
упругие е'е' и «необратимые» пластические е'Р) и скорость диссипации энергии
представляют в виде A/р)о,уе|-Р); см., например: Седов Л. И., Механика сплош-
сплошной среды, т. II, гл. X, § 3, «Наука», изд. 2, М., 1973.— Прим. ред.

5.7. ОПРЕДЕЛЯЮЩИЕ УРАВНЕНИЯ	189
ходит обратимый процесс, то диссипации энергии не будет; к то-
тому же dqldt = dq{R)/dt, так что, комбинируя E 40) и E.36), получаем
-?—НЧ + г-J-	<*¦«>
Для необратимых процессов, которые описываются уравнением
E.40), скорость производства энтропии можно найти из уравнения
E.41) '>. Таким образом,
4—r-f-+>«V	<*¦«>
Скаляр a'f'e,,- называется диссипативной функцией. Для необра-
необратимых адиабатических процессов (dg — 0), согласно второму за-
закону термодинамики, ds/dt>0. Тогда из E.42) следует, что дисси-
пативная функция является положительно определенной, так как
и р, и Т всегда положительны.
5.7. Определяющие уравнения.
Термомеханический и механический континуумы
В предыдущих параграфах этой главы было выведено несколько
уравнений, которые должны выполняться для Ьсех процессов или
движений, какие могут происходить в сплошной среде. Для термо-
термомеханической среды, где механические и тепловые явления взаимо-
взаимосвязаны, основными уравнениями будут следующие:
а) уравнение неразрывности E.4)
-§-+(р»*Ь=0, или -§- + V.(pv)=0; E.43)
б)	уравнения движения E.16)
аШ + Pbi = Р^> или Vx • 2 + pb = pv;	E.44)
в)	уравнение энергии E.32)
а1р{1—±с,с+г, или ^- = 2.S:D^pV.c+*.
E.45)
При предположении, что массовые силы Ьс и распределенные
источники тепла г заданы, уравнения E.43), E.44) и E.45) состав-
составляют систему пяти независимых уравнений, содержащих четыр-
четырнадцать неизвестных функций координат и времени. Неизвестными
являются: плотность р, три компоненты скорости vL (или, что равно-
') При этом делается существенное предположение, что E.41) выполняется
также и при необратимых процессах. В термодинамике E.41) иосит название
тождества Гиббса,— Прим. ред.

190	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
сильно, компоненты перемещения и,), шесть независимых компо-
компонент напряжения а,/, три компоненты вектора потока тепла ct
и плотность внутренней энергии и. В дополнение к этому должно
быть выполнено неравенство Клаузиуса — Дюгема E.38)
¦5--—f("H>°-	<5-46)
предписывающее положительность производства энтропии. Оно до-
добавляет еще две неизвестные — плотность энтропии s и абсолют-
абсолютную температуру Т. Значит, чтобы сделать систему замкнутой,
нужно' изыскать дополнительно еще одиннадцать уравнений. Шесть
из них известны как определяющие уравнения, которые характери-
характеризуют частные физические свойства изучаемой среды. Из остальных
пяти три будут соотношениями для задания закона теплопровод-
теплопроводности, а два —термодинамическими уравнениями состояния; напри-
например, калорическое уравнение состояния и уравнение для энтропии.
Характерная формулировка задачи для термомеханического кон-
континуума будет дана в следующей главе.
Следует отметить, что назначение определяющих уравнений
состоит в том, чтобы установить математические соотношения между
статическими, кинематическими и термодинамическими парамет-
параметрами, описывающими поведение материала при наличии механи-
механических и термодинамических воздействий. Так как реальные среды
реагируют на различные нагрузки крайне сложным образом, опре-
определяющие уравнения не пытаются отразить все наблюдаемые яв-
явления, связанные с конкретным материалом, а скорее служат для
того, чтобы ввести некоторые идеализированные среды, такие, на-
например, как идеально упругое тело или идеальная жидкость. Такие
идеализации, или, как они иногда называются, модели сред, очень
полезны тем, что они разумно отражают поведение реальных сред
в определенном интервале нагрузок и температур.
Во многих ситуациях взаимодействием механических и термо-
термодинамических процессов можно пренебречь; исследованием такого
типа является, например, теория несвязанной термоупругости.
В этом случае чисто механические процессы описываются уравне-
уравнениями E.43) и E.44). Система уравнений, образованная E.43)
и E.44), состоит из четырех уравнений с десятью неизвестными.
Нужны еще шесть определяющих уравнений, чтобы сделать систему
замкнутой. В несвязанной теории, где не учитывается взаимодей-
взаимодействие механических и тепловых процессов, определяющие уравнения
содержат только динамические (напряжения) и кинематические (ско-
(скорости, перемещения, деформации) параметры и часто представляют
собой соотношения между напряжениями и деформациями. Кроме то-
того, в такой теории поле температур обычно считается известным или,
быть может, задача теплопроводности решается отдельно и иезавн-

ЗАДАЧИ-С РЕШЕНИЯМИ	•9|
симо от механической задачи. При изотермических процессах темпе-
температура предполагается постоянной и задача является чисто меха-
механической.
ЗАДАЧИ С РЕШЕНИЯМИ
Уравнение неразрывности (§ 5.1)
5.1.	В гл. 4 описано безвихревое движение, для которого вектор
вихря скорости тождественно равен нулю. Найти вид уравнения
неразрывности для такого движения.
Согласно D.29), rot v = 0, если q = 0, и, следовательно, v становится гради-
градиентом скалярного поля ф (*(-, t); см. задачу 1.50. Таким образом, D; = ф,; и урав-
уравнение неразрывности E.3) имеет вид dp/dt + рф,^ = 0, или dp/dt + ру'2Ф = 0.
5.2.	Пусть функция Рц... (х, t) представляет любую скалярную,
векторную или тензорную величину, отнесенную к единице массы
сплошной среды, так что Р*;-... (х, t) = pP'iJ... (x, t). Показать,
что
V
По формуле D.52)
"It
9 dt ^ '¦'••¦ 1 dt + P <Э*,
v u
так как, согласно E.3), dp/dt -f- pvk k = 0.
5.3.	Доказать, что лагранжева форма d(pJ)/dt = 0 уравнения
неразрывности и эйлерова его форма dp/dt + pvk,k = 0 эквива*
лентны.
Выполним дифференцирование d (pJ)idt = (dp/dt) J + pdJ/dt = 0 и восполь-
воспользуемся результатом задач» 4.28 dJ/dt = Jvk k. Это дает d (pJ)ldt — J (dp/dt +
+ Pvk,k) = °-
5.4.	Показать, что поле скоростей v( = Axjr3, где jc,-jc,- == га
и А — произвольная константа, удовлетворяет уравнению нераз-
неразрывности несжимаемой жидкости.
Согласно E.5),,для несжимаемой жидкости ьк^ = 0. В нашем случае
следовательно, vkk = C — 3) [г3 = 0 и уравнение неразрывности несжимаемой
жидкости удовлетворяется.

192	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ МЕХ1НИКИ СПЛОШНОЙ.СРЕДЫ
5.5. Для поля скоростей с,- = xj{\ +1) показать, что рхгх2х3 =
Л\ХХ
В этом случае vk k = 3/A + г) и-, проинтегрировав E.3), получаем In p =
= — In A + fK -f- In С, где С — постоянная интегрирования. Так как р = р0" при
t = О, это равенство принимает вид р = ро/A + О3- Далее, интегрируя урав-
уравнения dxt/xi = dt/(\ + t) (суммирование no i не проводится), находим х;
*/(! + 0. откуда	^XX
Количество движения и момент количества движения.
Уравнения движения (§ 5.2—5.3)
5.6.	Непосредственным расписыванием обеих частей доказать
справедливость тождества е^а^е,- = 2^, использованного в фор-
формулах E.20) и E.21).
Согласно A.15) и B.8),
2* = ацв!- X ех + а18е! X е2 + о-13е! X е3 + • • • + 03зез X е3 =
/S	/S	Л
= (а2з — азг) ei + (o3i — Oi3) es + (а12 — а21) е3.
Раскрывая VijiPjk, приходим к тем же выражениям: а„3 —о3., при I = 1, о31 —
— сг13 при г = 2, <7i2 — O2i при / = 3.
5.7.	Пусть на континуум действуют распределенные массовые
моменты (т, на единицу объема). Доказать, что уравнения E.16)
остаются в силе, но тензор напряжений нельзя больше считать
симметричным.
Уравнения E.16) получены из условия равновеечя сил, поэтому наличие
моментов на них не влияет. Однако в E.19) появляются дополнительные члены,
так что
-д- J %kxiPvkdV = J e^Xjt^dS + J (e(/ft*/pbft + пц) dV,
Это можно свести к равенству j (е^-^Оу^ +«,) dV = 0 (см.задачу 2.9), и вследствие
произвольности объема V в данном случае будет выполняться соотношение
f«y*°/ft + т> = °-
5.8.	Теорема об изменении количества движения в дифферен-
дифференциальной форме (так называемой локальной форме, или «в малом»)
выражается уравнением д (pvc)/dt = pb( + (crl7 —рс(f;),/. До-
Доказать, что уравнения движения E.16) следуют из этого уравнения.
Выполняя указанное дифференцирование и перегруппировывая члены, по-
получаем
vi (dp/dt + p jVj + pvjj + p (dvi/dt + vjo^ = ph + ailf.
Первый член в левой части равен нулю, согласно E.4), а второй член равен рЯ{.
Таким образом, pa,- = pfc,- + cfy -, что совпадает с E.16).

ЗАДАЧИ С РЕШЕНИЯМИ	193
5.9. Показать, каким образом уравнение E.19) сводится к
форме E.20).
Подставим в E.19) для t^ выражение о кпр и применим теорему Гаусса —
Остроградского A.157) к получившемуся интегралу по поверхности:
j	dV = IT 18''ftp {x'Vk) dv'
Используя результат задачи 5.2 и выполняя дифференцирование, приводим
это уравнение к виду
xi l°Pk,p + Pfcft - №l - 9vivk) dV = 0.
Сумма членов в квадратных скобках равна нулю в силу E.16); кроме того, х-1ф —
= 6(-р и ^ijkVjVk = 0, так что окончательно получаем J 6yfta-fc dV = 0.
5.10.	При движении абсолютно твердого тела с неподвижной
точкой поле скоростей имеет вид vL = е^соуХд. Доказать, что для
такого движения уравнение E.19) сводится к известному уравнению
моментов динамики твердого тела.
Огева в уравнении E.19) стоит полный момент Mi всех поверхностных и массо-
массовых сил относительно начала отсчета. При ч(- = ei/ft@;Xft это уравнение пре-
преобразуется следующим образом:
Mi = -Jf J tiikXlpekptPiXiW = -?- \ wpP (M/e ~ 6'«V xixodV =
где /,-p = J p D>ipxqxq — xpXi)dV — тензор моментов инерции.
Энергия. Энтропия. Диссипативная функция (§ 5.4—5.6)
5.11.	Доказать, что для движения абсолютно твердого тела
с полем скоростей vt = е^дхо^ интеграл кинетической энергии
E.23) сводится к аналогичному выражению из динамики твердого
тела.
Из E.23) находим
К = J P ~Т~ dV = T J
1
--И'
V
2
v
или в символической записи К = (ш • I ¦ ш)/2.
7 Дж Мейз

194	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
5.12.	В некоторой точке сплошной среды даны тензоры скоростей
деформации и напряжений
1 6 4ч	/4 О—
Dtj = F 3 2 1 и аа = I 0-2
\4 2 5/	\— 1 7
Определить в этой точке величину к мощности напряжений DaGif.
Умножая каждый элемент Dy на соответствующий элемент тензора Оц и
складывая, получаем ^ = 4 + О — 4 + 0 — 6+14 — 4+14 +40 =58.
5.13.	Пусть аи = —рЬи\ показать, что мощность напряжений
можно представить выражением Д/т^ = -^—щ-.
По D.19) Dij — V(j— Уц, а так как Vip-ц = 0, то ОцОц = о,-;- (— рб//)=
= —ро,-;. Из уравнения неразрывности E.3) мы имеем f,-,-=—A/р) (dp/dQ,
Таким образом, окончательно получаем ОуОу = (р/р) (dpfdt) при ау = — рбу.
5.14. Найти вид уравнения энергии при условии, что ст„- =
= (— р + №Dkk) btj + 2[i*Z)i;-, а теплопроводность подчиняется зако-
закону Фурье С[ = — kT,t.
Из E.32)
Р -?- = (— р +
_ р Ф
где ID и Пр — соответственно первый и второй инварианты тензора скоростей
деформации.
5.15.	Пусть с% = —рб„. Написать уравнение для скорости
изменения удельной энтропии при обратимом термодинамическом
процессе.
В этом случае о,-/ = а|?' и уравнение E.41) с учетом результата задачи
..„¦„,¦.§—*—?~з-.
5.16.	Задана диссипативная часть тензора напряжений off =
= $DikDkr Найти диссипативную функцию и выразить ее через
инварианты тензора скоростей деформации D.
По формуле D.25) стЯр,-- = f>DikDkjDil; что является следом матрицы D3
(см. § 1.15) и может быть записано через главные значения D(I), DB), DC1.
Согласно A.138), след матрицы равен
DijDikDkj = D^j + Db{2) + Dp} = (D(I) + DB) + DC)K —
- 3 (D(I) + DB) + DC)) (D(I)DB) + DB)DC) + OC)D(I)) + 3D(I)DB)DC).
Отсюда полечим оФуеи = P [ID — 3IDIID + 3I1IDI.

ЗАДАЧИ С РЕШЕНИЯМИ
195
Определяющие уравнения (§ 5.7)
5.17. Пусть определяющие уравнения имеют вид аи- =
= Kr,pqDpq. Доказать, что из-за симметрии тензоров напряжений
и скоростей деформации тензор четвертого ранга Кцрц имеет не бо-
более 36 независимых компонент. Записать эти компоненты в виде
матрицы шестого порядка.
Так как ац = о/(-, то Kijpq = Kjipq; кроме того, Kcjpq = КцЧР, поскольку
Dij=Dji. Подобно внешнему произведению двух симметричных тензоров Ац и В-ц,
имеющих по шесть независимых компонент, тензор Kijpq будет иметь не более
36 различных компонент.
Обычно принято располагать компоненты КцрЧ следующим образом:
K2i
к.
^1182
^2222
^3322
Л328
^3122
/Cl228
Лизз
Л 22 33
Л"ззЗЗ
^2333
Л"з133
^1233
К1183
A2223
Л"з383
Аазаз
Л"з183
Kl223
Л"пз1
Л'ггз!
^3331
^8331
^3131
^1831
КШ2
^2212
^3318
^2318
К3И2
^1218
2311
5.18. Если предположить, что среда, имеющая определяющие
уравнения стG = KijpqDpq задачи 5.17, является изотропной,
так что тензор Kijpq имеет одинаковые компоненты в любой орто-
ортогональной декартовой системе коорди-
координат, то циклическим переименованием
осей координат 36 независимых компо-
компонент тензора Kvm можно сократить до
двух. Показать это.
Координатные направления можно переобо-
переобозначить шестью различными способами (рис. 5.2).
Для изотропии требуется, чтобы Kuss = Кц3э =
= ^2233 == ^2211 = КззИ = "^3322 И А1218 =
== ^1313 =: К2323 ~ КяЛЗЛ == "\3131 == ^3232- Эт° Ве"
дет к тому, что от 36 компонент остается 26.
Соответствующими отражениями и поворотами
осей координат эти 26 компонент в случае изо-
изотропии могут быть сведены к двум.	Рис. 5.2.
5.19. Для изотропной среды компоненты тензора KijPq могут
быть представлены в виде КцРп = Я,*б4убр(? + [а* F,-рб/,, -f 6,-,6/p). Исполь-
Использовать это выражение и записать определяющие уравнения Сц =
р
через К* и ц*.
= KijPQDpq
5.20. Доказать, что определяющие уравнения задачи 5.19
можно разбить на две группы аи = {ЗК* + 2jx*)DH и s,-y = 2\i*Djj,

196	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
где s,- и Dij — девиаторы тензоров напряжений и скоростей дефор-
деформации соответственно.
Подставим щ = S[j + f)ijOkf./3 и D,-/ = D|-;. + 6(-;Dftfc/3 в выражение о,у =
= X*6,-/Dftft + 2|.i*Di/ задачи 5.19. Получим следующее равенство: s(-/ -f- б^-от^/З =
= K*bijDkk + 2ц* (D|7 + 6,/Dfcft/3). Из него видно, что если i Ф j, то s,-/ = 2/д,*^
и, следовательно, Okk = C^* + 2|.i*) Dkk-
Смешанные задачи
5.21. Доказать, что -щ-[-^-) = (et/*afc./ + <7/»г./)/Р, где р —
плотность, а,- — ускорение и ^ — вектор завихренности.
Непосредственным дифференцированием найдем —=т— (—^—) = —	^т~ •
Но qi = Е^о^ r- + qjvt ¦ — qfi.j(ctA. задачу 4.32), а из уравнения неразрывности
E.3) следует, что р= —pt)f,-. Окончательно получаем
)
5.22.	Дано плоское течение несжимаемой жидкости v1 =
= A(x2i — xt)/r\ v2 = ABx1x2)/ri, v3 = 0, где г2 = х\ + х\. Доказать,
что такое поле скоростей удовлетворяет уравнению неразрывности.
Для несжимаемой жидкости уравнение неразрывности имеет вид E.5) vi( =
= 0. В данном случае D, [ = А [— 4хх (д^ — Х$Iгв + 2x1!ri\ и v2 2 = A [2xi/r* —
— Bxixf//-6]. Складывая, получаем г.'[ , + v22 = 0.
5.23.	Доказать, что поле скоростей задачи 5.22 является без-
безвихревым.
Для безвихревого течения в соответствии с D.29) необходимо выполнение
условия rot v = 0. Проверяем и видим, что в данном случае
rot v =
д/дх.
О
4ха (х\ - х|)/гв| е3 = 0.
5.24. Имеется плоский поток несжимаемой жидкости, в кото-
котором ох = —Ах2/г2, где г2 = х\ + х\. Найти во всем потоке ком-
компоненту v2, если v2 = 0 при xY = 0 для всех значений х2. Пока-
Показать, что движение безвихревое, а линии тока — окружности.
Уравнение неразрывности для несжимаемой жидкости E.5) v(i — 0 в данном
случае дает vl{ = — v2 2 = 2AxiXs/r*. Интегрируя его по ха и налагая упомяну-
упомянутые условия на D2, находим Vi = Ах\/г%.

ЗАДАЧИ С РЕШЕНИЯМИ	197
Для безвихревого движения нужно, чтобы rot v = 0. У нас
rot v = А [(*? - х$)!г* + (-*?+ л!)/'4] «з = 0.
В задаче 4.7 выведены уравнения линий тока dxi/vi = dxz/vz. Для данного
поля скоростей они имеют вид X\dx\ + Xidx% = 0, что после интегрирования дает
уравнения окружностей xf + xf = const.
5.25.	Определяющие уравнения для некоторой среды имеют
вид at/ = (— р + h*Dhk) 6i; + 2\i*Di/, где К* и [а* — постоянные.
Написать уравнения движения, выраженные через вектор ско-
скорости v(.
Уравнения движения E.16) ру,- = pb(- + а» у в этом случае имеют форму
р4- = рб,- — /71 6,-/ + №Dkkl&tj + 2ц* ?>,7>/. По определению 2D,y = i^. +
+ »/iiK?aK 4To'.Dftfc =» Dftft, 2Diy/ = i>u/ +' «/i(/. Поэтому
py,- = pbi — Pl + (Л* + ц*) оЛ,7 + p*viJf.
Это уравнение можно записать в символических обозначениях
р; = pb — Vp + (Я* + ц*) V (V ¦ v) + n*V2v.
5.26.	Вычислить материальную скорость изменения кинети-
кинетической энергии среды, занимающей объем V, и объяснить физиче-
физический смысл полученных интегралов.
Согласно E.23), dKldt = I pvflidV, Работа внешних поверхностных сил (в
v
единицу времени) равна \ Vitf^dS, что можно записать иначе: I ViCijnjdS. При-
S	S
S	S
меним к этому интегралу теорему Гаусса—Остроградского A.157) и воспользу-
воспользуемся уравнением движения E.16) Тогда I V(BijnjdS = I aijti dV + \ р (уfit —
S	v	V
— biVfidV. Отсюда получим
-J- = { pbcvidv - f o^jdV + J vtfidS.
V	V	S
Интегралы этой суммы представляют мощность массовых сил, внутренних поверх-
поверхностных сил и внешних поверхностных сил соответственно.
5.27. В несжимаемой среде, для которой off = к*Окк6^ +
+ 2|j,*Dl7, происходит безвихревое движение с потенциалом ско-
скоростей ф, так что v = grad ср. Найти диссипативную функцию
ofkh
Так как для несжимаемой жидкости D^k = vkk = 0, то в данном случае
°#Ч/ = tf>Dt, = (PDufin + 2ц'О(/) Dq = 2ц*О?/ЬG. Кроме того, v, = q>,,t и.
следовательно, скаляр D^D^ = ф,7ф ,-., а поэтому о^'О,-- = 2|.1*ф (-.фг
Из-за того что среда несжимаемая, а движение безвихревое, выполняются
соотношения ф(-( = 0 и 2фGф,7 = (ф ,-ф ,) .. = V2 (УфJ,

198	Гл. 5. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
Интересно отметить также, что
V* (ф2) = (фф)-й// = 2 (epiK//q> + 4Ф G/ф(- + <р_„<р#/;. + 2фш,уф>?/).
Это выражение при ф н = 0 сводится к 4ф ,-ф ,-. Тогда окончательно находим
ojf kl} = \i*S/2 (УфJ = |i*V* (ф2)/2.
5.28.	Для среды, в которой ау = — рб,,-, вводится понятие
удельной энтальпии h — и + р/р. Доказать, что, используя это
понятие, можно записать уравнение энергии в виде h — pip + Ts.
Уравнение энергии E.41) при данном законе напряжений имеет вид и =
= —p&[jD[-/p-{-Ts. Воспользуемся результатом задачи 5.13 и определением ft.
Тогда и — ft — р/р — рр/р2 = — рр/р2 + Ts. Сокращая одинаковые члены, нахо-
находим ft = р/р + Ts.
5.29.	Пусть среда задачи 5.25' движется как несжимаемая.
Написать уравнения движения, выраженные через вектор завих-
завихренности q при условии отсутствия массовых сил и постоянства
плотности.
В случае несжимаемости v • v = 0. При b = 0 уравнение движения задачи
5.25 примет форму рщ = —р,- + ц*"*//- Умножая векторно оператор у на это
уравнение, при р = const получаем epqiviq = — epqip.iq/p + _(^*/p) epqi \jjq. Но
epqiP.iq~®' ПОЭТОМУ> учитывая D.29), можно написать qp — (\i*lp) q^-, или
в символических обозначениях dq/dt = (|.i*/p) V2q.
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
5.30.	Доказать, что для вектора вихря скорости Q верна формула ~зг~(-~) =
_ Q (V ¦ v) J_ da
р ^ р dt
5.31.	Доказать, что течение с полем скоростей i^ = — 2x1x2x3,'ri, v2 = (х2{ —
— х^Хз/г*, v3 = x^r2, где гг = х\-\-х\, удовлетворяет условию несжимаемости.
Будет ли это течение безвихревым?
5.32.	Уравнение неразрывности в декартовых координатах х, у, г выглядит
так-
dpldt + д (pvx)/dx + д (риу)/ду + д (pvz)/dz = 0.
Доказать, что в цилиндрических координатах /•, 6, г оно примет вид
г (dpldt) + д (rpvr)ldr + д (руе)/<36 + /• (д (риг)/дг) = 0.
5.33.	Доказать, что течение с полем скоростей vr = A —г2) cos 6/г2, 1>е =
= A + г2) sinB/r2, vz = 0 удовлетворяет уравнению неразрывности в цилиндри-
цилиндрических координатах, если плотность р — константа.
5.34.	Доказать, что для любой скалярной, векторной или тензорной величи-
величины Рц (х, f) имеет место равенство
$ pU-°pqn<idS = J [°рЛ...л + рР'7- (»р - bP)] dV'

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ	19J
5.35.	Если в среде, кроме массовых сил Ь, действуют еще массовые моменты
h (на единицу массы), а, кроме напряжений t(n), еще пары напряжений g(n), то
уравнение моментов количества движения может быть записано в виде
~ [ р (т + х X v) dV = [ (h + x X b) dV + [ (g(n) + x X t(n)) dS,
di I	i	S
где tn — распределенный момент количества движения на единицу массы. Дока-
зать, что если n -G = g(n), то локальная форма этого уравнения такова: pdmldt =
= h + V • G + 2а.
5.36.	Среда задана своими определяющими уравнениями ац = — рб,/ +
+ PDiy + aDikPkj- Показать, что Оц = 3 (—р — 2а IID /3). Допустить при этом
несжимаемость Da = 0.
5.37.	Доказать, что для среды, в которой о,-; =—фц, соотношение E.41)
принимает вид du — Tds — pdv. (В этой задаче использовано обозначение v =
= 1/р — удельный объем.)
i i	do
5.38.	Пусть Tdsldt =	— = -гг- Удельной свободной энергией по"опре-
делению называется величина V = и — Ts. Доказать, что уравнение энергии
можно записать в виде pdWIdt + psdT/dt = OijDij.
5.39.	Имеется термомеханический континуум с определяющими уравне-
уравнениями
где Го — температура начального состояния. Доказать, что е^ == За (Г — Го),
если akk = 0.

Глава 6
Линейная теория упругости
6.1. Обобщенный закон Гуна. Функция энергии деформации
В классической линейной теории упругости предполагается,
что сами смещения и их градиенты настолько малы, что можно не
делать различия между их лагранжевым и эйлеровым представ-
представлениями. В соответствии с этим выражение тензора линейных де-
деформаций через вектор перемещения ы,- может быть записано в сле-
следующих эквивалентных формах:
F.1)
или
L = Е = 4" <uVx + VxU) = ~T(uVx + VxU) = -Т(uV + Vu)-
В дальнейшем будем, кроме того, пренебрегать тепловыми эффек-
эффектами, сопровождающими деформирование, если специально не ого-
оговаривается противное.
Для линейного упругого тела определяющие уравнения связы-
связывают тензор напряжений и тензор деформаций соотношением
ИЛИ 2 •= С: Е,	F.2)
которое называется обобщенным законом Гука. Коэффициенты это-
этого соотношения образуют тензор упругих констант Сцьп, кото-
который имеет 81 компоненту. Однако вследствие симметрии обоих
тензоров — и напряжений и деформаций — различных упругих
констант имеется не более 36. При записи закона Гука через эти
36 коэффициентов двойные индексы у компонент тензоров напряже-
напряжений и деформаций часто заменяют одинарными индексами, кото-
которые меняются от 1 до 6. В таких обозначениях
и	р - е 2е - 2е — f
cii — 1) ^23 —"" 32 — 4*
е2, 2еи = 2е31 = е8>	F.4)
е22
2е,„ = 2е
12 — ¦6t21

61. ОБОБЩЕННЫЙ ЗАКОН ГУКЛ ФУНКЦИЯ ЭНЕРГИИ ДЕФОРМАЦИИ	201
Закон Гука можно записать в виде
<Ук = Скмем (/С, М = 1,2, 3,4, 5,6),	F.5)
где 36 упругих констант обозначены теперь Скм, а заглавные
латинские буквы использованы в качестве индексов для того, что-
чтобы подчеркнуть, что эти индексы меняются от 1 до 6.
Если пренебречь тепловыми эффектами, то уравнение E.32)
примет вид
§ °° o	F-6)
Внутренняя энергия в этом случае оказывается чисто механической
величиной, которая называется энергией деформации (на единицу
массы). Из уравнения F.6) следует, что
du = — atldBih	F.7)
Если и считать функцией девяти компонент деформации и = и (е{/),
то дифференциал ее равен
du = ^- dec,:	F.8)
Сравнивая F.7) и F.8), замечаем, что •>
Введем функцию и*, такую, что
u* = pu;	F.10)
она называется плотностью энергии деформации (на единицу объе-
объема). В теории малых деформаций р в F.10) можно считать постоян-
постоянной, поэтому функция и* обладает следующим свойством:
<г1/ = р *!_=*?_.	F.11)
Состояние, в котором энергия деформации равна нулю, можно
выбрать произвольно. И так как напряжения должны обращаться
!) Формулы F.9) для упругого тела верны также и при учете тепловых эф-
эффектов. При этом вместо F.6) имеем
2
р
и поэтому
du = — Gi/dEij + dq, dq = Tds,
1	ди (е,7, s)	du (etJ, s)
-а,;=¦ /=-
р '' d?{j '	ds
см. также задачу 6.24, в которой показано, что в термоупругом теле всегда оц
df/dEjj, s=—df/dT, где f (ец,Т)—свободная энергия.— Прим. ред.

202
Гл 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
в нуль одновременно с деформациями, простейшим видом выраже-
выражения энергии деформации, обеспечивающим линейную связь между
напряжениями и деформациями, является квадратичная форма
U* = V2 CijkmtijEkrn.	F.1 2)
Принимая во внимание закон Гука F.2), это выражение можно
записать так:
u* = 1/totletl, или ы* = 7«2:Е.	F.13)
В обозначениях с одним индексом квадратичная форма F.12)
имеет вид
«* = 1/2Скл1екел.,	F.14)
причем Скм — Смк- Еслиф нкцня энергии деформации существует,
то вследствие симметрии Скм число независимых упругих констант
будет не более 21.
6.2. Изотропные и анизотропные среды.
Симметрия упругих свойств
Если упругие свойства среды не зависят от выбора системы коор-
координат, использованной для их описания, то такую упругую среду
называют изотропной. Среда, которая не является изотропной, на-
называется анизотропной. Упругие свойства твердого тела, подчиняю-
подчиняющегося закону Гука, выражены коэффициентами Скм, поэтому
в общем случае анизотропное тело имеет следующую матрицу
упругих констант:
12
3
с„
С2
С
34
с,
м
С35
слч
52
с16
36
м
30
F.15)
Если существует функция энергии деформации, то Скм
н 36 констант матрицы F.15) сводятся к 21.
Пусть в некоторой точке существует плоскость симметрии упру-
упругих свойств, т. е. упругие константы имеют одинаковые значения для
любой пары систем координат, которые получены одна из другой
отражением относительно указанной плоскости. Оси таких систем
координат называются «направлениями эквивалентных упругих
свойств». Если плоскость хгх2 — плоскость симметрии упругих
свойств (короче — плоскость упругой симметрии), то константы Скм
инвариантны относительно преобразования координат
М - Ху, Х2=Х2, А-з = — X-i,	F.16)

С 2. ИЗОТРОПНЫЕ И АНИЗОТРОПНЫЕ СРЕДЫ
203
которое показано на рис. 6.1.
Это преобразование описы-
описывается матрицей
 О О"
0 1 0 . F.17)
_0 0 — 1.
Подставляя компоненты мат-
матрицы F.17) в формулы B.27) и
C.78) преобразования тензо-
тензоров напряжений и деформа-
деформаций, находим, что матрица	Рис. 6.1.
упругих констант для среды,
обладающей симметрией относительно плоскости ххх^, имеет вид
12
W3
м
0
о
о
о
С3;
0
0
0
0
0
с44
см
о
о
о
о
'65
о
г
С2
^30
о
о
^06
F.18)
Если существует функция энергии деформации, то из 20 ненулевых
членов этой матрицы независимы только 13.
Если среда обладает тремя взаимно перпендикулярными плос-
плоскостями симметрии, то она называется ортотропной, а матрица уп-
упругих констант (в системе координат, в которой координатными
плоскостями являются плоскости симметрии) имеет форму
[Скм] =
Си
с21
0
0
0
С12
22
^32
0
0
0
Чз
^23
Сзз
0
0
0
0
0
0
с44
0
0
0
0
0
0
с55
0
0
0
0
0
0
с
F.19)
Здесь независимых постоянных 12 (или 9, если Скм — СМк).
Говорят, что в некоторой точке существует ось симметрии упру-
упругих свойств порядка Af, если существует набор направлений экви-
эквивалентных упругих свойств, которые могут быть совмещены поворо-
поворотом около оси на угол 2n/N. Некоторые случаи осевой и плоской
•симметрии эквивалентны.

204
Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
6.3. Изотропные среды. Упругие постоянные
Тела, у которых упругие свойства одинаковы по всем направле-
направлениям, обладают полной симметрией и называются изотропными.
В этом случае любая плоскость и любая ось являются плоскостью
и осью симметрии. Для изотропных сред число независимых упру-
упругих постоянных сводится к двум, и их матрица симметрична незави-
независимо от существования функции энергии деформации. Выбирая
в качестве двух независимых констант известные постоянные Ламе
Я, и ц, напишем матрицу F.19) для изотропной упругой среды:
[СКм] =
- 2ц
Я,
Я,
0
0
0
я,
Я, + 2ц
Я,
0
0
0
я.
Я, + 2и
0
0
0
0
0
. 0
0
0
0
0
0
0
0
0
0
0
0
0
и
F.20)
Закон Гука F.2) для изотропного тела через коэффициенты Я,
и ц записывается равенством
ог?/ =
+ 2\хеч, или 2 = Me + 2цЕ,
F.21)
где е = ekk = IE. Это соотношение нетрудно обратить и выразить
деформации через напряжения:
— к
или Е =
— X
2ц
2ц)
F.22)
где 0 = akk — In ¦— обозначение, по традиции используемое в тео-
теории упругости для первого инварианта тензора напряжений.
При простом одноосном растяжении в направлении оси хх можно
ввести технические упругие модули Е и v, которые служат коэффи-
коэффициентами в соотношениях ап = ?еи и е22 = е33 = —veu. Постоян-
Постоянная Е называется модулем Юнга, a v — коэффициентом Пуассона.
Через эти упругие постоянные закон Гука для изотропного тела
записывается следующим образом:
или, в обращенной форме,
_ 1 + v	v с
Ei	Ci
или s =
или Е = ¦
F.23)
:--^-10. F.24)

6.4. ПОСТАНОВКА СТАТИЧЕСКИХ И ДИНАМИЧЕСКИХ ЗАДАЧ	205
При изучении состояния равномерного гидростатического сжа-
сжатия вводят модуль объемного сжатия
или *=» + *.	F.25)
который связывает давление с величиной кубического расширения
при нагрузке такого типа. В случае так называемого состояния
чистого сдвига модуль сдвига G связывает касательные компоненты
напряжения и деформации. Коэффициент G фактически равен [х;
легко установить его связь с другими модулями:
|* = е = -2(Пй5-	F'26)
6.4. Постановка статических и динамических задач
теории упругости
При постановке статических задач для упругой однородной изо-
изотропной среды используются следующие уравнения, которые дол-
должны выполняться всюду внутри тела:
а)	уравнения равновесия
о,ч./ + Pbi = 0, или V • S + pb = 0,	F.27)
б)	закон Гука
ос, = Щ&кк + 2це,7, или 2 = А,1е+2цЕ,	F.28)
в)	соотношения, связывающие деформации с перемещениями,
ец = 4~ ("'J+ «/.«). или E = i-(uV+Vu). F.29)
Кроме того, на поверхности, ограничивающей тело, должны быть
удовлетворены заданные условия, наложенные на напряжения
и/или перемещения.
Краевые задачи теории упругости обычно классифицируют
по типу этих условий. Их разделяют на группы, для которых:
1)	на всей границе заданы перемещения,
2)	на всей границе заданы напряжения (поверхностные силы),
3)	на части границы заданы перемещения, а на остальной поверх-
поверхности — напряжения.
Во всех трех случаях предполагается, что всюду в теле массовые
силы известны.
Для тех задач, в которых на всей границе даны компоненты пере-
перемещения в виде функции
ul = gl(\), или u = g(X),	F.30)
выражение деформаций через перемещения F.29) можно подставить
в закон Гука F.28), а результат в свою очередь подставить в F.27).

206	Гл о ЛИНРПНАЯ ТЕОРИЯ УПРУГОСТИ
Так получаются основные уравнения для перемещений
\шс,и + (к + ц) Uj.it + pbi = 0,
или	F.31)
fxV2u + (А, + V) VV • u + pb = 0,
которые называются уравнениями Навье — Коиш1^. Решение задач
этого типа состоит в отыскании вектора перемещения щ, удовлет-
удовлетворяющего уравнению F.31) всюду внутри тела и условиям F 30)
на его границе.
Для тех задач, в которых на всей границе известны поверхност-
поверхностные силы
tf> = а^, или t(n) = 2 • n,	F.32)
комбинацией уравнений совместности C.104), закона Гука F.24)
и уравнений равновесия F.27) получим основные уравнения для
напряжений
аЧМ + [+v OkkJi + P (Kl + bi.i) + i2.v" 6,-,-pfcft.ft = 0.
или	F.33)
которые называются уравнениями совместности Бельтрами — Ми-
челла. Решение задач этого типа состоит в нахождении тензора на-
напряжений, который удовлетворяет уравнениям F.27) и F.33) всюду
внутри тела и условиям F.32) на границе.
Для задач, имеющих смешанные граничные условия, должна
решаться система уравнений F.27), F.28) и F.29). Решение дает
поле напряжений и перемещений для всех точек тела. На некоторой
части граничной поверхности компоненты напряжений должны
удовлетворять условиям F.32), а на оставшейся ее части перемеще-
перемещения должны удовлетворять условиям F.30).
При постановке динамических задач уравнения равновесия
F.27) нужно заменить уравнениями движения E.16):
Gij.i + pbi = pvt, или V • S -f pb = pv,	F.34)
и наряду с граничными условиями нужно задать еще начальные
условия. Основные уравнения для поля перемещений в этом случае
аналогичны уравнениям F.31) статики
+ (Я, + ц) ии- + pbc = рт, или
цУ2и + (Я, + \i)VV • u + pb = pii.
') В русской литературе эти уравнения обычно называются уравнениями
Ламе.— Прим. перев.

li.6. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ	207
Решение уравнений F.35) ищем в виде щ = u, (x, t). Оно должно
удовлетворять не только начальным условиям, которые обычно
записываются в виде равенств
щ — щ (х, 0) и щ — щ (X, 0),	F.36)
но и граничным условиям, наложенным либо на перемещения
«< = gi (х, 0» или u = g (x, t),	F.37)
либо на напряжения
if =-- $> (х, 0, или t5» = t5* (x, 0-	F-38)
6.5.	Теорема о суперпозиции. Единственность решений.
Принцип Сен-Венана
Вследствие того что в линейной теории упругости уравнения
и граничные условия линейны, можно использовать принцип су-
суперпозиции для получения новых решений из ранее найденных.
Если, например, off, uj" — решение системы F.27), F.28) и
F.29) при массовых силах, равных Ь[1\ a of/, up — решение
при массовых силах bj2), то au- = a\f + of/, ис = ы}4 + uf]
будет решением той же системы при массовых силах bt = b}{) -\- bf\
Единственность решения общей статической задачи теории упру-
упругости может быть установлена при помощи принципа суперпози-
суперпозиции и закона сохранения энергии. Доказательство единственности
включено в задачи к этой главе.
Принцип Сен-Венана касается разностей между напряжениями
и деформациями в некоторой области внутри упругого тела, вы-
вызванными двумя различными, но статически эквивалентными систе-
системами поверхностных сил, приложенных к определенной части
границы. Принцип утверждает, что в областях, достаточно далеких
от места приложения нагрузки, эти разности пренебрежимо малы.
Это допущение часто оказывает большую помощь при решении прак-
практических задач.
6.6.	Плоские задачи теории упругости.
Плоское напряженное состояние и плоская деформация
Во многих задачах теории упругости можно вполне удовлетво-
удовлетворительно обойтись двумя измерениями, или так называемой плос-
плоской теорией упругости. Имеется два общих типа задач такого рода.
Хотя эти два типа можно выделить, принимая определенные огра-
ограничения и допущения для полей напряжений и перемещений, часто
их вводят описательно при помощи типичных примеров. Для реали-
реализации плоского напряженного состояния тело должно представлять

208
Гл. 6 ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
собой пластину, у которой один размер много меньше, чем дру-
другие. Нагрузка распределена равномерно по толщине пластины
и действует в ее плоскости, как показано стрелками на рис. 6.2,а.
Для реализации плоской деформации тело должно иметь форму
цилиндра, когда один размер много больше, чем другие. Нагрузка
равномерно распределена вдоль оси наибольшего размера и действу-
действует перпендикулярно ей, как показано стрелками на рис. 6.2,6.
Рис. 6.2.
В задачах с плоским напряженным состоянием (рис. 6.2, а)
компоненты напряжения а33, а13, агз принимаются равными нулю
всюду, а остальные компоненты считаются функциями только хх
и х2,
<7«р *= craP (jflf х2) (а, Р = 1, 2).	F.39)
В соответствии с этим постановка задач для плоского поля напряже-
напряжений содержит следующие уравнения:
а) стар.р + фа = 0, или V • 2 + pb = 0,
б) е«р = -ЦЬ^- (гвр	J- 6«|
или Е = •
в) е«р = V2 ("о,р + «р.«), или Е = V21
-е2 и
S = | а12 а22 О
о о;
+
F.40)
F.41)
F.42)
F.43)
Из-за специальной формы тензора деформации в случае плоского
напряженного состояния шесть уравнений совместности C.104)

6.G. ПЛОСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ	209
для очень тонких пластин с достаточной точностью сводятся к одно-
одному уравнению
ец.22 + eZ2.ii = 2ei2.i2.	F.44)
Выписанную систему уравнений можно преобразовав и получить
основное уравнение для компонент перемещения иа:
^ " +	+ Ь °
2(l+v) ^ "« + 2A-V)
или	F.45)
2A +v) v »-г 2A—v)
где
Для задач о плоской деформации (рис. 6.2,6) компонента пере-
перемещения и3 принимается равной нулю, а остальные компоненты
считаются функциями только х1 и х2:
ua = ua(xltx2).	F.46)
В этом случае система уравнений, дающая постановку задачи,
имеет вид:
а)	а«р.р + Р&а = 0, или V • 2 + рЬ = 0,	F.47)
б)	ааР = A,8aPevv + 2цеар, или S = Me, + 2цЕ,	F.48)
_ _ К
стзз — vo'aa — 2 (Я + ц) аа'
в)	еар = 7г («а,Р + «р.а). ИЛИ Е = V2 ("V + V U).	F.49)
причем
cr12	0 \ /ец	е12	0\
ст2,	0 I	и Е= е12	е22	о). F.50)
0	а3з/ \0	0	О'
Из уравнений F.47), F.48), F.49) в случае плоской деформации
г.олучается соответствующая форма уравнений Навье:
или	F.51)
ц ^ и + (Я, + (х) V V • u + pb = 0.
Так же как при плоском напряженном состоянии, уравнения
совместности для плоских деформаций сводятся к одному урав-
уравнению F.44).

210	Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
Если силы, приложенные к ребру пластины на рис. 6.2,а, рас-
распределены по толщине не равномерно, а симметрично относительно
средней плоскости пластины, то нап/ яженное состояние называют
обобщенным плоским напряженным состоянием. При постановке
задач в этом случае переменные поля истинных величин оа$, eap и иа
нужно заменить напряжениями, деформациями и перемещениями,
осредненными по толщине пластины. Для таких осредненных пере-
переменных формулировка задач в случае обобщенного плоского на-
напряжения в сущности такая же, как при плоской деформации, если
Я заменить на величину
В курсах теории упругости иногда упоминается понятие обоб-
обобщенной плоской деформации, когда е33 в F.50) будет постоянной,
отличной от нуля.
6.7. Функция напряжений Эри
Если массовые силы отсутствуют или постоянны, то при решении
плоских статических задач теории упругости (задач о плоской де-
деформации или обобщенном плоском напряженном состоянии) час-
часто пользуются функцией напряжений Эри (если массовые силы от-
отличны от нуля, то их вклад в решение может быть учтен допол-
дополнительно при помощи принципа суперпозиции путем нахождения
частных интегралов системы линейных дифференциальных урав-
уравнений).
Для плоских статических задач при отсутствии массовых сил
уравнения равновесия сводятся к следующим:
сг«р.р = 0, или V • 2 = 0.	F.53)
Уравнения совместности, выраженные через компоненты напря-
напряжений (уравнения Бельтрами — Мичелла), дают
V* (ои + а22) = 0, ^ 0Х = 0.	F.54)
Из уравнений F.53) видно, что компоненты напряжений можно
представить частными производными функции напряжений Эри
Ф = Ф (xlt х2):
а11 = Ф.22, <Т12 = — ф,12, <*22 = Ф.И-	F.55)
При этом уравнения равновесия F.53) удовлетворяются тождествен-
тождественно, а условие совместности F.54) превращается в бигармоническое
уравнение
V2 (V2 ф) = V4<P = Ф.1Ш + 2ф,Ц22 + ф.2222 = 0.	F.56)
Функции, удовлетворяющие этому уравнению, называются бигар-
моническими. Пользуясь бигармоническими функциями с однознач-
однозначными вторыми производными, можно строить многочисленные

СТАТИЧЕСКИЕ ЗАДАЧИ В ПОЛЯРНЫХ КООРДИНАТАХ
211
решения плоских задач теории упругости, которые автоматически
удовлетворяют и уравнениям равновесия, и условиям совместности.
Конечно, эти решения нужно еще «подогнать» к заданным гранич-
граничным условиям.
6.8. Двумерные статические задачи теории упругости
в полярных координатах
По геометрическим соображениям некоторые двумерные стати-
статические задачи теории упругости удобно формулировать в поляр-
полярных координатах г и 0. После преобразования координат
A:1 = rcos0, Ar2 = rsin0	F.57)
компоненты напряжения, изображенные на рис. 6.3, будут удов-
удовлетворять уравнениям равновесия в полярных координатах
да,.
да,
С-6)
дг
дс.г
+ ¦
2а,
(/¦6)
2а,
\гв)
F.58)
F.59)
г dQ ^ дг ^ г -г^-">
где R и Q — отнесенные к единице объема компоненты массовых
сил в соответствующих направлениях.
Рис. 6.3.
Возьмем функцию напряжений Эри в виде Ф = Ф (г, 0) и выра-
выразим через нее компоненты напряжений
oM = ±™+_L™t	F.6О)
v ' /	•¦	si f	' *¦?	/7G
F.61)
F.62)
= дгФ/дг\
	д \ I дФ\
дг г \ 0Q ' '

212	Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
Условия совместности снова приводят к бигармоннческому уравне-
уравнению
V2 (V2 Ф) = V4 Ф = 0,	F.63)
г-72 д2 . 1 д . 1 <Э2
причем в полярных координатах v =-^т + — "йГ"^ Т5" IP"'
6.9.	Гикерупругость. Гипоупругость
В современной механике сплошной среды иногда используются
определяющие уравнения для сред, которые являются упругими
в специальном смысле. Материал называют гиперупругим, если для
него существует функция энергии деформации и, такая, что мате-
материальная производная от нее равна мощности напряжений в еди-
единице объема. Таким образом, определяющее уравнение такой среды
имеет вид
^Г = \ ач°ч = Т atjk"'	F-64)
где Dtj •— тензор скоростей деформации. С другой стороны, мате-
материал называют гипоупругим, если скорости напряжений являются
однородными линейными функциями скоростей деформации. В этом
случае в качестве определяющего берется уравнение
О?, = KiikmDkm,	F.65)
причем тензор скоростей напряжения а,У определяется выражением
°8 = ЧГ
где Уц. •— тензор завихренности.
6.10.	Линейная термоупругость
Если учитывать тепловые эффекты, то компоненты тензора
линейных деформаций можно представить суммой
et/ = ejf + e{P,	F.67)
в которой e\f — деформации, вызванные полем напряжений, а
е'Р — полем температур. Компоненты деформации элементарного
объема изотропного тела, вызванные изменением температуры от не-
некоторого начального значения То до Т, при отсутствии внешних сил
определяются формулой
ejP=a(T-T0)8?/,	F.68)
где а ¦— коэффициент линейного теплового расширения. Подстав-
Подставляя F.68) и F.22) в равенства F.67), находим выражения

6.10 ЛИНЕЙНАЯ ТЕРМОУПРУГОСТЬ	213
которые называются соотношениями Дюгамеля—Неймана. Равен-
Равенства F.69) можно обратить и написать определяющие уравнения
термоупругости в виде
оц = Щекк + 2це,,- - (ЗА, + 2fx) аЬч (Т — То).	F.70)
Теплопроводность в изотропном упругом теле подчиняется из-
известному закону теплопроводности Фурье
Cl = -kT.t,	F.71)
где скаляр k — коэффициент теплопроводности среды, который
должен быть положительным, чтобы обеспечить положительную
скорость производства энтропии. Если ввести удельную теплоем-
теплоемкость при постоянной деформации с<в) равенством
-с,., = рс(|*5Г	F.72)
и предположить, что внутренняя энергия является функцией ком-
компонент деформации га и температуры Т, то уравнение энергии
E.45) запишется в виде (см. задачу 6.24)
КГ,и = pc{v)f + (ЗЯ, + 2(х) оТён;	F.73)
F.73) называется уравнением притока тепла связанной термоупру-
термоупругости.
Система уравнений общей задачи термоупругости для изотроп-
изотропной среды состоит из:
а)	уравнения движения
<*tjj + pbi = щ, или у • ? + Pb = ",,	F.74)
б)	определяющего уравнения термоупругой модели
<т?/ = АЛ/е** + 2цр(у — (ЗА, + 2ц) айц (Т — То),
или	F.75)
S = Не + 2цЕ — (ЗЯ, + 2\i) al (T — Т„);
в)	выражения деформаций через перемещения
ei/ = V2 («../-+ НО, или Е = V2 (uV + V u); F.76)
г)	уравнения притока тепла
kTM = pc{v)f + C1 + 2ц) aTekk,
( }
Из этой системы нужно найти поля напряжений, деформаций и тем-
температур, удовлетворив указанным начальным и граничным условиям.
Условия совместности будут выполнены автоматически в силу F.76).
Существует широкий круг задач, в которых эффектами инер-
инерции и взаимосвязи тепловых и механических процессов можно

или	2 = Ш + 2цЕ (ЗЯ + 2ц) al G1 Т);	( '
2Н	Гл 6 ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
пренебречь. В таких случаях общая задача термоупругости распада-
распадается на две отдельные задачи, которые решаются последовательно,
но независимо. Так, для квазистатнческой задачи несвязанной
термоупругости (без учета теплообразования при деформации)
основные уравнения будут следующие:
а)	уравнение теплопроводности
kT.u = pciv)t, или fcV2r = pc@)f;	F.78)
б)	уравнения равновесия
Oij.j + pbi = 0, или V • 2 + pb = 0;	F.79)
в)	уравнения, связывающие тензоры напряжений и деформаций,
+ 2це„ - (ЗЯ, + 2fx) obi, (T - То),
+ 2цЕ — (ЗЯ, + 2ц) al G1 — То);
г)	выражение деформаций через перемещения
ei/ = 1/2(uij + u/.i). или E = V2(Vu + uV). F.81)
ЗАДАЧИ С РЕШЕНИЯМИ
Закон Гука. Энергия деформации. Изотропия (§ 6.1—6.3)
6.1.	Доказать, что плотность энергии деформации и* для изо-
изотропной гуковой среды можно выразить через тензор деформаций
в виде и* = Я, (tr ЕJ/2 + \хЕг: Е и через тензор напряжений в виде
и* = 1A + v) 2 : 2 — v (trSJ] I2E.
Подставляя F.21) в F.13), находим
и* = (Kf>tjekk + 2|хе,7) гц12 = 1е„в/у/2 + це^Е,,-,
или в символических обозначениях и* = К (tr ЕJ/2 + |хЕ : Е.
Подставляя F.24) в F.13), аналогично получаем
"* = о(/ [О + v) о?/ - vbtfbbWE = [A + v) с?/оу - чойоиУ2Е,
или в символических обозначениях и* = [A + v) Z : Z — v (tr SJ]/2?.
6.2.	Разложив каждый из тензоров напряжений и деформаций
на шаровые части и девиаторы, представить плотность энергии дефор-
деформации и* в виде суммы плотности энергии расширения u*{s) и
плотности энергии искажения формы (энергии дисторсии) h*d>.
Подставив C.98) и B.70) в формулу F.13), получим
«* = v, (*/+«WV3) to/ -1- 6рЛ//3) =
= V, (s,^ + оиел./3 + srte/f./3 + olte/7/3).
Вследствие того что e(i = s.( = 0, выражение для и* сводится к сумме а* =

ЗАДАЧИ С РЕШЕНИЯМИ	215
6.3.	Имеется состояние всестороннего равномерного сжатия
с тензором напряжений а,,- = —р8(/-. Получить формулы F.25)
для модуля объемного сжатия (отношения давления к изменению
объема).
Для тензора напряжений а(у=—рб?/. соотношение F.24) принимает вид
ef/ = [A + v) (— p6t/) + v6fу- (Зр) ]/f, откуда получаем еи= [— Зр (I + v) +
+ 9р\]/Е. Тогда К=—р/е.(=Е/3(\—2v). Аналогично из закона Гука
F.21) для данного случая имеем о.( = (ЗЛ + 2ц)ец = — Зр, так что К = (ЗЯ, +
+ ад/з.
6.4.	Выразить u(s) и u{D) задачи 6.2 через технические упру-
упругие модули К и G и компоненты деформаций.
В задаче 6.3 получено Оц — ЗКвц, и, следовательно,
*	Кгнгп12 = К AЕJ/2.
Представим компоненты напряжения по закону Гука F.21) и по формуле B.70):
°i/ = KSijEkk + 2^Ei/ = s«7 + CkAi13- А так как си = (ЗЯ + 2^) ги< то s'' =
=¦ 2|.i (е^- — ек/1)у/3). Таким образом,
Заметим, что плотность энергии расширения «(S) оказывается функцией только
К, а плотность энергии искажения формы и(?)) выражается через модуль сдвига
|х (или G).
6.5. В общем случае и* можно представить квадратичной фор-
формой и* — C*KMeKRM, коэффициенты С*КМ которой не обязательно
симметричны. Доказать, что это выражение можно записать в виде
F.14) и что ди*/дек = ак.
Преобразуем квадратичную форму следующим образом:
км мк
Теперь вычислим производную ди*/дц^:
ди*/двк = Ч2 Скм {екяем + b
6.6. Доказать, что для ортотропной упругой среды (с тремя ор-
ортогональными плоскостями упругой симметрии) матрица упругих
констант имеет вид F.19).
Пусть плоскость x\xi (или, что то же самое, х\х'2) является плоскостью упругой
симметрии (рис. 6.4). Тогда ак = Скмгм и одновременно с^ = Ск.Мг'щ-

216
Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
Матрица преобразования осей
будет
в оси
Г1 ° °1
[в?/]= 0 1 0 .
Lo о —iJ
Из B.27) и C.78)
¦>К, ек
ек =
ПРИ
К = 1, 2, 3, 6, вто время как 0^ ¦=» —ск>
е^=—ек при К = 4, 5. Так, например,
Рис. 6.4.
для cj =
получим
oj = а, = Сцб! + С12е2 + С13е3 — С14е4 — С16р6 + С1ве„.
Но, с другой стороны, ах = С,Л1еЛ1> т. е.
С,2е2 + С13е3 + С14е4
Эти два выражения для а1 = с/ совпадают только в том случае, когда С14 =
= С15 = 0. Точно так же из равенств с2 = а2, а3 = а3, а4 = —а4, с'5 = —а5,
с6 = ав следует, что С24 = С26 = С34 = С36 = Св4 =. Св6 = Са = С42 = С43 =
Если плоскость л:2л:3 (или х^) является второй плоскостью упругой симмет-
симметрии, так что ак = Скмвм и матрица преобразования к осям хс имеет вид
г-1 0 0-,
[ач]=\ 0 10,
L о о и
то из B.27) и C.78) получаем ак = ак, ек = — е.к при К = I, 2, 3, 4, тогда
как ск = — ак, ек = — ек при /( = 5, 6. Отсюда следует, что С1в = С2в =
Сзв = С45 = С64 = Св1 = Св2 = Свз = 0 и матрица упругих констант принимает
вид F.19). Читателю предлагается проверить, что упругая симметрия относи-
относительно (третьей) плоскости х^3 при такой матрице получается автоматически.
6.7. Подробно провести операцию по сведению матрицы упругих
констант F.19) для ортотропного материала к матрице для изо-
изотропной среды F.20).
В случае изотропии упругие свойства среды одинаковы во всех декартовых
системах координат. В частности, для осей, повернутых так, как изображено
на рис. 6.5, тот же способ, что в задаче 6.6, приводит к дальнейшему упрощению
матрицы F.19) за счет равенств Си = Сю = С33, С44 = С65 = CM и Ci2= C21 =
= С13 = С31 = С23 = С32- Наконец, для системы х(, полученной поворотом на
угол 45е вокруг оси х3 (рис. 6.6), матрица преобразования будет
1 /2 1 | 
-1/1  1/1 
. 0	0

ЗАДАЧИ С РЕШЕНИЯМИ
217
Рис. 6.5.
Рис. 6.6.
так что o'g = (сг — а,)/2 = (Си — С,2) (е2 — 6^/2 и е^ = е2 — е,. Но Cg = С44её,
поэтому 2С44 = Сц—См. Вводя обозначения ц =¦ С44 и Х = С12, приходим к
матрице F.20)
6.8.	Проделать операцию обращения закона Гука F.21), чтобы
получить соотношение F.22).
Равенство F.21) при ?=/ дает ап = (ЗА, + 2ц)ги; следовательно, 2це,.=
= ац — Щркь1(Ъ% + 2ц), или ъч ^ o,//Bj.i) - ЩрыП^ (ЗЯ + 2$].
6.9.	Выразить технические константы v и Е через постоянные
Ламе К и \х.
Из равенств F.25) видно, что ?/A — 2v) = ЗЯ + 2ц, а из F.26) ?/A + v) =
— 2j.i. Таким образом, (ЗЯ + 2ц) A — 2v) =2ц A + V), откуда v = К/ [2 (X + ц)].
Теперь опять воспользуемся F.26) и найдем Е = 2ц A + v) = |х (ЗА, + 2ц)/ (Я +
+ И)-
6.10.	Написать матрицу упругих констант для среды, имеющей
ось упругой симметрии порядка N=4. Считать при этом Скм =
С
Пусть осуо упругой симметрии будет ось
х3. Поворотом других осей на угол 6 =
= 2я/4 = я/2 относительно лг3 (рис. 6.7) по-
получим направления эквивалентных упругих
свойств при N = 4. Матрица такого преоб-
преобразования
[«?/1
г 0 1 <Ь
= -I 0 0 .
L о о iJ
Phj. 6.7.
и формулы B.27) и C.78) приводят к груп-
группе равенств О] = сг, с'2 = <у1, с3= а3, а4 =
= —а6. ag =а4, ag = —ав и г\ = е2,
62 = 6!, е3 == е3, е4 = — е5, е5 = е4, е6 = — е6. Они накладывают условия иа
коэффициенты Скм; так, например, из равенства о^ = а3 следуют равенства

218
Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
C3i = С36 = С36 = 0, C31=:CSi. Аналогично, используя остальные пять соотно-
соотношений для напряжений, запишем матрицу упругих констант так:
Си
сн
с13
0
0
с,„
С12
Си
Ci3
0
0
— с,„
С13
С13
C33
0
0
0
0
0
0
С44
0
0
0
0
0
0
С44
0
Cle
-си
0
0
0
с.
(с семью независимыми константами).
Статические и динамические задачи теории упругости
(§ 6.4-6.5)
6.11.	Вывести уравнения Навье F.31).
Заменим компоненты деформации в F.28) эквивалентными выражениями
через перемещения: Сц = М^щ^ + ц (",.,- + u/,i)- Таким образом, с,-^- = hikjtl +
+ A(ы,-•• + **.•(;)¦ Подставив это выражение в уравнения равновесия F.27) и
перегруппировав члены, получим нужное уравнение: ци[;-;- + (Я. + ц) и-^ + p6j=0.
6.12.	Доказать, что если V4/7, = 0, то компоненты перемещения
и1 = (^ -\- 2\i)Fcij,/\i(k + \i) — Fjtjil\i являются решением уравне-
уравнений Навье F.31) при отсутствии массовых сил.
Дифференцируя предполагаемое решение, найдем члены
2ц) FiM
Подставим их в уравнение F.31), что дает
(К + 2ц) F(Afc///(J. + и) - Qi -(К + 2ц) + (К + ц)] F/>/ftftl- =; 0.
Это уравнение удовлетворяется, если F( ккц = v4^i = 0.
6.13. Доказать, что при отсутствии массовых сил функции ui —
— ф,; + Eiiktyit.i удовлетворяют уравР1ению движения F.35), если
каждая из функций <р и г|з,- является решением трехмерного вол-
волнового уравнения.
Подставим функции щ в уравнение F.35):
Но ?iPqtyq,pjt = °> поэтому уравнение
((к + 2ц) <рм — рф),. + еф
удовлетворяется, если V2(j) = рф/(Я + 2ц) и
- рад/ = 0

ЗАДАЧИ С РЕШЕНИЯМИ	219
6.14.	Доказать, что полученное в задаче 6.13 волновое уравне-
уравнение c2V2cp = ф, где с2 = (К -\- 2{л)/р, имеет решение
m Blr + ct)+h(r — d)
ф=	_	,
где g и h —¦ произвольные функции своих аргументов, г г2 — хсхс.
В данном случае удобно воспользоваться выражением оператора Лапласа в
сферических координатах V2 = —2--^—у ~а—) » так как 4>=4>('-i0- Имеем
г2 (ду/дг) = г (g' + ft')—(g + ft), где штрих означает дифференцирование функ-
функций g и h по их аргументам. После повторного дифференцирования находим
V2q> = (g" + h")lr. Аналогично ф = (g'c—h'c)/r и ф = с2 (g" + ftj")/r. Теперь вид-
видно, что функция ф удовлетворяет уравнению с2У2ф = <р.
6.15.	Вывести уравнения Бельтрами — Мичелла F.33) и ука-
указать ту форму, которую они принимают в случае потенциальных
массовых сил, т. е. при pbt = cp.j.
Подставим соотношения F.24) в условия совместности деформаций C.103).
Получим
С + v) (cljikm + ckmlj - alKm - c/m ,ft) = v F,y6>ftm
где 0 = Ijj = O{[. Только шесть уравнений из написанных здесь 81 независимы.
Полагая т = k и используя уравнения равновесия F.27), можем написать
%м + ®,ц + р Фс,,- + &,-,<) = v Фчвшкк + ei(p/(i + v),
откуда находим 0ftft = — A + v)p6ftft/(l —v). Подстановка выражения для в kk
в предыдущее уравнение приводит к требуемому результату F.33).
Если p&j = ф>?, то р (b[f -\- bjt) = 2ф?/. и pbkk — фЛЙ = У2ф, так что урав-
уравнение F.33) принимает вид
V2al7 = е,7/A + v) + 2ф1?/ + vfi^WO -v) = 0.
Двумерные задачи теории упругости (§ 6.6—6.8)
6.16. Для плоских напряжений, действующих параллельно
плоскости хгх2, написать соотношение между напряжениями и де-
деформациями, используя коэффициенты Я, и \i. Показать, что эти
формулы совпадают с F.41).
В данном случае о33 = о13 = с23 = 0, а учитывая еще F.21), имеем е13 =
= е23 = 0 и е33 = — X (еи -\- е22)/(Я, + 2|л). Закон Гука F.21) записывается тог-
тогда в виде aap = 2K\.if>afitiyy/(X + 2ц) + 2|.ieap, где a, P, у =¦ 1, 2. Отсюда нахо-
находим ааа — 2[а (ЗЯ, + 2(.i) вуу/(К + 2ц). Теперь формулу для aap можно обратить
и найти
В частности, отсюда следует, что
- Ялту/2ц (ЗЯ. + 2ц) = -

220
Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
6.17.	Для плоской деформации, параллельной плоскости хгхг,
написать соотношение между напряжениями и деформациями,
используя коэффициенты v и Б. Показать, что эти формулы совпа-
совпадают с F.48).
В этом случае ы3 = 0 и, следовательно, е33 =¦ 0, а из F.24) а33 = v (ац +
-\-с2е) = hjaa/2 (К-\-\л). Теперь формула F.24) принимает вид
еар = A + v) аар/? _ v A + v) Ь^^Е.
откуда еаа = A -f- v) (I — 2\)ааа/Е. Обращая, окончательно находим
аа» = vEflope^/O + v) A - 2v) + ?е^р/A + v) = М^е^ + 2цеар.
6.18.	Вывести уравнения Навье для плоского напряженного
состояния F.45) и показать, что они эквивалентны соответствующим
уравнениям для плоской деформации F.51), если к заменить на
Я' = 2Хц/(% + 2ц).
Обращение равенства F.41) при учете F.42) дает
аар = Е (uaS + Up-a)/2 (I + v) + 2v?6apuv>v/[2 A - v*)].
Продифференцируем это по *р и подставим результат в уравнения равновесия
F.40); получим
?ыа.рр/[2 0 + v)l + ?"р,ра/[2 (• -^ + РЬа =
= |i ^ 2 «а + И @К + 2ц) «р Ва/(Х + 2|i) + рЬа = 0.
Если провести замену ц (ЗК + 2ц)/(Х + 2ц) = 2К\л/(К + 2ц) + ц = V + ц, то
уравнения F.45) совпадут с F.51).
6.19.	Найти связь между константами А и В, при которой
функция ф = Axixl + Bx\ будет функцией напряжений Эри.
Согласно F.56), функция ф должна быть бигармонической, т. е. Фпц +
+ 2Ф И22 + Ф.2222 = 0 + 24Лх2 + 1205*2 = 0. Это верно, если А = —5В.
6.20.	Доказать, что функцией напряжений Эри может служить
«1*2 1 , Р 2
Найти компоненты напряжения в области ху > 0, — с ¦< х2 < с.
R
А
Рис. 6.8.

ЗАДАЧИ С РЕШЕНИЯМИ	221
Вследствие того что ^ 4ф тождественно равно нулю, функция ф может слу-
служить функцией напряжения. Компоненты напряжения, вычисленные по фор-
формуле F.55), равны
аи = ф22 = — 3FXlx2/2c3 + Pile, a12 = - ф12 = — 3F (с2 — 4)/*с3.
а22 = фп = 0.
Такие напряжения возникают в консольной балке под действием продольной
нагрузки Р и поперечной нагрузки F иг конце балки (рис. 6.8).
6.21. В задаче 2.36 было показано, что при отсутствии массовых
сил уравнениям равновесия удовлетворяют функции ац =
= ?ipqZjmn%n.pm- Доказать, что функцией напряжений Эри в этом
случае служит ф33 = <р (лгх, х2), в то время как фп = ф22 = ф12 =
= Фи = Фгз = 0-
Компонента ф3з является единственной отличной, от нуля, и поэтому равен-
равенство oij=zipqzjmt^qnpm превращается в сц = е'^е^у^^, или
- В СИЛу Т0Г0 ЧТ0 <Рзз = Ф- aa?,F6	66
p,w .P
Поэтому компоненты напряжений выражаются че-
через функцию ф так:
°11 = Ф.П + Ф.22 — Ф.П = Ф.22, °12 = — Ф.12-
а22 = фи + ф22 — ф,22 = Ф,Ц.
6.22.	При решении задачи о диске радиу- о \N
са а, находящемся под действием вращающе- г'
го момента М, используется функция на-	^*— ~Т
пряжений Эри Ф = BQ в полярных коор-
координатах г, Э (рис. 6.9). Найти компоненты напряжения и величи-
величину константы В.
Вычислим компоненты напряжения. По формулам F.60) н F.61) в(ГГ\ =
= C/QQ. = 0, а из F.62) О/^)> = В/г2. Для равновесия моментов относительно
2я	2я
центра диска требуется, чтобы М = I a(re)a2d8 = I BdQ = 2пВ, Таким обра-
о	о
зом, В—М/2л.
Линейная термоупругость (§ 6.10)
6.23.	Обратив F.69), получить определяющие уравнения тер-
термоупругости F.70).
При i=j из F.69) имеем си = (Зк + 2ц) (e,-t- — За (Г — Го)). Разрешая
F.69) относительно о», находим
о?/ = 2це(/ + ЩръъНЗК + 2ц) - 2цовц (Г - Го) =
= 2це17 + My (eftfc - За (Г - Го)) - 2|хав?/ (Т - Тв) =
вц (Г - Го).

222	Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
6.24. Вывести уравнение энергии F.73) для термоупругости,
используя при этом функцию свободной энергии / = и — Ts.
Предположим, что свободная энергия является функцией деформаций и тем-
температуры f = / (el;-, Г). Подставим ее в уравнение E.41), т. е. в уравнение
pit = a[i-E,y + pTs, где точками обозначено дифференцирование по времени. Тог-
Тогда (а,у — рд//де(/) г(у — Р (s + df/дТ) t = 0. Так как члены в скобках не за-
зависят от скоростей изменения деформаций и температуры, то из последнего
равенства следует, что aj;- = pdf/de^- и s = — df/дТ.
Уравнение второго закона термодинамики для термоупругой среды имеет
вид Tds = dq, т. е.
Отсюда, в частности, видно, что Т {ds/dT) = с'"', где c(tl)—теплоемкость при
постоянных деформациях, когда е,- ¦ = 0. Воспользовавшись полученными выше
выражениями для s и а,у через /, получаем ds/dT = — cPf'dT2, т. е. c(t>) =
= _ Т (dPflffH) и да/дец = — 52//5е(/5Г =• — A,'р) (до^/дТ); поэтому
—г)
Из F.70) видно, что дац1дТ — — а (ЗА, -f- 2ц) 6^., поэтому
а это совпадает с F.73).
6.25. Используя соотношения F.13) и F.70), получить плот-
плотность энергии деформации для термоупругой среды.
Непосредственной подстановкой F.70) в формулу F.13) находим
- Т°> Еч'2 =
Смешанные задачи
6.26. Доказать, что плотность энергии искажения формы
для линейного упругого материала можно выразить через главные
значения напряжений следующим образом:
= [К - <т2J + (сгв - сг3J + (сг3 - спJ]/12G.
Как видно из результатов задачи 6.2, и,щ = s(/et../2 = s^JiG, что можно
записать через компоненты напряжений так:
(atJ — б^-о-рр, 3)/4G =
В главных напряжениях это выражение примет вид
°2 + <4 - (°1 + °2 + Оз) (^1 + °2 + О3) '3].'4G =
a| + а23 - a^ - c2c3 - OgaJ/3] 4G =

ЗАДАЧИ С РЕШЕНИЯМИ
223
6.27. Используя выводы задачи 6.1, доказать, что для упруго-
упругого материала диУде^ = Oj и ди*/дац = el7-.
В зацаче 6.1 было получено и* = Леке^-/2 -J- це^-е,-; поэтому
Аналогично, из равенства ы* = [A -+- v)o\yC(/. — va(.(.a^]/B?), полученного в за-
задаче 6.1, имеем
5«*/Лтр? = [2A+ v) o^l#,eA - v (онви + а/76р9)]/B?) =
6.28.	Представить плотность энергии деформации и* в виде
функции инвариантов деформации.
В задаче 6.1 установлено, что и* = Ъ.гиг~12 -f- це^е^. Но, согласно C.91),
1Е = е,ч- и ПЕ = (ВцЕц — е,-уе,-у)/2, и поэтому
и* = Х AЕJ/2 + ц [— 2ИЕ + (IEJ] = (A./2 + ц) AЕ)= - 2ц11Е.
6.29.	Цилиндрический вал
длины L и кругового сечения
радиуса а находится под дейст-
действием пары сил в торцевом сече-
сечении, как показано на рис. 6.10.
При этом отличными от нуля
будут компоненты напряжения
о13 = — Gax2, a23 = Gaxlt где
а — угол закручивания на еди-
единицу длины вала. Найти выра-
выражение для плотности энергии
деформации и полную энергию
деформации вала.
В силу результата задачи 6.1 и* = [A + v) 2: 2 — v(tr 2J]'B?). В данной
случае tr2-0 и 2:2 = 2G2aV2, где г = х? + х|. Поэтому и* = GaV2/2. Пол-
Полная энергия деформации находится в виде интеграла
а 2л L
U=[ u'dV = -^- Г Г Г r3drdQdx3 = GaVnL/4.
рис 6 10
J
0 0 0
2n a
Заметим, что так как Г = f f Ga
о о
= 0аа4л/2, то t/ =TaL/2, т. е.
о о
t/ равна работе внешнего момента.
6.30. Доказать, что упругие свойства (закон Гука и плотность
энергии деформации) среды, имеющей ось упругой симметрии по-
порядка N = 2, и среды с одной плоскостью упругой симметрии сов-
совпадают.

224
Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
Поворот осей на угол 8 = 2л/Л/ = 2л/2 = я приводит к направлениям эк-
эквивалентных упругих свойств. Но в точности к тому же положению мы прихо-
приходим при отражении относительно плоскости упругой симметрии.
6.31.	Доказать, что матрицу F.19), в которой Си = С22 = С33,
Ci4 — Съ& = С6в и С12 = С13 = С23, можно свести к виду F.20)
поворотом осей на произвольный угол
6 вокруг оси х5 (рис. 6.11).
Преобразование осей xi в оси х\ дается
матрицей
г cos8 sin8 От
[а,-у]= — sin6 cos 8 0 ,
L 0	0 U
Рис. 6.11.	а согласно B.27), имеем
а12 = {— sin 8 cos 8) о„ + (cos2 8 — sin2 8) а12 + (sin 8 cos 8) а22
или в обозначениях с одним индексом
а6 = (— sin 8 cos 8) ах + (cos3 8 — sin2 8) а„ + (sin 8 cos 8) а2.
Точно так же, используя формулу C.78) и учитывая F.4), получаем
е6 = (— 2 sin 6 cos G) ех + (cos2 8 — sin2 8) к„ ¦+- B sin 8 cos 8) е2.
Но для изотропного тела ag = C44eg, и, следовательно, в данном случае а2 —
—	a! = 2C44(e2 — et). Наконец, в соответствии с видом матрицы F.19) при ука-
указанных выше условиях будем иметь at = Cuei + С12 (е2 -f- ex) и a2 = Cue2 -|-
+ С12(е1 + е2), и, значит, ai~ol = (Си—С12) (е2 — ej. Таким образом, Си —
—	С12 = 2С44. Полагая С44 = р, С12 = К, Си = К -f- 2(j,, приходим к форме F.20).
6.32.	Упругое тело, подчиняющееся закону Гука, находится
в равновесии под действием массовых сил Ьс и поверхностных сил
/ч
/|п). Доказать, что полная энергия деформации равна половине
работы внешних сил на перемещениях ut.
Требуется доказать, что I pbiUidV -f- \ f| WjdS = 2 I u*dV. Рассмотрим сна-
v	s	v
чала интеграл по поверхности, "в котором проведем замену /[n) = c^/ij, и преоб-
преобразуем его по теореме Гаусса — Остроградского:
Ho olju[j=alj(eij-{-<x)lj) =
ким образом,
, а из уравнения равновесия
. — —pbi. Та-
Таf tfrUidS = - J pft.-B.-dV + 2 J (Otft
и теорема доказана.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ	225
6.33.	Воспользоваться результатом задачи 6.32, чтобы устано-
установить единственность решения статических задач линейной теории
упругости, допустив существование двух решений сг!1', и\1) и а<2>, ы'.2>.
В линейной теории упругости законно применение метода суперпозиции
решений, т. е. с?/-= а^—of), ы,- = ы[1)—u'2) тоже будет решением при 6,- =
= 0. Для этого нового решения, как установлено в задаче 6.32, \ tf^UidS =
s
— 2 \ u*dV. Так как оба исходных решения удовлетворяют граничным условиям,
i
интеграл в левой части равен нулю, потому что на границе '*"' = t\[) — <J2) в
соответствии с F.32) и щ = и\1' — ы|2) в соответствии с F.30). Таким образом,
\ u*dV — 0, но, поскольку и* — положительно определенная функция, это воз-
v
можно только тогда, когда е^ = e[.J.'—е[-2) = 0, или е'у' = е[2). Если деформа-
деформации для двух допущенных решений равны, то по закону Гука равны и напряже-
напряжения. Равны также перемещения с точностью до перемещений абсолютно твердого
тела. Таким образом, единственность установлена.
6.34.	Уравнения Навье F.31) можно представить в форме
которая в случае несжимаемости (v = V2) становится неопреде-
неопределенной. Для такого случая, используя уравнения равновесия,
доказать, что \iiti,n + ©,//3 + рб,- = 0.
Из уравнения F.24) следует, что е,-,-= A—2\)ац/Е, а при v = 1/г это
даст ец = utl = 0. Таким образом, соотношение F.24) имеет вид
2гЧ.1 = "•¦// + "/••¦/ = 2 (> + v) aij.i/E — 2vVfcfc,/?-
Ho Uj ji = 0 и E = 3G, когда v = 1/2; поэтому щ ц = — pbi/G — akk ?/30, или
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
6.35.	Доказать, что для однородной изотропной упругой среды главные оси
тензоров напряжений и деформаций совпадают.
6.36.	Получить выражение плотности энергии деформации и* для ортотроп-
ной упругой среды. Использовать при этом формулы F.14) и F.19).
Ответ: и* = (Сиб1 + 2С12е2 + 2C13zJ eJ2 -f (C22e2 + 2С23е3) е2/2 +
+ С33е| + С44е2 + Съъг\ + Сив2.
6.37.	Определить вид функции плотности энергии деформации для случаев:
а) плоского напряженного состояния, б) плоской деформации.
Ответ: а) и* ¦= [of, + of2 — 2vana22 + 2 A + v) af2l/2E;
б) и* = (ц + X!2) (ej, + e22) + Xeue22 + 2це22.
8 Дж. Мейз

226
Гл. 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
6.38.	Найти с (= const), при котором функции их = A sin—— (xl±ct),
Uj, =: и3 = 0 служат решением уравнения F.35) при отсутствии массовых сил.
Ответ: с = \г(\ + 2ц)/р.
6.39.	Доказать, что для изотропной линейно упругой среды плотность
энергии искажения формы равна «(*D) = (<7,-Д.у- — аи a;y3)/4G, а плотность энер-
энергии расширения равна u(s^ = 1\ВК
6.40.	Доказать, что 1/A + v) = 2 (X + ц)/Ш + 2ц) и v/(l — v) = К/(к + 2ц).
6.41.	Доказать, что для плоской деформации, параллельной плоскости
s, компонента массовой силы Ь3 & 0, а компоненты Ьу и Ы являются функ-
функциями только х\ и х2.
6.42.	Используя правило преобразования напряжений и деформаций, дока-
доказать, что упругие константы C,-/ftm являются компонентами декартова тензора
четвертого ранга, так что С'цкт = aipaiqakramsCpqrs.
6.43.	Доказать, что функция напряжений Эри ф = 2х\ -\- \2x\x\ — 6х| удов-
удовлетворяет бигармоническому уравнению V4q> = 0, и найти компоненты напряже-
напряжений, считая деформацию плоской.
f х\ — 3*5 —1ххх2	0
Ответ: atj = 24 I — 2хгх2 х\-\-х\	0
0	0 2v (x\ —;
6.44.	Найти деформации, вызванные напряжениями задачи 6.43, и доказать,
что уравнение совместности F.44) удовлетворяется.
Ответ:
(
— Ъх\ — 2v (х, —
о	о
6.45.	Для упругого тела, имеющего ось симметрии порядка N= 6, доказать,
что См = Си, С№ = С44, Ст = 2 (Си — Си), а из остальных упругих констаит
отличны от нуля только Ci3 и С33-
6.46.	Доказать, что в упругой среде при потенциальных массовых силах
рЬа=^ 'Ф='A3ауравнение совместности F.44) имеет вид V2aaa~ V2^' —v)
в случае плоской деформации или ^^аа = A + v)^2\j3 в случае плоского на-
напряженного состояния.
6.47.	Пусть V4f ,• = 0. Доказать, что функции щ = 2 A — v) V8F?/G — F/ /?/G
будут решением уравнений Навье F.31), если Ь[ з= 0 (см. задачу 6.12). Найти
компоненты напряжений, когда F =В(х2е1 — Xjt^/r, где г2 = xixi.
Ответ: ап = — a22 = eQGx^/r6, а33 = 0, а12 = 3QG (х| — xf)//-6, a13 =
= ^- а23 = ZQGx2x3lr*. где Q = 4В A — v)/G.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ	227
6.48.	Функция напряжений Эри задана в полярных координатах: Ф =
= О2 (cos 28—cos 2а), где С и а— постоянные. Найти величину С, если Ogg =
= 0, сгв = т при 8 = а и аее = 0, аг6 = — т при 6 = — а.
Ответ: С = т/ B sin 2а).
6.49.	Доказать что в задачах термоупругости при плоской деформации
Раз = v (ап + а22) - а? (Г - Тв) и
а при плоском напряженном состоянии е33 = v (au + (J22)/? -}- а (Г — Го) и
еар = A + ^) аар/? - v6apavv/? + бар (Г - Г0)а.
6.50. Доказать, что в термоупругости уравнение совместности F.44) можно
записать через функцию напряжений Эри ф = ф (xi, х?) в случае плоской дефор-
деформации в виде ^4Ф= — а?^72 (Г— Го)/A — v), а в случае плоского напря-
напряженного состояния — в виде у4ф = — a?^2 (T — То).
8*

Глава 7
Жидкости
7.1. Давление жидкости. Тензор вязких напряжений.
Баротропное течение
В любой жидкости г) в состоянии покоя вектор напряжения
tf на произвольном элементе поверхности коллинеарен нормали
п к поверхности и одинаков по величине для всех направлений в дан-
данной точке. Таким образом,
= — ponh или t(n) = S.n = —pon. G.1)
Здесь р0 — величина напряжения, или гидростатическое давление.
Отрицательный знак указывает на сжимающее действие напряжения
при положительном значении давления. Каждое направление явля-
является главным, и из G.1) следует, что
ос,- = — рА,; или 2 = — ро\.	G.2)
Это сферическое напряженное состояние, часто называемое гид-
гидростатическим сжатием. Из G.2) видно, что касательные компо-
компоненты напряжения равны нулю в покоящейся жидкости.
При движении компоненты касательных напряжений в общем
случае не равны нулю, и обычно в этом случае тензор напряжений
представляют суммой двух слагаемых
о„ = — pbj + Tij, или 2 = — р1 + Г,	G.3)
при этом Гц называют тензором вязких напряжений, ар — давле-
давлением.
Все реальные жидкости — сжимаемые и вязкие. Однако эти
свойства очень различны у разных жидкостей, и часто бывает воз-
возможно пренебречь этими эффектами в некоторых ситуациях без су-
существенной потери точности в расчетах, основанных на таких
предположениях. Согласно этому, невязкая, или так называемая
идеальная, жидкость — это такая жидкость, в которой хц тож-
тождественно равны нулю, даже если происходит движение. Напротив,
вязкие жидкости — это такие, для которых нужно учитывать т.,-/.
Для сжимаемых жидкостей давление р по существу то же самое,
что и в классической термодинамике. Согласно G.3), среднее
1) Понятие «жидкость» в этом тексте включает в себя как истинные жидкости,
так и газы.— Прим. перев.

7.2. ОПРЕДЕЛЯЮЩИЕ УРАВНЕНИЯ	229
нормальное напряжение дается формулой
VsP« = —Р + 73т», или 7>в = —/j + V,r.	G.4)
Для покоящихся жидкостей т,-; обращается в нуль, а р сводится
к р0, которое в этом случае равно взятому с обратным знаком сред-
среднему нормальному напряжению. Для несжимаемых жидкостей тер-
термодинамическое давление независимо от механических условий
не определяется, и для таких жидкостей р нужно рассматривать
как самостоятельную неизвестную механической природы.
В сжимаемых жидкостях давление р, плотность р и абсолютная
температура Т связаны уравнением состояния
Р = Р(Р,Т).	G.5)
Примером такого уравнения состояния может служить известный
закон совершенного газа
Р = PRT,	G.6)
где R — газовая постоянная. Процессы в жидкости, подчиняющие-
подчиняющиеся уравнению состояния, которое не содержит температуры, т. е.
имеет вид р = р (р), называются баротропными. Изотермический
процесс в совершенном газе— пример частного случая, в котором
выполняется предположение баротропии.
7.2. Определяющие уравнения. Стоксовы жидкости.
Ньютоновы жидкости
Наличие в жидкости вязких напряжений связано с диссипаци-
диссипацией энергии. При установлении определяющих соотношений для
жидкостей в общем случае считают, что тензор вязких напряжений
ту является функцией тензора скоростей деформации пц. Если
эта функциональная связь нелинейна, что символически можно
выразить формулой
ту =/у Фи), или r = f(D),	G.7)
то жидкость называется стоксовой. Если эта функция линейна, т. е.
имеет вид
T?> = ffi/p,DWl или r = K:D,	G.8)
где константы КуР<7 называются коэффициентами вязкости, то
жидкость называется ньютоновой. Некоторые авторы классифи-
классифицируют жидкости просто как ньютоновы и неньютоновы.
Определяющие уравнения для изотропной однородной ньюто-
ньютоновой жидкости можно получить из G.7) и G.3), следуя точно та-
такой же процедуре, которая была проделана с обобщенным законом
Гука для упругих сред в гл. 6. Окончательная их форма такова:
Щ = - pit, + ЖцОы + 2|i*D4,
или	G.9)
S	l A*l(tD 2*

230	Гл. 7. ЖИДКОСТИ
где А-* и ц* — коэффициенты вязкости жидкости. Из G.9) можно
найти среднее нормальное напряжение
4*>и = - Р + V3 C^* + 2ц*) Da = — р + y.*Dti,
или	G.10)
V, (tr S) = - р + % C1* + 2fi*) (tr D) = - р + х* (tr D),
где и* = 1/3 (Зк* + 2ц*) называется коэффициентом объемной вяз-
вязкости. Условие
и* = К* + */зИ* = 0,	G.11)
известное как условие Стокса, утверждает, что давление р опреде-
определяется как среднее нормальное напряжение в покоящейся сжима-
сжимаемой жидкости. В таком случае термодинамическое давление оп-
определено через механические напряжения.
Используя компоненты девиаторов st-/ = с,,- — 6(/-afcfc/3 и Df, =
= Dij — 6,jDftft/3, приведенные выше уравнения G.9) можно пе-
переписать следующим образом:
или	G.12)
S + Vsl (tr S) = - pi + I (&• + %!*•) (tr D) + 2n*D'.
Учитывая соотношения G.10), уравнения G.12) можно записать
в виде двух Групп уравнений:
sij = 2\JL*Dih или S = 2fi*D',	G.13)
Oti = — 3p + 3x*Du, или tr 2 = — Зр + Зи* (tr D); G.14)
первая из них относится к эффектам сдвига, а вторая дает соотноше-
соотношение для изменения объема.
7.3. Основные уравнения ньютоновой жидкости.
Уравнения Навье — Стокса — Дюгема
При постановке задач о движении ньютоновой жидкости (или
газа) основными уравнениями в эйлеровой форме будут следующие:
а) уравнение неразрывности E.3)
O, или p + p(Vx-v) = 0;	G.15)
б)	уравнения движения E.16)
a4.l + Ph = pwf, или Vx-2 + pb = pv;	G.16)
в)	уравнение энергии E.32)
оцОцусц^-г, или h = -^-S:D	?-
G.17)

7.3. УРАВНЕНИЯ НАВЬЕ ~ СТОКСА — ДЮГЕМА	231
г)	определяющие уравнения G.9)
at, = —p6t, + X*8tlDi* + 2ц*Д/,
или	G.18)
Z = —pI + k*I(trD) + 2n*D;
д)	уравнение состояния G.5)
Р = р(р,Т).	G.19)
Если учитываются тепловые эффекты, что очень часто бывает необ-
необходимо в задачах о движении жидкости, то требуются дополнитель-
дополнительные уравнения, а именно:
е)	закон теплопроводности Фурье F.71)
Ct^ — kTj, или c = -WT;	G.20)
ж)	калорическое уравнение состояния
и = и{р,Т).	G.21)
Система уравнений G.15) — G.21) содержит шестнадцать уравне-
уравнений с шестнадцатью неизвестными и поэтому является замкнутой.
Если определяющие соотношения G.18) подставить в уравнения
движения G.16) и воспользоваться определением 2Ау = (vtj +
+ Vf,i), то получатся так называемые уравнения движения Навье —
Стокса — Дюгема:
pvt = pb, — pj + (К* + ц*) иш + цХ/л
или	G.22)
pv = pb — Vp + {%* + ц*) V (V • v) + n*V2v.
Для несжимаемой жидкости (v,j = 0) уравнения G.22) сводятся
к уравнениям Навье—Стокса:
( pt р ]n или pv = pb — Vp + ц.*У 2v. G.23)
Если выполнено условие Стокса (К* = — 2/3Ц*). то для такой
сжимаемой среды из G.22) получаются уравнения Навье — Стокса
в форме
PVt = pbt —p.i + lUv*Vj.ji + ii*Vt.n,
или	G.24)
pv = pb — Vp + Vsi^V (V v) + (i*V 2v.
Уравнения Навье — Стокса G.23) вместе с уравнением нер з-
рывности G.15) образуют полную систему четырех уравнений
с четырьмя неизвестными: давлением р и тремя компонентами ско-
скорости vt. В каждой конкретной задаче решение этой системы дол-
должно еще удовлетворять граничным и начальным условиям, нало-
наложенным на напряжения и компоненты скорости. В вязкой жидкости
в качестве граничных условий на неподвижной непроницаемой

232	Гл. 7. ЖИДКОСТИ
поверхности принимается требование обращения в нуль нормальной
и касательной компонент скорости. Это условие вытекает из экспе-
экспериментально установленного факта прилипания, в результате ко-
которого жидкость приобретает скорость границы. Для невязкой
жидкости на неподвижной непроницаемой поверхности требуется
обращение в нуль только нормальной компоненты скорости.
Если уравнения Навье — Стокса записаны в безразмерной форме,
то появляются некоторые коэффициенты в виде комбинаций из
характерных значений параметров. Одним из наиболее важных
и чаще всего используемых таких коэффициентов является число
Рейнольдса N^, которое выражает соотношение между силами
инерции и силами вязкости. Так, если поток имеет следующие ха-
характерные параметры: линейный размер L, скорость V и плотность
р, то числом Рейнольдса является отношение
N{R)=VL/x,	G.25)
где v = (х*/р называется кинематическим коэффициентом вязкости.
Для очень больших значений числа Рейнольдса влиянием вязкости
на напряжения в уравнениях количества движения можно прене-
пренебрегать. В турбулентном потоке кажущиеся (турбулентные) на-
напряжения действуют в осредненном по времени потоке таким же
образом, как вязкие напряжения в ламинарном потоке. При от-
отсутствии турбулентности при больших NiR) силы инерции пре-
превосходят силы вязкости и жидкость ведет себя так, как будто она
невязкая. Способность потока поддерживать турбулентные дви-
движения устанавливается по числу Рейнольдса. Определяющие
уравнения G.18) применяются для описания реальных жидкостей
только в случае ламинарного течения.
7.4. Установившееся течение. Гидростатика.
Безвихревое течение
Движение жидкости будет установившимся, если компоненты
скорости не зависят от времени. При этом производные dvjdt рав-
равны нулю, а материальная производная по времени от скорости
dvi • dvi ,	dv ¦ dv , г; ,т пс\
Sf- = vi = -дГ + viv'-i• или ЧГ = v = "вГ + v ' VxV' G<26)
ЧГ = v = "вГ
упрощается и принимает вид
vt — VjVij, или v = v • Vxv.	G.27)
Если скорость всюду равна нулю, то уравнения Навье — Сток-
Стокса сводятся к равенству
pbt = p_i, или pb = Vxp,	G.28)
и описывают состояние гидростатического равновесия. При нали-
наличии баротропии, когда р = р (р), можно ввести по определению

7.5. ИДЕАЛЬНАЯ ЖИДКОСТЬ. УРАВНЕНИЕ БЕРНУЛЛИ	233
функцию давления
Р(Р) = \
' &Р	G.29)
Р
Ро
Если к тому же массовые силы потенциальны, т. е.
bt = — Q, i, или b = — VQ,	G.30)
то уравнение G.28) принимает вид
(Q + P).f = 0, или V(fi + P) = O.	G.31)
Течение, в котором тензор завихренности D.21)
=V2fv.V-V .v), G.32)
всюду равен нулю, называется безвихревым. Вектор завихренности
<7,- связан с тензором завихренности соотношением
<7,- = eiikVki, или q = V^;	G.33)
поэтому этот вектор также обращается в нуль в безвихревом потоке.
Кроме того,
qt = EijkVk.i, или q = V х v.	G.34)
Но равенство V х v = 0 выражает необходимое и достаточное усло-
условие существования потенциала скорости ц>, значит, вектор скорости
в безвихревом течении можно представить следующим образом:
fj = — Ф.1, или v = — Уф.	G.35)
7.5. Идеальная жидкость. Уравнение Бернулли.
Циркуляция
Если коэффициенты вязкости К* и ц* равны нулю, то жндкссть
называется невязкой или идеальной (без трения) и уравнения На-
вье — Стокса — Дюгема G.22) превращаются в уравнения
pvt = pbl—p,t, или pv = pb — Vp,	G.36)
которые называются уравнениями движения Эйлера. Для баротроп-
ной жидкости при потенциальных массовых силах условия G.29)
и G.30) можно ввести в уравнение G.36), в результате чего получит-
получится
щ = — (Q + P).i, или v = — V (Q + Р).	G.37)
При установившемся движении G.37) имеет следующую форму:
i,j = — (Q + P),it или v • Vv = — у (Q + Р). G.38)

234	Гл. 7. ЖИДКОСТИ
Если уравнения Эйлера G.37) проинтегрировать вдоль линии
тока, то получится известное уравнение Бернулли (см. задачу 7.17):
Q + Р + v%j2 + J (dv(ldt) dx, = С (t).	G.39)
При установившемся движении dvjdt = 0 и С (/) становится по-
постоянной Бернулли С, которая, вообще говоря, различна для раз-
разных линий тока. Но если течение является к тому же и безвих-
безвихревым, то постоянная С будет одной и той же во всем поле течения.
Когда из массовых сил действует только сила тяжести, то ее мож-
можно представить потенциалом Q = gh, raeg — постоянное ускорение
силы тяжести, aft — высота, отсчитываемая от некоторого уровня.
Величина hp = Pig характеризует так называемый напор давления,
a v2/2g = hv — скоростной напор. Уравнение Бернулли требует
постоянства полного напора вдоль линии тока. Для несжимаемой
жидкости это уравнение записывается следующим образом:
h + hp + hv = h + p/pg + v2/2g = const.	G.40)
По определению циркуляцией скорости по замкнутой жидкой
линии называют линейный интеграл
Гс = § vfixt, или Гс = § v • dx.	G.41)
По теореме Стокса A.153) или A.154) линейный интеграл G.41)
можно преобразовать в интеграл по поверхности:
Гс = f пы^йЗ, или Ге = f n • (V X v) dS, G.42)
= f пы^йЗ, или Ге = f n •
S	S
где п — единичный вектор нормали к поверхности S, натянутой
на данную линию. Если течение безвихревое, то V х v = 0 и цир-
циркуляция равна нулю. В этом случае подинтегральное выражение
в G.41) оказывается полным дифференциалом некоторой функции
dtp = — v • dx, а эта функция ц> представляет собой потенциал
скорости.
Материальную производную dYJdt от циркуляции по времени
можно найти, воспользовавшись формулой D.60). В приложении
к циркуляции G.41) эта формула дает
?с = § (i)idxi + VfdvJ, или Гс = § (v ¦ dx + v • dv). G.43)
Можно показать, что в баротропной невязкой жидкости при потен-
потенциальных массовых силах циркуляция постоянна. Это известная
теорема Кельвина (Томсона) о постоянстве циркуляции.
7.6. Потенциальное течение.
Плоское потенциальное течение
Термин потенциальное течение часто используют для обозна-
обозначения безвихревого движения, так как условие отсутствия вихрей
V х v = 0 является одновременно необходимым и достаточным

Г.6. ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ
235
для существования потенциала скорости ф, через который компо-
компоненты скорости определяются по формулам G.35). Для безвихре-
безвихревого течения сжимаемой жидкости уравнения Эйлера и уравнение
неразрывности в некоторых случаях могут быть линеаризованы
и совместно преобразованы, как это делается в акустике, к волно-
волновому уравнению
Ф =с2ф,«, или ф = сг\7г<р,	G.44)
где с — скорость звука в среде. В случае установившегося безвих-
безвихревого течения сжимаемой баротропной жидкости уравнения Эй-
Эйлера и уравнение неразрывности можно совместно преобразовать
к следующему виду:
(с26,7 — vfl,) v,.i = О, или c2V • v — v • (v • V v) = 0. G.45)
Это так называемые уравнения газовой динамики.
Для потенциального течения несжимаемой жидкости уравне-
уравнение неразрывности сводится к уравнению Лапласа
<р,н = 0, или У2ф = 0,	G.46)
и решение его обеспечит нахождение компонент скорости по форму-
формулам G.35). При этом должны также удовлетворяться граничные
условия для скорости, например, на неподвижной непроницаемой
границе ду/дп = 0. Вследствие линейности уравнения Лапласа
существенной чертой этой постановки задачи является возможность
использования метода суперпозиции решений.
В двумерном течении несжимаемой жидкости, параллельном
плоскости хххг, и3 = 0и уравнение неразрывности имеет вид
va,a = 0, или ^ • v = 0,	G.47)
где, как принято в этой книге, греческие индексы принимают зна-
значения 1 и 2. В соответствии с G.47) независимо от того, будет ли
течение безвихревым, можно ввести функцию тока яр = яр (хи х2),
такую, что
Va = — Еарз'Ф.р.	G.48)
Если плоское течение является к тому же еще и безвихревым,
т. е.
Va = — ф,а. ИЛИ V = — ^Ц>,	G.49)
то из равенств G.48) и G.49) видно, что функция тока и потенциал
скоростей удовлетворяют условиям Коши — Римана:
Ф.1=Я1'.2 И ф2 = —Я]5,1.	G.50)
Исключая ф и яр поочередно из уравнений G.50), легко показать,
что
ф.сса = 0, ИЛИ V2<P = 0»	G.51)
¦ф.сш = 0, или ^2ip = 0.	G.52)

236	Гл. 7. ЖИДКОСТИ
Таким образом, если течение безвихревое, то обе функции ц> и яр
являются гармоническими. В силу этого можно ввести комплекс-
комплексный потенциал
Ф (г) = ч> (*ь *«) + /ф (*lt x2),	G.53)
который будет аналитической функцией комплексного перемен-
переменного г = агх + ix2, а его производная dOldz определяет комплексную
скорость
dO/dz =—ы + щ.	G.54)
ЗАДАЧИ С РЕШЕНИЯМИ
Основные свойства жидкостей.
Ньютоновы жидкости (§ 7.1—7.3)
7.1.	Доказать, что девиатор sy тензора напряжений с,-/, удов-
удовлетворяющего соотношению G.3), равен 1ц — девиатору тензора
1ц, определенного тем же соотношением.
Из указанной формулы G.3) найдем аи = — Ър -f- xit\ следовательно,
hj = aif - <V<<fe/3 = — р6Ч + T'/ — 6'7 (— 3P + т**)/3 = X4 — V^/3 = ''У
7.2.	Определить среднее нормальное напряжение оц/3 в несжи-
несжимаемой стоксовой (нелинейной) жидкости, для которой т(> =
= aDij + fiDikDkj, причем а и Р — постоянные.
Из G.3) следует, что а^ = — р6?/- + aD(/- -J- $DikDkj, и поэтому а?(- =
= — Зр + aZ)j7- -j- §DikDkl. Но Z)/ft = Z)fo- и Z),7 = «,¦ t — 0 для несжимаемой
жидкости. Таким образом,
о„/3 = - р + {Ш?/Оч/3 = - р - 2Р IID/3,
где IID — второй инвариант тензора скоростей деформации.
7.3.	Адиабатическое (или изэнтропическое) течение идеального
(без трения) совершенного (подчиняющегося уравнению Клапейрона)
газа представляет собой баротропное течение и описывается уравне-
уравнением р =Cpk, где С и k — постоянные, причем k = cip)/c(v) —
отношение теплоемкостей при постоянном давлении и постоянном
объеме. Найти зависимости между температурой и плотностью,
а также между температурой и давлением для данного процесса.
Подставляя р = Ср в уравнение состояния G.6), находим соотношение меж-
между температурой и плотностью: р* /Г= R/C = const. Кроме того, из уравнения
р = (р/СI1 и опять из уравнения G.6) получим зависимость между температу-
температурой и давлением: р^-^^/Т = R/Cl>k = const.
7.4.	Написать определяющие уравнения для ньютоновой жид-
жидкости с нулевой объемной вязкостью и* = 0.

ЗАДАЧИ С РЕШЕНИЯМИ	237
При у* = 0, согласно G.11), X* = —2ц*/3 и из G.9) следует, что а{.=
= — рЬц — Bц*/3) btpkk + 2ц*?>(-;- Это выражение можно записать через девиатор
тензора скоростей деформации
Если ввести еще девиатор напряжений s,-,, то определяющие уравнения можно
представить двумя соотношениями &ц = 2ц "D^- и а,-? = — Зр.
7.5. Найти выражение для мощности напряжений сг,/Ау в нью-
ньютоновой жидкости с определяющими уравнениями G.9).
При определяющих уравнениях G.9) мощность напряжений по определению
равна
atPtl = ~ t*iPi\ + ЩРиРц + ^*DaDi, = ^ PDu + ^DuD
В символических обозначениях это равенство имеет вид
2 : D = — р (tr D) + К* (tr DJ + 2ц*Э : D.
Можно записать его через девиатор D-.:
+ 2ц* (D'y + btpuJS) iP\ + в?/ V3) =
или в символических обозначениях
X : D = — р (tr D) + к* (tr DJ + 2ц*Э': D'.
7.6.	Написать условия, при которых среднее нормальное дав-
давление Р(т) = — сг»73 равно термодинамическому давлению р
в ньютоновой жидкости.
Второе из определяющих уравнений G.14) дает p(ffl)—p=y.*Du. Таким
образом, Р(т. = р в следующих случаях: когда к* = 0 (т. е., как видно из G.11),
при К* = — 2/3Ц*) и когда DH = 0.
7.7.	Проверить правильность написания уравнений движения
Навье — Стокса — Дюгема ньютоновой жидкости G.22) и найти,
какой вид принимает уравнение энергии G.17) для этой жидкости,
если теплопроводность подчиняется закону Фурье G.20).
Учитывая, что Du = vu, соотношения G.18) можно написать в виде аг =
= — Pfyy + ^*Vw + I** К/ + vl.d'> тогда
Подставляя это выражение в G.16), непосредственно проверяем выполнение
G.22).
Подставим вышеупомянутые формулы для а{/ и закон Фурье G.20) в уравне-
уравнение энергии G.17) и найдем
После некоторых преобразовании получим
р'ы = - роу + Ь\ри + Ц* (fy + v/ti) (Vfj + оЛ,)/2 — kTfU + pz.

238
Гл. 7. ЖИДКОСТИ
Рис. 7.1.
7.8. Найти суммарную по-
поверхностную силу Tt, действу-
действующую на замкнутую поверх-
поверхность S, содержащую объем V
ньютоновой жидкости (рис. 7.1)
с нулевым коэффициентом объ-
объемной вязкости.
Элементарная поверхностная сила
равна dT{ = ^n'dS, а полная сила
2 определяется интегралом Tt= I <({п) dS,
который, используя свойства напря-
напряжений, можно представить в виде Г,- =
= \ov.n/d$. При учете результата зада-
s
s
чи 7.4 в случае нулевого коэффициента объемной вязкости получаем
s
Применив теорему Гаусса—Остроградского, это выражение можно записать так:
7.9. В осесимметричном потоке в направлении оси х3 скорость
является функцией х3 и г, где г2 = х\ + х\. Найти, какой вид
принимает при этом уравнение неразрывности, если вектор скорости
Л	Л	Л
представлен в форме v = qer + t/3e3, где er — единичный вектор
радиального направления.
Уравнение неразрывности в символических обозначениях имеет видЗр/д< +
+ V • (pv) = 0 (уравнение E.4)). В данном случае используем оператор V в ци-
цилиндрических координатах
V.(pv)= —
1 д (rpq) , д (pv3)
дг
+ ¦
Подставив его в E.4) и проведя некоторые упрощения, получим искомый вид
уравнения неразрывности:
г (dp/dl) + д (rpq)/dr + д (rpvj/dx3 = 0.
7.10. В двумерном течении, параллельном плоскости хгх2,
компонента скорости v3 и д/дх3 равны нулю. Написать для такого
случая уравнения Навье — Стокса и уравнение неразрывности не-
несжимаемой жидкости.
Уравнение G.23) при i = 3 дает pb3 = р3, а при с = 1, 2 дает pva = pba—
—-Pitt + ц*карр. Уравнение неразрывности G.15) принимает вид vai(x = 0.

ЗАДАЧИ С РЕШЕНИЯМИ	239
Если массовые силы равны нулю kv1 = v1 (xlt х2, 0. v2 = 0, p = р (xt, хг, t),
казанные у	^
и dvjdx1 = 0.
то указанные уравнения принимают вид pt^ = — dpldxy + |Л*
Установившееся течение. Гидростатика.
Безвихревое течение (§ 7.4)
7.11.	Будем считать атмосферный воздух совершенным газом,
температура которого меняется линейно с высотой Т = То — ах3,
где То — температура на уровне Земли, а координата х3 отсчиты-
вается от уровня Земли вверх. Определить атмосферное давление
как функцию х3 в условиях гидростатики.
В этом случае из уравнения состояния G.6) следует, что p—pR{T0— ах3).
Так как из массовых сил действует только постоянная сила тяжести Ь3 — — ?•
уравнение G.28) дает dp/dx3 = —pg = —pg/R (Го — а*з)- Разделяем переменные
и интегрируем: 1п р = (g/Ro.) In (То—ах3) -f- In С, где С—постоянная интегри-
интегрирования. Таким образом, р = С(Тв — ax3)e^Ra, и если р = р„ при х3 = 0, то С=
= p0T^e/Ra, и, следовательно, р = р0 A — ax3/TefIRa.
7.12.	Баротропная жидкость описывается уравнением состоя-
состояния р == ^-pfe, где К и k — постоянные. Жидкость остается в покое
в поле силы тяжести, действующей в направлении оси х3. Найти
распределение давления в жидкости в зависимости от х3, если
при х3 = 0 оно равно р0.
Из уравнения равновесия G.28) др/дх3 = — pg, др/дх1=др/дх2 = 0. Заме-
Заметим, что при отсутствии у массовых сил компонент bt и Ьг давление в направле-
направлениях ж, и хг постоянно. При р = (рА)''* уравнение равновесия дает р~1''dp =
= — gl-l/kdxs. Интегрируя его, находим (k/{k— I)) p{k~l)/k = — gh~l'kx3+ С.
Нор = р0при х3 = 0, откуда С = (k/(k—I)) P$~l^k- Таким образом, х3 =
= (kPo/(k - 1) gpB) A - (р/Ро)**-1'/*), где Ро = (PoIK)l'k.
7.13.	Широкий сосуд, наполненный несжимаемой жидкостью,
движется с постоянным ускорением а = й2ег + с3ез в поле силы
тяжести, направленном вдоль оси х3
(рис. 7.2). Найти наклон свободной
поверхности жидкости в сосуде.
Из уравнений равновесия G.28) dpldxt — 0>
др/дхг = ра2 и др/дх3 = — p(g — a3). Интегри-
Интегрируем: р = рагх2 + f {х3) и р = — р (g — а3) х3 +
+ h (х2), где / и h — произвольные функции своих
аргументов. Объединяя, получаем общую фор-
формулу для давления р = рагхг — р (g — а3) х3 +
+ ро, где ро — давление в начале координат на
свободной поверхности. Так как всюду на сво-
свободной поверхности р = ро, то уравнение иско-
иской бй	б	/ (	)/
р	р р ур
мой свободной границы будет Хг/х3 = (g — а3)/п2.	Рис. 7.2.
7.14. Если течение жидкости происходит очень медленно, так
что членами порядка квадрата скорости и выше можно пренебречь,
то получается предельный случай, который известен под названием

240	Гл. 7. ЖИДКОСТИ
ползущего движения. Доказать, что в таком случае в установив-
установившемся движении несжимаемой жидкости при нулевых массовых
силах давление является гармонической функцией, т. е. V2p = 0.
Уравнения Навье — Стокса G.23) для несжимаемой жидкости имеют вид
р (dvildt + v,V(j) = pb,- — р,- + Н-Ч-,//-
а для ползущих движений их можно линеаризовать, что дает
р (dvi/dt) = рб,— р,. + И-Ч-,//-
Отсюда видно, что при установившемся движении с нулевыми массовыми силами
р t. = (х* v( jj. Возьмем дивергенцию от обеих частей этого равенства: ри~
— \n*V[ ijj. Учитывая уравнение неразрывности vti = 0, получаем р lt = V3p =
= 0.
7.15.	Записать уравнение неразрывности и уравнения Навье —
Стокса — Дюгема для безвихревого движения через потенциал
скорости ф.
Согласно G.35), и,-= —ф,-, вследствие чего уравнение неразрывности прини-
принимает вид р — рУ2ф = 0. Уравнения G.22) при с,- = — ф t. запишутся следующим
образом:
— РФ,; = Pbi — р,- — (Я* + ц*) ф//; — ц*ф_ад,
или
— р (dffjldt + <Pik<tEik) = pbi — Pti — (Я* + 2(x*) ф//?.
Эти уравнения можно представить и в символических обозначениях:
— pV (d(p/dt + (УфJ/2) = pb — Vp — {к* + 2ц*) V (Уф).
7.16.	Найти функцию давления Р (р) при баротропном течении
жидкости с уравнением состояния р = Крк, где К и k — постоян-
постоянные.
По определению G.29)
f
Так как dp = hkpk~ldp, этот же результат можно получить и иным путем:
Идеальная жидкость. Уравнение Бернулли.
Циркуляция (§7.5)
7.17. Интегрированием уравнений Эйлера G.37) вдоль линий
тока получить уравнение G.39).

ЗАДАЧИ С РЕШЕНИЯМИ	241
Пусть dxc — элементарное перемещение вдоль линии тока. Возьмем скаляр-
скалярное произведение этого перемещения на G.37) и проинтегрируем:
J -i^- dxt + j vptjdxt + J QtfiXi + J Pjdxc = С @.
Так как Q tdx{ = dQ и P ^dxi = dP, последние два интеграла сразу находятся.
Кроме того, вдоль линии тока due,-= (vi/v)ds, где ds — элемент расстояния.
Таким образом, во втором интеграле
VjVt dxi = v-oi j (vi/v) ds = vfl[ y- {vjjv) ds = V(vt jdxj = v^dvi.
Поэтому I VjV; jdxi — I vcdvi = V2 V{ut = 1/i fz и G.39) получено.
7.18. Жидкость с уравнением состояния задачи 7.16 вытекает
из большого закрытого резервуара через гладкую тонкую трубку;
течение баротропное. Давление в резервуаре равно 7V атмосферам.
Определить скорость истечения газа, считая давление в струе
на выходе из резервуара равным атмосферному.
Применим интеграл Бернулли к установившемуся течению в двух точках:
А — в жидкости, покоящейся внутри резервуара, и В — на свободной поверх-
поверхности вытекающей струи. Уравнение G.39) дает QA + РА + 1/2vA = &в +
+ Рв + 1/ivB. Но vA = 0, и если пренебречь силой тяжести, то это уравнение
примет вид (см. задачу 7.16)
Ра Рв\ 1 ..2 .._.. t,2 _ 2fe РВ /nPb x
а Рв j z °	k~l Рв \ Ра
Так как р»/рл = (Pr/Pa)~~* == N , то окончательно
7.19. Доказать, что в невязкой баротропной жидкости при по-
потенциальных массовых силах скорость изменения циркуляции рав-
равна нулю (теорема Кельвина).
По формуле G.43) Гс = | (vidxi -\- v(dvi). Но для данного случая уравнения
G.37) сразу дают и,- = — (Q + Р),-, и поэтому
Ге = $ (— Q М — P/Xi + Vidvi) =
= — $ (dQ + dP — d (v*/2)) = — f d (Q + P— t)z/2) = 0
вследствие того, что подинтегральное выражение оказалось полным дифференциа-
дифференциалом.
7.20. Найти циркуляцию скорости по контуру квадрата хх =
= ±1. х% = ±1. х3 = 0 (см. рис. 7.3) в двумерном течении с полем
скоростей v = (л:г + хг) ег + (х\ — х8) еа

242
Гл. 7. ЖИДКОСТИ
-1
+1
X*
-1
Рис 7.3.
+1
Воспользуемся символической записью
формулы G.42) прн п = е3 и VXv=Bx1—
— 1) е3:
1 1
Ге= f \Bx1-l)dxldxi = -4.
К тому же результату можно прийти и из
формулы G.41):
Гс = (Ь v • dx ¦¦
l-l-i	i
= \0—xJdxt+§ (x1 + 1) dxt + f (l-Xi)dx2+ f
-ii	l	-I
Здесь интегрирование начинается в точке А н ведется против движения часовой
стрелки.
Потенциальное течение.
Плоское потенциальное течение (§ 7.6)
7.21.	Вывести уравнения газовой динамики G.45) и записать
эти уравнения через потенциал скорости <р.
Уравнение неразрывности E.4) для установившегося течения будет р cv. +
+ pfjj- = 0, а уравнения Эйлера G.36) дадут pv.-vi ¦ + р,- = О, если пренебречь
массовыми силами. Из условия баротропии р = р (р) следует dp = (dp/dp) dp,
или pj = (dp/dp) p i = c2p ,., где с — местная скорость звука. Подставляя это
выражение в уравнения Эйлера и умножая результат на V[, находим
-\-tPvip [ =0. Из уравнения неразрывности c2fjpt.= —c2f,-t-=—c
н тогда для уравнений движения окончательно получаем (с2б(у — Vivj) ty
Через потенциал скорости <p>t- = — и,- эти уравнения записываются следующим
образом: (c26t-;. — <р ,-ф j) ф t.;. = 0.
7.22.	Доказать, что функция <р = А (—х\— х\ + 2xf) удов-
удовлетворяет уравнению Лапласа. Найти компоненты скорости и опи-
описать движение..
Подстановкой ф в уравнение G.46) убеждаемся, что —2А—2А + 4Л = 0.
По формулам G.35) f, = 2Ахи чг = 2Ахг, v3 = —4Ах3. Используя результаты
задачи 4.7, видим, что линии тока в плоскости х1 имеют уравнение х%х3 — const,
а в плоскости jts уравнение х\х3 = const. Таким образом, поток направлен вдоль
оси х3 навстречу плоскости xYxz (натекание на твердую стенку).
y = 0.
7.23. Доказать, что функция тока
линии тока.
(xx, х2) постоянна вдоль
Из соотношений G.48) и дифференциального уравнения линии тока dx^v^ =
= dxjv2 (см. задачу 4.7) получаем — йхлAJ)>2 = dxjty^, нли ^idxl + il>>2d*a =
= d»J3 = 0. Таким образом, вдоль каждой линии тока ip = cpnst.

ЗАДАЧИ С РЕШЕНИЯМИ
243
7.24. Проверить, что функция <р = А (х? — х2) может служить
потенциалом скорости несжимаемой жидкости, и описать заданное
ею течение.	д?2
Данная функция ф удовлетворяет
уравнению G.46) тождественно, так
как 2А — 1А = 0. Компоненты ско-
скорости определяются формулами G.49):
V! = — UAxi, Vz = 2Ax2. Линии тока
получаются интегрированием урав-
уравнения dxjxi = — dxi/хг и представля-
представляют собой гиперболы х\Хг = С с взаим-
взаимно перпендикулярными асимптотами
(рис. 7.4). Эквипотенциальные линии
А (х\ — х%) = Ci образуют семейство
таких же гипербол, ортогональных
Н	G50) й
Линии
тона
Рис. 7.4.
р	р
линиям тока. Наконец, из G.50) най-
найдем функцию тока »|з = — 2AxiX2 + Со, которая оказывается постоянной вдоль
линий тока, как и утверждалось в задаче 7.23.
7.25.	Дан потенциал скорости <р = Ахх + Вхх/г2, где г2 =
= х\ + х\. Найти функцию тока ip для этого течения.
Согласно G.50), яр [ = —ф 2 = 2Вл:1л:г//-*, откуда интегрированием находим
¦!]> = —Вхг1гг + / (jtrs), где f(x2) — произвольная функция от хг. Продифференци-
Продифференцируем функцию тока: чр 2 = —В (х\ — х%)/г*-\-р (хг). Но из G.50) известно, что
¦ф2= ц х= а + В (—х\+ xl)/r*. Таким образом,/' {хг) = А и /(д;2) = Ахе + С.
Окончательно получаем яр = Ахг — Вхг/г2 + С.
7.26.	Дифференцированием комплексного потенциала Ф (г) =
= А/г получить компоненты скорости.
В данном случае dO/dz = —A/z2= — А'/(х1 + i*s)z, что после некоторых алгеб-
алгебраических преобразований можно записать следующим образом: dO/dz = — А (*[ —
— х%)/г* + i2Axlxi/rt. Таким образом,
Vx = А (х\ — ffy/r* и
Заметим еще, что если Ф = A/z = А (ж, —
и мы снова получаем
то ф = Axjr2, а г]з = — Ах2/г®,
«2 = — ф,2 =
Смешанные задачи
7.27. Вывести уравнение неразрывности для одномерного те-
течения несжимаемой жидкости в трубке тока (боковая поверхность
трубки тока образована линиями тока).
Пусть V — объем, заключенный между двумя произвольными сечениями А
и В трубки тока (рис. 7.5). Уравнение сохранения массы E.2) в интегральной
форме для этого объема при постоянной плотности р записывается в виде
С
J V • xdV = 0. Преобразуем этот интеграл по теореме Гаусса — Остроградского;

244
Гл. 7. ЖИДКОСТИ
это даст \ п • vdS = О, где п — еди-
едиРис. 7.5.
ничный вектор внешней нормали к
поверхности S, ограничивающей
объем V. Из-за того что на боко-
боковой поверхности n J. v, от инте-
интеграла остаются только члены
[ пл • vAdS + J nB ¦ vBdS = 0.
s'a -	Sb
Будем предполагать, что скорость распределена равномерно по сечению и перпен-
перпендикулярна плоскостям сечений SA и SB. Вследствие того что vB = —vBnB,
получим vA \ dS — vB \ dS = 0 или vASA = vBSB = const.
7.28.	В некоторой точке ньютоновой жидкости с нулевым коэф-
коэффициентом объемной вязкости задан тензор напряжений
,— Ь 2—1'
2—9 4
1 4 —;
Найти тензор xt/.
Для такой жидкости, согласно G.14), р = —a?t./3 = 6. Тогда из соотноше-
соотношения G.3) получаем
/—6 2—1\ /6 0 0\ / 0 2—Ь
T(-/=ot/--T-66,./, илитй-=[ 2—9 4j + |0 6 0j = | 2—3 41.
\_ 1 4—3/ \0 0 6/ V—1 4 3/
7.29.	Доказать, что тензоры а,-,- и Гц в формуле G.3) имеют
одни и те же главные оси.
Напишем полностью все соотношения G.3): ап — —p + tu, ass = —р +
+ т!2> °83 = —Р + Т33> °1! = Т12. °!3 = Т23- а13=т13- В ПИВНЫХ ОСЯХ X* ТвНЗО-
ра о,7 должны быть выполнены равенства а\2 = с^ — а*3 = 0. Но последние трн
уравнения из G.3) при этом дают al,= ti, = 0, если i Ф /. А это значит, что
оси х*- оказываются главными и для тензора т(-;- тоже.
7.30.	Для ньютоновой жидкости часто вводят диссипативный
потенциал Фо, определяемый формулой Фо=(к/2) DuDn +n*D'ijD't,:
Доказать, что dODldDi, = Tt-,-.
Пользуясь определением, находим
dOD/dDpq = (м/2) [Dl? (dDn/dDpq) + (dDu/dDpq) D/7] + 2ц*
Ho dD-i/dD 0=6,- б,- = б и 6D--/dD —д-„6- —б-.б /3. Поэтому

ЗАДАЧИ С РЕШЕНИЯМИ	245
Наконец, вследствие того, что и = Я* + 2р.*/3, получаем
d®DldDpq = Я*ер(?Оа. + 2|i*Dw = ти.
7.31.	Найти зависимость между давлением и плотностью в со-
совершенном газе при условиях задачи 7.11.
При х3 = 0 имеем р = р0 и р = р0. Уравнение состояния совершенно-
совершенного газа в нашем случае будет иметь вид р = pR (То — ах3) и, следовательно,
р0 = puRT0. Из зависимости давления от высоты, определенной в задаче 7.11
как р = р0 A — ax3/T0)g/Ra, можно получить р/ро= (T/T0)ie/Ra~l). Равенство
р =р0 A — ax3/T0)e/Ra представим в форме р/рв = (T/Tof/Ra, откуда Г/Го =
= (plpu)Ra^, и окончательно находим р/ро= (Р'Ро) ~ ?SK
7.32.	Доказать, что в баротропной невязкой жидкости при по-
потенциальных силах материальная производная от полной завихрен-
завихренности выражается формулой -п- f q^dV = f vtfjdS,.
v	s
'	d г
По формуле D.54), используя результат задачи 4.33, находим —тг \ i
til J
v
~ \ (¦etfifili-ht/fl>i)dSi. Но в нашем случае, согласно G.37), од = — (Q
s
Тогда по теореме Гаусса — Остроградского A.157) можно написать
= J
V
J ,/ft (Q + P),A/dV = 0
V
вследствие того, что подинтегральное выражение равно нулю (как произведение
симметричного и антисимметричного тензоров). Отсюда следует
7.33. Несжимаемая ньютонова жидкость движется внутри за-
закрытого покоящегося сосуда с твердыми стенками. Доказать, что
если массовые силы отсутствуют, то скорость изменения со вре-
временем кинетической энергии жидкости будет равна —(г* ^ qzdV
(q здесь означает модуль вектора завихренности).
Как было установлено в задаче 5.27, скорость изменения со временем кине-
кинетической энергии среды равна
dK г	г	г Г,
-jf = J pbfitdV - J cl/VijdV + \ о,/}п> dS.
V	V	S
В нашей задаче первый и третий интегралы обращаются в нуль, н для ньютоновой
жидкости, используя G.18), получаем
dK
1
V
V

246	Гл. 7. ЖИДКОСТИ
Но вследствие несжимаемости vt1- = Di( = 0; поэтому
J
= —^*\ &kjiQk) vtwidV = — И-* 9* tek/iViJ dV = — (x* ?
v	V	V
7.34. Доказать, что в идеальной жидкости при отсутствии мас-
массовых сил скорость изменения циркуляции Гс выражается инте-
интегралом
— J
По формуле G.43) Гс = ф fid*,- + ф VidVi. Но второй из интегралов обраща-
ется в нуль, так как ф d (Vgii8) = 0. Из уравнения G.36) при Ь,- = 0 имеем
Vi = —р 4/р; следовательно,
Ге = — ^ (p>ft/p) d«ft = —
Здесь использована формула G.42) для преобразования линейного интеграла
в интеграл по поверхности. Выполняя указанное дифференцирование, находим
'" = - J e«/fc
= - J «у*
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
7.35.	Даны определяющие уравнения изотропной жидкости о4- = —рб,- +
+ KcjpqDpy, где Kj/P? — постоянные, не зависящие от координат. Доказать,
что главные оси тензора напряжений и тензора скоростей деформации совпадают.
7.36.	Доказать следующее утверждение: если имеет место равенство
dp/dt ¦= 0, то в ньютоновой жидкости —°н/3 = р-
7.37.	Доказать, что определяющие уравнения ньютоновой жидкости с нуле-
нулевым коэффициентом объемной вязкости можно представить двумя группами
уравнений: st. = 2(x*Dl-- и —стй- = Зр.
7.38.	Доказать, что, используя вектор завихренности q, уравнения Навье —
Стокса для несжимаемой жидкости можно записать следующим образом: v =. b —
— Vp/p — v*V X q, где v* = ц*/р — кинематический коэффициент вязкости.
Показать, что для безвихревого движения эти уравнения приводятся к виду G.36).
7.39.	Движение жидкости происходит по радиусам со скоростью v = v {r, f),
где rz = x,-Xj. Доказать, что уравнение неразрывности имеет вид
7.40. Жидкость вращается как твердое тело с постоянной угловой скоростью
ш вокруг вертикальной оси х3- Из массовых сил действует только сила тяжести.
Доказать, что р/р — coVz/2 + gxa = const.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ	247
7.41.	Имеем совершенный газ в поле силы тяжести в условиях изотермии (при
постоянной температуре То). Доказать, что р/р„ = plp0 •= e~^RToX3\ где
р0 и р0 — плотность и давление при х* =. 0.
7.42.	Массовые силы потенциальны, т. е. 6,- = —Q (., и процесс баротропный.
Доказать, что для безвихревого движения можно проинтегрировать уравнения
Навье — Стокса — Дюгема и получить соотношение
-р (ftp/» + (V<p)f/2) + pQ + P + (X* + 2р.*) У2ф = / (О
(см. задачу 7.15).
7.43.	Показать, что в невязкой жидкости при потенциальных массовых силах
и постоянной плотности векторы скорости и завихренности связаны соотношением
hi — 9jvi j — 0- Доказать, что для стационарного потока той же жидкости и;-<?4 . =
7.44.	Доказать, что для баротропного процесса, в котором р = р (р) и функ-
функция Р (р) определена формулой G.29), выполняется равенство grad P = grad pip.
7.45.	Доказать, что уравнение Бернулли G.39) при установившемся движении
совершенного газа записывается в виде:
а)	Q + р In (pip) + W2 = const при изотермическом течении;
б)	Q+ [kl (k — 1)] (pip) + у!/2 = const при изэнтропическом течении.
7.46.	Доказать, что поле скоростей v1 = —Чх^х^г*, v2 = (х\ — х%) хя/г*,
и3 = х2''г2. где гг = х\ + д^ + *|, возможно при движении несжимаемой жидкости-
Будет ли это дпижение безвихревым?
Ответ: да.
7.47.	Потенциал скорости Ф (г) = ф + iif является аналитической функцией
комплексного переменного г = xt + ix2 = ге'е. Показать, что в полярных коорди-
дш 1 5ib	I dw	дй>
т —	1^ II	Z	L_
дг г дв г 36	дг '

Глава 8
Теория пластичности
8.1. Основные положения и определения
Упругие деформации, которые изучались в гл. 6, обладают
свойством полного восстановления недеформированного состояния
после снятия приложенных нагрузок. Кроме того, упругие деформа-
деформации зависят только от величины напряжений и не зависят от истории
деформирования или нагружения. Любая деформация, возникающая
как ответная реакция материала на приложенные нагрузки или из-
изменения в окружающей среде и не подчиняющаяся определяющим
законам классической теории упругости, может рассматривать-
рассматриваться как неупругая деформация. В частности, необратимые смещения,
которые получаются в результате скольжения или дислокаций на
атомном уровне и как следствие ведут к остаточным изменениям
размеров, называются пластическими деформациями. Такие дефор-
деформации имеют место только при интенсивности напряжения выше
некоторого порога, известного как предел упругости или предел
текучести. Будем обозначать этот предел оу.
Основные проблемы теории пластичности состоят в матема-
математической формулировке соотношений между напряжениями и де-
деформациями, соответствующих феноменологическому описанию
пластических деформаций, и в установлении правил определения
количественных критериев для указания начала наступления плас-
пластичности. С другой стороны, изучение пластических деформаций с
микроскопической точки зрения относится к области физики твер-
твердого тела.
Термин пластическое течение широко используется в теории
пластичности для обозначения процесса пластического деформиро-
деформирования. Однако в отличие от течения жидкости, при котором предпо-
предполагается движение частиц среды, понятие пластического течения
относится к непрерывному изменению суммарной деформации, а
скорость представляет собой скорость деформации. В самом деле,
твердое тело в состоянии пластичности может испытывать каса-
касательные напряжения, оставаясь в покое.
Многие основные понятия теории пластичности можно ввести
непосредственно, рассматривая диаграммы зависимости напряжений
от деформаций при испытании некоторого гипотетического мате-
материала на простое одноосное растяжение (или сжатие). Такая диа-
диаграмма представлена на рис, 8.1. На этой схеме а — условное напря-

8.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ОПРЕДЕЛЕНИЯ
249
жение (сила, деленная на начальную площадь сечения), тогда как
в качестве е можно взять либо обычную (техническую) относитель-
относительную деформацию, определяемую формулой
e = (L — L0)/L0,	(8.1)
где L — текущая длина образца, a Lo — его начальная длина, либо
натуральную (логарифмическую) относительную деформацию, опре-
определяемую формулой
е = In (L/Lo) = In A + е) = е — е*/2 + О (е3).	(8.2)
Для малых деформаций эти две их меры почти равны, как видно
из (8.2), и часто допустимо пренебрегать разницей между ними.
Предел текучести точка Р, соответствующая предельному на-
напряжению оу, разделяет кривую напряжение — деформация
на рис. 8.1 на упругую
область и пластическую
область. К сожалению,
предел упругости разные
авторы определяют по-
разному. Иногда он бе-
берется как предел пропор-
пропорциональности и лежит в
верхнем конце линейной
части кривой. Иногда
за него принимают точ-
точку /, которая назы-
называется пределом теку-
текучести Джонсона и по
определению представ-
представляет собой точку, где наклон кривой достигает 50% от своего пер-
первоначального значения. Есть и другие способы определения преде-
предела текучести. Так, один из них принимает за предел текучести
такое значение напряжения, которое дает 0,2% остаточной дефор-
деформации.
В начальной упругой области, которая может быть как линейной,
так и нелинейной, увеличение нагрузки заставляет точку, изобра-
изображающую напряженно-деформированное состояние, двигаться вверх
по кривой, а уменьшение нагрузки (разгрузка) ведет к движению
точки вниз по тому же самому пути. Таким образом, в упругой
области существует взаимно однозначное соответствие между на-
напряжением и деформацией.
В пластической области дело обстоит иначе. При разгрузке
от некоторого состояния, например В. на рис. 8.1, точка, изобража-
изображающая состояние, следует по пути ВС, практически параллельному
линейной упругой части кривой. В точке С, где напряжение дости-
достигает нуля, обнаруживается остаточная пластическая деформация гр.
Рис. 8.1.

250	Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
На рис. 8.1 символом е обозначена восстановленная упругая де-
деформация, соответствующая точке В. При повторной нагрузке
точка, изображающая состояние, движется из С обратно к В по пу-
пути, очень близкому к ВС, но не попадает точно в В'), и из-за поте-
потери энергии в цикле разгрузка — нагрузка образуется небольшая
петля гистерезиса. После возвращения к точке В требуется увели-
увеличение нагрузки, чтобы вызвать дальнейшую деформацию. Это
явление связано с так называемым свойством упрочнения материала.
Итак, ясно, что в пластической области напряжение зависит от
всей истории нагружения или деформирования среды.
Хотя известно, что температура оказывает существенное влия-
влияние на пластическое поведение реального материала, в теории плас-
пластичности часто принимают условие изотермии и считают темпера-
температуру просто параметром. Точно так же на практике в общепринятой
теории пластичности обычно пренебрегают влиянием скорости на-
нагружения на диаграмму напряжение—-деформация. В соответ-
соответствии с этим пластические деформации считаются не зависящими
от времени и изучаются отдельно от таких явлений, как ползучесть
и релаксация.
8.2. Идеализированные диаграммы пластического поведения
Многие из трехмерных теорий, изучающих пластическое пове-
поведение, можно рассматривать как некоторое обобщение ряда идеали-
идеализированных одномерных диаграмм зависимости напряжения от
деформации. Четыре из наиболее часто употребляемых диаграмм
такого рода представлены на рис. 8.2 вместе с простыми механиче-
механическими схемами осуществления каждой из них. В этих схемах пере-
перемещение массы М имитирует пластическую деформацию, а сила
F играет роль напряжения.
На рис. 8.2, а упругая область и явление упрочнения полностью
отсутствуют, тогда как на рис. 8.2, б существует упругая зона, пред-
предшествующая пределу текучести, а упрочнения нет. При отсутствии
упрочнения деформация называется идеально пластической. Пред-
Представления а и б наиболее полезны при изучении ограниченных
пластических деформаций, когда большие деформации запрещены.
На рис. 8.2, в упругая зона отсутствует, а упрочнение предполага-
предполагается линейным. Эта модель, так же как и модель, представленная
на рис. 8.2, г, широко используется при изучении не ограниченно-
ограниченного внешними условиями пластического течения.
Диаграммы напряжение—деформация, изображенные на рис. 8.2,
именуются в тексте кривыми растяжения. Кривая сжатия для неде-
формированного предварительно образца (при отсутствии истерии
]) Чтобы попасть точно в В, нужно было бы разгрузку продолжить несколько
дальше за нулевое напряжение.— Прим- перев.

8.2. ИДЕАЛИЗИРОВАННЫЕ ДИАГРАММЫ ПЛАСТИЧЕСКОГО ПОВЕДЕНИЯ	251
а
м \
У//////////////////////'/////////.
Су
У//////////////////////////////.
Л—VWW—
у//////////////////////////////.
У//////////////////////////////,
Рис. 8.2.
а — жестко-идеально-пластический материал; б — упруго-идеально-пластический
материал; в — жесткопластический материал с линейным упрочнением; г —
упругопластический материал с линейным упрочнением. Во всех механических
моделях существенно трение между массой М и горизонтальной плоскостью.
пластического деформирования) обычно представляет собой отраже-
отражение кривой растяжения относительно начала координат. Однако
если изменение напряжения на обратное (растяжения на сжатие
или наоборот) производится для материала, уже находящегося
в пластическом состоянии, то наблюдается определенное уменьшение
напряжения предела текучести при втором типе нагрузки. Это яв-
явление называется эффектом Баушингера и в этой книге рассматри-
рассматриваться не будет.

252	Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
8.3. Условия пластичности. Критерии Треска и Мизеса
Условие (или критерий) пластичности является важным обоб-
обобщением на трехмерное напряженное состояние понятия предела
текучести для одноосного растяжения. С математической точки
зрения условие пластичности представляет собой соотношение меж-
между компонентами напряжений в точке, которое должно быть выпол-
выполнено, когда в этой точке начинается пластическое поведение ').
В общем случае условие пластичности можно записать уравнением
/((*/) = Су,	(8.3)
где Су — постоянная текучести. Иногда это условие задают урав-
уравнением
в котором fx (oij) называется функцией текучести.
Для изотропного материала условие пластичности не должно
зависеть от направлений и поэтому может быть выражено в виде
функции инвариантов напряжения, или, что все равно, в виде
симметричной функции главных напряжений. Тогда равенство (8.3)
можно представить следующим образом:
f2(o"i, ог„, сгП1) = Cv.	(8.5)
Кроме того, эксперименты показывают, что для многих сред
(в частности, дла металлов) напряжение всестороннего сжатия не
вызывает пластических деформаций. Поэтому обычно считают, что
в условии пластичности фигурирует функция инвариантов девиа-
тора напряжений
МНю, Шю) = 0.	(8.6)
Из многочисленных условий пластичности, которые были пред-
предложены, два приемлемо просты математически и в то же время
достаточно точны, чтобы быть весьма полезными при изучении на-
начальной стадии пластичности изотропных материалов. Это усло-
условия (критерии) Треска и Мизеса.
1. Критерий текучести Треска (теория максимального каса-
касательного напряжения).
Согласно этому критерию, пластическое поведение начинается
тогда, когда максимальное касательное напряжение достигает за-
заданной величины Су. Проще всего критерий Треска записывается
в главных напряжениях. Так, при tfi > аи > От критерий Треска
в соответствии с формулой B.546) выглядит так:
lli (°i — ат) = Су = const.	(8.7)
1) Иногда (обычно для сред без упрочнения) это условие называют условием
(критерием) текучести. В дальнейшем будут использоваться оба эти термина	-¦
Прим- ред.

8.3. УСЛОВИЯ ПЛАСТИЧНОСТИ. КРИТЕРИИ ТРЕСКА И МИЗЕСА
253
Чтобы установить связь между постоянной текучести Су и пределом
текучести при простом растяжении оу, найдем максимальное каса-
касательное напряжение при простом растяжении в условиях пластич-
пластичности (например, при помощи кругов Мора; рис. 8.3,а). Оно
а	6
Рис. 8.3.
а — простое растяжение; б — чистый сдвиг.
оказывается равным о>/2. Поэтому критерий Треска выражается че-
через предел текучести при простом растяжении следующим образом:
O-I — стш = оу.	(8.8)
С той же целью установления величины постоянной CY можно ис-
использовать предел текучести в процессе, который называют чис-
чистым сдвигом. Так, если предел текучести при чистом сдвиге равен
k, то величина постоянной Су равна k (этот результат опять сразу
получается из кругов Мора на рис. 8.3, б) и критерий Треска запи-
записывается равенством
0-1 — (Тш = 2*.	(8.9)
2. Критерий текучести Мизеса (теория энергии искажения
формы)
Согласно этому критерию, пластическое поведение начинается
тогда, когда второй инвариант девиатора напряжений достигает
некоторого критического значения. Математически критерий Ми-
Мизеса записывается так:
— HsD = Cy,	(8.10)
или через главные напряжения так:
(or, _ „„)» + (а„ _ „,„)« + („„, _ ffIJ = 6Су- (8л j)
Рассматривая простое растяжение, легко показать, что (8.11) можно
записать в виде
{О\ — OiiV + (or,i — ошJ + (огщ — ст,)а = 2с? .	(8.12)
Критерий Мизеса (8.11) также можно записать и через величину
k — предел текучести при чистом сдвиге:
(СП — оги)а + (ог„ -с,„J + (ош -о,)8 = 6/га.	(8.13)

254
Гл 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
Существует несколько вариантов представления соотношений (8.12)
и (8.13), когда используются другие компоненты напряжения, от-
отличные от главных.
8.4. Пространство напряжений. П-плоскость.
Поверхность текучести
Пространство напряжений определяется тем, что в качестве
меры расстояний вдоль осей координат берутся величины на-
напряжений. В пространстве главных напряжений (пространстве
Хея—Вестергарда), изо-
изображенном на рис. 8.4,
по осям координат откла-
откладываются главные значе-
значения тензора напряжений.
Каждая точка такого
пространства соответст-
соответствует некоторому напря-
напряженному состоянию. Ра-
Радиус-вектор ОР любой
точки Р (cri, си, ош) мо-
может быть разложен на
две компоненты: О А —
вдоль прямой OZ, кото-
которая составляет равные
углы с осями коорди-
координат, и ОВ — в плоскос-
'О.
Рис. 8.4.
ти, перпендикулярной OZ и проходящей через начало координат (эта
плоскость известна под названием П-плоскости). Компонента вдоль
OZ, для которой С\ = он = сгш, представляет гидростатическое
давление, а компонента в П-плоскости — девиаторную часть на-
напряжения. Легко показать, что П-плоскость имеет уравнение
СП + огц + огш - 0.	(8.14)
В пространстве напряжений условие (8.5) f2 (аи Оц, Ощ) — Су
определяет некоторую поверхность; эта поверхность называется по-
поверхностью текучести. Если принять, что условие пластичности
не зависит от гидростатического напряжения всестороннего сжатия,
то соответствующие поверхности текучести являются цилиндрами
с образующими, параллельными OZ. Точки пространства напряже-
напряжений, которые лежат внутри цилиндрической поверхности текучести,
соответствуют упругому напряженному состоянию, а точки, лежа-
лежащие на поверхности текучести, представляют начальное пластиче-
пластическое напряженное состояние. Пересечение поверхности текучести
С П-плоскостью называется кривой текучести.

B.S. ПОВЕДЕНИЕ МАТЕРИАЛА ЗА ПРЕДЕЛОМ ТЕКУЧЕСТИ
255
Если посмотреть вдоль прямой OZ в направлении к началу ко-
координат — точке О, то станет ясно, что проекции осей коорди-
координат на П-плоскость оказываются расположенными симметрично под
углом 120° одна к другой, как показано на рис. 8.5, а. Кривые те-
текучести, соответствующие критериям Треска и Мизеса, изображены
на П-плоскости на рис. 8.5, б и 8.5, в. Кривые на рис. 8.5, б соот-
соответствуют уравнениям (8.7) и (8.11), и за основу (точку, через
которую должна проходить кривая) принято пластическое напря-
женное состояние при простом растяжении. В такой ситуации
окружность Мизеса радиуса ]/2/3 оу оказывается описанной около
правильного шестиугольника Треска. На рис. 8.5, в обе эти кривые
текучести имеют в качестве базиса предельное напряжение теку-
текучести k при чистом сдвиге. В этом случае окружность Мизеса впи-
вписана в шестиугольник Треска.
Положение на П-плоскости проекции произвольной точки на-
напряжения Р' (di, (Гц, am) находится непосредственным проектирова-
проектированием, так как каждая из осей координат пространства напряжений
составляет с П-плоскостью угол, косинус которого равен J/2/3.
Таким образом, компоненты девиаторной проекции равны A/2/3G1,
|/2/Зогц, 1^2/3 ащ). Решение обратной задачи — определение ком-
компонент напряжения для какой-либо точки П-плоскости — оказы-
оказывается не единственным, так как гидростатическая компонента
напряжения может принимать какое угодно значение.
8.5. Поведение материала за пределом текучести.
Изотропное и кинематическое упрочнение
Продолжение нагружения после достижения началь-
начального предела текучести приводит к пластическим дефор-
деформациям, которые могут сопровождаться изменениями перво-
первоначальной поверхности текучести. Если материал предполагается
идеально пластическим, то поверхность текучести не
изменяется в процессе пластического деформирования и
начальное условие пластичности остается в силе. Этому со-
соответствуют одномерные диаграммы напряжение—.деформация,

256
Гл 8 ТЕОРИЯ ПЛАСТИЧНОСТИ
изображенные на рис. 8.2,о и 8.2,6. Однако для материала с уп-
упрочнением пластическое деформирование в общем случае сопро-
сопровождается изменениями поверхности текучести. Для учета таких
изменений необходимо обобщить функцию текучести fx @4,) в фор-
формуле (8.4), чтобы она могла задавать изменения поверхности те-
текучести при деформировании (при этом поверхность текучести час-
часто называют поверхностью нагружения). Такое обобщение достига-
достигается введением функции нагружения
f'i (tfy, 4 К) = 0,	(8.15)
которая зависит не только от напряжений, но также и от пласти-
пластических деформаций е// и характеристик упрочнения, представлен-
представленных параметром К. Уравнение (8.15) дает поверхность нагружения,
что означает следующее: fi=0 определяет границу упругой зоны,
/i <0 соответствует упругой зоне внутри поверхности напружения,
a f* > 0 соответствует области вне^поверхности нагружения и смыс-
смысла не имеет.
Найдем полный дифференциал функции (8.15):
.«• dh j_. . dh л_р , dh АЬг	(8.16)
дК
Если /* = 0 и (dfi/dOij)doc,-< 0, то говорят, что имеет место про-
процесс разгрузки; если /Г = 0 и (д/'/дсг,-,) dcr,,- = 0, то мы имеем ней-
нейтральное нагружение; если fl = 0 и (dfi/doij) бац > 0, то происхо-
происходит процесс активного нагружения. Тот способ, каким пластические
деформации efj входят в функцию (8.15) в процессе нагружения,
определяется законом упрочнения. Здесь описываются два наибо-
наиболее простых из этих законов.
Начальные кривые
текучести
Рис. 8.6.
а — окружности Мизеса; б — правильные шестиугольники Треска.
Гипотеза изотропного упрочнения при нагружении постулирует,
что поверхность текучести просто увеличивается в размерах, со-

8.6. ТЕОРИЯ ПЛАСТИЧЕСКОГО ПОТЕНЦИАЛА	257
храняя при этом свою начальную форму. Кривые текучести в
П-плоскости для критериев Мизеса и Треска будут концентриче-
концентрическими окружностями и правильными шестиугольниками соответ-
соответственно (рис. 8.6).
При кинематическом упрочне-
упрочнении начальная поверхность теку-
текучести поступательно перемещается
в новое положение в пространстве
напряжений без изменений разме-	рис-
ров и формы. Тогда формулу (8.4),
задающую начальную поверхность текучести, нужно заменить сле-
следующей:
h К -«./) = 0,	(8.17)
где cty — координаты центра новой поверхности текучести. Если
упрочнение предполагается линейным, то
%	(8.18)
причем с — постоянная. В одномерном случае кривая текучести
Треска переносилась бы так, как показано на рис. 8.7.
8.6. Соотношения между напряжениями и деформациями в
пластическом состоянии. Теория пластического потенциала
Как только возникают пластические деформации, определяющие
уравнения теории упругости перестают быть верными. В силу того
что пластические деформации зависят от всей истории нагружения
материала, в теории пластичности соотношения между напряжением
и деформацией очень часто формулируют через приращения дефор-
деформации. Это так называемые инкрементальные теории, или теории
течения. Например, уравнения Леей — Мизеса, при записи которых
пренебрегают упругой частью деформации и предполагают, что
главные оси тензоров приращений деформации и напряжений совпа-
совпадают, связывают приращения полной деформации с компонентами
девиатора напряжений следующим образом:
detj = SifdK.	(8.19)
Здесь коэффициент пропорциональности dX дается в дифферент
циальной форме, чтобы подчеркнуть, что приращения деформации
связаны с конечными компонентами напряжений. Множитель dX
может меняться в процессе нагружения и является поэтому скаляр-
скалярной функцией, а не фиксированной постоянной. Соотношения (8.19)
представляют закон течения для жестко-идеально-пластического
материала.
Разложив приращения деформации на упругую и пластическую
части:
dztj = defj + def/	(8.20)
9 Дж. Мей:-

258	Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
и связав приращения пластической деформации с компонентами
девиатора напряжений:
def, = Si/dX,	(8.21)
мы приходим к уравнениям Прандтля—Рейсса. Формулы (8.21)
представляют закон течения упруго-идеально-пластического мате-
материала. Они устанавливают связь между приращениями пласти-
пластической деформации и девиатором текущих напряжений, но не дают
самих величин приращений деформации.
Функцию компонент напряжения g @7,), которая обладает сле-
следующим свойством:
d*r,= -$LdK	(8.22)
называют пластическим потенциалом. Для так называемого устой-
устойчиво пластического материала такая функция существует и тож-
тождественно совпадает с функцией текучести. Если к тому же функция
текучести взята в виде/^(с,,) = П2?>, то равенства (8.22) превраща-
превращаются в уравнения Прандгля — Рейсса.
8.7. Эквивалентное напряжение.
Эквивалентное приращение пластической деформации
Для математической формулировки закона упрочнения полезно
определить эквивалентное, или эффективное, напряжение ашв
формулой
(Тзкв = -~ {[@ц — Ом)г + (Osa — 0Г33J + @Ю — Oil)*] +
+ 6 @?2 + ста + о231)}*'¦ .	(8.23)
Кратко это выражение можно записать так:
<гэкв = \г5ь&№ = V— ЗПГо .	(8.24)
Подобным же образом вводится эквивалентное, или эффектив-
эффективное, приращение пластической деформации
deP3KS = B/в [(def, — de22)8 + (de& - rfef3J + (A& - def,J] +
+ 4/3[{de& + (de&)* + (de?)«]}v« .	(8.25)
Его компактная форма имеет вид
L \ГЧМЩ	(8.26)
Используя эквивалентные напряжения и приращения пласти-
пластической деформации, определенные соответственно формулами (8.24)

8.8. ГИПОТЕЗЫ УПРОЧНЕНИЯ	259
и (8.26), получим выражение для коэффициента dh из соотношения
(8.21):
8.8. Работа на пластических деформациях.
Гипотезы упрочнения
Скорость, с которой напряжения совершают работу на дефор-
деформациях, или так называемая мощность напряжений, была опреде-
определена для единицы объема формулой E.32) как OijDij. Согласно
D.25), de,-,- = Dijdt, поэтому можно ввести приращение работы
в единице объема:
dW = Oijdeu,	(8.28)
Применяя разложение (8.20), эту величину тоже можно	предста-
можно	представить суммой
dW = ati (def, + de?) = dWE + dWp .	(8.29)
Для пластически несжимаемого материала приращение	работы
на пластических деформациях будет равно
dWP = о^е?, = st/def,.	(8.30)
Если к тому же этот материал подчиняется уравнениям Прандтля —
Рейсса (8.21), то приращение работы на пластических деформаци-
деформациях представляется выражением
dWP = omiBdePKB ,	(8.31)
а (8.21) принимает вид
. р 3 dWp
de	S
(8.32)
Из всех гипотез, предложенных для расчета мгновенных пласти-
пластических напряжений при пластическом деформировании материала
с изотропным упрочнением, наибольшее распространение получили
две: энергетическая и деформационная. Энергетическая гипотеза
упрочнения заключается в том, что мгновенная поверхность теку-
текучести зависит только от полной работы на пластических деформа-
деформациях. Итак, через полную работу на пластических деформациях,
которая дается интегралом
Wp = 1афрц,	(8.33)
критерий пластичности выражается в символических обозначениях
равенством
h(oii) = F (W*),	(8.34)

260	Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
в котором точный вид функциональной зависимости должен быть
определен экспериментально. Деформационная гипотеза упрочне-
упрочнения состоит в том, что упрочнение определяется величиной пласти-
пластических деформаций. Через полную эквивалентную деформацию
«&b = JA&»	(8.35)
закон упрочнения в символических обозначениях представляется
соотношением
h Ш = И (е»),	(8.36)
в котором вид функциональной связи находится из эксперименталь-
экспериментальной зависимости напряжение — деформация при одноосном испы-
испытании материала. Можно показать, что для критерия Мизеса зако-
законы упрочнения (8.34) и (8.36) эквивалентны.
8.9. Деформационная теория пластичности
При изучении пластических деформаций наряду с теорией тече-
течения, которая основывается на уравнениях (8.19) и (8.21) и связы-
связывает приращения деформаций с напряжениями, существует так на-
называемая деформационная теория пластичности Генки, в которой
предполагается зависимость между напряжениями и полными де-
деформациями. Эти соотношения имеют вид
ei,=[<p-M/BG)]sl7,	(8.37)
е« = A —2v)c«/E.	(8.38)
Параметр Генки <р можно выразить через эквивалентные напряже-
напряжения и деформацию
ЭКГ
здесь е^в = У 2ef,-e^/3 и, таким образом,
8.10. Задачи упругопластичности
Ситуации, в которых и упругие, и пластические деформации,
возникающие в теле при нагружении, имеют примерно одинаковый
порядок, обычно относят к задачам упругопластичности. Много
широко известных задач такого типа встречается в теории балок
и теории кручения валов, а также в исследовании толстостенных
труб и оболочек, находящихся под давлением. В общем случае
постановка задач в упругой зоне, пластической зоне и на границе
между ними включает следующие соотношения.

8.11. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ЛИНИЙ СКОЛЬЖЕНИЯ	261
а)	Упругая область:
уравнения равновесия B.23),
связь между напряжениями и деформациями F.23) или
F.24),
граничные условия, наложенные на напряжения или пере-
перемещения,
условия совместности.
б)	Пластическая область:
уравнения равновесия B.23),
связи между напряжениями и приращениями деформации,
определяемые формулами (8.20), (8.21) и F.24),
условие совместности полных деформаций,
условие пластичности (8.8) или (8.11),
граничные условия на границе пластической области, если та-
таковая граница существует.
в) Граница между упругой и пластической областями:
условия непрерывности напряжений и перемещений.
8.11. Элементарная теория линий скольжения
при плоской пластической деформации
В неограниченном пластическом течении, например при про-
прокатке металла, часто допустимо пренебрегать- упругими деформа-
деформациями и рассматривать материал как жестко-идеально-пласти-
жестко-идеально-пластическую среду. Если течение в дальнейшем можно предполагать
таким, как в случае плоской деформации, то получающееся поле
скоростей можно изучать, пользуясь теорией линий скольжения.
Пусть ххх2 — плоскость течения; тогда
/ап о12 0 \
о22 0 .	(8.41)
\0 0 aj
и, так как упругими деформациями мы пренебрегаем, тензор ско-
скоростей пластической деформации будет равен
' ё12 0\
е22 0 •	(8-42)
\0 0 0'
Неизвестные в выражениях (8.41) и (8.42) являются функциями
только лс± и х2. Кроме того, известно; что
Ъ, = V. (vtJ + vj.i),	(8.43)
где ut •— компоненты скорости.

262
Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
При предполагаемых условиях плоской деформации имеем
de33 = 0. Тогда из уравнений Прандтля — Рейсса (8.21) для
напряжения а33 получим формулу
а33 = 1/2(о11+а22).	(8.44)
обычные обозначения теории линии скольжения
2 = k, находим главные значения
Используя
а33= — р и 1/(оп
с,2J/4 -f- (a12)
тензора напряжении (8.41):
= —p — k, аC) = — р.
(8.45)
Положение главных направлений тензора напряжений относитель-
относительно осей хххг показано на рис. 8.8, где tg 20 = 2а12/(ои— а22).
Направления площадок максимальных касательных напряжений
(см. § 2.11) образуют углы в 45° с главными осями тензора на-
напряжений. На рис. 8.8 соответствующие направления помечены
буквами а и р. Из это-
этого построения видно,что
0 — л/4 -f- ф и, следова-
следовательно,
= — ctg26. (8.46)
Для данного поля на-
х пряжений при пласти-
Рис 88	1 ческом течении можно
ввести в рассмотрение
два семейства кривых, в каждой точке идущих вдоль направлений
максимальных касательных напряжений. Эти кривые называются
линиями сдвига или линиями скольжения (в дальнейшем мы будем
называть их также ос-линиями и Р-линиями).
Рассматривая малый элемент, ограниченный двумя парами ли-
линий скольжения и изображенный на рис. 8.9, получим
ап = — р — k sin 2ф,
c22 = —p-\-ksm2(pt	v->-^'}
a12 = k cos 2ф.
Используя уравнения равновесия, можно показать, что
р -\- 2&ф = Сх постоянно вдоль ос-линии,
р — 2&ф = С2 постоянно вдоль Р-линии.
(8.48)
Что касается компонент скорости, то рис. 8.10 показывает,
как они связаны с положением а- и р-линий:
vt — va cos cp — v-, sin ф,
v2 = va sin ф + up cos <p.
(8.49)

ЗАДАЧИ С РЕШЕНИЯМИ
263
Для изотропной среды в теориях течения главные оси тензоров
напряжений и скоростей пластической деформации совпадают. По-
Поэтому если хх и x2 — направления линий скольжения, то ец и е22
Рис. 8.9.
равны нулю вдоль этих линий, так что
Ш~ (у« cos Ф — уР sin Ф
Рис. 8.10.
<p=D
Отсюда получаются соотношения
dvt — v2d(p = 0 на ос-линни,
dv2 -f- Vidy = 0 на C-линии.
(8.50)
(8.51)
(8.52)
(8.53)
Итак, для статически определимых задач поле линий скольже-
скольжения находится из (8.48); затем, используя это поле и соотношения
(8.52) и (8.53), можно построить поле скоростей.
ЗАДАЧИ С РЕШЕНИЯМИ
Основные понятия. Явление текучести (§ 8.1—8.4)
8.1. Используя определения (8.1) и (8.2), получить соотношение
между логарифмической и технической деформацией. Как связа-
связаны приращения этих величин?
Согласно (8.1), LJ,o = е + 1; тогда (8.2) дает е = In (e + 1). Дифференцируя
это равенство, находим de/de = 1/(е + 1) = LJL вследствие того, что dL =
8.2. При нагрузке Р в одномерном испытании образца истин-
истинное напряжение а = Р/А, в то время как техническое принимает-
принимается в виде 5 = Р/Ао, где Ао — начальная площадь сечения, a A —
текущая ее величина. Найти условие максимума нагрузки при плас-
пластическом деформировании с сохранением объема (A0L0 = AL).

264
Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
В нашем случае S = Р/Ао = (Р/А) (А/Ав) =* с (LJL) = а/ A + е) п учас-
участок максимальной нагрузки на S-e диаграмме находится там, где наклон ее равен
нулю (dSlde = 0). Дифференцирование дает dS/de = (daldz — а)/A + e)J. Это
выражение равно нулю, если do/de = а. Используя результат задачи 8.1, послед-
последнее условие можно записать в виде dolde = а/ A + е).
8.3.	В качестве меры влияния промежуточного главного напря-
напряжения на пластическое состояние часто используют параметр
Лоде ц = B(Тц — а — От) 1(о\—ащ). Доказать, что параметр
Лоде можно выразить через главные значения девиатора напряже-
напряжений формулой |я = 3sn/ (si — Shi).
Согласно B.71), а, = s, + ам и т. д., причем ам = аи/3. Тогда
(х = [2 (sn + ом) - (s, + ам) - (sUI + aM)]/[(Sl + aM) - (s,,, + aM)] =
= [3s,, -(s, + s,, + snl)]/(s, -sIM).
Ho s, + s,, + sin = l?c = 0, и, следовательно, ц = 3sn/ (sx — s,,,).
8.4.	Для напряженного состояния cju = о, ст22 = а33 = 0, а12 =
= Ti °2з — ai3 = 0, которое возникает при испытании на растя-
жение — кручение тонкостенной
трубы, получить кривые текучес-
текучести в плоскости сг-т в соответст-
Рис. 8.11.
вии с критериями Треска и Мизеса, если предел текучести при
простом растяжении равен oY.
В данном напряженном состоянии главные значения напряжений равны
01 = @+ V 4т2 + а2)/2, а„ = 0, аш = (а — /4т2 + а2)/2, как показывает диа-
диаграмма Мора на рис. 8.11. Таким образом, по формуле (8.8) найдем кривую теку-
текучести Треска К4т2 + а2 = Су, или а2 + 4т2 = Оу. Это эллипс в а-т плоскости.
Аналогично формула (8.12) дает кривую текучести Мизеса в виде эллипса аа+
+ Зт2 = Оу. Эллипсы текучести Мизеса и Треска для этого случая сравнивают-
сравниваются на рис. 8.12.
8.5. Преобразовать условие пластичности Мизеса (8.10) к форме
(8.11), т. е. записать его через главные напряжения.

ЗАДАЧИ С РЕШЕНИЯМИ
265
По формуле B.72) —Пх = —(s^sn -\- susul + «inSj), а, согласно B.71),
Sj = Oj — aM и т. д., причем ом = (а, + Оц + О|ц)/3- Отсюда
- H2d = - (а а„ + апаш + а,,,^) + (а, + а„ + сшJ/3 =т
= 2 (а1 + °П + °Ш — °1°П — аП аП1 — ОщОО/б.
Таким образом, (Oj—ап)а+(ац—ani)a + (aHi—OjJ = 6СУ.
8.6. Пусть ортогональная система координат OXYZ ориентирова-
ориентирована так, что плоскость XY совпадает с П-плоскостью, а осьащ лежит
в плоскости YOZ (см. рис. 8.13 и 8.4). Доказать, что поверхность
текучести Мизеса пересекает П-плоскость по окружности Мизеса
(рис. 8.5, б).
Таблица коэффициентов преобразования одной системы осей в другую нахо-
находится без труда и имеет следующий вид:
arccos(Vv/3)
у.
crccos\/2/3
X
Y
Z
ai
-П
-Г» 
aII
1/1 2
— 1 У 
aIIl
0
2 УЪ
Рис. 8.13.
+ Z!\Tb, a,, = X/V~2 -
Отсюда следует, что
Ol = — X/V~2 —
Тогда формула (8.12) сводится к уравнению
(— У~2Х)* + (Х1\Г2 - ЗК//"В)а + (Х/У1 + ЗК//"б)а = 24,
которое после упрощения приводит к окружности Мизеса ЗХа + ЗУ2 = 2сф,
изображенной на рис. 8.5, б.
8.7.	Используя преобразование координат задачи 8.6, доказать,
что уравнение (8.14) oi + an + ош =0 является уравнением
П-плоскости.
Подставляя в уравнение (8.14) выражения для Op an, аш, найденные в за-
задаче 8.6, получаем О1 + Оц+ош = У 3Z = 0, или Z — 0, а это и есть плос-
плоскость XY (П-плоскость).
8.8.	Для двуосного напряженного состояния, когда an = 0,
найти поверхности текучести Мизеса и Треска и сравнить их»
пользуясь диаграммой в плоскости /	/

266
Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
\
При ап = 0 критерий Мизеса
(8.12) записывается уравнением
9	,2 	 2
которое представляет эллипс
о,
с осями под углом 45° к указанным
координатным направлениям (aj/oy,
ffjjj/a^). Аналогично критерий Трес-
Треска, т. е- формула (8.8), вместе с
равенствами oln — an =ay, ац—al=ay приводит к шестиугольнику Трес-
Треска, образованному (рис. 8.14) отрезками АВ и ED с уравнениями (Oj/Oy) —
— (ani'av0 = ± 1, DC и FA с уравнениями о^ц/оу = ± 1 и 6С и EF с урав-
уравнениями a^cty = ± 1 соответственно.
8.9. В § 8.3 критерий Мизеса назван теорией энергии искаже-
искажения формы. Доказать, что если энергию искажения формы на еди-
единицу объема u*D) положить равной постоянной текучести Су, то
в результате получится критерий Мгкзеса в форме (8.12).
В задаче 6.26 было найдено выражение u^D. через главные напряжения:
"(D, = Ко, - а2J + (о, - cj* + (о, - OJ4/12G.
При одноосном растяжении или сжатии, когда а, = ау, а2 => аз = 0, из этой
формулы следует, что u*D) = aY /6G- Тогда CY = oy /60 и, как и прежде, кри-
критерий Мизеса выражается равенством (8.12).
Пластические деформации.
Упрочнение (§8.4—8.8)
8.10. Доказать, что уравнения Прандтля — Рейсса (8.21) со-
содержат в себе утверждение, что главные оси тензора приращений
пластической деформации совпадают с главными осями тензора
напряжений. Записать эти уравнения через главные напряжения.
Из формулы (8.21) видно, что в системе координат, в которой равны нулю
касательные напряжения, отсутствуют также и приращения пластической дефор-
деформации сдвига. В системе главных осей уравнение (8.21) принимает вид def/sj =
= defllsn — de^j 'sui = d%. Таким образом, def = (a( — cM) dX, de^ = (au —
— aM) dk и т. д. Последовательным вычитанием находим
ds?-deZ
jii-°iii
-¦= ок.

ЗАДАЧИ С РЕШЕНИЯМИ
267
8.11.	Доказать, что в случае плоской пластической деформа-
деформации, когда еаз = 0, de33 = 0 и о22 =. О, уравнения Леви — ЛЛизеса
(8.19) приводят к тождественному совпадению критериев теку-
текучести Треска и Мизеса (записанных через предел текучести при
чистом сдвиге k).
В нашем случае уравнения (8.19) записываются так:
deu = Bап — а33) d\!3, de22 = — (ап + а33) dh 3, 0 = 2о33 — аи.
При отсутствии касательных напряжений а, = ац. ои =033= аи/2, аш = 0 =
= а22. Тогда из формулы (8.9) находим критерий Треска в виде Oj—Ощ =
= ап = 2k, a из (8.13) получаем для данного случая критерий Мизеса (Оц'2J +
+ (— Оц/2J + (— ОцJ = 6ft2, или of, = 4/г2, т. е. au = 2k.
8.12.	Доказать, что из уравнений Прандтля— Репсса следует
равенство параметра Лоде ц (см. задачу 8.3) и величины
v = Bdef, - def - defi,,/^ - defj,).
Из соотношения (8.21) получаем
v = Bsn - s, - sIU) dX/(s, - sUI) d\ =
= B (Оц - оЛ1) - (a, - аЛ1) - (аш — aM))/((Ol - ам) — (аш - ам)) =
= Bаи - ai - °iii).'(°i - аш) = V-
8.13.	Доказать, что для второго инварианта девиатора на-
напряжений \\^D = sijSijl2 выполняется равенство dIIvD/do?/ = s,;-.
Пользуясь выражением для П? . находим
— fl«76OT/3- ТаКИМ обРазом- dllZDldapq==^>ipbjq—\(>pqi:SlSij = Sp(,' ПОСКОЛЬКУ
8.14.	Пусть пластический потенциал имеет вид g (a*/) = IIZd;
доказать, что соотношения (8.22) для пластического потенциала
превращаются в уравнения Прандтля — Рейсса.
Доказательство сразу следует из результата задачи 8.13, так как в этом слу-
случае dgfda^ = s,-;. и, следовательно, (8.22) сводятся к (8.21).
8.15.	Записать в развернутом виде выражение (8.24) и дока-
доказать, что эквивалентное напряжение аэкв можно записать в форме
(8.23).
Из равенства (8.24) имеем
=3 к j— V» '3) f°y - V

268	Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
Записывая его в развернутом виде, получаем
+ 6 (ог?2 + о^ + 40 — (°и + <г22 + <733J]/2 =
= [2 («п + <4 + <& — oua22 — ст22ст33 — ст33стц) + 6 (а
= K^ii — <%)' + (°22 — <%зJ + (<*зз — °иJ + 6 (о?2 + а|3
что и утверждается формулой (8.23).
8.16.	В теории пластического потенциала вектор приращения
пластической деформации перпендикулярен поверхности нагру-
жения (текучести) в любой регулярной точке; доказать, что если
удовлетворяется критерий Мизеса, то выполняются уравнения
йгР /si = den/sn = dem/sui-
Пусть числа Nlt N2, N3 задают направление нормали к поверхности теку-
текучести /i (af/.), т. е. эту нормаль можно характеризовать величиной N = grad flt a
для этого требуется, чтобы N1/(dfi/dal) — N^^dfjda^) ==Лг3/(й/г1/(?а111), причем,
согласно критерию Мизеса, ft = (ст, — апJ + (<7ц — ащJ + (ai ц — aiJ — 2a^.=>
= 0. Тогда dfJdO] = 2 BOj—ан—аш) = 6sj и т. д., а так как вектор при-
приращения пластической деформации направлен по нормали к f\, отсюда следует,
что rfef/s, = de/J/sn = de^n/slu.
8.17.	Найти отношения приращений пластических деформаций:
а) для простого растяжения, когда ои = ay; б) для двуосного на-
напряженного состояния, при котором au = — оу/^З, о22 =ау/\/Г3,
°зз = о12 = а23 = а13 = 0; в) для чистого сдвига при a12 = ay/V^3.
а) При данных условиях ац = Oj =Oy, au =oI]I = 0 и S! =2a^/3, sH =
s=sin=—ау/3. Используя результат задачи 8.16, находим def/2 = — de^/1 =
б)	В данном случае ах =ау/|^3, ап=0, аш = —а^/]Аз и sl = oy
sn = 0, Sjjj = — Oy/V 3. Таким образом, def/1 = — de^j/1, а третий член опус-
опускается, поскольку обычно предполагается, что при обращении в нуль знаменателя
и числитель тоже обращается в нуль.
в)	В этом случае Oj = ау/у^ 3, а„ = 0, а,и = —oY/V 3 и снова получаем
def7l=-de?,/l.
8.18. Найти приращение работы на пластических деформациях
dWp и приращение эквивалентной пластической деформации de^KB
для двуосного напряженного состояния an= —ау/У^З, о22=ау/\ 3,
a33 = о12 = а23 = аз1 = 0, если пластическая деформация проис-
происходит так, что def = С, где С—некоторая постоянная.
Выражение для приращения работы (8.30) в главных осях имеет вид dWp =
— Ojdef-f Oiidefi + 0п14ещ. Для указанного напряженного состояния результат
задачи 8.17 показывает, что def = — defjp dtpx = 0. Отсюда следует, что
dWp -= - ОуС/УИ + (о> \ 3) (— Q = — 2Соу/к .

ЗАДАЧИ С РЕШЕНИЯМИ	269
Используя формулу (8.25), находим
*&, = {2 [(<fcf - deft* + (defi - de^iI + Сеш ~ *fJ]}VV3 =
= {2 [C2 + C2 + 4C2]} v"/3 = 2С/У~3.
8.19.	Проверить правильность соотношения (8.32), доказав,
что приращение работы на пластических деформациях для мате-
материала Прандтля— Рейсса равно dWp = оэкъйгРкъ, как утверждает
формула (8.31).
Для материала Прандтля — Рейсса, удовлетворяющего уравнениям (8.21),
формула (8.30) дает Шр = s^s^d.%. Но, согласно (8.27), для такого материала
dh = 3de^B/2o3KB, и, следовательно, Шр = CstjSt/-/2) (dePKB(a3KB), а если учесть
определение (8.24), то последнее выражение упростится: dWp = o3KBde^B. Та-
Таким образом, в данном случае depKB = dWp/o3KB. Соотношение (8.32) теперь
сразу следует из формулы (8.21).
8.20.	Для материала, удовлетворяющего критерию текучести
Мизеса, в качестве функции текучести в законах упрочнения (8.34)
и (8.36) можно взять эквивалентное напряжение 0ЭКВ. Доказать,
что в этом случае выполняется равенство o3KBF' = Н', где F'
и Н' — производные характеризующих упрочнение функций по их
аргументам.
Закон упрочнения (8.34) в указанном случае принимает вндсэкв = F (Wp), и,
значит, da3KB = F'dWp- Аналогично закон упрочнения (8.36) записывается
следующим образом: аэкв = Н (efKB), и тогда da3KB = H'depKB. Таким образом,
F'dWp = H'de,pKB. А так как из формулы (8.31) (или задачи 8.19) известно, что
dWp = o3KBde^KB, сразу получаем o3KBf' =. Н'.
Деформационная теория пластичности (§ 8.9)
8.21.	Основу деформационной теории пластичности Генки со-
составляют следующие соотношения: е?;- = ef. + ef., причем ef. =
= efi + bcieg/3 = silfBG)+8li(l— 2v)akk/CE) и e? = cps?/. Дока-
Доказать, что эти равенства эквивалентны формулам (8.37) и (8.38).
Среди уравнений е^. = q>sl;. содержится и такое: ер = 0, а это означает, что
е^. = efj — ystj. Из равенства ztj = е^. + е^ следует, что тогда еу-;. = е?.. Из
того же самого равенства получается еще соотношение et/. + f>ijBkk/3 = eff- +
+ 6i7effc/3 + e!/' которое сводится к виду е^. = е^. + е^-=l4> +l/BG)]slj< а этой
есть (8.37). Кроме того, из равенства ги = е^ получаем ги = A — 2v) okk/E,
что представляет собой (8.38).
8.22.	Проверить тот факт, что параметр Генки ф можно пред-
представить формулой (8.39).

270
Гл. 8 ТЕОРИЯ ПЛАСТИЧНОСТИ
Возводя в квадрат и складывая компоненты тензоров в уравнении e?=(pS{.
задачи 8.21, приходим к следующему равенству: е^-е?. = «P^-s,-^ или q> =
= У Зе^е?-/2/аэкв. Умножая обе части последнего равенства на %, получ"аем
Ф = 3 )^2е?е?/3/2аэкв= 3<кв/2аэКв.
Задачи упругопластичности (§ 8.10)
8.23. Балка прямоугольного сечения из упруго-идеально-плас-
упруго-идеально-пластического материала находится под нагрузкой на чистый изгиб»
Рис. 8.15.
Пользуясь элементарной теорией балок, найти величину изгибаю-
изгибающего момента.М, действующего на конце балки, при которой упру-
упругое ядро балки простирается от —а до а, как показано на рис. 8.15.
В данной задаче единственным отличным от нуля напряжением будет изги-
изгибающее напряжение аи. В упругом ядре внутри балки (— а < х2< а) имеет место
равенство ап = Ееп = Ex2/R, где R — радиус кривизны изогнутой оси балки,
а Е — модуль Юнга. В пластической зоне аи = Оу. Таким образом,
с
М = 2
х2J bdx2 + 2
о
("
= be у (с2 — а2/3),
где Оу = Ea/R. т. е. использовано условие непрерывности напряжения на грани-
границе между упругой и пластической зонами. Из полученной формулы видно, что
М = 26с2ау/3, когда пластическая зона только появляется (при а = с), и М =•
= Ьс"Су, когда вся балка оказывается в пластическом состоянии (при а = 0).
8.24. Найти изгибающий момент для балки из материала с
кусочно-линейным упрочнением (так что за пределом текучести
ап = оу + A (en — oYIE)), на которую действует такая же на-
нагрузка, как в задаче 8.23.
Распределение напряжений в такой балке показано на рис. 8.16. Снова ей ¦=•
¦= x2IR, и, следовательно,
М = 2
о
2ЕЬа3

ЗАДАЧИ С РЕШЕНИЯМИ
271
Воспользовавшись, как и в задаче 8.23, условием cry = Ea/R, найдем
М = c2b0y A — А'Е)
8.25. Круглый вал радиуса с из упруго-идеально-пластиче-
упруго-идеально-пластического материала закручивается на концах --оментом Т, как показа-
показано на рис. 8.17. Найти величину
крутящего момента, при котором
внутри вала остается упругое яд- / /\$&с*ая_ *5><2%»
ро радиуса а.
Рис. 8.16-
Рис. 8.17.
В данном случае касательное напряжение а12 распределено следующим обра-
образом: а12 = krla при 0 < г < о и о,2 = k при а ^ г < с, где k — предел текучес-
текучести материала при чистом сдвиге. Тогда
а	с
Т = 2я (" (krs/a) dr + 2л С *r2dr = -^р. (с» — а2/4).
О	а
Таким образом, крутящий момент, характеризующий самое начало появления
пластической зоны (а — с), равен 7\ = ккс?12. Вал полностью находится в плас-
пластическом состоянии (а = 0) при Т2 = 2nk<?l2i =¦
= 4Г,/3.
8.26. Толстая сферическая оболочка,
размеры которой указаны на рис. 8.18,
находится под действием растущего
давления р0. Используя критерий Ми-
зеса, • найти то давление, при котором
впервые появится пластическое состоя-
состояние.
Из-за симметрии действующей нагрузки
главные напряжения являются компонентами в
сферических координатах а(ее) = aw = а1 =• аи,
щгг) =ош- Тогда критерий Мизеса (8.12) вы-	Рис 8.18.
глядит так: а(ев)—а(гЛ) = ау. Можно показать,
что компоненты напряжения в упругом состоянии представляются выражениями
<V) = - Ро Ф3/'* ~ 1)/F3/а3 - 1),
аЩ = а(ФФ) = Ро ФЧЪ* + 1)/F3/о3 - 1).

272	Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
Поэтому Оу =. Ъ№ро1[2гЩ?1<? — 1)], откуда рв = 2оу A — сР/Ь3)/^. Это то дав-
давление, при котором впервые появляется пластическое состояние на внутренней
границе оболочки (при г = а).
Теория линий скольжения (§8.11)
8.27. Проверить, что формула (8.45) действительно дает глав-
главные значения тензора напряжений (8.41), если принято условие
<*зз ~ @п + агг) /2 (формула (8.44)).
Главные значения тензора напряжений находятся из векового уравнения
B.37), которое в нашем случае имеет вид
,—а а12	О
з12 а22 — а О
= 0.
О	0 —р—а
Раскладывая определитель по третьему столбцу, получаем
(—р-а) [(сп — а) (а22 — а) — с?2] = (— р — а) [а2 — (аи + а22) а — а\2\ = 0.
Очевидно, корнями этого уравнения будут а = —р и
о = V2 (cn + а22) ± V^U ("и + о22J + а?2 = — Р ± к.
8.28.	Воспользовавшись условием постоянства предела теку-
текучести при чистом сдвиге к, подставить выражения (8.47) в уравне-
уравнения равновесия и, проинтегрировав, доказать справедливость со-
соотношений (8.48).
Уравнения равновесия дсгц/dxj + <Эа12/дх2 =.0и да12/дхг + да22/дл:2 = 0
после подстановки в них выражений (8.47) превращаются в следующие:
—	др/dXi —kB cos 2ф) (дф/djCi) + k (— 2 sin 2ф) (д<р/дх2) = 0,
—	k B sin 2ф) (ду/dxj) — бр/ах2 + k B cos 2ф) (д(р/дх2) = 0.
Если *! — координата вдоль ex-линии, а х2 — вдоль Р-линии, то ф=0 и
уравнения равновесия дают —dp/dxY— 2k (дф/dx,) = 0 вдоль ex-линии и — др/дх2+
+ 2k (дф/дх2) = 0 вдоль Р-линии. Эти уравнения сразу интегрируются, в резуль-
результате чего получаем р + 2/гф = Cj наа-линии и р — 2йф = С2 на Р-линии.
8.29.	При штамповке с вытяжкой без трения через квадратную
матрицу, приводящей к уменьшению сечения на пятьдесят процен-
процентов, линии скольжения заполняют веерообразную область, которая
состоит из радиальных прямых — Р-линий и дуг окружностей —
ос-линий (рис. 8.19). Найти компоненты скорости вдоль этих линий

ЗАДАЧИ С РЕШЕНИЯМИ	273
скольжения, выраженные через скорость подачи материала V
и полярные координаты гиб.
Вдоль прямых р-линий dq> -= 0, и по формуле (8.БЗ) находим dt>2 ¦= 0 или
1/г = const. Поскольку нормальная компонента скорости вдоль ВС непрерывна,
в данной задаче эта константа должна быть равна U cos В, т. е. у2 ¦= Ucos 8. Вдоль
круговых ex-линий Лр = d9. и по формуле (8-52) получаем
е
и1= С U cosG d6 = (/(sin В + l/j'l).
-Я/4
Смешанные задачи
8.30. Доказать, что условие пластичности Мизеса можно запи-
записать через октаэдрическое касательное напряжение стокт (см. зада-
задачу 2.22) следующим образом: стокт = V^ оу/3.
Октаэдрическое касательное напряжение через главные напряжения пред-
представляется формулой (см. задачу 2.22)
Чжт = V(°i ~ апJ + <°н - "inI + (°ш -°iJ-
Следовательно, согласно (8.12),
9<4т = (°1 - «I,J + (Оц - ОП1)« + (ОШ - О,)* = 24.
8.31.	Доказать, что уравнение (8.13), выражающее критерий
Мизеса, можно записать в виде s? + s?i + sin = 2fe2.
Согласно B.71), a, = Sj + ам и т. д.; тогда уравнение (8.13) сразу прини-
принимает форму
(SI - s,,J + (SII - s.nJ + (sin - siJ = №¦
Раскрывая скобки и перегруппировывая члены, это можно записать так: Sj +
+ sii + «ш - (si + sn + siiiJ/3 = 2*2- Ho si + SH + sni = hD = ° и требуе-
требуемое уравнение получено.
8.32.	При каком значении |я = Bац — ai — ащ) 1 (р\ — ощ)
(ц. — параметр Лоде) критерии Треска и Мизеса совпадают?
Из формулы, определяющей величину ц, имеем Оц = (at + от)№ +ц(О[ —
— аш)/2. Если подставить это выражение в критерий Мизеса (8.12), то после
некоторых алгебраических преобразований (см. задачу 8.42) получим а, — аш =
=» 2ау/У + [л.2. Критерий Треска записывается уравнением (8.8): а,—аи, =
= оу. Очевидно, если ц= 1, оба критерия совпадают. Когда 011=0!, то ц =
= 1; этот случай иногда называют цилиндрическим (осесимметричным) напряжен-
напряженным состоянием.
8.33.	Для напряженного состояния
/о т О
Oij = I т a О
\0 0 a

274
Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
где а и т —¦ постоянные, найти условия пластичности, соответ-
соответствующие критериям Треска и Мнзеса.
JleiKO показать, что главными значениями данного тензора напряжений будут
о, = a -f т. ац = а> аш ~с — х Тогда критерий Треска (8.8) щ — аш = ау
приводит к уравнению 2т = оу, критерий же Мизеса (8.12) дает т = оу/1 3.
Снова убеждаемся в том, что в обоих критериях фигурирует т и не фигурирует <т,
т. е. что гидростатическое давление никоим образом не влияет ни на характерис-
характеристики пластического состояния, ни на само наличие такого состояния.
8.34.	Доказать, что если уравнения Прандтля — Рейсса вы-
выполняются, то выполняется и условие несжимаемости материала
при пластической деформации. Записать эти уравнения через
мгноЕенные напряжения.
Из (8.21) видно, что deft = stid% = 0, так как sit = 12д зО, и, следова-
следовательно, условие несжимаемости defi = 0 выполняется.
Запишем уравнения Прандтля — Рейсса через компоненты тензора напряже-
напряжений: defj = (atj — 6(jckk'3) dK. Таким образом, def, = 2/3 [ац — (а22 + О33IЩ dX
и т. д. для нормальных компонент и dejg = a12d^ и т. д. для касательных.
8.35.	Используя критерий Мизеса, доказать, что в П-плоскости
компоненты девиатора напряжений на кривой текучести равны
si = I—2o\ cos@ — я/6)]/3, sn =[2aycos@ + л/6)]/3,
siii = Baysin0)/3,
где 6 = ardgYIX (определение X и V дано в задаче 8.6).
Радиус окружности текучести Мизеса равен }^2 '3 оу, так что по определе-
определению К = уТг/Зоу cos 9, Y = Y2/3oys\ti 9 на кривой текучести. Таблица коэф-
коэффициентов преобразования осей координат, приведенная в задаче 8.6, вместе с
равенствами О] = Sj-f-о^и и т- д- позволяет получить уравнения S]—stl =>
K = — 2aYsin 9.
= 0. Решая совместно
= — B/^) aKcos 9 и s, + s,, — 2sm = —
Известно также и уравнение П-плоскости s, + sn
Рис. 8.20.
эти три уравнения, приходим к требуе-
требуемым формулам, как может убедиться сам
читатель.
8.36. Упруго-идеально-пласти-
Упруго-идеально-пластический несжимаемый материал
находится под нагрузкой в усло-
условиях плоской деформации между
двумя жесткими пластинами, так
что а22 = 0 и е33 = 0 (рис. 8.20).
Используя критерий Мизеса, опре-
определить напряжение оп в момент
появления пластичности и соот-
соответствующую деформацию еи.

ЗАДАЧИ С РЕШЕНИЯМИ
27S
Соотношение, связывающее напряжение с деформацией в упругом состоянии
?езз = Озз — V (ап + Огг).
в данном случае сводится к уравнению о33 = \ап. Тогда главные напряжения
будут равны а, = 0, аи = — vau, аш = —ап. По формуле (8.12) мы имеем
(vatlJ + (On (I - v)J + (- auJ = йф.
ш
м\
Т
с
f
1
отсюда находим au = —ayl\ 1 — v — v (сжатие) на пределе текучести. Анало-
Аналогично из соотношения ?ец = au — v (a22 -)- a33) мы видим, что на пределе теку-
текучести 8.J j = — Оу A — V2)/? ]/1 — V — V2.
8.37. Балка прямоугольного сечения из упруго-идеально-
пластического материала подвергается нагрузке, приводящей к чис-
чистому изгибу (рис. 8.21).
Нагрузка возрастает
до такого значения
момента, что весь мате-
материал балки полностью
переходит в пластиче-	р „ 2
ское состояние. Найти
остаточное напряжение в балке после того, как изгибающий мо-
момент М снят.
Все сечение балки полностью оказывается в пластическом состоянии, когда
момент достигает значения М = Ьсгсу (см. задачу 8.23). При таком моменте
упругое напряжение в крайних волокнах было бы равно a = Mcll = 3ay/2,
где / = 26с3/3 — момент инерции сечения балки относительно оси х3.' Последую-
Последующее снятие момента М эквивалентно приложению соответственно распределенных
Зау/2	Оу/г
Uy
у
ау
в
о	6
Рис. 8.22.
а — пластическое напряжение; б — отрицательное упругое напряже-
напряжение; в — остаточное напряжение.
отрицательных упругих напряжений, что дает в результате остаточное напряже-
напряжение, представленное на рис. 8.22.
8.38. Толстостенная цилиндрическая труба, размеры которой
указаны на рис. 8.23, находится под действием внутреннего давле-
давления р0; труба закрыта с концов. Найти значение р0, при котором
впервые достигается предел текучести. Принять критерии текуче-
текучести: а) Мизеса, б) Треска.

276
Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
Рис. 8.23.
Рис. 8.24.
Компоненты напряжения в цилиндрических координатах (рис. 8.24) будут
главными напряжениями. Анализ упругого состояния позволяет показать, что
(fr2/2l)/Q	Ф2>* + 1)Q	/Q где Q =
V)	aF6) =
= (УУа2 —1).
а) В данном случае критерии Мизеса имеет вид
(V
или
(a(ee> - <W'2 + (a(Z2) - <
= Q*o2Y/3.
Предел текучести впервые достигается при г — а и р0 = {aYlV 3) A — a2/b2).
б) Критерий Треска сводится к равенству аFе) — а(/т) = оу, так как a(z^ —
промежуточное по величине из главных напряжений. Таким образом, 2pob2/r2 =
= Q<3y, и теперь предел текучести впервые достигается при г = а и р0 =
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
8.39.	Дан закон одномерной зависимости напряжение — деформация a a
с= Ке", причем Кип — постоянные, а е — истинная деформация. Доказать, что
максимальная нагрузка имеет место при е = п.
8.40.	Решить еще раз задачу 8.4, записав критерии Мизеса и Треска через
предел текучести при чистом сдвиге к, а не через оу.
Ответ: Мизес: (a/(/~3fc)J + (т/А;J = 1;
Треска: (о7B*)J + (т/А;J = 1.
8.41.	Приняв условия задачи 8.6, удостовериться в правильности геометри-
геометрического построения на рис. 8.5, в.
8.42.	Используя определение параметра Лоде (х (см. задачу 8.3) и критерий
Мизеса, доказать, что Oj — Ощ = 2oy/l/3 + |j.2.
8.43.	Доказать, что в П-плоскости, где 9 = arc tg Y/X (Л и У определены в
задаче 8.6), выполняется формула (х = — Y 3 tg 0.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
277
8.44. Доказать, что инварианты девиатора напряжений IIZ = st st -/2 и
Ш2?) = st,sjkshi/3 можно представить соответственно в виде П2 = (^ -f- «и
+ 4ц)/2 и HIj.D = (s? + *?i 4
8.45.	Доказать, что критерий Мизеса можно записать в форме
(ац — 022J + (а22 - а33J + (о33 - ОцJ + 6 {а?2 + а|3 + а|,) = 6й2.
8.46.	Используя метод решения задачи 8.17, найти отношения приращений
пластической деформации: а) для двуосного растяжения, когда аа = а22 = оу
б) для растяжения с кручением, когда ои = оу/2, о1а = оу/2.
Ответ: a) de,^ = de? = ^
б) def,/2 = - de? = - de3P3 = de?/3.
8.47. Проверить следующие эквивалентные выражения для приращения эф-
эффективной пластической деформации de^.B:
a)
6)
+2 (deP3J+2
[(def,-
(deP2-
Обратите внимание на то, что в обоих случаях de^ = dep, при одноосном
растяжении напряжением ап.
8.48.	Тонкостенная труба из упруго-идеально-пластического материала под-
подвергается нагрузке на растяжение и кручение. Первым прикладывается напряже-
напряжение вдоль оси трубы а = оу/2, которое остается постоянным, в то время как каса-
касательное напряжение т равномерно нарастает начиная от нуля. Основываясь
на критерии Мизеса, найти, при каком значении т начинается переход к пласти-
пластическому состоянию.
Ответ: т = оу/2.
8.49.	Балка треугольного поперечного сечения, изображенная на рис. 8.25,
подвергается нагрузке на чистый изгиб. Найти положение нейтральной оси бал-
,А
Рис. 8.25.
В
Рис. 8.26.
ки NA (ее расстояние Ь от вершины треугольника) в условиях, когда сечение цели-
целиком находится в пластическом состоянии.
Ответ: Ь = Ы].

278	Гл. 8. ТЕОРИЯ ПЛАСТИЧНОСТИ
8.50.	Показать, что тензор напряжений (8.41) имеет вид
(-Р k 0
°«7=( * —Р °
V 0 0 -vt
в системе координат, повернутой вокруг х3 на угол 9 (рис. 8.8).
8.51.	Линии скольжения образуют веерообразную область с углом раствора
30°; ех-лииии — дуги окружностей, Р-линии — радиусы (рис. 8.26). Давление
на линии АВ равно к. Найти давление на линии АС-
Ответ: р = k A + я/3).

Глава 9
Линейная вязко у пру гость
9.1.	Вязкоупругое поведение материала
Упругие тела и вязкие жидкости существенно различаются
своими свойствами при деформировании. Упругие деформируе-
деформируемые тела после снятия приложенных нагрузок возвращаются к свое-
своему естественному, или недеформированному, состоянию. В отличие
от них несжимаемые вязкие жидкости совсем не имеют тенденции
возвращаться после снятия нагрузки в исходное состояние. Кроме
того, напряжения в упругом теле евязаны„непосредственно с де-
деформациями, в то время как напряжения в вязкой жидкости зави-
зависят (за исключением гидростатической составляющей) от скоростей
деформации.
Поведение материала, которое объединяет в себе оба эти свой-
свойства— и упругости, и вязкости,— называют вязкоупругим. Упру-
Упругое тело и вязкая жидкость занимают крайние противоположные
точки в широком спектре вязкоупругих сред. Хотя вязкоупругие
материалы чувствительны к температуре, последующее изложение
ограничивается условиями изотермии й температура входит в урав-
уравнения только как параметр.
9.2.	Простейшие механические модели
вязкоупругого поведения
Линейную вязкоупругость для одномерного состояния удобно
трактовать при помощи механических моделей, которые наглядно
демонстрируют поведение различных вязкоупругих материалов. Эти
модели строятся из таких механических элементов, как линейно-
упругая пружина с модулем упругости G (массой этой пружины
пренебрегают) и вязкий элемент (демпфер} с коэффициентом вязкос-
вязкости т] (вязкий элемент представляет собой поршень, движущийся
в цилиндре с вязкой жидкостью). Как показано на рис. 9.1, сила
а, растягивающая пружину, связана с ее удлинением е формулой
о = вг.	(9.1)
Подобное же соотношение существует и для демпфера
а = т]ё,	(9.2)
где е = ckldt. Можно придать большую общность этим моделям
и устранить размерные эффекты, если в качестве а рассматривать
напряжение, а в качестве е — относительную деформацию.

280
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
Модель Максвелла вязкоупругого тела является комбинацией
пружины и вязкого элемента (демпфера), соединенных последова-
последовательно (рис. 9.2,а). Модель Кельвина или Фойхта представляет
собой параллельное соединение тех же элементов (рис. 9.2, бI). Соот-
о < о WWWWWWWW—*—»~<
Рис. 9.1.
а — линейный упругий элемент; б — вязкий элемент.
ношение между напряжением и деформацией (фактически содержа-
содержащее также и их скорости) для модели Максвелла дается формулой
а для модели Кельвина формулой
(j = Ge-
(9-3)
(9.4)
Эти уравнения являются по существу определяющими уравнениями
вязкоупругостн в одномерном случае. Полезно написать их в опе-
Рис. 9.2.
а — модель Максвелла; б — модель Кельвина.
раторной форме, используя линейный оператор дифференцирования
по времени dt = d/dt. Тогда уравнение (9.3) будет иметь вид
{dt/G + 1/т]} а = {а,} е,	(9.5)
') В дальнейшем, когда на основе моделей Максвелла и Кельвина будут стро-
строиться более сложные модели, для обозначения соответствующих «узлов» таких
многопараметрических моделей будут употребляться термины «узел Максвелла»
и «узел Кельвина>>-— При», ред.

9.2. МОДЕЛИ ВЯЗКОУПРУГОГО ПОВЕДЕНИЯ
281
а уравнение (9.4) примет форму
a={G + r\dt}e,	(9.6)
где соответствующие операторы выделены скобками.
Простые модели Максвелла и Кельвина не дают точного полного
описания поведения реальных сред. Усложненные модели обладают
большей гибкостью в отражении процессов в фактических материа-
г
г-*тт—
Чан	l-op-j
а	6
Рис. 9.3.
а — стандартное линейное твердое тело; б — трехпараметрическая модель вяз-
вязкой жидкости.
лах. Так, существует трехпараметрическая модель, состоящая из
двух упругих и одного вязкого элементов (рис. 9.3,а); она называ-
называется стандартным линейным твердым телом. Трехпараметри-
Трехпараметрическая модель вязкой жидкости, состоящая из двух вязких и одного
упругого элементов, представлена на рис. 9.3, б. Полезно заметить,
что с точки зрения формы записи определяющих уравнений ана-
аналогом стандартного линейного твердого тела, соответствующего
рис. 9.3, а, является узел Максвелла, параллельно соединенный
с упругим элементом, а аналогом модели вязкой жидкости, изобра-
изображенной на рис. 9.3, б, узел Максвелла, параллельно соединенный
с вязким элементом.
Четырехпараметрическая модель, состоящая из двух упругих
и двух вязких элементов, может рассматриваться как последова-
последовательно соединенные узел Максвелла и узел Кельвина (рис. 9.4).
fi,	1i
-4-е—vwww—°—ПТ-
г-Ц/VWVW—i
Рис. 9.4.
Существует несколько эквивалентных форм этой модели. Четырех-
Четырехпараметрическая модель способна описать все три основных типа
поведения вязкоупругой среды. Так, она объединяет в себе мгно-
мгновенную упругую реакцию (за счет свободного упругого элемента GJ,
вязкое течение (за счет свободного вязкого элемента т^) и, наконец,
запаздывающую упругую реакцию (за счет узла Кельвина).

282
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
Соотношение между напряжением и деформацией для любой
из трех- или четырехпараметрическнх моделей дается общей
формулой
Ръ*в -\- PiG -{- PqG = <?2е ~г" <?ie ~г" 9ое»	(9-7)
где величины /э,- и qt представляют собой комбинации коэффициентов
Сит] и зависят от способа соединения элементов в модели. В опе-
операторной форме соотношение (9.7) записывается так:
о	9
{PiPt + РА + Ро} о* = [q-fi't + qjdt + q0) e.	(9.8)
9.3. Обобщенные модели.
Линейное дифференциальное операторное уравнение
Обобщенная модель Кельвина состоит из совокупности ряда
узлов Кельвина, соединенных последовательно, как показано
на рис. 9.5. Полная деформация в такой модели равна сумме дефор-
-w/Av—,
I—WWW—,
—СЕ-
12
•—ОЕ-'
Рис. 9.5.
мапий в отдельных узлах. Тогда в операторной форме определяю-
определяющее уравнение в соответствии с (9.6) можно написать следующим
образом:
Аналогично, набор узлов Максвелла, соединенных параллельно,
как изображено на рис. 9.6, называется обобщенной моделью Макс-
1°
Рис. 9.6.
велла. В этом случае полное напряжение равно сумме напряжений
в каждом узле, т. е. в соответствии с (9.5) можно написать
о =
+
. (9.10)

9.4. ПОЛЗУЧЕСТЬ И РЕЛАКСАЦИЯ	283
Для обобщенных моделей соотношения (9.9) и (9.10) можно записать
так:
росг + PiO + Р& + ¦•¦ = <?ое + <?ie + <72е + •••, (9.11)
или более компактно так:
Это линейное дифференциальное операторное уравнение можно запи-
записать символически
{P}a={Q}e,	(9.13)
где операторы {Р} и {Q} определены формулами
9.4. Ползучесть и релаксация
Двумя основными экспериментами вязкоупругости являются
испытания на ползучесть и релаксацию. Их можно выполнить как
испытания на одномерное растяжение (сжатие) или на простой сдвиг.
Эксперимент на ползучесть состоит в мгновенном приложении
к образцу из вязкоупругого ма-
материала напряжения а0, которое
затем остается постоянным, и из-
измерении деформации как функции
времени (проявление ползучести).
В экспериментах на релаксацию
образец подвергается мгновенной
деформации е0, которая затем оста-	п
ется постоянной, в то время как	Рио 97-
проводятся измерения напряжения
как функции времени (эффект релаксации). Математически про-
процесс нагружения при ползучести и релаксации выражается еди-
единичной ступенчатой функцией [U (t — tfj j, определенной сле-
следующим образом:
О при t < U,
и изображенной на рис. 9.7.
Нагружение в опыте на ползучесть представляется функцией
(9.16)

284
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
причем [U (t)] — единичная ступенчатая функция со скачком в мо-
момент tt = 0. Деформация ползучести для модели Кельвина опре-
определяется решением дифференциального уравнения
е _ а„[1/@]
(9.17)
которое получается при подстановке функции (9.16) в уравнение
(9.4). Введенная здесь величина т = r\/G называется временем за-
запаздывания. Можно показать, что для любой непрерывной функции
времени / (t) верно интегральное соотношение
t	t
\ f (П IU(f -tj)dt' = [V{t-tJ\\f (Г) df, (9.18)
—м	t,
где f — переменная интегрирования. С помощью этого соотношения
можно проинтегрировать уравнение (9.17) и найти изменение де-
деформации со временем при ползучести для модели Кельвина
е@ = -§-A-е-*№@].	(9-19)
Закон нагружения в опытах на ползучесть вместе с соответствую-
соответствующей деформацией ползучести для моделей (материалов) Кельвина
и Максвелла представлены на рис. 9.8.
а	6	*
Рис. 9.8.
а — закон нагружения в опыте на ползучесть; б — деформация ползучести.
Релаксация напряжения, имеющая место в материале Максвел-
Максвелла после приложения деформации, меняющейся по закону
о 	 с MllfW	/Q ОГ\\
Ь —¦ со [U ^tjj,	\\i.Z\JJ
дается решением дифференциального уравнения
(9.21)
которое получено подстановкой производной по времени от функции
(9.20) в уравнение (9.3). Здесь [6(/)] = d [U(f)] /^ — функция,
называемая единичной импульсной функцией или дельта-функцией

9.5. ФУНКЦИЯ ПОЛЗУЧЕСТИ. ФУНКЦИЯ РЕЛАКСАЦИИ	285
Дирака. По определению это такая функция, для которой
(9.22а)
оо
J №U — tj)]dt = l.	(9.226)
Она равна нулю всюду, кроме t — tlt где, как видно из определения,
она должна иметь бесконечно большой пик. Можно показать, что
для любой непрерывной функции / (t) при t > tt выполняется ра-
равенство
t
J / (О [б (f - <i)l df = / (/J [U (t - y],	(9.23)
с помощью которого можно проинтегрировать уравнение (9.21)
и найти релаксацию напряжения для материала Максвелла
(9.24)
Релаксация напряжения для материала Кельвина получается
непосредственной подстановкой е = е0 [б (t)] в уравнение (9.4),
откуда
a(t) = Geo[U(t)] + r]eo[f>(t)].	(9.25)
Наличие дельта-функции в уравнении (9.25) указывает'на то, что
потребовалось бы бесконечное напряжение, чтобы вызвать мгновен-
мгновенную конечную деформацию в материале Кельвина.
9.5. Функция ползучести. Функция релаксации.
Интегралы наследственности
Деформация ползучести любого материала (модели), вызван-
вызванная нагрузкой специального вида о = а0 [U (/)], может быть запи-
записана в виде
е @ = 1> @ «о-	(9.26)
Введенная таким образом функция г]; (t) называется функцией
ползучести. Например, для обобщенной модели Кельвина (рис. 9.5)
функция ползучести определяется в соответствии с (9.19) формулой
* w = s Ji A ~~ e~tl%C) [U ш	(9-27)
где J[ = \IGl называется податливостью материала. Если число
узлов Кельвина неограниченно растет, так что А^ -»- оо и конечную
совокупность постоянных (т(, Jt) можно заменить непрерывной
функцией податливости J (т), то функция ползучести для модели

286
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
Кельвина принимает вид
оо
ф (I) = J / (т) (I — e-'A) dr.
о
(9.28)
Функция / (х) называется функцией распределения времен запаз-
запаздывания или спектром запаздывания.
По аналогии с ползучестью релаксация напряжения для любой
модели, подвергающейся деформации вида e = eo[U(f)], может
быть записана так:
a (t) = ф (f) e0;	(9.29)
Ф (/) называется функцией релаксации. Для обобщенной модели
Максвелла (рис. 9.6) функция релаксации в соответствии с (9.24)
определяется как
(9.30)
В этом случае при N ->¦ оо дискретный набор постоянных (G,, xt)
заменяется функцией G (т) и функция релаксации определяется
выражением
= G (т) е-"Чх.
(9.31)
Функция G (х) называется функцией распределения времен релак-
релаксации или спектром релаксации.
В линейной вязкоупругости имеет место принцип суперпози-
суперпозиции, т. е. полный «эффект» от суммы «причин» равен сумме «эффек-
«эффектов» от каждой из «причин». В силу этого если к материалу, для
_1	i
Рис. 9.9.
которого функция ползучести равна г|э (t), прикладывается напря-
напряжение со ступенчатым изменением во времени, как показано
на рис. 9.9, а, то деформация ползучести будет вычисляться

9.5. ФУНКЦИЯ ПОЛЗУЧЕСТИ. ФУНКЦИЯ РЕЛАКСАЦИИ	287
по формуле
е @ = аог|> (t) + orf (t - tt) + сг2г|> (t —12) + as^ (t - /s) =
^ (,	(9.32)
1=0
Тогда произвольный закон изменения напряжения а = a (t),
представленный на рис. 9.9, б, можно рассматривать как функцию,
состоящую из бесконечного числа ступенек, величина каждой из
которых равна da. Соответствующая деформация ползучести по
принципу суперпозиции дается интегралом
^P-^(t-t')df.	(9.33)
Такие интегралы часто называют интегралами наследственности,
так как деформация в любой момент времени оказывается завися-
зависящей от всей истории изменения напряжений.
Для материала первоначально «мертвого», т. е. полностью сво-
свободного от напряжений и деформаций в нулевой момент времени,
в формуле (9.33) можно заменить нулем нижний предел интеграла
и представить деформаиию ползучести в следующем виде:
t')dt'.	(9.34)
Если закон нагружения, кроме того, содержит в себе еще разрыв
в виде ступеньки величины ст0 в момент t = 0, то выражение (9.34)
обычно записывают следующим образом:
е @ = <*оЧ> @ + \ ^Р- №- f) dt'.	(9.35)
о
Проводя рассуждения, аналогичные тем, что были выше, по
принципу суперпозиции можно представить напряжение как функ-
функцию времени интегралом, содержащим указанную историю дефор-
деформации е (t) и функцию релаксации <р (t). Подобно (9.33), напряжение
дается выражением
J ^p<P(t-t')dl'.	(9.36)
Для материала, у которого в момент t = 0 отсутствуют напряжения
и деформации, интегралы, аналогичные тем, что были в (9.34) и

283
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
(9.35), соответственно будут равны
t
(9.37)
a(t) =
(t -1') df.
(9.38)
Поскольку для описания характерных вязкоупругих свойств
данного материала могут быть использованы в равной мере как
интеграл ползучести (9.34), так и интеграл релаксации (9.37),
должно существовать некоторое соотношение между функцией
ползучести гр (t) и функцией релаксации <р (/). Такое соотношение
в общем случае получить непросто, но, воспользовавшись преобра-
преобразованием Лапласа, которое по определению дается интегралом
(9-39)
можно показать, что указанные преобразования i|) (s) и tp(s) функций
¦ф @ и ф (t) связаны равенством
E) = 1/82,	(9.40)
где s— параметр преобразования.
9.6. Комплексные модули и податливости
Если образец из линейного вязкоупругого материала подверга-
подвергается одномерному (растяжение или сдвиг) нагружению по закону
о — о0 sin u>t, то в результате устанавливается деформированное со-
о, е 1
o=O(,sincct
Рис. 9.10.
стояние e = eosin(co? — б), т. е. деформация будет синусоидаль-
синусоидальной с той же частотой ы, что и напряжение, но по фазе отстанет от
напряжения на угол запаздывания б. В таком случае напряжение
и деформацию можно графически представить вертикальными

9.6 КОМПЛЕКСНЫЕ МОДУЛИ И ПОДАТЛИВОСТИ	289
проекциями векторов, имеющих постоянную длину и вращающих-
вращающихся с постоянной угловой скоростью со, как показано на рис 9.10.
Отношение амплитуд напряжения и деформации определяет
абсолютный динамический модуль <то/ео и абсолютную динамиче-
динамическую податливость е0/о0. Кроме того, совпадающие и не совпадаю-
совпадающие по фазе компоненты вращающихся векторов напряжения и де-
деформации на рис. 9.10, а используются для определения следую-
следующих коэффициентов:
а) модуль накопления	Gx = .a°cos.. t
б)	модуль потерь	G2 = a°sin6 ,
ео
в)	податливость накопления Jx = е°cos—,
г)	податливость потерь	Л = e°s'n— .
Обобщение приведенного выше описания поведения вязкоупру-
гого материала достигается представлением в комплексной форме
как напряжения
а* = о0еш,	(9.41)
так и деформации
е* = еое'^'-в>.	(9.42)
При использовании представлений (9.41) и (9.42) вводится комплек-
комплексный модуль G*(m), по определению равный величине
о*/е* = О* (/со) = (Со/в,,) е» = Gl + iG2,	(9.43)
действительная часть которой равн.а модулю накопления, а мнимая
часть — модулю потерь. Аналогично комплексная податливость
определяется формулой
в*/о* = J* (ш) = (eo/tfa) ег* =	G*
(9.44) Л*
/о
J»
где действительная часть рав-	°1
на податливости накопления,	,*
а мнимая часть — взятой с
обратным знаком податли-	Рис. 9.11.
вости потерь. На рис. 9.11
приведены векторные диаграммы G* и J* (заметим, что по опре-
определению G* = 1,7*).
К) Дж. Мейз

290	Гл. 9. ЛИНЕПНАЯ ВЯЗКОУПРУГОСТЬ
9.7. Трехмерная теория
При создании трехмерной теории линейной вязкоупругости
обычно принято рассматривать отдельно вязкоупругое поведение
в условиях так называемого чистого сдвига и чистого расширения.
Таким образом, эффекты искажения формы и изменения величины
объема изучаются независимо и затем их описания комбинируются,
чтобы построить общую теорию. Математически это обеспечивается
разложением тензоров напряжений и деформаций на их девиаторную
и шаровую части, для каждой из которых затем пишутся определя-
определяющие соотношения вязкоупругости. Разложение тензора напряже-
напряжений дано формулой B.70)
ац = sij + бцОик/З,	(9.45)
а разложение тензора малых деформаций — формулой C.98)
etf ='ft/ + буем/3.	(9.46)
Принимая обозначения, использованные в этих равенствах, запи-
запишем в операторной форме трехмерное обобщение определяющих
уравнений вязкоупругости (9.13):
{P)st, = 2[Q)et/	(9.47а)
и
{M}ati = 3{N}e{i,	(9.476)
где {Р}, {Q}, {М} и {N}—дифференциальные операторы, опреде-
определенные в соответствии с (9.14), а числовые множители введены для
удобства. Так как практически все материалы упруго реагируют
на умеренные гидростатические нагрузки, в качестве операторов
[М] и \N), связанных с расширением, обычно берут постоянные
и преобразуют соотношения (9.47) к виду
{Р} s,, = 2 {Q} e,h	(9.48а)
аа = ЗКеи,	(9.486)
где К — объемный модуль упругости.
Следуя тому же общему правилу разделения эффектов искаже-
искажения формы и изменения величины объема, напишем трехмерные
определяющие соотношения вязкоупругости в форме интегралов
ползучести
\w-t')^-df,	(9.49a)

9.8. АНАЛИЗ ВЯЗКОУПРУГОГО НАПРЯЖЕННОГО СОСТОЯНИЯ
•291
и интегралов релаксации
(9.50а)
(9.506)
Для того чтобы распространить на трехмерный случай описание
вязкоупругого процесса при помощи комплексного модуля, требу-
требуется ввести комплексный объемный модуль /\*. Уравнения, раз-
раздельно написанные для чистого сдвига и для чистого расширения,
таковы:
s'j = 2G* (ico) el, = 2{G1 + iGJ e'h	(9.51a)
a*u = 3/C* (ico) e« = 3 (Ki + iK2) e«.	(9.516)
(R)
9.8. Анализ вязкоупругого напряженного состояния.
Принцип соответствия
Задача исследования напряженного состояния в некотором
изотропном вязкоупругом теле, которое занимает объем V и
ограничено поверхно-
поверхностью S (рис. 9.12), ста-
ставится следующим обра-
образом. Пусть заданы мас-
массовые силы bit действу-
действующие внутри V, и пусть
на части St границы те-
тела известны внешние
поверхностные силы
t{"} (xk, t), а на части
S2 поверхности тела —
смещения поверхности
gt (xk, t). Тогда систе-
система, дающая постановку
задачи, состоит из сле-
следующих соотношений:
1)	уравнения движения (или равновесия)
<%/ + bi = 94	(9 52)
2)	соотношения, выражающие деформации через перемещения
2e,v = (uij + и1ш()	(9.53)
10*
Рис. 9.12.

292	Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
или скорости деформации через скорости
2ё(/ = К,+ 0W);	(9.54)
3)
граничные условия
) на
на
Sa;
Si,
(9.55)
(9.56)
4)	начальные условия
щ{хк,0)=иа,	(9.57)
М*».0)=»о;	(9.58)
5)	определяющие уравнения, записанные в одном из следующих
видов:
а) через линейные дифференциальные операторы, т. е. в форме
(9.48),
6)	через интеграл наследственности, т. е. в форме (9.49) или
(9.50);
в) через комплексный модуль, т. е. в форме (9.51).
Если форма тела и условия нагружения достаточно просты
и если поведение материала может быть представлено одной из
простейших моделей, то приведенную выше систему уравнений мож-
можно проинтегрировать непосредственно (см. задачу 9.22). Однако
для более общих условий обычно принято искать решение, поль-
пользуясь принципом соответствия упругой и вязкоупругой задач. Этот
принцип основывается на том, что система основных уравнений тео-
теории упругости и преобразования Лапласа по времени вышеприве-
вышеприведенной системы основных уравнений теории вязкоупругости запи-
записываются одинаково. Соответствующие уравнения для квазиста-
квазистатических изотермических задач, в которых черточки означают
преобразования Лапласа по времени, например
(xk,t)e-«dt,	(9.59)
сопоставлены в следующей таблице:
Уравнения теории	Преобразования уравнений
упругости	теории вязкоупругости
Йп)	на Si (Т.-/П/ = ?[п) на Sx
щ = g,	на S2 щ = gi на 52
вц = 2Get,	P (s) ВЦ = 2Q (s) et,
ац = ЗК&и	ои

ЗАДАЧИ С РЕШЕНИЯМИ	293
Из этой таблицы видно, что если G в уравнениях теории упругос-
упругости заменить на Q/P, то обе группы уравнений будут иметь одина-
одинаковую форму. В силу этого, если в решении соответствующей зада-
задачи теории упругости G заменить на QIP для вязкоупругого мате-
материала, то полученный результат будет преобразованием Лапласа
решения задачи теории вязкоупругости. Обратным преобразова-
преобразованием найдем само решение для вязкоупругого материала.
Этот принцип соответствия может быть установлен и для задач,
отличных от квазистатических. Более того, определяющие уравне-
уравнения не обязательно записывать через линейные дифференциальные
операторы, а можно брать в виде (9.49), (9.50) или (9.51). В предла-
предлагаемых далее конкретных задачах каждый раз будет указываться
форма, в которой следует использовать этот принцип.
ЗАДАЧИ С РЕШЕНИЯМИ
Простейшие механические модели вязкоупругого поведения
(§9.1-9.3)
9.1.	Проверить правильность соотношений между напряжения-
напряжениями и деформациями, данных формулами (9.3) и (9.4) для моделей
Максвелла и Кельвина соответственно.
В модели Максвелла (рис. 9.2, а) полная деформация равна сумме деформа-
деформации пружины и перемещения поршня в вязком элементе. Таким образом, е = es +
+ eD, а также е = es + eD- Так как напряжение в каждом элементе равно а,
формулы (9.1) и (9.2) позволяют найти е =¦ a/G+ о/г).
В модели Кельвина (рис. 9.2, б) а = as -\- oD и непосредственно из формул
(9.1) и (9.2) получаем а = т]е+ Ge.
9.2.	Использовать операторную форму соотношения между
напряжением и деформацией для модели Кельвина и получить
закон, связывающий напряжение и деформацию в стандартном ли-
линейном твердом теле (рис. 9.3,а).
В указанной модели полная деформация равна сумме деформаций упругого
элемента и элемента Кельвина, т. е. е = es + е^., или в операторной форме е ¦=¦
= a/Gl + a/{ G2 + т]2д/}. Отсюда находим
G* {G2 + T\*dt} e = {G2
и, следовательно,
9.3. Написать соотношение, связывающее напряжения и де-
деформации в четырехпараметрической модели (рис. 9,4). При гц ->-
->¦ оо сравнить с результатом задачи 9.2.

294
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
Для указанной модели полная деформация вычисляется как сумма е
ем, или в операторной форме как
е = o/{G2 + ЧвЭ*} + {dt + 1/TiJ olGx Щ.
Распишем оператора и сгруппируем члены:
При r\i -*¦ со это соотношение принимает вид a+(Gi +
+ G,G2'e/T]2, что эквивалентно результату, полученному в задаче 9.2.
9.4. Рассматривая модель, изображенную на рис. 9.13, как
частный случай обобщенной модели Максвелла, найти для нее со-
соотношение между напря-
напряжениями н деформациями.
Равенство (9.10) при N
= 2 дает
2	. .
	WVWWV	-|| [—
Рис. 9.13.
Выполняя указанные действия, получаем
о =
G,e
+
G2e
1/т2} e + G2 {й
Раскроем операторы и перегруппируем члены; это дает
G2) ё + (Gj/
e.
tj) ё.
9.5. Модель, изображенную на рис. 9.14, можно считать вы-
вырожденным случаем обобщенной модели Максвелла (N = 3) при
Gi — "Па = °°- Используя такие значения	о
коэффициентов в уравнении (9.10), напи-
написать соотношение между напряжениями и
деформациями для этой модели.
В данном случае уравнение (9.10) принимает
вид
a = т]хе + ¦
W
¦ +
{dt/G3
или
[dtlG3 + 1/тK} a = {df/G3 + lAb} ('Ni6 + G2e) + e.
Выполняя действия, указанные операторами, получаем
а
Рис. 9.14.
o/G3 + a/TK
что после интегрирования можно записать в форме
TKa + G& =
G3T)a) e + G2G3e.

1ЛДЛЧЙ С РЕШЕНЦЯМИ	295
Ползучесть и релаксация (§9.4)
9.6. Найти выражения для характеристик ползучести в моделях
Кельвина и Максвелла непосредственным интегрированием урав-
уравнений (9.17) и (9.21) соответственно.
Пользуясь интегрирующим множителем ef'x, из уравнения (9.17) находим
Ц 8
а применяя формулу (9.18), имеем
ее"х = (о0 [U (Q]/rj) Ы''-1^ = (ajG) (eift - 1) [U (t)\,
или е = (a0IG) A — e~t'%) [U (t)].
Возьмем dl% в качестве интегрирующего множителя в (9.21); тогда
о
и по формуле (9.23) получим
ae''x = Ge0 [U (t)], или а = Ge^-ilx \U (<)].
9.7. Найти деформацию ползучести для стандартного линейного
твердого тела (рис. 9.3,а).
В силу того что е = es+ e^-, деформация ползучести для данной модели,
согласно (9.1) и (9.19), вычисляется по формуле
е @ = [1/G! + A/Ог) A - е-«х')\ о0 [U ®].
Тот же результат можно получить, положив т]2 =. оо в обобщенной модели Кель-
2
вина (при N = 2), где деформация равна г =. 2 Ji A — е~'/т0 a0 [U (i) ], или не-
посредственным интегрированием закона, связывающего напряжения и деформа-
деформации для стандартного твердого тела. Читателю предлагается провести соответ-
соответствующие выкладки.
9.8. Эксперимент по исследованию обратной ползучести состоит
из нагружения, как в опыте на ползучесть: а — а0 сохраняется
некоторый период времени, а затем о
мгновенно снимается. Найти кривую
деформации обратной ползучести
для стандартного твердого тела а
(рис. 9 3,а) при законе нагружения,
изображенном на рис. 9.15.
Пока приложена нагрузка (т. е при t <	г
< 2т2). как найденов задаче9.7, деформация	Рис. 9.15.
^ еияется по закону
В момент t = 2т2 нагрузка снимается, а обращается в нуль и одновременно вос-
восстанавливается упругая деформация csJG^ При t > 2т2 изменение деформации

296
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЪ
описывается уравнением е + е/т2 = 0, которое отражает закон связи между на-
напряжением и деформацией для указанной модели прн а = 0 (см. задачу 9.2).
Решение этого дифференциального уравнения есть е = Сё~Т1%', где С — по-
постоянная, a T = t —2т2. При Г = 0 мы имеем е = С=о0A—e~~2)IG2,
следовательно,
е = а0 A — е~2) e~T/x4G2 = а0 (е2 — 1) e~'/TVG2 при t > 2т2.
9.9. Модель, изображенная на рис. 9.16, растягивается с по-
постоянной скоростью е = eo/ti, как показано на рис. 9.17. Найти
G
¦л/ww—Щ-
Рис. 9.16.
Рис. 9.17.
напряжение в такой модели при указанном процессе деформирова-
деформирования.
По результатам задачи 9.5 зависимость между напряжением и деформацией
в такой модели будет описываться уравнением a + a/т = r\e -f- 3Ge + Ge/x, а
для нашего случая уравнением a + a/т = SGeo'tx + Ge^/xt^. Проинтегрируем его
и найдем а = е0 Bт] -\- Gt)/^ + Сё~*1%, где С — постоянная интегрирования.
При t = 0 a = Tie,/*! и, следовательно, С = — vpo't-i. Таким образом, a =
,/!
— ie~''x)/'i- Заметим, что тот же результат получается при инте-
интеб
о(]	i
грировании уравнения другим способом:
9.10. Непосредственным интегрированием найти закон, свя-
связывающий напряжение и деформацию для стандартного линейного
твердого тела в процессе релаксации напряжения, если деформа-
деформация задана законом е = е0 [U (t)].
Запишем соотношение между напряжением и деформацией (см. задачу 9.2)
для данного случая в виде
6+$!+ G2) o/ifc = e0G ([6 (*)] + Gfi2 [U
Если воспользоваться интегрирующим множителем e<Ol+CaWTb, то
t
= 8oGi f [6 (t')
t
J
Вычисляя интегралы с помощью формул (9.18) и (9.23), находим
a = e0Gj (О, + Gl6-(Cl+G'» '/Чг) [I/ @1/@! + OJ.

ЗАДАЧИ С РЕШЕНИЯМИ	297
Функции ползучести и релаксации.
Интегралы наследственности (§ 9.5)
9.11. Найти функцию релаксации ф (f) для трехпараметриче-
ской модели, изображенной на рис. 9.18.
Соотношение между напряжением и деформацией для указанной модели
таково:
а + а/т2 = (Gt -f С2) ё + GtG2el42.
Тогда при е = е0 [U (()] и в = е0 [6 @] с помощью интегрирующего множителя
е'/*2 можем написать
t
ое«х' = е0 (G1 + GJ J e'7x'[6 @1 Л' +
Рис. 9.18.
Затем, пользуясь формулами (9.18) и (9.23), находим а = е0 (pi + G2e~t/X*) =
= еоФ(О- Заметим, что этот результат можно получить также, положив цг ~>
->оо в формуле (9.30) для обобщенной модели Максвелла.
9.12. Используя фундцию релаксации ф (t) для модели, предло-
предложенной в задаче 9.11, найти функцию ползучести по формуле 9.40.
Преобразованием Лапласа функции <р @ = ft + Gte~t^x' будет <р (s) =
¦= Gi/s + Gz/(s + 1/тг) (см. любую таблицу преобразований Лапласа). Тогда
по формуле 9.40 находим
(s) = (s + l/T2)/[GlS (s +
G2) т2).
Пользуясь таблицей преобразований Лапласа, легко обратить это выражение
и получить
Данный результат можно проверить интегрированием соотношения между напря-
напряжением и деформацией для указанной модели при законе иагружения, таком,
как в опытах на ползучесть.
9.13. К материалу Кельвина приложено напряжение, которое
линейно растет со временем, а затем долгое время сохраняет по-
постоянную величину о*! (рис. 9.19).
Вычислить вызванную им дефор-
		мацию, полагая при этом
Закон изменения напряжения
t,	t можно записать так:
Рис. 9.19.	о = U [U (О] — K{t — tJ[U(t — t

298
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
Подставляя его в уравнение (9.4), получаем
/	t	.
ее = — {J fer* [U (t')\ df - J («' - h) et>l% \U (f - <x)] df J .
Интегрируя с помощью (9.18), находим
е = (X/G) {(< + т (г-'/т - 1)) [U @1 - ((* ~h) + r (е^-™ - 1)) [U (t- ^)]}.
При f -»• оо это выражение сводится к виду е ¦= MJG = Oi/G.
9.14. Воспользовавшись интегралом ползучести (9.34) и функ-
функцией ползучести для модели Кельвина, проверить результат за-
задачи 9.13.
Для модели Кельвина г|з (i) .= A —e~"yGK формула (9.34) приводит к вы
ражению
в@
= f -^- W (П\ + г [в (П\ - [U V - 'i)l -
- (Г - h) [6 [? - h)\) A -е~ ('
которое с помощью (9.18) и (9.23) сводится к следующему:
е = _*_ I [U (
^	о	'i
Непосредственное вычисление этих интегралов подтверждает результат, получен-
полученный в задаче 9.13.
9.15. Применяя принцип суперпозиции, • найти реакцию мате-
материала Кельвина на закон нагружения, изображенный на рис. 9.20.
Указанное изменение нагрузки можно представить в виде последовательнос-
последовательности нагружений, заданных наклонными прямыми в плоскости a-t как показано
Рис. 9.20.
Рис. 9.21.
иа рис 9.21- В задаче 9.13 было найдено, что для нагружения такого типа дефор-
деформация вычисляется по формуле е = (k/G) [t+ т (е~'/х — 1)] [U {t)\; поэтому
в нашем случае она будет равна
е @ = (к/С) {(/ + т (е-'/г - I)) [U @] - ((< - Q +
+ т (е- С-'»>/т — 1)) [U {t — tj)] — ((t — 2tj) +
+ т (е- l'-2'-)/T - 1» [V (t - 2/01 + ((' - ЗУ +
Заметим, что е -> 0 при t -* оо.

ЗАДАЧИ С РЕШЕНИЯМИ	299
Комплексные модули и податливости (§ 9.6)
9.16. Найти комплексный модуль G* и угол запаздывания б
для модели Максвелла (рис. 9.2).
Запишем формулу (9.3) в виде а + а/т = Ge и подставим в нее выражения
(9.41) и (9.42). Получим iwsaeia>t + апеш/х = G/coe/ ^'-е), откуда а/6/е0 =
= G* = Gj'cot/A + /сот), или в стандартной форме
_ G ((о8т2 + /сот)
1 + со2т2
Из чертежа на рис. 9.11 находим tg6= G2/Gl = Gcot/Gco2t2 = 1/сот.
9.17.	Показать, что результат задачи 9.16 можно получить так-
также непосредственно из определения а/е = G* простой заменой
оператора dt на «о в уравнении (9.5).
После предложенной замены уравнение (9.5) примет вид (t'co/G + l/r\)o —
= toe, откуда находим
,	Gi'co	G/сот
а/е =	=
/со + I/T. I + /сот
как и прежде.
9.18.	На частном примере уравнения (9.10) для обобщенной
модели Максвелла показать справедливость правила, утверждаю-
утверждающего, что при параллельном соединении моделей их комплексные
модули складываются.
В задаче 9.17 для комплексного модуля модели Максвелла получено выра-
выражение G* = а/е = G/cot/A + /сот). Уравнение (9.10) можно записать в виде
01{dt}B	G2{dt)e
ГЛ. .1. 1/т 1 I" ГЯ. I I /_ I "Г *
Тогда комплексный модуль обобщенной модели Максвелла будет равен
"¦--ЯВГ+-Г&-+ - + -гт^г-°:+'«+ - +<*¦
9.19. Проверить соотношение ^ = 1/ [^ A + tgB6)] между
модулем накопления и податливостью накопления.
Согласно формулам (9.43) и (9.44), имеем J* = 1/G*, следовательно, Л —
- Ua = l/(Gi + (G2) = (Gi - /G2)/(G[ + Gip, т. е.
,	Gi1	1
1
	_
G\+G\ G, A + (GJGJ*) GiO
9.20. Для циклического нагружения (рис. 9.10) вычислением ин-
интеграла \fftie по одному циклу показать, что диссипация энергии
за один цикл прямо пропорциональна податливости потерь /а.

200	Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
Для векторов напряжения и деформации, изображенных иа рис. 9.10, вы-
вычисление интеграла lade за цикл дает
2я/и	2я/и
j o-jj-dt= \ (a0 sin o)Q еои cos (и/— ,6)d/ =
о
2п/а
'- aoeoco \ sin at (cos at cos 6 + sin at sin 6) dt =
о
2Я/0)	2я/ю
Трехмерная теория вязкоупругости.
Анализ напряженного состояния (§9.7—9.8)
9.21.	Комбинируя соотношения (9.48а) и (9.486), получить
определяющее уравнение с,-/ == б,-/ {#} ем + {S} е,-/ и найти вид опе-
операторов {R) и {S}.
Запишем (9.48а) в форме {Р} (at-y — 6^aftft/3) — 2 {Q} (е,у — б^е^/З) и за-
заменим aftft в этом выражении правой частью равенства (9.486). После некоторых
простых операции получим
°ц = «(/ {C/CP-2Q)/3P) Bkk + {2Q/P} г1}.
9.22.	Брус из материала Кельвина находится в состоянии од-
одноосного растяжения, так что ап — а0 [U (t)], а22 = оаз = а12 =
= с23 = о31 = 0, причем а0 постоянно. Найти деформацию еп
при таком законе нагружения.
Из равенства (9.486) для данного случая имеем Зе,-,- = a0 [U (t)]/K, а урав-
уравнение (9.48а) при / = /=1 дает {Р} (ou—ou/3) = {2Q} (en — eW3)- Но соот-
соотношение (9.6) показывает, что для материала Кельвина {Р} = 1 и {Q} =
{О+5}; поэтому в нашей задаче
2a0 [U @]/3 = 2{G + ф} (еи - а0 [U
или
ёи + ец/т = а0 [U ф] (ЗАГ + G)/9t)AT + а0 [6 @J/9AT.
Решая это дифференциальное уравнение, получаем
«и = а0 (ЗАГ + С) A - е-«х) [U @J/9ATG + ао?-'/т [(У @1/9/f;
при < -> со имеем ег1 -»• (ЗАГ + С) ao/9ATG = ao/?.
9.23. Материал Кельвина заполняет форму с жесткими стенка-
стенками, так что е22 = е33 = 0, когда прикладывается напряжение по
закону сц == — а0 [U (t)h см. рис. 9.22. Найти еи и возникающие
за счет наличия стенок компоненты напряжения o2s = о33.
В нашем случае eit = eu и <тгг = ass, поэтому для материала Кельвина равен-
равенство (9.486) имеет вид an + 2aM = З/feii, а из (9.48а) следует 2 (an — a22)/3 =
= 2С {1 + т5/} Bеи/3). Комбинируя эти соотношения, получаем дифференци-

ЗАДАЧИ С РЕШЕНИЯМИ
301
альиое уравнение
ёи + DG + 3/С) еп/4От = — Зст0 [U @]/4Gt,
которое после интегрирования дает
еи = — За0 [(/ @1 A — в~ <4С+ЗК) '/4CT)/DG +• 3/С).
Подставляя это выражение в равенство (9.48а) при I = / = 2, получаем
1 = Г
i	8G + 6АГ
9.24. Радиальная компонента напряжения в упругом полу-
полупространстве при действии концентрированной нагрузки Р, при-
приложенной в начале координат (рис. 9.23), выражается формулой
(V) = (Р/2п) [A - 2v) а (г, г) - р (г, г)],
где а и Р — известные функции. Пусть закон нагружения задан
функцией P = P0[U(t)]. Найти радиальную компоненту напря-
напряжения в полупространстве из вязкоупругого материала Кельвина,
пользуясь принципом соответствия.
Рис. 9.22.
Рис. 9.23.
Члену 1—2v в вязкоупругой среде соответствует оператор {3Q}/{3/(/> +
+ Q}; следовательно, для кельвиновского тела преобразование решения вязко-
упругой задачи будет
V) =
_ ЗР0
G+
а(л, г)-Р(л, г)
Это выражение можно обратить, представив его в виде суммы дробей и восполь-
воспользовавшись таблицами преобразований. В результате получим напряжение в вяз-
коупругой среде
ЗРПГ/ G . 3* .е-(ЗК+С„,)а(л>г) + р(Г(г)].
V) =
	. за:
3/C + G ¦*" 3/C+G
9.25. Принцип соответствия можно использовать для получе-
получения не только напряжений, но и перемещений. Перемещение по-
поверхности упругого полупространства, рассмотренного в задаче
9.24, по направлению оси г задано формулой йу(г=о) = Р A —
•— v^/Enr. Найти перемещение поверхности полупространства
из вязкоупругого материала в условиях упомянутой задачи.

302	Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
Оператор теории вязкоупругости, соответствующий члену A—v2)/?
упругого решения, будет {3/С+4QJ/4Q C/С+ Q)- Тогда для материала Кель-
Кельвина преобразование Лапласа перемещения дается выражением
-	P0C/C+4(G+T)s))
шB=0) 4n/-sCAT+G+T)s)(G+T)s) "
После довольно длительных преобразований и обращения получаем'
P0CAT+4G) Г 1	Зе-C1С+СIЛ1	ЗАГ+G ш]
шB=0)- 4л/-2 (ЗАГ + G) LG	3AT+4G	GCAT+4G)	J'
Заметим, что ^(Z=o) ¦= ^ ПРИ ' = 0 и что ^(Z=o) стремится к Ро A — \2)/Етхг,
т. е. к упругому смещению, при t -*¦ оо.
9.26. Предполагается, что равномерно нагруженная свободно
опертая балка изготовлена из материала Максвелла (рис. 9.24).
Найти изгибающее напряжение
^ сц и величину прогиба w (x±, t),
^1 если нагрузка задана в виде р =
-ZL-
Рис. 9.24.	Изгибающее напряжение для сво-
свободно опертой балки не зависит от
свойств материала, поэтому изгибающее напряжение и для упругого, и для вяз-
коупругого материала будет одним и тем же. Прогиб упругой балки определяется
формулой ш (Xj) = роа (xj/24EI, где a (xt)—известная функция, а / — момент
инерции поперечного сечения балки. Для материала Максвелла {Р} ={df-\- 1/т}
и {Q} = {Gdt}, так что преобразование Лапласа величины прогиба будет
24/ ('	9/CGs2
После обращения этого выражения получим
- = ^aixj I З/С/т + CK+G)s )
«л.о-^г- ж +
Прогиб ш (xlt 0) = роа (х1)/B4Е1) при / = 0 равен прогибу упругой балки.
9.27. Показать, что если материал считается несжимаемым
(v = 1/2), то при t -> оо напряжение о22. найденное в задаче 9.23,
стремится к а0 (среда ведет себя как жидкость).
В задаче 9.23 получено
.те = — о0 (9АГ - DG + ЗАЭ)/2 DG + ЗАГ) = - -
Это выражение можно записать через v в виде огв2|/^<»== — VCTo/(l—v)- Таким
образом, <т2г |^м = — <т0 при v = 1/2-
Смешанные задачи
9.28. Написать определяющее соотношение для комбинирован-
комбинированной модели Кельвина — Максвелла, представленной на рис. 9.25.
Вывести из него определяющие соотношения для модели Кельвина
и модели Максвелла,

ЗАДАЧИ С РЕШЕНИЯМИ
Для предложенной модели
303
е.
Выполняя указанное операторами
дифференцирование по времени,
имеем
0
	WWVW	-]j |
	WMW	1
G2 +
TJ/T))e+(Ga/T1)e.
Если в этом уравнении положить тJ >
e.
Рис. 9.25.
О (соединить параллельно с узлом Мак
свелла упругий элемент), то уравнение будет а + o/ti =¦ (Gt + GJ e + (G
Если к тому же и G2 = 0, то получаем определяющее соотношение для модели
Максвелла а + a/xi =¦ Gte. Аналогично если сначала положить G == 0 (соединить
параллельно с узлом Максвелла вязкий элемент), то уравнение будет иметь вид
<j-f o/ri = т]2ё'+ (GL -f- Tjs/TxJe, а когда н т]2 = 0, оно опять сводится к оп-
определяющему соотношению для модели Максвелла.
Если определяющее соотношение для этой четырехпараметрической модели
записать в виде
и положить % равным нулю, то в результате получается определяющее уравнение
для модели Кельвина a = тJё + G2e. Точно так же если Gt = 0, то уравнение
сводится к виду a = тJе + G2e и опять представляет модель Кельвина.
9.29. Воспользоваться принципом суперпозиции и получить
деформацию обратной ползучести для стандартного линейного твер-
ia	дого тела (рис. 9.3, а). Сравнить
результат с тем, что получено в
задаче 9.8.
-а0
2т,
При законе нагружения
(рис. 9.26), деформацию сразу можно за-
записать, воспользовавшись выражением,
найденным в задаче 9.7:
Рис. 9.26.
е = a0 A/Gt + A -e-'/T*)/G2 [U @1 -
- a0 A/Gi + A - е~ <'-2T*>/T»)/G2) [U (t - 2т„)].
В момент t > 2т2 обе ступенчатые функции равны единице, следовательно,
е = о0 (— е~'/т' + е~ <'-2t°>/t*)/G2 = a0 (e2 - 1) e-'/T'/G2,
что согласуется с результатом задачи 9.8.
9.30. Найти напряжение в модели, е
предложенной в задаче 9.9, при де-е
формации по закону, изображенному
на рис. 9.27. Показать, что в конце
концов все напряжение будет прихо-
приходиться на «свободный» упругий эле-
элемент.
i
Рис. 9.27.

304
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
Решение задачи 9.9 и принцип суперпозиции позволяют найти напряжение
в виде
а = е0 (т) B - е-"х) + Gf) [U (f)]/^ - е0 (т) B - <Г «~<'> х) +
+ G(t-ti))[U(t-t1)]/tv
Для моментов времени t > /a напряжение равно а = еот) (е'''т — 1) е~''т//, +Ge0,
а при /-»• со оно сводится к величине а= Ge0.
9.31. «Логарифмический спектр запаздывания» L определяется
через обычный спектр запаздывания J формулой L Aпт) = xJ (т).
Пользуясь этим определением, найти функцию ползучести гр (t)
как функцию от L Aпт).
Пусть 1пт = А, т. е. е = т; тогда dxIdX = е = х, или
Теперь формула (9.28) для функции г)) (/) позволяет написать
у @ = f Z. (In т) A — е~'/т) d (In т).
Аналогично если функция Н Aпт) =¦ \G (т) определяет логарифмический спектр
релаксации, то функцию <р (/), введенную формулой (9.31), можно представить
в виде
оо
Ф(/)= f ЯAпт)е-'/т^Aпт).
9.32. Для модели Максвелла
(рис. 9.2,а) найти модули на-
накопления и потерь G1 и G2 как
функции 1п сот и построить гра-
графики этих функций.
В задаче 9.16 установлено,что для
материала Максвелла
таким образом.
-1 0 1
Рис. 9.28.
Х=1п«т
где Я = In шт. При % = 0 имеем Gt = G/2, при К = схз имеем Gx — G и при
Я = —оо имеем Gt = 0. Таким же образом находим G2 = Ge /A+е2 ) и при
К = 0 имеем G2 = G/2, при Я, = ± оо имеем G2 = 0. Графики этих функций
приведены на рис. 9.28.
9.33. Найти вид оператора в определяющих соотношениях
вязкоупругости (9.48), соответствующего упругой постоянной v
(коэффициенту Пуассона).
При одноосном растяжении a1L = an. Формула (9.486) в этом случае
имеет вид е„/3 = ао/9К, а формула (9.48а) при подстановке i = / = 1 дает

ЗАДАЧИ С РЕШЕНИЯМИ
305
eu= {ЖР+ Q) aB/{9KQ). Точно так
же из (9.48а) при i = / = 2 получаем
е22 = {2Q— ЗРК) о„/{ 18ATQ}. Таким обра-
образом, в операторной форме можно написать
v = - еи/еи = {3PK—2Q}/WP +2Q}.
9.34. Цилиндр из вязкоупруго-
вязкоупругого материала помещен в плотно
пригнанную форму с жесткими
стенками (рис. 9.29), так что е(ГГ) =
= 0 (радиальные деформации от-
отсутствуют). При расширении ма-
материал ведет себя как упругий;	Рис 9.29.
функция ползучести равна гр =
= А + Bt + Сеи, где А, В, С, К — постоянные. Найти оаз (t),
если е33 = ё0 [U (t) ].
Для данной среды оц — ЪКъц, и в силу симметрии задачи это равенство
имеет вид 2ап + Озз = 3/(езз- Согласно формуле (9.50а), при i = / = 1 имеем
de:a
~~dT
¦ ф (t — /') dt'. Разрешая эту систему двух уравнений от-
носительно
находим
3 3
dt'
(f(t-t')dt'.
Функцию релаксации ф можно найти, пользуясь формулой (9.40). В результате
получим
ф = [('1 - л) г* - (г, - *
где /-, 2 = [>1А, — В ± У (АК + ВJ + 4BCAJ/2 (Л + С). Таким образом, оконча-
окончательно имеем
r\ — r%
и после интегрирования приходим к выражению
+ (', - Я) A - er'0/3r,l/(r1 - /,)) [t/ @].
9.35. Продольный изгиб стержня из вязкоупругого материала
в условиях ползучести в рамках линейной теории можно иссле-
исследовать при помощи принципа соответствия. Найти этим методом
величину прогиба w (xltf) шарнирно закрепленного на концах
стержня из материала Кельвина (рис. 9.30).
Прогиб упругого стержня описывается уравнением d2w/dx% + Pow/E/ = 0.
Для материала Кельвина Е следует заменить оператором [E-\-rfit], значит,
для стержня из вязкоупругого материала должно выполняться уравнение

306	Гл 9 ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
хг
Рис. 9.30.
[F + tK<}E2W5j^) + PqwII ¦= 0. Будем искать величину прогиба в виде про-
произведения w (xi.t) => К7 (дг^б ((). Тогда упомянутый оператор приведет к диф-
дифференциальному уравнению
(?6 + т]6) (d*W/dx§ + P0WQ// = 0,
откуда
б + П + Р<№1Е1 (cPW/dxfy] 6/т = 0,
где Т = Т]/?. Но нагрузка при продольном изгибе упругого стержня равна Рв =
= — El (d2W/dJC|)/W, поэтому можно записать последнее уравнение в
виде 6+ A + PjPg) G/t = 0, проинтегрировать и получить решение 6 =
«= е °	. Окончательно прогиб при продольном изгибе в условиях ползу-
ползучести определяется выражением w = We ° B
9.36. Сформулировать задачу о стационарных колебаниях бал-
балки из вязкоупругого материала, считая, что определяющие уравне-
уравнения этой среды заданы формулами (9.48).
Свободные колебания балки из упругого материала описываются уравнением
El (cPwldx\) + рА (дЧи/дР) = 0. Согласно (9.48), соответствующий Е оператор
уравнений теории вязкоупругости будет [9f(Q/CKP + Q)}. Если прогиб искать
в виде w(xlt t) = W (*i) В @, то дифференциальное уравнение колебаний вязко-
упругой балки можно расщепить на два уравнения — одно с производными по
пространственным координатам d^ldx* — №W = 0, а другое — с производными
по времени {ЩР + Q) (d*B/dP) + (НЧ/рА) {9KQ} F) = 0. Решение Wt простран-
пространственного уравнения дает форму t-ro главного колебания, а временное уравне-
" N ^.t
ние при k = k[ имеет решение 6j = ^ Ave " . гДе N зависит от порядка опе-
/¦=1
ратора. Общее решение представляется, таким образом, суммой w(xlt Q =
»=2 2 ^i (xi) Atie " f в которой %ij — комплексные величины.
f-l y=.l
ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
9.37.	Написать определяющее уравнение для четырехпараметрической моде-
модели, представленной на рис. 9.31.
Ответ: а + (GJ^ + G2/tJ + d/ru) а + (G^Ar]!^)) a = G^e + (GiGJr)^ к.
9.38.	Непосредственным интегрированием уравнения
ё + е/т2 = а0 [U @] (Gt + G2)/G^z + а0 [6 (t)]^
найти деформацию ползучести для стандартного линейного твердого тела (см.
ЗЯдачу 9.7).

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
307
-WWVW
1
-|
	VWWW	1
1
—V*
Рис. 9.31.
9.39. Вывести определяющие соотношения для модели Кельвина и для моде-
модели Максвелла из соотношения, установленного в задаче 9-5 для предложенной
в этой задаче четырехпараметрической модели.
Указание: положить &з = 0 и т. д.
	WMW
—www—Л
Рис. 9.32.
9.40. Воспользоваться уравнением (9.40) для нахождения функции i]) (Q,
если ф (/) = a (b/t)m и /п < 1.
Указание: положить т = 1—k, так что ф (/)
г,	i /л s'n лт
Ответ: ty (t) —
amn
I t
\b
9.41. Найти функцию ползучести и функцию релаксации для модели, изо-
изображенной на рис. 9.32.
Ответ: *|> (Q = 1/G2 - G1e-c''/<c'+c'» T'/G2 (Gt + G2), ф (t) = G2 + Gie-'/T«.
—WWW	J
e
Рис. 9.33.
«I
Рис. 9.34.
9.42. Найти G* для модели, представленной на рис. 9.33.
Ответ- G* =
Gi С + Ф") +
.
. jo(G2t2 + t)s A + т^со2))

308
Гл. 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ
9.43. В модели, предложенной в задаче 9.42, положить G, ^ Gt = G и
т]2 ¦= т)з = т) и определить закон изменения напряжения при деформировании
по закону, представленному на рис. 9.34.
Ответ: а=(ео//1) [G Bt —
о
Рис. 9.35.
о2г=0
т] D - A + <Л/Т)
при h<t< 2^.
Рис. 9.36
9.44. Вязкоупрутий материал с определяющим уравнением +Р +
Vei гДе а> Р> V — постоянные, подвергается нагружению в следующих усло-
усло[(/(Q]	0	0 ( 935) С	ЪК
+ Vi	> Р V	,
виях: ои = —<ro[(/(Q], а22 = 0, 633
найти ass@, ass@) и <т33(оо).
ру	у
(рис. 9.35). Считая, что Сц =
Ответ:
°
—2у
—2Р
2(ЗАГ+Р)
ЗкАГ —2у
г)'""]
где Я=(ЗаАГ+7)/(ЗАГ+Р).
9.45. Шарнирно закрепленный на концах стержень сделан из материала
Максвелла, для которого a -f- а/т = Ее. Начальная форма стержня задана вели-
величиной прогиба w = wfi'm (пх/l); приложенная сила равна P0{U (()] (рис. 9.36).
Найти величину прогиба ш (х, t) в следующие моменты времени как функцию
от Рв — нагрузки при продольном изгибе упругого стержня.
Ответ: w (x, t) =-- w0 sin {nx/t) e~

Список литературы
Бленд Д., Теория линейной вязкоу пру гости, «Мир», М., 1965.
Бэтчелор Дж., Введение в динамику жидкости, «Мир», М-, 1973.
Жермен П., Механика сплошных сред, «Мир», М., 1965.
Зоммерфельд А., Механика деформируемых сред, ИЛ, М., 1954.
Зоммерфельд А-, Термодинамика и статистическая физика, ИЛ, М., 1955.
Ильюшин А. А., Механика сплошной среды, Изд-во МГУ, М., 1971.
Ильюшин А. А., Ленский В. С, Сопротивление материалов, Физматгиз, М., 1959.
Ильюшин А. А-, Ломакин В. А., Шмаков А. П., Задачи и упражнения по меха-
механике сплошной среды, Изд-во МГУ, М., 1973.
Качанов Л- М., Теория ползучести, Физматгиз, М., 1960.
Кочин Н. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, ч. I и
II, Физматгиз, М., 1963.
Кристенсен Р., Введение в теорию вязкоупругости, «Мир», М., 1974.
Куликовский А. Г., Любимов Г. А., Магнитная гидродинамика, Физматгиз, 1962.
Лаидау Л. Д., Лифшиц Е. М., Механика сплошных сред, изд. 2, ГИТТЛ, М.,
1954.
Лойцянский Л. Г., Механика жидкости и газа, изд. 4, «Наука», М., 1973.
Ляв А., Математическая теория упругости, ОНТИ, М., 1935.
Мак-Коннел А. Дж., Введение в тензорный анализ, Физматгиз, М., 1963.
Милн-Томсон Л. М., Теоретическая гидродинамика, «Мир», М., 1964.
Новожилов В. В., Теория упругости, Судпромгиз, Л-, 1958.
Прагер В., Введение в механику сплошных сред, ИЛ, М., 1963.
Прагер В., Ходж Ф. Г., Теория идеально-пластических тел, ИЛ, М., 1956.
Праидтль Л., Гидроаэромеханика, ИЛ, М., 1949.
Седов Л. И., Введение в механику сплошной среды, Физматгиз, М., 1962.
Седов Л. И., Методы подобия и размерности в механике, изд. 7, «Наука», 1972.
Седов Л- И., Механика сплошной среды, т. 1—2, изд. 2, «Наука», М., 1973.
Сокольников И. С, Тензорный анализ, «Наука», М., 1971.
Соколовский В. В., Теория пластичности, ГИТТЛ, М.— Л., 1950.
Тимошенко С. П., Сопротивление материалов, т. I—II, «Наука». М.. 1965.
Тимошенко С. П., Теория упругости, ОНТИ, М-, 1934.
Хилл Р., Математическая теория пластичности, Гостехиздат, М., 1956.

Предметный указатель
Абсолютная температура 187
Абсолютно жесткое перемещение 119
Адиабатическое течение 236
Алгебраическое дополнение элемента
матрицы 32—33
Альтернирующий тензор 31
Базнс 17
—	ортонормированный 17
Бивектор 17
Вектор 10
—	вихря скорости 162
—	единичный 10
—	завихренности 162
—	линейного поворота 122
—	момента напряжений 70
—	напряжения 70
—	натяжения 70
—	нулевой 10
—	перемещения 114
	 относительного 121
	 на единицу длины 121
Векторы базисные 16
—, вычитание их 16
—	ковариантные 24
—	контравариантные 24
—, произведение нх векторное 12
	 двойное 13
	 неопределенное 13
	 скалярное 12
	смешанное 13
—	равные 10
—, сложение их 11
Вихревая линия 171
Время запаздывания 284
Гидростатическое сжатие 222
Гипотеза упрочнения деформашюн
иая 259, 260
	 энергетическая 259
Гистерезис 250
Давление 228
—	гидростатическое 228
Давление термодинамическое 229
Движение 157
—	безвихревое 191
—	ползущее 240
—	установившееся 160
Девиатор деформаций 131
—	напряжений 87
	, главные значения его 87
—	скоростей деформации 163
Дельта Кронекера 26, 28
Дельта-функция Дирака 284—28Г>
Деформации сдвига 125
	 технические 125
Деформация 112
—	бесконечно малая 120
—, градиент ее 116
—	идеально пластическая 250
—	изохорнческая 153
—	логарифмическая 249
—, мера ее 119
—	натуральная 249
—	неупругая 248
—	однородная 137
—	пластическая 248
—	плоская 132
—	полная 248
—	техническая 249
—	упругая 248
—	чистая 130
Диада 13
Диад произведение векторное 15
	дважды 15
	 скалярное 15
	дважды 15
	смешанное 15
Диадик 10, 13
—	антисимметричный 15
—, вектор его 14
—	единичный 14
—	самосопряженный 15
—	симметричный 15
—, скаляр его 14
Диадики взаимно обратные 15
—	равные 14
Дислокации 248

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
311
Жидкость вязкая 228
—	идеальная 228
—	ньютонова 229
—	неньютонова 229
—	стоксова 229
Закон Гука обобщенный 200
—	сохранения массы 180
	 энергии 185
—	теплопроводности Фурье 194, 213
—	механической 184
—	термодинамики первый 185
	 второй 187
—	течения 257
—	упрочнения 256
Инвариантность тензорных соотноше-
соотношений 9
Инварианты тензора 37
Индекс немой 20
•—, размерность его 20
—	свободный 20
Интегралы наследственности 287
—	ползучести 290
—	релаксации 290
Квадрика деформаций 128
—	Коши 128
Количество движения 181
Конфигурация сплошной среды 112
Концепция сплошности 68
Координаты материальные 113
—	пространственные 113
Коэффициент вязкости 229
	кинематический 232
	объемной 250
—	длины 125
—	относительного удлинения линей-
линейного элемента 123
—	Пуассона 204
—	расширения кубического 130
	линейного теплового 212
—	теплопроводности 213
Кривая растяжения (сжатия) 250
—	текучести 254
Критерий пластичности Мизеса 253
	 Треска 252
Круги Мора для деформации 132
	напряжения 82
Лагранжев способ описания движе-
движения 115
Линия сдвига 262
—	скольжения 262
—	тока 160
Масса 180
Материал, см. также Среда
—	анизотропный 68
—	вязкоупругий 279
—	гиперупругий 212
—	гипоупругий 212
—	жестко-идеально-пластическнй 251
—	жесткопластический 251
—	идеально пластический 250, 255
—	изотропный 68
—	однородный 68
—	пластический 248
—	с упрочнением 256
—	упруго-идеально-пластический 251
—	упругопластический 251
Матрица 32
—	вырожденная 32
—	диагональная 32
—	единичная 32
—	квадратная 32
—	обратная 33
—	ортогональная 33
—	присоединенная 33
—	тождественная 33
—	транспонированная 32
—	упругих констант 202
Матрица-столбец 32
Матрица-строка 32
Минор 33
Модель вязкоупругого тела Кельвина
(Фойхта) 280
	обобщенная 282
—	Максвелла 280
	обобщенная 282
—	трехпараметрическая 281
—	четырехпараметрическая 281
Модуль абсолютный динамический
289
—	комплексный 289
-- накопления 289
—	объемного сжатия 205
—	потерь 289
—	счвига 205
—	Юнга 204
Момент количества движения 183
	распределенный 199
Моменты поверхностных и массовых
пар распределенные 75
Мощность напряжений 259
Нагружение активное 257
—	нейтральное 256
Направления эквивалентных упругих
свойств 202
Напряжение касательное 72
	 октаэдрнческое 99
—	нормальное 72

312
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Напряжения главные 78
Напряженное состояние 71
	плоское 85, 94
	сферическое 228
	цилиндрическое 273
Неравенство Клаузиуса — Дюгема 188
Обозначения индексные 20
—	символические 10
Объем удельный 199
Октаэдрическая площадка 89, 98
Оператор замены 28
—	материального дифференцирования
по времени 159
Ось симметрии упругих свойств 203
Относительное удлинение 126
Параметр Генки 260
—	Лоде 264
Параметры состояния 186
П-плоскость 254
Плоская деформация 208
	обобщенная 210
Плоское напряженное состояние 207
	обобщенное 210
Плоскость симметрии упругих свойств
202
Плотность 69, 180
—	средняя 69
Поверхность линейных деформаций
128
—	нагружения 256
—	напряжений Коши 77
—	скоростей деформации 163
—	текучести 254
Податливость (материала) 285
—	абсолютная динамическая 289
—	комплексная 289
—	накопления 289
—	потерь 289
Поле скоростей 160
	 безвихревое 162
—	тензорное 38
	стационарное 38
Ползучесть 283
Полярное разложение тензора 126
Постоянная текучести 252
Постоянные Ламе 204
Потенциал векторный 180
—	диссипативный 244
—	комплексный 236
—	пластический 258
—	скорости 233
Поток тепла 185
Предел текучести 248
	Джонсона 249
Предел упругости 248
Преобразование координат ортого-
ортогональное 26, 28
Принцип напряжения Коши 70
—	Сен-Венана 207
—	соответствия упругой и вязкоупру-
гой задач 292
Приращения деформации 257
Произведение вектора на тензор 34
—	векторов, см. Векторы
—	диад, см. Диад произведение
—	тензоров внешнее 29
	 внутреннее 30
Производная по времени индивиду-
индивидуальная 158
	 материальная 158
—	полная 158
	 субстанциональная 158
Пространство напряжений 254
	главных 79, 254
—	Хея—Вестергарда 254
Процесс баротропный 229
—	изотермический 191
—	термодинамический 186
	обратимый 187
—	— необратимый 187
—	чистого сдвига 253
Работа внешних сил 185
—	внутренних поверхностных сил 185
—	на пластических деформациях 259
—	, приращение ее 259
Равновесие гидростатическое 232
Радиус-вектор 25
Разгрузка 256
Растяжение всестороннее равномерное
93
—	одноосное 93
Реакция упругая запаздывающая 281
	 мгновенная 281
Релаксация 283
Сдвиг простой 93
Силы массовые 69
—	поверхностные 69
Система координат декартсва 16
	 однородная 26
—	обозначений символическая (гиб-
бсова) 10
Скаляр 10
Скольжение 248
Скорость внутреннего производства
энтропии 188
—	изменения свойства локальная
(местная) 158
	конвективная 158

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
313
Скорость кубического расширения
176
—	комплексная 236
—	мгновенная частицы 158
—	сдвига 163
—	удлинения 163
	 относительного 163
Соглашение о суммировании 20
Соотношение Гамильтона — Кэли 38
Соотношение Дюгамеля — Неймана
213
—	между напряжениями и деформа-
деформациями 190
Состояния параметры 186
—	уравнения 186
—	функция 186
Спектр запаздывания 286
	логарифмический 304
—	релаксации 286
Способ описания движения лагранжев
115
	 эйлеров 185
Среда, см. также Материал
—	анизотропная 202
—	— идеализированная 190
—	изотропная 202
—, модель ее 190
—	несжимаемая 180
—	ортотропная 203
Стандартное линейное твердое тело
281
Тензор 9
—	альтернирующий 31
—	антисимметричный 34
—	вихря 161
—, главные значения его 37
	 направления его 36
	 оси его 36
—	градиента скорости 160
—	декартов 9, 26
—	деформаций бесконечно малых ла-
лагранжев 120
	 эйлеров 120
	 Грина 119
	конечных Альманси 119
	 Грина 119
	лагранжев 119
	 эйлеров 119
	Коши 118
	шаровой 131
—	завихренности 161
—, инварианты его 37
—	ковариантный 24, 25
—, компоненты его 9
	, закон их преобразования 9
—	кососимметричный 34
—	коэффициентов длины П7
Тензор Левн-Чнвиты 31
—	метрический 25
—	моментов, инерции 193
—	напряжений 72
	 вязких 228
—	— гидростатических 87
	, главные направления его 78
	 диссипативных 188
	, инварианты его 79
	консервативных 188
	, симметричность его 75
	шаровой 87
—	обычным 9
—	ортогональный 127
—	поворота линейного лагранжев 122
—	эйлеров 122
—, полярное разложение его 126
—, порядок его 9
—	приращений деформации 257
—, ранг его 9
—	ранга нулевого 10
	 первого 10, 20
	второго 10, 21
—, свертка его 30
—, свертывание его 30
—	симметричный 34
—	скоростей деформации 161
—	— —, главные значения его 163
	 — направления его 163
	, инварианты его 163
—	смешанный 25
—	упругих констант 200
—	фундаментальный пространства 25
—, характеристическое уравнение его
36
Тензоры сопряженные 13
Теорема Гаусса — Остроградского 41
—	об изменении количества движе-
движения 181—182
	момента количества движе-
движения 183
—	Кельвина (Томсона) 234
—	Рейнольдса о переносе 175
—	Стокса 40
Теория инкрементальная 257
—	линий скольжения 261
—	малых деформаций 120
—	несвязанной термоупругости 190
—	пластичности	деформационная
(Генки) 260
—	течения 257
Теплоемкость удельная 213
Тетрадик 10
Течение 112, 157
—	адиабатическое 236
—	безвихревое 233
—	вязкое 281
—	пластическое 248

314
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Течение потенциальное 234—235
Тождество Гиббса 189
Точка 112
Траектория 160
Транспозиция матрицы 32
Триадик 10
Триэдр единичных векторов 17
Трубка тока 243
Угол запаздывания 288
Узел Кельвина 280
—	Максвелла 280
Упрочнение 250, 256
—	изотропное 256, 259
—	кинематическое 257
—	линейное 257
Уравнение Бернулли 234
—	бигармоническое 210
—	волновое 218
—	калорическое 190
—	Лапласа 235
—	неразрывности 180, 189
—	характеристическое 36
—	энергии 190
—	для энтропии 190
Уравнения газовой динамики 235
—	движения 183, 189
—	^Ламе 206
—"Левц — Мизеса 257
—	Навье — Коши 206
—	Навье — Стокса 231
—	Навье — Стокса — Дюгема 231
—	определяющие 190
—	Прандтля — Рейсса 258
—	равновесия 75, 183
—	связанной термоупругости 213
—	совместности Бельтрами — Мичел-
ла 206
	 для лииейиых деформаций
133—134
	скоростей деформации 163
—	состояния 186
—	Эйлера 233
Ускорение 160
Условие Стокса 230
Условия Коши — Римана 235
Функция бигармоническая 2j*0
—	давления 232- 233
—	днссипативная 189
—	единичная импульсная 284- 285
	 ступенчатая 283
—	нагружеиия 256
ползучести 28F
—	распределения времен запаздыва-
запаздывания 286
	 релаксации 286
Функция релаксации 286
—	состояния 186
—	текучести 252
—	тока 235
—	Эри 210
Цилиндрическое напряженное состоя-
состояние 273
Циркуляция скоросги 234
Частица 112
Число Рейнольдса 232
Эйлеров способ описания движения
115
Эквивалентное напряжение 258
—	приращение пластической деформа-
деформации 258
Эксперимент на ползучесть 283
	обратную 295
	релаксацию 283
Элемент вязкий 280
—	упругий 280
Эллипсоид деформаций 128
	Коши 129
	 материальный 129
	пространственный 129
—	напряжений Ламе 80
Энергия внутренняя механическая 185
	 удельная 185
—	деформации 201
—	— , плотность ее 201
—	искажения формы (дисторсии) 214
—	кинетическая 184
—	расширения 214
—	свободная 222
—	— удельная 199
—	тепловая 185
—	химическая 185
—	электромагнитная 185
Энтальпия удельная 198
Энтропия 187
—, плотность ее 187
—	производство ее 185
—	удельная 187
Эффект Баушингера 251
Эффективное напряжение 258
—	приращение пластической дефор-
деформации 258
Якобиан (преобразования коорди-
координат) 24

Оглавление
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА		5
ПРЕДИСЛОВИЕ		7
К РУССКОМУ ИЗДАНИЮ 	 . .	8
Глава 1. МА ТЕМА ТИЧЕСКИЕ ОСНОВЫ
.1. Тензоры и механика сплошной среды		9
.2. Тензоры. Декартовы тензоры. Ранг тензора		9
.3. Векторы_и_?калзры_		10
.4. Бекторше сложение. Умножение вектора на скаляр		11
.5. Скялярнор и ^векторное произведени_а_векторов		12
.6. Диады и диадики 		13
.7. Системы координат. Базисные векторы. Триэдр единичных век-
векторов 		16
.8. Линейные векторные функции. Диадики как линейные вектор-
векторные операторы 		19
.9. Индексные обозначения. Интервал изменения индексов н согла-
соглашение в суммировании 		20
.10. Соглашение о суммировании в символических обозначениях	22
.11. Преобразование координат. Общее приятие тензора ....	23
.12. Метрический тензор. Декартовы тензоры		25
.13. Законы преобразования декартовых тензоров. Дельта Кроне-
кера. Условия ортогональности 		26
.14. Сложение декартовых тензоров. Умножение на скаляр ...	29
.15. Умножение тензоров 		29
.16. Векторное произведение. Тензор Леви-Чивиты. Бивектор . .	31
.17. Матрицы. Матричные представления декартовых тензоров . .	32
.18. Симметрия диадиков, матриц и тензоров 		34
.19. Главные значения и главные направления симметричных тен-
тензоров второго ранга		35
.20. Степени тензоров второго ранга. Соотношение Гамильтона —
Кэли 		37
.21. Тензорные поля. Дифференцирование тензоров 		38
.22- Криволинейные интегралы. Теорема Стокса 		39
.23. Теорема Гаусса — Остроградского 		41
Задачи с решениями 		41
Дополнительные задачи 		65
Глава 2. АНАЛИЗ НАПРЯЖЕННОГО СОСТОЯНИЯ		68
2.1.	Понятие сплошной среды 		68
2.2.	Однородность. Изотропия. Массовая плотность 		68
2.3.	Массовые силы. Поверхностные силы		69
2.4.	Принцип напряжения Коши. Вектор напряжения		69
JL5, Напряженное, состояние в точке. Тензор напряжений ...	71
2.6.	Связь между тензором напряжений и вектором напряжения	73
2.7.	Равновесие сил и моментов. Симметрия тензора напряже-
напряжений 		74

316	ОГЛАВЛЕНИЕ
2.8. Законы преобразования напряжений		75
2.fl. Поверхности напряжений Коши 		77
2.10.	Главные напряжения. Инварианты тензора напряжений. Эл-
Эллипсоид напряжений 		78
2.11.	Максимальное и минимальное касательное напряжение ...	80
2.12.	Круги Мора для напряжения		82
2.13.	Плоское напряженное состояние		85
2.14.	Девиатор и шаровой тензор напряжений 		87
Задачи с решениями		88
Дополнительные задачи *		109
Глава 3. ДЕФОРМАЦИИ		112
3.1.	Частицы и точки 		112
3.2.	Конфигурация сплошной среды. Деформация и течение ...	112
3.3.	Радиус-вектор. Вектор перемещения		112
3.4.	Лагранжевон эйлерово описания движения		115
3.5.	Градиенты деформации. Градиенты перемещения		116
3.6.	Тензоры деформаций. Тензоры конечных деформаций ....	117
3.7.	Теория малых деформаций. Тензоры бесконечно малых дефор-
деформаций 		120
3.8.	Относительное перемещение. Тензор линейного поворота.
Вектор поворота 	.-		121
3.9.	Геометрический смысл тензоров линейных деформаций . . .	123
3.10.	Коэффициент длины. Интерпретация конечных деформаций	125
3.11.	Тензоры коэффициентов длины. Тензор поворота 		126
3.12.	Свойства преобразовании тензоров деформаций 		127
3.13.	Главные деформации. Инварианты деформации. Кубическое
расширение 		129
3.14.	Шаровой тензор и девиатор деформаций 		131
3.15.	Плоская деформация. Круги Мора для деформации		132
3.16.	Уравнения совместности для линейных деформации ....	133
Задачи с решениями 		134
Дополнительные задачи 		155
Глава 4. ДВИЖЕНИЕ И ТЕЧЕНИЕ 		157
4.1.	Движение. Течение. Материальная производная		157
4.2.	Скорость. Ускорение. Мгновенное поле скоростей 		159
4.3.	Траектории. Линии тока. Установившееся движение ....	160
4.4.	Скорость деформации. Завихренность. Приращения дефор-
деформации 		160
4.5.	Физическая интерпретация тензоров скоростей деформации и
завихренности 		162
4.6.	Материальные производные по времени от элемента объема, эле-
элемента поверхности и линейного элемента 		163
4.7.	Материальные производные по времени от интеграла по объему,
интеграла по поверхности и линейного интеграла 		165
Задачи с решениями 	~ . . . .	167
Дополнительные задачи 		178
Глава 5. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ	180
5.1. Сохранение массы. Уравнение неразрывности 		180
Б.2. Теорема об изменении количества движения. Уравнения дви-
движения. Уравнения равновесия 		181
5.3.	Теорема об изменении момента количества движения ....	183
5.4.	Сохранение энергии. Первый закон термодинамики. Урав-
Уравнение энергии 		184

ОГЛАВЛЕНИЕ	317
5.5.	Уравнения состояния. Энтропия. Второй закон термодинамики	186
5.6.	Неравенство Клаузиуса— Дюгема. Диссипативная функция	187
5.7.	Определяющие уравнения. Термомеханический и механический
континуумы 		189
Задачи с решениями		191
Дополнительные задачи		198
Глава 6. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ		200
6.1.	Обобщенный закон Гука. Функция энергии деформации . .	200
6.2.	Изотропные и анизотропные среды. Симметрия упругих
свойств	i		202
6.3.	Изотропные среды.Упругие постоянные		204
6.4.	Постановка статических и динамических задач теории уп-
упругости		205
6.5.	Теорема о суперпозиции. Единственность решений. Принцип
Сен-Венана		207
6.6.	Плоские задачи теории упругости. Плоское напряженное со-
состояние и плоская деформация		207
6.7.	Функция напряжений Эри		210
6.8.	Двумерные статические задачи теории упругости в полярных
координатах		211
6.9.	Гиперупругость. Гипоупругость		212
6.10.	Линейная термоупругость 	'	212
Задачи с решениями	 . . '		214
Дополнительные задачи 		225
Глава 7. ЖИДКОСТИ		228
7.1.	Давление жидкости. Тензор вязких напряжений. Баротропное
течение 	*		228
7.2.	Определяющие уравнения. Стоксовы жидкости. Ньютоновы
жидкости 		229
7.3.	Основные уравнения ньютоновой жидкости. Уравнения На-
вье — Стокса — Дюгема 	,		230
7.4.	Установившееся течение. Гидростатика. Безвихревое течение	232
7.5.	Идеальная жидкость. Уравнение Бернулли. Циркуляция . .	233
7.6.	Потенциальное течение. Плоское потенциальное течение . .	234
Задачи с решениями 		236
Дополнительные задачи 		246
Глава 8. ТЕОРИЯ ПЛАСТИЧНОСТИ		248
8.1.	Основные положения и определения 		248
8.2.	Идеализированные диаграммы пластического поведения . .	250
8.3.	Условия пластичности. Критерии Треска и Мизеса ....	252
8.4.	Пространство напряжений. П-плоскость. Поверхность теку-
текучести	 . . .	254
8.5.	Поведение материала за пределом текучести. Изотропное и ки-
кинематическое упрочнение 		255
8.6.	Соотношения между напряжениями и деформациями в пласти-
пластическом состоянии. Теория пластического потенциала . . .	257
8.7.	Эквивалентное напряжение. Эквивалентное приращение плас-
пластической деформации 		258
8.8.	Работа на пластических деформациях. Гипотезы упрочнения	259
8.9.	Деформационная теория пластичности 		260
8.10.	Задачи упругопластнчности 		260

318	ОГЛАВЛЕНИЕ
8.11. Элементарная теория линий скольжения при плоской пласти-
пластической деформации 		261
Задачи с решениями		263
Дополнительные задачи		276
Глава 9. ЛИНЕЙНАЯ ВЯЗКОУПРУГОСТЬ		279
9.1.	Вязкоупругое поведение материала'		279
9.2.	Простейшие механические модели вязкоупругого поведения	279
9.3.	Обобщенные модели. Линейное дифференциальное операторное
уравнение 		282
9.4.	Ползучесть и релаксация		283
9.5.	Функция ползучести. Функция релаксации. Интегралы наслед-
наследственности 		285
9.6.	Комплексные модули и податливости 		288
9.7.	Трехмерная теория 		290
9.8.	Анализ вязкоупругого напряженного состояния. Принцип
соответствия 		291
Задачи с решениями		293
Дополнительные задачи		306
СПИСОК ЛИТЕРАТУРЫ		309
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ		310

Дж. Мейз
ТЕОРИЯ И ЗАДАЧИ
МЕХАНИКИ СПЛОШНЫХ СРЕД
Редактор Г. М. Ильичева. Художник Г. Д. Коняхина
Художественный редактор В. И. Шаповалов
Технический редактор Н. А. Иовлева
Корректор В. С. Соколов
Сдано а набор 29/V 1974 г. Подписано к печати Ю/Х 1974 г.
Бумага тип. № 3 60X90'/ie=!0 б. л. 20 печ. л. Уч.-нзд. л. 18,66.
Изд. № 1/7459. Цена I р. 50 к. Зак. 399.
ИЗДАТЕЛЬСТВО «МИР>
Москва, 1-й Рижский пер., 2.
Отпечатано в ордена Трудового Красного Знамени
Ленинградской типографии № 2 имени Евгении Соколовой
Союзполиграфпрома при Государственном комитете Совета
Министров СССР по делам издательств, полиграфин
и книжной торговли, 198052, Ленинград, Л-52,
Измайловский'проспект, 29, с матриц Головного предприятия
республиканского производственного объединения
«Полиграфкннга> Госкомиздата УССР,
г. Киев, ул. Довженко, 3.