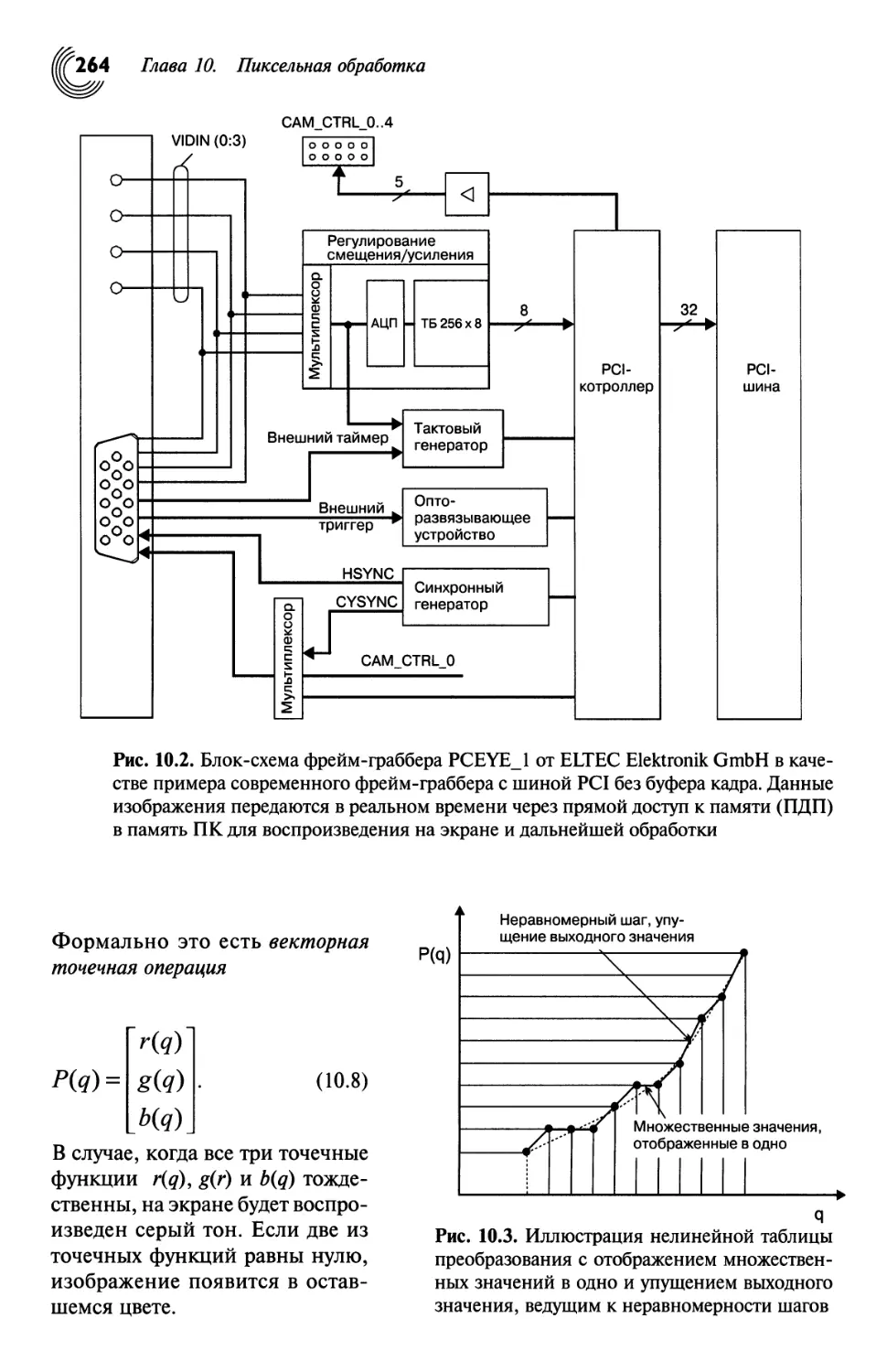
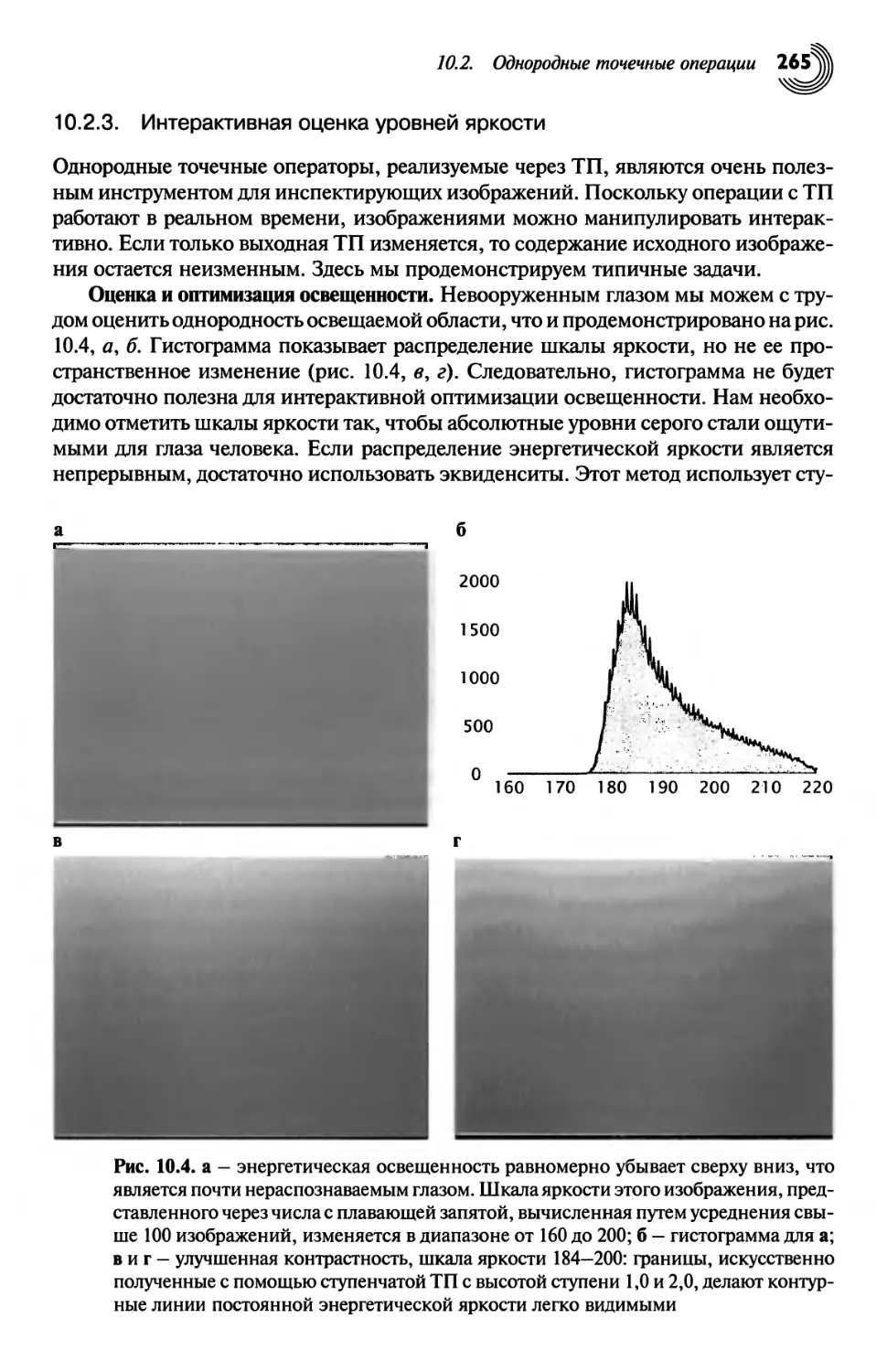
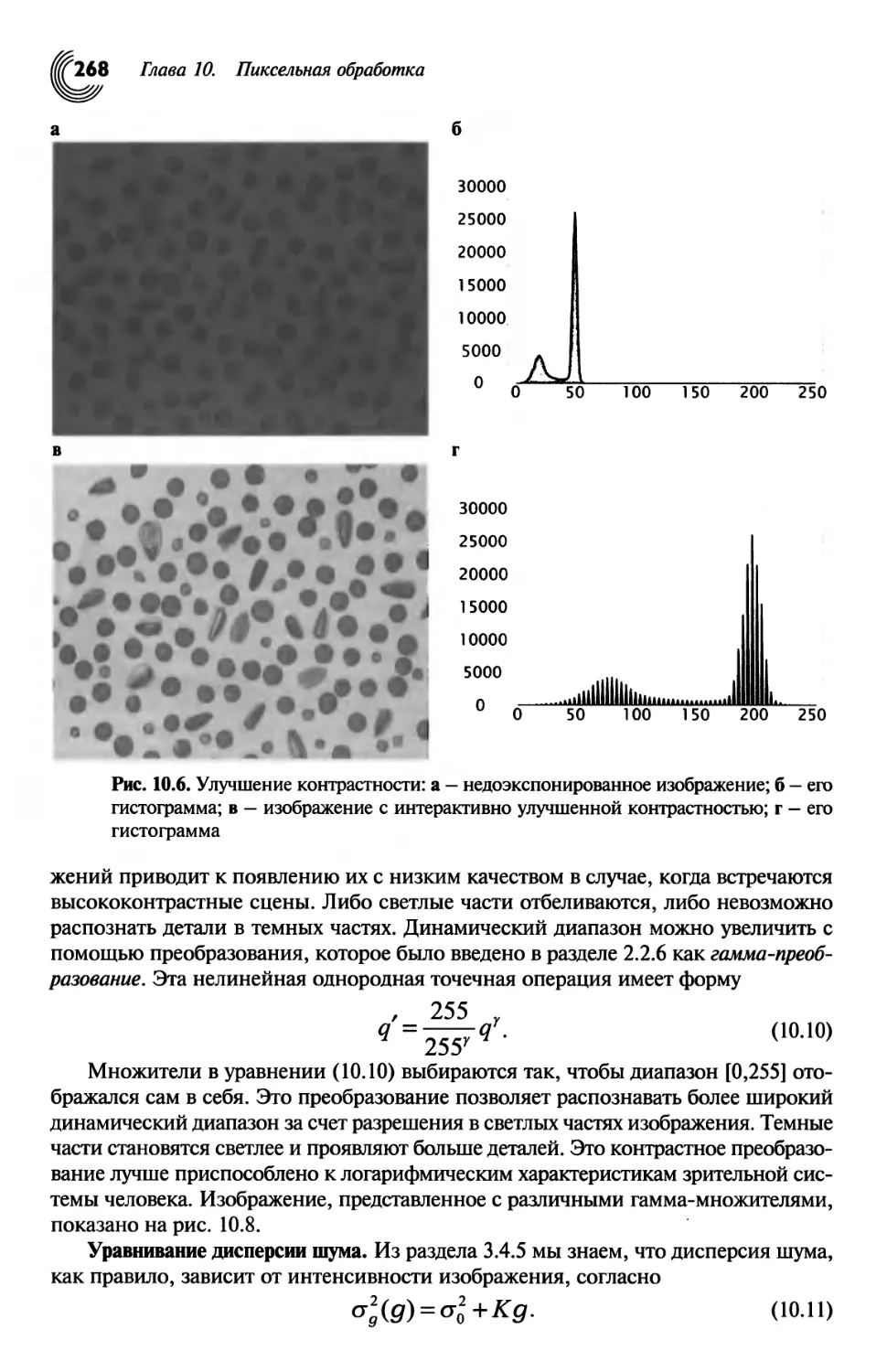
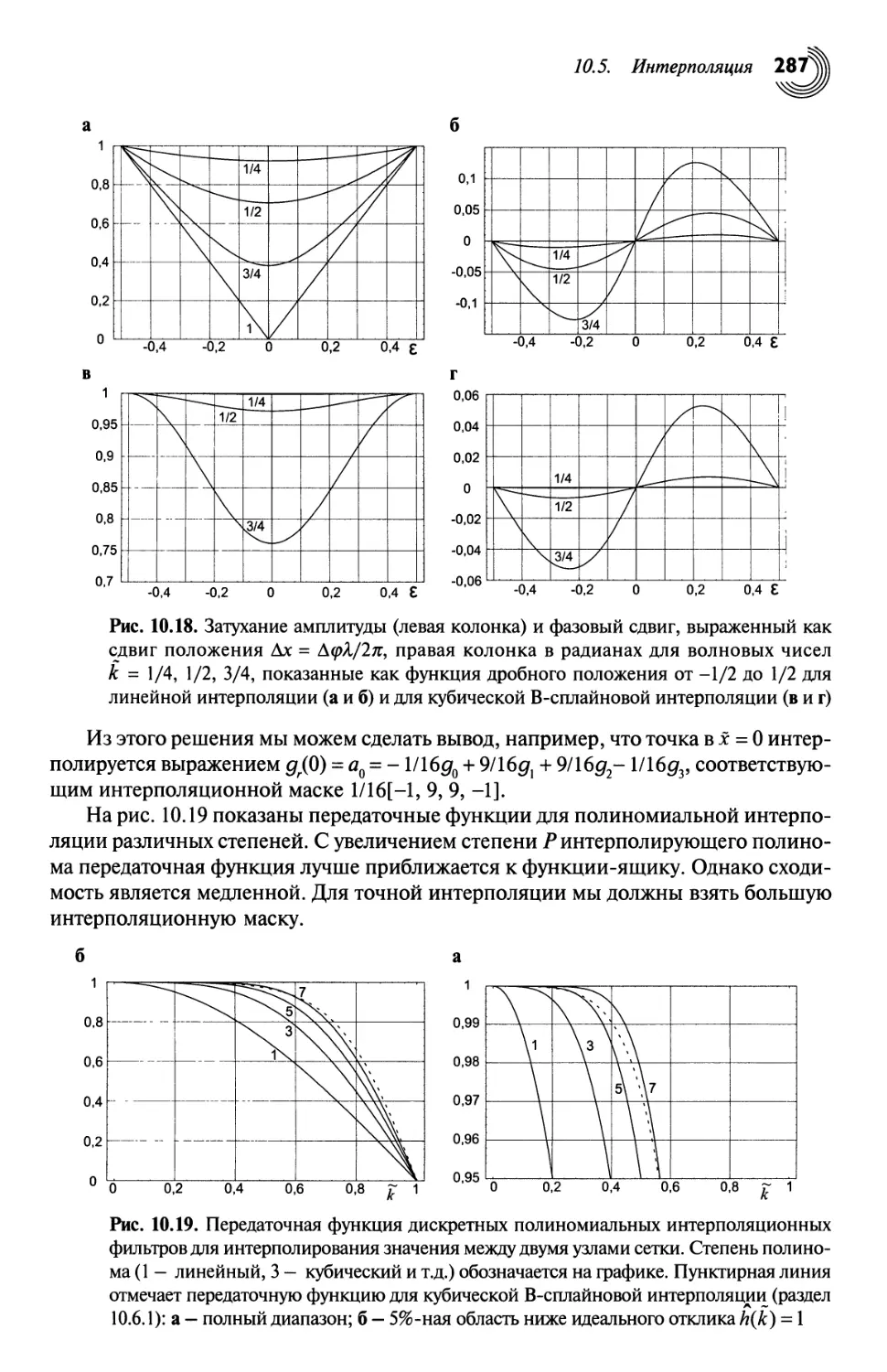
Автор: Яне Б.
Теги: учебное пособие переводная литература издательство техносфера цифровая обработка изображений
ISBN: 978-5-94836-122-2
Год: 2007
Текст
Яне Б.
Цифровая обработка изображений
Москва:
Техносфера, 2007. - 584с. ISBN 978-5-94836-122-2
С момента выхода первого издания, опубликованного в 1991 году, "Цифровая
обработка изображений" получила широкое применение в качестве учебного
пособия. В книге дается полный обзор процесса обработки от получения
изображения до выделения интересующих данных.
Каждая глава включает упражнения, которые помогут оценить понимание
материала, развить полученные навыки и дадут представление о реальных
задачах, связанных с обработкой изображений. Большое количество
интерактивных упражнений охватывает все рассмотренные в данном пособии темы.
К книге прилагается компакт-диск, содержащий программное обеспечение
heurisko, а также большую коллекцию изображений, которые могут быть
использованы при выполнении упражнений на компьютере.
Пособие адресовано всем, кто хочет овладеть практическими навыками работы
с изображениями.
Bernd Jahne
Digital Image
Processing
6th revised and extended edition
With 248 Figures ,15S Exercises, and CD-ROM
Ш Springer
© 2005, Springer-Verlag Berlin Heidelberg
© 2006, ЗАО «РИЦ «Техносфера» перевод на русский язык,
оригинал-макет, оформление
ISBN 978-5-94836-122-2
ISBN 3-540-24035-7 (англ.)
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ 11
ЧАСТЫ. ОСНОВЫ
ГЛАВА 1. ОБЛАСТИ ПРИМЕНЕНИЯ И ИНСТРУМЕНТАРИЙ 15
1.1. Инструмент в науке и технологии 15
1.2. Примеры применения 16
1.3. Иерархическая структура операций обработки
изображений 24
1.4. Обработка изображений и компьютерная графика 28
1.5. Междисциплинарная природа обработки изображений 29
1.6. Зрение человека и компьютерное зрение 30
1.7. Компоненты системы обработки изображений 32
1.8. Упражнения 37
1.9. Дополнительная литература 39
ГЛАВА 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ 41
2.1. Введение 41
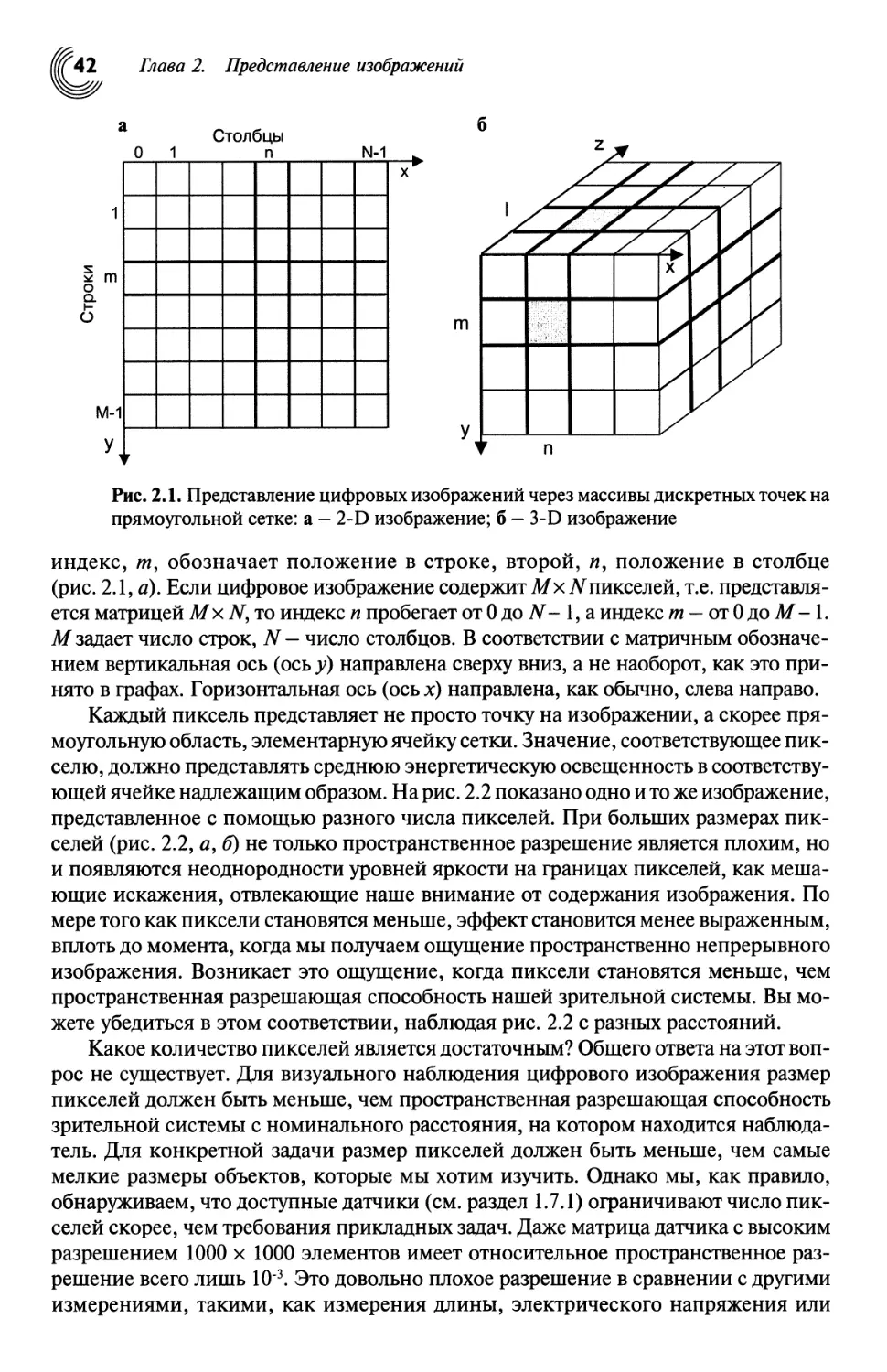
2.2. Пространственное представление цифровых изображений 41
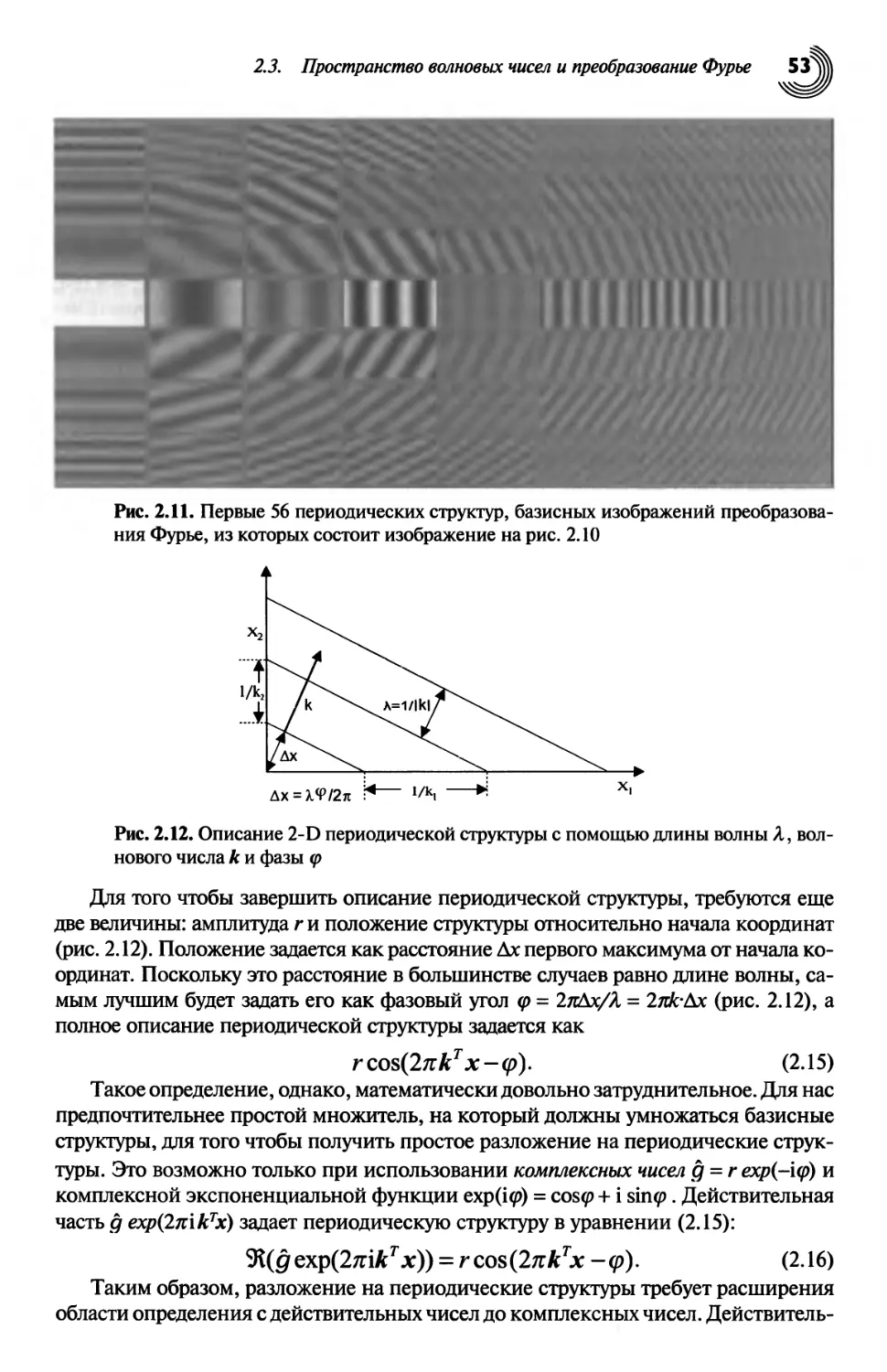
2.3. Пространство волновых чисел и преобразование Фурье 51
2.4. Дискретные унитарные преобразования 71
2.5. Быстрые алгоритмы для унитарных преобразований 76
2.6. Упражнения 87
2.7. Дополнительная литература 90
ГЛАВА 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И СЛУЧАЙНЫЕ ПОЛЯ 92
3.1. Введение 92
3.2. Случайные величины 93
3.3. Многомерные случайные величины 97
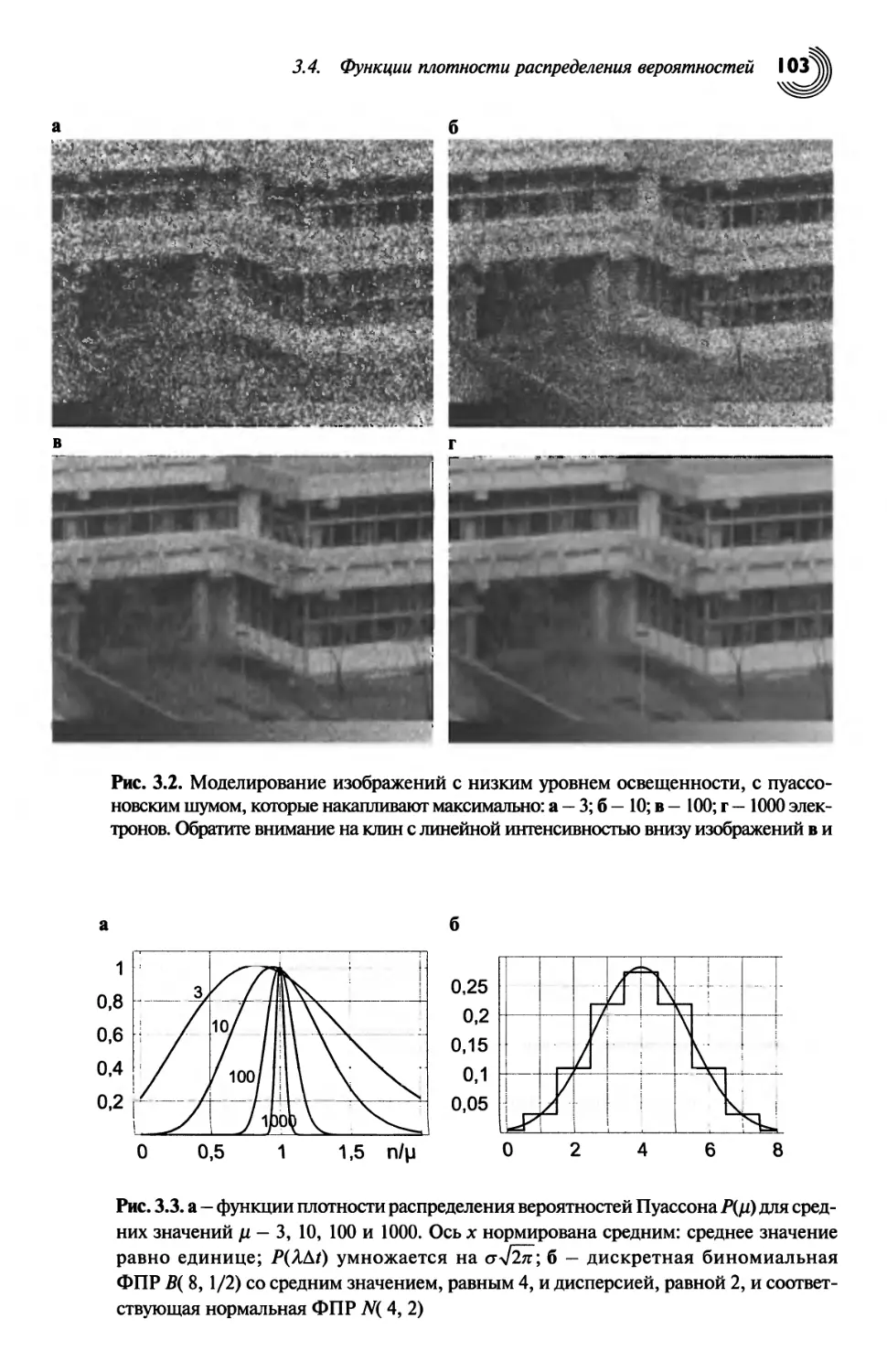
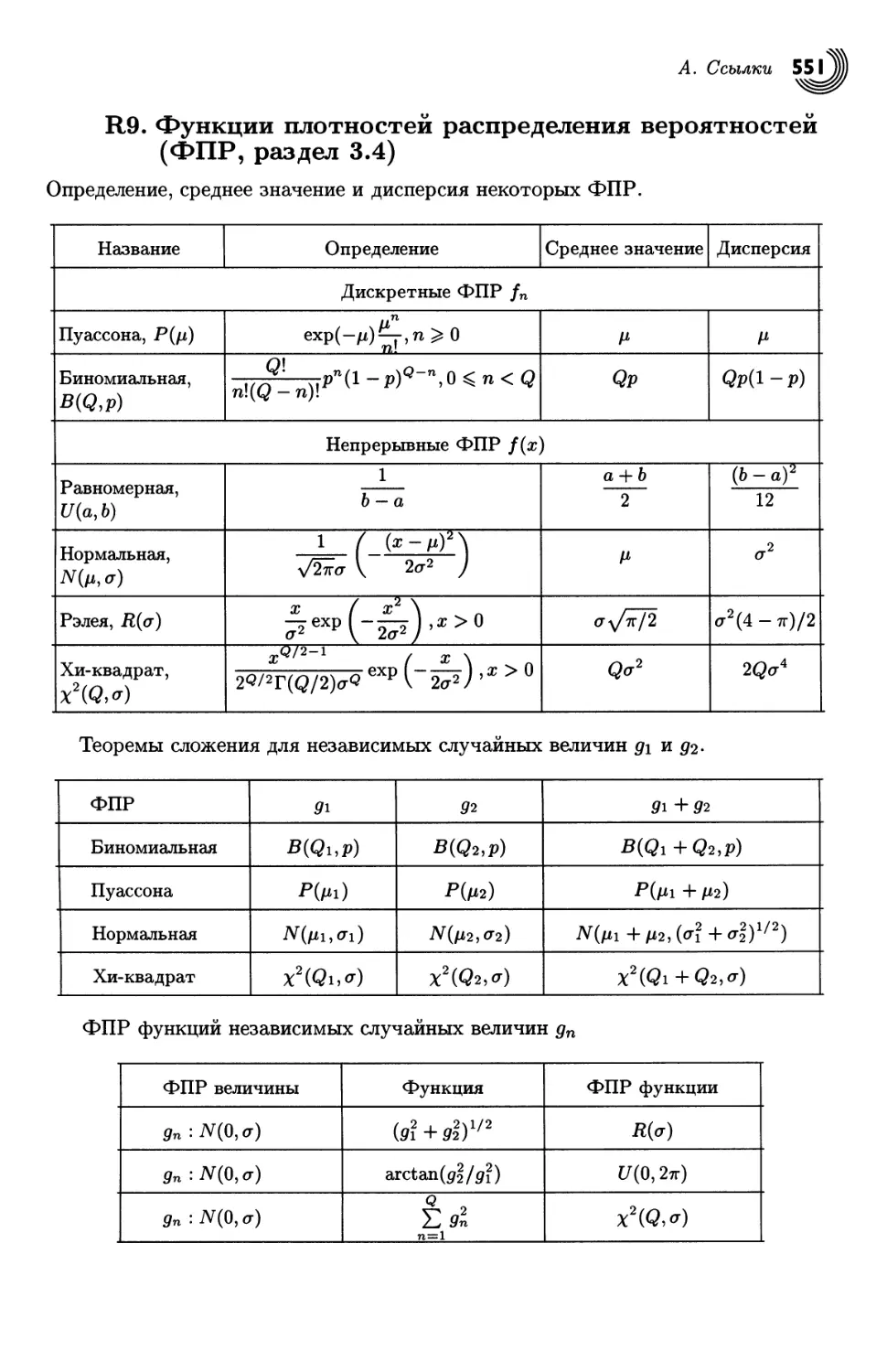
3.4. Функции плотности распределения вероятностей 101
3.5. Стохастические процессы и случайные поля 108
3.6. Упражнения 113
3.7. Дополнительная литература 115
ГЛАВА 4. ОПЕРАЦИИ НАД СОСЕДНИМИ ЭЛЕМЕНТАМИ 116
4.1. Основные свойства и назначение 116
4.2. Линейные инвариантные относительно сдвига фильтры 119
4.3. Фильтры порядковой статистики 129
4.4. ЛИС-фильтры: дополнительные свойства 130
4.5. Рекурсивные фильтры 132
4.6. Упражнения 141
4.7. Дополнительная литература 144
ГЛАВА 5. МНОГОМАСШТАБНОЕ ПРЕДСТАВЛЕНИЕ 145
5.1. Масштаб 145
5.2. Многосеточные представления 148
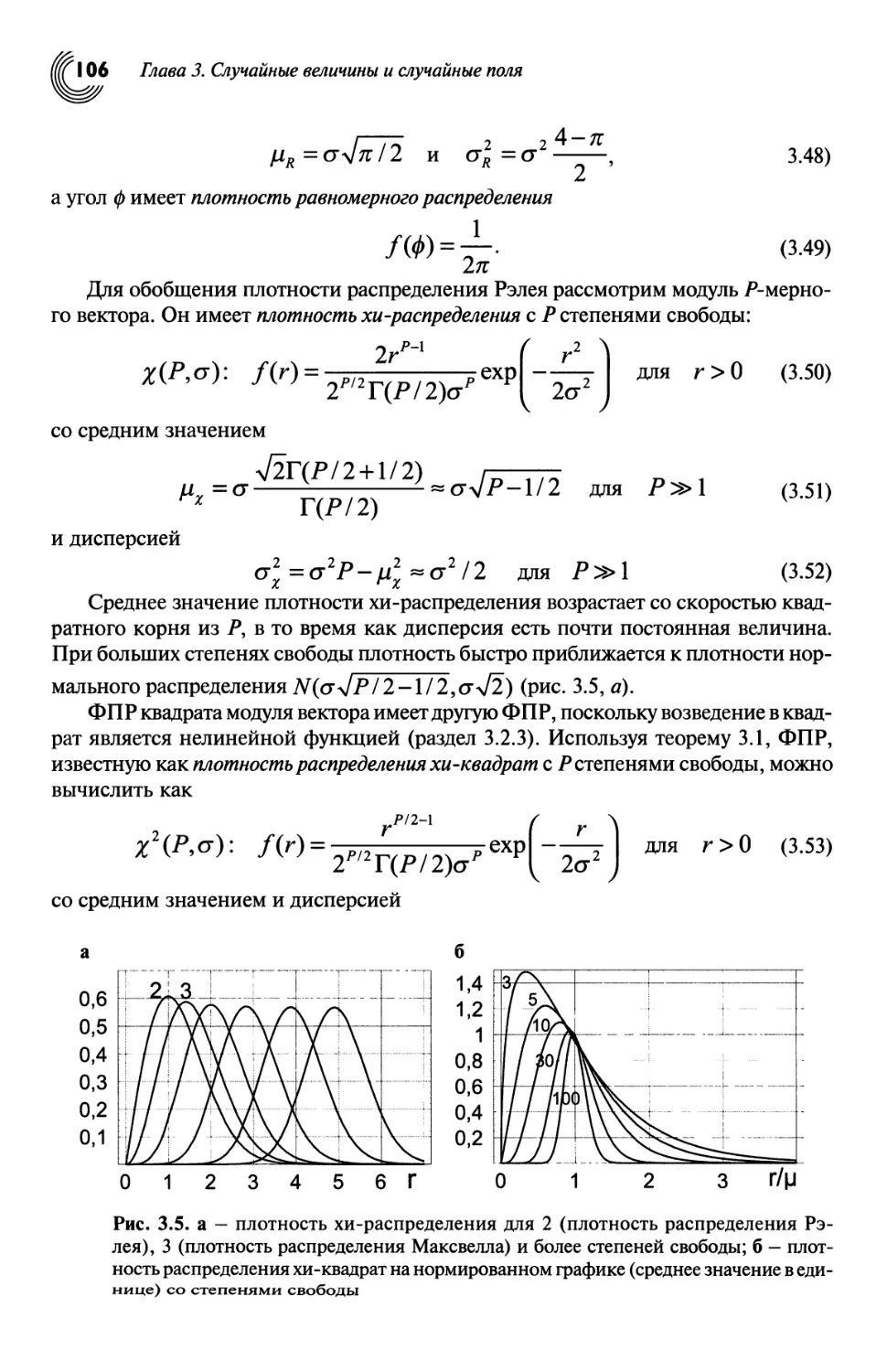
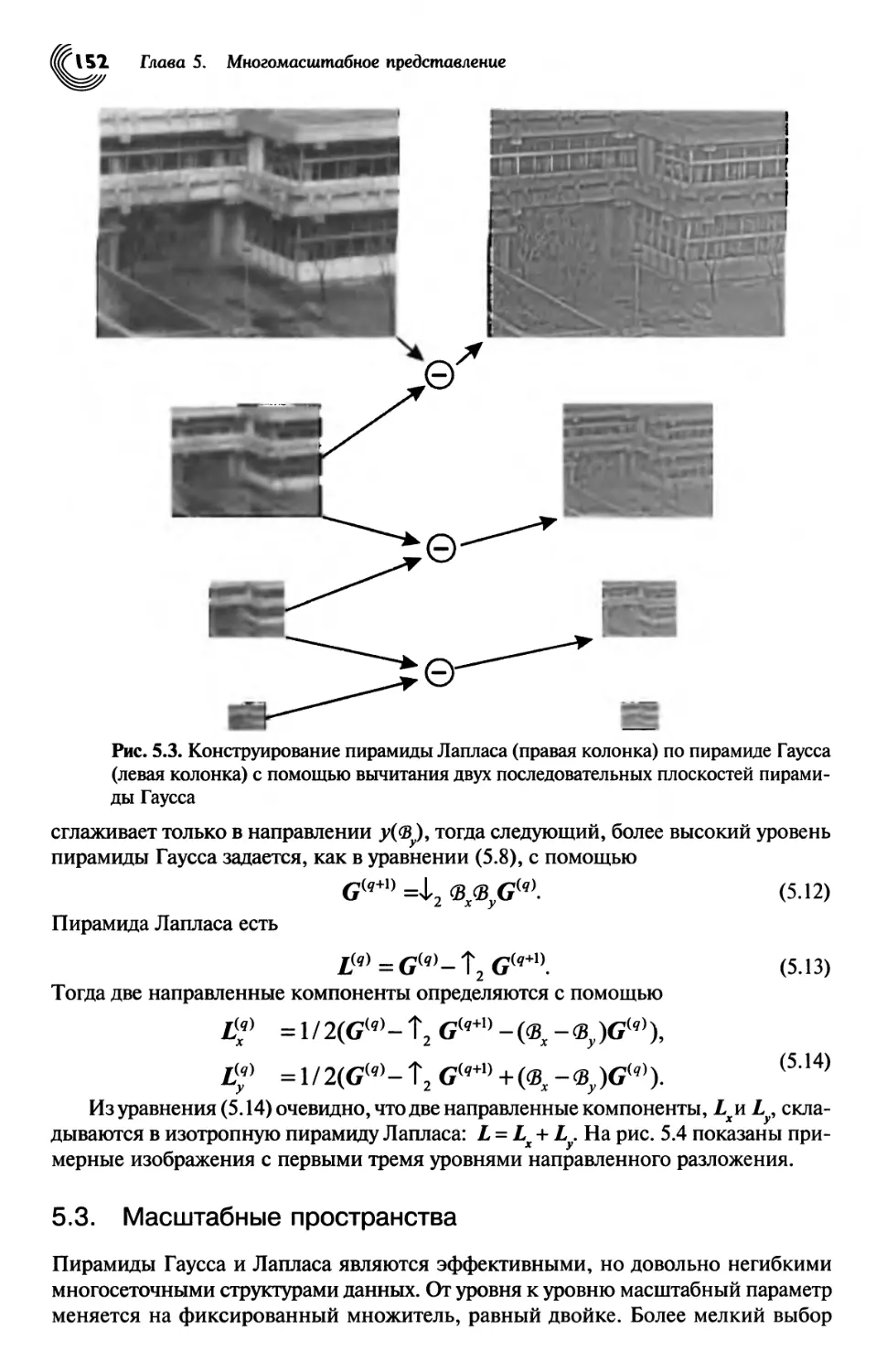
5.3. Масштабные пространства 152
5.4. Упражнения 161
5.5. Дополнительная литература 163
Содержание
ЧАСТЬ 2.
ГЛАВА 6.
6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
ГЛАВА 7.
7.1.
7.2.
7.3.
7.4.
7.5.
7.6.
7.7.
7.8.
7.9.
ГЛАВА 8.
8.1.
8.2.
8.3.
8.4.
8.5.
8.6.
8.7.
8.8.
ГЛАВА 9.
9.1.
9.2.
9.3.
9.4.
9.5.
9.6.
9.7.
ГЛАВА 10.
10.1.
10.2.
10.3.
10.4.
10.5.
10.6.
10.7.
ФОРМИРОВАНИЕ И ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА
ИЗОБРАЖЕНИЙ
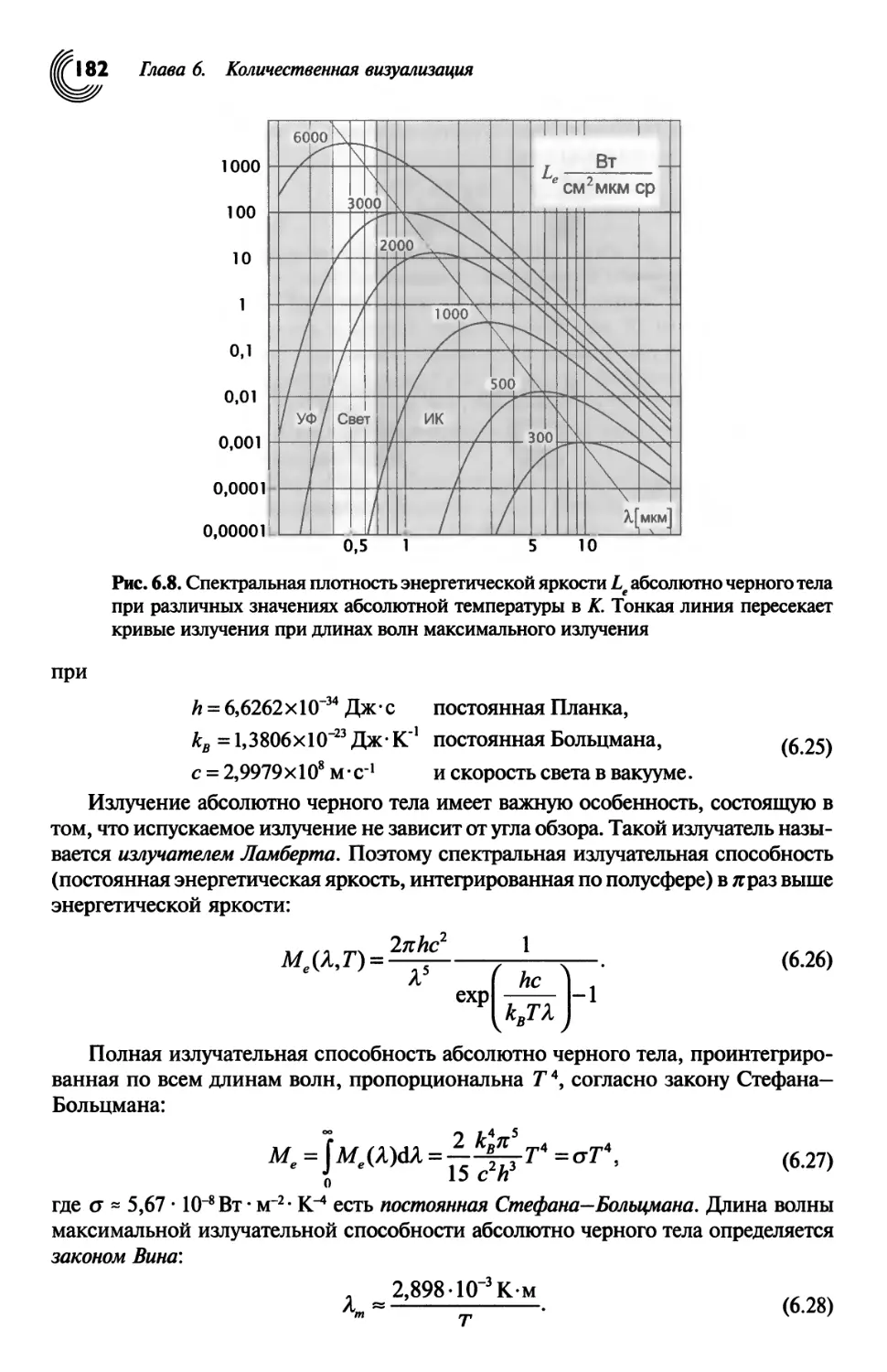
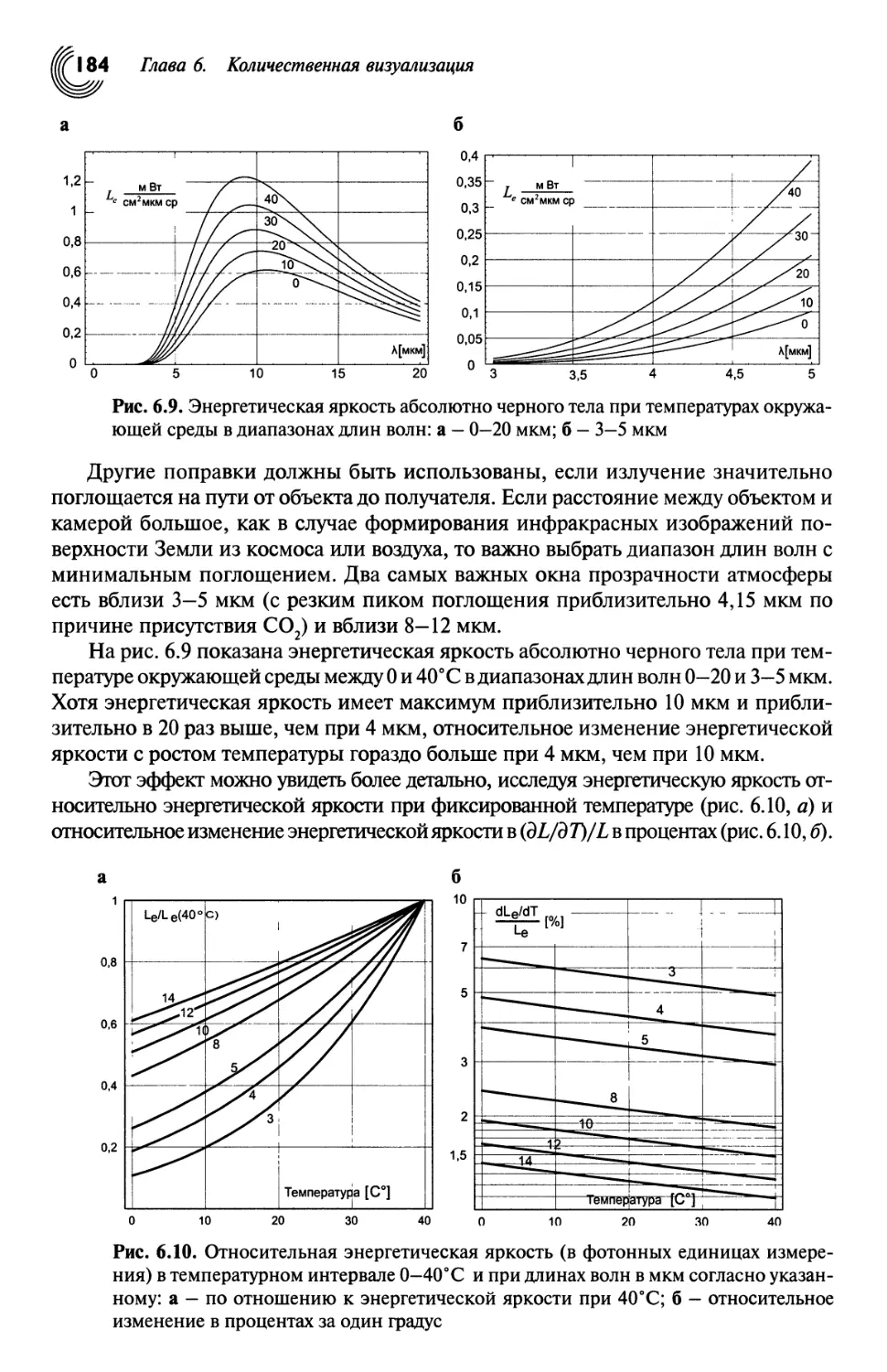
КОЛИЧЕСТВЕННАЯ ВИЗУАЛИЗАЦИЯ 164
Введение 164
Радиометрия, фотометрия, спектроскопия и цвет 166
Волны и частицы 175
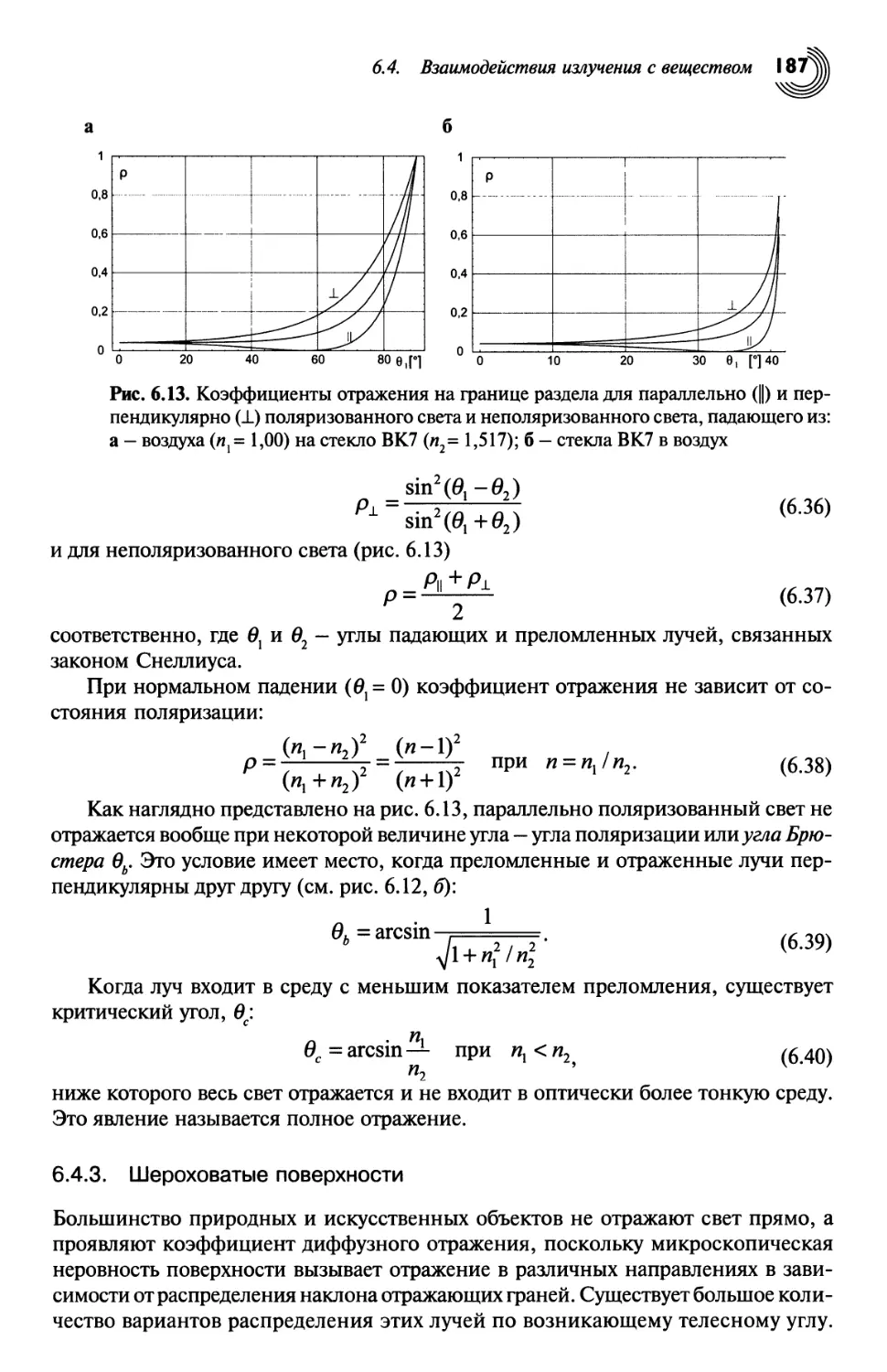
Взаимодействия излучения с веществом 180
Упражнения 193
Дополнительная литература 194
ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЙ 195
Введение 195
Мировые координаты и координаты камеры 195
Идеальное формирование изображений:
перспективная проекция 198
Реальное формирование изображений 201
Радиометрия формирования изображений 206
Теория линейных систем формирования изображений 209
Однородные координаты 218
Упражнения 220
Дополнительная литература 221
3-D ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЙ 222
Введение 222
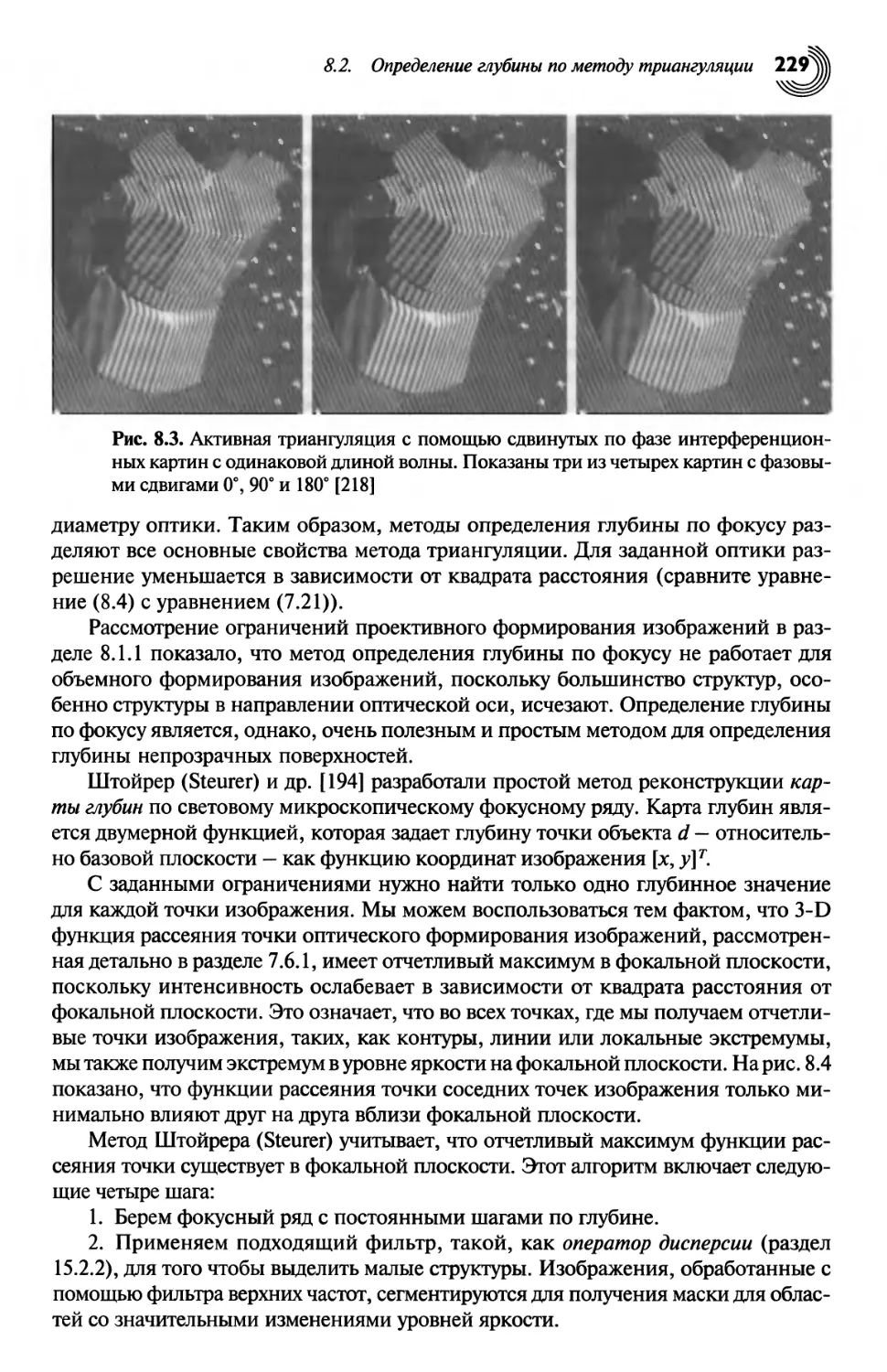
Определение глубины по методу триангуляции 225
Определение глубины по методу времени пролета 233
Определение глубины по фазе: интерферометрия 234
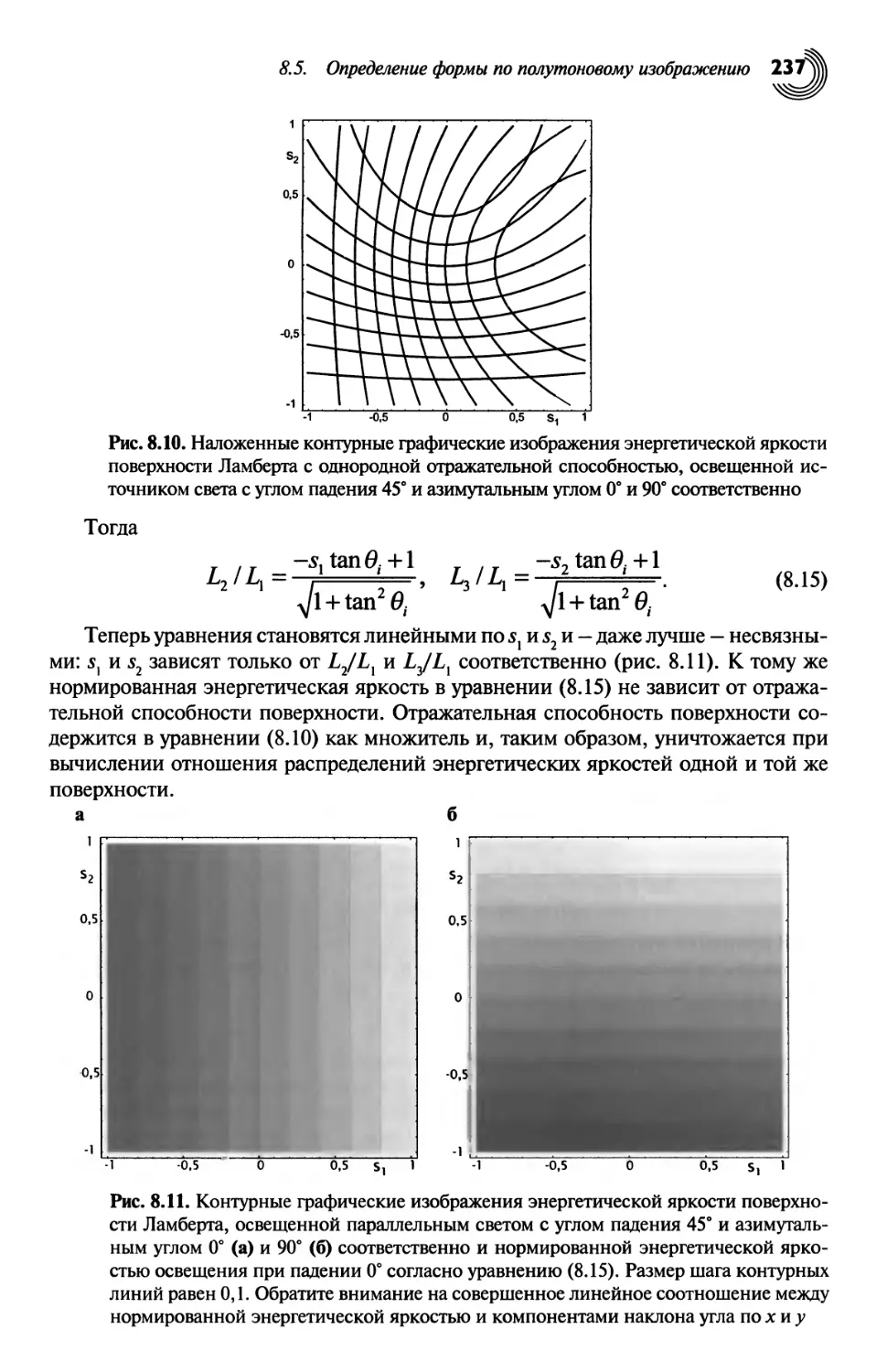
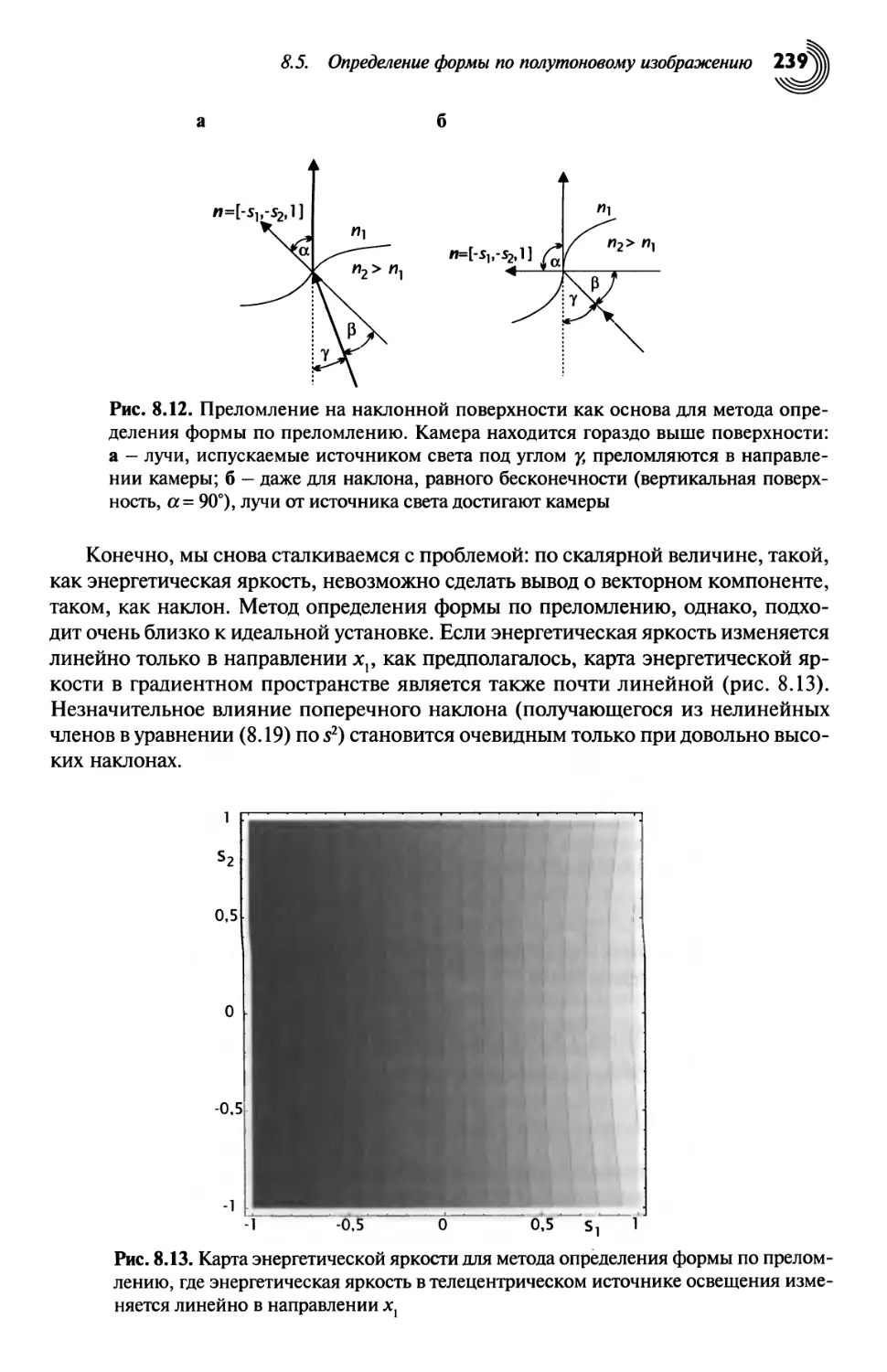
Определение формы по полутоновому изображению 234
Определение глубины по множественным проекциям:
томография 240
Упражнения 246
Дополнительная литература 247
ПРЕОБРАЗОВАНИЕ В ЦИФРОВУЮ ФОРМУ, ДИСКРЕТИЗАЦИЯ,
КВАНТОВАНИЕ 248
Определение и эффекты, связанные с преобразованием
в цифровую форму 248
Формирование изображений, дискретизация, отсечение 250
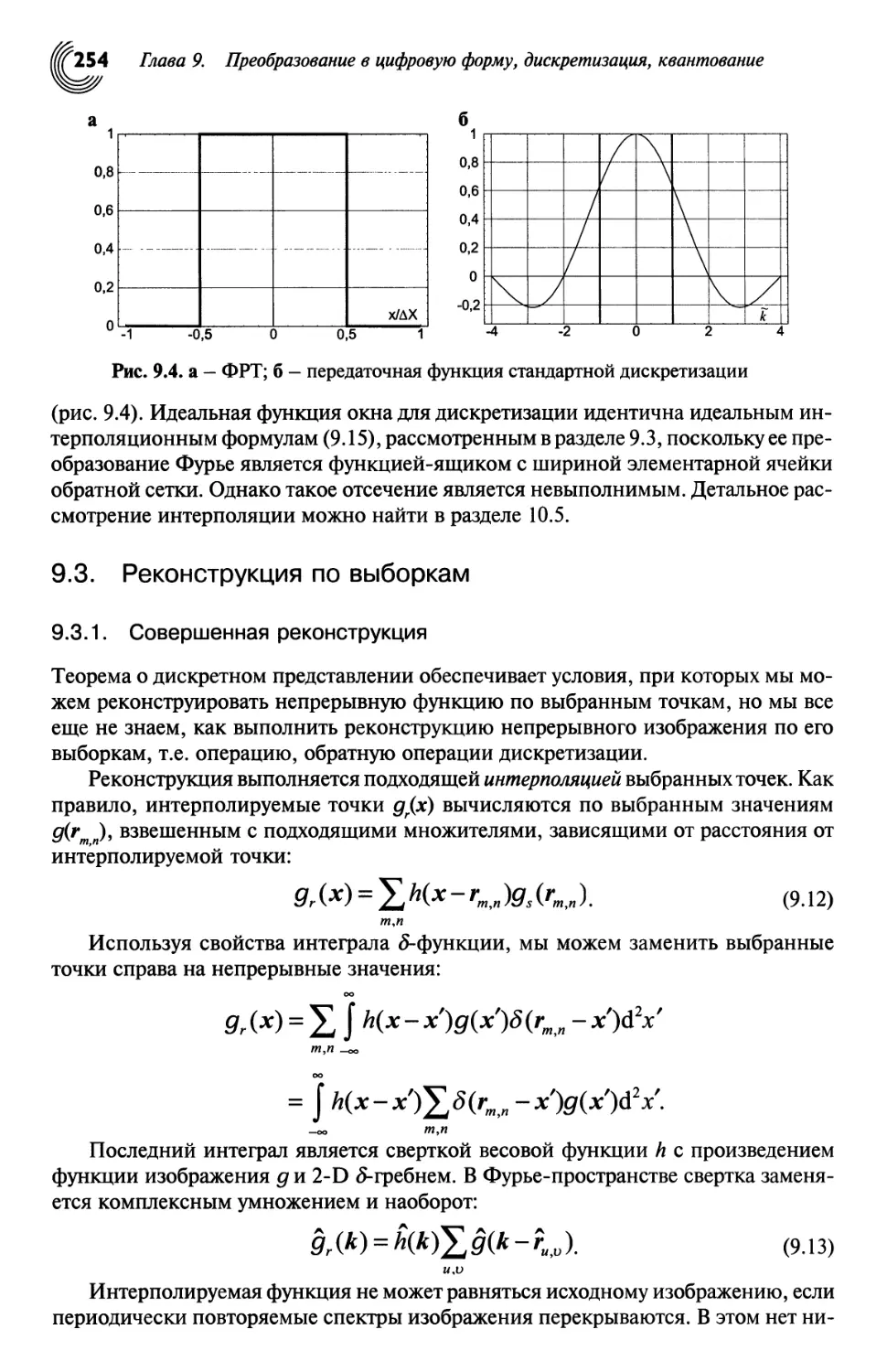
Реконструкция по выборкам 254
Многомерная дискретизация на неортогональных сетках 255
Квантование 257
Упражнения 259
Дополнительная литература 259
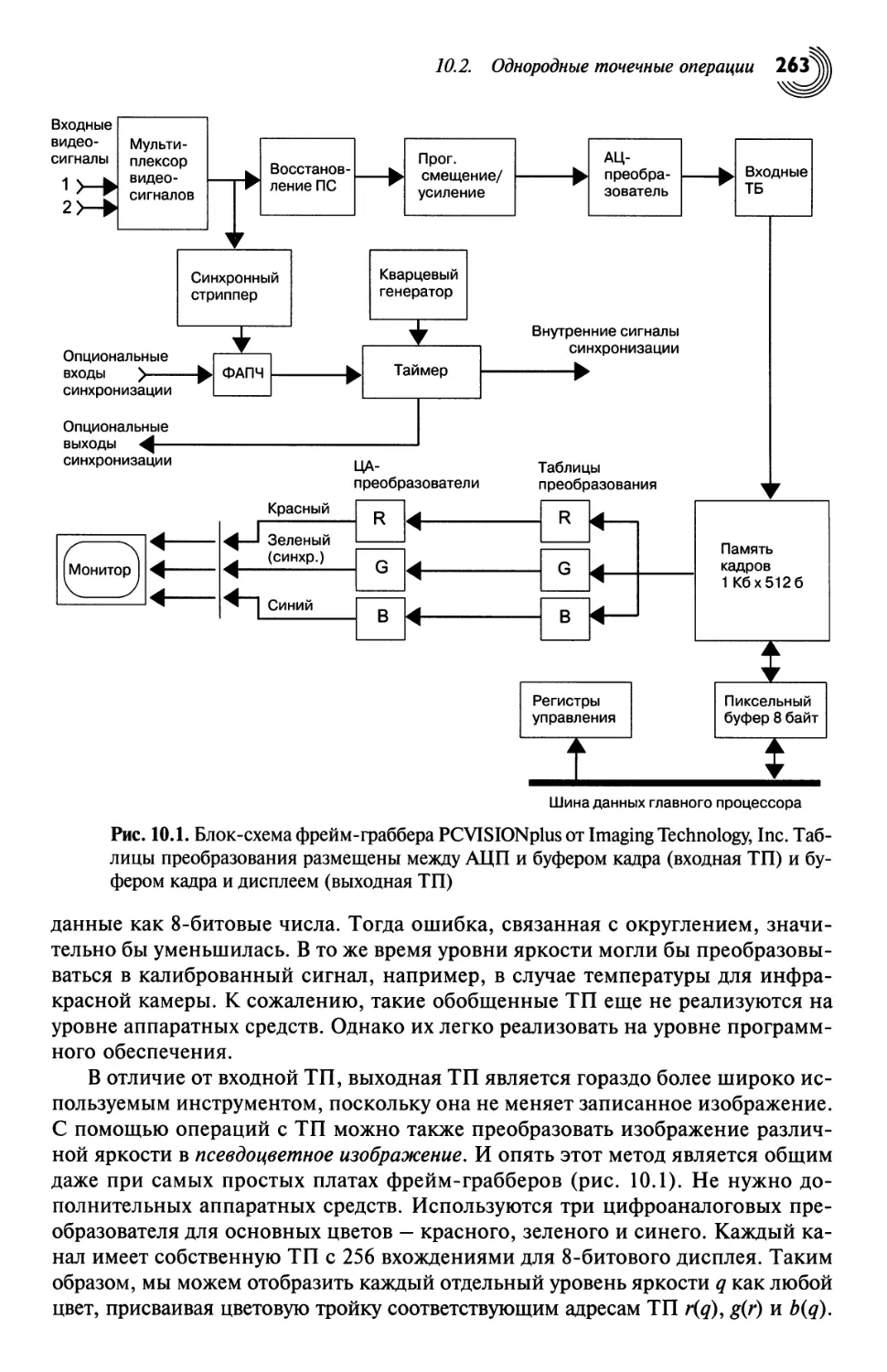
ПИКСЕЛЬНАЯ ОБРАБОТКА 260
Введение 260
Однородные точечные операции 261
Неоднородные точечные операции 271
Геометрические преобразования 277
Интерполяция 281
Оптимизированная интерполяция 288
Многоканальные точечные операции 293
Содержание
10.8. Упражнения 295
10.9. Дополнительная литература 297
ЧАСТЬ 3. ВЫДЕЛЕНИЕ ПРИЗНАКОВ
ГЛАВА 11. УСРЕДНЕНИЕ 298
11.1. Введение 298
11.2. Общие свойства усредняющих фильтров 298
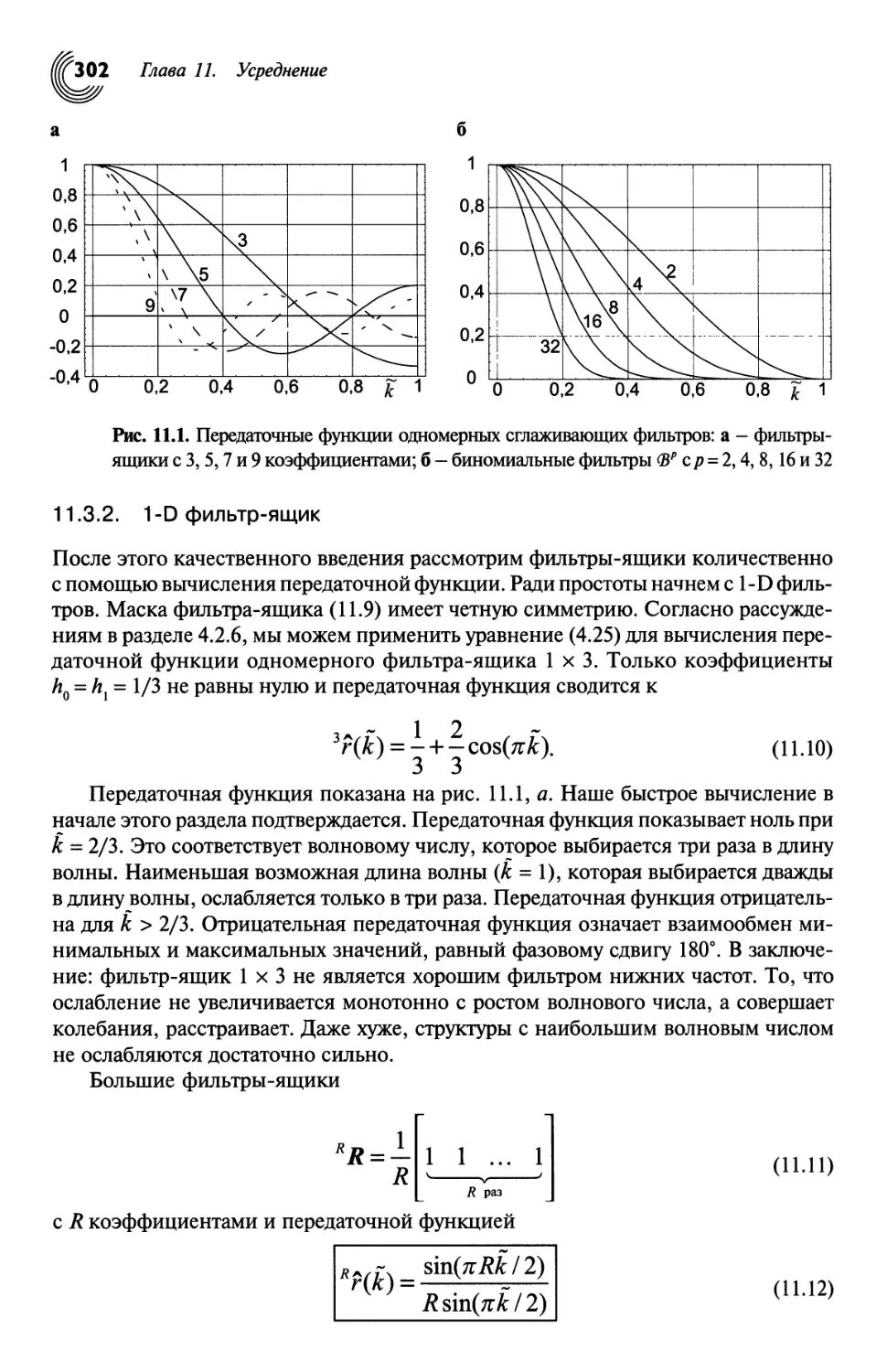
11.3. Фильтр-ящик 301
11.4. Биномиальный фильтр 305
11.5. Эффективное крупномасштабное усреднение 309
11.6. Нелинейное усреднение 320
11.7. Усреднение в многоканальных изображениях 326
11.8. Упражнения 327
11.9. Дополнительная литература 329
ГЛАВА 12. КОНТУРЫ 331
12.1. Введение 331
12.2. Дифференциальное описание изменений сигнала 332
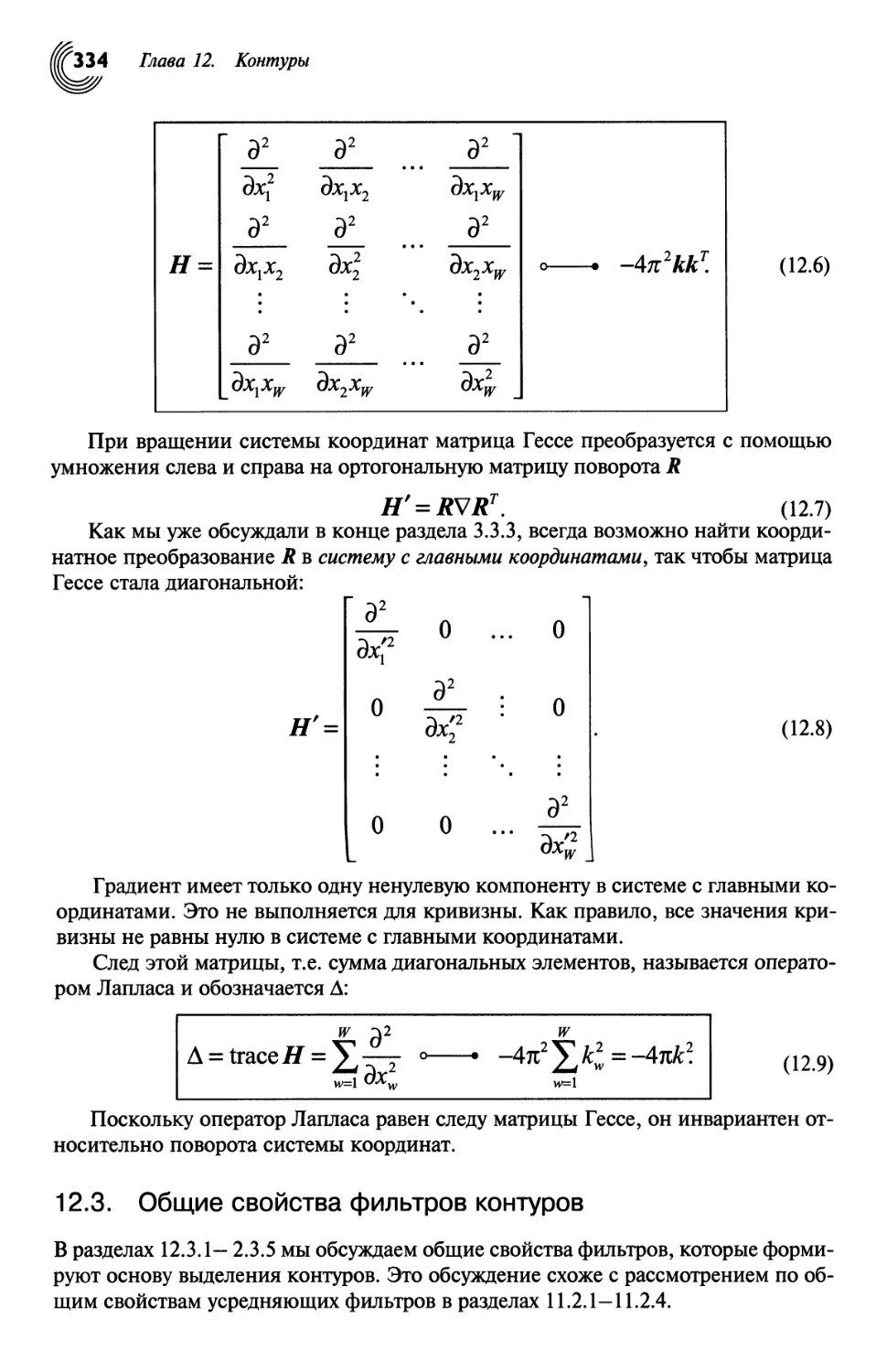
12.3. Общие свойства фильтров контуров 334
12.4. Определение контура по градиенту 337
12.5. Определение контура по переходу через нулевой уровень 344
12.6. Оптимизированное определение контуров 346
12.7. Регуляризованное определение контуров 348
12.8. Контуры в многоканальных изображениях 353
12.9. Упражнения 354
12.10. Дополнительная литература 356
ГЛАВА 13. ПРОСТЫЕ ОКРЕСТНОСТИ 357
13.1. Введение 357
13.2. Свойства простых окрестностей 358
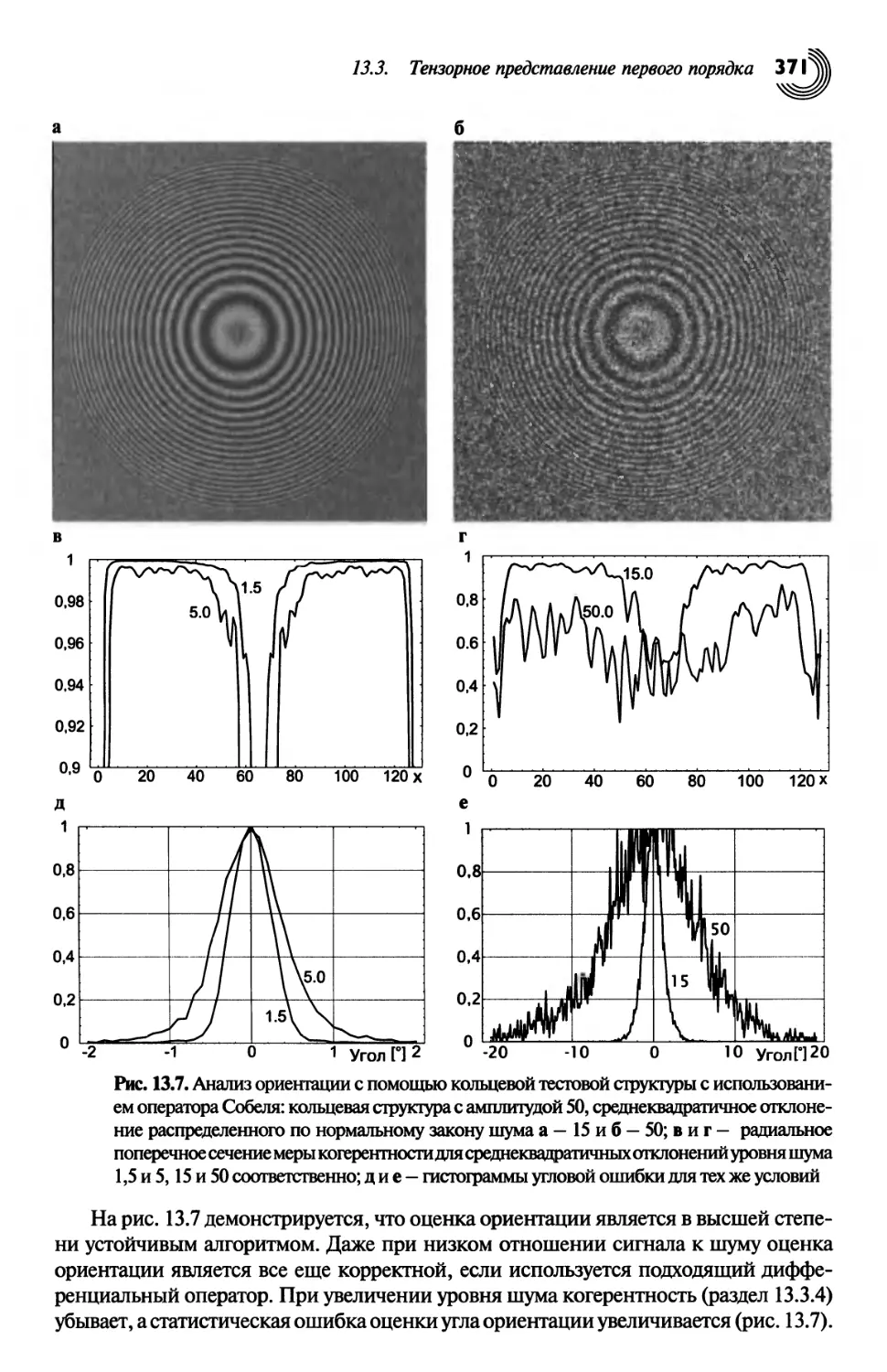
13.3. Тензорное представление первого порядка 362
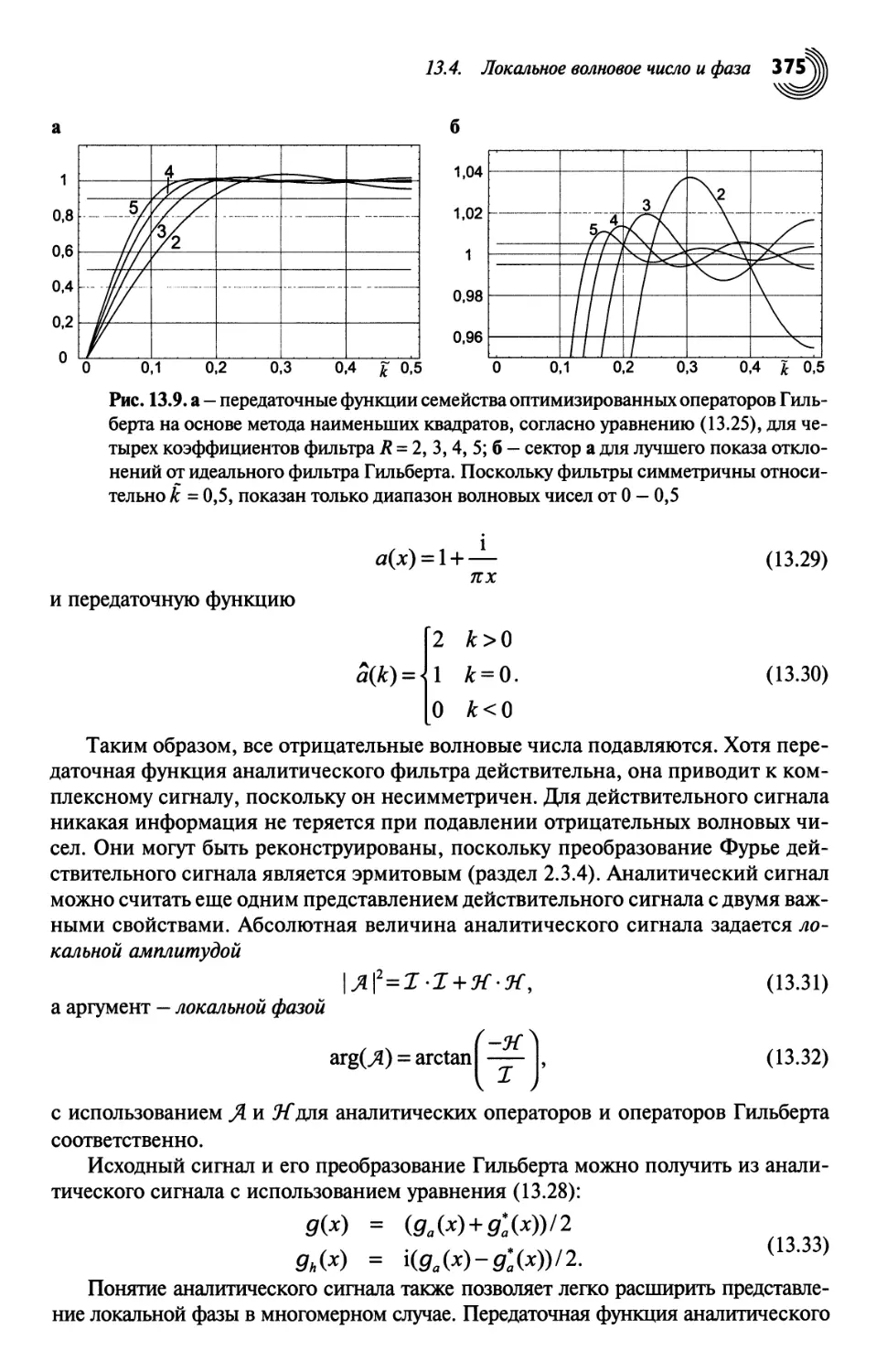
13.4. Локальное волновое число и фаза 372
13.5. Дополнительные тензорные представления 382
13.6. Упражнения 392
13.7. Дополнительная литература 394
ГЛАВА 14. ДВИЖЕНИЕ 395
14.1. Введение 395
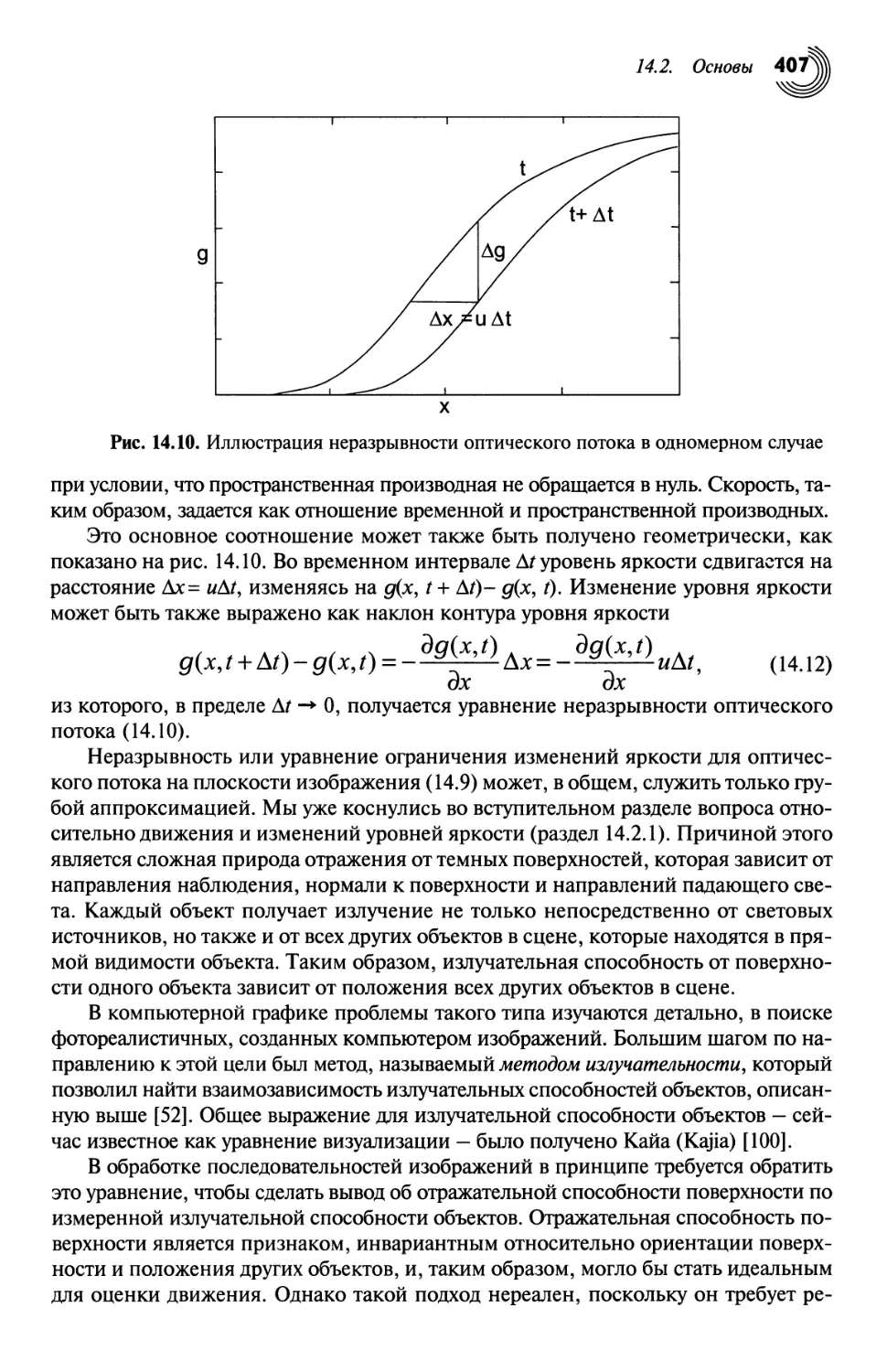
14.2. Основы 396
14.3. Дифференциальные методы первого порядка 410
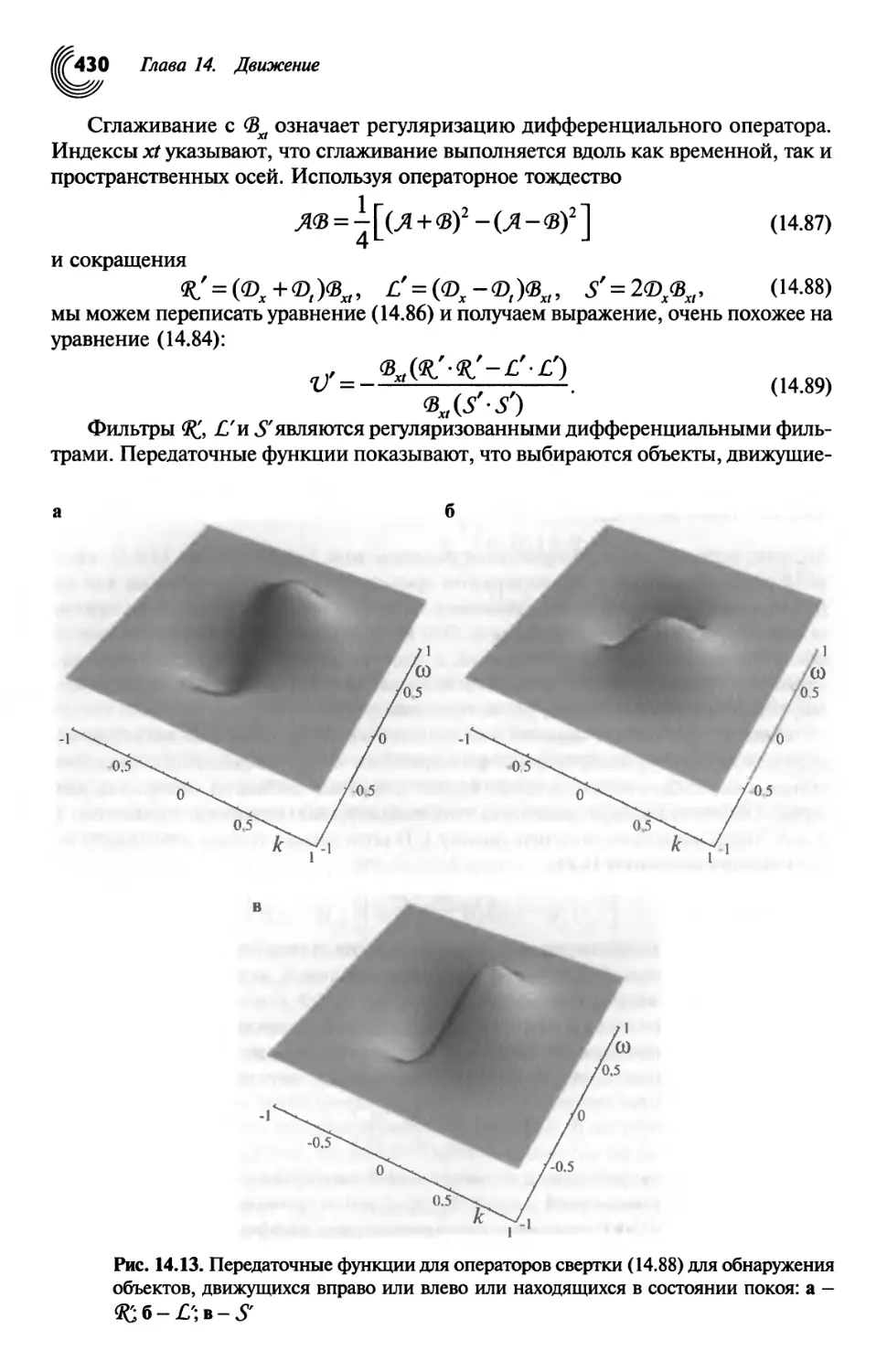
14.4. Тензорные методы 415
14.5. Корреляционные методы 420
14.6. Фазовый метод 423
14.7. Дополнительные методы 425
14.8. Упражнения 431
14.9. Дополнительная литература 432
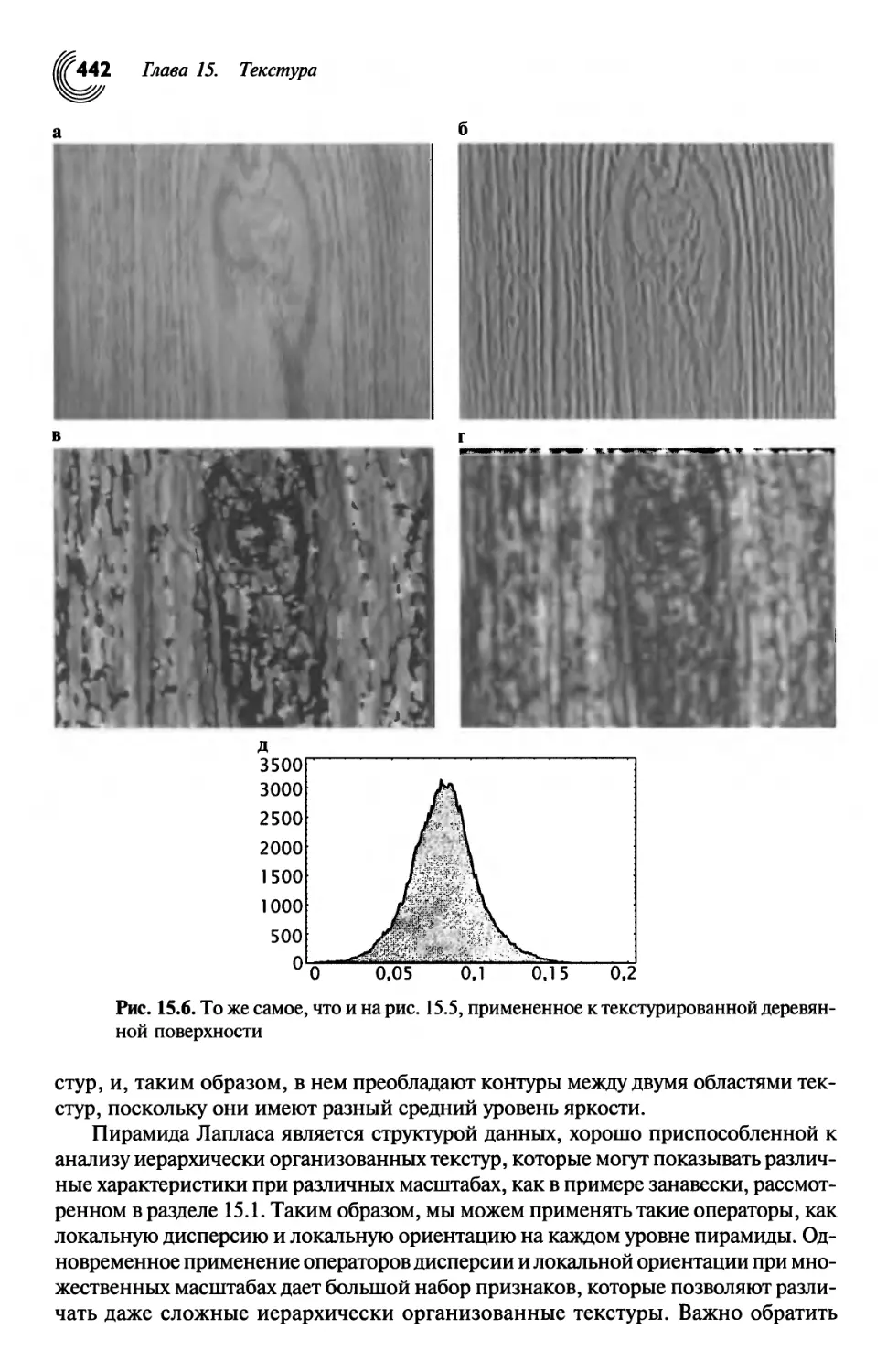
ГЛАВА 15. ТЕКСТУРА 433
15.1. Введение 433
15.2. Статистика первого порядка 436
15.3. Признаки текстуры, зависящие от поворота и масштаба 439
Содержание
15.4. Упражнения 443
15.5. Дополнительная литература 444
ЧАСТЬ 4. АНАЛИЗ ИЗОБРАЖЕНИЙ
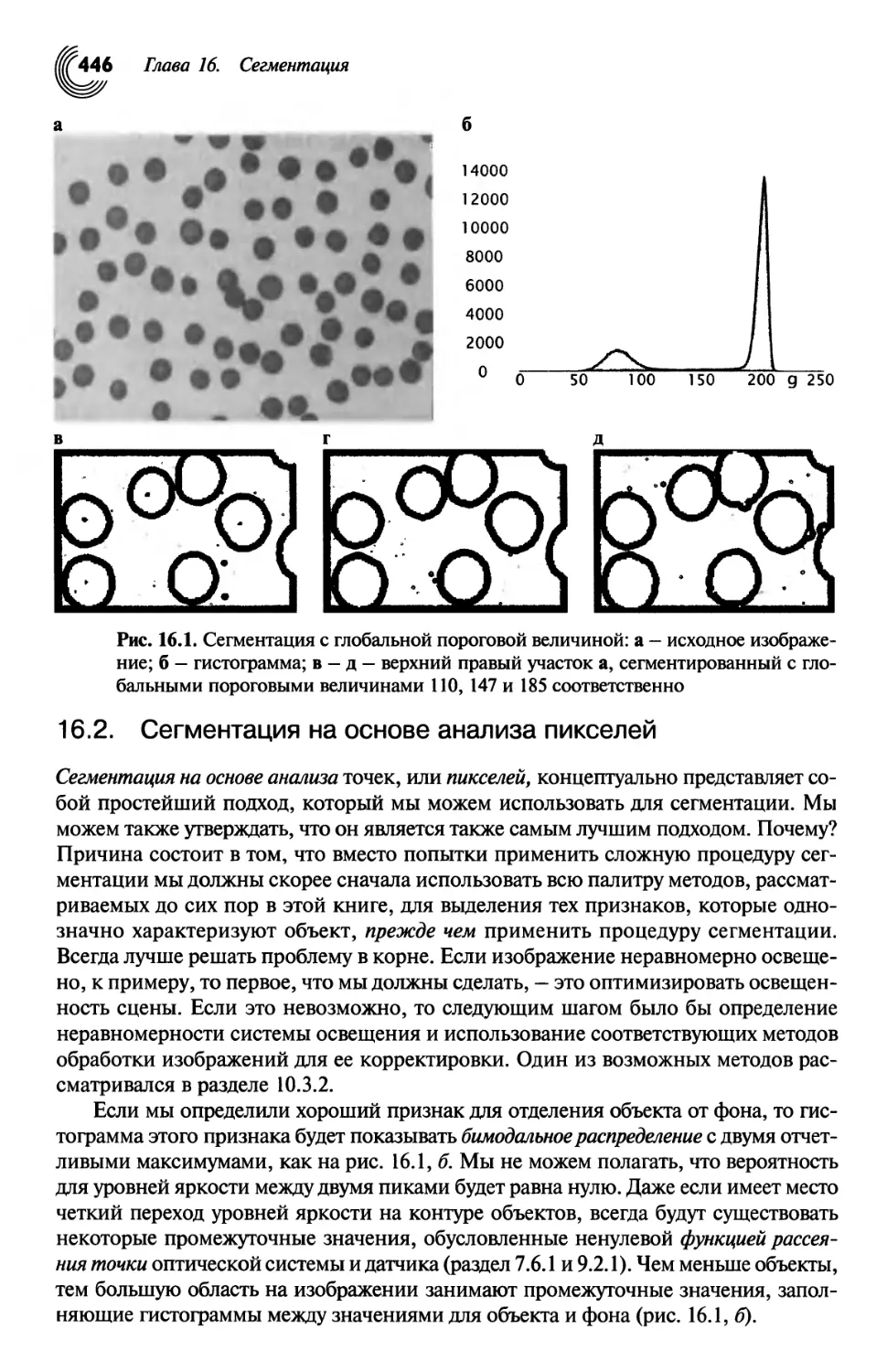
ГЛАВА 16. СЕГМЕНТАЦИЯ 445
16.1. Введение 445
16.2. Сегментация на основе анализа пикселей 446
16.3. Сегментация на основе анализа контуров 449
16.4. Сегментация на основе анализа областей 450
16.5. Сегментация на основе моделирования 454
16.6. Упражнения 457
16.7. Дополнительная литература 457
ГЛАВА 17. РЕГУЛЯРИЗАЦИЯ И МОДЕЛИРОВАНИЕ 458
17.1. Введение 458
17.2. Непрерывное моделирование I: вариационный подход 461
17.3. Непрерывное моделирование И: диффузия 469
17.4. Дискретное моделирование: обратные задачи 474
17.5. Обратная фильтрация 481
17.6. Дополнительные эквивалентные подходы 488
17.7. Упражнения 495
17.8. Дополнительная литература 496
ГЛАВА 18. МОРФОЛОГИЯ 497
18.1. Введение 497
18.2. Операции над соседними элементами на бинарных
изображениях 497
18.3. Общие свойства 499
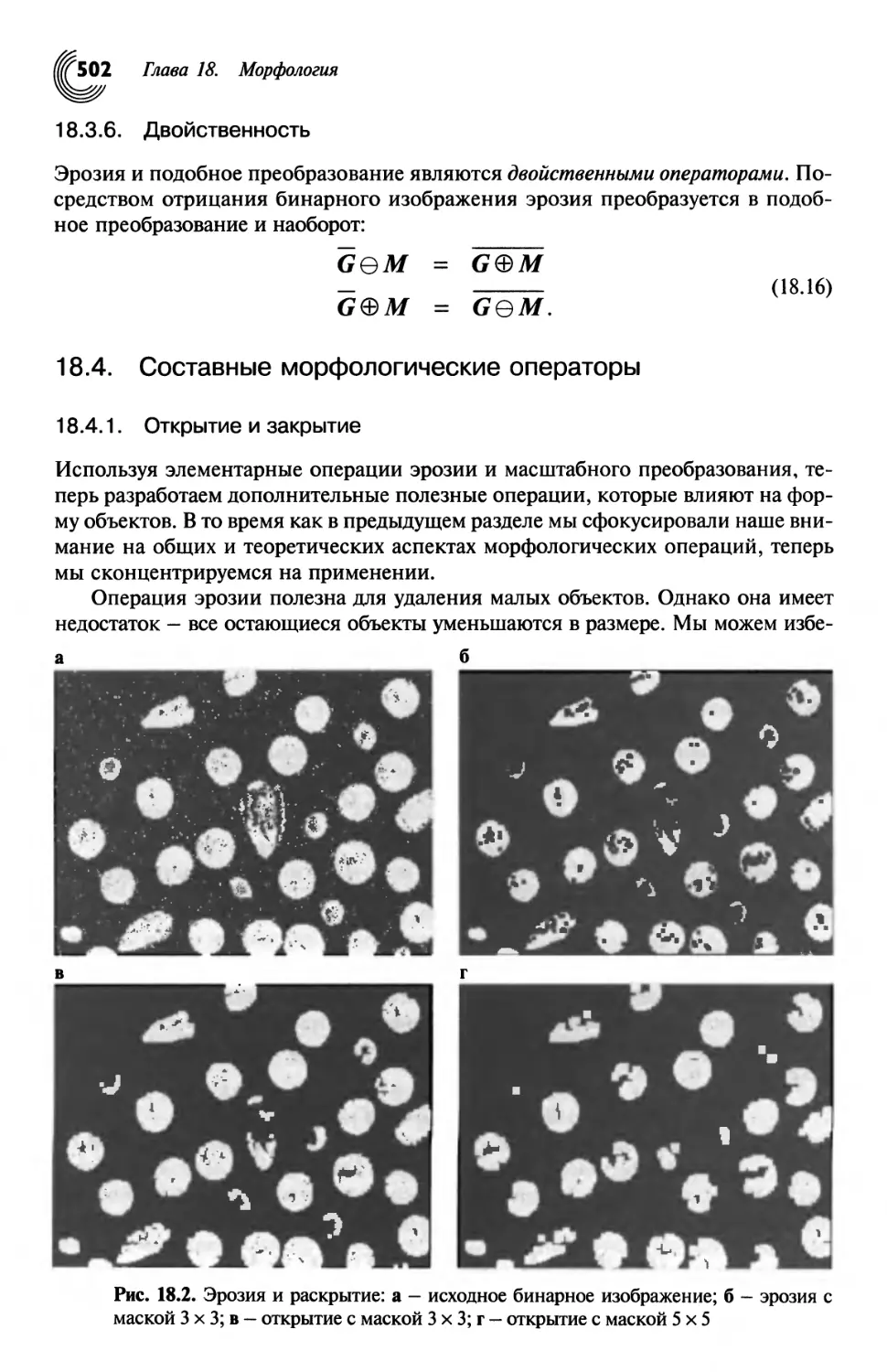
18.4. Составные морфологические операторы 502
18.5. Упражнения 508
18.6. Дополнительная литература 510
ГЛАВА 19. ПРЕДСТАВЛЕНИЕ И АНАЛИЗ ФОРМЫ 511
19.1. Введение 511
19.2. Представление формы 511
19.3. Признаки формы на основе анализа моментов 515
19.4. Фурье-дескрипторы 518
19.5. Параметры формы 523
19.6. Упражнения 525
19.7. Дополнительная литература .., 527
ГЛАВА 20. КЛАССИФИКАЦИЯ 528
20.1. Введение 528
20.2. Пространство признаков 531
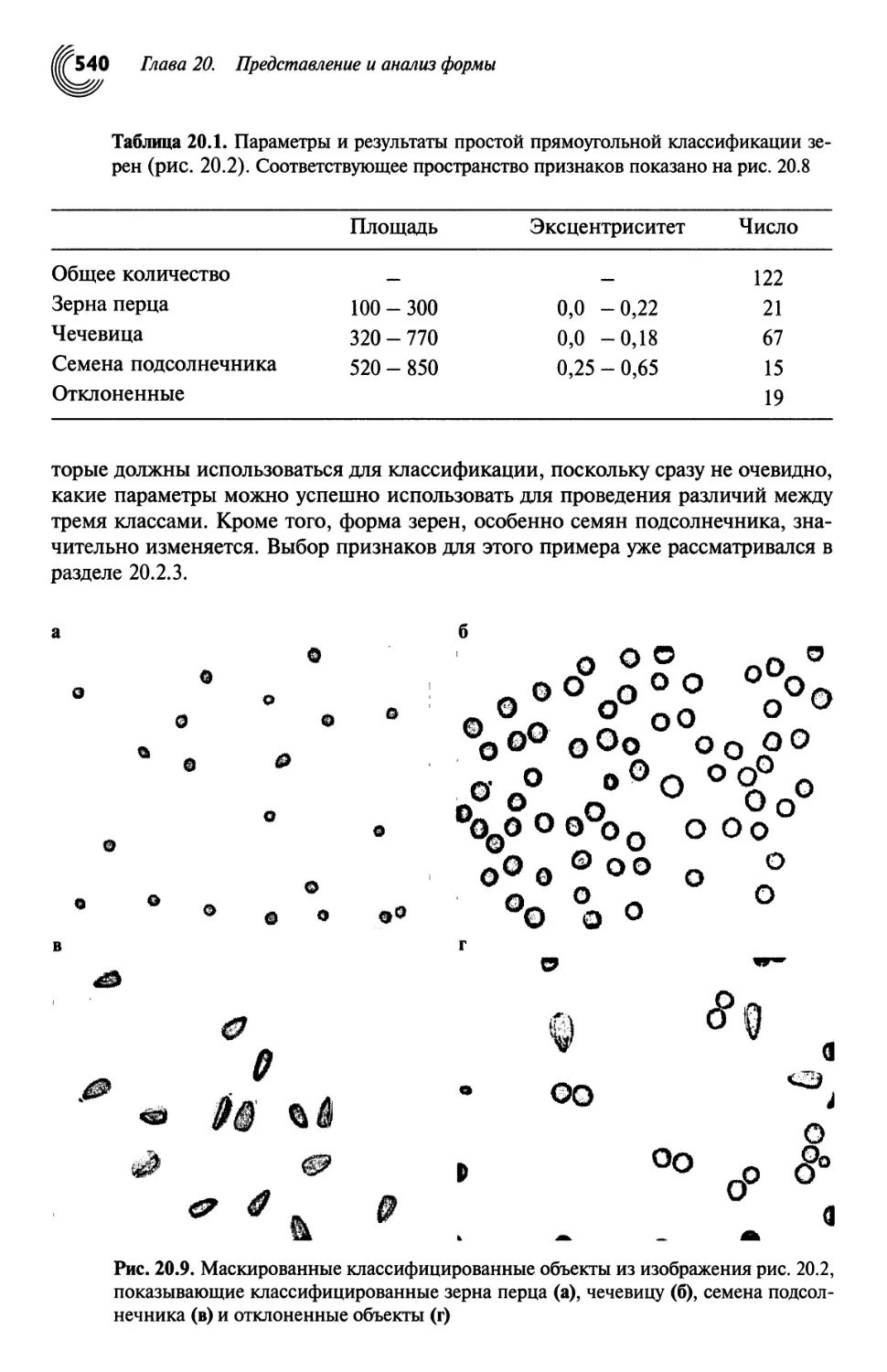
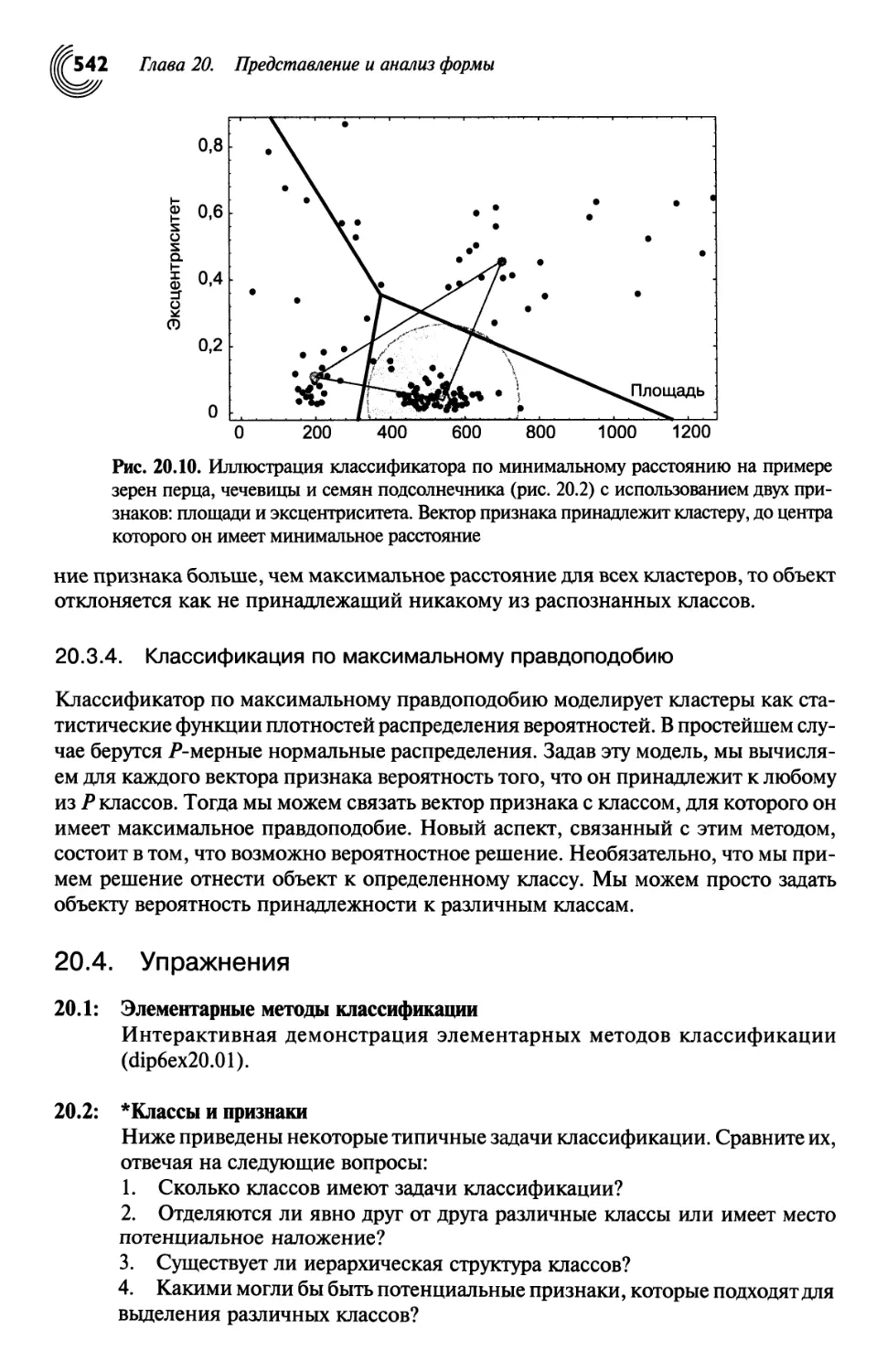
20.3. Простые методы классификации 537
20.4. Упражнения 542
20.5. Дополнительная литература 543
ЧАСТЬ 5 СПРАВОЧНАЯ ИНФОРМАЦИЯ
A. Ссылки 544
B. Обозначения 567
Библиография 575
ПРЕДИСЛОВИЕ
Шестое издание этого используемого во всем мире учебного пособия является
полностью исправленным и расширенным. По всему тексту вы встретите
многочисленные исправления, дополнения и обновления. Прежде всего, мне бы
хотелось обратить ваше внимание на два существенных изменения.
Во-первых, для того чтобы справиться с изучением постоянно развиваюш;ейся
области цифровой обработки изображений, весь текст данного учебного пособия
имеет четкое разделение на основной и дополнительный материалы. Наиболее
важные уравнения вьщелены рамкой. Дополнительные разделы расположены во
второй части каждой главы. Таким образом, вы можете, не пугаясь обилия
изложенного материала, сначала изучить основные принципы цифровой обработки
изображений. Впоследствии, выбрав наиболее интересующие вас темы, вы
можете расширить свои знания.
Вторым, наиболее существенным дополнением являются упражнения,
которые теперь включены в конец каждой главы. Эти упражнения помогут вам
оценить понимание материала, развить полученные навыки и дадут представление
о реальных задачах, связанных с обработкой изображений. Упражнения
помечены звездочками (от одной до трех), которые обозначают уровень их сложности.
Большое количество интерактивных упражнений на компьютере составляют
важную часть всех упражнений и охватьшают все рассмотренные в данном пособии темы.
Эти упражнения выполняются с использованием программного обеспечения,
предназначенного для обработки изображений, heurisko® (http://www.heurisko.de),
которое может быть найдено на прилагаемом к пособию компакт-диске. Таким
образом, вы можете самостоятельно практиковаться почти по всем темам и со всеми
алгоритмами, которые данная книга охватывает. Компакт-диск также содержит
большую коллекцию изображений, последовательностей образов и объемные
изображения, которые могут быть использованы при выполнении упражнений
на компьютере. Информацию о решении этих упражнений и о новых
упражнениях можно получить на домашней страничке автора http://www.bemd-jaehne.de.
Каждая глава заканчивается разделом «Дополнительная литература», в
котором заинтересованный читатель может найти дополнительные ссылки.
Приложение включает в себя две главы. Приложение А позволяет быстро обратиться к
часто используемому справочному материалу, а в приложении В приводится
детальный обзор используемых в данной книге обозначений. Полный текст книги
теперь доступен на прилагаемом компакт-диске. В текст включены гиперссылки,
что дает возможность гибкой работы с ним. Вы можете сразу же перейти из
оглавления в соответствующий раздел, от ссылок к библиографии, от предметного
указателя к соответствующей странице и к любой другой перекрестной ссылке.
Кроме того, возможно выполнение упражнений на компьютере прямо из
PDF-документа.
Я хотел бы выразить благодарность всем отдельным лицам и организациям,
которые предоставили визуальный материал для этой книги. Соответствующие
благодарности можно найти там, где данный материал используется. Мне
также хотелось бы выразить искреннюю благодарность персоналу издательства
Springer-Veriag за их постоянную заинтересованность в этой книге и за их
профессиональные рекомендации. Особенная благодарность моим друзьям из
Предисловие
AEON Verlag& Studio, Ганау, Германия. Создание этой книги и в особенности
прилагающегося компакт-диска было бы невозможным без их преданности и
профессиональных знаний.
И наконец, я приветствую любую конструктивную информацию от вас,
дорогие читатели. Я признателен за замечания по улучшению или дополнению и за
указания на ошибки, упущения или опечатки, которые, вопреки всем
приложенным усилиям, могли ускользнуть от внимания.
Гейдельберг, январь 2005 г. Бернд Яне
Из предисловия к пятому изданию
Как и четвертое, пятое издание является полностью исправленным и
расширенным. Весь материал теперь изложен в 20 главах вместо 16. Приблизительно треть
книги обозначена как дополнительный материал. Таким образом, вы можете
быстро и систематично изучить основной материал и впоследствии расширить свои
знания, обратившись к заинтересовавшим вас специальным темам.
Наиболее существенными дополнениями являются подробные обсуждения
случайных величин и случайных полей (глава 3), методов получения 3-D
изображений (глава 8) и подхода к получению регуляризованной параметрической
оценки, который объединяет методы, включающие обратные задачи, методы
адаптивных фишьтров, такие, как анизотропная диффузия, и вариационные подходы для
получения оптимальных решений при восстановлении, томографической
реконструкции, сегментации и определении движения изображений (глава 17). Каждая
глава теперь заканчивается разделом «Дополнительная литература», который
позволяет заинтересованному читателю получить дополнительные ссылки.
Полный текст книги теперь доступен на прилагаемом компакт-диске. В текст
включены гиперссылки, что дает возможность гибкой работы с ним. Вы можете
сразу же перейти из оглавления в соответствующий раздел, от ссылок к
библиографии, от предметного указателя к соответствующей странице и к любой другой
перекрестной ссылке.
Гейдельберг, ноябрь 2001 г. Бернд Яне
Из предисловия к четвертому изданию
В быстро развивающейся области, такой, как цифровая обработка изображений,
книга, первое издание которой появршось в 1991 году, потребовала полного
исправления только шесть лет спустя. Однако не изменилась проверенная
концепция, которая предлагает систематический подход к изучению цифровой
обработки изображений с использованием понятий и основных принципов, также
применяемых в других областях естествознания. Таким образом, читатель с
общими знаниями в естественной науке или инженерной дисциплине получает
быстрый доступ к сложному предмету обработки изображений. Книга охватывает
основы обработки изображений. Выбранные области изложены в деталях, чтобы
Предисловие
познакомить читателя с образом мышления при цифровой обработке
изображений и с некоторыми современными темами исследований. Где это возможно,
используются примеры и изображения для иллюстрации основных понятий.
Предполагается, что читатель знаком с элементарной матричной алгеброй и
преобразованиями Фурье.
Новое издание состоит из четырех частей. В части 1 рассмотрены основы,
необходимые для понимания процесса обработки изображений. Таким образом, это
издание не содержит математического приложения, как это было в предьщущих
изданиях. Часть 2, посвяш;енная получению и предварительной обработке
изображений, была расширена детальным рассмотрением формирования изображения.
Анализ движения включен в часть 3 как компонент вьщеления признаков.
Определение объектов, анализ формы объектов и классификация объектов
объединены в части 4, посвященной анализу изображений.
В целом эта книга не ограничивается рассмотрением обработки 2-D
изображений. Где возможно, темы изложены таким образом, что применимы и для
изображений более высокой размерности (объемные изображения,
последовательности изображений). Подобным образом цветные изображения рассматриваются как
частный случай многоканальных изображений.
Гейдельберг, май 1997 г. Бернд Яне
Из предисловия к первому изданию
Цифровая обработка изображений является захватывающей темой с некоторых
точек зрения. Человек воспринимает большую часть информации об окружающей
среде через зрение. В то время как в течение долгого периода изображения можно
было получить только с помощью фотографии, сейчас мы находимся на рубеже
другой технической революции, которая позволяет получать, обрабатывать и
оценивать изображения с помощью компьютера. Компьютеры развиваются
поразительными темпами, становясь более мощными и в то же время менее
дорогостоящими, так что цифровая обработка изображений получает все более широкое
распространение. Таким образом, обработка изображений становится
обязательным инструментом при анализе изображений во всех областях естествознания. Для
все большего числа ученых обработка изображений будет становиться ключевой
при изучении сложных научных проблем, за которые они и не мечтали взяться
каких-то там несколько лет назад. Открывается дверь для новых
междисциплинарных взаимодействий, объединяющих компьютерные науки с
соответствующими областями исследований.
Многие студенты, инженеры и исследователи во всех областях естественных
наук сталкиваются с необходимостью знать больше о процессе цифровой
обработки изображений. Данная книга предназначена именно для этой цели. Автор,
сам получивший образование в области физики, описывает цифровую обработку
изображений как новый инструмент в научных исследованиях. Книга начинается
с основ обработки изображений и приходит, в выбранных областях, к последним
достижениям. Такой подход дает возможность понять, как в действительности
происходит обработка изображения. При выборе материала следует руководство-
Предисловие
ваться потребностями исследователя, который хочет использовать методы
обработки изображений в своей области. Таким образом, цель данной книги -
попытаться предложить полный обзор обработки изображений от получения
изображения до вьщеления интересующих данных. Многие понятия и математические
инструменты, широко применяющиеся в естественных науках, используются
также и при цифровой обработке изображений. На подобные аналогии обращается
внимание, поскольку они позволяют читателям с общими знаниями в
естественных науках легко подойти ко многим сложным задачам в области цифровой
обработки изображений. Рассмотрение основных понятий дополняется примерами
применения в системах обработки изображений на базе ПК и готовых к
использованию реализаций важных алгоритмов.
Я очень обязан многим отдельным лицам, которые помогли мне в написании
этой книги. Я покажу это, проследив ее историю. В начале 1980-х годов, когда я
работал над физикой мелкомасштабного взаимодействия атмосферы с океаном в
институте физики окружающей среды в Университете Гейдельберга, стало
очевидным, что адекватное рассмотрение таких сложных явлений невозможно с
помощью точечных измерительных зондов. В результате было разработано несколько
методов расширенного измерения области. Тогда я начал искать коллег, имеющих
опыт цифровой обработки изображений, и методы получения физически
значимых данных из изображений. Первые контакты были установлены с Институтом
прикладной физики в Университете Гейдельберга и Немецким раковым
исследовательским центром в Гейдельберге. Я хотел бы искренне поблагодарить
профессора Билле, доктора Денглера и доктора Шмидта за неоднократные,
проливающие свет на многие вещи беседы и их сотрудничество.
Я хотел бы также поблагодарить профессора К.О. Мюниха, директора
Института физики окружающей среды. С самого начала он был готов прислушаться и
рассмотреть новые идеи по применению методов цифровой обработки
изображений в области физики окружающей среды. Благодаря его дальновидности и
существенной поддержке исследовательская группа «Цифровая обработка
изображений в физике окружающей среды» смогла плодотворно вести разработки в его
институте. Многие примеры, приведенные в этой книге, взяты из моих
исследований в Университете Гейдельберга и в Океанографическом институте им. Скрип-
пса. Я искренне благодарен за финансовую поддержку этих исследований от
Немецкого научного фонда. Европейского сообщества. Национального научного
фонда США и Министерства морских исследований США.
Гейдельберг, весна 1991 г. Бернд Яне
ЧАСТЫ
ОСНОВЫ
ГЛАВА 1
ОБЛАСТИ ПРИМЕНЕНИЯ
И ИНСТРУМЕНТАРИЙ
1.1. Инструмент в науке и технологии
с момента зарождения науки визуальное наблюдение играет главную роль. В то
время документально зафиксировать результаты эксперимента можно было лишь
с помощью устного описания и рисунков, сделанных вручную. Следующим
важным шагом стало изобретение фотографии, которое позволило документировать
результаты объективно. Тремя хорошо известными примерами научного
применения фотографии являются астрономия, фотограмметрия и физика частиц.
Астрономы получили возможность измерять положения и размеры звезд, а фотограм-
метристы создавать топографические карты по изображениям, полученным с воздуха.
Исследование бесчисленного количества изображений, полученных в водородных
пузырьковых камерах, привело к открытию многих элементарных частиц в
физике, но проводимые вручную процедуры оценки требовали больших затрат
времени. Были разработаны некоторые полу- или даже полностью автоматизированные
оптомеханические устройства, однако они были предназначены для конкретных
задач. По этой причине количественная оценка изображений не получила
широкого применения. Как правило, изображения использовались только для
документирования, качественного описания и иллюстрации наблюдаемых явлений.
Сегодня мы находимся на рубеже научной революции, возникшей благодаря
быстрому прогрессу в видео- и компьютерной технологиях. Персональные
компьютеры и рабочие станции стали достаточно мощными для обработки данных в виде
изображений. В результате мультимедийные аппаратные средства и программное
обеспечение успешно используются для обработки изображений,
последовательностей изображений и даже 3-D визуализации. Эта технология сейчас доступна
любому ученому или инженеру. И как следствие обработка изображений
развилась и продолжает дальше быстро развиваться из нескольких
специализированных методик в стандартный научный инструмент. Стандартные методы обработки
изображений теперь применяются практически во всех естественных науках и
технических дисциплинах.
Простой пример очевидно демонстрирует значение визуальной информации.
Представьте, что вы получили задание написать статью о новой технической
системе, к примеру, о новом типе солнечной электростанции. Описание этой
системы могло бы потребовать гигантских усилий, если бы вы не имели
возможности включить изображения и технические чертежи. Читатель же вашей
неиллюстрированной статьи испытал бы чувство досады. Он или она потратили
бы много времени, пытаясь понять, как новая солнечная электростанция
работает, и, в конце концов, пришли бы только к бледному представлению о том, как
она выглядит.
Глава L Области применения и инструментарий
Технические чертежи и фотографии солнечной электростанции могли бы
послужить неоценимой помощью для читателей вашей статьи. Они могли бы немедленно
представить эту станцию и смогли бы изучить на изображениях детали, которые не
были описаны в тексте, но которые привлекли бы их внимание. Картинки дают
гораздо больше информации — факт, который может бьпъ точно описан следующим
выражением: «картинка лучше тысячи слов» («а picture is worth а thousand words»).
Еще одно наблюдение представляет интерес. Если бы читатель позднее
услышал о новой солнечной электростанции, он или она смогли бы легко вспомнить,
как она выглядит, причем объект «солнечная электростанция» сразу же был бы
связан с изображением.
1.2. Примеры применения
в этом разделе рассматриваются примеры научного и технического применения
цифровой обработки изображений. Примеры иллюстрируют, что обработка
изображений позволяет исследовать сложные явления, которые не могли бы адекватно
оцениваться с помощью стандартных методов измерения.
1.2.1. Подсчет и измерение
Классической задачей цифровой обработки изображений является подсчет частиц и
измерение их распределения по размерам. На рис. 1.1 показаны три примера с очень
разными частицами: появляющееся под водой при разрушении волн пузырьки газа,
мыльные пузырьки и пигментные частрщы. Первой проблемой, возникающей в такого рода
задачах, является подбор соответствующей установки для освещения и формирования
изображений. Изображения пузырьков на рис. 1.1, й получены с помощью системы
телецентрического освещения и формирования изображершй. В этой установке главные
лучи направлены параллельно оптической оси. Следовательно, размер изображаемых
пузырьков не зависит от расстояния до них. Выборочный объем для измерений
концентраций определяется путем оценивания степени размытости в пузырьках.
Гораздо труднее измерить форму мыльных пузырьков, изображенных на
рис. 1.1,5, поскольку они прозрачны. Следовательно, пузырьки, расположенные
более глубоко, накладываются на изображения пузырьков на переднем слое.
Кроме того, пузырьки имеют отклонения от круглой формы, так что необходимо
определить подходящие параметры для описания их формы.
Еще один пример — измерение распределения по размерам цветных
пигментных частиц. Это распределение оказывает значительное влияние на качество и
свойства краски. Таким образом, измерение распределения является важной задачей
контроля качества. Изображение на рис. 1.1, в, полученное с помощью трансмиссионного
электронного микроскопа, иллюстрирует проблему, связанную с этой задачей
обработки изображений. Частицы имеют тенденцию собираться в группы.
Следовательно, необходимо распознать эти группы и, если возможно, разделить их, для
того чтобы не вызвать отклонений в определении распределения по размерам.
Почти каждый продукт, который мы используем сегодня, проверен на
наличие дефектов с помощью автоматической системы визуального контроля. Один из
классов задач включает проверку правильности размеров и положений.
Некоторые примеры таких изображений приведены на рис. 1.2. Здесь проверяются поло-
1.2. Примеры применения
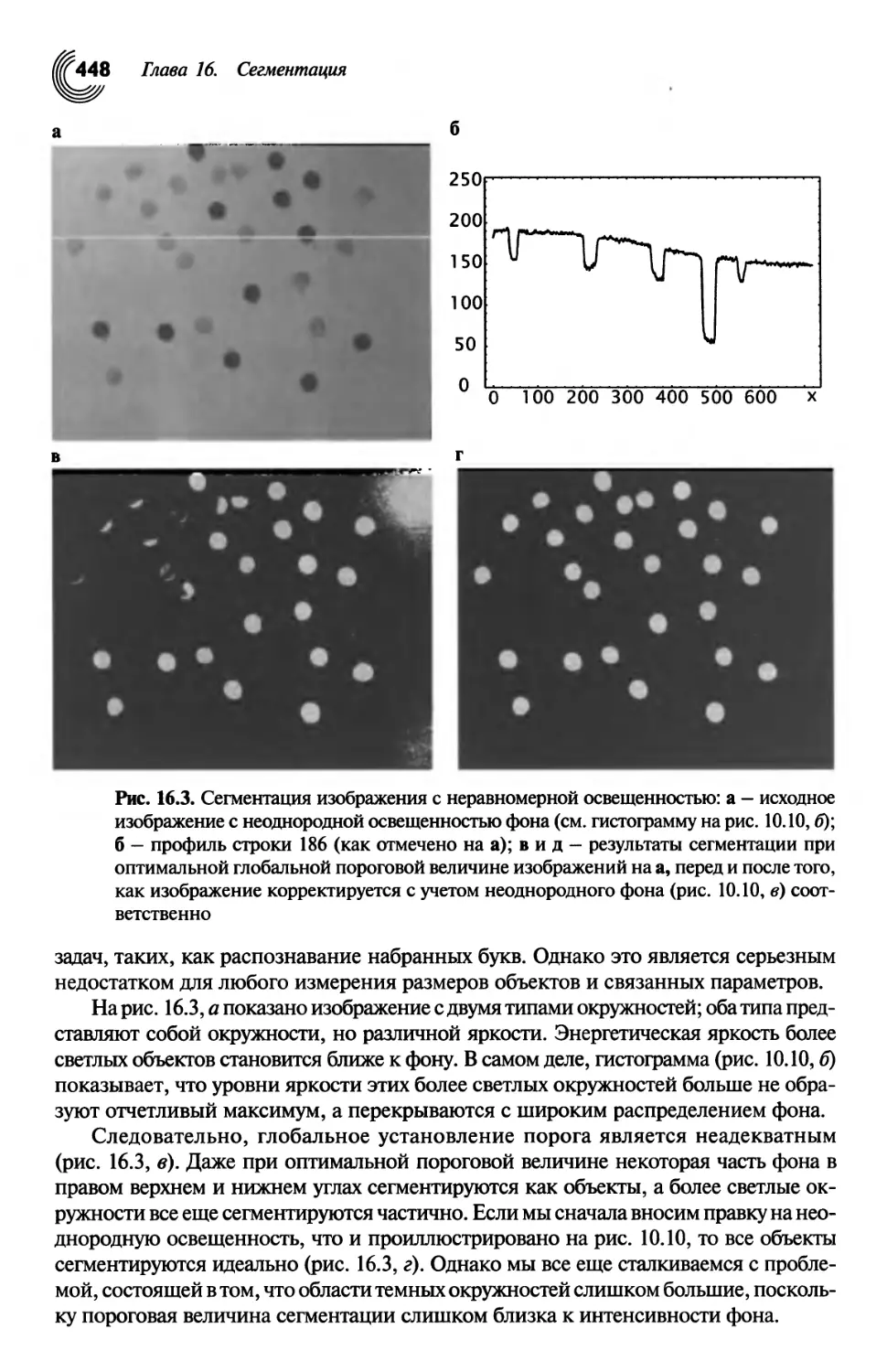
Рис. 1.1. Измерение частиц методами формирования изображений, а -
появляющиеся под водой при разрушении волн пузырьки сняты с использованием системы
телецентрического освещения и формирования изображений (Гайслер (GeiBler) и Яне
(Jahne) [57]); б - мыльные пузырьки; в - электронная микроскопия цветных
пигментных частиц (иллюстрации предоставлены доктором Клее (Dr. Юее), Хёхст
(Hoechst AG), Франкфурт)
У^'
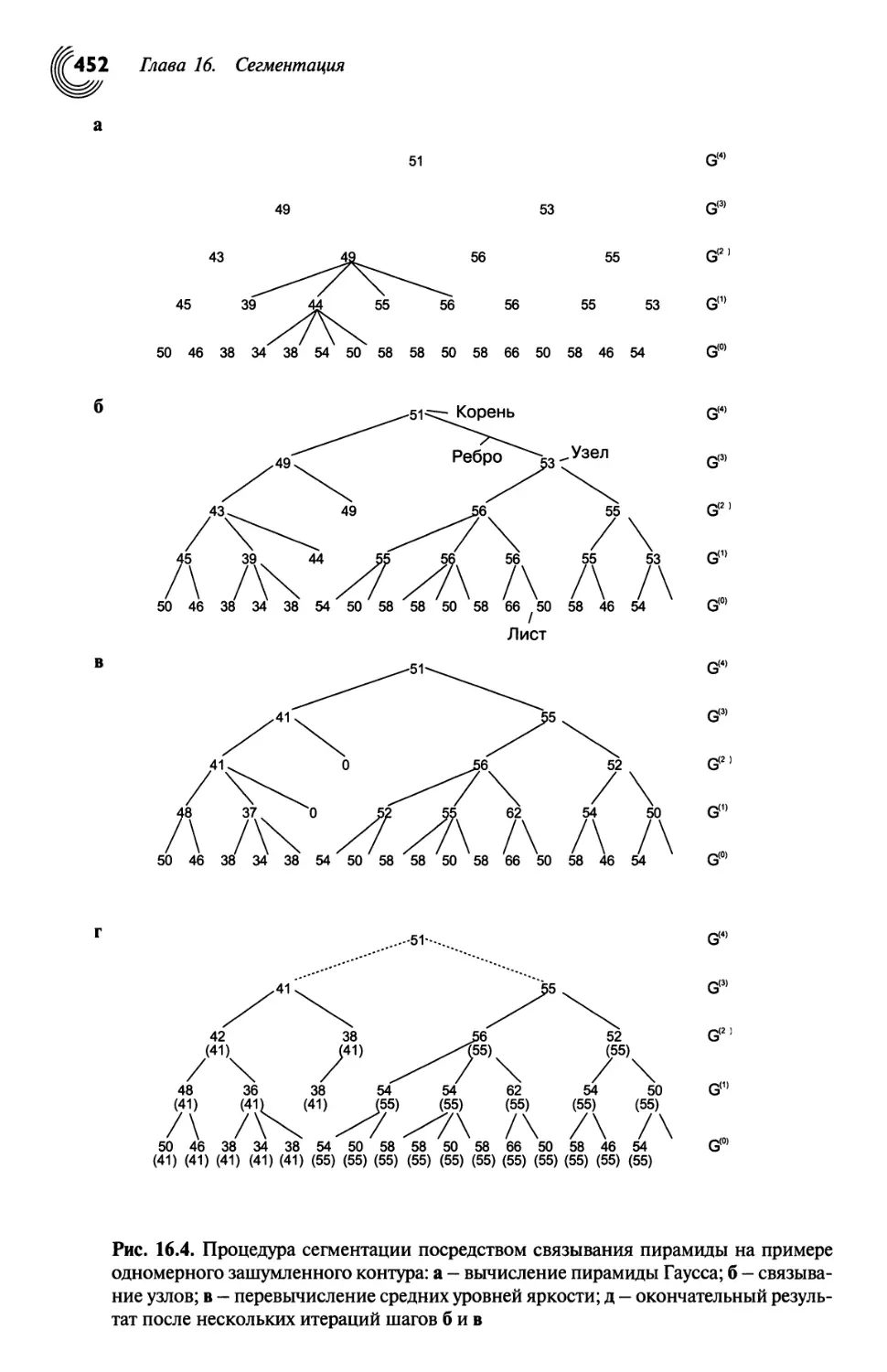
Рис. 1.2. Промышленные детали, которые проверяются с помощью системы
визуального контроля на правильность положения и диаметра отверстий. Иллюстрации
предоставлены Мартином фон Броке (Martin von Brocke), Робертом Бошем (Robert
Bosch), (GmbH).
жение, диаметр и округлость отверстий. Рис. 1.2, в показывает, что освещение
металлических деталей является непростой задачей. Контур отверстия слева
является частично светлым, и, таким образом, задача правильного определения и
измерения отверстий становится более сложной.
иГ 18 Глава 1. Области применения и инструментарий
б
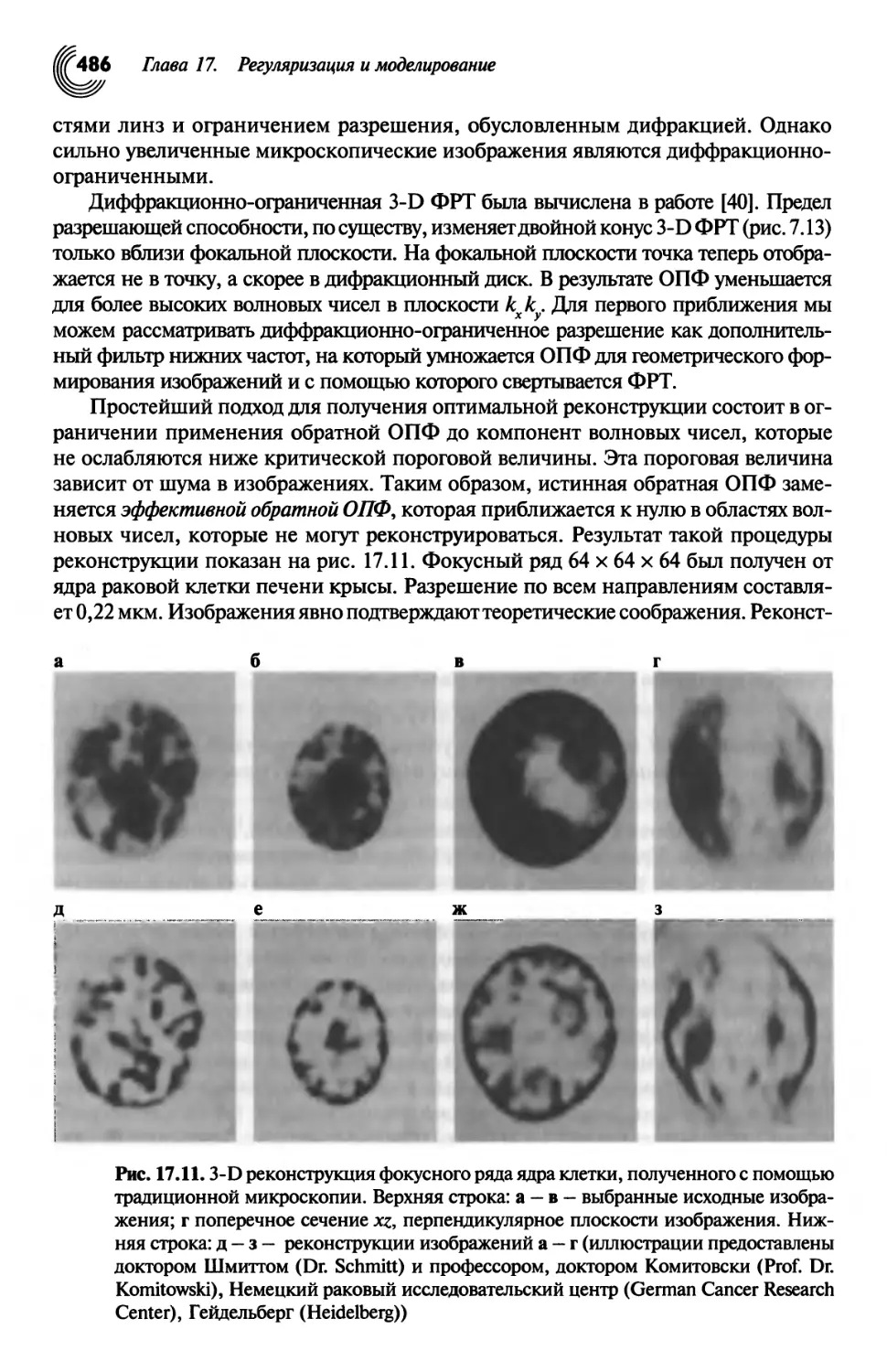
Рис. 1.3. Фокусная последовательность пресс-формы из полиметилметакрилата
(ПММА) с узкими прямоугольными отверстиями, полученная с помощью
конфокального метода, использующего статистически распределенные диаграммы ин-
тенсивностей. Изображения сфокусированы на следующих глубинах, измеряемых
от дна отверстий: а — 16 мкм; б — 480 мкм; в — 620 мкм (поверхность формы); г —
3-D реконструкция (иллюстрации предоставлены Шоерманном и др. (Scheuermann
etal.)[178])
1.2.2. Исследование 3-D пространства
В изображениях 3-D сцены проектируются на 2-D плоскость изображения. Таким
образом, глубинная информация теряется, и для восстановления топографии
поверхностей или объемных изображений требуются специальные методы
формирования изображений. В последние годы было разработано большое количество
разнообразных методов формирования дальностных и объемных изображений.
Поэтому методы обработки изображений также применяются к картам глубин и
объемным изображениям.
На рис. 1.3 показан процесс реконструкции пресс-формы для микроструктур,
изображения которой были получены с помощью специального типа
конфокального микроскопа [178]. Форма изготовлена из полиметилметакрилата (ПММА),
полупрозрачного пластмассового материала с гладкой поверхностью, так что она
является почти невидимой в стандартной микроскопии. Форма имеет узкие,
глубиной в 500 мкм прямоугольные отверстия.
1.2. Примеры применения
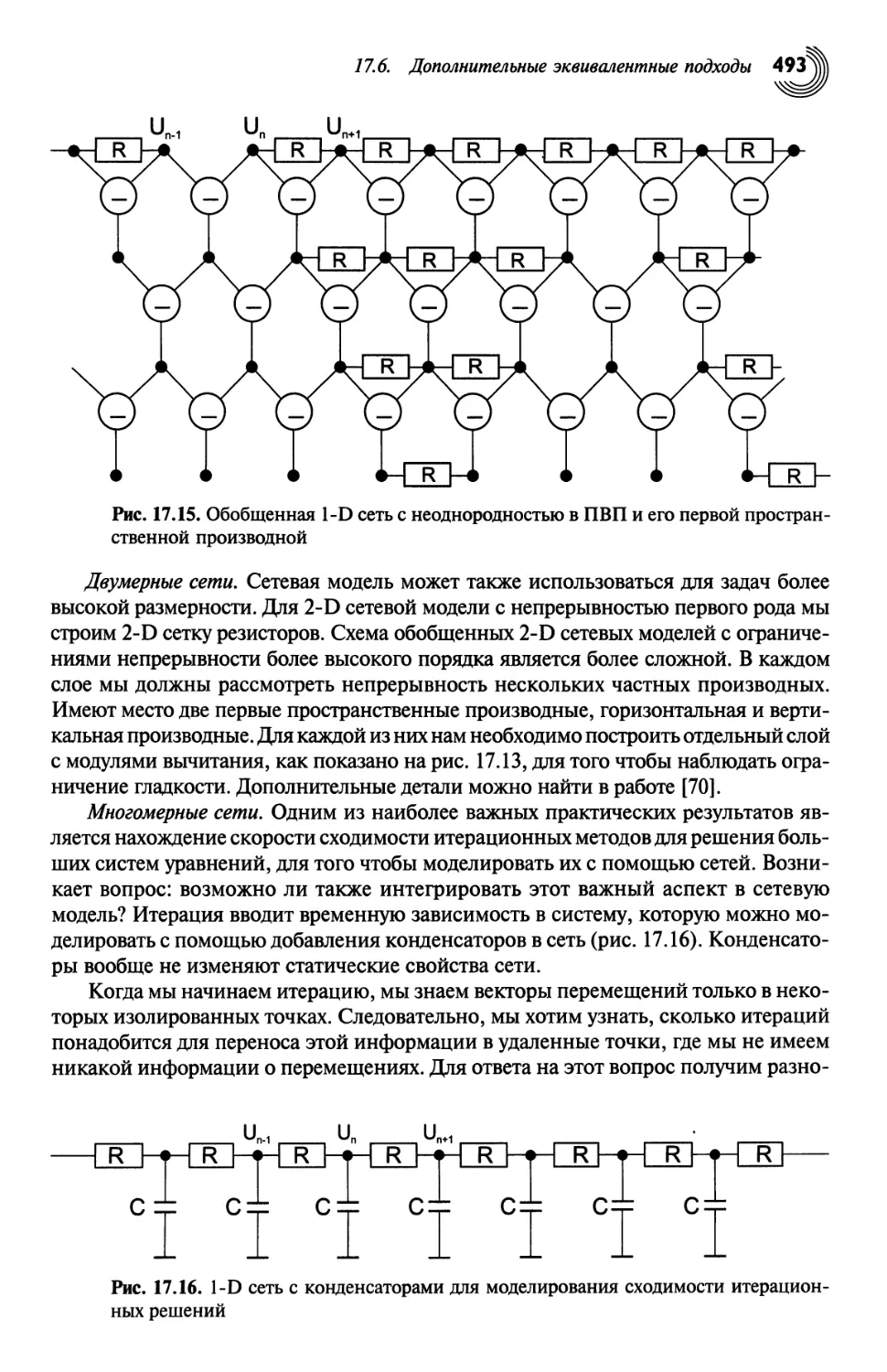
Рис. 1.4. Карта глубин листа растения, измеренная с помощью оптической
когерентной томографии. Иллюстрации предоставлены Йохеном Рестле (Jochen Restle),
Робертом Бошем (Robert Bosch), (GmbH).
Для того чтобы сделать прозрачный материал видимым, статически
распределенная диаграмма проецируется через оптику микроскопа на фокальную плоскость.
Эта диаграмма проявляется четкой только на частях, которые лежат в фокальной
плоскости. Диафамма становится более расплывчатой с увеличением расстояния
от фокальной плоскости. В фокусной последовательности, показанной на рис. 1.3,
можно видеть, что сначала диаграммы материала на дне отверстий становятся
четкими (рис. 1.3, а), а после того, как мы отодвигаем объект от оптики, последнее
изображение фокусируется на поверхности формы (рис. 1.3, в). Глубину
поверхности можно реконструировать с помощью поиска максимальной контрастности
для каждого пикселя в фокусной последовательности (рис. 1.3, г).
На рис. 1.4 показана карта глубин листа растения, изображение которого было
получено с помощью другого современного оптического метода — 3-D измерения,
известного как интерферометрия белого света или когерентная радиолокация. Этот
метод является интерферометрическим методом, который использует свет с
длиной когерентности всего лишь в несколько длин волн.
Таким образом, интерференционные картины возникают только при очень
коротких разностях хода в интерферометре. Этот эффект может использоваться для
измерения расстояний с точностью порядка длины волны используемого света.
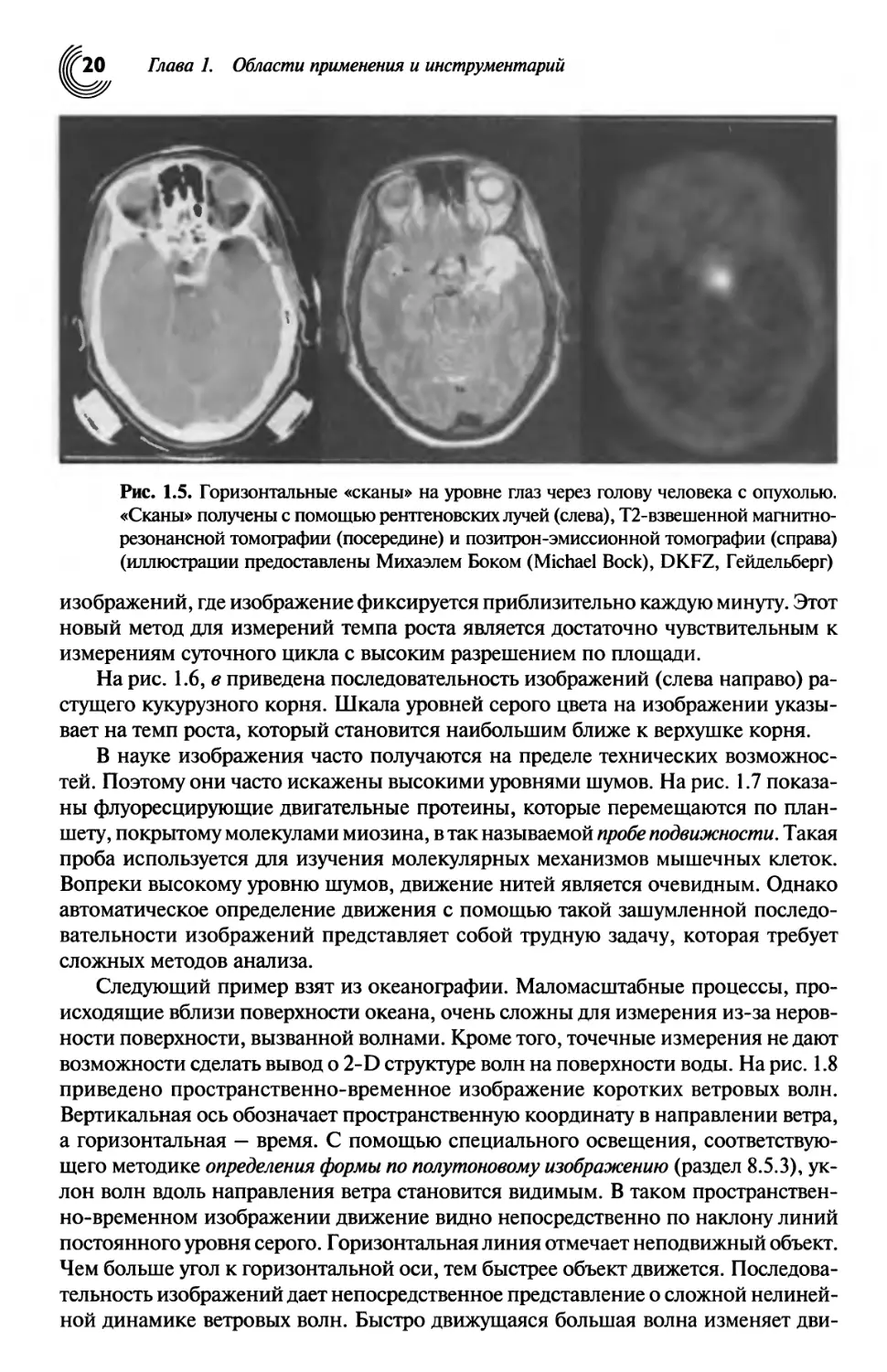
Медицинские исследования являются движущей силой в разработке
современных методов получения объемных изображений, которые позволяют заглянуть
внутрь 3-D объектов. На рис. 1.5 показан «скан» головы человека. Тогда как
рентгеновские лучи (компьютерная томография, КТ) преимущественно изображают
костные структуры, Т2-взвешенная магнитнорезонансная томография (МРТ)
показывает мягкие ткани, глаза и рубцовые ткани при высокой интенсивности сигнала.
При позитрон-эмиссионной томографии (ПЭТ) высокая интенсивность сигнала
наблюдается в местах нахождения опухоли, поскольку здесь аккумулируется
управляемое позитронное излучение.
1.2.3. Исследование динамических процессов
Исследование динамических процессов становится возможным с помощью
анализа последовательностей изображений. Гигантские возможности этого метода
проиллюстрированы несколькими примерами в этом разделе.
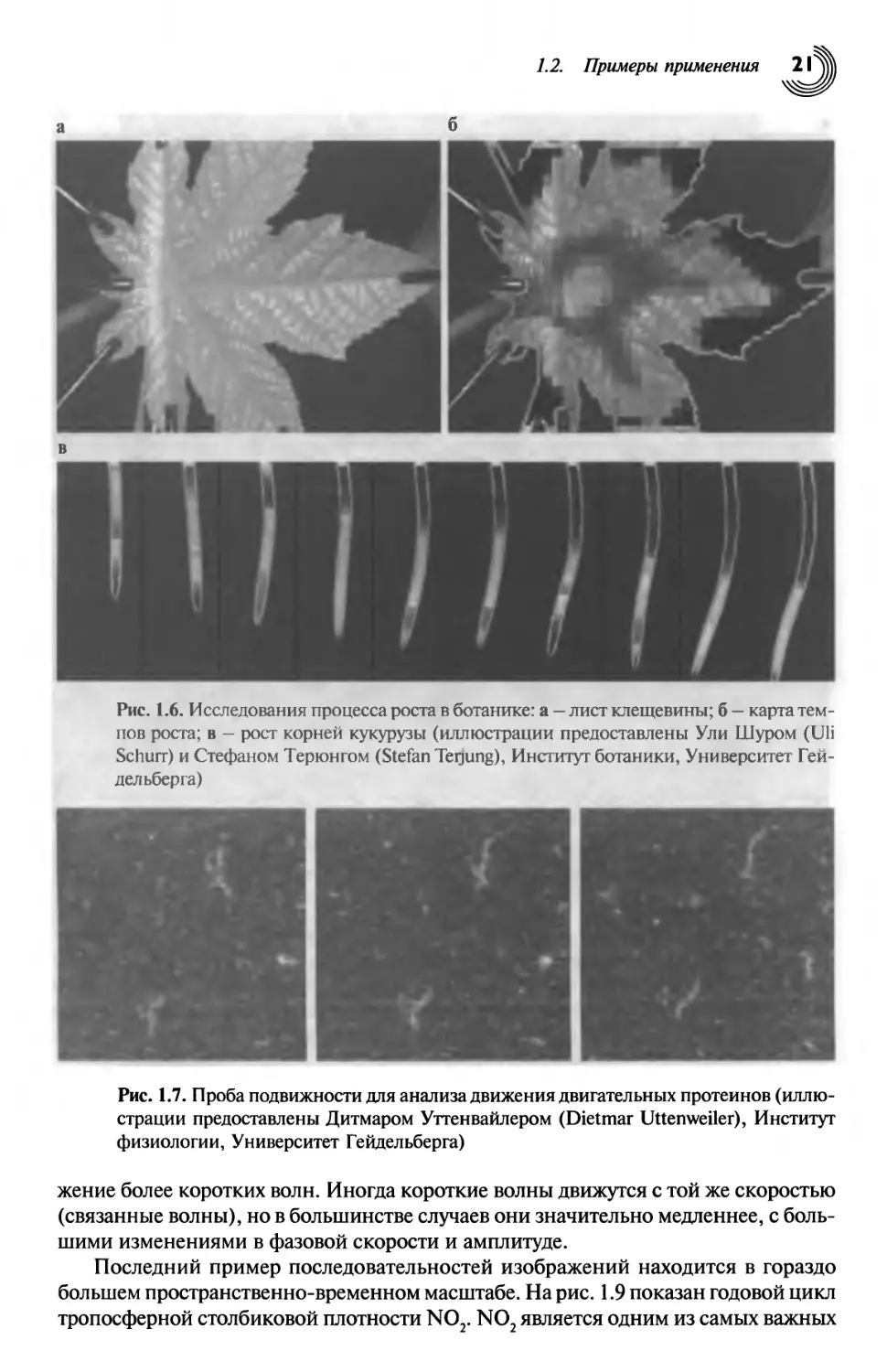
В ботанике центральной темой является изучение роста растений и механизмов,
контролирующих процессы роста. На рис. 1.6, а показан лист клещевины (Rizinus
plant leaf), для которого была составлена карта темпа роста (процентное увеличение
площади в единицу времени) с помощью цейтраферной последовательности
Глава 1. Области применения и инструментарий
Рис. 1.5. Горизонтальные «сканы» на уровне глаз через голову человека с опухолью.
«Сканы» получены с помощью рентгеновских лучей (слева), Т2-взвешенной магнитно-
резонансной томографии (посередине) и позитрон-эмиссионной томофафии (справа)
(иллюстрации предоставлены Михаэлем Боком (Michael Воск), DKFZ, Гейдельберг)
изображений, где изображение фиксируется приблизительно каждую минуту. Этот
новый метод для измерений темпа роста является достаточно чувствительным к
измерениям суточного цикла с высоким разрешением по площади.
На рис. 1.6, в приведена последовательность изображений (слева направо)
растущего кукурузного корня. Шкала уровней серого цвета на изображении
указывает на темп роста, который становится наибольшим ближе к верхушке корня.
В науке изображения часто получаются на пределе технических
возможностей. Поэтому они часто искажены высокими уровнями шумов. На рис. 1.7
показаны флуоресцирующие двигательные протеины, которые перемещаются по
планшету, покрытому молекулами миозина, в так называемой пробе подвижности. Такая
проба используется для изучения молекулярных механизмов мышечных клеток.
Вопреки высокому уровню шгумов, движение нитей является очевидным. Однако
автоматическое определение движения с помощью такой зашумленной
последовательности изображений представляет собой трудную задачу, которая требует
сложных методов анализа.
Следующий пример взят из океанографии. Маломасштабные процессы,
происходящие вблизи поверхности океана, очень сложны для измерения из-за
неровности поверхности, вызванной волнами. Кроме того, точечные измерения не дают
возможности сделать вывод о 2-D структуре волн на поверхности воды. На рис. 1.8
приведено пространственно-временное изображение коротких ветровых волн.
Вертикальная ось обозначает пространственную координату в направлении ветра,
а горизонтальная — время. С помощью специального освещения,
соответствующего методике определения формы по полутоновому изображению (раздел 8.5.3),
уклон волн вдоль направления ветра становится видимым. В таком
пространственно-временном изображении движение видно непосредственно по наклону линий
постоянного уровня серого. Горизонтальная линия отмечает неподвижный объект.
Чем больше угол к горизонтальной оси, тем быстрее объект движется.
Последовательность изображений дает непосредственное представление о сложной
нелинейной динамике ветровых волн. Быстро движущаяся большая волна изменяет дви-
Примеры применения
Рис. 1.6. Исследования процесса роста в ботанике: а — лист клещевины; б — карта
темпов роста; в — рост корней кукурузы (иллюстрации предоставлены Ули Шуром (Uli
Schurr) и Стефаном Терюнгом (Stefan Terjung), Институт ботаники, Университет Гей-
дел ьберга)
Рис. 1.7. Проба подвижности для анализа движения двигательных протеинов
(иллюстрации предоставлены Дитмаром Уттенвайлером (Dietmar Uttenweiler), Институт
физиологии, Университет Гейдельберга)
жение более коротких волн. Иногда короткие волны движутся с той же скоростью
(связанные волны), но в большинстве случаев они значительно медленнее, с
большими изменениями в фазовой скорости и амплитуде.
Последний пример последовательностей изображений находится в гораздо
большем пространственно-временном масштабе. На рис. 1.9 показан годовой цикл
тропосферной столбиковой плотности NO2. NO2 является одним из самых важных
22 Глава 1. Области применения и инструментарий
Рис. 1.8. Пространственно-временное изображение коротких ветровых волн при
скорости ветра: а — 2,5 м/с; б — 7,5 м/с. Вертикальная ось обозначает пространственную
координату в направлении ветра, горизонтальная координата — время
следовых газов в химии атмосферного озона. Главными источниками
тропосферного газа NO2 являются промышленность и транспорт, лесные пожары и пожары
небольших зарослей (горение биомассы), микробиологические выделения почвы
и освещение. Формирование изображений с помощью искусственных спутников
Земли предусматривает в первую очередь изучение распределения NO2 по
районам, определение источников и их годовых циклов.
Данные были вычислены по спектроскопическим изображениям, полученным со
спутника ERS2 прибором GOME. В каждом пикселе изображений был взят полный
спектр с 4000 каналами в ультрафиолетовом диапазоне и диапазоне видимости.
Полную атмосферную столбиковую плотность концентращ1и NO2 можно определить по
характеристическому спектру поглощения, на который, однако, накладываются
спектры поглощения других следовых газов. Следовательно, требуется сложный
нелинейный регрессионный анализ. Кроме того, должна вычитаться стратосферная
столбиковая плотность соответствующими алгоритмами обработки изображений.
Результирующие карты тропосферных столбиковых плотностей NO2 на рис. 1.9
показывают большое количество интересных деталей. Большршство вьщелений отно-
1.2. Примеры применения
Рис. 1.9. Карты тропосферных столбиковых плотностей NO2, показывающие четыре
средних значения по трем месяцам 1999 г. (иллюстрации предоставлены Марком Вени-
хом (Mark Wenig), Институт физики окружающей среды. Университет Гейдельберга)
(if 24 Глава 1. Области применения и инструментарий
Рис. 1.10. Задачи промышленного контроля: а - оптическое распознавание
символов; б — соединители. Иллюстрации предоставлены Мартином фон Броке (Martin
von Bocker), Робертом Бошем (Robert Bosch), (GmbH)
срггся к промышленно разврпым странам. Они показывают полный годовой цикл в
Северном полушарии с максимальным значением в зимний период.
1.2.4. Классификация
Еще одной важной задачей является классификация объектов, наблюдаемых на
изображениях. Классическим примером классификации является распознавание
символов (оптическоераспознавание символов, или ОРС). На рис. \Л0, а показано
типичное промышленное применение ОРС — распознавание метки на
интегральной схеме. Классификация объектов включает также распознавание различных
возможных расположений объектов для правильной обработки роботом. На
рис. 1.10, ^ соединители размещены произвольным образом на ленте конвейера.
Для правильного подбора и обработки необходимо также определить, передняя
или задняя сторона соединителя видна.
Классификация дефектов является еще одним важным применением. На
рис. 1.11 показаны некоторые типичные ошибки, обнаруживаемые при проверке
интегральных схем: неправильно отцентрированный накладной резистор
(рис. 1.11, fl) и нарушенные или пропущенные соединения контактов (рис. \Л1,б—е).
Применение классификации не ограничивается промышленными задачами.
На рис. 1.12 приведены некоторые наиболее удаленные галактики, когда-либо
запечатленные телескопом Хаббла. Галактики должны разделяться на различные
классы соответственно их форме и цвету и должны отделяться от других объектов,
например звезд.
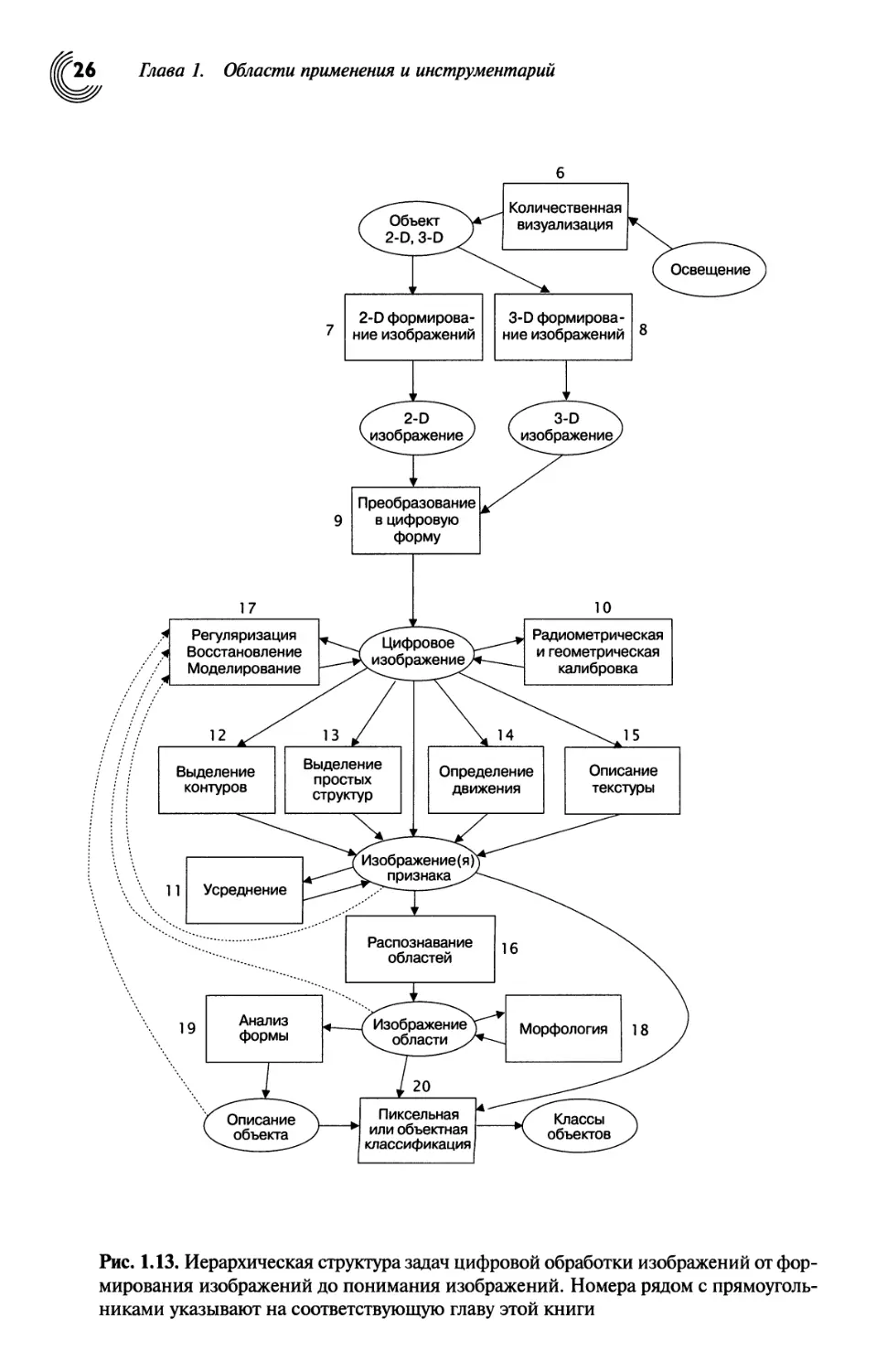
1.3. Иерархическая структура операций обработки изображений
Обработка изображений не является одношаговым процессом. Мы можем
обозначить несколько шагов, которые должны выполниться один за другим до тех пор,
пока мы не сможем вьщелить интересующие нас данные из наблюдаемой сцены.
Таким способом формируется схема иерархической обработки, представленная на
1.3. Иерархическая структура операций обработки изображений 25
iUHBHiJH
^
Рис. 1.11. Ошибки в припаивании и соединении интегральных схем. Иллюстрации
предоставлены Флорианом Рейшем (Florian Raisch), Робертом Боше (RobertBosch),
(GmbH)
Рис. 1.12. Изображение дальнего космоса, полученное телескопом Хаббла:
классификация удаленных галактик (http://hubblesite.org/)
рис. 1.13. Рисунок дает общее представление различных стадий обработки
изображений вместе с кратким описанием этой книги.
Обработка изображений начинается с получения изображения с помощью
подходящей, не обязательно оптической, системы формирования. В техническом или
научном применении мы можем выбрать соответствующую систему
формирования изображений. Кроме того, мы можем установить систему освещения, выбрать
наилучший диапазон длин волн и задать другие опции для фиксирования интере-
Глава 1. Области применения и инструментарий
Количественная
визуализация
2-D
формирование изображений
3-D
формирование изображений
Преобразование
в цифровую
форму
17
Регуляризация
Восстановление
Моделирование
10
Радиометрическая
и геометрическая
калибровка
Рис. 1.13. Иерархическая структура задач цифровой обработки изображений от
формирования изображений до понимания изображений. Номера рядом с
прямоугольниками указывают на соответствующую главу этой книги
1.3. Иерархическая структура операций обработки изображений
сующего нас признака объекта наилучшим образом на изображении (глава 6).
Формирование 2-D и 3-D изображений рассматриваются в главах 7 и 8. Раз
изображение получено, оно должно быть преобразовано в форму, которую можно
обрабатывать с помощью цифровых компьютеров. Этот процесс называется
преобразованием в цифровую форму и рассматривается в главе 9.
Первые этапы цифровой обработки, известные как предварительная
обработка изображений, могут включать несколько различных операций. Если датчик имеет
нелинейные характеристики, то их необходимо скорректировать. Подобным
образом яркость и контрастность изображения могут потребовать улучшения. Как
правило, также необходимы координатные преобразования для восстановления
геометрических искажений, внесенных при формировании изображения.
Радиометрические и геометрические корректировки являются элементарными
операциями пиксельной обработки, которые обсуждаются в главе 10.
Вся цепочка этапов обработки необходима для анализа и распознавания
объектов. Сначала должны применяться надлежащие процедуры фильтрации, для того
чтобы отличить интересующие нас объекты от всех других и от фона. По существу,
из изображения (или нескольких изображений) выделяются одно или больше
изображений признаков. Основными инструментами для этой задачи являются
усреднение (глава И), вьщеление контуров (глава 12), анализ простых окрестностей
(глава 13) и сложных структур, известных в обработке изображений как текстура.
Важным признаком объекта также является его движение. Методы для вьщеления
и определения движения рассматриваются в главе 14.
Затем объект должен быть отделен от фона. Это означает, что должны
распознаваться области постоянных признаков и неоднородностей с помощью
сегментации (глава 16). Эта задача может быть простой в случае, если объект хорошо
отделяется от фона по некоторым локальным признакам. Такое, однако, возможно
не часто. Тогда требуются более сложные методы сегментации. Эти методы
используют различные оптимизационные стратегии для минимизации отклонения
между данными изображения и заданной функцией модели, объединяющей
сведения об объектах на изображении.
Подобный математический подход можно использовать и для других задач
обработки изображений. Известные возмущения в изображении, к примеру обусловленные
расфокусировкой оптики, размытостью изображения, вызванной движением объекта,
погрешностями в датчике или погрешностями при передаче сигналов изображений,
могут корректироваться (восстановление изображений). С помощью непрямых методов
формирования изображений, таких, как томография, которые не дают прямого
изображения, можно реконструировать изображенрш (реконструкция изображений).
Зная геометрическую форму объекта, мы можем использовать морфологргчес-
кие операторы для ее анализа и модификации (глава 18) или вьщелить
дополнительную информацию, такую, как средний уровень яркости, площадь, периметр и
другие параметры формы объекта (глава 19). Эти параметры можно использовать
при классификации объектов (классификация, глава 20). Распознавание символов
в напечатанном и написанном от руки тексте является примером такой задачи.
Несмотря на то что разделение сложной задачи, такой, как обработка
изображений, на последовательность простых подзадач кажется логичным, неочевидно,
что такая стратегия работает вообще. Почему? Давайте рассмотрим простой
пример. Мы хотим обнаружить объект, который только незначительно отличается по
Глава 1. Области применения и инструментарий
уровню яркости от фона в зашумленном изображении. В этом случае мы не можем
ограничиться рассмотрением уровня яркости, чтобы отделить объект от фона.
Усреднение соседних точек изображения может уменьшить уровень шума. На
контуре объекта, однако, точки фона и объекта усредняются, приводя к
неправильным средним значениям. Если бы мы знали, где находится контур, то могли
бы прекратить усреднение на контуре. Но мы можем определить контур сразу
после усреднения, поскольку только тогда уровни яркости объекта существенно
отличаются от фона.
Мы можем надеяться избежать этого замкнутого круга с помощью
итерационного подхода. Просто применяем усреднение и сразу же проводим первую оценку
контуров объекта. Затем берем эту оценку для уточнения усреднения на контурах,
пересчитываем контуры и так далее. Однако открытым остается вопрос, сходится
ли эта итерация вообще, и если да, то является ли предел правильным.
В любом случае рассмотренный пример говорит о том, что более сложные
задачи обработки изображений требуют обратной связи. Последующие этапы
обработки возвращают параметры к предьщущим этапам. Тогда обработка не является
линейной вдоль цепочки, но может итерационно возвращаться к началу
несколько раз. На рис. 1.13 показаны некоторые возможные обратные связи. Обратная
связь может включать в себя обработку дополнительной информации,
полученной не из изображений.
Если задача обработки изображений не может быть решена с помощью
данного изображения, мы можем принять решение изменить освещение, приблизиться
к интересующему нас объекту или рассматривать его под более подходящим
углом. Такой тип подхода известен как активное зрение. В рамках интеллектуальной
системы, исследующей окружающую ее среду с помощью своих органов чувств,
мы можем также говорить о цикле действие-восприятие,
1.4. Обработка изображений и компьютерная графика
с некоторого времени обработка изображений и компьютерная графика
рассматриваются как две разные области. Знания в обеих областях значительно
расширились, и теперь могут рассматриваться более сложные задачи. Компьютерная
графика стремится достичь фотореалистических, полученных посредством компьютера
изображений трехмерных сцен, в то время как обработка изображений пытается
реконструировать трехмерную сцену из изображения, фактически полученного с
помощью камеры. В этом смысле обработка изображений выполняет операцию,
обратную операции компьютерной графики. В компьютерной графике мы
начинаем со сведений о форме и признаках объекта - нижняя часть рис. 1.13 - и
продолжаем работу вверх до тех пор, пока не получим двумерное изображение. Для того
чтобы владеть обработкой изображений или компьютерной графикой, мы, по
существу, должны исходить из одних и тех же знаний. Нам необходимо знать
взаимодействие освещения и объектов, как трехмерная сцена проектируется на плоскость
изображения, и т.д.
Тем не менее существует все еще немало различий между рабочей станцией
для обработки изображений и графической рабочей станцией. Однако мы можем
предположить, что, когда сходства и взаимосвязи между компьютерной графикой
и обработкой изображений будут лучше поняты и надлежащие технические сред-
1.5. Междисциплинарная природа обработки изображений
ства будут разработаны, мы увидим в будущем некоторый вид рабочей станции
общего назначения, которая сможет выполнять задачи компьютерной графики,
так же как задачи обработки изображений. Появление мультимедиа, т.е.
объединение текста, изображений, звука и фильмов, в дальнейшем ускорит объединение
компьютерной графики и обработки изображений. Термин «вычисления с
использованием графики» был введен в этом контексте [66].
1.5. Междисциплинарная природа обработки изображений
По своей природе наука обработки изображений является междисциплинарной в
некоторых аспектах. Во-первых, обработка изображений объединяет понятия из
различных наук. Прежде чем мы сможем обработать изображение, необходимо
знать, как цифровой сигнал связан с признаками изображаемых объектов. Сюда
включены различные физические процессы — от взаимодействия излучения с
веществом до геометрии и радиометрии формирования изображений.
Формирующий изображения датчик преобразует энергетическую освещенность падающего
излучения тем или иным образом в электрический сигнал. Затем этот сигнал
преобразуется в дискретные числа и обрабатывается цифровым компьютером для
выделения значимых данных. В эту последовательность процессов (см. также рис.
1.13) вовлечены многие области из физики, компьютерной науки и математики,
включая среди других оптику, физику твердого тела, разработку микросхем,
архитектуру компьютера, алгебру, анализ, статистику, теорию алгоритмов, теорию
графов, теорию систем и численную математику. С инженерной точки зрения
используются разработки теоретической и стекловолоконной оптики, электротехники и
проектирования программного обеспечения.
Обработка изображений частично пересекается с другими дисциплинами.
Задачи обработки изображений могут отчасти рассматриваться как задачи измерения,
которые являются частью науки метрологии. Задачи распознавания образов
включены в обработку изображений так же, как и в обработку речевой информации. Другими
дисциплинами, которые также связаны с обработкой изображений, являются
исследования нейронных сетей, искусственного интеллекта и зрительного восприятия.
Общим для этих областей является их сильная связь с биологическими науками.
Когда мы говорим о компьютерном зрении, мы имеем в виду компьютерную
систему, которая вътолушет такую же задачу, что и биологическая зрительная
система, для «определения по изображениям, что присутствует в мире и где это находится»
(«discover from images what is present in the world, and where it is») [132].
Противоположно, термин машинное зрение используется для системы, которая выполняет
зрительную задачу, такую, как проверка размеров и комплектности деталей в условиях
производства. В течение многих лет система технического зрения рассматривалась
только как пассивный наблюдатель. Как и в случае с биологическими
зрительными системами, система компьютерного зрения может также активно исследовать
окружающую ее среду при помощи, например, перемещения и регулирования угла
наблюдения. Мы называем это активным зрением.
Существует большое число специальных дисциплин, которые вследствие
исторических причин развивались отчасти независимо от основного течения в прошлом.
Одной из наиболее известных дисциплин является фотограмметрия (измерения по
фотографиям; основные применения: создание карт и обследование местности).
Глава 1. Области применения и инструментарий
Другими областями являются дистанционное зондирование, использующее
изображения, полученные с воздуха и из космоса, астрономия и рентгенография.
Еще одним важным аспектом междисциплинарной природы обработки
изображений является широкий спектр приложений. Практически не существует
области в естественных науках или технических дисциплинах, где бы не
применялась обработка изображений. Как мы увидели из примеров в разделе 1.2, она
получила большое значение в нескольких областях применения. Сильные связи с
таким большим количеством смежных наук дают плодородную почву для ее
дальнейшего быстрого развития вследствие постоянного притока методов и идей из
непрерывно увеличивающейся совокупности областей применения.
Последнее предостерегающее замечание: возможности междисциплинарного
подхода не являются лишь приятным приобретением. Это необходимость.
Недостаток знаний либо в области применения, либо в методологии обработки
изображений неизбежно ведет по меньшей мере к субоптимальным решениям и иногда
даже к полному провалу.
1.6. Зрение человека и компьютерное зрение
Мы не можем рассуждать об обработке изображений без рассмотрения зрительной
системы человека. Это кажется тривиальным утверждением, однако оно имеет далеко
идуш^1е последствия. Мы наблюдаем и оцениваем изображения, обрабатываемые
нашей зрительной системой. Без принятия во внимание этого элементарного факта мы
можем бьггь введены в сильное заблуждение при интерпретации изображений.
Первые простые вопросы, которые нам следует задать:
• Какие различия в интенсивности мы можем распознавать?
• Какое пространственное разрешение имеет наш глаз?
• Насколько точно мы можем оценивать и сравнивать расстояния и площади?
• Как мы воспринимаем цвета?
• По каким признакам мы можем обнаруживать и различать объекты?
Очевидно, что более глубокие знания могли бьггь очень полезны для
компьютерного зрения. Мы не будем приводить здесь обшдй обзор зрительной системы
человека. Целью является скорее познакомиться с элементарными соотношениями между
человеческим и компьютерным зрением. Мы обсудим свойства зрительной системы
человека в соответствующих главах. Здесь мы сделаем только несколько вводньех
замечаний. Детальное сравнение человеческого и компьютерного зрения можно найти
в работе Левине (Levine) [121]. Превосходным современным исследованием
человеческого зрения зшляется монография Ванделла (Wandell) [210].
Читатель может провести несколько экспериментов самостоятельно. На
рис. 1.14 приведены тестовые изображения для оценки расстояния и площади. У
нас не возникнет проблем в видении даже маленьких изменений в длине
параллельных линий на рис. 1.14, л. Сходное сравнение площадей на примере
окружностей является значительно более сложным (рис. 1.14, б). Другие примеры
показывают, как влияет на оценку контекст изображения. Такие явления известны как
оптические иллюзии. Два примера оценок длины показаны на рис. 1.14, в, г. Эти
примеры показывают, что зрительная система человека воспринимает контекст
через свою оценку длины. Следовательно, мы должны быть очень внимательны в
своих визуальных оценках длин и площадей на изображениях.
1.6. Зрение человека и компьютерное зрение 3 I
Рис. 1.14. Тестовые изображения для оценивания расстояний и площадей: а —
параллельные линии с разницей в длине до 5%; б - окружности с разницей в радиусе до 10%;
в - вертикальная линия кажется длиннее, хотя она имеет ту же длину, что и
горизонтальная линия; г - обман из-за перспекгавы: верхняя линия (на заднем плане) кажется
длиннее, чем нижняя линия (на переднем плане), хотя обе имеют одинаковую длину
Вторым вопросом является распознавание объектов в изображениях. Хотя
рис. 1.15 содержит только несколько линий и является плоским изображением, не
содержащим какой-либо непосредственной информации о глубине, мы сразу же
распознаем куб на правом и левом изображениях и его ориентацию в
пространстве. Единственными ключевыми моментами, по которым мы можем прийти к
этому заключению, являются скрытые линии и наши знания о форме куба.
Изображение посередине, на котором также показаны скрытые линии, двойственно.
Немного потренировавшись, мы можем переключаться между двумя
возможными ориентациями в пространстве.
Рис. 1.16 иллюстрирует поразительную особенность зрительной системы
человека. С легкостью мы видим четкие границы между разными текстурами на
рис. 1.16, А и сразу же распознаем цифру 5. На рис. 1.16, б мы распознаем белый
равносторонний треугольник, несмотря на то что части ограничивающих линий
отсутствуют.
По этим нескольким наблюдениям мы можем прийти к заключению, что
зрительная система человека является чрезвьгчайно мощной в распознавании
объектов, но менее подходящей для правильного измерения уровней яркости,
расстояний и площадей.
Рис. 1.15. Распознавание трехмерных объектов: три различных представления куба
с одинаковыми ребрами на плоскости изображения
32 Глава 1. Области применения и инструментарий
Рис. 1.16. а — распознавание границ между текстурами; б - «интерполяция»
границ объекта
По сравнению с потенциалом систем компьютерного зрения наши
возможности выглядят весьма скромно. Система цифровой обработки изображений может
выполнять элементарные или четко определенные фиксированные задачи
обработки изображений, такие, как производимый в реальном времени контроль качества в
промышленном производстве. Система компьютерного зрения также преуспела в
управлении машиной на высокой скорости на шоссе, даже с изменяющимися
рядами движения. Однако мы все еще очень далеки от универсальной системы
цифровой обработки изображений, которая способна «понимать» изображения на уровне
человека и реагировать разумно и гибко в реальном времени.
Стоит отметить еще одну связь между человеческим и компьютерным
зрением. Важные разработки в компьютерном зрении были сделаны в процессе
развития понимания зрительной системы человека. Мы встретимся с несколькими
примерами в этой книге: с пирамидой как эффективной структурой данных для
обработки изображений (глава 5), понятием локальной ориентации (глава 13) и
определением движения фильтрующими методами (глава 14).
1.7. Компоненты системы обработки изображений
Этот раздел кратко описывает возможности современных систем обработки
изображений. Система получения и обработки изображений общего назначения, как
правило, состоит из четырех неотъемлемых компонентов:
1. Системы получения изображений. В простейшем случае это может быть ПЗС-
камера, планшетный сканер или видеомагнитофон.
2. Устройство, известное как фрейм-граббер, для преобразования
электрического сигнала (обычно аналогового видеосигнала) системы получения
изображений в цифровой формат с возможностью последующего сохранения.
3. Персональный компьютер или рабочая станция, обеспечивающие процессы
обработки данных.
4. Программное обеспечение для обработки и анализа изображений.
1.7.1. Датчики изображений
Цифровая обработка требует, чтобы изображения были получены в виде
электрических сигналов. Эти сигналы можно оцифровать в последовательности чисел, ко-
1.7. Компоненты системы обработки изобра^юений 33
tm^TAiiT аигггАгчн^лмт/
Рис. 1.17. Современные полупроводниковые камеры: а — полная КМОП-камера на
микросхеме с цифровым и аналоговым выходом (иллюстрации предоставлены
К. Мейером (К. Meier), Институт физики им. Кирхгофа, Университет Гейдельбер-
га) [126]; б - профессиональная цифровая 12-разрядная ПЗС-камера, Pixelfly
(иллюстрации предоставлены РСО GmbH, Германия)
торые затем могут обрабатываться с помощью компьютера. Существует много
способов для преобразования изображений в дискретные числа. Здесь мы
сосредоточим свое внимание на видеотехнологии, поскольку это наиболее общий и
доступный подход.
Промежуточным этапом в технологии восприятия изображений было
изобретение матриц полупроводниковых фотодетекторов. Существует много типов
таких датчиков, причем наиболее общепринятым является прибор с зарядовой связью,
или ПЗС. Такой датчик состоит из большого числа фоточувствительных
элементов. Вначале каждый элемент накапливает электрические заряды, которые
генерируются поглощенными фотонами. Таким образом, накопленный заряд
пропорционален освещенности. На этапе считывания эти заряды последовательно
передаются через микросхему от датчика к датчику и, в конце концов,
преобразуются в электрическое напряжение.
С некоторого времени стали доступными датчики изображений на основе
комплементарных металлооксидных полупроводников (КМОП). Однако только недавно
эти устройства привлекли к себе должное внимание, поскольку качество
изображений, особенно равномерность чувствительностей отдельных сенсорных
элементов, теперь достигает качества ПЗС-датчиков изображений. КМОП-формирова-
тели изображений все еще не достигают стандартов ПЗС-формирователя в
некоторых свойствах, особенно при низких уровнях освещенности (более
высокий темповой ток). Однако они обладают некоторыми важными преимуществами
над ПЗС-формирователями изображений. Они потребляют значительно меньше
мощности, с их помощью можно быстро достигнуть подобласти, их можно
добавить к схемам для обработки изображений и преобразования сигналов.
Действительно, можно поместить всю камеру на отдельной микросхеме (рис. 1.17, а).
Последним, но не менее важным является то, что КМОП-датчики могут изготовляться
более дешево и, таким образом, открывают новые области применения.
Как правило, полупроводниковые датчики формирования изображений
являются универсальными и мощными устройствами.
• Точная и устойчивая геометрия. Отдельные сенсорные элементы
закрепляются на регулярной сетке. Геометрическое искажение практически отсутствует.
Кроме того, датчик не изменяется в размерах благодаря низкому коэффициенту
Глава 1. Области применения и инструментарий
линейного теплового расширения кремния (2 • lO'VK). Эти особенности
позволяют проводить прецезионные измерения размера и положения.
• Маленькие и прочные. Датчики являются маленькими и нечувствительными
к внешним влияниям, таким, как магнитные поля и вибрации.
• Высокая чувствительность. Квантовая эффективность, т.е. доля элементарных
зарядов, генерируемая одним фотоном, может быть близка к единице ()-R2 и :^R1).
Даже стандартные датчики формирования изображений, которые используются
при комнатной температуре, имеют низкий уровень шума, равный всего лишь
10—100 электронам. Таким образом, они показывают отличную чувствительность.
Охлажденные датчики формирования изображения могут использоваться с про-
должительностями экспонирования, составляюш;ими часы, без проявления
значительного теплового сигнала. Однако промышленные ПЗС при комнатной
температуре не могут использоваться для низких уровней освещенности из-за
термовозбужденных электронов. Но если ПЗС-устройства охлаждаются до низких
температур, то они могут экспонироваться часами. Такие устройства обычно
используются в астрономии и являются почти в 100 раз более чувствительными, чем
фотографические материалы.
• Широкое разнообразие. Датчики формирования изображений являются
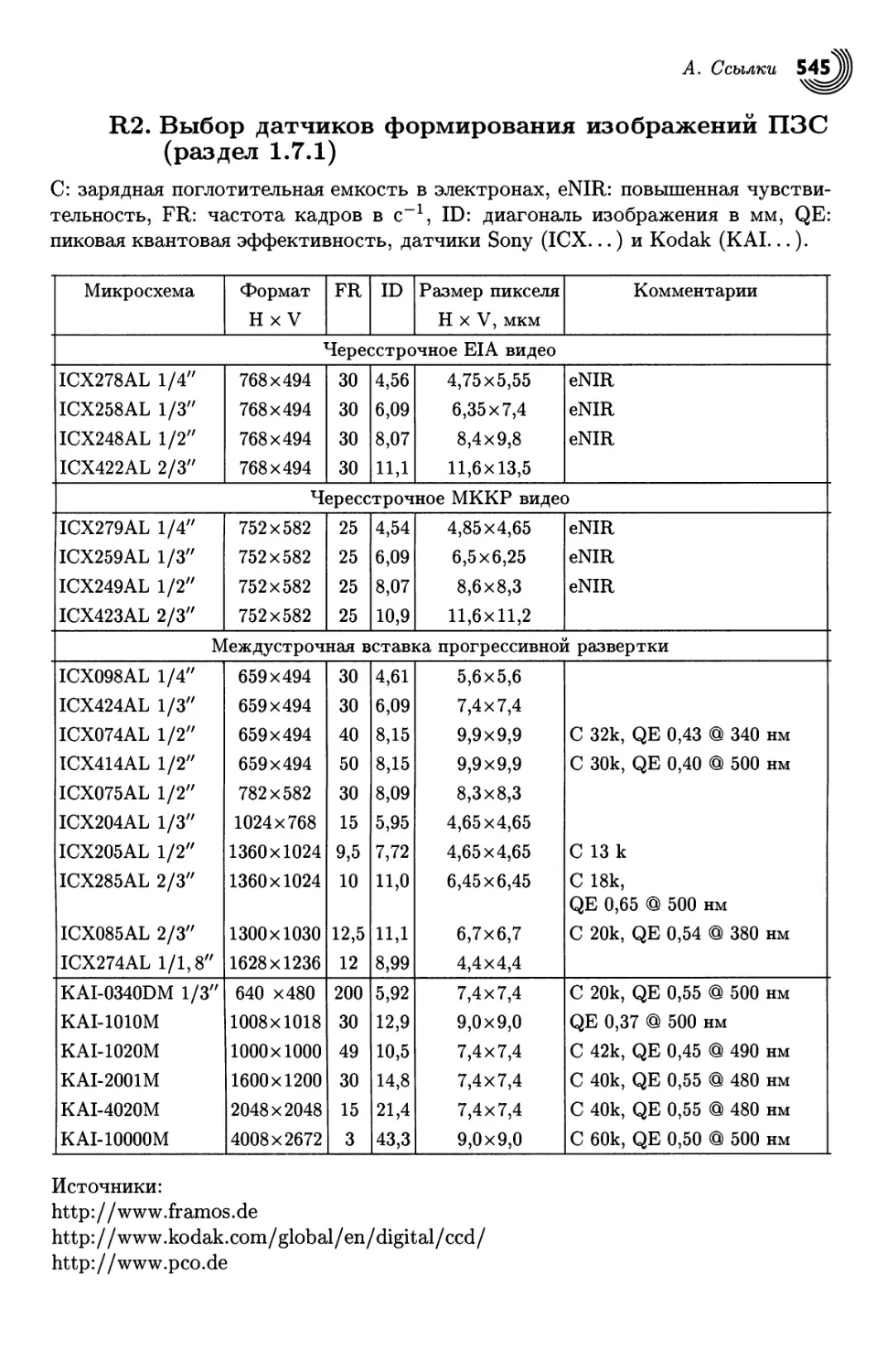
доступными в широком диапазоне разрешений и частот кадров ()^R2 и >Ш). Самый
большой на 2001 г. ПЗС-датчик разработан Pliilips. Это модульная конструкция
7к X 9к с сенсорными блоками 1к х 1к с пикселями 12 х 12 мкм [68]. Среди
доступных самых быстрых формирователей изображений с высоким разрешением есть
КМОП-датчик с активными пикселями 1280 х 1024 от Photobit с пиковой частотой
кадров в 500 Гц (скорость передачи данных 660 Мб/с) [152].
• Получение изображений за пределами прямой видимости.
Полупроводниковые формирователи изображений не ограничиваются диапазоном видимости
электромагнитного спектра. Стандартные кремниевые формирователи изображений
могут быть чувствительными далеко за пределами длин волн диапазона
видимости (400—700 нм) от 200 нм в ультрафиолетовой области до 1100 нм в ближней
инфракрасной области спектра. В инфракрасном диапазоне за пределами 1100 нм
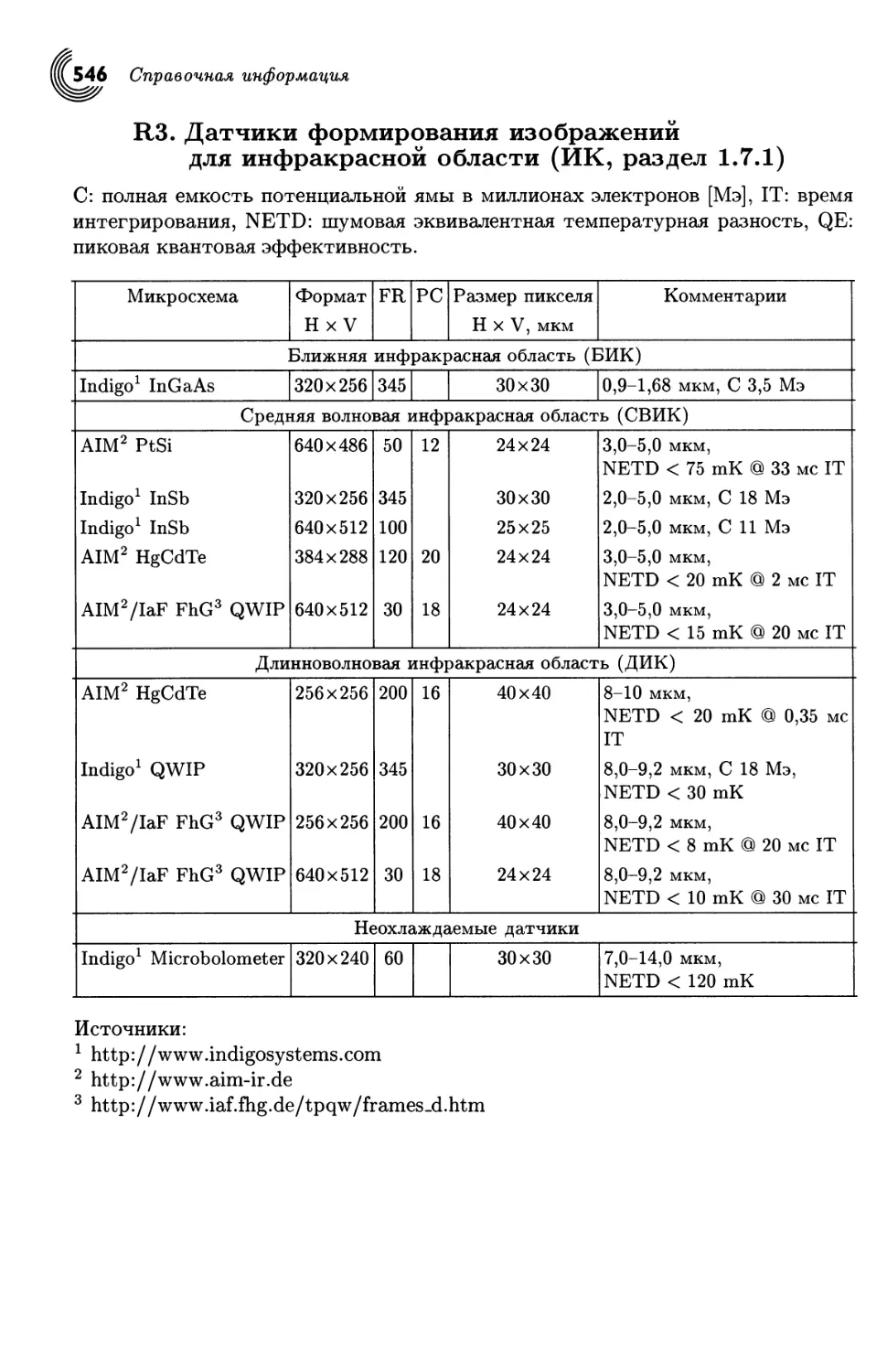
используются другие полупроводники, такие, как GaAs, InSb, HgCdTe (:^R3),
поскольку кремний становится прозрачным. Для более коротких длин волн
специально разработаны кремниевые формирователи изображений, они могут быть
чувствительными и в области длин волн рентгеновского излучения.
1.7.2. Получение и воспроизведение на экране изображений
Фрейм-граббер преобразует электрический сигнал, полученный от камеры, в
цифровое изображение, которое можно обрабатывать компьютером. Воспроизведение
изображений на экране и обработка сегодня не требуют каких-либо специальных
технических средств. С появлением графических пользовательских интерфейсов
воспроизведение изображений на экран стало составляющей частью
персонального компьютера или рабочей станции. Помимо воспроизведения полутоновых
изображений, имеющих до 256 уровней яркости (8 бит), также могут
воспроизводиться изображения в естественных цветах (до 16,7 миллиона цветов, 3 канала с
8 битами каждый) на недорогих системах на базе ПК с графическим дисплеем, с
разрешением до 1600 х 1200 пикселей.
1.7. Компоненты системы обработки изображений
Следовательно, современный фрейм-граббер больше не требует
собственного устройства для воспроизведения на экран. Ему необходимы только схемы для
преобразования в цифровую форму электрического сигнала от датчика
формирования изображений и хранения изображения в памяти компьютера.
Непосредственная передача данных изображения от фрейм-граббера в память (RAM)
микрокомпьютера стала возможной с 1995 г. с введением систем быстрых
периферийных шин, таких, как шина PCI. Эта 32-разрядная
высокопроизводительная 33 МГц шина имеет пиковую скорость передачи данных в 132 Мб/с. В
зависимости от контроллера PCI-шины на фрейм-граббере и чипсета на материнской
плате компьютера были зафиксированы поддерживаемые скорости передачи
данных между 15 и 80 Мб/с. Этого достаточно для передачи последовательностей
изображений в реальном времени в основную память, даже в случае цветных
изображений и изображений с большой скоростью передачи кадров. 64-разрядная
66 МГц PCI-шина второго поколения увеличивает скорости передачи данных в 4
раза до пиковой в 512 Мб/с. Цифровые камеры, которые передают изображения
непосредственно в ПК через стандартные цифровые интерфейсы, такие, как
Fireware (IEEE 1394), Camera link или даже быстрый Ethernet, упростят в
дальнейшем ввод изображений в компьютеры.
Скорости обмена данными со стандартными жесткими дисками, однако, ниже
10 Мб/с. Такие скорости не подходят для несжатого сохранения
последовательностей изображений, поступающих в реальном времени, на диске. Передача данных
в реальном времени с поддерживаемыми скоростями между 10 и 30 Мб/с
возможна с RAID-массивами.
1.7.3. Аппаратные средства компьютера для быстрой обработки изображений
Гигантский прогресс в компьютерной технологии в последние 20 лет позволил
цифровой обработке изображений получить широкое распространение среди
ученых и инженеров. Для того чтобы компьютер обш^его назначения был полезен
для обработки изображений, должны удовлетворяться четыре ключевых
требования: дисплей с высоким разрешением, допустимая пропускная способность
памяти, достаточная область памяти и достаточная вычислительная мощность.
Во всех четырех областях был достигнут критический уровень
производительности, который позволил обрабатывать изображения на стандартных аппаратных
средствах. В ближайшем будущем ожидается, что компьютеры общего
назначения смогут без проблем обрабатывать объемные изображения и/или
последовательности изображений. Дальше мы приведем краткое описание этих
ключевых областей.
Компьютеры общего назначения сейчас включают достаточную оперативную
память (RAM) для хранения многочисленных изображений. 32-разрядный
компьютер может обращаться к почти 4 Гб памяти. Этого достаточно для сложных задач
обработки изображений даже с большими изображениями. Сегодня также
доступны 64-разрядные компьютерные системы. Они обеспечивают достаточной RAM
сложные прикладные задачи с последовательностями изображений и объемными
изображениями.
В начале эры ПК жесткие диски имели вместимость лишь в 5-10 Мб,
сегодня дисковые системы с более чем в 10 000 раз большей емкостью запоминаю-
Глава 1. Области применения и инструментарий
щего устройства (40-200 Гб) являются стандартом. Таким образом, большое
количество изображений может храниться на диске, что стало важным требованием
для научной обработки изображений. Для постоянного хранения данных и
обмена с ПК, DVD играет важную роль как дешевая и универсальная среда для
хранения информации. Один DVD может хранить почти 5 Гб изображений, которые
могут быть считаны независимо от операционной системы на MS Windows,
Macintosh и UNIX платформах. Недорогие DVD-райтеры позволяют любому
создавать DVD.
В течение короткой истории микропроцессоров и персональных
компьютеров вычислительная мощность сильно выросла. С 1978 по 2001 г. тактовая
частота увеличилась в 300 раз, с 4,7 МГц до 1,6 ГГц. Скорость выполнения
элементарных операций, таких, как сложение и умножение чисел с
плавающей запятой, увеличилась даже больше, так как на современных CPU эти
операции имеют производительность лишь в несколько тактов вместо почти 100
на ранних процессорах. Таким образом, в течение менее 25 лет скорость
вычислений с плавающей запятой на отдельном процессоре увеличилась более
чем в 10 000 раз.
Обработка изображений смогла получить выгоду от этой разработки лишь
частично. На современных 32-разрядных процессорах стали чрезвычайно
неэффективными передача и обработка 8-битовых и 16-битовых изображений.
Ситуация изменилась только в 1997 г. с внедрением мультимедийных методов в ПК и
рабочие станции. Основная идея быстрой обработки изображений очень проста.
В современных процессорах для быстрой передачи и параллельной обработки
многочисленных изображений используются 64-битовые тракты данных. Этот
подход к выполнению параллельной обработки является формой понятия один
поток команд и много потоков данных (SIMD), В 16-разрядных машинах восемь
8-битовых, четыре 16-битовых или два 32-битовых потока данных могут
обрабатываться одновременно.
Sun была первой компанией, внедрившей понятие SIMD в компьютерную
архитектуру общего назначения с набором команд для работы с графикой (VIS) на
UltraSparc архитектуре [139]. В январе 1997 г. Intel ввел набор инструкций длямулъ-
тимедиарасширения (ММХ) для следующего поколения процессоров Pentium (Р55С).
Концепция SIMD была быстро принята другими производителями процессоров.
Motorola, к примеру, разработала набор инструкций AltiVec. Концепция стала
составляющей частью новых 64-разрядных архитектур, таких, как IA-64 архитектура
от Intel и x86-64 архитектура от AMD.
Таким образом, очевидно, что SIMD-обработка изображений стала
стандартной частью будущих микропроцессорных архитектур. Все больше и больше
задач обработки изображений могут быть выполнены в реальном времени на
стандартных микропроцессорах без необходимости каких-либо дорогостоящих и
громоздких специальных аппаратных средств. Однако все еще требуется
существенное усовершенствование компиляторов, прежде чем SIMD-методы могут
быть использованы обычным программистом. Сегодня пользователь также
зависит от библиотек, которые оптимизируются производителями аппаратных
средств для отдельных аппаратных платформ, или ему приходится погружаться в
изучение деталей архитектуры аппаратных средств ляя оптимизации
программирования.
1.8. Упражнения
1.7.4. Программное обеспечение и алгоритмы
Быстрый прогресс в аппаратном обеспечении компьютера может отвлечь наше
внимание от важности программного обеспечения и математической основы
базовых понятий обработки изображений. На ранних этапах развития обработка
изображений могла бы быть охарактеризована больше как «искусство», чем как наука.
Решение задачи находилось эмпирически. Алгоритм, созданный для разрешения
конкретной проблемы, не работал в других условиях. Современное положение
совершенно иное. Обработка изображений стремится созреть в хорошо развитую
науку. Глубокое понимание исследумых задач привело к более реалистической оценке
сегодняшних возможностей обработки и анализа изображений, которое во многих
отношениях является все еще далеким от возможностей человеческого зрения.
Широко распространенным заблуждением является то, что более надежная
математическая основа для обработки изображений представляет интерес только
для теоретиков и не имеет практического применения. Верно обратное.
Математический анализ позволяет разделить задачи обработки изображений на
решаемые и принципиально нерешаемые, что уже очень полезно. Алгоритмы обработки
изображений становятся предсказуемыми и точными, и в некоторых случа51х,
известны оптимальные решения. Новые математические методы часто приводят к
неизведанным подходам, которые гораздо быстрее или точнее, чем предыдущие
подходы, или помогают справиться с ранее труднорешаемыми задачами. Часто
ускорение, которое может быть получено быстрым алгоритмом, довольно
значительно. В некоторых случая[Х оно может достичь нескольких порядков величины.
Таким образом, быстрые алгоритмы делают многие методы обработки изображений
применимыми и заметно уменьшают стоимость аппаратных средств.
1.8. Упражнения
1.1: Программа просмотра последовательностей изображений
Интерактивный просмотр и контроль всех последовательностей
изображений и объемных изображений, используемых в этом пособии (dip6ex01.01).
1.2: * Задачи обработки изображений
На рис. 1.13 содержится систематическое описание иерархической
структуры процессов обработки изображений — от освещения до анализа объектов,
выделенных из полученных изображений. Определите, какие из этих
процессов на диаграмме необходимы для следующих задач:
1. Измерение распределения по размерам цветных пигментов (раздел 1.2.1,
рис. 1.1, <?).
2. Определение опухоли мозга в объемном изображении магнитнорезонанс-
ной томографии (раздел 1.2.2, рис. 1.5) и измерение ее размера и формы.
3. Исследование суточного цикла роста листьев растения (раздел 1.2.3,
рис. 1.6).
4. Оптическое распознавание символов (ОРС): чтение метки на
интегральной схеме (раздел 1.2.4, рис. 1.10, а).
5. Разделение галактик согласно их формам и спектрам на различные
классы (раздел 1.2.4, рис. 1.12).
Глава 1, Области применения и инструментарий
* Междисциплинарная природа обработки изображений
1. Какие другие науки предлагают методы, которые используются в
цифровой обработке изображений?
2. Какие области науки и техники используют методы обработки
изображений?
1.4: ** Сравнение компьютерного зрения и биологического зрения
В разделе 1.7 мы рассматриваем компоненты системы цифровой обработки
изображений. Попьггайтесь определить соответствующие компоненты
биологической системы зрения. Существует ли взаимно-однозначное соответствие, и
видите ли вы фундаментальные различия? Существуют ли компоненты, которые
еще не реализованы в системах компьютерного зрения, и наоборот?
1.5: * Количество данных в цифровой обработке изображений
В цифровой обработке изображений требуются большие объемы данных,
поскольку это, как правило, случай с анализом временных рядов. Оцените
количество данных, которое должно быть обработано в следующих реальных
прикладных задачах.
1. Последовательности изображений водной волны. В системе
ветер/волна последовательности изображений содержат ветровые волны на
поверхности воды (раздел 1.2.3, рис. 1.8). Используются две системы камер.
Каждая из них создает последовательности изображений с
пространственным разрешением в 640 Г 480 пикселей, 200 кадров/с и 8-битовым
разрешением данных. Последовательность измерений длится свыше 6 часов.
Каждые 15 минут 5-минутная последовательность создается непрерывно
с помощью обеих камер. Какова скорость передачи данных для записи в
реальном времени? Сколько данных необходимо сохранить за весь
6-часовой процесс?
2. Система промышленного контроля лазерной сварки. Сварка деталей в
промышленной производственной линии контролируется системой
высокоскоростных камер. Камера создает 256 х 256 изображений со скоростью
1000 кадров/с и разрешением 16 бит в пиксель за одну секунду, для того
чтобы контролировать сварку одной детали. Одна тысяча деталей проверяется
за час. Производственная линия работает непрерывно 24 часа и включает
шесть контрольных мест. Какое количество изображений должно быть
обработано за сутки и за год соответственно?
3. Система помощи водителю. Система помощи водителю определяет линию
дороги и дорожные знаки с помощью сети камер, которые имеют
пространственное разрешение в 640 х 480 пикселей и принимает 25 кадров/с. Камера
получает цветные изображения с помощью трех цветовых каналов —
красного, зеленого и синего. С какой скоростью должны обрабатываться
изображения в реальном времени?
4. Последовательности объемных изображений в медицине. Быстрые
компьютерные томографические системы для динамической медицинской
диагностики принимают объемные изображения с пространственным
разрешением 256 X 256 X 256 и частотой повторений 10 кадров/с. Данные имеют
16-битовую глубину. Какой должна быть скорость передачи данных (Мб/с)?
1.9. Дополнительная литература
1.9. Дополнительная литература
в этом разделе мы даем некоторые советы по дальнейшему чтению по обработке
изображений.
Начальные учебные пособия. «Руководство по обработке изображений» Русса
(Russ) [173] является отличным начальным введением в обработку изображений с
большим изобилием примеров применения и иллюстраций. Еще одним
начальным учебным пособием является работа Налва (Nalwa) [144]. Эта книга — на что и
указывает название - экскурс в компьютерное зрение.
Углубленные учебные пособия. Все еще достойным внимания является
классическое, теперь уже двадцатилетней давности учебное пособие «Цифровая
обработка изображений» Розенфельда (Rosenfeld) и Кака (Как) [172]. Еще одним
классическим, но отчасти устаревшим учебным пособием является книга Джейна (Jain)
[97]. Из других классических учебных пособий недавно были опубликованы
новые издания: Претт (Pratt) [157] и Гонсалес (Gonzalez) и Вудс (Woods) [62]. Учебное
пособие от ван дер Хайдена (van der Heijden) [205] рассматривает измерения,
основанные на изображениях, включающие оценивание параметров и распознавание
объектов.
Учебные пособия, охватывающие спещ1альные темы. Из-за
междисциплинарной природы (раздел 1.5) обработку изображений можно рассматривать с
совершенно разных точек зрения. Собрание монографий, которые фокусируются на
одном или другом аспекте обработки изображений, приведено здесь:
Тема
Ссылки
Датчики изображений
Магнитнорезонансное формирование
изображений
Геометрические аспекты компьютерного
зрения
Восприятие
Машинное зрение
Техническое зрение робота и компьютерное
зрение
Обработка сигналов
Получение изображений с помощью ИСЗ
и дистанционное зондирование
Анализ микроструктур
Промышленная обработка изображений
Классификация объектов и распознавание
образов
Высокоуровневое зрение
Холст (Hoist) [77], Ховель (Howell) [82] и
Джейнесик (Janesick) [99]
Яке (Нааске) и др. [67], Лианг (Liang) и Лау-
тербур (Lauterbur) [122], Митчелл (Mitchell)
и Коэн (Cohen) [138]
Фауджерес (Faugeras) [42], Фауджерес
(Faugeras) и Люонг (Luong) [43]
Маллот (MaUot) [129], Ванделл (Wandell) [210]
Джейн (Jain) и др. [98], Демант (Demant) и
др. [31]
Хорн (Нот) [81], Шапиро (Shapiro) и Сток-
ман (Stockman) [186], Форсис (Forsyth) и
Понс (Ponce) [54]
Гранлунд (Granlund) и Натссон (Knutsson)
[64],Лим(ит)[124]
Ричарде (Richards) и Джиа (Ла) [167], Скотт
(Schott) [181]
Осер (Ohser) и Мюклих (Mucklich) [147]
Демант (Demant) и др. [31]
Дуда (Duda) и др. [38], Шурманн (Schurman)
[182], Бишоп (Bishop) [10], Шоллкопф
(SchoUkopf) и Смола (Smola) [180]
Ульман (Ullman) [202]
Глава 1. Области применения и инструментарий
Зрение человека и компьютерное зрение. Эта тема детально рассматривается у
Левине (Levine) [121]. Отличной и современной работой является также
монография Ванделла (Wandell) [210].
Собрание статей. Отличный обзор обработки изображений с прямым доступом
к некоторым ключевым исходным статьям дается следующими сборниками:
«Цифровая обработка изображений» Челаппа (Chelappa) [22], «Данные по
компьютерному зрению: вопросы, принципы и парадигмы» от Фишлера (Fischler) и Фир-
шайна (Firschein) [47] и «Компьютерное зрение: принципы, достижения и
применение» от Кастюри (Kasturi) и Джейн (Jain) [103, 104].
Руководства. «Практическое руководство по обработке изображений для
научных применений» от Яне (Jahne) [89] дает ориентированный на задачи подход с
большим количеством практических процедур и подсказок. Современный обзор
компьютерного зрения можно найти в трехтомном «Руководстве по
компьютерному зрению и применениям» от Яне (Jahne) и др. [94]. Алгоритмы обработки
изображений и компьютерного зрения дают Восс (Voss) и Зюсе (SuBe) [209], Питас (Pitas)
[154], Паркер (Parker) [150], Умбаф (Umbaugh) [203] и Вилсон (Wilson) и Ритгер
(Ritter) [217].
ГЛАВА 2
ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ
2.1. Введение
Эта глава посвящена вопросу представления информации, содержащейся в
изображениях. Как и в следующих двух главах, здесь закладываются математические
основы низкоуровневой обработки изображений. В этой главе делается акцент на
двух ключевых моментах.
Во-первых, информация, содержащаяся в изображениях, может быть
представлена совершенно разными способами. Наиболее важными являются
пространственное изображение (раздел 2.2) и представление через волновое число
(раздел 2.3). Эти представления рассматривают пространственные данные с
разных точек зрения. Поскольку различные представления являются полными и
эквивалентными, они могут быть преобразованы одно в другое. Преобразование
между пространственным представлением и представлением через волновое число
является хорошо известным преобразованием Фурье, Это преобразование является
примером более общего класса оп^щиут — унитарных преобразований (раздел 2.4).
Во-вторых, мы рассматриваем, как эти представления могут быть обработаны
с помощью цифровых компьютеров. Как адекватным образом представить
изображения через массивы дискретных чисел? Как эффективно обрабатывать эти
данные? Можно ли получить быстрые алгоритмы для преобразования одного
представления в другое. Ключевым примером является быстрое преобразование Фурье,
рассматриваемое в разделе 2.5.
2.2. Пространственное представление цифровых изображений
2.2.1. Пиксель и вексель
Изображения образуют пространственное распределение энергетической
освещенности на плоскости. Математически говоря, пространственное распределение
энергетической освещенности можно описать как непрерывную функцию двух
пространственных переменных:
Е(х,,х^) = Е(х). (2.1)
Компьютеры обрабатывают не изображения, а только массивы дискретных
чисел. Таким образом, требуется представлять изображения в виде двумерных
массивов точек. Точка на 2-D сетке называется пикселем (pixel или pel). Эти названия
являются сокращениями понятия picture element (элемент изображения). Пиксель
представляет энергетическую освещенность в соответствующем месте сетки. В
простейшем случае пиксели располагаются на прямоугольной сетке. Положение
пикселя задается с помощью общепринятого обозначения для матриц. Первый
Глава 2. Представление изображений
г
1
^ m
о
о
М-1
у
1
и
г
1
Столбцы
п
N-1
i
X
Z
у у у.-'.
'Уу-ХУ
m
У
1
zq
г
у у у ^
П
X J
у
^
Рис. 2.1. Представление цифровых изображений через массивы дискретных точек на
прямоугольной сетке: а — 2-D изображение; б — 3-D изображение
индекс, т, обозначает положение в строке, второй, п, положение в столбце
(рис. 2.1, а). Если цифровое изображение содержит Мх 7Vпикселей, т.е.
представляется матрицей MxN, то индекс п пробегает от О до Л/^- 1, а индекс m - от О до 71/ -1.
Мзадает число строк, 7V— число столбцов. В соответствии с матричным
обозначением вертикальная ось (ось у) направлена сверху вниз, а не наоборот, как это
принято в графах. Горизонтальная ось (ось х) направлена, как обычно, слева направо.
Каждый пиксель представляет не просто точку на изображении, а скорее
прямоугольную область, элементарную ячейку сетки. Значение, соответствующее
пикселю, должно представлять среднюю энергетическую освещенность в
соответствующей ячейке надлежащим образом. На рис. 2.2 показано одно и то же изображение,
представленное с помощью разного числа пикселей. При больших размерах
пикселей (рис. 2.2, а, б) не только пространственное разрешение является плохим, но
и появляются неоднородности уровней яркости на границах пикселей, как
мешающие искажения, отвлекающие наше внимание от содержания изображения. По
мере того как пиксели становятся меньше, эффект становится менее выраженным,
вплоть до момента, когда мы получаем ощущение пространственно непрерывного
изображения. Возникает это ощущение, когда пиксели становятся меньше, чем
пространственная разрешающая способность нашей зрительной системы. Вы
можете убедиться в этом соответствии, наблюдая рис. 2.2 с разных расстояний.
Какое количество пикселей является достаточным? Общего ответа на этот
вопрос не существует. Для визуального наблюдения цифрового изображения размер
пикселей должен быть меньше, чем пространственная разрешающая способность
зрительной системы с номинального расстояния, на котором находится
наблюдатель. Для конкретной задачи размер пикселей должен быть меньше, чем самые
мелкие размеры объектов, которые мы хотим изучить. Однако мы, как правило,
обнаруживаем, что доступные датчики (см. раздел 1.7.1) ограничивают число
пикселей скорее, чем требования прикладных задач. Даже матрица датчика с высоким
разрешением 1000 х 1000 элементов имеет относительное пространственное
разрешение всего лишь 101 Это довольно плохое разрешение в сравнении с другими
измерениями, такими, как измерения длины, электрического напряжения или
2.2. Пространственное представление цифровых изображений 43
Рис. 2.2. Цифровые изображения состоят из пикселей. На квадратной сетке каждый
пиксель представляет квадратную область изображения. На рисунке приводится одно
и то же изображение с количеством пикселей: а — 3 х 4; б - 12 х 16; в - 48 х 64;
г - 192 X 256. Если изображение содержит достаточное количество пикселей,
кажется, что оно непрерывно
частоты, которые могут быть выполнены с относительными разрешениями
гораздо выше 10"^ Однако эти методы позволяют произвести измерение только в
отдельной точке, в то время как изображение 1000 х 1000 содержит один
миллион точек. Таким образом, мы проникаем в суть пространственных изменений
сигнала. Если мы рассмотрим последовательности изображений, станут
очевидными также временные изменения и, таким образом, кинематика и
динамика изучаемого объекта. Таким образом, изображения раскрывают целый
новый мир информации.
Прямоугольная сетка является всего лишь простейшей геометрией для
цифрового изображения. Возможны другие геометрические распределения
пикселей и геометрические формы элементарных ячеек. Поиск возможных
конфигураций является 2-D аналогом классификации кристаллической структуры
в 3-D пространстве — это процесс, который знаком специалистам в области физики
твердого тела, минералогии и химии. В кристаллах наблюдаются периодические
3-D структуры распределения их атомов, ионов или молекул, которые можно
классифицировать по их симметриям и геометрии элементарной ячейки. В 2-D
случае классификация дискретных сеток гораздо проще, чем в 3-D случае. Если
44 Глава 2 Представление изображений
Рис. 2.3. Три возможные регулярные сетки в 2-D: а - треугольная сетка; б -
квадратная сетка; в — гексагональная сетка
гп, п-1
т-1, п
т, п
т+1, п
т, п+1
т-1, п-1
т, п-1
т+1, п-1
т-1, п
т, п
т+1, п
т-1, п+1
т, п+1
т+1, п+1
1
Рис. 2.4. Окрестности на прямоугольной сетке: а - 4-компонентная окрестность;
б - 8-компонентная окрестность; в — темная область рассматривается как один объект
(связная область) при 8-компонентных окрестностях, но как два объекта при 4-ком-
понентных окрестностях
мы рассматриваем правильные многоугольники, существует только три воз-
можт>1х случая: треугольники, квадраты и шестиугольники (рис. 2.3).
3-D пространства (и даже пространства более высокой размерности) также
представляют интерес в обработке изображений. В трехмерных изображениях
пиксель превращается в воксель (voxel) — сокращение от volume element (элемент
объема). На прямоугольной сетке каждый воксель представляет средний уровень
яркости прямоугольного параллелепипеда. Положение вокселя задается тремя
индексами. Первый, — к, обозначает глубину, т — строку ил- столбец (рис. 2.1,6).
Декартова сетка, т.е. гиперкубический пиксель, является самым общим
решением для цифровых данных, поскольку это единственная геометрия, которая
может быть легко расширена на случай произвольных размерностей.
2.2.2. Окрестностные соотношения
Важным свойством дискретных изображений является их окрестностные
соотношения, поскольку они определяют то, что мы будем рассматривать как связную
область и, следовательно, как цифровой объект. Двумерная прямоугольная сетка
показывает, к сожалению, что существует два возможных способа определения
соседствующих пикселей (рис. 2.4, а, б). Мы можем рассматривать пиксели как
соседние элементы либо когда они имеют общее ребро, либо когда они имеют по
2.2. Пространственное представление цифровых изображений
4р+1
L
х^
/ / /
У
у^
и
уУ
у
у у
У^ / /
у
у
X
у
Рис. 2.5. Три вида окрестностей на 3-D кубической сетке: а — 6-компонентная
окрестность: воксели с общими гранями; б — 18-компонентная окрестность: воксели с
общими ребрами; в — 26-компонентная окрестность: воксели с общими углами
меньшей мере общий угол. Таким образом, пиксель имеет четыре или восемь
соседних элементов, и мы говорим о 4-компонентной окрестности или 8-компонент-
ной окрестности.
Оба типа окрестностей необходимы для правильного определения
объектов как связных областей. Область или объект называется связным, когда
можно достигнуть любого пикселя в области, переходя от одного соседнего
пикселя к следующему. Темный объект, изображенный на рис. 2.4, в, является одним
объектом при 8-компонентных окрестностях, но состоит из двух объектов при
4-компонентных окрестностях. Однако белый фон демонстрирует то же
свойство. Таким образом, мы имеем либо две пересекающиеся связные области при
8-компонентных окрестностях, либо две разделенные области при
4-компонентных окрестностях. Такая несовместимость может быть преодолена, если
положить, что объекты имеют 4-компонентные окрестности, а фон имеет
8-компонентные окрестности, или наоборот.
Эти сложности возникают не только с прямоугольной сеткой. С треугольной
сеткой мы можем определить 3-компонентные окрестности и 12-компонентные
окрестности, в которых соседние элементы имеют либо общее ребро, либо общий
угол соответственно (рис. 2.3, а). На гексагональной сетке, однако, мы можем
определить только 6-компонентную окрестность, поскольку пикселей, которые имеют
общий угол, но не имеют общего ребра, не существует. Соседствующие пиксели
всегда имеют одно общее ребро и два общих угла. Вопреки этому преимуществу,
гексагональные сетки почти не используются в обработке изображений, так как
датчики получения изображений образуют пиксели на прямоугольной сетке.
Фотодатчики на сетчатке человеческого глаза, однако, имеют гексагональную
форму [210].
В трехмерных пространствах окрестностные соотношения являются более
сложными. На сегодняшний момент существуют три способа описания
соседних элементов: воксели с общими гранями, общими ребрами и общими углами.
Эти определения вытекают в 6-компонентную окрестность, 18-компонентную
окрестность и 26-компонентную окрестность соответственно (рис. 2.5). И снова
мы вынуждены определить две разные окрестности для объектов и фона, для
того чтобы прийти к совместному определению связных областей. Объекты и
фон должны быть с 6-компонентными и 26-компонентными окрестностями,
соответственно, или наоборот.
Глава 2. Представление изображений
2.2.3. Дискретная геометрия
Дискретная природа цифровых изображений приводит к необходимости
переопределить элементарные геометрические свойства, такие, как расстояние, наклон
линии, и координатные преобразования — перемещение, вращение и
масштабирование. Эти величины требуются для определенрш и измерения геометрических
параметров объекта в цифровом изображении.
Для того чтобы рассматривать дискретную геометрию правильно, мы вводим
сеточный вектор, который представляет положение пикселя. Следующее
рассуждение ограничивается прямоугольными сетками. Сеточный вектор определяется в
2-D, 3-D изображениях и в 4-D пространственно-временных изображениях как
г =
пАх
тАу
9 ^/,/И,«
пАх
тАу
JAz
9 ^kj,m,n
пАх
тАу
lAz
kAt
1
(2.2)
Для измерения расстояния, кроме того, возможно перенести евклидово
расстояние из непрерывного пространства на дискретную сетку с помощью определения
d^{ry)=\\r-r\\=\{n--rifAx^^{m-myAy^Y' (2.3)
Эквивалентные определения можно дать для случаев более высоких
размерностей. В цифровых изображениях часто используются другие метрики. Расстояние
«городской квартал»
df^(r,/) = \n-n\'^\m-m'\ (2.4)
задает длину пути, если мы можем передвигаться только в горизонтальных и
вертикальных направлениях (4-компонентные окрестности). Противоположно,
расстояние «шахматная доска» определяется как максимум из горизонтального и
вертикального расстояний
d^ (г, /) = тах(| п-п1\т-т'\). (2.5)
Для практического применения только евклидово расстояние является значимым.
Это единственная метрика на множестве цифровых изображений, которая
сохраняет изотропию непрерывного пространства. При расстоянии «городской квартал», к
примеру, расстояния в направлении диагоналей длиннее, чем евклидово расстояние.
Кривая с одинаковыми расстояниями до некоторой точки не является окружностью,
а представляет собой кривую ромбовидной формы — квадрат, наклоненный на 45^
Перемещение на дискретной сетке определяется только в числах, кратных
пиксельным или воксельным расстояниям:
/1 . = И
т,п т\п^
(2.6)
Т.е. посредством прибавления сеточного вектора t^,^.
Подобным образом масштабирование возможно только для целых чисел,
кратных масштабному множителю посредством взятия каждого ^-го пикселя на
каждой/?-й линии. Поскольку эта дискретная операция масштабирования выполняет
подвыборку сетки, остается увидеть, является ли масштабированная версия
изображения все еще достоверным представлением.
2.2, Пространственное представление цифровых изображений
Рис. 2.6. Дискретная линия хорошо определяется только в направлениях осей и
диагоналей. Во всех других направлениях линия кажется ступенчатой негладкой
последовательностью пикселей
Вращение на дискретной сетке является невозможным, за исключением
нескольких тривиальных углов. Условием является то, что все узлы повернутой
сетки должны совпадать с узлами сетки. На прямоугольной сетке только повороты на
углы, кратные 180°, являются возможными, на квадратной сетке на углы, кратные
90°, а на гексагональной сетке на углы, кратные 60°.
Как правило, правильное представление даже простых геометрических
объектов, таких, как линий и окружностей, не является очевидным. Линии хорошо
определимы только при углах со значениями, кратными 45°, тогда как для всех
других направлений они появляются как негладкие, образующие ступенчатые
последовательности пикселей (рис. 2.6).
Все эти ограничения цифровой геометрии вызывают ошибки в положениях,
размерах и ориентациях объектов. Необходимо внимательно исследовать
последствия этих ошибок для последующей обработки (глава 9).
2.2.4. Квантование
При использовании компьютера, измеренной энергетической освещенности на
плоскости изображения необходимо поставить в соответствие ограниченное
число Q дискретных уровней яркости. Этот процесс называется квантованием. Число
требуемых уровней квантования в обработке изображений можно рассматривать
относительно двух критериев.
Первый критерий связан с тем, что наша зрительная система не способна
распознать ступени уровней яркостей, также как мы не можем увидеть отдельные
пиксели в цифровых изображениях. На рис. 2.7 демонстрируются изображения,
квантованные с различными ступенями уровней яркости. Очевидно, что низкое число
уровней яркости приводит к возникновению ложных: контуров и делает очень
сложным распознавание объектов, которые демонстрируют медленное
пространственное изменение в уровнях яркости. В напечатанных изображениях кажется, что 16
ступеней уровней яркости достаточно, однако на мониторе мы все еще увидели бы
ступени уровней яркости.
Как правило, данные изображения квантуются в 256 уровней яркости.
Тогда каждый пиксель занимает 8 бит или 1 байт. Этот битовый размер хорошо
подходит к архитектуре стандартных компьютеров, которые могут обращаться
к памяти побайтово. Кроме того, разрешающая способность является доста-
Глава 2. Представление изображений
Рис. 2.7. Иллюстрация квантования. Одно и то же изображение показано с
различными уровнями квантования: а—16;б — 8;в-4;г-2. Слишком маисе число
уровней квантования создает ложные контуры и приводит к частичному и полному
исчезновению признаков с низкой контрастностью
точно хорошей, для того чтобы создать иллюзию непрерывного изменения в
уровнях яркости, поскольку относительное разрешение нашей зрительной
системы по интенсивности не лучше, чем приблизительно 2%.
Другой критерий относится к задаче формирования изображений. Для
простого использования в машинном зрении, где нужно вьщелить и измерить
равномерно освещаемые объекты, достаточно только двух уровней квантования, т.е.
бинарное изображение. Другие области применения, такие, как спектроскопия
формирования изображений или медицинская диагностика с использованием
рентгеновских изображений, требуют разрешения слабых изменений в
интенсивности. Тогда стандартное 8-битовое разрешение являлось бы слишком низким.
2.2.5. Представление изображений со знаком
Обычно мы рассматриваем «яркость» (энергетическая освещенность или
энергетическая яркость) как величину положительную. Следовательно, кажется
естественным представить ее с помощью чисел без знака, изменяющихся в диа-
2.2. Пространственное представление цифровых изображений
пазоне чисел с 8-битовым представлением, к примеру, от О до 255. Однако
такое представление вызывает проблемы, как только мы начинаем выполнять
арифметические операции с изображениями. Вычитание двух изображений
является простым примером, который может дать отрицательные числа.
Поскольку отрицательные уровни яркости не могут быть представлены, они
прокручиваются и появляются как большие положительные значения. Число -1, например,
переходит в положительное значение 255, заданное так, что -1 по модулю 256 = 255.
Таким образом, мы сталкиваемся с проблемой двух разных представлений
уровней яркости, как 8-битовые числа со знаком и без знака. Соответственно, нам
необходимо иметь несколько вариантов каждого алгоритма: один для уровней
яркости со знаком, один для уровней без знака и другие для смешанных случаев.
Единственным решением этой проблемы является обработка уровней яркости
всегда как чисел со знаком. В 8-битовом представлении мы можем преобразовать
числа без знака в числа со знаком, используя вычитание 128:
q' = (q-l2S) mod 256, 0<9<256. (2.7)
Тогда интенсивность среднего уровня яркости 128 перейдет в ноль уровней
яркости, а уровни яркости ниже, чем это среднее значение, станут отрицательными.
По существу, мы рассматриваем уровни яркости при этом представлении как
отклонения от среднего значения.
Такая операция преобразует уровни яркости без знака в уровни яркости со
знаком, которые могут храниться и обрабатываться как таковые. Только для
воспроизведения изображений на экране мы должны преобразовать уровни яркости
снова в уровни без знака, используя обратную поточечную операцию:
^ = (^4128) mod 256, -128<^<128, (2.8)
которая является такой же операцией, как в уравнении (2.7), поскольку все
вычисления выполняются по модулю 256.
2.2.6. Восприятие яркости зрительной системой человека
Что касается квантования, важно знать, как человеческая зрительная система
воспринимает уровни и какие яркостные различия может распознавать. На рис. 2.8
продемонстрировано, что малый прямоугольник со средней яркостью кажется ярче на
шзгиоягошс^*
Рис. 2.8. Контекст определяет, насколько «ярким» мы воспринимаем объект. Оба
квадрата имеют одну и ту же яркость, но квадрат на темном фоне кажется ярче, чем
квадрат на светлом фоне. Оба квадрата кажутся одинаково яркими, только если они
соприкасаются
Глава 2. Представление изображений
Рис. 2.9. Высококонтрастная сцена, зафиксированная с помощью ПЗС-камеры с
линейным контрастом и малой (а), и большой (б) апертурой
темном фоне, чем на светлом, хотя его абсолютная яркость является одной и той
же. Такой обман исчезает только тогда, когда две области являются смежными.
Зрительная система человека проявляет скорее логарифмический, чем
линейный отклик. Это означает, что мы воспринимаем относительные и не
воспринимаем абсолютные различия с тем же успехом. В широком диапазоне уровней
яркости мы можем разрешить относительные различия, равные приблизительно 2%.
Это пороговое значение зависит от некоторых факторов, особенно от
пространственной частоты (длины волны) структуры, используемой для исследования. При
определенной длине волны яркостное разрешение является оптимальным.
Характеристики зрительной системы человека, рассмотренные выше,
полностью отличаются от тех, которыми обладает система компьютерного зрения. Как
правило, всего лишь 256 уровней яркости являются разрешенными. Таким
образом, оцифрованное изображение имеет гораздо более низкую динамику, чем
зрительная система человека. По этой причине качество оцифрованного
изображения, особенно сцены с высоким яркостным контрастом, кажется нам худшим по
сравнению с тем, что мы непосредственно видим. В цифровом изображении,
полученном из такой сцены с помощью линейного датчика изображения, либо
светлые части переэкспонированы, либо темные части недоэкспонированы.
Высококонтрастная сцена на рис. 2.9 демонстрирует это.
Несмотря на то что относительное разрешение намного лучше, чем 2% на
светлых частях, оно плохое на темных частях. При уровне яркости 10 яркостное
разрешение составляет всего лишь 10%.
Одно из решений, для того чтобы справиться с большой динамикой в сценах,
используется в видеокамерах, которые, как правило, преобразуют
энергетическую освещенность Е в уровень яркости д не линейно, а по экспоненциальному
закону:
д = Е\ (2.9)
Экспонента у показывает гамма-значение. Как праврито, у имеет значение 0,4. С
помощью такого преобразования можно приблизиться к логарифмической
характеристике зрительной системы человека. Диапазон контрастности значитель-
2.3. Пространство волновых чисел и преобразование Фурье
hIIIR ТгггРРггР BB~rff^'^^M?^ JlLLLL^K^
^^^Tj 11,1,,1.,.,1 I -t-j-^'jM»''-^^ Mill |П^^^^
-"^^Имг i 1 "^M^^^ffiTi—Г-^^^Ы" "i I ' ' —[""1 1 —U-U-^^B-|
^^^^^^^^^^^^^^ШшЩ I 1 I |IIIIIl]^^E—lX I I I I I ■иЦЛ.Х.ОГРДИ!]
Рис. 2.10. Изображение можно рассматривать состоящим из базисных изображений,
в которых только один пиксель не равен нулю
но улучшается. Если мы предположим минимальное относительное яркостное
разрешение, равное 10%, и 8-битовый диапазон шкалы серого цвета, мы получаем
диапазоны контрастности 25 и 316 при у= 1 и у= 0,4 соответственно.
Для многих научных применений, однако, существенным является то, что
сохраняется линейное соотношение между яркостью наблюдаемого объекта и
уровнем яркости в цифровом изображении. Тогда гамма-значение нужно положить
равным единице для таких применений.
2.3. Пространство волновых чисел и преобразование Фурье
2.3.1. Векторные пространства
В разделе 2.2 целью обсуждения было пространственное представление цифровых
изображений. Не упоминая этого явно, мы считали, что изображение состоит из
отдельных пикселей (рис. 2.10). Тогда мы можем составить любое изображение с
помощью базисных изображений, в которых лишь один пиксель имеет значение
единица, в то время как все остальные пиксели равны нулю. Обозначим такое базисное
изображение с единицей, расположенной в строке т и столбце «, с помощью
Г1
Р:
т = т' Ап = п
Ут\п
(2.10)
[О иначе.
Любое произвольное скалярное изображение можно тогда представить через
базисные изображения в уравнении (2.10) как
М-\ N-\
G = I,l9n.,r-"P,
(2.11)
w=0 и=0
где д^^ обозначает уровень яркости в положении (т, п).
Глава 2. Представление изображений
Можно легко убедиться, что базисные изображения '""Р формируют ортонор-
мированный базис, И наконец, введем внутреннее произведение (также известное как
скалярное произведение), которое может быть определено подобно скалярному
произведению векторов. Внутреннее произведение двух изображений Си Н
определяется как
М-\ N-\
(G\H) = j;^g„J„^„, (2.12)
/и=0 и=0
где обозначение внутреннего произведения, позаимствованное из квантовой
механики, используется для того, чтобы отличить его от умножения матриц, которое
обозначается GH.
Из уравнения (2.12) можно сразу же получить соотношение ортонормирован-
ности для базисных изображений '""Р:
М-\ N-\
УУ .
т=0 и=0
'^ " Р^ ^ ^ '" Р^ у, ^ ^v «,' ^и' .,"- (2.13)
Отсюда следует, что внутреннее произведение двух базисных изображений
равно нулю, если взяты два различных изображения. Скалярное произведение
базисного изображения самого на себя равно единице. Тогда MN базисных
изображений образуют Мх 7V-MepHoe пространство на множестве действительных чисел.
Аналогия к хорошо известным дву- и трехмерным векторным пространствам
М^и R^ поможет нам понять, как можно получить другие представления для
изображений. Изображение Л/х 7V представляет собой точку в векторном пространстве
размерностью Мх N, Если мы изменим координатную систему, то изображение
останется тем же, но изменятся его координаты. Это означает, что мы просто
рассматриваем одну и ту же часть информации с различных точек зрения. Из этого
элементарного факта мы можем прийти к следующим важным заключениям. Во-
первых, все представления эквивалентны друг другу. Каждое дает полное
представление изображения. Во-вторых, соответствующие координатные
преобразования позволят нам перейти от одного представления к другому и обратно.
Из всего многообразия всех возможных представлений, кроме
пространственного, только одно имеет огромное значение для обработки изображений. Его
базисными изображениями являются периодические структуры, а «координатное
преобразование», которое позволяет перейти к нему, известно как
преобразование Фурье. На рис. 2.11 показано, как одно и то же изображение, которое было
сформировано из отдельных пикселей на рис. 2.10, составляется из
периодических структур.
Периодическая структура, прежде всего, характеризуется расстоянием
между двумя максимумами или длиной повторения, длиной волны Я (рис. 2.12).
Направление структуры наилучшим образом описывается вектором, нормальным
к линиям постоянных уровней яркости. Если зададим длину этого вектора к
равной 1/Я:
|Л| = 1/Я, (2.14)
то длина волны и направление могут быть выражены одним вектором, волновым
числом ft. Компоненты ft = [к^, к^У непосредственно задают число длин волн в
единицу длины в соответствующем направлении. Волновое число ft может быть
использовано для описания периодических структур в случае любой размерности.
2.3. Пространство волновых чисел и преобразование Фурье
Рис. 2.11. Первые 56 периодических структур, базисных изображений
преобразования Фурье, из которых состоит изображение на рис. 2.10
Ах = ХФ/2л Г
Рис. 2.12. Описание 2-D периодической структуры с помощью длины волны Я,
волнового числа к и фазы (р
Для того чтобы завершить описание периодической структуры, требуются еще
две величины: амплитуда г и положение структуры относительно начала координат
(рис. 2.12). Положение задается как расстояние Ах первого максимума от начала
координат. Поскольку это расстояние в большинстве случаев равно длине волны,
самым лучшим будет задать его как фазовый угол (р = Itc^/X = 2лк-Ах (рис. 2.12), а
полное описание периодической структуры задается как
rcos(2nk^x-(p). (2.15)
Такое определение, однако, математически довольно затруднительное. Для нас
предпочтительнее простой множитель, на который должны умножаться базисные
структуры, для того чтобы получить простое разложение на периодические
структуры. Это возможно только при использовании комплексных чисел д = г exp(-i(p) и
комплексной экспоненциальной функции Qxp(i(p) = cos(p + i sin(p. Действительная
часть д ехр(2тк^х) задает периодическую структуру в уравнении (2.15):
Щдехр(2тк^х)) = rcos(27Tk^x -ср). (2.16)
Таким образом, разложение на периодические структуры требует расширения
области определения с действительных чисел до комплексных чисел. Действитель-
Глава 2. Представление изображений
позначное изображение тогда рассматривается как комплекснозначное
изображение с нулевой мнимой частью.
Предмет оставшейся части этой главы скорее математический, однако он
закладывает основу для представления и низкоуровневой обработки изображений.
После введения как непрерывного, так и дискретного преобразования Фурье в
разделах 2.3.2 и 2.3.3 мы обсудим все свойства преобразования Фурье, которые
являются значимыми в обработке изображений, в разделе 2.3.4. Воспользуемся тем,
что мы имеем дело с изображениями, что позволяет легко проиллюстрировать
некоторые сложные математические соотношения.
2.3.2. Одномерное преобразование Фурье
Сначала мы рассмотрим одномерное преобразование Фурье.
Определение 2.1 (1-D ПФ). Если д(х): R -► С является функцией, интегрируемой с
квадратом, т.е.
]\g(x)\'dx<oo^
тогда преобразование Фурье функции д(х), д(к) задается как
(2.17)
(2.18)
Преобразование Фурье отображает векторное пространство функций
интегрируемых с квадратом в само себя. Обратное преобразование Фурье функции д{к)
приводит к исходной функции д(х):
(2.19)
Преобразование Фурье можно записать в более компактной форме, если
использовать сокращение
w = e"'' (2-20)
и записать интеграл как внутреннее произведение:
{д{х) I h(x)) = J g\x)h(x)dx^
(2.21)
где * обозначает сопряженный комплекс. Тогда
9{k) = (w'"\g{x)). (2.22)
Функция W' может быть мысленно представлена как вектор, который
поворачивается против часовой стрелки по единичной окружности в комплексной
плоскости. Переменная t задает число оборотов.
Иногда также удобно использовать операторную форму записи для
преобразования Фурье:
g = <Fg и д = <р-'д. (2.23)
Функция и ее преобразование, пара преобразований Фурье, просто обозначается как
д(х) о . g(k).
2.3. Пространство волновых чисел и преобразование Фурье
Для дискретного преобразования Фурье (ДПФ), волновое число является теперь
целым числом, которое определяет, сколько длин волн помещается в интервале с N
элементами.
Определение 2.2 (1-D ДПФ). ДПФ отображает упорядоченный М-мерный кортеж из
комплексных чисел д^, комплекснозначный вектор
9=[9o^9i^-^9N-if^ (2.24)
в другой вектор д векторного пространства той же размерности N.
1
Л^-1
^ п=0
(
\
1п\гю
N
, 0<v<N.
(2.25)
Обратное преобразование задается как
Л^-1
9п=^9о^^Р
v=0
Ininv
N
0<n<N,
(2.26)
Причина, по которой мы используем здесь несимметричное определение для
ДПФ, объясняется в разделе 2.3.6.
И снова полезно использовать удобное сокращение для ядра ДПФ; сравните
уравнение (2.20):
1/дг (2т^
w^=w =ехр
N
(2.27)
Так же как и непрерывное преобразование Фурье, ДПФ можно рассматривать
как внутреннее произведение вектора д с набором из N ортонормированных
базисных векторов:
Тогда
*„=^K,w;.w-,...,w<;-""]'.
^"4|-»"^"=^<*"|«>=^*:«.
(2.28)
(2.29)
Обратите внимание на вторую компактную запись скалярного произведения в
правой части уравнения, использующую верхний индекс Т, который включается
для того, чтобы получить комплексно сопряженное значение первого вектора.
Уравнение (2.29) означает, что коэффициент д^ в Фурье-пространстве
получается при проектировании вектора д на базисный вектор Ь^. 7Vбазисных векторов
Ь^ являются ортогональными друг другу:
КК=^и-.'=\^ (2.30)
[U иначе.
Следовательно, множество векторов Ь^ образует ортонормированный базис
для векторного пространства. Это означает, что каждый вектор векторного
пространства может быть выражен как линейная комбинация базисных векторов
Глава 2. Представление изображений
'\/\/\/\г ^^\/\/\/\.
Рис. 2.13. Первые 9 базисных функций ДПФ для 7V= 16; а - действительная часть
(косинусная функция); б — мнимая часть (синусная функция)
Фурье-пространства. ДПФ вычисляет проекции вектора д на все базисные
векторы сразу, т.е. компоненты вектора д в направлении базисных векторов. В этом
смысле ДПФ является просто особым видом координатного преобразования в
М-мерном векторном пространстве. Математически ДПФ отличается от более
известных координатных преобразований, таких, как поворот в трехмерном
векторном пространстве (раздел 7.2.2), только тем, что векторное пространство
определяется на области комплексных чисел вместо вещественных и имеет гораздо
большую размерность.
Действительная и мнимая части базисных векторов являются дискретными
синусными и косинусными функциями разных длин волн (рис. 2.13). Индекс
V обозначает, сколько раз длина волны функции попадает в интервал [О, М].
Базисный вектор Ь^ является постоянным действительным вектором.
Проекция на этот вектор приводит к среднему значению элементов вектора д,
умноженного на v/V.
Помимо непрерывного и дискретного преобразований Фурье существуют еще
две другие формы, с которыми вы можете быть знакомы: ряд Фурье (РФ),
который отображает функцию на конечном интервале [О, Ах] в бесконечный ряд
коэффициентов, и бесконечное дискретное преобразование Фурье, которое
отображает бесконечный ряд комплексных чисел в конечный интервал [0,1/Ax] в
Фурье-пространстве. Поэтому в качестве иллюстрации сравним ДПФ с этими
преобразованиями (табл. 2.1).
2.3. Пространство волновых чисел и преобразование Фурье 5
Таблица 2.1. Сравнение непрерывного преобразования Фурье (ПФ), ряда
Фурье (РФ), бесконечного дискретного преобразования Фурье (БДПФ) и
дискретного преобразования Фурье (ДПФ) в одномерном случае (w == е^"")
Тип
Прямое преобразование
Обратное преобразование
ПФ:л:ДеМ
РФ:х€[0,Ах],
veZ
mO:n,VGZ^
oo
9(x)= jm^^'^dk
,vx/Ax
9ik) = X fi'«w-
■nkAx
1 N-\
^ и=0
9(х) = X 9t,w^
1/Ax
0
N-\
y=0
2.3.3. Многомерное преобразование Фурье
Преобразование Фурье может быть легко расширено для многомерных сигналов.
Определение 2.3 (Многомерное ПФ). Если д{х) \Ж —> С является функцией,
интегрируемой с квадратом, т.е.
] I д{х) Г дГх = {д(х) I д(х)) =|| д(х) \\1< -
тогда преобразование Фурье функций д(х), д(к) задается как
9(к) =
«образе
S'(^) =
oo
= \ g(x)Qxp(^-27cik'
)вание Фурье как
= J g(k)Qxp(^2mk^,
'x)d"'x
к)й"'к =
= (w^'*
= (w--'*
\9(x))\
1^(Л)).'
(2.31)
(2.32)
(2.33)
Скалярное произведение в экспоненте ядра х^к позволяет разложить
преобразование Фурье, т.е. можно записать как
,х'к
w*'^^
(2.34)
р=\
Дискретное преобразование Фурье рассматривается здесь для двумерного
случая. Расширение на случай больших размерностей не вызывает затруднений.
Глава 2. Представление изображений
Определение 2.4 (2-D ДПФ). 2-D ДПФ отображает комплекснозначные матрицы
размерностью MxNe комплекснозначные матрицы размерностью Мх N:
1 ^'^' { 2пти\
9и.о = Т^ 2.2.9'ш,„ ехр -— ехр
Ininv
N
или
1 М-\ {N-1
w
м
(2.35)
(2.36)
Во второй строке используется сокращение, определенное уравнением (2.27).
Так же как и в одномерном случае, ДПФ разлагает матрицу на множество из NM
базисных матриц, которые образуют Nx М-мерное векторное пространство на
поле комплексных чисел. Базисные матрицы имеют форму
1
^ 4Ш
MxN
W
W
W
о
W
(М-1)м
м
W
и 2и
W*;-'^"]. (2.37)
в этом уравнении базисные матрицы выражаются как векторное произведение
вектора-столбца на вектор-строку, которые образуют базисные векторы одномерных
ДПФ (уравнение 2.28). Это отражает сепарабельность ядра 2-D ДПФ.
Тогда снова 2-D ДПФ может быть записано как внутреннее произведение
^''.^>=-7T^K^>l^)'
л/Ш
(2.38)
где внутреннее произведение двух комплекснозначных матриц задается как
{(?|я)=х10:,„л.,„
/я=0 и=0
Обратное 2-D ДПФ задается как
М-\ N-\
9.Г. = SI^„,.wrw- =4Ш{В_„^_„ IG).
u=0 L>=0
(2.39)
(2.40)
2.3.4. Свойства преобразования Фурье
В этом разделе мы рассмотрим основные свойства непрерывного и
дискретного преобразований Фурье. Мы обращаем внимание на те свойства ПФ,
которые являются наиболее значимыми для обработки изображений. Вместе с
некоторыми основными парами преобразований Фурье (>-R5), эти общие свойства
(>-R4, >-R7) формируют мощную основу, с которой дополнительные свойства
2J. Пространство волновых чисел и преобразование Фурье
преобразования Фурье и преобразований многих функций могут быть получены
без особых усилий.
Периодичность ДПФ. Ядро ДПФ в уравнении (2.25) показывает
характеристическую периодичность:
ехр -
2n\{n^lN)
'n
ехр
In'm
IT
w
{n+lN) _ ^,^«
= w" V/eZ. (2.41)
Определения ДПФ ограничивают пространственную область и Фурье-область
до конечного числа значений. Если мы не учитываем это ограничение и
вычисляем прямое и обратное преобразования для всех целых чисел, то мы обнаруживаем
из уравнений (2.38) и (2.40) такие же периодичности для функций в пространстве
и Фурье-области:
область волновых чисел ди+км,о+ш = 9u,v' ^^' ^ ^ ^'
область пространства 9т^ш,п^ш = 9т,п ^ ^kje Z. (^-42)
Эти уравнения устанавливают периодическую повторяемость во всех
направлениях в обеих областях вне исходной области определения. Периодичность ДПФ
позволяет дать интересную геометрическую интерпретацию. В одномерном
случае граничные точки д^ ^ ид^ = д^ являются соседствующими точками. Мы можем
геометрически интерпретировать это свойство, нанеся точки вектора не на
конечную прямую, а на окружность, так называемое Фурье-кольцо (рис. 2.14, а). Это
представление имеет более глубокое значение, когда мы рассматриваем
преобразование Фурье как частный случай z-преобразования [148]. В двумерном случае матрица
переходит в тор (рис. 2.14, б), Фурье-тор.
Симметрии. Значимыми являются четыре типа симметрии для
преобразования Фурье:
четная 0("~^) = 9(^)^
нечетная 9(~^) - ~9(^)^
эрмитова д(-^) = б'*!-^). (2.43)
антиэрмитова 9(~^) ~ '~'9^{^)
б
■• тм^т км. йнф'зммпо ^мт
Рис. 2.14. Геометрическая интерпретация периодичности одно- и двумерного ДПФ
с помощью: а - Фурье-кольца; б - Фурье-тора
Глава 2. Представление изображений
Символ * обозначает комплексную сопряженность. Эрмитова симметрия
является важной, поскольку ядра ПФ (2.18) и ДПФ (2.25) являются эрмитовыми.
Любую функцию д{х) можно разложить на ее четную и нечетную части по
формулам / ч . / ч
.g(;,) = 2(f)z9(lil. (2.44)
Используя это разложение, преобразование Фурье можно разбить на косинусои-
дальное и синусоидальное преобразования:
д{к) = 2 J 'д{х) cos[2nk''x) d^x + 2i J 'g{x) s\n{2nk^x)d!^x^ (2.45)
0 0
Отсюда следует, что если функция является четной или нечетной, то ее
преобразование является также четной или нечетной функцией. Полные отношения симметрии:
действительная о • эрмитово
мнимая о • антиэрмитово
эрмитова о • действительное
антиэрмитова о—
четная о—
нечетная о—
действительная и четная о—
действительная и нечетная о—
мнимая и четная о—
мнимая и нечетная о—
мнимое
четное
нечетное (2.46)
действительное и четное
мнимое и нечетное
мнимое и четное
действительное и нечетное
ДПФ проявляет такие же симметрии, как ПФ (уравнения (2.43) и (2.46)). В
определении для четных и нечетных функций д{-х) = ±д{х) нужно лишь заменить х
соответствуюш;ими индексами: д^ = ±д^ или д^ _^ = ±д^ ^. Обратите внимание,
что благодаря периодичности ДПФ эти отношения симметрии могут также быть
записаны как
9-т,-п ^ —9т,п ~ 9м-т,М-п ~ —9т,п (2.47)
ДЛЯ четных (знак +) и для нечетных (знак -) функций. Это эквивалентно
перемещению центра симметрии из начала координат в точку [М/2, N/2Y.
Изучение симметрии имеет важные практические цели. Внимательное
рассмотрение симметрии позволяет сэкономить область памяти и ускорить алгориггмы.
Вещественные изображения относятся к такому случаю. Вещественные изображения могуг
быть сохранены в половине пространства как комплексные изображения. Из
отношения симметрии уравнения (2.46) мы можем заключить, что действительные функции
показывают эрмитово ДПФ:
9п ~ 9п ° * 9n-u ~ 9и 9
* ^ ^ ^ ^ ^ ♦ (2.48)
с7/и« %у тп <у M-u,N-u <Уии'
2.3. Пространство волновых чисел и преобразование Фурье
Комплекснозначные ДПФ от вещественных векторов, следовательно,
полностью определяются значениями в одном полупространстве. Другое
полупространство получается при отражении относительно центра симметрии [N/2],
Следовательно, нам необходимо такое же количество области памяти для ДПФ от
вещественного вектора, что и для самого вектора, поскольку необходимо хранить
только половину комплексного спектра.
В двумерном случае и случае более высоких размерностей дела обстоят не
намного сложнее. Преобразование Фурье от вещественного изображения
определяется полностью значениями одного полупространства, однако существует много
способов выбора полупространства. Это означает, что только один компонент
волнового числа офаничивается положительными значениями.
Преобразование Фурье от изображения Мх N можно представить через Мстрок
и Лу2+1 столбцов (рис. 2.15), предполагая, что Л/^четное. К сожалению, требуется
ЛУ2+1 столбцов, поскольку первый (/w = 0) и последний {т = М/2) столбцы
являются симметричными самим себе, согласно уравнению (2.48). Тогда кажется
невозможным переписать вещественное изображение с помощью его
комплексного преобразования Фурье, поскольку нам понадобится еще один столбец. Более
тщательное рассмотрение показывает, что такой подход тем не менее работает.
Первый и последний столбцы являются вещественными по причинам симметрии
^^oN-v ~ ^*ov ^ ^M/2N-v ~ ^*м/2 v ^' Слсдоватсльно, вещественную часть столбца М/2
можно хранить в мнимой части столбца 0.
В случае последовательностей вещественных изображений опять нам нужно
всего лишь полупространство для представления спектра. Физически имеет
наибольший смысл выбрать полупространство, которое содержит положительные
частоты. Противоположно случаю отдельного изображения мы получаем полное
пространство волновых чисел. Теперь мы можем определить пространственно
тождественные волновые числа Л и -Л как структуры, распространяющиеся в
противоположных направлениях.
Сепарабельность. Ядро преобразования Фурье является сепарабельным
(уравнение 2.34). Следовательно, преобразование сепарабельной функции является
также сепарабельным:
W W
Y[9iXp) о . Yidikp). (2.49)
р=\ /7=1
Это свойство является существенным при вычислении преобразований
многомерных функций из 1-D преобразований, поскольку многие из них являются сепара-
бельными.
Подобие. Теорема подобия определяет, как масштабирование координатной
системы влияет на преобразование Фурье. Лишь в одномерном случае функция
может быть масштабирована {х' = ах). В многомерном случае координатную
систему можно преобразовать более общим способом с помощью аффинного
преобразования {х'=Ах), т.е. новые базисные векторы являются линейными
комбинациями старых базисных векторов. Частным случаем является вращение
системы координат.
Теорема 2.1 (Подобие). Пусть а — ненулевое вещественное число, А — вещественная
обратимая матрица, aR — ортогональная матрица, представляющая вращение системы
координат (R~^ = BJ, UQiR = \). Тогда имеют место следующие отношения подобия:
62 Глава 2. Представление изображений
и
-1 М-1
-2 М-2
-М/2 М/2
М/2-1
>
"
)
0
III II
1 2 N/2-1
М/2-1.
V
N/2
-М/2"
-N/2
II I I
-1 О 1
Tl V
N/2-1
Рис. 2.15. a — полупространство, полученное при вычислении по алгоритму
преобразования Фурье в плоскости; начало отсчета волнового числа находится в нижнем
левом углу; б — ПФ с пропущенной половиной, дополненное и перераспределенное,
так что начало отсчета волнового числа находится в центре
(2.50)
Если функция сжата в пространственной области, она растянута в Фурье-области,
и наоборот. Вращение системы координат в пространственной области вызывает
идентичное вращение в Фурье-области.
Вышеупомянутые теоремы подобия неприменимы к дискретному
преобразованию Фурье, поскольку невозможно произвольное масштабирование и
вращение. Растяжение дискретной функции возможно только с помощью целого
множителя К (повышаюш,ая дискретизация), тогда вновь образованные дискретные
точки заполняются нулями:
^9^к)п =
\д^,^ n = 0,K,2K,.„(N-l)K
(2.51)
[О иначе.
Теорема 2.2 (Подобие, дискретный случай). Пусть д является комплекснознанным
вектором из N элементов uKeN. Тогда дискретное преобразование Фурье повышенно
дискретизированного вектора д^^^с KN элементами задается как
9гк
1 . . .
—д при gkN^^=g^.
(2.52)
Повышенная дискретизация с помощью множителя К, таким образом,
попросту сводится к ^-кратному повторению преобразования Фурье. Обратите внима-
2.3. Пространство волновых чисел и преобразование Фурье
ние, что из-за периодичности дискретного преобразования Фурье,
рассмотренного в начале этого раздела, g,^j^^^= д^.
Сдвиг. В разделе 2.3.1 мы рассматривали некоторые свойства базисных
изображений Фурье-пространства, комплексные экспоненциальные функции ехр(2шА:^дс).
Пространственный сдвиг этих функций приводит к умножению на фазовый множитель:
ехр(2л:1(л:-л:о)^А:) = ехр(-2л:1л:оА:)ехр(2л:1А:^л:). (2.53)
В качестве прямого следствия линейности преобразования Фурье мы можем
сформулировать следующую теорему о сдвиге:
Теорема 2.3 (Сдвиг). Если функция д(х) имеет преобразование Фурье д(к), тогда
д(х -jCq) имеет преобразование Фурье ехр(~2шлс^)5'(А:).
Таким образом, сдвиг в пространственной области не изменяет
преобразование Фурье, если не считать фазового изменения, зависящего от волнового
числа -2;гдс^А:.
Теорему сдвига можно также применить в Фурье-области. Сдвиг в Фурье-
области, д(к-к^), приводит к сигналу в пространственной области, который
модулируется комплексной экспоненциальной функцией с вектором волнового
числа к^: Qxp(27tixlx)g(x).
Свертка. Свертка является одной из самых важных операций при обработке
сигнала. Для непрерывного сигнала она определяется как
оо
ig*h)ix) = J hix')gix-x')d"'x\ (2.54)
В обработке сигнала функция h(x) обычно равна нулю везде, кроме небольшой
области вокруг нуля, и часто обозначается какмаска свертки. Таким образом,
свертка с функцией И(х) приводит к новой функции д\х), чьи значения являются, по
существу, взвешенным средним от д(х) в малой окрестности около х. Она
изменяет сигнал определенным образом, например, делает его более гладким. Поэтому
также называется фильтром.
Одно- и двумерная дискретные свертки определяются аналогично уравнению
(2.54) как
Л^-1 М-1 Л^-1
С7и ^^ п'<Уп-п'^ <Ут,п j^^ j^^ т'п'<Ут-т', п-п' /^ сс\
и'=0 т'=0 и'=0 V^. J j;
Теорема о свертке для ПФ и ДПФ утверждает:
Теорема 2.4 (Свертка). Если g(x)(g,G) имеет преобразования Фурье g{k)(g,G) и
h(x), (А, Н) имеет преобразования Фурье h(k)(h,H), тогда h'^g (h^g, H^G) имеет
преобразования Фурье й(к)д(к), (Nhg,MNHG):
ПФ: Кх)^д(х) о . h(k)g(kl
1-D ДПФ: h^g о . Nhg,
2-D ДПФ: H^G о • MNHG,
(2.56)
Таким образом, свертка двух функций означает умножение их преобразова
НИИ. Подобным образом свертка двух функций в Фурье-области означает умноже
Глава 2. Представление изображений
ние в пространственной области. Простота свертки в Фурье-пространстве
возникает из факта, что базисные функции Фурье-пространства, комплексные
экспоненциальные функции ехр(2шА:^дс) являются общими собственными функциями
всех операторов свертки. Это означает, что оператор свертки не изменяет эти
функции, если не считать умножения на некоторый множитель.
Из теоремы о свертке сразу становятся очевидными следующие свойства.
Свертка является:
коммутативной h^Q = ff^h,
ассоциативной h^^{h^^g) = {h^^h^^g, (2.57)
дистрибутивной относительно сложения {h^ + h^^g = h^^g -\r h^g).
Для того чтобы понять важность этих свойств свертки, мы отметим, что две
операции, которые на первый взгляд не выглядят таковыми, являются также
операциями свертывания: операция сдвига и все дифференциальные операторы.
В обоих случаях преобразование Фурье лишь умножается на комплексный
множитель. В случае операции сдвига это можно непосредственно увидеть из
теоремы о сдвиге (теорема 2.3). Маска свертки оператора сдвига 5 является
смещенным 5-распределением:
S{s)g{x) = 5{x-s)^g{x). (2.58)
Для частной производной функции в пространственной области теорема о
дифференцировании утверждает:
Теорема 2.5 (Дифференцирование). Если д(х) является дифференцируемой для всех х и
имеет преобразование Фурье д{к), тогда преобразование Фурье от частной
производной дд(х)/дх^ равно 27iik^g(k):
Inik^ д(к).
(2.59)
Теорема о дифференцировании вытекает непосредственно из определения
обратного преобразования Фурье в уравнении (2.33) при замене частной
производной интегралом Фурье.
Обратное преобразование Фурье от Ijdk^, т.е. соответствующей маске свертки,
не является больше обычной функцией (iTdk^ не является абсолютно
интегрируемой), а является производной от ^распределения:
2n:ik
^,. . й6(х) .. d
dx «-^0(Ьс
2\Л
ехр(-л:х^/а^)
а
(2.60)
Конечно, дифференцирование 5-распределения существует — как все свойства
распределения, - только в смысле предела последовательности функций, как и
показано в предьщущем уравнении.
Зная, что операторы производных и сдвигов являются операторами свертки,
мы можем использовать свойства, описанные в уравнении (2.57), для того чтобы
2.3. Пространство волновых чисел и преобразование Фурье
получить некоторые заключения. Поскольку любой оператор связки коммутирует
с оператором сдвига, связка является операцией, инвариантной относительно
сдвига. Кроме того, мы можем сначала продифференцировать сигнал, а затем
выполнить операцию свертывания, или наоборот, и получить один и тот же результат.
Свойства в уравнении (2.57) являются существенными для эффективного
вычисления операций свертывания.
Центральная предельная теорема. Центральная предельная теорема, главным
образом, известна благодаря своей значимости в теории вероятностей [149]. Однако
она также играет важную роль в обработке сигналов, поскольку является точной
формулировкой стремления каскадной свертки приблизиться к гауссовой форме
(<х ехр {-ах^)). Поскольку преобразование Фурье от гауссиана является также гаус-
сианом (>-R6), это означает, что как преобразование Фурье (передаточная функция),
так и маска свертки приближаются к виду гауссиана.
Таким образом, теорема о центральном пределе является центральной
благодаря исключительной роли функции Гаусса для обработки сигналов. Достаточные
условия, при которых теорема о центральном пределе является справедливой, могут
быть сформулированы различными способами. Мы используем здесь условия
из [149] и выражаем теорему по отношению к свертке.
Теорема 2.6 (Центральная предельная теорема). Пусть заданы N функций h^(x) с нулевым
оо оо ^ о
средним \xh^(x)dx и дисперсией (7^ = ^x^h^(x)dx с z = x/cr, С7^=Х^«> f^oeda
—оо —оо И=1
h= limAj*/22*...*^^ ос ехр(-zV2) (2.61)
/V—>оо > '
при условии
N
^ -> ^ (2.62)
и существует некоторое число а>2и конечная постоянная с, такая, что
j x''h„(x)dx<c<oo \/п (2.63)
Теорема имеет большое практическое значение, поскольку — особенно если h^
является гладкой — вид гауссиана аппроксимируется достаточно точно даже для
таких низких значений N, как 5.
Гладкость и компактность. Чем более гладкая функция, тем более компактным
является ее преобразование Фурье. Это обш;ее правило можно сформулировать
количественно, если мы выразим гладкость через число производных, которые
являются непрерывными, и компактность — через асимптотическое поведение при
больших значениях к. Тогда мы можем сформулировать: если функция д(х) и ее
первые п - 1 производные являются непрерывными, то ее преобразование Фурье
убывает по меньшей мере также быстро, как | к |"^"^'^ при больших к, т.е. lim |А:|"
9(к) = 0. '*'-°°
В качестве простых примеров мы можем взять функции-яш;ики и треугольные
функции (см. следующий раздел). Функция-ящик является разрывной (п = 0), ее
преобразование Фурье, sinc-функция, затухает со скоростью \k\-\ Противополож-
1\
lim У сг ^
Глава 2. Представление изображений
но треугольная функция является непрерывной, но ее первая производная
является разрывной. Следовательно, ее преобразование Фурье, sinc^-функция, затухает
более круто со скоростью | к |~^ Для того чтобы включить также импульсные
функции (5-распределения) в это отношение, мы должны отметить, что производные
от разрывных функций становятся импульсными. Следовательно, мы можем
сформулировать: если п-я производная от функции становится импульсной, то
преобразование Фурье этой функции затухает со скоростью | к |"".
Отношение между гладкостью и компактностью является расширением взаимности
между пространственной областью и Фурье-областью. То, что является сильно
локализованным в одной области, является широко распространенным в другой, и наоборот.
Соотношение неопределенностей. Этот общий закон взаимности находит еще
одно количественное выражение в классическом соотношении неопределенностей
или произведении продолжительности и ширины полосы. Эта теорема соотносит
среднеквадратичные ширину функции и ширину ее преобразования Фурье.
Среднеквадратичная ширина (Ах:)^ определяется как
]x^\g{x)f6x
\\9ix)f6x
\ XI д{х) f 6х
—оо
]\g{x)f6x
(2.64)
Это является, по существу, дисперсией от |gf(x)p, мерой ширины распределения
«энергии» сигнала. Соотношение неопределенностей утверждает:
Теорема 2.7 (Соотношение неопределенностей). Произведение дисперсии от, |д(л:)р,
(Ax)2m дисперсии от \д{к)^, {^У, не может быть меньше, чем 1/4 тт.
АхАк> 1/(4 я) (2.65)
Соотношения между компактностью и гладкостью и соотношение
неопределенностей дают некоторые основные правила для разработки линейных
операторов фильтров (свертки).
2.3.5. Фаза и амплитуда
Как описано выше, ДПФ можно рассматривать как координатное преобразование в
конечномерном векторном пространстве. Следовательно, изобразительная
информация полностью сохраняется. Обратное преобразование приводит снова к
исходному изображению.
В Фурье-пространстве мы смотрим на изображение с другой «точки зрения».
Каждая точка в Фурье-пространстве содержит две части информации: амплитуду
и фазу, т.е. относительное положение, периодической структуры. Если задана
такая композиция, мы задаемся вопросом: фаза или амплитуда содержит более
важную информацию по структуре в изображении или обе являются равнозначными?
Для того чтобы ответить на этот вопрос, мы проведем простой эксперимент. На
рис. 2.16, а, ^представлены два изображения. На одном показаны здания
Университета Гейдельберга, на другом — несколько строк из напечатанного текста. Над обоими
изображениями проводится преобразование Фурье, и затем фаза и амплитуда взаи-
2.3. Пространство волновых чисел и преобразование Фурье
мозаменяются так, как показано на рис. 2Л, в, г. Результат такого обмена является
удивительным. Оказывается, фаза определяет содержание для обоих изображений.
Из этого эксперимента мы можем заключить, что фаза преобразования Фурье
несет существенную информацию о структуре изображения. Амплитуда сама по
себе предполагает только то, что такая периодическая структура содержится в
изображении, но не определяет где. Мы также можем продемонстрировать этот
важный вывод с помощью теоремы о сдвиге (теорема 2.3, с. 61 и xRS). Сдвиг объекта в
пространственной области приведет только к сдвигу фазы в области волновых
чисел. Амплитуда не изменится. Если мы не знаем фазу его Фурье-компонентов, то
мы не знаем ни то, как выглядит объект, ни то, где он расположен.
Становится очевидным также, что энергетический спектр, т.е. амплитуда Фурье-
компонент в квадрате (см. также раздел 3.5.3), содержргг совсем немного
информации, поскольку вся фазовая информация потеряна. Если уровень яркости можно
связать с амплитудой физического процесса, скажем гармонического колебания, тогда
энергетический спектр дает распределение энергии в области волновых чисел.
б
elements (section 4J.2b).
f an optical system is a perspectK
^ models the imaging geometry ш
f described by the position of the
Focal length (section 4.3.2c). Forth
determine the distance range that
of field, section 4,3.2d) and to lear
id hypercentric optical systems {se
амплитуда
амплитуда
И1|Ш1111 ■..-.дтщш
I
Рис. 2.16. Иллюстрация значимости фазы и амплитуды в Фурье-пространстве для
содержания изображений: а, б - два исходных изображения; в — комбинированное
изображение, использующее фазу из изображения б и амплитуду из изображения а;
г — комбинированное изображение, использующее фазу из изображения а и
амплитуду из изображения б
Глава 2. Представление изображений
2.3.6. Альтернативные определения
В литературе встречаются некоторые вариации преобразования Фурье, которые
могут запутать и привести к многочисленным ошибкам. Это связано с
определением волнового числа. Определение волнового числа как величины, обратной
значению длины волны к = 1/Я является наиболее полезным для обработки сигнала,
поскольку к непосредственно дает число длин волн в единицу длины. В физике и
электротехнике, однако, определение, в которое входит множитель 2л:, является
более общепринятым: к - 2л:/Я. При таком обозначении можно определить две
формы преобразования Фурье: несимметричная форма:
д{к) = ^exp(ib) I g{x)Yg{x) = — ^exp(-ib) \д[к^ (2.66)
и симметричная форма
д[к) = -^^exp(ib) | д(х)^, д{х) = -j=(Qxp{-ikx) \д(к)У (2.67)
Поскольку все три варианта преобразования Фурье широко используются,
вероятно получение неправильных множителей в парах преобразования Фурье.
Правила перевода пар преобразований Фурье между тремя вариантами могут быть
выведены непосредственно из определений и описываются здесь:
^ = 1/Я, (2.22) д(х) о . д{к)
к = 2п1Х, (2.66) д{х) о . g(kl2n)
к = InIX, (2.67) д{х)о . g(kl4bi)ly[bi.
2.3.7. Практическое применение ДПФ
Единицы измерения. Для практического применения ДПФ важно рассмотреть
различные множители, которые могут использоваться в определении ДПФ, и
придать им четкое значение. Помимо определения в уравнении (2.29) два других, как
правило, используются:
1 Л^-1 1 N-\
^б) ^.=^Sw-;4 <^^ 9„ = I,<9.,
n=0
N-\
(2.69)
(B) 9.=t^T9„ — 9„=^Sw";0,.
Математически говоря, симметричное определение (а) является наиболее
элегантным, поскольку оно использует в обоих направлениях скалярное произведение с
ортогональными базисными векторами в уравнениях (2.28) и (2.29). На практике
2.3. Пространство волновых чисел и преобразование Фурье
определение (б) используется чаще всего, поскольку д^ дает среднее значение
вектора в пространственной области, не зависящее от его длины:
1 N-\ 1 N-\
^0 = Т7 X w^""9„ = Т? S ^«- (2-70)
Поэтому мы будем использовать (б) почти везде в этой книге.
На практике важно знать, какие пространственные или временные интервалы
использовались, чтобы произвести выборку дискретных сигналов. Только тогда
возможно корректно сравнивать ДПФ, которые были дискретизированы при
различных интервалах. Соотношение можно увидеть наиболее просто, если мы
аппроксимируем Фурье-интеграл в уравнении (2.18) суммой и произведем выборку
значений в пространственной и временной областях, используя х - «Ах, к - vbk и
AxAA:=l/7V:
д{рЫк) = J gf(x)exp(-2^:iuAAx)(k
—оо
~ ^ gf„ ехр (--2л:1^7иАхАА:) Ах
w=0
1 N-\
^ п=0
(2.71)
= NAxg^.
Эти уравнения показывают, что преобразование Фурье д^, вьшисленное с
помощью ДПФ, должно быть умножено на множитель NAx = 1/Ак, для того чтобы
соотнести его с единичным интервалом волнового числа. Без такого масштабирования
преобразование Фурье соотносится с интервалом Ак = l/(NAx) и, таким образом,
различается для сигналов, дискретизированных с различными частотами выборки.
Для двумерных и более высокой размерности сигналов выполняются
соответствующие соотношения:
д{оАк,,иАк,) « NAxMAyg^^=-^-^g^^^ (2.72)
Такое же масштабирование нужно применить к квадратам сигналов (энергии),
но не к квадратам множителей из уравнения (2.71). Этот результат следует из
теоремы Рэлея для непрерывных и дискретных сигналов (>-R4, )^R7):
Непрерьюные:
_oo -00 L»=0
l^\ ,2 ^\. ,2 (2.73)
Длс1феггаые: TT2^|S^„| =2^|9u| •
Теорема Рэлея гласит, что энергия сигнала может интегрироваться либо в
пространственной области, либо в Фурье-области. Для дискретных сигналов это
означает, что средняя энергия задается либо с помощью усреднения
прямоугольного сигнала в пространственной области, либо с помощью суммирования квадрата
Глава 2. Представление изображений
абсолютной величины сигнала в Фурье-области (если мы используем
определение (б) ДПФ в уравнении (2.69)). Из аппроксимации интеграла по квадрату
абсолютной величины в Фурье-области с помощью суммы в уравнении (2.73) мы
можем сделать вывод, что | g{vlsk) р ~ \д^р/А^.
Единицы измерения таких масштабированных, возведенных в квадрат
абсолютных величин в Фурье-пространстве есть -/м~^ или -/Гц для временного ряда, где •
обозначает единицы измерения квадрата сигнала.
Динамический диапазон. В то время как в большинстве случаев для
представления изображения достаточным является 256 уровней квантования, т.е. 1 байт за
пиксель, для преобразования Фурье-изображения нужен гораздо больший
динамический диапазон. Как правило, мы наблюдаем сильное убывание компонент
Фурье с увеличением значения волнового числа (рис. 2.15). Следовательно, по
меньшей мере необходимы 16-битовые целые числа или 32-битовые числа с
плавающей запятой для представления изображения в Фурье-области без
значительных ошибок округления.
Причиной такого поведения является значимость больших волновых чисел в
изображении. Если мы просто опустим их, то размоем изображение.
Уменьшение вызвано тем фактом, что относительная разрешающая способность
увеличивается. Рассмотрение относительных разрешений является естественным,
поскольку мы способны лучше различать относительные разности в расстоянии,
чем абсолютные. Мы можем, к примеру, легко увидеть разность в 10 см в 1 м, но
не в 1 км. Если мы применим это понятие к Фурье-области, то окажется более
естественным представить изображения в так называемой
логарифмически-полярной системе координат, как показано на рис. 2.17. Дискретная сетка в такой
системе координат разделяет пространство на угловые и In А: интервалы. Таким
образом, площадь элементарной ячейки пропорциональна к^. Для того чтобы
учесть это приращение площади, компоненты Фурье необходимо умножить на
к^ в этом представлении:
б
А Кз
►
к
Рис. 2.17. Разбиение Фурье-области на декартовы (а) и логарифмически-полярные (б)
интервалы
2.4, Дискретные унитарные преобразования 7
Рис. 2.18. Представление преобразованного Фурье-преобразованием изображения
на рис. 2.7 в декартовых (а) и логарифмически-полярных (б) координатах.
Изображен энергетический спектр | С^^ р, умноженный на к^. Шкапа уровней серого
является логарифмической и покрывает 6 десятых (см. также рис. 2.15)
J \g{kf dk,dk, = \k' \g{kf dhikdcp.
(2.74)
Если мы предположим, что энергетический спектр | д(к) р является плоским в
естественной логарифмически-полярной системе координат, он будет убывать со
скоростью кг^ в декартовых координатах.
Для изображения энергетических спектров обычно берут логарифм от
уровней яркости, для того чтобы сжать высокий динамический диапазон.
Рассмотрение логарифмически-полярных систем координат предполагает, что умножение
на к^ является ценной альтернативой. Подобным образом, представление в
логарифмически-полярной системе координат дает гораздо лучшую оценку
направлений пространственных структур и более мелких масштабов (рис. 2.18).
2.4. Дискретные унитарные преобразования
2.4.1. Общие свойства
В разделах 2.3.1 и 2.3.2 мы узнали, что дискретное преобразование Фурье можно
считать линейным преобразованием в векторном пространстве. Таким образом,
оно является всего лишь примером большого класса преобразований,
называемых унитарными преобразованиями. В этом разделе мы рассмотрим некоторые
Глава 2, Представление изображений
их общие свойства, которые помогут глубже проникнуть в суть обработки
изображений. Кроме того, мы приводим примеры других унитарных
преобразований, которые получили значение в цифровой обработке изображений.
Унитарные преобразования определяются для векторных пространств на поле
комплексных чисел, для которых определяется внутреннее произведение. Как
ПФ в уравнении (2.22), так и ДПФ в уравнении (2.29), по существу, вычисляют
скалярные произведения.
Основная теорема об унитарном преобразовании утверждает:
Теорема 2.8 (Унитарное преобразование). Пусть V - конечномерное векторное
пространство с внутренним произведением. Пусть U — взаимно-однозначное
линейное преобразование Ve само себя. Тогда следующие утверждения являются
эквивалентными:
1. и является унитарным,
2. и сохраняет внутреннее произведение, т.е. {д \h) =\Ug \ Unj, \/ g,h е V.
3. Обратная матрица к U, V^^ является сопряженной U: UIF= I.
4. Векторы-строки (и векторы-столбцы) [/образуют ортонормированный базис
векторного пространства V.
В этой теореме наиболее важные свойства унитарного преобразования уже
соотнесены друг с другом: унитарное преобразование сохраняет внутреннее
произведение. Это подразумевает, что еще одно важное свойство, норма, также
сохраняется:
\\91={9\9Г={ид\и9Г. (2.75)
Уместным будет рассматривать норму как длину или абсолютную величину
вектора. Вращение в М^или W является примером преобразования, в котором
сохранение длины векторов очевидно (сравните также рассмотрение однородных
координат в разделе 7.7).
Произведение двух унитарных преобразований i/, i/2 унитарно. Поскольку
тождественный оператор, как и обратный к унитарному оператору, является
унитарным, то множество всех унитарных преобразований на пространстве с
внутренним произведением является группой относительно операции композиции. На
практике это означает, что мы можем составить/разложить сложные унитарные
преобразования из/на более простые или элементарные преобразования.
Мы проиллюстрируем некоторые рассмотренные свойства унитарных
преобразований с помощью дискретного преобразования Фурье. Сначала рассмотрим
одномерное ДПФ в симметричном определении (2.69):
Это уравнение можно считать умножением матрицы W^^ размерностью NxM
на вектор д:
9=^^и9. (2.76)
Явно ДПФ для 8-мерного вектора задается как
2.4. Дискретные унитарные преобразования
\9о'
г'
02
г'
^4
г'
^6
l9i.
1
w«
w.
w«
w«
w
w
w
w
Wo
Wc
Wo
Wo
Wo W
Wo
Wo
Wo
w
Wo
Wo
7
8
6
8
5
8
4
8
3
w^
w^
w^
w^
„,6
w^
w^
Ws^
w^
„xl
Wo Wo
w
Wo
Wo
Wo
Wo
Wo
Wo
Wo
Wo
Wo
Wo
Wo
w^
Wo
Wo
Wo
Wo
Wo
Wo
w
w
w
w
w
w
Wo W
Wo Wo
w
o1
8
1
8
2
8
3
8
4
8
5
6
8
7
8 J
\^'\
bi
r'
r'
04
^5
W
I9i^
Мы воспользовались периодичностью ядра ДПФ (2.41), чтобы ограничить
экспоненты Wot о до 7. Матрица преобразования для ДПФ симметрична (W= W^\ W^
является обратным преобразованием.
Для двумерного ДПФ мы можем записать подобные уравнения, если отобразим
матрицу размерностью MxNb МЛ^-мерный вектор. Однако существует более
простой способ, если мы воспользуемся сепарабельностью ядра ДПФ как выражено в
уравнении (2.38). Используя матрицы JF^^размерностью МхМи Jf^размерностью
NxN, аналогично одномерному случаю, мы можем записать уравнение (2.76) как
1 М-\ N-\
IMN ш=0 «=0
или, в матричном обозначении,
1
^ _ w^ G W =
G =
MxN
W GW
(2.78)
МхЛ/ MxN NxN
Физики вспомнят о теоретических основах квантовой механики, которые
сформулированы для случая бесконечномерного векторного пространства с
внутренним произведением, - гильбертова пространства.
2.4.2. Косинус-преобразование, синус-преобразование и преобразование
Хартли
То, что дискретное преобразование Фурье отображает вещественные
изображения в комплекснозначные, часто является неудобным. Мы можем получить
вещественное преобразование, если разложим комплексное ДПФ на его
вещественную и мнимую части:
{^n)=^OS
2nnv
N
-hi sin
У
/
V
Innv
N
(2.79)
Ни косинусная, ни синусная части не являются полезными в качестве ядра
преобразования, поскольку эти функции не образуют полный базис векторного
пространства. Косинусные и синусные функции лишь стягивают подпространства
четных и нечетных функций соответственно.
Глава 2. Представление изображений
Эта проблема может быть решена с помощью ограничения
косинус-преобразования и синус-преобразования положительным полупространством в
пространственной области и Фурье-области. Тогда свойства симметрии не играют роли и два
преобразования определяются как
'д{к) = ^д{х)у12со^{2ккх)йх о . д(х) = j'g(A:)V2cos(2^b)dk
о о
оо оо
^gf(^) = Jgf(x)^/2sin(2л:Ь)dJC о . gf(x) = j'д(А:)л/2 8т(2л:Ь)ёк.
о о
(2.80)
Для соответствующих дискретных преобразований добавление тригонометрических
фушщий с полуцелыми длинами волн может образовать базисные векторы с
отсутствующей симметрией. Это эквивалентно удвоению базисной длины волны.
Следовательно, ядра для косинус- и синус-преобразований в 7У-мерном векторном пространстве есть
Чк
COS
^nnv^ ' ^ ^
N
5„„ = J sin
n{n + \){v + \)
V ^^1 J
(2.81)
Ha рис. 2.19, л, 5 показаны базисные функции одномерных косинусоидных и
синусоидных функций. Из графиков легко представить, что все базисные
функции ортогональны друг другу. Из-за удвоения периодов оба преобразования
теперь содержат четные и нечетные функции. Базисные функции с полуцелыми
длинами волн замещают функции с исходно отсутствующей симметрией.
Косинус-преобразование получило значение для сжатия данных изображения
[97]. Оно включается в стандартный алгоритм сжатия, предложенный
Объединенной группой экспертов по машинной обработке фотографических изображений
(Joint Photographic Experts Group — JPEG).
Преобразование Хартли (ПХ) — гораздо более элегантное решение, чем
косинус- и синус-преобразования, для преобразования, которое избегает
комплексных чисел. При помощи добавления косинусоидной и синусоидной функций мы
получаем несимметричное ядро:
cas2л:Aл: = cos(2л:fec) + sin(2л:Ь(:) = ^/2cos(2л:(Ax-"l/8)), (2.82)
которое подходит для преобразования по всей пространственной области:
^g{k)=^\g{x)cгs{2nkx)i^x о . д{х)^\^д{к)сг^{2пкх)^ (2.83)
—оо —оо
Соответствующее дискретное преобразование Хартли (ДПХ) определяется как:
yjN „=о yiN „=о
(2.84)
Базисные векторы для 7V= 8 показаны на рис. 2.19, в. Несмотря на элегантность
преобразования Хартли для вещественных сигналов, оно проявляет некоторые
недостатки по сравнению с преобразованием Фурье. Простая теорема о сдвиге для
преобразования Фурье больше не действует (теорема 2.3, с. 61). Сдвиг скорее при-
2.4. Дискретные унитарные преобразования 75
Рис. 2.19. Базисные функции одномерных унитарных пространств для N= 8:
а - косинус-преобразование; б - синус-преобразование; в — преобразование Хартли
водит к комбинации друг с другом базисных функций с положительными и
отрицательными волновыми числами:
л.
9п-п'
^д{к)со8{27скхо)л- ^g{-k)sm[27ckxQ),
^д^ cos{27rnv/N)+ ^д^_^ sm{2nnv/N).
(2.85)
Подобные сложности возникают и с теоремой о свертке для преобразования
Хартли (;^R8).
2.4.3. Преобразование Адамара
Базисные функции преобразования Адамара — ортогональные бинарные структуры
(рис. 2.20, а). Некоторые из этих структур являются регулярными прямоугольными
волнами, другие не являются таковыми. Преобразование Адамара эффективно с
точки зрения вьиислений, поскольку его ядро содержит только цифры 1 и -1. Таким
образом, для того чтобы вьиислить преобразование, необходимы только операции
сложения и вьиитания.
2.4.4. Преобразование Хаара
Базисные векторы всех преобразований, рассмотренных до сих пор,
характеризуются тем, что базисные функции распространяются по всему вектору или
изображению. Таким образом, мы обозначаем эти преобразования как
глобальные. Вся локальность теряется. Если мы имеем, например, два независимых
объекта в нашем изображении, тогда они одновременно распадутся на эти
глобальные структуры и не будут больше распознаваться как два отдельных
объекта в преобразовании.
Преобразование Хаара — это пример унитарного преобразования,
которое частично сохраняет локальную информацию, поскольку его базисные
функции являются парами импульсов, которые не равны нулю только в месте
импульса (рис. 2.20, ^. При преобразовании Хаара пространственное разрешение
Глава 2 Представление изображений
лучше для более мелких структур. Так же как в случае преобразования Адамара,
преобразование Хаара эффективно с точки зрения вычисления. Его ядро
включает только цифры -1, О и 1.
2.5. Быстрые алгоритмы для унитарных преобразований
2.5.1. Важность быстрых алгоритмов
Без эффективного алгоритма вычисления дискретного преобразования Фурье
будет невозможно использовать преобразование Фурье в обработке изображений.
При непосредственном применении уравнение (2.38) является чрезмерно
дорогостоящим. Каждая точка в преобразованном изображении требует 1SP-
комплексных умножений и Л^- 1 комплексных сложений (не учитывая вычисления коси-
нусоидных и синусоидных функций в ядре). В общем, нам необходимо выполнить
N^ комплексных умножений и N^(N^- I) комплексных сложений. Это сводится к
почти 87^^ операциям с плавающей запятой. Для изображения 512 х 512 это
приводит к 5 X 10^^ операциям. Процессор Pentium IV с 2 ГГц на ПК дает около 500
MFLOPs (миллионы операций с плавающей запятой в секунду), если
программируется на языке высокого уровня с оптимизирующим компилятором.
Отдельное ДПФ от изображения 512х512с5х10^' операциями может потребовать
около 1000 секунд или 0,3 часа, — это слишком медленно, чтобы представлять
какую-либо значимость для практического применения. Таким образом,
возникает крайняя необходимость минимизировать число вычислений путем
нахождения подходящего алгоритма. Это важная тема в компьютерной науке. Чтобы
найти такой алгоритм, мы должны изучить внутреннюю структуру исходной
задачи, ее вычислительную сложность и постараться выяснить, как можно ее
решить с минимальным числом операций.
В качестве наглядного примера рассмотрим следующую простую задачу
поиска. Друг живет в высотном здании с N этажами. Мы хотим узнать, на каком
этаже расположена его квартира. На наши вопросы мы будем получать ответы
только «да» или «нет». Сколько вопросов мы должны поставить, чтобы выяснить,
где он живет? Наиболее простым и самым прямым подходом является спросить
«Ты живешь на п-м этаже?» В лучшем случае: наша первоначальная догадка
является правильной, но наиболее вероятно, что это неверно, поэтому один и тот
же вопрос придется задавать с другими номерами этажей снова и снова. В
худшем случае мы должны задать точно N - I вопросов, в среднем N/2 вопросов.
При каждом вопросе мы можем только исключить одну из 7V возможностей — это
совершенно неэффективный подход.
Однако при вопросе: «Ты живешь в верхней половине здания?» мы можем
исключить половину возможностей одним вопросом. После ответа мы знаем, что он
живет либо в верхней, либо в нижней половине, и можем продолжить наш опрос в
такой же манере, разбивая оставшиеся возможности на две половины. При такой
стратегии нам потребуется гораздо меньше вопросов. Если число этажей
определяется степенью двойки, скажем 2', то нам потребуется ровно / вопросов. Таким
образом, для N этажей нам понадобится IdTV^ вопросов, где Id обозначает логарифм по
основанию 2. Стратегия, рекурсивно примененная здесь для получения более
эффективного решения задачи поиска, называется принципом «разделяй и властвуй».
2.5. Быстрые алгоритмы для унитарных преобразований
а
0
1
2
3
4
5
6
7
б
0
1
2
о
о
4
ц
А
D
7
/
Рис. 2.20. Первые 8 базисных функций одномерных унитарных преобразований для
7V= 16: а - преобразование Адамара; б — преобразование Хаара
Мерой вычислительной сложности задачи с N компонентами является
наибольшая степень N, которая возникает при подсчете операций, необходимых для
ее решения. Такая аппроксимация полезна, поскольку наибольшая степень А/^
мажорирует число операций, необходимых при больших N. Мы говорим о задаче
нулевого порядка О (Л/^), если число операций не зависит от ее размера, и о задаче
линейного порядка О (N), если число операций возрастает линейно с увеличением
размера. Это справедливо и для решений. Прямое решение задачи поиска,
рассмотренной в предьщущем примере, является решением порядка N, О (N),
стратегия «разделяй и властвуй» является решением порядка О (IdTV).
2.5.2. Одномерные двоичные алгоритмы БПФ
Сначала мы рассмотрим быстрые алгоритмы для одномерного ДПФ, обычно
имеющие сокращение алгоритмы БПФ для быстрого преобразования Фурье. Мы
положим, что размерность вектора определяется степенью двойки, 7V= 2'.
Поскольку прямое решение, согласно уравнению (2.29), является О (N^), кажется полезным
использовать стратегию «разделяй и властвуй». Если мы сможем разложить
преобразование на две части с векторами размером N/2, то уменьшим число операций
cffjxo 2{N/2y = N^/2. Эту процедуру можно применять рекурсивно Id iVpa3, до тех
пор пока мы не получим вектор размером 1, чье ДПФ является тривиальным,
поскольку ничего вообще не нужно делать. Конечно, эта процедура работает, только
если возможно разделение и число дополнительных операций для соединения
разделенных преобразований не превышает порядка О (N).
Результат рекурсивного разделения является интересным. Нам не нужно
выполнять ДПФ вообще. Весь алгоритм для вычисления ДПФ сводится к
рекурсивным стадиям композиций. Если эти композиции порядка О (N), то вычисление
Глава 2. Представление изображений
ДПФ в итоге составит О (MdN), поскольку нужно выполнить IdiV композиций. В
сравнении с прямым решением порядка О (N^), это потрясающая экономия в
числе операций. Для N=2^^= 1024 оно уменьшается почти в 100 раз.
Мы разделяем вектор на два вектора, отдельно выбирая четные и нечетные
элементы (рис. 2.21):
Л^-1
9и =
/2-1
«=0
N/2-1
= X 9^2. ехр
^ Ininv ^
N
г
1к\1т \
N
NI2-\
S dln^l^^V
^ Ininv ^
«=0
2m(2n-\-l)v
V
N
п=0
N12
+ ехр --
2n'\v
IT
\NI2-\
X9^2«+iexp
/7=0
)
2mnv
' N/2
(2.86)
Обе суммы образуют ДПФ с N' = N/2. Вторая сумма умножена на фазовый
множитель, который зависит только от волнового числа v. Наличие фазового
множителя следует из теоремы сдвига, поскольку нечетные элементы сдвигаются на
одно место влево.
В качестве примера возьмем базисный вектор с i; = 1 и N= 8 (рис. 2.21). С
нечетными выборочными точками функция показывает фазовый сдвиг к/4. Этот
фазовый сдвиг полностью компенсируется фазовым множителем в уравнении (2.86):
ехр(-2л:1и/Л^) = ехр(-л:1/4).
Операциями, необходимыми для комбинации частичных преобразований
Фурье являются лишь одно комплексное умножение и одно комплексное сложение,
т.е. О (N). Однако некоторые, более детальные рассмотрения необходимы,
поскольку ДПФ над половинчатыми векторами дает только N/2 значений. Для того чтобы
посмотреть, как работает композиция из 7V значений, мы отдельно изучим
значения i; от О до N/2 - 1 и от N/2 jioN-l. Частичные преобразования над четными и
нечетными выборочными точками сокращенно обозначаются ^д^ и "д^
соответственно. Для первой части мы можем взять лишь разделение, как выражено в
уравнении (2.86). Для второй части, v'= v + N/2, изменяется только фазовый
множитель. Прибавление N/2 приводит к смене знака:
Все точки выборки
Четные
точки выборки
■ ■*..„.,„^^ 1 1 1 г
J 1 1 ' ^^--4
Нечетные
точки выборки
^л
Рис. 2.21. Разложение вектора на два вектора, содержащих четные и нечетные
выборочные точки
2.5. Быстрые алгоритмы для унитарных преобразований
(
ехр
2^i(u + iV/2)l { Iniv
К ^ У
= -ехр
ИЛИ W„^ ^ = -W^^
У
N
Воспользовавшись этой симметрией, мы можем записать:
0u= S^o+w^ 5^u I о<и<Л/^/2. (2.87)
Преобразования Фурье для индексов vhv + N/2 отличаются лишь в знаке
второго слагаемого. Таким образом, для композиции двух слагаемых нам лишь нужно
одно комплексное умножение. Разделение теперь применяется рекурсивно. Два
преобразования Л72-мерных векторов делятся снова на два преобразования каждый.
Мы получаем подобные выражения как в уравнении (2.86), с единственной
разницей, заключающейся в том, что фазовый фактор удваивается до Qxp[-(27dv)/(N/2)].
Четные и нечетные части четного вектора содержат точки {О, 4, 8, ..., N/2 - 4} и
{2, 6, 10,..., N/2 - 2} соответственно.
На последнем шаге мы раскладываем вектор с двумя элементами на два
вектора с одним элементом. Поскольку ДПФ от вектора с одним элементом
является тождественной операцией уравнению (2.29), нет необходимости в
дополнительных вычислениях.
После того как разложение закончено, мы можем использовать уравнение
(2.87) рекурсивно с соответствующими фазовыми множителями, чтобы
скомпоновать исходные векторы шаг за шагом в обратном порядке. На первом шаге мы
составляем векторы с всего лишь двумя элементами. Таким образом, нам лишь
потребуется фазовый множитель для i;=0, который равен единице.
Следовательно, первый шаг композиции имеет очень простой вид:
9 о = 90-^91
(2.88)
9o^N/2=9l = 9o''9v
Алгоритм, который мы рассмотрели, называется прореживающим во времени
алгоритмом БПФ, поскольку сигнал прореживается в пространственной области.
Все шаги алгоритма БПФ показаны на схеме прохождения сигнала на рис. 2.22 для
N=8. Левая половина схемы показывает шаги прореживания. Первый столбец
содержит исходный вектор, второй — результат первого шага разложения на два
вектора. Векторы с четными и нечетными элементами помещены в нижних и
верхних половинах. Это разложение продолжается до тех пор, пока мы не получим
векторы с одним элементом.
В результате разложения элементы вектора располагаются в новом
порядке. Это все действия, которые выполняются на этапах разложения. Не
требуется никаких вычислений. Мы можем легко понять новую схему упорядочения,
если представим индексы вектора с помощью дуальных чисел. На первом шаге
разложения мы упорядочиваем элементы согласно младшему биту, сначала —
четные элементы (младший бит является нулевым), затем — нечетные
элементы (младший бит равен единице). С каждым дальнейшим шагом разложения
бит, который управляется сортировкой, смещается влево на одно место. В
конце концов, мы получаем сортировку, в которой упорядочение битов является
Глава 2. Представление изображений
Эо
000
91
001
92
010
93
011
94
100
95
101
9б
110
97
111
9о
92
94
9б
9i
9з
95
97
9о
000
lot)
""дГ
010
110
—--^^
■ ^т^
1^®
Рис. 2.22. Схема прохождения сигнала двоичного разреживающего во времени
алгоритма преобразования Фурье для 7V= 8 (для дальнейшего разъяснения смотри текст)
полностью обратным. Элемент с индексом 1 = OOI2, например, будет в
положении 4 = IOO2, и наоборот.
Следовательно, последовательность шагов разложения можно выполнить с
помощью одной операции, чередуя элементы на обьиных положениях и положениях с
инвертированием битов. Такое переупорядочение известно как инверсия битов.
Дальнейшие шаги с правой стороны схемы прохождения сигнала
показывают пошаговую композицию для векторов удвоенного размера. Композиция
для двумерных векторов задается уравнением (2.88). Операции изображаются с
помощью стрелок и точек, имеющих следующее значение: точки представляют
цифру, элемент вектора. Эти точки называются узлами схемы прохождения
сигнала. Стрелки переносят цифры от одной точки в другую. В процессе
переноса цифра умножается на множитель, написанный рядом со стрелкой. Если
сопутствующий множитель пропущен, то умножение не требуется. Значение
узла есть сумма значений, перенесенных с предыдущего уровня.
Элементарная операция алгоритма БПФ включает только два узла. Нижний
узел умножается на фазовый фактор. Сумма и разность двух значений
переносятся на верхний и нижний узлы соответственно. Из-за скрещивания путей сигнала
эта операция обозначается как бабочкообразная операция.
Мы проникнем в суть алгоритма БПФ еще глубже, если проследим вычисление
отдельного элемента. На рис. 2.23 показываются пути сигнала для д^ и д^. Для
каждого уровня мы возвращаем число узлов, вносящих вклад в вычисление пар.
На последней стадии вовлечены все элементы. Путь прохождения сигнала для
д^ И д^ является тождественным, за исключением последней стадии, таким
образом, хорошо демонстрируя эффективность алгоритма БПФ.
Все фазовые множители на пути прохождения сигнала для д^ являются
единичными. Как и следует из уравнения (2.29), д^ содержит сумму всех элементов вектора д:
9о = [(5^0 + 94) + (92 + 9б)\ + K9i + 5^5) + (5^3 + S^y)!,
в то время как на последней стадии для д^ сложение заменяется вычитанием:
94=\(9o+94) + (92'^9в)]-\(9^-^95)-^(9з-^9l)l
2.5. Быстрые алгоритмы для унитарных преобразований
90
000
91
001
92
010
9з
011
94
100
95
101
9б
110
1 97
111
9о
92
94
9б
9i
9з
95
97
90
000
9i
001
92
010
9з
011
94
100
95
101
9б
110
97
111
9о
92
94
9б
9i
Эз
95 1
97
00?)
loi
92
010
9б
110
9i
001
95
101
011
97
111
1 9о
Q0Q
lot)
010
9б
110
1 9i
001
95
1 101
9з
011
97
111
1—-—""^
— '
1__^_—^
--^^^^
^J——'—^
-^
1^^-—""^
-—'^^^
1 щ^^
—
® §0
Рис. 2.23. Путь прохождения сигнала для вычисления д^ и д^ с помощью
разреживающего во времени ангоритмоа БПФ для 8-мерного вектора
В разделе 2.4 мы изучили, что ДПФ — это пример унитарного преобразования,
которое, как правило, выполняется с помощью умножения унитарной матрицы на
вектор. Что в таком контексте означает алгоритм БПФ? График прохождения
сигнала на рис. 2.22 показывает, что вектор преобразуется за несколько шагов.
Следовательно, матрица унитарного преобразования разбивается на несколько матриц
частичных преобразований, которые применяются одна за другой.
Если мы возьмем алгоритм для Л/^= 8, как показано на рис. 2.22, то унитарная
матрица раскладывается на три более простых преобразования с помощью
разреженных унитарных преобразований:
00
9х
9i
9ъ
9,
9s
9в
9i
1
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
1
1
0
0
0
-1
0
0
0
0
w''
0
0
0
-w-'
0
0
0
0
W-'
0
0
0
-W-'
0
0
0
0
мГ
0
0
0
—w
Глава 2. Представление изображений
1
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
1
0
-1
0
0
0
0
0
0
i
0
-i
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
1
0
-1
0
0
0
0
0
0
i
0
-i
10 0 0 1 о
10 0 0-1 о
0 0 10 0 о
0 0 10 0 о
0 10 0 0 1
0 10 0 0-10
0 0 0 10 о
0 0 0 10 о
0
0
1
-1
0
0
0
0
0]
0
0
0
0
0
1
-ij
Г^о]
г'
гЧ
03
гМ
гЧ
06
ХяЛ
Читатель может убедиться, что эти матрицы преобразований отражают все
свойства одиночного уровня алгоррггма БПФ. Разложение матриц подчеркивает, что
алгоритм БПФ можно рассматривать как остроумный метод разложения матрицы
унитарного преобразования на разреженные частичные унитарные преобразования.
2.5.3. Меры для быстрых алгоритмов
В соответствии с требуемым числом арифметических операций существует много
других быстрых алгоритмов преобразования Фурье, которые еще более
эффективны. Большинство из них основано на алгебре многочленов и теории чисел.
Углубленное рассмотрение этих алгоритмов приведено в [11]. Однако простое число
арифметических операций не является единственной мерой для эффективного
алгоритма. Мы должны также рассматривать и некоторые другие факторы.
Доступ к данным требует дополнительных операций. Рассмотрим простой
пример сложения двух векторов. Здесь помимо сложения выполняются следующие
операции: необходимо вьиисление адресов соответствующих элементов; два
элемента считываются в регистры, а результат этих сложений записывается обратно в
память. В зависимости от архитектуры используемых аппаратных средств эти пять
операций создают значительные накладные расходы, которые могут занять
гораздо больше времени, чем само сложение. Следовательно, алгоритм со сложной
схемой доступа к элементам вектора мог бы добавить значительные накладные
расходы к арифметическим операциям. В результате более простой алгоритм с большим
количеством арифметических операций, но с меньшими накладными
издержками может оказаться быстрее.
Еще одним фактором в оценке алгоритмов является количество необходимой
области памяти. Это включает не только пространство для кода, но также и
область памяти для промежуточных результатов или таблиц констант. Например, так
называемый алгоритм БПФ на месте, который может выполнять преобразование
Фурье на некотором изображении без использования области памяти
промежуточного хранения для изображения, является очень выгодным. Часто существует
компромисс между областью памяти и скоростью. Многие целочисленные алгоритмы,
например, предварительно вычисляют комплексные фазовые множители w"^и
хранят их в статически размещаемых таблицах.
2.5. Быстрые алгоритмы для унитарных преобразований
В значительной степени эффективность алгоритмов зависит от архитектуры
компьютера, используемой для их выполнения. Если умножение выполняется
либо в программном обеспечении, либо с помощью микропрограммной
команды, то оно гораздо медленнее, чем сложение или обращение к памяти. В этом
случае целью быстрых алгоритмов является уменьшение числа умножений, даже
за счет большего количества сложений или более сложного доступа к памяти.
Такая стратегия не имеет смысла на некоторых современных высокоскоростных
архитектурах, в которых конвейерное сложение и умножение чисел с
плавающей запятой занимает всего лишь один такт. Чем быстрее выполняются
операции на процессоре, тем больше доступ к памяти становится узким местом.
Быстрые алгоритмы должны теперь рассматривать эффективные схемы обращения
к памяти. Решающим является то, что очень много вычислений может
выполняться над одним и тем же набором данных. Таким образом, эти данные могут
храниться в быстрой промежуточной области памяти, известной как
сверхоперативная кэш-память, и не требуется прямого доступа к гораздо более медленной
общей памяти (RAM).
После такого детального рассмотрения алгоритма мы можем теперь оценить
необходимое число операций. На каждой стадии композиции выполршются N/2
комплексных умножений и 7Vкомплексных сложений. В общем, нам понадобится
7V/21diVкомплексных умножений и TVldTVкомплексных сложений. Более глубокий
анализ показывает, что мы можем сэкономить еще больше умножений. На первых
двух шагах композиции возникают лишь тривиальные умножения на 1 или i
(сравните рис. 2.22). Для дальнейших шагов число тривиальных операций уменьшается
в 2 раза. Если бы наш алгоритм смог избежать всех тривиальных умножений, то
число умножений свелось бы к (A/2)(ld7V- 3).
Алгоритм БПФ является классическим примером быстрого алгоритма, Вьршсли-
тельная экономия является огромной. Для вектора с 512 элементами необходимо
всего лишь 1536 вместо 262 144 комплексных умножений по сравнению с прямым
вычислением согласно уравнению (2.29). Число умножений уменьшилось в 170 раз. С
использованием алгоритма БПФ дискретное преобразование Фурье не может больше
считаться дорогостоящей с точки зрения вычислений операцией, поскольку для
каждого элемента вектора необходимо всего лишь несколько операций. Для вектора с 512
элементами необходимо вьиислить для каждого пикселя всего лишь 3 комплексных
умножения и 8 комплексных сложений, соответствующих 12 веществеьшым
умножениям и 24 вещественным сложениям.
2.5.4. Четверичный прореживающий во времени алгоритм БПФ
Разработав один быстрый алгоритм, мы все еще не знаем, является ли этот
алгоритм оптимальным или можно найти более эффективные алгоритмы. В
действительности мы использовали только один частный случай — стратегию «разделяй и
властвуй». Вместо разбиения вектора на две части мы могли бы выбрать любое
другое разделение, скажем, на Р Q-мерных векторов, если N= PQ. Этот тип
алгоритмов называется алгоритмом Кули—Таки (Cooly-Tukey) [11].
Другим часто используемым разбиением является четверичный алгоритм БПФ.
Мы можем разложить вектор на четыре компонента:
Глава 2. Представление изображений
1У I t—1
9u = Z 5'4„
I
w:
п=0
4«+1 ^ N
N/4-\ TV/4-1
,-4/7D
74n+2 "" N
4n+3^N
Для получения более простых уравнений мы будем использовать сокращения,
как и в случае двоичного алгоритма, и обозначим частичные преобразования с
помощью ^д,..., д^. Воспользуемся симметрией w^"^, тогда преобразования в четверти
каждого из векторов определяются формулами:
9о
9v+N/4
9v+N/2
9t)+2N/4
или в матричном обозначении
fl'u+w^, S'u+w^v g^+^N 9u
0^ I :,,r-i^l^ ,,r~2i;2'i.
-iw
-3u 3;^
N
9„
9o
9v+N/4
9v+N/2
9u+iNI4
1 1
1 -i
1 -1
1 i
1
-1
1
-1
1
i
-1
-i
w
9v
-u 1 -
9u
w
N
-2u 2 A
Л^
9u
L'^T'g.
Для сложения элементов вектора, состоящих из 4-компонентных кортежей,
понадобятся 12 комплексных сложений и 3 комплексных умножения. Мы можем
уменьшить число сложений в дальнейшем путем разложения матрицы на две более
простые матрицы:
9и
9u+N/4
9v+N/2
9v+3N/4,
1
0
1
0
0
1
0
1
1
0
-1
0
о
-i
О
i
1
1
0
0
0
0
1
1
1
-1
0
0
о
о
1
"1
W
W
W
9и
-ul-
-2v 2
N
-3u з;:.
9.
N
9и
Первое умножение матриц дает промежуточный результат, который можно
использовать в нескольких операциях на второй стадии. Таким образом, мы
экономим четыре сложения. Мы можем применить это разложение рекурсивно log^TV
раз. Как и в двоичном алгоритме, понадобятся только тривиальные умножения
на первом шаге композиции. На всех остальных шагах умножения возникают
для 3/4 части точек. В общем, Ъ/AN{[og^- 1) = 3/87V(ld7V- 2) комплексных
умножений и 2Nlog^N= TVldN комплексных сложений необходимы для четверичного
алгоритма. В то время как число сложений остается равным, умножений
требуется на 25% меньше, чем для двоичного алгоритма.
2.5. Быстрые алгоритмы для унитарных преобразований
^><>Ы>.
90
000
юЬ
92
010
110
~97~
001
95
101
9з
011
97
111
90
92
94
9б
9i
9з
95
97
9о
000
9i
001
92
010
93
011
lot)
95
101
110
97
111
Рис. 2.24. Схема прохождения сигнала двоичного прореживающего по частоте
алгоритма БПФ для 7V = 8
2.5.5. Двоичное прореживающее по частоте БПФ
Прореживающее по частоте БПФ является еще одним примером алгоритма Кули—
Хаки. Теперь мы разбиваем Л^-мерный входной вектор на N/2 первые и N/2 вторые
компоненты. Такое разбиение разделяет выходной вектор на его четные и
нечетные компоненты:
Nll-\
дю =
Z {9п-^9п^И12)'^~Ю2
«=0
N/2-1
Qlu+l "" 2^ ^N \9п Gn+NIl)
(2.89)
w
N12-
и=0
Рекурсивное применение этого разбиения приводит к битовой инверсии
элементов в выходном векторе, но не во входном векторе. В качестве примера на
рис. 2.24 приведена схема прохождения сигнала для N= 8. Из сравнения с
прореживающей во времени схемы прохождения сигнала (рис. 2.22) видно, что все шаги
выполняются в обратном порядке. Даже элементарные бабочкообразные
операции прореживающего в частоте алгоритма являются обратными к бабочкообраз-
ной операции в прореживающем во времени алгоритме.
2.5.6. Многомерные алгоритмы БПФ
Как правило, существует два возможньис способа формирования быстрых
алгоритмов в случае многомерных дискретных преобразований Фурье. Во-первых, мы
можем разложить многомерное ДПФ на 1-D ДПФ и использовать быстрые
алгоритмы для них. Во-вторых, мы можем обобщить подходы 1-D ДПФ для более
высоких размерностей. В этом разделе мы продемонстрируем примеры обоих
возможных способов.
Разложение на 1-D преобразования. Двумерное ДПФ можно разбить на два
одномерных ДПФ благодаря сепарабельности ядра. В 2-D случае уравнения (2.38) мы
получим
9и,о =
1
Л/-1
N-\
/ ^Ут
(
п^М
/я=01
и=0
Inmv
N
М
/
ехр
/-"
2тти
М
(2.90)
Глава 2. Представление изображений
Внутреннее суммирование образует Af 1-D ДПФ от строк, внешнее — Л^ 1-D
ДПФ от столбцов, т.е. 2-D ДПФ вычисляется как Л/преобразований строк, за
которыми следуют 7V преобразований столбцов.
Строковое преобразование
^ и=0
1
М-1
Столбцовое преобразование Эии^ — zli9 о ^^Р
2жто
N
1п\ти ^
М
Аналогичным образом Ж-мерное ДПФ можно составить из ^одномерных ДПФ.
Многомерное разложение. Разложение также непосредственно возможно в
многомерных пространствах. Мы продемонстрируем такие алгоритмы с помощью
простого случая 2-D двоичного прореживающего во времени алгоритма.
Мы раскладываем М х 7V матрицу на четыре подматрицы, взяв только каждый
второй пиксель в каждой второй строке (рис. 2.25). Это разложение дает
у и,и
9u,v+N/2
9u*M/2,v
9u+M/2,o+N/2 _
"1
1
1
1
1
-1
1
-1
1
1
-1
-1
1]
-1
-1
1 J
Г 0,0*
9u,o
„ -и 0,1 Д
W^ 9и,и
^ М Уи,и
1 —и —и \ \ ^
Верхние индексы перед д обозначают соответствующее частичное
преобразование. 2-D двоичный алгоритм очень похож на 1-D четверичный алгоритм. Так
же как для 1-D четверичного алгоритма (раздел 2.5.4), мы можем уменьшить число
сложений с 12 до 8 с помощью факторизации матрицы:
1111
1 -1 1 --1
11-1-1
1-1-1 1
10 10
0 10 1
10-10
0 10-1
110 0
1-10 0
0 0 11
0 0 1-1
2-D двоичный алгоррггм для Nx TV матрицы требует (3/47V2)ldiV комплексных
умножений, на 25% меньше, чем разделение на два 1-D двоичных БПФ. Однако
многомерное разложение имеет недостаток в том, что схема обращения к памяти
является более сложной, чем для 1-D преобразования Фурье. При разделении на 1-D
преобразования обращение к памяти становится локальным, приводя к более
высокой частоте успешных обращений к кэш-памяти, чем при распределенном
доступе многомерного разложения.
2.5.7. Преобразование Фурье для действительных изображений
До сих пор мы рассматривали только преобразование Фурье комплекснозначных
сигналов. Те же самые алгоритмы можно также использовать для действительньис
сигналов. Однако тогда они менее эффективны, поскольку преобразование Фурье
2.6. Упражнения
0
2
0
2
0
2
0
2
1
3
1
3
1
3
1
3
0
2
0
2
0
2
0
2
1
3
1
3
1
3
1
3
0
2
0
2
0
2
0
2
1
3
1
3
1
3
1
3
0
2
0
2
0
2
0
2
1
3
1
3
1
3
1
3
Рис. 2.25. Разложение матрицы изображения на четыре разбиения для 2-D
двоичного алгоритма БПФ
действительного сигнала является эрмитовым (раздел 2.3.4) и, таким образом,
только половина коэффициентов Фурье независима. Это соответствует выводу, что к
тому же половина сигнала, а именно мнимая часть, является нулевой.
Очевидно, что можно получить еще один множитель двойку в скорости
вычислений для Д ПФ действительных данных. Самый легкий способ сделать это заключается
в вычислении двух действительных 1-D последовательностей одновременно. Эту идею
можно легко применить к ДПФ изображений, поскольку необходимо вычислить
большое количество 1-D ДПФ. Таким образом, мы можем подставить первую строку х в
действительную часть, а вторую строку у— в мнимую часть и получить комплексный
вектор Z = дс + iy. Из свойств симметрии, рассмотренных в разделе 2.3.4, мы
заключаем, что преобразования действительных и мнимых частей отображаются в
Фурье-пространстве в эрмитовы и антиэрмитовы части. Таким образом, преобразования Фурье
двух действительных Л/-мерных векторов определяются по формуле
x„=l/2(i„+z;.J, %=l/2(z,-z;_J. (2.91)
2.6. Упражнения
2.1: Пространственное разрешение изображений
Представление изображений с интерактивно регулируемым числом точек
((Iip6ex02.01).
2.2: Квантование изображений
Представление изображений с интерактивно регулируемым числом
уровней квантования (dip6ex02.02).
2.3: Восприятие яркости в зависимости от контекста
Интерактивная демонстрация зависящего от контекста восприятия
яркости зрительной системы человека (dip6ex02.03).
2.4: Контрастное разрешение зрительной системы человека
Интерактивное исследование для определения контрастного разрешения
зрительной системы человека (dip6ex02.04).
2.5: Гамма-значение
Интерактивное регулирование гамма-значения для воспроизведения
изображения на экране (dip6ex02.05).
Глава 2. Представление изображений
2.6: "^Контрастное разрешение при логарифмическом датчике формирования
изображений
Вычислите относительное яркостное разрешение /^дУд\ вызванное
процессом преобразования в цифровую форму (Ад' =1), датчика формирования
изображений с логарифмическим откликом вида
g=a^+a^\ogg
и диапазоном контрастности 10^ для 8- и 10-битового разрешения.
Минимальный уровень яркости д отображается в д' = О, а в 110^ раз более
высокий максимальный уровень яркости либо в д' = 255, либо в д' = 1023.
2.7: Разделение на периодические структуры
Интерактивная демонстрация разбиения изображения на периодические
структуры, т.е. базисные функции преобразования Фурье (dip6ex02.06).
2.8: Преобразование Фурье
Интерактивное обучение для преобразования Фурье (dip6ex02.07).
2.9: Диапазон контрастности изображений, обработанных преобразованием Фурье
Интерактивное обучение для вычисления преобразования Фурье и
диапазона контрастности изображений, обработанных преобразованием Фурье
(dip6ex02.07).
2.10: Фаза и амплитуда преобразования Фурье
Интерактивное обучение для понимания значения и важности амплитуды и
фазы преобразования Фурье изображений (dip6ex02.9).
2.11: "^Теорема о сдвиге преобразования Фурье
Докажите теорему о сдвиге (теорема 2.3, с. 61) преобразования Фурье.
2.12: "^^Пары преобразований Фурье
Вычислите преобразование Фурье следующих функций в
пространственной области, используя пары преобразований Фурье, перечисленные в
>-R5 и >-R6, и основные теоремы преобразования Фурье (раздел 2.3.4 и
:^R4):
yjlna
5) i;;^^''"'
X у
^ х'
1g'
2 2 ^
_^ J^
2
J
2< 2(7^
2.6. Упражнения
в) cos^{k^x), ^\х\^{к^х)\
\\-\x\ IX |< 1
г) Л(х) = < (треугольная функция);
О иначе.
д) cos(/rojc) ехр
2а'
(волновой пакет).
С некоторыми функциями возможны различные способы вычисления
преобразования Фурье. Тщательно перечислите все шаги вашего решения и
укажите, какую теорему вы использовали.
2.13: *ДПФ
С помощью этого упражнения легко познакомиться с 1-D дискретным
преобразованием Фурье.
1. Вычислите базисные функции ДПФ для векторов с 4 и 8 элементами.
2. Вычислите преобразование Фурье вектора [4 12 1]^.
3. Вычислите преобразование Фурье вектора [1 4 1 2 ]^ чтобы увидеть, как
работает теорема о сдвиге (теорема 2.3, с. 61).
4. Вычислите преобразование Фурье вектора [40102010]^, чтобы
увидеть, как работает теорема о подобии в дискретном случае (теорема 2.2,
с. 60).
5. Выполните свертку вектора [4 1 2 1 ]^с [2 1 О 1 ] V4 и вычислите
преобразование Фурье второго вектора и свернутых векторов, чтобы увидеть, как
работает дискретная теорема о свертке (теорема 2.4, с. 61).
2.14: **Теорема о дифференцировании ДПФ
В то время как почти все теоремы непрерывного ПФ можно легко
перенести на дискретное ПФ (сравните )^R4 с xR7), в случае с теоремой о
дифференцировании существуют проблемы, поскольку дифференцирование
может аппроксимироваться только с помощью конечной разности в
дискретном пространстве. Докажите теорему для центральной конечной
разности для 1-ОДПФ
(9'..i-0.-i)/2 о . {^m{2nvlN)g^
и покажите, что эта теорема является аппроксимацией к теореме о
дифференцировании для непрерывного ПФ.
2.15: **Инвариантные нары преобразования Фурье
Какие функции являются инвариантными относительно непрерывного
преобразования Фурье, т.е. не изменяют свой вид, за исключением
масштабного множителя? (Подсказка: проверьте )^R6 в справочной инфор-
Глава 2. Представление изображений
мации этой книги). Имеют ли эти инвариантные пары преобразований
Фурье особую важность для обработки сигнала?
2.16: **Симметрии преобразования Фурье
Докажите следующие соотношения симметрии для пары преобразований
Фурье:
Пространственная область Фурье-область
эрмитова g(-Jc)= g*(jc) действительная д'{к)= д{к)
действительная gf*(jc) = д{х) эрмитова д{-к) = g'ik)
действительная и четная действительная и четная
действительная и нечетная мнимая и нечетная
сепарабельная: g(x)h{x^ сепарабельная: g{k)h{k^
осесимметричная д{\ х\) осесимметричная д{\ к\)
2 17: ^'^'^Троичный алгоритм БПФ
Имеет ли троичный алгоритм БПФ тот же порядок 0(MdAO, что и двоичные
и четверичные алгоритмы? Большее или меньшее число вычислительных
шагов необходимо?
2.18: ***БПФ действительных сигналов
В разделе 2.5.7 мы рассматривали, как можно эффективно вычислить
преобразование Фурье от действительного изображения. Возможен еще один
метод. Он основывается на том же принципе разложения, что и двоичный
алгоритм БПФ (раздел 2.5.7, уравнение (2.86)). Действительный вектор
разбивается на два. Считается, что точки с четными номерами являются
действительной частью комплексного вектора. По этому вектору вычисляется
преобразование Фурье. Покажите, как преобразование Фурье
действительного вектора можно вьиислить по преобразованию Фурье комплексного
вектора. (Этот метод имеет существенное преимущество в том, что он может
применяться для отдельного действительно вектора, в отличие от метода,
описанного в разделе 2.5.7.)
2.7. Дополнительная литература
Классическим учебным пособием по преобразованию Фурье — и все еще
одним из самых лучших - является книга Брейсвелла (Bracewell) [13]. Отличным
2 7. Дополнительная литература
источником для изучения различных преобразований является «Handbook on
transforms» от Поуларикаса (Poularikas) [156]. Для основ линейной алгебры,
особенно унитарных преобразований, читатель отсылается к одному из
современных учебных пособий по линейной алгебре, например, Мейера (Meyer) [137],
Энтона (Anton) [5] или Лея (Lay) [118]. Стоит обратить внимание на
историческую статью Кули (Cooley) и Таки (Тикеу) [25] о создании первого быстрого
алгоритма преобразования Фурье. Монография Блахута (Blahut) [11] охватывает
разнообразие быстрых алгоритмов для преобразования Фурье. Ахо (Aho) и др.
[3] дают общий обзор разработки и анализа алгоритма очень ясным и
понятным способом. Можно также порекомендовать исчерпывающее учебное
пособие Кормена (Cormen) и др. [26]. Оба учебных пособия включают БПФ.
ГЛАВА 3
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
СЛУЧАЙНЫЕ ПОЛЯ
3.1. Введение
Цифровую обработку изображений можно рассматривать как подобласть
цифровой обработки сигналов. По существу, все методы для получения и анализа
измерений и их ошибок можно также использовать для обработки изображений. В
частности, любое измерение - например, размер, положение объекта или его
средний уровень яркости - можно получить лишь с определенной точностью, и
оно применимо только в том случае, если можно также оценить его
недостоверность. Этим важным фактом, известным любому ученому или инженеру, часто
пренебрегали в самом начале развития обработки изображений. Использование
эмпирических и плохо обоснованных методов не позволяло получить
достоверные оценки погрешностей. К счастью, знания в области обработки изображений
значительно продвинулись вперед. На сегодняшний день доступны многие
хорошо обоснованные методы обработки изображений, которые включают
достоверные оценки ошибок.
В этом отношении необходимо вьщелить два важных класса погрешностей.
Статистическая ошибка описывает разброс измеренной величины при условии,
что одно и то же измерение повторяется снова и снова, как и показано на рис. 3.1.
Соответствующая мера ширины распределения определяет статистическую
ошибку, его центр и среднее измеренное значение.
Однако это среднее значение может находиться гораздо дальше от истинного, чем
значение, задаваемое статистически допустимыми пределами. Такое отклонение
называется систематической ошибкой. С разницей между систематическими и
статистическими ошибками тесно связаны понятия точный и правильный. Точное, но
неправильное измерение появляется в случае, когда статистическая ошибка малая, а
систематическая ошибка большая (рис. 3.1, а). Если верно обратное, т.е.
статистическая ошибка большая, а систематическая ошибка малая, то отдельные измерения
широко разбрасываются, но их среднее значение близко к истинному (рис. 3.1, б).
Легко, по крайней мере в принципе, получить оценку статистической ошибки,
повторяя одно и то же измерение много раз. Однако гораздо сложнее контролировать
систематические ошибки. Они часто связаны с недостатком в понимании
измерительной установки и процедуры. Неизвестные или неконтролируемые параметры,
влияющие на процедуру измерения, могут легко привести к систематическим
ошибкам. Типичными источниками систематических ошибок являются погрешности
калибровки или зависящие от температуры изменения параметра в экспериментальной
установке без регулятора температуры.
В этой главе мы познакомимся с тем, как обрабатывать данные изображений -
как статистические величины или случайные величины. Начнем мы со
статистических свойств измеряемого уровня яркости в отдельном элементе датчика или
3.2. Случайные величины
Точное, но неправильное измерение
Неточное, но правильное измерение
Статистическая
неопределенность
Отдельное
измерение
Среднее
значение
Систематическая
ошибка
Истинное
значение
Статистическая
неопределенность
Рис. 3.1. Иллюстрация систематической (а) и статистической (б) ошибок,
демонстрирующая различие между точностью и правильностью измерения положения в
2-D изображениях. Статистическая ошибка определяется распределением
отдельных измерений, в то время как систематическая ошибка — это разность между
истинным значением и средним значением от измеренных значений
пикселе в разделе 3.2. Тогда мы можем применять классические понятия
статистики, используемой для обработки точечных измерений. Эти методы, как правило,
используются в большинстве научных дисциплин. Такой тип используемой
статистики также известен как статистика первого порядка, поскольку она
рассматривает только статистику отдельной точки измерения.
Операции обработки изображений используют измеренные уровни яркости для
вычисления новых величин. В простейшем случае только уровень яркости в
отдельной точке берется как входное значение так называемыми точечными
операциями. В более сложных случаях берутся уровни яркости от многих пикселей для
вычисления новой точки. В любом случае необходимо знать, как статистические
свойства, в особенности точность вычисляемой величины, зависят от точности
взятых для вычисления этой величины уровней яркости. Другими словами,
необходимо установить, как ошибки распространяются в процессе выполнения
операций обработки изображений. Таким образом, темой раздела 3.3 являются
многомерные случайные величины и распространение ошибок.
В качестве последнего шага мы обратимся к временным рядам случайных
величин (стохастические процессы) и пространственным массивам случайных
величин (случайным полям) в разделе 3.5. Это позволит нам рассматривать случайные
процессы в Фурье-области.
3.2. Случайные величины
3.2.1. Функция плотности распределения вероятностей и гистограммы
Представьте экспериментальную установку, с помощью которой мы получаем
изображение определенного объекта. Измеряемой величиной в некоторой точке на плоскости
изображения (пикселе) является энергетическая освещенность. Из-за статистической
природы наблюдаемого процесса каждое измерение даст различное значение.
Глава 3. Случайные величины и случайные поля
Это означает, что наблюдаемый сигнал характеризуется не отдельным значением, а
скорее функцией плотности распределения вероятностей {ФПР) f{g). Эта функция
определяет вероятность появления значения д. Измеряемая величина, которая обуслов-
ливаетх^я случайным процессом, обозначается как случайная величина, или коротко СВ.
В дальнейшем мы рассматриваем непрерывные и дискретные случайные
величины и вероятностные функции вместе. Нам понадобятся дискретные вероятности,
поскольку только дискретные числа могут обрабатываться с помощью цифрового
компьютера. Дискретные значения получаются после процесса квантования,
который был введен в разделе 2.2.4. Многие уравнения этого раздела содержат
непрерывную формулировку слева и их дискретные аналоги справа. В непрерывном
случае /(gf)dg задает неотрицательную вероятность получить при измерении значение
в интервале от ддо gf + dgf. В дискретном случае мы можем получить при измерении
лишь конечное число Q значений д(д=1, 2,..., Q) с вероятностью/. Как правило,
значение пикселя хранится в одном байте, так что мы можем измерить Q = 256
различных уровней яркости. Поскольку полная вероятность появления вообще любого
значения равна 1 по определению, ФПР должна удовлетворять требованию
]f(g)dg = l Х/.=1. (3.1)
-со д=\
Интеграл от ФПР
F(g)=^jfig')dg\ F^=t,f,^ (3.2)
известен как функция распределения. Поскольку ФПР является неотрицательной
функцией, функция распределения монотонно возрастает от О до 1.
Как правило, распределение вероятностей неизвестно заранее. Скорее оно
оценивается по измерениям. Если наблюдаемый процесс является однородным, т.е.
если он не зависит от положения пикселя на изображении, то существует простой
способ оценить ФПР, используя гистограмму.
Гистограммой изображения является список (вектор), который содержит один
элемент для каждого уровня квантования. Каждый элемент содержит число
пикселей, уровень яркости которых соответствует индексу элемента. Гистограммы
можно легко вычислить для данных любой размерности. Сначала положим вектор
гистограммы равным нулю. Затем мы просматриваем каждый пиксель изображения,
сопоставляем его уровень яркости с индексом в списке и увеличиваем
соответствующий элемент списка на единицу. Действительный алгоритм просмотра зависит от
того, как хранится изображение.
Оценка функции плотности распределения вероятностей может быть также
получена для данных изображений с более высоким разрешением, например, 16-битовых
изображений или изображений с плавающей запятой. Тогда диапазон возможных
значений разбивается на Q интервалов одинаковой ширины. Значением, связанным с
интервалом, является центр интервала, несмотря на то что мы выбираем значения
между иьггервалами, увеличивая соответствующие элементы списка. Если мы не
принимаем такого допущения, то величины, вычисляемые по гистограмме, например
средние значения, искажаются.
3.2. Случайные величины
3.2.2. Среднее значение, дисперсия и моменты
Двумя основными параметрами, которые описывают СВ д, являются ее среднее
значение (также известное как математическое ожидание) и ее дисперсия. Среднее
значение 1Л=Ед определяется как
(3.3)
Среднее значение можно также определить, не зная функцию плотности
распределения вероятностей явно, путем усреднения бесконечного числа
измерений:
А^ = Ь^^^-- (3.4)
^ р=\
Поскольку мы не можем получить бесконечное число измерений,
определение среднего значения по уравнению (3.4) сохраняет оценку с остаточной
неопределенностью, которая зависит от формы ФПР, т.е. типа случайного
процесса и числа измерений.
Дисперсия а^ = vargf = EUg- jn) 1 позволяет оценить степень отклонения
измеренных значений от среднего значения:
-«о 9=1
(3.5)
ФПР может характеризоваться более детально с помощью величин, подобных
дисперсии, — центральных моментов п-го порядка /и^ = Е Ug — lu) 1:
оо Q
Ип = 1{9-иУЯ9)^д, Ип=^(9,-и)У,. (3.6)
-оо q=\
Первый центральный момент равен по определению нулю. Второй момент ji^
равен дисперсии а^. Третий момент ц^, асимметрия, является мерой
несимметричности ФПР относительно среднего значения. Если ФПР является функцией с
четной симметрией, f[-{g-jLi)) = f(g - /л), то третий и все моменты более
высокого нечетного порядка исчезают.
3.2.3. Функции случайных величин
Любая операция обработки изображений изменяет сигнал д в отдельных
пикселях. В простейшем случае д в каждом пикселе преобразуется в h с помощью
функции/?: h =р(д). Такая функция известна в обработке изображений как
точечный оператор. Поскольку g является СВ, h будет также СВ, и нам
необходимо знать ее ФПР, для того чтобы определить статистические свойства
изображения после его обработки.
Глава 3. Случайные величины и случайные поля
Очевидно, что ФПРу^ от h имеет такой же вид, как ФПР/ от д, если/? является
линейной функцией: А = а^ + di^g:
\а,\ I а J
где обратное линейное соотношение g = p'\h) : д = (h - a^la^ используется для
выражения д как функции от А.
Из уравнения (3.7) интуитивно видно, что в общем случае нелинейной функции
р{ф наклон flj заменится на первую производную/7'(gf) (утр(д). Дополнительные
сложности возникают, если обратная функция имеет больше, чем одну ветвь. Простым и
важным примером является функция h = д^,у которой две обратные функции
gfj 2 = i\lh. В таком случае ФПР от h складьшается из всех ветвей обратной функции.
Теорема 3.1 (ФПР функции от случайной величины). Если f^ является ФПР
случайной величины д, и р является дифференцируемой функцией h = р(д), тогда ФПР
случайной величины h определяется соотношением
(3.8)
\F\bJsn I
где д^ — S действительных корней h =р{д).
Монотонная функция/? имеет единственную обратную функцию/?"Чй). Тогда
уравнение (3.8) сводится к
fhih)= \ _, . (3.9)
\Р(Р (h))\
Следующая встречающаяся в обработке изображений задача связана с
распределениями вероятностей. У нас есть сигнал д с некоторой ФПР, и мы хотим
преобразовать g с помощью подходящего преобразования в h таким образом, чтобы А
имела конкретное распределение вероятностей. Эта задача является обратной к
той, которую мы рассматривали до сих пор, и она имеет на удивление простое
решение. Преобразование
h = F-'(F^(g)) (3.10)
преобразует/^(д)-распределенную случайную величину д в/^(А)-распределен-
ную случайную величину А. Решение является особенно простым для
преобразования в равномерное распределение, поскольку тогда F~^ является постоянной
функцией и А = Fg(g),
Теперь рассмотрим среднее значение и дисперсию функций от случайных
величин. По определению, согласно уравнению (3.3), среднее значение для А есть
оо
Eh = n^ = jhff,ih)(ih. (З.п)
—оо
Однако мы можем также выразить среднее значение непосредственно исходя
из функции/?(gf) и ФПР/^(д):
оо
Eh = Е{р(д)) = j p(9)f,ig)dg. (З.12)
3.3. Многомерные случайные величины
Интуитивно мы можем предположить, что среднее значение h можно
вычислить по среднему значению д: Eh =р(Ед). Однако это возможно только в случае,
если р является линейной функцией. Если р(д) аппроксимируется многочленом
P(9) = P(^lg) + PX^lg)(g-Mg) + P\^lgX9-^lg)^2 + ..., (3.13)
Ц,'-р{Цд) + р\^1д)(У112. (3.14)
ol^\p\^lg)\ о]
Из этого уравнения видно, что /х^ ^ p{ii) является хорошей аппроксимацией
только в случае, когда и кривизна функции р{д), и дисперсия д малы, т.е. р{д) может
хорошо аппроксимироваться линейной функцией на отрезке [jU - Зет, /i + За].
Оценка первого порядка дисперсии для h определяется соотношением
(3.15)
Это выражение является точным только для линейных функций/?.
Следующие простые соотношения для средних значений и дисперсий следуют
непосредственно из вышеизложенного рассмотрения (а — константа):
Е(ад) = аЕд, var(agf) = а'vargf, \ггд=^Е(д^)-{Ед)\ (3.16)
3.3. Многомерные случайные величины
при обработке изображений мы имеем дело с большим количеством случайных
величин. Операции обработки изображений вычисляют новые величины по
значениям во многих пикселях. Таким образом, важно рассмотреть статистику
многомерных СВ. В данном разделе мы сделаем первый шаг и рассмотрим, как можно
манипулировать статистическими свойствами многомерных СВ и функций от
многомерных СВ.
3.3.1. Совместная функция плотности распределения вероятностей
Сначала нам необходимо рассмотреть, как могут быть описаны случайные
свойства многомерных СВ. Как правило, случайные свойства двух СВ, д^ и д^, не могут
быть описаны их отдельными OnP,/(gfj) и/(д^). Скорее нужно определить
совместную функцию плотности распределения вероятностей/(д^, д^. Только тогда,
когда две случайные величины являются независимыми, т.е. если вероятность, что д^
примет определенное значение, не зависит от значения д^, совместная ФПР
может быть вычислена по отдельным ФПР, известным как маргинальные ФПР:
f(9i.9^2) = Л, (01 )/д, (92) <=> 9i^92 - независимые. (3.17)
Для Р случайных величин д — случайного вектора д — совместная функция
плотности распределения вероятностей ecTb/(gfp д^, ..., д) =f{g). Рслучайньгх:
величин называются независимыми, если совместная ФПР может быть записана
как произведение маргинальных ФПР:
р
fi9) = Y[fg^{9p) <^ 9р -независимые, р = 1, ...,Р. (зл8)
/7=1
Глава 3. Случайные величины и случайные поля
3.3.2. Ковариация и корреляция
Ковариация показывает, в какой степени колебания двух СВ — g и g - связаны
друг с другом. В расширенном определении дисперсии в уравнении (3.5)
ковариация определяется как
^p,=E[{g^-^i^){g^-^^)) = E{g^g^)-E{g^)E{g^). (3.19)
Для Р случайных величин ковариации образуют симметричную матрицу РхР,
ковариационную матрицу Z = covgf. Диагональ этой матрицы содержит дисперсии Р
случайных величин.
Коэффициент корреляции связывает ковариацию с соответствующими
дисперсиями:
с,,=^, где |с|<1. (3.20)
Р й
Две СВ — д ид — называются некоррелированными, если ковариация а равна
нулю. Тогда согласно уравненрым (3.19) и (3.20) для некоррелированных СВ
выполняются следующие соотношения:
^ря=^^ ^ря= О О Е(д^д^) = Е(д^)Е(д^)^ 9р.9,- некоррелированные.
(3.21)
Из последнего из этих условий и уравнения (3.17) очевидно, что независимые СВ
являются некоррелированными.
На первый взгляд кажется, что легко манипулировать только
статистическими свойствами независимых СВ. В этом случае нам необходимо рассматривать
только маргинальные ФПР отдельных случайных величин вместе с их средним
значением и дисперсией. В большинстве случаев нужно рассматривать
взаимосвязь случайных изменений величин, что и выражается ковариационной
матрицей Z. Однако, поскольку ковариационная матрица является симметричной,
можно всегда найти систему координат, т.е. линейную комбинацию СВ, в которой
ковариационная матрица является диагональной и, следовательно, СВ являются
некоррелированными.
3.3.3. Линейные функции от многомерных случайных величин
В дополнение к рассмотрению функций от одной СВ в разделе 3.2.3 можно
выразить среднее значение функции от многих случайных величин h =р(д^, 5^2' •••» 9)
непосредственно из совместной ФПР:
Eh= j р(д,, 02' •••'9p)f(9i^ 9i. -. 9р)^9А92 - ^9р. (3.22)
Из этого общего соотношения следует, что среднее значение любой линейной
функции
р
^^И^р9р (3.23)
р=\
определяется как линейная комбинация средних значений СВ д:
3.3. Многомерные случайные величины
/7=1 1 р=\
(3.24)
Обратите внимание, что это соотношение является общим результатом. Мы
не делали предположения, что СВ являются независимыми и он не зависит от типа
ФПР. В частном случае уравнение (3.24) включает простые соотношения
Е{д,+92) = Ед,+Ед,, Е(д,+а) = Ед,+а. (3.25)
Дисперсия функций от многих СВ не может быть вычислена так просто даже в
линейном случае. Пусть д есть вектор из Р случайных величин, А — вектор из Q
случайных величин, которые являются линейной комбинацией Р случайных
величин д,М- матрица коэффициентов размерностью QxP,a.a — вектор-столбец с
Q коэффициентами. Тогда
к = Мдл^а с E(h) = ME(g) + a (3.26)
в расширении к уравнению (3.24). Если P=Q, то уравнение (3.26) можно
интерпретировать как координатное преобразование в Р-мерном векторном
пространстве. Следовательно, неудивительно, что симметричная ковариационная матрица
преобразуется как тензор второго порядка [149]:
соу(Л) = Mcov(flf)M ^.
(3.27)
Для того чтобы продемонстрировать применение уравнения (3.27), мы
рассмотрим три примера.
Дисперсия среднего от случайных величин. Сначала рассмотрим вычисление
дисперсии среднего д от случайных величин с одинаковым средним значением и
дисперсией (т^ Предположим, что случайные величины являются
некоррелированными. Тогда матрица Ми ковариационная матрица cov д имеют вид
М =-^[1,1,1,...,!] и cov(flf) =
О
О
о о .
Подставляя эти выражения в уравнение (3.27), получаем
9 р
О
о
= g'L
(3.28)
Таким образом, дисперсия g^ пропорциональна Р ^ а среднеквадратичное
отклонение Gg убывает со скоростью только Р "^/^ Это означает, что мы должны взять
в 4 раза больше измерений, для того чтобы удвоить точность измерения среднего.
Это не выполняется в случае коррелированных СВ. Если СВ являются полностью
коррелированными (с^^ = 7, о^^ = <7 ^), в соответствии с уравнением (3.27),
дисперсия среднего равна дисперсии отдельных СВ. В этом случае невозможно
уменьшить дисперсию с помощью усреднения.
Глава 3. Случайные величины и случайные поля
Дисперсия суммы некоррелированных случайных величин с неравными
дисперсиями. Внеся незначительное изменение, мы возьмем Р некоррелированных СВ с
неравными дисперсиями с^ и вьгаислим дисперсию суммы случайных величин. В
уравнениях (3.25) мы уже установили, что среднее значение суммы равно сумме средних
значений (даже для коррелированных случайных величин). Аналогичным образом,
как и в предыдущем случае, можно показать, что для некоррелированных
случайных величин дисперсия суммы равна также сумме отдельных дисперсий:
р р
var]£gf^=Xvargf^. (3.29)
/7=1 р=\
Линейные комбинации многомерных случайных величин. В качестве третьего
примера возьмем Q случайных величин А^, которые являются линейной комбинацией
Р некоррелированных случайных величин д с равными дисперсиями а^\
\=alg. (3.30)
Тогда векторы а ^образуют строки матрицы Мразмерности PxQb уравнении
(3.26), а ковариационная матрица А примет в соответствии с уравнением (3.27) вид
cov(/i) = (j'MM^=o-^
т
«Г«2
«Г«е
т
а, 02
г
а2<12
«[«е •
.. afog
.. alaQ
.. ag«g
(3.31)
Из этого уравнения мы можем сделать два вывода. Во-первых, дисперсия СВ h
задается как а ^а , т.е. как сумма квадратов коэффициентов
ст^(/;^) = ст\\. (3.32)
Во-вторых, несмотря на то что случайные величины д являются
некоррелированными, две случайные величины, h^ и h^, являются некоррелированными
только в случае, если скалярное произведение векторов коэффициентов, а ^а равно
нулю, т.е. если векторы коэффициентов ортогональны. Таким образом, только
ортогональные матрицы преобразования Мъ уравнении (3.26) оставляют
некоррелированные случайные величины некоррелированными.
Для коррелированных случайных величин можно заключить, что всегда
можно применить подходящее преобразование М, для того чтобы получить набор
линейных комбинаций случайных величин, которые являются
некоррелированными. Это следует из элементарной теоремы линейной алгебры: любая симметричная
квадратная матрица может быть приведена к диагональному виду
преобразованием, которое называется преобразованием главных компонентов [15, 215].
Некоррелированный набор линейных комбинаций образует оси системы главных
компонент и известен как набор собственных векторов матрицы. Собственные векторы
удовлетворяют условию
cov(h)ep=Gle^.
(3.33)
3.4. Функции плотности распределения вероятностей
Это означает, что умножение ковариационной матрицы на собственный вектор
сводится к умножению на скалярную величину. Этот множитель называется
собственным значением, соответствующим собственному вектору е . Для
ковариационной матрицы/?-м собственным значением является дисперсия а^ в
направлении собственного вектора е.
3.3.4. Нелинейные функции от многомерных случайных величин
Вышеизложенный анализ дисперсии для функций от многомерных случайных
величин можно расширить на случай нелинейных функций при условии, что функция
является достаточно линейной в окрестности среднего значения. Как и в разделе 3.2.3, мы
разложим нелинейную функцию р (д) в ряд Тейлора в о1фестности среднего значения:
Р др
Р=1 ^9q
(3.34)
Сравнив это уравнение с уравнением (3.26), находим, что матрица Мс
размерностью PxQ должна быть заменена матрицей
/ =
Эр,
^9х
др2
^9i
^Pq
^9i
dp,
^92
Эрз
^92
^Pq
^9г
dp,
^9p
Эр2
^9p
^Pq
^9p
(3.35)
известной как матрица Якоби преобразования А =р(д). Таким образом, ковариа-
ция для А определяется соотношением
coy(h) ^ J C0Y(g)J
(3.36)
3.4. Функции плотности распределения вероятностей
в предьщущих разделах мы получили некоторые общие свойства случайных
величин без каких-либо сведений о распределениям вероятностей. В этом разделе мы
рассматриваем некоторые определенные функции плотностей распределения
вероятностей, которые представляют важность при обработке изображений.
В качестве введения к обработке ФПР рассмотрим ФПР от функций многомерных
случайных величин. Ограничим наше рассмотрение двумя простыми случаями.
Сначала рассмотрим сложение двух случайных величин. Если две случайные величины д^ и д^
являются независимыми, то результирующая функция плотности распределения
вероятностей аддитивной суперпозиции g = 3i + 02 определяется интегралом свертки
Рд(9)= jPg,Wpg^(g-h)dh.
(3.37)
Глава 3. Случайные величины и случайные поля
Это общее свойство вытекает из мультипликативной природы суперпозиции
вероятностей. Вероятность р (д) получить при измерении значение д равно
произведению вероятностей получить при измерении д^= hn д^ = д - h. Интеграл в
уравнении (3.37) требуется сам по себе, поскольку мы должны рассмотреть все
комбинации значений, которые приводят к сумме д.
Теперь можно применить такую же процедуру к произведению двух
случайных величин, если преобразовать произведение двух случайных величин в
сложение, используя логарифм: Ingf = Ingfj + Ing^. Функции плотности распределения
вероятностей логарифма от СВ можно вычислить, применив уравнение (3.9).
3.4.1. Распределение Пуассона
Сначала рассмотрим процедуру получения изображений. Формирующий
изображение элемент датчика, который освещается с некоторой интенсивностью,
принимает в течение некоторого интервала времени А^ - времени экспонирования — в
среднем N электронов путем поглощения фотонов. Таким образом, средний
поток фотонов в единицу времени Я определяется соотношением
Я = —. (3.38)
А/
Из-за случайного характера потока фотонов в течение каждой экспозиции
поглощается разное число фотонов. Случайный процесс, в котором мы насчитываем
в среднем ДА/ событий, известен как пуассоновский процесс P{)[At).
Такой процесс имеет распределение с дискретной плотностью вероятностей
Р(ЯАО: /„=ехр(-ЯАО^^
1ием и дисперсией
|jU = AA/ и (Т^=ЯА/.
, «>0
(3.39)
(3.40)
На рис. 3.2 показаны смоделированные изображения с низким уровнем
освещенности, с пуассоновским шумом. При малых средних значениях ФПР
Пуассона наблюдается асимметрия с более длинным хвостом (рис. 3.3, а). При среднем
значении (100) функция плотности становится симметричной.
Типрмный элемент ПЗС-датчика изображения (раздел 1.7.1, >- R2 )
накапливает порядка 10 000 и больше электронов, которые порождаются при поглощении
фотонов. Таким образом, среднеквадратичное отклонение числа накапливаемых
электронов составляет 100, или 1%. Из этой цифры можно сделать заключение,
что даже совершенный элемент датчика изображения, который не создает
дополнительного электронного шума, показывает значительный уровень шума как раз в
соответствии с лежащим в основе пуассоновским процессом.
Пуассоновский процесс обладает следующими важными свойствами:
1. Среднеквадратичное отклонение а не является постоянной величиной, а
равно квадратному корню из числа событий. Следовательно, уровень шума
зависит от сигнала.
2. Можно показать, что непересекающиеся экспозиции являются
статистически независимыми событиями [149, раздел 3.4]. Это означает, что мы можем брать
3.4. Функции плотности распределения вероятностей 103
Рис. 3.2. Моделирование изображений с низким уровнем освещенности, с пуассо-
новским шумом, которые накапливают максимально: а — 3; б — 10; в — 100; г — 1000
электронов. Обратите внимание на клин с линейной интенсивностью внизу изображений в и
п о<^ 1
0.2
0,15
0,1
0,05
1—:
J7
\Л
f/
А.
Ч
Л 1
ъ
W
О
8
Рис. 3.3. а - функции плотности распределения вероятностей Пуассона P()U) для
средних значений jU - 3, 10, 100 и 1000. Ось х нормирована средним: среднее значение
равно единице; P(XAt) умножается на G^Jln\ б — дискретная биномиальная
ФПР В( 8, 1/2) со средним значением, равным 4, и дисперсией, равной 2, и
соответствующая нормальная ФПР N{ 4, 2)
Глава 3. Случайные величины и случайные поля
изображения, полученные с помощью одного и того же датчика в разное время,
как независимые случайные величины.
3. Пуассоновский процесс является аддитивным: сумма двух независимых
распределенных по закону Пуассона случайных величин со средними значениями ji^
и /^2 является также распределенной по закону Пуассона со средним значением и
дисперсией ^и^ + ii^.
3.4.2. Нормальные и биномиальные распределения
Многие процессы с непрерывными случайными величинами можно адекватно
описать с помощью нормальной или гауссовой плотности распределения М(ц, а), со
средним значением /j. и дисперсией а^:
(3.41)
Из уравнения (3.41) можно видеть, что нормальное распределение полностью
описывается средним значением и дисперсией.
Дискретным аналогом нормального распределения является биномиальное
распределение B(Q, р):
(3.42)
Натуральное число Q обозначает число возможных исходов, а параметр ^ б ]0,1 [
определяет вместе с Q среднее значение и дисперсию:
ILi = Qp и CJ =Qp(l-p)
(3.43)
Даже для среднего значения Q биномиальное распределение оказывается очень
близким гауссову распределению, как и показано на рис. 3.3, б.
В дополнение к уравнению (3.41) совместная функция плотности
нормального распределения вероятностей N(ji, X) для многомерных случайных величин, т.е.
случайного вектора д со средним значением fi и ковариационной матрицей Z,
определяется соотношением
N(fi^): f(g) =
1
(2яY^^^[d^
exp
{g-tiyir\g-ti)
(3.44)
/
На первый взгляд это выражение выглядит ужасно сложным. Но на самом деле это
не так. Мы лишь должны учесть, что симметричная ковариационная матрица
становится диагональной при повороте в систему с главными осями. Тогда совместная
функция плотности нормального распределения становится сепарабельной функцией
М)-П
1
/
(2л:(т)
2ч1/2
ехр
2(у1
2 \
(3.45)
с дисперсиями а ^ вдоль главных осей (рис. 3.4, а), а компоненты д' являются
случайными величинами.
3.4. Функции плотности распределения вероятностей
Рис. 3.4. Двумерные плотности нормального распределения: а - коррелированные
случайные величины с о^=о^ = 1 и г,2 = -0,5; б - изотропные некоррелированные
^2
случайные величины с дисперсиями с^
= ст/ = 1
в случае некоррелированных случайных величин с равными дисперсиями а^
распределение N(fx, Z) сводится к изотропной функции плотности нормального
распределения вероятностей N(iu, а) (рис. 3.4, б):
N(H.CJ): f(g) =
1
Г
{2па')
2\Р/2
ехр
l(g-A^)
|2 Л
(3.46)
3.4.3. Центральная предельная теорема
Существенная значимость нормального распределения вытекает из центральной
предельной теоремы (теорема 2.6, с. 63), которую мы рассматривали относительно
каскадной свертки в разделе 2.3.4. Здесь мы сделаем акцент на ее важности для случайных
величин при обработке изображений. Теорема о центральном пределе утверждает, что
при условиях, которые почти всегда выполняются в задачах обработки изображений,
ФПР суммы случайных величин стремится к нормальному распределению. Как мы и
рассматривали в разделе 3.3, при обработке изображений часто вычисляются
взвешенные суммы от многих значений. Следовательно, эти связанные величины имеют
функцию плотности нормального распределения вероятностей.
3.4.4. Другие распределения
Несмотря на значимость нормального распределения, другие функции плотности
распределения вероятностей также играют определенную роль при обработке
изображений. Они возникают, когда случайные величины связываются нелинейными
функциями.
В качестве первого примера рассмотрим преобразование декартовых координат
в полярные. Возьмем случайный вектор д = [gfj, д^^с независимыми 7V(0, cj)-pacnpe-
деленными компонентами. Тогда можно показать [149, раздел 6.3], что модуль этого
вектора г=^(д^, д^У^^ и полярный угол ф =diTctSin(g^/g^) являются независимыми
случайными величинами. Модуль имебт плотность распределения Рэлея
R{CJ): /(г) = —ехр
2g'
для г>0
(3.47)
со средним значением и дисперсией
06 Глава 3, Случайные величины и случайные поля
Ик
= (Тл/л:/2
2 2
4-я-
3.48)
а угол 0 имеет плотность равномерного распределения
2п
Для обобщения плотности распределения Рэлея рассмотрим модуль Р-мерно-
го вектора. Он имеет плотность хи-распределения с Р степенями свободы:
(3.49)
XiP.G): fir) =
со средним значением
2г
р-1
2''''Г(Р/2)(т^
ехр
„2 Л
2сг'
для г > о (3.50)
>/2Г(Р/2 + 1/2) /„ ,,^ „ ,
Ц,=<т-—5^ ^«CTVP-1/2 для Р»1
^' ПРИ)
(3.51)
И дисперсией
(7j=o-^P-juJ«CT^/2 для Р»1 (3.52)
Среднее значение плотности хи-распределения возрастает со скоростью
квадратного корня из Р, в то время как дисперсия есть почти постоянная величина.
При больших степенях свободы плотность быстро приближается к плотности
нормального распределения N(ay/P/2 — l/2,(jyf2) (рис. 3.5, а).
ФПР квадрата модуля вектора имеет другую ФПР, поскольку возведение в
квадрат является нелинейной функцией (раздел 3.2.3). Используя теорему 3.1, ФПР,
известную как плотность распределения хи-квадрат с Р степенями свободы, можно
вычислить как
Р/2-\
х\Р,о): Пг) = -
2^''Г(Р/2)ст''
со средним значением и дисперсией
ехр
2<г'
для г > о (3.53)
0,6
0,5
0,4
0,3
0,2
0,1
__2^.а_1 .,, L,„ :. _
б
1,4
1,2
1
0,8
0,6
0,4
0,2
1
6 Г
к/^
/ЗОН
/ / Г Г
^пл^
1 1
^^^з===_г
о 1 2 3 Г/М
Рис. 3.5. а — плотность хи-распределения для 2 (плотность распределения
Рэлея), 3 (плотность распределения Максвелла) и более степеней свободы; б —
плотность распределения хи-квадрат на нормированном графике (среднее значение в
единице) со степенями свободы
3.4. Функции плотности распределения вероятностей
IU^,=G^P И С7\ =2С7^Р. 3.54)
Сумма квадратов случайных величин представляет особую важность для
получения ошибки при оценивании выборочной дисперсии:
1 ^ _ _ 1 ^
^'=ir^Y(9n-9f с д = -Уд, 3.55)
Папоулиз (Papoulis) [149, раздел 8.2] показал, что нормированная выборочная
дисперсия
а'
г
=1
'9„-9^'
V
(3.56)
имеет плотность распределения хи-квадрат с Р- 1 степенями свободы. Таким
образом, среднее значение выборочной дисперсии равно а^ (несмеп1енная
оценка), а дисперсия равна 2&/{Р - 1). При малых степенях свободы
плотность распределения хи-квадрат показывает значительные отклонения от
плотности нормального распределения (рис. 3.5, б). Для степеней свободы
больших чем 30 плотность распределения является в хорошей
аппроксимации нормально распределенной. Достоверная оценка дисперсии требует
большого количества измерений. При Р= 100 относительное среднеквадратичное
отклонение дисперсии все еще равно приблизительно 20% (при
среднеквадратичном отклонении от среднеквадратичного отклонения оно составит
половину, 10%).
3.4.5. Шумовая модель для датчиков изображений
После детального рассмотрения случайных величин теперь мы можем закончить
простой шумовой моделью для датчика изображения. В разделе 3.4.1 мы показали,
что фотонный сигнал в отдельном пикселе распределен по закону Пуассона. За
исключением низкоуровневых условий формирования изображений, при которых
только незначительное количество электронов накапливается в отдельном элементе
датчика, пуассоновское распределение хорошо аппроксимируется нормальным
распределением N(Q^^^Q^), где Q^— число электронов, поглощенных за время
экспозиции. Не каждый падающий фотон вызывает возбуждение электрона. Доля
электронов, возбуждаемых излучением фотонов на элемент датчика (Q^),
называется квантовой эффективностью 7j:
п — ^^
^~'0~' (3-57)
Электронные схемы включают некоторые другие источники шумов. Для
практических целей важно лишь знать, что эти источники шумов являются нормально
распределенными и независимыми от фотонного шума. Следовательно, общее
число порожденных единиц заряда и их дисперсии равны
Глава 3. Случайные величины и случайные поля
PixelflyQE/c204, 1,70 ms, low gain, 270xs3706
A602f/c066, 4.30 ms, gain 1
500 1000 1500 2000 2500 3000 3500 4000
g'
Рис. 3.6. Шумовая дисперсия как функция от дискретного уровня яркости для а —
Pixelfly QE от РСО с Sony interline CCD ICX285AL, 12 бит, сг^ =2,2 (8 е-)\ б - Basler
A602f с Micron MT9V403 CMOS, 8 бит, ст^ =0,61 (91 е-) [90]
Предположим, что электронные схемы линейны. Тогда результирующий
цифровой сигнал д определяется соотношением
g = KQ. (3.59)
Коэффициент преобразования К представляет собой безразмерную величину
и выражает полное усиление сигнала в битах/единица заряда. Дисперсию
цифрового сигнала легко вычислить, используя равенство Gq^
(3.29), (3.40) и (3.59):
Q и уравнения (3.15),
<=^Чо+^Ч=^о+^^-
(3.60)
Уравнение (3.60) прогнозирует линейный рост дисперсии с увеличением
цифрового сигнала д. Измерения, как правило, хорошо согласуются с этой простой
моделью (рис. 3.6). Интересно, что шум имеет здесь преимущество. Коэффициент
преобразования ЛГ можно определить из соотношения для о'^{д), не зная каких-
либо деталей об электронных схемах.
3.5. Стохастические процессы и случайные поля
Полученная на данный момент статистика не учитьюает пространственные и
временные соотношения между точками многомерного сигнала. Если мы хотим проводить
статистический анализ контекста изображений, то должны рассматривать все
изображение как статистическую величину, известную как случайное поле в случае
пространственных данных и как стохастический процесс в случае временных радов.
В случае изображения Мх N случайное поле состоит из матрицы
размерностью Мх N, чьи элементы являются случайными величинами. Это означает, что
совместная функция плотности распределения вероятностей имеет MN
переменных. Среднее значение случайного поля задается тогда, как сумма по всем
возможным состояниям q:
G„,„ = J,f,(G)G^
?=i
(3.61)
3.5. Стохастические процессы и случайные поля
Если у нас есть Q уровней квантования, то каждый пиксель может принимать
Q разных состояний. Сложение по всем Мх N пикселям дает Q^^ состояний G .
Получаем ужасающее представление, оказывающееся бесполезным из-за
невероятного количества возможных комбинаций. Таким образом, мы должны найти
более простые представления для обработки многомерных сигналов как случайных
полей. В этом разделе мы подойдем к этой проблеме практическим способом.
Начнем с оценки среднего значения и дисперсии случайного поля. Мы можем
сделать это таким же образом, как и в случае для одной величины (уравнение (3.55)),
взяв среднее значение G от Р измерений при одних и тех же условиях и вычислив
среднюю величину как
— 1 ^
р^ Р (3.62)
^ р=\
Такой вид усреднения известен как среднее по ансамблю. Оценка дисперсии,
выборочной дисперсии, задается соотношением
*^^=-^ГтХК"^)- (3.63)
На этой стадии нам уже известны среднее значение и дисперсия в каждом
пикселе на изображении. Из этих значений можно сделать некоторые интересные
заключения. Можно исследовать однородность обеих величин при заданных
условиях, например, при постоянном уровне освещенности.
3.5.1. Корреляционные и ковариационные функции
В качестве второго шага соотнесем теперь уровни яркости в различных местах на
изображениях друг с другом. Мерой корреляции уровней яркости является
среднее значение произведения уровней яркости в двух местах — автокорреляционная
функция
R (m,n:m\n) = G G ,,. (3.64)
Как и в уравнениях (3.62) и (3.63), возьмем среднее по ансамблю.
Автокорреляционная функция не имеет широкого применения, если
изображение содержит детерминированную часть с аддитивным шумом с нулевым средним
значением:
G' = G + N, с G^ = G и W = Q (3-65)
Тогда можно вычесть среднее значение, с тем чтобы адекватно
охарактеризовать свойства случайной части сигнала:
С (m,n:m\n) = (G -G )(G^^-G,\ (3.66)
Эта функция называется автоковариационной функцией. При нулевом сдвиге
(т=^т' ип=п) она дает дисперсию в пикселе [т, nY, а для всех других сдвигов —
ковариацию, которая была введена в разделе 3.3.2, уравнение (3.19). Новым здесь
является то, что автоковариационная функция включает пространственные
соотношения между различными точками на изображении. Если автоковариация
равна нулю, то случайные свойства соответствующих точек являются
некоррелированными.
Глава 3. Случайные величины и случайные поля
Автоковариационная функция, определенная уравнением (3.66), все еще
является неудобной, поскольку она является четырехмерной. Следовательно, даже
эта статистика используется лишь для ограниченного числа сдвигов, например
коротких расстояний, поскольку мы полагаем, что случайные свойства удаленных
точек являются некоррелированными.
Все становится проще, если статистика не зависит явно от положения точек,
что характерно для однородного случайного поля. Тогда автоковариационная
функция становится инвариантной относительно сдвига:
Сдд (m-\-k,n + l;m'-\r к, п + /)
= Сдд{т,п\т\п)
= Сдд (т -т\п- п\ 0,0) (3.67)
= Cgg{0,Q\rn-m,n-n\
Последние два тождества получаются, если положить {к, I) ={-т\ -п") и
(к, Г) = (-т, -п). Это также означает, что дисперсия шума С (т, п; т, п) не зависит
больше от положения на изображении и является равной во всех точках.
Поскольку автокорреляционная функция зависит только от расстояния между
точками, она сводится от четырех- к двумерной функции. К счастью, многие
стохастические процессы являются однородными. Из-за инвариантности
относительно сдвига автоковариационную функцию в случае однородного случайного поля
можно оценить с помощью пространственного усреднения:
1 М-\ N-\
Сдд{т,п) = —— X S(^^V ~^;«V)(<^;.4;.,«4« ~<^;«4;«y-bJ. (3.68)
J^y m'=On=0
Как правило, необязательно, что пространственное усреднение приведет к
среднему значению, являющемуся средним по ансамблю. Случайное поле, которое
удовлетворяет этому критерию, называется эргодическим.
Другая трудность касается индексирования. Как только (т, п) ф (О, 0),
индексы пробегают по диапазону матрицы. Тогда мы должны рассматривать
периодическое расширение матрицы, что и было описано в разделе 2.3.4. В этом случае
имеет место циклическая корреляция. Теперь проиллюстрируем значение
автоковариационной функции. Рассмотрим изображение, которое содержит
детерминированную часть плюс однородный шум с нулевым средним значением (смотри
уравнение (3.65)). Примем дополнительное предположение, что все точки являются
статистически независимыми. Тогда среднее значение равно детерминированной
части, и автоковариация исчезает, за исключением нулевого сдвига, т.е. нулевого
расстояния между пикселями:
С^д=ст^'"'Р или С^^{т,п) = су 8J„. (3.69)
При нулевом сдвиге автоковариация равна дисперсии шума. Таким образом,
мы можем исследовать, являются ли отдельные точки изображений статистически
некоррелированными. Это представляется важным, поскольку степень
корреляции между точками изображений определяет статистические свойства операций
обработки изображений, как и рассматривалось в разделе 3.3.3.
Подобным образом, как и в случае коррелирования одного изображения с
самим собой, мы можем коррелировать два различных изображения, Си Н, друг с
3.5. Стохастические процессы и случайные поля
другом. Эти изображения могут быть либо из разных сцен, либо из изображений
динамической сцены, полученных в различное время. По аналогии с уравнением
(3.68) взаимнокорреляционная функция и взаимноковариационная функция
определяются соотношениями
1 М-\ N-\
^9Н <'"'"> = 1^ X S G.v^„4.,„4„. (3.70)
1
М-1 Л^-1
Cgh{m,n) = -— X E(^-v ~<^.v)(^.w,«w -^;«w,«w)- (3-71)
Взаимнокорреляционная операция очень похожа на свертку (раздел 2.3.4, )^R7).
Единственным различием является знак индексов {т\ л) во втором члене.
3.5.2. Случайные поля в Фурье-пространстве
В предыдущих разделах мы исследовали поля в пространственной области. Приняв
во внимание значимость преобразования Фурье в обработке изображений (раздел 2.3),
мы теперь перейдем к рассмотрению случайных полей Фурье-области. Для
простоты ограничим рассмотрение здесь 1-D случаем. Все доводы, приведенные в этом
разделе, однако, можно аналогично применять для любой размерности.
Преобразование Фурье требует рассмотрения комплексных чисел. Однако это
не вызовет дополнительных сложностей, поскольку случайные свойства
действительной и мнимой частей можно обрабатывать отдельно. Определения для
среднего значения остаются такими же, однако определение ковариации требует
незначительного изменения по сравнению с уравнением (3.19):
С,,=^((0,-//,)*(0,-Л,)), (3.72)
где * означает сопряженный комплекс. Это определение обеспечивает то, что
дисперсия
о1=Е[{д^-^^)*{д^-ц^)) (3.73)
остается действительным числом.
1-D преобразование Фурье отображает вектор д G С^ в вектор д е С^.
Компоненты д задаются как скалярное произведение с ортонормированными
базисными векторами векторного пространства С^ (сравните уравнения (2.29) и (2.30)):
а =Ь^д с ЬЧ=8 .. (3.74)
С/о о CJ и и и—и
Таким образом, комплексные случайные величины в Фурье-пространстве
являются не чем иным, как линейными комбинациями случайных величин в
пространственной области. Если мы предположим, что случайные величины в
пространственной области являются некоррелированными с равной дисперсией (однородное
случайное поле), то придем к далеко идущему заключению. В соответствии с
уравнением (3.74) векторы коэффициентов Ь^ являются ортогональными друг другу с
единичным квадратом модуля. Следовательно, в результате рассмотрения функций
многомерных случайных величин в разделе 3.3.3 (смотри уравнение (3.32)) мы
можем заключить, что случайные величины в Фурье-области остаются
некоррелированными и имеют такую же дисперсию, как и в пространственной области.
Глава 3. Случайные величины и случайные поля
3.5.3. Энергетический спектр, спектр взаимной корреляции и когерентность
В разделе 3.5.1 мы выяснили, что случайные поля в пространственной области
характеризуются авто- и взаимнокорреляционными функциями. Теперь рассмотрим
случайные поля в Фурье-пространстве.
Корреляция в пространственной области соответствует умножению в Фурье-
пространстве на комплексно сопряженные функции ()-R4):
G * G о • Р,, (к) = д{к) * д(к) (3.75)
и
G * Н о . р^^ (к) = д(к) * kk)- (3.76)
В ЭТИХ уравнениях корреляция сокращенно обозначается символом • подобно
свертке, для которой мы используем символ *. При более простом обозначении
спектры записываются как непрерывные функции. Это соответствует переходу к
бесконечно протяженному случайному полю (раздел 2.3.2, табл. 2.1).
Преобразование Фурье автокорреляционной функции называется
энергетическим спектром Р . Энергетический спектр является действительной величиной.
Его название связано с тем, что он представляет собой распределение мощности
физического сигнала в Фурье-области по частотам и волновым числам, если
квадрат амплитуды сигнала соотносится с энергией сигнала. Если энергетический
спектр усреднен по нескольким изображениям, то он образует сумму квадратов
независимых случайных величин. Если случайные величины имеют плотность
нормального распределения, то энергетический спектр имеет в соответствии с
рассуждением в разделе 3.4.4 плотность распределения хи-квадрат.
Автокорреляционная функция поля некоррелированных случайных величин
равна нулю во всех точках, за исключением начала координат, т.е. может быть
описана 5-функцией (уравнение (3.69)). Следовательно, ее энергетический спектр
является константой (>-R7). Такой вид шума называется белым шумом.
Преобразование Фурье взаимнокорреляционной функции называется
спектром взаимной корреляции /*;,. В отличие от энергетического спектра, это
комплексная величина. Действительные и мнимые части обозначаются со- и
квадратный спектр соответственно.
Для понимания значения спектра взаимной корреляции будет полезным
определить другую величину, функцию когерентности Ф:
Ф (к) = . П 771
По существу, функция когерентности содержит информацию о подобии двух
изображенийj^Покажем это, положив, что изображение Н— сдвинутая копия
изображения G: h(k) = g(k)Qxp(—ikx^). В этом случае функция когерентности
равна единице, а спектр взаимной корреляции Р ^ сводится к
Рд,{к) = />^ДЛ)ехр(-1Лд:,). (3.78)
Поскольку Р — действительная величина, мы можем вычислить сдвиг jc^
между двумя изображениями по фазовому множителю ехр(-1Азс^).
Если не существует фиксированной фазовой связи периодической
составляющей между двумя изображениями, тогда когерентность уменьшается. Если фазо-
3.6. Упражнения
вый сдвиг является распределенным по случайному закону от изображения к
изображению в некоторой последовательности, то векторы взаимной корреляции на
комплексной плоскости имеют случайные направления и при сложении дают ноль.
Тогда в соответствии с уравнением (3.77) когерентность также равна нулю.
3.6. Упражнения
3.1: Шум в изображениях и последовательностях изображений
Интерактивное моделирование распределенного по пуассоновскому
закону шума, аддитивного распределенного по нормальному закону шума и
мультипликативного распределенного по нормальному закону шума;
вычисление среднего значения и дисперсии (dip6ex03.01).
3.2: **Пуассоновское распределение и нормальное распределение
Датчик изображения получает излучение, постоянное в пространстве и
времени. В течение времени экспозиции в среднем порождаются 9 и 100
единиц заряда. В дальнейшем будем полагать, что датчик является идеальным,
т.е. электронные схемы не создают дополнительного шума.
1. Вычислить абсолютное среднеквадратичное отклонение и относительное
среднеквадратичное отклонение (а//л) для обоих случаев.
2. Насколько распределение Пуассона отклоняется от нормального
распределения при одной и той же дисперсии?
Ответьте на этот вопрос, вычислив функции плотности распределения
вероятностей для значений /л - па при п е {-3, -2, -1,0, 1,2, 3}.
3.3: "^Биномиальное и нормальное распределения
Биномиальное распределение B(Q, 1/2) быстро сходится с увеличением Q к
нормальному распределению. Проверьте это утверждение, сравнив все
значения биномиальных распределений 5(4,1 /2) и 5(8,1/2) с нормальным
распределением при равных среднем значении и дисперсии.
3.4: "^Равномерное распределение
Случайная величина (СВ) имеет функцию плотности равномерного
распределения (ФПР) в интервале от д ло д + Ад. ФПГ равна нулю вне этого
интервала. Вычислить среднее значение и дисперсию этой СВ.
3.5: "^^Функции плотности распределения вероятностей, среднее значение и дисперсия
Пусть gjH заявляются некоррелированными случайными величинами с
нулевым средним значением ()U=0) и дисперсией ст^ = 1. Вычислить ФПР,
среднее значение и дисперсию для следующих случайных величин:
1) h=g, + 9r
2) h=ag^-\- Ь{аиЬ являются детерминированными константами);
3) h=g^ + g,l
4) h=g^;
5) h = yjg^ + gl (модуль вектора [g^, gJO;
6) A = avctan(g^/g) (угол вектора [g^, gJO-
Глава 3. Случайные величины и случайные поля
"^Распространение ошибки
Пусть д является СВ со средним значением д и дисперсией с\ ФПР
неизвестна. Вычислить, если возможно, дисперсию и относительную ошибку
(Jfj/ h следующих случайных величин h, полагая, что дисперсия
достаточно мала, так что нелинейностью следующих функций можно пренебречь:
1) А =9^;
2) h^yfg;
3) h = l/g',
4) A=ln(g).
3.7: Центральная предельная теорема
Интерактивное моделирование с целью продемонстрировать центральную
предельную теорему (dip6ex03.02).
3.8: "^"^Выбор датчика изображений
В разделе 3.4.5 мы рассматривали простую линейную шумовую модель для
датчиков формирования изображений, которая оказалась пригодной. У нас
есть две камеры под рукой со следующими шумовыми характеристиками:
Камера А: ст^ = 1,0 + 0,1д.
Камера В: а ^ = 2,5 + 0,025gf.
Обе камеры получают сигналы с 12-битовым разрешением. Таким образом,
уровни яркости д могут принимать значения между О и 4095. Обе камеры
имеют квантовую эффективность, равную 0,5. Какая из этих камер
наиболее подходит для следующих задач:
1. Измерение высоких уровней яркости с наилучшим возможным
относительным разрешением.
2. Измерение наименьшего возможного излучения.
Для того чтобы получить корректное решение, вычислите среднее
квадратичное отклонение при наивысшем дискретном уровне яркости
{д = 4095) и самом низком уровне (темное изображение, д =0). Далее
вычислите число фотонов, которое равно среднему квадратичному
отклонению темного изображения.
3.9: "^"^Раснространение ковариации
Линейный датчик имеет пять элементов. На первом шаге обработки
сигналы двух соседствующих сигналов усредняются (так называемое скользящее
среднее). В соответствии с разделом (3.3.3) этот процесс относится к
линейному преобразованию
2
110 0 0
0 110 0
0 0 110
0 0 0 11
9
3.7. Дополнительная литература
Вычислить ковариационную матрицу h, полагая, что д есть вектор из пяти
некоррелированных случайных величин с равной дисперсией s ^ Также
вычислить дисперсию среднего значения А ((А, + ^2 + A3 "*" ^4)/^) ^ сравнить ее
с дисперсией среднего значения д ({д^ + 5^2 "^ б'з "^ 9^4"*" ЭзУ^)-
Проанализируйте результаты!
3.7. Дополнительная литература
Введение в случайные сигналы дано Рисом (Rice) [164]. Детальный обзор теории
вероятностей и случайных величин можно найти в книге Папоулиса (Papoulis) [ 149].
Учебное пособие Розенфельда и Кака (Rosenfeld and Как) [172] дает хорошее
введение в стохастические процессы по отношению к обработке изображений.
Спектральный анализ рассматривается в работе Марпла (Маф1е Jr.) [131].
ГЛАВА4
ОПЕРАЦИИ НАД СОСЕДНИМИ
ЭЛЕМЕНТАМИ
4.1. Основные свойства и назначение
4.1.1. Распознавание объектов и операции над соседними элементами
Анализ пространственных соотношений уровней яркости в малой окрестности дает
первый ключ к распознаванию объектов на изображениях. В качестве простого
примера давайте рассмотрим сцену, содержащую объекты с равномерной
энергетической яркостью. Если уровень яркости не изменяется в малой окрестности, то
окрестность принадлежит объекту. Однако если уровень яркости существенно
изменяется, то контур объекта пересекает окрестность. Таким образом, мы
распознаем области постоянных уровней яркости и контуров.
Однако обработка только отдельных пикселей на изображении с помощью
точечных операций не обеспечивает такой информацией. В главе 10 мы детально
показываем, что такие операции являются полезными только в качестве
первоначального шага обработки изображений для правки неоднородных и нелинейных
откликов датчика формирования изображения, интерактивного манипулирования
изображениями для обследования или улучшения визуального впечатления.
Необходим новый класс операций, который объединяет пиксели малой
окрестности соответствующим образом и в качестве результата формирует новое
изображение. Операции такого вида относятся к общему классу операций над соседними
элементами. Эти операции являются основным инструментарием при низкоуровневой
обработке изображений. По этой причине мы рассматриваем в данной главе
возможные классы операций над соседними элементами и их свойства.
Результатом любой операции над соседними элементами является по-прежнему
изображение. Однако его содержимое изменено. Правильно вьшолненная операция над
соседними элементами для вьщеления контуров, к примеру, должна показывать
высокие уровни яркости в пикселях, которые принадлежат контуру объекта, при этом для
всех других пикселей, независимо от их уровня яркости, должна показывать низкие
уровни. Этот пример иллюстрирует, что при применении оператора формирования
окрестности информация в целом теряется. Мы больше не можем сделать вьюод об исходных
уровнях яркости. По этой причине операции над соседними элементами также
называют фильтрами. Они позволяют вьщелить некий интересуюыщй нас признак из
изображения. Изображение, получаемое при применении оператора формирования
окрестности, следовательно, носит также название изображение признака.
Очевидно, что операции, объединяющие соседние пиксели для
формирования нового изображения, могут выполнять совершенно разные задачи обработки
изображений:
• Вьщеление простых локальных структур, таких, как контуры, углы, линии
и области постоянных уровней яркости (главы 12 и 13).
4.1. Основные свойства и назначение
• Определение движения (глава 14).
• Анализ текстуры (глава 15).
• Реконструкция изображений, полученных непрямыми методами
формирования изображений, такими, как томография (глава 17).
• Восстановление изображений, имеющих плохое качество вследствие де-
фокусирования, размытости при дврхжении объекта или любых похожих
нежелательных изменений в процессе получения изображений (глава 17).
• Корректировка нарушений, вызванных нежелательными изменениями
при получении изображений или передачи. Такие нежелательные изменения
приводят к искаженным уровням яркости для некоторых отдельных пикселей
(глава 17).
4.1.2. Общее определение
Оператор формирования окрестности А^ берет значения в окрестности точки,
выполняет некоторые операции над ними и присваивает полученный результат
обратно пикселю. Эта операция повторяется для всех точек сигнала.
Определение 4.1 (Непрерывный оператор формирования окрестностей). Непрерывный
оператор формирования окрестностей отображает многомерный непрерывный
сигнал д{х) в самого себя следующей операцией:
g'(x) = N({g(x')}Mx-x)e М), (4.1)
где М — компактная область.
Область М называется маской, окном, областью поддержки или структурным
элементом операции над соседними элементами. При вычислении д\х) размер и
форма М определяют операцию над соседними элементами, задавая входные
значения д в области М, начало которой сдвигается в точку jc. Операция над
соседними элементами Л^сама по себе здесь не определяется. Она может быть любого вида.
Из соображений симметрии маска часто является симметричной и имеет начало в
центре симметрии.
Определение 4.2 (Дискретный оператор формирования окрестностей). Дискретный
оператор формирования окрестностей отображает матрицу размерностью MxNe
саму себя следующей операцией:
G:,„ = A^(G„--.y-„,V[m>r€ М), (4.2)
где М является теперь дискретным множеством точек.
Выражения, эквивалентные определению 4.2, можно легко записать и для
других размерностей, не равных двум. Хотя уравнения (4.1) и (4.2) в любом случае не
определяют вид выполняемой операции над соседними элементами, они все же
позволяют выявить общую структуру всех операций над соседними элементами.
4.1.3. Размер маски и симметрия
Первой характеристикой операции над соседними элементами является размер
окрестности. Окно может быть прямоугольным или иметь любую другую форму.
Мы также должны определить относительно окна положение пикселя, которому
Глава 4. Операции над соседними элементами
будет присвоен результат операции. Что же касается симметрии, наиболее
естественным решением является поместить результат операции в пиксель,
соответствующий центру маски с нечетным размером (2Л + 1) х {2R +1).
Маски, имеющие четный размер, кажутся неподходящими для операций над
соседними элементами, поскольку в этом случае не существует пикселя, который
лежит в центре маски. Если результат операции над соседними элемерггами просто
приписать обратно пикселям, которые расположены между исходными пикселями
в центре маски, то мы тем не менее можем использовать их. Таким образом,
результирующее изображение сдвигается на половину пиксельного расстояния в каждом
направлении. Из-за этого сдвига характеристические изображения, вычисленные с
помощью масок с четным размером, не следует комбинировать с исходными
уровнями яркости, поскольку это может привести к значительным ошибкам. Если мы
используем несколько масок параллельно и комбинируем результирующие
характеристические изображения, то маски должны быть либо с четным размером, либо с
нечетным размером в одном и том же направлении. В противном случае выходные
структуры не совпадают.
4.1.4. Запись в операторной форме
В случае использования операторов формирования окрестностей полезным
будет ввести запись в операторной форме. Таким образом, сложные составные
операции над соседними элементами становятся легкими для понимания. Все
операторы будем обозначать каллиграфическими буквами, такими, как (В, ®, Н, S.
Оператор Н преобразует изображение G в изображение G'=HG. Такое
обозначение используется для непрерывных и дискретных сигналов любой
размерности и дает компактное, независящее от представления обозначение операций
обработки сигналов.
Запись операторов один за другим обозначает последовательное применение.
Самый правый оператор применяется первым. Показатель степени выражает
последовательное применение одного и того же оператора:
Ж7{ ,.,9{ = Я\ (4.3)
^ V '
Рраз
Если оператор действует на одиночное изображение, то операнд, который
находится справа в уравнениях, можно опустить. Таким образом, операторные
уравнения можно записывать без объектов действия. Кроме того, мы будем использовать
скобки обычным способом для того, чтобы контролировать порядок выполнения. Мы
можем записать основные свойства операторов простым к восприятию способом,
например,
коммутативность ^ ^ = ^ Я|,
ассоциативность Я^{9{^9{) = {Я^Я)Я^, (4.4)
дистрибутивность относительно сложения {J{ + J{^ 9{^=Н^!К^ + ^2*^з*
Другие операции, такие, как сложение, можно также использовать в такой
операторной форме записи. Однако нужно быть внимательными с любой
нелинейной операцией. Как только вводится нелинейный оператор, порядок, в котором
выполняются операторы, должен быть точно определен.
4.2. Линейные инвариантные относительно сдвига фильтры I 19
Простым примером нелинейного оператора является поточечное
перемножение изображений, бинарный точечный оператор. Поскольку этот оператор
возникает достаточно часто, его обозначают специальным символом, центрированной
точкой (•). Этот символ требуется для того, чтобы отлР1чить его от
последовательного применения операторов. Операторное выражение (В (® • 3)), к примеру,
означает: применение операторов (D и ® к одному и тому же изображению,
перемножение результатов поточечно и применение оператора ® к произведению изображений.
Без круглых скобок выражение (8© • (D могло бы означать: применение оператора
(D^ к изображению и применение операторов ®^ и (В к одному и тому же
изображению и дальнейшее перемножение результатов поточечно. Использованное
операторное обозначение, таким образом, определяет приоритет унитарных операторов
над бинарными операторами. При необходимости для большей ясности
используется указатель места заполнения объекта, на который действует оператор,
обозначаемый символом «:». При использовании указателя места заполнения
вышеупомянутая операторная комбинация запишется в виде Ф (©: • ®:).
В оставшейся части этой главы мы обсудим два самых важных класса
операций над соседними элементами: линейные инвариантные относительно сдвига
фильтры (раздел 4.2) и фильтры порядковых статистик (раздел 4.3).
Дополнительный раздел посвящен специальному подклассу линейных инвариантных
относительно сдвига фильтров, известных как рекурсивные фильтры (раздел 4.5).
4.2. Линейные инвариантные относительно сдвига фильтры
4.2.1. Дискретная свертка
Сначала сфокусируем внимание на вопросе, как можно комбинировать уровни
яркости пикселей в малой окрестности.
Элементарная комбинация пикселей в окне задается операцией, которая
умножает каждый пиксель в пределах маски фильтра на соответствующий весовой
множитель маски, складывает произведения и записывает сумму на место
центрального пикселя:
^jj^ j^^ т п *J т—т ,п—п
т=-г п=-г
г г
J^ j^ -т ,-п <Ут+т ,п+п
т =-гп =-г
(4.5)
В разделе 2.3.4 дискретная свертка была определена уравнением (2.55) как
Утп ^ ' / ' т'п'Ут-т, п-п \^-^)
т = О и = О
Оба определения эквивалентны, если примем во внимание периодичность в
пространственной области, определенную уравнением (2.42). Из уравнения (2.42)
можно сделать вывод, что отрицательные индексы эквивалентны положительным
коэффициентам согласно соотношениям
9-п~ 9м-п^ 9-п-т~ 9м-п,М-п1- (4-^)
Глава 4. Операции над соседними элементами
Ограничение суммы в уравнении (4.5) отражает тот факт, что элементы
матрицы Яравны нулю, за исключением нескольких точек маски фильтра {2R +1) х {2R +1).
Таким образом, последнее представление является гораздо более практичным и
дает лучшее понимание фильтрующей операции. Например, следующие маска
фильтра 3 X 3 и матрица Я размерностью AfxTV эквивалентны
0 -1
1 0.
2 1
-2
-1
0
=
0.
1
0
0
-1
-1
0
0
0
-2
0 .
0 .
0 .
0 .
0 .
. 0
. 0
. 0
. 0
. 0
1
2
0
0
0
(4.8)
Ж-мерная фильтрующая операция может быть записана с помощью упрощенной
векторной индексации:
Уп / ' -пУп
n=-R
(4.9)
при п = [п^, Пу ... ,п^], R= [R^, R^, ..., R^], где g^ есть элемент Ж-мерного сигнала
а Обозначение сумм в этом уравнении является сокращенной записью для
X = X £ - X ■ (4.10)
П =—R Mj =—R\ ^2 ~~^2 ^W ~~^W
Векторная индексация, введенная здесь, позволяет записывать большую часть
соотношений для сигналов произвольной размерности простым способом.
4.2.2. Симметрии
Что касается симметрии, можно вьщелить два класса фильтров: четные и
нечетные фильтры с условием по одному или более направлениям:
hr..=±Kr, и h „=±/г^„, (4.11)
—т,п тп т,—п тп^ ^ '
где знаки + и - определяют четную и нечетную симметрию. Исходя из этого
определения, можно сразу же упростить уравнение (4.5), для того чтобы вычислять
одномерные фильтры более эффективно:
четная:
г
п=1
г
нечетная: 9пт - 2w ^«' ^9т.п-п' ~ Qm.nW ) •
(4.12)
п=]
Суммы пробегают только по половине маски фильтра, не включая
центральный пиксель, который должен обрабатываться отдельно, поскольку он не имеет
симметричного аналога. Его можно опустить в случае нечетного фильтра, поскольку
коэффициент в центральном пикселе равен нулю, согласно уравнению (4.11).
В 2-D случае уравнения становятся более сложными, поскольку теперь
требуется учитывать симметрию в каждом направлении отдельно. 2-D фильтр с
четной симметрией в обоих направлениях сводятся к
4,2. Линейные инвариантные относительно сдвига фильтры
9т,п ~ ^Оо9тп
г
"'" 2ш^ '^т'О \9т-т,п ''" 9т+т',п )
г г (4.13)
J^^ jt^ тп \^ т—т ,п—п \Ут—т,п+п
т=\ п'-\
Ут+т\п-п' Ут+т',п+пу'
2-D фильтры могут иметь разные типы симметрии в различных направлениях.
Например, они могут быть нечетными в горизонтальных направлениях и четными
в вертикальных направлениях. Тогда
г
Ут,п ~ ^^^Оп\Ут,п-п^Ут,п+п)
п'=\
г г
"*" 2ш^^'^тп \9т-т\п-п " 9т-т,nW (4.14)
т'=\ Г1=\
+9п,..'г,-п+9п,.п,'.„.Л
Уравнения для более высоких размерностей еще более сложны [89].
4.2.3. Вычисление свертки
Операция дискретной свертки настолько важна, что заслуживает детального
изучения, чтобы понаблюдать, как она работает. Прежде всего, нас могли бы
смутить отрицательные знаки индексов т'и «'для маски или для изображения
в уравнении (4.5). Это всего лишь означает, что мы отображаем или маску, или
изображение относительно центра симметрии, прежде чем накладываем маску
на изображение.
Ознакомимся с причиной этого отображения в разделе 4.2.5. Если мы хотим
вычислить результат свертки в точке [т, пУ, то центрируем отображенную маску в
этой точке, выполняем свертку и записываем результат обратно на место [т, nY
(рис. 4.1). Эта операция выполняется для всех пикселей изображения.
Вблизи фаницы изображения, когда маска фильтра простирается на контур,
мы сталкиваемся со сложностями, поскольку упускаем некоторые точки
изображения. Теоретически корректный способ решения этой проблемы в соответствии
со свойством периодичности, рассмотренный в разделе 2.3.4 (особенно уравнение
(2.42)), должен учитывать, что конечные матрицы изображений нужно
рассматривать как периодически повторяемые. Следовательно, когда достигаем левой
границы изображения, мы берем пропущенные точки изображения с правой
границы изображения. Мы говорим о циклической свертке. Только этот тип сведется к
умножению в Фурье-пространстве (раздел 2.3).
122 Глава 4. Операции над соседними элементами
m
•
0
1
2
-1
0
1
-2
-1
0
m-1
m
m+1
n-1 n n+1
"m
"pfl
тЩ
frf
H
i1
Tn
TTj
Tm
Рис. 4.1. Иллюстрация операции дискретной свертки с маской фильтра 3x3
На практике этот подход выбирается редко, поскольку периодическое
повторение является искусственным, по существу, относящимся к выборке данных
изображения в Фурье-пространстве. Взамен мы добавляем пограничную область к
изображению с половиной ширины маски фильтра. В эту пограничную область записываем
нули или экстраполируем тем или иным образом уровни яркости по уровням
яркости на контуре изображения. Самым простым типом экстраполяции является
запись уровней яркости пикселей контура в пограничную область. Хотя этот подход
дает меньшее визуальное искажение на контуре изображения, чем циклическая
свертка, мы вносим ошибки на контуре изображения в пограничную область с
шириной, равной половине размера маски фильтра. Если мы выбираем какой-либо тип
метода экстраполяции, пиксели контура получают слишком большой вес. Если
положим пограничную область равной нулю, то введем горизонтальные и
вертикальные контуры на границе изображения.
В заключение отметим: не существует совершенного метода для корректной
обработки пикселей, близких к контурам, с помощью операций над соседними
элементами. Тем или иным образом вносятся ошибки. Единственным надежным
способом избежать ошибок является гарантия того, что интересующие объекты
сохраняют безопасное расстояние от контура, равное, по крайней мере, половине
размера наибольшей маски, используемой при обработке изображения.
Уравнение (4.5) указывает на то, что ни один из вычисленных уровней яркости
G'^^ не войдет в вьиисление в других соседних пикселях. Таким образом, если мы
хотим выполнить фильтрующую операцию в плоскости, то сталкиваемся с
проблемой. Предположим, что мы выполняем свертку от линии к линии и слева
направо. Тогда уровни яркости для всех пикселей, расположенных выше и с левой
стороны от текущего пикселя, являются уже переписанными результатами,
полученными предьщущими вьиислениями (рис. 4.2).
Следовательно, нам необходимо хранить уровни яркости в этих местах в
соответствующем буфере. Эффективные алгоритмы для выполнения этой задачи
описаны в работах [89] и [94, том 2, глава 5].
Число элементов, содержащихся в маске, значительно возрастает при
увеличении размера и размерности. Ж-мерная маска с линейным размером R содержит
R^ элементов. Чем выше размерность, тем быстрее увеличивается число
элементов с ростом размера маски. В случае высоких размерностей даже малая
окрестность включает сотни и тысячи элементов.
4.2. Линейные инвариантные относительно сдвига фильтры 123
0
1
2
►
4
\т
Рис. 4.2. Свертка изображения с помощью сканирующего перемещения маски от
линии к линии по изображению. В затемненных пикселях уровень яркости уже
заменен суммой свертки. Таким образом, уровни яркости в затемненных пикселях,
которые попадают в маску фильтра, необходимо хранить в дополнительном буфере
Сложной задачей при создании эффективных схем вычислений является
уменьшение числа вычислений с 0{R}^ до более низкого порядка. Это означает, что
число вычислений больше не пропорционально Л^, а скорее пропорционально более
низкой степени R. Конечной целью является получение вычислительных схем,
которые возрастают только линейно с ростом размера маски {0{R})) или вообще не
зависят от размера маски (P{R^)).
4.2.4. Линейность и инвариантность относительно сдвига
Линейные операторы определяются принципом суперпозиции.
Определение 4.3 (Принцип суперпозиции). Если GuG' есть два W-мерных комплекс-
позначных сигнала, а и b — две комплекснозначные скалярные величины, а Н—
оператор, то оператор является линейным тогда и только тогда, когда
Я(аС + ЬС) = a!HG + бЯС'. (4.15)
Можно обобщить определение 4.3 на случай суперпозиции многих входных данных:
Я
J,^,G, =Х«.^ь
(4.16)
Принцип суперпозиции утверждает, что мы можем разложить сложный
сигнал на более простые составляющие. Мы можем применить линейный оператор
к этим составляющим и затем образовать результирующий отклик из откликов
составляющих.
Другим важным свойством оператора является инвариантность относительно
сдвига (также известным, как трансляционная инвариантность или однородность).
Это означает, что отклик оператора явно не зависит от положения на
изображении. Если мы сдвигаем изображение, то выходное изображение остается тем же
самым, за исключением примененного сдвига. Можно сформулировать это
свойство более изящно, если записать оператор сдвига "'"S как
Глава 4. Операции над соседними элементами
'""sg„'„' = g„'-„,„'-„. (4.17)
Тогда можно определить оператор, инвариантный относительно сдвига следующим
образом:
Определение 4.4 (Инвариантность относительно сдвига). Оператор является
инвариантным относительно сдвига тогда и только тогда, когда он коммутирует с
оператором сдвига S:
^{гпп(.^тп^^ (4.18)
Из определения операции свертки (4.5) и (4.9) очевидно, что она является как
линейной, так и инвариантной относительно сдвига. Такой класс операторов
называется линейными инвариантными относительно сдвига операторами (ЛИС-опе-
раторами). В контексте временных рядов то же самое свойство известно как
линейные, не изменяющиеся во времени (ЛИВ). Обратите внимание, что оператор
сдвига '""iS сам по себе является ЛИС-оператором.
4.2.5. Функция рассеяния точки
Линейность и инвариантность относительно сдвига позволяет легко понять
отклик оператора свертки. Согласно 2.3.1, можно разложить любое дискретное
изображение (сигнал) на отдельные точки или базисные изображения '""Р
(уравнение (2.10)):
М-\ N-\
G = Y1.GS"P- (4.19)
Линейность свидетельствует о том, что мы можем применить оператор к
каждому базисному изображению и затем сложить получающиеся изображения.
Инвариантность относительно сдвига свидетельствует о том, что отклик на каждое из
точечных изображений остается тем же самым, за исключением сдвига. Таким
образом, если нам известен отклик на точечное изображение, то мы можем
вычислить отклик на любое изображение.
Следовательно, отклик на точечное изображение имеет особое значение. Он
известен как функция рассеяния точки (ФРТ) (в случае временных рядов часто
обозначается как импульсная характеристика, отклик на импульсное возмущение).
ФРТ свертки или ЛИС-оператора тождественна его маске
г г
/ "V^ "^ h ^^ — и
г^тп / / ^^^ -т\-п Jrm+m\n+n' т,п (4.2U)
т =-г п =-г
И полностью описывает оператор свертки в пространственной области.
ФРТ предлагает другой, хотя и эквивалентный взгляд на свертку. Сумма
свертки в уравнении (4.5) говорит о том, что каждый пиксель становится линейной
комбинацией соседних пикселей. ФРТ указывает на то, что каждый пиксель
рассеивается в окрестности, согласно заданной ФРТ.
4.2.6. Передаточная функция
В разделе 2.3 мы обсудили возможность представления изображения в
Фурье-области. Это представление имеет особую важность для линейных фильтров, посколь-
4.2. Линейные инвариантные относительно сдвига фильтры
ку операция свертки сводится к умножению в Фурье-области в соответствии с те-
оремой о свертке (теорема 2.4, с. 61):
flf*/l
^Ngh, G^H
MNGH
(4.21)
Наличие множителей TV и AfTV следует из определения дискретного
преобразования Фурье согласно уравнению (2.69, б). Поэтому включим множители Nvi MN,
соответственно в определение передаточной функции. Это означает, что во всех
дальнейших уравнениях Nh и MNH заменяются киН соответственно.
Преобразование Фурье от маски свертки или ФРТ известно как
передаточная функция (ПФ) линейного фильтра. Передаточная функция имеет важное
практическое значение. Для каждого волнового числа она задает множитель,
на который умножается периодическая структура при использовании
фильтрующей операции.
Обратите внимание, что этот множитель является комплексным числом (раздел
2.3.1). Таким образом, периодическая структура чувствительна не только к
изменению в амплитуде, но также и к фазовому сдвигу:
9и,о = К,о9и,о = h exp(i%)r^ exp(i(p^)
= V^exp[i(()9,+(p^)],
(4.22)
где комплексные числа представлены во второй части уравнения через свои
модули и фазы как комплексные экспоненты.
Симметрия масок фильтров, согласно рассмотренному в разделе 4.2.2,
значительно упрощает передаточную функцию. Тогда мы можем объединить
соответствующие симметричные члены в преобразовании Фурье от ФРТ:
IS. I
2nmv
n=-R
K + Y.K-
N
(при h_„.=±h^.)
exp
V
V
2тпо
N
±ехр
Ininu
N
(4.23)
Эти уравнения могут быть дальше упрощены заменой дискретного волнового
числа масштабированным непрерывным волновым числом
k = 2u/N, при -N/2<v<N/2. (4-24)
Масштабированное волновое число к ограничено интервалом [-1, 1[.
Волновое число на границе этого интервала соответствует максимальному волновому
числу, которое удовлетворяет теореме дискретизации (раздел 9.2.3).
Используя уравнение Эйлера ехр(Ьс) = cos л: + i sin х, сводим уравнение (4.23)
для случая 1-D четных и нечетных фильтров к виду:
четные:
h(k) = к^+ 2^/г„. соз(пкк),
R
нечетные: h(k) = -2i]^ h^^ sm(n7rk).
n=\
(4.25)
Глава 4. Операции над соседними элементами
Соответственно маска (2Л + 1) х {2R + 1) с четной горизонтальной и
вертикальной симметрией приводит к передаточной функции:
h{k) = h,
т
д л.
R R
т=\
(4.26)
н- 4^ ]^ /z^w cos(n7ik^) со8(т'л-^2 )•
/и'=1 «'=1
Подобные уравнения применимы для других комбинаций симметрии.
Уравнения (4.25) и (4.26) очень полезны, поскольку они дают
непосредственную зависимость между коэффициентами маски фильтра и передаточной
функцией. Они будут нашим основным инструментом при изучении свойств фильтров для
конкретных задач обработки изображений в главах 11-15.
4.2.7. Дополнительные свойства
В этом разделе рассмотрим некоторые дополнительные свойства операторов
свертки, которые будут полезными при обработке изображений и сигналов.
Свойство 4.1 (Коммутативность). ЛИС-операторы являются коммутативными:
9т'=э{'я:, (4.27)
т.е. порядок, в котором применяются операторы свертки к изображению, не имеет
значения. Это свойство легко доказать в Фурье-области, поскольку там эти
операторы сводятся к коммутативному умножению.
Свойство 4.2 (Ассоциативность). ЛИС-операторы являются ассоциативными:
Я'!И''' = !}{, (4.28)
Поскольку ЛИС-операции являются ассоциативными, мы можем составить
сложный оператор из простых операторов. Подобным образом мы можем
попытаться разложить заданный сложный оператор на более простые операторы. Это
характерное свойство является существенным для эффективного выполнения
операторов свертки. В качестве примера рассмотрим оператор
14 6 4 1
4 16 24 16 4
6 24 36 24 6
4 16 24 16 4
14 6 4 1
(4.29)
Нам придется выполнить 25 операций умножения и 24 операции сложения
для каждого пикселя с такой маской свертки. Однако можно легко показать, что
мы можем разложить эту маску на горизонтальную и вертикальную маски:
4,2, Линейные инвариантные относительно сдвига фильтры
14 6 4 1
4 16 24 16 4
6 24 36 24 6
4 16 24 16 4
14 6 4 1
= [14 6 4 1]'
(4.30)
Применяя две свертки с меньшими масками одну за другой, мы выполним
только 10 операций умножения и 8 операций сложения для каждого пикселя
при применении операции к полному изображению. Маски фильтров,
которые могут быть разложены на одномерные маски вдоль осей, называются сепа-
рабельными масками. Мы будем обозначать одномерные операторы с помощью
индекса, указывающего ось. Тогда можно записать сепарабельный оператор Ф
в трехмерном пространстве:
(В = (В,(Бу(В^. (4.31)
В случае одномерных масок, имеющих ортогональные направления, свертка
сводится к векторному произведению. Сепарабельные фильтры тем более
эффективны, чем выше размерность пространства. Давайте в качестве примера
рассмотрим маску фильтра 9x9x9. Непосредственное выполнение могло бы потребовать
729 операций умножения и 728 операций сложения для каждого пикселя, в то
время как сепарабельная маска того же размера потребует всего лишь 27 умножений и
24 сложения, приблизительно в 30 раз меньшее количество операций.
Свойство 4.3 (Дистрибутивность относительно сложения). ЛИС-операторы
являются дистрибутивными относительно сложения:
Я'+ !}{'' = Я. (4.32)
Поскольку ЛИС-операторы являются элементами одного и того же
векторного пространства, к которому они применяются, мы можем определить сложение
операторов через сложение векторных элементов. Благодаря этому свойству мы
можем также включить операторные сложения и вычитания в нашу общую
операторную форму записи, введенную в разделе 4.1.4.
4.2.8. Распространение ошибки при фильтрации
Фильтры применяются к измеряемым данным, которые показывают шум.
Поэтому важно знать, как статистические свойства отфильтрованных данных могут быть
получены из свойств исходных данных. В принципе мы решили эту задачу в
разделе 3.3.3. Ковариационная матрица линейной комбинации д'-Мд случайного
вектора д определяется, согласно уравнению (3.27), как
cov(flf') = Mcov(g)M^
(4.33)
Теперь необходимо применить этот результат к частному случаю свертки.
Сначала рассмотрим только 1-D сигналы. Положим, что ковариационная матрица
сигнала однородна, т.е. зависит только от расстояния между точками, а не от
положения самого по себе. Тогда дисперсия сг^ для всех элементов одинакова. Кроме
Глава 4. Операции над соседними элементами
того, значения, находящиеся на диагоналях, также равны, и ковариационная
матрица принимает простую форму:
cov(flf) =
'-1
G
(4.34)
где индекс обозначает расстояние между точками и ст^ = а I Как правило, ковари-
ация уменьшается с увеличением пиксельного расстояния. Часто только
ограниченное число ковариаций а отлично от нуля. В случае статистически
некоррелированных пикселей только ст^ = <т ^ не равна нулю.
Поскольку линейные комбинации, описываемые матрицей М, обладают
особой формой свертки, матрица имеет такой же вид, как однородная
ковариационная матрица. Для фильтра с тремя коэффициентами матрица М сводится к
М =
к
f\
0
0
0
Л-,
К
К
0
0
0
Л-.
К
fh
0
0
0
h-г
ho
К
0 ...
0 ...
0 ...
А., ...
К ...
(4.35)
Отбросив граничные эффекты, матричные умножения в уравнении (4.33)
сводятся к операциям свертки. Введем автоковариационный вектор а= [..., (J_j, ст^, (Т^ ..у.
Тогда уравнение (4.33) можно записать в виде
CT'=~h^CT^h = a^~h^h = CF^(h*h), (4.36)
где h — отраженная маска свертки: ~h = А^. На последнем шаге мы заменили свертку
корреляцией. Свертку стс А • А можно заменить корреляцией, поскольку
автокорреляционная функция от действительной функции есть функция четной симметрии.
В случае некоррелированных данных автоковариационный вектор является
дельта-функцией и автоковариационный вектор шума отфильтрованного вектора
сводится к
С7' = ог^(Л*Л). (4.37)
Для фильтра с R коэффициентами 2R-1 значений автоковариационного
вектора теперь не равны нулю. Это означает, что в отфильтрованном сигнале пиксели
с максимальным расстоянием R-1 теперь коррелируют друг с другом.
Поскольку ковариационный вектор свернутого сигнала может описываться
корреляцией, мы можем также вычислить изменение в спектре шума, т.е.
энергетический спектр шума, вызванного операцией свертки. Это требуется для
Фурье-преобразования уравнения (4.36) с учетом теоремы о корреляции (>-R7). Тогда мы получаем
а'= а*(А*А) о . о\к) = Ъ{кЩЦ
(4.38)
4.3. Фильтры порядковой статистики
Это означает, что спектр шума свернутого сигнала определяется умножением
спектра шума входных данных на квадрат передаточной функции фильтра. С
уравнениями (4.36) и (4.38) у нас есть все для того, чтобы вычислить изменения
статистических параметров сигнала (дисперсию, автоковариационную матрицу и спектр
шума), вызванные операцией фильтрации. Возвращаясь назад от уравнения (4.38),
мы можем заключить, что уравнение (4.36) применимо не только для 1-D
сигналов, но и для сигналов произвольной размерности.
4.3. Фильтры порядковой статистики
Рассмотрение вопроса объединения пикселей в результате привело к важному
понятию линейных инвариантных относительно сдвига систем. Таким образом,
хотелось бы думать, что мы уже изучили все, что нам необходимо знать для этого
типа операции обработки изображений. Однако это не так. Существует еще один
класс операций, который действует по совершенно другому принципу.
Мы могли бы охарактеризовать свертку с маской фильтра взвешиванием и
суммированием. Процедуры сравнения и выбора характеризуют класс операций
объединения соседних пикселей, который мы рассмотрим сейчас. Такой фильтр называется
фильтром порядковой статистики. В этом случае мы берем все уровни яркости
пикселей, которые принадлежат маске фильтра, и сортируем их по возрастанию уровней
яркости. Такая сортировка является общей для всех фильтров порядковой
статистики. Они отличаются только тем, из какого места в списке выбирается уровень
яркости, который записывается в центральный прпссель. Фильтрующая операция, которая
выбирает среднее значение, называется медианным фильтром. На рис, 4.3 показано,
как работает медианный фильтр. Фильтры, выбирающие минимальные и
максимальные значения, обозначаются как фильтры минимума и максимума соответствеьшо.
Медианный фильтр является нелинейным оператором. Для простоты
рассмотрим одномерный случай с трехэлементным медианным фильтром. Легко найти два
вектора, для которых медианный фильтр не является линейным. Сначала
применим медианный фильтр к сумме двух сигналов. Это в результате дает
М{[... 0 10 0 ...] + [... 0 0 10 ...]) = [... 0 110 ...].
Затем применим медианный фильтр сначала к двум компонентам, прежде чем
складывать результаты:
Ml.. 0 10 0 ...]-\-9\il.. 0 0 10 ...]=[... 0 0 0 0 ...].
Отсортированный список
39
35
34
32
33
33
34
33
36
31
32^
37
98
32
36
^
36
36
35
34
^
33
34
36
31
31
34
32
35
32
m
35
34
32
33
33
Ч
33
36
31
32
37
36
32
36
35
36
36
35
34
36
33
34
36
31
31
34
32
35
32
Входные данные Выходные данные
Рис. 4.3. Иллюстрация принципа фильтров порядковой статистики на примере
медианного фильтра 3x3
Глава 4. Операции над соседними элементами
Результаты обоих вычислений различны. Это доказывает, что медианный
фильтр является нелинейным.
Есть некоторые существенные различия между фильтрами свертки и
фильтрами порядковой статистики. Самым важным является то, что фильтры порядковой
статистики принадлежат классу нелинейных фильтров. Следовательно, гораздо
сложнее понять их общие свойства. Поскольку фильтры порядковой статистики не
выполняют арифметических операций, а выбирают пиксели, мы никогда не
столкнемся с проблемами округления. Эти фильтры отображают дискретное множество
уровней яркости само в себя.
4.4. ЛИС-фильтры: дополнительные свойства
4.4.1. Свертка, линейность и инвариантность относительно сдвига
В разделе 4.2.4 мы убедились, что оператор свертки является линейным ршвариант-
ным относительно сдвига оператором. Но является ли также верным обратное -
любой линейный инвариантный относительно сдвига оператор является также и
оператором свертки? В этом разделе мы собираемся доказать это утверждение. В наших
рассуждениях в разделе 4.2.5 мы уже познакомились с функцией рассеяния точки не-
прерьгоных и дискретных операторов. Здесь введем формальное определение
функции рассеяния точки для оператора Нпг. Мх 7У-мерном векторном пространстве:
Н = Я''Р, (4.39)
Теперь можно использовать линейность (4.16), инвариантность относительно
сдвига (4.18) оператора Ни определение импульсной характеристики (4.39) для
вычисления результата действия оператора на произвольное изображение G в
пространственной области:
(^G)„„ =
=
=
z=
=
=
zz
=
я
-
"m-1 n-\
II^^v""'"'^
_w'=0 «'=0
Гм-\м-\
\m9.w^'"'"'P
Lw'=0 п=0
'М-\ N-\
IIs'.v^'"'"'^"
_/и'=0 п=0
ГМ-1 N-\
SS^.v""'"'^^"
~M-\N-\ "1
II ^.v""'"'^
_w'=0 w'=0 J
M-1 Л^-1
^ ' j^^ <^m'n m-m\n-n
m'=0 n=0
M-\ N-\
s
jr^ ^m-m ,n-n m ,)
-i~l
ИЗ уравнения (4.16)
-*Jm«
линейность
Jmn
P ИЗ уравнения (4.17)
J/ИИ
»pl
J/ИИ
из уравнения (4.39)
гии
из уравнения (4.17)
т" = т-т
ft /
п" п -п-п
4.4. ЛИС-филыпры: дополнительные свойства
Эти преобразования доказывают, что линейный инвариантный относительно
сдвига оператор должен обязательно быть операцией свертки в пространственной
области. Не существует другого типа оператора, который является как линейным,
так и инвариантным относительно сдвига.
4.4.2. Обратные операторы
Можем ли мы обратить фильтрующую операцию так, чтобы можно было получить
обратно исходное изображение из отфильтрованного изображения? Этот вопрос
является существенным, поскольку ухудшение качества, вызванное размытием
изображения при движении или при расфокусированной оптике, может также
рассматриваться как фильтрующие операции (раздел 7.6.1). Если обратный оператор
существует и если известна функция рассеяния точки ухудшения качества, то мы можем
реконструировать исходное ненарушенное изображение. Задача обращения
фильтрующей операции называется обращением свертки или обратной фильтрацией.
Рассматривая фильтрующую операцию в Фурье-области, легко заметить, что
можно реконструировать только те волновые числа, для которых передаточная
функция фильтра не обращается в ноль. На практике условие обращения
фильтрующей операции еще более строгое из-за ограниченного качества сигналов
изображений. Если волновое число является затухающим ниже критического
уровня, который зависит от шума и квантования (раздел 9.5), то оно не будет обратимым.
Очевидно, что эти условия значительно ограничивают возможности
непосредственной обратной фильтрации. Задача обратной фильтрации рассматривается
дальше в главе 17.5.
4.4.3. Собственные функции
Следующим, что нас интересует, является вопрос: существуют ли специальные
виды изображений £, которые сохраняются линейным инвариантным относитель- ♦
но сдвига оператором, за исключением умножения на скалярную величину.
Интуитивно очевидно, что эти изображения имеют особую важность для ЛИС-опера-
торов. Математически это означает
НЕ = ХЕ, (4.40)
Вектор (изображение), который удовлетворяет этому условию, называется
собственным вектором (собственным изобра:ясением) или характеристическим
вектором оператора, масштабный множитель Я — собственным значением или
характеристическим значением оператора.
Для того чтобы найти собственные изображения ЛИС-операторов,
рассмотрим оператор сдвига S. Совершенно очевидно, что для действительных
изображений существует только тривиальное собственное изображение, а именно
постоянное изображение. Однако для комплексных изображений существует целое
множество собственных изображений. Мы можем найти его, как только
рассмотрим свойство сдвига комплексной экспоненциальной функции:
которое определяется соотношением
Глава 4, Операции над соседними элементами
kl ciuv
S''"W = exp
^ 2ткиЛ ( 2k\Iv\,
exp :^ I
V
V
N )
^. (4.42)
М
Последнее уравнение прямо утверждает, что комплексные экспоненциальные
функции "''Жявляются собственными функциями оператора сдвига.
Собственными значениями являются комплексные фазовые множители, которые зависят от
индексов волнового числа (и, v) и сдвига {к, /). Когда сдвиг равен одной длине волны,
(к, [) = (М/и, N/v), фазовый множрггель сводится к 1, чего и следовало ожидать.
Теперь любопытно узнать, имеет ли любой линейный инвариантный
относительно сдвига оператор такое доступное множество собственных изображений.
Оказывается, что все линейные инвариантные относительно сдвига операторы
имеют одно и то же множество собственных изображений. Мы можем доказать
это утверждение, сославшись на теорему о свертке (раздел 2.3, теорема 2.4, с. 61),
которая утверждает, что свертка является поточечным умножением в
Фурье-пространстве. Таким образом, каждый элемент представления изображения в Фурье-
пространстве 9ии умножается на комплексную скалярную величину /г„„. Каждая
точка в Фурье-пространстве представляет базисное изображение, а именно
комплексную экспоненциальную функцию "^И^в уравнении (4.41), умноженную
на скалярную величину 5,..,. Следовательно, комплексные экспоненциальные
функции являются собственными функциями любого оператора свертки.
Собственными значениями являются тогда элементы передаточной функции, А„„. В
заключение можно записать
П9и.ГЮ = кАГ1^. (4.43)
То, что собственные функции ЛИС-операторов являются базисными
функциями Фурье-области, объясняет, почему свертка сводится к умножению в Фурье-
пространстве и подчеркивает центральную значимость преобразования Фурье для
обработки изображений.
4.5. Рекурсивные фильтры
4.5.1. Введение
Поскольку свертка требует большого числа операций, встает вопрос: возможно ли
или даже выгодно ли включать уже свернутые соседние уровни яркости в свертку в
следующем пикселе. В таком случае мы могли бы выполнять свертку с меньшим
числом операций. Фактически мы можем выполнять свертки с гораздо меньшими
вычислительными усилиями и к тому же с большей гибкостью. Однако такие
фильтры, которые нзiзывзютcя рекурсивными фильтрами, являются гораздо более
трудными в понимании и обработке, особенно в многомерном случае.
Для получения первого впечатления рассмотрим очень простой пример.
Простейший l-D-рекурсивный фильтр, который мы можем представить, имеет обпщй вид
9:=ссд:_,+(1-а)д„. (4.44)
Этот фильтр берет часть (1 - а) от ранее вычисленного значения и часть а от
текущего пикселя. Рекурсивные фильтры, в отлрмие от нерекурсивных фильтров,
действуют в определенном направлении, в нашем примере — слева направо. В слу-
4.5. Рекурсивные фильтры
чае временных радов преимущественное направление кажется естественным,
поскольку текущее положение сигнала зависит только от предыдущих значений.
Фильтры, которые зависят только от предыдущих значений сигнала, называются
причинными фильтрами. В случае пространственных данных, однако, не существует
преимущественных направлений. Следовательно, необходимо искать способы
построения фильтров с четной и нечетной симметрией, поскольку они требуются для
обработки изображений, из рекурсивных фильтров.
При рекурсивных фильтрах функция рассеяния точки не является больше
тождественной маске фильтра, а должна вычисляться. Из уравнения (4.44) можно
вычислить функцию рассеяния точки или импульсную характеристику фильтра, как
отклик фильтра на дискретную дельта-функцию (раздел 4.2.5):
Г1 п = 0
Рекурсивно применяя уравнение (4.44), получаем
д:,=0, д',=\-а, д[ = {\-а)а, ..., д[={\-а)а\ (4.46)
Это уравнение иллюстрирует три типичных общих свойства рекурсивных фильтров.
• Во-первых, импульсная характеристика является бесконечной (рис. 4.4),
несмотря на конечное число коэффициентов. При | а | < О она убывает
экспоненциально, но никогда не достигает нуля. Противоположно импульсная
характеристика нерекурсивных фильтров свертки всегда конечна. Она равна размеру маски
фильтра. Поэтому иногда вьщеляют два типа фильтров: фильтры с конечной
импульсной характеристикой (КИХ-фильтры) и фильтры с бесконечной импульсной
характеристикой (БИХ-фильтры).
• КИХ-фильтры всегда устойчивы. Это означает, что импульсная
характеристика является конечной. Тогда отклик фильтра на любой финитный сигнал
конечен. Это не выполняется для БИХ-фильтров. Устойчивость рекурсивных
фильтров зависит от коэффициентов фильтра. Фильтр в уравнении (4.44) является
неустойчивым при I а I > 1, поскольку тогда импульсная характеристика расходится.
В простом случае уравнения (4.44) легко понять неустойчивость фильтра. Однако,
как правило, гораздо сложнее анализировать устойчивость рекурсивных
фильтров, особенно в двумерном случае или в случае более высокой размерности.
• Любой рекурсивный фильтр можно заменить нерекурсивным фильтром, в
общем, с маской бесконечного размера. Его маска определяется функцией
рассеяния точки рекурсивного фильтра. Обратное заключение не выполняется. Это
можно увидеть из самого факта, что нерекурсивные фильтры всегда устойчивы.
4.5.2. Передаточная функция, z-преобразование и устойчивая характеристика
После такого вводного примера мы готовы к более формальному обсуждению/?е-
курсивных фильтров. Рекурсивные фильтры включают результаты от предьщущих
сверток в соседних точках в сумму свертки и, таким образом, становятся
направленными. Мы рассматриваем здесь только 1-D рекурсивные фильтры. Общее
уравнение для фильтров, движущихся слева направо, имеет вид
9п =-Х«""0«-'.'+ Z ^'9п-п-
n=-R
(4.47)
134 Глава 4. Операции над соседними элементами
Рис. 4.4. Функция рассеяния точки рекурсивного фильтра д[ = осд'^_^ + {\-а)д^ для
а- а=1/2;б-а=15/16
В то время как окрестность нерекурсивной части (коэффициенты И) является
симметричной относительно центральной точки, рекурсивная часть
(коэффициенты а) использует только предварительно вычисленные значения. Такой
рекурсивный фршьтр называется причинным фильтром.
Если мы перенесем рекурсивную часть в левую сторону уравнения, то
получим, что рекурсивный фильтр эквивалентен следующему разностному уравнению,
также известному как процесс ARMA (5, R) (авторегрессионный процесс скользящего
среднего):
S R
S ^п'9^' = S ^«'^«-' ^ ^0 = 1. (4.48)
и'=0 n'=-R
Передаточную функцию такого фильтра с рекурсивной и нерекурсивной
частями можно вычислить, применив дискретное преобразование Фурье (раздел 2.3.2)
и воспользовавшись теоремой о сдвиге (теорема 2.3, с. 61). Тогда
S R
дХк)^ а„. Qxp{-2mn''k) =д{к)^ h^. ехр {-2п\пк), (4.49)
«'=0 п=-К
Таким образом, передаточная функция равна
h{k) =
д{к)
^ й^, ехр(-2л:ш'А:)
n=-R
^^^^ Y,^n'^M-^n\nk)
и'=0
(4.50)
Нули числителя и знаменателя обусловливают свойства передаточной
функции. Таким образом, ноль в нерекурсивной части передаточной функции
приводит к нулю в передаточной функции, т.е. исчезновению соответствующего
волнового числа. Ноль в рекурсивной части приводит к полюсу в передаточной функции,
т.е. бесконечному отклику.
Определение нулей и, таким образом, более глубокий анализ передаточной
функции невозможны из уравнения (4.50). Необходимо расширение, подобное
расширению от действительных чисел до комплексных, которое использовалось
при введении преобразования Фурье (раздел 2.3.2). Видно, что выражения как для
4.5. Рекурсивные фильтры 135^
числителя, так и для знаменателя являются многочленами относительно
комплексной экспоненциальной функции exp(27ci/:) вида
S
2;^Дехр(~2л:1Л:))". (4.51)
Комплексная экспоненциальная функция имеет модуль, равный единице, и,
таким образом, покрывает единичную окружность в комплексной плоскости. Нули
многочлена не обязательно располагаются на единичной окружности, а могут быть
произвольными комплексными числами. Следовательно, полезным будет
расширить полином так, чтобы он покрывал всю комплексную плоскость. Это
возможно при использовании выражения z = r ехр(2шА:), которое описывает окружность
радиуса г на комплексной плоскости.
При таком расширении мы получаем многочлен комплексного числа z. По
существу, мы можем использовать фундаментальный закон алгебры, который
утверждает, что любой многочлен степени Л^ можно разложить на А^ множителей,
состоящих из корней или нулей многочлена:
N N
J^a^ ^^^z'^fKl-r^z"^). (4.52)
и=0 п=]
С помощью уравнения (4.52) можно разложить рекурсивные и нерекурсивные
части многочленов в передаточной функции на следующие произведения:
п=0
R
п=0
2R
(4.53)
n=-R n=0 n=l
Используя z = r exp(2nik), передаточную функцию окончательно можно
записать как
2R
h{z) = h_,z'^ .
П(1-<'^'')
п''=\
(4.54)
Каждый из множителей с^, и rf^„ является нулем соответствующего многочлена
{z =с , или z = d „).
Включение множителя г в расширенную передаточную функцию приводит к
расширению преобразования Фурье, z-преобразованию, которое определяется как
9(z)=t9.^-\
(4.55)
Z-преобразование ряда д^ можно рассматривать как преобразование Фурье ряда
д^г" [124]. Z-преобразование является ключевым математическим инструментом
для понимания 1-D рекурсивных фильтров. Оно является дискретным аналогом
преобразования Лапласа. Детальные рассмотрения z-преобразования приводятся
Оппенхаймом (Oppenheim)H Шафером (Schafer) [148] и Поуларикасом (Poularikas)
[156]; 2-D z-преобразование рассматривается Лимом (Lim) [124].
Глава 4. Операции над соседними элементами
Сейчас мы проведем анализ передаточной функции более детально.
Разложение передаточной функции является значительным преимуществом, поскольку
каждый множитель может рассматриваться как отдельный фильтр. Таким
образом, каждый рекурсивный фильтр может быть разложен в каскад простых
рекурсивных фильтров. Поскольку все множители имеют вид
/„(^) = 1-с/„ехр(-2;г1Л), (4.56)
а импульсная характеристика фильтра должна быть действительной, то
передаточная функцры должна быть эрмитовой, т.е.Д-А:) = /*(А:). Это возможно только в
случае, когда или ноль d^ является действительным, или существует пара
множителей при комплексно-сопряженных нулях. Это условие дает начало двум
основным типам рекурсивных фильтров —релаксационному фильтру viрезонансному
фильтру, которые детально рассматриваются в разделах 4.5.5 и 4.5.6.
4.5.3. Рекурсивные фильтры более высокой размерности
Рекурсивные фильтры могут быть также описаны в случае более высоких
размерностей с помощью такого же вида уравнения, как (4.47); к тому же передаточная
функция и 2-преобразование рекурсивных фильтров более высокой размерности могут
быть записаны почти таким же образом, как в уравнении (4.50). Однако, как
правило, невозможно получить разложение z-преобразования, каквуравнении (4.54) [124].
Из (4.54) можно сразу же прийти к заключению, что возможным будет разложить
сепарабельные рекурсивные фильтры, поскольку тогда многочлены более высокой
размерности могут бьггь разложены на 1-D многочлены. Тезисно описав
математические трудности, присущие рекурсивным фильтрам более высокой размерности,
ограничим дальнейшее рассмотрение 1-D рекурсивными фильтрами.
4.5.4. Симметричная рекурсивная фильтрация
Применение фильтра, который использует только предьщущие данные,
естественно и полезно в случае обработки в реальном времени временных рядов, но не имеет
большого смысла в случае обработки пространственных данных. В
пространственных данных не существует понятий «до» и «после». Еще хуже зависящий от сигнала
пространственный сдвиг (задержка), связанный с рекурсивными фильтрами.
С помощью одного рекурсивного фильтра невозможно построить так
называемый ноль-фазовый фильтр с четной передаточной функцией. Необходимо
объединить многочисленные рекурсивные фильтры. Комбинация должна в качестве
результата давать или ноль-фазовый фильтр, подходящий для операций сглаживания,
или производный фильтр, который сдвигает фазу на 90^ Таким образом,
передаточная функция должна быть или чисто вещественной, или чисто мнимой (раздел 2.3.4).
Начнем с 1-D причинного рекурсивного фильтра, который имеет
передаточную функцию ^ ^
"^hik) = a(k) + ib(k). (4.57)
Верхний индекс + обозначает, что фршьтр действует в положительном
координатном направлении. Передаточная функция такого же фильтра, но
действующего в противоположном направлении, является похожей. Заменяем ^ на -^ и
учитываем, что а(-к) = а(-\-к) и b(-k) = b(k), поскольку передаточная функция
действительной ФРТ является эрмитовой (раздел 2.3.4), и получаем
4.5. Рекурсивные фильтры 137
-h{k) = a{k)-\b{ky (4.58)
Таким образом, при изменении направления фильтра на противоположное
меняется только мнимая часть передаточной функции.
Теперь у нас есть три возможных варианта объединения передаточных
функций (уравнения (4.57) и (4.58)) или в чисто вещественную, или в чисто мнимую
передаточные функции:
сложение %{к) = — ( ^h{k) + ~h{k) 1 = а{к),
вычитание ^й(^) = ^('т - -Щ)) = Чк\ (4.59)
умножение Щ) = ^h{k) ~kk) = а^ {к) + Ъ^ (к).
Сложение и умножение (последовательное применение) фильтров,
двигающихся налево и направо, дают фильтры четной симметрии и действительную
передаточную функцию, в то время как вычитание дает фильтр нечетной симметрии и
чисто мнимую передаточную функцию.
4.5.5. Релаксационные фильтры
Простой рекурсивный фильтр, рассмотренный в разделе 4.5.1,
9п=^,9п^,-^К9п при а,=а, h,=(l--a) (4.60)
и функция рассеяния точки
О иначе
(4.61)
является релаксационным фильтром. Передаточная функция фильтра,
действующего или в прямом, или в обратном направлениях, согласно (4.50), с учетом (4.60),
определяется соотношением
~г{к) = — при аеШ. (4 62)
1-аехр(+л:1А:)
Передаточная функция уравнения (4.62) является комплексной и может быть
разложена на действительную и мнимую части как
*Я(А^) = = Г(1 - а cos Trie) + ia sin тгк], (4.63)
1-2асо8л:А: + а •- -•
Согласно уравнению (4.59), можно вычислить передаточную функцию г для
результирующего симметричного фильтра, если применить релаксационные
фильтры последовательно в положительном и отрицательном направлениях:
при
\т=
'm-rik)=Y
^=-^
{l-af _ 1
-2acos7tk+a^ {l + P)-PcosKk\
и a = ^! .
(4.64)
(1-ar
а
1
0,8
0.6
0,4
0,2
Глава 4. Операции над соседними элементами
|^^:^^^ч^ 11
\ \ \ ^
1 \ Л \ 3/4
\ \ 7/8 V
\l5/16 \ \
31/32 \ \ \
1 ^^^^^S:^
-2,5
-2
-1,5
-0,5 _ О
log к
^1/2/
^-1/4^
~ -1/8
-1/16
0.2
0.4
0,6
0,8
Рис. 4.5. Передаточная функция релаксационного фильтра д'„ -ад^^^ -l-(l-a)gf„,
примененного сначала в прямом и затем в обратном направлениях, для а —
положительных, б — отрицательных значений а
Из уравнения (4.61) можно прийти к заключению, что релаксационный фильтр
является устойчивым, если | а | < 1, соответственно j3 G ]-1/2, оо[. Как уже
упоминалось, передаточная функция равна единице при малых волновых числах. Ряд
Тейлора относительно к имеет вид
Кк)-\-
а . -2 а(1 + 10а+а^), .-4
Если а является положительным, то фильтр является фршьтром нижних
частот (рис. 4.5, а). Это можно установить, изменяя а. Если а приближается к 1, то
усредняющее расстояние становится бесконечным. Для отрицательных а фильтр
увеличивает большие волновые числа (рис. 4.5, б).
Этот фильтр является дискретным аналогом дифференциального уравнения
первого порядка j-i-T>^ = 0, описывающего релаксационный процесс со временем
релаксации т= -А//1па.
Примером может служить простая резисторно-конденсаторная схема,
показанная на рис. 4.6, б. Дифференциальное уравнение для этого фильтра можно
получить из закона Кирхгофа о сумме токов. Ток, проходящий через резистор от V. к
J/q, должен равняться току, втекающему в конденсатор. Поскольку ток, текущий в
конденсатор, пропорционален производной по времени от напряжения И^,
приходим к дифференциальному уравнению первого порядка
и
СИ
б
Черный ящик
ю
Uo
ho
r\
\J
1 R 1 A
L_J!_J ^
'I
Щ
r\
\J
oH
4r
Рис. 4.6. Анагюговый фильтр для временного ряда: а — модель «черного ящика»:
сигнал и. подается в неизвестную систему, и на выходе мы измеряем сигнал И^, б -
резисторно-конденсаторная схема в качестве простого примера аналогового
фильтра нижних частот; в — затухающий резонансный фильтр, состоящий из индуктора I,
резистора R и конденсатора С.
4.5. Рекурсивные фильтры
i
/
^
»=S*-
1 I15/16
'/\
7/8 \\
3/4 n\
77Г^^
'
0,2
0,4
0,6
0,8
б
Ф
-0,5
-1
-1,5
-2
-2,5
-3
-3,5
Я/2
я
J 5/16
U7/8
\l/2
0,2
0,4
0,6
0,8
к I и u,z u,*f и,о и,о 1 I
Рис. 4.7. а — абсолютная величина; б — фазовый сдвиг передаточной функции
резонансного фильтра в соответствии с уравнением (4.67) для ка= 1/4 и указанных значений г
R dt '
а постоянная времени определяется соотношением т = RC.
(4.66)
4.5.6. Резонансные фильтры
Второй, основной тип рекурсивного фильтра, который мы определили из
рассмотрения передаточной функции в разделе 4.5.2, имеет пару комплексно
сопряженных нулей. Следовательно, передаточная функция этого фильтра, действующего в
прямом и обратном направлениях, равна
'т =
1
(1 - г exp(i лгА:^) ехр(+iл:А:))(1 - г ехр(ЧлгА:^) ехр(+iл:А:))
1 (4.67)
1 - 2г cos{nk^) ехр(+ ink) -I- г^ exp(T2i7r^)
Вторая строка уравнения показывает, что этот рекурсивный фильтр имеет
коэффициенты Aq = 1, flfi = -2rcos(nkQ) и «2 =^^ так что
д: = д„ +2rcos(;r^o)^:.i -r'g'^.r (4.68)
Из передаточной функции в уравнении (4.67) мы приходим к заключению,
что этот фильтр является полосовым фильтром с волновым числом полосы
пропускания, равным ± icf, (рис. 4.7). Для г= 1 передаточная функция имеет два
полюса в ^ = ±k^.
Импульсная характеристика этого фильтра равна, согласно [148],
г"
Кп =
sin л: А:,
— $т[(п + 1)7гк^] п>0
"О (4.69)
О п<0-
Это означает, что фильтр действует как затухающий осциллятор. Параметр Ц^
определяет волновое число колебаний, а параметр г является коэффициентом
затухания (рис. 4.8). Фильтр является устойчивым только при г < \.
а
1
0,75
0,5
0,25
О
-0,25
-0,5
-0,75
-1
140 Глава 4. Операции над соседними элементами
б
1
0,75
0,5
0,25
О
-0,25
-0,5
-0,75
-1
IF
ППт
10
15
20 П
I
ЦР^Ши"
О 10 20 30 П40
Рис. 4.8. функция рассеяния точки рекурсивного резонансного фильтра в
соответствии с уравнением (4.68) для а — А:п = 1/4, г = 3/4; б - ^ = 1/4, г = 15/16
Если мы двигаем фильтр туда и обратно, то результирующий фильтр имеет
действительную передаточную функцию s{k) = '^s(kys(k), которая определяется
соотношением
1
sik).
(4.70)
(1-2гсо8[л:(^-4)] + г')(1-2гсо8[л:(^ + ^о)] + ^')
Передаточную функцию этого фильтра можно нормировать, так что ее
максимальное значение станет равным 1 в полосе пропускания, положив коэффициент
нерекурсивного фильтра h^ равным (l-r^) sm(n:kQ). Тогда получаем следующую
модифицированную рекурсию:
д'„ = (l-r')smiKk,)g„'^2rcos(nkM.^, -r^Q.-.r (4.71)
Вследствие симметрии множители становятся наиболее простыми в случае
резонансного волнового числа, равного к^ = 1/2. Тогда рекурсивный фильтр равен
9>i^-r')g„-r'g'„,,=g„-r\g^^g'„^,) (4.72)
С передаточной функцией
(4.73)
Кк)--
1 + /+2г^со8(2л:^)'
Максимальный отклик этого фильтра при к - 1/2 равен единице, а
минимальный отклик при А: = О и А: = 1 равен [(1 - г^)1{\ л- r^)Y.
Этот резонансный фильтр является дискретным аналогом линейной системы,
описываемой дифференциальным уравнением второго порядка у-\-1хул-(о1у-^^
затухающим гармоническим осциллятором, таким как LRC схема на рис. 4.6, е.
Циклическая собственная частота (о^ и постоянная времени т реального
осциллятора связаны с параметрами дискретного осциллятора, r\iK соотношением [89]
г = ехр(-Д/ /т) и ^0 = (o^tu I п-
(4.74)
4.5.7. ЛИС-фильтры и теория систем
Последний пример затухающего осциллятора иллюстрирует тот факт, что существует
тесная связь между дискретными фильтрующими операциями и аналоговыми фи-
4.6. Упражнения
зическими системами. Таким образом, цифровые фильтры являются моделями
реальных физических процессов. Они моделируют реакцию соответствующей
системы на данный входной сигнал д, В действительности мы будем пользоваться этой
аналогией при рассмотрении формирования изображений в главе 7. Там мы
определим, что получение изображений с помощью однородной оптической системы
полностью описывается ее функцией рассеяния точки и что процесс
формирования изображений можно описывать сверткой. Оптическое получение
изображений вместе с физическими системами, такими, как электрические фильтры и
осцилляторы всех видов, могут, таким образом, рассматриваться как представление
абстрактного типа процесса или системы, называемой лм//ей«ой инвариантной
относительно сдвига системой, рши коротко ЛИС,
Это обобщение является очень полезным для обработки изображений,
поскольку можно описывать как формирование изображений, так и обработку
изображений как операции свертки с тем же формализмом. Кроме того, наблюдаемые
изображения могут возникать из физического процесса, который можно смоделировать
линейной инвариантной относительно сдвига системой. Тогда метод определения,
как система работает, может быть проиллюстрирован с использованием модели
«черного ящика» (рис. 4.6, а). Термин «черный ящик» означает, что мы не знаем
устройства наблюдаемой системы или законов, которые управляют ею. Мы можем
определить их путем зондирования системы некими сигналами (входными сигналами) и
наблюдения отклика при измерении некоторых других сигналов (выходных
сигналов). Если окажется, что система линейна, то она будет полностью описываться
импульсной характеристикой.
Многие биологические и медицинские эксперименты проводятся таким
образом. Биологические системы являются, как правило, настолько сложными, что
исследователи часто возбуждают их с помощью сигналов и наблюдают отклики
для того, чтобы определить, как они работают, и построить модель. По этой
модели можно начать более детальное исследование для обнаружения того, как
функции наблюдаемой системы могли бы быть реализованы. Таким образом были
обнаружены многие свойства биологических зрительных систем. Однако будьте
внимательны - модель не является реальностью! Она изображает только аспект,
который мы исследуем с помощью используемых сигналов.
4.6. Упражнения
4.1: Общие свойства операторов свертки
Интерактивная демонстрация общих свойств линейных инвариантных
относительно сдвига операторов (dip6ex04.01).
4.2: *1-D свертка
Исследуйте следующие 1-D маски свертки:
2 1];
а)
б)
в)
г)
д)
е)
1/4 [1 2 1];
1/4 [10 2 0 1];
1/16 [12 3 4 3
1/2 [1 0 -1];
[1 -2 1];
[10-2 0 1].
4.3:
Глава 4. Операции над соседними элементами
Вопросы и задания:
1. Какую симметрию проявляют эти маски свертки?
2. Вычислите передаточные функции. Попытайтесь получить простейшее
возможное уравнение, используя тригонометрические тождества для
половинных и двойных углов.
3. Проверьте вьшисленные передаточные функции, применяя маски к
постоянной структуре уровней яркости {к = 0)
... 1 1 1 1 1 1 ...,
структуре уровней яркости с максимально возможным волновым числом
... 1-11-11-11 ...,
и ступенчатому контуру
... О О О О О 1 1 1 1 1 ...
**2-D свертю!
Ответьте на те же вопросы, что и в упражнении 4.2, для следующих 2-D
масок сверток:
а)
в)
1
/Г
о
'1 2 1]
2 4 2
1 2 ij
б)
1 2 1
0 0 0
-1 -2 -1
1 2
2 -12
1 2
1 О -1
0 0 0
-1 О 1
Проверьте, являются ли маски сепарабельными или могут быть составлены
иным образом из 1-D масок свертки упражнения 4.2. Это поможет вам
сохранить много вычислительных усилий!
4.4:
"^Коммутативность и ассоциативность свертки
Покажите с помощью применения масок свертки а и б из упражнения 4.2 к
ступенчатому контуру
... 0 0 0 0 0 11111 ...,
что свертка является коммутативной и ассоциативной.
4.5: "^Маски свертки с четным числом коэффициентов
Для фильтров с четным числом коэффициентов (2R) также возможно
определить фильтры с четной и нечетной симметрией, если мы представим, что
результат свертки расположен на промежуточной сетке. Маску свертки
можно записать как
[А.^,..., h_j,..., AJ.
Справочная часть (>-Rll) задает уравнения для передаточных функций этих
масок.
1. Докажите эти уравнения путем применения сдвига, равного половине
сеточного расстояния, к общему уравнению для передаточной функции из (4.23).
4.6. Упражнения 143
2. Вычислргге передаточные функции двух элементарных масок [1 1 ]/2
(среднее значение двух соседних точек) и [ 1 -1] (разность двух соседних точек).
4.6: ^^Манипуляции масками свертки
Исследуйте, как передаточная функция маски свертки с (2R +
1)-коэффициентами изменяется, если изменить коэффициенты следующим образом:
1. Дополнительный фильтр
h' =S -h.
п п п
Пример: изменение [1 1 1]/Здо[-1 2 -1]/3.
2. Частичное изменение знака
п четное
п нечетное.
Пример: [1 2 1]/4 изменяется до [-1 2 -1]/4.
3. Расширение
/ \Ki2 ^ четное
[О п нечетное.
Пример: [1 2 1]/4 изменяется до [1 0 2 0 1]/4.
4.7: ***Обратная свертка
Существует ли обратный оператор для следующих операторов свертки?
а) 1/6 [1 4 1];
б) 1/4 [1 2 1];
в) 1/3 [1 1 1].
Являются ли эти обратные операторы снова операторами свертки? (См.
раздел 4.4.2) Если да, то имеют они особую структуру?
4.8: "^"^Изменение статистики 1-D сигналов с помощью свертки
Вычислите автоковариационный вектор некоррелированного временного
ряда с постоянной дисперсией сг^ для всех элементов, которые были
свернуты с помощью фильтров а, г и д из упражнения 4.2. Проанализируйте
результаты, особенно для дисперсии свернутого временного ряда.
4.9: Рекурсивные релаксационные фильтры
Интерактивная демонстрация рекурсивных релаксационных фильтров
(dip6ex04.02).
4.10: Рекурсивные резонансные фильтры
Интерактивная демонстрация рекурсивных резонансных фильтров
(dip6ex04.03)
4.11: "^^Устойчивость рекурсивных фильтров
1. Какой из следующих рекурсивных фильтров (раздел 4.5) является
устойчивым?
а) g:=-l/4g:.,+5/4g„;
Глава 4. Операции над соседними элементами
б) g:=5/4g:_,-l/4g„;
в) g:=-l/4g:_,+3/4g,;
г) g:=-5/4g:_2-i/4g,.
Ответьте на этот вопрос, вьиислив функцию рассеяния точки.
2. Вычислите передаточные функции этих фильтров.
4.12: "^"^Физические системы и рекурсивные фильтры
Физические системы можно рассматривать как реализацию рекурсивных
фильтров. Вычислите функцию рассеяния точки (импульсную
характеристику) и передаточную функцию следующих физических систем:
1. Каскадный электрический фильтр нижних частот, включающий две
стадии, каждая с резистором R и конденсатором С.
2. Пружинный маятник с массой т, жесткостью пружины D (К= Dx) и
коэффициентом трения к{К= kux/dt).
4.13: ^"^Полосовой фильтр
Разработайте полосовой фильтр со следующими свойствами:
1. Волновое число пропускания должно быть ^ = 0,5.
2. Полоса пропускания диапазона пропусканрш должна быть регулируемой.
Фильтр должен работать и как рекурсивный, и как нерекурсивный.
(Подсказка: возьмите фильтр [~1 0 2 0 -1] как стартовую точку для
нерекурсивного выполнения. Как можно использовать этот фильтр для получения
меньшей ширины полосы?)
4.7. Дополнительная литература
Классические понятия фильтрации дискретных временных рядов, особенно
рекурсивных фильтров и z-преобразования, рассматриваются в работах Оппенхайма
(Oppenheim) и Шафера (Schafer) [148], Проакиса (Proakis) и Манолакиса (Manolakis)
[159], 2-D фильтрация - в книге Лима (Lim) [124]. Детальный обзор по
нелинейным фильтрам, особенно медианным фильтрам, дается Хуангом (Huang) [83] и
Питасом (Pitas) и Венетсанополосом (Venetsanopoulos) [155].
ГЛАВА 5
МНОГОМАСШТАБНОЕ ПРЕДСТАВЛЕНИЕ
5.1. Масштаб
5.1.1. Введение
Операции над соседними элементами, рассмотренные в главе 4, могут служить
только отправной точкой при анализе изображений. Этот класс операторов способен
вьщелять локальные признаки в областях с размерами в несколько пикселей.
Очевидно, что изображения содержат информацию в гораздо больших масштабах. Для
того чтобы выделять признаки объекта на большой площади, нам необходимы
соответственно маски фильтров больших размеров. Однако использование масок
больших размеров приводит к значительному увеличению вычислительных
затрат. Если мы используем маску размера R^ в PF-мерном изображении, то число
операций пропорционально R^. Таким образом, увеличение масштаба вдвое
приводит к четырех- и восьмикратному увеличению числа операций в двумерных и
трехмерных изображениях соответственно. При масштабе, увеличенном в 10 раз,
количество вычислений увеличивается в 100 и в 1000 раз для двумерных и
трехмерных изображений соответственно.
Взрыв вычислительных затрат является только поверхностным
представлением о проблеме с более глубокими корнями. Покажем это на простой задаче
определения контуров и линий при различных разрешениях. Рассмотрим строку
одного и того же изображения, размытую в различной степени (рис. 5.1). Определим
соответствующий масштаб как расстояние, на которое размыто изображение, и
проанализируем различия уровней яркости по этому расстоянию.
Сначала исследуем различия уровней яркости при высоком разрешении, в
масштабе, равном всего лишь расстоянию в один пиксель (рис. 5Л, а, б). При таком
мелком масштабе над изменением в уровнях яркости преобладает зашумленный
фон изображения. Любое определение изменений уровней яркости, вызванных
контрастом между объектами и фоном, получается неаккуратным и ошибочным.
Проблема вызвана масштабным рассогласованием: уровни яркости изменяются
на больших масштабах, чем использовали операторы при их определении.
В случае низкого разрешения (рис. 5.1,5, ё) линии размыты настолько, что контраст
значительно уменьшился. Кроме того, две близко расположенные линии в левой части
сигнала слились в один объект при такой низкой разрешающей способности. Поэтому
определение контуров и лрший является снова субоптимальным. Однако при
разрешении, сравнимом с шириной линии, определение линий уже кажется оптимальным
(рис. 5.1, в, г). Шум значительно понизился по сравнению с самым мелким масштабом
(рис. 5.1, flf), а контраст между линией и фоном не уменьшился, как на рис. 5 Л, д.
Из рассмотрения этого примера мы можем сделать заключение, что
выделение некоторых признаков в изображении является оптимальным при опре-
Глава 5. Многомасштабное представление
Ijllll 1
1 '
1 1
50
100
150
200
250
Рис. 5.1. Линии и контуры при: а - высоком; в — среднем; д - низком разрешениях;
б, г, е — разность между соседними пикселями при определении контуров а, в и д,
соответственно
деленном масштабе. Этот масштаб зависит, конечно, от характерных размеров,
содержащихся в определяемом объекте. Поэтому оптимальная обработка
изображения требует представления изображения при различных масштабах. Для того
чтобы удовлетворить этому требованию, необходимо многомасштабное
представление изображений. В этой главе мы сначала проиллюстрируем соотношение
между пространственным представлением изображений и представлением через
волновое число с этой точки зрения (раздел 5.1.2). Затем обратимся к эффективным
многосеточным представлениям, таким как Гауссова пирамида (раздел 5.2.2) и
пирамида Лапласа (раздел 5.2.3). И в заключение в разделе 5.3 введем понятие
масштабного пространства, с непрерывным масштабным параметром. Обсудим, как
диффузионный процесс может сформировать масштабное пространство, и
опишем его основные свойства.
5.1.2. Пространственное представление относительно представления через
волновое число
В главе 2 мы детально обсуждали представление изображений в пространственной
области и области волновых чисел. В этом разделе мы снова рассмотрим оба
представления с перспективой формирования многомасштабного представления изображения.
5.7. Масштаб
Если мы представим изображение на сетке в пространственной области, то не
будем иметь никакой информации о волновых числах, содержащихся в некой
точке на изображении. Мы знаем положение с точностью до сеточной постоянной
Ах, но локальное волновое число на этом месте может находиться где угодно в
диапазоне возможных волновых чисел от О до МАк = 2пМ/Ах.
В случае представления через волновое число мы имеет обратную ситуацию.
Каждый пиксель в этой области представляет одно волновое число при самом
высоком разрешении волновых чисел, возможном для данного размера
изображения. Однако всякая информация о положении является потерянной, поскольку
каждый пиксель в пространстве волновых чисел представляет периодическую
структуру, которая распространена по всему изображению.
Вышеприведенное рассуждение показывает, что представления изображения
либо в пространственной области, либо в области волновых чисел образуют две
противоположные крайности. Мы можем оптимизировать либо
пространственное разрешение, либо разрешение волновых чисел, но информация в другой
области будет полностью потеряна. Для многомасштабного представления
изображений необходим вид совместного разрешения, который предусматривает разделение
на различные диапазоны волновых чисел (масштабы), но все еще сохраняет
пространственное разрешение, насколько это возможно.
5.1.3. Преобразование Фурье, реализуемое посредством организации окна
Одним из способов получить совместное пространственно-волновое
представление является преобразование Фурье, реализуемое посредством организации окна. Как
следует из названия, преобразование Фурье не применяется ко всему
изображению, а только к части изображения, которая формируется умножением
изображения на оконную функцию w(x). Оконная функция имеет максимум в дс = О и
монотонно убывает с ростом | jc | к нулю. Максимум оконной функции устанавливается
в каждой точке jc изображения для вычисления преобразования Фурье посредством
организации окна для каждой точки:
д(х,к^) = j g(x)w(x-x)Qxip(-2mkQx)dx'\ (5.i)
Интеграл в уравнении (5.1) выглядит почти как интеграл свертки (уравнение
(2.54), )^R4). Для преобразования его в интеграл свертки обратим внимание на то,
что w(-k) =w(k), и преобразуем вторую часть уравнения (5.1) к виду:
5.2)
w(л:'-л:)exp(~2л:iA:ox') =
= w{x - х') ехр[2тк^(х - л:')) ехр(-2л:1А:оЛ:).
Тогда мы можем записать уравнение (5.1) как свертку:
д{х,к^) = (g{x)^w(x)Qxp(2mk^x))Qxp(-2n:ikQx)' (5.3)
Это означает, что локальное преобразование Фурье соответствует свертке с
комплексным ядром свертки ^(л:)ехр(2я1А:^дс) за исключением фазового
множителя Qxp(-27nk^x). Используя теорему о сдвиге (теорема 2.3, с. 61, >^R4), можно
вычислить, что передаточная функция ядра свертки есть
w(x)exp(2mkQx) о • wik-k^y (5.4)
Глава 5. Многомасштабное представление
Это означает, что ядро свертки ^(дс)ехр(2я1ЛрДс) является полосовым фильтром с
пиковым волновым числом Лр. Ширина полосы пропускания обратно
пропорциональна ширине оконной функции. Таким образом, пространственные и волновые
разрешения взаимосвязаны друг с другом. В качестве примера возьмем оконную
функцию Гаусса
ехр
^ х' ^
V "J
Ее преобразование Фурье (>-R4, >-R5) равно
(5.5)
-j^-QXv(-2K'eGl\ (5.6)
Следовательно, произведение среднеквадратичных отклонений в
пространственной области и области волновых чисел (ст^^ = \/{Апо^)) является постоянной
величиной: 1/(4;г). Этот факт устанавливает классическое соотношение
неопределенностей (теорема 2.7, с. 64). Оно утверждает, что произведение
среднеквадратичных отклонений любой пары преобразований Фурье больше или равно 1/(4;г).
Поскольку оконная функция Гаусса достигает теоретического минимума, она
является оптимальным выбором; лучшее волновое разрешение не может
достигаться с заданным пространственным разрешением.
5.2. Многосеточные представления
5.2.1. Введение
Если мы хотим обрабатывать сигналы в различных масштабах, это можно сделать
наиболее эффективным способом в многосеточном представлении. Основная идея
проста. В то время как мелкие размеры требуют полного разрешения, крупные
размеры можно представить при более низком разрешении. Это приводит к
масштабному пространству со все уменьшающимися изображениями, по мере того как
масштабный параметр увеличивается. В следующих двух разделах мы обсудим
пирамиду Гаусса (раздел 5.2.2) и пирамиду Лапласа (раздел 5.2.3). В этом разделе мы
только рассматриваем основы многосеточных представлений. Оптимальные
многосеточные сглаживающие фильтры подробно рассматриваются в разделе 11.5,
после того как мы познакомимся со сглаживающими фильтрами.
Эти пирамиды являются примерами многосеточных структур данных,
которые были введены в цифровую обработку изображений в ранние 1980-е и привели
к огромному увеличению в скорости многих алгоритмов обработки изображений
в цифровой обработке изображений с того времени.
5.2.2. Гауссова пирамида
Если мы хотим уменьшить размер изображения, то не можем просто выполнить
подвыборку изображения, взяв, к примеру, каждый второй пиксель в каждой
второй линии. Если мы сделаем так, то пренебрежем теоремой о дискретном
представлении (раздел 9.2.3). Например, структура, которая выбирается три раза в длину
5.2. Многосеточные представления
волны в исходном изображении, будет выбрана только полтора раза в
изображении после выполнения подвыборки и, таким образом, появится как структура с
наложением спектров, как мы рассмотрим в разделе 9.1. Следовательно, все
структуры, которые выбираются меньше, чем четыре раза в длину волны, должны
подавляться с помощью соответствующего сглаживающего фильтра для
обеспечения правильного изображения после выполнения подвыборки. Для формирования
масштабного пространства это означает, что уменьшение размера должно
сопровождаться соответствующим сглаживанием. Как правило, требование для
сглаживающего фильтра можно сформулировать как
В{к) = 0 ^к^>-, (5.7)
где г есть частота подвыборки в направлении р-й координаты.
Комбинированное сглаживание и уменьшение размера можно выразить в
отдельном операторе, используя следующее обозначение для вычисления р + 1-го
уровня пирамиды Гаусса по/?-му уровню:
G^'^=G, G^'^'^=(B,,G^'\
(5.8)
Число за I в индексе обозначает частоту подвыборки. 0-м уровнем пирамиды
является исходное изображение.
Если мы повторяем операции сглаживания и подвыборки итерационно, то
получаем ряд изображений, который называется пирамидой Гаусса. От уровня к
уровню разрешение уменьшается в 2 раза; размер изображений уменьшается
соответственно. Следовательно, мы можем рассматривать ряд изображений,
упорядоченный в форме пирамиды, как проиллюстрировано на рис. 5.2.
Пирамида не требует большой области памяти. Как правило, если мы
рассматриваем формирование пирамиды по Ж-мерному изображению с множителем
подвыборки, равным двойке и Мпикселями в каждом координатном направлении, то
общее число пикселей задается как
М"'
<М
w
2^-1 (5.9)
Для двумерного изображения всей пирамиды необходимо только на 1/3
больше пространства, чем для исходного изображения, для трехмерного
изображения - только на 1/7 больше. Вычисление пирамиды является также равно
эффективным. К каждому уровню пирамиды применяется один и тот же сглаживающий
фильтр. Таким образом, для вычисления всей пирамиды необходимо только в 4/3
и 8/7 раза больше операций, чем для первого уровня двумерного и трехмерного
изображений соответственно.
Пирамида вносит большие масштабы в диапазон локальных операций над
соседними элементами с малыми ядрами. Кроме того, эти операции
выполняются эффективно. Если пирамида вычислена, мы можем выполнять операции
над соседними элементами на больших масштабах на верхних уровнях
пирамиды - из-за меньших размеров изображения — гораздо эффективнее, чем для
более мелких масштабов.
Пирамида Гаусса образует ряд изображений, отфильтрованных с помощью
фильтров нижних частот, в которых предельные волновые числа уменьшаются в 2
150 Глава 5. Многомасштабное представление
^^ШЯ
Рис. 5.2. Пирамида Гаусса: а — схематическое представление - квадраты шахматной
доски, соответствующие пикселям; б - пример
раза (октава) от уровня к уровню. Таким образом, только более крупные детали
остаются в более мелких изображениях (рис. 5.2). Всего несколько уровней
пирамиды необходимы для покрытия всех возможных волновых чисел. Для
изображения NxNмы можем вычислить, самое большее, пирамиду с ldN+ 1 уровнем.
Наименьшее изображение состоит из единственного пикселя.
5.2.3. Пирамида Лапласа
Из пирамиды Гаусса можно получить другой тип пирамиды — пирамиду Лапласа,
которая приводит к последовательности изображений, отфильтрованных с помощью
полосовых фильтров. В отличие от преобразования Фурье, пирамида Лапласа
приводит только к грубому волновому разложению без направленного разложения. Все
волновые числа, независимо от их направления, внутри диапазона, равного
приблизительно октаве (множитель, равный двойке), содержатся в одном уровне пирамиды.
Из-за низкого волнового разрешения мы можем сохранить хорошее
пространственное разрешение. Каждый уровень пирамиды содержит только согласующиеся
размеры, которые выбираются несколько раз (от 2 до 6) в длину волны. Таким
образом, пирамида Лапласа является эффективной структурой данных, хорошо
адаптированной к пределам произведения волнового и пространственного разрешений,
устанавливаемым соотношением неопределенностей (раздел 5.1.3 и теорема 2.7, с. 64).
Для того чтобы получить ее, мы вычитаем два уровня пирамиды Гаусса. Это
требует повышающей выборки изображения на более грубом уровне. Эта
операция выполняется оператором растяжения ]^. Степень растяжения или
повышающей выборки обозначается цифрой после t в индексе, в обозначении, подобном
оператору сжатия в уравнении (5.8).
Растяжение значительно сложнее, чем уменьшение размера, поскольку нужно
интерполировать недостающую информацию. Для увеличения размера в 2 раза во
5.2. Многосеточные представления
всех направлениях, сначала нужно интерполировать каждый второй пиксель в
каждой строке, а затем каждую вторую строку. Интерполяция рассматривается детально
в разделе 10.5. С помощью введенного обозначения образование/?-го уровня
пирамиды Лапласа можно записать как
L^p^=G^p^-^^G^p-'\ L^'^=G^'\
(5.10)
Пирамида Лапласа является эффективной схемой полосового разложения
изображения. Центральное волновое число делится пополам от уровня к уровню.
Последнее изображение пирамиды Лапласа, L^^\ является изображением G^^\
отфильтрованным с помощью фильтра нижних частот, содержащее только самые
крупные структуры.
Пирамида Лапласа имеет существенное преимущество, так как исходное
изображение можно быстро реконструировать по последовательности изображений в
пирамиде Лапласа с помощью рекурсивного растяжения изображений и их
суммирования. Рекурсия является обратной к рекурсии в уравнении (5.10). В
пирамиде Лапласа с /? + 1 уровнями уровень р (вычисление начинается с нуля) является
самым грубым уровнем пирамиды Гаусса. Тогда уровень р - 1 пирамиды Гаусса
можно реконструировать с помощью
G(n=lin^ (;(.-!) ^jr,(p-l)+^^(;.
(5.11)
Обратите внимание, что это как раз инверсия схемы конструирования для
пирамиды Лапласа. Это означает, что даже если интерполяционные алгоритмы,
требуемые для растяжения изображения, содержат ошибки, они влияют только на
пирамиду Лапласа, а не на реконструкцию пирамиды Гаусса по пирамиде
Лапласа, поскольку используется один и тот же алгоритм. Рекурсия в уравнении (5.11)
повторяется нижними уровнями, пока снова не достигается уровень О, т.е.
исходное изображение. Как проиллюстрировано на рис. 5.3, все более мелкие и мелкие
детали становятся видимыми в течение процесса реконструкции. Из-за
прогрессирующей реконструкции деталей пирамида Лапласа используется как
компактная схема для сжатия изображений. Сегодня доступны более эффективные схемы
на основе вейвлет-преобразований, но они работают по принципам, схожим с
принципами пирамиды Лапласа.
5.2.4. Направленно-пирамидальное разложение
В многомерных сигналах направленное разложение является таким же важным,
как масштабное разложение. Направленные разложения требуют подходящих
направленных фильтров. В идеале, все направленные компоненты должны сводиться
к полному изображению. Комбинированное разложение изображения в пирамиду
и на каждом уровне по направленным компонентам известно как
направленно-пирамидальное разложение [86]. Как правило, такое разложение является сложной
проблемой разработки фильтров. Поэтому мы иллюстрируем здесь направленно-
пирамидальное разложение только с простой и эффективной схемой разложения
с двумя направленными компонентами.
Сглаживание выполняется сепарабельными сглаживающими фильтрами,
одним фильтром, который сглаживает только в направлении х((В), и другим, который
(^IS2 Глава 5. Многомасштабное представление
Рис. 5.3. Конструирование пирамиды Лапласа (правая колонка) по пирамиде Гаусса
(левая колонка) с помощью вьиитания двух последовательных плоскостей
пирамиды Гаусса
сглаживает только в направлении у((В), тогда следующий, более высокий уровень
пирамиды Гаусса задается, как в уравнении (5.8), с помощью
Пирамида Лапласа есть
G^'^'^ =L (В (В G^'\
2 X у
£(^)^^(^)_t^^(^+l)^
(5.12)
(5.13)
(5.14)
Тогда две направленные компоненты определяются с помощью
4'^ = 1 / 2(G^'^ - Т^ G^'^'^ - {(В^ - (By )G^'^ \
Lf = 1 / 2(G^'^ - Т2 G^'^'^ + (®, - cBy )G^'^).
Из уравнения (5.14) очевидно, что две направленные компоненты, 1^и L ,
складываются в изотропную пирамиду Лапласа: Z = £^ + £ . На рис. 5.4 показаны
примерные изображения с первыми тремя уровнями направленного разложения.
5.3. Масштабные пространства
Пирамиды Гаусса и Лапласа являются эффективными, но довольно негибкими
многосеточными структурами данных. От уровня к уровню масштабный параметр
меняется на фиксированный множитель, равный двойке. Более мелкий выбор
5.3 Масштабные пространства 153
Рис. 5.4. Первые три плоскости направленно-пирамидального разложения рис. 5.6, а:
показанные строки являются плоскостями О, 1 и 2, столбцы L, L^, L согласно
уравнениям (5.13) и (5.14)
масштаба невозможен. В этом разделе мы рассматриваем более общую схему,
масштабное пространство, которая допускает непрерывный масштабный параметр.
Как мы уже увидели на примере преобразования Фурье с организацией окна в
разделе 5.1.3, введение характеристического масштаба добавляет новую
координату в представление данных изображений. Помимо пространственного
разрешения мы имеем новый параметр, который характеризует текущий уровень
разрешения данных изображения. Масштабный параметр обозначается как ^. Структура
данных, которая состоит из последовательности изображений с различными
разрешениями, известна как масштабное пространство; мы записываем д(х, t) для
обозначения масштабного пространства изображения д(х).
Далее, в разделе 5.3.1 мы рассматриваем физический процесс - диффузию,
которая подходит для генерации масштабного пространства. Затем мы
рассматриваем общие свойства масштабного пространства в разделе 5.3.2.
5.3.1. Диффузное масштабное формирование
Образование масштабного пространства требует процесса, который может
размывать изображения до контролируемой степени. Диффузия является процессом пе-
Глава 5. Многомасштабное представление
реноса, который стремится уравнять разности в концентрациях [27]. В физике
диффузионные процессы управляют передачей тепла, вещества и импульса, ведущей
к постоянно возрастающему выравниванию пространственных разностей. Если мы
отождествляем время с масштабным параметром ^, то диффузионный процесс
устанавливает масштабное пространство.
Для того чтобы применить диффузионный процесс к многомерному сигналу с
размерностью W, мы рассматриваем уровень яркости дкак концентрацию
химического вещества. Элементарный закон диффузии утверждает, что плотность
потока у имеет направление, противоположное градиенту концентрации Vg и
пропорциональна ему:
j = -DVg, (5.15)
где константа D известна как коэффициент диффузии. Используя уравнение
неразрывности
получаем
|w,=o,
| = V(Z)Vg).
(5.16)
(5.17)
Для случая однородного диффузионного процесса {D не зависит от положения),
уравнение сводится к
^9
Э/
= DAg,
где
W Д2
(5.18)
(5.19)
есть оператор Лапласа. Легко показать, что общее решение этого уравнения
эквивалентно свертке со сглаживающей маской. И наконец, мы выполняем
пространственное преобразование Фурье, которое приводит к
ot
(5.20)
с использованием теоремы 2.5 (с. 62), и сводит уравнение к линейному
дифференциальному уравнению первого порядка с общим решением
g{k,t) = exp(-4n'D\к \' t)g(k,0), (5.21)
где д(к, 0) является изображением, преобразованным с помощью преобразования
Фурье, в начальный момент времени.
Умножение изображения в Фурье-пространстве на функцию Гаусса в
уравнении (5.21) эквивалентно свертке с той же функцией, но обратной ширины
(теорема 2.4, с. 61, >-R4 и>-К6). Таким образом,
Г I ,. |2 Л
g(x,t) =
1_^
[2nc7\t)]
WI2
ехр
\х\'
2o\t)
'g{x,Qi)
(5.22)
при
5.3. Масштабные пространства
G{t) = 42Dt, (5.23)
Уравнение (5.23) показывает, что степень сглаживания, выраженная
среднеквадратичным отклонением, возрастает только со скоростью квадратного корня
из времени. Следовательно, мы устанавливаем масштабный параметр ^ равным
квадрату среднеквадратичного отклонения:
^=2Dt. (5.24)
Важно обратить внимание на то, что эта формулировка масштабного
пространства действительна для изображений любой размерности. Она может также
расширяться на последовательности изображений. Масштабный параметр не
тождественен времени, хотя мы использовали для его получения физический диффузионный
процесс, который происходит во времени. Если мы вычисляем масштабное
пространственное представление последовательности изображений, полезно
масштабировать временную координату с помощью характеристической скорости и^, с
тем чтобы она имела такую же размерность, как пространственные координаты:
t' = UQt. (5.25)
Мы добавляем эту координату к пространственным координатам и получаем
новый координатный вектор:
л: = [х,, Х2, u^tf или X = [Хр ^2, Хз, u^tf. (5.26)
Подобным образом мы расширяем вектор волнового числа с помощью
масштабированной частоты:
k=[k^,k2,v/щУ или к = [к^,к2,к^,у/щУ, (5.27)
С учетом уравнений (5.26) и (5.27) все уравнения, полученные ранее,
например, уравнения (5.21) и (5.22), можно также применять к масштабным
пространствам последовательностей изображений. Для дискретных пространств,
конечно, не требуется такое масштабирование. Оно автоматически устанавливается с
помощью пространственных и временных интервалов выборки: и^ = Ах/ At,
В качестве иллюстрации на рис. 5.5 показывается масштабное пространство
некоторых характерных одномерных сигналов: зашумленные контуры и линии,
периодическая структура, случайный сигнал и строка изображения. Эти примеры
прекрасно демонстрируют общее свойство масштабных пространств. С увеличением
масштабного параметра t, сигналы становятся все более и более размытыми, больше
и больше деталей теряются. Эту особенность можно легче всего увидеть с помощью
передаточной функции масштабного пространственного преобразования в
уравнении (5.21). Передаточная функция всегда положительна и монотонно убывает с
увеличением масштабного параметра t, для всех волновых чисел. Это означает, что
никакие структуры не усиливаются. Все структуры ослабляются с увеличением ^, и
более мелкие структуры всегда быстрее, чем более крупные структуры. В пределе
^-►00 масштабное пространство сходится к постоянному изображению со средним
уровнем яркости. Определенный признак существует только на определенном
масштабном диапазоне. На рис. 5.5, а мы можем наблюдать, что контуры и линии
исчезают и два объекта сливаются в один.
Для двумерных изображений непрерывное представление масштабного
пространства дает трехмерную структуру данных. Следовательно, на рис. 5.6
показываются отдельные изображения для различных масштабных параметров ^,
согласно указанному.
156 Глава 5. Многомасштабное представление
Рис. 5.5. Масштабное пространство некоторых одномерных сигналов: а - контуры и
линии; б — периодическая структура; в - случайный сигнал; г — строка 10 из
изображения, показанного на рис. 11.6, а. Вертикальная координата является масштабным
параметром ^
5.3.2. Общие свойства масштабного пространства
В этом разделе мы рассматриваем некоторые общие свойства масштабных
пространств. Более конкретно, мы хотим узнать, какому типу условий должно
удовлетворять ядро фильтра, образующее масштабное пространство. Мы рассмотрим
два основных требования. Во-первых, никакие новые детали не должны
добавляться с увеличением масштабного параметра. С точки зрения теории
информации мы можем сказать, что содержание информации в сигнале должно
непрерывно уменьшаться с увеличением ^.
Второе свойство связано с общим принципом масштабной
инвариантности. Это, по существу, означает, что мы можем начать сглаживание сигнала при
любом масштабном параметре в масштабном пространстве и все еще получить
то же масштабное пространство. Здесь мы приведем только некоторые
основные идеи относительно этих элементарных свойств без доказательств. Для
детального рассмотрения теории масштабных пространств мы отсылаем к
недавней монографии по линейной теории масштабных пространств Линдеберга
(Lindeberg) [125].
5.3. Масштабные пространства 157
Рис. 5.6. Масштабное пространство одномерного изображения: а - исходное
изображение; б, в, г — при масштабных параметрах ст 1, 2 и 4 соответственно
Линейный однородный и изотропный диффузионный процесс имеет,
согласно уравнению (5.22), ядро свертки
и передаточную функцию (уравнение (5.21))
|2 Л
2^
(5.28)
В(к,^) = ехрМл:' IЛ I' (^ /2). (5.29)
В этих уравнениях мы заменили явную зависимость от времени масштабным
параметром ^, используя уравнение (5.24). Не зависящим от представления
образом мы обозначаем порождающий масштабное пространство оператор как
«(^). (5.30)
Свойство убывания информации масштабного пространства с ^ можно
сформулировать математически различными способами. Мы выразим его здесь с
помощью принципа максимума-минимума, который утверждает, что локальные
экстремумы не должны усиливаться. Это означает, что уровень яркости в локальном
максимуме или минимуме не должен увеличиваться или уменьшаться
соответственно. Для диффузионного процесса это является интуитивным свойством. На-
Глава 5. Многомасштабное представление
пример, в задаче переноса тепла горячее пятно не должно становиться горячее
или холодное пятно холоднее. Ядро Гаусса уравнения (5.28) удовлетворяет
принципу максимума-минимума.
Второе важное свойство масштабного пространства связано с принципом
масштабной инвариантности. Мы хотим начать порождающий процесс при любом
масштабном параметре и получить то же самое масштабное пространство.
Математически мы можем сформулировать это свойство как
(В(^,Ж^,) = ®(«^,+<^2)- (5-31)
Это означает, что сглаживание масштабного пространства при масштабе ^j с
помощью оператора с масштабом Ъ,^ эквивалентно применению масштабного
пространственного оператора с масштабом ^j + ^2 к исходному изображению. В качестве
альтернативы мы можем утверждать, что представление на более грубом уровне ^j можно
вьиислить по представлению на более мелком уровне с помощью применения
Щ,) = Щ,-^,)Щ,) при ^,>^, (5.32)
Исходя из уравнений (5.28) и (5.29), мы можем легко проверить, что уравнения
(5.31) и (5.32) верны. В математике свойства уравнений (5.31) и (5.32)
рассматриваются как свойство полугруппы.
Может возникнуть вопрос: существуют ли порождаюище масштабное
пространство ядра, которые удовлетворяют и принципу максимума-минимума и свойству
полугруппы. Ответ на этот вопрос может стать неожиданным. Ядро Гаусса является
единственным ядром свертки, которое удовлетворяет обоим критериям и является к тому
же изотропным и однородным [125]. Эта особенность ставит ядро свертки Гаусса и,
как мы увидим далее, его дискретный аналог — биномиальное ядро — на уникальное
место в теории обработки изображений. Это будет детально разобрано в разделе 11.4.
Всегда поучительно рассмотреть противоречащий пример. Наиболее простым
сглаживающим ядром для W^-мерного изображения, известным как скользящее
среднее, является фильтр-ящик
1 W
R(x,^) = —Yln
с передаточной функцией
'х..
1«
(5.33)
Это ядро не удовлетворяет ни принципу максимума-минимума, ни свойству
полугруппы. На рис. 5.7 сравниваются масштабные пространства периодического
сигнала с изменяющимся волновым числом, порожденные с помощью ядра
Гаусса и ядра-ящика. На рис. 5.7, Остановится очевидным, что ядро-ящик не
удовлетворяет принципу максимума-минимума, поскольку структуры убывают до тех пор,
пока полностью не удаляются, а затем появляются снова.
5.3.3. Квадратичные и экспоненциальные масштабные пространства
Вопреки математической привлекательности порождения масштабных пространств
с помощью ядра свертки Гаусса, этот подход имеет один значительный
недостаток. Среднеквадратичное отклонение сглаживания увеличивается только со ско-
5.3. Масштабные пространства
I
11III1I1II
Рис. 5.7. Масштабное пространство 1-D сигнала с изменяющимся волновым
числом, вычисленное с помощью: а — ядра Гаусса; б — ядра-ящика. Масштабный
параметр пробегает сверху вниз
ростью квадратного корня из времени, см. уравнение (5.23). Следовательно,
масштабный параметр^ пропорционален квадрату среднеквадратичного отклонения.
Это приводит к нелинейности масштабной координаты. В то время как
сглаживание протекает быстро для мелких масштабов, оно становится все более и более
медленным для более крупных масштабов.
Существует простое средство решения этой проблемы. Нам нужен
диффузионный процесс, где постоянная диффузии увеличивается в зависимости от
времени. Сначала мы рассмотрим коэффициент диффузии, который возрастает
линейно в зависимости от времени. Этот подход приводит к дифференциальному
уравнению
Пространственное преобразование Фурье приводит к
дд{к)
(5.35)
Э/
=-4ж'D^t\ к \' д{к).
(5.36)
Это уравнение имеет общее решение
gik,t) = exp{-2n'D/ \ к \')д{к,0),
(5.37)
которое эквивалентно свертке в пространственной области. Таким образом,
g{x,t) =
1
2nD/
exp
|2 Л
2D/
*g{x,0).
(5.38)
Из этих уравнений мы можем записать ядро свертки и передаточную функцию
в такой же форме, как в уравнениях (5.28) и (5.29), с единственным исключением —
масштабный параметр равен
^,=D/. (5.39)
Теперь среднеквадратичное отклонение сглаживания пропорционально
времени для диффузионного процесса, который увеличивается линейно по времени.
Поскольку масштабный параметр t, пропорционален квадрату времени,
обозначим это масштабное пространство как квадратичное масштабное пространство.
Глава 5. Многомасштабное представление
Это модифицированное масштабное пространство по-прежнему удовлетворяет
принципу максимума-минимума и свойству полугруппы.
Для более ускоренного сглаживания мы можем построить экспоненциальное
масштабное пространство, т.е. масштабное пространство, где логарифм
масштабного параметра увеличивается линейно в зависимости от времени. Мы используем
коэффициент диффузии, который увеличивается экспоненциально во времени:
-^ = D,Qxp{t/T)Ag. (5.40)
ot
И снова получаем ядро свертки и передаточную функцию, как в уравнениях
(5.28) и (5.29), теперь с масштабным параметром
(^^=2Дтехр(//г). (5.41)
5.3.4. Дифференциальные масштабные пространства
Интерес к дифференциальным масштабным пространствам обусловлен тем, что
мы хотим выбрать оптимальные масштабы для обработки признаков в
изображениях. В дифференциальном масштабном пространстве делается акцент на
изменении изображения в зависимости от масштаба. Мы используем
передаточную функцию масштабного пространственного ядра уравнения (5.29), которая
также применима для квадратичных и логарифмических масштабных
пространств. Общее решение для масштабного пространства можно записать в
Фурье-пространстве как
д(к,^) = ехр(-2я' \ к f ^)д(к,0). (5.42)
Дифференцирование этого сигнала относительно масштабного параметра ^ дает
Щ^й = -2ж' I к f схр(-2п' I к f 4)д(к,0) = -2л' \ к f д(к,а (5.43)
о?
Умножение на -| к рэквивалентно второй пространственной производной (xR4),
оператору Лапласа. Таким образом, мы можем записать в пространственной области
' =^Agf(x,.^). (5.44)
Уравнения (5.43) и (5.44) образуют основное свойство дифференциального
масштабного пространства. Дифференциальное масштабное пространство
эквивалентно взятию второй пространственной производной с оператором
Лапласа и, таким образом, приводит к изотропному полосному разложению
изображения. Передаточная функция при масштабе ^ равна
~2л:' I к f ехр(-2л:' | к f ^). (5.45)
Для малых волновых чисел передаточная функция пропорциональна -| к р. Она
достигает максимума при
е Л
max t-
и затем убывает экспоненциально.
(5.46)
5.4. Упражнения
5.3.5. Дискретные масштабные пространства
Построение дискретного масштабного пространства требует дискретизации
уравнения диффузии. Мы начнем с дискретизации одномерного уравнения диффузии
Производные заменяются дискретными разностями следующим образом:
Эх' Дх'
Это приводит к следующей итерационной схеме для вычисления дискретного
масштабного пространства с е = Z)A(^ / Ах :
д(х,<^ + А<^) = бд(х + Ах,<^) + (1-2б)д(х,<^)+ебг(х-Ах,<^) (5.49)
или с помощью дискретных координат (^-*/, х-*^п)
'"S'„ =е'9'„., +(1-2е)'д„ +€'бг„_,. (5.50)
Линдеберг (Lindeberg) [125] показал, что эта итерация приводит к дискретному
масштабному пространству, которое удовлетворяет принципу
максимума-минимума и свойству полугруппы тогда и только тогда, когда
б <1/4. (5.51)
Предельный случай е < 1/4 приводит к особенно простой итерации
'^'0„=l/4'0„.,+l/2'g„+l/4'6f„_, (5.52)
Каждый шаг вычисления масштабного пространства задается пространственным
сглаживанием сигнала с маской В^ = [\ 2 1]/4. Мы можем также сформулировать
обш;ий порождающий масштабное пространство оператор в уравнении (5.49),
используя оператор свертки (В. Записанный в операторной форме, введенной в 4.1.4,
оператор одного итерационного шага для порождения дискретного масшггабного
пространства есть
(l-4€)J + 4€«^ при €<1/4, (5.53)
где J обозначает тождественный оператор.
Это выражение является значимым, поскольку оно может быть
непосредственно расширено до случая более высокой размерности путем замены (В^
сглаживающим оператором соответственно более высокой размерности. Маска свертки В^
является простейшей маской в классе сглаживающих биномиальных фильтров. Эти
фильтры будут рассматриваться детально в разделе 11.4.
5.4. Упражнения
5.1: Пирамиды
Интерактивная демонстрация пирамид Гаусса и Лапласа (dip6ex05.01).
Глава 5. Многомасштабное представление
^^Сглаживающие фильтры для пирамид Гаусса
Первые статьи о пирамидах Бюрта (Burt) и Адельсона (Adelson) [19] и Бюрта [18]
использовали сглаживающие фильтры с 5 коэффшдиентами, например, фильтры
[14 6 4 1]/16, [12 3 2 1]/9.
Эти фильтры сначала применялись в горизонтальном направлении, а затем
в вертикальном направлении.
1. Удовлетворяют ли эти фильтры условию, выраженному уравнением (5.7),
состоящему в том, что передаточная функция должна быть равна нулю для
^1>1/2или4>1/2?
2. Возможно ли вообще, чтобы фильтр с конечной функцией рассеяния
точки мог удовлетворять этому условию точно!
5.3: **Поетроение пирамиды Гаусса
Пирамида Лапласа могла бы быть также построена согласно следующей
схеме как альтернатива уравнению (5.10):
Сглаженный р-и уровень пирамиды Гаусса просто вычитается из себя без
применения понижающей выборки. Понижающая выборка применяется
только для вычисления (р + 1)-го уровня пирамиды Гаусса.
1. Определите уравнение, которое эквивалентно уравнению (5.11), для того
чтобы построить пирамиду Гаусса по пирамиде Лапласа.
2. Видите ли вы какое-либо преимущество или недостаток этой схемы по
сравнению со схемой, описанной уравнениями (5.10) и (5.11)?
5.4: "^"^^Пирамида с более низким масштабным разрешением
Одна из проблем общепринятых пирамид заключается в уменьшении размера в
каждом направлении на фиксированный множитель, равный двум. Некоторые
прикладные задачи требуют более низкого масштабного разрешения.
Как могли бы вы образовать пирамиду, у которой размер в обоих направле-
НИ51Х уменьшается не в 2 раза, а в V2 раза?
(Подсказка: вам нужно найти схему, которая выбирает только каждый
второй пиксель из 2-D изображения).
5.5: Масштабное пространство
Интерактивная демонстрация различных масштабных пространств и их
свойств (dip6ex05.02).
5.6: "^"^Дискретное масштабное пространство с использованием фильтров-ящиков
Дискретное масштабное пространство должно быть построено с
использованием фильтров-ящиков (скользящее среднее) с увеличивающейся длиной
фильтра. Длина фильтра определяется масштабным параметром ^ = 2R +1.
Ответьте на следующие вопросы:
1. Удовлетворяется ли принцип максимума-минимума?
2. Является ли масштабное пространство инвариантным относительно
масштаба, т.е. удовлетворяет ли оно свойству полугруппы
5.5. Дополнительная литература
5.5. Дополнительная литература
Обработка изображений методом с переменной разрешающей способностью
получила развитие в ранние 1980-е. Превосходный обзор этих работ дается Розен-
фельдом (Rosenfeld) [171]. Линейные масштабные пространства детально
описываются монографией Линдеберга (Lindeberg) [125], нелинейные масштабные
пространства, включая неоднородную и изотропную диффузию, Вайкертом
(Weickert) [214]. Читатели, интересующиеся недавним развитием теории
масштабных пространств, отсылаются к докладам международных конференций по
теме «Масштабные пространства»: 1997 [197], 1999 [145], 2001 [106], 2003 [106] и
2005 [107] гг.
ЧАСТЬ 2
ФОРМИРОВАНИЕ И ПРЕДВАРИТЕЛЬНАЯ
ОБРАБОТКА ИЗОБРАЖЕНИЙ
ГЛАВА 6
КОЛИЧЕСТВЕННАЯ ВИЗУАЛИЗАЦИЯ
6.1. Введение
Система формирования изображений накапливает излучение, испускаемое
объектами, для того, чтобы сделать их видимыми. Излучение состоит из потока частиц,
электромагнитных или акустических волн. В классическом компьютерном зрении
сцены и освещение анализируются так, как они заданы, однако зрительные
системы, используемые в науке и промышленности, требуют иного подхода. Здесь
первостепенной задачей является установление количественного соотношения
между интересующим нас признаком объекта и испускаемым излучением. Целью этих
усилий является отображение интересующего нас признака объекта с
минимально возможным искажением яркости с помощью других параметров.
На рис. 6.1 показано, что и на падающий луч, и на луч, испускаемый объектом по
направлению к камере, могут влиять дополнительные процессы. Положение объекта
может быть смещено при преломлении испускаемого луча. Рассеяние и поглощение
падающих и испускаемых лучей приводит к ослаблению потока излучения,
вызываемое не самим наблюдаемым объектом, а окружающей средой, которая, таким
образом, искажает наблюдение. Для надлежащей работы важно обеспечить,
чтобы эти дополнительные влияния минимизировались и чтобы получаемое излучение
было непосредственно связано с интересуюпщм нас признаком объекта. В случаях,
когда отсутствуют какие-либо влияния на освещение или установку, мы можем,
кроме того, выбрать излучение наиболее подходящего вида и диапазон длин волн.
Как указано в разделах 1.2 и 6.4, существует большое количество явлений при
формировании изображений объектов и признаков объектов, включающих
самоиспускание, вынужденное излучение (флуоресценция), отражение, поглощение и
рассеяние излучения. Эти явления зависят от оптических свойств материала
объекта и от структуры поверхности объекта. По существу, можно отделить явления,
связанные с поверхностью и вызванные неоднородностью оптических свойств на
поверхности объектов, и явлениями, связанными с объемом объектов.
Очеврщно, что сложность процедур количественной визуализации сильно зависит
от задачи обработки изображения. Если нашей целью является только проведение
точного геометрического измерения объектов, то достаточно установить освещение, при
котором объекты равномерно освещаются и явно отличаются от фона. В этом случае не
6.1. Введение
Объект (наблюдаемый)
при отражении, преломлении,
испускании, поглощении или рассеянии
Рассеяние
Падающий луч
(от источника света)
Путь освещения
Рассеяние
Испускаемый луч
(по направлению к камере)
Путь наблюдения
Рис. 6.1. Схематическая иллюстрация взаимодействия между излучением и
веществом с целью визуализации объекта. Соотношение между испускаемым по
направлению к камере излучением и признаком объекта может быть нарушено рассеянием,
поглощением и преломлением падающего и испускаемого лучей
требуется установления количественных соотношений между интересующими нас
признаками объектов и излучением, испускаемым по направлеюпо к камере.
Однако если мы хотим измерить определенные признаки объекта, такие, как
плотность, температура, ориентация поверхности или концентрация химриеского
вещества, то необходимо знать точное соотношение между выбранным
признаком и испускаемым излучением. Простым примером является распознавание
объекта по его цвету, т.е. спектральная зависимость коэффициента отражения.
Однако в большинстве прикладных задач соотношение между
интересующими нас параметрами и испускаемым излучением гораздо менее очевидно. В
изображениях, полученных из космоса, к примеру, легко распознать городские зоны,
леса, реки, озера и сельскохозяйственные области. Но по каким признакам мы
распознаем их? И даже более важный вопрос: почему на изображениях они
выглядят именно так?
Подобным образом в медицинских исследованиях одним из самых общих
вопросов, связанных с диагнозом, основанным на изображениях, является
определение патологических отклонений. Надежное решение требует хорошего
понимания отношения между биологическими параметрами, которые определяют
патологическое отклонение, и их возникновением на изображениях.
Итак, по существу, нужно ответить на два вопроса для успешной установки
системы формирования изображения:
1. Как энергетическая яркость объекта (испускаемый поток энергии
излучения в телесный угол) зависит от интересующих нас параметров объекта и условий
освещения?
2. Как энергетическая освещенность на плоскости изображения (плотность
потока энергии излучения), полученная оптической системой, зависит от яркости объекта?
В этой главе обсуждается первый из этих вопросов, второй вопрос
рассматривается в разделе 7.5.
Глава 6. Количественная визуализация
6.2. Радиометрия, фотометрия, спектроскопия и цвет
6.2.1. Термины, используемые в радиометрии
Радиометрия является разделом оптики, описывающим и измеряющим излучение
и его взаимодействие с веществом. Из-за двойственной природы излучения
радиометрические термины относятся либо к энергии, либо к частицам; в случае
электромагнитного излучения частицы — это фотоны (раздел 6.3.4). Если
требуется сделать различие между этими двумя типами, то для радиометрических
терминов используются индексы ей р.
Радиометрия не является сложным предметом. Однако она стала предметом,
сбивающим с толку, вслед за различным, неточным и часто даже неправильным
использованием ее терминов. Кроме того, радиометрия преподается не так часто
и не так полно, как другие предметы оптики. Таким образом, наука о радиометрии
является менее распространенной. Однако она является очень важным предметом
для формирования изображения. Геометрическая оптика только сообщает нам,
где расположено изображение объекта, тогда как радиометрия предоставляет
информацию о том, сколько энергии излучения было получено от объекта.
Энергия излучения. Поскольку излучение является формой энергии, оно
совершает работу. Тело, поглощающее излучение, нагревается. Излучение может
освобождать электрические заряды в подходящем материале, разработанном для
определения излучения. Энергия излучения обозначается Q и задается в единицах
измерения Вт • с (джоуль) или числом частиц (фотонов).
Поток излучения. Мощность излучения, т.е. энергия в единицу времени,
известна как поток излучения и обозначается Ф:
Ф = -^. (6.1)
at
Этот термин важен для описания полной энергии, испускаемой источником
света в единицу времени. Его единицей измерения является джоуль/с (Дж • с~'),
ватт (Вт) или фотоны в секунду (с"0-
Плотность потока излучения. Поток излучения на единицу площади, плотность
потока, известна под двумя названиями:
dO dO
энергетическая освещенность Е = , светимость М = . (g 2)
Энергетическая освещенность, Е, равна потоку излучения, падающего на
поверхность, на единицу площади, к примеру, на датчик, который преобразует
энергию излученрш в электрический сигнал. Единицей измерения энергетической
освещенности является Вт • м"^ или фотоны на единицу площади и в единицу времени
(м"2- с~^). Если излучение испускается с поверхности, то плотность потока
излучения называется светимостью или излучательной способностью и обозначается М.
Телесный угол. Понятие телесного угла является первостепенным для
понимания углового распределения излучения. Рассмотрим компактный источник в
центре сферы радиусом R, испускающий излучение наружу по направлениям,
образующим конус (рис. 6.2, а). Границы конуса описывают площадьу4 на сфере. Телесный
угол (Q), измеряемый в стерадианах (ср), равен площади ^4, поделенной на квадрат
радиуса (Q = A/R^), Хотя стерадиан является безразмерной величиной, лучше ис-
6.2. Радиометрия, фотометрия, спектроскопия и цвет 167
Сфера
Рис. 6.2. а - определение телесного угла; б — определение яркости, мощности
излучения, испускаемого на единицу площади поверхности (L4, спроектированную в
направлении распространения, на единицу телесного угла Q
пользовать его явно в случае, когда радиометрический термин, относящийся к
телесному углу, может быть спутан с соответствующим термином, в котором не
важно направление. Телесные углы, соответствующие всей сфере и полусфере, равны
Ак и 2п соответственно.
Сила излучения. (Полный) поток излучения в единицу телесного угла,
испускаемый источником, называется силой излучения Г.
Очевидно, что этот термин имеет значение только при описании компактных
или точечных источников, т.е. в случае, когда расстояние от источника гораздо
больше, чем его размер. Эта область также часто называется полем источника в
дальней зоне. Сила излучения также используется для описания световых лучей.
Энергетическая яркость. Для распределенного источника излучение на
единицу площади в направлении светимости и в единицу телесного угла является
важной величиной (рис. 6.2, б):
d4dQ d4ocos0d«' ^^'^^
Излучение может либо быть испущенным с поверхности, либо проходить
через поверхность, либо падать на поверхность. Энергетическая яркость L зависит
от угла падения на поверхность, в (рис. 6.2, б), и азимутального угла 0. Для
плоской поверхности 0 и 0 принадлежат интервалам [О, л/2] и [О, 2 п] соответственно.
Важно понимать, что энергетическая яркость относится к единице площади в
направлении светимости, йА = dA^ • cos0 . Таким образом, эффективная площадь, с
которой испускается излучение, увеличивается с ростом утла падения.
Единицами измерения яркости, связанной с понятиями энергии и фотона, являются
Вт • м"^ • ср"^ и с"^ • м"2 • ср"^ соответственно.
Часто энергетическую яркость — особенно падающую энергетическую яркость —
называют яркостью. Лучше не использовать этот термин вообще, поскольку он
создает путаницу между энергетической яркостью и энергетической освещенностью.
Глава 6. Количественная визуализация
Хотя обе величины имеют одну и ту же размерность, они совершенно разные.
Энергетическая яркость L описывает угловое распределение излучения, в то время как
энергетическая освещенность Е интегрирует энергетическую яркость, падающую
на элемент поверхности, по диапазону телесного угла, соответствующему всем
направлениям, по которым он может получать излучение:
Ttllln
Е = ^Цв,ф)cosedQ= j jL{в,ф)cosвsmвdвdф, (6.5)
а 0 0
Множитель cose возникает потому, что единица площади для энергетической
яркости связана с направлением светимости (рис. 6.2, б), в то время как
энергетическая освещенность относится к единице площади параллельной поверхности.
6.2.2. Спектрорадиометрия
Поскольку любое взаимодействие вещества и излучения зависит от длины волны
или частоты излучения, необходимо обрабатывать все радиометрические
величины как функции от длины волны. Следовательно, область определения всех этих
величин — единичный интервал длин волн. В качестве альтернативы также
возможно использование единичных интервалов частот или волновых чисел.
Волновое число обозначает число длин волн в интервале единичной длины (см.
уравнение (2.14) и раздел 2.3.6). Для того чтобы сохранить различие спектральных величин,
определим зависимость явно, например L(X), L(v) и L(k).
Радиометрические термины, рассмотренные в предьщущем разделе,
описывают свойства излучения в терминах энергии и числа фотонов. Фотометрия
связывает те же самые величины с восприимчивостью к ним человеческого глаза.
Фотометрия представляет важность для научного понимания формирования
изображений в двух отношениях: во-первых, фотометрия дает количественный
подход к радиометрическим величинам на основе того, как их воспринимает
человеческий глаз. Во-вторьпс, фотометрия служит моделью для описания отклика
любого типа датчика излучения, используемого для преобразования
энергетической освещенности в электрический сигнал. Ключевым в понимании фотометрии
является взгляд на спектральную чувствительность человеческого глаза. Что
касается всего остального, то в фотометрии нет ничего нового.
6.2.3. Спектральные выборочные методы
Спектроскопическое формирование изображений является в принципе мощным
инструментом для определения объектов и их свойств, поскольку почти все
оптические константы материалов зависят от длины волны излучения. Проблема,
связанная со спектроскопическим формированием изображений, заключается
в том, что добавляется еще одна координата к формированию изображений и
требуемое количество данных соответственно увеличивается. Следовательно,
важно провести дискретизацию спектра с минимальным числом выборок,
достаточным для выполнения требуемой задачи. Здесь мы введем несколько общих
спектральных выборочных стратегий. В следующем разделе мы к тому же
рассматриваем цветовое зрение человека с позиции одной из реализаций
спектральной выборки.
6.2. Радиометрия, фотометрия, спектроскопия и цвет
Выборка по линиям представляет собой метод, в котором каждый канал
выбирает только узкий спектральный диапазон (рис. 6.3, а). Этот метод полезен, если
необходимо получить изображения процессов, которые связаны с испусканием
или поглощением в определенных спектральных линиях. Этот метод является очень
избирательным. Один канал «видит» только определенную длину волны и
нечувствителен - по крайней мере, в той степени, с которой такая узкополосная
фильтрация может быть реализована технически, — ко всем другим длинам волн.
Таким образом, этот метод подходит для формирования изображений весьма
ограниченного класса явлений рши отдельных химических веществ. Он не может
быть использован для получения оценки общей энергетической яркости от
объектов, поскольку упускает большинство длин волн.
Выборка по полосам является подходящим методом, если необходимо получить
изображение общей энергетической яркости в определенном диапазоне длин волн
и еще некоторое разрешение по длине волны (рис. 6.3, б). В идеале отдельные
полосы имеют постоянную чувствительность и соседствуют друг с другом. Таким
образом, выборка по полосам дает оптимальное разрешение с несколькими
каналами, но не позволяет каким-либо образом различать длины волн внутри
отдельной полосы. Спектральное разрешение, достижимое с помощью такого метода,
ограничивается шириной спектральных полос датчиков.
Во многих случаях возможно получить модель спектральной плотности
энергетической яркости некоторого объекта. Тогда можно найти лучший спектральный
выборочный метод, который, по существу, производит выборки не определенных
длин волн, а скорее параметров модели. Этот метод известен как спектральный
метод на основе использования модели.
Проиллюстрируем этот общий подход с помощью простого примера. Он
наглядно представляет метод для измерения средней длины волны произвольного
спектрального распределения ф (Я) и полного потока излучения в некотором
диапазоне волновых чисел.
Эти величины определяются как
ф = —^\ф{Х)АХ и Я=]я0(Я)(1Я/]0(A)dA. (6.6)
Во втором уравнении спектральное распределение умножается на длину
волны Я. Следовательно, нам необходим датчик, который имеет чувствительность,
изменяющуюся линейно в зависимости от волнового числа. Возьмем два
сенсорных канала со следующей линейной спектральной чувствительностью, как
показано на рис. 6.3, в\
- + Я
2
^0
^>
(6.7)
где R - чувствительность датчика; Я - нормированная длина волны:
70 Глава 6. Количественная визуализация
б
в
А
f N /' N
Al А;
Аз
Ai А2 A3
Ai
А2
Рис. 6.3. Примеры спектральной выборки: а — выборка по линиям; б — выборка по
полосам; в — выборка, предназначенная для определенной модели спектрального
диапазона, в этом примере — для отдельной спектральной линии неизвестной длины юлны
/
я =
я-
Л^+Я;
/(^-Л).
(6.8)
X равна нулю в середине и ±1/2 на границах интервала.
Сумма чувствительностей двух каналов не зависит от длины волны, в то время
как разность прямо пропорциональна длине волны и изменяется от -/?„ при Х = Х^
до Лц при Я = Я^:
R^(X) = R,(X)-R,(X) = 2Xr,. ^^-^^
Следовательно, сумма сигналов двух датчиков, R^ и R^, задает полный поток
излучения, в то время как средняя длина волны задается как 2Я = (R^ - ^2)7(^1 + ^2)*
Помимо этих двух величин датчики не показывают каких-либо дополнительных
деталей о спектральном распределении.
6.2.4. Цветовое зрение человека
Зрительная система человека реагирует только на электромагнитное излучение,
имеющее длины волн в диапазоне между приблизительно 360 и 800 нм. Она очень
нечувствительна при длинах волн между 360 и приблизительно 410 нм и между
720 и 830 нм. Даже для людей, не имеющих дефектов зрения, имеет место
некоторое изменение в спектральной чувствительности. Таким образом, диапазон
видимости в электромагнитном спектре (свет, рис. 6.6) является отчасти
неопределенным.
Сетчатка глаза, на которую проектируется изображение, содержит два общих
класса рецепторов — палочки и колбочки. Фотопигменты на внешних сегментах
рецепторов поглощают излучение. Поглощенная энергия затем преобразуется в
нейронные электрохимические сигналы, которые передаются через
последовательные нейроны и зрительный нерв к мозгу. Три различных типа
фотопигментов в колбочках делают их чувствительными к различным спектральным
диапазонам и, таким образом, обеспечивают цветовое зрение (рис. 6.4, б). Зрение при
помощи колбочек является активным только при высоких и средних уровнях
освещения и называется фотопинеским зрением. При низких уровнях освещения
зрение осуществляется с помощью палочек. Такой тип зрения называется ско-
топическим зрением.
0,6
0,4
0,2 -
6.2. Радиометрия, фотометрия, спектроскопия и цвет
0,8
0.6
0,4
0,2
—
■ ■
„i /
■и
¥-\
'^
\
\
,__Ч
Л[нм]
/ В
У/
1/
1 G
/
\ '\
\
\
\
R
\А[нм]
400
500
600
700
400 450 500 550 600 650 700
Рис. 6.4. а — относительная спектральная чувствительность «стандартного» глаза
человека согласно установленному МКО в 1980 г. при средних и высоких уровнях
энергетической освещенности (фотопическое зрение, К(Я), сплошная линия) и низких
уровнях энергетической яркости (скотопическое зрение, V\X), пунктирная линия);
данные из [117]; б - относительные чувствительности колбочек глаза человека
согласно Де Марко (DeMarco) и др. [32]
На первый взгляд могло бы показаться невозможным измерение спектральной
чувствительности глаза количественным способом, поскольку мы можем
полагаться только на субъективное представление того, как глаз человека воспринимает
«энергетическую яркость». Однако спектральную чувствительность человеческого глаза
можно измерить, воспользовавшись тем фактом, что он может воспринимать
различия в яркости очень чувствительно. Основываясь на обширных исследованиях со
многими людьми, в 1924 г. 1\/1еждународная комиссия по освеш;ению (1VIK0)
установила стандарт для спектральной чувствительности визуального наблюдателя при
фотопических условиях, который незначительно исправлялся несколько раз позже.
На рис. 6.4 показаны значения 1980 г. Кривая относительной спектральной
чувствительности для скотопического зрения, V\X), имеет подобную форму, но
максимальное значение сдвигается с приблизительно 555 до 510 нм (рис. 6.4, а).
Физиологические измерения могут дать только функцию относительной
спектральной световой эффективности. Следовательно, необходимо установить новую единицу
измерения для световых величин. Этой новой единицей измерения является кандела;
она является одной из семи фундаментальных единиц измерения метрической системы
(Systeme Internationale - SI, ]У[еждународная система единиц, СИ). Кандела задается
как сила света монохроматического источника с частотой 5,4 х 10^^ Гц и силой
излучения 1/683 Вт/ср. Нечетный множитель 1/683 имеет исторические причины, поскольку
кандела была ранее определена независимо от фотометрических величин.
С помощью этого определения силы света и способности глаза распознавать
небольшие изменения в яркости можно измерить силу света любого источника
света путем сравнения его со стандартным источником света. Однако такой
подход связывал бы световые величины с отдельным наблюдателем. Поэтому гораздо
лучше использовать стандартную функцию относительной спектральной
световой эффективности. Тогда любая световая величина может быть вычислена по
соответствующей ей радиометрической величине как:
780 нм
лм
б. =683-^ j Q{X)V{X)&X фотопическое,
380нм
780НМ
а-=1754^ j Q{X)V'{X)dX скотопическое,
(6.10)
Глава 6. Количественная визуализация
где К(Я) - спектральная световая эффективность при дневном зрении (фотопи-
ческое). Список со всеми фотометрическими величинами и их радиометрические
эквиваленты можно найти в Дополнении А (>-R15). Единицей измерения
светового потока, фотометрргческой величины, эквивалентной потоку излучения
(единицы измерения Вт), является люмен (лм).
Исходя из спектральных выборочных методов, изложенных выше, цветовое
зрение человека может рассматриваться как смесь выборки по полосам и выборки
на основе модели. Чувствительности охватывают различные полосы с
максимальными значениями чувствительностей при 445, 535 и 575 нм соответственно, но
они значительно перекрывают друг друга (рис. 6.4, б). В отличие от наших
примеров моделей, три сенсорных канала неравноотстоящие и не могут быть просто
линейно связаны. На самом деле цветочувствительность человеческого глаза
нечетна и все включенные нелинейности сильно усложняют науку о цветовом зрении.
Здесь мы приведем только некоторые основные факты, так как они могут быть
полезны при обработке цветных изображений.
В случае трехцветных датчиков очевидно, что цветовой сигнал охватывает 3-D
пространство. Каждая точка в этом пространстве представляет один цвет. Ясно,
что многие спектральные распределения, известные как метамерные цветовые
стимулы, или просто метамеры, отображаются в одну точку в цветовом
пространстве. Как правило, мы можем записать сигнал s., полученный датчиком со
спектральной характеристикой чувствительности Я(Х), как
5. =|/гДЯЖЯ)(1Я. (6.11)
В случае датчиков с тремя основными цветами получается тройка значений,
часто называемая трехцветный стимул.
Один из самых важных вопросов в колориметрии связан с тем, как создать
систему, представляющую цвета как линейную комбинацию некоторых базисных или
основных цветов. Набор из трех спектральных распределений ф.(Х) представляет
набор из трех основных цветов и приводит к массиву откликов, которые можно
описать с помощью матрицы Р:
РУ=\ЯХЩ{Щ?С. (6.12)
Каждый вектор/>.= (р^., р^., р^) представляет трехцветный стимул основных
цветов в 3-D цветовом пространстве. Очевидно, что могут быть представлены
только цвета, которые являются линейной комбинацией базисных векторов/?.:
s = Rp,+Gp^+Bp^ с 0<R,G,B<h (6.13)
где коэффициенты обозначены R, Ои Ви указывают на три основных цвета -
красный, зеленый и синий. Только в случае, если три базисных вектора р.
составляют ортогональный базис, все цвета могут быть представлены как их
линейная комбинация. Одна возможная и легко реализуемая система трех
основных цветов сформирована с помощью монохроматических цветов - красного,
зеленого и синего, с длинами волн 700, 546,1 и 435,8 нм, согласно стандарту,
принятому МКО в 1931 г. В дальнейшем стала использоваться система основных
цветов, согласованная с нормами Европейского телевещательного союза,
состоящая из красного, зеленого и синего (люминофора), - стандартных цветов
изображений, выводимых на дисплей.
6.2. Радиометрия, фотометрия, спектроскопия и цвет
При данном значительном наложении спектральной чувствительности трех
типов колбочек (рис. 6.4, б), особенно в зеленой части спектра, очевидно, что не
существует основных цветов, которые могут образовать цветовые системы. Цвета,
которые можно представить, лежат внутри параллелепипеда, образованного тремя
базисными векторами основных цветов. Чем больше основные цвета являются
коррелированными друг с другом, т.е. чем меньше угол между двумя из них, тем меньше
цветовое пространство, которое может быть представлено ими. Математически цвета,
которые не могут быть представлены с помощью набора основных цветов, имеют по
меньшей мере один отрицательный коэффициент в уравнении (6.13).
Одним из компонентов в 3-D цветовом пространстве является интенсивность.
Если цветовой вектор умножается на скаляр, изменяется только его интенсивность,
но не цвет. Таким образом, все цвета могли бы быть нормированы по
интенсивности. Эта операция сводит 3-D цветовое пространство к 2-D цветовой плоскости
или диаграмме цветности:
R G ^ В
^ = ' S= г. ^ ^> ^= г. ^ ^^ (6.14)
R^G^B
R + G + B
R + G + B
с r + g + 6 = l. (6.15)
Достаточно использовать только две компоненты — rug. Третья компонента
задается как Ь= \ - г-gB соответствии с уравнением (6.15). Таким образом, все
цвета, которые могут быть представлены тремя основными цветами — R, Ои В,
ограничены треугольником в А^-пространстве, показанном на рис. 6.5, а. Как уже
упоминалось, некоторые цвета не могут быть представлены основными цветами.
Граница всех возможных цветов задается видимыми монохроматическими
цветами от густо-красного до синего. Линия монохроматических цветов образует U-
образную кривую в /^-пространстве. Поскольку все цвета, которые лежат на
прямой линии между двумя цветами, могут быть получены как аддитивная смесь этих
цветов, пространство всех возможных цветов покрывает площадь, заполненную
U-образной спектральной кривой и прямой линией смешивания между ее двумя
конечными точками для синего и красного цветов (пурпурная линия).
Для того чтобы избежать отрицательных значений цветовых координат, часто
выбирается новая система координат с виртуальными основными цветами, т.е.
основными цветами, которые не могут быть представлены какими-либо
физическими цветами. Эта цветовая система известна как цветовая система XYZи
строится таким образом, что включает только кривую монохроматргческих цветов с
только положительными коэффициентами (рис. 6.5, в) и задается следующим линейным
координатным преобразованием:
X
Y
Z
0,490 0,310 0,200
0,177 0,812 0,011
0,000 0,010 0,990
(6.16)
Обратное преобразование из цветовой системы XYZ в цветовую систему RGB
задается матрицей, обратной к матрице в уравнении (6.16).
Цветовые системы, рассматривавшиеся до сих пор, не относятся
непосредственно к человеческому восприятию цвета. По значениям rg или ху мы не можем
непосредственно получить цвета, такие, как зеленый или синий. Естественный
Глава 6. Количественная визуализация
V
0.5
-1
Л>
\
\
\
»500
Чзеленый
Хсиний
\
\
\
\ 570
"Ч жёлтый
Ч
/■•■■■
/
»590
\opai
линия постс1янногс| цвета
1жев
кра(
-1 -0,5 О О,
Рис. 6.5. Диаграмма цветности, изображенная в rg-цветовом пространстве (а);
wv-цветовом пространстве (б); ху-цветовом пространстве (в); затемненные
треугольники указывают цвета, которые могут быть образованы путем аддитивного
цветового смешивания, используя основные цветаЯ,ОиВ
вид описания цветов включает помимо светимости (интенсивности), тип цвета,
такой, как зеленый или синий (цветовой тон), и чистоту цвета (насыщенность). Из
чистого цвета мы можем получить любую степень насыщенности путем
смешивания его с белым.
Цветовой тон и насыщенность можно вьщелить по диаграммам цветности
путем простых координатных преобразований. Опорной точкой является точка
белого в середине диаграммы цветности (рис. 6.5, б). Если мы нарисуем линию из
этой точки к чистому (монохроматическому) цвету, то она образует линию
смешивания чистого цвета с белым и является, таким образом, линией постоянного
цветового тона. Насыщенность увеличивается линейно от точки белого до чистого
цвета. Точка белого задана на А^-диаграмме цветности как w = [1/3, 1/3]^.
Цветовая система, которая имеет центр в точке белого, называется системой
цветовых контрастов. По системе цветовых контрастов мы можем сделать вывод о
цветовой системе тон—насыщенность (цветовой тон, насыщенность и плотность;
HIS), просто используя полярные системы координат. Тогда насыщенность
пропорциональна радиусу, а цветовой тон - углу (рис. 6.5, б).
До сих пор наука о цветах является легкой. Все действительные сложности
возникают из-за необходимости приспосабливать цветовую систему оптимальным
образом для устройств воспроизведения, печати, передачи с помощью телевизи-
6.3. Волны и частицы
онных сигналов или для корректировки нечетного цветового разрешения
зрительной системы человека, которое очевидно на диаграммах цветности простых
цветовых пространств (рис. 6.5). Эти необходимости привели к сбивающему с толку
разнообразию различных цветовых систем.
6.3. Волны и частицы
Можно выделить три главных типа излучения: электромагнитное излучение,
корпускулярное излучение с атомными и субатомными частицами и акустические
волны. Хотя на первый взгляд эти три формы излучения могут показаться
совершенно разными, они обладают многими общими свойствами, что касается
формирования изображений. Во-первых, изображения объектов могут быть
получены с помощью любого типа излучения, испускаемого ими и накапливаемого
подходящей системой формирования изображений. Во-вторых, все три формы
излучения проявляют волновой характер, врслючая корпускулярное излучение. Длина
волны Я равна расстоянию одного цикла колебаний в направлении распространения.
Длина волны также определяет предельное разрешение системы формирования
изображений. Согласно эмпирическому правилу, только структуры большие, чем длина
волны излучения, могут быть разрешены.
Очевидно, что при условии использования различных типов излучения могут
быть получены изображения совершенно разных свойств объектов.
Следовательно, для правильной установки системы формирования изображений необходимо
знать некоторые свойства различных форм излучения. Это и является целью
данного раздела.
6.3.1. Электромагнитные волны
Электромагнитное излучение состоит из переменных электрических и магнитных
полей. В электромагнитной волне эти поля направлены перпендикулярно друг другу
и к направлению распространения. Они классифицируются по частоте v и по длине
волны Я. В свободном пространстве все электромагнитные волны распространяются
со скоростью света, с ~ 3 х 10^ м • с"^ Скорость распространения устанавливает
соотношение между длиной волны Я и частотой v электромагнитной волны как
\Ху = с.\ (6.17)
Частота измеряется числом периодов в секунду (Гц или с'О, а длина волны в
метрах (м).
Как наглядно показано на рис. 6.6, электромагнитные волны покрывают
огромный диапазон частот и длин волн в 24 порядка. Только крошечная доля,
приблизительно 400—700 нм, около одной октавы, входит в диапазон видимости, часть,
к которой чувствителен человеческий глаз. Классификация, обычно
используемая для электромагнитных волн (рис. 6.6), является отчасти искусственной и
обусловлена главным образом историческими причинами в соответствии со способом,
которым эти волны формируются или распознаются.
В сущности, электрические и магнитные поля электромагнитной волны
взаимодействуют с электрическими зарядами, электрическими токами, электрическими
полями и магнитными полями в среде. Однако основная природа электромагнитных
волн остается той же, только распространение волны замедляется, и волна затухает.
176 Глава 6. Количественная визуализация
Длина
Частота волны
[м]
[Гц]
1024
1021
101
1015
101
1 ГГц 109
1 МГц 106 I
103
102
10-
10-
-121
10-^
10"
10-
ю^
10°
Энергия
фотона
[эВ]
1фм 10^
1пм 10^
1А
1нм lo^
1мкм 1
1мм 10-^'
1 t Чм 10"
1км Ю"^-
10-
Ткосмические
|лучи
1ГэВ <-
. 0,94 ГэВ, энергия покоя протона, нейтрона
Гамма-лучи
1МэВ
\ Жесткие
Рентгеновские
лучи
' Мягкие
Ультрафиолетовая
■ ^ область (УФ)
Гимая (свет)
ИК-
спектро-
Инфракрасная скопия
• область (ИК) <
8 МэВ, энергия связи/нуклон
1 МэВее^, образование пар
0,5 МэВ, энергия покоя электрона
комптоновское рассеяние
Диаметр атомов
постоянные кристаллических решеток
твердых тел
Фотоэлектрический эффект, электронные
переходы внутренних электронов в
электронные переходы внешних электронов
УФ-спектроскопия/спектроскопия в
видимой области
Молекулярные колебания, тепловое
излучение при температурах окружающей сре-
■ ды (300 К)
4 4
Полоса
Микроволны
Радиоволны
11ЧВЧ
ЮСВЧ
9 УВЧ
8 0ВЧ
7ВЧ
6 04
5НЧ
4 0НЧ
ЗТЧ
2ЧНЧ
3 к, космическое фоновое излучение
молекулярное врашение
Электрон-спиновый резонанс
Ядерный магнитный резонанс
— 20 кГц
Звуковые частоты
— 50 Гц
Рис. 6.6. Классификация электромагнитного спектра с помощью шкал длины
волны, частоты и энергии фотона
Самый простой случай возникает, когда среда изотропна и реагирует на
возмущение электрических и магнитных полей, вызванное электромагнитной
волной, линейным образом. Тогда влияние среды выражается через комплексный
показатель преломления, т] = л + i;^. Действительная часть, п, или показатель
преломления обыкновенной волны, равен отношению скорости света, с, к
скорости распространения и в среде, п = с/и. Мнимая компонента, т], -х, относится к
затуханию амплитуды волны.
6.3. Волны и частицы
Как правило, показатель преломления зависит от частоты или длины
электромагнитной волны. Следовательно, скорость распространения волны больше не
является независимой от длины волны. Этот эффект называется дисперсией, а
волна называется дисперсионной волной.
Показатель преломления и коэффициент затухания являются двумя главными
параметрами, характеризующими оптические свойства среды. В контексте
формирования изображений они могут быть использованы для определения
химического состава или любого другого физического параметра, влияющего на него.
Электромагнитные волны являются, как правило, линейным явлением. Это
означает, что мы можем разложить любую волновую картину на базисные, такие,
как плоские гармонические волны. Или, обратно, мы можем наложить любые две
или больше электромагнитные волны и не сомневаться в том, что это
по-прежнему электромагнитные волны.
Этот принцип суперпозиции нарушается только для волн с очень высокими
напряженностями поля. В этом случае вещество больше не действует на
электромагнитную волну линейным образом, а порождает нелинейные оптические явления.
Эти явления стали очевидными только совсем недавно с появлением очень
интенсивных световых источников, таких, как лазер. Известным нелинейным явлением
является удвоение частоты света. Этот эффект теперь широко используется в
лазерах для производства выходных лучей двойной частоты (половина длины волны).
С точки зрения количественной визуализации эти нелинейные эффекты
открывают новый восхитительный мир для визуализации специфических явлений и свойств
материалов.
6.3.2. Поляризация
Принцип суперпозиции можно использовать для объяснения поляризации
электромагнитных волн. Поляризация определяется ориентацией вектора
электрического поля Е. Если этот вектор ограничен плоскостью, как в предыдущих примерах
плоской гармонической волны, то излучение называется плоскополяризованным или
линейно поляризованным. В общем случае электромагнитные волны не
поляризованы. Для обсуждения общего случая рассмотрим две волны, распространяющиеся
в направлении z, одна с компонентой электрического поля в направлении х, а
другая с компонентой электрического поля в направлении у. Амплитуды Е^ и Е^
являются константами, а ф есть разность фаз между двумя волнами. Если 0 = О, то
вектор электромагнитного поля ограничен плоскостью. Угол ф этой плоскости
относительно оси х определяется как
0 = arctan--f. (6.18)
^1
Еще один частный случай возникает, если разность фаз 0=± 90° и ^j = Е^, тогда
волна называется циркулярно поляризованной. В этом случае вектор электрического
поля вращается вокруг направления распространения, совершая один оборот за
период волны. Общий случай, где и разность фаз не равна ± 90°, и амплитуды
обеих компонент не равны, называется эллиптически поляризованной. В этом случае
вектор Е вращается по эллипсу, т.е. с изменяющейся амплитудой, вокруг
направления распространения. Важно обратить внимание на то, что любой тип
поляризации может быть составлен из лучей с правой круговой поляризацией и левой
Глава 6. Количественная визуализация
круговой поляризацией. Лучи с левой круговой поляризацией и правой круговой
поляризацией с одной и той же амплитудой, к примеру, при комбинировании
образуют луч с линейной поляризацией. Направление плоскости поляризации
зависит от фазового сдвига между циркулярно поляризованными лучами.
6.3.3. Когерентность
Важным свойством некоторых электромагнитных волн является их когерентность.
Говорят, что два луча излучения являются когерентными, если существует
систематическая зависимость между фазами векторов электромагнитного поля. Если
эта зависимость является случайной, то излучение является некогерентным.
Очевидно, что некогерентное излучение накладывается иным образом, чем
когерентное излучение. В случае когерентного излучения возможен деструктивный вывод,
в том смысле, что волны гасят друг друга в некоторых местах, где фазовый сдвиг
равен 180°.
Обычные источники света являются некогерентными. Они испускают не одну
непрерывную плоскую волну, а скорее волновой пакет с короткими длинами волн
и без определенной фазовой зависимости. Противоположно, лазер является
когерентным световым источником.
6.3.4. Фотоны
Электромагнитное излучение обладает свойствами частиц в дополнение к
свойствам, характеризуемым волновым движением. Электромагнитная энергия
квантуется, так как для заданной частоты ее энергия может быть только числом,
кратным величине hv — кванту действия, в которой h есть постоянная Планка:
Ё=Ы (6.19)
Квант электромагнитной энергии называется фотоном.
В любом взаимодействии излучения с веществом, является ли это
поглощением излучения или испусканием излучения, энергия может изменяться только в
числах, кратных этим квантам. Энергия фотона часто определяется в единицах
энергии электрон-вольтах (эВ). Это кинетическая энергия, которую мог бы
приобрести электрон, ускоряясь при прохождении через разность потенциалов в один
вольт. Фотон желтого цвета, к примеру, имеет энергию приблизительно 2 эВ. Рис.
6.6 включает шкалу энергии фотона в эВ. Чем выше частота электромагнитного
излучения, тем более очевидной становится его корпускулярная природа,
поскольку его кванты энергии становятся больше. Энергия фотона может быть больше
энергии, связанной с массой покоя элементарной частицы. В этом случае
существует возможность самопроизвольного преобразования электромагнитной
энергии в массу в форме пары частиц. Хотя фотон не имеет массы покоя, с ним
связывается понятие момента, поскольку он движется со скоростью света и имеет
конечную энергию. Момент, р, задается как
;? = Л/Я. (6.20)
Квантование энергии электромагнитных волн важно для формирования
изображений, поскольку чувствительный детектор излучения может измерить
поглощение отдельного фотона. Такие детекторы называются счетчиками фотонов.
Таким образом, наименьшее количество энергии, которое может быть определено,
6.3. Волны и частицы
равно hv. Случайная природа поступления фотонов на детектор порождает
неопределенность («шум») в измерении энергии излучения. Число фотонов,
подсчитанное в единицу времени, является случайной величиной с распределением
Пуассона, рассмотренное в разделе 3.4.1. Если #равно среднему числу подсчитываемых
фотонов в заданном интервале времени, то распределение Пуассона имеет
среднеквадратичное отклонение a». Следовательно, измерение потока
излучения со среднеквадратичным отклонением в 1% требует подсчета 10 000 фотонов.
6.3.5. Излучение частицы
В отличие от электромагнитных волн, в большинстве случаев корпускулярное
излучение движется со скоростью меньшей, чем скорость света, поскольку частицы
имеют ненулевую массу покоя. Что касается формирования изображений,
наиболее важный тип корпускулярного излучения состоит из электронов, он также
известен как бета-излучение, испускаемое радиоактивными элементами. Другие типы
важных корпускулярных излучений состоят из нейтронов, положительно
заряженных ядер атома водорода или протонов, ядер атома гелия или альфа-частиц,
которые имеют двойной положительный заряд.
Корпускулярное излучение также проявляет волновой характер. Длина волны
А и частота v непосредственно связаны с энергией и моментом частицы:
V = E/h — условие частот Бора,
^ UI т. " (6.21)
A^hl р - соотношение для длины волны де-Броиля.
Эти соотношения такие же, как и для фотона (уравнения (6.19) и (6.20)). Их
значимость для целей формирования изображений заключается в том, что
частицы, как правило, имеют излучение с гораздо более короткими длинами волн.
Электроны, к примеру, с энергией 20 кэВ имеют длину волны приблизительно 10~'^ м,
или 10 пм, - меньшую, чем диаметр атомов (рис. 6.6), и приблизительно в 50 000
раз меньшую, чем длина волны света. Поскольку разрешаюш;ая способность
любой системы формирования изображений, за исключением систем поля в
ближней зоне, ограничена размерами порядка длины волны излучения (раздел 7.6.3),
системы формирования изображений, основанные на электронах, такие, кгк
электронный микроскоп, имеют гораздо более высокую потенциальную разрешающую
способность, чем любой световой микроскоп.
6.3.6. Акустические волны
В отличие от электромагнитных волн, акустическим или упругим волнам
необходим носитель. Акустические волны распространяют упругие деформации. Так
называемые продольные акустические волны формируются при изотропном давлении,
вызывающем равномерное сжатие и, таким образом, деформацию в направлении
распространения. Локальная плотность р, локальное давление/? и локальная
скорость i; описываются одним и тем же волновым уравнением
-bt^^""^'^ З^Г-Ар при и = ^—, (6.22)
где и — скорость звука; р^ — статическая плотность; /J^^ — адиабатическая
сжимаемость. Адиабатическая сжимаемость задается как относительное изменение объе-
Глава 6. Количественная визуализация
ма, вызванное равномерным давлением (сила/единица площади) при условии, что
нет теплообмена:
1 &V
Таким образом, скорость звука связана универсальным образом с упругими
свойствами среды. Чем меньше плотность и сжимаемость, тем выше скорость
звука. Акустические волны распространяются гораздо медленнее, чем
электромагнитные волны. Их скорость в воздухе, воде и железе при 20° равна 344, 1485 и
5100 м/с соответственно. Слышимая акустическая волна с частотой 3 кГц имеет
длину волны в воздухе приблизительно 10 см. Однако акустические волны с
гораздо более высокой частотой, известные как ультразвук, могут иметь длины волн в
диапазоне микрометра. При использовании подходящих акустических линз
возможна ультразвуковая микроскопия.
Если звук или ультразвук используются для формирования изображений, важно
указать, что распространение звука является гораздо более сложным в твердых
телах. Во-первых, твердые тела, как правило, не изотропны, а упругость твердого
тела не может быть описана скалярной сжимаемостью. В самом деле, требуется
тензор для описания свойств упругости. Во-вторых, поперечные силы, в отличие
от сил давления, порождают также поперечные акустические волны, где
деформация перпендикулярна направлению распространения, как и в случае с
электромагнитными волнами. Таким образом, звуковые волны различных мод
распространяются в твердом теле с различными скоростями.
Вопреки всем этим сложностям, скорость звука зависит только от плотности и
упругих свойств среды. Следовательно, акустические волны не проявляют
дисперсию (в рамках механики сплошной среды, т.е. для длин волн гораздо больших, чем
расстояния между атомами). Поэтому волны разных частот распространяются с
одной и той же скоростью. Это важный базовый факт для методов формирования
акустических изображений.
6.4. Взаимодействия излучения с веществом
Взаимодействие излучения с веществом является основой для любого метода
формирования изображений. По существу, можно вьщелить два класса взаимодействий
излучения с веществом. Первый класс связан с неоднородностями оптических
свойств на поверхности раздела двух различных сред (рис. 6.7, а). Второй класс
связан с рассмотрением объема и зависит от оптических свойств вещества
(рис. 6.7, б). В этом разделе мы дадим краткий обзор наиболее важных явлений.
Целью является — дать читателю обзор многих возможных способов измерения
свойств материалов с помощью методов формирования изображений.
6.4.1. Тепловыделение
Испускание электромагнитного излучения имеет место при любой температуре и
является, таким образом, повсеместной формой взаимодействия между веществом
и электромагнитным излучением.
Причиной самопроизвольного испускания электромагнитного излучения
является тепловое движение молекул, которое увеличивается с ростом температуры.
6.4. Взаимодействия излучения с веществом 181
Поверхностное Вынужденное
излучение излучение
Отражение
!ЛОмление
МА,0,Д)
Рассеяние
Вынужденное
излучение
Поглощение ^п\ Преломление,
E(\i) ЦЛе,0е,Фе)
Вращение
плоскости
поляризации
(оптическая активность)
^ а(Л)
Щ = -a(A)ds
* Vnortou
Удвоение,
утроение
частоты
Градиент
показателя
преломления
Нелинейный эффект,
двухфотонные процессы
Рис. 6.7. Основные возможности взаимодействия излучения и вещества: а — на
поверхности объекта, т.е. в местах неоднородности оптических свойств; б -
отнесенные к объему
В процессе испускания излучения тепловая энергия преобразуется в
электромагнитное излучение, и вещество охлаждается в соответствии с универсальным
законом сохранения энергии.
Существует верхний уровень тепловыделения. Согласно законам
термодинамики, доля излучения при определенной волне, которая поглощается,
должна быть повторно испущена: таким образом, существует верхний предел
испускания, когда коэффициент поглощения равен единице. Совершенный
поглотитель - и, таким образом, максимальный излучатель — называется
абсолютно черным телом.
Корректное теоретическое описание излучения абсолютно черного тела План-
ком в 1900 г. потребовало предположения, что излучение испускается и
поглощается дискретными квантами энергии £" = Av. Спектральная энергетическая
яркость излучения абсолютно черного тела с абсолютной температурой равна
(рис. 6.8)
к(УЛ =
2hv'
1
ехр
' hv^
-1
^ДЯ,г) =
Ihc^
1
ехр
' he ^
-1
(6.24)
182 Глава 6. Количественная визуализация
1000
100
10
1
0,1
0,01
0,001
0,0001
0,00001
t
60
и
/
р<
1
00
/
/
/
/
1
с
^
зооо}
}е
2<
т
и
i
fj°\-
fl \
100
И ик
1
/
/
\
о\^
\:
50С
к
м
II
Rt
см^мкм ср
J0
г^
f\
\
i
х^
мкм]
0,5
1
10
Рис. 6.8. Спектральная плотность энергетической яркости L^ абсолютно черного тела
при различных значениях абсолютной температуры в К. Тонкая линия пересекает
кривые излучения при длинах волн максимального излучения
при
(6.25)
h = 6,6262x10"^"* Джс постоянная Планка,
kg =1,3806X10"^^ Дж• К'^ постоянная Больцмана,
с = 2,9979X10^ м • с-^ и скорость света в вакууме.
Излучение абсолютно черного тела имеет важную особенность, состоящую в
том, что испускаемое излучение не зависит от угла обзора. Такой излучатель
называется излучателем Ламберта, Поэтому спектральная излучательная способность
(постоянная энергетическая яркость, интегрированная по полусфере) в я раз выше
энергетической яркости:
2nhc^ 1
МДЯ,Г) = -
ехр
he
kJX
(6.26)
-1
Полная излучательная способность абсолютно черного тела,
проинтегрированная по всем длинам волн, пропорциональна Т "*, согласно закону Стефана-
Больцмана:
i 15 с h
(6.27)
где G ~ 5,67 • 10"^ Вт • м~^* К"^ есть постоянная Стефана—Больцмана, Длина волны
максимальной излучательной способности абсолютно черного тела определяется
законом Вина:
^_.2.898.10-К.м^ («g)
6.4. Взаимодействия излучения с веществом
Максимальная светимость при комнатной температуре (300 К) находится в
инфракрасной области спектра (около 10 мкм), а при 3000 К (лампа накаливания)
в ближней инфракрасной области спектра (около 1 мкм).
Реальные объекты испускают меньше излучения, чем абсолютно черное
тело. Отношение излучения реального объекта к излучению абсолютно
черного объекта называется (удельным) коэффициентом излучения т и зависит от
длины волны.
Излучение в инфракрасной области спектра и в области микроволн можно
использовать для получения изображений температурного распределения объектов.
Это применение формирования изображений известно как термография.
Термическое формирование изображений усложняется тем, что действительные
объекты не являются совершенными черными телами. Поэтому они частично отражают
излучение от окружающей среды. Если объект имеет коэффициент излучения 6,
то доля 1 - 6 полученного излучения возникает из окружающей среды, искажая
результаты измерения температуры. При упрощающем предположении, что
окружающая среда имеет постоянную температуру Г, можно оценить влияние
отраженного излучения на измерение температуры. Полная энергетическая яркость,
испускаемая объектом, Е, равна
^ = бС77Ч(1-€)(тГ;. (6.29)
Можно интерпретировать эту энергетическую яркость, как возникшую от
абсолютно черного тела с наблюдаемой температурой Г':
аГ' =€(7ГЧ(1-б)с77;'. (6.30)
Преобразование относительно F приводит к
Г^Т
^+(1-0:^
4^/4
(6.31)
в пределе малых температурных разностей (АГ= Г - Т <^ Т) уравнение (6.31)
сводится к
Г-бГ + (1-€)Г^ или Г-Г«(1-б)АГ. (6.32)
Из этого упрощенного уравнения мы можем сделать заключение, что 1%
отклонения т от единицы приводит к температурной погрешности 0,01 К при
разности между температурой объекта и температурой окружающей среды в 1 К. Даже
для почти совершенного черного тела, такого, как поверхность воды со средним
коэффициентом излучения приблизительно 0,97, это соотношение приводит к
значительным ошибкам в измерениях абсолютной температуры. Видимая
температура ясного неба может легко быть на 80 К холоднее, чем температура
поверхности воды при 300 К, приводя к -0,03 • 80 К = -2,4 К отклонению в измерении
абсолютной температуры поверхности воды.
Это отклонение может, согласно уравнениям (6.31) и (6.32), быть
скорректировано, если известна средняя температура окружающей среды. Также
искажаются измерения относительной температуры, хотя в менее значимой степени.
Допуская постоянную температуру окружающей среды в пределе (Г - Г) <$^ Г, мы
можем сделать заключение из уравнения (6.32), что
ЭГ-бЭГ при (Г^-Г)«Г, (6.33)
которое означает, что измеряемые разности температур в 6 раз меньше, чем в
реальности.
Глава 6. Количественная визуализация
1.2
1
0,8
0,6
0,4
0.2
О
мВт
^ см^мкм ср
) / ,
4^\
зо\\
"1Г\^
^^^^^
Л[мкм]
10
20
б
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
О
'
X м Вт
^ см ^ мкм ср
.^<^
/40
/ ■//зо
^ ^^20
^^^^0
^^^^^^--^^
Л[мкм]
3,5
4.5
Рис. 6.9. Энергетическая яркость абсолютно черного тела при температурах
окружающей среды в диапазонах длин волн: а — 0-20 мкм; б — 3—5 мкм
Другие поправки должны быть использованы, если излучение значительно
поглощается на пути от объекта до получателя. Если расстояние между объектом и
камерой большое, как в случае формирования инфракрасных изображений
поверхности Земли из космоса или воздуха, то важно выбрать диапазон длин волн с
минимальным поглощением. Два самых важных окна прозрачности атмосферы
есть вблизи 3—5 мкм (с резким пиком поглощения приблизительно 4,15 мкм по
причине присутствия СО2) и вблизи 8—12 мкм.
На рис. 6.9 показана энергетическая яркость абсолютно черного тела при
температуре окружающей среды между О и 40** С в диапазонах длин волн 0—20 и 3—5 мкм.
Хотя энергетическая яркость имеет максимум приблизительно 10 мкм и
приблизительно в 20 раз выше, чем при 4 мкм, относительное изменение энергетической
яркости с ростом температуры гораздо больше при 4 мкм, чем при 10 мкм.
Этот эффект можно увидеть более детально, исследуя энергетическую яркость
относительно энергетической яркости при фиксированной температуре (рис. 6.10, а) и
относительное изменение энергетической яркости в (dL/dT)/L в процентах (рис. 6.10, ^.
а б
10
0,8
0.4
Le/Le(40°
14^^^
i^^^^^^^i
С)
Температура [С°]
1 dLi^/dT
.И^1%]
Ц-.^,..1
н ^
1
1 —
Темпер
1 ]
_ 3
4
5
!•
1
1
^■^^ J-
^^Щ
^ J
'__
атура [С ]
о 10 20 30
Рис. 6.10. Относительная энергетическая яркость (в фотонных единицах
измерения) в температурном интервале 0-40°С и при длинах волн в мкм согласно
указанному: а — по отношению к энергетической яркости при 40°С; б - относительное
изменение в процентах за один градус
6.4. Взаимодействия излучения с веществом
В то время как энергетическая яркость при 20°С изменяется только приблизительно
на 1,7%/К при длине волны 10 мкм, она изменяется приблизительно на 4%/К при
длине волны 4 мкм. Эта более высокая относительная чувствительность позволяет
использовать диапазон длин волн 3—5 мкм для измерений малых температурных
разностей, хотя абсолютная энергетическая яркость гораздо ниже.
Некоторые изображения, иллюстрирующие применение термографии,
представлены на рис. 6.11.
6.4.2. Преломление, отражение и пропускание
На границе раздела двух оптических сред, согласно закону Снеллиуса, проходящий
луч преломляется, т.е. меняет направление (рис. 6.12):
Рис. 6.11. Некоторые примеры термофафии: а — здание Университета Гейдельберга
(Heidelberg University), полученное в холодный зимний день; б — сцена улицы; в —
взгляд внутрь ПС; г — человек с зажигалкой
86 Глава 6. Количественная визуализация
Падающий;
.луч
Нормаль
к поверхности
•У
п\ Преломленный
^2 \ луч
Отраженный
П2>п
0 Р Отраженный
П1<П2
Прошедший
Рис. 6.12. а — луч изменяет направление на поверхности раздела двух оптических
сред с разными показателями преломления; б - параллельно поляризованный свет
полностью проходит и не отражается, если угол между отраженным и прошедшим
лучами составляет 90° С. Это условие имеет место при переходах как из оптически
более тонкой среды, так и оптически более толстой среды
^'^. (6.34)
Sin02 W,
где 0J и ©2 есть углы падения и преломления. Преломление является основой для
прозрачных оптических элементов (линз), которые могут формировать
изображение объекта. Это означает, что все лучи, испускаемые от точки объекта и
проходящие через оптический элемент, сходятся в другой точке на плоскости изображения.
Зеркальная поверхность ведет себя как зеркало. Свет, излученный в
направлении (в., (р), отражается обратно в направлении (в., срл к). Это означает, что
угол отражения равен углу падения и что падающий и отраженный лучи и
нормаль к поверхности лежат в одной плоскости. Отношение отраженного потока
излучения к падающему на поверхность потоку называется коэффициентом
отражения р.
Зеркальное отражение имеет место, когда все параллельные падающие лучи
отражаются как параллельные лучи. Поверхность необязательно должна быть
абсолютно гладкой для зеркального отражения благодаря волновой природе
электромагнитного излучения. Достаточно, чтобы остаточные неровности поверхности
являлись значительно меньше, чем длина волны. Коэффициент отражения р
зависит от угла падения, показателей преломления, п^и п^, двух сред,
пересекающихся на границе раздела, и состояния поляризации излучения. Свет называется
параллельно или перпендикулярно поляризованным, если вектор электрического
поля параллелен или перпендикулярен плоскости падения, т.е. плоскости,
содержащей направления, отражения и нормали к поверхности.
Уравнения Френеля определяют коэффициент отражения для параллельно
поляризованного света:
" tan'(6),+6>2)'
для перпендикулярно поляризованного света
(6.35)
6.4. Взаимодействия излучения с веществом 187
Р I
I ±
60
80е,п
1
0.8
0,6
0,4
0.2
О
Р
20
30 0, П40
Рис. 6.13. Коэффициенты отражения на границе раздела для параллельно (||) и
перпендикулярно (±) поляризованного света и неполяризованного света, падающего из:
а — воздуха (п^ = 1,00) на стекло ВК7 {п^= 1,517); б — стекла ВК7 в воздух
и для неполяризованного света (рис. 6.13)
(6.36)
(6.37)
соответственно, где 0, и 0^ - Углы падающих и преломленных лучей, связанных
законом Снеллиуса.
При нормальном падении (0, = 0) коэффициент отражения не зависит от
состояния поляризации:
Р =
{n,-n,f {n-\f
{n,+n,f {n + \f
при П = Щ1П2
(6.38)
Как наглядно представлено на рис. 6.13, параллельно поляризованный свет не
отражается вообще при некоторой величине угла — угла поляризации или угла Брю-
стера в^. Это условие имеет место, когда преломленные и отраженные лучи
перпендикулярны друг другу (см. рис. 6.12, б):
Когда луч входит в среду с меньшим показателем преломления, существует
критический угол, 0,:
Of^ =arcsin-
в^ = arcsin — при «J < «2
(6.40)
ниже которого весь свет отражается и не входит в оптически более тонкую среду.
Это явление называется полное отражение.
6.4.3. Шероховатые поверхности
Большинство природных и искусственных объектов не отражают свет прямо, а
проявляют коэффициент диффузного отражения, поскольку микроскопическая
неровность поверхности вызывает отражение в различных направлениях в
зависимости от распределения наклона отражающих граней. Существует большое
количество вариантов распределения этих лучей по возникающему телесному углу.
Глава 6. Количественная визуализация
Некоторые материалы создают сильные эффекты рассеяния в прямом
направлении, в то время как другие рассеивают почти равномерно во всех направлениях.
Часть материалов демонстрируют тип смешанной отражательной способности,
которая является частично зеркальной из-за отражения на гладкой поверхности
и частично диффузной, вызванной отражением тела. В этом случае свет
проникает частично в объект, где он рассеивается в местах оптических неоднороднос-
тей. Часть этого рассеянного света снова покидает объект, вызывая диффузное
отражение. Для получения изображений объектов, которые не испускают сами
излучения, но пассивно отражают падающий свет, существенно знать, как свет
отражается.
Как правило, соотношение между падающей и испускаемой энергетической
яркостью может быть выражено как отношение энергетической яркости,
испускаемой при полярном угле в^ и азимутальном угле ф^, и энергетической освещеьшости,
полученной при угле падения в.. Это отношение называется функцией
распределения двунаправленного отражения (ФРДО) или распределением коэффициента
отражения, поскольку оно главным образом зависит от углов как падающей, так и
возбуждающей энергетической яркости:
Для совершенного зеркала (зеркальное отражение) / равна нулю повсюду,
кроме ft= 0 иф = ж-\- ф., следовательно,
Ав,А)=т-ют-^-Фд- (6-42)
Другим предельным случаем является совершенный рассеиватель,
отражающий падающее излучение равномерно по всем направлениям независимо от угла
падения. Такая поверхность известна как излучатель Ламберта или отражатель
Ламберта. Энергетическая яркость такой поверхности не зависит от направления
визирования:
L^=-E, или т,ФЛА) = -- (6.43)
К к
6.4.4. Поглощающая способность и пропускаемость
Излучение, распространяющееся в веществе, более или менее поглощается и
преобразуется в различные формы энергии, в особенности в тепло. Поглощающая
способность пропорциональна силе излучения в тонком слое dx. Следовательно,
^^ = -а(Я,х)/. (6.44)
оос
Коэффициент поглощения а является свойством среды и зависит от длины
волны излучения. Он является обратной длиной с единицами измерения м"^
Проинтегрировав уравнение (6.44), можно вычислить затухание излучения на
расстоянии от О до х.
( X \
/(х) = /(0)ехр
V о
или, если среда однородна (т.е. а не зависит от положения х'), то
-\a{X,x)dx
(6.45)
6.4. Взаимодействия излучения с веществом
1{х) = 1(0) ехр(-а (Я)х). (6.46)
Экспоненциальное затухание излучения в однородной среде, выраженное
уравнением (6.46), часто рассматривается как закон Ламберта—Бера или закон Буге.
Пройдя расстояние \/а, излучение ослабляется до \/е от его исходного значения.
Интефал по траектории от коэффициента поглощения
T{x^,x^) = ja{x)dx' (6 47)
^1
приводит к безразмерной величине, которая известна как оптическая толщина или
оптическая глубина. Оптическая глубина является логарифмическим выражением
затухания излучения и означает, что вдоль пути от точки х^ до точки х^ излучение
затухает до е~\
Если излучение распространяется в составной среде, то часто только одно
химическое вещество, по крайней мере при определенных длинах волн,
ответственно за затухание излучения. Следовательно, имеет смысл связать коэффициент
поглощения с концентрацией этого вещества:
г п Г 1 1
а=£с, [£] = \ -и (6.48)
L моль • м J
где с — концентрация в моль/л, £ известно кгк молярный коэффициент поглощения.
Простое линейное соотношение уравнение (6.48) выполняется для очень
широкого диапазона интенсивности излучения, но нарушается при очень высокой
интенсивности, например, поглощение очень интенсивных лазерных лучей. С этой
точки зрения вводится область нелинейных оптических явлений.
Поскольку коэффициент поглощения является отличительным оптическим
признаком химических веществ, он может использоваться в прикладных задачах
формирования изображений для определения химических веществ и измерения
их концентраций.
И наконец термин пропускаемость означает долю излучения, которая остается
после того, как излучение прошло некоторый путь в среде. Часто пропускаемость
и коэффициент пропускания вносят путаницу. В отличие от пропускаемости,
термин коэффициент пропускания относится к отдельной поверхности. Он означает
долю излучения, которая не отражается, а входит в среду.
6.4.5. Рассеяние
Ослабление излучения при рассеянии можно описать с помощью тех же понятий,
как и в случае потери излучения при поглощении. Коэффициент рассеяния
определяется как
ра)-\^. <б.49,
/ ох
Это обратная длина с единицей измерения м"^ Если в среде излучение затухает
как при поглощении, так и при рассеянии, то можно объединить эти два объекта в
коэффициент затухания к* (Я):
^(Я) = а(Я) + /?(Я). (6.50)
Хотя кажется, что рассеяние подобно поглощению, это гораздо более сложное
явление. Вышеуказанную формулу можно использовать, только если излучение от
Глава 6. Количественная визуализация
отдельных случаев рассеяния складывается некогерентно в некоторой точке,
удаленной от частиц. Сложность явления рассеяния связана с тем, что рассеянное
излучение (без дополнительного поглощения) никогда не теряется. Рассеянный свет
может быть рассеян более чем один раз. Следовательно, доля его может заново
войти в исходный луч. Вероятность того, что энергетическая яркость будет рассеяна на
некоторой длине пути более чем один раз, связана непосредственно с полным
затуханием при рассеянии вдоль пути луча или оптической глубиной т. Если т меньше
чем 0,1, то менее чем 10% энергетической яркости рассеивается.
Общее количество рассеянного света и анализ углового распределения
связаны с оптическими свойствами рассеивающей среды. Следовательно, рассеяние
вызывается оптической неоднородностью среды. В дальнейшем рассуждении
будем предполагать, что малые сферические частицы с радиусом г и показателем
преломления п внесены в однородную оптическую среду.
Рассеяние частицей описывается поперечным сечением. Оно определяется,
исходя из отношения потока, удаленного частицей, к потоку, падающему на частицу:
С7^^=ф^фпг'. (6.51)
Поперечное сечение имеет единицы измерения площади. Оно может
рассматриваться как эффективная площадь рассеивающей частицы, которая полностью
рассеивает падающий поток излучения. Следовательно, коэффициент
эффективности при рассеивании Q^ определяется как поперечное сечение, отнесенное к
геометрическому поперечному сечению рассеивающей частицы:
Q,=C7j(nr'y (6.52)
Угловое распределение рассеянного излучения задается дифференциальным
поперечным сечением dcr/dQ, т.е. плотностью потока, рассеянного в единичном
телесном угле. Полное поперечное сечение задается как интеграл по сфере от
дифференциального поперечного сеченрш:
'^^4ia (6.53)
-.=я
dQ
Соотношение между коэффициентом рассеяния j3 из уравнения (6.49) и
рассеивающим поперечным сечением можно получить следующим образом. Пусть р
есть число частиц в единице объема. Следовательно, полное эффективное
рассеивающее поперечное сечение охватывает площадь р • а. Эта площадь задает долю
площади, которая удаляет падающий поток и, таким образом, равна
коэффициенту рассеяния Д*
р = рс7^ (6.54)
На рассеяние малыми частицами наиболее существенно влияет отношение
размера частицы к длине волны излучения, выраженное в безразмерном размере
частицы q = 2;гг/Я= 2кгк. Если ^ <^ 1 (рэлеевское рассеяние), то рассеяние является очень
слабым и пропорционально Я"^:
/284
J кг =-д
п'^1
(6.55)
|«'+2|
Для q^ I рассеяние можно описать с помощью геометрической оптики. Если
частица полностью отражает падающее излучение, то рассеивающее поперечное
сечение равно геометрическому поперечному сечению (<7 / я г^ = 1), а дифферен-
6.4. Взаимодействия излучения с веществом
циальное поперечное сечение является постоянной величиной (изотропное
рассеяние, dcr/dQ = г^/2).
Рассеяние частиц с размерами, приблизительно равными длине волны
излучения (рассеяние Ми), является очень сложным из-за эффектов дифракции и
интерференции света, рассеянного от различных участков поверхности частицы.
Дифференциальное поперечное сечение сильно изменяется с ростом угла рассеяния и в
большинстве случаев имеет прямое направление, в то время как рэлеевское
рассеяние является достаточно изотропным.
6.4.6. Оптическая активность
Оптический материал вращает плоскость поляризации электромагнитного
излучения. Вращение пропорционально концентрации оптически активного
материала, с, длине пути d:
(p = y(X)cd^ (6.56)
Постоянная /известна как удельное вращение и имеет единицы м^- моль или
см^- г"^; она сильно зависит от длины волны излучения. Как правило, удельное
вращение значительно больше при более коротких длинах волн.
Двумя хорошо известными оптически активными материалами являются
кристаллы кварца и сахарный растюр. Оптическую активность, включая измерение
зависимости от длины волны, можно использовать для определения химических веществ и
измерения их концентраций. Что касается визуализации, то оптическая активность является
значимой, поскольку она может вызываться различными внешними силами, среди
которых электрические поля (эффект Керра) и магнитные поля (эффект Фарадея).
6.4.7. Люминесценция
Люминесценцией называется испускание излучения от материалов, которое
возникает из-за излучательного перехода от возбужденного состояния в нижнее
состояние. Флуоресценцией является люминесценция, характеризуемая короткими про-
должительностями возбужденного состояния (порядка наносекунд), в то время как
термин фосфоресценция используется в случае более длительных продолжительно-
стей (от миллисекунд до минут).
Люминесценция — чрезвычайно гибкий процесс, поскольку может вызываться
различными явлениями. В хемилюминесценции энергия, необходимая для формирова-
шля возбужденного состояния, берется из энергии, вьщеляемой химической
реакцией. Хемилюминесценция, как правило, обладает только низкими эффективностями
(т.е. число фотонов, испускаемое одной взаимодействующей молекулой), порядка 1%
или даже ниже. Пламя является классическим примером низкоэффективного хеми-
люминесцентного процесса. Биолюминесценцией является хемилюминесценция в
живых организмах. Светляки и свечение морских микроорганизмов являются хорошо
известными примерами. Реакция светляка включает энзиматическое окисление лу-
циферина. В отличие от большинства хемилюминесцентных процессов, эта реакция
преобразует почти 100% химической энергии в энергию излучения. Низкоуровневые
биолюминесцентные процессы являются общими для многих существенных
биологических процессов. Формирование их изображений становится все более важным
инструментом для изучения биологических процессов.
Глава 6. Количественная визуализация
Маркировка биомолекул с помощью флуоресцентных красителей становится
еще одним в большей мере сложным инструментом биохимии. Стала возможной
даже маркировка отдельных хромосом или последовательностей генов в
хромосомах с помощью флуоресцентных красителей.
Люминесценция всегда должна заканчиваться другими процессами, которые
деактивируют возбужденное состояние без испускания излучения. Известным де-
зактивационным процессом без испускания излучения является перенос энергии
при столкновении молекул.
Некоторые типы молекул, особенно электроотрицательные молекулы, такие,
как кислород, являются очень эффективными при дезактивации возбужденных
состояний в столкновениях. Этот процесс именуется термином гашение. Наличие
гасящих молекул заставляет флуоресценцию уменьшаться. Следовательно,
измерение флуоресцентной энергетической освещенности можно использовать для
измерения концентрации гасящих молекул. Зависимость флуоресцентной
интенсивности от концентрации гасителя задается уравнением Стерна—Вольтера'.
Lo 1 + Лс^
L — флуоресцентная энергетическая яркость; L^ — флуоресцентная
энергетическая яркость в отсутствии гасителя; С — концентрация гасителя; к — константа
гашения, зависящая соответствующим образом от продолжительности
флуоресцентного состояния. Эффективное гашение требует, чтобы возбужденное
состояние имело достаточно долгую продолжительность.
Флуоресцентный краситель, подходящий для гашения растворенным
кислородом, —масляная кислота из косточки (РВА) [206]. Относительная флуоресцентная
энергетическая яркость РВД как функция растворенного кислорода, показана на рис. 6.14
[141]. Флуоресценция возбуждается импульсным азотным лазером при 337 нм.
Изменение во флуоресценции является достаточно слабым, но достаточно большим для
обеспечения надежных измерений концентрации растворенного кислорода.
6.4.8. Эффект Доплера
Разность скоростей между излучающим источником и получателем приводит к
тому, что получатель измеряет частоту, отличную от той, которая испускается ис-
£5
100
80
60
40
20
п
8
10 12
14
Оз, концентрация в мг/л
Рис. 6.14. Гашение флуоресценции масляной кислоты из косточки растворенным
кислородом: измерения и совпадение с уравнением Стерна—Вольмера (пунетирная линия) [ 140]
6.5, Упражнения 193
точником. Это явление известно как эффект Доплера. Сдвиг частоты прямо
пропорционален разности скоростей в соответствии с
с-и^к . (и -и У к
Уг= jr^s или Av=v, -v,= / 1 , (6.58)
с-щк \-щк1с
Tjntk =А: /1 А: I; v^ — частота источника; v^ — частота, измеренная в получателе; к —
волновое число излучения; с — скорость распространения излучения; м^ и м^ —
скорости источника и получателя относительно среды, в которой
распространяется волна. Только компонента скорости по направлению к получателю
вызывает сдвиг частоты.
Если источник движется по направлению к получателю («/ft > 0), то частота
увеличивается по мере того, как волновые фронты начинают быстрее двигаться
друг за другом. Критический предел достигается, когда источник движется со
скоростью распространения излучения. Тогда излучение остается позади
источника. При малых скоростях относительно скорости распространения волны сдвиг
частоты прямо пропорционален относительной скорости между источником и
получателем:
^v = {щ-u^)k. (6.59)
Относительный сдвиг частоты Ас»/ со задается непосредственно отношением
разности скоростей по направлению к получателю и скорости распространения волны:
^Jj^ZJ^^ (6.60)
V С
Для электромагнитных волн скорость относительно «среды» не представляет
важности. Теория относительности определяет частоту
V, ^ пи 1
""' r{\-u'klc) "^"^ ^ 4^-{\u\lcf' ^^'^^^
Для малых скоростей {\и\ = с) это уравнение сводится также к уравнению (6.59)
при и = и^ - и^. В этом случае акустические и электромагнитные волны могут
обрабатываться одинаково по отношению к сдвигу частоты из-за относительной
скорости между источником и получателем.
6.5. Упражнения
6.1: "^Радиометрические величины
Какие радиометрические величины описывают следуюш;ие процессы:
1) полная радиометрическая энергия, испускаемая световым источником;
2) радиометрическая мощность, испускаемая световым источником с
единицы площади в единичный телесный угол;
3) радиометрическая энергия, получаемая на единицу площади в единицу
времени датчиком формирования изображений, и
4) радиометрическая энергия, получаемая на единицу площади в течение
времени экспозиции датчиком формирования изображения?
6.2: "^Энергетическая освещенность
Световой источник устанавливается на поверхность плоской фигуры и
испускает изотропно 1 Вт радиометрической мопщости в полусферу. Какую долю этой
Глава 6. Количественная визуализация
мопщости получает элемент датчика формирования изображений 10 х 10 мкм^
на расстоянии 1 м? Какова энергетическая освещенность элемента датчика?
6.3: ^Смешивание цветов
Могут ли быть получены чистые (монохроматические) цвета с помощью
аддитивного смешивания трех цветов — красного, зеленого и синего?
6.4: *Метамерные цвета
Представьте датчик для определения цвета объекта с тремя каналами —
красным, зеленым и синим, который имеет спектральную чувствительность,
соответствующую или выборке по линиям, или выборке по полосам (рис. 6.3, б) в
разделе 6.2.3. Для каждого из двух типов датчиков определите, по крайней мере,
три спектральных распределения, которые должны как можно больше
отличаться друг от друга и которые приводят к одинаковому восприятию цвета.
6.5: *Цветовой круг
Почему мы ошущаем цветовые переходы от красного к желтому, зеленому и
синему и снова обратно к красному на цветовом круге как непрерывный
переход без разрывов? Физически существует разрыв в длине волны, если
мы идем от синего к красному.
6.6: "^Признаки объектов и излучение
Какие параметры излучения, испускаемого объектом и получаемого
камерой, могут дать нам информацию о признаках наблюдаемого объекта?
6.7: **Фотоны
Сколько фотонов получает элемент датчика формирования изображений
10х Юмкм^, который облучается с £= 0,1 м • Вт/см^ (приблизительно 1/1000
энергетической освещенности прямого солнечного света) в течение 1 мс?
(Подсказка: постоянная Планка А = 6,626 • 10"^"^ Дж • с).
6.6. Дополнительная литература
Эта глава охватьгоает большое количество тем, которые не являются центральными
для обработки изображений, но важны для правильного получения изображений. Вы
можете освежить или расширить свои знания об электромагнитных волнах с помошью
одного из классических учебньк пособий по этому предмету, например, Ф. С. Кроу-
форд (F. S. Crawford) [41], Хект (Hecht) [74] или TayH(Towne) [201]. Стюарт (Stewart)
[195] и Друри (Drury) [37] обращаются к взаимодействию излучеьшя с веш;еством в
области дистанционного зондирования. Ричарде (Richards) [165] дает обзор методов
формирования изображений через электромагнитный спектр. Тема формирования
инфракрасных изображений стала предметом исследований и рассматривается
детально Гауссоргус (Gaussoigues) [56] и Холст (Hoist) [79]. Пратт (Pratt) [157] дает хорошее
описание цветового зрения относительно обработки изображений. Практические
аспекты фотометрии и радиометрии охвачены Де Кузе (DeCusaris) в [30]. Самой
старейшей областью применения количествершой визуализации является гидродашамика.
Обзор визуализации потока с помопц>ю большого количества изображений дан в [ 143].
ГЛАВА?
ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЙ
7.1. Введение
Формирование изображений включает три главных аспекта. Первый — по сути
своей геометрический. Вопрос заключается в том, где мы находим объект на
изображении. По существу, все методы формирования изображений проектируют
трехмерное пространство тем или иным образом на двумерную плоскость изображения.
Таким образом, формирование изображений можно рассматривать как проекцию
из 3-D в 2-D пространство. Исчезновение одной координаты ведет к серьезной
потере информации о геометрии наблюдаемой сцены. Однако мы бессознательно и
постоянно ощущаем, что наша зрительная система воспринимает трехмерное
представление достаточно хорошо, так что мы можем понимать трехмерный мир вокруг
нас и взаимодействовать с ним. Легкость, с которой задача реконструкции
выполняется биологическими зрительными системами, могла бы убедить нас, что это
простая задача. Но, как мы увидим в главах 8 и 17, это не так-то просто.
Второй аспект - радиометрический. Насколько «ярким» является изображаемый
объект и как яркость в изображении зависит от оптических свойств объекта и системы
формирования изображений? Радиометрия системы формирования изображений
рассматривается в разделе 7.5. Для повторения основ радиометрии см. раздел 6.2.
И наконец, третий вопрос состоит в том, что случается с изображением, когда
мы представляем его с помощью массива дискретных чисел для обработки на
цифровом компьютере? Как процессы, которые трансформируют непрерывное
изображение в такой массив, известные как преобразование в цифровую форму и
квантование, ограничивают разрешение в изображении или вносят помехи? Эти вопросы
исследуются в главе 9.
7.2. Мировые координаты и координаты камеры
7.2.1. Определение
В основном положение объектов в 3-D пространстве можно описать двумя
различными способами (рис. 7.1). Во-первых, мы можем использовать систему координат,
которая относится к наблюдаемой сцене. Эти координаты называются мировыми
координатами и обозначаются какX = [Х^\ Х^'^ ^/]^- КоординатыХ^'иХ^'описывают
горизонтальные, ^Х/- вертикальное положения, соответственно. Иногда
альтернативное общепринятое обозначение с помощью координат без индексов
X' = [X', Т, Z'] ^ оказывается удобнее. Оба обозначения используются в этой книге.
Вторую систему - с координатами камеры X = [Х^, Х^, X^Y— можно привязать к
камере, наблюдающей сцену. Ось Х^ совмещается с оптической осью системы
камеры (рис. 7.1). Физики знакомы с такими рассуждениями. Общепринято рассмат-
Глава 7. Формирование изображений
Координаты камеры
Мировые координаты
Рис. 7.1. Иллюстрация взамосвязи мировых координат и координат камеры
ривать физические явления в различных системах координат. В элементарной
механике, например, движение изучается относительно двух наблюдателей, одного в
состоянии покоя, другого — движущегося вместе с объектом.
Перемещение из мировых координат в координаты камеры, как правило,
требует перемещения и поворота. Сначала мы сдвигаем начало отсчета мировой
системы координат в начало отсчета системы координат камеры с помощью вектора
перемещения Г (рис. 7.1). Затем изменяем ориентацию сдвинутой системы
поворотами относительно соответствующих осей, с тем чтобы она совпала с системой
координат камеры. Математически перемещение можно описывать векторным
вычитанием, а поворот умножением координатного вектора на матрицу:
X=^R{X'-T) (7.1)
7.2.2. Поворот
Поворот системы координат имеет две важные особенности. Он не изменяет
длину или норму вектора и сохраняет систему координат ортогональной. Такое
преобразование известно в линейной алгебре как ортонормированное преобразование.
Коэффициенты в матрице преобразования имеют интуитивно понятные
значения. Их можно увидеть, когда мы применяем преобразование к единичным
векторам Е в направлении координатных осей. Для F, к примеру, мы получаем
е:=ае,=
а,,
Uy
а
21
а
22
а
31
а
32
а,
а
а
ь]
'23
'зз]
гг
0
[о
=
«и"
а,,
«31 _
(7.2)
Таким образом, столбцы матрицы преобразования задают координаты базисных
векторов в новой системе координат. Зная это свойство, легко сформулировать
условие ортонормированности, которое должно выполняться матрицей поворота R\
3
R^R = I или X^b,^/-=^it-b (7.3)
где /обозначает единичную матрицу, чьи элементы равны единице и нулю на
диагональных и недиагональных местах соответственно. Используя уравнение (7.2),
это уравнение просто утверждает, что преобразованные базисные векторы
остаются ортогональными:
ё7ё;=5,_,. (7.4)
7.2, Мировые координаты и координаты камеры
Рис. 7.2. Поворот мировых координат Хв координаты камеры Xz использованием
трех углов Эйлера (0, в, у/) с помощью последовательных поворотов относительно
осей: а - Лз'; б - ^/'; в - Х;\
В уравнении (7.3) три матричных элемента из девяти остаются независимыми.
К сожалению, оказывается, что зависимость между матричными элементами и
тремя параметрами для описания поворота является достаточно сложной и
нелинейной. Общая процедура включает три угла поворота Эйлера (0, в, у/). В
литературе существует большая путаница относительно определения угла Эйлера. Мы
следуем стандартному математическому подходу. Мы используем правые системы
координат и считаем углы поворота положительными в направлении против
часовой стрелки. Поворот от сдвинутой мировой системы координат в систему
координат камеры раскладывается на три шага (см. рис. 7.2, [60]).
1. Поворот вокруг оси Х^'на. угол ф, Х" = ЯфХ':
^ =
COS0 sin0 О
-sinф cosф О
О 0 1
2. Поворот вокруг оси А^''на угол в, Х^ = RqX^:
10 О
(7.5)
Re =
О COS0
О -sin0
sin0
COS0
(7.6)
(7.7)
3. Поворот вокруг оси ЛГз^ на угол \i/,X = R^X'^:
Г cosy/ sin I// О
R^ = -sin I// cosy/ 0
[0 0 1
Каскадное применение трех поворотов R ,R^,R^ — дает матрицу
COS у/ cos ф - cos О sin ф sin у/ cos i// sin 0 + cos в cos ф sin y/ sin в sin y/
-sini//cos0-cos0sin0cosi// -siny/sin^ + cos^cos^cosv/ sin0cosi//
sin 0 sin 0 -sin0cos0 cos0
Глава 7. Формирование изображений
Обратное преобразование из координат камеры в мировые координаты
задается матрицей, транспонированной к вышеуказанной матрице. Поскольку
матричное умножение не является коммутативным, вращение также не является
коммутативным. Следовательно, важно не менять местами порядок, в котором
выполняются повороты.
Вращение является коммутативным только в пределе бесконечно малого
поворота. Тогда косинусные и синусные члены сводятся к 1 и е соответственно. Этот
предел имеет некоторые практические применения, поскольку незначительные
вращательные смещения являются обычными.
Поворот вокруг оси ^3, например, может быть
X = R^X' =
1
-S
0
е 0
1 0
0 1
X'
или
X, = Х[-\-еХ'^
■^2 ^ 2—^-^\»
X. =
х;
В качестве примера рассмотрим поворот точки [Х^', О, 0]^. Она поворачивается
в точку [JSTj \ еХ^ \ 0] ^, тогда как правильным было бы \Х^' cos г, Х^' sin г, 0] ^.
Разложение тригонометрической функции в ряд Тейлора до третьего порядка дает ошибку
в определении положения [ Xjle-X^ \ l/6e^Zj', 0] ^. Для изображения 512 х 512 (Xj' < 256
для центрированного вращения) и предельной ошибки 1/20 пикселя едолжно быть
меньше, чем 0,02, или 1,15\ Это все еще значительный поворот, вертикально
сдвигающий строки до ± еЛГ' = ± 5 пикселей.
7.3. Идеальное формирование изображений: перспективная
проекция
7.3.1. Камера-обскура
Основные геометрические аспекты формирования изображений оптической
системой хорошо моделируются с помощью камеры-обскуры. Формирующим
изображения элементом этой камеры является бесконечно малое отверстие (рис. 7.3).
Отдельный световой луч, идущий из точки объекта с координатами [А",, Х^, Х^,
который проходит через это отверстие, пересекает плоскость изображения в
[jCj, х^, -dy. При этом условии изображение объекта формируется на плоскости
Плоскость
изображения
Фокальная
плоскость
Плоскость
объекта
Рис. 7.3. Формирование изображений с помощью камеры-обскуры
7.3. Идеальное формирование изображ:ений: перспективная проекция
изображения. Зависимость между 3-D пространством и 2-D координатами
изображения [х^, ^2]^ задаются соотношением
х,=-^, х,=-^. (7.8)
Две мировые координаты, параллельные плоскости изображения
масштабируются множителем d'/Xy Следовательно, координаты изображения [х,, ^2]^
содержат только отношения мировых координат, по которым невозможно сделать
заключение ни о расстоянии, ни об истинном размере объекта.
Прямая линия в мировом пространстве проектируется на прямую линию на
плоскости изображения. Эту важную особенность можно доказать простым
геометрическим рассмотрением. Все световые лучи, испускаемые от прямой линии,
проходят через отверстие малого диаметра. Следовательно, они все лежат на
плоскости, которая образуется прямой линией и отверстием малого диаметра. Эта
плоскость пересекается с плоскостью изображения по прямой линии.
Все точки объекта на луче, проходящем через отверстие малого диаметра,
проектируются в отдельную точку на плоскости изображения. В сцене с несколькими
прозрачными объектами объекты проектируются друг в друга. Тогда мы не можем
сделать вывод о трехмерной структуре сцены вообще. Мы не можем даже
распознать форму отдельных объектов. Этот пример демонстрирует, насколько много
информации теряется при проектировании 3-D сцены на 2-D плоскость изображения.
Большинство естественных сцен, однако, содержат непрозрачные объекты.
Здесь наблюдаемое 3-D пространство, по существу, сводится к 2-D поверхностям.
Эти поверхности можно описывать двумя двумерными функциями - д(х^, х^) и
Х^{х^, х^) — вместо общего описания 3-D скалярного изображения различной
яркости д(Х^, Х^у Х^. Поверхность в пространстве полностью проектируется на
плоскость изображения при условии, что не более одной точки поверхности лежит на
одном и том же луче, проходящем через отверстие малого диаметра. Если это
условие не выполняется, то части поверхности остаются невидимыми. Этот эффект
называется скрытием. Скрытое 3-D пространство можно сделать видимым, если
поместить точечный источник света в само отверстие малого диаметра (рис. 7.4).
Тогда невидимые части сцены лежат в тени тех объектов, которые ближе к камере.
До тех пор пока мы можем исключать скрытие, нам необходима только карта
глубин Х^{х^, х^ для реконструкции 3-D формы сцены полностью. Одним из
способов получить ее, который также используется нашей зрительной системой,
является стереоскопическое формирование изображений, т.е. наблюдение сцены с
помощью двух датчиков с различных точек зрения (раздел 8.2.1).
Скрытое пространство
Объект 1/ . ,
Объект 2
Центр
проекций
Скрытая поверхность
Рис. 7.4. Скрытие более удалершых объектов и поверхностей перспективной проекцией
Глава 7. Формирование изображений
Плоскость изображения
Рис. 7.5. Перспективная проекция с помощью рентгеновских лучей
7.3.2. Проективное формирование изображений
Формирование изображений с помощью камеры-обскуры является, по существу,
перспективной проекцией, поскольку все лучи должны пройти через одну
центральную точку—отверстие малого размера. Таким образом, модель камеры-обскуры очень
схожа с формированием изображений с помощью проникающих лучей, таких, как
рентгеновские лучи, испускаемые от точечного источника (рис. 7.5). В этом случае
объект находится между центральной точкой и плоскостью изображения.
Уравнение проекции соответствует уравнению (7.8), за исключением знака:
Г^1
1
X,
\х.
->
X
1
X.
=
L -^ _1
L 3 J
Г^'л^,]
^3
d'X,
1
1^3 J
(7.9)
Координаты изображения, поделенные на расстояние до изображения d^,
называются обобщенными координатами изображения:
(7.10)
Обобщенные координаты изображения являются безразмерными и
обозначаются тильдой. Они равны тангенсу угла относительно оптической оси системы, при
котором наблюдается объект. Эти координаты явно учитывают ограничения
проекции на плоскость изображения. По этим координатам мы не можем сделать вывод
об абсолютных положениях, а можем узнать только угол, под которым объект
проектируется на плоскость изображения. Такие же координаты используются в
астрономии. Общее уравнение (7.9) для перспективной проекции тогда сводится к
х =
X,
X.
2.
А',
L 3 J
-^JC =
\^л
^
X,
1
L^bJ
(7.11)
Мы будем использовать это упрощенное уравнение проекции в дальнейших
рассуждениях. Для оптического формирования изображений мы только должны
включить знак минус или, если говорить геометрически, отобразить изображение
относительно начала отсчета системы координат.
7.4. Реальное формирование изображений
1А, Реальное формирование изображений
7.4.1. Основная геометрия оптической системы
Модель камеры-обскуры является чрезмерным упрощением системы
формирования изображения. Камера-обскура формирует изображение объекта на любом
расстоянии, в то время как реальная оптическая система формирует четкое
изображение только в пределах определенного диапазона расстояний. К счастью, геометрию
даже для сложных оптических систем можно по-прежнему моделировать с
помощью незначительной модификации перспективной проекции, как
проиллюстрировано на рис. 7.6 и 7.7. Фокальная плоскость должна заменяться двумя главными
плоскостями. Две главные плоскости пересекают оптическую ось в главных точках.
Оказывается, луч, направленный к первой главной точке, после прохождения через
систему возникает из второй главной точки без углового отклонения (см. рис. 7.6).
Расстояние между главными плоскостями, таким образом, моделирует осевую
протяженность оптической системы.
Оптическая система
Параллельные световые лучи f
Фокальная точка
Главные
р.^ТОЧКИ-^.д^„
Переднее фокусное
расстояние
- Эффективное-
фокусное
расстояние
] / Параллельные световые лучи
N Эффективное—►
[ фокусное
расстояние
Рис. 7.6. Модель «черного ящика» оптической системы
Объект
Оптическая
система
Изображение
Рис. 7.7. Оптическое формирование изображений с использованием оптической
системы, смоделированной с помощью ее главных точек P^^^P^vl фокальных точек F^ и F^.
Система формирует изображение, которое находится на расстоянии cf'позади F^, от
объекта, который находится на расстоянии d перед F^
Глава 7. Формирование изображений
Как проиллюстрировано на рис. 7.6, лучи между главными плоскостями
всегда параллельны, а параллельные лучи, входящие в оптическую систему слева и
справа, пересекаются во второй и первой фокальных точках соответственно. Для
практических целей полезными являются также следующие определения:
эффективное фокусное расстояние равно расстоянию от главной точки до
соответствующей фокальной точки. Переднее фокусное расстояние и заднее фокусное расстояние
равны расстояниям от первой и второй поверхностей оптической системы до
первой и второй фокальных точек соответственно.
Соотношение между расстоянием до объекта и расстоянием до изображения
становится очень простым, если они измеряются от фокальных точек (рис. 7.7):
dd'=f
(7.12)
Это представление Ньютона для уравнения изображения. Возможно, более
известная форма Гаусса использует расстояния относительно главных точек:
1 1 1
d' + f d^f f
(7.13)
7.4.2 . Линейное и осевое увеличение
Линейное увеличение т^ оптической системы задается отношением размера
изображения, X, к размеру объекта, Х\
f d' f + d'
X d f f+d
(7.14)
Линейное увеличение m^ пропорционально d': d'=fm. и обратно
пропорционально d: d' = f/m.. Следовательно, легко вычислить расстояние до объекта (d) и
расстояние плоскости изображения до фокальной плоскости (d) по заданному
увеличению. Три наглядных примера: объект на бесконечности (т^ = 0): d'= О,
увеличение 1/10 (т^ = 1/10): (d'=f/lO), взаимно-однозначное формирование
изображений: (т^ = 1): d'= d =/.
Труднее определить осевое увеличение, которое связывает положения
плоскости изображения и плоскости объекта друг с другом, т.е. задает увеличение вдоль
оптической оси. Выясним, как изменится сдвиг плоскости изображения, если
сместить точку в пространстве объекта вдоль оптической оси. В отличие от линейного
увеличения, осевое увеличение не является постоянной величиной вдоль
оптической оси. Поэтому осевое увеличение определяется только в пределе малых
изменений. Возьмем незначительно измененные положения объекта и изображения
d + АЛГ3 и d'- АХ3 и внесем их в уравнение (7.12). Тогда разложение в ряд Тейлора до
первого порядка по АХ^ и Ах^ (полагая, что AX^<^d и Ax^^^d") дает
АХ,
d'
d
и осевое увеличение /я задается соотношением
т,
а
d'
Д5
d
f
d'
d"
^
f
2
= m,.
/
(7.15)
(7.16)
7Л Реальное формирование изображений
7.4.3. Глубина фокуса и глубина поля
Уравнения изображений (7.12) и (7.13) определяют соотношение между
расстояниями до объекта и изображения. Если плоскость изображения незначительно
сдвигается или объект становится ближе к объективу, изображение не делается
бесполезным. Оно скорее становится размытым. Степень размытости зависит от
отклонения от расстояний, задаваемых уравнением изображения.
Понятия глубины фокуса и глубины поля основываются на том, что
определенная степень размытости не влияет на качество изображений. Для цифровых
изображений она, естественно, задается размером элементов датчика. Не имеет
смысла разрешать малые структуры. Вычислим размытость в рамках
геометрической оптики, используя изображение точечного объекта, как проиллюстрировано
на рис. 7.8, а. На плоскости изображение точечного объекта формируется в виде
точки. Она размывается до диска с радиусом б с увеличением расстояния от
плоскости изображения. Вводя относительную апертуру я оптической системы, как
отношение фокусного расстояния и диаметра апертуры объектива 2г
/
мы можем выразить радиус диска размытости как
1 /
б =•
2п. f^-d
-Ах.
(7.17)
(7.18)
Глубина фокуса
Объект
Изображение
Апертурная диафрагма
-Глубина поля
Объект
Диск размытости
Изображение
Апертурная диафрагма
Рис. 7.8. Иллюстрация глубины фокуса (а) и глубины поля с использованием
точечного объекта, находящегося на оси (б)
Глава 7. Формирование изображений
где АХз есть расстояние от (сфокусированной) плоскости изображения. Диапазон
положений плоскости изображения [d'- /SXy сГ-¥ Ах^], для которого радиус диска
размытости ниже, чем е, известен как глубина фокуса.
Уравнение (7.18) можно разрешить относительно АХз и получить
АХз =2f2y
/
б = 2«у^(1+т^)б,
(7.19)
где nil ^ линейное увеличение, как описано уравнением (7.14). Уравнение (7.19)
иллюстрирует решающую роль числа п^и увеличения для глубины фокуса. Только
эти два параметра определяют для заданного е глубину фокуса и глубину поля.
Даже больш[ую важность для практического применения, чем глубина фокуса,
представляет глубина поля. Глубиной поля является диапазон положений объекта,
для которого радиус диска размытости остается ниже пороговой величины е при
фиксированной плоскости изображения (рис. 7.8, б), С помощью уравнений (7.12)
и (7.19) мы получаем
Г ^^ f
^±АЛГ,=-
В пределе bJC^ J уравнение (7.20) сводится к
АЛГз "^ 2«^
\-\-mi
6.
т.
(7.21)
Если глубина поля включает бесконечное расстояние, то минимальное
расстояние для четкого изображения равно
(7.22)
J
4«^(1 + т^)б
4w^€
Типичная ПЗС-камера высокого разрешения имеет элементы датчика,
которые составляют в размере приблизительно 10 х 10 мкм. Таким образом, мы можем
учитывать радиус диска размытости, равный 5 мкм. Предполагая объектив с
относительной апертурой, равной 2, и фокусным расстоянием 15 мм, согласно
уравнению (7.21), мы имеем глубину поля, равную ± 0,2 м при расстоянии до объекта 1,5
м, а, согласно уравнению (7.22), глубина поля простирается от 5 м до
бесконечности. Этот пример иллюстрирует, что даже с такой малой относительной апертурой
и довольно коротким расстоянием мы можем получить большое поле фокуса.
Для больших увеличений, как в микроскопии, глубина поля очень мала. При
nij ^1 уравнение (7.21) сводится к
АХз«
2п^е
(7.23)
При 50-кратном увеличении (т^ = 50) и п^= 1 мы получаем экстремально
низкую глубину поля, равную только 0,2 мкм.
Как правило, общее понятие глубины поля и глубины фокуса, как рассмотрено
здесь, является применимым только в пределах геометрической оптики. Оно может
использоваться только для размьшания, которое значительно больше, чем
размывание, вызьшаемое аберрациями или дифракцией оптической системы (раздел 7.6.3).
7.4. Реальное формирование изображений
Нормальное формирование
изображений
Объект
Pl=P2
Внутренняя стенка
J Диафрагма
Оптическая система
Изображение
Телецентрическое формирование
изображений
Объект
Переднее
поперечное сечение
I
Диафрагма!
оптическая система
Изображение
Рис. 7.9. а — стандартное рассеивающее формирование изображений с
использованием диафрагмы в главной точке; б — телецентрическое формирование
изображений с использованием диафрагмы во второй фокальной точке. Справа наглядно
показано, как короткая цилиндрическая труба, ось которой совмещена с оптической
осью, изображается с помощью соответствующей установки
7.4.4. Телецентрическое формирование изображений
В стандартной схеме сходящийся пучок света входит в оптическую систему. Эта
установка обнаруживает при измерениях существенный недостаток (рис. 7.9, а).
Объект кажется больше, если он ближе к объективу, и меньше, если он дальше от
объектива. Поскольку невозможно сделать вывод о глубине объекта по его
изображению, тогда либо объект должен быть с точно известной глубиной, либо
ошибки при измерениях неизбежны.
Смещение апертурной диафрагмы из главной точки в первую фокальную
точку решает проблему, система формирования изображения заменяется
телецентрическим объективом (рис. 7.9,6). При установлении диафрагмы в этой точке
главные луни (лучи, проходящие через центр апертуры) параллельны оптической оси в
пространстве объекта. Следовательно, незначительные изменения в положении
объекта не меняют размер изображения объекта. Чем дальше он от
сфокусированного положения, тем более оно размыто. Однако центр диска размытости не
меняет положения.
Телецентрическое формирование изображений стало важным принципом в
машинном зрении. Его недостатком, конечно, является то, что диаметр
телецентрического объектива должен быть по меньшей мере размера объекта,
изображение которого получают. Это делает телецентрическое формирование изображений
очень дорогостоящим для больших объектов.
На рис. 7.9 иллюстрируется, как цилиндр, совмещенный с оптической осью, с
тонкой стенкой виден посредством стандартного объектива и телецентрического
объектива. Стандартное формирование изображений видит поперечное сечение и
внутреннюю стенку, а телецентрическое формирование изображений — только
поперечное сечение.
Глава 7. Формирование изображений
Рассмотрение телецентрического формирования изображений подчеркивает
важность диафрагм в конструкции оптических систем, факт, который часто не
рассматривается надлежащим образом.
7.4.5. Геометрическое искажение
Реальная оптическая система вызывает отклонения от совершенной
перспективной проекции. Самые очевидные геометрические искажения можно наблюдать с
помощью простых сферических линз, как, например, бочкообразные рши
подушкообразные изображения квадратов. Даже при скорректированной системе линз
эти эффекты полностью не подавляются.
Этот тип искажения можно легко понять, рассмотрев симметрии. Поскольку
системы линз имеют цилиндрическую симметрию, концентрические окружности
испытьюают только искажение в радиусе. Это искажение можно аппроксимировать
соотношением
в зависимости от того, является к^ положительным или отрицательным, будут
наблюдаться бочкообразные и подушкообразные искажения в изображениях квадратов.
Торговые ТВ-объективы проявляют радиальное отклонение нескольких точек
изображения (пикселей) на краю датчика. Если искажение корректируется с помощью
уравнения (7.24), то остаточная ошибка составляет менее чем 0,06 точек изображения [119].
Такая высокая степень корректировки, вместе с геометрической
устойчивостью современных ПЗС-датчиков, объясняет точность до фрагментов пикселя в
измерениях расстояния и площади без использования дорогостоящих специальных
объективов. Ленц (Lenz) [120] рассматривает дополнительные детали, которые
влияют на геометрическую точность ПЗС-датчиков.
Искажения также возникают, если неплоские поверхности проектируются на
плоскость изображения. Эти искажения доминируют в получении изображений с
воздуха и с помощью ИСЗ. Таким образом, коррекция геометрического
искажения в изображениях является основным разделом в дистанционном
зондировании и фотограмметрии.
Точная коррекция геометрических искажений требует сдвига точек
изображения на доли расстояния между двумя точками изображения. Мы будем иметь дело
с этой проблемой далее в разделе 10.5, после того как составим знания,
необходимые для ее подробного рассмотрения.
7.5. Радиометрия формирования изображений
Недостаточно знать только геометрию формирования изображений. Равно
важным является рассмотрение того, как энергетическая освещенность на плоскости
изображения связана с энергетической яркостью изображаемых объектов и какие
параметры оптической системы влияют на эту зависимость. Для рассмотрения
фундаментальных основ радиометрии, особенно всех терминов, описывающих
свойства излучения, мы отсылаем к разделу 6.2.
Путь излучения от источника света до плоскости изображения включает
цепочку процессов (см. рис. 6.1). В этом разделе мы концентрируем наше внимание
7.5. Радиометрия формирования изображений 207
Проектируемая апертура
Площадь
изображения ,
Площадь объекта А
с энергетической яркостью L
Оптическая система
Рис. 7.10. Оптическая система принимает плотность потока, которая соответствует
произведению энергетической яркости объекта и телесного угла, образованного
проектируемой апертурой, если смотреть от объекта. Поток, испускаемый от площади
объекта А, отображается на площадь изображения А'
на линии наблюдения (сравните рис. 6.1) — нас интересует, как излучение,
испускаемое от изображаемого объекта, накапливается системой формирования
изображений.
7.5.1. Энергетическая яркость объекта и энергетическая освещенность
изображения
Оптическая система накапливает часть излучения, испускаемого объектом (рис. 7.10).
Мы полагаем, что объект является однородным излучателем Ламберта с
энергетической яркостью L. Со стороны объекта кажется, что апертура оптической системы
образует определенный телесный угол Q. Проектируемая круглая площадь
апертуры равна к г ^ cos0 на расстоянии {d -\-f) I cosft Тогда, согласно уравнению (6.4), поток
Ф = АШ. = А
пг
'cos'0
(7.25)
входит в оптическую систему. Излучение, испускаемое с площади А,
проектируемой на плоскость объекта, т.е. А/со%в, отображается на область у!'. Следовательно,
поток Q должен делиться на площадь у1'для вычисления энергетической
освещенности изображения Е\ Согласно уравнению (7.14), отношение площадей можно
выразить как
^/cos0_ 1 __ if + df
А' mf if + dy
(7.26)
Далее предполагаем, что оптическая система имеет коэффициент
пропускания t. Подстановка уравнения (7.26) в уравнение (7.25) окончательно приводит к
следующему соотношению энергетической яркости объекта/энергетической
освещенности изображения:
: tn I ,. 1 cos^ в L. (7.27)
Е' =
А'
f^d'
Глава 7. Формирование изображений
Эта фундаментальная зависимость утверждает, что энергетическая
освещенность изображения пропорциональна энергетической яркости объекта. Это
является основой для линейности оптического формирования изображений.
Оптическая система описывается двумя простыми величинами: ее (полным) коэффициентом
пропускания t и отношением апертурного радиуса к расстоянию изображения от
первой главной точки. Для удаленных объектов d ^/, (Г <^f уравнение (7.27) сводится к
(7.28)
с использованием относительной апертуры л^ (уравнение (7.17)). Для реальных
оптических систем уравнения (7.27) и (7.28) являются только приближением. Если
часть падающего пучка отсекается дополнительными апертурами или
ограниченными диаметрами линз (виньетирование), снижение является еще более
резким при больших углах 0. Однако тщательная разработка положения апертуры
может сделать снижение менее резким, чем cos'^ft Поскольку остаточная
отражательная способность поверхностей линз также зависит от угла падения,
истинное снижение зависит сильно от разработки оптической системы и наилучшим
образом определяется экспериментально с помощью подходящей
калибровочной установки.
7.5.2. Инвариантность энергетической яркости
Поразительный вывод о простой связи энергетической освещенности
изображения с энергетической яркостью объекта базируется на фундаментальной
инвариантности. Изображение имеет энергетическую яркость так же, как реальный объект.
Оно может приниматься как источник излучения последующими оптическими
элементами. Фундаментальная теорема радиометрии гласит, что энергетическая
яркость изображения равна энергетической яркости объекта, умноженной на
коэффициент пропускания оптической системы.
Теорему можно доказать, используя предположение, что поток излучения Ф
через оптическую систему сохраняется, за исключением потерь на поглощение в
системе с коэффициентом, меньшим, чем единица. Телесные углы, которые
образуют объект и изображение в оптической системе, равны
a = A,l{d + ff и a' = A,l{d' + f)\ (7.29)
где А^ - эффективная площадь апертуры.
Поток, испускаемый от площади А объекта, принимается площадью
А' =^(rf4y)V(rf+/)2 на плоскости изображения (рис. 7.11, а). Следовательно,
энергетические яркости равны
L = -^-=-^-(^+/)2
QA J^A
И следующая инвариантность сохраняется:
L' = tL для п=п, (7.31)
7.6. Теория линейных систем формирования изображений 209
Главные плоскости
А, ^/
Оптическая система
Рис. 7.11. Иллюстрация инвариантности энергетической яркости: а — произведение
АО. является одинаковым в пространстве объекта и изображения; б — изменение
телесного угла, когда пучок лучей входит в оптически более плотную среду
Инвариантность энергетической яркости такого вида действительна, только если
объект и изображение находятся в средах с одинаковым показателем преломления
{п '= п). Если пучок лучей с энергетической яркостью L входит в среду с более высоким
показателем преломления, то энергетическая яркость увеличивается, поскольку лучи
наклоняются к оптической оси (рис. 7.11, б). Таким образом, общее отношение
энергетической яркости и квадрата показателя преломления остается инвариантным:
L4n^=tLln\ (7.32)
Из инвариантности энергетической яркости мы можем немедленно сделать
вывод, что энергетическая освещенность на плоскости изображения есть
E' = L'Q' = L'7V
= ья81п а = tinsm а .
(7.33)
Это уравнение не учитывает снижение в зависимости от cos'^^ в уравнении
(7.27), поскольку мы не рассматриваем наклонные главные лучи.
Инвариантность энергетической яркости значительно упрощает вычисление
энергетической освещенности изображения и распространение излучения через
сложные оптические системы. Ее фундаментальную важность можно сравнить с
основным принципом геометрической оптики: излучение распространяется
таким образом, что оптический путь nd (реальный путь, умноженный на показатель
преломления) принимает экстремальное значение.
7.6. Теория линейных систем формирования изображений
в разделе 4.2 мы рассматривали линейные инвариантные относительно сдвига
фильтры (операторы свертки) как одно из применений теории линейных систем.
Формирование изображений является еще одним примером, который может
описываться с помощью этого важного понятия. Здесь мы будем обсуждать
оптическое формирование изображений, исходя из понятий 2-D и 3-D функции
рассеяния точки (раздел 7.6.1) и оптической передаточной функции (раздел 7.6.2).
Глава 7. Формирование изображений
7.6.1. Функция рассеяния точки
Ранее было показано, что точка в 3-D пространстве объекта не отображается в точку
в пространстве изображения, а отображается на более или менее протяженную
область с изменяющимися интенсивностями. Очеввдно, функция, которая
описывает формирование изображений точки, является существенной
характеристикой системы формирования изображений и называется функцией рассеяния точки
(ФРТ). Мы полагаем, что ФРТ не зависит от положения. Тогда оптическое
формирование изображений можно рассматривать как линейную инвариантную
относительно сдвига систему (LSI) (раздел 4.2).
Если мы знаем ФРТ, то можем вычислить, как будет изображаться любой
произвольный объект. Для выполнения этой операции мы рассматриваем объект, как
разложенный на отдельные точки. На рис. 7.12 иллюстрируется этот процесс.
Точка X' на плоскости объекта проектируется на плоскость изображения с
распределением интенсивности, соответствующим функции рассеяния точки Л. С
помощью д](х') мы обозначаем значения интенсивности на плоскости объекта g'Q(X'),
проектируемые на плоскость изображенР1я, но без каких-либо дефектов в
процессе формирования изображения. Тогда интенсивность точки х на плоскости
изображения вычисляется с помощью интегрирования вкладов от передаточных
функций, которые имеют свои максимумы в дс' (рис. 7.12):
д^ (х) = J дХх'Щх - x')d'/ = (д: * h)(x).
(7.34)
Операция в уравнении (7.34) известна как свертка. Операции свертывания
играют существенную роль в обработке изображений. Операции свертывания
включаются не только в формирование изображений, но также и во многие операции
обработки изображений. В случае формирования изображений свертка,
очевидно, «размывает» изображение и уменьшает разрешение.
до(Х'
до(Х")
Плоскость
объекта
Рис. 7.12. Формирование изображений с помощью свертки с функцией рассеяния
точки h(x). Точка в ^'на плоскости объекта приводит к распределению
интенсивности с максимумом в соответствующей точке х'на плоскости изображения. В точке х
на плоскости изображений вклады от всех точек х\ т.е. g\{x')h{x - х"), должны
интегрироваться
7.6. Теория линейных систем формирования изобраэюений
Этот эффект операций свертывания можно легче всего продемонстрировать с
помощью структур изображений, которые показывают периодические вариации
уровней яркости. Пока длина повторяемости, длина волны этой структуры больше,
чем ширина ФРТ, она не будет испытывать существенных изменений. Однако по
мере того как длина волны убывает, амплитуда вариаций уровней яркости будет
убывать. Мелкие структуры, в конце концов, будут размыты до такой степени, что
они перестанут быть видимыми. Эти соображения подчеркивают важную роль
периодических структур и, естественно, приводят к введению преобразования Фурье,
которое раскладывает изображение на периодические вариации уровней яркости,
которые оно содержит (раздел 2.3).
Предыдущие рассуждения показали, что формирование двумерного
изображения на плоскости изображения описывается явно ее ФРТ. В дальнейшем мы
расширим это понятие до трехмерного случая и явно вычислим функцию
рассеяния точки в пределах геометрической оптики, т.е. с совершенной системой линз и
без дифракции. Этот подход мотивируется необходимостью понять трехмерное
формирование изображений, особенно в микроскопии, т.е. как точка в 3-D
пространстве объекта отображается не только на 2-D плоскость изображения, но и в
3-D пространство изображения.
Сначала рассмотрим, как фиксированная точка в пространстве объекта
проектируется в пространство изображения. Из рис. 7.8 мы делаем вывод, что радиус
диска размытости определяется соотношением
6,=-^. (7.35)
Индекс / у е указывает на пространство изображения. Затем заменяем радиус
апертуры г максимальным углом, при котором линза накапливает свет от
рассматриваемой точки, и получаем
dr.
б^=-^Хз1апа. (7.36)
Это уравнение дает нам контур ФРТ в пространстве изображения. Она
представляет собой двойной конус с осью Хз в центре. Вершины обоих конусов
совпадают в начале координат. Вне двух конусов ФРТ равна нулю. Об интенсивности
внутри конуса мы можем сделать вывод из закона сохранения энергии излучения.
Поскольку радиус конуса возрастает линейно в зависимости от расстояния до
плоскости фокуса, интенсивность внутри конуса убывает квадратично. Таким
образом, ФРТ h.{x) в пространстве изображений задается соотношением
h^x) = ^ ' jjAhj:l2)_
я(-^- Хз tan а)^ 2-^х^ tan а
d. d.
- ^0 П "^ ^^-З^)
7t(-^ztanaf 2-^^ztana
d, d,
Глава 7. Формирование изображений
где /q — сила света, накопленная линзой от точки; П - функция-ящик, которая
определяется как
[О иначе.
Последнее выражение в уравнении (7.37) записывается в цилиндрических
координатах {г, ф, z) для учета круговой симметрии ФРТ относительно оси Ху Во
втором шаге рассмотрим, чему ФРТ в пространстве изображений соответствует
в пространстве объектов, поскольку нас интересует, как эффекты
формирования изображений проектируются обратно в пространство объектов. Мы должны
рассмотреть как линейное, так и осевое увеличение. Во-первых, изображение и,
таким образом е, больше, чем объект в d. / d^ раз. Во-вторых, мы должны найти
плоскости в пространствах объектов и изображений, соответствующие друг
другу. Эта задача уже была решена в разделе 7.4.2. Уравнение (7.16) связывает
изображение с координатами камеры. В сущности, обратно проектируемый радиус
диска размытости, б^, задается соотношением
6^ =Х^1дпа,
а ФРТ, обратно проектируемая в пространство объектов, соотношением
(7.39)
К(Х)=^
я (Х, tana)
П
П
R
2Х^ tan а n{Z tan а У 1Z tan а
(7.40)
Двойной конус ФРТ, обратно проектируемый в пространство объектов,
показывает тот же угол разворота, что и линза (рис. 7.13). В сущности, А^(х) в уравнении
(7.40) задает эффект оптического формирования изображений, с условием
пренебрежения геометрическим масштабированием.
1 к,
\
0,5\
о\
-0,51
Рис. 7.13. а — 3-D ФРТ; б — 3-D ОПФ оптического формирования изображений с
использованием линзы, обратно проектируемая в пространство объектов.
Аберрациями линзы и эффектами дифракции пренебрегаем
7.6. Теория линейных систем формирования изображений
7.6.2. Оптическая передаточная функция
Свертка с ФРТ в пространственной области является довольно сложной
операцией. В Фурье-пространстве, однако, она выполняется как умножение
комплексных чисел. В частности, свертка 3-D объекта д\{Х) с ФРТ hj^X) соответствует в
Фурье-пространстве умножению преобразованного с помощью преобразования
Фурье объекта д'^ (к) на преобразованную с помощью преобразования Фурье ФРТ,
оптическую передаточную функцию (ОПФ) h^(k).B этом разделе мы
рассматриваем ОПФ в пространстве объектов, т.е. проектируем изображенный объект обратно
в пространство объектов. Тогда формирование изображений можно описать с
помощью схемы:
Изображенный Формирование Объект
объект изображений
Пространственная область Qoi^) = К(^) * 0о(^) (7 41)
л "^ А.
Фурье-Область д^(к) = h^(k) - д^{к).
Это соответствие означает, что мы можем описать оптическое изображение с
помощью либо функции рассеяния точки, либо оптической передаточной
функции. Оба описания являются полными. Как и в случае с ФРТ, ОПФ имеет
наглядное значение. Поскольку Фурье-преобразование раскладывает объект на
периодические структуры, ОПФ показывает, как оптический процесс формирования
изображений изменяет эти периодические структуры. ОПФ, равная единице для
отдельной длины волны, означает, что на эту структуру не оказывается влияния
вообще. Если ОПФ равна нулю, то она исчезает полностью. Для значений между О
и 1 она затухает соответственно. Поскольку ОПФ, как правило, является
комплексным числом, не только амплитуда периодической структуры может
изменяться, но также и ее фаза. Прямое вычисление ОПФ является затруднительным.
Здесь используются некоторые особенности преобразования Фурье, особенно
его линейность и сепарабельность, для разложения ФРТ на соответствующие
функции, которые легче можно преобразовать. Демонстрируются две возможности.
Они являются также, в более общем смысле, наглядными, поскольку
иллюстрируют некоторые важные особенности преобразованрш Фурье.
Первый метод вычисления ОПФ раскладывает ФРТ в пучок 5-линий,
пересекающихся в начале системы координат. Они равномерно распределяются в
поперечном сечении двойного конуса. Мы можем считать 5-линию одним световым
лучом. Без дальнейших вычислений мы знаем, что это разложение определяет
корректное квадратичное убывание в ФРТ, поскольку то же число 5-линий
пересекает квадратично возрастающую область. Преобразование Фурье 5-линии является
5-плоскостью, которая перпендикулярна линии (>-R5). Таким образом, ОПФ
состоит из пучка 5-плоскостей. Они пересекают плоскость к^к^ по линии через
начало координат к пространства при величине угла, равной самое большее а. Поскольку
преобразование Фурье сохраняет вращательную симметрию, ОПФ имеет также
круговую симметрию относительно оси ку ОПФ заполняет все
Фурье-пространство, за исключением двойного конуса с углом к/2-а.Ъ этом секторе ОПФ равна
нулю. Точные значения ОПФ в ненулевой части сложно получить с помощью это-
Глава 7. Формирование изображений
го метода разложения. Мы сделаем вывод о ней с помощью еще одного подхода,
основанного на сепарабельности преобразования Фурье. Рассмотрим двойной
конус как слои дисков с изменяющимися радиусами, которые возрастают с
ростом Щ. На первом шаге мы выполняем преобразование Фурье только в плоскости
х^х^. Это преобразование дает функцию с двумя координатами в ^-пространстве и
одну координату в х-пространстве, {к^, к^, х^), соответственно (q, ср, z) в
цилиндрических координатах. Поскольку ОПФ-уравнение (7.40) зависит только от г (осевая
симметрия относительно оси z), двумерное преобразование Фурье соответствует
одномерному преобразованию Ханкеля нулевого порядка [13]:
/г(г, z) =
П(-
h(q,z) = /(
J^(2nzqtQna)
)
(7.42)
nzqtana
Преобразование Фурье диска, таким образом, приводит к функции, которая
содержит функции Бесселя J, (>^R5).
В качестве второго шага мы выполняем недостающее одномерное
преобразование Фурье в направлении z. Уравнение (7.42) показывает, что h{q,z) является
функцией Бесселя в направлении z. В этот раз, однако, преобразование Фурье
является одномерным. Таким образом, мы получаем не функцию диска, а функцию
окружности (>^R5):
J^(2nx)
2{^-,r
п
Г1гЛ
\ /
(7.43)
Если мы, наконец, применим теорему о масштабировании преобразования
Фурье ()^R4),
если
тогда
мы получаем
h(q,k^) =
2L
п l^tana
fix)
f{ax)
1-
fik).
\a\
v«/
(7.44)
kl
q^ tan^ a
Ч1/2
/
/
П
V
2^ tan a
(7.45)
Большая часть ОПФ равна нулю. Это означает, что пространственные
структуры с соответствующими направлениями и длинами волн полностью исчезают. В
частности, это выполняется для всех структур в направлении z, т.е.
перпендикулярных плоскости изображения. Такие структуры полностью теряются и не могут
реконструироваться без дополнительных сведений.
Мы можем увидеть только 3-D структуры, если они также содержат структуры,
параллельные плоскости изображения. Например, возможным является разрешить
точки или линии, которые расположены друг над другом. Мы можем объяснить
это явление в х-пространстве, так же как в /^-пространстве. ФРТ размывает точки
7.6. Теория линейных систем формирования изображений
и линии, но они могут все еще выделяться, если они не слишком близко
расположены друг к другу.
Точки или линии являются протяженными объектами в Фурье-пространстве,
т.е. константами и плоскостями. Такие протяженные объекты частично
совпадают с ненулевыми частями ОПФ и, таким образом, не исчезнут полностью.
Периодические структуры вплоть до угла а к плоскости к^^^ который просто
соответствует углу разворота линзы, не удаляются ОПФ. Интуитивно понятно, что можно
распознать все 3-D структуры, которые в действительности исследуются. Все, что
нам необходимо, - это, по крайней мере, один луч, который перпендикулярен
волновому числу структуры и, таким образом, проходит в направлении постоянных
уровней яркости.
7.6.3. Дифракционно-ограниченные оптические системы
Свет - это электромагнитное излучение и, по существу, субъект волновых
явлений. Когда параллельный пучок света входит в оптическую систему, он не может
сфокусироваться в точку, даже если исключены аберрации. Дифракция в апертуре
оптической системы размывает пятно в фокусе до размеров по меньшей мере
порядка длины волны света. Оптические системы, для которых аберрации
подавлены до такой степени, что они значительно ниже, чем эффекты дифракции,
называются дифракционно-ограниченными.
Строгое рассмотрение дифракции, согласно уравнениям Максвелла, является
математически достаточно сложным ([12], [39, главы 9 и 10] и [85, глава 3]).
Дифракцию плоского волнового фронта в апертуре линз, однако, можно
рассматривать в простой аппроксимации, известной как дифракция Фраунгофера. Это ведет к
фундаментальному соотношению.
Мы полагаем, что апертура оптической системы пронизывается плоским
волновым фронггом, идущим от объекта на бесконечности (рис. 7.14). Эффект совершенной
линзы заключается в том, что она изгибает плоский волновой фроьгг в сферический
волновой фронт с его началом в фокальной точке на оптической оси. Дифракция в
конечной апертуре линзы заставляет свет двигаться в других направлениях. Этот
эффект можно учесть, применяя принцип Гюйгенса на апертурной плоскости. Этот
Плоский волновой фронт Сферический волновой фронт
f
Оптическая система Плоскость изображения
Рис. 7.14. Дифракция плоского волнового фронта в апертурной диафрагме
оптической системы. Оптическая система преобразует входящий плоский волновой фронт в
сферические волновые фронты во всех направлениях, сходящихся на плоскости
изображения. Для дополнительных подробностей см. текст
Глава 7. Формирование изображений
принцип утверждает, что каждую точку волнового фронта можно принять за
начало новой совпадающей по фазе сферической волны. Все эти волны
накладываются на плоскости изображения, чтобы сформировать изображение входящей
плоской волны. Длины путей от точки лс'на апертуре изображения до фокальной точки
и до точки с отклонением х на плоскости изображения (рис. 7.14) задаются
соотношениями
s = ylx"+/'+f и s' = ^(x'-xf+(/-yf+f (7.46)
соответственно. Разность между этими двумя путями, при условии, что х <^ /(т.е.
пренебрегаем квадратичными членами по х и у), дает
хх''\-уу'
S -S ^ —
/
Эта разность путей приводит к фазовой разности
_2^{s'-s) _ 2п(хх'+уу') _ 2ж(хх')
(7.47)
(7.48)
/Я /Я /Я
ДЛЯ длины волны я.
Теперь мы полагаем, что y/'ix) есть распределение амплитуды волнового
фронта на апертурной плоскости. Обратите внимание, что это более общий подход, чем
использование простой функции-ящика для апертурной диафрагмы. Мы хотим
рассмотреть обобщающий случай произвольно изменяющейся амплитуды
волнового фронта Р1ЛИ любого типа апертурных функций. Если мы используем комп-
лекснозначное у/' (х), то также возможно учесть эффекты, которые приводят к
фазовому сдвигу в апертуре.
Тогда наложение сферических волн у/' (х) на плоскости изображения с
фазовым сдвигом, заданным уравнением (7.48), дает
оо оо
\1/(х)= j jy/\x)exp
—оо —оо
-2т —
V
/я
2,У
d'x
(7.49)
Это уравнение означает, что амплитудно-фазовое распределение у/ (х) на
фокальной плоскости является просто 2-D преобразованием Фурье (см. уравнение
(2.32)) от амплитудно-фазовой функции уг'{х) на апертурной плоскости.
Для круглой апертуры амплитудное распределение задается соотношением
V/'(jc') = n
2г
(7.50)
где г — радиус апертуры. Преобразование Фурье уравнения (7.50) задается
функцией Бесселя первого порядка (>"R4):
Wi.x) = Wb
1^(2лхг/ fX)
(7.51)
лхг I /я
Энергетическая освещенность Е на плоскости изображения задается
квадратом амплитуды:
E{x)^xi,{x)f=xi,l
I,{2nxrlfX)
nxrIfX
\2
(7.52)
7.6. Теория линейных систем формирования изображений
Дифракционная картина имеет центральное пятно, которое содержит 83,9%
энергии и окружающие кольца с убывающей интенсивностью (рис. 7.15, а).
Расстояние от центра диска до первого кольца равно
Дх = 0,6Ь^Я = 1 22Яа2
/'
(7.53)
При этом расстоянии можно легко вьщелить две точки (рис. 7.15, б). Это есть
критерий Рэлея для разрешения оптической системы. Разрешение оптической системы
можно интерпретировать, исходя из углового разрешения входящей плоской волны и
пространственного разрешения на плоскости изображения. Приняв во внимание
критерий Рэлея (уравнение (7.53)), угловое разрешение А0 = Ах//задается как
А0о=О,61-. (7.54)
г
Таким образом, угловое разрешение не зависит вообще от фокусного
расстояния, а зависит только от апертуры оптической системы по отношению к длине
волны электромагнитного излучения.
В отличие от углового разрешения, пространственное разрешение Ах на
плоскости изображения зависит, согласно уравнению (7.53), только от отношения
радиуса апертуры линзы к расстоянию/от изображения объекта до главной точки.
Вместо относительной апертуры мы можем использовать в уравнении (7.53)
числовую апертуру, которая определяется как
п =«sin0n =—.
(7.55)
п
f
Мы полагаем теперь, что показатель преломления позади изображения п
может отличаться от 1. Здесь в^ есть угол разворота светового конуса, проходящего от
центра плоскости изображения через апертуру линзы. Тогда
Ax = 0,6l4. (7.56)
Следовательно, абсолютное разрешение на плоскости изображения не
зависит вообще от фокусного расстояния системы, а только зависит от числовой
апертуры конуса изображений.
]
0 8
0 6
0 1
0,2
0
-3 -
1
/
/
/
2 -
Л.
\
1 (
/\
1
)
1
\
\
\
1 3
Рис. 7.15. а - энергетическая освещенность Е{х) дифракционной картины («диск
Эйри») на фокальной плоскости оптической системы с равномерно освещаемой
круглой апертурой, согласно уравнению (7.52); б — иллюстрация разрешения
изображения двух точек на расстоянии х/{п^ Я) = 1,22
Глава 7. Формирование изображений
Поскольку путь света может обращаться, те же аргументы применяются для
плоскости изображения. Пространственное разрешение на плоскости объекта
зависит только от числовой апертуры конуса объектов, т.е. угла разворота конуса,
входящего в апертуру линзы:
Я
АХ = 0,61-
(7.57)
Эти простые соотношения полезны для оценки выполнения оптических систем.
Поскольку максимальная числовая апертура оптических систем равна
приблизительно единице, не могут разрешаться структуры меньшие, чем полудлина волны.
7.7. Однородные координаты
в компьютерной графике используется элегантный формализм однородных
координат [42,52,134] для описания всех преобразований, которые мы рассматривали до сих
пор, т.е. перемещения, поворота и перспективной проекции, в унифицированном виде.
Этот формализм является значимым, поскольку весь процесс формирования
изображений можно выразить единственной матрицей 4x4.
Четырехкомпонентный столбцовый вектор представляет однородные координаты
X'= [tX[,tX'^,tX[,tY. (7.58)
из которого получаются обьршые трехмерные координаты с помощью деления первых
трех компонент однородных коордашат на четвертую. Любое произвольное
преобразование можно получить предварительным умножением однородных координат на
матрицу Мразмерностью 4 х 4. В частности, мы можем получить координаты изображения
X = [sx^,sx2, sx^.sf (7.59)
с помощью
X = MX. (7.60)
Поскольку матричное умножение ассоциативно, мы можем рассматривать
матрицу М, как состоящую из многих матриц преобразования, выполняющих такие
элементарные преобразования, как перемещение, поворот вокруг координатных осей,
перспективная проекция и масштабирование. Матрицы для элементарных
преобразований имеют вид:
Т =
R. =
1
0
0
0
1
0
0
0
0 0
1 0
0 1
0 0
0
COS0
sin0
0
т,
Тг
Тг
1
0
-sinO
COS0
0
0
0
0
1
перемещение на [7],Г2 Г3] ,
поворот вокруг оси Xj на 0,
(7.61)
7.7. Однородные координаты 219
^.=
^.=
5 =
COS0 о sin0 О
0 10 0
-sin0 О cos^ О
О 0 0 1
COS!// -sini// о О
siny/ cosi/' О О
О 0 10
О 0 0 1
О О
О О
поворот вокруг оси ^2 на ф,
поворот вокруг оси Xj на i//,
Р =
О
О
о
о
1
о о
о
о
о
1
масштабирование,
перспективная проекция.
О О -\/d' 1
Формулировка перспективной проекции незначительно отличается от
определения в уравнении (7.11). Предварительное умножение однородного вектора
на Рдает выражение
iJi I , tJi 2 ? ^-^ "^ 9 ^ '
-}Т
(7.62)
по которому мы получаем координаты изображения делением на четвертую
координату
X
d'
d'-X.
X.
d'
d'-X,
(7.63)
Из этого уравнения мы можем видеть, что плоскость изображения
помещается в начало отсчета, поскольку если Х^ = О, то и координаты изображения, и
мировые координаты тождественны. Центр проекции сдвинут в [О, О, -d'Y.
Полные преобразования из мировых координат в координаты изображения
могут состоять из этих элементарных матриц. Страт (Strat) [196], например,
предложил следующее разложение:
M = CSPRRRT.
(7.64)
Глава 7. Формирование изображений
Масштабирование 5 и кадрирование (перемещение) С являются
преобразованиями, имеющими место в двумерной плоскости изображения. Страт [196]
показал, как полные параметры преобразований из координат камеры в мировые
координаты можно определить неитерационным образом по набору калибровочных
точек внешней камеры, чьи положения в пространстве точно известны. Таким
образом, можно получить абсолютную калибровку внешних параметров камеры:
положения и ориентации — и внутренних параметров: точки отверстия
оптической оси, фокусного расстояния и размера пикселя.
7.8. Упражнения
7.1: ^'^Формирование изображений с помощью камеры-обскуры
1. Каким является соотношение между координатами объекта и
изображения для камеры-обскуры?
2. Какой геометрический объект является изображением прямой линии с
точками AviE, треугольника с точками А,БиВи плоского, и неплоского квадрата?
3. Предположите, что вы знаете длину прямой линии и положение А одного
из концов в мировых координатах. Возможно ли тогда определить вторую
точку конца Б по координатам изображения а и ^?
7.2: "^Геометрия формирования изображений с помоидью рентгеновских лучей
Можно ли описать формирование изображений посредством рентгеновских
лучей, которые исходят из отдельной точки и измеряются на проекционном
экране, также с помощью проективного формирования изображений? В этом
случае объект располагается между источником рентгеновских лучей и
проекционным экраном. Каково в этом случае соотношение между координатами
изображения и мировыми координатами? Подготовьте набросок геометрии.
7.3: ^'^^Глубина ноля при рентгеновском формировании изображений
Возможно ли ограничить глубину поля при рентгеновском формировании
изображений? (Подсказка: вы не можете использовать какую-либо линзу для
рентгеновских лучей.) Глубина поля связана с тем, что линза собирает лучи
от точки объекта, которые распространяются в диапазоне направлений. Как
можно использовать этот принцип с системой, которая не формирует
изображение? Исследуемый объект не движется.
7.4: "^Высокая глубина поля
Вы сталкиваетесь со следующей проблемой. Объект должен измеряться с
максимально возможной глубиной поля. Условия освещенности, которые не
могут меняться, офаничивают апертуру «^максимальным значением 4. Объект
имеет протяженность 320 х 240 мм^ и должен заполнять весь размер
изображения при получении изображения с расстояния 2,0 ± 0,5 м. В вашем
распоряжении две камеры с разрешением 640 х 480 пикселей. Пиксельный размер
одной камеры составляет 9,9 х 9,9 мкм^, размер другой камеры 5,6 х 5,6 мкм^
(>-R2). Вы можете использовать любое фокусное расстояние линзы. Вопросы:
1. Какое фокусное расстояние вы выберете?
2. Какая из двух камер дает большую глубину поля?
7.9. Дополнительная литература
1.5: "^Диффракционно-ограниченное разрешение
При какой апертуре «^дифракционно-ограниченное разрешение равно
размеру элемента датчика? Используйте элементы датчиков с размерами
4,4 X 4,4 мкм^ и 6,7 х 6,7 мкм1 Что происходит при больших значениях п^
7.9. Дополнительная литература
в этой главе рассматриваются только основные принципы методов
формирования изображений. Более детальное рассмотрение можно найти в работе Яне (Jahne)
или Ричардса (Richards) [165]. Геометрические аспекты формирования
изображений также представляют важность для компьютерной графики и, следовательно,
детально рассматриваются в стандартных учебных пособиях по компьютерной
графике, например. Ватт (Watt) [211] или Фоли (Foley) и др. [52]. Больше деталей
относительно теоретической оптики можно найти в следующих учебных пособиях:
Изука (lizuka) [85] (особенно об оптике Фурье) и Смит (Smith) [191]. Ридл (Riedl)
[168] сфокусировал свое внимание на разработке инфракрасной оптики. В этой
главе была подчеркнута важность теории линейных систем для описания
оптических систем. Теория линейных систем имеет широкое применение в науке и
технике, см., например, Клозе (Close) и Фредерик (Frederick) [24] или Дорф (Dorf) и
Бишоп (Bishop) [36].
ГЛАВА 8
3-D ФОРМИРОВАНИЕ ИЗОБРАЖЕНИЙ
8.1. Введение
в этой главе мы рассматриваем различные методы формирования изображений,
нацеленные на восстановление глубинной координаты, которая теряется при
проектировании объекта на плоскость изображения. Эти методы принадлежат к двум категориям.
Они либо восстанавливают только глубинную координату поверхности в 3-D
пространстве, либо предусматривают полную реконструкцию объемных объектов. Часто оба
понятия глубинного формирования изображений и объемного формирования изображений на-
зьшаются 3-D формированием изображений. Это вызьшает большую путаницу.
Но даже более сбивающим с толку является широкое разнообразие как
методов глубинного формирования изображений, так и методов объемного
формирования изображений. Поэтому эта глава не будет детально рассматривать все
доступные методы. Она скорее фокусируется на основных принципах. Удивительно
это или нет, но суш;ествует только несколько принципов, на которых основано
широкое разнообразие методов 3-D формирования изображений. Если вы знаете
их, то легко понять, как они работают и какую точность вы можете ожидать.
Мы начинаем с рассмотрения основного ограничения проективного
формирования изображений для 3-D видения (раздел 8.1.1), затем даем краткий обзор
основных принципов глубинного формирования изображений (раздел 8.1.2) и
объемного формирования изображении (раздел 8.1.3). По одному разделу
посвящено каждому из основных принципов 3-D формирования изображений:
определение глубины по методу триангуляции (раздел 8.2), определение глубины по
методу времени пролета (раздел 8.3), определение глубины по фазе (интерферометрия)
(раздел 8.4), определение формы по теням, фотограмметрическая система
стереоскопического зрения (раздел 8.5), и томография (раздел 8.6).
8.1.1. Основное ограничение проективного формирования изображений
Как мы уже детально рассмотрели в разделах 7.6.1 и 7.6.2, проективная оптическая
система является линейной инвариантной относительно сдвига системой,
которую можно описывать функцией рассеяния точки (ФРТ) и оптической
передаточной функцией (ОПФ).
3-D ОПФ для геометрической оптики показывает наилучшим образом
ограничения проективной системы формирования изображений (см. раздел 7.6.2):
%Дз) =
2L
t 1 2 V/2
О
п 19tana I
к
1-2 2
а Хш\ а ,
V ^ J
/
П
h
ylqXdina .
(8.1)
Символы qvik^ обозначают радиальную и осевую компоненты вектора волнового
числа соответственно. Два серьезных ограничения 3-D формирования
изображений сразу же следуют из формы 3-D ОПФ.
8.1. Введение
Полная потеря в широком диапазоне волновых чисел. Как показано на рис. 7.23, б,
3-D ОПФ является осесимметричной относительно оси к^ (направление z) и не
равна нулю только внутри конуса с углом ± а относительно плоскости ху.
Структуры с широким диапазоном волновых чисел, особенно относительно оси z,
полностью теряются. Мы можем «видеть» только структуры в тех направлениях, по
которым оптика накапливает лучи.
Потеря контрастности при высоких волновых числах. Согласно уравнению (8.1),
ОПФ обратно пропорциональна радиальному волновому числу д. Следовательно,
контрастность периодической структуры ослабляется пропорционально ее
волновому числу. Поскольку это свойство ОПФ действительно для всех оптических
систем формирования изображений, включая зрительную систему человека,
возникает вопрос: почему мы можем видеть мелкие структуры вообще?
Ответ содержится в более тщательном исследовании геометрической структуры
наблюдаемых объектов. Большинство объектов в естественной окружающей среде
являются непрозрачными. Таким образом, мы видим только поверхности, т.е. мы не
наблюдаем реальные 3-D объекты, а только 2-D поверхностные структуры. Если мы
отображаем 2-D структуру на 2-D плоскость изображения, то 3-D ФРС также
сводится к 2-D функции. Математически это означает умножение ФРГ на ^плоскость,
параллельную наблюдаемой поверхности. Следовательно, диск размытости,
соответствующий расстоянию от линзы до поверхности, теперь задает 2-D ФРГ. Ограничение до
2-D поверхностей, таким образом, сохраняет интенсивность всех структур с длинами
волны большими, чем диск. Мы можем видеть их с той же контрастностью.
Мы приходим к тому же заключению в Фурье-пространстве. Умножение 3-D
ОПФ на 5-плоскость в х-пространстве соответствует свертке 3-D ОПФ с 5-линией
вдоль оптической оси, т.е. интегрирование в соответствующем направлении. Если
мы интегрируем 3-D ОПФ вдоль координаты к, то, в действительности получаем
константу, не зависящую от радиального волнового числа q:
,.а„а ^
±10. Г
^ Janaktana
I ^tana
dz' = 4 (8.2)
Для решения интеграла, сделаем замену z''=z' /(q tana), которая дает интеграл
по единичной полуокружности.
В заключение: есть существенное различие между поверхностным
формированием изображений (и, таким образом, глубинным формированием изображений) и
объемным формированием изображений. ОПФ для поверхностных структур не
зависит от волнового числа. Однако для объемных структур мы все еще сталкиваемся с
проблемой убывания ОПФ в зависимости от радиального волнового числа.
Наблюдая такие структуры глазом или с помощью камеры, мы не сможем видеть
мелкие детали. Проективные системы формирования изображений не
разрабатываются для изображения истинных 3-D объектов. Следовательно, объемное
формирование изображений требует иных методов.
8.1.2. Основные принципы глубинного формирования изображений
Глубинное формирование изображений отдельной непрозрачной поверхности
требует некоторой дополнительной информации, помимо яркости в каждом пикселе
изображения, для того чтобы получить глубинное изображение или дальностную
Глава 8. 3-D формирование изображений
картину. Мы можем вьщелить четыре основных принципа глубинного
формирования изображений, известных как определение глубины по парадигмам.
Определение глубины по методу триангуляции. Если мы наблюдаем объект с двух
различных точек обзора, разделенных базовой линией й, то объект будет виден под
разными углами к базовой линии из двух положений. Этот метод известен как
триангуляция и составляет один из основных методов в геодезии и картографии.
Метод триангуляции лежит в основе удивительно широкого разнообразия
методов. На первый взгляд эти методы кажутся настолько разными, что сложно
поверить, что они основаны на одном и том же принципе.
Определение глубины по методу времени пролета. Это еще один простой
принцип измерения расстояния. Посылается сигнал, он распространяется с
характеристической скоростью до объекта, отражается и возвращается обратно к камере.
Время прохождения прямо пропорционально сумме расстояний между
отправителем и объектом и объектом и получателем.
Определение глубины по фазе: интерферометрия. Интерферометрию можно
рассматривать как особый вид измерения расстояния по методу времени полета. Этот
метод измеряет расстояния в долях длины волны излучения с помощью измерения
не только амплитуды (энергии) излучения, но также и его фазы. Фазовые
измерения возможны с помощью наложения когерентного излучения (раздел 6.3.3),
ведущего к высоким интенсивностям в случае, когда два накладывающихся волновых
фронта совпадают по фазе (усиливающая интерференция), и к низким
интенсивностям, когда они показывают фазовый сдвиг 180** (;г, ослабляющая интерференция).
Свет имеет длины волн между 400 и 700 нм (раздел 6.3.1 и рис. 6.6). Следовательно,
интерферометрические измерения расстояния с помощью света разрешают
расстояния в нанометрическом диапазоне (10"^ м) - малой доле длины волны.
Определение глубины по когерентности. Еще одной характеристикой излучения
является длина когерентности (раздел 6.3.3), т.е. максимальная разность хода, при
которой все еще возможно когерентное наложение. Длину когерентности можно
легко измерить благодаря возможности создавать интерференционные картины.
Длины когерентности могут составлять всего несколько длин волн. Методы
определения глубины заполняют промежуток в диапазоне расстояний, который может из-
мерзпъся между интерферометрическими методами и методами времени полета.
Определение формы по полутоновому изображению. Форму поверхностей
можно также определить по локальной ориентации поверхностных элементов. Это
выражается математически поверхностью к нормали. Тогда, конечно, абсолютная
глубина поверхности теряется, но глубинный профиль можно вычислить
интегрированием угла наклона поверхности. Вывод о нормали к поверхности можно
сделать по обработке полутонов, поскольку энергетическая яркость поверхности
зависит от угла падения осветительного источника.
8.1.3. Основные принципы объемного формирования изображений
Любой метод определения глубины, который может измерять множественные
глубины одновременно, также полезен для объемного формирования изображений.
Способность измерять множествершые глубины является, таким образом, еще одной
характеристикой метода глубинного формирования изображений. В дополнение к
методам глубинного формирования изображений имеют место два новых базовых
принципа для объемных изображений:
8.2. Определение глубины по методу триангуляции
Расслаивание освещенности. В проектном формировании изображений мы не
знаем, из какой глубины исходит энергетическая освещенность, накопленная на
плоскости изображения. Она могла бы быть из любого места проекционного луча
(см. раздел 7.3.1 и рис. 7.3). Однако освещение может регулироваться таким
образом, чтобы только определенный диапазон глубин получал свет. Тогда мы знаем, из
какой глубины исходит энергетическая освещенность на плоскости изображения.
При исследовании глубины освещенности можно получить объемное изображение.
Определение глубины по множественным проекциям: томография. Отдельная
проекция содержит только частичную информацию от объемного объекта. Вопрос,
следовательно, заключается в том, возможно ли получить множественные
проекции от различных направлений и объединить различные компоненты частичной
информации для полного 3-D изображения. Такие методы определения глубины по
множественным проекциям известны как томография,
8.1.4. Характеризация методов 3-D формирования изображений
Глубинное формирование изображений характеризуется двумя базовыми
величинами — глубинным разрешением а, и диапазоном глубин Az. Глубинное разрешение
обозначает статистическую ошибку измерения глубины и, таким образом,
минимальную разрешимую разность глубин. Обратите внимание, что систематическая
ошибка измерения глубины может быть гораздо больше (см. рассуждение в
разделе 3.1). То, как разрешение зависит от расстояния z, является важной
характеристикой метода глубинного формирования изображений. Существенно, например,
является ли разрешение равномерным, т.е. независимым от глубины, или убывает
в зависимости от расстояния z.
Диапазон глубин Az равен разности между минимальной и максимальной
глубинами, которые можно измерить методом глубинного формирования
изображений. Следовательно, отношение диапазона глубин и глубинного разрешения, Az/cr
обозначает динамический диапазон глубинного формирования изображений.
8.2. Определение глубины по методу триангуляции
Наблюдение одного и того же объекта из различных точек обзора, разделенных
базовым вектором й, приводит к различным углам наблюдения. Тем или иным образом
это различие в угле наблюдения приводргг к сдвигу на плоскости изображения,
известному как диспаратность, по которому можно сделать вьгеод о глубине объекта.
Измерения глубины на основе триангуляции включают широкое разнообразие
различных методов, которые на первый взгляд не имеют ничего общего, но они все
же основываются на одном и том же принципе. В этом разделе мы рассмотрим
стереоскопию (раздел 8.2.1); активную триангуляцию, где одна из двух камер
заменяется световым источником (раздел 8.2.2); определение глубины по фокусу (раздел 8.2.3)
и конфокальную микроскопию (раздел 8.2.4). В разделе, посвященном
стереоскопии, мы также рассмотрим базовую геометрию триангуляции.
8.2.1. Спектроскопия
Наблюдение сцены из двух различных точек обзора позволяет определить
расстояние до объектов. Установка с двумя датчиками формирования изображений на-
226 Глава 8. 3-D формирование изображений
Левая камера
Правая камера
Рис. 8.1. Стереоскопическая установка камер
зывается системой стереоскопического зрения. Многие биологические
зрительные системы осуществляют восприятие глубины таким способом. Рис. 8.1
иллюстрирует, как можно определить глубину с помощью стереоскопической установки
камер. Две камеры размещаются поблизости друг от друга с параллельными
оптическими осями. Вектор расстояния b между двумя оптическими осями называется
стереоскопическим базисом. Объект спроектируется на различные места плоскости
изображения, поскольку он наблюдается с незначительно отличных углов.
Различие в положении обозначается как диспаратность или параллакс, р. Его легко
вычислить по рис. 8.1:
•= х--х=а— а— = 6—.
Хз Х^ Х^
(8.3)
Параллакс обратно пропорционален расстоянию Х^ до объекта (ноль для
объекта на бесконечности) и обратно пропорционален стереоскопическому базису и
фокусному расстоянию камер (d'^fjim удаленных объектов). Таким образом,
оценка расстояния становится сложнее с увеличением расстояния. Это можно увидеть
более явно, если использовать закон распространения ошибки (раздел 3.3.3) для
вьиисления Х^:
;f,=^
bd'
X
р ' р bd "^
Следовательно, абсолютная чувствительность для оценки глубины убывает со
скоростью квадрата расстояния. В качестве примера возьмем стереосистему со
стереоскопическим базисом 200 мм и объективами с фокусным расстоянием 100 мм.
Тогда при расстоянии Юм изменение в параллаксе составляет приблизительно
200 мкм/м (приблизительно 20 пикселей/м), в то время как оно составляет только
2 мкм/м (0,2 пикселя/м) при расстоянии 100 м.
Параллакс является векторной величиной и параллелен стереоскопическому
базису й. Таким образом, если две камеры точно ориентированы, то мы знаем
направление параллакса заранее. С другой стороны, мы не можем вычислить параллакс во всех
случаях. Если сектор изображения не проявляет изменения уровней яркости в
направлении стереобазиса, то мы не можем определить параллакс. Эта проблема является
частным случаем так называемой апертурной проблемы, которая также имеет место в
определении движения и будет рассматриваться детально в разделе 14.2.2.
Информация о глубине, содержащаяся в стереоизображениях, может
пониматься непосредственно с помощью ряда методов. Во-первых, левое и правое
стереоизображения можно представить на одном изображении, если одно по-
8.2. Определение глубины по методу триангуляции
казывается в красном свете, а другое - в зеленом. Наблюдатель использует очки
с красным фильтром для правого и зеленым фильтром для левого глаза. Таким
образом, правый глаз наблюдает только зеленое, а левый глаз только красное
изображение. Недостаток этого так называемого анаглифного метода — в
невозможности использовать цветные изображения. Однако этот метод не требует никаких
специальных аппаратных средств, и стереоизображения могут экспонироваться
на любом RGB-мониторе или быть напечатанными с помощью стандартных
принтеров.
Вертикальная спектроскопия также подразумевает наблюдение цветных
стереоизображений [114]. Два составляющих изображения устанавливаются друг над
другом. При наблюдении посредством призменных очков, которые преломляют
верхнее изображение в правый глаз, а нижнее изображение в левый глаз, оба
изображения объединяются в 3-D изображение.
Другие стереоскопические формирователи изображений используют
специальные аппаратные средства. Общий принцип состоит в демонстрации левого и
правого стереоизображения с быстрым чередованием на мониторе и
переключением направления поляризации экрана одновременно. Наблюдатель носит
поляроид ные очки, которые отфильтровывают надлежащие изображения для левого и
правого глаза. Однако анаглифный метод обладает наибольшим потенциалом для
большинства применений, поскольку он может использоваться при почти любой
рабочей станции обработки изображений, при этом единственной
дополнительной частью аппаратных средств являются красно-зеленые очки. Увлекательный
обзор научного и технического использования стереоизображений дается
Лоренцем (Lorenz) [127].
8.2.2. Определение глубины с помощью активной триангуляции
Вместо стереоскопической установки камер одна камера может заменяться
источником света. Для восстановления глубины необходимо тогда определить в каждом
пикселе, из какого направления приходит освещение. Эти сведения
эквивалентны сведениям о диспаратности. Таким образом, метод активной триангуляции
разделяет все основные особенности со стереосистемой, которую мы обсуждали в
предьщуш;ем разделе.
Сложные методы были разработаны в последние годы для кодировки световых
лучей однозначным образом. Как правило, используются световые проекторы,
которые проектируют интерференционные картины с полосами,
перпендикулярными базовой линии триангуляции на сцену. Отдельной картины недостаточно для
определения положения картины на плоскости изображения однозначным
образом, но при последовательности интерференционных картин с различными
длинами волн, каждое горизонтальное положение на плоскости изображения светового
проектора можно определить с помощью однозначной последовательности темных
и светлых полос. Частичный ряд из шести таких картин показан на рис. 8.2.
Такая последовательность интерференционных картин имеет также
преимущество в том, что в пределах динамического диапазона камеры определение
интерференционных картин становится независимым от коэффициента отражения
объекта и от зависящей от расстояния энергетической освещенности светового
проектора. Проблема затемнения, которая очеввдна по тени за кофеваркой эсп-
рессо на рис. 8.2, остается.
3-D формирование изображений
Рис. 8.2. Активная триангуляция с помощью проектирования ряда
интерференционных картин с различными длинами волн для двоичного кодирования
горизонтального положения [218]
Двоичное кодирование посредством последовательности интерференционных
картин перестает работать для мелких интерференционных картин. Для
определения положения с высоким разрешением, как показано на рис. 8.3, сдвинутые по
фазе картины одной и той же длины работают гораздо лучше и в результате дают
положение с точностью до фрагментов пикселя на плоскости изображения
светового проектора. Поскольку фазовый сдвиг является однозначным только в
пределах длины волны интерференционной картины, на практике часто используется
гибридный код, который определяет грубое положение с помощью двоичного
кодирования и точное положение с помощью фазового сдвига.
8.2.3. Определение глубины по фокусу
Ограниченное поле глубин реальной оптической системы (раздел 7.4.3) является
еще одним методом для глубинного оценивания. Изображение объекта
формируется без размывания, только если он находится в пределах поля глубин. На
первый взгляд этот метод не похож на метод определения глубины по
триангуляции. Однако он имеет точно такую же геометрию, как метод триангуляции.
Единственное различие состоит в том, что вместо двух используется много лучей, а
радр1ус размытого круга заменяет диспаратность. База триангуляции соответствует
8.2. Определение глубины по методу триангуляции
Рис. 8.3. Активная триангуляция с помощью сдвинутых по фазе
интерференционных картин с одинаковой длиной волны. Показаны три из четырех картин с
фазовыми сдвигами 0% 90** и 180" [218]
диаметру оптики. Таким образом, методы определения глубины по фокусу
разделяют все основные свойства метода триангуляции. Для заданной оптики
разрешение уменьшается в зависимости от квадрата расстояния (сравните
уравнение (8.4) с уравнением (7.21)).
Рассмотрение ограничений проективного формирования изображений в
разделе 8.1.1 показало, что метод определения глубины по фокусу не работает для
объемного формирования изображений, поскольку большинство структур,
особенно структуры в направлении оптической оси, исчезают. Определение глубины
по фокусу является, однако, очень полезным и простым методом для определения
глубины непрозрачных поверхностей.
Штойрер (Steurer) и др. [194] разработали простой метод реконструкции
карты глубин по световому микроскопическому фокусному ряду. Карта глубин
является двумерной функцией, которая задает глубину точки объекта d —
относительно базовой плоскости - как функцию координат изображения [х, уУ.
С заданными ограничениями нужно найти только одно глубинное значение
для каждой точки изображения. Мы можем воспользоваться тем фактом, что 3-D
функция рассеяния точки оптического формирования изображений,
рассмотренная детально в разделе 7.6.1, имеет отчетливый максимум в фокальной плоскости,
поскольку интенсивность ослабевает в зависимости от квадрата расстояния от
фокальной плоскости. Это означает, что во всех точках, где мы получаем
отчетливые точки изображения, таких, как контуры, линии или локальные экстремумы,
мы также получим экстремум в уровне яркости на фокальной плоскости. На рис. 8.4
показано, что функции рассеяния точки соседних точек изображения только
минимально влияют друг на друга вблизи фокальной плоскости.
Метод Штойрера (Steurer) учитывает, что отчетливый максимум функции
рассеяния точки существует в фокальной плоскости. Этот алгоритм включает
следующие четыре шага:
1. Берем фокусный ряд с постоянными шагами по глубине.
2. Применяем подходящий фильтр, такой, как оператор дисперсии (раздел
15.2.2), для того чтобы вьщелить малые структуры. Изображения, обработанные с
помощью фильтра верхних частот, сегментируются для получения маски для
областей со значительными изменениями уровней яркости.
Поверхность
Глава 8. З-В формирование изображений
3. В маскированных областях
выполняем поиск максимальной
величины разности во всех
изображениях фокусного ряда.
Изображение, в котором возникает
максимум, задает глубинное
значение для карты глубин. С
помощью интерполяции значений
глубинное положение максимума
можно определить более точно,
чем с глубинным разрешением
ряда изображений [178].
4. Поскольку карта глубин не будет плотной, требуется интерполяция. Штой-
рер (Steurer) использовал метод наращивания областей с идущей следом
адаптивной фильтрацией нижних частот, которая применяется только к
интерполируемым областям, для того чтобы не повредить непосредственно вычисленные
значения глубин. Однако допустимы другие надежные методы, такие, как
нормированная свертка (раздел 11.6.2) или любой метод, описанный в разделе 17.2.
Рис. 8.4. Суперпозиция функции рассеяния точки
двух соседних точек на поверхности
Рис. 8.5. а — фокусный ряд с 16 изображениями металлической поверхности, взятый
с глубинными расстояниями 2 мкм; фокальная плоскость становится глубже слева
направо и сверху вниз; б — глубинная карта, вычисленная по фокусному ряду.
Глубина кодируется интенсивностью. Объекты, которые ближе к наблюдателю,
показаны светлее (Штойрер (Steurer) и др.)
8.2. Определение глубины по методу триангуляции
Этот метод был успешно использован для определения структуры поверхностей
обработанных металлических участков. На рис. 8.5 показывается, что были
достигнуты хорошие результаты. Можно видеть стружку, которая проектируется с
поверхности. Кроме того, на поверхности видны явные следы процесса шлифовки.
Этот метод работает, если только поверхность демонстрирует мелкие детали.
Если это не выполняется, то можно применять конфокальный метод освещения
Шойерманна (Scheuermann) и др. [178], который проектирует статистические
диаграммы в фокальную плоскость (сравните раздел 1.2.2 и рис. 1.3).
8.2.4. Конфокальная микроскопия
Объемное микроскопическое формирование изображений крайне важно для
материаловедения и наук о жизни. Следовательно, возникает вопрос: возможно ли
изменить процесс формирования изображений и, таким образом, функцию
рассеяния точки так, чтобы оптическая передаточная функция не обращалась больше в
ноль, особенно в направлении z.
Ответом на этот вопрос является конфокальная лазерная сканирующая
микроскопия. Ее основной принцип заключается в освещении только точек в фокальной
плоскости. Это достигается с помощью сканирования лазерного пучка по
плоскости изображения, которая фокусируется с помощью оптики микроскопа на
фокальной плоскости (рис. 8.6). Поскольку используется одна и та же оптика для
формирования изображений и освещения, распределение интенсивностей в
пространстве объекта задается приближенно с помощью функции рассеяния точки
микроскопа. (Имеют место незначительные различия, поскольку лазерный свет
является когерентным.) Только тонкий слой вблизи фокальной плоскости
получает сильную освещенность. Вне этого слоя освещенность убывает в зависимости
от квадрата расстояния от фокальной плоскости. Таким образом, вклады от
расфокусированных объектов вне фокальной плоскости сильно подавляются и
искажения уменьшаются. Однако можем ли мы получить полностью свободную от
искажений реконструкцию? Мы воспользуемся двумя независимыми взглядами для
ответа на этот вопрос.
Давайте сначала представим периодическую структуру в направлении z. В
стандартной микроскопии эта структура теряется, поскольку все глубины освещаются
с равной энергетической яркостью. В конфокальной микроскопии, однако, мы
можем по-прежнему наблюдать периодическое изменение в направлении z из-за
Образец
Микрообъектив
Дихроичный Апертура
расщепитель пучка
Фокальная Сканирующее Лазерный
плоскость устройство
микроскопа
возбуждающий
свет
Детектор
Рис. 8.6. Принцип конфокальной лазерной сканирующей микроскопии
Глава 8, 3-D формирование изображений
сильного убывания интенсивности освещения при условии, что длина волны в
направлении z не слишком мала.
Тот же факт можно проршлюстрировать, используя ФРТ. ФРТ конфокальной
микроскопии задается как произведение пространственного распределения ин-
тенсивностей и ФРТ оптического формирования изображений. Поскольку обе
функции убывают со скоростью z"^ ФРТ конфокального микроскопа убывает со
скоростью z~^. Эта, гораздо более резкая локализация ФРТ в направлении z
приводит к ненулевой ОПФ в направлении z вплоть до предела разрешения по z.
Превосходное 3-D формирование изображений конфокальной лазерной
сканирующей микроскопии демонстрируется на рис. 8.7. Изображение, полученное с
помощью стандартной микроскопии, показывает кристалл в форме квадратной
пирамиды, которая является четкой только в основании пирамиды (рис. 8.7, а),
В направлении вершины пирамиды контуры становятся более размытыми.
Противоположно, отдельное изображение, полученное с помощью конфокальной
Рис. 8.7. Демонстрация конфокальной лазерной сканирующей микроскопии
(КЛСМ): а — кристалл в форме квадратной пирамиды, изображенный с помощью
стандартной микроскопии, сфокусированной на основании пирамиды; б - схожий
объект, изображенный с помощью КЛСМ: только узкий контурный диапазон
высот, 2,5 мкм над основанием квадратной пирамиды, является видимым; в -
изображение, составленное из сканирования по диапазону глубин 6,2 мкм КЛСМ
изображений. Изображения представлены Карлом Цайсом Йена (Carl Zeiss Jena),
Общество с ограниченной ответственностью (GmbH, Германия).
8J. Определение глубины по методу времени пролета 233
лазерной сканирующей микроскопии, отображает только совсем узкий диапазон
высот (рис. 8.7, б). Изображение, составленное из сканирования по глубине 6,2
мкм с помощью сложения всех изображений, показывает четкое изображение для
всего диапазона глубин (рис. 8.7, в). Можно наблюдать многие мелкие детали,
которые не видны на изображении, полученном с помощью стандартной
микроскопии. Лазерный сканирующий микроскоп нашел широкое применение в
медицинских и биологических науках и исследовании материалов.
8.3. Определение глубины по методу времени пролета
Методы времени полета измеряют задержку, вызванную временем, за которое
сигнал проходит определенное расстояние. Если сигнал посылается с позиции
камеры, то он должен пройти в 2 раза большее расстояние между камерой и объектом,
отражающим сигнал. Следовательно, задержка т определяется соотношением
Iz
т=—, (8.5)
с
где с — скорость распространения сигнала. Из уравнения (8.5) очевидно, что
статистическая ошибка измерения глубины не зависит от расстояния до объекта. Она
зависит только от точности измерения задержки:
сх с
Z- —> G,-—G. (8.6)
2 ' 1 '
Это составляет существенное преимущество над методами триангуляции
(уравнение (8.4)).
При использовании метода времени пролета сразу же вспоминают об
импульсной модуляции, т.е. измерении времени полета путем испускания и получения
короткого импульса. Максимально измеримое расстояние зависит от частоты, с
которой посылаются импульсы к объекту. Для электромагнитных волн измерения
задержки очень затруднительны. Поскольку скорость света с равна 3-10^ м/с,
задержка составляет только 6,7 не на метр.
Импульсная модуляция является только одним из многих методов модуляции
сигнала для измерений времени полета. Еще одним значимым методом является
модуляция непрерывной волной (НВ-модуляция). В этом методе сигнал
модулируется периодически, и задержка измеряется как фазовый сдвиг между исходящим и
входящим сигналами:
z^-^ф ^ a^=^G^, (8.7)
где V — частота модуляции. Диапазон глубин задается при условии, что фаза может
измеряться однозначно только в диапазоне ±п:
Az = —= —. (8.8)
2v 2
Одним из самых существенных недостатков периодической модуляции, таким
образом, является ограниченный диапазон глубин. Эту проблему удается
преодолеть с помощью псевдошумовой модуляции, где амплитуда сигнала модулируется
случайно. Этот метод комбинирует высокое разрешение НВ-модуляции с
большим диапазоном расстояний импульсной модуляции.
Глава 8. 3-D формирование изображений
8.4. Определение глубины по фазе: интерферометрия
Интерферометрию можно рассматривать как частный случай модуляции
непрерывной волной. Модуляция задается непосредственно частотой
электромагнитного излучения. Кроме того, полезно рассматривать интерферометрию как
частный случай метода измерения диапазона, поскольку требуется когерентное
излучение (раздел 6.3.3). Из-за высоких частот света фазы уходящего и падающего
излучения не могут измеряться непосредственно, измеряются только изменения
амплитуды, вызванные когерентной оптической суперпозицией уходящего и
падающего света.
Ошибка в определении глубины и диапазон глубин для интерферометричес-
ких измерений расстояний задается просто уравнениями (8.7) и (8.8) и
соотношениями с = vA (раздел 6.3.1):
4л: 4л: ^ 2
Из-за малых длин волн света (0,4—0,7мкм) интерферометрические измерения
являются чрезвычайно чувствительными. Ограниченный диапазон глубин,
равный всего лишь половине длины волны, может быть преодолен с помощью
многоволновой интерферометрии.
Второй класс интерферометрических методов измерения дальности базируется
на свойствах излучения с длиной когерентности, равной всего лишь нескольким
длинам волн. Тогда интерференционные картины имеют место только для
короткого расстояния в несколько длин волн и могут, таким образом, быть использованы
для измерения глубины в сканирующей системе. Этот тип интерферометрии
известен как интерферометрия в белом свете или когерентная радиолокация.
8.5. Определение формы по полутоновому изображению
Методы определения формы по полутоновому изображению не дают
представления о глубине, а позволяют сделать вывод о нормали к поверхностям и, таким
образом, формируют совершенно новый класс методов реконструкции
поверхностей. Очевидно, что методы определения формы по полутоновому изображению не
могут дать информацию об абсолютных расстояниях.
8.5.1. Определение формы по полутоновому изображению для
поверхностей Ламберта
Сначала мы применим этот метод для диффузных отражающих непрозрачных
объектов. Ради простоты мы полагаем, что поверхность объекта Ламберта
освещается параллельными лучами. Энергетическая яркость L поверхности Ламберта
(раздел 6.4.3) не зависит от угла наблюдения и задается соотношением
L = ^^Ecosy, (8.10)
где Е — энергетическая освещенность; у— угол между нормалью к поверхности
и направлением освещения. Соотношение между нормалью к поверхности и
падающим и испускаемым излучением можно легче всего понять в градиент-
8.5. Определение формы по полутоновому изображению
ном пространстве. Это пространство образуется градиентом высоты поверхности
а{Х, Y):
s = Va =
= [s^,S2]'
да да
дХ'д¥_
Этот градиент непосредственно связан с нормалью к поверхности п соотношением
(8.11)
п =
да да
~дХ'~д¥'
-лТ
= [-5p-52,lf
(8.12)
Это уравнение показывает, что градиентное пространство можно понимать как
плоскость, параллельную плоскости ЛГКна высоте Z = 1, если мы обратим
направления осей Хи Y. Координаты Хи У, где вектор нормали к поверхности и другие
направленные векторы пересекают эту плоскость, являются соответствующими
координатами в градиентном пространстве.
Геометрия отражения Ламберта в градиентном пространстве иллюстрируется
на рис. 8.8. Без потери общности мы устанавливаем направление источника света
как направление х. Тогда направление света задается вектором /= (tan в., О, 1 )^, а
энергетическая яркость L поверхности можно выразить как
1=еШЕ.
пЧ _р{Х)
-S, tan 0+1
п
\п\\1\
п
>
+ tan^
e,^\ + sl+sl
(8.13)
Контурное графическое изображение распределения энергетической яркости
в градиентном пространстве показано на рис. 8.9, а для источника света с углом
падения в. = 0°. В случае светового источника в зените контурные линии равной
энергетической яркости обозначают линии с постоянным абсолютным наклоном
S = (s^ + ^2^) ^/^. Однако изменения энергетической яркости в зависимости от
наклона поверхности малы, особенно для низких поверхностных наклонов. Наклонное
освещение приводит к гораздо более высокому контрасту в энергетической
яркости (рис. 8.9, б). При наклонном освещении, однако, максимальный
поверхностный наклон в направлении, противоположном источнику света, ограничен ж/2 - в,
когда нормаль к поверхности перпендикулярна направлению света.
При единственном источнике освещения информация о нормали к
поверхности является неполной, даже если поверхностная отражательная способность
известна. Задается только компонент нормали к поверхности в направлении изме-
Нормаль к поверхности
Направление света
Рис. 8.8. Вычисление энергетической яркости, проиллюстрированное в
градиентном пространстве для поверхности Ламберта, освещаемой удаленным источником
света с углом падения в. и азимутальным углом 0., равным нулю
236 Глава 8. 3-D формирование изображений
Рис. 8.9. Контурное фафическое изображение энергетической яркости поверхности
Ламберта с однородной отражательной способностью, освещенной параллельным
светом, показанное в градиентном пространстве для наклонов поверхности между -1 и 1.
Энергетическая яркость нормируется энергетической яркостью для плоской
поверхности: а — нулевой угол падения в = О"; расстояние между контурными линиями
составляет 0,05; б - наклонное освещение с углом падения 45° и азимутальным углом 0°;
расстояние между контурными линиями равно 0,1
нения освещенности. Таким образом, поверхностная реконструкция с
единственным источником освещения образует сложную математическую проблему, которая
не будет рассматриваться здесь. В следующем разделе мы рассматриваем, сколько
источников освещения из различных направлений требуется для однозначного
решения задачи определения формы по полутоновому изображению. Этот метод
известен как фотометрическая система стереоскопического зрения.
8.5.2. Фотограмметрическая система стереоскопического зрения
Кривые контурные линии на рис. 8.9 указывают на то, что соотношение между
наклоном поверхности и энергетической яркостью является нелинейным. Это
означает, что даже если мы рассматриваем два разных направления освещения
одной и той же поверхности (рис. 8.10), наклон поверхности не может определяться
однозначно. Это имеет место, когда кривые контурные линии пересекают друг друга
в более чем одной точке. Только третья экспозиция с еще одним направлением
освещения сделала бы решение единственным.
Использование трех экспозиций также дает значительное преимущество
потому, что отражательная способность поверхности может быть исключена при
нормировании энергетических яркостей. В качестве примера мы освещаем поверхность
Ламберта с помощью одного и того же источника света с трех разных направлений:
/,=[0,0, if,
/2=[tan0,,O,lf,
/3 = [О, tan ^„ if.
(8.14)
8.5. Определение формы по полутоновому изображению 237
Рис. 8.10. Наложенные контурные графические изображения энергетической яркости
поверхности Ламберта с однородной отражательной способностью, освещенной
источником света с углом падения 45* и азимутальным углом 0° и 90* соответственно
Тогда
-Van^+l
ТьЙап^
^/^^ = "-2tan0,^
^l + tan^0.
(8.15)
Теперь уравнения становятся линейными по 5j и ^2 и — даже лучше —
несвязными: 5j и ^2 зависят только от L^/L^ и L^/L^ соответственно (рис. 8.11). К тому же
нормированная энергетическая яркость в уравнении (8.15) не зависит от
отражательной способности поверхности. Отражательная способность поверхности
содержится в уравнении (8.10) как множитель и, таким образом, уничтожается при
вычислении отношения распределений энергетических яркостей одной и той же
поверхности.
а б
0,5
■^^^^^^^Bf
-0.5
0.5
Рис. 8.11. Контурные графические изображения энергетической яркости
поверхности Ламберта, освещенной параллельным светом с углом падения 45° и
азимутальным углом 0° (а) и 90° (б) соответственно и нормированной энергетической
яркостью освещения при падении 0° согласно уравнению (8.15). Размер шага контурных
линий равен 0,1. Обратите внимание на совершенное линейное соотношение между
нормированной энергетической яркостью и компонентами наклона угла по л: и д^
Глава 8. 3-D формирование изображений
8.5.3. Определение формы по преломлению для зеркальных поверхностей
Для зеркальных поверхностей методы определения формы по полутоновому
изображению, рассмотренные в разделе 8.5.1, не работают совсем, поскольку свет
отражается в камеру, только когда угол падения от источника света равен углу
отражения. Таким образом, требуются протяженные источники света. Тогда оказывается,
что для прозрачных зеркальньгх: поверхностей методы определения формы по
преломлению являются более выгодными, чем методы определения формы по
отражению, поскольку энергетическая яркость выше, нелинейности зависимости между
наклоном и энергетической яркостью ниже, и можно измерить более крутые
наклоны поверхности.
Метод определения формы по преломлению требует особого освещения,
поскольку нет значительных изменений энергетической яркости, за исключением
небольшой доли света, отраженного от поверхности. Основой метода
определения формы по преломлению является телецентрическая система освещения,
которая преобразует пространственное распределение энергетической яркости в
угловое распределение энергетической яркости. Тогда все, что мы должны сделать, -
это вычислить отношение между наклоном поверхности и углом преломленного
пучка и использовать источник света с подходящим пространственным
распределением энергетической яркости.
На рис. 8.12 иллюстрируется оптическая геометрия для простого случая, когда
камера размещается гораздо выше, а источник света ниже прозрачной
поверхности среды с более высоким показателем преломления. Соотношение между
наклоном поверхности s и углом у определяется согласно Яне (Jahne) и др. [97], как
«tan/ .^
5 = tana = . ^4tany
«-A/l + tan^y
при п = п^/п J. Обратное соотношение равно
Г 2 ^
l + -tanV
V 2
Jn'+{п'-l)s' -I 1 г, 3 2^
tan/ =s г «—5'
1- — S
32
(8.16)
(8.17)
В принципе метод определения формы по преломлению работает для
наклонов вплоть до бесконечного (вертикальные поверхности). В этом предельном
случае луч к камере скользит по поверхности (рис. 8.12, б) и
1ту = у1п^-\. (8.18)
Закон преломления, таким образом, заставляет световые лучи наклоняться в
определенном направлении относительно наклона поверхности воды. Если мы
делаем энергетическую яркость источника света зависимой от направления
световых пучков, наклон поверхности воды становится видимым. Детали построения
такой системы описываются Яне (Jahne) и др. [97]. Здесь мы просто полагаем, что
энергетическая яркость световых лучей пропорциональна 1апув направлении х^
Тогда мы получаем соотношение
8.5. Определение формы по полутоновому изображению 239
ff=[-Si,-S2,l]
M-5i.-5^1]^^
Рис. 8.12. Преломление на наклонной поверхности как основа для метода
определения формы по преломлению. Камера находится гораздо выше поверхности:
а — лучи, испускаемые источником света под углом /, преломляются в
направлении камеры; б - даже для наклона, равного бесконечности (вертикальная
поверхность, а= 90°), лучи от источника света достигают камеры
Конечно, мы снова сталкиваемся с проблемой: по скалярной величине, такой,
как энергетическая яркость, невозможно сделать вывод о векторном компоненте,
таком, как наклон. Метод определения формы по преломлению, однако,
подходит очень близко к идеальной установке. Если энергетическая яркость изменяется
линейно только в направлении Xj, как предполагалось, карта энергетической
яркости в градиентном пространстве является также почти линейной (рис. 8.13).
Незначительное влияние поперечного наклона (получающегося из нелинейных
членов в уравнении (8.19) по s^) становится очевидным только при довольно
высоких наклонах.
Рис. 8.13. Карта энергетической яркости для метода определения формы по
преломлению, где энергетическая яркость в телецентрическом источнике освещения
изменяется линейно в направлении х^
Глава 8. 3-D формирование изображений
Нормирование в формировании изображения можно также использовать в
методе определения формы по преломлению. Цветные изображения имеют три
независимых основных цвета - красный, зеленый и синий. Для всех трех каналов
мы можем определить положение в телецентрической системе освещения — и,
таким образом, наклон поверхности воды — однозначно и все еще иметь одну
степень свободы, оставленную для корректировок. При цветовом формировании
изображений мы также имеем преимущество, так как все три освещения берутся
одновременно. Таким образом, могут наблюдаться и движущиеся объекты.
Однозначное кодирование положения с помощью цвета можно получить,
например, с помощью следующих цветовых клиньев:
G{s) = {\l2 + cs,)E,{s),
(8.20)
R{s) = {\l2-cl2{s,+s,))E,{s),
B(s) = (m-c/2(s,-s,))E,(s).
Мы снова предположили линейное соотношение между одной компонентой
наклона и энергетической яркостью, с нелинейными изотропными коррекциями
вида 5j£q(5); с — калибровочный коэффициент, связывающий измеренную
энергетическую яркость с наклоном поверхности.
Теперь мы имеем три направления освещения для определения двух
компонент наклона. Таким образом, мы можем взять одно для компенсации
нежелаемого пространственного изменения Е^, Это можно сделать с помощью
нормирования трех цветовых каналов по сумме всех каналов G + R + В:
2
G-^-R + B 3
B-R 2 (8-21)
= —cs..
G+R+B 3
Тогда положение на клине, из которого возникает свет, задается как
1 2G-R-B 3 B-R ^^_
^1 = , ^2= . (8.22)
' 1с G + R + B ' IcG + R^B
По этим значениям положения компоненты наклона по х и з^ можно
вычислить согласно уравнению (8.19).
8.6. Определение глубины по множественным проекциям:
томография
8.6.1. Принцип
Томографические методы не создают 3-D изображение объекта непосредственно, а
позволяют реконструировать 3-D форму объектов, используя подходящие методы.
Томографические методы можно рассматривать как расширение спектроскопии. С
помощью спектроскопии можно сделать вывод только о глубине поверхностей, но
не о 3-D форме прозрачных объектов. Интуитивно мы можем предположить, что
необходимо наблюдать такой объект из как можно большего числа направлений.
8.6. Определение глубины по множественным проекциям: томография 241
Рис. 8.14. а - параллельная проекция; б - проекция с расходящимся пучком в
томографии
Томофафические методы используют излучение, которое проникает в объект
из разных направлений. Если мы используем точечный источник (рис. 8.14, б), то
наблюдаем перспективную проекцию или проекцию с расходящимся пучком на
экране позади объекта, как в оптическом формировании изображений (раздел 7.3).
Такое изображение берется по различным направлениям проектирования с помощью
вращения точечного источника и проекционного экрана вокруг объекта. Подобным
образом мы можем использовать параллельную проекцию (рис. 8.14, а), которую
легче анализировать, но сложнее осуществлять. Если объект поглощает излучение,
то потеря интенсивности, измеренная в проекции на экране, пропорциональна длине
пути луча в объекте. 3-D форма объекта не может реконструироваться по одной
проекции. Необходимо измерить проекции по всем направлениям с помощью
поворота источника излучения и проекционного экрана вокруг объекта.
Как и в других методах, томография может использовать взаимодействие
между веществом и излучением. Наиболее широко распространенным применением
является трансмиссионная томография. Механизм формирования изображений
основывается на поглощении излучения, например, рентгеновских лучей. Другие
методы включают эмиссионную томографию, томографию на отраженных волнах
и времяпролетную томографию (особенно с ультразвуком) и сложные методы
формирования изображений, у[сполъъую\щ[^ магнитный резонанс (MP).
8.6.2. Преобразование Радона и теорема о Фурье-слое
Что касается реконструкции, то важно обратить внимание, что проекции под всеми
углами 1^ можно рассматривать как еще одно 2-D представление изображения.
Одной координатой является положение в проекционном профиле г, другой —
угол I? (рис. 8.15). Следовательно, мы можем рассматривать параллельную
проекцию как преобразование изображения в другое 2-D представление. Реконструкция
тогда просто означает применение обратного преобразования. Решающий вопрос.
242 Глава 8. 3-D формирование изображений
Проекционный
пучок
Рис. 8.15. Геометрия проекционного пучка
следовательно, заключается в описании томографического преобразования
математически и исследовании, существует ли обратное преобразование.
Проекционный пучок характеризуется углом 1?и смещением г (рис. 8.15). Угол t>
является углом между плоскостью проекций и осью х. Кроме того, мы полагаем,
что мы нарезаем 3-D объект параллельно плоскости лу. Тогда скалярное
произведение между вектором х на проекционном пучке и единичным вектором
ii = [cos5,sin5f, (8.23)
нормальным к проекционному пучку, является постоянной величиной и равно
смещению г пучка
A(:#i-r = xcosi9-l->;sini9-r = 0. (8.24)
Проективная интенсивность Р(г, iS) определяется интегрированием вдоль
проекционного пучка:
Р(г,Э)= J g(x)ds= J {g(x)d(x^cos3 + X2sin9-r)d^x, (8.25)
путь -oo -oo
5-распределение в этом уравнении сводит двойной интеграл к проекционному
пучку в направлении г>, который имеет расстояние гот центра системы координат.
Проективное преобразование 2-D функции д(х) на Р(г, т}) называется в честь
математика Радона как преобразование Радона,
Для того чтобы лучше понять свойства преобразования Радона,
проанализируем его в Фурье-пространстве. Преобразование Радона можно понимать как
частный случай линейной инвариантной относительно сдвига фильтрующей
операции — проекционный оператор. Все уровни яркости вдоль проекционного пучка
суммируются. Следовательно, функция рассеяния точки проекционного
оператора является 5-линией в направлении проекционного пучка. В Фурье-области эта
операция свертки соответствует умножению на передаточную функцию, которая
является 5-линией (2-D) или 5-плоскостью (3-D), нормальной к 5-линии в
пространственной области (см. >-R5). Таким образом, проекционный оператор
вырезает из спектра линию или плоскость, перпендикулярную проекционному пучку.
Это элементарное соотношение можно вычислить легче всего, без потери
общности, в повернутой системе координат, в которой проекционное направление
8.6. Определение глубины по множественным проекциям: томография
совпадает с осью у\ Тогда координата г в Р{г, i}) совпадает с х\ а t>становится
нулевым. В этом частном случае преобразование Радона сводится к интегрированию
вдоль направления у':
оо
P(x\0)=jg(x,y)dy\ (8.26)
—оо
Преобразование Фурье проекционной функции можно записать как
оо
P(k^.,0) = J Р(х\0)Qxp(-2mk^.x)dx'. (8.27)
Заменяя Р{х\ 0) определением преобразования Радона, из уравнения (8.26)
получаем
hk,.0)=]\]g(x\yW
Qxp(-27iik^y)dx\ (8.28)
Если мы вставим множитель ехр(-2л:Юз;') = 1 в этот двойной интеграл, то
поймем, что интеграл является 2-D преобразованием Фурье от д(х', у) для к ,= 0:
Р(к^г ,0) = \ \ д(х\ у') ехр(-2Tri^^.x') ехр(~2л:10j^')dx:'dy'
-- (8.29)
= д(К.оу
Обратное преобразование в исходную систему координат окончательно дает
Р(Я.^) = д(к)5(к-(кп)п), (8.30)
где д — координата в А:-пространстве в направлении т},з,п — нормальный вектор,
введенный в уравнении (8.23). Спектр проекции идентичен спектру исходного
объекта на пучке, нормальном направлению проекционного пучка. Этот важный
результат называется теоремой о Фурье-слое или проекционной теоремой.
8.6.3. Отфильтрованная обратная проекция
Если проекции со всех направлений доступны, то полученные слои спектра
покрывают полный спектр объекта. Обратное преобразование Фурье тогда
приводит к исходному объекту. Отфильтрованная обратная проекция использует этот
подход с незначительной модификацией. Если бы мы просто сложили спектры
отдельных проекционных пучков для получения полного спектра объекта, то
спектральная плотность для малых волновых чисел была бы слишком высокой,
поскольку пучки находятся ближе друг к другу при малых радиусах. Таким
образом, мы должны скорректировать спектр с помощью подходящего весового
множителя. В непрерывном случае геометрия очень проста. Плотность
проекционных пучков пропорциональна | к \'\ Следовательно, спектры проекционных
пучков должны умножаться на | Л |. Таким образом, отфильтрованная обратная
проекция является двухшаговым процессом. Сначала отдельные проекции
нужно отфильтровать, прежде чем выполнять реконструкцию с помощью
суммирования обратных проекций.
На первом шаге мы, таким образом, умножаем спектр каждого проекционного
направления на подходяшую весовую функцию w{\ к |). Конечно, эта операция мо-
Глава 8. 3-D формирование изображений
жет также выполняться как свертка с обратным преобразованием Фурье от w(| к |),
w{r). Из-за этого шага процедура называется отфильтрованной обратной проекцией.
На втором шаге выполняется обратная проекция, и каждая проекция задает
слой спектра. Сложение всех отфильтрованных спектров дает полный спектр.
Поскольку преобразование Фурье является линейной операцией, мы можем
складывать отфильтрованные проекции в пространственной области. В
пространственной области каждая отфильтрованная проекция содержит часть объекта, которая
постоянна в направлении проекционного пучка. Таким образом, мы можем
спроектировать обратно соответствующий уровень яркости отфильтрованной
проекции вдоль направления проекционного пучка и прибавить его к вкладам от всех
других проекционных пучков.
После наглядного описания принципа алгоритма формирования
отфильтрованной обратной проекции получим метод для непрерывного случая. Начнем с
преобразования Фурье объекта и запишем обратное преобразование Фурье в
полярных координатах {q, -&), для того чтобы воспользоваться теоремой о Фурье-слое:
In оо
д{х) = \ \ qg(q,3)Qxp[27j:iq(x^ cosi9 +Х2 sini9)]d^d0. (8.31)
о о
в этой формуле спектр уже умножается на волновое число q. Пределы
интегрирования, однако, все еще не являются правильными, чтобы применяться к
теореме о Фурье-слое (уравнение (8.30)). Координата q должна пробегать от -оо до оо,
at? — только от О до тс. В уравнении (8.31) мы интегрируем только по половине
пучка — от начала координат до бесконечности. Мы можем составить полный
пучок по двум половинным пучкам при углах ^ и i? + тс. Таким образом, мы
расщепляем интеграл в уравнении (8.31) на два, по диапазонам углов [О, к[ и [тс, 2тс[, и
получаем
д(х) = \ \ qg(q,3)Qxp[2mq(x^ cos 5 +Х2 sini9)]d^di9
о о
Я" оо
+ \\qg(-q,3')Qxp[--2mq(x^cosS'-\-X2sin3')]dqd3\
о о
используя следующие тождества:
9' = 9-\-7г, g(-q,S) = g{q,9'% cos(,90 = -cos(,9), sm(9') =-sin{9).
Теперь мы можем заново объединить ^ва интеграла, если заменим q на -q во
втором интеграле и заменим g(q,9) на P(q,S), согласно теореме о Фурье-слое
(уравнение (8.30)):
д(х) ={ {\q\P(q,9)Qxp[2niq{x^cos9 +Х2sini9)]d^di9. (8.32)
о -оо
Уравнение (8.32) задает обратное преобразование Радона и является основой
для алгоритма получения отфильтрованной обратной проекции. Внутренний
интеграл выполняет обратную проекцию отдельной проекции:
P'=<F-\\q\TP), (8.33)
8,6, Определение глубины по множественным проекциям: томография
^обозначает 1-D оператор преобразования Фурье. Р'есть проекционная
функция Р, умноженная в Фурье-пространстве на | ^ |. Если мы выполняем эту
операцию как свертку в пространственной области, то можем формально записать
P' = ['F-\\q\)]*P. (8.34)
Внешний интеграл в уравнении (8.32) по углу т}
п
д{х) = \р'{г,&)йЭ (8.35)
О
суммирует обратно спроектированные и отфильтрованные проекции по всем
направлениям и, таким образом, формирует реконструированное изображение. Обратите
внимание, что отфильтрованный проекционный профиль F{r, tS) в уравнении (8.35)
должен рассматриваться как 2-D функция для построения 2-D объекта д(х). Это означает,
что проекционный профиль проектируется обратно в проекционном направлении.
8.6.4. Дискретная отфильтрованная обратная проекция
Существуют некоторые еще нерассмотренные нами детали, которые вызывают
серьезные проблемы для реконструкции в бесконечном непрерывном случае. Во-
первых, мы видим, что невозможно реконструировать среднее значение объекта.
Из-за умножения на | А | в Фурье-области (уравнение (8.32)) д(0) уничтожается.
Во-вторых, совершенно невозможно реконструировать объект бесконечного
размера, поскольку любой проекционный пучок даст бесконечные значения.
К счастью, все эти сложности исчезают, когда мы переходим от бесконечного
непрерывного случая к конечному дискретному случаю, где объекты имеют
ограниченный размер. На практике ограничение размера задается расстоянием между
источником излучения и детектором. Разрешение проекционного профиля
ограничивается комбинированными эффектами протяженности источника излучения
и разрешением матрицы детекторов на проекционной плоскости. И, наконец, мы
можем взять только ограниченное число проекций. Это соответствует
дискретизации угла 1? в представлении изображения Радона.
Проиллюстрируем рассмотренное в этом разделе примером. Мы можем узнать
многое о проекции и реконструкции с помощью рассмотрения реконструкции
простейшего объекта — точки, поскольку преобразование Радона (уравнение (8.25))
и его обратное преобразование являются линейными преобразованиями. Тогда
проекции со всех направлений равны (рис.8.16, а) и показывают четкий максимум
в проекционных функциях Р(г, г?). На первом шаге алгоритма построения
отфильтрованной обратной проекции Р сворачивается с фильтром | А |. Результатом
является модифицированная проекционная функция Р', которая тождественна
функции рассеяния точки фильтра | к | (рис. 8.16, б).
На втором шаге обратные проекции складываются на изображении. Из рис. 8.16, в
мы можем увидеть, что в положении точки в изображении складываются
максимумы от всех проекций. Во всех других положениях в изображениях отфильтрованные
обратные проекции накладьюаются друг на друга уничтожающим образом, поскольку
они показывают отрицательные и положительные значения. Если проекционные
направления достаточно близки друг к другу, то они уничтожают друг друга, за
исключением точки в центре изображения. На рис. 8.16, в также демонстрируется, что
недостаточное число проекций приводит к звездообразным структурам искажений.
246 Глава 8. 3-D формирование изображений
Рис. 8.16. Иллюстрация алгоритма получения отфильтрованной обратной проекции на
примере точечного объекта: а — проекции с различных направлений; б — фильтрация
проекционных функций; в — обратная проекция: сложение отфильтрованных проекций
Простой пример реконструкции точки по ее проекциям также полезен для
иллюстрации важности фильтрации проекций. Давайте представим, что происходит
в случае, когда мы опускаем этот шаг. Тогда бы мы сложили 5-линии как обратные
проекции, которые вращаются вокруг положения точки. Следовательно, мы не
получили бы точку, а получили бы вращательно-симметричную функцию,
которая убывает со скоростью | дс |"^ В результате реконструированные объекты были
бы значительно размытыми.
8.7. Упражнения
8.1: Стереоскопия
Интерактивная демонстрация реконструкции карт глубин по
стереоизображениям (dip6ex08.01).
8.2: "^Стереоскопическое зрение человека
Оцените, насколько хорошо зрительная система человека может оценивать
глубину. Положите фокусное расстояние глаза равным 17 мм, а стерео-
базу — равной 65 мм.
Ответьте на следующие вопросы:
8.8. Дополнительная литература
1. При каком расстоянии параллакс равен пространственному
разрешению глаза? Положите, что глаз является дифракционно-ограниченной
оптической системой (раздел 7.6.3) с апертурой 3 мм.
2. Насколько большим является среднеквадратичное отклонение оценки
глубины при расстоянии 0,5 и 5 м, если мы полагаем, что
среднеквадратичное отклонение измерения параллакса составляет четверть
пространственного разрешения глаза?
8.3: Определение глубины по фокусу
Интерактивная демонстрация реконструкции изображений с большим
полем глубин и карт глубин по фокусному ряду (dip6ex08.02).
8.4: Томография
Интерактивная демонстрация преобразования Радона и томографической
реконструкции с использованием отфильтрованной обратной проекции;
демонстрация искажений при реконструкции (dip6ex08.03).
8.5: **Искажения при томографии
На практике часто требуется проводить томографию как можно с меньшим
числом проекций. Представьте, что угловые интервалы становятся все
больше и больше. Рассмотрите, что происходит, используя точечный объект с
распределением Гаусса и среднеквадратичным отклонением с.
1. Когда начинаются искажения и на что они похожи?
2. Где эти искажения возникают сначала?
3. Вы можете заключить из этих наблюдений, является ли разрешение
томографической системы независимой от положения?
8.6: ***Томография с несколькими проекциями
При особых классах объектов можно применять томографические методы
только с несколькими проекциями. Исследуйте следуюпцие примеры и
определите, сколько требуется проекций для полной реконструкции:
1. Произвольный осесимметричный объект.
2. Произвольно сформированный объект без отверстий (только одна
поверхность), состоящий из однородного материала.
3. Несколько малых объектов, которые не накладываются друг на друга ни
в одной проекции. Вам нужно только определить центр тяжести этих
объектов и их объем.
8.8. Дополнительная литература
Часть с семью главами «Руководства по компьютерному зрению и
применениям» («Handbook of Computer Vision and Applications») посвящена 3-D
формированию изображений [94, т. I, ч. IV]. Клетте (Юette) и др. [109] рассматривают 3-D
компьютерное зрение, фокусируясь на стереоскопическом зрении,
фотометрическом стереоскопическом зрении и определении формы по полутоновому
изображению.
ГЛАВА 9
ПРЕОБРАЗОВАНИЕ В ЦИФРОВУЮ ФОРМУ,
ДИСКРЕТИЗАЦИЯ, КВАНТОВАНИЕ
9.1. Определение и эффекты, связанные с преобразованием
в цифровую форму
Последним шагом формирования цифрового изображения является
преобразование в цифровую форму. Это означает выборку уровней яркости в дискретном
множестве точек, которые можно представить матрицей. Дискретизация может
иметь место уже в датчике, преобразующем накопленные фотоны в
электрический сигнал. В стандартной трубчатой камере изображение выбирается по
линиям, поскольку электронный пучок сканирует формирующую изображения
трубку от линии к линии. ПЗС-камера уже имеет матрицу дискретных датчиков.
Каждый датчик является выборочной точкой на 2-D сетке. Стандартный
видеосигнал, однако, является опять аналоговым сигналом. Следовательно, мы
теряем горизонтальную выборку, поскольку сигнал от линии датчиков
преобразуется снова в аналоговый сигнал.
На первый взгляд кажется, что преобразование в цифровую форму
непрерывного изображения является огромной потерей информации, поскольку
непрерывная функция сводится к функции на сетке узлов. Поэтому возникает
вопрос: какой критерий мы можем использовать для обеспечения адекватности
представления непрерывного изображения по выбранным точкам, без потери
информации. Мы также хотим знать, как и до какой степени мы можем
реконструировать непрерывное изображение по выбранным точкам. Мы подойдем к этим
вопросам с помощью иллюстраций искажений, которые получаются при
неправильной дискретизации.
Интуитивно ясно, что дискретизация ведет к уменьшению разрешения, т.е.
структуры, имеющие размеры, равные расстоянию выборки и меньше, будут
потеряны. Может показаться удивительным, что значительные искажения
возникают, если мы дискретизируем изображение, которое содержит мелкие структуры.
На рис. 9.1 показан простой пример. Преобразование в цифровую форму
моделируется наложением 2-D сетки на объект, включающий две линейные сетки с
различными сеточными постоянными. После дискретизации кажется, что обе сетки
имеют сеточные постоянные с различной периодичностью и направлением. Этот
вид искажения изображений называется муар-эффектом.
То же явление, называемое наложением спектров, известно для
одномерных сигналов, особенно временных рядов. На рис. 9.2 показан сигнал с
синусоидальным колебанием. Он выбирается с расстоянием выборки, которая
незначительно меньше, чем его длина волны. В результате мы будем наблюдать
торазцо большую длину волны. Всякий раз, когда мы преобразуем в цифровую
форму аналоговый сигнал, возникают эти проблемы. В этом отношении обра-
p. 7. Определение и эффекты, связанные с преобразованием в цифровую форму 249
Рис. 9.1. Муар-эффект: а — исходное изображение с двумя периодическими
структурами: верхняя - /г = [0,21; 0,22]^, нижняя — Л= [0,21; 0,24]^; б — каждая четвертая;
в - каждая пятая точка выбирается в каждом направлении соответственно
ботка изображений является только частным случаем более общей области
науки — теории сигналов.
Поскольку эффект наложения спектров продемонстрирован на примере
периодических сигналов, ключевым к пониманию и, таким образом, избеганию
является анализ процесса преобразования в цифровую форму в
Фурье-пространстве. Далее мы будем выполнять этот анализ шаг за шагом. В результате мы
сможем сформулировать условия, при которых выбранные точки являются
корректным и полным представлением непрерывного изображения в так
называемой теореме о дискретном представлении. Следующие рассуждения не являются
строгим математическим доказательством теоремы о дискретном
представлении, а являются, скорее, наглядным подходом.
Рис. 9.2. Демонстрация эффекга наложения спекгров: колебательный сигнал
выбирается с расстоянием выборки Ах, равной 9/10 длины волны. Результатом является
длина волны, возникающая при наложении, которая в 10 раз больше расстояния выборки
Глава 9. Преобразование в цифровую форму, дискретизация, квантование
9.2. Формирование изображений, дискретизация, отсечение
Нашей стартовой точкой является бесконечное непрерывное изображение д{х),
которое мы хотим отобразить в матрицу G. В этой процедуре мы будем учитывать
процесс формированры изображений, рассмотренный в разделе 7.6. Тогда мы
можем вьщелить три отдельных шага: формирование изображений, дискретизацию и
ограничение до конечной матрицы изображения.
9.2.1. Формирование изображений
Преобразование в цифровую форму нельзя рассматривать без процесса
формирования изображений. Оптическая система, включающая датчик, влияет на сигнал
изображения, так что мы должны учитывать этот процесс.
Преобразование в цифровую форму означает, что мы дискретизируем
изображение в определенных точках дискретной сетки, г^^ (раздел 2.2.3). Если мы
ограничиваем рассмотрения прямоугольными сетками, то эти точки можно записать в
соответствии с уравнением (2.2):
г^ „ = [mAxj, «Ахз f при m.neZ, (9.1)
Как правило, мы не накапливаем интенсивность освещенности точно в этих
точках, а скорее в определенной области вокруг них. В качестве примера возьмем
ПЗС-камеру, которая состоит из фотодиодов без каких-либо нечувствительных к
свету полос между ними. Далее полагаем, что фотодиоды одинаково
чувствительны по всей области. Тогда сигнал в узлах сетки является интегралом по площади
отдельных фотодиодов:
(w+l/2)Axi (п+\/2)Ах2
9(г.,„)= J j gXx)dx,dx,. (9.2)
(m-l/2)Axi («-1/2)AX2
Эта операция включает свертку с прямоугольной функцией-ящиком и
дискретизацию в узлах сетки. Эти два шага можно отделить. Мы можем выполнить сначала
непрерывную свертку, а затем дискретизацию. Таким образом, мы можем обобщить
процесс формирования изображений и отделить его от процесса дискретизации.
Поскольку свертка является ассоциативной операцией, мы можем объединить
процесс усреднения ПЗС-датчика с ФРТ оптической системы (раздел 7.6.1) в отдельный
процесс свертки. Следовательно, мы можем описьшать процесс формирования
изображений в пространственной области и Фурье-области с помошд>ю следующей операции:
оо
gix)=jgXx')Kx-x)d'x о . g{k) = g\k)h\k), (9.3)
где h(x) и h{k) — результирующие ФРТ и ОПФ соответственно, а д\х) можно
рассматривать как изображение различной яркости, которое могло бы получиться с
помощью совершенного датчика, т.е. оптической системы (включающей датчик),
чья ОПФ тождественна единице и чья ФРТ является 5-функцией.
Как правило, процесс формирования изображений приводит к размыванию
изображения; мелкие детали теряются. В Фурье-пространстве это ведет к ослаблению
высоких волновых чисел. Формируется результирующее яркостное изображение
с ограниченной полосой пропускания.
9.2. Формирование изображений, дискретизация, отсечение
9.2.2. Дискретизация
Теперь мы выполним дискретизацию. Дискретизация означает, что теряется вся
информация, за исключением узлов сетки. Математически этот процесс состоит в
умножении непрерывной функции на функцию, которая равна нулю везде, за
исключением узлов сетки. Эта операция может выполняться с помощью умножения
функции изображения д(х) на сумму 5-функций, размещенных в узлах сетки г^^
(уравнение (9.1)). Эта функция называется двумерным 5-гребнем или функцией
«ложе гвоздей». Тогда дискретизацию можно выразить как
где
1
при w,UG Z И пА:^ = (9.5)
Ах
- узлы так называемой обратной сетки, которая играет значимую роль в физике
твердых тел и кристаллографии. Согласно теореме о свертке (теорема 2.4, с. 61),
умножение изображения на 2-D 5-гребень соответствует свертке преобразования Фурье от
изображения, спектра изображения, с другим 2-D 5-гребнем, чьи сеточные
постоянные являются обратными к сеточным постоянным в пространстве х (см. уравнения
(9.1) и (9.5)). Плотная дискретизация в пространстве х приводит к крупной сетке в
пространстве к, и наоборот. Следовательно, дискретизация приводит к
воспроизведению спектра изображения в каждом узле сетки г^ ^ в Фурье-пространстве.
9.2.3. Теорема о дискретном представлении
Теперь мы можем сформулировать условие, при котором мы не получаем
искажения сигнала при дискретизации, известное как теорема о дискретном
представлении. Если спектр изображения является настолько протяженным, что части его
перекрываются с периодически повторяемыми копиями, тогда перекрывающиеся
части чередуются. Мы не можем вьщелить, получаются ли спектральные
амплитуды из исходного спектра в центре или из одной из копий. Для того чтобы не
получить каких-либо искажений, мы должны избежать наложения.
Надежное условие для избегания наложения состоит в следующем: спектр
должен ограничиваться областью, которая имеет протяженность вокруг
центрального узла сетки вплоть до линий, разбивающих область между центральным узлом
сетки и всеми остальными узлами. В физике твердых тел эта зона называется
первой зоной Бриллюэна [108].
На прямоугольной fF-мерной сетке это дает в результате простое условие,
состоящее в том, что максимальное волновое число, при котором спектр
изображения не равен нулю, должно ограничиваться до менее чем половиной сеточных
постоянных обратной сетки.
Теорема 9.1 (Теорема о дискретном представлении). Если спектр непрерывной
функции д{к) является спектром с ограниченной полосой пропускания, т.е.
д(к) = 0 \/\kJ>akJ2, (9.6)
тогда он может реконструироваться точно по выборкам с расстоянием
Ах =1/рЛ„, (9.7)
Глава 9. Преобразование в цифровую форму, дискретизация, квантование
•
•
•
• 1 к^
k^j
• 1 •
Рис. 9.3. Объяснения муар-эффекта на примере периодической структуры, которая
не удовлетворяет условию дискретизации
Другими словами, мы корректно получим периодическую структуру, только
если возьмем по меньшей мере две выборки в длину волны. Максимальное
волновое число, которое может дискретизироваться без ошибок, называется
волновым числом Найквиста или предельным волновым числом. Далее мы будем часто
использовать безразмерные волновые числа, которые масштабируются
предельным волновым числом. Обозначим это масштабирование тильдой:
k =
К.
пкЛ
= 2^,,.Ах:,.
(9.8)
В этом масштабировании все компоненты волнового числа к^ попадают в
интервал ]-1, 1[.
Теперь мы можем объяснить муар-эффекты и эффекты из-за наложения
спектров. Начнем с периодической структуры, которая не удовлетворяет условию
дискретизации. Исходный спектр содержит единственный пик, который отмечен
длинным вектором к на рис. 9.3.
Из-за периодического повторения дискретизированного спектра имеется
точно один пик, в к\ который лежит в центральной ячейке. На рис. 9.3 показано, что
этот пик имеет не только другую длину волны, но, в общем случае, и другое
направление, что и наблюдается на рис. 9.1.
Наблюдаемое волновое число Л'отличается от истинного волнового числа к на
сеточный вектор перемеш;ения г^ ^ на обратной сетке. Индексы w и d должны
выбираться так, чтобы удовлетворять условию
I к^ + иик^ I < пкуИ
\к^+ипк^\ < ukjl, ^^-^^
Согласно этому условию, мы получаем волновое число, возникающее при
наложении спектра,
к[ = к,-пк,^91\0пк,-пк, = -\1\0ик,
для одномерного примера на рис. 9.2, как мы только что наблюдали.
(9.10)
9.2. Формирование изображений, дискретизация, отсечение 253
Теорема о дискретном представлении, согласно сформулированному выше,
является в действительности слишком строгим требованием. Достаточным и
необходимым условием является то, что периодические повторения спектров
изображений не должны перекрываться.
9.2.4. Ограничение до конечного окна
До сих пор дискретизированное изображение является все еще бесконечным в
размере. На практике мы можем работать только с конечными матрицами
изображений. Таким образом, последним шагом является ограничение изображения
до конечного размера окна. Простейшим случаем является умножение дискре-
тизированного изображения на функцию-ящик. Более обобщенно, мы можем
взять любую функцию окна w(jc), которая равна нулю для достаточно больших
значений х:
9i(x) = gXx)'w(x) о . g,(k) = gXk)^w(k). (9.11)
В Фурье-пространстве спектр дискретизированного изображения будет
сворачиваться с преобразованием Фурье функции окна. Давайте рассмотрим пример
оконной функции-ящика детально. Если окно в пространстве х включает Мх N
выборочных точек, его размер равен МАх^х NAx^. Преобразование Фурье от 2-D
функции-ящика есть 2-D sine функция (>-R5). Главный пик sine функции имеет
полуширину 1/(М AXj) X \/(N Ах^). Узкий пик в спектре изображения станет 2-D
sine функцией. Как правило, разрешение в спектре будет уменьшаться до
значения порядка полуширины sine функции.
В итоге дискретизация приводит к ограничению волнового числа, в то время
как ограничение размера изображения определяет волновое разрешение. Таким
образом, размеры в пространственных областях и областях волновых чисел
являются обратными друг к другу. Разрешение в пространственной области
определяет размер в области волновых чисел, и наоборот.
9.2.5. Стандартная дискретизация
Тип дискретизации, рассмотренный в разделе 9.2.1, с использованием примера
идеальной ПЗС-камеры называется стандартной дискретизацией. Здесь среднее
значение элементарной ячейки приписывается соответствующей выборочной
точке. Эта дискретизация является видом регулярной дискретизации, поскольку
каждая точка непрерывного пространства является одинаково взвешенной. Мы
могли бы склониться к предположению, что стандартная дискретизация
согласуется с теоремой о дискретизации. К сожалению, это не так (рис. 9.4). Для
волнового числа Найквиста преобразование Фурье функции-ящика равно все еще
1/V2. Первое пересечение нулевого уровня возникает при двойном волновом
числе Найквиста. Следовательно, муар-эффекты будут наблюдаться при
использовании ПЗС-камер. Эффекты являются даже более вьщеленными, поскольку
только малые доли, — как правило, 20% от площади чипа для камер с
построчным переносом — являются светочувствительными [120].
Сглаживание по большим областям с окном-ящиком не дает большой пользы,
поскольку преобразование Фурье окна-ящика убывает только со скоростью кг^
254 Глава 9. Преобразование в цифровую форму, дискретизация, квантование
1
0,8
0,6
0,4
0.2
О
Х/ДХ
-0,5
0,5
1
0,8
0,6
0,4
0,2
О
-0,2
Mil
Км nJz
I Г I I I I 11^1
-4-2024
Рис. 9.4. а — ФРТ; б — передаточная функция стандартной дискретизации
(рис. 9.4). Идеальная функция окна для дискретизации идентична идеальным
интерполяционным формулам (9.15), рассмотренным в разделе 9.3, поскольку ее
преобразование Фурье является функцией-ящиком с шириной элементарной ячейки
обратной сетки. Однако такое отсечение является невыполнимым. Детальное
рассмотрение интерполяции можно найти в разделе 10.5.
9.3. Реконструкция по выборкам
9.3.1. Совершенная реконструкция
Теорема о дискретном представлении обеспечивает условия, при которых мы
можем реконструировать непрерывную функцию по выбранным точкам, но мы все
еще не знаем, как выполнить реконструкцию непрерывного изображения по его
выборкам, т.е. операцию, обратную операции дискретизации.
Реконструкция выполняется подходящей интерполяцией выбранных точек. Как
правило, интерполируемые точки дрс) вычисляются по выбранным значениям
д(г^„), взвешенным с подходящими множителями, зависящими от расстояния от
интерполируемой точки:
9Лх) = ^Кх-г^^дЛГт,п).
(9.12)
Используя свойства интеграла 6-функции, мы можем заменить выбранные
точки справа на непрерывные значения:
9Л^) = I J Kx^x')g(x')5(r^„-x')dV
= J h(x-x)^d(r^„-x)g(x)dh\
Последний интеграл является сверткой весовой функции h с произведением
функции изображения д и 2-D 5-гребнем. В Фурье-пространстве свертка
заменяется комплексным умножением и наоборот:
9rik)^kk)J,g{k-iJ.
(9.13)
Интерполируемая функция не может равняться исходному изображению, если
периодически повторяемые спектры изображения перекрываются. В этом нет ни-
9.4, Многомерная дискретизация на неортогональных сетках
чего нового; это именно то, что утверждает теорема о дискретном представлении.
Интерполируемая функция изображения равна исходной функции изображения,
если только весовая функция является функцией-ящиком с шириной
элементарной ячейки обратной сетки. Тогда эффекты дискретизации — все повторяемые и
сдвинутые спектры — удаляются, и только исходный спектр с ограниченной
полосой пропускания остается, а уравнение (9.13) принимает вид
д^{к) = Щк,Ах„к,Ах,)д(к). (9.14)
Тогда интерполяционная функция является обратным преобразованием
Фурье функции-ящика, - sine функцией (>^R5):
h(x) = sinc(Xi / Ax:,)sinc(x2 / AxJ. (9.15)
9.3.2. Дискретизация с повышенной частотой
К сожалению, эта функция убывает только при стремлении к нулю 1/х.
Следовательно, корректная интерполяция требует большой области изображения;
математически она должна быть бесконечно большой. Это условие можно ослабить,
если мы «переполним» теорему о дискретном представлении, т.е. обеспечим,
чтобы g{k) равнялась нулю уже до того, как мы достигнем волнового числа Найквис-
та. Согласно уравнению (9.13), мы можем тогда выбрать h(k) произвольно в
области, где д обращается в нуль. Мы можем использовать эту свободу для построения
интерполяционной функции, которая убывает более быстро в пространственной
обрасти, т.е. имеет интерполяционную маску с минимальной длиной. Мы можем
также начать с заданных интерполяционных формул. Тогда отклонение ее
преобразования Фурье от функции-ящика говорит нам, до какой степени структуры
будут искажаться как функции волнового числа. Подходящие интерполяционные
функции будут рассматриваться детально в разделе 10.5.
Принцип дискретизации с повышенной частотой представляет важность не
только для построения эффективных интерполяционных функций. Он также
существен для разработки любого типа точного фильтра с малыми масками
фильтров (см. главы 11 и 12). Как правило, мы должны найти баланс между частотой
передискретизации, которая увеличивает число данных точек, и требованиями к
разработке фильтров. Практический опыт показывает, что частота выборки
между 3 и 6 выборками в длину волны, т.е. 1,5—3-кратная передискретизация,
является хорошим компромиссом.
9.4. Многомерная дискретизация на неортогональных сетках
До сих пор, дискретизация рассматривалась только для прямоугольных 2-D сеток.
Здесь мы увидим, что ее можно легко распространить на более высокие
размерности и неортогональные сетки. Требуется два дополнения.
Во-первых, Ж-мерные сеточные векторы должны определяться с
использованием набора Ж необязательно ортогональных базисных векторов А^, которые
покрывают W^-мерное пространство. Тогда вектор на решетке задается с помощью
r„=[n^b^,n^b^,...,n^b^fTipiin = [n,,n^,...,n^l n^eZ. (9.16)
В последовательностях изображений одной из этих координат является время.
Во-вторых, для некоторых типов решеток, например треугольная сетка, требуется
Глава 9. Преобразование в цифровую форму, дискретизация, квантование
больше чем одна точка. Таким образом, для общих регулярных решеток должно
рассматриваться Р точек для каждой элементарной ячейки. Каждая из точек
элементарной ячейки определяется вектором смещения s .
Следовательно, требуется дополнительная сумма по всем точкам в
элементарной ячейке, и уравнение (9.4) развивается до
Р п
в этом уравнении диапазоны суммирования опущены.
Расширенная теорема о дискретном представлении непосредственно
получается из преобразования Фурье от уравнения (9.17). В этом уравнении
непрерывный сигнал умножается на сумму 5-гребней. Согласно теореме о свертке (теорема
2.4, с. 61), это приводит к свертке преобразования Фурье сигнала и суммы 5-греб-
ней в Фурье пространстве. Преобразование Фурье 5-гребня является снова 5-греб-
нем (>-R5). Поскольку свертка сигнала с дельта-распределением просто повторяет
значение функции в нулевой точке дельта-функций, преобразование Фурье диск-
ретизированного сигнала является просто суммой сдвинутых копий
преобразования сигнала:
^.(*.v) = ^^g(*-rjexp(-27ci*^s^). (9.18)
р ^
Фазовый множитель exp(-27ciA:^5) получается из сдвига точек в элементарной
ячейке Has , согласно теореме о сдвиге (теорема 2.3, с. 61). Векторы i;,
г^=ц*1+иДн-... + и^)6^ npnu^eZ (9.19)
являются точками обратной решетки. Элементарные векторы смещений в
пространственной области и Фурье-области связаны друг с другом соотношением
blK^5,_,.. (9.20)
Это, по существу, означает, что элементарный вектор смещения в
Фурье-области перпендикулярен всем векторам смещения в пространственной области, за
исключением соответствующего вектора. Кроме того, модули соответствующих
векторов связаны друг с другом обратным соотношением, поскольку их скалярное
произведение равно единице. В 3-D пространстве элементарные перемещения
обратной решетки можно, следовательно, вычислить с помощью
£ к ХЬ,,,^ (9.21)
Индексы в предыдущем уравнении вычисляются по модулю 3, а Ь^^Ь^ х Ь^
является объемом исходной элементарной ячейки в пространственной области. Все
эти уравнения знакомы физикам в области твердых тел или кристаллографам [ 108].
Математики знают решетку в Фурье-области как двойственный базис или взаимный
базис векторного пространства, образованного неортогональным базисом. Для
ортогонального базиса все векторы двойственного базиса появляются в том же
направлении, что и соответствующие векторы, а модуль задается соотношением
|Л^ I = 1 /1 й^ I. Тогда часто длина базисных векторов обозначается с помощью Ах^, а
длины обратных векторов как ик^ = 1 / Дх^. Таким образом, ортогональный базис
двойственен сам себе.
9.5. Квантование 257
Реконструкция непрерывного сигнала выполняется снова подходящей
интерполяцией значений в выбранных точках. Теперь интерполируемые значения gj^x)
вьиисляются по значениям, выбранным в #*^+5 , взвешенным с подходящими
множителями, которые зависят от расстояния от интерполируемых точек:
9rix) = Yb9sir,^Sp)Kx-r^ -s^). (9.22)
р «
Используя свойства интеграла ^распределений, мы можем заменить
выбранные точки с правой стороны непрерывными значениями и затем поменять
местами суммирование и интегрирование:
оо
9rix) = j;^\g{x')h{x-x')5{r„+s^-x')u''x
Р «
= \
Р п
Последний интеграл является сверткой весовой функции h с функцией, которая
равна сумме произведений функции изображения д на сдвинутые 5-гребнями. В
Фурье-пространстве свертка заменяется комплексным умножением, и наоборот.
Если мы далее применим теорему о сдвиге и то, что преобразование Фурье
5-гребня является опять 5-гребнем, мы окончательно получим
g,{k) = h{k)^^g{k-l)Qxv{-2nik's^). (9.23)
Р О
Интерполированный сигнал д^ может равняться исходному сигналу д, если
только периодические повторения не перекрываются. Это в точности то, что утверждает
теорема о дискретном представлении. Преобразование Фурье идеальной
интерполяционной функции равно функции-ящику, которая равна единице внутри первой
зоны Бриллюэна и нулю за пределами, что исключает все повторения и оставляет
исходный сигнал с ограниченной полосой пропускания д без изменений.
9.5. Квантование
9.5.1. Эквидистантное квантование
После преобразования в цифровую форму (раздел 9.2) пиксели все еще
показывают непрерывные уровни яркости. Для использования компьютера мы должны
отобразить их в ограниченное число Q дискретных уровней яркости:
[0,oo[^2_^{gf^,gfj, ...,gfg_J = G.
Этот процесс называется квантованием, и мы уже рассматривали некоторые
его аспекты в разделе 2.2.4. В этом разделе мы рассматриваем погрешности,
связанные с квантованием. Квантование всегда вносит ошибки, поскольку истинное
значение д заменяется одним из уровней квантования д^. Если уровни
квантования равно распределены с расстоянием А.д и если все уровни яркости равно
возможны, то дисперсия, вводимая квантованием, определяется как
Глава 9. Преобразование в цифровую форму, дискретизация, квантование
Это уравнение показывает, как мы выбираем уровень квантования. Мы берем
уровень д, для которого расстояние от уровня яркости д, \д - д \ меньше, чем
соседние уровни квантования gf^, и g^^j. Среднеквадратичное отклонение а^
приблизительно в 0,3 раза больше, чем расстояние между уровнями квантования Ад.
Квантование с неравномерно распределенными уровнями квантования
является сложным для реализации в любой системе обработки изображений.
Более легкий способ получить неравномерно распределенные уровни использует
равномерно распределенное квантование — оно преобразует сигнал
интенсивности, прежде чем выполнять квантование, с помощью нелинейного усилителя,
например логарифмического. В случае логарифмического усилителя можно
получить уровни, чья ширина увеличивается пропорционально в зависимости от
уровня яркости.
9.5.2. Точность квантованных уровней яркости
Что касается квантования, возникает вопрос точности, с которой мы можем
измерить уровень яркости. На первый взгляд ответ на этот вопрос кажется тривиальным
и определяется уравнением (9.24): максимальная ошибка равна половине
расстояния между двумя уровнями квантования, а средняя ошибка равна приблизительно
0,3 уровня квантования.
Но что, если мы измеряем значение неоднократно? Это могло бы случиться,
если мы возьмем много изображений одного и того же объекта или если мы имеем
объект постоянного уровня яркости и хотим измерить средний уровень яркости
объекта с помощью усреднения по многим пикселям.
По законам статистического распространения ошибки (раздел 3.3.3) мы
знаем, что ошибка среднего значения убывает с ростом числа измерений согласно
1
среднего Г7Т 5 V>'*^*^/
где о— среднеквадратичное отклонение отдельных измерений, а 7V— число взятых
измерений. Это уравнение говорит нам, что если мы берем 100 измерений, то
ошибка должна быть всего лишь приблизительно 1/10 от ошибки индивидуальных
измерений.
Применим ли этот закон к нашему случаю? Да или нет — зависит от случая, и
ответ оказывается парадоксальным. Если бы мы измеряли с помощью
совершенной системы, т.е. без какого-либо шума, мы всегда получали бы одно и то же
квантованное значение и, следовательно, результат не мог бы быть точнее, чем
отдельные измерения. Однако если измерения зашумлены, мы получили бы разные
значения для каждого измерения. Вероятность отражает среднее значение и
дисперсию зашумленного сигнала, и, поскольку мы можем измерить распределение,
можем оценить как среднее значение, так и дисперсию.
В качестве примера возьмем среднеквадратичное отклонение шума равным
уровню квантования. Тогда среднеквадратичное отклонение отдельного измерения
приблизительно в 3 раза больше, чем среднеквадратичное отклонение, обусловленное
9.6. Упразднения 259
квантованием. Однако уже при 100 измерениях среднеквадратичное отклонение
среднего значения составляет только 0,1 или в 3 раза ниже, чем отклонение квагггования.
Поскольку в изображениях мы можем легко получить большое количество
измерений с помощью пространственного усреднения, существует возможность
измерить средние значения со среднеквадратичными отклонениями, которые
гораздо меньше, чем среднеквадратичное отклонение квантования в уравнении (9.24).
Точность также ограничивается, однако другими — систематическими —
ошибками. Наиболее значимым источником является неравномерность квантовых
уровней. В реальных квантователях, таких, как аналого-цифровой преобразователь,
уровни квантования являются неравномерно удаленными с систематическими
отклонениями, вплоть до половины интервала квантования. Таким образом,
требуется тщательное исследование аналого-цифрового преобразователя для оценивания
того, что в действительности ограничивает точность измерений уровней яркости.
9.6. Упражнения
9.1: Теорема о дискретном представлении
Интерактивная иллюстрация теоремы о дискретном представлении
(dip6ex09.01).
9.2: Стандартная дискретизация
Интерактивная иллюстрация стандартной дискретизации (dip6ex09.02).
Муар-эффект
Интерактивная иллюстрацр1я муар-эффекта на примере периодических
сигналов (dip6ex09.03).
9.3: **Дискретная выборка
Что происходит с дискретным преобразованием Фурье 1-D сигнала д, если
использовать только каждую вторую точку сигнала? Попытайтесь
сформулировать дискретную теорему о выборке для этого случая и доказать ее.
Сравните ее с теоремой для выборки непрерывного сигнала.
9.4: Квантование, шум и усреднение
Интерактивная демонстрация систематических и статистических ошибок
при оценивании средних значений с квантованными сигналами при
различных уровнях шума (dip6ex09.04).
9.7. Дополнительная литература
Теория выборок подробно рассмотрена в работе Поуларикаса (Poularikas) [156,
раздел 1.6]. Детальный отчет по выборке случайных полей — также при случайных
расстояниях - дается Папоулисом (Papoulis) [149, раздел 11.5]. Раздел 9.5
рассматривает только квантование с равными интервалами. Квантование с неравными
интервалами изложено в книге Розенфельда (Rosenfeld) и Кака (Как) [172].
ГЛАВА 10
ПИКСЕЛЬНАЯ ОБРАБОТКА
10.1. Введение
После того как получено цифровое изображение, первые шаги предпроцессорной
обработки включают два класса операций — точечные операции и геометрические
операции. В сущности, эти два типа операций определяют, «каким» является
пиксель и «где» он.
Точечные операции изменяют уровни яркости в отдельных пикселях, в
зависимости от уровня яркости и, возможно, от положения пикселей. Как правило,
такой вид операций выражается как
G' =Р (G ). (10.1)
Индексы при функции Р обозначают возможную зависимость точечной
операции от положения пикселя.
В отличие от точечных операций, геометрические операции изменяют только
положение пикселя. Пиксель, расположенный в положении дс, перемещается в
новое положение х'. Соотношение между двумя координатами задается
геометрической отображающей функцией
х=М{х). (10.2)
Точечные и геометрические операции являются комплементарными
операциями. Они применимы для коррекций элементарных искажений процесса
формирования изображений, таких, как нелинейная и неоднородная радиометрическая
чувствительность датчиков формирования изображений или геометрических
искажений системы формирования изображений. Мы применяем точечные
операции для правки и оптимизации освещенности изображения, определения потери
значимости и переполнения, улучшения и расширения контрастности,
усреднения изображений, внесения правки на неоднородное освещение или выполнения
радиометрической калибровки (10.2.3—10.3.3).
Геометрические операции включают два основных шага. В большинстве
прикладных задач отображающая функция (10.2) не задается явно, а должна быть
получена из соответствий между исходным объектом и его изображением (раздел
10.4.4). Если изображение искажено геометрическим преобразованием, то
пиксели на исходных и искаженных изображениях почти никогда не накладываются друг
на друга. Таким образом, требуется интерполяция уровней яркости в этих
пикселях по соседним пикселям. Эта важная задача детально рассматривается в разделе
10.5, поскольку выполнение точной интерполяции не является тривиальным.
Точечные и геометрические операции представляют интерес не только для
элементарных шагов предпроцессорной обработки. Они также являются
неотъемлемой частью многих сложных операций над изображениями, особенно при вьщеле-
нии признаков (главы 11—15). Однако обратите внимание, точечные операции и
10.2. Однородные точечные операции
геометрические операции не подходят для корректировки эффектов оптической
системы, описываемых ее функцией рассеяния точки. В этом случае требуются
сложные методы реконструкции, которые рассматриваются в главе 17. Точечные
операции и геометрические операции ограничиваются выполнением простых
радиометрических и геометрических коррекций.
10.2. Однородные точечные операции
10.2.1. Определения и основные свойства
Если точечная операция не зависит от положения пикселя, она называется
однородной точенной операцией и записывается
С =P(G ). (10.3)
Точечная операция отображает множество уровней яркости в самого себя. Как
правило, точечные операции являются необратимыми, поскольку два различных
уровня яркости могут быть отображены в один. Таким образом, точечная
операция в большинстве случаев приводит к не подлежащей восстановлению потере
информации. Точечная операция
[ О q<t
К примеру, выполняет простую глобальную пороговую операцию. Все уровни
яркости ниже пороговой величины /'устанавливаются равными нулю (черный цвет),
а все выше и равные пороговой величине — равными самому высокому значению
Q - 1 (белый цвет). Следовательно, эта точечная операция не может быть
обращена. Примером обратимой точечной операции является отрицание изображения.
Эта операция вычисляет изображение с перевернутой шкалой яркости, как в
случае с фотонегативом, согласно
РЛя) = а-^-Я- (10.5)
Операция, обратная операции отрицания, является еще одним отрицанием:
рлРм{я))=а-'^-(а-'^-я)=я- (10-5)
Еще одним примером обратимой точечной операции является
преобразование между представлениями уровней яркости со знаком и без знака (раздел 2.2.5).
10.2.2. Таблицы преобразования
Прямое вычисление однородных точечных операций, согласно уравнению (10.3)
может быть очень дорогостоящим. Продемонстрируем это на следующем
примере. 14-битовая шкала яркости изображения 1024 х 1024 ПЗС-камеры высокого
разрешения должна быть представлена в виде 8-битовой логарифмической шкалы
яркости, охватывающей 10"^'^ от 1 до 16 383. Следующая точечная операция выполняет
это преобразование:
Р(9) = 59,30 Ig^. (10.7)
Прямое выполнение потребовало бы следующих операций для каждого
пикселя: преобразование целого числа в число с плавающей запятой, вычисление
логарифма, умножение на 59,30 и преобразование числа с плавающей запятой в
Глава 10. Пиксельная обработка
8-битовое целое число. Все эти операции должны быть повторены свыше
миллиона раз для изображения 1024 х 1024.
Ключевой момент для более эффективного выполненры заключается в том, что
если мы посмотрим, то увидим, что область определения любой точечной операции
состоит только из ограниченного числа Q уровней квантования. В случае
преобразования 14-битовой шкалы в 8-битовую логарифмическую шкалу мы имеем
максимум 16 384 различных входных значения. Это означает, что большая часть одного
миллиона вьиислений просто повторяется в среднем 64 раза. Мы можем избежать
ненужного повторения предварительным вычислением P(q) для всех 16 384
возможных уровней яркости и сохранением вьгаисленных значений в 16 384-элементной
таблице. Тогда вычисление точечной операции сводится к замещению уровня
яркости элементом в таблице с индексом, соответствующим уровню яркости.
Такая таблица называется таблицей преобразования (ТП). Следовательно,
однородные точечные операции эквивалентны операциям с таблицами
преобразования. Таблицы преобразования являются тем более эффективными, чем меньше
число уровней квантования. В случае стандартных 8-битовых изображений
таблицы содержат всего лишь 256 значений. Но в большинстве случаев по-прежнему
эффективным является использование таблиц преобразований с 65 536
вхождениями при 16-битовых изображениях.
В большинстве систем обработки изображений и фрейм-грабберов ТП
реализуются на уровне аппаратных средств. Имеются два возможных места для ТП
на платах фрейм-грабберов, наглядно представленных на рис. 10.1. Входная ТП
размещается между аналого-цифровым преобразователем и буфером кадра.
Выходная 777 размещается между буфером кадра и цифроаналоговым преобразователем
для выходных данных изображения в форме аналогового видеосигнала, например
для монитора. Входная ТП позволяет выполнять точечную операцию до того,
как изображение сохраняется в буфере кадра. С помощью выходной ТП
точечная операция может выполняться и наблюдаться на мониторе. Таким образом,
мы можем интерактивно выполнять точечные операции без модификации
записанного изображения. Многие современные фрейм-грабберы больше не
включают буфер кадра. С появлением систем с быстрыми периферийными шинами
(такими, как шина PCI с пиковой частотой 132 Мбайт/с, см. раздел 1.7)
оцифрованные изображения могут передаваться непосредственно в память ПК (рис. 10.2).
С таким фрейм-граббером воспроизведение изображения на экран выполняется
на плате графических изображений компьютера. Следовательно, фрейм-граббер
включает только входную ТП.
Использование входных ТП ограничено. Нелинейные функции ТП приводят
к потере уровней яркости или отображению последовательных значений в одно
(рис. 10.3). Таким образом, вносятся искажения, которые приводят к увеличению
ошибок при последовательной обработке, например, вьиислений средних
значений и распознавании контуров. Очевидно, что, по существу, нарушаются резкость
контуров и точность изменений уровней яркости.
Входные ТП были бы полезными также для нелинейных точечных операций,
если бы 8-битовые входные значения отображались бы в выходные значения
более высокой точности, например в 16-битовые целые числа или 32-битовые числа
с плавающей запятой, или если бы сигнал камеры преобразовывался в цифровую
форму с более высоким разрешением, например 12-битовые, и затем выходные
10.2. Однородные точечные операции
Входные
видеосигналы
2
Мультиплексор
видеосигналов
Восстановление ПС
Прог.
смещение/
усиление
АЦ-
преобра-
зователь
Входные
ТБ
Синхронный
стриппер
Кварцевый
генератор
Опциональные
входы )
синхронизации
Опциональные
выходы ^
синхронизации
ФАПЧ
Таймер
Внутренние сигналы
синхронизации
►
ЦА-
преобразователи
Таблицы
преобразования
Красный
Монитор
<
^
^
^
^—I Зеленый
(синхр.)
*л
Синий
Память
кадров
1 Кбх512б
Регистры
управления
Пиксельный
буфер 8 байт
Шина данных главного процессора
Рис. 10.1. Блок-схема фрейм-граббера PCVISIONplus от Imaging Technology, Inc.
Таблицы преобразования размещены между АЦП и буфером кадра (входная ТП) и
буфером кадра и дисплеем (выходная ТП)
данные как 8-битовые числа. Тогда ошибка, связанная с округлением,
значительно бы уменьшилась. В то же время уровни яркости могли бы
преобразовываться в калиброванный сигнал, например, в случае температуры для
инфракрасной камеры. К сожалению, такие обобш;енные ТП еще не реализуются на
уровне аппаратных средств. Однако их легко реализовать на уровне
программного обеспечения.
В отличие от входной ТП, выходная ТП является гораздо более широко
используемым инструментом, поскольку она не меняет записанное изображение.
С помощью операций с ТП можно также преобразовать изображение
различной яркости в псевдоцветное изображение. И опять этот метод является общим
даже при самых простых платах фрейм-грабберов (рис. 10.1). Не нужно
дополнительных аппаратных средств. Используются три цифроаналоговых
преобразователя для основных цветов — красного, зеленого и синего. Каждый
канал имеет собственную ТП с 256 вхождениями для 8-битового дисплея. Таким
образом, мы можем отобразить каждый отдельный уровень яркости q как любой
цвет, присваивая цветовую тройку соответствующим адресам ТП r{q), g{r) и b{q).
Глава 10. Пиксельная обработка
О
О
о
о о
САМ CTRL 0..4
VIDIN (0:3)
О О О О О
о о о о о
т
Регулирование
смещения/усиления
АЦП U ТБ 256x8
Внешний таймер
Тактовый
генератор
Внешний
триггер
HSYNC
8
Опто-
развязывающее
устройство
LJ
CYSYNC
Синхронный
генератор
САМ CTRL О
PCI-
котроллер
32
PCI-
шина
Рис. 10.2. Блок-схема фрейм-граббера PCEYE_1 от ELTEC Elektronik GmbH в
качестве примера современного фрейм-граббера с шиной PCI без буфера кадра. Данные
изображения передаются в реальном времени через прямой доступ к памяти (ПДП)
в память ПК для воспроизведения на экране и дальнейшей обработки
Формально это есть векторная
точечная операция
P{q)Ag{q)V (10.8)
Wq)_
В случае, когда все три точечные
функции r{q), g(r) и b(q)
тождественны, на экране будет
воспроизведен серый тон. Если две из
точечных функций равны нулю,
изображение появится в
оставшемся цвете.
P(q)
Неравномерный шаг,
упущение выходного значения
Множественные значения,
отображенные в одно
Рис. 10.3. Иллюстрация нелинейной таблицы
преобразования с отображением
множественных значений в одно и упущением выходного
значения, ведущим к неравномерности шагов
10.2. Однородные точечные операции
10.2.3. Интерактивная оценка уровней яркости
Однородные точечные операторы, реализуемые через ТП, являются очень
полезным инструментом для инспектирующих изображений. Поскольку операции с ТП
работают в реальном времени, изображениями можно манипулировать
интерактивно. Если только выходная ТП изменяется, то содержание исходного
изображения остается неизменным. Здесь мы продемонстрируем типичные задачи.
Оценка и оптимизация освещенности. Невооруженным глазом мы можем с
трудом оценить однородность освещаемой области, что и продемонстрировано на рис.
10.4, а, б. Гистограмма показывает распределение шкалы яркости, но не ее
пространственное изменение (рис. 10.4, в, г). Следовательно, гистограмма не будет
достаточно полезна для интерактивной оптимизации освещенности. Нам
необходимо отметить шкалы яркости так, чтобы абсолютные уровни серого стали
ощутимыми для глаза человека. Если распределение энергетической яркости является
непрерывным, достаточно использовать эквиденситы. Этот метод использует сту-
Рис. 10.4. а - энергетическая освещенность равномерно убывает сверху вниз, что
является почти нераспознаваемым глазом. Шкала яркости этого изображения,
представленного через числа с плавающей запятой, вычисленная путем усреднения
свыше 100 изображений, изменяется в диапазоне от 160 до 200; б — гистограмма для а;
в и г - улучшенная контрастность, шкала яркости 184—200: границы, искусственно
полученные с помощью ступенчатой ТП с высотой ступени 1,0 и 2,0, делают
контурные линии постоянной энергетической яркости легко видимыми
Глава 10. Пиксельная обработка
пенчатый тип однородной точечной операции, производящих отображение
некоторого диапазона шкал яркости в одну. Эта точечная операция достигается путем
обнуления р наименее значимых разрядов с помощью операции логического м:
q' = P{q) = qA{2''-V), (10.9)
где Л обозначает логическое (побитовое) w, а верхнее подчеркивание обозначает
отрицание. Эта точечная операция ограничивает разрешение jxoQ-p разрядов и,
таким образом, 2^~^ уровней квантования. Теперь переход между оставшимися
уровнями квантования достаточно большой для восприятия глазом, и мы видим
контурные линии равной абсолютной шкалы яркости на изображении (рис. 10.4). Мы
можем попытаться гомогенизировать освещенность, образовав насколько
возможно большое расстояние между контурными линиями.
Еще одним подходом для маркировки абсолютных уровней яркости является так
называемое псевдоцветное изображение, которое уже обсуждалось в разделе 10.2.2. С
помощью этого метода уровень яркости q отображается для воспроизведения на
экране в тройку RGB. Поскольку цвет гораздо более распознаваем глазом, он
поможет обнаружить абсолютные уровни яркости.
Выявление потери значимости и переполнения. Явления потери значимости и
переполнения уровней яркости оцифрованного изображения часто остаются
незамеченными и вызывают серьезные отклонения при дальнейшей обработке,
например, для средних уровней яркости объектов или центра тяжести объекта. В
большинстве случаев такие области не могут распознаваться непосредственно. Они
могут стать очевидными только в текстурированных областях, когда текстура
отбеливается. Потеря значимости и переполнение легко определяются по
гистограммам через сильные пики при минимальных или максимальных уровнях
яркости (рис. 10.5). С помощью псевдоцветового отображения можно получить
некоторые самые низкие и самые высокие уровни яркости, к примеру, в синем и
красном цветах соответственно. Тогда уровни яркости, опасно близкие к
пределам, немедленно возникают из изображения и могут избегаться путем коррекции
апертуры объектива освещения или коэффициента усиления цепи входных
видеосигналов фрейм-граббера.
Улучшение контрастности. Из-за плохих условий освещенности часто случается,
что изображения бывают недодержанными. Тогда изображение является слишком
темным и имеет низкую контрастность (рис. 10.6, а). На гистограмме (рис. 10.6, б)
показано, что изображение содержит только небольшой диапазон уровней
яркости при низких значениях уровней яркости. Внешний вид изображения
значительно улучшается, если мы применим точечную операцию, которая отображает
малый диапазон шкалы яркости в диапазон полной контрастности (например, с
помощью операции: ^'= Aq для q<64H q'= 255 для q > 64) (рис. 10.6, в). Мы только
улучшаем внешний вид изображения, но не качество изображения само по себе.
На гистограмме показано, что разрешение уровней яркости по-прежнему
остается таким же (рис. 10.6, г).
Качество изображения можно улучшить. Самым хорошим способом является
увеличение энергетической освещенности объекта с помощью использования
более мощного светового источника или разработки оптимальной установки
освещения. Если это невозможно, мы все еще можем увеличить коэффициент усиления
аналогового усилителя сигнала. Все современные платы обработки изображений
включают усилитель, чей коэффициент усиления и смещение могут устанавли-
10.2, Однородные точечные операции 267
50 ТОО 150 200 250
slements (section 4.3,2b).
f an optical system is a perspectix
i) models the imaging geometry ^<
r described by the position of the
Focal length (section 4.3,2c). For th
determine the distance range thai
of field, section 4.3,2d) and to learji
id hypercentric optical systems (s
r-^'
6000
5000
4000
3000
2000
1000
0 ,
50
100
150 200 250
Рис. 10.5. Определение потери значимости и переполнения в оцифрованных
изображениях по гистограммам: а - изображение с потерей значимости; б - его
гистограмма; в - изображение с переполнением; г - гистограмма
ваться профаммным обеспечением (см. рис. 10.1 и 10.2). С увеличением
коэффициента усиления и смещения яркость и разрешение изображения улучшаются, но
только за счет повышения уровня шумов (раздел 3.4.5).
Расширение контрастности. Часто интерес представляет анализ слабых различий
энергетической освещенности, которые выходят за пределы разрешения зрительной
системы человека или используемой аппаратуры отображения информации. Это
особенно важно, если изображение печатается. Для того чтобы наблюдать слабые
различия, мы расширяем интересующий нас малый диапазон шкалы яркости до полного
доступного диапазона. Все уровни яркости вне этого диапазона устанавливаются
равными минимальному и максимальному значениям. Эта операция требует, чтобы
уровни яркости интересующего нас объекта попадали в диапазон, выбранный для
расширения. Пример расширения контрастности показан на рис. 10.7, а, б. Клин внизу
изображений, имеющих значения в диапазоне от О до 255, прямо указывает, какая
часть диапазона шкалы яркости имеет улучшенную контрастность.
Сжатие диапазона. По сравнению со зрительной системой человека цифровые
изображения имеют значительно меньший динамический диапазон. Если
требуется минимальное разрешение 10%, уровни яркости не должны быть меньше 10.
Следовательно, максимальный динамический диапазон в 8-битовом изображении
равен всего лишь 255/10 ~ 25. Низкий диапазон контрастности цифровых изобра-
Глава 10. Пиксельная обработка
liiiiUUUkUMl
ТОО 150 200 250
Рис. 10.6. Улучшение контрастности: а — недоэкспонированное изображение; б - его
гистограмма; в - изображение с интерактивно улучшенной контрастностью; г - его
гистограмма
жений приводит к появлению их с низким качеством в случае, когда встречаются
высококонтрастные сцены. Либо светлые части отбеливаются, либо невозможно
распознать детали в темных частях. Динамический диапазон можно увеличить с
помощью преобразования, которое было введено в разделе 2.2.6 как
гамма-преобразование. Эта нелинейная однородная точечная операция имеет форму
, 255 ,
я =5^?'. (10.10)
Множители в уравнении (10.10) выбираются так, чтобы диапазон [0,255]
отображался сам в себя. Это преобразование позволяет распознавать более широкий
динамический диапазон за счет разрешения в светлых частях изображения. Темные
части становятся светлее и проявляют больше деталей. Это контрастное
преобразование лучше приспособлено к логарифмическим характеристикам зрительной
системы человека. Изображение, представленное с различными гамма-множителями,
показано на рис. 10.8.
Уравнивание дисперсии шума. Из раздела 3.4.5 мы знаем, что дисперсия шума,
как правило, зависит от интенсивности изображения, согласно
ст1(д) = ст',+Кд,
(10.11)
10.2, Однородные точенные операции 269
l^ggSS пи»*^^'-' 'EciiiKniii'
iniwi"''"^ Щшяю
Рис. 10.7. б — г — расширение контрастности изображения, показанного на а.
Расширенный диапазон можно изучить по изменению клина шкалы яркости внизу изображения
Статистический анализ изображений и операций над изображениями
является, однако, гораздо легче, если шум не зависит от уровней яркости. Только тогда
все методы определения распространения ошибки, рассмотренные в разделе 3.3.3,
действительны. Поэтому нам необходимо применить нелинейное преобразование
уровней яркости h{g) таким образом, чтобы дисперсия шума стала постоянной.
Для первого порядка дисперсия h{g) равна
<у1-
V
<i9).
(10.12)
согласно уравнению (3.36) [53]. Если мы положим а^ равной константе, то получим
4^49)
Интегрирование дает
' dg'
h{9) = cf,\
lyl^W)
+ С.
(10.13)
270 Глава 10. Пиксельная обработка
и
IflriHiiP гшря^штш ^^ipip
Рис. 10.8. представление изображения с различными гамма-значениями: а — 0,5;
б- 0,7; в-1,0; г-2,0
При линейной функции дисперсии (10.11) интеграл в уравнении (10.13)
приводит к
2сг,
К
(10.14)
Мы используем два свободных параметра, о"^ и С, для отображения значений А
в интервал [О, Y9mmi ^ получаем
yKg^J^
(10.15)
Нелинейное преобразование становится особенно простым для идеального
датчика формирования изображений с сТр= 0. Тогда нужно применить
преобразование квадратного корня для получения интенсивности, независящей от
дисперсии шума:
У
К9) = г499^ и <^/,=tV^
(10.16)
10.3. Неоднородные точенные операции 271
10.3. Неоднородные точечные операции
Однородные точечные операции являются только подклассом точечных
операторов. В общем, точечная операция зависит также от положения пикселя на
изображении. Такая операция называется неоднородной точечной операцией.
Неоднородные точечные операции, в большинстве случаев, относятся к процедурам
калибровки. Как правило, вычисление неоднородных точечных операций
требует гораздо больше времени, чем вычисление однородной точечной операции.
Мы не можем использовать таблицы преобразования, поскольку точечная
операция зависит от положения пикселя, и вынуждены вычислять функцию для
каждого пикселя.
Вычитание фонового изображения без объектов или освещения является
простым примером неоднородной точечной операции, которая записывается как
Утп тпУУтпу Утп тп^
где b — фоновое изображение.
(10.17)
10.3.1. Усреднение изображений
Одной из самых простых неоднородных точечных операций является усреднение
изображений. В некоторых прикладных задачах формирования изображений
имеют место высокие уровни шумов. Известные примеры включают термическое фор-
мирование изображений (раздел 6.4.1) и все применения, где накапливается только
ограниченное число фотонов (см. рис. 3.2 и раздел 3.4.5).
На рис. 10.9, а показаны разности температур на поверхности воды установки
ветровых волн, охлаждаемой при скорости ветра 1,8 м/с с помощью испарения.
Из-за существенного уровня шума почти не вьщеляются малые температурные
колебания. Взятие среднего значения по нескольким изображениям значительно
уменьшает уровень шума (рис. 10.9, б).
Рис. 10.9. Уменьшение шума с помощью усреднения изображения: а — отдельное
тепловое изображение малых температурных колебаний на поверхности воды,
охлаждаемой с помощью испарения; б — то же самое изображение, усредненное по
16 изображениям; полный диапазон уровней яркости соответствует температурному
диапазону 1,1 К
Глава 10. Пиксельная обработка
Погрешность среднего (раздел 3.3.3), взятая по 7V выборкам, задается как
Если мы возьмем среднее от К изображений, то уровень шума уменьшится в
\i4k Р^з по сравнению с отдельным изображением. Взятие, таким образом,
среднего значения по 16 изображениям уменьшит уровень шума в 4 раза. Однако
уравнение (10.18) действительно только в случае, если среднеквадратичное
отклонение о значительно больше, чем среднеквадратичное отклонение, относяш;ееся к
квантованию (раздел 9.5).
10.3.2. Коррекция неоднородного освещения
Каждая реальная прикладная задача решает проблему неравномерной
освещенности наблюдаемой сцены. Даже если мы потратим много усилий, оптимизируя
установку освещения, все еще будет трудно получить абсолютно равномерную
энергетическую освещенность объекта. Трудно разрешаемая проблема вызывается
маленькими частицами пыли на оптическом пути, особенно на стеклянном окне,
близком к датчику ПЗС. Из-за расстояния от окна до формирователя
изображения, эти частицы — если они не слишком большие — размываются до такой
степени, что не являются непосредственно ввдимыми. Но они тем не менее поглощают
часть света и, таким образом, вызывают падение в уровне освещенности в малой
области. Эти эффекты нелегко увидеть в сцене с высоким контрастом и большим
количеством деталей, но они становятся очеввдными в случае однородного фона
(рис. 10.4, а, б). Некоторые датчики формирования изображений, особенно
дешевые КМОП-датчики, также проявляют неравномерную чувствительность
отдельных фоторецепторов, которая добавляется к неоднородности изображения. Эти
искажения могли бы очень ограничить качество изображений. Перечисленные
эффекты приводят к тому, что становится сложнее отделить объект от фона, и
вносят систематические ошибки в последовательные шаги обработки изображений.
Тем не менее возможно откорректировать эти эффекты, если мы знаем
природу искажения и можем получить подходящие опорные изображения. В
дальнейшем мы изучим два случая. В первом мы полагаем, что уровень яркости на
изображении является результатом неоднородной энергетической освещенности и
отражательной способности или пропускаемости объекта. Кроме того, мы можем
получить опорное изображение без поглощающих объектов или с объектом
постоянной отражательной способности. Опорное изображение можно также
вычислить в случае, когда малые объекты случайно распределены на изображении.
Тогда достаточно вычислить среднее изображение по большому количеству
изображений с объектами. Неоднородная освещенность может быть
скорректирована делением изображения на опорное изображение:
G' = c GIR. (10.19)
Константа с требуется для представления нормированного изображения с
помощью снова целых чисел. Если объекты поглощают свет, то константа с, как
правило, выбирается близкой к максимальному целому значению. На рис. 10.10, д
демонстрируется, что эффективное уменьшение воздействия неоднородной
освещенности возможно при использовании этого простого метода.
10.3. Неоднородные точечные операции 273
а
50 200
12000
10000
8000
6000
4000
2000
.
А
\
II 1
11
N
'
^<^
50
100
150 200
250
1 "^CiCiCi
10000
8000
6000
4000
2000
0
0
5
0
1
00 1
50 2
1
00
250
Рис. 10.10. Коррекция неравномерной освещенности с помощью неоднородной
точечной операции: а — исходное изображение; б — его гистограмма; в — фоновое
изображение; г — его гистограмма; д — деление изображения на фоновое
изображение; е —его гистограмма
10.3.3. Двухточечная радиометрическая калибровка
Простое формирование изображенР1я отношения, описанное выше, неприменимо,
если необходимо также вносить правки на ненулевой неоднородный фон, под
воздействием, к примеру, фиксированного структурного шума датчика ПЗС. В этом слу-
Глава 10. Пиксельная обработка
чае требуются два опорных изображения. Этот метод также применяется для
простой двухточечной радиометрической калибровки датчика формирования
изображения с нелинейным откликом. Некоторые задачи измерения изображений
требуют абсолютной или относительной радиометрической калибровки. Как только
такая калибровка получена, мы можем сделать вывод об энергетической яркости
объектов по измеренным уровням яркости.
Во-первых, возьмем темное изображение В без какой-либо освещенности. Во-
вторых, возьмем опорное изображение R с объектом постоянной энергетической
яркости, например фотометрическим шаром. Тогда нормированное изображение,
скорректированное как на фиксированный шум структуры, так и на
неоднородную чувствительность, задается как
G' = c^^ (10.20)
R-B
На рис. 10.11 показаны с улучшенной контрастностью темное изображение и
опорное изображение камеры ПЗС с аналоговыми выходными данными. Можно
наблюдать типичные искажения сигнала. Колебание сигнала на левом краю
темного изображения получается от электронных помех, в то время как темные
маленькие шарики на опорном изображении вызываются частицами пыли на
стеклянном окне перед датчиком. Улучшение, обусловленное радиометрической
калибровкой, можно явно увидеть на рис. 10.12.
10.3.4. Нелинейная радиометрическая калибровка
Иногда величина, измеряемая датчиком формирования изображения, связана
нелинейным образом с измеряемым уровнем яркости. Очевидным примером
является термофафия. В таких случаях требуется нелинейная радиометрическая
калибровка. Здесь температура испускаемого объекта определяется по его энергетической
яркости с использованием уравнений Планка (раздел 6.4.1).
Мы определим практическую процедуру калибровки для температуры
окружающей среды. Из-за нелинейного соотношения энергетР1ческой яркости и температуры
Рис. 10.12. Двухточечная радиометрическая калибровка с помощью темного и
опорного изображений из рис. 10.11: а — исходное изображение; б - калиброванное
изображение; в калиброванном изображении темные пятна, вызванные частицами пыли,
больше не видны
10.3. Неоднородные точечные операции 275
недостаточно простой двухточечной калибровки с линейной интерполяцией. Хаусэ-
кер (HauBecker) [71 ] показал, что квадратичное соотношение является достаточно
точным для малого температурного диапазона, скажем, от О до 40** по шкале Цельсия.
Следовательно, требуется три калибровочные температуры, которые обеспечиваются
блоком калибровки абсолютно черного тела с регулируемой температурой.
Калибровка дает три калибровочных изображения G^, G^h G^c известными
температурами Г,, Т^и Ту Температурное изображение Г произвольного
изображения G можно вычислить с помощью квадратурной интерполяции как
j.^ AG, AG, ^_ AG, AG, ^ ^ Afi AG, ^
AG,,-AG,, ' AG,,'AG,, ' AG,,-AG,, '
при AG, = G-G, и AG,/ = G,-G^ (10.22)
Символ • указывает на поточечное умножение изображений, для того чтобы
отличать его от матричного умножения. На рис. 10.13, а, б, с показаны три
калибровочных изображения. Инфракрасная камера смотрит на калибровочную цель через
зеркало, которое ограничивает поле зрения на границах изображения. Это является
причиной резких температурных изменений, которые видны на границах
изображений на рис. 10.13, а, в. Процедура калибровки удаляет остаточные
неоднородности (рис. 10.13, г, е), которые проявляются на исходных изображениях.
10.3.5. Отсечение
Еще одним важным применением неоднородных точечных операций является
операция, известная как отсечение. До того как мы можем вычислять ДПФ от
изображения, изображение должно быть умножено на оконную функцию. Если мы
опустим этот шаг, спектр будет искажен сверткой спектра изображения с
преобразованием Фурье от функции-ящика sinc-функцией (см раздел 2.3, >^R5), которая
приводит к тому, что пики спектра становятся звездообразными структурами вдоль
координатных осей в Фурье-пространстве (рис. 10.14, б). Мы можем также
объяснить эти искажения с помощью периодического повторения изображений
конечной области, эффекта, который рассматривался вместе с теоремой о дискретном
представлении в разделе 9.2.3. Периодическое повторение приводит к
нарушениям непрерывности на горизонтальных и вертикальных краях изображения,
которые вызывают соответственно высокие спектральные плотности вдоль осей л: и >; в
Фурье-области.
Для того чтобы избежать этих искажений, мы должны умножить изображение
на оконную функцию, которая постепенно приближается к нулю по направлению
к контурам изображения. Оптимальная оконная функция должна сохранять
высокое спектральное разрешение и проявлять минимальные искажения в спектре,
т.е. ее ДПФ должно убывать как можно быстрее. Это несовместимые требования.
Хорошее спектральное разрешение требует полной оконной функции. Такое окно,
однако, резко убывает на границах, вызывая медленное убывание боковых
лепестков его спектра.
Внимательно выбранное окно является решающим для спектрального анализа
временного ряда [131,148]. Однако в цифровой обработке изображений это является
менее важным из-за гораздо более низкого динамического диапазона уровней яркости.
276 Глава 10. Пиксельная обработка
Рис. 10.13. Трехточечная калибровка инфракрасных температурных изображений: на
а — в показаны изображения кагшбровочных объектов, сделанных из апюмршиевых
блоков, при температурах 13,06; 17,62 и 22,2° по шкапе Цельсия. Изображения являются
расширенными в контрастности до узкого диапазона 12-битового цифрового выходного
диапазона инфракрасной камеры: а - 1715—1740; б - 1925-1950; в - 2200-2230 - и
показывают некоторые остаточные неоднородности, особершо вертикальные полосы; г -
калиброванное изображение с использованием трех изображений: а — в — при квадратичной
интерполяции; д — исходное; е - калиброванное изображение температурных
микромасштабных колебаний на поверхности океана (площадь приблизительно 0,8 х 1,0 м^)
Простое косинусное окно
Г
W^^ = sin
Ttm
sin
^nn^
N
0<m<M, 0<n<N
(10.23)
выполняет эту задачу хорошо (рис. 10.14, в, г).
Непосредственное выполнение операции отсечения требует больших
временных затрат, поскольку нам пришлось бы вычислять косинусную функцию 2MN
раза. Гораздо более эффективным является выполнение вычислений оконной
функции один раз, сохранение изображения окна и использование его затем для вьиис-
ленрш многих ДПФ. Определив, что функция окна (10.23) является сепарабельной.
10.4. Геометрические преобразования ТП
Рис. 10.14. Влияние отсечения на дискретное преобразование Фурье: а — исходное
изображение; б — ДПФ а без использования оконной функции; в — изображение,
умноженное на косинусное окно; г — ДПФ в с использованием косинусного окна
т.е. результат двух функций W^^ = "^w^ • 'w^, можно смягчить требования
хранения. Тогда нам необходимо вычислить только М плюс iV значений столбцовых
и строчечных функций ""w^ и 'w^ соответственно. В результате достаточно
хранить только столбцовые и строчечные функции. Уменьшенное пространство
хранения получается за счет дополнительного умножения для каждого пикселя
при операции окна.
10.4. Геометрические преобразования
в оставшейся части этой главы мы рассматриваем геометрические операции как
комплементарные точечным операциям. Сначала мы рассматриваем
элементарные геометрические преобразования, такие, как аффинное преобразование
(раздел 10.4.2), перспективное преобразование (раздел 10.4.3) и получение параметров
преобразования с помощью методов согласования в конечном числе точек. Затем
мы фокусируем свое внимание в разделе 10.5 на интерполяции, которая возникает
как главная проблема для быстрой и точной реализации геометрических операций
на дискретных изображениях. И наконец, в разделе 10.6.3 мы кратко обсуждаем
быстрые алгоритмы для геометрических преобразований.
278 Глава 10. Пиксельная обработка
а
/
L/
N,
/
Входное
изображение
Выходное
изображение
б
\
т:
Входное
изображение
Выходное
изображение
Рис. 10.15. Иллюстрация прямого отображения (а) и обратного отображения для
пространственного преобразования изображений (б)
10.4.1. Прямое и обратное отображения
Геометрические преобразования определяют зависимость между точками на двух
изображениях. Это соотношение можно выразить двумя способами. Либо
координаты выходного изображения, х\ могут быть определены как функция входных
координат, JC, либо наоборот:
х=М{х) или х = М ^{х).
(10.24)
где М определяет отображающую функцию, а М~^ — ее обратную функцию. Два
выражения (10.24) порождают два главных вида пространственного
преобразования: прямое отображение и обратное отображение,
С помощью прямого отображения пиксель входного изображения
отображается в выходное изображение (рис. 10.15, а). Как правило, пиксель входного
изображения лежит между пикселями выходного изображения. В случае прямого
отображения не подходит только задать значение входного пикселя ближайшему
пикселю в выходном изображении (поточечное отображение или отображение
методом «ближайшего соседа»). Тогда может случиться, что преобразованное
изображение содержит дыры, поскольку значение никогда не присваивается
пикселю на входном изображении, или значение присваивается более одного
раза точке на выходном изображении. Подходящий метод распределяет
значение входного пикселя нескольким выходным пикселям. Самая простая
процедура рассматривает пиксели как квадраты и берет долю площади входного
пикселя, которая покрывает выходной пиксел в качестве весового множителя.
Каждый выходной пиксель накапливает соответствующие доли входных
пикселей, которые, если отображение непрерьгоно, складываются, чтобы покрыть весь
выходной пиксель.
С помощью обратного преобразования координаты точки на выходном
изображении отображаются обратно во входное изображение (рис. 10.15, б). Очевидно,
что эта схема избегает дыр и наложений в выходном изображении, поскольку все
пиксели сканируются последовательно. Теперь возникает проблема
интерполяции во входном изображении. Координаты выходного изображения, в общем
случае, не попадают в пиксель во входном изображении, а лежат между пикселями.
Таким образом, его правильные значения должны быть интерполированы по
окружающим пикселям. Как правило, обратное отображение - более гибкий метод,
поскольку легче выполнять различные типы интерполяционных методов.
/
/
.::2\
Перемещение
Поворот
10.4. Геометрические преобразования
Подобное
преобразование
поверхности
Растяжение
Сдвиговое
деформирование
Рис. 10.16. Элементарные геометрические преобразования для элемента плоской
поверхности: перемещение, поворот, подобное преобразование, растяжение и
сдвиговое деформирование
10.4.2. Аффинное преобразование
Аффинное преобразование является линейным координатным преобразованием,
которое включает элементарные преобразования перемещения, вращения,
масштабирования, растяжения и сдвигового деформирования (рис. 10.16), и может быть
выражено векторным сложением и матричным умножением
У
а,
а.
а,
а
hl'l
22 J
Гх
1У\
+
41
14
(10.25)
*21
При однородных координатах (раздел 7.7) аффинное преобразование
записывается с помощью одного матричного умножения как
а,
Gy
а
21
О
а
11
О
t.
1
(10.26)
Аффинное преобразование имеет шесть степеней свободы: две для
перемещения (t^, О и по одной для вращения, масштабирования, растяженры и
сдвигового деформирования (tz,,, а^^, а^^ и а^^. Аффинное преобразование отображает
треугольник в треугольник, а прямоугольник в параллелограмм. Следовательно,
оно также относится к трехточечному отображению. Таким образом, очевидно,
что использование аффинного преобразования ограничено. Более общие
искажения, такие, как при отображении прямоугольника в произвольный
четырехугольник, не являются аффинными преобразованиями.
10.4.3. Перспективное преобразование
Перспективная проекция является основой оптического формирования
изображений согласно рассмотренному в разделе 7.3. Аффинное преобразование
соответствует параллельной проекции и может использоваться только как модель для
оптического формирования изображений в пределе малого поля зрения. Общее
перспективное преобразование наиболее удобно записывается с помощью
однородных координат (раздел 7.7) как
Глава 10. Пиксельная обработка
WX
/ /
wy
W
а
а.>
а,.
а
21
L^3i
а
22
а
23
а
32
1
WX
wy
W
или
Х' = РХ,
(10.27)
Два дополнительных коэффициента, а^^ и а^^, не присутствующие в аффинном
преобразовании (10.26), описывают перспективную проекцию (сравните с
уравнением (7.61) в разделе 7.7).
Записанное в стандартных координатах перспективное преобразование
согласно уравнению (10.27) выглядит
а^,х + а^^у + \
у ^^21^ + ^223^ + ^23
^31^ +«32^^ + 1
(10.28)
В отличие от аффинного преобразования, перспективное преобразование
нелинейно. Однако оно сводится к линейному преобразованию использованием однородных
координат. Перспективное преобразование отображает линии в линии, но только
линии, параллельные плоскости проекции, остаются параллельными. Прямоугольник
отображается в произвольный четырехугольник. Следовательно, перспективное
преобразование также рассматривается как четырехточечное преобразование.
10.4.4. Определение коэффициентов преобразования с помощью
согласования в конечном числе точек
Как правршо, коэффициенты преобразования, согласно описанному в разделах 10.4.2
и 10.4.3, неизвестны. На самом деле мы имеем множество соответствующих точек
между объектом и пространством изображения. В этом разделе мы изучим, как
сделать вывод о коэффициентах преобразования по множеству соответствующих
точек. Для аффинного преобразования нам необходимы три неколлинеарные точки
(для отображения треугольника в треугольник). С этими тремя точками уравнение
(10.26) приводргг к следующему виду линейной системы уравнений:
f
1
/
^2
/
У2
1
/ ~
X,
Уг
1
=
а.
а,.
= а
21
а
22
О
Лл Л"у •Ai'i
Ух Уг Уъ
1 1 1
(10.29)
или Р'= АР,
из которой А можно вычислить как
А = Р'р-\
Матрица, обратная к матрице Р, существует в случае, когда три точки
^3 — линейно независимы. Это означает геометрически, что они не должны лежать
на одной прямой. При более чем трех соответствующих точках параметры аффин-
(10.30)
(10.31)
10.5. Интерполяция 281
ного преобразования могут быть найдены с помощью следующей системы уравне
НИИ в смысле наименьших квадратов (раздел 17.4):
р'рТ(^ррту
А =
FP' =
РР^ =
(10.32)
при
^^Уп П X .УпУп 7 лУп
Х^„ 1л N .
Преобразование, обратное аффинному преобразованию, является также
аффинным. Матрица преобразования обратного преобразования задается обратной
матрицей А~^.
Определение коэффициентов для перспективной проекции незначительно
более сложное. Задав четыре или больше соответствующих точек, можно определить
коэффициенты перспективного преобразования. В завершение переписываем
уравнение (10.28) как
^ _, / / (10.33)
Для 7V точек это приводит к линейной системе уравнений с 2А^ уравнениями и
8 неизвестными вида
Ух
Уг
Ух
0
Уг
0
Xf)
1
0
1
0
1
0
X,
0
^2
0
0
Ух
0
Уг
0
0
1
0
1
0
/
-^Ух
/
-^гУг
-УхХх
-УхУх
-УгА
-УгУг
-У^х'и
j;;J [о о о х^ j;^ 1 --х^у^ -Уг^у'Л
которая может быть решена как задача о наименьших квадратах.
а,
12
а.
13
а.
2\
а
22
а
23
а
31
а
■32
10.5. Интерполяция
10.5.1. Общее понятие
Другим важным аспектом дискретных геометрических операций помимо
преобразования является интерполяция. Интерполяция требуется, поскольку
преобразованные точки сетки входного изображения, в обп];ем, не совпадают больше с
точками сетки выходного изображения, и наоборот.
Глава 10. Пиксельная обработка
Основой интерполяции является теорема о дискретном представлении
(раздел 9.2.2). Эта теорема утверждает, что цифровое изображение полностью
представляет непрерывное изображение при условии, что выполняются условия
дискретизации. Вкратце это означает, что каждая периодическая структура, которая
имеет место на изображении, должна выбираться по меньшей мере дважды в
длину волны. Из этого основного факта легко, по крайней мере в принципе,
разработать основу для интерполяции: сначала реконструируем непрерывное
изображение и затем выполняем новую выборку в новых точках сетки. Эта процедура
работает только до тех пор, пока новая сетка имеет равный или более узкий шаг
сетки. Если он шире, то будет возникать наложение. В этом случае изображение
должно предварительно фильтроваться, прежде чем оно заново дискретизируется.
Хотя создается впечатление, что эти процедуры являются простыми и
прямыми, это вовсе не так. Проблема связана с тем, что реконструкция непрерывного
изображения по дискретизированному изображению на практике становится
довольно сложной и может выполняться только приближенно. Таким образом, нам
необходимо рассмотреть, как оптимизировать интерполяцию при заданных
определенных ограничениях. В этом разделе мы сначала увидим, почему идеальная
интерполяция невозможна, и затем обсудим различные практические подходы в
разделах 10.5.2 - 10.6.2.
В разделе 9.3.1 мы сформулировали, что реконструкцию непрерывной
функции по выборочным точкам можно рассматривать как операцию свертки
9r(^) = ^9(Xm,n)Kx-x^J,
(10.34)
где непрерывная интерполяционная маска h является sine функцией
, , . sin пх. I Дх, sin nxj I Ах.
К^) = 7—^ 7—^. (10.35)
жх^ I Ах, пх^ I Ах^
Передаточная функция функции рассеяния точки в уравнении (10.35)
является функцией-ящиком с шириной 2^^ = 1/Ах:^ (уравнения (9.8) и (9.14)):
к{к) = ЩК12,кг12) при к= 2к„Ах^- (10.36)
Об интерполяционной природе ядра свертки (10.35) можно сделать вывод из
следующих свойств. Интерполируемые значения в уравнении (10.34) в точках
сетки х^^ должны воспроизводить точки сетки и не зависеть от какой-либо другой
точки сетки. Из этого условия мы можем получить интерполяционное условие:
[1 т = 0,п = 0
^(^т,п) = \^ ' (10.37)
[U иначе
Интерполяционная маска в уравнении (10.35) удовлетворяет этому
интерполяционному условию. Любая рштерполяционная маска должна, следовательно, иметь
нулевое пересечение во всех точках, за исключением нулевой точки, где она равна единице.
Вывод о том, что интерполяция является операцией свертки и, таким образом,
может описываться передаточной функцией в Фурье-пространстве (10.36), дает
нам доступный инструмент для оценки ошибок, связанных с интерполяционным
методом. Передаточная функцрш типа «ящик» для идеальной интерполяционной
функции просто означает, что все волновые числа внутри диапазона возможных
10.5. Интерполяция 283
волновых чисел | ft^ | < 1/(2Ах:^) не испытывают ни фазового сдвига, ни затухания
амплитуды. Также никакие волновые числа вне разрешенного интервала не
присутствуют в интерполированном сигнале, поскольку передаточная функция там равна нулю.
Идеальная интерполяционная функция в уравнении (10.34) является сепара-
бельной. Следовательно, интерполяцию можно легко сформулировать для
изображений более высокой размерности. Мы можем ожидать, что все решения
интерполяционной задачи будут также сепарабельными. Следовательно, нам нужно
рассмотреть только 1-D интерполяционную задачу. Раз она решена, мы также
имеем решение для «-мерной интерполяционной задачи.
Важным частным случаем является интерполяция для промежуточных точек
сетки, находящихся между существующими точками сетки. Эта схема удваивает
разрешение и размер изображения во всех направлениях, в которых она
применяется. Тогда непрерывное интерполяционное ядро сводится к дискретной маске
свертки. Поскольку интерполяционное ядро (10.35) является сепарабельным, мы
можем сначала интерполировать промежуточные точки в строке в
горизонтальном направлении, прежде чем мы применим вертикальную интерполяцию к
промежуточным строкам. В трехмерном случае третья 1-D интерполяция добавляется
в направлении z или /. Интерполяционные ядра одинаковы во всех направлениях.
Нам необходимо непрерывное ядро h{x) только при полуцелых значениях для х/Ах.
Из уравнения (10.35) мы получаем дискретное идеальное интерполяционное ядро
/2 =
{-Xy-'l 111 1 (-1Г'2
(10.38)
{1т-1)71 Ъп п п Ъп (1т-\)к
с коэффициентами чередующихся знаков.
10.5.2. Интерполяция в Фурье-пространстве
Интерполяция сводится к простой операции в Фурье-области. Как показано с
помощью уравнения (10.36), передаточная функция идеального интерполяционного
ядра является функцией-ящиком, которая равна нулю за пределами волновых
чисел, которые можно представить. Этот основной вывод предлагает следующую
интерполяционную процедуру в Фурье-пространстве:
1. Увеличиваем матрицу преобразованного с помощью преобразования
Фурье изображения. Если матрица Мх Af увеличивается до матрицы М'х М\ то
изображение в пространственной области также увеличивается до изображения М'х М\
Из-за взаимности преобразования Фурье размер изображения остается без
изменений. Только пространство между пикселями уменьшается, приводя к более
высокому пространственному разрешению:
МАк^М'М о . Ах = — >Ах' = —^. (10.39)
МАк М'Ак
2. Заполняем дополнительную область в Фурье-пространстве нулями и
вычисляем обратное преобразование Фурье.
Теоретически эта процедура приводит к прекрасно интерполированному
изображению. К сожалению, она имеет три недостатка:
1. Преобразование Фурье от конечного изображения подразумевает
циклическое повторение изображения в пространственной области и Фурье-области.
Глава 10. Пиксельная обработка
Таким образом, свертка, выполненная с помощью преобразования Фурье,
является циклической. Это означает, что на контуре изображения свертка продолжает
изображение на противоположной стороне. Поскольку реальный мир не является
периодическим, а интерполяционные маски являются большими, это может
привести к значительным искажениям интерполяции даже на довольно больших
расстояниях от контуров изображения.
2. Преобразование Фурье можно вычислить эффективно только для
определенного числа значений для М\ Наиболее известными являются быстрые
двоичные алгоритмы, которые можно применять только к изображениям размера М'- 2^
(раздел 2.5.2). Следовательно, интерполяция на основе использования
преобразования Фурье является медленной для чисел М', которые не могут выражаться как
произведение большого числа малых множителей.
3. Поскольку преобразование Фурье является глобальным преобразованием,
оно может применяться только к масштабированию. Согласно обобщенной
теореме подобия (теорема 2.1, с. 60), оно могло бы также применяться к повороту и
аффинным преобразованиям. Но тогда задача интерполяции сдвигается из
пространственной области в область волновых чисел.
10.5.3. Линейная интерполяция
Линейная интерполяция является классическим подходом к интерполяции.
Интерполируемые точки лежат на участках прямых, соединяющих соседние узлы сетки.
Для того чтобы упростить выражение, мы используем в дальнейшем
нормированные пространственные координаты х = х/ Ах. Расположим два узла сетки в -1/2 и
1/2. Это дает интерполяционное уравнение
д(х) = ^"^ ^-"^ +{д^,^ -д-т)^ для | jc| < 1/2. (10.40)
Из сравнения уравнения (10.40) с уравнением (10.34) мы можем заключить,
что непрерывная интерполяционная маска для линейной интерполяции равна
/^(х) =
[l-|jc| |х| < 1
(10.41)
[О иначе
Ее интерполяционная природа проиллюстрирована на рис. 10.17.
Передаточная функция интерполяционной маски для линейной интерполяции, треугольная
1/2(91,2+g-iJ
б
Линейное интерполяционное ядро
Рис. 10.17. Иллюстрация линейной интерполяции: а — при х = О берется среднее
значение между gf,/2 и 5^-1/2' ^ ~ "Р^ X = О, gf,/2 повторяется
10,5, Интерполяция 285
функция Aj(x) в уравнении (10.41), равна квадрату sine функции ()^R5)
сравнение с идеальной передаточной функцией для интерполяции (10.36)
показывает, что линейная интерполяция вносит два искажения:
1. В то время как малые волновые числа (и особенно среднее значение к =0)
интерполируются правильно, большие волновые числа незначительно
уменьшаются в амплитуде, приводя к некоторой степени сглаживания. При к = 1
передаточная функция уменьшается приблизительно до 40%: /г,(1) = (2/л:У ~ 0,4.
2. Поскольку h^{k) не равна нулю при волновых числах к > I, вносятся
некоторые ложные большие волновые числа. Если непрерывно интерполированное
изображение заново дискретизировать, то это даст небольшое наложение
спектров. Первый боковой лепесток имеет амплитуду, равную (2/Зл:У ~ 0,045.
Если мы интерполируем только промежуточные узлы сетки в х = О, то
непрерывная интерполяционная функция (10.41) сводится к дискретной маске свертки
со значениями в х = [... -3/2 -1/2 1/2 3/2 ...]. Поскольку уравнение (10.41) равно
нулю для X > 1, мы получаем простую интерполяционную маску Н= 1/2[ 11 ] с
передаточной функцией
h^(k) = cosnk/2, (10.43)
Передаточная функция является действительной, так что никаких фазовых
сдвигов не возникает. Значительное ослабление амплитуды при более высоких
волновых числах, однако, показывает, что структуры с высокими волновыми
числами интерполируются некорректно. Фазовые сдвиги возникают при всех других
значениях, кроме промежуточных узлов сетки при х = 0. Исследуем фазовый сдвиг
и затухание амплитуды линейной интерполяции при произвольных дробньгх
целых сдвигах € € [-1/2, 1/2]. Интерполяционная маска для точки е равна тогда
[1/2 - б, 1/2 + б]. Маска содержит симметричную часть [1/2,1/2] и
антисимметричную часть [-6, б]. Следовательно, передаточная функция является комплексной и
имеет форму
h^(e,k) = cosn:k/2 + 2iesm7rk/2. (10.44)
Для того чтобы оценить ошибку в фазовом сдвиге, полезно компенсировать
линейный фазовый сдвиг Аср = блк, вызванный перемеш;ением б.
Согласно теореме о сдвиге (теорема 2.3, с. 60, >-R4), требуется умножить
уравнение (10.44) на Qxp(i6Kk): тогда мы получаем
h^(e,k) = (cos7rk/2-\-2iesinnk/2)Qxp(-ie7rk)' (10-45)
Только для /I = о и 6 = 1/2 передаточная функция является действительной:
^ (О, k) = cosnk/2, /г, (1 / 2, ^) = 1; но при всех других дробных сдвигах ненулевые
фазовые сдвиги остаются, как наглядно представлено на рис. 10.18. Фазовый сдвиг
А(р выражается как сдвиг положения Ах соответствующей периодической
структуры, т.е. Ах = А(рХ/2к= А(р/(пк).
286 Глава 10. Пиксельная обработка
10.5.4. Полиномиальная интерполяция
При заданных существенных ограничениях линейной интерполяции, как
рассмотрено в разделе 10.5.3, мы задаемся вопросом: выполняются ли интерполяционные
схемы более высокого порадка лучше? Основной принцип линейной
интерполяции заключался в том, что строилась прямая линия, проходящая через две точки.
Таким же образом мы можем использовать полином степени Р, который должен
проходить через Р+ 1 точек с Р+ 1 неизвестными коэффициентами а:
р
дД^) = Х^Р^''- (10.46)
По причинам симметрии в случае четного числа узлов сетки мы
устанавливаем их положение в полуцелые значения
^р =
2р-Р
(10.47)
Из условия интерполяции в узлах сетки дХ^р) = д^ мы получаем линейную
систему уравнений сР+\ уравнениями и Р+ 1 неизвестными а следующего вида,
когда Р является нечетным:
00
9{Р-\)/2
9(Р+\)/2
9р
1 -PI2 РЧА -P4S
1 -1/2
1 1/2
1/4 -1/8
1/4 1/8
1 Р/2 РЧА P4S
On
а.
(10.48)
из которой мы можем определить коэффициенты полинома. Для кубического
полинома (Р= 3) система уравнений имеет вид
с решением
Г^о'
191
02
19, _
Г«о]
Г'
«2
к J
"1
-3/2 9/4 -27/8"
1 -1/2 1/4 -1/8
1 1/2 1/4 1/8
1 3/2 9/4 27/8_
_ 1
~48
-_3 27 27 -3]
2 -54 54 -2
12 -12 -12 12
-8 24 -24 8]
Г«о1
Г'
Г'
\[^i\
'9o^
9х
02
М
(10.49)
(10.50)
10.5. Интерполяция 2Ы
в
0,8
0,6
0,4
0.2
О
1
0,95
0,9
0,85
0,8
0.75
0,7
-}--■
-(
3.4
-
3,2
1/4
'V2
3/4
l\
(
3
0,2
/
0.4 z
\
1/2
1/4
^4
-0.4
-0.2
0,2
0,4 £
0.1
0.05!
О
-0,05
-0.1
0.06
0,04
0.02
О
-0,02
-0,04
-0.06
h
N
"--^
-0.4
1/4
1/2
3/4
-0.2
0
0.2
ч
0,4 £
1/4
~Ш
3/4
-0,4
-0,2
0,2
0,4 £
Рис. 10.18. Затухание амплитуды (левая колонка) и фазовый сдвиг, выраженный как
сдвиг положения Ах = ^.(рХ/2к, правая колонка в радианах для волновых чисел
^ = 1/4, 1/2, 3/4, показанные как функция дробного положения от -1/2 до 1/2 для
линейной интерполяции (а и б) и для кубической В-сплайновой интерполяции (в и г)
Из этого решения мы можем сделать вывод, например, что точка в х = О
интерполируется выражением дДО) = «о ~ ~ ^I^^9q + 9/16gf, -f 9/1602-1/16^35
соответствующим интерполяционной маске 1/16[-1, 9, 9,-1].
На рис. 10.19 показаны передаточные функции для полиномиальной
интерполяции различных степеней. С увеличением степени Р интерполирующего
полинома передаточная функция лучше приближается к функции-ящику. Однако
сходимость является медленной. Для точной интерполяции мы должны взять большую
интерполяционную маску.
б
0.8
0,6
0,4
0,2
О
^\5
7
\
\V
0,2
0,4
0.6
0,8
1
0.99
0.98
0.97
0.96
0.95
1 \3 \\\
\ \ 5\ Л7
0.2
0.4
0,6
0,8 ^ 1
Рис. 10.19. Передаточная функция дискретных полиномиальных интерполяционных
фильтров для интерполирования значения между двумя узлами сетки. Степень
полинома (1 - линейный, 3 - кубический и т.д.) обозначается на фафике. Пунктирная линия
отмечает передаточную функцию для кубической В-сплайновой интерполяции (раздел
10.6.1): а — полный диапазон; б — 5%-ная область ниже идеального отклика h{k) = 1
Глава 10. Пиксельная обработка
10.6. Оптимизированная интерполяция
10.6.1. Интерполяция с помощью сплайн-функций
Помимо своей ограниченной точности полиномиальная интерполяция имеет еще
один существенный недостаток: интерполированная кривая не является
непрерывной в узлах сетки уже в своей первой производной. Это обусловливается тем,
что для каждого интервала между узлами сетки берется новый полином. Таким
образом, только интерполированная функция является непрерывной в узлах
сетки, но не производные.
Сплайны позволяют избежать этого недостатка с помощью дополнительных
ограничений для неразрывности производных в узлах сетки. Из широких классов
сплайнов мы будем рассматривать здесь только один класс — В-сплайны. Поскольку
В-сплайны являются сепарабельными, достаточно рассмотреть свойства 1-D
В-сплайнов. Исходя из обработки изображений, самым легким подходом к
сплайнам является их свойство свертки. Ядро В-сплайновой кривой Р-го порядка
образуется с помощью свертывания функции-ящика Р+ 1 раз с самой собой (рис. 10.20, а):
чР+1
/Зр(х) = П(х)*...*П(х)
Рр{к) =
sin nkll
(nk/2)
(10.51)
(Р+\) раза
Передаточная функция функции-ящика является sine функцией (>-R5).
Следовательно, передаточная фунюция В-сплайна Р-го порядка равна
Рр(к) =
sin nkll
{nkll)
(10.52)
На рис. 10.20, б показывается, что В-сплайновая функция не образует
подходящую интерполяционную функцию. Передаточная функция начинает убывать
слишком рано, указывая на то, что В-сплайновая интерполяция выполняет
слишком большое усреднение. Кроме того, В-сплайновое ядро не удовлетворяет
интерполяционному условию (10.37) для Р> 1.
1
0,8
0.6
0.4
0,2
О
-0.2
, "^"^
/
/л
' 1
/
1
1
1'''
л
\
\1
ч\
0
\
V
\
^О V ^
1
0.8
0.6
0.4
0.2
О
-0.2
"У
/ /
/ '''''
/1!'
1!'
/>
3
1\
)\ \
^^^\ \
Рис. 10.20. а — В-сплайновые интерполяционные ядра, образованные с помощью
каскадной свертки ядра-ящика порядка О (ближайший соседний элемент), 1
(линейная интерполяция), 2 (квадратический В-сплайн) и 3 (кубический В-сплайн);
б — соответствующие передаточные функции
10.6. Оптимизированная интерполяция 289
В-сплайны можно использовать для интерполяции, только если сначала
дискретные узлы сетки преобразуются таким образом, что последующая свертка с
В-сплайновым ядром возвращает исходные значения в узлах сетки. Это
преобразование известно как В-сплайновое преобразование и строится из следующего условия:
0/^) = X^A(^-^J при gf^xj = gf(xj.
(10.53)
Если произвести центрирование относительно узла сетки, то В-сплайновое
интерполяционное ядро не равно нулю только для трех узлов сетки.
Коэффициенты /Зз(-1) = А,> Р^{^) = До и /Зз(1) = Д равны 1/6, 2/3 и 1,6. Свертка этого ядра с
неизвестными значениями В-сплайнового преобразования с^ должна дать в результате
исходные значения д^ в узлах сетки. Следовательно,
д = с^Р^ или Qn-zli ^nwPn.
(10.54)
и'=-1
Уравнение (10.54) образует разреженную линейную систему уравнений
4 1 О ••. О 1
1 4 1 О ••. О
9о
9х
?Af-l.
1
~6
0
■•
0
1
1
0
4
1
0
1
4
1
0
0
■-.
1
4
1
0
1
4
■^N-X
(10.55)
с использованием циклических граничных условий. Определение В-сплайнового
преобразования, таким образом, требует решения линейной системы уравнений с
А^неизвестными. Однако специальный вид системы уравнений как операции
свертки предусматривает более эффективное решение. В Фурье-пространстве
уравнение (10.54) сводится к
9 = Р.с.
(10.56)
Передаточная функция для р^ равна Д (^) = 2 / 3 +1 / 3 cos(;r^). Поскольку эта
функция не имеет нулей, мы можем вычислить с с помощью обратной фильтрации
(раздел 4.4.2), т.е. свертывания д с маской, которая имеет передаточную функцию
Ь-,\к) = Ш = ——1 .. (10.57)
2/34-1/Зсо8л:Л:
Такая передаточная функция имеет вид рекурсивного фильтра (раздел 4.4.2),
который применяется сначала в прямом и затем в обратном направлениях со
следующей рекурсией [204]:
д: = g^-{2S){gl,-g„)
с'„ = д[-(2-4ъ){с„,,-д:).
(10.58)
Глава 10. Пиксельная обработка
Вся операция требует только двух действий умножения и четырех - сложения.
В-сплайновая интерполяция применяется после В-сплайнового
преобразования. В непрерывном случае с использованием уравнения (10.51) это приводит к
эффективной передаточной функции
. - sin4rt-/2)/(rf-/_2)- „0.59)
(2/3 + 1/Зсо8л:Л:)
По существу, В-сплайновое преобразование выполняет усиление высоких
волновых чисел (при ^ = 1 в 3 раза). Это компенсирует сглаживание В-сплайновой
интерполяции в значительной степени.
Исследуем эту компенсацию в узлах сетки и в промежуточных узлах. Из
уравнения кубического В-сплайнового интерполирующего ядра (10.51) (см. также рис.
10.20, а) интерполяционные коэффициенты для узлов сетки и промежуточных
узлов сетки равны
1/6 [1 4 1] и
1/48 [1 23 23 1] ^^^-^^^
соответственно. Следовательно, передаточные функции равны
2/3 + 1/Зсо8л:^ и
23/24со8(л:^/2) + 1/24со8(Зл:^/2) ^^^*^^^
соответственно. В узлах сетки передаточная функция полностью компенсирует -
как ожидалось — применение В-сплайнового преобразования (10.57). Таким
образом, интерполяционная кривая проходит через значения в узлах сетки. В
промежуточных узлах эффективная передаточная функция для кубической
В-сплайновой интерполяции тогда равна
5 ,,, ^ Гч 23 / 24 С08(л:^ / 2) +1 / 24 со8(Зл:^ / 2)
2/3 + 1/Зсо8л:А:
Затухание амплитуды и фазовые сдвиги, выраженные как сдвиг положения в
пиксельных расстояниях, показаны на рис. 10.18, в, г. Обратите внимание на то,
что сдвиг связан с промежуточной сеткой. Сдвиг и затухание амплитуды равны
нулю в узлах сетки [-0,5, 0,5]^. В то время как затухание амплитуды максимально
для промежуточного узла, сдвиг положения также равен нулю в промежуточном
узле по причинам симметрии. К тому же при волновом числе к = 3/4 фазовый сдвиг,
к сожалению, только приблизительно в 2 раза меньше, чем для линейной
интерполяции (рис. 10.18, 6), Он является все еще существенным с максимумом
приблизительно 0,13.
Это значение является слишком высоким для алгоритмов, которые должны
быть точными в диапазоне 1/100 пикселя. Если невозможно применить лучшую
интерполяцию, это означает, что максимальное волновое число должно быть
ниже 0,5. Тогда максимальный сдвиг составляет ниже 0,01, а затухание
амплитуды меньше 3%.
Обратите внимание, что эти замечания по фазовым сдвигам применимы
только для произвольных дробных сдвигов. Для пикселей на промежуточной сетке сдвиг
положения вообще не происходит. В этом частном случае, который нередко воз-
10.6. Оптимизированная интерполяция
никает в обработке изображений, например, для вычислений пирамид (глава 5)
оптимизация интерполяционных фильтров является достаточно легкой,
поскольку нужно минимизировать только затухание амплитуды по интересующему нас
диапазону волновых чисел.
10.6.2. Интерполяция по методу наименьших квадратов
Разработка фильтров для интерполяции — как любая задача разработки фильтров —
может рассматриваться математически более строгим образом как задача
оптимизации. Общая идея заключается в изменении коэффициентов фильтра таким
образом, что отклонение от идеальной передаточной функции достигает минимума.
Для нерекурсивных фильтров передаточная функция является линейной
относительно коэффициентов h\
кк) = ^КЛ(к), (10.63)
г=]
Пусть идеальная передаточная функция есть h (к)- Тогда оптимизационная
процедура должна минимизировать интеграл
lw(k)
£/^.XW M/W dk. (10.64)
о \\г=\ ) I
В этом выражении была введена весовая функция w{k), которая позволяет
контролировать оптимизацию для определенного диапазона волновых чисел. В
уравнении (10.64) учитывается произвольная L^-норма. В большинстве случаев
берется 12-норма, которая минимизирует сумму квадратов.
Для L^-HopMbi задача минимизации приводит к линейной системе уравнений
для R коэффициентов фильтра, которую можно легко решить:
Mh = d (10.65)
при d =
и М =
h,f.
где было использовано сокращение
А, /Ч
h J\Ji
J\J1 Jl
J\Jr JiJR
e(^) = jw(^)-e(^)d^
J\Jr
JlJR
/r
(10.66)
для произвольной функции e{k).
Гибкость оптимизационного метода наименьших квадратов для разработки
фильтров определяется свободным выбором весовой функции w{k), а тщательное
рассмотрение свойств симметрии и других особенностей фильтра — выбором пе-
Глава 10. Пиксельная обработка
редаточной функции в уравнении (10.63). Для иллюстрации рассмотрим
следующие два подхода:
h(k) = ^h^ COS
r=l
2r~l
Л
Tvk
(10.67)
h(k) = cos
— nk
2
\
+
COS
(i!^.k
-COS
(10.68)
Оба фильтра в результате дают симметричную маску за счет выбора
косинусной функции. Уравнение (10.68) гарантирует, что й(0) = 1, т.е. средние уровни
яркости сохраняются при интерполяции. Это получено путем приравнивания
первого коэффициента, Ар единице минус сумма всех других. Уравнение (10.67) не
использует это ограничение. На рис. 10.21 сравниваются оптимальные
передаточные функции с обоими подходами для Л = 3.
Фильтры в этом случае оптимальнее, чем полиномиальные и кубические
В-сплайновые интерполяции (см. рис. 10.19). Дополнительная степень свободы
для уравнения (10.67) приводит к значительно лучшим решениям для диапазона
волновых чисел, где весовая функция максимальна. Еще более подходящие
интерполяционные маски можно получить с помощью использования комбинации
нерекурсивных и рекурсивных фильтров, как в случае с кубической В-сплайновой
интерполяцией:
cos(l/2л:^) + 2,^Jcos((2r~3)/2 л:^)-cos(l/2 пк)\
h(k) = -
г=2
l-a+acos
н
(10.69)
При рекурсивных фильтрах оптимизация методом наименьших квадратов
становится нелинейной, поскольку й^{к) в уравнении (10.69) нелинейна относительно
параметра а рекурсивного фильтра. Тогда требуется итерационный подход для решения
оптимизационной задачи. На рис. 10.21, в, г показаны передаточные функции для R =
2. Более детальное рассмотрение интерполяционных фильтров, включающее
таблицы с оптимизированными фильтрами, можно найти в книге Яне (Jahne) [89].
10.6.3. Быстрые алгоритмы для геометрических преобразований
Благодаря этому исчерпывающему рассмотрению по интерполяции мы хорошо
оснащены для создания быстрых алгоритмов для различных геометрических
преобразований. По существу, все быстрые интерполяционные алгоритмы
используют следующие два принципа: эффективное вычисление, использующее
интерполяционные коэффициенты, и разбиение на 1-D геометрические преобразования.
Во-первых, требуется большое количество вычислений интерполяционных
коэффициентов для дробных сдвигов. Для каждого сдвига требуются отличные
интерполяционные коэффициенты. Таким образом, мы должны разрабатывать
преобразования таким образом, чтобы нам понадобились только постоянные
10.7. Многоканальные точечные операции
1
0,8
0.6
0.4
0.2
О
/
у
\
"^,,
л
\^
\ \
\\
\\
\\
0,2
0.4
0.6 0.8 1
1,01
1.005
1
0.995
0,99
N^^
/-"^
/
i
0,2 0.4
0.6 0,8
Рис. 10.21. Передаточная функция интерполяционных ядер, оптимизированных с
помощью метода взвешенных наименьших квадратов (уравнения (10.67) и
уравнения (10.68) с /? = 3 (сплошная линия) и уравнения (10.69) для R=2 (пунктирная
линия)). Весовая функция, используемая для оптимизации, показана на а — тонкой
сплошной линией; б — показывает узкий сектор графического изображения в а для
лучшего оценивания малых отклонений от идеальных значений
сдвиги для определенного прохода преобразования. Если это невозможно, то
может быть все еще эффективно предварительно вычислить интерполяционные
коэффициенты для различных дробных шагов и сохранить их для дальнейшего
использования.
Во-вторых, мы узнали в разделе 10.5.1, что интерполяция является сепарабель-
ной процедурой. Принятие во внимание этого основного факта значительно
уменьшает число операций. В большинстве случаев возможным является разделение
двумерных и более высокой размерности геометрических преобразований в ряд
1-D преобразований.
10.7. Многоканальные точечные операции
10.7.1. Определения
Точечные операции можно обобщить до многоканальных точечных операций без
особых затруднений. Операция по-прежнему зависит только от значений
отдельного пикселя. Единственное различие состоит в том, что она зависит от векторных
входных данных вместо скалярных. Выходное изображение тоже может быть
многоканальным изображением. Для однородных точечных операций, которые не
зависят от положения пикселя в изображении, мы можем записать
G^P{G) при (10.70)
Ь =LCjo,C7p ...,C7^, ...,Cj^_J,
где G\ и G^- компоненты / и /: многоканальных изображений G'nGc Ln A^
каналами соответственно.
Линейные операторы являются важным подклассом многокомпонентных
точечных операторов. Это означает, что каждый компонент многоканального
изображения С является линейной комбинацией компонент многоканального
изображения G: ^_j
^;=Ё^А, (10.71)
Глава 10. Пиксельная обработка
где Р^^ являются постоянными коэффициентами. Следовательно, общая линейная
многокомпонентная точечная операция задается матрицей коэффициентов Р. Тогда
мы можем записать уравнение (10.71) в матричном обозначении как
G' = PG. (10.72)
Если компоненты многоканальных изображений в точечной операции не
взаимосвязаны друг с другом, то все коэффициенты в Р, за исключением компонент
на диагонали, становятся нулевыми. Для АГ-канальных входных и выходных
изображений остаются только ^различных точечных операций, по одной для каждого
канала. Матрица точечньвс операций окончательно сводится к стандартной
скалярной точечной операции, когда одна и та же точечная операция применяется к
каждому каналу многокомпонентного изображения.
Для равного числа выходных и входных изображений линейные точечные
операции можно интерпретировать как координатное преобразование. Если матрица
коэффициентов в уравнении (10.72) имеет ранг R<K,to многоканальная точечная
операция проектирует ^-мерное пространство в Л-мерное подпространство.
Как правило, линейные многоканальные точечные операции довольно легко
обрабатывать, поскольку они могут описываться непосредственно с помощью
понятий линейной алгебры. Для квадратных матриц, например, мы можем легко
задать условие существования операции, обратной к многоканальной операции, и
вычислить ее. Для нелинейных многокомпонентных точечных операций
линейные коэффициенты в уравнениях (10.71) и (10.72) должны заменяться
нелинейными функциями
Gi=Pi(Gq.G^, ....(^^-i). (10.73)
Нелинейные многокомпонентные точечные операции не могут
обрабатываться общим способом, в отличие от линейных операций. Таким образом, они
должны рассматриваться отдельно. Сложность можно значительно уменьшить, если
возможно разделить данную многоканальную точечную операцию на линейные и
нелинейные части.
10.7.2. Бинарные точечные операции
Операции, в которые входят только два изображения, носят название бинарных
точечных операций. Бинарные однородные точечные операции можно выполнять
как операции с таблицами преобразования (ТП). Как правило, любую бинарную
операцию над изображениями можно выразить как
GL=PiG.nMn..). (10.74)
Если уровни яркости двух входных изображений принимают Q различных
значений, то существует Q^ комбинаций входных параметров и, таким образом,
различных выходных значений. Таким образом, для 8-битовых изображений
требуется вычислить 64 килобайта значений. Это все еще на четверть меньше, чем при
прямом вычислении для каждого пикселя в изображении 512 х 512. Все
возможные результаты бинарной операции можно хранить в большой ТП LcQ^=64
килобайтами элементов следующим образом:
L(2'p + q) = P(p,q), 0<p,q<Q. (10.75)
Старшие и младшие байты адреса ТП определяются уровнями яркости в
изображениях G и Я соответственно.
10.8. Упражнения 295
Некоторые системы обработки изображений содержат 16-битовую ТП в
качестве модулярного обрабатывающего элемента. Вычисление бинарной точечной
операции с помощью либо аппаратной, либо программной ТП является часто
значительно быстрее, чем прямое выполнение, особенно если операция является
комплексной. К тому же легче контролировать исключительные ситуации, такие, как
деление на ноль или потеря значимости и переполнение.
Бинарная точечная операция может использоваться для выполнения двух
точечных операций одновременно. Фазу и модуль (г, /) комплекснозначного
изображения, например, можно вычислять одновременно с помощью одной бинарной
операции с ТП, если мы также ограничиваем выходные данные 8 битами:
128 ^'^
I у V
r^-^f- -{■ arctan
п
I
vO
> 0<rJ<Q (10.76)
Модуль возвращается в старший байт, а фаза, масштабируемая до интервала
[-128,127], в младший байт.
10.8. Упражнения
10.1: Улучшение контрастности
Интерактивная демонстрация улучшения контрастности с помощью
таблиц преобразования (dip6exl0.01).
10.2: Контроль неоднородной освещенности
Интерактивная иллюстрация возможностей для объективного
контролирования неоднородной освещенности с использованием однородных
точечных операций (dip6exl0.02).
10.3: Определение переполнения
Интерактивная демонстрация определения потери значимости и
переполнения с использованием гистограмм (dip6exl0.03).
10.4: Однородные точечные операции
Интерактивная демонстрация однородных точечных операций (dip6ex 10.04).
10.5: ^Таблицы преобразования
Таблицы преобразования можно использовать для быстрого вычисления
однородных точечных операций. Определите уравнения для вычисления
таблиц преобразования следующих точечных операций. Изображения
имеют 0= / дискретных значений. Ответьте на вопрос: можно ли обратить
точечную операцию?
1. Отрицательное изображение (белый становится черным и наоборот).
2. Таблица преобразования, которая определяет потерю значимости и
переполнение уровней яркости. Потеря значимости должна отмечаться в
синем цвете, переполнение — в красном. (Подсказка: цветные выходные
данные требуют трех таблиц преобразования, по одной для красного, зеленого
и синего (аддитивное цветовое смешивание).
^296 Глава 10. Пиксельная обработка
3. Улучшение контрастности: малый диапазон из S уровней яркости должен
быть отображен в полный диапазон уровней яркости из f уровней яркости.
10.6: "^Коррекция нелинейных калибровочных кривых
С помопцью таблиц преобразования можно корректировать калибровочные
кривые.
1. Запишите полную таблицу преобразования для следующей
калибровочной кривой:
д=а^^а,д')-а^д\
где а^ = О, «J = 0,7 и а^ = 0»02 с 16 различными уровнями яркости (4 бита,
уровни яркости от О до 15). Пожалуйста, обратите внимание на то, что
существуют различные возможности для округления: а) отбрасывание
(ближайшее более низкое целое) и б) округление до ближайшего значения
(целое число, которое ближе всего к числу с плавающей запятой).
2. Какие типы ошибок возникают при округлении?
3. Как уменьшить ошибки при округлении, если датчик преобразует
сигнал д в цифровую форму внутри с 16 битами (уровни яркости от О до 63) и
вьщает ^ как 4-битовые значения? Запишите модифицированную таблицу
преобразования, которая охватывает этот случай.
10.7: ^'^Вьписление полярньк координат с помопц>ю таблицы преобразования
Бинарные функции (функции с двумя входными значениями) можно
эффективно вьиислять с использованием таблиц преобразования.
1. Определите уравнения для вычисления таблицы преобразования,
которая вычисляет полярные координаты по декартовым координатам с Р-би-
товым разрешением:
г = (х' +y^f\ ф = (2''-' /п)ггс1т(у/х),
2. Сколько элементов имеет таблица преобразования?
10.8: Усреднение зашумленных последовательностей изображений
Интерактивная демонстрация усреднения зашумленных
последовательностей изображений; вьгаисление изображения дисперсии (dip6exl0.05).
10.9: Коррекция неоднородной освещенности
Интерактивная демонстрация коррекции неоднородной освеш;енности с
использованием неоднородных точечных операций (dip6exl0.06).
10.10: Оконные функции с преобразованием Фурье
Интерактивная демонстрация использования оконных функций с
преобразованием Фурье (dip6exl0.07).
10.11: Интерполяция
Интерактивная демонстрация точности различных интерполяционных
методов при масштабировании с точностью до фрагмента пикселя, сдвиге или
повороте изображений (dip6exl0.08).
10.9. Дополнительная литература
10.12: "^Линейная и кубическая интерполяция
Косинусный сигнал выбирается либо четыре, либо восемь раз в длину
волны. Какой вид сигнала получается при реконструкции непрерывного
сигнала по этим дискретизированным сигналам с помощью либо линейной,
либо кубической интерполяции?
10.9. Дополнительная литература
Холст (Hoist) [78, 80] и Биберман (Biberman) [8] занимаются радиометрической
калибровкой датчиков и камер в видимой и инфракрасной областям спектра.
Детальное рассмотрение интерполяционных фильтров, включающее таблицы с
коэффициентами фильтров и эффективные алгоритмы для геометрических
преобразований, можно найти в книге Яне (Jahne) [89, глава 8]. Читатели, которые
интересуются математической основой интерполяции, отсылаются к Давису (Davis)
[29] и Ланкастеру (Lancaster) и Залкаскасу (Salkauskas) [115]. Вольберг (Wolberg)
[219] дает изложение по геометрическим преобразованиям.
ЧАСТЬ 3
ВЫДЕЛЕНИЕ ПРИЗНАКОВ
ГЛАВА 11
УСРЕДНЕНИЕ
11.1. Введение
в этой главе мы рассмотрим операции над соседними элементами для
выполнения элементарной задачи усреднения. Эта операция представляет особую важность
для низкоуровневой обработки изображений. Она является одним из
строительных блоков для более сложных операторов вьщеления признаков, рассмотренных
в главах 13 — 15.
В простейшем случае объекты распознаются как области постоянной
энергетической яркости, т.е. уровней яркости. Тогда усреднение определяет
соответствующие средние значения уровней яркости внутри объекта. Этот подход, конечно,
подразумевает простую модель содержания изображения. На самом деле
интересующие нас объекты должны характеризоваться постоянными уровнями яркости,
которые явно отличаются от фона и/или других объектов.
Однако это предположение редко выполняется в реальных задачах.
Интенсивность, как правило, меняется в некотором диапазоне. Эти изменения могут быть
собственным признаком объекта или могут быть вызваны процессом
формирования изображений. Типичными случаями являются шум, неравномерная
освещенность или неоднородный фон.
В сложных случаях невозможно отделить объекты от фона с помощью только
одного признака. Тогда вычисление более чем одного признака по одному и тому
же изображению может быть действенным подходом. Это приводит к
многокомпонентному или векторному изображению признака.
Подобная ситуация возникает, когда более чем одно изображение берется из
сцены, как в случае с цветными изображениями или любым типом многоспект-
ралъного изображения. Следовательно, задача усреднения должна также
применяться к векторным изображениям. В последовательностях изображений
усреднение расширяется на временную координату до пространственно-временного
усреднения.
11.2. Общие свойства усредняющих фильтров
Свертка обеспечивает основу для всех элементарных усредняющих фильтров. Эти
фильтры обладают некоторым числом общих свойств, которые рассматриваются в
этом разделе.
77.2 Общие свойства усредняющих фильтров 299
11.2.1. Нулевой сдвиг
Что касается распознавания объектов, наиболее важной характерной
особенностью сглаживающего оператора свертки является то, что он не должен сдвигать
положение объектов. Любой сдвиг, введенный оператором предварительной
обработки, вызвал бы ошибки в оценках положения и, возможно, других
геометрических признаков объекта. Для того чтобы не вызывать сдвига, передаточная
функция фильтра должна быть действительной. Фильтр с этим свойством
известен как фильтр с нулевой фазой, поскольку он не вносит фазовый сдвиг ни в
какую из периодических компонент изображения. Действительная передаточная
функция подразумевает симметричную маску фильтра (раздел 2.3). Ж-мерная
симметричная маска свертки определяется как
1-D: h_„=h„,
2-D* h =h h =h
^ ^' '-m,n ''■m,n^ "'m,-n "^m,n^ (111)
3-D: rl-i^m^n^ '^hm,n^ '^l-m^n^ '^Lm.n'> '^Lm.-n ~'^Lm.n'
Соотношения симметрии также значительно облегчают вычисление
передаточных функций, поскольку в уравнениях остается только косинусный член
комплексной экспоненциальной функции из преобразования Фурье. Передаточная
функция для 1-D симметричных масок с нечетным числом коэффициентов
(27?+ 1) равна
h{k) = /?o + 2^/г^ cos{vnk).
D=l
(11.2)
При четном числе коэффициентов (27?) передаточная функция 1-D
симметричной маски определяется как
h{k) = 2^ h^ cos((u -1 / 2)пк\
v=\
(11.3)
Обратите внимание, что волновые числа равны полуцелым числам v= 1/2, 3/2,...,
поскольку по причинам симметрии результат свертки с маской четного размера
лежит на промежуточной сетке.
Для 2-D симметричной маски с нечетным числом коэффициентов в обоих
направлениях мы получаем соответственно:
h{k) = /2^0
г ^ R
+ 2^ h^^ co^{vnk^) + X ^«0 ^osiunk^)
R R
+ 4^ ^ h^^ cos(vnk^) cos(imk2).
(11.4)
u=\ u=l
Дополнительное обсуждение свойств симметричных масок вплоть до
трехмерного случая можно найти в работе Яне (Jahne) [89].
300 Глава 77. Усреднение
11.2.2. Сохранение среднего значения
Сглаживающий оператор должен сохранять среднее значение. Это условие
свидетельствует о том, что передаточная функция для нулевого волнового числа равна
единице или, эквивалентно, что сумма всех коэффициентов маски равна единице:
1-D: ад=1 J^K=\,
п
2-D: т = 1 ХХ^.«=1'
-" " (11.5)
3-D: ад = 1 ХЕЕ^/.«=1-
1 т п
11.2.3. Монотонно убывающая передаточная функция
Интуитивно мы ожидаем, что сглаживающий оператор ослабляет меньшие
масштабы более интенсивно, чем крупные. Более конкретно сглаживающий оператор
не должен полностью уничтожать определенный масштаб, в то время как
меньшие размеры все еще остаются в изображении. Математически говоря, это
означает, что передаточная функция убывает монотонно с ростом волнового числа:
h{kj)<h{k^), если к^^>к^, (11.6)
Мы можем наложить более строгое условие, состоящее в том, что для самых
высоких волновых чисел передаточная функция тождественна нулю:
1-D: А(1) = 0,
2-D: Л(^р1) = 0, Й(1Д2) = 0, (117)
3-D: А(^1Д2Д) = 0. й(^р1Дз) = 0. h{\,k^,k^) = 0.
Наряду с условием монотонности и сохранением среднего значения, это
означает, что передаточная функция убывает монотонно от единицы до нуля для
каждого усредняющего фильтра.
11.2.4. Изотропия
В большинстве прикладных задач сглаживание должно быть одинаковым во всех
направлениях, для того чтобы не отдавать предпочтение какому-либо
направлению. Таким образом, и маска фильтра, и передаточная функция должны быть
изотропными. Следовательно, маска фильтра зависит только от модуля
расстояния от центрального пикселя, а передаточная функция от модуля волнового
числа:
h{x) = h(\x\) и h{k) = h{\k\l (11.8)
В дискретном пространстве, конечно, это условие может выполняться только
приблизительно. Следовательно, построение дискретных масок с минимальным
отклонением от изотропии является важной конструкторской целью.
11.3. Фильтр-ящик 30 i
11.3. Фильтр-ящик
11.3.1. Введение
Очевидно, что сглаживающие фильтры будут усреднять пиксели внутри малой
окрестности. Простейший метод должен складывать все пиксели внутри маски
фильтра и делить сумму на число пикселей. Такой простой фильтр называется фильтр-
ящик. Фильтры-ящики являются наглядным примером правильной разработки
фильтра. В качестве введения рассмотрим фильтр-ящик 1x3:
'^ = ^[1 1 1]. (11.9)
Множитель 1/3 масштабирует результат суммы свертки, для того чтобы
сохранить среднее значение (раздел 11.2.2). В противном случае уровень яркости в
области с постоянными уровнями яркости не сохраняется. Применим эту маску к
вертикальному контуру:
О О 1 1 ••• ••. О 1/3 2/3 1
О О 1 1 ••• *1[1 1 1]= ... О 1/3 2/3 1
О О 1 1 ••• ••• О 1/3 2/3 1
Как и ожидалось для сглаживающей операции, резкая граница
преобразовалась в линейное изменение сглаживающего фильтра с постепенным переходом от
О до 1. Сглаживающие фильтры ослабляют структуры с высокими волновыми
числами. Давайте проверим это сначала с помощью вертикальной структуры с
длиной волны, равной расстоянию трех пикселей:
1-211-21... 000000
1-211-21 ... *-[1 1 1]= О О О О О О
1-211-21... 000000
Оказывается, что фильтр-ящик 1x3 полностью удаляет структуру с длиной
волны 3. Как уже рассматривалось в разделе 11.2.3, мы ожидаем, что все структуры
с длиной волны выше определенной пороговой величины удаляются хорошим
сглаживающим фильтром. Это не выполняется для фильтра-ящика 1x3. Структура с
длиной волны 2 ослабляется только в три раза:
1-11-1 ... ... -1/3 1/3 -1/3 1/3
1 _1 1 ^1 ... *i[l 1 1]= ... ^1/3 1/3 -1/3 1/3..
1-11-1 ... ... -1/3 1/3 -1/3 1/3..
Глава 11. Усреднение
а
1
0.8
0.6
0.4
0.2
О
-0,2
-0.4
П\\\
\\
\\
9
\ \5
\7 \
' ^ \
\^
\7;
' "^
0,2
0,4
0,6
0.8 k 1
б
1
0,8
0.6
0.4
0,2
О
"1 32
\б\
^
.4 \
0,2
0,4
0.6
0,8 k 1
Рис. 11.1. Передаточные функции одномерных сглаживающих фильтров: а - фильтры-
ящики с 3, 5,7 и 9 коэффициентами; б — биномиальные фильтры (В^ ср = 2,4,8,16 и 32
11.3.2. 1-D фильтр-ящик
После этого качественного введения рассмотрим фильтры-ящики количественно
с помощью вьиисления передаточной функции. Ради простоты начнем с 1-D
фильтров. Маска фильтра-ящика (11.9) имеет четную симметрию. Согласно
рассуждениям в разделе 4.2.6, мы можем применить уравнение (4.25) для вычисления
передаточной функции одномерного фильтра-ящика 1x3. Только коэффициенты
Aq = Aj = 1/3 не равны нулю и передаточная функция сводится к
/ч ~ 1 2
^г(к) = - Ч- — С08(л:А:).
3 3 <"■""
Передаточная функция показана на рис. 11.1, л. Наше быстрое вычисление в
начале этого раздела подтверждается. Передаточная функция показывает ноль при
к = 2/3. Это соответствует волновому числу, которое выбирается три раза в длину
волны. Наименьшая возможная длина волны (^ = 1), которая выбирается дважды
в длину волны, ослабляется только в три раза. Передаточная функцрш
отрицательна для к > 2/3. Отрицательная передаточная функция означает взаимообмен
минимальных и максимальных значений, равный фазовому сдвигу 180°. В
заключение: фильтр-ящик 1 X 3 не является хорошим фильтром нижних частот. То, что
ослабление не увеличивается монотонно с ростом волнового числа, а совершает
колебания, расстраивает. Даже хуже, структуры с наибольшим волновым числом
не ослабляются достаточно сильно.
Большие фильтры-ящики
R
1 1
R раз
С R коэффициентами и передаточной функцией
лл,
Я(А:) =
sm(nRk/2)
Rsm(nk/2)
(11.11)
(11.12)
11.3. Фильтр-ящик 303
не проявляют значительного улучшения (рис. 11.1, й). Наоборот, колебательное
поведение является более выраженным и ослабление только пропорционально
волновому числу. Для больших масок фильтров дискретная маска с Я
коэффициентами приближается к непрерывной функции-ящику ширины R.
Следовательно, передаточная функция аппроксимирует sine функцию (>-R5) при низких
волновых числах (Л = 1):
R^
г(к)^
sminRkll)
nRk/2
= sinc(M/2).
(11.13)
11.3.3. 2-D фильтр-ящик
Теперь вернемся к двумерным фильтрам-ящикам. Чтобы упростить арифметику,
воспользуемся тем, что фильтр является сепарабельным и раскладывает ее на
вертикальные и горизонтальные 1-D компоненты:
'R = 'R, *
п _1
"1 1 1]
1 1 1
_1 1 Ij
3^
1]*-
^ 3
Передаточная функция одномерных фильтров определяется уравнением (11.10)
(заменяя к^ на к у для вертикального фильтра). Поскольку свертка в
пространственной области соответствует умножению в области волновых чисел, передаточная
функция R равна
- + -С08(л:А:,)
3 3'
-Н- —С08(л:а:^)
3 3 "^
(11.14)
11.3.4. Оценка
Из уравнения (11.14) и рис. 11.2, а мы можем заключить, что 2-D фильтры-яищки
являются также плохими фильтрами нР1жних частот. Больший фильтр, например,
фильтр с маской 7x7 (рис. 11.2, б), не вьшолняется хоть насколько-нибудь лучше.
Помимо недостатков, уже обсуждавшихся для одномерного случая, мы сталкиваемся
с проблемой, состоящей в том, что передаточная функция не является изотропной, т.е.
она зависит, дня заданного волнового числа, от направления волнового числа.
Когда мы применяем фильтр-ящик к произвольному изображению, все эти
недостатки влияют на изображение, но их сложно выразить количественно.
Однако они немедленно обнаруживаются, если мы используем тщательно
разработанное тестовое изображение. Это изображение содержит концентрические
синусоидальные кольца. Длина волны колец убывает с ростом расстояния от центра. С
помощью этого тестового изображения мы отображаем Фурье-область в
пространственное изображение. Таким образом, мы можем непосредственно видеть
передаточную функцию, т.е. изменение в амплитуде и фазовый сдвиг, когда
применяем фильтр. Когда мы производим свертку этого изображения с помощью
фильтра-ящика 5x5 или 9x9, отклонения от изотропной передаточной функции
становятся легко видимыми (рис. 11.3). Мы можем наблюдать волновые числа,
Глава и. Усреднение
Рис. 11.2. Передаточные функции двумерных фильтров-ящиков, показанные в псев-
до-3-D графическом отображении: а — фильтр-ящик 3 х 3; б - финьтр-ящик 7x7
которые полностью исчезают, и превращение максимумов уровней яркости в
минимумы уровней яркости, и наоборот, в некоторых областях, указывающее на фазовый
сдвиг в 180°, вызванный отрицательными значениями в передаточной функции.
Из этого опыта мы можем извлечь важный урок. Мы не должны оценивать
свойства фильтрующей операции по ее влиянию на произвольные изображения,
даже если мы думаем, что они, как кажется, выполняются корректно. Очевидно,
глаз воспринимает скорее качественное впечатление, но для количественного
выделения признаков изображения требуется количественный анализ свойств
фильтра. Он включает тщательный анализ передаточной функции и применения
фильтров к специально разработанным тестовым изображениям.
Теперь мы возвращаемся к вопросу о том, что не удалось в случае с фильтром-
ящиком. Мы могли бы попьггаться разработать лучший сглаживающий фильтр
непосредственно в пространстве волновых чисел. Идеальный сглаживающий фильтр
отсекал бы все волновые числа, которые выше определенного порогового значения.
Мы могли бы использовать эту идеальную передаточную функцию и вычислить маску
фильтра с помощью обратного преобразования Фурье. Однако мы сталкиваемся с
двумя проблемами, которые можно понять без явных вычислений. Обратное
преобразование Фурье от функции-ящика представляет собой sine функцию. Это
означает, что коэффициенты убывают прямо пропорционально расстоянию от
центрального пикселя. Мы были бы вынуждены работать с большими масками фильтров.
Кроме того, фильтр имеет недостаток в том, что он сильно отклоняется на контурах.
11.3.5. Быстрое вычисление
Вопреки всем недостаткам фильтров-ящиков, они проявляют одно значительное
преимущество. Согласно следующему уравнению, свертку с помощью
одномерного фильтра-ящика можно вьиислить независимо от его размера с помощью
только трех операций как рекурсивную фильтрующую операцию:
1
9т =9.
т-\
\Ут+г Ут-г-\)'
(11.15)
2г + 1
Эту рекурсию можно понять с помощью сравнения вычислений для свертки в
соседних пикселях. Когда маска-ящик сдвигается на одно положение вправо, она
11.4. Биномиальный фильтр
Рис. 11.3. Тестовый пример сглаживания с помощью фильтра-ящика 5x5 (верхний
правый квадрант) и 9 х 9 (нижний левый квадрант), использующий тестовое
изображение с концентрическими синусоидальными кольцами. Максимальное волновое
число к на контуре структуры равно 0,6
содержит тот же весовой коэффициент для всех пикселей, за исключением
последнего и первого. Таким образом, мы можем просто взять результат предьщущей
свертки - (д^.,), вычесть первый пиксель, который непосредственно сдвигается из
маски, — (S'^.^.i), и добавить уровень яркости в пикселе, который непосредственно
вошел в маску, - {д^^). Таким образом, вьиисление фильтра-ящика не зависит от
его размера, а число вычислений равно О(а^). Только одно сложение, одно
вычитание и одно умножение требуются для вычисления результата фильтра.
11.4. Биномиальный фильтр
11.4.1. Основы
Из нашего опыта с фильтрами-ящиками мы можем заключить, что разработка
фильтров является сложной оптимизационной задачей. Если мы выбираем малую
прямоугольную маску фильтра, получаем плохую передаточную функцию. Если
мы начинаем с идеальной передаточной функции, то получаем большие маски
фильтров и отклоняющиеся отклики фильтров. Причиной такого поведения
является фундаментальное соотношение между гладкостью и компактностью пары
преобразований Фурье (раздел 2.3.4). Граница образует разрыв. Разрыв приводит
к импульсу в первой производной. Преобразование Фурье от импульса
равномерно распространяется по всей Фурье-области. Согласно интегральному свойству
преобразования Фурье (раздел 2.3), интегрирование производной в
пространственной области означает деление на Л в Фурье-области (>-R5). Тогда мы знаем без
какого-либо детального вычисления, что в одномерном случае огибающая
преобразования Фурье от функции, которая проявляет разрывы в пространственной
Глава 11. Усреднение
области, будет уменьшаться со скоростью 1с^ в области волновых чисел. Именно
это мы обнаружили для функции-ящика. Ее преобразованием Фурье является sine
функция (>-R5).
Учитывая этот важный вывод, мы можем разработать лучшие сглаживающие
фильтры. Одним из условий является то, что маски фильтра должны постепенно
приближаться к нулю.
11.4.2. 1-D биномиальный фильтр
Здесь мы введем класс сглаживающих фильтров, которые удовлетворяют этому
критерию и могут вычисляться очень эффективно. Кроме того, эти фильтры
являются отличным примером того, как можно построить более сложные фильтры по
простым компонентам. Простейшей и самой элементарной сглаживающей
маской, которую мы можем представить, является
В = ]^[\ 1]. (11.16)
Она усредняет уровни яркости двух соседних пикселей. Мы можем применить
эту маску R раз в строке на одном и том же изображении. Это соответствует маске
фильтра
^[' '1'1' ']•■■■*[' '] ,11.17,
R раз
ИЛИ, записанное как операторное уравнение,
<^''=тЛ. (11.18)
R раз
Рис. 11.4. Тестовый пример сглаживания с помощью биномиальных фильтров Ф"* и
(В'^, использующий тестовое изображение с концентрическими синусоидальными
кольцами
11.4. Биномиальный фильтр 30
Некоторыми примерами результирующих масок фильтров являются:
5'=1/4[1 2 1],
5'=1/8[1 3 3 1],
В'=\1\6[\ 4 6 4 1], (11.19)
Л'=1/256 [1 8 28 56 70 56 28 8 1].
Из-за симметрии представляют интерес только маски фильтров с нечетным
размером.
Маски содержат значения дискретного биномиального распределения. В
действительности итерационная композиция маски с помош;ью последовательной
свертки с маской 1/2[1 1] эквивалентна вычислительной схеме треугольника Паскаля:
R
0
1
2
3
4
5
6
7
8
/
1
1/2
1/4
1/8
1/16
1/32
1/64
1/128
1/256
1
1 8
1
1 1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
7 21 35 35 21 7
28 56 70 56 28
1
8 1
<j'
0
1 4
1 2
3/4
1
5/4
3/2
7/4
2
(11.20)
где R обозначает порядок бинома; /— масштабный множитель 2"^; а^ —
дисперсию, т.е. эффективную ширину маски.
Вычисление передаточной функции биномиальной маски является также очень
простым, поскольку нам нужно знать только передаточную функцию <В.
Передаточная функция Ф'^ тогда задается как R-я степень:
b\k) = cos\nk/2\
(11.21)
которая может аппроксимироваться для малых волновых чисел с помопцью
b\k) = l-ji7tkf +
^3R^-2R^
384
\(пкУ+0(к').
(11.22)
Графическое представление передаточной функции на рис. 11.1,5
показывает, что биномиальные фильтры являются гораздо лучшими сглаживающими
фильтрами, чем фильтры-ящики. Передаточная функция убывает монотонно и
достигает нуля при наибольщем волновом числе. Наименьшая маска, <В^, имеет
308 Глава 11. Усреднение
полуширину к/2. Это является периодической структурой, которая выбирается
четыре раза в длину волны. Для больших масок как передаточная функция, так и
маски фильтров близки к распределению Гаусса с эквивалентной дисперсией.
Большие маски приводят к меньшим полуширинным волновым числам, согласно
соотношению неопределенностей (раздел 2.3.4).
11.4.3. 2-D биномиальный фильтр
Двумерные биномиальные фильтры могут быть составлены из горизонтального и
вертикального 1-D фильтров:
(B^zzcBfcgJ. (11.23)
Наименьшая маска такого вида является биномиальным фильтром 3 х 3 (Л = 2):
В'=-[1 2 1]*1
4^ ^ 4
_1_
16
1 2
2 4
1 2
1]
2
ij
(11.24)
Передаточная функция 2-D биномиального фильтра (В"с(Л+1)х(Л+1)
коэффициентами легко получается из передаточных функций 1-D фильтров (11.21) как
Ь" = Ць^ = cos''(пку/2)008" (пк^ II), (11.25)
и соответственно для 3-D фильтра как
Ь'' = b^b^b^ = cos'' (як^ 12) cos'' {пк^ 12) cos'' {пк^ 12). (И .26)
Рис. 11.5. Передаточная функция двумерных биномиальных фильтров: а - (В^; б -
анизотропия В^{к,в) - В^(к,0) на диаграмме {к,в);в — (В^\т — анизотропия для (В^^ как на б
11.5. Эффективное крупномасштабное усреднение
Передаточные функции (В^ и (В* показаны на рис. 11.5. Уже малый фильтр 3x3
является удивительно изотропным. Большие отклонения от кольцевых контурных
линий можно распознать только для больших волновых чисел, когда
передаточная функция уменьшилась до 0,3 (рис. 11.5, а). Это свойство можно показать с
помощью разложения уравнения (11.25) в ряд Тейлора, используя
цилиндрические координаты к = [к,вУ'.
Zr , Rr r^i 2R^-R^ -4 Л cos 40. ~4
b^^l--(nkf+ (TvkY ^7^(^^) . (11-27)
о zjo /oo
Только член второго порядка является изотропным. Противоположно член
четвертого порядка содержит анизотропную часть, которая увеличивает передаточную
функцию в направлении диагоналей (рис. 11.5, а). Больший фильтр (большее К)
является менее анизотропным, поскольку изотропный член с к увеличивается
квадратично с ростом R, в то время как анизотропный член с ксо$4в увеличивается только
линейно с ростом R. Уже фильтр 5x5 (рис. 11.5,6) является удивительно
изотропным. Несущественная анизотропия биномиальных фильтров становится также
очевидной при применении к тестовому изображению на рис. 11.4.
11.4.4. Оценка
На рис. 11.6, б, в показано сглаживание с помощью двух различных биномиальных
фильтров. Мы наблюдаем, что контуры становятся размытыми. Мелкие структуры,
например в ветвях дерева, теряются. Сглаживание подавляет шум. Биномиальные
фильтры могут значительно уменьшать уровень шума Гаусса с нулевым средним
значением (раздел 3.4.2), но только за счет размывания деталей (рис. 11.7, а, в).
Двоичный шум (также называемый импульсным шумом), который вызывает
ложные уровни яркости для нескольких случайно распределенных пикселей (рис. 11.7,
б) (например, из-за ошибок при передаче), весьма плохо подавляется линейными
фильтрами. Изображения размываются, но ошибка, вызываемая двоичным
шумом, не удаляется, а только распределяется.
11.4.5. Быстрое вычисление
Мы заканчиваем наше рассмотрение биномиальных фильтров некоторыми
замечаниями по быстрым алгоритмам. Непосредственное вычисление маски фильтра
(7? + 1) X (Л + 1) требует (Л + 1)^ умножений и (Л + 1)^ - 1 сложений. Если мы
раскладываем биномиальную маску на элементарные сглаживающие маски 1/2[ 1 1] и
применяем эту маску в горизонтальных и вертикальных направлениях R раз каждую, то
нам необходимо только 2R сложения. Все умножения могут обрабатываться гораздо
эффективнее, как операции сдвига. Например, вьшисление биномиального
фильтра 17 х 17 требует только 32 сложения и некоторые операции сдвига в сравнении с
289 умножениями и 288 сложениями, необходимыми для прямого подхода.
11.5. Эффективное крупномасштабное усреднение
Вопреки эффективному выполнению биномиальных сглаживающих фильтров (В'
путем каскадной свертки с помощью (В, количество вычислений разительно уве-
31 о Глава 11. Усреднение
Рис. 11.6. Применение сглаживающих фильтров: а - исходное изображение; б - фильтр-
ящик 5 X 5; в — фильтр-ящик 9 х 9; г — биномиальный фильтр 17 х 17 (<В'^); набор
рекурсивных фильтров (11.38), действующих в горизонтальных и вертикальных
направлениях; д — R=2;e-R=16
личивается для сглаживающих масок с низкими предельными волновыми
числами, поскольку среднеквадратичное отклонение фильтров пропорционально
квадратному корню из R, согласно (3.43):
(j = yjR/4. (11.28)
Давайте рассмотрим сглаживающую операцию по окружности с радиусом
всего лишь приблизительно 1,73 пикселя, соответствующую дисперсии а^ = 3. Со-
11,5. Эффективное крупномасштабное усреднение 31 I
Рис. 11.7. Подавление шума с помощью сглаживающих фильтров: а — изображение из
рис. 11.6, А с шумом Гаусса; б - изображение с двоичным шумом; в — изображение а и
г - изображение б, отфильтрованные с помощью биномиа^хьного фильтра 9x9 ((В^);
д - изображение а и е ~ изображение б, отфильтрованные с помощью медианного
фильтра 3x3 (раздел 11.6.1)
гласно уравнению (11.28), нам необходимо применить (В^^ который — даже в
эффективном сепарабельном выполнении — требует 24 (36) сложения и 2 (3)
операции сдвига для каждого пикселя в 2-D (3-D) изображении. Если мы хотим
сгладить по двойному расстоянию (ст^ = 12, радиус ~ 3,5, Ф"*^), то число сложений
увеличивается в 4 раза до 96 (144) для каждого пикселя в 2-D (3-D) пространстве.
Глава 11. Усреднение
11.5.1. Многошаговое усреднение
Проблема медленного крупномасштабного усреднения происходит от малого
расстояния между пикселями, усредняемыми в элементарной маске В = 1/2[1 1]. Для
того чтобы преодолеть эту проблему, мы можем использовать один и тот же
элементарный усредняющий процесс, но с более удаленными пикселями и увеличить
среднеквадратичное отклонение для сглаживания соответственно. В двумерном
случае могут быть применены следующие маски вдоль диагоналей (о* • v2):
в -1
1 О О
0 2 0
О О 1
^-i
О О 1
0 2 0
1 О О
или с двойной шириной шага вдоль осей (ст • 2) и в трехмерном случае
(11.29)
В,^=^[1 0 2 0 1], В,^=^
'А
(11.30)
Нижние индексы в этих масках обозначают шаговую ширину и координатное
направление. В^^^ усредняет уровни яркости в двух соседних пикселях в
направлении главной диагонали. В^ вычисляет среднее значение двух пикселей на
расстоянии 2 в направлении х. Среднеквадратичное отклонение этих фильтров
пропорционально расстоянию между пикселями. Наиболее эффективными реализациями
являются многошаговые маски вдоль осей. Они имеют дополнительное
преимущество — из-за сепарабельности алгоритмы могут применяться к данным
изображений произвольной размерности.
Проблема, связанная с этими фильтрами, состоит в том, что они выполняют
подвыборку. Следовательно, они больше не являются фильтрами для больших
волновых чисел. Если мы возьмем, к примеру, симметричный 2-D фильтр (В\^(В\у, то
сможем эффективно работать на сетке с удвоенной сеточной постоянной в
пространственной области. Следовательно, обратная сетка в пространстве волновых
чисел имеет половину ширины сетки, а передаточная функция периодически
повторяется один раз в обоих направлениях (рис. 11.8). Как правило, нулевые линии
передаточной функции масок с большей шириной шага отражают эту обратную
сетку. Для свертки с двумя соседними пикселями в направлении двух диагоналей
обратная сетка поворачивается на 45°. Сеточная постоянная обратной сетки в V2
раза меньше, чем сеточная постоянная исходной сетки.
Используемые по отдельности, эти фильтры не приносят большой пользы. Но
мы можем использовать их в каскаде, начиная с непосредственно соседних пикселей.
Тогда нулевые линии передаточных функций, которые лежат по-разному для
каждого пиксельного расстояния, эффективно влияют на то, что передаточная
функция приближается к нулю для больших диапазонов волновых чисел.
11.5. Эффективное крупномасштабное усреднение 313
Рис. 11.8. Передаточная функция биномиальной маски, примененной: а - в
диагональном направлении ((В\^у(В\у)\ б - с двойной шириной шага в направлениях осей
Каскадная многошаговая биномиальная фильтрация приводит к
значительному увеличению выполнения для крупномасштабного сглаживания. Для
нормальной сепарабельной фильтрации число вычислений пропорционально о^{0 (сг^)).
Для многошаговой биномиальной фильтрации оно зависит только логарифмически
от а{0 (IdcT^)), если выполняется каскад фильтрующих операций с рекурсивным
удвоением ширины шага:
(В
25-1 •• • 8х 4х 1х X
S раз
Такая маска имеет среднеквадратичное отклонение
сг'=/г/4+/г+4/г+...+4^"^/г = —(4^-1)
S раз
12
(11.31)
(11.32)
и передаточную функцию
5-1
Ylcos^'il'-'nk),
5=0
(11.33)
Таким образом, для 5шагов требуется только iWсложений, в то время как
среднеквадратичное отклонение растет экспоненциально со скоростью л]Rill-2^.
С помощью параметра R мы можем регулировать степень изотропии и степень
остаточных неоднородностей в передаточной функции. Очень эффективное
выполнение задается при использовании R = 2 (^ = 1/4[1 2 1] в каждом направлении).
Однако остаточные боковые пики при высоких волновых числах с максимальными
амплитудами до 0,08 являются по-прежнему значительными возмущениями (рис.
11.9,^,5, рис. 11.10, л, б).
С помощью следующих больших масок с нечетным размером (R = 4,
В^ = 1/16[1 4 6 4 1] в каждом направлении) эти остаточные боковые пики при
высоких волновых числах хорошо подавляются ниже 0,005 (рис. 11.9, в, г, рис. 11.10, в, г).
Глава и. Усреднение
Рис. 11.9. Передаточная функция каскадных многошаговых биномиальных
фильтров и их анизшропия: а - (B^^Bf; б - 4'ДЧ^, ^) ~ ^2 ДЧ^, 0); в - ®2®'; г - 4'^^^
Анизотропия показана в полярных координатах {к, 0) как отклонение от
передаточной функции в направлении х
Это приблизительно соответствует разрешению 8-битовых изображений и
должно быть, следовательно, достаточным для большинства задач. С помощью
по-прежнему больших масок они могут подавляться и далее. На рис. 11.11 показаны
первые четыре шага многошагового усреднения с маской В ^, иллюстрирующие, как
быстро сглаживание достигает больших масштабов.
11.5.2. Многосеточное усреднение
Многошаговое каскадное усреднение можно далее улучшить с помощью
преобразования его в метод с переменной разрешающей способностью. Идея
многосеточного сглаживания очень проста. Когда включается маска с большим шагом, эту
операцию можно применять на соответственно более крупной сетке. Это
означает, что для последней операции, перед использованием маски с большим шагом,
необходимо вычислить свертку только в точках сетки, используемых следующим
оператором с более крупной сеткой.
Эта выборочная процедура обозначается с помощью специального
синтаксиса в индексе оператора. О^^ означает: применить оператор в направлении х и
сдвинуть маску на два пикселя в направлении х. Таким образом, выходные данные
оператора фильтра имеют только половину пикселей входных данных в направлении х.
11.5. Эффективное крупномасштабное усреднение 315^
б
Рис. 11.10. Каскадное многошаговое усреднение с удвоением ширины шага
согласно уравнению (11.31), примененное к кольцевой тестовой структуре: а - Ф^'^^',
б - (В/(В^^(В^\ в - (В^%'; г - (В^%%'
Многосеточное сглаживание делает число вычислений, по существу,
независимым от среднеквадратичного отклонения сглаживающей маски. Мы снова
рассматриваем последовательность 1-D биномиальных фильтров:
(В'
i2
•®:42«:х2
S раз
Поскольку (В^ 12 захватывает R операций, последовательность операторов захватывает
х\2
\
<2R.
Как и в случае многошагового подхода (11.32), среднеквадратичное
отклонение последовательности операторов равно
316 Глава 11, Усреднение
Рис. 11.11. Каскадное многошаговое усреднение с удвоением ширины шага согласно
уравнению (11.31), примененное к изображению рис. 11.6, а с: а — одним; б —
двумя; в — тремя; г — четырьмя шагами с использованием фильтра В'^
12
(11.34)
Таким образом, сглаживание до любой степени захватывает не больше, чем в 2
раза больше операций, что сглаживание при первом шаге! Как и в случае для
многошаговых биномиальных фильтров, среднеквадратичное отклонение возрастает
в 2 раза. Также — как только В^(к) = 0 V^ > 1/2 — передаточные функции
фильтров становятся такими же, как для многошаговых фильтров.
11.5.3. Рекурсивное усреднение
Совершенно иной подход к крупномасштабному усреднению задается
рекурсивной фильтрацией, введенной в разделе 4.5. Рекурсия, в сущности, задает фильтру
свертки бесконечную функцию рассеяния точки. Основным преимуществом
рекурсивных фильтров является то, что они могут легко «настраиваться», как мы уже
продемонстрировали с помощью простого фильтра нижних частот в разделе 4.5.5.
В этом разделе акцент делается на разработку усредняющих фильтров,
соответствующих критериям, которые мы обсудили ранее в разделе 11.2, особенно свой-
77.5. Эффективное крупномасштабное усреднение 31
ству о нулевом сдвиге (раздел 11.2.1), которое не удовлетворяется причинными
рекурсивными фильтрами.
По существу, рекурсивные фильтры работают так же, как нерекурсивные
фильтры. В принципе мы можем заменить любой рекурсивный фильтр с помощью
нерекурсивного фильтра, чья маска тождественна функции рассеяния точки
рекурсивного фильтра. Реальной проблемой является разработка рекурсивного фильтра, т.е.
определение коэффициентов фильтра для требуемой передаточной функции.
В то время как теория одномерных рекурсивных фильтров составляет
стандартные сведения в цифровой обработке сигнала (например, книга Оппенхайма
(Oppenheim) и Шафера (Schafer) [148]), разработка двумерных фильтров
по-прежнему понимается неадекватно. Основной причиной является фундаментальное
различие между математикой одномерных и более высокой размерности z-преоб-
разований и полиномов [124].
Вопреки этим теоретическим проблемам, рекурсивные фильтры могут
успешно применяться в цифровой обработке изображений. Для того чтобы избежать
проблем разработки фильтров, мы будем использовать только очень простые
рекурсивные фильтры и составлять из них более сложные фильтры подобно
способу, которым мы построили класс биномиальных фильтров из элементарной
сглаживающей маски 1/2[1 1]. Таким образом, мы получим класс рекурсивных
фильтров, который может не быть оптимальным с точки зрения разработки
фильтров, но являться полезным в практических применениях.
В первом шаге композиции мы объединяем причинные рекурсивные фильтры
в симметрические фильтры. Начнем с общего одномерного рекурсивного фильтра
с передаточной функцией
^A = a{k)V\b{k). (11.35)
Индекс + обозначает направление действрш фильтра в положительном
координатном направлении. Передаточная функция того же фильтра, но
действующего в противоположном направлении, есть
~A = a{k)-ib{k), (11.36)
Изменяется только знак мнимой части передаточной функции, поскольку он
соответствует нечетной части функции рассеяния точки, в то время как
действительная часть соответствует четной части.
У нас теперь есть два возможных пути для объединения фильтров,
действующих в прямом и обратном направлениях, в симметричные фильтры, полезные для
усреднения:
/V 1г.^_^П
сложение ^ ="" ^ + ^ = ^(^)'
вычитание А= А~А = а (к)-\-Ь (к).
Оба метода дают действительные передаточные функции и, таким образом,
четные фильтры с нулевым сдвигом, которые подходят для усреднения.
В качестве элементарного рекурсивного сглаживающего фильтра мы
используем двухэлементный фильтр нижних частот, который уже изучили в разделе 4.5.5:
'A:G:„=G:,„,,+a(G„„-G;„,,) при 0<а<1 (11.38)
С импульсной характеристикой
318 Глава 11. Усреднение
V х'т.п
\а{\-аУ п>0,т = 0
(1.39)
О иначе.
Передаточную функцию этого фильтра можно легко вычислить, приняв в
расчет то, что преобразование Фурье уравнения (11.39) образует геометрический ряд:
^. (11.40)
1-(1--а)ехр(+1л-А:)
Это соотношение является допустимым только приближенно, поскольку мы
оборвали бесконечную сумму в уравнении (11.39) при n = N-l из-за
ограниченного размера изображений.
Последовательная фильтрация с фильтрами, действующими слева и справа,
соответствует умножению передаточной функции
л. ^ л. ^
^(A:)=4W4W«
а
a^+2(l-a)(l-cos(nk)y
(11.41)
Передаточная функция проявляет хар^актеристики, ожидаемые для фильтра
низких частот (рис. 11.12). При ^ = О, А^(к) = 1; для малых к передаточная
функция уменьшается пропорционально к^:
A^^l-^-^(nkf Л«1
а
и имеет волновое число половинного значения lcc{A^{kJ = 1/2):
к «—arcsin-
а
а
(11.42)
(11.43)
п yj2{\-a) y/ln'
где последняя аппроксимация допустима только для а <^ 1. При самом высоком
волновом числе, ^ = 1, передаточная функция уменьшается до
Л(1) =
а
■г- (11-44)
4(1-а) + а'
В отличие от биномиальных фильтров, она не равна точно нулю, но
достаточно мала даже для малых значений а (рис. 11.12).
1
0.8
0,6
0.4
0.2
О
А\
А \
г\ \
г \
1/'^6^ _>.
\l/2
0,2
0.4
0,6
0,8 ^ 1
Рис. 11.12. Передаточная функция рекурсивного фильтра нижних частот (11.41) для
различных значений а = 1/2, 1/4, 1/8 и 1/16
11.5. Эффективное крупномасштабное усреднение
Двумерные фильтры можно составить из одномерных фильтров, действующих
в горизонтальных и вертикальных направлениях:
Этот фильтр (рис. 11.13, а, б) является значительно менее изотропным, чем
биномиальные фильтры (рис. 11.5). Высокие волновые числа ослабляются
гораздо меньше в координатных направлениях, чем в других направлениях. Однако
рекурсивные фильтры имеют большое преимущество в том, что вычислительные
усилия не зависят от степени усреднения. При простом рекурсивном фильтре первого
порядка мы можем получить степень усреднения с помощью соответствующего
выбора параметра фильтра а (уравнение (11.43)). Изотропию рекурсивных
фильтров можно в дальнейшем улучшить с помощью действия дополнительных
фильтров вдоль диагоналей:
Л'=ЛЛЛ-.Л.,- (11.46)
Индексы x-yvix + y обозначают главную и второстепенную диагонали
соответственно. Передаточные функции таких фильтров показаны на рис. 11.13, в, г.
В отличие от нерекурсивных фильтров, вычислительные усилия не зависят от
предельного волнового числа. Если а = 2' в уравнении (11.38), то фильтр можно
вычислить без какого-либо умножения:
<^:„=K„«-2'-c7:,„„+G,„]-2-', />1. (11.47)
Двумерному фильтру ^ необходимо только 8 сложений и операций сдвига для
каждого пикселя, в то время как фильтру Л', действующему в четырех направлени-
*-Г\/Т'1*Шг?^*'-^1^¥?^^'ТШ^
Рис. 11.13. Передаточные функции двумерных рекурсивных фильтров нижних
частот: а-у?с а= 1/2; б - анизотропия а: А(к,в)-А{к,п1А)\ b-J?'c а= 1/2;
г-анизотропия в: 2(/г, в)-2(^,0)
Глава 11. Усреднение
ях, необходимо в 2 раза больше операций. Однако этот фильтр не является более
эффективным, чем многосеточный подход с биномиальными масками (раздел
11.5.2), который является гораздо более изотропным фильтром.
11.6. Нелинейное усреднение
Линейные усредняющие фильтры, рассмотренные до сих пор, размывают
контуры. Более того, если маска сглаживающего оператора пересекает контур объекта,
то он содержит пиксели как от объекта, так и от фона, давая бессмысленный
результат от фильтра. То же самое имеет место, если вычисляются средние значения,
когда определенное число пикселей в изображении проявляют ложные значения,
например, из-за ошибки передачи. Вопрос, следовательно, заключается в том,
возможно ли выполнить усреднение, которое не пересекает границы объекта или
которое игнорирует определенные пиксели. Такую процедуру можно применять,
конечно, только если мы уже определили контуры или какой-либо возмущенный
пиксель. В этом разделе мы рассмотрим три типа нелинейных усредняющих
фильтров: классический медианный фильтр (раздел 11.6.2); взвешенное усреднение,
также известное как нормированная свертка (раздел 11.6.6); и управляемое
усреднение (раздел 11.6.3), где мы контролируем направление и/или степени
усреднения с помощью локального содержания окрестности.
11.6.1. Медианный фильтр
Линейные фильтры эффективно подавляют шум Гаусса, но плохо работают в
случае двоичного шума (рис. 11.7). Используя линейные фильтры, которые
взвешивают и суммируют, мы полагаем, что каждый пиксель несет некоторую полезную
информацию. Пиксели, возмущенные ошибками при передаче, теряют исходный
уровень яркости. Линейное сглаживание не исключает эту информацию, а
переносит ее на соседние пиксели. Таким образом, подходящая операция для
обработки таких искажений должна распознавать эти пиксели и исключать их.
Это как раз то, что делают фильтры порядковой статистики (раздел 4.3).
Пиксели внутри маски сортируются, и выбирается один пиксель. В частности,
медианный фильтр выбирает среднее значение. Поскольку двоичный шум полностью
изменяет уровень яркости, маловероятно, что он будет показывать средний уровень
яркости в окрестности. Таким образом, средний уровень яркости окрестности
используется для восстановления уровня яркости возмущенного пикселя.
Следующие примеры иллюстрируют влияние медианного фильтра v\i
размером 1x3:
М [•••
см [...
М [•••
12 3 7 8 9 •••]
1 2 102 4 5 б---]
0 0 0 9 9 9-]
= [•••
= [•••
= [•••
12 3 7 8 9---],
12 4 5 5 6 •••],
0 0 0 9 9 9 •••]
Как и ожидалось, медианный фильтр исключает отклонения. Две другие
структуры уровней яркости — монотонно возрастающее линейное изменение и контур
между двумя платами постоянного уровня яркости — сохраняются. Таким
образом, медианный фильтр эффективно исключает двоичный шум без значительного
11.6. Нелинейное усреднение
размывания изображения (рис. 11.7, г). Шум Гаусса уничтожается менее
эффективно (рис. 11.7, е).
Наиболее важные детерминистические свойства одномерного медианного
фильтра 2N-\- 1 можно сформулировать, используя следующие определения.
• Постоянная окрестность — область с 7V+ 1 равными уровнями яркости.
• Контур - монотонно возрастающая или убывающая область между двумя
постоянными окрестностями.
• Импульс - область, самое большее, 7V точек, окруженных постоянной
окрестностью с одним и тем же уровнем яркости.
• Корень или фиксированная точка — сигнал, который сохраняется при
операции медианного фильтра.
С помощью этих определений детерминистические свойства медианного
фильтра можно описать очень компактно:
• Постоянные окрестности и контуры являются фиксированными точками.
• Импульсы удаляются.
Итерационная фильтрация изображения с помощью медианного фильтра
приводит к изображению, содержащему только постоянные окрестности и контуры.
Если возмущаются только единичные пиксели, то медианного фильтра 3x3
достаточно для их удаления.
Статистические свойства медианного фильтра можно проиллюстрировать с
помощью изображения, содержащего только постоянные окрестности, контуры и
импульсы. Импульсный энергетический спектр импульсов является равномерным
(белый шум). Поскольку медианный фильтр удаляет импульсы, энергетический спектр
убывает однородно. Вклад контуров в определенное волновое число не удаляется.
Этот пример также подчеркивает нелинейную природу медианного фильтра.
11.6.2. Взвешенное усреднение
В разделе 3.1 мы увидели, что уровни яркости в пикселях, как и любые другие
экспериментальные данные, могут характеризоваться отдельными ошибками,
которые должны рассматриваться в дальнейшей обработке. В качестве введения, мы,
сначала рассматриваем усреднение набора из Л/^ независимых данных д^ со
среднеквадратичными отклонениями а^. Из элементарной статистики известно, что
подходящее усреднение требует взвешивания каждой точки данных д^ с обратной
дисперсией w^= l/o"^^. Тогда оценка среднего значения задается соотношением
в ТО время как среднеквадратичное отклонение равно
^5=i/ii/^«- (11-49)
Чем ниже статистическая ошибка отдельной точки данных, тем выше вес в
уравнении (11.48).
Применение взвешенного усреднения к обработке изображений известно как
нормированная свертка [64]. Усреднение теперь расширяется до локальной
окрестности. Каждый пиксель входит в сумму свертки с весовым множителем, соотне-
Глава и. Усреднение
сенным с ним. Таким образом, нормированная свертка требует двух изображений.
Одним является изображение, которое обрабатывается, другим изображение с
весовыми множителями.
По аналогии с уравнениями (11.48) и (11.49) нормированная свертка
определяется соотношением
_, H*{W G)
и = ,
(11.50)
где Н— любая маска свертки; G — изображение; которое обрабатывается; W—
изображение с весовыми множителями. Нормированная свертка с маской Н, по
существу, преобразует набор из изображения G и весового изображения Wb новое
изображение G и новое весовое изображение W =Н* W, которое может подвергаться
дальнейшей обработке.
В этом смысле нормированная свертка не представляет ничего сложного или
особенного. Она является просто адекватным рассмотрением пикселей с
пространственно изменяющимися статистическими ошибками. «Стандартную» свертку
можно рассматривать как частный случай нормированной свертки. Тогда всем
пикселям присваивается один и тот же весовой множитель и не требуется
использовать весовое изображение, поскольку множитель остается постоянным.
Гибкость нормированной свертки определяется выбором весового
изображения. Весовое изображение не обязательно связано с ошибкой. Оно может
использоваться для выбора и/или усиления пикселей с определенными признаками.
Таким образом, нормированная свертка становится универсальным нелинейным
оператором.
В качестве примера на рис. 11.14 показано зашумленное изображение,
которое фильтруется с помощью нормированной свертки с использованием весового
изображения, препятствующего сглаживанию на контурах.
11.6.3. Управляемое усреднение
Идея управляемых фильтров состоит в создании маски свертки, зависящей от
локальной структуры изображения. Это является общим понятием, которое не
ограничивается усреднением, а может применяться к любому типу процесса свертки.
Основная идея управляемых фильтров заключается в следующем. Управляемый
фильтр имеет некоторые свободно регулируемые параметры, которые
контролируют фильтрацию. Они могли бы определять различные свойства, такие, как
степень сглаживания, направление сглаживания или и то и другое. Не
составляет труда записать маску фильтра с управляемыми параметрами. Мы уже сделали
это для рекурсивных фильтров в уравнении (11.38), где параметр а определяет
степень сглаживания. Однако свертывание изображения с масками, которые
отличны в каждом пикселе, не является эффективным с точки зрения вычислений.
Тогда преимущество, связанное с тем фактом, что маски являются сепарабель-
ными, не может больше использоваться.
Альтернативный подход заключается в поиске базиса из нескольких фильтров
и использовании этих фильтров для вьгаисления набора отфильтрованных
изображений. Тогда эти изображения интерполируются с использованием
регулируемых параметров. В операторной форме записи это читается как
11,6 Нелинейное усреднение 323
Рис. 11.14. Взвешенное усреднение, использующее интенсивность контуров для пре-
пятствования усреднения на контурах: а - изображение из рис. 11.6, л с добавленным
шумом Гаусса; б - весовое изображение после 5 сверток; изображение после в — двух
и г - пяти нормированных сверток, использующих биномиальную сглаживающую
маску (В^ (сравните с рис. 11.7)
(11.51)
где ^ —/?-й фильтр; f^{a) — скалярная интерполяционная функция от
управляющего параметра а. Должны быть решены две проблемы при использовании
управляемых фильтров. Во-первых, и самое основное, неявным является то, что такой
фильтровый базис Н существует вообще. Во-вторых, должно быть найдено
соотношение между управляющими параметрами а и интерполяционными
коэффициентами ^. Если первая проблема решена, то мы, в большинстве случаев,
получаем решение второй без особых затруднений.
В качестве примера построим направленный сглаживающий фильтр с
передаточной функцией
\{к,в) = \- f{k)QOs\e -в^У (11.52)
В этом уравнении используются цилиндрические координаты (к, в) в Фурье-
области. Фильтр в уравнении (11.52) является полярным сепарабельным фильт-
324 Глава 77. Усреднение
ром с произвольной радиальной функцией/(А:). Эта радиальная компонента
обеспечивает произвольную изотропную сглаживающую фильтрацию. Управляемый
угловой член задается с помощью cos^(0 - в^. Структуры, ориентированные в
направлении 0Q, остаются в изображении, в то время как структуры
перпендикулярные 0Q являются полностью отфильтрованными. Угловая ширина направленного
сглаживающего фильтра равна ±45".
Разложим косинусную функцию в уравнении (11.52) на
тригонометрические функции, которые зависят либо только от 0, либо от управляющего угла 0^,
и получим
^^^A:,0) = l--/(A:)[l + cos(20o)cos(20) + sin(20o)sin(20)] (11.53)
с базисными фильтрами
h=\~f{k), h,=~f(k)cos(2e), h,=~fik)sm(2e) (11.54)
И интерполяционными функциями
/гЮ = 1 Л(0о) = со8(20о), M9,) = sm(29,). (11.55)
Таким образом, требуется три базисных фильтра. Фильтр Л, является
изотропным сглаживающим фильтром, другие два — направленными фильтрами. Хотя
уравнения для этого семейства управляемых направленных сглаживающих
фильтров просты, нелегко реализовать полярные сепарабельные базисные фильтры,
поскольку они не являются сепарабельными в декартовой системе координат и,
таким образом, требуют тщательной оптимизации.
Тем не менее возможно выполнить даже этот управляемый сглаживающий
фильтр с базисными фильтрами 3x3 (рис. 11.15). Из-за свойств симметрии
передаточных функций мы имеем небольшую альтернативу выбора коэффициентов
фильтров и окончательно приходим к следующим базисным фильтрам:
' 32
1 2 1
2 20 2
1 2 1
' 32
0-4 0
4 0 4
0-4 0
' 32
-2 0 2
0 0 0
2 0-2
'^ 1 1
/г, = — +—cos^ (яk^ 12) cos^ {пк212)
h^ =-(со8(л:^,)-со8(;г^2))
2 7.2
«1-
к'к
8 '
cos(20),
8 (11.56)
}ц =-(со8(л:(А:, +k2))-cos{n{k^ -^2))) ~ sin(20).
Из рис. 11.16 очевидно, что эта простая реализация хорошо работает вплоть до
средних волновых чисел. При высоком волновом числе {к > 0,5) направленный
фильтр работает гораздо хуже.
11.6. Нелинейное усреднение 325
Vl^?asM*4WK( и it Гг'Ы
1U Н7ПГЛ la idrtrt^nM^U*-!!'
(И*
н v^f^^
Рис. 11.15. Передаточные функции для трех базисных фильтров для направленного
сглаживания согласно уравнению (11.56)
r*v'., м ;п ;rj!H MrUiOlv
Рис. 11.16. Передаточные функции для управляемого сглаживающего фильтра,
согласно уравнению (11.53), использующего базисные фильтры (11.56): сглаживание в
0°, 22,5° и 45° косих
Глава 11. Усреднение
11.7. Усреднение в многоканальных изображениях
На первый взгляд кажется, что нет ничего особенного в отношении усреднения
многоканальных изображений: просто применяем сглаживающую маску к
каждому из Р каналов отдельно:
G' =
Ig;-
Г
к.
= H*G =
Н *
Н *
Н *
(11.57)
Это простое понятие можно расширрггь до нормированной свертки,
рассмотренной в разделе 11.6.2. Если одно и то же сглаживающее ядро применяется ко
всем компонентам, то достаточно использовать одно общее весовое изображение,
которое может быть добавлено как (Р+ 1)-я компонента многокомпонентного
изображения:
<?;
G'2
G'p
W
\H*(W■G^))/(H*W)1
(H*(W-G2y)/(H*W)\
(H*(W-Gp))/iH*W)\
H*W \
(11.58)
Частный случай многокомпонентных изображений задается в случае, когда они
представляют признаки, которые могут отображаться в угловых координатах. Как
правило, такие признаки учитывают направление контура или фазу
периодического сигнала. Признаки такого вида являются циклическими и не могут быть
корректно представлены в декартовьис координатах. К тому же они не могут
усредняться в этом представлении. Представьте углы +175** и -179^ Средний угол равен
178°, поскольку -179° = 360° - 179°= 181° близко к 175°, а не (175° - 179°)/2 = -2°.
Циклические признаки, такие, как углы, следовательно, лучше представлять
как единичные векторы в виде щ = [cos в, sine]^.
В этом представлении они могут корректно усредняться, как и показано на
рис. 11.17. Средний вектор имеет правильное направление, а его модуль, как
правило, меньше 1:
к+«^.
)/2 =
cos[(02-0i)/2].
(11.59)
Для разности углов 180° средний вектор имеет нулевой модуль. Убывание
модуля среднего вектора имеет интуитивное объяснение. Чем больше разброс угла,
тем меньше достоверность среднего значения. В самом деле, если все направления
равно вероятны, то суммарный вектор обращается в ноль, в то время как он
возрастает в длине, когда разброс мал.
11.8. Упражнения 3 2
Рис. 11.17. Усреднение циклической величины, представленной как нормальный
вектор Hq =[cos0,sin0]^ на единичном векторе. Средний вектор (Я^^ +Пд^)12 имеет
правильное направление {9^ + в^/2, но его модуль убывает в зависимости от угла
Эти рассуждения можно расширить до усреднения циклических признаков.
И наконец, мы устанавливаем модуль вектора равным достоверности величины,
которая представляется с помощью угла наклона вектора. Таким образом,
короткие векторы добавляют немного, а длинные векторы добавляют больше в
процедуру усреднения.
Эта форма взвешенной свертки является очень привлекательной, поскольку, в
отличие от нормированной свертки (раздел 11.6.2), она не требует занимающего
много времени деления. Конечно, она работает только с признаками, которые
можно адекватно отобразить в угловой форме.
В заключение мы рассмотрим меру, характеризующую разброс в направлении
векторов. На рис. 11.17 показывается, что для малого разброса суммарный вектор
только незначительно меньше, чем сумма модулей векторов. Таким образом, мы
можем определить угловую меру когерентности как
с = ' ', (11.60)
|G|
где Н- произвольный сглаживающий оператор свертки. Эта мера равна единице,
если все векторы в окрестности, охватьгоаемой оператором свертки, имеют одно и
то же направление, и равна нулю, если они равномерно распределены. Это
определение меры когерентности работает не только в одномерных, но также и в
многомерных векторных пространствах. В одномерных векторных пространствах
(скалярные изображения) мера когерентности равна, конечно, всегда единице.
11.8. Упражнения
11.1: Фильтры-ящики и биномиальные фильтры
Интерактивная демонстрация сглаживания с фильтрами-ящиками и
биномиальными фильтрами (dip6ex 11.01).
11.2: Многошаговое сглаживание с фильтрами-ящиками и биномиальными фильтрами
Интерактивная демонстрация многошагового сглаживания с фильтрами-
ящиками и биномиальными фильтрами (dip6ex 11.02).
Глава 77. Усреднение
11.3: *Фильтр-ящик
Фильтр-ящик детально рассматривался в разделе 11.3. Ответьте на
следующие вопросы:
1. Почему фильтры-ящики являются плохими сглаживающими
фильтрами? Перечислите все причины.
2. Улучшаются ли плохие признаки, если применить фильтры несколько
раз? Возьмите фильтр-ящик 3 х 3 в качестве примера.
3. Каким является результирующий фильтр, если применить фильтр-ящик
несколько раз к изображению?
11.4: **Разработка фильтров
Фильтр должен быть разработан с малой маской и оптимальными
сглаживающими свойствами. Используйте маску с коэффициентами: [а, j3, у].
Фильтр должен обладать следующими свойствами:
а) сохранение среднего значения;
б) отсутствие сдвига структур уровней яркости;
в) устранение структур с наибольшим возможным волновым числом.
Вопросы и задачи:
1. Определяются ли коэффициенты фильтра а, j8 и /однозначно?
2. Вычислите передаточную функцию фильтра.
3. Какие ограничения накладываются на фильтр с пятью
коэффициентами: [а, Д у, 5, б]?
4. Вычислите передаточную функцию фильтра.
5. Какие значения могут принимать оставшиеся свободные параметры,
чтобы передаточная функция оставалась монотонно убывающей для всех
волновых чисел?
6. Какие коэффициенты имеют соответствующие маски фильтров для
предельных значений?
11.5: "^^Быстрое вычисление сглаживающих фильтров
Исследуйте число вьиисленрш (сложеьшй и умножений) для нескольких
методов, чтобы свернуть изображение со следующей 2-D сглаживающей маской:
в'='
14 6 4 1
4
6
4
1
16
24
16
4
24
36
24
6
16
24
16
4
4
6
4
1
256
и с эквивалентной 3-D маской:
1. Вычисление без какой-либо оптимизации с непосредственным
использованием уравнения свертки.
1L 9. Дополнительная литература
2. Избегая любых необязательных умножений, приняв во внимание, что
многие коэффициенты имеют одно и то же значение.
3. Разложение на 1-D маски.
4. Разложение 1-D масок на элементарную маску 1/2[1 1].
Есть ли у вас какие-либо другие идеи для эффективных вычислительных
схем?
11.6: "^"^Поглощение шума с помощью сглаживания
1. Докажите, что невозможно улучшить отношение сигнала к шуму для
произвольного отдельного волнового числа с помощью линейного
сглаживающего фильтра Н. (Подсказка: запишите изображение G как сумму части,
относящейся к сигналу, -5'- и части, относящейся к шуму, -7V).
2. Рассмотрите «белый шум» (равномерно распределенный по всем
волновым числам) и спектр сигнала, который равномерно распределен только до
половины максимального волнового числа. Возможно ли теперь
улучшение отношения сигнала к шуму, проинтегрированное по всем волновым
числам? Какую форму имеет передаточная функция, которая
оптимизирует отношение сигнала к шуму?
11.7: ***Передаточная функция 1-D фильтра-ящика
Докажите равенство (11.12) для передаточной функции 1-D
фильтра-ящика. (Подсказка: существует, по меньшей мере, два способа сделать это. Один
состоит в том, чтобы записать передаточную функцию так, чтобы она
могла рассматриваться как геометрическая последовательность
aJ^\-\-q + q^ + ...-\-q"'^)c суммой a^iq""- \)/{q - 1). Другое решение
основывается на рекурсивном вычислении фильтра-ящика, заданном уравнением
(11.15)).
11.8: "^Адаптивное сглаживание
Простой адаптивный сглаживающий фильтр, который уменьшает
сглаживание на контуре, имеет вид
(l-a)J+a®=T+a(®-T),
где а € [О, 1] зависит от крутизны контура, например, а= /7(7^+ \^gV)'
Ваполните следующие задания полагая, что Фесть биномиальный фильтр
3x3:
1. Вычислите явно девять коэффициентов адаптивных фильтров 3x3 как
функцию от а.
2. Сравните вычислительные затраты это прямого выполнения
адаптивного фильтра с выполнением его как управляемого фильтра. Не принимайте
во внимание затраты на вычисление а.
11.9. Дополнительная литература
Статьи Симондса (Simonds) [188] и Веллса (Wells) [216] рассматривают быстрые
алгоритмы для больших ядер Гаусса. Читатели, заинтересованные общими
принципами эффективных алгоритмов, отсылаются к учебным пособиям Ахо
(Aho) и др. [4] или Седжевика (Sedgewick) [183]. Блахут (Blahut) [11] имеет дело
Глава 77. Усреднение
с быстрыми алгоритмами для цифровой обработки сигналов. Классические
методы разработки фильтров, особенно БИХ-фильтра, рассматриваются в
стандартных учебных пособиях по обработке сигналов, например, в книгах Проакиса
(Proakis) и Манолакиса (Manolakis) [159] или Оппенхайма (Oppenheim) и Шафера
(Schafer) [148]. Лим (Lim) [124] особенно уделяет внимание разработке 2-D БИХ-
фильтров. Детальное описание детерминистических и статистических свойств
медианных фильтров можно найти в работе Хуанга (Huang) [83] или Аке и др. [6].
Они также детально рассматриваются в монографии по нелинейным
цифровым фильтрам Питасом (Pitas) и Венетсанопоулосом (Venetsanopoulos) [155].
Монография Гранлунда (Granlund) и Натссона [64] по обработке сигналов для
компьютерного зрения касается также вопроса о взвешенном усреднении
(нормированная свертка, раздел 11.6.2). Понятие управляемого фильтра (раздел 11.6.3)
было введено статьями Фримана (Freeman) и Симонселли и др. [187].
ГЛАВА 12
КОНТУРЫ
12.1. Введение
Задача выделения контуров требует использования операторов над соседними
элементами, которые чувствительны к изменениям и подавляют области постоянных
уровней яркости. Таким образом, формируется изображение признака, в котором
те части изображения, где возникают изменения, становятся светлыми, в то время
как все остальные части остаются темными.
Говоря математическим языком, идеальный контур является разрывом
пространственной функции уровней яркости д{х) плоскости изображения.
Очевидно, что это только абстракция, которая часто не соответствует реальности.
Таким образом, первая задача выделения контуров должна определять свойства
контуров, содержащихся в анализируемом изображении. Только смоделировав
контур, мы сможем определить, насколько точно и при каких условиях удастся
вьщелить контур и оптимизировать выделение контуров.
Вьщеление контуров всегда основывается на дифференцировании в той или иной
форме. В дискретных изображениях дифференцирование заменяется
дискретными разностями, которые только аппроксимируют дифференцирование. Ошибки,
связанные с этими аппроксимациями, требуют тщательного рассмотрения. Они
вызывают серьезные эффекты, которые не ожидаются вначале. Двумя самыми
серьезными ошибками являются: анизотропное вьщеление контуров, т.е. контуры
не вьщеляются одинаково хорошо во всех направлениям, и ошибочное
оценивание направления контуров.
В то время как определение контуров очевидно в скалярных изображениях, в
многокомпонентных или векторных изображениях существуют различные
возможности (раздел 12.8). Контур может быть признаком, который проявляется
только в одной компоненте или во всех. Вьщеление контура также становится
более сложным в многомерных изображениях. В трехмерном случае, например,
объемные области отделяются поверхностями, а контуры становятся разрывами
в ориентации поверхностей.
Еще одним важным вопросом является надежность оценок контуров. Мы
хотим не просто обнаружить контур, а узнать, насколько он значим. Таким образом,
нам нужна мера для интенсивности контура. Тесно связанным с этой проблемой
является вопрос оптимального вьщеления контуров. Раз контурные детекторы не
только обеспечивают распознавание контуров, но и оценивают объективную меру
достоверности, различные контурные детекторы можно сравнивать друг с другом,
и оптимизация вьщеления контуров становится возможной.
Глава 12. Контуры
1
0,8
0,6
0,4
0,2
0
1
1
>-«i.-VUT»^%^-»r.4^»«^_<V-^
■^ ■ ' ■
:
1
1
1
1
. ^■^-^''•''■■'*-'^'-'^-''^^^ _.
0,2
0,1
0
-0,1
-0,2
0
':
:
50
100
150
200
250
:
^л-л^чл^ ■
\
■
50
100
150
200
250
0,2
0,1 t
О [
-0,1 [
-0,2 [
>*^M/^^#vfJi^^
о 50 100 150 200 250
Рис. 12.1. Зашумленный 1-D контур и его первая и вторая производные
12.2. Дифференциальное описание изменений сигнала
Усредняющие фильтры подавляют структуры с высокими волновыми числами.
Выделение контуров требует фильтрующей операции, которая подчеркивает
пространственные изменения в значениях сигнала и подавляет области с
постоянными значениями. На рис. 12.1 иллюстрируется, что дифференциальные операторы
подходят для такой операции в одномерном случае. Первая производная
показывает экстремум на контуре (максимальный положительный и отрицательный подье-
мы), в то время как вторая производная пересекает ноль (обращающаяся в ноль
кривизна), где контур имеет свой самый крутой подъем и спуск. Оба критерия
можно использовать для вьщеления контуров.
В случае более высокой размерности описание изменения сигнала гораздо
сложнее. Во-первых, мы рассматриваем 2-D изображения. Здесь мы можем
выделить контуры, углы, линии и локальные экстремумы как подходящие
признаки для обработки изображений. Для контура должно присутствовать большое
изменение значения сигнала перпендикулярно направлению контура. Но в
направлении контура изменения незначительны. Однако если кривизна в
направлении, перпендикулярном градиенту, максимальна, то контур становится углом.
Линия характеризуется нулевыми первой и второй производной вдоль линии, и,
в отличие от контура, вместо наклона кривизна растет перпендикулярно
направлению линии. Локальные экстремумы характеризуются нулевыми первыми
производными, но высокой кривизной во всех направлениях.
В трехмерном случае, т.е. для объемных изображений, ситуация становится
сложнее. Теперь появляются поверхности с сильным изменением первого порядка в
12.2. Дифференциальное описание изменений сигнала
направлении, перпендикулярном поверхности, и небольшими величинами наклона
и кривизны в двух направлениях в пределах поверхности. На контуре изменения
сигнала незначительны только в направлении контура, а на вершине угла сигнал
изменяется во всех направлениях.
Из-за этого большого множества различных признаков для описания локальных
изменений в многомерных сигналах важно более тесное рассмотрение основных
математических свойств дифференциальных операторов, прежде чем мы построим
надлежащие операторы над соседними элементами для вьщеления этих признаков.
12.2.1. Дифференцирование первого порядка и градиент
Оператор частной производной р-то порядка соответствует умножению на {liviky в
пространстве волновых чисел (раздел 2.3, >-КА)\
(12.1)
Частные производные первого порядка по всем направлениям Ж-мерного
сигнала образуют Ж-мерный градиентный вектор:
v =
"э э _э_'
Эх,'Эх/ 'Эх„
т
0 • 2т1\к.
(12.2)
При повороте системы координат оператор градиента преобразуется как
любой другой вектор с помощью умножения на ортогональную матрицу поворота R
(раздел 7.2.2):
V' = RV- (12.3)
Дифференцирование первого порядка в конкретном направлении, так
называемая производная по направлению [15], задается как скалярное произведение между
градиентом и единичным вектором п, имеющим это направление:
э
Модуль градиентного вектора
дп
/ т \1/2
|VH|V||,= (v^v) =
W
w=l
_э^
Эх.
V
V
/
ч1/2
(12.4)
(12.5)
инвариантен относительно поворота системы координат. Если мы поворачиваем
систему координат так, чтобы градиентный вектор стал параллельным
направлению новой осих', все остальные компоненты градиентного вектора исчезают,
производная по направлению достигает максимального значения и равна модулю
градиентного вектора.
12.2.2. Дифференцирование второго порядка и кривизна
Вторые производные определяют кривизну. Все возможные комбинации частных
дифференциальных операторов второго порядка Ж-мерного сигнала формируют
симметричную матрицу размерностью WxW, известную как матрица Гессе:
334 Глава 12, Контуры
н =
' Ь'
dxf
д'
дх^Х2
д'
ОХ-уЛцг
д'
дх^Х2
д'
дх1
д'
\j\'2'^w
д'
\ЭЛ>лЛ>ц^
д'
иХ2Хцг
д'
Эд:^
0 . -4л:'М^
(12.6)
При вращении системы координат матрица Гессе преобразуется с помощью
умножения слева и справа на ортогональную матрицу поворота R
H' = RVR\ (12.7)
Как мы уже обсуждали в конце раздела 3.3.3, всегда возможно найти
координатное преобразование R в систему с главными координатами, так чтобы матрица
Гессе стала диагональной:
О
Н' =
Ьх['
0
0
_Э^
о
дх['
О
Ъх2
(12.8)
Градиент имеет только одну ненулевую компоненту в системе с главными
координатами. Это не выполняется для кривизны. Как правило, все значения
кривизны не равны нулю в системе с главными координатами.
След этой матрицы, т.е. сумма диагональных элементов, называется
оператором Лапласа и обозначается А:
W ^2
А = trace/Г = ^:—- о-
w=l
Эх!
и=1
(12.9)
Поскольку оператор Лапласа равен следу матрицы Гессе, он инвариантен
относительно поворота системы координат.
12.3. Общие свойства фильтров контуров
в разделах 12.3.1- 2.3.5 мы обсуждаем общие свойства фильтров, которые
формируют основу вьщеления контуров. Это обсуждение схоже с рассмотрением по
общим свойствам усредняющих фильтров в разделах 11.2.1—11.2.4.
12.3. Общие свойства фильтров контуров
12.3.1. Нулевой сдвиг
Что касается вьщеления контуров, наиболее важной особенностью
дифференциального оператора свертки является то, что он не должен сдвигать положение
объекта. Для сглаживающих фильтров это ограничение потребовало введения
действительной передаточной функции и симметричной маски свертки (раздел 11.2.1). Для
дифференциального фильтра первого порадка действительная передаточная
функция не имеет смысла, поскольку экстремальные значения должны отображаться
в пересечения нулевого уровня, а самые крутые наклоны — в экстремальные
значения. Это отображение подразумевает фазовый сдвиг 90\ Следовательно,
передаточная функция дифференциального фильтра первого порядка должна быть
мнимой. Мнимая передаточная функция подразумевает антисимметричную
маску фильтра. Антисимметричная маска фильтра определяется как
h.„=-K. (12.10)
Для маски свертки с нечетным числом коэффициентов это означает, что
центральный коэффициент равен нулю.
Дифференциальный фильтр второго порядка определяет кривизну.
Экстремумы в значениях функции должны совпадать с экстремумами в кривизне.
Следовательно, дифференциальный фильтр второго порядка должен быть симметричным,
как сглаживающий фильтр. Все свойства симметричных фильтров, рассмотренные
для сглаживающих фильтров, также применимы к этим фильтрам (раздел 11.2.1).
12.3.2. Подавление среднего значения
Дифференциальный фильтр любого порядка не должен показывать отклик на
постоянные значения или смещение в сигнале. Это условие подразумевает, что
сумма коэффициентов должна быть равна нулю и что передаточная функция равна
нулю для нулевых волновых чисел:
1-D: ад = 0, J^h„=0,
п
2-D: А(0) = 0, Y;^h^=0,
т п (12.11)
3-D: ед = 0, XSS^/.«=0-
I т п
К тому же дифференциальный фильтр второго порядка не должен реагировать на
постоянный наклон. Это условие не подразумевает дополнительных: ограничений,
поскольку его можно получить из симметрии фильтра и условия нулевой суммы (12.11).
12.3.3. Свойства симметрии
Свойства симметрии заслуживают дополнительного рассмотрения, поскольку они
формируют основу для более эффективного вычисления свертки путем уменьшения числа
умножений и упрощения вычислений передаточных функций. Условие нулевого
сдвига (раздел 12.3.1) подразумевает, что дифференциальный фильтр первого порядка, как
правило, имеет 1-D маску нечетной симметрии с 2iJ = 1 или 2R коэффициентами:
[h,,,..,h,A-h,,'".-K] или [h,,...,h,,-h,,.,.,-hj,l (12.12)
Глава 12. Контуры
Следовательно, вычисление свертки сводится к
R R
9п =^K'(9n-n'-'9nw) или g'„^v2 =^K'(9n^i-n'-gnw). (12.13)
Для 2R+1 {2R) коэффициентов фильтра требуется только R умножений.
Число сложений, однако, по-прежнему равно 2R- I.
Соотношения симметрии также значительно облегчают вычисление
передаточных функций, поскольку в этих уравнениях остаются только синусные члены
комплексной экспоненциальной функции из преобразования Фурье.
Передаточные функции для 1-D нечетной маски равны
g(k) = 2i^h^sm(uKk) или g(k) = 2i^h^sm[(v-l/2)nkl (12.14)
Для дифференциальных фильтров второго порядка мы можем использовать
все уравнения, полученные для усредняющих фильтров в разделе 11.2.1, так как
они характеризуют четную симметрию в направлении дифференцирования.
12.3.4. Неселективное дифференцирование
Интуитивно мы ожидаем, что дифференциальный оператор усиливает меньшие
масштабы сильнее, чем более крупные, поскольку, согласно уравнению (12.1),
передаточная функция идеального дифференциального оператора/?-го порядка в
направлении W соответствует {InikJ^. Следовательно, мы могли бы утверждать, что
передаточная функция хорошего дискретного дифференциального оператора
должна аппроксимировать идеальные передаточные функции в уравнении (12.1)
настолько близко, насколько это возможно.
Однако это условие является слишком сильным ограничением. Причина
заключается в следующем. Представьте, что мы применяем сглаживающий
оператор к изображению, прежде чем применить дифференциальный оператор. Мы
могли бы все еще распознавать точечную операцию как дифференцирование.
Средний уровень яркости подавляется, и оператор по-прежнему чувствителен только к
пространственным изменениям уровней яркости.
Следовательно, идеальная передаточная функция в уравнении (12.1) могла бы
ограничиваться малыми волновыми числами с помощью разложения
передаточной функции в ряд Тейлора в нуле волнового числа. Это приводит к следующим
условиям для дифференциального 1-D оператора/?-го порядка:
f л ^
д'Кк)
дк'
= ({пУр\д^_р, с р'<р + 1 (12.15)
|*=о
В двумерном случае нам нужно сделать различие между направлениями хиу:
х:
У-
d''*'h{k)
Ьк[дк1
dkldkl
= (тУр\д^_^5^ с r + s<p + l,
(12.16)
р-г S
к=0
= (тУр\д^5 с г + 5</7 + 1.
12.4. Определение контура по градиенту 337
Эти условия можно преобразовать в пространственную область, применяя
теорему моментов преобразования Фурье (>-R4). Уравнение (12.15) для 1-D
дифференциальных операторов преобразуется в
X«4=i^!^.-/' (12.17)
и уравнение (12.16) для 2-D дифференциального оператора в
п т
п т
В качестве примера для двумерного дифференциального оператора второго
порядка в направлении х эти условия приводят к
п т п т п т
ХХ'^'"Л„,.=о, Х2«\.=2, SS'«\.=o,
п т п т п т (12.19)
п т п т
Эти условия включают подавление среднего значения, как рассматривалось в
разделе 12.3.2, и также усиливают условия симметрии, которые получаются из
свойства нулевого сдвига (раздел 12.3.1).
12.3.5. Изотропия
Для хорошего вьщеления контуров важно, чтобы отклик оператора не зависел от
направления контура. Если это выполняется, то мы говорим об изотропном
контурном детекторе. Изотропию контурного детектора можно анализировать наилучшим
образом с помощью его передаточной функции. Наиболее общая форма для
изотропного дифференциального оператора порядка/? задается соотношением
кк) = {2шк„уЬ{\к\) с 6(0) = 1 и уД|Л|) = 0. (12.20)
Офаничения для дифференциальных операторов кратко изложены в
Дополнении А {yR24 и УК15).
12.4. Определение контура по градиенту
12.4.1. Принцип
В терминах изменений первого порядка контур определяется как экстремум
(рис. 12.1). Таким образом, выделение контуров с помощью
дифференциальных операторов первого порядка означает поиск самых резких изменений, т.е.
максимумов модуля градиентного вектора (уравнение (12.2)). Следовательно,
нужно вычислить первые частные производные по всем направлениям. В
операторной форме записи градиент можно записать как векторный оператор. В
2-D и 3-D пространстве получаем
Глава 12. Контуры
© =
X
или ® =
X
CD
у
(12.21)
Поскольку градиент является вектором, его модуль (уравнение (12.5))
инвариантен относительно поворота системы координат. Это является необходимым
условием для изотропного вьщеления контуров. Вычисление модуля градиента можно
выразить в 2-D пространстве с помощью операторного уравнения
ll/2
|©|=[
® •© +®,.
(12.22)
Символ • обозначает поточечное умножение изображений, которые
получаются из фильтрации с помощью операторов Ф>^и ©^ соответственно (раздел 4.1.4).
Подобным образом квадратный корень выполняется поточечно в
пространственной области. Согласно уравнению (12.22), применение оператора | Ф | к
изображению G означает следующую цепочку операций:
1) фильтруем изображение G независимо с помощью Ф^ и (D;
2) возводим в квадрат уровни яркости двух результирующих изображений;
3) складываем результирующие изображения и
4) вычисляем квадратный корень из суммы.
На первый взгляд кажется, что вычисление модуля градиента является
дорогостоящим с вычислительной точки зрения. Поэтому он часто аппроксимируется
выражением
® h ® J н- ®,.
(12.23)
Однако эта аппроксимация является анизотропной даже для малых волновых
чисел. Она вьщеляет контуры вдоль диагоналей в V2 раза более чувствительно, чем
вдоль главных осей. Вычисление модуля градиента можно, однако, эффективно
выполнить как бинарный точечный оператор с помощью таблицы преобразованрш
(раздел 10.7.2).
12.4.2. Ошибка в абсолютной величине и направлении
Главной проблемой, связанной со всеми типами контурных детекторов, является
то, что на дискретной сетке дифференциальный оператор может только
аппроксимироваться. При этой аппроксимации в основном возникает два типа ошибок
(рис. 12.2). Во-первых, вьщеление контуров становится анизотропным, т.е.
вычисление модуля оператора градиента зависит от направления контура. Во-вторых,
направление контура отклоняется от истинного. Для обоих типов ошибок полезно
ввести меры ошибок. Все меры ошибок вычисляются по передаточным функциям
фильтрующего оператора градиента.
Модуль градиента тогда задается соотношением
Щ=[1{к)'^1{к)'')'\
(12.24)
где d{k) — векторная передаточная функция оператора градиента. Анизотропию в
модуле градиента можно тогда выразить отклонением модуля от модуля градиента
в направлении х, которое задается соотношением
12.4. Определение контура по градиенту
Единичный вектор
в направлении градиента
f. Ошибка в модуле
в направлении j
Градиент в направлении X
^Х
Рис. 12.2. Иллюстрация ошибки в модуле и направлении вектора градиента
e^ik) = \d{k)\-\d^{k)\. (12.25)
Эта мера ошибки может использоваться для сигналов любой размерности.
Подобным образом можно вьиислить ошибку в направлении градиента. По
компонентам градиента вычисленный угол ф' 2-D градиентного вектора равен
ф =arctan:s"^^ .
Ошибка в величине угла, следовательно, задается соотношением
eф(k,ф) = aIctan-
dAkA)
■Ф.
(12.26)
(12.27)
В случае более высокой размерности отклонение угла может быть в различных
направлениях. Но даже в таком случае мы можем найти ошибку определения
направления, используя скалярное произведение между единичным вектором в
направлении истинного градиентного вектора и вычисленного градиентного
вектора 5U) (рис. 12.2):
cose^ =
k^d(k)
d(k)\
\к\
(12.28)
В отличие от меры ошибки угла (уравнение (12.27)) для двумерного случая, эта
мера ошибки имеет только положительные значения. Она является скалярной
величиной и, таким образом, не может определять направление отклонения.
Существует широкое разнообразие решений для контурных детекторов. Мы
детально рассмотрим некоторые из них в разделах 12.4.3—12.6.
12.4.3. Дискретные разности первого порядка
Метод дискретных разностей первого порядка является самым простым из всех
подходов для вычисления градиентного вектора. Для первой частной
производной в направлении х можно использовать одну из следующих аппроксимаций для
дд(х^, х^)/дх^:
Глава 12. Контуры
левая разность
правая разность
центральная разность
Axj
gf(Xi+AypX2)-gf(XpXj
Axj
gf(Xi + AxpX2)-5f(Xi -Axi,X2)
2Ax:j
Рис. 12.3. Применение симметричных дифференциальных фильтров первого
порядка (D^ и (D к тестовому изображению, показанному на рис. 11.4
(12.29)
Эти аппроксимации соответствуют маскам фильтров:
левая "Z)^=[L —1],
правая "^D^ = [1 -1.],
центральная D2^ = 1 / 2[1 О -1].
Нижний индекс • обозначает центральный пиксель асимметричных масок с
двумя элементами. Только последняя маска показывает свойства симметрии,
требуемые в разделе 12.3.3. Мы можем также рассматривать двухэлементные маски,
соответствующие левой и правой разностям, как нечетные маски при условии, что
результат не сохраняется в положении правого или левого пикселя, а сохраняется
точно посередине между двумя пикселями. Это соответствует сдвигу сетки на
половину пиксельного расстояния. Передаточная функция для левой разности тогда равна
X = exp(i7C^^ /2)[l--exp(47C^j] = 2isin(K^^ /2), (12.31)
где первый член получается из сдвига на половину узловой точки сетки.
(12.30)
12А. Определение контура по градиенту 341^
б
Рис. 12.4. Выделение контуров с помощью дифференциальных фильтров: а —
исходное изображение; б — оператор Лапласа £; в — горизонтальная производная (D^,
г - вертикальная производная Ю^^, д — модуль градиента (Ю^- Ф^+ (D^^- Ю^ У'\
е - сумма модулей виг, согласно уравнению (12.23)
Используя уравнение (12.14), получим передаточную функцию оператора
центральной разности
л ~ /*/
d^^ =isin(^A:^) = isin(7cA:cos0). (12.32)
Этот оператор можно вычислить по
А. = "^х'«.=[1. -1]*1/2[1 1.] = 1/2[1 О -1].
Глава 12. Контуры
Дифференциальные операторы первого порядка в других направлениях
задаются подобными уравнениями. Передаточная функция фильтра центральной
разности в направлении у задается, например, соотношением
л ~ ~
d2y =isin(7C^^) = isin(^A:sin0). (12.33)
Применение (D^ к кольцевой тестовой структуре на рис. 12.3 иллюстрирует
свойства, зависящие от направления, и фазовый сдвиг на 90° этих фильтров. На рис.
12.4 показано вьщеление контуров с помощью этих фильтров, модуль градиента и
сумма модулей (D^ и (D^^.
К сожалению, эти простые разностные фильтры являются всего лишь
плохими аппроксимациями для контурного детектора. Из уравнений (12.32) и
(12.33) мы делаем вывод, что модуль и направление градиента задается
соотношением
|rf|=(sin^(K^cos0)H-sin^(7C^sin0)) (12.34)
и
., ^ sin^(7C^sin0) ^^^..^
ф =arctan ^^^= ^, (12.35)
sin(7i;A:sin0)
где волновое число записывается в полярных координатах {к, ф). Результирующие
ошибки показаны на псевдо 3-D графическом отображении на рис. 12.5 как
функция от модуля волнового числа и угла к оси х. Модуль градиента быстро убывает от
истинного значения. Разложение в ряд Тейлора выражения (12.34) по к дает для
относительной ошибки в модуле
еЛ,Ф)" ^^sin' 2ф + 0ф). (12.36)
Убывание является анизотропным; оно медленнее в диагональном
направлении. Ошибки в направлении градиента являются также большими (рис. 12.5, б). В
то время как в направлении осей и диагоналей ошибка равна нулю, в
направлениях между ними она достигает значений приблизительно ±10° при к = 0,5. Разложе-
Рис. 12.5. а - анизотропия модуля; б - ошибка в направлении фадиента на основе
симметричного градиентного оператора [Ю^, ^jx^^- Параметрами являются модуль
волнового числа (от О до 1) и угол к оси х (от О до я/2)
12.4. Определение контура по градиенту
ние в ряд Тейлора выражения (12.35) по к дает ошибку в величине угла, согласно
уравнению (12.27), в приближении для малых к\
{nkf
24
Как видно на рис. 12.5, б, ошибка в величине угла равна нулю для ф = пк/А при
« € Z, т.е. для 0= 0^ 45% 90% ...
e.(A:,0)--^^^^^sin40 + O(A:'). (12.37)
12.4.4. Определение контуров на основе сплайнов
Преобразование на основе кубических В-сплайнов, рассмотренное в разделе 10.6.1
для интерполяции, дает непрерывное представление дискретного изображения,
которое непрерывно также по его первой и второй производным:
5^3W = X^«A(^-«X (12.38)
п
где Р^{х) есть кубическая В-сплайн-функция, определенная в уравнении (10.51).
По этому непрерывному представлению легко вычислить пространственную
производную от дрс)\
^дЛ^) v^ дВЛх-п)
^^ = Е^«-^^^^ -' (12.39)
ох „ ох
Для дискретного дифференциального фильтра нам нужны только
производные в узлах сетки. Из рис. 10.20, а можно видеть, что кубическая
В-сплайн-функция покрывает самое большее пять узлов сетки. Максимум сплайн-функции
возникает в центральном узле сетки. Следовательно, производная в этой точке равна
нулю. Она также равна нулю в двух внешних узлах сетки. Таким образом,
производная не равна нулю только в левом и правом соседних узлах центрального узла.
Следовательно, производная в узле сетки х^ сводится к
Эдз(^)
. , =(^..i-^.-i)/2. (12.40)
ох
Таким образом, вычисление первой производной, основанное на кубическом
В-сплайновом преобразовании, является на самом деле эффективным решением.
Мы применяем сначала кубическое В-сплайновое преобразование в направлении
производной, которую вычисляем (раздел 10.6.1), и затем оператор Ю^. Тогда
передаточная функция задается соотношением
D=i ^ '^ ^ =1Пк-1 ^ + 0(A:J). (12.41)
' 2/3 + l/3cos(K^J ' 180
Ошибки в модуле и направлении градиентного вектора, основанные на
В-сплайновом дифференциальном фильтре, показаны на рис. 12.6. Они значительно
меньше, чем для простых разностных фильтров (рис. 12.5). Это можно увидеть более
наглядно из разложений Тейлора для относительных ошибок в модуле градиента
еЛк,ф) - -^sin^ 2ф + 0{Р) (12.42)
и ошибки в величине угла
Глава 12. Контуры
Рис. 12.6. а — анизотропия модуля; б — ошибка в направлении фадиента на основе
кубического В-сплайнового дифференциа1П>ного оператора согласно уравнению (12.41).
Параметрами являются модуль волнового числа (от О до 1) и угол к оси л: (от О до п/2)
Лк.Ф)-
(пкУ
sm4ф + 0(k').
(12.43)
Слагаемые ошибок теперь содержатся только в членах с к (и более высокой
степени к). Сравните также уравнения (12.42) и (12.43) с уравнениями (12.36) и (12.37).
12.5. Определение контура по переходу через нулевой уровень
12.5.1. Принцип
Контуры дают пересечения нулевого уровня во вторых производных (рис. 12.1).
Следовательно, вторые производные по всем направлениям можно просто
сложить для образования линейного изотропного контурного детектора с
передаточной функцией -(пкУ (уравнение (12.9)), известного как оператор Лапласа. Из
рис. 12.1 также очевидно, что не каждый переход через нулевой уровень
соответствует контуру.
Только пики до и после нуля, которые значительно выше уровня шума,
указывают на действительные контуры. Из рис. 12.1 мы также можем заключить, что
вьщеление контуров с помощью оператора Лапласа, очевидно, гораздо более
чувствительно к шуму в сигнале, чем выделение контуров с использованием подхода,
основанного на использовании градиента.
12.5.2. Фильтр Лапласа
Мы можем непосредственно получить дифференциальные операторы второго
порядка с помощью двукратного применения операторов первого порядка
©2 = -®/©^. (12.44)
В пространственной области это означает
[1. -1]*[1 -1.] = [1 -2 1]. (12.45)
Дискретный оператор Лапласа £= <D^-\- Ф^ для 2-D изображений, таким
образом, имеет маску фильтра
12.5. Определение контура по переходу через нулевой уровень 345
£ = [1 -2 1] +
1
-2
1
=
0 1 0
1 -4 1
0 1 0
(12.46)
и передаточную функцию
1{к) = -4 sin'(71^^ /2)-4 sin' {nk^l2\ (12.47)
Как и другие дискретные аппроксимации операторов, оператор Лапласа
является изотропным только для малых волновых чисел (рис. 12.7, а)\
?(к,ф) = -{пкУ + — {пкУ +—со$4ф(пкУ -^Оф).
48 48
(12.48)
Существует много других способов построения дискретной аппроксимации для
оператора Лапласа. Интересной возможностью являются биномиальные маски. С
помощью уравнения (11.25) мы можем аппроксимировать все биномиальные
маски для достаточно малых волновых чисел с помощью
b'^ik) ^\-^(ЫУ+0(к'). (12.49)
Из этого уравнения мы можем заключить, что любой оператор (В^ - J образует
оператор Лапласа для малых волновых чисел. Например,
чфт<^Н
Рис. 12.7. Передаточные функции дискретных операторов Лапласа и их
анизотропия: а - £ уравнение (12.46); б - 1(к,в)-1(к,0); в - £'уравнение (12.50); г -
1\к,в)-1Хк,0)
Глава 12. Контуры
L' = 4iB^-I) = -
1 2 1
2 4 2
1 2 1
—
0 0 0
0 4 0
0 0 0
1
1
~4
1
2
1
2 1
-12 2
2 1
(12.50)
с передаточной функцией
/V) = 4cos'(7C^,/2)cos'(7C^/2)-4 (12.51)
является еще одним примером дискретного оператора Лапласа. Для малых
волновых чисел он может аппроксимироваться с помощью
?(к,ф) « -(nkf + — (71^)' - — cos4^(71^)40(Р). (12.52)
32 96
Для больших волновых чисел передаточные функции обоих операторов
Лапласа показывают значительные отклонения от идеального лапласиана, -(пкУ.
£'является значительно менее анизотропным, чем L.
12.6. Оптимизированное определение контуров
в этом разделе рассматриваются дифференциальные фильтры первого порядка,
которые были оптимизированы с использованием метода наименьших квадратов,
уже применявшегося в разделе 10.6.2 для оптимизации интерполяционных
фильтров. Основная идея в использовании одномерной маски фильтра 2R-\-lc нечетной
симметрией в соответствующем направлении w и изменении коэффициентов -
чтобы передаточная функция аппроксимировала идеальную передаточную
функцию дифференциального фильтра, ink^, с минимальным отклонением. Таким
образом, целевая функция равна
КК) = тК (12.53)
И передаточная функция одномерного фильтра 2Л + 1 с Л неизвестными
коэффициентами равна
M^w) = -iZH ^^pnkj, (12.54)
Как в случае для интерполяционных фильтров в разделе 10.6.2,
коэффициенты определяются таким образом, чтобы ^d{k) показывала минимальное
отклонение от t{k) в смысле наименьших квадратов:
\w{kj\^j-KK)\
dA:
(12.55)
Зависящая от волнового числа весовая функция w(k) определяет взвешивание
отдельных волновых чисел.
Одно из полезных дополнительных ограничений должно заставить
передаточную функцию равняться тк для малых волновых чисел. Это ограничение
уменьшает степень свободы на единицу для фильтра с R коэффициентами, так что
только iJ - 1 могут изменяться. Результирующие уравнения равны
^ ^ R
V = Чsin(л:^^)--i^2J^(sin(uл:^J~usin(л:^^)) (12.56)
г;=2
12.6. Оптимизированное определение контуров 34
Рис. 12.8. а - анизотропия модуля; б — ошибка в направлении градиента на основе
оптимизированного по методу наименьших квадратов дифференциального
фильтра, согласно уравнению (12.56), для/?=3 Ц =-0,597949, t/^ =0,189835, flfj =-0,0357216).
Параметрами являются модуль волнового числа (от О до 1) и угол к оси л: (от О до п/2)
dr=l-t,vd^.
(12.57)
i;=2
Как показывает сравнение рис. 12.6 и 12.8, фильтр демонстрирует значительно
более низкую ошибку, чем фильтр, построенный с помощью кубической
В-сплайновой интерполяции.
Дифференциальные фильтры можно далее улучшить с помощью компенсации
убывания в передаточной функции посредством рекурсивного релаксационного
фильтра, действующего в прямом и обратном направлениях (раздел 4.5.5,
рис. 4.5, б). Тогда результирующая передаточная функция равна
^ R
(^'^)^ = \^ ^ (12.58)
\ + P-PQOs{nkJ
с дополнительным параметром Д На рис. 12.9 показаны ошибки в модуле и
направлении градиента для R-2.
% кл^^тжх^штщ
Рис. 12.9. а — анизотропия модуля; б — ошибка в направлении градиента на основе
рекурсивного дифференциального фильтра по методу наименьших квадратов,
согласно уравнению (12.58), для Л = 2 (j3 = -0,439496, d^ = -0,440850, d^ = -0,0305482).
Параметрами являются модуль волнового числа (от О до 1) и угол к оси х (от О до я/2)
348 Глава 12. Контуры
Более детальное рассмотрение по разработке оптимальных
дифференциальных фильтров, включая таблицы с коэффициентами фильтров, можно найти в
работе Яне (Jahne) [89].
12.7. Регуляризованное определение контуров
12.7.1. Принцип
Контурные детекторы, рассмотренные до сих пор, все еще плохо справляются с
задачей, особенно в зашумленных изображениях. Из-за малых размеров масок они
наиболее чувствительны к высоким волновым числам. При высоких волновых
числах часто имеет место больше шума, чем сигнала в изображениях. Другими
словами, мы еще не рассматривали важность размеров для обработки изображений,
как было показано в разделе 5.1.1. Таким образом, путь к оптимальным
контурным детекторам лежит в регулировке контурных детекторов по размеру
(диапазону волновых чисел) с максимальным отношением сигнала к шуму.
Следовательно, мы должны разработать фильтры, которые выполняют дифференцирование в
одном направлении, но также сглаживают сигнал во всех других направлениях.
Сглаживание является особенно эффективным в многомерных сигналах,
поскольку оно не размывает контуры по всем направлениям, перпендикулярным
направлению градиента. Дифференциальные фильтры, которые включают
сглаживание, также известны как регуляризованные контурные детекторы, поскольку
они приводят к устойчивым решениям для некорректно поставленных задач
оценивания производных по дискретным сигналам.
1
^^v=-
X у 2
1
1
-1
-1
1
и DB=-
М у X
1
-1
1
-1
12.7.2. Поперечно-сглаживающий оператор 2x2
Наименьший поперечно-сглаживающий оператор имеет следующие маски 2 х 2:
(12.59)
и передаточные функции
dj^y (k) = 2i sm(Kk^ 12) со8(л:^^ / 2)
^ ^ - ~ - (12.60)
^y^x (^) = 2i sm{nky 12) co^{nk^ 12).
Здесь нет ничего, что можно оптимизировать с этой маской фильтра. Фильтры
/>^ = [1 -1] и Z)^ = [1 -1]^ не подходят для формирования оператора градиента,
поскольку D^ и Dy сдвигают результат свертки на половину сеточной постоянной в
направлениях хиу соответственно.
Ошибки в модуле и направлении градиента для малых волновых чисел равны
еЛк,Ф)«-^^вт4ф + 0(.к').
(12.61)
(12.62)
12.7. Регуляризованное определение контуров
Рис. 12.10. а — анизотропия модуля; б - ошибка в направлении градиента на основе
поперечно-сглаживающего контурного детектора 2x2 (уравнение (12.59)).
Параметрами являются модуль волнового числа (от О до 1) и угол к оси X (от О до я/2)
Ошибки значительно ниже (в 2 раза для малых волновых чисел) по сравнению
с градиентным вычислением, основанным на простом разностном операторе
D^ = 1/2[1 О -1] (рис. 12.5 и 12.10), хотя возникают анизотропные члены в
слагаемых того же порядка в уравнениях (12.36) и (12.37).
12.7.3. Контурный детектор Собеля
Оператор Собеля является наименьшим разностным фильтром с нечетным
числом коэффициентов, который усредняет изображение в направлении,
перпендикулярном дифференцированию:
2х у g
1
2
1
0
0
0
-1]
-2
-ij
Кв>\
1
0
-1
2
0
-2
1]
0
-IJ
(12.63)
Ошибки в модуле и направлении градиента на основе уравнения (12.63)
показаны на рис. 12.11. Улучшение по простому симметричному дифференциальному
оператору (рис. 12.5) схоже с поперечно-сглаживающим разностным оператором
(рис. 12.10). Разложение Тейлора по волновому числу приводит к тем же
аппроксимациям (сравните уравнения (12.61) и (12.62)):
еЛк,ф)''-^вт'2ф + 0{Р)
ДЛЯ ошибки модуля и
eф{k.ф)--^sm4ф + 0(k')
(12.64)
(12.65)
для направления градиента. Сравнения с соответствующими уравнениями для
простого разностного фильтра (12.36) и (12.37) показывают, что и анизотропия, и
ошибка в величине угла оператора Собеля в 2 раза меньше. Однако ошибка возрастает
со скоростью квадрата волнового числа. Ошибка в направлении градиента Собеля
составляет все еще до 5" при волновом числе 0,5. Для многих задач такая большая
ошибка недопустима.
350 Глава 12, Контуры
Рис. 12.11. а — анизотропия модуля; б - ошибка в направлении градиента на основе
контурного детектора Собеля (уравнение (12.63)). Параметрами являются модуль
волнового числа (от О до 1) и угол к оси х (от О до л/2)
12.7.4. Производные гауссиана
Хорошо известным общим классом регуляризованных дифференциальных
операторов является класс производных сглаживаюш;его оператора Гаусса. Такой фильтр,
например, использовал Кении (Canny) [21] для оптимального выделения
контуров, он известен также как контурный детектор Кении. На дискретной решетке
этот класс операторов лучше всего аппроксимируется производной
биномиального оператора (раздел 11.4) как
^^'^>® =©, Ф^ (12.66)
С неквадратными Ж-мерными масками (2R+3) х {2R +1)^"^ и передаточной функцией
^^'Х W = ism{KkJllcos''{nkJ2l (i2.67)
Удивительно, оказывается, что этот фильтр является плохим выбором,
поскольку его анизотропия является такой же, как в случае для простого симметричного
разностного фильтра. Это можно сразу же увидеть для направления градиента.
Сглаживающий член одинаков для обоих направлений и, таким образом,
уничтожается в уравнении (12.27). Оставшиеся члены являются такими же, как в случае
для симметричного разностного фильтра.
Таким же образом разностные операторы с размером /?^типа Собеля
'^W WW XX ^
(12.68)
с Ж-мерной маской (2R+ 1)*''и передаточной функцией
%(к) = Шп(пк,/2)1[со8"'(лк,/2) (12.69)
vv=l
показывают такую же анизотропию при том же волновом числе, как и оператор
Собеля 3x3.
12.7.5. Оптимизированные регуляризованные контурные детекторы
Не составляет труда получить оптимизированный регуляризованный
дифференциальный оператор со значительно меньшей ошибкой в оценке контуров. Срав-
12.7. Регуляризованное определение контуров
нение уравнений (12.35) и (12.65) показывает, что два фильтра имеют ошибки
определения угла в противоположных направлениях. Таким образом, оказывается, что
оператор Собеля выполняет слишком много поперечных сглаживаний, в то время
как симметричный разностный оператор выполняет слишком мало.
Следовательно, мы можем предполагать, что комбинация обоих операторов может привести к
гораздо более низкой ошибке. В самом деле, легко уменьшить поперечное
сглаживание с помощью увеличения центрального коэффициента. Яне (Jahne) и др. [96]
показывают, используя нелинейный оптимизационный метод, что операторы
1/4/),дз5;+/)=^
l/4D,(3Bl^I) =
32
3 0-3
10 о -10
3 0-3
3 10 3
0 0 0
-3 -10 -3
(12.70)
имеют минимальную ошибку в величине угла (рис. 12.12). Подобная оптимизация
возможна для регуляризованных дифференциальных фильтров большего размера.
12.7.6. LoG- и DoG-фильтры
Фильтры Лапласа имеют тенденцию значительно увеличивать уровень шума,
поскольку передаточная функция пропорциональна квадрату волнового числа.
Таким образом, лучший контурный детектор может быть найден с помощью
выполнения сначала сглаживания изображения и затем применения фильтра Лапласа.
Это приводит к виду регуляризованного вьщеления контуров и классу фильтров,
называемых фильтрами Лапласа—Гаусса (Laplace of Gaussian filter, LoG) или
операторами Марра—Хилдрета [133].
Рис. 12.12. а - анизотропия в модуле; б — ошибка в направлении градиента на основе
оптимизированного контурного детектора Собеля (12.70). Параметрами являются
модуль волнового числа (от О до 1) и угол к оси X (от О до л/2)
352 Глава 12. Контуры
В дискретном случае LoG-фильтр аппроксимируется с помощью выполнения
сначала сглаживания изображения с биномиальной маской и затем применения
дискретного фильтра Лапласа. Таким образом, мы имеем оператор L<S^ с
передаточной функцией
LB'(k) = -4[sin'(^^, /2) + 8т'(л:^/2)]со8^(л:^^ /2)со8^(л:^/2). (12.71)
Для малых волновых чисел эта передаточная функция может
аппроксимироваться с помощью
LB'(k4)^-i^kf-^
11 1
— + -/? + — cos(40)
16 8 48
(7tk)\
(12.72)
В разделе 12.5.2 мы увидели, что фильтр Лапласа может даже лучше
аппроксимироваться с помощью операторов типа Ф^ -1. Если применить дополнительное
сглаживание, эта аппроксимация для фильтра Лапласа приводит к разности
гауссова типа фильтра Лапласа, или 1)оС-фильтрам:
А{(В' -J)(B^ =4((В^^^ -сВ'). (12.73)
DoG-фильтр 4((В''^' - ^0 имеет передаточную функцию
- 4со8^(л:^^/2)со8^(л:^/2),
(12.74)
которая может аппроксимироваться для малых волновых чисел соотношением
А{В'^^ -В'){к,ф)^-{пкУ +
3 1 1
+ - /7 СО8(40)
32 8 96
{пк)\ (12.75)
Передаточные функции LoG- и DoG-фильтров сравниваются на рис. 12.13.
Очевидно, что DoG-фильтр значительно более изотропный. Фильтр с даже еще
меньшим отклонением в изотропии можно получить, сравнив уравнения (12.72) и
*^Г^
Рис. 12.13. Псевдо-3-D фафическое изображение передаточной функции: а - LoG-
фильтра £в^; б - DoG-фильтра 4(Ф^ - ®^)
12.8. Контуры в многоканальных изображениях
(12.75). Анизотропные члены с cos 40 имеют разные знаки. Таким образом, они
могут легко компенсироваться с помощью комбинации LoG- и DoG-операторов
вида 2/3DoG + l/3LoG, которая соответствует оператору (8/ЗФ^ - 8/3 J - 1/3£)Ф^.
DoG- и LoG- фильтрующие операторы имеют некоторое значение для
зрительной системы человека [132].
12.8. Контуры в многоканальных изображениях
в многоканальных изображениях значительно более сложным является анализ
контуров, чем выполнение усреднения, которое было рассмотрено в разделе 11.7.
Основная сложность состоит в том, что разные каналы могут содержать
противоречивую информацию о контурах. В канале А градиент может иметь отличное
направление, чем в канале В. Простое сложение градиентов по всем каналам
ivg.w
(12.76)
р=\
здесь неприменимо. Может случиться, что градиенты в двух каналах имеют
противоположные направления и, таким образом, уничтожают друг друга. Тогда сумма
градиентов по всем каналам равнялась бы нулю, хотя отдельные каналы имели бы
ненулевые градиенты и мы не смогли бы отличить этот случай от случая
постоянных областей в обоих каналах.
Таким образом, более подходящей мерой полной интенсивности контуров
является сумма квадратов модулей градиентов по всем каналам:
р W
iv^,r=IS
Эх...
\2
(12.77)
р=1 p=\w=\y ^
Хотя это выражение определяет полезную оценку общей интенсивности
контуров, оно все еще не рещает проблему противоречивых контурных направлений.
Анализ того, как контуры распределены в Ж-мерном многоканальном
изображении с Р каналами, возможен с помощью следующей симметричной матрицы 5
размерностью WxW, где Жесть размерность изображения):
где /известна как матрица Якоби. Эта матрица Р х ^определяется как
(12.78)
J =
^9х М
дх, Эх,
ддр ддр
^9х
Э%
^9р
Эх, Эх2 Эх^
(12.79)
Глава 12. Контуры
Таким образом, элементами матрицы S являются
^ki
^f^9,^9.
(12.80)
p-l OXj^ OXj
Поскольку 5 является симметричной матрицей, мы можем привести ее к
диагональному виду с помощью подходящего координатного преобразования. Тогда
мы можем записать
S' =
[dx:j
о
о
о
о
• о
•. о
Эх'
\2
/ -1
(12.81)
В случае идеального контура только один диагональный элемент матрицы не
будет равен нулю. Это направление, перпендикулярное разрыву. Во всех других
направлениях он будет равен нулю. Таким образом, 5 является матрицей с рангом
один в этом случае.
Противоположно, если контуры в различных каналах распределены случайно
по всем направлениям, то все диагональные элементы будут неравными нулю и
равны между собой. Таким образом, в принципе возможно отличить случайные
изменения, вызванные шумом, от когерентных контуров. След матрицы S
W Р
w=l
Эх..
V
(12.82)
задает меру интенсивности контуров, которую мы уже определили в уравнении
(12.77). Она не зависит от ориентации контура, поскольку след симметричной
матрицы инвариантен относительно поворота системы координат.
12.9. Упражнения
12.1: Выделение контуров и линий
Интерактивная демонстрация вьщеления контуров и линий с помощью
нескольких контурных детекторов, основанных на дифференциальных
фильтрах первого и второго порядков (dip6exl2.01).
12.2: Выделение контуров и линий на пирамидах
Интерактивная демонстрация вьщеления контуров и линий с помощью
нескольких дифференциальных фильтров первого и второго порядков при
различных масштабах на пирамидах (dip6exl2.02).
12.9. Упражнения 355
12.3: "^Разностные фильтры первого порядка
Перед вами часто используемые разностные фильтры первого порядка в
направлении х:
1
1
0
0
0
-1
-1
-1
1
' в) 8
1 0
2 0
1 0
-1
-2
-1
а)-[1 О -1], б) 6
1. Вычислите передаточные функции трех фильтров.
2. Сравните и опишите свойства трех фильтров.
3. Какой фильтр наиболее подходит для вьщеления контуров? Обоснуйте
свой выбор.
12.4: "^Плохой разностный фильтр первого пор51дка
Почему разностный фильтр первого порядка
[1 -1],
1
-1
является плохим фильтром для вычисления 2-D градиента и для выделения
контуров?
12.5: "^"^Разностный фильтр первого порядка Роберта
Роберт предложил фильтр
1 О
О -1
О 1
-1 О
для вычисления 2-D градиента и выделения контуров.
1. В каких направлениях эти фильтры выделяют контуры?
2. Вычислите передаточную функцию этих фильтров.
3. Сравните качество этого фильтра с фильтром из упражнения 12.4.
12.6: "^^Неизвестные фильтры
Вот некоторые неизвестные фильтры:
а) ^[1 2 О -2 -1], б) ^[1 О
О О
-2 О 1],
в)з
1 1
1 -8
1 1
г) 2
0-10
-1 -6 -1
0-10
которые необходимо проанализировать.
1. Вычислите передаточную функцию этих фильтров.
2. Являются ли они разностными фильтрами первого или второго порядка?
3. Как они сопоставляются с фильтрами, описанными в этой главе?
Глава 12. Контуры
12 J: "^"^Разработка разностных фильтров второго порядка
Воспользуйтесь всеми необходимыми свойствами для разностного
фильтра второго порядка, чтобы показать, что может существовать только один
такой фильтр с тремя коэффициентами ([ар у]).
Если фильтр имеет пять коэффициентов, то остается один свободный
параметр. Каковы коэффициенты этого фильтра и какова его передаточная
функция, если применить дополнительное ограничение: фильтр должен
уничтожать структуры с самым высоким волновым числом (А(1) = 0)?
12.8: ***Изотропия 2-D градиентного фильтра
Изотропия фильтров играет большую роль в обработке изображений.
Сглаживающие фильтры должны сглаживать мелкие структуры одинаково во
всех направлениях, а дифференциальные фильтры должны выделять
контуры во всех направлениях одинаково хорошо.
Исследуйте изотропию простого градиентного фильтра
D^=\/2[l О -1], /) =1/2
1
О
-1
посредством разложения двух передаточных функций в ряд Тейлора вплоть
до третьего порядка по волновому числу.
(Подсказка: изотропия означает, что модуль градиента одинаков во всех
направлениях и что направление градиента вычисляется корректно (раздел
12.4.2). Вычисление станет проще, если выразить волновые числа в
полярных координатах: к^=к cos (р,к^=к sin ср.)
12.10. Дополнительная литература
Доступно громадное множество литературы по проблемам вьщеления контуров.
Мы дадим здесь только немногие выбранные ссылки. Развитие области
вьщеления контуров, основанного на разностных фильтрах первого порядка, можно
подробно проследить по некоторым ключевым работам. Кении (Canny) [21]
сформулировал оптимальный контурный детектор, основанный на производных гауссиана,
Дерихе (Deriche) [34] ввел быстрое рекурсивное выполнение контурного
детектора Кении (Canny), Лансер (Lanser) и Экштайн (Eckstein) [116] улучшили
изотропию рекурсивного фильтра Дерихе (Deriche), а Яне (Jahne) и др. [96] предложили
нелинейную оптимизационную стратегию для контурных детекторов с
оптимальной изотропией. На вьщеление контуров, основанное на разности второго
порядка (нулевые пересечения), сильно повлияло биологическое зрение.
Изыскательская работа описана Марром (Магг) и Хильдретом (Hildreth) [133] и Марром (Магг)
[132]. Недавние исследования унифицированной базы для операторов над
соседними элементами можно найти в книгах Коендеринка (Koenderink) и ван Дорна
(van Doom) [113] и Данильссона (Danielsson) и др. [28].
ГЛАВА 13
ПРОСТЫЕ ОКРЕСТНОСТИ
13.1. Введение
в последних двух главах мы познакомились с операциями над соседними
элементами для выполнения усреднения и вьщеления контуров. Фактически мы изучили
только самые простые структуры в локальных окрестностях: постоянные области
и неоднородности. Однако локальные окрестности могут также содержать более
сложные структуры. В этой главе мы рассматриваем самый простой класс таких
структур, которые мы назовем простыми окрестностями. В качестве введения
исследуем, какие типы простых структур можно использовать для того, чтобы
сделать объект отличимым от фона для зрительной системы человека.
Наша зрительная система может легко распознавать объекты, которые
отличаются от фона не по среднему уровню яркости, а только по ориентации или масштабу
структуры, что и продемонстрировано на рис. 13.1. Для того чтобы вьшолнить задачу
распознавания с помощью системы цифровой обработки изображений, нам нужны
операторы, которые определяют ориентацию и масштаб структуры. После такой
операции полутоновое изображение преобразуется в изображение признака. В
изображении признака мы можем вьщелять структуры, которые отличаются орие1ггацией или
масштабом, таким же образом, каким мы может вьщелить уровни яркости.
Мы обозначаем локальные окрестности, которые могут быть описаны
ориентацией как простые окрестности. Разработка подходящих операторов для
ориентации и масштаба является важным и необходимым требованием для анализа
более сложных структур. Интересно следующее наблюдение: значение одной и той
же локальной структуры может быть совершенно различным, что и
проиллюстрировано на рис. 13.2 для 2-D изображений:
• В самом простом случае наблюдаемая сцена состоит из объектов и фона с
равномерной энергетической яркостью (рис. 13.2, а). Тогда изменение уровней
яркости в локальной окрестности указывает на то, что встретился контур объекта, а
анализ ориентации приводит к ориентации контура.
• На рис. 13.2, б объекты отличаются от фона ориентацией текстуры. Теперь
локальная пространственная структура не показывает контур, а характеризует
текстуру объектов. Анализ текстуры будет рассмотрен в главе 15.
• В последовательностях изображений локальная структура в
пространственно-временной области определяется движением, что и изображено на рис. 13.2, в
для 2-D пространственно-временного изображения. Движение является важным
признаком для определения объектов и будет рассматриваться детально в главе 14.
Хотя эти три примера относятся к полностью различным данным
изображений, для них является общим то, что локальная структура характеризуется ориен-
358 Глава 13. Простые окрестности
Рис. 13.1. Объект можно отделить от фона, поскольку он отличается по: а — уровню
яркости; б — ориентации структуры; в — масштабу структуры
N о
XXX
Рис. 13.2. Три различные интерпретации локальных структур в 2-D изображениях:
а — контур между однородными объектом и фоном; б — ориентация структуры; в -
ориентация в 2-D пространственно-временном изображении, указывающая на наличие
скорости 1-D объектов
тацией, т.е. уровни яркости изменяются локально в одном направлении. В этом
смысле понятие ориентации является расширением понятия контуров.
13.2. Свойства простых окрестностей
13.2.1. Представление в пространственной области
Математическое описание локальной окрестности наилучшим образом
производится с помощью непрерывных функций. Этот подход имеет два существенных
преимущества. Во-первых, гораздо легче формулировать понятия и изучать их
свойства аналитически. Если соответствующее дискретное изображение
удовлетворяет теореме о дискретном представлении, все результаты, полученные от
непрерывных функций, остаются действительными, поскольку дискретизированное
изображение является точным представлением функции уровней яркости.
Во-вторых, мы можем теперь сделать различие между ошибками, присущими
выбранному подходу, и ошибками, которые вносятся только дискретизацией.
Локальная окрестность с идеальной локальной ориентацией
характеризуется тем, что уровень яркости изменяется только в одном направлении. Во всех
остальных направлениях он остается постоянным. Поскольку уровни яркости
13.2. Свойства простых окрестностей
постоянны вдоль линий, локальная ориентация также обозначается как
линейная симметрия [9]. Термин простая окрестность совсем недавно был введен
Гранлундом (Granlund) и Натссоном (Knutsson) [64]. Если задать ориентацию
системе координат вдоль главных направлений, то уровни яркости становятся
1-D функцией только от одной координаты. Как правило, мы будем
обозначать направление локальной ориентации с помощью единичного вектора Я,
перпендикулярного линиям постоянных уровней яркости. Тогда простая
окрестность математически представляется как
д(х) = д(х^п1 ^ (13.1)
где скалярное произведение обозначаем просто как х^п. Мы будем использовать
это упрощенное обозначение по всей главе. Выражение (13.1) также
действительно для данных изображения с размерностью, больше чем два. Проекция вектора jc
на единичный вектор п приводит к тому, что уровни яркости зависят только от
скалярной величины — координаты в направлении п (рис. 13.3). Легко проверить,
что это представление корректно, с помощью вычисления градиента:
Vg(x^ii) =
щдХх'п)
п^дХх'п)
= пд\х^п)
(13.2)
С помощью д' мы обозначаем производную от д по скалярной величине
х^п. в гиперплоскости, перпендикулярной градиенту, значения остаются
локально постоянными, уравнение (13.2) доказывает, что градиент лежит в
направлении п.
Рис. 13.3. Иллюстрация линейной симметричной или простой окрестности. Уровни
яркости зависят только от координаты, заданной единичным вектором п
Глава 13. Простые окрестности
13.2.2. Представление в Фурье-области
Простая окрестность также имеет специальную форму в Фурье-пространстве. Для
того чтобы получить ее, сначала предположим, что все изображение описывается
уравнением (13.1), т.е. п не зависит от положения. Тогда из того факта, что
простая окрестность является постоянной во всех направлениях, за исключением л,
мы делаем вывод, что преобразование Фурье должно быть ограничено линией.
Направление линии задается п\
д(х^п) о . д(к)д(к-п(к^п)), (13.3)
где к обозначает координату в Фурье-области в направлении й. Аргумент в 5-функ-
ции равен нулю, только когда к параллелен й. Во втором шаге теперь
ограничиваем уравнение (13.3) локальной окрестностью, умножая д(х^п) на оконную
функцию w(x - jCq) в пространственной области. Таким образом, мы выбираем
локальную окрестность вокруг дс^. Размер и форма окрестности определяется
оконной функцией. Оконная функция, которая постепенно убывает к нулю,
уменьшает влияние пикселей как функция их расстояния от внешних пикселей.
Умножение в пространственной области соответствует свертке в Фурье-области
(раздел 2.3). Таким образом.
w(x-XQ)-g{x п) о • w(k)^g(k)5(k-n(k п)),
(13.4)
где w{k) — преобразование Фурье от оконной функции.
Ограничение до локальной окрестности, таким образом, размывает линию в
Фурье-пространстве до «колбасовидной» формы. Из-за обратимости размеров
между двумя областями ее толщина обратно пропорциональна размеру окна. Из
этого элементарного соотношения мы уже можем качественно прийти к
заключению, что оценка точности ориентации непосредственно связана с отношением
размера окна к длине волны самой малой структуры в окне.
13.2.3. Векторное представление локальных окрестностей
Для подходящего представления простых окрестностей важно сначала отделить
ориентацию от направления. Направление определяется на полном угловом
диапазоне 2л: (ЗбО**). Два вектора, ориентированных в противоположных направлениях,
т.е. отличающихся на 180**, являются различными. Вектор градиента, к примеру,
всегда имеет направление, в котором уровни яркости увеличиваются. Относительно
светлого объекта на темном фоне это означает, что градиент на контуре является
направленным к объекту. Противоположно, для описания локальной
окрестности угловой диапазон 360° не имеет смысла. Мы не можем сделать различие между
структурами, которые поворачиваются на 180°. Если структура повернута на 180°,
то она по-прежнему имеет то же направление. Таким образом, направление
простой окрестности отличается от направления градиента. В то время как для
контура объекта градиенты, направленные в противоположные направления, являются
противоречащими и несовместными, для направления простой окрестности это
непротиворечивая информация.
Для того чтобы вьщелить два типа «направлений», мы будем говорить об
ориентации во всех случаях, где требуется угловой диапазон только в 180°. Ориентация
является по-прежнему, конечно, циклической величиной. Увеличение ориентации
13.2. Свойства простых окрестностей 36
Рис. 13.4. Представление локальной ориентации как вектора: а — вектор ориентации;
б — усреднение векторов ориентации из области с однородной ориентацией; в — то же
самое для области со случайно распределенной ориентацией
выше 180° переводит ее назад к 0\ Следовательно, подходящее представление
ориентации требует удвоения угла.
После этого обсуждения принципов представления ориентации мы готовы
подумать о подходящем представлении простых окрестностей. Очевидно,
скалярная величина с просто удвоенным углом ориентации не подходит.
Представляется, что будет полезным добавить меру достоверности, которая описывает, насколько
хорошо окрестность аппроксимирует простую окрестность. Скалярная величина
и мера достоверности должны быть сопоставлены для формирования вектора. Мы
установим абсолютную величину вектора, равную мере достоверности, а
направление вектора — двойному углу ориентации (рис. 13.4, а). Это векторное
представление ориентации имеет два существенных преимущества.
Во-первых, оно является более подходящим для дальнейшей обработки, чем
отдельное представление ориентации с помощью двух скалярных величин.
Возьмем, например, усреднение. Векторы складываются с помощью
выстраивания их в цепь, и результирующий вектор суммы является вектором из начальной
точки первого вектора в конечную точку последнего вектора (рис. 13.4, б). Вес
отдельного вектора в векторной сумме задается его длиной. Таким образом,
достоверность измерения ориентации адекватно принимается в расчет. Векторное
представление локальной ориентации проявляет подходящие свойства усреднения. В
области с однородным представлением вектора выстраиваются в большой вектор
(рис. 13.4, б), т.е. определенную оценку ориентации. Однако в области со
случайно распределенной ориентацией результирующий вектор остается малым,
указывая на то, что присутствует несущественная локальная ориентация (рис. 13.4, в).
Во-вторых, сложно воспроизвести ориентацию как полутоновое изображение.
В то время как ориентация является циклической величиной, представление
через шкалу яркости проявляет неестественный скачок между самым малым углом и
самым большим. Этот скачок преобладает во внешнем представлении
изображений ориентации и, таким образом, не дает хорошего представления о
распределении ориентации. Вектор ориентации может быть хорошо представлен, однако как
цветное изображение. Кажется естественным отобразить меру достоверности в
яркость, а угол ориентации как тон цвета. Наше внимание привлекают светлые
части на изображениях, где мы можем хорошо различать цвета. Чем темнее цвет,
тем сложнее становится различать цвета визуально. Таким образом, наше
зрительное впечатление совпадает с информацией об ориентации на изображении.
Глава 13, Простые окрестности
13.3. Тензорное представление первого порядка
13.3.1. Структурный тензор
Векторное представление, рассмотренное в разделе 13.2.3, не является полным.
Хотя оно подходит для представления ориентации простых окрестностей, оно не
может сделать различие между окрестностями с постоянными значениями и
изотропным распределением ориентации (например, некоррелированный шум). Оба
случая приводят к вектору ориентации с нулевой абсолютной величиной.
Поэтому очевидно, что адекватное представление изменений уровней яркости в
локальной 01фестности должно бьпъ более сложным. Такое представление должно бьпъ
способным определять однозначную ориентацию (заданную единичным вектором п) и
отличать постоянные окрестности от окрестностей без локальной ориентации.
Подходящее представление может быть введено следующей оптимизационной
стратегией для определенрш ориентации простой окрестности. Оптимальная
ориентация определяется как ориентация, которая проявляет наименьшие
отклонения от направлений градиента. Подходящая мера отклонения должна трактовать
градиенты, направленные в противоположных направлениях, одинаково.
Квадрат скалярного произведения, вектора градиента и единичного вектора,
представляющего локальную ориентацию Я, удовлетворяет этому критерию:
{Wg'nf =\Vgf cos\Z(Vg,n)). (13.5)
Эта величина пропорциональна квадрату косинуса угла между вектором
градиента и вектором ориентации и является, таким образом, максимальной, когда
Vgnn параллельны или антипараллельны, и равна нулю, если они
перпендикулярны друг другу. Следовательно, следующий интеграл максимизируется в Ж-мер-
ной локальной окрестности:
jw(x-x){Vg(xynfd'^x, (13.6)
где оконная функция w определяет размер и форму окрестности вокруг точки х, по
которой усредняется ориентация. Задача максимизации должна решаться для
каждой точки X, Уравнение (13.6) можно переписать следующим образом:
n^Jn —> maximum (137)
при
/ = \w(x-x'){Vgix')Vg{xr)d"'x',
где VgVg^ обозначает векторное (декартово) произведение. Компоненты этого
симметричного тензора Wx JV, носящего название структурного тензора, равны
оо
^9(х) дд{х)
дх^ дх^
Гх\
(13.8)
Эти уравнения указьгоают на то, что тензор является адекватным представлением
локальной поверхности первого порядка. Термин «первый порядок» имеет двойное
значение. Во-первых, включены только первые производные. Во-вторьос, только
простые окрестности могут описываться в том смысле, что мы можем анализировать, в
каком направлении(51х) изменяются уровни яркости. Более сложные структуры,
такие, как структуры с многочисленными ориентациями, не могут вьщеляться.
13.3, Тензорное представление первого порядка
Сложность уравнений (13.7) и (13.8) отчасти затемняет их простое значение.
Тензор является симметричным. С помощью вращения системы координат он может быть
приведен к диагональному виду. Тогда уравнение (13.7) сводится в 2-D случае к
J' = [n,.K]
-^maximum. (13.9)
Единичный вектор п' = [cos0 sin0]B направлении в определяет значения
f = J{^ cos^ в + J22 sin^ в-
Без потери общности предположим, что /j^ ^/зг* Тогда очевидно, что
единичный вектор п' = [1 0]^ максимизирует уравнение (13.9). Максимальное значение
равно /|j. В заключение отметим, что этот подход не только дает тензорное
представление для локальной окрестности, но также и предлагает способ для
определения ориентации. По существу, мы должны решить так называемую задачу на
собственные значения. Собственные значения Я^ и собственные векторы е^
матрицы размерностью Wx ^определяются как
Je =Я ^ . (13.10)
^ W WW ^ ^
Собственный вектор е^ тензора / является, таким образом, вектором,
который не изменяет направления при умножении на матрицу /, а только
умножается на скалярный множитель, собственное значение Я^. Это подразумевает, что
структурный тензор становится диагональным в координатной системе, которая
образуется собственными векторами (13.9). Для нашего дальнейшего
рассмотрения важно помнить следующие основные свойства собственных значений
симметричной матрицы:
1. Собственные значения являются действительными и неотрицательными.
2. Собственные векторы образуют ортогональный базис.
Согласно задаче максимизации, сформулированной здесь, собственный
вектор к максимальному собственному значению задает ориентацию локальной
окрестности.
13.3.2. Классификация собственных значений
Значение тензорного представления становится очевидной, если мы
классифицируем собственные значения структурного тензора. Классифицирующим
критерием является число собственных значений, которые равны нулю. Если
собственное значение равно нулю, то это означает, что уровни яркости в направлении
соответствующего собственного вектора не изменяются. Число нулевых
собственных значений также тесно связано с рангом матрицы. Ранг матрицы
определяется как размерность подпространства, для которого Лсу^О. Пространство, для
которого Лс = О обозначается как нулевое пространство. Размерность нулевого
пространства равна размерности матрицы минус ранг матрицы и равна числу
нулевых собственных значений. Мы выполним анализ собственных значений для
дву- и трехмерного случаев. В дву- и трехмерном случаях мы можем выделить
случаи, кратко изложенные в табл. 13.1 и 13.2 соответственно.
В реальных задачах собственные значения должны быть ниже критической
пороговой величины, которая определяется уровнем шума на изображении. Их
равенство нулю не столь важно.
Глава 13. Простые окрестности
Таблица 13.1. Классификация собственных значений структурного тензора в 2-D
изображениях
Условие
Ранг (J)
Описание
; _ ^ _ Q О Оба собственных значения равны нулю.
Среднеквадратичный модуль градиента (Aj + Х^ равен
нулю. Локальная окрестность имеет постоянные
значения
Я, >05 Я2 =0 1 Одно собственное значение равно нулю. Значения не
изменяются в направлении соответствующего
собственного вектора. Локальная окрестность является
простой 01фестностью с идеальной ориентацией
Я, > О, Я^ > О 2 Оба собственных значения не равны нулю. Уровни
яркости изменяются во всех направлениях. В
частном случае Я, = Х^ мы говорим об изотропной
структуре уровней яркости, поскольку она изменяется
одинаково во всех направлениях
13.3.3. Вектор ориентации
С помощью простой свертки и точечных операций, рассмотренных в предыдущем
разделе, мы вьиислили компоненты структурного тензора. В этом разделе мы
решаем задачу на собственные значения для определения вектора ориентации. В
двумерном случае мы можем легко решить задачу на собственные значения. Угол
ориентации можно определить с помощью вращения тензора инерции в системе
координат с главными осями:
[;
Л
0
0
к\
'cos^
sin0
-sin^ 1
COS0 J
Wu
W
Л2
•^22 J
Г cos^
[-sin0
sin^
COS0
Используя тригонометрические тождества sin20 = 2sin0 cos0 и cos2e = cos^S - sin^0,
матричные умножения приводят к
COS0 -sin0
sin0 COS0
X О
О Я,
Уц cos в - ^12 si^ ^ Jii sin 0 + У12 cos в
-J22 sin в + J^2 C^S ^ Л2 C^S ^ "*■ «^12 Si^ ^
Jj 1 cos^ в + ^22 sin в - Ji2 20
l/2(yii-J22)sin20 + yi2COs20
[1/2(У11 -/22)511120 + Ji2 COS 20 Уц sin^ 0 + У22 cos^ 0 + J12 sin20j
Теперь мы можем сравнить коэффициенты матрицы левой и правой частей
уравнения. Поскольку матрицы являются симметричными, мы имеем три уравне-
13.3. Тензорное представление первого порядка 365
Таблица 13.2. Классификация собственных значений структурного тензора в 3-D
(объемных) изображениях
Условие
Ранг (J)
Описание
Ai>0, Я2=Аз=0
О
\>0, Я2>0, Лз=0 2
Д^>0, Я2>0, Аз>0 3
Уровни яркости не изменяются ни в одном
направлении; постоянные окрестности
Уровни яркости изменяются только в одном
направлении. Это направление задается
собственным вектором к ненулевому значению.
Окрестность включает границу между двумя
объектами или слоистую текстуру. В
пространственно-временном изображении это
означает постоянное движение пространственно
ориентированной структуры («плоская волна»)
Уровни яркости изменяются в двух
направлениях и являются постоянными в третьем.
Собственный вектор к нулевому собственному
значению задает направление постоянных
уровней яркости
Уровни яркости изменяются во всех трех
направлениях.
ния с тремя неизвестными, 0, \ и Х^. Хотя система уравнений является
нелинейной, она может легко быть решена для ft
Сравнение недиагональных элементов с обеих сторон уравнения
l/2(y,i-y22)sin20 + y,2COs20 = O (13.11)
позволяет выразить угол ориентации
tan 20 =
и.
12
•^22 *^\\
(13.12)
Без определения каких-либо предварительных условий мы получили
ожидаемое удвоение угла ориентации. Поскольку tan20 определяется из частного, мы
можем рассматривать делимое как компоненту з^, а делитель как компоненту л:
вектора и можем сформировать вектор ориентации о, согласно определению Гранлунда
(Granlund) [63]:
0 =
•^22 "'U
2J,.
(13.13)
Аргумент этого вектора задает угол ориентации и модуль — меру
достоверности для локальной ориентации.
Результат уравнения (13.13) является примечательным в том смысле, что
вычисление компонента вектора ориентации по компонентам тензора ориентации
требует только одного вычитания и одного умножения на двойку. Поскольку эти
Глава 13. Простые окрестности
компоненты вектора ориентации нужны нам для дальнейших шагов обработки,
нам не нужен угол ориентации или модуль вектора. Таким образом, решение
задачи на собственные значения по двум направлениям является тривиальным.
13.3.4. Когерентность
Вектор ориентации сводит локальную структуру к локальной ориентации. Из трех
независимых компонент симметричного тензора используются по-прежнему
только две. Когда нам не удается наблюдать ориентированную структуру в
окрестности, мы не знаем, встречаются ли изменения уровней яркости или распределенные
ориентации. Эта информация включается в еще не использованную компоненту
тензора, /^^ + J^^, которая определяет среднеквадратичную абсолютную величину
градиента. Следовательно, хорошо оснащенный структурный тензор должен
включать также третью компоненту. Подходящей линейной комбинацией является
(13.14)
Этот структурный оператор содержит две компоненты вектора ориентации и,
в качестве дополнительной компоненты, среднеквадратичную абсолютную
величину градиента, которая является параметром, инвариантным относительно
поворота. Сравнивая последнюю с модулем вектора ориентации, можно вьщелить
область постоянного уровня яркости и изотропную структуру уровней яркости без
преимущественной ориентации. В первом случае обе возведенные в квадрат
величины равны нулю, во втором — только модуль вектора ориентации. В случае
совершенно ориентированной структуры обе величины равны. Поэтому оказывается,
что их отношение является хорошей мерой когерентности с^ для локальной
ориентации:
s =
"'и "'""'22
•^22 ""*^11
•
с. =■
(13.15)
*^11 "'" *^22 А "'" ^2
Когерентность изменяется в диапазоне от О до 1. Для идеальной локальной
ориентации {Х^ = О, Aj > 0) она равна единице, для изотропной структуры уровней
яркости (А, = Х^>0) она равна нулю.
13.3.5. Цветовое кодирование 2-D структурного тензора
В разделе 13.2.3 мы рассматривали цветовое представление вектора ориентации.
Вопрос состоит в том, возможно ли также адекватно представить структурный
тензор как цветное изображение. Симметричный 2-D тензор имеет три независимые
области информации (13.14), которые хорошо подходят трем степеням свободы,
пригодным для представления цвета, например, яркости, тона и насыщенности.
Цветовое представление структурного тензора требует всего лишь две
незначительные модификации по сравнению с цветовым представлением для вектора
13,3. Тензорное представление первого порядка
ориентации. Во-первых, вместо длины вектора ориентации возведенный в
квадрат модуль градиента отображается в интенсивность. Во-вторых, мера
когерентности (13.15) используется как насыщенность. В цветовом представлении для
вектора ориентации насыщенность всегда равна единице. Угол вектора ориентации
по-прежнему представляется как тон.
На практике полезна незначительная модификация этого цветового
представления. Возведенный в квадрат модуль градиента демонстрирует изменения
слишком большие, чтобы воспроизводиться на экране в узком динамическом
диапазоне дисплейного экрана всего лишь с 256 уровнями яркости. Следовательно,
требуется подходящее нормирование. Основной идеей этого нормирования
является сравнение возведенного в квадрат модуля градиента с уровнем шума. Как
только градиент становится гораздо выше уровня шума, он рассматривается как
существенная часть информации. Такой подход предполагает следующее нормирование
интенсивности /:
/ = —^и±:к^, (13.16)
где а^ - оценка среднеквадратичного отклонения уровня шума. Это
нормирование обеспечивает быстрый переход яркости от единицы, когда модуль градиента
больше, чем о^, к нулю, когда градиент меньше, чем о;. Множитель у используется
для оптимизации воспроизведения на экране.
13.3.6. Реализация
Структурный тензор (раздел 13.3.1) или тензор инерции (раздел 13.5.1) может быть
вычислен непосредственно как комбинация линейной свертки и нелинейных
точенных операций. Частные производные в уравнениях (13.8) и (13.64)
аппроксимируются дискретными дифференциальными операторами. Интегрирование,
взвешенное с оконной функцией, заменяется сверткой со сглаживающим фильтром,
который имеет форму оконной функции. Если мы обозначим дискретный
оператор в частных производных относительно координаты/? с помощью оператора ©,,
а (изотропный) сглаживающий оператор с помощью (В, то локальную структуру
изображения различной яркости можно вычислить с помощью структурного
тензорного оператора
J^^=CB{(D^(D^l (13.17)
Уравнение записывается в операторной форме. Попиксельное умножение
обозначается • для отделения его от последовательного применения операторов
свертки. Уравнение (13.17) говорит о том, что компонент J тензора
вычисляется свертыванием изображения с помощью <D и (D независимо, умножением двух
изображений попиксельно и сглаживанием результирующего изображения с
помощью (В.
Эти операторы действительны на изображениях любой размерности W> 2. В W-
мерном изображении структурный тензор имеет W{W-\-1)/2 независимых компонеигг
и, следовательно, 3 в 2-D, 6 в 3-D и 10 в 4-D изображениях. Эти компоненты лучше
всего сохранять в многоканальных изображениях с W{W-\-1)/2 компонентами.
Сглаживающие операции поглощают наибольшее число операций.
Следовательно, быстрые алгоритмы должны, во-первых, использовать быстрый сглажива-
Глава 13. Простые окрестности
юищй алгоритм. Быстрый алгоррггм можно создать на основе общего наблюдения -
признаки более высокого порядка всегда показывают более низкое разрешение, чем
признаки, по которым они вычислены. Это означает, что структурный тензор может
сохраняться на более 1фупной сетке и, таким образом, в меньшем изображении.
Удобная и подходящая частота подвыборки должна уменьшить размер в 2 раза с помош5>ю
сохранения только каждого второго пикселя в каждой второй строке.
Эти процедуры приводят нас естественным образом к многосеточным
структурам данных, которые рассматривались детально в главе 5. Многошаговое
усреднение рассматривается детально в разделе 11.5.1.
Хранение признаков более высокого порядка в крупных масштабах имеет еще
одно существенное преимущество. Любая последовательная обработка
ускоряется просто тем фактом, что обрабатывается гораздо меньшее количество пикселей.
Линейное уменьшение размера в 2 раза приводит к уменьшению числа пикселей и
вьиислений в 4 раза в двумерном случае и в 8 раз — в трехмерном случае.
На рис. 13.5 иллюстрируются все шаги для вычисления структурного тензора и
получаемых величин с использованием кольцевой тестовой структуры. Эта
тестовая структура особенно подходит для анализа ориентации, поскольку содержит
все виды ориентации и волновых чисел в одном изображении.
Точность угла ориентации сильно зависит от выполнения дифференциальных
операторов. Прямое выполнение алгоритма с использованием стандартной маски
дифференциального фильтра 1/2[1 О -1] (раздел 12.4.3) или оператора Собеля
(раздел 12.7.3) приводит к удивительно большим ошибкам (рис. 13.6, б) с
максимальной ошибкой в величине угла ориентации более чем У** при волновом числе к = 0,7.
Ошибка зависит и от волнового числа, и от ориентации локальной структуры. Для
углов ориентации в направлениях осей и диагоналей ошибка исчезает. Большая
ошибка и структура распределения ошибки получается для передаточной
функции дифференциального оператора. Передаточная функция проявляет
существенное отклонение от передаточной функции идеального дифференциального
фильтра для высоких волновых чисел (раздел 12.3). Согласно уравнению (13.12), угол
ориентации зависит от отношения производных. Вдоль осей одна из производных
равна нулю и, таким образом, ошибки не возникают. Вдоль диагоналей
производные в направленияххиу являются такими же. Следовательно, ошибка
сокращается также в отношении производных.
Ошибка угла ориентации может быть значительно подавлена, если
использовать лучшие дифференциальные фильтры. На рис. 13.6 показана ошибка в оценке
ориентации с использованием двух примеров: оптимизированного оператора
Собеля (раздел 12.7.5) и оптимизированного оператора на основе наименьших
квадратов (раздел 12.6).
Небольшое дополнительное усилие в оптимизации дифференциальных
фильтров, таким образом, окупится в точной оценке ориентации. Остаточная угловая
ошибка менее чем 0,5° является достаточной почти для всех прикладных задач.
Различные дифференциальные фильтры, рассмотренные в разделах 12.4 и 12.7, дают
возможность достичь равновесия вьшислительных усилий и точности.
Важным свойством любого алгоритма обработки изображений является qto
устойчивость. Этот термин обозначает чувствительность алгоритма к шуму.
Важно ответить на два вопроса. Во-первых, какова погрешность
оцениваемых признаков в изображениях с шумом? Для того чтобы ответить на этот воп-
13.3. Тензорное представление первого порядка 369
а
..miiLi^^
1.11.111П111.1шшш Штттпш
шшшй
Рис. 13.5. Шаги для вычисления структурного тензора: а — исходная круговая
тестовая структура; б — горизонтальное отклонение Ф>^; в — вертикальное отклонение ®;
г - е - усредненные компоненты для структурного тензора /jj = <Ъ (ф^- ®J,
/22 = ® (®,* ©,), /,2 = ® (Ф,* Ф,); ж - возведенный в квадрат модуль градиента
/j, + /22' 3 - компонента х вектора ориентации /jj - /22» и — компонента з^ вектора
ориентации 2J^^, к - угол ориентации из [-я/2,7г/2], отображенный в интервал
шкалы яркости из [0,255]
370 Глава 13. Простые окрестности
Рис. 13.6. Систематические ошибки оценки угла ориентации с использованием
дифференциальных операторов: а — исходная круговая тестовая структура с
максимальным нормированным волновым числом к = 0,7; распределения ошибок для б —
оператора Собеля (угловой диапазон ±7" в 16 дискретных шагов); в -
оптимизированный оператор Собеля; г — оптимизированный оператор на основе наименьших
квадратов (угловой диапазон ±7** в 16 дискретных шагов) с г = 3
рос, используются законы статистики для исследования распространения
ошибок. В этом контексте шум делает оценки только недостоверными, но не
ошибочными. Среднее значение — если мы делаем достаточное число оценок - по-прежнему
вычисляется корректно. Однако возникает второй вопрос. В зашумленных
изображениях оператор может также привести к искаженным результатам, т.е.
среднее значение может содержать значительное отклонение от правильного
значения. В наихудшем случае алгоритм может даже стать неустойчивым и дать
ничего не значащие результаты.
13.3. Тензорное представление первого порядка 371
гч
1.5
и
П!
1
0,8
0.6
0.4
0.2
20 40 60 80 100 120 X
100 120 X
1
0.98
0.96
0.94
0.92
0.9
Д
1
0.8
0.6
0.4
0.2
1 Угол П 2 -20 -10 О 10 УголП20
Рис. 13.7. Анализ ориентации с помощью кольцевой тестовой структуры с
использованием оператора Собеля: кольцевая структура с амплитудой 50, среднеквадратичное
отклонение распределенного по нормальному закону шума а - 15 и б - 50; в и г - радиальное
поперечное сечение меры когерентности для среднеквадратичных отклонений уровня шума
1,5 и 5,15 и 50 соответственно; дне — гистограммы угловой ошибки для тех же условий
На рис. 13.7 демонстрируется, что оценка ориентации является в высшей
степени устойчивым алгоритмом. Даже при низком отношении сигнала к шуму оценка
ориентации является все еще корректной, если используется подходящий
дифференциальный оператор. При увеличении уровня шума когерентность (раздел 13.3.4)
убывает, а статистическая ошибка оценки угла ориентации увеличивается (рис. 13.7).
\\5.0
1.5\ \
Глава 13. Простые окрестности
13.4. Локальное волновое число и фаза
13.4.1. Фаза
До сих пор в этой главе мы рассматривали детально анализ простых
окрестностей относительно их ориентации. В этом разделе мы продолжим рассмотрение
еще одного элементарного свойства простых окрестностей. В главе 5 мы делали
акцент на важности масштаба для обработки изображений. Таким образом, мы
должны не только осведомляться, в каких направлениях изменяются уровни
яркости. Мы должны также задаваться вопросом: насколько быстро изменяются
уровни яркости? Этот вопрос приводит нас к понятию локального волнового
числа. Ключевым в определении локального волнового числа является фаза сигнала. В
качестве введения мы обсудим простой пример и рассмотрим одномерный
периодический сигнал
0W = 0oCOs(b). (13.18)
Аргумент косинусной функции известен как фаза периодического сигнала:
ф{х) = кх. (13.19)
Это выражение показывает, что фаза является линейной функцией
координаты и волнового числа. Таким образом, получаем волновое число
периодического сигнала путем вычисления первой пространственной производной от
фазового сигнала
-^^ = к. (13.20)
ох
Эти простые рассуждения делают новый акцент на важной роли фазы в
обработке изображений, которую мы уже рассматривали в разделе 2.3.5. Будем
рассматривать два родственных подхода для определения фазы сигнала:
преобразование Гильберта (раздел 13.4.2) и квадратурный фильтр (раздел 13.4.5), прежде чем
вводить эффективные методы для вычисления локального волнового числа по
фазовым градиентам.
13.4.2. Преобразование Гильберта и фильтр Гильберта
Для того чтобы объяснить принцип вычисления фазы сигнала, возьмем снова
пример простого периодического сигнала из предыдущего раздела. Предположим, что
существует оператор для задержки сигнала на 90^ Этот оператор преобразовал бы
сигнал д(х) = д^со^(кх) в сигнал дХх) = - д^$т(кх), что и проиллюстрировано на
рис. 13.8. Используя оба сигнала, можно вычислить фазу д(х)
ф(д(х)) = arctan
(-дХ^)]
(13.21)
д(х)
Поскольку в уравнение (13.21) входит только отношение д\х) и д{х), в
действительности фаза не зависит от амплитуды. Если мы примем во внимание
знаки двух функций дХх) и д(х), то можно вычислить фазу по полному
диапазону в 360°.
Таким образом, все, что нам надо для определения фазы сигнала, - это
линейный оператор, который сдвигает фазу сигнала на 90°. Такой оператор известен как
13.4. Локальное волновое число и фаза
Рис. 13.8. Применение фильтра Гильберта к кольцевой тестовой структуре: верхний
левый квадрат - в горизонтальном направлении; нижний правый квадрат — в
вертикальном направлении
фильтр Гильберта Я или оператор Гильберта Я и имеет передаточную функцию
h{k) =
i к>0
О А: = 0.
Ч k<Q
(13.22)
Абсолютная величина передаточной функции равна единице, поскольку
амплитуда остается неизменной. Поскольку фильтр Гильберта имеет чисто мнимую
передаточную функцию, она должна иметь нечетную симметрию для
производства действительных сигналов. Следовательно, положительные волновые числа
сдвигаются на %\к/2), а отрицательные волновые числа на -90°(-^/2). Частный
случай имеет место для нулевого волнового числа, где передаточная функция
также равна нулю. Это исключение можно проиллюстрировать следующим образом.
Сигнал с нулевым волновым числом является постоянным. Он может
рассматриваться как косинусная функция с бесконечным волновым числом, выбранным при
нулевой фазе. Следовательно, сигнал, преобразованный фильтром Гильберта,
является соответствующей синусной функцией при нулевой фазе, т.е. ноль.
Из-за нарушения непрерывности передаточной функции фильтра Гильберта в
начале координат ее функция рассеяния точки имеет бесконечную протяженность
A(jc) = "—.
пх
Свертку с уравнением (13.23) можно записать как
д{х')
, . If д{х) . ,
п ■' X -X
(13.23)
(13.24)
Глава 13. Простые окрестности
Это интегральное преобразование известно как преобразование Гильберта [128].
Поскольку маска свертки фильтра Гильберта является бесконечной,
невозможно разработать точный дискретный фильтр Гильберта для произвольных
сигналов. Это представляется возможным в случае, если мы ограничим класс сигналов,
к которым он применим. Поэтому берется следующий подход для разработки
эффективной реализации фильтра Гильберта.
Во-первых, фильтр должен точно сдвигать фазу на я/2. Это требование
необходимо потому, что мы не можем допустить ошибку в фазе, поскольку она
содержит информацию о положении. Волновое число, зависящее от фазового сдвига,
должно вызывать ошибки, зависящие от волнового числа. Это требование
выполняется любым ядром свертки с нечетной симметрией.
Во-вторых, требование равенства единице абсолютной величины может быть
ослаблено, если фильтр Гильберта применяется к сигналу с ограниченной
полосой частот, например, к пирамиде Лапласа. Тогда фильтр Гильберта должен
показывать абсолютную величину, равную единице, в диапазоне полосы
пропускания используемого фильтра с ограниченной полосой частот. Этот подход избегает
разрывов в передаточной функции при нулевом волновом числе и, таким образом,
приводит к ядрам свертки конечного размера.
Оптимизированные фильтры Гильберта получаются с помощью тех же самых
методов наименьших квадратов, использовавшихся ранее для интерполирующих
фильтров (раздел 10.6.2) и дифференциальных фильтров первого порядка (раздел 12.6).
Из-за нечетной симметрии фильтра Гильберта используется следующая
формулировка:
/?(^) = 2i]^/?„sin((2u-l)^:^). (13.25)
и=1
Обратите внимание, что мы использовали только синусные функции с
нечетными волновыми числами. Это приводит к тому, что передаточная функция также
становится симметричной относительно к = 1/2, а маска фильтра с
чередующимися нулями имеет вид
[КА ...,/2„0,/^,0,-А,,0,-/г„ ...,0,-А,]. (13.26)
Маска имеет AR-\ коэффициентов, 2Л - 1 из которых равны нулю. На рис. 13.9
показаны передаточные функции, оптимизированные методом наименьших
квадратов для Л = 2, 3, 4, 5. Фильтр с Л = 4 (маска с 15 коэффициентами)
h = {0,6208; 0,1683; 0,0630; 0,0191}, (13.27)
к примеру, имеет погрешность амплитуды, лишь незначительно большую, чем 1%
в волновом диапазоне [0.16, 0.84] и, согласно условию, не имеет ошибки фазы.
Свертка с такой маской требует 4 умножения и 7 сложений/вычитаний.
13.4.3. Аналитический сигнал
Действительный сигнал и его преобразование Гильберта можно объединить в ком-
плекснозначный сигнал как
9а=д-'^9н- (13.28)
Этот комплекснозначный сигнал обозначается как аналитическая функция или
аналитический сигнал. Согласно уравнению (13.28), аналитический фильтр имеет
функцию рассеяния точки
а
1
0.8
0,6
0.4
0,2
О
13.4. Локальное волновое число и фаза
4
ъ7у7
ш
1,04
1,02
1
п оя
и,90
и,эО
5^
/ / 1
/ / /
з/
ч N(\
\2
^^У^ ^"^—
0,1
0,2
0,3
0,4 k 0,5
0,1
0,2
0,3
0.4 k 0.5
Рис. 13.9. а - передаточные функции семейства оптимизированных операторов
Гильберта на основе метода наименьших квадратов, согласно уравнению (13.25), для
четырех коэффициентов фильтра Л = 2, 3, 4, 5; б — сектор а для лучшего показа
отклонений от идеального фильтра Гильберта. Поскольку фильтры симметричны
относительно ^ = 0,5, показан только диапазон волновых чисел от О — 0,5
а{х) = 1 + —
кх
и передаточную функцию
а{к)^
к>0
к^О.
к<0
(13.29)
(13.30)
Таким образом, все отрицательные волновые числа подавляются. Хотя
передаточная функция аналитического фильтра действительна, она приводит к
комплексному сигналу, поскольку он несимметричен. Для действительного сигнала
никакая информация не теряется при подавлении отрицательных волновых
чисел. Они могут быть реконструированы, поскольку преобразование Фурье
действительного сигнала является эрмитовым (раздел 2.3.4). Аналитический сигнал
можно считать еще одним представлением действительного сигнала с двумя
важными свойствами. Абсолютная величина аналитического сигнала задается
локальной амплитудой
а аргумент — локальной фазой
\ЛЫХ'Х + Я'Я,
arg(j?) = arctan
-Я
(13.31)
(13.32)
с использованием Л и ^для аналитических операторов и операторов Гильберта
соответственно.
Исходный сигнал и его преобразование Гильберта можно получить из
аналитического сигнала с использованием уравнения (13.28):
9{х) = {9Лх) + 9*Лх))/2
9н(х) = К9а(х)-д:(х))/2. ^^^-^^^
Понятие аналитического сигнала также позволяет легко расширить
представление локальной фазы в многомерном случае. Передаточная функция аналитического
Глава 13. Простые окрестности
оператора использует только положительные волновые числа, т.е. только половину
Фурье-пространства. Если мы расширим это разбиение на многомерный случай, то
мы имеем более чем один вариант разделения Фурье-пространства на два
полупространства. Вместо волнового числа мы можем взять скалярное произведение
вектора волнового числа к и любого единичного вектора п и погасить полупространство,
для которого скалярное преобразование ftw является отрицательным:
а(к) =
2 кп>0
1 кп = 0, (13.34)
О кп<0
Единичный вектор п задает направление, в котором применяется фильтр
Гильберта. Определение (13.34) для передаточной функции аналитического сигнала
подразумевает, что оператор Гильберта может применяться только к направленно
отфильтрованным сигналам. Этот результат получается из следующих
соображений. Для одномерных сигналов мы увидели, что дискретный фильтр Гильберта
плохо работает для малых волновых чисел (рис. 13.9). В многомерном случае это
означает, что фильтр Гильберта непригоден, если kn = I. Таким образом, чтобы
избежать ошибок, нельзя использовать волновые числа, почти ортогональные к
направлению фильтра Гильберта.
Этот факт делает применение фильтров Гильберта и, таким образом,
определение локальной фазы в многомерных сигналах значительно более сложными.
Недостаточно использовать изображения, отфильтрованные с ограниченной
полосой частот, например, пирамиду Лапласа (раздел 5.2.3). В дополнение изображения,
отфильтрованные с ограниченной полосой частот, должны быть далее разложены
на направленные компоненты. Количество направленных компонент должно
соответствовать размерности пространства.
13.4.4. Моногенный сигнал
Расширение преобразования Гильберта от 1-D сигнала до сигналов более высокой
размерности не является удовлетворительным, поскольку его можно применять
только к направленно отфильтрованным сигналам. Для волновых чисел, близких к
плоскости разделения, преобразование Гильберта не работает. Таким образом,
требуется изотропное расширение преобразования Гильберта. Очевидно, что
скалярнозначное преобразование для многомерного сигнала не может быть и
изотропным, и иметь нечетную симметрию.
Векторнозначное расширение аналитического сигнала удовлетворяет обоим
требованиям. Оно известно как моногенный сигнал и было введено в теорию
обработки сигнала Фельсбергом (Felsberg) и Соммером (Sommer) [44]. Моногенный
сигнал конструируется по исходному сигналу и его преобразованию Рисса.
Передаточная функция задается как
fe = i7^. (13.35)
\к\
Модуль вектора А равен единице для всех значений к. Преобразование Рисса
является, таким образом, изотропным. Оно также имеет нечетную симметрию,
поскольку
13.4. Локальное волновое число и фаза
h(-k) = -h(k) (13.36)
Преобразование Рисса можно применять к сигналу любой размерности. Для
1-D сигналов оно сводится к преобразованию Гильберта.
Для 2-D сигнала передаточную функцию для преобразования Рисса можно
записать с использованием полярных координат как
-»т
kcosO ksine
A(ifc) = i
(13.37)
\k\ \k\ J
Эта передаточная функция подобна передаточной функции для оператора
градиента (раздел 12.2.1, уравнение (12.2)). Она отличается тем, что передаточная
функция для преобразования Рисса делится на абсолютную величину волнового
числа.
Маска свертки или ФРГ преобразования Рисса задается как
А(д:) = --^. (13.38)
2к\х\
Исходный сигнал и сигнал, свернутый с помощью преобразования Рисса,
могут быть объединены для 2-D сигнала в 3-D моногенный сигнал:
9jx) = [p.qi.q2f при p=^g,q,=h,^g.q2=K''g^ (13.39)
Локальная амплитуда моногенного сигнала задается как норма вектора
моногенного сигнала, как и в случае аналитического сигнала (уравнение (13.31)):
lff.l' = /+9i'+?2. (13.40)
Моногенный сигнал не только дает оценку для локальной фазы ф как для
аналитического сигнала. Моногенный сигнал определяет также оценку локальной
ориентации в с помощью следующих соотношений:
р = асо8ф, q^=asinфcosв, ^^ =(2sin0sin0. (13.41)
Таким образом, мы можем сделать заключение, что моногенный сигнал
объединяет оценку локальной ориентации и локальной фазы. Это имеет большое
значение для обработки изображений, поскольку два наиболее важных признака
локальной окрестности, локальная ориентация и локальное волновое число, могут
быть оценены единым образом.
13.4.5. Квадратурный фильтр
Квадратурные фильтры являются альтернативным подходом к получению пары
сигналов, которые отличаются только на фазовый сдвиг 90\к/ 2). Легче всего
ввести комплексную форму квадратурных фильтров. По существу, передаточная
функция квадратурного фильтра также равна нулю для ЛЯ < О, как и передаточная
функция аналитического фильтра. Однако абсолютная величина передаточной функции
не равна единице, а может быть любой произвольной действительной функцией
A(ft):
q(k) = \ ^ (13.42)
[ О иначе.
Таким образом, квадратурный фильтр также преобразует действительный
сигнал в аналитический сигнал. В отличие от аналитического оператора,
применяется взвешивание волнового числа. По комплексной форме квадратурного фильтра
378 Глава 13. Простые окрестности
(13.43)
мы можем получить пару действительных квадратурных фильтров, обнаружив, что
они являются частью уравнения (13.42) с четной и нечетной симметрией. Таким
образом,
5ДЛ) = (q(k)+q(-k))/2,
дЛк) = (q(k)-q(-k))/2.
Четная и нечетная части пары квадратурных фильтров показывают фазовый сдвиг
на 90** и могут, таким образом, быть использованы для вьиисления локальной фазы.
Квадратурные фильтры могут также разрабатываться на основе моногенного
сигнала (раздел 13.4.4). Квадратурные фильтры имеют на одну компоненту
больше, чем размерность сигнала. Передаточная функция равна
кк) = [дЛк), iklik)/\k\f. (13.44)
Самой известной парой квадратурных фильтров является фильтр Габора. Фильтр
Габора является фильтром с ограниченной полосой частот, который выбирает
определенный диапазон длин волн вокруг центральной длины волны А^, используя
функцию Гаусса. Комплексная передаточная функция фильтра Габора равна
О иначе.
(13.45)
Если I kji G^ > 3, то уравнение (13.45) сводится к
д(А) = ехр(-|Л-Ао1'^'/2). (13.46)
С использованием соотношений (13.43) передаточная функция для четной и
нечетной компонент задается как
дДЛ) = 1[ехр(-|Л-Л„Г<т,^2) + ехр(-|Л + Л„Го-//2)],
1г / л , ч / л , чп (13.47)
gSk) = -[ехр(-|Л-Л„Гс7,^/2)-ехр(-|Л + А„Го-;/2)].
Функции рассеяния точки этих фильтров могут быть легко вычислены с
помощью теоремы о сдвиге (теорема 2.3, с. 61, >-R4):
д^{х) = со8(ЛоЛ:)ехр
\х\
2 \
д_(х) = isin(A:oJc)exp
2а?
1^
2 Л
2(7
(13.48)
или объединены в комплексную маску фильтра:
д(дг) = ехр(1ЛоДг)ехр
/ I |2 Л
2а!
(13.49)
Фильтры Габора полезны для полосовой фильтрации изображений и
выполнения анализа изображений в пространственной области/области волновых чисел. На
рис. 13.10 иллюстрируется их применение [Ример (Riemer), 1991; Ример и др., 1991].
Изображение с короткими ветровыми волнами на поверхности воды раскладьшает-
13,4. Локальное волновое число и фаза 379
Рис. 13.10. Анализ изображений (а — 40 х 30 см) ветровых волн на поверхности воды.
Интенсивность пропорциональна компоненте в направлении ветра уклона волн.
Четная часть (б, г, е) и возведенная в квадрат абсолютная величина (энергия — в, д, ж)
преобразованных с помощью фильтра Габора изображений с центральной длиной
волны при 48, 24 и 12 мм соответственно
Глава 13. Простые окрестности
ся на множество фильтров Габора. Центральная длина волны к^ была установлена
в направлении х, параллельном направлению ветра. Фильтры имели центральную
длину волны на октавных расстояниях при длинах волн 1,2; 2,4 и 4,8 см. Ширина
полосы была установлена пропорциональной центральному волновому числу.
Левая колонка изображений на рис. 13.10 показывает фильтрование с
помощью четного фильтра Габора, правая колонка - локальную амплитуду, которая
непосредственно связана с энергией волн. Отфильтрованные изображения
показывают, что волны с различной длиной волны частично связаны. В областях, где
большие волны имеют большие амплитуды, также небольшие волны
(капиллярные волны) имеют большие амплитуды. Энергия волн неравномерно
распределена по поверхности воды.
Расширение этого анализа до последовательностей изображений дает
прямое представление о нелинейных процессах взаимодействия волна-волна. На
рис. 13.11 показана временная эволюция одной строки изображений из рис. 13.10.
Как мы детально покажем в разделе 14.2.4, уклон структур в этих
пространственно-временных изображениях к временной оси прямо пропорционален скорости
движущихся объектов.
Рис. 13.11. Анализ пространственно-временной части длительностью 5 с в
направлении ветра последовательности изображений от коротких ветровых волн на
поверхности воды. Временная ось вертикально ориентирована. Четная часть (а - в) и
возведенная в квадрат абсолютная величина (энергия - г - е), преобразованных с
помощью фильтра Габора изображений с центральной длиной волны при 48, 24 и 12 мм
соответственно
13.4. Локальное волновое число и фаза
Хорошо видно, что малые волны модулируются большими волнами и что
групповая скорость (скорость волновой энергии) малых волн меньше, чем фазовая
скорость капиллярных волн.
13.4.6. Определение локального волнового числа
Для того чтобы определить локальное волновое число, нам всего лишь нужно
вычислить первую пространственную производную от фазового сигнала (раздел 13.4.1,
уравнение (13.20)). Эта производная должна применяться в том же направлении, в
котором применялся фильтр Гильберта или квадратурный фильтр. Фаза задается
либо как
ф(х) = arctan
9(х)
либо как
ф(х) = arctan
дЛх)
(13.50)
(13.51)
где q^ и q обозначают сигналы, отфильтрованные с помощью четной и нечетной
частей квадратурного фильтра.
Однако прямое вычисление частных производных по уравнениям (13.50) и
(13.51) нецелесообразно из-за свойственных им разрывов в фазовом сигнале. Фаза,
вычисленная с помощью арктангенса, ограничивает фазу до основного интервала
[-7С, п] и, таким образом, неизбежно приводит к свертыванию фазы от пдо -же
соответствующими разрывами.
Флит (Fleet) [48] показал, что этой проблемы можно избежать, если вычислить
фазовый градиент непосредственно по градиентам q_^(x) и q_(x). В результате
2 Л ■ (13.52)
Р +^
Эта формулировка фазового градиента также устраняет необходимость
использования тригонометрических функций для вычисления фазового сигнала, и
алгоритм вычислений, основанный на ней становится, следовательно, значительно
более быстрым.
Гораздо более сложным является вьиисление локального волнового числа по
моногенному сигналу (раздел 13.4.4), поскольку нам необходимо использовать три
сигнала для 2-D сигналов. Из (13.41) получаем два различных уравнения для фазы:
к = V0(jc) = V arctan(-/7(jc) / q{x)) = -
01 = arccot
I pcosO
9i
02 = arccot
psinO^
?2
(13.53)
J
Необходимо объединить эти уравнения, поскольку каждое из них в
отдельности не дает результата для определенных направлений. Решением является
использование производной по направлению (раздел 12.2.1). Когда мы дифференцируем
фазу по направлению вектора волнового числа, мы непосредственно получаем
модуль вектора волнового числа:
k = ^ = cose^ + sine^^^
дк
дх
ду
(13.54)
Глава 13. Простые окрестности
Члены cosO и sinO также могут быть получены из уравнения (13.41):
2 2
cos'0 = -^^ и sin'0 = -/^. (13.55)
Тогда модуль вектора волнового числа приводится к виду
/+?1 +^1
Компоненты вектора к = [к cos в, h sin в\ могут быть вычислены после
объединения уравнений (13.56) и (13.54).
13.5. Дополнительные тензорные представления
в этом разделе мы исследуем несколько альтернативных подходов для описания
локальной структуры с помощью тензоров. Метод тензора инерции в разделе 13.5.1
рассматривает локальную структуру в Фурье-пространстве. Основным акцентом в
этом разделе является, однако, синтез тензорных методов с квадратурными
фильтрами. Это методы, которые комбинируют анализ локальной ориентации и
локального волнового числа.
13.5.1. Тензор инерции
Для начала рассмотрим, как выглядит идеально ориентированная структура
уровней яркости (уравнение (13.1)) в пространстве волновых чисел. Мы можем
вычислить преобразование Фурье от уравнения (13.1) легче, если повернем ось х в
направлении п. Тогда функция уровней яркости будет постоянной в направлении х^.
Следовательно, преобразование Фурье сводится к 5-линии в направлении п (>-R5).
Это кажется многообещающим для определения локальной ориентации в
Фурье-области, поскольку все, что мы должны вычислить, так это ориентацию
линии, на которой спектральные плотности не равны нулю. Бигюн (Bigun) и Гран-
лунд (Granlund) разработали следующую процедуру:
• Использовать оконную функцию для выбора малой локальной окрестности
из изображения.
• Преобразовать с помощью преобразования Фурье вырезанное изображение.
Чем меньше выбранное окно, тем более размытым будет спектр {соотношение
неопределенностей, теорема 2.7, с. 64). Это означает, что даже при идеальной
локальной ориентации мы получим полосовидное распределение спектральной энергии.
• Определить локальную ориентацию путем построения прямой по
спектральному распределению плотности. Это даст угол локальной ориентации по наклону
линии.
Критическим шагом этой процедуры является построение прямой по
спектральному распределению плотности в Фурье-области. Мы не можем решить эту задачу
точно, поскольку она является, как правило, переопределенной, а можем только
минимизировать меру ошибки. Стандартной мерой ошибки является квадрат модуля
вектора (норма 1.^, см. уравнение (2.75) в разделе 2.4.1). При построении прямой мы
минимизируем сумму квадратов расстояний от точек данных до линии:
j d\k,n) I д{к) f d^A: -^ minimum. (13.57)
Рис. 13.12. Расстояние до
точки в пространстве волновых
чисел от линии в направлении
единичного вектора Я
13.5. Дополнительные тензорные представления
Функция расстояния записывается
сокращенно с помощью d{kn). Интеграл пробегает по всему
пространству волновых чисел; волновые числа
взвешиваются со спектральной плотностью | д(к) р.
Уравнение (13.57) не ограничивается двумерным
случаем, а, как правило, действительно для
локальной ориентации или линейной симметрии в Ж-мер-
ном пространстве. Из рис. 13.12 можно сделать
заключение, что вектор расстояния rf равен
d = k-{k^n)n. (13.58)
Квадрат расстояния тогда задается как
\(1\^=\к-{к'п)Щ = \к\'-{к'пу.{\Ъ.59)
Для того чтобы выразить расстояние более явно как
функцию вектора л, перепишем его следующим
образом:
\df=n\l{k^k)-{kk^))n, (13.60)
где /- единичная диагональная матрица. Подставляя это выражение в уравнение
(13.57), получаем
(13.61)
где/
п J п -^minimun,
симметричный тензор с диагональными элементами
J>Y.]K\9ik)fA4
цФр-
и недиагональными элементами
•^;.=~J^Ai^wi'd4 р^^^
(13.62)
(13.63)
Тензор /' аналогичен хорошо известной физической величине, тензору инерции.
Если мы заменим волновые координаты пространственными координатами, а
спектральную плотность I д{к) р — удельной плотностью р, то уравнения (13.57) и (13.61)
образуют уравнение для вьиисления инерции тела, вращающегося вокруг оси п.
С помощью этой аналогии мы можем переформулировать задачу определения
локальной ориентации. Мы должны найти ось, вокруг которой тело вращения,
сформированного из спектральной плотности в Фурье-пространстве, вращается с
минимальной инерцией. Это тело могло бы иметь различные формы. Мы можем
соотнести его форму с различными решениями, которые мы получаем для
собственных значений тензора инерции и, таким образом, для решения задачи о
локальной ориентации (табл. 13.3).
Мы получили подход на основе тензора инерции в Фурье-области. Теперь
покажем, как вычислить коэффициенты тензора инерции в пространственной области.
Интегралы в уравнениях (13.62) и (13.63) содержат члены вида
и
Интегралы по этим членам равны внутренним рши скалярным произведениям
функций \к д(к). Поскольку внутреннее произведение сохраняется при преобразовании
Глава 13. Простые окрестности
Таблица 13.3. Классификация собственных значений структурного тензора в 3-D
(объемных) изображениях
Условие
Объяснения
Идеальная локальная
ориентация
Изотропная структура
уровней яркости
Постоянные уровни
яркости
Тело вращения является линией. При вращении
вокруг этой линии инерция обращается в ноль.
Следовательно, собственный вектор к нулевому
собственному значению совпадает с
направлением линии. Другой собственный вектор
ортогонален линии, а соответствующее собственное
значение не равно нулю и задает ось вращения для
максимальной инерции
В этом случае тело вращения имеет вид плоского
изотропного диска. Преимущественного
направления не существует. Оба собственных значения
равны, а инерция одна и та же при вращении
вокруг всех осей. Мы не можем найти минимум
Тело вращения вырождается в точку в начале
координат пространства волновых чисел. Инерция равна
нулю при вращении вокруг любой оси.
Следовательно, оба собственных значения обращаются в ноль
Фурье (>-R4), мы можем также вычислить соответствующие интегралы в
пространственной области. Умножение д{к) на iA: в области волновых чисел соответствует юятию
первой пространственной производной в направлении х в пространственной области:
J'pp{x) = ^jw(x-x)
дФр.
d^x'
(13.64)
В уравнение (13.64) мы уже включили взвешивание с оконной функцией w для
выбора локальной окрестности.
Структурный тензор (13.8), рассмотренный в разделе 13.3.1 , и тензор инерции
тесно связаны:
/' = trace(/)/-J. (13.65)
Из этой зависимости видно, что обе матрицы имеют один и тот же набор
собственных векторов. Собственные значения Я соотносятся как
K=t.\-K^ K=i.\-K' (13.66)
q=\ q=\
Следовательно, мы можем выполнять анализ с любой из этих двух матриц. Для
тензора инерции направление локальной ориентации задается минимальным
собственным значением, но для структурного тензора оно задается максимальным
собственным значением.
13.5. Дополнительные тензорные представления
13.5.2. Дополнительные эквивалентные подходы
В своей статье, посвященной анализу ориентированных структур, Касс (Kass) и
Виткин (\Mtkin) выбирают на первый взгляд абсолютно иной метод. Однако
оказывается, что он эквивалентен методу тензора, что будет показано в дальнейшем.
Они начали с идеи использования направленных дифференциальных фильтров с
помощью дифференцирования разности фильтров Гаусса (DoG, раздел 12.7.6)
(записанных в операторной форме)
где (Bj и ®2 обозначают гауссовы сглаживающие маски с различными
дисперсиями. Направление, в котором производная по направлению является
максимальной в среднеквадратичном смысле, задает ориентацию, имеющую нормальное
направление к линиям постоянных уровней яркости. Этот подход приводит к
следующему выражению для дисперсии производной по направлению:
^(0) = (В((2?,(0)-(^(0)). (13.67)
Производная по направлению возводится в квадрат и затем сглаживается с
помощью биномиального фильтра. Это уравнение можно также интерпретировать через
инерщпо объекта как фушащю угла. Соответствующий тензор инерщш имеет вид
^(0) = [cos0 sin0]
= [cos0 sin0]
(13.68)
L-cB(^-^) Ф(^-^)^
Таким образом, подход Касса (Kass) и Виткина (W^tkin) тождествен общему
методу на основе тензора инерции, рассмотренному в разделе 13.5.1. Они только
использовали особый вид дифференциального фршьтра.
Не будучи знакомыми либо с более ранней работой Бипона (Bigun) и Гранлунда
(Granlund), либо современной работой Натссона (Knutsson), Рао (Rao) и Шунка
(Schunck) [162] и Рао (Rao) [161], они предложили такой же структурный тензор
(обозначив его как тензор момента), как тот, который мы рассматривали в разделе 13.3.1.
13.5.3. Полярные сепарабельные квадратурные фильтры
Квадратурные фильтры дают еще один способ анализа простых окрестностей и
определения как локальной ориентации, так и локального волнового числа.
Исторически это был первый метод анализа локальных структур, впервые рассмотренный
в работе Гранлунда (Granlund) [63]. Методы на базе тензора инерции и
структурного тензора в действительности позже появились в литературе [9, 101, 161, 162].
Основной идеей метода на основе использования набора квадратурных
фильтров является выделение структур в определенных диапазонах волновых чисел и
направлений. Для того чтобы определить локальную ориентацию, мы должны
применить весь набор направленных фильтров, в котором каждый фильтр
чувствителен к структурам различной ориентации. Затем мы сравниваем отклики фильтров
и получаем максимальный отклик фильтра от направленного фильтра, чье
направление наилучшим образом совпадает с направлением локальной структуры.
Подобным образом набор квадратурных фильтров для различных диапазонов
волновых чисел может быть установлен для определения локального волнового числа.
Глава 13. Простые окрестности
Если мы получаем явный максимум в одном из фильтров, но всего лишь
малый отклик в других, то локальная структура содержит локально
ориентированную структуру. Если различные фильтры дают сравнимые отклики, то окрестность
содержит распределение ориентированных структур.
До сих пор понятие кажется не вызывающим затруднений, но, однако,
необходимо решить некоторое число коварных проблем. Каким свойствам должны
удовлетворять направленные фильтры, для того чтобы обеспечить точное определение
локальной ориентации, если это вообще возможно? Для вычислительной
эффективности нам нужно использовать минимальное число фильтров для
интерполяции угла локальной ориентации. Каково это минимальное число?
Понятия, введенные в этом разделе, основаны на работах Гранлунда (Granlund)
[63], Натссона (Knutsson) [ПО] и Натссона и др. [112]. Несмотря на то что методы
на основе использования набора квадратурных фильтров были сформулированы
этими авторами для многомерного случая, мы будем рассматривать только
одномерный случай.
Сначала мы рассмотрим разработку квадратурных фильтров, которые подходят
для определения как локальной ориентации, так и локального волнового числа. Это
ведет к полярным сепарабельным квадратурным фильтрам (раздел 13.5.3). Во
втором шаге мы покажем, как вектор ориентации, определенный в разделе 13.3.3,
может быть построен с помощью простого векторного сложения откликов
квадратурных фильтров (раздел 13.5.4). Подобным образом в разделе 13.5.5 мы изучим
вычисление локального волнового числа. И наконец, раздел 13.5.6 подводит итог,
показывая, что структурный тензор можно также вычислить с помощью набора
квадратурных фильтров. Таким образом, тензорные методы, рассмотренные в
первой части этой главы (раздел 13.3), и метод на основе использования набора
квадратурных фильтров отличаются только в некоторых тонких вопросах, но в других
отношениях дают идентичные результаты.
При соответствующем наборе направленных фильтров каждый фильтр
должен представлять собой повернутую копию всех других. Это требование
подразумевает, что передаточная функция фильтров может быть разложена на угловую
часть й{ф) и волновую часть rik). Такой фильтр называется полярным
сепарабельным и может быть удобно представлен в полярных координатах
д(к,ф) = г(кЩф), (13.69)
где к = yjk^ + kl и 0 = arctan(A:2Aj) равны абсолютной величине и аргументу
волнового числа соответственно. Для набора направленных фильтров только угловая
часть передаточной функции представляет важность, в то время как радиальная
часть должна быть одинаковой для каждого фильтра, но может иметь
произвольный вид. Обратное верно для случая набора фильтров для определения
локального волнового числа.
Натссон (Knutsson) [НО] предложил следующий базовый квадратурный фильтр:
г{к) = ехр
(Ink-lnk^f
' (5/2)'1п2
С08^'(ф-ф,) \ф-ф,\<л/2 (13.70)
О иначе.
]3.5. Дополнительные тензорные представления
В этом уравнении используется комплексное обозначение квадратурных
фильтров (раздел 13.4.5). Фильтр имеет направление под углом ф^. Единичный вектор в
этом направлении есть d^ = [cos 0^, sin ф^].
Фильтр непрерывен, поскольку косинусная фунвдия равна нулю в плоскости
разбиения двух полупространств (\ф - 0J = я/2 или d^k = 0). При использовании
единичного вектора d^ в направлении фильтра угловая часть фильтра может быть
также записана как
d(k) = \^ (13.71)
[О иначе.
Константа к^ в уравнении (13.70) обозначает пиковое волновое число.
Константа В определяет полуширину волнового числа в числе октав, а / - угловое
разрешение фильтра. В логарифмической шкале волновых чисел фильтр имеет форму
функции Гаусса. Поэтому радиальная часть имеет логарифмически нормальную форму.
Для действительного четного и мнимого нечетного фильтров пары квадратичных
фильтров радиальная часть является одной и той же, и только угловая часть отличается:
1(ф) = cos" (ф-ф,)
d_{(t)) = icos"(0-0t)sigti(cos(^-^,)).
(13.72)
На рис. 13.13 показаны радиальная и угловая части передаточной функции для
различных kg и 0^. Набор направленных фильтров получается с помощью
подходящего выбора различных ф^:
тек
ф,=— к = 0,1,...,к-\. (13.73)
К
Натссон (Knutsson) использовал четыре фильтра с 45° приращениями в
направлениях 22,5\ 67,5', 112,5° и 157,5°. Эти направления имеют преимущества в том,
что нужно разработать только одно ядро фильтра. Ядра для фильтра в других
направлениях получаются отображением относительно осей и диагоналей.
Эти фильтры были разработаны в пространстве волновых чисел.
Коэффициенты фильтра получаются обратным преобразованием Фурье. Если мы выбираем
довольно малую маску фильтра, то уменьшаем число ненулевых коэффициентов
фильтра. Это вызывает отклонения от идеальной передаточной функции.
1
0,8
0.6
0.4
0.2
О
""Л
V
г
.
г
\
у
[Р
у.
/л
1
^
^
0,2
0.4
0.6
0.8 ^ 1
Рис. 13.13. а - радиальная; б - угловая части квадратурного фильтра, согласно
уравнению (13.70), с/ =1и5 = 2в различных направлениях и с различными пиковыми
волновыми числами
Глава 13. Простые окрестности
Следовательно, Натссон (Knutsson) модифицировал коэффициент ядра
фильтра, используя процедуру оптимизации таким образом, что он приближается к
идеальной передаточной функции как можно ближе. Оказывается, что
необходима, по крайней мере, маска фильтра 15 х 15 для получения хорошей
аппроксимации ожидаемой передаточной функции.
13.5.4. Определение вектора ориентации
Локальная ориентация может быть вычислена по откликам четырех квадратурных
фильтров с помощью векторного сложения. Идея этого подхода проста. Мы
присваиваем отдельным направляющим фильтрам вектор ориентации. Модуль
вектора соответствует отклику квадратурного фильтра. Направление вектора задается
двойным углом направления фильтра (раздел 13.3.3). В этом представлении
каждый отклик фильтра показывает, насколько хорошо ориентация структуры
совпадает с направлением фильтра. Оценка вектора ориентации тогда задается как
векторная сумма откликов фильтров.
Используя представление с комплексными числами для вектора ориентации,
мы можем записать отклик для фильтра в направлении ф^ как
е^, =ieiexp(2i0J. (13.74)
Тогда вектор ориентации как векторная сумма откликов фильтров может быть
записана как
к-\
о=1е..
(13.75)
л=о
На рис. 13.14 иллюстрируется, почему необходимо удвоение угла для
векторного сложения, чтобы получить вектор ориентации. Взят пример, где отклики от
всех четырех фильтров равны. В этом случае окрестность содержит структуры во
всех направлениях. Следовательно, мы не наблюдаем локальную окрестность, а
векторная сумма всех откликов фильтров обращается в нуль. Это происходит, если
Рис. 13.14. Вычисление локальной ориентации с помощью векторного сложения
четырех откликов фильтров. Показан пример, где окрестность является изотропной
относительно ориентации: все четыре отклика фильтров равны. Углы векторов
равны направлениям фильтров (а) и двойным направлениям фильтров (б)
13.5, Дополнительные тензорные представления
мы удваиваем угол ориентации (рис. 13.14, б), и не происходит, если мы опускаем
этот шаг (рис. 13.14, а).
После этих, скорее качественных, рассуждений мы будем доказывать, что
можем вычислить локальную ориентацию точно в случае, когда локальная
окрестность идеально ориентирована в произвольном направлении ф^. В результате мы
также узнаем минимальное число необходимых фильтров. Мы можем упростить
вычисления с помощью всего лишь рассмотрения угловых членов, поскольку
отклики фильтров показывают одну и ту же зависимость от волнового числа.
Нетерпеливый читатель может пропустить это доказательство.
Используя уравнения (13.74), (13.70) и (13.73), мы можем записать угловую часть
отклика к-то фильтра как
а^{ф^)--^х^{2п\к1 К)со^^^{ф^-пк1 К),
Косинусная функция раскладывается в сумму двух комплексных
экспоненциальных функций:
^*(0o) = ^exp(2;ri^/^[exp(i(0o-;r^//^)) + exp(-i(0„-^^/ii:))f
1 ^'
—ехр(2шА://:)Х
^ у=0
J
exp(i/(^„ - nklK))QX^{-i{2l - m,-nklK))
1 ^'
^21^
v^y
expOO- - /)20о)ехр(2я:1(1 + l-j){klK)).
Теперь суммируем векторы всех ^Г-направленных фильтров:
S^*=:^I|^n^''P^i(^-^)2^o)Iexp(2;ri(H-/-y)(^/^)).
jt=0 ^ 7=0\J ) к=0
Комплексная двойная сумма может быть найдена, если мы внимательно
проанализируем внутреннюю сумму по к. Если у = / + 1, то экспонента равна нулю.
Следовательно, сумма равна К. В противном случае сумма представляет
геометрический ряд с множителем exp(27ii(l -^-l-JXk/K)), а сумма
к-\
J^Qxpi2mil + l-j)ik/K)) = -
l-exp(2m(l + l-j))
*=о l-Qxp(2m(l + l-J)/Ky ^^^-"^^^
Мы можем использовать уравнение (13.76), только если знаменатель ¥= О
У/ = 0,1,..., 2/; следовательно, К> 1 + /. При этом условии сумма обращается в ноль.
Этот результат имеет простую геометрическую интерпретацию. Сумма состоит из
векторов, которые равномерно распределены на единичной окружности. Угол
между двумя последовательными векторами равен 2пк/К.
В заключение: внутренняя сумма в уравнении (13.76) сводится к Кддя] = / + 1,
в противном случае она равна нулю. Поэтому сумма по j содержит только член с
J = 1+1, Окончательный результат
^ 2П
*=о
/ + 1
exp(i2^o)
(13.77)
показывает вектор с удвоенным углом локальной ориентации. Утверждение доказано.
Глава 13. Простые окрестности
Доказательство точности методов векторного сложения определяет также
минимальное требуемое число направляющих фильтров. Из/>Ои/Г>/+ 1 мы
заключаем, что, по крайней мере, К= 3 направленных фильтров необходимы. Мы можем
также проиллюстрировать это условие интуитивно. Если у нас есть только два фильтра
(АГ= 2), то векторные отклики этих двух фильтров принадлежат линии (рис. 13.15, а).
Таким образом, определение ориентации невозможно. Только с тремя или четырьмя
фильтрами вектор суммы может указьюать во всех направлениях (рис. 13.15,5, в),
С помощью подобного вывода мы можем доказать еще одно важное свойство
направленных квадратурных фильтров. Суммирование по передаточным
функциям А^фильтров приводит к изотропной функции для К>1\
^21^
^С08'\ф-7Ск/К) = ^
к=0
k'j
к (2/)!
2'^ /Р
(13.78)
Другими словами, преимущественного направления не существует. Сумма всех
откликов фильтров определяет отклик, инвариантный относительно ориентации.
Это к тому же более глубокая причина, почему мы можем определить локальную
ориентацию точно с помощью очень ограниченного числа фильтров и простой
линейной процедуры, такой, как векторное сложение.
13.5.5. Определение локального волнового числа
Логарифмически нормальная форма радиальной части наборов квадратурных
фильтров является ключевой для непосредственной оценки локального
волнового числа узкополосного сигнала. Согласно уравнению (13.70), мы можем записать
радиальную часть передаточной функции наборов квадратурных фильтров как
(ln^i:-ln^,)'
гДА:) = ехр
(13.79)
2с7Чп2
Исследуем отношение выходных данных двух различных радиальных
центральных частот, к^ и к^, получим:
(]nk-]nk,f -(lnk-lnk,f
-L -
ехр
ехр
ехр
2стЧп2
2(^k^-\rik,)\xvk^W k^-W к,
2с7'1п2
(1п^,-1пА:^)[1п^-1/2(1п^,+1пА:^)]
С74п2
ехр
\xv{kl^,)\xvikjk,)
стМп2
^ >^ln(^2/^i)/(<TMn2)
к
у^к^к^
Как правило, отношение двух различных радиальных фильтров
непосредственно связано с локальным волновым числом. Соотношение становится особенно
13.5. Дополнительные тензорные представления
Рис. 13.15. Векторное сложение откликов фильтров от & направленных фильтров
для определения локальной ориентации; а - К= 2; б - К= 3; в - К= 4; вектор суммы
выделен более толстой линией
простым, если отношение волновых чисел двух фильтров равно двум (к^/к^ = 2 и
а= 1). Тогда
'2 _
13.5.6. Определение структурного тензора
(13.80)
В этом последнем разделе мы свяжем метод на основе использования набора
квадратурных фильтров, рассмотренного в разделе 13.5, с тензорным методом (раздел 13.3).
Показано, что структурный тензор может быть вычислен по откликам этих
фильтров. Гранлунд (Granlund) и Натссон (Knutsson) [64] представляют общее
уравнение для вычисления структурного тензора по откликам квадратурных тензоров:
J(x)^'^Q,g{x)(ad,®d,-pil (13.81)
где Qf^gix) - выходные данные (амплитуда) к-то квадратурного фильтра; / -
единичная матрица. В двумерном случае а = 4/3 и j3 = 1/3.
Продемонстрируем эту зависимость с помощью набора квадратичных
фильтров с тремя фильтрами (минимальное число). Три фильтра направлены под 0°, 60°
и 120°. Таким образом, единичные векторы направлений равны:
do = [l,Of,
d, = [l/2,V3/2f,
rfj = [-l/2,yj3/2f.
При этих значениях для 3^ уравнение (13.81) можно записать как
J(x) = QoQix)
+ Q^9{x)
+ QiQix)
(13.82)
"1 0
0 -1/3
0 1/7з"
I/n/З 2/3 _
0 -1/л/з^
-1/л/З
2/
3 \
(13.83)
Глава 13. Простые окрестности
Матрицы определяют взнос отдельных квадратичных фильтров в
соответствующие элементы структурного тензора. Для изотропно ориентированной
структуры выходные данные от всех квадратурных фильтров одинаковы. Если положим
входные данные равными q{x), то уравнение (13.83) приводит к корректному
структурному тензору для изотропно ориентированной структуры:
J{x) =
(13.84)
'q{x) О 1
О q{x)\
Обратно, для ориентированной структуры отклик равен q{x)cos\(f)^ - 0^), и мы
получаем
cos^(0o) sin(20o)/2
J{x) = q{x)
sin(20o)/2 sin'(0o)
(13.85)
Это корректная форма структурного тензора для идеально ориентированной
структуры в направлении ф^, (Это можно показать, к примеру, с помощью
проверки равенства нулю определителя матрицы и вычисления угла ориентации
согласно уравнению (13.12)).
Существует одна незаметная, но важная разница между методом
квадратурного фильтра и методом структурного тензора. Метод квадратурного тензора не
требует какого-либо усреднения для вычисления элементов структурного тензора.
Однако усреднение является существенным элементом прямого метода. Без
усреднения мера когерентности (см. уравнение (13.15) в разделе 13.3.4) всегда
равнялась бы единице.
13.6. Упражнения
13.1: Анализ локальной ориентации
Интерактивная демонстрация анализа локальной ориентации с
использованием различных дифференциальных операторов первого порядка
(dip6exl3.01).
13.2: Локальная ориентация и шум
Интерактивная демонстрация влияния шума на локальную ориентацию
(dip3exl3.02).
13.3: ^Ориентация и направление
Объясните разницу между ориентацией и направлением и приведите, по
крайней мере, один пример векторного оператора обработки изображений,
который образует либо направленный вектор, либо вектор ориентации.
13.4: **Усреднение структурного тензора
1. Почему требуется усреднять компоненты структурного тензора по
некоторой окрестности (уравнения (13.8) и (13.17))? Или зададим вопрос
по-другому: какую информацию предоставил бы структурный тензор без
усреднения?
2. Знаете ли вы какие-либо тензорные операторы обработки, которые не
требуют усреднения?
13.6 Упражнения 393
13.5: Анализ локальной ориентации при наложении структур
В разделе 13.3 мы детально рассмотрели, что при идеально
ориентированной структуре структурный тензор имеет ранг, равный только единице. Легко
вычислить вектор ориентации (амплитуду и угол ориентации), а
когерентность равна единице. Как выглядит структурный тензор, если две идеально
ориентированные структуры с различными направлениями
накладываются? Без ограничения общности вы можете полагать, что две структуры
ориентированы под углом ±в/2 к оси X. Пусть амплитуды различны. Вы можете
предположить синусоидальный сигнал.
1. Какой угол ориентации вычисляется структурным тензором?
2. Какое значение имеет когерентность?
3. Проанализируйте результаты.
13.6: Фильтр Гильберта
Интерактивная демонстрация различных фильтров Гршьберта (dip6exl3.01).
13.7: **Маска свертки для фильтров Гильберта
1. Какие общие условия требуются для маски свертки, которая должна быть
фильтром Гильберта на некотором диапазоне волновых чисел?
2. Может идеальный фильтр Гильберта, т.е фильтр, который имеет идеальную
передаточную функцию фильтра Гильберта для всех волновых чисел, бьггь
реализован с помощью маски свертки с бесконечным числом коэффициентов?
13.8: Локальная фаза и волновое число
Интерактивная демонстрация определения локальной фазы и волнового
числа с использованием преобразования Гильберта и квадратурных
фильтров (dip6exl3.04).
13.9: **Локальная амплитуда, фаза и волновое число
Локальная фаза, амплитуда и волновые числа являются
характеристическими признаками, которые подходят для описания локальных свойств
сигналов. Вычислите эти три характеристики для следующих простых 1-D
сигналов с использованием преобразования Гильберта:
1) синусная волна: fl^sin кх\
2) синусная волна с гармоникой: a^sm кх + ар.кх при а^ <^ а^\
3) суперпозиция двух синусных волн с равными амплитудами и почти
равными волновыми числами:
а sin[(/:^M /)2х] + а sin[(A:_М /)2x] при М «: А:.
Проанализируйте вычисленные результаты.
13.10: Локальная фаза и волновое число с помощью преобразования Рисса
Интерактивная демонстрация определения локальной фазы и волнового
числа с использованием преобразования Рисса (dip6exl3/05).
13.11: **Простой 1-D квадратурный фильтр
Является ли простая пара фильтров
Глава 13. Простые окрестности
[-10 2 0 -1]/4 8 [1 О -1]/2
полезной парой квадратурных фильтров?
1. Вычислите передаточную функцию обоих фильтров.
2. Вычислите фазовую разность между двумя фильтрами.
3. Сравните амплитуды обеих передаточных функций.
13.7. Дополнительная литература
Подход на базе квадратурного фильтра (раздел 13.5) детально изложен в
монографии Гранлунда (Granlund) и Натссона (Knutsson) [66], метод тензора инерции
(раздел 13.5.1) — в статье Бигюна (Bigun) и Гранлунда [10]. Поуларикас (Poularikas)
[158] объясняет математические основы преобразования Гильберта. Обсуждение
расширения аналитического сигнала до многомерных сигналов (раздел 13.4.4) было
опубликовано только недавно Фельсбергом (Felsberg) и Соммером (Sommer) [64].
Математические основы моногенного сигнала и геометрическая алгебра для
компьютерного зрения содержатся в работе Соммера [195].
ГЛАВА 14
ДВИЖЕНИЕ
14.1. Введение
Анализ движения долгое время являлся специализированной тематикой, которая
не имела особого значения в общей теории обработки изображений. Это
разделение имело две причины. Во-первых, методы, используемые для анализа движения
в последовательностях изображений, были совершенно иными. Во-вторых,
большой объем памяти и вычислительная мощность, требуемые для обработки
последовательностей изображений, привели к тому, что анализ последовательностей
изображений был доступен только некоторым специализированным институтам,
которые могли позволить себе купить дорогостоящее специализированное
оборудование. Обе причины больше не актуальны. Из-за общего развития в области
обработки изображений более передовые методы, используемые в анализе
движения, больше не отличаются от тех, что используются для других задач обработки
изображений. Быстрый прогресс в аппаратных средствах и алгоритмах делают
анализ последовательностей изображений теперь выполнимым даже на стандартных
персональных компьютерах и рабочих станциях.
Поэтому мы рассматриваем движение в этой главе только как еще один
признак, который можно использовать для распознавания, характеризации и
различения объектов и понимания сцен. В действительности движение является
значительным признаком. Мы можем сравнить интеграцию анализа движения в
основную область обработки изображений с переходом от фотосъемки к
киносъемке. Только анализ последовательностей изображений позволяет нам распознавать
и анализировать динамические процессы. Таким образом, становятся
доступными перспективные возможности для научных и инженерных задач, включая
изучение потока транспорта, процессов биологического роста от молекулярного
уровня до уровня экосистемы, суточных, годовых и междугодичных изменений,
промышленных процессов; движения автономных средств передвижения и
роботов, — и это только незначительное число областей применения.
Вкратце все, что вызывает временные изменения или делает их видимыми в
нашем мире, является потенциальным предметом анализа последовательностей
изображений.
Анализ движения остается по-прежнему перспективной задачей и требует
некоторых особых знаний. Поэтому мы рассматриваем основные проблемы и
принципы анализа движения в разделе 14.2. Затем возвращаемся к различным методам
определения движения. Как и во многих других областях обработки изображений,
литература заполнена множеством подходов. Этой книге не следует усиливать
путаницу. На самом деле мы сделаем акцент на основных принципах и постараемся
представить различные понятия единым образом как фильтрующие операции на
396 Глава 14. Движение
Рис. 14.1. а — г — две пары изображений со строительной площадки новой главной
клиники в Университете Гейдельберга. Какие изменения произошли от левых к
правым изображениям?
пространственно-временных изображениях. Таким образом, взаимозависимости
между различными понятиями станут очевидными.
В этом смысле мы будем рассматривать дифференциальные (раздел 14.3),
тензорные (раздел 14.4), корреляционные (раздел 14.5) и фазовые методы (раздел 14.6)
как элементарные оценки движения.
14.2. Основы
14.2.1. Изменения движения и уровней яркости
Иьпуитивно мы связываем движение с изменениями. Поэтому мы начнем наше
обсуждение по анализу движения с рассмотрения различий между двумя
изображениями последовательности. На рис. 14.1, а и 5 показана пара изображений
строительной площадки при Университете Гейдельберга. Существуют различия между
левыми и правыми изображениями, которые неочевидны из прямого сравнения.
Однако если мы вычтем одно изображение из другого, то различия немедленно
становятся видны (рис. 14.3, а), В нижней левой части изображения сдвинулся
грузовик, в то время как находящаяся прямо позади машина, очевидно,
припаркована. В центре изображения мы обнаруживаем очертания пешехода, который едва
14.2. Основы 39/
Рис. 14.2. От а к г — две пары изображений внутри лаборатории. Какие изменения
можно увидеть между левыми и правыми изображениями?
виден на исходных изображениях. Оказывается, светлые пятна в строке на
верхней части изображения - это мотоциклисты, движущиеся по кольцевой дороге.
По перемещению двойных контуров мы можем оценить, что они движутся
быстрее, чем пешеход. Даже из такого качественного описания очевидно, что анализ
движения значительно помогает нам в понимании этой сцены. Было бы гораздо
сложнее определить расположение кольцевой дороги без наблюдения
движущихся мотоциклистов.
На рис. 14.1, в и г показана та же сцена. Теперь мы можем распознать
изменения даже в исходных изображениях. Если посмотрим на контуры изображения, то
заметим, что изображения незначительно сдвинуты в горизонтальном
направлении. Что случилось? Очевидно, камера для съемки была установлена под
различными углами. На разностном изображении рис. 14.3,5все контуры объектов
появляются как светлые линии. Однако изображение затемнено в местах, где
пространственные изменения уровней яркости малы. Следовательно, мы можем
определить движение только в частях изображения, которые проявляют
изменения уровней яркости. Это простое наблюдение указывает на решающую роль
пространственных изменений уровней яркости для определения движения.
Итак, мы можем суммировать наш опыт с помощью утверждения, что
движение может вызвать временные изменения уровней яркости. К сожалению,
обратное заключение, что все временные изменения уровней яркости обусловли-
Глава 14. Движение
Рис. 14.3. Разность между: а - изображениями а и б на рис. 14.1; б - изображениями
вигнарис. 14.1
Рис. 14.4. Разность между: а -
вигнарис. 14.2
изображениями а и б на рис. 14.2; б - изображениями
ваются движением, является неверным. На первый взгляд пара изображений
на рис. 14.2, а и ^выглядит идентичной. Но тем не менее разностное
изображение рис. 14.4, а обнаруживает, что некоторые части на верхнем изображении
светлее, чем на нижнем. Очевидно, что изменилась освещенность. В
действительности лампа, находящаяся за пределами показанного изображаемого
сектора, была выключена до того, как было получено изображение на рис. 14.2, б.
Можем ли мы сделать вывод о том, где находится лампа? На разностном
изображении мы замечаем, что не все поверхности являются одинаково светлыми.
Поверхности, которые ориентированы по направлению к камере, показывают
приблизительно одну и ту же яркость на обоих изображениях, в то время как
поверхности, смотрящие в левую сторону, значительно светлее.
Следовательно, мы можем сделать заключение, что лампа расположена слева за пределами
изображаемого сектора.
Еще одна пара изображений (рис. 14.2, виг) иллюстрирует гораздо более
сложную сцену, хотя мы не изменяли освещенность. Мы всего лишь закрыли дверь
лаборатории. Конечно, мы видим сильные различия уровней яркости там, где
расположена дверь. Однако изменения уровней яркости растягиваются на пол вблизи
14.2. Основы 399'
Рис. 14.5. Иллюстрация апертурной проблемы в анализе движения: а —
неопределенность векторов перемещения на границе; б — однозначность вектора
перемещения в угле
двери и на объекты, расположенные слева от двери (рис. 14.4, б). Поскольку мы
закрываем дверь, мы изменяем также освещенность в близости двери, особенно
ниже двери, так как в эту область отражается меньше света.
14.2.2. Апертурная проблема
Итак, мы установили, что оценка движения тесно связана с пространственными и
временными изменениями уровней яркости. Обе величины могут легко быть
получены с помощью локальных операторов, которые вычисляют пространственные
и временные производные. Такой оператор «видит» только маленький сектор
наблюдаемого объекта, равный размеру его маски. Мы можем проиллюстрировать
этот эффект наложением маски или апертуры на изображение.
На рис. 14.5, а показан контур, который сдвинулся из положения сплошной
линии на первом изображении в положение пунктирной линии на втором
изображении. Движение от изображения один к изображению два можно описать
вектором перемещения (ВП). В этом случае мы не можем определить перемещение
однозначно. Вектор перемещения мог бы соединить одну точку контура на первом
изображении с любой другой точкой контура на втором изображении (рис. 14.5,
а). Мы можем определить только компоненту ВП по нормали к контору, в то
время как компонента, параллельная контуру, остается неизвестной. Эта
неопределенность известна как апертурная проблема.
Однозначное определение ВП возможно, только если угол объекта находится
внутри маски нашего оператора (рис. 14.5, б). Это указывает на то, что мы можем
получить только неполную информацию о движении от локальных операторов.
14.2.3. Проблема соответствия
Апертурная проблема вызывается тем, что мы не можем найти соответствующую
точку на контуре в следующем изображении последовательности, поскольку у нас
нет средств выделения различных точек на контуре. В этом смысле мы можем
понимать апертурную проблему как частный случай более общей проблемы —
проблемы соответствия. Вообще говоря, эта проблема заключается в том, что мы не
можем найти однозначно соответствующие точки в двух последовательных
изображениях последовательности. В этом разделе мы рассматриваем дополнительные
примеры проблемы соответствия.
400 Глава 14. Движение
>
Рис. 14.6. Р1ллюстрация проблемы соответствия: а
объект; б — регулярная сетка
деформируемый двумерный
На рис. 14.6, а показан двумерный деформируемый объект — капля краски, -
который расширяется постепенно. Сразу же становится очевидным, что мы не
можем получить какое-либо однозначное определение вектора перемещения даже
на контуре капли. Во внутренней части капли мы не можем получить какую-либо
оценку перемещений, поскольку нет видимых характерных признаков, которые
мы могли бы проследить.
Мы могли бы предположить, что проблема соответствия не возникнет с
твердыми телами, которые проявляют большое количество изменений уровней
яркости. Решетка, как пример периодической структуры, показанная на рис. 14.6, б,
демонстрирует, что это не так. Как только мы наблюдаем перемещение решетки с
помощью локального оператора, мы не можем дифференцировать перемещения,
которые отличаются на числа, кратные постоянной решетки. Только в случае, когда
мы наблюдаем всю решетку, перемещение становится однозначным.
Еще один аспект проблемы соответствия выявляется, если изображение
включает объекты одинаковой формы. Типичным примером является случай, когда
маленькие частицы помещаются в поле потока, для того чтобы измерить поле
скоростей (рис. 14.7). В таком случае частицы неотличимы, и мы, как правило, не
можем сказать, какие частицы соответствуют друг другу. Мы можем найти
решение этой проблемы, если возьмем последовательные изображения при таких
коротких временных интервалах, что средний вектор перемещения значительно
меньше, чем среднее расстояние частиц. С такими дополнительными сведениями мы
можем найти ближайшего соседа частицы на следующем изображении. Такой
подход, однако, никогда не будет освобожден от ошибок, поскольку расстояние
между частицами является статистически распределенным.
Эти простые примеры ясно демонстрируют основные проблемы анализа
движений. На более высоком уровне абстракции мы можем утверждать, что
физическое соответствие, т.е. реальное соответствие реальных объектов, может не быть
идентичным визуальному соответствию на изображении. Проблема имеет две
стороны. Во-первых, мы можем найти визуальное соответствие без существования
физического соответствия, как в случае объектов или периодических объектных
структур, которые являются неотделимыми. Во-вторых, физическое соответствие,
как правило, не подразумевает визуального соответствия. Это тот случай, когда
объекты не проявляют отличительных признаков или когда мы не можем
распознать визуальное соответствие из-за изменений освещенности.
14.2. Основы 401
^ •^
•"•- •-
•^•^ Фю
•^ Ф^©
•«
• О
• о ^ • о
о
• о •
• о
• о о • о
• • о
о
• о
Рис. 14.7. Проблема соответствия с неотличимыми частицами: а — среднее расстояние
между частицами больше, чем средний вектор перемещения; б - обратный случай.
Закрашенные и незакрашенные окружности — частицы на первом и втором изображениях
14.2.4. Движение как ориентация в пространственно-временных
изображениях
Рассуждение в разделах 14.2.1-14.2.3 показало, что анализ движения только по двум
последовательным изображениям сопровождается серьезными проблемами.
Возникает вопрос: можно ли преодолеть эти проблемы или по крайней мере
некоторые из них, если мы расширим анализ до более чем двух последовательных
изображений? С двумя изображениями мы можем получить только «моментальный
снимок» поля движения. Мы не знаем, как движение продолжается во времени.
Мы не можем измерить ускорения и не можем наблюдать, как части объектов
появляются или исчезают, по мере того как объект дврскется перед ними.
В этом разделе мы рассматриваем основы анализа последовательностей
изображений в многомерном пространстве, образованном одной временной и от
одной до трех пространственными координатами. Следовательно, мы говорим об
изображении пространства-времени, пространственно-временном изображении или
просто xt пространстве.
Мы можем рассматривать трехмерное пространственно-временное
изображение как стопку последовательных изображений, которые могут быть
представлены как куб изображений, как показано на рис. 14.9. На каждой видимой грани куба
мы отображаем поперечное сечение в соответствующем направлении. Так, слой xt
показан на верхней фани, а слой yt — на правой грани куба. Слои были взяты при
глубинах, отмеченных белыми линиями на передней грани, которая показывает
последнее изображение последовательности.
В пространственно-временном изображении пиксели расширяются до
векселей, т.е. они представляет уровень яркости в маленьком элементе объема с растяже-
НР1ЯМИ Ах, Ау и А^. Здесь мы сталкиваемся с пределами нашего визуально
воображения, когда пытаемся правильно понять 3-D данные (сравните с рассуждениями в
разделе 8.1.1). Следовательно, нам необходимо соответствующие представления
таких данных, чтобы сделать интересующие нас существенные признаки видимыми.
Для анализа движения в пространственно-временных изображениях мы
сначала рассмотрим простой пример с одной пространственной и одной временной
координатами (рис. 14.8, а). Неподвижный 1-D объект проявляет вертикально
ориентированные структуры уровней яркости. Если объект движется, то он сдвигает-
Глава 14. Движение
V
1
п
/
ф»/
у
Рис. 14.8. Пространственно-временные изображения: а — двумерное
пространственно-временное изображение с одной пространственной и одной временной
координатой; б — трехмерное пространственно-временное изображение
ся от изображения к изображению и, таким образом, проявляется как наклонная
структура уровней яркости. Скорость непосредственно связана с ориентацией в
пространственно-временных изображениях. В простом примере 2-D
пространственно-временного изображения она определяется как
w = ~tan<j9, (14.1)
где (р — угол между осью / и направлением, в котором уровни яркости являются
постоянными. Знак минус в уравнении (14.1) появляется по причине того, что
углы положительны в направлении против часовой стрелки. Расширение до
двумерного по пространству случая не вызывает затруднений и проиллюстрировано
на рис. 14.8, б\
и = -
(14.2)
Углы (р^иср определяются аналогично углу между компонентами векторахиу
в направлении постоянных уровней яркости и осью /.
Практический пример для такого вида анализа показан на рис. 14.9. Движение
происходит приблизительно в вертикальном направлении, так что поперечное
сечение yt можно рассматривать как 2-D пространственно-временное изображение.
Движение сразу же становится очевидным. Когда машины останавливаются на
светофоре, линии горизонтально ориентированы, и фазы с ускоренной и
постоянной скоростью могут быть легко распознаны.
В итоге мы приходим к важному заключению, что движение проявляется как
ориентация в пространственно-временных изображениях. Этот
фундаментальный вывод формирует основу для анализа движений в пространстве xt.
Основным концептуальным различием к подходам, использующим два
последовательных изображения, является то, что скорость оценивается непосредственно как
ориентация в непрерывных пространственно-временных изображениях, а не как
дискретное перемещение.
14.2. Основы 403'
Рис. 14.9. 3-D последовательность изображений, продемонстрированная с
использованием сцены уличного движения на Ганауер Ландштрассе (Hanauer LandstraBe),
Франкфурт-на-Майне (Frankfurt/Main), представленная как кубоид изображений.
Временная ось уходит в глубину, указывая по направлению к наблюдателю. На
правой стороне куба показан слой yt, отмеченный вертикальной белой линией на ху
изображении, в то время как верхняя грань показывает слой xt, отмеченный
горизонтальной линией (Яне [88])
Эти два понятия отличаются больше, чем это кажется на первый взгляд.
Алгоритмы для оценки движения теперь могут быть сформулированы в непрерывном
пространстве xt и изучены аналитически, до применения подходящей
дискретизации. Таким образом, мы можем явно вьщелить главные изъяны подхода по
ошибкам, вызванным дискретизацией.
Используя больше, чем два изображения, можно ожидать более устойчивое и
точное определение движения. Это является решающим результатом для научных
задач, сформулированных в главе 1.
Этот подход к анализу движения имеет много общего с проблемой
реконструкции 3-D изображений по проекциям (раздел 8.6). Действительно, мы можем
рассматривать геометрическое определение скорости путем наблюдения
прозрачного трехмерного пространственно-временного изображения с различных точек
зрения. При правом угле наблюдения мы смотрим вдоль контуров движущегося
объекта и получаем скорость по величине угла между направлением наблюдения
и временной осью.
Если мы наблюдаем только контуры объекта, мы не можем определить
такой угол наблюдения однозначно. Мы можем изменять компоненту угла вдоль
контура произвольно и по-прежнему смотреть вдоль контура. Таким образом,
апертурная проблема, рассмотренная в разделе 14.2.2, проявляется с другой
точки зрения.
Глава 14. Движение
14.2.5. Движение в Фурье-области
Вводя пространственно-временную область, мы получаем значительное
преимущество, состоящее в том, что мы можем также анализировать движение в
соответствующей Фурье-области — пространстве kv. В качестве введения
рассмотрим пример последовательности изображений, в которой все объекты
движутся с постоянной скоростью. Такая последовательность д{х, i) может
описываться как
g(x,t) = g(x-ut). (14.3)
Преобразование Фурье от этой последовательности
g(k,v) = jjg(x-ut)Qxp[-2ni{kX'-vt)]d^xdt, (14.4)
t X
Производя замену
х' = х-Ш,
получаем
g(/r,v) = j jg(x)Qxp{-27tikx')
Qxp(-2mkut) exp(2;ri vt)d^x'dt.
Внутренний интеграл охватывает пространственные координаты и приводит к
пространственному преобразованию Фурье д(к) изображения д(х). Внешний
интеграл по временной координате сводится к 5-функции:
g(k,v) = §ik)d(ku-v). (14.5)
Это уравнение утверждает, что объект, движущийся со скоростью и,
захватывает только двумерное подпространство в трехмерном пространстве kv. Таким
образом, это линия и плоскость в двумерном и трехмерном случаях
соответственно. Уравнение для плоскости задается непосредственно аргументом 5-функции
в уравнении (14.5):
у^Ли. (14.6)
Эта плоскость пересекает плоскость к^к^ нормально к направлению скорости,
поскольку в этом направлении внутреннее произведение ки обращается в ноль.
Наклон плоскости — двухкомпонентный вектор дает скорость
Индекс к в операторе градиента обозначает, что частные производные
вычисляются относительно компонент к
Из этих соображений становится очевидным, по крайней мере в принципе,
как можно определить скорость в последовательности изображений,
показывающей постоянную скорость. Мы вычисляем преобразование Фурье от
последовательности и затем определяем наклон плоскости, на которой расположен спектр
последовательности. Мы можем сделать это наилучшим образом, если сцена
содержит мелкомасштабные структуры, т.е. высокие волновые числа, которые
распределены по многим направлениям. Мы не можем определить наклон плоскости
однозначно, если спектр лежит на прямой вместо плоскости. По прямой в Фурье-
пространстве мы только получаем компоненту наклона плоскости в направлении
пространственной локальной ориентации. Таким образом, мы сталкиваемся с апер-
турной проблемой (раздел 14.2.2) в пространстве kv.
14.2. Основы 405'
14.2.6. Оптический поток
Примеры, рассмотренные в разделе 14.2.1, показали, что движение и изменение
уровней яркости не эквивалентны. В этом разделе мы хотим определить колипчественно
это соотношение. В связи с этим два термина представляют важность: поле движения
и оптический поток. Поле движения в изображении — это действительное движение
объекта в 3-D сцене, спроектированное на плоскость изображения. То есть
величина, которую мы хотели бы вьщелить из последовательности изображений.
Оптический поток определяется как «поток» уровней яркости на плоскости изображений.
Это то, что мы наблюдаем. Оптический поток и поле движений равны, если объекты
не изменяют энергетическую освещенность на плоскости изображений в процессе
движения в сцене. Хотя это кажется разумным на первый взгляд, более полный
анализ показывает, что это точно выполняется только в очень ограниченных случаях.
Таким образом, основной вопрос заключается в том, насколько существенными
являются отклонения, чтобы на практике мы могли действовать в соответствии с
эквивалентностью оптического потока и поля движения.
Два классических примера, где спроектированное поле движений и
оптический поток не равны, были приведены Горном (Нот) [81]. Первым примером
является вращающаяся сфера с однородной поверхностью любого вида. Такая сфера
может вращаться вокруг любой оси, проходящей через ее центр тяжести, не
вызывая поля оптического потока. Противоположным примером является та же самая
сфера в состоянии покоя, освещаемая движущимся источником света. Теперь поле
движений равно нулю, но изменения в уровнях яркости, обусловленные
движением источника света, вызывают ненулевое поле оптического потока.
С этой точки зрения будет полезным прояснить различные обозначения для
движения относительно последовательностей изображений, поскольку
существует большая путаница в литературе и используется большое количество
различных терминов. Оптический полок или поток изображений кажутся очевидным
движением на плоскости изображений на основе визуального восприятия и имеют
размерность скорости. Обозначим оптический поток с помощью/= [/j, /J^. Если
оптический поток определяется по двум последовательным изображениям, он
появляется как вектор перемещения (ВП) от признаков на первом изображении
до признаков на втором. Сжатое представление векторов перемещения известно
как поле векторов перемещений (ПВП) 5 = [ 5,, s^. Аппроксимация оптического
потока может быть получена делением ПВП ка временной интервал между двумя
изображениями. Важно обратить внимание на то, что оптический поток
является понятием, свойственным непрерывному пространству, в то время как поле
векторов перемещений является его дискретным аналогом. Поле движения и =
[w,, «2!^= [w,v]^Ha плоскости изображения является проекцией 3-D физического
поля движения на плоскость изображения.
Понятие оптического потока происходит из гидрогазодинамики. В случае
изображений движение заставляет уровни яркости, т.е. оптический сигнал,
«течь» по плоскости изображения именно так, как элементы объема движутся в
жидкостях и газах. В гидрогазодинамике уравнение неразрывности играет
важную роль. Оно выражает закон сохранения массы в потоке. Можем ли мы
сформулировать подобное уравнение неразрывности для уровней яркости и при
каких условиях они сохраняются?
Глава 14. Движение
В гидрогазодинамике уравнение неразрывности для плотности р жидкости
задается как
ot ot
(14.7)
Это уравнение действительно для двумерных и трехмерных потоков. Оно
определяет сохранение массы в жидкости в дифференциальной форме. Временные
изменения в плотности уравновешены дивергенцией от плотности потока up. С
помощью интегрирования уравнения непрерывности по произвольному элементу
объема мы можем записать уравнение в интегральной форме:
Эр „. .^ ,.. Э
n^ + V(iip) dF = —JpdF+|)piida = 0. (14.8)
F V / V A
Интеграл по объему был преобразован в поверхностный интеграл вокруг
объема с использованием интегральной теоремы Гаусса, da — вектор, нормальный к
элементу поверхности йА. Интегральная форма уравнения неразрывности явно
утверждает, что временное изменение массы вызывается результирующим потоком
в объеме, проинтегрированном по всей поверхности объема.
Как мы можем получить подобное уравнение неразрывности для оптического
иотока/^Vgf — известное kslk уравнение ограничения изменений яркости (УОИЯ) или
ограничение оптического потока (ООП) — в компьютерном видении? Величиной
аналогичной плотности р является энергетическая яркость £" или уровень яркости
д. Однако нам следует быть внимательными и исследовать члены в уравнении (14.7)
более тщательно. Левый дивергентный член/Vgf описывает временное изменение
яркости, обусловленное движущимся градиентом уровней яркости. Второй член с
дивергенцией поля скоростей д\укажется неясным. Он мог бы вызывать
временное изменение даже в области с постоянной энергетической освещенностью, если
дивергенция поля потока не равна нулю. Такой случай возникает, к примеру,
когда объект удаляется от камеры. Энергетическая освещенность на плоскости
изображений остается постоянной при условии, что энергетическая освещенность
объекта не изменяется. Накопленная энергетическая яркость убывает со
скоростью квадрата расстояния от объекта. Однако это полностью компенсируется,
поскольку спроектированная площадь объекта уменьшается на тот же множитель.
Таким образом, мы опускаем последний член в уравнении неразрывности для
оптического потока и получаем
ot
(14.9)
В одномерном случае неразрывность оптического потока принимает простую
форму
из которой мы непосредственно получаем одномерную скорость
(14.10)
•^ dt/ дх'
(14.11)
14.2. Основы AOf
1 1
А
|- /
/ Ах >/|
—^ \ —— 1
t^
Ад/
J At
1
/f+At
1
J
-^
Рис. 14.10. Иллюстрация неразрывности оптического потока в одномерном случае
при условии, что пространственная производная не обращается в нуль. Скорость,
таким образом, задается как отношение временной и пространственной производных.
Это основное соотношение может также быть получено геометрически, как
показано на рис. 14.10. Во временном интервале А/ уровень яркости сдвигается на
расстояние Ах:= и At, изменяясь на д{х, t-\- At)- д(х, t). Изменение уровня яркости
может быть также выражено как наклон контура уровня яркости
дх дх
(14.12)
из которого, в пределе А/ -► О, получается уравнение неразрывности оптического
потока (14.10).
Неразрывность или уравнение ограничения изменений яркости для
оптического потока на плоскости изображения (14.9) может, в общем, служить только
грубой аппроксимацией. Мы уже коснулись во вступительном разделе вопроса
относительно движения и изменений уровней яркости (раздел 14.2.1). Причиной этого
является сложная природа отражения от темных поверхностей, которая зависит от
направления наблюдения, нормали к поверхности и направлений падающего
света. Каждый объект получает излучение не только непосредственно от световых
источников, но также и от всех других объектов в сцене, которые находятся в
прямой видимости объекта. Таким образом, излучательная способность от
поверхности одного объекта зависит от положения всех других объектов в сцене.
В компьютерной фафике проблемы такого типа изучаются детально, в поиске
фотореалистичных, созданных компьютером изображений. Большим шагом по
направлению к этой цели был метод, называемый методом излучательности, который
позволил найти взаимозависимость излучательных способностей объектов,
описанную выше [52]. Общее выражение для излучательной способности объектов —
сейчас известное как уравнение визуализации — было получено Кайа (Kajia) [100].
В обработке последовательностей изображений в принципе требуется обратить
это уравнение, чтобы сделать вывод об отражательной способности поверхности по
измеренной излучательной способности объектов. Отражательная способность
поверхности является признаком, инвариантным относительно ориентации
поверхности и положения других объектов, и, таким образом, могло бы стать идеальным
для оценки движения. Однако такой подход нереален, поскольку он требует ре-
Глава 14. Движение
конструкции 3-D сцены, прежде чем обращение уравнения визуализации может
быть получено вообще.
Поскольку, как правило, не существует адекватного уравнения
неразрывности для оптического потока, важно сравнить дополнительные члены с членами в
стандартном У0Р1Я. Все остальные члены, по существу, зависят от темпа
изменений некоторого числа величин, но не от градиентов яркости. Если градиент
уровня яркости большой, то влияние дополнительных членов становится малым.
Таким образом, мы можем заключить, что определение скорости является наиболее
надежным для крутых контуров уровней яркости, в то время как оно может
значительно искажаться в областях с малыми градиентами уровня яркостей. Это
заключение согласуется с данными Верри (Verri) и Поггио (Poggio) [207, 208], где они
указывают на различие между оптическим потоком и полем движения.
Важно еще одно наблюдение. Несомненно верным является то, что
исторический подход определения векторов перемещений лишь по двум
последовательным изображениям является неустойчивым. В общем случае мы не способны
понять, происходит ли изменение уровней яркости в результате перемещения или по
какой-то другой причине. Однако оптическое течение становится более
устойчивым в пространственно-временных изображениях. Мы продемонстрируем это с
помощью двух примеров.
Во-первых, возможно отделить изменения уровней яркости, вызванные
глобальными изменениями освещенности, от изменений, вызванных движением. На
рис. 14.11 показана последовательность изображений статической сцены,
полученная с частотой пять кадров в минуту. Два пространственно-временных слоя
(рис. 14.11, а, в), обозначенных с помощью двух белых горизонтальных линий на
рис. 14.11, покрывают период приблизительно 3,4 часа. Верхняя линия охватывает
высотное здание и небо. По небу можно видеть, что оно частично облачное, но
иногда имело место прямое солнечное освещение. Нижняя линия пересекает
несколько окон на крыше, стены и крыши домов.
В обоих слоях изменения освещенности проявляются как полосы, которые
отчетливо накладываются на вертикальные полосы, указывая на статическую
сцену. Горизонтальные структуры указывают на объект, двигающийся с бесконечной
скоростью, эти структуры можно исключить, например, с помощью
направленной фильтрации, без внесения возмущений в анализ изображений.
Второй пример демонстрирует, что определение движения по-прежнему
возможно в пространственно-временных изображениях, если имеют место
препятствия и локальная освещенность объекта меняется, поскольку он поворачивается.
На рис. 14.12 показана сцена уличного движения на окраине Ганау (Hanau),
Германия. Из последнего изображения последовательности (рис. 14.12, а) мы видим,
что уличный перекресток со светофором наблюдается через ветви дерева,
расположенного справа на переднем плане. Одна дорога проходит горизонтально слева
направо со светофором слева.
Пространственно-временной слой (рис. 14.12) вырезан через
последовательность изображений по горизонтальной линии, указанной на рис. 14.12, а. Он
обнаруживает различные препятствия: следы машин исчезают под статическими
вертикальными структурами веток дерева и дорожных знаков. Мы также можем видеть,
что временной след фургона показывает значительные изменения, поскольку он
повернул на уличном перекрестке и условия освещенности изменились, тогда как
14.2. Основы 409'
в
^н^^
и
f
BHIHi
Рис. 14.11. Статическая сцена с изменениями освещенности: а — поперечное
сечение xt по помеченной сверху строке (область неба) на б; б — первое изображение
последовательности; в - поперечное сечение х/по помеченной снизу строке (область
крыши) на б; временная ось покрывает 3,4 часа и направлена вниз (Яне (Jahne) [88])
сейчас он движется вдоль сцены. Тем не менее временной след является
непрерывным и обещает надежную оценку скорости.
Мы можем сделать заключение, что наилучшим подходом является
придерживаться стандартного УОИЯ для оценок движения и использовать его для
разработок оценок движения в этой главе. Из-за широкого разнообразры дополнительных
членов все еще кажется, что этот подход является наиболее резонным и наиболее
широко применимым, поскольку он содержит фундаментальное ограничение.
410 Глава 14. Движение
Рис. 14.12. Сцена уличного движения на окраине Ганау (Hanau), Германия; а —
последнее изображение последовательности; б — поперечное сечение xt по помеченной
линии на а; временная ось покрывает 20,5 секунды и направлена вниз (Яне (Jahne) [88]).
14.3. Дифференциальные методы первого порядка
14.3.1. Основы
Дифференциальные методы являются классическим подходом для определения
движения по двум последовательным изображениям. Эта глава рассматривает
вопрос о том, как эти методы можно применять к пространственно-временным
изображениям. Уравнение неразрывности для оптического потока (раздел 14.2.6),
вкратце УОИЯ или ООП, является стартовой точкой для дифференциальных методов:
14.3. Дифференциальные методы первого порядка
^ + fVg = 0. (14.13)
ot
Это одиночное скалярное уравнение содержит Жнеизвестных векторных
компонент в W^-мерном пространстве. Таким образом, мы не можем определить
оптический поток/= [/j, /J^однозначно. Скалярное произведение /^Vgравно модулю
градиента уровня яркости, умноженного на компоненту / в направлении
градиента, т.е. нормальную к локальному контору уровня яркости:
/'V6r = /JVg|.
Таким образом, мы можем определить только компоненту оптического
потока, нормальную к контуру. Это хорошо известная апертурная проблема, которую
мы качественно рассматривали в разделе 14.2. Из уравнения (14.13) получаем
Л=—^/|Vg. (14.14)
Следовательно, невозможно определить полный вектор с помощью производных
первого порядка в одиночной точке в пространственно-временном изображении.
14.3.2. Решение методом наименьших квадратов первого порядка
Вместо одиночной точки мы можем использовать малую окрестность для
определения оптического потока. Мы полагаем, что оптический поток является постоянным
в этой области, и рассматриваем в этом разделе, при каких условиях возможно
однозначное определение оптического потока. Мы все еш;е имеем две неизвестные
/= \fx> f^^^ но также имеем ограничение неразрывности (14.13) для оптического
потока во многих точках. Такая система не может быть решена точно, а может быть
решена только с помощью минимизирования функционала ошибки. Мы ищем
решение, которое минимизирует уравнение (14.13) внутри локальной окрестности в
смысле наименьших квадратов. Таким образом, интеграл свертки
\\e\f,= ]w{x-x\t-t')[f,g^{x') + f,g^{x') + g,{x)fd'x'At' (14.15)
—00
должен быть минимизирован. Обратите внимание, что/= [/,, ^2!^ является
постоянным внутри локальной области. Он зависит, конечно, как || е \\ от jc. Ради более
компактных уравнений мы опускаем явную зависимость д^, д и gf^ от jc' в следующрсс
уравнениях. Частную производную дд/Ьр сокращенно обозначаем с помощью д.
В этом интеграле квадрат остаточного отклонения от ограничения
неразрывности суммируется по области, определяемой размером оконной функции w. Для
того чтобы упростить уравнения дальше, мы используем следующее сокращение
для этой процедуры взвешенного усреднения:
\^f2'=[fi9Af29y^9t) ->minimum.
(14.16)
Оконная функция w определяет размер окрестности. Это делает подход
наименьших квадратов очень гибким. Усреднение в уравнении (14.15) может, но не
должно расширяться во временном направлении. Если мы выбираем
прямоугольную окрестность с постоянным взвешиванием для всех точек, то мы в конце
приходим к простому методу совпадения блоков. Это соответствует усреднению с фильт-
Глава 14. Движение
ром-ящиком. Однако из-за плохих усредняющих свойств фильтров-ящиков
(раздел 11.3), оказывается, что усреднение с весовой функцией, которая убывает с
ростом расстояния точки [х, tY от [дс, tY, является более подходящим подходом. В
непрерывном пространстве усреднение с фильтром Гаусса является хорошим
выбором. Для дискретных изображений наиболее подходит усреднение с
биномиальным фильтром (раздел 11.4).
Уравнение (14.16) может быть решено приравниванием частных производных
Э]|£|
!
= ^9y(fi9.+f29y+9,h^
(14.17)
нулю. Из этого условия получаем линейную систему уравнений
\9x9x 9x9у \
19x9у 9у9у\
\А'
Ш
9x9, \
9у9,\
(14.18)
или более компактно в матричном обозначении
Gf = g, (14.19)
Члены QpQq представляют собой регуляризованные оценки, которые состоят
из свертки и нелинейных точечных операций. В операторной форме записи мы
можем заменить его с помощью
®(®^-®^), (14.20)
где (D — подходящий дискретный дифференциальный оператор первого порядка в
направлении/7 (глава 12), а (В — оператор усреднения (глава И). Таким образом,
операторное выражение в уравнении (14.20) включает следующую
последовательность операторов обработки изображений:
1) применяем операторы свертки 0 и (D к изображению для получения
изображений с производными первого порядка в направлениях/? и q\
2) умножаем два дифференциальных изображения поточечно;
3) сворачиваем результирующее изображение с маской усреднения (В.
Обратите внимание, что точечная операция является нелинейной операцией.
Следовательно, ее нельзя поменять местами с усреднением.
Линейная система (14.18) может быть решена, если можно обратить матрицу.
Это выполняется, если определитель матрицы не равен нулю:
detG = д^д^ЯуЯу -g^Qy' ф 0. (i4.2i)
Из этого уравнения мы можем сделать вывод о двух условиях, которые должны
выполняться:
1. Не все частные производные д^ и д^ должны бьпъ равны нулю. Другими словами,
окрестность не должна состоять из области с постоянными уровнями яркости.
2. Градиенты в окрестности не должны иметь одинаковое направление. Если
бы это выполнялось, то мы могли бы выразить д с помощью д^, за
исключением постоянного множителя, и определитель матрицы G в уравнении (14.21)
обратился бы в ноль.
14.3. Дифференциальные методы первого порядка 413
Решение для оптического потока/ может быть записано явно, поскольку
легко обратить матрицу G размерностью 2x2:
G =
1
detG
При /=G^gfполучаем
'А
9у9у -9x9.
-9.9у 9х9х
или detG^^O.
(14.22)
1
detC?
9х9,9у9у-9у9,9х9у
(14.23)
9у9,9х9х-9х9,9х9у
Решение выглядит по-прежнему сложным. Оно может быть значительно
упрощено, если мы примем во внимание, что G является симметричной матрицей.
Любая симметричная матрица может быть приведена к диагональному виду с
помощью поворота системы координат в так называемую систему координат с глав-
ными осями. Тогда матрица G сводится к
G' =
9х'9х
О
О
9у'9у
(14.24)
определитель det С = g^.gfyg -о ., а оптический поток равен
fv]
fr\
9x9,
9х'9х'
9Wt
9/9/j
(14.25)
Это уравнение отражает количественным образом качественное рассмотрение
апертурной проблемы, обсуждаемой в разделе 14.2.2. Главные оси ориентируются
по направлениям максимальных и минимальных среднеквадратичных
пространственных изменений уровней яркости, которые перпендикулярны друг другу.
Поскольку матрица С является диагональной, оба изменения являются
некоррелированными. Теперь мы можем вьщелить три случая:
1) д^д^ > О, д д ' >0: пространственные изменения уровней яркости по
всем направлениям. Тогда обе компоненты оптического потока могут быть
определены;
2) д^д/ > О, д д ' =0: пространственные изменения уровней яркости
только в направлении х' (перпендикулярно контуру). Тогда только компонента
оптического потока в направлении х' может быть определена (апертурная
проблема). Компонента оптического потока, параллельная контуру,
остается неизвестной;
^) 9х'9х ~ д д ' ~^'- ^^^ пространственных изменений уровней яркости ни в
одном направлении. В случае постоянной области ни одна компонента
оптического потока не может быть определена вообще.
Глава 14. Движение
Важно обратить внимание, что матрица G определяет тип решения метода
наименьших квадратов. В этой матрице возникают только пространственные
производные и не возникают временные производные. Это означает, что
пространственные производные и, таким образом, пространственные структуры изображений
полностью определяют, можно ли оценить оптический поток и как точно.
14.3.3. Анализ ошибок
Шум может вносить систематическую ошибку в оценку оптического потока. Здесь
мы покажем, как можно проанализировать влияние шума на определение
оптического потока самым обш;им образом. Положим, что сигнал изображений
состоит из структуры, двигающейся с постоянной скоростью м, на который
накладывается изотропный шум с нулевым средним значением:
дХх, t) = д{х - ш) + п{х, t). (14.26)
Это является самым общим подходом, поскольку мы не полагаемся на какой-
либо особый вид структуры уровней яркости. Выражение д(х- ut) свидетельствует
только о том, что произвольная пространственная структура движется с постоянной
скоростью и. Таким образом, функция с тремя параметрами д{х^, х^, t) сводится к
функции со всего лишь двумя параметрами д(х^ - u^t, x^-u^t). Далее мы
предполагаем, что частные производные функции шума не являются коррелированными друг
с другом или частными производными структур изображения. Поэтому мы
используем условия
^ = 0,
а частные производные равны
Vg =Vg-hVn д\ = -uS/g + Э,«,. (14.28)
Эти условия приводят к оценке оптического потока
п п =ст 5
р q п p-q^
0Л=О'
(14.27)
/ = u{VgVg^ +VrNn^y^VgVg\ (14.29)
Ключевым в понимании этого матричного уравнения является то, что
матрица шума VnVn^ является диагональной в любой системе координат из-за
условий, установленных уравнением (14.27). Следовательно, мы можем преобразовать
уравнение в систему координат с главными осями, в которой Vg Vgf ^ является
диагональной. Тогда получаем
г- _
/=«
9:
^+gI
О
о
^/+^«
9х
О
О
Если дисперсия шума не равна нулю, матрица, обратная к первой матрице,
существует всегда, и мы получаем
/ = «
9/^о1
О
О ^=^
9/
9/ +^„
(14.30)
14Л Тензорные методы 415
Это уравнение показывает, что оценка оптического потока отклоняется по
направлению к более низким значениям. Если дисперсия шума равна
приблизительно квадрату модуля градиента, то оценочные значения равны только половине
истинных значений. Таким образом, дифференциальный метод является примером
неустойчивого метода, поскольку он разрушается в зашумленных
последовательностях изображений.
Однако если шум является незначительным, то оценка оптического потока
является корректной. Этот результат находится в противоречии с широко
распространенным заявлением, что дифференциальные методы не дают точных
результатов, если пространственные структуры уровней яркости не могут быть
адекватно аппроксимированы рядом Тейлора первого порядка (см., к примеру, [189]).
Кеарней (Kearney) и др. [105], например, предоставили анализ градиентного
метода и сделали заключение, что он дает ошибочные результаты, как только
пространственные производные второго порядка становятся супхественными.
Эти противоречивые сведения разрешаются, если мы анализируем
дополнительные ошибки в оценке оптического потока, которые вносятся неадекватной
дискретизацией операторов частных производных (см. рассмотрение по
оптимальным дифференциальным фильтрам в разделе 12.4). Ошибка в оценке оптического
потока непосредственно связана с ошибкой в направлении дискретных
операторов градиента (сравните также рассмотрение по оценкам ориентации в разделе
13.3.6). Следовательно, точные оценки оптического потока требуют тщательно
оптимизированных дифференциальных операторов, таких, как
оптимизированные регуляризованные операторы градиента, рассмотренные в разделе 12.7.5.
14.4. Тензорные методы
Тензорный метод для анализа локальной ориентации уже детально обсуждался в
разделе 13.3. Поскольку движение образует локально ориентированные структуры
в пространственно-временных изображениях, все, что нам нужно сделать, это
расширить тензорный метод на трехмерный случай. Сначала мы вернемся к
оптимизационному критерию, используемому для тензорного подхода в разделе 14.4.1,
для того чтобы отделить этот метод от дифференциального метода (раздел 14.3).
14.4.1. Стратегия оптимизации
В разделе 13.3.1 мы сформулировали, что оптимальная ориентация описывается как
ориентация, которая проявляет наименьшие отклонения от направления
градиентных векторов. Мы ввели квадрат скалярного произведения градиентного вектора и
единичный вектор, представляющий локальную ориентацию, Я как адекватную меру:
{S/g'nf =1 Чд f cos' (Z(V£?,«)). (14.31)
Эта мера может использоваться в векторных пространствах любой
размерности. Для того чтобы определить ориентацию в пространственно-временных
изображениях, мы берем пространственно-временной градиент
V п = 1^ М ^^
и записываем
= \д.,9у^9,^ (14.32)
Глава 14. Движение
{V,,g'nf ^V^,gf cos'{Z(y^,g,n)).
Для анализа 2-D ориентации мы максимизировали выражение
ч2
(14.33)
\w{x-x)[Vg{xyn) dV = (Vg/i)', (14.34)
для того чтобы найти оптимальную ориентацию. Для анализа движения в
пространственно-временных изображениях нас интересует направление не максимальных,
а минимальных изменений уровней яркости. Обозначим эту ориентацию с
помощью единичного вектора 'ё^ = [е^^, е^^, е^^. Этот 3-D вектор, согласно рассуждениям
в разделе 14.2.4 (14.2), связан с 2-D вектором скорости соотношением
/=
1
(14.35)
•^33 1*^32,
По аналогии с уравнением (14.34) мы, следовательно, минимизируем
j w{x -x,t- О (V^,gf(x', ff ёз )'d"'x'd/' (14.36)
или в более компактном обозначении
{^.9%)
^ minimum.
(14.37)
Оконная функция w теперь также расширяется на временную координату и
определяет размер и форму окрестности вокруг точки [jc, t] ^, в которой усредняется ори-
ентацрш. Уравнение (14.37) нужно сравнить с соответствующим выражением,
которое минимизируется с помощью дифференциального метода (уравнение (14.16)):
{/^9 + 9.) ■ (14.38)
Обратите внимание на тонкую разницу между двумя оптимизационными
стратегиями уравнений (14.37) и (14.38). Обе стратегии являются задачами по методу
наименьших квадратов для определения скорости таким образом, что отклонение
от неразрывности оптического потока становится минимальным. Два метода,
однако, отличаются в параметрах, которые оцениваются. Оказывается, что оценка
3-D единичного вектора является так называемой полной задачей по методу
наименьших квадратов [84]. Этот метод больше подходит для задачи, поскольку все
компоненты пространственно-временного градиента должны иметь
статистические ошибки, а не только временную производную, как в уравнении (14.38).
По аналогии с рассуждением в разделе 13.3.1 мы можем заключить, что
определение оптического потока в пространственно-временном изображении
является эквивалентным нахождению собственного вектора F3 наименьшего
собственного значения Х^ структурного тензора /:
|- -,
\j=
9x9. 9х9у 9x9, \
9x9у 9у9у 9у9, 1'
9x9, 9у9, 9,9, \
(14.39)
где д д прир, q € {х, у, t} задается как
14.4. Тензорные методы
9p9,ix,t) = jw(x- X, t - t')g^ (x, t')g^ {x, t')u^xdt'. (14.40)
С этой точки зрения мы можем снова сравнить тензорный метод с
дифференциальным методом. В то время как тензорный метод, по существу, выполняет анализ
собственных значений симметричного тензора с помощью шести регуляризован-
ных произведений пространственных и временных производных,
дифференциальный метод использует те же произведения, но только пять из них. Таким образом,
дифференциальный метод пропускает д^ д^. Мы увидим в следующем разделе, что
этот дополнительный член дает возможность тензорному методу определять,
проявляет ли локальная окрестность постоянную скорость, или нет. Это не
представляется возможным при дифференциальном методе.
14.4.2. Анализ собственных значений
К сожалению, анализ собственных значений симметричного тензора 3 х 3 не
является таким простым, как для симметричного тензора 2 х 2. В двумерном случае мы
могли бы решить задачу на собственные значения непосредственно. В разделе 13.3.3
мы преобразовали три независимые компоненты симметричного тензора 2 х 2 в
три параметра: ориентация, инвариантная относительно поворота достоверность
и мера когерентности (раздел 13.3.4).
Симметричный тензор 3x3 теперь содержит шесть независимых компонент, и
нам нужно найти соответствующее число параметров, которые адекватно
описывают локальную структуру пространственно-временного изображения. И снова
полезным будет разложить эти шесть параметров в зависящие от поворота и
инвариантные относительно поворота параметры.
Как уже упоминалось, решение задачи на собственные значения не может быть
выполнено быстро. Оно требует подходящего численного алгоритма. Мы не будем
приводить детали этой задачи, поскольку она не является тривиальной, но она
является стандартной задачей вычислительной математики, для которой имеется
несколько эффективных решений [Пресс (Press) и др., 1992; Голуб (Golub) и ван
Лоан (van Loan), 1989]. Таким образом, мы будем полагать в дальнейшем, что
решили задачу на собственные значения и получили набор из трех ортонормирован-
ных собственных векторов и трех собственных значений. С помощью решения
задачи на собственные значения мы, по существу, получили систему координат с
главными осями, в которой структурный тензор является диагональным и
содержит собственные значения в качестве диагональных элементов:
/'=
я, о о
о А^ о
О О Х^
(14.41)
Без ограничения общности собственные значения упорядочиваются в
порядке убывания:
\>Х^>Х,>0. (14.42)
Система координат с главными осями образуется с помощью собственных
векторов. Поворот в эту систему координат требует трех независимых параметров,
что мы и рассмотрели в разделе 7.2.2. Таким образом, три из щести параметров ис-
Глава 14. Движение
пользуются для описания ее ориентации в пространственно-временной области. Эта
информация содержится в трех ортонормированных собственных векторах.
Остающиеся параметры являются тремя инвариантными относительно
поворота собственными значениями. Теперь мы покажем, как различные классы
локальных структур в пространственно-временных изображениях могут
дифференцироваться с помощью значений трех собственных значений. Этот подход поможет
нам также осуществить эффективное выполнение анализа на основе тензора.
Можно вьщелить четыре различных класса в пространственно-временном
изображении в соответствии с рангом от О до 3 для структурного тензора:
Постоянный уровень яркости. Все элементы и собственные значения
структурного тензора равны нулю:
Я^=Я2=/1з=0. (14.43)
Ранг тензора также равен нулю. Поэтому скорость не может быть получена
вообще. Это условие легко понять. Сумма собственных значений должна быть ниже
критического уровня, определяемого уровнем шума в последовательности
изображений. Поскольку сумма собственных значений равна следу тензора, никакого
анализа собственных значений не требуется для выяснения этого условия:
trace(/) = Y,3p9p < Г, (14.44)
р=\
где 7 — подходящая мера для уровня шума в последовательности изображений.
Для всех точек, где выполняется условие (14.44), анализ собственных значений
можно полностью пропустить.
Пространственная ориентация и постоянное движение. В этом случае два
собственных значения равны нулю, поскольку уровни яркости изменяются только в
одном направлении:
Ai>0 и Я2=/1з=0. (14.45)
Ранг тензора равен единице. Пространственная структура уровней яркости
проявляет линейную симметрию. Это условие можно опять легко определить без
выполнения анализа собственных значений, поскольку определитель главного
подтензора 2x2 должен быть ниже пороговой величины 7^:
9.9.9у9у-9.9у <У . (14.46)
Собственный вектор F,, относящийся только к ненулевому (т.е. наибольшему)
собственному значению, ориентирован по направлению максимального
изменения уровней яркости. Таким образом, он задает как пространственную
ориентацию, так и скорость в этом направлении. Обратите внимание, что может быть
получена только нормальная скорость, т.е. скорость в направлении пространственного
градиента, по причине апертурной проблемы (раздел 14.2.2). Пространственная
ориентация задается двумя пространственными координатами собственного вектора
F, наибольшего собственного значения. Поскольку оптический поток имеет это
направление, он задается как
f = f!l
^2 . „2
(14.47)
a модуль нормального оптического потока сводится к
14.4. Тензорные методы
Распределенная пространственная структура и постоянное движение. В этом
случае только одно собственное значение равно нулю:
\,Х^>0 и Дз=0- (14.49)
Поскольку движение является постоянным, система координат с главными
осями движется со сценой. Собственный вектор 1^ с нулевым собственным
значением имеет направление постоянных уровней яркости в
пространственно-временной области. Таким образом, оптический поток задается как
f-^
^г,
^3.
(14.50)
а его модуль как
Распределенная пространственная структура и непостоянное движение. В этом
случае все три собственных значения больше, чем ноль, а ранг тензора равен трем:
?i,,X^,l,>Q. (14.52)
Никакой полезной оценки оптического потока не может бьпъ получено в этом случае.
После этой детальной классификации вернемся к вопросу о том, какие три
инвариантные относительно поворота параметра могут быть вьщелены из
структурного тензора для получения полезного описания локальной структуры, не зависящего
от скорости и пространственной ориентации параметров шкалы яркости.
Мера достоверности. Первым параметром является снова мера достоверности,
которая определяет меру изменений уровней яркости. У нас есть две
возможности. Мы можем взять либо среднеквадратичный пространственный градиент (след
верхнего подтензора 2x2), либо среднеквадратичный пространственно-временной
градиент. С практической точки зрения среднеквадратичный пространственный
градиент должен быть предпочтительнее, поскольку он не изменяется в
последовательности, если скорость увеличивается. Среднеквадратичный пространственный
градиент, однако, увеличивается с ростом скорости, поскольку добавляется более
высокий временной градиент. Таким образом, среднеквадратичный
пространственный градиент является лучшей мерой достоверности:
Сс=9.9. + 9у9у' (14.53)
Пространственная мера когерентности. В качестве второй меры возьмем уже
известную меру когерентности из анализа 2-D локальных окрестностей (раздел
13.3.4) и обозначим ее здесь как пространственную меру когерентности:
(9.9.-9у9У+49.9
у/ ZfxZfy
с^ = 1 ' ——. (14.54)
(9.9. + 9у9у)
Ее значение находится между О и 1 и решает, можно ли определить только
нормальный оптический поток или обе компоненты оптического потока.
Глава 14. Движение
Полная мера когерентности. И наконец, нам нужна дополнительная мера,
которая свидетельствует о том, встретилась ли нам локальная окрестность с
постоянной скоростью, или нет. Эта мера должна быть независящей от
пространственной когерентности. Следующая мера, использующая наибольшие и наименьшие
собственные значения, удовлетворяет этому условию:
^г =
(14.55)
Полная мера когерентности равна единице, как только собственное
значение Aj равно нулю. Другие два собственных значения могут тогда принимать
любые другие значения. Полная когерентность достигает нуля, если все три
собственных значения равны нулю. В отличие от других двух мер, с^ и с^, полная
когерентность требует анализа собственных значений, поскольку для ее
вычисления необходимы наименьшие и наибольшие значения. Существует одно
предостережение, связанное с этой мерой: она также равна единице при
пространственно-ориентированной структуре и непостоянном движении. Однако этот частный
случай может быть распознан из условия, что и пространственная, и полная
когерентности равны единице, но что только одно собственное значение равно
нулю. Еще одним простым критерием является то, что собственный вектор к
нулевому собственному значению лежит в плоскости ху. Это подразумевает, что
^33 = О, так что, согласно уравнению (14.50), мы получили бы бесконечное
значение для вектора оптического потока.
14.5. Корреляционные методы
14.5.1. Принцип
Как и в случае с дифференциальным методом, корреляционный метод является
подходом, который возникает из анализа перемещения между двумя
последовательными изображениями. Для того чтобы найти характеристический признак из
первого изображения во втором изображении, мы берем первое изображение
gif) = 01 и сравниваем его со вторым изображением g(t^ = 92^ пределах
определенного диапазона поиска. В пределах этого диапазона мы ищем положение
оптимального подобия между двумя изображениями. Когда мы считаем два признака
подобными? Мера подобия должна быть устойчива к изменениям в
освещенности. Таким образом, две пространственные структуры признаков подобны, если они
отличаются только на постоянный коэффициент а, который отражает разницу в
освещенности. На языке векторных пространств с внутренним произведением это
означает, что два вектора признаков д^ и д^ параллельны. Это может выполняться
тогда и только тогда, когда имеет место равенство в неравенстве Коши—Шварца
I оо 1^ оо
J 9х (х)д2 (х - s)d'x\ < J gff (x)d^x j gl (лг - s)A^x. (14.56)
|—oo I —oo —oo
Другими словами, нам нужно максимизировать коэффициент взаимной корреляции
14.5, Корреляционные методы 421
ф) =
\g,{x)g^{x-s)6'x
\ gl{x)d^x\ gl{x-s)&^x
ч1/2
(14.57)
J
Коэффициент взаимной корреляции является полезной мерой подобия. Она
равна нулю при полностью неподобных (ортогональных) структурах и достигает
максимума, равного единице при подобньис признаках.
Так же как и для дифференциального метода (раздел 14.3), коррел5Щионный
метод может быть выполнен с помощью комбинирования свертки и точечных
операций. Первый шаг должен ввести оконную функцию w в определение коэффициента
взаимной корреляции. Это окно перемещается по изображению для вычисления
локального коэффрщиента взаимной корреляции. Тогда уравнение (14.57) становится
r{x,s) = -
J w{x - х)д^ (х)д2 (х - s)dh'
ч1/2
1 w(x - x')gf (jc')d^/ j w(x - x)gl {x - s)di^x
—oo —oo
или в более компактной форме записи, уже использованной в разделах 14.3.2 и 14.4.1:
(14.58)
r{x,s) =
g,{x)g^{x-s)
-il/2
gl{x)gl{x-s)\
—> maximum.
(14.59)
Результирующий коэффициент взаимной корреляции является
четырехмерной функцией, зависящей от положения на изображении х и сдвига s.
14.5.2. Быстрый итерационный поиск максимума
Очевидно, что корреляционный метод, согласно рассмотренному до сих пор,
является очень дорогостоящей операцией. Значительное ускорение можно получить,
если мы ограничим вычисление быстрым подходом к поиску положения
максимума г, поскольку это все, что нас интересует.
Одним из способов прямого вычисления положения максимума является
аппроксимация функции взаимной корреляции рядом Тейлора. Разложим коэффициент
взаимной корреляции в разложение Тейлора второго порядка в положении максимума 5,
+^xv(^)('^l"^l)('^2~^2)
где Н— матрица Гессе, введенная в уравнении (12.6).
(14.60)
Глава 14. Движение
Нам неизвестно положение максимума коэффициента корреляции. Таким
образом, полагаем, что производные второго порядка являются
постоянными, достаточно близкими к положению максимума, и вычислим его в
положении предыдущей итерации 5^'^ Если у нас нет другой информации, то мы
устанавливаем начальную оценку равной нулю: s^^^ = 0. Пока мы еще не нашли
положение максимума коэффициента корреляции, будет существовать
остаточное отклонение в 5^'\ которое можно вычислить с помощью взятия
производной (14.60):
Vr{s^'^) = H{s^'^){s^'^ -S). (14.61)
При условии, что матрица Гессе является обратимой, мы получаем
следующую итерацию:
^(/^1) ^ ^(0 -H-'is^'^y^ris^^) при s^'^ = 0. (14.62)
Этот вид итерации известен как итерация Ньютона-Рафсона [158]. Для того
чтобы вычислить сдвиг, нам нужно вычислить только первые и вторые частные
производные от коэффициента взаимной корреляции.
14.5.3. Оценка и сравнение
В отличие от дифференциальных методов, которые основываются на
неразрывности оптического потока, корреляционный подход нечувствителен к
изменениям интенсивностей между двумя изображениями. Это делает
корреляционные методы очень полезными для обработки стереоизображений, где всегда
возникают незначительные изменения интенсивности между левым и правым
изображениями из-за двух используемых различных камер. В
действительности быстрый поиск максимума, описанный в разделе 14.5.2, является
стандартным подходом для определения стереонесоответствия. Квам (Quam) [160]
использовал его с «груботочной» стратегией контроля, а Нишихара (Nishihara)
[146] — в модифицированной версии, берущей знак лапласиана от гауссиана
как признак. Он представил точность разрешения приблизительно 0,1 пикселя
для малых перемещений. Геллес (Gelles) и др. [58] измерили движения в клетках с
точностью приблизительно 0,02 пикселя, используя корреляционный метод.
Однако они использовали более дорогостоящий подход, вычисляя центроид
ограниченной функции взаимной корреляции. Подход на основе использования модели
Диля (Diehl) и Буркхардта (Burkhardt) [35] может быть понят как расширенный
корреляционный подход, поскольку он учитывает также вращение и другие
формы движения.
Корреляционный метод отличается от всех других методов, рассмотренных в
этой работе, тем, что он концептуально основывается на сравнении только двух
изображений. Даже если мы расширим корреляционный метод с помощью
множественных корреляций до более чем двух кадров, он останется дискретным
подходом с дискретным шагом. Таким образом, ему недостает элегантности других
методов, которые были сформулированы в непрерывном пространстве, до того
как они выполнялись для дискретных изображений. Кроме того, очевидно, что
расширение до группы кадров будет слишком дорогостоящим с вычислительной
точки зрения.
14.6. Фазовый метод
14.6. Фазовый метод
14.6.1. Принцип
За исключением дорогостоящего корреляционного метода, все другие методы,
которые вычисляют оптический поток, являются более или менее чувствительными к
временным изменениям освещенности. Таким образом, мы ищем признак,
который содержит важную информацию в изображениях относительно анализа
движения. Флит (Fleet) и Эпсон (Jepson) [51] и Флит [48] предложили использование фазы
для вычисления оптического потока. Мы уже обсудили решающую роль фазы в
разделах 2.3.5 и 13.4.1. В разделе 2.3.5 мы продемонстрировали, что фаза
преобразования Фурье сигнала несет существенную информацию. Изображение можно все еще
распознать, когда потеряна информация об амплитуде, но не когда потеряна фаза
[124]. Глобальное освещение изменяет амплитуду сигнала, но не его фазу.
В качестве введения в фазовый метод рассмотрим плоскую 1-D волну с
волновым числом к и частотой v, распространяющуюся с фазовой скоростью и - v/k:
g{x,t) = д^ ехр[-2л:1(0(л:,О)] = д^^^^[-2п\{кх-у()\ (14.63)
Положение и, таким образом, также перемещение задается фазой. Фаза
зависит как от пространственных, так и от временной координат. Для плоской волны
фаза изменяется линейно во времени и пространстве:
ф(х,0 = 27г(кх -vt) = 27г(кх -ukt), (14.64)
где /: и V являются волновым числом и частотой структуры соответственно.
Вычисление временной и пространственных производных от фазы, т.е.
пространственно-временной градиент, дает и волновое число, и частоту движущейся
периодической структуры:
'к
^J =
= 2;г
-V
Тогда скорость задается как отношение частоты к волновому числу:
к
(14.65)
(14.66)
Эта формула очень похожа на оценку на основе оптического потока
(уравнение (14.11)). В обоих случаях скорость задается как отношение временной и
пространственных производных. Прямое вычисление частных производных по
фазовому сигналу не рекомендуется из-за свойственных разрывов в фазовом сигнале
(ограничение до основного интервала [-я, я[). Как мы рассмотрели в разделе 13.4.6,
возможно вычислить фазовые градиенты прямо по выходным данным пары
квадратурных фильтров. Если мы обозначим пару квадратурных фильтров с помощью
р(х, t) и q{x, О, то пространственно-временной фазовый градиент задается как
(сравните с уравнением (13.52))
V,,^(x,0=^^^'^^^-f'^t''T^''^'''^- (14.67)
p\x,t) + q\x,t)
Используя уравнение (14.66), фазовый получаемый оптический поток/равен
/ = ■
ря, - т
РЧ. - 1Р.
(14.68)
Глава 14, Движение
14.6.2. Оценка и сравнение
На первый взгляд кажется, что фазовый метод не предлагает ничего нового.
Однако замена уровня яркости фазой является значительным усовершенствованием,
поскольку фаза гораздо меньше зависит от освещенности, чем уровень яркости
сам по себе. При использовании только фазового сигнала амплитуда изменений
уровней яркости может меняться без влияния на оценки скорости вообще.
До сих пор мы только рассматривали идеальную структуру уровней яркости.
Как правило, изображения состоят из структур уровней яркости с разными
волновыми числами. Из такой структуры мы не можем получить полезные фазовые
оценки. Следовательно, нам нужно разложить изображение на множество диапазонов
волновых чисел.
Это подразумевает, что фазовый метод не является подходящим для
обработки двумерных сдвигов. Это, по существу, 1-D понятие, которое измеряет
движение линейно-ориентированной структуры, например плоской волны, в
направлении градиентов уровней яркости. Из этого факта Флит (Fleet) и Эпсон (Jepson)
[50] получили новую парадигму для анализа движения. Изображение
раскладывается с помощью направленных фильтров, и в каждом из компонентов
определяются нормальные скорости.
2-D поле движения тогда составляется из этих нормальных скоростей. Этот
подход имеет преимущество в том, что композиция для полного поля движения
откладывается на второй шаг обработки, который может быть приспособлен к врщу
движения, имеющего место в изображениях. Следовательно, этот подход может
также обрабатывать более сложные случаи, такие, как наложение прозрачных
объектов при дврокении.
Флит и Эпсон [50] используют набор фильтров Габора (раздел 13.4.5) с угловым
разрешением 30° и шириной полосы 0,8 октавы для направленного разложения.
В качестве альтернативы можно использовать полосовое разложение и фильтр
Гильберта (раздел 13.4.2). Мотивацией для этой идеи служит то, что разложение с
набором фильтров Габора, согласно методу, предложенному Флитом и Эпсоном,
не позволяет легко реконструировать исходное изображение. Передаточные
функции ряда фильтров Габора не сводятся к единичной передаточной функции, но
проявляют колебания, согласно данным Римера (Riemer) [169].
Полосовое разложение, к примеру использование пирамиды Лапласа [18.19],
не разделяет этот недостаток (раздел 5.2.3). К тому же оно является более
эффективным с вычислительной точки зрения. Однако мы сталкиваемся с проблемой,
состоящей в том, что никакое направленное разложение не получено.
Яне (Jahne) [86, 87] показал, как понятие пирамиды Лапласа может быть
эффективно расширено в направленно-пирамидальное разложение. Каждый уровень
пирамиды далее раскладывается на две или четыре направленные компоненты,
которые непосредственно сводятся к соответствующему изотропно
отфильтрованному уровню пирамиды (см. также раздел 5.2.4).
14.6.3. От нормального потока к 2-D потоку
Поскольку фазовый метод определяет только нормальный оптический поток,
требуется метод для определения двумерного оптического потока по нормальному
потоку. Основное соотношение между нормальным и 2-D потоком является еле-
14,7. Дополнительные методы
дующим. Положим, 4Tof^ является нормальным вектором потока. Он является
результатом проекции 2-D вектора потока/в направлении нормального потока.
Таким образом, мы можем записать:
Л=7х/. (14.69)
где /l - единичный вектор в направлении нормального потока. Из уравнения (14.69)
- очевидно, что мы можем определить неизвестный 2-D оптический поток по
методу наименьших квадратов, если у нас есть больше, чем одна оценка нормального
потока в различных направлениях. Подобным образом, как в разделе 14.3.2, этот
подход приводит к линейной системе уравнений
JLxJLx JLxJl
LxJ Ly
JlxJlv JlvJi
LyJLy
/2
J LxJ 1.
J LxJ 1.
при
Л.Л. = J>v(:c - xV - OA,A,d^^'dr'
14.7. Дополнительные методы
(14.70)
(14.71)
(14.72)
14.7.1. Дифференциальные методы второго порядка
Основной недостаток дифференциального метода первого порядка в том, что нераз-
рьгоность оптического потока определяет только одно ограничение для двух
неизвестных компонент скорости (раздел 14.3.1). До сих пор мы могли компенсировать
этот недочет с помощью моделирования скорости и, таким образом,
использования всей окрестности для определения одной оценки вектора оптического потока
(раздел 14.3.2).
Альтернативный подход заключается в использовании множественных
изображений признаков или многоканальных изображений. Тогда мы можем иметь
два или более независимых ограничения в одном и том же месте и, таким образом,
можем определить обе компоненты оптического потока в отдельной точке.
Однако существенным моментом является то, что новый признак должен внести
действительно новую информацию в изображение. Она не поможет вообще, если
новый признак тесно связан с уже используемыми.
Таким образом, мы приходим к важному обобщению дифференциального
метода. Мы можем применить любую предварительную обработку к последовательностям
изображений или вьщелить произвольные изображения признаков и применить все
методы, рассмотренные до сих пор. Если неразрывность оптического потока
сохраняется для исходного изображения, то она сохраняется также для любого
изображения признака, полученного из исходного изображения. Мы можем применять
нелинейные точечные операторы так же, как любой оператор над соседними элементами.
Рассмотрим сначала метод Джайроси (Girosi) и др. [59]. Они применили
неразрывность оптического потока к двум изображениям признаков, а именно к
горизонтальной и вертикальной пространственным производным:
Глава 14. Движение
f^gy+gy, = 0.
Использование горизонтальных и вертикальных дифференцированных
изображений, таким образом, приводит к дифференциальному методу второго
порядка с решением
(14.73)
f = -H~Wg,, если detH^O,
(14.74)
д^
дхх
дху
ду
д^^
дуу \
=-
д,
д^,
ду,
где Н— матрица Гессе, как и определено в уравнении (12.6).
Если мы также учитываем стандартное уравнение оптического потока, мы
окончательно приходим к переопределенной линейной системе уравнений с тремя
уравнениями и двумя неизвестными:
(14.75)
В этом отношении объединение изображений, полученных от разных
датчиков, может быть перспективным методом. Маркэнди (Markandey) и Флинчбауф
(Flinchbaugh) [130], к примеру, использовали многоспектральное формирование
изображений, одно видимое и одно ИК-изображения. Обработка
последовательностей изображений сцен, освещаемых с помощью источников света из разных
направлений, была изучена Вудхамом (Woodham) [220]. Этот подход является
особенно интересным, поскольку он имеет потенциальную возможность для
определения зеркальных отражений и, таким образом, исключения важного источника
ошибок в оценивании движения.
14.7.2. Дифференциальное геометрическое моделирование
Рассуждения в последних разделах явно показали, что пространственная
структура уровней яркости обусловливает определение движения. Дифференциальный
метод первого порядка не учитывает адекватно этот основной факт, поскольку мы
основывались только на первых пространственных производных.
Дифференциальные методы второго порядка обеспечивают прямое решение при условии, что
матрица Гессе может обращаться (уравнение (14.73)). В этом разделе мы подходим
к дифференциальным методам с другой точки зрения, используя
дифференциальную геометрию. Мы полагаем, что структура уровней яркости в двух
последовательных изображениях отличается только на постоянное перемещение s\
g{x-\l2sj,) = g{x^-\l2sj^). (14.76)
Этот подход является еще одной формулировкой уравнения неразрывности,
предполагающей только перемещение изображения и пренебрегающей каким-
либо вращением или деформацией поверхностных элементов. Мы просто
полагаем, что поле скоростей не изменяется в малой окрестности. Ради симметрии
мы делим перемещение поровну между двумя изображениями. Предположив, что
вектор перемещения s и размер поверхностного элемента малы, мы можем
разложить уровень яркости в обоих изображениях в точке дс=О в ряд Тейлора. Сначала
14,7, Дополнительные методы
рассмотрим разложение первого порядка, т.е. аппроксимируем распределение
уровней яркости плоскостью:
gf(x±l/25) = Sfo+Vgf-(A:±l/25). (14.77)
Плоскости в обоих изображениях должны быть тождественны, за
исключением перемещения s. Упорядочим слагаемые в уравнении (14.77) по
возрастанию степеней дс, для того чтобы иметь возможность выполнить сравнение
коэффициентов
gf(jc±l/25) = gfo±l/2Vgf5+ Vgx. (14.78)
смещение наклон
Первый и второй члены содержат смещение и наклон плоскости
соответственно. Теперь мы можем оценить перемещение s^ip^qYva условия, что обе
плоскости должны быть тождественны. Следовательно, два коэффициента должны быть
тождественны, и мы получаем два уравнения:
g,it,)-gM = l/2(Vg(t,) + Vg(t,))s,
VgrCO = V0(/,). ^^^-^^^
Второе уравнение утверждает, что градиент должен быть равным в обоих
изображениях. В противном случае соответствие плоскости
пространственного уровня яркости не кажется пригодным представлением. Первое уравнение
соответствует неразрывности оптического потока (14.9). В уравнении (14.79)
временная производная выражается дискретным образом как разность
средних уровней яркости в обоих изображениях. Еще одно уточнение также
обусловливается преобразованием в цифровую форму по времени. Градиент
заменяется средним градиентом обоих изображений. Кроме того, мы используем
поле вектора перемещения (ПВП) s вместо оптического потока/. Как и
ожидалось, соответствие плоскости распределения уровней яркости не дает ничего
нового. Мы по-прежнему можем только оценить компоненту скорости в
направлении градиента уровня яркости.
Следовательно, разложение в ряд Тейлора уравнения (14.76) до второго
порядка дает
g{x±l/2s) = д,
+ g^-(x±\/2s,) + g^-(y±l/2s,)
+ l/2g^-(x±\/2sy+l/2g^-(y±l/2s,f
+ g^-(x±V2s,)(y±l/2s,).
Нагель (Nagel) [142] выполнил очень схожее моделирование геометрии
уровня яркости, разложив его в ряд Тейлора до второго порядка. Однако он
получил довольно сложные нелинейные уравнения, которые могут быть легко
решены только для особых условий. Он назвал их угол уровня яркости и экстремум
уровня яркости. Причина разных результатов заключаются в подходе к
решению. Нагель (Nagel) сравнивает разложение Тейлора в двух изображениях в
смысле наименьших квадратов, в то время как здесь выполняется
непосредственное сравнение коэффициентов.
Сравнение коэффициентов разложения второго порядка приводит, в общем,
к шести уравнениям. Квадратичные члены дают три уравнения, которые утвер-
Глава 14. Движение
ждают, что все вторые пространственные производные должны совпадать в
обоих изображениях:
9:^(0 =
9yy(tl) --
9^{Ч) --
'- 9ЛЧ\
= 9yy{h\
-- 9^it2)-
Если это не выполняется, то либо разложение второго порядка для
распределения уровней яркости не соответствует адекватно распределению уровней
яркости, либо предположение о постоянном перемещении в окрестности не является
верным. Сравнение коэффициентов членов нулевого и первого порядков
приводит к следующим трем уравнениям:
-(5'o(^2)-5'o(^i)) = ^{9Ah) + 9M)s,
<9ЛЧ)-9ЛЧ))
<9y(t2)-9y(0)
+-(9yit^) + 9yit,))s„
9хх^1+9ху^2'
9yyS2-^9^s^.
(14.81)
Удивительно, но сравнение коэффициентов для члена нулевого порядка
(смещение) приводит к такому же результату, как соответствие плоскости (14.79). Это
означает, что ПВП вьиисляется корректно с помощью простого соответствия
плоскости, даже если распределению уровней яркости больше не соответствует
адекватно плоскость, а соответствует многочлен второго порядка.
Два других уравнения образуют простую линейную систему уравнений с двумя
неизвестными:
9хх 9:
9
ху
ху
1уу
^9у(О-9у(0
(14.82)
Мы можем легко обратить левую матрицу 2x2, как мы обращали матрицу, при
условии, что д^д - (д У не обращается в ноль. Следовательно, возможно
оценить перемещение между двумя изображениями по локальной окрестности, если
мы примем во внимание кривизну распределения уровней яркости. Мы еще не
обсудили условия, которым должно удовлетворять распределение уровней яркости,
для того чтобы уравнение (14.81) являлось обратимым. Это выполняется, если
встречается либо экстремум уровня яркости, либо угол уровня яркости. Как уже
упоминалось, эти термины придумал Нагель (Nagel) [142]. В экстремуме уровня
яркости (так же как в седловой точке) обе главные кривизны не равны нулю. Таким
образом, уравнение (14.82) может быть решено. В угле уровня яркости только одна
главная кривизна равна нулю, но градиент в этом направлении не равен нулю.
Таким образом, первое и второе уравнения из уравнения (14.81) можно
использовать для определения обоих компонентов вектора оптического потока.
При дифференциальном геометрическом методе сглаживание не требуется,
поскольку используются вторые производные только в одной точке. Однако для
14.7. Дополнительные методы
более устойчивой оценки производных часто используются регуляризованные
дифференциальные операторы, как рассмотрено в разделе 12.7. Поскольку операции
свертки являются коммутативными, это сглаживание могло бы также
применяться после вычисления производных.
Разность в первых пространственных производных между двумя
изображениями в моменты времени t^vit^B правом векторе в уравнении (14.82) является
дискретной аппроксимацией временной производной, которая может заменяться
оператором временной производной. Тогда вектор перемещения должен заменяться
вектором оптического потока. Таким образом, непрерывная формулировка
дифференциального геометрического метода приводит к
9^
9ху
9ху\
9уу\
\л'
ш
9х,
9у,
(14.83)
14.7.3. Пространственно-временные модели энергии
Модели, использующие квадратурные фильтры вида Табора (раздел 13.4.5),
являются общепринятыми в биологическом зрении. Они являются основой для так
называемых пространственно-временных моделей энергии [1, 2, 75]. Этот термин
можно запросто неправильно понять. Это не кинетическая энергия движущихся
объектов, которая с ними связывается, а энергия (квадрат амплитуды) сигнала в
датчике в определенном интервале ксо. Здесь мы хотим сравнить этот тип модели с
дифференциальным методом, рассмотренным ранее.
Одна из простейших моделей для зрительного восприятия 1-D движения
использует только три квадратурных фильтра. Этот набор направленных фильтров
обнаруживает объекты, движущиеся вправо или влево, и объекты, которые не
движутся. Обозначим квадрат величины этих квадратурных операторов с помощью ^
LviS. Тогда мы можем получить оценку 1-D оптического потока с помощью
использования оператора [1,2]:
г)^— . (14.84)
S
Можно определить интересную взаимосвязь этого подхода с
дифференциальным методом (раздел 14.3.2), так что дифференциальный метод можно также
понимать как метод вьщеления энергии.
Мы выполняем это сравнение здесь для анализа 1-D движения, т.е. в 2-D
пространственно-временном изображении. В этом случае решение дифференциального
метода можно записать в операторной форме записи, согласно уравнению (14.25), как
(14.85)
Перепишем это уравнение с незначительной модификацией для сглаживания
изображений с биномиальной маской (В^^, прежде чем применять
дифференциальные операторы, т.е. воспользуемся регуляризованным дифференциальным
оператором (раздел 12.7):
v=-
®хД(®А)-(®А)]
(14.86)
430 Глава 14. Движение
Сглаживание с (В^ означает регуляризацию дифференциального оператора.
Индексы xt указывают, что сглаживание выполняется вдоль как временной, так и
пространственных осей. Используя операторное тождество
A(B = U{A + (Bf -iЛ-фf^^
(14.87)
и сокращения
<г?,' = (Ф,+©,)«,„ £' = (Ф,-Ф,)С8,„ У = 2©,<8„, (14.88)
мы можем переписать уравнение (14.86) и получаем выражение, очень похожее на
уравнение (14.84):
(Bi^'-<lC-L'-L')
"' -. (14.89)
V' = --
Фильтры <!R^, £'и У являются регуляризованными дифференциальными филь
трами. Передаточные функции показывают, что выбираются объекты, движущие
Рис. 14.13. Передаточные функции для операторов свертки (14.88) для обнаружения
объектов, движущихся вправо или влево или находящихся в состоянии покоя: а -
(гСб-£';в-У
14.8. Упражнения 431
ся вправо, влево и находящиеся в состоянии покоя. Эти фильтры не являются
квадратурными фильтрами. Возведение в квадрат откликов фильтров и дальнейшее
сглаживание с <В^^, однако, приблизительно приводит к независящему от фазы
определению квадрата амплитуды, как в случае с квадратурным фильтром при
определенных условиях. Давайте предположим мелкомасштабную периодическую
структуру. Дифференциальные фильтры будут сохранять эти структуры, но
удалять средний уровень яркости. Последовательное возведение в квадрат
результатов фильтров с нулевым средним значением приводит к среднему уровню яркости
со значением половины квадрата амплитуды изменений уровней яркости и
быстрому пространственному колебанию уровней яркости с двойным волновым
числом (половина длины волны). Если последовательное сглаживание удаляет эти
быстрые колебания, то получается независящий от фазы отклик на фильтр, так же
как в случае с квадратурным фильтром. В отличие от квадратурных фильтров, этот
результат может достигаться только в областях, где размеры структур являются
настолько мелкими, что удвоенное волновое число может удаляться с помощью
сглаживающего фильтра.
14.8 Упражнения
14.1: Точность анализа движения
Интерактивная демонстрация точности некоторых методов для
определения поля движения с использованием тестовых последовательностей с
известными значениями скорости, выходных результатов ошибок,
исследования влияния шума и временной субдискретизации (dip6exl4.01).
14.2: Анализ движения
Интерактивная демонстрация различньос методов для анализа движения на
примере реальных последовательностей изображений (dip6exl4.02).
14.3: ^'^Ускоренное движение
При ускоренном движении уравнение неразрывности оптического потока
можно расширить следующим образом:
(f+at)S/g + g,=0.
1. Сформулируйте переопределенную линейную систему уравнений для
оптического потока/и ускорения а (4 параметра в 2-D изображениях) с
помощью подхода, подобного изложенному в разделе 14.3.2.
2. Покажите, что невозможно определить ускорение, если
последовательность содержит только два изображения.
14.4: "^"^Дифференциальный метод второго порядка
Дифференциальный метод второго порядка определяет оптический поток
без дополнительного усреднения по уравнению (14.74). При каких
структурах уровней яркости возможно определить оптический поток по
уравнению (14.74) однозначно? Покрывает ли метод все типы структур уровней
яркости второго порядка, при которых принципиально возможно
определить полный вектор оптического потока?
Глава 14. Движение
14.9. Дополнительная литература
Доступны следующие монографии по анализу движения: Синг (Singh) [189],
Флит (Fleet) [49] и Яне (Jahne) [88]. Хороший обзор анализа движения можно
также найти в обзорных статьях Беаухемина (Beauchemin) и Баррона (Barron)
[7] и Яне (Jahne) и Хаусекера (HauBecker) [93, глава 10]. Последняя статья
также включает оценивание полей движения более высокого порядка. Читатели,
заинтересованные в визуальном определении движения в биологических
системах, отсылаются к монографии, изданной под редакцией Смита (Smith) и
Сноудена (Snowden) [190]. Расширение анализа движения до оценивания
параметров динамических процессов и изменения освещенности описываются в
работах Хаусекера (HauBecker) и Флита (Fleet) [73], Хаусекера (HauBecker) [72]
и Яне (Jahne) [91]. Методы для анализа различных типов сложного движения
рассматриваются в книге Яне (Jahne) и др. [88].
ГЛАВА 15
ТЕКСТУРА
15.1. Введение
в главах 11 и 12 мы изучали сглаживание и вьщеление контуров, а в главе 13 —
простые окрестности. В этой главе мы воспользуемся этими важными
строительными блоками и расширим их для анализа сложных структур, известных в обработке
изображений как текстура. В действительности текстуры наглядно показывают
разницу между искусственным миром объектов, чьи поверхности характеризуются
только их цветом и свойствами отражательной способности, и миром
формирования реальных изображений.
Наша зрительная система способна с легкостью распознавать и различать
текстуры, что можно увидеть из рис. 15.1. Оказывается, гораздо сложнее
охарактеризовать и вьщелить скорее «диффузные» свойства текстуры с помош;ью точно
определенных параметров, которые позволяют компьютеру выполнять эту задачу.
В этой главе мы методично исследуем операторы для анализа и проведения
различий между текстурами. Эти операторы способны описывать даже сложные
структуры с помощью всего лишь нескольких величин. Таким образом, мы
сводим задачу распознавания текстур к простой задаче различения уровней яркости.
Как мы можем описать текстуру? Произвольная структура, которая
распространяется на большую область в изображении, безусловно, не распознается как
текстура. Таким образом, основным свойством текстуры является малая
элементарная структура, которая повторяется периодически или квазипериодически в
пространстве, как рисунок на обоях. Таким образом, достаточно описать малую
элементарную структуру и правила повторения. Последние задают
характеристический размер текстуры.
Анализ текстуры можно сравнить с анализом структуры твердых тел -
тематикой, изучаемой в физике твердых тел, химии и минералогии. Физики в области
твердых тел должны определить повторяющуюся структуру и распределение
атомов в элементарной ячейке. Анализ структуры усложняется тем, что и структуры,
и периодическое повторение могут проявлять существенные случайные
флуктуации, что и показано на рис. 15.1.
Текстуры можно организовывать иерархическим образом, т.е. они могут
выглядеть совершенно по-разному при различных масштабах. Хорошим примером
является занавеска, показанная на рис. 15.1, а. В самом мелком масштабе наше
внимание фокусируется на отдельных нитях (рис. 15.2, а). Тогда
характеристическим размером является толщина нитей. Они также имеют преобладающую
локальную ориентацию. На следующем, более грубом уровне мы распознаем петли сети
(рис. 15.2, б). Характеристический размер здесь показывает размер петель. На этом
уровне локальная ориентация является хорошо распределенной. И наконец, на
Глава 15. Текстура
Рис. 15.1. Примеры текстур: а - занавеска; б — дерево; в - собачий мех; г -
древесностружечная бумага; д — е — одежда
еще более грубом уровне мы больше не распознаем отдельные петли, но
наблюдаем складки занавески (рис. 15.2, г). Они характеризуются еще одним
характеристическим размером, показывающим период складок и их ориентацию. Эти
рассуждения подчеркивают важность многомасштабного текстурного анализа. Таким
образом, многомасштабные структуры данных, на что и указывалось в первой
части этой книги (глава 5), являются существенными для текстурного анализа.
Как правило, два класса текстурных параметров представляют важность.
Текстурные параметры могут быть или не быть инвариантными относительно
75.1. Введение
Рис. 15.2. Иерархическая организация текстуры, продемонстрированная посредством
представления изображения занавески на рис. 15.1, л при различных разрешениях
поворота и масштаба. Эта классификация обусловливается задачей, которую мы
должны выполнить.
Представьте типичную промышленную или научную задачу, в которой мы
хотим распознать объекты, которые случайно ориентированы в изображении.
Нас не интересует ориентация объектов, но интересует их отличие друг от
друга. Следовательно, текстурные параметры, которые зависят от ориентации, не
представляют интереса. Мы могли бы по-прежнему использовать их, но только
если объекты имеют форму, которая затем позволит нам определить их
ориентацию. Мы можем использовать подобные аргументы для признаков,
инвариантных относительно масштаба. Если интересующие нас объекты
расположены на различных расстояниях от камеры, текстурный параметр, используемый
для их распознавания, должен быть также инвариантным относительно
масштаба. В противном случае распознавание объекта будет зависеть от расстояния.
Однако если текстура изменяет свои характеристики в зависимости от
масштаба, как в примере с занавеской на рис. 15.1, а, текстурные признаки,
инвариантные относительно масштаба, могут не существовать вообще. Тогда
использование текстур для характеризации объектов на различных расстояниях
становится сложной задачей.
В вышеприведенных примерах нас интересовали объекты сами по себе, а
не их ориентация в пространстве. Ориентация поверхностей является
ключевым признаком для другой задачи обработки изображений — реконструкции
трехмерной сцены по двумерному изображению. Если мы знаем, что
поверхность объекта показывает однородную структуру, мы можем анализировать
ориентацию и размеры текстуры для нахождения ориентации поверхности в
пространстве. Для этого необходимы характеристические размеры и
ориентации текстуры.
Текстурный анализ является одной из тех областей в обработке изображений,
которой все еще недостает фундаментальных знаний. Поэтому литература
содержит много различных эмпирических и полуэмпирических подходов к
текстурному анализу. Здесь эти подходы не повторяются. Противоположно представляется
довольно простой подход к текстурному анализу, который строит сложные
текстурные операторы по элементарным операторам.
Для текстурного анализа используются только четыре фундаментальных
текстурных оператора:
• среднее значение;
• дисперсия;
Глава 15. Текстура
• ориентация;
• масштаб,
которые применяются на различных уровнях иерархической структуры
последовательности обработки изображений. Раз мы, скажем, вычислили локальную
ориентацию и локальный масштаб, оператор усреднения и оператор дисперсии
можно применять снова, но на этот раз не к среднему значению и дисперсии уровней
яркости, а к локальной ориентации и масштабу.
Эти четыре основных текстурных оператора можно сгруппировать в два класса.
Среднее значение и дисперсия являются независящими от поворота и масштаба, в
то время как операторы ориентации и масштаба только определяют ориентацию и
масштаб соответственно. Это важное разделение между параметрами,
инвариантными или неинвариантными относительно масштаба и поворота, значительно
упрощает текстурный анализ. Значение этого подхода заключается в ортогональности
набора параметров, простоте и возможности применения его иерархично.
15.2. Статистика первого порядка
15.2.1. Основы
Все текстурные признаки, основанные на статистике первого порядка
распределений уровней яркости, являются по определению инвариантными относительно
перестановки пикселей. Следовательно, они не зависят от ориентации объектов и —
пока мелкие признаки не исчезают при низких разрешениях ~ от размера объекта.
Следовательно, этот класс текстурных операторов инвариантен относительно
поворота и масштаба.
Инвариантность статистики первого порядка относительно перестановок
пикселей имеет, однако, существенный недостаток. Текстуры с различными
пространственными конфигурациями, но с одним и тем же распределением уровней
яркости не могут различаться. Вот простой пример. Текстура с черными и белыми
полосами равной ширины и текстура с черно-белой шахматной доской имеют одно
и то же бимодальное распределение, но абсолютно разную пространственную
конфигурацию текстуры.
Таким образом, многие текстуры не могут различаться с помощью
параметров, основанных на статистике первого порядка. Требуются дополнительно
другие классы текстурных параметров для лучшего различения разных текстур.
15.2.2. Локальная дисперсия
Все параметры, которые отклоняются от статистики уровней яркости отдельных
пикселей, как правило, не зависят от ориентации объектов. В разделе 3.2.2 мы
изучали, как характеризовать распределение уровней яркости с помощью среднего
значения, дисперсии и моментов высокого порядка. Для использования в текстурном
анализе требуется, чтобы оценка этих параметров усреднялась по локальной
окрестности. Это приводит к новому оператору, оценивающему лол:а/гь«у/о дисперсию.
В простейшем случае мы можем выбрать маску и вычислить параметры только
по пикселям, содержащимся в этом окне М. Оператор дисперсии, например,
тогда задается соотношением
15.2. Статистика первого порядка 437
тп р л ^^ \Ут-т',п-п' Umn) • (15.1)
Сумма пробегает по Р точкам изображения окна. Выражение вт» обозначает
среднее значение уровней яркости в точки [т, п] ^, вычисленное по тому же окну М\
-9^-ЛЪ W.-
Р ГТ^
^ т,пеМ
(15.2)
Важно отметить, что оператор дисперсии является нелинейным. Однако он
напоминает общий вид операции над соседними элементами — свертку.
Объединяя уравнения (15.1) и (15.2), мы можем показать, что оператор дисперсии
является комбинацией линейной свертки и нелинейных точечных операций
1
Р-1
J^ <^т-т, п-п I jrj j^ Ут-т, п-п
т[ ПЕ. М
J J
(15.3)
или в операторной форме записи
1^ = (2^(J-J)-((^-^). (15.4)
Оператор ^ обозначает сглаживание по всем точкам изображения
фильтра-ящика размера окна М. Оператор / является тождественным оператором.
Следовательно, оператор / •/ выполняет нелинейную точечную операцию, а
именно возведение в квадрат уровней яркости в каждом пикселе.
Окончательно оператор дисперсии вычитает квадрат сглаженного уровня яркости из
сглаженных возведенных в квадрат уровней яркости. Из рассуждений о
сглаживании в разделе 11.3 мы знаем, что фильтр-ящик не является подходящим
сглаживающим фильтром. Таким образом, мы получаем более подходящий
оператор дисперсии, если заменяем фильтр-ящик (?^с помощью
биномиального фильтра Ф
^ = (B(J-J)-(®-(B). (15.5)
Мы знаем, что оператор дисперсии является изотропным. Он также не зависит
от масштаба, если окно больше, чем самый большой размер в текстурах и если
никакие мелкие размеры текстуры не исчезают, когда объекты располагаются
дальше от камеры. Это означает, что инвариантный относительно масштаба
текстурный оператор существует только, если текстура сама по себе инвариантна
относительно масштаба.
Применение оператора дисперсии (15.5) с ^^ к нескольким изображениям
показано на рис. 15.3. На рис. 15.3, а оказывается, что оператор дисперсии является
изотропным контурным детектором, поскольку исходное изображение содержит
области с более или менее равномерными уровнями яркости.
Другие три примера на рис. 15.3 показывают изображения дисперсий от тек-
стурированных поверхностей. Оператор дисперсии может отличить области с
мелкими горизонтальными полосами на рис. 15.1, д от более равномерных
поверхностей. Они появляются как равномерные светлые области на изображении
дисперсии (рис. 15.3, 6). Оператор дисперсии не может сделать различие между
двумя текстурами на рис. 15.3, в. Поскольку разрешение все еще выше, чем
характеристический повторяющийся размер текстуры, оператор дисперсии не дает
равномерную оценку дисперсии в текстуре. Древесно-стружечная бумага (рис. 15.3, г)
438 Глава 15. Текстура
Рис. 15.3. Оператор дисперсии, примененный к различным изображениям: а — рис. 11.6, а\
б-рис. 15.1, д\ в —рис. 15.1, е\ г —рис. 15.1, г
также дает неравномерный отклик на оператор дисперсии, поскольку структура
проявляет значительные случайные флуктуации.
15.2.3. Моменты высокого порядка
Помимо дисперсии мы могли бы также использовать моменты высокого порядка
распределения уровней яркости, что и рассматривалось в разделе 3.2.2, для более
детального описания. Значимость этого подхода можно проиллюстрировать с
помощью примеров двух совершенно различных распределений уровней яркости,
нормального и биномиального распределений:
р{9) =
1
у/Ъгсг
ехр
9-9^
2а'
\ р\9) = \{5{д+су) + 5{д-а))^
Оба распределения показывают одинаковое среднее значение и дисперсию.
Поскольку оба распределения обладают четной симметрией, все нечетные
моменты равны нулю. Таким образом, третий момент (асимметрия) равен также
нулю. Однако четвертый и все четные моменты более высокого порядка двух
распределений различны.
15.3. Признаки текстуры, зависящие от поворота и масштаба 439
т^ tW^"^
^Я^^
зо Soc^^^F
IXru ^шкЯ
'"Inhrv'iM'T '
д^^л!
4?fe3?
fy|5^irs*y
^^яЯ
r^?0*v9^'s
^^l^'SX^^
Sr*Or^v-Sr
i'
VuV/
Рис. 15.4. Когерентность локальной ориентации: а - куска ткани с областями
горизонтальных полос (рис. 15.1, д); б - меха собаки (рис. 15.1, в); в - занавески (рис. 15.1, а);
г — древесно-стружечных обоев (рис. 15.1, г)
15.3. Признаки текстуры, зависящие от поворота и масштаба
15.3.1. Локальная ориентация
Поскольку локальная дисперсия уже обсуждалась детально в главе 13, сейчас мы
рассмотрим только несколько примеров для иллюстрации значимости локальной
ориентации для текстурного анализа. Поскольку эта книга содержргг только полутоновые
изображения, мы покажем изображения когерентности локальной ориентации.
На рис. 15.4 показана мера когерентности для локальной структуры, как
определено в разделе 13.3. Эта мера равна единице для идеально ориентированной
текстуры, где уровни яркости изменяются только в одном направлении, и нулю для
распределенных структур уровней яркости. Мера когерентности близка к единице
в областях куска ткани рубашки с горизонтальными полосами (рис. 15.4, а) и в
густых частях меха собаки (рис. 15.4, б).
Анализ ориентации занавески (рис. 15.1, й) приводит к интересной структуре
когерентности (рис. 15.4, в). Когерентность является высокой вдоль отдельных
нитей и низкой — в углах, где две нити пересекают друг друга, или в большей части
области между ними. Когерентность локальной ориентации изображения дре-
Глава 15. Текстура
весностружечной бумаги (рис. 15.1, г) не приводит к равномерному изображению
когерентности, поскольку эта структура не показывает преобладающей
локальной ориентации.
15.3.2. Локальное волновое число
В разделе 13.4 мы рассматривали детально вычисление локального волнового числа
по паре квадратурных фильтров посредством либо фильтра Гильберта (раздел 13.4.2),
либо квадратурных фильтров (раздел 13.4.5). В этом разделе мы применяем эти
методы для вычисления характеристического размера текстуры с использованием
направленно-пирамидального разложения как направленного полосового
фильтра, за которым следует фильтрация Гильберта.
Кусок ткани рубашки на рис. 15.5, а показывает различные горизонтальные
полосы в определенных частях. Это изображение сначала фильтруется с помощью
полосового фильтра с использованием уровней один и два вертикальной
компоненты направленно-пирамидального разложения изображения (рис. 15.5, б). На
рис. 15.5, в показана оценка локального волнового числа (компонента в
вертикальном направлении).
Все области, в которых амплитуда соответствующей структуры (рис. 15.5, г)
незначительно выше, чем уровень шума, скрываются. Во всех областях с
горизонтальными полосами было вычислено волновое число. Гистограмма на рис. 15.5, д
показывает, что пиковое локальное волновое число равно приблизительно 0,133.
Эта структура выбирается приблизительно 7,5 раз в длину волны. Обратите
внимание на длинный шлейф распределения по направлению к коротким
волновым числам. Таким образом, второстепенная, более крупная структура
содержится в текстуре. Она в действительности задается малыми диагональными полосами.
На рис. 15.6 показан тот же анализ для текстурированной деревянной
поверхности. В этот раз текстура более случайная. Тем не менее возможно определить
локальное волновое число. Хотя важно скрыть области, в которых не присутствуют
существенные амплитуды отфильтрованного с помощью полосового фильтра
изображения. Если скрывание не выполнится, то оценка локального волнового числа
будет значительно искажена. При скрывании определяется довольно узкое
распределение локального волнового числа с пиком при волновом числе 0,085.
15.3.3. Пирамидальный анализ текстуры
Пирамида Лапласа является альтернативой оператору локального волнового
числа, поскольку она приводит к полосовому разложению изображения. Это
разложение не вычисляет непосредственно локального волнового числа, но мы можем
получить последовательность изображений, которые показывают текстуру при
различных масштабах.
Оператор дисперсии принимает очень простую форму для пирамиды Лапласа,
поскольку средний уровень яркости, кроме самого грубого уровня, равен нулю:
V = (B{&^'&^). (15.6)
На рис. 15.7 демонстрируется, как появляются различные структуры из
рис. 15.1, в на различных уровнях пирамиды Лапласа. В двух самых мелких
масштабах на нулевом и первом уровнях пирамиды (рис. 15.7, а, б) над дисперсией до-
15.3. Признаки текстуры, зависящие от поворота и масштаба 44
О
0,05
0.1 0,15 0,2
Рис. 15.5. Определение характеристического размера текстуры с помощью
вычисления локального волнового числа: а — исходная структура; б — направленная
полосовая фильтрация с использованием уровней один и два вертикальной компоненты
направленно-пирамидального разложения; в — оценка локального волнового числа
(все структуры ниже определенной пороговой величины скрываются черным); г —
амплитуда локального волнового числа; д — гистофамма распределения локального
волнового числа (единицы: число периодов в пиксель)
минирует сама текстура. Наиболее выделенным признаком становится
дисперсия вокруг круглых петель в одной из двух структур. На втором уровне
пирамиды Лапласа (рис. 15.7, в) круглые петли сглаживаются и дисперсия становится
малой в этой текстуре, в то время как дисперсия по-прежнему существенна в
областях с более крупными вертикально и диагонально ориентированными
петлями. Третий уровень (рис. 15.7, г) является слишком грубым для обеих тек-
442 Глава 15. Текстура
0.05 0.1 0.15 0.2
Рис. 15.6. То же самое, что и на рис. 15.5, примененное к текстурированной
деревянной поверхности
стур, и, таким образом, в нем преобладают контуры между двумя областями
текстур, поскольку они имеют разный средний уровень яркости.
Пирамида Лапласа является структурой данных, хорошо приспособленной к
анализу иерархически организованных текстур, которые могут показывать
различные характеристики при различных масштабах, как в примере занавески,
рассмотренном в разделе 15.1. Таким образом, мы можем применять такие операторы, как
локальную дисперсию и локальную ориентацию на каждом уровне пирамиды.
Одновременное применение операторов дисперсии и локальной ориентации при
множественных масштабах дает большой набор признаков, которые позволяют
различать даже сложные иерархически организованные текстуры. Важно обратить
15.4. Упражнения 443^
Рис. 15.7. Применение оператора дисперсии к уровням от О до 3 пирамиды Лапласа
изображения из рис. 15.1, е
внимание, что применение этих операций на всех уровнях пирамиды увеличивает
число вычислений только в 4/3 раза для 2-D изображений.
15.4. Упражнения
15.1: Статистические параметры для текстурного анализа
Интерактивная демонстрация статистических параметров для текстурного
анализа (dip6exl5.01).
15.2: Локальная ориентация для текстурного анализа
Интерактивная демонстрация текстурного анализа с использованием
структурного тензора для анализа ориентации (dip6exl5.02).
15.3: Текстурный анализ с использованием пирамид
Интерактивная демонстрация текстурного анализа с помощью
многомасштабного подхода на пирамидах (dip6exl5.03).
15.4: "^"^Признаки для текстурного анализа
Какие признаки подходят для текстурного анализа? Попытайтесь перечне-
Глава 15. Текстура
лить признаки систематическим образом, начиная с самого простого
возможного, такого, как средний уровень яркости, и продолжая все более и
более сложными текстурами. Кратко объясните ваш подход.
15.5: **Структурный тензор для текстурного анализа
Какие типы текстуры можно различать с помощью структурного тензора, и
какие типы нельзя?
(Подсказка: используйте примеры структур, ведущих к одним и тем же
признакам для объяснения, какие текстуры не могут различаться с помощью
структурного тензора.)
15.6: "^"^Инвариантные текстурные признаки
Покажите, какой из перечисленньгх текстурных признаков является
инвариантным при изменении масштаба, поворота и изменении яркости
изображения:
1. Оператор дисперсии: (G - BG)^.
2. Локальная гистограмма уровней яркости в определенной окрестности.
3. Локальная гистограмма первой производной в направлении х.
4. Модель градиента уровня яркости.
5. Угол вектора ориентации.
6. Когерентность локальной ориентации.
7. Дисперсия угла вектора ориентации.
Возможно ли получить признаки, которые зависят от яркости
изображения, инвариантные относительно изменений яркости? Если да, то как?
15.5. Дополнительная литература
Учебные пособия Джейна (Jain) [97, раздел 9.11] и Претта (Pratt) [157, глава 17]
имеют дело с текстурным анализом. Дополнительными ссылками для текстурного
анализа являются монография Рао (Rao) [161], учебное пособие Яне (Jahne) и др.
[94, том 2, глава 12], и периодические издания семинара по текстурному анализу
под редакцией Буркхардта (Burkhardt) [16].
ЧАСТЬ 4
АНАЛИЗ ИЗОБРАЖЕНИЙ
ГЛАВА 16
СЕГМЕНТАЦИЯ
16.1. Введение
Все операции обработки изображений, рассмотренные в предыдущих главах,
имели своей целью лучшее распознавание интересующих нас объектов, т.е.
нахождение подходящих локальных признаков, которые позволяют нам отличить
их от других объектов и от фона. Следующий шаг заключается в проверке
каждого отдельного пикселя для того, чтобы выяснить принадлежит ли он к
интересующему нас объекту, или нет. Эта операция называется сегментацией и
образует бинарное изображение. Пиксель имеет значение единицы, если он
принадлежит объекту; в противном случае он равен нулю. Сегментация
представляет собой операцию, находящуюся на границе между низкоуровневой
обработкой изображений и анализом изображений. После сегментации мы знаем,
какой пиксель к какому объекту принадлежит. Изображение разбивается на
области, и мы понимаем неоднородности как границы между областями.
После сегментации мы можем также провести анализ формы с помощью
операций, таких, как операции, рассмотренные в главе 19.
В этой главе мы рассматриваем некоторые типы элементарньис методов
сегментации. По существу, мы можем иметь в виду некоторые основные понятия для
сегментации. Методы на основе анализа пикселей (раздел 16.2) используют
только уровни яркости отдельных пикселей. Методы на основе анализа областей
(раздел 16.4) анализируют уровни яркости в более крупных областях. И наконец,
методы на основе анализа контуров (раздел 16.3) вьщеляют контуры и затем стараются
следовать им. Общим ограничением всех этих подходов является то, что они
основаны только на локальной информации. И даже в таком случае они используют
эту информацию частично. Методы на основе анализа пикселей не
рассматривают даже локальную окрестность. Методы на основе анализа контуров ищут только
неоднородности, в то время как методы на основе анализа областей проводят
анализ однородных областей. В случаях, когда мы знаем геометрическую форму
объекта, можно применять сегментацию на основе моделей (раздел 16.5). Мы
рассматриваем подход к преобразованию Хафа, который исходит непосредственно из
полутоновых изображений (раздел 16.5.3).
446 Глава 16. Сегментация
а
»• • •• • •
.• •• V» •<
•».
14000
12000
10000
8000
6000
4000
2000
50
100
150 200 g 250
Рис. 16.1. Сегментация с глобальной пороговой величиной: а — исходное
изображение; б — гистофамма; в — д — верхний правый участок а, сегментированный с
глобальными пороговыми величинами ПО, 147 и 185 соответственно
16.2. Сегментация на основе анализа пикселей
Сегментация на основе анализа точек, или пикселей, концептуально представляет
собой простейший подход, который мы можем использовать для сегментации. Мы
можем также утверждать, что он является также самым лучшим подходом. Почему?
Причина состоит в том, что вместо попытки применить сложную процедуру
сегментации мы должны скорее сначала использовать всю палитру методов,
рассматриваемых до сих пор в этой книге, для вьщеления тех признаков, которые
однозначно характеризуют объект, прежде чем применить процедуру сегментации.
Всегда лучше решать проблему в корне. Если изображение неравномерно
освещено, к примеру, то первое, что мы должны сделать, — это оптимизировать
освещенность сцены. Если это невозможно, то следующим шагом было бы определение
неравномерности системы освещения и использование соответствующих методов
обработки изображений для ее корректировки. Один из возможных методов
рассматривался в разделе 10.3.2.
Если мы определили хороший признак для отделения объекта от фона, то
гистофамма этого признака будет показывать бимодальное распределение с двумя
отчетливыми максимумами, как на рис. 16Л, б. Мы не можем полагать, что вероятность
для уровней яркости между двумя пиками будет равна нулю. Даже если имеет место
четкий переход уровней яркости на контуре объектов, всегда будут существовать
некоторые промежуточные значения, обусловленные ненулевой функцией
рассеяния точки оптической системы и датчика (раздел 7.6.1 и 9.2.1). Чем меньше объекты,
тем большую область на изображении занимают промежуточные значения,
заполняющие гистограммы между значениями для объекта и фона (рис. 16.1, б).
76.2 Сегментация на основе анализа пикселей
!lements (section 4.3.2b).
f ar optical system is a perspecti\
j) rrodels the imaging geometry a
' described by the position of the
btd\ length (section 43.2c). Forth
determine the distance range thai
of f eld, section 4.3.2d) and to learl
d h/percentric optical systems (se|
0 50 100 150 200 250 300 350У
Рис. 16.2. Сегментация изображения с неоднородным фоном: а - исходное
изображение; б - профиль столбца 55 (как отмечено на а); в - д - первые 64 столбца а,
сегментированного с глобальными пороговыми величинами 90, 120 и 150 соответственно
Как мы можем определить оптимальную пороговую величину в этой
ситуации? В случае, показанном на рис. 16.1, это легко, поскольку и фон, и объект
показывают довольно равномерные уровни яркости. Таким образом, мы
получаем хорошую сегментацию для большого диапазона пороговых величин, между
низким порогом 110, когда объекты начинают приобретать дыры (рис. 16.1, в), и
высоким порогом 185, близким к значению фона, когда некоторые пиксели фона
определяются как пиксели объекта.
Однако более тщательное рассмотрение рис. \6Л,в-д показывает, что размер
сегментированных объектов значительно изменяется в зависимости от уровня
пороговой величины. Таким образом, выбор корректной пороговой величины
является решающим для безошибочного определения геометрических признаков
объекта. Это невозможно без сведений о типе контура между объектом и фоном. В
простом случае симметричного контура корректная пороговая величина задается
средним уровнем яркости между пикселями фона и объекта.
Эта стратегия перестает действовать, как только фон становится
неравномерным или если изображение содержит объекты с различными уровнями яркости
(рис. 16.2 и 16.3). На рис. 16.2, б сегментированные буквы являются тоньше на
верхней, более светлой части изображения. Такое отклонение допустимо для некоторых
448 Глава 16. Сегментация
ш
1
* щ
б
250
200
150
100
50
0
О 100 200 300 400 500 600 х
Рис. 16.3. Сегментация изображения с неравномерной освещенностью: а - исходное
изображение с неоднородной освещенностью фона (см. гистограмму на рис. 10.10, б);
б — профиль строки 186 (как отмечено на а); в и д - результаты сегментации при
оптиманьной глобальной пороговой величине изображений на а, перед и после того,
как изображение корректируется с учетом неоднородного фона (рис. 10.10, в)
соответственно
задач, таких, как распознавание набранных букв. Однако это является серьезным
недостатком для любого измерения размеров объектов и связанных параметров.
На рис. 16.3, а показано изображение с двумя типами окружностей; оба типа
представляют собой окружности, но различной яркости. Энергетическая яркость более
светлых объектов становится ближе к фону. В самом деле, гистофамма (рис. 10.10, б)
показывает, что уровни яркости этих более светлых окружностей больше не
образуют отчетливый максимум, а перекрываются с широким распределением фона.
Следовательно, глобальное установление порога является неадекватным
(рис. 16.3, в). Даже при оптимальной пороговой величине некоторая часть фона в
правом верхнем и нижнем углах сегме1ггируются как объекты, а более светлые
окружности все еще сегментируются частично. Если мы сначала вносим правку на
неоднородную освещенность, что и проиллюстрировано на рис. 10.10, то все объекты
сегментируются идеально (рис. 16.3, г). Однако мы все еще сталкиваемся с
проблемой, состоящей в том, что области темных окружностей слишком большие,
поскольку пороговая величина сегментации слишком близка к интенсивности фона.
16.3. Сегментация на основе анализа контуров 449
16.3. Сегментация на основе анализа контуров
16.3.1. Принцип
Мы увидели в разделе 16.2, что даже при совершенной освеш;енности сегментация
на основе анализа пикселей приводит к отклонению размера сегментированных
объектов в случае, когда объекты проявляют изменения в своих уровнях яркости
(рис. 16.2 и 16.3). Более темные объекты будут становиться слишком малыми, а
более светлые — слишком большими. Изменения в размере обусловлены тем, что уровни
яркости на контуре объекта изменяются постепенно от значения фона к значению
объекта. Отклонения в размере не происходит, если мы берем среднее значение
уровней яркости объекта и фона в качестве пороговой величины. Однако этот подход
возможен, только если все объекты показывают один и тот же уровень яркости или
если мы применяем различные пороговые величины для каждого объекта.
Метод сегментации на основе анализа контуров можно использовать, чтобы
избежать отклонения в размере сегментированного объекта без использования сложной
схемы установления пороговой величины. Сегментация на основе анализа
контуров основывается на том, что положение контура задается экстремумом первой
производной или пересечением нулевого уровня второй производной (рис. 12.1).
Таким образом, все, что нам требуется сделать, так это найти локальные максимумы в
интенсивности контуров и проследить максимум вдоль контура объекта.
16.3.2. Отклонение при неравномерной освещенности
В этом разделе мы изучим погрешность различных методов сегментации
вследствие неоднородности фона и изменяющейся яркости объекта. Предположим, что
контур объекта можно адекватно моделировать с помощью ступенчатого контура,
который размывается функцией рассеяния точки h{x) с четной симметрией. Ради
простоты мы моделируем 1-D случай. Тогда яркость объекта на изображении с
контуром в начале отсчета можно записать как
g{x) = gQ\h{x)dx при \h(x)dx = \. (16.1)
Далее предположим, что интенсивность фона можно моделировать
параболическим изменением вида
b(x) = bf^+b^x + b2X^. (16.2)
Тогда полная интенсивность в изображении задается соотношением
X
д{х) = 001 h(x)dx + bQ +b^x + b2X^. (16.3)
Первая и вторая производные равны
9,ix) = 9oKx) + b^+2b2X,
9:a(x) = 9oK(x) + 2b^.
В окрестности максимума мы можем аппроксимировать функцию рассеяния
точки h(x) параболой: h(x) ~ h^- h^^. Тогда
9х W == 9оК - 9о^х^ + А + 2^2^'
5'x.W==-25'oV + 262.
(16.4)
Глава 16. Сегментация
Положение контура определяется как ноль второй производной. Следовательно,
отклонение в оценке положения контура, х^, определяется из уравнения (16.5) как
Из уравнения (16.6) мы можем заключить:
1. Сегментация на основе анализа контура не показывает отклонения в
определении положения контура, даже если интенсивность фона изменяется линейно.
2. Сегментация на основе анализа контура не показывает отклонения в
зависимости от интенсивности д^ контура, как это происходит в случае с сегментацией
на основе анализа интенсивности (раздел 16.2).
3. Сегментация на основе анализа контура отклоняется только кривизной в
интенсивности фона. Отклонение непосредственно связано с отношением
кривизны в интенсивности фона к максимальной кривизне функции рассеяния
точки. Это означает, что отклонение является более высоким для размытых контуров.
Отклонение также обратно пропорционально интенсивности объекта и, таким
образом, серьезно влияет только на объекты со слабой контрастностью.
16.3.3. Слежение по контуру
Сегментация на основе анализа контура является последовательным методом. В
отличие от сегментаций на основе анализа пикселей и особенно на основе анализа
областей, она не может вьшолняться параллельно на всех пикселях. Следующий
выполняемый шаг скорее зависит от результатов предьщущих шагов. Типичный подход
состоит в следующем. Изображение сканируется по линиям для нахождения
максимумов модуля градиента. Когда встречается максимум, алгоритм слежения старается
следовать за максимумом градиента вокруг объекта, пока не приходит опять в
начальную точку. Затем поиск начитается для следующего максимума градиента. Подобно
сегмеьггации на основе анализа областей, сегментация на основе анализа контуров
принимает во внимание то, что объект характеризуется смежными пикселями.
16.4. Сегментация на основе анализа областей
16.4.1. Принципы
Методы на основе анализа областей фокусируют наше внимание на важном
аспекте процесса сегментации, которым мы пренебрегали при методах на основе
анализа точек. Там мы классифицировали пиксель как пиксель объекта,
производя оценку исключительно по его уровню яркости независимо от контекста. Это
означало, что изолированные точки или малые области могут
классифицироваться как пиксели объекта, если не брать во внимание, что важной характеристикой
объекта является его связность,
В этом разделе мы не будем рассматривать такие стандартные методы, как
методы «расщепления и слияния» или методы наращивания областей.
Заинтересованные читатели отсылаются к работе Розенфельда (Rosenfeld) и Кака (Как) [172]
или Джейн (Jain) [97]. Здесь мы рассматриваем скорее метод, который имеет своей
целью решение одной из центральных проблем процесса сегментации.
16.4. Сегментация на основе анализа областей
Если мы используем не исходное изображение, а изображение признака для
процесса сегментации, то признаки представляют не отдельный пиксель, а малую
окрестность в зависимости от размеров масок используемых операторов. На
контурах объектов, однако, где маска включает как пиксели от объекта, так и от фона,
не может вычисляться никакой признак, который мог бы быть полезным.
Корректная процедура заключалась бы в ограничении размера маски на контуре до точек
либо объекта, либо фона. Но как это может быть выполнено, если мы можем
разделить объект и фон только после вычисления признака?
Очевидно, что эта проблема не может быть решена одним шагом. Ее можно
решить, итерационно используя процедуру, в которой вьиисление признака и
сегментация выполняются поочередно. В общем, действуем следующим образом. На
первом шаге мы вычисляем признаки, не обращая внимания на какие-либо
границы объекта. Затем выполняем предварительную сегментацию и опять вьиисля-
ем признаки, теперь с использованием результатов сегментации для ограничения
масок операций над соседними элементами на контурах объекта либо пикселями
объекта, либо фона, в зависимости от расположения центрального пикселя. Для
улучшения результатов мы можем повторять вычисление признаков и
сегментацию до тех пор, пока процедура не сойдется к устойчивому результату.
16.4.2. Связывание пирамиды
Бюрт (Burt) [18] предложил алгоритм связывания пирамиды как эффективное
выполнение комбинированного алгоритма сегментации и вычисления признаков.
Мы продемонстрируем его с использованием наглядного примера зашумленного
ступенчатого контура (рис. 16.4). В этом случае вычисленный признак является
просто средним уровнем яркости. Алгоритм включает следующие шаги:
1. Вычисление пирамиды Гаусса. Как показано на рис. 16.4, а, уровни яркости
четырех соседних пикселей усредняются для формирования пикселя на
следующем, более высоком уровне пирамиды. Это соответствует операции сглаживания
с фильтром-ящиком.
2. Сегментация посредством связывания пирамиды. Поскольку каждый пиксель
вносит вклад в каждый из двух пикселей на более высоком уровне, мы можем
теперь решить, к какому из них он наиболее вероятно принадлежит. Решение
принимается просто - посредством сравнения уровней яркости и выбора пикселя,
близкого к нему. Связь изображается на рис. 16.4, б посредством соединения
ребрами двух пикселей. Эта процедура повторяется по всем уровням пирамиды. В
результате связи в пирамиде образуют новую структуру данньсс. Начиная с вершины
пирамиды, один пиксель соединяется с несколькими пикселями на следующем,
более низком уровне. Такая структура данных называется деревом в
компьютерной науке. Связи называются/7ефал^«; точки данных являются уровнями яркости
пикселей и обозначаются как узлы или вершины. Узел на самом высоком уровне
называется корнем дерева, а узлы без дальнейших связей называются листьями
дерева. Узел, связанный с узлом на более низком уровне, обозначается
kslkродительский узел этого узла. Соответственно каждый узел, связанный с узлом на более
высоком уровне, определяется как дочерний узел этого узла.
3. Усреднение связанных узлов. Далее, результирующая структура связей
применяется для перевычисления средних уровней яркости теперь с использованием
452 Глава 16. Сегментация
49
51
53
43
45 39 44 55 56 56
55
55 53
50 46 38 34 38 54 50 58 58 50 58 66 50 58 46 54
Q(4)
Q(3)
Q(2,
Q(1)
Q(0)
-51^:::гКорень
Ребро^з^Узел
/5 39^ 44 55 56 56 55 53
\ /\\ /f Ж i\ /\ /\
50 46 38 34 38 54 50 58 58 50 58 66 50 58 46 54 G<°^
Лист
...-51-
Q(4)
^41 >
Q(3)
42
(41)
38
(41)
48
36
38
54
.6
55)^
52
(55)
54
62
54
50
Qd)
(41) (41) (41) j55) (55) (55) (55) (55)
/\ /\4 У/^/\ /\ /\ /\ ^„,
50 46 38 34 38 54 50 58 58 50 58 66 50 58 46 54 G^°'
(41) (41) (41) (41) (41) (55) (55) (55) (55) (55) (55) (55) (55) (55) (55) (55)
Рис. 16.4. процедура сегментации посредством связывания пирамиды на примере
одномерного зашумленного контура: а — вычисление пирамиды Гаусса; б —
связывание узлов; в — перевьгаисление средних уровней яркости; д - окончательный
результат после нескольких итераций шагов бив
16.4. Сегментация на основе анализа областей
только связанных пикселей (рис. 16.4, в), т.е. новый уровень яркости каждого
родительского узла вьршсляется как средний уровень 51ркости из всех дочерних узлов. Эта
процедура начинается на самом низком уровне и продолжается по всем уровням пирамиды.
Последние два шага итерационно повторяются до тех пор, пока мы не
достигаем устойчивого результата, показанного на рис. 16.4, г. Анализ дерева связей
позволяет увидеть результат процедуры сегментации. На рис. 16.4, б мы
распознаем два поддерева, которые имеют корни на третьем уровне пирамиды. На
следующем, более низком уровне возникают четыре поддерева. Но различия в уровнях
яркости на этом уровне значительно меньше. Таким образом, мы заключаем, что
структура уровней яркости, очевидно, разбивается на две области. Тогда мы
получаем окончательный результат процедуры сегментации посредством переноса
уровней яркости в корнях двух поддеревьев к связанным узлам на самом низком
уровне. Эти значения показаны как числа, заключенные в круглых скобках, на
рис. 16.4, г.
Применение алгоритма сегментации посредством связьгоания пирамиды к
двумерным изображениям показаны на рис. 16.5. Оба примера иллюстрируют то, что даже
очень зашумленные изображения могуг успешно сегментироваться с помощью этой
процедуры. Не существует ограничения по форме сегментируемой области.
Процедура связывания пирамиды соединяет сегментацию и эффективное
вычисление средних признаков для вьщеленных объектов с помощью построения дерева по
пирамиде. Также является преимуществом, что нам не нужно знать число уровней
сегментации заранее. Они содержатся в структуре дерева. Дополнительные детали
сегментации посредством связывания пирамиды рассматривается в работах Бюрта и др.
(Burt) [20], Питикейнена (Pietikainen) и Розенфельда (Rosenfeld) [153].
Рис. 16.5. Зашумленные изображения: а — танка и в - клетки крови,
сегментированные с помощью алгоритма связывания пирамиды в двух (б) и трех (г) областях
соответственно [18]
Глава 16. Сегментация
16.5. Сегментация на основе моделирования
16.5.1. Введение
Все методы сегментации, рассмотренные до сих пор, используют только
локальную информацию. В разделе 1.6 (рис. 1.16) мы обратили внимание на
замечательную способность зрительной системы человека распознавать объекты, даже если
они не представляются полностью. Очевидно, что информация, которая может
собираться от локальных операторов формирования окрестностей, недостаточна
для выполнения этой задачи. Вместо этого нам требуются определенные сведения
относительно геометрической формы объектов, которые могут затем
сравниваться с локальной информацией.
Такой ход мыслей приводит к сегментации на основе моделирования. Она может
применяться, если мы знаем точную форму объектов, содержащихся в
изображении. Мы рассматриваем здесь только простейший случай: прямые линии.
16.5.2. Пространство параметров; преобразование Хафа
Подход, рассмотренный здесь, вьщеляет линии, даже если они нарушаются шумом
или видны только частично. Начнем с предположения, что мы имеем
сегментированное изображение, которое содержит линии этого типа. Тот факт, что точки
лежат на прямой, приводит к важному ограничению, которое можно использовать
для определения параметров прямой линии. Для всех точек [х^, 3^„]^ на прямой
линии должно выполняться следующее условие:
Л=^о+^Л' (16.7)
где а^иа^ — смеш;ение и наклон линии. Мы можем рассматривать уравнение (16.7)
также, как условие для параметров а^иа^:
Уп 1
а^= — ^0. (16.8)
Это опять является уравнением для линии в новом пространстве, образованном
параметрами а^ и «^ В этом пространстве линия имеет смещение у^ /х^ и наклон -1А^.
При одной заданной точке мы уже перестаем иметь свободный выбор а^иа^,
поскольку параметры должны удовлетворять уравнению (16.8).
Пространство, образованное параметрами модели а^иа^, называется
модельным пространством. Каждая точка сводит модельное пространство к линии.
Таким образом, мы можем нарисовать линию в модельном пространстве для
каждой точки в пространстве данных, как проиллюстрировано на рис. 16.6. Если все
точки лежат на прямой линии в пространстве данных, то все линии в модельном
пространстве пересекаются в одной точке, которая задает параметры а^иа^
линий. Поскольку участок линии содержит большое количество точек, мы
получаем надежную оценку двух параметров линии. Таким образом, линия в
пространстве данных отображается в точку в модельном пространстве. Это
преобразование из пространства данных в модельное пространство через
уравнение модели называется преобразованием Хафа. Оно представляет собой
универсальный инструмент для выделения линий, даже если они нарушаются или
являются неполными.
16.5. Сегментация на основе моделирования 455
10
5
У
0
-5
-
о/^
1 1
Эо
1
2а^'
-6-4-20246
X
Рис. 16.6. Преобразование Хафа для прямых линий: [л:, >^]^ пространство данных (а)
отображается в \а^, а у модельное пространство (б)
На практике хорошо известное уравнение прямой линии, заданное
уравнением (16.6), не используется. Причина просто заключается в том, что наклон линии
может становиться бесконечным и, таким образом, не подходит для дискретного
модельного пространства. Более пригодная параметризация прямой линии
задается посредством использования двух различных параметров с конечными
значениями. Одна из возможностей состоит в том, что берется угол наклона линии и
расстояние до линии от центра системы координат. При этих двух параметрах
уравнение прямой линии можно записать как
nx^d или xcos0 + j;sin0 = J, (16.9)
где п — вектор нормальный к линии; Q — угол этого вектора к оси х системы
координат изображения.
Недостатком метода преобразования Хафа для вьщеления линий являются
большие вычислительные усилия. Для каждой точки в изображении мы должны
вычислять линию в пространстве параметров и увеличивать каждую точку в
модельном пространстве, через которое проходит линия.
16.5.3. Быстрое преобразование Хафа на основе ориентации
Существенное ускорение преобразования Хафа можно получить, используя
дополнительную информацию из низкоуровневой обработки изображений. Анализ
локальных окрестностей с помощью метода структурного тензора не только вьщеляет
контуры, но также и задает их наклон. Следовательно, мы имеем две порцрш информации
для каждой точки в изображении, если она лежит на контуре: точку, через которую
проходит контур, и ее ориентацию. Это уже полностью описывает линию.
Следовательно, каждая точка на линии в пространстве изображения больше
не соответствует линии, как рассмотрено в разделе 16.5.2, а соответствует
отдельной точке в пространстве параметров. Взаимно-однозначное соответствие
значительно ускоряет вычисление преобразования Хафа. Для каждой точки в
изображении нам необходимо добавить только одну точку к пространству параметров.
Глава 16. Сегментация
Рис. 16.7. Быстрое преобразование Хафа на основе ориентации: а, б - неравномерно
освещенные зашумленные квадраты; в, г — модельное пространство Хафа с
расстоянием d (горизонтальная ось) и углом в (вертикальная ось) линий в соответствии с
уравнением (16.9) для а, б соответственно
Применение преобразования Хафа на основе ориентации демонстрируется на
рис. 16.7. На рис. 16.7, л, 5 показываются зашумленные изображения с квадратом.
Для вьщеления контуров прямоугольника не требуется никакой сегментации. Мы
просто вычисляем компоненты структурного тензора с использованием методов,
описанных в разделе 13.3.6. Тогда для каждой точки в изображении, вий,
вычисляются согласно уравнению (16.9).
В качестве весового множителя для вклада точки в пространство параметров
мы используем длину вектора ориентации. Таким образом, точки взвешиваются в
соответствии с мерой достоверности для локальной ориентации и, таким образом,
интенсивности контура. В пространстве параметров Хафа (рис. 16.7, в, г)
появляются четыре кластера в соответствии с четырьмя различными линиями квадрата.
Кластеры возникают парами, поскольку две линии параллельны друг другу и
отличаются только расстоянием до центра изображения. Обратите внимание, как
хорошо работает метод даже при высоких уровнях шума.
16.6. Упражнения
16.6. Упражнения
16.1: Простые методы сегментации
Интерактивная демонстрация простых методов сегментации (dip6exl6.01).
16.2: Преобразование Хафа
Интерактивная демонстрация преобразования Хафа (dip6exl6.02).
16.3: "^"^Сегментация с постоянным фоном
Все методы сегментации сталкиваются с проблемой систематических
ошибок. Предположите, что изображение содержит объекты с различной, но
постоянной яркостью. Фон имеет постоянную яркость h. Для следующих
вьиислений достаточно использовать два объекта с яркостями д^ и д^.
Объекты имеют ширину / > 5 и свертываются прямоугольной функцией рассеяния
точки с шириной 5 пикселей в течение процесса получения изображения.
Сигнал изображения содержит аддитивный «белый шум» с нулевым
средним при дисперсии g I
Доступны три подхода к сегментации:
Р - сегментация на основе анализа пикселей с постоянной глобальной
пороговой величиной на уровне яркости t\
G - сегментация на основе анализа контуров на базе дифференциальных
фильтров первого порядка. Положение контура задается максимальным
значением модуля градиента;
L - сегментация на основе анализа контуров на базе дифференциальных
фильтров второго порядка. Положение контура задается пересечениями
нулевого уровня оператора Лапласа.
Ответьте на следующие вопросы для трех методов сегментации:
1. Какое различие яркости требуется для того, чтобы отделить объекты от
фона статистически значимым образом? (Различие между пороговыми
величинами и уровнями сигнала должно быть, по крайней мере, в 3 раза
больше среднеквадратичного отклонения с шума.)
2. Возможно ли, что один из методов вызывает систематическую ошибку в
размере объекта? Если да, то вычислите систематическую ошибку и
сравните ее для различных методов.
16.4: "^Сегментация с изменяющимся фоном
Ответьте на те же вопросы, что и для упражнения 16.3 со следующей
моделью изображения: объект с постоянной яркостью д и неоднородным
фоном с квадратичным изменением:
(Подсказка: достаточно рассмотреть задачу в одномерном случае.)
16.7. Дополнительная литература
Питас (Pitas) [154, глава 6] и Умбаф (Umbaugh) [203, раздел 2.4] описывают
различные стандартные алгоритмы для сегментации. Форсис (Forsyth) и Понс (Ponce)
[54, глава 14] рассматривают сегментацию с помощью кластеризации.
ГЛАВА 17
РЕГУЛЯРИЗАЦИЯ И МОДЕЛИРОВАНИЕ
17.1. Введение
17.1.1. Объединение локального анализа и глобальных знаний
Метод сегментации на основе моделирования, рассмотренный в разделе 16.5,
является первым шагом к интеграции глобальной информации в процесс
распознавания объектов. Однако он недостаточно гибкий, так как требует точной
параметризации объектов для распознавания. Для реальных объектов определение такого
явного типа модели часто бывает невозможным.
В этой главе мы рассматриваем самый общий подход для связывания локальной и
глобальной ршформации, который не требует явной модели объекта. Взамен он
использует гибкие ограничения для учета информации глобального типа. Основная идея
заключается в уравновешивании двух противоположных требований. С одной
стороны, модель должна воспроизводить установленные данные изображения настолько
близко, насколько это возможно. Это требование известно как ограничение подобия. С
другой стороны, смоделированные данные должны удовлетворять некоторым
глобальным ограничениям, которые могут быть получены из общих сведений о наблюдаемой
сцене. В простейшем случае это может бьпъ ограничением гладкости.
Как правило, получить точное решение не представляется возможным.
Поскольку все реальные данные изображений включают некоторую
неопределенность, точное соответствие данных не имеет смысла. Мы скорее предполагаем
некоторое отклонение вычисленных данных модели отданных изображения, которое
может быть сопоставимо с ожидаемым среднеквадратичным отклонением шума,
содержащегося в данных.
Таким образом, мы приходим к глобальной оптимизационной задаче. Оба типа
ограниченрш должны объединяться соответствующим образом для поиска
решения, которое имеет минимальную ошибку при заданной норме погрешности.
Этот общий подход можно применять к широкому диапазону задач анализа
изображений, включающих такие разные задачи, как
• восстановление изображений с ухудшенным в процессе формирования
изображений качеством (глава 7);
• вычисление карт глубин по стереоскопическим изображениям или с
использованием любого другого датчика формирования изображений на основе методов
триангуляции (глава 8.2);
17.1. Введение
• вычисление карт глубин по методу определения формы по полутоновому
изображению или фотометрической системы стереоскопического зрения (глава 8.5);
• реконструкция изображений по методам 3-D формирования изображений,
таким, как томография (раздел 8.6), которые не дают прямых изображений;
• вычисление движения или полей векторов перемещений по
последовательностям изображений (глава 14);
• разбиение изображений на области {сегментация, глава 16);
• вычисление границ объектов {активные контуры или змеи).
Большинство вычисляемых признаков являются скалярными полями, но
некоторые из них, такие, как поле движения или нормали к поверхностям, являются
векторными полями. Следовательно, полезным будет расширить методы
моделирования изображений на векторные величины.
Прежде чем мы начнем, полезно рассмотреть назначение и пределы
моделирования (раздел 17.1.2). После детального рассмотрения общего подхода
вариационного моделирования изображений в разделе 17.2 мы рассмотрим в разделе 17.2.5
важный вопрос: как можно адекватно учесть неоднородности в глобальных
ограничениях гладкости? Вариационный подход приводит к дифференциальным
уравнениям в частных производных, которые эквивалентны уравнениям переноса,
учитывающим диффузию и реакцию. Таким образом, рассмотрение диффузионных
моделей в разделе 17.3 дает еще один интересный взгляд на задачу моделирования
изображений.
Во второй части этой главы мы обращаемся к дискретной части моделирования
изображений и показываем, что она может пониматься как дискретная обратная
задача (раздел 17.4). Электрические сети служат наглядным примером (раздел 17.6.2).
В разделе 17.5 мы в заключение показываем на примере обратной фильтрации, как
можно эффективно решать обратные задачи.
17.1.2. Назначение и пределы моделей
Термин модель отражает тот факт, что любое природное явление можно описать
только с определенной степенью точности и корректности. Моделирование является
одним из самых мощных инструментов во всех естественных науках для поиска
простейшего и самого общего отображения, которое тем не менее описывает
наблюдения с минимальными отклонениями. Небольшое число основных законов физики
описывают количественным образом чрезвычайно широкий диапазон явлений.
По тем же самым соображениям модели являются полезным и действенным
подходом для задач обработки изображений. Однако модели должны использоваться
осторожно. Даже если кажется, что данные полностью согласуются с модельными
предположениями, нет гарантии, что эти модельные предположения корректны.
На рис. 17.1 показан наглядный пример: модельные предположения
учитывают плоский черный объект, лежащий на белом фоне, который равномерно
освещается (рис. 17.1, а). Объект можно явно распознать по низким уровням яркости
на изображении, а неоднородности между высокими и низкими значениями
обозначают контуры объекта.
Однако если черный объект имеет толщину, которой нельзя пренебречь, а сцена
освещается наклонным параллельным световым пучком (рис. 17.1, в), то мы
получаем точно такой же тип профиля, как в случае на рис. 17.1, а. Таким образом, мы
460 Глава 17, Регуляризация и моделирование
9t
Тонкий черный объект
Белый \
—X J
Профиль уровней яркости
Белый ! Белый
Чернаый
Освещение
Толстый черный объект //
гГ'-Т
D
Белый
Черный
^^
Белый
Положение х
—i-
Белый
Затененная область
Неправильное распознавание контура
Рис. 17.1. Демонстрация систематической ошибки, которая не может быть
обнаружена по воспринимаемому изображению: а, в - наброски условий объекта и
освещения; б, г — результирующие профили уровней яркости для айв соответственно
Гистограмма
Рис. 17.2. Демонстрация систематического отклонения от модельного
предположения (объект - черный, фон - белый), которое не может быть обнаружено по
гистограмме изображения
не распознаем какое-либо отклонение по модельному предположению. Однако
только правый контур определяется правильно. Левый контур сдвигается влево из-за
затененной области, приводя к изображению, слишком большому для этого объекта.
На рис. 17.2 показан еще один случай. Черное плоское тело занимает
половину изображения на белом фоне. Гистограмма (распределение уровней яркости) явно
показывает бимодальную форму с двумя пиками равной высоты. Это
свидетельствует о том, что, по существу, в изображении возникают только два уровня
яркости, причем более низкий распознается как черный объект, а более высокий -
как белый фон, каждый из которых занимает половину изображения.
Это не означает, однако, что любая бимодальная гистограмма возникает из
изображения, в котором черный объект занимает половину изображения на белом
фоне. Возможны многие другие интерпретации. Например, мог бы также иметь
место белый объект на черном фоне. Такая же бимодальная гистограмма также
получается из изображения, в котором как объект, так и фон состоят из черных и
17.2. Непрерывное моделирование I: вариационный подход
белых полос. В последнем случае процедура сегментации, которая относит все
пиксели ниже определенной пороговой величины к объекту, а остальные к фону,
не выделила бы искомый объект, а вьщелила бы черные полосы. Эта простая
процедура работает, только если удовлетворяется модельное предположение, что
объекты и фон обладают равномерной яркостью.
Два примера, рассмотренные выше, ясно демонстрируют, что даже в простых
случаях мы можем столкнуться с ситуациями, где кажется, что модельные
предположения удовлетворяются — что и оценивается с помощью изображения или
величин, полученных из изображения, таких, как гистограммы, — но в действительности
это не так. В то время как довольно легко увидеть несостоятельность модельного
предположения в этих простых случаях, это может быть довольно
затруднительным, если не невозможным, в более сложных случаях.
17.2. Непрерывное моделирование I: вариационный подход
Как рассматривалось во введении (раздел 17.1.1), математически хорошо
обоснованный подход к моделированию изображений требует установки функции
модели и функционала ошибок, который измеряет остаточные отклонения
полученных при измерении данных от вычисленных данных модели.
Для сегментации изображений подходящая моделирующая функция может быть
кусочно-гладкой целевой функциейДдс). Области с постоянными значениями
соответствуют сегментированным объектам, а неоднородности к границам объекта.
Свободные параметры этой функции модели являлись бы уровнями яркости в
различных областях и на фаницах между областями. Границы между объектами и уровни
яркости областей должны изменяться таким образом, чтобы отклонение между
функцией модели Ддс) и данными изображения д{х) было минимальным.
Глобальные ограничения этого примера сегментации являются довольно
жесткими. Ограничения гладкости являются более общими. Они стремятся
минимизировать пространственные изменения признака. Эта концепция гораздо более
общая, чем использование некоторой конкретной модели, подразумевающей, что
признак должен быть постоянным, как в вышеупомянутом примере сегментации,
или изменяться только линейно.
Такие глобальные ограничения можно рассматривать общим образом с
использованием вариационного исчисления. Прежде чем мы обратимся к применению
вариационного исчисления в моделировании изображений, полезным будет начать
с более простого примера из физики.
17.2.1. Временные вариационные задачи: простой пример
Вариационное исчисление нашло широкое применение во всех естественных
науках. Оно особенно хорошо известно в физике. Все основные понятия
теоретической физики можно сформулировать как принципы экстремума. Вероятно, самым
известным является принцип Гамильтона, который приводит к уравнению Лагран-
жа в теоретической механике [60].
В качестве простого примера рассмотрим движение материальной точки. В
случае отсутствия внешних сил материальная точка будет двигаться с постоянной
скоростью. Чем больше масса, тем большая сила требуется для изменения ее ско-
462 Глава 17. Регуляризация и моделирование
рости. Таким образом, масса стремится уменьшить скорость в то время, как
частица проходит через изменяющееся в пространстве и времени потенциальное поле
V{x, t), которое прикладывает силу F= F(x, t) к частице. Принцип Гамильтона
утверждает, что движение происходит по траектории, для которой следующий
интеграл является экстремумом:
\-mxf-V(x,t)dt. (17.1)
i^
Временная производная от х обозначается в уравнении (17.1) с помощью х^.
Функция в интеграле известна как функция Лагранжа L(x, х^, t). Функция Лагран-
жа зависит от координаты х и времени t через потенциал V(x, t) и от временной
производной координаты, т.е. от скорости, через кинетическую энергию mx'^/l
материальной точки.
Вышеуказанное интегральное уравнение решается с помощью уравнения
Эйлера—Лагранжа
dL^d_d£^ d
Эх d/Эх," или коротко 4-^4, =0. (17.2)
С помощью этого уравнения интегральное уравнение (17.1) можно
преобразовать в дифференциальное для заданной функции Лагранжа.
В качестве наглядного примера вычислим движение материальной точки в поле
гармонического потенциала V(x) = ех^/2. Функция Лагранжа этой системы равна
1 9 1 9
L{x,x^,t) = T -V = -m{xJ—ex". (17.3)
Производные функции Лагранжа равны
dL дЬ d dL
^- = -ос, -:— = тх^, —-— = тх^^. (17.4)
ах ах^ at дх^
Из уравнения Эйлера (17.2) получаем простое дифференциальное уравнение
второго порядка
тх,^-\-€Х = 0. (17.5)
Это дифференциальное уравнение второго порядка описывает гармонические
колебания материальной точки в потенциале с циклической частотой со = у/е/т.
17.2.2. Пространственные и пространственно-временные вариационные
задачи
В обработке изображений требуется сформулировать вариационную задачу для
изменяющихся по пространству и времени переменных. Траектория
материальной точки x(t) - скалярная функция - должна быть заменена пространственной
функцией или пространственно-временной Дл:), т.е. скалярно-векторной
функцией от векторной переменной. Для последовательностей изображений одним из
компонентов х является время t.
Следовательно, функция Лагранжа теперь зависит от векторной переменной х.
Кроме того, она не будет просто функцией, явно зависящей отДдс) и х. Будут
существовать дополнительные члены, зависящие от пространственных (и, возможно.
17.2. Непрерывное моделирование I: вариационный подход 463
временной) частных производных от /. Они появятся, как только мы потребуем,
чтобы/в точке зависела от/в окрестности. В заключение общая формулировка
функционала ошибок eif) как вариационный интеграл для д читается
£(/) = jl(/,/^ ,л:)(к^ -> minimum. (17.6)
а
Интеграл по площади вычисляется по некоторой области изображения Q € М^.
Уравнение (17.6) уже содержит информацию о том, что экстремум является
минимумом, так как /должна показывать минимальное отклонение от заданных
функций в определенных точках с дополнительными ограничениями.
Соответствующее уравнение Эйлера—Лагранжа равно
W
Вариационный подход можно также расширить до векторных признаков,
таких, как скорость в последовательностях изображений. Тогда функция Лагранжа
зависит от векторного признака /= [/,,/2,...,/ У, частных производных от каждой
компоненты/ признака по всем направлениям (/* )^ и явно от координаты jc:
£(/) = Jl(/,(/^)^ ,x)dx^ ^minimum.
(17.8)
Из этого уравнения получаем уравнение Эйлера—Лагранжа для каждой
компоненты / векторного признака:
(17.9)
17.2.3. Ограничения подобия
Член подобия используется для того, чтобы сделать смоделированный признак
подобным измеренному признаку. Для простой задачи сегментации, в которой
объекты могут различаться по их уровню яркости, измеренным признаком
является уровень яркости сам по себе, а член подобия задается S соотношением
Щ,х) = S{f,x) =11 f{x)-g{x) \\„. (17.10)
Это просто означает, что отклонение между смоделированным признаком и
измеренным изображением по норме L^ должно быть минимальным. Наиболее
часто используемой нормой является норма L^, приводящая к хорошо известному
подходу метода наименьших квадратов (НК). Для линейной задачи
восстановления исходное изображение Ддс) ухудшается операцией свертки с функцией
рассеяния точки понижения качества h{x) (для дополнительных подробностей см. раздел
17.5). Таким образом, измеренное изображение д(х) задается соотношением
g{x) = h{x)^f{x). (17.11)
Для того чтобы получить минимальное отклонение между измеренными и
реконструированными изображениями, член подобия равен
S{f,x)^h{x)*f{x)-g{x)\\„. (17.12)
Глава 17. Регуляризация и моделирование
В качестве последнего примера рассмотрим ограничение подобия для
определения движения. В разделе 14.3.2 мы рассмотрели, что оптический поток должен
удовлетворять уравнению ограничения яркости (14.9):
f{x,t)Vg{x,t)^gXx,t) = 0, (17.13)
и использовали подход, который минимизировал отклонение от оптического
потока в смысле наименьших квадратов (уравнение (14.15)). При норме L^ мы
получаем следующий член подобия:
S{f,x,t)=\\fVg + gX- (17.14)
Это уравнение просто выражает, что уравнение неразрывности для оптического
потока (14.9) должно удовлетворяться настолько хорошо, насколько возможно в
смысле наименьших квадратов. Обратите внимание, что подобие теперь также
зависит от времени, поскольку задача минимизации расширяется от изображений
до пространственно-временных изображений.
Из следующего примера мы узнаем, что ограничения подобия в одиночку не
имеют большого применения с вариационным подходом. Используем задачу
определения движения с нормой L^ (наименьшие квадраты). Функция
Лагранжауравнения (17.14) зависит только от оптического потока/ Для вычисления уравнений
Эйлера—Лагранжа нам нужно только рассмотреть частные производные от члена
подобия уравнения (17.14) относительно компонент оптического потока, dL/df:
Lf=2{fVg + g,)g^. (17.15)
Подстановка уравнения (17.15) в уравнение Эйлера—Лагранжа (17.9) дает
(f^9 + 9,)9.=0^ (f'^9 + 9,)9y=0 (17.16)
ИЛИ, записанное как векторное уравнение,
{f^9 + 9,)^9 = ^- (17-17)
Эти уравнения свидетельствуют, что оптический поток не может определяться в
случае, когда пространственный градиент Vg равен нулевому вектору. В противном
случае они дают не больше ограничений, чем неразрывность оптического потока. Этот
пример наглядно демонстрирует ограниченные возможности применения локальных
офаничений подобия. Они дают только изолированные локальные решения без каких-
либо ограничений на пространственное изменение оптического потока. Это
результат формулировки задачи без учета связей между соседними точками. Таким образом,
для успешного решения задачи необходимо включение глобальных ограничений.
Следовательно, требуется прибавить еще один член к функции Лагранжа,
который также зависит от производных от/
L{f. V/, л:) = 5(/, X) + R{f, V/, л:).
(17.18)
17.2.4. Глобальные ограничения гладкости
Одним из самых элементарных глобальных регуляризаторов является гладкость.
Для большого количества задач в обработке изображений имеет смысл
потребовать, чтобы моделируемая величина изменялась медленно в пространстве и
времени. Для задачи сегментации это требование означает, что объект
определяется как связная область с постоянными или медленно изменяющимися
признаками. Более того, глубина поверхности и поле скоростей движущегося
объекта непрерывны по меньшей мере в большинстве точек.
17.2. Непрерывное моделирование I: вариационный подход
Следовательно, мы теперь ищем подходящий регуляризатор R для
прибавления к функции Лагранжа, чтобы получить пространственно гладкие решения.
Такой член требует пространственных частных производных смоделированного
признака. Простейший член, содержащий только первые производные, для скалярного
признака /в 2-D изображении равен
/?(/,,/J = a^(/>/;) = a^|V/r. (17.19)
Для векторного признака/= [/p/J^
/?(v/i,v/,)=a^(l у/; г+1V/, Г). (17.20)
В этом дополнительном члене частные производные возникают как сумма
квадратов. Это означает, что мы оцениваем член гладкости по той же норме (норма L^ -
сумма наименьших квадратов), как и член подобия. Кроме того, в этой
формулировке все частные производные являются равно взвешенными. Множитель а^
указывает на относительный вес члена гладкости в сравнении с членом подобия.
Полный функционал оишбок по методу наименьших квадратов для определения
движения, включающий члены подобия и гладкости, задается тогда соотношением
Д/,УА,У/;,л:) = (/Уд + д,)Ча^(|У/;Г+|7Лр).
(17.21)
Подстановка этой функции Лагранжа в уравнение Эйлера—Лагранжа (17.9) дает
следующее дифференциальное уравнение:
(У9/ + 9,)9у -а'(Ш^+Ш„) = 0 ^^^'^^^
ИЛИ подытоженное в векторном уравнении:
\
Член подобия
Vgf- о^ =0.
Член гладкости
(17.23)
Легко понять, как оптический поток получается из этой формулы. Сначала
представьте, что интенсивность сильно изменяется в определенном направлении. Член
подобия тогда становится доминирующим над членом гладкости, и скорость будет
вьиисляться в соответствии с локальным оптическим потоком. И наоборот, если
изменение интенсивности мало, то член гладкости становится доминирующим.
Локальная скорость будет вьиисляться таким образом, чтобы она являлась настолько
близкой к скорости в окрестности, насколько это возможно. Другими словами,
векторы потока интерполируются по ближайшим векторам потока.
Этот процесс можно далее проиллюстрировать предельным примером.
Давайте рассмотрим объект с постоянной интенсивностью, движущийся на
черном фоне. Тогда член подобия полностью исчезает внутри объекта, в то время
как на границе скорость, перпендикулярная границе, может быть вычислена
только по этому члену. Это давняя и хорошо известная задача в физике: задача о
вычислении потенциальной функции (без стоков и источников, А/=0) при
заданных граничных условиях на контуре объекта. Это уравнение известно кзкуравнение
Лапласа. Мы можем сразу же сделать вывод о форме решения в областях, где член
подобия равен нулю. Поскольку вторые производные равны нулю, первые про-
Глава 17, Регуляризация и моделирование
странственные производные являются постоянными. Это приводит к
смоделированному признаку/, который изменяется линейно в пространстве.
17.2.5. Управление гладкостью
Обсудив основные свойства ограничений гладкости, рассмотрим, как мы можем
адекватно рассматривать пространственные и временные неоднородности при этом
подходе. В задаче сегментации смоделированный признак будет разрывным на
контуре объекта. То же самое выполняется для оптического потока. Ограничение
гладкости, как мы формулировали его до сих пор, не учитывает неоднородности.
Мы использовали глобальное ограничение гладкости и, таким образом, получили
глобально гладкое поле. Таким образом, нам необходимо разработать методы,
которые позволят нам выделять и моделировать неоднородности адекватно.
Сначала мы рассмотрим основные возможности для изменения задачи
минимизации в пределах выбранных рамок. Для того чтобы сделать это, перепишем
интегральное уравнение (17.6), используя знания о значении функции Лагранжа,
полученной в последнем разделе:
J {S{f) + Л(Д) )d^x-»Minimum. (17.24)
Член подобия Член гладкости
Для учета неоднородностей возможны два подхода:
1. Ограничение области интегрирования. Область интегрирования
является одним из возможных способов для решения проблемы неоднородностей в
признаке/. Если область интегрирования содержит неоднородности, то
получаются некорректные значения. Таким образом, должны быть найдены
алгоритмы, которые осуществляют поиск контуров в/и как следствие
ограничивают область интегрирования сегментированными областями. Очевидно, что это
сложная итерационная процедура. Во-первых, контуры в изображении сами по
себе не обязательно совпадают с контурами в признаке/. Во-вторых, до
вычисления поля признака/доступна только разреженная информация, так что
разбиение не представляется возможным.
2. Модификация члена гладкости. Модификация члена гладкости — еще один
способ решения проблемы неоднородностей. В точках, где предполагается
неоднородность, ограничение гладкости может ослабляться или даже исчезать. Это
допускает неоднородности. И опять это представляет собой итерационный
алгоритм. Член гладкости должен включать функцию управления, которая отключает
ограничение гладкости в соответствующих условиях. Это свойство называется
управляемой гладкостью [198].
Далее мы рассматриваем два подхода, которые модифицируют область
интегрирования для определения движения. Модификация члена гладкости детально
рассматривается в разделе 17.3.
Интегрирование вдоль замкнутых кривых пересечений нулевого уровня. Хилд-
рет (Hildreth) [76] использовал изображение, обработанное с помощью
фильтра Лапласа, и ограничил какие-либо дальнейшие вычисления пересечениями
нулевого уровня. Этот подход мотивируется тем, что пересечения нулевого
уровня отмечают контуры уровней яркости (раздел 12.3), т.е. признаки, в которых
мы можем вычислить компоненту скорости, нормальную к контуру. Большое
77.2 Непрерывное моделирование I: вариационный подход 46
Рис. 17.3. Два изображения гамбургского такси. Видеоизображения предоставлены
факультетом компьютерных наук (Computer Science Department) Гамбургского
университета и используются в качестве тестовой последовательности для обработки
последовательностей изображений
преимущество подхода заключается в том, что предварительный выбор
перспективных признаков значительно уменьшает объем вычислений.
С помощью выбора пересечений нулевого уровня ограничение гладкости
ограничивается некоторой контурной линией. Это кажется полезным, поскольку
пересечение нулевого уровня, вероятнее всего, принадлежит объекту, но не
пересекает границ объекта. Однако это не обязательно выполняется. Если пересечение
нулевого уровня принадлежит объекту, то скорость вдоль контура не должна
показывать нарушения непрерывности. Выбор линии вместо области для ограничения
гладкости заменяет интегрирование по площади интегрированием по линии вдоль
контура s:
j>{(nf-Af +сс' [Ulf+((f2)sf]}^ -^ minimum, (17.25)
где п - единичный вектор, нормальный к контуру; f^ — скорость, нормальная к
контуру.
Производные скоростей вьиисляются в направлении контура. Компонента,
нормальная к контуру, задается непосредственно членом подобия, в то время как
компонента скорости, параллельная контуру, должна быть получена из ограничения
гладкости вдоль всего контура. Хилдрет (Hildreth) [76] вычислил решение линейной
системы уравнений (17.25), итерационно используя метод сопряженных фадиентов.
Несмотря на свою элегантность, ориентированный на контуры метод имеет
существенные недостатки. Нет гарантии, что пересечение нулевого уровня
принадлежит объекту. Таким образом, мы не можем полагать, что поле оптического
потока является непрерывным вдоль пересечения нулевого уровня. Поскольку для
вычисления поля оптического потока используются только контуры, можно
вычислить локально только один компонент вектора перемещения. Таким образом,
все признаки, такие, как максимумы уровней яркости или углы уровней яркости,
которые допускают однозначное локальное определение вектора перемещения,
игнорируются.
Ограничение интегрирования сегментированными областями. Ориентированный
на области подход не упускает такие точки, но по-прежнему старается ограничить
468 Глава 17. Регуляризация и моделирование
\ \ ч \
\ ч ч ч
Ч Ч Ч Ч N Ч
\ Ч Ч Ч Ч Ч
ч ч V ч ч ч
ч \ Ч ч ч ч
ч ч ч ч ч ч
• ».Л>-4;'>*. >
Рис. 17.4. Определение ПВП в сцене такси (рис. 17.3) с использованием метода
динамической пирамиды: а — в — три уровня поля оптического потока с использованием
глобального офаничения гладкости; г - конечный результат оптического потока с
использованием ориентированного на области ограничения гладкости (с согласия М. Шмидта
(М. Schmidt) и Дж. Денглера (J. Dengler), Gemian Cancer Research Center, Heidelberg)
гладкость в пределах объекта. И снова для разложения изображения на области
можно использовать пересечения нулевого уровня или любой другой метод
сегментации (глава 16). Ограниченная по областям гладкость просто пренебрегает
ограничением неразрывности на границах области. Простейший подход к этому виду
ограничения состоит в разделении областей интегрирования и оценивании их по
отдельности.
Как и следовало ожидать, офаниченное по областям ограничение гладкости
приводит к полю оптического потока с разрывами на границах областей (рис. 17.4, г),
которое явно отличается от глобально гладкого поля оптического потока на рис. 17.4, в.
Мы сразу же распознаем такси по границам оптического потока.
Однако мы также видим, что машина сегментируется дополнительно на области
с различным полем оптического потока, что и обнаруядавается табличкой такси на
крыше машины и задним и боковыми окнами. Малые области особенно хорошо
проявляют поле оптического потока, значительно отличающееся от поля в более
крупных областях. Таким образом, простое, ограниченное по областям
ограничение гладкости не отражает того, что могут существовать отделимые области внутри
объекта. Поле оптического потока может быть сильно гладким вдоль этих границ.
17.3, Непрерывное моделирование II: диффузия
17.3. Непрерывное моделирование II: диффузия
в этом разделе мы рассматриваем непрерывное моделирование с новой точки
зрения. Функционал ошибок на основе метода наименьших квадратов для
определения движения (17.23)
■«'Д/ = 0 (17.26)
можно рассматривать как стационарное решение диффузионно-реакционной системы
с однородной диффузией, если постоянная а^ отождествляется с коэффициентом
диффузии D:
J'^'t,
\^9. (17.27)
Стандартное нестационарное дифференциальное уравнение (в частных
производных) для однородной диффузии (см. уравнение (5.18) в разделе 5.3.1)
дополняется еще одним членом источника, относящимся к ограничению подобия.
Интенсивность источника пропорциональна отклонению от ограничения оптического
потока. Таким образом, этот член стремится сдвинуть значения/, чтобы
удовлетворить условию ограничения оптического потока.
После этого вводного примера мы можем сформулировать соотношение
между вариационным функционалом ошибок и диффузионно-реакционными
системами в общем виде. Уравнение Эйлера—Лагранжа
W
Е^Л.-^/=0. (17.28)
которое минимизирует функционал ошибок для скалярной
пространственно-временной функцииДдс), дс 6 Q
е(,/) = \Щ,/,^,х)дос'', (17.29)
О.
можно рассматривать как установившееся состояние диффузионно-реакционной
системы
Далее мы будем детально рассматривать аспект моделирования, которого мы
до сих пор только коснулись в разделе 17.2.5, а именно локальную модификацию
члена гладкости. Говоря языком диффузионной модели, это означает локально
изменяющийся коэффициент диффузии в первом члене в правой части уравнения
(17.30). Из вышеизложенного рассуждения мы знаем, что для каждого подхода к
локально изменяющемуся коэффициенту диффузии существует соответствующий
вариационный функционал ошибок, который минимизируется
диффузионно-реакционной системой.
В разделе 5.3.1 мы рассматривали однородный диффузионный процесс,
который образовывал представление изображения с переменной разрешающей
способностью, известное как линейное масштабное пространство. Если ограничение
гладкости задается зависимым от локальных свойств содержания изображения.
Глава 17. Регуляризация и моделирование
таких, как градиент, тогда неоднородный диффузионный процесс приводит к
образованию нелинейного масштабного пространства. Что касается моделирования,
интересный момент здесь состоит в том, что сегментация может выполняться без
члена подобия.
17.3.1. Неоднородная диффузия
Простейший подход к пространственно изменяющемуся сглаживающему члену,
который учитывает неоднородности, заключается в уменьшении коэффициента
диффузии на контурах. Таким образом, коэффициент диффузии становится
зависимым от интенсивности контуров, что и задается с помощью модуля градиента
£)(/) = £)(|V/p). (17.31)
При локально изменяющемся коэффициенте диффузии
диффузионно-реакционная система принимает вид
y;=V(Z)(|V/p)V/)-I,. (17.32)
Обратите внимание, что неправильным будет записать Д| V f\^)Af, Это можно
увидеть из дифференцирования нестационарного уравнения диффузии в разделе 5.3.1.
С учетом уравнения (17.32) член регуляризации R в функции Лагранжа равен
R = R(\Vfn (17.33)
где коэффициент диффузии равен производной функции R:D=R\ Это можно
легко доказать, подставив уравнение (17.33) в уравнение (17.28).
В работе [151] была использована следующая зависимость коэффициента
диффузии от модуля градиента:
;i2
D(\ V/1) = D, -, -, (17.34)
где Я — регулируемый параметр. Для малых значений градиентов \Wf\<^X, D
приближается к Dq, для больших значений градиентов \Vf\» А, D стремится к нулю.
Хотя эта идея кажется простой и понятной, с ней также связаны проблемы.
Зависящий от функциональной зависимости D от V/*диффузионный процесс
может стать неустойчивым, приводя даже к увеличению крутизны контуров.
Надежный способ избежать этой проблемы заключается в использовании регуляризо-
ванного градиента, полученного из сглаженного варианта изображения, что и
показано в [213]. В этой работе коэффициент диффузии
D = D,
1-ехр
т
(\ViB'*f){x)\/Xy
/J
(17.35)
Это уравнение подразумевает, что для малых значений модулей градиента
коэффициент диффузии является постоянным. При определенной пороговой
величине модуля градиента коэффициент диффузии быстро убывает к нулю. Чем выше
показатель степени т, тем круче переход. Для значений, используемых в [213], /и=4
ис^ = 3,31488, коэффициент диффузии убывает от 1 при 1УП/А = 1 до
приблизительно 0,15 при \Vf\/X = 2. Обратите внимание, что в уравнении (17.35) выбран
регуляризованный градиент, поскольку градиент не вычисляется
непосредственно по изображению Ддс), а вычисляется по изображению, сглаженному с помощью
17.3. Непрерывное моделирование II: диффузия
биномиальной сглаживающей маски <BF. Правильно выбранный регуляризован-
ный градиент делает устойчивым неоднородный сглаживающий процесс и
позволяет избежать неустойчивостей и увеличения крутизны контуров.
Простая явная дискретизация неоднородной диффузии использует регуляризо-
ванные дифференциальные операторы, что и рассмотрено в разделе 1.7. На первом
шаге фадиентное изображение вычисляется с помощью векторного оператора
®1
(17.36)
На втором шаге градиентное изображение поточечно умножается на оператор
управления S, который вычисляет коэффициент диффузии в соответствии с
уравнением (17.34) или уравнением (17.35):
sn
sn
2J
(17.37)
Изображение управления Нравно единице в постоянных областях и
уменьшается до малых значений на контурах. На третьем шаге оператор градиента
применяется повторно
[®Р®2]
5®1
^(D,{S(D,)-\-CD^{S'(D^).
(17.38)
В работе [213] была использована более сложная неявная схема решения.
Однако эта схема является более дорогостоящей с вычислительной точки зрения и
менее изотропной, чем явная схема в уравнении (17.38), если используются
операторы градиента, которые оптимизируются для изотропии, что и рассматривалось
в разделе 12.7.5.
Даже еще более простое, но только приближенное выполнение неоднородной
диффузии управляет биномиальным сглаживанием, используя оператор
X+S'{(B-X), (17.39)
Оператор 5 вычисляет изображение управления со значениями от нуля до единицы.
На рис. 17.5 показано применение неоднородной диффузии для сегментации
зашумленных изображений. Тестовое изображение содержит треугольник и
прямоугольник. Стандартное сглаживание значительно подавляет шум, но приводит к
существенному размыванию контуров (рис. 17.5, б). Неоднородная диффузия не ведет
к размыванию контуров и по-прежнему приводит к совершенной сегментации
квадрата и треугольника (рис. 17.5, в). Единственным недостатком является то, что
контуры сами по себе остаются зашумленными, поскольку сглаживание там подавляется.
17.3.2. Анизотропная диффузия
Как мы увидели в примере, рассмотренном в конце последнего раздела,
неоднородная диффузия имеет существенный недостаток — диффузия останавливается
полностью и во всех направлениях на контурах, оставляя контуры
зашумленными. Однако контуры размываются только диффузией, перпендикулярной им;
диффузия, параллельная им, является даже выгодной, поскольку она делает
устойчивыми контуры.
/^472 Глава 17. Регуляризация и моделирование
Рис. 17.5. а - исходное изображение, сглаженное с помощью линейной диффузии
(б), неоднородной, но изотропной диффузии (в) и анизотропной диффузии (г) [213]
Подход, который делает диффузию независимой от направления контуров,
известен как анизотропная диффузия. При этом подходе поток больше не параллелен
градиенту. Следовательно диффузия больше не может описываться скалярным
коэффициентом диффузии, как в уравнении (5.15). Теперь требуется тензор диффузии:
j = -DVf = -
д, д
12
д, д
'12
22
Л
2 J
(17.40)
С тензором диффузии диффузионно-реакционная система принимает вид
f,=V(D(VfVf)Vf)-L^, (17.41)
а соответствующий регуляризотор в функции Лагранжа равен
/г = traced (V/V/^) (17.42)
npvLD= R\
17.3. Непрерывное моделирование II: диффузия
Свойства тензора диффузии можно увидеть лучше всего, если симметричный
тензор привести в систему с главными осями с помощью поворота системы
координат. Тогда уравнение (17.40) сводится к
J =-
d;
о
о D'
fi
D[f;'
(17.43)
Диффузия по двум направлениям осей теперь разделяется. Два коэффициента
на диагонали, D^ и D^, являются собственными значениями тензора диффузии. По
аналогии с изотропной диффузией общее решение для однородной анизотропной
диффузии можно записать как
f(x,t) =
1
2nG{(t)(J2(t)
exp
.у2 л
2а;(0 J
/
= ехр
.п \
У
2a,(t)
'/(х,0)
(17.44)
в пространственной области при сг[(/) = yjw^ и cjzit) = -y/lDj/.
Это означает, что анизотропная диффузия эквивалентна каскадной свертке с
двумя 1-D гауссовыми ядрами свертки, которые устанавливаются в направлениях
главных осей тензора диффузии. Если одно из двух собственных значений тензора
диффузии значительно больше другого, то диффузия имеет место только в
направлении соответствующего собственного вектора. Таким образом, уровни яркости
сглаживаются только в этом направлении. Пространственное расширение — как
для любого диффузионного процесса — пропорционально квадратному корню из
коэффициента диффузии (уравнение (5.23)).
Используя эту особенность анизотропной диффузии, легко разработать
диффузионный процесс, который преимущественно сглаживает только вдоль
контуров, но не перпендикулярно контурам. С помощью следующего подхода
блокируется только сглаживание через контуры [213]:
f ^ \
D[ = 1-ехр
(|V(5'*/)W|/Ar
(17.45)
А'
= 1.
Как показано в работе [177], эффективное и точное явное выполнение
анизотропной диффузии снова возможно с регуляризованным дифференциальным
оператором первого порядка, оптимизированным для минимальной анизотропии:
[®„Фз]
Ol2
Ol2
»>22
(17.46)
при
<D,(J„ • Ф, + 5,2 • ®2) + ^2^2 • ®1 + «^22 • ®2)-
^12
У12 ^:
22,
COS0
-sine
sin0
COS0
О
О
COS0 -sin0
sin0 COS0
Spq, S( и Sj - изображения управления со значениями между нулем и единицей,
которые направляют диффузию параллельно контурам в каждой точке изображения.
S{vi ^2 непосредственно вьиисляются из уравнения (17.45), а направление контуров
и угол в можно получить, например, из структурного тензора (раздел 13.3).
Глава 17. Регуляризация и моделирование
Применение анизотропной диффузии показывает, что теперь - в отличие от
неоднородной диффузии — контуры также сглаживаются (рис. 17.5, г). Однако
сглаживание вдоль контуров имеет недостаток — углы контуров теперь размываются,
как в случае с линейной диффузией. Этого не происходило при неоднородной
диффузии (рис. 17.5, в).
17.4. Дискретное моделирование: обратные задачи
Во второй части этой главы мы обращаемся к дискретному моделированию.
Дискретное моделирование можно, конечно, получить с помощью непосредственной
дискретизации дифференциальных уравнений в частных производных,
получающихся при использовании вариационного подхода. В действительности мы уже
сделали это в разделе 17.3 с помощью итерационных дискретных схем для
неоднородной и анизотропной диффузии.
Однако, анализируя дискретное моделирование независимо, мы получаем
дополнительное понимание. Теперь мы смотрим на моделирование с другой точки
зрения и рассматриваем его как линейную дискретную обратную задачу, В качестве
введения начнем со знакомой задачи линейной регрессии и затем разовьем
теорию дискретного обратного моделирования.
17.4.1. Простой пример: линейная регрессия
Соответствие прямой линии множеству точек экспериментальных данных х, у
является простым примером дискретной обратной задачи. Как проиллюстрировано
на рис. 17.6, величина ;; измеряется как функция переменной х, В этом случае
нашей моделью является прямая линия с двумя параметрами — смещением а^ и
наклоном а^:у = а^+а^х, С множеством из Q точек данных [Хд, yqVB итоге мы
приходим к линейной системе уравнений
(17.47)
которую можно сокращенно записать как
Mp = d. (17.48)
Матрица М размерностью Qx2 обозначается как модельная матрица или
расчетная матрица. Эта матрица отражает как тип модели (здесь линейную
регрессию), так и выбранные независимые точки измерения Хд, Вектор модели или
вектор параметров р содержит параметры модели, которые необходимо оценить, а
вектор данных d — измеренные данные Хд,
Если мы имеем только две точки данных, которые не совпадают, х^ ф х^, то мы
получаем точное решение линейной системы уравнений. Если доступны более двух
точек данных, то мы имеем больше уравнений, чем неизвестных. Мы говорим, что
система уравнений является переопределенной обратной задачей, В этом случае, как
правило, больше не представляется возможным получить точное решение. Мы
[l Xj 1
1 ^2
V ^q\
=
' уЛ
у^
Уа\
17.4. Дискретное моделирование: обратные задачи 475
10
5
У
0
-5
-
6
О
У^О
1
-4
о
о
1
-2
о
(
о
а
0
D
О
/° 1
О
1
2
i 0 J
Jai 1
1
4
6
Рис. 17.6. Иллюстрация линейной регрессии методом наименьших квадратов
можем только вьиислить оценку параметров модели р^^ в смысле минимального
отклонения данных d от данных, прогнозируемых с помощью модели d^^^ = Mp^^^.
Это отклонение можно выразить с помощью вектора ошибок е:
e = d-d^^^=d-Mp^^,, (17.49)
17.4.2. Нормы ошибок
Для того чтобы минимизировать вектор ошибок, нам необходима подходящая мера.
Мы можем использовать нормы, которые рассматривали при использовании
векторных пространств с внутренним произведением в разделе 2.3.1. Как правило,
норма L Q-мерного вектора е определяется как
\е\\„=
ч1/и
q=\
(17.50)
Частным случаем является норма Lj
\\e\l=max\e^\. (17.51)
Норма L^ используется чаще; она равна корню из суммы квадратов
отклонений элементов вектора ошибок
f Q V''
1^112 =
^=1
(17.52)
Более высокие нормы оценивают более высокие отклонения с более
существенным взвешиванием. Статистика точек данных определяет, какая норма должна
использоваться. Если измеренные точки данных з^ имеют плотность нормального
распределения (раздел 3.4.2), то должна использоваться норма L^ [136].
476 Глава 17, Регуляризация и моделирование
17.4.3. Решение методом наименьших квадратов
Переопределенная линейная обратная задача решается в смысле минимальной
нормы L^ вектора ошибок с помощью
Pcst=(^^^y ^^^ при ||^||2=|l<'-^/'estlHn^inin[ium. (17.53)
Это решение можно сделать приемлемым с помощью следующей
последовательности операций:
= d
(м^м)'
(17.54)
при условии, что существует матрица, обратная к МР'М,
В оставшейся части этого раздела мы выводим решение переопределенной
дискретной линейной обратной задачи (уравнение (17.48)), которое
минимизирует норму L^ вектора ошибок. Следовательно, мы явно вычисляем решение,
минимизируя норму L^ вектора ошибок е (уравнение (17.49)):
Q f р Л( ^ ^
^=1
р=1
р'=1
Разложение суммы и перестановка местами двух суммирований приводит к
Р Р Q
Iklli = ^^^Рр'Рр'^^^яр'^яр-
р'^Хр'^Х
q^\
г у, у,
(17.55)
р=1
q^\
Найдем минимум этого выражения, вычислив частные производные
относительно параметров/;^, которые должны оптимизироваться. Только выражения А и
В в уравнении (17.55) зависят от/?^:
ЪА ^ ^ ^
Фк /=1р'=1 «'=1
Р Q Р Q
р'=\ q=\ р'=1 q'=l
V'Wp'
= 4.р,Ь
р'=\ q'=l
— = lY.'^^'A'-
Фк 9=1
17.4. Дискретное моделирование: обратные задачи
Сложим обе производные и приравняем результат к нулю:
Э||^||^ ,^ Д л^ ^ п
^— = ^LPpL'^,'krn,y--2^rn^,,d^. = 0.
Для того чтобы выразить суммы как операции умножения матрицы на
матрицу и матрицы на вектор, заменяем матрицу Мв обоих слагаемых на ее
транспонированную матрицу ЛГ:
р Q Q
Z Рр X К'^яУ - S К'^я'=о
И окончательно получаем матричное уравнение
М' Мр^^^М' d. (17.56)
PxP P
P
Это уравнение можно решить, если квадратная и симметричная матрица ЛГМ
размерностью РхРявляется обратимой. Тогда
Р^^,=(М^МУ'МЧ. (17.57)
Матрица (ЛГЛ/)"*АГ известна как обобщенное обращение M-^ матрицы М.
МАЛ. Геометрическая иллюстрация
Прежде чем мы изучим методы решения больших линейных систем уравнений,
полезным будет проиллюстрировать линейные системы уравнений
геометрически, /^параметров модели/i образуют Р-мерное векторное пространство. Это
пространство можно рассматривать как пространство всех возможных решений
обратной задачи с Р параметрами модели. Теперь мы задаемся вопросом, что
означает иметь одну точку данных d^. Согласно уравнению (17.48), одна точка
данных приводит к одному линейному уравнению, включающему в себя все
параметры модели/>
р
Ъ'^ярРр^^я ™" ^яР = ^я (17-58)
к=р'
Это уравнение можно рассматривать как скалярное произведение строки q
модельной матрицы т^ на вектор модели/^. В пространстве моделей это
уравнение образует Р - 1-мерную гиперплоскость всех векторов/?, которая имеет
нормальный вектор т^ и расстояние d^ от начала отсчета пространства моделей. Таким
образом, линейное уравнение устанавливает взаимно-однозначное соответствие
между точкой данных в пространстве данных и{Р- 1)-мерной гиперплоскостью в
пространстве моделей. Это отображение точек данных в пространство моделей
называется преобразованием Хафа, которое мы ввели в разделе 16.5.2. Каждая
точка данных сводит пространство возможных решений к (Р - 1)-мерной
гиперплоскости в пространстве моделей.
На рис. 17.7, а иллюстрируется решение линейной системы уравнений с тремя
неизвестными. При трех уравнениях три плоскости пересекаются в единственной точке
478 Глава 17. Регуляризация и моделирование
Рис. 17.7. Геометрическая иллюстрация решения линейной системы уравнений с тремя
неизвестными с использованием преобразования Хафа: а — точно разрешимая система
уравнений; б — переопределенная система уравнений с неединственным решением
при условии, что соответствующая модельная матрица 3x3 является обратимой. Даже
в переопределенном случае решение необязательно должно быть единственным. На
рис. 17.7, б показан случай пяти плоскостей, пересекающихся по линии. Тогда
решение не является единственным, но только ограничено линией. Если эта линия
ориентирована вдоль одной из осей, то соответствующий параметр модели может
принимать любое значение; однако два других параметра модели фиксируются.
В случае произвольно ориентированной линии все усложняется. Тогда
фиксируются параметрические комбинации, нормальные к линии, но не фиксируется
параметрическая комбинация, представленная вектором в направлении линии.
Используя разложение по сингулярным значениям [61, 158], мы можем решать
сингулярные линейные системы уравнений и отделять разрешимые параметрические
комбинации от неразрешимых.
Переопределенная линейная система уравнений, которая не имеет
единственного решения, не является математической редкостью. Она является скорее
общей задачей в обработке изображений. Мы уже сталкивались с ней, к примеру, в
определении движения с апертурной проблемой (раздел 14.3.2).
17.4.5. Ошибка параметров модели
Переопределенная линейная система уравнений, которая была решена с помощью
минимизирования нормы L^, допускает анализ ошибок. Мы можем изучать не
только отклонения между моделью и данными, но также и ошибки оценки вектора
параметров модели/>^^^.
Среднее отклонение между измеренными и прогнозируемыми точками
данных непосредственно связано с нормой вектора ошибок. Дисперсия равна
1 „ ,., 1
а =
к|р=.
\d-Mp^
i2
Wr
(17.59)
Q-P Q-P
Для того чтобы не вносить ошибку в оценку дисперсии, мы делим норму на
степень свободы 0 - Р, а не на Q.
Согласно уравнению (17.57), оценка вектора параметров/>^^^ является
линейной комбинацией вектора данных d. Следовательно, мы можем применить закон
распространения ошибки (уравнение (3.27)), полученный в разделе 3.3.3. Ковариа-
17.4. Дискретное моделирование: обратные задачи
ционная матрица (определение см. уравнение (3.19)) оценки вектора параметров
р^^^ с использованием (^)^ = Д^^4^ задается соотношением
cov(/i,3t) = (М^М)'' М'' coy(d)M( М^Му\ (17.60)
Если отдельные элементы в векторе данных rf являются некоррелированными и
имеют одинаковую дисперсию ст^, т.е. cov(d) = a^I, то уравнение (17.60) сводится к
cov(/i,J = (M^M)"'a^ (17.61)
В этом случае {NfMy^ непосредственно является, за исключением множителя
а^, ковариационной матрицей параметров модели. Это означает, что
диагональные элементы содержат дисперсии параметров модели.
17.4.6. Регуляризация
До сих пор функционал ошибок (17.52) содержит только ограничение подобия и
не содержит никакого ограничения регуляризации или сглаживающего
ограничения. Для многих дискретных обратных задач, таких как линейная регрессия,
рассмотренная в разделе 17.4.1, регуляризация параметров не имеет смысла. Однако
если оцениваемые параметры являются элементами временного ряда или
пикселями изображения, ограничение гладкости имеет смысл. Подходящий параметр
гладкости может быть тогда нормой временного ряда или изображения,
свернутого с помощью дифференциального фильтра:
\\r\\,=\\h*pt- (17.62)
Говоря языком матричной алгебры, свертку можно выразить операцией
умножения вектора на матрицу:
II I-112=11 Яр 11^. (17.63)
Вследствие операции свертки матрица /Г имеет особый вид. Только
коэффициенты вблизи диагонали являются ненулевыми, а все значения в направлении
диагонали одинаковы.
В качестве примера рассмотрим тот же критерий гладкости, который мы также
использовали в вариационном подходе (раздел 17.2.4), - первую производную. Его
можно аппроксимировать, к примеру, сверткой с фильтром правой разности,
который приводит к матрице
"-1 1 О О ... О'
Я =
0-11 о ... о
о о -1 1 ... о
(17.64)
Минимизация суммарного функционала ошибок с использованием нормы L^.
(17.65)
\\et=\\d-Mpt^a'\\Hpt
Подобие
Гладкость
приводит к следующему решению методом наименьших квадратов [136]:
р^^^=(М^М-^а^Н^ну' МЧ.
(17.66)
Глава 17. Регуляризация и моделирование
Структура решения подобна решению методом наименьших квадратов в
уравнении (17.53). Член гладкости просто создает дополнительный член a^IFH,
В следующем разделе мы изучим, как отобразить изображение в вектор так,
чтобы мы могли также применять дискретные обратные задачи к изображениям.
17.4.7. Алгебраическая томографическая реконструкция
В этом разделе мы рассматриваем пример дискретной обратной задачи,
которая учитывает данные изображения: реконструкцию по проекциям (раздел 8.6).
Для того чтобы применять дискретную обратную теорию, как и рассматривалось
до сих пор, данные изображения должны отображаться в вектор, - вектор
изображения. Это отображение легко выполняется с помощью перенумерования
пикселей матрицы изображения от строки к строке (рис. 17.8). Таким образом,
матрица изображения Мх 7Vпреобразуется в вектор-столбец с размерностью Р= Л/х N\
р = [т^,т2, ...уГПр, ....Шр^ . (17.67)
Теперь мы берем отдельный проекционный пучок, который пересекает
матрицу изображения (рис. 17.8). Тогда мы можем приписать весовой множитель
каждому пикселю вектора изображения, который представляет вклад пикселя в
проекционный пучок. Мы можем объединить эти множители в Q-мерном векторе дд.
9q "[^ЭдЛ^Эда^ —^9q,p9 —^9q,p\ *
(17.68)
Полное испускание или поглощение вдоль ^-го проекционного пучка d^
можно тогда выразить как скалярное произведение двух векторов дд ир:
р
^Я^^9д^р^р='9дР. (17.69)
Если Q проекционных пучков пересекают матрицу изображения, то мы
получаем линейную систему уравнений из Q уравнений и Р неизвестных:
т,
^ы*^
т2
ГПз
/
/
/
/
/
/
у
/
/
/
^
m^i
глгм
fTlMN
Рис. 17.8. Иллюстрация йигебраической реконструкции по проекциям:
проекционный пучок flf^ пересекает матрицу изображения. Все пиксели, соответствующие
пучку, вносят вклад в проекцию
17.5. Обратная фильтрация
Х = ^^. „7.70,
Вектор данных d содержит измеренные проекции, а вектор параметровр содержит
значения пикселей матрицы изображения, которые должны реконструироваться.
Расчетная матрица Л/дает зависимость между этими двумя векторами, описывая, как в
отдельной установке проекционные пучки пересекают матрицу изображения. С
помощью соответствующих весовых множителей мы можем непосредственно учесть
ограниченную разрешающую способность детектора и размер источника излучения.
Алгебраическая томографическая реконструкция является общим и гибким
методом. В отличие от метода отфильтрованной обратной проекции (раздел 8.6.3),
он не ограничивается параллельной проекцией. Пучки могут пересекать матрицу
изображения любым образом и могут даже быть изогнутыми. К тому же мы
получаем оценку ошибок реконструкции.
Однако алгебраическая реконструкция включает в себя решение больших
линейных систем уравнений. Здесь полезно проиллюстрировать огромный размер этих
систем уравнений. В типичной задаче вектор модели учитывает все пиксели
изображения. Даже при среднем разрешении, например 256 х 256 пикселей, пришлось бы
вьиислять матрицу, обратную к матрице 65 536 х 65 536. Эта матрица содержит
приблизительно 4 • 10^ точек и не вмещается в память любых даже самых мощных
компьютеров. Таким образом, требуются альтернативные методы решения.
17.4.8. Дополнительные примеры обратных задач
Задачи такого вида являются довольно распространенными в анализе
экспериментальных данных в естественных науках. Экспериментаторы смотрят на дискретную
обратную задачу следующим образом. Они проводят эксперимент, из которого
получают набор результатов измерений и объединяют их в Q-мерный вектор данных rf.
Эти данные сравниваются с моделью наблюдаемого процесса. Параметры этой
модели задаются Р-мерным вектором модели/i. Теперь полагаем, что зависимость между
вектором модели и вектором данных можно описать как линейную. Тогда она
может быть выражена модельной матрицей М, и мы получаем уравнение (17.70). Для
обработки изображений обратные задачи являются также распространенными. Они
не только включают полный список задач, рассмотренных во введении этой главы
(раздел 17.1.1), но также и оптимизацию фильтров. В этой книге рассматриваются
оптимизированные методом наименьышх квадратов фильтры для интерполяции
(раздел 10.6.2) и вьщеления контуров (разделы 12.6 и 12.7.5).
17.5. Обратная фильтрация
Теперь изучим класс обратных задач, которые распространены в обработке
сигналов, и покажем способ быстрых итерационных решений больших обратных задач.
17.5.1. Восстановление изображений
Совершенной системы формирования изображений не существует вследствие
неустранимых физических ограничений. Следовательно, изображения не являются
тождественными их оригиналу. Поскольку научное применение всегда наклады-
Глава 17. Регуляризация и моделирование
вает ограничения, существует необходимость вносить поправки на пределы
резкости изображений. Люди также совершают ошибки в управлении системами
формирования изображений. Изображения, смазанные движением объектов или камеры,
размытые из-за неправильной настройки фокуса, механически неустойчивой
оптической системы, или с ухудшенным качеством вследствие неисправных или
неправильно используемых оптических систем, являются более распространенными, чем
можно подумать. Известным недавним примером был дефект в оптике
космического телескопа Хаббла, где ошибка в тестовых процедурах для главного зеркала
привела к значительной остаточной аберрации телескопа. Коррекция известного и
неизвестного ухудшения качества изображения называется восстановлением.
Возникает вопрос: можно ли удалить эффекты ухудшения качества, и если да, то
в какой степени? Конечно, очевидно, что информация, которая больше совсем не
присутствует в изображении с ухудшенным качеством, не может быть
восстановлена. Чтобы разъяснить этот момент, давайте предположим предельный случай -
только средний уровень яркости изображения сохраняется. Тогда реконструкция его
содержания никаким образом не будет представляться возможной. Таким образом,
мы можем надеяться, что искажение только частично удаляет интересующую нас
информацию, даже если мы больше не можем непосредственно «ввдеть» ее.
В разделах 7.6 и 9.2.1 мы увидели, что, как правило, любая оптическая система,
включающая преобразование в цифровую форму, может рассматриваться как
линейная, инвариантная относительно сдвига система и, таким образом, описываться
в хорошем приближении функцией рассеяния точки и передаточной функцией.
Первая задача состоит в определении и описании ухудшения качества
изображения настолько точно, насколько это возможно. Это можно сделать с помощью
проведения анализа системы формирования изображений либо теоретически, либо
экспериментально, используя некоторые подходящие тестовые изображения. Если
это не представляется возможным, то изображение с ухудшенным качеством
остается единственным источником информации.
17.5.2. Обзор искажений изображений
При огромном разнообразии способов формирования изображений (глава 7)
существует много причин для ухудшения качества изображения. Несовершенства
оптической системы, известные как аберрации линз, ограничивают резкость
изображений. Однако даже с совершенной оптической системой резкость
ограничивается дифракцией электромагнитных волн в апертурной диафрагме линзы. В то
время как эти типы ухудшения качества являются свойством данной оптической
системы, размывание вследствие расфокусировки является распространенной
несогласованностью, которая ограничивает резкость в изображениях.
Дополнительными причинами размывания в изображениях являются нежелательные
движения и вибрации системы камер в течение времени экспонирования. Особенно
системы с узким полем обзора (телеобъективы) очень чувствительны к этому типу
ухудшения качества изображений. Размывание может также возникать в случае,
когда объекты перемещаются больше чем на пиксель в плоскости изображения в
течение времени экспонирования.
Расфокусировка и аберрации линз рассматриваются в этом разделе вместе,
поскольку они непосредственно связаны с оптической системой. Эффект размыва-
17.5. Обратная фильтрация
ния, или аберрации, выражается функцией рассеяния точки h(x) и оптической
передаточной функцией (ОПФ) h(k) (см. раздел 7.6). Таким образом, соотношение между
объектом д(х) и изображением д\х) в пространственной области и Фурье-области равно
g\x) = (h*g)(x) о . gXk) = kk)g{k). (17.71)
Аберрации линз являются, как правило, более сложными для обработки.
Большинство аберраций сильно увеличиваются в зависимости от расстояния от
оптической оси и не являются, таким образом, инвариантными относительно сдвига и
не могут описываться с помощью независящей от положения ФРТ. Однако
аберрации изменяются медленно и непрерывно в зависимости от положения в
изображении. До тех пор пока результирующее размывание ограничивается областью, в
которой мы можем считать аберрацию постоянной, мы можем все еще
рассматривать их с использованием теории линейных, инвариантных относительно сдвига
систем. Единственное различие состоит в том, что ФРТ и ОПФ изменяются
постепенно в зависимости от положения.
Если расфокусировка является доминирующим размывающим эффектом, то
ФРТ имеет форму апертурной диафрагмы. Поскольку большинство апертурных
диафрагм можно аппроксимировать окружностью, то функция описывает диск.
Преобразование Фурье от диска с радиусом г является функцией Бесселя ввда (>-R5):
1
пг
П
Г
х\
1г
\
J,{lK\k\r)
(ПЛ2)
п\к\г
Эта функция Бесселя, как показано на рис. 17.9, а, имеет ряд нулей и, таким
образом, полностью уничтожает определенные волновые числа. Этот эффект
можно наблюдать на рис. 17.9, б, который показывает расфокусированное
изображение кольцевой тестовой структуры.
В то время как размывание вследствие расфокусировки и аберраций линз
стремится быть изотропным, размывающие эффекты при движении одномерны, как
показано на рис. 17.10, б. В простейшем случае движение остается постоянным в
Рис. 17.9. а ~ передаточные функции для размывания в форме диска. Параметры для
различных кривых равны радиусу диска размытости; б — расфокусированное
изображение кольцевой тестовой структуры
484 Глава 17. Регуляризация и моделирование
Рис. 17.10. Моделирование размьюания при движении с использованием кольцевой
тестовой структуры: а — малое и б — большое размывание в горизонтаньном направлении
течение экспонирования. Тогда ФРТ размытости, вызванной движением, равна
одномерной функции-ящика. Без потери общности сначала положим, что
движение имеет направление вдоль оси х. Тогда (>-R4, >-R5)
иш
^ X ^
wA/
о . А^ДА:) = sinc(bAO, (17.73)
где и — модуль скорости; А^ — время экспонирования. Длина размытости равна
Ax=uAt.
Если скорость и ориентирована в другом направлении, то уравнение (17.73)
можно обобщить до
hBi(x) = -
1
u\At
-П
^ хй ^
\u\At]
\5(их) о . hsi(k)==smc(kuAt), (17.74)
где и = и /1 и I — единичный вектор в направлении размытости, вызванной движением.
17.5.3. Обращение свертки
Общим для расфокусировки, размытости при дврокении и 3-D формирования
изображений такими методами, как фокусный ряд или конфокальная
микроскопия (раздел 8.2.4), является то, что функция объекта д(х) свертывается с помощью
функции рассеяния точки. Следовательно, основная процедура для
реконструирования или восстановления функции объекта одна и та же. По существу, это
процедура обращения свертки или обратная фильтрация, поскольку эффект
свертки с помощью ФРТ должен быть обратимым. При заданных простых
соотношениях в уравнении (17.71), обратная свертка является в принципе несложной
процедурой. Эффект оператора свертки Я' уничтожается применением обратного
оператора !ff'\ В Фурье-пространстве мы можем записать:
С,=-^ = Я->.(7'. (17.75)
н
Реконструированное изображение G^ определяется тогда с помощью
применения обратного преобразования Фурье:
17.5. Обратная фильтрация
Gj^=T-^H'^ TG\ (17.76)
Процедура реконструкции состоит в следующем. Обработанное с помощью
преобразования Фурье изображение, TG, умножается на функцию, обратную ОПФ,
Н~\ и затем преобразуется обратно в пространственную область. Обратная
фильтрация может также выполняться в пространственной области с помощью свертки с
маской, которая задается обратным преобразованием Фурье от обратной ОПФ:
С^=(У"^Я"^)*С'. (17.77)
На первый взгляд обратная фильтрация кажется простой. Однако в
большинстве случаев бесполезно или даже невозможно применять уравнения (17.76) и (17.77).
Причина несостоятельности связана с тем, что ОПФ зачастую равна нулю в
широких диапазонах. Оптические передаточные функции для размытости при движении
(уравнение (17.74)) и расфокусировки (уравнение (17.72)) имеют протяженный
нулевой диапазон. В этих областях обратная ОПФ становится бесконечной.
Но не только нули ОПФ вызывают проблемы, все диапазоны, в которых ОПФ
становится малой, делают это. Этот эффект относится к влиянию шума. Для
количественного анализа положим следующую простую модель формирования
изображений:
G' = H^G + N о . д' = Н G + N. (17.78)
Уравнение (17.78) утверждает, что шум прибавляется к изображению, после
того как изображение ухудшается в качестве. При использовании этой модели,
согласно уравнению (17.75), обратная фильтрация дает
G,=H-' G' = G + H-' N (17.79)
при условии, что НфО. Это уравнение утверждает, что восстановленное
изображение равно восстановленному исходному изображению G плюс шум, усиленный
с помощью Н~\
Если Н стремится к нулю, то Я"^ становится бесконечной, и то же происходит
с уровнем шума. Уравнения (17.78) и (17.79) также утверждают, что отношение
сигнала к шуму не улучшается, а остается таким же, поскольку шум и полезная
информация в изображении умножаются на одинаковый множитель.
Из этого мы можем заключить, что обратная фильтрация совсем не улучшает
качество изображения. Более обобщенно, ясно, что никаким линейным методом
улучшения не добиться. Все, что мы можем сделать с помощью линейных
методов, так это усилить структуры, ослабленные при ухудшении качества, вплоть до
момента, когда уровень шума не достигнет критического уровня.
В качестве примера рассмотрим 3-D реконструкцию по микроскопическому
фокусному ряду. Фокусным рядом является стопка из микроскопических
изображений, в которой мы исследуем сфокусированную глубину. Вследствие
ограниченной глубины поля (раздел 7.4.3) только объекты в тонкой плоскости
изображаются четко. Следовательно, мы получаем 3-D изображение. Однако оно искажено
функцией рассеяния точки оптического формирования изображений.
Определенные структуры полностью отфильтровываются, а размытые объекты
накладываются на четко изображенные объекты. Мы можем теперь использовать обратную
фильтрацию, чтобы попытаться ограничить эти искажения. Очевидно, что точное
знание ФРГ существенно для хорошей реконструкции. В разделе 7.6.1 мы
вычислили 3-D ФРТ оптического формирования изображений, пренебрегая погрешно-
486 Глава 17. Регуляризация и моделирование
стями линз и ограничением разрешения, обусловленным дифракцией. Однако
сильно увеличенные микроскопические изображения являются диффракционно-
ограниченными.
Диффракционно-ограниченная 3-D ФРГ была вьршслена в работе [40]. Предел
разрешающей способности, по существу, изменяет двойной конус 3-D ФРГ (рис. 7.13)
только вблизи фокальной плоскости. На фокальной плоскости точка теперь
отображается не в точку, а скорее в дифракционный диск. В результате ОПФ уменьшается
для более высоких волновых чисел в плоскости к^к. Для первого приближения мы
можем рассматривать диффракционно-ограниченное разрешение как
дополнительный фильтр нижних частот, на который умножается ОПФ для геометрического
формирования изображений и с помощью которого свертывается ФРГ.
Простейший подход для получения оптимальной реконструкции состоит в
ограничении применения обратной ОПФ до компонент волновых чисел, которые
не ослабляются ниже критической пороговой величины. Эта пороговая величина
зависит от шума в изображенршх. Таким образом, истинная обратная ОПФ
заменяется эффективной обратной ОПФ, которая приближается к нулю в областях
волновых чисел, которые не могут реконструироваться. Результат такой процедуры
реконструкции показан на рис. 17.11. Фокусный ряд 64 х 64 х 64 был получен от
ядра раковой клетки печени крысы. Разрешение по всем направлениям
составляет 0,22 мкм. Изображения явно подтверждают теоретические соображения. Реконст-
Рис. 17.11.3-D реконструкция фокусного ряда ядра клетки, полученного с помощью
традиционной микроскопии. Верхняя строка: а - в - выбранные исходные
изображения; г поперечное сечение xz, перпендикулярное плоскости изображения.
Нижняя строка: д — з — реконструкции изображений а — г (иллюстрации предоставлены
доктором Шмиттом (Dr. Schmitt) и профессором, доктором Комитовски (Prof. Dr.
Komitowski), Немецкий раковый исследовательский центр (German Cancer Research
Center), Гейдельберг (Heidelberg))
17.5. Обратная фильтрация
рукция значительно улучшает разрешение в плоскости изображения ху, в то время
как разрешение в направлении z — что и следовало ожидать — явно хуже.
Структуры, которые изменяются в направлении z, полностью уничтожаются в фокусном
ряде сверткой с ФРТ оптических изображений и, следовательно, не могут
реконструироваться.
17.5.4. Итерационная обратная фильтрация
Итерационные методы формируют интересный вариант обратной фильтрации,
поскольку они дают управление над степенью применяемой реконструкции. Пусть
J{- оператор размывания. Введем новый оператор Н' =1 - Н. Тогда обратный
оператор
^"' =^^ (17.80)
МОЖНО аппроксимировать разложением Тейлора
!К~^ = J + .7/'4.7/''4.7/''^ + ... (17.81)
или, записанным явно для ОПФ в непрерывной Фурье-области,
й-ЧЛ) = 1 + АЧА'Чй'Ч.... (17.82)
Для того чтобы понять, как работает итерация, рассмотрим периодические
структуры. Сначала возьмем структуру, которая только незначительно
ослабляется. Это означает, что h только немного меньше единицы. Таким образом, h' мала,
а итерация быстро сходится.
Другой предельный случай имеет место, когда периодическая структура почти
исчезла. Тогда h' близка к единице. Следовательно, амплитуда периодической
структуры увеличивается на одну и ту же величину с каждым итерационным
шагом (линейная сходимость). Эта процедура имеет существенное преимущество в
том, что мы можем остановить итерацию, как только картины распределения
шумов становятся заметными.
Прямое применение итерации не имеет большого смысла, поскольку
увеличивающиеся показатели степени масок сверток становятся больше и, таким
образом, вычислительные усилия возрастают от шага к шагу. Более эффективная
схема, известная как итерация Ван Циттерта, использует схему Горнера для
вычисления полиномов:
G,=G\ G,,,=G'+{\-H)*G,. (17.83)
в Фурье-пространстве легко исследовать сходимость этой итерации. Из
уравнения (17.83)
g,{k) = g\k)f^{\-kk))\ (17.84)
/=о
Это уравнение образует геометрический ряд с начальным значением щ=д vi
множителем q = \-h. Ряд сходится, только если | ^ |=11 - А | < 1. Тогда сумма
определяется соотношением
дЛк) = С1^-г^^ = 9(к) (17.85)
\-q h(k)
Глава 17. Регуляризация и моделирование
и сходится к точному значению g'/h,K сожалению, это условие для сходимости не
выполняется для всех передаточных функций, которые имеют отрицательные
значения. Следовательно, итерация Ван Циттерта не может применяться к
размыванию при движении и к расфокусировке.
Незначительная модификация итерационного процесса, однако, делает
возможным его использование также для ухудшений качества с частично
отрицательными передаточными функциями. Простой прием состоит в применении
передаточной функции дважды. Передаточная функция h^ каскадного фильтра Н*Н
положительна.
Модифицированная итерационная схема имеет вид
G,=H^G\ G,^,^H^G'+{I-H^H)^G,. (17.86)
При а^=Ьд И9 = 1-А итерация опять сходится к точному значению
hmgj^(k) = limhg—Ц^^—- = ^, если |1-А^|<1. (17.87)
17.6. Дополнительные эквивалентные подходы
Этот последний раздел показывает дополнительные эквивалентные подходы к
моделированию, которые проливают свет на моделирование с различных точек
зрения. В качестве еще одного подхода рассматриваются модели упругости в
разделе 17.6.1, а в качестве интересного дискретного подхода — модели
электрических сетей (раздел 17.6.2).
17.6.1. Модели упругости
На этой стадии нашего рассуждения полезно рассмотреть аналогичную
физическую задачу, которая дает дополнительное понимание того, как ограничения
подобия и гладкости уравновешивают друг друга. В физической модели эти два члена
соответствуют двум видам сил.
И снова мы будем использовать пример определения оптического потока.
Рассмотрим изображение как рисуемое на упругой мембране. Движение будет сдвигать
мембрану от изображения к изображению. В особенности неравномерное
движение вызывает незначительное расширение или сжатие мембраны. Член подобия
работает в качестве внешней силы, которая пытается натянуть мембрану по
направлению к соответствующему вектору перемещения (ВП). Внутренние упругие
силы распределяют эти деформации непрерывно по всей мембране, создавая
гладкое поле вектора перемещений (ПВП).
Давайте сначала рассмотрим внешние силы более детально. Не имеет
большого смысла задавать деформации жесткими в точках, где мы можем определить ВП
для оценки перемещения. Вместо этого мы допускаем отклонения от ожидаемых
перемещений, которые могут быть тем больше, чем более неопределенным
является определение ВП. Физически это аналогично паре пружин, чья жесткость
пропорциональна достоверности, с которой можно вычислить перемещение. Начало
отсчета системы пружин устанавливается в соответствии с вычисленным векто-
17.6. Дополнительные эквивалентные подходы
ром перемещения. Поскольку мембрана является двумерной, требуются две пары
пружин. Направление системы пружин устанавливается согласно локальной
ориентации (раздел 13.3). На контуре можно вычислить только перемещение,
нормальное к контуру (апертурная проблема, раздел 14.2.2). В этом случае требуется
только одна пара пружин — перемещение, параллельное контуру, не является
результатом действия восстанавливающей силы.
Внешние силы пружин уравновешиваются внутренними упругими силами,
стремящимися сгладить различные деформации. Давайте вновь взглянем на
уравнение Эйлера—Лагранжа оптического потока (17.23) с этой точки зрения. Мы
можем теперь понимать это уравнение следующим образом:
(ygf+QtWg^- ^W =0, (17.88)
Внешняя сила Внутренняя сила
где а^ — коэффициент эластичности. В выражении для внутренних сил возникают
только вторые производные, поскольку постоянный градиент оптического потока
не приводит к равнодействующей внутренних сил.
Свойства упругости мембраны выражаются отдельной постоянной.
Дополнительное проникновение во внутреннюю структуру мембраны задается функцией
Лагранжа (уравнение (17.19)):
L(f,f,^,x) = a'(m\'+\Vf,\') + (Vgf + g,f. (17.89)
^ V ' ' ^ '
Т, энергия деформации - К, потенциал
Функция Лагранжа состоит из потенциала внешней силы как результата
неразрывности оптического потока и энергии, отнесенной к внутренним силам. Это
слагаемое называется, таким образом, энергией деформации. Эта энергия
появляется на месте кинетической энергии в классическом примере функции Лагранжа,
поскольку минимум ищется не по времени, а по пространству.
Энергия деформации может раскладываться на несколько слагаемых, которые
тесно связаны с различными напряженно-деформируемыми состояниями:
'■(/.,) 4
L Подобное преобразование
(17.90)
((/х-Шу) НШу+ш.) Н(Л)у-(/2Х)
V ^ / V ^
Сдвиговое преобразование Поворот
Ясно, ЧТО свойства упругости мембраны оптимально совпадают с
кинематикой движения. Каждая возможная деформация, которая может возникать
вследствие различных состояний 2-D движения на плоскости изображения, являются
равно взвешенными.
Физически такая мембрана не имеет смысла. Дифференциальное уравнение
для реальной физической мембраны иное [45]:
/-(A + Ai)V(Vii)-AiAii = 0. (17.91)
Упругость физической мембраны описывается двумя постоянными — Я и д.
Глава 17, Регуляризация и моделирование
Равенство Я = -jU невозможно; в результате дополнительный член V(Vii) (в
сравнении с модельной мембраной для ПВП) никогда не обращается в нуль. Если нет
поперечного сжатры, то А может быть только нулевой.
С модельной мембраной только растяжение является непрерывным, но не
первая производная. Разрывы возникают точно в тех точках, где внешние силы
прикладываются к мембране. Это получается непосредственно из уравнения (17.23).
Локально приложенная внешняя сила соответствует 5-распределению в члене
подобия. Интегрируя уравнение (17.23), мы получаем разрыв в первых производных.
Эти соображения подвергают сомнению ограничения гладкости,
рассмотренные до сих пор. Мы знаем, что движение плоских поверхностных элементов не
приводит к таким разрывам. Гладкости первой производной можно достичь, если
учесть вторые производные в члене гладкости (уравнение (17.23)) или энергии
деформации (уравнение (17.89)). Физически такая модель аналогична тонкой
упругой пластине, которая не может складываться как мембрана.
17.6.2. Сетевые модели
В этом разделе мы рассматриваем еще один метод на основе электротехнических
аналогий — сетевое моделирование. Преимущество этого метода в том, что он
является дискретной моделью, которая непосредственно соответствует дискретному
получению изображений. Этот раздел следует работам [69, 70]. Изучение сетевых
моделей стало популярным, поскольку сетевые структуры можно выполнять
непосредственно на таких массовых параллельных компьютерных системах, как
Connection МасЫпе в Массачусетском технологическом институте (MIT) [70] или
в аналоговых сверхбольших интегральных схемах (СБИС) [135].
Одномерные сети. Сначала рассмотрим простой 1-D случай. Перемещение
соответствует электрическому напряжению. Непрерывность достигается посредством
соединения соседних пикселей с помощью электрических резисторов. Таким
образом, мы строим линейную резисторную цепь, как показано на рис. 17.12. Мы можем
вызвать перемещение в пикселе до определенного значения, приложив потенциал в
соответствующем пикселе. Если в резисторной цепи имеется только один источник
напряжения, то вся сеть находится под этим постоянным напряжением. Если еще
один потенциал прикладывается ко второму узлу сети и все соединительные
резисторы одинаковы, то мы получаем линейное изменение напряжения между двумя
точками. В итоге сеть резисторов обеспечивает непрерывность в напряжении, в то
время как применение напряжения в определенном узле определяет подобие.
Существуют различные типы граничных условий. С одной стороны, мы
можем приложить определенное напряжение к контуру резисторной цепи и, таким
образом, получить определенное значение вектора перемещения на контуре
изображения. С другой стороны, мы можем не создавать никакого соединения. Это
эквивалентно существованию первой пространственной производной, равной
нулю на контуре. Напряжение на контуре тогда равно напряжению в ближайшем
соединении к источнику напряжения.
В моделях упругости (раздел 17.6.1) мы не считали величину перемещения
равной значению, получающемуся непосредственно из ограничения подобия, а
допускали некоторую эластичность, рассматривая перемещение с помощью модели
пружины. Подобным образом мы подводим напряжение V^^ к узлу п не непосред-
R
17.6. Дополнительные эквивалентные подходы
и,
On
1-Н R hH R Н-Н
R
Un
Рис. 17.12. Простая 1-D сеть для 1-D гладкого ПВП [70]
R
R
ственно, а через резистор 5^ (рис. 17.12). Мы считаем сопротивление
пропорциональным неопределенности вектора перемещения.
Разностное уравнение для сетевой модели задается по следующему правилу:
сумма всех токов должна взаимно уничтожаться в каждом узле сети. Используя
обозначения, приведенные на рис. 17.12, получаем для узла п сети
Un-U.n
и-и_, . и-и
п+\ _
= 0.
(17.92)
S„ R R
Второе и третье слагаемые образуют дискретный дифференциальный
оператор ф2 (см раздел 12.5.2). Таким образом, уравнение (17.92) приводит к
5 " R дх'
(17.93)
Это уравнение является 1-D формой уравнения (17.23). Для лучшего
сравнения перепишем это уравнение для 1-D случая:
i^.gf
\9
-а^и^О.
дх'
(17.94)
Теперь мы можем провести аналогию между векторами перемещения и
сетевой моделью. Применение потенциала U^ соответствует вычислению локальной
скорости по -(Э^д)/(Э^д). Члены подобия и гладкости взвешиваются с обратным
сопротивлением (проводимостью) 1/5и 1/R вместо квадрата градиента (д^дУ и а^.
Обобщенные сети. Теперь обратимся к вопросу о том, как интегрировать
непрерывность первых производных в сетевую модель. Харрис (Harris) [69]
использовал активный модуль вычитания, который вычисляет разность двух сигналов.
Все три соединения элемента служат как входами, так и выходами. В двух
произвольных входах мы подводим напряжение и получаем соответствующее выходное
напряжение в третьем соединении.
Такой модуль требует активных электронных компонентов [69]. На рис. 17.13
показывается, как этот модуль вьиитания интегрируется в сеть. Он вычисляет
разностное напряжение между двумя соседними узлами. Эти разности — а не
напряжения сами по себе — вставляются в резисторную сеть.
Таким образом, мы получаем сеть, которая сохраняет первую производную
непрерывной. Мы можем обобщить этот подход для получения сетей, которые
сохраняют производные более высокого порядка непрерывными, с помощью
добавления нескольких слоев с модулями вьиитания (рис. 17.14).
492 Глава 17. Регуляризация и моделирование
Рис. 17.13. Дискретная сетевая модель для 1-D скалярного признака с гладкими
первыми производными [70]
ш 1 F
•. Г
>;
Г"
ч
X
1 р 1 J
1 Гл 1 Ч
\
3
R_
f
L
У
|„.1
\\Л
\
Rb
1 1
\7
/
f
1 1 f
\ Li
х
Р 1—-
\
\ 1 ч
L
^ b
^
^^"R~h№
>:
Н R Ь
>:
"^ \)
i
i\
И1
м
Н R N
X
1 1 р ' '^
р 1 п
i
у\1
^ \/
i
м
>:
? 1 J
л 1 1
f
\\ f
X
RhJ
/
1 1 F
f \ Г
1
^ b*
/
M '
>^
? i 1
л 1 1
?
^
^
?
P" 1
1 l_
Ъ i D 1 J
ПК iv 1 ^
^^
D U-4
^
R r:*^ r
i
\/
/
F
M
1 1 г
1. 1 ^
\
7 1 1
'Ы
^
If
r
1
. 1 о 1 -
\ 1 V 1 \
^ 1 Ч
^
r
H R H»-
\:
Э 1 l_
^
i-T/^
/
и Rk
\^
/
1 1 p 1 Л. 1 n 1
9 \ n
' 1 ГЧ 1
Рис. 17.14. Обобщенная сеть для 1-D ПВП, которая сохраняет производные более
высокого порядка гладкими [70]
Неоднородности в сетях, Поля векторов перемещения обнаруживают
неоднородности на контурах движущихся объектов. Неоднородности можно легко
реализовать в сетевой модели. В простой сети с непрерывностью нулевого порядка
(рис. 17.12) мы просто удаляем соединительный резистор между двумя соседними
узлами для образования скачка потенциала между этими двумя узлами. Для того
чтобы научиться управлять гладкостью (раздел 17.2.5), мы можем также
проанализировать нелинейную сетевую модель с нелинейными резисторами. Мы могли бы
предположить неоднородности в крутых градиентах в поле скоростей. Если
сопротивление возрастает в зависимости от напряжения, то мы получаем механизм
для образования предполагаемых неоднородностей. Эти краткие суждения
иллюстрируют гибкость и вариабельность сетевых моделей.
Интеграция неоднородностей является более сложной в обобщенной сети.
Здесь мы можем разместить неоднородности на каждом уровне сети, т.е. мы
можем сделать либо ПВП, либо любую из его производных разрывными с
помощью удаления резистора на соответствующем уровне. Нам необходимо
удалить все резисторы более глубоких узлов, которые соединены с точкой разрыва
(рис. 17.15). В противном случае производные более высокого порядка
остаются непрерывными и заставляют производные более низкого порядка
становиться непрерывными.
17,6. Дополнительные эквивалентные подходы 493
i-CEh
Рис. 17.15. Обобщенная 1-D сеть с неоднородностью в ПВП и его первой
пространственной производной
Двумерные сети. Сетевая модель может также использоваться для задач более
высокой размерности. Для 2-D сетевой модели с непрерывностью первого рода мы
строим 2-D сетку резисторов. Схема обобщенных 2-D сетевых моделей с
ограничениями непрерывности более высокого порядка является более сложной. В каждом
слое мы должны рассмотреть непрерывность нескольких частных производных.
Имеют место две первые пространственные производные, горизонтальная и
вертикальная производные. Для каждой из них нам необходимо построить отдельный слой
с модулями вычитания, как показано на рис. 17.13, для того чтобы наблюдать
ограничение гладкости. Дополнительные детали можно найти в работе [70].
Многомерные сети. Одним из наиболее важных практических результатов
является нахождение скорости сходимости итерационных методов для решения
больших систем уравнений, для того чтобы моделировать их с помощью сетей.
Возникает вопрос: возможно ли также интегрировать этот важный аспект в сетевую
модель? Итерация вводит временную зависимость в систему, которую можно
моделировать с помощью добавления конденсаторов в сеть (рис. 17.16).
Конденсаторы вообще не изменяют статические свойства сети.
Когда мы начинаем итерацию, мы знаем векторы перемещений только в
некоторых изолированных точках. Следовательно, мы хотим узнать, сколько итераций
понадобится для переноса этой информации в удаленные точки, где мы не имеем
никакой информации о перемещениях. Для ответа на этот вопрос получим разно-
|-»Ч R I—]Н R hf-H
и„.
C:i: Сф Сф Сф
Рис. 17.16. 1-D сеть с конденсаторами для моделирования сходимости
итерационных решений
(17.96)
Глава 17, Регуляризация и моделирование
стное уравнение для резисторно-конденсаторной цепи, как показано на рис. 17.16.
Оно задается по правилу: сумма всех токов, втекающр1х в узел, должна равняться
нулю. В дополнение нам необходимо знать, что ток, втекающий в конденсатор,
пропорционален его емкости Си временной производной напряжения dU/dt\
-^^ 2. + -J211 и-с—^ = 0 (17.95)
R R dt
или
ди„ ^ (Axf д'и„
dt RC Эх^ *
Во втором уравнении мы ввели Ах как пространственное расстояние между
соседними узлами, для того чтобы сформулировать пространственную
производную. К тому же RC= т, где т — временная постоянная отдельной
резисторно-конденсаторной схемы. Уравнение (17.96) является дискретной 1-D формулировкой
одного из наиболее важных уравнений в естественных науках — уравнения
переноса или диффузии, которое мы детально рассматривали в разделах 5.3.1 и 17.3. Мы
можем ответить на вопрос относительно временной постоянной, необходимой для
сглаживания поля вектора перемещения на определенном пространственном
масштабе, без явного решения уравнения (17.96). Давайте предположим
существование пространственно изменяющегося потенциала с длиной волны Я,
экспоненциально убывающего в зависимости от временной постоянной г^, которая зависит от
длины волны Я (сравните раздел 5.3.1):
U(x) = C/o(x)exp(~//r)exp(ib:). (17.97)
Подставляя это выражение в уравнение (17.96), получаем
(Axkf 4n\Axf
^я=77т=. 2.л 42^'- (17.98)
С помощью этого результата мы можем ответить на вопрос относительно
времени сходимости итерации. Время сходимости соответствует квадрату
длины волны структуры. Следовательно, уравновешивание уровней яркости на
двойном расстоянии займет в 4 раза больше времени. Давайте произвольно
предположим, что нам необходим один итерационный шаг для
уравновешивания соседних узлов. Тогда нам потребуется 100 итерационных шагов для
уравновешивания узлов, которые находятся на расстоянии 10 пикселей. Если
потенциал известен только в изолированных точках, то этот подход сходится
слишком медленно, чтобы быть полезным.
Многосеточные структуры данных, которые мы рассматривали в главе 5,
являются эффективным инструментом для ускорения сходимости итерации. На более
грубых уровнях пирамиды удаленные точки становятся гораздо ближе друг к
другу. В пирамиде только с шестью уровнями расстояния уменьшаются в 32 раза.
Таким образом, мы можем вычислять крупномасштабные структуры ПВП со
скоростью сходимости, которая приблизительно в 1000 раз быстрее, чем на исходном
изображении. Мы не получаем каких-либо мелкомасштабных изменений, но
можем использовать грубое решение как начальную точку для итерации на
следующем, более мелком уровне.
Таким образом, мы можем улучшать решение от уровня к уровню и прийти к
решению с максимальным разрешением на самом нижнем уровне пирамиды. Вы-
77.7. Упразднения 495
числения на всех более высоких уровнях пирамиды не добавляет существенных
накладных расходов, поскольку число пикселей на всех уровнях пирамиды только
приблизительно на одну треть больше, чем на самом нижнем уровне. Вычисление
ПВП сцены такси (рис. 17.3) с помощью этого метода показано на рис. 17.4.
17.7. Упражнения
17.1: Неоднородная и анизотропная диффузия
Интерактивная демонстрация сглаживания с использованием
неоднородной и анизотропной диффузии (dip6exl7.01).
17.2: Регуляризованный анализ движения
Интерактивная демонстрация некоторых методов для регуляризованного
анализа движения (dip6exl7.02).
17.3: Итерационная обратная фильтрация
Интерактивная демонстрация итерационной обратной фильтрации;
получение тестовых изображений с размытостью при движении и
расфокусировкой (dip6exl7.03).
17.4: **Плоская регрессия
Изучите регрессию функции изображения с помощью плоскости с
использованием метода наименьших квадратов, рассмотренного в разделе 17.4.1:
d{x,y)^a^-\'a^X'\'a^y,
Вопросы:
1. Определите переопределенную систему уравнений {Gm = d).
2. При каких условиях переопределенная система уравнений приводит к
единственному решению методом наименьших квадратов? Рассмотрите
свойства матрицы G^G, которую нужно обратить. (Подсказка: на этот
вопрос легко ответить, если привести симметричную матрицу к
диагональному виду (главной системе координат).)
3. При каких условиях параметры плоского соответствия
являются статистически некоррелированными? (Подсказка: вам понадобится
ковариационная матрица т, которая задается соотношением со\(т) = (G^G)-^a^
для статистргчески некоррелированных данных с равной дисперсией а I)
4. Решите явно систему уравнений для случая 3x3 = 9 точек, данных на
квадратной сетке с расстоянием Ах, которая центруется относительно
начала отсчета. Как точность регрессионньЕХ параметров т зависит от
расстояния Ах?
5 Можете ли вы выразить оценку трех регрессионных параметров т = [а^, а^, а^] ^
как операции свертки? Если да, то вычислите соответствуюшде маски сверток.
17.5: "^Обратная фильтрация
Рассмотрите следующие функции рассеяния точки для 1-D размывания:
1. Я=[1/3, 1/3, 1/3] (маска-ящик).
2. Н=[1/4, 1/2, 1/4] (биномиальная маска).
Глава 17. Регуляризация и моделирование
3. Я= [1/8, 3/4, 1/8].
Вопросы и задания:
• Возможно ли удалить размывание обратной фильтрацией?
• Если да, то определите передаточную функцию обратной фильтрации.
• Если да, определите маску свертки обратного фильтра (Подсказка:
разложение в ряд.)
17.6: "^"^Итерационная обратная фильтрация
Предположим, что изображение С размывается сверткой с маской Я, и
обозначим ряд итерационно восстановленных изображений символом С^. Три
хорошо известные схемы имеют вид:
Итерация Ван Циттерта:
Стабилизированная итерация Ван Циттерта:
G,=^H^G\ G^^, = H^G'+{I-H^H)^Gj^,
Регуляризованная итерация:
G,=H^G\ G,^,^H^G'+(B-H^H)^G,
(/означает тождественный оператор; В — сглаживающую маску).
Используйте следующие маски ухудшения качества
1) Я=[1/3, 1/3, 1/3] (маска-ящик);
2) Я= [1/8, 3/4, 1/8]
для ответа на следующие вопросы:
• Сходится ли итерация?
• Если да, то к какому пределу?
(Подсказка: на вопросы можно легко ответить в Фурье-пространстве!)
17.8. Дополнительная литература
Предмет этой главы основывается на матричной алгебре. Голуб (Golub) и ван Лоан
(van Loan) [63] дают превосходный обзор по матричным вычислениям.
Вариационные методы (раздел 17.2) излагаются Яне (Jahne) и др. [96, том 2, глава 16] и
Шнорром (Schnorr) и Вайкертом (Weiclcert) [181]. Использование модели
мембраны (раздел 17.6.1) впервые было изложено Бройтом (Broit) [15], который
применил ее в компьютерной томографии. Позднее она была использована и расширена
Денглером (Dengler) [35] для обработки последовательностей изображений.
Сегодня модели упругости - широко используемый инструмент в совершенно
разных областях обработки изображений, таких, как моделирование и контурное
слежение [104], реконструкция 3-D объектов [202] и реконструкция поверхностей [201].
Анизотропная диффузия (раздел 17.3) и нелинейные масштабные пространства
являются действующей исследовательской темой. Превосходное рассмотрение
дается Вайкертом (Weickert) [215] и Яне (Jahne) и др. [96, том 2, глава 15].
Оптимальные фильтры для быстрой анизотропной диффузии рассматриваются
Шарром (Scharr) и Вайкертом (Weickert) [179] и Шарром (Scharr) и Уттенвайлером
(Uttenweiler) [178].
ГЛАВА 18
МОРФОЛОГИЯ
18.1. Введение
в главах 16 и 17 мы рассматривали процесс сегментации, который вьщеляет объекты
из изображений, т.е. распознает, какие пиксели принадлежат к каким объектам.
Теперь мы можем выполнить следующий шаг и проанализировать форму
объектов. В этой главе мы рассматриваем класс операций над соседними элементами на
бинарных изображениях, морфологические операторы, которые модифицируют
и анализируют форму объектов.
18.2. Операции над соседними элементами на бинарных
изображениях
18.2.1. Бинарная свертка
В нашем рассмотрении цифровой обработки изображений операторы,
связывающие пиксели в малой окрестности, возникали как универсальный и мощный
инструмент для скалярных и векторных изображений (глава 4). Результат такой
операции в бинарных изображениях может б^1ть только нулем или единицей.
Следовательно, операторы формирования окрестностей для бинарных
изображений будут влиять на форму объекта, добавляя пиксели к объекту или исключая
пиксели из объекта. В разделах 4.2 и 4.3 мы рассматривали две основные операции
для объединения соседних пикселей изображений различной яркости: свертку
(«взвешивание и суммирование») и фильтрацию порядковой статистики
(«упорядочение и выбирание»). Для бинарных изображений мы не имеем большого
выбора в отношении того, какой тип операций выполнять. Мы можем объединять
пиксели только с помощью логических операций булевой алгебры. Мы могли бы ввести
бинарную свертку с помощью замены операции умножения пикселей
изображения и маски операцией Я, а суммирование операцией ИЛИ:
9L= \/ V ^mW^9n
7т+т,п+п
-Rn=-R
(18.1)
Л и V обозначают логические операции И и Я/Ш соответственно. Бинарное
изображение Gсвертывается с симметричной маскойМразмером 2R-\-lx2R-\-l,
Обратите внимание, что, в отличие от операций свертки, маска не отражается
относительно начала отсчета (см. раздел 4.2.5).
Что эта операция выполняет? Давайте предположим, что все
коэффициенты маски устанавливаются равными «единице». Если один или более пикселей
объекта, т.е. «единиц», находятся внутри маски, то результат операции будет
равен единице, в противном случае он равен нулю (рис. 18.1, а, б). Следова-
Глава 18. Морфология
ШШШ Ш шШш
IНИI nfflniHIII III I ИНН I I
Рис. 18.1. б — преобразование подобия и в - эрозия бинарного объекта на а с
маской 3x3. Уданенные (эрозия) и добавленные (преобразование подобия) пиксели
показаны в более светлом цвете
тельно, объект будет расширяться. Малые дыры или щели будут заполняться, а
контурная линия будет становиться более гладкой, как показано на рис. 18.2, 5.
Оператор, определенный уравнением (18.1), известен как оператор
масштабных преобразований.
Интересно, что мы можем получить тот же эффект, если применим фильтр
порядковой статистики (см. раздел 4.3) к бинарным изображениям. Давайте
возьмем оператор максимума. Тогда максимум будет равен единице, если одна или
более «единиц» находятся внутри маски как раз, как в случае с бинарной
операцией свертки в уравнении (18.1).
Оператор минимума производит противоположный эффект. Теперь результат
равен единице, только если маска полностью принадлежит объекту (рис. 18.1, в).
Таким образом, объект стирается. Объекты меньшие, чем маска, полностью
исчезают, а объекты, соединенные только малым мостом, станут разъединенными.
Эрозия объекта может также выполняться с использованием бинарной свертки с
операциями логического И\
9L= /\ Л ^mW^9n
-R n=-R
(18.2)
Для изображений более высокой размерности уравнения (18.1) и (18.2) просто
необходимо дополнить еще одним циклом для каждой координаты. В 3-D
пространстве оператор масштабных преобразований равен, к примеру,
R R R
9lmn=\J V \1 ^1тп'^9м\т^т\п^' (18.3)
l'=-Rm=-Rn=-R
Перенося понятия операций над соседними элементами для изображений
различной яркости на бинарные изображения, мы получили важный инструмент для
оперирования с формой объектов. Мы уже увидели на рис. 18.1, что эти операции можно
использовать для заполнения малых дыр и щелей или удаления малых объектов.
Размер маски обусловливает эффект операторов, поэтому маску часто
называют структурным элементом. Например, операция эрозии работает как сеть,
которая имеет дыры в форме маски. Все объекты, которые проходят в отверстие, будут
проскальзывать и исчезать из изображения. Объект остается, только если, по край-
18.3. Общие свойства
ней мере, в одной точке маска полностью покрывается пикселями объекта. В
противном случае он исчезает.
Оператор, который влияет на форму объектов, называется морфологическим
оператором. Название происходит из тематики морфологии, которая описывает
форму объектов в биологии и геофизических науках.
18.2.2. Операции на множествах
Мы использовали довольно нетрадиционный способ для введения
морфологических операций. Как правило, эти операции определяются как операции на
множествах пикселей. Рассмотрим G как множество всех пикселей матрицы, которые не
равны нулю. Af есть множество ненулевых пикселей маски. С помощью М обозначим
маску, сдвинутую со своей опорной точкой (как правило, но необязательно, это ее
центр) в пиксель/?. Тогда эрозия определяется как
GeM = {p:M^(^G}
и подобное преобразование как
G®M = {p:MnG^0},
(18.4)
(18.5)
Эти определения эквивалентны уравнениям (18.1) и (18.2) соответственно. Мы
можем теперь выразить эрозию множества пикселей G посредством множества
пикселей Мкак множество всех пикселей/?, для которых М полностью
содержится в G. Противоположно подобное преобразование G посредством М есть
множество всех пикселей, для которых пересечение между G и М не равно пустому
множеству. Поскольку теоретико-множественный подход ведет к более компактным
и наглядным формулам, мы будем использовать его и впредь.
Уравнения (18.1) и (18.2) все еще остаются важными для выполнения
морфологических операторов с помощью логических операций. Операторы эрозии и
масштабных преобразований можно рассматривать как элементарные
морфологические операторы, из которых можно построить другие, более сложные
операторы. Их свойства детально изучаются в следующем разделе.
18.3. Общие свойства
Морфологические операторы разделяют большинство, но не все свойства,
которые мы уже рассмотрели для линейных операторов свертки в разделе 4.2.
Свойства, рассмотренные ниже, не ограничиваются 2-D изображениями, а, как
правило, имеют силу для Л^-мерных данных изображения.
18.3.1. Инвариантность относительно сдвига
Инвариантность относительно сдвига следует непосредственно из определения
операторов эрозии и масштабных преобразований как сверток с бинарными
данными в уравнениях (18.1) и (18.2). Используя оператор сдвига 5, как определено в
уравнении (4.17), и операторную форму записи, мы можем записать
инвариантность относительно сдвига любого морфологического оператора 5W как
Глава 18. Морфология
Mr"SG) ="""5(^01 (18.6)
18.3.2. Принцип суперпозиции
Что означает принцип суперпозиции для бинарных данных? Для изображений
различной яркости он определяется как
Я(аС + ЬС) = аЯС + ЫНС: (18.7)
Множители аиЬнс имеют смысла для бинарных изображений; сложение
изображений соответствует объединению или логическому ИЛИ изображений. Если
принцип суперпозиции имеет силу для морфологических операций М на
бинарных изображениях, он имеет вид
M{GkjG') = {MG)kj{MG') или !M(GvG') = (MG)v(MG'). (18.8)
Операция Gv G' означает поточечную операцию логического ИЛИ элементов
матриц G и G\ Как правило, морфологические операторы не являются
аддитивными в смысле уравнения (18.8). В то время как операция масштабного
преобразования согласуется с принципом суперпозиции, эрозия не делает этого. Эрозия
объединения двух объектов равна, как правило, надмножеству объединения двух
эродированных объектов:
(GuG')eM 3 (GeM)u(G'eM)
{GkjG')@M = {G®M)Kj{G'®My
(18.9)
18.3.3. Коммутативность и ассоциативность
Морфологические операторы, в общем, не являются коммутативными:
м,®м^=м^®м,, но м.ем^ФМ^ем,. (i8.io)
Мы можем видеть, что эрозия не является коммутативной, если мы берем
частный случай М, ^Mj. Тогда эрозия М^ посредством М^ дает пустое множество.
Однако как маски эрозии, так и маски масштабных преобразований,
последовательно примененные в каскаде к одному и тому же изображению, являются
коммутативными:
(GeM,)eM^ =Ge(M,®M^) =(GeM^)eM,,
(G®M,)®M^ =G®{M,®M^) =(G®M^)®M^,
(18.11)
Эти уравнения важны для выполнения морфологических операций. Как
правило, каскадная операция с к структурными элементами Mj, М^, •••» Л/^
эквивалентна операции со структурным элементом Л/= М^ eMj 0... Ф Л/^. Итак,
мы можем раскладывать большие структурные элементы тем же самым
образом, как мы раскладывали линейные, инвариантные относительно сдвига
операторы. Важным примером является составление сепарабельных структурных
элементов с помощью горизонтальных и вертикальных элементов М= М^®М.
Еще одним менее тривиальным примером является составление больших од-
18.3. Общие свойства
номерных структурных элементов из структурных элементов, включающих
большое количество нулей:
[1 1 1]е[1 О 1] = [1 1111]
[1111 1]е[1 0 0 0 1]=[1 11111111]
[11111111 1]е[1 0000000 1] (18.12)
=[11111111111111111]
Таким образом, мы можем строить большие экспоненциально растущие
структурные элементы с минимальным числом логических операций так же, как
мы строили большие маски сверток посредством каскадирования в разделе 11.5.
Гораздо более сложным является получение изотропных, т.е. в форме круга,
структурных элементов. Проблема состоит в том, что преобразование подобия
горизонтальных и вертикальных структурных элементов всегда приводят к
структурному элементу в форму прямоугольника, но не к круглой маске. Однако круглая
маска может аппроксимироваться с помощью одномерных структурных
элементов, действующих в большем количестве направлений, чем только вдоль осей.
Как в случае со сглаживающими масками сверток, большие структурные
элементы можно эффективно строить с помощью каскадирования многошаговых
масок.
18.3.4. Монотонность
Эрозия и подобное преобразование являются монотонными операциями
G,^G^ ^ G.eM^G^eM. ^^^'^^^
Монотонность означает, что отношения включения инвариантны
относительно эрозии и подобного преобразования.
18.3.5. Дистрибутивность
Линейные, инвариантные относительно сдвига операторы являются
дистрибутивными относительно сложения. Соответствующие дистрибутивности для эрозии и
подобного преобразования относительно объединения и пересечения двух
изображений Gj и G^ являются более сложными:
iG,nG^)®M с (G,®M)n(G^®M)
(G,nG,)eM = (G,eM)n(G,eM) ^^^-^"^^
и
{G,^G^)®M = {G,®M)u(G^®M)
iG,uG,)eM 3 (G,eM)u(G,eMy ^^^'^^^
Эрозия дистрибутивна относительно операции пересечения, в то время как
подобное преобразование дистрибутивно относительно операции объединения.
502 Глава 18. Морфология
18.3.6. Двойственность
Эрозия и подобное преобразование являются двойственными операторами.
Посредством отрицания бинарного изображения эрозия преобразуется в
подобное преобразование и наоборот:
сем = G@M
G®M = GQM,
(18.16)
18.4. Составные морфологические операторы
18.4.1. Открытие и закрытие
Используя элементарные операции эрозии и масштабного преобразования,
теперь разработаем дополнительные полезные операции, которые влияют на
форму объектов. В то время как в предыдущем разделе мы сфокусировали наше
внимание на общих и теоретических аспектах морфологических операций, теперь
мы сконцентрируемся на применении.
Операция эрозии полезна для удаления малых объектов. Однако она имеет
недостаток - все остающиеся объекты уменьшаются в размере. Мы можем избе-
б
Рис. 18.2. Эрозия и раскрытие: а - исходное бинарное изображение; б
маской 3 X 3; в - открытие с маской 3 х 3; г — открытие с маской 5x5
эрозия с
18.4. Составные морфологические операторы
жать этого эффекта посредством масштабного преобразования изображения
после эрозии с помощью того же структурного элемента. Эта комбинация операций
называется операцией открытия (opening operation)
GoM = (GeM)®M, (18.17)
Открытие отсеивает все объекты, которые ни в одной точке полностью не
вмещают структурный элемент, но избегает общего уменьшения размера объектов
(рис. 18.2, в, г). Она является также идеальной операцией для удаления линий с
толщиной меньшей, чем диаметр структурного элемента. Обратите также
внимание на то, что границы объектов становятся более гладкими.
Противоположно оператор масштабных преобразований увеличивает
объекты и закрывает малые дыры и щели. Общее увеличение объектов с размером
структурного элемента можно обратить с помощью следующей эрозии (рис. 18.3, г и (3).
Эта комбинация операций называется операцией закрытия (closing operation)
G^M = (G@M)eM. (18.18)
Изменение площади объектов с помощью различных операций можно
обобщить с помощью следующих соотношений:
GeM^GoMi^G^G^M^G®M. (18.19)
Рис. 18.3. Подобное преобразование и закрытие: а - исходное бинарное
изображение; б — подобное преобразование с маской 3 х 3; в — закрытие с маской 3x3;
г - закрытие с маской 5x5
Глава 18. Морфология
Открытие и закрытие являются идемпотентными операциями:
G^M = {G^M)^M
GoM = (GoM)oM,
т.е. повторное применение закрытия и открытия с тем же структурным элементом
не производит каких-либо дальнейших эффектов.
(18.20)
18.4.2. Оператор попадание-промах
Оператор попадание-промах возникает из вопроса: возможно ли выделять
объекты определенной формы? Оператор эрозии удаляет только объекты, которые ни
в одной точке не вмещают полностью структурный элемент, и, таким образом,
удаляет объекты самых различных форм. Выделение определенной формы
требует комбинации двух морфологических операторов. В качестве примера
рассмотрим выделение объектов, содержащих горизонтальные строки из трех
последовательных пикселей.
СИ!
ш
ш
1 Ц
е
■
Рис. 18.4. Иллюстрация оператора попадание-промах для выделения всех объектов,
содержащих горизонтальные строки из трех последовательных пикселей: а —
исходное изображение; во всех последующих изображениях черные пиксели исходного
изображения показаны как светло-серые пиксели, а черные пиксели есть пиксели со
значением 1, образованные соответствующим оператором; б — фон, эродированный
маской 3x5 (уравнение (18.22)); в - фон, эродированный маской 3x7 (уравнение (18.24));
г — объект, эродированный маской 1x3 (уравнение (18.21)); д - пересечение б и г,
вьщеляющее объекты с горизонтальными строками из 3 последовательных пикселей;
е — пересечение виг, вьщеляющее объекты с горизонтальными строками из от 3 до 5
последовательных пикселей в свободном фоне 3x7
18.4. Составные морфологические операторы
Если мы подвергаем изображение эрозии с маской 1x3, которая соответствует
форме объекта
М, =[1 1 1], (18.21)
мы удалим все объекты, которые меньше, чем целевой объект, но сохраним также
все объекты, которые больше, чем маска, т.е. где сдвинутая маска является
подмножеством объекта G (М с G, рис. 18.4, г). Таким образом, нам теперь нужна
вторая операция для удаления всех объектов больших, чем целевой объект.
Это можно сделать с помощью проведения анализа фона исходного
изображения. Таким образом, мы можем использовать в качестве второго шага
эрозию фона с маской М^ размером 3 х 5, в которой все коэффициенты равны
нулю, за исключением пикселей фона, окружающих объект. Это
отрицательная маска для объекта:
(18.22)
Тогда эродированный фон содержит все пиксели, в которых фон имеет форму
М^ или большую (М cG, рис. 18.4, б). Это соответствует теперь объектам,
имеющим искомую форму или меньшую. Поскольку первая эрозия получает все
объекты равные или большие, чем целевой объект, пересечение изображения,
эродированного с Mj, и фона, эродированного с М^, дает все центральные пиксели объектов
с горизонтальными строками из трех последовательных пикселей (рис. 18.4, (3). В
общем, оператор попадание-промах определяется как
2 ~
11111
10 0 0 1
11111
G®{M,,M^) = {GeM,)n{GeM^)
при
(18.23)
Условие М^пМ^:
0 является необходимым, поскольку в противном случае
оператор попадание-промах привел бы к пустому множеству.
Оператор попадание-промах является гибким инструментом, с которым мы
можем вьщелять объекты заданной определенной формы. Универсальность
оператора попадание-промах можно легко продемонстрировать, используя еще одну
маску промаха:
Мз =
1111111
О
1
о
1
о
1
о
1
о
1
(18.24)
Эрозия фона с этой маской оставляет все пиксели в бинарном изображении,
где объединение маски Mj с объектом равно нулю (рис. 18.4, в). Это может
выполняться только для объектов с горизонтальными строками от одного до пяти
последовательных пикселей в фоне размером 3x7. Таким образом, оператор
попадание-промах с Л/| и iWj дает все пиксели объектов с горизонтальными строками от 3
до 5 последовательных пикселей в фоне размером 3x7 (рис. 18.4, с).
Глава 18. Морфология
Поскольку маски попадания и промаха оператора попадание-промах
являются дизъюнктивными, они могут объединяться в одну маску, используя
обозначение попадания (1), промаха (-1) и безразличного состояния (0). Комбинированная
маска отмечается 1, где маска попадания равна единице; О, где маска промаха
равна единице; и х, где обе маски равны нулю. Таким образом, маска
попадание-промах для вьщеления объектов с горизонтальными строками из от 3 до 5
последовательных пикселей равна
М =
-1 -1 -1 -1 -1 -1 -1
-10 1110-1
-1 -1 -1 -1 -1 -1 -1
(18.25)
Если маска попадание-промах не имеет пикселей безразличного состояния,
то она выделяет объекты точной формы, заданной пикселями маски с 1. Если
пиксели безразличного состояния присутствуют в маске попадание-промах, то
пиксели с 1 задают минимум, а объединение пикселей с 1 и пикселей безразличного
состояния - максимум вьщеляемых объектов.
В качестве еще одного примера — маска попадание-промах
М,=
-1 -1 -1
-1 1 -1
-1 -1 -1
(18.26)
определяет изолированные пиксели. Таким образом, операция G/ G ® М^ удаляет
изолированные пиксели из бинарного изображения. Символ / представляет
оператор разности множеств.
Оператор попадание-промах вьщеляет определенные формы, только если маска
промаха окружает маску попадания. Если маска попадания соприкасается с
контуром маски попадание-промах, то выделяются только определенные формы на
краю объекта. Маска попадание-промах
(18.27)
Мс =
0
1
-1
1
1
-1
-1
-1
-1
к примеру, выделяет нижние правые углы объектов.
18.4.3. Выделение границ
Морфологические операторы можно также использовать для вьщеления фаниц
бинарного объекта. Эта операция является значимой, поскольку граница является полным и,
кроме того, компактным представлением геометррш объекта, по которой можно вьще-
лить дополнительные параметры формы, как мы рассматриваем далее в этой главе.
Граничные точки упускают по меньшей мере один из своих соседних элементов.
Таким образом, оператор эрозии с маской, содержащей все возможные
соседние элементы, удаляет все граничные точки. Эти маски для 4-компонентной и
8-компонентной окрестности равны
18.4. Составные морфологические операторы 507
Мь.=
Го
1
[0
1
1
1
0]
1
oj
Л/.8 =
Г1
г
^1
1
1
1
1]
1
ij
(18.28)
Граница тогда получается с помощью разности множеств (оператор /) между
объектом и эродированным объектом:
дС = GI{GeM^)
(18.29)
= Gn{GeM,)
= Gn{G®M^).
Как показывает уравнение (18.29), граница также задается как пересечение
объектов с расширенным фоном. На рис. 18.5 показаны 4- и 8-связные границы,
выделенные по бинарным объектам с использованием уравнения (18.28).
Граница фона задается подобно с помощью масштабного преобразования
объекта и вычитания его:
dGs=(G®Mf^)/G. (18.30)
"^
,0
с
2^
<£) ^ 0
) ооУо о
о
о
с
0
1
1
ч
0
о
о /
с
Oi
(1 \_У
:i с^^г, tJ
Рис. 18.5. Выделение фаниц с помощью морфологических операторов: а — исходное
изображение; б — 8-связные и в — 4-связные границы, вьщеленные с
использованием М^^ и M^g соответственно, (уравнение (18.28)); г — 8-связная граница фона,
выделенная с использованием уравнения (18.30)
Глава 18. Морфология
18.4.4. Преобразования расстояний
Граница состоит из всех точек с нулевым расстоянием до контура объекта. Если
мы снова применяем выделение границ к объекту, эродированному с маской
(18.28), то мы получаем все точки с расстоянием, равным единице, до границы
объекта. Рекурсивное применение процедуры вьщеления границ, таким образом,
задает расстояние всех точек от объекта до границы. Такое преобразование
называется преобразованием расстояния и может записываться как
D=\JiiGeMr')i{GeMi)-n\, (18.31)
п=\
где операция • обозначает поточечное умножение бинарного изображения а2-го
контура расстояния на число п.
Это прямое преобразование расстояния имеет два серьезных недостатка. Во-
первых, оно представляет собой медленную итерационную процедуру. Во-вторых,
оно не дает предпочтительное евклидово расстояние, а задает — в зависимости от
выбранной связности окрестности — расстояние «городской квартал» или
«шахматная доска» (раздел 2.2.3).
К счастью, доступны быстрые алгоритмы для вычисления евклидова
расстояния. Евклидово преобразование расстояния является важным преобразованием,
поскольку оно вводит изотропию для морфологических операций. Все
морфологические операции страдают от того, что евклидово расстояние не является
естественной мерой на прямоугольной сетке. Структурные элементы в форме
квадрата, к примеру, наследуют расстояние «шахматная доска». Последовательное
масштабное преобразование с такими структурными элементами придают
объектам вид, все более и более похожий на квадраты.
Евклидово преобразование расстояния можно использовать для выполнения
изотропных операций эрозии и масштабных преобразований. Для операции
эрозии с радиусом г мы сохраняем только пиксели с расстоянием, большим, чем г в
объекте. Подобным образом изотропное преобразование подобия можно
выполнять посредством вычисления евклидова преобразования расстояния фона и
затем изотропной эрозии фона.
18.5. Упражнения
18.1: Элементарные морфологические операторы
Интерактивная демонстрация элементарных морфологических операторов,
таких, как эрозия, масштабное преобразование, открытие и закрытие
(dip6exl8.01).
18.2: ^Коммутативность морфологических операторов
Проверьте, являются ли морфологические операторы эрозии и
масштабного преобразования коммутативными, и докажите ваш вывод.
(Подсказка: если один из операторов не коммутативный, то представьте
противоположный пример.)
18.3: Оператор попадание-промах
Интерактивная демонстрация оператора попадание-промах (dip6exl8.02).
18.5. Упражнения 509
18.4: Морфологическое выделение границ
Интерактивная демонстрация морфологического выделения границ
(dip6exl8.03).
18.5: Морфологические операции с полутоновыми изображениями
Интерактивная демонстрация морфологических операторов с
полутоновыми изображениями (dip6exl8.04).
18.6: "^Открьггие и закрьггие
Открытие и закрытие являются двумя наиболее важными
морфологическими операторами.
1. Что происходит, если применить открытие или закрытие с одним и тем
же структурным элементом несколько раз?
2. Каким является структурный элемент для оператора открытия,
который должен удалять все горизонтальные линии с шириной всего лишь в
один пиксель?
18.7: "^Комбинация морфологических операторов
Какой вид операции выполняется, если вы:
1) вычитаете эродированное бинарное изображение из исходного
бинарного изображения;
2) вьиитаете исходное бинарное изображение из расширенного изображения;
3) вычитаете эродированное изображение из расширенного изображения?
Какое различие суш;ествует между этими тремя комбинированными
морфологическими операторами?
18.8: ^'^Разложение морфологических операторов
Большие маски сверток могут часто раскладываться на некоторое число
более малых масок и, таким образом, выполняться гораздо более
эффективно. Возможно ли то же самое также с морфологическими масками
(структурными элементами)? Исследуйте этот вопрос на следуюш;их
примерах:
1)
[1 1 1] и
2)
[1 1 1] и [1 О О 1 О О 1]
18.9: "^Выделение объектов с использованием оператора попадание-промах
Оператор попадание-промах можно использовать для вьщеления объектов
с определенной формой.
1. Покажите на некоторых примерах, что маска попадание-промах
Глава 18. Морфология
-1 -1 -1
-1 1 -1
-1 -1 -1
вьщеляет изолированные пиксели.
2. Какие объекты вьщеляются с помощью следующих двух масок
попадание-промах?
[О 1 -1] и [-1 1 0]
18.6. Дополнительная литература
Авторитетным источником теории морфологической обработки изображений
является монография, написанная основателем морфологии изображений Зерра
(Serra) [184]. Более практические аспекты охватываются Яне (Jahne) и Хаусэ-
кером (HauBecker) [93, глава 14] и Зойлле (Soille) [192]. Между тем,
морфологическая обработка изображений является сформировавшейся тематикой с
основательной теоретической основой и широким диапазоном применения, как
можно видеть из недавних трудов конференций, например, доклады Зерра
(Serra) и Зойлле (Soille) [185].
ГЛАВА 19
ПРЕДСТАВЛЕНИЕ И АНАЛИЗ ФОРМЫ
19.1. Введение
Все операции, рассмотренные в главах 11—15, вьщеляли признаки из
изображений, которые опять представляются как изображения. Даже морфологические
операции, рассмотренные в главе 18, которые анализируют и модифицируют форму
сегментированных объектов в бинарных изображениях, действуют таким же
образом. Очевидно, однако, что форму объектов можно представлять в гораздо более
компактном виде. Вся информация относительно формы объекта, к примеру,
содержится в его граничных пикселях.
Поэтому в разделе 19.2 мы обращаемся к вопросу: как представлять
сегментированный объект? Мы изучим представление бинарных объектов с помощью кода
длин серий (раздел 19.2.1), квадрадерева (раздел 19.2.2) и цепного кода (раздел 19.2.3).
Два дополнительных представления объектов — моменты и Фурье-дескрипторы —
являются настолько значимыми, что мы посвящаем им целые разделы (разделы
19.3 и 19.4).
Компактное представление для формы объектов не имеет широкого
использования, если вычисление его отнимает много усилий и если вычисление
параметров формы непосредственно из него представляется громоздким. Поэтому мы
обращаемся также к вопросу вьщеления параметров формы по различным
представлениям формы в разделе 19.5.
Параметры формы вьщеляются из объектов для описания их формы,
сравнения ее с формой эталонных объектов или разделения объектов по классам
различных форм. В этом отношении возникает важный вопрос: как можно сделать
параметры формы инвариантными относительно определенных преобразований?
Объекты можно наблюдать с различных расстояний и из различных точек
наблюдения. Таким образом, представляет интерес нахождение параметров формы,
которые инвариантны относительно масштаба и поворота или даже относительно
аффинной или перспективной проекции.
19.2. Представление формы
19.2.1. Код длин серий
Компактным, простым и широко используемым представлением изображения
является код длин серий. Код длин серий получается с помощью следующей процедуры.
Изображение сканируется по линиям. Если линия содержит последовательность из/7
равных пикселей, то мы не сохраняем одно и то же значение р раз, а сохраняем один
раз значение пикселя и указьшаем, что оно возникает/? раз (рис. 19.1). Таким образом,
большие однородные сегменты линий могут храниться очень эффективно.
Для бинарных изображений код может быть особенно эффективным, поскольку
имеют место только два значения пикселей — ноль и единица. Поскольку за пос-
Глава 19. Представление и анализ формы
Изображение различной яркости
Исходная линия (hex): 12 12 12 20 20 20 20 25 27 25 20 20 20 20 20 20
Код (hex): 82 12 83 20 2 25 27 25 85 20
б
Бинарное изображение
Исходная линия (hex): 1111110001110010000011111111
Код (hex) 0 6 3 3 2 15 8
Рис. 19.1. Демонстрация кода длин серий для изображения различной яркости (а),
бинарного изображения (б).
ледовательностью нулей всегда следует последовательность единиц, нет
необходимости хранить значение пикселя. Нам необходимо хранить только число раз,
которое значение пикселя встречается. Однако мы должны быть внимательны в
начале линии, поскольку она может начинаться с единицы или нуля. Эту
проблему можно разрешить, если мы предположим, что линия начинается с нуля. Если
линия должна начинаться с последовательности единиц, то мы начинаем код длин
серий с нуля для указания того, что линия начинается с последовательности
нулевых нулей (рис. 19.1, б).
Код длин серий подходит для компактного хранения изображений. Он стал
составной частью нескольких стандартных форматов изображений, например,
форматов TGA или TIFF. Однако код длин серий менее полезен для непосредственной
обработки изображений, поскольку он не является объектно-ориентированным.
В результате кодирование длин серий более полезно для компактного хранения
изображений. Но не все виды изображений могут успешно сжиматься с помощью
этой схемы. Преобразованные в цифровую форму полутоновые изображения, к
примеру, всегда содержат некоторый шум, так что вероятность для достаточно
длинных последовательностей пикселей с одинаковым уровнем яркости очень мала.
Однако можно достичь высоких коэффициентов сокращения данных при
бинарных изображениях и многих видах полутоновых и цветных изображений,
формируемых с помощью компьютера.
19.2.2. Квадрадеревья
Коды длин серий, рассмотренные в разделе 19.2.1, являются
построчно-ориентированным представлением бинарных изображений. Таким образом, они
кодируют скорее одномерные, чем двумерные данные. Фактически двумерные структуры
не рассматриваются вообще. Противоположно квадрадерево основывается на
принципе рекурсивного разложения пространства, как проиллюстрировано на
рис. 19.2 для бинарного изображения.
Сначала все изображение раскладывается на четыре равных по размеру
квадранта. Если один из квадрантов не ограничивает однородную область, т.е. квадрант не
вмещается полностью в объект или фон, то он вновь последовательно делится на
четыре подквадранта. Разложение останавливается, если встречаются только
однородные квадранты или если квадранты в конечном счете вмещают только один
пиксель.
19.2. Представление формы 513
Рис. 19.2. Представление бинарного изображения с помощью квадрадерева
областей: а — последовательное деление бинарного изображения на квадранты; б —
соответствующее квадрадерево областей
Рекурсивное разложение можно представить через структуру данных,
известную в компьютерной науке как дерево (рис. 19.2, б). На верхнем уровне дерева, в
корне, начинается разложение. Корень соответствует целому бинарному
изображению. Он соединяется через ребра с четырьмя дочерними узлами, которые
представляют слева направо квадранты NW, NE, SW и SE. Если квадрант не нуждается
в дополнительном последовательном делении, то он представляется
терминальным узлом или листом в дереве. Его называют черным в случае, когда квадрант
принадлежит объекту, и белым — в противном случае и указывают черным и белым
квадратом соответственно. Узлы, не являющиеся листами, требуют дальнейшего
последовательного деления и, говорят, являются серыми и изображаются былыми
кружками (рис. 19.2, б).
Квадранты можно кодировать, например, с помощью обхода дерева, берущего
начало в корне, преимущественно в глубину. Требуется хранить только тип узла с
использованием символов b (черный), w (белый) и д (серый). Мы начинаем код со
значения корневого узла. Затем перечисляем значения дочерних узлов слева
направо. Каждый раз, когда мы встречаем серый узел, мы продолжаем кодирование на
один уровень ниже в дереве. Это правило применяется рекурсивно. Это означает,
что мы возвращаемся на более высокий уровень в дереве только после того, как
посещаемая ветвь полностью закодирована вплоть до самого низкого уровня. По этой
причине это кодирование называется преимущественным в глубину.
Пример квадрадерева, показанный на рис. 19.2, 5, приводит к коду
ggwwgwwwbbwggwbwbbwgwbwwgbwgbbwww.
Код становится более читаемым, если мы включаем левую круглую скобку
каждый раз, когда мы опускаемся на один уровень в дереве, и правую круглую скобку
когда мы вновь поднимаемся:
gf(g(wwg(www6)6)wg(g(w6w6)fewg(w6ww))g(Z>wgf(66ww)w)).
Однако код является единственным также без круглых скобок. Квадрадерево
является компактным представлением бинарного изображения, если оно
содержит большое количество листов на высоких уровнях. Однако в худшем случае,
например, случае регулярной шахматной структуры, все листья располагаются на
самом нижнем уровне. Тогда квадрадерево содержит столько же листьев, сколько
Глава 19. Представление и анализ формы
пикселей и, таким образом, требует гораздо больше байтов области памяти, чем
прямое представление бинарного изображения в виде матрицы.
Квадрадерево областей, рассмотренное здесь, представляет только одну из
многих возможностей для рекурсивного пространственного разложения.
Трехмерные бинарные изображения можно рекурсивно раскладывать подобным образом.
3-D изображение последовательно делится на восемь равных по размеру октантов.
Результирующая структура данных называется октадеревом областей. Квадраде-
ревья и октадеревья получили существенную важность в геоинформационных
системах и компьютерной графике.
Квадрадеревья являются более подходящим методом кодирования для
изображений, чем построчно-ориентированный код длин серий. Но они являются
менее подходящими для анализа изображений. Довольно трудно выполнять анализ
формы непосредственно по квадрадеревьям. Не углубляясь в дополнительные
детали, это можно видеть из того простого факта, что объект, сдвинутый на один
пиксель в любом направлении, приводит к полностью отличному квадрадереву.
Квадрадеревья областей разделяют свой наиболее важный недостаток с кодом длин
серий: метод является глобальным разложением изображения, но не представляет
компактным образом объекты, вьщеляемые из изображений.
19.2.3. Цепной код
В отличие от кода длин серий и квадрадеревьев, цепной код является относ5пцейся к
объектам структурой данных для эффективного представления границы бинарного
объекта на дискретной сетке. Вместо хранения положений всех граничных пикселей
мы выбираем начальный пиксель и храним только его координату. Если мы
используем алгоритм, который сканирует изображение по линиям, то это будет самый
верхний левый пиксель объекта. Тогда мы следуем границе в направлении часовой
стрелки. В 4-компонентной окрестности существуют 4, а в 8-компонентной окрестности 8
возможных направлений прохода, которые мы можем кодировать с помощью
3-битового или 2-битового кода, как указано на рис. 19.3. Вьщеленные границы
показываются на рис. 19.4 для 4-компонентной окрестности и 8-компонентной окрестности.
Цепной код демонстрирует некоторое число очевидных преимуществ над
матричным представлением бинарного объекта.
Во-первых, цепной код является компактным представлением бинарного
объекта. Давайте предположим объект в форме диска с диаметром R пикселей. В прямом
матричном представлении нам необходимо хранить ограничивающий прямоугольник
а б
2 1
3 '
\
, \
/
у
у
\/
/ ►»
\
2-4-
-►о
Рис. 19.3. Кодирование направлений в 8-компонентной окрестности (а) и
4-компонентной окрестности (б)
19.3. Признаки формы на основе анализа моментов 515
/[
/~
"л1
к
JI
и
А
Ч И
г\
г
JJ
г
J
~]
L
"1
1
1
JJ
Рис. 19.4. Граничное представление с помощью цепного кода: а — 8-компонентная
окрестность; б - 4-компонентная окрестность
объекта (раздел 19.5.4), т.е. приблизительно R^ пикселей, которые хранятся в R^
битах. Ограничивающим прямоугольником является наименьший прямоугольник,
вмещающий объект. Если мы используем 8-связную границу, то диск имеет
приблизительно TtR фаничных точек. Цепной код nR точек можно хранить в
приблизительно Зтг/? битах. Для объектов с диаметром больше 10 цепной код является
более компактным представлением.
Во-вторых, цепной код является представлением бинарного объекта,
инвариантным относительно перемещения. Это свойство облегчает сравнение объектов.
Однако цепной код не является инвариантным ни относительно поворота, ни
относительно масштаба. Это значимый недостаток для распознавания объектов, хотя
цепной код может тем не менее использоваться для выделения параметров,
инвариантных относительно поворота, например, площади объекта.
В-третьих, цепной код является полным представлением объекта или кривой.
Следовательно, мы можем, по крайней мере в принципе, вычислять любой
признак формы по цепному коду.
Как показано в разделе 19.5, мы можем вычислять некоторое число
параметров формы, включая периметр и площадь, более эффективно, используя
представление через цепной код, чем в матричном представлении бинарного изображения.
Ограничение здесь, конечно, состоит в том, что цепной код является цифровой
кривой на дискретной сетке и, по существу, описывает границы объекта только в
пределах точности дискретной сетки.
Если объект не является связным или если он имеет дыры, то нам требуется
больше одного цепного кода для его представления. Мы должны также учитывать, что
окружает граница - объект или отверстие. Реконструкция бинарного изображения
по цепному коду представляет собой легкую процедуру: мы можем нарисовать
очертание объекта и затем использовать операцию заполнения для его закраски.
19.3. Признаки формы на основе анализа моментов
19.3.1. Определения
В этом разделе мы представляем систематР1ческий подход для описания формы
объектов. Сначала мы определяем моменты для изображений различной яркости и бинар-
Глава 19. Представление и анализ формы
ных изображений и затем показьшаем, как вьщелять полезные параметры формы из
этого подхода. Мы рассмотрим подобным образом Фурье-дескрипторы в разделе 19.4.
Мы использовали моменты в разделе 3.2.2 для описания функции плотности
распределения для уровней яркости. Здесь мы расширяем это описание до
двумерного случая и описываем моменты функции уровней яркости д{х) объекта как
i"p,, =|(^1 -^Г(^2 -Т,Уд{х)А'х, (19.1)
где
^ = \х,д{х)&^х1\д{х)&^х. (19.2)
Интегрирование учитывает площадь объекта. Вместо уровня яркости мы
можем использовать более обобщенно любой признак на основе пикселей для
вычисления моментов объекта. Вектор х = (jc, ^^) называется центром масс объекта
по аналогии с классической механикой. Рассмотрим д(х) как плотность р(х)
объекта; тогда момент нулевого порядка fi^^ становится общей массой объекта.
Все моменты, определенные в уравнении (19.1), связаны с центром масс.
Следовательно, они часто обозначаются как центральные моменты. Центральные
моменты инвариантны относительно перемещения и, таким образом, являются
полезными признаками для описания формы объектов.
Для дискретных бинарных изображений вьиисление моментов сводится к
^p,<,=Y,ix,-Xy{x,-Y,y. (19.3)
Суммирование включает в себя все пиксели, принадлежащие объекту. Для
описания формы объекта мы можем использовать моменты на основе или
бинарных изображений, или полутоновых изображений, или изображений
признаков. Моменты на основе полутоновых изображений или изображений
признаков отражают не только геометрическую форму объекта, но также и распределение
признаков внутри объекта. По существу, они, как правило, отличаются от
моментов на основе бинарных изображений.
19.3.2. Моменты, инвариантные относительно масштаба
Часто необходимо использовать параметры формы, которые не зависят от размера
объекта. Это всегда требуется, если должны сравниваться объекты, наблюдаемые
с различных расстояний. Моменты можно нормировать для получения
параметров формы, инвариантных относительно масштаба, следующим образом. Если мы
масштабируем объект д(х) множителем а, д'{х) = д(х/а), то его моменты
масштабируются соотношением
Г'р,д ^ H'p,q
Тогда мы можем нормировать моменты с помощью момента нулевого
порядка, /Iqq, для получения моментов, инвариантных относительно масштаба
-^ Ир,,
А*о,о
Поскольку момент нулевого порядка бинарного объекта задает площадь объекта
(уравнение (19.3)), нормированные моменты масштабируются площадью
объекта. Моменты второго порядка (/? + ^ = 2), например, масштабируются с помощью
квадрата площади.
19.3. Признаки формы на основе анализа моментов 517
Рис. 19.5. Главные оси тензора инерции объекта для поворота вокруг центра масс
19.3.3. Тензор моментов
Анализ формы за пределами измерений площади начинается с моментов второго
порядка. Момент первого порядка просто задает площадь или «общую массу»
бинарного объекта или объекта различной яркости соответственно. Центральные
моменты первого порядка равны нулю по определению.
Аналогия с механикой вновь полезна для понимания значения моментов
второго порядка jU2 Q, )Uq 2 ^ Ml г ^"^ содержат слагаемые, в которых функция уровней
яркости, т.е. плотность объекта, умножается на квадраты расстояний от центра
масс. Точно такие же члены учитываются также в тензоре инерции, который
рассматривался в разделе 13.5.1 (см. уравнения (13.62) и (13.63)). Три момента
второго порядка образуют компоненты тензора инерции для поворота объекта вокруг его
центра масс:
У =
(19.4)
/^2,0 М,1
""/^1,1 /^0,2
Вследствие этой аналогии мы можем перенести все результаты из раздела 13.3
на описание формы с помощью моментов второго порядка. Ориентация объекта
определяется как угол между осью х и осью, вокруг которой объект может вращаться
с минимальной инерцией. Это есть собственный вектор минимального
собственного значения. Объект является наиболее вытянутым в этом направлении (рис. 19.5).
Согласно уравнению (13.12), этот угол определяется соотношением
1 2а,,
0 = -arctan -^—. (19.5)
^ /^2,0 ~ /^0,2
В качестве меры для эксцентриситета е мы можем использовать величину,
которую мы определили какмеру когерентности для локальной ориентации (13.15):
Эксцентриситет изменяется в диапазоне от О до 1. Он равен нулю для круглого
объекта и единице для объекта в форме линии. Таким образом, он представляет луч-
Глава 19. Представление и анализ формы
ше определенную величину, чем округлость со своим ненормированным
диапазоном (раздел 19.5.3).
Описание формы с помощью моментов второго порядка в тензоре моментов,
по существу, моделирует объект как эллипс. Объединение трех моментов второго
порядка в тензор наглядно приводит к двум инвариантным относительно
поворота членам — следу тензора, или ii^^ + ^i^^, который задает радиальное
распределение признаков в объекте, и эксцентриситету (19.6), которое измеряет округлость,
и одному члену, который измеряет ориентацию объекта. Моменты
предусматривают полное описание формы [163]. Описание формы становится тем более
детальным, чем более высокого порядка используются моменты.
19.4. Фурье-дескрипторы
19.4.1. Декартовы Фурье-дескрипторы
Фурье-дескрипторы, подобные цепному коду, используют границу объекта. В
отличие от цепного кода, Фурье-дескрипторы не описывают кривые на дискретной
сетке. Они могут формулироваться для непрерывных или дискретизированных
кривых. Рассмотрим замкнутую граничную кривую, схематически изображенную
на рис. 19.6. Мы можем описывать ее параметрически, взяв в качестве параметра
длину траектории/? от начальной точки [х^, у^'^.
Довольно нелегко образовать граничную кривую с равноудаленными
выборками. Дискретные фаничные кривые, подобно цепному коду, имеют существенные
недостатки. В 8-компонентной окрестности выборки не являются
равноудаленными. В 4-компонентной окрестности выборки равноудалены, но граница является
рваной, поскольку участки граничной кривой могут идти только в горизонтальных
и вертикальных направлениях. Следовательно, периметр стремится быть слишком
длинным. Поэтому формирование непрерывной граничной кривой по точкам на
прямоугольной сетке не кажется хорошей идеей. Единственная альтернатива
состоит в вьщелении граничных кривых объекта с точностью до фрагментов пикселя не-
Рис. 19.6. Иллюстрация параметрического представления замкнутой кривой.
Параметр/? определяет длину траектории от начальной точки [х^, у^в направлении против
часовой стрелки. Также показана равномерная дискретизация кривой с /^точками
19.4, Фурье-дескрипторы
посредственно из полутоновых изображений. Но это не является легкой задачей.
Таким образом, точное определение Фурье-дескрипторов по контурам в
изображениях все еще остается перспективной исследовательской задачей.
Непрерывная граничная кривая имеет вид х(р) и у(р). Мы можем объединить
эти две кривые в одну кривую с помощью комплексной функции z(p) =х(р) + \у(р).
Эта кривая является циклической. Если Р есть периметр кривой, тогда
z{p + nP) = z(p) neZ. (19.7)
Циклическую или периодическую кривую можно разложить в ряд Фурье (см.
также табл. 2.1). Коэффициенты ряда Фурье задаются соотношением
5, =-J^(p)exp
d/7 ugZ.
(19.8)
V " J
Периодическую кривую можно реконструировать по коэффициентам Фурье с
помощью
^2n\vp^
z(p) = X ^^^ ^^Р
V
(19.9)
У
Коэффициенты z ^ известны как декартовы Фурье-дескрипторы граничной
кривой. Их значения очевидны. Первый коэффициент
1 1 *
2
Р
(19.10)
о ^0 -'о
определяет средний вихрь или центроид границы. Второй коэффициент
описывает окружность
(2тр^
z^(p) = z,Qxp
V
= Tj exp(i()r)i + 2nip IP).
(19.11)
J
Радиус A-j и начальная точка при угле ср^ определяются соотношением z^ = r^Qxp(i(p^).
Коэффициент Z J также приводит к окружности
z_^{p) = r_, exp(i(p_i -ImpIP), (19.12)
но эта окружность прослеживается в противоположном направлении (по часовой
стрелке). С использованием обоих комплексных коэффициентов совместно, в
сумме четырех параметров, можно сформировать эллипс с произвольными
полуосями а и й, ориентацией i^ главной оси а и начальным углом (р^ на эллипсе. В качестве
примера возьмем (jo, = <р_, = 0. Тогда
Zj +Z_j =(ri +r_j)-COS
2np
|H-i(rj -r_j)sin
(2np\
(19.13)
Это параметрическая форма эллипса, где оси лежат вдоль координатных осей,
а начальная точка - на оси х.
Из этого описания очевидно, что Фурье-дескрипторы всегда должны быть
парными. Образование пар коэффициентов более высокого порядка также приводит
к эллипсам. Однако эти эллипсы циклически повторяются п раз. При добавлении
к основному эллипсу первой пары это означает, что Фурье-дескрипторы более
высокого порядка добавляют все больше и больше деталей к граничной кривой.
Глава 19. Представление и анализ формы
Рис. 19.7. Реконструкция формы буквы L (а) и буквы Т (б) с 2, 3, 4 и 8 парами Фурье-
дескрипторов
Для дальнейшей иллюстрации показана реконструкция букв Ти Lc
возрастающим числом Фурье-дескрипторов (рис. 19.7). Пример показывает, что
требуются только несколько коэффициентов для описания даже довольно сложных форм.
Фурье-дескрипторы можно также легко вычислять по дискретизированным
границам z^. Если периметр замкнутой кривой равен Р, то нужно взять N выборок
на равных расстояниях P/N (рис. 19.6). Тогда
. 1 ^^ ( 1к\ую ^
\
N
(19.14)
Все другие уравнения имеют силу также для дискретизированных границ.
Дискретизация только заменяет ряд Фурье на дискретное преобразование Фурье с Л^
волновыми коэффициентами, которые пробегают от О до Л/^- 1 или от -N/2 до N/
2 - 1 (см. также табл. 2.1).
19.4.2. Полярные Фурье-дескрипторы
Альтернативный подход к Фурье-дескрипторам использует другую параметрити-
зацию фаничной линии. Вместо длины траектории р используется угол в между
радиусом, проведенным из центроида в точку на границе, и осью х. Таким
образом, мы непосредственно описываем/?^fdw>'c объекта как функцию угла. Теперь нам
требуется только действительная последовательность, #•, с Л^ равноугольными
выборками для описания границы. Коэффициенты дискретного преобразования
Фурье этой последовательности
. 1 « ( Ininv ^
известны как полярные Фурье-дескрипторы границы. Здесь первый
коэффициент, ?Q, равен среднему радиусу. Полярные Фурье-дескрипторы не могут
использоваться для всех типов границ. Радиальная граничная параметритизация
г{в) должна быть однозначной. Вследствие этого существенного ограничения
мы фокусируем дальнейшее рассмотрение Фурье-дескрипторов на декартовых
Фурье-дескрипторах.
(19.15)
19.4. Фурье-дескрипторы
.....й
-10
11»
5 10
.1
-10 -5
5
10
-10
10
-10
10
Рис. 19.8. Влияние симметрии объекта на его Фурье-дескрипторы: а - буква L; б -
линия; в — треугольник; г — квадрат. Показаны абсолютные величины
Фурье-дескрипторов от i;= -16 до 1;= 16
19.4.3. Симметричные объекты
Можно легко выделить симметрии в Фурье-дескрипторах. Если контур имеет
т-осевую симметрию, тогда только z^^^ могут быть неравными нулю. Это
демонстрируется на рис. 19.8 на примере Фурье-дескрипторов вертикальной линии,
треугольника и квадрата. Если один контур является зеркальным контуром другого,
то их Фурье-дескрипторы являются комплексно сопряженными друг к другу.
Фурье-дескрипторы можно также использовать для незамкнутых границ.
Чтобы сделать их замкнутыми, мы просто прослеживаем кривую вперед и назад.
Такие кривые легко распознать, поскольку их площадь равна нулю. Из уравнения
(19.17) мы можем тогда заключить, что \z_J= \zj. Если след начинается в одном из
концов, то даже z_ = z .
19.4.4. Инвариантное описание объектов
Инвариантность относительно перемещения. Положение объекта ограничивается
единственным коэффициентом z^. Все другие коэффициенты являются
инвариантными относительно перемещения.
Инвариантность относительно масштаба. Если контур масштабируется
коэффициентом а, то все Фурье-дескрипторы также масштабируются а. Если контур
объекта с ненулевой площадью прослеживается против часовой стрел1си, то первый
коэффициент всегда неравен нулю. Таким образом, мы можем просто масштабировать
Глава 19. Представление и анализ формы
все Фурье-дескрипторы с помощью | z J для получения инвариантных
относительно масштаба дескрипторов формы. Обратите внимание, что эти
масштабированные дескрипторы являются все еще полными.
Инвариантность относительно поворота. Если контур поворачивается против
часовой стрелки на угол ср^, то Фурье-дескриптор z^ умножается на фазовый
множитель Qx^(\v(p^ согласно теореме о сдвиге для Фурье-преобразования (теорема 2.3,
с. 61, >-R4). Теорема о сдвиге позволяет легко построюъ инвариантные
относительно поворота Фурье-дескрипторы. Например, мы можем соотнести фазы всех
Фурье-дескрипторов с фазой Z J, ф,, и вычесть фазовый сдвиг v(p^ из всех
коэффициентов. Тогда все остающиеся дескрипторы инвариантны относительно поворота.
Как Фурье-дескрипторы (раздел 19.4), так и моменты (раздел 19.3)
обеспечивают основу для инвариантных относительно масштаба и поворота параметров
формы. Фурье-дескрипторы являются более универсальным инструментом.
Однако они ограничивают описание объекта граничной линией, в то время как
моменты полутоновых объектов чувствительны к пространственному распределению
уровней яркости в объекте.
В идеале параметры формы описывают форму объекта полностью и
единственным образом. Это означает, что различные формы не должны отображаться в один
и тот же набор признаков. Инвариантное относительно масштаба и поворота, но
неполное описание формы задается абсолютной величиной Фурье-дескрипторов.
На рис. 19.9 показано, как различные формы отображаются в этот дескриптор
формы, при применении Фурье-дескрипторов букв Т и L и случайного изменения фазы.
Только полный набор Фурье-дескрипторов образует единственное описание
формы. Обратите внимание, что для каждой инвариантности теряется одна
степень свободы. Для инвариантности относительно перемещения мы не учитываем
первый Фурье-дескриптор z^ (две степени свободы). Для инвариантности
относительно масштаба мы устанавливаем абсолютную величину второго
Фурье-дескриптора, Zj, равным единице (одна степень свободы), а для инвариантности
относительно поворота мы соотносим все фазы с фазой z, (еще одна степень свободы).
При всех трех инвариантах теряются четыре степени свободы.
Рис. 19.9. Важность фазы для описания формы с помощью Фурье-дескрипторов.
Помимо исходных букв показаны три случайные модификации фазы с
неизмененной абсолютной величиной Фурье-дескрипторов
19.5. Параметры формы
Преимуществом Фурье-дескрипторов является то, что эти инварианты просто
содержатся в первых двух Фурье-дескрипторах. Если мы нормируем все другие
Фурье-дескрипторы с помощью фазы и абсолютной величины второго
Фурье-дескриптора, то получим полное инвариантное относительно перемещения,
поворота и масштаба описание формы объектов. Не учитывая Фурье-дескрипторы более
высокого порядка, мы можем постепенно выпускать мелкие детали из описания
формы управляемым образом.
Различия в форме можно измерять, используя тот факт, что
Фурье-дескрипторы формируют комплекснозначный вектор. Метрика для различий в форме тогда
задается модулем разностного вектора:
d^'= I \К-К\. (19.16)
\)=-NI2
В зависимости от того, какое нормирование мы применяем к
Фурье-дескрипторам, эта метрика будет инвариантна относительно масштаба и/или поворота.
19.5. Параметры формы
После рассмотрения различных способов представления бинарных объектов,
выделенных из данных изображения, мы обращаемся к вопросу: как описывать
форму этих объектов? Этот раздел рассматривает элементарные геометрические
параметры, такие, как площадь и периметр.
19.5.1. Площадь
Одним из наиболее тривиальных параметров формы является площадь А объекта. В
цифровых бинарных изображениях число пикселей, принадлежащих изображению,
задает площадь. Так, вычисление площади объекта, представленного в матричном
виде или через список пикселей, означает просто подсчет числа пикселей. Площадь
также задается как момент нулевого порядка бинарного объекта (уравнение (19.3)).
На первый взгляд кажется, что вычисление площади объекта, который
описывается его цепным кодом, является сложной операцией. Однако верно обратное.
Вычисление площади по цепному коду выполняется гораздо быстрее, чем подсчет
пикселей, поскольку граница объекта содержит только малую долю пикселей
объекта и требует только две операции сложения в пикселе границы.
Алгоритм работает так же, как численное интефирование. Мы предполагаем
горизонтальную базовую линию, проведенную в произвольном вертикальном
положении в изображении. Затем мы начинаем интегрирование площади в самом верхнем
пикселе объекта. Расстояние от этой точки до базовой линии равно В. Мы следуем
границе объекта и увеличиваем площадь объекта согласно цифрам в табл. 19.1.
Если мы, например, движемся вправо (8-цепной код 0), то площадь
увеличивается на В. Если мы движемся вверх вправо (цепной код 1), то площадь также
увеличивается на В, но 5 должно также увеличиваться, поскольку расстояние между
граничным пикселем и базовой линией увеличилось. Для всех движений влево
площадь уменьшается на В. Таким образом, мы вычитаем площадь между нижней
граничной линией объекта и базовой линией, которая была учтена в вычислении
площади при движении вправо. Однако цепной код должен располагаться в сере-
Глава 19. Представление и анализ формы
Таблица. 19.1. Вычисление площади объекта по цепному коду. Вначале
устанавливаем площадь равной 1. С каждым шагом площадь и параметр В увеличиваются в
соответствии со значением цепного кода [221]
4-цепной код
0
1
2
3
8-цепной
0
1
2
3
4
5
6
7
код
Увеличение площади
+В
+В
0
-в
-в
-в
0
+в
Увеличение В
0
1
1
1
0
-1
-1
-1
дине пикселя. Следовательно, он не определяет площадь, которая равна числу
пикселей объекта. Линия с толщиной в один пиксель не имеет площади, квадрат 2x2
имеет площадь, равную единице. Вначале площадью! устанавливается равной нулю.
Площадь можно также вычислить по Фурье-дескрипторам. Она задается
соотношением
N/2-\
А = к X i^l^ul'- (19.17)
ч=-М/2
Это представляет собой быстрый алгоритм, который требует самое большее
столько же операций, сколько точек на граничной линии кривой.
Фурье-дескрипторы имеют дополнительное преимущество в том, что мы можем вычислять
площадь для определенной степени гладкости с помощью определенного количества
Фурье-дескрипторов. Чем больше Фурье-дескрипторов мы берем, тем более
детальной является граничная кривая, как продемонстрировано на рис. 19.7.
19.5.2. Периметр
Периметр является еще одним геометрическим параметром, который может легко
получаться из цепного кода границы объекта. Нам просто необходимо вьиислить
длину цепного кода и принять во внимание, что шаги в диагональных направлениях
больше в у/2 раза. Тогда периметр р задается цепным кодом при 8-компонентной
окрестности:
р = п^+у/2п^, (19.18)
где п^ип^ — число четных и нечетных шагов цепного кода соответственно. Шаги с
нечетным кодом имеют диагональное направление.
В отличие от площади, периметр является параметром, который чувствителен
к уровню шума в изображении. Чем более зашумлено изображение, тем более
неровной и, таким образом, более длинной будет становиться граница объекта в
процедуре сегментации. Это означает, что нужно быть внимательными в сравнении
периметров, которые были вьщелены из разных изображений. Мы должны быть
уверены, что гладкость границ в изображениях является сравнимой.
К сожалению, не существует простой формулы для вьиисления периметра по
Фурье-дескрипторам, поскольку вычисление периметра эллипсов содержит эллип-
19.6. Упражнения
тические интефалы. Однако периметр получается непосредствеьшо из построения
граничной линии с равноудаленными выборками и хорошо аппроксимируется числом
выборочных точек, умноженным на среднее расстояние между точками.
19.5.3. Округлость
Площадь и периметр являются двумя параметрами, которые описывают размер
объекта тем или иным образом. Для того чтобы сравнивать объекты, наблюдаемые
с различных расстояний, важно использовать параметры формы, которые не
зависят от размера объекта на плоскости изображения. Округлость с является одним из
простейших параметров этого типа. Она определяется как
(19.19)
с=Р-
Округлость является безразмерным числом с минимальным значением
4к -12,57 для окружностей. Округлость равна 16 для квадрата и 12л/3-20,8 для
равностороннего треугольника. Как правило, она стремится к большим
значениям для вытянутых объектов.
Площадь, периметр и округлость являются параметрами формы, которые не
зависят от ориентации объектов на плоскости изображения. Таким образом, они
полезны для вьщеления объектов независимо от их ориентации.
19.5.4. Ограничивающий прямоугольник
Еще одним простым и полезным параметром для грубого описания размера объекта
является ограничивающий прямоугольник. Он определяется как прямоугольник,
который просто является достаточно большим для вмещения всех пикселей
объекта. Он определяет также грубое описание формы объекта. В отличие от площади
(раздел 19.5.1), однако, он не инвариантен относительно поворота. Его можно
сделать инвариантным относительно поворота, если объект поворачивается в
стандартную ориентацию, например используя ориентацию тензора моментов (раздел
19.3.3). В любом случае ограничивающий прямоугольник является полезным
признаком, если требуется любая дальнейшая объектно-ориентированная
пиксельная обработка, такая, как вьщеление пикселей объекта для дальнейших целей.
19.6. Упражнения
19.1:
^^Представление бинарньк объектов
Вычислите по бинарному объекту на квадратной сетке, показанной ниже,
код длин серий, цепной код при 4-компонентной окрестности и цепной
код при 8-компонентной окрестности. Определите, сколько байтов
потребуется для хранения его в различных кодах.
Глава 19. Представление и анализ формы
19.2: **Периметр
Вычислите непосредственно по кодам в упражнении 19.1 периметр
объекта. Сколько требуется вьиислительных шагов?
19.3: **Площадь
Вычислите непосредственно по кодам в упражнении 19.1 площадь объекта.
Сколько требуется вычислительных шагов?
19.4: Элементарные параметры формы
Интерактивная демонстрация элементарных параметров формы, таких, как
площадь и эксцентриситет (dip6exl9.01).
19.5: Параметры формы на основе моментов
Интерактивная демонстрация анализа формы на основе моментов
(dip6exl9.02).
19.6: Фурье-дескрипторы
Интерактивная демонстрация свойств Фурье-дескрипторов (dip6exl9.03).
19.7: ^Декартовы и полярные Фурье-дескрипторы
Доступны два типа Фурье-дескрипторов: декартовы дескрипторы и
полярные дескрипторы.
1. В каких отношениях эти два дескриптора отличаются?
2. Подходят ли оба дескриптора для всех типов контуров объектов?
19.8: **Свойства Фурье-дескрипторов
Декартовы Фурье-дескрипторы являются важным инструментом для
описания контуров, поскольку по ним можно легко выделять многие
геометрические признаки. Предположим объект, который является односвязным
и, таким образом, имеет единственную замкнутую границу. Ответьте на
следующие вопросы:
1. Как можно вьщелить объект в форме линии? (Подсказка: замкнутая
кривая означает, что она идет от начальной точки линии к конечной точке и
обратно.)
2. Как можно найти симметричный объект и определить его ось симметрии?
3. Можете ли вы определить наклон контура по Фурье-дескрипторам?
4. Можете ли вы сгладить контур, используя Фурье-дескриптор?
19.9: ^'^Выделение равнобедренных треугольников
Как можно вьщелить равнобедренные треугольники с помощью
Фурье-дескрипторов? Вьщелите следующие случаи:
1. Равнобедренный треугольник с одинаковой ориентацией.
2. Треугольники различного размера, но с одинаковой ориентацией
(инвариантное относительно масштаба распознавание).
3. Треугольники различного размера и различной ориентации
(инвариантное относительно масштаба и инвариантное относительно поворота
распознавание).
19.7 Дополнительная литература
19.10: ***Моменты и Фурье-дескрипторы
Исследователи все еще спорят: Фурье-дескрипторы или моменты
являются лучшим методом для описания формы объектов? Каково ваше мнение?
Исследуйте в особенности проблему различных инвариантных
дескрипторов формы и ответьте на вопрос: сколько параметров требуется для
описания сложной формы?
19.7. Дополнительная литература
Пространственные структуры данных, особенно различные древовидные
структуры, и их применение детально рассматриваются в монографиях Самета (Samet)
[174, 175]. Подробное рассмотрение анализа формы на основе моментов с
акцентом на инвариантные признаки формы можно найти в монографии Райсса (Reiss)
[163]. Инварианты на основе уровней яркости рассматриваются Буркхардтом
(Burkhardt) и Сиггелковым (Siggelkow) [17].
ГЛАВА 20
ПРЕДСТАВЛЕНИЕ И АНАЛИЗ ФОРМЫ
20.1. Введение
Когда выделяются объекты с помощью подходящих операторов и описывается их
форма (глава 19), обработка изображений достигает своей цели для определенных
классов прикладных задач. Для других прикладных задач остаются нерешенными
дополнительные задачи. В этом введении мы исследуем некоторые примеры,
которые демонстрируют, как задачи обработки изображений зависят от вопросов,
которые мы ставим.
Во многих прикладных задачах обработки изображений требуется
проанализировать размер и форму частиц, таких, как пузырьки, аэрозоли, капли,
пигментные частицы или адра клеток. В этих случаях интересующие нас параметры явно
описываются и непосредственно измеряемы по полученным изображениям. Мы
определяем площадь и форму каждой частицы, которые вьщеляются с
использованием методов, рассмотренных в разделах 19.5.1 и 19.3. Знание этих параметров
позволяет ответить на все интересующие нас вопросы. По выбранным данным мы
можем, например, вычислять гистограммы площадей частиц (рис. 20.1, в). Этот
пример является типичным для широкого класса научных задач. Параметры
объектов, которые можно оценивать непосредственно и однозначно по данным
изображения, помогают ответить на поставленные вопросы.
Другие прикладные задачи являются более сложными в том смысле, что
требуется вьщелить различные классы объектов в изображении. Простейший случай
задается типичной задачей промышленного контроля. Находятся ли размеры
детали в пределах заданного допуска? Упускаются ли какие-либо детали? Видны ли
какие-либо дефекты, такие, как царапины? В результате анализа проверенная
деталь либо проходит тест, либо приписывается к определенному классу ошибок.
Приписывание объектов в изображениях к определенным классам является,
подобно многим другим аспектам обработки изображений и анализа,
несомненно, междисциплинарной задачей, которая характерна не для анализа
изображений, а для самого общего типа методов. В этом отношении анализ изображений
является частью более общей тематики, известной k^lkраспознавание образов.
Классическим применением распознавания образов, которое всем известно, является
распознавание речи. Произнесенные слова содержатся в 1-D акустическом
сигнале (временной ряд). Здесь задача классификации состоит в распознавании фонем,
слов и предложений по разговорному языку. Соответствующей задачей в
обработке изображений является распознавание текста, распознавание букв и слов по
написанному тексту, также известное как оптическое распознавание символов (ОРС).
Общая сложность классификации связана с тем, что зависимость между
интересующими нас параметрами и данными изображения неочевидна. Объекты,
которые требуется классифицировать, не связаны непосредственно с определенным
диапазоном значений отдельного признака и должны распознаваться по их
оптической сигнатуре в изображении. По каким признакам, например, мы можем вьще-
20.1. Введение
500
1000 1500 2000
Рис. 20.1. Шаги анализа распределения размеров частиц (чечевица): а — исходное
изображение; б — бинарное изображение; в — распределение площадей
лить чечевицу, зерна перца и семечки подсолнечника, показанные на рис. 20.2?
Соотношение между оптическими сигнатурами и классами объектов, как правило,
требует тщательного анализа. Проиллюстрируем сложные соотношения между
признаками объектов и их оптическими сигнатурами на двух дополнительных примерах.
«Умирание леса» (крупномасштабное повреждение леса вследствие кислотного
дождя и другого загрязнения окружающей среды) является одной из многих
больших проблем, с которой сталкиваются специалисты в науке об окружающей среде.
В дистанционном зондировании задача состоит в картировании и
классифицировании степени повреждения в лесах по полунению изображений с воздуха и с
помощью ИСЗ. В этом примере зависимость между различными классами повреждения
и признаками в изображениях является менее очевидной. Необходимы детальные
исследования для обнаружения этих сложных зависимостей. Изображения,
полученные с воздуха, должны сравниваться с исследованиями на земле. Можно
предположить, что нам потребуется более одного признака для распознавания
определенных классов повреждения леса.
Существует много подобных задач в медицине и биологии. Одним из
стандартных вопросов в медицине является разделение между понятиями «здоровый» и
«больной». И опять очевидно, что мы не можем ожидать простой зависимости между
этими двумя классами объектов и признаками наблюдаемых объектов на изображениях.
В качестве еще одного примера возьмем объекты, показанные на рис. 20.3. У
нас не возникнет проблем в распознавании того, что все объекты, кроме одного.
Глава 20, Представление и анализ формы
Рис. 20.2. Задача классификации: какие из зерен относятся к зернам перца,
чечевицы, семенам подсолнечника или не относятся ни к одним из трех? А - исходное
изображение; б - бинарное изображение после сегментации
являются лампами. Как могла бы система машинного зрения выполнить эту
задачу? Какие признаки мы можем вьщелить из этих изображений, которые помогают
нам распознавать лампу? В то время как у нас не возникает проблем в
распознавании ламп на рис. 20.3, мы чувствуем себя довольно беспомощными в отношении
вопроса: как решить эту задачу, используя компьютер? Очевидно, что эта задача
сложна. Мы распознаем лампу, поскольку мы уже видели многие прочие лампы
прежде и так или иначе запомнили этот опыт и способны сравнивать эти
накопленные знания с тем, что мы видим на изображении. Но как эти знания
накапливаются и как выполняется сравнение? Очевидно, что это не просто база данных с
геометрическими формами, мы также знаем, в каком контексте или окружении
появляются лампы и для чего они используются. Исследования проблем такого
рода являются частью тематики, называемой искусственным интеллектом,
сокращенно обозначаемой как ИИ.
Что касается научного использования, представляет интерес еще один аспект
классификации. Поскольку методы формирования изображений находятся среди
дврокущих сил прогресса в экспериментальных естественных науках, часто
происходит так, что на изображениях появляются неизвестные объекты, для которых пока
не придумана схема классификации. Одной из целей обработки изображений
является определение классов для этих новых объектов. Следовательно, нам нужны
методы классификации, которые не требуют каких-либо предварительных данных.
Подводя итог, мы заключаем, что классификация включает две основные задачи:
1. Соотношение между признаками изображения (оптическая сигнатура) и
искомыми классами объектов должно исследоваться настолько детально, насколько
это возможно. Эта тема частично изложена в публикациях по проблемам
соответствующей научной области и частично в работах по теории формирования
изображений, т.е. оптике, как рассмотрено в главах 6—8.
2. Из множества возможных признаков изображения мы должны выбрать
оптимальный набор, который позволяет однозначно выделять различные классы
объектов с минимальными усилР1ями и настолько незначительным числом
ошибок, насколько это возможно с помощью подходящего метода систематизации. Эта
задача, известная как классификация, является предметом этой главы. Мы касаем-
20.2. Пространство признаков 531
Рис. 20.3. Как мы распознаем, что все, кроме одного из этих объектов, являются
лампами?
ся здесь только некоторых основных вопросов, таких, как выбор надлежащих типа
и числа признаков (раздел 20.2), и разрабатываем некоторые простые методы
классификации (раздел 20.3).
20.2. Пространство признаков
20.2.1. Классификация на основе пикселей в сравнении с классификацией
на основе объектов
Можно вьщелить два типа процедур: классификация на основе пикселей и
классификация на основе объектов. В сложных случаях сегментация объектов не
представляется возможной при использовании единственного признака. Тогда требуется
использование множественных признаков и процесса классификации, чтобы решить,
какой пиксель к какому типу объекта принадлежит.
Гораздо более простая классификация на основе объектов может
использоваться, если различные объекты четко отделяются от фона, не соприкасаются и не
перекрывают друг друга. Следует использовать, если это вообще возможно,
классификацию на основе объектов, поскольку в этом случае обрабатывается гораздо
меньше данных. Тогда все признаки на основе анализа пикселей, рассмотренные
в главах 11—15, такие, как средний уровень яркости, локальная ориентация,
локальное волновое число и дисперсия уровней яркости, могут усредняться по всей
Глава 20. Представление и анализ формы
области объекта и использоваться как признаки, описывающие свойства
объектов. К тому же мы можем использовать все параметры, описывающие форму
объектов, рассмотренные в главе 19. Иногда требуется применять оба процесса
классификации: во-первых, классификацию на основе пикселей для отделения объектов
друг от друга и фона и, во-вторых, классификацию на основе объектов для
использования также геометрических свойств объектов для классификации.
20.2.2. Кластер
Набор из Р признаков образует Р-мерное пространство М, обозначаемое как
пространство признаков или пространство измерений. Каждый пиксель или объект
представляется как вектор признака в этом пространстве. Если признаки
правильно представляют класс объектов, то все векторы признаков объектов из этого класса
должны находиться поблизости друг от друга в пространстве признаков. Мы
рассматриваем классификацию как статистический процесс и приписываем Р-мер-
ную функцию плотности распределения каждому классу объектов. В этом смысле
мы можем оценить эту функцию распределения вероятностей посредством взятия
выборок из данного класса объектов, вычисления вектора признака и увеличения
соответствующей точки в дискретном пространстве признаков. Эта процедура
соответствует вычислению обобщенной Р-мерной гистограммы (раздел 3.2.1). В
случае, когда класс объекта показывает узкое распределение вероятностей в
пространстве признаков, мы говорим о кластере. Разделение объектов по данным классам
объектов будет возможным, если кластеры для различных классов объектов
хорошо отделяются друг от друга. При менее подходящих признаках кластеры
перекрывают друг друга или, даже хуже, кластеров может не существовать вообще. В
этих случаях безошибочная классификация не представляется возможной.
20.2.3. Выбор признаков
Начнем с примера классификации различных зерен, показанных на рис. 20.2, на
три класса: зерна перца, чечевица и семена подсолнечника. На рис. 20.4, а, б
показаны гистограммы двух признаков — площади и эксцентриситета (уравнение (19.6)
в разделе 19.3.3). В то время как гистограмма площади показывает два пика,
только один пик может наблюдаться в гистограмме эксцентриситета. В любом случае
ни один из двух признаков в отдельности недостаточен для вьщеления трех
классов — зерен перца, чечевицы и семян подсолнечника. Если мы берем одновременно
оба параметра, то мы можем вьщелить по меньшей мере два кластера (рис. 20.4, в).
Эти два класса можно распознать как зерна перца и чечевицу. Оба вида зерен
являются почти круглыми и, таким образом, показывают малый эксцентриситет
между О и 0,2. Следовательно, оба класса сливаются в один пик на гистограмме
эксцентриситета (рис. 20.4, б). Семена подсолнечника не образуют плотный кластер,
поскольку они значительно отличаются по форме и размеру. Но очевидно, что они
могут быть схожими по размеру с чечевицей. Таким образом, недостаточно
использовать только площадь в качестве признака.
На рис. 20.4, в мы можем также выделить несколько систем оконтурирова-
ния. Во-первых, имеют место некоторые малые объекты с высоким
эксцентриситетом. Это объекты, которые только частично видны на контурах изображения
20,2, Пространство признаков
A^f-gwA
Площадь
1000
1500 2000
Эксцентриситет
0,4 0,6
0,8
Рис. 20.4. Признаки классификации различных зерен (рис. 20.2) для перца,
чечевицы и семян подсолнечника: гистограмма признаков площади (а) и эксцентриситета
(б); двумерное пространство с обоими признаками (в)
(рис. 20.2).Также имеют место пять больших объектов в местах, где
соприкасающиеся зерна чечевицы сливаются в крупные объекты. Эксцентриситет этих объектов
также большой, и отделение их от семян подсолнечника с использованием только
двух простых параметров — площади и эксцентриситета, может быть невозможно.
Качество признаков является решающим для хорошей классификации. Что это
означает? На первый взгляд мы могли бы подумать, что наилучшим решением было
бы рассмотрение как можно большего числа признаков. Как правило, это не так.
На рис. 20.5, а показано одномерное пространство признаков с тремя классами
объектов. Признаки первого и второго классов разделены, в то время как
признаки второго и третьего классов значительно перекрываются. Второй признак
необязательно улучшает классификацию, как продемонстрировано на рис. 20.5, б.
Кластеры второго и третьего классов все еще перекрываются. Тщательное
рассмотрение распределения в пространстве признаков объясняет: второй признак не
говорит нам ничего нового. Таким образом, два признака являются сильно
коррелированными.
Стоит сделать два важных дополнительных замечания. Часто не придают
значения тому, сколько различных классов можно выделить при нескольких
параметрах. Давайте предположим, что один параметр может разделять только два
класса. Тогда десять признаков могут разделять 2'^ = 1024 класса объектов. Этот простой
пример иллюстрирует высокий потенциал разделения только нескольких па-
534 Глава 20. Представление и анализ формы
со
1-
g
о
со
т
-
-
-
1
1/Д
/ 1
1
2/\
X 1 ^
1
^ \ 1
-
-
-
Рис. 20.5. а — одномерное пространство признаков с тремя классами объектов; б -
расширение пространства признаков с помощью второго признака. Площади,
затемненные серым цветом, указывают области, в которых вероятность для
определенного класса больше нуля. На а и б показаны одинаковые классы объектов
раметров. Существенной проблемой является равномерное распределение
кластеров в пространстве признаков. Следовательно, важно найти правильные
признаки, т.е. тщательно изучить зависимость между признаками объектов и
признаками в изображениях.
20.2.4. Выделение классов в пространстве признаков
Даже если мы берем наилучшие доступные признаки, возможны классы, которые
не могут разделяться. В таком случае всегда стоит напомнить, что разделение
объектов по хорошо определенным классам - это только модель реальности. Часто
переход от одного класса к другому может быть не резким, а скорее постепенным.
Например, аномалии в клетке могут присутствовать в изменяющейся степени,
причем не существует двух отчетливых классов, «нормальный» и
«патологический», а скорее имеет место непрерывный переход между ними. Таким образом, мы
не можем надеяться обнаружить хорошо разделенные классы в пространстве
признаков в каждом случае. Мы можем прийти к двум заключениям. Во-первых, не
существует гарантии, что мы обнаружим хорошо разделенные классы в
пространстве признаков, даже если выбраны оптимальные признаки. Во-вторых, эта
ситуация может заставить нас пересмотреть классификацию объектов. Либо два
класса объектов могут быть в действительности только одним классом, либо методы
визуализации для разделения их могут быть неадекватными.
В такой важной задаче, как оптическое распознавание символов (ОРС), мы имеем
отчетливые классы. Каждый символ является хорошо определенный классом. В то
время как большинство литер легко вьщелить, некоторые, например, заглавная
«О» и цифра «О» или литеры «I» и «1» и цифра «1», являются очень схожими, т.е.
находятся близко друг от друга в пространстве признаков (рис. 20.6). Такие
хорошо определенные классы, которые почти не отличаются в своих признаках, ставят
серьезные проблемы для задачи классификации.
20.2. Пространство признаков
1990, Oil, Island, L7R 4А6
Рис. 20.6. Иллюстрация распознавания литер с очень схожей формой, таких, как
заглавная «О» и цифра «О» или литеры «I» и «1» и цифра «1»
Как мы можем отделить заглавную литеру «О» от цифры «О» или «1» от
заглавной «I»? Мы можем дать два ответа на этот вопрос. Во-первых, можно изменить
шрифты, чтобы сделать литеры лучше отличимыми друг от друга. В самом деле,
специальные наборы шрифтов разработаны для автоматизированного
распознавания символов.
Во-вторых, можно внести дополнительную информацию в процесс
классификации. Однако это требует, чтобы классификация не останавливалась на уровне
отдельных литер; она должна распространяться до уровня слов. Тогда легко
установить правила для лучшего распознавания. Одно простое правило, которое
помогает отделить литеру «О» от «О», состоит в том, что буквы и цифры не
сочетаются в слове. В качестве контрпримера к этому правилу возьмем британские и
канадские почтовые индексы, которые содержат сочетание литер и цифр. Любой,
кто не имеет большого опыта чтения этих необьиных сочетаний, имеет серьезные
проблемы в их чтении и запоминании. В качестве еще одного примера заглавная
«I» может отделяться от нижнего регистра «1», так как заглавные литеры
возникают только как первая литера в слове или в слове из всех заглавных литер.
Закончим этот раздел следующим замечанием: постановка вопроса: возможна
ли вообще классификация для данной задачи в соответствии либо со своей
природой, либо с типом возможных признаков? — является по меньшей мере настолько
же важной, если не более, чем надлежащий выбор метода классификации.
20.2.5. Преобразование к главным осям
Рассмотрение в предыдущем разделе предполагало, что мы должны выбирать
признаки объектов очень внимательно. Каждый признак должен вносить новую
информацию, которая ортогональна тому, что мы уже знаем относительно классов
объектов; т.е. классы объектов с подобным описанием в одном признаке должны
отличаться в другом признаке. Другими словами, признаки должны быть
некоррелированными. Корреляцию признаков можно изучать с помощью
статистических методов, рассмотренных в разделе 3.3, при условии, что распределение
признаков для разных классов известно (контролируемая классификация).
Важной величиной является взаимная ковариация двух признаков, т^ и т^, из
Р-мерного вектора признака для одного класса объектов, которая определяется как
^p,=^-'Wp)K-mJ. (20.1)
Если взаимная ковариация <т равна нулю, то говорят, что признаки являются
некоррелированными или ортогональными. Член
является мерой для дисперсии признака. Хороший признак для определенного
класса объектов должен показывать малую дисперсию, указывающую на узкую
Глава 20. Представление и анализ формы
протяженность кластера в соответствующем направлении пространства признака.
С Р признаками мы можем сформировать симметричную матрицу с
коэффициентами G
рд^
ковариационную матрицу
Е =
'\р
42
'22
'2Р
'\Р
'IP
' РР
(20.3)
Диагональные элементы ковариационной матрицы содержат дисперсии Р
признаков, в то время как недиагональные элементы образуют взаимные ковариации.
Подобно любой симметричной матрице, ковариационную матрицу можно
привести к диагональному виду (разделы 3.3.2 и 13.3). Эта процедура называется
преобразованием к главным осям. Ковариационная матрица в системе координат с
главными осями имеет вид
г=
о
о
о
'22
О
о
РР
(20.4)
Приведение к диагональному виду показывает, что мы можем найти новую
систему координат, в которой все признаки являются коррелированными. Эти новые
признаки являются линейными комбинациями старых признаков и являются
собственными векторами ковариационной матрицы. Соответствующими
собственными значениями являются дисперсии преобразованных признаков. Наилучшие
признаки показывают наименьшую дисперсию; признаки с большими дисперсиями не
имеют большой пользы, поскольку они разбросаны в пространстве признаков и,
таким образом, мало привносят в разделение различных классов объектов. Таким
образом, ими можно пренебрегать без значительного ухудшения классификации.
Тривиальным, но наглядным примером является случай, когда два признака
почти тождественны, как проиллюстрировано на рис. 20.7. В этом примере
признаки AWj и т^ для класса объектов являются почти тождественными, поскольку все
точки в пространстве признаков расположены вблизи главной диагонали, и оба
признака показывают большую дисперсию. В системе координат с главными
осями aw'2 = aw j - т^ является хорошим признаком, поскольку он показывает узкое
распределение, в то время как т\ является настолько бесполезным, насколько сами
т^ит^. Следовательно, мы можем свести пространство признаков от двумерного
случая к одномерному без какого-либо ущерба.
Таким образом, мы можем использовать преобразование к главным осям для
уменьшения размерности пространства признаков и найти меньший набор
признаков, который действует также хорошо. Это требует анализа ковариационной
матрицы для всех классов объектов. Пренебречь можно только теми признаками, где
анализ для всех классов дает одинаковые результаты. Чтобы избежать непонимания,
надо отметить — преобразование к главным осям не может улучшить качество разде-
20.3, Простые методы классификации 537
Рис. 20.7. Иллюстрация коррелированных признаков и преобразования к главным осям
ления. Если набор признаков не может разделить два класса, тот же самый набор
признаков, преобразованный в систему с главными осями, не будет делать этого
также. При заданном наборе признаков мы можем только найти оптимальный подна-
бор и, таким образом, уменьшить вычислительные затраты классификации.
20.2.6. Контролируемая и неконтролируемая классификация
Мы можем рассматривать задачу классификации как анализ структуры
пространства признаков. Один объект рассматривается как структура в пространстве
признаков. Как правило, мы можем провести различие между процедурами
контролируемой классификации и неконтролируемой классификации. Контроль процедуры
классификации означает предварительное определение кластеров в пространстве
признаков с известными объектами, с использованием учебных областей для
распознавания кластеров. Тогда мы знаем число классов, их расположение и
протяженность в пространстве признаков.
При неконтролируемой классификации сведения о классифицируемых
объектах не предполагаются. Мы вычисляем структуры в пространстве признаков по
объектам, которые хотим классифицировать, и тогда выполняем анализ кластеров
в пространстве признаков. В этом случае мы не знаем даже число классов заранее.
Они получаются из числа хорошо разделенных кластеров в пространстве
признаков. Очевидно, что этот метод является более объективным, но он может привести
к менее подходяш;ему разделению.
В завершение мы говорим об изучающих методах, если пространство признаков
обновляется с каждым новым объектом, который классифицируется. Изучающие
методы могут компенсировать любые временные тенденции в признаках объектов.
Такие тенденции могут обуславливаться простыми причинами, такими, как
изменения освеш;енности, легко возникающие в промышленной среде вследствие
изменений дневного света, изнашивания или загрязнения установки освещения.
20.3. Простые методы классификации
в этом разделе мы рассмотрим различные методы классификации. Они могут
использоваться как для контролируемой, так и неконтролируемой классификации.
Методы отличаются только способом, используемым для связывания классов с
кластерами в пространстве признаков (раздел 20.2.6).
Глава 20. Представление и анализ формы
Раз кластеры вьщеляются любым из двух способов, дальнейший процесс
классификации тождествен для обоих из них. Новый объект дает вектор признака,
который связывается с одним из классов или отклоняется как неизвестный класс.
Различные методы классификации отлР1чаются только способом, которым
кластеры моделируются в пространстве признаков.
Обш;им для всех классификаторов является отображение типа «множество -
один» из пространства признаков М в пространство решений D. Пространство
решений содержит Q элементов, каждый из которых соответствует классу,
включая возможный класс отклонений для нераспознаваемых объектов. В случае
детерминированного решения элементы в пространстве решений являются
двоичными числами. Тогда только один из элементов может равняться единице;
все другие должны равняться нулю. Если классификаторы образуют
вероятностное решение, то элементы пространства решений являются
действительными числами. Тогда сумма всех элементов в пространстве решений должна
равняться единице.
20.3.1. Классификация просмотром
Этот метод является простейшим методом классификации, однако в некоторых
случаях также наилучшим, поскольку он не выполняет никакое моделирование
кластеров для различных классов объектов, которое никогда не может быть
совершенным. Основной подход классификации просмотром очень прост. Берем
пространство признаков, как оно есть, и отмечаем в каждой ячейке, к какому классу
она принадлежит. Как правило, значительное количество ячеек не принадлежит к
какому-либо классу и, таким образом, отмечается как 0.
В случае, когда кластеры от двух классов перекрываются, мы имеем две
возможности. Во-первых, мы можем взять тот класс, который показывает более
высокую вероятность в этой ячейке. Во-вторых, мы могли бы утверждать, что
безошибочная классификация невозможна при этом векторе признака, и отметить
ячейку нулем. После такой инициализации пространства признаков
классификация сводится к простой операции поиска просмотром (раздел 10.2.2). Берется
вектор признака т и ищется в многомерной таблице преобразования, чтобы увидеть,
к какому классу, если это имеет место, он принадлежит.
Без сомнения, это быстрый метод классификации, который требует
минимального количества вычислений. Недостатком метода — как в случае со
многими другими быстрыми методами - является то, что он требует огромных
объемов памяти для таблиц преобразований. Пример: трехмерное пространство
признаков со всего лишь 64 интервалами для каждого признака требует
64 X 64 X 64 = 1/4 Мб памяти, - если требуются не больше 255 классов, то
достаточно одного байта для хранения всех индексов классов. Мы можем заключить,
что метод с использованием таблицы преобразования является выполнимым
только для пространств признаков низкой размерности. Это предполагает, что
уменьшение числа признаков даст нужный результат. В качестве альтернативы
полезны признаки с узким распределением значений признака для всех
классов, поскольку тогда довольно малый диапазон значений и, таким образом,
малое число интервалов для каждого признака существенно уменьшают
требования к объему памяти.
20.3. Простые методы классификации
20.3.2. Прямоугольная классификация
Прямоугольный классификатор дает простое моделирование кластеров в
пространстве признаков. Кластер одного класса моделируется ограничивающим
прямоугольником, тесно окружающим область, покрываемую кластером (рис. 20.8).
Очевидно, что прямоугольный метод является довольно грубым моделированием. Если
мы предполагаем, что кластеры являются многомерными нормальными
распределениями, тогда кластеры имеют эллиптическую форму. Эти эллипсы довольно
хорошо вписываются в прямоугольники в случае, когда оси эллипса параллельны
осям пространства признаков. В двумерном пространстве признаков, например,
эллипс с полуосями avib имеет площадь тшЬ, окружающий прямоугольник —
площадь АаЬ. Это довольно неплохо.
В случае, когда признаки коррелированы друг с другом, кластеры
превращаются в длинные узкие объекты вдоль диагоналей в пространстве признаков. Тогда
прямоугольники вмещают много свободного пространства и имеют тенденцию
гораздо больше пересекаться, делая невозможной классификацию в
перекрывающихся областях. Однако можно избежать коррелированных признаков, применяя
преобразование к главным осям (раздел 20.2.5).
Вычисления, требуемые для прямоугольного классификатора, тем не менее
являются умеренными. Для каждого класса и для каждого измерения
пространства признаков должны выполняться две операции сравнения для решения,
принадлежит ли вектор признака классу, или нет. Таким образом, максимальное
число операций сравнения для Q классов и Р-мерного пространства признаков
составляет 2PQ. Тогда как классификатор просмотра требовал только Р
вычислений адресов; число операций не зависело от числа классов.
В заключение этого раздела рассмотрим реальную задачу классификации. На
рис. 20.2 было показано изображение с тремя различными видами зерен, а именно
семенами подсолнечника, чечевицей и зернами перца. Этот простой пример
показывает многие свойства, которые типичны для задачи классификации. Хотя три
класса хорошо определены, необходимо тщательное рассмотрение признаков, ко-
о
Q.
I-
I
О
СО
0,8
0,6
0,4
0,2
0
•
•
•
•
•
•
•
• • •
.
•
••
• •
•
•
• •
1 ilii^ife^:'!^
• • •
•
•
•
•
Площадь
200 400 600 800 1000 1200
Рис. 20.8. Иллюстрация прямоугольного классификатора различных зерен (рис. 20.2)
для перца, чечевицы и семян подсолнечника с использованием двух признаков:
площади и эксцентриситета
Глава 20. Представление и анализ формы
Таблица 20.1. Параметры и результаты простой прямоугольной классификации
зерен (рис. 20.2). Соответствующее пространство признаков показано на рис. 20.8
Общее количество
Зерна перца
Чечевица
Семена подсолнечника
Отклоненные
Площадь
100 - 300
320 - 770
520 - 850
Эксцентриситет
0,0 -0,22
0,0 -0,18
0,25 - 0,65
Число
122
21
67
15
19
торые должны использоваться для классификации, поскольку сразу не очевидно,
какие параметры можно успешно использовать для проведения различий между
тремя классами. Кроме того, форма зерен, особенно семян подсолнечника,
значительно изменяется. Выбор признаков для этого примера уже рассматривался в
разделе 20.2.3.
@
О
9
О
т^
I
б
о <> ° лО ®
^ШО qOO 0"о^
т^1 *^оО °
fP о о On"
*^0 О О эЯэ - - "^
0®0 ® ОО
©Oq oof
^ Or
о Со
о
0 о
о
о
^1
©о
Оо
о
Рис. 20.9. Маскированные классифицированные объекты из изображения рис. 20.2,
показывающие классифицированные зерна перца (а), чечевицу (б), семена
подсолнечника (в) и отклоненные объекты (г)
20.3. Простые методы классификации 541
На рис. 20.8 иллюстрируется прямоугольная классификация с
использованием двух признаков: площади и эксцентриситета. Затененные
прямоугольники отмечают прямоугольники, используемые для различных классов. Условия
для трех прямоугольников суммируются в табл. 20.1. В качестве
окончательного результата классификации на рис. 20.9 показаны четыре изображения. На
каждом из изображений только объекты, принадлежащие одной из
промежуточных сумм из табл. 20.1 и относящиеся к соответствующей маске. Из 122
объектов распознаны 103 объекта. Таким образом, 19 объектов отклонены. Они
не могли быть приписаны ни к одному из трех классов вследствие одной из
следующих причин:
• Два или более объектов располагались настолько близко друг к другу, что
слились в один объект. Тогда значения площади и/или эксцентриситета
слишком высокие.
• Объект располагался на контуре изображения и, таким образом, был виден
только частично. Это приводит к объектам с относительно малой площадью, но
высоким эксцентриситетом.
• Три больших семечка подсолнечника были отклонены вследствие
слишком большой площади. Если бы мы увеличили площадь для класса семян
подсолнечника, тогда также слившиеся зерна чечевицы были бы распознаны как
семена подсолнечника. Таким образом, этой ошибки классификации можно
избежать, только если избежать сливания объектов с использованием более
продвинутого метода сегментации.
20.3.3. Классификация по минимальному расстоянию
Классификатор по минимальному расстоянию является еще одним простым
способом для моделирования кластеров. Каждый кластер просто представляется
своим центром масс т . Основанное на этой модели, простое разделение
пространства признаков задается поиском минимального расстояния от вектора признака
до каждого класса. Для выполнения этой операции мы вычисляем расстояние
вектора признака т до каждого центра кластера т :
dl = \т-т^ f=Y,^rn^-mj\ (20.5)
р=\
Тогда признак приписывается к классу, до которого он имеет кратчайшее
расстояние.
Геометрически этот подход разбивает пространство признаков, как
проиллюстрировано на рис. 20.10. Границы между кластерами являются
гиперплоскостями, перпендикулярными векторам, соединяющим центры кластеров, на
расстоянии полпути между ними.
Классификатор по минимальному расстоянию, подобно прямоугольному
классификатору, требует числа вычислений, которое пропорционально размерности
пространства признаков и числу кластеров. Он представляет собой гибкий метод,
который может моделироваться разнообразными способами.
Размер кластера мог бы приниматься во внимание посредством введения
масштабного множителя в вычисление расстояния (20.5). Таким образом, признак
должен быть ближе к узкому кластеру, чтобы связываться с ним. Во-вторых, мы
можем определить максимальное расстояние для каждого класса. Если расстоя-
Глава 20. Представление и анализ формы
0
I-
О
Q.
X
о
со
0,8
0,6
0,4
0,2
0
—1 ■ ^г-" ■ 1 -
• \
•
•
• •
^
•
•
Г
Ш%
'
^
Г9
•,
^•/
—1 ■ ■ 1 i 1
• •
•
••
1 •
/ ^^^^
^ f
•
•
1 ■ 1
• 1
• \
'
^Площадь
200
400 600 800
1000 1200
Рис. 20.10. Ишхюстрация классификатора по минимальному расстоянию на примере
зерен перца, чечевицы и семян подсолнечника (рис. 20.2) с использованием двух
признаков: площади и эксцентриситета. Вектор признака принадлежит кластеру, до центра
которого он имеет минимальное расстояние
ние признака больше, чем максимальное расстояние для всех кластеров, то объект
отклоняется как не принадлежаш;ий никакому из распознанных классов.
20.3.4. Классификация по максимальному правдоподобию
Классификатор по максимальному правдоподобию моделирует кластеры как
статистические функции плотностей распределения вероятностей. В простейшем
случае берутся Р-мерные нормальные распределения. Задав эту модель, мы
вычисляем для каждого вектора признака вероятность того, что он принадлежит к любому
из Р классов. Тогда мы можем связать вектор признака с классом, для которого он
имеет максимальное правдоподобие. Новый аспект, связанный с этим методом,
состоит в том, что возможно вероятностное решение. Необязательно, что мы
примем решение отнести объект к определенному классу. Мы можем просто задать
объекту вероятность принадлежности к различным классам.
20.4. Упражнения
20.1: Элементарные методы классификации
Интерактивная демонстрация элементарных методов классификации
(dip6ex20.01).
20.2: ^Классы и признаки
Ниже приведены некоторые типичные задачи классификации. Сравните их,
отвечая на следующие вопросы:
1. Сколько классов имеют задачи классификации?
2. Отделяются ли явно друг от друга различные классы или имеет место
потенциальное наложение?
3. Существует ли иерархическая структура классов?
4. Какими могли бы быть потенциальные признаки, которые подходят для
вьщеления различных классов?
20.5. Дополнительная литература 543
Задачи классификации:
А Изображения получены от пузырьков, появляющихся под водой при
разрушении волн. Цель состоит в измерении распределения по размерам
пузырьков.
B. Задача заключается в отделении клеток опухоли от здоровых клеток в
микроскопических изображениях клеток.
C. Задача состоит в разделении удаленных точечных объектов на звезды,
галактики и квазары с использованием телескопических изображений.
Изображения получены в спектральном диапазоне от видимой области до
ближней инфракрасной области спектра с 10—12 каналами.
D. Оптическое распознавание символов (ОРС): автоматическая система
формирования изображений должна считывать числа по формам,
случайным образом содержащим цифровые знаки от О до 9, десятичную точку и
знаки плюс и минус.
E. Задача заключается в создании карт использования земли, для того
чтобы вьщелять площади застройки, улицы, леса, поля и т.д.
20.3: "^Требования к хранению и вычислительные усилия
Сравните требования к хранению и вычислительные усилия для
следующих задач классификации. Предположите, что вы имеете четыре признака
с разрешением 6 бит и четыре известных класса. Методы классификации:
1) метод просмотра;
2) прямоугольный метод;
3) метод минимального расстояния;
4) метод максимального правдоподобия.
20.5. Дополнительная литература
Классификация рассматривалась в этой главе только вводным образом, без
теоретических основ. Заинтересованные читатели, которые предпочитают углубить свои
знания в этой области, отсылаются к некоторой более продвинутой литературе.
Из огромного количества литературы по классификации упомянем здесь только
некоторые учебные пособия и монографии. Двумя из наиболее успешных учебных
пособий являются работы Дуда (Duda) и др. [40] и Вебба (Webb) [214]. Оба учебных
пособия делают акцент на статистических подходах. Книга Шурманна (Schurmann)
[184] показывает уникальным образом общие понятия методов классификации,
основанных на классических статистических методах и на нейронных сетях.
Применение нейронных сетей для классификации детально изложено Бишепом (Bishop)
[11]. Одно из самых недавних продвижений в классификации, так называемые
вспомогательные векторные машины, очень читаемо вводится Кристианини (Christianini)
и Шаве-Тейлором (Shawe-Taylor) [24] и Шоллкопфом (Schollkopf) и Смола (Smola)
[182].
ЧАСТЬ V
Справочная информация
А. Ссылки
R1. Выбор датчиков формирования
изображений КМОП (раздел 1.7.1)
С: зарядная поглотительная емкость в электронах, FR: частота кадров в с~^,
PC: пиксельная частота в МГц, QE: пиковая квантовая эффективность.
Микросхема
1 Micron^
MT9V403
Fillfactory^
IBIS54-1300
Fillfactory^
IBIS4-4000
Fillfactory^
LUPA1300
Micron^ MV40
Micron^'^
MT9M413
Micron^ MV02
IMSHDRCVGA^
PhotonFocus^
Формат
HxV
FR
PC
Размер пикселя
HxV, мкм
Линейный отклик
656x491
1280x1024
2496x1692
200
30
4,5
66
40
Линейный отклик с
1280x1024
2352x1728
1280x1024
512x512
450
240
600
4000
40
80
80
80
Логариф
640x480
1024x1024
25
150
8
80
9,9x9,9
6,7x6,7
11,4x11,4
: высокой часто!
12,0x12,0
7,0x7,0
12,0x12,0
16,0x16,0
мический отклиь
12x12
10,6x10,6
Комментарии
QE 0,32 @ 520 нм
QE 0,30-0,35 @ 600 нм,
СбОк
С 150к
ой кадров
16 параллельных портов
16 параллельных
10-разрядных портов
QE 0,27 @ 520 нм, С бЗк,
10 параллельных
10-разрядных портов
16 параллельных
10-разрядных портов
QE 0,29 @ 600 нм, С 200к,
линейный отклик при низких
уровнях освещенности с
регулируемым переходом к
логарифмическому отклику
Источники:
^ http://www.photonfocus.com
^ http://www.fillfactory.com
^ http://www.photobit.com
^ http://www.ims-chips.de
^ http://www.pco.de
А. Ссылки
R2. Выбор датчиков формирования изображений ПЗС
(раздел 1.7.1)
С: зарядная поглотительная емкость в электронах, eNIR: повышенная
чувствительность, FR: частота кадров в с~^, Ш: диагональ изображения в мм, QE:
пиковая квантовая эффективность, датчики Sony (ICX...) и Kodak (KAI...).
Микросхема
ICX278AL 1/4"
ICX258AL 1/3"
ICX248AL 1/2"
|lCX422AL 2/3"
ICX279AL 1/4"
ICX259AL 1/3"
ICX249AL 1/2"
|lCX423AL 2/3"
1 и
ICX098AL 1/4"
ICX424AL 1/3"
ICX074AL 1/2"
ICX414AL 1/2"
ICX075AL 1/2"
ICX204AL 1/3"
ICX205AL 1/2"
ICX285AL 2/3"
ICX085AL 2/3"
|lCX274AL 1/1,8"
KAI-0340DM 1/3"
KAI-IOIOM
KAM020M
KAI-2001M
KAI-4020M
|kai-ioooom
Формат
Hx V
FR
ID
Размер пикселя
Н X V, мкм
Чересстрочное EIA видео
768x494
768x494
768x494
768x494
30
30
30
30
4,56
6,09
8,07
11,1
Чересстроч
752x582
752x582
752x582
752x582
25
25
25
25
4,54
6,09
8,07
10,9
Междустрочная встав!
659x494
659x494
659x494
659x494
782x582
1024x768
1360x1024
1360x1024
1300x1030
1628x1236
640 х480
1008x1018
1000x1000
1600x1200
2048x2048
4008x2672
30
30
40
50
30
15
9,5
10
12,5
12
200
30
49
30
15
3
4,61
6,09
8,15
8,15
8,09
5,95
7,72
11,0
11,1
8,99
5,92
12,9
10,5
14,8
21,4
43,3
4,75x5,55
6,35x7,4
8,4x9,8
11,6x13,5
Комментарии
eNIR
eNIR
eNIR
ное МККР видео |
4,85x4,65
6,5x6,25
8,6x8,3
11,6x11,2
<а прогрессивно!
5,6x5,6
7,4x7,4
9,9x9,9
9,9x9,9
8,3x8,3
4,65x4,65
4,65x4,65
6,45x6,45
6,7x6,7
4,4x4,4
7,4x7,4
9,0x9,0
7,4x7,4
7,4x7,4
7,4x7,4
9,0x9,0
eNIR 1
eNIR
eNIR
i развертки
С 32k, QE 0,43 @ 340 нм
С 30k, QE 0,40 @ 500 нм
С 13 к
с 18k,
QE 0,65 @ 500 нм
С 20k, QE 0,54 @ 380 нм
С 20k, QE 0,55 @ 500 нм
QE 0,37 @ 500 HM
С 42k, QE 0,45 @ 490 нм
С 40k, QE 0,55 @ 480 нм
С 40k, QE 0,55 @ 480 нм
С 60k, QE 0,50 @ 500 нм |
Источники:
http://www.framos.de
http://www.kodak.com/global/en/digital/ccd/
http://www.pco.de
546 Справочная информация
R3. Датчики формирования изображений
для инфракрасной области (ИК, раздел 1,7.1)
С: полная емкость потенциальной ямы в миллионах электронов [Мэ], IT: время
интегрирования, NETD: шумовая эквивалентная температурная разность, QE:
пиковая квантовая эффективность.
Микросхема
Формат
Hx V
FR
PC
Размер пикселя
Н X V, мкм
Комментарии
Ближняя инфракрасная область (БИК)
Indigo^ InGaAs
320x256
345
30x30
0,9-1,68 мкм, С 3,5 Мэ |
Средняя волновая инфракрасная область (СВИК)
АШ^ PtSi
Indigo^ InSb
Indigo^ InSb
AIM2 HgCdTe
AIMVlaFFhG^ QWIP
640x486
320x256
640x512
384x288
640x512
50
345
100
120
30
12
20
18
24x24
30x30
25x25
24x24
24x24
Длинноволновая инфракрасная облает
AIM^ HgCdTe
Indigo^ QWIP
AIMVlaFFhG^ QWIP
AIM^/IaF FhG^ QWIP
256x256
320x256
256x256
640x512
200
345
200
30
16
16
18
40x40
30x30
40x40
24x24
Неохлаждаемые датчики
Indigo^ Microbolometer
320x240
60
30x30
3,0-5,0 мкм,
NETD < 75 тК @ 33 мс IT
2,0-5,0 мкм, С 18 Мэ
2,0-5,0 мкм, С И Мэ
3,0-5,0 мкм,
NETD < 20 шК @ 2 мс IT
3,0-5,0 мкм,
NETD < 15 тК @ 20 мс IT |
ь (ДИК)
8-10 мкм,
NETD < 20 шК @ 0,35 мс
IT
8,0-9,2 мкм, С 18 Мэ,
NETD < 30 шК
8,0-9,2 мкм,
NETD < 8 тК @ 20 мс IT
8,0-9,2 мкм,
NETD < 10 тК @ 30 мс IT
7,0-14,0 мкм, 1
NETD < 120 шК 1
Источники:
^ http://www.indigosystems.com
^ http://www.aim-ir.de
^ http://www.iaf.fhg.de/tpqw/frames_d.htm
А. Ссылки 547
R4. Свойства W-мерного преобразования Фурье
(раздел 2.3.4)
р(ж) о—•^(fe) и h{x) о—• h(k) есть пары преобразования Фурье:
оо
д{к) = / д{х)ехр f-27rifc^ajj d^a: = (exp (27rik^x] \g{x)\ ,
— oo
где s — действительное ненулевое число; a и b — комплексные константы; А —
матрица размерностью W xW, R — ортогональная матрица поворота {R~^ = R ,
detH = 1).
Свойство
Линейность
Подобие
Обобщенное подобие
Поворот
Сепарабельность
Сдвиг в ж-пространстве
Конечная разность
Сдвиг в ^-пространстве
Модуляция
Дифференцирование
в ж-пространстве
Дифференцирование
в fc-пространстве
Определенный интеграл,
среднее значение
Моменты
Свертка
Пространственная
корреляция
Умножение
Внутреннее произведение
Пространственная область
ад{х) -Ь bh(x)
g(sx)
д{Ах)
g{Rx)
w
П gw(xw)
g{x - xo)
g{x -h жо/2) - g{x - жо/2)
Q-K.-p{2'K\k^x)g{x)
cos{2'Kk^x)g{x)
dgjx)
dxp
—27Г1Хрд{х)
7 9{x')d'^x'
— OO
oo
— OO
OO
/ h{x')g{x-x')d'^x'
— OO
OO
/ h{x')gix'+x)d^x'
— OO
h{x)g{x)
OO
/ g*{x)h{x)d^x
— OO
Фурье-область
ag{k) + bh{k)
9{k/s)/\sr
g{{A-^fk)ldetA |
g{Rk) 1
w
П 9w{kw)
гу=1
exp(—27rifc^xo)^(fe)
2isin(7r«Jfc)§(fc)
g{k - ко) 1
{g(k-ko)-^g{k^ko))l2 |
2шкрд{к)
dgjk)
dkp
m
/ i Y^^ (d'^^''g{k)\
V27ry V дк^дк^ J
0
h{k)g{k) 1
g%k)h{k) 1
J h{k')g{k-k')d^k' 1
— OO
OO
/ g*(k)h{k)d^k
— OO 1
548 Справочнал информация
R5. Элементарные пары преобразований для
непрерывного преобразования Фурье
2-D- и З-В-функции отмечены f и J соответственно.
Пространственная область
Дельта, 6{х)
константа, 1
cos(A;oa:)
sm{kox)
sgn(2:) = <
1 ж^О
-1 ж <0
Ящик, П(ж) = <
1 \х\ < 1/2
^ 0 \х\^ 1/2
Д«-'^"(^)
Шар, • П (й)
Бесселя, —^
X
ехр{ \х\),
слру^
\^\)
Фурье-область
константа, 1
Дельта, b{k)
]^(Ь(к-к^)Л-Ь(к^и))
L{S{k-ko)-S{k-\-ko)) 1
—i
тгк
stac« = 2;ge
Бесселя, —^^—,.,
7ГГ|«|
sin(|fc|)-|fc|cos(|fc|)
\k\4ii7r)
2(1-^)^/^п(^)
2 27Г +
1 + (27гА:)2' (1 + (27г|А;|)2)з/2 |
R6. Функции, инвариантные
преобразования Фурье
относительно
Пространственная область
Фурье-область
Гауссова, ехр(—тгж^ж)
Гауссова, ехр(—Trfc^fc)
Жрехр(—тгж^ж)
-ikp ехр{—'кк^ к)
sech(7rx) =
ехр(7га;) -Ь ехр(—тгж)
8есЬ(7гА;) =
ехр(7гА;) -\- ехр(—тгА;)
Гипербола, |ж| ^^^
ifci
-W/2
1-D (5-гребень, П1(ж) = ^ 5{х — п)
Ш{к)= Х; S{k-v)
А. Ссылки 549,
R7. Свойства 2-D ДПФ (раздел 2.3.4)
G и Н — комплекснозначные матрицы размерностью М х N, G и Н — их
преобразования Фурье,
M-17V-1
9u,v = j^ Yl XI ^m,nw^'^''w^'''^, WAT = ехр(27г1/А^),
m=0 n=0
M-lN-1
a И b — комплекснозначные константы. Растяжение и повторение посредством
множителей X, L G N дают матрицы размерностью КМ х LN. Доказательства
смотри в книгах Кули (Cooley) и Таки (Тикеу) [27], Поуларикаса (Poularikas) [158].
Свойство
Среднее значение
Линейность
Пространственное растяжение
(повышающая дискретизация)
Повторение (растяжение
частоты)
Сдвиг
Модуляция
Конечные разности
Свертка
Пространственная корреляция
Умножение
Внутреннее произведение
Норма
Пространственная
область
1 М-1 N-1
мм ^ ^ "^^
М1\ гп=0 п=0
аС-\-ЬН
9Кт,Ьп
gm,n{9kM+m,lN+n = 9гп,п)
Ут — 771' ,п — п'
и'т v'n
^М ^N 9гп,п
(pm+l,n — ^m-l,n)/2
)/2
M-1 N-1
/ J / J i^m'n'9rn — ra',n — n'
m'=0 n'=0
M-1 iV-1
/ V / ^ '^m'n'9m-\-m',n-\-n'
m'=0 n'=0
9mnhmn
M-1 iV-1
m=0 n=0
M-1 N-1
m=0 n=0
Область
волновых чисел
90,0
аСЛ-ЬН
guv/(KL)
{9kM+u,lN-\-v = 9u,v) 1
9Ku,Lv
^M ^N 9uv
9u — u',v—v'
ism{27ru/M) guv
i sm{27rv/N) guv
MNhuvguv
MNhuvglv
M-1 N-1
/ J / J i^u'v'gu — u',v — v'
u'=0 v'=0
M-lN-1
it=0 г;=0
M-liV-1
E E \9u.\'
u=0 v=0 1
550 Справочнал информация
R8. Свойства непрерывного l-D-преобразования
Хартли (раздел 2.4.2)
д{х) о—•^(fc) и h{x) о—• h{k) есть пары преобразований Хартли: R i-^ М,
оо
д{х) cas(27r/;:x) dx о—• д(
ОС
^(fc) са8(27гА:ж) dfc
при
cas27rfcx = cos(27rfcx) + sin(27rA:a:),
где s — действительное ненулевое число; а и b — действительные константы.
Свойство
Линейность
Подобие
Сдвиг
в ж-пространстве
Модуляция
Дифференцирование
в ж-пространстве
Определенный
интеграл,
среднее значение
Свертка
Умножение
Автокорреляция
Пространственная
область
ад{х) + bh{x)
g{sx)
д{х - хо)
cos{2T:kox)g{x)
дхр
оо
— ОО
оо
/ h{x')g{x-x')dx'
— оо
h(x)g{x)
оо
/ gix')gix'-^x)dx'
— оо
Фурье-область
ад(к) + bh(k)
9{k/s)/\s\
cos{27rkxo)g{k) — sm{27rkxo)g{—k)
{д{к-ко)-\-д{к-^ко))/2
—2тткрд{—к)
т
[g{k)h{k) + g{k)h{-k)+ 1
+д(-к)Нк) - g(-k)hi-k)]/2
[д{к) * h{k) + д{к) * h{-k)+ 1
+д{-к) * h{k) - д(-к) * h(-k)]/2
[дЦк) + дН-к)]/2
1. Преобразование Фурье, выраженное исходя из преобразования Хартли:
т = 2 {'т + "gi-k)) - ^ CsCfc) - '^gi-k)).
2. Преобразование Хартли, выраженное исходя из преобразования Фурье:
'^g{k) = Ке[д{к)] - 1т[9{к)] = ^Ш + Пк)) + '^{д{к) - 9*{к)).
А. Ссылки 551
R9. Функции плотностей распределения вероятностей
(ФПР, раздел 3.4)
Определение, среднее значение и дисперсия некоторых ФПР.
Название
Определение
Среднее значение Дисперсия
Дискретные ФПР /п
Пуассона, Р(/х)
exp(-/i)^,n^ О
Биномиальная,
Q\
n\{Q-n)\
p^(l-p)^-^,0^n<Q
Qp
Qp{i-P)
Непрерывные ФПР f(x)
Равномерная,
U{a,b)
a-\-b
12
Нормальная,
•\/27Г.
1 / {x-WY
Рэлея, R{(7)
^^^Ч'^)-^"^^
(Ту/7г/2
,<5/2-l
(72(4-7г)/2
Хи-квадрат,
2Q/^r{Q/2)crQ
exp
(-2&)'^>°
Qa^
2Q<7^
Теоремы сложения для независимых случайных величин gi и 32-
ФПР
Биномиальная
Пуалсона
Нормальная
Хи-квадрат
91
B(Qup)
РЫг)
N{ni,ai)
x4Qu<r)
92
B{Q2,P)
РЫ
N{(12,02)
x4Q2,a)
91+52 1
B{Qi+Q2,p)
Pit4+fi2)
iV(Mi+p2,(<T?+cri)^/^) 1
x4Qi+Q2,Ct) I
ФПР функций независимых случайных величин дп
ФПР величины
9n:N{0,a)
\ 9n--N{0,a)
9п:Щ0,(т)
Функция
igf^giy^'
arctan(^i/p?)
Q
n=l
ФПР функции
R{a) 1
U(0,2n)
x'(Q,<t) 1
552 Справочная информация
RIO. Распространение опхибок
(разделы 3.2.3, 3.3.3 и 4.2.8)
fg — ФПР случайной величины (СВ) д] а и b — константы; д' = р{д) —
дифференцируемая монотонная функция с производной dp/dg и обратной функцией
9=р-Ч9')-
Пусть д — вектор с Р случайными величинами с ковариационной матрицей
cov(^); д' — вектор с Q случайными величинами и с ковариационной матрицей
cov(^'); М — матрица размерностью QxP;a — вектор-столбец с Q элементами.
1. ФПР, среднее значение и дисперсия линейной функции д' = ад Л- Ь:
2. ФПР монотонной дифференцируемой нелинейной функции д' — р{д):
/Лр-Чд'))
fg'ig')
\Мр-'{9'))1Н'
3. Среднее значение и дисперсия дифференцируемой нелинейной функции
/^.'«РЫ + f-^^, <^1
Mf^g)
dg
2
-l-
4. Ковариационная матрица линейной комбинации случайных величин,
д' = Мд + а.
cov(^') = Mcov(flf)M^.
5. Ковариационная матрица нелинейной комбинации случайных величин,
д' = p{9)'
coY{g') « Jcov{g)J с матрицей Якоби J, jq^p = ■^-^.
6. Однородное стохастическое поле: свертка случайного вектора фильтром h:
д' = hi^g (раздел 4.2.8)
а) С автоковариационным вектором с.
с' = а.{Н^.к)с>-Фс{к) = с{к)\к{к)\'^;
б) С автоковариационным вектором с = cr'^Sn (некоррелированные
элементы) .
с' = a\hi.h) о-Фс{к) = a^\h{k)\^.
А. Ссылки 553
R11. lD-линейные инвариантные относительно сдвига
фильтры (разделы 4.2.6, 11.2 и 12.3)
1. Передаточная функция l-D-фильтра с нечетным числом коэффициентов
(2Д -I-1, [h-R,..., h-i, /lo, /ii,..., Hr])
а) Общий случай:
R
h{k) = y^ hy'exp{—mv'k).
v'=-R
б) Четная симметрия {h
R
hy = ho + 2 y^ hyf cos(7n;'fc).
в) Нечетная симметрия {h-y = —hy):
R
hy = —2i yj hyf sm{7rv^k).
v'=l
2. Передаточная функция l-D-фильтра с четным числом коэффициентов
(2Д, [h-R,..., ft-i, /ii,..., Лд], результаты свертки располагаются на
промежуточной сетке).
а) Четная симметрия {h
R
hy = 2Y^ hy' С08(7г(г;' - l/2)fc).
6) Нечетная симметрия {h-y = —hy):
R
hy = -2i ^ hy' 8ш(7г(г;' - l/2)fc).
3. Передаточная функция двух элементарных фильтров:
а) Усреднение двух соседних точек:
В = [1 l]/2o-#b(fc) = cos(7rfc/2);
б) Разность двух соседних точек:
Di = [1 - l]c^#di(fc) = 2isin(7rfc/2).
^554 Справочная информация
R12. 1-D рекурсивные фильтры (раздел 4,5)
1. Общее уравнение фильтра
S R
п"=1 n'=-R
2. Общая передаточная функция
R
^ hn' ехр(—Trin'fc)
h{k) = ^^ -.
Y^ an" exp(—7rin"fc)
3. Разложение на множители передаточной функции с использованием 2:-пре-
образования и фундаментального закона алгебры
П {I'Cn'Z-^)
h{z) = h.Rz''^ .
П {l-dn"Z-^)
п"=1
4. Релаксационный фильтр:
а) Уравнение фильтра (|а| < 1)
9п = о^9пц:1 + (1 - «)^п;
б) Функция рассеяния точки
^"^ \ О иначе.
в) Передаточная функция симметричного фильтра (последовательное
действие фильтра в положительном и отрицательном направлениях)
^(^^ = тттЛ—Г' (m = i,fw = YT2e)
1+ Р — PCOSTTK \ >■ + ^Р /
при
2а 1 + /3 - v/rT2^ - , , ,^ ,
^=(13^' " = ^ ' ^е]-1/2,оо].
5. Резонансный фильтр с единичным откликом при резонансном волновом
числе ко в пределе слабого затухания 1 — г <^ 1:
а) Уравнение фильтра (коэффициент затухания г G [0,1[, резонансное
волновое число fco ^ [ОД])
р;, = (1 - Г^) sin(7rfco)Pn + 2Г COS(7rfeo)pn:Fl ~ '^^9'п^2'
А. Ссылки 555
б) Функция рассеяния точки
и _ / (1 - ^^)^" sin[(n 4- l)7rfco] n ^ О,
^^""1 О п<0;
в) Передаточная функция симметричного фильтра (последовательное
действие фильтра в положительном и отрицательном направлениях)
.(j^) ^ Sin^(7rfco)(l-r^)^
(l - 2r cos[7r(fc - fco)] + гА (л - 2rcos[7r(fc + ко)] + гА '
г) Для слабого затухания передаточную функцию можно
аппроксимировать соотношением
s(fc) « :—г /,. о,г для 1 - г < 1;
д) Полуширина ДА:, определенная соотношением s(fco + ^k) = 1/2,
Afc« (1 -г)/тт,
R13. Пирамиды Гаусса и Лапласа (раздел 5.2)
1. Построение пирамиды Гаусса G^^\G^^\ ..., G^^^ с Р + 1 плоскостями
посредством итерационного сглаживания и подвыборки в два раза по всем
направлениям
G^^^ = G, G^^+^^ = <Bi2G^^\
2. Условие для сглаживающего фильтра для избегания наложения спектров
В{к)=0 Vifcp^i
3. Построение пирамиды Лапласа ПЛОСКОСТЯМИ по
пирамиде Гаусса
Последняя плоскость пирамиды Лапласа является последней плоскостью
пирамиды Гаусса.
4. Интерполяционные фильтры для операции повышающей дискретизации |2
(у R22).
5. Итерационная реконструкция исходного изображения по пирамиде
Лапласа. Вычисляем
начиная с самой высокой плоскости (р = Р). Когда используется тот же
оператор повышающей дискретизации, как в случае для построения
пирамиды Лапласа, реконструкция является совершенной, за исключением
ошибок округления.
Справочная информация
6. Направленно-пирамидальное разложение на две направленные компоненты:
4^> = l/2(i(^)-(«:,-®^)G(^^);
i^,^) = l/2(i(^) + («^ - e^)G(^)).
R14. Основные свойства электромагнитных волн
(раздел 6.3)
1. Частота и (циклы в единицу времени) и длина волны А (длина периода)
связаны фазовой скоростью с (в вакууме скорость света с = 2,9979 х
X 10^ м/с):
Ai/ = с.
2. Классификация ультрафиолетовой, видимой и инфракрасной областей
электромагнитного спектра (см. также рис. 6.6).
Название
ВУФ (вакуумная УФ)
УФ-С
УФ-В
|УФ-А
Видимая (свет)
ОБИК (очень ближняя ИК)
БИК (ближняя ИК)
ТИК (тепловая ИК)
СИК (средняя ИК)
1 ДИК (дальняя ИК)
Диапазон длин волн
30-180 нм
100-280 нм
280-315 нм
315-400 нм
400-700 нм
0,7-1,0 мкм
0,7-3,0 мкм
3,0-14,0 мкм
3-100 мкм
100-1000 мкм
Комментарии
Сильно поглощаемая воздухом;
требует вакуумного оборудования
Стандартное определение МКО
Стандартное определение МКО
Стандартное определение МКО
Видимая человеческим глазом
ИК-диапазон длин волн, на
который реагируют стандартные
кремниевые датчики изображений
Диапазон наибольшего
испускания при температурах
окружающей среды
3. Энергия и импульс корпускулярного излучения, такого, как /3-излучение
(электроны), а-излучение (ядра гелия), нейтроны и фотоны
(электромагнитное излучение):
и = E/h условие частот Бора,
А = h/p соотношение длины волны де Бройля.
А. Ссылки
R15. Радиометрические и фотометрические термины
(раздел 6.2)
AAq — элемент площади поверхности; в — угол падения; П — телесный угол. Для
терминов, относящихся к энергии, фотону и радиометрии, часто используются
индексы е, р и I/ соответственно.
Термин
Энергия
Поток энергии
(мощность)
Плотность
падающего потока
энергии
Плотность
возбуждающего
потока энергии
Поток энергии
в телесный угол
Плотность потока
энергии в
телесный угол
Энергия/площадь
Относящийся
к энергии
Энергия излучения Q
[Вт • с]
Поток излучения
Энергетическая
освещенность
Энергетическая
светимость (излучательная
способность)
Сила излучения
/=^[Вт.ср-Ч
Энергетическая яр-
КОСТЬ L — dUdAo cos в
[Вт-М-2.Ср-1]
Плотность энергии
[Вт . С • м^]
Относящийся
к фотону
Число фотонов [1]
Поток фотонов
[с-Ч
Энергетическая
освещенность
фотонов [м"^ • с~^]
Плотность потока
фотонов
[м-^.с-Ч
Интенсивность
фотонов [с~^ • ср~^]
Энергетическая
яркость фотонов
[м-2.С-^.Ср-^]
Плотность фотонов
[м-Ч
Радиометрическая
величина
Световая энергия
[лм • с] 1
Световой поток
[люмен (лм)]
Освещенность
[лм/м^ = люкс(лк)]
Светимость [лм/м^]
Сила света [лм/ср =
= кандела(кд)] |
Яркость [кд • м~^]
Экспонирование
[лм • с • м~^ = лк • с]
Вычисление световых величин по соответствующей радиометрической
величине с помощью спектральной световой эффективности V{\) для дневного
(фотопического) зрения:
780 нм
(?„ = 68з|^ / Q{\)V{\)d\.
380 нм
Таблица со значениями от МКО 1980 г. спектральной световой эффективности
V{\) для фотопического зрения.
1Л[нм]
380
390
400
410
420
430
1440
V{\)
0,00004
0,00012
0,0004
0,0012
0,0040
0,0116
0,023
Л[нм]
450
460
470
480
490
500
1510
уЩ
0,038
0,060
0,091
0,139
0,208
0,323
0,50з]
Л[нм]
520
530
540
550
560
570
|580
V{\)
0,710
0,862
0,954
0,995
0,995
0,952
0,870
Л[нм]
590
600
610
620
630
640
650
пЩ
0,757
0,631
0,503
0,381
0,265
0,175
0,107
Л[нм]
660
670
680
690
700
710
1720
v{\) ■■]
0,061
0,032
0,017
0,0082
0,0041
0,0021
0,00105]
Л[нм]
730
740
750
760
770
780
V{\)
0,00052
0,00025
0,00012
0,00006
0,00003
0,000015
Справочная информация
R16. Цветовые системы (раздел 6.2.4)
1. Цветное зрение человека на основе трех типов колбочек с максимальными
чувствительностями при 445, 535 и 575 нм (рис. 6.4, б),
2. Цветовая система RGB: аддитивная цветовая система с тремя основными
цветами — красным, зеленым и синим. Это могут быть либо
монохроматические цвета с длинами волн 700, 646,1 и 435,8 нм, либо красный, зеленый и
синий люминофор, как использовано в jRGB-мониторах (например, в
соответствии с нормой Европейского союза телевещания). Не все цвета могут
быть представлены с помощью цветовой системы RGB (см. рис. 6.5, о).
3. Диаграмма цветности: сведение 3-D цветового пространства к 2-D
цветовой плоскости с нормированием по интенсивности:
R О ^ В
9 =
г =
R + G + B'
R-^G + B'
b =
R + G + B'
Достаточно использовать две компоненты г и д: b =^ 1 — г — д,
4. Цветовая система XYZ (рис. 6.5, в): аддитивная цветовая система с тремя
виртуальными основными цветами X, F и У, которая может представлять
все возможные цвета и задается следующим линейным преобразованием из
цветовой системы RGB Европейского союза телевещания:
X
У
Z
0,490 0,310 0,200
0,177 0,812 0,011
0,000 0,010 0,990
R
G
В
5. Цветовой контраст или система YUV: цветовая система с началом отсчета
в точке белого (рис. 6.5, б).
6. Цветовая система тон-насыщенность (HSI): цветовая система,
использующая полярные координаты в цветоразностной системе. Насыщенность
определяется радиусом, цветовой тон — углом.
R17. Тепловыделение (раздел 6.4.1)
1. Спектральная излучательная способность (закон Планка):
27гЛс2 1
Ме(А,Т) =
А5
ехр
[квТх)
при
h = 6,6262 • 10"^^ Дж • с постоянная Планка,
кв = 1,3806 • 10"^^ Дж • К~^ постоянная Больцмана и
с = 2,9979 • 10^ м • с~^ скорость света в вакууме.
2. Полная излучательная способность (закон Стефана-Больцмана):
М, = ^!^Т^ = аТ^ при а«5,67.10-«Вт.м-2.К-^
15 с^д**
А. Ссылки 559
3. Длина волны максимальной излучательной способности (закон Вина):
2898 К • мкм
R18. Взаимодействие излучения с веществом
(раздел 6.4)
1. Закон преломления Снеллиуса на границе двух оптических сред с
показателями преломления пх и пг:
sin^i ^ П2
sin 02 Til '
где ^1 и ^2 — углы падения и преломления соответственно.
2. Коэффициент отраоюения р: отношение отраженного потока излучения к
падающему потоку на поверхности.
а) Уравнения Френеля задают коэффициент отражения для параллельно
поляризованного света:
_ tan^(gi -62)
^""tan2(ei-f02)'
б) для перпендикулярно поляризованного света:
в) и для неполяризованного света:
^ 2 *
3. Коэффициент отражения при нормальном падении {вг = 0) для всех
состояний поляризации:
4. Полное отражение. Когда луч входит в среду с более низким показателем
преломления, вне критического угла вс весь свет отражается, и ни один луч
не входит в оптически более тонкую среду:
вс = arctan — при щ <П2-
П2
^560 Справочная информация
R19. Оптическое формирование изображений
1. Перспективная проекция с использованием модели камеры-обскуры
d'Xi d'X2
Аз Аз
Отверстие располагается в начале отсчета мировой системы координат
[Xi, Хг,Хз]^, d! есть расстояние от плоскости изображения до центра
проекций, ось Хз располагается перпендикулярно плоскости изображения.
2. Уравнение изображения (форма Ньютона и Гаусса):
где d 1Л. d' — расстояния от объекта и изображения до передней и задней
фокальных точек оптической системы соответственно (см. рис. 7.7).
3. Линейное увеличение
XI f d'
'^^ = x; = d = 7'
4. Осевое увеличение
d' Р d'2 2
5. Относительная апертура п/ оптической системы равна отношению
фокусного расстояния и диаметра апертуры линзы:
^^ = 2г-
2г
6. Глубина фокуса (пространство изображения):
Джз = 2п/ и-|-у]б = 2п/(И-т0б.
7. Глубина поля (пространство объекта).
Удаленные объекты (ДХз < d) ДХз « 2п/ ^^е.
dmin ДЛЯ диапазона, включаюш;его бесконечность, dmin ^
4п/€
Микроскопия (ш/ > 1) ДХз w —^.
mi
8. Разрешение дифракционно-ограниченной оптической системы: угловое
разрешение
Угловое разрешение Дбо = 0,61-.
г
Разрешение по плоскости на плоскости изображения Дж = 0,61-7-
г»'
п'
Разрешение по плоскости на плоскости объекта ДХ = 0,61—.
Па
А. Ссылки 561
Разрешение определяется критерием Рэлея (см. рис. 7.15, 6); Па и п'^
числовые апертуры со стороны объекта и со стороны изображения светового
конуса, входящего в оптическую систему:
. 2п пг
Па^ ть sm 6^0 = — = ~~г ?
п/ /
п — показатель преломления.
9. Соотношение энергетической освещенности на плоскости изображения Е'
с энергетической яркостью объекта L (см. рис. 7.10):
/ ^ \2 cos^e
Е' = ^7Г ( -: I cos^ 9L « t'K—Ty-L для d > /.
R20. Однородная точечная операция (раздел 10.2)
Точечная операция, которая не зависит от положения пикселя:
1. Отрицание
2. Определение потери значимости и переполнения с помощью
псевдоцветового [г, д^ Ь] отображения:
( [0,0,(9-1] (синий) д = 0,
Puo{q) = I [q, q, q] (серый) g € [1, Q - 2],
{ [Q -1,0,0] (красный) q = Q -I,
3. Контрастное растяжение диапазона [^1,^2]:
Pcsiq) = {
О q<qu
{q-qi){Q-l)
q^ [^1,92],
q2 -qi
Q-1 q>q2'
R21. Процедуры калибровки
1. Уравнивание шума (раздел 10.2.3). Если дисперсия шума зависит от
интенсивности изображения, то она может уравниваться нелинейным
преобразованием на шкале серого
Ко) ^^h j
562 Справочная информация
С двумя свободными параметрами ah и С При линейной функции
дисперсии (раздел 3.4.5)
преобразование принимает вид для д е [О, рта
V^prg +Кд-ао
Но) = 7Рп
V^O + ^^max - СТО
^/1 =
н-^ ft G [О, 75'тах]
7-ft^^max/2
y^Crg -h Kgmsix - СТО
2. Линейная фотометрическая калибровка (раздел 10.3.3). Берутся два
калибровочных изображения, темное изображение В без какой-либо
освещенности и опорное изображение R с объектом постоянной энергетической
яркости. Нормированное изображение, скорректированное с учетом как
фиксированного структурного шума, так и неоднородной
чувствительности, задается соотношением
G-B
G' = c
R-B
R22. Интерполяция (раздел 10.5)
1. Интерполяция непрерывной функции по выборочным точкам на
расстояниях ^х^ является операцией свертки:
9т{х) = ^g{xn)h{x - Хп).
п
Воспроизведение узлов сетки приводит к интерполяционному условию
Л(Жп) = I Q
п = 0,
О иначе.
2. Идеальная интерполяционная функция
W W
h{x) = J^ smc{xu)/Axu,)o—9h{k) = Y[ Щки}/2).
w=l w=l
3. Дискретные 1-D интерполяционные фильтры для интерполяции
промежуточных узлов сетки, находяш;ихся на равном расстоянии между суш;еству-
ющими узлами:
1 Тип
Линейная
Кубическая
Кубическая В-сплайновая
Маска
1 1
/2
[-199-1
/16
[ 1 23 23 1 ] /48
[з-л/3, уД-2]
Передаточная функция
cos(7r^/2)
9 cos(7r^/2) - cos(37r^/2)
23 cos(7rfc/2) -1- cos(37rifc/2) 1
16-h8cos(7rfc)
^Рекурсивный фильтр, примененный в прямом и обратном направлениях (см. раздел
10.6.1).
А. Ссылки 563
R23. Усредняющие фильтры свертки (глава 11)
1. Краткое изложение общих ограничений для усредняющих фильтров свертки:
Свойство
Сохранение среднего
значения
Нулевой сдвиг,
четная симметрия
Монотонное убывание
от единицы до нуля
Изотропия
Пространственная
область
п
h-n = hn
—
h{x) = hi\x\)
Область волновых чисел
^(0) = 1
Im (h{k)^ = 0
h{k2) ^ ^(^i) если ^2 > ^1J
Mfc)€[0,l]
ft(fe) = ft(|Jfc|) 1
2. 1-D сглаживающие фильтры-ящики:
Маска
1 "Я = [1 1 1 ]/3
1 *й=[1 1 1 l]/4
1 ''R = [ 1 ... 1 ]/R
L Яраз
Передаточная функция
3 + 3 ^^^(^^)
cos(7r^) cos(7rfc/2)
8т(7гЯА;/2)
Rsm{nk/2)
Подавление шума^
^ « 0,577
л/3
1/2 = 0,5
1
ч/Д
^Для «белого шума».
3. 1-D сглаживающие биномиальные фильтры:
Маска
1 В^ = [ 1 2 1 1/4
|в' = [ 1 4 6 4 1 1/16
В^'^
ПФ
COS*(7rfc/2)
cos^(7rfc/2)
cos2«(7rJfc/2)
Подгюление шума^
J|« 0,612 1
VS"«'^23
/Г(Д + 1/2)у/^^/ 1 Y*f 1 \\
\y/^r(R + l)J ^\RitJ \ 16Rj\
^Для «белого шума».
564 Справочнал информация
R24. Дифференциальные фильтры свертки первого
порядка (глава 12)
1. Краткое изложение общих ограничений для дифференциального фильтра
первого порядка в направлении Xw для W-мерных сигналов; w'
обозначает любое из возможных направлений; п — векторную индексацию
(раздел 4.2.1):
Свойство
Нулевое среднее значение
Нулевой сдвиг,
нечетная симметрия
Первая производная
Изотропия
Пространственная
область
п
п
Область волновых чисел
h{k)\ =0
lfc=0
Re (Я(/Ь)) = 0
dh(k)
= 7ri<5ii,/_^
fc=0
h{k) — mkwb{\kV)
при 6(0) = 1, Vfcb(|fc|) = 0
2. Дискретные разностные фильтры первого порядка:
Название
Vx
Центральная разность, V2x
Кубический В-сплайновый Т)2х f^
Маска
[ ,
1 -1
1 0 -1
1
и —1
\/3, \/3-
/2
/1
-2
t
Передаточная функция
2isin(7rfcx/2)
isin(7rfcx)
. sin(7rfcx) 1
2/3 + l/3cos(7r^x)
^Рекурсивный фильтр, примененный в прямом и обратном направлениюс (см. раздел 10.6.1).
А. Ссылки 565
3. Регуляризованные дискретные разностные фильтры первого порядка
Название
2x2, Ра.®!/
Собеля, Р2х®у
Оптимизированный
Собеля Р2х(3(8^+Х)/4
Маска
1
2
1
8
1
32
1 -1
1 -1 1
10-1
2 0-2
1 1 0 -1 1
3 0-3
10 0 -10
3 0-3
Передаточная функция
2isin(7rfcx/2) cos(7r^3,/2)
i sin(7rfcaj) cos^ (tt^j,/2)
isin(7r^a:)(3cos^(7rfcj,/2) + l)/4
4. Характеристики выполнения контурных детекторов: угловая ошибка,
ошибка модуля и подавление шума для «белого шума». Три значения в двух
столбцах ошибок определяют ошибки для диапазона волновых чисел 0-0,25,
0,25-0,5 и 0,5-0,75 соответственно.
Название
Vx
\ V2X
V2x^1l
1 Vx^y
1 V2x^l
|р2х(3®^+Х)/4
Угловая ошибка [°]
1,36 4,90 12,66
0,02 0,33 2,26
0,67 2,27 5,10
0,67 2,27 5,10
0,15 0,32 0,72
Ошибка модуля
0,026 0,151 0,398
0,001 0,023 0,220
0,013 0,079 0,221
0,012 0,053 0,070
0,003 0,005 0,047
Коэффициент шума
V^« 1,414
1/\/2 « 0,707
v/31n3/7r« 1,024
1
л/3/4 « 0,433 1
\/59/16 « 0,480
566 Справочная информация
R25. Дифференциальные фильтры свертки второго
порядка (глава 12)
1. Краткое изложение общих ограничений для дифференциального фильтра
второго порядка в направлении х^ для W-мерных сигналов; w'
обозначает любое из возможных направлений; п — векторную индексацию
(раздел 4.2.1):
Свойство
Нулевое среднее значение
Нулевой наклон
Нулевой сдвиг,
четная симметрия
Вторая производная
Изотропия
Пространственная область
п
п
h-n = hrt
п.
Область волновых чисел
К{к)
= 0
fc=0
д%{к) 1
dkyji 1
= 0
fc=0
Im (Н{к)\ = 0
дЩк)
= —27Г Sy}f-^
lfc=0
h{k) = — (7Г^гу)^Ь( fc ) при
2. Дискретные разностные фильтры второго порядка:
Название
1-D Лапласа Vx
2-D Лапласа С
2-D Лапласа £'
Маска
[1-21]
1
4
■ 0 1 0 1
1-4 1
0 1 0 J
Г 1 2 1]
2 -12 2
L 1 2 1 J
Передаточная функция
-4sin^(7rfcx/2)
-4sin^(7rL/2) - 4sm^{'Kky/2)
4cos^(7r^x/2) cos^(7rfcy/2) - 4
Б. Обозначения
Б. Обозначения
Вследствие междисциплинарной природы цифровой обработки изображений не
существует согласованной и общепринятой терминологии, как в других
областях. Возникают две основные проблемы:
- Противоречивая терминология. Различные специалисты используют
различные обозначения (и даже названия) для одних и тех же терминов.
- Двусмысленные обозначения. Вследствие большого количества терминов,
используемых в обработке изображений и областях, к которым она имеет
отношение, одно и то же обозначение используется ц,ля многочисленных
терминов.
Простого решения для этой затруднительной ситуации нет, иначе оно было
бы доступно. Таким образом, необходимо найти разумный компромисс. В этом
учебном пособии используются следующие указания:
- Придерживаться общепринятых стандартов, В качестве первого
указания были приняты во внимание обозначения, рекомендованные
международными организациями (такими, как Международная организация по
стандартизации, ИСО), также было проведено сравнение нескольких основных
руководств [48, 125, 130, 158]. Кроме того, были сделаны взаимные
проверки с несколькими стандартными учебными пособиями из различных
областей [14, 63, 150, 160]. Только в некоторых противоречивых ситуациях
используются отклонения от общепринятых обозначений.
- Использовать наиболее компактное обозначение, В случаях, когда была
возможность различных обозначений, использовалась наиболее
компактное и исчерпывающее обозначение. В редких случаях оказалось полезным
использовать более одного обозначения для одного и того же термина.
Например, иногда более удобным является использование векторных
компонент с индексами (ж = [xi,X2]^), а иногда использовать х = [х^у]'^.
- Допускать двусмысленные обозначения. Одно и то же обозначение
может иметь различные значения. Это не так плохо, как кажется на первый
взгляд, поскольку смысл обозначения становится ясным из контекста.
Для того чтобы познакомить читателей, имеющих различные
предварительные знания, с обозначениями, используемыми в этой книге, мы приведем здесь
некоторые замечания по нетипичным обозначениям.
Волновое число. К сожалению, существуют различные определения термина
волновое число:
27Г 1
к' = ^ и к=^, (Б.1)
Л Л
Физики обычно учитывают множитель 27г в определении волнового числа:
fc' = 27г/А, по аналогии с определением циклической частоты и = 27г/Т =
= 27Г1/. В оптике и стереоскопии, однако, оно определяется как величина,
обратная длине волны без множителя 27г (т. е. число длин волн в единице
длины) и обозначается г> = А~^.
Справочная информация
Мнимая единица. Мнимая единица обозначается здесь с помощью i. В
электротехнике и связанных областях общепринятым является обозначение j.
Временные ряды, матрицы изображений. Стандартное обозначение для
временного ряда [150], х[п]^ слишком громоздко для использования с
многомерными сигналами: p[A:][m][n]. Поэтому выбирается более компактное
обозначение Хп и дк,т,п-
Частные производные. В случаях, когда это не приводит к путанице,
частные производные сокращенно обозначаются посредством введения индекса:
дд/дх = дх9 = 9х'
Шрифт
e,i,d,w
а,6,...
9i '•') ^5 ж,...
G,HyJ,...
в,7г,^-,...
N,Z,R,C
Акценты
fc,n,...
1 rV , rv, t/C/ , . • .
\ GJ{k),...
Нижний индекс
9n
1 Qmn
1 9p
9pq
Описание
Прямые символы имеют конкретное значение; примеры: е для
основания натурального логарифма, i — \/--Т, символ для производных:
dp,w = e2^^
Курсив (нежирный): скалярная величина
Строчный жирный курсив: векторная величина^ т.е. координатный
вектор, временной ряд, строка матрицы, ...
Прописной жирный курсив: матрица, тензор^ т. е. дискретное
изображение, 2-В-маска свертки, структурный тензор; также
используемый для сигналов с более чем двумя размерностями
Каллиграфические буквы указывают на независящий от
представления оператор
Буквы с задней панелью обозначают множества чисел или других
величин
Описание
Черта указывает на единичный вектор
Тильда указывает на безразмерную нормированную величину (от
величины с размерностью)
Крьппка указывает на величину в Фурье-области
Описание
Элемент п вектора д
Элемент т, п матрицы G
Компактное обозначение для первой частной производной
непрерывной функции д в направлении р: дд{х)/дхр
Компактное обозначение для второй частной производной
непрерывной функции д{х) в направлениях р и q: д^д{х)/(дхрдхд)
Б. Обозначения 569
Верхний индекс
А \А ^
А^,а^
а^Ь, {а\Ь)
а*
1 ^*
Индексирование
K,L,M,N
k^l^m^n
r,s,u,v
Р
Q
R
W
p,q,w
Функция
COS (ж)
ехр(ж)
\d{x)
ln(a:)
Ig(^)
sin (ж)
sine (ж)
det(G)
diag(G)
trace(G)
cov(^)
1 E{g),y3i{G)
Описание
Обращение квадратной матрицы А; обобщенное обращение
(неквадратной) матрицы А 1
Транспонирование матрицы или вектора (включает сопряжение для
комплексных чисел)
Скалярное произведение двух векторов
Сопряженный комплекс
Сопряженный комплекс и транспонирование матрицы
Описание
Протяженность дискретных изображений в направлениях f, z, у и х
Индексы дискретных изображений в направлениях t, z, у и х
Индексы дискретных изображений в Фурье-области в направлениях
t, Z, у и X
Число компонент в многоканальном изображении; размерность
пространства признаков, число компонент, плоскостей пирамиды или
точек данных
Число уровней квантования, число классов объектов или число
параметров регрессии
Размер масок для операторов формирования окрестностей
Размерность изображения или пространства признаков
Индексы компоненты в многоканальном изображении, размерности
в изображении, уровня квантования или признака
Описание
Косинусная функция
Экспоненциальная функция
Логарифмическая функция по основанию 2
Логарифмическая функция по основанию е
Логарифмическая функция по основанию 10
Синусная функция
5шс-функция: sinc(a;) = sin(7rx)/(7rx)
Определитель квадратной матрицы
Вектор с диагональными элементами квадратной матрицы
След квадратной матрицы
Ковариационная матрица случайного вектора
Ожидание (среднее значение) и дисперсия
Справочная информация
Операторы^
изображений
*
•
е,е
°'*
(8)
V,A
1 и,п
с,с
0
is
ь
Описание
Поточечное умножение двух изображений
Свертка
Корреляция
Морфологические операторы эрозии и масштабных преобразований
Морфологические операторы открытия и закрытия
Морфологический оператор попадание-промах
Булевы операторы ИЛИ и И
Объединение и пересечение множеств
Множество является подмножеством, подмножеством или равным
Оператор сдвига
Оператор выборки или уменьшения: берем только каждый s-й
пиксель, строку и т. д.
Оператор растяжения или интерполяции: увеличиваем разрешение в
каждом координатном направлении в s раз, новые точки
интерполируются по имеюпщмся точкам
Символ
Определение [единицы]
Значение
Греческие символы
а
Р
\б{х),6п
А
б
е
к
V
Л
V
Vx
1 ^
1
Ф
Фе
[м-1]
[м-Ч
W „2
[1]
[м]
[м-Ч
\_dxi ' • • • ' dxw \
[м]
[с-Ч, [Гц] (герц)
n + ie,[l]
[1]
[рад], П
[рад], [1
Коэффициент поглощения
Коэффициент рассеяния
Непрерывное, дискретное (^-распределение
Оператор Лапласа
Удельный коэффициент излучения
Радиус диска размытости
Коэффициент затухания, сумма
коэффициентов поглощения и рассеяния
Оператор градиента
Длина волны
Частота
Оператор поворота
Комплексный показатель преломления
Квантовая эффективность
Фазовый сдвиг, разность фаз
Азимутальный угол
Б. Обозначения
1 *
Фе,Фр
\p^PhP±
1 ^
О'х
а
(Тз
т
т
т
в
вь
Ос
Ое
вг
Символ
fi
ш
[Дж/с], [Вт], [с-'], [лм]
[Вт], [с-1], [лм]
[1]
[кг/м*]
5,6696 • 10-* Вт • м-^ • К-"
[м^]
[1]
[1]
[с]
[рад], [°]
[рад], [°]
[рад], [°]
[рад], [1
[рад], [1
Определение [единицы]
[ср] (стерадиан)
ш = 27П/, [с-1], [Гц]
Поток излучения или световой поток
Поток излучения на основе энергии, на основе
фотона и световой поток
Коэффициент отражения для неполяризован-
ного, параллельно поляризованного и
перпендикулярно поляризованного света
Плотность
Среднеквадратичное отклонение случайной
величины X
Постоянная Стефана-Больцмана
Эффективная площадь рассеяния
Оптическая глубина (толщина)
Пропускаемость
Временная постоянная
Угол падения
Угол Брюстера (угол поляризации)
Критический угол (для полного отражения)
Полярный угол
Угол падения
Значение
Телесный угол
Циклическая частота
Римские символы
А
а, а
т
в
в
(В
с
с
d
d'
d{k)
D
D
1 ^
e
[м^]
а = xtt = uty [м/с^]
[В . с/м^]
2,9979 • 10^ м-с-^
[м]
М
[м^/с]
l,6022.10-^^ А-с
Площадь
Ускорение
Передаточная функция биномиальной маски
Магнитное поле
Биномиальная маска фильтра
Биномиальный оператор свертки
Скорость света
Множество комплексных чисел
Диаметр (апертура) оптики, расстояние
Расстояние в пространстве изображения
Передаточная функция D
Коэффициент диффузии
Разностная маска фильтра первого порядка
Разностный фильтр первого порядка
Элементарный электрический заряд
Справочнал информация
е
Е
1 ^
ё
fje
fbjf
f
f
1 ^
G
1 ^
h
1 ^
i
1 /
1 /
Символ
1 I
I
J
\ кв
1 ^
к
к
К,
I\.r
к.
к,
L
\ ^
1 -^
2,718281...
[Вт/м^], [лм/м^], [лк]
[В/м]
[1]
[м]
М
[Н] (ньютон)
6,6262 -10 ^Мж • с
й/(2х)[Дж-с]
^=т
[Вт/ср], [лм/ср]
[А]
Определение [единицы]
1,3806 • 10-^' Дж/К
1/А, [м-1]
[м-Ч
кАх/тг
[1/моль]
Ф^/Фе, [лм/Вт]
Ф^/Р, [лм/Вт]
[1]
[ВтДм^.ср)], [1/(м2-ср)],
[лм/(м2 • ср)], [кд/м^]
Основание натурального логарифма
Плотность падающего потока энергии
излучения (энергетическая освещенность) или
плотность падающего потока энергии света
(освещенность)
Электрическое поле
Единичный собственный вектор матрицы
(Эффективное) фокусное расстояние
оптической системы
Заднее и переднее фокусное расстояние
Оптический поток
Вектор признака
Сила
Матрица изображения
Общая маска фильтра
Постоянная Планка (квант действия)
Мнимая единица
Сила излучения или сила света
Электрический ток
Значение
Единичная матрица
Тождественный оператор
Структурный тензор, тензор инерции
Постоянная Больцмана
Модуль волнового числа
Волновое число (число длин волн в единице
длины)
Волновое число, нормированное на
максимальное волновое число, которое может выбираться
(волновое число Найквиста)
Постоянная гашения
Световая эффективность излучения
Световая эффективность системы освещения
Индикаторная постоянная равновесия
Плотность потока излучения (энергетическая
яркость) или плотность светового потока
(яркость) в телесном угле
Маска фильтра Лапласа
Оператор Лапласа
Б. Обозначения 573
m
m
m
М
Me
Мр
1 м
п
Па
1 'г/
п
N
Р
Р
рН
Q
<3з
Символ
г
1 f*m,n
^Р.9
Я
Я
R
S
\ ^
1 *
1 *
^
ге
t/
V
V{\)
[кг]
[1]
[ВтМ, [1/(с.м2)]
[Вт/м^]
[1/(с.м2)]
[1]
[1]
f/d, [1]
[1]
[кг • м/с], [Вт • м]
[Н/м^]
[1]
[Вт-с] (джоуль),
[лм • с] число фотонов
[1]
Определение [единицы]
м
Гт,п = [тДх, пДу]^
rp,q = \pl^x,qld.yf
Ф/s, [А/Вт]
[А]
[К]
м
[1]
[м/с]
[м/с]
[В]
[м1
[лм/Вт]
Масса
Увеличение оптической системы
Вектор признака
Плотность возбуждающего потока энергии
излучения (светимость, излучательная
способность)
Светимость на основе энергии
Светимость на основе фотона
Пространство признаков
Показатель преломления
Числовая апертура оптической системы
Апертура оптической системы
Единичный вектор, нормальный к поверхности
Множество натуральных чисел: {0,1,2,...}
Импульс
Давление
Значение рН, отрицательный логарифм
концентрации фотонов
Энергия излучения или световая энергия
Коэффициент эффективности рассеяния
Значение
Радиус
Вектор перемещения на сетке
Вектор перемещения на обратной сетке
Чувствительность детектора излучения
Маска фильтра-ящика
Множество действительных чисел
Сигнал датчика
Абсолютная температура
Время
Коэффициент пропускания
Скорость
Вектор скорости
Напряжение, электрический потенциал
Объем
Спектральная световая эффективность для фо-
топического зрения человека
574 Справочная информация
ПА)
W
1 WTV
X
X
Z, Z+
[лм/Вт]
g27ri
exp(27ri/iV)
[X,yf, [xuX2f
[X,Y,ZfAXuX2,Xsf
Спектральная световая эффективность для
скотопического зрения человека
Координаты изображения в пространственной
области
Мировые координаты
Множество целых чисел, положительных целых
чисел
ЛИТЕРАТУРА
1. т. A:harya and R-S. Tsai. JPEG2000 Standard for Image Compression .Wiley, New York, 2005.
2. E. H. Adelson and J. R. Beigen. The extraction of spatio-temporal energyin human and machine
vision. In Proceedings Workshop on Motion: Representation and Analysis, May 1986, Charleston,
South Carolina, pp. 151-155. IEEE Computer Society, Washington, 1986.
3. A V. Aho, J. E. Hopcroft, and J. D. Ullman. The Design and Analysis of Computer Algorithms.
Addison Wesley, Reading, МД 1974.
4. A V. Aho, J. E. Hopcroft, and J. D. Ullman. The Design and Analysis of Computer Algorithms.
Addison-Wesley, Reading, МД 1974.
5. J. Anton. Elementary Linear Algebra. John >Mley & Sons, New York, 2000.
6. G. R. Arce, N. С Gallagher, and T. A Nodes. Median filters: theory for one and two dimensional
filters. JAI Press, Greenwich, USA 1986.
7. S. Beauchemin and J. Barron. The computation of optical flow. ACM Computing Surveys,
27(3):433-467, 1996.
8. L. M. Biberman, ed. Electro Optical Imaging: System Performance and Modeling. SPIE,
Bellingham, WA 2001.
9. J. Bigun and G. H. Granlund. Optimal orientation detection of linear symmetry. In Proceedings
1ССГ87, London, pp. 433-438. IEEE, Washington, DC, 1987.
10. С M. Bishop. Neural Networks for Pattern Recognition. Clarendon, Oxford, 1995.
11. R. Blahut. Fast Algorithms for Digital Signal Processing. Addison-Wesley, Reading, MA 1985.
12. M. Bom and E. Wolf. Principles of Optics. Cambridge University Press, Cambridge, UK, 7th
edn., 1999.
13. R. Bracewell. The Fourier Transform and its Applications. McGraw-Hill, New York, 2nd edn.,
1986.
14. C. Broit. Optimal registrations of deformed images. Diss., Univ. of Pennsylvania, USA 1981.
15. I. N. Bronshtein, K. A Semendyayev, G. Musiol, and H. Muehlig. Handbook of Mathematics.
Springer, Beriin, 4th edn., 2004.
16. H. Burkhardt, ed. Workshop on Texture Analysis, 1998. Albert-Ludwigs- Universitat, Freiburg,
Institut fur Informatik.
17. H. Burkhardt and S. Siggelkow. Invariant features in pattern recognition - fimdamentals and
applications. In С Kotropoulos and I. Pitas, eds.. Nonlinear Model-Based Image/Video
Processing and Analysis, pp. 269-307. John Wiley & Sons, 2001.
18. P. J. Burt. The pyramid as a structure for efficient computation. In Rosenfeld, ed., Multiresolution
image processing and analysis, vol. 12 oi Springer Series in Information Sciences, pp. 6—35.
Springer, New York, 1984.
19. P. J. Burt and E. H. Adelson. The Laplacian pyramid as a compact image code. IEEE Trans.
COMM, 31:532-540, 1983.
20. P. J. Burt, T H. Hong, and A Rosenfeld. Segmentation and estimation of image region properties
through cooperative hierarchical computation. IEEE Trans. SMC, 11:802-809, 1981.
21. J. E Canny. A computational approach to edge detection. PAMI, 8:679— 698, 1986.
22. R. Chelappa Digital Image Processing. IEEE Computer Society Press, Los Alamitos, CA 1992.
23. N. Christianini and J. Shawe-Taylor. An Introduction to Support Vector Machines. Cambridge
University Press, Cambridge, 2000.
24. C. M. Close and D. K. Frederick. Modelling and Analysis of Dynamic Systems. Houghton Mifflin,
Boston, 1978.
576 Литература
J. W. Cooley and J. W. Tukey. An algorithm for the machine calculation of complex Fourier
series. Math. ofComput., 19:297-301, 1965.
26. T. H. Gormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms. MIT
Press, Cambridge, МД 2nd edn., 2001.
27. J. Crank. ТЪе Mathematics of Diffusion. Oxford University Press, New York, 2nd edn., 1975.
28. P.-E. Danielsson, Q. Lin, and Q.-Z. Ye. Efficient detection of second degree variations in 2D
and 3D images. Technical Report LiTH-ISYR- 2155, Department of Electrical Engineering,
Linkoping University, S- 58183 Linkoping, Sweden, 1999.
29. P. J. Davis. Interpolation and Approximation. Dover, New York, 1975.
30. С DeCusaris, ed. Handbook of Applied Photometry. Springer, New York, 1998.
31. C. Demant, B. Streicher-Abel, and P. Waszkewitz. Industrial Image Processing. Viusal Quality
Control in Manufacturing. Springer, Berlin, 1999. Includes CD-ROM.
32. P. DeMarco, J. Рокоту, and V. С Smith. Full-spectrum cone sensitivity functions for X-
chromosome-linked anomalous trichromats. /. of the Optical Society, A9:1465—1476, 1992.
33. J. Dengler. Methoden und Algorithmen zur Analyse bewegter Realweltszenen im Hinblick aufein
Blindenhilfesystem. Diss., Univ. Heidelberg, 1985.
34. R. Deriche. Fast algorithms for low-level vision. IEEE Trans. PAMI, 12(1): 78-87, 1990.
35. N. Diehl and H. Burkhardt. Planar motion estimation with a fast converging algorithm. In
Proc. 8th Int. Conf Pattern Recognition, ICPR'86, October 27-31, 1986, Paris, pp. 1099-1102.
IEEE Computer Society, Los Alamitos, 1986.
36. R. C. Dorf and R. H. Bishop. Modem Control Systems. Addison-Wesley, Menlo Park, СД 8th
edn., 1998.
37. S. A Drury. Image Interpretation in Geology. Chapman & Hall, London, 2nd edn., 1993.
38. R. О Duda, P E. Hart, and D. G. Stork. Pattern Classification. Wiley, New York, 2nd edn., 2001.
39. M. A H. Elmore, W. С Physics of Waves. Dover Publications, New York, 1985.
40. A Erhardt, G. Zinser, D. Komitowski, and J. Bille. Reconstructing 3D light microscopic images
by digital image processing. Applied Optics, 24:194- 200, 1985.
41. J. F. S. Crawford. Waves, vol. 3 of Berkely Physics Course. McGraw-Hill, New York, 1965.
42. О Faugeras. Three-dimensional Computer Vision. A Geometric Vewpoint. MIT Press, Cambridge,
МД 1993.
43. О Faugeras and Q.-T. Luong. Ihe Geometry of Multiple Images. MIT Press, Cambdridge, МД 2001.
44. M. Felsberg and G. Sommer. A new extension of linear signal processing for estimating local
properties and detecting features. In G. Sommer, N. Kruger, and C. Perwass, eds.,
Mustererkennung 2000,22. DAGM Symposium, Kiel, Informatik aktuell, pp. 195—202. Springer,
BerUn, 2000.
45. R. Feynman. Lectures on Physics, vol. 2. Addison-Wesley, Reading, Mass., 1964.
46. D. G. Fink and D. Christiansen, eds. Electronics Engineers' Handbook. McGraw-Hill, New
York, 3rd edn., 1989.
47. M. A Fischler and О Firschein, eds. Readings in Computer Vision: Issues, Problems, Principles,
and Paradigms. Morgan Kaufmann, Los Altos, СД 1987.
48. D. J. Fleet. Measurement of Image Velocity. Diss., University of Toronto, Canada, 1990.
49. D. J. Fleet. Measurement of Image Velocity. Юuwer Academic Publisher, Dordrecht, 1992.
50. D. J. Fleet and A D. Jepson. Hierarchical construction of orientation and velocity selective
filters. IEEE Trans. PAMI, ll(3):315-324, 1989.
51. D. J. Fleet and A D. Jepson. Computation of component image velocity from local phase
information. Int. J. Сотр. Vision, 5:77-104, 1990.
Литература 57
52. J. D. Foley, A van Dam, S. K. Feiner, and J. F. Hughes. Computer Graphics, Principles and
Practice. Addison Wesley, Reading, МД 2nd edn., 1995.
53. W. Forstner. Image preprocessing for feature extraction in digital intensity, color and range
images. In A Dermanis, A Griin, and F. Sanson eds., Geomatic Methods for the Analysis of Data
in the Earth Sciences, vol. 95 of Lecture Notes in Earth Sciences. Springer, Beriin, 2000.
54. D. A Forsyth and J. Ponce. Computer Vision, a Modem Approach. Prentice Hall, Upper Saddle
River, NJ, 2003.
55. W. T. Freeman and E. H. Adelson. The design and use of steerable filters. IEEE Trans. PAMI,
13:891-906, 1991.
56. G. Gaussorgues. Infrared Thermography. Chapman & Hall, London, 1994.
57. P. GeiBler and B. Jahne. One-image depth-from-focus for concentration measurements. In E.
P. Baltsavias, ed., Proc. ISPRS Intercommission workshop from pixels to sequences, Zurich, March
22-24, pp. 122-127. RISC Books, Coventry UK, 1995.
58. J. Gelles, B. J. Schnapp, and M. P. Sheetz. Tracking kinesin driven movements with nanometre-
scale precision. Nature, 331:450-453, 1988.
59. F. Girosi, A Veni, and V. Torre. Constraints for the computation of optical flow. In Proceedings
Workshop on Visual Motion, March 1989, Irvine, CA, pp. 116-124. IEEE, Washington, 1989.
60. H. Goldstein. Classical Mechanics. Addison-Wesley, Reading, МД 1980.
61. G. H. Golub and C. F. van Loan. Matrix Computations. The John Hopkins University Press,
Baltimore, 1989.
62. R. С Gonzalez and R. E. Woods. Digital image processing. Prentice Hall, Upper Saddle River,
NJ, 2nd edn., 2002.
63. G. H. Granlund. In search of a general picture processing operator. Сотр. Graph. Imag. Process.,
8:155-173, 1978.
64. G. H. Granlund and H. Knutsson. Signal Processing for Computer Vision. Юuwer, 1995.
65. L. D. Griffin and M. Lillhom, eds. Scale Space Methods in Computer Vision, vol. 2695 of Lecture
Notes in Computer Science, 2003. 4th Int. Conf. Scale- Space'03, Springer, Berlin.
66. M. GroB. Visual Computing. Springer, Berlin, 1994.
67. E. M. Haacke, R. W. Brown, M. R. Thompson, and R. Venkatesan. Magnetic Resonance Imaging:
Physical Principles and Sequence Design. John Жй^у & Sons, New York, 1999.
68. M. Halloran. 700 x 9000 imaging on an integrated CCD wafer - affordably. Advanced Imaging,
Jan.:46-48, 1996.
69. J. G. Harris. The coupled depth/slope approach to surface reconstruction. Master thesis, Dept.
Elec. Eng. Comput. Sci., Cambridge, Mass., 1986.
70. J. G. Harris. A new approach to surface reconstruction: the coupled depth/slope model. In 1st
Int. Conf Сотр. Vis. (ICCV), London, pp. 277- 283. IEEE Computer Society, Washington,
1987.
71. H. HauBecker. Messung und Simulation kleinskaliger Austauschvorgange an der Ozeanoberfl^he
mittels Thermographic. Diss., University of Heidelberg, Germany, 1995.
72. H. HauBecker. Simultaneous estimation of optical flow and heat transport in infrared imaghe
sequences. In Proc. IEEE Workshop on Computer Vision beyond the Visible Spectrum, pp. 85—93.
IEEE Computer Society, Washington, DC, 2000.
73. H. HauBecker and D. J. Fleet. Computing optical flow with physical models of brightness
variation. IEEE Trans. PAMI, 23:661-673, 2001.
74. E. Hecht. Optics. Addison-Wesley, Reading, МД 1987.
75. D. J. Heeger. Optical flow from spatiotemporal filters. Int. J. Сотр. Vis., 1:279-302, 1988.
578 Литература
76. Е. С. Hildreth. Computations underlying the measurement of visual motion. Artificial
Intelligence, 23:309-354, 1984.
77. G. С Hoist. CCD Arrays, Cameras, and Displays. SPIE, Bellingham, WA 2nd edn., 1998.
78. G. С Hoist. Testing and Evaluation of Infrared Imaging Systems. SPIE, Bellingham, WA, 2nd
edn., 1998.
79. G. С Hoist. Common Sense Approach to Thermal Imaging. SPIE, Bellingham, WA 2000.
80. G. С Hoist. Electro-optical Imaging System Performance. SPIE, Bellingham, WA 2nd edn., 2000.
81. B. K. Horn. Robot Vision. MIT Press, Cambridge, MA 1986.
82. S. Howell. Handbook of CCD Astronomy. Cambridge University Press, Cambridge, 2000.
83. T. S. Huang, ed. Two-dimensional Digital Signal Processing II: Transforms and Median Filters,
vol. 43 of Topics in Applied Physics. Springer, New York, 1981.
84. S. V. Huffel and J. Vandewalle. The Total Least Squares Problem — Computational Aspects and
Analysis. SIAM, Philadelphia, 1991.
85. K. lizuka Engineering Optics, vol. 35 of Springer Series in Optical Sciences. Springer, Berlin, 2nd
edn., 1987.
86. B. Jahne. Image sequence analysis of complex physical objects: nonlinear small scale water
surface waves. In Proceedings 1ССУ87, London, pp. 191-200. IEEE Computer Society,
Washington, DC, 1987.
87. B. Jahne. Motion determination in space-time images. In Image Processing Ш, SPIE Proceeding
1135, international congress on optical science and engineering, Paris, 24-28 April 1989, pp. 147—152,
1989.
88. B. Jahne. Spatio-temporal Image Processing. Lecture Notes in Computer Science. Springer,
Berlin, 1993.
89. B. Jahne. Handbook of Digital Image Processing for Scientific Applications. CRC Press, Boca
Ilaton, FL, 1997.
90. B. Jahne. \feigleichende Analyse modemer Bildsensoren fiir die optische Messtechnik. In Sensoren
und Messsysteme 2004, vol. 1829 of VDIBerichte, pp. 317-324. VDI Verlag, Dusseldorf, 2004.
91. B. Jahne, ed. Image Sequence Analysis to Investigate Dynamic Processes, Lecture Notes in
Computer Science, 2005. Springer, Berlin.
92. B. Jahne, E. Barth, R. Mester, and H. Scharr, eds. Complex Motion, Proc. 1th Int. Workshop,
Gijnzburg, Oct. 2004, vol. 3417 of Lecture Notes in Computer Science, 2005. Springer, Berlin.
93. B. Jahne and H. HauBecker, eds. Computer Vision and Applications. A Guide for Students and
Practitioners. Academic Press, San Diego, 2000.
94. B. Jahne, H. HauBecker, and P. GeiBler, eds. Handbook of Computer Vision and Applications.
Volume I: Sensors and Imaging. Volume II: Signal Processing and Pattern Recognition. Volume
III: Systems and Applications. Academic Press, San Diegoi, 1999. Includes three CD-ROMs.
95. B. Jahne, J. Ю1пке, and S. Waas. Imaging of short ocean wind waves: a critical theoretical
review. /. Optical Soc. Amer. A, 11:2197-2209,1994.
96. B. Jahne, H. Scharr, and S. Korgel. Principles of filter design. In B. Jahne, H. HauBecker, and
P. GeiBler, eds.. Computer Vision and Applications, volume 2, Signal Processing and Pattern
Recognition, chapter 6, pp. 125—151. Academic Press, San Diegoi, 1999.
97. A K. Jain. Fundamentals of Digital Image Processing. Prentice-Hall, Englewood Cliffs, NJ, 1989.
98. R. Jain, R. Kasturi, and B. G. Schunck. Machine Vision. McGraw-Hill, New York, 1995.
99. J. R. Janesick. Scientific Charge-Coupled Devices. SPIE, Bellingham, WA 2001.
100. J. T. Kajiya The rendering equation. Computer Graphics, 20:143-150, 1986.
101. M. Kass and A W^tkin. Analysing oriented patterns. Сотр. Vis. Graph. Im. Process., 37:362-385,
1987.
Литература 579
102. М. Kass, А Wtkin, and D. Terzopoulos. Snakes: active contour models. In Proc. 1st Int. Conf.
Сотр. Vis. (ICCV), London, pp. 259-268. IEEE Computer Society, Washington, 1987.
103. B. Y. Kasturi and R. С Jain. Computer Vision: Advances and Applications. IEEE Computer
Society, Los Alamitos, 1991.
104. B. Y. Kasturi and R. С Jain, eds. Computer Vision: Principles. IEEE Computer Society, Los
Alamitos, 1991.
105. J. K. Kearney, W. B. Thompson, and D. L. Boley. Optical flow estimation: an error analysis of
gradient-based methods with local optimization. IEEE Trans. PAMI, 9 (2):229-244, 1987.
106. M. Kerckhove, ed. Scale-Space and Morphology in Computer Vision, vol. 2106 of Lecture Notes
in Computer Science, 2001.3rd Int. Conf. Scale- Space'Ol, Vancouver, Canada, Springer, Berlin.
107. R. Kimmel, N. Sochen, and J. Weickert, eds. Scale-Space andPDEMethods in Computer Vision,
Lecture Notes in Computer Science, 2005. 5th Int. Conf. Scale-Space'05, Springer, Berlin.
108. С Kittel. Introduction to Solid State Physics. Wiley, New York, 1971.
109. R. Юette, A Koschan, and K. Schluns. Computer Vision. Three-Dimensional Data from Images.
Springer, New York, 1998.
110. H. Knutsson. Filtering and Reconstruction in Image Processing. Diss., Linkoping Univ, Sweden,
1982.
111. H. Knutsson. Representing local structure using tensors. In The 6th Scandinavian Conference
on Image Analysis, Oulu, Finland, June 19-22, 1989.
112. H. E. Knutsson, R. Wilson, and G. H. Granlund. Anisotropic nonstationary image estimation and
its applications: part I - restoration of noisy images. IEEE Trans. COMM, 31(3):388-397,1983.
113. J. J. Koenderink and A J. van Doom. Generic neighborhood operators. IEEE Trans. PAMI,
14(6):597-605, 1992.
114. С Koschnitzke, R. Mehnert, and R Quick. Das KMQ- Verfahren: Medienkompatible Vbertragung
echter Stereofarbabbildungen. Forschungsbericht Nr. 201, Universitat Hohenheim, 1983.
115. R Lancaster and K. Salkauskas. Curve and Surface Fitting. An Introduction. Academic Press,
London, 1986.
116. S. Lanser and W. Eckstein. Eine Modifikation des Deriche-Verfahrens zur Kantendetektion.
In B. Radig, ed., Mustererkennung 1991, vol. 290 of Informatik Fachberichte, pp. 151—158. 13.
DAGM Symposium, Munchen, Springer, Berlin, 1991.
117. Laurin. The Photonics Design and Applications Handbook. Laurin Publishing CO, Pittsfield,
МД 40th edn., 1994.
118. D. C. Lay Linear Algebra and Its Applications. Addison-Wesley, Reading, МД 1999.
119. R. Lenz. Linsenfehlerkorrigierte Eichung von Halbleiterkameras mit Standardobjektiven fiir
hochgenaue 3D-Messungen in Echtzeit. In E. Paulus, ed., Proc. 9. DAGM-Symp.
Mustererkennung 1987, Informatik Fachberichte 149, pp. 212-216. DAGM, Springer, Berlin,
1987.
120. R. Lenz. Zur Genauigkeit der Videometrie mit CCD-Sensoren. In H. Bunke, О Kiibler, and
P. Stucki, eds., Proc. 10. DAGM-Symp. Mustererkennung 1988, Informatik Fachberichte 180,
pp. 179-189. DAGM, Springer, Berlin, 1988.
121. M. Levine. Vision in Man and Machine. McGraw-Hill, New York, 1985.
122. Z.-P. Liang and P. С Lauterbur. Principles of Magnetic Resonance Imaging: A Signal Processing
Perspective. SPIE, Bellingham, WA 1999.
123. D. R. Lide, ed. CRC Handbook of Chemistry and Physics. CRC, Boca Raton, FL, 76th edn.,
1995.
124. J. S. Lim. Two-dimensional Signal and Image Processing. Prentice-Hall, Englewood Cliffs, NJ,
1990.
580 Литература
125. Т. Lindeberg. Scale-space Theory in Computer Vision, Юи>¥ег Academic Publishers, Boston,
1994.
126. M. Lx)ose, K. Meier, and J. Schemmel. A self-calibrating single-chip CMOS camera with
logarithmic response. IEEE J. Solid-State Circuits, 36(4), 2001.
127. D. Lorenz. Das Stereobild in Wissenschaft und Technik, Deutsche Forschungs- und
Versuchsanstalt fur Luft- und Raumfahrt, Koln, ObeфfafFenhofen, 1985.
128. V. K. Madisetti and D. B. WilUams, eds. The Digital Signal Processing Handbook, CRC, Boca
Ilaton, FL, 1998.
129. H. A Mallot. Computational Vision: Information Processing in Perception and Visual Behavior.
The MIT Press, Cambridge, МД 2000.
130. V. Markandey and B. E. Flinchbaugh. Multispectral constraints for optical flow computation.
In Proc. 3rd Int. Conf. on Computer Vision 1990 (ICCV90), Osaka, pp. 38-41. IEEE Computer
Society, Los Alamitos, 1990.
131. S. L. Маф1е Jr. Digital Spectral Analysis with Applications. Prentice-Hall, Englewood Cliffs,
NJ, 1987.
132. D. Marr. Vision. W. H. Freeman and Company, New York, 1982.
133. D. Marr and E. Hildreth. Theory of edge detection. Proc. Royal Society, London, Sen B, 270:187-
217, 1980.
134. E. A Maxwell. General Homogeneous Coordinates in Space of Three Dimensions. University Press,
Cambridge, 1951.
135. С Mead. Analog VLSI and Neural Systems. Addison-Wesley, Reading, МД 1989.
136. W. Menke. Geophysical Data Analysis: Discrete Inverse Theory, vol. 45 of International Geophysics
Series. Academic Press, San Diego, 1989.
137. С D. Meyer. Matrix Analysis and Applied Linear Algebra. SIAM, Philadelphia, 2001.
138. D. G. Mitchell and M. S. Cohen. MRIPrinciples. Saunders, Philadelphia, 2nd edn., 2004.
139. A Z. J. Мои, D. S. Rice, and W. Ding. VIS-based native video processing on UltraSPARC. In
Proc. IEEE Int. Conf on Image Proc, ICIF96, pp. 153-156. IEEE, Lausanne, 1996.
140. T. Munsterer. Messungvon Konzentrationsprofilen geldsterGase in derwasserseitigen Grenz^chicht.
Diploma thesis, University of Heidelberg, Germany, 1993.
141. T. Munsterer, H. J. Mayer, and B. Jahne. Dual-tracer measurements of concentration profiles in
the aqueous mass boundary layer. In B. Jahne and E. Monahan, eds., Air-Water Gas Transfer,
Selected Papers, 3rd Intern. Symp. on Air-Water Gas Transfer, pp. 637-648. AEON, Hanau, 1995.
142. H. Nagel. Displacement vectors derived from second-order intensity variations in image
sequences. Computer Vision, Graphics, and Image Processing (GVGIP), 21:85—117, 1983.
143. Y. Nakayama and Y. Tanida, eds. Atlas of Visualization III CRC, Boca Raton, FL, 1997.
144. V. S. Nalwa A Guided Tour of Computer Vision. Addison-Wesley, Reading, МД 1993.
145. M. Nielsen, P. Johansen, O. Olsen, and J. Weickert, eds. Scale-Space Theories in Computer
Vision, vol. 1682 of Lecture Notes in Computer Science, 1999. 2nd Int. Conf. Scale-Space'99,
Corfu, Greece, Springer, Berlin.
146. H. K. Nishihara Practical real-time stereo matcher. Optical Eng., 23:536- 545, 1984.
147. J. Ohser and F. Miicklich. Statistical Analysis of Microstructures in Material Science. >\^ley,
Chicester, England, 2000.
148. A V. Oppenheim and R. W Schafer. Discrete-time Signal Processing. Prentice-Hall, Englewood
cuffs, NJ, 1989.
149. A Papoulis. Probability, Random Variables, and Stochastic Processes. McGraw-Hill, New York,
3rd edn., 1991.
Литература 581
150. J. R. Parker. Algorithms for Image Processing and Computer Vision. John Wiley & Sons, New
York, 1997. Includes CD-ROM.
151. P. Perona and J. Malik. Scale space and edge detection using anisotropic diffusion. In Proc.
IEEE сотр. soc. workshop on computer vision (Miami Beach, Nov. 30-Dec. 2, 1987), pp. 16-20.
IEEE Computer Society, Washington, 1987.
152. Photobit. PB-MV13 20 mm CMOS Active Pixel Digital Image Sensor. Photobit, Pasadena,
СД Aigust 2000. www.photobit.com.
153. M. Pietikainen and A Rosenfeld. Image segmentation by texture using pyramid node linking.
SMC, 11:822-825, 1981.
154. I. Pitas. Digital Image Processing Algorithms. Prentice Hall, New York, 1993.
155. I. Pitas and A N. Venetsanopoulos. Nonlinear Digital Filters. Principles and Applications. Юuwer
Academic Publishers, Norwell, МД 1990.
156. A D. Poularikas, ed. Ibe Transforms and Applications Handbook. CRC, Boca Raton, 1996.
157. W. K. Pratt. Digital image processing, PIKS Inside. Wiley, New York, 3^ edn., 2001.
158. W. H. Press, B. P. Flannery, S. A Teukolsky, and W. T. Vetterling. Numerical Recipes in C: The
Art of Scientific Computing. Cambridge University Press, New York, 1992.
159. J. G. Proakis and D. G. Manolakis. Digital Signal Processing. Principles, Algorithms, and
Applications. McMillan, New York, 1992.
160. L. H. Quam. Hierarchical waф stereo. In Proc. DARPA Image Understanding Workshop, October
1984, New Orleans, LA, pp. 149-155,1984.
161. A R. Rao. A Taxonomy for Texture Description and Identification. Springer, New York, 1990.
162. A R. Rao and B. G. Schunck. Computing oriented texture fields. In Proceedings CVPR'89, San
Diego, CA, pp. 61-68. IEEE Computer Society, Washington, DC, 1989.
163. T. H. Reiss. Recognizing Planar Objects Using Invariant Image Features, vol. 676 of Lecture notes
in computer science. Springer, Berlin, 1993.
164. J. A Rice. Mathematical Statistics and Data Analysis. Duxbury Press, Belmont, СД 1995.
165. A Richards. Alien Vision: Exploring the Electromagnetic Spectrum with Imaging Technology. SPIE,
Bellingham, WA 2001.
166. J. A Richards. Remote Sensing Digital Image Analysis. Springer, BerUn, 1986.
167. J. A Richards and X. Jia Remote Sensing Digital Image Analysis. Springer, BerUn, 1999.
168. M. J. Riedl. Optical Design Fundamentals for Infrared Systems. SPIE, Bellingham, 2nd edn., 2001.
169. K. Riemer. Analyse von Wasseroberflachenwellen im Orts-Wellenzahl- Raum. Diss., Univ.
Heidelberg, 1991.
170. K. Riemer, T. Scholz, and B. Jahne. Bildfolgenanalyse im Orts- Wellenzahlraum. In B. Radig,
ed., Mustererkennung 1991, Proc. 13. DAGMSymposium Munchen, 9.-11. October 1991, pp. 223-
230. Springer, Berlin, 1991.
171. A Rosenfeld, ed. Multiresolution Image Processing and Analysis, vol. 12 of Springer Series in
Information Sciences. Springer, New York, 1984.
172. A Rosenfeld and A С Как. Digital Picture Processing, vol. I and II. Academic Press, San Diegoi,
2nd edn., 1982.
173. J. С Russ. The Image Processing Handbook. CRC, Boca Raton, FL, 4th edn., 2002.
174. H. Samet. Applications of Spatial Data Structures: Computer Graphics, Image processing, and
GIS. Addison-Wesley, Reading, MA, 1990.
175. H. Samet. The Design and Analysis of Spatial Data Structures. Addison-Wesley, Reading, МД
1990.
582 Литература
176. Н. Scharr and D. Uttenweiler. 3D anisotropic diffusion filtering for enhancing noisy actin
filaments. In B. Radig and S. Florczyk, eds., Pattern Recognition, 23rd DAGM Stmposium,
Munich, vol. 2191 of Lecture Notes in Computer Science, pp. 69—75. Springer, Berlin, 2001.
177. H. Scharr and J. Weickert. An anisotropic diffusion algorithm with optimized rotation invariance.
In G. Sommer, N. Kriiger, and С Perwass, eds., Mustererkennung 2000, Informatik Aktuell,
pp. 460-467. 22. DAGM Symposium, Kiel, Springer, Berlin, 2000.
178. T. Scheuermann, G. Pfundt, P. Eyerer, and B. Jahne. Oberflachenkonturvermessung
mikroskopischer Objekte durch Projektion statistischer Rauschmuster. In G. Sagerer, S. Posch,
and E Kummert, eds., Mustererkennung 1995, Proc. 17. DAGM-Symposium, Bielefeld, 13.-15.
September 1995, pp. 319-326. DAGM, Springer, BerUn, 1995.
179. C. Schnorr and J. Weickert. Variational image motion computations: theoretical framework,
problems and perspective. In G. Sommer, N. Kriiger, and С Perwass, eds., Mustererkennung
2000, Informatik Aktuell, pp. 476- 487. 22. DAGM Symposium, Kiel, Springer, Beriin, 2000.
180. B. Schollkopf and A J. Smola Learning with Kernels, Support Vector Machines, Regularization,
Optimization, and Beyond. MIT Press, Cambridge, МД 2002.
181. J. R. Schott. Remote Sensing. The Image Chain Approach. Oxford University Press, New York, 1997.
182. J. Schurmann. Pattern Classification. John Wiley & Sons, New York, 1996.
183. R. Sedgewick. Algorithms in C, Part 1-4. Addison-Wesley, Reading, МД 3rd edn., 1997.
184. J. Serra Image analysis and mathematical morphology. Academic Press, London, 1982.
185. J. Serra and P. Soille, eds. Mathematical Morphology and its Applications to Image Processing,
vol. 2 of Computational Imaging and Vision. Юuwer, Dordrecht, 1994.
186. L. G. Shapiro and G. С Stockman. Computer Vision. Prentice Hall, Upper Saddle River, NJ, 2001.
187. E. P. Simoncelli, W. T. Freeman, E. H. Adelson, and D. J. Heeger. Shiftable multiscale
transforms. IEEE Trans. IT, 38(2):587-607, 1992.
188. R. M. Simonds. Reduction of large convolutional kernels into multipass applications of small
generating kernels. /. Opt. Soc. Am. A, 5:1023-1029,1988.
189. A Singh. Optic Flow Computation: a Unified Perspective. IEEE Computer Society Press, Lx)s
Alamitos, СД 1991.
190. A T. Smith and R. J. Snowden, eds. Visual Detection of Motion. Academic Press, London, 1994.
191. W. J. Smith. Modem Optical Design. McGraw-Hill, New York, 3rd edn., 2000.
192. P. Soille. Morphological Image Analysis. Principles and Applications. Springer, Berlin, 2nd edn., 2002.
193. G. Sommer, ed. Geometric Computing with Clifford Algebras. Springer, Berlin, 2001.
194. J. Steurer, H. Giebel, and W Altner. Ein lichtmikroskopisches Verfahren zur
zweieinhalbdimensionalen Auswertung von Oberflachen. In G. Hartmann, ed., Proc. 8. DAGM-
Symp. Mustererkennung 1986, Informatik- Fachberichte 125, pp. 66—70. DAGM, Springer,
BerUn, 1986.
195. R. H. Stewart. Methods of Satellite Oceanography. University of California Press, Berkeley, 1985.
196. T. M. Strat. Recovering the camera parameters from a transformation matrix. In Proc. DARPA
Image Understanding Workshop, pp. 264—271, 1984.
197. B. ter Haar Romeny, L. Florack, J. Koenderink, and M. \^ergever, eds. Scale-Space Theory in
Computer Vision, vol. 1252 of Lecture Notes in Computer Science, 1997. 1st Int. Conf, Scale-
Space'97, Utrecht, The Netherlands, Springer, Berlin.
198. D. Terzopoulos. Regularization of inverse visual problems involving discontinuities. IEEE Trans.
PAMI, 8:413-424, 1986.
199. D. Terzopoulos. The computation of visible-surface representations. IEEE Trans. PAMI, 10
(4):417-438, 1988.
Литература 583
200. D. Terzopoulos, A Witkin, and M. Kass. Symmetry-seeking models for 3D object reconstruction.
In Proc. 1st Int. Conf. Сотр. Vis. (ICCV), London, pp. 269-276. IEEE, IEEE Computer Society
Press, Washington, 1987.
201. D. H. Towne. Wave Phenomena. Dover, New York, 1988.
202. S. Ullman. High-level Vision. Object Recognition and Visual Cognition. The MIT Press,
Cambridge, МД 1996.
203. S. E. Umbaugh. Computer Vision and Image Processing: A Practical Approach Using CVIPTools.
Prentice HaU PTR, Upper Saddle River, NJ, 1998.
204. M. Unser, A Aldroubi, and M. Eden. Fast B-spline transforms for continuous image
representation and Ы^троЫюп. IEEE Trans. PAMI, 13: 277-285, 1991.
205. F. van der Heijden. Image Based Measurement Systems. Object Recognition and Parameter
Estimation. Wley, Chichester, England, 1994.
206. W. M. Vaughan and G. Weber. Oxygen quenching of pyrenebutyric acid fluorescence in water.
Biochemistry, 9:464,1970.
207. A Verri and T. Poggio. Against quantitative optical flow. In Proceedings ICCV87, London, pp.
171-180. IEEE, IEEE Computer Society Press, Washington, DC, 1987.
208. A Verri and T. Poggio. Motion field and optical flow: quaUtative properties. IEEE Trans. PAMI,
11 (5):490-498, 1989.
209. K. Voss and H. SuBe. Praktische Bildverarbeitung. Hanser, Munchen, 1991.
210. B. A Wandell. Foundations of Vision. Sinauer Ass., Sunderland, МД 1995.
211. A Watt. 3D Computer Graphics. Addison-Wesley, Workingham, England, 3rd edn., 1999.
212. A Webb. Statistical Pattern Recognition. Wiley, Chichester, UK, 2002.
213. J. Weickert. Anisotropic Diffusion in Image Processing. Dissertation, Faculty of Mathematics,
University of Kaiserslautem, 1996.
214. J. Weickert. Anisotropic Diffusion in Image Processing. Teubner, Stuttgart, 1998.
215. E. W Weisstein. CRC Concise Encyclopedia of Mathematics. CRC, Boca Raton, FL, 2nd edn.,
2002.
216. I. Wells, W M. Efficient synthesis of Gaussian filters by cascaded uniform filters. IEEE Trans.
PAMI, 8(2):234-239, 1989.
217. J. N. Wilson and G. X. Ritter. Handbook of Computer Vision Algorithms in Image Algebra. CRC,
Boca Raton, FL, 2nd edn., 2000.
218. G. Wiora Optische 3D-Messtechnik: Pra'zise Gestaltvermessung mit einem erweiterten
Streifenprojektionsverfahren. Dissertation, Fakultat flir Physik und Astronomic, Universitat
Heidelberg, 2001. http://www.ub.uni-heidelberg.de/archiv/1808.
219. G. Wolberg. Digital Image Warping. IEEE Computer Society, Los Alamitos, СД 1990.
220. R. J. Woodham. Multiple light source optical flow. In Proc. 3rd Int. Conf. on Computer Vision
1990(ICCV90), Osaka, pp. 42-46. IEEE Computer Society, Los Alamitos, 1990.
221. P. Zamperoni. Methoden derdigitalen Bildsignalverarbeitung. Vieweg,Braunschweig, 1989.