Методы статистического анализа в управлении - Сулицкий В.Н.

1 Представление данных в статистическом анализе

2 Группировка и графическое представление данных

7 Распределения непрерывных случайных величин

12 Распределение хи квадрат и его применение в выборочном методе

13 Корреляция и простая линейная регрессия

16 Статистические методы и модели в прогнозировании

17 Статистические методы обоснования управленческих решений в условиях неопределенности

Автор: Сулицкий В.Н.

Теги: экономические науки основные понятия стоимость капитал фонды рынок: суть и структура экономика менеджмент системы управления статистический анализ

ISBN: 5-7749-0234-Х

Год: 2002

Похожие

Анализ и статистическая динамика систем автоматического управления. Методы ТАУ. Том 1

Методы морфологического анализа изображений

Статистические методы интеллектуального анализа данных

Макроэкономика

Текст

В.Н. Сулицкий
МЕТОДЫ
СТАТИСТИЧЕСКОГО
АНАЛИЗА
в УПРАВЛЕНИИ
УДК 330.101.541(075.8)
ББК 65.012.2я73
С89
Об авторе:
Сулицкий Владимир Николаевич - окончил механико-
математический факультет МГУ, доктор экономических наук,
кандидат технических наук, профессор, зав. кафедрой высшей
математики и статистики факультета ‘'Информационные технологии
в бизнесе” Академии народного хозяйства
при Правительстве Российской Федерации
Сулицкий В.Н.
С89 Методы статистического анализа в управлении: Учеб,
пособие. — М.: Дело, 2002. — 520 с.
ISBN 5-7749-0234-Х
Учебное пособие содержит системное изложение методов приклад-
ного статистического анализа в применении к количественному обо-
снованию решений В доступной форме, не требующей значительной
математической подготовки, ихтагаются основы математико-статис-
тических расчетов в менеджменте, экономике и бизнесе. Приведены
многочисленные примеры таких расчетов для практических ситуаций,
взятых из рахтичных областей управленческой деятельности.
Учебное пособие предназначено для студентов экономических спе-
циальностей, преподавателей, менеджеров, предпринимателей и слу-
шателей, занимающихся в сети переподготовки управленческих кад-
ров.
УДК 330.101.541(075.8)
ББК 65.012.2я73
ISBN 5-7749-0234-Х
© Издательство “Дело”, 2002
ОГЛАВЛЕНИЕ
Предисловие........................................... 10
Глава 1. ПРЕДСТАВЛЕНИЕ ДАННЫХ В СТАТИСТИЧЕСКОМ
АНАЛИЗЕ.................................................11
1.1. Основные направления статистического анализа.......11
1.2. Количественные измерения статистических данных.......13
1.3. Уровни измерения данных............................14
1.4. Сбор данных........................................15
1.5. Формирование и виды выборки....................... 17
Основные положения главы /................................20
Глава 2. ГРУППИРОВКА И ГРАФИЧЕСКОЕ
ПРЕДСТАВЛЕНИЕ ДАННЫХ ..................................23
2.1. Ряд распределения................................. 23
2.2. Графическое представление ряда распределения.......32
2.3. Диаграммы как способ графического |Цедставления
статистических данных...................................39
Основные положения главы 2..............................42
Глава 3. ИЗМЕРЕНИЕ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ................44
3.1. Вычисление центральных значений .для несгрунпированных
.данных.................................................45
3.1.1. Средняя арифметическая......................45
3.1.2. Медиана................................... 48
3.1.3. Мода........................................50
3.2. Оценка характеристик центральной тенденции для сгруппи-
рованных .данных........................................52
3.2.1. Средняя арифметическая для ряда распределения.52
3.2.2. Медиана для сгруппированных данных..........53
3.2.3. Оценка моды для сгруппированных данных......55
3.2.4. Сравнение типов средних при анализе центральной
тенденции..........................................56
Основные положения главы 3..............................59
3
Глава 4. ИЗМЕРЕНИЕ ВАРИАЦИИ..............................61
4.1. Основные характеристики вариации.................. 62
4.1.1. Размах колебаний.............................62
4.1.2. Среднее линейное отклонение..................63
4.1.3. Дисперсия и среднее квадратическое (стандартное)
отклонение..........................................65
4.1.4. Интерпретация стандартного отклонения на основе
неравенства Чебышева................................71
4.1.5. Коэффициент вариации.........................71
4.2. Измерение вариации на основе порядковых характеристик .... 73
4.2.1. Размах квартилей и квартильное отклонение....74
4.2.2. Размах процентилей...........................77
4.3. Характеристики формы кривой распределения...........78
Основные положения главы 4...............................80
Глава 5. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ....................83
5.1. Основные понятия теории вероятностей ................83
5.1.1. Общее понятие вероятности....................83
5.1.2. Объективный и субъективный подходы к определе-
нию вероятности. Закон больших чисел................84
5.2. Основные правила действий над вероятностями ........87
5.2.1. Типы событий. Алгебра событий................87
5.2.2. Правила сложения вероятностей................90
5.2.3. Условная вероятность. Правила умножения вероят-
ностей ............................................ 93
5.2.4. Таблица сопряженности и дерево возможных
исходов.............................................96
5.2.5. Формула полной вероятности. Теорема Байеса...99
5.3. Основные формулы комбинаторного анализа............. 102
5.3.1. Перестановки................................102
5.3.2. Принцип умножения......................... 103
5.3.3. Сочетания...................................104
Основные положения главы 5............................... 105
Глава 6. ДИСКРЕТНЫЕ РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ........................................... 109
6.1. Случайные величины ................................. 109
6.2. Ряд распределения дискретной случайной величины..... 110
6.3. Характеристики дискретной случайной величины ....... 112
6.3.1. Математическое ожидание...................... 112
6.3.2. Дисперсия и стандартное отклонение...........114
6.3.3. Графическое представление распределения дискрет-
ной случайной величины..............................117
6.4. Биномиальный закон распределения ................. 117
6.4.1. Биномиальные вероятности..................... 118
4
6.4.2. Математическое ожидание и дисперсия биномиаль-
ной случайной величины............................. 123
6.5. Гипергеометрическое распределение....................... 125
6.5.1. Распределение гипергсометрических вероятностей.... 125
6.5.2. Математическое ожидание и дисперсия гипергео-
метрического распределения..........................127
6.5.3. Использование биномиального закона для замены
гипергеометрического распределения..................127
6.6. Распределение Пуассона................................ 128
6.6.1. Распределение вероятностей пуассоновской
случайной величины................................. 128
6.6.2. Математическое ожидание и дисперсия пуас-
соновской случайной величины...................... 129
6.6.3. Замена биномиального распределения распределе-
нием Пуассона..................................... 131
6.7. Функции и комбинации случайных величин.................. 132
6.7.1. Математическое ожидание и дисперсия функций
случайной величины..................................132
6.7.2. Сумма и произведение независимых случайных
величин.............................................135
Основные положения главы 6................................... 138
Глава 7. РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ
ВЕЛИЧИН ..................................................... 141
7.1. Непрерывные случайные величины. Функция и плотность
распределения. Числовые характеристики............... 141
7.2. Равномерное распределение .............................. 145
7.3. Нормальный закон распределения..................... 149
7.3.1. Кривая нормального распределения и ее свойства... 149
7.3.2. Площади под кривой нормального распределения... 153
7.3.3. Вероятность попадания на заданный промежуток.
Стандартное нормальное распределение................156
7.3.4. Нормальное распределение как замена биномиаль-
ного распределения................................. 163
7.4. Экспоненциальное распределение.......................... 166
Основные положения главы 7................................... 169
Глава 8. ОЦЕНКА ПАРАМЕТРОВ................................... 172
8.1. Точечные оценки..................................... 172
8.1.1. Критерии качества точечных оценок................ 173
8.2. Распределение выборочных средних. Центральная предель-
ная теорема 174
8.3. Интервальные оценки генеральной средней................. 182
8.3.1. Общие принципы построения доверительных
интервалов........................................ 183
5
8.3.1.1. Вычисление доверительных интервалов при из-
вестном генеральном стандартном отклонении ... 186
8.3.1.2. Вычисление доверительных пределов при неиз-
вестном генеральном стандартном отклонении
Использование 1-распределения Стьюдента.... 189
8.3.1.3. Общие правила определения доверительных
интервалов...................................... 196
8.3.1.4. Объем выборки и точность интервальной
оценки средней.................................................. 197
8.3.2. Доверительные интервалы для разности средних двух
генеральных совокупностей (случай двух больших
независимых выборок)................................... 199
8.3.3. Доверительные интервалы для разности средних
(случай двух малых независимых выборок).................200
8.3.4. Объем выборки и допустимая ошибка оценки раз-
ности генеральных средних...............................204
8.4. Оценка долей.....................................!......205
8.4.1. Распределение выборочных долей (пропорций).......205
8.4.2. Доверительные интервалы для доли................207
8.4.3. Объем выборки и допустимая ошибка оценки доли ... 208
8.4.4. Доверительные интервалы для разностей долей......210
8.4.5. Объем выборок и допустимая ошибка разности
долей...................................................212
Основные положения главы 8...................................213
Глава 9. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО
СРЕДНИХ......................................................217
9.1. Общая постановка задачи проверки гипотез.
Нулевая гипотеза и статистические критерии..............217
9.1.1. Критическая область. Уровень значимости.........219
9.1.2. Ошибки первого и второго вида...................222
9.1.3. Двусторонние и односторонние проверки гипотез
относительно средней....................................224
9.2. Проверка гипотез относительно средней: случай одной
генеральной совокупности,.....................................226
9.2.1. Значение генерального стандартного отклонения
известно................................................226
9.2.2. Значение генерального стандартного отклонения
неизвестно: большая выборка.............................227
9.2.3. Значение генерального стандартного отклонения
неизвестно: малая выборка...............................229
9.3. Проверка гипотез относительно разности средних двух
генеральных совокупностей.....................................231
9.3.1. Случай больших выборок..........................231
9.3.2. Случай малых выборок............................235
9.3.3. Сравнение средних двух нормальных совокупностей
на основе пар наблюдений................................239
Основные положения главы 9...................................241
6
Глава 10. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО ДОЛЕЙ ... 245
10.1. Проверка гипотез относительно доли одной генеральной
совокупности..................................................245
10.1.1. Двусторонняя проверка...........................245
10.1.2. Односторонние проверки..........................247
10.1.3. Поправка на конечность генеральной
совокупности............................................249
10.2. Проверка гипотез относительно разности долей двух
генеральных совокупностей ....................................251
10.2.1. Двусторонняя проверка...........................251
10.2.2. Односторонние проверки..........................254
Основные положения главы 10........................................................... 257
Глава 11. ДИСПЕРСИОННЫЙ АНАЛИЗ...............................258
11.1. Общая схема однофакторного анализа.....................258
11.2. Межгрупповая и внутригрупповая дисперсии...............261
11.3. Сравнение межгрупповой и внутригрупповой дисперсий
на основе ^-распределения.....................................264
11.4. Проверка гипотез относительно дисперсий двух генераль-
ных совокупностей ............................................ 268
Основные положения главы 11................................,...........‘J.............. 271
Глава 12. РАСПРЕДЕЛЕНИЕ х2 И ЕГО ПРИМЕНЕНИЕ
В ВЫБОРОЧНОМ МЕТОДЕ..........................................274
12.1. Распределение х2 и оценка генеральной дисперсии........274
12.2. Проверка гипотез относительно дисперсии и стандартного
отклонения....................................................279
12.3. х2-распределение как критерий согласия.................281
12.4. Проверка гипотез относительно формы распределения .....286
12.5. Таблица сопряженности .................................292
Основные положения главы 12..................................297
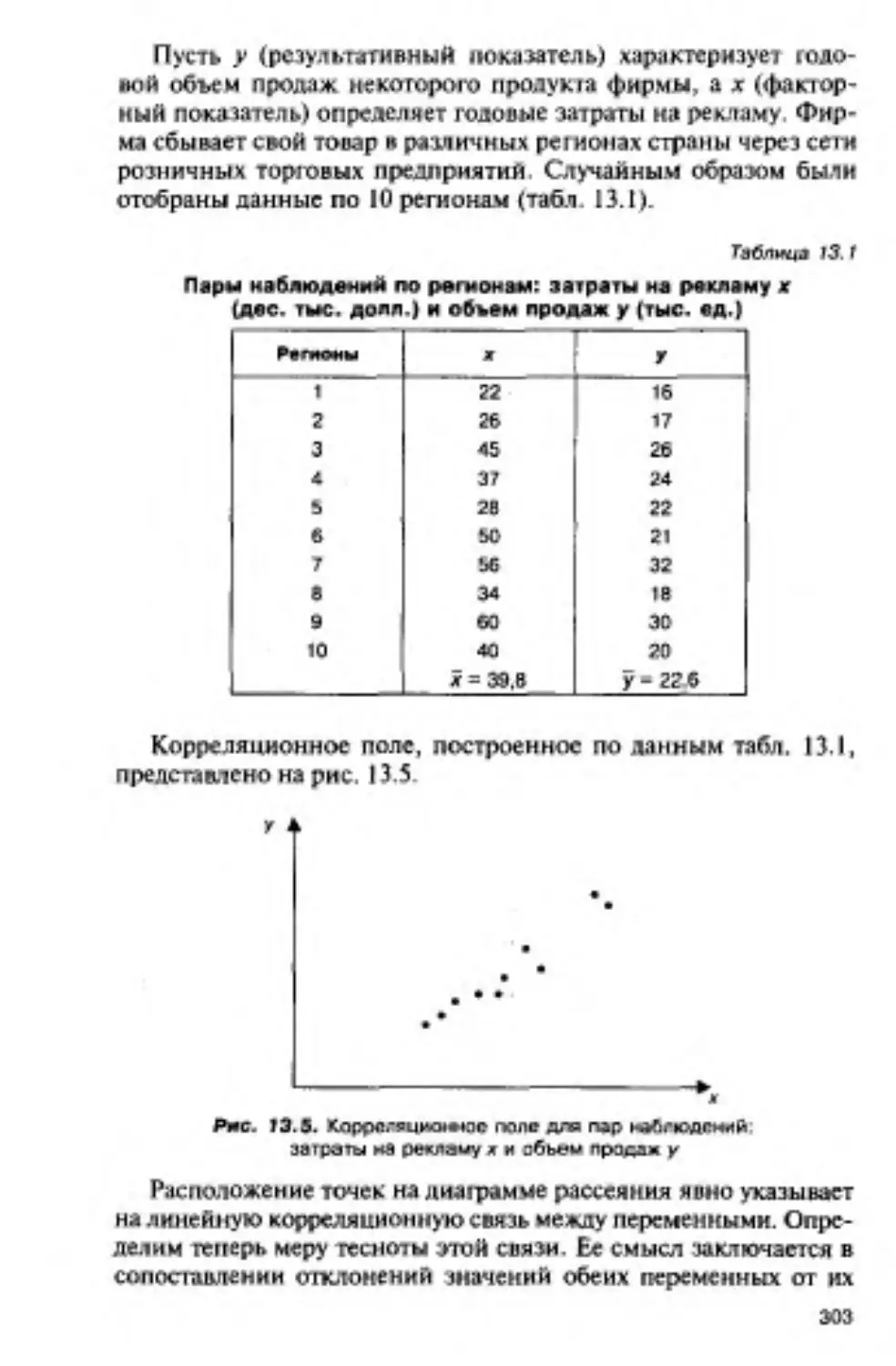
Глава 13. КОРРЕЛЯЦИЯ И ПРОСТАЯ ЛИНЕЙНАЯ
РЕГРЕССИЯ.................................................. 299
13.1. Линейная корреляция....................................299
13.1.1. Корреляционная связь и корреляционное поле.....299
13.1.2. Коэффициент корреляции.........................302
13.1.3. Существенность выборочного коэффициента кор-
реляции ................................................307
13.1.4. Ранговый коэффициент корреляции................309
13.2. Простой линейный регрессионный анализ .................314
13.2.1. Уравнение простой регрессии. Метод наименьших
квадратов...............................................314
13.2.2. Стандартная ошибка регрессии...........;........317
7
13.2.3. Доверительные интервалы уравнения
регрессии.......................................319
13.2.4. Коэффициент детерминации...................325
13.2.5. Проверка существенности коэффициента
регрессии.......................................327
13.2.6. Возможные ошибки при практическом использо-
вании корреляционно-регрессионного анализа.......329
Основные положения главы 13.............................331
Глава 14. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ.......................334
14.1. Уравнение множественной линейной регрессии........334
14.2. Оценка качества множественной регрессии: стандартная
ошибка и коэффициент множественной детерминации......338
14.3. Проверка статистической значимости множественной
регрессии............................................342
14.4. Подбор переменных в модель множественной регрессии .347
14.5. Проверка допущений относительно статистических свойств
ошибок регрессии. Критерий Дарбина—Уотсона...........351
14.6. Множественная линейная регрессия как модель прогнози-
рования .............................................357
14.7. Нелинейная регрессия..............................359
Основные положения главы 14.............................366
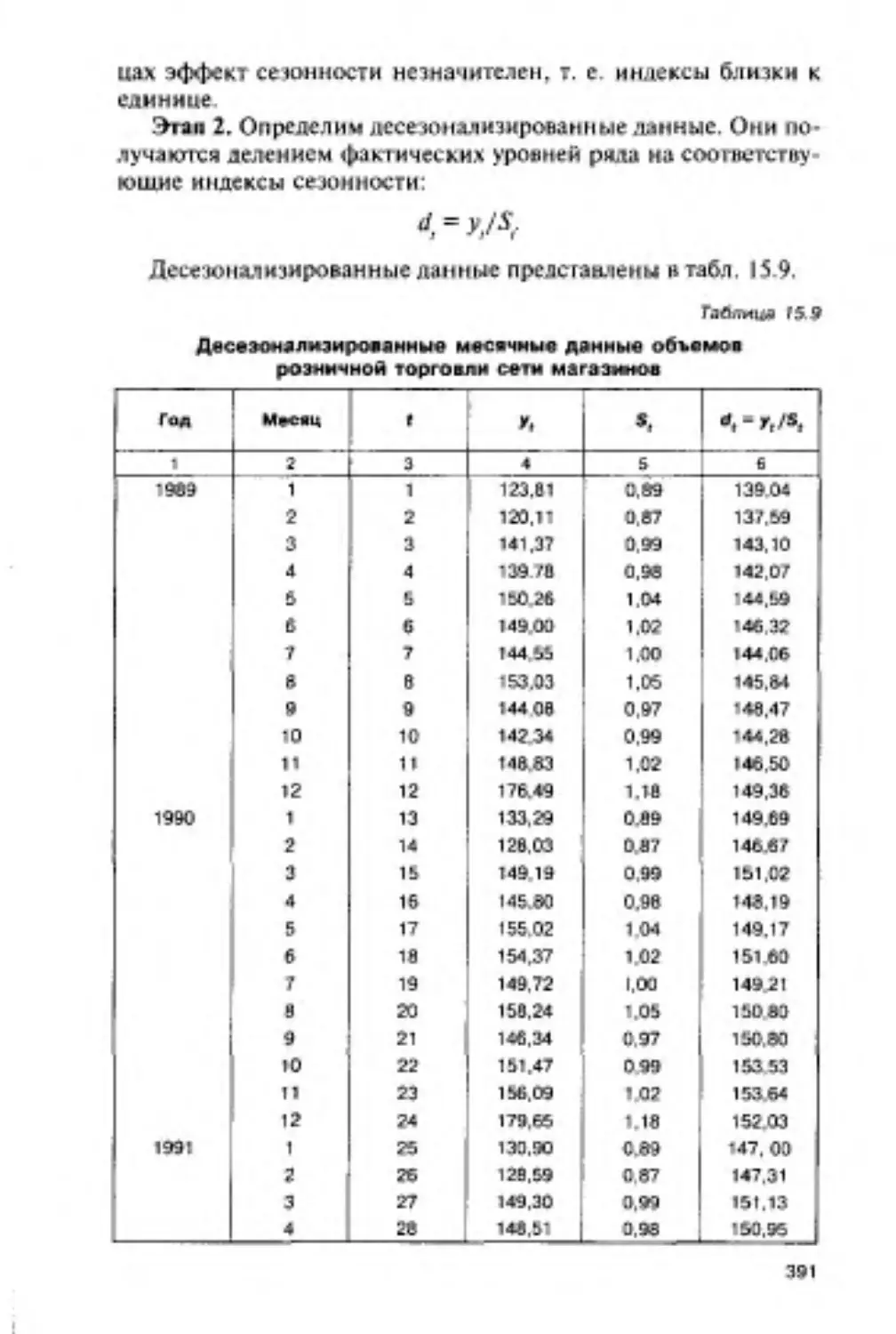
Глава 15. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ ..................369
15.1. Компоненты временного ряда........................369
15.2. Анализ тренда...............................L... 372
15.3. Измерение циклической компоненты..................376
15.4. Определение сезонной составляющей............... 378
15.5. Дессзонализацня данных и сезонное прогнозирование.384
15.6. Процедура общей декомпозиции временного ряда......386
Основные положения главы 15.............................398
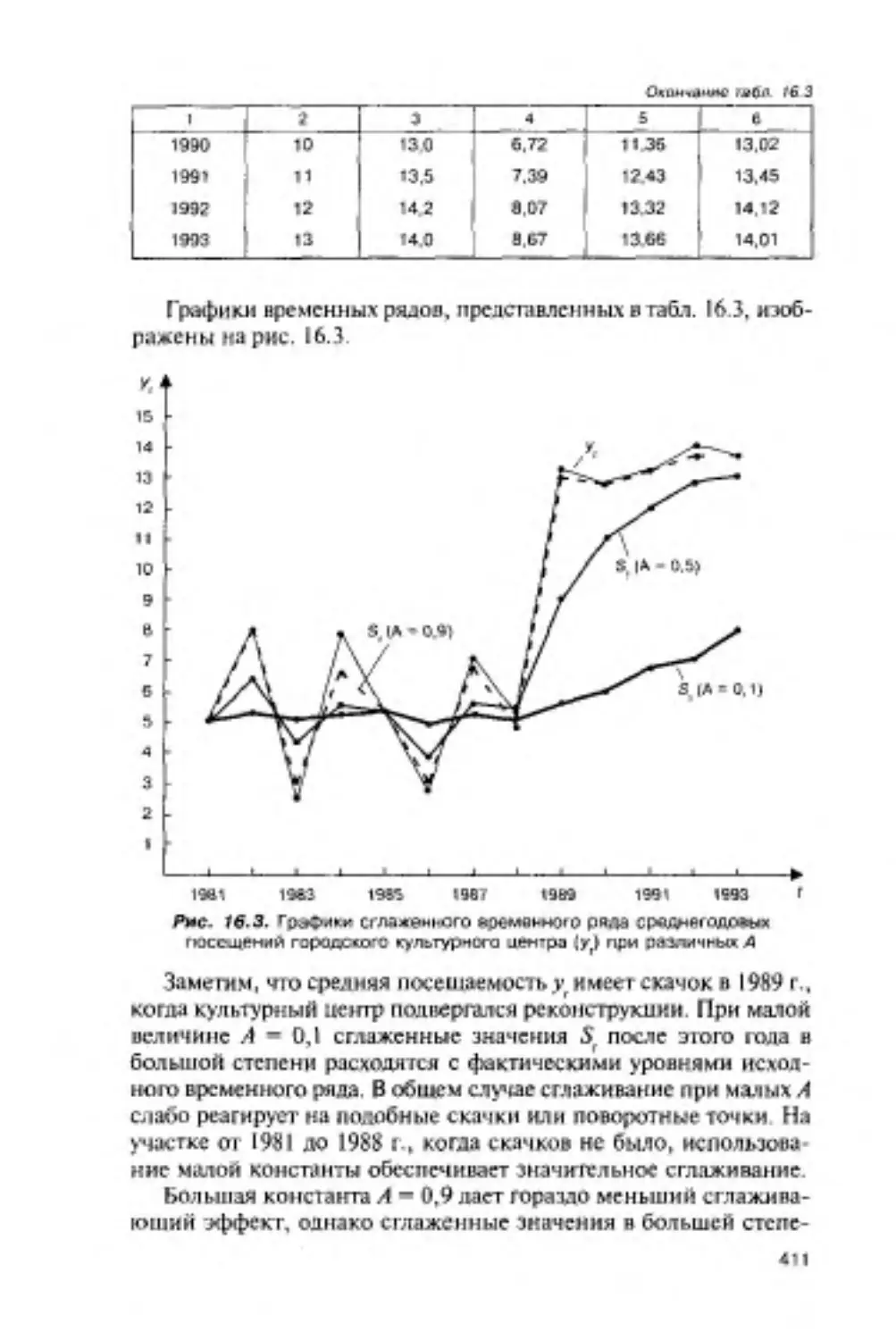
Глава 16. СТАТИСТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ
В ПРОГНОЗИРОВАНИИ..................................... 401
16.1. Простейшие модели.................................402
16.2. Методы экспоненциального сглаживания..............407
16.2.1. Простое экспоненциальное сглаживание.......407
16.2.2. Экспоненциальное сглаживание с учетом
тренда..........................................415
16.2.3. Экспоненциальное сглаживание с учетом
одновременно тренда и сезонности......................421
16.2.4. Измерение ошибок и сравнение методов прогно-
зирования .......................................428
8
16.2.5. Сравнительная оценка методов экспоненциального
сглаживания и сглаживающих констант..............431
16.3. Авторегрессионные модели прогнозирования........435
16.3.1. Коэффициент автокорреляции и определение
лагированных переменных модели...................438
16.3.2. Выявление и устранение нестационарности вре-
менных рядов..............................441
16.4. Искусственные переменные в линейной регрессионной
модели................................................443
16.5. Проблема устранения автокорреляции ошибок.......448
Основные положения главы 16...........................451
Глава 17. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБОСНОВАНИЯ
УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ В УСЛОВИЯХ
НЕОПРЕДЕЛЕННОСТИ......................................455
17.1. Описание проблемной ситуации....................456
17.2. Критерии выбора оптимального варианта действии
при неизвестных вероятностях состояний природы........462
17.2.1. Максиминный критерий Валвда..............462
17.2.2. Минимаксный критерий Севиджа........... 463
17.2.3. Максимаксный критерий....................464
17.2.4. Комбинированный критерий пессимизма—опти-
мизма Гурвица..............................465
17.3. Выбор решений при известных вероятностях состояний
природы ..............................................466
17.3.1. Критерий максимального ожидаемого выигрыша .... 466
17.3.2. Критерий минимальных условных потерь.....469
17.3.3. Анализ чувствительности..................470
17.3.4. Измерение риска..........................471
17.4. Исследование проблемы с помощью дерева решений .474
17.4.1. Общие принципы построения дерева решений..474
17.4.2. Использование теоремы Байеса для уточнения
вероятностей состояний природы.............476
Основные положения главы 17...........................484
Приложения ......................................... 489
Литература............................................518
Моей дочери Ксении посвящаю
ПРЕДИСЛОВИЕ
Учебное пособие написано на основе курсов, прочитанных
автором на различных факультетах и в рамках программ в Акаде-
мии народного хозяйства при Правительстве РФ. Пособие может
быть полезным для студентов экономических специальностей и
слушателей системы переподготовки профессиональных управ-
ленческих кадров. Автор стремился дать последовательное изло-
жение вероятностных и статистических методов, делая основной
акцент на их практическом использовании в менеджменте и биз-
несе. Каждое формальное понятие теории вероятности и матема-
тической статистики поясняется на практических примерах из
различных областей управленческой деятельности. В конце посо-
бия представлен список некоторых отечественных и зарубежных
работ, посвященных прикладным вопросам математико-статис-
тического анализа. Приведенные иностранные источники послу-
жили основой для разработки большинства примеров по исполь-
зованию статистических методов в практических ситуациях.
Решение задач статистического анализа связано со значи-
тельными объемами вычислений. Проведение реальных много-
вариантных статистических расчетов без использования ком-
пьютера практически невозможно. Это прежде всего относится
к задачам корреляционно-регрессионного анализа и статисти-
ческого прогнозирования. В ряде примеров, относящихся к дан-
ным темам (главы 13—16), промежуточные расчеты были сде-
ланы с помощью статистических пакетов прикладных программ.
В настоящее время разработано достаточное количество уни-
версальных и специализированных программных средств для
статистического анализа данных. С наиболее популярными из
них можно ознакомиться, например, в книге: Тюрин Ю.И.,
Макаров А.А. Статистический анализ данных на компьютере/
Под. ред. В.Э. Фигурнова. — М.: ИНФРА-М, 1998.
Ю
Г J ПРЕДСТАВЛЕНИЕ ДАННЫХ
В СТАТИСТИЧЕСКОМ
АНАЛИЗЕ
1.1. ОСНОВНЫЕ НАПРАВЛЕНИЯ
СТАТИСТИЧЕСКОГО АНАЛИЗА
В статистическом анализе можно выделить два основных на-
правления. Одно из них представляет собой статистическое опи-
сание (описательная статистика) какого-либо явления на ос-
нове только тех данных, которые были собраны. Например, к
методам статистического описания относится представление
данных в виде различных типов таблиц и графиков, которые
служат как бы фотографиями исследуемого явления в различ-
ных ракурсах. г>ги методы также включают получение обобщен-
ных показателей, характеризующих свойства и структуру ис-
следуемых данных. Описательная статистика упорядочивает и
систематизирует имеющуюся информацию, облегчает понима-
ние изучаемого явления. Наиболее ярким примером статисти-
ческого описания служат результаты переписи населения, пред-
ставленные в виде соответствующих таблиц, графиков и
показателей распределения населения по демографическим и
социальным признакам.
Другое направление статистического анализа (аналитичес-
кая статистика) — обработка собранных данных с целью про-
ведения анализа и получения статистических выводов отно-
сительно исследуемого массового явления. При этом данное
явление, как правило, характеризуется значительно боль-
шим количеством данных, чем участвует в обработке. Реша-
ющую роль здесь играют математико-статистические методы.
Они позволяют анализировать и интерпретировать массивы
полученных данных независимо от их качественного содер-
жания. Например, это могут быть значения показателей, от-
ражающих различные массовые явления в экономике и биз-
несе. Массовым явлениям соответствуют статистические co-
ll
вокупности, в рамках которых они проявляются. Статисти-
ческая совокупность — это масса отдельных качественно од-
нородных единиц или элементов. Элементами статистичес-
кой совокупности могут быть отдельные индивиды или их
группы, а также какие-либо объекты: предприятия отрасли,
единицы продукции, акции, транспортные средства, стра-
ны и т. д. Если совокупность состоит из всех элементов, кото-
рые соответствуют данному явлению, то в этом случае ис-
пользуется термин “генеральная совокупность”. В то же вре-
мя термин “выборка”, или “выборочная совокупность”,
используется для обозначения части (подмножества) гене-
ральной совокупности. Состав генеральной совокупности пол-
ностью определяется соответствующим явлением. Пусть цель
статистического исследования — выявление мнения избира-
телей, живущих в крупном регионе страны, относительно
избрания определенного кандидата на пост губернатора дан-
ного региона. В этом случае генеральная совокупность вклю-
чает в себя всех жителей региона, имеющих право голоса.
Численность такой совокупности для крупного региона мо-
жет составлять более миллиона человек. Очевидно, оператив-
но организовать опрос всех потенциальных избирателей, т. е.
провести обследование всех единиц совокупности, практи-
чески невозможно, так как это требует значительных затрат
людских, материальных и финансовых ресурсов. Поэтому в
подобных случаях для изучения свойств генеральной сово-
купности обследуют некоторую ее часть — выборку, извле-
ченную случайным образом. Например, в рассматриваемой
ситуации для проведения опроса имеет смысл случайным об-
разом отобрать приемлемое число респондентов (проблема
численности выборки будет рассмотрена в гл. 8) — взрослых
жителей региона. Случайный отбор предполагает, что до его
осуществления все взрослые жители (единицы генеральной
совокупности) имели равные возможности для включения в
число респондентов (выборку). С помощью случайного отбо-
ра формируется случайная выборка, которая лежит в основе
выборочного метода. С этим методом в статистическом ана-
лизе ассоциируется целое направление — получение статис-
тического заключения. Оно связано с использованием мето-
дов математической статистики для обоснования наиболее
правдоподобных выводов о характерных признаках генераль-
ной совокупности только с помощью данных случайной вы-
борки.
12
1.2. КОЛИЧЕСТВЕННЫЕ ИЗМЕРЕНИЯ
СТАТИСТИЧЕСКИХ ДАННЫХ
Пусть в качестве статистической совокупности рассматри-
вается множество семей, живущих в некотором округе. На-
пример, это делается с целью проведения маркетинговых ис-
следований некой торговой фирмой, которая собирается
организовать на территории округа сеть магазинов. Очевидно,
для определения покупательной способности местного насе-
ления одним из важнейших показателей будет годовой доход
каждой семьи. Можно сказать, что каждой единице совокуп-
ности (семье) соответствует значение некоторого варьирую-
щего признака (сумма годового семейного дохода). Вариация
(изменение) признака отражает тот факт, что он принимает
различные значения у различных единиц совокупности. Се-
мейный доход является не единственным варьирующим при-
знаком, характеризующим элементы совокупности. Так, при-
знаками семьи могут служить количество детей дошкольного
или школьного возраста, общая площадь квартиры или дома,
наличие автомобиля, удовлетворенность работой коммуналь-
ных служб и т. п. В общем случае для каждой статистической
совокупности может существовать множество варьирующих
признаков, имеющих количественное или качественное зна-
чение. Кроме того, при изучении совокупности часто рассмат-
риваются количественные обобщенные характеристики, на-
пример: общая численность совокупности; процент единиц
совокупности, обладающих данным свойством; средние по-
казатели по ряду признаков. Численные данные, являющиеся
измерителями всей совокупности этих характеристик и вари-
ации признаков, представляют собой ту исходную информа-
цию, которой оперирует статистический анализ. Некоторые
методы обработки данных рассчитаны на определенный вид
данных. В этой связи перед изложением этих методов имеет
смысл рассмотреть главные характерные признаки числовых
данных. Анализируемые данные можно разделить на две ос-
новные категории: дискретные и непрерывные.
Дискретные данные выражаются в виде целых положитель-
ных чисел. Например, это могут быть результаты опроса груп-
пы лиц по поводу согласия с каким-либо фактом, где степень
согласия кодируется по следующей системе: 1 — полностью
согласен, 2 — согласен, 3 — нейтрален, 4 — не согласен, 5 —
полностью не согласен. В основном дискретные данные возни-
кают в тех случаях, когда есть необходимость подсчета каких-
13
либо единиц, например при определении числа детей в семье;
числа автомобилей, проезжающих в течение 5 минут через же-
лезнодорожный переезд; числа младенцев, родившихся в тече-
ние дня в городе, и т. п.
В отличие от дискретных непрерывные данные могут непре-
рывно заполнять некоторый промежуток. Например, пусть в
качестве данных рассматривается вес посылок, прибывающих
в некоторое почтовое отделение. Теоретически вес каждой по-
сылки может быть выражен в килограммах с любой точностью
(это зависит от точности весов), т. е. представлен в виде деся-
тичного числа с бесконечным числом знаков после запятой.
Непрерывные данные могут принимать любые значения в за-
данных пределах. В рассматриваемом случае каждая посылка
может иметь любой вес в пределах нормативов, установленных
для приема посылок в почтовых отделениях. Непрерывные дан-
ные также могут быть получены при измерении роста, веса и
возраста индивида; диаметра подшипника; срока годности при-
бора; времени обслуживания клиента и т. д.
Важно отметить, что дискретные данные могут выражать
значения не только дискретных переменных, но и некоторых
непрерывных. Так, когда говорят о возрасте человека, то, как
правило, имеют в виду целое число прожитых лет.
1.3. УРОВНИ ИЗМЕРЕНИЯ ДАННЫХ
Численные данные не только делятся на дискретные и не-
прерывные, но и классифицируюся по уровням измерения,
которые определяют тип шкалы измерений. Выделяют четыре
типа шкал: шкала наименований, порядковая шкала, шкалы
интервалов и отношений.
Шкала наименований используется для описания качествен-
ных данных, характеризующих принадлежность элементов со-
вокупности к каким-либо классам. Всем объектам одного класса
присваивается одно и то же число, а объектам разных классов —
разные числа. Например, при распределении людей по полу:
мужчина - 1, а женщина = 2; при классификации человеческих
глаз по цвету: голубой = 1, зеленый = 2, коричневый = 3; при
учете фирм — производителей автомобилей: "Форд" = 1, “Дже-
нерал моторе" = 2, "Крайслер" = 3. Смысл шкалы наименова-
ний — присваивание каждому классу определеного кода. Эта про-
цедура необходима для организации и хранения поиска
информации в компьютерных системах. Однако проводить ка-
кие-либо вычисления на основе данных такого типа не имеет
«4
смысла. Так, утверждение о том, что средний цвет глаз равен
2,73, абсурдно.
Порядковая шкала используется для упорядочения (ранжи-
рования) объектов (например, распределение мест среди участ-
ников какого-либо состязания или конкурса). Числа в шкале
определяют порядок следования объектов, однако не дают воз-
можности установить, на сколько или во сколько раз один
объект предпочтительней другого. Если участник конкурса А
занял первое место, участник В — третье, участник С — пятое
и участник D — седьмое, то это не означает, что D по отноше-
нию к С стоит гак же близко, как В по отношению к Л. В шкале
порядка отсутствуют понятия масштаба и начала отсчета.
Для определения меры различия между значениями при-
знака, присущего разным элементам совокупности, использу-
ется шкала интервалов. Классическим примером интервальной
шкалы является измерение температуры в градусах по Фарен-
гейту или Цельсию. Ясно, что разница между 15 и 10‘С та же,
что и между 17 и 12’С. В общем случае шкала интервалов может
иметь произвольные точки отсчета и масштаб.
Шкала отношений является частным случаем шкалы интер-
валов. В отличие от шкалы интервалов она имеет фиксирован-
ную точку отсчета. В этой шкале можно измерять, во сколько
раз значение признака, характеризующего одну единицу сово-
купности, превосходит значение признака для другой едини-
цы. Это невозможно сделать, пользуясь шкалой интервалов.
Например, нельзя утверждать, что температура 20*С в два раза
выше темсратуры 10’С, так как температура О’С не означает
отсутствия температуры вообще. В шкале отношений измеря-
ются, например, площадь, длина, вес, денежные потоки. Ну-
левая точка отсчета в шкале отношений означает полное от-
сутствие измеряемого признака.
Использование типа шкалы при измерении признака зави-
сит от самой природы этого признака. Если он носит качествен-
ный характер, то измерения производятся в шкалах наименова-
ний и порядка (качественные данные), если количественный,
го применяются шкалы интервалов и отношений (количествен-
ные данные).
1.4. СБОР ДАННЫХ
Методы статистического заключения оперируют выбороч-
ными данными. Справедливость получаемых выводов относи-
тельно свойств генеральной совокупности зависит от каче-
15
ства исходных данных, подвергаемых обработке, т. е. их точ-
ности и способности в достаточной мере отражать свойства
анализируемой статистической совокупности. Очевидно, это
качество зависит от источников и способов сбора данных, а
также правильности составления выборки. Анализируемые дан-
ные можно разделить на две категории — первичные и вто-
ричные.
Первичные данные собираются непосредственно в резуль-
тате проведения специально ориентированных опросов, ин-
тервью, наблюдений и экпериментальных исследований. Тра-
диционным методом сбора первичных данных является
составление вопросника, предназначенного для изучения фак-
торов и условий, влияющих на исследуемую проблему. Этбт
вопросник целенаправленно распространяется среди выбороч-
ной группы лиц, представляющих, по мнению исследователя,
всю совокупность людей, которые заинтересованы в данной
проблеме. Полученные ответы кодируются и вводятся в память
компьютера для последующей обработки. Результаты расчетов
являются основой для получения заключения относительно ис-
следуемой проблемы.
Вторичные данные собираются из различных информаци-
онных источников: периодических печатных изданий финан-
сового, экономического и социологического характера, пуб-
ликуемых годовых финансовых и бухгалтерских отчетов фирм
и банков, котировок акций, биржевых сводок, показателей
различных внутренних и внешних рынков и т. п. Как видно,
вторичные данные всегда предварительно собираются, запи-
сываются и публично представляются в определенной форме.
Приобрести вторичные данные, как правило, дешевле, чем
организовать сбор первичных данных. Однако в большинстве
случаев содержание, точность и новизна вторичных данных не
могут быть в полной мере адекватны объектам конкретного
статистического исследования. Это связано с тем, что в основе
их сбора и публикации были заложены другие, более общие
цели и задачи. Поэтому в статистическом анализе стараются по
возможности использовать первичные данные, которые, на-
пример, регулярно могут собираться специальными агентства-
ми (сеть таких агентств стабильно функционирует в развитых
странах).
Важно понимать тот факт, что эффективность решений в
бизнесе, принимаемых на основе выборочного метода, в пол-
ной мере зависит от качества исходной информации. На практи-
16
ке получение детальных и адекватных первичных данных не
всегда бывает технически возможным или требует значитель-
ных затрат. Поэтому при выборе типов данных для статистичес-
кого анализа следует соотносить надежность и соответствие
изучаемой проблеме первичных данных с доступностью и удоб-
ством в получении вторичных данных.
1.5. ФОРМИРОВАНИЕ И ВИДЫ ВЫБОРКИ
Основная цель формирования выборки — эффективное ис-
пользование ее состава данных в качестве входной информации
для статистического анализа в целях получения наиболее прав-
доподобных статистических выводов о свойствах генеральной со-
вокупности. Поэтому важнейшим требованием, которое должно
выполняться при организации выборки, является репрезента-
тивность. Репрезентативность, или представительность, означа-
ет, что выборка должна в максимальной степени (как в “капле
воды") отражать свойства и структуру генеральной совокупнос-
ти. Она достигается с помощью объективного отбора, т. е. прави-
ла равных возможностей попадания в выборку элементов гене-
ральной совокупности. Тип выборки определяется способом
отбора данных. Различают простой случайный отбор, отбор по
заранее определенному принципу и их комбинацию. Если из ге-
неральной совокупности численностью Nединиц отбирается слу-
чайным образом п единиц, то такой отбор называется простым
случайным отбором, или собственно случайным. Например, про-
стой случайный отбор реализуется при розыгрышах различных
лотерей. В результате простого случайного отбора формируется
простая случайная выборка, или собственно случайная выборка
(часто используют термин “случайная выборка”). Схема просто-
го случайного отбора предполагает регистрацию элементов со-
вокупности, например в виде списков, реестров, картотек, кви-
танций и т. п. Если регистрация в том или ином виде проведена,
то для формирования простой случайной выборки можно ис-
пользовать таблицу случайных чисел, которая может быть взята
в готовом виде или сгенерирована с помощью компьютерной
программы.
Пример. Рассмотрим ситуацию, когда аудитору требуется полу-
чить случайную выборку из 50 записей финансовой отчетности
фирмы, состоящей из 1000 записей, пронумерованных пос-
17
ледовательно от 1 до 1000. В данном случае он может воспользо-
ваться таблицей случайных чисел, представленной в Приложе-
нии 1.
Зафиксируем произвольную позицию в таблице, например
ряд 5, колонка 3 (24127). Далее составим список из 50 случай-
ных чисел, произвольным образом двигаясь по таблице. В каж-
дом выбранном пятизначном числе для отделения дробной
части поставим запятую между третьим и четвертым знаками
и затем округлим полученное дробное число до ближайшего
целого. Например, первое выбранное число 24127 запишем в
виде 241,127 и затем округлим его до 241. Отобранные таким
образом трехзначные числа будут порядковыми номерами за-
писей финансовой отчетности, образующих случайную вы-
борку.
Кроме собственно случайного отбора существуют и другие
методы организации выборки. Например, к ним относятся си-
стематический, экспертный, районированный и многоступен-
чатый отборы.
Систематический отбор предполагает формирование вы-
борки согласно некоторому плану. Он может использоваться,
когда получение простой случайной выборки затруднительно
или связано с большими издержками. Например, пусть гене-
ральная совокупность состоит из 2000 накладных, которые
хранятся в специальных выдвижных ящиках. Пусть требуется
осуществить случайный отбор 100 накладных для бухгалтерс-
кой проверки. Теоретически следует пронумеровать все наклад-
ные числами от 0 до 1999 и, используя таблицу случайных
чисел, отобрать среди них случайным образом 100 номеров.
Очевидно, эта процедура займет достаточно много времени.
Гораздо проще было бы, выдвигая ящики и механически про-
сматривая подряд все накладные, отбирать из них каждую
двадцатую. Систематический отбор может привести к тем же
результатам, что и случайный, если элементы генеральной
совокупности хорошо перемешаны. Однако если элементы рас-
положены в определенном порядке, то фактор случайности
уже не будет решающим.
При экспертном отборе в выборку включаются те едини-
цы, свойства которых в наибольшей степени соответствуют
целям исследования. Исследователь считает, что он включа-
ет в выборку именно такие элементы, что полученные на ее
18
основе выборочные характеристики будут наилучшими оцен-
ками соответствующих характеристик генеральной совокуп-
ности. Очевидно, экспертный отбор будет эффективен в слу-
чае небольших выборок и из небольших генеральных сово-
купностей. Используя экспертный отбор, исследователь
должен хорошо знать свойства отдельных элементов гене-
ральной совокупности. Экспертный отбор чаще всего приме-
няется в торговле.
Районированный отбор является разновидностью случайного.
При этом исследователь делит генеральную совокупность на
несколько “районов” и элементы, составляющие выборку, от-
бираются случайным образом не из всей генеральной совокуп-
ности как целого, а из каждого “района” отдельно. При опре-
деленных предпосылках районированный отбор может дать более
высокую точность результатов, чем простой случайный отбор.
Точность будет зависеть от того, как было проведено “райони-
рование”. Общая оценка анализируемого параметра генераль-
ной совокупности находится (с помощью специальных спосо-
бов) как объединение выборочных оценок по каждому “району”.
Часто для статистического анализа представляет интерес оценка
параметров не только для всей совокупности, но и для отдель-
ных “районов”. Районированный отбор используется при со-
циологических опросах, когда районирование может произво-
диться по территориальному, социальному и демографическому
признакам.
При многоступенчатом отборе реализуется процедура несколь-
ких последовательных случайных отборов, причем извлечение
единиц в выборку происходит на последней стадии озбора. На-
пример, необходимо обследовать областные города. Такой отбор
может быть проведен в три ступени: единицы отбора первой
ступени — края, единицы отбора второй ступени — области,
единицы отбора третьей ступени (составляющие выборку) —
Областные города. Данный метод не увеличивает точность оцен-
ки по сравнению с простым случайным отбором, но его приме-
нение может существенно сократить затраты на проведение об-
следования.
С уществует еще несколько методов отбора выборки, кото-
рые по сути являются комбинацией описанных выше спосо-
бов В дальнейшем в статистических заключениях будем счи-
шть, что выборка получена на основе простого случайного
отбора.
19
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 1
Статистический анализ направлен на изучение количествен-
ного аспекта массовых явлений. В нем можно выделить два ос-
новных направления: описательная и аналитическая статисти-
ка. Описательная статистика представляет собой статистическое
описание какого-либо явления на основе только тех данных,
которые были собраны. К методам статистического описания
относится представление данных в виде таблиц, графиков и
обобщающих показателей.
В основе аналитической статистики лежит статистическое
заключение или выборочный метод. Это направление связано с
использованием методов математической статистики. Осново-
полагающими понятиями здесь являются генеральная совокуп-
ность и выборочная совокупность (выборка). Генеральная сово-
купность включает в себя все единицы, которые соответствуют
данному явлению. Термин “выборка” используется для обозна-
чения части генеральной совокупности. Методология этого на-
правления заключается в том, что с помощью математико-ста-
тистических методов на основе данных выборки делаются
выводы о признаках и свойствах генеральной совокупности. При
этом выборка должна удовлетворять требованию случайности,
т. е. отбор элементов в нее должен производиться случайным
образом.
Единицы генеральной совокупности могут характеризоваться
некоторым варьирующим признаком, который изменяется от
одной единицы совокупности к другой. Признаки могут иметь
количественное и качественное содержание. Количественные
измерения значений признака, а также различных обобщен-
ных показателей совокупности представляют собой исходные
данные для статистического анализа. Анализируемые данные
можно разделить на две основные категории — дискретные и
непрерывные. Дискретные данные выражаются в виде целых
положительных чисел. Они используются для кодирования и
подсчета каких-либо единиц. Непрерывные данные непрерыв-
но заполняют некоторый промежуток. Они получаются при
измерении непрерывных переменных (например, времени, га-
баритов изделий и т. д.).
Численные данные классифицируются по уровням изме-
рения, которые определяют тип шкалы измерений. Выделяют
шкалу наименований, порядковую шкалу, шкалы интервалов
и отношений. Шкала наименований используется для описа-
20
ния качественных данных, характеризующих принадлежность
элементов совокупности к каким-либо классам или категори-
ям; порядковая шкала — для упорядочения (ранжирования)
объектов; шкалы интервалов и отношений — для определе-
ния меры различия между значениями признака. С помощью
последних можно измерять, на сколько (шкала интервалов)
и во сколько раз (шкала отношений) значение признака, ха-
рактеризующего одну единицу совокупности, превосходит зна-
чение признака для другой единицы. Использование типа шка-
лы зависит от содержания измеряемого признака. Если он носит
качественный характер, то прибегают к шкалам наименова-
ний и порядка (качественные данные), если количественный —
к шкалам интервалов и отношений (количественные данные).
По источникам получения данные можно классифицировать
как первичные и вторичные. Первичные данные собираются
непосредственно в результате проведения специально ори-
ентированных опросов, интервью, наблюдений и экспери-
ментальных исследований. Вторичные данные собираются из
различных информационных источников: периодических пе-
чатных изданий финансового, экономического и социоло-
гического характера. Вторичные данные всегда предварительно
собираются, записываются и публично представляются в оп-
ределенной форме. Первичные данные, как правило, более
адекватны анализируемой проблеме, однако их получение
менее удобно и требует больших затрат по сравнению со вто-
ричными.
Для выборочного метода важнейшим условием является реп-
резентативность (представительность) выборки. Она означает,
что выборка должна в максимальной степени отражать свой-
ства и структуру генеральной совокупности. Репрезентативность
достигается с помощью объективного отбора, т. е. принципа
равных возможностей попадания в выборку единиц генераль-
ной совокупности. Тип выборки определяется способом отбора
данных. Если из генеральной совокупности элементы, состав-
ляющие выборку, отбираются случайным образом, то такой
отбор называется случайным, или собственно случайным. В ре-
зультате формируется простая случайная выборка, или собствен-
но случайная выборка.
Кроме простого случайного отбора существуют другие спо-
собы организации выборки, например: систематический, экс-
пертный, районированный и многоступенчатый отборы. Сис-
тематический по своей сути является механическим отбором,
21
который производится по какому-либо плану. Например, если
каждому элементу генеральной совокупности приписать поряд-
ковый номер, то в выборку может попасть каждый пятый эле-
мент. Экспертный отбор заключается в выборке по субъектив-
ному мнению исследователя. Он решает, какие элементы
должны составлять выборку, чтобы полученные выборочные
характеристики дали наилучшую оценку соответствующей ха-
рактеристики генеральной совокупности. При районированном
отборе случайная выборка извлекается не из всей генеральной
совокупности как целого, а из двух или нескольких “районов”,
на которые исследователь делит всю генеральную совокупность.
Метод многоступенчатого отбора включает ряд стадий или сту-
пеней, при этом извлечение единиц совокупности в выборку
происходит на последней стадии.
TAAZA
ГРУППИРОВКА
И ГРАФИЧЕСКОЕ
ПРЕДСТАВЛЕНИЕ ДАННЫХ
2.1. РЯД РАСПРЕДЕЛЕНИЯ
В предыдущей главе были рассмотрены основные понятия,
связанные с представлением и сбором статистических данных.
Собранные данные являются исходной информацией для про-
ведения статистических исследований. Как правило, эта инфор-
мация представляет собой хаотический набор данных. Очевид-
но, начальным этапом се обработки должна быть систематизация
беспорядочной массы чисел с целью придания ей удобной фор-
мы и структуры для проведения первичного анализа, смысл
которого заключается в оценке данных в связи с исследуемой
проблемой и облегчении сравнения с другими данными того же
рода. Например, пусть имеются две совокупности данных, одна
из которых отражает доходы всех семей страны А, а другая —
страны В. Численность каждой совокупности может составлять
несколько миллионов числовых значений. Требуется сделать об-
щие заключения о структуре распределения семейных доходов
каждой страны и провести сравнительный анализ семейных до-
ходов этих стран. Ясно, что без определенной обработки и обоб-
щения всей этой огромной массы чисел никакой анализ невоз-
можен. Необходимо сжать исходную информацию, т. е. представить
ее в виде существенно меньшего по численности набора дан-
ных, которые было бы легко и удобно интерпретировать.
Основным способом обобщения и сжатия статистической
информации является группировка данных или построение ряда
распределения. Ряд распределения (вариационный ряд) пред-
ставляет собой упорядоченное распределение единиц совокуп-
ности на группы по какому-либо варьирующему признаку, име-
ющему количественное выражение. Каждой группе соответствует
определенная частота, т. е. количество единиц совокупности, для
которых значения признака принадлежат этой группе.
23
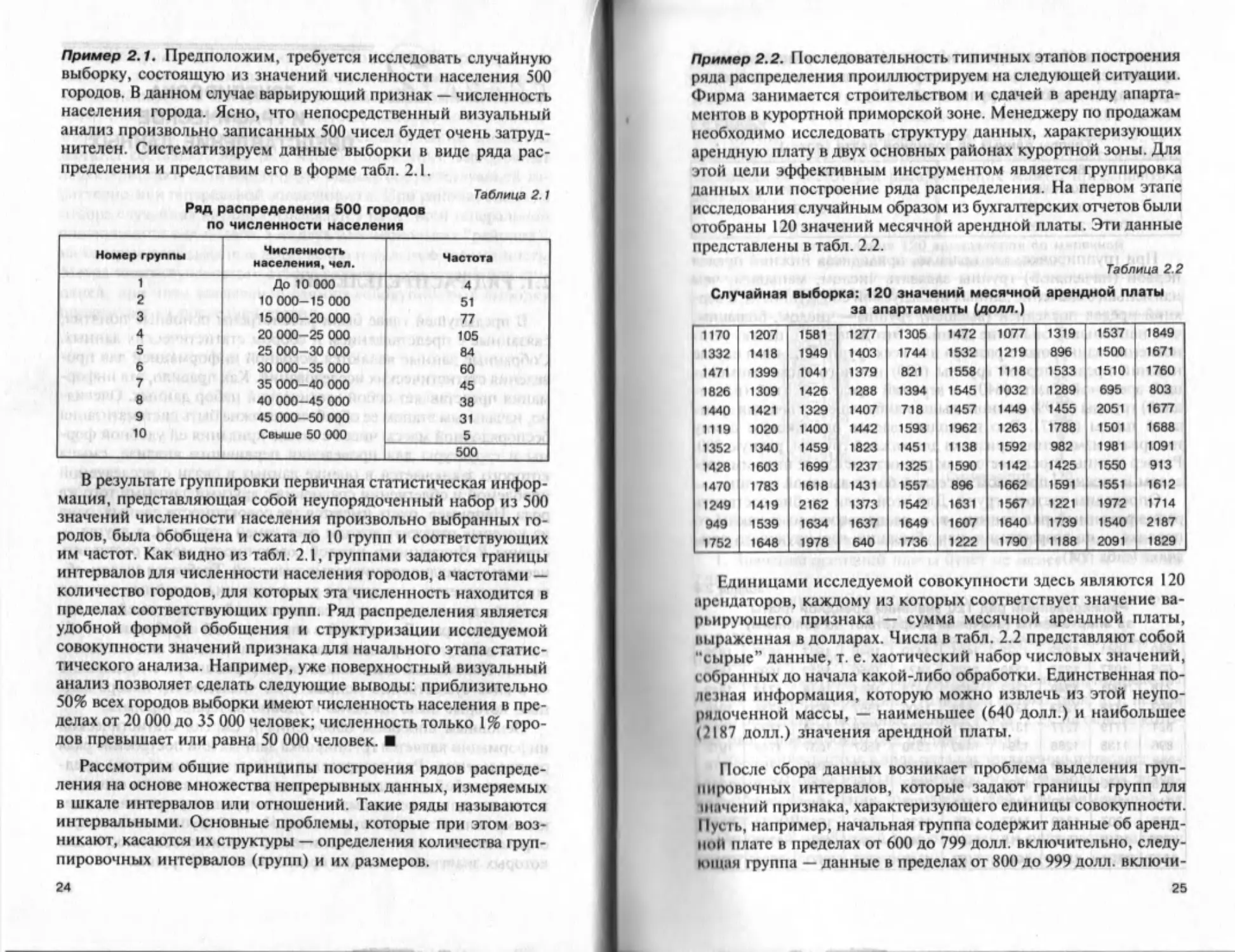
Пример 2.1. Предположим, требуется исследовать случайную
выборку, состоящую из значений численности населения 500
городов. В данном случае варьирующий признак — численность
населения города. Ясно, что непосредственный визуальный
анализ произвольно записанных 500 чисел будет очень затруд-
нителен. Систематизируем данные выборки в виде ряда рас-
пределения и представим его в форме табл. 2.1.
Таблица 2.1
Ряд распределения 500 городов
по численности населения
Номер группы Численность населения, чел. Частота
1 До 10 000 4
2 10 000-15 000 51
3 15 000-20 000 77
4 20 000-25 000 105
5 25 000 30 000 84
6 30 000-35 000 60
7 35 000-40 000 45
8 40 000-45 000 38
9 45 000-50 000 31
10 Свыше 50 000 5
500
В результате группировки первичная статистическая инфор-
мация, представляющая собой неупорядоченный набор из 500
значений численности населения произвольно выбранных го-
родов, была обобщена и сжата до 10 групп и соответствующих
им частот. Как видно из табл. 2.1, группами задаются границы
интервалов для численности населения городов, а частотами —
количество городов, для которых эта численность находится в
пределах соответствующих групп. Ряд распределения является
удобной формой обобщения и структуризации исследуемой
совокупности значений признака для начального этапа статис-
тического анализа. Например, уже поверхностный визуальный
анализ позволяет сделать следующие выводы: приблизительно
50% всех городов выборки имеют численность населения в пре-
делах от 20 000 до 35 000 человек; численность только 1% горо-
дов превышает или равна 50 000 человек.
Рассмотрим общие принципы построения рядов распреде-
ления на основе множества непрерывных данных, измеряемых
в шкале интервалов или отношений. Такие ряды называются
интервальными. Основные проблемы, которые при этом воз-
никают, касаются их структуры — определения количества груп-
пировочных интервалов (групп) и их размеров.
24
Пример 2.2. Последовательность типичных этапов построения
ряда распределения проиллюстрируем на следующей ситуации.
Фирма занимается строительством и сдачей в аренду апарта-
ментов в курортной приморской зоне. Менеджеру по продажам
необходимо исследовать структуру данных, характеризующих
арендную плату в двух основных районах курортной зоны. Для
этой цели эффективным инструментом является группировка
данных или построение ряда распределения. На первом этапе
исследования случайным образом из бухгалтерских отчетов были
отобраны 120 значений месячной арендной платы. Эти данные
представлены в табл. 2.2.
Таблица 2.2
Случайная выборка: 120 значений месячной арендной платы
за апартаменты (долл.)
1170 1207 1581 1277 1305 1472 1077 1319 1537 1849
1332 1418 1949 1403 1744 1532 1219 896 1500 1671
1471 1399 1041 1379 821 1558 1118 1533 1510 1760
1826 1309 1426 1288 1394 1545 1032 1289 695 803
1440 1421 1329 1407 718 1457 1449 1455 2051 1677
1119 1020 1400 1442 1593 1962 1263 1788 1501 1688
1352 1340 1459 1823 1451 1138 1592 982 1981 1091
1428 1603 1699 1237 1325 1590 1142 1425 1550 913
1470 1783 1618 1431 1557 896 1662 1591 1551 1612
1249 1419 2162 1373 1542 1631 1567 1221 1972 1714
949 1539 1634 1637 1649 1607 1640 1739 1540 2187
1752 1648 1978 640 1736 1222 1790 1188 2091 1829
Единицами исследуемой совокупности здесь являются I20
арендаторов, каждому из которых соответствует значение ва-
рьирующего признака — сумма месячной арендной платы,
выраженная в долларах. Числа в табл. 2.2 представляют собой
"сырые" данные, т. е. хаотический набор числовых значений,
собранных до начала какой-либо обработки. Единственная по-
лезная информация, которую можно извлечь из этой неупо-
рядоченной массы, — наименьшее (640 долл.) и наибольшее
(2I87 долл.) значения арендной платы.
После сбора данных возникает проблема выделения груп-
пировочных интервалов, которые задают границы групп для
(ничений признака, характеризующего единицы совокупности.
Пусть, например, начальная группа содержит данные об аренд-
ной плате в пределах от 600 до 799 долл, включительно, следу-
ющая группа — данные в пределах от 800 до 999 долл, включи-
25
тельно и т. д. Каждая группа имеет нижний и верхний пределы,
причем верхний предел каждой группы отличается от нижнего
предела последующей группы (табл. 2.3).
Таблица 2.3
Группы данных об арендной плате (долл.)
600-799 1400-1599
800-999 1600-1799
1000-1199 1800-1999
1200-1399 2000-2199
При группировке, как правило, приходится нижний предел
первой (начальной) группы задавать числом, меньшим, чем
наименьшее значение данных исследуемой совокупности, а вер-
хний предел последней (высшей) группы— числом, большим,
чем наибольшее значение данных. Это делается с целью уста-
новления одинакового размера для всех групп. В данном случае
нижний предел первой группы (600) немного ниже наимень-
шей арендной платы (640), а верхний предел десятой (после-
дней) группы (2199) немного выше наибольшего значения арен-
дной платы (2187). Это позволяет задать одинаковую длину
интервала изменения признака для каждой группы, равную 200.
Размер группы определяется как разность между ее нижним пре-
делом и нижним пределом соседней более высокой группы.
Определим частоты групп. Для этой цели удобно составить
ранжированный ряд данных, т. е. расположить их в каком-то
порядке — по возрастанию или убыванию варьирующего при-
знака (табл. 2.4).
Таблица 2.4
Ранжированный ряд 120 значений арендной платы
за апартаменты (значения возрастают по колонкам)
640 1041 1222 1332 1421 1470 1545 1607 1677 1826
695 1077 1237 1340 1425 1471 1550 1612 1699 1829
718 1091 1249 1352 1426 1472 1551 1618 1714 1849
803 1118 1263 1373 1428 1500 1557 1631 1736 1949
821 1119 1277 1379 1431 1501 1558 1634 1739 1962
896 1138 1288 1394 1440 1510 1567 1637 1744 1972
896 1142 1289 1399 1442 1532 1581 1640 1752 1978
913 1170 1305 1400 1449 1533 1590 1648 1760 1981
949 1188 1309 1403 1451 1537 1591 1649 1783 2051
982 1207 1319 1407 1455 1539 1592 1662 1788 2091
1020 1219 1325 1418 1457 1540 1593 1668 1790 2162
1032 1221 1329 1419 1459 1542 1603 1671 1823 2187
26
Просматривая данные табл. 2.4 последовательно по колон-
кам, легко подсчитать количество чисел (т. е. число арендато-
ров), попавших в границы каждой группы. Так, например, в
интервал от 600 до 799 попадают числа 640, 695, 718 (частота
1-й группы — 3); в интервал от 800 до 999 — числа 803, 821,
896, 896, 913, 949, 982 (частота 2-й группы — 7) и т. д. После
определения частот ряд распределения можно представить в
виде табл. 2.5.
Таблица 2.5
Ряд распределения 120 арендаторов по месячной
арендной плате за апартаменты
Месячная арендная плата, долл. Частота
600-799 3
800-999 7
1000-1199 11
1200-1399 22
1400-1599 40
1600-1799 24
1800-1999 9
2000-2109 4
Сумма частот — 120
На основе ряда распределения, представленного в табл. 2.5,
менеджер по продажам может сделать следующие заключения.
1. Значение арендной платы будет не менее 600 и не более
2200 долл.
2. Подавляющее большинство арендаторов платят за апарта-
менты в пределах от 1000 до 1800 долл, в месяц.
3. Наибольшее число арендаторов принадлежат группе с гра-
ницами 1400—1599 долл.
Следует отметить, что при группировке данных происходит
потеря части информации. Пользуясь только табл. 2.5, нельзя
точно определить исходные данные (табл. 2.2), на основе кото-
рых был сформирован ряд распределения.
Обобщение данных в виде ряда распределения позволяет сде-
лать выводы относительно наименьших и наибольших значе-
ний признака, а также зон наибольшей или наименьшей их
концентрации.
Основной проблемой при построении ряда распределения
является проблема построения группировочных интервалов.
27
В частности, возникает вопрос определения границ между груп-
пами. Для ряда распределения (табл. 2.5) границы каждой груп-
пы задавались его нижним и верхним пределами: 600—799, SOO-
999 и т. д. Значения арендной платы были округлены до
ближайших целых чисел. Например, величина 799,5 округля-
лась до 800 и попадала во вторую группу, а все значения свыше
799, но меньше, чем 799,5, округлялись до 799 и относились к
первой группе. Таким образом, группа 600—799 фактически со-
стоит из всех значений от 599,5 (включительно) до 799,5 (не
включая 799,5). Аналогично следующая группа 800—999 содер-
жит на самом деле значения от 799,5 (включительно) до 999,5
(не включая 999,5). В отличие от пределов, которые иногда на-
зывают номинальными границами, фактические границы груп-
пы являются ее точными границами. Точная нижняя граница
группы располагается посередине между ее нижним пределом
и верхним пределом предыдущей группы, а точная верхняя —
между ее верхним пределом и нижним пределом последующи
группы.
Для сравнения пределов групп и их точных границ рассмот-
рим ряд распределения, представленный в табл. 2.6.
Таблица 2.6
Пределы и точные границы групп ряда распределения
(табл. 2.5)
Пределы групп Точные границы групп Частота
600 799 599.5—799,5 (не включая) 3
800 999 799,5-999,5 (не включая) 7
1000—1199 999,5—1199,5 (не включая) 11
1200-1399 1199,5—1399,5 (не включая) 22
1400-1599 1399,5—1599,5 (не включая) 40
1600-1799 1599,5—1799,5 (не включая) 24
1800-1999 1799,5—1999,5 (не включая) 9
2000-2199 1999,5—2199,5 (не включая) 4
Следует отметить, что размер группы можно определить,
вычитая ее нижний предел из нижнего предела последующей
группы, а также вычитая ее соответствующую точную ниж-
нюю границу из соответствующей точной нижней границы
последующей группы.
Выбор размеров групп или их числа является наиболее труд-
ной проблемой построения ряда распределения. Решая этот воп-
рос, следует руководствоваться принципом: необходимо выби-
28
рать такое число групп, чтобы распределение данных внутри
каждой группы было как можно ближе к равномерному. В этом
случае среднюю точку группы можно рассматривать как ти-
пичную величину признака, представляющую весь интервал
изменения признака в границах данной группы. Средняя точка
вычисляется как полусумма нижнего и верхнего пределов груп-
пы или ее точных нижней и верхней границ. Среднюю точку
часто называют меткой группы, и ею пользуются в вычислени-
ях и построениях графиков, где она представляет все данные,
принадлежащие этой группе.
Очень важно, особенно при графической иллюстрации груп-
пировки, чтобы все группы имели одинаковый размер. Однако
при этом могут получиться “пустые группы” или группы, ко-
торым соответствуют “провалы” в распределении частот. Тогда
возникает небходимость построения ряда распределения с раз-
ными по размеру группами. Особенно это касается больших по
размеру неоднородных совокупностей. В этом случае построен-
ный ряд содержит такое большое количество однородных ipynn,
что это смазывает общую структуру данных и сильно затрудня-
ет дальнейший статистический анализ.
Пример 2.3. В табл. 2.7 представлен ряд распределения количе-
ства налоговых поступлений в зависимости от величины скор-
ректированного (для уплаты налогов) валового дохода инди-
видов в некоторой условной стране.
Таблица 2.7
Распределение количества налоговых поступлений
в зависимости от величины скорректированного
валового дохода (долл.)
Группы скорректированных валовых доходов Число налоговых поступлений, тыс. ед.
До 2 000 135
2 000-2 999 3 399
3 000-4 999 8 179
5 000- 9 999 19 740
10 000-14 999 15 539
15 000-24 999 14 944
25 000 49 999 4 451
50 000-99 999 699
100 000-499 999 162
500 000 999 999 3
1 000 000 и свыше 1
29
Как видно из табл. 2.7, в случае выбора одинакового размера
для всех групп (например, 1000) ряд распределения имел бы
такое громадное их число, что это сделало бы его практически
бесполезным для анализа.
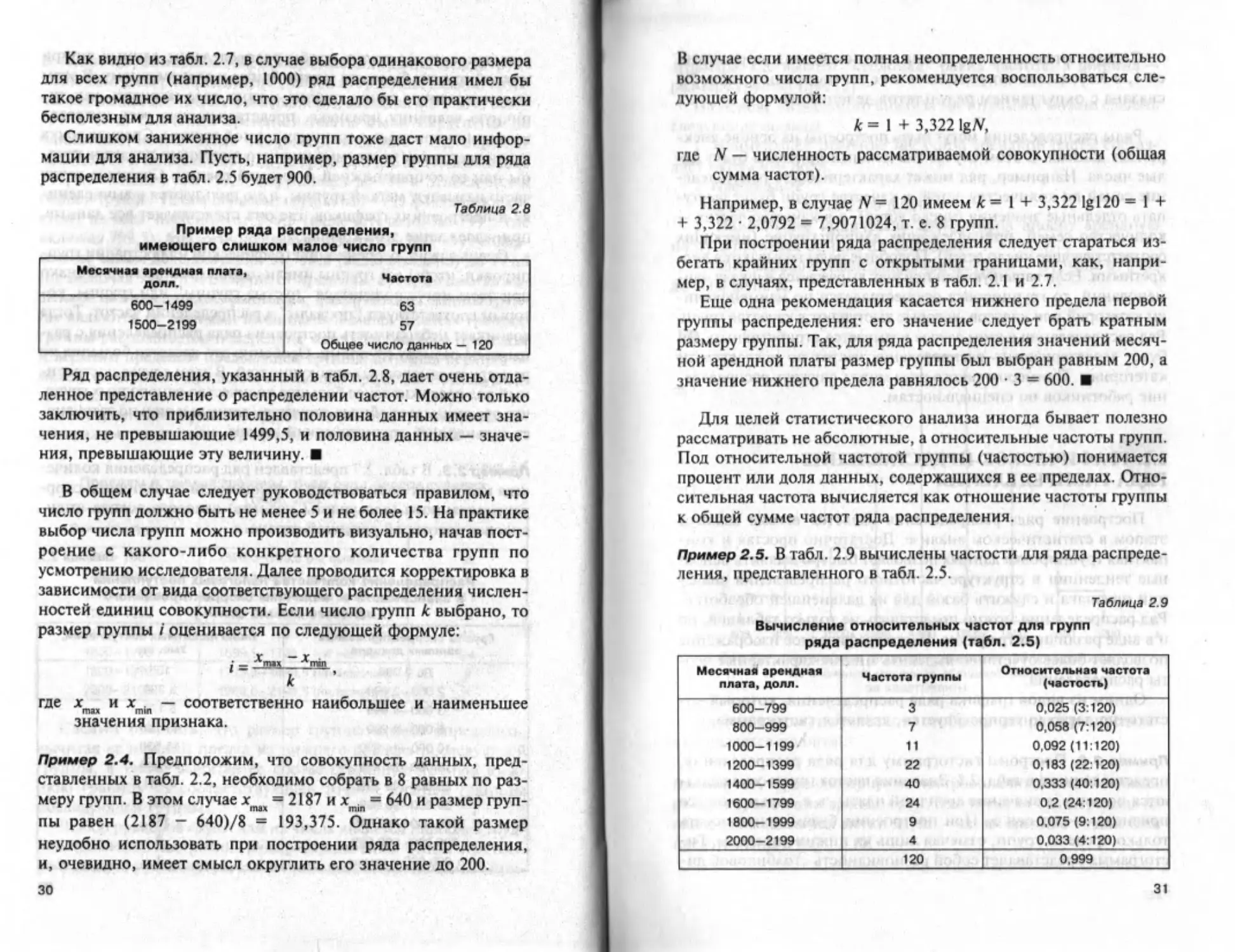
Слишком заниженное число групп тоже даст мало инфор-
мации для анализа. Пусть, например, размер группы для ряда
распределения в табл. 2.5 будет 900.
Таблица 2.8
Пример ряда распределения,
имеющего слишком малое число групп
Месячная арендная плата, долл. Частота
600—1499 1500-2199 63 57 Общее число данных — 120
Ряд распределения, указанный в табл. 2.8, дает очень отда-
ленное представление о распределении частот. Можно только
заключить, что приблизительно половина данных имеет зна-
чения, не превышающие 1499,5, и половина данных — значе-
ния, превышающие эту величину.
В общем случае следует руководствоваться правилом, что
число групп должно быть не менее 5 и не более 15. На практике
выбор числа групп можно производить визуально, начав пост-
роение с какого-либо конкретного количества групп по
усмотрению исследователя. Далее проводится корректировка в
зависимости от вида соответствующего распределения числен-
ностей единиц совокупности. Если число групп к выбрано, то
размер группы / оценивается по следующей формуле:
i - inm.
к
где х их.— соответственно наибольшее и наименьшее
max min
значения признака.
Пример 2.4. Предположим, что совокупность данных, пред-
ставленных в табл. 2.2, необходимо собрать в 8 равных по раз-
меру групп. В этом случае хмх = 2187 и xmin = 640 и размер груп-
пы равен (2187 — 640)/8 = 193,375. Однако такой размер
неудобно использовать при построении ряда распределения,
и, очевидно, имеет смысл округлить его значение до 200.
зо
В случае если имеется полная неопределенность относительно
возможного числа групп, рекомендуется воспользоваться сле-
дующей формулой:
к = 1 + 3,322 lg/V,
где N — численность рассматриваемой совокупности (общая
сумма частот).
Например, в случае ^ = 120 имеем к = I + 3,322 Igl20 = 1 +
+ 3,322 • 2,0792 = 7,9071024, т. е. 8 групп.
При построении ряда распределения следует стараться из-
бегать крайних групп с открытыми границами, как, напри-
мер, в случаях, представленных в табл. 2.1 и 2.7.
Еще одна рекомендация касается нижнего предела первой
группы распределения: его значение следует брать кратным
размеру группы. Так, для ряда распределения значений месяч-
ной арендной платы размер группы был выбран равным 200, а
значение нижнего предела равнялось 200 • 3 = 600.
Для целей статистического анализа иногда бывает полезно
рассматривать не абсолютные, а относительные частоты групп.
Под относительной частотой группы (частостью) понимается
процент или доля данных, содержащихся в ее пределах. Отно-
сительная частота вычисляется как отношение частоты группы
к общей сумме частот ряда распределения.
Пример 2.5. В табл. 2.9 вычислены частости для ряда распреде-
ления, представленного в табл. 2.5.
Таблица 2.9
Вычисление относительных частот для групп
ряда распределения (табл. 2.5)
Месячная арендная плата, долл. Частота группы Относительная частота (частость)
600-799 3 0,025 (3:120)
800-999 7 0,058 (7:120)
1000-1199 11 0,092 (11:120)
1200-1399 22 0,183 (22:120)
1400-1599 40 0,333 (40:120)
1600-1799 24 0,2 (24:120)
1800-1999 9 0,075 (9:120)
2000-2199 4 0,033 (4:120)
120 0,999
31
Следует отметить, что сумма частостей должна равнять-
ся 1, а небольшая погрешность в ее вычислении в табл. 2.9
связана с округлением результатов делений.
Ряды распределения могут быть построены на основе диск-
ретных данных. В этом случае значениями признака будут це-
лые числа. Например, ряд может характеризовать распределе-
ние семей по количеству детей: в качестве групп будут высту-
пать отдельные значения (число детей), а в качестве частот —
количество семей, принадлежащих данной группе (имеющих
соответствующее число детей). Подобные ряды называются дис-
кретными. Если варьирующий признак выражается в шкале наи-
менований, то группировка осуществляется по наименовани-
ям категорий или классов, которые выступают в качестве групп.
Ряд распределения в этом случае называется атрибутивным. Он
будет характеризовать распределение частот по исследуемым
категориям. Примером такого ряда может служить распределе-
ние работников по специальностям.
2.2. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
РЯДА РАСПРЕДЕЛЕНИЯ
Построение ряда распределения является весьма важным
этапом в статистическом анализе. Достаточно простая и ком-
пактная группировка данных позволяет быстро выявить основ-
ные тенденции в структуре частотного распределения значе-
ний признака и служить базой для их дальнейшей обработки.
Ряд распределения можно представить не только таблицей, но
и в виде различных (рафиков. Часто графическое изображение
позволяет более отчетливо выделить многие характерные чер-
ты распределения.
Одним из видов графика ряда распределения, который до-
статочно легко интерпретируется, является гистограмма.
Пример 2.6. Построим гистограмму дтя ряда распределения,
представленного в табл. 2.5. Значения частот групп откладыва-
ются по оси у, а значение арендной платы, т. е. варьирующего
признака, — по оси х. При построении будем использовать
только пределы групп, отмечая лишь их нижние пределы. Ги-
стограмма представляет собой разновидность столбиковой ди-
32
аграммы. где высота “столбика” равна частоте, а ширина —
размеру группы (рис. 2).
На основе визуального анализа гистограммы можно сделать
следующие выводы.
I. Наименьшее значение месячной арендной платы состав-
ляет около 600 долл.
2. Наибольшее
значение — около 2200 долл.
3. Наибольшее количество арендаторов вносит арендную
плату в пределах от 1200 до 1800 долл.
4. Наибольшая концентрация арендаторов — в группе от 1400
до 1600 долл.
Рис 2.1. Гистограмма ряда распределения 120 арендаторов
по значению месячной арендной платы
за апартаменты
Другим видом графического отображения ряда распределе-
ния является полигон.
Пример 2.7. Проиллюстрируем построение полигона на приме-
ре о распределении арендаторов. В отличие от гистограммы на
оси х откладываются метки групп, т. е. их средние точки. Они
представлены в табл. 2.10.
зз
Таблица 2.10
Группы, их средние точки и частоты
(данные для построения полигона)
Пределы группы Средняя точка Частота
600-799 699.5 3
800-999 899,5 7
1000-1199 1099,5 11
1200-1399 1299,5 22
1400-1599 1499,5 40
1600-1799 1699.5 24
1800-1999 1899,5 9
2000-2199 2099,5 4
График полигона (рис. 2.2) строится следующим образом.
На оси х откладываются средние точки групп. Из каждой точки
восстанавливается к оси х перпендикуляр, длина которого рав-
на частоте группы. Затем верхние концы соседних перпендику-
ляров соединяются отрезками прямых. Для того чтобы график
полигона был замкнут, вводятся дополнительные фиктивные
группы: самая нижняя группа размером 200 (400—599) со сред-
ней точкой 499,5 и самая верхняя группа того же размера 200
(2200—2399) со средней точкой 2299,5.
Рис. 2.2. Г рафик полигона для распределения
120 арендаторов апартаментов
34
Графическое представление ряда распределения в виде гис-
тограммы или полигона позволяет получить быстрый визуальный
анализ основных характеристик распределения данных: наиболь-
шее и наименьшее значения, точки концентрации и т. д.
Следует отметить, что гистограмма имеет определенные пре-
имущества по сравнению с полигоном в смысле большей на-
глядности изображения групп. На гистограмме каждая группа
четко обозначена соответствующим столбиком: высота столби-
ка дает представление о частоте группы, ширина столбика и его
расположение на оси х — о размере и границах группы. Однако
использование графика полигона будет более предпочтительным
при сравнительном анализе двух и более рядов распределений.
Пример 2.8. Обратимся опять к ситуации с арендаторами. Слу- •
чайная выборка из 120 арендаторов была составлена из лиц,
снимающих апартаменты в двух различных районах курортной
зоны (обозначим их район 1 и район 2). Пусть менеджера по
продажам интересует сравнительный анализ условий сдачи в
аренду апартаментов в этих районах. Предположим, что слу-
чайная выборка была разделена на две совокупности, в одну из
которых вошли лица, арендующие апартаменты в районе 1, а в
другую — в районе 2. Для каждой группы арендаторов постро-
им отдельный ряд распределения и соответствующий ему гра-
фик полигона. Оба графика поместим на одной координатной
плоскости (рис. 2.3).
Рис. 2.3. Графики полигонов для рядов распределений
двух районов курортной зоны
35
Из рис. 2.3 видно, что величина месячной арендной платы в
районе 2 в целом выше, чем в районе I.
В примере 2.8 исследуемые ряды распределений имеют оди-
наковые размеры групп и приблизительно равные общие суммы
частот. Выполнение этих условий дает возможность визуально
сравнивать формы графиков полигонов. В случае когда общие
суммы частот (т. е. численности совокупностей, на основе кото-
рых были построены ряды распределений) значительно отлича-
ются друг от друга, следует величины абсолютных частот заме-
нить на их относительные значения (относительные частоты).
Ряд распределения, а также гистограмма и полигон не дают
возможности ответить на вопросы, подобные следующим. Сколь-
ко единиц совокупности имеет значение признака, превыша-
ющее заданное число? Какой процент составляют единицы
совокупности, значения признака которых меньше определен-
ной величины?
Для ответа на подобные вопросы вычисляются кумулятив-
ные (накопленные) частоты ряда распределения и строится
график кумулятивного частотного полигона, который иногда
называют кумулятой. Кумулятивный частотный полигон, или
просто кумулятивный полигон, используется для оценки чис-
ла наблюденных значений, которые превышают или остаются
меньше некоторой величины. В этой связи различают два типа
кумулятивных полигонов: “меньше, чем ...” и “более, чем ...”.
Пример 2.9. Построим кумулятивный полигон типа “меньше,
чем ...” для ряда распределения арендаторов (табл. 2.6). Три че-
ловека платят за апартаменты в пределах от 600 до 799 долл.,
т. е. попадают в 1-ю группу. Учитывая точные границы 1-й груп-
пы, можно утверждать, что величина арендной платы для каж-
дого из них находится в интервале от 595,5 до 799,5 долл, (не
включая 799,5). Кроме того, очевидно, что нет ни одного арен-
датора, платившего менее 599,5 долл, в месяц. Поэтому можно
выделить следующие группы, имеющие только точные верх-
ние границы: 0 арендаторов попали в группу “меньше, чем
595,5 долл.”; 3 арендатора попали в группу “меньше, чем 795,5
долл.”. Прибавим к 3 арендаторам 1-й группы 7 арендаторов
2-й группы (800—999). Очевидно, эти 10 арендаторов попадают
в новую группу “меньше, чем 999,5 долл.”. Кумулятивная час-
тота этой группы будет равна 10. Аналогично вычисляются ку-
мулятивные частоты остальных групп: последовательно сумми-
руются частоты групп исходного ряда распределения (табл. 2.11).
36
Таблица 2.11
Вычисление кумулятивных частот для кумулятивного полигона
типа “меньше, чем ...”
Месячная арендная плата, долл. Частоты групп Кумулятивные частоты Вычисления
Меньше, чем 599.5 0 0
Меньше, чем 799,5 3 3
Меньше, чем 999,5 7 10 3+7
Меньше, чем 1199,5 11 21 3+7+11
Меньше, чем 1399,5 22 43 3+7+11+22
Меньше, чем 1599,5 40 83 И т. п.
Меньше, чем 1799,5 24 107
Меньше, чем 1999,5 9 116
Меньше, чем 2199,5 4 120
Для построения полигона типа “меньше, чем ...” на коор-
динатной плоскости отметим точки, имеющие в качестве абс-
цисс точные верхние границы групп, а в качестве ординат —
соответствующие им кумулятивные частоты. Отрезки прямых,
соединяющие каждые две соседние точки, образуют график
полигона (рис. 2.4). Для удобства проведения анализа на <рафи-
ке поместим две оси ординат: слева — ось кумулятивных час-
тот, справа — ось кумулятивных частостей, выраженных в про-
центах.
Рис. 2.4. Кумулятивный полигон типа ‘меньше, чем ..."
37
На основе построенного полигона можно сделать следую-
щие оценки. Пусть, например, задается процент арендаторов
у0, для которого требуется найти пороговое значение месячной
арендной платы х0. Через точку у0 проведем прямую, парал-
лельную оси х, до пересечения с линией полигона. Затем из
точки пересечения опустим перпендикуляр на ось х, который
пересечет се в искомой точке х0 (рис. 2.4).
На графике, представленном на рис 2.4, в качестве конк-
ретных значений у(|были выбраны 50 и 75%. Им соответствова-
ли пороговые точки х0— 1500 и 1675 долл. Таким образом, 50%
арендаторов (60 человек) платят в месяц менее 1500 долл, и
75% (90 человек) — менее 1675 долл.
При построении другого типа кумулятивного полигона “бо-
лее, чем...” суммируются частоты групп в обратном порядке:
от высшей группы к низшей, а на оси х откладываются точные
нижние границы групп.
Пример 2. Ю. Построим кумулятивный полигон типа “более,
чем...” для ряда распределения арендаторов. Вычислим для
этого кумулятивные частоты от высшей группы к низшей
(табл. 2.12).
Таблица 2.12
Вычисление кумулятивных частот для кумулятивного полигона
типа “более, чем ..."
Арендная плата, долл. Частоты групп Кумулятивные частоты Вычисления
Более чем 599.5 3 120 4+9+24+40+22+11+7+3
Более чем 799.5 7 117 4+9+24+40+22+11+7
Более, чем 999,5 11 110 4+9+24+40*22+11
Более, чем 1199,5 22 99 4+9+24+40+22
Более, чем 1399,5 40 77 4+9+24+40
Более, чем 1599,5 24 37 4+9+24
Более, чем 1799,5 9 13 4+9
Более, чем 1999,5 4 4 4
Более, чем 2199,5 0 0 0
Отметим на оси х точные нижние границы групп и восста-
новим из них перпендикуляры, длины которых соответствуют
кумулятивным частотам (рис. 2.5).
38
Рис. 2.5. Кумулятивный полигон типа 'более, чем ...*
Предположим, что нужно определить, сколько арендаторов
платят за месяц более 1500 долл. Тогда из точки х = 1500 вос-
становим перпендикуляр до пересечения с полигоном. Затем
из точки пересечения опустим перпендикуляр на ось у, кото-
рый пересечет ее примерно в точке у = 57. Это означает, что не
менее чем 57 человек арендуют апартаменты более чем за
1500 долл, в месяц.
2.3. ДИАГРАММЫ КАК СПОСОБ ГРАФИЧЕСКОГО
ПРЕДСТАВЛЕНИЯ СТАТИСТИЧЕСКИХ ДАННЫХ
Гистограмма, полигон и кумулятивный полигон являются
разновидностями специального типа статистических графиков,
которые называются диаграммами. Диаграммы удобно исполь-
зовать для сравнительного анализа значений различных стати-
стических показателей, наглядного представления их динами-
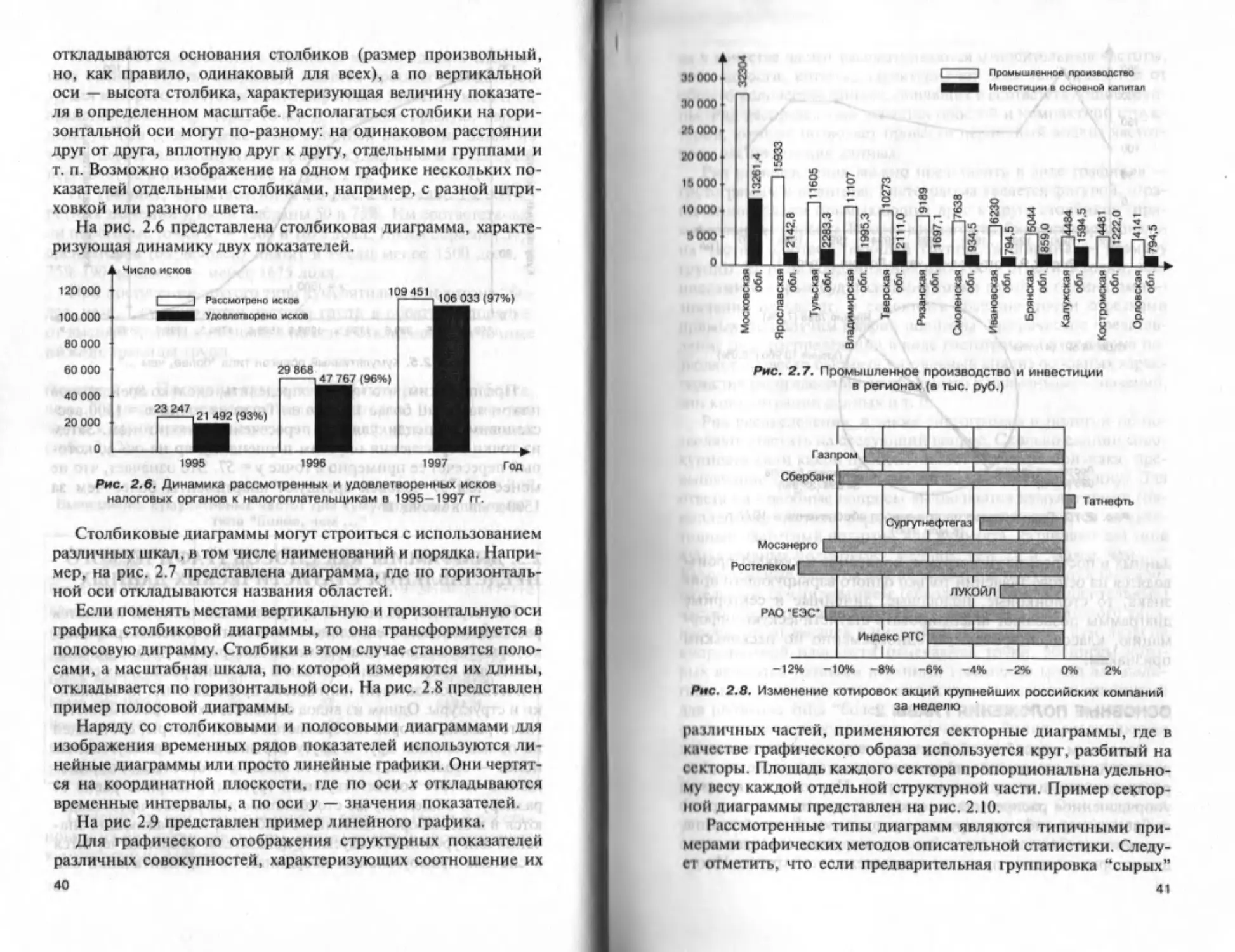
ки и структуры. Одним из видов столбиковых диаграмм является
гистограмма, которая изображается в виде фигуры, состоящей
из примыкающих друг к другу вертикальных прямоугольных
полос — столбиков, где высота каждого столбика пропорцио-
нальна частоте соответствующей группы, а ширина равна ее
размеру. В общем случае столбиковые диаграммы представля-
ются в виде набора отдельных столбиков, изображающих зна-
чения или уровни исследуемого показателя. Столбики чертятся
в системе прямоугольных координат: по горизонтальной оси
39
откладываются основания столбиков (размер произвольный,
но, как правило, одинаковый для всех), а по вертикальной
оси — высота столбика, характеризующая величину показате-
ля в определенном масштабе. Располагаться столбики на гори-
зонтальной оси могут по-разному: на одинаковом расстоянии
друг от друга, вплотную друг к другу, отдельными 1руппами и
т. п. Возможно изображение на одном графике нескольких по-
казателей отдельными столбиками, например, с разной штри-
ховкой или разного цвета.
На рис. 2.6 представлена столбиковая диаграмма, характе-
ризующая динамику двух показателей.
Рис. 2.6. Динамика рассмотренных и удовлетворенных исков
налоговых органов к налогоплательщикам в 1995—1997 гг.
Столбиковые диаграммы могут строиться с использованием
различных шкал, в том числе наименований и порядка. Напри-
мер, на рис. 2.7 представлена диаграмма, где по горизонталь-
ной оси откладываются названия областей.
Если поменять местами вертикальную и горизонтальную оси
графика столбиковой диаграммы, то она трансформируется в
полосовую диграмму. Столбики в этом случае становятся поло-
сами, а масштабная шкала, по которой измеряются их длины,
откладывается по горизонтальной оси. На рис. 2.8 представлен
пример полосовой диаграммы.
Наряду со столбиковыми и полосовыми диа<раммами для
изображения временных рядов показателей используются ли-
нейные диаграммы или просто линейные графики. Они чертят-
ся на координатной плоскости, где по оси х откладываются
временные интервалы, а по оси у — значения показателей.
На рис 2.9 представлен пример линейного графика.
Для графического отображения структурных показателей
различных совокупностей, характеризующих соотношение их
40
Рис. 2.7. Промышленное производство и инвестиции
в регионах (в тыс. руб.)
Рис. 2.8. Изменение котировок акций крупнейших российских компаний
за неделю
различных частей, применяются секторные диаграммы, где в
качестве графического образа используется круг, разбитый на
секторы. Площадь каждого сектора пропорциональна удельно-
му весу каждой отдельной структурной части. Пример сектор-
ной диаграммы представлен на рис. 2.10.
Рассмотренные типы диаграмм являются типичными при-
мерами графических методов описательной статистики. Следу-
ет отметить, что если предварительная группировка “сырых”
41
Рис. 2.10. Производство программного обеспечения в 1977 г.
(в млн экю)
данных и построение гистограмм, полигонов и кумулят произ-
водятся на основе значений только одного варьирующего при-
знака, то столбиковые, полосовые, линейные и секторные
диаграммы позволяют анализировать статистическую инфор-
мацию, классифицированную одновременно по нескольким
признакам.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 2
Основным способом обобщения и сжатия несистематизи-
рованной статистической информации является построение ряда
распределения, или вариационного ряда. Под этим понимается
упорядоченное распределение единиц совокупности на груп-
пы по какому-либо варьирующему признаку. Каждой группе
соответствует частота, т. е. количество единиц совокупности,
для которых значения признака принадлежат этой группе. Иног-
да
да в качестве частот рассматриваются относительные частоты,
или частости, которые характеризуют доли или проценты от
общего количества данных, попавших в соответствующие груп-
пы. Ряд распределения является простой и компактной струк-
турой, которая позволяет провести первичный анализ частот-
ного распределения данных.
Ряд распределения можно представить в виде графиков —
гистограммы и полигона. Гистограмма является фигурой, огра-
ниченной рядом примыкающих друг к другу столбиков (пря-
моугольных полосок). Высота каждого столбика пропорциональ-
на частоте соответствующей группы, а ширина — размеру
группы. Если на координатной плоскости отметить точки, абс-
циссами которых будут средние точки групп, а ординатами —
значения их частот, и соединить соседние точки отрезками
прямых, то получим график полигона. Графическое представ-
ление ряда распределения в виде гистограммы и полигона по-
зволяет провести быстрый визуальный анализ основных харак-
теристик распределения: наибольшего и наименьшего значений,
зон концентрации данных и т. п.
Ряд распределения, а также гистограмма и полигон не по-
зволяют ответить на следующий вопрос. Сколько единиц сово-
купности (или какой процент) имеет значения признака, пре-
вышающие (или не превышающие) заданную величину? Для
ответа на подобные вопросы вычисляются кумулятивные (на-
копленные) частоты ряда распределения и строится кумуля-
тивный частотный полигон, или кумулята. Рахтичают два типа
кумулятивных полигонов: “меньше, чем ...” и “более, чем ...”.
Кумулятивные частоты для первого типа получаются последо-
вательным суммированием (абсолютных или относительных)
частот групп от низшей группы к высшей, а для второго типа,
наооборот, от высшей к низшей. Для построения кумуляты на
координатной плоскости отмечаются точки, абсциссы кото-
рых являются точными верхними границами групп для поли-
гона типа “меньше, чем...” или точными нижними границами
для полигона типа “более, чем...”, а ординаты — значениями
соответствующих кумулятивных частот. Линия, соединяющая
эти точки, является кумулятивным полигоном.
В описательной статистике кроме гистограмм, полигонов и
кумулят используются другие разновидности диаграмм: стол-
биковые, полосовые, линейные и секторные. Они являются
удобным инструментом для анализа динамики показателей и
соотношения структурных частей исследуемых объектов.
ИЗМЕРЕНИЕ
ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ
В первых двух главах рассматривались типы статистических
данных, способы их измерения и обобщения. Систематизация
массы “сырых” данных в виде ряда распределения, его графи-
ческое представление в форме гистограммы, полигона и куму-
ляты, а также построение линейных, столбиковых, полосовых
и секторных диаграмм — все эти средства являются удобным
инструментарием для первичного визуального анализа свойств
совокупности.
Для того чтобы перейти к рассмотрению методов статисти-
ческого заключения, прежде всего следует изучить основные
количественные характеристики статистических совокупнос-
тей. Дело в том, что важнейшим направлением аналитичес-
кой статистики является оценка ключевых числовых характе-
ристик, отражающих свойства генеральной совокупности. Эти
характеристики, вычисленные на основе выборочных данных,
будут оценочными для соответствующих характеристик гене-
ральной совокупности, т. е. приближенно отражать свойства
генеральной совокупности. Каждая выборка представляет со-
бой некоторую часть большей по размеру генеральной сово-
купности. При статистическом анализе это обстоятельство все-
гда следует иметь в виду, даже если о генеральной совокупности
совсем не упоминается. Условимся в дальнейшем все те конк-
ретные характеристики, которые были вычислены на основе
данных генеральной совокупности, называть параметрами, а
вычисленные на основе выборочных данных — статистиками.
В этой главе будут рассмотрены количественные характерис-
тики, измеряющие центральную тенденцию распределения
данных. Центральная тенденция характеризует свойство дан-
ных скапливаться вокруг какого-то центрального значения.
Пусть центральная тенденция ярко выражена, т. е. данные в
подавляющем большинстве концентрируются около некото-
44
рого центрального значения, или центра. Тогда значение цен-
тра можно рассматривать как наиболее типичное для всей со-
вокупности. Это означает, что центр обладает способностью
представлять всю совокупность, и его можно использовать в
качестве сравнительной характеристики при сопоставлении
двух или более совокупностей, состоящих из качественно од-
нородных данных. Основными характеристиками, измеряю-
щими положение центра, в статистическом анализе являются
средняя арифметическая, медиана и мода.
3.1. ВЫЧИСЛЕНИЕ ЦЕНТРАЛЬНЫХ ЗНАЧЕНИЙ
ДЛЯ НЕСГРУППИРОВАННЫХ ДАННЫХ
3.1.1. Средняя арифметическая
Чаше всего для измерения центральной тенденции исполь-
зуется средняя арифметическая, которую, как правило, назы-
вают просто средней. Для “сырых”, т. е. несгруппированных,
данных средняя арифметическая получается суммированием всех
значений совокупности и делением этой суммы на общее чис-
ло данных.
Пусть выборочная совокупность состоит из л наблюдений:
Хр х2,..., хя. Тогда формула для вычисления средней арифмети-
ческой будет иметь вид
где х обозначает выборочную среднюю арифметическую (чи-
тается “х с чертой”);
л — численность, или объем, выборки;
х — любое из л значений совокупности;
S — знак суммирования (в статистической литературе ин-
Я
деке суммирования часто опускается, т. е. £х = х,).
i=i
Величина х является статистикой, так как она вычислена на
основе выборочных данных. Соответствующим параметром для
нее будет средняя генеральной совокупности ц, которая вы-
числяется по аналогичной формуле:
где N — численность, или объем, генеральной совокупности.
45
Генеральная средняя обозначается греческой буквой р. В даль-
нейшем будем придерживаться следующего принципа в обо-
значениях: все статистики (количественные выборочные харак-
теристики) будем обозначать латинскими буквами, а параметры
(количественные характеристики генеральной совокупности) —
греческими.
Пример 3.1. Автоматическая производственная линия напол-
няет пузырьки одеколоном. Случайным образом были отобра-
ны пять наполненных пузырьков, в которых чистый вес одеко-
лона составил 85,4, 85,3, 84,9, 85,4 и 85 г. Найти средний вес
одеколона в пузырьке для данной выборки из пяти наблюде-
ний.
По формуле (3.1) находим
_ 85,4 + 85,3 + 84,9 + 85.4 + 85 426 ое _
'*---------------------------.85,2 г.
Следовательно, средний арифметический вес для выборки
из пяти пузырьков составляет 85,2 г.
Средняя арифметическая обладает следующими свойствами.
I. Средняя арифметическая может быть вычислена в шкалах
интервалов и отношений (например, в таких шкалах измеря-
ются доходы, возраст, вес, габариты и т. п.).
2. При вычислении средней арифметической необходимо
использовать все данные рассматриваемой совокупности.
3. Множество данных может иметь единственное значение
средней арифметической (далее в главе будет показано, что
другой тип средней может иметь два или более значений для
одной и той же совокупности).
4. Средняя арифметическая является очень удобной характе-
ристикой для сравнения двух или более совокупностей, одина-
ковых по качественному составу значений признака (напри-
мер, при сравнении прозводительности труда работников
первой смены с производительностью труда работников вто-
рой смены на одном предприятии).
5. Средняя арифметическая есть единственная мера цент-
ральной тенденции, для которой сумма отклонений каждого
значения от нее всегда равна нулю. Математически это свой-
ство можно записать следующим образом:
£(х-х) = 0.
46
Пример 3.2. Средняя арифметическая чисел 3, 8 и 4 равна 5.
Вычислим сумму отклонений этих чисел от 5:
£(х-х) = (3-5) + (8-5) + (4-5) = -2 + 3-1=0.
При использовании средней арифметической в статистичес-
ком анализе всегда следует иметь в виду свойство 2. Если одно
или два крайних значения совокупности сильно отличаются от
всех остальных данных (крайнее правое значительно больше и
(или) крайнее левое значительно меньше всех остальных), то
средняя арифметическая не будет типичной величиной, пред-
ставляющей все множество данных.
Пример 3.3. Пусть годовые доходы пяти предпринимателей со-
ставляют 62 900, 61 600, 62 500, 60 800 и 1 200 000 долл. Сред-
ний арифметический годовой доход будет 289 560 долл. Оче-
видно, он не отражает доходы всей группы предпринимателей,
гак как все предприниматели, кроме одного, имеют доход в
интервале от 60 000 до 63 000 долл.
Особой формой средней арифметической является взвешен-
ная средняя арифметическая. Она вычисляется в случае, когда
изучаемая статистическая совокупность велика и ее можно раз-
бить на группы, имеющие постоянное значение признака.
Пусть вся совокупность разбита на л групп, имеющих зна-
чения признака хг,..., хяс численностями w(, (значе-
ния весов). Взвешенная средняя арифметическая вычисляется
по формуле
Н-.Х. + МЧХ» +... + W.X.
xw = —L-1--—--------—. (3.3)
W1 + w2+... + wB
Пример 3.4. Почасовая оплата продавцов на фирме дифферен-
цирована и составляет 6,5; 7,5 и 8,5 долл. Известно, что 14 про-
давцов имеют ставку 6,5 долл.; 10 — 7,5 и 2 — 8,5 долл. В каче-
стве средней арифметической почасовой ставки в данном случае
выступает взвешенная средняя арифметическая:
6,514 + 7,510 + 8,5-2 _ _.
х =--------------------» 7,04.
* 14 + 10 + 2
Таким образом, средняя почасовая ставка составляет при-
близительно 7,04 долл.
47
3.1.2. Медиана
При описании основных свойств средней арифметической
отмечалось, что выбор ее в качестве центра не имеет смысла,
если есть одна или две величины, одна из которых значительно
больше, а другая значительно меньше, чем все остальные дан-
ные. В этом случае в качестве более точной меры центральной
тенденции выбирается другой, структурный тип средних, ко-
торые определяются не как результат арифметических действий
над значениями признака. К такому типу относится медиана.
Для иллюстрации необходимости такого выбора рассмот-
рим следующую ситуацию.
Пример 3.5. Предположим, что некто хочет купить квартиру в
определенном районе. Из рекламы он получил информацию о
том, что в наличии имеется несколько апартаментов и их сред-
няя цена составляет 110 000 долл. Однако бюджет данного лица
позволяет купить квартиру по цене в пределах от 60 000 до 75 000
долл. На первый взгляд может показаться, что предлагаемые ва-
рианты ему не по карману. В действительности же на продажу
было предложено пять квартир по следующим ценам: 60 000,
65 000, 70 000, 80 000 и 275 000 долл. Очевидно, что средняя
арифметическая цена 110 000 долл, не является представитель-
ной для данного набора цен. Как раз более типичная цена нахо-
дится в пределах личного бюджета заинтересованного лица.
В подобных случаях следует в качестве центра рассматривать
другой тип центральной величины, которая называется медиа-
ной. Медиана характеризует величину, обладающую свойством:
слева от медианы находится ровно половина всех данных, ко-
торые меньше ее, и справа — половина всех данных, которые
ее больше. Для определения медианы следует из всего множе-
ства данных составить ранжированный ряд, т. е. упорядочить
данные либо последовательно по возрастанию: от наименьше-
го значения к наибольшему, либо, наоборот, последовательно
по убыванию: от наибольшего к наименьшему. Если последо-
вательно пронумеровать все члены упорядоченного (ранжиро-
ванного) ряда, то в качестве медианы берется средний по но-
меру член этого ряда.
В примере 3.5 упорядочим цены на квартиры по возраста-
нию и убыванию:
60 000, 65 000, 70 000, 80 000, 275 000;
275 000, 80 000, 70 000, 65 000, 60 000.
48
Как видно, медианной ценой в данном случае будет 70 000
долл., так как эта величина стоит в середине ранжированного
ряда. Заметим, что слева и справа от нее находится одинаковое
количество данных. Поэтому на величину медианы не оказыва-
ют влияние значения крайних членов ранжированного ряда,
т. е. наименьшее и наибольшее значения всей совокупности дан-
ных. Так, например, если бы самая дорогая квартира стоила
90 000 или даже 1 000 000 долл., то медианная цена не измени-
лась бы. Аналогично, если бы цена самой дешевой квартиры
была 20 000 или 50 000 долл., то медианная цена оставалась бы
по-прежнему равной 70 000 долл.
Отметим, что медианная цена располагается на третьем мес-
те ранжированного ряда. В рассмотренном случае число данных
было нечетным (равно 5). Ввиду этого номер среднего члена ран-
жированного ряда вычисляется как (п +1)/2 : (5 +1)/2 = 3.
В случае четного числа данных медиана находится как полусум-
ма двух средних членов ранжированного ряда, которые распо-
лагаются на местах с номерами п/2 и п/2 +1.
Пример 3.6. За восемь дней представлены следующие данные,
отражающие количество пациентов, которые были на приеме
у врачей одной поликлиники: 52, 86, 49, 43, 35, 11, 31, 30.
Требуется определить медиану.
Составим ранжированный ряд по возрастанию: 11, 30, 31,
35, 43, 49, 52, 86.
Медианой является полусумма чисел, находящихся на
4 (8/2)-м и 5 (8/2 + 1)-м местах ранжированного ряда:
(35 + 43)/2 = 39.
Заметим, что сама медиана (число 39) нс входит в совокуп-
ность данных, для которой она была вычислена.
В общем случае если число данных четно, то медиана не
обязательно будет входить в их состав.
Можно выделить следующие основные свойства медианы.
1. Если имеется одно или два крайних значения, которые
сильно отличаются от всех остальных, то это не влияет на ве-
личину медианы.
2. Так же как и для средней арифметической, значение ме-
дианы является единственным для данной совокупности зна-
чений признака.
3. Медиана может быть определена, даже если представлены
не все данные. Необходимо, чтобы были известны их общее
49
число, расположение и точные данные только о тех значени-
ях, которые располагаются вблизи медианной величины.
4. Медиана может быть определена для данных, измеряемых
как в шкалах отношений и интервалов, так и в порядковой
шкале.
Пусть, например, респонденты дают оценку некоторому
явлению по следуюшей шкале, включающей пять градаций:
отлично, хорошо, удовлетворительно, плохо, очень плохо. До-
пустим, что респондентов было пять человек. Один из них дал
оценку “отлично”, один — “хорошо”, один — “удовлетвори-
тельно”, один — “плохо” и один — “очень плохо”. Медианная
оценка в данном случае будет “удовлетворительно”, так как
половина ответов характеризует явление ниже, чем “удовлет-
ворительно”, а половина — выше.
5. При большом количестве данных процедура нахождения
медианы является более трудоемкой, чем вычисление средней
арифметической, так как требует предварительной ранжиров-
ки всего множества значений признака.
3.1.3. Мода
Под модой понимается наиболее часто встречающаяся ве-
личина в рассматриваемом множестве значений признака. Как
и медиана, она принадлежит к структурному типу средних.
Мода не всегда яазяется мерой центральной тенденции, так
как по определению необязательно должна находиться в центре
данного множества значений. Мода часто используется, напри-
мер, в швейной и обувной отраслях, где рассматриваются такие
понятия, как наиболее распространенные размеры различных
типов одежды и обуви. В данном случае представляет интерес не
средний размер, а тот, который носит наибольшее число людей.
Мода может быть полезной в случае данных, представлен-
ных в шкале наименований. Например, автомобильную фирму
может интересовать, какая марка автомобиля имеет наиболь-
шее количество рекламаций.
Пример 3.7. Рассмотрим множество данных: 4, 8, 7, 6, 9, 8,
19, 5, 8.
Мода будет равна 8, так как 8 встречается наибольшее чис-
ло раз, равное 3.
Множество данных может иметь несколько мод в случае,
если несколько значений повторяется одинаковое (самое боль-
50
шое) количество раз. Если множество имеет две моды, то оно
называется бимодальным, если мод больше двух, то — поли-
модальным.
Пример 3.8. Пусть выборка состоит из возрастов 13 служащих
небольшого предприятия (в голах): 22, 27, 30, 30, 30, 30, 34,
58, 60, 60, 60, 60, 65. Данное множество имеет две моды: 30 и
60 лет. Часто наличием двух мод характеризуется неоднород-
ность исследуемой совокупности. Очевидно, в данном случае
генеральная совокупность работников может быть составлена
из двух качественно различных групп: группы молодых работ-
ников, которые были недавно наняты, и группы работающих
на предприятии уже долгое время.
Предположим, что рассматривается выборка достаточно
большого объема, для которой построены ряд распределения и
полигон с большим числом групп. Сгладим ломаную линию
графика полигона с помощью плавной кривой. Если сглажен-
ный график будет иметь два отдельных пика, но разной высо-
ты (рис. 3.1), то такое распределение будет называться бимо-
дальным.
Аналогично если число локальных пиков графика рас-
пределения, имеющих необязательно одинаковую высоту,
больше двух, то такое распределение называется полимо-
дальным.
Множество данных может вообще не иметь моды, если все
значения признака повторяются одинаковое количество раз.
51
Отметим основные характерные свойства молы.
1. Наличие одного или двух крайних значений признака,
сильно отличающихся от всех остальных значений, не влияет
на величину моды.
2. Мода совпадает с точкой наибольшей плотности данных.
3. В отличие от средней арифметической и медианы мода
может иметь несколько значений.
4. Мода может существовать для совокупностей значений
признака, которые измеряются в шкалах наименований, по-
рядка, интервалов и отношений.
3.2. ОЦЕНКА ХАРАКТЕРИСТИК ЦЕНТРАЛЬНОЙ
ТЕНДЕНЦИИ ДЛЯ СГРУППИРОВАННЫХ ДАННЫХ
3.2.1. Средняя арифметическая
для ряда распределения
При оценке средней арифметической для данных, сгруппи-
рованных в виде ряда распределения, все величины одного груп-
пировочного интервала представляются его средней точкой.
Средняя арифметическая оценивается по формуле
(3.4)
п
где х — средняя арифметическая;
хс — средняя точка группы;
f — частота группы;
л = Е/— общая сумма частот (общее число данных).
Пример 3.9. Вычислим среднюю арифметическую для ряда рас-
пределения, представленного в табл. 2.10.
Средняя точка первой группы (699,5) представляет одно-
временно три значения месячной арендной платы, входящие в
эту группу. Можно сказать, что эти значения аппроксимируют
(т. е. приближают) в целом величину 3 • 699,5 = 2098,5, которая
является частью суммарной арендной платы для всех 120 аренда-
торов, попавших в выборку. Аналогично средняя точка 899,5
представляет все семь значений арендной платы для второй
группы, а величина 7 • 899,5 = 6296,5 аппроксимирует часть
общей суммы арендной платы. Этот процесс можно продол-
жить для всех оставшихся групп (табл. 3.1).
52
Таблица 3.1
Пример вычисления средней арифметической
для сгруппированных данных
Месячная арендная плата (группы), долл. Частота t Средняя тонка хв
600-799 3 699,5 2098,5
800-999 7 899.5 6296,5
1000-1199 11 1099,5 12094,5
1200-1399 22 1299,5 28589
1400-1599 40 1499.5 59980
1600-1799 24 1699,5 40788
1800-1999 9 1899,5 17095,5
2000-2199 4 2099,5 8398
Общая сумма 120 = л 175340
Средняя арифметическая равна 175340/120 = 1461,17.
При вычислении средней арифметической для сгруппиро-
ванных данных происходит потеря информации. Она связана с
тем, что отдельные данные, на основе которых строился ряд
распределения, были неизвестны и заменены на значения сред-
них точек соответствующих групп. Например, вычисленное зна-
чение средней арифметической в предыдущем примере отлича-
ется от ее точного значения 1457,93, полученного на основе
“сырых” данных (см. табл. 2.2).
Таким образом, средняя арифметическая, вычисленная на
основе сгруппированных данных, является оценкой точного
значения средней арифметической для несгруппированных
(“сырых”) данных. Среднюю арифметическую затруднительно
вычислить для ряда распределения, имеющего хотя бы одну
крайнюю группу с открытой границей.
Пример 3.10. Пусть ряд распределения индивидов по величине
годового дохода имеет группу “100 000 долл, и более”, причем
в эту группу попали 10 человек. Очевидно, этой информации
недостаточно, чтобы определить, близки ли их доходы, на-
пример, к 100 000, 500 000 или 1 600 000 долл.
3.2.2. Медиана для сгруппированных данных
При вычислении медианы для ряда распределения, как и в
случае средней арифметической, можно получить только ее
оценочное значение. Для этой цели нужно определить группу,
53
в которой находится медианное значение, и внутри медианно-
го интервала провести интерполяцию для оценки положения
медианы. При этом предполагается, что данные внутри меди-
анного интервала располагаются равномерно.
Формула для вычисления медианы будет иметь вил
л г-
—-cF
Ма - / ц. 2__; п.
где L — точная нижняя граница медианной группы;
л — сумма частот всех классов (общее число данных);
f— частота медианной группы;
cF — кумулятивная (накопленная) частота группы, не-
посредственно предшествующей медианной;
i — размер медианного интервала.
Для использования формулы (3.5) необходимо выявить груп-
пу, в которой содержится медиана. Это можно сделать на осно-
ве значений кумулятивных частот групп.
Пример 3.11. Найдем медиану для ряда распределения, пред-
ставленного в табл. 2.11, где вычислены также кумулятивные
частоты. По определению слева и справа от медианы должно
находиться по 50% всех данных, т. е. по 60 значений арендной
платы. Очевидно, медианным интервалом будет тот, кумуля-
тивная частота которого впервые будет равна или превзойдет
половину всех значений л/2 (в данном случае величину, рав-
ную 60). Из табл. 2.11 видно, что медиану содержит интервал
1400—1599, так как его кумулятивная частота равна 83, в то
время как кумулятивная частота предыдущей группы (1200—
1399) равна 43, т. е. меньше 60. Отсюда следует, что точная
нижняя граница (£) медианного интервала — 1399,5, а точная
верхняя — 1599,5.
Проведем интерполяцию внутри группы 1399,5—1599,5 в
предположении, что все значения месячной арендной пла-
ты, которые ей принадлежат, равномерно располагаются
между ее точными границами. Если рассматриваемые 120
арендаторов упорядочить по возрастанию месячной аренд-
ной платы, то между 43-м и 60-м по порядку членами ран-
жированного ряда будет содержаться 17 значений. Медиан-
ная группа содержит 40 значений, поэтому медиана должна
54
располагаться в точке, равной 17/40 расстояния между 1399,5
и 1599,5. Это расстояние равно размеру группы, т. е. 200. От-
сюда получаем, что 17/40 200 = 85 следует прибавить к
нижней точной границе 1399,5. Оценочное значение для ме-
дианы равно 1484,5. Этот результат можно также получить,
используя формулу (3.5) (L = 1399,5, п = 120, cF = 43,
/= 40, г = 200):
—44 17
Me = 1399,5 + - • 200 = 1399,5 + — • 200 =
40 40
= 1399,5 + 85 = 1484,5 долл.
Вычисленная величина 1484,5 представляет собой некоторую
оценку точного значения медианы — 1464,5, которое определя-
ется на основе ранжированных первичных данных табл. 2.4. По-
грешность возникает в связи с предположением о равномерно-
сти распределения данных в медианной группе, которое в общем
случае редко выполняется.
Медиану можно определить по формуле (3.5) и для ряда
распределения с относительными или процентными частота-
ми групп. Абсолютные величины частот (/) и кумулятивных
частот (cF) заменяются при этом на их соответствующие отно-
сительные значения (частости). Сумма процентных частот рав-
на 100, поэтому по 50% данных должно находиться слева и
справа от значения медианы.
Медиана может быть вычислена для ряда распределения,
имеющего крайнюю группу с открытой границей, при усло-
вии, что она не принадлежит к этой группе.
3.2.3. Оценка моды для сгруппированных данных
По определению модой является такое значение, которое
встречается наиболее часто в рассматриваемой совокупности
значений признака. Для сруппированных данных оценкой моды
может являться средняя точка группировочного интервала, име-
ющего максимальную частоту.
Пример 3.12. Выборка, составленная из данных о ежедневных
продажах изделий фирмы, была сгруппирована в виде ряда
распределения, представленного в табл. 3.2.
55
Таблица 3.2
Ряд распределения ежедневных продаж фирмы
Ежедневные продажи (ед.) Частоты
80-90 5
90-99 9
100-109 20
110-119 8
120-129 6
130-139 2
Для определения моды распределения выделим группу с
наибольшей частотой (100—109) и найдем ее середину: 104,5.
Таким образом, если бы в наличии были первичные данные,
то, вероятно, наиболее типичный объем продаж приблизи-
тельно составлял 104—105 изделий вдень.
Так же как и медиана, мода может быть определена для
рядов распределений с крайними группами, имеющими от-
крытые границы.
3.2.4. Сравнение типов средних при анализе
центральной тенденции
Одной из проблем статистического анализа является опре-
деление такого типа средней (т. е. средней арифметической, ме-
дианы или моды), который в наибольшей степени характери-
зовал бы положение центра.
Для решения этой проблемы рассмотрим полигон исследу-
емого ряда распределения, построенный на основе выбороч-
ных данных. Их значения могут быть неточными, так как связа-
ны со случайными ошибками наблюдения, которые искажают
основную закономерность распределения генеральной совокуп-
ности. Пусть число данных (объем выборки) возрастает и одно-
временно уменьшаются размеры группировочных интервалов.
В результате зигзаги полигона начнут сглаживаться, и в преде-
ле ломаная линия графика полигона будет представлять собой
плавную кривую. Эта кривая называется кривой распределения
и теоретически отражает распределение генеральной совокуп-
ности при условии полного устранения случайных ошибок
выборочных наблюдений. На практике для получения кривой
распределения полигон, построенный на основе эмпиричес-
ких данных, сглаживается визуально (например, сглаженный
56
полигон представлен на рис. 3.1). По форме кривой распределе-
ния можно делать выводы относительно характеристик цент-
ральной тенденции. Если кривая имеет симметричную форму
(рис. 3.2), то в этом случае мода, медиана и средняя арифмети-
ческая совпадают. Проблема выбора средней, представляющей
центральную тенденцию, решается сама собой.
Рис. 3.2. Кривая симметричного распределения
Если распределение асимметрично, то различают положи-
тельную и отрицательную асимметрию. В случае положитель-
ной (правосторонней) асимметрии график кривой распреде-
ления имеет “хвост”, вытянутый вправо (рис. 3.3).
Рис.3.3. Кривая распределения с положительной (правосторонней)
асимметрией
Наибольшее значение из всех трех характеристик принима-
ет средняя арифметическая. Это связано с тем, что на нее в
значительной степени влияет несколько больших величин, т. е.
значения, максимально удаленные вправо. Следующей по ве-
57
личине после средней арифметической обычно идет медиана,
и наименьшее значение принимает мода. В случае если положи-
тельная асимметрия ярко выражена, средняя арифметическая
не может служить в качестве наилучшей средней для характе-
ристики центральной тенденции. Более представительными здесь
будут медиана и мода.
При отрицательной (левосторонней) асимметрии наблюда-
ется обратная картина (рис. 3.4).
Рис. 3.4. Кривая распределения с отрицательной (левосторонней)
асимметрией
В этом случае “хвост” кривой распределения вытянут влево
и средняя арифметическая принимает наименьшее значение,
так как на нее влияет несколько небольших значений, макси-
мально удаленных влево. Мода будет иметь наибольшее значе-
ние среди всех трех характеристик. Как видно, если распреде-
ление имеет достаточно сильную отрицательную асимметрию,
то аналогично случаю положительной асимметрии средняя
арифметическая не является представительной средней вели-
чиной.
Когда распределение имеет достаточно сильно выраженную
асимметрию (положительную или отрицательную), медиана
часто является лучшей мерой центральной тенденции, так как
обычно расположена между средней арифметической и модой.
На медиану почти не влияет, как на моду, частота отдельного
значения, и она не зависит, как средняя арифметическая, от
отдельных крайних величин распределения.
Пусть имеется достаточно большое количество данных для
того, чтобы построить гладкую кривую распределения (сгла-
женный полигон). В этом случае расстояние между медианой и
средней арифметической составляет примерно одну треть рас-
стояния между средней арифметической и модой.
58
Если значения двух из трех типов средних известны, то ве-
личина неизвестной средней может оцениваться с помошью
следующих формул: Mo = х - 3(i - Me), (3.6) _ ЗМе-Мо х , ') 2 .. 2х + Мо Me = , (3.8)
Выбор типа средней в статистическом анализе часто зави-
сит от предметной области исследования. Например, для при-
нятия решений в социальной сфере важным показателем явля-
ется среднее арифметическое количества детей в семье. В то же
время конструктора автомобиля может больше интересовать
модальное количество детей (число детей, которое имеет наи-
большее количество семей), когда он приступает к разработке
новой модели.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 3
Выборочный метод предполагает обоснование статистичес-
ких заключений о свойствах генеральной совокупности по дан-
ным выборки. Количественные характеристики, приближенно
отражающие эти свойства и вычисленные на основе выбороч-
ных данных, называются статистиками. Те же характеристики,
полученные на основе данных генеральной совокупности, на-
зываются параметрами.
В главе рассматриваются различные типы средних величин,
отражающие центральную тенденцию, т. е. свойство быть цент-
ром, около которого в наибольшей степени концентрируются
все данные совокупности. Наиболее часто встречающейся сред-
ней в статистическом анализе является средняя арифметичес-
кая, или просто средняя. Она определяется как сумма всех зна-
чений, деленная на общее катичество данных. Для несгруппи-
рованных данных средняя арифметическая вычисляется по
формулам (3.1) и (3.2).
Особым случаем средней арифметической является взвешен-
ная средняя арифметическая (3.3). Она вычисляется, когда мно-
жество данных велико и его можно разбить на группы одина-
ковых значений. Для сгруппированных данных оценочное
значение средней арифметической находится по формуле (3.4).
59
В некоторых случаях в качестве центра имеет смысл рас-
сматривать не среднюю арифметическую, а медиану. Под ме-
дианой понимается величина, слева и справа от которой нахо-
дится по половине всех данных. В отличие от средней
арифметической она не зависит от крайних значений, сильно
отличающихся от всех остальных. Для данных, представленных
в виде ряда распределения, оценка медианы находится из со-
отношения (3.5).
Иногда наиболее подходящей характеристикой для выраже-
ния точки наибольшей плотности данных является мода. Она
представляет собой наиболее часто встречающуюся величину в
данной совокупности. Возможны случаи, когда может быть не-
сколько мод. Если совокупность имеет две моды, то она назы-
вается бимодальной, если более двух, то — полимодальной.
Медиана и мода суть структурные средние, они не являются
результатами арифметических действий над значениями при-
знака, входящими в исследуемую совокупность.
Для сгруппированных данных в качестве оценки моды рас-
сматривается средняя точка группировочного интервала, име-
ющего наибольшую частоту.
В статистическом анализе может возникнуть проблема — ка-
кой из перечисленных средних следует отдать предпочтение при
выборе центральной величины. Для этой цели рассматривается
форма графика сглаженного полигона, называемого кривой
распределения. В случае симметричной кривой средняя ариф-
метическая, медиана и мода совпадают. Если кривая распреде-
ления достаточно сильно вытянута вправо (положительная, или
правосторонняя, асимметрия) или влево (отрицательная, или
левосторонняя, асимметрия), то средняя арифметическая не
является типичным представителем всей совокупности данных.
Более представительными здесь будут структурные средние —
медиана или мода. Кроме того, выбор средней зависит от каче-
ственного содержания исследуемого явления.
Средняя арифметическая, медиана и мода связаны соотно-
шением: расстояние между медианой и средней арифметичес-
кой составляет примерно одну треть расстояния между сред-
ней арифметической и модой. Если значения двух из трех типов
средних известны, то величина неизвестной средней оценива-
ются с помощью формул (3.6)—(3.8).
ИЗМЕРЕНИЕ ВАРИАЦИИ
В предыдущей главе были рассмотрены различные типы сред-
них. Каждая из них определялась как наиболее типичная вели-
чина для всего множества данных, т. с. представляющая при-
близительно центр этого множества.
Предположим, что средняя (например, средняя арифмети-
ческая) уже вычислена. Далее возникает вопрос, насколько
надежно она представляет в целом исследуемую совокупность.
Другими словами, необходимо оценить в количественной форме
степень представительности полученной средней. Очевидно, чем
плотнее и ближе концентрируются данные вокруг средней ариф-
метической, тем она более надежна или представительна. На-
оборот, если данные сильно отклоняются от средней, то ее
надежность низкая.
В статистическом анализе для характеристики разброса дан-
ных относительно центра распределения часто используется
термин “вариация”.
Пример 4.1. На рис. 4.1 представлен график кривой распределе-
ния возрастов служащих некой фирмы.
Рис. 4.1. Кривая распределения возрастов служащих фирмы
61
Как видно, возраст служащих изменяется в диапазоне от 18
до 75 лет. Такой значительный разброс говорит о том, что сред-
няя (40 лет) не является представительной для всего распреде-
ления возрастов.
Необходимость измерения вариации может возникнуть при
сравнительном анализе двух или более распределений.
Пример 4.2. Пусть двое рабочих производят на станке одинаковые
детали. В течение 9 дней выпуск деталей первым рабочим имел
следующее распределение: 49, 48, 50, 49, 50, 51, 50, 51, 52.
Для второго рабочего распределение выпуска деталей по дням
имело вид: 40, 47, 50, 47, 53, 50, 60, 53, 50.
Средний дневной выпуск деталей для обоих рабочих одина-
ков и составляет 50 штук. Однако степень разброса ежедневных
выпусков деталей для второго рабочего значительно выше, чем
для первого: выпуск деталей в течение дня у первого рабочего
колеблется в пределах от 48 до 52, в то время как у второго —
от 40 до 60. Ясно, что средний ежедневный выпуск в количе-
стве 50 деталей является гораздо более типичным для первого
рабочего.
В общем случае при сравнении нескольких распределений
вычисления средних в качестве сравнительных характеристик,
как правило, недостаточно. Очевидно, наряду со средней в ста-
тистическом анализе следует рассматривать количественные
показатели, характеризующие вариацию данных.
4.1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИИ
4.1.1. Размах колебаний
Простейшей, грубой характеристикой является размах ко-
лебаний (R):
где х — максимальное значение во множестве данных;
х — минимальное значение во множестве данных,
min
Пример 4.3. Дадим количественное обоснование выводам, по-
лученным в примере 4.2, используя при этом понятие размаха
колебаний. Для первого рабочего R = 52 — 48 = 4, для второ-
го — R = 60 — 40 = 20. Как видно, размах колебаний для перво-
62
го рабочего в пять раз меньше, чем для второго. Это говорит о
том, что производимые ежедневно первым рабочим количе-
ства деталей более плотно концентрируются около значения
средней арифметической (50 штук) по сравнению с количе-
ствами деталей, производимыми ежедневно вторым рабочим.
Иначе говоря, средняя, равная 50, будет более представитель-
ной для первого рабочего.
Если данные представлены уже в сгруппированном виде, т. е.
в виде ряда распределения, то величина размаха колебаний оце-
нивается как разность между верхним пределом высшей (после-
дней) группы и нижним пределом низшей (первой) группы
(иногда вычисляют разность между точной верхней границей
высшей группы и точной нижней границей низшей группы).
Пример 4.4. Пусть 40 значений почасовых ставок (долл.) сгруп-
пировано в виде ряда распределения:
Почасовые ставки Частота
6-9 10
10-13 21
14-17 9
Размах колебаний составляет
R = 17 - 6 = 11 долл, или R - 17,5 - 5,5 = 12 долл.
4.1.2. Среднее линейное отклонение
Размах колебаний зависит только от двух значений — наи-
большего и наименьшего. На его величину совершенно не вли-
яют остальные значения. Поэтому размах колебаний является
очень грубой оценочной характеристикой вариации.
Этот серьезный недостататок учитывается при вычислении
среднего линейного отклонения. Среднее линейное отклоне-
ние (d) определяется как средняя арифметическая из абсолют-
ных значений отклонений от средней арифметической. Для
выборочных данных среднее линейное отклонение вычисляет-
ся по формуле
м.2)
п
где х — данные (значения признака элементов выборки);
х — выборочная средняя арифметическая;
п — объем выборки.
63
В формуле (4.2) фигурируют абсолютные величины откло-
нений всех данных от средней, т. е. среднее линейное отклоне-
ние учитывает все значения рассматриваемого множества дан-
ных. Отрицательные значения игнорируются, гак как берутся
их абсолютные значения. В этой связи среднее линейное откло-
нение часто называют средним абсолютным отклонением.
Если бы в формуле (4.2) обозначения модуля отсутствова-
ли, то вычислялась бы алгебраическая сумма положительных и
отрицательных отклонений от средней. Значение этой суммы
всегда равно нулю, так как положительные и отрицательные
отклонения всегда взаимно погашаются (это следует из свойств
средней арифметической, представленных в разделе 3.1.1). Оче-
видно, такая характеристика не имела бы смысла в статисти-
ческом анализе.
Пример 4.5. Рассматривается выборка из пяти упаковок това-
ра, имеющих следующий вес (кг): 103, 97, 101, 106, 103. Опре-
делим среднее линейное отклонение по формуле (4.2). Для это-
го сначала вычислим среднюю арифметическую:
х = (103+97+101 +106+1ОЗ)/5 = 102 кг.
Для вычисления среднего линейного отклонения необходи-
мо произвести следующие действия (табл. 4.1):
а) из каждого значения веса вычесть среднюю арифмети-
ческую и взять абсолютную величину разности;
б) просуммировать все абсолютные отклонения от средней;
в) сумму абсолютных отклонений разделить на общее число
данных.
Таблица 4.1
Вычисление среднего линейного отклонения
Вес к, кг х - X Ijt-kI
103 +1 1
97 -5 5
101 -1 1
106 4 4
103 1 1
12
= 2,4 кг.
d =
64
Полученный результат можно легко интепретировать: вес
упаковок отклоняется от среднего арифметического веса в сред-
нем на 2,4 кг.
Среднее линейное отклонение обладает одним важным свой-
ством. Пусть среднее линейное отклонение рассматривается
относительно не средней арифметической, а медианы, т. е. вы-
числяется по формуле
- Ух - Мс|
d = —-------L (4.3)
п
В этом случае значение среднего линейного отклонения бу-
дет наименьшим, т. е. меньше, чем от средней арифметической
и любой другой величины. Это означает, что среднее линейное
отклонение обладает свойством минимальности относительно
медианы.
4.1.3. Дисперсия и среднее квадратическое
(стандартное) отклонение
Определение дисперсии и среднего квадратического откло-
нения также основано на вычислении отклонений от средней
арифметической. Однако вместо абсолютных значений в вы-
числительных формулах фигурируют квадраты величин откло-
нений.
Дисперсия определяется как средняя арифметическая квад-
ратов отклонений от средней арифметической. Формула для
дисперсии, вычисляемой на основе данных генеральной сово-
купности, имеет следующий вид:
о ------------• (4.4)
где о2 — генеральная дисперсия;
х — значение признака;
ц — генеральная средняя;
N — объем генеральной совокупности.
Пример 4.6. Пусть распределение возрастов пяти больных, на-
ходящихся в изоляторе больницы, следующее: 38, 26, 13, 41 и
42 года. Требуется определить дисперсию, рассматривая приве-
денные данные как генеральную совокупность.
Все действия и результаты вычислений сведем в табл. 4.2.
65
Таблица 4.2
Вычисление генеральной дисперсии
Возраст х, лет х-р (х-в)1
38 + 10 100
26 -2 4
13 -15 225
41 + 13 169
22 -6 36
— — —
140 0 534
Н= = 140/5 = 28 лет
N
i У(х-Ц)2
СТ- = = 534/5 = 106,8.
N
Из соотношения (4.4) можно вывести более удобную для
вычислений формулу:
В данной формуле не требуется вычислять разности, харак-
теризующие отклонения от средней, что упрощает расчеты.
Используем формулу (4.5) для вычисления дисперсии в
примере 4.6:
2 382 + 262 +132 + 412 + 222 /38 + 26+13 + 41 + 22
О =----------------------------------------------
5 5
= 4454/5 - (140/5)2 = 106,8.
Как видно, результаты вычислений по формулам (4.4) и
(4.5) совпадают.
Дисперсию, так же как размах колебаний и среднее абсо-
лютное отклонение, можно использовать для сравнения двух
или более совокупностей по степени вариаиии.
Пример 4.7. По расчетам примера 4.6 дисперсия распределения
возрастов больных составляет 106,8. Предположим, что диспер-
сия распределения возрастов пациентов, лежащих в онкологи-
ческом отделении, равна 342,9. Так как 106,8 < 342,9, то, оче-
видно, степень вариации возрастов для пациентов изолятора
меньше, чем для больных раком. Это означает, что возрасты
66
пациентов изолятора концентрируются ближе к средней ариф-
метической по сравнению с возрастами больных раком. Поэто-
му средний возраст 28 лет является более представительной
величиной для больных изолятора, чем неизвестное значение
среднего возраста больных онкологического отделения.
Значения размаха колебаний и среднего абсолютного откло-
нения легко интерпретируются. Размах колебаний — это раз-
ность между наибольшим и наименьшим значениями, а среднее
абсолютное отклонение — средняя арифметическая абсолютных
отклонений данных от средней. Однако неясно, как интерпре-
тировать дисперсию для одной совокупности. Так, в примере 4.6
единицей измерения дисперсии, равной 106,8 для возрастов па-
циентов, будет не “год”, а “год в квадрате”. Для того чтобы мера
вариации данных, характеризуемая дисперсией, выражалась в
тех же единицах, что и исходные данные, имеет смысл из зна-
чения дисперсии извлечь квадратный корень. Например, корень
квадратный из 106,8 приблизительно равен 10,3 года.
Корень квадратный из дисперсии называется средним квад-
ратическим отклонением, или стандартным отклонением. Со-
ответственно записываются формулы для его вычисления:
а =
или
Формулы (4.4)—(4.7) предназначены для вычисления пара-
метров, т. е. характеристик генеральной совокупности. В них
фигурируют значения: N — объем генеральной совокупности
иц — средняя генеральная.
Рассмотрим аналогичные формулы для вычисления соот-
ветствующих статистик, т. е. подобных характеристик, опреде-
ляемых на основе выборочных данных. Очевидно, для этого не-
обходимо заменить величину объема генеральной совокупности
/V на объем выборки п, а значение генеральной средней ц — на
значение выборочной средней х. Однако такая механическая
замена не будет правомерной. В математической статистике до-
казывается, что отклонения от выборочной средней в боль-
шинстве случаев меньше соответствующих отклонений от ге-
неральной средней. Поэтому оценки дисперсии и стандартного
отклонения (т. е. значения статистик) в среднем будут зани-
67
женными, т. е. смещенными. Для получения более точных (не-
смещенных) оценок знаменатель формулы (4.4) заменяют не
на л, а на л - 1. Отсюда следует, что формула для вычисления
выборочной дисперсии будет иметь вид
2 У(Х-Х)2
* = U, (4.8)
п-1
где л2 — обозначение выборочной дисперсии;
х — выборочные данные;
х— выборочная средняя;
п — объем выборки.
Аналогом формулы (4.5) для выборки является
у 2
s =--------°—. (4.9)
л -1
Пример 4.8. Рассматриваются почасовые ставки для выборки
из пяти работников-совместителей некоторого предприятия: 2,
10, 6, 8, 9 долл. Требуется определить дисперсию.
Вычислим значение средней:
х = (2 + 10 +6 + +8 + 9)/5 = 35/5 = 7 долл.
Все последующие вычисления сведем в табл. 4.3.
Таблица 4.3
Вычисление выборочной дисперсии
По формуле (4.8) По формуле (4.9)
Почасовые ставки х, долл. к - X ж»
2 -5 25 4
10 3 9 100
6 -1 1 36
8 1 1 64
9 2 4 81
— — — —
И о II 5 м 1 3 С GJ С । । 01 II " hi о ** II 0 40 285 s2=— а_. л-1 ^285-35*75 |0
68
Выборочное стандартное отклонение определяется как ко-
рень квадратный из выборочной дисперсии:
|У(х-х)2
s = \ " (4.10)
V л -1
или
Пример 4.9. Определим стандартное отклонение для примера 4.8:
з =-710 = 3,16 долл.
Вычисленное стандартное отклонение измеряется в долла-
рах (т. е. в тех же единицах, что и исходные данные), так как
было получено извлечением квадратного корня из величины,
измеряемой “долларами в квадрате”.
Так же как и дисперсия, стандартное отклонение использу-
ется при сравнении степени разброса данных около средней в
двух или более совокупностях. Чем меньше его значение, тем
ближе располагаются данные к средней или тем более предста-
вительна эта средняя.
В случае сгруппированных данных стандартное отклонение
может быть оценено на основе формул (4.10) и (4.11). Для этой
цели следует все значения х, принадлежащие одной группе,
заменить на среднюю точку хг величину Ех2 — на Ъ/х* и ве-
личину Ех — на Е/х (f — частота группы, L/= л). Тогда фор-
мула для оценки стандартного отклонения примет вид
где х вычисляется по формуле (3.4).
Пример 4.10. Множество станков предприятия было сгруппи-
ровано по времени износа в виде следующего ряда распределе-
ния:
69
Время износа, лет Количество станков
2—4 2
5-7 5
8-10 10
11-13 4
14-16 2
Используя формулу (4.12), оценим стандартное отклонение
и дисперсию. Результаты вычислений сведем в табл. 4.4.
Таблица 4.4
Износ, лет f ч **
2-4 2 3 6 18
5—7 5 6 30 180
8-10 10 9 90 810
11-13 4 12 48 576
14-16 2 15 30 450
23 45 204 2034
2034,__________________
s _ _ 23__ - , 2034-1809,3913 =
1 23-1 ~~Ч 22
= .10,209486 = 3,195 года.
Дисперсия оценивается как квадрат стандартного отклоне-
ния:
s2 = 10,209.
Дисперсия и стандартное отклонение обладают свойством
минимальности относительно средней арифметической. Это
означает, что сумма квадратов отклонений данных от средней
арифметической будет всегда меньше, чем от произвольного
значения. Иначе говоря, подставляя в формулы (4.4) и (4.6)
вместо величины ц (или в формулы (4.8) и (4.10) вместо зна-
чения х) любое другое значение, в результате получим вели-
чину, большую, чем вычисленную для ц (или для х ).
Средняя арифметическая — наиболее часто используемая
статистика (параметр) в статистическом анализе. Ввиду этого,
а также свойства минимальности дисперсия и стандартное от-
клонение являются наиболее важными характеристиками ва-
риации.
70
4.1.4. Интерпретация стандартного отклонения
на основе неравенства Чебышева
Используя величину стандартного отклонения, можно про-
вести более глубокий анализ разброса данных. Для этой цели
служит неравенство Чебышева, доказанное в теории вероятно-
стей. В терминах статистической совокупности оно имеет сле-
дующую трактовку.
Для любой совокупности доля значений, попадающих в
интервал х ±As (или ц + кв для генеральной совокупности),
будет равна, по крайней мере, 1 — 1Д2, где к — любое число,
большее 1.
Пример 4.11. Средний недельный доход группы менеджеров
составляет х = 500 долл., стандартное отклонение j = 40 долл.
Пользуясь неравенством Чебышева, найти нижнюю границу
для процента работников, имеющих доход в пределах от 400 до
600 долл.
Интервал от 400 до 600 можно представить как интервал от
(500 - 100) до (500 + 100), или 500 ±100.
Как видно, к = 100/40 = 2,5, и в силу неравенства Чебышева
минимально возможный процент равен
= = —= 0,84.
5 А2 25 25
2 )
Отсюда следует, что не менее 84% всех менеджеров имеют
недельный доход в заданных границах.

Ценность неравенства Чебышева заключается в том, что оно
будет верно для любого частотного распределения данных. Так,
исходя из этого неравенства, можно утверждать, что на интер-
вале с границами х ±2$ содержится, по крайней мере, 3/4 (75%)
всех данных, а на интервале с границами х ±3з — 8/9 (89,9%)
всех значений.
Неравенство Чебышева верно для любой совокупности не-
зависимо от формы кривой распределения.
4.1.5. Коэффициент вариации
Пусть для выборочной совокупности, которая представляет
собой группу служащих одной организации, рассматриваются
значения двух качественно различных признаков: годовой до-
71
ход и невыход на работу в течение года. Первый признак изме-
ряется в долларах, второй — в днях. Предположим, что стан-
дартное отклонение для первого признака равно 1200 долл., а
для второго — 4,5 дня. Возникает проблема непосредственного
сравнения этих двух совокупностей по степени вариации. Было
бы бессмысленно в качестве сравнительных характеристик рас-
сматривать стандартные отклонения, так как они выражены в
разных единицах (заключение о том, что 1200 долл, больше,
чем 4,5 дня, является абсурдным). В этой связи для сравнения
двух или более совокупностей используется специальная ха-
рактеристика, которая не зависит от единиц измерения при-
знака. Она называется коэффициентом вариации и является
относительной безразмерной величиной, выражаемой в долях
или процентах. Коэффициент вариации (к) вычисляется как
отношение среднего квадратического отклонения к средней
арифметической:
к= — или к = -100%. (4.13)
X X
Коэффициент вариации полезно использовать при сравни-
тельном анализе нескольких совокупностей в двух случаях:
1) данные измеряются в качественно различных единицах;
2) данные совокупностей измеряются в одинаковых едини-
цах, но значения средних арифметических существенно отли-
чаются друг от друга.
Пример 4.12. Группа менеджеров фирмы окончила курсы повы-
шения квалификации. По окончании курсов было проведено те-
стирование, результаты которого оценивались по специальной
балльной шкале. После обобщения результатов было установле-
но, что средний результат составляет 200 баллов при стандарт-
ном отклонении 40 баллов. Дополнительные исследования по-
казали, что средний стаж работы на фирме для данной группы
менеджеров — 20 лет при стандартном отклонении 2 года.
Требуется сравнить вариации двух совокупностей значений
признаков: результаты тестирования и значения стажа работы.
Вычислим по формуле (4.13) коэффициент вариации для
множества балльных оценок:
40
t = —100% = 20%.
200
Таким образом, стандартное отклонение составляет 20% от
средней арифметической. Аналогично определим коэффици-
ент вариации для значений стажа работы:
72
* = — •100% = 10%.
20
Стандартное отклонение составляет 10% от средней ариф-
метической.
Можно сделать вывод, что совокупность оценок тестирова-
ния имеет ббльшую вариацию по сравнению с совокупностью
данных о стаже работы.
Ту же самую процедуру можно использовать для случая оди-
наковых единиц измерений, но значительно отличающихся
величин средних.
Пример 4.13. Средний годовой доход высших менеджеров од-
ной крупной фирмы составляет х = 500 000 долл, при стан-
дартном отклонении з = 50 000 долл. Средний годовой доход
неквалифицированных служащих этой фирмы — 12 000 долл,
при s = 1200 долл. Для сравнительного анализа вариаций было
бы сомнительно использовать величину стандартного откло-
нения (т. е., исходя из того, что 50 000 > 1200, утверждать,
что вариация для высших менеджеров выше, чем для неква-
лифицированных служащих).
Для высших менеджеров имеем
* = 50000 ,100% = 10%
500000
Для неквалифицированных служащих
ПОО
к = —~ 100% = 10%.
12 000
Отсюда следует, что множества имеют одинаковую вариа-
цию.
4.2. ИЗМЕРЕНИЕ ВАРИАЦИИ НА ОСНОВЕ
ПОРЯДКОВЫХ ХАРАКТЕРИСТИК
К порядковым характеристикам относятся значения, зани-
мающие определенное место в ранжированном ряду. Из ранее
рассмотренных характеристик таковыми являются наибольшее
и наименьшее значения, а также медиана. К другим порядко-
вым характеристикам относятся квартили и процентили.
Рассмотрим их использование для анализа разброса дан-
ных.
73
4.2.1. Размах квартилей и квартильное отклонение
Под квартилями понимаются значения, которые делят весь
ранжированный в порядке возрастания ряд на четыре равные
по численности группы. Так, ниже первого квартиля ((?) ле-
жит 25% всех данных. Между первым (О,) и вторым (QJ квар-
тилями также располагается 25% всех данных. Отсюда получа-
ем, что ниже и выше второго квартиля лежит по 50% общей
численности, т. е. он совпадает с медианой: Q2 = Me.
Между вторым и третьим квартилями, а также выше третье-
го расположено 25% всех значений.
В качестве меры разброса рассматривается расстояние меж-
ду третьим и первым квартилями, которое называется разма-
хом квартилей. Размах квартилей вычисляется по формуле
По определению между Q2 и должно лежать 50% всех дан-
ных рассматриваемой совокупности. Очевидно, чем меньше
расстояние между и (размах квартилей), тем ближе к
средней располагаются данные.
Если данные сгруппированы в виде ряда распределения, то
для оценки второго квартиля, т. е. медианы, можно использо-
вать формулу (3.5). Для расчетов первого и третьего квартилей
выводятся аналогичные формулы:
--cF
Ql=L+^——i,
(4.14)
где L — точная нижняя граница группы, содержащей первый
квартиль;
п — сумма частот всех групп (общее число данных);
f — частота группы, содержащей первый квартиль;
cF — кумулятивная частота группы, непосредственно пред-
шествующей группе, содержащей первый квартиль;
i — размер группировочного интервала, в котором содер-
жится первый квартиль;
Зп _
----cF
Q3 = L+-±y-----i, (4.15)
где L — точная нижняя граница группы, в которой содержит-
ся третий квартиль;
п — сумма частот всех групп (объем совокупности);
74
f — частота группы, содержащей третий квартиль;
cF— кумулятивная частота группы, непосредственно пред-
шествующей группе, в которой содержится третий квар-
тиль;
/ — размер группировочного интервала, содержащего тре-
тий квартиль.
Так же как и в случае медианы (второго квартиля), для оп-
ределения точной нижней границы L в формулах (4.14) и (4.15)
необходимо использовать кумулятивные частоты.
Пример 4.14. Вычислим размах квартилей для ряда распределе-
ния, представленного в табл. 2.11.
По определению первого квартиля Q, слева от него должно
находиться 25% всех данных, т. е. 30 значений (л = 120). Очевид-
но, группой, содержащей Q, будет такая группа, кумулятив-
ная частота которой равна или превосходит 30. Из табл. 2.11
видно, что первый квартиль содержит группа 1200—1399 долл.,
так как ее кумулятивная частота равна 43, а кумулятивная ча-
стота предыдущей группы — 21. Для искомой группы точная
нижняя граница L = 1199,5 долл., частота / = 22 и размер
/ = 200 долл. По формуле (4.14) найдем оценку для первого
квартиля:
125-2!
С, =1199.5 + ^-----200= 1281,32 долл.
Для группы, содержащей третий квартиль Q)t кумулятивная
частота должна быть равна или впервые превзойти 75% всех дан-
ных (л = 120), т. е. 90. Такой группе будет соответствовать интер-
вал 1600—1799 долл., имеющий кумулятивную частоту 107 (для
предшествующей группы cF = 83). Отсюда L = 1599,5 долл.,
f = 24, / = 200 долл. Проведем расчет по формуле (4.15):
5^5-83
= 1599,5 + —4------200 = 1657,51 долл.
3 24
Найдем оценку для размаха квартилей:
Q = G, - С, = 1657,83 - 1281,32 = 367,51 долл.
Иногда наряду с размахом квартилей рассматривают полу-
размах, или квартильное отклонение, равное половине рас-
стояния между третьим и первым квартилями:
?=(CJ-(21)/2. (4.16)
75
В примере 4.14 квартильное отклонение равно q = 376,51/2 =
= 188,26 долл.
Значения первого и третьего квартилей могут быть прибли-
женно определены на основе графика кумулятивного полигона.
Пример 4.15. Выборка, состоящая из торговых работников
фирмы, сгруппированных по годовым доходам, была пред-
ставлена в виде кумулятивного полигона типа “меньше, чем
...” (рис. 4.2).
Рис. 4.2. Оценка первого и третьего квартилей
с помощью кумулятивного полигона
На рис. 4.2 по левой вертикальной оси откладывается чис-
ленность торговых работников, а по правой — проценты от их
общего числа, равного 800. По горизонтальной оси графика
отмечаются годовые доходы. По определению первым кварти-
лем будет такая точка на горизонтальной оси, ниже которой
расположено 25% всех значений годовых доходов. Она находит-
ся следующим образом: на вертикальной оси процентов отме-
чается точка 25 (она соответствует '/ от 800, т. е. 200 на верти-
кальной оси численностей), далее из этой точки проводится
горизонталь до пересечения с (рафиком кумулятивного поли-
гона и затем вертикаль до пересечения с горизонтальной осью
годовых доходов. Точка пересечения вертикали с осью доходов
есть первый квартиль. На графике видно, что он равен пример-
но 30 000.
Аналогично находится третий квартиль. На оси процентов
отмечается точка 75, из нее проводится горизонталь до пересе-
чения с графиком кумулятивного полигона, далее из точки их
пересечения опускается перпендикуляр на горизонтальную ось
(ось доходов), который пересекает ее приблизительно в точке
40 000.
76
4.2.2. Размах процентилей
Так же как три квартиля делят все распределение на 4 рав-
ные по численности группы, процентили делят его на 100 рав-
ных по количеству данных частей. Формулы для процентилей
записываются аналогично формулам для квартилей:
^-cF
= L + 100-
(4.17)
где Рк — обозначение Л-го процентиля (к = 1,2, ..., 99);
L — точная нижняя граница группы, содержащей к-й про-
центиль;
к — порядковый номер процентиля;
cF— кумулятивная частота группы, предшествующей груп-
пе, содержащей Jt-й процентиль;
f — частота группы, в которой содержится к-й процен-
тиль;
i — размер группового интервала, содержащего к-й про-
центиль.
В качестве размаха процентилей на практике часто рассмат-
ривается расстояние между 10-м и 90-м процентилями:
(4.18)
90 W
Исходя из обшей формулы процентилей (4.17), формулы
для 10-го и 90-го процентилей будут иметь вид
I^-cF
PI0 = L + -^---i,
(4.19)
^-cF
P9O=L + -lfi2--------
i.
(4.20)
Очевидно, между 10-м и 90-м процентилями содержится
80% всех значений распределения.
Пример 4.16. Рассмотрим ряд распределения, представленный
в табл. 2.11. Вычислим для него размах процентилей, измеряе-
мый расстоянием между 90-м и 10-м процентилями.
По формуле (4.18) рассчитаем 10-й процентиль. Для этой
цели необходимо определить группу, в которой он содержится.
77
Кумулятивная частота этой группы должна быть равна или впер-
вые превзойти 10% всех данных (л = 120), т. е. 12. Из табл. 2.11
видно, что такой группой является интервал 1000—1199 долл,
(кумулятивная частота ее равна 21, в то время как кумулятив-
ная частота предыдущей группы равна 10). Подставляя данные
в формулу (4.19), получим
1^-ю
Р10 = 999,5 + —----200 = 1035,9 долл.
Группа, содержащая 90-й процентиль, должна иметь куму-
лятивную частоту, которая равняется или превышает 90% всех
данных, т. е. 108. Этой группой будет интервал 1800—1999 долл.
Вычислим 90-й процентиль по формуле (4.20):
90^20-107
Р90 = 1795,5 + --К&--200 = 1821,7 долл.
По формуле (4.18) вычислим размах процентилей:
Р = 1821,7 - 1035,9 = 785,8 долл.
Интерпретируя результаты, можно сказать, что 80% всех
арендаторов платят за апартаменты приблизительно от 1035,9
до 1821,7 долл.
4.3. ХАРАКТЕРИСТИКИ ФОРМЫ
КРИВОЙ РАСПРЕДЕЛЕНИЯ
Наряду с количественными характеристиками центральной
тенденции и разброса данных можно ввести измерители степе-
ни асимметрии распределений.
В разделе 3.2.4 рассматривались симметрия и различные типы
асимметрии кривых распределений. Если распределение симмет-
рично, то, очевидно, асимметрия равна нулю. В этом случае сред-
няя арифметическая, медиана и мода совпадают: х = Me = Мо.
Если во множестве данных одно или несколько значений
существенно превышают все остальные значения, то имеет
место положительная асимметрия. В этом случае средняя ариф-
метическая будет больше медианы и моды. Наоборот, если одно
или несколько значений существенно меньше всех остальных,
то возникает отрицательная асимметрия. В этом случае средняя
арифметическая остается меньше медианы и моды.
78
Для измерения степени асимметрии вводится коэффициент
асимметрии
$ (4.21)
s
где х — средняя арифметическая;
Me — медиана;
з — стандартное отклонение.
Коэффициент асимметрии колеблется в пределах от -3
до +3.
Если St > 0, то асимметрия положительна; если Sk < 0, то
асимметрия отрицательна; если = 0, то распределение будет
симметричным.
Пример 4.17. Данные о времени пребывания пациентов в кар-
диологическом отделении больницы были сгруппированы в виде
ряда распределения. Среднее арифметическое время лечения
составляло 28 дней, а медианное время — 23 дня. Вычисленное
стандартное отклонение равнялось 4,2 дня. Необходимо опре-
делить, является ли данное распределение симметричным или
имеющим положительную (отрицательную) асимметрию. Для
ответа на поставленные вопросы вычислим коэффициент асим-
метрии:
_ _3(х-Ме) 3 (28-25) _ , .
□ 1 —--------—----------—
* S 4.2
Величина коэффициента асимметрии +2,14 свидетельствует
о значительной положительной асимметрии. По-видимому, не-
сколько пациентов оставались на лечении значительно доль-
ше, чем все остальные. Это повлияло на то, что значение сред-
ней арифметической превысило медиану и моду.
Для симметричных распределений вводится понятие курто-
зиса. Под куртозисом понимается крутость кривой распределе-
ния, которая определяется сопоставлением с кривой нормаль-
ного распределения (оно достаточно подробно рассматривается
в гл. 7). Если вершина распределения находится выше вершины
нормального распределения, то оно называется высоковершин-
ным, или островершинным. Если же она находится ниже, рас-
пределение называется низковершинным, или плосковершин-
ным. На рис. 4.3 показаны кривые нормального, островершинного
и плосковершинного распределений.
79
В качестве меры крутости рассматриваются специальные
показатели, которые характеризуют отклонение вершины фак-
тического распределения от вершины нормального распреде-
ления. Формулы для вычисления этих показателей достаточно
сложны и в данной работе не рассматриваются.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 4
В главе рассматривались вопросы количественного измере-
ния вариации, или разброса данных. Одной из характеристик
вариации является размах колебаний, который вычисляется как
разность между наибольшим и наименьшим значениями (фор-
мула (4.1)). Размах колебаний — грубая характеристика, зави-
сящая только от двух значений всего множества данных. Более
точным показателем, зависящим от всех значений, является
среднее линейное отклонение. Оно вычисляется как средняя
арифметическая абсолютных величин отклонений от средней
(формула (4.2)). Если в качестве средней выбирается медиана,
то среднее линейное отклонение будет наименьшим. Среднее
линейное отклонение часто называют средним абсолютным от-
клонением. Другой тип характеристики разброса относительно
средней арифметической представляет собой дисперсия. Ее
определение основано на вычислении среднего значения для
квадратов отклонений. Дтя генеральной совокупности диспер-
сия вычисляется по формуле (4.4), а для выборки — по форму-
ле (4.8). В формуле для выборочной дисперсии в знаменателе
стоит число, равное общему числу данных, уменьшенному на
единицу (в отличие от формулы для генеральной дисперсии
80
(4.4), где знаменатель равен объему генеральной совокупнос-
ти). Это делается с целью корректировки оценки выборочной
дисперсии, которая получается заниженной в связи с заме-
ной генеральной средней на выборочную среднюю. Диспер-
сия не очень удобная характеристика при сравнительном ана-
лизе, так как выражается в единицах измерения, которые
имеют неясный смысл: квадрат единицы измерения первич-
ных данных. Более удобно пользоваться стандартным откло-
нением, которое вычисляется как корень квадратный из дис-
персии (формулы (4.6) и (4.10)). Стандартное отклонение
измеряется в тех же единицах, что и значения исходной сово-
купности.
Для более глубокого анализа разброса данных около сред-
ней можно использовать неравенство Чебышева, которое име-
ет следующую трактовку: для любой совокупности доля значе-
ний. попадающих в интервал л ±ks (или ц ±к<з) для генеральной
совокупности), будет равна по крайней мере 1 - l/к2, где к —
любое число, большее 1.
При сравнительном анализе двух или более совокупностей
по степени вариации данных возникает проблема, связанная с
единицами измерения признаков элементов различных сово-
купностей или с ситуацией, когда средние совокупностей зна-
чительно отличаются друг от друга. Для решения этой пробле-
мы вводится относительная характеристика — коэффициент
вариации. Он равен отношению стандартного отклонения к
средней арифметической.
Степень вариации измеряется также с помощью порядко-
вых характеристик, т. е. значений, занимающих определенные
места в ранжированном ряду. К ним относятся квартили и про-
центили. Квартили делят ранжированный по возрастанию ряд
на четыре равные по численности группы, а процентили — на
КМ) равных частей. В качестве характеристик разброса часто рас-
сматривают размах квартилей и размах процентилей. Под раз-
махом квартилей понимается расстояние между третьим и пер-
вым квартилями. На этом отрезке концентрируется 50% всех
данных совокупности. Для ряда распределения оценка первого
и третьего квартилей осуществляется по формулам (4.14) и (4.15).
Половина размаха квартилей называется квартильным откло-
нением. Под размахом процентилей часто понимают длину
интервала между 90-м и 10-м квартилями. На нем располагает-
ся 80% общего числа данных. Для ряда распределения оценка
всех процентилей производится по формуле (4.17).
81
Для характеристики формы кривой распределения исполь-
зуется коэффициент асимметрии, который вычисляется по
формуле (4.21). Он изменяется в границах от -3 до +3 и равен
нулю для симметричного распределения. Знак коэффициента
асимметрии отражает направление асимметрии (положитель-
ная или отрицательная).
Куртозис характеризует крутость распределения, которая
определяется сопоставлением кривой фактического распределе-
ния с кривой нормального распределения. Если вершина рас-
пределения находится выше вершины нормального распределе-
ния, то оно называется высоковершинным, или островершинным.
Если же она находится ниже, то распределение называется низ-
ковершинным, или плосковершинным.
ЭЛЕМЕНТЫ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
Главная задача аналитической статистики состоит в том,
чтобы сделать максимально правдоподобные выводы о свой-
ствах и характеристиках генеральной совокупности на основе
доступной части данных из этой совокупности. При этом все-
гда существует риск, что эти выводы будут неправильными
ввиду неполноты имеющейся информации. Отсюда возникает
проблема количественных оценок степени этого риска. Наибо-
лее адекватным научным подходом в данном случае является
использование понятий и методов теории вероятностей. Тео-
рию вероятностей можно назвать “наукой о неопределеннос-
ти” или “математикой случайного”.
5.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
5.1.1. Общее понятие вероятности
В быту и профессиональной деятельности человек постоянно
сталкивается с такими понятиями, как вероятность или шансы
чего-то, что еще не произошло, но может произойти. Напри-
мер, прогноз погоды, возможность выигрыша любимой коман-
ды, шансы продвижения нового товара, оценка будущего ва-
лютного курса и т. д. В практической жизни слова “вероятность”
и “шансы” имеют одинаковый смысл. Они выражают степень
уверенности в том, что некоторое событие должно произойти.
Понятие события является основополагающим в теории ве-
роятностей. Всякое событие появляется в результате некоторо-
го опыта или испытания. Для проведения опыта необязательно
наличие каких-либо лабораторных условий, как, например, для
исследования химической реакции. Под опытом (или испыта-
нием) в теории вероятностей понимаются всякие действия,
83
связанные с наблюдениями и измерениями. Событие рассмат-
ривается как один или несколько возможных исходов данного
испытания. Обычно события обозначают прописными буква-
ми: А, В, С и т. п.
Рассмотрим описания нескольких опытов и соответствую-
щих событий.
I. Опыт: бросание двух игральных костей; событие А — вы-
падение на костях суммы очков, равной 7; В — выпадение сум-
мы очков, большей 8; С — выпадение двух четверок.
2. Опыт: сдача студентом предстоящего экзамена; событие
А — сдал, В — не сдал.
3. Опыт: поворот ключа в замке зажигания автомобиля, со-
шедшего с конвейера; событие А — двигатель запустился, В —
двигатель не запустился.
4. Опыт: наблюдение за числом автомобилей, прибывающих
на стоянку; событие А — ни одного автомобиля, В — 1 автомо-
биль, С — 2 автомобиля и т. д.
Под определением вероятности всегда понимается вычис-
ление вероятности какого-либо события. Например, пусть бро-
саются две игральные кости (опыт). Тогда вероятность того,
что сумма выпавших очков на костях будет равна 7 (событие
А), есть вероятность, что произойдет событие А (или просто
вероятность события А). Эта вероятность обозначается Р(А).
Вероятности событий выражаются числом, заключенным
между 0 и 1. Если вероятность события равна 1, то это собы-
тие обязательно произойдет. Такое событие называется досто-
верным. Чем ближе вероятность события к единице, тем оно
достовернее. Так, событие, что любой человек рано или по-
здно умрет, является достоверным, т. е. имеет вероятность,
равную 1.
Событие, которое не может произойти ни при каких обсто-
ятельствах, называется невозможным. Его вероятность равна 0.
Например, выпадение 8 очков при бросании игральной кости
является невозможным событием. Чем ближе вероятность со-
бытия к нулю, тем это событие менее вероятно.
5.1.2. Объективный и субъективный подходы
к определению вероятности. Закон больших чисел
Объективный подход имеет две основные схемы вычисле-
ния вероятности: классическое определение вероятности и ста-
тистическая вероятность.
84
Классическое определение вероятности основано на поня-
тии случаев. Под случаями понимаются все возможные исходы
опыта, которые равновозможны (равновероятны) и являются
взаимоисключающимися (т. е. никакие два из них не могут по-
явиться вместе в данном опыте). Если появление определенно-
го случая влечет за собой появление некоторого события А, то
этот случай называется благоприятствующим этому событию.
Классическое определение вероятности основано на схеме слу-
чаев. Вероятность события А вычисляется как отношение числа
случаев, благоприятствующих событию А, к общему числу слу-
чаев:
Число случаев, благоприятствующих событию А
Р\А)в л— • (5.1)
Общее число случаев
Пример 5.1. Рассмотрим опыт — бросание игральной кости. Дан-
ный опыт имеет ровно шесть единственно возможных, равно-
вероятных и взаимоисключающихся исходов (случаев): выпа-
дение вверх грани с соответствующим количеством очков от 1
до 6. Ясно, что вероятность каждого случая равна '/t, так как
выпадение определенного числа очков есть единственный бла-
гоприятствующий этому событию случай. Следует отметить, что
сумма вероятностей всех случаев будет всегда равна 1. Возьмем
более сложное событие, заключающееся в выпадении четного
числа очков. Тогда данному событию будуг благоприятствовать
уже три случая: выпадение 2, 4 и 6 очков. Исходя из классичес-
кого определения вероятности (5.1) вероятность выпадения чет-
ного числа очков будет равна 3/6 = 1/2 = 0,5.
Классическое определение вероятности применимо только
тогда, когда реализуется схема случаев. Однако во многих ситу-
ациях, связанных с производством, экономикой и бизнесом,
возможные исходы опыта могут быть не обязательно равнове-
роятными и взаимоисключающимися.
Пример 5.2. Пусть некоторая деталь выгачивается на станке (про-
ведение испытания). В качестве возможных исходов будем рас-
сматривать два единственно возможных и взаимоисключающих-
ся события — выпуск детали в допуске и выпуск бракованной
детали. Если станок хорошо налажен, то, очевидно, вероят-
ность производства годной детали будет превышать вероятность
выпуска бракованной детали. Следовательно, в данной ситуа-
ции использование схемы случаев становится невозможным.
85
Другим объективным подходом к вычислению вероятности
является статистическая вероятность. Пусть в прошлом было
произведено достаточно большое количество опытов, где в
результате каждого из них наблюдалось появление или непояв-
ление события А. Если отношение частоты, т. е. количества по-
явления события А, к общему числу опытов приближается к
некоторой величине, то эта величина принимается за вероят-
ность события А. Обозначим число проведенных опытов через
п, а частоту появления события А — через т. Тогда формула
статистической вероятности будет иметь вид
Р(А) — т/п. (5.2)
Формула (5.2) выражает относительную частоту события А,
которая является оценочным значением вероятности. Чем боль-
шее количество опытов произведено, тем точнее оценка. Ста-
тистическая вероятность является одним из проявлений закона
больших чисел в теории вероятностей. В широком смысле под
законом больших чисел понимается свойство устойчивости
массовых явлений, которое проявляется при большом числе
опытов. При этом конкретные особенности каждого отдельно-
го случайного явления почти не сказываются на среднем ре-
зультате массы таких явлений. В теории верятностей закон боль-
ших чисел объединяет ряд теорем, в каждой из которых
доказывается, что при определенных условиях средние харак-
теристики большого числа опытов приближаются к некоторым
определенным константам. В частности, доказывается, что при
большом числе опытов относительная частота события при-
ближается к вероятности этого события.
Пример 5.3. Статистическая отчетность в здравоохранении по-
казала, что за последние годы на каждые 883 смерти приходит-
ся 24 смерти вследствие автомобильных аварий, 182 — вслед-
ствие заболевания раком, 333 — заболеваний сердца. Используя
статистическую вероятность, определить вероятность того, что
причиной смерти любого умершего, выбранного случайным
образом, является:
автомобильная авария (событие А}),
онкологические заболевания (событие AJ,
заболевания сердца (событие Л3).
Оценим вероятности данных событий по формуле (5.2):
РЦ) = 24/883 = 0,027, /\AJ = 182/883 = 0,206,
АЛ3) = 333/883 = 0,377.
86
Вычисленные величины являются относительными часто-
тами событий. Их надо рассматривать как оценочные значения
вероятностей. Под испытанием в данном случае понимается слу-
чайный выбор какого-либо умершего и установление причины
его смерти.
Для использования объективного подхода к определению
вероятности необходимо наличие либо схемы случаев, либо
информации о появлении события в прошлом. Если эти усло-
вия не выполняются, то объективный подход становится не-
возможным. В этом случае единственный путь определения ве-
роятности — субъективная оценка. Субъективная вероятность
основывается на индивидуальном или коллективном мнении
людей, которые выступают в роли экспертов. Они высказыва-
ют свои оценки вероятности события на основе какой-либо
информации, а также своего опыта и интуиции. Субъективная
вероятность отражает степень уверенности отдельного челове-
ка или группы лиц в том, что данное событие произойдет.
В качестве примеров, отражающих необходимость получения
субъективной вероятности, можно рассмотреть следующие за-
дачи:
оценить вероятность того, что данная команда выиграет пер-
венство страны по футболу;
оценить вероятность того, что объем продаж нового про-
дукта в течение года составит более 1000 штук.
5.2. ОСНОВНЫЕ ПРАВИЛА ДЕЙСТВИЙ
НАД ВЕРОЯТНОСТЯМИ
5.2.1. Типы событий. Алгебра событий
Всякое событие, которое рассматривается в теории вероят-
ностей, является случайным, т. е. оно может произойти или не
произойти.
События Ан В называются совместимыми, если в условиях
опыта появление одного события не исключает появления дру-
гого. Если возможно появление только одного из событий, т. е.
они не могут появиться вместе в одном опыте, то эти события
называются несовместимыми.
Пример 5.4. Рассматривается множество деталей двух сортов. Слу-
чайным образом вынимается одна деталь. Появление детали оп-
87
ределенного сорта является случайным событием. Пусть событие
А заключается в появлении детали первого сорта, а событие В —
в появлении детали второго сорта. Ясно, что эти события несов-
местимы. Если испытание заключается в случайном выборе двух
деталей, то события А и Сбудут совместимыми.
Определение двух совместимых или несовместимых собы-
тий можно распространить и на группу, состоящую из несколь-
ких событий. В этом случае для любых двух событий этой груп-
пы должно соответственно выполняться условие совместимости
или несовместимости.
Суммой, или объединением, п событий Л(, Л2, .... назы-
вается случайное событие, состоящее в том, что в результате
опыта произойдет хотя бы одно из этих событий. Сумма собы-
тий обозначается следующим образом:
А. + А, + ... + А .
I 2 к
Пример 5.5. Событие D. состоящее в выпадении нечетного числа
очков при бросании игральной кости, является суммой собы-
тий А. В, С:
D = А + В + С,
где А — выпадение 1 очка,
В — выпадение 3 очков,
С — выпадение 5 очков
Несовместимые события Лр Av ..., Ая образуют полную груп-
пу, если одно из зтих событий должно обязательно осуществить-
ся. Ясно, что сумма вероятностей полной группы событий рав-
на единице:
АЛ,) + АЛ2) + ... + АЛ,) = ь
Если полная группа событий состоит из двух событий, то
эти события называются противоположными. Событие, проти-
воположное событию А, обозначается А. Для противоположных
событий верно соотношение
АЛ) + АЛ) = 1. (5.3)
Пример 5.6. Пусть событие Л состоит в выпадении четного числа
очков при бросании игральной кости. Тогда противоположное
событие Л заключается в выпадении нечетного числа очков.
88
Произведением, или пересечением, событий А , Аг ..., Ап
называется случайное событие (обозначается A Ar..Aj, кото-
рое состоит в том, что в результате испытания произойдут все
эти события.
Пример 5.7. Пусть испытание заключается в том, что по мише-
ни производятся три выстрела. Событие Af характеризуется по-
паданием в мишень только при первом выстреле, событие Л2 —
только при втором выстреле, событие Л, — только при третьем
выстреле.
Произведением событий Лр Л, и Л3 будет событие С= AtA2A},
которое означает, что при трех выстрелах будет ровно три по-
падания.
Наглядную геометрическую интерпретацию действий над
двумя случайными событиями Л и Я дает диаграмма Венна. Для
построения диаграммы Венна представим все возможные исхо-
ды испытания в виде совокупности точек некоторого квадрата.
Событие Л (или В) заключается в том, что выбранная про-
извольным образом точка квадрата лежит внутри соответству-
ющего круга. Противоположное событие Л (или В) заключает-
ся в том, что выбранная произвольным образом точка лежит
вне соответствующего круга. Заштрихуем соответствующие со-
бытия и получим геометрическую интерпретацию производи-
мых действий над событиями (рис. 5.1).
Рис. 5.1. Диаграмма Венна:
а — событие А. б — событие В; а — событие А; г — событие В; д — сумма совмести-
мых событий Див; е - произведение совместимых событий Див; ж - несовмести-
мые события Див
89
Два случайных события называются зависимыми друг от
друга, если вероятность появления одного из них изменяется в
зависимости от появления или непоявления другого.
Пример 5.8. В ящике находится 25 деталей. Среди них — 23
годные и 2 бракованные. Пусть испытание состоит в том, что
одна деталь случайным образом выбирается из ящика и не
возвращается обратно. Событие А заключается в том, что при
первом отборе вынимается годная деталь, а событие В — при
втором отборе вынимается дефектная деталь. Тогда вероятность
события В будет зависеть от того, произошло событие А или
нет. В самом деле, если при первом испытании была вынута
годная деталь, то вероятность, что при втором испытании
будет извлечена бракованная деталь, равна 2/24 = 1/12, а
если при первом испытании была извлечена бракованная,
то — 1/24.
Два события называются независимыми, если вероятность
появления одного из них не зависит от появления или непояв-
ления другого.
Пример 5.9. Подбрасываются две монеты. Под событием А, по-
нимается выпадение цифры для первой монеты, под событием
А} — выпадение герба для второй монеты. Ясно, что вероят-
ность появления события Я,(Я2) никак не влияет на появление
события Я2(Л,).
5.2.2. Правила сложения вероятностей
Если события А и В несовместимы, то вероятность суммы
этих событий (т. е. вероятность того, что произойдет или собы-
тие А, или событие В) равна сумме вероятностей наступления
каждого события:
Р[А + В) = ЛЯ) + Р[В). (5.4)
Аналогично это правило распространяется на сумму п не-
совместимых событий:
ЛЯ, + Я2 + ... + Ая) = ЛЯ,) + ЛЯ2) +...+ ЛЯ,). (5.5)
Из этого правила следует, что сумма вероятностей един-
ственно возможных и несовместимых событий равна 1.
90
Пример 5.10. Автомат заполняет пластиковые пакеты смесью
овощей. Большинство наполненных пакетов имеет стандартный
вес. Однако ввиду небольших отклонений в размерах кусочков
овощей часть пакетов имеет перевес, а часть — недовес. Резуль-
таты проверки большого числа наполненных пакетов (4000)
были сведены в табл. 5.1.
Таблица 5.1
Результаты проверки весов автоматически
наполненных пакетов
Тип пакета Событие Число пакетов Вероятость события
Недовес А 100 0.025(100:4000)
Стандартный вес В 3600 0,9 (3600 4000)
Перевес С 300 0,075 (300:4000)
Требуется определить, чему равна вероятность того, что
наугад вынутый пакет окажется нестандартного веса (будет иметь
или недовес, или перевес). В табл. 5.1 событие “недовес” обо-
значено буквой А, а событие “перевес” — буквой С. Требуется
найти вероятность суммы событий А и С.
По формуле (5.5) имеем
Р(А + О = ЛЛ) + ЛО = 0,025 + 0,075 - 0,1.
Заметим, что события А, В, С являются несовместимыми.
Иначе говоря, любой случайным образом выбранный пакет
будет иметь либо стандартный вес, либо недовес, либо перевес.
Отсюда получаем
Р{А + В + С) = Р(А) + Р(В) + ЛО = 1
Случайные события не всегда бывают несовместимыми.
В случае двух совместимых событий правило сложения вероят-
ностей принимает вид (теорема сложения вероятностей)
Р(А + В) = Р(А) + Р(В) - Р[АВ). (5.6)
Теорема сложения вероятностей, выраженная формулой (5.6),
является общим правилом сложения вероятностей как для со-
вместимых, так и для несовместимых событий. В случае несовме-
стимых событий их произведение будет невозможным событи-
ем, т. е. вероятность произведения этих событий будет равна нулю:
Р[АВ) = 0. В этом случае формула (5.6) примет вид (5.5).
91
Пример 5.11. Из 200 студентов 120 факультативно изучают ан-
глийский язык и 100 немецкий. Какова вероятность того, что
произвольным образом выбранный студент изучает или анг-
лийский, или немецкий? Какова вероятность, что он не изу-
чает ни английский, ни немецкий?
Вероятность, что студент изучает английский (событие А),
равна /\А) = 120/200 = 0,6. Вероятность, что студент изучает
немецкий (событие В), равна Р{В) = 100/200 = 0,5. Нас инте-
ресует вероятность суммы событий. Если использовать формулу
(5.4) для несовместимых событий, то вероятность суммы со-
бытий Р(А + В) = Р(А) + f\B) = 1,1. Это невозможно, так как
вероятность любого события не может превышать 1. Единствен-
ное объяснение данного факта состоит в том, что некоторые
студенты изучают оба языка и были просчитаны дважды. Пусть
таких студентов оказалось 60. Тогда вероятность того, что сту-
дент изучает оба языка одновременно, равна 60/200 = 0,3. Для
определения вероятности суммы событий воспользуемся фор-
мулой (5.6):
Р(А + В) = ЛЛ) + Р(В) - 1\АВ) = 120/200 +
+ 100/200 - 60/200 = 160/200 = 0,8.
Событие, что студент не изучает ни английский, ни немец-
кий, будет противоположным событию А + В. Обозначим его
А + В Ввиду (5.3) сумма вероятностей противоположных со-
бытий равна I:
Р(А + В) + Р(АТ~В) = 1.
Отсюда вероятность события, что случайным образом выб-
ранный студент факультативно не изучает ни одного языка,
равна Pt А + В) = 0,2. Группа таких студентов составляет 40
человек.
Описанную ситуацию можно наглядно проиллюстрировать
с помощью диаграммы Венна (рис. 5.2).
Р(АВ) - 0.3
Рис. 5.2. Диаграмма Вонна для ситуации со студентами, изучающими
английский (событие А), немецкий (событие S) и оба языка одновременно
(событие АВ)
92
5.2.3. Условная вероятность.
Правила умножения вероятностей
В примере 5.8 был рассмотрен случай зависимых событий,
связанных со случайным выбором бракованной или годной
детали. Было показано, что вероятность выбора годной или бра-
кованной детали при втором отборе зависит от того, какая де-
таль (годная или бракованная) была выбрана в первый раз. Ве-
роятность события вычисленная при условии осуществления
другого события Аг называется условной вероятностью. Она
обозначается PiAt/A2). В примере 5.8 были вычислены две ус-
ловные вероятности:
вероятность выбора дефектной детали при втором отборе
(событие В) при условии, что в первый раз была выбрана год-
ная деталь (событие А), т. е. Pi В/А) = 1/12;
вероятность выбора при втором отборе бракованной детали
при условии, что в первый раз была выбрана также бракован-
ная деталь, т. е. Pi В/А) = 1/24.
Если события Ли В независимые, то условная вероятность
одного из них при условии, что другое произошло, будет рав-
на безусловной вероятности первого из событий:
Р[А/ В) = Р(А), (5.7)
PiB/A) = PiB). (5.8)
Соотношения (5.7) и (5.8) следуют из определения незави-
симых событий.
Пусть события А и Я являются независимыми. Тогда вероят-
ность, что оба эти события произойдут в результате одного
испытания (т. е. произведения АВ), равна произведению веро-
ятностей этих событий:
Pi АВ) = PiA)PiB). (5.9)
Формула (5.9) характеризует частный случай правила ум-
ножения вероятностей.
Пример 5.12. Из стандартной колоды игральных карт (52 кар-
ты) случайным образом последовательно с возвратом выбира-
ются две карты. Какова вероятность, что одна карта будет ко-
ролем, а другая — пиковой масти?
93
Пусть выбор короля является событием Л, а выбор карты
пиковой масти — событием В. Ввиду того что выбор каждой
карты осуществляется с возвратом, то события А и В будут не-
зависимыми. Искомая вероятность равна вероятности произве-
дения событий А и В, т. е. в данном случае верна формула (5.9).
Найдем вероятность Р(А). Событию А (выбор короля) благо-
приятствуют 4 случая. Отсюда Р(А) = 4/52 = 1/13. Событию В
(выбор карты пиковой масти) благоприятствует 13 случаев:
ЛЛ) = 13/52 = 1/4.
По формуле (5.9) имеем
ЛЛ5) = Р(А)/\В) = 1/13 • 1/4 = 1/52.
Следует отметить, что выполнение одного из соотношений
(5.7), (5.8), (5.9) является необходимым и достаточным усло-
вием независимости событий А и В.
Пример 5.13. Рассмотрим следующие события:
Л — компания Procter and Gamble выпустит новое моющее
средство, которое в будущем году займет по крайней мере 5%
рынка;
В — компания General Motors введет новую линию произ-
водства компактных автомобилей.
Очевидно, что от того, свершится или не свершится собы-
тие В, никаким образом не зависит появление или непоявле-
ние события Л, т. е. 1\А/В) = Р(А). Отсюда следует, что события
Л и В независимые.
Заменим теперь событие Л на новое событие: компания Toyota
предполагает сокращение в следующем году объема продаж ма-
лолитражных автомобилей. В данном случае было бы неправильно
полагать, что Р(А/В) = Р(А). Здравый смысл подсказывает, что
условная вероятность f\A/B) будет больше, чем безусловная
вероятность Р(А).
Заметим, что вопрос о конкретных значениях величин F\A/B)
и Р[А) не обсуждается. Было только установлено, что эти вероят-
ности не равны: f\A/B) * ЖЛ), что является доказательством
зависимости данных событий.
Рассмотрим теперь общее правило умножения вероятнос-
тей, которое учитывает случай зависимых событий А и В. Это
правило, или теорема об умножении вероятностей, выражает-
ся в виде следующей формулы:
94
Р(АВ) = f\A)P(B/A) = P(B)P(A/B).
(5.10)
Иначе говоря, вероятность того, что события А и В могут
совместно произойти в результате испытания, равна произве-
дению безусловной вероятности события Л (Я) и условной ве-
роятности события В (А).
Пример S. 14. В коробке находится 10 шаров: 3 белых и 7 черных.
Из коробки вынимают наугад один за другим два шара, при-
чем первый вынимается без возврата. Какова вероятность того,
что оба шара окажутся белыми?
Пусть событие А состоит в выборе первого белого шара, а
событие В — в выборе второго белого шара. Очевидно, необхо-
димо определить вероятность совпадения этих двух событий,
т. е. вероятность их произведения Р{АВ). Для того чтобы исполь-
зовать формулу (5.10), следует найти безусловную вероятность
Р(А) и условную Р(В/А).
При выборе первого шара появлению белого шара благо-
приятствуют 3 случая, следовательно, Р(А) = 3/10. Если собы-
тие А произошло, то при втором выборе появлению белого
шара соответствуют 2 случая из 9. Отсюда Р[В/А) = 2/9.
По формуле (5.10) найдем вероятность Р(АВ);
3 2
Р(АВ) = Р(А)Р(В/А) = — • -«0.07.
Статистический смысл этой вероятности состоит в том, что
если данный опыт повторить 100 раз, то в семи исходах следует
ожидать появления одного за другим двух белых шаров.
Теорему умножения вероятностей можно распространить и
на случай трех событий:
Р(АВС) = Р(А)Р(В/А)Р(С/АВ). (5.11)
Пример 5.15. Пусть соблюдаются условия примера 5.14 и выни-
маются последовательно три шара, причем первые два без воз-
врата. Используя формулу (5.11), определить, какова вероят-
ность, что все три шара окажутся белыми.
Величины /\А) и 1\В/А) уже были вычислены в примере
5.14. Определим вероятность события, что при третьем выборе
появится белый шар при условии, что в результате двух преды-
95
луших были также вынуты белые шары, т. е. найдем величину
Р[С/АВ). Данному событию благоприятствует один случай из
восьми, следовательно, Р(С/АВ) = 1/8.
По формуле (5.11) вычислим вероятность появления трех
белых шаров:
3 2 1 1
КАВС) = F\A)P{B/A)P(C/AB) = = — «0,00833.
1U V о 1ZU
Заметим, что в примере 5.15 вычисление условной вероят-
ности зависело от принципа организации отбора. В данном слу-
чае отбор производился по схеме невозврашенного шара, т. е.
те элементы, из которых формировалась выборка, уже не воз-
вращались в генеральную совокупность. Такая выборка, эле-
менты которой отбираются из генеральной совокупности с
соблюдением принципа случайности и не возвращаются в ге-
неральную совокупность, называется выборкой без возвраще-
ния, или бесповторной . Если выборка формируется по схеме с
возвращением отобранных элементов в генеральную совокуп-
ность, то она называется выборкой с возвращением или по-
вторной.
5.2.4. Таблица сопряженности и дерево
возможных исходов
Общее правило умножения вероятностей применяется при
анализе так называемой таблицы сопряженности, которую удоб-
но использовать для статистических заключений. Для иллюст-
рации этого понятия рассмотрим следующую ситуацию.
В некой компании был проведен социологический опрос.
Цель опроса — выяснить, желают ли служащие остаться на
фирме или намерены перейти на другую работу. В анонимной
анкете необходимо было указать стаж работы на фирме и в
форме “да/нет” ответить на вопрос: “Перейдете ли вы в дру-
гую компанию, если вам будет предложена работа на таких
же (или чуть лучше) условиях, которые вы имеете на нашей
фирме?”
Результаты анализа ответов 200 работников были сведены в
таблицу, которая называется таблицей сопряженности (табл. 5.2).
В ней отражается перекрестная классификация работников по
двум признакам: стаж работы на фирме и намерения остаться
или переменить место работы.
96
Таблица 5.2
Таблица сопряженности признаков: стаж работы
и намерения относительно перемены места работы
Намерения Стаж работы, годы
До 1 1-5 5-10 Более 10 Итого
Собираются остаться Собираются перейти 10 25 30 15 5 10 75 30 120 80
200
Данные таблицы сопряженности позволяют вычислять ве-
роятности потенциальных предпочтений: продолжать работать
на фирме или нет в сочетании со стажем. Например, вычислим
вероятность того, что случайным образом выбранный работ-
ник остается на фирме (событие Я) и одновременно имеет стаж
более 10 лет (событие В). Из табл. 5.2 видно, что общее число
работников, собирающихся остаться, равно 120. Поэтому
Р(А) = 120/200 = 3/5. Далее необходимо вычислить условную
вероятность Р(В/А), т. е. вероятность того, что служащий со ста-
жем более 10 лет останется на фирме, несмотря на предложе-
ние новой работы на таких же (или немного лучше) условиях.
По данным табл. 5.2 из 120 потенциально остающихся работ-
ников 75 имеют стаж более 10 лет, следовательно, Р{В/А) =
= 75/120 = 15/24.
По формуле (5.10) вычисляем искомую вероятность:
3 5
Р(АВ) = Р{А)Р[В/А) = - - = 0,375.
D о
Наряду с таблицей сопряженности полезным инструмен-
том для вычисления условных вероятностей и вероятностей
произведений событий является дерево возможных исходов.
Подобное дерево, построенное на основе таблицы сопря-
женности 5.2, представлено на рис. 5.3. Выделим свойства и
принципы построения, которые присущи любому другому де-
реву возможных исходов.
1. Начальная точка в левой части диаграммы обозначает
“ствол” дерева.
2. Из ствола выходят две “ветви”, которые формируют пер-
вый уровень дерева и соответствуют двум возможным исходам:
верхняя ветвь — “собираются остаться”, нижняя ветвь — “со-
бираются перейти”. Безусловные вероятности этих событий
указаны на соответствующих ветвях.
97
1-5
6-10
5
120
75
120
Стаж
10 работы
120
30
120
<1
120 ’0
200 120 " 0,05
120 30
200 120 S
120 5
200 120 ’ 0,025
120 75 „
200 120 0,375
>10
80 15
200 80 = 0,075
80 25 „ ,
200 80 “ 0,125
80 30 „
200 80 "0,15
80 ’0 „ „
200 80 0,05
1.00
Рис. 5.3. Дерево возможных исходов для таблицы сопряженности 5.2
3. Второй уровень дерева образуют восемь ветвей: из нижней
и верхней ветвей первого уровня “растут” по четыре ветви,
характеризующие возможные исходы, связанные со стажем
работы на фирме (менее 1 года, 1—5 лет, 6—10 лет, свыше 10
лет). Соответствующие условные вероятности записаны у каж-
дой ветви. Для данной проблемы дерево возможных исходов
имеет два уровня.
4. Любой путь из исходной точки в концевую точку послед-
него уровня (в данном случае второго) будет характеризовать-
ся произведением событий на соответствующих ветвях, обра-
зующих этот путь. Вероятность каждого такого произведения
вычисляется как произведение вероятностей, соответствующих
ветвям рассматриваемого пути. Эти вероятности указаны на
диаграмме справа около концевых точек дерева. Например, ве-
роятность события, что наугад выбранный работник не со-
98
бирается уходить с работы и имеет стаж менее одного года,
нычисляется как произведение:
120 10
200 120
= 0,05.
Ввиду того что концевые точки дерева характеризуют все
возможные исходы, которые получаются в результате испыта-
ния, сумма их вероятностей, очевидно, равняется единице.
5.2.5. Формула полной вероятности. Теорема Байеса
Полная вероятность события А вычисляется на основании
его условных вероятностей. Пусть событие А может произойти
тогда и только тогда, когда имеет место одно из нескольких
несовместимых событий Ае А.,..., Ап (называемых гипотезами).
Тогда полная вероятность события А равна сумме слагаемых,
где каждое из них есть произведение вероятности гипотезы на
вероятность события А при условии осуществления этой гипо-
тезы, и сумма берется по всем гипотезам:
Р(А) - PlAJPtA/AJ + Р(А2)Р(А/А2) + ... + ЛЛл)АЛ/Ля). (5.12)
Пример 5.16. Пусть имеются 3 одинаковых ящика. В каждом
ящике содержится по 10 деталей, причем из них в 1-м ящи-
ке — 2 бракованные детали, во 2-м — 3, в 3-м — 4. Опреде-
лим вероятность того, что при выборе наудачу одной детали
из произвольно взятого ящика деталь окажется годной (со-
бытие Л).
Гипотезой в данном случае является отбор детали из соот-
ветствующего ящика: At — выбор детали из ящика I, А2 — вы-
бор детали из ящика 2, А3 — выбор детали из ящика 3. Ввиду
того что выбор ящика случайный, имеем = ЛЛ2) =
• ДЛЭ) = 1/3.
Условные вероятности отбора годной летали по гипотезам
таковы: PtA/AJ = 8/10, Р(А/А2) = 7/10, PIA/AJ = 6/10.
Полная вероятность события А вычисляется по формуле
(5.12):
Р(А) = PtAJPtA/AJ + Р(А2)Р(А/А2) + Р(А2)Р(А/А}) =
= 1.А + 1.2 + 1.А=21=о,7.И
3 10 3 10 3 10 30
99
Р(А/А) =------- Р^А'У
Р(\)Р(А/А,)+Р(А2)Р(А/А2) +
Формула полной вероятности является основой для теоре-
мы Байеса, или теоремы о вероятности гипотез. Эта теорема
позволяет оценить величину вероятности какого-либо предпо-
ложения после того, как получен определенный результат ис-
пытания. По теореме Байеса вероятность гипотезы А после ис-
пытания равна произведению вероятности этой гипотезы до
испытания на вероятность события по этой гипотезе, деленно-
му на полную вероятность события А (сумму таких произведе-
ний по всем гипотезам Л , Ар ..., AJ:
---------------, (5.13)
... + /’(Ав)Р(А/Д1)
где Р(А./А) — вероятность гипотезы Л после испытания, или
апостериорная вероятность;
Р(А ) — вероятность гипотезы AI (i — 1,...,л) до испыта-
ния, или априорная вероятность;
Р(А/А) (I = 1,2,...,л) — вероятность события А в предпо-
ложении, что гипотеза Л. осуществилась.
На основе теоремы Байеса можно корректировать априор-
ные вероятности гипотез (т. е. принятые до испытания) по ре-
зультатам уже произведенного испытания (т. е. получить значе-
ния апостериорных вероятностей).
Пример 5.17. Фирма производит компоненты для электропри-
боров в три рабочие смены. Известно, что 50% всех компонен-
тов производится в течение 1-й смены, 20% — в течение 2-й
смены, 30% — в течение 3-й смены. Дополнительный анализ
качества производимых компонентов показал: 6% компонентов,
сделанных за 1 -ю смену, являются дефектными; 8% компонентов,
выпускаемых в течение 2-й смены, дефектны; доля дефектных
компонентов за 3-ю смену составила 15% (ночная смена).
1. Требуется определить, какова вероятность, что наугад ото-
бранный компонент из обшей партии, произведенной за три
смены, окажется дефектным?
2. Предположим, что в результате проверки отобранного слу-
чайным образом компонента было установлено, что он дефект-
ный. Какова в этом случае вероятность того, что этот компонент
был произведен: а) в 1-ю смену; б) во 2-ю смену; в) в 3-ю
смену?
Будем рассматривать случайный отбор дефектного компо-
нента как событие А. Систему гипотез составляют следующие
события:
100
A. — компонент произведен в 1-ю смену, А2 — компонент
произведен во 2-ю смену, Л3 — компонент произведен в 3-ю
смену. Из процентного распределения выпуска компонентов по
рабочим сменам следует: Р(А^ = 0,5; НА2) = 0,2; Р(А2) = 0,3.
Эти вероятности являются априорными.
Условные вероятности отбора дефектного компонента по
гипотезам находятся на основе результатов анализа качества
выпускаемых компонентов по сменам:
KA/AJ = 0,06; Р(А/А2) = 0,08; Р(А/А}) = 0,15.
Величина 1\А/А) означает вероятность, что компонент, вы-
пускаемый в смену i (i = 1, 2, 3), будет дефектным. По формуле
полной вероятности (5.12) найдем вероятность события А:
НА) = KAJHA/AJ + НА2)НА/А2) + НА2)НА/А2) =
= 0,5 • 0,06 + 0,2 • 0,08 + 0,3 • 0,15 = 0,091.
Таким образом, 9,1% всех выпускаемых за три смены дета-
лей будут дефектными. Предположим, что в результате испы-
тания событие А произошло (в результате проверки случайным
образом отобранного компонента было установлено, что он
дефектный).
Скорректируем априорные вероятности с учетом получен-
ной информации о результатах испытания (стало известно, что
собыгис А произошло). Для этой цели используем формулу Бай-
еса (5.13):
Р(А/Л)=-----------------------------------------
Р(А)Я(Л/А)+Р(Лг)Р(Л/Л.)+Р(Л!>Р(Л/Л,)
где (=1,2,3.
Подставляя в формулу (5.14) соответствующие вычислен-
ные значения вероятностей, получим апостериорные вероят-
ности:
0,5 0.06
‘wT' °'33;
0,2 0,08
=-0091 = °’18;
0,3 0.15
°’495
101
Величина РЩА) означает вероятность того, что если слу-
чайным образом отобранная деталь оказалась дефектной, то
она сделана в /-ю смену (/ = 1, 2, 3).
5.3. ОСНОВНЫЕ ФОРМУЛЫ
КОМБИНАТОРНОГО АНАЛИЗА
При классическом подходе определения вероятности требу-
ется найти общее количество случаев (равновероятных и взаи-
моисключающихся исходов испытания), а также число случа-
ев, благоприятствующих данному событию. Часто вычисление
искомого количества случаев удобно проводить по формулам
комбинаторного анализа. Рассмотрим основные из них.
5.3.1. Перестановки
Пусть требуется найти количество способов расположения
совокупности объектов на одной линии. Например, сколькими
способами могут 10 человек встать в очередь друг за другом?
Сколько существует различных автомобильных номеров,
имеющих структуру: буква — 3 цифры — 2 буквы?
В данном случае рассматривается линейное размещение
объектов, которые располагаются подобно отдельным точкам
на прямой. Перестановкой некоторого количества объектов
называется любое линейное размещение этих объектов в опре-
деленном порядке.
Пусть число объектов равно п. Тогда число способов их рас-
положения на одной линии равно
л! = п (л - I) (л - 2)...3 -2 1.
Символ л! читается как “л факториал” и обозначает произ-
ведение всех натуральных чисел от 1 до л. По определению счи-
тается 0! = 1.
Каждое линейное расположение л объектов является пере-
становкой из л объектов. Если в перестановке участвуют все л
объектов, то она называется перестановкой из л элементов по
л. Общее число возможных перестановок из л элементов по л
вычисляется по формуле
Ля=Л/=л!, (5.15)
где А и А ” — обозначения числа перестановок из л элементов
по л. "
102
Пример 5.18. Сколькими способами можно расставить на пол-
ке в ряд 5 книг?
По формуле (5.15) имеем Л5 = Л55 = 5 • 4 • 3 • 2 • 1 = 120.
Следовательно, существует 120 различных комбинаций рас-
становки в ряд на книжной полке пяти книг.
Рассмотрим теперь случай, когда перестановка образуется
не из всего множества элементов, а только из его части.
Предположим, что из п элементов отбирается к элементов
(к<п), из которых образуют перестановку. Такая перестановка
называется перестановкой из п элементов по к. Общее число
различных перестановок из п элементов по к обозначается Апк и
вычисляется по формуле
А* = п\/(п - к)\ = п(п - I )...(л - к + 1). (5.16)
Пример 5.19. Студенту необходимо сдать 4 экзамена в течение
7 дней. Сколькими способами можно составить расписание эк-
заменов, если учитывать, что в один день он может сдавать
только один экзамен?
Каждый отдельный вариант расписания представляет собой
перестановку из 7 элементов (дней) по 4. По формуле (5.16)
вычислим общее число вариантов:
Л/ = 7!/3! = (7 6 • 5 4 • 3 • 2 • 1)/(3 • 2 • I) =
= 7 6 • 5 • 4 • 1 = 840.
5.3.2. Принцип умножения
Пусть требуется выполнить одно за другим к действий. Пер-
вое действие можно выполнить л( способами; после того как
первое действие выполнено, второе действие может быть вы-
полнено л2 способами; после того как выполнено второе дей-
ствие, третье действие можно выполнить л, способами, и так
далее до Л-го действия, которое можно выполнить пк способа-
ми. Принцип умножения заключается в том, что при этих усло-
виях все к действий могут быть выполнены вместе п} п2... пк
способами.
Пример 5.20. При продаже новых автомобилей предлагаются раз-
личные варианты цвета кузова без крыши, отдельно крыши и
обивки салона: в первом случае имеется 8 цветов (л(), во вто-
ром — 10 цветов (л2) и в третьем — 4 цвета (л5). Определить
103
количество возможных комбинаций цветов для одного автомо-
биля.
Исходя из принципа умножения общее число сочетаний цве-
тов для одного автомобиля составит: л, п2 л, = 8 • 10 4 = 320.
5.3.3. Сочетания
Сочетанием называется набор элементов, рассматриваемых
без учета порядка их следования. Пусть рассматривается мно-
жество из п элементов. Сочетанием из п элементов по к (к<п)
называется его произвольное неупорядоченное подмножество,
содержащее к элементов. Общее число таких подмножеств (со-
четаний) определяется по формуле
<517>
к\(п-ку.
где С* — обозначение числа сочетаний из п элементов по к.
20 19...2-1
Пример 5.21. Из партии, включающей 20 деталей, случайным
образом для проверки выбираются 3 детали. Партия содержит 6
дефектных деталей. Какова вероятность, что в число отобран-
ных деталей войдут: 1) только дефектные детали (событие Л);
2) только годные детали (событие В); 3) одна дефектная и две
годные детали (событие С).
Для данной ситуации подходит классическое определение
вероятности. В качестве системы случаев рассматриваются раз-
личные подмножества, состоящие из трех деталей, отобран-
ных из партии. Иначе говоря, случаем является сочетание из 20
элементов (деталей) по 3. Тогда общее число случаев вычисля-
ется по формуле (5.17):
С1 - 20' 20 19...21 _ 20-19-18 _
20 ЗМ7! 3-2-1-17-16-15...21 3-2-1
= 20-19-3 = 1140.
Определим число случаев, благоприятствующих событию А.
Очевидно, оно равняется числу подмножеств из трех деталей,
каждое из которых состоит только из дефектных деталей. Ввиду
того что партия содержит 6 бракованных деталей, все подмно-
жества должны включать какие-либо три детали из их числа.
Количество таких подмножеств, очевидно, соответствует чис-
лу сочетаний из 6 элементов по 3, т. е. величине
С?= —= 20.
6 3!-3!
104
Таким образом, количество случаев, благоприятствующих
событию А, равно 20, а общее количество случаев — 1140. От-
сюда Р[А) = 20/1140 = 0,017. Аналогично находится вероят-
ность события В. Количество годных деталей — 14. Поэтому число
благоприятствующих случаев равно
С,4 = —- = 364.
14 3!11!
Следовательно, Р(В) = 364/1140 = 0,319. Для вычисления
количества исходов, благоприятствующих событию С, следует
воспользоваться принципом умножения. Формирование выбор-
ки из трех деталей в данном случае можно рассматривать как
результат двух действий. Первое действие заключается в отборе
из партии одной бракованной детали, второе — двух годных
деталей. Ясно, что количество способов, с помощью которых
можно реализовать первое действие, — C<J, а количество спо-
собов для второго действия — С\. Согласно принципу умноже-
ния, общее число благоприятствующих случаев равно
' С^С|24=—^^- = 546.
6 14 11-51-2М2!
Отсюда получаем, что вероятность события С вычисляется
следующим образом:
Р(О = 546/1140 = 0,479.
Следует отметить, что формирование подмножества из трех
деталей, извлеченных из партии в 20 деталей, можно рассмат-
ривать как случайную бесповторную выборку. В этом случае
объем выборки равен 3, объем генеральной совокупности — 20.
Поэтому вероятность любой бесповторной выборки есть 1/С^.
Очевидно, в общем случае вероятность бесповторной вы-
борки объема л, т. е. полученной по принципу невозвращения
отобранного элемента обратно в генеральную совокупность
численностью N(n<N), равна 1/С£ .
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 5
Понятие вероятности определяет меру возможности появ-
ления некоторого события в результате опыта (испытания). Под
опытом понимаются некоторые действия, связанные с наблю-
дениями и измерениями. Событие рассматривается как один
105
или несколько возможных исходов данного опыта. Вероятность
может принимать наибольшее значение, равное I. Это означа-
ет, что событие обязательно произойдет, т. е. является досто-
верным. Наименьшее значение вероятности равно 0, что соот-
ветствует невозможному событию, которое никогда не прои-
зойдет.
Можно выделить три подхода к определению вероятности.
Одним из объективных подходов является классическое опре-
деление вероятности. Оно применяется только в тех случаях,
когда реализуется схема случаев. Под случаями понимаются
единственно возможные, равновероятные и несовместимые ис-
ходы испытания. Вероятность события определяется как отно-
шение числа случаев, благоприятствующих данному событию,
к общему числу случаев.
Другой объективный подход — определение статистической
вероятности. Он используется, когда не может быть реализова-
на схема случаев. Пусть в прошлом было проведено достаточно
большое количество опытов, в результате которых наблюда-
лось появление или непоявление некоторого события. Если от-
ношение частоты появления данного события к общему числу
опытов приближается к некоторой величине, то эта величина
принимается за вероятность события.
Третьим подходом к определению вероятности является
субъективное оценивание вероятности, т. е. субъективная веро-
ятность. Он используется, когда схема случаев не выполняется
и недостаточно информации о прошлых испытаниях.
Суммой, или объединением, событий называется событие,
состоящее в том, что в результате опыта произойдет хотя бы
одно из этих событий. Два события называются совместимыми,
если в условиях опыта появление одного события не исключа-
ет появления другого. Если в результате опыта возможно появ-
ление только одного из событий, то эти события называются
несовместимыми. Если речь идет о совместимости или несов-
местимости трех или более событий, то условие совместимос-
ти или несовместимости выполняется для любых двух из них.
Несовместимые события образуют полную группу, если одно
из этих событий обязательно должно осуществиться.
Сумма вероятностей событий, входящих в полную группу,
равна 1. Если полная группа состоит из двух событий, то эти
события называются противоположными. Произведением, или
пересечением, нескольких событий называется событие, кото-
рое состоит в том, что в результате испытания произойдут все
эти события. Для несовместимых событий вероятность суммы
106
этих событий равна сумме вероятностей наступления каждого
события (формула (5.4)). В обшсм случае двух совместимых или
несовместимых событий правило (теорема) сложения вероят-
ностей формулируется следующим образом: вероятность сум-
мы двух событий равна сумме вероятностей каждого события
минус вероятность произведения этих событий (формула (5.6)).
Два события называются независимыми, если вероятность по-
явления одного из них не зависит от появления или непоявле-
ния другого. Вероятность произведения двух независимых со-
бытий равна произведению вероятностей этих событий. Два
события называются зависимыми, если вероятность появления
одного из них изменяется в зависимости от появления или не-
появления другого. Пусть рассматриваются два зависимых со-
бытия. Вероятность одного из зависимых событий, вычислен-
ная при условии осуществления другого, называется условной
вероятностью этого события. Общее правило (теорема) умно-
жения вероятностей гласит: вероятность произведения двух со-
бытий равна произведению безусловной вероятности одного
из них на условную вероятность другого (формула (5.10)). В слу-
чае независимых событий условная вероятность события равна
его безусловной вероятности. Если рассматриваются три собы-
тия, то правило нахождения вероятности их произведения за-
дается формулой (5.11).
На условную вероятность влияет способ организации слу-
чайной выборки. Если отбор элементов производится без их
возвращения в генеральную совокупность, то она называется
выборкой без возвращения, или бесповторной выборкой. Если
отбор прозводится с возвратом, то формируется выборка с воз-
вращением, или повторная выборка. Теорему умножения веро-
ятностей удобно использовать при анализе ситуаций, которые
можно описывать с помощью таблицы сопряженности или де-
рева возможных исходов.
Пусть событие может произойти тогда и только тогда, когда
имеет место одно из нескольких несовместимых событий (на-
)ываемых гипотезами). В этом случае полная вероятность этого
события равна сумме слагаемых, где каждое слагаемое есть
произведение отдельной гипотезы на вероятность данного со-
бытия при условии осуществления этой гипотезы (формула
(5.12)). На основе полной вероятности формулируется теорема
Байеса (формула (5.13)): вероятность каждой гипотезы после
испытания равна произведению вероятности этой гипотезы до
испытания на условную вероятность события по этой гипоте-
1С, деленному на полную вероятность события. С помощью те-
107
оремы Байеса производится корректировка априорных вероят-
ностей гипотез (т. е. оцененных до проведения испытания). После
того как испытание было проведено и результат стал известен,
делается новая, более правдоподобная оценка вероятностей ги-
потез, которые называются апостериорными.
Для вычисления необходимого количества случаев при клас-
сическом определении вероятности часто используются поня-
тия и формулы комбинаторного анализа. Перестановкой п о^гъек-
тов (элементов) называется любое линейное размещение этих
объектов (элементов). Число перестановок из п элементов оп-
ределяется по формуле (5.15). Перестановкой из п элементов
по к (к<п) называется перестановка из какого-либо Л-элемент-
ного подмножества этих элементов. Число перестановок из п
элементов по к определяется по формуле (5.16).
Пусть требуется выполнить одно за другим к действий. Пер-
вое действие можно выполнить п} способами; после того как
первое действие выполнено, второе действие может быть вы-
полнено л2 способами; после того как выполнено второе дей-
ствие, третье действие можно выполнить л способами, и так
далее до к-ro действия, которое можно выполнить пк способа-
ми. Принцип умножения заключается в том, что при этих усло-
виях все к действий могут быть выполнены вместе п} п2... пк
способами.
Сочетанием назывется множество из п элементов, рассмат-
риваемых без учета порядка их следования. Сочетанием из п
элементов по к (к<п) называется произвольное неупорядочен-
ное ^-элементное подмножество этого множества. Число соче-
таний из п элементов по к вычисляется по формуле (5.17).
ДИСКРЕТНЫЕ
РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ
6.1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
В предыдущей главе рассматривалось понятие случайного
события, которое является исходом некоторого испытания. Если
исходы могут быть количественно измерены (например, общее
число очков, выпавших на двух игральных костях), то пред-
ставление этих исходов и их вероятностей удобно анализиро-
вать, используя понятие случайной величины.
Случайная величина — это функция, которая ставит в соот-
ветствие каждому исходу испытания определенное численное
значение. Ввиду того, что исход испытания является случай-
ным событием, заранее неизвестно, какое именно значение
примет случайная величина.
Если все значения случайной величины могут быть заранее
перечислены, то такая величина называется дискретной.
Пример 6.1. Пусть на станке вытачиваются детали. Число бра-
кованных деталей, которые будут произведены на следующей
неделе, является случайной величиной, гак как точно неизве-
стно, какое значение она примет. Однако можно перечислить
все ее возможные значения: 0, 1,2,п, где п — общее число
деталей, которое будет произведено на станке. Следовательно,
рассматриваемая случайная величина является дискретной.
Другим типом случайной величины является непрерывная
случайная величина. Для нее в отличие от дискретной величи-
ны нельзя заранее перечислить все возможные значения, кото-
рые она может принять. Значения непрерывной случайной ве-
личины непрерывно заполняют некоторый промежуток.
Пример 6.2. Рассмотрим две случайные величины: X — прогноз
числа дождливых дней в определенном месяце в данном реги-
109
оне, Y— прогноз уровня дождевых осадков за этот период. Ясно,
что X — дискретная случайная величина, a Y — непрерывная
(теоретически она может принять любое неотрицательное зна-
чение).
Данная глава посвяшена описанию дискретных случайных
величин. Свойства и характеристики непрерывных величин бу-
дут рассмотрены в гл. 7.
6.2. РЯД РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Обозначим через Xдискретную случайную величину, кото-
рая может принимать одно из п единственно возможных значе-
ний хр хг,..., хп. Ввиду того что X — случайная величина, любое
значение х. (/= 1, 2,..., п) возможно, но не достоверно. Сможет
принимать каждое из этих значений с некоторой вероятнос-
тью:
Р(Х = х,) = />|( Р(Х = х,) = рг..., /\Х = хя) = х„.
В результате испытания случайная величина X обязательно
примет одно из значений х (/ = 1,2. п). Следовательно, п
событий, каждое из которых заключается в том, что Xприни-
мает конкретное значение, равное х (X = х, i = 1, 2,..., п),
образуют полную группу событий.
Отсюда .
п п
£p(x=xi)=2}ft=i. (6.1)
<=i i=i
Из соотношения (6.1) можно заключить, что суммарная
вероятность случайной величины равна 1 и она как бы распре-
делена между всеми отдельными ее значениями. Случайная ве-
личина X считается заданной с вероятностной точки зрения,
если точно известно это распределение вероятностей. Будем
полагать, что задан закон распределения дискретной случай-
ной величины, если точно известны все ее значения, которые
получаются в результате испытания, а также вероятности, с
которыми она принимает соответствующие значения. Закон
распределения дискретной случайной величины, который еще
называется рядом распределения, можно представить в виде
табл. 6.1.
110
Таблица 6.1
Закон (ряд) распределения дискретной случайной величины
Значения X ... X
Вероятности Р(Х = х,) Pi Pi ... рп
Пример 6.3. Пусть опыт заключается в трехкратном подбрасы-
вании монеты. Рассмотрим случайную величину X, значения
которой определяются количеством выпадений герба.
Требуется записать ряд распределения этой случайной ве-
личины. Очевидно, Xможет принимать четыре единственно воз-
можных значения: 0, 1,2, 3. Определим распределение вероят-
ностей, т. е. Р{Х = 0), Р(Х = 1), 1\Х = 2), 1\Х = 3). Для этого
используем схему случаев. При однократном подбрасывании
монеты возмджны два равновероятных исхода — герб и цифра
При трехкратном подбрасывании общее число случаев нахо-
дится по принципу умножения (раздел 5.3.2), т. е. 2 • 2 • 2 = 8.
Если представить каждый случай как последовательность
выпадений гербов и цифр, то все случаи можно записать в сле-
дующем виде:
Ц Ц Ц, Г Г Ц, Ц Г Ц, Г Ц Ц, Г Г Ц, Г Ц Г, Ц Г Г, Г Г Г.
Тогда:
событию X = 0 благоприятствует 1 случай (ЦЦЦ);
событию X — 1 - 3 случая (ЦЦГ, ЦГЦ, ГЦЦ);
событию X = 2-3 случая (ГГЦ, ГЦГ, ЦГГ);
событию Х= 3 — 1 случай (ГГГ).
Запишем распределение вероятностей:
Р(Х = 0) = 1/8, Р(Х = 1) = 3/8, Р[Х = 2) = 3/8,
Р(Х = 3) = 1/8.
Ряд распределения случайной величины Xбудет иметь вид
Значения X (X = х,) 0 1 2 3
Вероятности Р(Х = х() 1/8 3/8 3/8 1/8
Заметим, что в примере 6.3 использовалась схема случаев,
т. е. классическое определение вероятности. Предположим, что
число опытов (трехкратные бросания монеты) будет достаточ-
но большим и при этом наблюдаются относительные частоты
соответствующих событий (отношения числа опытов, в резуль-
П1
тате которых герб выпадал определенное количество раз, к
общему числу опытов). При стремлении числа опытов к беско-
нечности значения относительных частот по закону больших
чисел будут стремиться к соответствующим вероятностям, по-
лученным по схеме случаев.
Чем больше опытов наблюдается, тем относительные час-
тоты будут более точными оценками вероятностей.
Можно сказать, что в терминах статистического подхода к
определению вероятности распределение вероятностей диск-
ретной случайной величины получается в результате подсчета
относительных частот отдельных событий при бесконечном
числе опытов. Под отдельным событием в данном случае пони-
мается тот факт, что в результате опыта случайная величина
принимает одно из возможных своих значений.
6.3. ХАРАКТЕРИСТИКИ ДИСКРЕТНОЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
6.3.1. Математическое ожидание
В гл. 3 было рассмотрено понятие средней арифметической
для выборочной и генеральной совокупностей. Введем анало-
гичное понятие средней для дискретной случайной величины.
Рассуждения будем проводить для случайной величины, пред-
ставленной в примере 6.3. Пусть монета подбрасывается три
раза подряд и фиксируется, сколько раз выпал герб, т. е. значе-
ние величины X. Затем этот опыт повторяется и опять записы-
вается число выпадения герба. Предположим, что опыт был
повторен 10 раз и результаты подсчетов выпадения герба в каж-
дом опыте были следующие:
2, 1, 1, 0, 2, 3, 2, I, 1, 3.
Найдем среднюю арифметическую (статистику), рассмат-
ривая результаты наблюдений как выборочные данные:
- 2+1+1+0+2+3+2+1+1+3 , z _
х ------------------------= 1,6 герба.
10
Можно сказать, что в результате проведения опытов герб в
среднем выпадал 1,6 раза.
Значение 1,6 можно было бы получить как среднюю взве-
шенную величину, если использовать в качестве весов относи-
тельные частоты значений:
112
X -
01 + 14 + 2 3 + 32
10 ’
1 . , 4 л 3 2
-----F 1-----к 2-----+ 3‘------
10 10 10 10
Как видно, относительная частота представляет собой долю
общего числа опытов, в которых случайная величина прини-
мает соответствующее возможное значение.
Пусть число опытов бесконечно возрастает. Рассмотрим,
какова в этом случае будет средняя. Будем полагать, что все
опыты следуют непрерывно один за другим и длятся одинако-
вое время.
Случайная величина дописывается следующим образом:
X = 0 с вероятностью 1/8,
X = 1 с вероятностью 3/8,
X = 2 с вероятностью 3/8,
Х= З'с вероятностью 1/8.
Предположим, что процесс проведения опытов бесконечен
(длится бесконечное время) и за ним непрерывно осуществля-
ются наблюдения (отмечаются количества выпадения герба).
Тогда распределение вероятностей можно интерпретировать как
долю общего времени наблюдений, когда случайная величина
X принимает соответствующие значения: 1/8 всего времени на-
блюдается Х= 0; 3/8 всего времени — Х= 1; 3/8 всего време-
ни — X = 2; 1/8 всего времени — X - 3.
Если рассматривать вероятности как значения относитель-
ных частот при бесконечном числе опытов, то среднюю слу-
чайной величины X можно вычислить так:
13 3 1
0 - + 1- + 2- + 3- = 1,5 герба.
8 8 8 8
Заметим, что 1,5 не является возможным значением случай-
ной величины X, оно только характеризует то значение, кото-
рое X может принимать в среднем при очень большом числе
опытов.
В общем случае пусть задан закон распределения дискрет-
ной случайной величины X, т. е. она принимает значения х,
х хя с вероятностями Р(Х = х,) = Ах,) = р}, Р(Х = х2) =
Ах2) = р2... Р(Х = х) = F\xJ = ря. Тогда среднее значение
случайной величины X вычисляется по формуле
Е(Х) = Ц = £х,Р(Х =xi)='^xipi =^x</’(*i)=2}x/’(x). (6.2)
i=l i=l i=l
Обозначение ц вводится по аналогии со средним значением
генеральной совокупности. В теории вероятностей среднее зна-
нз
чение случайной величины чаще называют ее математическим
ожиданием, используя при этом запись ц = Е(Х). Математичес-
кое ожидание является аналогом центра распределения гене-
ральной совокупности, т. е. характеризует наиболее типичное
значение для всего распределения, около которого концент-
рируется основная масса возможных значений случайной ве-
личины X.
6.3.2. Дисперсия и стандартное отклонение
Для того чтобы определить, насколько тесно располагаются
значения случайной величины около ее математического ожи-
дания, существуют специальные характеристики — дисперсия
и стандартное отклонение, которое еще называют средним квад-
ратическим отклонением. Они определяются по аналогии с
соответствующими характеристиками для статистических со-
вокупностей. Вычислим по формуле (4.8) выборочную диспер-
сию для совокупности из десяти значений, представляющих
результаты подсчета выпадения герба при 10 трехкратных под-
брасываниях монеты (раздел 6.3.1):
2 У(х--?)2 (2-1.6)2+(1-1.6)2+... + (3-1,6)2
л-1 10-1
= (O-1.6)2-1 + (1-1,6)2-4 + (2-1,6)2 3-ь(3-1,6)2-2 = Q
10-1
Чтобы определить дисперсию, в числителе находится сумма
произведений квадратов отклонений данных от средней на со-
ответствующие частоты значений.
Вычислим стандартное отклонение s =^'0,944 = 0,97. Пусть
число опытов будет достаточно большим. В этом случае для вы-
числения дисперсии и стандартного отклонения можно исполь-
зовать формулу (4.4), где знаменатель равен общему числу опы-
тов N. При бесконечном числе опытов (У-и») относительные
частоты будут стремиться к вероятностям, а выборочная сред-
няя — к математическому ожиданию. Отсюда очевидны форму-
лы для дисперсии и стандартного отклонения случайной вели-
чины X:
о2 = ^(х<-ц)2Р(х|) = £(х-ц)2Р(х), (6.3)
1-1
о = ^£(х-ц)2Р(х). (6.4)
114
Выражение (6.3) можно интерпретировать как математичес-
кое ожидание квадрата отклонения случайной величины от ее
математического ожидания:
д2 = Е(Х-ц)2.
Формулу (6.3) можно записать в более удобном для прове-
дения вычислений виде:
Л
о2 = Sх'2 ) - и2 = Е( X 2) - Е( X )2. (6.5)
<1
Пример 6.4. Фирма продает новые автомобили. Известно, что
наиболее интенсивная продажа бывает по субботам. На основа-
нии данных о проданных автомобилях за ряд прошедших суб-
бот менеджер оценил возможные субботние продажи и рас-
пределение вероятностей.
Пусть случайная величина Xозначает количество автомоби-
лей, продаваемых по субботам. Закон распределения X, кото-
рый установил менеджер, имеет вид
Значения X“к 0 1 2 3 4
Вероятности Р(х) 0,1 0.2 0.3 0,3 0.1
Как видно, 10% составляют субботы, в течение которых не
было продано ни одного автомобиля; 20% — субботы, за кото-
рые объем продаж составил 1 автомобиль в день; 30% — 2 ав-
томобиля в день, 30% — 3 автомобиля в день, 10% — 4 автомо-
биля в день.
Определим, какое количество автомобилей в среднем ожи-
дает продавать менеджер в будущем по субботам. Другими сло-
вами, необходимо, используя формулу (6.2), вычислить мате-
матическое ожидание случайной величины X:
ц = Е(Х) =£хР(х)= 0 0,1 + 1 • 0,2 + 2 • 0,3 +
+ 3 • 0,33 + 4-0,1 » 2,1.
Величину 2,1 можно интерпретировать следующим образом:
в течение большого числа суббот в среднем будут продавать по
2,1 автомобиля.
Следует особо подчеркнуть, что 2,1 не является точным зна-
чением продаж, которые ожидают совершать в течение каждой
отдельной субботы Это только средняя дневная величина, ко-
торая ожидается в течение большого количества суббот.
115
Вычислим дисперсию случайной величины X. Для этого удобно
промежуточные вычисления по формуле (6.3) свести в табл. 6.2.
Таблица 6.2
Расчет дисперсии
Продажи х Вероятность Р(х) х-р (х -1»)1 (х - p)»F(x)
0 0.1 0-2,1 4,41 0.441
1 0.2 1-2.1 1.21 0,242
2 0.3 2-2,1 0,01 0,03
3 0,3 3-2.1 0,81 0,243
4 0.1 4-2.1 3,61 0,361 о2 = 1,29
Стандартное отклонение определим по формуле (6.4):
ст = \'ст* =л/1,29= 1,14 автомобиля. Вычислим также диспер-
сию по упрошенной формуле (6.5):
о2 = £х2Р(х)-р2 = О2 • 0,1 + I2 • 0,2 + 22 • 0,3 +
+ З2 0,3 + 42 • 0,1 - 2,12 = 1,29.
Дисперсия является характеристикой вариации или разбро-
са данных около математического ожидания. Ее можно исполь-
зовать для сравнительного анализа нескольких случайных ве-
личин, принимающих качественно схожие значения.
Пример 6.5. Продолжим ситуацию примера 6.4. Менеджер той
же автомобильной фирмы, но в другом регионе установил на
основе собранных данных, что средние субботние продажи
составляют также 2,1 автомобиля, но дисперсия о2 = 1,91.
Очевидно, в первом случае (о2 = 1,29) значения продаж
более тесно располагаются около величины 2,1, представляю-
щей математическое ожидание субботних продаж.
Если рассматривать математическое ожидание как прогноз-
ную величину, то, очевидно, дисперсия будет отражать меру
риска или надежность прогноза: чем меньше дисперсия, тем
надежнее прогноз. Когда дисперсия нулевая, случайная вели-
чина перестает быть случайной, так как с вероятностью 1 она
будет принимать в каждом опыте одно и то же значение. Так,
можно сделать вывод, что прогноз продаж, сделанный менедже-
116
ром в примере 6.4, более надежен, чем прогноз, полученный
менеджером в примере 6.5 (1,29 < 1,91).
6.3.3. Графическое представление распределения
дискретной случайной величины
Распределение может быть представлено в виде линейного
графика, где по оси х откладываются возможные значения слу-
чайной величины X, а по оси у — величины вероятностей Лх)
Пример 6.6. Пусть испытание заключается в двукратном под-
брасывании монеты. При одном подбрасывании может выпасть
либо герб, либо цифра. Под случайной величиной Xбудем по-
нимать число выпаданий цифры при двух подбрасываниях. По-
строим график распределения случайной величины X.
Возможные исходы испытания: Г Г, Ц Г, Г Ц, Ц Ц. Возмож-
ные значения случайной величины X: 0, 1, 2. Распределение ве-
роятностей: ДХ- 0) = 1/4, Р(Х = 1) = 2/4, 2) = 1/4. На
рис. 6.1 представлен график распределения X.
Рис. 6.1. Графическое представление распределения дискретной
случайной величины X: выпадание цифры при двукратном
подбрасывании монеты
6.4. БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
Дискретная случайная величина Xбудет иметь биномиаль-
ный закон распределения, если выполняются следующие ус-
ловия.
I. Имеет место эксперимент, который заключается в после-
довательном повторении п опытов.
2. В результате каждого опыта могут произойти два един-
ственно возможных и взаимно исключающихся исхода — два
117
противоположных события: появление или непоявление неко-
торого события А. Эти события можно рассматривать как “ус-
пех” (появление А) или “неудача” (непоявление А).
3. Все п проводимых опытов являются независимыми.
4. Величина вероятности “успеха” в каждом из п опытов ос-
тается постоянной (обозначается р).
5. Случайная величина X характеризует число “успехов”,
которые имеют место при п испытаниях.
Пример 6.7. Социологический опрос, проведенный в одном го-
роде, показал, что 30% всего взрослого населения читают го-
родскую вечернюю газету. Случайным образом выбираются че-
тыре взрослых городских жителя. Покажем, что если под
случайной величиной X понимать число читающих вечернюю
газету среди этих четырех человек, то X подчиняется биноми-
альному закону распределения.
Определим, удовлетворяет ли рассматриваемая ситуация ус-
ловиям биномиального распределения, т. е. проверим выполне-
ние каждого из вышеуказанных условий.
I. В данном случае число опытов п = 4, где каждый опыт
состоит в случайном выборе одного взрослого жителя.
2. В результате каждого опыта имеют место два единственно
возможных и взаимно исключающихся исхода — человек чита-
ет газету (“успех”) и человек не читает газету (“неудача”).
3. Опыты являются независимыми, так как выбор людей осу-
ществляется случайным образом.
4. Вероятность “успеха” при проведении каждого из четырех
опытов постоянна: р = 0,3.
5. Случайная величина Д'принимает значения, равные числу
“успехов” в результате проведения п опытов (л = 4).
Как видно, все условия для биномиального распределения
выполнены, т. е. можно утверждать, что случайная величина X
распределена по биномиальному закону.
6.4.1. Биномиальные вероятности
Пусть рассматривается схема опытов, удовлетворяющая ус-
ловиям биномиального распределения. Чтобы вычислить рас-
пределение вероятностей, необходимо подсчитать общее чис-
ло событий, каждое из которых является исходом п испытаний
и заключается в том, что “успех” наблюдался определенное
число раз. Например, пусть монета подбрасывается четыре раза
118
подряд (л = 4). Сколькими способами могут выпасть два герба?
Иначе говоря, требуется подсчитать число событий, где каж-
дое событие характеризуется выпаданием двух гербов при че-
тырех подбрасываниях монеты (в двух оставшихся подбрасыва-
ниях естественно выпадает цифра). Очевидно, таких событий
будет шесть: ГГЦЦ, ГЦГЦ, ГЦЦГ, ЦГГЦ, ЦГЦГ, ЦЦГГ.
Рассмотрим теперь следующую задачу. Сколькими способа-
ми из группы, включающей четырех человек, можно выбрать
двух человек, если порядок людей в выборке неважен? Обо-
значим людей в группе /, /,, /3, /4. Тогда задача выбора по два
человека будет иметь шесть вариантов решений. Сравним их с
вариантами выпадания двух гербов при четырех подбрасыва-
ниях монеты.
Выпадание двух гербов при
четырех подбрасываниях монеты
ГГЦЦ
ГЦГЦ
ГЦЦГ
ЦГГЦ
ЦГЦГ
ЦЦГГ
Выбор двух человек из группы,
состоящей из четырех человек
Как видно, существует взаимно однозначное соответствие
между вариантами: порядковые номера двух подбрасываний
монеты, в которых выпал герб, в общей последовательности
четырех подбрасываний соответствуют номерам двух выбран-
ных индивидов. Очевидно, в обоих случаях мы составляем под-
множество из двух элементов, выбираемых из множества, со-
стоящего из четырех элементов. Количество таких подмножеств
равно числу сочетаний из 4 элементов по 2 (формула 5.17):
’ (4-2)!-2!
Данный вывод можно распространить на общий случай. Пусть
осуществляется п подбрасываний монеты (проведение п опы-
тов). Требуется подсчитать количество вариантов, в каждом из
которых герб выпадал ровно к раз (“успех” появлялся ровно к
раз). Очевидно, эту задачу можно свести к подсчету числа вы-
борок, состоящих из к человек, взятых из группы в составе п
человек: к порядковых номеров подбрасываний монеты, в ко-
торых выпал герб, соответствуют номерам к отобранных инди-
видов (порядок индивидов в выборке неважен). Очевидно, ис-
комое число вариантов будет с*
п
119
Сформулируем этот вывод для любой схемы, удовлетворя-
ющей условиям биномиального распределения. Пусть прово-
дится п независимых опытов, в каждом из которых может по-
явиться (успех) или не появиться (неудача) некоторое событие
А. Тогда количество вариантов, в которых событие А (успех)
появляется ровно к раз (к < л), равняется числу сочетаний из л
элементов по к, т. е. С*.
Предположим, что вероятность “успеха” в каждом опыте
равна р. Тогда вероятность “неудачи”, очевидно, равняется
q = 1 ~ р. Рассмотрим один из вариантов, когда в л опытах
“успех” появляется ровно к раз. Его можно рассматривать как
сложное событие, которое является произведением л незави-
симых простых событий: к “успехов” и (л - к) “неудач”. Тогда
вероятность этого произведения равна р*(1 - />)*"* = рк<?'к.
В общем случае число рахтичных произведений, где каждое
произведение соответствует варианту появления ровно к “ус-
пехов” в л опытах, будет С*. Отсюда получаем, что вероят-
ность события, что при л испытаниях “успех” наступит ровно
к раз (к < л) (обозначим ее Р{к, л)), является вероятностью
суммы событий, где каждое слагаемое есть один из вариантов
произведения к “успехов” и (л - к) “неудач”:
Р(*,л) = С*р*(1-рГ* =С*АЯ*. (6.6)
Например, вероятность события, что при четырех подбра-
сываниях монеты герб выпадет ровно 2 раза, вычисляется сле-
дующим образом:
Р(2,4) = С42
=6.±Л.
16 8
Выражение (6.6) задает распределение вероятностей для
биномиальной случайной величины X
л = 0 с вероятностью Спр q = q ,
Х = 1 с вероятностью C'nplqn~',
X = 2 с вероятностью C2p2qn2,
(6.7)
X = л с вероятностью C^pnqn " = рп.
120
Распределение (6.7) определяет дискретную случайную ве-
личину X, распределенную по биномиальному закону, где л —
число испытаний, р — вероятность появления события А (“ус-
пеха") в результате каждого опыта, q = I - р — вероятность
ненаступления события А (“неудачи”), к — число появлений
события А (“успехов”) (к < п). Для биномиальной X как для
любой дискретной случайной величины сумма вероятностей
равна 1: „
We*=1
i=0
।
Пример 6.8. В примере 6.7 случайная величина X, распределен-
ная по биномиальному закону, характеризовала число читаю-
щих вечернюю городскую газету среди случайным образом ото-
бранных четырех жителей. Определим ряд распределения
величины X. В данном случае число опытов л = 4 (случайный
отбор четырех человек). Событие А (“успех”) заключается в том,
что отобранный случайным образом человек читает вечернюю
газету. Вероятность АЛ) ~ Р = 03, так как по результатам со-
циологического опроса 30% всего взрослого населения города
читают вечернюю газету. Вероятность противоположного собы-
тия А (человек не читает вечернюю газету) равна АЛ) = q =
- I - 0,3 = 0,7.
Определим вероятности, что среди случайным образом ото-
бранных четырех человек читают вечернюю газету: I) 0 чело-
век; 2) 1 человек; 3) 2 человека; 4) 3 человека; 5) 4 человека.
Эти вероятности вычисляются по формуле (6.6):
АО,4) = Сд 0,3° 0,74 =0,74 =0.2401;
А 1,4) = С\ 0,3' 0,7’ =0,4116;
А2,4) = Сд • 0,32 0,72 = 0,2646;
АЗ,4) = Сд 0,3’- 0,71 =0,0756;
А4,4) = С4 0,34 0,7° =0,3* =0,0081.
Запишем ряд распределения для случайной величины X:
Х-ж 0 1 2 3 4
Ах) 0,2401 0,4116 0,2646 0,0756 0.0061
Заметим, что ^Р(х,4) = 1.
121
Значения вероятностей имеют вполне определенную стати-
стическую интерпретацию. Например, Л2,4) = 0,2646 означа-
ет, что если много раз случайным образом набирать группы из
четырех жителей, то 26,5% всех отобранных групп будут вклю-
чать ровно два человека, которые читают вечернюю газету.
Пусть нас интересует событие, что случайная величина X не
превзойдет некоторого значения к. Так, для ситуации примера
6.8 определим вероятность, что среди выбранных случайным
образом четырех человек не более двух читают вечернюю газе-
ту. Вероятность данного события PtX'i 2). Она является суммой
вероятностей событий, что случайная величина X примет одно
из значений 0, 1,2:
Р(Х<. 2) = Р[Х = 0) + Р[Х = I) + Р[Х = 2) =
* АО,4) + Л1,4) + Л2.4) = 0,2401 + 0,4116 + 0,2646 =
= 0,9163.
В общем случае вероятность события, что случайная вели-
чина X, распределенная по биномиальному закону, примет
значения, не превышающие к (к < л), вычисляется следующим
образом:
Р(Х<к) = Р(0,п) + Л1Л) + ... + /\к,п) =
-<7"+CiW-’+...+C*pV-*. (6.8)
Выражение (6.8) является накопленной вероятностью, ко-
торая получается суммированием величин 1\х) для соответ-
ствующих значений х. Она характеризует вероятность того, что
при п опытах событие А наступит не более к раз.
Соответственно вероятность события, что случайная величи-
на Xпримет значение, превышающее к (т. е. вероятность, что в п
опытах событие А появится более чем к раз), определяется так:
Р(Х> к) = 1 - 1\Х< к). (6.9)
В примере 6.8 вычислим по формуле (6.9) вероятность со-
бытия, что среди выбранных четырех человек более двух чита-
ют вечернюю газету:
Р(Х>2) = 1 - /\Х<2) = 1 - 0,9163 = 0,0837.
Заметим, что вероятности Р(к,п), вычисляемые по формуле
(6.6), можно получить как члены разложения бинома:
122
/ . _ В . z-,I l _B“1 i i ''1 j Л
(p + <?) =p +Cnpq +.- + Cn p q + q
Для удобства вычислений в Приложении 2 приведены таб-
лицы биномиальных вероятностей для п = 1, 2,..., 20, 25 и
р = 0,05; 0,1; 0,2; 0,9; 0,95. Каждая таблица соответствует
определенному значению п. В строках таблицы задаются вели-
чины к (к<п), в столбцах — значения вероятности р. На их пере-
сечении находим биномиальную вероятность С*рп(\- р)п * .
»
6.4.2. Математическое ожидание и дисперсия
биномиальной случайной величины
Математическое ожидание дискретной случайной величи-
ны находится по формуле (6.2). В случае биномиального рас-
пределения необходимо вычислить выражение
ц = £ XiP(x,) = о • С°пр V +1 • С'„p'q-1 +... + п • с; Pnq°.
м
Так, в примере 6.8 математическое ожидание числа читаю-
щих вечернюю газету среди отобранных случайным образом
четырех жителей города определяется следующим образом:
ц = 0 0,2401 + 1 • 0,4116 + 2 • 0,2646 +
+ 3 • 0,0756 + 4 • 0,081 = 1,2.
Можно доказать, что для математического ожидания бино-
миальной величины верна следующая формула:
ц = пр. (6.10)
Для ситуации примера 6.8 математическое ожидание можно
было бы вычислить гораздо проще по формуле (6.10):
ц = 4 - 0,3 = 1,2 чел.
В общем случае дисперсия дискретной случайной величины
X определяется по формулам (6.3) и (6.5).
Для биномиального распределения можно доказать:
о2 = (0 - лр)2С„ р0^'1 + (1 - np)2c\plqn-} +... +
+ (n-np)2C"pnq0 = np(l-p) = npq. (6 1 D
123
Стандартное отклонение соответственно определяется так:
а = -]пр( 1 - р j = -jnpq. (6.12)
Для ситуации в примере 6.8 вычислим дисперсию и стан-
дартное отклонение по формулам (6.11) и (6.12):
о2 = 4 • 0,3 0,7 = 0,84,
о = ai'0,84 = 0,92 чел.
Пример 6.9. Анализ большого количества деклараций о доходах
показал, что одна из десяти деклараций заполнена с ошибка-
ми. Пусть случайная величина Xпредставляет собой число дек-
лараций с ошибками среди 20 выбранных случайным образом
деклараций.
Требуется определить:
1) какова вероятность события, что по крайней мере три
декларации будут содержать ошибки?
2) какова вероятность события, что не более чем в одной
декларации содержатся ошибки?
3) математическое ожидание, дисперсию и стандартное от-
клонение случайной величины X.
Случайная величина X имеет параметры: п = 20, р = 0,1.
Событие А заключается в наличии ошибок при заполнении
декларации (“успех”). Вероятность, что по крайней мере три
декларации содержат ошибки, будет вычисляться с использо-
ванием формул (6.8) и (6.9):
ЛЛ>3) = 1 - Р(Х<3) = 1 - Р(Х$2) =
= 1 - [ Л0,20) + Я 1,20) + Р(2,2О)1.
Вероятности Л0.20), Л 1,20) и Л2.20) определим по таб-
лице Приложения 2 (л = 20; р = 0,1; к = 0,1,2);
Р[Х^З) = 1 - (0,122 + 0,27 + 0,285) = 0,323.
Вероятность события, что среди 20 случайно отобранных
деклараций будет не более одной, содержащей ошибки, опре-
деляется по формуле (6.10):
Р (Х<, 1) = Л0.20) + Л1.20) = 0,122 + 0,27 - 0,392.
Математическое ожидание равно:
ц - пр = 20 • 0,1 = 2 декларации.
124
Это означает, что для большого количества случайных вы-
борок объемом в 20 деклараций средняя величина дефектных
деклараций в одной выборке равняется 2.
Дисперсия вычисляется по формуле (6.11):
ст2 = пр( I - р) = 20 • 0,1 • 0,9 = 1,8.
Соответственно стандартное отклонение рассчитывается по
формуле (6.12):
а = yjnp(l - р)- \ 1,8 = 1,34 декларации.
6.5. ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
6.5.1. Распределение гипергеометрических вероятностей
Другим типом распределения дискретной случайной вели-
чины, который часто соответствует ситуациям, связанным с
организацией выборок, является гипергеометрический закон
распределения. Он имеет большое сходство с биномиальным
распределением: опыт повторяется п раз, причем каждый опыт
имеет только два исхода — появление или непоявление собы-
тия А (успех или неудача).
Для использования гипергеометрического распределения
должны выполняться следующие условия.
1. Численность генеральной совокупности равна N. В ней име-
ется к элементов “успехов” и (2V- £) элементов “неудач”.
2. Выборка состоит из п элементов и является бесповторной.
3. Случайная величина X, распределенная по гипергеомет-
рическому закону, характеризует количество “успехов” в п
опытах (т. е. в случайной выборке, состоящей из п элементов).
Основное отличие от биномиального закона состоит в том,
что опыты не являются независимыми. Поэтому вероятность
“успеха” в каждом опыте зависит от результатов предыдущих
опытов. Такая ситуация возникает, когда случайная выборка
отбирается из конечной генеральной совокупности по схеме
без возвращения^
Сходство с ситуацией, которая описывается биномиальным
распределением, заключается в подсчете числа “успехов”. Од-
нако если выполняются условия гипергеометрического распре-
деления, то генеральная совокупность обязательно конечна
(имеет объем N) и известно число “успехов” (к) и “неудач”
(N - к), которые составляют генеральную совокупность.
125
Пусть /\х) обозначает вероятность события X = х, т. е. веро-
ятность, что в п опытах (выборке из п элементов) “успех” по-
явится ровно п раз. Распределение вероятностей для гипергсо-
мегрического закона выражается в виде соотношения
Р(х)а....С Jf*. (6.13)
здесь N — объем генеральной совокупности (общее число “ус-
пехов и “неудач”);
п — объем случайной выборки (число опытов);
к — количество “успехов”;
N - к — количество “неудач”;
х = а, а + 1, а + 2.Ь, где а — максимальное значение из
чисел Онп + к— N(a = max (0,л + к — Л)), b — минималь-
ное значение из чисел к и п (b = min (к,л)), Дх) = 0 для
всех остальных значений х.
Пример 6.10. Партия из 50 чипов (N) для компьютеров содер-
жит 5 дефектных (к) и 45 годных чипов (N — к). Из партии
случайным образом отбирается 10 чипов (л) для проверки. Ка-
кова вероятность, что в выборке будет ровно 1 дефектный чип?
Пусть событие А (“успех”) характеризует дефектный чип, а
противоположное событие А (“неудача”) — годный чип. При
отборе первого чипа вероятность, что он будет дефектным,
можно записать следующим образом:
Р(А в 1-м опыте) = 5/50 = 0,1.
Условные вероятности события А во втором опыте следую-
щие:
ДЛ/ А в 1-м опыте) = 4/49 = 0,082;
ДЛ/ Л в 1-м опыте) = 5/49 = 0,102.
Как видно, вероятность появления “успеха” (дефектность
чипа) во втором опыте зависит от результататов первого опыта
(отбора первого чипа). Следовательно, рассматриваемая ситуа-
ция удовлетворяет условиям гипергеометрического распреде-
ления.
По формуле (6.13) найдем вероятность Д1):
Д1) =
Cj-C?5 = 5-45110140!
С'® 9136150!
= 0,431.
Иначе говоря, 43% всех выборок по 10 чипов, взятых из
каждой партии, состоящей из 50 чипов, будут иметь ровно один
дефектный чип.
126
6.5.2. Математическое ожидание и дисперсия
гипергеометрического распределения
Можно доказать, что математическое ожидание гипергео-
метрической случайной величины X вычисляется по формуле
М = (6.14)
/V
где /V — объем генеральной совокупности;
п — объем выборки;
к — число “успехов” в генеральной совокупности.
Соответственно выражение для дисперсии имеет вид
аг _ *.¥,.* (6.15)
№(W-1) I N Л Л/Лл,-17
где обозначения те же, что и в формуле (6.14).
Для ситуации примера 6.10 вычислим математическое ожи-
дание, дисперсию и стандартное отклонение. Имеем N = 50,
к = 5, п = 10.
По формуле (6.14) получим
ц = 10 5/50 = 1 чип.
По формуле (6.15) вычислим дисперсию:
2 5-45 10-40
о =-----=-----= 0,735.
502 49
Отсюда получаем а = \'0,735 = 0,857 чипа.
Таким образом, теоретически наблюдая непрерывный бес-
конечный процесс составления случайных выборок по 10 чи-
пов в каждой, отбираемых из партии в 50 чипов, мы обнару-
жим в среднем по одному дефектному чипу в каждой выборке
(ц = 1). При этом стандартное отклонение как мера вариации
равна о = 0,857 (дисперсия о2 = 0,735).
6.5.3. Использование биномиального закона
для замены гипергеометрического распределения
Пусть выполняется условие, что объем выборки п не превы-
шает 5% от объема генеральной совокупности N (n/N < 0,05).
В этом случае биномиальное распределение с достаточной точ-
ностью заменяет гипергеометрическое.
127
Вычислим отношение:
Число “успехов” в генеральной совокупности п
? Объем генеральной совокупности W
Тогда величина X, характеризующая число “успехов" в вы-
борке, будет приблизительно распределена по биномиальному
закону с параметрами: п — число опытов и р — вероятность
“успеха” в каждом опыте.
Пример 6.11. Пусть в ситуации примера 6.10 рассматривается
партия из 500 чипов (N), из которой отбирается случайным обра-
зом 10 чипов (и). В этом случае выполняется условие n/N < 0,05,
так как 10/500 = 0,02. Известно, что число дефектных чипов (“ус-
пехов”) к в партии составляет 50. Отсюда р — 50/500 = 0,1. Слу-
чайную величину X, которая принимает значения, равные числу
дефектных чипов в выборке, можно считать распределенной по
биномиальному закону с параметрами п = 10 и р = 0,1. Опреде-
лим вероятность, что выборка содержит ровно I дефектный чип.
Она будет равна биномиальной вероятности Л 1,10) = 0,387 (При-
ложение 2).
6.6. РАСПРЕДЕЛЕНИЕ ПУАССОНА
6.6.1. Распределение вероятностей пуассоновской
случайной величины
Данное распределение часто используется при исследовании
ситуаций, когда требуется оценить число появлений некоторого
события за определенный промежуток времени или на задан-
ной пространственной области. Например, такие ситуации воз-
никают при регистрации дорожно-транспортных происшествий
на определенном участке дороги; оценке числа абонентов теле-
фонной сети, получивших при вызове сигнал “занято”; опреде-
лении числа повреждений в изоляции кабеля; определении чис-
ла слабых звеньев в различного рола цепях и т. п.
В дальнейшем ограничимся рассмотрением пуассоновской
случайной величины, характеризующей появление опреде-
ленного числа “успехов” в течение заданного промежутка
времени.
Распределение Пуассона имеет вид
Р(Х =х) = Р(х) = £^—, (6.16)
х!
128
где X — пуассоновская случайная величина;
х = 0, 1, 2,...;
е — константа (число е — основание натурального лога-
рифма, приблизительно равное 2,71828);
ц — математическое ожидание (среднее значение) числа
появлений'“успеха” за рассматриваемый промежуток вре-
мени (определяется исходя из условий конкретной ситуа-
ции).
Распределение Пуассона имеет заметное сходство с бино-
миальным распределением. В обоих случаях рассматриваются
опыты, каждый из которых может иметь только два исхода —
появление или непоявление некоторого события А (“успех” или
“неудача”). Опыты независимы друг от друга, и вероятность р
успешного исхода остается постоянной в каждом опыте. В При-
ложении 3 приведена таблица, где представлены значения пу-
ассоновских вероятностей Р(х) для х — 1, 2.. 24 (строки
таблицы) и ц = 0,005; 0,01; 0,02;..; 0,09; 0,1; 0,2;...; 9,9; 10 (столб-
цы таблицы), стоящие на пересечении соответствующих строк
и столбцов.
В отличие от биномиального распределения для пуассоновс-
кой случайной величины Xчисло опытов п не является фикси-
рованным числом и она может принимать бесконечное множе-
ство целых неотрицательных значений: х = 1,2, 3,... (каждый
опыт может длиться очень малый промежуток времени). Теоре-
тически предполагается, что п стремится к бесконечности
(объем выборки бесконечен), а вероятностьр стремится к нулю,
но при этом величина пр = ц должна оставаться постоянной.
Для пуассоновской величины характерно, что число “успехов”
в одном большом интервале не зависит от их числа в непе-
ресекающемся с ним другом интервале.
6.6.2. Математическое ожидание и дисперсия
пуассоновской случайной величины
Математическое ожидание равно ц, что следует из опреде-
ления распределения Пуассона, заданного соотношением (6.16).
Это утверждение можно было бы доказать, используя общую
формулу (6.2) для математического ожидания дискретной слу-
чайной величины:
И» £хр(х) = 0е’и +1цеи+2-£-^~ + 3—... = ц.
129
Дисперсия для распределения Пуассона равна математичес-
кому ожиданию, т. е. о2 = ц. Это также можно доказать, исполь-
зуя формулу (6.3):
о2 = £(х -Ц)2 р(х) = ц2 • е~ц + (1 - Ц)2цг + (2 - ц)2 = Н-
Особо отметим, что для пуассоновской случайной величи-
ны имеет место следующее свойство. Пусть случайная величина
рассматривается на определенном промежутке времени. Если
этот промежуток увеличится (уменьшится) в некоторое число
раз, то точно в такое же число число раз увеличится (умень-
шится) математическое ожидание случайной величины. Пока-
жем это на следующем примере.
Пример 6.12. На станции автосервиса в течение получаса оформ-
ляют заказы на мелкий ремонт автомобилей в среднем у четы-
рех клиентов. Требуется определить:
I) какова вероятность, что ровно 4 клиента сделают заказы
в течение получаса?
2) какова вероятность, что более чем 1 клиент сделает заказ
в течение получаса?
3) какова вероятность, что ровно 6 клиентов сделают зака-
зы в течение часа?
В данном случае ситуация моделируется с помощью пуассо-
новского процесса, где ц = 4. Вычисления будем проводить,
используя таблицу Приложения 3.
43 4е*4
1. ЛТ = 4) = Л4) 0,1954.
4!
Следовательно, непрерывно наблюдая за оформлением за-
казов в течение многих получасовых периодов, можно убедить-
ся, что 19,5% всего времени наблюдения заказы будут оформ-
лять ровно 4 клиента.
2. Р(Х > 1) = Р(Х й 2) = 1 - Р(Х = 1) - f\X = 0) =
, 4°е~* 4'е4
= 1-------------- = 1 - 0,183 - 0,0733 = 0,9084.
3. Ввиду того что интерват наблюдения увеличился в 2 раза
(с получаса до одного часа), ц = 2 • 4 = 8. Тогда
о<>«
/ХХ = 6) =—— = 0,1221.
о!
130
6.6.3. Замена биномиального распределения
распределением Пуассона
В ситуациях, когда выполняются условия биномиального рас-
пределения, вычисления вероятностей при большом числе опы-
тов достаточно трудоемкие. Однако они значительно упроща-
ются, если биномиальную случайную величину X заменить на
пуассоновскую с тем же математическим ожиданием. При боль-
шом числе опытов и малой вероятности р такая замена дает
достаточно точный результат. На практике наиболее благопри-
ятны условия, когда п > 20, р < 0,05 и пр < 7.
На рис. 6.2 представлены графики распределений вероятно-
стей для биномиальной величины с параметрами п = 20,
р = 0,1 (т. е. ц = пр = 2) и для пуассоновской с ц = 2.
Рис. 6.2. Графики распределения Пуассона (ц 2) и биномиального
распределения (п = 20, р = 0,1)
Можно сказать, что распределение Пуассона — это бино-
миальное распределение при большом числе опытов и малой
вероятности р.
Пример 6.13. Пусть рассматривается ситуация примера 6.10,
только объем партии значительно увеличился и составляет 2500
чипов (Л0- Из партии случайным образом отбирается 100 чипов
(л) для тестирования. Вся партия принимается в производство,
если среди отобранных 100 чипов окажется не более одного
дефектного. Если предположить, что 5% всех чипов в партии
являются дефектными, то определить, какова вероятность, что
партия будет принята.
131
Рассмотрим отношение n/N= 100/2500 = 0,04 < 0,05. Следо-
вательно, в данной ситуации можно использовать биномиаль-
ное распределение вместо гипергеометрического.
Биномиальное распределение имеет параметры п - 100,
р = 0,05.
Для определения вероятности приемки партии необходимо
вычислить:
Лприемки) = /1(0,100) + Л1,100) =
= С’оо • 0,05° • 0,95100 + С]ж • 0,05* • 0,95" = 0,037.
Очевидно, вычисления достаточно трудоемки. Расчеты можно
значительно упростить, если использовать распределение Пу-
ассона с математическим ожиданием ц = пр = 100 0,05 = 5.
Условия для замены являются благоприятными: п > 20,
р = 0,05, пр = 5 < 7. Используя Приложение 3, получим
Лприемки) = ДО) + Л1) = 0,0067 + 0,0337 = 0,0404.
Как видно, результат замены (0,0404) достаточно близок к
0,037 — значению биномиальной случайной величины.
6.7. ФУНКЦИИ И КОМБИНАЦИИ
СЛУЧАЙНЫХ ВЕЛИЧИН
6.7.1. Математическое ожидание и дисперсия
функций случайной величины
Пусть X — случайная величина, численное значение кото-
рой зависит от испытания. Если каждое значение Xразделить
на 5, то в зависимости от исхода испытания мы получим чис-
ла, которые характеризуют случайную величину Х/5. Аналогич-
но, возведя значение X в квадрат, получим случайную величи-
ну X1; линейное преобразование X даст случайную величину
аХ+ b и т. д. В общем случае некоторое преобразование значе-
ний Xявляется функцией Дх). Пусть случайная величина Xимеет
ряд распределения:
Х-х, xi *2 Жп
ЖХ = хД Р. Pi Рп
где 5jPi=1-
i=i
132
Очевидно, математическое ожидание случайной величины
ДЛ) можно вычислить по формуле
I
л
E(/(X)] = Sa/U). (6.18)
<-i
Заметим, что формула (6.18) была получена не на основе
какой-либо информации о законе распределения зависимой от
Л'случайной величины ДА), а непосредственно из ряда распре-
деления случайной величины X.
пример 6.14. Пусть случайная величина X имеет ряд распреде-
ления
X -1 2 4 8
р. 0.1 0,4 0,3 0,2
Определим Е(Х2 — 1).
По формуле (6.18) имеем
Е(Х2- 1) = ((-I)2- 1)0,1 + (22- 1) 0,4 + (42 - 1) 0,3 +
+ (82— 1) 0,2 = 0 0,1 + 3 0,4 + 150,3 + 63 0,2 = 16,3.
Рассмотрим линейную функцию Y = аХ + Ь, где X — слу-
чайная величина с рядом распределения (6.17). Найдем мате-
матическое ожидание Е(У) по формуле (6.18):
П ЯП
Е(Г ) = + Ь)р, = + ^Ьр, =
1=1 1-1 г-1
п л
= a^xtPl+b^p,=aE(X) + b. (6.19)
i=i «=1
Из (6.19) следует, что если Ь = 0, то
Е(ах) = аЕ(х). (6.20)
Соотношение (6.20) означает, что константу можно выно-
сить за знак математического ожидания.
Если а = 0, то из (6.12) получим Е(Ь) = Ь, т. е. математичес-
кое ожидание константы равно этой константе.
Данный результат имеет следующую вероятностную интер-
претацию. Константа не является случайной величиной, одна-
ко условно ее можно рассматривать как случайную величину,
133
которая принимает одно возможное значение b с вероятнос-
тью 1. Отсюда
Е(Л) = 61 = Ь.
Пусть случайная величина имеет дисперсию o2(J). Вычис-
лим дисперсию о2(К) линейной функции Y= аХ + Ь, исполь-
зуя (6.19):
ст2( Y) = £|(ах,, + Ь) - Е(аХ + 6)[2 Pi = £[ах,+ b - «Е( X) - Ь]2р, =
1-1 i=l
« „ (6.21)
= £ [ах, - аЕ( X )J2 Pi =а2 £ Ц - Е( X )]2 р, = а2 а2 (X).
««I i«l
Если b = 0, то (6.21) можно переписать:
сг(аХ) = rfoXX). (6.22)
Соотношение (6.22) означает, что константу можно вынес-
ти за знак дисперсии, возведя ее в квадрат. Как следствие ра-
венства (6.22) имеем
<j(aX) = lala(A'),
т. е. константу можно выносить за знак стандартного отклоне-
ния в виде ее абсолютной величины.
Определим дисперсию константы Ь. По определению дис-
персии
о2(6) = Е[(6 - Е(6))2] = Е[(6 - 6)21 = Е(0) = 0.
Следовательно, дисперсия константы равна нулю.
Пример 6.15. Автомат фасует чай в пакетики. Средний вес па-
кетика — 2 г со стандартным отклонением 0,05 г. Пакетики в
свою очередь пакуются в пачки по 25 штук. Определить сред-
ний вес чая в пачке и соответствующее стандартное отклоне-
ние.
Пусть X — случайная величина, характеризующая вес паке-
тика с чаем. Тогда случайная величина 25Хбудет характеризо-
вать вес пачки. Отсюда если Е(%) = 2 г, то Е(25Х) = 25Е(ЛГ) =
=25-2 = 50 г. По условию о{Х) = 0,05 г. Следовательно, а(25Л)=
= |25| о(Х) = 25 0,05 = 1,25 г.
134
Пусть/(А*) и g(X) — любые функции случайной величины
X. Можно показать, что математическое ожидание суммы фун-
кций равно сумме математических ожиданий каждой функции:
Е(Я%) + g(X)) = E(/t¥)) + Е(£(Х)).
6.7.2. Сумма и произведение независимых
случайных величин
Случайные величины Хи У называются независимыми, если
закон распределения каждой из них не зависит от того, какое
значение приняла другая. Формально можно записать, что если
х — любое возможное значение случайной величины X, а у —
величины Y, то Хи У будут независимыми, если выполняется
условие
f\X = х и У=у) = ДХ = х)ЛУ = у).
Покажем, что для любых двух случайных величин (как неза-
висимых, так и зависимых) выполняется равенство
Е(ЛГ + У) = Е(Х) + Е(У),
т. е. математическое ожидание суммы двух случайных величин
равно сумме их математических ожиданий.
Пусть случайные величины X и У имеют следующие ряды
распределений:
X ... *л У У| Уг ... уп
р, Pl р2 ... Рл Ч. Pl ... РЛ
Рассмотрим случайную величину Z = X + У и запишем ее
ряд распределения:
Z х^Уу х,+Уг ... *1^5», ... *2+Кл ... VKn
р РЫ РЪ ... р^т ... РгРп, ...
Математическое ожидание E(Z) вычисляется как сумма про-
изведений (х + yt\Pfif Запишем (х, + y^pfl. = хр^ + у^р,.
При составлении суммы, определяющей математическое
ожидание E(Z), сгруппируем слагаемые следующим обра-
зом:
135
<7,(Р,х, +рЛ + р3х3+... +рЛ)
+ ^Л + ед + ед+-+/’Л>
+
?.О’Л + РЛ + /’А+ • +^х.)
+ Р&М + ед + «Л + - + VJ (6.23)
р2( V, + ед + ?»У3 + ... +<7Х>-
+
+ ед + ед + -+vJ w Е<* )(<?. + ч2 + «з + - +<?„) +
+ Е( У) (р, + р2 +л + ... + ря) = Е(Х) + Е( Г).
Соотношение (6.23) обобщается на произвольное число сла-
гаемых:
=ЕЕ<Х<)-
i*i
То есть математическое ожидание суммы нескольких слу-
чайных величин равно сумме их математических ожиданий.
Если Хм Y — независимые случайные величины, то анало-
гично можно показать, что
Е(ХУ) = Е(Х)Е(У). (6.24)
Для независимых Xи Убудет верно соотношение
а\Х+ У) = о2(Х) + о2(У). (6.25)
Докажем (6.25). Ввиду (6.5) можно записать
oV+ У) • Е|(Х + Г)2] - (Е(Х + Г)]2 = Е(Г + 2АТ+ Г2) -
- [Е(Х) + Е(Г)]2 = Е(Х2) + 2Е(ЛТ) + £(№)- Е(ЛГ2) -
- 2Е(ЛГ)Е(Г) - Е(Г2) = Е(Л2) - E(J)2 + 2(E(XY) -
- Е(Х)Е(У)) + Е(Г2) - Е(У)2 = а\Х) + 0 + о2(У).
136
Таким образом, если X и У — зависимые случайные величи-
ны, то равенство Е(% + У) = Е(Х) + Е(У) останется верным.
Однако соотношения (6.24) и (6.25) будут верными только
при условии независимости случайных величин X и У.
Ввиду равенств (6.22) и (6.25) можно записать:
а2(Х — У) = а2(Х + (~1)У) = а2(Х) + сН((—1)У) =
= <ЛХ) + (-1)2 <Т2(У) = <?(%) + а2(Г).
То есть для независимых случайных величин дисперсия раз-
ности равна сумме дисперсий. Обобщая полученные соотноше-
ния для суммы и разности двух независимых случайных вели-
чин, можно сделать следующие выводы относительно алгебраи-
ческой суммы нескольких случайных величин:
математическое ожидание алгебраической суммы случайных
величин (необязательно зависимых) равно соответствующей
алгебраической сумме их математических ожиданий;
дисперсия алгебраической суммы нескольких независимых
случайных величин равна сумме их дисперсий.
Пример 6.16. Некоторый товар укладывается в одинаковые ящи-
ки. Средний вес товара составляет 10,5 кг со стандартным от-
клонением 0,8 кг. Средний вес ящика — 3,5 кг со стандартным
отклонением 0,1 кг. Требуется определить средний вес напол-
ненного ящика, соответствующие стандартное отклонение и
дисперсию.
Путь X — случайная величина, характеризующая вес това-
ра, уложенного в ящик, а У — случайная величина, соответ-
ствующая весу отдельного ящика. Ясно, что Хи У — независи-
мые случайные величины. Средний вес наполненного ящика
равен
E(J+ У) = E(J) + Е(У) = 10,5 + 3,5 = 14 кг.
Найдем дисперсию:
а\Х + У) = а2(Х) + о2(У) = 0,82 + 0,12 = 0,65 кг2.
Определим стандартное отклонение:
о(Х + У) = <65" = 0,806 кг.
Пример 6.17. Пусть X— случайная величина, характеризующая
число очков, которое выпадает при бросании игральной кос-
ти; У — случайная величина, значением которой является коли-
137
чество выпадений гербов при подбрасывании четырех монет.
Требуется определить: математическое ожидание, дисперсию и
стандартное отклонение случайной величины Z = 2Х - Y + 4.
Величина X имеет ряд распределений
X 1 2 3 4 5 6
р 1/6 1/6 1/6 1/6 1/6 1/6
Вычислим Е(А'):
Е(Х) = 1/61 + 1/6 2 + 1/6-3 + 1/6 4 + 1/6 5 + 1/6 6 = 3,5.
Определим ст2^):
<ЛХ) = Е(Х}) - Е(ЙГ)2 = 1/61» + 1/6 2» + 1/6 3» + 1/6 42 +
+ 1/6-5» + 1/6-62 - (3,5)» =
= 91_12£ = 35=2_Н
6 4 12 12’
Случайная величина У распределена по биномиальному за-
кону с параметрами л = 4, р = 1/2. Следовательно,
Е(У) = пр = 4 1/2 - 2,
о2(У) = лр(1 - р) = 41/21/2 = 1.
Определим E(Z):
E(Z) = E(2J - Г + 4) = Е(2Х) - Е(У) + Е(4) =
“ 2Е(ЛГ) - Е(Г) + 4 = 2-3,5 -2 + 4 = 9.
Вычислим o2(Z) и o(Z):
o2(Z) = о2 (2 А" - Y +4) = <j2(2X) + crV) + а2(4) =
11 2
= 4а2(Х) + о2(У) + 0 = 4-2^ + 1 = 12^12,67.
o(Z) = 3,56.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 6
При описании случайных событий удобно использовать по-
нятие случайной величины, под которой понимается функ-
ция, ставящая в соответствие каждому исходу испытания чис-
138
ленное значение. Исход испытания является случайным собы-
тием, поэтому заранее неизвестно, какое значение примет слу-
чайная величина. Если все значения случайной величины мо-
гут быть перечислены, то она называется дискретной. Если
значения случайной величины непрерывно заполняют некото-
рый промежуток и все эти значения невозможно перечислить,
то она называется непрерывной. Дискретная случайная вели-
чина с вероятностной точки зрения считается заданной, если
известен ее закон (ряд) распределения. Ряд распределения пред-
ставляет собой таблицу возможных значений случайной вели-
чины с соответствующими вероятностями. Одной из характе-
ристик случайной величины является математическое ожидание
(среднее значение). Оно вычисляется по формуле (6.2) и опре-
деляет положение центра распределения, около которого кон-
центрируется основная масса значений. Их разброс около ма-
тематического ожидания измеряется с помощью дисперсии
(формула 6.3). Дисперсия вычисляется как математическое ожи-
дание квадрата отклонения значений случайной величины от
ее математического ожидания. Для выражения разброса в еди-
ницах измерения исходной случайной величины используется
стандартное отклонение (среднее квадратическое отклонение),
которое вычисляется как корень квадратный из дисперсии. Чем
меньше величина дисперсии или стандартного отклонения, тем
более плотно значения случайной величины располагаются
около математического ожидания.
Дискретная случайная величина, распределенная по бино-
миальному закону, характеризует количество появлений неко-
торого события А в п независимых опытах. При этом предпола-
гается, что каждый опыт имеет только два исхода — появление
(“успех”) или непоявление (“неудача”) события А. “Успех” в
каждом опыте появляется с постоянной вероятностью р. Рас-
пределение вероятностей для биномиального распределения
выражается членами разложения бинома.
Пусть опыты зависимы, известны численность генеральной
совокупности (N) и число “успехов” (к), содержащихся в ней.
В этом случае для оценки вероятности появления ровно х успе-
хов в выборке из п элементов используется гипергеометричес-
кое распределение (формула (6.13)).
Если производится много независимых опытов, каждый из
них имеет два противоположных исхода (“успех” и “неудача”)
и вероятность “успеха” в каждом опыте мала, то вероятность
появления определенного числа “успехов” следует рассчиты-
вать на основе распределения Пуассона (формула (6.16)). Это
139
распределение часто используется при исследовании ситуаций,
когда требуется оценить число появления некоторого события
за определенный промежуток времени. На практике в случае
возникновения трудностей при вычислениях возможна замена
одного распределения другим. Так, если для гипергеометри-
ческого распределения выполняется отношение n/N < 0,05, то
оно достаточно точно приближается биномиальным. Замена
биномиального распределения пуассоновским дает хорошие
результаты при условиях, что л > 20, р < 0,05 и пр < 7.
Пусть рассматривается функция от случайной величины.
Математическое ожидание этой функции можно вычислить,
зная только закон распределения исходной случайной величи-
ны (формула (6.18)). Если случайная величина умножается на
константу, то эту константу можно выносить за знак матема-
тического ожидания, а если возвести в квадрат, то за знак дис-
персии. Математическое ожидание алгебраической суммы слу-
чайных величин равно соответствующей алгебраической сумме
их математических ожиданий. Случайные величины называют-
ся независимыми, если закон распределения каждой из них не
зависит от того, какое значение приняла другая. Дисперсия ал-
гебраической суммы нескольких независимых случайных вели-
чин равна сумме дисперсий. Математическое ожидание произ-
ведения независимых случайных величин равно произведению
их математических ожиданий.
РАСПРЕДЕЛЕНИЯ
НЕПРЕРЫВНЫХ
СЛУЧАЙНЫХ ВЕЛИЧИН
7.1. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
ФУНКЦИЯ И ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ.
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
В гл. 6 было дано общее определение случайной величины.
Отмечалось, что случайные величины могут носить дискрет-
ный и непрерывный характер. Были рассмотрены основные за-
коны распределения дискретных случайных величин, которые
часто используются в прикладном статистическом анализе.
Данная глава будет посвящена описанию непрерывных слу-
чайных величин и их законов распределения.
Дискретная случайная величина является прерывной, т. е.
все ее возможные значения отделены друг от друга конечными
интервалами и могут быть заранее перечислены. Возможные же
значения непрерывной случайной величины непрерывно за-
полняют некоторый промежуток и не могут быть заранее пере-
числены.
Примерами непрерывных случайных величин могут служить
сроки службы различных товаров: электрических лампочек,
батареек, автомобильных покрышек, электроприборов и т. п.
Так, срок службы каждого из перечисленных товаров может
измеряться промежутком времени от нуля до некоторой ко-
нечной верхней границы. В общем случае непрерывные случай-
ные величины могут характеризовать результаты измерений:
длительности процесса, веса, длины, площади, высоты, на-
пряжения в электросети и т. д.
Теоретически (предполагается, что возможна любая точность
измерений) результат измерения может быть выражен любым
действительным числом, взятым из некоторого промежутка.
Дискретная случайная величина в вероятностном смысле
будет полностью определена, если задан ее ряд распределения.
141
Для непрерывной случайной величины записать таблицу ряда
распределения невозможно, так как она должна включать все
ее возможные значения (непрерывная случайная величина имеет
бесконечное множество значений, которые невозможно пере-
числить). Поэтому для характеристики распределения вероят-
ностей непрерывной случайной величины удобно воспользо-
ваться не вероятностью события X- х, а вероятностью события
Х<х, где х — некоторая текущая переменная. Очевидно, веро-
ятность того, что Х<х, зависит от текущей переменной х и явля-
ется некоторой функцией от х. Эта функция называется функ-
цией распределения случайной величины х и обозначается Дх):
F(x)~P(X<x). (7.1)
Функция распределения F(x) называется также интеграль-
ной функцией распределения или интегральным законом рас-
пределения.
Функция распределения может существовать как для непре-
рывных, так и для дискретных случайных величин. С вероятно-
стной точки зрения функция распределения полностью харак-
теризует случайную величину, т. е. является одной из форм закона
распределения.
Рассмотрим основные свойства функции распределения (7.1).
1. Так как значение вероятности неотрицательно и не может
быть больше единицы, то 0 < Дх) < 1.
2. Функция распределения есть неубывающая функция, т. е.
при х2 >Xj имеем Дх2) 2 FlxJ.
3. Предельное значение функции распределения при х -» —<»
равно нулю, а при х -> +°° равно единице.
В случае дискретной случайной величины X, заданной ря-
дом распределения, Fix') для каждого х есть сумма вероятнос-
тей значений X, которые лежат до точки х: Дх) = Р(Х<х) =
= ^Р(Х = х,), где неравенство х<х под знаком суммы пока-
то ,
зывает, что суммирование распространяется на все те значе-
ния х, которые меньше х. Отсюда следует, что вероятность Дх)
увеличивается скачками всякий раз, когда х проходит через
одно из возможных значений х( величины X (между двумя со-
седними значениями х( и х функция Дх) постоянна). Таким
образом, график функции Дх) является ступенчатой кривой
(рис. 7.1).
142

Рис. 7.1. Г рафик функции распределения F(x)
для дискретной случайной величины
Для непрерывной случайной величины функция распреде-
ления представляет собой функцию, непрерывную и диффе-
ренцируемую во всех точках. Ее график является плавной кри-
вой, имеющей касательную в любой точке (рис. 7.2).
Рис. 7.2. График функции распределения непрерывной
случайной величины
На практике часто возникают ситуации, когда требуется
определить вероятность того, что случайная величина прини-
мает значения, находящиеся в некотором промежутке, напри-
мер от а до р. Другими словами, требуется определить вероят-
ность события а<*<0. Было отмечено, что F(x) имеет
производную в любой точке х. По определению производной
F(x + Ax)-F(x) ,
hm =-------т---------г- (л).
Дх
143
Введем обозначение
Лх) = Г(х).
Функция Дх) характеризует плотность, с которой распре-
деляются значения вероятности случайной величины в данной
точке. Она называется плотностью распределения непрерыв-
ной случайной величины X. Ее также называют дифференци-
альной функцией распределения. Очевидно, вероятность собы-
тия, что случайная величина X примет значение, лежащее в
границах от а до 0, равна
₽
Ла<х<0) = / /(х) dx = Л 0) - Да). (7.2)
а
График кривой, изображающей плотность распределения,
называется кривой распределения. Приближением кривой рас-
пределения является сглаженный полигон, рассматриваемый
ранее как кривая частотного распределения данных.
Рассмотрим кривую распределения заданной случайной ве-
личины х и отметим участок, ограниченный абсциссами а и 0.
Тогда ввиду (7.2) площадь, ограниченная частью кривой, опи-
рающейся на отрезок [а, 0], и прямыми х = а и х = 0, будет
характеризовать вероятность попадания случайной величины X
на промежуток (а, 0) (рис. 7.3).
л*) 4
Рис. 7.3. Графическая интерпретация вероятности попадания значения
непрерывной случайной величины на промежуток от а до fl
Плотность распределения является одной из форм закона
распределения. Однако она не является универсальной и суще-
ствует только для непрерывных случайных величин.
Отметим основные свойства плотности распределения.
144
I. Плотность распределения есть неотрицательная функция,
т. е. Дх) > 0. Отсюда график кривой распределения не может
лежать ниже оси абсцисс.
2. Интеграл в бесконечных пределах от плотности распреде-
ления равен единице:
н»
J/(x)dx=l. (7.3)
-♦о
Геометрически это означает, что площадь, ограниченная
кривой распределения и осью абсцисс, равна единице.
Количественные характеристики непрерывной случайной
величины выражаются в виде интегралов. Так, математическое
ожидание (среднее значение) вычисляются как интеграл:
♦«>
ц = Е(х)= |х/(х)<й. (7.4)
—OQ
Аналогично дисперсия определяется как математическое
ожидание квадрата отклонения значения случайной величины
х от ее математического ожидания:
ст2 = |(x-g)2/(x)dx. (7.5)
—оо
Отсюда получаем, что стандартное отклонение есть
J+<~
J(x - n)2/(x)dx . (7.6)
Для непрерывных случайных величин верны все свойства,
указанные в разделе 6.7 для математических ожиданий и дис-
персий функций и комбинаций дискретных случайных величин.
7.2. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ
Иногда в практических ситуациях встречаются непрерыв-
ные случайные величины, распределение которых удовлетво-
ряет условию: значения случайной величины внутри опреде-
ленных границ равновероятны. Иначе говоря, плотность
распределения является постоянной величиной. Такие случай-
ные величины называются равномерно распределенными или
распределенными по закону равномерной плотности.
145
Пусть дана случайная величина X, равномерно распреде-
ленная на промежутке от а до р. Запишем для нее выражение
плотности распределения Лх). Плотность постоянна и равна с
на промежутке (а, Р) и нулю вне этого промежутка (т. с. обра-
зует прямоуголиник):
Лх) =
с при а < х < р,
О прих<а или х^р.
Ввиду (7.4) площадь, ограниченная кривой распределения,
равна единице:
с(а - Р) = I или с = -о
а-р
Тогда плотность распределения имеет вид (рис. 7.4)
1
- при а<х<р,
р а (7.7)
О прих^а или х>р.
Ф) м
Лх) =
X
Рис. 7.4. Кривая плотности равномерного распределения
Формула (7.8) является математическим выражением зако-
на равномерной плотности на промежутке (а, Р).
Вероятность попадания значения случайной величины на
промежуток, находящийся внутри отрезка (а, Р), вычисляется
по формуле
P(a<x<h)=f-^- = ^. (7.8)
JP-a p-а
а
Графически выражение (7.8) представляет собой площадь
прямоугольника, заштрихованного на рис. 7.5.
146
Пх) л
По формулам (7.4)—(7.6) найдем математическое ожида-
ние, дисперсию и стандартное отклонение:
• <79>
<710)
ст= |(Р~а); (7.11)
V 12 Т/з
Пример 7.1. На фармацевтической фирме установлена автомати-
ческая линия, наполняющая пузырьки некоторыми лекарствами.
Случайным образом отбирается 150 наполненных лекарством пу-
зырьков и измеряется объем лекарства в каждом пузырьке. Оказа-
лось, что он колеблется в пределах от 19 до 21 мл. Для определе-
ния вида распределения построим гистограмму, где по оси ординат
отложим относительные частоты (оценки вероятности), а по оси
абсцисс — значения объема лекарства в пузырьке (рис. 7.6).
Очевидно, форма гистограммы свидетельствует, что распре-
деление объемов лекарств, содержащихся в пузырьках, близко
к равномерному. Согласно (7.7), плотность этого распределе-
ния имеет вид (график плотности распределения представлен
на рис. 7.7)
Лх)
1
21-19
при 19 < х< 21,
0 при х < 19 или х > 21.
147
Относительная
частота
для выборки из 150 пузырьков
Рис. 7.7. Кривая плотности распределения объемов лекарства
в пузырьках
Вычислим средний объем лекарства в пузырьках, наполня-
емых на автоматической линии, по формуле (7.9):
19 + 21 „
Ц =----— = 20 мл.
2
Дисперсия и стандартное отклонение вычисляются соответ-
ственно по формулам (7.10) и (7.11):
ст2 ,(21-19/ _ 1
12 3’
1
СТ =
148
Пусть требуется определить вероятность, что случайно вы-
бранный пузырек будет содержать объем лекарства, заключен-
ный между 19,5 и 20,5 мл. Используем для этого формулу (7.8):
20,5-19,5
/К19,5 <х< 20,5) = =0,5.
Следовательно, объем лекарства в 50% всех пузырьков, на-
полняемых на автоматической линии, находится в пределах от
19,5 до 20,5 мл.
7.3. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
В практических ситуациях равномерно распределенные не-
прерывные случайные величины встречаются достаточно ред-
ко. Как правило, массовые явления в различных сферах дея-
тельности подчиняются нормальному закону распределения.
Этот закон играет исключительно важную роль в статистичес-
ком анализе. Главная его особенность состоит в том, что он
является предельным законом, к которому приближаются дру-
гие законы распределения при определенных условиях, часто
встречающихся на практике.
В математической статистике доказывается, что сумма боль-
шого числа независимых (или слабо зависимых) случайных
величин распределяется почти нормально. При этом слагаемые
случайные величины могут подчиняться каким угодно законам
распределения. Чем больше число слагаемых случайных вели-
чин, тем ближе к нормальному будет распределение их суммы.
Большинство массовых явлений формируется как наложе-
ние многих отдельных причин (факторов). Каждая из них но-
сит, как правило, случайный характер, т. е. является случайной
величиной, подчиненной какому-либо закону. При сложении
большого числа причин особенности их распределений ниве-
лируются и сумма оказывается подчиненной нормальному за-
кону.
На практике, например, нормальному закону подчинены по-
грешности различного рода измерений, отклонения от установ-
ленного стандарта при производстве какой-либо детали и т. д.
7.3.1. Кривая нормального распределения и ее свойства
Нормальный закон распределения характеризуется плотно-
стью распределения, имеющей вил
149
Д*) =
___1 , 2в1
О\'2л
(7.12)
Как видно из формулы (7.12), для построения кривой нор-
мального распределения необходимо знать два параметра ц и о.
Кривая распределения по нормальному закону имеет сим-
метричную колоколообразную форму (рис. 7.8).
Рис. 7.8. Кривая нормального распределения
Максимальная ордината кривой нормального распределе-
ния, равная —1= , соответствует точке х = ц. По мере удаления
<ь/ 2п
от точки ц значение плотности распределения падает и асимп-
тотически приближается к оси абсцисс.
Можно доказать, что для случайной величины X, распреде-
ленной по нормальному закону (7.12), значение ц есть матема-
тическое ожидание (центр распределения), а о — стандартное
отклонение (мера разброса данных около центра).
Пусть все возможные значения случайной величины рас-
сматриваются как генеральная совокупность. Если Д'распреде-
лена нормально, то распределение случайной выборки из этой
совокупности будет близко к нормальному. Поэтому на прак-
тике при проверке нормальности распределения строят гис-
тограмму на основе полученных данных, которые рассматри-
ваются как случайная выборка из всех возможных значений
некоторой случайной величины X. Далее сравнивают форму сгла-
женного графика гистограммы, приближенно отражающего вид
кривой распределения случайной величины X, с кривой нор-
мального распределения.
Пример 7.2. Фирма производит электрические лампочки. Объек-
том исследования является срок их службы (время непрерыв-
но
ного горения), который можно рассматривать как случайную
величину X. Случайным образом выбирают 200 лампочек и про-
водят специальное тестирование для определения их сроков
службы. На основе данных тестирования была построена гис-
тограмма (по оси ординат откладывались относительные час-
тоты, а по оси абсцисс — сроки службы) и сглаживающая ее
кривая (рис. 7.9).
Рис. 7.9. Гистограмма распределения 200 лампочек по сроку их службы
Сглаживающая прямая характеризует кривую распределения
сроков службы всех лампочек, выпускаемых фирмой. Как вид-
но, ее форма очень близка к кривой нормального распределе-
ния с центром 400 ч.
В общем случае существует не одно распределение, а беско-
нечное семейство нормальных распределений, так как вид кри-
вой нормального распределения полностью определяется зна-
чениями параметров ц и о. Каждой паре значений ц и а
соответствует отдельное нормальное распределение.
На рис. 7.10 представлены кривые распределений работни-
ков трех фирм по стажу работы. Все кривые имеют одинаковые
средние значения ц = 20 лет, но разные стандартные отклоне-
ния.
Как видно из рис. 7.10, чем больше значение стандартного
отклонения о, тем более пологая и растянутая вдоль оси абс-
цисс кривая распределения. Наоборот, при уменьшении о кри-
вая распределения сжимается вдоль оси абсцисс и вытягивает-
ся вверх вдоль оси ординат.
151
Рис. 7.10, Кривые нормальных распределений,
имеющих одинаковые математические ожидания, но разные
стандартные отклонения
На рис. 7.I I представлены кривые двух нормальных распре-
делений с разными средними, но с одинаковыми стандарт-
ными отклонениями. Одна из кривых характеризует распределе-
ние по росту студенток некоторого университета (ц( = 1,65 м),
а другая — студентов (ц2 = 1,76 м).
Рис. 7.11. Кривые нормальных распределений, имеющих одинаковые
стандартные отклонения, но разные средние значения
Таким образом, если изменять математическое ожидание р
нормального распределения, не изменяя при этом стандарт-
ное отклонение о, то кривая распределения будет перемещать-
ся вдоль оси абсцисс, не меняя своей формы. Следовательно,
математическое ожидание ц определяет положение кривой нор-
мального распределения на оси абсцисс, а стандартное откло-
нение о — ее форму. Все возможные значения нормального
распределения случайной величины X представляют собой ге-
неральную совокупность. На практике, как правило, возможно
получение лишь выборочных значений X. Поэтому значения
152
параметров ц и о заменяют на значения соответствующих ста-
тистик х и 5. Так, в примере 7.2 средний срок службы 150
электрических лампочек равен х ” 400 ч. Предположим, что
было вычислено стандартное отклонение s = 50 ч. Ясно, что
для генеральной совокупности (всего множества выпущенных
лампочек) значения параметров ц и о будут отличаться от со-
ответствующих вычисленных статистик. Однако можно пред-
положить, что х достаточно близко к ц, a s — к о. Тогда теоре-
тическая кривая нормального распределения будет приближать-
ся к кривой
. <rs>
/(х) = - Ue ь’
зу12п
5OV2n
(л-400)1
250’
7.3.2. Площади под кривой нормального распределения
Исходя из свойства (7.3) площадь между всей кривой нор-
мального распределения с любыми параметрами ц и о и осью
абсцисс равна 1: .
2о’ dr = l.
Это соответствует вероятности достоверного события, что
нормально распределенная величина ^обязательно примет одно
из своих возможных значений.
Будем откладывать на оси абсцисс интервалы с центром ц и
границами (ц - о, ц + о), (ц — 2о, ц + 2о) и (ц + Зо, ц — Зо).
Площади, находящиеся под кривой распределения любого нор-
мального закона, обладают следующими свойствами (рис. 7.12).
1. Площадь под кривой, распределенная на интервале от
ц - о до р 4- о (или ц ±о), составляет 68,27% всей площади,
ограниченной всей кривой. Это означает, что на этом участке
сосредоточено 68,27% всех значений распределения.
2. Площадь под кривой распределения на участке от ц - 2о
до ц + 2о составляет 95,45% площади под всей кривой. Это
означает, что на этом участке располагается около 95,45% всех
значений распределения.
3. Площадь под кривой распределения на интервале от
ц — Зо до ц + Зо (ц ±3о) составляет 99,73% площади под
всей кривой, т. е. практически вся кривая располагается над
участком ц ±3о, следовательно, практически все значения
распределения сосредоточены в границах трех о по обе сто-
роны от ц.
153
Рис. 7.12. Доли площадей под кривой нормального распределения
над участками м ±в, м т2о, ц ±3а
Перечисленные выше свойства площадей под кривой нор-
мального распределения используются при выяснении, явля-
ется ли изученное распределение нормальным. Для различных
статистических заключений наиболее часто берутся следующие
пределы:
ц ±1,64 ст — ограничивает площадь, равную 90% площади
под кривой;
ц ±1,96 ст - 95%;
р ±2,5 о - 99%.
Кривая нормального распределения является симметричной.
Это означает, что площадь под кривой на участке от ц до +«>
(или от -о» до ц) составляет половину (50%) площади под
всей кривой. Аналогично площадь над участком от ц до ц + ст
(или от ц - о до ст) приблизительно равна 0,34 (34%) площади
под всей кривой; площадь над участком от р до ц + 2ст (или от
И - 2о до ц) — 0,475 (47,5%); площадь над участком от ц до
ц + Зо (или от ц - За до ц) — 0,5 (50%).
Следует еще раз отметить, что перечисленные выше про-
порции площадей будут верны для всех нормальных законов
распределения независимо от значений параметров ц и о. Они
могут использоваться при проверке соответствия исследуемого
распределения нормальному закону.
Пример 7.3. Специальное тестирование большого количества
батареек показало, что их средний срок службы —19 ч. Распре-
деление сроков службы батареек предполагается нормальным.
Значение стандартного отклонения равно 1,2 ч.
Можно утверждать: 1) примерно 68,27% всех батареек име-
ют срок службы в границах от 17,8 до 20,2 ч (19±11,18);
154
2) средний срок службы примерно 95,45% всех батареек зак-
лючен в пределах от 16,6 до 21,4 ч (19±21,8);
3) около 99,73% всех батареек имеют срок службы в преде-
лах от 15,4 до 22,5 ч ( 19±3-1,2).
Любой интервал с центром в точке ц можно рассматривать
как промежуток вида ц±го, где г>0 — любое положительное
действительное число (необязательно целое). В этом случае рас-
стояние между математическим ожиданием ц и любой точкой на
оси абсцисс определяется в единицах стандартного отклонения.
Рассмотрим две различные кривые нормального распреде-
ления. Одна из них характеризуется параметрами ц, и в(, а дру-
гая — ц, и о2. Пусть г— положительное число. Для первой кри-
вой построим интервал а для второй — ц2±го2. Тогда
площади между соответствующими кривыми и отрезками бу-
дут составлять одинаковые доли общих площадей кривых. Вви-
ду симметрии одинаковые доли площадей будут соответство-
вать также интервалам pf+ rat и ц2+ го2 (или — и
Таким образом, для всего семейства нормальных кривых
будет верно следующее свойство площадей, ограниченных этими
кривыми: если для каждой кривой измерять расстояние между
математическим ожиданием ц и какой-либо точкой на оси абс-
цисс в единицах стандартных отклонений о, то все площади,
заключенные между кривыми и интервалами ц±га (г>0 — оди-
наковое для всех кривых число, характеризующее длину ин-
тервала в масштабе стандартного отклонения о), будут состав-
лять одинаковые доли площадей соответствующих кривых.
Рис. 7.13. Площади, ограниченные нормальными кривыми
и отрезками ц + 1,5с
155
Пример 7.4. На рис.7.13 представлены три кривые нормально-
го распределения с разными параметрами ц и о: распределение
1 (р( 100, = 45), распределение 2 (ц, = 60, о, = 30), рас-
пределение 3 (цз = 50, оз = 20). Для каждой кривой справа от р
на оси абсцисс отметим отрезок ц+1,5а. Все заштрихованные
площади, ограниченные кривыми и отмеченными отрезками,
будут составлять одинаковые доли площадей кривых.
7.3.3. Вероятность попадания на заданный промежуток.
Стандартное нормальное распределение
Используя соотношение (7.2), можно определить вероятность
попадания значения случайной величины X, распределенной
по нормальному закону с параметрами ц и о, на произволь-
ный участок (а, 0):
Р (in)'
Р(а<. х<0) = —I— fe 2о’ dx. (7.13)
Стл/2л *
а
Геометрически вероятность (7.13) соответствует площади,
заключенной между кривой распределения и промежутком (а,
0). Она равна некоторой доле площади, ограниченной всей
кривой (т. е. некоторой доле 1).
Пример 7.5. Пусть случайная величина X, взятая из примера 7.2,
имеет параметры ц = 400, о = 50. Тогда для определения вероят-
ности события, что взятая наугад лампочка будет иметь срок
службы в пределах от 300 до 360 ч, следует вычислить интеграл:
360 (х-400)1
f е 250 dx. (7.14)
300
что соответствует заштрихованной площади на рис. 7.14.
Л300<х<360) = —I
300 360 400
Рис. 7.14. Геометрическое выражение вероятности Р(300<х<360)
Вычисление с необходимой точностью интегралов типа (7.13)
в каждом конкретном случае (например, (7.14)) является трудо-
емкой процедурой. Поэтому на практике при вычислении вероят-
156
ности Я(а<х<Р) поступают следующим способом: рассматрива-
ют соответствующую площадь под кривой нормального распре-
деления. Затем эту площадь представляют как алгебраическую сум-
му площадей определенного вида, значения которых рассчитывают
заранее. Данный способ основан на свойствах площадей, ограни-
ченных кривой нормального распределения и отрезком между
средним значением ц и какой-либо точкой на оси абсцисс, при-
чем длина этого отрезка должна выражаться в единицах стандар-
тного отклонения ст. Как было отмечено в п. 7.3.2, доли площадей
под кривыми нормального распределения, ограниченных отрез-
ками ц ± га, где ц и а принимают любые значения, а г>0 имеет
постоянное значение для всех кривых, будут равны между собой.
Поэтому имеет смысл составить таблицу площадей данного вида
для одного специального нормального распределения и сопос-
тавлять с ним кривую любого другого нормального распределе-
ния. Для этой цели любой нормальный закон с параметрами цист
можно стандартизировать, используя преобразование
Z=—(7.15)
о
где х — значение случайной величины X, распределенной по
нормальному закону с параметрами ц и о;
ц — математическое ожидание X,
а — стандартное отклонение данного распределения;
Z — число стандартных отклонений, содержащихся на от-
резке между ц и х.
Преобразование (7.15) называется стандартизацией нормаль-
ного закона распределения. Оно позволяет перейти от конкрет-
ных единиц размерности случайной величины X (например,
единиц измерения денежных потоков, габаритов физических
тел, времени, экономических показателей и т. д.) к безразмер-
ному масштабу. Величина 7для любого нормального распреде-
ления характеризует отклонение от математического ожидания
ц в единицах стандартного отклонения а.
Математически выражение (7.15) можно рассматривать как
преобразование переменной х в переменную Z. При этом лю-
бой нормальный закон с параметрами ц и а приводится к виду
1 ~
Ж--4-е 2. (7.16)
У2Л
Функция (7.16) представляет собой плотность нормального
распределения с параметрами ц = 0 и ст = 1. Она характеризует
стандартный нормальный закон распределения.
157
Для стандартного нормального распределения в Приложе-
нии 4 представлена специальная таблица. В ней указаны доли
площади, ограниченной кривой стандартного нормального
распределения и заключенной между ц = 0 и различными зна-
чениями Z>0 (т. е. соответствующие положительным отклоне-
ниям от средней). Ввиду симметричности кривой нормального
распределения площади под кривой, расположенной по одну
сторону от средней, эквивалентны соответствующим площа-
дям по другую сторону. Это позволяет использовать таблицу
Приложения 4 для нахождения площадей, соответствующих от-
рицательным отклонениям от средней. По этой таблице можно
определить вероятность попадания значений стандартной нор-
мальной величины в промежуток (0; Z).
Пример 7.6. Пусть требуется определить вероятность, что стан-
дартная нормально распределенная случайная величина при-
мет значение в интервале между —1,5 и 1,62, т. е. вычислить
/X~1,5<Z<1,62). Это означает, что необходимо вычислить пло-
щадь под кривой распределения, ограниченную интервалом
(-1,5; 1,62). Эта площадь заштрихована на рис. 7.15.
-1.5 0 1,62
Рис. 7.15. Заштрихованная площадь соответствует вероятности
P(-1,5<Z<1.S2)
Искомую площадь можно представить в виде двух частей
(различная штриховка на рис. 7.15). Одна площадь ограничена
интервалом (-1,5; 0), а другая — интервалом (0; 1,62). Соответ-
ственно вероятность f\-\,5<Z<\,62) является суммой вероят-
ностей Р(— 1,5<Z<0) и /XO<Z<1,62). Вероятность P(0<Z<l,62)
определяется по таблице Приложения 4. Для этого в колонке Z
находится строка, соответствующая значению 1,62. Затем на
пересечении этой строки с колонкой 0,02 находится значение
искомой площади 0,4474. Как видно из таблицы, значение Z
должно указываться с точностью не более двух знаков после
запятой (колонка Z задает точность до первого знака после
запятой, остальные колонки уточняют значение Z до второго
знака).
Дтя того чтобы найти площадь, соответствующую интервалу
(—1,5; 0), т. е. отрицательному отклонению от средней ц = 0, сле-
дует учесть свойство симметричности кривой нормального рас-
158
пределения. Очевидно, искомая площадь будет соответствовать
площади, ограниченной интервалом (0; 1,5), в правой половине
кривой. Она находится по таблице для Z = 1,5 и равна 0,4332.
Искомая вероятность вычисляется как сумма: 0,4474 + 0,4332 =
= 0,8806.
Таким образом, вероятность события, что случайная вели-
чина, распределенная по стандартному нормальному закону,
примет значение в границах от -1,5 до 1,62, равна 0,8806.
Пример 7.7. Для стандартного нормального распределения зре-
буется вычислить вероятности: a) AZ>1,82); б) /\Z<-0,78);
в) Л 1,73<Z< 1,96).
а) Вероятности P(Z>1,82) соответствует площадь, ограни-
ченная бесконечным интервалом (1,82; +~). Из рис. 7.16 видно,
что величину этой плошали можно получить, если вычесть из
половины площади, всей кривой (т. е. из 0,5) значение площа-
ди, ограниченной интервалом (0; 1,82). Площадь между 0 и 1,82
вычисляется по таблице Приложения 4. Она соответствует значе-
нию Z— 1,82 и равна 0,4656. Отсюда AZ>1,82) = 0,5 - 0,4656 =
= 0,0344.
б) Ввиду симметрии кривой распределения вместо площа-
ди, ограниченной интервалом (-«>; -0,78) (рис. 7.16), можно
рассматривать площадь под интервалом (0,78; +<»). Тогда по ана-
логии со случаем а имеем p(Z<—0,78) = 0,5 — P(0<Z<0,78)=
= 0,5 - 0,2823 = 0,2177.
в) Искомая площадь ограничена интервалом 1,73<Z<1,96.
По таблице можно вычислить площади под интервалами
(0; 1,73) и (0; 1,96). Из рис. 7.16 видно, что искомая площадь
представляется как разность этих площадей, что соответствует
разности вероятностей:
P(0,73<Z<l,96) = 7XO<Z<1,96) - fl(0<Z<l,73) =
= 0,475 - 0,4582 = 0,0168.
а
Рис. 7.16. Заштрихованные площади соответствуют вероятностям:
a) ₽(Z>1,82); б) Я(2<0.78). в) Pf1,73<Z<1.96)
159
Используя преобразование (7.15) и данные таблицы пло-
щадей под кривой стандартного нормального распределения
(Приложение 4), можно по аналогии с примерами 7.5 и 7.6
вычислять необходимые вероятности для произвольного нор-
мального распределения.
Пример 7.8. Вернемся к примеру 7.5 и вычислим вероятность
(7.14). Для этой цели границы интервала (300; 360) в распреде-
лении с параметрами ц = 400 и о = 50 переведем с помощью
преобразования (7.15) в соответствующие границы для стан-
дартного нормального распределения:
_ _ 300 - 400 _
Zi —--------— ”2,
1 50
„ _ 360 - 400 ___
4S-) —------ — ~U,O.
2 50
Отсюда получаем, что площадь ограниченная интервалом
(300; 360) для исследуемого распределения, будет эквивалент-
на площади, ограниченной интервалом (—2; -0,8) для стан-
дартного нормального распределения. В свою очередь эта пло-
щадь будет равна площади, ограниченной отрезком между 0,8
и 2 для правой половины кривой стандартного нормального
распределения (рис. 7.17).
Рис. 7.17. Геометрическое представление эквивалентных площадей:
а) Р(300<2<360); б) P[-2<Z<-0,6). •) P(0.8<Z<2)
Вероятность P(0,8<Z<2) вычисляется как разность площа-
дей:
Л0,8<7<2) = Л0<7<2) - fl(0<Z<0,8) =
= 0,4772 - 0,288 = 0,1892.
Вычисленную вероятность можно интерпретировать следу-
ющим образом: 18,9% всех лампочек имеют срок службы, за-
ключенный в пределах от 300 до 360 ч.
160
Пример 7.9. Средний месячный доход большой группы менед-
жеров составляет ц = 1000 долл, со стандартным отклонением
о = 100 долл. Какова доля менеджеров, имеющих доход в пре-
делах от 840 до 1200 долл.?
Для решения задачи необходимо вычислить вероятность
Я(840<Л’<1200), где X — случайная величина, распределенная
по нормальному закону с параметрами ц = 1000 и о = 100.
Найдем границы интервала для стандартного нормального рас-
пределения, который соответствует интервалу (840; 1200). Най-
дем точку Z, в которую перейдет точка х в 840 в результате
преобразования (7.15):
, 840-1000 -160
1 100 100
Аналогично определим точку Zr соответствующую х = 1200:
1200-1000
Z.’X “ — L.
2 100
Площади, соответствующие обоим распределениям, за-
штрихованы на рис. 7.18.
1000 1200
Рис. 7.18. Геометрическая интерпретация эквивалентных площадей:
а) P(840<Z< 1200). б) Р(-1.6<2<2)
Из рис. 7.186 видно, что искомую площадь можно рассмат-
ривать как сумму двух площадей (вероятностей): P[-\,6<Z<2)
= = A-1.6<Z<0) + P(0<Z<2).
Из симметрии кривой распределения относительно ц = О
следует
a-i.6<z<o) = ao<z<i,6).
Вероятности P(O<Z<1,6) и A(0<Z<2) находятся по таблице
Приложения 4: P(0<Z< 1,6) = 0,4452 (соответствует значению
Z = 1,6), P(0<Z<2) = 0,4772 (соответствует значению Z = 2).
Суммируя две площади, получим P(-1,6<Z<2) =
= P(840<Z<1200) = = 0,4452 + 0,4772 = 0,9224.
Итак, вероятность случайным образом выбрать менеджера,
имеющего месячный доход от 840 до 1200 долл., равна 0,9224.
Это означает, что 92,24% всех менеджеров имеют доходы в ука-
занных пределах.
звз
В примерах 7.7—7.9 рассматривались ситуации, которые сво-
дились к нахождению доли площади (вероятности), соответству-
ющей событию, что случайная величина X примет значение,
большее (или меньшее), чем некоторая заданная величина х.
В содержательном смысле это означает, что требовалось най-
ти, какой процент всех наблюдаемых значений превышает (или
меньше) определенную величину х.
Рассмотрим теперь в некотором смысле обратную задачу.
Пусть требуется определить такое значение х, правее (или ле-
вее) которого располагается заданный процент всех значений.
В терминах вероятности проблему можно сформулировать так:
найти такое значение х, что нормально распределенная слу-
чайная величина X примет значение Х>х (или Х<х) с заданной
вероятностью р\
f\X>x) = р (Р(Х<х) = />).
Геометрически это означает, что на оси абсцисс требуется
найти такую точку х, которая отделяла бы заданную долю пло-
щади под кривой распределения.
Пример 7.10. Фирма производит автомобильные шины нового
типа. Специальное тестирование показало, что средний пробег
шины до ее износа равен 47 900 км при стандартном отклоне-
нии 2050 км. Руководству фирмы необходимо оценить величи-
ну гарантийного пробега при условии, что при этом пробеге
будет заменено не более 5% всех используемых шин. Геометри-
ческая иллюстрация данной проблемы представлена на рис. 7.19.
Точках характеризует искомый гарантийный пробег. Она отсе-
кает заштрихованный “хвост” распределения, площадь кото-
рого составляет 5% всей площади кривой.
х = ? 47 900
Рис. 7.19. Геометрическая интерпретация решения:
х — искомый гарантийный пробег шины (км)
Если площадь заштрихованного “хвоста" равна 0,05, то пло-
щадь, ограниченная интервалом (х; 47 900), очевидно, будет
0,5 - 0,05 = 0,45. Следовательно, задача сводится к нахожде-
нию такого отрицательного отклонения от ц, которое ограни-
162
чивало бы площадь, равную 0,45. Запишем преобразование
(7.15) для искомой величины х:
х-47900
2050
(7.17)
В равенстве (7.17) две неизвестные величины — Z и х. По
условию доля площади, ограниченной интервалом (Z; 0), рав-
на 0,45. В таблице Приложения 4 найдем значение, ближайшее
к 0,45. Как видно из таблицы, существуют два ближайших зна-
чения, равноотстоящих от 0,45: 0,4505 и 0,4495. Им соответ-
ствуют значения Z: 1,65 и 1,64. Возьмем среднее значение меж-
ду ними: 1,645. Так как Zнаходится в левой половине кривой,
то на самом деле Z= —1,645. Подставляя Z = -1,645 в (7.17),
получим уравнение относительно х
-1,645 =
х-47900
2050
Отсюда
-1,645 • 2050 = х - 47900,
х = 44 528 км.
Полученный результат имеет следующую содержательную ин-
терпретацию. Пусть фирма утверждает, что гарантийный пробег
шин нового типа равен 44 528 км. В этом случае можно ожидать,
что только 5% всех шин, находящихся в эксплуатации, будет
заменено еще до окончания гарангийного пробега.
7.3.4. Нормальное распределение как замена
биномиального распределения
Нормальное распределение иногда можно использовать в ка-
честве биномиального. Основная проблема, которая при этом
возникает, заключается в том, что дискретное биномиальное
распределение должно заменяться непрерывным нормальным
законом распределения. Эта проблема легко решается с помо-
щью корректирующей величины, которая называется поправ-
кой на непрерывность. Смысл этой поправки поясним на сле-
дующем примере.
Пусть монета подбрасывается 10 раз (число опытов п = 10).
Требуется вычислить вероятность того, что герб в этом случае
выпадет 5, 6, 7 или 8 раз. Вероятность “успеха” (выпадение
герба) в каждом опыте р = 0,5, а вероятность “неудачи” (выпа-
дение цифры) q = 1 - р = 0,5. Отсюда получаем, что рас-
163
сматриваемая случайная величина будет иметь параметры
ц = пр = 10 0,5 =5, о = Jnpq = -./100,5 • 0,5 = Л/2Л = 1,58.
Рассмотрим случайную величину, распределенную по нор-
мальному закону, но имеющую те же параметры: ц. = 5, ст = 1,58.
Построим графики обеих случайных величин и совместим их на
одной координатной плоскости (рис. 7.20). График биномиаль-
ной случайной величины строится как гистограмма, в которой
столбики симметричны относительно целых значений 0, 1,2,
.... 10. Ширина каждого столбика равна I, а высота — соответ-
ствующей биномиальной вероятности. Гистограмма сглаживает-
ся кривой нормального распределения
Рис. 7.20. Графики биномиального и нормального распределений
с параметрами ц = 5, о = 1.58
Построенная гистограмма обладает следующими свойства-
ми: площадь каждого столбика равна соответствующей бино-
миальной вероятности, а ее общая площадь — I.
Например, вероятность события, что из I0 бросаний монеты
герб выпадет ровно 5 раз, равна площади столбика, имеющего в
качестве основания интервал от 5 -0,5 до 5 +0,5 (заштрихован-
ная полоска на рис. 7.20). Величина 0,5 характеризует поправку
на непрерывность. Она прибавляется к 5 и вычитается из 5. Ис-
пользуя таблицу вероятностей для биномиального распределе-
ния (Приложение 2), вычислим вероятность суммы событий:
Лх = 5) + Р(х = 6)+Лх = 7) + Лх = 8) =
= 0,2461 + 0,2051 + 0,1172 + 0,0439 = 0,6123.
Вычисленная вероятность равна сумме площадей соответ-
ствующих столбцов гистограммы биномиального распределе-
ния. Как видно из рис. 7.20, она приблизительно соответствует
164
плошали под кривой нормального распределения, ограничен-
ной интервалом (4,5; 8,5). Найдем значение этой площади, ис-
пользуя преобразование (7.15). Вычислим:
Z, = ^—- = -0,32;
1,58
=8^ = 2,21.
2 1,58
Z
Ввиду симметрии площадь, ограниченная интервалом
(-0,32; 0), равна площади, ограниченной интервалом (0; 0,32).
По таблице Приложения 4 площади для Z= 0,32 и Z = 2,21
будут равны соответственно 0,1255 и 0,4864. Суммируя, полу-
чаем 0,1255 + 0,4864 = 0,6119.
Сравнивая значения 0,6123 и 0,6119, видим, что ошибка
аппроксимации меньше, чем 0,1%.
В общем случае наиболее благоприятные условия замены
биномиального распределения нормальным имеют место тог-
да, когда число опытов п сравнительно велико, а генеральная
доля р не слишком велика и не слишком мала. Для практичес-
ких расчетов достаточно, чтобы выполнялись условия: лр>5 и
л(1 - р)>5. В этом случае сглаживающая кривая графика бино-
миального распределения будет близка к нормальной кривой.
Пусть X — биномиальная случайная величина, которая ха-
рактеризуется числом опытов п и вероятностью “успеха” р. Тогда
правила использования поправки на непрерывность можно за-
писать в следующем виде:
1) Р(Х <b)= Р (Z<('b +0,5)-~^);
ст
2) Р(Х >a) = P(Z>^0,5^); (7.18)
п
3) Р(а<Х <b)-P(^^^^<Z<---°'5)-M).
ст ст
где ц = пр\
о = %/пр(1-р);
Z — случайная величина, распределенная по нормально-
му закону.
Пример 7.11. Администрация сети ресторанов национальной
кухни провела социологический опрос посетителей. В результа-
те было выяснено, что обычно 70% новых посетителей повто-
165
ряют свой визит. Пусть в течение некоторой недели было отме-
чено, что 80 человек посетили рестораны в первый раз. Какова
вероятность, что по крайней мере 60 из них посетят ресторан
еще раз?
Для вычисления искомой вероятности требуется вычислить
и сложить биномиальные вероятности:
С^ОЛ.З2" + С“О,761О,3*’ +... + С,® О,78оО,3°.
Очевидно, в данном случае имеет смысл заменить биноми-
альное распределение нормальным, поскольку выполняются
все условия:
пр = 80 0,7 = 56>5; л(1 - р) = 80 0,3 = 24>5.
Найдем параметры аппроксимирующего нормального рас-
пределения:
ц = пр = 800,7 = 56;
о = - р) = -у'80 • 6,7-03 = <16,8 = 4.1.
Для замены биномиального распределения нормальным вос-
пользуемся правилом 2 из списка правил (7.18). Вычислим:
„ (я-0,5)-ц (60-0,5)-56 _ 59,5-56 ЛО<
о 4,1 4.1
По таблице Приложения 4 найдем долю ллощаци под кри-
вой стандартного нормального распределения, ограниченную
отрезком между 0 и 0,85. Она равна 0,3023. Вычтем эту величи-
ну из 0,5: 0,5 - 0,3023 = 0,1977.
Следовательно, вероятность того, что 60 или более человек
из 80 новых посетителей посетят еще раз ресторан националь-
ной кухни, равна 0,1977.
7.4. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Экспоненциальное показательное распределение использу-
ется в различных приложениях статистического анализа, на-
пример при оценке времени между заказами на телефонной
линии, между прибытиями транспорта и т. п., а также при ана-
лизе сроков службы компонент, составляющих некоторый аг-
регат. В разделе 6.6 рассматривалось распределение Пуассона,
которое часто используется для характеристики числа поступ-
166
лений каких-либо заказов или прибытий (числа появления “ус-
пехов”) каких-либо объектов в течение определенного перио-
да времени. Если случайная величина ^представляет собой число
появлений “успеха” в течение периода Т и распределена по
закону Пуассона, то случайная величина X, характеризующая
промежутки времени между двумя последовательными “успе-
хами”, будет иметь экспоненциальное распределение. Экспо-
ненциальная случайная величина имеет много приложений при
моделировании ситуаций, описывающих процесс ожидания
людей или объектов, стоящих в очереди на различного рода
обслуживание. Случайная величина, распределенная по экспо-
ненциальному закону, имеет кривую графика экспоненциаль-
ной функции
/(х) = Ае-Ах, (7.19)
где А — константа.
Вид кривой распределения типа (7.19) представлен на рис.
7.21. Можно доказать, что общая площадь, ограниченная этой
кривой, равна 1: +<ю
A je-x,dr = l.
о
Рис. 7.21. Кривая экспоненциального распределения
При увеличении текущей переменной х вероятность собы-
тия, что значение экспоненциальной случайной величины бу-
дет не меньше х, убывает по экспоненциальному закону. Пусть
х = х0, тогда можно показать, что
Р(х>х0) = А = (7.20)
167
Геометрической интерпретацией вероятности (7.20) явля-
ется площадь, ограниченная кривой распределения и интерва-
лом х 2 х0 (рис. 7.22).
*□ а
Рис. 7.22. Геометрическая интерпретация вероятности Р(ж i
Параметр А имеет следующую содержательную интерпрета-
цию. Пусть рассматривается пуассоновская случайная величина
с параметром А, т. е. А соответствует среднему числу появлений
“успехов” за единицу времени. Рассмотрим соответствующую
экспоненциальную случайную величину, характеризующую зна-
чения промежутков времени между последовательными “успе-
хами”. Тогда величина 1/А будет представлять собой среднее время
между появлениями двух последовательных “успехов".
В общем случае можно показать, что значение 1/А является
математическим ожиданием экспоненциальной случайной ве-
личины, которая равна также ее стандартному отклонению:
ц = A Jxe’^dx»-, (7.21)
о
В практических ситуациях, где используется экспоненциаль-
ное распределение, значение параметра А либо известно, либо
каким-то образом определяется.
Пример 7.12. Владелец крупного косметического салона счита-
ет, что наибольшую прибыль он получает в случае обслужива-
ния клиентов, посещающих салон произвольным образом, а
не делающих заказ на обслуживание заранее. Из прошлого опыта
известно, что среднее число клиентов, которые обслуживались
в течение часа, составляет А = 4.
168
Требуется определить:
I) если в салон вошел клиент, то какова вероятность, что
следующий клиент придет в течение 30 мин?
2) если ^обозначает время между появлениями двух клиен-
тов, которые придут один за другим, то каково будет матема-
тическое ожидание и стандартное отклонение случайной вели-
чины А?
Для решения задачи 1 следует промежуток времени 30 мин
исчислять как 0,5 ч, так как размерность А — 4 ед. за час. Тогда
искомая вероятность есть Р(х<0,5). Исходя из (7.20), получим
Р(х > 0,5) = е’4Д5=е~2 = 0,135.
Очевидно,
Р(х < 0,5) = 1 - Р(х г 0,5) = 1 -0,135 = 0,865.
Следовательно, вероятность, что в течение 30 мин после
прихода первого клиента салон посетит второй клиент, равна
0,865. Иначе говоря, 86,5% всего времени работы салона про-
межутки между приходами клиентов не превышают 30 мин. Ре-
шение задачи 2 получим на основе соотношений (7.21):
11
И = о = — = - ч (т. е. 15 мин).
А 4
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 7
Рассматриваются характеристики, свойства и основные за-
коны распределений непрерывных случайных величин. Возмож-
ные значения непрерывной случайной величины непрерывно
заполняют некоторый промежуток и не могут быть перечисле-
ны заранее как в случае дискретных случайных величин. Поэто-
му для характеристики распределения вероятностей непрерыв-
ной случайной величины пользуются не вероятностью события
X = х, а вероятностью события Х<х, где х — некоторая теку-
щая переменная. Вероятность, что Х<х, зависит от текущей
переменной х и является некоторой функцией от х. Эта функ-
ция называется функцией распределения непрерывной случай-
ной величины X. Ее также называют интегральной функцией
распределения или интегральным законом распределения. Функ-
ция распределения является универсальной характеристикой
как для непрерывных, гак и для дискретных случайных вели-
169
чин. С вероятностной точки зрения функция распределения пол-
ностью характеризует случайную величину, т. е. является одной
из форм закона распределения. График функции распределе-
ния непрерывной случайной величины есть плавная кривая,
имеющая касательную в любой точке. Ее значения лежат в ин-
тервале от 0 до 1.
В практических задачах иногда встречаются непрерывные
случайные величины, распределенные по закону равномерной
плотности. Такие величины еще называются равномерно рас-
пределенными. Для равномерно распределенной случайной ве-
личины имеются определенные границы, внутри которых все
значения равновероятны, т. е. плотность распределения являет-
ся постоянной величиной на всем промежутке изменения слу-
чайной величины.
Исключительно важную роль играет в статистическом ана-
лизе нормальный закон распределения. Сумма достаточно боль-
шого числа независимых (или слабо зависимых) случайных
величин распределена почти по нормальному закону, причем
слагаемые случайные величины могут подчиняться каким угодно
законам распределения. Это свойство широко реализуется на
практике, так как большинство массовых явлений формирует-
ся как наложение многих отдельных факторов (причин).
Нормальный закон распределения характеризуется плотно-
стью вероятности, имеющей вид (7.12). Существует бесконеч-
ное семейство нормальных распределений, каждое из которых
задается двумя параметрами — математическим ожиданием ц и
стандартным отклонением а. Кривая нормального распределе-
ния имеет симметричную относительно ц колоколообразную
форму. Значением ц определяется положение кривой распреде-
ления, а величиной о — форма этой кривой. Чем больше р, тем
больше кривая распределения смещена вправо по оси абсцисс.
С увеличением о кривая растягивается вдоль оси абсцисс, а
при уменьшении — сжимается и вытягивается вверх вдоль оси
ординат.
Независимо от значений параметров ц и о для всех нор-
мальных кривых сохраняются единые пропорции для площа-
дей, ограниченных этими кривыми и определенными интерва-
лами на оси абсцисс. Так, вся площадь между любой нормаль-
ной кривой и осью абсцисс будет равна I, а площади, ограни-
ченные промежутками ц±го(г>0), будут одинаковыми для всех
кривых при фиксированном г. Эти свойства площадей можно
использовать для вычисления вероятностей попадания значе-
ния случайной величины X, распределенной по нормальному
170
закону, на заданный промежуток (а, р). Для этой цели любой
нормальный закон можно стандартизировать с помощью пре-
образования (7.15). При этом переменная х переходит в пере-
менную Z, а исходное нормальное распределение с любыми
параметрами ц и о преобразуется в стандартное нормальное
распределение с параметрами ц = 0, о = 1. Используя симмет-
рию кривой нормального распределения и свойства площадей
под нормальными кривыми, можно с помощью преобразова-
ния (7.15) необходимую площадь под любой нормальной кри-
вой перевести в соответствующую площадь под кривой стан-
дартного нормального закона распределения. Для него рассчи-
тана таблица специальных площадей, ограниченных кривой
стандартного распределения и интервалом между ц и Z, где
Z>0.
Учитывая симметрию кривой стандартного нормального
распределения и рассматривая любую площадь как алгебраи-
ческую сумму площадей, ограниченных интервалом (0; Z), по
таблице Приложения 4 можно найти искомую площадь.
При определенных условиях нормальное распределение ис-
пользуется в качестве биномиального распределения в случае,
если расчет биномиальных вероятностей затруднен. Основная
проблема, которая здесь возникает, заключается в том, что
дискретное биномиальное распределение заменяется непрерыв-
ным нормальным законом распределения. Поэтому при замене
вводится специальная корректировочная величина, которая
называется “поправкой на непрерывность”. Правила использо-
вания этой поправки задаются соотношениями (7.18).
В различных прикладных задачах, связанных с ситуациями,
когда люди или объекты образуют очередь на какое-либо об-
служивание, а также когда требуется оценить время между при-
бытиями транспорта или сроки службы компонентов, состав-
ляющих некоторый агрегат, используется экспоненциальное
распределение. Случайная величина, распределенная по экс-
поненциальному закону, имеет кривую плотности, которая
является графиком экспоненциальной функции. Вид этой функ-
ции задается уравнением (7.19).
ОЦЕНКА ПАРАМЕТРОВ
8.1. ТОЧЕЧНЫЕ ОЦЕНКИ
Проблема оценки является особенно актуальной в приклад-
ном статистическом анализе, связанном с принятием реше-
ний в бизнесе, экономике и других сферах общественной дея-
тельности. Например, производители не знают точно, сколько
новых товаров они продадут в будущем году; администрация
учебного заведения точно не знает, сколько студентов посту-
пят на первый курс в новом учебном году, и т. д.
Существуют два типа оценок — точечные и интервальные.
Рассмотрим вначале точечный тип оценок. Под точечной оцен-
кой понимается отдельное число (называемое точкой), кото-
рое используется в качестве оценки параметра генеральной
совокупности. Например, выборочная средняя х, вычисленная
по формуле (3.1), есть точечная оценка средней генеральной
совокупности ц, а выборочная дисперсия з2 и стандартное от-
клонение з, вычисленные соответственно по формулам (4.8) и
(4.10), являются точечными оценками параметров а2 и а.
Пример 8.1. Для определения емкости автомобильных аккуму-
ляторов нового типа было проведено специальное исследова-
ние. Оно заключалось в запуске двигателя до тех пор, пока те-
стируемый аккумулятор не садился. Такое исследование было
проведено для выборки, состоящей из 40 случайным образом
выбранных аккумуляторов. Результатами были следующие ко-
личества запусков:
26 27 26 20 21 42 30 22 22 21 26 9 21 22 28 26
19 16 20 32 18 23 32 26 21 41 19 31 21 22 16 23
30 21 37 28 39 30 21 23
Данные 40 аккумуляторов были выбраны из очень большой
партии, которую теоретически можно рассматривать как бес-
конечную генеральную совокупность.
172
Точечная оценка для средней арифметической такова:
х= (26 + 27 + 26 + ... + 23)/40 = 1000/40 = 25 запусков.
Точечные оценки для дисперсии и стандартного отклоне-
ния:
? = [(26 - 25)2 + (27 - 25)2 +...+ (23 - 25)21/39 =
= 2031/39 = 52,077,
5 = 752.077 = 7,216.
8.1.1. Критерии качества точечных оценок
Различные статистики могут служить оценками истинных па-
раметров генеральной совокупности. Чтобы оценить их качество,
в статистическом анализе рассматриваются четыре критерия.
1. Несмещенность. Пусть из данной генеральной совокупнос-
ти извлекается большое количество выборок. На основе значе-
ний каждой из них рассчитывается точечное значение оценки
параметра генеральной совокупности (т. е. статистики). При этом
статистика называется несмещенной, если все выборочные
значения располагаются симметрично относительно истинно-
го значения оцениваемого параметра. В этом случае математи-
ческое ожидание распределения статистики будет равно ис-
тинному значению параметра. Далее будет показано, что такая
картина наблюдается для распределения выборочных средних,
которое является нормальным (т. е. симметричным), а матема-
тическое ожидание распределения выборочных средних равно
математическому ожиданию генеральной совокупности (т. е. ге-
неральной средней).
2. Эффективность. Будем рассматривать дисперсию как сред-
ний квадрат отклонения или ошибки выборочной средней. Тог-
да стандартное отклонение можно рассматривать как ее стан-
дартную ошибку. Вместо выборочной средней в формулу
дисперсии или стандартного отклонения подставим любую дру-
гую статистику (например, медиану). Стандартное отклонение,
вычисленное относительно этой статистики, будем называть стан-
дартной ошибкой статистики. Критерий эффективности харак-
теризует минимальность стандартной ошибки статистики, ис-
пользуемой в качестве точечной оценки параметра генеральной
совокупности. Иначе говоря, стандартная ошибка эффективной
оценочной статистики должна быть меньше стандартной ошиб-
ки любой другой статистики, выбираемой в качестве точечной
173
оценки. Например, в разделе 4.13 отмечалось, что дисперсия и
стандартное отклонение обладают свойствами минимальности
относительно средней арифметической. Поэтому выборочная
средняя будет эффективной оценкой генеральной средней.
3. Состоятельность. Говорят, что оценка истинного значения
параметра является состоятельной, если по мере увеличения
объема выборки ее значение приближается к истинному значе-
нию параметра. Например, состоятельной оценкой является вы-
борочная средняя.
4. Достаточность. Оценка является достаточной, если при ее
вычислении используется вся содержащаяся в выборке инфор-
мация. Иначе говоря, для вычисления любой другой оценки
нельзя будет извлечь из выборки дополнительную информа-
цию об истинном значении оцениваемого параметра.
Выборочная средняя является наилучшей оценкой генераль-
ной средней. Она удовлетворяет всем четырем критериям.
Критерии качества оценок могут служить не только для вы-
бора, но и для улучшения оценок. Пример тому формула (4.8)
для вычисления выборочной дисперсии, в которой для кор-
ректировки смещенности выборочных дисперсий (заниженно-
сти) в знаменателе величина п заменяется нал - 1.
Следует отметить, что лучшими оценками для параметров
генеральной совокупности соответствующие статистики быва-
ют не всегда. Рассмотрим, например, генеральную совокуп-
ность, имеющую симметричное распределение. В этом случае
средняя арифметическая и медиана совпадают. Возьмем в каче-
стве оценок медианы выборочную медиану и выборочную сред-
нюю. Обе эти оценки будут несмещенными и состоятельными
оценками медианы. Однако ввиду свойства минимальности стан-
дартной ошибки средней арифметической выборочная сред-
няя будет более эффективной оценкой медианы.
8.2. РАСПРЕДЕЛЕНИЕ ВЫБОРОЧНЫХ СРЕДНИХ.
ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
Реализация выборочного метода, т. е. получения статисти-
ческого заключения относительно характеристик и свойств всей
генеральной совокупности на основе выборочных значений,
обязательно предполагает простой случайный отбор. Предпо-
ложим, что условие формирования простой случайной выбор-
ки будет всегда выполняться. Нас в этом случае интересует связь
между некоторой выборочной характеристикой (статистикой)
и определенным параметром всей совокупности. Маловероят-
174
но, что значение статистики точно совпадает со значением па-
раметра. Разность между этими величинами будем называть
ошибкой выборки.
Пример 8.2. Генеральная совокупность состоит из 5 работников.
Эффективность их работы была оценена с помощью некоторо-
го теста. Результаты теста были представлены в специальной
балльной шкале: 97, 103, 96, 99, 105. Вычислим средний балл
для всей совокупности (генеральную среднюю):
И = (97 + 103 + 96 + 99 + 1О5)/5 = 500/5 = 100.
Рассмотрим две выборки, состоящие из двух значений каж-
дая: 97, 105 и 103, 96. Вычислим для каждой из-них значение
среднего балла (статистики): xf = (97 + 105)/2 = 101,х2 = (103 +
+ 96)/2 = 99,5. В первом случае ошибка выборки будет х - р -
= 101 — 100 = 1, а во втором — xj — д = 99,5 - 100 = -0,5.
Каждая из разностей (1 и -0,5) является ошибкой, или погреш-
ностью, которая будет допущена, если в качестве оценочного
значения генеральной средней взять соответствующую выбороч-
ную среднюю (т. е. точечную оценку генеральной средней).
Возникает проблема, как на основе выборки дать макси-
мально точную оценку генеральной средней. Для этой цели
рассмотрим выборочное распределение этой статистики или
распределение выборочных средних. Зафиксируем объем вы-
борки и возьмем из исследуемой генеральной совокупности
все возможные выборки данного объема. Затем для каждой из
этих выборок вычислим среднюю и составим распределение
частот, т. е. дисретный ряд распределения. Далее полученное
распределение будем анализировать как распределение выбо-
рочных средних. '
Пример 8.3. Семь работников фирмы (генеральная совокуп-
ность) имеют следующие почасовые ставки:
№ работников Почасовые ставки (долл.)
1 7
2 9
3 8
4 8
5 7
6 8
7 9
175
Требуется определить генеральную среднюю, построить рас-
пределения выборочных средних и генеральной совокупности.
Провести сравнительный анализ этих распределений.
Вычислим среднюю почасовую ставку для генеральной со-
вокупности:
ц = (7+ 9 + 8 + 8 + 74-8 + 9)/7 = 8 долл.
Чтобы построить распределение выборочных средних, рас-
смотрим все возможные выборки, состоящие из четырех чело-
век, из семи данных работников. Очевидно, количество таких
выборок определяется числом сочетаний из 7 элементов по 4:
С* - 7!/(4!-3!) = 35. Все они вместе с выборочными средними
представлены'втабл. 8.1.
Таблица 8.1
Выборки объема л = 4 из совокупности объема N = 7
и выборочные средние
№ работников в выборке Почасовые ставки, долл. Выборочные средние, долл.
1 2 3
1234 7. 9, В. 8 32/4 = 8
1235 7. 9. 8. 7 31/4 7,75
1236 7, 9, 8. 8 32/4 = 8
1237 7, 9, 8, 9 33/4 8,25
1245 7. 9. 8, 7 31/4 = 7,75
1246 7, 9. 8, 8 32/4 = 8
1247 7, 9, 8, 9 33/4 = 8,25
1256 7. 9, 7, 8 31/4 = 7,75
1257 7, 9, 7, 9 32/4 8
1267 7. 9, 8. 9 33/4 = 8,25
134 5 7. 8, 8, 7 30/4 = 7.5
1346 7, 8. 8. 8 31/4 = 7,75
1347 7, 8, 8. 9 32/4 = 8
1356 7, 8. 7, 8 30/4 = 7,5
13 57 7, 8, 7, 9 31/4 = 7,75
1367 7. 8. 8, 9 32/4 8
14 56 7, 8, 7, 8 30/4 = 7,5
1 457 7. 8, 7, 9 31/4 = 7,75
1467 7. 8, 8. 9 32/4 = 8
1567 7. 7, 8. 9 31/4 = 7,75
2345 9, 8. 8. 7 32/4 - 8
2347 9, 8. 8. 8 33/4 = 8.25
176
Окончание табл в 1
1 2 3
2356 9. 8. 8, 9 34/4 = 8,5
2357 9. 8. 7, 8 32/4 = 8
2367 9, 8. 8, 9 34/4 = 8.5
2436 9. 8. 8. 8 33/4 = 8,25
24 56 9, 8. 8, 9 34/4 8.5
24 57 9, 8, 7, 8 32/4 = 8
2467 9, 8. 7, 9 33/4 = 8.25
2567 9, 7. 8, 9 33 /4 = 8.25
34 56 8, 8. 7, 8 31/4 = 7.75
3457 8, 8, 7, 9 32/4 = 8
3467 8. 8. 8. 9 33/4 = 8,25
3567 8. 7, 8, 9 32/4 8
4 567 8, 7, 8, 9 32/4 = 8
Вычислим среднюю распределения выборочных средних,
приведенного в табл. 8.1, как сумму всех выборочных средних,
деленную на общее число выборок:
ц. = (8 + 7,75 + ... + 8)/35 = 280/35 = 8 долл.,
где обозначает среднюю распределения выборочных сред-
них.
Подсчитаем частоты и частости (вероятности) возможных
отдельных значений выборочных средних и результаты пред-
ставим в виде дискретного ряда распределения — распределе-
ния выборочных средних (табл. 8.2).
Таблица 8.2
Распределение выборочных средних
(объем выборок л = 4; объем генеральной совокупности N = 7)
Выборочные средние, долл. Частота Вероятность
7.5 3 3/35 = 0.0857
7.75 8 8/35 = 0.2286
8 13 13/35 0,3714
8.25 8 8/35 = 0,2286
8,5 3 3/35 = 0.0857
35 35/35 = 1
Из табл. 8.2 видно, что распределение выборочных средних
отражает, по существу, закон распределения некоторой диск-
ретной случайной величины.
177
Запишем теперь частотное распределение первичных дан-
ных о почасовых ставках, т. е. распределение генеральной сово-
купности (табл. 8.3).
Таблица 8.3
Распределение генеральной совокупности
Почасовые ставки Частота Вероятность
7 2 2/7 = 0,2857
8 3 3/7 = 0,4286
9 2 2/7 = 0,2857
7 7/7 = 1
Графики распределений, приведенных в табл. 8.2 и 8.3, ука-
заны на рис. 8.1.
Рис. 8.1. Распределение а) генеральной совокупности (объем N = 7);
б) выборочных средних (объем выборок п - 4)
Проведя сравнительный анализ распределений, можно сде-
лать следующие выводы.
1. Средняя генеральной совокупности равна средней выбо-
рочных средних, т. е. р = щ = 8. Это утверждение будет всегда
справедливо в случае, если рассматриваются все возможные
выборки заданного объема, отобранные из данной генераль-
ной совокупности.
178
2. Из рис. 8.1 видно, что разброс данных в распределении
выборочных средних меньше, чем в распределении генераль-
ной совокупности. Так, выборочная средняя варьирует в пре-
делах от 7,5 до 8,5, значения генеральной совокупности — в
пределах от 7 до 9.
3. Графики распределений генеральной совокупности и вы-
борочных средних имеют сходство с нормальным распределе-
нием (если начертить огибающие кривые).
Рассмотрим теперь ситуацию, когда распределение генераль-
ной совокупности значительно отличается от нормального.
Пример 8.4. Пусть стаж работы пяти администраторов фирмы
имеет равномерное распределение:
Администраторы Стаж работы, годы Частота Вероятность
1 20 1 1/5
2 22 1 1/5
3 26 1 1/5
4 24 1 1/5
5 28 1 1/5
Вычислим средний стаж работы: ц = (20 + 22 + 26 + 24 +
+ 28)/5 = 24 года.
Построим распределение выборочных средних при объеме
выборок п = 2. Число таких выборок из 5 администраторов бу-
дет Cj = 5!/(2!-3!) « 10. Состав выборок и выборочные средние
представлены в табл. 8.4.
Таблица 8.4
Выборочные средние для всех выборок (л = 2),
извлеченных из генеральной совокупности (N = 5)
Выборки, состоящие из двух администраторов Стаж работы Выборочные средние
1 2 20. 22 21
1 3 20. 26 23
1 4 20. 24 22
1 5 20. 28 24
23 22. 26 24
24 22, 24 23
25 22. 28 25
34 26. 24 25
3 5 26. 28 27
4 5 24. 28 26
179
Вычислим среднюю выборочных средних:
Mi =(21 + 23 + ... + 26)/10 = 24.
Представим данные табл. 8.4 в виде распределения (табл. 8.5).
Таблица 8.5
Распределение выборочных средних
для совокупности выборок (л - 2)
Выборочные средние Частота Вероятность
21 1 0,1
22 1 0,1
23 2 0.2
24 2 0.2
25 2 0.2
26 1 0.1
27 1 0.1
10 1
Графики распределения генеральной совокупности и выбо-
рочных средних указаны на рис. 8.2.
• б
-Illi 1.1.11111
20 22 24 26 28 21 22 23 24 25 26 27
Рис. 8.2. Распределение а) выборочной совокупности (N = 5),
б) выборочных средних (л = 2)
Как видно из графиков распределений (рис. 8.2), разброс
данных для генеральной совокупности выше, чем для выбо-
рочных средних. В первом случае значения колеблются в грани-
цах от 20 до 28 лет, а во втором — от 21 до 27 лет. Если прове-
сти сглаживающую кривую для графика б, то она будет иметь
сходство с кривой нормального распределения.
В примерах 8.2 и 8.3 размеры генеральной совокупности и вы-
борок были взяты небольшими в целях упрощения вычислений.
Тем не менее отчетливо проявились следующие закономерности.
1. Если генеральная совокупность распределена нормально,
то распределение выборочных средних также будет иметь нор-
мальный закон распределения. В этом можно убедиться, если
нарисовать сглаживающие кривые для почасовых ставок работ-
ников, представленных в примере 8.2 (рис. 8.3).
180
Выборочные средние
почасовых ставок
Ямс. 8.3. Сглаженные распределения генеральной совокупности
(Л/ = 7) и выборочных средних (л = 4)
2. В случае если распределение генеральной совокупности не
является нормальным, распределение выборочных средних все
равно оказывается близким к нормальному. Это видно из гра-
фиков распределений примера 8.4 (рис. 8.2),
Отмеченные закономерности не случайны, так как в дан-
ном случае выполняются условия центральной предельной те-
оремы, если рассматривать повторную выборку объема п как
совокупность п независимых случайных величин, имеющих одно
и то же распределение. Тогда центральная предельная теорема
имеет следующую трактовку.
Для генеральной совокупности со средней ц и дисперсией
ст5 распределение выборочных средних для всех возможных вы-
борок с возвращением объема л, составленных из этой гене-
ральной совокупности, будет нормальным со средней м и
О2 _
дисперсией —. При этом предполагается, что объем выборки
л
л достаточно большой.
Центральная предельная теорема играет исключительную
роль в статистическом анализе, поэтому имеет смысл более
подробно пояснить ее основные положения.
I. Если объем выборки л достаточно велик, то распределе-
ние выборочных средних будет почти нормальным. Данное ут-
верждение будет справедливым независимо от вила распреде-
ления генеральной совокупности, откуда извлекаются выборки.
Например, теорема будет верна, когда генеральная совокуп-
ность имеет нормальное, асимметричное или равномерное рас-
пределение.
2. Из приведенных примеров следует, что средняя генераль-
ной совокупности ц и средняя выборочных средних равны
между собой. Если генеральная совокупность имеет достаточно
181
большой размер и из нее извлечено достаточно большое коли-
чество выборок, то величина средней выборочных средних бу-
дет близка к генеральной средней.
3. Дисперсия распределения выборочных средних определя-
ется по формуле
2 О'
- П
где о2 — генеральная дисперсия;
п — объем выборки.
Величина стандартного отклонения
of=% (8.1)
•уп
называется стандартной ошибкой средней.
Возникает вопрос, какое значение п считать достаточно боль-
шим. В примере 8.2 объем выборок был небольшой (и = 4), тем
не менее распределение выборочных средних оказалось близко
к нормальному. Это произошло ввиду того, что генеральная
совокупность, откуда извлекались выборки, имела распреде-
ление, близкое к нормальному. Чем сильнее распределение ге-
неральной совокупности отличается от нормального, тем боль-
шее влияние оказывает увеличение объема выборки на точность
результата. При статистических заключениях считается, что
использование центральной предельной теоремы дает прием-
лемые результаты, если объем выборки нс меньше 30.
8.3. ИНТЕРВАЛЬНЫЕ ОПЕНКИ
ГЕНЕРАЛЬНОЙ СРЕДНЕЙ
Из распределения выборочных средних табл. 8.2 видно, что
только 37,14% всех значений статистик совпадает с истинным
значением параметра — генеральной средней. В общем случае,
когда рассматривается одна небольшая случайная выборка из боль-
шой по объему генеральной совокупности, полное совпадение
точечной опенки с истинным значением параметра будет мало-
вероятным. На практике большую ценность в статистическом ана-
лизе представляют интервальные оценки, когда определяется
интервал, внутри которого с известной вероятностью находится
истинное значение параметра. Такой интервал называется дове-
рительным интервалом, его границы — доверительными преде-
лами, а связанная с ним вероятность — доверительной вероягно-
стью, измеряющей степень доверия к этому интервалу.
182
8.3.1. Общие принципы построения
доверительных интервалов
Нахождение доверительных пределов для оценки средней
арифметической генеральной совокупности основывается на
центральной предельной теореме и свойствах площадей под
кривой нормального распределения (раздел 7.3.2). Согласно цен-
тральной предельной теореме, при определенных условиях рас-
пределение выборочных средних будет близко к нормальному.
Средняя выборочного распределения совпадает с генеральной
средней ц, откуда извлекаются выборки, а стандартная ошиб-
ка средней определяется по формуле (8.1).
Возьмем значение генеральной средней ц, а затем приба-
вим к нему и отнимем от него величину 1,96вг . Тогда, как
отмечалось в разделе 7.3.2, 95% всей площади под кривой рас-
пределения выборочных средних будет ограничено интервалом
(ц - 1,96в;; ц + 1.96 ). Это означает, что 95% всех значений
выборочных средних лежит в пределах от ц — 1,96д;
до ц + 1,96 ст-. Они являются доверительными пределами, ко-
торые соответствуют доверительной вероятности, равной 95%.
Рассмотрим геометрическую интерпретацию данного факта.
Возьмем несколько выборок, извлеченных из генеральной со-
вокупности, и рассчитаем для них средние значения х. Для каж-
дой выборочной средней построим 95-процентный доверитель-
ный интервал (рис. 8.4).
Рис. 8.4. Построение доверительных интервалов
183
Из рис. 8.4 видно, что интервалы, соответствующие выбор-
кам 1, 2, 3 и 5, содержат значение средней генеральной сово-
купности р, а в интервал для выборки 4 значение ц не попало.
В общем случае верно следующее утверждение. Если взять мно-
го выборок и для каждой из них подобным образом построить
доверительные пределы, то в среднем 95% всех интервалов бу-
дет содержать истинное значение генеральной средней. Напри-
мер, если рассмотреть 1000 выборок, то следует ожидать, что
примерно для 950 из них доверительные интервалы включат
истинное значение параметра.
В практических ситуациях, как правило, возможно получе-
ние данных, соответствующих только одной выборке опреде-
ленного размера. При этом статистические заключения отно-
сительно доверительного интервала для ц делаются на основе
единственной точечной оценки х (выборочной средней) и
а
величины стандартной ошибки средней
В общем виде доверительный интервал, соответствующий
доверительной вероятности 95%, имеет вид
jt ± 1,96
ст
(8.2)
Доверительный интервал (8.2) можно определить в терми-
нах доверительной вероятности:
Я л-1,96 <р<х + 1,96 П-
I -Jn
= 0,95.
Аналогично ставя в соответствие доверительной вероятнос-
ти площадь под кривой нормального распределения, ограни-
ченную интервалом (ц-пз--, ц+ га,) (г > 0), можно постро-
ить интервалы с заданной доверительной вероятностью.
В связи со свойствами площадей, ограниченных кривыми
нормального распределения и интервалами ц ± гст. в качестве
значения г можно рассматривать значение Z для стандартного
нормального распределения. Тогда доли площади будут равны
между собой и, в частности, равны доле площади, заключен-
ной между кривой стандартного нормального распределения
(ц = 0, о = I) и интервалом (-г, г).
Пусть Z
ХВОСТОВОЙ ’
— такое значение Z, справа от которого площадь
части кривой равна а/г. При определении довери-
тельных интервалов величину а называют уровнем доверия или
184
значимости. Доверительная вероятность определяется как
1 — а (или (1 - а) 100%).
Геометрическая интерпретация уровня значимости и дове-
рительной вероятности представлена на рис. 8.5.
Рис. в. 5. Площади под кривой нормального распределения,
соответствующие уровню доверия (значимости) а и доверительной
вероятности (1 - а): а) произвольное нормальное распределение;
б) стандартное нормальное распределение (ц = 0, в = 1)
Значения Z;J для любого а находятся из таблицы Приложе-
ния 4.
Для нахождения доверительных пределов с уровнем значи-
мости а (или доверительной вероятностью I - а) следует ум-
м °
ножить величину Z;, на стандартную ошибку средней -у- и
затем полученный результат вычесть и прибавить к значению
точечной оценки средней (т. е. выборочной средней):
i±Zal2-~. (8.3)
В соответствии с формулой доверительного интервала (8.3)
нижний и верхний доверительные пределы будут ограничивать
интервал
Смысл доверительной вероятности можно представить в виде
соотношения
p(x-Za/2-^<»<i + Za/2 (8.4)
\ л/Л 'Jn )
Кроме доверительных интервалов с вероятностью 0,95 (95%)
в практических задачах часто используются интервальные оцен-
ки с вероятностями 0,9 (90%) и 0,99 (99%).
185
В случае если а = 90%, доверительные пределы определяют-
ся соотношением
х±1,64
(8.5)
При доверительной вероятности 99% оценочный интервал
будет иметь вид
х±2,58 (8.6)
у/п
В терминах доверительной вероятности доверительные ин-
тервалы (8.5) и (8.6) будут соответственно иметь следующую
интерпретацию:
р! л-1,64 -?=<ц<л + 1,64 °
I -ул
п
Р[ х - 2,58 < Ц < X + 2,58-Я=
. -Ул -Ул
= 0,9(90%);
= 0,99(99%).
Очевидно, чем больше доверительная вероятность (степень
уверенности в том, что истинное значение генеральной сред-
ней принадлежит соответствующему доверительному интерва-
лу), тем шире доверительный интервал. Это в свою очередь оз-
начает уменьшение точности оценивания.
В практических приложениях при построении доверитель-
ных интервалов выделяют два случая:
значение стандартного отклонения генеральной совокупно-
сти о известно;
значение о неизвестно.
8.3.1.!. Вычисление доверительных интервалов
при известном генеральном стандартном отклонении
На практике иногда возникают ситуации, когда значение
генеральной средней приходится оценивать много раз подряд.
При этом значение стандартного отклонения генеральной со-
вокупности о может быть вычислено заранее и есть основание
предполагать, что оно не изменяется. Тогда при оценке ц имеет
смысл использовать это известное значение, чтобы не оцени-
вать его заново по каждой новой выборке.
Пусть генеральная совокупность распределена нормально со
средней ц и стандартным отклонением о. Тогда стандартная
186
ошибка средней равна = ~г~ (п ~ объем выборки). По цснт-
-\Г/1
ральной предельной теореме распределение выборочных сред-
них будет нормальным со средней ц и стандартным отклонени-
CI
ем - ~г~ •
•Jn
Необходимым условием выполнения указанных свойств яв-
ляется также неограниченность размера генеральной совокуп-
ности, откуда извлекаются выборки. На практике часто огра-
ниченная, но большая по объему совокупность теоретически
рассматривается как бесконечная. При этом предполагается, что
эта гипотетическая совокупность формируется под постоянным
влиянием тех же факторов, что определяли состав, свойства и
структуру действующей ограниченной совокупности.
Общая формула для построения доверительных пределов в
случае бесконечной генеральной совокупности и известного
значения а имеет вил (8.3), а се частные случаи для довери-
тельных вероятностей 90, 95 и 99% — соответственно вил (8.5),
(8.2) и (8.6). Объем выборки п при этом не оказывает суще-
ственного влияния на адекватность результатов опенки, полу-
ченных на основе данных формул.
Пример 8.5. Компания производит определенный тип электри-
ческих приборов. Ранее были проведены исследования сроков
службы приборов, которые показали, что стандартное откло-
нение ст для большой партии приборов составляет 50 ч. Из про-
изведенной партии была извлечена выборка объемом п = 10
приборов, для которых сроки службы имели следующие значе-
ния, выраженные в часах:
308, 419, 432, 362, 302, 440, 430, 375, 383.
На основе выборочных данных определим доверительные
интервалы для среднего срока службы прибора при вероятнос-
тях 90. 95 и 99%.
Вычислим выборочную среднюю:
х = (308 + 419 + ... + 383)/1О = 384 ч.
Доверительные пределы с вероятностью 90% вычисляются
по формуле (8.5):
384 ± 1,64
50
/10
= 384 ±16 = 368-ь 400.
187
Отсюда с вероятностью 90% можно утверждать, что истин-
ное значение среднего срока службы прибора содержится в
интервале от 368 до 400 ч.
По формуле (8.3) вычисляется интервал с доверительной
вероятностью 95%:
384 ±1,96
50
716
= 384 131 = 353 + 415.
Следовательно, с вероятностью 95% можно быть уверен-
ным, что средний срок службы для всей партии приборов на-
ходится в пределах от 353 до 415 ч.
Определим доверительный интервал, соответствующий ве-
роятности 99% (формула (8.6)):
38412,58 В =384141 = 343 + 425.
^10
Ввиду бесконечности генеральной совокупности можно счи-
тать, что случайные выборки извлекаются из нее по принципу
“с возвращением" (повторная выборка). Однако на практике ча-
сто требуется проводить статистические заключения для огра-
ниченной генеральной совокупности, имеющей заданный обьем
N. В этом случае имеет место отбор элементов в выборку по прин-
ципу “без возвращения элементов в генеральную совокупность”
(бесповторная выборка). Это в свою очередь влияет на величину
стандартной ошибки средней. Она уменьшается и принимает вид
о । N — п
@ г Г Л J ''
* .'п У N-1
(8.7)
V Л N-n
Корректирующий множитель J——- называется поправ-
V N -1
кой на конечность генеральной совокупности. Его включение в
формулу для вычисления стандартной ошибки средней являет-
ся обязательным. Однако если объем выборки п мал по сравне-
нию с размером генеральной совокупности N, значение кор-
ректирующего множителя будет близко к единице и он не
повлияет на стандартную ошибку средней. При расчетах во всех
случаях, когда и<0,05Х корректирующий множитель полага-
ется равным единице. Он учитывается, когда n>0,05/V, т. е. объем
выборки составляет более 5% от объема генеральной совокуп-
ности.
188
Общая формула для доверительных пределов при условии
л>0,057¥будет иметь вид
<«»
-Jn i N -1
Пример 8.6. Рассмотрим ситуацию примера 8.5. Предположим,
что партия произведенных приборов имеет размер W = 100,
тогда объем выборки п — 10 будет превышать 5% объема гене-
ральной совокупности: n/W = 0,1 >0,05. Поэтому при определе-
нии доверительных пределов следует учитывать поправку на
конечность генеральной совокупности. Вычислим стандартную
ошибку средней по формуле (8.7):
о [N-n= 50 1100-10 _ 50 190 = 50
7Й V/V-l ~7ioY 100-1 "710^99 3,16*
= ,0,909 = 50 0.95 = 15.82 • 0,95 = 15.03ч.
3,16 3,16
Используя формулу (8.8), найдем доверительные пределы
(измеряемые в часах), соответствующие доверительным веро-
ятностям 90, 95 и 99%:
364 ± 1,64 15,03 = 384 ± 25 = 359 + 409,
364 ± 1,96 • 15,03 = 384 ± 29 = 355 + 413,
364 ± 2,58 15,03 = 384 ± 39 = 345 + 423.
8.3.1.2. Вычисление доверительных пределов при неизвестном
генеральном стандартном отклонении. Использование
t-распределения Стьюдента
Пусть исследуется генеральная совокупность, распределен-
ная по нормальному закону, и известно значение стандартно-
го отклонения а. В этом случае независимо от объема выборок п
распределение выборочных средних х будет нормальным со
о о In —п
стандартной ошибкой (или = ~Г Л'1Я ко’
нечной генеральной совокупности) и средней, равной гене-
ральной средней ц. Тогда, как было показано в 7.3.3, величина
Л g будет иметь стандартное нормальное распределение.
Заметим, что нормальность Z получается ввиду того, что из
189
нормально распределенной величины выборочной средней х
вычитается постоянная и полученная разность делится на по-
стоянную.
Полагая Z = Zy, где а — заданная доверительная вероят-
ность. по формулам (8.3) и (8.8) можно построить соответ-
ствующий доверительный интервал для оценки значения р.
Предположим теперь, что значение о неизвестно. В этом слу-
чае оно заменяется соответствующей статистикой, т. е. выбо-
рочным стандартным отклонением х, и тогда стандартная ошиб-
ка средней вычисляется по формулам
(для бесконечной генеральной совокупности),
- s Z2*
5з ~ Tn \ n-i
(для конечной генеральной совокупности).
Полагая, что объем выборки постоянный, рассмотрим те-
X —ц
перь величину = —" . Очевидно, знаменатель этого выра-
жения уже не будет постоянным, так как значение si не
является одинаковым для всех различных выборок заданного
объема. Поэтому величину Z в этом случае нельзя считать
нормально распределенной. Она подчиняется другому зако-
ну распределения, который получил название /-распределе-
ния Стьюдента.
Обозначение Z, используемое для стандартной нормальной
величины, заменяется буквой /, которая обозначает отноше-
ние
Величина (8.9) распределена по закону /-распределения. В
действительности существует целое семейство /-распределений.
Каждое отдельное распределение этого семейства соответству-
ет фиксированному объему выборки л. Степень отклонения
/-распределения от нормального связана с объемом выборки
л, для которой вычисляется величина стандартного отклоне-
ния х Чем меньше объем выборки, тем больше отклонение от
нормальности.
При малых выборках (л<30) использование распределения
Z для интервальных оценок средней возможно только при из-
вестном о.
190
Кривая /-распределения (рис. 8.6) имеет симметричную плос-
ковершинную форму (см. раздел 4.3). Чем меньше объем вы-
борки п, тем более пологой будет кривая /-распределение.
С ростом объема выборки кривая /-распределения сжимается
по оси абсцисс и вытягивается вдоль оси ординат. При л > 30
она почти полностью совпадает с кривой стандартною нор-
мального распределения.
Рис. 8.6. Сравнение кривых стандартного нормального распределения
и /-распределения
Как видно из рис. 8.6, в “хвостовых" частях /-распределения
заключены большие плошали по сравнению с соответствую-
щими “хвостами" распределения Z Поэтому при фиксирован-
ной доверительной вероятности интервал, построенный на
основе /-распределения, будет шире соответствующего интер-
вала, вычисленного на основе распределения Z. Отсюда при
неизвестном о и л<30 использование распределения Z ведет к
существенным погрешностям. Наоборот, с увеличением объе-
ма п /-распределение будет приближаться к стандартному нор-
мальному закону.
В практических приложениях считают, что в случае большой
выборки, т. е. когда п > 30, /-распределение почти совпадает со
стандартным нормальным распределением. Поэтому если вы-
борка большая и о неизвестно, то для построения доверитель-
ных интервалов можно пользоваться распределением Z, а в
качестве стандартной ошибки средней рассматривать статис-
s
тику Хх —~ . Тогда для бесконечной генеральной совокупнос-
ти формула вычисления доверительных пределов с доверитель-
ной вероятностью 1 — а имеет вид
* S f v vi
x±Za/2 г или \ x-Za/2~f=-,x+Za,2 > . (8.10)
УЛ I л/Л Ул I
191
В случае конечной генеральной совокупности объема Л/при
условии n/N>0,05 следует учитывать поправку на конечность
генеральной совокупности:
, _ s । N -п
X±ZanTn^- ,8">
I
Пример 8.7. На фирме работают несколько тысяч служащих.
Предполагается, что показатели их недельных заработков рас-
пределены нормально. Составлена случайная выборка из 49 слу-
жащих. Средний недельный заработок служащих в выборке ра-
вен 110 долл, со стандартным отклонением 10,5 долл. Требуется
найти 95-процентные доверительные пределы для среднего не-
дельного заработка всех служащих фирмы.
В данном случае генеральную совокупность составляют все
служащие фирмы. Ее объем можно считать бесконечным. Обьсм
выборки п = 49 превышает 30, следовательно, можно исполь-
зовать формулу (8.10) для вычисления искомых пределов. Ис-
ходными данными задачи будут х = 110 долл., s - 10,5 долл.,
I — а = 0,95, Z,,= 1,96. Получим
110± 1,96 10,5 = 11011,96—= 11011,96-1,5 =
.49 7
= 11012,94 = 107,06+112.94.
Таким образом, с уверенностью на 95% можно утверждать,
что средний недельный заработок служащего фирмы заключа-
ется в пределах от 107 до 113 долл.
Пример 8.8. Пусть рассматривается та же ситуация, что и в
предыдущем примере, только общее число служащих фирмы
составляет W= 645 человек. В этом случае n/N - 49/645 = 0,07>0,05.
Поэтому для вычисления 95-процентных доверительных пре-
делов следует учитывать поправку на конечность генеральной
совокупности, т. е. воспользоваться формулой (8.11):
110± 1,96 10,5 /145 49 = 11011,961,5— =
V49 V 145-1 12
= 11012,94 0,82 = 11012,41 = 107,6+112,4.
С вероятностью 95% можно утверждать, что средний недель-
ный заработок служащего фирмы находится в пределах от 108
до 112 долл.
192
В статистике с каждым отдельным /-распределением связы-
вают определенное понятие — число степеней свободы, кото-
рое в свою очередь тесно связано с объемом выборки. Число
степеней свободы определяется при нахождении различных ста-
тистик, например средней, дисперсии и т. д. Под числом степе-
ней свободы понимается количество данных, которые входят в
формулу для вычисления статистики и которые могут свободно
изменяться, сохраняя при этом заданную величину статистики.
Например, число степеней свободы для средней арифмети-
ческой будет df = п - 1 (где df — обозначение числа степеней
свободы). Действительно, пусть выборка состоит из четырех
значений х(, х2, х3, х4, а средняя х = 5. Это означает, что верно
соотношение -1 *- -2 £ = 5. Очевидно, можно задавать лю-
бые три значения х, четвертое значение при этом всегда будет
единственным, так как вычисляется из данного равенства в
качестве неизвестного. Поэтому в данном случае df = 4 - 1 = 3.
При вычислении площадей, заключенных под кривыми
/-распределения, используется специальная таблица, подобная
таблице для распределения Z. Она представлена в Приложении 5.
Если в Приложении 4 указаны доли общей площади под кри-
вой, заключенные между ц = 0 и Z>0, то в аналогичной табли-
це для /-распределения представлены доли площади между />0
и +оо. По сравнению с таблицей для распределения Zтаблица
для /-распределения сильно сжата. Имеется в виду, что каждую
строку таблицы Приложения 5 можно развернуть в целую таб-
лицу, эквивалентную таблице для распределения Z Сжатие
каждой таблицы в одну строку достигается путем указания зна-
чений /лишь для некоторых долей плошали кривой. Значения
долей соответствуют столбцам таблицы Приложения 5, а ее
строки — числу степеней свободы. Как видно, при увеличении
числа степеней свободы характеристики /-распределения при-
ближаются к характеристикам стандартного нормального рас-
пределения Z. В последней строке для df = +«> эти характерис-
тики полностью совпадают.
Например, в этой строке доле площади, равной 0,01, соот-
ветствует значение / = 2,326. По таблице Приложения 4, учи-
тывая округление, найдем, что доля площади, заключенной
между ц = 0 и Z = 2,33, равна 0,4901, т. е. 0,5 — 0,01 = 0,49.
Пусть — такое значение />0, которое отсекает долю
площади под “хвостовой” частью кривой /-распределения, со-
ответствующего числу степеней свободы df = п — 1, которая
193
равна а/2. По таблице площадей под кривыми /-распределения
(Приложение 5) значение г и_| находится на пересечении
строки, соответствующей df = п — I, и столбца, соответствую-
щего а/2.
Тогда доверительные пределы при доверительной вероят-
ности I — а и объеме выборки п находятся по формуле
(8.12)
УЛ
Доверительные пределы ограничивают интервал
(- * 5 5
х ^а/2л-1 /" • ±^а/2л-1 •
\ УЛ УЛ /
Еще раз отметим, что формулой (8.12) следует пользовать-
ся, если значение а неизвестно и л<30. В этой связи /-распреде-
ление получило название распределения малых выборок.
Пример 8.9. Предполагается, что значения уровня напряжения
на выходе трансформатора подчиняются нормальному закону.
Было произведено 18 измерений выходного напряжения:
10,85; 11,4; 10,81; 10,81; 10,23; 9,49; 9,89; 10,11; 10,57; 11,21;
10,1; 11,22; 10,31; 11,24; 9,51; 10,52; 9,92; 8,33.
Требуется найти 95-процентные доверительные пределы для
среднего уровня выходного напряжения трансформатора.
Точечная оценка для р:
- 10,85+ 11,4+ ... + 8,33
х =--------------------= 10,331.
18
Точечная оценка для о:
I (10,85 -10,331)2 + (11.4 -10,331)2 +... + (8,83 -10.331)2 _
s =,-----------------------------------------------= о,/о/.
V 17
Заданная доверительная вероятность I — а = 0,95. Отсюда
а = 0,05, т. е. а/2 = 0,025. Число степеней свободы df = л - 1 =
= 18 - 1 = 17. По таблице Приложения 5 найдем значение
/оои.17 ~ 2.Н» которое находится на пересечении строки
df - 17 и столбца 0,025.
По формуле (8.12) определим доверительные пределы с
вероятностью 95%:
10,331 ±2,11 9^ = 10,331 ±0,381 = 9,95 +10,71.
-./18
194
Следовательно, на 95% можно быть уверенным, что сред-
ний уровень напряжения на выходе трансформатора заключен
в пределах от 9,95 до 10,71 В-
Пусть выборка объема л<30 извлекается из конечной гене-
ральной совокупности размера N. Если п a 0.05/V, то в формулу
In -п
(8.10) следует ввести корректирующий множитель — п0‘
правку на конечность генеральной совокупности:
s W-п
•»±'а/2и.-1
(8.13)
Пример в. 10. Дирекция электростанции хочет оценить средний
недельный расход угля в течение года. Для этой цели было ото-
брано Ю недельных показателей расхода угля из I50 показателей,
накопленных за 3 года. Средний показатель по выборке оказался
равным х - 11 400 т со стандартным отклонением s = 700 т.
Пользуясь 95-процентными доверительными пределами, дать
оценку среднего недельного расхода угля на электростанции.
Объем выборки п удовлетворяет условию л>0,05/У, так как
Ю>0,05-150 = 7,5. Следовательно, для вычисления доверитель-
ных пределов можно воспользоваться формулой (8.I3).
Вычислим оценочное значение для стандартной ошибки
средней:
з Г/У-л_7ОО П50-10_ 700 |Т40
/nNN-i 710 V 150-1 3,1627144
= 221,38 0,97 = 214,59.
По таблице Приложения 5 определим значение t „ , при
л= 10иа = 0,05:гооИ;, = 2,262.
По формуле (8.13) найдем пределы:
11400 +2,262 • 214,59 = 11400 ±485,4 = 10914,6-11885,4.
Таким образом, с вероятностью 95% можно быть уверен-
ным, что средний недельный расход топлива — от 10 914,6 до
И 885,4 т.
195
8.3.1.3. Общие правила определения доверительных
интервалов
В итоге сформулируем несколько правил вычисления дове-
рительных интервалов для генеральной средней ц.
1. Рассматривается случайная выборка объемом п, полученная
из генеральной совокупности, распределенной по нормальному
закону. Известно значение стандартного отклонения генеральной
совокупности о. Пусть генеральная совокупность либо бесконеч-
на, либо конечна и имеет объем N, но при этом выполняется
условие л<0,05У Тогда доверительный интервал с уровнем дове-
рия а (т. е. до не ригельной вероятностью 1 — а) имеет вид
.г ± Za/2 • -т—.
Ул
2. Рассматривается случайная выборка объема п, полученная
по принципу “без возвращения” в генеральную совокупность.
Пусть генеральная совокупность нормальна, конечна (объем
Л) и л>0,05У Известно значение а. Тогда доверительный ин-
тервал с уровнем доверия а имеет вид

СТ I N -п
/л N .N^\'
3. Рассматривается случайная выборка, объем которой л>30.
Она получена из нормальной генеральной совокупности. Пусть
генеральная совокупность либо бесконечна, либо имеет объем
N при условии л<0,05У Значение о неизвестно. Вычислим вы-
борочное значение стандартного отклонения s. Тогда довери-
тельный интервал с уровнем доверия а имеет вид
x±Z •
ЛХГ-а/2
4. Пусть из конечной нормальной совокупности объема N
извлекается бесповторная выборка размера л>30. При этом
лй 0,05Л'и значение а неизвестно. Вычислено выборочное стан-
дартное отклонение з. Тогда доверительней интервал с уров-
нем доверия а имеет вид
a±Z„,2
з - л
5. Пусть объем случайной выборки л< 30. Генеральная сово-
купность, откуда получена выборка, распределена по нор-
196
мальному закону. Она бесконечна или конечна с объемом N.
При этом выполняется условие п <0,05N. Значение о неизвест-
но и вычислено выборочное значение з. Тогда доверительный
интервал с уровнем доверия а имеет вид
л1П
6. Пусть случайная выборка, полученная по принципу “без
возвращения”, имеет объем п< 30. Генеральная совокупность
нормальна и имеет конечный объем N, а также выполняется
условие п> 0,05М Значение ст неизвестно, и вычислено выбо-
рочное значение х. Тогда доверительный интервал с уровнем
доверия а имеет вид
з \N -п
Х±Гп . ----
л V N-1
7. В случае если распределение генеральной совокупности
достаточно близко к нормальному, для вычисления довери-
тельных пределов можно использовать первые шесть правил.
Если распределение генеральной совокупности сильно отли-
чается от нормального (например, сильно асимметрично или
равномерно), то первые четыре правила также могут быть при-
емлемыми на практике. В этом случае использование правил 5
и 6 для малых выборок (п< 30) не имеет смысла.
8.3.1.4. Объем выборки и точность интервальной
оценки средней
Точность оценки средней, т. е. ширина доверительного ин-
тервала, зависит от объема выборки. Очевидно, с увеличением
_ з
объема п значение стандартной ошибки средней 5;=-т—
уменьшается. Это в свою очередь приводит к сужению дове-
5
рительного интервала ,x±Zal2-j— или к повышению точности
* у1П
оценки средней при заданной доверительной вероятности. Отсю-
да следует, что при достаточно большом п доверительный ин-
тервал будет настолько узким, что его можно рассматривать в
качестве точной генеральной средней ц. Однако на практике
получение выборки большого объема сопряжено со значитель-
ными затратами на исследования. Поэтому имеет смысл оп-
197
ределить такой объем выборки л, которого было бы достаточ-
но для обеспечения допустимой ошибки.
Пусть Е = Za/2 — допустимая ошибка. Выразим отсюда
-Jn
значение п:
Z2 s2
(814)
С
Таким образом, если известно значение выборочного стан-
дартного отклонения s (например, в результате предваритель-
ных или пробных исследований), то, задаваясь доверитель-
ной вероятностью 1 — а и допустимой ошибкой Е, с помощью
выражения (8.14) можно вычислить необходимый объем вы-
борки.
Следует отметить, что иногда может быть известно значе-
ние генерального стандартного отклонения о. В этом случае
при вычислении п в выражение (8.14) вместо ? следует под-
ставить о2.
Пример В.11. Торговая фирма хочет открыть супермаркет на
территории некоторого округа. Для проведения маркетинговых
исследований руководству фирмы необходимо иметь инфор-
мацию о головых доходах семей, живущих в данном округе. Пред-
варительные обследования показали, что доходы варьируются
в пределах от 9000 до 29 000 долл. Однако для более надежных
прогнозов необходима точность в размере 200 долл, с довери-
тельной вероятностью 95%. Требуется определить, сколько се-
мей нужно обследовать, чтобы получить заданную точность
оценки. Для определения стандартного отклонения з было про-
ведено пробное обследование 50 семей. В результате была полу-
чена оценка стандартного отклонения s = 3000 долл.
По формуле (8.14) найдем необходимый объем выборки:
п =
1,962-30002
2ОО2
= 864,36.
Очевидно, выборка из 865 семей может обеспечить задан-
ную ошибку.
Следует отметить, что точность оценки необходимого объе-
ма п будет зависеть от достоверности информации о величине
стандартного отклонения г.
198
8.3.2. Доверительные интервалы для разности средних
двух генеральных совокупностей (случай двух больших
независимых выборок)
Рассмотрим две различные генеральные совокупности (тео-
ретически бесконечные): совокупность 1 и совокупность 2. Пусть
совокупность 1 имеет параметры ц] и о^, а совокупность 2 — ц2
и о22. Булем из каждой генеральной совокупности извлекать не-
зависимые случайные выборки постоянных объемов. При этом
процедура формирования выборок строится следующим обра-
зом: вначале извлекается случайная выборка постоянного объема
nf из совокупности I, затем независимо от нее из совокупнос-
ти 2 извлекается случайная выборка постоянного объема л, и
т. д. Если выборки большие, т. е. л, > 30 и л2£ 30, то, очевидно,
по центральной предельной теореме независимо от законов рас-
пределения генеральных совокупностей 1 и 2 соответствующие
распределения выборочных средних будут нормальными с па-
ст, ст,
раметрами ц , -j-L и ц2, .
У я| у п2
Пусть первое из выборочных распределений характеризу-
ет случайную величину Хр а второе — Х2. Рассмотрим раз-
ность случайных величин X — Хг Очевидно, она является
2 2
нормальной с параметрами - ц2 и °L + (см. раздел 6.7.2).
«1 «2
Это означает, что распределение разностей выборочных сред-
них двух генеральных совокупностей нормальное и имеет
„2 _,2
2 СТ. &•>
параметры = ц, - ц2 и о,- =-»- + -1.
Пусть имеется информация только о двух случайных неза-
висимых выборках, полученных из рассматриваемых генераль-
ных совокупностей 1 и 2. Так, выборка из совокупности 1 имеет
объем Лр среднее значение х( и дисперсию з(2, а выборка из
совокупности 2 — объем я , среднее значение х и дисперсию
2 4 2
V-
Построим доверительный интервал для разности генераль-
ных средних ц1 - ц2. Очевидно, точечной оценкой для нее бу-
дет разность выборочных средних x(-x2, а оценкой стандарт-
I? 7
ной ошибки разности — Х.,, ял~ + ~-
V"l П2
199
Отсюда получаем, что доверительный интервал для разно-
сти средних двух генеральных совокупностей имеет вид
(xt-x2)±Za/2 - + ^- (8.15)
V ”| П2
или
| 9* I Т*" <S*
(X! - х2) - Zal2 > ' + < р, -ц2 < (Л, - х2) + Zal2 р- + - . (8.16)
1J Л] /Ij J Л| л>
Пример В. 12. Фирма имеет филиалы в двух разных городах. Ру-
ководству фирмы необходимо выяснить, как отличаются друг
от друга средние почасовые ставки малоквалифицированных
рабочих в этих филиалах. В первом филиале была сделана слу-
чайная выборка из 200 рабочих. Для нее были вычислены сле-
дующие значения статистик: х, = 8,93 долл., 5, = 0,4 долл.
Во втором филиале случайная выборка имела объем
Wj= 175, статистики: х2 = 9,1 долл., = 0,6 долл.
Определим 95-процентный доверительный интервал для
разности средних. По формуле (8.15) имеем
(8,93-9,1) ± 1,96д!^ + —2
I 200 175
= -0,17 ±1,96 0,053 =
= -0,17 ±0,104 = -0,274 + -0,066.
Как видно, с вероятностью 95% можно утверждать, что сред-
няя ставка во 2-м филиале превышает среднюю ставку в 1-м
филиале на 0,07—0,27 долл.
8.3.3. Доверительные интервалы для разности средних
(случай двух малых независимых выборок)
Если при интервальной оценке разности двух генеральных
средних используются малые выборки (л^ЗО, л2<30), то рас-
пределение разностей выборочных средних может значительно
отличаться от нормального. Например, это будет в том случае,
когда распределения исходных генеральных совокупностей силь-
но отличаются от нормального. Как известно, при малых вы-
борках большую точность при оценке средних лает /-распреде-
ление. Формула для вычисления доверительных интервалов в
этом случае будет иметь вид
200
(xt
(8.17)
где /— значение /, соответствующее уровню значимости
а й числу степеней свободы, которое вычисляется по фор-
муле
И| -1 л2 -1
Результаты вычислений по формуле (8.18) следует округ-
лять до целой части, так как число степеней свободы характе-
ризуется целым положительным числом.
Пример В. 19. Руководство компании по перевозке грузов хочет
определить, какой тип покрышек для грузовых автомобилей
более надежен в эксплуатации. В результате проведенного ана-
лиза рынка покрышек были отобраны два типа: тип 1 и тип 2.
Для того чтобы осуществить выбор между ними, было решено
провести проверку покрышек на специальном оборудовании.
Покрышки разных типов ставились на задние колеса грузовика.
Грузовик заезжал задними колесами на свободно вращающие-
ся специальные металлические валики. После включения пере-
дачи колеса катились по валикам, что приводило к быстрому
износу покрышек. При этом засекалось точное время, за кото-
рое каждая покрышка приходила в негодность. Обстоятельства,
связанные со сроками и ресурсами, позволили проверить только
по 15 покрышек каждого типа. В результате испытаний были
получены две независимые выборки, каждая из которых вклю-
чала 15 временных значений.
После обобщения данных каждой выборки были вычисле-
ны средние значения и стандартные отклонения (в часах):
х, = 3,33, з, = 0,68; х2= 3,98, з2 = 0,38.
Требуется определить 90-процентный интервал для разно-
сти ц. - р2, где ц, характеризует среднее время до полного
износа для всех покрышек типа I, а ц2 — для всех покрышек
типа 2.
201
Для того чтобы использовать формулу (8.17), вначале необ-
ходимо определить число степеней свободы или вычислить
выражение (8.18):
0,682 О!38* f
^__L15 15 .
Г 2 Т2 Г 2 П2
О,682 О,382
15 15
14 + 14
0.04042
= 21,9.
0,0000679 + 0,00000662
Округляя, получим <#= 21. Используя таблицу г-распреде-
ления (Приложение 5), найдем /00, 2| = 1,721 (а = 1).
По формуле (8.17) вычислим доверительный интервал:
О^2.О.382 =Ч)1б5±о,35 = -1 + Ч),3.
(3,33- 3,98) ± 1,721..
V 15 15
Таким образом, среднее время до полного износа покры-
шек типа 2 превышает среднее время до полного износа по-
крышек типа 1 в пределах от 0,3 ч (т. е. 18 мин) до 1 ч с вероят-
ностью 90%. Выбор очевиден — покрышки типа 2 имеют
больший срок эксплуатации.
На практике в некоторых случаях следует учитывать условие
равенства дисперсий исходных генеральных совокупностей,
т. е. о « о » о. Например, такая ситуация может возникнуть
при исследовании производственных процессов с долговремен-
ным циклом производства. Тогда, основываясь на прошлых на-
блюдениях, с достаточной степенью достоверности можно ут-
верждать, что дисперсия генеральной совокупности 1 равна
дисперсии генеральной совокупности 2.
Если известно, что обе генеральные совокупности имеют
одинаковые дисперсии, то возникает проблема оценки общей
дисперсии на основе выборочных дисперсий 1/и $22. В качестве
аппроксимирующего значения можно рассматривать среднюю
взвешенную величину значений 5(2и s22’
52 = + (п2~Од2 (8.19)
«I + п2 -1
Заметим, что комбинированная из выборочных дисперсий
величина ? будет ближе к дисперсии той выборки, которая имеет
больший объем. Если объемы выборок равны (л, = л, = л), то
комбинированная выборочная дисперсия равна средней ариф-
202
метической значений S(2 и s2. Стандартная ошибка разности сред
них примет вил
f_ + £_=j ± + -L. (8.20)
"1 "2 V "I п2
Число степеней свободы, соответствующее статистике t, в
данном случае равно df = л) + я - 2. С учетом выражения (8.20)
формула для доверительных интервалов имеет вид
(8.21)
(-4 “ *2) ^а/2;п,+л,-2
где ? вычисляется по формуле (8.19).
Следует отметить, что в случае равенства дисперсий вычис-
ление числа степеней свободы для статистики t значительно
облегается. На практике, если не оговаривается условие нера-
венства дисперсий (о,2 * о22), можно полагать, что они равны.
При этом пофешность будет несущественной.
Пример 8.14. Пусть рассматривается ситуация, представленная
в примере 8.13, причем предполагается, что дисперсии гене-
ральных совокупностей сроков износа для покрышек типа I и
типа 2 равны. Определить 90-процентный доверительный ин-
тервал для ц, - щ.
По формуле (8.21) вычислим комбинированную выбороч-
ную дисперсию:
2 (15-1)0,682+(15-1)0,3«1 8,495
15 + 15-2 28
Определим стандартную ошибку разности средних:
j = Дзоз = 0,55 ч.
По таблице Приложения 5 найдем значение 1, соответству-
ющее числу степеней свободы df=n} + я2 — 2 = 28, при уровне
значимости а = 0,01: = 1,701.
Используя формулу (8.21), найдем доверительный интер-
вал:
1 1 2
(3,33 - 3,98) ± 1,701 0,55 J - + — = -0,65 ± 1.701 0,2 =
V15 15
= -0,65 ± 0,34 = -0,99 + -0.31.
203
Как видно, вычисленный доверительный интервал незна-
чительно отличается от интервала, полученного в примере 8.15.
Следует отметить, что он немного уже, т. е. использование сред-
ней взвешенной дисперсии дает более точную интервальную
оценку разности генеральных средних.
8.3.4. Объем выборки и допустимая ошибка оценки
разности генеральных средних
В выражении (8.15) величина Za/2л L+i прибавляется к
V И| П2
точечной оценке разности генеральных средних и вычитается
из нее. Обозначим Е = 2ay2.i-L+ - . Тогда Е характеризует
V Л1 Л2
ошибку интервальной оценки или ширину доверительного
интервала. Очевидно, чем меньше Е, тем уже доверительный
интервал и меньше погрешность оценки. Зададимся допусти-
мым значением ошибки Е и предположим, что обе выборки
имеют одинаковый о^ъем: л( = п2~ п. Определим в этом случае,
какое значение объема л обеспечивает заданную ошибку Е.
Имеем
E = Za/2M + ^
V л л
(8.22)
Из (8.22) выразим л:
п = (8.23)
Е2
Отметим, что общий объем двух выборок равен л( + л2 = 2л.
Пример В. 15. Две научно-исследовательские лаборатории не-
зависимо друг от друга занимаются разработкой и производ-
ством таблеток для больных артритом. Таблетки предназначены
для снятия боли в период приступов болезни.
Были проведены испытания действия обоих типов таблеток.
Действие первых типов таблеток было опробовано на 50 боль-
ных. Оказалось, что он снимает боль в среднем в течение 8,5 ч
(х,) со стандартным отклонением 1,8 ч (S]). Для таблеток, про-
изведенных второй лабораторией и действие которых было оп-
робовано на 40 больных, результаты такие: х2 = 7,9 ч, х2 = 2,1 ч.
204
Определим ошибку разности двух средних для 95-процент-
ного доверительного интервала:
г = 1.96, /+ — = 1,96/0,0648 + 0,1102 = 1,96 0,418 = 0,82.
*’* У 50 50 4
Определим доверительный интервал:
(8,5 - 7,9) ±0,82 = 0,6 ±0,82 = -0,22+1,42.
Как видно, полученная точность недостаточна для досто-
верного сравнительного анализа эффективности обоих типов
таблеток.
Пусть требуется, чтобы допустимая ошибка не превышала
0,5 ч. По формуле (8.23) вычислим, каков должен быть в этом
случае объем каждой выборки:
1,962(1,82 + 2.I2) 3,842(3,24 + 4,452) 3,842-7,692 110,
О,52 0,25 0,25
Таким образом, для получения нужной точности следует
опробовать действие таблеток каждого типа на 118 больных. Об-
щая выборка составит 236 больных.
8,4, ОЦЕНКА ДОЛЕЙ
8.4.1. Распределение выборочных долей (пропорций)
Под долей (или пропорцией) понимается относительная или
процентная характеристика, определяющая часть элементов
совокупности, обладающих некоторым признаком (свойством).
В статистическом анализе часто требуется оценить доли появ-
ления “успехов” в генеральной совокупности. Например, ста-
тистические обследования проводятся правительством с целью
определения уровня безработицы в стране, который выража-
ется как процент безработных по отношению к активному на-
селению.
Чтобы определить точечную оценку доли, следует подсчи-
тать число “успехов” в совокупности (т. е. выявить число эле-
ментов, обладающих данным признаком), а затем вычислить
отношение этого числа к общему количеству элементов в сово-
купности. При этом должно выполняться условие дихотомнос-
ти генеральной совокупности. Это означает, что ее можно раз-
205
бить на две части: те элементы, которые обладают данным при-
знаком, и все остальные элементы, которые им не обладают
(например, все активное население делится на безработных и
имеющих работу на данный момент времени). Можно пока-
зать, что выборочная доля является наилучшей оценкой гене-
ральной доли, т. е. удовлетворяет критериям несмешенности,
эффективности, состоятельности и достаточности.
Рассмотрим следующую ситуацию. Для выявления обществен-
ного мнения относительно усиления мер по охране окружаю-
щей среды правительство крупного региона организовало со-
циологической опрос. Были опрошены 2000 человек, из которых
1600 высказались за принятие более жестких мер. Точечная оцен-
ка доли населения региона, которая выступает за принятие более
жестких мер, такова: р = 1600/2000 = 0,8. Иначе говоря, при-
близительно 80% всего населения региона выступают за ужес-
точение мер по охране окружающей среды.
Как было показано в разделе 6.4, распределение вероятнос-
тей числа “успехов” характеризуется биномиальным законом
распределения. Математическое ожидание и стандартное откло-
нение биномиальной случайной величины определяются соот-
ветственно по формулам ц = пр, а2 = npq, где п — число испы-
таний, р — вероятность появления “успеха”, q = 1 — р —
вероятность “неудачи”.
Величина ц = пр отражает среднее ожидаемое число “успе-
хов ”. Для того чтобы получить соответствующую долю, эту ве-
личину следует разделить на п: пр/п = р.
Величина р, таким образом, определяет ожидаемую долю
или, что то же самое, среднюю распределения выборочных
долей: = р.
Аналогично для вычисления стандартного отклонения рас-
пределения выборочных долей величину о = yjnpq следует раз-
делить на п:
_ Jnpg _ Ipq _ Ip(l-p)
* п У п N п
Величина о? называется стандартной ошибкой доли.
В отличие от средней арифметической, расчет которой про-
изводится в непрерывном масштабе, при вычислении доли
получаются дискретные данные, связанные с подсчетом коли-
чества “успехов”. Распределение этих данных подчиняется би-
номиальному закону, т. е. является дискретной случайной ве-
личиной. Поэтому теоретически при оценке долей следует
206
пользоваться биномиальным распределением. Однако на прак-
тике использование биномиального распределения сопряжено
со значительными трудностями как теоретического, так и вы-
числительного характера. В разделе 7.3.4 отмечалось, что при
определенных условиях (лр>5 и л(1 - р)>5) биномиальное рас-
пределение достаточно точно приближается к нормальному. Это
позволяет применять центральную предельную теорему, рас-
сматривая при больших выборках распределение выборочных
долей как нормальное со средней Цр = р и стандартным откло-
_ jp(l-p)
нением ------------
V л
Величина генеральной доли р является оцениваемой вели-
чиной. Поэтому на практике в выражение для стандартной
ошибки доли вместо р подставляется ее точечная оценка р:
5р ~
Р(1 ~ Р)
л
(8.24)
Величина является оценочным значением стандартной
ошибки доли.
8.4.2. Доверительные интервалы для доли
Доверительные интервалы для доли генеральной совокуп-
ности можно найти по формуле, аналогичной формуле (8.3)
для генеральной средней:
P±Zal2s-p. (8.25)
где р — выборочная доля (точечная оценка генеральной доли);
з. — оценочное значение стандартной ошибки доли;
п — объем выборки;
а — уровень доверия (значимости);
Z „ — значение стандартного нормального распределения,
ограничивающее правую “хвостовую” часть кривой рас-
пределения с долей площади а/2.
Учитывая (8.24), формулу (8.25) можно записать следую-
щим образом:
Р ^а/2
рО-р)
П
(8.26)
207
Пример в. 16. Аудиторская проверка финансовой деятельности
фирмы за год показала, что среди 250 случайно выбранных
платежных поручений 12 содержат ошибки, допущенные при
оформлении счетов. Определить доверительные пределы с до-
верительной вероятностью 90% для доли неправильно оформ-
ленных в течение года платежных поручений (общий объем
оформленных за год платежных поручений составил несколько
тысяч).
Вычислим точечную оценку доли:
р = —-=0,048.
г 250
Доверительная вероятность 1 - а = 0,9(90%), тогда Z^., ” 1,64.
По формуле (8.26) вычислим соответствующий доверитель-
ный интервал:
i 0 048 0 95’
0,048 ± 1,64. ’ — = 0,048 ± 1,64 • 0.013 = 0,048 ± 0,022.
V 250
Отсюда получаем доверительные пределы:
0,0264-0,07.
Можно утверждать, что с вероятностью 90% доля непра-
вильно оформленных платежных поручений содержится в гра-
ницах от 0,026 до 0,07 (или в пределах от 2,6 до 7%).
Формула (8.26) будет верна, если объем генеральной сово-
купности очень большой (теоретически может считаться беско-
нечным). В общем случае, если объем генеральной совокупности
конечен и равен N, а объем выборки п составляет более 5%
объема# (n/N > 0,05), то в формулу для доверительного интер-
\N -п
вала (8.26) следует ввести коэффициент J» характеризу-
ющий поправку на конечность генеральной совокупности.
8.4.3. Объем выборки и допустимая ошибка
оценки доли
Аналогично тому, как был определен объем выборки, обес-
печивающий допустимую погрешность при оценке средней,
можно определить объем выборки для допустимой ошибки
доли.
208
Ошибка доли имеет вид
Е = 7 Ip^-p)
Е Ла/2 -у
V И
Отсюда
ns7i/2P^-P\ (8.27)
Е2
Таким образом, если известна какая-нибудь точечная оцен-
ка доли р, то при заданной ошибке Е можно вычислить необ-
ходимый объем выборки.
Если рассматривать величину р как переменную, то выра-
жение (8.27) будет достигать максимума при р = 1/2. Тогда верх-
ней границей для п будет
Z2
л=а';. (8.28)
4Е2
С помощью формулы (8.28) можно найти такой объем вы-
борки, который заведомо обеспечивает ошибку, не превыша-
ющую допустимое значение Е:
p±ZaJ&^J^ (8.29)
\ л V /V — 1
Пример 8.17. Автоматический станок производит детали. Из
500 деталей, произведенных станком, случайным образом было
отобрано 80 деталей. Из них 4 оказались нестандартными. Опре-
делить 95-процентный доверительный интервал для вероятно-
сти изготовления станком нестандартной детали.
По условию задачи объем генеральной совокупности N —
500, объем выборки л = 80. В качестве точечной оценки вероят-
ности можно рассматривать относительную частоту появления
нестандартной детали в выборке р 4/80 = 0,05.
Так как n/N = 80/500 = 0,16>0,05, то следует учитывать по-
правку на конечность генеральной совокупности. Вычислим
доверительный интервал по формуле (8.29):
0,05±1,96
V 80 V 500-1
= 0,05 ± 1,96 • 0,024 • 0,917 = 0,05 ± 0,43 = 0,007 + 0,093.
Отсюда с вероятностью 95% можно утверждать, что вероят-
ность события, что автомат произведет нестандартную деталь,
209
заключена в пределах от 0,007 до 0,093 (или процент нестан-
дартных деталей, произведенных станком, находится в преде-
лах от 0,07 до 9,3%).
Пример 8.18. Администрация крупного региона хочет оценить
мнение избирателей относительно переизбрания действующе-
го губернатора на новый срок. Предварительный опрос несколь-
ких сотен избирателей показал, что примерно 40% из них под-
держивают действующего губернатора. Сколько избирателей
необходимо опросить, чтобы ошибка прогноза составляла 2%
с вероятностью 95%?
Так как имеется некоторая оценка доли р = 0,4, то можно
использовать формулу (8.27):
1.962 0,4 0,6
О,О22
= 2304,96 = 2305 чел.
Вычисленное значение п может быть завышено или заниже-
но в зависимости от точности оценки р . В случае если бы не
было логически приемлемой информации о значении доли р,
то можно было положить р = 1/2 и, используя формулу (8.28),
получить верхнюю границу для п:
п = —'= 2401 чел.
4 0,022
8.4.4. Доверительные интервалы для разностей долей
Пусть требуется вычислить доверительный интервал для раз-
ности долей, взятых из двух разных генеральных совокупнос-
тей.
Для обеих генеральных совокупностей рассмотрим распре-
деления выборочных долей. Если значение генеральной доли
совокупности 1 равно р, а для совокупности 2 — р, то при
выполнении условий п Pt>5 и я((1 - р)>5, '^Р-^ и л2(1 - р2)>5
оба распределения выборочных долей будут близки к нормаль-
ному. Каждое распределение приблизительно соответствует
нормальной случайной величине с параметрами = р(.
Pi(l ~ Pi)
".
°э,=
и = Р2. <*-Рг
, Р2(1~Рг)
п2
Очевидно, если выборки из различных совокупностей неза-
висимы, то распределение разности выборочных средних мож-
п =
210
но рассматривать как разность этих случайных величин. Она так-
же будет распределена приблизительно нормально с параметра-
мн = р, - oU - < + 05, = М + .
П| л2
Величина в = .£l1 + £iC!—£11 является стандарт-
” V ”1 Л2
ной ошибкой разности средних.
На практике почти всегда имеется информация только о
двух независимых выборках, взятых из разных совокупностей,
т. е. известны выборочные доли р, и р2. Поэтому средняя и
дисперсия распределения разности выборочных долей оцени-
ваются соответствующими статистиками
Л| л2
Оценочной величиной стандартной ошибки будет
. ₽;(!.--&>. (8.30)
' П Л! Л2
Исходя из нормальности распределения можно записать
формулу для доверительных интервалов:
(8.3D
1 "1 "г
Пример В. 19. Две конкурирующие фирмы выпускают двигате-
ли для грузовых автомобилей. Каждая фирма осуществляет так-
же ремонт своих двигателей. Выпускаемые двигатели имеют га-
рантийный срок эксплуатации. Доля двигателей, которые
ремонтируются по гарантии в общей совокупности ремонти-
руемых за определенный период двигателей, характеризует сте-
пень надежности двигателей каждой фирмы. Требуется опреде-
лить 90-процентный доверительный интервал для разности этих
долей, соответствующих различным фирмам.
Рассмотрим две независимые случайные выборки, каж-
дая из которых содержит 100 отремонтированных двигате-
лей, выпущенных одной из фирм за определенный период.
Оказалось, что для фирмы 1 из 100 двигателей 28 были в
гарантийном ремонте, а для фирмы 2 этот показатель со-
ставлял 32 из 100.
211
Вычислим значения точечных оценок долей:
р, = 28/100 = 0,28, р2 = 32/100 = 0,32.
Определим оценку стандартной ошибки по формуле (8.30):
0,28 0.72 0,36~6ф8
s- - =, —-----— + —----’— = 0,059.
* V 100 100
Для доверительной вероятности 1 — а = 0,9 значение
^=,’64‘
По формуле (8.31) вычислим:
(0,28 - 0,32) ±1,64 0,059 = -0,04 ±0,097 = -0,137+0,057.
По данному доверительному интервалу нельзя установить,
какая из двух фирм выпускает более надежные двигатели. С ве-
роятностью 90% можно только утверждать, что для фирмы 1
доля двигателей, сломавшихся в период гарантийного срока,
может быть на 13,7% ниже и на 5,7% выше соответствующей
доли двигателей фирмы 2.
8.4.5. Объем выборок и допустимая ошибка
разности долей
Согласно формуле (8.30) ошибка разности двух долей будет
иметь вид
E=z ЕЕЕЩЗЕЫ. (8.32)
V "I "2
Полагая в (8.32) п = л = и, можно записать:
п = Zg/afciO-PO+PzCl-Pz)] (8.33)
Е2
Пример 8.20. Торговая фирма проводит маркетинговые иссле-
дования рынка пищевых продуктов. В частности, руководство
фирмы интересует отношение покупателей к двум сортам чая.
Для выяснения данного факта были произведены две случай-
ные выборки численностью 100 покупателей каждая. Покупа-
телям, попавшим в 1-ю выборку, задавали вопрос, нравится
ли им сорт 1, а покупателям из 2-й выборки — сорт 2. В 1-й вы-
борке положительно ответили на вопрос 69 человек, во 2-й —
54 человека. Определить, каков должен быть объем каждой вы-
212
борки, чтобы точность оценки разности долей покупателей,
одобряющих разные сорта чая, была ±5% с вероятностью 95%.
Вычислим: р} = 69/100 = 0,69, />, = 54/100 = 0,54.
По формуле (8.33) найдем:
_ 1,962 (0,69 0,31 + 0,54 0,46) _ 3,842(0,214 + 0,248) =
П ~ О.О52 0,0025
= = 7Ючел.
0,0025
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 8
Под точечной оценкой понимается отдельное число (назы-
ваемое точкой), которое используется как оценка параметра
генеральной совокупности. Различные статистики могут слу-
жить оценками истинных параметров генеральной совокупно-
сти. Для оценки их качества в статистическом анализе рассмат-
риваются четыре критерия: несмещенность, эффективность,
состоятельность и достаточность. Статистика является несме-
щенной, если при вычислении большого количества точечных
выборочных оценок их значения располагаются примерно сим-
метрично относительно истинного значения оцениваемого па-
раметра. При этом математическое ожидание распределения
статистик будет равно значению оцениваемого параметра. Кри-
терий эффективности характеризует минимальность стандарт-
ной ошибки статистики, используемой для оценки. Это озна-
чает, что стандартная ошибка должна быть меньше стандартной
ошибки всех других возможных оценок. Оценка является состо-
ятельной, если при увеличении объема выборки значения ста-
тистик стремятся к истинному значению оцениваемого пара-
метра. Оценка является достаточной, если при ее вычислении
используется вся содержащаяся в выборке информация.
Значение отдельной статистики очень редко совпадает с
истинным значением оцениваемого параметра. Разность между
этими величинами называется ошибкой выборки. Пусть в каче-
стве искомого параметра рассматривается средняя арифмети-
ческая генеральной совокупности. Выборочная средняя будет
наилучшей оценкой генеральной средней, так как удовлетво-
ряет всем четырем критериям качества оценок. Возникает про-
блема, как на основе случайной выборки дать максимально
точную оценку генеральной средней. Зафиксируем объем вы-
борки и возьмем из генеральной совокупности все возможные
213
выборки данного объема. Затем для каждой из них вычислим
среднюю и составим распределение выборочных средних. По
центральной предельной теореме можно утверждать: для гене-
ральной совокупности со средней ц и дисперсией о1 распреде-
ление выборочных средних для всех возможных выборок боль-
шого объема (п > 30),составленных из ее элементов, будет
нормальным со средней ц и дисперсией и2/п.
На основе центральной предельной теоремы возможно по-
строение интервальных оценок параметров генеральной со-
вокупности, в частности доверительных интервалов для гене-
ральной средней. Под доверительным интервалом понимается
интервал, внутри которого с известной вероятностью нахо-
дится истинное значение параметра. Границы этого интервала
называются доверительными пределами, а связанная с ними
вероятность — доверительной вероятностью, которая изме-
ряет степень доверия к этому интервалу. Имея в виду свойства
площадей под кривой нормального распределения и утверж-
дения центральной предельной теоремы, можно вывести фор-
мулы для доверительных интервалов. При нахождении дове-
рительных пределов задаются уровнем значимости или доверия
а. Доверительная вероятность тогда вычисляется как 1 - а (или
(I - а)-100%). В случае больших выборок п> 30 или при усло-
вии заданного значения генеральной дисперсии о2 рассмат-
ривается стандартное нормальное распределение Z. Для него
определяется величина Za/2 >0, справа от которой доля пло-
щади под “хвостовой” частью кривой равна а/2. Для нахожде-
ния доверительных пределов с доверительной вероятностью
1 — а на основе одной случайной выборки объема п величину
Z^ следует умножить на стандартное отклонение (называе-
мое стандартной ошибкой средней) и затем полученный ре-
зультат вычесть и прибавить к значению выборочной средней
х (формула(8.3)).
Если объем выборки п > 30, а значение о неизвестно, то ве-
личина стандартной ошибки в формуле (8.3) заменяется на
величину $ — выборочное стандартное отклонение (формула
(8.10)).
Для малых выборок (л<30) при определении доверительных
интервалов использование стандартного нормального распре-
деления приводит к значительным погрешностям. В этом слу-
чае используется /-распределение Стьюдента, которое дает боль-
шую точность оценки. При этом рассматривается величина
/и;, * (, которая соответствует /-распределению при числе сте-
214
пеней свободы df = п - I и справа от которой доля плошади
под “хвостовой” частью кривой равна а/2. Под числом степе-
ней свободы понимается количество данных выборки, кото-
рые могут свободно изменяться, сохраняя при этом заданную
величину статистики.
При вычислении доверительных пределов с заданным уров-
нем значимости а на основе выборки объема я<30 величина Z
в формуле (8.10) заменяется на величину г , ((формула (8.12)).
В случае когда объем генеральной совокупности N конечен и
объем выборки составляет более 5% от объема генеральной
совокупности («>0,05АО, при вычислении доверительных пре-
делов следует учитывать поправку на конечность генеральной
совокупности J------. Во всех формулах для доверительных
J N -1
интервалов она умножается на стандартную ошибку средней.
В практических исследованиях часто возникает необходимость
определить такой объем выборки, который обеспечивал бы
заданную ошибку оценки. Под ошибкой оценки понимается
ширина доверительного интервала. При заданной ошибке и
доверительной вероятности объем выборки определяется по
формуле (8.14).
Доверительные интервалы для разности двух средних, взя-
тых из разных генеральных совокупностей, определяются по
формуле (8.15). В этом случае точечной оценкой является раз-
ность двух выборочных средних, где каждая выборка берется
из соответствующей генеральной совокупности (выборки пред-
полагаются большими и независимыми). Стандартная ошибка
разности средних равна корню квадратному из суммы квадра-
тов стандартных ошибок каждой средней.
В случае двух малых выборок («,<30, «2<30) используется
формула (8.17), где стандартная ошибка умножается на вели-
чину t (число степеней свободы «увычисляется по формуле
(8.18)>.
На практике при оценке разности двух средних иногда сле-
дует учитывать условие равенства дисперсий генеральных со-
вокупностей. В этом случае в качестве оценки обшей дисперсии
рассматривается средняя взвешенная величина значений вы-
борочных дисперсий, которая вычисляется по формуле (8.19).
В формуле для доверительных интервалов (8.21) она умножает-
ся на величину / соответствующую числу степеней свобо-
ды df = л, + л — 2. Объем каждой выборки, обеспечивающий
215
заданную ошибку для оценки разности двух средних, рассчи-
тывается по формуле (8.23).
Под долей, или пропорцией, понимается относительная ха-
рактеристика, определяющая часть элементов совокупности,
обладающих некоторым признаком или свойством. Определе-
ние точечной оценки доли — это подсчет числа “успехов” в
совокупности (т. е. выявление числа элементов, обладающих
данным признаком) и вычисление отношения этого числа к
общему количеству элементов в совокупности. При этом долж-
но выполняться условие дихотомности генеральной совокуп-
ности, т. е. ее можно разбить на две части: элементы, которые
обладают данным признаком, и все остальные элементы, ко-
торые им не обладают.
В общем случае при определении доверительных интервалов
долей следует использовать биномиальное распределение. Од-
нако при определенных условиях (пр>5 и л(1 - />)>5) биноми-
альное распределение достаточно точно аппроксимируется нор-
мальным. Аналогично распределению выборочных средних для
определения доверительных интервалов долей рассматривает-
ся распределение выборочных долей. Это распределение будет
близко к нормальному со средней р, равной генеральной доле,
и стандартным отклонением, вычисляемым по формуле (8.24).
На практике доверительные интервалы для доли определяются
на основе одной выборки и значение генеральной доли р заме-
няется на выборочное р. В случае бесконечной генеральной со-
вокупности доверительный интервал для доли вычисляется по
формуле (8.26). Если генеральная совокупность конечна, а объем
выборки составляет более 5% от объема генеральной совокуп-
ности, то необходимо учитывать поправку на конечность гене-
ральной совокупности (формула (8.29)). При определении ми-
нимального объема выборки, обеспечивающего заданную
ошибку оценки, можно воспользоваться формулами (8.27) и
(8.28).
При интервальной оценке разности долей, взятых из двух
различных генеральных совокупностей, рассматривается раз-
ность двух распределений выборочных долей. Точечной оцен-
кой в этом случае является разность выборочных долей, а стан-
дартной ошибкой — корень квадратный из суммы дисперсий
этих распределений (формула (8.30)). Для определения объема
каждой выборки, обеспечивающего заданную ошибку интер-
вального оценивания, можно использовать формулу (8.33).
ПРОВЕРКА ГИПОТЕЗ
ОТНОСИТЕЛЬНО СРЕДНИХ
9.1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ПРОВЕРКИ
ГИПОТЕЗ. НУЛЕВАЯ ГИПОТЕЗА
И СТАТИСТИЧЕСКИЕ КРИТЕРИИ
Оценка генеральной совокупности осуществлялась на осно-
ве заранее собранных выборочных данных. В качестве точечных
оценок рассматривались соответствующие выборочные статис-
тики (выборочная средняя или доля). Проверка гипотез пред-
полагает обратную последовательность действий. Еше до полу-
чения выборочных данных выдвигается предположение
(гипотеза) о точном значении некоторого параметра генераль-
ной совокупности. Затем собираются выборочные данные, об-
разующие случайную выборку. На их основе вычисляется оце-
ночная статистика и проверяется, насколько правдоподобна
выдвигаемая гипотеза (т. е. правильность предположения о том,
что принятое значение параметра является истинным). Гипоте-
зу о нулевой разности между предполагаемым и истинным зна-
чениями параметра генеральной совокупности называют нуле-
вой гипотезой.
Расхождение между выборочной статистикой и истинным
значением параметра связано с фактором случайности выбор-
ки. Интуитивно ясно, что чем меньше по абсолютной величи-
не разность между ними, тем более правдоподобна нулевая
гипотеза и, наоборот, если статистика и параметр сильно от-
личаются друг от друга, то степень правдоподобия уменьшает-
ся. Часто на практике расхождение между вычисленной стати-
стикой и гипотетическим значением параметра бывает очень
большим. В такой ситуации невозможно объективно подтвер-
дить или опровергнуть нулевую гипотезу, руководствуясь толь-
ко здравым смыслом и интуицией. Возникает необходимость в
разработке формальной процедуры, обеспечивающей количе-
217
ственное обоснование принимаемого решения. Данные рассуж-
дения поясним на следующем примере.
Пример 9.1. Крупная торговая фирма имеет несколько филиа-
лов в различных городах страны. На фирме работают более ты-
сячи продавцов. Для проверки эффективности их работы была
создана специальная система тестов. Руководство фирмы пред-
полагает, что 90% продавцов работают эффективно. Возникает
проблема, как проверить эту гипотезу, если сплошная провер-
ка продавцов невозможна в силу ограниченности средств.
Для решения задачи используем выборочный метод. Для этого
случайным образом отберем приемлемое для статистических
заключений количество продавцов и проведем среди них тес-
тирование, затем по результатам выборочной проверки сдела-
ем заключение о правильности предположения, что ровно 90%
всего состава продавцов работают эффективно.
Пусть результаты тестирования показали, что 95% продав-
цов успешно прошли испытание. Очевидно, в этом случае ну-
левая гипотеза будет достаточно правдоподобной. Предполо-
жим, что проверку прошли только 46% продавцов. Тогда здравый
смысл подсказывает, что есть достаточные основания для не-
принятия нулевой гипотезы.
Как видно, в обоих случаях нет четкого формального пра-
вила или критерия для подтверждения или неприятия нулевой
гипотезы. Заключения делались только на основе здравого смыс-
ла и интуиции. Пусть, например, значение выборочной про-
центной доли — 88%, тогда принятие решения о правильности
нулевой гипотезы на уровне здравого смысла будет очень за-
труднительным.
Формальная процедура проверки гипотез заключается в ус-
тановлении критических пределов для оценки значимых от-
клонений вычисленной статистики от гипотетического значе-
ния параметра генеральной совокупности.
Если выборочное значение статистики попадает внутрь про-
межутка, ограниченного критическими пределами, то откло-
нение считается статистически незначимым и нулевая гипоте-
за принимается. Если же разность столь велика, что статистика
выходит за критические пределы, то отклонение считается ста-
тистически значимым и нулевая гипотеза отвергается. При этом
решение принимается с некоторой вероятностью, так как раз-
ность между выборочной статистикой и гипотетическим зна-
чением параметра является случайной величиной. Эта величи-
218
на называется статистическим критерием (или просто крите-
рием). Таким образом, критерий является разностью между
распределением выборочных статистик и константой — гипо-
тетическим значением параметра генеральной совокупности.
Отсюда следует, что как случайная величина он будет распре-
делен по тому же закону, что и выборочная статистика.
В общем случае возможна проверка гипотез относительно
произвольного параметра в условиях любого статистического
критерия. В этой главе нас будет интересовать проверка гипотез
относительно генеральной средней. Как было показано в гл. 8,
соответствующие выборочные распределения выборочных сред-
них могут быть двух типов: нормальное распределение и г-рас-
пределение Стьюдента. Выбор критерия зависит от объема вы-
борки, а также от того, известно или нет значение генерального
стандартного отклонения о.
9.1.1. Критическая область. Уровень значимости
Пусть выдвигается нулевая гипотеза относительно парамет-
ра генеральной совокупности. Рассмотрим соответствующее рас-
пределение выборочных статистик. Рассуждения теперь будем
проводить для проверки гипотез относительно средней, пола-
гая, что объем выборки достаточно большой (л > 30).
В этом случае согласно центральной предельной теореме
распределение выборочных средних является нормальным. Если
нулевая гипотеза верна, то значения статистик располагаются
симметрично относительно гипотетической средней. Пусть ге-
неральная совокупность, откуда извлекались выборки объема
л, имеет параметры ц и о2. Тогда распределение выборочных
средних характеризуется средней Ц, = ц и стандартным от-
клонением (стандартной ошибкой) =
sill
Построим критические пределы для проверки нулевой ги-
потезы, используя понятие доверительных пределов для оцен-
ки средней. Так, можно утверждать, что внутри промежутка
+ ) сосредоточено (I — а)% всех выбороч-
ных средних. Доля плошали под кривой распределения, огра-
ниченная этим промежутком, также будет равна (I — а).
Если вычисленная статистика находится в доверительных
пределах, то можно записать:
H-2o/2aj<i<p + Za/2or. (9.1)
219
Используя понятие доверительной вероятности, соотноше-
ние (9.1) можно интерпретировать так:
P(M-Ze72ai<x<H+Ze/2ai) = l-a. (9.2)
Очевидно, вероятность того, что значения рассматриваемых
статистик выйдут за доверительные пределы, будет равна уров-
ню значимости а:
Р(х<ц~2а/2о5 или х>ц + Za/2oa) = а. (9.3)
Рассмотрим теперь формальную постановку задачи провер-
ки гипотез относительно генеральной средней.
Пусть до сбора выборочных данных была выдвинута нулевая
гипотеза относительно средней. Нулевая гипотеза обозначается
символом Н(), и ее формальная запись имеет вид
Н0:ц=ц0. (9.4)
Запись (9.4) читается так: нулевая гипотеза заключается в
предположении, что значение средней генеральной совокуп-
ности равно цц. В результате сравнения с выборочным значени-
ем средней нулевая гипотеза может быть отвергнута. В этом слу-
чае принимается альтернативная гипотеза, которая обозначается
Н(. Ее запись имеет вид
(9.5)
Выражение (9.5) читается так: альтернативная гипотеза зак-
лючается в том, что генеральная средняя не равна ц0.
После того как сформулированы нулевая и альтернативная
гипотезы, необходимо задать правило, по которому принима-
ется решение о принятии или непринятии нулевой гипотезы.
Это правило следует из соотношений (9.2) и (9.3). Если а дос-
таточно мало, то получение большого отклонения выборочной
статистики от истинного значения параметра будет маловеро-
ятным событием. Пусть, например, a = 5% (или a = 0,05). Тогда
такая большая разность будет наблюдаться в среднем в 5 из 100
случайных выборок. Поэтому проверка гипотез всегда привя-
зывается к определенному уровню значимости, т. е. формули-
ровка задачи обязательно предполагает задание уровня значи-
мости, при котором проверяется нулевая гипотеза. Если
выполняется условие (9.2), то говорят, что нулевая гипотеза
принимается или не отвергается с уровнем значимости а. Вы-
ражение “не отвергается” будет более точным, так как прини-
220
мать гипотезу можно в случае, если известно точное значение
параметра. Если выполняется условие (9.3), то говорят, что
нулевая гипотеза не принимается или отвергается с уровнем
значимости а.
Таким образом, доверительные пределы играют роль кри-
тических пределов. Между ними находится область принятия
нулевой гипотезы, а вне них — критическая область, или об-
ласть непринятия гипотезы (рис. 9.1).
Рис. 9.1. Области принятия или непринятия нулевой гипотезы
относительно средней при уровне значимости а
Полагая ц = ц0, преобразуем соотношение (9.1) к виду
-Za/i<^<Za/2. (9.6)
Соотношение (9.6) можно переписать:
^<Za/2. (9.7)
Соотношение (9.7) задает критические пределы и область
принятия гипотезы для стандартного распределения Z, где
Z = -—— характеризует отклонение выборочной средней от
гипотетической средней в единицах стандартной ошибки сред-
ней.
Критическая область задается условием
^^а/2. (9.8)
221
На практике проверка гипотезы производится при следую-
щих уровнях значимости:
« 0.01 0,05 0.1
ZV2 2.58 1.96 1,64
Пример 9.2. Автоматический станок производит болты. Извест-
но, что дойна болтов распределена по нормальному закону с
дисперсией 0,16 мм2. Станок должен быть налажен на выпуск
болтов со средней дойной 20 мм. Из большой партии болтов,
произведенных за смену на станке, была извлечена выборка из
25 болтов. Средняя длина выбранных болтов оказалась равной
20 мм. Требуется проверить при 5-процентном уровне значимо-
сти нулевую гипотезу о том, что станок производит болты со
средней дойной 20 мм, т. е. не требует переналадки.
Запишем формальную постановку задачи проверки гипотез:
Ио: = 20 мм,
Н: цо * 20 мм.
Параметры задачи имеют следующие значения: п = 25,
х =20,1 мм, а2 = 0,16 мм2 (ст = 0,4 мм), а = 0,05, Z(l(|,5 = 1,96.
Вычислим критерий Z:
Z = = 20,*~2° = 1,25.
о 0,4
т
Ввиду того что |Z| = 1,25 < 1,96, статистика попадает в об-
ласть принятия нулевой гипотезы. Следовательно, нулевая ги-
потеза Нп не отвергается с уровнем значимости 5%.
9.1.2. Ошибки первого и второго вида
При проверке гипотезы необходимо прийти к решению:
принимается гипотеза Hfl или отвергается (т. с. принимается
альтернативная гипотеза Нр. При этом возможны ошибки двух
видов:
непринятие правильной гипотезы (т. е. непринятие нуле-
вой гипотезы, в то время как она верна) — ошибка первого
вида;
принятие неправильной гипотезы (принятие нулевой гипо-
тезы, в то время как она неверна) — ошибка второго вида.
222
Всегда в принятии нулевой гипотезы есть риск совершить
ошибку второго вида, а в ее отклонении — ошибку первого
вида. Как было отмечено, установление критических пределов
всегда предполагает задание уровня значимости а. Очевидно, а
есть вероятность попадания выборочной статистики в зону не-
принятия нулевой гипотезы при условии правильности этой
гипотезы. Иначе говоря, проверка значимости непосредствен-
но отражает степень риска появления ошибки первого вида, т.
е. характеризует вероятность совершения этой ошибки в при-
нятии решений.
Ошибка второго вида зависит от того, насколько правдопо-
добна альтернативная гипотеза. Пусть, например, нулевая ги-
потеза (Н(): ц = ц0) неверна, а истинное значение средней
ц = ц Тогда ошибка второго вида будет характеризоваться по-
паданием значения выборочной средней в заштрихованную
область на рис. 9.2.
Рис. 9.2. Геометрический смысл ошибки второго вида: заштрихованная
площадь равна вероятности ошибки второго вида (Р)
Из рис. 9.2 видно, что чем больше площадь области принятия
нулевой гипотезы (т. е. чем шире промежуток (Цо~^а/2ао'
ц0 + Za/2o0)), тем больше площадь пересечения под кривыми
двух распределений, характеризующая ошибку второго вида.
С другой стороны, с увеличением области принятия нулевой
гипотезы уменьшается суммарная площадь под “хвостовыми”
частями соответствующей кривой распределения. Как раз эта пло-
щадь и характеризует ошибку первого вида. Таким образом, если
уменьшается вероятность ошибки первого вида (т. е. уровень зна-
чимости а), то одновременно увеличивается вероятность ошиб-
ки второго вида р, связанной с принятием нулевой гипотезы,
которая в действительности неверна.
В данной работе вычисление ошибки второго вида не рас-
сматривается.
223
9.1.3. Двусторонние и односторонние проверки гипотез
относительно средней
Пусть альтернативная гипотеза задается выражением (9.5).
Это означает, что альтернативой нулевой гипотезе может быть
либо выполнение неравенства ц < ц0, либо неравенства
ц > ц0.Тогда существуют два симметричных критических преде-
ла и, как видно из рис. 9.1, две соответствующие области не-
принятия гипотезы под “хвостовыми” частями кривой распре-
деления. Подобные проверки называются двусторонними.
Возможны также односторонние проверки гипотез. В этом
случае рассматривается альтернативная гипотеза (Н() о том,
что истинное значение параметра не просто отличается, а боль-
ше (или меньше) гипотетического значения. Так, возможны
две постановки задачи односторонней проверки гипотез:
Но;М = Мо,
Н,:ц>мв. (9.9)
Но; Н = Н0.
Н,:ц<м0. (9.10)
Выражение (9.9) ((9.10)) характеризует предположение: вы-
борочная средняя значимо больше (меньше) гипотетичес-
кого значения средней.
В отличие от двусторонней проверки односторонней соот-
ветствует только один критический предел. Так, в случае (9.9),
когда проверяется значимость превышения выборочной сред-
ней гипотетического значения, критический предел будет за-
даваться неравенством
х>В0 + гаЛ, (9.11)
или
(9.12)
Vn
где Za характеризует такое значение Z для стандартного
нормального распределения, которое отделяет правую
“хвостовую” часть кривой с долей площади, равной а%
(рис. 9.3).
224
Рис 9.3. Односторонняя проверка гипотезы Н,: ц>ц0:
а) произвольное нормальное распределение.
б) стандартное нормальное распределение
Если производится проверка предположения о том, что
выборочная средняя значимо меньше гипотетической средней,
то критическая область задается неравенством
isn.-z.4-. ОН)
у п
или
(9.14)
где величина —Za отделяет левую “хвостовую” часть кривой
стандартного нормального распределения, площадь под ко-
торой составляет а% всей площади кривой.
Величина Z задается уровнем значимости а. На практике
при односторонних проверках чаще всего используют следую-
щие значения:
a 0.01 0,05 0,1
±z s2,33 ±1,64 si,58
Пример 9.3. Рассмотрим условия примера 9.2. Пусть теперь тре-
буется проверить гипотезу, что станок производит болты со
средней длиной, превышающей 20 мм. Задача в этом случае
записывается так:
Но: ц0 = 20 мм,
Н(: ц0 > 20 мм.
Параметры задачи те же, за исключением значения крити-
ческого предела Za, который равен Z00i= 1,64. Величина крите-
рия Z меньше критического предела:
Z- 1,25 < 1,64.
225
Следовательно, гипотеза Но принимается с 5-процентным
уровнем значимости. Это говорит о том, что предположение о
разладке станка (т. е. о том, что он производит болты со сред-
ней длиной, превышающей 20 мм) не подтвердилось.
9.2. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО
СРЕДНЕЙ: СЛУЧАЙ ОДНОЙ ГЕНЕРАЛЬНОЙ
СОВОКУПНОСТИ
9.2.1. Значение генерального стандартного
отклонения известно
Пусть выборка объема п берется из бесконечной или очень
большой генеральной совокупности, распределенной по нор-
мальному закону (или близкому к нему). Стандартное отклоне-
ние генеральной совокупности известно и равно о. В этом слу-
чае независимо от объема выборки критическая область для
двусторонней проверки находится из соотношения (9.8).
Если требуется односторонняя проверка, то критические
области задаются соотношениями (9.11), (9.12) или (9.13),
(9.14).
В примерах 9.2 и 9.3 рассматривалась ситуация, когда вы-
полнялись перечисленные выше условия: распределение зна-
чений длины болтов предполагалось нормальным и было из-
вестно значение а = 0,04 мм. Следует отметить, что в данных
примерах гипотеза проверялась на основе малой выборки (л
= 25<30).
Если нормальная совокупность конечна и имеет объем N,
то следует проверить соотношение между N и объемом выбор-
ки л. В случае л > 0,05А при вычислении стандартной ошибки
средней необходимо учитывать поправку на конечность гене-
„ ст |Л/-л _ „ „
ральнои совокупности, т. е. стк =-?—л- Тогда критерий Z
•Jn \ N-I
для проверки гипотез имеет вид:
Z = — М— (915)
ст । N - п
Tn V А-1
Пример 9.4. Рассмотрим условия примеров 9.2 и 9.3. Будем пред-
полагать, что партия, откуда была извлечена выборка объема
226
25, составляет 300 болтов. Таким образом, n/N = 25/300 =
= 0,0833>0,5.
Вычислим поправочный множитель:
_ 130°-25 -092
V /V -1 V 299
Критерий Z определим по формуле (9.15):
z= 2ОЛ-_2О= 0,1 =
2d. о 92 °”074 ’
5 ’
Следовательно, при а =0,05 двусторонняя и односторонняя
проверки показывают, что нулевая гипотеза не может быть от-
вергнута.
9.2.2. Значение генерального стандартного отклонения
неизвестно: большая выборка
На практике значение стандартного отклонения генеральной
совокупности о, как правило, неизвестно. В этом случае его можно
заменить на соответствующую статистику — выборочное стан-
дартное отклонение з. При этом для адекватности результата
проверки объем выборки должен быть не менее 30. Стандартная
ошибка средней заменяется оценочным значением:
s
°iasi = -T-
•sin
Величина Z вычисляется следующим образом:
Z = ^do. (9.16)
s
-Jn
Если генеральная совокупность относительно_мала и вы-
з Гл/ -п
полняется соотношение л>0,05Л/, то «j = “p-klT,-Т- Тогда
критерий Z имеет вид ™ “
Z = —. (9.17)
5 UV-fl
7л V N-1
Пример 9.5. Фирма выпускает компоненты для электронных при-
боров со средним сроком службы 100 ч. После того как была
227
введена новая технология производства, случайным образом было
проверено 100 компонентов. Результаты теста показали, что сред-
ний срок службы равен 102,5 ч с дисперсией 99 ч2. Требуется
проверить гипотезу о том, что новая технология способствовала
увеличению среднего срока службы компонентов. В данном слу-
чае следует провести одностороннюю проверку на превышение:
Н0:ц= 100,
Н(:ц> 100.
Значение о неизвестно, поэтому вычислим значение 5. Ве-
личина выборочной дисперсии известна (? = 99). Отсюда
5 = V99 = 9,95 ч. По формуле (9.16) вычислим значение Z:
102,5-100 2,5 _
9,95 0,995
10
Критическим пределом при уровне значимости 5% является
ZOI)5= 1,64. Таким образом, 2,51 >1,64, что свидетельствует о том,
что нулевая гипотеза о равенстве средних с 5-процснтным уров-
нем значимости отвергается: принимается предположение, что
новая технология удлинила срок работы компонентов.
Пример 9.6. Фермер выращивает кур. В течение нескольких лет
средний вес кур составлял 1,85 кг. За последние месяцы на
ферме было выращено 350 кур с использованием корма нового
типа. Случайным образом фермер отобрал 35 кур и определил,
что их средний вес равен 2,03 кг со стандартным отклонением
0,8 кг. Фермеру нужно выяснить, повлияло ли использование
нового корма на увеличение среднего веса кур. Проверку сле-
дует вести при а = 0,05.
Данная ситуация предусматривает одностороннюю провер-
ку на превышение. Задача имеет следующие параметры:
N — 350, п = 35, ц0 = 1,85 кг, х = 1,93 кг,
5 = 0,8 кг, Za = 1,64.
Так как n/N = 35/350 = 0,1 >0,05, то критерий Z вычисляет-
ся с учетом поправочного множителя по формуле (9.17):
Z = 2,03-1,85 _ 0,18 _ 37
0,8 }350 -35 0.76
г/35 V 350-1
228
Имеем Z=2,5I>),64. Следовательно, нулевая гипотеза (Но:
ц = 1,85 кг) отвергается, а альтернативная об увеличении сред-
него веса кур (Н^ ц >1,85 кг) не отвергается при а = 5%.
9.2.3. Значение генерального стандартного отклонения
неизвестно: малая выборка
Как было показано в разделе 8.3.1.2, в случае малых выбо-
рок (л<30) при неизвестном о для опенки параметров следует
использовать /-распределение. Аналогично для проверки нуле-
х — ц
вой гипотезы вычисляется /-критерий / =—- , который
'!п
сравнивается по абсолютной величине с критическим значением
U.-r Критический предел определяется из таблицы площа-
дей кривой /-распределения (Приложение 5). Он находится на
пересечении строки, соответствующей числу степеней свобо-
ды df = п — 1, и столбца, соответствующего а/2, т. е. доли
отсекаемой площади в “хвостовой” части /-распределения.
Область принятия нулевой гипотезы в случае двусторонней
проверки задается соотношением

</а/2и-1-
(9-18)
Соответственно критическая область задается неравенством
*-Цо
(9.19)
S/a/2»-l’
Для односторонней проверки критическая область задается
неравенствами без модуля. Если проверяется гипотеза о значи-
мом превышении выборочной средней значения генеральной
средней, то критическая область задается неравенством
(9.20)
fn
где / _ (является критическим пределом, отделяющим под кри-
вой /-распределения (df= п — 1) правую “хвостовую” часть,
площадь под которой составляет а% площади всей кривой.
229
Аналогично для проверки значимости отклонения влево
область непринятия нулевой гипотезы характеризуется соотно-
шением
s " (9.21)
/п
где значение -tu я_ (отделяет левый “хвост” с площадью, рав-
ной а% площади под всей кривой /-распределения при
df= л - I. Для нахождения качения / _, можно исполь-
зовать таблицу Приложения 5, соответствующую двухсто-
ронним проверкам.
Если генеральная совокупность конечна, имеет объем N, а
размер выборки п > 0,057V, то стандартная ошибка средней
т
в неравенствах (9.18)—(9.21) умножается на коррек-
-ул I----
„ N-n
тирующий множитель J—------, характеризующим поправку на
V N -1
конечность генеральной совокупности.
Пример 9.7. Известно, что средний срок службы определенно-
го типа батареек для часов составляет 305 дней и подчиняется
нормальному закону. Рассматриваемый тип батареек был усо-
вершенствован с целью продления срока службы. Случайным
образом было выбрано 20 батареек нового типа, которые были
протестированы. Результаты проверки показали, что средний
срок службы новых батареек равен 3! I дням со стандартным
отклонением 12 дней. При 5-процентном уровне значимости
требуется проверить, что средний срок новых батареек превы-
шает 305 дней.
В данном случае осуществляется односторонняя проверка,
задаваемая соотношениями (9.18) и (9.19). Критический пре-
дел задается значением / = 1,729 (Приложение 5). Вычис-
лим /:
„Ц13О5.2,„6.
/20
Следовательно, нулевая гипотеза ( Н : ц = 305) отвергается
в пользу альтернативной гипотезы (Н ; ц>305). Можно утверж-
дать с 5-процентным уровнем значимости, что средний срок
службы батареек увеличился.
230
Пример 9.В. В магазин поступила партия из 300 килограммовых
пакетов сахара. Возникло подозрение, что средний вес пакетов
в партии существенно отличается от I кг. Для проверки случай-
ным образом было выбрано и взвешено 20 пакетов. Их средний
вес оказался равным 920 г со стандартным отклонением 75 г.
Требуется проверить данное предположение, используя 1-про-
центный уровень значимости.
Параметры задачи: ц0= 1000 г, х = 920 г, 5 = 75 г, п = 20,
У = 300, а = 0,01.
Проверим соотношение n/N = 20/300=0,067>0,05. Следова-
тельно, при вычислении значения г следует учитывать поправ-
ку на конечность генеральной совокупности:
t - = ?20-1000 _ -80 = _348
fN-n 75 1280 23,73 0,97
TnVN-l 710 V299
Определим критические пределы для двусторонней провер-
ки по таблице Приложения 5: ±/0 00$. „ = ±2,86.
Так как |-3,48|> 2,861, то нулевая гипотеза (Но: ц= 1000) не
может быть принята с уровнем значимости, равным 1%.
Следовательно, предположение о том, что средний вес па-
кета значимо отличается от 1кг (т. е. альтернативная гипотеза Н :
ц # 100), является правильным.
В данном случае, очевидно, имеет смысл сделать односто-
роннюю проверку, т. е. проверить альтернативную гипотезу, что
средний вес пакетов в партии меньше 1 кг (Н : ц< 100). Крити-
ческим пределом тогда будет значение -г00)Так как
-3,48<-2,539, то это предположение принимается с 1-процен-
тным уровнем значимости.
9.3. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО
РАЗНОСТИ СРЕДНИХ ДВУХ ГЕНЕРАЛЬНЫХ
СОВОКУПНОСТЕЙ
»
9.3.1. Случай больших выборок
На практике достаточно часто приходится сравнивать сред-
ние двух различных генеральных совокупностей. Например, две
фирмы выпускают батарейки для бытовых приборов. Требуется
определить, какая фирма выпускает батарейки с большим сред-
ним сроком службы.
231
Пусть рассматриваются две различные генеральные совокуп-
ности с параметрами и ц2,ог Из каждой совокупности из-
влекаются большие случайные независимые выборки фикси-
рованного объема соответственно и п. Тогда соответствующие
распределения выборочных средних будут нормальными с па-
раметрами
Очевидно, разность этих распределений является случайной
величиной, распределенной по нормальному закону со сред-
ней р.! — ц2 и дисперсией, равной сумме дисперсий:
_2
X, “Xj X,
Л1 «2
Таким образом, распределение разности выборочных сред-
них будет нормальным с параметрами
10^ ст2
Н,-Ц2.ог г = +
' ’ V«i л2
При проверке гипотезы о значимости разности между вы-
борочными средними рассматривается нулевая гипотеза
(9.22)
В случае двусторонней проверки альтернативная гипотеза
имеет вид
Н(:р, *ц2.
При односторонней проверке возможны случаи:
(9.23)
Н,:ц1<ц2. (9.24)
Пусть х( — средняя выборки объема л, из первой генераль-
ной совокупности, х2— средняя выборки объема л, из второй
генеральной совокупности.
Вычислим отношение Z для проверки нулевой гипотезы
(9.22):
Z =
Л1 л2
(х, —х2)-(ц,-ц2)
(9.25)
232
Для двусторонней проверки нулевая гипотеза не отвергает-
ся с уровнем значимости а, если выполняется условие
и=
< Za/2-
(9.26)
Критическая область задается соответственно неравенством
Za,2-
(9.27)
Для односторонних проверок критические пределы для уров-
ня значимости а будут соответственно ±Za. Так, при альтерна-
тивной гипотезе (9.23) соотношения для областей принятия и
непринятия нулевой гипотезы будут иметь вид
Z = .\~Хг <Za, (9.28)
'j «1 «2
z = 2 Za. (9.29)
\ л, л2
Для альтернативной гипотезы (9.24) соответствующие об-
ласти задаются неравенствами
Z» .ЛгЛ, 2-Za, (9.30)
\ "1 п2
Z = -^-^2—^-Za. (9.31)
I О? СГ
V «1 «2
Если анализируемые генеральные совокупности распреде-
лены нормально, то соотношения (9.26)—(9.31) можно исполь-
зовать при проверки гипотез и в случае малых выборок (л^ЗО,
л2<30).
На практике значения стандартных отклонений о, и о2для
енеральных совокупностей часто бывают неизвестны. Для боль-
ших выборок возможна замена их значений на соответствую-
233
щие выборочные статистики и Тогда критерий Z в выра-
жениях (9.26)—(9.31) примет вид
• <9з2>
"1 «2
Пример 9.9. Две независимые автоматизированные линии вы-
пускают кабель. Для обеих линий средняя длина кабеля должна
быть одинаковой. Предполагается, что длина кабеля в обоих
случаях распределена нормально со стандартными отклонени-
ями оа1мио«1,5м. Возникло предположение, что линии
выпускают кабель с различной средней длиной. Требуется про-
верить данное предположение с уровнем значимости а = 0,05.
Для этой цели были рассмотрены две случайные выборки: одна
выборка состояла из 15 кусков кабеля, произведенных на пер-
вой линии, другая — из 13 кусков, выпускаемых второй лини-
ей. Для первой выборки средняя длина кабеля оказалась равной
52 м, для второй — 51м.
Обозначим среднюю длину кабеля, выпускаемого первой
линией, ц^а второй —
Тогда задачу проверки гипотезы формально можно записать
так:
Но: Н, =
Н,: Ц1 * Ц,.
Задача имеет следующие исходные данные: х,= 52 м, х2 =
51 м, 0,= I м, о(= 1,5 м, л( = 15, л2= 13, ZOO25 = 1,96.
Вычислим величину Z:
Z- ,52~51 - 1 - 1 -2СИ
l|2 1.52 70.067 + 0,173 0,49 ’
V 15 + 1Т
Отсюда |Z| = 2,04> 1,96, т. е. нулевая гипотеза не может быть
принята при уровне значимости 5%. Следовательно, предположе-
ние о том, что линии производят куски кабеля разной средней
длины, оправдалось с 5-процентным уровнем значимости.
Пример 9.10. Исследуем ситуацию, представленную в примере
8.15, как задачу проверки гипотез. Пусть две научно-исследо-
вательские лаборатории независимо друг от друга занимаются
разработкой лекарственных препаратов для больных, страдаю-
234
ших артритом. Таблетки, произведенные первой лаборатори-
ей, были опробованы на 90 больных в период сильных присту-
пов боли. В среднем прием таблетки обеспечивал снятие боли в
течение 8,5 ч со стандартным отклонением 1,8 ч. Действие таб-
леток второй лаборатории, опробованное на 80 больных, обес-
печивало снятие боли в среднем на 7,9 ч со стандартным от-
клонением 2,1 ч. Требуется при 5-лроцентном уровне значимости
проверить предположение о том, что период действия табле-
ток второй лаборатории значимо меньше, чем период действия
таблеток первой лаборатории.
Формальная запись задачи проверки гипотез будет иметь вид
Но: и, = и2,
Н,: < И|.
Параметры задачи: х(= 8,5 ч, х2- 7,9 ч, $ 1,8 ч, $2 = 2,1 ч,
л, = 90, „,-80,2^-1,64.
Вычислим Z:
7,9-8,5 _ -0,6
I1.82 2.12 70’036 + 0,055
J 90 + 80
Следовательно, —1,99<-1,64 и нулевая гипотеза не может
быть принята с уровнем значимости, равным 5%, т. е. выска-
занное предположение подтверждается с 5-процентным уров-
нем значимости.
9.3.2. Случай малых выборок
Пусть объемы выборок, которые берутся из рахтичных ге-
неральных совокупностей, меньше 30. В этом случае процедура
проверки гипотез относительно разности генеральных средних
мало чем отличается от случая больших выборок. Единственное
отличие состоит в том, что критическая область определяется
на основе /-распределения Стьюдента.
В качестве критерия оценки рассматривается отношение
•= (9-33>
i£l + £l
V «1 П2
Отношение (9.33) имеет приблизительно /-распределение
для числа степеней свободы, задаваемого формулой (8.18).
235
Пример 9.11. Рассмотрим ситуацию примера 8.13. Пусть требу-
ется проверить гипотезу, что средние сроки износа покрышек
двух типов не равны между собой:
Но: И, = Н2,
Н,: h * h-
Воспользуемся формулой (9.33):
t_ 3,3-3,98 _-0.65^ 325
^0,682 t 0,38~ 0.2
V 15 + 15
Чисто степеней свободы, найденное по формуле (8.18), равно
df = 21. Проведем проверку с IО-пропентным уровнем значи-
мости, т. е. критическая область задается неравенством
= 1,721. Так как |—3,25|> 1,721, то нулевая гипотеза не может
быть принята. Следовательно, предположение о том, что сред-
ние сроки износа двух типов покрышек не равны между собой,
подтверждается с уровнем значимости 10%.
Рассмотрим теперь одностороннюю проверку, т. е. предпо-
ложение, что покрышки типа В имеют больший срок износа,
чем типа Л:
Но: М1 = и2;
Н,: ц, < ц2.
В этом случае критический предел задается величиной
tQ 1 21 = -1,323, т. е. проверяется условие К—10)21. Ввиду того что
—3,25 < —1,323, нулевая гипотеза о равенстве сроков износа
отвергается и принимается альтернативная гипотеза о превы-
шении срока износа покрышек типа В.
Особый случай представляет ситуация, когда дисперсии ге-
неральных совокупностей равны: о(2 = о22. Такая ситуация дос-
таточно часто встречается в производственных процессах с дол-
госрочным циклом. В таких случаях обработка статистических
данных за предыдущие периоды времени подтверждает равен-
ство дисперсий.
Кроме того, подобная ситуация может возникнуть при про-
верке гипотезы о том, что выборки были получены из одина-
ковых или одной и той же генеральной совокупности. Тогда про-
верку следует производить в предположении, что о,2 = о22 = о.
На практике, если нет очевидных аргументов, указывающих
236
на то, что дисперсии не равны, можно вполне допускать их
равенство.
Пусть объем выборок не превышает 30 и выполняются усло-
вия:
I) выборки извлекаются из двух различных генеральных со-
вокупностей независимо друг от друга;
2) обе генеральные совокупности приблизительно нормаль-
ные;
3) дисперсии совокупностей равны.
Рассмотрим выборочное распределение разностей выбороч-
ных средних, принадлежащих различным совокупностям. Об-
щая дисперсия генеральной совокупности неизвестна, но она
может быть оценена, если вычислены выборочные дисперсии
j(2 h'j22. Если л( и л, — соответствующие объемы выборок, то в
качестве оценки общей генеральной дисперсии можно рассмат-
ривать взвешенную среднюю величину
s2 (»i ~ D*? + («2 ~
(л,-1) + (л2-1)
где л( — 1 и л2 - I — степени свободы соответственно для вы-
борок из первой и второй совокупностей.
Так как дисперсии равны, то выборочное распределение
разностей выборочных средних будет иметь дисперсию
+ f! = ± +
х,-х’ Л] л2 л, + л2 - 2 [ л, л2 J
Соответственно стандартное отклонение или стандартная
ошибка разности средних такова:
= ± + |±71. (,.34)
11 ч Л| + л2 - 2 Л] л2 J ул, л2
Если средние генеральных совокупностей совпадают, то
можно считать, что обе выборки берутся из одной или одина-
ковых совокупностей.
Пусть рассматривается задача проверки гипотез:
Но: Ц, = ц2,
Н,: м, * м2.
237
В качестве критерия возьмем величину
t = . (9.35)
(И,-1)*?-Ь("2-1)4Г 1 + ±1
Л| + п2 - 2 л1 л2 J
При уровне значимости а величина сравнивается со значе-
нием где df = + л2 - 2.
Если И<Га/2 я . _2, то нулевая гипотеза не может быть от-
вергнута с уровнем2 значимости а. В случае |г^г , . „ _ 2 раз-
ность средних попадает в критическую зону и нулевая гипотеза
Но отвергается при уровне значимости а. Для односторонних
проверок рассматриваются соответствующие критические пре-
делы ±1
“• "1 "2 ~ *
Пример 9.12. Проверим гипотезу примера 9.11 в предположе-
нии, что дисперсии сроков износа покрышек обоих типов рав-
ны между собой. Найдем взвешенную среднюю дисперсию и
стандартное отклонение:
2 (15-1)0.682 + (15-1)0,382 _ 8,495
15 + 15-2 28
5 = 70,303=0,55.
По формуле (9.34) найдем стандартную ошибку разности
= 0,55
£ 1
15 + 15
= 0,2.
Вычислим значение критерия оценки:
х.-х, 3,33-3,98
t = —г---=— =----------= -3.25.
I 1 1 0,2
5 — +---
V «1 п2
Критическое значение г при а = 0,1 находится для df = 28:
'0.0,2 = ‘.701.
Следовательно, |-3,25| = 3,25> 1,701 и нулевая гипотеза от-
вергается.
Аналогично осуществляется односторонняя проверка, для
которой критическое значение равно f01 м = -1,313. Отсюда
следует, что гипотеза Но отвергается, а предположение о пре-
вышении срока износа покрышек типа В над сроком покрышек
238
типа А принимается с 10-процентным уровнем значимости. Как
видно, предположение о равенстве дисперсий двух совокупно-
стей никак не повлияло на результаты проверок, которые сов-
пали с результатами примера 9.11 (где предполагалось, что
°.2*°АВ
9.3.3. Сравнение средних двух нормальных совокупностей
на основе пар наблюдений
Ранее при сравнении двух выборочных средних необходи-
мым условием было получение выборок из двух нормальных
совокупностей независимо друг от друга. Однако часто возни-
кает ситуация, когда элементы выборок рассматриваются по-
парно. Например, пара наблюдений соответствует одному и тому
же городу, моменту времени, супружеской паре или даже од-
ному и тому же лицу.
Пусть имеется п пар наблюдений:
Ц.У,). (х2,у2),..., (хя,уя).
Рассмотрим разности, соответствующие каждой паре:
= Xj - у, = х2 — у,,..., dn — хп — уя. Проблему сравнения
двух совокупностей данных сведем к анализу одной совокуп-
ности, состоящей из разностей d. Для этой цели вычислим вы-
борочное стандартное отклонение разностей
где d = ~-----выборочная средняя разностей,
л
Ввиду того что каждый элемент пары берется из нормаль-
ной генеральной совокупности, распределение выборочных
разностей будет также нормальным. Предположим, что нужно
проверить гипотезу о том, что средняя этого распределения
равна Do, тогда задачу проверки гипотез можно записать так:
Но: М, = Д>.
239
Если число рассматриваемых пар п £30, то для проверки
можно использовать стандартное нормальное распределение.
В случае л <30 в качестве критерия используется /-распределе-
ние Стъюдента. При этом проверяется отношение
которое сравнивается со значениями /-распределения при
dfx п - I и заданном уровне значимости а. Если |/.|>/и.,„ J,, то
гипотеза Но отвергается с уровнем значимости а. Односторон-
ние проверки выполняются аналогично: Н : ц <Л (/>/ )
либо Н(: ^>D0(td<-/__,).
Пример 9.13. Руководство отдела маркетинговых исследований
фирмы, торгующей пищевыми продуктами, должно принять
решение о форме упаковки для быстрого завтрака (овсяные
хлопья). Было предложено два вида упаковки: прямоугольная
коробка и цилиндрический контейнер. Пробное исследование
проводилось в 10 супермаркетах, где в каждом супермаркете на
противоположных сторонах торговой секции выставлялись на
полках упаковки соответствующей формы (на каждой стороне —
упаковки одной и той же формы). Цель исследований — понять,
существует ли разница в продажах для упаковок разных типов?
Проверку гипотез следует осуществлять при а = 0,05.
Данные о продажах в 10 супермаркетах были объединены в
пары:
Супермаркеты 1 2 3 4 5 6 7 8 9 10
Коробка (шт.) 194 152 160 172 110 137 126 176 145 118
Цилиндр (шт.) 184 161 153 184 123 155 111 156 129 105
Определим соответствующие разности пар элементов выбо-
рок и вычислим их квадраты.
Супермаркеты 1 2 3 4 5 6 7 8 9 10 сумма
d 10 -9 7 -12 -13 -18 15 20 16 13 29
d2 100 81 49 144 169 324 225 400 256 169 1917
Пусть ц — средняя разностей между продажами упаковок
различной формы. Требуется проверить нулевую гипотезу:
Нв: Ма=^о=О.
Н,:ц^0.
240
Вычислим:
/n '1917-292/10
n-1 V 9
Вычислим /-отношение (9.36):
2.9-0 Л,.а
ta — "“жи" = 0,643.
14,72/^'40
По таблице Приложения 5 найдем г = 2,262.
Так как |zj =0,643<2,262, то гипотеза Но не может быть от-
вергнута. Таким образом, нет достаточных оснований предпо-
лагать, что форма упаковки влияет на продажу.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 9
В отличие от оценки параметров проверка гипотез предпо-
лагает обратную последовательность действий. Еще до получе-
ния выборочных данных выдвигается предположение (гипоте-
за) о точном значении некоторого параметра генеральной
совокупности. Затем собираются выборочные данные, образу-
ющие случайную выборку. На ее основе вычисляется оценоч-
ная статистика и проверяется, насколько правдоподобна вы-
двигаемая гипотеза относительно того, что принятое значение
параметра является правильным. Гипотеза о нулевой разности
между предполагаемым и истинным значениями параметра ге-
неральной совокупности называется нулевой гипотезой.
При проверке нулевой гипотезы оценивается статистичес-
кая значимость разности между вычисляемым выборочным зна-
чением статистики и предполагаемым истинным значением
параметра. Расхождение возникает в связи со случайностью
выборки. Формальная процедура оценки гипотез заключается в
установлении критических пределов для оценки значения от-
клонения от истинного значения параметра. Если выборочное
значение попадает внутрь промежутка, ограниченного крити-
ческими пределами (область принятия гипотезы), то нулевая
гипотеза принимается. Если же значение статистики выходит
за критические пределы (область непринятия гипотезы), то
отклонение считается статистически значимым и нулевая ги-
241
потеза отвергается. Решение о принятии или непринятии нуле-
вой гипотезы характеризуется некоторой вероятностью, так как
разность между выборочной статистикой и гипотетическим
значением параметра является случайной величиной, которая
называется критерием. При проверке гипотез относительно сред-
ней генеральной совокупности возможны два вида критериев:
нормальное распределение и /-распределение Стьюдента. Нор-
мальное распределение имеет место, если известно значение
генерального стандартного отклонения или в случае больших
выборок (яг30). При малых выборках (л<30) и неизвестном
значении о распределение выборочных средних точнее прибли-
жается /-распределением.
Пусть нулевая гипотеза Но заключается в предположении,
что значение генеральной средней равно Ц0(Н0: ц= цп).В ре-
зультате сравнения с выборочным значением нулевая гипотеза
может быть отвергнута и принята альтернативная гипотеза
которая заключается в том, что генеральная средняя не равна
р.о( Н(: цх ц0). Для определения критических пределов в приня-
тии решений о правильности нулевой гипотезы вычисляется
отношение — Нй или (если о неизвестно).
о s
-7»
В случае больших выборок величина данного отношения
подчиняется стандартному нормальному закону распределения
и обозначается Z. Если то гипотеза Но принимается;
если lZfeZa/2, то отвергается с уровнем значимости а. В данном
случае а характеризует риск, что правильная гипотеза Но будет
отвергнута. Проверка гипотез всегда привязывается к опреде-
ленному уровню значимости.
При проверке правильности гипотезы Но возможны ошиб-
ки двух видов: непринятие правильной гипотезы (ошибка пер-
вого вида) и принятие ложной гипотезы (ошибка второго вида).
Вероятностью ошибки первого вида является уровень значи-
мости а. Ошибка второго вида Р зависит от того, насколько
правдоподобна альтернативная гипотеза Нг При уменьшении
вероятности ошибки первого вида одновременно возрастает
вероятность ошибки второго вида.
Пусть альтернативная гипотеза задается в виде Н,: ц > ц0
(или Н: ц < ц0), т. е. рассматривается гипотеза о том, что истин-
ное значение параметра не просто отличается, а больше (мень-
ше) гипотетического значения. В этом случае осуществляется од-
242
посторонняя проверка гипотез, т. е. рассматривается только один
из критических пределов ±Za. Если Z>+Za, то принимается ги-
потеза Н[: ц > ц0; если Z<-Z, то гипотеза Hj: ц< ц0.
При малых выборках и неизвестном о распределение отно-
шений Л будет приближаться /-распределением Стьюден-
л/л
та, соответствующим числу степеней свободы df= п - 1. В этом
случае критериальное отношение обозначается t. Для двусто-
ронней проверки критическая область (область непринятия Но)
задается соотношением ,» где а — уровень значимости.
Если генеральная совокупность конечна, имеет объем У и
при этом выполняется условие n>0,05W, то в знаменатель крите-
риального отношения Z (или /) вводится поправочный мно-
j N — п -
житель J——который характеризует поправку на конеч-
ность генеральной совокупности.
На практике часто приходится сравнивать средние двух раз-
личных генеральных совокупностей. Нулевая гипотеза при этом
характеризует равенство средних: Hft: = цп. В качестве альтер-
нативных гипотез можно рассматривать соответствующие од-
ностороннюю и двустороннюю проверки:
Н,: и, * U2,
Н,: ц, > Ь.
Н,: р, < ц2.
Критериальное отношение будет иметь вид (9.25), если из-
вестны дисперсии генеральных совокупностей, или (9.32), если
они неизвестны. Проверка производится по тем же правилам,
что и в случае одной генеральной совокупности. В случае малых
выборок и неравенства генеральных дисперсий число степеней
свободы /-распределения вычисляется по формуле (8.18). Если
полагать, что генеральные дисперсии равны, то в качестве об-
шей дисперсии можно рассматривать взвешенную среднюю двух
выборочных дисперсий. Вид критерия в этом случае задается
выражением (9.35).
При сравнении средних двух генеральных совокупностей
обязательным условием является независимость получения
выборок из каждой совокупности. Если это условие нарушает-
ся, то рассматриваются пары связанных наблюдений. В этом
случае сравнение двух совокупностей сводится к сравнению
243
разностей, вычисленных для каждой пары. Генеральные сово-
купности предполагаются нормальными, поэтому выборочное
распределение разностей также будет нормальным. Пусть нуле-
вая гипотеза заключается в том, что среднее значение распре-
деления разностей предполагается равным D№. Тогда задача про-
верки имеет вид
Н»: = Do,
Hrl*? Do-
Если число пар п >30, то в качестве критерия используется
распределение Z. В случае п< 30 адекватным критерием являет-
ся ^-распределение.
ПРОВЕРКА ГИПОТЕЗ
ОТНОСИТЕЛЬНО ДОЛЕЙ
10.1. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО
ДОЛИ ОДНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
10.1.1. Двусторонняя проверка
Теорию и методы построения доверительных интервалов,
изложенные в разделе 8.4, можно использовать для определе-
ния критических пределов в задачах проверки гипотез относи-
тельно долей.
Теоретически распределение выборочных долей наиболее
адекватно характеризуется биномиальным законом распреде-
ления. Однако при больших выборках возможна замена бино-
миального распределения выборочных долей нормальным рас-
пределением с теми же параметрами. Такая замена дает вполне
приемлемые результаты, если одновременно выполняются ус-
ловия пр>5 и л(1 - р)>5, где п — объем выборки, ар — значе-
ние генеральной доли.
Пусть выдвигается нулевая гипотеза На относительно того,
что доля генеральной совокупности р принимает определенное
значение. Тогда задача двусторонней проверки имеет следую-
щую формальную запись:
Но:р = /’о-
НГР*РО.
Распределение выборочных долей для больших выборок за-
данного объема п приближается нормальным законом со сред-
ним значением, равным генеральной доле р, и стандартной
ошибкой о- = . В расчетах будем полагать, что гене-
ральная доля р равна гипотетическому значению р1}.
245
Как и в случае средней, проверка гипотез осуществляется
на основе только одной выборки. Пусть значение выборочной
доли равно р . Рассмотрим отношение Z, имеющее стандарт-
ный нормальный закон распределения:
<ю.1>
V п
Область принятия нулевой гипотезы Н() и критическая об-
ласть задаются (ври уровне значимости а) соответственно ус-
ловиями
Р~Ро
РоО-Ро)
п
Пример 10.1. Руководство телевизионной редакции утвержда-
ет, что ее специальную тематическую передачу регулярно смот-
рят, по крайней мере, 20% телезрителей. Специальная социо-
логическая служба провела опрос 2000 телезрителей. Среди
респондентов 390 человек подтвердили, что они достаточно
часто смотрят данную передачу. Следует ли доверять утвержде-
нию руководства редакции, если при проверке использовать
5-процентный уровень значимости?
Вначале проверим, выполняются ли условия использования
нормального распределения: пр = 2000 0,2 = 4ОО>5, 2000(1 —
- 0,2) = 2000 0,8 = 16ОО>5.
Запишем постановку задачи двусторонней проверки:
Но: р = 0,2,
Н,: pt 0,2.
Параметры задачи: п - 2000 (число респондентов), р0 = 0,2
(значение заявленной доли телезрителей, смотрящих переда-
чу), а = 0,05(Z0O25 = 1,96).
246
Вычислим выборочную долю: Р = - 0,195.
Определим значение отношения (10.1):
„ 0,195-0,2 -0,005
Z = —I =-------= -U,5o.
0,2 0,8 0,0099
V 2000
Таким образом, нулевая гипотеза не может быть отвергнута
при 5-процентном уровне значимости, так как |-0,56|<1,96. Ут-
верждению редакции можно доверять при 5-проиентном уров-
не значимости.
10.1.2. Односторонние проверки
Пусть альтернативная гипотеза Н( характеризует не просто
отличие гипотетического значения параметра от истинного, а
указывает направление этого отклонения:
Н,:р>р0, (10.2)
Н, :/></,,. (10.3)
Рассмотрим случай (10.2). Область принятия нулевой гипо-
тезы задается соотношением
/7? <za,
PoU-Po)
ч л
а критическая область — неравенством
Р-Р0- *Za.
РрО-Ро)
\ л
Значение а характеризует уровень значимости, а величина Z.
имеет тот же смысл, что и в соотношении (9.12) (рис. 9.3).
Аналогично записываются неравенства соответственно для
области принятия нулевой гипотезы и критической области в
случае альтернативной гипотезы (10.3):
Pq(I-Pq)
N
247
,PH s-za.
iPq(I-Pq)
V N
Пример 10.2. Геологоразведочное объединение рассматривает воп-
рос о покупке большой партии специальных компьютеров, пред-
назначенных для наблюдения за сейсмической активностью ре-
гиона. Эти компьютеры должны работать в экстремальных
условиях низких температур. Компания-производитель утверж-
дает, что не менее 80% выпушенных компьютеров может устой-
чиво работать при температуре -20’С. Объединение собирается
сделать закупку, если утверждение фирмы будут подтверждено
независимым тестированием. Для проверки случайным образом
отобрали 30 компьютеров. В результате тестирования 9 компью-
теров были забракованы. Можно ли доверять утверждениям фир-
мы при 5-процентном уровне значимости?
Прежде всего выясним, выполняются ли условия для ис-
пользования нормального распределения: пр = 30 0,8 = 24>5,
л( I - р) = 300,2 = 6>5.
Задача проверки гипотез сводится к односторонней (лево-
сторонней) проверке:
Н0:/>>0,8,
Н, : р < 0,8.
Нулевая гипотеза Н(| в данном случае формулируется как
“равно или больше", а критическая область задается левой “хво-
стовой” частью кривой стандартного нормального распределе-
ния, ограниченной критическим пределом -Zo. = —(,64 (отсе-
кающим “хвост” с долей площади, равной 0,05).
Вычислим выборочное значение доли. Известно, что из 30
тестируемых компьютеров 21 (30 — 9) успешно прошел про-
- 21 m
верку. Отсюда Р = ~~ = О, 7.
Вычислим отношение (10.1): Z = । । । = —= -1,37.
|°>80'2 °’073
f 30
Так как —1,37>—1,64, то нулевая гипотеза не может быть
отвергнута при 5-процентном уровне значимости. Следователь-
но, объединение может произвести закупку партии компьюте-
ров.
248
Пример 10.3. Руководство компании, которая производит кет-
чуп, решает вопрос о производстве новой марки продукта. Идея
производства нового продукта возникла год назад. Тогда были
проведены маркетинговые исследования, которые показали,
что 5% домохозяйств одобряют новую марку. Для выявления
отношения к новому кетчупу в настоящее время было опроше-
но 6000 домохозяйств, 635 из них заявили, что хотели бы ку-
пить новый продукт. Требуется определить при 2-процентном
уровне значимости, возрос ли интерес покупателей к новому
кетчупу.
В данном случае рассматривается правосторонняя проверка
гипотез:
Но:р = О,05;
Н, : р > 0,05
при уровне значимости а = 0,02.
Объем выборки п = 6000. При этом выполняются условия
пр = 6000 0,05 = ЗОО>5 и л(1 - р) = 6000 0,95 = 5700>5. По
таблице Приложения 4 найдем величину критического преде-
ла: ZOI)2 = 2,05 (соответствует значению 0,4798, ближайшему к
0,48, таблицы площадей, ограниченных кривой стандартного
нормального распределения). Определим выборочную долю:
Вычислим значение критерия Z по формуле (10.1):
„ 0,056 - 0,05 0,006
Z = । =-------= 2,14.
[0,05 0,95 0,0028
\ 6000
Ввиду того что 2,14>2,05, нулевая гипотеза не может быть
принята с уровнем значимости 2%, т. е. при данном уровне
значимости можно считать, что интерес покупателей к новой
марке кетчупа возрос.
10.1.3. Поправка на конечность генеральной
совокупности
Пусть генеральная совокупность конечна и имеет объем N.
При этом объем выборки л, на основе которой вычисляется
выборочная доля р , составляет не менее 5% от объема N. Как
249
и в случае распределения выборочных средних, стандартная
ошибка статистики (теперь доли) умножается на поправочный
l~N -п
множитель J——т:
V N -1
_ - 1ро(1~Р^ Р^“п
? X л Vn-г
Критерий Z принимает вид
Z = -----ILZES-——. (10.4)
iPo(l-Po) \N-n
У п NN-1
Если объем выборки л составляет менее 5% от объема гене-
ральной совокупности N, то поправку на конечность можно не
учитывать.
Пример 10.4. Компания хочет закупить партию калькуляторов
в количестве 2500 штук. По условию закупки количество де-
фектных калькуляторов не должно превышать 4%. Случайным
образом было отобрано 150 калькуляторов. После проверки 13
из них оказались дефектными. Требуется определить, выполня-
ется ли условие закупки при уровне значимости а = 0,05.
Рассмотрим правостороннюю проверку гипотез:
Но : р<. 0,04;
Н, : р > 0,04.
Проверим выполнение условий правомерности использова-
ния нормального распределения: пр = 150 0,04 = 6>5, л(р) =
= 150 0,96= 144>5. Вычислим выборочную долю:
13
р = — = 0,087.
150
Ввиду того что N/n = 150/2500 =0,06>0,05, необходимо учи-
тывать поправку на конечность генеральной совокупности. По-
этому отношение / следует вычислить по формуле (10.4):
_ 0,087 - 0,04 0,047
|0Д)4 0,96 12500-150 0,016
V 150 V 2500-1
250
Как видно (2,94> 1,96), гипотеза Нп отвергается, а альтерна-
тивная гипотеза о превышении процента дефектных калькуля-
торов критического значения (4%) принимается при 5-про-
центном уровне значимости. Следовательно, компания вправе
отказаться от закупки.
10.2. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО
РАЗНОСТИ ДОЛЕЙ ДВУХ ГЕНЕРАЛЬНЫХ
СОВОКУПНОСТЕЙ
10.2.1. Двусторонняя проверка
Пусть рассматриваются две генеральные совокупности и сто-
ит вопрос о сравнении долей этих совокупностей. Будем отби-
рать из совокупности 1 все возможные выборки объема л(, а из
совокупности 2 — объема п2, причем выборки из различных
совокупностей являются независимыми. Пусть значение гене-
ральной доли для совокупности 1 - р, а для совокупности
2 Тогда если одновременно выполняются условия «^^5 и
л,(1 ~ Р1)>5, л2/’2>5 и л;(1 - р2)>5, то, как отмечалось в разделе
8.1.4, распределение разностей выборочных долей будет нор-
мальным. Стандартная ошибка разности долей будет вычисляться
как корень квадратный из суммы дисперсий двух выборочных
распределений:
п _ |ptU-Pt) . Рг^-Рг)
п, п2 •
При проверке гипотез информация о точных значениях па-
рамегров р и р2 отсутствует, поэтому стандартная ошибка раз-
ности средних ст-заменяется на оценочное значение
где фигурируют статистики р} и р2.
+ (10.5)
А у П| п2
Рассмотрим нулевую гипотезу Но, смысл которой заклю-
чается в том, что предполагается равенство долей двух сово-
купностей (Н#: />! = р2). Очевидно, в случае правильности ну-
левой гипотезы лучшей точечной оценкой должна быть
комбинированная оценка, полученная на основе выборочных
долей р} и рг
251
Пусть Х} — число единиц в выборке из совокупности 1, об-
ладающих данным свойством (число “успехов”), а X, — число
_ X 1 _ X,
“успехов” в выборке из совокупности 2. Тогда Р] = —Ч р-, = —
«1 л2
Рассмотрим комбинированную величину
р = Х1 + Х2 = л1Р|+я2Р2
И| + л2 л( + л2
(10.6)
Величина (10.6) является взвешенной средней величиной
долей pt и р2, где в качестве статистических весов выступают
объемы выборок л, и лг Подставляя вместо значений статистик
р, и р2 величину (10.6) в формулу (10.5), получим оценку для
стандартной ошибки средней:
Sp-Pi
P(l~P)+Р(1~Р) _
«1 л2
Р(1"Р)
1 + ±
Л| л2
Z-критерий для проверки нулевой гипотезы относительно
разности средних двух генеральных совокупностей будет иметь
вид
Z =
(Pi -Р2)-<Р1 -Р2)
Jp(l-p)[—+~ |
V n2 J
(Ю.7)
Если в качестве альтернативной гипотезы Н, рассматривать
предположение о неравенстве долей, то задачу двусторонней
проверки можно записать так:
Но:Л ~Рг
Н1-Р^Рг
При уровне значимости а область принятия гипотезы Но бу-
дет задаваться условием
р(1-р)[—+ —
I "I л2
< ^-а/2-
252
Соответственно критическая область задается неравенством
Пример 10.5. Два типа лекарств были опробованы на двух раз-
личных группах пациентов. Лекарство типа А принимала груп-
па пациентов, состоящая из 60 человек, из которых 20 испыта-
ли положительное воздействие. Группа из 70 человек принимала
лекарство типа В. Из этой группы 25 пациентов испытали по-
ложительный эффект. При 5-процентном уровне значимости
определить, имеется ли различие в эффективности двух типов
лекарств.
Пусть мера эффективности лекарства заключается в величи-
не пропорции пациентов, испытавших положительный эффект
от приема лекарства. Для проверки нулевой гипотезы о равен-
стве пропорций вычислим величину средней взвешенной доли
по формуле (10.6):
Условия нормальности распределений выборочных долей вы-
полняются:
Л|Р = 6ОО,35 = 21>5и г, и1- р) = 60 0,65 = 39> 5,
л2р = 70 0,35 = 29,5,
л2(1-р) = 7ОО,65 = 45,5>5.
Пусть рх — генеральная доля пациентов, испытавших поло-
жительный эффект от лекарства типа А, а рг — от лекарства
типа В. Запишем задачу проверки гипотез:
H0:Pi =Р2.
НгЛ*^-
Вычислим выборочные значения долей:
20 1
Р1 60 3
= 0,33 ;р2=^ = 0,36.
253
Определим по формуле (10.7) значение Z:
z= ..ОЗЗгОЛб =Ч)34
Jo,35O,65f— + --1
V I 60 70 J
Так как |z| = |-0,34| = 0,34 < 1,96, то нулевая гипотеза о ра-
венстве двух типов лекарств принимается при а = 0,05.
10.2.2. Односторонние проверки
Пусть альтернативная гипотеза Н при сравнении долей двух
генеральных совокупностей имеет вид Н(: >/>г или Н(: р, < рг
Тогда
Но:Л =Рг
^C-P^Pr <Ю.8)
Область принятия гипотезы Но для задачи (10.8) при уровне
значимости а задается соотношением
....<za.
.'р(1-р)| — + — I
V I Л| «2 I
а критическая область — условием
Р(1-Р)| —+ —1
V”l «2 J
Задача левосторонней проверки имеет вид
Но:Л =Рг
НхР<<рг (10.9)
Область принятия гипотезы Но и критическая область для
задачи (10.9) при уровне значимости а будут задаваться соот-
ветственно неравенствами
254
Р\-Ръ
р(1-р)| —+—
1 Л| n2
<-Za.
Пример 10.6. Компания производит жестяные консервные бан-
ки для хранения соков. Банка считается некондиционной, если
она не круглой формы или имеет вмятины. Банки произво-
дятся в две смены (дневная и вечерняя). В отделе качества про-
дукции подозревают, что доля некондиционных банок, про-
изводимых в дневную смену, меньше, чем в вечернюю. Для
проверки данного предположения случайным образом было
отобрано по 500 банок, произведенных в каждой смене. В ре-
зультате проверки оказалось, что для дневной смены 70 ба-
нок были некондиционными, а для вечерней смены — 110.
Проверить предположение отдела качества при 5-процентном
уровне значимости.
Пусть Р] — генеральная пропорция некондиционных банок,
выпушенных в дневную смену, ар, - в вечернюю смену.
Задача односторонней проверки будет иметь вид
но: Л = Р2<
Н,: р, < р2.
По условию задачи л( = 500, = 70 и п2 = 500, Х2 = 110.
Вычислим выборочные пропорции и комбинированную общую
пропорцию:
р{ = — = 0,14; р, = — = 0,22;
500 500
_ 500 0,14 + 500 0,22 180 Л,о
р =-----------------------=------= (J.1 о.
500 + 500 1000
Выборки достаточно большие и являются независимыми,
что дает право использовать Z-критерий:
Z =
0.14-0,22
= 22^08 =_329
0,0243
Отсюда -3,29<—1,96, что свидетельствует о том, что Но от-
вергается, а следовательно, предположение отдела качества
подтверждается при a = 0,05.
255
Пример 10.7. Торговая фирма собирается открыть сеть магази-
нов в двух регионах. Для организации торговли важно иметь
сведения о численности семей, живущих в этих регионах. Есть
предположение, что доля семей в регионе I, имеющих в своем
составе более четырех человек, превышает долю подобных се-
мей в регионе 2. В рамках маркетинговых исследований в реги-
оне I была составлена случайная выборка из 180 домохозяйств,
а в регионе 2 выборка содержала 155 домохозяйств. Оказалось,
что число семей, в составе которых более четырех человек, для
региона I — 89, а для региона 2 — 61. Можно ли на основе этих
данных заключить, что доля семей с численностью более че-
тырех человек в регионе 1 выше? При оценке следует исполь-
зовать уровень значимости а = 0,05.
Определим выборочные доли для регионов:
р. = -- = 0,47; р, = — = 0,39.
1 180 'п 155
Вычислим комбинированную долю:
. 89 + 61 150
р =--------=----= 0,45.
' 160 + 155 335
Проверим, выполняются ли условия использования крите-
рия Z:
Л]Р = 180 0,45 = 81 > 5 и П](1-р) = 180 0,55 = 99>5;
п2р = 155 0,45 = 69,75>5 и
л2(1-р) = 155 0.55 = 85,25>5.
Проверка гипотез будет правосторонней:
^Р^Рг
Н,: р, > р2.
Вычислим Z:
Ввиду того что 1,85> 1,64, гипотеза Но не может быть приня-
та при 5-процентном уровне значимости. Подтверждается пред-
положение о том, что доля семей, в составе которых более 4
человек, в регионе I выше.
256
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 10
Содержание нулевой гипотезы Н. в задачах проверки гипо-
тез относительно генеральной доли заключается в предполо-
жении, что доля генеральной совокупности р принимает опре-
деленное значение pQ (Но: р = р0). Если объем выборки п
достаточно большой (выполняются условия пр>5 и л(1 - р)>5),
то распределение выборочных долей будет приблизительно нор-
мальным. Поэтому для проверки нулевой гипотезы можно ис-
пользовать стандартное нормальное распределение, вычисляя
Р Рп
значение критерия Z = । "— и сравнивая его с соот-
IPo(I-Pq)
V л
ветствующими критическими значениями. Если осуществляет-
ся двусторонняя проверка при уровне значимости а, т. е. рас-
сматривается альтернативная гипотеза Н(: р * pQ, то критерий
Z сравнивается по абсолютной величине с Z . При односто-
ронних проверках (Н( : р > р0 или Н1 : р < р0) величина Z
сравнивается соответственно с +Zu (или -Za).
Если генеральная совокупность конечна и имеет объем N, то
в случае выполнения условия л/^0,05 следует учитывать по-
правку на конечность генеральной совокупности. Для этого не-
обходимо стандартную ошибку доли домножить на поправоч-
ный множительу. Если n/N<0,05, то поправку на
конечность можно не учитывать.
Пусть рассматриваются две генеральные совокупности и
необходимо провести сравнение долей этих совокупностей. Пусть
р. и р2 — соответственно доли первой и второй совокупности.
Если из совокупностей извлекаются независимые выборки до-
статочно больших объемов (пр >5 и л((| — pt)>5, пру>5 и
л (1 - р2)>5), то распределение разностей выборочных средних
будет близко к нормальному. Пусть в качестве нулевой гипоте-
зы рассматривается Н(: = р тогда при вычислении стандарт-
ной ошибки разности средних следует рассматривать взвешен-
ную среднюю выборочных средних pt и р2: р = + п2Р2
И1+л2
Критерий оценки будет иметь вид (10.7).
При односторонних проверках (Н( : или Н( : pt < р2)
критерий Z сравнивается соответственно с +Za или —Z.
J J ДИСПЕРСИОННЫЙ
АНАЛИЗ
11.1. ОБЩАЯ СХЕМА
ОДНОФАКТОРНОГО АНАЛИЗА
Одна из важнейших проблем статистического анализа, ко-
торая очень часто возникает на практике, — выявление влия-
ния различных факторов на исследуемый показатель. Для ре-
шения подобных задач используется дисперсионный анализ.
В зависимости от числа влияющих факторов дисперсион-
ный анализ может быть однофакторным и многофакторным.
Мы будем рассматривать только однофакторный дисперсион-
ный анализ. Метод дисперсионного анализа был создан для
обработки результатов агрономических опытов при исследо-
вании влияния различных типов удобрений на урожайность.
Данный подход затем стал широко использоваться в различ-
ных сферах деятельности, в том числе экономике, управле-
нии и бизнесе.
Пусть, например, несколько фирм выпускает электричес-
кие лампочки и требуется проанализировать, отличаются ли
средние сроки службы лампочек, произведенных различными
фирмами. В данной ситуации можно провести аналогию: уро-
жайность, измеряемая в центнерах на гектар, будет соответ-
ствовать сроку службы лампочек, выраженному в часах, а раз-
личные типы удобрений — торговым маркам фирм. В случае
двух фирм задача сводится к проверке гипотез относительно
разности средних двух генеральных совокупностей. Дисперси-
онный анализ используется, когда требуется одновременно
сравнить генеральные средние нескольких совокупностей (число
фирм больше двух).
Предположим, имеются три различные торговые марки элек-
трических лампочек Л, В и С, соответствующие трем различ-
ным фирмам. Пусть требуется проверить, имеются ли различия
258
в средних сроках службы лампочек этих фирм. Случайным об-
разом отберем по четыре лампочки каждой марки и протести-
руем их для выяснения срока службы. Пусть результаты испы-
тания, измеренные в часах, были сгруппированы по торговым
маркам в следующем виде:
Марка А: 30, 31, 32, 33
Марка В: 40, 41, 42, 43
Марка С: 50, 51, 52, 53
Отметим данные о сроках службы на оси времени:
АВС
--НН-----НН----НН-------►
Без всяких статистических заключений ясно, что лампочки
марки С горят дольше, чем лампочки марки В, которые в свою
очередь горят дольше, чем лампочки марки А. Очевидно, сред-
ние сроки службы лампочек различных марок отличаются друг
от друга.
Предположим теперь, что результаты тестирования были
другими:
Марка А. 30, 40, 50, 60
Марка В. 31, 31, 51, 61
Марка С: 32, 42, 52, 62
Отметим полученные данные на оси времени:
АВС АВС АВС АВС
--НН---НН---НН---НН-----►
Во втором случае, очевидно, трудно сделать вывод о значи-
мости различия между средними сроками службы лампочек
марок А, В, С. Причина заключается в том, что величина вари-
ации (разброса) значений внутри группы для каждой марки
гораздо больше, чем вариация между группами. В первом же
случае наоборот: вариации между группами значительно выше,
чем разброс внутри группы.
Данный принцип сравнения двух дисперсий, одна из кото-
рых характеризует вариацию внутри групп, а другая — между
группами, является методологической основой дисперсионно-
го анализа. При этом обязательно должны выполняться следу-
ющие условия относительно генеральных совокупностей, для
которых проводится сравнение средних:
1) распределения генеральных совокупностей нормальные
или близкие к нормальным;
259
2) все генеральные совокупности имеют одинаковую дис-
персию, которая в общем случае может быть неизвестной.
Если данные условия выполняются для ситуации с лампоч-
ками. то можно предположить, что в первом случае данные
были взяты из нормальных совокупностей, распределения ко-
торых могли иметь вид, указанный на рис. 11.1.
30 40 50
Рис. 11.1. Случай большой вариации между группами
Второй случай мог бы характеризоваться распределениями,
представленными на рис. 11.2.
30 40 50 60
Рис. 11.2. Случай большой вариации внутри групп
Как видно, в обоих случаях генеральные и средние не со-
впадают. Однако во втором случае (рис. 11.2) правильное зак-
лючение, сделанное только на основе визуального анализа
выборочных данных, будет неочевидным. Исследуемую ситуа-
цию можно рассматривать как проблему проверки гипотез. Обо-
значим средние сроки службы лампочек марок А, В, С соответ-
ственно ц , ц и Тогда нулевая гипотеза будет иметь вил
Но = Нс •
Под альтернативной гипотезой понимается условие
Hj : среди ц4, ця, цс имеется хотя бы одна, не равная двум
остальным.
Формально дисперсионный анализ можно рассматривать как
задачу проверки гипотез относительно равенства средних п
260
нормальных генеральных совокупностей, имеюших одинако-
вую дисперсию:
Но : h = Р, = - = = Ц.
Н, : не все ц , ц2,..., pvравны между собой.
Если нулевая гипотеза окажется правильной, то это будет
означать, что все совокупности идентичны, т. е. являются од-
ной и той же нормальной совокупностью со средней ц и дис-
персией ст2.
Процедура проверки нулевой гипотезы заключается в вы-
числении с помощью двух различных подходов оценочного
значения дисперсии, которая должна быть общей для всех ге-
неральных совокупностей. Первый подход основан на предпо-
ложении, что нулевая гипотеза верна, т. е. имеет место равен-
ство средних генеральных совокупностей. При втором подходе
исходят из того, что верна альтернативная гипотеза. Если рас-
хождение между оценками дисперсии значимо, то предполо-
жение о равенстве генеральных средних считается неправиль-
ным и нулевая гипотеза отвергается. Наоборот, если расхождение
будет незначимо, то нулевая гипотеза не отвергается.
11.2. МЕЖГРУППОВАЯ И ВНУТРИГРУППОВАЯ
ДИСПЕРСИИ
В дисперсионном анализе сравниваются две оценки гене-
ральной дисперсии — межгрупповая и внутригрупповая дис-
персии.
Предположим, что все значения признака элементов гене-
ральной совокупности разбиты на несколько групп. Каждую
группу можно рассматривать как отдельную выборку. Напри-
мер, общая совокупность лампочек может быть разбита на три
группы, соответствующие трем различным маркам А, В, С.
Значением признака здесь является срок службы каждой лам-
почки. Пусть в общем случае значения признака нормальной
генеральной совокупности с параметрами цист2 разбиты на к
групп. Каждую группу можно рассматривать как отдельную
выборку. Вычислим значения выборочных средних и диспер-
сий: Х|,Х2.и J|2.i2...5*.
Рассмотрим совокупность выборочных средних как некото-
рую выборку и вычислим выборочную дисперсию:
261
где
i-1

*-l
(11.1)
— средняя выборочных средних.
к
Величина (11.1). очевидно, является оценкой дисперсии
распределения выборочных средних, т. е. квадрата стандартной
ошибки средней:
Sr «о? =
(11.2)
(113)
(114)
ст У ст2
!п J п
Обозначим оценочное значение генеральной дисперсии а2.
Тогда из соотношения (11.2) получим
-2 2 £«(^-^)2
ст = ns- = -------
х к-1
Использование формулы (11.3) для оценки генеральной
дисперсии будет возможным, если группы или выборки, на
которые была разбита генеральная совокупность, имеют оди-
наковый объем л. В общем случае группы разбиения генераль-
ной совокупности могут иметь различные объемы. Пусть объем
Ай выборки будет л (/ = 1,..., к). Умножим каждый квадрат откло-
нения (х, -х)2 на соответствующий объем л( и скорректируем
оценку (11.3) с учетом различных объемов групп:
ст2 _ £”<(<<-*)2
к-1
Величина (11.4) называется межгрупповой дисперсией. Она
характеризует различия в величине изучаемого признака, ко-
торые возникают под влиянием фактора (признака), заложен-
ного в основу группировки. Так, в ситуации с лампочками в
качестве такового фактора фигурировала сортировка лампочек
по трем торговым маркам А, В и С.
Определим внутригрупповую дисперсию, которая является
второй оценкой генеральной дисперсии. Для Ай группы дис-
персия вычисляется по формуле выборочной дисперсии
s2 =
л,-1
(115)
где X, — средняя выборки /.
262
Величина л — 1 в выражении (11.5) характеризует число
степеней свободы для дисперсии г2. Общее число степеней
свободы по всем выборкам будет равно сумме
(л, - 1) + (л2- 1) + ...+ (л4 - 1) =
= (Л[ + л, + ... + nt) - к = лт - к,
где л обозначает общую сумму объемов выборок (лт= Ел.).
Внутригрупповая дисперсия вычисляется как средняя взвешен-
ная величина выборочных дисперсии, где в качестве весов высту-
пают удельные веса степеней свободы соответствующих выборок;
ст
л, -1'
Vt-1,
(116)
2
Внутригрупповая дисперсия характеризует вторую оценку
обшей генеральной дисперсии ст2. Она отражает случайные из-
менения признака, происходящие под влиянием других неуч-
тенных факторов и не зависящие от фактора, положенного в
основу группировки.
Проверка нулевой гипотезы в дисперсионном анализе про-
водится по следующему принципу. Пусть гипотеза Но верна
(Но: = ц2 = ... = цг). Это означает, что фактор группировки
не должен оказывать влияния на выделение групп, так как
все группы берутся из одной и той же генеральной совокуп-
ности (или образуют лишь одну исходную генеральную сово-
купность). Иначе говоря, можно полагать, что выделения групп
как бы не существует (межгрупповая дисперсия равна нулю),
а имеет место только внутригрупповая дисперсия, совпадаю-
щая с обшей генеральной дисперсией о2.
Предположим теперь, что верна альтернативная гипотеза
Нр т. е. существует, по крайней мере, одна совокупность, сред-
няя которой отличается от средних других совокупностей. В этом
случае фактор, заложенный в основу группировки, оказывает
значительное влияние на выделение групп. Средние значения
групп существенно отличаются друг от друга, в то время как
каждая группа характеризуется внутренней однородностью.
Очевидно, дисперсия общей совокупности, составленной из
таких групп, должна совпадать с межгрупповой дисперсией,
отражающей разнородность общей совокупности.
Дисперсионный анализ основан на следующем фундамен-
тальном правиле: если межгрупповая дисперсия статистически
значимо превышает внутригрупповую, то делается вывод, что
групповые средние значимо различны, т. е. нулевая гипотеза Но
отвергается.
263
11.3. СРАВНЕНИЕ МЕЖГРУННОВОЙ
И ВНУТРИГРУППОВОЙ ДИСПЕРСИЙ
НА ОСНОВЕ Г-РАСПРЕДЕЛЕНИЯ
После того как значения межгрупповой и внутригрупповой
дисперсий вычислены, возникает проблема их сравнения. Она
осуществляется на основе F-критерия (критерия Фишера), ко-
торый еще называют F-статистикой, или F-отиошением. F-m-
ношение представляет собой отношение оценок и v обшей
дисперсии, полученных из независимых выборок, элементы
которых взяты из одной или нескольких совокупностей с оди-
наковой дисперсией: ,
Г = Д-. (11.7)
32
F-отношение подчиняется закону F-распределсния Фишера.
Существует целое семейство F-распределений, каждое из ко-
торых характеризуется двумя параметрами: степенями свобо-
ды, соответствующими числителю и знаменателю отношения
(11.7). Кривая F-распределсния всегда расположена в положи-
тельной полуплоскости с областью определения от 0 до + оо
(рис. 11.3). При возрастании значения /кривая неограниченно
приближается к оси х, но никогда не пересекает ее. Все F-рас-
пределения имеют положительную асимметрию и стремятся к
симметричной форме при неограниченном возрастании степе-
ней свободы. F-распределение является непрерывным, поэто-
му данные совокупностей, которые анализируются на его ос-
нове, должны быть непрерывными и изменяться, по крайней
мере, в шкале интервалов.
Рис. 11.3. Кривые F-распределений: 1 — 29 степеней свободы
в числителе и 28 в знаменателе; 2—19 степеней свободы в числителе
и 6 в знаменателе; 3 — 6 степеней свободы в числителе и 6 в знаменателе
264
Для F-отношения при разных сочетаниях степеней свободы
числителя и знаменателя построены таблицы критических зна-
чений (пределов), которые могут быть превзойдены с различ-
ной вероятностью (уровнем значимости). Так, в Приложении 6
представлены таблицы для уровней значимости а = 0,05 и
а = 0,01.
Гипотеза, которая проверяется с помощью F-критерия, за-
ключается в том, что независимые выборки были взяты из од-
ной и той же нормальной совокупности или из нормальных
совокупностей с равными дисперсиями. При вычислении
F-отношения по формуле (11.7) для проверки этой гипотезы
за з(2 берется ббльшая из оценок ^2 и з22, т. е. з(2 > з22. Число
степеней свободы, соответствующих большей оценке з(2 (чис-
лителю), определяет колонка таблицы, а число, соответствую-
щее меньшей оценке з22 (знаменателю), — строка таблицы. Так
как всегда полагается з(2 > зЛ то значение F-отношения будет
больше 1. Поэтому таблицы Приложения 6 соответствуют все-
гда критическим пределам односторонней проверки гипотезы
о значимости превышения з(2 над з22.
В дисперсионном анализе в качестве F-критерия рассматри-
вается отношение
Межгрупповая дисперсия (118)
Внутригрупповая дисперсия ’
В отношении (11.8) числителю соответствует число степе-
ней свободы, равное к — 1 (к — число групп), а знаменателю —
л — к (лт — общая сумма объемов групп).
Если величина F-критерия, выраженного формулой (11.8),
превзойдет критическое значение Fand (где а — уровень значимо-
сти, л = к - 1 — число степеней свободы числителя, с/= л_ - 1 —
число степеней свободы знаменателя), взятое из соответствую-
щей таблицы Приложения 6, то нулевая гипотеза о равенстве
средних (Но : = ц. = ... = pj отвергается с уровнем значимо-
сти а.
Пример 11.1. Руководство кадровой службы компании хочет про-
анализировать эффективность трех различных методов подготовки
персонала. Для этой цели после завершения курсов повышения
квалификации была составлена случайная выборка из 16 работ-
ников, которая была разбита на три группы в соответствии с
методами обучения. С помощью специальных тестов была изме-
рена их дневная производительность. Результаты тестирования,
выраженные в специальной шкале, были сведены в табл. 11.1.
265
Таблица 11.1
Данные о дневной производительности работников,
сгруппированных по методам обучения
Метод 1 Метод 2 Метод 3
15 22 18
18 27 24
19 18 16
22 21 22
11 17 15
85 105 114
х, = 85/5 = 17 Xj 105/5 = 21 Х3 = 114/6= 19
л, = 5 л2 = 5 Л3 = 6
Используя данные табл. 11.1, следует сделать заключение,
влияют ли различные методы обучения на производительность
работников. Формальная постановка задачи сводится к провер-
ке гипотезы о том, что средние значения дневной производи-
тельности работников в группах, соответствующих трем раз-
личным методам подготовки, равны между собой. Формальная
запись задачи проверки гипотез имеет вид
Ио: И, = = ц,,
Н( : не все у , g2, ц, равны между собой.
Нулевая гипотеза Но будет верна в случае, если выборочные
(групповые) средние статистически незначимо отличаются друг
от друга. Если же расхождения будут значимы, то принимается
альтернативная гипотеза Н . Эго означает, что методы подго-
товки оказывают сильное влияние на производительность ра-
ботников и поэтому следует скорректировать программы под-
готовки персонала.
Данная задача является задачей дисперсионного анализа.
В табл. 11.1 представлены значения производительности работни-
ков, сгруппированных по трем методам подготовки, и вычисле-
ны групповые средние. Вычислим среднюю выборочных средних:
_ х. + х2 + х» 17 + 21 + 19
х = -1—а—-А =----------= 19.
3 3
По формуле (11.4) определим межгрупповую дисперсию:
а - *11*1 Г*)2 + л2(хг-х)2+л3(х3-х)2 _
3-1
= 5(17- 19)2 +5(21-19)2 +6(19-19)2 = 40 =
2 2
266
Другой оценкой общей дисперсии будет внутригрупповая
дисперсия. Для ее определения необходимо вычислить группо-
вые дисперсии. Их вычисление сведено в табл. 11.2.
Таблииа 11.2
Вычисление групповых дисперсий
Метод 1 (х, “ 17) Метод 2 (х, - 21) Метод 3 (х, - 1»)
х - ж, (* - *,)* х - xt (х - X,)2 х - ж3 (» - *>)*
15- 17- -2 (-2)г = 4 22-21-1 1»-1 18 - 19 = -1 (-D2- 1
18- 17= 1 12- 1 27 - 21 = 6 62 = 36 24 - 19 = 5 5’ = 25
19-17-2 22 = 4 18- 21 = -3 (-3)2 = 9 19 - 19 = 0 02-0
22 - 17 = 5 52 = 25 21-21-0 О2 = 0 16 - 19 = -3 (-3)2 - 9
11 - 17 = -6 (-6)2 = 36 17-21 --4 (-4)2 = 16 22 - 19 = 3 15-19 = 4 З2- 9 42 = 16
Х(х-х« )2 =70 £(х-х2)2-62 £(х-х})2=12
-V ——— = г *2 ж з,2-^ •*з>\
«1 -I "2 -1 "3 -1
70 = = 4 17J 66 Ж = 4 15,5 60 = —— = 5 12
По формуле 11.6. вычисляем внутригрупповую дисперсию:
а _ (л, - Ф,+(лг ~ + (из ~ =
л, + л2 + л3 - 3
417,5 + 415,5 + 512 192
=-------------------=----= 14,77.
5 + 5 + 6-3 13
Определим /"-отношение:
Пусть руководство кадровой службы хочет проверить нуле-
вую гипотезу при уровне значимости а = 0,05.
Для этой цели воспользуемся соответствующей таблицей
Приложения 6. Число степеней свободы числителя, соответ-
ствующее колонке таблицы, равно к — 1=3-1= 2, а число
степеней свободы знаменателя, определяющее строку табли-
цы, равно ^л,-Л = 16-3 = 13. На пересечении выделенных
267
строки и столбца найдем значение критического предела
Foai |3 = 3,81. Так как F— 1,35<3,81, то нулевая гипотеза при-
нимается (рис. 11.4).
Рис. 11.4. Области принятия и непринятия нулевой гипотезы при уровне
значимости 0,05 на основе F-раслределения
В итоге руководство кадровой службы может сделать вывод,
что при 5-процентном уровне значимости различные методы
подготовки не оказывают существенного влияния на произво-
дительность работников.
11.4. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО
ДИСПЕРСИЙ ДВУХ ГЕНЕРАЛЬНЫХ
СОВОКУПНОСТЕЙ
F-распределение может также использоваться для проверки
гипотезы о равенстве дисперсий двух нормальных совокупнос-
тей. При этом можно рассматривать одностороннюю и двусто-
роннюю проверки. Для односторонней проверки постановка
задачи имеет вид
Но:о>2 = стЛ
Гипотеза проверяется по F-критерию, где в качестве Г-от-
ношения берется отношение выборочных дисперсий и $22,
которые являются оценками соответственно генеральных дис-
персий о(2 и о22:
г-4
s2
Данная F-статистика распределена по закону F-распрсдслс-
ния с — 1 степенями свободы в числителе и пг~ 1 степеня-
268
ми свободы в знаменателе, где л( — объем выборки из первой
совокупности, а л — из второй. Проверка производится при
заданном уровне значимости а, т. е. критическим пределом бу-
дет величина F
® «|-1; л2-1
Пример 11.2. На автомобильном заводе работают две конвей-
ерные линии. Руководство отдела контроля качества хочет оп-
ределить, имеется ли однородность в количестве дефектов для
автомобилей, сходящих с первого и второго конвейеров. Для
этой цели были сделаны две случайные выборки: 20 автомоби-
лей из числа сошедших с первой линии и 16 автомобилей со
второй. Оказалось, что для первой линии среднее число дефек-
тов на один автомобиль было 10 с дисперсией 9, а для вто-
рой — 11 с дисперсией 25.
Требуется сделать заключение, значимо ли превышение ва-
риации числа дефектов для второй линии при уровне значимо-
сти а = 0,05. Если превышение будет значимым, то, очевидно,
следует провести переналадку работы конвейеров.
Исходные данные задачи: $2 = 9, л) = 20, з* = 25, л2 = 16.
Запишем задачу односторонней проверки:
Но: а,2 « о22,
Hi: < > °Л
Вычислим F-отношение, где в числитель поставим большую
выборочную дисперсию:
Числителю соответствует л2 - 1 = 16 - 1 = 15 степеней сво-
боды, знаменателю — л( — 1 = 20 - 1 = 19. Критическое значе-
ние F005 |5 = 2,23. Так как 2,78>2,23, то превышение значимо
и нулевая гипотеза Но отвергается с 5-процентным уровнем
значимости.
Как видно, при односторонней проверке рассматривается
только верхний критический предел, отделяющий правосто-
ронний “хвост” распределения — критическую область, соот-
ветствующую непринятию нулевой гипотезы. Процедура дву-
сторонней проверки аналогична, однако возникает проблема
определения нижнего критического предела, отделяющего ле-
вую “хвостовую” часть критической области.
269
Пусть F(a, п, d) — значение F, соответствующее п степеням
свободы числителя, d степеням свободы знаменателя и отделя-
ющее правой “хвост” F-распределения с долей площади а. Для
него верно следующее соотношение:
1
F(a,n,d) =-----------,
F(l-a,d,n)
(11.9)
Величина - a, d, п) в формуле (11.9) характеризует ниж-
ний критический предел, ограничивающий область в левой
части распределения с долей площади I — а. Таким образом,
определение нужного нижнего критического предела для дву-
сторонней проверки сводится к нахождению табличного зна-
чения F-статистики, которая является для него обратной вели-
чиной.
Пример 11.3. Большая фармацевтическая фирма разрабатывает
два типа препарата для местной анестезии. Препарат вводится
с помощью инъекций. Для принятия решения о запуске препа-
ратов в производство необходимо сравнить вариацию средних
сроков действия препаратов. Под сроком действия подразуме-
вается время, прошедшее от момента инъекции до начала дей-
ствия анестезии. Ввиду сходства в химическом составе двух пре-
паратов ожидалось, что степень вариации будет одинаковой у
обоих препаратов.
Для проверки этой гипотезы действие препарата 1 было ис-
пытано на выборке из 31 пациента (и, = 31), а препарата 2 —
на выборке из 41 пациента (п, = 41). Выборочная дисперсия в
первом случае была = 1296, а втором — j22 = 784. Фирма
хочет проверить предположение о равенстве вариаций при 2-
процентном уровне значимости.
Формальная запись задачи имеет вид
Н,: о/ * о/.
Вычислим F-статистику:
F = 4 = 1~- = 165.
sj 784
Эта статистика соответствует F-распределению с 30 - 1 =
= 31-1) степенями свободы числителя и 40 (я} - I » 41 - I)
270
степенями свободы знаменателя. Так как проверка должна быть
двусторонней при а “ 0, 02, то нижний и верхний критические
пределы должны отделять области, имеющие доли площади,
равные 0,01. Верхний предел F00i. 0 найдем непосредственно
по таблице для а = 0,01 Приложения 6: F001 30. w = 2,2. Однако
величины нижнего предела F ?t) в этой таблице нет. Исходя
из соотношения (11.9), можно записать:
^0.99.30.40 - ~----= ЧЧ = 0’4}
^o.oi.wjo
Следовательно, значение F-статистики попадает в область
принятия гипотезы Но (рис. 11.5).
Рис. 11.5. Область принятия нулевой гипотезы
при уровне значимости а “ 0,02
Нулевая гипотеза Но принимается при 2-процентном уров-
не значимости. Следовательно, предположение о равенстве ва-
риаций сроков действия препаратов подтвердилось.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 11
Дисперсионный анализ используется для выявления влия-
ния различных факторов на результативный показатель. Если
влияющий фактор единственный, то дисперсионный анализ
называется однофакторным, если факторов несколько — мно-
гофакторным. В главе приведены основные принципы и мето-
ды однофакторного анализа. Формально дисперсионный ана-
лиз можно рассматривать как задачу проверки гипотез, где
нулевая гипотеза Но заключается в предположении о равенстве
нескольких генеральных средних.
271
Если Но верна, то это означает, что все совокупности иден-
тичны, т. е. являются одной и той же генеральной совокупно-
стью со средней ц и дисперсией о3. Процедура проверки нуле-
вой гипотезы заключается в вычислении с помощью двух
различных методов оценки общей дисперсии. Первый подход
основан на предположении, что нулевая гипотеза верна. Вто-
рой подход предполагает, что верна альтернативная гипоте-
за, которая за-ключается в том, что не все генеральные сред-
ние имеют одинаковые значения. Если расхождение между
оценками значимо, то нулевая гипотеза отвергается. В диспер-
сионном анализе одной из опенок общей дисперсии является
межгрупповая дисперсия, а другой — внутригрупповая дис-
персия. Пусть все значения признака элементов генеральной
совокупности разбиваются на несколько групп. Каждую груп-
пу можно рассматривать как отдельную выборку. Под меж-
групповой дисперсией (формула (11.4)) понимается диспер-
сия выборочных средних относительно их среднего значения,
где каждый квадрат отклонения умножается на объем соот-
ветствующей группы. Она характеризует различия в величине
изучаемого признака, которые возникают под влиянием фак-
тора, заключенного в основу группировки. Внутригрупповая
дисперсия вычисляется как средняя взвешенная величина
выборочных дисперсий, где в качестве весов выступают удель-
ные веса степеней свободы соответствующих выборок (фор-
мула (11.6)). Она отражает случайные изменения признака,
происходящие под влиянием других неучтенных факторов и
не зависящие от фактора, положенного в основу группиров-
ки. Дисперсионный анализ основан на следующем правиле:
если межгрупповая дисперсия статистически значимо превы-
шает внутригрупповую, то делается вывод, что групповые
средние значимо различны, т. е. нулевая гипотеза Но отверга-
ется. Сравнение дисперсий осуществляется с помощью F-ста-
тистики, которая представляет собой отношение межгруппо-
вой дисперсии к внутригрупповой. Распределение F-статистик
является F-распределением, которое соответствует (к — 1)
степеням свободы в числителе (к — число групп) и (лт — к)
степеням свободы в знаменателе (лт — общая сумма объемов
групп). Значение F-статистики сравнивается с соответствую-
щим критическим значением где а—• заданный
уровень значимости. Критические значения находятся изтаб-
272
лип Приложения 6. Если F-отношение превышает критичес-
кое значение, то превышение межгрупповой дисперсии счи-
тается значимым при заданном уровне значимости.
F-распределение также используется для проверки гипотезы
о равенстве дисперсий двух нормальных совокупностей. При этом
можно рассматривать одностороннюю и двустороннюю провер-
ки. При двусторонней проверке возникает проблема определе-
ния нижнего критического предела, отделяющего область, име-
ющую долю площади а/2, где а — уровень значимости. Для его
определения можно использовать соотношение (11.9).
РАСПРЕДЕЛЕНИЕ х2
И ЕГО ПРИМЕНЕНИЕ
В ВЫБОРОЧНОМ МЕТОДЕ
12.1. РАСПРЕДЕЛЕНИЕ %2
И ОЦЕНКА ГЕНЕРАЛЬНОЙ ДИСПЕРСИИ
Пусть Z, Z2,..., Zv — независимые случайные величины,
каждая из которых распределена по стандартному нормально-
му закону с параметрами ц( = О, О( = I (/ = 1. v).
Рассмотрим случайную величину, равную сумме квадратов
этих величин и имеющую особое распределение, называемое
хи-квадрат (х2):
X2=Z2 + Z2+... + Zv2. (12.1)
Распределение х2 всегда неотрицательно, зависит только
от значения V, которое называется числом степеней свободы
и полностью определяет конкретное распределение Сред-
нее значение х 2 равно V, а стандартное отклонение — 2v. На
рис. 12.1 представлены графики нескольких распределений для
различных значений v. При возрастании v распределение стре-
мится к нормальному.
Рис. 12.1. Кривые распределений х\ Для v = 2, 4 и 10
274
Для распределения х2. как и для любого непрерывного рас-
пределения, вероятность попадания значения случайной вели-
чины в определенный промежуток характеризуется соответству-
ющей площадью под кривой распределения. Форма кривой
распределения х2 зависит от числа степеней свободы. Как и для
семейства /-распределений, была рассчитана таблица площа-
дей под кривыми распределений х2. соответствующих различ-
ным степеням свободы. Эта таблица представлена в Приложе-
нии 7. Ее строки задают степени свободы, обозначаемые df, а
столбцы — определенные доли (а) для площадей под правыми
“хвостовыми” частями кривой, которые ограничиваются зна-
чением х^фис. 12.2). Эти значения находятся на пересечении
соответствующих строк и столбцов (рис. 12.2).
Рис. 12.2. Геометрическая интерпретация величины Х2[[СЛ
Пример 12.1. Используя кривую х2 для df= 12, вычислим веро-
ятность Лх2> 18,5494) и Лх2<6,3038). В таблице Приложения 7
в строке, соответствующей df 12, найдем значение 18,5494.
Оно находится в столбце х201П0, т. е. ограничивает правый “хвост”
кривой с долей площади 0,1 (рис. 12.3).
Таким образом, Лх2> 18,5494) = 0,1. Аналогично значение
6,3038 находится в строке “df = 12” и в столбце х20,. т. е. вероят-
ность, что х,|2> 6,3038, будет Лх212>6,3038) = 0,9 (рис 12.4).
Ввиду того что правее 6,3038 доля площади под кривой равна
0,9, а правее 18,54494 — 0,1, очевидно, Л6,3038$х2|2^ 18,5494)=
= 0,9-0,1 =0,8.
275
Пример 12.2. Используя данные примера I2.1, определить преде-
лы а и Ь, которые удовлетворяют условию Р(а <Х?а<Ь) - 0,95. При
этом а и bдолжны отделять “хвосты” с одинаковыми площадями.
Очевидно, площади левого “хвоста” (ограниченного пре-
делом а) и правого “хвоста” (ограниченного пределом Ь) дол-
жны быть равны (I — 0,95)/2 = 0,025. Относительно величины
а это означает, что справа от нее должна находиться область с
площадью, равной I - 0,025 = 0,975. Следовательно, а = Х20,7?|2-
По таблице Приложения 6 найдем а - х2.... = 4,40, Ь =
= Х2о.ОИ;12 = 23,3 (рис. 12.5).
Рис. 12.5. Геометрическая интерпретация Р^а <х*,2<Ь) = 0,095
Распределение х2 можно определить другим способом. Рассмот-
рим случайную выборку хр х2,.... хя, взятую из нормальной гене-
ральной совокупности с параметрами ц и о2. Тогда статистика
? = (|22)
ст ст ст
будет распределена по закону х2„-
Если ц неизвестно, то в качестве оценки рассмотрим выбо-
рочную среднюю х , которую подставим в (12.2) вместо ц:
2(х,-х)2 (х2-х)2 (*„-х)2 _
* ст2 ст2 ст2 "
- +(х2 ~*>2 + ••• + (*, ~*)2 (12.3)
276
Числитель выражения (12.3) является числителем в форму-
ле для выборочной дисперсии:
2
5 = “-------.
Л-1
Отсюда
2_(л-1)?
* „2
(12.4)
где г является несмещенной оценкой генеральной дисперсии и2.
По определению несмещенности математическое ожидание
распределения оценочных статистик должно быть равно оце-
ниваемому параметру, т. е. Е(з2) = о2. Следовательно, ввиду (12.4)
имеем
е(х2) = е
о2
= —Е(?) = л-1.
Таким образом, распределение статистики (12.4) можно
рассматривать как распределение х\.г Потеря одной степени
свободы произошла ввиду того, что в формуле для выборочной
дисперсии s2 фигурирует выборочная средняя х , которая свя-
зывает одну из переменных х, х.,..., хя (при известных значени-
ях х, х2,.., хд| и х значение хя будет единственным).
При построении доверительных интервалов для генераль-
ной дисперсии о2 следует рассмотреть распределение выбо-
рочных дисперсий J2. Для этого будем извлекать из нормаль-
ной генеральной совокупности с параметрами ц и о случайные
выборки объема л и вычислять соответствующие выборочные
дисперсии J2. Из формулы (12.4) видно, что выборочное рас-
пределение зг можно определить на основе распределения
Очевидно, оно зависит от величин л и а2 и его можно
использовать для построения доверительных интервалов при
оценке о2.
Например, рассмотрим выборку объема л = 13, что соот-
ветствует #=12. Для данных примера 12.2 было установлено,
что
Ж4.40<х2<23,3) = 0,95.
На основе соотношения (12.4) можно записать:
Р 4,40 <
12s2
_2
<23,3 =0,95.
277
или
12?
23,3
12?'
4,40
= 0,95.
Это означает, что 95-процентный доверительный интервал
12s2 12s2
имеет пределы -----;----.
23,3 4,40
По аналогии можно выразить доверительные пределы для
а2 при доверительной вероятности 1 — а и объеме выборки п:
(я-1)т2е (я-1)з2
„2 ’
Ха/2л-1 Х1-ц/2л-1
(12.5)
Соответственно доверительный интервал для стандартного
отклонения имеет вид
(я-l)s2. । (я-l)s2
Ха/2;л-1 у Х|-а/2л-1
(12.6)
Пример 12.3. Фасовочный автомат наполняет пакеТики специя-
ми. Стандартный вес наполненного пакетика должен быть 50 г.
Одним из показателей качества работы автомата является ве-
личина вариации весов пакетиков. Чтобы определить степень
вариации, была извлечена случайная выборка из 15 пакетиков
с весами (в граммах):
51,2 ; 47,5; 50,8; 51,5; 49,5; 51,1; 51,3; 50,7;
46,7 ; 49,2; 52,1; 48,3; 51,6; 49,2; 51,5.
Для этих данных х = 50,15 г и s = 1,65 г. Вычислить 90-про-
центный доверительный интервал для дисперсии о2 и стандар-
тного отклонения о. Предполагается, что веса пакетиков рас-
пределены нормально.
Требуемая доверительная вероятность I - а = 0,9, т. е. уро-
вень значимости а = 0,1. Число степеней свободы df= п - I =
= 15 - I = 14. Отсюда доверительные пределы для ст2 находятся
из выражения (12.5):
14 • 1,65^. 14-1.652 V Г 14 1.652.14-1.652"
XO.05J4 Xo,9J;l4 , k ^,7 >
278
Соответственно 90-процентный доверительный интервал
для о:
(71,61; Д8) = (1,27; 2,41),
т. е. с вероятностью 90% можно утверждать, что стандартное
отклонение о изменяется в пределах от 1,27 до 2,41 г.
12.2. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО
ДИСПЕРСИИ И СТАНДАРТНОГО ОТКЛОНЕНИЯ
Во многих приложениях приходится решать вопрос, превы-
шает ли дисперсия или стандартное отклонение определенное
значение. Например, вариация параметров выпускаемой про-
дукции может служить характеристикой стабильности работы
оборудования. В подобных ситуациях проблему можно свести к
проверке гипотез. Так, возможна постановка задачи двусторон-
ней проверки:
Но: о = о2,
Н,: о2 # о/.
В качестве критерия оценки рассматривается статистика
2 (л-1)№ п
X =-----/—. При уровне значимости а критическими пре-
°о
делами будут значения % (левый предел) и X (пра-
вый предел). Нулевая гипотеза Но отвергается, если х2>^^г
или xJ<x’1HVfc,.r
Пример 12.4. Психолог изучает возможности обучения детей
до-школьного возраста. Его интересует максимальное время, в
течение которого ребенок может быть внимателен и сосредо-
точен. Исследования показали, что разброс указанных проме-
жутков времени для пятилетних детей характеризуется диспер-
сией а2 = 64. Для выборки из 20 шестилетних детей s2 — 28.
Необходимо сделать заключение при а = 0,05, отличаются ли
вариации значений промежутков внимательности для пятилет-
них и шестилетних детей.
Рассмотрим задачу двусторонней проверки:
Нв: а2 = 64,
Н,: о2 #64.
279
Вычислим статистику х2:
64
Критические пределы задаются значениями: Х2О,„19 =
= 8,90655, Х^ои и” 32,8523, которые находятся по таблице
Приложения 7. Ввиду того что 8,31 <8,90655, гипотеза Но отвер-
гается при уровне значимости 5%, т. е. подтверждается гипотеза
о различии вариаций.
Если альтернативная гипотеза характеризует одностороннее
отклонение, то возможны два типа задач:
Но: о = оД
Н(: о1 > о02 (или о2<о02).
Соответственно нулевая гипотеза Н(| отвергается, если
Х2>Х2и;я.1 (или Х,<Х21НС„1).
Пример 12.5. Предприятие точных приборов выпускает элект-
ронные весы. Весы считаются качественными, если стандарт-
ное отклонение при взвешивании 500-граммовой гирьки зна-
чимо меньше 1 мг. На новых весах взвешивание было
произведено 30 раз, причем выборочное стандартное отклоне-
ние оказалось 0,73 мг. Определить, являются ли данные весы
достаточно точными при а = 0,01.
Исходные параметры: oQ = 1, з = 0,73, п = 30. В данном
случае ставится задача односторонней проверки:
Но: а =1,
Н(: о < 1
или
Но: о2 =1,
Н,: о2 < I.
Вычислим статистку %2:
,,29^ = 1
1!
280
По таблице Приложения 7 найдем критический предел
Х2|.„ „ । = X20W|9 ~ 14,2565. Так как 15,45> 14,2565, то нулевая
гипотеза не может быть отвергнута с уровнем значимости 1%
(рис. 12.6).
Рис. 12.6. Геометрическая интерпретация области принятия нулевой
гипотезы для односторонней проверки при а = 0,01
12.3. х2-РАСГ1Р£ДЕЛЕНИЕ
КАК КРИТЕРИИ СОГЛАСИЯ
В разделе 12.2, а также в главах 9, 10 рассматривались гипо-
тезы относительно отдельных параметров генеральных совокуп-
ностей, причем данные этих совокупностей измерялись, по
крайней мере, в шкале интервалов (например, вес, доход, воз-
раст и т. д.).
Рассмотрим теперь следующую си туацию. Пусть высказыва-
ется предположение о законе распределения исследуемой ге-
неральной совокупности. На основе выборочных данных стро-
ится частотное распределение значений признака (например,
в виде ряда распределения). Возникает задача проверки нуле-
вой гипотезы о том, что расхождение между предполагаемым
(теоретическим) распределением и наблюдаемым (эмпиричес-
ким) распределением незначимо. Критерии, с помощью кото-
рых проверяется эта гипотеза, называются критериями согла-
сия. Один из таких критериев, основанный на распределении
X2, получил название критерия согласия х2 или критерия со-
гласия Пирсона. Его преимущество по сравнению с другими
критериями состоит в том, что он позволяет оперировать дан-
ными, выраженными как в шкалах интервалов и отношений,
так и в шкалах наименований и порядка. Как было показано в
гл. 1, шкала наименований характеризует такой тип измерения
данных, когда они могут классифицироваться только по ка-
ким-либо категориям. Шкала порядка позволяет судить о том,
что одна категория данных по рангу выше, чем другая.
281
Критерии проверки гипотез, связанные с данными, изме-
ряемыми в шкалах наименований и порядка, называются не-
параметрическими или свободными от распределений. Это оз-
начает, что статистические критерии, которые при этом
используются, не зависят от определенного распределения, ко-
торому могут принадлежать выборочные данные. Пригодность
же рассмотренных ранее критериев зависела от правильности
предположения о распределении генеральной совокупности,
откуда бралась выборка. Например, /-критерий, строго говоря,
можно использовать, если выполняется условие нормальности
генеральной совокупности.
В этой связи критерий согласия х2 является наиболее удоб-
ным и часто используемым непараметрическим критерием.
Применим его как критерий согласия для сравнения наблюда-
емого распределения частоте ожидаемым (теоретическим) рас-
пределением.
Пусть имеет место ситуация, когда требуется сравнить серию
наблюдаемых значений признака (полученных в результате экс-
перимента) с соответствующей серией значений, которая рас-
сматривается в качестве гипотетической. Последовательность
значений, входящих в серию, распределим по определенным
категориям. Например, детали, производимые на станке, будем
сортировать на годные и дефектные; служащих компании разо-
бьем на возрастные группы; сгруппируем данные об объемах
продаж продукции фирмы по регионам; специалистов с выс-
шим образованием распределим по специальностям. Каждая ка-
тегория будет характеризоваться частотой, т. е. числом данных, в
нее попавших в результате эксперимента. Распределение наблю-
даемых частот по категориям является результатом случайного
выбора, если эксперимент представляет собой последователь-
ное проведение независимых опытов.
Пусть эксперимент удовлетворяет следующим условиям
1. Эксперимент состоит из п независимых повторных опытов
(испытаний).
2. Каждый опыт может иметь к исходов, причем каждый ис-
ход точно попадает в одну из к категорий.
3. Вероятности осуществления исходов рг рг,..., рк в каждом
опыте остаются неизменными, и выполняется соотношение
Р, + р2+...
Очевидно, если к = 2, то схема эксперимента будет биноми-
альной: имеются два исхода — “успех” и “неудача” с соответ-
ствующими вероятностями р} = р и р, = 1 — р. Когда к>2, схема
называется полиномиальной. В условиях полиномиальной ситу-
282
ации можно определить к случайных величин О, Оу..., Ок как
к наблюдаемых значений частот:
О = наблюдаемое число значений, попавших при п опытах
в категорию 1;
О, = наблюдаемое число значений, попавших при п опытах
в категорию 2;
Ot = наблюдаемое число значений, попавших при п опытах
в категорию к.
Наблюдаемые частоты являются оценками ожидаемых час-
тот Ер Е2,..., Et, которые вычисляются следующим образом:
Е1 = л/>р Е2 = пр2.Ед = npt. (12.7)
Для полиномиальной схемы рассмотрим следующую стати-
стику, имеющую распределение %2:
(12.8)
Распределение (12.8) соответствует числу степеней свободы
df ~ к — 1, где к — число категорий.
Статистику (12.8) можно использовать в качестве критерия
проверки гипотез для решения следующей задачи.
Пусть рассматривается ситуация с полиномиальной схемой
эксперимента. Точные значения вероятностей исходов ру ру
..., pk неизвестны. Выдвигается гипотеза о том, что эти вероят-
ности имеют конкретные значения р{ = />(°, рг = рк = р*.
По результатам эксперимента требуется при определенном уров-
не значимости либо подтвердить, либо опровергнуть эту гипо-
тезу. Формальная запись задачи:
Р. = Р°> Pi = Рг..Р> = Р^
Н : по крайней мере одно из значений pt не совпадает с
гипотетическим.
На основе наблюдаемых значений частот О{, Оу..., Ot вы-
числим точные оценки вероятностей исходов (ру ру ..., рк)'.

О{ _ О2 _
— .Р2=— Pk =
п п п
(12.9)
283
Если нулевая гипотеза верна, то, очевидно, расхождения
между оценками р (i = и соответствующими гипотети-
ческими вероятностями р° (i = должны быть статисти-
чески незначимыми. Если же верна альтернативная гипотеза,
то, наоборот, следует ожидать значимых расхождений. Ввиду
(12.7) и (12.9), значимость отклонений будет эквивалентна
значимости расхождений между соответствующими наблюдае-
мыми и ожидаемыми частотами. Она определяется с помощью
Х2-критерия (12.8): если х2>Х2(1 t l. то нулевая гипотеза Но от-
вергается при уровне значимости а. Таким образом, критичес-
ким пределом здесь служит значение х t ( (а— уровень значи-
мости, к — число категорий). Если Jc = 2, то использовать
Х2-критерий нс имет смысла, так как можно осуществить обыч-
ную проверку гипотез с помощью Z-критерия. Однако когда
число категорий к больше 2, то следует рассматривать несколь-
ко Z-критериев отдельно для каждой пропорции. Поэтому ис-
пользовать критерий согласия х* гораздо удобнее, так как он
позволяет оценить отклонения всех пропорций одновременно.
Пример 12.6. Исследования, проведенные в прошлом году в
области медицинской статистики, показали, что имело место
следующее процентное распределение людей по возрасту, ре-
гулярно принимающих лекарства от расстройств желудка:
Возрастные кате- гории 18-24 25-34 35-44 45-44 55-64 55 и старше
Процент 5,7 16,4 20 15 16,2 26,7
В текущем году были проведены новые исследования. Для
случайной выборки численностью 150 человек, регулярно при-
нимающих данные лекарства, частотное распределение по
возрастным категориям имеет вид
Возрастные кате- гории 18-24 25-34 35-44 45-44 55-64 55 и старше
Процент 12 19 39 23 26 31
Используя 5-процентный уровень значимости, определить,
изменилось ли возрастное распределение людей, регулярно
принимающих лекарства.
Исходные данные задачи:
объем выборки п = 150;
число категорий к = 6;
гипотетические пропорции: р ° = 0,057; р,° = 0,164;
р,° = 0,2; р° = 0,15; = 0,162; р“ = 0,267.
284
Наблюдаемые частоты: О{ = 12, О2 = 19, О, = 39, ОА = 23,
(\ = 26, = 31.
Уровень значимости: а = 0,05.
Гипотезы, которые требуется проверить:
Н#: рх°= 0,057, />2°= 0,164, />3° = 0,2, р4° = 0,15, р5° = 0,162,
р4° = 0,267;
Н : по крайней мерс, одно из равенств гипотезы Но не вы-
полняется.
Вычислим ожидаемые частоты:
Е( = р*п = 0,057 • 150 = 8,55, Е2 = р2°п = 0,164 • 150 = 24,6,
Е, = р*п = 0,2 • 150 = 30, Е, = р4пп = 0,15 • 150 = 22,5,
Е, = 0,162- 150 = 24,3,
Е = 0,267- 150 = 40,05.
о
Вычислим статистику х2 по формуле (12.8):
2 _ у (£ -БУ _ (12-8.55)2 + (19-24.6)2 + (39-30)2 +
Z ~ Е; 8,55 24,6 30
х (23-22.5)2 х (26-24.3)2 . (31-40.05)2 _ _ м
22,5 24,3 40,05
По таблице Приложения 7 найдем критический предел
X2 ... = Х2Л„< « = 11,0705. Следовательно, х2 = 7,34<11,0705 и
нулевая гипотеза Н ( не может быть отвергнута при уровне зна-
чимости 5%. Таким образом, при уровне значимости а = 0,05
можно утверждать, что процентное распределение по возраст-
ным категориям людей, регулярно принимающих лекарства от
расстройства желудка, не изменилось.
При вычислении статистики по формуле (12.8) мы опреде-
ляем разность между двумя частотами (О — Е), относящимися
к одной категории, возводим ее в квадрат и делим на ожидае-
мую частоту Е. Если одно из значений Е очень мало (напри-
мер, меньше 5), то соответствующее отклонение может быть
достаточно большим и в значительной степени повлиять на
конечный результат вычислений статистики х2- Иначе говоря,
небольшое значение ожидаемой частоты для какой-то одной
категории может сильно поднять величину х2» что вполне мо-
жет привести к неоправданному непринятию гипотезы Hft. Чтобы
предотвратить такую возможность, следует соблюдать правило:
ожидаемая частота Е должна быть не меньше 5.
285
В ситуации, если одна или несколько ожидаемых частот ока-
жутся меньше 5, следует укрупнить соответствующие катего-
рии таким образом, чтобы ожидаемая частота каждой новой
категории была не меньше 5.
12.4. ПРОВЕРКА ГИПОТЕЗ ОТНОСИТЕЛЬНО
ФОРМЫ РАСПРЕДЕЛЕНИЯ
Критерий согласия х2 можно использовать для проверки на
“согласие” наблюдаемого распределения с каким-либо конкрет-
ным распределением. Например, могут возникнуть ситуации, когда
нужно определить, насколько согласуется наблюдаемое распре-
деление частот с ожидаемым распределением при условии, что
ожидаемое распределение имеет биномиальный, равномерный,
нормальный или любой другой закон распределения.
Пример 12.7. Плавкие электрические предохранители укладыва-
ются в пачки по 20 штук в каждую. Отдел контроля качества
утверждает, что в среднем только около 10% предохранителей в
пачке дефектны. Случайным образом отбирают 41 пачку предох-
ранителей. Результаты подсчета дефектных предохранителей были
систематизированы в виде следующего распределения:
Число дефектных предохранителей в лачке Число пачек с данным числом дефектных предохранителей
0 7(0,) 12(Ог)
1
2 Ю(О3)
3 7(О4)
4 1(О5)
5 2(О6)
>5 2(О7)
Если верить утверждению отдела качества, то рассматри-
ваемая выборка должна была извлечена из генеральной сово-
купности, имеющей биномиальный закон распределения с
р = 0,1. Требуется проверить это утверждение при а = 0,05.
Данная ситуация описывается полиномиальным эксперимен-
том. Проведен 41 независимый опыт, каждый из которых со-
стоял в том, что случайным образом отбиралась пачка предох-
ранителей. Исходом опыта является количество дефектных
предохранителей в пачке.
286
Ввиду того что частоты Os, О'и О, меньше 5, объединим
три последние категории в одну. Тогда в соответствии с числом
исходов можно выделить пять следующих категорий:
категория 1 — наблюдается 0 дефектных предохранителей в
пачке (О( = 7);
категория 2 — 1 дефектный предохранитель в пачке (О2 = 12);
категория 3 — 2 дефектных предохранителя (О3 = 10);
категория 4 — 3 (О4 = 7);
категория 5 — более 3 (О5 = 5).
Запишем гипотезы:
Но: данные распределены по биномиальному закону с р = 0,1;
Н : закон распределения не соответствует биномиальному
закону с р — 0,1.
Предположим, гипотеза Но верна. Рассмотрим биномиаль-
ное распределение с параметрами п = 20 и р = 0,1. В данном
случае опыт заключается в проверке каждого предохранителя в
пачке, состоящей из 20 предохранителей. Вероятность появле-
ния дефектного предохранителя (“успеха”) равна 0,1.
Пусть X — биномиальная случайная величина с данными па-
раметрами. Рассмотрим следующие биномиальные вероятности:
р0= р(Х = 0) = С?о 0,9м, Р] = р(Х — 1) = Сго • 0,1 • 0,9*’,
Рг = р(Х = 2) = С& • 0,12 • 0,9", р} = р(Х = 3) =
= С& • 0,Р • 0,9”, р4 - р(Х= 4) = С^о • 0,14 • 0,9",
Р, = । “ (Л + Р2 + Pj + р4).
Найдем значения р. по таблице Приложения 2 и выразим
гипотезы в следующем виде:
Но: />, = 0,122, р2 = 0,27, Pj = 0,285, р4 = 0,19, />5 = 0,133;
Н(: по крайней мере, одно значение р не равно соответ-
ствующей биноминальной вероятности.
Вычислим ожидаемые частоты:
Е( =41 -0,122 = 5,22; Е, = 41 0,27 = 11,07; Е, - 41 -0,285 =
= 11,68; Е4 = 4 0,19 = 7,79; Е5 = 41 -0,133 = 5,45.
Сравним наблюдаемые частоты с ожидаемыми по крите-
рию х2: , - ,
2 = (7-5,22)2 (12-11.07)2 (10-11,68)2
Х 5,22 + 11,07 + 11,68 +
( (7-7,79)2 t (5-5,45)2 =
7,79 5,45
287
По таблице Приложения 7 найдем критическое значение:
Х2ОО5 4 ~ 9,48773. Так как 1,23<9,48773, то нулевая гипотеза не
может быть отвергнута при а - 0,05.
В примере 12.7 осуществлялась проверка на согласие наблю-
даемого распределения с биномиальным распределением, при-
чем параметрр был известен. Часто возникает ситуация, когда
необходимо проверить на согласие наблюдаемое распределе-
ние с конкретным распределением, однако параметры теоре-
тического распределения не представлены.
Пример 12.8. Менеджер по продажам телефонных автоответчи-
ков предполагает, что недельные продажи подчиняются зако-
ну распределения Пуассона. Данные о продажах за 50-недель-
ный период были обобщены в следующем виде:
Число проданных единиц Число модель Число проданных единиц Число недель
0 1 5 7
1 3 6 5
2 6 7 3
3 11 8 4
4 10 >8 0
50
Рассмотрим, как можно проверить гипотезу о согласии с
распределением Пуассона при а = 0,1:
Но: недельные продажи распределены по закону Пуассона;
Н : недельные продажи не распределены по закону Пуас-
сона.
Распределение Пуассона имеет один параметр:
цЛе-и
Р(Х=л) = *Ц-,
ли
где х = 0,1,2,... характеризует число единиц, проданных за не-
делю.
Значение ц представляет собой среднее значение пуассонов-
ской случайной величины. Вычислим его оценку на основе вы-
борочных данных:
. 01 + 1-3+2-6+3 11 + 410+5-7 + 6-5 + 7-3 + 8-4
|1 --------------------—---------------------= 4.1.
50
288
Подставим |1 = 4,1 в функцию вероятностей:
где х~ 0,1,2,....
Используя таблицу Приложения 3, найдем оценки пуассо-
новских вероятностей и вычислим оценочные значения ожи-
даемых частот Е:
X Р(Х = X» Е О
0 0,0166 0,0166 50 = 0,83 1
1 0,0679 0,0679 50 = 3.39 3
2 0,1393 0,1393 50» 6.97 6
3 0,1904 0,1904 50 = 9,52 11
4 0,1951 0,1951 50 = 9,76 10
5 0,16 0.16 50 = 8 7
6 0,1093 0,1093 50 = 5.46 5
7 0,064 0,064 50 3.2 3
8 0,0328 0,0328 50 = 1,64 4
>8 0,0246 0,0246 50 = 1,23 0
1 50 50
Заметим, что величина Р(Х>8) = 1 - (0,0166 + 0,0679 +...+
+ 0,0328) = 0,0246.
Проверим, все ли значения ожидаемых частот Е больше или
равны 5. Очевидно, необходимо объединить первые три катего-
рии (0,83 + 3,39 + 6,97 = 11,19) и последние три категории
(3,2 + 1,64 + 1,23 = 6,07).
Вычислим ^’-статистику:
X Е О (О-в) (О - Е)2/Е
s2 11.9 10 -1,19 0,127
3 9,59 11 1,48 0,23
4 9,76 10 0,24 0,006
5 8 7 -1 0,125
6 5,46 5 -0,46 0,039
г7 6,07 7 0,93 0,142
50 50 0 0,669

289
В общем случае, если необходимо провести оценку неизвест-
ных параметров, число степеней свободы для критерия согла-
сия вычисляется по формуле
df = (число категорий) — 1 — (число оценочных
параметров).
В данном случае для распределения Пуассона был оценен
один параметр. Поэтому df= 6 - 1 - 1 = 4. По таблице Прило-
жения 7 найдем
Х2о.|;4 = 7,779.
Отсюда х2 ~ 0,669<7,779, и нулевая гипотеза не может быть
отвергнута при а = 0,1. То есть выборочные данные согласуются
с распределением Пуассона, имеющим параметр ц = 4,1.
Пример 12.9. В архиве метеослужбы некоторого региона хра-
нятся данные о годовых дождевых осадках за 120 лет. Выдвига-
ется гипотеза, что высота осадков имеет нормальное распреде-
ление. Для проверки данной гипотезы был составлен ряд
распределения (высота осадков измерялась в дюймах):
Высота осадков X, дюймы Число лет (частота), f Относительная частота р
25-29.99 3 3/120 = 0,025
30—34,99 14 14/120 = 0.117
35-39.99 31 3/120 = 0,258
40-44,99 31 31/120 = 0.258
45-49,99 29 29/120 = 0,242
50-54.99 8 8/120 = 0,067
55-59,99 3 3/20 = 0,025
60 -64,99 1 1/120 = 0,008
Требуется проверить гипотезы:
Но: высота годовых дождевых осадков распределена нормально,
Hf распределение высоты дождевых осадков отличается от
нормального.
Группы ряда распределения можно рассматривать как кате-
гории, а частоты (/) — как наблюдаемые частоты.
Если предположить, что нулевая гипотеза верна, то следует
вычислить ожидаемые частоты, рассматривая данное распре-
деление как нормальное. Для проведения расчетов необходимо
знать параметры ц и о предполагаемого нормального распреде-
ления. Вычислим оценки этих параметров на основе сгруппи-
290
рованных данных. Среднее значение ряда вычисляется по фор-
муле (3.3):
_ 27,5-3 + 32,5-14 + 37,5-31 + 42,5-31 + ... + 62.5-1 .....
х =-----------------------------------------= 42.06.
120
Дисперсия оценивается по формуле (4.12):
г _ (27Л - 42.O6)2 + (32,5 - 42,06)2 +... + (62,5 - 42,О6)2 _
120-1
Рассмотрим нормальный закон с параметрами ц = 42,06 и
о = \40.425 = 6,348.
Будем использовать стандартное нормальное распределение
7для вычисления вероятностей попадания случайной величи-
ны в группировочные интервалы ряда распределения.
Из соотношения (7.12) определим значение Z, соответству-
ющее границам групп ряда распределения, и по таблице При-
ложения 4 найдем вероятности:
25<Х<30 R-2.68 <2<-1,9) ’ 0,025
30<х<35 ₽(-1,9<Z<—1,13) = 0,1005
35<Х<40 Р(-1,13<Z<-0,32) = 0,2453
40<х<45 Р(-0.32<2< 0,46) - 0,3027
45<х<50 Р{0,46<2< 1,25) = 0,2172
50<х<55 P(1,25<Z<2.04) = 0,0849
55<х<60 P(2,04<Z<2.82) = 0,0183
60<Х<65 P(2.82<Z) = 0,0024
Теперь вычислим ожидаемые частоты, т. е. ожидаемые коли-
чества лет, когда высота осадков будет находиться в границах
групп ряда распределения. Если рассматривать данные за 120
лет как выборку объема п = 120 из нормальной генеральной
совокупности с параметрами ц = 42,06 и а = 6,358, то ожида-
емые частоты вычисляются следующим образом:
Группы, дюймы Ожидаемые частоты
25-30 0,025 120 = 3
30-35 0,1005 120 = 12,06
35-40 0,2453 120 = 29,44
40-45 0,3027 120 = 36,22
45-50 0,2172 120 = 26,06
50-55 0,0849 120 = 10,19
55-60 0,0183 120 = 2.2
60-65 0,0024 120 = 0,29
291
Объединим первые три группы и последние три группы в
общие категории, чтобы все ожидаемые частоты были не мень-
ше 5.
Получим следующее распределение ожидаемых (вычислен-
ных в предположении, что данные взяты из нормальной сово-
купности) и наблюдаемых (полученных на основе архивных
данных) частот:
Группы (категории) Ожидаемые Наблюдаемые частоты О
частоты Е
25-35 15.06 17
35-40 29.44 31
40-45 36.32 31
45-50 28,06 29
50-65 12.68 12
Вычислим статистику:
2 _ (17-15.06)2 + (31-29.44)2 + (31-36.32)2 +
* 15,06 29,44 36,32
(29-26.06)2 (12-12.68)2 ..в
26,06 12,68
В ситуации, когда число категорий — л, а ожидаемое рас-
пределение имеет к параметров, число степеней свободы опре-
деляется по формуле
df = п - к - 1.
В данном случае п = 5 и к = 2 (два параметра ц и о). Поэтому
5 - 2 - 1 “ 2.
Из таблицы Приложения 7 видно, что х2 = 1.48 меньше всех
значений х2. соответствующих df - 2. Следовательно, нулевая
гипотеза Но не может быть опровергнута, т. е. можно утверж-
дать, что годовая высота осадков распределена нормально с
параметрами ц = 42,06 и а = 6,358.
12.5. ТАБЛИЦЫ СОПРЯЖЕННОСТИ
В предыдущих разделах было рассмотрено использование
критерия х2 в качестве критерия согласия наблюдаемого рас-
пределения с ожидаемым распределением. При этом данные
распределяются по различным категориям. Такое распределе-
ние является одномерным, т. е. данные характеризуются только
292
одним признаком, например принадлежностью к торговой мар-
ке, возрастом, производственным стажем и т. д.
Часто возникают ситуации, когда одни и те же данные мо-
гут соответствовать двум различным признакам, например про-
фессия покупателя и его отношение к определенному типу то-
вара. Если данные классифицируются по одному признаку, то
все категории наблюдаемых частот можно расположить в од-
ной строке (или в одном столбце). В случае двумерной класси-
фикации, когда она производится одновременно по двум при-
знакам, категории частот образуют таблицу сопряженности. Ее
можно использовать для выяснения зависимости между при-
знаками. Это означает, что требуется определить, оказывает ли
влияние положение элемента в распределении по одному при-
знаку на его положение в распределении по другому признаку.
Заключение о зависимости признаков можно сделать на осно-
ве критерия х2-
Пример 12.10. Фирма выпускает электронный прибор. Одним из
компонентов прибора является специальная схема, которая про-
изводится в виде съемной платы. Анализ проверок выпускаемых
плат показал, что в основном могут иметь место три типа неис-
правностей: отсутствие какого-либо элемента схемы (тип 1), по-
вреждение основания платы(тип 2), неправильное соединение
элементов схемы (тип 3). Платы выпускаются тремя видами обо-
рудования (А, В, С). Оборудование А на 90% управляется компь-
ютером и выпускает в 2 раза больше плат за день, чем В и С,
которые управляются компьютером на 50%. Требуется опреде-
лить, имеется ли связь между типом неисправности и видами
используемого оборудования. Для этой цели было обследовано
500 дефектных плат: 250, выпущенных на оборудовании А, и по
125, выпущенных на Bn С. Распределение частот было система-
тизировано в виде таблицы сопряженности (табл. 12.1).
Таблица 12.1
Таблица сопряженности двух признаков:
тип неисправности платы и вид оборудования
Оборудование Тип неисправности
1 2 3 Итого
А 50 80 120 250
В 60 55 10 125
С 65 45 15 125
Итого 175 180 145 500
293
Требуется проверить гипотезы:
Но: типы неисправностей не зависят от вида выпускающего
оборудования,
Н,: типы неисправностей зависят от вида выпускающего
оборудования.
Каждая пара признаков в таблице образует клетку, в кото-
рой помещается число неисправных плат, обладающих данной
парой признаков. Если верна нулевая гипотеза, т. е. признаки не
связаны между собой, то платы должны быть разбросаны слу-
чайным образом по двум распределениям. Визуальный анализ
табл. 12.1 показывает, что третий тип неисправностей в боль-
шей степени присущ оборудованию А. Однако если рассматри-
вать 500 отобранных плат как случайную выборку, то эта зави-
симость может объясняться просто выборочной ошибкой.
Предположим, что зависимость между признаками отсут-
ствует. Тогда пропорции в распределении плат по типам неис-
правностей для всех видов должны быть одинаковыми. Они со-
впадают с общими пропорциями для всей выборки. Вычислим
значения этих пропорций. Как видно из табл. 12.1, для типа 1
общее число плат в выборке составляет 175. Тогда ожидаемая
пропорция вычисляется как отношение р} = 175/500. Отсюда
ожидаемая частота (ожидаемое количество дефектных плат),
соответствующая сочетанию признаков “оборудование А” и
“неисправность типа 1 ”, должна быть равна р (общее количе-
ство плат, выпущенных на оборудовании А), т. е. 175 • 250/500 =
= 87,5. Аналогично вычисляем ожидаемые частоты для сочета-
ний признаков “оборудование В" и “неисправность типа 1”,
“оборудование С" и “неисправность типа 1” (общее количе-
ство плат в выборке для В и С равно 125): 175 • 125/500 = 43,75.
Общая пропорция для неисправностей типа 2 (табл. 12.1)
является отношением общего числа плат с неисправностями
типа 2 к объему выборки: р, = 180/250. Соответствующие ожи-
даемые частоты для сочетаний признака “неисправностей типа
2” с признаками “оборудование А”, “оборудование В”, “обо-
рудование С” вычисляются следующим образом:
180 • 250/500 = 90, 180 125/250 = 45, 180 • 125/250 = 45.
Общее число плат, имеющих неисправности типа 3, равно
145 (табл. 12.1). Пропорция, соответствующая этому признаку:
р} = 145/500. Вычислим соответствующие ожидаемые частоты
для комбинаций с признаками “оборудование А”, “оборудова-
ние В” и “оборудование С”: 145 • 250/250 = 72,5; 145 • 125/500 =
= 36,25; 145 • 125/500 = 36,25.
294
Из логики вычисления ожидаемых частот следует правило
их расчета на основе таблицы сопряженности 12.1. Рассмотрим
каждую наблюдаемую частоту как некоторый элемент таблицы
сопряженности. В столбце “Итого” найдем сумму по строке, в
которой расположен рассматриваемый элемент, а в строке
“Итого” — сумму по столбцу этого элемента. Ожидаемая часто-
та получается как отношение произведения указанных сумм к
обшей сумме всех частот.
Для удобства сравнения наблюдаемых и ожидаемых частот
поместим их в одну табл. 12.2, где рядом с наблюдаемой часто-
той в скобках стоит соответствующая ожидаемая частота.
Таблица 12.2
Наблюдаемые и ожидаемые (в скобках) частоты сопряженности
признаков “вид оборудования” и “тип неисправностей"
Оборудование Тип неисправности
1 2 3 Итого
А 50 (87,5) 80 (90) 120 (72,5) 250
В 60 (47,75) 55(45) 10 (36,25) 125
С 65 (43,75) 45 (45) 15 (36,25) 125
Итого 175 180 145 500
Вычислим х2-критерий по данным табл. 12.2:
2 = (5O-87.5)2 + (80-90)* + (120-72,5)* +
Х 87,5 + 90 + 72,5
+ (60-47,75)* + (55-45)* (10 - 36,25)* +
47,75 45 36,25
(65-43,75)* (45-45)* + (15-36,25)* _
+ 43,75 + 45 36.25
= 16,071 + 1,111 + 31,121 + 6,036 + 2,222 +19,09 +
+ 10,321 + 0+12,457 = 98,35.
Для нахождения критического значения, ограничивающего
область принятия нулевой гипотезы, следует определить число
степеней свободы соответствующего распределения %2. Число сте-
пеней свободы определяется как число данных, которые входят
в формулу для вычисления статистики и могут свободно изме-
няться. В каждой строке табл. 12.1 содержатся три значения час-
тот, связанные суммой, представленной в строке “Итого”. По-
этому число свободных данных в каждой строке равно 3-1=2.
295
Аналогично, в каждом столбце содержатся три значения с изве-
стной суммой. Поэтому число свободных данных для каждого
столбца равно 3-1=2. Отсюда общее число степеней свободы
для всей таблицы определяется так: (3 - 1) (3 — 1) = 4.
Пусть уровень значимости проверки гипотез а = 0,1 .Тогда по
таблице Приложения 7 найдем критическое значение х2О]4 =
= 7,78. Так как 98,35>7,78, то нулевая гипотеза отвергается при
а = 0,1.
В итоге можно сделать вывод, что совокупности дефектных
плат, выпускаемых на оборудовании А, В, С, не являются одно-
родными относительно трех типов неисправностей. Типы не-
исправностей неравномерно распределяются среди дефектных
плат, выпускаемых на различном оборудовании. Очевидно, зна-
чительное количество неисправностей третьего типа для плат,
выпускаемых на оборудовании А, не является случайным.
Рассмотрим общий случай использования критерия х2 для
проверки однородности наблюдаемых частот, сгруппирован-
ных в таблицу сопряженности. Пусть таблица сопряженности
имеет вид
°11 °12 •••
°21 °22 ...
•
°Л2 ... ®пт Л» °nt
Хоп Хов ... ES о.
Рис. 12.7. Общий вид таблицы сопряженности:
О, — наблюдаемые частоты, i — индекс строки (/ 1.п),
/ — индекс столбца (J = 1.т)
Таблица сопряженности на рис. 12.7 имеет л строк и т столб-
цов, где располагаются наблюдаемые частоты, т. е. рассматри-
вается л значений признака 1 и т значений признака 2. В край-
нем правом столбце таблицы, который носит вспомогательный
характер, вычисляются суммы частот по строкам. В нижней
(вспомогательной) строке вычисляются суммы частот по столб-
цам.
296
Ожидаемая частота, стоящая в г-й строке и к-м столбце (Е^,
вычисляется как произведение суммы наблюдаемых частот по
r-й строке на сумму наблюдаемых частот по jt-му столбцу, от-
несенное к обшей сумме наблюдаемых частот:
т п
5Х So.
Е„ = С, . (12.10)
М J-I
На практике следует придерживаться правила* величины Е*
должны быть не меньше 5. В противном случае следует объеди-
нить некоторые категории частот таблицы сопряженности, что-
бы данное условие выполнялось.
Число степеней свободы для статистики х2 определяется по
формуле
#»(л-l) (m-1). (12.11)
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 12
Распределение х2 характеризует случайную величину, рав-
ную сумме квадратов независимых стандартных нормальных ве-
личин. Оно зависит только от количества слагаемых v, входя-
щих в эту сумму, которое называется числом степеней свободы
и которое полностью определяет конкретное распределение х,2.
Среднее значение распределения у 2 равно v, а стандартное
отклонение — 2v. Распределения х' образуют семейство рас-
пределений, где каждое отдельное распределение соответству-
ет определенному числу степеней свободы. Так же как для се-
мейства /-распределений, рассчитана таблица площадей под
кривыми распределений х2 (Приложение 7).
Распределение х2 можно использовать для построения дове-
рительных интервалов дисперсии нормальной генеральной со-
вокупности. Эго связано с тем, что распределение выборочных
дисперсий ? можно определить на основе распределения х2„Р
где п — объем выборки (выражение (12.4)). Доверительные ин-
тервалы для дисперсии и стандартного отклонения определя-
ются соответственно по формулам (12.5) и (12.6).
Распределение х2 можно использовать для проверки гипотез
о равенстве дисперсии гипотетическому значению. В качестве
критерия оценки рассматривается статистика (12.4).
297
Распределение х2 можно рассматривать в качестве критерия
согласия наблюдаемого распределения выборочных данных с
теоретическим (ожидаемым) распределением генеральной со-
вокупности, откуда была взята выборка. Пусть требуется срав-
нить серию наблюдаемых значений признака (полученных в
результате эксперимента) с соответствующей серией значений,
которая рассматривается в качестве гипотетической. Последо-
вательность значений, входящих в серию, распределим по оп-
ределенным категориям. Каждая категория будет характеризо-
ваться частотой, т. е. числом данных, попавших в нее в результате
эксперимента. Распределение наблюдаемых частот по катего-
риям является результатом случайного выбора, если экспери-
мент представляет собой последовательное проведение неза-
висимых опытов. Наблюдаемыми частотами характеризуются
оценки ожидаемых частот. Сравнение на согласие наблюдае-
мых и ожидаемых частот производится по критерию х2, где
необходимая статистика вычисляется из соотношения (12.8). Она
имеет число степеней свободы, равное к — 1, где к — число
категорий. Если ожидаемые частоты вычислять, предполагая
конкретный закон распределения, то с помощью х2-критерия
можно проверять гипотезу относительно формы распределе-
ния (например, проверка на согласие с равномерным, бино-
миальным или нормальным законом распределения).
Может возникнуть ситуация, когда одни и те же данные
должны соответствовать двум различным признакам. В случае
двумерной классификации наблюдаемые частоты образуют таб-
лицу сопряженности. Ее можно использовать для выяснения
зависимости между признаками. Это означает, что требуется
определить, оказывает ли влияние положение элемента в рас-
пределении по одному признаку на его положение в распреде-
лении по другому признаку. Если такой зависимости нет, то
значения должны быть разбросаны случайным образом по двум
распределениям. Ожидаемые частоты вычисляются по формуле
(12.7). Сравнение ожидаемых и наблюдаемых частот таблицы
сопряженности осуществляется по критерию (12.8).
-J3

КОРРЕЛЯЦИЯ И ПРОСТАЯ
ЛИНЕЙНАЯ РЕГРЕССИЯ
В предыдущих главах рассматривались методы, позволяющие
обобщать все множество значений одной случайной перемен-
ной либо в виде графика (например, гистограммы), либо в
виде сводной количественной характеристики (например, сред-
ней).
Переменная в данном случае представляет собой признак,
характеризующий элементы генеральной совокупности. Значе-
ния признака могут измеряться или наблюдаться в результате
эксперимента и далее входить в случайную выборку, представ-
ляющую генеральную совокупность.
Будем теперь рассматривать ситуацию, когда генеральная
совокупность и выборка состоят из измерений не одной, а двух
переменных и при этом требуется описать, как связаны эти
переменные.
13.1. ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ
13.1.1. Корреляционная связь н корреляционное поле
Можно выделить два типа связи между парой переменных.
Первый тип — функциональная (или детерминированная)
связь — выражается в виде формульной зависимости. В этом слу-
чае одна из переменных полагается независимой, а другая —
зависимой. Зная точное значение независимой переменной и
подставляя его в связующую формулу, получим единственное
значение зависимой переменной. Рассмотрим другой тип свя-
зи, который проявляется как тенденция, т. е. в общем, при
массовых наблюдениях. Такая связь называется статистической.
Ее частным случаем является корреляционная связь. При кор-
реляционной связи изменение независимой переменной влия-
299
ет на изменение среднего значения зависимой переменной
Будем обозначать л независимую переменную (факторный по-
казатель), у — зависимую переменную (результативный пока
затель). Для корреляционной связи значению факторного по-
казателя х ставится в соответствие нс единственное значение
результативного показателя у, как при функциональной свя-
зи, а некоторое распределение значений у.
Корреляционно-регрессионный анализ заключается в уста-
новлении степени тесноты связи (корреляционный анализ) и
ее формы, т. с. аналитического выражения, связывающего пе-
ременные (регрессионный анализ).
Первым шагом в проведении исследования является по-
строение специального графика, называемою корреляционным
полем, или диаграммой рассеяния. На координатной плоско-
сти по оси абсцисс отэстадывается значение факторною пока-
зателя, а по оси ординат — соответствующее значение резуль-
тативного показателя. На плоскости отмечается точка, для
которой отложенные по осям значения являются координата-
ми Каждой паре наблюдений (х, у) будет соответствовать точ-
ка корреляционного поля Чем теснее связь между переменны-
ми, тем более плотно точки должны располагаться вокруг
некоторой линии. Эта линия будет графиком аналитической
зависимости между переменными. Если точки корреляционно-
го поля беспорядочно разбросаны на координатной плоско-
сти. го это означает отсутствие тесной взаимосвязи между пе-
ременными.
Прнхюр 13.1. Рассмотрим взаимосвязь между весом человека х
и его ростом у. Пусть имеются пары наблюдений 10 случайно
выбранных человек :
х. кг. 67.3 68.3 70,9 70 65,9 68,2 71,8 74 71,9 69.5
у, и: 1,74 1,69 1.82 1,79 1,61 1,83 1,95 1,92 1,81 1,75
Соответствующее корреляционное поле представлено на
рис 13.1.
Визуальный анализ графика на рис 13 1 показывает, что за-
висимость между переменными вполне реальна В данном слу-
чае в качестве ее аналитического выражения может выступать,
например, прямая с положительным угловым коэффициентом
В общем случае если с увеличением или уменьшением фак-
торного показателя наблюдается концентрация значений ре-
зао
Рис. 13.1. Корреляцио1*«се папе записимосзм роста от веса удивила
(полами те (иная корреляция)
зультзтинного показателя окаю прямой с положительным на
клоном. то говорят. что имеет место линейная положительная
корреляционная связь, или просто положительная корреляция.
Если факторный показатель изменяется в одном направлении,
а соответствующие значения результативного показателя рас-
полагаются достаточно тесно около прямой, имеющей отри-
цательный угловой коэффициент, то такая связь называется
линейной отрицательной корреляционной связью, или просто
отрицательной корреляцией На рис 13.2 представлен график
корреляционного поля для пар наблюдений, х — затраты на
фильтрацию вредных выбросов в атмосферу ну- концентра*
ния вредных примесей в атмосфере. Отрицательная корреляция
здесь очевидна
Рве. 13.2. Пример отрифпяльмоА коррслтцы
ж - »чр«-ы на фильтрацию «рохгъ» воВюоссе » жгиосферг.
Г псм4»-траигй >p«ahui мидетв и Атмосфере
Корреляционное поле на рис. 13.3 характеризует отсутствие
какой-либо корреляции.
301
Рте. 13.3. Пример отсутствия корреляции
Корреляция может быть не обязательно линейной (рис. 13.4).
Рте. ГЭ.4. Пример нелинейной коррелыионной сейм
В данной главе мы булем рассматривать методы анализа ли-
нейной корреляции, которые также при определенных усло-
виях можно использовать и случае нелинейной корреляции.
13.1.2. Коэффициент корреляции
Пусть расположение точек корреляционного поля наводит
нас на мысль, что имеет место линейная корреляция. Это пред-
положен ие, основанное на визуальном анализе, носит предва-
рительный характер Очевидно, необходима объективная коли-
чественная характеристика, определяющая тесноту линейной
связи между переменными. То есть требуется определить, в ка-
кой степени мы можем оценивать связь результативного пока-
зателя с факторным » виде прямой линии. Для измерения тес-
ноты линейной корреляционной связи вычисляется коэффи-
циент корреляции Его смысл и вывод вычислительной формулы
рассмотрим на следующем примере.
эог
Пусть у (результативный показатель) характеризует годо-
вой объем продаж некоторою продукт фирмы, а х (фактор-
ный показатель) определяет годовые затраты на рекламу. Фир-
ма сбывает свой товар в различных ретионах страны через сети
розничных торговых предприятий Случайным образом были
отобраны данные по 10 регионам (табл. 13.1).
Таблица 13.1
Пары наблюдений по регионам: затраты на рекламу х
(дее. тыс. долл.) и объем продаж у (тыс. ед.)
Ьпюыы М Г
1 22 16
2 26 17
3 45 26
4 37 24
5 2В 22
в ЬО 21
7 Ь6 32
в 34 IB
9 60 3D
10 40 20
Х = 39.8 у-гав
Корреляционное поле, построенное по данным табл. 13.1,
представлено на рис. 13.S.
Рис. T3.S. Корр«.-яцио*-«ит поле для пар ньПгкхпений
заняты на рекламу я и пбьем продаж у
Расположение точек на диаграмме рассеяния явно указывает
на линейную корреляционную связь между переменными. Опре-
делим теперь меру тесноты этой связи. Ее смысл заключается в
сопоставлении отклонений значений обеих переменных от их
ЗОЭ
средних (в табл. 13.1 указаны значения л =39,8 и у =22,6). Эти
отклонения приведены в табл. 13.2.
Таблица 13.2
Отклонения от средних факторного
и результативного показателей

JT - X У" У
22 - 39,8 = -17,8 16 - 22,6 = -6,6
26 - 39.8 = -13,8 17 - 22,6 = -5,6
45 - 39,8 = 5,2 26 - 22,6 = 3.4
37 - 39.8 - -2.8 24 - 22,6 - 1,4
28 - 39.8 = -11,8 22 - 22,6 = -0.6
50 - 39,8 = 10,2 21-22,6 = -1,6
56 39,8- 16.2 32 - 22,6 - 9,4
34 - 39,8 = -5.8 18 - 22,6 = -4,6
60 - 39,8 = 20,2 30 - 22,6 = 7.4
40 - 39,8 = 0.2 20 - 22,6 = -2,6
Заметим, что в табл. 13.2 преобладают пары отклонений с
одинаковым знаком. Эго говорит о том, что отклонения от сред-
ней в одном направлении значений факторного показателя вы-
зывают в большинстве случаев отклонения от средней в ту же
сторону значений результативного показателя. Таким образом,
вычисление пар отклонений от средних позволяет сопоставить
эти отклонения с учетом знака. Однако их сопоставление с уче-
том размера невозможно, так как отклонения факторного и
результативного показателей измеряются в разнокачественных
единицах. Так, для х это денежные единицы, а для у — физи-
ческие единицы, т. е. единицы товара. В общем случае независи-
мо от ситуации данного примера сравнение отклонений, как
правило, невозможно адекватно провести даже и тогда, когда
переменные измеряются в одинаковых единицах. Эго связано с
тем, что размеры отклонений зависят от величин самих при-
знаков. Например, один из показателей выражается трехзнач-
ными числами, а другой — двузначными. Поэтому при сопос-
тавлении имеет смысл абсолютные отклонения заменить на
относительные в каждой паре (х, у). Сделать это можно по ана-
логии со стандартным нормальным распределением, когда от-
клонение от средней нормировалось, т. е. делилось на величину
стандартного отклонения (см. раздел 7.3.3).
Нормировав отклонения для обеих переменных, т. е. разде-
лив их на соответствующие стандартные отклонения, мы смо-
жем попарно сравнить их друг с другом в масштабах стандарт-
304
ных отклонений. В табл. 13.3 представлены стандартные откло-
нения и нормированные отклонения затрат на рекламу и объем
продаж.
Таблица 13.3
Нормированные отклонения затрат на рекламу (х)
и объем продаж (у)
-17.8/12.2 = -1,46 -6,6/5.12 = -1,29
-13.8/12,2 = -1,13 -5,6/5,12 = -1,09
5,2/12,2 = 0,43 3.4/5.12 = 0,66
-2,8/12,2 = -0,23 1,4/5.12 = 0,27
-11,8/12,2 = -0,97 -0,6/5,12 = -0,12
10,2/12,2 = 0,84 -1,6/5,12 = -0,31
16,2/12,2= 1,33 9,4/5,12 =1,84
-5,8/12,2 = -0,47 -4,6/5,12 = -0.9
20,2/12,2= 1,66 7,4/5,12= 1,44
0,2/12,2 = 0,016 -2.6/5,12 = - 0,51
S, = 12,2 Зк=5,12
В качестве обобщающего показателя тесноты линейной свя-
зи двух переменных рассмотрим среднее произведение норми-
рованных отклонений:
«у
^(х-хХу-у)
ПЗх5у
(13.1)
где х — значение факторного показателя (независимой пере-
менной);
у — значение результативного показателя (зависимой пе-
ременной);
— выборочное стандартное отклонение факторного по-
казателя;
s? — выборочное стандартное отклонение результативного
показателя;
п — количество пар наблюдений (объем выборки).
Величина (13.1), обозначаемая г, называется выборочным
коэффициентом корреляции, который варьируется от —1 до
+ 1, так как каждое нормированное отклонение меньше еди-
ницы ввиду определения стандартного отклонения. Знак и ве-
личина коэффициента корреляции зависят от знака суммы
L(x - х )(у - у), стоящей в числителе отношения (13.1). Если
преобладают отклонения с одинаковыми знаками, то коэффи-
305
iihcht корреляции имеет знак плюс, если, наоборот. преобла-
лают отклонения с разными знаками, то коэффициент корре-
ляции будет отрицательным Чем больше абсолютная величина
каждого отклонения, тем больше абсолютная величина суммы
Х(х — i) (у — >) или абсолютная величина коэффициента
корреляции Приближение коэффициента корреляции к к I (или
I) означает увеличение степени тесноты линейной положи-
тельной (или отрицательной» корреляционной связи Если имеет
место полная линейная корреляция, т. с. переменные сказаны
линейным функциональным соотношением у “ b0 + b х, то
легко показать, что коэффициент корреляции ранен + i при
6, > 0 и -I при 4, < 0.
На диаграмме рассеяния эти случаи характеризуются распо-
ложением точек на прямой линии (рис. 13.6).
Рис. 13.6. Случаи гипчей коэреля1,ии:
1 - патнай гспигитет^тад eupjMUMuHw
- 1 го<«нэч ото««дагсгънзч *сррогкщ><«>
Котла коэффициент корреляции близок к нулю, линейная
корреляционная связь отсутствует.
Типичная диаграмма рассеяния в этом случае представлена
на рис 13 3 Следует подчеркнуть, что близость коэффициента
корреляции к нулю нс означает отсутствие какой-либо связи
вообще. Коэффициент корреляции является индикатором только
линейной связи Поэтому при небольшом по абсолютной вели-
чине значении коэффициента корреляции может существовать
какая-то достаточно тесная нелинейная связь (например, та-
кой случай представлен на рис. 13.4).
Вычислим по формуле 13,1 и Данным табл 13 3 коэффнци
ент корреляции
(-1,46) (-U9)+(-M3) (-LO9)e...+<W6 (-O,3l) _0
10
306
Как видно, между затратами на рекламу и объемом продаж
существует достаточно тесная линейная положительная корре-
ляционная связь, 1 е. с ростом затрат на рекламу объем прола*
в среднем возрастает
Формулу (13.1) можно преобразовать к более простому для
вычисления виду
<13.2)
Формула (13.2) не содержит нормированных отклонений от
средних, а оперирует только суммами, что облегчает процесс
вычислении.
13.1.3. Существенность выборочного коэффициента
корреляции
Вычисление выборочного коэффициента корреляции осу-
ществляется на основе выборочных данных, т. е. г является ста-
тистикой или оценкой некоторого параметра. Таким парамет-
ром, очевидно, будет генеральный коэффициент корреляции,
вычисляемый на основе всех значений генеральной совокуп-
ности. Формула для вычисления генерального коэффициента
корреляции (р) имеет вид
(13.3)
где и, — генеральная средняя значений факторного показате-
ля зг,
)i — генеральная средняя значений результативного пока-
зателя у;
о — генеральное стандартное отклонение значений фак-
торного показателя х;
в — генеральное стандартное отклонение значений ре-
зультативного показателя у;
N — объем генеральной совокупности
Выборочный коэффициент корреляции г, как правило, вы-
числяется по данным малых выборок {п < 30). Ввиду случайных
причин значение сможет существенно отличаться от генераль
ного коэффициента корреляции р. Например, может возник-
путь ситуация, когда линейной корреляции нет (т. е. истинное
.307
значение р - 0), а по яыборочным данным значение г суще
огненно отличается от нуля
Так, на рис 13 7 представлено корреляционное поле гене-
ральной совокупности. где разброс точек явно отражает отсут-
ствие линейной связи Однако в выборку попали точки (отме-
ченные на графике крестиками), которые расположены прак-
тически на одной прямой, имеющей положительный наклон
Поэтому следует ожидать, что выборочный коэффициент кор-
реляции будет близок к единице.
V > .
Яке. 13.7. Гсюмефмчйская мнтерлряга^в ямПорки
искажэошгй истинное з начете генерш*ы<мо мюффмияен»»
корреляции: р О, г • 1
В этой связи для выборочною коэффициента корреляции г
необходима оценка существенности, или статистической зна-
чимости. Она заключается в том, что проверяются гипотезы:
Но: р — 0 (линейная связь между хну отсутствует);
Н, р » 0 (линейная связь между х и у существует).
При п < 30 проверку нулевой гипотезы Н„ можно произво-
дить с помощью Г- критерия:
г-0
<-—•.
а,
где г — наблюдаемое (выборочное) значение коэффициента
корреляции,
р = 0 — гипотетическое значение генерального коэффи-
циента корреляции;
з — оценка стандартной ошибки коэффициента корреля-
ции, т. е стандартного отклонения распределения выбо-
рочных коэффициентов корреляции.
Величина S, вычисляется по формуле
зов
Отсюда величина /-критерия примет вид
(13 4)
г ле г выборочный коэффициент корреляции,
л — объем выборки
Статистика (13.4) имеет распределение, близкое к /-рас-
пределению, соответствующему п - 2 степеням свободы. При
заданном
величина
уровне значимости а критическим значением будет
'.а.-/-
> то коэффициент вы-
борочной корреляции / будет существенным, или значимым.
Пример 13.2. Оценим существенность коэффициента корреля-
ции, измеряющего тесноту линейной связи между х (затраты
на рекламу) и у (объем продаж), вычисленного в разделе 13.2.
Условия -задачи: г “ 0.843. л ” 10 Вычислим /-статистику по
формуле (13.4):
0,843 -0843
/ = =----= 4.44
fl-OMf 049
V 10-2
Пусть а ”0.05. Из таблицы Приложения 5 найдем критичес-
кий предел / , = 2,306. Ввиду того что 4,44>2,306. нулевая
гипотеза Н„ о равенстве генеральною коэффициента корреля-
ции нулю отвергается с уровнем значимости 5%
13.1.4. Ранговый коэффициент корреляции
Коэффициент корреляции, рассмотренный в разделе 13.1 2,
вычисляется для переменных, измеряемых в шкале интервалов
или отношений Для оценки корреляции между признаками,
которые выражаются в порядковой шкале, рассматривается
специальный ранговый коэффициент корреляции Под рангом
понимается порядковый номер значения признака в ранжиро-
ванном ряду Рассмотрим значения пар наблюдений (х, у):
зов
Составим ранжированный ряд из значений х (например,
по возрастанию) и найдем их ранги: наибольшему значению
присвоим ранг I, второму по величине - 2 и г. д. Булем обозна-
чат. ранг элемента г . Диалогично определим ранги для значе-
ний у. Заменим пары наблюдений (х, у) соответствующими
рангами (г , г ):
rl
* S ч
У г’«
Предположим, что как среди г О' = 1, 2,..., л), гак и среди
г (| • I, 2,.... л) нет одинаковых:
'' Используя формулу (13 2), запишем выражение коэффици-
ента корреляции между переменными, представленными в ран
говой (порядковой) шкале:

(13 5)
По предположению ранги для х (г ) И у (г ) являются раз,лич-
ными числами от 1 до л Поэтому можно записать:
1?’ -,2+2’ ♦-* "2
Отсюда определим подкоренные выражения в знаменателе
формулы (13.5):
_ л(л + 1К2л +1) _ лг(л + 1)г а Жл1-!)
6 4л 12
Ввиду того что ab= ' |а2 + Ь‘ -(а-6)’) .будет верно соотно-
шение г _
_ л(л + >Х2я + 1) 1 y* 12
6 '
где </ = г — г .
• »,
310
Тогда выражение в числителе формулы (13 5) имеет вил
Ev,.-E^>-=^4S'A
В результате преобразований коэффициент корреляции (13.5)
выразится формулой
л(л'-1) 1« j
и(и2-1) я<в’-1)
(13 6)
12
тле величины d обозначают разности рангов.
Формула (13 6) определяет ранговый коэффициент корре-
ляции Спирмена, обозначаемый г.
Преимущество коэффициента корреляции рангов состоит в
том, что на его основе оценивается коррелироваиность чисто
качественных признаков, не имеющих точного количествен-
ного измерения. Например, с помощью экспертов можно про-
ранжировать кандидатов на занятие определенной должности
по различным деловым и личным качествам. Коэффициент
Спирмена изменяется от -I до I. В случае полного совпадения
рангов гиг козффииие1гг г - I. что означает полную поло-
жительную корреляцию. Если имеет место полная противопо-
ложность рангов, то г = -1 и между переменными существует
полная отрицательная корреляционная связь В случае г - О
корреляционная связь отсутствует
Пример 13.3. Комитет по здравоохранению проводит иссле-
дование 11 крупнейших городов страны с целью выявления
наиболее существенных факторов, влияющих на рост легоч-
ных заболеваний у городских жителей. С помощью специаль-
ных тестов эти города были проранжированы по двум крите-
риям (г = I означает “худший", г “ 11 — "лучший"): коли-
чество легочных заболеваний на 100 тыс. жителей и уровень
загрязненности воздуха. Затем определялся ранговый коэф-
фициент корреляции Спирмена для оценки степени тесноты
связи ыежду легочными заболеваниями и загрязненностью
воздуха Промежуточные вычисления были сведены в табли-
цу (табл. 13.4).
эн
Тзбшиим 13.4 вмЧИСЛВНИЯ РАНГОВОГО коэффициента ворролвцин
и загрязненностью воздуха (X) по 11 городам |Г)
Город 4, • г - Г
Г, 5 4 1 1
Г, 4 7 -3 9
7 9 -2 4
3 1 2 4
г9 г -1 1
ге 11 10 1 1
гт 2 3 1 1
10 5 5 М
г_ 8 5 2 4
с. 6 8 -2 4
Г.1 9 11 2 4 1<Г‘- 5в
Используя данные табл. 13.4, вычислим ранговый коэффи-
циент корреляции по формуле (13.6):
г = I - 6 58/11 - <112 — I) = I - 348/1320 =
- 1 - 0,264 = 0,736
Величина коэффициента Спирмена (0,736) характеризует
высокую положительную корреляцию между появлением легоч-
ных болезней и загрязненностью воздуха в крупных городах
На практике могут возникнуть ситуации, когда среди зна-
чений признаков Xи Уесть равные между собой В этом слу-
чае несколько одинаковых значений образует связные ран-
ги. которые полагаются равными средней арифметической
их порядковых номеров в ранжированном ряду. Например,
если на 5-м и 6-м местах расположены одинаковые значения
признака, то все они будут иметь одинаковый рант , ранный
5,5((5 ♦ 6)/2 - 5,5).
Пример Г3.4. На фирме была проведена аттестация 10 менед
жеров среднего звена. С помошью специальных тестов и систе-
мы показателей эффективности работы подразделений были
получены значения рейтингов менеджеров. Кадровую службу
интересует, насколько величина рейтинга связана со стажем
работы на фирме Для вычисления коэффициента Спирмена
данные о рейтингах и стаже были переведены в ранги Все про-
312
межуточные вычисления коэффициента ранговой корреляции
прелетлклены в табл 13.5.
ГаДлица 13 5
Промежуточные вычисление для определение
коэффициента ранговой корреляции между рейтингом (X)
и стажем работы (У)
Намял ары Райгммг Стаж работы Раит Л Рыж V Ж <Р
(X) in г
1 3 10 4,5 3.5 1 1
2 5 11 5,5 9 -2.5 6.25
3 1 1 1 1 0 0
4 4 3 5 2 3 0
5 8 5 10 4.5 5,5 30.25
6 3 4 3,5 3 0.5 0.25
7 6 13 8 10 -2 4
8 2 6 2 6 4 16
9 5 9 6.5 7 0.5 0.25
10 7 10 9 8 1 1 £ й’-ва
По формуле (13.6) вычислим г:
г = I - 6 68/10 (101 - 1) - 1 - 0,412 - 0.588.
Таким обратом, существует средняя степень связи между
рейтингом менеджера и его стажем работы на фирме.
Отметим. что если число связных рангов достаточно вели-
ко. то в формулу (13.6) следует ввести корректирующий фак-
тор. Пусть г обозначает ранговую корреляцию между признака
ми X и ) В случае связных рангов коэффициент Спирмена
выражается по формуле
г =1_ (137)
(л’-н-12ЛХл’-"-12Я)’
гае л=112Е‘а)-лР;
j - номера связок по порядку для признака X.
А — число одинаковых рангов в у-й связке по X;
к номера связок по порядку для признака t;
в( — число одинаковых рангов в К-й связке no У.
333
13.2. ПРОСТОЙ
ЛИНЕЙНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
13.2.1. Уравнение простой регрессии.
Метод наименьших квадратов
После того как установлено существование и вывалена сте-
пень тесноты линейной святи, возникает проблема определе-
ния конкретного вида этой зависимости. Геометрически это оз-
начает, что нужно подобрать такую прямую, которая нанлучшим
образом сглаживала бы точки корреляционного поля На рис
13.1 и 13 2 это было сделано "на глаз" по принципу, чтобы все
точки одновременно находились хак можно ближе к прямой
Уравнение прямой, сглаживающей точки корреляционного
поля, называется уравнением простой (парной) регрессии, а
сама прямая — линией регрессии.
Если у — зависимая переменная, ах— независимая, то на-
хождение зависимости у от х будем называть определением per
рессии у на х.
Формальным аналитическим метолом определения уравне-
ния регрессии является метод наименьших киалратов. Рассмот-
рим сначала геометрическую интерпретацию этого метода.
Р>*с. 13.9. Геометрическая мг’щш »-зим*?»-ъц.мк «вадрэюв
На рис. 13.8 представлена искомая линия регрессии, на ко-
торую из каждой точки корреляционного поля опушены от-
резки, преттендикулярныс оси х Длины отрезков d},...,
характеризуют- расстояния от точек до прямой регрессии.’Пусть
критерием иаилучшей сглаживающей прямой будет миними-
зация суммы квадратов расстояний:
тптп<</|‘ ♦ di я-<(?♦..,♦</*) nrin£<tf. (13.8)
<-т
31-1
Прямая, построенная по критерию (1.18), будет линией рег-
рессии, полученной методом наименьших квадратов.
Рассмотрим аналитическую процедуру метода наименьших
квадратов,
Пусть имеется совокупность из я пар наблюдений: (х, у,).
Ц, ур,-. (*.. У)
Запишем искомое уравнение регрессии в виде
у-*„+4,х, (13.9)
где и Л] — искомые величины, а у (читается “у с крыш-
кой") характеризует оценку у при заданном х, когда Ьа и
(т| определены
Сумму квадратов расстояний (5) можно записать так:
$ = = £(у-у)’=Е(у, -ь,»,)1. (в.ю)
»т
Будем рассматривать 5 как функцию двух переменных Ьа и
найдем такие их значения, которые минимизируют сумму
квадратов расстояний Для атого продифференцируем выраже-
ние (13.10) отдельно по 4,и i и приравняем частные произ-
водные к нулю: л
т~-=-з£( У, - - Мт)=О.
«Ъ .-I
. (13.11)
дГ = -2^ х,(у,-Ат-Ь,х,)ж0.
"И м
Из (13.11) следует система так называемых нормальных урав-
нений я В
=2л- (13.12)
1-1 г-4
(|3|3>
1=1 1*1 4*1
Неизвестные значения Ьл и Ь находятся как решение систе-
мы нормальных уравнений (13.12) и (13.13):
п п
315
Величина 4, является угловым коэффициентом линии рег-
рессии Он называется коэффициентом регрессии Если неза-
висимая переменная х возрастает на единицу, то зависимая
переменная у в этом случае возрастает в среднем на b единиц
при b > 0 (или убывает в среднем на 4, единиц при bt < 0).
Величина 4П является ординатой пересечения прямой регрес-
сии с осью у, т. е характеризует значение зависимой перемен-
ной у при х “ 0. Для регрессионного анализа 4(1 не имеет осо-
бого смысла В отличие от него коэффициент регрессии 4( более
информативен и играет значительную роль в прикладном ана-
лизе.
Разделим обе части нормального уравнения (13.12) на л:
или у - 4в 4, х .
(13 16)
Соотношение (13.16) показывает, что линия регрессии (13.9)
проходит через точку (х , у). Отсюда можно записать другой
вил уравнения регрессии:
У — У -Ь,(х— х).
(13.17)
Пример 13.в. Вычислим коэффициенты уравнения регрессии
по данным табл. 13.1. Для этого проведем необходимые проме-
жуточные вычисления и сведем их в таблицу:
я Г У И
22 16 352 484
26 17 442 Б76
45 26 1170 2075
37 24 088 1369
28 22 616 704
50 21 1050 254»
56 32 1792 3136
34 18 612 1156
60 30 1 вгю 3600
40 20 800 1600
зэв 226 9522 1/330
316
По формуле (13.14) вычислим 6:
. 9522-398-226/10 ....
Л =-----------z---” U.J 34
17334)-398’/10
На основе (13.15) определим 6а:
. 226 „„.398
10 10
Уравнение регрессии имеет вил
у - 8,51 + 0,354х.
Коэффициент регрессии 0,354 означает, что возрастание на
10 000 лолл затрат на рекламу (х возрастает на 1) сопровожда
ется в среднем ростом на 354 единицы объема продаж (у возра-
стает в среднем на 0,354). Свободный член 8,51 не несет ника-
кой полезной информации. Он соответствует объему продаж
при нулевых затратах на рекламу. Однако уравнение регрессии
было построено на основе выборочных данных, где фактор-
ный показатель х изменялся в пределах от 22 000 до 60 000 долл.
Поэтому данная линейная зависимость совершенно необяза-
тельно сохраняется за границами этого промежутка
13.2.2. Стандартная ошибка регрессии
Полученное на основе метода наименьших квадратов урав-
нение регрессии можно использовать для предсказания значе-
ний у в зависимости от значений х. Ясно, что эти предсказания
не будут точны, так как уравнение регрессии задает связь меж-
ду переменными только в среднем. На рис. 13.8 данные наблю-
дений (точки корреляционного поля) разбросаны вдоль пря-
мой регрессии Расстояния </ раины абсолютным величинам
ошибок оценок фактических значений yf полученных с помо-
щью уравнения у = ba + 6,x. Обозначим ошибку е:
е, = у,-у,,г= (13.18)
Ошибки (13.18) называют также остатками Если точка на-
блюдения находится выше примой регрессии, то остаток будет
положительным, если ниже — отрицательным.
Рассмотрим пару наблюдений в исходных данных приме-
ра 13.5 :х — 44), у “ 20. На основе уравнения регрессии у = 8.51 +
+ 0.354л вычислим оценочное значение у при х " 44):
317
у = 8,51 + 0,354 40 - 22.67
Величина остатка такова:
у - у - 20 - 22,67 - -2,67.
Линия регрессии, построенная по методу наименьших квад-
ратов, обладает свойством: сумма всех остатков равна нулю
Действительно, рассмотрим уравнение регрессии, представ-
ленное в виде (13.17):
у " у + *, (х-х).
Тогда остаток е выражается следующим обратом
*, = У, - У,” (/, ~ У) - *,(х -х )•
Вычислим сумму* остатков, имея в виду свойство средней
арифметической:
X*. = У; - И ) =£(>, ~У1~Ь> Ё<*. -X) = о.
.-I ы >•<
Следовательно, остатки для прямой, построенной по мето-
ду наименьших квадратов. взаимно погашаются. Это говорит о
том, что точки наблюдений в одинаковой степени разбросаны
по обе стороны от сглаживающей прямой регрессии.
После определения уравнения регрессии возникает пробле-
ма опенки надежности этого уравнения, если его использовать
для предсказания значений у. Очевидно, чем меньше в целом
разброс точек наблюдений около прямой регрессии, тем на-
дежней будет уравнение как оценочная функция В качестве меры
разброса можно рассмотреть аналог стандартного отклонения,
только отклонения вычислять не от средней, а от оценочной
прямой. Такая характеристика называется стандартной ошиб-
кой оценки (регрессии) и вычисляется по формуле
(13 19)
где у — наблюдаемые значения независимой переменной;
у — оценочные значения, полученные из уравнения рег-
рессии и соответствующие каждому у;
л — число точек наблюдения. участвующих в вычислении
линии регрессии.
318
Заметим, что в соотношении (13.19) сумма квадратов ос-
татков делится не на и, а на и - 2. Это связано с тем, что 2
степени свободы были потеряны при оценке с помощью урав-
нения регрессии, которое задается величинами Ь„ и ht, вычис-
ленными на основе и пар наблюдений
Очевидно, чем меньше величина стандартной ошибки рег-
рессии, тем ближе располагаются точки наблюдений к прямой
ретрессии (тем лучше прямая сглаживает точки корреляцион-
ного поля).
Если 5 ,= 0, то это означает, что построенная прямая явля-
ется наилучшей сглаживающей прямой. В этом случае все точки
наблюдений располагаются на прямой, т. е. нет ни одной точ-
ки. отклоняющейся от линии регрессии
пример 13.6. Вычислить стандартную ошибку регрессии для
уравнения регрессии у ” 8,51 + 0,354х, используя исходные
данные примера 13.5. Все промежуточные вычислении сведем в
таблицу:
я F г 0-й’
22 16 16,3 -0.3 0,09
» 17 17,71 -0.71 0.504
45 26 24,44 1.56 2.434
37 24 21,61 2,39 5.712
28 22 16,42 3.58 12Л16
50 21 26.21 -5.21 77 144
56 32 2833 367 13.469
34 18 20.54 -2,54 6,452
60 30 29 75 0 25 0,063
40 20 22,67 -2.67 7,129
0 758»
Стандартная ошибка регрессии вычисляется по формуле
(13.19):
5 у'9'476 -3.078
гл У 6
13.2.3. Доверительные интервалы уравнения регрессии
Рассмотрим использование уравнения регрессии в качестве
модели прогнозирования Эта модель описывает взаимосвязь
независимой переменной х и зависимой переменной у лишь в
319
среднем, поэтому фактические значения у, как правило, не
будут совпадать с точечными оценочными (т с прогношымн)
значениями у.
Рассмотрим причины этих отклонений.
Уравнение линейной регрессии (13.9) является выборочным,
т. е. величины и t>t рассчитываются по методу наименьших
квадратов на основе выборки. Предположим, уравнение рег-
рессии определяется по данным генеральной совокупности и
имеет вид
у-0„ + Р,х (13.20)
Тогда р„ и р, можно рассматривать как параметры, а b и
Ьп — соответственно их оценочные статистики.
Генеральное уравнение (13.20) характеризует сглаживающую
прямую, полученную по методу наименьших квадратов Так же
как и выборочное уравнение, оно описывает взаимосвязь не
ременных в среднем, в общем. Среди причин, вызывающих
отклонения фактических значений от сглаживающей прямой,
можно выделить
влияние других факторов, не учтенных в модели;
ошибки измерения;
случайные возмущения.
Запишем уравнение регрессии как модель, учитывающую
подобные отклонения:
у-Я. + Р.х+е, (13.21)
где с — случайная ошибка, вызванная указанными причинами
В модели (13.21) фактическое значение у складывается из
двух компонент — детерминированной (Р( + р,х) и случайной
(е). Уравнение (13 20) характеризует некоторое среднее значе-
ние у при заданном значении х, равное оценочному значению
у. Уравнение (13.21) отражает индивидуальные значения ус
учетом возможных отклонений от средних, т. е, от линии гене-
ральной регрессии.
Для того чтобы использовать модель (13.21) для предсказа-
ния значений у, необходимо сделать следующие допущения:
— каждому значению х соответствует распределение наблю-
даемых значений у, которое является нормальным. Иначе
говоря, генеральная совокупность фактических значений
у нормально распределена вокруг линии генеральной рег-
рессии (рис. 13.9);
320
— все распределения у имеют одинаковую дисперсию вок-
руг всей прямой генеральной регрессии, т. е. дисперсия
остается постоянной при возрастании х;
— ошибка г является случайной величиной со средней, рап-
ной нулю, причем последовательные значения г незави-
симы друг от друга и имеют одинаковую дисперсию
Рис Т.З.Я. -кюмапь-пя.’ рас-средеойний у дла трех плможгых ихачммй *
вокруг гмиия генерального уравнения ре<реоони
Таким образом, при построении парной линейной регрес-
сии предполагается, что для каждого индивидуального значе-
ния у. будет верно соотношение
(13.22)
Исходя из допущений относительно случайных последова-
тельных ошибок г, можно записать:
Е<е,> - 0;
ЕХед) • E<t,)F.(ep = 0 (i * Д
Е(«,) - Е|(е, - 0) (с, - 0)1 = o’;
me i,J — 1,..., л — номера наблюдений.
Кроме того, из допущений относительно генерального
уравнения линейной регрессии получим
Е(у.) - Е(Р. + р,х, + с.) ’ р, + р,х + Е («,) - р„+ р,х - у..
Отсюда и месм
Е«у, - ЕТу )й_т - Е(>У)1 = Е(у, ~ У, >0', - У,)|* Е(се)) » o’.
Итак, если предположить линейную корреляционную связь
между переменными х и у, то дисперсия распределения у вок-
321
рут прямой генеральной регрессии совпадает с дисперсией слу-
чайных ошибок е
На практике ввиду наличия только выборочной информа-
ции построить теоретическую модель (13.21) не представляет-
ся возможным. Поэтому мы вынуждены пользоваться выбороч-
ным уравнением 03 9), в кагором значения 6, и 4, являются
статистическими оценками соотве гстауюших параметров р, и
(3„ теоретической модели
Таким образом, при определении доверительных пределов
для индивидуального значения у (т. е при определении интер-
вала, где с доверительной вероятностью будет содержаться
фактическое значение у для данною значения хф) с помо-
щью выборочного уравнения (13.9) обшая дисперсия прогноза
+ btx будет складываться из трех дисперсий: диспер-
сии. определяющей разброс точек наблюдений вокруг теоре-
тической прямой, дисперсий статистик blt и Z>,
Дисперсия разброса о’ оценивается как квадрат стандарт-
ной ошибки регрессии
221-Х.
п-2
Можно показать, что оценка дисперсии Ь* вычисляется по
формуле 2
а оиенкд дисперсии bt (см раздел 13.2.5) — по формуле
Если представить уравнение в виде у = у + Ь^х -х), то
дисперсия прогноза уЦ,) будет иметь вид (обозначение з})
Стандартное отклонение .г,называйся стандартной ошиб-
кой прогнозирования:
з х, '| + 1+ <Х?)2 (13.23)
322
Винду (13.23) и допущения о нормальности распределения
у вокруг прямой генерального уравнения регрессии можно оп-
ределить доверительный интервал для индивидуального значе-
ния у при заданном значении х.
Для больших выборок (л г 30) при доверительной вероят-
ности I — а доверительный интервал вычисляется по формуле
у +2^днлиуЦ) ±Z^ I) ♦ 1 у <5^2^.(1324)
I л-2 1J л >(д-*Г
В случае малых выборок (л < 30) стандартное нормальное
распределение Z заменяется на /-распределение при л - 2:
У ,11ИЦа-г1 <11251
’ п~г \ п хс-»-*)*
Пример /17. Рассмотрим уравнение регрессии, полученное в при-
мере 13.5, и вычислим 95-процентный доверительный интервал
для объема продаж у при затратах на рекламу xt “ 35 тыс, долл.
Вычислим точечную оценку у (-\,)
у UQ = 8,51 + 0,354 35 = 20,9 (20 900 ед.).
Величина стандартной ошибки регрессии (или стандартное от-
клонение. харакгеризуюшее разброс точек наблкиения около при
мой регрессии) была вычислена в примере 116:5 3,078.
Для определения стандартной ошибки прогнозирования
необходимо вычислить сумму квадратов отклонений хотсред-
ней х . Воспользуемся для ЭТОГО формулой L(x - х “
г, (*1
= 2jc ——**, в которую подставим соответствующие зна-
чения. вычисленные в примере 13.5:
Е(х -X )’ = 17330 » 1489,6.
Значение средней х равно
п 10
По таблице Приложения 5 найдем • 2,306.
323
В результате, используя формулу (13.25), получим
_ Г« (35-39Л)2
20.9 ±2.306 3,078 *й - 20.9 ±7.49 -
= 13,41 +28,39.
Таким образом, с вероятностью 95% можно утверждать: если
затраты на рекламу составляют 35 тыс. долл., то ожидаемый
обмм продаж будет в гранииах от 13 410 до 28 390 ед.
Как видно из формул (13.24) и (13.25). ширина довери-
тельного интервала прогноза зависит от объема выборки я. Ес-
тественно, что с ростом л точность прогноза повышается (до-
верительный интервал сужается). Очевидно, наибольшая
точность будет иметь место, когда прогнозируется значение у
при условии, что х = л . В этом случае стандартная ошибка про-
гнозирования принимает наименьшее значение:
На рис. 13.10 показан график доверительных границ прогно-
за Они представлены в виде ветвей гиперболы, расположен-
ных ныше и ниже прямой регрессии
Рис. Г3. to. Дрмритслк.>«4П границы прппяаза
Как видно на рис. 13.10. наиболее ужа я часть между МТМ
ми графика наблюдается при х =лг. Доверительные границы
расширяются по мере удаления значений хот х .
324
13.2.4. Коэффициент детерминации
Уравнение регрессии позволяет оценить, в какой степени
изменяются значения зависимой переменной в зависимости от
изменения независимой переменной Величина стандар!ной
ошибки регрессии определяет степень разброса точек наблю-
дений вокруг прямой регрессии. Коэффициент корреляции яв-
ляезся отвлеченным показателем, характеризующим тесноту
связи между переменными, если эта связь линейная
Рассмотрим теперь показатель, который измеряет интенсив-
ность связи, т. е. определяет, в какой степени изменением неза-
висимой переменной обьясняется изменчивость (вариация)
зависимой переменной. Определение интенсивности связи ос-
новано на разложении на два слагаемых суммы квадратов от-
клонений зависимой переменной от средней, сумма квадратов
характеризует общее рассеяние под воздействием всех факто-
ров, влияющих на зависимую переменную у.
Представим отклонение для индивидуального значения у. в
виде суммы:
У,~у = (У, _У) * О’,- у,). (13.26)
где у — оценочное значение, вычисленное с помощью урав-
нения регрессии у, “ 6, * 6.x,
Если возвести обе части равенства (13.26) в квадрат, то
можно показать, что сумма квадратов отклонений по всем вы-
борочным точкам представляется и виде
£( V - У)г = £(> - >)2 ♦ X < 3- Я’- (• 3-27)
Первая компонента в правой части равенства (13.27) харак-
теризует отклонения расчетных величин у от средней у. Вви-
ду того что у “ Ь. ♦ Ь'Х, эта сумма квадратов отклонений
обусловлена регрессией, т е. объясняется изменением незави-
симой переменной х Вторая компонента отражает отклонения
фактических значений у от оценочных значений, вычисленных
на основе уравнения регрессии В этом случае сумма квадратов
отклонений относительно регрессии измеряет ту часть общего
рассеяния, которая обусловлена всеми факторами, за исклю-
чением х
Если разделить обе части равенства (13 27) на п, то мы по-
лучим фундаментальное соотношение, характеризующее раз-
ложение общей дисперсии значений у
325
Из соотношения (13.28) следует, что общая дисперсия ре-
зультативного показателя у является суммой двух компонент пер-
вая характеризует ту часть обшей дисперсии, которая объясняет
ся факторным показателем х, а вторая — необъясним кую часть
обшей дисперсии. Это положение иллюстрируется на рис. 13.11.
Я*с. 13.11. Разложение обил*О огклонемия у от у
<у “ у) — пЛыг.нинсля честь |<*Г^Л«Н*Л»ИМ|»» г |,
|у и часть. и«)ОХ4пст«мя вепки фаа-ирам*'. .м левлоче-ыем м|
Ввиду уравнения (I3.I7), полученною по методу наименьших
квадратов. точный прогноз будет всегда при х “ х : у ( х) “ >•
Как видно из рис I3.l I, отклонение (у ' у) зависит от того,
насколько значение факторною показателя х отклонилось от х
Иначе говоря, оно объясняется изменением X В то же время от
клоненне (у - у) никак нс объясняется вариацией независимой
переменной х Именно величина лото отклонения имеет решаю-
щее значение для прогнозирования Если бы вариация независи-
мой переменной объяснялась только изменением х, то все откло-
нения (у _ у) были бы равны нулю и все точки наблюдений
располагались на прямой регрессии.
Рассмотрим отношение объясненной дисперсии к общей
дисперсии (обозначим его г1):
2 - £(У~ У)2 _, _ £(У~У>2
^(у-у)г Х<У-У)’
<13 29)
Величина г’ называется коэффициентом детерминации. Он
характеризует удельный вес (процент) общей дисперсии. ко-
торый объясняется уравнением ретрессии (или изменением
факторного показателя х). Чем больше этот удельный нее, тем
в большей степени вариация у объясняется изменениями пере-
менной х, и. следовательно, связь между ними является более
интенсивной.
Можно показать, что значение коэффициента детермина-
ции равно квадрату коэффициента корреляции (выбор обозна-
чения г1 связан именно с этим фактом)
В регрессионном анализе оба коэффициента играют важную
роль. Каждый из них имеет преимущество по отношению к дру-
гому
Так, знак коэффициента корреляции «-определяет направ-
ление корреляционной связи.
Значение коэффициента легерминацин изменяется от 0 до
1 и никак ие указывает на направление связи.
В то же время коэффициент детерминации измеряет интен-
сивность связи, г. е процент обшей вариации результативного
показателя у, объясняемый изменением факторного показате-
ля х.
Пример 13. в. Вычислим коэффициент детерминации для урав
нения регрессии примера 13.5, характеризующего зависимость
объема продаж (у) от затрат на рекламу (х): у - 8,51 ♦ 0,354х.
В разделе 13.2 был рассчитан коэффициент корреляции
г - 0,843. Тогда коэффициент детерминации равен г1 “
-0,843'= 0,71.
Это означает, что 71% общей вариации (дисперсии) про-
даж объясняется изменением затрат на рекламу.
Очевидно, величина I - г1 = 0,29 означает, что 29% общей
дисперсии остается необъясненной
13.2.5. Проверка существенности коэффициента
регрессии
Уравнение регрессии было получено на основе выборочных
пар наблюдений. Очевидно, выборочное уравнение у "1, + Ь х
не будет совпадать с теоретическим у - Ри + ₽,х, которое мог-
ло быть получено по данным генеральной совокупности. В уран
нении репрессии связь между переменными характеризуется ко-
эффициентом регрессии Ь По аналогии с комрфкциенгом
корреляции необходимо проверить, существует ли эта связь на
самом деле или истинный коэффициент регрессии Р равен нулю.
Иначе говоря, следует оценить существенность выборочного
згт
коэффициента регрессии А, г. е. проверить нулевую гипотезу о
том, что = 0. Если />, несуществен, то использование выбо-
рочною уравнения для дальнейшею анализа и прогнозирова-
ния не имеет- смысла
Оценка существенности сводится к проверке гипотез
Но: ₽, =0;
Н,:Р,-0.
При малых выборках (и < 30) следует использовать /-крите-
рий:
где s* — стандартная ошибка выборочного коэффициента
регрессии.
Величина а является оценочным значением стандартного
отклонения распределения выборочных коэффициентов рег-
рессии. При больших выборках распределение будет нормаль-
ным с математическим ожиданием Е(5 ) = В и дисперсией
2 а’ 2 У(у-у)г
<?ь ==—8 . (Р, = 1,11 ---- — дисперсия ошибки гене-
ральной регрессии). Оценочным значением для а; будет
величина квадрата стандартной ошибки регрессии = л1.
определяемая по формуле (13.19). Сэстовагетыю.

Отсюда /-критерий (/-статистики) вычисляется по формуле

<13 30)
При уровне значимости а критический предел задается зна-
чением Если |/| г (,ЯлГ то нулевая гипотеза Н„ отперта
стся, т е коэффициент регрессии Л. сушествен при уровне
значимости а.
Прммвр 13.9. Проверитьсушсс/иеннос/ь коэффициент? регрес-
сии для уравнения у — 8,51 + 0,354х (пример 13.5) при а “0.05.
зав
Вычислим I критерий, подставив » формулу (I3.J0) значе-
ния: ft, “ 0,354. s “ 3.078 (пример 13 6) и S(x - i)1 “ 1489,6
(пример 13.7):
0.354
I =------ -/ - 4.44
3.078/./1489,6
Критическое значение /пм,, “ 2.306
Отсюда |/| " 4.44 > 2,306. и. следовательно, коэффициент
регрессии 6, = 0,354 существен при а = 0.05.
13.2.6. Возможные ошибки при практическом
использовании корреляционно-регрессионного анализа
Корреляционно-регрессионный анализ является эффектив-
ным инструментом статистического анализа Однако следует от-
метить основные ошибки, которые возникают при его исполь-
зовании и которые могут привести к неправильным выводам.
Прогнозирование вне гравии изменения наблюдаемых данных
Эта ошибка заключается я использовании уравнения рег-
рессии в качестве прогнозной функции, когда в уравнение
подставляется значение независимой переменной, выходящее
за границы изменения выборочных значений х. При прогнози-
ровании следует всегда помнить, что уравнение регрессии яв-
ляется экстраполяционным, т. е. оно отражает зависимость,
которая действует только в диапазоне изменения данных, на
основе которых оно было получено
Причинность и статистическая зависимость
Корреляционно-регрессионный анализ позволяет выявить и
оценить статистическую связь между переменными. Однако ста-
тистическая зависимость еще не означает существование при
чинной связи между переменными. Например, если мы гово
рим, что в данном году существует коррелвиия между прибылью
предприятия й затратами на научно-исследо-ваггельские разра-
ботки (НИР), то это не означает, что прибыль в данном году
была вызвана затратами на НИР Реальными причинами при-
были могут быть, например, состояние экономики в данном
году, затраты на рекламу и другие причины Поэтому вывод о
том, ‘гго при возрастании затрат на НИР следует ожидать не-
медленного роста прибыли, будет неверным.
329
Перенесение прошлых тенденции на будущее
При использовании уравнения регрессии в прогнозирова-
нии следует иметь в виду, что исторические данные, участвую-
щие в определении уравнения, могут отражать такие условия и
факторы, которые к моменту прогнозирования уже не оказы-
вают значительного влияния на результативный показатель.
Например, пусть рассматривается регрессия объема производ-
ства на численность работников Прямая, вычисленная на ос-
нове данных за периоды, взятые несколько лет назад, может
иметь больший угол наклона (коэффициент регрессии), чем
прямая, полученная на основе наблюдений за ближайшие пе-
риоды. Причиной этого является эффект от изменения техно-
логии производства.
Величина случайной ошибки, характеризующая разброс
наблюдений вокруг прямой регрессии, также может изменять-
ся от года к году.
Интерпретация коэффициента корреляции
Коэффициент корреляции иногда пугают с коэффициен-
том детерминации, рассматривая его значение как процент ва-
риации у, который обьясняеюя уравнением регрессии Напри-
мер, если г “ 0,6. то неверно утверждать, что 60% обшей
вариации у объясняется регрессией. На самом деде этот про-
цент равен 36%, так как г1 = 0,36. Коэффициент детерминации
г1 озень часто трактуется как процент изменения переменной
у по причине изменения переменной х 'Это неверно, так как г1
измеряет, насколько хорошо одна переменная объясняет дру-
гую только в статистическом, а не в причинном смысле.
Выявление нереальных святей
Используя методы регрессионного анализа, иногда можно
выявить связи между переменными, которые противоречат здра-
вому смыслу При этом даже если одна переменная не является
причинным фактором, вызывающим изменение другой, часто
полагают, что существует какой-то общий фактор для обеих
переменных. Вполне возможно, например, обнаружить статис-
тическую связь между километражем на I литр потребляемого
бензина для восьми автомобилей и расстояниями от Земли до
восьми планет Солнечной системы. Ясно, что эта связь будет
бессм ысленной
Имея сззответствуюшую базу данных, можно строить рег-
рессии между различными парами переменных и получать нео-
жиданные связи. Поэтому регрессионный анализ должен сочс-
330
тать здравый смысл и качественное исследование переменных
Обнаруженные неожиданные связи следует перепроверять,
используя новые данные, прежде чем пытаться найти им объяс-
нения.
ОСНОВНЫЕ ПОЛОЖЕНИЯ ГЛАВЫ 13
Статистическая сеть между двумя переменными проявля-
йся как тенззенция, т. е. в общем, при массовых наблюдениях.
Ее частным случаем является корреляционная связь. При кор-
реляционной связи изменение независимой переменной влия-
ет на изменение среднего значения зависимой переменной.
Корреляционно-регрессионный анализ заключается в установ-
лении степени тесноты связи и се формы, т. с. аналитического
выражения, связывающею переменные.
Будем обозначать х независимую переменную (факторный
показатель), у — зависимую переменную (результативный по-
казатель). Пусть имеется совокупность пар наблюдений (х, у).
Представим каждую пару наблюдений как точку с координата-
ми (х. у) на координатной плоскости. Данные точки образуют
корреляционное пате, или диаграмму рассеяния Чем теснее
связь между переменными, тем более плотно точки распола-
гаются вокруг некоторой линии. Эта линия является трафиком
аналитической зависимости между переменными F-сли точки
корреляционного пазя беспорядочно разбросаны на коорди-
натной плоскости, то это означает отсутствие тесной взаимо-
связи между переменными.
Если точки корреляционного поля концентрируются вдоль
некоторой прямой, то корреляционная связь линейная Пря-
мая с положзттсльны.м наклоном характеризует положительную
корреляционную связь (положительную корреляцию), а с от-
рицательным — отрицательную корреляционную связь (отри-
цательную корреляцию). Количественной мерой тесноты ли-
нейной количественной связи между переменными является
коэффициент корреляции г, который вычисляется по формуле
(13.1) Значение гизменяется от -1 до +1. Приближение сто к
-Г I или -1 означает увеличение степени тесноты линейной связи
(соответственно положительной или отрицательной). Ехли
г" I, то имеет место полная линейная корреляция, т. е пере-
менные связаны функциональным соотношением у " А, э Ь^х.
Когда г близок к нулю, линейная корреляционная связь отсут-
ствует.
331
Коэффициент г является выборочной статистикой, или
оценкой генерального коэффициента корреляции о, вычислен
ного на основе пар наблюдений генеральной совокупности (фор-
мула (13.3)). Поэтому для выборочного коэффициента корре-
ляции необходима проверка существенности, или статистичес-
кой значимости. Она заключается в том, что проверяется нулевая
гипотеза Ht: р = 0. Проверка производится на основе г-крите-
рии (13.4) для малы* выборок
Коэффициент корреляции вычисляется для переменных,
измеряемых в шкапе интервалов или отношений Для оценки
корреляции между признаками, выраженными в порядковой
шкале, рассматривается ранговый коэффициент корреляции
Спирмена (формула (13.6)). Под рангом понимается порядко-
вый номер значения признака в ранжированном ряду Одина-
ковым значениям при знака соответствуют связные ранги, ко
торые полагаются равными средней арифметической порядко-
вых номеров значений в ранжированном ряду. Если связных
рангов много, то коэффициент ранговой корреляции вычис-
ляется по формуле (13.7).
После выявления существования и степени тесноты линей-
ной связи возникает проблема определения конкретного вида
этой зависимости. Геометрически это означает, что нужно по-
добрать такую прямую, которая нанлучшим образом опалива-
ла бы точки корреляционного поля. Аналитическим методом
определения уравнения регрессии является метол наименьших
квадратов, тле в качестве критерия наилучшей сглаживающей
прямой выступает минимизация суммы квадратов расстояний
от точек корреляционного поля до этой прямой. Коэффициен-
ты уравнения регрессии у = 6, + b х получаются как решения
системы нормальных уравнений (13.12) и (13 13) и выражают-
ся формулами (13 14) и (13 15) Коэффициент b называется
коэффициентом ретрессин. Если независимая переменная х воз
растает в среднем на единицу, то зависимая переменная у в
этом случае возрастает в среднем на А. единиц при 6, > 0 (или
убывает на 6, единиц при Л. < О).
Оценкой точности уравнения регрессии является стандарт-
ная ошибка регрессии, вычисляемая по формуле (13.19). Она
харазстсризуст разброс точек наблюдений окало прямой рег-
рессии. Уравнение регрессии можно рассматривать в качестве
модели прогнозирования. Эта модель описывает взаимосвязь
независимой переменной х и зависимой переменной у лишь в
среднем, поэтому фактические значения у. как правило, нс
будут совпадать с точечными оценочными (прогнозными) эна-
332
ченнями v Поэтому очень важно получить интервальную оцен-
ку прогноза. т е. найти доверительный интервал, где с довери-
тельной вероятностью будет содержаться фактическое значе-
ние у. При допущении о нормальности распределения у вокруг
прямой ретрессии доверительный интервал определяется по
формуле (13 24) при п > 30 и по формуле (13.25) при и < 30.
Ширина доверительного интервала прогноза зависит от объе-
ма выборки л. С ростом и точность прогноза повышается. Наи-
большая точность достигается, котла прогнозируется значение
у при .» “ х
Показателем интенсивности связи, который измеряет, в
какой степени изменением независимой переменной объясня-
ется изменчивость (вариация) зависимой переменной, являет-
ся коэффициент детерминации г*. Он вычисляется как отно-
шение части обшей дисперсии, объясненной регрессией, к общей
дисперсии к характеризует удельный вес (пропегп) обшей дис-
персии, который объясняется уравнением регрессии (или изме-
нением факторного показателя л). Значение коэффициента лс-
термншшки равно квадрату коэффициента корреляции.
Уравнение регрессии у= + Ь.х. полученное на основе
выборочных пар наблюдений, является выборочным, Оно от-
личается от теоретического уравнения у w Р, + Р.х. которое
могло быть получено по данным генеральной совокупности,
««этому необходима проверка на существенность коэффици-
ента регрессии б. т. с. проверка нулевой гипотезы Но: р, = О
При малых выборках (л < 30) лтя проверки следует использо-
вать /-критерий (13.30). Если А, не существен, то использова-
ние выборочного уравнения для прогнозирования и анализа не
имеет смысла, гак как оно не отражает реальной связи между
переменными
ГЛАВА
МНОЖЕСТВЕННАЯ
РЕГРЕССИЯ
14.1. УРАВНЕНИЕ МНОЖЕСТВЕННОЙ
ЛИНЕЙНОЙ РЕГРЕССИИ
Используя уравнение парной регрессии к качестве модели
прогнозирования, мм учитываем влияние на результативный
показатель тол ько одного факторного показателя. Однако в боль-
шинстве практических ситуаций такой подход будет слишком
упрощенным, гак как изменение зависимой переменной в зна-
чительной степени связано с влиянием нескольких факторов
Очевидно, следует обобщить уравнение парной регрессии,
включив в него до1Н1ЛНите.'1ы<ые факторные переменные. В злом
случае мы получим уравнение (модель) множественной ли-
нейной регрессии
у “ А,+ ₽Л + Ал * - * ₽Л + Е- <14 »
где xt, X,,..., xt — независимые (факторные) переменные;
е — ошибка, ассоциируемая с моделью
В уравнении (14.1) выражение ₽, + р,х, + + ... + Рд
является детерминированной компонентой, а отклонение от
нее характеризуется случайной ошибкой г В случае парной рег-
рессии графиком лстерминиронанной компоненты Рп + Р,х яв-
ляется прямая линия, а е отражает разброс точек наблюдения
около нее. Для множественной регрессии, включающей две не-
зависимые переменные, детерминированной компонентой бу-
дет плоскость у = ро + р,л, + РуХ^рис 14.1).
В общем случае, когда чисто независимых переменных Гхыыие
2, построение графика детерминированной компоненты (т. е.
гиперплоскости) невозможно.
ззз
Рис М. 1. Геомегр^чесдек ии»ерпрвта14ня модели множественном линий
мой регрессии, окг4оча»сщсН две факторные переменные х, и я.
По аналогии с парной линейной регрессией получение опе-
нок Ь*> Лр...» Ьк для 0П, 0. 0, осуществляется с помощью
метода наименьших квадратов по критерию
Zo - ь„ - - *А “ — “ */,)’ " min. (14.2)
Приравняв частные производные левой час,и равенства
(14.2) по переменным Ли, 6,,..., fct к нулю, получим систему к + 1
нормальных уравнений Решение этой системы характеризует
искомые опенки 40, Л,
В качестве примера рассмотрим определение нормальных
уравнений в случае регрессии у на три факторные переменные
a,, Xj, х,. Оценочное уравнение множественной регрессии бу-
дет иметь вил
у-Л0+*Л**А+6А
Пусть имеются данные наблюдений но переменным:
У *1 х>
У, у> У. л.а Х(„ Лп хм хв ч
335
Запишем частный случай кри1ерия метода наименьших квад-
ратов (14.2).
S(y - А, - blxl - А/, - ft,*,)1 “
= Z О', ~ Ьа ~ Мн " *А ~ “ т|П'
••1
S - S(b,. А,. A,. ft,) - j (у,- ft„ - bf,, - bfy~ ft,*,.)1.
1=1
Обозначим - Sy. У, *> - S*. У a’ -*;,
i-i i-i .-I
“ Sy*, 2^*у*и = S**, (j, к = 1, 2. 3).
i-i (->
Тогда нормальные уравнения будут иметь вид
~ "2<У‘ -"*»-^Ех1'6гЕЛ»_й1ЕЛ’,'°-
«Л»
=2(^.М |-А>ХТ' -A)5zitt
«3
=2(£у* 2 - х2 - «у £ »|.т2 - ft, £*j - *i X * г* j) = О.
пАч
" *2(y.Wf5-Ai1^Vj-6,yilx3-/»,^x2xi-6j^xJ2)«0.
d/>5
Оценки А„, ft,, 6;, А, будут решением системы
nbt + А,Х*, + A,Sx, + A^jr, = Sy,
6,S*, + ft,St,1 ♦ A;Sr, + A,S*^t, - Sy*,, (14.3)
AjSt, + A, Sr,л, + Ь£х}‘ + 6,Se,л, “ Sy*(.
A„S*,+ A.S*,*, + А^Ьсу*, + AjS»,1 •= Sy*,.
Следует отметить, что системы нормальных уравнений, по-
добные (14.3). решаются с ломошью компьютера
В предыдущей славе был проведен простой корреляциоиио-
регрессионный аналит зависимости объема продаж (у) от зат-
рат на рекламу (*) Коэффициент корреляции между * и у был
равен г = 0,843 и оказался существенным По методу наимень-
ших квадратов было определено уравнение парной линейной
336
регрессии у = 8,51 + 0,354х с коэффициентом детерминации
г' = 0.71 Проверка на существенность коэффициента регрес-
сии bt = 0,354 показала, что уравнение отражает реальную связь
между переменными
Предположим, есть основание считать, что объем продаж
зависит также еще от двух факторных переменных: х, — коли-
чество сетей предприятий розничной торговли (например, се-
тей магазинов), продающих продукт фирмы в регионе, и х, —
уровень безработицы в регионе.
Построим регрессионную модель
y = 8,+ ft|x,+ 4Л+*Л,
где у — оценка объема продаж (тыс ед );
х, — затраты на рекламу (дес тыс. долл );
х; — число сетей предприятий розничной торговли (ел );
х3 — уровень безработицы (Ж).
Значения 6. 6,, 6, являются оценками (),. ₽г
Данные по регионам были дополнены наблюдениями по
переменным х, и х,:
У V. Я9 *>

1 16 22 2 4
2 17 26 2 В
3 26 4S 3 7
4 24 37 4 0
5 22 28 4 г
6 21 50 3 10
7 32 56 Б 8
в 18 34 3 в
9 30 60 5 2
10 20 40 3
Предста