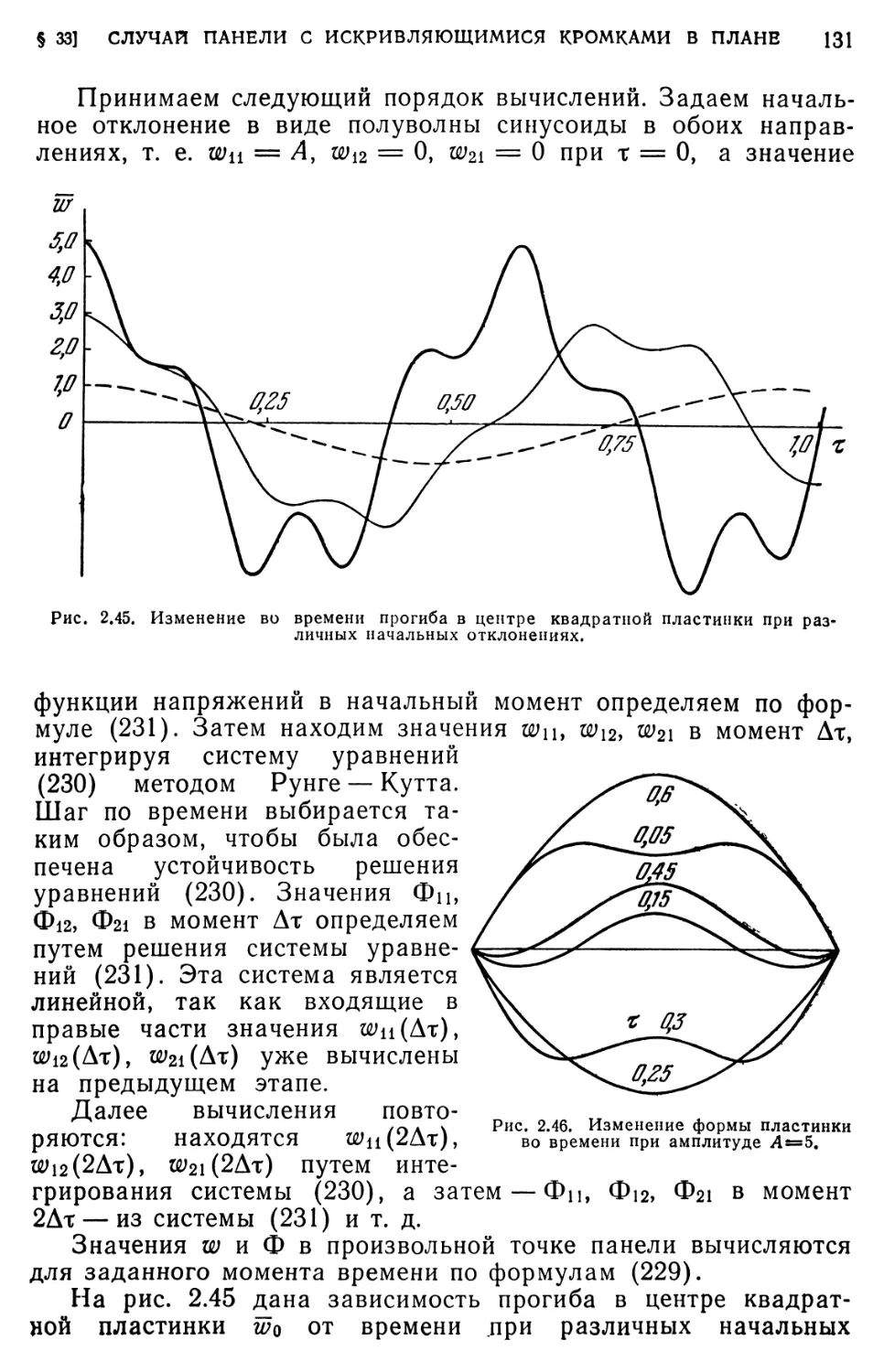
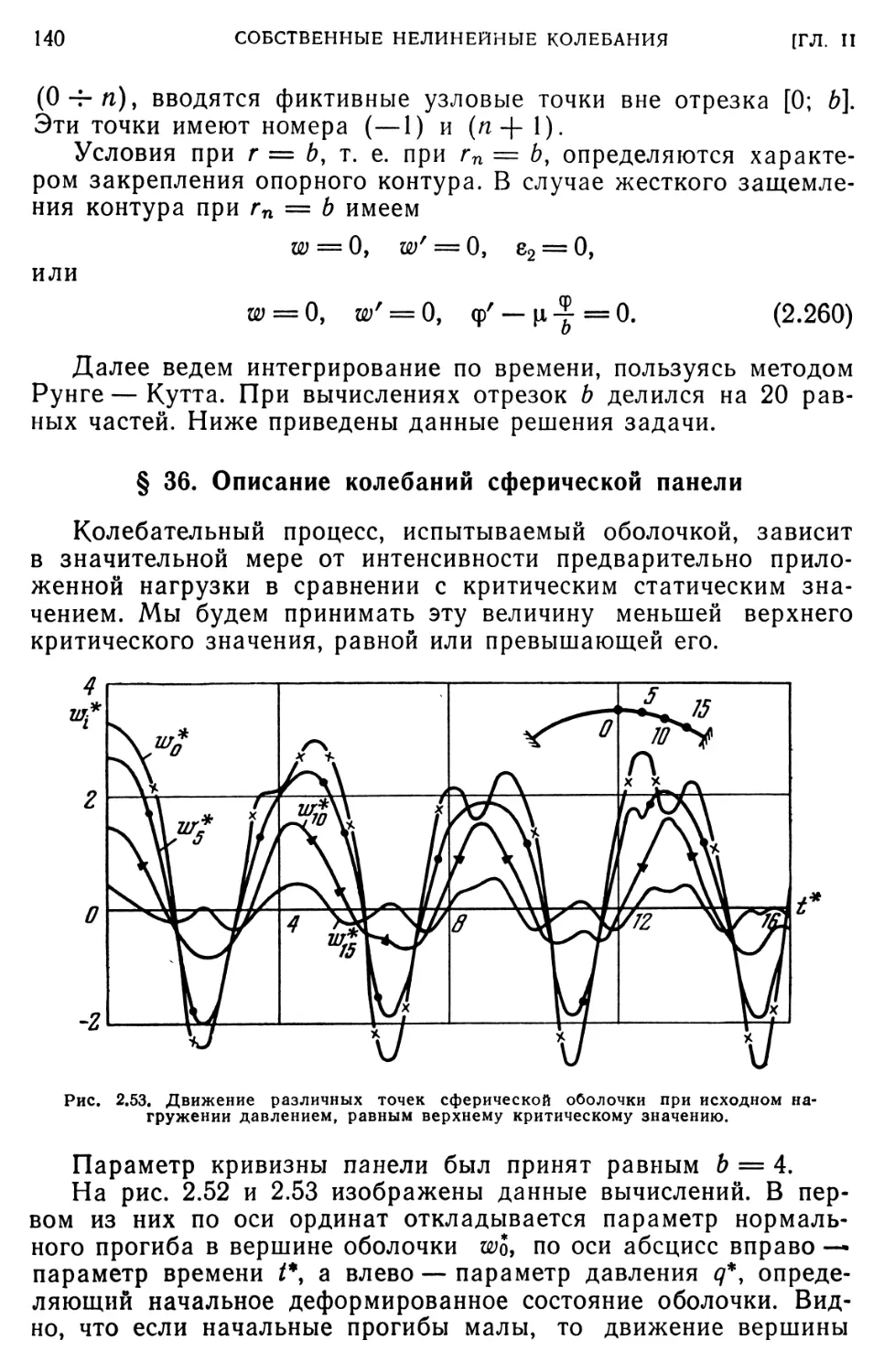
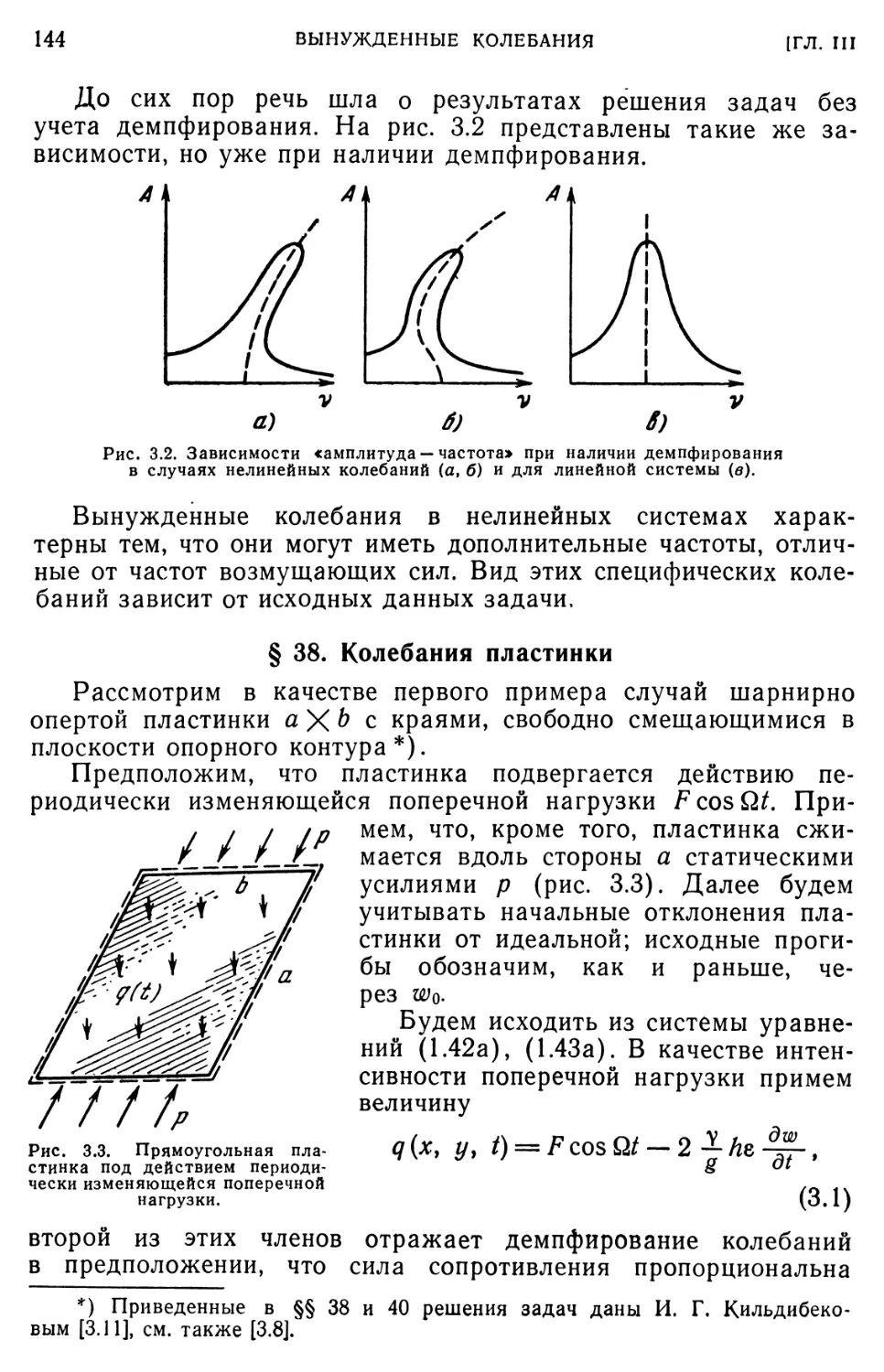
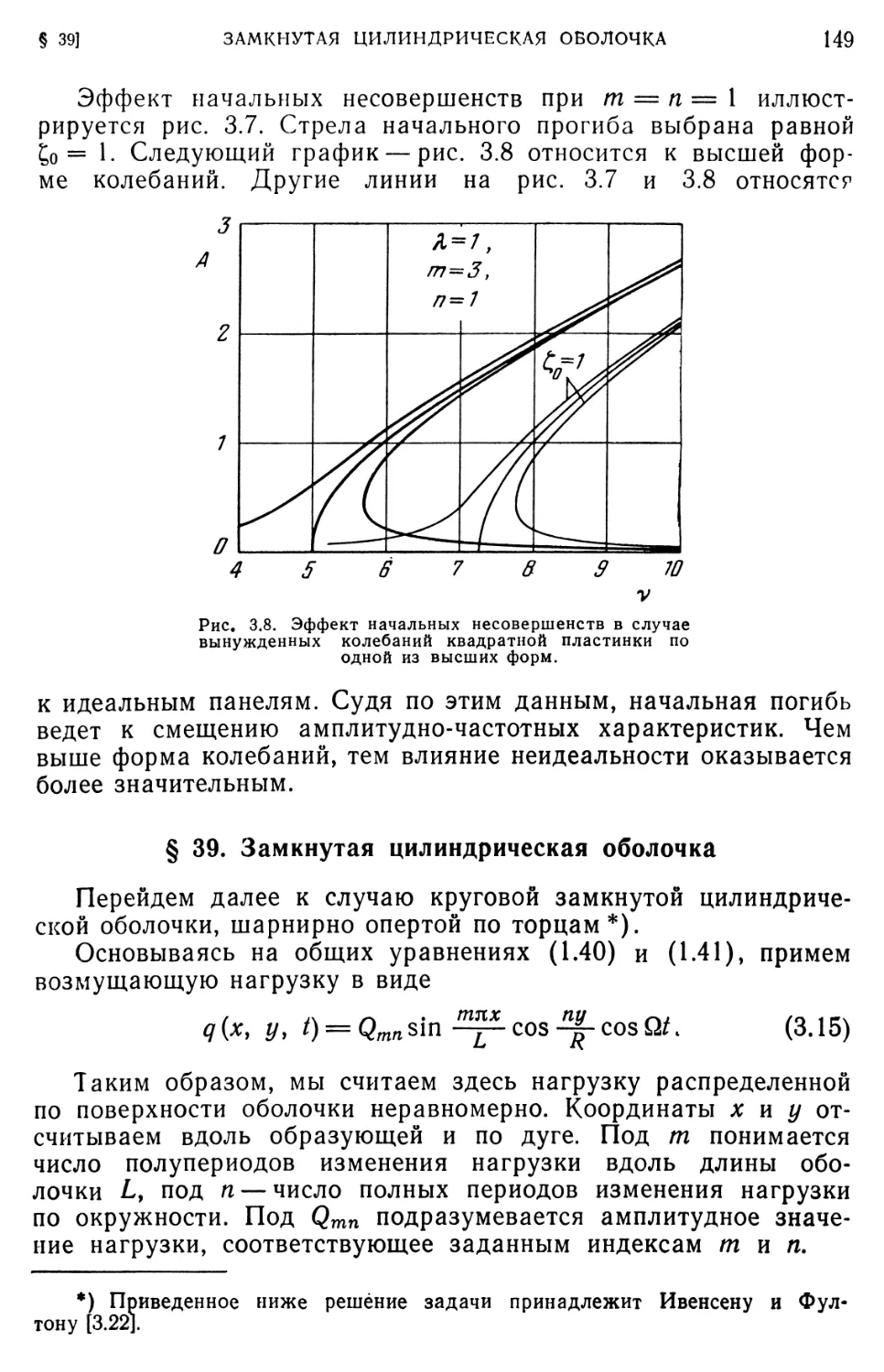
Текст
А. С. ВОЛЬМИР
НЕЛИНЕЙНАЯ ДИНАМИКА ПЛАСТИНОК И ОБОЛОЧЕК
ИЗДАТЕЛЬСТВО «НАУКА» ГЛАВНАЯ РЕДАКЦИЯ ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1972
531 В 71
УДК 531.3
Нелинейная динамика пластинок и оболочек, В о л ь м и р А. С., Главная редакция физико-математической литературы изд-ва «Наука», 1972 г., 432 стр.
В первой части книги излагается общая нелинейная теория динамики пластинок и оболочек на основе гипотезы Кирхгофа — Лява, а также модели типа Тимошенко. Далее исследуются собственные, вынужденные, параметрические колебания и автоколебания тонкостенных систем; в вводных разделах приведены данные для практических расчетов, основанные на линеаризованных зависимостях. Вторая часть книги посвящена поведению пластинок и оболочек при действии быстро изменяющихся во времени и ударных нагрузок с учетом процесса распространения волн деформации. Рассмотрены упругие и упруго-пластические задачи. Приведены результаты экспериментов.
Илл. 263, табл. 4, библ. ссылок 560.
Арнольд Сергеевич Вольмир Нелинейная динамика пластинок и оболочек М., 1972 г., 432 стр. с илл.
Редактор И, Г. Кильдибеков Техн. редактор К. Ф. Брудно Корректор И. Я. Кришталь
Сдано в набор 181V 1972 г. Подписано к печати 31Х 1972 г. Бумага 60 X90,в, тип. 1. Физ. печ. л. 27. Условн. печ. л. 27. Уч.-изд. л. 27,65. Тираж 5700 экз. Т-16842. Цена книги 1 р. 98 к. Заказ 142
Издательство «Наука»
Главная редакция физико-математической литературы 117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография 2 имени Евгении Соколовой Главполиграфпрома Государственного комитета Совета Министров СССР по делам издательств, полиграфии и книжной торговли, измайловский проспект, 29.
2-4-2
161—72
ОГЛАВЛЕНИЕ
Предисловие. 7
Глава I. Общие зависимости нелинейной теории оболочек 9
§ 1. Классификация динамических задач нелинейной теории пластинок и оболочек 9
§ 2. Некоторые сведения об оболочках 10
§ 3. Описание моделей оболочки. 13
§ 4. Деформации и перемещения. 16
§ 5. Напряженное состояние. Связь между усилиями и деформациями. 21
§ 6. Приближенные уравнения движения 24
§ 7. Уравнения в перемещениях 27
§ 8. Граничные и начальные условия 30
§ 9. Модель оболочки с учетом сдвига и инерции вращения. Деформации и перемещения 31
§ 10. Напряженное состояние с учетом поперечного сдвига. 34
§ 11. Вариационное уравнение.37
§ 12. Переход к уравнениям в перемещениях и граничным условиям 42
§ 13. Некоторые варианты динамических уравнений 45
§ 14. Более полные соотношения между деформациями и перемещениями 52
§ 15. Уравнения движения 60
§ 16. Оболочки за пределами упругости 65
Глава II. Собственные нелинейные колебания 72
§ 17. Свойства собственных нелинейных колебаний 72
§ 18. Прямоугольная пластинка, шарнирно опертая по краям. Линейная задача 74
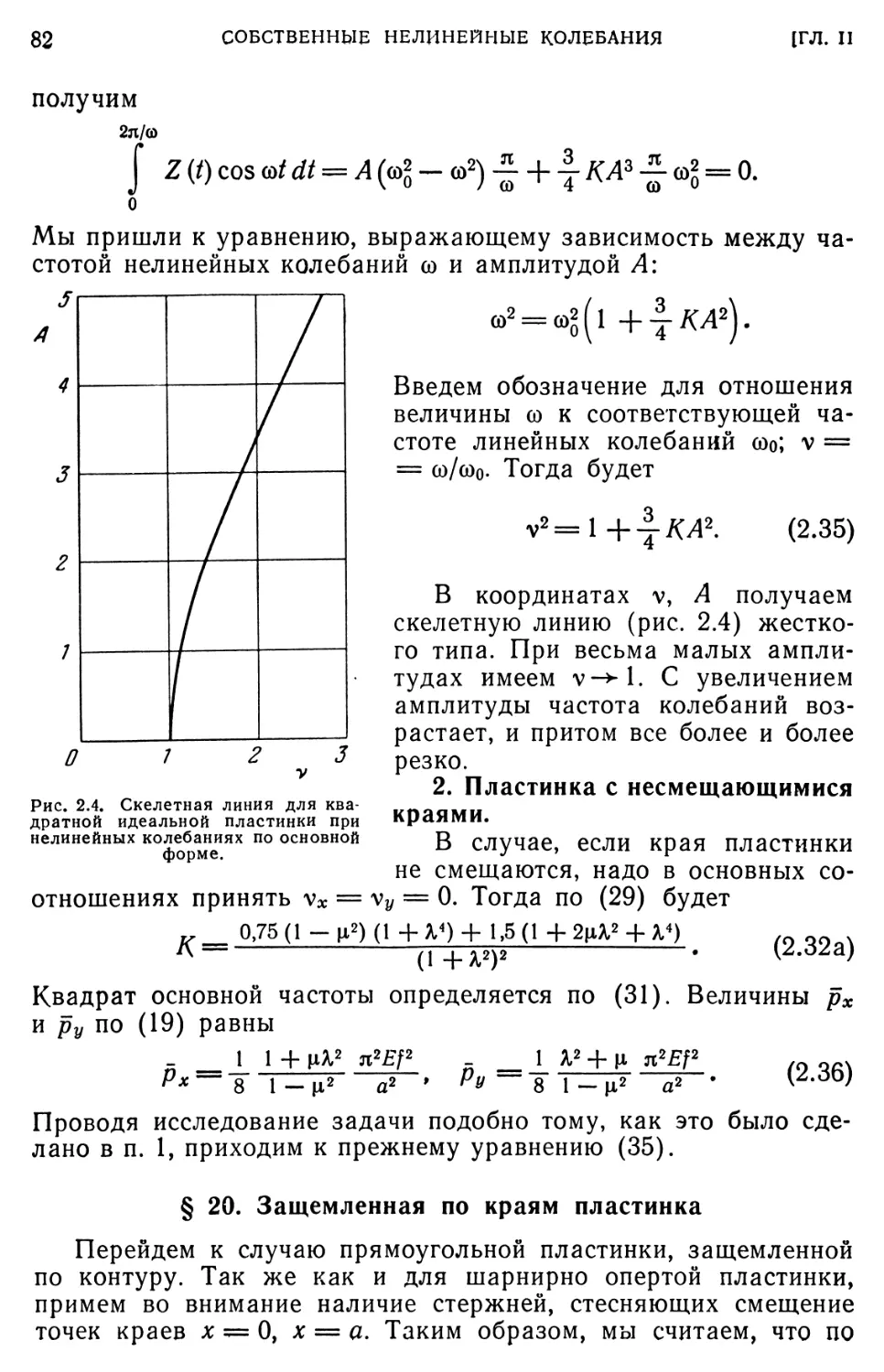
§ 19. Нелинейная задача. Метод Бубнова — Галеркина 75
§ 20. Защемленная по краям пластинка 82
§ 21. Метод гармонического баланса 86
§ 22. Метод возмущений 87
§ 23. Точное решение.89
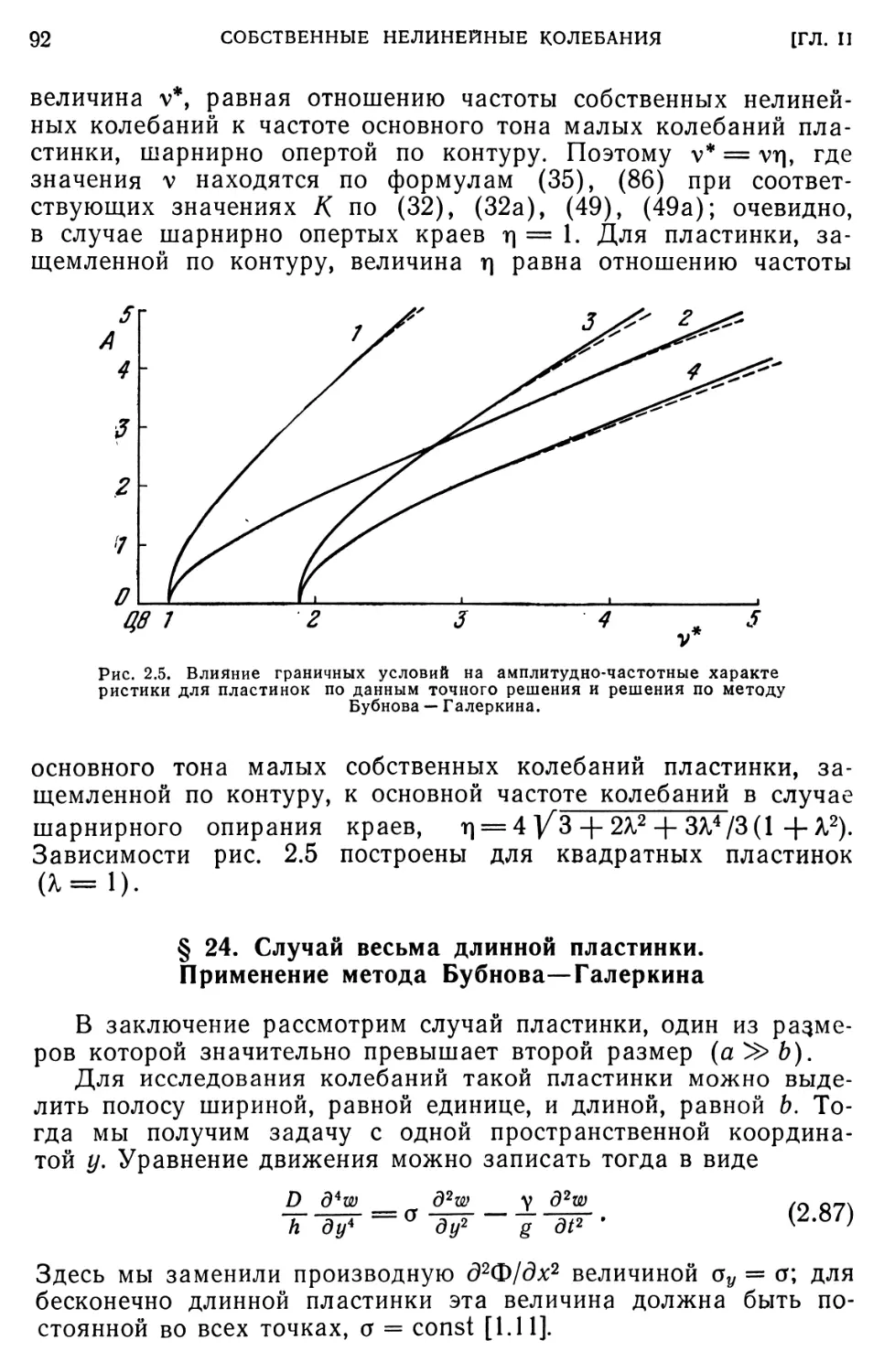
§ 24. Случай весьма длинной пластинки. Применение метода Бубнова— Галеркина 92
§ 25. Приложение метода конечных разностей 94
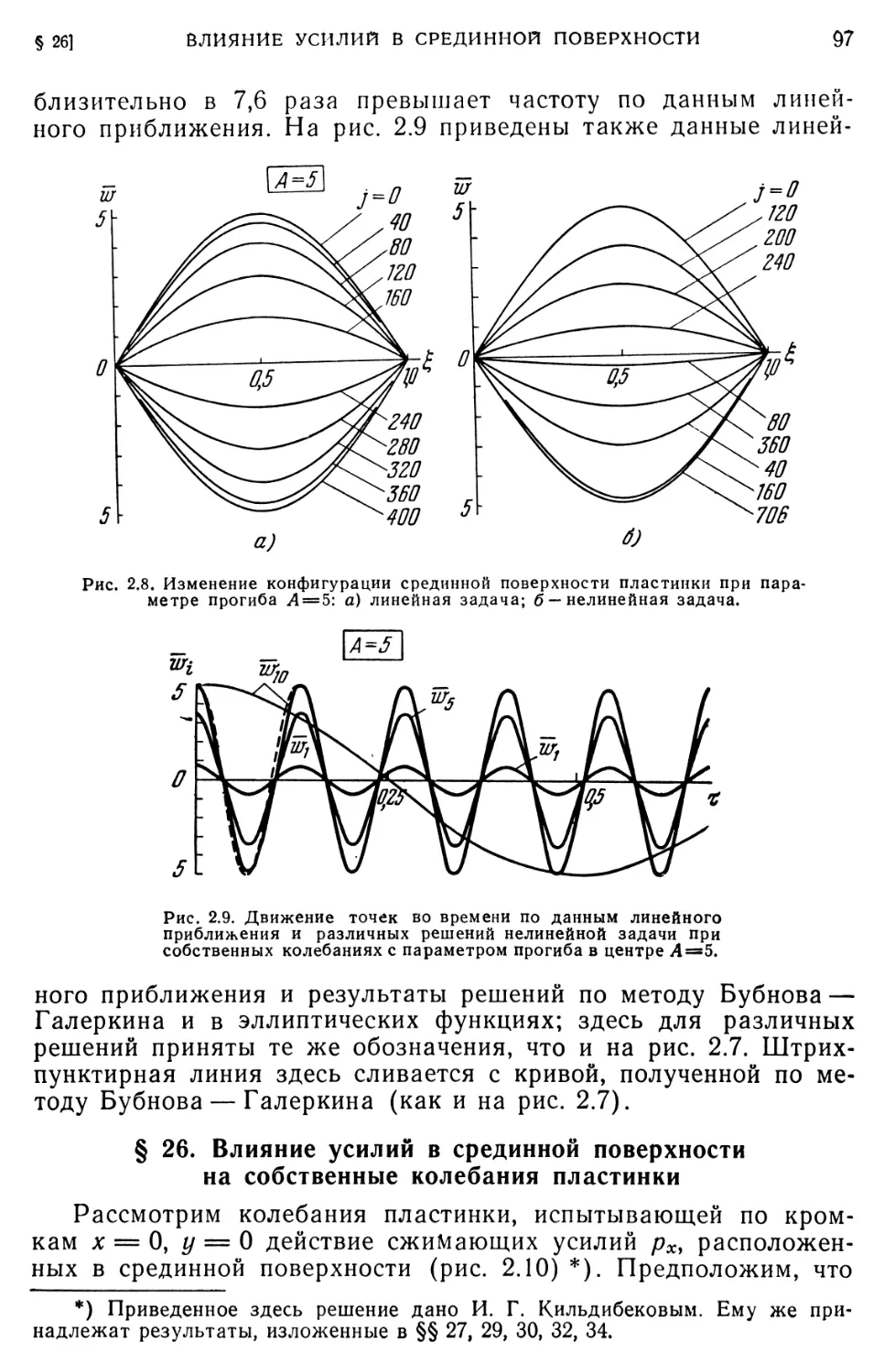
§ 26. Влияние усилий в срединной поверхности на собственные колебания пластинки 97
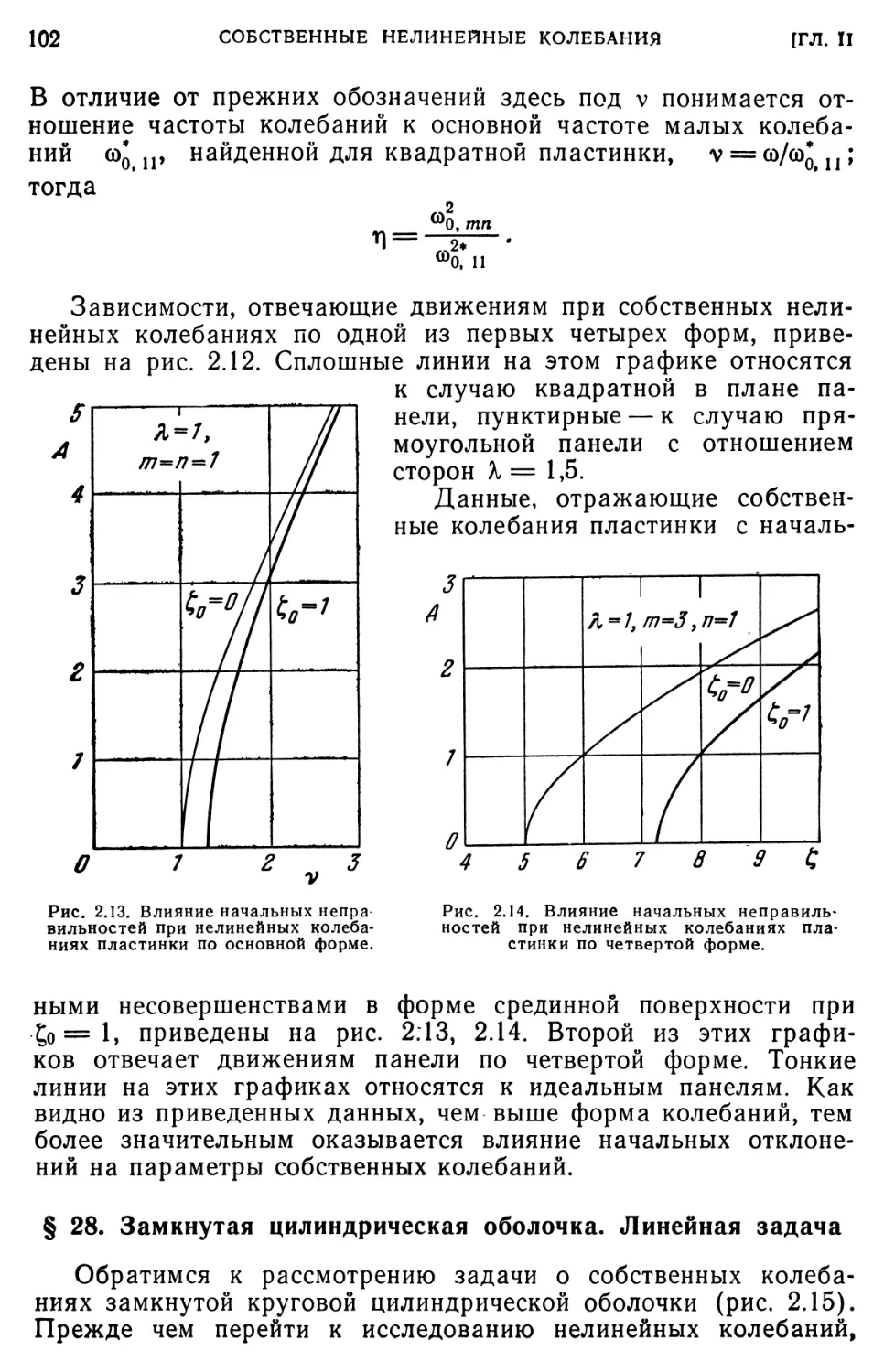
§ 27. Эффект начальных неправильностей 100
§ 28 Замкнутая цилиндрическая оболочка. Линейная задача. 102 § 29. Замкнутая цилиндрическая оболочка. Нелинейная задача.111
§ 30. Удлиненная цилиндрическая панель. Метод Бубнова — Галеркина 116
4
ОГЛАВЛЕНИЕ
§ 31. Удлиненная цилиндрическая панель. Метод конечных разностей 118
§ 32. Круговая цилиндрическая панель с конечным отношением сторон. 124
§ 33. Случай панели с искривляющимися кромками в плане. Уточненное решение 127
§ 34. Случай панели двоякой кривизны 132
§ 35. Пологая сферическая панель. Решение методом прямых. 136 § 36. Описание колебаний сферической панели. 140
Глава III. Вынужденные колебания 142
§ 37. Характер вынужденных нелинейных колебаний пластинок и
оболочек. 142
§ 38. Колебания пластинки. 144
§ 39. Замкнутая цилиндрическая оболочка 149
§ 40. Случай цилиндрической панели. 153
§ 41. Экспериментальные данные по нелинейным колебаниям и
устойчивости подкрепленных панелей в акустическом поле. 154 § 42. Сферическая панель 158
Глава IV. Параметрические колебания. 161
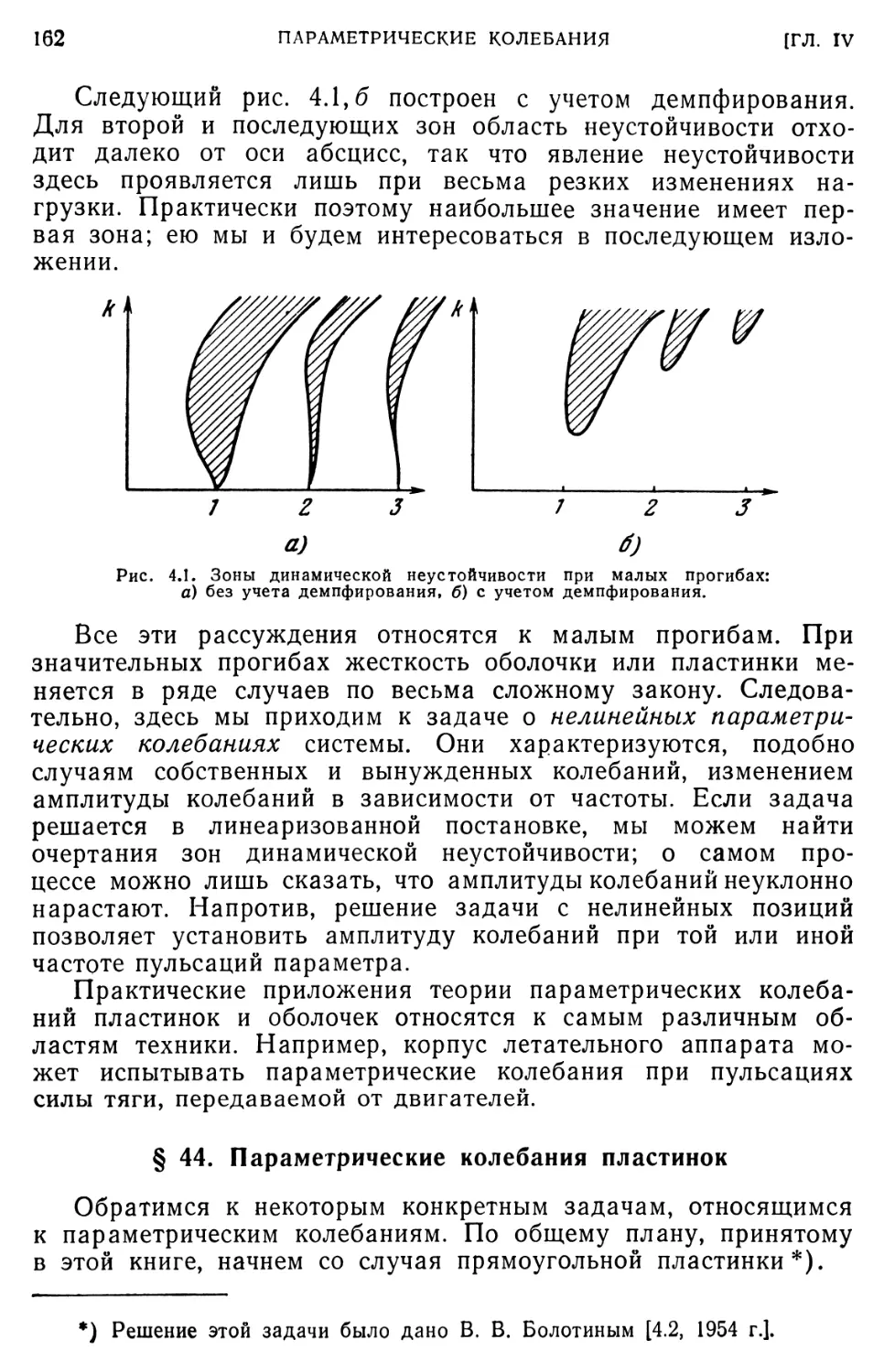
§ 43. Особенности параметрических колебаний.161
§ 44. Параметрические колебания пластинок 162
§ 45. Замкнутая цилиндрическая оболочка при пульсирующем внешнем давлении • 168
§ 46. Поведение цилиндрической панели при пульсирующей сжимающей нагрузке. 170
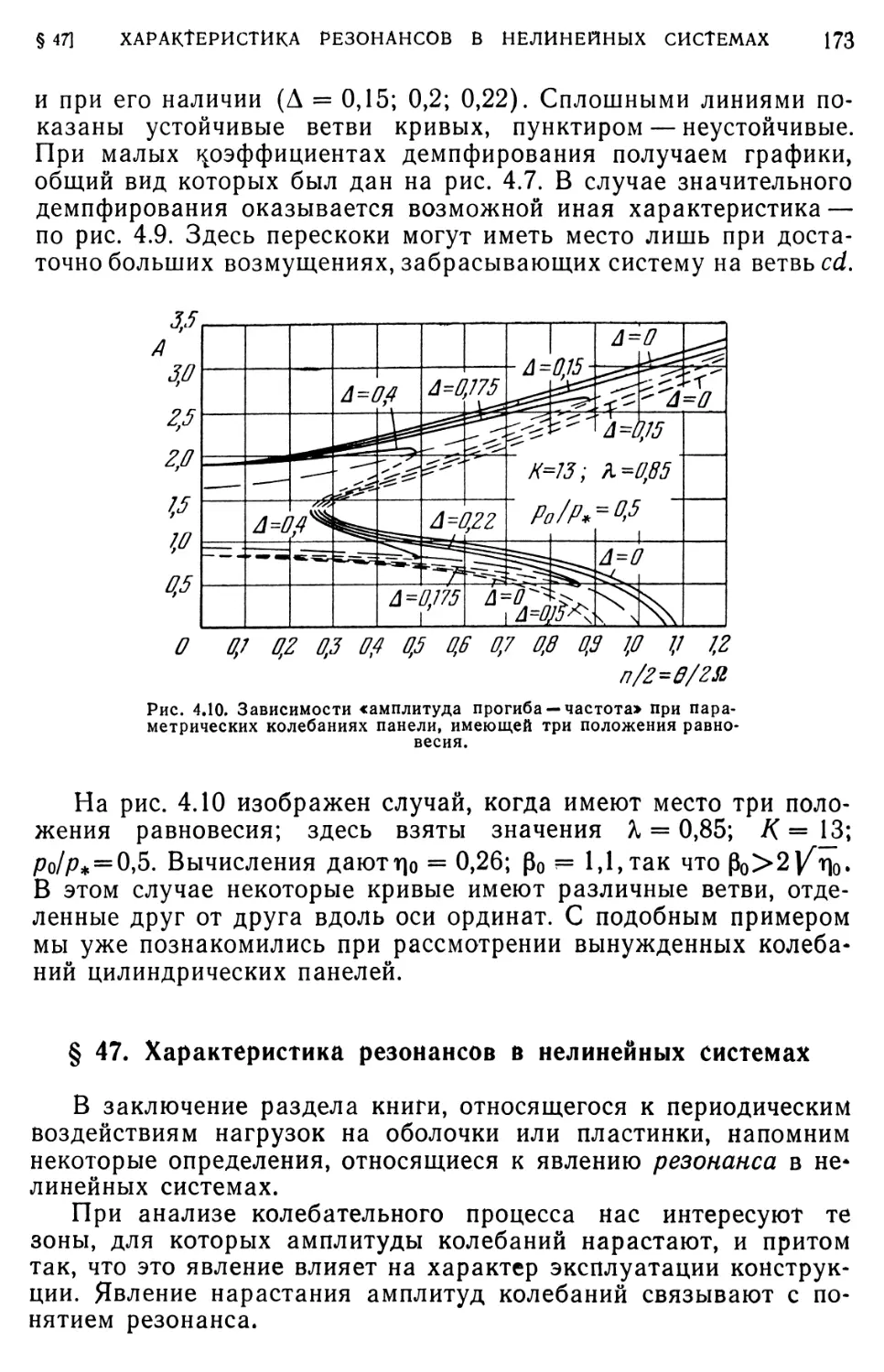
§ 47. Характеристика резонансов в нелинейных системах. 173
Глава V. Автоколебания. 175
§ 48. Основные понятия 175
§ 49. Нелинейный флаттер пластинки 176
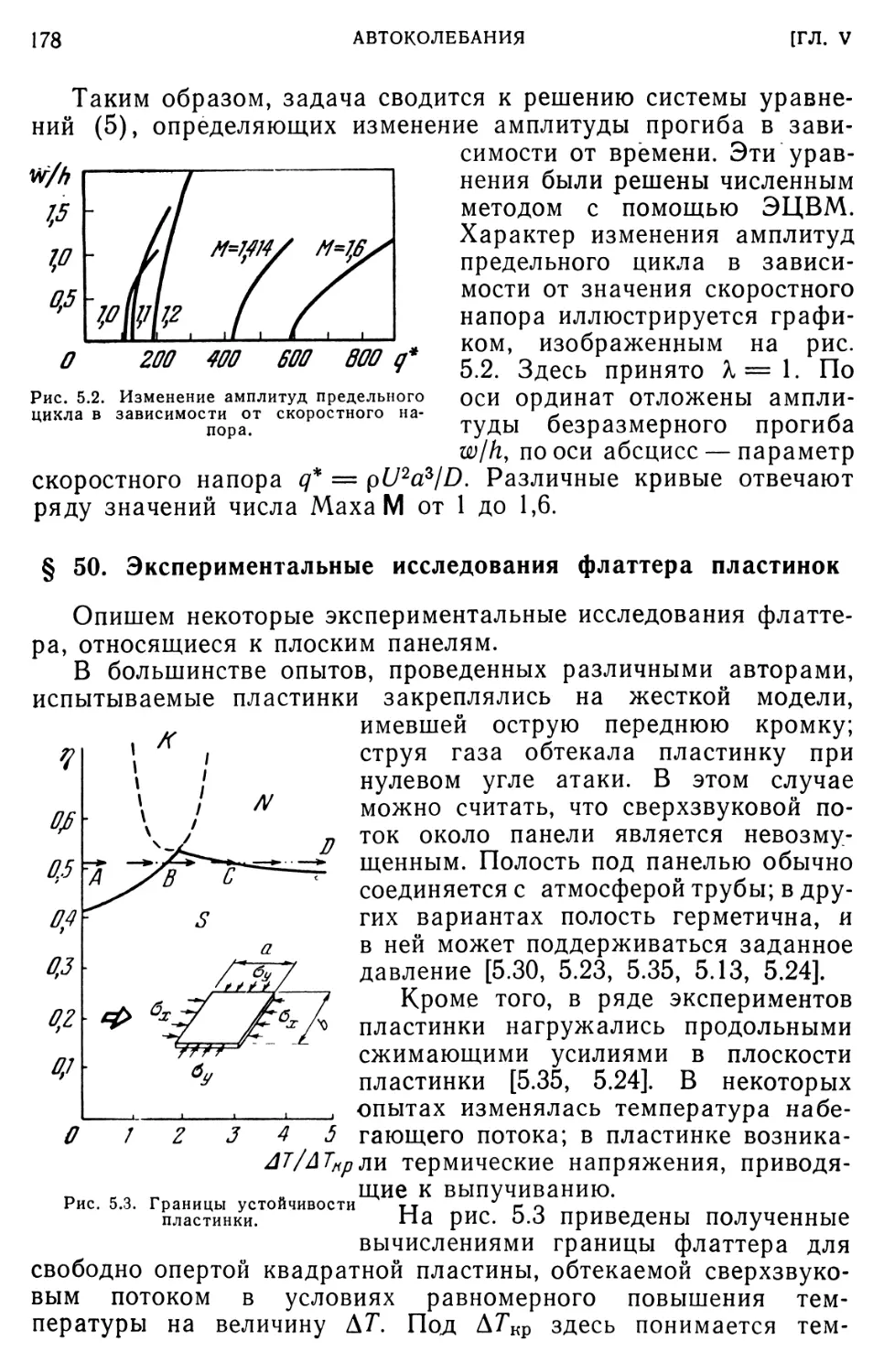
§ 50. Экспериментальные исследования флаттера пластинок.178
§ 51. Квазистатическая задача для замкнутой цилиндрической оболочки. 179
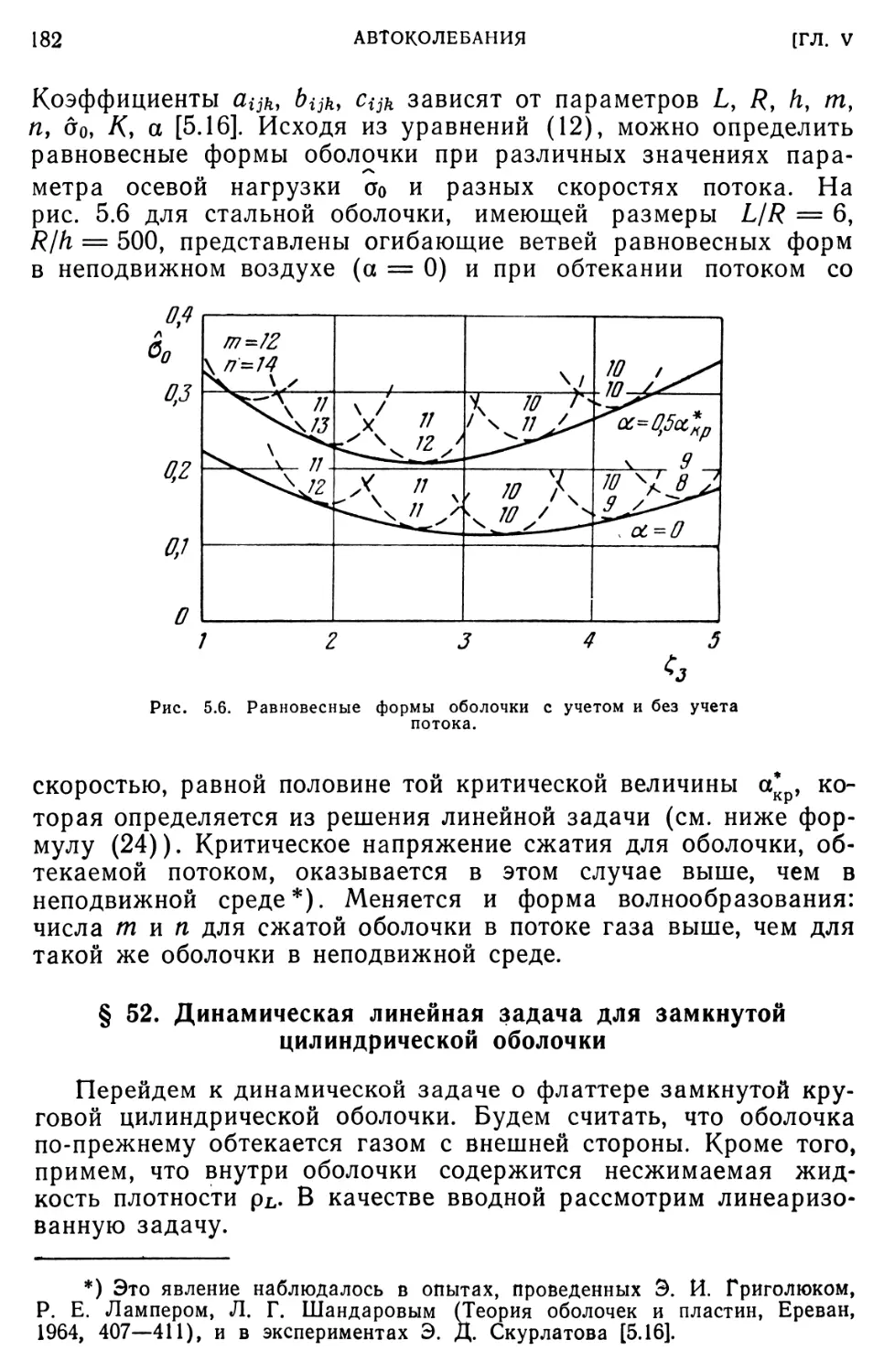
§ 52. Динамическая линейная задача для замкнутой цилиндрической оболочки. 182
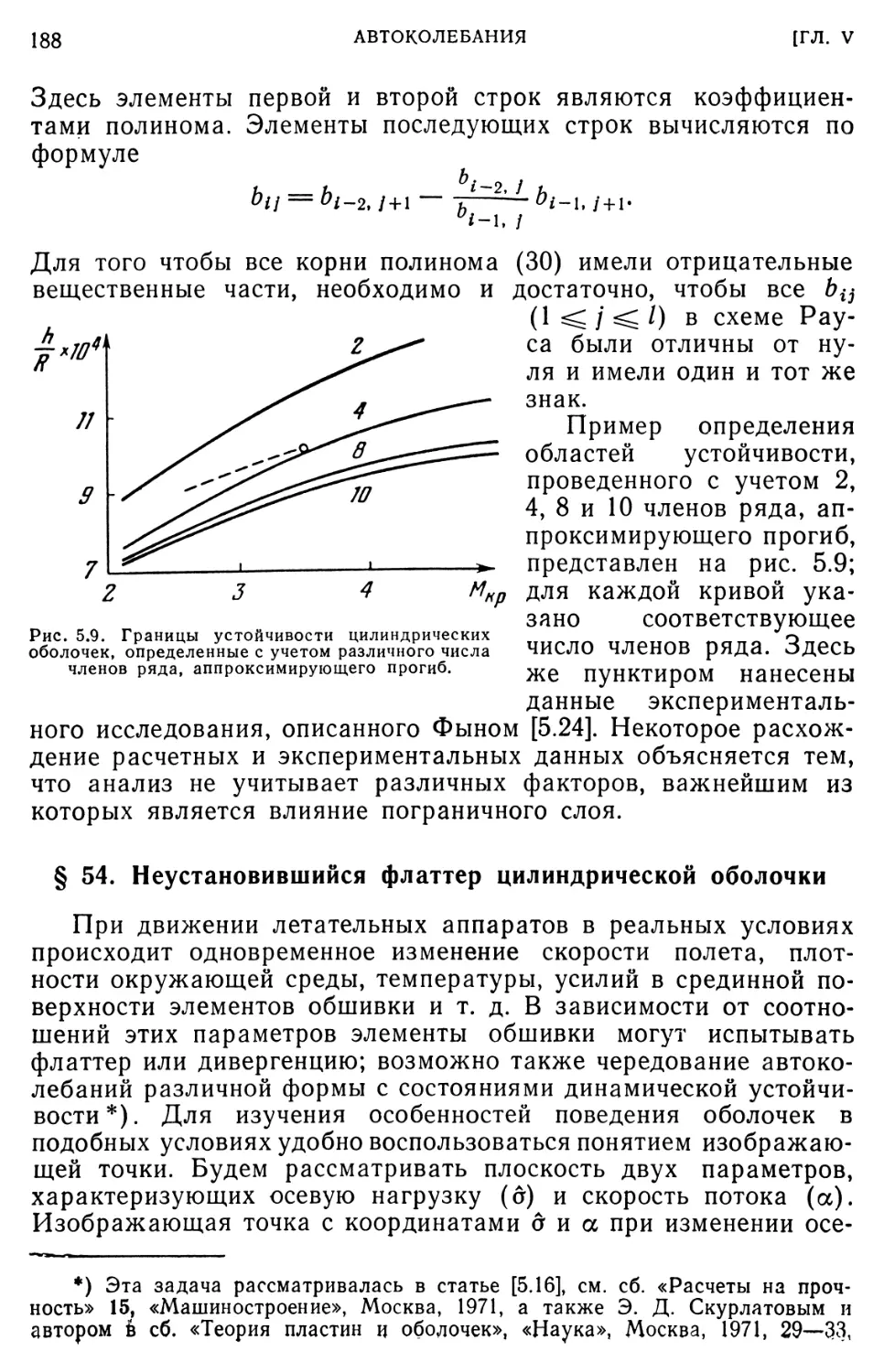
§ 53. Уточненное решение линейной динамической задачи. 187 § 54. Неустановившийся флаттер цилиндрической оболочки. 188
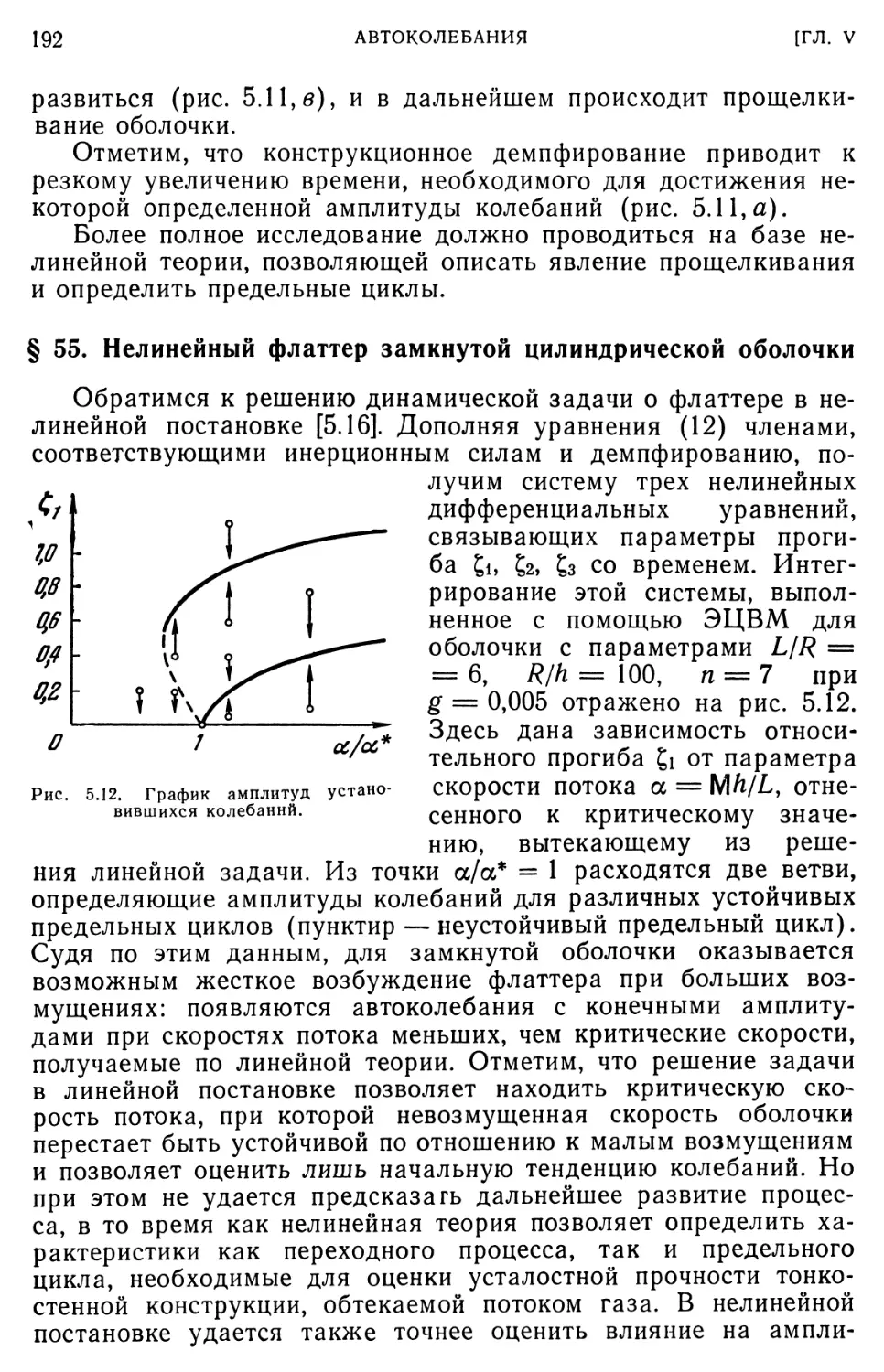
§ 55. Нелинейный флаттер замкнутой цилиндрической оболочки. 192
§ 56. Флаттер цилиндрической оболочки с бегущей в окружном направлении волной 193
§ 57. Дивергенция и флаттер цилиндрической оболочки с учетом
пограничного слоя 195
§ 58. Флаттер цилиндрической оболочки при изменяющемся давлении в набегающем потоке 201
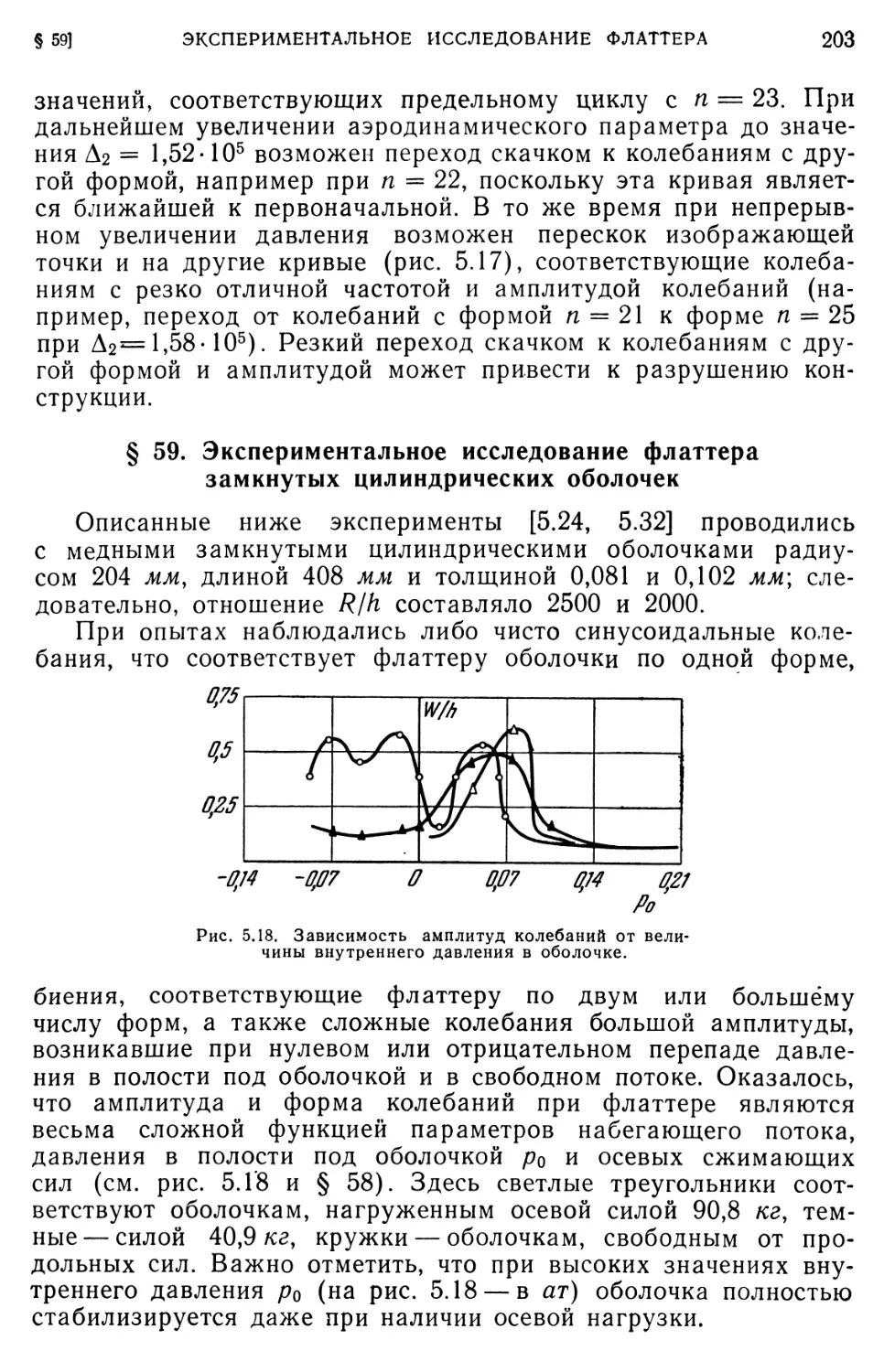
§ 59. Экспериментальное исследование флаттера замкнутых цилиндрических оболочек. 203
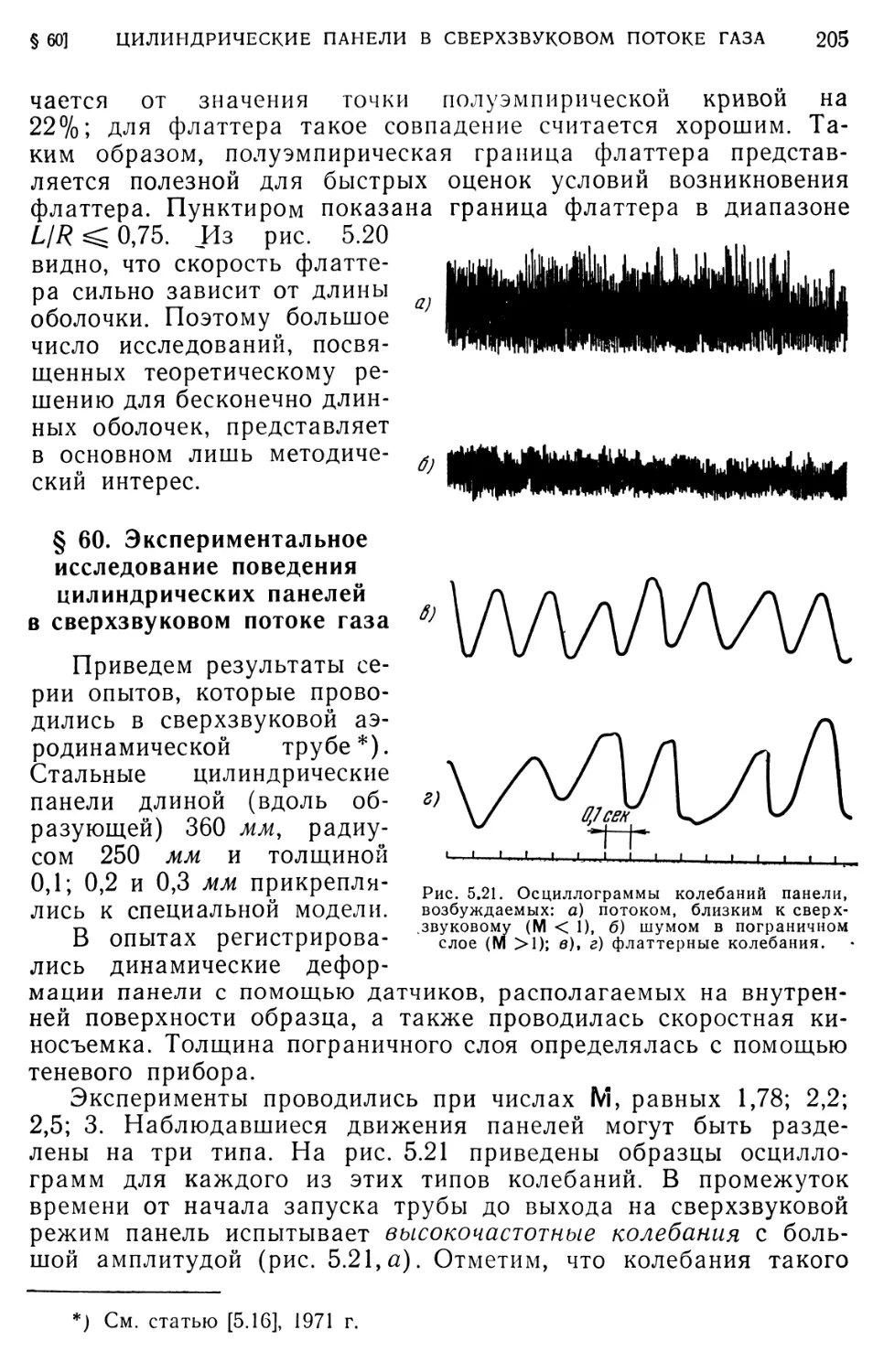
§ 60. Экспериментальное исследование поведения цилиндрических
панелей в сверхзвуковом потоке газа 205
Глава VI. Критерии динамической устойчивости оболочек и пластинок 212
§ 61. Основные определения 212
§ 62. Различные виды импульсных нагрузок.215
§ 63. Понятия динамической критической нагрузки и динамического
коэффициента 217
§ 64. Другие возможные подходы к задаче 218
ОГЛАВЛЕНИЕ
5
Глава VII. Выпучивание оболочек и пластинок при динамическом
нагружении 221
§ 65. Постановка задачи. Исходные уравнения. 221
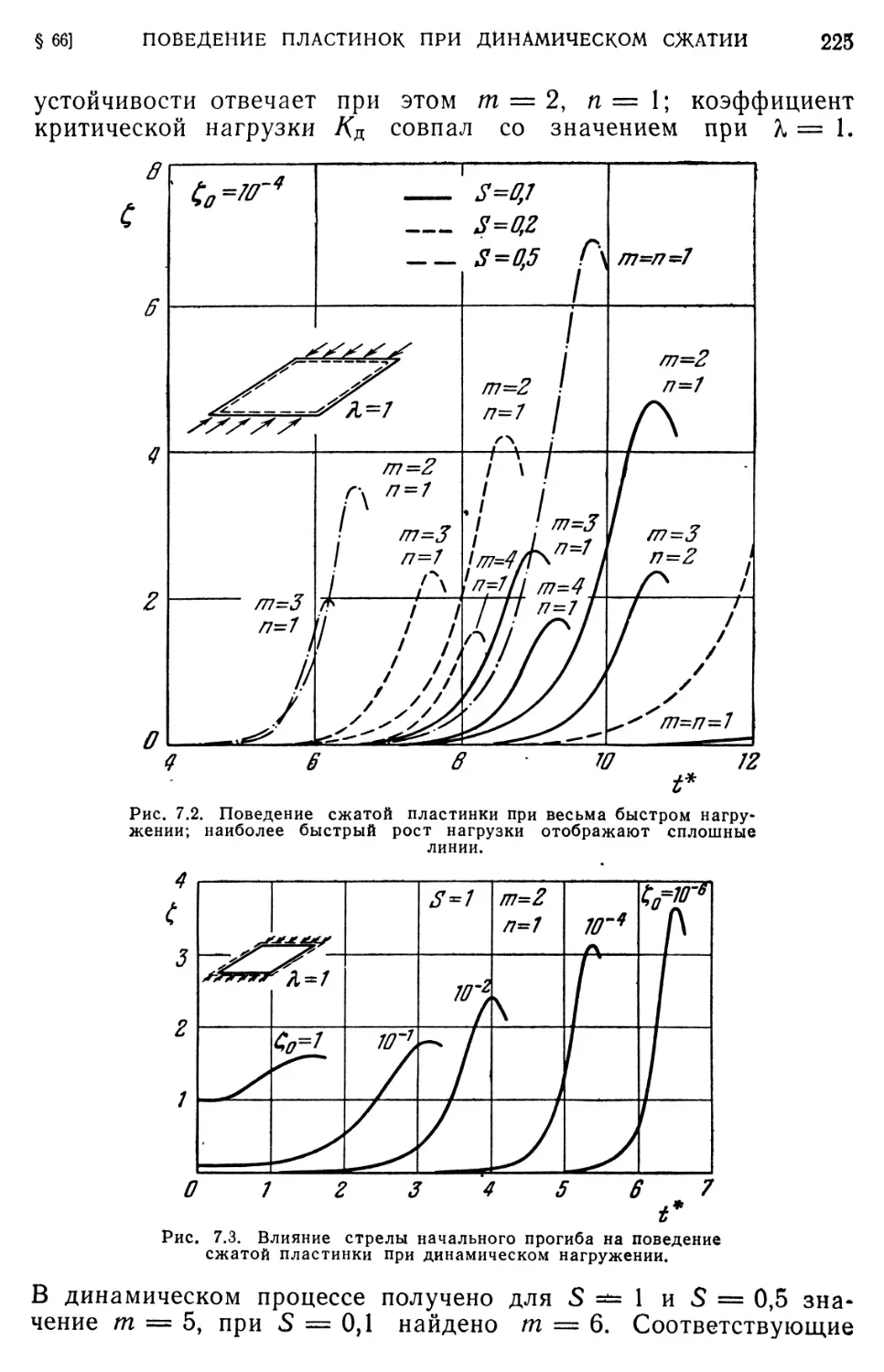
§ 66. Поведение пластинок при динамическом сжатии 221
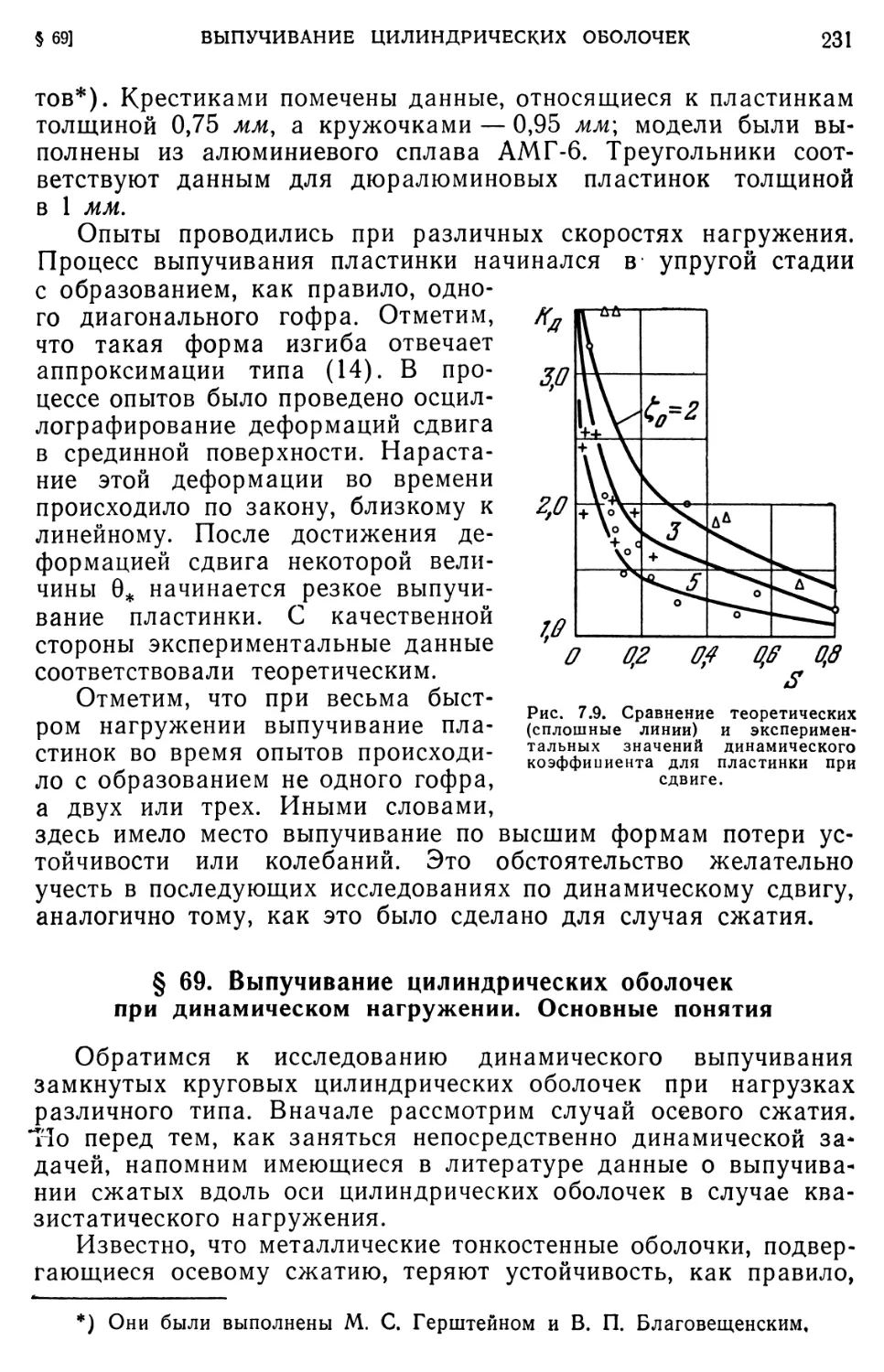
§ 67. Влияние формы импульса на поведение пластинки. 226 § 68. Динамическое выпучивание пластинок при сдвиге. 228 § 69. Выпучивание цилиндрических оболочек при динамическом нагружении. Основные понятия 231
§ 70. Цилиндрические оболочки при динамическом приложении осевого сжатия. 233
§ 71. Цилиндрические оболочки при внешнем давлении 238
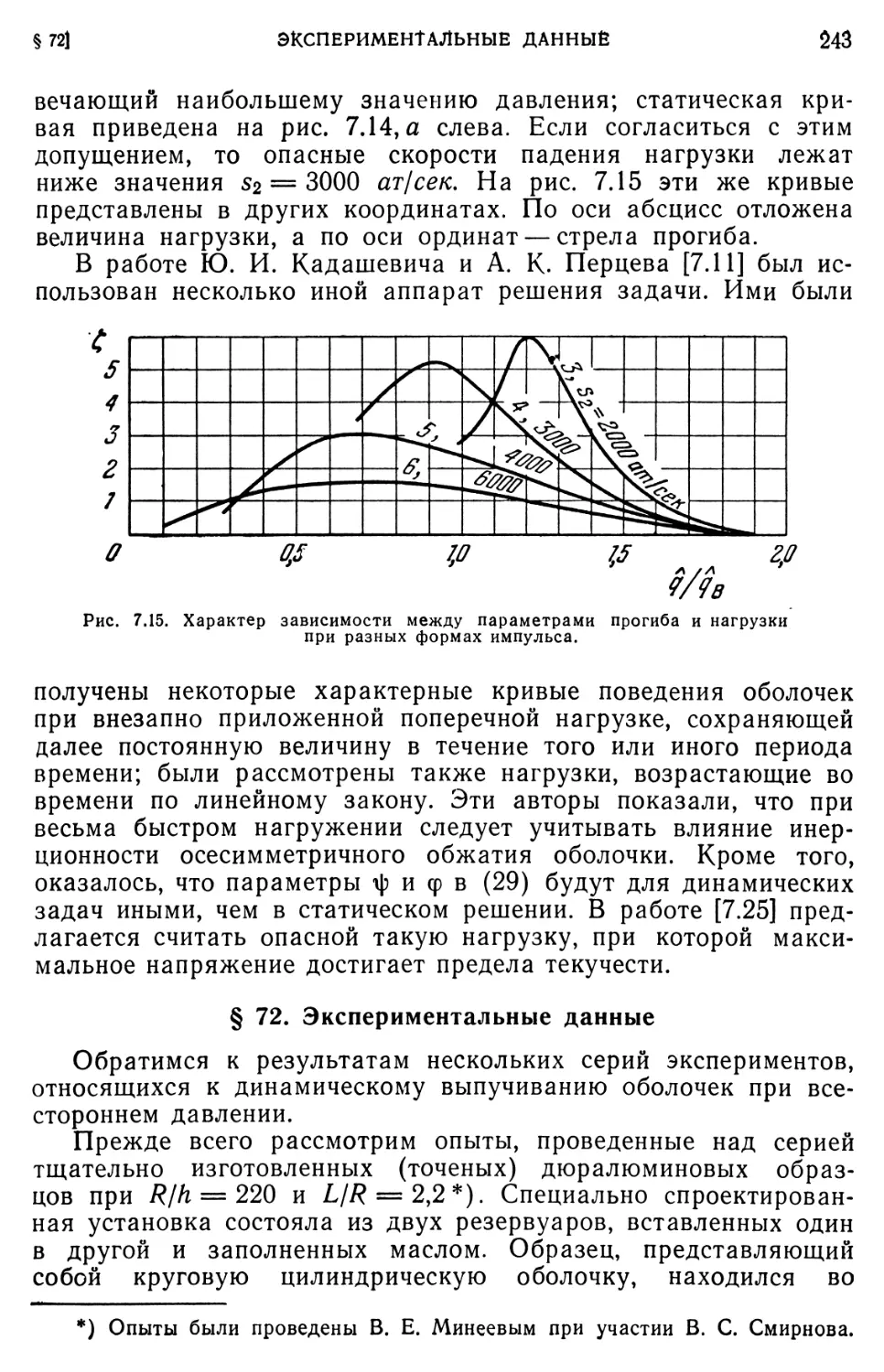
§ 72. Экспериментальные данные 243
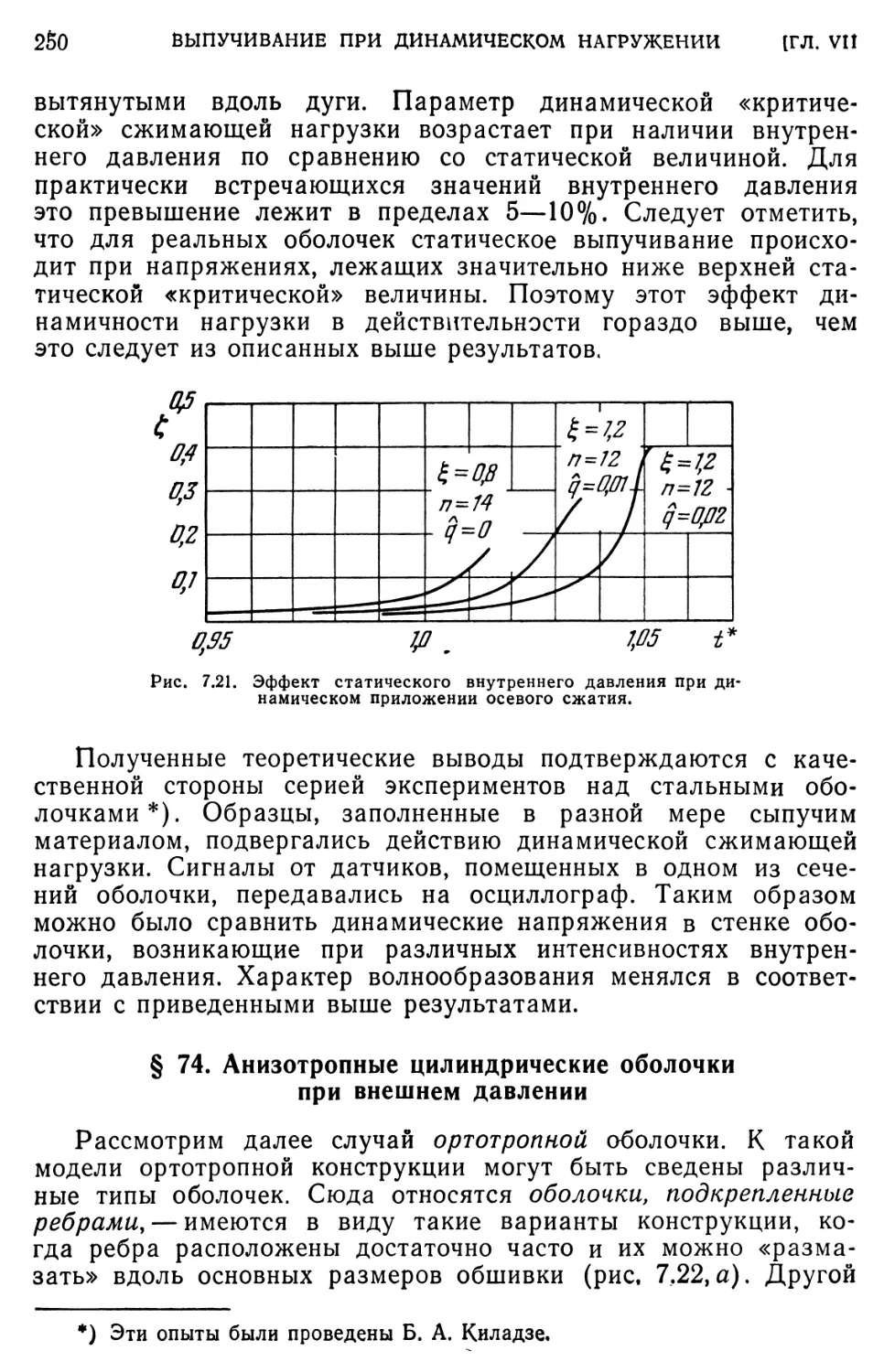
§ 73. Эффект внутреннего давления 247
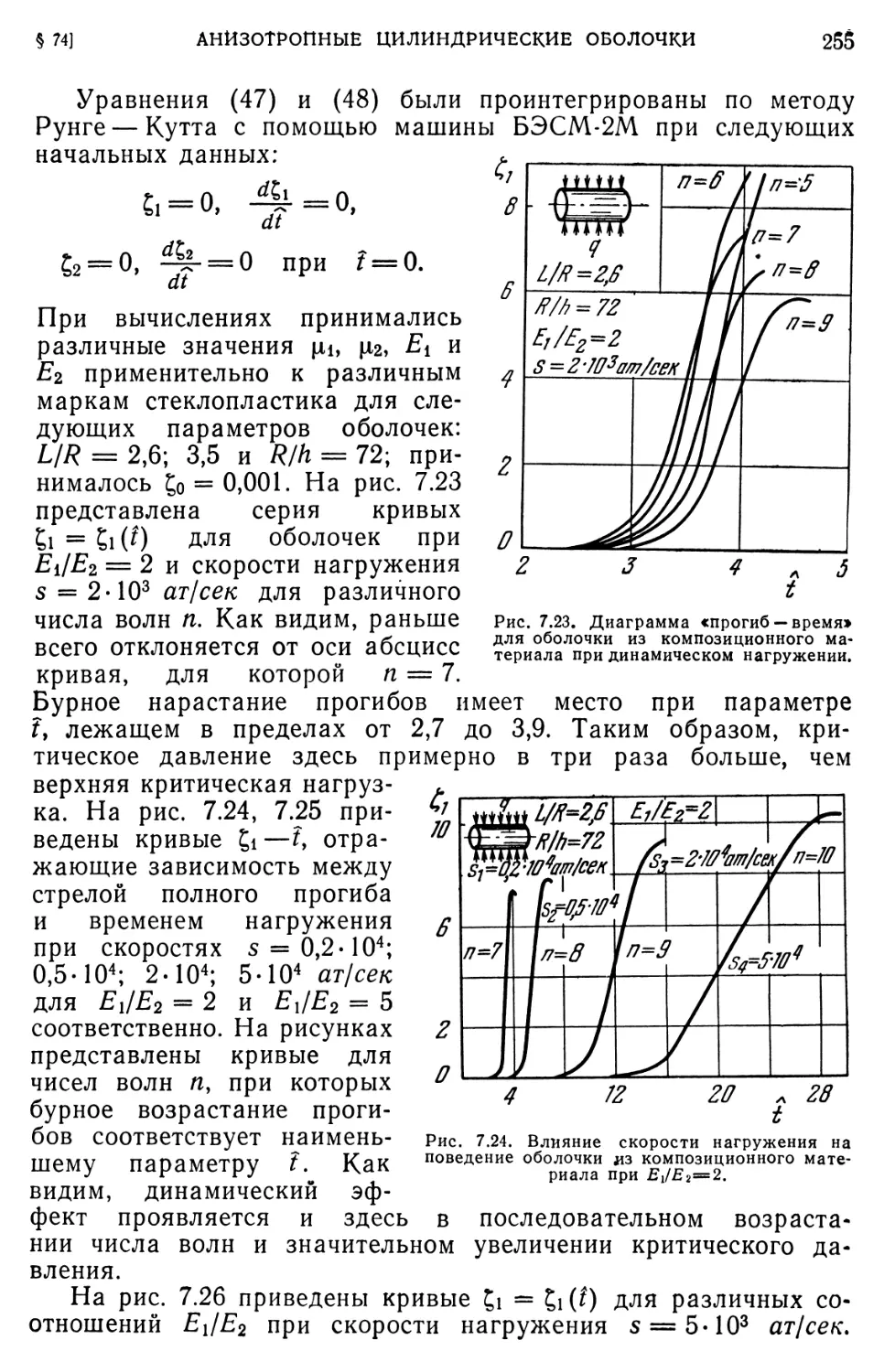
§ 74. Анизотропные цилиндрические оболочки при внешнем давлении 250
§ 75. Анизотропные конические оболочки при осевом нагружении 257
§ 76. Цилиндрическая панель при динамическом сжатии 263
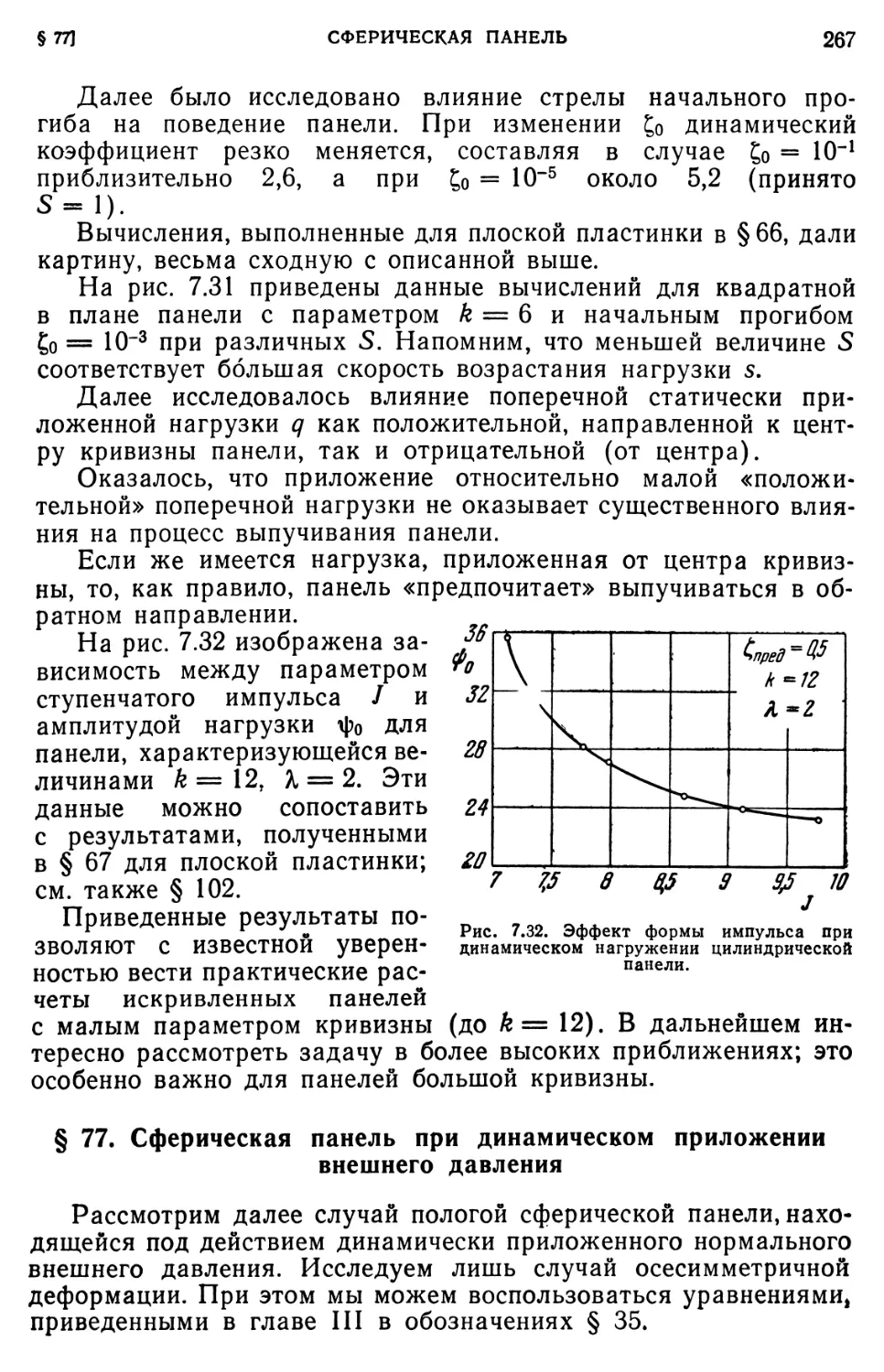
§ 77. Сферическая панель при динамическом приложении внешнего
давления. 267
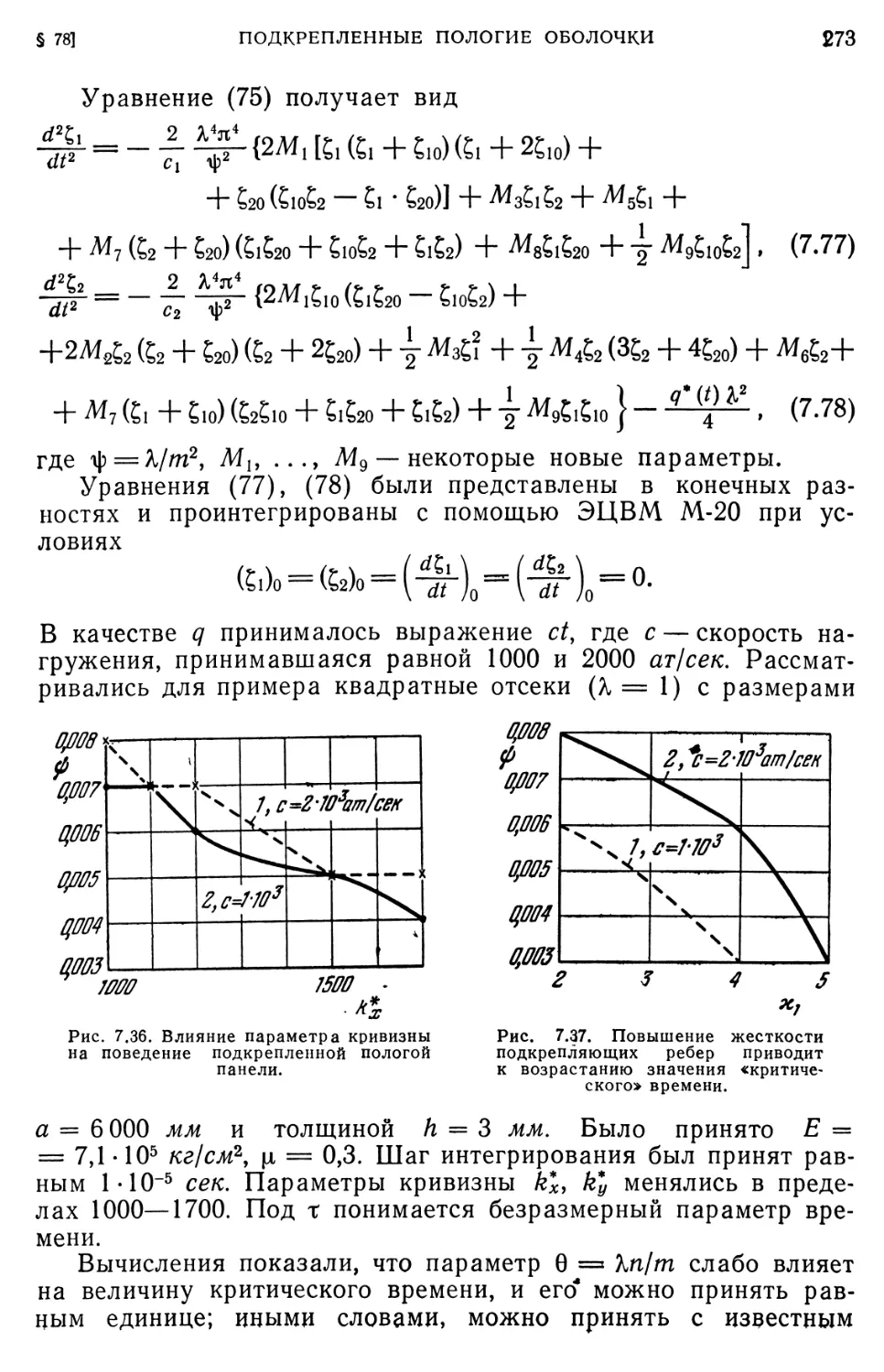
§ 78. Подкрепленные пологие оболочки положительной кривизны. 270
§ 79. Цилиндрическая оболочка при быстром нагреве 275
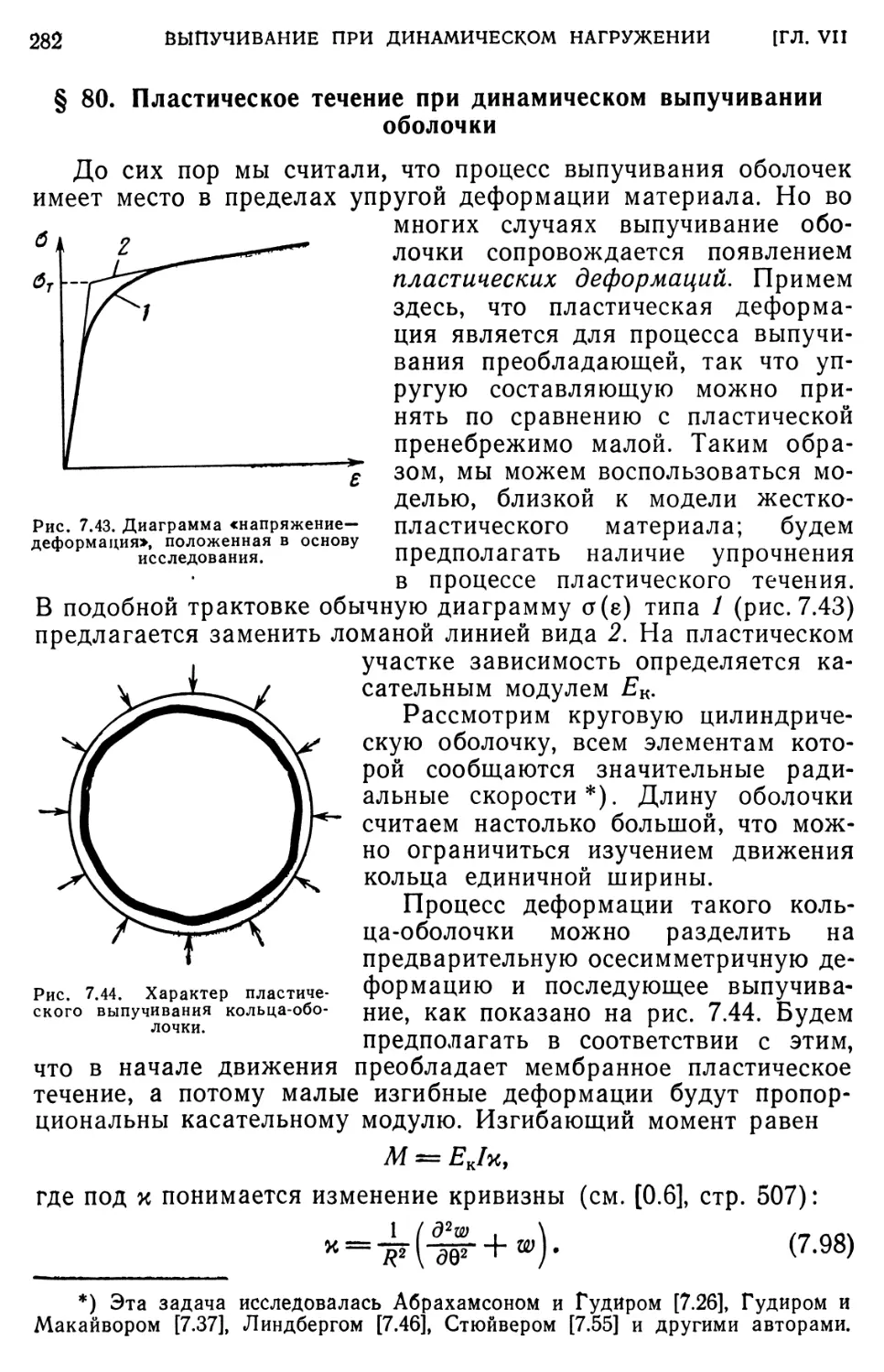
§ 80. Пластическое течение при динамическом выпучивании обо- -
лочки 282
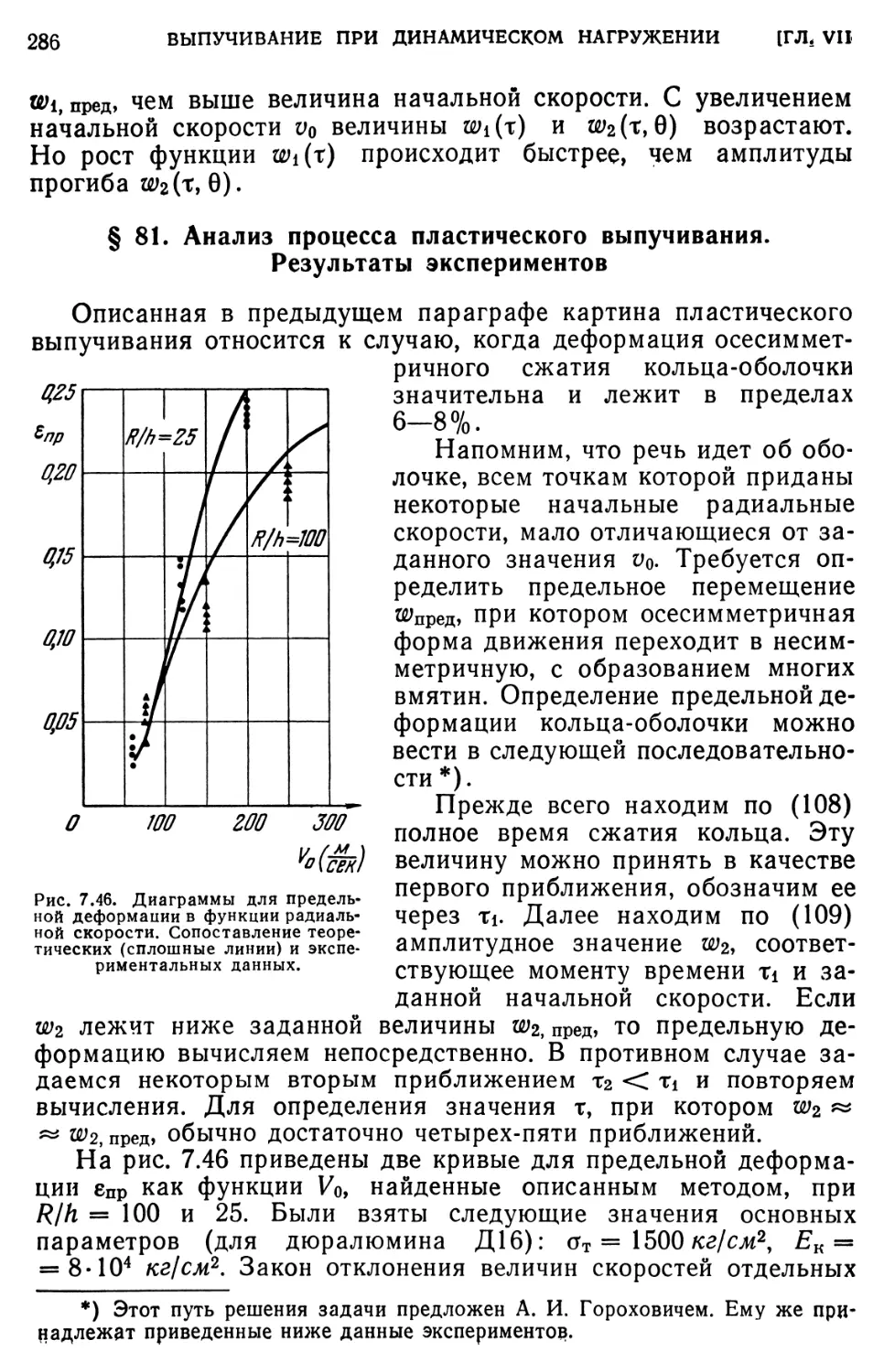
§ 81. Анализ процесса пластического выпучивания. Результаты
экспериментов. 26
Глава VIII. Поведение оболочек при ударе 288
§ 82. Особенности задач о поведении оболочек при ударном нагружении. 288
§ 83. Стержень при продольном ударе. 289
§ 84. Выпучивание стержня с начальной погибью. 291
§ 85. Различные подходы к задаче. Экспериментальные данные. 296
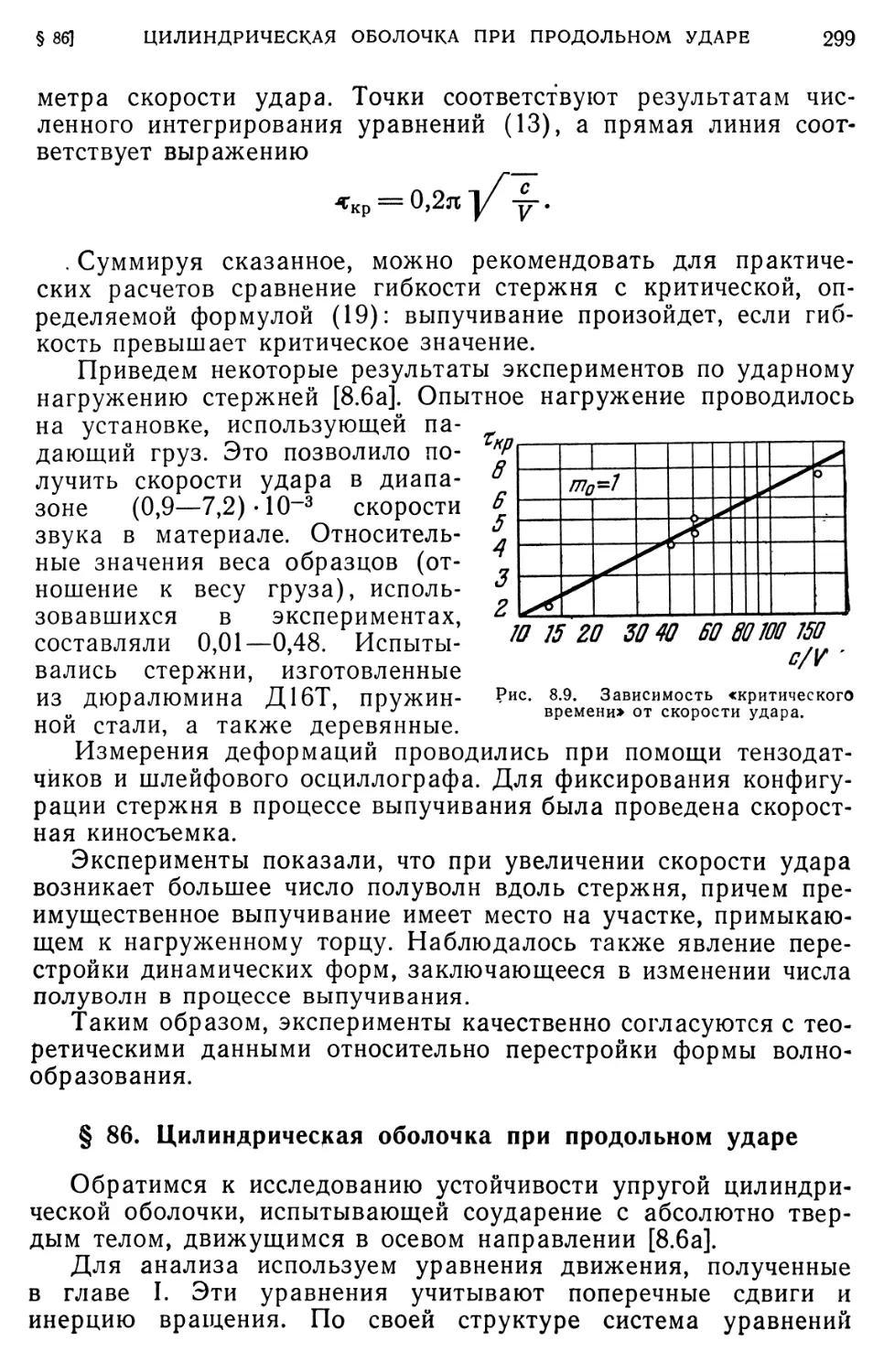
§ 86. Цилиндрическая оболочка при продольном ударе 299
§ 87. Случай неосесимметричного выпучивания 304
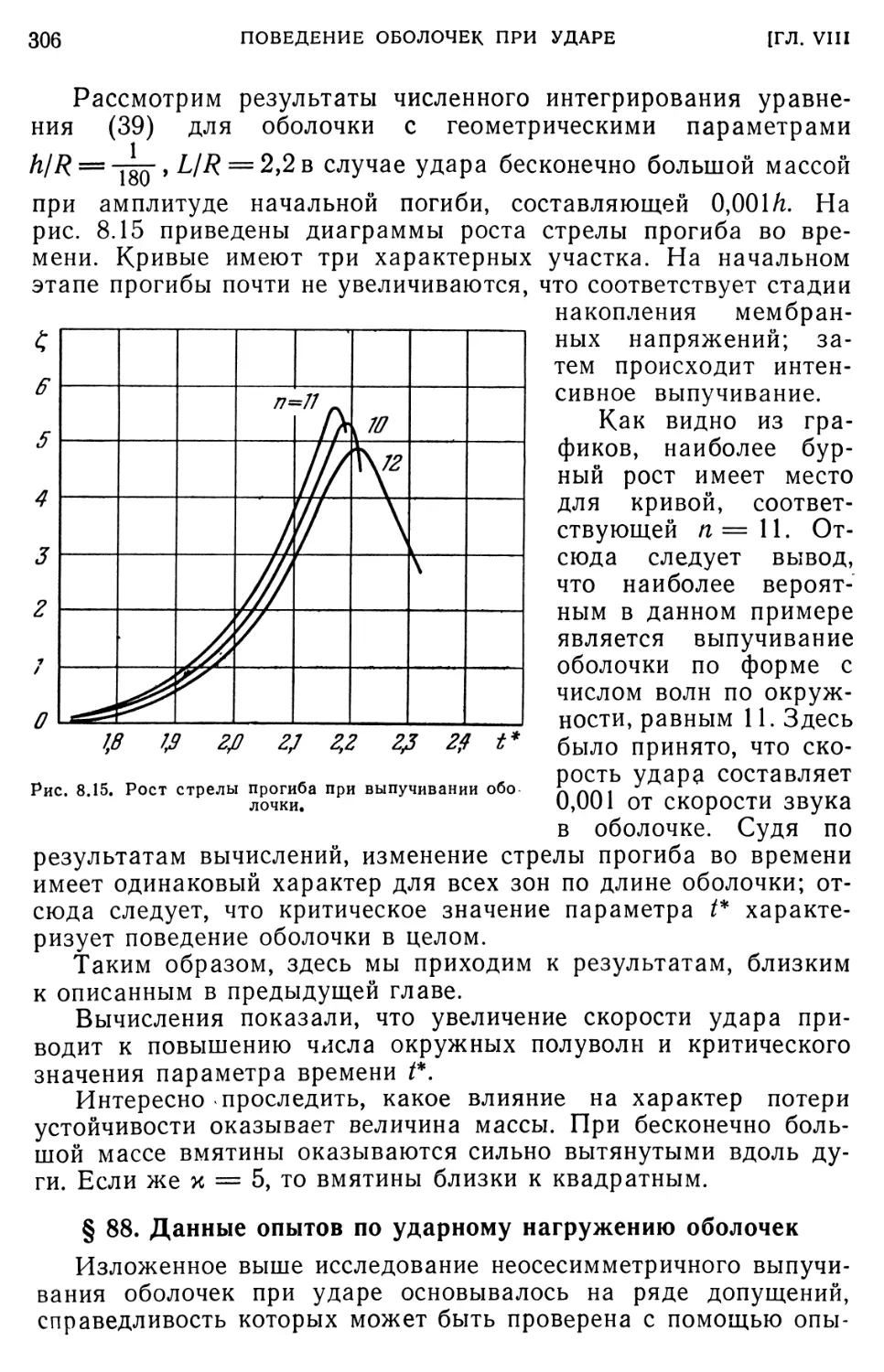
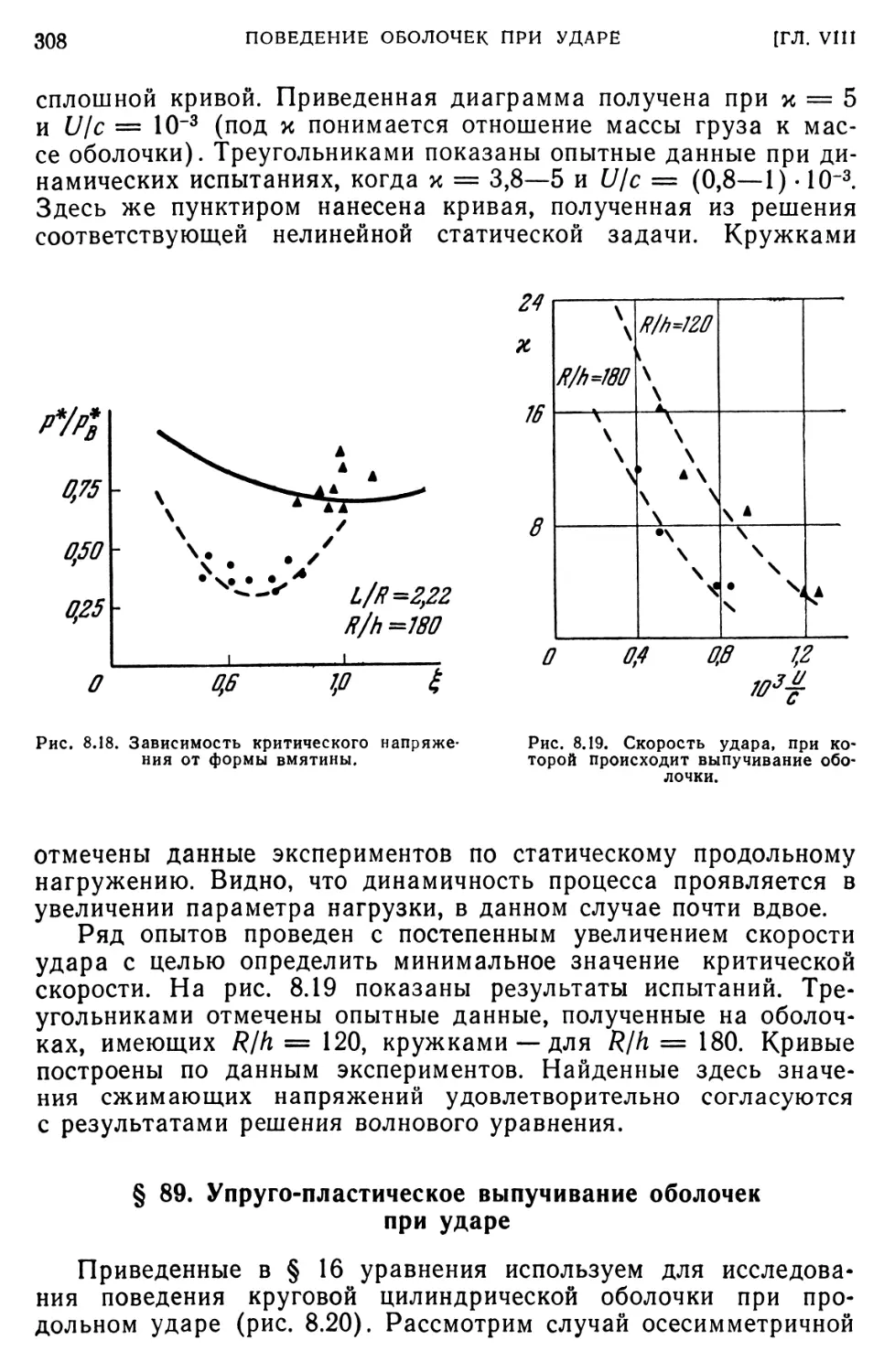
§ 88. Данные опытов по ударному нагружению оболочек. 306 § 89. Упруго-пластическое выпучивание оболочек при ударе. 308
§ 90. Коническая оболочка при продольном ударе 315
§ 91. Двухслойная оболочка. Общие зависимости 318
§ 92. Решение задачи о поведении двуслойной оболочки. 325
§ 93. Выпучивание цилиндрических оболочек при тепловом ударе 329
Глава IX. Поведение пластинок и оболочек при действии подвижной
нагрузки 334
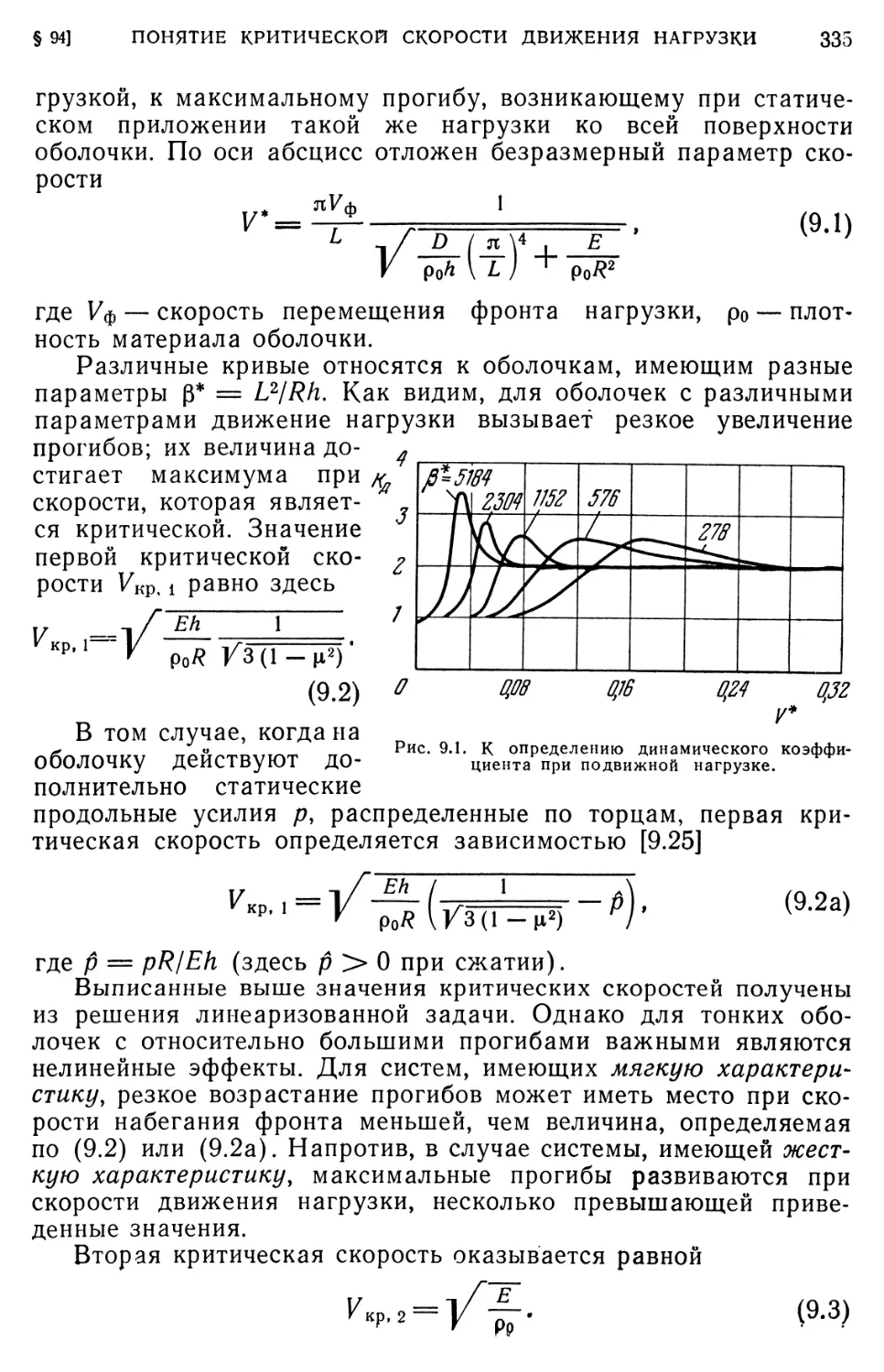
§ 94. Общие положения. Понятие критической скорости движения
нагрузки. 334
§ 95. Решение линеаризованной задачи 336
§ 96. Замкнутая цилиндрическая оболочка при действии подвижной
волны давления. Применение метода Бубнова — Галеркина 340
§ 97. Решение задачи с помощью метода конечных разностей. 344
§ 98. Применение метода конечных разностей к уравнениям в перемещениях 346
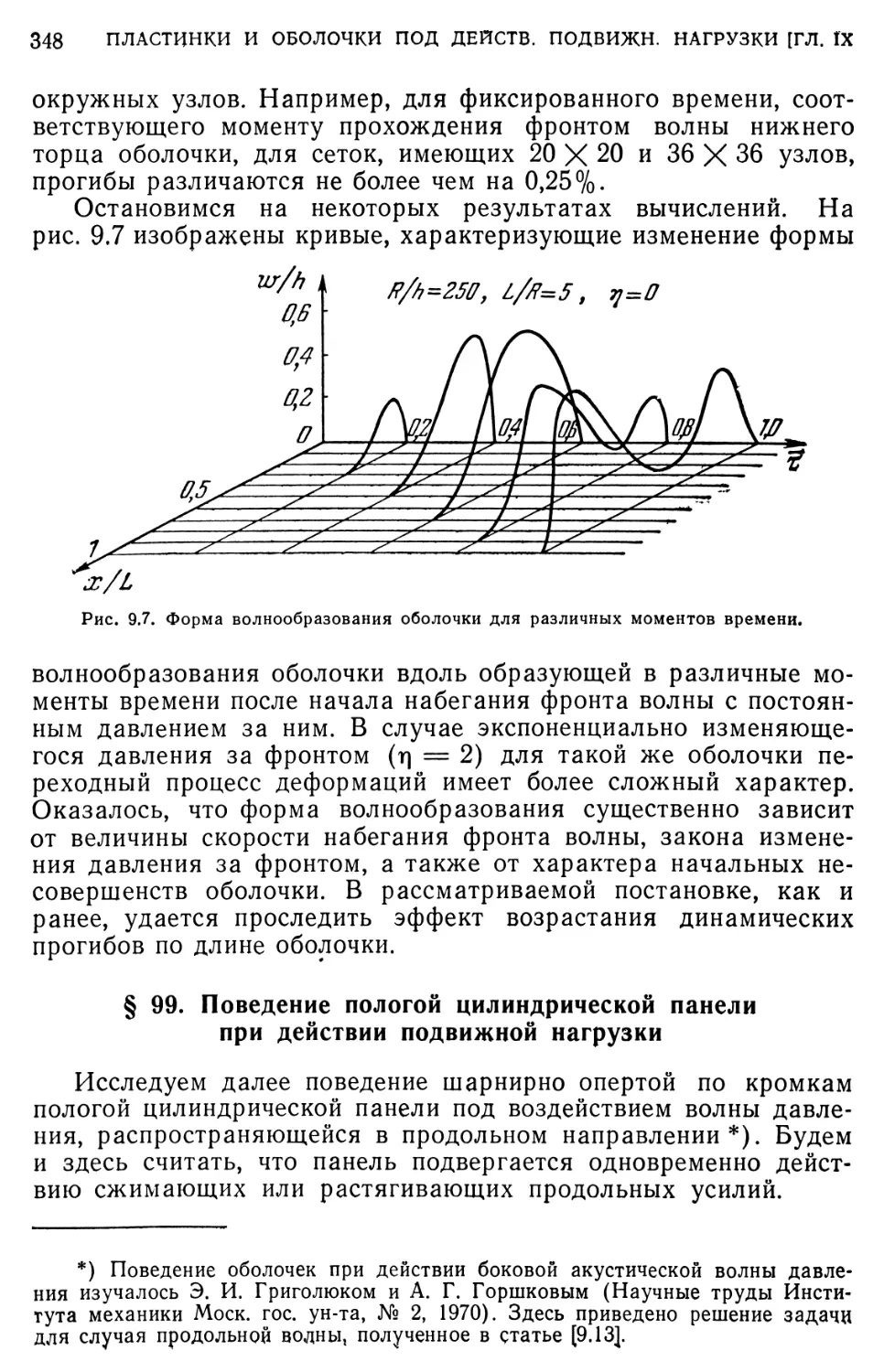
§ 99. Поведение пологой цилиндрической панели при действии
подвижной нагрузки. 348
§ 100. Особенности поведения нелинейной системы при подвижной
нагрузке. 350
§ 101. Поведение цилиндрической панели при действии подвижных
пульсирующих скачков давления -,, 352
б
ОГЛАВЛЕНИЕ
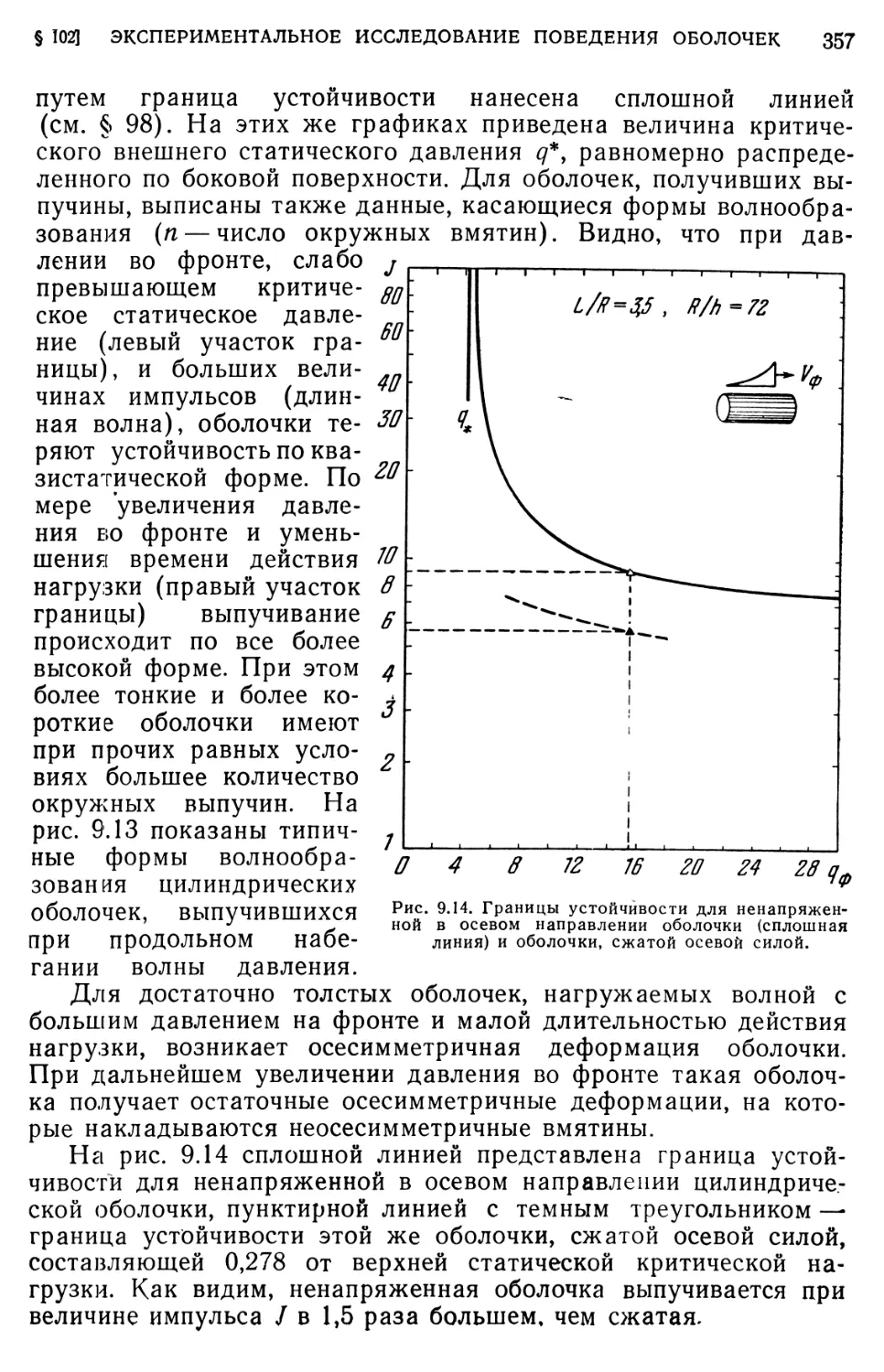
§ 102. Экспериментальное исследование поведения оболочек при
действии подвижных волн давления 355
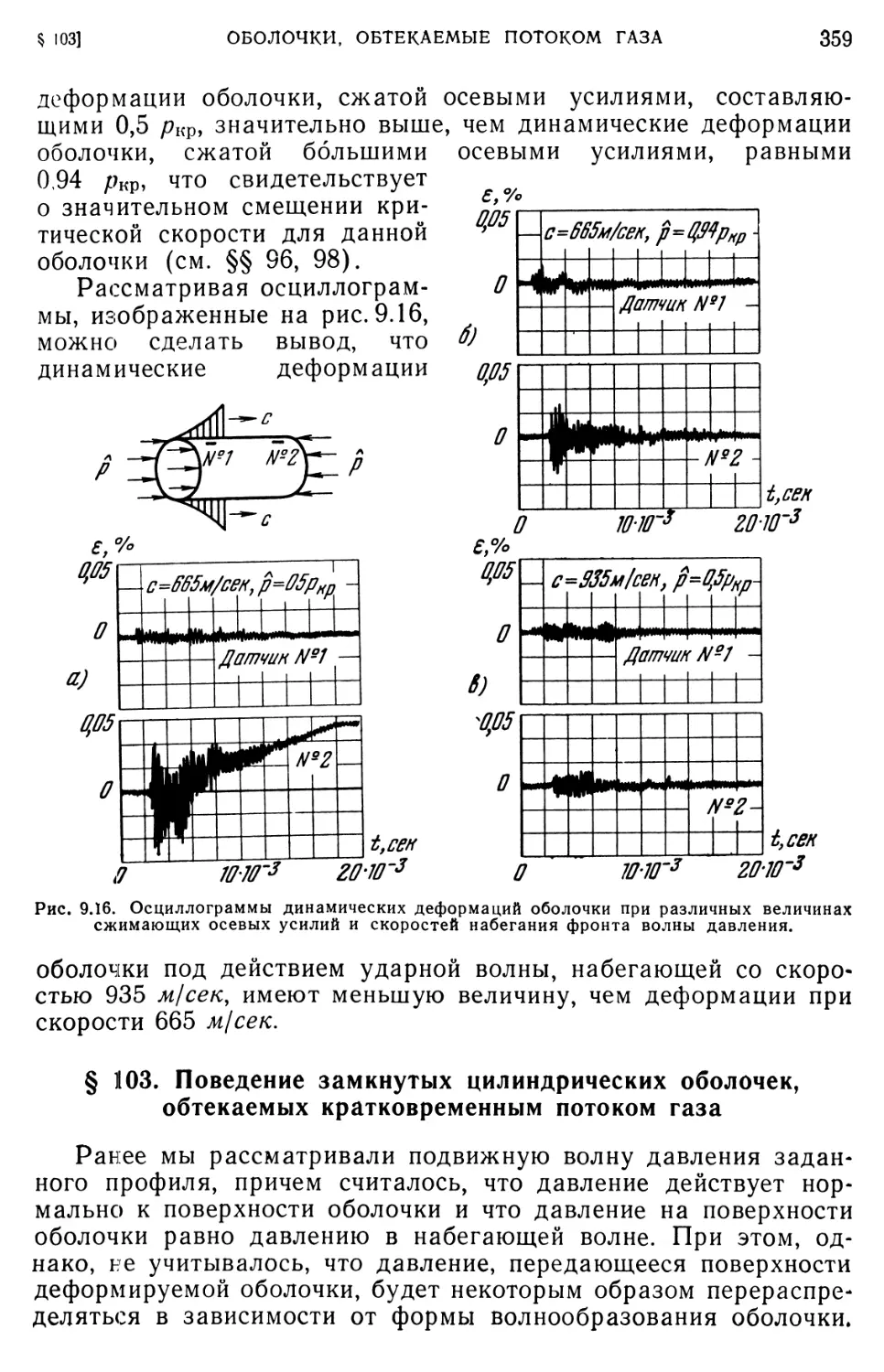
§ 103. Поведение замкнутых цилиндрических оболочек, обтекаемых
кратковременным потоком газа 359
§ 104. Экспериментальное исследование поведения оболочек при — подвижных пульсирующих скачках давления 362
Глава X. Задачи статистической динамики 364
§ 105. Характеристика задач и методов исследования 364
§ 106. Пластинка в акустическом поле. Закон распределения прогиба 367 § 107. Распределение экстремумов прогиба для пластинки. 373 § 108. Акустические колебания цилиндрической оболочки. Модель
системы со многими степенями свободы 374
§ 109. Цилиндрическая панель. Вероятностные параметры прогиба 378 § 110. Плотность вероятности экстремумов прогиба для системы
с прощелкиванием 381
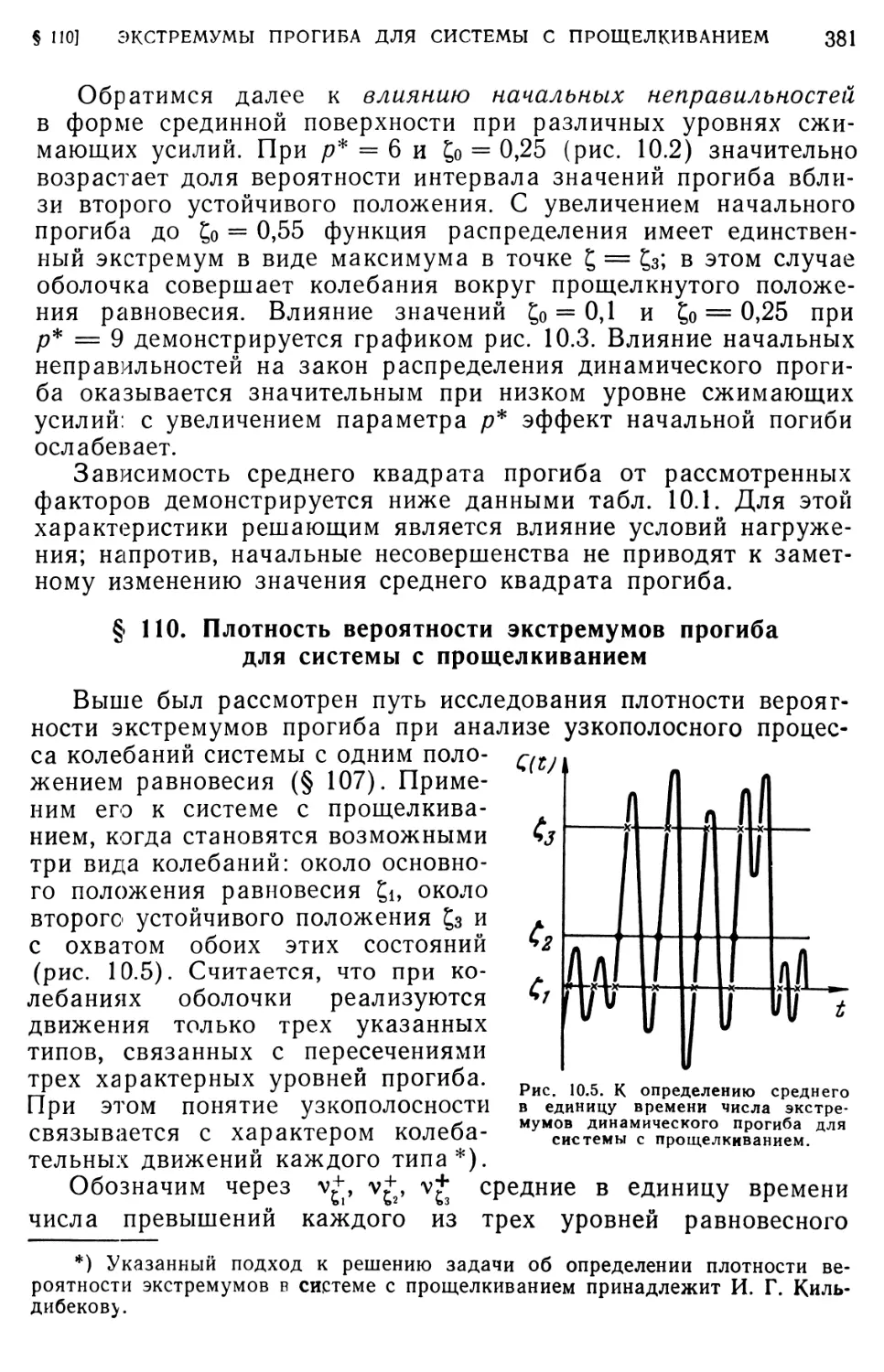
§ 111. Трактовка узкополосного процесса для системы с прощелкиванием 383
§ 112. Описание напряженного состояния панели. Плотность вероятности напряжений 386
§ ИЗ. Закон распределения экстремумов напряжений для системы
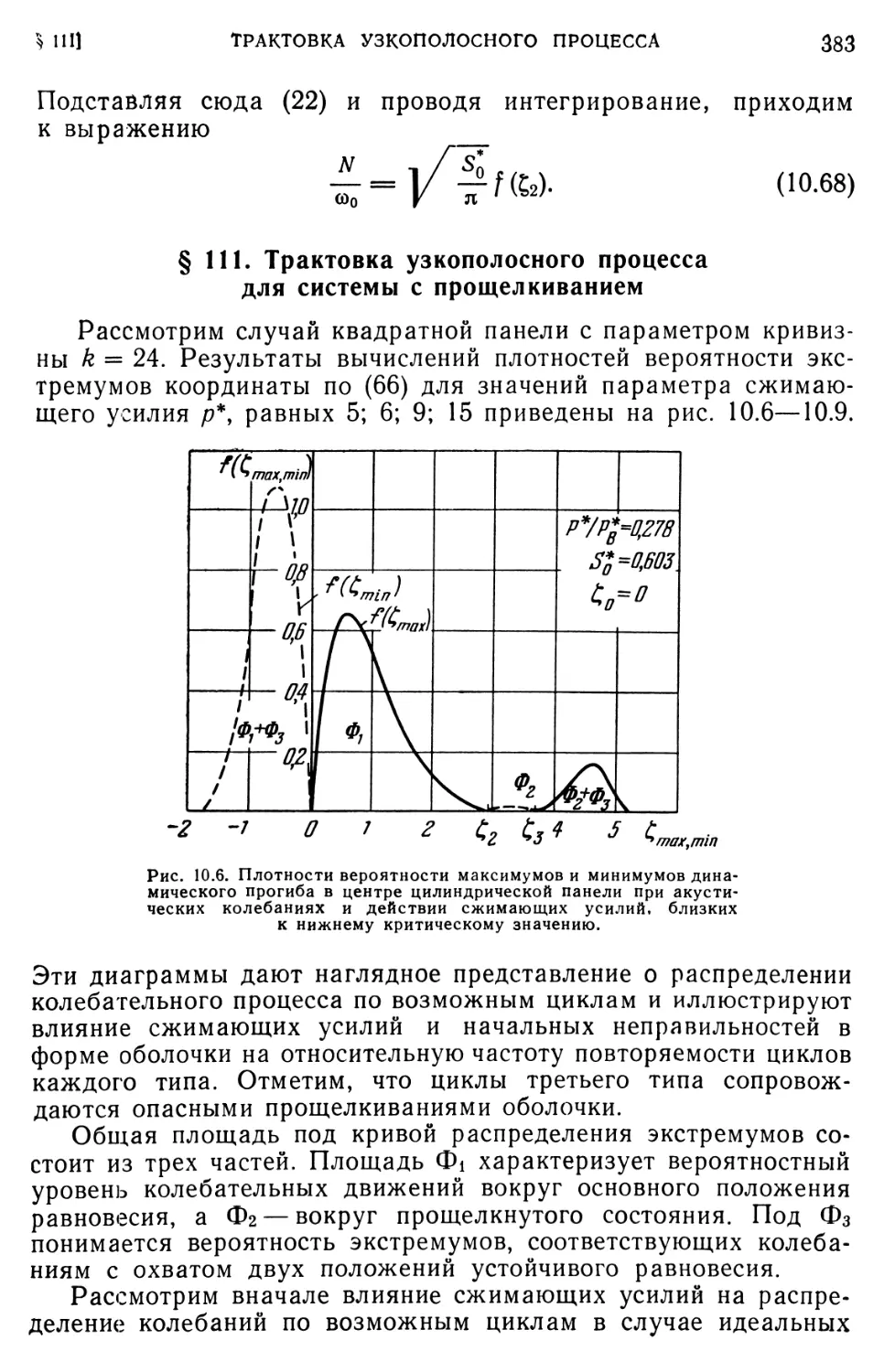
с прощелкиванием. Анализ возможных циклов 391
§ 114. Пологая оболочка 397
§ 115. Задачи для дальнейших исследований 404
Литература 405
ПРЕДИСЛОВИЕ
Настоящая книга посвящена нелинейным динамическим задачам теории пластинок и оболочек.
На протяжении трех последних десятилетий внимание авторов, занимавшихся теорией тонких пластинок и оболочек, было привлечено главным образом к задачам статики. Сюда относятся известные работы по методам сведения статической трехмерной теории твердых деформируемых тел к двумерной, по статической устойчивости оболочек в малом и большом, по медленно развивающейся ползучести пластинок и оболочек и т. д. Хотя эти проблемы далеко нельзя считать решенными, накопленные в литературе теоретические и экспериментальные данные позволяют уже теперь с достаточной уверенностью вести практические расчеты многих реальных конструкций.
В настоящее время центр исследований по теории пластинок и оболочек перемещается в область динамики. Это объясняется прежде всего запросами авиационной и космической техники; напомним, что именно эти области вызвали тот значительный прогресс в теории оболочек, свидетелями которого мы являемся. Однако изучение динамического поведения конструкций имеет существенное значение также для судостроения, инженерных сооружений и т. д.
Наиболее опасным для тонкостенных конструкций типа оболочек является сочетание статических нагрузок с разного типа динамическими воздействиями. Такие комбинированные нагрузки особенно часто влекут за собой прощелкивания хлопки оболочки, во многих случаях чередующиеся одно за другим и приводящие к образованию усталостных трещин. Разрушение конструкции наступает при этом иногда за весьма короткий срок.
Описание процесса прощелкивания оболочки может быть выполнено лишь с позиций геометрически нелинейной теории. Но исчерпание несущей способности оболочек нередко связано с накоплением пластических деформаций, поэтому важным является изучение и физически нелинейных систем. Таким образом, нелинейные задачи динамики пластинок и оболочек представляют большой практический интерес.
До последнего времени нелинейная динамика пластинок и оболочек была сравнительно мало освещена в литературе. Ниже изложены данные теоретических и экспериментальных исследований в этой области, полученные на протяжении последних лет
8
ПРЕДИСЛОВИЕ
автором и его сотрудниками. Наряду с этим сделана попытка систематизировать имеющуюся литературу и привести такие результаты, которые могут быть непосредственно использованы в практических расчетах.
Книга делится на десять глав.
Глава I содержит основные уравнения динамической теории пластинок и оболочек большого прогиба. Отметим, что общей нелинейной теории оболочек был посвящен в последние тридцать лет ряд фундаментальных исследований. Анализ этих работ выходит за рамки данной книги. В первой главе представлены лишь те математические модели, которые используются в дальнейшем при решении конкретных задач.
В главах II—V исследуются различные виды колебательных движений пластинок и оболочек. Отдельные конкретные задачи, относящиеся к собственным и вынужденным колебаниям, представлены здесь, по-видимому, впервые. В некоторых случаях мы отказываемся от обычной модели в виде системы с одной степенью свободы, характерной для большинства предыдущих работ по нелинейным колебаниям упругих систем. В разделе, относящемся к автоколебаниям, основное внимание уделено новым данным по панельному флаттеру.
Главы VI—IX посвящены описанию поведения тонкостенных систем при динамическом нагружении. Сюда относится анализ деформации пластинок и оболочек при быстром и весьма быстром, ударном, воздействии нагрузок различного характера.
Наконец, в главе X изложены некоторые задачи динамики оболочек и пластинок, требующие статистического подхода.
Данная книга примыкает к предыдущим монографиям автора: «Гибкие пластинки и оболочки» Москва, 1956 г. и «Устойчивость деформируемых систем» Москва, 1967 г. Автор стремился к тому, чтобы по возможности избежать повторений; ниже без вывода приведены многие соотношения со ссылкой на книги 1956 и 1967 гг. Это особенно относится к главам книги VI—VIII и X, тесно связанным с соответствующими разделами монографии «Устойчивость деформируемых систем». Библиография по этим главам относится к литературе, опубликованной главным образом после 1967 г.
Нумерация формул и иллюстраций дана по главам; в ссылках на формулы внутри глав номера их опущены.
Рукопись книги была внимательно просмотрена Л. И. Балабухом, сделавшим ряд ценных указаний. Большой труд по редактированию рукописи был выполнен И. Г. Кильдибековым. Автор искренне благодарит их, а также всех лиц, оказавших ему помощь при подготовке отдельных разделов книги.
А. С. Вольмир
И то, что носится в колеблющихся очертаньях,
Пусть закрепится в прочных мыслях.
Гёте, «Фауст».
ГЛАВА I
ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК
§ 1. Классификация динамических задач нелинейной теории пластинок и оболочек
На протяжении последних десятилетий теория оболочек, являющаяся естественным продолжением и обобщением теории пластинок, получила широкое развитие. В монографиях
В. 3. Власова 1.10, А. Л. Гольденвейзера 1.131 Н. А. Кильчевского 1.15, А. И. Лурье 1.18, X. М. Муштари и К. 3. Галимова 1.21, В. В. Новожилова 1.22, А. Лява 1.32, С. П. Тимошенко 1.38 содержатся основные зависимости современной теории оболочек; в них дано также решение многих конкретных примеров. Но в этих книгах рассмотрены главным образом статические задачи. Между тем в настоящее время все более актуальными становятся задачи о динамическом поведении пластинок и оболочек. Сюда относятся исследования периодических или близких к периодическим колебаний тонкостенных конструкций, включающих пластинки и оболочки, и их неустановившейся деформации при быстром и ударном нагружении.
Изучение колебаний оболочек было начато еще Рэлеем в его «Теории звука». В последнее время труды в этой области опубликованы Н. А. Алумяэ, Л. И. Балабухом, В. В. Болотиным,
Э. И. Григолюком и другими авторами. В имеющейся литературе речь идет, как правило, о малых колебаниях упругих оболочек, когда соотношения между деформациями и перемещениями, с одной стороны, и деформациями и усилиями, с другой, могут быть приняты линейными. Правда, и в такой постановке подобные задачи оказываются весьма трудными. Если малые колебания пластинок сопровождаются лишь появлением напряжений собственно изгиба, то в случае оболочки к ним присоединяются цепные напряжения. В зависимости от очертания оболочки и условий закрепления мы получаем тот или иной спектр частот и форм колебаний. Для одних видов колебаний
10 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
оказываются преобладающими изгибные усилия, для других — цепные. Характер напряженного состояния при колебаниях может сильно меняться вдоль главных размеров оболочки по мере удаления от края.
Особый раздел теории колебаний представляет собой исследование нелинейных колебаний, имеющих важные специфические свойства. Такого рода движения могут возникать в пластинках и оболочках при больших перемещениях, когда деформации и перемещения связаны нелинейными соотношениями. С другой стороны, деформации могут лежать за пределами применимости закона Гука и нелинейно зависеть от усилий.
В настоящей книге мы будем интересоваться именно нелинейными колебаниями пластинок и оболочек. Эта область представляет собой одну из частей общей нелинейной механики твердых деформируемых тел, или, в более широких рамках, нелинейной механики сплошных сред.
Второй круг вопросов, изучаемый в этой книге и получающий все более широкие практические приложения, относится к поведению пластинок и оболочек при импульсных воздействиях. В то время как при рассмотрении периодических колебаний может идти речь о некотором установившемся движении системы, в задачах о динамическом нагружении наибольшее внимание привлекают неустановившиеся, переходные, процессы. Такой процесс заключается обычно в скачкообразном переходе — перескоке системы от установившегося движения одного типа к некоторому другому движению. Подобное явление особенно характерно для оболочек и носит название хлопка или прощелкивания. Хлопок оболочки сопровождается, как правило, значительными перемещениями. Поэтому изучение поведения пластинок и оболочек при импульсных воздействиях будет достаточно полным лишь в том случае, если оно ведется для больших прогибов, с позиций нелинейной теории. Впрочем, в некоторых примерах начальная стадия переходного процесса может быть исследована и с помощью линеаризованных зависимостей.
Обратимся к исходным соотношениям динамики пластинок и оболочек.
§ 2. Некоторые сведения об оболочках
В дальнейшем мы будем исследовать тонкие оболочки — тела, одно из измерений которых толщина оболочки значительно меньше двух других. Толщину оболочки мы будем, как правило, предполагать постоянной. Поверхность, делящая пополам толщину оболочки, называется срединной поверхностью. В случае, если срединная поверхность представляет собой плоскость, мы получим тонкую пластинку.
§ 2
НЕКОТОРЫЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
11
Оболочки могут быть классифицированы по очертанию срединной поверхности. Простейшими примерами служат цилиндрические рис. 1.1, а или конические рис. 1.1,6 оболочки
Рис. 1.1. Отрезок замкнутой круговой оболочки: а цилиндрической, б конической.
с круговым поперечным сечением. На рисунках отмечены прямые линии, расположенные вдоль длины оболочки — меридианы, и окружности поперечных сечений — параллели. Проведем нормаль к срединной поверхности N, а затем различным образом ориентированные плоскости, содержащие N рис. 1.2. В пересечении этих плоскостей с поверхностью мы получим кривые линии — нормальные сечения срединной поверхности.
Для характеристики поверхности важно определить в каждой ее точке наибольший и наименьший радиусы кривизны этих сечений. Легко видеть, что наибольшим радиусом кривизны будут в обоих случаях обладать меридианы: центры кривизны для них будут лежать на бесконечности. Если же провести плоскости, нормальные к меридиональным, то полученные таким образом линии будут иметь наименьший радиус кривизны. Соответствующие центры кривизны будут расположены в точках пересечения нормали с осью симметрии. Для круговой цилиндрической оболочки наименьший радиус кривизны совпадает с радиусом поперечного сечения.
Третий пример оболочки простейшей формы — сферическая оболочка. Здесь радиусы кривизны всех нормальных сечений равны между собой.
12 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ffiOPHH ОБОЛОЧЕК ГЛ. 1
Приведенные выше примеры оболочек являются частными случаями оболочек вращения. На рис. 1.3 показано сечение меридиональной плоскостью срединной поверхности оболочки вращения произвольной формы. Изобразим и на этом рисунке
нормаль N на ней будут лежать центры кривизны нормальных сечений.
Пусть центр кривизны линии меридиана лежит в точке Си центр кривизны сечения плоскостью, нормальной к меридиональной, будет находиться в точке С2 пересечения нормали с осью симметрии. Обозначим соответствующие радиусы кривизны через pi и р2. Можно показать, что один из них является наибольшим, а другой — наименьшим по сравнению с радиусами кривизны всех нормальных сечений, проходящих через данную точку т. Направления этих двух нормальных сечений с экстремальными свойствами определяют для точки т так называемые главные направления. Если теперь провести линии, касательные
к которым будут в каждой точке срединной поверхности совпадать с главными направлениями, то мы получим так называемые линии кривизны. Для оболочки вращения линиями кривизны будут меридианы и параллели.
В самом общем случае оболочки произвольной конфигурации можно таким же образом установить в каждой точке срединной поверхности главные направления и соответствующие главные радиусы кривизны pi и р2 рис. 1.4. Если центры кривизны Ci и С2 лежат по одну сторону от срединной поверхности-, то условимся придавать радиусам pi и р2 одинаковый знак, а в противном случае — разные знаки.
Произведение главных кривизн k 1pi и 21р2 для данной точки носит название гауссовой кривизны поверхности или короче — кривизны поверхности: Г 12; полусумма — средней кривизны: k l2ki k2. Цилиндрическая и коническая оболочки имеют срединную поверхность нулевой кривизны. Сферическая оболочка имеет положительную кривизну.
С,
Рис. 1.4. Отрезки оболочки отрицательной кривизны слева и положительной кривизны справа.
Рис. 1.3. Центры кривизны нормальных сечений оболочки вращения.
§31
ОПИСАНИЕ МОДЕЛЕЙ ОБОЛОЧКИ
13
Если же обратиться к тороидальной оболочке рис. 1.5, то в одной части поверхности она будет иметь положительную кривизну точка Л, а в другой — отрицательную точка В.
Оболочки и пластинки находят на протяжении последних десятилетий все большее распространение в технике. Корпус космического корабля представляет собой конструкцию, состоящую из оболочек вращения различного вида — цилиндрических, конических, сферических. Фюзеляж самолета можно рассматривать в целом — вместе с подкрепляющими ребрами — как цилиндрическую оболочку. Крыло самолета также можно представить как оболочку или пластинку, имеющие в различных направлениях разную жесткость.
Оболочками являются корпус реактивного двигателя, кузов цельнометаллического вагона, корпус подводной лодки и т. д. Оболочки также часто встречаются в инженерных д
сооружениях в виде различных ре- рис 15 Тороидальная оболочка
зервуаров, Трубопроводов, куполь- Кругового сечения имеет в точке А r'r г о л о положительную кривизну, в точке
НЫХ И ИНЫХ ПОКрЫТИИ ЗДанИЙ и пр. В —отрицательную.
Подобные конструкции могут испытывать, наряду со статическими усилиями, быстро изменяющиеся нагрузки. Поведение конструкций при действии таких нагрузок обладает рядом особенностей. Поэтому исследование поведения оболочек и пластинок при динамических воздействиях является весьма актуальным.
§ 3. Описание моделей оболочки
При установлении модели, представляющей в теоретических исследованиях реальные оболочки, мы должны сделать ряд допущений.
Начнем с характеристики конструкции оболочки и ее материала. В технических приложениях, о которых было кратко сказано выше, встречаются оболочки самой разнообразной структуры. Сюда относятся, например, двух- и трехслойные оболочки; конструкции из композиционных материалов типа стеклопластика, графитопластика или боропластика; оболочки, подкрепленные ребрами.
Описание динамического поведения таких оболочек является весьма сложным. В качестве наиболее простой модели мы рассмотрим в данной главе однослойные оболочки, изготовленные из однородного изотропного материала.
14 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. 1
Но такой однородный изотропный материал может обладать различными свойствами.
Если учитывать эффекты пластической или вязкопластической деформации, то мы должны были бы исходить из нелинейных соотношений между напряжениями, деформациями и скоростями изменения этих величин во времени. Мы же будем, как правило, считать материал упругим и подчиняющимся закону Гука.
Надо иметь в виду, что механические характеристики материала при высоких скоростях деформации могут иметь значения, резко отличающиеся от статических. Модуль упругости несколько увеличивается, а предел пропорциональности, предел текучести, временное сопротивление могут возрасти на 50 и более.
Будем в дальнейшем рассматривать оболочки постоянной толщины h.
Отличительной особенностью общих зависимостей, относящихся к тонким оболочкам, является сведение уравнений трехмерной задачи теории упругости к уравнениям для двух измерений. При этом для однослойной однородной оболочки координатную систему естественно связать со срединной поверхностью оболочки. Мы можем, например, в качестве основных
координатных направлений принять линии кривизны срединной поверхности.
Одним из путей приведения £ трехмерной задачи к двумерной является принятие гипотезы недеформируемых нормаН21 1г лей гипотезы Кирхгофа —
Лява. Она состоит в том, что
Рис. 1.6. Элемент оболочки под действием птобпр ипттпкнп нппмяпкнпр к внешней нагрузки и внутренних усилий. ЛЮООС ВОЛОКНО, НОрМЗЛЬНОе К
срединной поверхности до деформации, остается после деформации прямым и нормальным к срединной поверхности в ее новом очертании; вместе с тем длина волокна вдоль толщины оболочки остается неизменной. Дополнительное допущение состоит в том, что нормальными напряжениями в направлении нормали к срединной поверхности можно пренебречь по сравнению с основными напряжениями.
Под основными напряжениями в теории оболочек понимают нормальные и касательные напряжения в самой срединной поверхности и в слоях оболочки, ей параллельных.
Рассмотрим элемент оболочки, вырезанный сечениями вдоль координатных линий g, г рис. 1.6 и подвергающийся, вообще говоря, действию поперечной нагрузки интенсивностью q. Нормальные усилия в каждом из этих сечений можно привести к силам Nt и N2, с одной стороны, и изгибающим моментам Ми М2,
ОПИСАНИЕ МОДЕЛЕЙ ОБОЛОЧКИ
15
с другой светлыми стрелками на рисунке изображены вектормоменты. Касательные усилия приводятся к сдвигающим усилиям Г12, Т21 и крутящим моментам Нi2, 21.
Обратимся теперь к поперечным силам Qu Q2, представленным на рис. 1.7, а. Они являются равнодействующими касательных усилий, лежащих в самих сечениях, ц рис. 1.7,6 и направленных вдоль нормали к срединной поверхности. Того же
Рис. 1.7. Поперечные силы в сечениях оболочки а как результирующие касательных усилий б.
типа касательные усилия возникают в поперечных сечениях балок, подвергающихся поперечному изгибу.
В статических задачах внутренние силы, действующие на элемент оболочки, уравновешивают внешнюю поперечную нагрузку следующим образом. С одной стороны, равновесие достигается за счет усилий в срединной поверхности. Это показано на рис. 1.8 на примере искривленной панели: нормальные усилия N в сечениях панели дают равнодействующую, уравновешивающую внешнюю нагрузку.
Если при этом в сечециях оболочки отсутствуют изгибающие и крутящие моменты, то оболочку можно охарактеризовать как безмоментную. С другой стороны, в плоской пластинке при малых прогибах равновесие элемента может быть получено лишь за счет разности поперечных сил Q рис. 1.9, в свою очередь связанных с изгибающими и крутящими моментами. В общем случае моментной оболочки имеет место совместное действие усилий в срединной поверхности, поперечных сил и моментов.
В интересующих нас задачах динамики мы должны, пользуясь принципом Даламбера, ввести в рассмотрение силы
Рис. 1.8. В оболочке внешняя поперечная йагрузка уравновешивается частично за счет усилий в срединной поверхности.
Взаимные им касательные усилия действуют в слоях, параллельных срединной поверхности.
16 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
инерции. Определим прежде всего силы инерции, соответствующие перемещениям элементов оболочки вдоль нормали. Обозначая нормальные перемещения — прогибы — через w, мы получим силу инерции, приходящуюся на единицу объема, равной —ygd2wdt2 где у — удельный вес материала, g — ускорение силы тяжести, t — время. Аналогично находятся силы инерции, отвечающие перемещениям и, v.
Обратимся к деформациям, связанным с усилиями различного типа. Усилия N вызывают удлинения или укорочения вдоль координатных линий g, г, усилия Т — сдвиг элемента в срединной поверхности. Эффект моментов М проявляется в изменении кривизн оболочки, а моментов Н — в скручивании элемента. Что же касается деформаций сдвига, связанных с поперечными силами и соответствующими касательными напряжениями т, то этими деформациями обычно пренебрегают.
Очерченную схему напряженного и деформированного состояния оболочки, основанную на гипотезе Кирхгофа — Лява, можно считать моделью первого приближения. Она оказалась удобной при решении многих статических и динамических задач; полученные при этом результаты в ряде случаев достаточно точны для практических приложений.
Перейдем к анализу основных соотношений динамической теории оболочек для такой модели.
§ 4. Деформации и перемещения
Рассмотрим более подробно деформированное состояние оболочки произвольного очертания в предположении, что прогибы точек срединной поверхности могут быть одного порядка с толщиной оболочки. Будем пользоваться в дальнейшем декартовыми координатами х, у, z. Координатные линии х, у условимся совмещать с линиями кривизны срединной поверхности. Линию г направим вдоль нормали к срединной поверхности к центру кривизны. Примем ниже правую систему координат. Обозначим перемещения точек срединной поверхности по направлениям х, уу z через и, v, w.
Поставим перед собой целью выразить соотношения между деформациями и перемещениями. Перемещения точек срединного слоя вдоль координатных линий являются функциями координат х, у и времени t: и их, y9t, v vx, y,t, это же
Рис. 1.9. В пластинке и оболочке внешняя нагрузка уравновешивается отчасти за счет поперечных сил.
ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ
17
относится к прогибам w wx, y,t. Перемещения произвольной точки с координатой до деформации z, которые обозначим через uzxy у, zy t и
т. д., примем равными
dw дх dw
и — и — z -
V V — Z
W W.
ду
1.1
Рис. 1.10. Деформация элемента оболочки по гипотезе Кирхгофа — Лява.
Первая из этих зависимостей иллюстрируется рис.
1.10, где изображено сечение оболочки плоскостью, касательной к линиям х и z.
При деформации оболочки происходит поворот нормали к линии х на такой же угол dwdx, на какой поворачивается касательная I к той же линии. Это следует из гипотез Кирхгофа — Лява. Знаки в выражениях 1 соответствуют принятой нами системе отсчета.
Перейдем к определению деформаций в некотором слое, параллельном срединной поверхности и удаленном от нее на
Рис. 1.11. Деформации в слое оболочки, параллельном срединной поверхности.
расстояние z. Деформации удлинения в направлении линий у обозначим через ъгх, ггу, а деформацию сдвига — через Y. Величины е®, е, у2 зависят от перемещений uz, vz, wz.
Сначала определим составляющие деформации е, е, обусловленные перемещениями uz, vz. Выделим элемент ABCD
18 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
данного слоя оболочки сечениями, нормальными к линиям, у рис. 1.11. Точка А, координаты которой пусть будут х, у, получает перемещения иz, vz для точки В с координатами х dx, у перемещения равны uz duzdxdxt vz dvzdxdx. Для точки С с координатами х, у dy получим величины иг • duzdydy, vz dvzdydy.
Новая длина элемента dx после деформации составит
Л,т- dx dxf 4£dxf4-,
или
»Г4£Ш'-
Разложим это выражение в ряд; считая выражение, стоящее в квадратных скобках, малым по сравнению с единицей, поdx лучим
,-< 1 7 2 1ГГ
Деформация удлинения, зависящая от иг vzt будет
Рис. 1.12. Составляющие де¬
формаций в срединной по- duz, 1 I duz 2. 1 dvz 2, ч
верхности, связанные с pa- 6Z г 7- I —jr-1 —г— а
диальными перемещениями. х ОХ 2 ОХ J 2 ОХ
По аналогии выражение для деформации удлинения вдоль линии у найдем в виде
dvz, 1 dvz 2, 1 I dvz 2
8„
дх 1 2
1 до 2, 1 dvz 2
2 дх 2 ду Определим теперь составляющие деформаций е, е, связанные с общим перемещением к центру кривизны или от него элемента в сечении, нормальном к линии у рис. 1.12. Если длина элемента первоначально равна dx pd0, то после смещения она составит рx — wdQx. Соответствующая деформация элемента оказывается равной
ъг - р. —gL — kxw. аО
Рх dvx Рх
Здесь принято wz w. Аналогично для координатной линии у получим
гу — kyw> ЬО
Речь идет о проекции элемента слоя на плоскость, касательную к линиям ху у в точке А,
§ 4 ДЕФОРМАЦИЙ И ПЕРЕМЕЩЕНИЯ 19
В дальнейшем мы будем считать величины kx и ky для рассматриваемого участка оболочки постоянными.
Найдем далее деформации удлинения, возникающие при изменении прогиба вдоль координатных линий. Если прогиб в точке А по направлению z равен w рис. 1.13, то прогибы точек В и С составят соответственно w dwdxdx и wdwjdydy. Пренебрегая искривлением малого элемента, найдем его новую длину
-Н'ШТ- <с>
Поступая так же, как и при выводе выражения а, находим dsi dx 1 y4f
Отсюда получим деформацию равной
r—dsidx 1 dw2,
X dx 2 дх • >
Для линии у по аналогии
ч-4г- <ь>
Перейдем к определению деформации сдвига yz. Первую составляющую этой деформации, зависящую от перемещений uzt vz, найдем как разность величин прямого угла между сторонами dx, dy до деформации и угла, который эти стороны составляют после деформации рис. 1.11:
z диг, dvz
Составляющую деформации сдвига, соответствующую прогибу w, найдем, обратившись к рис. 1.13.
Здесь показано, как искажается при деформации прямоугольный треугольник со сторонами dx, dy. Пользуясь выражением типа с, определим квадраты длин сторон после деформации:
И здесь рассматривается проекция элемента слоя. См. предыдущую сноску.
20 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Квадрат третьей стороны В2С2 будет равен
влгт 1 жТш 1 П-
Здесь с точностью до малых высшего порядка можно принять dsds2 dxdy.
С другой стороны, сопоставляя длины отрезков ВВ2 и СС2, получим
Сравнивая выражения е и f и принимая cos — yz j yz,
будем иметь
Используя полученные результаты, выпишем полные выражения для деформаций удлинения и сдвига в слое оболочки, удаленном на расстояние z от срединной поверхности:
Так как мы изучаем деформацию тонких гибких оболочек и пластинок, то можно принять, что углы поворота dwzdx, dwzdy, связанные с прогибом, значительно превышают значения производных дидх, диду и т. д., относящихся к деформациям в массиве материала. Будем считать, что квадраты производных dwzdx2 одного порядка с составляющими duzjdx и т. д; тогда квадратами производных типа дигдх2 этих выражений можно пренебречь. Мы приходим к более простым соотношениям
.В2С2f dx2 dy2 ■dy — dxj. f
z duz. dvz. dw dw
У ду ' дх ' dx dy
1.3
Воспользуемся далее выражениями 1 для перемещений
ЙАПРЯЖЕННОЁ СОСТОЯНИЙ
21
произвольном точки по толщине; тогда получим
1.4
ди, dv. dw dw 0 d2w
Введем обозначения ех, гу и у для деформаций в срединной поверхности при г 0; они будут равны
Полные деформации произвольной точки по толщине е, е и уъ складываются из деформаций в срединной поверхности гх, еу, у и деформаций изгиба,, для которых введем обозначения гх, и, и, Уи- Деформации изгиба равны
Важно отметить, что деформации в срединной поверхности по 5 не являются независимыми; они выражаются через одни и те же функции и, v, w. Дифференцируя вторую из зависимостей 5 дважды по х, первую — дважды по у, а третью — последовательно по х и у, после простых преобразований придем к следующему уравнению совместности или неразрывности деформаций в срединной поверхности: д2ех
§ 5. Напряженное состояние. Связь между усилиями и деформациями
В пределах сделанных нами допущений можно рассматривать напряженное состояние оболочки как результат наложения трех состояний. Одно из них соответствует так называемым цепным или мембранным напряжениям; в дальнейшем мы будем
1.5
ди. dv. dw dw
ду дх дх ду
—
ду2 1 ахл охоу axayj ах оу оу ох
1.8
Перейдем к исследованию напряженного состояния оболочки.
22 общие зависимости нелинейной теории оболочек гл. i
часто называть их напряжениями в срединной поверхности, Второе отвечает напряжениям изгиба — нормальным и касательным, — изменяющимся вдоль толщины по. линейному закону; «нейтральный» слой, в котором напряжения изгиба равны нулю, совпадает со срединным. Эти два напряженных состояния вместе взятые определяют «классические» усилия. Наконец, третье состояние соответствует поперечным касательным напряжениям. В рассматриваемом варианте теории учитываются лишь результирующие этих напряжений; более подробно они исследуются в другом варианте, приведенном ниже § 9.
Выделим элемент оболочки, грани которого совпадают с касательными к линиям х и у. На рис. 1.14 показаны цепные напряжения: нормальные а, оу и касательные т. Если выделить
Рис. 1.14. Цепные мембранные напряжения в се чениях оболочки.
Рис. 1.15. Изгибающие и крутящий моменты в сечениях оболочки.
Рис. 1.16. Поперечные силы и соответствующие им касательные напряжения в сечениях оболочки.
участки граней, имеющие длину, равную единице, то мы сможем определить отвечающие этим напряжениям нормальные усилия NXt Ny и касательное усилие Т:
N х Gxhf Ny а „г, Т tl
1.9
Обратимся к напряжениям изгиба. Обозначим нормальные напряжения через ох, и, оу, и, касательные — через ти. Очевидно, им будут соответствовать изгибающие моменты МХу Му и кру¬
§ 5
НАПРЯЖЕННОЕ СОСТОЯНИЕ
23
тящий момент Н рис. 1.15. Эти величины, приходящиеся на единицу длины граней элемента, будут равны
Л2 Л2 Л2
Мх J oXtllzdz, Му J Oytllzdzy Я J xnzdz. 1.10
—г2
-Л2
-Л2
Напряжения поперечного сдвига, изображенные на рис. 1.16, будем обозначать через хх2, хуг они связаны с поперечными силами QX1 Qy, приходящимися на единицу длины сечения, зависимостями
А2 Л2
Qx f T’xzdz Qy:: 'tyzdz. 1.11
-Л2 -Л2
Таким образом, интегральные характеристики усилий и локальные напряжения связаны зависимостями 9 — 11.
При выводе соотношений, связывающих усилия и моменты с деформациями, будем здесь исходить из предположения, что деформации лежат в пределах действия закона Гука.
Для деформаций в срединной поверхности можно выписать известные соотношения
Ох ву
гЁ 1Г'
Gy Х
гу — В ТГ
21fl л кп ц т, 1,12
где G — модуль упругости при сдвиге. Отсюда
IX2 ® Ь М1®» 2 У “Ь xi
1 —I т 21 ц
1.12а
N„
Учитывая зависимости 5 и 9, находим Eh
1
тЩг
Eh dv,, 1 dw2.
ди ■ dv. dw dw
dy ‘ dx ‘ dx dy'
T
21 Ц
1.13
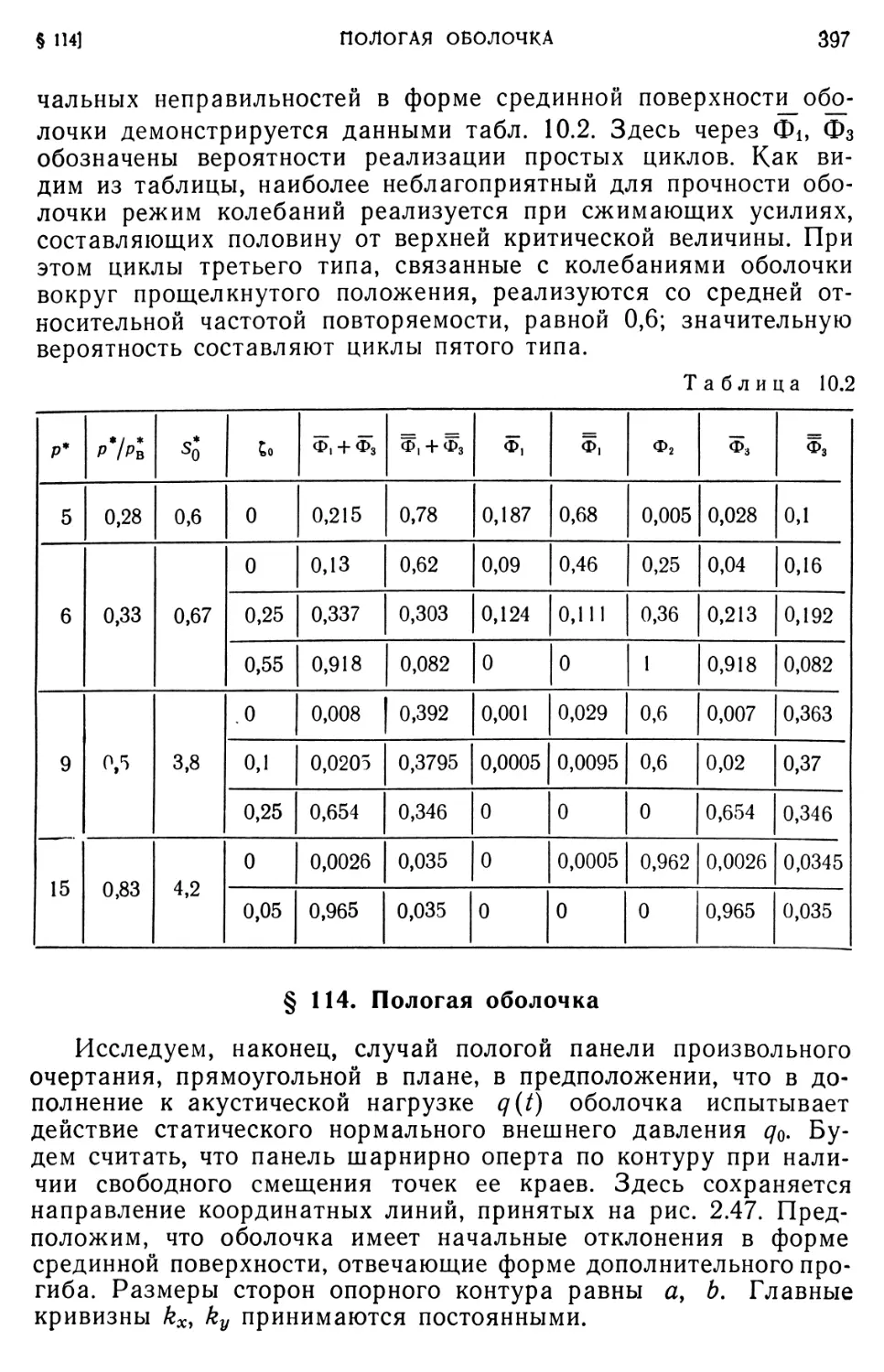
24
ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Далее определим напряжения в произвольной точке с координатой г
Выражения для изгибающих и крутящих моментов 10 с учетом зависимостей 6 примут вид
Через D обозначена цилиндрическая жесткость оболочки
Зависимости поперечных сил Qx и Qy от перемещений здесь не приводятся, поскольку для их вывода в этой модели используются условия равновесия элемента; соответствующие выражения будут даны в следующем параграфе.
Перейдем к составлению уравнений движения элемента оболочки hdxdy, по граням которого действуют усилия в срединной поверхности, моменты и поперечные силы рис. 1.17. Интенсивность заданных внешних нагрузок, приложенных к элементу по направлениям х, у, z, обозначим соответственно через А ру, q.
Будем пользоваться принципом Даламбера и присоединим к заданным силам и динамическим реакциям соседних элементов оболочки усилиям и моментам силы инерции. Составляющие результирующей силы инерции по направлениям х, у, z будут
1.15
§ 6. Приближенные уравнения движения
Инерцию вращения элемента hdxdy относительно направлений х и у в этой модели оболочки учитывать не будем,
ПРИБЛИЖЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
25
Уравнение движения элемента в проекциях на направление касательной к линии х имеет вид
N Щ dxdy-Ndy Qrdy-
-< IFF йхж l£dxdy T dydx-
V Л21
— Tdx px dxdy —j-h dx dy — 0,
или
dNx, дТ d n dw. у u d2u n 1 i
dfwшQi.mpxghdF0- 1 •17
Подчеркнутый пунктиром член в уравнении может оказаться значительным лишь при образовании весьма крупных вмятин.
Рис. 1.17. Элемент оболочки под действием изгибающих и крутящих моментов и поперечных сил.
Между тем в задачах, которые будут рассматриваться нами в дальнейшем, деформация оболочки обычно сопровождается появлением сравнительно мелких вмятин, размеры которых малы по сравнению с радиусами кривизны оболочки. Поэтому уравнение проекций на касательную к линии х можно записать в виде
dNx. дТ, y h д2и _п п
Такое предположение характерно для теории пологих оболочек, кото¬
рой мы здесь пользуемся.
26 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИЙ ОБОЛОЧЕК ГЛ. 1
Аналогичным образом выпишем уравнение в проекциях на направление касательной к линии у:
дТ dNy у d2v
■77 Ti P>-7hT>r 0- U9>
Далее составим уравнение в проекциях всех сил на направление нормали к срединной поверхности. После упрощений получим
dQx dQu d j dw dw -аГ -ЗГ Л М, -5
. d rr dw I dw i V i d2w л,л ллч
Перейдем к уравнениям моментов относительно касательных к линиям у и х. В' соответствии со сделанным в начале параграфа допущением эти уравнения не содержат членов, связанных с инерцией вращения элемента. Первое из них имеет вид
Mx dxdy-Mxdy H -dydx— Н dx — qdxdy-- — Qx -dxdy dx —
dQy dx y d2w dx
jjj- dy dx-2 — h dx dy -y 0.
Отбрасывая малые высшего порядка, после упрощений будем иметь
-f—Q,«0. 1.21
Второе из уравнений моментов по аналогии запишется следующим образом:
•£ ТГ-<Ь°- Пользуясь зависимостями 15, 21 и 22, получаем значения поперечных сил
Qx-D-i- V2W,
dx
«.—D ■§-,■
1.23
Здесь V2 -02 двумерный оператор Лапласа.
§ 7 УРАВНЕНИЯ В ПЕРЕМЕЩЕНИЯХ 27
Исключая Qx и Qy из уравнения 20 с помощью 21 и 22 и выписывая снова 18 и 19, получаем следующую систему уравнений:
dNx. дТ. у и д2и Л 1 сл
-jf >i P-JhF 0’ -24
дТ dNv V дЧ
дГ pyjhm 0’ 1-25
д2Мх д2Ми д2Н
2Жд кхЫх кУЫУ
, д кт dw. rr dw. д rr, dw. Ar dw. у и d2w Л
N TW ibV Ny q-ghiw0-
1.26
Уравнения 24—26 описывают движение элемента оболочки. К ним должны быть присоединены граничные и начальные условия.
§ 7. Уравнения в перемещениях
Выразим усилия, входящие в уравнения 24—26, через перемещения и, v, w с помощью зависимостей 13, 15 и 23. Из уравнения 24 найдем
д2и, 1 — и' д2и, 1 м> d2v и,, ч dw_,
2 ду2 ' 2 dxdy ' х У' дх дх2
dw d2w, 1 М- dw d2w, 1 — ц dw d2w f
dx dx2 ' 2 dy dx dy 2 dx dy1
1 - l2 n V 1 27
Eh px g E dt2 U
Аналогичным образом из уравнения 25 получим
l l d2u, d2v, 1 — ц d» ttU и dw
2 dxdy dy2 2 dx2 WKx-TKy ду 1-
, dw d2w, 1 ii dw d2w, 1 — ц dw d2w.
О Л v ■ О Л -и2 I
дг d2 ' 2 d dxdy x 2 dy dx2
JLEFLPy-J-Lr°- 0-28>
В уравнениях 27—29 и в дальнейшем в 80—84, отброшены некоторые члены высшего порядка малости.
28 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Уравнение движения в проекциях на нормаль к срединной поверхности 26 будет таким:
-yj V4o> — kx llky ky
, tul I i О и U kx nky dw2 ky ikx dwy
2Mkxkyw 2 2—Ы -
d dw f du. dv <t f 1,
dx dx Ц dy w J
, 1 — Li dw I du. dv d dw Г du, dv,,,, 4 1,
2 Ту дх ду ду Г dx dy kv W
■ 1 — ц do du ■ dv Y 1 - i« у 1 - ц» d»a>,
2 йд: dy алг Jj Eh £ <32 1 I1-»
Здесь v-V’V«_£r 2-3£i -£.
Если можно рассматривать динамический процесс без учета распространения упругих волн, то уравнения 24—26 упрощаются. Становится возможным отбросить инерционные члены в первых двух уравнениях. Эти два уравнения будут удовлетворяться при отсутствии усилий рх и ру, если ввести функцию напряжений в срединной поверхности Ф по формулам
Nx а2Ф Ny d2 Ф Т d2 Ф
°х 7Г 1уг <yyT dxrf Х Т - dx dy 9 30
Выразив в 8 деформации в срединной поверхности через усилия, а затем — через Ф, приводим уравнение совместности деформаций к виду
-Ф -Uw,w-kx-ky-. 1.31
Здесь введен оператор Lw, w:
Уравнение движения элемента оболочки примет вид
D Г74 т гтл и 2Ф I и 2Ф I Я У d2w п ооч
Tv w Lw,0 kx-gjT ky-r J — j-gjr, 1.33
где
w d2w d2Ф. d2w d2Ф 0 d2w d2Ф OA,
Hw> Ф-'Wdyr dyrdxr “ Жду Txdy ’ 034
§7
УРАВНЕНИЯ В ПЕРЕМЕЩЕНИЯХ
29
Окончательно получаем следующие уравнения:
1.36
1.35
Здесь под V понимается оператор
1.37
В дальнейшем мы будем часто рассматривать оболочки с начальными неправильностями в форме срединной поверхности. Примем, что начальные прогибы малы по сравнению с основными размерами оболочки, но вместе с тем сравнимы с ее толщиной. Приведем без вывода уравнения, соответствующие 35, 36 и составленные с учетом начальных прогибов Wo w0x, у:
-1у4ф —w — Lw0> дао _ V w — w0. 1.39
Обратимся к некоторым частным случаям.
Для круговой цилиндрической оболочки при kx 0, ky 1, где R — радиус кривизны срединной поверхности, получим следующие уравнения:
При исследовании сферической оболочки радиуса R при kx — kyR будем иметь уравнения
-f V«® - W0 LW, ф ±у2ф М2
-Lv4<P — w — Lw0, да0 —V2ny — ш0. 1.43
JjL V4 w — w0 L w, Ф -i-
-Lу4Ф —jLw,w — Lw0, a>0
В случае пластинки получим
£v4w-w0 Lw, <b ±--V-Lt i.42a
-Lv— w — Lw0, to0. 1.43a
См. книгу 0.6, стр. 505.
30 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Другой путь преобразования исходных уравнений 24 — 26 состоит во введении так называемой динамической функции напряжения в срединной поверхности; этот вариант описан в книге 0.6, стр. 792—796.
§ 8. Граничные и начальные условия
При интегрировании уравнений движения мы должны исходить из определенных граничных и начальных условий.
Если пользоваться гипотезой прямых нормалей, то для каждой точки контура необходимо удовлетворить четырем граничным условиям. В самом деле, если известны перемещения иу v, w точек контурной линии, то этим определяется положение этой линии в пространстве после деформации. Нормаль, проведенная в любой точке контура, может переместиться поступательно вместе с этой точкой и повернуться на некоторый угол в плоскости, нормальной к контурной линии. Следовательно, положение нормали после деформации оболочки фиксируется с помощью четырех величин 1.11.
Перечислим некоторые граничные условия, характерные для практических задач; здесь принято, что внешние усилия не меняют своего направления при деформации оболочки. Выпишем их для края оболочки х const; условия, относящиеся к краю у const, получим взаимной заменой х на у, и на v.
1. Точки края пластинки не получают нормальных перемещений. В этом случае
w 0. 1-44
2. Край защемлен и касательная к срединной поверхности
не получает поворота. Тогда должно быть
4 0- 1-45
3. Край шарнирно оперт. При этом
Мх 0. 1.46
Это условие можно переписать в виде
d2w. d2w п п ла ч
1.46а
4. Точки незагруженного края свободно смещаются вдоль оси z. При этом должно быть равно нулю давление на подкрепляющее ребро см. 1.11, стр. 41:
дН. dw, г dw
§ g МОДЕЛЬ ОБОЛОЧКИ С УЧЕТОМ СДВИГА И ИНЕРЦИИ ВРАЩЕНИЯ 31
5. Точки края не смещаются вдоль нормали к граничной линии. При этом
и 0. 1.48
6. Точки незагруженного края свободно смещаются вдоль нормали к граничной линии. В этом случае надо положить
Nx 0. 1.49
7. Точки края не смещаются вдоль граничной линии. Должно быть
v 0. 1.50
8. Точки незагруженного края свободно смещаются вдоль граничной линии. Следует положить
Г 0. 1.51
Граничные условия, относящиеся к перемещениям, являются геометрическими. В то же время условия, формулируемые для усилий и моментов, могут быть названы динамическими.
При интегрировании основных уравнений должны быть удовлетворены также начальные условия, относящиеся к перемещениям и скоростям точек срединной поверхности оболочки.
§ 9. Модель оболочки с учетом сдвига и инерции вращения.
Деформации и перемещения
В предшествующих параграфах приведены основные зависимости, относящиеся к модели оболочки, основанной на гипотезах Кирхгофа — Лява. Как уже отмечалось, использование этой модели первого приближения позволяет достичь достаточной точности при решении ряда практических задач.
Однако в некоторых случаях эта схема оказывается недостаточно полной. Например, в теории трехслойных оболочек, средний слой которых весьма податлив по отношению к сдвигу, нельзя пренебрегать деформациями, соответствующими касательным напряжениям вдоль нормали. По отношению к пакету слоев в целом гипотеза прямых нормалей оказывается уже неприемлемой. Это относится также к оболочкам из композиционных материалов со связующим, обладающим относительно малой жесткостью на сдвиг.
Другой пример, особенно важный для дальнейшего изложения, относится к динамическим процессам в оболочках, связанным с распространением волн деформаций. Речь идет о деформации, возбуждаемой вследствие удара или каким-либо иным образом в некоторой зоне оболочки и передающейся затем в различных направлениях вдоль срединной поверхности. В этом
32 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
случае мы должны принять во внимание силы инерции, соответствующие перемещениям и и v. Учитывая эти силы инерции, мы можем описать волновые процессы, связанные с удлинениями укорочениями в срединной поверхности.
Но при этом остается в стороне описание передачи поперечных усилий, связанных с локальным действием нормальных нагрузок. Такой процесс может происходить как самостоятельный, либо вместе с распространением волн растяжения — сжатия. При этом важное значение приобретают деформации сдвига, связанные с поперечными силами Q или напряжениями т. Кроме того, следует учесть инерцию вращения элементов оболочки; если обозначить углы поворота касательных к линиям £, ц через 0£ и 0п> то моменты сил инерции для призмы с размерами вдоль и г, равными 1, будут при этом уКд20д2 и Yl£Kd20Tid2, где y£J — массовый момент инерции рассматриваемого объема относительно соответствующих осей; I г312.
Следовательно, в дополнение к «классическим» деформациям и силам инерции мы вводим деформации, связанные с поперечными силами, и инерцию вращения. Такую картину напряженного и деформированного состояния можно рассматривать как модель второго приближения.
В литературе эту модель обычно связывают с именем С. П. Тимошенко, предложившего ее в применении к теории изгиба балок. Важно отметить, что уравнения движения для модели второго приближения получаются гиперболического типа; именно такие уравнения описывают явление распространения волн.
Недостаток теорий Кирхгофа — Лява и Тимошенко состоит в том, что они построены на гипотезах, которые, по крайней мере на первый взгляд, носят интуитивный характер. Другой путь построения основных зависимостей теории тонких оболочек состоит в разложении перемещений либо напряжений в ряды степенные или функциональные по нормальной координате и удержании определенного отрезка этого ряда в зависимости от требуемой точности и характера задачи.
Рассмотрим теперь те особенности, которые вносит в анализ учет деформации поперечного сдвига. Для принятой нами модели Тимошенко характерно четкое разделение перемещений, вызванных «классическими» усилиями, с одной стороны, и по¬
Дальнейшие работы в этой области принадлежат в приложении к пластинкам Я. С. Уфлянду 1.236, к оболочкам — С. А. Амбарцумяну 1.5 и другим авторам.
Классификация различных методов построения теории тонких оболочек приведена в работах А. Л. Гольденвейзера 1.13а, Н. А. Кильчевского 1.15, Л. Я, Айнолы и У. К. Нигула 1.2 и других авторов.
§ 9 МОДЕЛЬ ОБОЛОЧКИ С УЧЕТОМ СДВИГА И ИНЕРЦИИ ВРАЩЕНИЯ 33
перечными касательными силами, с другой. На рис. 1.18 изображено сечение срединной поверхности оболочки плоскостью, касательной к линиям х и z в точке К.
На рисунке отмечена касательная к линии х. При деформации оболочки касательная поворачивается на угол, равный в пределах относительно малых перемещений дтдху по направлению от линии х к z. Если бы точки, расположенные вдоль толщины оболочки и лежавшие до деформации на нормали
к линии х, остались на повернувшейся нормали, то новое их положение определилось бы линией т. Но деформации сдвига, связанные с поперечными силами, вызывают нарушение прямолинейности. Соответствующий «интегральный» угол поворота отрезка нормали обозначим через р; будем придавать ему знак плюс при положительном направлении поперечных усилий см. рис. 1.18. Тогда окончательный угол поворота отрезка нормали у срединной поверхности будет Р—dwdx. Вводя такие же обозначения для углов поворота в плоскости, касательной к линиям z и х, получим окончательно
Примем условно, что нормаль к недеформированной срединной поверхности поворачивается в целом на эти углы, не искривляясь. Далее, будем считать, что нормаль при таком повороте не меняет своей длины; это допущение входит в систему гипотез Кирхгофа — Лява. Перемещения произвольной точки нормали с координатой до деформации z будут теперь равны
дш
дх
I
Рис. 1.18. Деформация элемента оболочки по гипотезе типа Тимошенко.
1.52
uz — u--zx, vz v ztyy, wz w. 1.53
34 Общие зависимости нелинейной теории оболочек гл. i
Этим зависимостям можно было бы придать более симметричную структуру, принимая элемент вдоль нормали деформируемым по закону wz w -f- г — некоторая функция х, у, t.
Однако это повлекло бы за собой усложнение последующих соотношений.
Чтобы найти величины деформаций в слое оболочки, удаленном на z от срединной поверхности, подставим в соотношения 3, которые справедливы и для данной модели, зависимости 53.
Вместо 4 получим
или, с учетом выражений 5 для деформаций в срединной поверхности,
Рассмотрим теперь напряжения и усилия, действующие в оболочке.
§ 10. Напряженное состояние с учетом поперечного сдвига
Как было показано в § 5, напряженное состояние оболочки в общем случае соответствует напряжениям в срединной поверхности, классическим напряжениям изгиба и поперечным касательным напряжениям.
Зависимости 9 для усилий в срединной поверхности приводят к выражениям 13, связывающим эти силы с перемещениями.
Напряжениям изгиба и сдвига соответствуют изгибающие и крутящий момент 10. Учитывая зависимости 14 и 55, получаем из 10 следующие выражения для моментов:
— ди
ду дх дх ду Z ду дх 9
ду
1.54
1.55
1.56
§ 10 НАПРЯЖЕННОЕ СОСТОЯНИЕ С УЧЕТОМ ПОПЕРЕЧНОГО СДВИГА 35
Поперечные касательные напряжения ххг и хуг связаны с попе речными силами Q и Qy выражениями
т Xz jQJz, xyz jQyfz. 1.57
Функция fz характеризует закон распределения напряжений Ххг и Хуг по толщине оболочки. Эта функция является четной:
fz f—z, а
что соответствует симметричному относительно срединной поверхности распределению напряжений tz. Отсюда следует также
Л2
J fzzdz 0. b
—Л2
Интегрируя 57 по толщине оболочки, мы должны получить зависимости 11.
Отсюда вытекает следующее свойство функции fz:
Л2
1 fzdz 1. с
—Л2
Наконец, введем обозначение
Ы 2
Р—I J f4zdz• d>
-А2
Подробнее о величине k2 речь пойдет ниже.
В соответствии с законом Гука мы должны были бы принять зависимость между напряжениями тхуг и деформациями сдвига Р и р в виде
Tjt2 21 ц Vе 21 ц Р» 1.58
Сопоставляя эти соотношения с выражениями 57, находим < ■>,, 1аИ
Однако в соответствии с 52 мы считаем углы поперечного
сдвига постоянными по толщине оболочки и равными
Р Ф» Ру “г • 1.60
36 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Примем условие эквивалентности, выражающееся в равенстве работы поперечных сил, найденной с использованием гипотезы неискривляемых нормалей, работе касательных усилий:
Подставляя в левую часть значение х по 60, а в правую-т2 по 58 и р по 59, найдем
Учитывая введенное обозначение d, записываем для Qx и по аналогии для Qy:
Значения коэффициентов k2 зависят от вида функций fz в 57. Напомним, что в теории изгиба балок мы получаем в случае прямоугольного сечения параболический закон изменения поперечных касательных напряжений по высоте. Они оказываются равными нулю в крайних точках сечения и максимальными в точках «нейтрального» слоя. Аналогичную картину распределения напряжений хг мы должны были бы получить для участка сечения оболочки, имеющего вид прямоугольника h-1. Тогда функция fz приобретает вид
Эта зависимость удовлетворяет условиям а, Ь, с, а величина k2 по выражению d оказывается равной 56. Именно такую величину принимают для k2 в уточненной теории пластинок
С. А. Амбарцумян 1.5а и Э. Рейсснер 1.36; у С. П. Тимошенко
1.37 фигурируют значения k2 23 и 89. Первая из этих величин принята также Я. С. Уфляндом 1.236.
Миндлин 1.33 предложил определять k2 для пластинки, исходя из сравнения скорости распространения упругих волн на основе принятой модели и соответствующей скорости, найденной с помощью трехмерных уравнений теории упругости. Рэлей
1.35 и Лэмб 1.31 показали, что зависимость между скоростью
1.61
1.63
ВАРИАЦИОННОЕ УРАВНЕНИЕ
37
с распространения изгибных волн и скоростью cs волн сдвига при длинах волн А,—0 получает вид
Для скорости распространения волн в пластинке получено с учетом сдвига и инерции вращения при Я,—►О
4 1 — ak2 1 — k2 2 — k22 при 0<Jfe<l. 1.66
Исследование этой зависимости показывает, что k2 должно меняться по закону, очень близкому к линейному, от значения
0,76 при коэффициенте Пуассона 0 до 0,91 при х 0,5.
Другую величину для k2 получаем путем сравнения частот первой антисимметрической формы колебаний прямоугольной удлиненной пластинки, найденных по точной теории о ncjh и по зависимостям, учитывающим эффекты сдвига и инерции вращения со csJ127i. Тогда будет k2 — n2j 12, что близко к величине 56, предложенной С. А. Амбарцумяном и Э. Рейсснером. При л 0,176 значение k2 по 66 совпадает с величиной я212. Вообще говоря, коэффициент k2 целесообразно выбирать, исходя из того, какая именно форма колебаний или волновых движений является существенной в рассматриваемой задаче.
Экспериментальное определение коэффициента сдвига принадлежит Файлону; им получено k2 89. Можно считать, что это значение хорошо согласуется с 66, так как материал, для которого проводились эксперименты, — фотоупругое покрытие — имел высокий коэффициент Пуассона.
Выведем уравнения движения оболочки с учетом сдвига и инерции вращения, а также соответствующие граничные условия, исходя из энергетических предпосылок.
Сравни книгу 1.11, стр. 53, в которой для вывода основных дифференциальных уравнений статики гибких пластинок был использован принцип возможных перемещений. Приведенный ниже вывод принадлежит М. С. Герштейну.
4с Vс — ас2 с2 — с2 2с — с22 1.64
при 0 < ccs < 1, где
с2 k2c2s.
По 64 и 65 находим для k2 уравнение
1.65
§ 11. Вариационное уравнение
38 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Рассмотрим процесс движения на отрезке времени между моментами U и U. Сравним для этого отрезка времени различные траектории движения точек системы между начальным и конечным положениями. Истинные траектории отличаются от других возможных совместимых со связями траекторий тем, что для первых должно выполняться условие
и
J бс - 6П б'Г dt 0. 1.67
и
Здесь под К понимается кинетическая энергия системы, под П — потенциальная энергия и под 6'W— сумма элементарных работ внешних сил.
В том случае, когда все силы, действующие на систему, имеют потенциал, равенство 67 получает вид
.
65 6 К — П dt 0,
0
где
S J K-Tldt
и
— действие по Гамильтону. Это последнее равенство выражает известный принцип Гамильтона — Остроградского.
Определим вначале вариацию потенциальной энергии деформации оболочки 6П. Величина П представляет собой сумму энергий, соответствующих деформации в срединной поверхности Пс, с одной стороны, и деформации изгиба и поперечного сдвига Пи с другой:
П ПС НИ.
Энергия Пс равна
п° уЯ Nxex Nyeu Ту dxdy.
Вводя выражения для деформаций 5, получим
“.-тШМ£--П
,£- т ■Ш т £• w ■
1.68
§ 11 ЁАРИАЦИОННОЕ УРАВНЕНЙЕ
Энергия Пи выражается следующим образом:
п.-Ш-£.£ £ £
Q,-4>, Q,- 4>,dxdn. 1.69
Кинетическая энергия оболочки равна, с учетом энергии вращения элемента,
«ЧИШ£24гГ
£тгГтИтг1'ixi«- с-70
Элементарная работа внешних сил будет
b'W J J рх 6и ру bv q dw dx dy. 1.71
Рассмотрим участок оболочки, ограниченный координатными линиями х аи х а2, у Ьх, у — Ь2. Определим частную вариацию энергии, считая изменяющейся только функцию и; тогда найдем
bi а.2
6JI J J nx Ьи Т 6« dx dy.
bi а,
Интегрируя по частям, получим
Ьг Лг bz О2
биП J Nxtofidy J T6ub’dx-j J Dbudxdy.
bi fli b ax
1.72
Обратимся к интегралу по времени от вариации кинетической энергии оболочки. И здесь будем рассматривать случай, когда варьируется только функция и. Тогда для отрезка времени от момента t0 до tx будет
to to b a
В результате интегрирования по частям найдем
t Ьг Да t bz flj
J 6uKdt уЛ J Jj-budxdy — -J- h J J J budxdydt.
t, bt ei ' U b, a,
1.73
40 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. 1
Предоставляем читателю найти аналогичные выражения для вариаций по v:
и
60П, bvKdt.
U
Далее будем варьировать функцию углового перемещения tyx. Тогда по выражению 69
Ъч a-i
бфд.П J -376 Н-щ; И — Qx bdxdy.
Ь ах
Применяя и здесь интегрировани-е по частям, получим
Ъч
МХЬЪЛУУ
Ьх
a<i b di
jiHMtXyx- J J ¥L-Qxbqxdxdy. 1.72а
а, Ьх а,
Для вариации кинетической энергии будем иметь
i-S- И т 6Ц -
to b <Л
t bz di
gT2 J J J p-b'bxdxdydt. 1.73a
U b CL
Аналогичным образом найдутся вариации
бфП, J byKdt.
и
Вариация потенциальной энергии при варьировании функции прогиба w может быть найдена из выражений 68 и 69:
bi 0.2
6ШП J J -kxNx bw -kyNy bw Nx bw
»'W-£f6w W W-Kto
Qx -§; bw Qy-§t dx dy‘
§ II ВАРИАЦИОННОЕ УРАВНЕНИЕ 41
Интегрируя по частям, получим
6ШП J nx -Ц- T6w dy b 1
:т ж N> w'‘“Г ■is IQ-< •
a, 1 b
CL'i Ct2
JQybwldx- kxNx kyNy Anx r
fli b, a,
d j dw dw dQx dQyl
T-Wfl>w rf’™d’“ly- >-72ь>
Для кинетической энергии найдем
t, b2 а2
J bwK dtY h J J -p- 6a> dx dy —
t' b d 0
t b2 a 2
fh J J Wbjodxdydu 1J3b
U bx a,
Подставим все полученные выражения в уравнение 67 соответствующее принципу Гамильтона—Остроградского. Тогда придем к следующему вариационному уравнению:
tx Ъч ач
Ш£'-£
и b di
I дТ dNy у d2v дх ду рУ g ШЧ 60
,,Мыт
I д т dw I л; dw I dQx. dQy I Y 1
di T-w Ny-dil r r i-Th Ж 6W
lrdw -- т' a--•'ix'd«'dt -
t a2 0 d
— Mybtyy — H6a5 dx dt —
42 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. 1
U Ь,
_ J jfifx6u T6v Nx2L T- Qx6w-
to b
— Мх ьух — Н 61“’ dy dt -f-
Ъ ах
Ъх ах
h2 dtyx dtyy V‘,
12 Ыг “ЗГ бгМ Iudx йУ °- 1.-74
В этом уравнении усилия в срединной поверхности Nx, Ny, Т, моменты Мх, Му, Н и поперечные силы Qx, Qy связаны с перемещениями соответственно формулами 13, 56 и 63. Так как вариации 6ut dv и т. д., рассматриваемые как функции, произвольны, то множители при каждой из вариаций в первом интеграле должны быть равны нулю. Отсюда вытекают следующие пять дифференциальных уравнений движения:
Первые три уравнения здесь аналогичны уравнениям 18 — 20, а два последних отличаются от уравнений 21, 22 тем, что теперь учитывается инерция вращательного движения элемента относительно направлений х и у.
Выразив усилия через перемещения и, v, w и углы и с помощью зависимостей 13, 56 и 63, получим новую сцетему уравнений движения в перемещениях.
д_0х
дх
§ 12. Переход к уравнениям в перемещениях и граничным условиям
§ 12 ПЕРЕХОД К УРАВНЕНИЯМ В ПЕРЕМЕЩЕНИЯХ 43
Из 75 и 76 найдем уравнения, совпадающие с 27 и 28:
ди, l-ii ди. l i d2v,,, Lvj»,
2 дхду х у дх
, dw d2w, 1 fi dw d2w, 1 — i dw d2w.
О Я О Л г 2 I
дх дх2 2 ду дхду 2 дх ду'
I 1 - „ V 1 - и2 ди о- I от
£Л Р g Е dt2 ’ 80
LJL
d d
., i — у, и.и и uw I
W “2“ aF а7
ддо д2ау, 1 и- dw d2w. 1 — i dw d2w,
ду ду2 2 дх дхду 2 ду дх2
I 1 Н>2 п Y_ 1 М-2 д2а п 1 о 1
Eh Р У g Е dt2 I1®1
Уравнение движения в проекциях на нормаль к срединной поверхности приобретает вид
v, М„ £ <»„ и, -
- « г2ц,». £2 -£
££<>£-».>.Нт£££
if'W l5-»» '»
■ 1 - ц dw 1 ди ■ dv. 1 - цг у 1 - цг <Эга> __ п м
2 дх ду дх Eh q g Е dt U‘ L82
Преобразуем далее уравнения моментов 78 и 79. Первое из них будет иметь вид
dsib l — й дЧ 1 й <Э211У 2 1 — i dw
дх 2 ду 2 дхду bft А2 I ах у и2 а2,фЛ Л л
Т д >
Второе уравнение приводится к следующему:
44
ОБЩИЕ ЗАВИСИМОСТИ НЁЛЙНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Мы получили систему уравнений 80 — 84 в перемещениях, позволяющую исследовать колебательные движения и процессы распространения упругих волн в оболочке с учетом эффектов сдвига и инерции вращения. Выпучивание оболочки в процессе ударного нагружения также описывается этими уравнениями.
Интегрирование уравнений движения производятся с учетом граничных и начальных условий.
Второй и третий интегралы в вариационном уравнении 74 позволяют сформулировать пять граничных условий для ка¬
ждого края оболочки. Выпишем их для края оболочки х const.
1. Заданы угол поворота элемента нормали вокруг оси у или изгибающий момент:
,ф;с 'ф® или МХ М°Х. 1.85
2. Заданными являются угол поворота элемента нормали
вокруг оси х или крутящий момент:
г ф° или Я Я°. 1.86
3. Заданы нормальное перемещение точек контура или величина внешнего‘поперечного усилия:
w w° или Qx Nx- T- 1.87
4. Заданными являются перемещение точек контура срединной поверхности в направлении оси х или величина внешнего сжимающего усилия
и и° или Nx x. 1.88
5. Заданы перемещение точек контура срединной поверхно¬
сти вдоль оси у или внешнее касательное усилие:
t; i;0 или Т Т°. 1.89
В § 8 отмечалось, что при использовании гипотез Кирхгофа—Лйва положение элемента нормали в крайнем сечении после деформации определяется четырьмя параметрами. Соответственно на каждом участке контура формулируется по четыре граничных условия. В том случае, когда в рассмотрение вводится деформация поперечного сдвига, число степеней свободы элемента нормали увеличивается до пяти за счет того, что теперь допускается независимый поворот его вокруг оси х на границе х const.
НЕКОТОРЫЕ ВАРИАНТЫ ДИНАМИЧЕСКИХ УРАВНЕНИЙ
45
Поясним сказанное на примере. Пусть торец цилиндрической оболочки оперт на жесткую в своей плоскости диафрагму, помещенную внутри оболочки, так что точки внутреннего контура неподвижны. При использовании уравнений сдвиговой модели необходимо уточнить, являются ли точки внешнего контура сечения также неподвижными. Если это так, то имеет место условие 0, в противном случае следует принять Н 0. Отметим, что возникновение крутящего момента в оболочке типа Тимошенко не обязательно связано с кручением срединной поверхности.
Если пренебречь поперечным сдвигом и положить р-г Л Л dw,, дdw, дбш
'Фж —0, то получим — -6фя, --
—62- Исключая в вариационном уравнении бф и при помощи этих соотношений, получим вместо 75 — 79 уравнения, соответствующие гипотезам Кирхгофа — Лява см. § 6.
Мы составили уравнения в перемещениях и, v, w, пользуясь вариационным методом. Далее мы выписали уравнения, содержащие функцию прогиба w и функцию напряжений в срединной поверхности Ф. В качестве искомых функций могут быть выбраны, вообще говоря, перемещения, деформации, усилия в самых различных сочетаниях. Соответствующие варианты основных уравнений и граничных условий могут быть получены при этом единообразно, с использованием знакомого нам вариационного уравнения; но оно должно быть дополнено некоторыми членами, содержащими множители Лагранжа. Для случая, когда основными функциями являются w и Ф, это сделано в книге автора 1.11, стр. 53.
Общий метод построения «универсального» вариационного уравнения был предложен К. Фридрихсом К. Friedrichs, Nachrichten der Ges. d. Wiss. zu Gottingen, 1929, 13—20; этот метод изложен в книге Р. Куранта и Д. Гильберта «Методы математической физики», М., 1963, стр. 224 R. С о u г a n t,
D. Hilbert, Methoden d. Math. Physik 1, Berlin, 1931. В применении к нелинейной теории оболочек, с использованием теории Кирхгофа — Лява, этот вопрос подробно обсуждался Н. П. Абовским в ряде работ.
§ 13. Некоторые варианты динамических уравнений
Выясним, каким образом модель, описываемая уравнениями предыдущих параграфов, связана с иными моделями, исследованными в литературе.
Начнем с линеаризованной задачи, относящейся к пластинкам малого прогиба, без учета деформаций в срединной
46 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
поверхности. Уравнения 80 — 84 примут в этом случае вид С.90
f 1.91
Г72. 1 fi д дх ду 1 — м 'j
V 2 дх 1 ду дх Л2 ду »
Y I — М-2 д2Фи
“У е 1-92
Введем функции <р и д с помощью зависимостей
♦.—££■ -•£-£■ «-93
тогда получим
Взяв производные от 91 по л и от 92 по у и складывая их, найдем
Это равенство удовлетворяется, если положить
V» 6a-t-Xii o. 1.95
Дифференцируем теперь 91 по у, а 92 — по х и вычтем
второе равенство из первого. Тогда будем иметь
- ifl О - -2-1-±Л>. fr 0. 1.96
Наконец, подстановкой 94 в 90 получим
-97
Мы пришли к системе уравнений 95 — 97, в той или иной форме неоднократно обсуждавшейся в литературе.
См. работу В. Н. Москаленко 1.19.
§13
НЕКОТОРЫЕ ВАРИАНТЫ ДИНАМИЧЕСКИХ УРАВНЕНИЙ
47
Приняв в уравнениях 80 — 84 kx 0, ky 1, а также пренебрегая перемещениями v и и отбрасывая нелинейные члены, придем к системе трех уравнений, полученных Германом и Мирским 1.28 для случая осесимметричного волнового движения цилиндрической оболочки. Пренебрегая влиянием поперечного сдвига, эти авторы получили систему двух уравнений, соответствующих моментной теории оболочек. Если не учитывать инерцию вращения и перейти к —► оо, то перемещения w и и в уравнениях разделяются. Движение в направлении z описывается классической теорией пластинок, а движение вдоль х — теорией продольного удара.
Далее из приведенных выше уравнений можно в случае цилиндрической оболочки получить уравнения для исследования осесимметричной деформации при ударе. Уравнения, описывающие осесимметричный волновой процесс в цилиндрической оболочке, с учетом сдвига и инерции вращения, были получены для линеаризованной задачи Нахди и Купером 1.34.
При выводе уравнений движения мы предполагали, что параметры, определяющие геометрию любого слоя оболочки, совпадают с параметрами срединной поверхности. Поставим перед собой целью получить уточненный вариант уравнений, основанных на гипотезе Кирхгофа — Лява, но с учетом изменения геометрических параметров от слоя к слою по толщине оболочки. Это обстоятельство может сказаться при решении некоторых важных для практики задач динамики и устойчивости.
Рассмотрим слой оболочки, отстоящий на расстоянии z от срединной поверхности —г2 г Л2. Будем учитывать изменение кривизны для данного слоя по сравнению с кривизной срединной поверхности. Тогда выражения для деформаций будут следующими:
1 duz
1 — kxz дх
'У 1 — kyz ду
1.98
1 диг
1 dvz 1 — kzz дх
По гипотезе прямых нормалей мы должны принять ууг угх 0. Развертывая эти выражения см. книгу 0.6, стр. 485, получим
48
ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Для точек прямого волокна, нормального к срединной поверхности, производные duzdz и dvzdz должны сохранять постоянные значения, равные
диг du
dvz dv
dz dz
dz dz z dz dz z
Но, с другой стороны, принимая z 0 в 99, получим ди kx 1 dw
dz
dv
dz
1 — kxz by 1 — kyz
a —
v —
1 — kxz dx 1 dw 1 — kyz dy
1.100
1.101
Сравнивая 100 и 101, найдем
uz 1 — kxz a — z
dw
dx
dw
Z 1 ow
v 1 -kyzv wz w. j
Тогда выражения для деформаций примут вид
du kx _ d2w
1.102
dx 1 — kxz
dv ky
dy 1 — kyz
w
w —
1 — kxz dx2
z d2w
1 — kyz dy2
1 — kxz du 1 — kuz dv d2w
— kyz dy 1 — kxz dy dxdy
l — kyz 1 — kxz '
1.103
Нормальные и касательные усилия, приходящиеся на единицу длины дуги, будут равны
А 2 А2
Nx J ах 1 — kyz dz, Тху J xz 1 — kyz dz,
-hi 2 Л2
-A2
A2
N
y J Gzyl — kxzdz, Tyx J T2l —kxzdz.
— A2
-A2
1.104
В общем случае, при kx Ф kyy т. е. Ri Ф R2, где kx lRu ky l2, касательные усилия Txy и Тух оказываются различными. Если учесть, что для тонких оболочек г <С Ri и г <С 2> можно в выражениях 104 принять
1 — zkx
тогда получим Тху Тух 7
1, 1 — zky « 1;
г 13
НЕКОТОРЫЕ ВАРИАНТЫ ДИНАМИЧЕСКИХ УРАВНЕНИЙ
49
Выпишем выражения для изгибающих и крутящих моментов, приходящихся на единицу длины граней элемента:
Л2 Л2
Мх J о — kyzzdz, нху j x2l — kyzzdz,
-Л2
Л2
-Л2
Л2
Му J огу 1 — kxzzdz9 Нух J xz — kxzzdz.
-Л2
-Л2
1.105
Напряжения поперечного сдвига, изображенные на рис. 1.16, будем обозначать через тХ2, туг. Они связаны с поперечными силами Qx и Qy зависимостями
Л2 Л2
Qx j XZZy Qy: j yzdz.
1.106
-Л2
-Л2
Будем и здесь считать, что для некоторого слоя оболочки, отстоящего на z от срединной поверхности, связь между напряжениями и деформациями подчиняется закону Гука
< т8 ’ атж к> тг 2-Тй V.
1.107
Тогда, с учетом 103 и 107, соотношения 104 будут иметь вид:
50 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. 1
Выражения для изгибающих и крутящих моментов примут Mx -D ц ky ц J kx kx — ky да,
вид:
Af,
пГд2ау. д2ш. у dv. д«, - и, 1
, — Ddjr V'-M кЩ ш М'ky —kxw,
HxyD
Hyx -D
i-ц
1 -ц
2 а а< 2Лг’
d2w
2 ал: а< кУ дх ЦУ 2к> ду 2 L дх ду
1.109
При вычислении усилий встречающиеся в результате интегрирования логарифмы разложены в ряд с сохранением первых трех членов.
Уравнения равновесия элемента в проекциях на направление касательной к линиям х и у по аналогии с 18 имеют вид dNx дТХи у д2и
L ду х®х >rPxg dF
дх дТ Ху
dNu
у d2v kyQy Ру yh дТГ 0-
1.110
ду 1 ду rvyy • ГУ g dt2
Уравнение в проекциях на направление нормали к срединной поверхности будет
■ЕГ “5Г 4«л,« »А,» '37 л,’5Г Тп-Щг
Мты-ж-тн-0- с-1
Уравнения моментов относительно касательных к линиям х и у имеют вид
■ Qx
дМх дНух
дх
дНхь
ду
дМу
дх ' ду Qj 0Выразим из этих уравнений Qx и Qy:
nd3w I dw I и д2ц и ctu
Qx— Dldx дхду2 kv дх2 у х'
1.112
— х д2и 2ду2
д, дЧ
Kfi
2 ЛУ дх ду kx k кУ> дх ’
п Г dw, d3w,, d2v 1 — ii,u 0, 4 d2v,
®У _dx2dyr xdy2 2 kx2kedx2 I 1 H, d2u
' 2 x дхду
kyky — kxy
1.113
§13 НЕКОТОРЫЕ ВАРИАНТЫ ДИНАМИЧЕСКИХ УРАВНЕНИЙ 51
Подставляя выражения 112 в 111, получим д2Мх д7Ми д2
д ду дШЯ у Н у kN kNv
MN‘T'’wiT>'£N>w
0. U14
Выразим далее усилия, входящие в уравнения 110, через перемещения и, v, w с помощью зависимостей 108, 113. Пренебрегая некоторыми членами, содержащими k3x, k и т. п., получим
J2 xky'j ■I2'-l 3kxky 36 j. i±£ i ь ь л. ь.
2 12 RxRydxdy Ry 12 dx3
-1- 12 • 2 2 jdjdi,2 Vtx-TVKy dx -f-
1i-1i£ly0> 0.НБ
ЧР 1 72 kЛ> ШГу 1 12 kxky W
13If
j.iifb.--E — k JLzjM __„ь
12 Г» 2 2 j d2di K 12 <ty3 I Jjziii- 1 - цг V d2v _ n n n Eh Py Eg dt2 ° I'llo
Исключая нелинейные члены из 114, придем к уравнению
kyh д3и Л2 3 —ц 1—ц <33и
12 дх3Г 12 Vх 2 кУ 2 дхду2
. Л2, 3 — ц, 1 — ц <53t>. kxh d3v
-f 12 V 2 K 2 дхду 12 dy3
— £ Рку — fej, ikx — kl -f- 2nkxky -f k2y w
kx- ky kl - kl w -g- WAw kx kx -ky-
I и U и d2w 1 — „ I 1 — V <2да n 1 it7
6 kyky kx dy2 Eh q E s d2 0. 1.117
52
ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Приведенные уравнения в случае kx 0, ky R совпадают с уравнениями Флюгге для цилиндрической оболочки.
§ 14. Более полные соотношения между деформациями и перемещениями
В предыдущих параграфах был приведен вывод уравнений движения элемента оболочки, основанных на модели типа Тимошенко. Уравнения оказались нелинейными, так как в них
учитывались большие перемещения точек срединной поверхности оболочки. Эти уравнения могут быть использованы для изучения процесса выпучивания оболочек, происходящего при распространении упругих волн в материале под действием динамических нагрузок. В выписанные выше соотношения введены главные нелинейные члены, необходимые при решении большинства практических задач. Однако в некоторых случаях могут оказаться существенными и другие члены, которыми мы при выводе пренебрегали. Поэтому целесообразно получить более полные нелинейные уравнения движения оболочки с тем, чтобы при решении конкретных задач вводить в них те или иные упрощения.
Для вывода таких уточненных зависимостей воспользуемся тензорной формулировкой основных соотношений теории оболочек с учетом эффекта сдвига и инерции вращения.
Рассмотрим упругое тело, с которым связана система криволинейных координат х i 1, 2, 3. Выберем в качестве исходной некоторую точку пространства О рис. 1.19 и обозначим через Rx радиус-вектор произвольной точки Р. Считая R дифференцируемой функцией переменных х получим
dR -rdxl. 1.118
дхг
В соответствии с принятым в тензорном анализе правилом
W. F 1 u g g е, Stresses in shells, Berlin 1960, 219, 233.
Подобный вывод был сделан Хэбипом 1.27. В более полном виде уравнения движения получены JT. Я. Айнола 1.1. В приводимой здесь форме они исследованы М. С. Герштейном.
Рис. 1.19. Векторы, образующие базис криволинейной системы координат.
§ 14 ПОЛНЫЕ СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЯМИ И ПЕРЕМЕЩЕНИЯМИ 53
суммирования по дважды повторяющемуся — «немому» индексу выражение 118 означает
дхг дхт
В дальнейшем будем применять следующую запись для каждого из трех векторов, входящих в а:
17 «<- Ь
Очевидно, каждый из векторов направлен по касательной к координатной линии хк Для каждой точки тела векторы Ri образуют некомпланарную тройку, которая является базисом системы координат. Эти векторы характеризуют изменение радиуса-вектора R при перемещении вдоль координатных линий из данной точки Р. В декартовой системе векторы г будут ортами координатных линий.
Обозначим через dR бесконечно малый вектор PQ в предположении, что положение точки Q определяется координатами х -J- dx
Длину вектора PQ обозначим через ds. Пользуясь определением скалярного произведения, находим
ds2 dRdR. 1Л19
В свою очередь
dR Rt dx1. 1.120
Из 119 и 120 получаем для квадрата расстояния между двумя бесконечно близкими точками выражение
ds2 RiRk dx1 dxk gikdxl dxk, 1.121
где
gik — gki RiRki > 1> 2, 3. 1.122
Правую часть 121 называют метрической квадратичной формой, а величины gih — ковариантными компонентами метрического тензора.
При использовании криволинейных координат наряду с базисом 118 координатной системы вводят в рассмотрение ее сопряженный базис, состоящий из векторов R При этом
RiRk 6, 1.123
где 6 — символ Кронекера:
f 1 пРи lk.
1 0 при i ф k.
Подробнее о применяемом ниже тензорном аппарате см., например, книгу И. Н. Векуа «Основы тензорного анализа», Тбилиси, 1967.
54 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Любой вектор можно представить как линейную комбинацию векторов ь 2, Rs или U1, R2, R3.
Например, Ri представим как линейную комбинацию векторов Rly R2y R3, пользуясь зависимостями 122 и 123:
Rt gikRk. 1.124
Напомним, что выражение в правой части означает сумму, так
что соотношению 124 отвечают следующие зависимости:
Ri gRl “Ь §i2R2 “h gR3
R2 §2R1 И- §22R2 4” g2sR3>
3 311 832R2 4 £33R3 •
Решая эту систему равенств относительно векторов, получим
Rk gkiRh 1Л25
где для gki по 123 справедливо соотношение
gik gki RiRk 1Л26
Рис. 1.20. Основной и сопря- Величины ghi являются контравариженный кись системы антными компонентами метрического
тензора. С ковариантными компонентами они связаны зависимостью
gijglk bl 1.127
В качестве иллюстрации рассмотрим некоторый вектор А на плоскости рис. 1.20; ь R2 — базис системы координат, R1, R2 — ее сопряженный базис.
Вектор А можно выразить в виде
A ARi или A AiRl. 1.128
Таким образом, контравариантные компоненты А и ковариантные компоненты А дают два различных представления одного и того же вектора А. Умножим скалярно обе части равенств 128 на базисные векторы Rh и Rh:
Ak ARk, Ak ARk. 1.129
Из этих равенств с помощью 124 и 125 получим
или 1.130
Такая операция опускания или поднятия индексов, примененная здесь к компонентам векторов, распространяется на тензоры любого ранга.
§ 14 ПОЛНЫЕ СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЯМИ И ПЕРЕМЕЩЕНИЯМИ 55
Вернемся к рассмотрению упругого тела, базисные векторы и метрический тензор которого до деформации выражаются соотношениями 118 и 122. Охарактеризуем деформированное состояние тела с помощью разности квадратов линейного элемента после деформации ds и до деформации ds0. Исходя из соотношения 121, получим
ds2 — ds2 2уц dx1 dxf> 1.131
где
Vi”YGtj-gt; 1.132
величины Gij и gij являются ковариантными компонентами метрического тензора соответственно после и до деформации. Функции уij являются симметричными компонентами ковариантного тензора деформации.
Выразим компоненты деформации через вектор перемещения. Пусть радиус-вектор точки тела после деформации будет
R R uf
где и я1, х2, х3, t—вектор перемещения. Базисные векторы R и метрический тензор после деформации на основании Ь и 122 определяются соотношениями
Ri Rt j' Gij — Rtkj. 1.133
Тогда компоненты тензора деформации 132 будут иметь вид
Yij — RiRj ““ RiRjу и uf “ t1
I Rjut uiuj 1.134
Перейдем к рассмотрению тонкостенной оболочки. Обозначим через г я1, х2 и nxi>x2 радиус-вектор некоторой точки срединной поверхности недеформированной оболочки и орт нормали, проходящей через эту точку. Под Xх и х2 понимаются криволинейные координаты в срединной поверхности.
Радиус-вектор произвольной точки оболочки, удаленной от срединной поверхности вдоль нормали на расстояние х3 z будет
R rx x2 znx х2. 1.135
Базисные векторы, связанные с системой координат оболочки по Ь, будут
Г« ’ 4 17 °> Р Ь 2. 1.136
53
ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Введем в рассмотрение компоненты тензоров первой и второй квадратичной форм:
Первая квадратичная форма характеризует см. книгу 0.6, стр. 472, 474 длины дуг, углы между кривыми и площади областей на поверхности. Вторая квадратичная форма позволяет определить нормальные кривизны поверхности.
В силу формул Вейнгартена будет
§а а “Ь а г
Введем допущение о неизменности метрики по толщине оболочки, т. е. будем считать, что zba <С 1. Тогда базисные векторы и метрические тензоры примут вид
Напомним, что векторы га и п ортогональны, и гап 0. Представим вектор перемещения произвольной точки в виде
Зависимости, характеризующие распределение перемещений по толщине оболочки, запишутся в виде
В тензорном анализе вместо обычных частных производных вводятся в рассмотрение ковариантные и контравариантные производные. Особенность ковариантного и контравариантного дифференцирования состоит в том, что, применяя эти операции к тензору, снова получаем тензор.
См. книгу И. Н. Векуа, указанную выше, стр. 80.
Здесь и ниже применен индекс у 1,2; его не следует смешивать с обозначением ytj для компонент тензора деформаций.
1.137
1.138
Тогда
К Га 2Па — Га 2ЬауГЧ,
1.139
и — иага и3П иага и3п,
1.140
1.141
1.142
> 4 ПОЛНЫЕ СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЯМИ И ПЕРЕМЕЩЕНИЯМИ 57
Ковариантные производные компонент иУ, иу вектора и связаны с частными производными следующими зависимостями:
Va„v rV>, 1.143а
diiy, о
аиуГсгуИр. 1.143Ь
Знаком Va обозначается операция ковариантного дифференцирования. Величины типа Гр называются символами Кристоффеля второго рода:
pY rY У Y.
1 ap — 1 pa — T Tap — Т Гра.
В ортогональных декартовых координатах символы Кристоффеля равны нулю, и ковариантные производные совпадают с обычными частными производными.
Производная от базисного вектора гу по координате ха имеет вид
Гуад Ьо.П. 1.143с
Аналогично этому
U -rV3 n. 1.143d
Формулы 143с и 143d носят название деривационных формул Гаусса.
Пользуясь этими формулами, а также формулой Вейнгартена 138, преобразуем зависимость 141 к виду
«а Va«v rV иУКуП Va«3 « — «3ЬаугЧ
V0«v “ изКу гу П иУЬау Va«3. 1.144
Введем обозначения
®ау аЦу 1.145
и представим 144 в виде
a VY 1.146
Подставляя выражения 139 и 146 в 134, придем к следующим соотношениям принято е еа:
Yap 2 ”1 ра “Ь '2 еар “Ь ера “Ь ваЗруар»
Ya3 Y '■«Из па„ а„а3 у а еа1
Y33 -j 2и«з ы3ы3 •
1.147
58 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. 1
Перемещения иа будем считать меняющимися вдоль толщины оболочки по закону
«а »а '> 2. О 2фа '» 2, 0- 1-148а
Что же касается перемещения и3, то, как мы условились ранее, примем
u3 wxl, х2, t. 1.148b
Введем выражения 148 и 145; получим прежде всего
®ар ар Зар ар 4 2аФр> 1 149
где
eap Vaop — bafiw. 1.150
Далее
V V 2VpiJja, 1
8a va ov Zt>V — blw el zVa13V. J
Наконец, имеем
■a Uybafi Va«3 0a -f zbayV,
ftp uyba p -f VpM3 Dp Zbfiytf. Здесь мы ввели обозначение
1.151а
1.153
®a bayVV 1.152
Подставляя последние соотношения в 147 и пренебрегая членами, содержащими г2, как малыми высшего порядка, получим следующие выражения для деформаций:
Yap i Кр р« elePY ®«®р ZVa VA
eaVfil5Y epYVal3V ©афу ftaWptv.
Ya3 y«>a Фа Vay Z баФ фафу»
Y33 ЛГ
Закон Гука в общем случае можно выписать в форме
а«Э Еаь а, р,. 1,2, 3, 1.154
где тензор упругости £af>v8 для изотропных тел равен
£W-V 2lgvVe. Ы55
§ 14 ПОЛНЫЕ СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЯМИ И ПЕРЕМЕЩЕНИЯМИ 59
Усилия и моменты на единицу длины сечения оболочки выражаются следующим образом:
Л2 А2 А2
Г odz, лгр Г z<sdz, Qa — Г <та3 dz. 1.156
-Л2 -А2 -Л2
Для изотропного тела соотношение 154 принимает также вид
<т°е IQgrt 2цуар- 1.157
о
Здесь Я и л — коэффициенты Ляме, 0 — объемное расширение:
e g“V 1.158
В 157 мы приняли
Yap gV<g»y6.
Учитывая 139, имеем: ga — cia вместо 155 находим
£°м XaV 2IavVe a, р,. 1,2. 1.159
Выражение для узз через Yap находится из обычного условия
а33 0 и подставляется в соотношение для aap. При интегрировании по 156 используются зависимости для деформаций 153. Как известно, параметры Ляме равны
Ei ° Е
Х 1ц1-2ц ’ 21 ц '
Таким образом, находим
М-i., <VA «„vy
d.161
<г”2гтдг“. 4’« 4'4,. 1-162
Здесь
Papv5 aaV6 evcpe.
Под caP понимаются компоненты дискриминантного тензора, под k2 — известный коэффициент сдвига.
60 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Закон распределения напряжений по толщине оболочки выражается зависимостями
a«P i-JVaV, 2, t §-MaHx х2, О, 1Л63
oai jQaxx2,tfz, a33 0. 1.164
Под f понимается функция, о которой говорилось в § 10; она удовлетворяет условиям
Л2 г2 hi 2
f—z fz, J J fdz 1, -jr- J f2dz -p-, J zfdz 0.
-ft2 -ft2 -Л2
1.165
§ 15. Уравнения движения
Для вывода уравнений движения воспользуемся и здесь принципом Гамильтона — Остроградского. Соответствующее уравнение, аналогичное 67, будет
и
J <ЬК - 611 б'Г dt 0. 1.166
и
Потенциальная энергия деформации П для трехмерного тела
п jj olikdV.
V
Здесь dV — элементарный объем. Для криволинейных координат в случае оболочки будет принято а ЦаЦ 1:
hi 2
П у J <Jaafl 2a-ya3dSdz, 1.167
S —Л2
где dS — элемент площади срединной поверхности.
Подставим сюда выражения для напряжений 163, 164 и значения деформаций 153. С учетом 165 найдем
П4 у Na® еа еа £a£3v ЮаЮр
Y Мае Vu V6ala YVa1Jv bl<i>av
bl Qa “a Уу dS- i • 168
§ 15 УРАВНЕНИЯ ДВИЖЕНИЯ 61
Представим это выражение как сумму трех функций:
П ПС ПИ Псдв.
Составляющая Пс соответствует энергии деформации в срединной поверхности; Пи — энергии деформации изгиба; ПСДв — энергии деформации поперечного сдвига.
Пользуясь соотношениями 150 и 152, перепишем выражения для этих составляющих в виде
псJ J Vayp - wbai 1 evvpyv coa Vpay ©v dS,
1.169
n„7 J Va 4- V4v - blwVa
1“ dS, 1.170
псдв J J Q“ Va® vabay ipvVauY - dS. 1.171
s
Кинетическая энергия в общем случае определяется с помощью выражения
Шу ди, ди1 1-WfdV.
V
Для оболочки получим, подставляя сюда 148:
KYJh J 2,M>adS. 1.172
s
Точками обозначены производные по времени.
Элементарная работа внешних сил равна
b'W J ра 6va q 6w ma ds -f
s
JWe6o„ d® gie6i„rfc. 1.173
С
Здесь С — контур недеформированной оболочки, к которому приложены составляющие внешней нагрузки N и 9£а. Под ра, q и та понимаются интенсивности распределенных внешних нагрузок — тангенциальной, поперечной и моментной.
62 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Найдем вариации полной потенциальной энергии по переменным va, wy га. После вычислений, аналогичных предыдущим стр. 39, получим
6VU 1J бI el ftp ЛГЧ«а e<AJ dc -
С
- т J VaaP Vp av - bfafT1 VY VA -
- fyfaM1 - blQa VaQa 6yp ds, 1.174 бшП -J Qa«a 6oM“PllY«p б ay dc —
С
- у J VaQa b4Na Va Naop
s
VpAfaptv MaSVav bQaбю ds, 1.175 б„,П — 1J б 4 пр 6v dc -
С
- 4 J fVoAiae -Qa- - VYAf°v4 - MavcoY Афу rfs. 1.176
s
Здесь na — компонент единичного вектора нормали к контуру недеформированной оболочки.
Вариация кинетической энергии равна
б J 6t>a ш бку -h -фаcfs —
to S
и
— J-jj J 0аб0а йбда -фабг>ай5<. 1.177
to S
Просуммируем вариации потенциальной энергии 174'— 176 и вместе с выражениями 173 и 177 подставим в 166. Ввиду произвольности вариаций 6va, бw, бга условием выполнения зависимости 166 будет равенство нулю множителей при
§ 1Л УРАВНЕНИЯ ДВИЖЕНИЯ 63
этих вариациях. Отсюда вытекают уравнения движения V«AT - blQa VY “v - baNay V« VYMav -
- V. Gl>PQa-ЛуР рР 0, 1.178
V«Q b4Na Vp cDaWaf5 bleayNafi Vp YMap
VafaYMap bUzQ fhw q 0, 1.179
VaMap—Qp—6aQa VY eMav - 6a<»YMaY- те 0, 1.180 где I h32.
Граничные условия связывают усилия и перемещения на контуре оболочки с нагрузками, приложенными по контуру. Принимая бар ф 0, будем иметь
еТщ MapVvrta i3aQe«a - 0. 1.181
Далее при 8w ф 0
Qa«a ©aa4 N 0 1.182
и при 6-фу ф 0
Afap6j e2rtp-9tv 0. 1.183
Рассмотрим случай, когда координатные линии в срединной поверхности оболочки являются линиями кривизны. Тогда будет b 0. Кроме того, будем рассматривать декартовы координаты и считать кривизны вдоль координатных линий постоянными: b — kx, bt ky. Представим для этого случая уравнения движения 178 — 180 в скалярной форме.
Для примера преобразуем первый из членов, входящих в уравнение 178. Получим
VaNa lNlfi--V2N.
Для Р 1 будет
V,tf»V2tf21 NX,X T„
при р 2
VlN V2N22 Tx Ny,y.
Нижний индекс после запятой обозначает переменную, по которой производится дифференцирование.
Следующий член в 178 может быть представлен в виде
ftSQe-ftfQ4rfQ.
64 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Например, при Р1
ь< ikxQx.
Наконец, для третьего члена имеем
VY e<aNay V, efW1 eW' V2 efN12 efyV22.
При p 1 будет
Vj eJW11 4V21 V2 eN'2 eN22
, x Nx -- ut yT, x “h, x xw T -f- Uf yNt у.
Выполняя аналогичные операции над остальными членами, придем к таким уравнениям:
Nx,x Т_у — kxQx Nх и, х — kxw -f- Tut у, х
Т и, х kxW “h Ut yNy у kx Nx wy x -“ kxti -J-’
T wt у kyv Гаг'Фл:, Htyx, y, x
Htyx, x Mytyx, y, y — kX Mxtyxkx Htyyky
“Ь xQx,x b xQ, у h P_x 0> 1.184
Qx,X Qy, У kxNx kyNy Nx wt X kxll
Wj, kyV TtX T ш kxu Ny w, у kyVl у
kx Nxut x — kxw ut yT kyv,xT vty — kyw Ny
4“ xkxtyx Hkytyy' X “f HkXtyX -f- M ykytyy' у -j-
kx Mдс'Фх, X Htyx, y “b ky Hytyy, X Ф, y -J-
kxQxx kyQytyy — -jhwtit -f q 0, 1.185
MXtX H — Qx — Qxu,x-- kxw — QyUtу
-j- Hи, у h Mx ц, x kxW, x ”1“ yll у H Ut x kxw у
—kxMx wtJC—kxu Hwty kyv — jlx, tt tnx 0. 1.186
Под ргс, q и mx понимаются интенсивности соответствующих распределенных нагрузок.
Кроме того, по аналогии с 184 и 186 могут быть выписаны еще два уравнения.
Мы получили уравнения в более полном виде по сравнению с теми, которые были составлены нами ранее. Члены, фигурировавшие в предыдущих уравнениях 75 — 79, здесь подчеркнуты. Сохранение только этих слагаемых аналогично предположению о малости производных от тангенциальных компонент
060Л0ЧКИ ЗА ПРЁДЕЛАМИ УПРУГОСТИ
65
вектора перемещения по сравнению с производными нормального прогиба, принятому для пологих оболочек.
Перейдем к граничным условиям для края х const. Принимая в 181 —183 пi 1, я2 0, получим следующие пять граничных условий:
NX1 utX — kxw Tuty у -J-
Qxx-N°x°> <U87
Nxv,x — kyw Mxytx Htyy,y
QX-T° 0, 1.188
Qjc,x h kxuNjc “h, у 4 kyvT
Mxkxx Hkyx-Qx 0, 1.189
Mx 0 ut x — kxw Hu,y — M°x 0, 1.190
Mxv,xHlv,y - kyw - H° 0. 1.191
Здесь через x и T° представлены внешние усилия в срединной поверхности, приложенные по краю х const, через
Q — поперечное усилие, через М°х п Н° — интенсивности моментных нагрузок.
Мы снова пришли к пяти динамическим граничным условиям, которые соответствуют кинематическим параметрам и, v, w, tyx и В условиях 187 — 191 по-прежнему участвуют «основные» усилия NXy Г, QXy Мх и Я; напомним, что такой же результат мы получили выше § 12. Но теперь граничные усилия получены в уточненном виде; имевшиеся ранее члены подчеркнуты. Геометрические граничные условия совпадают с теми, какие фигурируют в 81 — 89.
В дальнейшем изложении мы будем пользоваться, как правило, моделью Кирхгофа — Лява. Она позволяет с известным приближением описать интересующие нас динамические процессы— в том числе такие, которые сопровождаются распространением упругих волн. Однако для некоторых задач мы используем модель второго приближения; постараемся при этом выявить особенности одной и другой модели в связи с применением различных методов решения.
§ 16. Оболочки за пределами упругости
Обратимся теперь к случаю, когда деформации оболочки являются упруго-пластическими. При рассмотрении этого случая мы должны воспользоваться той или иной теорией пластичности. Как известно, в литературе используются соотношения,
бб ОБЩИЕ ЗАЁИСИМОСТИ НЕЛИНЕЙНОЙ fEOPHH ОБОЛОЧЕК ГЛ. основанные на различных теориях: течения, деформационной, локальных деформаций и других. Для исследования динамических задач до настоящего времени применялись главным образом первые две из этих теорий. В данной книге мы будем пользоваться как теорией течения глава VII, так и деформационной теорией глава VIII. Мы остановимся здесь более подробно
на зависимостях деформационной теории.
Будем исходить из диаграммы ае, полученной из опытов с одноосным растяжением образца из данного материала рис. 1.21. При малых деформациях большинство конструкционных материалов деформируется упруго. Тангенс угла наклона касательной к кривой ае в точках начального участка отвечает модулю упругости Е. Проведем в некоторой точке А касательную к кривой; в этом случае прямая АВ уже не проходит через начало координат и свойства материала в точке А могут быть охарактеризованы двумя параметрами: касательным модулем Ек dode и секущим модулем Ес ае. Очевидно, Ек и Ес являются функциями деформации. Коэффициент Пуассона л в упругой области для многих материалов лежит между 0,25 и 0,33. При возникновении пластических деформаций величина х быстро возрастает, приближаясь к предельному значению i 0,5.
В случае сложного напряженного состояния вводится понятие интенсивности напряжений ст и интенсивности деформаций ес
«1 — Yf V”-<,f о,- atf «, - ® j1 в ы, 4 ■'гЛ
Y-- '»-«,' '«-'•’ ТМ. ll,>
1192
Эти выражения являются инвариантными, т. е. сохраняют величину при изменении ориентации системы координат. Допустим, что интенсивность деформаций в данной точке возрастает и выполняется условие простого нагружения. Тогда компоненты тензоров напряжения и деформаций связаны между собой
О £
Рис. 1.21. К определению основного, секущего и касательного модулей.
ОБОЛОЧКИ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
67
зависимостями
»-7в—
у o' 0 <ур оу 5,
е2-т 0:
2 Ес
<y2-s,
Уху р Ъху> Уyz р ЪугУ Ухг— р Ъх
1.193
Под 0 понимается объемная деформация
® — ех еу
под S —среднее нормальное напряжение
<х <Уу <г 0
они связаны зависимостью
0:
31-2Х о Е
Для несжимаемого материала 0 0.
В соответствии с принимаемой моделью оболочки выражения Oi и будут иметь разный вид. В дальнейшем будет рассмотрена прежняя модель типа Тимошенко, учитывающая поперечные сдвиги; в этом случае в 192 следует положить только ez — 0, Gz 0. После очевидных преобразований получим выражения для интенсивностей деформаций и напряжений, которые будут использоваться в дальнейшем:
охоу <1 3 xly Х2хг Х2уг, e‘yVe2x еЛ г1 7 ty YL уг •
1.194
Если же в некоторой точке происходит уменьшение интенсивности деформаций, то соотношения 193 должны быть заменены другими, относящимися к разгрузке.
68 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
Считая, что в процессе разгрузки изменяются только упругие составляющие деформации, можно записать:
т4е4л - <4 ей’
ау ТЕ TeJ - е1 Тгх •
Ху <у ТЕЧху-У'х«' J 1Л95
Xz T'Xz iEVXz-yXz’
VVt£y-y;z;
звездочкой отмечены напряжения и деформации в данной точке в момент начала разгрузки. Очевидно, что в упругой области соотношения 193 и 195 совпадают с обобщенным законом Гука.
Области активных пластических деформаций и разгрузки разграничены поверхностью dejdt 0.
Обратимся теперь к уравнениям типа Тимошенко, полученным в § 12. Очевидно, что уравнения движения элемента оболочки в усилиях и моментах останутся без изменения и при наличии пластических деформаций; изменятся только выражения, связывающие усилия и моменты с перемещениями.
Имея в виду, что деформации е, е,. связаны соотношениями типа 55
, дх. I
вв 2 —. еу гугд1Г' 1
дх
дх ду __
Уху Ь z ду дх 9
ху
Угуг У
Уг’
1.196
ду дх
перепишем выражение для интенсивности деформаций в виде 1.197
где
Р0 1 «А еуТ Х, Ууг Y 1у,
Р'5Г е 2гу тг« Те ТV« W w •
_ dt 2,
•Эф дОру ду2 1 j
дх ду ду 4 V
dt
ЩГ
дх Г
Эта задача была исследована в линейной постановке М. П. Галиным Инж. сб. 31, 1961; приведенные ниже зависимости получены В. А. Фельдштейном.
ОБОЛОЧКИ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
69
Как нетрудно убедиться, поверхности, разграничивающие области активных пластических деформаций и разгрузки, имеют вид
В общем случае в интервале —А2 z Л2 могут находиться оба корня полинома 198. Первый из них отвечает границе между зонами первичного нагружения А и разгрузки В рис. 1.22, а второй — между зонами разгрузки и вторичных пластических деформаций С противоположного знака. z<i
Допустим, что на началь-
никновению области разгрузки. Кроме того, динамический процесс может сопровождаться волной разгрузки. В дальнейшем деформации растяжения, вызванные изгибом, могут превзойти предел текучести, образуя область вторичных пластических деформаций. В этой зоне определяющие соотношения могут быть выписаны, исходя из теории циклических нагружений.
Однако использование этой связи весьма затруднительно при интегрировании уравнений, так как требует хранить в памяти вычислительной машины полную информацию о напряженном состоянии в объеме, занимаемом оболочкой, на протяжении всего времени интегрирования. Поэтому в дальнейшем используются два предположения. Примем, во-первых, что разгрузка происходит по линейному закону. Это положение, по-видимому, справедливо при исследовании переходных процессов в случае нагрузок, не носящих ярко выраженного колебательного характера со значительными амплитудами. Тогда можно считать, что вибрации не успевают развиться и сопровождаются изменением лишь упругих составляющих напряжений.
Далее примем, что разгрузка в разных слоях вдоль нормали начинается в момент ее начала в некотором характерном слое, например в срединной поверхности. В этом
1.198
ной стадии деформирования, когда изгиб оболочки незначителен, в ней преобладают усилия сжатия. С развитием прогибов внешние волокна оболочки удлиняются относительно первоначально сжатого состояния, что приводит к воз-
Рис. 1.22. Зоны первичного нагружения А, разгрузки В и вторичных пластических деформаций С.
В. В. М о с к в и т и н, Пластичность при переменных нагружениях, изд. МГУ, 1965.
70 ОБЩИЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ ОБОЛОЧЕК ГЛ. I
случае приходится запоминать только параметры напряженного состояния срединной поверхности.
Перейдем к выводу выражений для усилий и моментов. Интегрируя напряжения и их моменты по толщине оболочки, получим усилия и моменты в области активных пластических деформаций материал считаем несжимаемым, л 0,5:
Особенностью выражений 199 является то обстоятельство, что в отличие от упругой задачи, усилия, действующие на гранях элемента оболочки, зависят не только от деформаций растяжения срединной поверхности, но и от параметра изгиба; в свою очередь моменты определяются как изгибом, так и растяжением. Это связано с нелинейностью распределения напряжений по толщине оболочки, определяемой кривой нагружения аг-г.
Аналогично определяются усилия и моменты в зоне разгрузки:
Nx -l е 1Геи Т И ’
е у6 2 у у
Qx — з 1Ухг> Цу з iYyz>
1.199
мх у 2 в з х у X».
iW»4'28J'Te 3 х» ТХ'
где
Nx Nx-- 2 8» в 2 ®у'
Tr± Eh чп
М М'х Щ- Т X» Т » ■
1.200
СЁОЛОЧКЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
Выражения для Ny> Qy и Му выписываются по аналогии; звездочкой отмечены соответствующие величины в момент начала разгрузки.
Как уже было сказано, уравнения движения, записанные в усилиях и моментах, совпадают с 75 — 79. Полные уравнения движения в перемещениях оказываются весьма громоздкими, поэтому приводить их здесь не будем. Впрочем, при численном интегрировании уравнений по методу, который будет в дальнейшем использован, в них нет необходимости: удобнее строить алгоритм решения путем последовательного вычисления производных от перемещений, деформаций, напряжений, усилий и моментов и подстановки их в уравнения, полученные в § 11.
ГЛАВА II
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ § 17. Свойства собственных нелинейных колебаний
Рассмотрение конкретных задач, относящихся к периодическим движениям пластинок и оболочек, мы начнем с исследования собственных свободных колебаний. Если известен характер собственных колебаний конструкции, то можно судить
о присущих ей внутренних свойствах, проявляющихся при действии внешних возмущений.
Как известно, пластинка или оболочка представляют собой системы с бесконечно большим числом степеней свободы. В применении к задаче о колебаниях это означает, что число собственных частот бесконечно велико, причем каждой частоте отвечает и определенная форма колебаний.
В случае собственных линейных колебаний амплитуды перемещений той или иной точки системы не зависят от частоты и при возникновении колебаний определяются лишь начальными условиями. Эти условия включают отклонения элементов пластинки или оболочки от положения равновесия и их скорости в начальный момент времени. Такие особенности линейных колебаний объясняются тем, что параметры жесткости системы принимаются неизменными. Но из теории пластинок и оболочек вытекает, что характеристики жесткости могут считаться постоянными лишь при малых прогибах. Тогда можно считать, что внутренние силы сводятся к напряжениям собственно изгиба.
Если же прогибы сравнимы с толщиной пластинки, надо принимать во внимание мембранные напряжения. По обычной классификации мы переходим при этом от жестких пластинок к гибким. Для гибких пластинок параметры жесткости являются переменными и зависят от прогиба. Это относится также к абсолютно гибким пластинкам мембранам; напряжениями изгиба в них пренебрегают по сравнению с напряжениями в срединной поверхности.
• Эта классификация была введена И. Г. Бубновым 0.5. См. также книгу 1.11, стр. 13.
§ 17 СВОЙСТВА СОБСТВЕННЫХ НЕЛИНЕЙНЫХ КОЛЕБАНИЙ
73
Для оболочек, как мы видели в главе I, напряженное состояние включает, вообще говоря, усилия изгиба и усилия в срединной поверхности уже при малых прогибах. Однако и здесь деформации при больших прогибах характеризуются изменением соотношения между этими усилиями.
Но так как частота собственных колебаний связана с параметрами жесткости системы, для гибких пластинок или оболочек частота должна зависеть от того, насколько система отклоняется от положения равновесия или, иными словами, зависеть от амплитуды колебаний. Это обстоятельство является наиболее характерным для тонкостенных конструкций, получающих большие перемещения.
Решение нелинейных динамических задач, в которых независимыми переменными являются время и пространственные координаты, сравнительно сложно даже при условии применения современных электронных цифровых машин. Поэтому в настоящее время ограничиваются, как правило, исследованием низших тонов колебаний и прежде всего основного тона. При рассмотрении таких задач часто приводят пластинку или оболочку к системе с одной степенью свободы, аппроксимируя тем или иным образом их изогнутую поверхность.
В случае пластинки зависимость между характерным прогибом А и частотой, отнесенной к частоте линейной системы — этот параметр обозначен через v, — имеет вид, показанный на
a d
Рис. 2.1. Возможные варианты зависимости между характерным прогибом и частотой собственных нелинейных колебаний.
рис. 2.1, а. С увеличением амплитуды частота возрастает. Система с такой характеристикой называется жесткой. Для оболочки аналогичная зависимость может быть иной, см. рис. 2.1,6. Начальный участок здесь отклоняется к оси ординат, и соответствующая характеристика определяется как мягкая.
Линию v, Л называют скелетной кривой. Она отражает основные свойства деформируемой системы; вокруг этой кривой, как мы увидим в главе III, группируются различного типа диаграммы для вынужденных колебаний системы.
74 СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ГЛ. II
Рассмотрим задачи, относящиеся к собственным колебаниям пластинок и оболочек. Дальнейшее изложение проводится следующим образом. Вначале решаются «классические» задачи с представлением пластинки или оболочки как систем с одной степенью свободы. Здесь мы получаем общее представление о характере колебаний и влиянии различных факторов на амплитудно-частотные характеристики. Далее для различных задач даются уточненные решения с применением численных методов. При этом картина колебаний пластинки или оболочки становится более полной; оказывается возможным проследить за сложным процессом движения различных точек системы. Эти особенности проявляются особенно ярко в случае открытых оболочек большой кривизны.
Для наиболее важных задач в качестве исходных данных проводится решение линеаризованных вариантов с определением частот и форм малых колебаний.
§ 18. Прямоугольная пластинка, шарнирно опертая по краям.
Линейная задача
Начнем с простейшего случая прямоугольной пластинки, шарнирно опертой по краям. Прежде всего рассмотрим задачу в линейной постановке.
Обозначим через а, b стороны пластинки. Координатные оси ху у направим вдоль сторон опорного контура.
Воспользуемся линейным вариантом основных уравнений 1.35, 1.36 при kx ky 0:
fv°- ад
Для прогиба выберем выражение
т. тпх. ппу п пх
sin—-— sin —2.2
Подставляя это выражение в равенство
J JtVw±snsndKdy 0,
о о
получим
жЧ»»“0; <2-3>
здесь £ fth. Квадрат частоты собственных колебаний при малых прогибах равен
п4т4 1 “о” °2h2
со2 V а L 2 4
wo, тп т2 1 - ц2 а2Ь2 9 к
§ 19 НЕЛИНЕЙНАЯ ЗАДАЧА. МЕТОД 6УБНОВА-ГАЛЕРКИНА 75
где Я а6, с — скорость распространения продольных упругих волн в материале пластинки:
С VEgy- 2.5
На рис. 2.2 показан характер волнообразования квадратной пластинки при колебаниях по первым трем формам. В этом случае пластинка совершает колебания по наинизшей частоте
с образованием одной полуволны по направлению каждой стороны рис. 2.2,а, следующей, более высокой частоте соответствуют две полуволны по одному направлению и одна полуволна по другому рис. 2.2,6, третьей частоте отвечают две полуволны по каждому из направлений рис. 2.2, в и т. д.
§ 19. Нелинейная задача. Метод Бубнова—Галеркина
Исследуем нелинейные колебания применительно к рассмотренному выше случаю прямоугольной пластинки, шарнирно опертой по краям. Что касается граничных условий для перемещений и усилий в срединной плоскости, то здесь мы будем считать, что кромки пластинки связаны с упругими, неискривляющимися в плоскости пластинки ребрами, препятствующими взаимному сближению кромок. В качестве предельных мы рассмотрим при этом случаи свободно сближающихся прямолинейных кромок, с одной стороны, и неподвижных кромок, с другой.
Предположим, что отношение сторон пластинки X аЬ лежит в пределах 1 X 2. Отнесем площадь сечения упругих ребер, окаймляющих пластинку, к длине соответствующей стороны. Пусть координатные оси х, у будут направлены вдоль сторон а, Ь. Примем, что на единицу длины сторон b и а приходятся площади сечения ребер Fx и Fv введем обозначения
hFx Vxi hFy Vy.
См. книгу 0.6, стр. 294.
Эта задача рассматривалась Чу и Германом 2.28, Гринспоном 2.371 и другими авторами. Здесь приводятся результаты, полученные И. Г. Кильдибековым.
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ГЛ. II
Воспользуемся основными уравнениями 1.35, 1.36 при
kx ky 0.
•f-V<w Lw, Ф- 2.6
-LvQ>-jLw,w. 2.7
Оператор Lw, Ф определяется по 1.34.
Удовлетворяя условиям шарнирного опирания 1.44, 1.46а, выберем для прогиба выражение
w f sin sin. 2.8
Подставляя 8 в правую часть уравнения 7, получим
т cosT -sin T
или
-г-у,ф-7Рс03с05- <2-9>
Частное решение уравнения 9 выпишем в виде
Ф, Л cos- В cos-2-. 2.10
Коэффициенты Ау В определяем, вычисляя V4Di и сравнивая левую и правую части 9:
л — РЛ_±1 r-fJL1i
32 62 ’ П 32 а2 '
Далее, решение однородного уравнения У4Ф 0 представим следующим образом:
ф2£ V-
2 2 2 '
где рХу ру — внешние усилия, прикладываемые к пластинке через краевые ребра; рх и ру считаются положительными при растяжении.
Окончательно
_ _ 2 Гя2 2ял; 6 2 2пу 1 р2 pw2
Ф Е32-т «» — Ы “>-r-J £T- V- <2'П>
Напряжения в срединной поверхности равны
д2Ф п я2 2 2я. _
а- -д-Е-8-т C0S Р’
д2Ф г я2 2 2я, _ о 1 о
-£-8-Ш cos — Р’ 2-12
5гФ „
Т “ дх ду
§ 19 НЕЛИНЕЙНАЯ ЗАДАЧА. МЕТОД БУБНОВА-ГАЛЕРКИНА 77
Отметим, что касательные напряжения т оказываются равными нулю для всех точек пластинки. Если нормальные напряжения являются сжимающими по всей кромке влияние первого члена, то они окажутся максимальными у кромок и минимальными в серединах сторон.
Найдем взаимное смещение краев у О, у 6. Для некоторого волокна, параллельного оси х> сближение концов будет равно
а
4 -17л <2-13>
О
Сопоставляя формулы 1.5 при kx 0 с 1.12, находим
а
. 1 Г<9гФ <92Ф Еdw УЛ. г,,о ч
Е J ду дх2 2 Id dx' 2.13а
О
Подставляя сюда значения ш, Ф по 8 и 11, получим после интегрирования
2.14
Аналогично
Эти значения Д и Ау должны быть равны упругим деформациям ребер. Обозначим через ах, р и ау>р напряжения в распорках положительные при сжатии; тогда
А а, А У Ь. 2.16
Из условий равновесия узлов, в которых ребра скреплены с пластинкой, имеем
h h <x.p Pxj VxPx, Oy.p Py-j VyPx- 2.17
Тогда
vxPx o' V'Py’
,ti I 2.18
-Pv-VPx-
78
СОБСТВЕННЫЙ НЁЛИНЕЙНЫЁ колёбАнйя
ГЛ. И
Отсюда
21 V,
Рх — Е-
f2
— ц2 I ’
86 I vl v,-i2 b.
„2 —F 1 Vjc
— JH Jl U £2
Py tl'W 1 v,l Vy- I •.
Введем безразмерные параметры
„•—£±1Y — 1— r—L
Px E hi • py E hj ’ b ® h '
будем иметь
2.19
2.20
f
Px
1 Vj,
X2
-t2 2 b >
8 1 v 1 y — Ц2
„2 р-Ч-lv,
py 81 v 1 y - H2
2.21
Мы выписали основные соотношения для задачи о собственных колебаниях прямоугольной пластинки. Эти соотношения приводят к дифференциальному уравнению в частных производных относительно функции w w х, у, t. Точное решение уравнения, взятого в его исходном виде, отсутствует. Но имеется ряд методов, которые позволяют провести приближенное интегрирование уравнения при тех или иных граничных условиях. На рассматриваемом нами простейшем примере познакомимся с несколькими из таких приближенных методов и прежде всего с методом Бубнова — Галеркина. Выполним решение в два этапа. На первом этапе применим метод Бубнова — Галеркина к уравнению 6 для некоторого фиксированного момента времени t. Обозначим через X выражение
д2Ф d2w ду2 дх2
— 2
д2Ф d2w
дхду дхду
<52ф d2w дх2'Туг
Y d2w g dt2
2.22
Эта функция, судя по уравнению, должна быть тождественно равна нулю для координат х, уу отвечающих всем точкам пластинки. Но мы не будем стремиться к выполнению этого условия для всех ху у, а ограничимся некоторым интегральным соот¬
См. И. Г. Бубнов, Отзыв о сочинениях профессора Тимошенко 1913 г. и Строительная механика корабля, ч. 2 1914 г., а также Б. Г, Г алеркин, Стержни и пластинки, Вестник технологов 1915 г.
§ 19
НЕЛИНЕЙНАЯ ЗАДАЧА. МЕТОД БУБНОВА—ГАЛЕРКИНА
79
ношением. В общем случае аппроксимируем функции wxfyit в виде ряда
где гг — некоторые, наперед заданные и независимые функции х, у, которые, будучи подставлены вместо w в равенства типа 1.44, 1.46а, удовлетворяют граничным условиям задачи; fi — параметры, зависящие лишь от t.
По методу Бубнова — Галеркина выпишем п уравнений типа
интегрирование ведется по всей площади пластинки F.
В нашем решении вместо ряда 23 фигурирует выражение 8, и функция г1 будет
Пользуясь выражениями для w по 8, Ф по 11 и по 25, получим
Здесь принято f f. Подставляя 26 в 24 и интегрируя, приходим к уравнению
Переходя к безразмерным параметрам 20 и подставляя вместо р и ру их выражения по 21, получим
п
W,11 f2Л2 • • • fnVn 2 fгЛь 2.23
i1
J J Xty dx dy 0, i—l,2,.,n, 2.24
F
ЛЛ. JIU
Tli sin — sin —r.
11 a b
nx. 7tu
с i n 2.25
sinsin--. 2.26
nx. nu
ctn _
L”L
h 4
n Eh 17 1 V
8 Ь 1у1г,-ц2
. 1 vy. n4 Eh4 11 X2 1
4 b 1 vlvy-nJ
80
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
От исходного нелинейного уравнения в частных производных 6 четвертого порядка мы пришли хотя снова и к нелинейному уравнению, но уже в обыкновенных производных, и притом второго порядка. Представим его в виде
Если отбросить в 28 нелинейный член, содержащий £3, то мы придем к уравнению 3, если принять m — n 1:
описывающему малые колебания пластинки. Параметр со представляет здесь квадрат основной частоты собственных малых колебаний пластинки:
где под с понимается величина по 5.
Но нашей целью является изучение колебаний пластинки при амплитудах, сравнимых с толщиной; поэтому нам надо вернуться к исходному нелинейному уравнению 28. Исследование этого уравнения представляет собой простейшую из классических задач общей теории нелинейных колебаний механических систем.
Отметим, что если представить уравнение 28 в виде
то функция F£ будет определять упругую характеристику системы во всем диапазоне рассматриваемых амплитуд. В нашем
■g-co2itmo,
2.28
где под К понимается выражение
2.30
или
2.31
“i ®gFg 0, F£ l CS2,
НЕЛИНЕЙНАЯ ЗАДАЧА. МЕТОД БУБНОВА-ГАЛЕРКИНА
81
примере эта характеристика является симметричной относительно £, и притом жесткой рис 2.3, а. Собственные колебания такой системы, как будет показано ниже, отвечают скелетной линии жесткого типа. В случае оболочек упругая кривая может иметь вид, показанный на рис. 2.3, б, чем и объясняется изменение в характере амплитудно-частотных зависимостей см. § 32.
Итак, поставим перед собой цель провести интегрирование уравнения 28, содержащего теперь лишь одну независимую переменную— время; в этом и состоит второй этап решения задачи. Рассмотрим сначала случай пластинки со свободно перемещающимися прямолинейными кромками.
1. Пластинка со свободно смещающимися краями.
Решение, отвечающее этому варианту, получим, принимая в приведенных выше зависимостях рх ру 0. Но если учесть, что величина прогиба отлична от нуля, то из 18 вытекает vx Vy оо. По 29 тогда будет
31-ц»1Я«
41 К22 V.OZ
Рис. 2.3. Возможные варианты упругих характеристик.
К-
Квадрат первой частоты малых колебаний по-прежнему определяется по 31.
Представим прогиб в виде функции
£ A cos at, 2.33
где А — безразмерная амплитуда, со — частота колебаний. Обозначим левую часть уравнения 28 через Z:
Z 0 ■“' “о 1 £2 С 2.34
На втором этапе решения задачи проведем интегрирование по
полному периоду колебаний Т 2ясо. Иными словами, выпи¬
шем равенство типа
2я'ю
I Z t cos cot dt 0.
Принимая во внимание соотношения
2ясо 2ясо
I
cos2 со tdt '9 J
9
cos4 dt
Зя 49 9
82
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
1ГЛ. II
получим
2л0
J Z 0 cos CD dt A <D-СО2-J 4 U3 £ ю 0.
О
Мы пришли к уравнению, выражающему зависимость между частотой нелинейных колебаний со и амплитудой А:
cd2 cd2i КА2.
Введем обозначение для отношения величины о к соответствующей частоте линейных колебаний coo; v cdcdo. Тогда будет
v2l ±КА
2.35
В координатах v, А получаем скелетную линию рис. 2.4 жесткого типа. При весьма малых амплитудах имеем v->l. С увеличением амплитуды частота колебаний возрастает, и притом все более и более резко.
2. Пластинка с несмещающимися краями.
В случае, если края пластинки не смещаются, надо в основных соотношениях принять v vy 0. Тогда по 29 будет
«г _ 0,75 1 - »л 1 V 1,5 1 2цХ2 V
А 1Я22 • ' а;
Квадрат основной частоты определяется по 31. Величины рх и ру по 19 равны
1 1 цЯ2 n2Ef2 - _ 1 i n2Ef2 а2
Рис. 2.4. Скелетная линия для квадратной идеальной пластинки при нелинейных колебаниях по основной форме.
Рх 8 1-цг
Ру
2.36
8 1 - ц2 «2 ’
Проводя исследование задачи подобно тому, как это было сделано в п. 1, приходим к прежнему уравнению 35.
§ 20. Защемленная по краям пластинка
Перейдем к случаю прямоугольной пластинки, защемленной по контуру. Так же как и для шарнирно опертой пластинки, примем во внимание наличие стержней, стесняющих смещение точек краев х 0, х а. Таким образом, мы считаем, что по
§ 20 ЗАЩЕМЛЕННАЯ ПО КРАЯМ ПЛАСТИНКА §3
краям пластинки действуют усилия, средние значения которых
равны рх и ру. Вместе с тем условимся, что точка каждого края
перемещается свободно вдоль самого края, так что касательные усилия по контуру должны и здесь обратиться в нуль. Отношение сторон аb будем считать лежащим в пределах 1 <а6< 1,5.
По-прежнему воспользуемся основными уравнениями в форме 6, 7. Исследуя низшую форму колебаний, аппроксимируем прогиб с помощью выражения
w sin2 rx sin2 sy, 2.37
где г л;а, s nb.
Уравнение совместности деформаций принимает вид
У4Ф -g-fW cos 2 rx cos 2 sy — cos 4 rx — cos 4 sy
cos 4rx cos 2sy cos 2rx cos 4sy — 2 cos 2rx cos 2sy. 2.38
Решение этого уравнения
ф Е W т cos 2гх 17 cos 2sy
5l2 i C0S 4rx 5 C0S 4s Ж тгЧГ cos 4rx cos 2sy
V'f 45» cos 2r cos 4s — 16 £ S22 cos 2rx cos 2srJ £ ££. 2.39
Напряжения в срединной поверхности будут о» — Ef2'2 -§■ cos 2s« — cos 4sy
T '4НТ7 C0S 4rX C0S 2StJ C0S 2rX C0S 4s —
4 r2 s2j2 cos 2га: cos 2sy J -f- px, 2.40
о у — £2s21 -g- cos 2rx — -2 cos 4r
T cos 4rx cos f2 4'a»« cos 2rx cos 4s —
— 4 522 COS 2rx cos 2sy Py, 2.41 <Э2Ф „f, rV Г 1 ■ Л ■ n I
T -— lwFFsin4rxsin2s
ri 4522 sin 2rx sin 4sy — g2-T sin 2rx sin 2sy. 2.42
При ajb > 1,5 можно получить удовлетворительные результаты, рассматривая пластинку как бесконечно длинную см. 1.11.
84
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
Как видим, условие равенства нулю касательных усилий на кромках выполняется.
Для взаимного смещения кромок х 0, х а находим по 13а выражение
3
bx r2f2a
Р X t-Py
а.
32 7 Е
Аналогично для кромок у 0, у Ь
А 2f2 и РУ РРХ 1
AyMSfb Е Ь-
2.43
2.44
Используя зависимости 16 между смещениями Д, Ау и напряжениями <т, р, ву,р в упругих распорках, получим
о», р vxpx 32- Er2f2 — рх — цру,
з
Gy, р УуРр 39 Es2f2 ру ьр х>
2.45
Здесь приняты обозначения по 17. Отсюда безразмерные параметры р, ру по 20 будут
lVy
2
3 я2
32 vx I2
Ь»
. _ Зя и 1 v ру 32 1 vx 1 v, - Ц2 S •
2.46
Используем уравнение, составленное по методу Бубнова — Галеркина
2.47
J J X sin2 rx sin2 sy dx dy 0.
Находим функцию X по формуле 22. Подставляя выражения 37 и 39 для w и Ф, приходим к громоздкому выражению, приведенному в книге 1.11, стр. 111. Подставляя это выражение в 47, после интегрирования получим
d
16я4>
— h
g ‘ dt2 1 9а4
, 2л4Eh3 17
3 2Х2 3V £ ig- р, Х2рИ £
За2
9 а2Ь2
f _LZ_ а2 Г-LI
32Я2 л 132
1
1
1 А,22 4 14А,22 т44 Я22
1
»
'гЗ.
Рассмотрим далее различные частные задачи.
2.48
5 so защемленная Но каям Пластинка 85
1. Пластинка со свободно смещающимися краями.
Для этого варианта должно быть рх ру 0. Уравнение движения 48 приводится к прежнему виду 28, под К теперь должна пониматься величина
1,5а.4 1 ц2 Г 17 1. 1 г 1, 11. 1 Д “ 31А4 2А2 I 32 V1 ' А4 4 _4 A,22 14A22J lA22 J ‘
2.49
Квадрат основной частоты малых колебаний для защемленной пластинки будет
»г1тгрг<32131,>
или
”5 - т- Г--Р Д- 3 2У w>- <2-5°
Сравнивая 31 и 50, находим отношение частоты колебаний защемленной пластинки к соответствующей частоте шарнирно опертой пластинки:
®0 заш 16 з 2А2 ЗА.4
Т Л. Я2Т2-- 2.51
ш0. шарн 9 U Л ;
Для квадратной пластинки будет
ф.«з>55. 2.52
«Ч шарн
Приближенному решению задачи отвечает прежняя формула 35, где К должно быть найдено по 49.
2. Случай неподвижных кромок.
В этом случае надо принять v 0. Тогда находим по 46
п’ — — Г2
v 32 1 - ц2 1-
. _ Зя2 Я2
Ру 32 1 - ц2 6
2.52а
Уравнение 48 приводится к виду 28. Квадрат частоты выражается по формуле 50, а значение К в 28 определяется в виде
у 1,5А4 1 — ц2 Г 17 л., 1, 1 Г 1, 1 1 ■
А 31 Л4 2А2 132 -Г_Л4_Г4 14 A22 r 1 4А22 J г
■ — I
1, 9 А,2 А4 >
1 - И2 J
1 А,22 16 1 — ц2 • 2.49а
86
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
§ 21. Метод гармонического баланса
Решение задач о нелинейных колебаниях пластинок состоит, как мы видели, в приведении на первом этапе основного уравнения в частных производных к обыкновенному дифференциальному уравнению, а на втором — к интегрированию этого последнего уравнения. Второй этап решения может быть выполнен наряду с методом Бубнова — Галеркина с помощью ряда других приемов. Один из них носит название метода гармонического баланса.
Выпишем уравнение 28 в виде
-з£ юС 0 2.53
и примем
F0 Z K. 2.54
Так как величина £ зависит от, то и F является здесь неявной
функцией.
Выберем решение уравнения в форме
£ A cos со
и подставим это выражение в 53. Тогда будет
- соМ cos со со20F 0. 2.55
Разложим функцию Ft в ряд по косинусам и, желая срав¬
нить коэффициенты при cos со, ограничимся в разложении первым членом
Ft В j cos со. 2.56
Тогда по 55 получим
со2 2.57
Коэффициент разложения Вi равен
2ясо
В J F cos со dt
и
2JTC0
--- J A cos со КА3 cos3 со cos со dt А 1 КА2 j.
о
Обоснование этого метода дано в книге Н. М. Крылова и Н. Н. Боголюбова 0.11.
§22 МЕТОД ВОЗМУЩЕНИЙ 87
Окончательно находим:
<D2 co2lС42. 2.58
Мы пришли к результату, полученному выше методом Бубнова—Галеркина.
§ 22. Метод возмущений
Обратимся снова к уравнению типа 28. Его решение может быть также проведено с помощью так называемого метода возмущений, сводящегося к замене нелинейного уравнения системой линейных связанных между собой дифференциальных уравнений.
Введем безразмерный параметр времени т со и представим уравнение 28 в виде
о23- ш 3 0, 2.59
где х ®о.
Считая, что величина К является достаточно малой, примем X также в качестве малого параметра и разложим по степеням этой величины функции Сию:
S So X£i 3C2S2 •••> со б0 х©1 ГЧ ••• 2.60
Подставляя 60 в 59 и приравнивая нулю коэффициенты при
одинаковых степенях, получим следующую систему линейных
уравнений:
® «o 0, 2.61
со2, - 2й0о0 - 2.62
точки над буквой обозначают дифференцирование по т. Тогда мы получаем цепь последовательных задач, заключающихся в интегрировании уравнений 61, 62 и т. д.
Кроме того, должно быть выполнено условие периодичности
£<т 2я £т. 2.63
Для примера выберем начальные условия
£0 Л, £ 0 0, 2.64
и примем
£о0 А £,0£20. 0, 1
So 0 ti 0. 0, j 2-ЬЬ
h т 2я h т, t 0, 1,2,. 2.66
88 СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ГЛ. II
Начнем с первой задачи, заключающейся в интегрировании
уравнения 61. Решение его представим в виде
£0 Bcos-T Csin--T. 2.67
©о ©о
Из условий 65 и 66 находим
В А, С 0, ©о <о0.
Таким образом, будет
go A cos т. 2.68
Перейдем к уравнению 62. Подставляя значение £0 по 68, получим
®о 0>i Ь £i 2о0со, Л cos т — A3 cos3 т. 2.69
Представляя cos3t приближенно выражением
cos3 т cos т -j- cos Зт,
находим
®о t £i 2®о®1 Т 2 А cos т Т Аcos Зт- 2.70
В случае, если коэффициент при cost будет отличен от нуля,
решение уравнения окажется содержащим член типа 'Tsinr. Но функция £it периодическая, поэтому должно быть
гйосй, — 1 А2 0 и со, 2.71
Решение уравнения 70 принимает вид
£i б cos т Ci sin т Ц—cos Зт. 2.72
32Dq
Из начальных условий 65 находим
32с0а
Тогда окончательно будет
А3
32©о
— cos т cos Зт. 2.73
Таким образом, найденное решение после подстановки значения х ооС получает вид
С А 1 - JL ка2 cos т ± КА3 cos Зт, 2.74 ф со01 1-СЛ2. 2.75
§ 23 ТОЧНОЕ РЕШЕНИЕ 89
Далее, ограничиваясь членами, содержащими малый параметр, находим
<D2 <o2l-042. 2.76
Эта зависимость между со2 и Л совпадает с той, которая была получена предыдущими путями. Но выражение для £ содержит теперь дополнительный член, отвечающий утроенной частоте.
§ 23. Точное решение
Решение уравнения 28, отвечающее начальным условиям £ Л, £ 0 при О, выражается через эллиптический косинус
£ Лсп,, где У®0УТШ,
Определим период Т для этого решения.
В силу того, что
1 dY dt dl 2 dl '
уравнение 28 приводится к виду
Tf1 <0o0 0. 2.77
Предположим, что движение пластинки в момент t — О характеризуется значениями прогиба и скорости, равными £<0 А, £<0 0. Интегрируя 77, получим
С А
Т чгУ >2J>M <d2Jf £ dl. 2.78
а ;
Согласно 78 при движении панели кинетическая энергия равна разности потенциальной энергии, соответствующей начальному положению £ Л, £0 и потенциальной энергии в рассматриваемый момент. Эта доля потенциальной энергии пропорциональна площади, заштрихованной на рис. 2.3, а. Выражение 78 определяет скорость £ для любого положения панели.
90 СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕЁАНИЯ ГЛ 11
Учитывая, что движение панели в рассматриваемый момент времени соответствует уменьшению прогиба, из уравнения 78 получим
dt- r dlA 2.79
20 о J
0 di
с
В результате интегрирования 79 получим время, необходимое для перехода пластинки в положение £ из положения А:
С
-J -г— 2,80
Fldl
С
yf 2«»oJ
Ввиду симметрии упругой характеристики время движения пластинки от положения £ А к положению £ 0 будет равно четверти периода, поэтому период равен
А
Т 4J——1 -4 л <2'81>
А у 2cojFSdS 0 у 2cog J FS
С С
Подставляя сюда выражение для F£ по 54, получим
А
Т> 4 I о оо
<°° о Вводя обозначения
г 4 s 2-
придадим выражению 82 форму
Юо J
О l-r'l-i-s у «Г»
-V 1 1_г21±£ г2
§ 23 ТОЧНОЕ РЕШЕНИЕ 91
Приведем это выражение к виду, удобному для вычислений с помощью таблиц. Эллиптический интеграл
f, dx -W, ф. 2.84
J а2-т2 62 т2 с с 7 '
Здесь Facy ср—эллиптический интеграл первого рода. Его
значения в зависимости от ас, ф приводятся в таблицах в со¬
ответствии со следующими обозначениями:
c2 a2 b2, sin2 ф aipiX2 Х2 ■
Сравнивая 83 и 84, получим
а2 1, fe2 l±i. 211±£ 2ls
S 9 S S х, sin2 ф 1, ф -у» и окончательное выражение для периода будет
’тЬ-т- 2'85
©О
VT-S
Полагая здесь s 1, получим выражение для периода малых колебаний
т 2л
J° — '
Отношение частоты нелинейных колебаний к частоте малых колебаний v Т0Т получает вид
п 4 s J су од
v — 2, - я. 2.86
РУ 215 Т
На рис. 2.5 приведены амплитудно-частотные зависимости по 86 для ряда граничных условий сплошные линии: 1 — шарнирное опирание при свободном смещении краев; 2 — шарнирное опирание при отсутствии взаимного смещения краев; зависимости 3, 4 относятся к аналогичным вариантам граничных условий защемленной по контуру пластинки. На этом же графике пунктирными линиями приведены соответствующие зависимости, отвечающие рассмотренным выше решениям см.§§ 19, 20 по методу Бубнова — Галеркина. На рис. 2.5 используется
См., например, Янке и Эмде, Таблицы функций, изд. 3-е, Физматгиз» Москэа, 1959,
92
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
величина v, равная отношению частоты собственных нелинейных колебаний к частоте основного тона малых колебаний пластинки, шарнирно опертой по контуру. Поэтому v vr, где значения v находятся по формулам 35, 86 при соответствующих значениях К по 32, 32а, 49, 49а; очевидно, в случае шарнирно опертых краев г 1. Для пластинки, защемленной по контуру, величина ц равна отношению частоты
Рис. 2.5. Влияние граничных условий на амплитудно-частотные характе ристики для пластинок по данным точного решения и решения по методу Бубнова — Г алеркина.
основного тона малых собственных колебаний пластинки, защемленной по контуру, к основной частоте колебаний в случае шарнирного опирания краев, г 413 2Х2 ЗЯ431 А,2.
Зависимости рис. 2.5 построены для квадратных пластинок
1.
§ 24. Случай весьма длинной пластинки.
Применение метода Бубнова—Галеркина
В заключение рассмотрим случай пластинки, один из размеров которой значительно превышает второй размер а>Ь.
Для исследования колебаний такой пластинки можно выделить полосу шириной, равной единице, и длиной, равной Ь. Тогда мы получим задачу с одной пространственной координатой г. Уравнение движения можно записать тогда в виде
D d4w d2w y d2w
h dy4 dy2 g dt2 • Здесь мы заменили производную д2Фдх2 величиной оу сг; для бесконечно длинной пластинки эта величина должна быть постоянной во всех точках, а const 1.11.
§ 24 СЛУЧАЙ ВЕСЬМА ДЛИННОЙ ПЛАСТИНКИ 93
Воспользуемся методом Бубнова — Галеркина. Аппроксимируя прогиб выражением
wf sin--, 2.88
получим
2.89
О
Далее приходим к уравнению
2-90
Условие равновесия подвижного края имеет вид 1.11, стр. 74
oh opFejl, 2.91
где
.I, у£<»■ 2-91а>
О
причем v hFeд. Отсюда
а -i2 1 v wf2' 292
Если опоры неподвижны, будет v 0, в случае абсолютно
подвижных краев v oo.
Подставляя 92 fe 90, получим
X и -L п — f -L — -ЁL fз __ о 2 93
g п dt2 и Ь ' 4 Ь4 1 - ц2 1 v ' и W-Уо
Уравнение 93 приводится к виду
-gf cod 2 0, 2.94
где
ch я2 гг 3 л л ““VHd-Ml ТТ7’ <2-94а
Здесь о0, как и ранее, — основная частота собственных колеба¬
ний системы.
При неподвижных краях будет С 3, в случае абсолютно подвижных краев К 0.
Перейдем к случаю полосы с защемленными краями. Представляя прогиб в виде
w f sin2--, 2,95
94
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
получим тем же путем уравнение
-rD£f -r-£.-0- 2.96
Определяя а по прежним формулам, найдем
‘’“тттЫЯ- <2-97>
Подставляя 97 в 96, получим
1. и d2f 4. £ Eh 1 1 «з л л qq
g dt2 3 b ' 3 b4 1 — ц2 1 v ' 2.Щ
Это уравнение приводится к форме 94, где
2 ch я2 3
Юо -Т-ГТ7’ К:
3 l -ц2 Ь2 ’ 41 v
В случае неподвижных краев К 34. При абсолютно подвижных опорах по-прежнему К — 0.
§ 25. Приложение метода конечных разностей
Обратимся к решению задачи, рассмотренной в предыдущем параграфе, с помощью метода конечных разностей.
В случае несмещающихся краев v 0 из уравнения 91а определяется величина а, и исходное соотношение 87 получает вид
ъ
D dw Е ldwjfdu, y__dh_ о 2QQ4
h ду4 26 1 — и-2 J <ty j '
о
Примем безразмерные величины
Е1’ т Т’ 2.100
где Г — период малых собственных колебаний Т 2ясо0; величина coo определяется по формуле 94а. Тогда уравнение 99 приводится к виду
d4w
d2w С dw 2. п2 d2w л о 1Л1
д4 дг J д db 4 дх2 0, 2.101
о
Здесь мы рассмотрим случай шарнирно опертых краев; соответствующие граничные условия имеют вид
w 0, --0 при £ 0, 1—1. 2.102
Это решение принадлежит И. Г. Кильдибекову, С. В. Медведевой и автору; ими же рассмотрены задачи, изложенные в § 31.
25
приложение МЕТОДА КОНЕЧНЫХ РАЗНОСТЁЙ
95
Примем следующие начальные условия:
dw
oy 4sin:iT£, 0 при т 0.
2.103
Соответствующее решение линейной задачи для основной формы собственных колебаний, как известно, имеет вид
w A sin cos т. 2.104
Теперь исследуем нелинейные колебания с помощью метода конечных разностей.
Представим уравнение 101, а также граничные и начальные условия задачи в конечных разностях. Шаг по времени sx 1m, шаг по координате 1п. Для узла, будет
т i2, — 4wi u J 6®,. — 4Wi-, f Wi-2,, 2.105
9V
T F Wi< ■ — t t wl<
<7T S.
Граничные условия задачи
гй0> 0,
w
п, I
0,
wu, — 2w0, 0 для точки 0,
sS
-Т — 2i5«. “’«-l. для точки il.
Из условий 108 с учетом 107 имеем
—®i. WnUj — Wn-Ut.
Начальные условия 103 будут
й, о Л sin я sj • г'> г 1, 2,., «— 1,
”t. 1
У 1
-- 0.
2.106
2.107
2.108
2.108а
2.108Ь 2.108с
Результаты вычислений приведены на рис. 2.6—2.9. При вычислениях число шагов вдоль координаты было принято п 20, отношение шагов sTs 140.
Рис. 2.6, б отражает конфигурацию срединной поверхности в различные моменты времени, обозначенные на графике номе рами интервалов разбиения вдоль оси времени. Значение ам плитуды прогиба в центре принято равным А 1. На этом же графике приведены результаты линейной задачи рис. 2.6,а. Как видно, частота колебаний по данным линейного приближения оказывается существенно ниже. Это обстоятельство более
96
СОБСТВЕННЫЙ НЕЛИНЕЙНЫЙ КОЛЕБАНЙЙ
ГЛ. II
наглядно демонстрируется рис. 2.7; эти данные отражают движение различных точек пластинки во времени.
Через гйю обозначается кривая изменения по времени стрелы прогиба; этой точке отвечает значение t 10. Тонкая линия
Рис. 2.6. Конфигурация срединной поверхности пластинки для различных моментов времени при параметре прогиба Л 1: а линейная задача; б нелинейная задача.
отображает изменение стрелы прогиба во времени по данным линейного приближения. Отношение частоты колебаний, полученной по методу конечных разностей, к частоте в линейной задаче равно 1,8.
На рис. 2.7 пунктирной линией приведена зависимость для стрелы прогиба, полученная по методу Бубнова — Галеркина, штрих-пунктирнойв эллиптических функциях.
Графики, аналогичные рассмотренным выше, приведены на рис. 2.8, 2.9. Эти данные относятся к случаю колебаний с амплитудой прогиба в центре А 5. В этом случае частота нелинейных колебаний, полученная по методу конечных разностей, при
ВЛИЯНИЕ УСИЛИЙ в СРЕДИННОЙ ПОВЕРХНОСТИ
97
близительно в 7,6 раза превышает частоту по данным линейного приближения. На рис. 2.9 приведены также данные линей-
Рис. 2.8. Изменение конфигурации срединной поверхности пластинки при параметре прогиба А 5: а линейная задача; б —нелинейная задача.
Рис. 2.9. Движение точек во времени по данным линейного приближения и различных решений нелинейной задачи при собственных колебаниях с параметром прогиба в центре А5.
ного приближения и результаты решений по методу Бубнова — Галеркина и в эллиптических функциях; здесь для различных решений приняты те же обозначения, что и на рис. 2.7. Штрихпунктирная линия здесь сливается с кривой, полученной по методу Бубнова — Галеркина как и на рис. 2.7.
§ 26. Влияние усилий в срединной поверхности на собственные колебания пластинки
Рассмотрим колебания пластинки, испытывающей по кромкам х 0, у 0 действие сжимающих усилий рх, расположенных в срединной поверхности рис. 2.10. Предположим, что
Приведенное здесь решение дано И. Г. Кильдибековым. Ему же принадлежат результаты, изложенные в §§ 27, 29, 30, 32, 34.
98
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
одновременно по краям пластинки у О, у Ъ действуют со стороны подкрепляющих ребер усилия в срединной поверхности, средняя интенсивность которых равна ру. Значения рх и ру
без черты здесь считаются положительными при сжатии. Касательные усилия в срединной поверхности будем считать равными нулю по всем четырем кромкам.
1- Случай шарнирно опертых кромок.
Вначале рассмотрим случай, когда кромки пластинки шарнирно оперты. Решая задачу в первом приближении по методу Бубнова — Галеркина, как это было сделано в § 19, примем для w прежнее аппроксимирующее выражение 8. Подставляя это выражение в правую часть уравнения 7 и ин-
Рис. 2.10. Пластинка под действием сжимающих усилий в срединной поверхности.
тегрируя,
ности:
находим функцию напряжений в срединной поверх-
f2 ГI а2 Ь2 2я’1 рху2 РиХ2
ф£жт «—« ™-г-Ч— -т-; с-109»
по сравнению с 11 здесь лишь изменяются знаки перед рх и ру. Далее уравнение 24 принимает вид
У-Н2 g п dt2
ач ' Я12Ч-РхЛ2Р,;-Я2з0.
2.110
Принимая продольные края пластинки смещающимися свободно, мы должны положить ру — 0. Тогда окончательное уравнение НО перейдет в следующее:
лт
о-в
ато.
2.111
Здесь р рх pb2l Eh. Параметр рр ния равен
. _ я2 1 А,22 ркр 12А.2 1 — ц2-
Под К в 111 понимается коэффициент
0,75 1 — ц2 1 А4
-£Г
критического напряже-
1Л2 1
2.112
2.113
§26
ВЛИЯНИЕ УСИЛИЙ В СРЕДИННОЙ ПОВЕРХНОСТИ
99
Квадрат основной частоты собственных колебаний пластинки при малых прогибах с учетом сжимающих усилий будет
1 -
Рх
Ркр
2.114
где под понимается выражение 30. Формулу 30 можно также переписать в виде
, 2.115
2 о c2h2 < ПРкрШ2
величины ркр и с определяются по
112 и 5.
Зависимость между амплитудой и частотой колебаний находим по формуле
v2 1 -КА2
4ч. 2.116
Ркр>
пользуясь новыми выражениями для и К рис. 2.11; здесь nojiv понимается отношение частоты колебаний пластинки к собственной частоте основного тона колебаний без учета сжимающих усилий. Тонкая линия отвечает случаю рх 0.
Как видим, влияние сжимающих усилий на амплитудно-частотные характеристики системы является значительным.
Если продольные края пластинки неподвижны Ду 0, то из уравнения 15, изменив знаки перед рх и ру> находим
2.117
Рис. 2.11. Влияние сжимающих усилий в срединной поверхности пластинки на амплитудно-частотную характеристику.
р я2 п2
Ру — VPx Е 8 Ь '
Подставляя это выражение в 110, приходим к прежнему по виду дифференциальному уравнению 111 с заменой 112 на следующее:
„• 2iw 2im
ркр. 1 12Я,2 1 цА2 1 — Ц2' V-b.noj
Величина К определяется по формуле К-
i22l
' Ркр, I
Выражение для квадрата основной частоты остается прежним 114 с заменой рр на £р>1
0,751 —ц2 1 ЗУ Рх
2.119
100 СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ГЛ. II
Отметим, что статический вариант зависимости 110 приводит к следующим значениям для рх в закритической области: при смещающихся кромках
p-d-Sfx »T -w>t : <2-'2°>
при неподвижных кромках
l xT „да ТГ »•
Обратимся к варианту защемленных кромок пластинки.
2. Случай защемленных кромок.
Повторяя выкладки п. 1 и принимая аппроксимирующее выражение для прогиба в виде
w f sin2 rxsn2sy, г тсау 5 я6, 2.122
приходим в случае подвижных продольных кромок к прежним зависимостям § 20, но с введением в некоторые формулы коэффициента 1 — РРкр 2» как в п Величина р 2 ПРИ этом равна
. 2 3 v -1Л
р;,.—т—i-ii.—<2-123>
В случае неподвижных продольных кромок величина К равна
—.».<■-■ ±
31,< 2Л2 1 А
' Ркр, 3 1
■Т 4 Я,22 1 4Л22 1 А,22 2-124
а значение р ъ будет
2 2 зл2-р-
Ркр, з “9 1 _ Ц2 1 цЯ,2 • 2.125
§ 27. Эффект начальных неправильностей
Основные уравнения, учитывающие начальные несовершенства в форме срединной поверхности, примем в виде
Z.a>, w0, Ф — ph- 0, 2.126
гу2У2Ф-1ш12ш0, ю,, 2.127
оператор L определяется по формуле 1.34, через Wi обозначается дополнительный прогиб.
§27
ЭФФЕКТ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ
101
Исследуем случай пластинки, шарнирно опертой по контуру, совершающей колебания с образованием тип полуволн вдоль координатных линий х, у. Примем следующие выражения для дополнительного и начального прогибов:
р. тлх. плу W —f Osin-—sin—2.
г. mnx. w0 f0sm—-sm
b
плу
2.128
2.129
Функция напряжений в срединной поверхности находится из уравнения 127 в виде
п2Х2
cos 2.130
Применение метода Бубнова — Галеркина приводит к следующему уравнению собственных колебаний пластинки: d dt2
2.131
принимаем безразмерные величины £ fith, Zo foh. Квадрат частоты собственных колебаний при малых прогибах со2 тп определяется по формуле 4. г Значение а в уравнении 131 а будет
а1
2.132
величины р и К определяются
в виде
Р-
К
2.133
0,75l-n2l--v
' IH
Рис. 2.12. Амплитудно-частотные характеристики для различных форм собственных нелинейных колебаний квадратной и прямоугольной пластинок.
2.134
Приближенное решение уравнения 131 примем в виде ЗЗ1. Используя приведенный выше метод решения, получим
v - а т КА2 Ч ° 135
См. статью 3.11.
102
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. и
В отличие от прежних обозначений здесь под v понимается отношение частоты колебаний к основной частоте малых колебаний <>oflP найденной для квадратной пластинки, v ©©J п; тогда
Зависимости, отвечающие движениям при собственных нелинейных колебаниях по одной из первых четырех форм, приведены на рис. 2.12. Сплошные линии на этом графике относятся
к случаю квадратной в плане па-
Рис. 2.13. Влияние начальных непра Рис. 2.14. Влияние начальных неправиль
вильностей при нелинейных колеба- ностей при нелинейных колебаниях пла
ниях пластинки по основной форме. стиики по четвертой форме.
ными несовершенствами в форме срединной поверхности при £о1, приведены на рис. 2:13, 2.14. Второй из этих графиков отвечает движениям панели по четвертой форме. Тонкие линии на этих графиках относятся к идеальным панелям. Как видно из приведенных данных, чем выше форма колебаний, тем более значительным оказывается влияние начальных отклонений на параметры собственных колебаний.
§ 28. Замкнутая цилиндрическая оболочка. Линейная задача
Обратимся к рассмотрению задачи о собственных колебаниях замкнутой круговой цилиндрической оболочки рис. 2.15. Прежде чем перейти к исследованию нелинейных колебаний,
§ 28 ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА. ЛИНЕЙНАЯ ЗАДАЧА ЮЗ
остановимся на особенностях собственных колебаний при малых прогибах.
Пусть L — длина оболочки, R — радиус кривизны срединной поверхности, координатные линии х, у направим соответственно вдоль образующей и дуги.
Опуская нелинейные члены в исходных уравнениях 1.40, 1.41, при р yg, <7 0, получим для идеальной оболочки w0 0:
D V74™. I л d2w 1 д2ф 0 10д
h V w р df2 — R дх2, 2.136
— У4ф — 2 137
Е R дх2 У-14
В случае шарнирного опирания -примем следующее выражение для прогиба: wft sin-sin-; 2.138 р
Рис. 2.15. Круговая цилиндрит — ЧИСЛО полуволн ПО длине ОООЛОЧ- ческая оболочка.
ки, п — число полных волн по окружности. Узловые линии для различных форм колебаний показаны на рис. 2.16.
Подставляя 138 в 137 и проводя интегрирование для случая р 0, получим
J г2 522 sin rx sin sy, 2.139
где
t'l ’ R
тл п _ «
S R' 2.140
Воспользуемся методом Бубнова — Галеркина и положим
L 2ПН
J J X sin rx sin sydxdy 0, 2.141
о о
где
<2Л42>
Из равенства 141 с учетом 138, 139 получим следующее
уравнение:
-§- со£ 0. 2.143
Здесь и ниже рассматриваются формы с п 2. Поведение оболочки при п < 2 характеризуется несколько отличными свойствами; см., например, статью Форсберга К. Forsberg, AIAA J. 7, 2, 1969.
104
СОБСТВЕННЫЕ ИЁЛИНЕЙНЫЁ КОЛеБАНЙЯ
ГГЛ. II
Здесь £ fth. Величина со;- равна квадрату частоты собственных колебаний оболочки при малых прогибах
'■■£ а
02
02Ti Eh
2.144
Т1—значение критического усилия для оболочки, вытекающее из решения линейной задачи об устойчивости оболочки при
осевом сжатии, Т кр pKpEhR. Безразмерная величина в формуле 144
л _ 1 1 022
Ркр —
121—ц2 О2
О2
Л
1 О22 к • 2-145 Параметры волнообразования
tnjiR
tiL
Л ’
n2h
R
2.146
77
772
7 3
Ixi ly
ly — длины полуволн вдоль образующей и дуги соответственно. Минимальное значение
рв
1
31 -1 '
имеет место при
2
0,605 2.147
Рис. 2.16. Узловые линии для различных форм колебаний круговой цилиндрической оболочки.
ч» 1Г-
V 121 -ц2 3,3. 2148
Через с обозначается скорость распространения продольных волн в материале оболочки по 5.
Результаты вычислений частоты собственных колебаний по 144 приведены на рис. 2.17—2.19, а и 2.19,6. Здесь принят безразмерный параметр частоты
соп о
1 Do L2
ch
2.149
На графике рис. 2.17 приведены значения этого параметра в зависимости от числа полных волн в окружном направленйи п при пг — 1 для оболочки с параметрами LR 2, Rh 1500.
Данные рис. 2.17—2.19, а и 2.19,6 принадлежат И. Г. Кильдибекову 2.12.
Рис. 2.17. Зависимость частотного параметра оболочки при малых прогибах от числа окружных волн.
Рис. 2.19а. Зависимость частотного параметра оболочки при малых колебаниях от числа полуволн вдоль образующей и полных волн вдоль окружности при малом числе г.
LR
Рис. 2.18. Расчетные данные для определения минимальной частоты малых собственных колебаний оболочки.
Рис. 2.196. Частотный параметр для оболочки при большом числе окружные волн п.
106
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
Минимальное значение параметра частоты собственных колебаний со min для рассматриваемой оболочки отвечает значению п 10.’
Результаты вычислений минимальных значений т 1 частотного параметра coj mln для оболочек в широком диапазоне параметров LR, Rh даны на рис. 2.18. Здесь же приведены для отдельных значений LR соответствующие числа волн п.
Данные рис. 2.19а, 2.196 отражают изменение параметра coj по 149 в зависимости от числа полуволн по длине оболочки т для ряда фиксированных значений п принято LR 2, Rh
Приведем далее результаты уточненного решения задачи. При этом, воспользуемся уравнениями главы I стр. 51. Для круговой цилиндрической оболочки они приобретают вид
1500.
дЧ I I I к d‘u I
2 I ' д<р2
1 ц d2v., d3w
2 арф д£3
1 ц д2у
2 д£дф
дъи 1 — ц, дъи ди - 3 — ц, д3о
д3 2 д дф2 д Т 2 dg2d<p
ди 3 •— ji 4 d3v
af 2 ag2 Зф
“■ау А: v4® 25f “>v2-- °, 2.150
где
YR2 i - f2
gE
Общее решение этих уравнений выпишем в виде
2.151
Здесь приводятся результаты, полученные Форсбергом К- Forsbgrg, AIAA J. 2, 12, 1964.
§ 28 ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА. ЛИНЕЙНАЯ ЗАДАЧА Ю7
Постоянные As определяются из граничных условий на каждом торце оболочки:
Подставляя выражения 151 в 150, получим уравнение
где ау Ьу су d — действительные числа.
Решение получает вид
w Cj --С2еа C3cos 6 C4sin C5cosd£C6sin
ес С7 cos dl С8 sin dQ cos щ еш. 2.154
Аналогичные выражения для и и v содержат комбинации постоянных С8у а также действительных и мнимых частей параметров а8у Ps. Величины as, зависят от Яв, hRt ц, г, со, они вычисляются после решения уравнения 153.
Удовлетворяя краевым условиям, получаем восемь уравнений относительно неизвестных Cs, содержащих параметры а, 6, су d. Представление этих параметров в аналитической форме невозможно, и задача решается численно. При заданных параметрах А, LR, ы, числе волн п, системе краевых условий, задаваясь некоторой начальной оценкой для частоты соо, путем итерации находятся те значения частоты, при которых определитель системы обращается в нуль.
Для фиксированных тип существуют три собственные частоты с различным отношением амплитуд u> vf w. Асимптотическими значениями этих частот будут соответственно соол, «>0,2» ®о.з- Значение cd0, i отвечает изгибным движениям кольца
ОУтах «»тах. И 0, <00,,<В0. ft2 fl212 R2 П2 tt2 — 1 2п2 1.
При продольных колебаниях w v 0, a»0i2<»0i 2 1 —цп22. В случае колебаний растяжения — сжатия кольца vmilx nwmix,
2.152b 2.152с 2.152d
2.152а
о 0 или Т Niv — 0.
4 SseK 8«К Ss2K gs0 0, 2.153
где
Корни уравнения 153
А — ± a, ± iby ± с ± idу
108
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
и 0, <D0 зсо0 kf п2 1. Величина со2 k EgR21 — ц2 отвечает квадрату низшей собственной частоты в случае растяжения — сжатия кольца при плоской деформации.
Если пренебречь продольными и тангенциальными силами инерции, фиксированным т, п будет соответствовать лишь одно значение со, близкое к наименьшей из трех частот оболочки.
,10
О0
0,5
0,2
0,1
OftS
0J02
ЩП
74
Ч
—Вар.1
ныоо
—Ой
р. и
71
slff
-Rh
Rh-
Ш
501
7yv
л
7
г
л
7
я
--Z
цг qs Ifi г 5 ю 20
LR
Рис. 2.20. Значения минимальной собственной частоты колебаний при малых прогибах для шарнирно опертой и защемленной оболочки без продольного закрепления.
ы0
Ц5
0,2
OJ
0,05
0,02
Ofll
0,005
apoz
0,001
пго
74
—бар.1 —Bap.Z 8ар.З
15
16
3J
1Z
ч
>Г
г
Rh
50i
8 и
4
Xv
5
X
4
X
я
3
О, Z op 1,0 2 5 10 ZO 50 100
LR
Рис. 2.21. Минимальные частоты оболочки в случае шарнирного опирания торцов при различных условиях закрепления от продольных смещений.
Приведенные ниже данные получены с учетом всех трех инерционных членов.
На рис. 2.20—2.24 приведены минимальные частоты огибающие семейств частотных кривых, построенных для постоянных значений п при т 1. Здесь приведены результаты для граничных условий в соответствии с табл. 2.1. В отличие от значения со по 149 принят безразмерный параметр частоты
00:
vU — Ц2
Eg
2.155
указанные параметры связаны соотношением
©оя2 У — ц2
On
2.156
На рис. 2.20 сравниваются значения минимальной собственной частоты для шарнирно опертой сплошная линия и защемленной оболочки штрих-пунктирная линия без продоль¬
§ 28 ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА. ЛИНЕЙНАЯ ЗАДАЧА Ю9
ного закрепления варианты 1 и 6, табл. 2.1. Увеличение минимальной частоты за счет заделки весьма мало. Это влияние заделки проявляется только для коротких оболочек LR <
С 1. Приведенные выше результаты, полученные по методу Бубнова — Галеркина рис.
2.18, весьма близки к соответствующим данным рис. 2.20 для варианта 1. Так, при LR 2, следуя графику рис.
2.18, для минимальных частот получим по 156, приняв Rh 20, величину соо 0,264, в случае Rh 500 значение со0 0,052, а при Rh 5000 будет шо 0,016.
На рис. 2.21 приводится сравнение минимальных частот в случае шарнирного опирания торцов при различных
Рис. 2.22. Минимальные частоты по данным двух решений в случае защемления при отсутствии торцевых смещений.
W
ш0
5
o,z
0,1
0,05
0,0Z
w
0,5
0,2
0,7
qo5
apz
7го
L 7-
“Г г г ■■ I ■■
4 —Вар. 7 _ Вар. 4
73
2>,
h
Ч
Jh20
Xl.J 1 п20
'2
к
1 1 ■' г - ■
4 Вар. 3
Ыв
4
N
Sap. 4
Вар. 5
73
VS
ч
V
ч
V
ф
Ъ-20
1 1 O.Z Ц5 yj Z 50 ZO
so mo
LR
Рис. 2.23. Влияние краевых условий для тангенциального перемещения на минимальные частоты колебаний оболочки при шар-, нирном закреплении торцов.
0,5
о,г 0,1 0,05
qpz
1,0
0,5
0,2
0,1
Ц05
цог
74
— вар 6 Вар. 8
j4
3
Ч1
ZO
i
tth5W 1 1 £20
6
П—4
— Вар. 7
— Sap. 0 Sap. Э
75
ч
О
N
V
Rh 20
i
Лг5Щ '
0,Z 0,5 10 Z 5
10 ZO 50 100 LR
Рис. 2.24. Влияние краевых условий для тангенциального перемещения в случае защемления торцов.
условиях продольной заделки. Это условие оказывает заметное влияние даже для очень длинных оболочек. Для большей части
110
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
Таблица 2.1
ва¬
Условия опирания
Граничные условия
рианта
х0
x—L
1
Шарнирное опирание со свободным смещением в продольном направлении и при отсутствии смещения в дуговом
w 0 v 0 Мх 0 Nx 0
о о о о
IIIIIIII
2
Шарнирное опирание со свободным продольным смещением на одном торце и с неподвижным вторым торцом
w — 0 t> 0 Мх 0 Nx 0
w 0 v 0 Мх 0 и — 0
3
Шарнирное опирание при неподвижных торцах
О О О О
II II II II
§ a
w 0 и 0 о 0 Мх 0
4
Шарнирное опирание без закрепления точек торцевых сечений в дуговом направлении
О О О О
II II II II
IIIIIIII
о о о о
5
Шарнирное опирание с закреплением в продольном направлении, но без закрепления в окружном направлении
О О О О
IIIIIIII
§ а
о о о о
IIIIIIII
§ з.
6
Защемление без продольного закрепления
w — 0 дх
v 0 Nx 0
О О О О
II II II II
'О 1
7
Защемление при отсутствии смещений торцевых сечений
о о о о
II II IIII
О о о о
II II II II
8
Защемление без закрепления в окружном направлении
w — 0 0
дх
Nx 0 Т 0
w 0 дх
ых 0
Т 0
9
Защемление с продольным закреплением, но без закрепления в окружном направлении
о о оо
II II II II § э
w 0
JL 0
дх и 0 Г 0
10
Шарнирное опирание без продольного закрепления на одном торце, защемление с продольным закреплением — на другом
о о о о
IIII II II
а о х ч
8 5 5
w 0 t; 0
L 0
дх
и 0
§ 29 ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА. НЕЛИНЕЙНАЯ ЗАДАЧА 111
диапазона значений параметров оболочки минимальная собственная частота для варианта 3 приблизительно на 40—60 выше, чем для варианта 1.
На рис. 2.22 приведены результаты решения в сравнении с приближенным решением Арнольда и Варбартона пунктир для варианта 7. Они обычно превышают точные значения в пределах 2.
Снижение частоты собственных колебаний при изменении краевых условий по тангенциальному перемещению v отражается на рис. 2.23, 2.24.
§ 29. Замкнутая цилиндрическая оболочка. Нелинейная задача
Рассмотрим задачу в нелинейной постановке, предполагая, что оболочка испытывает действие усилий осевого сжатия р рис. 2.15, равномерно распределенных по торцам. Воспользуемся основными уравнениями в виде
V4 w - w0 L w, Ф - Р-. 2.157
±VG> -±Lw,w-Lw0, w0—, 2.158
где ay —полный прогиб, w Wi w0y w0 — начальный прогиб. Оператор L определяется по формуле 1.34.
Дополнительный и начальный прогибы аппроксимируем выражениями, отражающими характер волнообразования при потере устойчивости в большом при осевом сжатии в случае шарнирного опирания 0.6
W fi sin rx sin sy f2 sin2 rx, 2.159
wo — fuo sin tx sin sy f2,0 sin2 rx, 2.160
где приняты обозначения по 140.
Подставляя 159, 160 в уравнение 158, получим
-L У4Ф -J r2s2fi, 2fu о cos 2rx cos 2sy —
— у r cos 2n< r2s2 fj2,2. о fju o sin Zrx sin sy —
— r2s2 fif2 fif2, o fJuo — -r sin rx sin sy. 2.161
R. N. Arnold, G. B. War bur ton, Proc. Roy. Soc., A197 1949. 238—256; Proc. Inst. Mech. Engrs 167 1953, 62—80,
См. статью 2.12.
112 СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ГЛ. II
Интегрируя 161, определяем функцию напряжений в срединной поверхности
ТГ ШГ“Ь 2f 1, о — -дг cosгх
2 fi fi 2ь оcos sy 9r2 s2y 12 12,0 21, 0 X
X sin 3rx sin sy r2 ‘ siy - r2 - r2s2ff2 f,f2.0 f2f,, 0 X
X sin nr sin sy — 2.162
По методу Бубнова — Галеркина удовлетворяем равенствам
L 2я R
J J Xsnrxsnsydxdy Ot 2.163
о о
L2nR
J J X sn2 гх dx dy — О, 2.164
о о
где
Х D-VHw-w0-Lw-- >-. 2.165
Подставляя сюда выражения 159, 160, 162 и используя равенства 163, 164, получим следующие уравнения движения оболочки значение Т см. стр. 104:
dt2 77 0 а0 Ь
- Ф.Са Ш1 - С, -£• о' 0, 2.166
:1 Т; К1 а2 4i Ф£ Ш2
-Cs-Cs. о 0, 2.167
где введены безразмерные величины
у- _fl 0_ f.2._ 5- fl> 0 2» О о 1 AQ
fei— h > £2— > £1,0— fj' 2’° — h'
Под Cj понимается квадрат частоты собственных колебаний оболочки при малых прогибах по 144. Параметры волнообразования О, г отвечают формулам 146. Значения С2, Т2 равны
C2i-r2c2-, 2.169
Т2 — -4 — 9 i _ jj2 з2А2 • 2.170
§ 29 ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА. НЕЛИНЕЙНАЯ ЗАДАЧА 113
Остальные величины в уравнениях 166, 167 будут °i s' о г2 s22 Rh 2.0
Г S 9г2 s22 г2 s22 2. ° ’ 2-171
a2YrS 9г2 s22 г2 s221.о2 2.172
2-173
2-174
n —fr1 s I rV 1 g -
D‘ U 4 Rh Rh r2 s22 J fel’ 0
rs 9r2 s22 r2 s22 i. 02. о 2-175
rs gr2 _J_ -S22 r2 __ S22 Si, 01 » 2.176
2r4s2, I s2
Ф1
r2 s22Rh ' 4 Rh
2rs 9r2 s22 r2 s22 J 2, о » 2-177
Г S 9r2 s22 r2 s22 'P ’ 2.178
02 -0i> я2 ук1. ф2 уф1.,Ф2 -,ФЛ» 2.179
где С ЧГЧГ2, причем
-12 1 — Ц2 r2S22 A2 S22 2-l 2-180
2 91 — ц2 r4t ЗЯ2г2 — Тт- 2.181
Приведем результаты предварительных исследований, полагая в полученных выше выражениях £2 — 0> Si.oS2,o 0Задача сводится к рассмотрению уравнения 166; в рассматриваемом случае оно принимает вид
d4i со 1 -L S 5C.S3 - 0. 2.182
1 г 1 _L 2 i Т7 7ГТ U.183
di2
Значение по 174 можно представить в виде
1 О4
16 Г,
1 И
l -—l
121-ц2 1
V Tj
114
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
Уточненное по сравнению с 182 уравнение получим, определяя величину £2 из статического варианта 167. Тогда можно
Рис. 2.25. Амплитудно-частотные зависимости для различных форм собственных нелинейных колебаний оболочки.
принять приближенно £2 <p2£2; подставляя это значение в 166, приходим в случае идеальной оболочки к уравнению
С, 1 - - ф,ф2 - х С Ч 0. 2.182а
Примем решение уравнения 182 в виде
£ Л cos at. 2.184
Удовлетворяя далее условию ортогональности результата подстановки этого решения в уравнение 182, получим
v2l TXH2>
где
©о
V'-t’
2.185
2.186
На основе уравнения 182а получим вместо 185 следующую зависимость:
v2 1 — -ф1Ф2 — хЛ2 -’’1фИ4- 2.185а
Особенности нелинейных колебаний оболочки по 185 демонстрируются рис. 2.25—2.29. На рис. 2.25 приведены ампли-
§29 ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА. НЕЛИНЕЙНАЯ ЗАДАЧА Ц5
тудно-частотные характеристики собственных нелинейных колебаний для оболочки с параметрами LR 2, Rjh — 1500. Для
О 1 г 3 4 v 5
Рис. 2.26. Скелетные линии при нелинейных колебаниях оболочек для минимальных частот при различных значениях ЦК.
Рис. 2.27. Скелетные линии при нелинейных колебаниях оболочек для минимальных частот при различных значениях Rfh.
рассматриваемой оболочки минимальная частота собственных колебаний при малых прогибах отвечает числу волн п 10 см. рис. 2.17. Следующие, более высокие частоты колебаний
Рис. 2.28. Влияние параметра волнообразования на амплитудно-частотные характеристики.
0.5
7.5
г
v
Рис. 2.29. Влияние числа волн в окружном направлении на амплитудночастотные характеристики.
отвечают числам волн лг 11,9, 12, 13, 8, 14, 15, 7 и т. д. в соответствии с правой и левой ветвями кривой рис. 2.17. Рис. 2.25 определяет зависимость амплитуды от частоты при нелинейных колебаниях оболочки с числами волн, отвечающими спектру частот малых колебаний в соответствии с рис. 2.17. На этом
116
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
графике для величины v вместо 186 принято отношение частоты колебаний к минимальной частоте п 10, т. е. v со©о, mjn Таким образом, точки пересечения кривых рис. 2.25 с осью абсцисс определяют отношение частоты собственных колебаний оболочки при малых прогибах,к минимальной частоте.
На рис. 2.26, 2.27 приведены амплитудно-частотные зависимости по 185, 186 для волнообразования, отвечающего минимальным частотам малых колебаний в соответствии с данными рис. 2.18. Первый из этих графиков построен для оболочек с параметрами LR 1, 2, 3 при Rh 1500. Второй график отражает влияние параметра Rh при LR 2.
Влияние характера волнообразования на амплитудно-частотные зависимости характеризуется рис. 2.28 и 2.29. График рис. 2.28 построен для случаев, когда соотношение между параметрами волнообразования и г отвечает значению по 148, при котором величина верхнего значения параметра критической нагрузки при осевом сжатии оболочки рв 0,605. На рис. 2.29 показано влияние числа волн по окружности при отношении длин полуволн Ф 2.
§ 30. Удлиненная цилиндрическая панель.
Метод Бубнова—Галеркина
Переходя к задачам о собственных колебаниях панелей, рассмотрим вначале случай, когда сторона пологой панели радиуса R вдоль образующей значительно превышает размер b
вдоль дуги. Как и в случае плоской полосы, примем, что панель скреплена с ребрами и при колебаниях напряжения в срединной поверхности оу не зависят от координаты у оу а. Задачу сводим к исследованию колебаний полосы шириной, равной единице, и имеющей размер вдоль дуги, равный b рис. 2.30.
Уравнение движения 1.35 принимает вид
Рис. 2.30. Удлиненная пологая цилиндрическая панель.
D d4w hW
d2w. a
i d2w л P-57T °-
2.187
Выражение для прогиба в случае шарнирного закрепления примем в форме
пУ О 1 QQ
§30 УДЛИНЕННАЯ ПАНЕЛЬ. МЕТОД БУВНОВА-ГАЛЕРКИНА Ц7
Величину а найдем из условия закрепления краев. Взаимное сближение А принимаем равным нулю:
ъ
Д 17 0. 2.189
о
Из выражений 1.5 и 1.12 имеем
° 1 2 I dw 2. w л 1ПЛ.
ду Е ц 2ду R’ 2.189а
Отсюда
Т61- “Т2 dy j-jdy. 2.190
о о
Подставляя выражение 188 для прогиба, найдем
«—-грт-й-4т- <2Л91>
Используя далее процедуру Бубнова — Галеркина
ъ
ЛР d4w Е я2 Р 2 f d2w
h ду4 1 — jx2 4 Ь2 я R ду2
о
Е я2 f2 2 f. у d2w 1. пу л, _Я1-ц24 Ь2 п a2iSinX °» 2-192
получим следующее уравнение движения:
-g- «>£- К2 л£» 0, 2.193
где величина квадрата частоты при малых колебаниях определяется по формуле
я4 c2h2
< 12 П — и.2 64 я6 29 2.194
12 1 — ы2 64
параметр кривизны k b2Rh, с YEgy. Величины р и rj равны
3fe8 ’ 2Л95
— 4- — к2
12 я3
4 1 55—• 2196
i 71'
Для отыскания амплитудно-частотной характеристики нелинейных колебаний примем
£ Лсозсо. 2.197
118 СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ГЛ. II
Проводя здесь интегрирование по четверти периода 2.10, получим
у21--рЛ тИ2. 2.198
Исследуя случай панели с защемленными краями, задаемся следующим выражением для прогиба:
w f sin2--.
Аналогичным путем находим выражение для <т: а- ё—Ц 1 -ц2 2R 4 Ьг ’
Уравнение движения приводится к виду 193, где
2 _ я4 cW 16. 8k2
0 12 1 — ц2 Ь4 3 я4 '
Для величин р и г имеем выражения
ft — l2k
р 2 16, 8k2 ’
712 Ы 1
4
<П 16 86
3 я4
§ 31. Удлиненная цилиндрическая панель.
Метод конечных разностей
Обратимся к решению задачи о колебаниях панели, шарнирно закрепленной по краям, с применением метода конечных разностей.
Определяя а из выражения 190 и подставляя в 187, получим следующее уравнение в частных производных:
D d4w Е Г Г,dw 2, Г w, 1 d2w
TW 1 i2b 2 J аУ — r ay
L о о J
- f«-i T -«• <2-204>
L о 0-1
2.199
2.200 2.201
2.202
2.203
§ 31 УДЛИНЕННАЯ ПАНЕЛЬ. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 119
Вводя безразмерные величины w wjh, уb, т tT, где Т 2jtcob а со0 определяется по 194, приходим к уравнению
1
2.205
Если в уравнении 187 и соотношении 189а пренебречь нелинейными членами, то получим следующее уравнение для исследования задачи в линейном приближении:
-rt1 24S- iF12fe2 0- 2-206
о
При интегрировании уравнений 205, 206 в конечных разностях были приняты граничные и начальные условия по 102, 103. Число шагов вдоль координаты g по-прежнему было принято равным п 20, отношение шагов sxst 140.
Проведем анализ полученных результатов. Оценим прежде всего влияние величины прогибов, задаваемых начальными условиями, на собственные колебания панелей различной кривизны.
Рассмотрим данные рис. 2.31 —2.38. На этих графиках время т отнесено к периоду собственных колебаний при малых прогибах, найденному с учетом кривизны соответствующей панели по формуле 194.
На рис. 2.31 показаны прогибы точек срединной поверхности панели с параметром k 10 в различные моменты времени, обозначенные на графике номерами шагов вдоль координаты т по данным решения линейной задачи на основе 206 и нелинейной — в соответствии с 205 при амплитуде стрелы прогиба А 0,1. Как видим, в этом случае получаются весьма близкие результаты. Движение центральной точки i 10 по двум решениям отражается рис. 2.32; тонкая линия отвечает линейной задаче. Здесь же показано движение другой точки i 1; оно совпадает по частоте с законом движения центральной точки. Как видим, это значение частоты соответствует вычисленному по формуле 194.
В отличие от случая k 0, рассмотренного в § 25, движение панели с параметром k 10 рис. 2.31 характеризуется изменением формы дополнительных прогибов срединной поверхности, задазаемой начальными условиями.
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ.
Рис, 2.31. Изменение формы прогибов во времени для пологой оболочки с параметром кривизны £ 10 при исходной амплитуде прогиба в центре Л0,1: а по данным линейного приближения, б по данным решения нелинейной задачи.
Рис. 2.32. Движение различных точек во времени по данным решения линейной и нелинейной задач для оболочки с параметром k 0 при амплитуде прогиба Л —0,1.
Иг
а
А5
б
Рис. 2.33. Изменение формы прогибов во времени для пологой оболочки С параметром кривизны k 10 при амплитуде исходной формы Л5: а линейная задача, б нелинейная задача.
УДЛИНЕННАЯ ПАНЕЛЬ. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Рис. 2.34. Изменение стрелы прогиба во времени по данным решения линейной и нелинейной задач для оболочки с параметром 10 при амплитуде прогиба А 5.
Ш
АЦ
ш
Рис. 2.35. Изменение формы прогибов во времени для пологой оболочки с параметром кривизны 24 при амплитуде прогиба в центре Л 0,1: а линейная задача, б нелинейная задача.
Рис. 2.36. Закон движения различных точек во времени по данным двух решений для оболочки с параметром 24 при амплитуде прогиба в центре Л0,1.
122
COBCf ВЁННЫЁ НЁЛЙНЕЙНЫЁ КОЛЕБАНИЯ
ГЛ. II
При амплитуде А 5 рис. 2.33 решение нелинейной задачи приводит к иным результатам по сравнению с линейным вариантом. В первом случае выявляется возрастание частоты собственных колебаний оболочки при больших прогибах. Это
Рис. 2.37. Изменение формы прогибов для оболочки с параметром 24 при амплитуде прогиба в центре А5: а линейная задача, б нелинейная
задача.
Рис. 2.38. Закон движения центральной точки по двум решениям для оболочки с параметром k—24 при амплитуде прогиба в центре А5.
обстоятельство более наглядно демонстрируется данными рис. 2.34, где показано изменение стрелы прогиба во времени по данным линейной тонкая линия и нелинейной задач. Значение частоты нелинейных колебаний равно v 1,52; определяя частоту по формуле 198, находим v 1,28.
Аналогичные данные для панели с параметром кривизны k 24 приведены на рис. 2.35—2.38. В этом случае даже при малых прогибах А 0, 1 наблюдается резкое изменение формы, задаваемой в виде полуволны синусоиды в момент т О
§31
УДЛИНЕННАЯ ПАНЕЛЬ. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
123
рис. 2.35. Этим графиком демонстрируется одинаковый характер движения оболочки по данным двух решений. На рис. 2.36 сравниваются эти решения для центральной точки; здесь же
Рис. 2.39. Влияние параметра кривизны оболочки на частоту нелинейных колебаний при амплитуде прогиба в центре Л 1.
нанесена кривая двжения другой точки 1. В отличие от рассмотренного выше случая k — 10, здесь даже при малых прогибах движение оболочки носит нерегулярный характер. Особенности проявляются также при сравнительном рассмотрении движения разных точек, характеризующегося различной частотой.
При этом частота центральной точки оказывается несколько ниже значения по 194, а для второй точки — существенно выше этого значения.
При амплитуде 45 собственные колебания оболочки отвечают движениям около прощелкнутого положения равновесия рис.
2.37, б; это не выявляется в линейной задаче рис.
2.37, а. Различие в характере движения центральной точки по этим решениям показано на рис. 2.38.
Как видно из сравнения рис. 2.9, 2.34, эффект возрастания частоты при больших прогибах по отношению к частоте колебаний панели соответствующей кривизны при малых прогибах претерпевает заметное снижение по мере увеличения параметра кривизны.
Рис. 2.40. Влияние параметра кривизны оболочки на частоту нелинейных колебаний при амплитуде прогиба в центре Л—5.
124
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
С другой строны, с ростом амплитуды прогиба сглаживается различие в значениях частот нелинейных колебаний для панелей разной кривизны. Это демонстрируется рис. 2.39, 2.40 для амплитуд А 1 и А 5; во всех этих случаях время т отнесено к периоду малых колебаний плоской панели в соответствии с формулой 94а. При А 5 увеличение параметра кривизны приводит к некоторому снижению частоты собственных нелинейных колебаний.
§ 32. Круговая цилиндрическая панель с конечным отношением сторон
Рассмотрим случай колебаний пологой круговой цилиндрической панели с конечным отношением сторон рис. 2.41.
Примем, что края панели шарнирно оперты и что они смещаются свободно вдоль дуги и вдоль образующей; при этом кромки панели в срединной поверхности остаются прямолинейными.
По криволинейным кромкам панели действуют сжимающие усилия р, равномерно распределенные по ширине.
Пусть R — радиус срединной поверхности панели, а, b — размеры сторон опорного контура в плане, h — толщина. Расположение ко-
Рис. 2.41. Круговая цилиндрическая ОрДИНаТНЫХ ОСеЙ ПОКаЗЭНО НЭ
панель с конечным отношением Сто- г су л
рон под действием осевых сжимаю- рИС. Z.41.
щих усилий. Исходные уравнения примем в
виде 1.40, 1.41.
Решая задачу в первом приближении, прогиб w аппроксимируем в виде
w ft sin sin. 2.207
Подставляя 207 в уравнение совместности деформаций 1.41, определяем функцию напряжений в срединной поверхности
Ф e.pvcos cosM.
2.208
где Х аЬ. Удовлетворяя далее соотношению 1.40 по методу Бубнова — Галеркина, получаем следующее обыкновенное диф¬
§32
КРУГОВАЯ ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ
125
ференциальное уравнение, описывающее собственные колебания панели:
принято t> fxthy х со, р pb2Eh2, рв pQb2Eh2. Параметр рв верхнего критического напряжения равен
параметр кривизны k b2Rh. Квадрат основной частоты собственных колебаний идеальной панели при малых прогибах без учета сжимающих усилий определяется в виде
При действии усилий осевого сжатия панель получает новую устойчивую равновесную форму в области больших прогибов. Поэтому становятся возможными три типа колебательных движений: около основного положения равновесия около прощелкнутого положения £3 и скачкообразные перемещения оболочки от одного положения устойчивого равновесия к другому хлопки оболочки, связанные с пересечением уровня, отвечающего неустойчивому положению равновесия.
Возможные равновесные положения панели определяются корнями уравнения 209 в статическом варианте.
При р < 2 Y Л оболочка имеет единственное положение равновесия, около которого происходят колебания; при Р > 2 Y система имеет три положения равновесия.
Упругие характеристики панелей с различными параметрами кривизны k приведены на рис. 2.42 в соответствии с соотношением
Как видим, во всех этих случаях оболочка имеет единственное положение равновесия.
-5т 4 f1 - А- £ - Р£2 т£3 о, 2.209
а т о рв
„ я2 1 Л22. кгX2
рв 12Л2 1 — и-2 я2 1 Л22 ’
2.210
о о С П
со2 я2рв-,
2.211
где c — YEgjy. Под Р и понимаются величины
2.212
2.213
t 0,75W 1 А4,
где
2.214
f с—с—ps2e
2.215
126
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
Для панели, испытывающей осевое сжатие, из уравнения
215 при f£ 0 находится диаграмма равновесных форм
идеальной панели, определяющая равновесные точки при произвольном уровне осевого нагружения; соответствующая диаграмма £ для панели с параметром кривизны k 24 приведена на рис. 2.43. Параметр верхней критической нагрузки в этом случае равен рв18; нижнее критическое значение 4,6-
Перейдем к исследованию амплитудно-частотных зависимостей. Принимая приближенное решение уравнения 209 в виде
£ Лсоэт 2.216
и удовлетворяя условию ортогональности результата подстанов-
Рис. 2.42. Упругие характеристики панелей с различными параметрами кривизны.
О 1 Z 3 4 5 С
Рис. 2.43. Диаграмма равновесных форм для оболочки с параметром k24.
Рис. 2.44. Влияние параметра кривизны оболочки на амплитудно-частотные зависимости.
ки этого решения в 209 к функции cos т по четверти периода, получим выражение типа 198
v21--r T2'
где
со0
74'
2.217
2.218
§ 33 СЛУЧАЙ ПАНЕЛИ С ИСКРИВЛЯЮЩИМИСЯ КРОМКАМИ В ПЛАНЁ 127
Амплитудно-частотные характеристики для панелей различной кривизны при отсутствии начальных усилий сжатия приведены на рис. 2.44.
§ 33. Случай панели с искривляющимися кромками в плане.
Уточненное решение
Рассмотрим решение той же задачи о панели конечных размеров в несколько иной постановке. Будем считать, что шарнирно закрепленные кромки цилиндрической панели свободно искривляются, оставаясь в плоскости опорного контура. Размеры сторон панели в плане обозначим здесь через 2а и 26. Начало координат расположим в центре, а оси х и у направим соответственно вдоль сторон 2а и 2Ь.
Безразмерные параметры введем в виде
Здесь TQ — период основного тона малых колебаний квадратной шарнирно опертой пластинки. Формулу 31 для частоты собственных колебаний основного тона в случае квадратной пластинки представим в виде
Тогда безразмерный параметр времени определится следующим образом:
Исходные уравнения для цилиндрической панели в безразмерных параметрах примут форму черточки над безразмерными параметрами опускаем
2 д4Ф. 0 д<Ф 1 дФ _ Л дх дх2ду2 X2 ду
2.219
-t. 2.220
J i d2w. d2w д2и
L 4 У дх2 дх2 ду‘
, d2w d2w d2w
дх2 ду2 дх di
2.221
д2Ф d2w, д2Ф d2w 0 д2Ф d2w
ду2 дх2 дх2 ду2 дхду дхду
<92ф d2w 1 л2
дхду дхду J 16А,2
я2 d2w Ш2‘д:х29
Приведенные ниже данные получены А. А. Логвинской, В. В. Рогале вичем и автором, ДАН СССР 205, 2 1972, 44—46.
128 СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ГЛ. II
Интегрирование этих уравнений должно вестись с учетом граничных и начальных условий.
При свободном шарнирном опирании краев граничные условия имеют вид
д2хю д2Ф д2Ф л,
W дхг дуг дхду При х±1>
d2w д2Ф д2Ф л t
w-W -d7dj 0 ПРИ
Эти условия могут быть представлены в форме
d2w дФ л о> -ЖгФг 0 при х±1,
d2w -ч дФ л а, а ф 7 0 ПРИ У±1-
Начальные условия примем в виде
л dw п п
w A, -57 — 0 при т 0,
где А — начальное отклонение от положения равновесия в центре панели.
Для решения задачи выберем путь, несколько отличающийся от принятого в § 32: будем применять метод Бубнова — Галеркина не только к уравнению равновесия, но и к уравнению совместности деформаций.
Рассмотрим решение задачи в первом приближении и по координатным, и по временной функциям.
Граничные условия удовлетворяются точно, если положить
W х, у, т W т cos cos, I
z z j 2.222 Фх, У у т Фц т1 cos лх 1 cos яу, J
Подставим 222 в уравнения 221 и применим к каждому из них процедуру Бубнова — Галеркина.
Из уравнения совместности деформаций получим зависимость между функцией напряжений и прогибом
ф 1 2 о 99Q
11 9я4 3 2А,2 ЗА,4 у П 83 2л2 3я4 11’
а уравнение движения примет вид
я2Я2 12и - 121 -ц2§Л2Фи 4Я2я11Фи--0.
2.224
Подставим значения функции напряжений 223 в уравнение 224; получаем обыкновенное нелинейное дифференциальное
§ 33 СЛУЧАЙ ПАНЕЛИ С ЙСКРЙВЛЯЮ1ЦЙМЙСЯ КРОМКАМИ В ПЛАНЕ 129
уравнение
где
■-Enawn-yw2npw3i0
2.226
4096Я4
а _ я2Я2 I2 с 81я6 3 22 32Л4 «.
Y с РС
Ь2
3V у’
Зя2 3 2Л2 ЗА,4 я2Л4
2 3 2А,2 ЗЛ4 ’
С 121 -Ц2.
Ьуу
2.226
Второй этап решения состоит в интегрировании уравнения 225. Приведем решение в первом приближении и по временной функции, полагая колебания гармоническими.
Представим решение уравнения 225, как это было принято в § 19, в виде
w t A cos соty 2.227
удовлетворяющем начальным условиям задачи.
Дальнейшее исследование по временной функции проведем с помощью метода Бубнова — Галеркина. Тогда получим прежнюю формулу для определения частоты колебаний цилиндриче ской панели, отнесенной к частоте малых колебаний квадратной шарнирно опертой пластинки:
V а м2.
2.228
Рассмотрим уточненное решение задачи, аппроксимируя изогнутую поверхность пластинки или оболочки с помощью нескольких параметров. Такое решение даст возможность проследить за изменением формы изогнутой поверхности по времени. В этом случае вычисления усложняются, и для их выполнения должны быть привлечены электронные цифровые машины.
Ниже приведено решение по. методу Бубнова — Галеркина в третьем приближении по координатным функциям; интегрирование по времени выполнено методом Рунге — Кутта.
Представим функции w и Ф в виде рядов, удовлетворяющих приведенным выше граничным условиям:
ЛХ лу, ЛХ Зли I
W wn COS COS -у- W12 cos -тр cos I Злх ли
w2l cos — COS -f-
Ф Ф i 1 -J- COS fix 1 -- COS Ш “f Ф12 1 — cos 2nx X
X 1 COS Jty-f Ф21 0 cosnl — cos2jiy.
2.229
130
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. и
2.230
Применяя метод Бубнова — Галеркина одновременно к обоим основным соотношениям, получаем три уравнения движения
-- Я2 dxwn-cd< Ф„ 0,8Ф12 0,8Ф21
с2 2 wn 2Ф,, Ф12 Ф21 2ш12 ЗФ,, Ф12—4,5Ф21
2ш21 ЗФп-4,5Ф12 Ф21,
я2d2wX2 - cd40,2ФИ 0,16Ф2 - у Ф21
ск2 2w ЗФц Ф12 — 4,5Ф21 18ш12Фц Ф2
25да21 0,64Ф„ — Ф12 — Ф21,
— я2 d3w2i — cd4 1,8Фц 12 ”Ь 1>44Ф21 j
сХ2 2wu ЗФц — 4,5Ф12 -f- Ф2
25ш12 0,64Фи — Ф12 — Ф21 18йУ21 Ф„ Ф12,
и три уравнения совместности деформаций
rf5On 2Ф12 2А4Ф21 d8 -Jg wn ш12 0,05ву21 —
T2wn wu 3wu 3wv 9K2 О 16ЮЛ,
2Ф„ d6012 ds wu 215012-7 ®2i -
- Ж ®U ®I1 2ш12 - 9®2i 9wli - 25йУ12ш21,
2Л4ФП й7Ф21 ds ■-jg- wu — ш 12 0,04ay2I —
- ■ К wn - 9ш12 2wv 9ау12 - 2ба»12ю21.
Здесь приняты обозначения:
dt - к2 12, d2 - A.2 92, d3- 9Х2 l2, dk d5 2A4 2 X2 l2, d6 32Я4 2 Д4А2 l2, d7 32 2A4 A2 42, ds -ky.
2.231
256Я2, 9я4
Уравнения 230 представляют собой систему обыкновененых дифференциальных уравнений, а уравнения 231—систему алгебраических уравнений.
§ 33 СЛУЧАЙ ПАНЕЛИ С ИСКРИВЛЯЮЩИМИСЯ КРОМКАМИ В ПЛАНЕ 131
Принимаем следующий порядок вычислений. Задаем начальное отклонение в виде полуволны синусоиды в обоих направлениях, т. е. Wu Л, w 12 0, w21 0 при т 0, а значение
Рис. 2.45. Изменение во времени прогиба в центре квадратной пластинки при различных начальных отклонениях.
функции напряжений в начальный момент определяем по формуле 231. Затем находим значения wn, wi2, w21 в момент Ат, интегрируя систему уравнений 230 методом Рунге — Кутта.
Шаг по времени выбирается таким образом, чтобы была обеспечена устойчивость решения уравнений 230. Значения Фц,
Ф12, Ф21 в момент Ат определяем путем решения системы уравнений 231. Эта система является линейной, так как входящие в правые части значения ШцАт, до 12 Ат, 1021 Ат уже вычислены на предыдущем этапе.
Далее вычисления повторяются: находятся Шц2Ат,
1С>12 2Ат, 2i2At путем интегрирования системы 230, а затем 2Дт — из системы 231 и т. д.
Значения w и Ф в произвольной точке панели вычисляются для заданного момента времени по формулам 229.
На рис. 2.45 дана зависимость прогиба в центре квадратной пластинки wo от времени при различных начальных
Рис. 2.46. Изменение формы пластинки во времени при амплитуде Л5.
Фи, Ф12, Ф21 в момент
132
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
отклонениях. При А 1 колебания пластинки являются гармоническими, а форма изогнутой поверхности сохраняется первоначальной. Полученное решение практически, как оказалось, совпадает с решением в первом приближении.
Если начальное отклонение превышает толщину пластинки, то колебания резко отличаются от чисто гармонических. При этом и форма колебаний в некоторые моменты времени существенно отличается от полуволны синусоиды рис. 2.46; эти данные получены при амплитуде А 5.
Отметим, что наблюдается рост периода колебаний по сравнению с первым приближением. К такому же результату пришел Э. И. Григолюк 2.10, рассматривая решение во втором приближении по координатным функциям, но предполагая, что пластинка совершает гармонические колебания при любом начальном отклонении.
§ 34. Случай панели двоякой кривизны
Перейдем к исследованию случая пологой панели произвольного очертания срединной поверхности, прямоугольной в плане
рис. 2.47.
Будем считать, что панель шарнирно оперта по контуру при наличии свободного смещения точек ее краев вдоль линий кривизны дс, у.
Допустим, что оболочка имеет начальные отклонения в срединной поверхности, отвечающие форме дополнительного прогиба.
Размеры сторон опорного конту-
Рис 2.47. Пологая панель’ двоякой Р В ™3He рЗВНЫ d Ь. ГлаВНЫв КРИкривизны. визны оболочки kx, ky предпо-
лагаются постоянными.
Динамические уравнения нелинейной теории пологих оболочек выпишем в виде 1.38, 1.39:
V4 w — w0 — Lw, Ф kx ky — р--, 2.232 --L у<ф — j L w, w — L w0, йу0 —
2-233
Для полного и начального прогибов примем выражения
W ft sinsin-у-, Wq U sinsin2.234
§ 34 СЛУЧАЙ ПАНЕЛИ ДВОЯКОЙ КРИВИЗНЫ 133
Из уравнения 233 определяется функция напряжений в срединной поверхности
ф. У, о —- ft » vcos -Т-
f£ sinsin- , i
1 E I v■f sinsin T ■ <2-235>
Пользуясь методом, использованным выше, получим следующее обыкновенное дифференциальное уравнение колебаний оболочки:
-g- 002 аГ - т£3 0; 2.236
здесь £ flth, i0 f0h, flf — f0; ю2 —квадрат основной частоты собственных колебаний идеальной панели при малых прогибах:
2.237
n2c2h2 wo a2b2
где
jf — я2 1 A,22 1 А2 ь2 о 238
12Я2 1 -i2 n2X22 K • V-too
Через с по-прежнему обозначается скорость распространения продольных волн в материале оболочки; ХаЬ. Безразмерные параметры кривизны оболочки равны
<2.239
Для величин а, р, т получаем выражения
л2 2, „ 16А,4’ Г 8 1
а 1 l2F¥L з1 ii5 L1 TTWJ-
16k Г. 8А.4 „
лГ L1 1 л22 J1 2-240
й 2 116Ч г1, 8 1,
Р— 2У I я4 2 lA.22J'r
16fe Г 1 8А,4 1 9, 1
T2-TiwJ--I l,£»’ <2241>
Ч 0'75-2Р 1'' 2.242
134
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
Если полагать, что оболочка испытывает действие статического давления qo, то получим упругую характеристику в виде
<7о « — К2 Л3> 2.243
где параметр д0 выражается через интенсивность статического давления qo по формуле
16А.2М4 ППлл
wt q°- 2.244
В частном случае сферической оболочки надо принять kx kv lR величина k по 239 будет равна k — 2b2Rh.
О г 4 6 8 10
t
Рис. 2.48. Диаграммы равновесных форм для идеальных панелей различной кривизны.
Зависимости до£ для сферических панелей при X ab 1 приведены на рис. 2.48, 2.49. Графики рис. 2.48, построенные при различных k, представляют собой диаграммы равновесных форм для идеальных панелей £о 0. Как видим, при значениях к, равных 36, 48, 60, становится возможным прощелкивание оболочки при действии статического поперечного давления q0i превышающем нижнее критическое значение qH. При k 48 величина дн 0,87; верхнее значение этого параметра равно q в — 1,18.
•Влияние начальной погиби для панели с параметром k 48 видно из рис. 2.49, здесь принято £0 0; 0,1; 0,25; 0,5.
Исследуя собственные колебания оболочки, примем решение уравнения 236 в виде 197. Пользуясь использованным выше методом, получим следующее уравнение для определения амплитудно-частотной характеристики
’’“‘-■s.w H. <2-246>
СЛУЧАИ ПАНЕЛИ ДВОЯКОЙ КРИВИЗНЫ
138
где
Va
СОо
2.246
Данные вычислений, относящихся к идеальной панели при kl ky 24, приведены сплошными линиями на рис. 2.50. Для
¥
12 10 0,8 о,в
Ofl
O.Z
У
1
kZ0o-
48
Ц25
>Ио”фО-
Ш-Ж
— 7
чХЙ
1
It II 5 С
У
' и
О 2 4 S В 10
е
Рис. 2.49. Влияние начальной погиби на диаграмму равновесных форм.
Рис. 2.50. Амплитудно-частотные зависимости для пологих оболочек различной кривизны.
сравнения здесь приведены случаи пластинки kx — kl 0 и цилиндрической панели 0, ky — 24. Соответствующие зависимости для панелей с начальными неправильностями в форме срединной поверхности при £0 0,5 обозначены пунктирными линиями.
136
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. I
§ 35. Пологая сферическая панель. Решение методом прямых
В заключение рассмотрим собственные колебания пологой сферической оболочки кругового очертания. Общие уравнения для этого случая имеют вид 1.42, 1.43. Учитывая линейное демпфирование, перепишем их в виде при w0 0
под F понимается величина ФЛ. Введем следующие безразмерные параметры:
Здесь под R и с понимается радиус кривизны срединной поверхности и радиус панели в плане.
С помощью введенных параметров уравнения 247 и 248 запишутся следующим образом:
В уравнениях 249 и 250 звездочки для упрощения записи опущены.
Изгибающие моменты, усилия в срединной поверхности, перемещения и деформации выражаются через функции F и w. Введем и для них безразмерные параметры:
Результаты, изложенные здесь, получены Н. В. Валишвили и В. Б. Сил киным Изв. ВУЗ’ов, Машиностр., 2, 1969, 24—28.
£>V-1-V2F LF, w q 2.247
JL V47 — V2o> — у Z. да, w, 2.248
-e, 2.247
V4w V2
2.249
2.250
§ 35 ПОЛОГАЯ СФЕРИЧЕСКАЯ ПАНЕЛЬ. РЕШЕНИЕ МЕТОДОМ ПРЯМЫХ 137
В приведенных выражениях оХу т — полные напряжения, а
ои ого — соответственно главные напряжения и интенсивность
напряжений у поверхности оболочки. Формулы для М2, N2 и т. д. запишутся по аналогии.
В дальнейшем будем пользоваться цилиндрической системой координат. При этом длину радиуса-вектора обозначим через г, а полярный угол — через р. Формулы перехода от декартовой системы координат к цилиндрической можно получить, совместив ось х первой системы с радиусом-вектором г.
Производные от w по х и у выражаются через производные от w по г и р следующим образом:
dw dw dw 1 dw d2w d2w
dx dr dy r d5 ' dx2 dr2
d2w d2w 1 dw d2w 1 dw. 1 d2w
dxdy rdrdfi d TyrTdF l2'
Оператор S72w равен
d2w - d2w d2w - 1 dw. 1 d2w
V W dx2 dy2 dr2 тТдГ 'гтдг
_d_ I dw 1 d2w
r dr v dr r2 ap2
Аналогично выражаются производные от функции усилий F. В цилиндрических координатах уравнения 249 и 250 примут вид
vvf ± ££ -L -
V W V Г -Г дг2 г дг2 -Г Г2 J
0 d2w 1 dw d2F 1 dF.
r dr d r2 d j r dr dp r2 ap J t
W —»‘—SL74r F -»>
В дальнейшем будем исследовать лишь осесимметричную деформацию оболочки. При этом все соотношения значительно упрощаются, так как функции w и F будут зависеть только от переменных г и t. Уравнение 252 переходит в следующее:
Id d 1 d dF 1 _d_ dw I dw d2w opro
r dr Г dr r dr Г dr r dr Г dr r dr dr2 '
Умножив правую и левую части уравнения 253 на г и проинтегрировав его, получим следующее соотношение:
d d dF dw. 1 dw 2, n A
r'dFTdFrdFrd TVdF C
138 СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ГЛ. II
Для замкнутых в вершине оболочек функция Ct обращается в нуль.
Введем новую разрешающую функцию ф dFdr. Производные по г в дальнейшем будем обозначать штрихом, по t — точкой.
Окончательно получим следующую систему уравнений:
w' I w w' I i I w' i
W — w — — — тг ф1 — w — еш 4, 2.254
Ф »'1- 2-255
Для усилий и деформаций получаем выражения
N2 ф',
е, и' — w j ад'2 7- — Цф'> г2 у' — i-y и т. д.
Исследуем собственные осесимметричные колебания панели, защемленной по контуру рис. 2.51, предполагая, что на нее
п р едв арительно дей ствует давление заданной интенсивности q. Считаем, что в начальный момент времени давление падает внезапно до нуля. Определим последующее движение оболочки.
Исходное состояние оболочки определяется из решения статической нелинейной задачи. В уравнениях 254 и 255 опускаем производные по времени и интегрируем 254. Постоянная интегрирования для рассматриваемого случая обращается
в нуль. Таким образом, получаем уравнения
е т - уг Ф :1 ■ 2qr, 2.256
Ф 01» <2-257>
где 0 dwdr.
Рис. 2.51. Пологая сферическая панель под действием равномерного давления.
§ 35 ПОЛОГАЯ СФЕРИЧЕСКАЯ ПАНЕЛЬ. РЕШЕНИЕ МЕТОДОМ ПРЯМЫХ 139
Эта задача может быть решена, например, с помощью алгоритма, изложенного в работе Н. В. Валишвили.
Рис. 2.52. Движение вершины сферической оболочки при различных видах нагружения в исходном положении.
Далее переходим к основным уравнениям 254 и 255, описывающим движение элемента оболочки. Эти уравнения преобразуются с помощью формул центральных конечных разностей:
ъ1-ъ- М
2Д
2Дг
vti-2wt wt-i гД2
Ф 1
2А
Ф wi2 - 4тш 6wt - 4 wt_2
п А4
w,, л — 2 w., 2 w,, — w •
— — Ц - еш 2.258
ФИ1 7 _ т -
2;259
где А bщ п — число участков, на которое разделяется радиуг панели.
Для формулировки граничных условий в вершине и на опорном контуре, наряду с узловыми точками, номер которых равен
См. Прикл. матем. и мех., 6 1968.
140
СОБСТВЕННЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГЛ. II
0-т-м, вводятся фиктивные узловые точки вне отрезка 0; Ь. Эти точки имеют номера —1 и г 1.
Условия при г 6, т. е. при rn b, определяются характером закрепления опорного контура. В случае жесткого защемления контура при rn b имеем
w 0, w' 0, е2 0,
или
w 0, w' 0, ф'-м,-0. 2.260
Далее ведем интегрирование по времени, пользуясь методом Рунге—Кутта. При вычислениях отрезок b делился на 20 равных частей. Ниже приведены данные решения задачи.
§ 36. Описание колебаний сферической панели
Колебательный процесс, испытываемый оболочкой, зависит в значительной мере от интенсивности предварительно приложенной нагрузки в сравнении с критическим статическим значением. Мы будем принимать эту величину меньшей верхнего критического значения, равной или превышающей его.
Рис. 2.53. Движение различных точек сферической оболочки при исходном нагружении давлением, равным верхнему критическому значению.
Параметр кривизны панели был принят равным 6 4.
На рис. 2.52 и 2.53 изображены данные вычислений. В первом из них по оси ординат откладывается параметр нормального прогиба в вершине оболочки wl, по оси абсцисс вправо — параметр времени t а влево — параметр давления q, определяющий начальное деформированное состояние оболочки. Видно, что если начальные прогибы малы, то движение вершины
§ 36
ОПИСАНИЕ КОЛЕБАНИЙ СФЕРИЧЕСКОЙ ПАНЕЛИ
141
оболочки близко к гармоническому. В качестве примера на рис. 2.52 приводится график движения вершины оболочки при начальном напряженном и деформированном состояниях, определенными точкой. Этой точке соответствует q 0,19 и начальное значение параметра нормального прогиба в вершине Wo 0,515 или Wo 0,163i. При этом безразмерный период колебаний равен Т 4,3. Заметим, что верхняя критическая нагрузка для рассматриваемой оболочки равна q 0,56, а максимальный период линейных свободных колебаний в соответствии с решением задачи в функциях Бесселя равен Т 5,3. Практически такое же значение периода получается при численном решении системы уравнений 254, 255, если в них опустить нелинейные члены.
Приведенные на рис. 2.52 графики показывают, что при значениях давления, близких к критическому, движение вершины оболочки имеет весьма сложный характер.
На рис. 2.53 приводятся графики движения отдельных точек оболочки при исходном давлении, равном верхнему критическому q 0,56. Как видим, отдельные точки срединной поверхности оболочки движутся несинхронно.
В итоге получаем примерно ту же картину, что и для цилиндрической панели см. § 31 при решении задачи в конечных разностях.
Задачи о собственных колебаниях пластинок или оболочек, рассматриваемых как системы со многими степенями свободы, ждут дальнейшего тщательного исследования.
См. книгу О. Д. Ониашвили 0.16.
ГЛАВА III
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
§ 37. Характер вынужденных нелинейных колебаний пластинок и оболочек
Проведенное в предыдущей главе рассмотрение собственных колебаний пластинок и оболочек позволяет нам перейти к исследованию других типов колебаний. Хотя собственные колебания и изучались без учета демпфирования, в реальных системах они быстро затухают из-за внутреннего трения в материале, сопротивления среды и т. д. Поэтому исследование собственных колебаний является важным, как уже было сказано, не только само по себе, сколько для оценки поведения системы при наличии внешних возмущающих сил того или иного характера. Настоящая и следующая главы будут посвящены случаю действия периодических внешних воздействий.
Для упругих систем, обычно изучаемых в курсах теории колебаний, различают «обычные» и «параметрические» нагрузки. Первые из них изменяются независимо от колебаний самой системы, они фигурируют в уравнениях, описывающих движение системы, как некоторые функции времени и пространственных координат. Нагрузки второго типа входят в уравнения в виде некоторых параметров.
Нагрузкам первого типа соответствуют вынужденные колебания, • второго типа — параметрические. Обратимся сначала к вынужденным колебаниям. Надо, правда, сказать, что в гибких пластинках и оболочках нагрузки «обычного» типа — например, нормальное давление — могут вызывать периодически изменяющиеся усилия в срединной поверхности; тогда возникнут вибрации параметрического типа.
Вынужденные колебания, в отличие от собственных, уже не являются затухающими. При некоторых условиях амплитуды колебаний, а вместе с тем деформации и напряжения в пластинке или оболочке, резко возрастают. Подобные колебания могут быть опасными для реальных конструкций. Они часто
ХАРАКТЕР КОЛЕБАНИЙ ПЛАСТИНОК И ОБОЛОЧЕК
143
приводят к образованию усталостных трещин даже в случаях, когда напряжения остаются лежать в пределах упругости.
Если рассмотреть пластинку как систему с одной степенью свободы, то мы получим характерные диаграммы «амплитуда перемещений — частота», изображенные на рис. 3.1, а. Под Q понимается частота возмущающих сил, под соо — собственная
а б в
Рис. 3.1. Зависимости «амплитуда-частота» для случаев нелинейных колебаний а, б и для линейной системы в.
частота малых колебаний системы; v Qcoo- Пунктиром показана скелетная линия, относящаяся к собственным колебаниям. Сплошные линии соответствуют вынужденным колебаниям. Как видим, кривые «амплитуда — прогиб» для вынужденных колебаний «следят» за линией, отвечающей собственным колебаниям. При постепенном увеличении частоты возмущающей нагрузки мы получаем последовательное повышение амплитуды, этот процесс отвечает левой ветви кривой. Если же идти в обратном направлении от высоких частот, то изменение амплитуд имеет своеобразный характер, описываемый правой ветвью кривой. Следовательно, одной и той же частоте могут соответствовать вынужденные колебания различного характера. При некоторых условиях может произойти перескок изображающей точки от одной ветви кривой к другой, сопровождающийся резким изменением амплитуды колебаний системы; для реальной пластинки такой процесс носит характер хлопка. В случае системы со многими степенями свободы описание движения значительно усложняется.
Если же речь идет об оболочке, склонной к прощелкиванию, то в простейшем случае, когда имеется в виду система с одной степенью свободы, скелетная линия пунктир, как мы видели выше § 32, имеет вид, показанный на рис. 3.1,6, и содержит «падающий» участок. Линии, характеризующие амплитуды колебаний, получают теперь иную форму сплошные кривые.
На рис. 3.1, в изображены аналогичные характеристики, относящиеся к линейной системе с одной степенью свободы.
144
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
ГЛ. III
До сих пор речь шла о результатах решения задач без учета демпфирования. На рис. 3.2 представлены такие же зависимости, но уже при наличии демпфирования.
А >
А>
А
s'
п
ft
П
1
J I
Г
а
б
В
Рис. 3.2. Зависимости «амплитуда —частотаэ при наличии демпфирования в случаях нелинейных колебаний а, б и для линейной системы в.
Вынужденные колебания в нелинейных системах характерны тем, что они могут иметь дополнительные частоты, отличные от частот возмущающих сил. Вид этих специфических колебаний зависит от исходных данных задачи,
§ 38. Колебания пластинки
Рассмотрим в качестве первого примера случай шарнирно опертой пластинки аХ с краями, свободно смещающимися в плоскости опорного контура.
Предположим, что пластинка подвергается действию периодически изменяющейся поперечной нагрузки FcosQt. При у р мем, что, кроме того, пластинка сжимается вдоль стороны а статическими усилиями р рис. 3.3. Далее будем учитывать начальные отклонения пластинки от идеальной; исходные прогибы обозначим, как и раньше, через w0.
Будем исходить из системы уравнений 1.42а, 1.43а. В качестве интенсивности поперечной нагрузки примем величину
dw
дГ 3.1
второй из этих членов отражает демпфирование колебаний в предположении, что сила сопротивления пропорциональна
Приведенные в §§ 38 и 40 решения задач даны И. Г, Кильдибековым 3.11, см. также 3.8.
л
Рис. 3.3. Прямоугольная пластинка под действием периодически изменяющейся поперечной нагрузки.
qx, у, t F cosQ —2
КОЛЕБАНИЯ ПЛАСТИНКИ
145
скорости dwdt; е — коэффициент демпфирования. Принимаем здесь, что нагрузка равномерно распределена по всей площади пластинки. Примем аппроксимирующую функцию для полного прогиба в виде
с,ч. тпх. пли 0
w f t sin - sin. 3.2
Будем полагать, что начальные прогибы распределены по аналогичному закону:
о. тпх. пли 0
00 о sin—— sin—jp. 3.3
Подставляя 2 и 3, как обычно, в правую часть уравнения совместности деформаций 1.43а, находим
тг1-W- <»•«>
Здесь аb, под m понимается число полуволн в направлении образующей, под п — число полуволн вдоль дуги. Применяя далее метод Бубнова — Галеркина к уравнению 1.42а, приходим к следующему обыкновенному дифференциальному уравнению, описывающему в первом приближении нелинейные колебания пластинки:
Ч1 -£-К«0-
--ЧоР 0, 3.5
Ро
принято
С9НГ. £о Т’ Р'Ш>
wt27c0S0 3'6
Величина р0 равна значению параметра сжимающих усилий р, вытекающему из решения линейной задачи об устойчивости пластинки при сжатии
я2т2 -1я22 п — ' Ш ' Ч 7
Ро 12Я2 1 — И-2 •
146
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
ГЛ. Ш
При определении собственно критического сжимающего усилия в этой формуле следует положить п 1 и найти число т, придающее 7 наименьшее значение. Квадрат частоты собственных колебаний при малых прогибах для линейной системы равен
где с — скорость распространения продольных волн в матери-
Отметим, что для «идеальных» пластинок при £о 0 коэффициент а оказывается равным 1, а р 0.
Если рассмотреть квазистатическую задачу и в уравнении 5 опустить члены, зависящие от t, то придем к следующему уравнению:
3.8
але оболочки: c V Egly, — удельный вес материала. Далее, в 5 фигурируют параметры
3.9
т£3-Р£2 а-Л- <7.
Ро,
ЗЛО
где
3.11
Исходя из И, мы можем определить статические состояния, около которых происходят собственные колебания пластинки.
i 88
КОЛЕБАНИЯ ПЛАСТИНКИ
147
Следующий шаг решения динамической задачи заключается в интегрировании уравнения 5. Представим приближенное решение в виде
£ AcosQt. 3.12
Подставим 12 в уравнение 5 и выпишем условие ортогональности результата подстановки к функции cosQt по полному периоду:
2я
J L it cos Qt dt 0, 3.13
где
<
■-
X
X3-PS2 aD-
-<»l тп-Ло-Ht. 3.13а P 0
Рис. 3.4. Амплитудно-частотные зависимости для основного типа колебаний в случаях квадратной и прямоугольной пластинок.
Выполняя вычисления, получим следующую зависимость между амплитудой прогиба и частотой :
v2--Vt2 atf - 0, 3.14
где К — коэффициент, зависящий от способа определения безразмерной частоты v.
Мы получаем зависимости, близкие к показанным на рис. 3.1, а. Рис. 3.5 соответствует одной из высших форм колебаний при т 3, п 1. В качестве базы при вычислении значения v везде принята частота основного тона линейных колебаний квадратной пластинки без учета сжимающих усилий; тогда v Qw0> п, К — со0, тпщ, п21 — Р1ро- Как видим, нелинейный характер колебаний выражен для высших форм более ярко, чем для основного тона.
Влияние статических усилии сжатия на вынужденные колебания квадратной пластинки отражено на рис. 3.6. Уровень сжимающих усилий выбран равным 0,9 от статического критического значения.
Такого вида результат имеет место при нечетных значениях тип.
148
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
ГЛ. lit
Результаты вычислений по уравнению 14 приведены ниже. На рис. 3.4 изображены амплитудно-частотные кривые, отно-
v
Рис. 3.5. Амплитудно-частотные зависимости для одной из высших форм колебаний квадратной и прямоугольной пластинок.
сящиеся к случаям панелей с отношением сторон X 1 и 1,5 при числах полуволн т — п 1, т. е. для основного тона ко-
0 1 2 3 4 0 1 Z 3 4
v v
Рис. 3.6. Влияние сжимающих усилий на Рис. 3.7. Влияние начальных несовершенств
вынужденные колебания квадратной пла- на вынужденные колебания квадратной стинки по основной форме. пластинки по основной форме.
лебаний. Здесь нанесены скелетные линии, относящиеся к собственным колебаниям, и характеристики вынужденных колебаний для определенного уровня поперечной нагрузки 8,9.
ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА
149
Эффект начальных несовершенств при т — п 1 иллюстрируется рис. 3.7. Стрела начального прогиба выбрана равной £о 1. Следующий график — рис. 3.8 относится к высшей форме колебаний. Другие линии на рис. 3.7 и 3.8 относятся
4 5 6 7 в 3 70
v
Рис. 3.8. Эффект начальных несовершенств в случае вынужденных колебаний квадратной пластинки по одной из высших форм.
к идеальным панелям. Судя по этим данным, начальная погибь ведет к смещению амплитудно-частотных характеристик. Чем выше форма колебаний, тем влияние неидеальности оказывается более значительным.
§ 39. Замкнутая цилиндрическая оболочка
Перейдем далее к случаю круговой замкнутой цилиндрической оболочки, шарнирно опертой по торцам.
Основываясь на общих уравнениях 1.40 и 1.41, примем возмущающую нагрузку в виде
qx> У у 0 Qmn sin cos cos Qt. 3.15
Таким образом, мы считаем здесь нагрузку распределенной по поверхности оболочки неравномерно. Координаты х и у отсчитываем вдоль образующей и по дуге. Под т понимается число полупериодов изменения нагрузки вдоль длины оболочки L, под п — число полных периодов изменения нагрузки по окружности. Под Qmn подразумевается амплитудное значение нагрузки, соответствующее заданным индексам тип.
Приведенное ниже решение задачи принадлежит Ивенсену и Фултону 3.22.
150 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ГЛ. Ш
Мы будем интересоваться колебаниями оболочки изгибного типа и примем п 2. Прогиб оболочки аппроксимируем выражением
,ч л,ч. тпх пи, п2 -2 J4. 2 тя 0 цч
«К, У> f Antsm—j—cos-Z- -jgAntsin —. 3.16
Такого же типа зависимость была использована нами в § 29 при исследовании собственных колебаний. Отличие состоит в выборе коэффициента при втором члене. Здесь он ставится заранее в зависимость от числа волн п и от первого параметра. Сопоставляя 2.159 и 16, находим отношение
U _ 1 пЧАп fx — 41 r A h ;
Предполагается, что при п 2 роль этого второго члена в 16 мала, и что она является значительной при п2 порядка Rh.
Подставляем 16 в правую часть уравнения 2.158. Интегрируем это уравнение и определяем функцию Ф. Далее применяем процедуру метода Бубнова — Галеркина по отношению к уравнению 2.157. Тогда приходим к следующей зависимости:
•0 5 -1Г Is 5 ж2 - Ч4 COS VT. 3.17
Здесь введены безразмерные параметры
£ 4’ т ’ 3.18
h yh
Под v понимается безразмерная частота
v£L. 3.19
о0 — частота колебаний для соответствующей линейной си¬
стемы и определяется по 2.144; это выражение представим в виде
а -f Eg Г <И пЧ1Пуа о ш
vR2 L <2 О2 12 I — ц.2 Jj ’
Б качестве основных параметров, определяющих поведение нелинейной системы, служат величины
<иГ __ а 1
2 _ '2 с — И»г1г 16 121-ц2
Ч — I R ’ S Г О4 т2«»г121 1Ф I2 121 -ц2 J
02
1
. _ 3ft4 Ul2 9Ф21Ч
0— 16 Г Ф4 тг О2 I2
L О2 О2 12 1 - Ц2 J
3.21
§ 39
ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА
151
Коэффициент д характеризует форму волнообразования:
nRn
Lm
3.22
и представляет собой отношение длины полуволны в направлении дуги к длине полуволны вдоль образующей. Величины т, О, аналогичные принятым здесь, использовались нами в главе II при изучении собственных колебаний. Примем далее
£ i4cosvr. 3.23
Тогда уравнение 17 приведется к следующему:
1 -v2M---v43
3sr2
• Л3 -л4М5 Сл
16. 4 <1, 8 ч-‘ тп- 3.24
Мы получили амплитудно-частотную характеристику Лй вынужденных колебаний, зависящую от амплитуды возмущающей нагрузки Gmn. При Gmn 0 мы придем к соотношению
6
А
5
Рис. 3.9. Амплитудно-частотные зависимости мягкого типа в случае замкнутой цилиндрической оболочки.
Рис. 3.10. Влияние параметров волнообразования на амплитудно-частотные зависимости в случае замкнутой цилиндрической оболочки.
<4v, отвечающему собственным колебаниям. В § 29 мы получили подобное же уравнение, исследуя задачу в иной постановке. При этом учитывались два самостоятельных параметра в выражении для прогиба, отражающем характер выпучивания оболочки в большом; один из этих параметров определялся из статического варианта соответствующего уравнения движения.
На рис. 3.9 изображены кривые, отвечающие 24 при Gmn 0,1; г2 0,01; -в 0,1. Пунктиром представлена скелетная линия, отвечающая Gmn 0. Как видим, при выбранных параметрах оболочки амплитуды собственных колебаний возрастают с уменьшением частоты, в отличие от случая плоской пластинки. Следовательно, здесь мы имеем нелинейность
152
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
ГЛ. Ill
иного типа, чем для пластинки; вся кривая получается «падающей», как на одном из участков кривой рис. 3.1,6. Слабая
Рис. 3.11. Эффект отношения длин полуволн на амплитудно-частотные характеристики нелинейных колебаний для цилиндрической оболочки.
0,4 0,8
Рис. 3.12. Зависимость «амплитуда прогиба — частота» для круговой цилиндрической оболочки в сравнении с данными экспериментов.
12 If а 0,4
0,8 1,2 6
7,В 2,0
V
Рис. 3.13. Амплитудно-частотные зависимости для круговых цилиндрических панелей различной кривизны: а идеальная панель, б оболочка с начальной погибью.
нелинейность, характерная для рис. 3.9, относится к относительно длинным цилиндрам с тонкой стенкой. В других случаях нелинейность может быть выражена более резко.
СЛУЧАЙ ЦИЛИНДРИЧЕСКОЙ ПАНЕЛИ
153
На рис. 3.10 и 3.11 представлена зависимость характера скелетных кривых от параметров г и О. Эти графики свидетельствуют о значительном влиянии величины г на поведение системы.
Наконец, рис. 3.12 иллюстрирует экспериментальные данные, полученные Олсоном 3.22 для вынужденных колебаний. Сплошная линия отвечает скелетной кривой по 24 при значениях параметров, взятых для моделей Олсона. Как видим, характер зависимостей для вынужденных колебаний, изображенный на рис. 3.9, находит подтверждение.
Надо оговориться, впрочем, что для оболочек иного типа решение задачи может привести к графикам типа рис. 3.1,6, 3.13.
§ 40. Случай цилиндрической панели
Исследуем далее случай пологой цилиндрической панели; собственные колебания подобной системы мы рассматривали в § 32. Примем и здесь, что панель сжата статическими усилиями р вдоль образующей.
Воспользуемся обычными уравнениями 1.40, 1.41; для интенсивности нагрузки q выберем выражение 1, учитывающее эффект демпфирования. Аппроксимируем полный и начальный прогиб в виде 2 и 3, предполагая здесь, что выпучивание панели происходит по одной полуволне в направлении образующей и по дуге т ti 1.
Дополненное выражение 4 для Ф получает форму К аЬ
® r-f2cos 1Lc os
ikr TirW <f - '.15i sin i p,f. 3.25
После применения метода Бубнова — Галеркина к уравнению 1.40, придем снова к соотношению 5. Но вместо р следует подставить параметр верхнего критического напряже ния, равный по 2.210
. я21>.2 ■ W, 3 6
12Л2 1 — ц2 я2 1 Л22 ’
под k понимается параметр кривизны k — b2Rh. Величины а,
р, т оказываются здесь равными
«-1 1 х<С5-Jfii тгпйф.
Р_Ч-4 _«___9.1Я-5с, 13.27
Ч Ч'1П
154
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
ГЛ. III
Выражение для будет по 2.214
Частота собственных колебаний соо определяется выражением
Вторую стадию решения задачи построим по тому же плану, что и в случае пластинки § 38. Принимая ££ по 12, выписываем условие ортогональности по аналогии с § 32 и приходим при е 0 к амплитудно-частотной характеристике
Значение q вычисляется аналогично И.
На рис. 3.13 показаны кривые j4v, построенные по 29 для цилиндрических панелей различной кривизны. Рис. 3.13, а относится к случаям идеальных панелей при двух значениях параметра кривизны; принято q 0,3. Для панели с параметром k 24 здесь рассматривается два случая — при отсутствии осевого сжатия и при значении параметра осевых усилий, составляющих 12 от верхней критической величины. В последнем случае амплитудно-частотные характеристики состоят из нескольких изолированных участков, что отражает наличие у системы второго устойчивого положения равновесия. Колебаниям около основного положения равновесия отвечает ветвь cmd, верхние ветви отвечают колебаниям со значительными амплитудами.
Данные рис. 3.13,6 демонстрируют влияние начальной погиби на амплитудно-частотные зависимости при параметре кривизны k — 24 в случае р 0; для сравнения здесь же штрих-пунктирными линиями приведены кривые для идеальной панели. Начальные неправильности, направленные к цент ру кривизны, как бы «спрямляют» амплитудно-частотные кривые; начальная погибь, направленная от центра кривизны, приводит к усилению нелинейных эффектов.
§ 41. Экспериментальные данные по нелинейным колебаниям и устойчивости подкрепленных панелей в акустическом поле
Приведенные в предыдущем параграфе результаты отражают характерные особенности поведения элементов конструкций, испытывающих вибрации под действием давлений в пол акустического излучения.
Исследованиям этих задач в статистической постановке посвящена глава X.
2.211.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
165
Как показывают экспериментальные данные, деформации оболочек при интенсивном акустическом нагружении имеют существенно нелинейный характер. Это особенно относится к элементам конструкций, несущим одновременно с акустическими воздействиями дополнительные усилия типа осевого сжатия или внешнего давления, действие которых может привести к выпучиванию конструкции. В подобных случаях нагружения, кроме проблемы усталостного разрушения, не менее важное значение имеет вопрос о влиянии акустических нагрузок на несущую способность подкрепленной конструкции.
Обратимся к результатам экспериментальных исследований акустической прочности и несущей способности подкрепленных цилиндрических панелей из дюралюмина. Рассмотрим данные по усталостной выносливости, особенностям напряженного состояния и характеру разрушения панелей в условиях акустического нагружения при различных уровнях статического осевого сжатия.
Образцы представляли собой цилиндрические панели, подкрепленные в продольном направлении тремя ребрами два по краям и одно в центре. Отношение сторон для ячеек гладкой части после закрепления по криволинейным кромкам на приспособлении составляло Я 2 при параметре кривизны k
b2Rh 10 см. § 30.
Вначале проводились статические испытания при действии только усилий осевого сжатия. По результатам экспериментов на трех образцах были установлены средние значения крити1еских нагрузок местной потери устойчивости обшивки и определена статическая несущая способность.
Динамические испытания были проведены с использованием сирены и акустической камеры, создающих поле давлений
Приведенные здесь экспериментальные данные были получены i. Г. Кильдибековым совместно с А. А. Мицюком 3.11а.
Рис. 3.14. Оболочка после потери несущей способности при осевом сжатии в акустическом поле: а вид со стороны гладкой части обшивки; б вид со стороны подкрепляющих ребер.
156
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
ГЛ. III
с ярко выраженным узкополосным энергетическим спектром при резком преобладании уровня пульсаций первой гармоники. Первоначально проводились резонансные испытания. При низком уровне звукового давления путем плавного изменения частоты была установлена частота основного тона собственных колебаний 0 370 гц. Эта частота фиксировалась по резкому возрастанию показаний тензодатчиков.
а
Ф в ■: Щ:'я
Рис. 3.15. Характер усталостного разрушения образца после акусти-4 ческого воздействия при одновременном действии осевых сжимающих усилий: а вид со стороны обшивки, б — д зоны разрушения.
Определение несущей способности панелей при действии акустической нагрузки производилось следующим образом. Первоначально панели нагружались усилием осевого сжатия, соответствующим 0,7 от среднего значения статической несущей способности, и затем в процессе акустического воздействия проводилось дальнейшее медленное увеличение осевого усилия
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
157
а
до момента потери несущей способности. При этом характер нарастания осевой нагрузки соответствовал статическим испытаниям. Фиксировался момент потери несущей способности по аналогии со статическими испытаниями. Критические нагрузки были определены при уровне звукового давления в 164—168 56 и спектре пульсаций, сосредоточенном в окрестности частоты 300 гц. Снижение несущей способности по отношению к результатам статических испытаний составило в среднем 7.
Фотография одного из образцов к моменту потери несущей способности при акустическом нагружении приведена на рис. 3.14. Отличие этих случаев нагружения от статических испытаний проявилось в углублении выпучин обшивки и ослаблении заклепочных соединений.
Образец другой серии подвергался акустическому нагружению при уровне 164—16856 с преобладающей частотой 370 гц и одновременном действии статического усилия осевого сжатия Р выбранное значение Р отвечало критической нагрузке местной потери устойчивости. Ресурс — время до появления первой трещины — составил 7 мин.
Последующее нагружение панели в течение 4 мин вызвало усталостное разрушение при значительном распространении трещин вдоль заклепочных швов и повреждении участка обшивки, включающего концентраторы напряжений. Вид образца после суммарного акустического воздействия в течение И мин приведен на рис. 3.15. Здесь же показаны зоны усталостного разрушения.
На рис. 3.16 приведена фотография образца после испытаний при акустическом нагружении в режиме плавающей частоты ё диапазоне 10-500 гц в течение 8 мин при том же уровне звукового давления. Усилие осевого сжатия и в этом случае было равно критической нагрузке выпучивания общивкц,
Ф
Рис. 3.16. Вид образца после испытания при акустическом нагружении с другим режимом при одновременном действии осевых сжимающих усилий: а фотография образца со стороны обшивки; б, в зоны усталостного разрушения.
158
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
ГЛ. III
Значительное повреждение обшивки рис. 3.16, зона А произошло в зоне концентратора; другая зона разрушения сосредоточена вдоль заклепочного шва.
Анализ осциллограмм, соответствующих напряжениям в образцах, показывает, что акустическое напряжение панелей при отсутствии осевого сжатия приводит к появлению в конструкции переменных напряжений с амплитудным значением цикла в пределах оа 200-н 400 кгсм2 наибольшее значение аа в проведенных испытаниях оказалось равным 765сгсж2.
Значительное возрастание напряжений происходит при акустическом нагружении и одновременном действии усилия осевого сжатия, равного критическому значению местной потери устойчивости. Для одного из образцов рис. 3.15 значение оа достигало величины 1000 кгсм2 при среднем значении цикла ат 250 кгсм2. Это возрастание уровня напряжений, по-видимому, связано с прощелкиванием панели от одного положения устойчивого равновесия к другому, а также колебаниями около второго положения устойчивого равновесия. В одном из экспериментов максимальное значение напряжений было близким к пределу текучести материала и составило атах 2500 кгсм2 при амплитудном значении цикла оа 1050 кгсм2.
По результатам частотного анализа осциллограмм были зарегистрированы частоты изменения напряжений, вдвое превышающие частоту акустического воздействия. Это объясняется особенностью нелинейных колебаний, связанной с развитием прогибов, составляющих до пяти толщин оболочки.
Вернемся к случаю сферической панели, о собственных колебаниях которой говорилось в §§ 35 и 36. Имеется в виду панель, круговая в плане с жестко защемленным опорным контуром. Исследуем осесимметричные вынужденные колебания панели. При этом примем, что интенсивность внешнего давления, постоянная вдоль радиуса, изменяется по одному из следующих законов в безразмерных параметрах § 35:
В этих выражениях амплитудные значения нагрузки взяты, с одной стороны, лежащими заметно ниже верхней критической нагрузки <7 0,56, с другой — близкими к ней. Период внешнего воздействия в первых двух случаях превышает период свободных линейных колебаний оболочки, а в третьем и четвертом — ниже этого значения.
§ 42. Сферическая панель
3.30
СФЕРИЧЕСКАЯ ПАНЕЛЬ
159
На рис. 3.17 и 3.18 приведены результаты вычислений для оболочки с параметром кривизны к 4 см. § 35. При
Z
-7
4
1. ущ
2.у0,5ш
А
3. yurf 1 у 0,25vj
V
Л
II
1
1 1 1
г Г
ш
м
ilf
з
X V
и
1Н
hTi
Рис. 3.17. Движение полюса пологой сферической оболочки при различных законах изменения интенсивности внешней нагрузки.
численном решении задачи, выполненном по описанному в § 35 алгоритму, начальные значения перемещений и скоростей
Эти данные принадлежат Н. В. Валишвили и В. Б. Силкину.
160
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
ГЛ. III
считались равными нулю. Демпфирование здесь не учитывалось; принималось Ь 0.
На рис. 3.17 приводятся графики движения вершины оболочки во времени. Номера кривых на графиках соответствуют номеру закона изменения нагрузки по 30.
Приведенные на рис. 3.17 результаты свидетельствуют
о том, что только для первой задачи решение имеет периодический характер. При этом период колебаний вершины оболочки близок к периоду изменения возмущающей нагрузки 4я. Для остальных законов изменения нагрузки полученные решения не являются строго периодическими — трудно установить определенные значения периода и амплитуды колебаний. Выделение периодических решений рассматриваемых задач возможно различными путями. Прежде всего можно подобрать соответствующим образом начальные значения перемещений и скоростей. Но этот способ оказывается сложным. По-видимому, целесообразно выделить периодические решения, учитывая в уравнениях движения эффект демпфирования.
Судя по полученному решению, отдельные точки срединной поверхности оболочки совершают движение, не синхронное движению вершины. На рис. 3.18 приводятся графики движений характерных точек оболочки для четвертой задачи. Как видим, рассматриваемые точки совершают сложное движение. При этом они в некоторые моменты времени находятся в противофазе. Это говорит о том, что исследование пологих оболочек как систем с одной степенью свободы при конечных перемещениях может привести к существенной погрешности.
Таким образом, мы приходим к выводам, аналогичным тем которые были сделаны в главе II.
ГЛАВА IV
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ § 43. Особенности параметрических колебаний
Как мы уже знаем из главы III, параметрические колебания возникают при периодическом изменении «особенных» нагрузок. В основные дифференциальные уравнения задачи величины, характеризующие такие нагрузки, входят в качестве параметров.
Представим себе для примера закрепленную известным образом по краям пластинку. Пусть она подвергается действию сжимающих усилий вдоль одной из сторон, меняющихся периодически во времени; тогда могут иметь место параметрические колебания. Основное состояние конструкции при подобных колебаниях характеризуется перемещениями точек срединной поверхности в самой этой поверхности. При определенных соотношениях частоты пульсаций нагрузки и частоты собственных колебаний подобное основное состояние становится неустойчивым, и возникают нарастающие нормальные перемещения.
При решении задачи в линейной постановке оказывается, что таким неустойчивым зонам основного состояния соответствуют прогибы, нарастающие от цикла к циклу. Важно отметить, что первая зона такой динамической неустойчивости лежит вблизи частоты пульсаций нагрузки, составляющей удвоенную частоту собственных колебаний конструкции; здесь имеется в виду система с одной степенью свободы.
На рис. 4.1, а изображены примерные границы зон динамической неустойчивости. По оси абсцисс отложено отношение удвоенной частоты собственных колебаний 2Я к частоте пульсаций нагрузки 0; рассматривается система с одной степенью свободы. По оси ординат откладывается величина 6, зависящая от характера пульсаций нагрузки; она представляет собой отношение амплитуды переменной части нагрузки к ее среднему значению. Заштрихованы первая область динамической неустойчивости, отвечающая точке на оси абсцисс с координатой 2Й0 1, вторая и третья зоны, при 2Q0 2; 3. Этот график относится к случаю, когда демпфирующие факторы не учитываются.
162
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. IV
Следующий рис. 4.1,6 построен с учетом демпфирования. Для второй и последующих зон область неустойчивости отходит далеко от оси абсцисс, так что явление неустойчивости здесь проявляется лишь при весьма резких изменениях нагрузки. Практически поэтому наибольшее значение имеет первая зона; ею мы и будем интересоваться в последующем изложении.
а б
Рис. 4.1. Зоны динамической неустойчивости при малых прогибах: а без учета демпфирования, б с учетом демпфирования.
Все эти рассуждения относятся к малым прогибам. При значительных прогибах жесткость оболочки или пластинки меняется в ряде случаев по весьма сложному закону. Следовательно, здесь мы приходим к задаче о нелинейных параметрических колебаниях системы. Они характеризуются, подобно случаям собственных и вынужденных колебаний, изменением амплитуды колебаний в зависимости от частоты. Если задача решается в линеаризованной постановке, мы можем найти очертания зон динамической неустойчивости; о самом процессе можно лишь сказать, что амплитуды колебаний неуклонно нарастают. Напротив, решение задачи с нелинейных позиций позволяет установить амплитуду колебаний при той или иной частоте пульсаций параметра.
Практические приложения теории параметрических колебаний пластинок и оболочек относятся к самым различным областям техники. Например, корпус летательного аппарата может испытывать параметрические колебания при пульсациях силы тяги, передаваемой от двигателей.
§ 44. Параметрические колебания пластинок
Обратимся к некоторым конкретным задачам, относящимся к параметрическим колебаниям. По общему плану, принятому в этой книге, начнем со случая прямоугольной пластинки.
Решение этой задачи было дано В. В. Болотиным 4.2, 1954 г.
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ ПЛАСТИНОК
163
Пусть по сторонам b к пластинке приложены сжимающие усилия рх, изменяющиеся во времени по закону
Рх Ро Pt cos 0. 4.1
Под ро здесь понимается постоянная часть нагрузки, под pt — амплитуда переменной части. Таким образом, те усилия р, которые по рис. 3.3 были как бы пассивными и лишь способствовали деформации пластинки под действием периодической поперечной нагрузки, теперь в свою очередь самостоятельно раскачивают систему.
Будем считать пластинку шарнирно опертой по краям и примем, что стороны а остаются неподвижными. Что касается сторон 6, то предположим, что одна из сторон х а свободно смещается относительно второй 0, фиксированной в плоскости ху обе эти стороны во время движения пластинки продолжают быть прямолинейными.
Если рассматривать пластинку как систему с одной степенью свободы и аппроксимировать изогнутую поверхность с помощью выражения
w ft sin sin, 4.2
то мы можем использовать для решения задачи все выкладки главы II. Рассматривая собственные колебания прямоугольной пластинки, мы воспользовались методом Бубнова — Галеркина и пришли окончательно — с учетом усилий в срединной плоскости— к уравнению 2.110
т5§И-»тягсго; <4-3>
под £ по-прежнему понимается отношение Л, Я а6. Если считать, что продольные края остаются неподвижными Аг 0, то для ру мы получаем выражение 2.117
<4-4
Уравнение 3 для рассматриваемого случая примет вид, о Л Рх<., 0,751-ц21ЗЯ4
164 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ ГЛ. IV
с — по-прежнему скорость звука в материале пластинки. Обозначив множитель при £3 через г
0,75 1-ц21 ЗУ,,
Л 1 ®о>.оа;
приходим к уравнению
4.7
dt Ркр Под р’ в 5 и 7 понимается, как обычно, безразмерный параметр нагрузки
р; тгт- W-«
Критическое напряжение ркр определяем из 3, опуская инерционный и нелинейный члены, тогда, считая ру арх, найдем
Рк» ЬЧХ2 1 цА.2 1
Параметр рр будет по 2.118
и2 IV2 иш
ркр 12Л2 1 - цг 1цА,2 ’ 4Ю
Переходя к безразмерным параметрам в 1, получим
Рх Р'о Рcos е- 4Л1
Таким образом, в уравнении 7 должны фигурировать сжимающие усилия, изменяющиеся во времени по закону 11. Окончательно приходим к уравнению
- 41- --°-■ Т- -- g Ч£3 0. 4.12
СМ кр •
Введем обозначение Q для частоты собственных колебаний пластинки как системы с одной степенью свободы, испытывающей статическое действие постоянной составляющей р0:
Q2 cog Л >-. 4.13
' Ркр'
Далее назовем коэффициентом возбуждения величину
§ 44 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ ПЛАСТИНОК 165
характеризующую соотношение между переменной составляющей нагрузки и средним значением точнее — разностью между эйлеровым и средним значениями, см. рис. 4.2. Пользуясь этими обозначениями, представим 12 в виде
-g- Q2l-fecoseOS t£> 0. 4.15
Мы пришли к классическому уравнению, описывающему параметрические колебания системы с одной степенью свободы при единственном параметре нелинейности г. Отбрасывая член, содержащий т, получаем обычное уравнение Матье, соответствующее линейной системе. Свойства этого уравнения хорошо известны. Как уже говорилось в § 43, для линейной системы в области неустойчивости будет иметь место последовательное возрастание амплитуды. Мы будем интересоваться первой зоной неустойчивости вблизи 0 2Q. Для такой области, подобно тем, которые заштрихованы на рис. 4.1, а, амплитуды колебаний будут неограниченно увеличиваться.
Если же речь идет о нелинейной системе, то амплитуды оказываются ограниченными. Их можно определить следующим образом. Введем новый параметр времени
1 щЛ m 4.16
г Р Р
и обозначим
6 4.17
Тогда уравнение по 15 примет вид
- 1_£соз--ф 6> 0. 4.18
Примем функцию £ для частот, лежащих вблизи Q0 12,
Э виде
cos fijsin-. 4.19
Рис. 4.2. К определению коэффициента возбуждения системы.
106 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
Воспользуемся формулами 4
ГЛ. IV
sin3 х -j- 3 sin х — sin 3, cos3 x 3 cos x cos Sx,
НеуслойчиЗясть
sin x cos2 x sin x sin 3, sin2 д; cos x cos x — cos 3.
Тогда, отбрасывая члены с утроенной частотой, получим
Ai cos х В sin v3 А2 А cos х sin, где
а2а в1
Следовательно,
£3 Л2 л, cos В, sin j.
С другой стороны, применим соотношения
cos 2х cos x — -j cos х -f cos 3;
cos 2x sin x -i- — sin x sin 3x.
S22 здесь сохраним лишь первые члены. Тогда Рис. 4.з. границы пер- Уравнение 18 можно выписать в форме
М1 -i£--T TM2coslir
вой зоны неустойчиво сти при линейных параметрических колебаниях прямоугольной пластинки.
4Q2 2 1 4
02, k
f -6A2sin-- 0. 4.20
4Q2 ' 2
Принимая А Ф 0 и Вх ф 0, приравниваем нулю выражения в скобках; будем иметь
е2
1
4Q2
J-W 4 ТМ2 °-
4.21
Если нелинейный член в 18 отсутствует 6 0, мы получаем по 21 границы первой зоны неустойчивости
— л 1 — — — f 1 4- —
2Q V 2 ’ 2Й V 1 2
ИЛИ
в k е
2Q 4 ’ 2Q
1т-
4.22
4.22а
Для всех значений 02Q, лежащих в этих пределах, амплитуды колебаний неограниченно возрастают; соответствующие линии изображены на рис. 4.3, сплошные линии отвечают 22, пунктирные — 22а.
§ 441 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ ПЛАСТИНОК 167
Но в разбираемом случае б ф 0. Следовательно, для А нахо¬
дим определенные значения
<4-23>
зависящие от параметра нелинейности б и коэффициента возбуждения. График Л2024Й2, соответствующий 23, показан на рис. 4.4; мы получаем прямые сплошные линии, Аг наклоненные к оси абсцисс под углом 45°, «коридор» между ними имеет ширину k.
Решая задачу в линейной постановке, получим полосу шириной kt изображенную пунктирными ли- q -j j £ ег4л2
ниями: амплитуды здесь 2 2
неограниченно возрастают. Рис 4 4 3ависимости «амплитуда_частота>
ВЫЯСНИМ Далее, какой при параметрических колебаниях пластинки.
эффект оказывает линейное
демпфирование. Вводя соответствующий член в 16, приходим к уравнению
2е -§ Q2l - k cos 61 g rtf 0. 4.24
Вводя переменную tx по 16, получим
f2it1-cosi''S£J0’ 4-25>
где 6 определяется по 17. Выражая по-прежнему £ в виде 19, приходим к уравнениям при А Л В
Л1 мгBl-5l<:osgi-
М1 “ w 1 т“ - ■л, £sl TS о- <4-26>
Условия Ахф0, Вф 0 приводят теперь к уравнению
168
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. IV
При отсутствии нелинейного члена в 24, когда 6 0, границы первой зоны неустойчивости теперь определялись бы уравнением
_ 2 1 — — 1 — — 0
Z 4Й2 1 Q2 1 4
е
16Q4
или приближенно
6 1 f 1 __ -f k2 4е2
2Q У V 4 Q2
4.28
Кривая, найденная по 28 для некоторого значения е, изображена на рис. 4.3 штрих-пунктирной линией.
Вернемся к нелинейной задаче. Величина Л, исходя из полного уравнения 27, определяется следующим образом:
Рис. 4.5. Влияние демпфирования на параметрические колебания пластинки.
1 ±
т-тЙГ- <4-29>
Новый график для А2 изображен на рис. 4.5. Считая А 0, находим ширину полосы вдоль оси абсцисс; она равна теперь
2 Yk24 — 4e2Q2. Как видим, границы неустойчивости при наличии затухания сближаются. Вместо сплошного коридора по рис. 4.4 мы получаем здесь петлю. Правая граница k зоны устойчивых колебаний определяется абсциссой пунктир:
4Q2
k2a2
: 16е2•
§ 45. Замкнутая цилиндрическая оболочка при пульсирующем внешнем давлении
Перейдем к задаче о поведении замкнутой цилиндрической оболочки, испытывающей пульсирующее нормальное давление. Эта задача имеет актуальные приложения в современной технике.
Общий план решения задачи оставим тем же, что и при обсуждении вынужденных колебаний. Аппроксимируем прогиб с помощью выражения а яL, р nR:
w ft sin ах sin у г sin2 ах ф‘ 4.30
Приведенные здесь результаты принадлежат В. Ц. Гнуни 4.3.
ОБОЛОЧКА ПРИ ПУЛЬСИРУЮЩЕМ ВНЕШНЕМ ДАВЛЕНИИ
169
Повторяя выкладки, приведенные в книге 0.6, стр. 764, приходим к следующему уравнению, аналогичному 12:
С4 С0 - q01С С32 С, С,£3 —0. 4.31
Здесь Со С2 С4
далее введены параметры
r -L с —М.
h ’ s nL ' L2 Величину можно с известным приближением найти из ре¬
шения нелинейной статической задачи см. 0.6, стр. 790. Далее примем qt q°cosQt. Тогда уравнение 31 можно переписать в виде
-g- 2е ■§■ Q2 1 — k cos 9; — с£3 К5 0, 4.32
где
Для случая nRriL < 2,66 находим зависимость между квадратом амплитуды установившихся колебаний А2 и квадратом отношения 02Я2, изображенную на рис. 4.6. Петля на этом гра- А фике сходна с той, которую мы получили для пластинки рис. 4.5, но имеет «падающий участок». Очевидно, в этом случае возможны хлопки оболочки
Рис. 4.6. Зависимость «амплитуда — ОТ ОДНИХ УСТОЙЧИВЫХ уСТаНОВИВ- частота» при параметрических колебаШИХСЯ положений К другим. На- ииях круговой цилиндрической обо-
пример, идя из области низких
частот к более высоким, можно наблюдать перескоки, показанные стрелками на рис. 4.7, а. Напротив, при уменьшении частоты мы получаем скачки, изображенные на рис. 4.7,0.
вгЯг
Iе
я21 l22S 1
121-ц2 1
I I22 ■ я» 1 у.
2 о, jg fc2 Sy
1 22 1 9225’ Сз 4 l 1622'
yR2 gSr1 ’
170
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. IV
Интересным является исследование параметрических колебаний цилиндрических оболочек, наполненных жидкостью.
Рис. 4.7. К характеристике поведения круговой цилиндрической оболочки при параметрических колебаниях, связанных с явлением срыва: а при увеличении частоты, б при уменьшении частоты.
Подобная задача обсуждается с позиций, близких к описанным выше, в работе 4.6; там же приведены данные некоторых экспериментов.
§ 46. Поведение цилиндрической панели при пульсирующей сжимающей нагрузке
В заключение распространим результаты, полученные в § 44 для пластинки, на случай цилиндрической панели, сжатой вдоль образующей.
Будем считать, что края панели шарнирно оперты, а по дуговым кромкам действуют равномерно распределенные сжимающие усилия р ро ptcos Qt. Примем, что нормальные и касательные усилия, действующие по продольным кромкам, в среднем обращаются в нуль.
Выпишем основные уравнения в обычной форме 1.40,
1.41. Прогиб аппроксимируем с помощью выражения
w f t sin sin -у-, 4.33
принимая в качестве первого приближения, что для пологой панели в направлениях каждой из сторон а, Ь образуется по одной полуволне. Подставляя 33 в уравнение 1.41, находим функцию Ф. Далее, применяя процедуру метода Бубнова — Галеркина по отношению к уравнению 1.40, получаем следующее уравнение wq 0, Я аb:
тк2е - f ■ р« Pt cos -
-s§lTwfJS-1i',-a <4М>
Эта задача обсуждалась Г. В. Мищенковым 4.4.
§ 46 ПАНЕЛЬ ПРИ ПУЛЬСИРУЮЩЕЙ СЖИМАЮЩЕИ НАГРУЗКЕ 171
Под ©о по-прежнему подразумевается частота собственных колебаний, равная по 2.211
<•>• <4-35>
Здесь под К и F подразумеваются величины
А'—22 Р_
Rh ’
Далее введем обозначения
K-ж- F<1 -wwi- 4'36
Pt
i-Й, <4-37>
1 Р
з1 — и-2 1 а,4 ft 16 1 — jx2 а2 г 1. 8 4 F f j Ро L 1 Я22 J
4.38
Фигурирующие здесь величины встречались нам в § 32 при рассмотрении собственных колебаний. При £ придем к уравнению
-g- 2е -§■ Q2 1 — к cos 0 С — Q2 0. 4.39
В случае С 0 мы получим случай пластинки; коэффициент р0 будет равен нулю.
Если исключить из 39 динамические члены, то будем иметь уравнение
1-К-ро£2 £3 0. 4.40
Корни этого уравнения соответствуют трем возможным положениям равновесия. При Р0 > 2т возможны колебания около начального состояния равновесия, относительно прощелкнутого состояния и с охватом этих двух состояний см. § 32.
Обратимся теперь к динамической задаче. Будем по-прежнему интересоваться главной зоной неустойчивости и примем выражение для £ в виде
л I я 6. п. 6
£ А0 A, cos В sin -у.
Обычным путем приходим к уравнениям
А> ЛоА А1 Т 2 Р А> у 2
J 4.41
-Л„4 В,4 0.
172
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. IV
где п 0Q, А 2е£2, п0 — безразмерная частота собственных колебаний, определяемая из уравнения
411 VI2 А0Зц0А0 - 2р0;
под А понимается, как и ранее, амплитуда установившихся колебаний. Из первого уравнения 41 находим
Л2 2Л0-Мо“3,1о“1
Зтоо — Р
Два других уравнения при А ф О, Вх Ф О дают
Отсюда
— яА
яД
г2
k
0.
п2 no — 2Д2 ±2Vh- «оА2 А4. При отсутствии затухания
4.42
4.43
4.44
4.45
что совпадает с 22.
На рис. 4.8 даны амплитудно-частотные кривые, построенные по приведенным выше зависимостям для квадратной панели при
К — 13 и рор 0,45; коэффициенты го и Ро, вы-
3.0
V
ZJJ
7,5
10
0.5
д-
0
' У
у
л
д
-02
0,15
ЛА
0
1
д
opz
У
'•
У
S
К13; Л 7
w
vv
РоРЬ
ч
N 1
численные по 38, будут при этом Tio 0,26, Ро 0,8. В этом случае имеют место колебания лишь
d
Я
0,6 0,7 О,В 0,3 1fl 1,1
1,2 1,3 Ifl
п2 0231
вгяг
Рис. 4.8. Амплитудно-частотные зависимости в случае параметрических колебаний цилиндрической панели.
Рис. 4.9. Поведение оболочки при параметрических колебаниях в случае значительного демпфирования.
вокруг одного положения равновесия. Рис. 4.8 содержит кривые, построенные в допущении об отсутствии демпфирования А 0
§ 47 ХАРАКТЕРИСТИКА РЕЗОНАНСОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ 173
и при его наличии Д 0,15; 0,2; 0,22. Сплошными линиями показаны устойчивые ветви кривых, пунктиром — неустойчивые. При малых коэффициентах демпфирования получаем графики, общий вид которых был дан на рис. 4.7. В случае значительного демпфирования оказывается возможной иная характеристика — по рис. 4.9. Здесь перескоки могут иметь место лишь при достаточно больших возмущениях, забрасывающих систему на ветвь cd.
3.5
А
3.0
2.5
2.0
15
10
0,5
О OJ 0,2 0,3 Оfl 0,5 0,6 0,7 0,0 0,3 1,0 1J 1,2
п2вгя
Рис. 4.10. Зависимости «амплитуда прогиба —частота» при параметрических колебаниях панели, имеющей три положения равновесия.
На рис. 4.10 изображен случай, когда имеют место три положения равновесия; здесь взяты значения Я 0,85; С 13; Рор 0,5. Вычисления даютто 0,26; р0 1,1,так что p0>2Alo В этом случае некоторые кривые имеют различные ветви, отделенные друг от друга вдоль оси ординат. С подобным примером мы уже познакомились при рассмотрении вынужденных колебаний цилиндрических панелей.
§ 47. Характеристика резонансов в нелинейных системах
В заключение раздела книги, относящегося к периодическим воздействиям нагрузок на оболочки или пластинки, напомним некоторые определения, относящиеся к явлению резонанса в не линейных системах.
При анализе колебательного процесса нас интересуют те зоны, для которых амплитуды колебаний нарастают, и притом так, что это явление влияет на характер эксплуатации конструкции. Явление нарастания амплитуд колебаний связывают с понятием резонанса.
4
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
ГЛ. IV
При разложении в ряд Фурье нелинейных составляющих в уравнениях колебаний и приведении уравнений к разрешающей форме в них появляются члены с комбинационными частотами типа nQ ± rnQ, где 0 — частота изменения нагрузки внешняя частота, Q — основная частота собственных колебаний, п и т — некоторые целые числа. Поэтому, в отличие от линейных систем, в нелинейных задачах резонансы наступают при различных сочетаниях частот: г£2 « 0, где г и q — взаимно простые целые числа 0.21; эти сочетания зависят от характеристик системы.
Случай 0 Q носит название главного или обыкновенного резонанса; мы им интересовались для вынужденных колебаний.
Напротив, для параметрических колебаний наибольшее значение имеет случай, когда частота собственных колебаний равна дробной части внешней частоты £2 02; такой резонанс называют параметрическим.
Могут иметь практическое значение и колебания с частотным соотношением Q 0. Эти колебания относятся к обертонам внешней частоты.
Сложные задачи о. разнообразных резонансах в нелинейных системах применительно к пластинкам и оболочкам разработаны слабо; они представляют значительный теоретический и практический интерес.
ГЛАВА V
АВТОКОЛЕБАНИЯ
§ 48. Основные понятия
Следующим важным типом колебаний, к которому мы теперь обратимся, являются автоколебания. Под ними понимаются незатухающие колебания, возбуждаемые силами, зависящими от деформации самой вибрирующей системы: поэтому такие колебания называют самовозбуждающимися. Энергию для поддержания автоколебаний доставляет некоторый внешний источник.
Одним из наиболее важных видов автоколебаний в технике являются вибрации типа флаттера. Колебания такого вида возникают в случае воздействия на деформируемую систему газового потока. При обтекании конструкции поток оказывает различное действие на нее в зависимости от положения системы. Так, например, крыло летательного аппарата при деформации, возникающей в тех или иных режимах полета, получает различные давления от набегающего газового потока. Изменение геометрии крыла, связанное с деформацией, в свою очередь ведет к увеличению или уменьшению давления в различных точках крыла. Таким образом, мы получаем связанную систему «упругая конструкция — газовый поток», непрерывно меняющую свои характеристики. При некоторых параметрах этой системы амплитуды перемещений крыла, имеющие колебательный характер, резко возрастают. Деформации, возникающие при флаттере, весьма опасны для конструкции, так как быстро приводят к потере прочности и развитию усталостных трещин.
Надо различать так называемый «классический» флаттер, сопровождающийся общей изгибно-крутильной деформацией крыла или совместными перемещениями крыла и элеронов, деформацией фюзеляжа и оперения, и «панельный» флаттер, характеризующийся местным выпучиванием участков обшивки крыла или фюзеляжа между подкрепляющими элементами. Панельный флаттер может иметь место для обшивки конструкции летательных аппаратов различного типа. Особенно большое
176
АВТОКОЛЕБАНИЯ
ГЛ. V
значение такой тип флаттера приобретает при сверхзвуковых и гиперзвуковых скоростях полета.
В настоящее время проблема флаттера становится особенно актуальной для авиационных конструкций в связи с увеличением размеров летательных аппаратов и повышением скоростей полета.
§ 49. Нелинейный флаттер пластинки
Рассмотрим вначале задачу о флаттере шарнирно опертой по всем краям плоской прямоугольной пластинки, имеющей длину по потоку а и ширину Ь. Предположим, что пластинка обтекается с одной стороны сверхзвуковым потоком газа, характеризующимся скоростью U рис. 5.1. Координатные линии х, у, z расположим соответственно вдоль сторон а, 6 и по нормали к поверхности пластинки.
Уравнения, описывающие поведение пластинки, выпишем в виде 1.42а, 1.43а, считая w0 0:
-Lv4<i> — jLw, зу;
5.1
под Yo подразумевается удельный Первое уравнение содержит член,
вес материала пластинки, характеризующий давление на пластинку со стороны газового потока; под v понимается удельный вес газа, ф — потенциал скоростей. При составлении уравнений 1 использована линеаризованная теория невязкого потенциального течения. Функция Ф должна удовлетворять уравнению
вместе с тем решение должно быть подчинено граничному условию
д<р дг
Рис. 5.1. Пластинка, обтекаемая потоком.
dw тг dw
zo— dt U дх
5.3а
у поверхности пластинки и условию
дер
dz г> 0
0
5.3Ь
вне пластинки; под с понимается скорость звука в невозмущенном потоке газа.
См. работу Е. N. Dowell, Nonlinear oscillations of a fluttering plate, AIAA Paper 67-13, 1967.
§ 49 НЕЛИНЕЙНЫЙ ФЛАТТЕР ПЛАСТИНКИ 177
Воспользуемся далее методом Бубнова — Галеркина. Функцию прогиба аппроксимируем с помощью ряда
®2'»sin'Tlsin'L- 5-4
т
Здесь принимается, что в направлении ширины пластинки образуется всегда одна полуволна; число полуволн по длине равно т. Подставляя 4 в уравнения 1, с учетом 2 и 3, при¬
ходим к следующей системе уравнений, записанных здесь в безразмерном виде:
fmn4 т Я22 - Зя< 1 - ц2 If т2А К2В СА< 47ngn2Qm. ml, 2,. 5.5
Г
Под fm понимается безразмерная амплитуда т-й составляющей прогиба, под т — безразмерное время; X аb. Коэффициенты Л,., С зависят от параметров пластинки и характеристик материала. Через Qrm обозначаются выражения типа
1 1
1 Г Г Рг — роо • тпх. пи J J —r-sm — sm--dxdy,
О о
где рг — давление, возникающее за счет появления компоненты прогиба
-. гпх. пи
wr Ar sin sin —г,
ГГ а £ »
Роо — давление в набегающем потоке, р yg.
Коэффициенты Qrm имеют вид
s
Qrm fr is srm 4®- Drm fr s HrM s - s ds
0
s
5.6
0
где T5F,;
Srm, Drm, Hrm, Л™ — некоторые функции M и. Если опустить интегралы, входящие в уравнение 6, то оставшиеся члены дают значения Qrw, соответствующие поршневой теории.
178
АВТОКОЛЕБАНИЯ
ГЛ. V
Таким образом, задача сводится к решению системы уравнений 5, определяющих изменение амплитуды прогиба в зависимости от времени. Эти уравнения были решены численным методом с помощью ЭЦВМ. Характер изменения амплитуд предельного цикла в зависимости от значения скоростного напора иллюстрируется графиком, изображенным на рис. 5.2. Здесь принято Х. По оси ординат отложены амплитуды безразмерного прогиба wh, по оси абсцисс — параметр скоростного напора q рU2azD. Различные кривые отвечают ряду значений числа МахаМ от 1 до 1,6.
ВОО д
Рис. 5.2. Изменение амплитуд предельного цихла в зависимости от скоростного напора.
§ 50. Экспериментальные исследования флаттера пластинок
Опишем некоторые экспериментальные исследования флаттера, относящиеся к плоским панелям.
В большинстве опытов, проведенных различными авторами, испытываемые пластинки закреплялись на жесткой модели,
имевшей острую переднюю кромку; струя газа обтекала пластинку при нулевом угле атаки. В этом случае можно считать, что сверхзвуковой поток около панели является невозмущенным. Полость под панелью обычно соединяется с атмосферой трубы; в других вариантах полость герметична, и в ней может поддерживаться заданное давление 5.30, 5.23, 5.35, 5.13, 5.24.
Кроме того, в ряде экспериментов пластинки нагружались продольными сжимающими усилиями в плоскости пластинки 5.35, 5.24. В некоторых опытах изменялась температура набегающего потока; в пластинке возника-
Ofi
0,5
О
0,3
о,г 0,1
Рис. 5.3. Границы устойчивости пластинки.
3 4 5
АТй Тнр ли термические напряжения, приводящие к выпучиванию.
На рис. 5.3 приведены полученные вычислениями границы флаттера для свободно опертой квадратной пластины, обтекаемой сверхзвуковым потоком в условиях равномерного повышения температуры на величину АТ. Под ДГкр здесь понимается тем¬
§ 51 КВАЗИСТАТИЧЕСКАЯ ЗАДАЧА ДЛЯ ЗАМКНУТОЙ ОБОЛОЧКИ
179
пература, при которой происходит статическое выпучивание пластинки. Через ц обозначено r V' 2 1 Из рис. 5.3
видно, что автоколебания отсутствуют для пластинки в плоском или выпученном состоянии области К и N соответственно при больших значениях аэродинамического параметра и равномерном увеличении температуры; в то же время при меньших значениях аэродинамического параметра изображающая точка будет перемещаться из области статической устойчивости точка А во флаттерную область S точка В, где возникнут автоколебания. При дальнейшем увеличении температуры система «пластина-поток» выйдет из флаттерной области точка С, и произойдет статическая потеря устойчивости точка D; выпученная панель при этом оказывается динамически устойчивой.
§ 51. Квазистатическая задача для замкнутой цилиндрической оболочки
Перейдем к рассмотрению поведения замкнутой круговой цилиндрической оболочки, обтекаемой с внешней стороны сверхзвуковым потоком газа; невозмущенную скорость струи U будем считать направленной вдоль образующей. Предположим, что оболочка, кроме того, испытывает статическое действие равномерных ежи мающих усилий во вдоль длины рис. 5.4.
Явление панельного флаттера,
о котором ядет речь в данной главе, часто проявляется наряду с монотонным выпучиванием оболочки, которое не имеет колебательного характера и может рассматриваться как квазистатический процесс. В авиационной литературе подобный процесс принято называть дивергенцией. Явления дивергенции и флаттера могут в отдельных случаях чередоваться при изменении скорости газовой струи, либо величины сжимающих усилий. Поэтому мы исследуем сначала явление дивергенции. При этом аэродинамические силы определим по поршневой теории см. книгу 0.6, § 225.
Рассмотрим вначале эту задачу как геометрически линейную, считая прогибы оболочки малыми по сравнению с толщиной»
Рис. 5.4. Цилиндрическая оболочка под воздействием потока газа и осевых усилий.
Эта задача была решена Э. Д. Скурлатовым 5.16. Ему же принадлежат теоретические и экспериментальные результаты, изложенные ниже в §§ 52—55, 57, 60, см. сб. «Переходные процессы деформации оболочек и пластин», Тарту, 1967.
180 АВТОКОЛЕБАНИЯ ГЛ. V
Основные уравнения примем в виде см. 0.6, стр. 858:
TV4-il£-«-§££• I
-Lv«d_-L. 5'7
Е R дх2 9 Как легко видеть, эти уравнения представляют собой линеаризованный вариант уравнений 1.40, 1.41 при о>0 —д2Фду2 величину q примем по формуле поршневой теории также в линеаризованном виде,
Mdw
-37-
Решение ищем в виде 0.6:
w х, у, t fm, п t sin ах sin у „ sin ух sin у, 5.8
где а ттсL, у пг 1яL, р nR; m — число полуволн вдоль образующей, п — число волн в окружном направлении. Подставляя 8 во второе из уравнений 7, найдем выражение для функции напряжений в срединной поверхности:
Ф > У у t — lx sin ах sin pу 2 sin y sin py, 5.9
где
i f i __ У2Е £
1 R a2 p22 1 m> n’ 2 R y2 P221 mu n'
Используя 8 и 9 в первом уравнении системы 7 и применяя метод Бубнова — Галеркина, придем к системе двух алгебраических уравнений относительно ш, п и fm1, п. Введем безразмерные величины
fm,n «. fml, ti МА
fern, п fo > fem1. ft »
„ _ mm 1 1 — ц2 „ _ 121—ц,2 L2 2
A— 12m Eh4 я4 ’ A— я2 Rh m ’
121 — Ц2 Z,2 « I 2 д Д2 Жт1’
<12 m2 W2l2,121->п414
•«. Lm »<« 7
Тогда система уравнений примет вид
CO
,2
5.9a
m1,
Приравнивая нулю определитель системы уравнений 9а, найдем верхнее критическое усилие сжатия как минимальный
Величину а не следует смешивать со встречающимся ниже пара¬
метром а.
. 511
КВАЗИСТАТИЧЕСКАЯ ЗАДАЧА ДЛЯ ЗАМКНУТОЙ ОБОЛОЧКИ
181
корень следующего уравнения:
К - -2tqc, «1 < м ±
«,. л - <. ЛГ - «W,K,. 5.10
Если поток отсутствует а 0, соотношение 10 совпадает с выражением для верхнего критического значения параметра осевых сжимающих усилий, щ
Анализ соотношения 10 при водит к заключению, что газовый поток может стабилизировать оболочку, сжимаемую в продольном направлении рис.
5.5.
Рассмотрим ту же задачу в нелинейной постановке, для чего воспользуемся общими уравнениями типа 1.40,
1.41. Так как прогибы и их производные входят сюда в степени не выше третьей, то аэродинамические силы будем определять по формуле третьего приближения см. 0.6, стр. 835. Выражение для прогиба зададим в виде ряда
W ху у у t fx t sin ax sin p у
f2 t sin yx sin pyf3 0 sin2 a.
5.11
Дальнейшие вычисления аналогичны проведенным для линейной задачи, но являются весьма громоздкими. Минуя промежуточные выкладки, выпишем уравнения в окончательном безразмерном виде:
1001 “Ь 0102 “Ь 10113 3001 ”1 12012 ”Ь
а 0213 “Ь 0302 ”1“ а210 12 Ь 01223
1001 Ь 30£l ”Ь 0302 Ь 21012 Ь 12012
Ю2С1Й 012аЙ 0,
С0013 200 “1“ С022 “Ь 0023 ”Ь 201 4”
“Ь 0213 4 111123 - 0
140
125
ПО
0,95
В
л
р
С
0,50
т1 — п4
775 7 4
т1
74
ъ §
II II -fc
т1 715
т3 4а
А
00
0,02
ЦОЗ Цр4 ос
Рис. 5.5. Зависимость параметра осевых сжимающих усилий от скорости потока.
5.12
182
АВТОКОЛЕБАНИЯ
ГЛ. V
Коэффициенты агд, bh, Cijk зависят от параметров L, R, А, т, г, а0, С, а 5.16. Исходя из уравнений 12, можно определить равновесные формы оболочки при различных значениях параметра осевой нагрузки о»о и разных скоростях потока. На рис. 5.6 для стальной оболочки, имеющей размеры LR 6, Rh 500, представлены огибающие ветвей равновесных форм в неподвижном воздухе а 0 и при обтекании потоком со
Ofl
л
0,3
0,2
0,1 о
1 Z 3 4 5
3
Рис. 5.6. Равновесные формы оболочки с учетом и без учета потока.
скоростью, равной половине той критической величины ар, которая определяется из решения линейной задачи см. ниже формулу 24. Критическое напряжение сжатия для оболочки, обтекаемой потоком, оказывается в этом случае выше, чем в неподвижной среде. Меняется и форма волнообразования: числа тип для сжатой оболочки в потоке газа выше, чем для такой же оболочки в неподвижной среде.
§ 52. Динамическая линейная задача для замкнутой цилиндрической оболочки
Перейдем к динамической задаче о флаттере замкнутой круговой цилиндрической оболочки. Будем считать, что оболочка по-прежнему обтекается газом с внешней стороны. Кроме того, примем, что внутри оболочки содержится несжимаемая жидкость плотности рх,. В качестве вводной рассмотрим линеаризованную задачу.
Это явление наблюдалось в опытах, проведенных Э. И. Григолюком, Р. Е. Лампером, Л. Г. Шандаровым П'еория оболочек и пластин, Ереван, 1964, 407—411, и в экспериментах Э. Д. Скурлатова 5.16.
mIZ
J
V
N
W 11
;
X
X 1Z '
Уч,£лУ
Ч. 10
к0,5сср
Я
■ ш 'ч
w V 82
§ 62 ДИНАМИЧЕСКАЯ ЛИНЕЙНАЯ ЗАДАЧА ДЛЯ ЗАМКНУТОЙ ОБОЛОЧКИ 183
В выражение для нормальной составляющей нагрузки q включим силы инерции, диссипативные силы, давление газа и давление жидкости, заполняющей оболочку:
vn d2w V - dw у, дер.
4 -Thwlher Pl tf' 5ЛЗ
где в — коэффициент затухания, р — внешнее давление газа, срь — потенциал скоростей, yL — удельный вес жидкости, заполняющей оболочку, yo и y — по-прежнему значения удельного веса материала оболочки и газа.
Перейдем к цилиндрическим координатам х, 0, г.
Потенциал скоростей фх, жидкости, содержащейся в оболочке, должен удовлетворять уравнению
д2Ф, 1 дф, д2ф, 1 д2ф,
-а Т-£ -5 7г-з£“0- <5Л4>
Одно из граничных условий имеет вид дф, dw
-дГ --5Г при rR; 5Л5
другие условия относятся к кромкам х 0, х L; кроме того, функция фх, должна быть конечна при г 0.
Представляя функцию w, характеризующую форму колебаний оболочки, в виде
w fm.n 0 sin — COS пв, 5.16
найдем следующее решение уравнения 14:
A ИМ I тПГ • ШПХ л г
<Pi Ат, ntIn -£- J Sin —J— cos M0. 5.17
Здесь ln — модифицированная функция Бесселя первого рода
С ИНДеКСОМ 1X fm, п И Ат, п
— искомые функции времени. Используя условие 15, определим величину Л„
1771, П
7 dfT • <5-18
mnln aR dt
Подставляя 18 в 17, найдем выражение для потенциала скоростей
СГ т W р- 1 q
где К mnRL. Неустановившееся давление жидкости на стенку оболочки будет определяться формулой
дфг prR d2w d2w
Pl — — Pi — —— m,, 5.20
dt m Inm dt2 L dt2 ’ V ’
184
АВТОКОЛЕБАНИЯ
ГЛ. V
где ть — присоединенная масса жидкости, соответствующая колебаниям оболочки с образованием п волн в окружном направлении и т полуволн по образующей. Таким образом, инерционный член типа у0ghd2wdt2 заменим величиной
-22-hK —
g dt2 >
где
mLg
Km,n 1
Yo
Идя тем же путем, что и в § 51, получим следующие уравнения движения:
т, п ”Ь §т, Jam, п “Ь Р 1 й t,m< „ Qm1. л i'W, п
£т1, п 4“ §т 1» лСт1» п “Ь
IK. - • <т '>'“ £«,. «т. °'
где
48хРооМ L3 1 — ц2 тт 1
5.21
Q
Еагт п hA я 12т
121 И-2 1 7J- - dmtn
2 2 rw Wm1, П я ®«,п ЛЛ От§я
точками обозначены производные по времени. Под gm, п и gmi,n понимаются коэффициенты затухания, соответствующие различным формам колебаний. В дальнейшем примем gmt n gm, n g. Представляя решение 21 в виде
U П Fm. пеКх, £wli n Fm1, Пт, 5.22
получим систему однородных линейных алгебраических уравнений относительно Fm, п и Fmit п. Приравнивая нулю определитель системы, найдем характеристическое уравнение
А,4 2 g i Ъ2 — Ьъ — 64 g2 g b Ь2 — Ь3 — Ь4 Я
bb2 — b2b — bi4 -j- 6364 —— 65 0; 5.23
здесь
1. ixi «. 6лт2а
Кт,п Кт,п Кт,п и б'о т О2 Д 1 1 т2 т2
4 Ст1, л. ® Кт,пКт >п 1 2т2
Невозмущенная форма равновесия оболочки будет устойчивой, если все действительные части характеристических показателей отрицательны, и станет неустойчивой, если среди характеристц-
§ 52 ДИНАМИЧЕСКАЯ ЛИНЕЙНАЯ ЗАДАЧА ДЛЯ ЗАМКНУТОЙ ОБОЛОЧКИ 185
ческих показателей окажется хотя бы один, обладающий положительной вещественной частью. Применяя критерий Рауса — Гурвица, определим параметр а, соответствующий критической скорости флаттера:
а
где
1 -f 2т УКт,пКт,п 1Q2 р>2 2_i_ 02 fl2 _Lfl2
'2тт S У VDml, п
5.24
48>фоо L п tt2 1 —бопг2а
о ъо-кроо 1,.2 й2 L “_и
rrFf2 A4 ' ГП,П К
п га 'т, л
— 2
02
ит1, п
Ст 1, гс
Далее минимизируем величину а по числу волн в окружном направлении г, считая п достаточно большим. Результаты вычислений приведены на рис. 5.7. Здесь даны критические числа
Рис. 5.7. График для критических скоростей потока в случае цилиндрической оболочки с учетом демпфирования и присоединенной массы жидкости.
акР ПРИ различных значениях сжимающих до > 0 и растягивающих а0 < 0 усилий, а также с учетом пунктир и без учета сплошные линии эффектов присоединенной массы жидкости и демпфирования колебаний. На рис. 5.8 показаны границы устойчивости для оболочек, имеющих различные значения LR и hR, полых пунктир и заполненных жидкостью сплошные линии. Из рис. 5.7 и 5.8 следует, что демпфирование в данном случае стабилизирует оболочку. При наличии осевых сжимающих усилий, изменяющихся в рассмотренных пределах,
186
АВТОКОЛЕБАНИЯ
ГЛ. V
критическая скорость флаттера резко снижается, а при растяжении, напротив, возрастает. Учет присоединенной массы жидкости приводит здесь к некоторому повышению критической скорости; отметим, что форма колебаний при этом также меняется.
При исследовании функции аря оказывается, что она имеет два минимума, причем первый минимум характерен для длинных оболочек, а второй — для коротких. При уменьшении длины оболочки число волн вдоль образующей падает; в то же
0,00 fiff
0JJ09 0,005 0,004
0002
0 1 2 3 4 5 0 7 0
М
пмр
Рис. 5.8. Границы устойчивости полых и заполненных жидкостью цилиндрических оболочек.
время возрастает число волн в окружном направлении. Исходя из допущения, что п > п, из соотношения 24 можно получить приближенную зависимость для определения числа волн в окружном направлении, соответствующего минимальной критической скорости флаттера:
п6 5я2-2т l. 5.25
при этом минимальная критическая скорость описывается зависимостью
infer- иг- <•>
Пример. Определить критические параметры для медной оболочки радиусом 204 мм, длиной 408 мм и толщиной стенки 0,1 мм. Используя зависимости 25 и 26, получим
п' — 20, А Г W
h _2EgVW - 1 J
При опытах с подобными оболочками 5.24 были получены достаточно близкие величины:
h U£«KM-J
Т '
7
Нет флаттера
оУу у У
6 S'
у
Ъ'б
1 7
LR-10 'Jy _.в в 7
х 'Os',
_ ——
LRB '
-,а. U
У
70
70
73
LR4
74
Флаг
Timep
§ 53 УТОЧНЕННОЕ РЕШЕНИЕ ЛИНЕЙНОИ ДИНАМИЧЕСКОЙ ЗАДАЧИ 187
Следует помнить, что зависимости 25 и 26 были получены, исходя из двучленной аппроксимации прогиба оболочки. Рассматривая данные, полученные при расчетах с большим числом степеней свободы, можно найти следующие оценки критической скорости, справедливые при LR > 3 hR13 и небольшом сжатии оболочки вдоль оси. Для первого минимума
где ох — осевое напряжение.
§ 53. Уточненное решение линейной динамической задачи
Для уточненного решения линейной задачи необходимо учитывать в разложении 4 большее число членов ряда. Ввиду громоздкости вычислений при определении границ устойчивости возникает необходимость в использовании ЭЦВМ. Рассмотрим алгоритм, позволяющий определять границу устойчивости в плоскости двух параметров hR и М в случае учета в ряде 4, аппроксимирующем прогиб, многих членов и при отличном от нуля демпфировании 5.16. Решение системы уравнений типа 21, определяемое в виде 22, приводит к характеристическому определителю значения К и С даны на стр. 190:
Применим далее критерий Рауса, который весьма удобен для применения ЭЦВМ, так как требует проведения однотипных операций. Была принята такая последовательность действий. По полиному 30 строится схема Рауса
Эти данные принадлежат Э. И. Григолюку, Р. Е. Ламперу и Л. Г. Шандарову 5.10, 1969 г.
См. также статьи 5.16, 1967 г.
5.27
для второго минимума
5.28
П — О, 1,2 5.29
которому соответствует характеристический полином
Ь2К “f 12 Н 22 • • • 0. 5.30
Ь ь12 ь13
Ь2 b22 b2z
Ьц 62 63
61, 1 bl1,2 6 1,з
188
АВТОКОЛЕБАНИЯ
ГЛ. V
Здесь элементы первой и второй строк являются коэффициентами полинома. Элементы последующих строк вычисляются по формуле
Ьц bi-2, 1 i 2’bi-1, i.
°i-1,
Для того чтобы все корни полинома 30 имели отрицательные вещественные части, необходимо и достаточно, чтобы все Ъ
1 <;<; в схеме Рауса были отличны от нуля и имели один и тот же знак.
Пример определения областей устойчивости, проведенного с учетом 2, 4, 8 и 10 членов ряда, аппроксимирующего прогиб, представлен на рис. 5.9; для каждой кривой указано соответствующее число членов ряда. Здесь же пунктиром нанесены данные экспериментального исследования, описанного Фыном 5.24. Некоторое расхождение расчетных и экспериментальных данных объясняется тем, что анализ не учитывает различных факторов, важнейшим из которых является влияние пограничного слоя.
§ 54. Неустановившийся флаттер цилиндрической оболочки
При движении летательных аппаратов в реальных условиях происходит одновременное изменение скорости полета, плотности окружающей среды, температуры, усилий в срединной поверхности элементов обшивки и т. д. В зависимости от соотношений этих параметров элементы обшивки могут испытывать флаттер или дивергенцию; возможно также чередование автоколебаний различной формы с состояниями динамической устойчивости. Для изучения особенностей поведения оболочек в подобных условиях удобно воспользоваться понятием изображающей точки. Будем рассматривать плоскость двух параметров, характеризующих осевую нагрузку а и скорость потока а. Изображающая точка с координатами а и а при изменении осе¬
Эта задача рассматривалась в статье 5.16, см. сб. «Расчеты на прочность» 15, «Машиностроение», Москва, 1971, а также Э. Д. Скурлатовым и автором h сб. «Теория пластин и ободочек», «Наука», Москва, 1971, 29—33,
Рис. 5.9. Границы устойчивости цилиндрических оболочек, определенные с учетом различного числа членов ряда, аппроксимирующего прогиб.
§ 54 НЕУСТАНОВИВШИЙСЯ ФЛАТТЕР ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 189
вых продольных усилий и скорости потока будет перемещаться в плоскости а, а. Некоторое представление о поведении оболочки при достаточно медленном изменении какого-либо параметра можно получить, анализируя взаимное расположение границ установившегося флаттера и дивергенции, представленных на рис. 5.10. Допустим, что сжимающие усилия малы и лежат ниже критического значения а
0,6. При возрастании параметра скорости а и а const изображающая точка перемещается в плоскости графика на уровне линии ab. Оболочка будет оставаться устойчивой вплоть до значения а, соответствующего точке Ьу где возникает флаттер. Пусть теперь величина а остается постоянной, и в оболочке возникают сжимающие усилия. Тогда, идя по линии ей, приходим в точку, соответствующую дивергенции оболочки. При более высоком значении а const и возрастающем сжатии изображающая точка движется по линии fe, пересекающей последовательно области флаттера, соответствующие колебаниям с различной формой, и области динамической устойчивости.
В реальных системах, обладающих конструкционным демпфированием, для установления амплитуд колебаний, соответствующих флаттеру, необходимо некоторое время. Например, если время, в течение которого достигается критическое значение дв движение по линии ikf сравнимо с несколькими периодами собственных колебаний оболочки, то флаттерные движения, возможно, не успевают развиться и наступит квазистатическая потеря устойчивости. Поэтому при изучении нестационарного флаттера необходимо учитывать время пребывания изображающей точки в области флаттера. Отметим, что здесь рассматривается нагружение в течение времени, большего
0,002 HP04 0JJ06 0JJ08 0,010 OJflZ Щ
Рис. 5.10. Границы установившегося флаттера и дивергенции для цилиндрической оболочки.
190
АВТОКОЛЕБАНИЯ
ГЛ. V
периода нескольких собственных колебаний или нескольких десятков собственных колебаний ненагруженной оболочки, так что процесс мало отличается от статического и не приводит к повышению параметра верхней критической нагрузки ав.
Нестационарный флаттер цилиндрической оболочки в линейной постановке будет описываться уравнениями типа 21 с переменными коэффициентами:
< „£«.„-«. т nf Q, „
ОО оо
к т а т — 0, 5.31
11 0
где
Zm,n -tfL> от -щ-«тт, а --Мт,
ri к L2 ч о „, 2tn4L4 — i2
Q W 2л2Е h2 п “Ь R2h2n4A 1
>1 21 nLYl2 48 1 — Ы2L4, ч
Л 1т Ы ' К т,
5.32
'm, я, »
пп если п, т ± 1 — нечетные,
т2 - 21
0, если п, m ± 1 — четные,
0, если п.
Для исследования уравнений 31 здесь используется метод численного интегрирования, причем основное внимание уделяется различным законам изменения во времени параметра продольной нагрузки а при фиксированных значениях скорости потока а. Составленная для ЭЦВМ программа реализовала метод Рунге — Кутта с переменным, автоматически выбираемым шагом интегрирования. Некоторые результаты вычислений представлены на рис. 5.11. Рассматривалась оболочка с параметрами LR 6, Rh 100, п 6 при g 0,001 и начальных условиях
£i£2 °>4, ti£2 0 при т 0.
На рис. 5.11 нанесены огибающие амплитуд колебаний и линии, соответствующие различным законам нагружения бг а т. Движения с экспоненциально возрастающими амплитудами могут рассматриваться как флаттерные. Пунктирными линиями на рис. 5.11 выделены зоны, соответствующие области установившегося флаттера на рис. 5.10 при движении изображающей точки по траектории ik.
§ 64 НЕУСТАНОВИВШИЙСЯ ФЛАТТЕР ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 191
При докритической скорости потока варьировалась скорость нагружения и разгрузки, а также время пребывания изображающей точки в зоне флаттера. Сопоставление кривых переходного процесса при различных законах нагружения приводит к заключению, что изменение продольного сжатия может привести
Рис. 5.11. Изменение амплитуд колебаний цилиндрической оболочки для различных законов нагружения во времени осевыми силами.
как к колебаниям с возрастающей амплитудой рис. 5.11,а,г, если изображающая точка находится достаточно долго во флаттерной области, так и к затухающим движениям рис. 5.11,6, в, если флаттерная область проходится быстро. Таким образом, увеличение усилий сжатия оболочки может привести к прекращению уже начавшегося флаттера. При возрастании нагрузки в течение времени, соизмеримого с несколькими периодами колебаний оболочки, флаттерные движения не успевают
192
АВТОКОЛЕБАНИЯ
ГЛ. V
развиться рис. 5.11,в, и в дальнейшем происходит прощелкивание оболочки.
Отметим, что конструкционное демпфирование приводит к резкому увеличению времени, необходимого для достижения некоторой определенной амплитуды колебаний рис. 5.11,а.
Более полное исследование должно проводиться на базе нелинейной теории, позволяющей описать явление прощелкивания и определить предельные циклы.
§ 55. Нелинейный флаттер замкнутой цилиндрической оболочки
Обратимся к решению динамической задачи о флаттере в нелинейной постановке 5.16. Дополняя уравнения 12 членами, соответствующими инерционным силам и демпфированию, получим систему трех нелинейных дифференциальных уравнений, связывающих параметры прогиба £i, £2, £з со временем. Интегрирование этой системы, выполненное с помощью ЭЦВМ для оболочки с параметрами LR 6, Rh 100, п 7 при g 0,005 отражено на рис. 5.12. Здесь дана зависимость относительного прогиба £1 от параметра скорости потока а МhL, отнесенного к критическому значению, вытекающему из решения линейной задачи. Из точки аа 1 расходятся две ветви, определяющие амплитуды колебаний для различных устойчивых предельных циклов пунктир — неустойчивый предельный цикл. Судя по этим данным, для замкнутой оболочки оказывается возможным жесткое возбуждение флаттера при больших возмущениях: появляются автоколебания с конечными амплитудами при скоростях потока меньших, чем критические скорости, получаемые по линейной теории. Отметим, что решение задачи в линейной постановке позволяет находить критическую скорость потока, при которой невозмущенная скорость оболочки перестает быть устойчивой по отношению к малым возмущениям и позволяет оценить лишь начальную тенденцию колебаний. Но при этом не удается предсказать дальнейшее развитие процесса, в то время как нелинейная теория позволяет определить характеристики как переходного процесса, так и предельного цикла, необходимые для оценки усталостной прочности тонкостенной конструкции, обтекаемой потоком газа. В нелинейной постановке удается также точнее оценить влияние на ампли-
Рис. 5.12. График амплитуд установившихся колебаний.
ФЛАТТЕР ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
1S3
туды автоколебаний таких факторов, как конструкционное демпфирование, внутренний наддув, а также описать флаттер с бегущей в окружном направлении волной, наблюдавшийся в опытах и не описываемый линейной трактовкой. Эти вопросы будут рассмотрены ниже.
§ 56. Флаттер цилиндрической оболочки с бегущей в окружном направлении волной
Выше было показано, что, рассматривая динамическую задачу в нелинейной постановке, можно определить «нижнюю» критическую скорость флаттера, которая не может быть найдена с помощью линейной теории. Здесь мы рассмотрим задачу о возникновении флаттера с бегущей в окружном направлении волной, который также может быть описан с нелинейных позиций 5.22. Бегущие в окружном направлении волны наблюдались в опытах, описанных в работе 5.32. Иногда эту волну называют «псевдобегущей», поскольку во внешнем потоке на первый взгляд отсутствуют какие-либо факторы, ее вызывающие. Можно предположить, что причиной возникновения бегущей волны является нелинейный характер колебаний цилиндрической оболочки. Явление такого типа было обнаружено при исследовании вынужденных нелинейных колебаний тонкого кольца. Поскольку нелинейные колебания цилиндрической оболочки с большими длинами волн в осевом направлении близки по своему характеру к колебаниям тонкого кольца, то весьма вероятно, что подобное явление возникает при флаттере замкнутой оболочки. Если у тонкого кольца возбудить резонансные колебания с формой типа cos nQ и постепенно увеличивать амплитуду колебаний за счет увеличения амплитуды возбуждающей силы, то при некотором критическом значении амплитуды внезапно возбудится форма типа sin п0. Последняя накладывается на форму вида cos г0 таким образом, что образуется псевдобегущая волна. Критическое значение амплитуды снижается при увеличении числа окружных волн п и при снижении эффекта диссипации в кольце. Можно ожидать, что сходные в качественном отношении результаты могут быть получены при колебаниях цилиндрической оболочки в случае больших значений п при малых т.
Будем использовать уравнения типа 1.40, 1.41 в форме Nx, Nq — усилия в осевом и окружном направлениях:
Nq Л2™ 1 Л2Т>
г
дх2 дд2 d2w d2w 1
дзё wl
, 5.34
•. 5.33
194
Автоколебаний
rtfi. V
где аэродинамическое давление р аппроксимируется линейным приближением поршневой теории.
Аппроксимируем прогибы оболочки, колеблющейся с образованием бегущей в окружном направлении волны, с помощью выражения, содержащего четыре члена:
w х, 0, t А sin А2 t sin Cos пв
1 Bt fysin B2 t sin sin nQ
w Ai Wsin чг A2 0sin -г
-s,0sin- S20sin-2. 5.35
В соотношение 35 включены члены, содержащие n24R, так что решение удовлетворяет условию периодической непрерывности окружного перемещения v. Применяя процедуру метода
Бубнова — Г алеркина, получим систему четырех нелинейных обыкновенных дифференциальных уравнений. Эти уравнения ре-шались методом гармонического баланса, а также интегрировались численно. Как и в § 55, интегрирование по времени продолжалось до тех пор, пока амплитуды либо падали до нуля, либо достигался один из установившихся предельных циклов; изуча0 I Z лась также устойчивость пре-
дельных циклов.
На рис. 5.13 представлены ре-
Рис. 5.13. Амплитуды предельных цик- ЗУЛЬТЭТЫ ВЫЧИСЛеНИЙ, ПрОВедеНлов для флаттера с бегущей в окруж J г
ном направлении волной. НЫХ ДЛЯ НеКОТОрЫХ ХараКТерИС-
тик оболочки и потока. Здесь показан характер изменения амплитуды предельного цикла, полученного в предположении, что демпфирование отсутствует. Можно показать, что конструкционное демпфирование лишь незначительно изменяет амплитуды предельного цикла для флаттера с бегущей волной. Значения Ai и Д2 выписаны ниже, на стр. 202.
Отметим, что минимальные значения амплитуды предельных циклов флаттера, приведенные на рисунке, составляют примерно
4 — 5 толщин оболочки. В то же время наблюдавшиеся в опытах с подобными оболочками прогибы имеют величины порядка
§ 57 ДИВЕРГЕНЦИЯ И ФЛАТТЕР С УЧЕТОМ ПОГРАНИЧНОГО СЛОЯ 195
одной-двух толщин. Следует ожидать, что величина прогиба, полученного теоретически, уменьшится, если полагать оболочку не шарнирно опертой, а защемленной по кромкам, как это имело место в эксперименте. Кроме того, удерживая в выражении, аппроксимирующем прогиб, большее число членов ряда, можно получить уточненное решение. Такое исследование должно быть проведено в дальнейшем.
§ 57. Дивергенция и флаттер цилиндрической оболочки с учетом пограничного слоя
Для выяснения роли пограничного слоя при дивергенции и панельном флаттере замкнутой круговой цилиндрической оболочки воспользуемся идеализированной схемой, предложенной Фыном 5.24. Представим пограничный слой в виде кольцевой области равномерного дозвукового течения, расположенной между оболочкой и однородным сверхзвуковым потоком. Толщину дозвуковой области обозначим через б, скорость течения — через Ub рис. 5.14.
Допустим также, что рассматриваемая упругая цилиндрическая оболочка конечной длины L является частью бесконечно длинного цилиндра. Задача состоит в отыскании аэродинамического давления на
поверхность оболочки, возникающего в результате малых отклонений ее от невозмущенной формы. Возмущения потока, порождаемые деформациями оболочки, будем считать малыми. Для потенциала возмущенной скорости внутри пограничного слоя выпишем линеаризованное уравнейие см. 5.24
д2Ф6 1 дФЬ
с6 ах at ах dr2 г dr
при 6,
Рис. 5.14. Пограничный слой на поверхности цилиндрической оболочки, обтекаемой потоком газа.
1 д2Ф6, 9 М6 дФ6 п2дФ6_
2 dt2 с dxdt 6 дх2
L д2ф6 к оо
r2 dQ2 5-36
где с6 — скорость звука в пограничном слое, Фб — потенциал скорости в области пограничного слоя, Мб UJcb — число Маха в пограничном слое, Р 1 — Mj.
Потенциал Ф6 связан с функцией нормального прогиба условием непроницаемости стенок
<Ф6
дг
dw
dw
rR
dt
dx
5.37
196 АВТОКОЛЕБАНИЯ ГЛ. V
Кроме того, на поверхности раздела между дозвуковым и сверхзвуковым потоками при г R б значения давления и скорости, нормальной к поверхности, должны быть непрерывными. Обозначая через w малое радиальное перемещение поверхности раздела, запишем условие непрерывности радиальной скорости
дФь — dw JL г J dw К
Т гб - дГ и дГ • <5-38
Условие непрерывности давления на границе раздела выпишем в виде Ф и роо относятся к внешнему потоку:
5.39
при г R б.
Представляя перемещения стенки оболочки в форме
wxt 0, t w0ei<df cos л0 sin ал:, 5.40
где а тпЬ, т — число полуволн в продольном направлении, запишем решение уравнения 36 в виде
ф«, Г, 6, 0 cosneexpiC6Me-X1l„n,
ClYn М1 “ехр ркжЯ2 w BJn Ь е
С2К„ц2- 5.41
где п, Уп — функции Бесселя. Произвольные постоянные, входящие в 41, определяются из граничных условий. Опуская промежуточные выкладки, выпишем окончательное выражение для возмущенного давления на стенку цилиндра:
р х, г, 0, t еш cos n0 Атп cos ах Атп sin ал:, 5.42
где коэффициенты Атпу Атп зависят от параметров пограничного слоя и набегающего потока. При отсутствии пограничного слоя б 0 аэродинамическое давление по 42 совпадает с выражением, полученным по поршневой теории.
В § 51 было установлено, что статическая потеря устойчивости оболочек, обтекаемых сверхзвуковым потоком газа, происходит при больших осевых усилиях, чем в отсутствие потока. Попытаемся определить, какова роль идеализированного пограничного слоя в подобной задаче. Выражение для аэродина¬
§ 57 ДИВЕРГЕНЦИЯ И ФЛАТТЕР С УЧЕТОМ ПОГРАНИЧНОГО СЛОЯ 197
мической нагрузки 42 после очевидных преобразований примет вид
р х, R, 0 Wop™-- cos nQ Bmn cos ax Bmn sin a, 5.43
где
p П n2ri3 Б nins — n2 _
I „ q’ mn 1« l-Mx6p6M6, т2л,
<4 aR'fb, «3 06 n — Aj,
Д Мб6 „ Мб й_ яРооМ Л-М8’ Vх Щ’ 1 — м хвр6м6аг
Приводя систему 7 к одному уравнению, получим
DVw г f4- V<p 0. 5.44
Рассмотрим случай шарнирного опирания. Прогиб оболочки будем аппроксимировать двумя членами ряда:
w fmn sin ах cos nQ fmi. n sin Y c°s nQ. 5.45
Применяя к 44 метод Бубнова — Галеркина и проводя некоторые преобразования, придем к системе двух алгебраических уравнений, близких к 9а:
« n - V2 фД«£«. я - <рВти „Ст1, „ 0,
К1. » - 6оа т 2 ф5т1- „1 Ст1, „ ■ 5.46
'nmi<p5m>„Sm.„ 0,.
где
_ <Р— DRn4 '
Приравнивая нулю определитель системы уравнений 46, разрешим его относительно параметра продольных усилий д0:
2am т 1 т n m 1 ±
± £Й,,,„т-ОД.„я 122-4тт 1фВт. „Вт1>„-5.47
198
АВТОКОЛЕБАНИЯ
ГЛ. V
Зависимость 47 по форме совпадает с полученным ранее соотношением 10, но входящие сюда величины имеют другие значения:
Можно показать, что при отсутствии пограничного слоя б 0 соотношение 47 переходит в равенство 10.
На рис. 5.15 представлены в графической форме результаты вычислений при LR 6, Rh 100, £ 2-106 кгсм2, М6 0,5, т 3, п 5, выполненных по 47. Варьировалась
толщина пограничного слоя и скорость течения в дозвуковой зоне 5.16.
Анализ результатов вычислений, проведенных для оболочек с размерами, изменяющимися в широких пределах, приводит к заключению, что увеличение толщины пограничного слоя или уменьшение скорости течения в дозвуковой области приводит к значениям верхних критических усилий ав, несколько меньшим, чем при 6 0. Эти данные указывают на то, что рассматриваемая модель пограничного слоя отражает в первом приближении физические условия, характерные для реального пограничного слоя.
Перейдем к задаче о флаттере круговой цилиндрической оболочки при наличии пограничного слоя. Воспользуемся линеаризованным уравнением 1.40; аэродинамическую нагрузку р будем учитывать по 42:
Ц66
0
0j68
Ц60
0,64
0,62
0,601
О 4 8 72 16 20 М
а
О 4 6 72 76 20 И
б
Рис. 5.15. Границы дивергенции цилиндрической оболочки: а для различных значений толщин пограничного слоя, б для различных чисел Маха в пограничном слое.
§ 57 ДИВЕРГЕНЦИЯ И ФЛАТТЕР С УЧЕТОМ ПОГРАНИЧНОГО СЛОЯ 199
Перемещение стенок оболочки аппроксимируем следующим рядом.
Подставляя 49 в 48 и применяя метод Бубнова — Галеркина, получим систему однородных линейных относительно ат алгебраических уравнений. Определитель этой системы
имеет комплексные элементы., Значения числа М и частоты колебаний со, при которых одновременно обращаются в нуль действительная и мнимая части определителя, соответствуют нейтральному состоянию оболочки. Превышение этой скорости приводит к колебаниям с возрастающей по времени амплитудой.
Определение критических значений М и со обычно производится весьма трудоемким графическим методом 5.19. Здесь используется другой путь решения задачи, требующий значительно меньшего числа операций для расчета каждого варианта, что особенно важно при исследовании влияния многих параметров. Он состоит в том, что система двух алгебраических нелинейных относительно М и со уравнений, получившихся в результате приравнивания нулю действительной и мнимой частей определителя 50, решалась методом Ньютона. В качестве первого приближения в случае очень тонкого пограничного слоя использовались результаты решения задачи, обсуждавшейся в § 52. Процесс обычно быстро сходился, и полученные новые значения М и со использовались как начальное приближение в задаче с новым значением толщины пограничного- слоя б Аб.
Параметры пограничного слоя б и U6 можно определять также следующим образом. Необходимо, чтобы между применяемой приближенной и «точной» моделями существовало энергетическое соотретствие. Под «точной» понимается модель, описываемая либо теоретически на основе уравнений вязкой жидкости, либо экспериментально. Таким образом, для определения параметров б и U6 можно рассматривать две задачи
оо
w еш cos пв 2 т sin ах>
5.49
т1
w — Вю — дафЛ,
1 t ft 11 tl
о
А
g£ — Во — А да Ф А _
2, п 2, п
0
©2 — В© — 96а Ф А.
5.50
Эти результаты принадлежат Л. В. Селезовой Канд. дисс., Киевский гос. ун-т, 1969; они относятся к обтеканию плоской границы.
200
АВТОКОЛЕБАНИЯ
ГЛ. V
стационарного обтекания границы — идеальной жидкостью с кусочно-постоянным профилем скоростей и обтекание вязкой жидкостью. Если приближенные или точные решения последней задачи иву известны, то из условий сохранения полного вихря и количества движения в указанных двух задачах однозначно определяются параметры U6 и 6.
В случае кусочно-постоянного профиля скоростей выражение для полного вихря имеет вид 0 < б < у:
Ух Ух
J rot2udy - U — U6b0y — 6dy — U — U6; a
0 0
здесь бо — б — дельта-функция Дирака. Величина yx должна выбираться из условия
I ‘'•
yJL
Для количества движения имеем
Киб9б6и9У16. Ь
70
ff
5
4
Z
Устойчивость
Неустойчивость
О 0,001 0,002
<fR
Рис. 5.16. Зависимость относительной толщины оболочки, необходимой для предотвращения флаттера, от толщины пограничного слоя и числа Маха набегающего потока.
С учетом выражений а и Ь условия сохранения вихря и количества движения записываются в виде
У
1 dy-U-V>, с
о
Ух
uBpBdy СвРбб -f Up г, — б, d
Из уравнений с.и d получаем выражения, определяющие Ut и б при р„ pep:
Щ
ТГ
6_
L
-i
див
ду
dy,
«в dy
'
е
О
див
ду
dy
Некоторые результаты определения границ флаттера с учетом четырех членов ряда для цилиндрических оболочек, имею
§ 58 СЛУЧАЙ ИЗМЕНЯЮЩЕГОСЯ ДАВЛЕНИЯ В НАБЕГАЮЩЕМ ПОТОКЕ 201
щих пограничный слой различной толщины, приведены на рис. 5.16; принято LR 2, £ 1,1 • 106 кгсм2у п 22, Мб 0,5, оо р6 0,12 кгсм2. Полученные данные подтверждают вывод, сделанный в работах Фына 5.24 и Андерсона 5.19 о стабилизирующем влиянии дозвукового идеализированного пограничного слоя. Можно предположить, что стабилизирующий эффект, полученный с использованием идеализированной схемы пограничного слоя, является завышенным. Этот вопрос желательно исследовать дополнительно.
§ 58. Флаттер цилиндрической оболочки при изменяющемся давлении в набегающем потоке
Ранее предполагалось, что давление и скорость набегающего на оболочку сверхзвукового потока являются неизменными. В то же время представляет практический интерес задача о поведении оболочек при обтекании потоком с изменяющимися во времени параметрами, например давлением см. также § 103.
Будем исходить из уравнений 33, 34, описывающих поведение замкнутой цилиндрической оболочки 5.32. Решение уравнений движения представим в более сложном виде:
w i 0 sin ах -f f2 t sin 2ax sinP f t sin ax -f f2 sin 2ax2f
a тлL, p nR, 5.51
в предположении, что m 1. Множитель n24R выбран с тем, чтобы удовлетворить условию периодичности окружного перемещения v. Применяя процедуру метода Бубнова — Галеркина, придем к следующей системе уравнений:
TF 4'Jl <5.
1 ь з 2 тгfetf«э
4фФ 4ЗДЬ J-
- «Cl ей Ч5 - l f й 7 U — 0, 5.52а
<ънФт
tF 4' т°2 4Фт
4ASi£.-§l - «Ь 16с 6
Дй, l f t у d - 0, 5.52b
202
АВТОКОЛЕБАНИЯ
ГЛ. V
где
л _ KPoog Л _ 8хМроо£ в
1 YohCoo ’ 3YoLh ’
a, by с — некоторые коэффициенты, зависящие от параметров оболочки.
Уравнения 52 интегрировались численно с помощью ЭЦВМ, а также решались методом гармонического баланса. Вычисления были выполнены для медной оболочки с параметрами, приведенными в предыдущем параграфе при различных значениях давления в набегающем потоке и постоянном числе
Маха, равном 3. Как видно из рис. 5.17, для выбранной аппроксимации прогиба изменение амплитуд предельных циклов с увеличением давления в потоке носит более сложный характер, но при этом оказывается, что участки кривых, имеющие отрицательный угол наклона, соответствуют неустойчивым предельным циклам. Несмотря на непрерывное увеличение давления в набегающем потоке, амплитуды предельных циклов могут изменяться скачком.
Проследим поведение оболочки при плавном увеличении давления в набегающем потоке. При достижении аэродинамическим параметром Д2 величины, равной 1,41 • 105, некоторое возмущение оболочки например, вызванное шумом в турбулентном пограничном слое, приведет к автоколебаниям с формой п 23. При небольшом увеличении Д2 амплитуды колебаний начнут увеличиваться по экспоненциальному закону до
2 r-Nr
Аг-МГ5
Рис. 5.17. Изменение амплитуд предельных циклов оболочки в зависимости от давления в набегающем потоке.
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ФЛАТТЕРА
203
значений, соответствующих предельному циклу с п 23. При дальнейшем увеличении аэродинамического параметра до значения Д2 1,52 • 105 возможен переход скачком к колебаниям с другой формой, например при п 22, поскольку эта кривая является ближайшей к первоначальной. В то же время при непрерывном увеличении давления возможен перескок изображающей точки и на другие кривые рис. 5.17, соответствующие колебаниям с резко отличной частотой и амплитудой колебаний например, переход от колебаний с формой п 21 к форме п 25 при Д2 1,58-105. Резкий переход скачком к колебаниям с другой формой и амплитудой может привести к разрушению конструкции.
§ 59. Экспериментальное исследование флаттера замкнутых цилиндрических оболочек
Описанные ниже эксперименты 5.24, 5.32 проводились
с медными замкнутыми цилиндрическими оболочками радиусом 204 мм, длиной 408 мм и толщиной 0,081 и 0,102 мм следовательно, отношение Rh составляло 2500 и 2000.
При опытах наблюдались либо чисто синусоидальные колебания, что соответствует флаттеру оболочки по одной форме,
Рис. 5.18. Зависимость амплитуд колебаний от величины внутреннего давления в оболочке.
биения, соответствующие флаттеру по двум или большему числу форм, а также сложные колебания большой амплитуды, возникавшие при нулевом или отрицательном перепаде давления в полости под оболочкой и в свободном потоке. Оказалось, что амплитуда и форма колебаний при флаттере являются весьма сложной функцией параметров набегающего потока, давления в полости под оболочкой р0 и осевых сжимающих сил см. рис. 5.18 и § 58. Здесь светлые треугольники соответствуют оболочкам, нагруженным осевой силой 90,8 кг, темные — силой 40,9 кг, кружки — оболочкам, свободным от продольных сил. Важно отметить, что при высоких значениях внутреннего давления 0 на рис. 5.18 — в ат оболочка полностью стабилизируется даже при наличии осевой нагрузки.
204
АВТОКОЛЕБАНИЯ
ГЛ. V
Были получены данные по определению форм колебаний при флаттере. Форма в продольном направлении соответствует колебаниям по одной, двум
Wh 3
о
о
о°
О
О
<°
Оо
<5Ь
оо
ООО <
6
о
°о°С
о
1 оо
о
в
или трем полуволнам синусоиды, причем узловые окружности располагались неравномерно. Отмечено наличие волн, бегущих в окружном направлении; теоретическое обоснование этого явления проведено ранее в § 56.
В опытах с оболочками, которые выпучивались при действии осевого сжатия с образованием ромбовидных вмятин, начинался интенсивный флаттер на гладких участках оболочки. В то же время оболочка, потерявшая устойчивость под действием внешнего давления, не была подвержена флаттеру.
На рис. 5.19 представлена экспериментально полученная
зависимость амплитуды флаттера цилиндрической оболочки от
параметра
р U2
70 7Z ос
Рис. 5.19. Полученная в опытах зависимость «прогиб — аэродинамическая нагрузка».
ю4
10'
10
10
0.1
—I f f
2Е У М2 - 1 h ’
Флаттер
Давление внутри оболочки изменялось при этом в широких пределах. Как только давление в свободном потоке превышает определенное критическое значение, наблюдается достаточно резкое увеличение амплитуды.
На рис. 5.20 показана зависимость параметра потока от LR, под X по-
121-ц2 pU2R
нимаетсявеличинал —.
VbA2 - 1 Eh3 Сплошная кривая была проведена по средним значениям вычисленных величин Я; она представляет границу флаттера в области LR 0,75. Светлыми знаками представлены результаты вычислений, полученных другими авторами; видно, что они хорошо согласуются с полуэмпирической кривой. Темный кружок
представляет экспериментальную точку границы флаттера.
Экспериментальное значение динамического давления отли¬
Нет флаттера
0 2 4
6 0 70 LF
Рис. 5.20. Полуэмпирическая граница флаттера для цилиндрических оболочек.
§ 60 ЦИЛИНДРИЧЕСКИЕ ПАНЕЛИ В СВЕРХЗВУКОВОМ ПОТОКЕ ГАЗА 205
чается от значения точки полуэмпирической кривой на 22; для флаттера такое совпадение считается хорошим. Таким образом, полузмпирическая граница флаттера представляется полезной для быстрых оценок условий возникновения флаттера. Пунктиром показана граница флаттера в диапазоне LR 0,75. Из рис. 5.20 видно, что скорость флаттера сильно зависит от длины оболочки. Поэтому большое число исследований, посвященных теоретическому решению для бесконечно длинных оболочек, представляет в основном лишь методический интерес.
§ 60. Экспериментальное исследование поведения цилиндрических панелей в сверхзвуковом потоке газа
Приведем результаты серии опытов, которые проводились в сверхзвуковой аэродинамической трубе.
Стальные цилиндрические панели длиной вдоль образующей 360 мм, радиусом 250 мм и толщиной 0,1; 0,2 и 0,3 мм прикреплялись к специальной модели.
В опытах регистрировались динамические деформации панели с помощью датчиков, располагаемых на внутренней поверхности образца, а также проводилась скоростная киносъемка. Толщина пограничного слоя определялась с помощью теневого прибора.
Эксперименты проводились при числах М, равных 1,78; 2,2; 2,5; 3. Наблюдавшиеся движения панелей могут быть разделены на три типа. На рис. 5.21 приведены образцы осциллограмм для каждого из этих типов колебаний. В промежуток времени от начала запуска трубы до выхода на сверхзвуковой режим панель испытывает высокочастотные колебания с большой амплитудой рис. 5.21, а. Отметим, что колебания такого
ч jNrlPr I
VWvWvv
Рис. 5.21. Осциллограммы колебаний панели, возбуждаемых: а потоком, близким к сверхзвуковому М < 1, б шумом в пограничном слое М >1; в, г флаттерные колебания.
См. статью 5.16, 1971 г.
206
АВТОКОЛЕБАНИЯ
ГГЛ. V
типа были зарегистрированы на тонкостенных летательных аппаратах при прохождении трансзвуковой области; они возбуждаются пульсирующими скачками уплотнения и срывами потока 9.22. Пусковой скачок, представляющий собой движущуюся в направлении потока волну давления, обычно приводит к
движения являются результатом суперпозиции двух или большего числа синусоидальных колебаний рис. 5.21, в, г.
При действии сжимающих усилий стенки панели, обтекаемые потоком газа с дофлаттерной скоростью, вначале совершают незаметные на глаз высокочастотные колебания, о которых говорилось выше; затем для панелей, имеющих начальные неправильности формы, возникают отдельные зоны, совершающие слабые колебания. Дальнейшее медленное увеличение сжатия приводит к колебаниям, охватывающим область, прилегающую к заднему шпангоуту. Амплитуда этих колебаний невелика, но заметно возрастает с увеличением интенсивности осевого сжатия, далее в движение приходит вся поверхность панели. Колебания имеют при этом вид стоячих волн с одной окружной узловой линией, расположенной примерно в среднем сечении панели, и с максимальными амплитудами у задней кромки. Дальнейшее увеличение сжимающих усилий приводит к колебаниям с большими амплитудами; у задней кромки па-
прощелкиванию испытываемой панели рис. 5.22, если для ее сохранения не принимается специальных мер введение растягивающих усилий.
Рис. 5.22. Характерная форма волнообразования при воздействии подвижной волны давления.
После установления сверхзвукового обтекания со скоростью потока, меньшей критической скорости флаттера для испытываемой панели, отмечались случайные колебания с относительно низким уровнем амплитуд, вызываемые шумом в пограничном слое рис. 5.21,6. Если скорость потока была зафлаттерной, то устанавливались колебания с большими амплитудами. Величина амплитуд зависит от степени превышения скоростью потока критической скорости флаттера. Эти
§ 60 ЦИЛИНДРИЧЕСКИЕ ПАНЕЛИ В СВЕРХЗВУКОВОМ ПОТОКЕ ГАЗА 207
нели развиваются трещины, имеющие типичную крестообразную форму рис. 5.23. Поток вырывает отдельные участки
оболочки; в дальнейшем разрушение быстро распространяется
по направлению к передней кромке.
В ряде опытов наблюдалось явление, попытка теоретического объяснения которого была предпринята в § 54: интенсивные колебания панели после некоторого небольшого увеличения усилий сжатия внезапно прекращались.
Последующий рост сжимающих усилий приводил к колебаниям с другой ампли¬
тудой и частотой; при снижении усилий устанавливались колебания прежнего типа. Качественно поведение панели в этом случае
может иллюстрироваться рис. 5.10. Характер движений зависит от положения изображающей точки, определяющей состояние системы «оболочка — поток», в различных областях устойчивости или неустойчивости.
При дальнейшем увеличении сжимающей нагрузки Рис. 5.23. Типичная картина разрушения па-
пппнруппит ртятииргкяя пп. нели При Флаттерных колебаниях в сверхзву-
проислиди L1 d 1 HHcLKdH I1U ковом потоке направление потока — снизу—
теря УСТОЙЧИВОСТИ оболоч- вверх,
ки, характеризующаяся образованием серии ромбовидных выпучин, расположенных в области, примыкающей в заднему шпангоуту. Статическая потеря
устойчивости панели в потоке газа дивергенция всегда про¬
исходила при несколько большей величине осевых усилий, чем для тех же панелей без потока см. § 51.
На рис. 5.24 представлены некоторые результаты, полученные в описываемых опытах для панелей толщиной 0,2 мм при М 3;' приводятся также теоретические данные, соответствующие вычислениям с учетом двух кривая 1 и шести кривая 2 членов ряда 4. Здесь через р обозначено
Кружки соответствуют началу колебаний с малой амплитудой, охватывающих область у задней кромки панели, точки —
208
АВТОКОЛЕБАНИЯ
ГГЛ. V
интенсивным движениям с большой амплитудой всей панели у кромки амплитуды достигали 5—6 мм. Усилия, при которых происходит статическая потеря устойчивости, обозначены треугольником, прямоугольник отвечает экспериментальному критерию Фына см. § 59, рис. 5.19.
В реальных условиях между поверхностью обшивки летательного аппарата и обтекающим ее сверхзвуковым потоком
имеется вязкий пограничный
Ц12
0,10
i
црв
щ
0,04
цог
‘-'V
Рис. 5.24. Сопоставление экспериментальных и теоретических данных для панели, сжатой в осевом направлении и обтекаемой сверхзвуковым потоком газа.
слои; толщина его зависит от параметров потока и от конфигурации конструкции. Наличие пограничного слоя, как мы видели, является существенной причиной расхождения теоретических и экспериментальных данных. Было установлено, что толщина турбулентного пограничного слоя составляет 6—7 мм при М 3 и неT сколько меньшую величину при М 2,5. Однако при М 2,5 наблюдаются более интенсивные колебания панели; разрушение наступает быстрее, чем при М 3, что свидетельствует о значительном влиянии пограничного слоя на характер процесса. Отметим для сравнения, что в опытах Олсона и Фына 5.32 толщина пограничного слоя несколько превышала 10 мм и флаттерные колебания не приводили к разрушению стенок оболочки в течение всего эксперимента. По-видимому, пограничный слой влияет не только на величину критической скорости флаттера, но и на амплитуды колебаний; поэтому при использовании результатов экспериментов следует учитывать особенности течения в области, примыкающей к поверхности обшивки.
Остановимся на некоторых результатах исследования нестационарного флаттера, возникающего при действии продольных осевых сил, изменяющихся во времени по различным законам. Такого типа нагрузки могут возникнуть в авиационных конструкциях при действии порывов ветра, температурных и других факторов. При полете со скоростью, близкой к флаттерной, малые по величине и не опасные для статической прочности нагрузки могут вызвать вибрации, ведущие к усталостному разрушению обшивки.
Опыты показали, что характер движения упругой поверхности в процессе изменения осевых усилий зависит от закона
§ 60 ЦИЛИНДРИЧЕСКИЕ ПАНЕЛИ В СВЕРХЗВУКОВОМ ПОТОКЕ ГАЗА 209
изменения этих усилий во времени. Этот вывод качественно подтвержден вычислениями, приведенными в § 54.
Увеличение параметра осевого сжатия приводит к понижению критической скорости флаттера; если же система находится в критической области малое время, автоколебания могут не вызвать разрушения оболочки.
На рис. 5.23 была показана панель, нагружавшаяся усилиями осевого сжатия по закону, близкому к изображенному на рис. 5.11, а. При некотором значении продольных сил, соответствующих переходу изображающей точки в область неустойчивости, возникают флаттерные колебания. В дальнейшем, вплоть до разрушения, продольные силы оставались постоянными. Разрушение панели начиналось через 2—3 сек после момента установления бурных флаттерных колебаний с образованием крестообразных трещин у задней кромки и распространялось по направлению к передней кромке.
Панель, изображенная на рис. 5.25, нагружалась монотонно возрастающими усилиями сжатия рис. 5.11,6, в, причем флаттерные зоны были пройдены в течение двух секунд. Когда величина осевых сил превысила критическое значение, наступила статическая потеря устойчивости. За время прохождения области флаттера в результате интенсивных колебаний образовались трещины у задней кромки панели; последующее возникновение больших выпучин у задней кромки, вызванных осевым сжатием, приводило к прекращению флаттерных движений. Стабилизация оболочки может быть объяснена тем, что часть панели, примыкающая к задней кромке, становится как бы гофрированной, а для оставшейся гладкой части в результате уменьшения длины критическая скорость будет значительно большей. Отметим, что на всех панелях, испытывавших в течение некоторого времени флаттерные колебания, после прекращения эксперимента оставались поля мелких волнообразных вмятин. Объяснение этого явления будет дано ниже в § 103 главы IX,
Рис. 5.23. Форма волнообразования и типичные повреждения панели, сжимаемой непрерывно возрастающими продольными усилиями и обтекаемой сверхзвуковым потоком газа.
210
АВТОКОЛЕБАНИЯ
ГЛ. V
Панель, показанная на рис. 5.26, подвергалась более быстрому нагружению усилиями осевого сжатия. Нижнее критическое усилие было достигнуто в течение 0,3 сек с момента начала нагружения; при этом в области заднего шпангоута образовались глубокие выпучины, повышающие ее устойчивость по отношению к воздействию потока. При этом панель
сохраняет некоторую несущую способность. В данном опыте флаттерные колебания не были зарегистрированы ни в процессе нагружения, ни после образования больших вмятин, хотя при возрастании
осевых сил изображающая точка, характеризующая состояние системы, очевидно, пересекла те же флаттерные. зоны, что и в предыдущем
опыте.
Таким образом, на некоторых режимах полета небольшое по величине усилие сжатия может привести к флаттерным колебаниям обшивки с образованием трещин, в результате чего в условиях сверхзвукового полета может произойти полное разрушение обшивки. В то же время усилия, превышающие критическую величину и вызывающие появление выпучин, могут быть менее опасны.
В предыдущих разделах главы мы рассматривали поведение пластинок и оболочек в сверхзвуковом потоке газа и пользовались при этом преимущественно поршневой теорией.
Однако аппарат, которым располагает современная аэродинамика для решения задач аэроупругости, гораздо более широк.
Для сверхзвуковых течений, если речь идет о линеаризованных зависимостях, решение может быть дано с помощью численных методов. Обоснование и развитие их дано в известных работах Е. А. Красилыциковой «Крыло конечного размаха в сжимаемом потоке» М., Гостехиздат, 1952, Дж. Майлса «Потенциальная теория неустановившихся сверхзвуковых течений» М., Физматгиз, 1963, С. М. Белоцерковского, Н. А. Кудрявцевой, Б. Н. Федотова Изв. АН СССР, МЖГ,, 2, 1969, С. М. Белоцерковского, С. А. Попыталова там же,
Рис. 5.26. Форма выпучивания панели при более быстром нарастании продольных сжимающих сил и одновременном обтекании сверхзвуковым потоком.
§60 ЦИЛИНДРИЧЕСКИЕ ПАНЕЛИ В СВЕРХЗВУКОВОМ ПОТОКЕ ГАЗА 211
2, 1970 и подытожено в монографии С. М. Белоцерковского, Б. К. Скрипача и В. Г. Табачникова «Крыло в нестационарном потоке газа» «Наука», М., 1971. В основу решения положено общее уравнение для потенциала возмущений, трактуемое с позиций метода источников. Аэродинамические характеристики, относящиеся к каждому элементу несущей поверхности, определяются с учетом влияния всех остальных элементов в процессе движения конструкции. Особенно важно то обстоятельство, что при этом принимается во внимание предыстория процесса.
Для случая дозвуковой скорости потока оригинальные методы решения задач нестационарной аэродинамики развиты С. М. Белоцерковским в книге «Тонкая несущая поверхность в дозвуковом потоке газа» «Наука», М., 1965; см. также статьи С. М. Белоцерковского Изв. АН СССР, МЖГ, 1 и 6, 1966, Г. А. Колесникова там же, 6, 1967, С. М. Белоцерковского и Г. А. Колесникова там же, 5, 1969. Эти методы базируются на теории присоединенных и свободных вихрей; они также систематически изложены в указанной выше монографии С. М. Белоцерковского, Б. К. Скрипача, В. Г. Табачникова.
Использование приведенных в указанных работах зависимостей для сверхзвуковых и дозвуковых течений целесообразно не только в случае автоколебаний, но и при исследовании переходных процессов, рассматриваемых в последующих главах данной книги.
ГЛАВА VI
КРИТЕРИИ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ ОБОЛОЧЕК И ПЛАСТИНОК
§ 61. Основные определения
Перейдем к исследованию процесса выпучивания оболочек и пластинок при апериодических воздействиях. В начале главы I мы говорили о таких задачах, — взятых для примера из авиационной практики, — которые связаны с изучением периодических колебаний тонкостенных конструкций. Не менее важными являются задачи, связанные с быстро протекающим переходным процессом, приводящим к выпучиванию оболочки или пластинки.
Приведем и здесь некоторые примеры. Корпус летательного аппарата подвергается на старте действию силы тяги, вызывающей на протяжении короткого промежутка времени значительные продольные сжимающие усилия. При этом возникает опасность выпучивания конструкции. Конструкция летательного аппарата испытывает также динамические нагрузки при резких изменениях режима полета. Элементы корпуса авиационного двигателя воспринимают в некоторых случаях кратковременные изменения внешнего давления.
Характер выпучивания пластинки или оболочки при быстром нагружении может быть совершенно отличен от поведения конструкции при статической потере устойчивости. Это объясняется влиянием сил инерции, соответствующих перемещениям при выпучивании. Конструкция «не успевает» получить перемещения, отвечающие резко изменяющейся нагрузке. Такое «запаздывание» вызывает изменение нагрузки, при которой происходит бурное выпучивание оболочки или пластинки по сравнению с эйлеровой статической величиной. Для оболочки несущая способность конструкции может при этом, как мы увидим, превзойти в той или иной мере не только «ближнюю» нижнюю кри¬
На это обстоятельство было впервые обращено внимание в работе М. А. Лаврентьева и А. Ю. Ишлинского 6.7.
§61
бСНОЁНЫЁ ОПРЕДЕЛЕНИЙ
213
тическую статическую нагрузку, но и верхнюю критическую величину.
В дальнейшем мы будем условно различать случаи динамической и ударной нагрузок. Примем, что нагрузка является динамической, если при решении задачи могут быть приняты во внимание лишь силы инерции, соответствующие нормальным перемещениям прогибам. При этом мы оставляем вне поля зрения механизм передачи нагрузки вдоль конструкции, считая, что вызываемые ею усилия в срединной поверхности устанавливаются как бы мгновенно. «Запаздывание» процесса выпучивания проявляется при этом особенно ярко. Для металлических конструкций время приложения импульса оказывается при этом порядка 10-2—10_3 сек. При более медленных процессах динамический эффект оказывается выраженным весьма слабо.
В случае же ударной нагрузки мы будем в дополнение к силам инерции, соответствующим прогибам, учитывать влияние сил инерции вдоль тех или иных направлений в срединной поверхности оболочки или пластинки. Иными словами, явление выпучивания будет изучаться совместно с исследованием процесса передачи основных усилий. Характерное время приложения нагрузки составляет при этом для металлических конструкций 10-4 — 10_6 сек.
Рассмотрим более подробно характерную диаграмму зависимости параметра прогиба — перемещения, характеризующего процесс выпучивания, — от параметра нагрузки. Предположим, что нагрузка возрастает монотонно во времени. На рис. 6.1 по оси абсцисс отложен параметр нагрузки р или времени t, вдоль оси ординат — характерное перемещение f.
Вид диаграммы — р или f — t зависит от того, является ли оболочка или пластинка идеальной, либо она имеет начальные несовершенства. Мы будем исходить из модели неидеальной системы. Тогда график f — р будет отображать колебательное движение конструкции вплоть до момента, когда параметр нагрузки достигнет верхней статической критической величины. Пусть этот участок соответствует отрезку ОА. Начиная с точки Л, диаграмма получает иной вид: характерный изгиб монотонно возрастает во времени или с увеличением нагрузки. Наибольший
Рис. 6.1. Зависимость между параметрами прогиба и нагрузки при динамическом сплошная линия и статическом нагружении пунктир.
Это понятие пояснено ниже, в § 69.
214
КРИТЕРИИ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
ГЛ. VI
интерес здесь представляет темп возрастания прогиба. Вначале прогибы увеличиваются слабо, и диаграмма f — р близка к оси абсцисс. Но в некоторый момент времени, отвечающий известному значению нагрузки, происходит бурное возрастание прогиба; на диаграмме рис. 6.1 этому этапу отвечает участок ВС. Для оболочек мы наблюдаем на участке ВС прощелкивание к новой, изогнутой форме равновесия. На рис. 6.1 пунктиром показана кривая, соответствующая статическому поведению конструкции и включающая верхнюю и нижнюю критические точки ри pi закритический участок р2С отвечает устойчивым равновесным формам оболочки с большими прогибами. Динамический процесс заключается, как видим, в перескоке конструкции к новым устойчивым статическим формам; в дальнейшем — на участке CD — должны происходить нелинейные колебания вокруг этих равновесных состояний.
Динамическое прощелкивание оболочки может происходить различными путями в зависимости от формы выпучивания. С практической точки зрения нас интересуют те формы волнообразования, которым отвечает наиболее раннее выпучивание. Предположим, что мы рассматриваем различные формы волнообразования. При этом необходимо найти на диаграмме типа рис. 6.1 такие кривые, для которых фронт нарастания прогибов является наиболее ранним.
В таком исследовании нас прежде всего интересует неустановившийся, переходный процесс движения оболочки или пластинки на участке ВС. Эксперименты показывают, что динамическое прощелкивание оболочки завершается, как правило, появлением пластических деформаций вдоль линий, разделяющих выпучины, и при продолжающемся нагружении — образованием трещин вдоль этих линий. Правда, для материалов типа композиционных, характеризующихся линейным законом деформации вплоть до разрушения, картина выпучивания оказывается иной. Здесь динамическое выпучивание при относительно слабых импульсах не вызывает остаточных деформаций. Однако при достаточно интенсивных ударных нагрузках в оболочках из подобных материалов появляются трещины, расположенные вдоль ребер исчезнувших вмятин.
Общий характер волнообразования при динамическом выпучивании, судя по данным опытов, оказывается близким к тому, который имеет место в случае статической потери устойчивости оболочки или пластинки. Например, при осевом сжатии цилиндрической оболочки образуются такой же формы ромбические вмятины, как и при медленном нагружении. Однако размеры вмятин меняются: они зависят от вида импульса, приложенного к оболочке. Кроме того, узкие участки, разделяющие вмятины, в динамическом процессе выражены более резко.
РАЗЛИЧНЫЕ ВИДЫ ИМПУЛЬСНЫХ НАГРУЗОК
215
Мы говорили до сих пор о случае, когда конструкция имеет начальные неправильности формы. Задача при этом сводится к определению функций, характеризующих деформированное и напряженное состояние системы в зависимости от времени. Мы получим здесь задачу, в которой требуется определить перемещения точек срединной поверхности оболочки и зависящие от них величины при заданных граничных и начальных условиях. Можно представить себе и такой случай, когда конструкция является идеальной, но получает некоторые начальные скорости. Наконец, может иметь место и комбинированный вариант — при наличии исходных неправильностей формы и начальных скоростей. Кроме того, отдельные импульсы могут быть приложены и в другие моменты времени, уже в процессе деформации конструкции.
Появляется вопрос, как можно судить о степени опасности для конструкции того или иного импульса с падающим участком. Автором этих строк было предложено 0.6 в этом случае исследовать полную диаграмму f — Р для оболочки или пластинки. Общий вид ее может быть таким, как изображено на рис. 6.2. Характерный прогиб сначала возрастает, а потом, при снижении нагрузки, начинает падать. Будем условно считать, что в процессе приложения импульса конструкция получила опасные деформации, если характерный параметр прогиба f достиг некоторой предельной величины пр. В качестве пр можно принимать, например, прогиб, соответствующий появлению в статическом процессе пластических деформаций либо, скажем, величину, равную толщине оболочки или пластинки. Если использовать такой критерий и уровень Пр охарактеризовать штрих-пунктирной линией рис. 6.2, то динамический процесс, отвечающий пунктирной линии, надо считать опасным, а сплошной линии — безопасным.
§ 62- Различные виды импульсных нагрузок
До сих пор мы рассматривали случай, когда нагрузка меняется монотонно во времени. Но реальные динамические усилия с параметром р, воспринимаемые теми или иными конструкциями, могут зависеть от времени t по самым разнообразным законам. На рис. 6.3 изображены различные варианты диграммы р — t.
и опасного пунктир.
216
КРИТЕРИИ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
ГЛ. VI
Рис. 6.3, а соответствует линейному закону возрастания р этот случай мы часто будем рассматривать в главе VII. Говоря о непрерывном увеличении нагрузки, мы имеем при этом в виду, что важный для нас процесс прощелкивания оболочки происходит на восходящем участке диаграммы нагружения; дальнейшим поведением конструкции мы не интересуемся. Решающее влияние на положение фронта бурного выпучивания пластинки или оболочки оказывает, при прочих равных условиях, скорость 5 возрастания нагрузки, характеризуемая углом наклона
Я
t
р
г
д
е
Рис. 6.3. Возможные диаграммы, изображающие зависимость между параметрами нагрузки и времени.
прямой ОА к оси абсцисс. С увеличением s эффект запаздывания усиливается. Диаграмма рис. 6.3,6 состоит из двух участков: на первом из них нагрузка возрастает по линейному закону, на втором — остается постоянной.
Остановимся более подробно на форме импульса по рис. 6.3, в. Здесь нагрузка сначала возрастает до некоторого уровня со скоростью Su cl затем падает с некоторой иной скоростью 52. Поведение конструкции оказывается зависящим при этом от той и другой величин. Допустим, что при достаточно большом значении Si на первом из этих участков конструкция не претерпела прощелкивания. Если скорость на втором участке снижается сравнительно медленно — скорость s2 мала, — выпучивание может произойти именно здесь. Поэтому характер «падающего» участка является таким же существенным, как и «восходящего».
Такие же предположения можно сделать по отношению к следующим вариантам зависимости р — по рис. 6.3. При этом можно увязать характер поведения оболочки с общим очертанием кривой р — t и величиной импульса, определяемой площадью диаграммы; это будет сделано в главе VII.
63 ПОНЯИЯ ДИНАМИЧЕСКОЙ КРИТИЧЕСКОЙ НАГРУЗКИ 217
§ 63. Понятия динамической критической нагрузки и динамического коэффициента
Рассматривая процесс динамического выпучивания конструкции, мы обращаем прежде всего внимание на положение зоны бурного выпучивания пластинки или оболочки. В литературе часто применяют по отношению к этому участку диаграммы f — р термин «динамическая потеря устойчивости». Однако здесь следует соблюдать осторожность. Вопрос о характере устойчивости движения оболочки на различных участках требует специального исследования. Судя по данным вычислений, малым изменениям начальных перемещений и начальных скоростей будут соответствовать сколь угодно малые изменения в очертании кривых f — р.
Будем в дальнейшем трактовать участок прощелкивания как процесс наступления динамической неустойчивости, так как здесь происходит резкое изменение характера волнообразования оболочки или пластинки.
В таком же условном смысле можно говорить о понятии динамической критической нагрузки, определяемой положением участка ВС на рис. 6.1. Но участок этот может быть очерчен различным образом; поэтому естественно попытаться более определенно условиться относительно величины «критического» усилия или «критического» промежутка времени. Один из возможных подходов заключается здесь в установлении положения точки перегиба характерной кривой f — р на этом участке и определении критической динамической нагрузки как абсциссы этой точки. Другое предположение заключается в определении абсциссы некоторой «средней» точки участка ВС.
Некоторые авторы считают критическую динамическую нагрузку достигнутой в тот момент, когда стрела прогиба доходит до величины, равной толщине пластинки или оболочки. Такое предложение основывается на том, что этой точке примерно соответствует достижение приведенным напряжением предела текучести материала.
Можно определить наибольшую величину интенсивности напряжений в срединной поверхности или интенсивности полных напряжений с учетом усилий изгиба и сопоставить ее с пределом текучести.
Если определена так или иначе динамическая «критическая» нагрузка, то мы можем ее сравнить с соответствующей статической величиной. В дальнейшем мы будем пользоваться понятием динамического коэффициента Сд. Под этой величиной понимается отношение динамической «критической» нагрузки к верхней статической критической нагрузке, вычисленной для идеальной оболочки или пластинки с теми же параметрами.
218
КРИТЕРИИ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
ГЛ. Vt
либо для конструкции с теми же начальными несовершенствами. В случае, если сопоставляются экспериментальные данные, уместно, по нашему мнению, находить динамический коэффициент как отношение полученной в опыте динамической нагрузки, отвечающей резкому выпучиванию, к критической нагрузке для такой же оболочки, найденной при статических испытаниях.' Отметим, что в качестве базисной величины здесь может быть выбрана также теоретически вычисленная верхняя статическая критическая нагрузка.
§ 64. Другие возможные подходы к задаче
Итак, мы условились все понятия, относящиеся к динамическому прощелкиванию, относить к несовершенным конструкциям. Естественно задать вопрос: нельзя ли определить динамическую критическую нагрузку и для идеальной системы, рассматривая ее как предельный случай конструкции с начальными несовершенствами. На это можно лишь ответить, что в рамках принятой математической модели идеальная конструкция не может быть рассмотрена: в течение всего процесса быстрого нагружения дополнительные прогибы будут отсутствовать. Правда, при решении задачи с помощью цифровых машин можно ожидать, что в качестве возмущений будут служить погрешности вычислительного процесса. Но в проделанных автором и его сотрудниками примерах оказалось, что такие «импульсы» не оказывают сколько-нибудь существенного влияния на вид диаграммы f — р.
В литературе, однако, предложены и другие подходы к задаче, относящиеся уже к идеальным конструкциям. Один из таких путей удобнее всего опиния ежа- сать в применении к задаче о поведении стержня с одстержня ним неподвижным концом А в случае приложения ко при ударе, второму концу В продольной ударной нагрузки рис. 6.4. Допустим, что в момент удара элемент стержня у торца В получает некоторую деформацию сжатия, которая затем в виде волны распространяется по стержню. В различные моменты времени деформация сжатия охватывает разные участки стержня. Можно предположить, что в процессе удара потеря устойчивости происходит на том же участке стержня ВС, который отвечает эйлеровой статической нагрузке. Возникает вопрос, какие граничные условия следует принимать для рассматриваемого участка. На это следует ответ, что один из кон¬
Рис. 6.4. Характер выпучива-
См. G. Gerard, Н. Becker, J. Aeron. Sci. 19, Яг 1 1952, 58—62,65.
ДРУГИЕ ВОЗМОЖНЫЕ ПОДХОДЫ К ЗАДАЧЕ
219
цов В надо считать шарнирно закрепленным, а второй С, например, — упруго защемленным. На вопрос, потеряет ли стержень устойчивость в процессе распространения продольной упругой волны, здесь можно ответить утвердительно, если вычисленная длина участка ВС окажется меньше полной длины стержня АВ.
Такой подход является интуитивным; его можно оценить лишь в результате анализа динамического процесса выпучивания. Исследования, проведенные для стержня с начальной погибью, показывают см. книгу 0.6, стр. 304, что действительно после удара на том участке стержня, который охватывается упругой волной, образуется одна полуволна. Но реальный процесс выпучивания стержня гораздо более сложен, чем у той модели, которую мы разбираем. Упругая волна отражается от закрепленного конца и затем, после некоторых последовательных отражений, стержень разбивается на известное число участков с возрастающим дополнительным прогибом. Длина такого участка зависит от обстоятельств удара; интересно отметить, что при некоторых предположениях она оказывается примерно равной той длине, которая отвечает эйлеровой статической критической силе. Но такой результат является, по-видимому, случайным.
Подобный путь приведения динамической задачи к квазистатической нашел приложение и в применении к оболочкам. Допустим, что докритические усилия в срединной поверхности оболочки определяются с учетом сил инерции из динамических соотношений. Что же касается самого процесса выпучивания, то в таком варианте исследования влияние сил инерции из рассмотрения выпадает. На этом пути мы можем получить неожиданные результаты. Так, например, в случае приложения мгновенного импульса система получает, как известно, деформации, вдвое превышающие статические. Следовательно, система в такой интерпретации задачи должна потерять устойчивость в динамическом процессе уже в тот момент, когда ее деформации достигнут половины максимальной величины. Если вычислить по предложенному ранее методу динамический коэффициент, то он окажется равным 0,5. Между тем многочисленные опыты показывают, что при динамическом приложении нагрузки несущая способность конструкции оказывается, как правило, выше, чем в случае медленно возрастающих усилий; динамический коэффициент должен превышать единицу. Таким образом, при подобном подходе докритические усилия определяются из решения динамической задачи, в то время как самый процесс выпучивания рассматривается со статических позиций.
Другой подход заключается в исследовании задачи о выпучивании конструкции при динамическом приложении нагрузки
220
КРИТЕРИИ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
ГЛ. VI
с позиций теории параметрического резонанса. Как мы знаем из главы IV, в случае приложения к упругой конструкции нагрузки, имеющей периодическую составляющую, система может оказаться динамически неустойчивой. Она начинает совершать колебания с нарастающей амплитудой: возникает ряд зон неустойчивости; наибольшую опасность представляет первая из них, отвечающая наименьшей частоте. В данной и последующих главах выражение «динамическая устойчивость» не связывается с теорией параметрических колебаний.
По-видимому, теория параметрического резонанса может служить для описания процесса перекачки энергии продольного движения элементов конструкции — в случае осевого сжатия — в энергию поперечных колебаний. По-существу, такое явление перехода энергии мы должны наблюдать и при динамическом выпучивании. Эта идея требует дальнейшего исследования.
В следующих двух главах книги будет рассмотрено поведение оболочек и пластинок при динамическом и ударном нагружении. Мы будем придерживаться той линии, которая была намечена в этой главе. Речь при этом идет о несовершенных системах; они исследуются с позиций нелинейной теории по уравнениям, приведенным в главе I. Из-за трудностей, связанных с применением каких-либо аналитических методов, мы будем использовать в основном различные численные методы с широким применением цифровых машин.
ГЛАВА VII
ВЫПУЧИВАНИЕ ОБОЛОЧЕК И ПЛАСТИНОК ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ
§ 65. Постановка задачи. Исходные уравнения
В настоящей главе будут рассмотрены такие случаи динамического выпучивания, при которых можно пренебречь волновым характером распространения основных усилий по объему конструкции. Будем считать, что эти усилия пронизывают конструкцию как бы мгновенно, изменяясь во времени по заданному закону. Задача состоит в том, чтобы проследить за поведением оболочки или пластинки под действием таких нагрузок в предположении, что, как правило, конструкция имеет начальные несовершенства.
Выпишем основные зависимости для подобной задачи, исходя из уравнений главы I. Вводя функцию напряжений Ф ху у, t по соотношениям 1.30, придем к следующей системе уравнений по 1.38 и 1.39:
D Г74 т rfs I и 2Ф,, д2Ф, q у d2w 1 ч
Y V w — Wq L w, Ф kx ду2 ky дх2 — -J2, 7.1
-L V40 — jLw, w — Lw0, КУ0 —
t, d2W — Wq _, 32W — Wq 0,
KX dy2 Ky dx2 • ‘-t
Здесь операторы Lw, Ф и Lw,w соответствуют выражениям
1.32 и 1.34. Напомним, что через kx и ky обозначены главные кривизны срединной поверхности, которые считаются постоянными, через w и Wo — полный и начальный прогибы, через q — поперечное давление.
§ 66. Поведение пластинок при динамическом сжатии
В качестве первого примера рассмотрим случай пластинки ауЬ, сжатой в одном направлении см. рис. 2.10 вдоль стороны а. Примем вначале, что усилия сжатия р возрастают
пропорционально времени по закону р st рис. 6.3,а. Решим
222 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
эту задачу с помощью метода Бубнова — Галеркина. Основные уравнения 1 и 2 примут вид
--V<w-w0 Lw, ф±-±°Ъ, 7.3
-1у4Ф Lw0, а»о — Lw, да. 7.4
Считая пластинку близкой к квадратной и полагая ее шарнирно закрепленной по всем краям, примем в качестве аппроксимирующих функций выражения
£. тлх. плу с. тлх. пли -ч
w f sinsin —, Wq о sin — sin —, 7.5
где тип — числа полуволн вдоль а и Ъ. Подставляя соотно¬
шения 5 в 4, находим края а сближаются свободно:
ф £ f2 — fo п2 I а2 2тлх t j m2 b2 2плу ру2
32
Г п2 I а2 2тлх jm2fb2 2плу ру2
•« Ыcos—Ы Ыcos— J-т--
Далее, пользуясь методом Бубнова — Галеркина по отношению к уравнению 3, получим следующую зависимость:
- тгТ Кт’ '■’Г « - W ■'- is ¥ S'»• <7-7>
Здесь обозначено о величине а см. стр. 264:
9- J_ f О О — •
h ° h ’ Л — Ь
через р и q выражены величины
р by •_ q Ь4
Р £ г q Eh
Опуская в 7 нелинейный и инерционный члены, приходим к известной формуле для безразмерного критического напряжения при X 1, 2, 3.
Ркр
_кр т2_ я2 78ч
— Е hi 31 -ц2 •
Приведенные в §§ 66, 67, 76 решения задач для пластинки и цилиндрической панели принадлежат Е. А. Вольмир ДАН СССР 201, 6, 1971, 46—48; ранее в книге 0.6 был рассмотрен один частный пример.
66 ПОВЕДЕНИЕ ПЛАСТИНОК ПРИ ДИНАМИЧЕСКОМ СЖАТИИ 223
С другой стороны, отбрасывая нелинейные члены, получаем уравнение малых колебаний ненагруженной пластины, при £о 0 будет
Р Кт п2 » уЬ' dK Q
кР 4 Egn2h2 dt2
Квадрат основной частоты равен для квадратной пластинки
< 7.9
Введем обозначение f для параметра времени
7.10
Ркр Ргр
тогда придем к обыкновенному дифференциальному уравнению для стрелы прогиба
1
,Д«-«ЖМ£тМ-
-'f
2 Г - 16.а< 0. 7.11
Ркряш
Под 5 понимается величина
с з яcEhz 2 t
S 7.12
где с — скорость звука в материале пластинки, определяемая по 2.5. Сопоставляя выражения 9 и 12, находим, что VS pJsEhbf.
Интегрирование уравнения 11 выполнялось с помощью метода Рунге — Кутта. Результаты вычислений, выполненных с помощью цифровой машины БЭСМ-2М, отражаются графиками, приведенными на рис. 7.1 —7.3. В дальнейшем мы будем определять динамическую «критическую» нагрузку по данным главы VI, исходя из критерия бурного выпучивания системы.
Рис. 7.1 относится к случаю квадратной пластинки X ab 1 с начальной стрелой прогиба £0 Ы04; считаем, что поперечная нагрузка отсутствует, q 0. Сплошными линиями изображены кривые £, отвечающие S 1 и т 1, 2, 3. Как видим, развитие бурных прогибов начинается раньше всего при т 2, п 1. Таким образом, здесь следует ожидать развития динамических прогибов при двух полуволнах по длине. Напомним, что статическая потеря устойчивости квадратной пластинки происходит при т п 1. Коэффициент динамичности, равный отношению динамической «критической»
24 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЁНИЙ Vtl
нагрузки к статической, оказывается в рассматриваемом случае равным Сд 5. В случае S 10 пунктирные линии «критической» оказывается форма выпучивания по тем же двум полуволнам т 2, но коэффициент Сд здесь будет около 3.
Штрих-пунктирной линией на рис. 7.1 нанесена квазистатическая зависимость между усилием и стрелой прогиба при закритической деформации.
О 1 2 3 4 5 6 7 8
t
Рис. 7.1. Диаграмма «прогиб— время» для сжатой пластинки при динамическом нагружении; сплошные линии относятся к более быстрому росту нагрузки.
На рис. 7.2 приведен аналогичный график для S 0,5; 0,2 и 0,1; в этих случаях «критическое» значение Сд составляет соответственно 6; 7,3; 8,5.
Исследовалось влияние на поведение квадратной пластинки дополнительной статической поперечной нагрузки. Для случая, когда S 1 и q 1, «критическое» число полуволн т оказалось равным т 1, в то время как при q 0 было т 2.
Таким образом, при наличии поперечной нагрузки эффект появления высших форм выпучивания ослабевает. Соответствующее значение Сд при q 1 составляет 4,25, между тем как при q 0 было Сд 5.
Рассмотрен такой случай удлиненной пластинки, когда 2. Как показали вычисления, статическая форма потери
§ 66 ПОВЕДЕНИЕ ПЛАСТИНОК ПРИ ДИНАМИЧЕСКОМ СЖАТИИ 225
устойчивости отвечает при этом т — 2, п 1; коэффициент критической нагрузки Кд совпал со значением при К 1.
в
с
в
и
г
о
4 6 В W 12
t
Рис. 7.2. Поведение сжатой пластинки при весьма быстром нагружении; наиболее быстрый рост нагрузки отображают сплошные
Рис. 7.3. Влияние стрелы начального прогиба на поведение сжатой пластинки при динамическом нагружении.
1
II
1
S0,1
3ff,Z
30,5 Г
77 7 7
т2 1 п 1 1
Л '
II
т—2 г п1
I
п—7 1
• L.s
1
> т4
773
772 j
Г
II II
и ' 1 1, 1'
Г 7
77
ш
f
У
тп1
В динамическом процессе получено для S 1 и S 0,5 значение т 5, при 5 0,1 найдено т 6. Соответствующие
226
ВЫПУЧИВАНИЕ ПРИ ДЙНАМИЧЁСКОМ НАГРУЖЕНИИ ГЛ. VII
значения Сд составили 4,9; 5,8; 8,4. Если сравнить эти величины с теми же коэффициентами при К 1, то получим примерно те же значения. Отсюда можно сделать предварительный вывод, что найденные для квадратной пластинки значения коэффициента динамичности можно с небольшой погрешностью распространить на прямоугольные пластинки иной конфигурации.
По рис. 7.3 можно проследить эффект стрелы начального прогиба на поведение пластинки. Здесь даны «критические» кривые £ при 5 1 для последовательно уменьшающихся £о, начиная от 1 до 1 • 10_б.
§ 67. Влияние формы импульса на поведение пластинки
Обратимся теперь к. задаче, аналогичной рассмотренной в § 66, но в отличие от нее не будем ограничивать характера изменения осевой сжимающей нагрузки законом р st, а допустим, что она может быть задана произвольной функцией времени р ср0- Здесь удобно ввести другой безразмерный параметр времени т coot под соо понимается наинизшая частота собственных колебаний незагруженной пластинки по 9. Принимая во внимание соотношение
и ч Ь23 — Ц1
р ф0 фт-.
приведем 11 к виду при q' 0 £-£ох2 «22
£о-4 фй
Ко0; 7.13
под S понимается выражение
о М31-Цга’
° n4h3cE
Далее мы будем пользоваться безразмерной функцией времени ф т Sq> т.
Пользуясь 13, исследуем случай ступенчатого импульса
г0 ПрИ OTTq,
О при т > т0.
На рис. 7.4 приведены данные вычислений для одного и того же параметра г0 5, но импульсов различной продолжительности; принято to 1 • 10_3, К 2. «Критическое» число полу¬
Рис. 7.4. Характер кривых «прогиб — время» при импульсе ступенчатой формы.
f1
1>т
§ 67 ВЛИЯНИЕ ФОРМЫ ИМПУЛЬСА НА ПОВЕДЕНИЕ ПЛАСТИНКИ 227
волн ткр оказалось в данном случае не зависящим от продолжительности импульса и равным 7; пир по-прежнему равно 1.
В дальнейшем условно примем критерий «опасного» значения импульса фото, исходя из заданного максимального
76
то 72
8
4
О
6 6,5 7 7,5 в в<5 9
J
Рис. 7.5. Области безопасных импульсоп ступенчатой формы для сжатой пластинки.
значения прогиба. Будем находить те сочетания величин нагрузки J0 и импульса, при которых впервые достигается некоторая предельная амплитуда прогиба. На рис. 7.5 представлены соответствующие кривые для тех случаев, когда предельными считаются прогибы £ 1 и £ 0,5.
Как видим, опасными являются тем меньшие импульсы, чем выше уровень нагрузки. Интересно отметить, что на левом участке «предельные» значения импульса остаются почти неизменными.
На рис. 7.6 приведены такие же данные для случая экспоненциального импульса по рис. 6.3, е, заданного законом гэт Ае°>Ъх. Нанесенные на рис. 7.6 кривые соответствуют предельным значениям прогиба С 0,5; 0,8; 1; здесь также величина импульса, приложение которого необходимо для достижения того или иного прогиба, уменьшается с увеличением амплитуды нагрузки А.
40
4
5Z
24
76 8
6 6,4 6J3 7,2 7,6 8J7
J
Рис. 7.6. Области безопасных импульсов экспоненциального вида для сжатой пластинки.
228
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
§ 68. Динамическое выпучивание пластинок при сдвиге
Перейдем к случаю, когда прямоугольная пластинка подвергается динамическому действию усилий сдвига, равномерно распределенных по ее кромкам. Задачи такого типа встречаются, например, в судовых конструкциях, когда на корпус судна действуют динамические нагрузки, возникающие при ударе волн, при прохождении акустической волны и т. д. Аналогичные нагрузки могут иметь место в панелях обшивки летательного аппарата.
Примем пластинку шарнирно опертой по краям и предположим, что кромки сближаются свободно. Будем пользоваться попрежнему методом Бубнова — Галеркина.
Следуя решению статической задачи см. 1.11, стр. 157, выберем аппроксимирующее выражение для прогиба в виде
Эта формула относится к случаю, когда стороны пластинки а и Ь мало отличаются по величине. Дальнейшая процедура выкладок та же, что в § 66. В результате интегрирования уравнения 2 находим функцию Ф в виде
под s понимается интенсивность касательных усилий. Далее, применяя к 3 процедуру Бубноваг—• Галеркина, приходим к системе нелинейных дифференциальных уравнений
w fn sin sin f22 sin -
7.14
Ф £
;2
11 32 а2Ь2
22 32а2Ь2
a4 COS
J_,Cos — 0-cosf-
fuf224aW
sxy; 7.15
16jx4A,2
А» 92 9X2 14 „2 ■ 9A,2 l2 A.2 92 bife2-t-
2 2.U _28 V 0
121— Ц2 X2 9я2 2
7.16
X2 92 9Л2 l2 fir. 4л1 X2 1
9A,2 l2 A,2 92 WW f з i _ ц2
7.17
Эта задача была исследована М. С. Герштейном 7.9а.
Для упрощения мы не приводим здесь члены в уравнениях, связанные с начальными неправильностями.
§ 68 ДИНАМИЧЕСКОЕ ВЫПУЧИВАНИЕ ПЛАСТИНОК ПРИ СДВИГЕ 229
Здесь введены обозначения
0 S Eh2 '
ab
Если в приведенных выше уравнениях отбросить инерционные члены, а также нелинейные составляющие, то можно определить приближенное значение критического статического напряжения сдвига:
Рассмотрим далее динамическую задачу, принимая, что взаимное смещение кромок по направлению стороны а происходит с постоянной скоростью. Сдвиг, соответствующий этому смещению, будет
так же определяется йуо.
Перемещение и находится по аналогии с решением статической задачи 1.11, стр. 159. Далее определяем «средние» смещения сторон у 0 и у 6, которые затем подставляем в 17а. После несложных преобразований и приведения к безразмерному виду получим
где tQtabh2rKp—безразмерный параметр времени. Вводя 18 в 16 и 17, приходим к системе обыкновенных нелинейных уравнений относительно £i,
Если предполагать, что рассматриваемая пластинка имеет начальный прогиб, описываемый выражением
т,
кр
Зя4 Л212 128 1 — p.2 X
где
0 — j Jlysssb йуо — Q.
Здесь йуъ — «среднее» смещение стороны у — Ь:
7.17а
а
Г 16А,2
X2 - 9ц 9Яа I2 9 9 — цЯ» X 9а » » 9Я2 929Я2О2
7.18
230
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
то вместо системы 16, 17 следует записать новые уравнения движения. Для квадратной Я 1 пластинки из материала с коэффициентом Пуассона ц 0,32 они после упрощений приобретают вид
7.19
-gi- S 0,124 Й - £, 0,4691 0,368 ft, - Zo -
at
— 1,09 If £2 0,
-5 1,98£ 0,4692 5,882 - 1,09£1 0, dt
где
<•
Численное интегрирование уравнений системы 19 было выполнено методом Рунге — Кутта.
Результаты вычислений представлены на рис. 7.7 и 7.8 для случая, когда стрела начального прогиба составляет £0 0,01
S
4
У
к
уа>5
<
9 А 1 У
i х
1 ✓
1
i
Рис. 7.7. Кривые «стрела прогиба — время» для квадратной пластинки, подвергающейся динамическому сдвигу 52.
О 2 4 6 8 70
t
Рис. 7.8. Амплитуды различных форм волнообразования для удлиненной пластинки при динамическом сдвиге S0,5; 2; 6.
при разных значениях 5. Сплошными линиями нанесены графики £i; для одного варианта S 2 изображена также функция £2 t. Пунктиром отмечены соответствующие статические зависимости. Общий характер кривых соответствует случаю сжатия, описанному в § 66.
На рис. 7.9 сплошными линиями показаны теоретические значения динамического коэффициента Сд в зависимости от стрелы начального прогиба. Здесь же приведены результаты опы-
ВЫПУЧИВАНИЕ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
231
тов. Крестиками помечены данные, относящиеся к пластинкам толщиной 0,75 мм, а кружочками — 0,95 мм; модели были выполнены из алюминиевого сплава АМГ-6. Треугольники соответствуют данным для дюралюминовых пластинок толщиной в 1 мм.
Опыты проводились при различных скоростях нагружения. Процесс выпучивания пластинки начинался в упругой стадии с образованием, как правило, одного диагонального гофра. Отметим, что такая форма изгиба отвечает аппроксимации типа 14. В процессе опытов было проведено осциллографирование деформаций сдвига в срединной поверхности. Нарастание этой деформации во времени происходило по закону, близкому к линейному. После достижения деформацией сдвига некоторой величины 0 начинается резкое выпучивание пластинки. С качественной стороны экспериментальные данные соответствовали теоретическим.
Отметим, что при весьма быстром нагружении выпучивание пластинок во время опытов происходило с образованием не одного гофра, а двух или трех. Иными словами, здесь имело место выпучивание по высшим формам потери устойчивости или колебаний. Это обстоятельство желательно учесть в последующих исследованиях по динамическому сдвигу, аналогично тому, как это было сделано для случая сжатия.
3.0
2,0
7.0
у
v
°у
X
О
02 0,4
0,0 0,8 S
Рис. 7.9. Сравнение теоретических сплошные линии и экспериментальных значений динамического коэффициента для пластинки при сдвиге.
§ 69. Выпучивание цилиндрических оболочек при динамическом нагружении. Основные понятия
Обратимся к исследованию динамического выпучивания замкнутых круговых цилиндрических оболочек при нагрузках различного типа. Вначале рассмотрим случай осевого сжатия. Но перед тем, как заняться непосредственно динамической задачей, напомним имеющиеся в литературе данные о выпучивании сжатых вдоль оси цилиндрических оболочек в случае квазистатического нагружения.
Известно, что металлические тонкостенные оболочки, подвергающиеся осевому сжатию, теряют устойчивость, как правило,
Они были выполнены М. С. Герштейном и В. П. Благовещенским,
232
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
с образованием ромбических вмятин. Эти вмятины образуют обычно два-три пояса; в некоторых же опытах удается получить вмятины, охватывающие почти всю поверхность оболочки. Объяснение этому явлению может быть дано с геометрических позиций. Оболочка выпучивается главным образом внутрь, к центру кривизны, так как срединная поверхность не получает при такой деформации значительных деформаций растяжения — сжатия.
Изгибание оболочки не является непрерывным и происходит в процессе резкого прощелкивания. Если представить себе все же, что равновесные формы оболочки непрерывно следуют одна за другой, то мы в первом приближении получим диаграмму «параметр прогиба — нагрузка», изображенную на рис. 6.1 пунктирной линией. В действительности картина выпучивания оболочки оказывается гораздо более сложной. Явление хлопка сопровождается трансформацией форм выпучивания. Если проследить за этим явлением с помощью скоростной киносъемки, то окажется, что число волн вдоль окружности падает, а затем в некоторых случаях вновь начинает возрастать. Таким образом, вместо одной плавной кривой рис. 6.1 мы получаем серию кривых, отвечающих различным числам волн. В литературе по статической устойчивости оболочек в большом было принято строить огибающую этих кривых; далее определялась нижняя критическая нагрузка по точке, соответствующей минимуму р для наинизшей из кривых. Однако последние данные заставили пересмотреть эту процедуру, по крайней мере в применении к практическим расчетам. Оказалось, что уточнение вычислений приводит к существенному уменьшению нижней критической нагрузки, и в пределе эта величина приближается к нулю. Но отдаленные кривые pf соответствуют весьма значительным прогибам, превышающим толщину оболочки в десятки и сотни раз. С другой стороны, можно показать, что переход к этим отдаленным равновесным ветвям требует преодоления весьма высокого энергетического барьера. Исходя из этих данных, автором книги было предложено ввести понятие ближней нижней критической нагрузки. Если рассмотреть экспериментальные данные, относящиеся к реальным оболочкам, то окажется, что они укладываются главным образом в область, лежащую между верхней критической нагрузкой и той величиной, которая отвечает ближней нижней критической нагрузке.
См. более подробно об этом в книге 0.6, стр. 534 и в монографии А. В. Погорелова «Геометрические методы в нелинейной теории упругих оболочек», М., 1967.
На это обстоятельство обратил внимание Л. И. Балабух в 1952 г
См. также статью Джонса AIAA Journ. 5, 9, 1966.
ДИНАМИЧЕСКОЕ ПРИЛОЖЕНИЕ ОСЕВОГО СЖАТИЯ
233
Вернемся к динамической задаче. Как уже было сказано в главе VI, характер кривой pf при импульсном нагружении может резко отличаться от статических ветвей. Задача и здесь сводится к интегрированию с помощью тех или иных приближенных методов, уравнений типа 1 и 2. При этом мы будем, как правило, аппроксимировать прогиб и функцию напряжений с помощью таких выражений, которые соответствуют статическим решениям первого приближения, но с учетом возможного изменения числа узловых линий в различных направлениях.
§ 70. Цилиндрические оболочки при динамическом приложении осевого сжатия
Рассмотрим случай замкнутой круговой цилиндрической оболочки, скрепленной по торцам с жесткими на изгиб шпангоутами. Будем считать, что оболочка подвергается быстрому приложению осевой нагрузки, равномерно распределенной по ее торцам. Поставим перед собой цель определить поведение оболочки во времени, считая, как мы условились, что приложенные к торцам усилия «мгновенно» пронизывают всю оболочку.
Примем следующий план решения задачи. Используя вариационный метод и аппроксимируя выражение для прогиба, сведем задачу к нахождению зависимости параметров прогиба от времени. Иными словами, пойдем по тому же пути, что и в случае пластинки.
Выражение для полного прогиба примем в виде
f. птх. пу. о тлх. wf sin sin— -фsin h <pl. 7.20
Через L и R здесь обозначены длина оболочки и радиус кривизны срединной поверхности. Под т понимается число полуволн вдоль длины, под п — число волн по окружности.
В дальнейшем мы будем считать, что начальный прогиб по
своей форме находится как бы в «резонансе» с формой допол¬
нительного прогиба, и аппроксимируем начальные отклонения выражением
с. я тх. пу -,. о тлх, т
w0 fo sm sin-jf- sin2 —J- qpj. 7.21
Отметим, что выражения 20 и 21 соответствуют решению статической задачи об устойчивости оболочки в первом приближении см. 0.6, стр. 526. Первый из членов в скобках отвечает форме потери устойчивости оболочки в малом, а также форме малых изгибных колебаний. Второй член учитывает преимущественное направление выпучивания оболочки к центру кривизны. Третий член отражает радиальные перемещения точек концевых сечений.
234 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
Подставим выражения 20 и 21 в правую часть уравнения 2 при kx 0, ky 1R. После интегрирования находим
Ф - Е к, cos К, cos К, sin sin
K,sinS-sin-. 7.22
Коэффициенты К>., К4 равны
к_ 1 Г-оР. f f о2 2f-f01
мт
2 - - <Р2
K2f2-a Ki-f-s2-fiH
Щт 9а т Р22
к _ «т f h «тР22о
Дз“ а р2 а р22 V’
где ат тпЩ р nR. Под р понимается средняя интенсивность сжихмающих усилий, приложенных к торцам оболочки.
Далее выпишем условие замкнутости оболочки для перемещения v:
2nR
д0 dy 0. 7.22а
I
ду
о
Сравнивая выражения для гуу записанные через прогиб и функцию напряжений, находим:
dv 1 д2Ф д2Ф 1 dw 2 1 dw0 2. w w0
ду Е дхг ду 2 ду Т ду R R ’
Подставляя сюда 20—22, с учетом предыдущих соотношений находим
<р - т Р2.
Таким образом, величина ф оказывается выраженной через параметр г, значения f и f0.
Воспользуемся далзе методом Бубнова — Галеркина в применении к уравнению 1. Основные уравнения имеют вид
L2nR
J J £sin amsinp dxdy 0, 7.23
о
L2nR
J J X sin2 amx dx dy 0; 7.24
о о
L2nR
0 0
§ 70 ДИНАМИЧЕСКОЕ ПРИЛОЖЕНИЕ ОСЕВОГО СЖАТИЯ 235
здесь X будет
X 2. V4 w _ w0 - L w, Ф - -jL -J. 7.24a
После интегрирования уравнения 23 находим р Со 1 —if с, S2 - с2 S - £2 г>2 -
1 d2t £2 £2
-Сза-У С-Сз---ф, 7.25
где
• 11 If
1 42ц 121 — и2 im
2
Ьт
16 й
C_e”iW 0Wn’
с,_ж1 I■•
_ ■« 1 „ _ I»
> 5 —'
Egr fm ’ l fj-
Введенные безразмерные параметры равны
г — L r—h. л — mnR — ат
ь г » h 9 nL р ’
р R oh
р Е h 9 т1 —п •
Если из уравнения 25 исключить инерционный член и положить £о 0> то мы придем к решению статической задачи для оболочки идеальной формы. Принимая во внимание лишь члены, линейные ютносительно £, найдем параметр р равным
л-г- 1 1 2М -
Р -Со 12 l — Ц2 т Л 1 2 п —
-ЩТ Т- <7“>
Это отвечает формуле 13.39 книги 0.6. Минимизируя р по параметру х 1т2ц1т> получим
Рв,77- ИЛИ при ц 0,3, pBz 0,605. 7.27
у 6 1 — ц2
236
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ, VII
Если же учесть в статической задаче нелинейные члены, то данный вариант решения приводит к параметру нижнего критического напряжения н 0,15в 0,09; он соответствует значению 1т 0,6. Это означает, что при достижении сжимающим напряжением «ближнего» нижнего критического значения отношение дугового размера вмятины nRn к осевому размеру Lm составляет 0,6; иными словами, вмятины ромбовидной формы оказываются вытянутыми вдоль дуги. Отметим, что здесь речь идет о нижней точке огибающей ряда кривых р£, определяемых при различных тип.
Обратимся вновь к динамической задаче. Примем, подобно случаю пластинки, что внешние усилия возрастают по закону р st, и введем безразмерные параметры
«-г-
Тогда уравнение 25 примет вид
1 d Uf, C-CoU 1 IImV2 2
0 S,2 U 9>2k 4fpT I1 uSi2
ГтЬ-йЬ0- <7-28>
Уравнение 28 было проинтегрировано методом Рунге — Кутта с помощью цифровой машины. При этом была принята форма вмятин, которая отвечает наименьшему верхнему критическому напряжению; здесь речь идет о предельных значениях параметров формы волнообразования, найденных из решения нелинейной задачи при £о 0, когда Параметр гэ, харак¬
теризующий удельный вес «несимметричной» составляющей прогиба в 20, был принят тем же, что и в соответствующей статической задаче для оболочки совершенной формы, поэтому второе из уравнений 23, 24 в решении не учитывалось. Результаты представлены на рис. 7.10 и относятся к оболочке Rh 180, LR 2,2. По оси абсцисс отложены значения
t Р Р Рв Рв'
где рв — наименьшее верхнее критическое напряжение, а по оси ординат — параметр стрелы прогиба £. Различные серии кривых относятся к динамическому нагружению, происходящему при постоянной скорости увеличения нагрузки 5 МО6; 2-106;
ДИНАМИЧЕСКОЕ ПРИЛОЖЕНИЕ ОСЕВОГО СЖАТИЯ
237
5-10е кгсм2-сек. Каждая кривая характеризуется некоторым числом волн п, указанным на графике. Как видим, бурный рост имеет место ранее всего в первом случае при п 11, во втором при п 12, в третьем при п 13.
s-2'W 6кгсм2сек
С
з
2
7
О
7,0 7,7 7,2 7f3 7f7 7,5 7,6 7,7 7,0 t
Рис. 7.10. Диаграммы «характерный прогиб —время» для замкнутой цилиндрической оболочки при осевом сжатии.
На рис. 7.11 теоретические значение Сд, в зависимости от скорости нагружения s, сопоставлены с экспериментальными. Коэффициент динамической перегрузки Сд был получен делением величины нагрузки, при которой происходило динамическое выпучивание, на статическое значение, также найденное из опытов. Сплошная кривая проведена через точки, полученные интегрированием уравнения 28 при So 0,001. Рассмотрение графика показывает, что данные испытаний характеризуются большим разбросом, но в общем следуют теоретической кривой. Отметим, что и в других случаях достаточно хорошее соответствие экспериментальных данных для тщательно изготовленных оболочек с теоретическими имеет место, если в вычислениях принять параметр начального прогиба равным приблизительно £0 0,001. В динамическом процессе испытанные оболочки
Рис. 7.11. Теоретические значения динамического коэффициента для сжатой цилиндрической оболочки сплошная линия в сравнении с данными опытов Rlh «180, LR2,2.
Опыты были проведены С. Н. Кирюшиной, ей же принадлежат приведенные выше вычисления.
238
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
выпучивались, как видим, при нагрузке, превышающей статическую от 10 до 60, в зависимости от скорости нагружения. Хотя меньшая из этих величин невелика и лежит в пределах разброса опытов, верхний предел характеризует заметное повышение несущей способности оболочки.
Другие авторы, занимавшиеся этой же задачей, аппроксимировали прогиб с помощью несколько иного выражения:
р. тпх. пу. о тпх.9 пу
W I I Sin —Sin-j Sin2 -—SlIT ft •
В выкладках, проведенных тем же путем, было принято, что волны являются квадратными.
§ 71. Цилиндрические оболочки при внешнем давлении
Перейдем к другой важной задаче — о поведении замкнутой круговой цилиндрической оболочки при динамическом приложении равномерно распределенного внешнего давления. Подобно тому как это было сделано в § 70, считаем оболочку скрепленной по торцам со шпангоутами, форма которых при деформации конструкции остается круговой. В приведенных ниже выкладках мы будем, собственно, рассматривать несколько более общую задачу для случая всестороннего давления. Иными словами, предположим, что оболочка снабжена днищами и что давление действует с одинаковой интенсивностью на боковую поверхность и днища.
Случай быстрого нагружения внешним давлением характерен, например, для оболочек в конструкциях авиационных двигателей.
Решая задачу по тому же плану, что и в § 70, примем для полного и начального прогибов следующие аппроксимирующие выражения:
£. пх. пу,,. О ЛХ. W f sin -J- sin -ф sin2 — -f ф,
7 29
r. nx. ny. О nx • ay0 osin — sin-- isin2-r- cpj.
Эти выражения построены подобно 20, 21 и отличакртся от них лишь тем, что число полуволн по длине принято равным т 1; это соответствует данным исследования статической за¬
См. работы В, Л. Агамирова и автора 7.1, а также О. И. Тере бушко 7.22.
§ 71 ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ ПРИ ВНЕШНЕМ ДАВЛЕНИИ 239
дачи и опытов. Подставляя 29 в уравнение типа 2 и интегрируя его, получим
Ф £ cos Кч cos ЩУ K3sin-sin--
7,30
Коэффициенты Ки • • • > Кь определяются прежними выражениями см. стр. 234, но с заменой ат на а, где а яL; под Р и здесь подразумевается величина р nR. Через q обозначена интенсивность внешнего давления; предпоследний член в 30 отвечает напряжению ai qRh в срединной поверхности, вызванному давлением на боковую поверхность, а последний член — напряжению аг qR2hf вызванному давлением на днища.
Пользуясь далее условием замкнутости, как и в § 70, получим
Ф — >Р2 £ О — т 7-31
Уравнения метода Бубнова — Галеркина выпишем по-прежнему в виде
L 2л R
J J X sin а х sinfiy dxdy 0,
о о
L 2nR
J J X sin2 ах dxdy 0,
7.32
где под X понимается выражение 24а.
Выполняя интегрирование первого из уравнений 32, будем иметь
4 С0 1 -C3S-£oH-C4l 7.33
Коэффициенты Со,. С5 равны
г 2 Г S6 I 1122д1
2 £2 U2l226т 121-ц2 2 °Г
-> L±11a С 2я22 Г 1. 1 Т.
1 8 2 2 I2 2 2 L 1 £22 1 922 J
с — 1 Г о- _iL_l
3 22 i2 L1 1 22J
r 24 r _ 2Ytf2 1, Rh
1 5222 2 ’ Egr 2 2 ’ ° L2’
240
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ 1ГЛ. VII
Здесь мы в дополнение к обозначениям § 70 пользуемся безразмерными параметрами
t-3-т- <7-34>
Исключая из 33 инерционный член и принимая £0 0> придем к уравнению, отвечающему решению линейной статической задачи
Л -Г— 2 Г V 1 П£22 J
кр Со 2 2 122Л 121— ji2 Чг I'-oD
Минимизируя Кр по г или, иными словами, по числу волн г, определим верхнее критическое давление qB см. стр. 545 книги 0.6, где рассмотрен случай только радиального давления.
Вернемся к динамической задаче, принимая далее, что параметр -ф условно считается тем же, что и в статическом решении. Будем считать и здесь, что интенсивность давления возрастает по закону q st, и введем параметр времени
stR2 _ _ q.
Eh2Q в <7в тогда уравнение 33 примет вид
dK db
-в
S2-3 S-S0S2 С-Со Ко 1
2 3N2 Nt N£ Ni J — U’ ',сЮ
где значения Ль Л2, N3 см. 0.6, стр. 766;
Rh л I 1 л 6N2, п C3No
би- B Cl7’ В2-С2-, с,лЦ. ±е- о_
'4 2<в
Уравнение 36 для безразмерной стрелы прогиба было проинтегрировано численным методом при следующих начальных данных:
£ £°’ if10 Для г0-
Вычисления были проведены применительно к дюралюминовым оболочкам при исходных данных с 5 • 105 смсек, 0,3, £ 7,75105 кгсм1. Кроме того, принималось RL 0,45, Rh 112, б 1,8 ‘10-3.
§ 71 ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ ПРИ ВНЕШНЕМ ДАВЛЕНИИ 241
На рис. 7.12 представлен график, отражающий зависимость между стрелой полного прогиба и временем нагружения или нагрузкой для случая <.
£0ЫО-3. Первая ли- Д
ния слева отвечает реше- нию статической задачи для 0. На графике 7,5
изображена огибающая различных кривых, отве- 5 чающих тому или иному числу волн п. Верхнее критическое давление ' имеет место при числе волн п6, нижнее — при п 5. На том же рис. 7.12 нанесены кривые, найденные для случаев динамического нагружения при
Дин.
£
II1
'о
Н
ч
0
J
я
<о
У
7
У
V
V
1
J
У
О
4
6t 7
Рис. 7.12. Зависимость «характерный прогиб —время» для замкнутой цилиндрической оболочки при внешнем давлении.
скоростях s 0,2-104; 1 • 104; 2-104 атсек. На рисунке и здесь приведены кривые для тех чисел волн, при которых бурное возрастание прогибов соответствует наименьшему параметру. Динамический эффект, как видно из рисунка, проявляется в последовательном возрастании числа волн и значительном увеличении критического давления.
Сравнение данных, относящихся к случаю динамического приложения осевого сжатия см. рис. 7.11 и всестороннего давления, показывает, что во втором из этих случаев эффект динамичности проявляется более резко.
Это можно пояснить особенностями волнообразования: при преобладании внешнего давления вдоль длины оболочки образуется обычно одна полуволна, в то время как случай сжатия характеризуется наличием мелких вмятин как вдоль окружности, так и по длине. В первом случае, по-видимому, элементы оболочки получают относительно большие ускорения, и эффект сил инерции более ощутим.
График, представленный на рис. 7.13, содержит кривые, аналогичные изображенным на рис. 7.12, но для случая
72.5
70
75
2,5
р
Дцп.
i
1
t
О
-ч
Г
1
X
,Г
ч
У
У
Л
у
I
У
г 3 4 л 5 t
Рис. 7.13. График, отображающий в сочетании с предыдущей фигурой влияние начальной погиби на поведение оболочки.
242
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
большей начальной погиби £00,1. При сравнимых значениях скорости s здесь проявляются менее высокие формы потери устойчивости, чем в случае £о 0,001; меньшими примерно в 1,5 раза оказываются и критические значения давления. Общий вид кривых несколько иной: фронт бурного нарастания прогиба выражен не так резко, как при £о 0,001.
Рассмотрим далее более сложную программу нагружения оболочки. Предположим, что система подвергается нагружению давлением, возрастающим со скоростью s 2000 атсек и достигающим величины, равной 80 от критической динамической величины. При этом в процессе нагружения оболочка не получает заметных прогибов. Примем, что в дальнейшем нагрузка меняется по различным законам рис. 7.14,6. Вариант
1 совпадает с тем, который был разобран ранее: здесь нагрузка продолжает нарастать с прежней скоростью. В варианте 2 нагрузка на втором этапе остается по¬
стоянной. В остальных вариантах 3—9 нагрузка падает по линейному за¬
кону; скорость падения нагрузки обозначена через s2 и меняется от 2 • 103 до 2-104 атсек. На рис. 7.14, а показаны графики изменения стрелы прогиба во времени. Несмотря на то, что в вариантах 3—9 нагрузка падает, стрела про¬
гиба до известного предела нарастает, после чего начинает уменьшаться.
Поведение оболочки при разгрузке характеризуется величиной максимального прогиба. В главе VI мы условились считать, что оболочка выпучивается в период разгрузки, если максимальная стрела прогиба превышает статический прогиб', от¬
Рис. 7.14. Поведение оболочки, характеризуемое графиками а для различных форм импульса, показанных на рис. б.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЁ
243
вечающий наибольшему значению давления; статическая кривая приведена на рис. 7.14, а слева. Если согласиться с этим допущением, то опасные скорости падения нагрузки лежат ниже значения s2 3000 атсек. На рис. 7.15 эти же кривые представлены в других координатах. По оси абсцисс отложена величина нагрузки, а по оси ординат — стрела прогиба.
В работе Ю. И. Кадашевича и А. К. Перцева 7.11 был использован несколько иной аппарат решения задачи. Ими были
о я 10 it5 г,о
Л Л
Фв
Рис. 7.15. Характер зависимости между параметрами прогиба и нагрузки при разных формах импульса.
получены некоторые характерные кривые поведения оболочек при внезапно приложенной поперечной нагрузке, сохраняющей далее постоянную величину в течение того или иного периода времени; были рассмотрены также нагрузки, возрастающие во времени по линейному закону. Эти авторы показали, что при весьма быстром нагружении следует учитывать влияние инерционности осесимметричного обжатия оболочки. Кроме того, оказалось, что параметры г и ср в 29 будут для динамических задач иными, чем в статическом решении. В работе 7.25 предлагается считать опасной такую нагрузку, при которой максимальное напряжение достигает предела текучести.
§ 72. Экспериментальные данные
Обратимся к результатам нескольких серий экспериментов, относящихся к динамическому выпучиванию оболочек при всестороннем давлении.
Прежде всего рассмотрим опыты, проведенные над серией тщательно изготовленных точеных дюралюминовых образцов при Rh 220 и LR 2,2. Специально спроектированная установка состояла из двух резервуаров, вставленных один в другой и заполненных маслом. Образец, представляющий собой круговую цилиндрическую оболочку, находился во
Опыты были проведены В. Е. Минеевым при участии В. С. Смирнова.
244
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
внутреннем резервуаре; верхний торец образца оставался открытым. Отверстие в днище внутреннего резервуара закрывалось клапаном, связанным с системой пружин. В наружном резервуаре создавалось повышенное давление в пределах от 5 до 50 ат при этом сжималась находящаяся в верхней части резервуара газовая «подушка». При внезапном открытии клапана во внутреннем резервуаре происходил гидравлический удар, передававшийся на образец; с известным приближением можно считать, что образец подвергался при этом динамическому нагружению всесторонним внешним давлением. Изменение во времени давления в нескольких точках резервуара измерялось специальными датчиками, сигналы от которых фиксировались на ленте шлейфового осциллографа. Датчики омического сопротивления, наклеенные на наружную и внутреннюю поверхности образца, позволяли определить деформации удлинения в соответствующих точках; показания датчиков также передавались на осциллограф. При испытаниях варьировалась разность давлений во внешнем и внутреннем резервуарах, а также время открытия клапана, что позволило получить различные скорости нарастания давления в пределах от
2 • 103 до 6,5 • 103 атсек.
Оказалось, что при динамическом нагружении общий характер глубоких вмятин, обращенных главным образом к центру кривизны, тот же, что при статическом; однако конфигурация вмятин несколько меняется: при динамическом приложении давления они имеют очертание, близкое к прямоугольному.
На рис. 7.16 экспериментальные данные сопоставлены с результатами, полученными в § 71 для оболочек с теми же размерами. По оси абсцисс отложена скорость 5 в атсек, по оси ординат — коэффициент динамической перегрузки Сд. Сплошной линией соединены точки, полученные расчетом для £о 0,001. Треугольниками нанесены экспериментальные данные для первоначально совершенных оболочек, кружками — для оболочек с начальной погибью. Судя по графику, эксперименты подтвердили теоретические выводы, по крайней мере с качественной стороны. Некоторые отклонения опытных значений критического давления для оболочек «идеальной формы» вверх от теоретической кривой можно объяснить тем, что в экспериментах края оболочек были защемлены и что к силам инерции
47 3
2
7
аа
“1 '
k А
4
•
•
•
0 7 2 3
5 6
S
Рис. 7.16. Сопоставление теоретических данных по динамическому выпучиванию цилиндрических оболочек при всестороннем сжатии с результатами экспериментов.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
245
массы оболочки присоединились силы инерции прилегающего слоя жидкости.
Опыты над стальными оболочками были выполнены В. В. Сорокиным см. 0.6, стр. 775; параметры оболочек составили Rh 200, LR 2,9. Оболочки, снабженные вставными днищами, помещались в резервуар, заполненный жидкостью. По свободной поверхности жидкости производится удар падающим грузом. Изменение высоты падения груза позволяло варьировать скорость нарастания всестороннего давления, передававшегося на оболочку. Как показали результаты испытаний, при статическом нагружении оболочка получила шесть вмятин по окружности, при динамическом нагружении с различными скоростями — восемь и девять вмятин.
На рис. 7.17 приведены результаты исследований, выполненных Вудом и Ковэлом 7.61. Защемленная по торцам цилиндрическая оболочка нагружалась на одном конце постоянным осевым усилием, а затем подвергалась воздействию быстро возрастающего до постоянной величины осесимметричного гидростатического давления. Время нарастания давления до максимальной величины составляло 0,003 сек. Опасная деформация образцов при статических и динамических испытаниях характеризовалась появлением больших вмятин и исчерпыванием несущей способности по отношению к осевой нагрузке. Далее образец возвращался в устойчивое положение при нулевом перепаде давления, после чего изменялась величина осевой нагрузки и вновь прикладывалась серия скачков внешнего давления. Величина давления постепенно увеличивалась до тех пор, пока не наступала опасная деформация образца. Таким путем были определены максимальные значения скачкообразно возрастающего давления, при воздействии которого отсутствовала опасная деформация. На рис. 7.17 приведена зависимость Р — q, где Р — осевая нагрузка в кг, q — максимальное значение перепада давления в ат. Эти данные относятся к оболочке с параметрами LR 2, Rh — 800, ft 0,13 мм.
В лабораторных условиях трудно получить заданный закон изменения внешней нагрузки. Рассмотрим некоторые установки, позволяющие осуществить такое нагружение. На
О 0,28 0,56 0,84 JJ2 Ц 103-q
Рис. 7.17. Опасные значения параметра динамического гидростатического давления при одновременном действии статических осевых усилий.
Эти данные принадлежат Ю. К. Бивину и А. А. Найда, Прикл. мех. 6, 10 1970, 28—34.
246 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
рис. 7.18 представлен общий вид камеры давления экспериментальной установки, с помощью которой удается получить различные законы нагружения. Полость В камеры 1 заполняется жидкостью. Давление на об¬
разец создается при перемещении поршня 4 вниз по цилиндру 3. Движение поршня определяется скоростью массы М в момент соприкосновения с крешером 5, жесткостью крешера и сопротивлением перемещению поршня со стороны прокладки 6. Если полость А заполнена воздухом, то можно регулировать момент начала сброса давления в полости В,
Рис. 7.18. Эскиз установки, предназначенной для испытаний моделей цилиндрических оболочек 2 на всестороннее динамическое сжатие.
на всестороннее динамическое сжатие оболочек 3.
подбирая толщину мембраны 5. Измерение давления в камере производится датчиками 7.
Далее рассмотрим электрогидравлический способ создания всестороннего давления. При его использовании легко можно регулировать величину создаваемого импульса давления с помощью электрогидравлического эффекта. Общий вид камеры для испытания моделей на воздействие импульсной нагрузки показан на рис. 7.19. Один из электродов 2 камеры 1 зазем¬
ЭФФЕКТ ВНУТРЕННЕГО ДАВЛЕНИЯ
247
ляется, а другой присоединяется к разряднику. При пробое разрядника между электродами возникает искра. В результате в этой зоне резко повышается давление. Образуется волна давления, которая затем со скоростью звука проходит вдоль камеры. Величина и характер изменения нагрузки на испытуемую конструкцию 3 во времени зависит от многих обстоятельств. Главными из них являются энергия, накопленная в конденсаторах, расстояние между электродами, плотность среды, заполняющей камеру, расстояние от зоны разряда, жесткость камеры, электрические характеристики цепи разряда и т. д. При прочих равных условиях давление в волне будет больше, если между электродами взрывается проводник. Если волна сжатия разрушает диафрагму 4, то импульс нагрузки на модель будет меньше. Используя вставки 5 разной конфигурации, можно заметно изменять характер нагрузки во времени.
§ 73. Эффект внутреннего давления
Рассмотрим далее случай, когда наряду с динамической осевой сжимающей нагрузкой замкнутая круговая цилиндрическая оболочка испытывает статически приложенное внутреннее давление различной интенсивности.
Напомним прежде всего те результаты, к каким приводит исследование той же задачи в квазистатической постановке. Если рассматривать случай комбинированного нагружения с линейных позиций, то окажется, что внутреннее давление относительно малой интенсивности не должно влиять на верхнюю критическую нагрузку осевого сжатия. Если же исходить из нелинейных уравнений и пользоваться процедурой определения ближних нижних критических нагрузок см. § 69, то мы получим, что внутреннее давление существенно сказывается на несущей способности оболочки. По мере увеличения параметра внутреннего давления ближняя нижняя критическая нагрузка возрастает и при известной интенсивности давления приближается к верхнему значению. Эти результаты подтверждаются данными экспериментов.
Для решения соответствующей динамической задачи надо дополнить уравнение типа 28 членом, отвечающим внутреннему давлению интенсивности q. По-прежнему предполагаем, что сжимающая нагрузка изменяется по закону
См. об этом подробно в книге 0.6, стр. 573.
Подобная задача была рассмотрена А. В. Севастьяновым Мех. тв. тела, Ко з, 1968. Здесь приведены результаты, полученные Б. А. Киладзе и автором 7.6а.
248
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ
ГЛ. VI'
р st. Тогда вместо 28 получим
1 If __ £ £ — «п У f>2 £2 £ S dt2 IV 2 £ 165в 1» _ 1ТГ ll2m2 1 92 5 _ о2
JlP71Tw’,tt-ts
гтУ-к-А-Н7-37
Здесь, в дополнение к обозначениям § 70, введена величина q qR2Eh2.
Интегрирование уравнения 37 было по-прежнему проведено методом Рунге — Кутта. В качестве начальных условий были выбраны те же, что и в § 70: £ £0 и £ О.при t 0. В процессе вычислений варьировалось отношение Rh в пределах от 100 до 1000, интенсивность внутреннего давления q — от нуля до двух. Параметр стрелы начального прогиба £0 во всех случаях был выбран равным 1 • 103. Скорость нагружения s менялась в пределах от 1 • 106 кгсм2 сек до
5 • 106 кгсм2-сек. Параметр g, характеризующий форму волнообразования при прощелкивании оболочки, варьировался от 0,4 до 3. Отметим, что возрастание значения g связано с удлинением вмятин вдоль дуги. В каждом варианте вычислений были найдены зависимости £ —, соответствующие различным числам волн п вдоль дуги. При этом определялось то число волн, для которого бурное нарастание прогибов наступало раньше всего.
Данные вычислений представлены для примера в виде графиков на рис. 7.20. Здесь выбраны значения Rh — 200 и s 2 • 106 кгсм2-сек. Все кривые перестроены таким образом, что в качестве базы взято верхнее критическое статическое напряжение рв. Первый из графиков рис. 7.20, а относится к случаю отсутствия внутреннего давления. Здесь бурное нарастание прогибов имеет место раньше всего при 0,8 и 114, а параметр «критического» времени равен кР 1,006. Иными словами, здесь превышение верхнего критического значения при динамическом выпучивании составляет 0,6. Из следующего графика рис. 7.20,6, относящегося к случаю 0,01, видно, что динамическое прощелкивание имеет место при другом параметре £1,2, и числе волн п 12. Статическая критическая величина здесь превзойдена на 2,5. Наконец, на рис. 7.20, в представлена зависимость £ — t для случая q 0,02. Бурное выпучивание должно произойти в этом примере при параметре 1,2 и п 12. Превы¬
ЭФФЕКТ ВНУТРЕННЕГО ДАВЛЕНИЯ
249
шение верхней статической «критической» нагрузки составляет при этом 4,5.
Приведем далее данные, относящиеся к большим значениям При q 0,2 динамическая «критическая» нагрузка
Рис. 7.20. Диаграммы «прогиб — время» при динамическом сжатии при отсутствии внутреннего давления а и при наличии статического давления малой б и большой в интенсивности.
оказывается выше верхней статической на 10,3, при q 0,5 на 12,1, прк-- 1—на 23 и при q 2 — на 34.
На рис. 7.21 сопоставлены окончательные результаты, относящиеся к случаям <7 0, 0,01; 0,02. Здесь указаны «критические» параметры £ и п при Rh 200 и s 2 -106 кгсм2-сек.
Таким образом, при наличии статического внутреннего давления характер волнообразования оболочки резко меняется по сравнению со случаем чистого динамического сжатия. Чем выше внутреннее давление, тем вмятины оказываются более
250
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
вытянутыми вдоль дуги. Параметр динамической «критической» сжимающей нагрузки возрастает при наличии внутреннего давления по сравнению со статической величиной. Для практически встречающихся значений внутреннего давления это превышение лежит в пределах 5—10. Следует отметить, что для реальных оболочек статическое выпучивание происходит при напряжениях, лежащих значительно ниже верхней статической «критической» величины. Поэтому этот эффект динамичности нагрузки в действительности гораздо выше, чем это следует из описанных выше результатов.
0,95 V. i
Рис. 7.21. Эффект статического внутреннего давления при динамическом приложении осевого сжатия.
Полученные теоретические выводы подтверждаются с качественной стороны серией экспериментов над стальными оболочками. Образцы, заполненные в разной мере сыпучим материалом, подвергались действию динамической сжимающей нагрузки. Сигналы от датчиков, помещенных в одном из сечений оболочки, передавались на осциллограф. Таким образом можно было сравнить динамические напряжения в стенке оболочки, возникающие при различных интенсивностях внутреннего давления. Характер волнообразования менялся в соответствии с приведенными выше результатами.
§ 74. Анизотропные цилиндрические оболочки при внешнем давлении
Рассмотрим далее случай ортотропной оболочки. К такой модели ортотропной конструкции могут быть сведены различные типы оболочек. Сюда относятся оболочки, подкрепленные ребрами, — имеются в виду такие варианты конструкции, когда ребра расположены достаточно часто и их можно «размазать» вдоль основных размеров обшивки рис, 7,22,а. Другой
Эти опыты были проведены Б. А. Киладзе,
АНИЗОТРОПНЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
251
класс подобных конструкций — однослойные или многослойные оболочки из композиционных материалов с непрерывными волокнами из стекла, бора, углерода, графита, бериллия и т. д. рис. 7.22,6.
Исследуем поведение замкнутой круговой цилиндрической ортотропной оболочки, подвергающейся динамическому действию равномерно распределенного по боковой поверхности внешнего нормального давления, изменяющегося во времени по закону q qt. Допустим, как и в предыдущих вариантах
решения задач, что оболочка шарнирно скреплена со шпангоутами, точки которых могут получать некоторые радиальные перемещения, причем шпангоуты остаются круговыми. Считаем, что главные направления жесткости совпадают с образующей цилиндра и дугой поперечного сечения. Упругие свойства ортотропных оболочек характеризуются модулями Ех и Е2 по направлениям х и у, модулем сдвига G и коэффициентами Пуассона jii, ji2- Отметим соотношение £21 Е- Уравнение движения элемента оболочки имеет вид см. книгу 0.6, стр. 580
здесь w и Wq — полный и начальный прогибы; у — удельный вес материала оболочки; D2 — жесткости при изгибе в осевом и кольцевом направлениях; Dz — приведенная жесткость; DG — жесткость при кручении:
Г -сП 1-4 П2П
121 -чх2’ 172 12 1 — ШМ-г 9
Exh п _ Е2
Ds — £12 2 Dq,
Это решение принадлежит Л. Н. Сметаниной.
252
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
Выпишем далее уравнение совместности деформаций:
и Л’ иу- ил иу ил иу- ил иу
где
1 д2 w — w0 к дх2
7.39
Граничные условия для прогиба w будут: w 0, О
при х 0у L.
Аппроксимирующие выражения для полного и начального прогибов выберем по-прежнему в виде
Считаем снова, что форма начального волнообразования, характеризуемая параметрами г и ф, находится в «резонансе» с волнообразованием оболочки в процессе деформации, и что единственным заранее заданным параметром является величина fo. Как мы уже знаем, при внешнем давлении оболочка выпучивается вдоль образующей по одной полуволне, поэтому в дальнейшем будем принимать т 1. Подставим выражения 40 и 41 в правую часть 39. После интегрирования полученного уравнения приходим к следующему выражению для функции напряжений:
Ф Cj cos 2ах -f С2 cos 2ру С3 sin Зах sin ру
w f sin ах sin p г sin2 ах ф, wq fo sin ax sin y гэ sin2 ax ф,
7.40
7.41
где
C4 sin ax sin y — x2; 7.42
§ 74 АНИЗОТРОПНЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ 253
Последний член в выражении 42 отвечает напряжениям в срединной поверхности, определенным по безмоментной теории.
Перемещение v должно удовлетворять условию замкнутости 22а. Сравнивая выражения для гу через перемещения, с одной стороны, и через функцию Ф — с другой, находим
dv 1 д2Ф д2Ф 1 dw 2. 1 dwQ 2. w — w0
ду Е2 дх2 ду2 2 ду 2 ду ' R
Пользуясь выписанными выше выражениями 40 — 42, находим
<R2 I f fo пр2 Ф
ф EM-h 8 -Т
Таким образом, параметр ф оказывается выраженным через f и г.
Для нахождения зависимости между параметрами прогиба и изменяющейся во времени нагрузкой выпишем уравнения Лагранжа типа
дТ ■■Ql• 7.43
-f—V
dt dq,j
В качестве обобщенных координат выберем параметры прогиба q £i, 2 в качестве обобщенных сил — величины
Г „ п Й.
Ql — as, и Qa — •
Здесь введены безразмерные параметры
f f — fo r _ f — fo fcl h > fe2 ft
9 — 9 д — Я I
nLhVExE2 ' Я V EtEt V A Кинетическая энергия системы Г равна
L 2я R
J <М4>
о о
в безразмерном виде
ji 4
пШУТйЪ
Полная потенциальная энергия системы Э определяется как сумма потенциальной энергии деформации срединной поверхности и потенциальной энергии изгиба, за вычетом работы
254 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
внешних усилий. Находим
л л4 А2,,20, Я1Д4л,20
У1_ 16Д 6, 6о
I I а I п АК
г8 Х2 п1 Со - « т-тт-, 7.45
Q2 2£2 А V С, 2£02 Я, 2-Mi£, 2£0 1 81
5 I60QIV. 7.46
Выше были введены обозначения
Rh n2h
h • ъ nL ' U'
дл — е JL., й-т£, «■ 1
Г £„
я,' VExEt’ VEtEt ’ 121 -n,i2’
1
Я
816« 961--2ма Д2 ’
JL - 1
2 —,.
Г 2д-5--2ц,д Дг X3 I4Q 2n2Q2 A.
Примем, что давление q меняется во времени по закону q st при этом предположим, что выпучивание оболочки происходит на восходящей ветви импульса давления. Введем безразмерный параметр времени ; тогда уравнение Лагранжа для переменной £i примет вид
d 1, л2 С, Со MEi2 _ 4S, С, g0 х
rf2 4 Т2 Cl So2 dt 1 4 tl2 1 So2
x
t _ li4 д2 Sl 1 So A, я2 Дё4П 6,-26061
где
16Д<„ <MSi 6o М1±ЖЫи__±_Н, 7.47
Второе уравнение 43 для £2 будет ■Ф- - А-AiV Cl 2So2 я, Я2 -
- £i 2£о 1 84Я2 £2А 16QS2V 0. 7.48
АНИЗОТРОПНЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
255
Уравнения 47 и 48 были проинтегрированы по методу Рунге — Кутта с помощью машины БЭСМ-2М при следующих начальных данных:
Ь 0,
£2 0, О
w dt
о,
dt
при 0.
в
г
о
ТТПТТ
ч
LR 2,S
П6 j
' jn5
Iff-7
хПв
ffh 72 I U £,£z2 1 S2'W3amcen П 1
ш
w
4
Рис. 7.23. Диаграмма «прогиб —время» для оболочки из композиционного материала при динамическом нагружении.
При вычислениях принимались различные значения jlxi, лг, Et и Еч применительно к различным маркам стеклопластика для следующих параметров оболочек:
LR 2,6; 3,5 и Rh 72; принималось 0,001. На рис. 7.23 представлена серия кривых £i £i0 Для оболочек при
EiE2 2 и скорости нагружения 5 2• 103 атсек для различного числа волн п. Как видим, раньше всего отклоняется от оси абсцисс кривая, для которой п 7.
Бурное нарастание прогибов имеет место при параметре f, лежащем в пределах от 2,7 до 3,9. Таким образом, критическое давление здесь примерно в три раза больше, чем верхняя критическая нагруз- ка. На рис. 7.24, 7.25 при- ведены кривые Si—отра- ™
жающие зависимость между стрелой полного прогиба и временем нагружения при скоростях s 0,2-104;
0,5-104; 2-104; 5-104 атсек для EiE2 2 и ЕЕ2 5 соответственно. На рисунках представлены кривые для чисел волн я, при которых бурное возрастание прогибов соответствует наименьшему параметру. Как видим, динамический эффект проявляется и здесь в последовательном возраста нии числа волн и значительном увеличении критического давления.
На рис. 7.26 приведены кривые Si — ti0 для различных соотношений EJE2 при скорости нагружения s 5• 103 атсек.
Рис. 7.24. Влияние скорости нагружения на поведение оболочки из композиционного материала при EiE2s 2.
256
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
Первая кривая слева отражает зависимость £1 £1 t для изотропных оболочек, остальные кривые — для оболочек с различной степенью анизотропии. По мере увеличения степени анизотропии вся кривая перемещается вправо, в сторону больших
10 6
г
О 6 IZ IB Z4 зо зв
УУ
t
Рис. 7.25. Эффект скорости нагружения в случае отношения Ех1Е2Ь.
€
9
Ufi2J6 ЭМ 72
1
. n1.
T' ' 773
»£i£z5
1
76
Г 1 1
f
1 p2-6ysjz- А
A
7iW
Ш
Г1г<мдУ
значений. На рис. 7.27 даны кривые, устанавливающие зависимость между коэффициентом динамической перегрузки и скоростью нагружения 5 для различных соотношений EiE2upn
JO
ь
5
3
1
О
<7
S5'10samCBH
ч'-г ' —i tn7
UifcZ
Г
I WfS
i
jnO
1 A
4
V
7 t
Рис. 7.26. Влияние отношения модулей EiE2 на поведение оболочки при динамическом нагружении.
Рис. 7.27. Динамический коэффициент для оболочки из композиционного материала при различных скоростях нагружения.
EiE2. Из графиков видно, что коэффициент Сд растет по мере увеличения скорости нагружения и степени анизотропии. Имеется в виду, что направление волокон, соответствующих большему модулю Е, совпадает с направлением образующей.
§751
АНИЗОТРОПНЫЕ КОНИЧЕСКИЕ ОБОЛОЧКИ
257
§ 75. Анизотропные конические оболочки при осевом нагружении
Круговые конические оболочки входят в конструкции реактивных двигателей, летательных аппаратов, резервуаров и т. д. Исследование устойчивости конических оболочек оказывается более трудным, чем в случае цилиндрических оболочек, так как структура исходных уравнений является
номерно распределенными по контуру усилиями ри рг рис. 7.28. Предполагается, что известен закон изменения внешней силы во времени. Подкрепляющие ребра предполагаются симметричными относительно срединной поверхности обо-
Выпишем уравнения совместности и движения элемента такой оболочки в проекциях на нормаль, исходя вначале из линеаризованных зависимостей см. 0.6, стр. 643:
Здесь введены следующие обозначения: 0i 0-cosa; а — угол наклона образующей к основанию конуса; h — толщина оболочки; Ль h2 — приведенные толщины подкрепленной оболочки
Это решение получено А. А. Соломоненко.
лочки. Если считать ребра расположенными достаточно часто, то их жесткость можно распределить
по длине шага и воспользо¬
ваться моделью ортотропной оболочки.
более сложной. Приведем решение задачи о динамической устойчивости конструктивно ортотропной усеченной конической оболочки, нагруженной вдоль образующих рав-
Рис. 7.28. Круговая коническая оболочка, подкрепленная стрингерами и шпангоутами.
258 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИЙ ГЛ Vtt
в направлении координат s и 0 соответственно; ь 2—моменты инерции стрингеров и шпангоутов, вычисленные относительно осей, лежащих в срединной поверхности оболочки; Ьи Ъ2 — расстояния между стрингерами и шпангоутами; ф— функция усилий в срединной поверхности; w — дополнительный прогиб;
л г 1 п EI2
U 12 1 — ц2 ' Ul— bx ’ С2““ Ъ2 9
у4 d4w. 2 d3w 1 d2w. 1 dw, 2 d4w
ds4 s ds3 s ds2 s3 ds s2 ds2 00
2 dzw, 4 д2до. 1 d4w
.3 Лг ЛЛ2 4 лл2
s4 dQf ' s4 6Щ
r d4w. 2 d3w
Lw ds4 ygjr;
1 d4w, 2 d2w, 1 dw 1 d2w
T 1
T rt и w 1 z и w. 1 uw 1
2 s4 <e s4 ae s3 ds s2 a
Функцию прогиба, возникающего в оболочке при выпучивании, представим в виде
оу sin • sin P20> 7.51
где
р, —, р2 -—, z0 In —, z ln —; 7.52
Zq COS X Si f Si 9 N J
m — число полуволн вдоль образующей оболочки, п — число волн по окружности, Si — расстояние от вершины конуса до меньшего основания, s2— расстояние от вершины до большего основания. Введем новые переменные
s sxez ф ф22. 7.53
Тогда уравнение совместности с учетом 51 принимает сле¬
дующий вид:
_ d4<pi, а3ф,. а2ф,, дф,, а4ф. <э3ф,.
1 1F 2 eF 3 IF 417 5 iTaef 6 aTief r7 -f r8 -д ф — E • h • Si - fi • tg a X 7 00 <эе
XPi Pi sinfl — cosPsinPaQi- 7.54
Здесь f, r2,., r8 — некоторые функции величин ц, h, hi и hi. Решение уравнения 54 выпишем в форме
<рх Kl sin frz sin 020 2CosPiZsinp2ei- 7.55
§ 751 АНИЗОТРОПНЫЕ КОНИЧЕСКИЕ ОБОЛОЧКИ 259
Здесь
KiEhsJt P,P»p»t e«Ltga,
Pi Р2
C2 £W, Pi Pp, tg a,
Pi P2
Pi riPi - гзР rl rM r£b
P2 p.r2pl-r4 r6p'
Уравнение движения после введения в него зависимостей 51 и 53 перепишется в виде
DVw CXLш C2Z,; да — s, tg a 3 2 e3
s■ p•“жe2z ste4zphww°> <7-56
где
V74 dAw A dzw, л d2w,
Vf w —r — 4 —r 4 -—■
1 dz4 dz3 a2
i о d4w д d3w,, д2ш, а4ад
a2ae2 аае2 ае сюр
f а4оу „ а3ш, к л а
®:15Г 41ST 5 -W 2дГ>
т ч а4оу, 0 а2ш. п dw d2w
им-щ22--17-
Далее пользуемся методом Бубнова — Галеркина, считая варьируемым параметр Д; соответствующее уравнение имеет вид
20 2jtcosa
J J lFzsinp12sinp20,rf2frf01 O.
о о
После интегрирования получим уравнение, связывающее параметр прогиба и изменяющуюся во времени нагрузку:
д 3 E2s2 s2t
dt2 2 р s ss s24 Рв’ 7'57
здесь введены обозначения
p f j л mn cos a pj
260
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
р — параметр верхнего критического усилия при статическом нагружении конической оболочки. Если исследуемые оболочки удовлетворяют условиям
Если, далее, исходить из нелинейных уравнений, то функцию, аппроксимирующую дополнительный прогиб, можно выбрать в виде
w fe2:sinp12sinp201 'Ф sin2 Р. 7.58
Выполняя операции в той же последовательности, что и выше, получим уравнения, устанавливающие зависимость между параметрами прогиба и изменяющейся во времени нагрузкой:
где Кл, KZ, Сп —Функции р„ р2, iy ft, hlf ft2. Под £ понимается безразмерный параметр полного прогиба.
Если на оболочку действует линейно изменяющаяся во времени нагрузка p — st, то после введения в уравнение 59
р2»1 и Р>1,
то
2h tgg r9fl4 2d2 ri0
■
где
г91 121-ц2-А_. rI0 1 121
- К Щ К S3 - Щ Ф2 -
- к;¥ - Ф- К - Й0Ч>; 7.59
к с3 - sq ч>3к; з - к2 к; s2 - ф f t g«
k'8z2 - - tofs2a
-ltga K'n £2 - Oo ■§■ tg a, 7.60
§ 75 АНИЗОТРОПНЫЕ КОНИЧЕСКИЕ ОБОЛОЧКИ 261
безразмерного параметра времени приходим к следующему уравнению:
■» it р
Ehpl Р;'
• Q п - 5 - Q - ЯЛ3 - Ш - Q2 S5 - £3 Q3£3 - Шу QS - Щ у; 7.61
о 1 р22 _fbM_ сЕ_2.3
Ц 3 3 4 S Рв’
о в_£_. L q JL
«Ж Рв ’ «Ж р ’
здесь
h tgct 3 fttga К4
„ о2л2 ' 4 0 о2,2 ™
12 Рв 512 Рв
02 Г Г Г2, »41
1 4 4ф2 л 4r8J'
Г Й6А4 Г Г14 Г8г 4 Г» 2 “ Рг к',04 Г8« г82 »2г22 Г6;
е»Чг.ъ4 г.<
к:
2
81г,<Н 9гъ г в
Pl 81r,d4 9r5d2 г82 902 9г22 г621 Р24 г 14 г5'в'2 Гв
ft2
;р.2
4 2
г У Г5д2 Г82 д2 г22 Гб2 '
Г riPl2 2. p4-i4 r5d2 r8 1
L 4 т Р г4 Гь r82 ft2 д2 Г62J
Параметр -ф определяем из решения соответствующей статической задачи. Сопоставляя равенства 59 и 60, получим кубическое уравнение относительно гэ:
к1 - Кз У - tg a Kl Kl tС Кт tV
1 Г I 42 I 72 1 I
Мв s2 s2 31_12 М3 62Аз
Сз с - S tg2a- к: - ; g2j-
-±tgafi Cio rnk2--tga-p:. 7.62
s, ргО у Л
262
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
Следуя далее предложению Н. А. Алфутова, можно считать, что параметр «несимметричной» составляющей прогиба t>
2fl
t
w
Ц5
О
S11L
1вкгсм
i сек
oL 70 6 if—0,75
770
£.2,5■
706нгсм ced
j -Ц
i
'■10вкг
7M 'CBH
i
J
Z7
29
J
J
, —
is 2,0 25 3,0 3,5 4,0 4,5 5,0 5,5 6,0
Рис. 7.29. Зависимость между параметром прогиба и временем для конической оболочки при осевом сжатии.
пропорционален «симметричной» составляющей, i> a£; коэффициент а определяется по формуле
wK‘K:K'i'‘a
-2 з<>-; tg« вытекающей из 62. Здесь введены обозначения:
. г1р22 г2 ьг р гРг’®'2 г2
Д9_4г г. 4г г2 >
ф4г,©4 г5е2 л8
Д“ ” ЙМ4 r52 rsf 2г22 г62’
4h
vh
Гп Ь,Н3 ’ Г>2 — ‘мз
Уравнение 61 окончательно запишется в виде
J _ Q • _ Qj _ Q3. а - ЩI - С-д - Q2c« - Ща -j-QAt3-Z2Zoa Q,
§ 76 ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ ПРИ ДИНАМИЧЁСКОМ СЖАТИИ 263
Это уравнение интегрировалось численным методом. Начальные условия были выбраны в виде d£dt 0, £ £о при 0. На рис. 7.29 приведены кривые £Г> полученные при следующих данных: а 70°, 19,9 сл, s2 7S, см, R2 25 см,
Н 50 см, h 0,05 см. Параметры подкрепления: гх 0,954, 2 3,53, г5 2,054, г6 4,16, г8 0,866, г9 2,69, г101,57, Г 1,05, г12 0,135. В качестве материала оболочек был принят хромансиль. Амплитуда начальной погиби £01.Ю“3. Параметр формы волнообразования считался равным -в 0,75.
Скорости нагружения приняты s МО6; 2,5 10е; 5 106 кгсм-сек. Каждая кривая соответствует определенному числу волн, указанному на графиках. Как видим, бурный рост прогибов имеет место в первом случае при п 21, во втором при п 27, а в третьем при п 32. Таким образом, с ростом скорости нагружения возрастает число окружных волн п. Одновременно с этим увеличивается критическое время нагружения.
§ 76. Цилиндрическая панель при динамическом сжатии
Перейдем к рассмотрению цилиндрической панели, подвергающейся действию динамических усилий сжатия вдоль образующей. Будем решать задачу в первом приближении, пользуясь методом Бубнова — Галеркина. Рассмотрим сначала случай, когда усилие сжатия р возрастает во времени по закону р з st, и будем предполагать, что динамическое выпучивание панели происходит до того, как нагрузка достигает своего максимального значения. Выберем в качестве аппроксимирующих функций для полного и начального прогибов выражения
р. тпх. ппу £. тпх. ппи ллч
w fsm—— sm-f-, Wq f0 sin —-— sin —. 7.63
Стороны а и b ориентированы соответственно вдоль образующей и по дуге панели. Под т понимается число полуволн вдоль стороны а, под п — вдоль Ь. Подставляя выражения 63 в правую часть уравнения типа 2 и интегрируя его, находим функцию Ф в виде
ф4 Г - R v f f I г
ЭТ »тУ й ■ ‘W--■■•У ■-■ <М4>
Далее применяем метод Бубнова — Галеркина по отношению к уравнению 1. Выполняя интегрирование, приходим к
264 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
следующей зависимости:
, „ 32 knm Г X 2. ч f я2 т, пХ2,
'а 3 я2 L «2 Яга2 J 1 121 - ц2 Я т 1
тг т><1«> -dSk«-£tfh£rS-o- w
Здесь введены безразмерные параметры: £ fA, £0 f0, А, a6, b2Rhy p pb2Eh2, q qbAEhA, — радиус кривизны срединной поверхности. Коэффициент а равен 1, если тип нечетные; если же хотя бы один из этих параметров четный, то a 0.
Отбросив в уравнении 65 инерционный и нелинейные члены и считая £о0> придем для безразмерного верхнего критического напряжения при квазистатическом нагружении при Х 1 к выражению
<7-66>
Введем обозначение t для безразмерного параметра времени по формуле
r — J. 7.67
Ркр Ркр
Уравнение 65 получает вид
1 d. S- g0
S dt2
1 й ьт“‘‘ - >4т‘ п< - <'128-
- <■« £, 8£<1 - Ю -1 192 - £У 0; 7.68
здесь через р обозначено р 4я4 31 — jx2 k2f а под 5 понимается величина
5 Ркр-2' 7-69
с — скорость звука в материале панели. В случае плоской пластинки выражение для критического напряжения запишется в форме 8
<7-70>
§ 76 ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ ПРИ ДИНАМИЧЕСКОМ СЖАТИИ 265
а уравнение движения приводится к виду И
т й-£отт 2
-’SC 61 — 12т —
xV°- <7-71
Интегрирование уравнения 65 проводились с помощью метода Рунге — Кутта на ЭЦВМ БЭСМ-2М; шаг по безразмерному времени принимался равным 0,01. Предварительно была исследована практическая сходимость решения; дальнейшее уменьшение шага не оказывало сколько-нибудь заметного влияния на результаты вычислений.
Описанный выше алгоритм был применен для решения ряда конкретных задач. Прежде всего исследовалось поведение панели в зависимости от ее геометрических характеристик. На рис. 7.30 представлены результаты вычислений для удлиненных панелей и квадратных в плане. В обоих случаях параметр начального прогиба равен £0 Ю3, параметр скорости нагружения составляет S 0,1. Этому значению 5 в случае дюралюминовой панели толщиной h порядка 0,1 см и параметром k 6 отвечает скорость возрастания «физического» усилия s 2,2-105 кгсм2-сек. Отметим, что каждой кривой на рис. 7.30, б соответствует свой масштаб вдоль оси абсцисс: в выражении для параметра рркр под ркр понимается для каждого значения кривизны k величина верхнего критического статического усилия по 66. Это дает возможность непосредственно по построенным эпюрам определять коэффициент динамичности Сд, равный отношению условной критической нагрузки к верхнему статическому значению.
На рис. 7.30 приведены лишь кривые, соответствующие «критическому» числу полуволн тКр, т. е. кривые, у которых участок, характеризующий фронт бурного выпучивания, лежит ближе всего к оси ординат. Как и следовало ожидать, значения гакр, отвечающие удлиненной панели с отношением сторон X 2, вдвое больше значений ткр для квадратной в плане панели Я 1. Из этих данных вытекает, что длина панели практически не оказывает влияния на значение коэффициента динамичности. Вместе с тем коэффициент динамичности уменьшается с ростом параметра кривизны панели. Это можно объяснить тем, что искривленная панель имеет склонность к прощелкиванию, что отражается на снижении ее несущей способности по сравнению с пластинкой или панелью меньшей кривизны.
Вся серия вычислений показала, что «критическое» число полуволн вдоль дуги п1.
3 4 5 В 78
t
Рис. 7.30. График «прогиб —время» для круговой пологой цилиндрической панели при динамическом приложении осевого сжатия в случаях a A,s2 и б
Рс. 7.31. Влияние скорости нагружения на поведение цилиндрической панели при осевом
§77
СФЕРИЧЕСКАЯ ПАНЕЛЬ
267
Далее было исследовано влияние стрелы начального прогиба на поведение панели. При изменении £0 динамический коэффициент резко меняется, составляя в случае £о Ю”1 приблизительно 2,6, а при £0 Ю“5 около 5,2 принято
S-1.
Вычисления, выполненные для плоской пластинки в § 66, дали картину, весьма сходную с описанной выше.
На рис. 7.31 приведены данные вычислений для квадратной в плане панели с параметром k 6 и начальным прогибом £0 Ю3 при различных S. Напомним, что меньшей величине S соответствует большая скорость возрастания нагрузки s.
Далее исследовалось влияние поперечной статически приложенной нагрузки q как положительной, направленной к центру кривизны панели, так и отрицательной от центра.
Оказалось, что приложение относительно малой «положительной» поперечной нагрузки не оказывает существенного влияния на процесс выпучивания панели.
Если же имеется нагрузка, приложенная от центра кривизны, то, как правило, панель «предпочитает» выпучиваться в обратном направлении.
На рис. 7.32 изображена зависимость между параметром ступенчатого импульса и амплитудой нагрузки 0 для панели, характеризующейся величинами k 12, 2. Эти данные можно сопоставить с результатами, полученными в § 67 для плоской пластинки; см. также § 102.
Приведенные результаты позволяют с известной уверенностью вести практические расчеты искривленных панелей с малым параметром кривизны до k 12. В дальнейшем интересно рассмотреть задачу в более высоких приближениях; это особенно важно для панелей большой кривизны.
§ 77. Сферическая панель при динамическом приложении внешнего давления
Рассмотрим далее случай пологой сферической панели, находящейся под действием динамически приложенного нормального внешнего давления. Исследуем лишь случай осесимметричной деформации. При этом мы можем воспользоваться уравнениями, приведенными в главе III в обозначениях § 35.
Рис. 7.32. Эффект формы импульса при динамическом нагружении цилиндрической панели.
268-
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
Обратимся прежде всего к тому закону изменения давления, который подробно изучался в предыдущих разделах главы: предположим, что интенсивность равномерно распределенного давления q меняется во времени по линейному закону q at.
Рис. 7.33. График движения вершины сферической панели при динамическом приложении внешнего давления.
Выясним, как будет протекать процесс выпучивания оболочки при различных скоростях нагружения. Метод интегрирования основного уравнения принят тем же, что и в § 35.
Вычисления были проведены для оболочки с жестко защемленным опорным контуром, имеющим параметр пологости b 4 см. § 35. Некоторые результаты вычислений приводятся на рис. 7.33. Сплошные линии представляют графики движения вершины оболочки при различных скоростях нагружения оболочки, определяемых величиной а. По оси абсцисс откладывается параметр нагрузки, но можно считать, что графики построены в измененном масштабе для параметра времени. Здесь учитываются силы вязкого сопротивления среды. Штрих-пунктирные линии представляют такие же графики, но при отсутствии сил сопротивления.
Приведенные результаты свидетельствуют о том, что при некотором значении нагрузки происходит перескок оболочки на
Приведенные ниже данные получены Н. В. Валишвили.
§77
СФЕРИЧЕСКАЯ ПАНЕЛЬ
269
отдаленную равновесную ветвь, после чего начинаются нелинейные колебания. Эти колебания при наличии сил вязкого сопротивления среды быстро затухают. Увеличение скорости нагружения приводит, как это было показано в предыдущих параграфах, к затягиванию процесса перескока; поэтому с увеличением скорости нагружения возрастает и нагрузка, соответствующая моменту перескока. К аналогичному эффекту приводит и наличие сил вязкого сопротивления среды.
Рис. 7.34. Перемещения вершины сферической панели при различных формах ступенчатого импульса.
Естественно, при наличии сил вязкого сопротивления размах колебаний около нового равновесного состояния оказывается меньшим, чем при их отсутствии.
Перейдем к случаю, когда при t 0 к панели прикладывается равномерное давление, которое в дальнейшем остается постоянным во времени. Решение задачи осуществляем с помощью системы уравнений, в которой принимаем q const, а начальные перемещения и скорости считаем нулевыми. Некоторые результаты вычислений приводятся на рис. 7.34. По оси ординат на фигуре откладывается параметр нормального перемещения вершины оболочки, а по оси абсцисс — параметр времени. Первые три кривые построены для оболочки с параметром пологости b 3,5 при следующих значениях параметра давления: q 0,3 кривая, q 0,4 кривая 2, q 0,5 кривая 3. Заметим, что для рассматриваемой оболочки верхнее критическое давление равно qB 0,6.
270
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
Приведенные результаты показывают, что если давление мало по сравнению с критическим, то движение вершины оболочки происходит по закону, близкому к гармоническому кривая 1. Вблизи критического давления период колебаний оболочки резко возрастает, а движение приобретает сложный характер: одновременно с медленным основным процессом имеет место движение с малым периодом около положения, определяемого основным состоянием системы кривая 3.
Кривые 4 и 5 построены соответственно для оболочек с параметрами Ь 2 и Ь 3 при q 0,5. Видно, что с уменьшением параметра b период колебаний уменьшается если процессы рассматриваются при одной и той же нагрузке.
Следует заметить, что во всех рассмотренных задачах колебания совершаются около положения, смещенного от начального недеформированного состояния оболочки к центру кривизны оболочки.
§ 78. Подкрепленные пологие оболочки положительной кривизны
Практически важным является исследование поведения пологой оболочки положительной кривизны, подкрепленной упругими ребрами рис. 7.35, при динамическом нагружении нормальным давлением. Будем для общности предполагать, что ребра расположены либо с внутренней, либо с внешней стороны, несимметрично относительно срединной поверхности.
Выражения для усилий, приходящихся на единицу длины контура и приведенных к срединной поверхности оболочки, могут быть представлены в следующем виде:
Nx Bxzx t 1B2Zy A Q-2,
T-Bb М, -о -С,™А,,, у>Ал,
H Dl-,0 «,■■;
выражения для Ny и My можно выписать по аналогии.
Эти задачи решались как с автоматическим выбором шага в зависимости от заданной точности, так и с постоянным шагом Д 10-3. При решении каждой из задач было сделано более 13 000 шагов, причем счет был устойчив.
Эта задача ранее рассматривалась для цилиндрической оболочки О. И. Теребушко. Здесь приведены данные С. А. Тимашева; ему принадлежат также уравнения 72, 73; см. сб. «Строительная механика», 158, Свердловск, 1968.
§ 781 ПОДКРЕПЛЕННЫЕ ПОЛОГИЕ ОБОЛОЧКИ 271
Здесь введены параметры
n Eh j EF1 Еh > EJ тт GKi
1 - Ц2, — 1 - х2 9 1 — ' 1 — 1Х 9 1 — U 9
где под Fit Su Ji, Ki понимаются площадь сечения, статический момент, моменты инерции сечения ребра первого направления
X
Рис. 7.35. Подкрепленная пологая панель положительной кривизны.
на изгиб и кручение. Под h и k понимаются расстояния между ребрами первого и второго направлений.
Деформации в срединной поверхности будут равны
е
д,<1- К - А< 1г - М» 4jr ■
ОТ Ph
V1 -цв ПРИ S T
Основные нелинейные уравнения относительно функций прогиба и функции напряжений в срединной поверхности принимают вид в безразмерных параметрах
P.1.-.’ 2D<x-j»L w _
д2Ф d2w л 2 I д2Ф d2w 2 о а2Ф d2w 2 I
v2 2 Яу Я Л v Л д2 дл;2 1 дл:2 dz2 дхду дхду
wя2 lYiV2 1 -1121
- V2 - Y. 4- Y. - v2 V. 7.72
<2W 2,2 12 d4W0, <Э2Ш d2ffi>,2
Л Л дхду дх ду2 Л
- —У'а>- ’V ft • 7.М
272 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
Усилия NXy Ny, Т связаны с безразмерной функцией напряжений зависимостями
м _ д2Ф Ehz д. _ д2Ф Eh т _ д2Ф Eh3
Nx ду2 b2 ’ дх2 а2 ' 1 дхду аЪ 9
В приведенных выше зависимостях принято:
х ха, X ab, w why
6 ЕЕ19 6 2 ££2, 263 21 М- — И' 6i б2,
по аналогии напишутся выражения для у, kyy ky, D2. Под уо понимается удельный вес материала оболочки.
При ребрах, расположенных симметрично относительно срединной поверхности yi Y2 0> и из 72, 73 получается
обычная система уравнений для оболочек с конструктивной анизотропией.
Перейдем к решению задачи о процессе выпучивания оболочки. Предположим, что дополнительный и начальный прогибы аппроксимируются выражениями
w w — w0 £1 sin mnx sin tiny £2 sin2 mnx sin2 tiny, w0 £10 sin mnx sin tiny £20 sin2 sin2 nny.
Далее составим уравнения Лагранжа типа 43 d I дт _дТ__дЭ_
dtd4, dqf dqt> I'-'V
где через Э обозначена по-прежнему потенциальная энергия
системы.
Функция напряжений Ф определяется из 73: ф С sin ах sin у -f- С2 cos 2ах С3 cos 2ах cos 2fiy
С4 cos 2р у С5 cos Аах С6 cos 4р у С7 cos 4cu cos 2р у
С8 cos 2ах cos 4Ру С9 sin Зал: sin ру 7.76
здесь Си С9 — некоторые коэффициенты, зависящие от параметров системы.
7.74
§ 78 ПОДКРЕПЛЕННЫЕ ПОЛОГИЕ ОБОЛОЧКИ 273
Уравнение 75 получает вид
1 £i £1 £10 Si 2Sio
£20 S10S2 — Si £20 Н 31 £2 sSi
М7 £2 Н £20 £i£20 £ю£2 £i£2 “t“ s£i£20 4“ 2 9£ю£г » 7.77 2Mii° CiSso SloS2
2 M£2 fe £20 fe 2S20 4- ЛГ3С1 4 2 420 M£2
7 Ci £10 C2C10 “Ь C1C20 Ci2 2 gSiSio I'
4't b2
7.78
где 'ф Яя2> Afj, M9 — некоторые новые параметры.
Уравнения 77, 78 были представлены в конечных разностях и проинтегрированы с помощью ЭЦВМ М-20 при условиях
<;,><,<hk-o.
В качестве q принималось выражение ct, где с — скорость нагружения, принимавшаяся равной 1000 и 2000 атсек. Рассматривались для примера квадратные отсеки Я 1 с размерами
DJJ08
0,007'
ЦРОБ
0fl05
Q004
11003
ч
N
1
1,с
7Jm
m
Ч
ч
ч
vr
2с
1103
Щ8
Р
ЦР07
0,006
0105
Q004
2, фс2-10amсек
'V'
cN03
ч
Ч
ч
V-
ч
ч
ч
WOO
1500
г
Рис. 7.36. Влияние параметра кривизны на поведение подкрепленной пологой панели.
Рис. 7.37. Повышение жесткости подкрепляющих ребер приводит к возрастанию значения «критического» времени.
а 6 000 мм и толщиной h 3 мм. Было принято Е 7,ЫО5 кгсм2, М- 0,3. Шаг интегрирования был принят равным МО-5 сек. Параметры кривизны kx, ky менялись в пределах 1000—1700. Под т понимается безразмерный параметр времени.
Вычисления показали, что параметр 0 Ыпг слабо влияет на величину критического времени, и его можно принять равным единице; иными словами, можно принять с известным
274
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
7, сш2’703
2,с7703
8
10
Рис. 7.38. Эффект амплитуды начальной погиби по отношению к форме волнообразования пологой панели.
приближением, что при выпучивании образуются квадратные волны. Параметр гэ Хт2, таким образом, характеризует форму волнообразования при выпучивании.
Увеличение параметра кривизны kx или ky приводит к повышению числа полуволн рис. 7.36. Возрастание параметра, характеризующего жесткость подкрепляющих ребер, связано с резким уменьшением величины ф и повышением значения «критического» времени. Это видно из рис. 7.37.
Графики, приведенные на рис. 7.38, 7.39, демонстрируют влияние амплитуды начальной погиби на форму волнообразования. Рассматриваемые оболочки оказались более чувствительными к «несимметричной» составляющей начальной погиби. Так, увеличение амплитуды «симметричной» погиби от значения 0,1 до 1 привело к уменьшению числа т с 13 до 11; такое же изменение амплитуды «несимметричной» погиби связано с падением числа полуволн от 13 до 9 г 0,012.
Интересно, что по данным рис. 7.40 оболочка имеет тенденцию к выпучиванию к центру кривизны: составляющая прогиба £2 резко возрастает значительно раньше, чем £i.
Полученные в этом параграфе результаты имеют предварительный характер. Желательно подробнее рассмотреть влияние подкреплений и начальных несовершенств на величину «критического» времени и формы выпучивания.
Рис. 7.39. Влияние одного из параметров начальной погиби на поведение пологой панели.
С, Л г
Рис. 7.40. Изменение параметров волнообразования во времени для пологой панели.
ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА ПРИ БЫСТРОМ НАГРЕВЕ
275
§ 79- Цилиндрическая оболочка при быстром нагреве
Обратимся теперь к задаче о поведении замкнутой цилиндрической изотропной оболочки, находящейся в условиях быстро нарастающего во времени теплового воздействия.
Выпишем основные соотношения термоупругости нелинейной теории пологих оболочек с учетом начальных неправильностей формы, дополнив их инерционным членом, соответствующим нормальным перемещениям :
9 дМ3 Г д3 w — Wq. д3 w — Wq 1. Г д2М3 д2 w — w0 t ду L дуъ дх2 ду j дх2 дх2 ‘
Ш2iWl W I- <—-Л'
L», Ф L<Ф, М, •£•■§£ £г«А - ягу WH.-». я-1 V“'•. 7.79
' ■ ад' I® ■ „ ш, 1д>ф. а»д.
Do дх дх3 дх ду2 ду ду3 дх2 ду
. д2Ф аш,. „ <2ф д2м,, а2Ф аш,,,_.
■“ дх2 дх2 дхду дхду ду2 ду2 Ф, М
Mi, Щ -gr М„ JVe-j Lw, w - Lw0, »o
. d2 w — w0 d2M2. 0 d2M2 d2w d2w0.
ду2 dx2 1 дхдудх ду дхду , d2 w — w0 д2М2 1 дх2 ду2 RJ 7‘80
где величины Мь М2 и т. д. определяются с помощью выра¬
жений:
1 - - 1 лл 20
Мх D, М2 D, М3
Jo w Do
Л2 Л2
N0 J kzQzEzdz, Мв J 6z02£z dz; 7.81
-Л2 -Л2
Эта задача была решена А. Т. Пономаревым.
См. В. J1. Бажанов, И. И. Гольденблат, Н. Л. Николаенко,
А. М. С и н ю к о в, Расчет конструкций на тепловые воздействия, сМашиностроение», М., 1969, стр. 286.
276
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
здесь
ft2 ft2 ft2
D0 J Ezdzt J Ezzdz, D2 j Ezz2dz
-Л2 —Л2 -Л2
£2 — модуль упругости в точке с координатой г, вычисленный для данной температуры, 0 — температура, kz — коэффициент линейного расширения. Примем далее, что температура, оставаясь постоянной вдоль образующей оболочки и в окружном направлении, изменяется только вдоль толщины: 0 02. При этом величины Z0, Du D2, NQ и Mq будут постоянными; уравнения 79 и 80 в случае q 0 примут вид
- тг V2V2 w — w0 L Ф, да -g-'j-p' — ■j ---Wo. 7.82 M,V2V20 -1 L w, w - L w0, ш0 - -2wd w0-. 7.83
Для примера рассмотрим поведение оболочки, шарнирно скрепленной с несмещающимися в продольном направлении опорами и неравномерно нагретой по толщине, под действием быстро изменяющегося во времени теплового потока. Кроме того, будем считать, что точки торцов оболочки свободно перемещаются в радиальном направлении.
Выберем по-прежнему выражения для полного и начального прогибов в форме 40 и 41. Подставляя их в уравнение 83, определим, как обычно, функцию Ф:
Ф £>о CKicos 2a К2 cos 2у Кз sin ах sin у
ху2
К4 sin Зад: sin ру Н, 7.84
где Nx — — р — эквивалентное сжимающее усилие, определяемое из принятого нами условия
L
efl7-0- <7'85>
о
Коэффициенты — С4 определяются аналогично тому, как это было в § 70.
Используя уравнения Лагранжа типа 75, составим основные зависимости между параметрами прогиба и изменяющими¬
§ 79 ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА ПРИ БЫСТРОМ НАГРЕВЕ 277
ся во времени эквивалентными сжимающими усилиями. Введем обозначения:
ы — 2. по Я
6 D0 А ’ О0 А ’ ’
f f о » to ft t ft' mnR
fel— h > felO — b2 — 5— nL ’
Далее выпишем выражение для полной энергии системы:
9 UeUa-W, 7.86
где £с — потенциальная энергия деформации срединной поверхности; Uu — потенциальная энергия изгиба, W — работа внешних сил. Составляющие Uc, Uu и. W находим из выражений
L 2я R
о о
L 2JlR
о 0
и Мз Г Г М——2
и“ 21 - ц2 J J I дх2 ду2 о о
L2nR
•шт ГГ д2Ф d2w. д2Ф d2w. 0 д2Ф d2w,,
2J J I ду2 дх2 дх2 ду2 2 'Wddxddxdy о о
L 2nR
M2NQ Г Г d2w, d2w “ТГ-J J -wwdxdy-
о о
L 2nR
-rrl J 17.88
0 0
L 2nR
W -N,M,.j j 7.89
278 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
Тогда, учитывая введенные обозначения, уравнения в безразмерной форме запишем в виде
Qi j _3ц2 Л1 £2 Si 2£о Si So П6Ч-1 1 221 —
- jr<8 « - ЗД чЛОД. ay j Л12 С 2SI с, 30 2- 2 Щ- - 4. 7.90
4 - ЛЪ j Л С 202 9S1» тИгГг
j_±Jl £i£i 2£o Г,, 86 1 S 2g0 »,
4 i6i2 L1 i i22J JVe с, 2
jTll2-S,ySo2 S 2SES2. 7.91
Далее представим зависимость для дополнительного прогиба в безразмерной форме:
W — w0 h sin ах sin Ру Сг sin2 ах Я, 7.92
где
Используя условие замкнутости оболочки типа 22а, находим параметр прогиба А,:
Я vlN°x -1S2 - J- «1 Si 2So. 7.93
Вводя зависимость 92 с учетом 93 в 44, получим безразмерное выражение для кинетической энергии
f f tf2 S2 4 si n2s. Si So2
i цг - ixNUt Si So. 7.94
где
т RMi rpt
1 — nLh 1 •
ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА ПРИ БЫСТРОМ НАГРЕВЕ
279
точки над буквой обозначают, как обычно, производные по времени. Далее выпишем первое уравнение Лагранжа в виде
С. г 1 £о тtl2 W ЗД
41J Л2 Si Co2J 1
— 2£o 92 12 g2 2 2 2 4-
lFt2C, Ql g28j4,2-
- j л2 £, - 2Q £, 2 —I 0. 7.95
Здесь введены параметры
_xt _ с 2 2Л4
S-U l4,ti £o,j’
где к — коэффициент температуропроводности, с — скорость распространения звука в материале. Примем, что параметр £2 в уравнении 95 в первом приближении будет для динамического процесса таким же, как и для статического в случае совершенной оболочки £0 0, и найдется из соотношения
«■—гЬг 7-96
где
L - U I 84 1.
Ll 1б2 L i2d2J
_ 1 V 1 1. г 1. 1 I
16 I2 Л 2,Р L 92 I2 £2 I2 J’
L3-
1212, I2 IIм» l-ц V 2 12т 1 -ц2 Ч®
4г,2
Мы пришли снова к обыкновенному нелинейному дифференциальному уравнению второго порядка 95, которое связывает между собой параметры прогиба £ь £2, температурное усилие Ne и время т. Для нахождения зависимости £1 £it необходимо та.кже найти изменение температурного усилия во времени Ne Nq t с помощью формулы 81. Для этого в дополнение к выражению 95 надо решить температурную задачу.
Так как оболочка считается тонкостенной и подвергается равномерному воздействию теплового потока, то в дальнейшем
280 ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
распространением тепла в меридиональном направлении будем пренебрегать и рассмотрим задачу о распространении тепла в одномерной постановке. Тогда уравнение теплопроводности выпишем в виде 0.6, стр. 309
дв д26 „ g-v
dt К dz2 ’
проинтегрируем его при следующих граничных и начальном условиях:
1г°- 2т- § const 24> >0’
0 0 для t 0.
Для нахождения поля температур по толщине оболочки было использовано известное решение. Интегрирование соотношения 95 было проведено с помощью метода конечных разностей при начальных условиях
£i — £o Si 0 при т 0.
Было принято, что температура вдоль толщины оболочки распределяется по линейному закону
0 а0 — b0z>
где
0102 t — 02
о — 2 ’ °° h •
Через 01 и 02 здесь обозначены соответственно температура наружной и внутренней поверхности. При этом модуль упругости будет являться также функцией координаты z:
Ег аЕг bEzz,
где aEz аЕ — bEa0, bEz bEbQ. Например, для дюралюмина Д16Т можно считать
аЕ 7,29 • 105 кгсм2у ЬЕ 551 кгсм2 • °С.
Такую же зависимость выпишем и для коэффициента линейного расширения k:
ak 60-
Далее имеем
kz akz — bkzzy akz ak a0bk.
Приведенная температурная жесткость оболочки, неравномерно нагретой по толщине, имеет вид
D2Dq - D h3 l2a - фй2
1-ц2£>о 144а г 1 — ц.2 '
ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА ПРИ БЫСТРОМ НАГРЕВЕ
281
7 к и ал
Вычисления были проведены на примере дюралюминовых оболочек для различных сочетаний геометрических характеристик и параметров теплового потока, при начальном у прогибе £о 0,001. Для различных параметров вычислялось значение и определялось распределение температуры по толщине оболочки при шаге аргумента Ат, равном 0,01. Далее находились значения и г, для которых фронт прогиба соответствовал наименБ- шему значению т, и коэффициент температурной перегрузки Сд, равный
р»—г
n1Z Rh 180 tg-W
мгсен Ч'
77
и
Я.
'см2сек
10
П11 1
нал
сек
10
г
1
12
J
J
Nq
Рис. 7.41, Диаграммы «прогиб — время» для цилиндрической оболочки при различных тепловых потоках.
Под Nqb понимается верхнее температурное критическое статическое усилие, отвечающее при заданном g наименьшему числу волн п.
На рис. 7.41 для значения Rh 180 представлены три группы кривых £it при разных тепловых потоках. Анализ данных на рис. 7.41 показывает, что наиболее вероятная форма выпучивания оболочки, например при q 2 ккалсм2- сек, будет отвечать числу волн п 12 вместо п 10 для
статического нагружения. Рис, 7.42 отражает зависимость между Сд и соотношением hR для разных qt. Как видим, эффект динамичности наиболее резко сказывается для более тонких оболочек.
Рис. 7.42. Влияние относительной толщины оболочки при быстром нагреве на значения динамического коэффициента.
282
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ. VII
§ 80. Пластическое течение при динамическом выпучивании
оболочки
До сих пор мы считали, что процесс выпучивания оболочек имеет место в пределах упругой деформации материала. Но во
многих случаях выпучивание оболочки сопровождается появлением пластических деформаций. Примем здесь, что пластическая деформация является для процесса выпучивания преобладающей, так что упругую составляющую можно принять по сравнению с пластической пренебрежимо малой. Таким образом, мы можем воспользоваться моделью, близкой к модели жесткопластического материала; будем предполагать наличие упрочнения в процессе пластического течения. В подобной трактовке обычную диаграмму сге типа 1 рис. 7.43 предлагается заменить ломаной линией вида 2. На пластическом
участке зависимость определяется касательным модулем Ек.
Рассмотрим круговую цилиндрическую оболочку, всем элементам которой сообщаются значительные радиальные скорости. Длину оболочки считаем настолько большой, что можно ограничиться изучением движения кольца единичной ширины.
Процесс деформации такого кольца-оболочки можно разделить на предварительную осесимметричную де-
Рис. 7.44. Характер пластиче- формацию И ПОСЛедуЮЩее ВЫПуЧИВаского выпучивания кольца-обо- ние как показано на рис. 7.44. Будем
лочки. r J
предполагать в соответствии с этим, что в начале движения преобладает мембранное пластическое течение, а потому малые изгибные деформации будут пропорциональны касательному модулю. Изгибающий момент равен
М а EJx,
где под х понимается изменение кривизны см. 0.6, стр. 507:
“>• <7-98>
Эта задача исследовалась Абрахамсоном и Гудйром 7.26, Гудиром и Макайвором 7.37, Линдбергом 7.46, Стюйвером 7.55 и другими авторами.
Рис. 7.43. Диаграмма «напряжениедеформация», положенная в основу исследования.
§ 80 ПЛАСТИЧЕСКОЕ ТЕЧЕНИЕ ПРИ ДИНАМИЧЕСКОМ ВЫПУЧИВАНИИ 283
Через Л312 обозначим момент инерции поперечного сечения;
0 — угловая координата. Рассматривая элемент кольца рис. 7.45, получаем
«-7ЧГ’
где Q — поперечная сила, dy— элемент дуги.
Уравнение, описывающее поперечное перемещение, будет
где под дфду понимается переменная кривизна:
Ц-т 7-00
р — интенсивность давления, N ovh — окружное мембранное усилие. Подставляя 100 в 99 и исключая Q и М с помощью предыдущих соотношений, придем к уравнению
Рис. 7.45. Усилия, приложенные к элементу кольца.
EKI d'w, д2и>, Г 1. 1 д2т. 1
R <04 д02 N R R2 д W
-р-1А
d2w
dt2
7.101
Вводя безразмерные параметры
W
w
1 ch
t,
7.102
т Vhn' ‘ re »
СЬ£,,_4.
приходим к уравнению при р 0 звездочка при w опущена
4£ £ <sl>£ r«’l> 0. 7.103
Это уравнение относится к идеальному кольцу; влияние начальных несовершенств здесь учитывать не будем.
Предположим, что всем точкам кольца сообщены некоторые дчальные радиальные скорости, близкие к Vq. Зададим их
284
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ
ГЛ. VII
величину с помощью ряда
где
7.104а
7.104
Решение уравнения 103 при начальных условиях 104 выпишем в виде
Отметим, что уравнение 103 не учитывает изменения окружного усилия в процессе сжатия кольца см. 0.6, стр. 164.
Первый член решения 105 определяет осесимметричную деформацию кольца в любой момент времени. Если бы начальные скорости в любой точке кольца были одними и теми же, то деформации кольца оказались бы осесимметричными и определялись из уравнения 106. В соответствии с уравнением 106 процесс сжатия кольца продолжается до момента времени, определяемого наименьшим корнем уравнения
Второй член 105 характеризует величину ожидаемых отклонений от круговой формы кольца. Возможность появления заметных волн связана с тем, что в члены первой строки уравнения 107 входят гиперболические функции shpnxy достигающие больших значений в пределах длительности деформирования кбльда.
7.105
7.106
0 00 2 «я cos П0 -ь рп sin п0 4
оо
0„ V ct„ cos nQ Pn sin габ sin pnX. 7.107
Prt
nr
Под г понимается наибольшее число, меньшее s: при п г р2п га2 — 1 s2 — га2, при га г 1 р га2 — 1 га2 — s2.
7.108
§ 80 ПЛАСТИЧЕСКОЕ ТЕЧЕНИЕ ПРИ ДИНАМИЧЕСКОМ ВЫПУЧИВАНИИ 285
Гармонические же функции sinpnt, входящие в члены второй строки выражения 107, не оказывают существенного влияния. на рост волн. Поэтому можно считать, что
пг
w2 т, 6 « о0 У « cos «е Рп sin «9. 7.109
Pfl
п
Если известна начальная скорость V0 и закон ее отклонения от равномерности по 104, то для любого момента времени можно найти из 106 величину осесимметричных деформаций wu а из уравнений 107 или 109 величину ожидаемых отклонений от круговой формы поперечного сечения w2.
В том случае, когда задана предельная деформация кольца
можно, сопоставляя выражения 106 и 108, найти минимально необходимую для достижения этой деформации начальную скорость
2®, «■-£--4-£3. 7. ПО
Если же известен и характер распределения начальных скоростей по 104, то, подставив значения v0 и т, найденные из 108 и 110, в уравнения 107 или 109, можно определить ожидаемые отклонения от круговой формы кольца после его обжатия при минимально необходимой для получения заданной деформации начальной скорости.
Рассмотрим влияние изменения начальной скорости на величину предельной осесимметричной деформации. Используя 106 и 109, выпишем отношение Wixw2x,Q в виде
, ч — cos st — 1 — sin st
Wj т _ Vp S T, 9 >k
7, ctn cos Pn sin Я0 -—
Pn
ti—
7Л11
Так как произведение sx всегда меньше я2, то 0<cosst< 1, a —-sin5T>0. Следовательно, числитель выражения 111, а
вместе с тем и отношение с увеличением v0 возрастают.
Это означает, что заданному допустимому отклонению от круговой формы поперечного сечения w2, ДОп соответствует тем большая предельная степень осесимметричной деформации
286
ВЫПУЧИВАНИЕ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ ГЛ< VII
Wi, пред, чем выше величина начальной скорости. С увеличением начальной скорости Vo величины Wix и w2t, 0 возрастают. Но рост функции wix происходит быстрее, чем амплитуды прогиба w2т, 0.
§ 81. Анализ процесса пластического выпучивания.
Результаты экспериментов
Описанная в предыдущем параграфе картина пластического выпучивания относится к случаю, когда деформация осесимметричного сжатия кольца-оболочки значительна и лежит в пределах
6-8.
Напомним, что речь идет об оболочке, всем точкам которой приданы некоторые начальные радиальные скорости, мало отличающиеся от заданного значения v0. Требуется определить предельное перемещение пред, при котором осесимметричная форма движения переходит в несимметричную, с образованием многих вмятин. Определение предельной деформации кольца-оболочки можно вести в следующей последовательности.
Прежде всего находим по 108 полное время сжатия кольца. Эту величину можно принять в качестве первого приближения, обозначим ее через ri. Далее находим по 109 амплитудное значение w2y соответствующее моменту времени т4 и заданной начальной скорости. Если w2 лежит ниже заданной величины w2y пред, то предельную деформацию вычисляем непосредственно. В противном случае задаемся некоторым вторым приближением х2 < Ti и повторяем вычисления. Для определения значения т, при котором w2 «
и>2, пред, обычно достаточно четырех-пяти приближений.
На рис. 7.46 приведены две кривые для предельной деформации еПр как функции 10, найденные описанным методом, при Rh 100 и 25. Были взяты следующие значения основных параметров для дюралюмина Д16: сгт 1500 кгсм2, Ек 8-104 кгсм2. Закон отклонения величин скоростей отдельных
Этот путь решения задачи предложен А. И. Гороховичем. Ему же принадлежат приведенные ниже данные экспериментов
Рис. 7.46. Диаграммы для предельной деформации в функции радиальной скорости. Сопоставление теоретических сплошные линии и экспериментальных данных.
АНАЛИЗ ПРОЦЕССА ПЛАСТИЧЕСКОГО ВЫПУЧИВАНИЯ
28
точек от значения основной скорости был принят в виде
с максимальным значением отклонения ±2,5.
На том же рис. 7.46 нанесены экспериментальные точки для моделей из того же материала. Опыты проводились на установке для штамповки изделий импульсным магнитным полем.
Рис. 7.47. Кадры скоростной киносъемки процесса упруго-пластического выпучивания.
В таких установках давление, действующее на заготовку, достигает 1000—4000 кгсм2. Время действия импульса внешнего давления измеряется десятками микросекунд. Эксперименты были проведены для колец, имевших следующие размеры: R 37 мм, h 1,5 мм и R 50 мм, h 1 мм.
На рис. 7.46 точки относятся к отношению Rh 25, а треугольники — к отношению Rh 100. Сплошные линии отвечают теоретическому решению. Как видим, согласование теоретических и опытных данных удовлетворительное.
Интересными являются результаты высокоскоростной киносъемки. На рис. 7.47, а—д показаны кадры, соответствующие первой стадии деформации — осесимметричному обжатию кольца. Кадры е—к отображают вторую стадию образования волн и процесс увеличения их амплитуды. Наконец, на кадрах п, р можно наблюдать третью стадию — разрушение колец.
ГЛАВА VIII
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
§ 82. Особенности задач о поведении оболочек при ударном нагружении
Перейдем ко второму классу задач, относящихся к динамическому выпучиванию тонкостенных конструкций. Как было сказано в главе VI, здесь мы будем учитывать волновой характер распространения деформаций.
Наиболее выпукло подобные задачи формулируются в случае, если конструкция удлиненного очертания подвергается действию продольного удара. Правда, в чистом виде при эксплуатации конструкций, содержащих оболочки, этот вид нагружения встречается сравнительно редко. Однако его исследование является практически важным по следующим причинам. При резких перегрузках оболочка испытывает со стороны укрепленных на ней массивных элементов конструкции нагружение, близкое к ударному. Кроме того, при модельных экспериментах динамическое продольное нагружение проще всего реализуется именно в виде удара. Поэтому изучение особенностей поведения оболочек при ударе необходимо для правильной постановки экспериментов.
Наконец, исследование удара весьма интересно в теоретическом отношении, так как в этом случае наиболее ярко проявляется динамичность процесса деформации, который может быть охарактеризован минимальным числом параметров.
При продольном ударе с большой скоростью деформации сопровождаются рядом сложных физических явлений: проявлением реологических свойств материала, температурными и химическими изменениями и т. п. Подробные сведения о физической стороне ударных процессов содержатся в монографии Гольдсмита 8.16. Кроме того, в малой окрестности торца напряженное состояние является существенно трехмерным. Поэтому с самого начала следует оговорить, какие именно стороны явления будут в дальнейшем изучены.
СТЕРЖЕНЬ ПРИ ПРОДОЛЬНОМ УДАРЕ
289
Прежде всего, учитывая, что скорости продольного удара, которым могут подвергаться оболочки в конструкциях, например, летательных аппаратов, сравнительно невелики, допустимо воспользоваться моделью упругого или упруго-пластического тела, не чувствительного к скорости деформирования. Кроме того, будем пренебрегать местными эффектами, связанными с трехмерностью напряженного состояния. В этой постановке удар определяется приданием некоторой определенной скорости одному из торцов стержня или оболочки и соотношением масс оболочки и груза.
Таким образом, случаи удара, которые будут рассмотрены в этой главе, существенно отличаются от тех, которые возникают, например, при исследовании задачи о пробивании, где перечисленные выше физические эффекты и соображения
о структуре материала являются определяющими.
В качестве примеров резкого нагружения, относящихся к конструкциям летательных аппаратов, можно привести воздействие волны давления, удар при посадке, взаимное влияние скрепленных элементов при кратковременных перегрузках и т. д. По отношению к судовым конструкциям также возможны действие волн давления, столкновение с жесткой преградой и т. п. Аналогичные примеры можно привести и по отношению к оболочкам наземных транспортных конструкций.
Некоторые общие положения, характерные для задач удара в постановке, принятой в дальнейшем, изложим на простейшем примере о продольных деформациях упругого стержня, испытывающего ударное нагружение.
Приведем элементарные зависимости, относящиеся к динамике идеальных стержней при продольном ударе. Рассмотрим стержень, один конец которого закреплен, а другой испытывает соударение с абсолютно твердым телом массы т, движущимся до встречи со стержнем со скоростью U. Принимая, что стержень и груз соприкасаются по параллельным плоскостям и отказываясь от учета местных деформаций в месте контакта, будем изучать изменение сжимающих напряжений в стержне в процессе удара вплоть до отделения груза от стержня.
Дифференциальное уравнение для перемещений стержня вдоль оси х рис. 8.1 имеет вид
§ 83. Стержень при продольном ударе
д2и _ 1 д2и дх2 с2 dt2 9
8.1
где
290
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
Решение этого уравнения должно удовлетворять условиям
8.2
их, 0 0, 4т-, 0 £ при х 0, 4т- 0 при >0,
д л> dt
ди
dt2 к1 дх
94 0,04--М. «,0 о.
dm
Здесь к — отношение массы груза к массе стержня. Время отсчитывается от момента соударения. Известно, что решение уравнения 1 можно принять в виде
и л;, t ct — x f2 ct, 8.3
где fi и f2— произвольные дважды дифференцируемые функции своих аргументов. Это решение получает наглядную интерпреgfc. dzu тацию, если предположить, что прибор, реР dt2 гистрирующий перемещения и деформации, определяемые функцией fi, движется со скоростью с от подвижного края к защемленному. В этом случае в точках, где находится прибор, х cty fi const; поэтому показания прибора не будут меняться. Следовательно, fi определяет волну деформации, распространяющуюся в стержне в на-
Рис. 8.1. К задаче о про- г г г j г
дольном ударе для прямо- правлении от места удара к закрепленному линейного стержня. торцу, а с есть скорость распространения
фронта волны, являющаяся с точки зрения акустики скоростью звука в стержне. Точно так же устанавливается смысл функции г, представляющей собой волну, отраженную от неподвижного края. Местная скорость частиц стержня и деформация определяются производными
V -f cf'ct — x cf'2ct х, я» > 8.4
е -а7 — f'ct x f2ct x; j
здесь штрихи означают дифференцирование по аргументам, стоящим в скобках.
Рассмотрим начальный период деформации 0 t 1с. Полагая 2 0 и х 0, получим уравнение для нахождения перемещений нагруженного торца
f П гП0 0, где f ct. 8.5
ВЫПУЧИВАНИЕ СТЕРЖНЯ С НАЧАЛЬНОЙ ПОГИБЫО
291
Используя граничные условия, получим для скорости перемещения подвижного торца стержня и соответствующей деформации следующие выражения:
V 0, t uf' 0 Uer,
v 8-6 е0, t — —.
Отсюда следует, что в момент соударения элемент стержня, примыкающий к торцу, подверженному удару, получает деформацию, равную отношению местной скорости верхней точки стержня к скорости звука в нем.
Перемещение крайней точки стержня определяется зависимостью
И 0, tUj -e-t’W. 8.7
Если масса груза значительно превышает массу стержня и можно считать к — оо, то при U const по 6 будет
и 0, t Ut.
Чтобы перейти к периоду времени <c:ct 21, нужно использовать функцию 2 и граничное условие на неподвижном крае. Таким образом, прямое интегрирование уравнения 1 приводит к функциям, вид которых изменяется по истечении отрезка времени, равного периоду прохождения упругой волны по длине стержня. Способ построения этих функций дан в книге А. И. Лурье 8.10. Используются и другие способы решения, наиболее употребительным из которых является метод характеристик.
Характерная кривая для деформации в фиксированной точке стержня при продольном ударе имеет вид экспоненты, спадающей во времени, на которую в моменты, кратные с, накладываются скачки. Показатель экспоненты определяется соотношением масс к. Продолжительность контакта зависит от величин U и к. Отделение происходит в тот момент, когда деформация у торца обращается в нуль, что соответствует прохождению через положение равновесия.
§ 84. Выпучивание стержня с начальной погибью
Зависимости, приведенные в предыдущем параграфе, относятся к стержню, деформирующемуся без изгиба. Рассмотрим теперь стержень, в котором, кроме деформаций сжатия, могут возникать также изгибные деформации,
292
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
В дальнейшем мы будем интересоваться вопросом о поведении стержня, один из торцов которого испытывает соударение с абсолютно твердым телом.
Классическая теория устойчивости стержней, сжатых статической продольной силой, базируется на элементарной теории изгиба, использующей гипотезы плоских сечений, нормальных к нейтральной оси.
Уравнение поперечных колебаний имеет четвертый порядок, причем скорость распространения возмущений, определяемых его решением, неограниченно возрастает с уменьшением длины волны. Это несоответствие физическим представлениям о конечной скорости распространения возмущений объясняется несовершенством принятой модели, свойственной элементарной теории изгиба стержней. При изучении выпучивания в процессе удара подобное противоречие может оказаться существенным; поэтому воспользуемся уточненной моделью изгиба, учитывающей поперечный сдвиг и инерцию вращения элемента стержня. Такие уравнения мы назвали в главе I уравнениями типа Тимошенко. Кроме того, откажемся от предположения о нерастяжимости нейтральной оси и добавим уравнение продольных колебаний, выведенное в предыдущем параграфе.
Предполагая, что прогибы могут быть соизмеримыми с характерным размером поперечного сечения, воспользуемся нелинейными зависимостями при составлении выражений, связывающих деформации с перемещениями.
Предположим, что полный прогиб стержня v складывается из трех составляющих — начального прогиба v0, а также прогибов v и, отвечающих соответственно изгибу и поперечному сдвигу. Тогда деформация удлинения волокон, деформация сдвига и изменение кривизны будут
Рассмотрим «равновесие» элемента стержня, вырезанного двумя близкими плоскостями, перпендикулярными к недеформированной нейтральной оси рис. 8.2. Проектируя усилия, действующие на элемент в продольном направлении, получим уравнение здесь Yo — удельный вес материала:
8.8
дх ' дх2
8.9
Приведенные здесь данные принадлежат И- Г- Кильдибекову и автору, см. ДАН СССР 167, 4, 1966.
§ 84 ВЫПУЧИВАНИЕ СТЕРЖНЯ С НАЧАЛЬНОЙ ПОГИБЬЮ 293
совпадающее по существу с рассмотренным в § 83. Уравнение движения элемента в нормальном направлении имеет вид
дх дхудх g г at2 и> 'бли'
п d2V
где уже второй член нельзя записать в виде так как
сжимающие напряжения являются переменными по длине стержня. Точки на рисунке соответствуют производным по времени.
Составим далее уравнение вращения элемента в плоскости ху вокруг поперечной оси, проходящей через центр тяжести:
Ж--0
'££-«•»>
В 9 — 11 обозначено: продольная сила
Р —EFs, поперечная сила Q k2FGy, изгибающий момент М Е1. Относительно коэффициента k2 см. главу I. Подставляя в 9 — 11 зависимости 8 и пренебрегая членами
третьего порядка, приходим к следующей системе нелинейных уравнений относительно продольного и нормального перемещений:
JLJ-4--U--Yl 1 д2« 1 д Г до0 УП
дх L дх ‘ 2 дх J с2 dt2 2 дх LI дх ’
д'у _1, 1_ d4v. 1 ду _
дх4 с2 с дх2dt2 с2с З4
V ' 8.12
i2 дх I l дх 2 дх 2 dx J dx J
. 1 d2v d4v0
i2c2 dt2 dx
Здесь введены обозначения:
— скорость распространения волн сдвига в стержне, i YlF -• радиус инерции сечения.
х
■Fdxii
:dx
Рис. 8.2. К выводу уравнений для продольнопоперечного движения стержня.
294
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛг VIII
Вводя безразмерные параметры:
приведем уравнения 12 к безразмерному виду
д2и д2и dl2 дх2 1
Если концы стержня свободно поворачиваются, то граничные и начальные условия имеют вид
Учитывая, что в интересующий нас период неустановившегося изгиба стержня прогибы сравнительно невелики, мы опустили в 13 нелинейные члены в первом уравнении, а также члены третьего порядка малости относительно производных от перемещений. Таким образом, задача приводится к интегрированию нелинейной системы 13 при начальных и граничных условиях 14, 15. Для интегрирования уравнений используется метод сеток в виде явной разностной схемы, аппроксимирующей исходные уравнения с точностью порядка квадрата шага.
Известно, что алгоритм явной разностной схемы приводит задачу к вычислению значений искомых функций для каждого последующего временного слоя по известным значениям функций в предыдущие моменты времени при помощи рекуррентных соотношений. При реализации вычислений на ЭЦВМ было обращено особое внимание на соотношение шагов по и т. Оказа¬
и 1, т 0,
1>1, т 0, 8.14
о 0, т О,
и£> 0 0, £, 0 V при 0, -§70 при 10,
о 6, 0 v0, £6, 0 0.
8.15
ВЫПУЧИВАНИЕ СТЕРЖНЯ С НАЧАЛЬНОЙ ПОГИБЬЮ
295
-0,005
Рис. 8.3. Конфигурация упругой линии, отвечающей дополнительным прогибам стержня при выпучивании.
лось, что при числе интервалов разбиения по длине от 16 до 60 шаг по нормированному времени т должен составлять 0,2—0,9 от шага по осевой координате
Приведем результаты вычислений, выполненных на машине БЭСМ-2М. На рис. 8.3 изображены упругие линии стержня, искривленного первоначально по одной полуволне синусоиды. Приведенные кривые относятся к различным моментам времени т. Видно, что в начальный период упругая линия стержня имеет четко выраженный характер бегущей волны. Вслед за ударом возникают две полуволны, амплитуды которых возрастают. В последующий период происходит «стабилизация» узловых точек и прогибы стержня приобретают форму стоячей волны. Проследим за процессом ее установления.
Зависимости т рис. 8.4 для различных полуволн
различны, однако во всех случаях можно определить «критическую длину» г’кр тахгт, которая является максимальной за все время выпучивания. Вычисления показали, что эти длины полуволн практически не связаны с величиной начальной погиби, т. е. остаются почти неизменными при варьировании в широких пределах.
Важно отметить, что начало уменьшения длины первой полуволны относится к моменту возникновения новой, «нулевой», полуволны, примыкающей к торцу, когда стержень как бы прощелкивает в противоположную сторону.
Длины полуволн, достигнув максимума, начинают
сходиться к одному и тому же значению. На этом заканчивается переходной этап выпучивания стержня. Ряд исследований, появившихся после указанной выше работы М. А. Лаврен
0,5
-
Of
1
А
0,3
- 1
г,мр
ол
-
0,1
h
1
О
7
Z
u-in
h
h
h
Ц
Г
О
Г”1
Ы
7,кр
7 t
Рис. 8.4. Пакет критических длин полуволн.
296
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЁ
ГЛ. VH
тьева и А. Ю. Ишлинского, относятся лишь к этапу установившегося выпучивания. Однако в действительности явление поперечного изгиба, вызванного продольным ударом, сильно осложнено переходными процессами.
§ 85. Различные подходы к задаче. Экспериментальные данные
В работах 8.15, 8.9, 8.11, 8.12 был развит критерий устойчивости стержней при ударе, основывающийся на интуитивном представлении о существовании некоторого участка стержня, для которого сжимающие напряжения в прямой волне являются эйлеровыми критическими. Примем, что на всем участке возможного выпучивания деформация равна е Vic. Если считать, что левый край этого участка шарнирно оперт, а правый жестко защемлен, то критическая деформация, определяемая известной формулой Эйлера, равна гэ n2i2vL2 v 0,7, где L — длина полуволны, подлежащая определению. Отсюда легко получить критическую гибкость стержня
Выпучивание начинается в момент времени, называемый критическим:
где X li — гибкость всего стержня, закрепленного шарнирно.
Согласно этой концепции выпучивание должно наступить, если I 0,7LKP или X А.
Другой возможный подход к задаче вытекает из результатов М. А. Лаврентьева и А. Ю. Ишлинского, согласно которым число полуволн выпучивания выражается целым числом, ближайшим к туГв2еэ> где еэ я2Д2. Следовательно, критическая гибкость в пределах одной полуволны оказывается равной
A nVcV
8.16
и критическую длину участка выпучивания
8.17
8.18
А я2 VcV,
8.19
длина полуволны
8.20
а параметр критического времени
8.21
См. ссылку на стр. 212.
§ 85 РАЗЛИЧНЫЕ ПОДХОДЫ К ЗАДАЧЕ. ЭКСПЕРИМЕНТАЛЬН. ДАННЫЕ 297
Рис. 8.5. Нарастание амплитуды критической полуволны при динамическом выпучивании.
Отметим, что если принять в описанном выше приближенном решении v 0,7, то оба подхода приводят к одинаковым численным результатам.
Вернемся к нашей задаче и сравним полученные данные с только что приведенными зависимостями. Если найти среднегеометрическую величину критических длин главных полуволн первой и второй, то при v 0,75 она окажется близкой к LKp по 17 и 20.
Однако приведенные данные показывают, что в неустановившейся стадии речь должна идти не об одной полуволне, а о целой серии полуволн.
Как же можно практически использовать результаты, относящиеся к длинам критических полуволн На рис. 8.5 см. также рис. 8.4 изображена амплитуда. первой полуволны в зависимости 0 от времени т. Видно, что пока ее длина it возрастает, амплитуда увеличивается медленно и кривая Ai — т обращена выпуклостью кверху. В момент, когда расстояние между узловыми точками достигает критического значения, начинается интенсивное возрастание амплитуды основной полуволны. Очевидно, этот момент может быть интерпретирован как критическое время, зависящее от обстоятельств удара.
Дальнейшее изучение выпучивания упругого стержня при продольном ударе было проведено в работе Б. А. Гордиенко 8.6а. Здесь использовались уравнения движения, аналогичные 13. Интегрирование уравнений проводилось также по методу конечных разностей.
Анализ результатов вычислений, проведенных при различных скоростях удара, показал, что процесс выпучивания стержня имеет три характерные стадии. Вслед за ударом начинается изгиб стержня по одной полуволне, длина которой возрастает
игг»
6
Рис. 8.6. Упругая линия стержня при ударе: а начальная стадия выпучивания, б развитие прогибов по форме начальной погиби.
298
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
с течением времени рис. 8.6. По мере распространения фронта деформаций по длине стержня, если начальная погибь имеет более одной полуволны на рис. 8.6 выбран случай, когда число полуволн т0 5, возникают новые полуволны. Длины этих
полуволн непостоянны, однако перемещение узловых точек про¬
исходит в малых окрестностях узлов в форме начального прогиба. Это дает основание считать волны близкими к стоячим.
Вторая стадия заканчивается равномерным возрастанием прогибов, повторяющих форму начальных несовершенств. Начиная с некоторого момента времени тКр, происходит трансформация форм движения, заключающаяся в следующем. Если
Рис. 8.7. Трансформация динамических форм: а возникновение новых полуволн, б исчезновение «избыточных» полуволн.
I 0 1 В 7 8 3 10 X
Рис. 8.8. Изменение длин полуволн в процессе выпучивания.
число полуволн начальной погиби т0 оказывается меньшим величины -т>»то происходит скачкообразный переход
стержня к форме, содержащей большее число полуволн, чем начальный прогиб. В тех случаях, когда т0 > т, происходит противоположное явление — исчезновение «избыточных» полуволн. И в первом и во втором случаях после трансформации упругая линия приобретает одно и то же число полуволн, определяемое параметрами стержня, скоростью удара и не зависящее от формы и амплитуды начальной погиби рис. 8.7. Процесс перестройки формы выпучивания отчетливо виден на рис. 8.8, где приведена зависимость длин полуволн от времени.
Характерно, что на третьей стадии происходит интенсивное развитие прогибов, поэтому можно принять начало перестройки формы упругой линии в качестве «критического времени». На рис. 8.9 показана зависимость критического времени от пара¬
§ 861 ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА ПРИ ПРОДОЛЬНОМ УДАРЕ 299
метра скорости удара. Точки соответствуют результатам численного интегрирования уравнений 13, а прямая линия соответствует выражению
кр 0,2я у •
. Суммируя сказанное, можно рекомендовать для практических расчетов сравнение гибкости стержня с критической, определяемой формулой 19: выпучивание произойдет, если гибкость превышает критическое значение.
Приведем некоторые результаты экспериментов по ударному нагружению стержней 8.6а. Опытное нагружение проводилось на установке, использующей падающий груз. Это позволило получить скорости удара в диапазоне 0,9—7,2 • 103 скорости звука в материале. Относительные значения веса образцов отношение к весу груза, использовавшихся в экспериментах, составляли 0,01—0,48. Испытывались стержни, изготовленные из дюралюмина Д16Т, пружинной стали, а также деревянные.
Измерения деформаций проводились при помощи тензодатчйков и шлейфового осциллографа. Для фиксирования конфигурации стержня в процессе выпучивания была проведена скоростная киносъемка.
Эксперименты показали, что при увеличении скорости удара возникает большее число полуволн вдоль стержня, причем преимущественное выпучивание имеет место на участке, примыкающем к нагруженному торцу. Наблюдалось также явление перестройки динамических форм, заключающееся в изменении числа полуволн в процессе выпучивания.
Таким образом, эксперименты качественно согласуются с теоретическими данными относительно перестройки формы волнообразования.
§ 86. Цилиндрическая оболочка при продольном ударе
Обратимся к исследованию устойчивости упругой цилиндрической оболочки, испытывающей соударение с абсолютно твердым телом, движущимся в осевом направлении 8.6а.
Для анализа используем уравнения движения, полученные в главе I. Эти уравнения учитывают поперечные сдвиги и инерцию вращения. По своей структуре система уравнений
10 15 ZO 30 40 60 80100 150 cV '
Рис. 8.9. Зависимость «критического времени> от скорости удара.
300
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
описывает распространение волн сжатия — растяжения и изгиба — сдвига.
Предварительно рассмотрим задачу в упрощенной постановке: будем пренебрегать волновыми процессами в срединной поверхности, а также сдвигами и инерцией вращения.
Считая в 1.29 v 0 и дидх —V, получим условное соотношение, описывающее изгибные колебания оболочки:
здесь безразмерные координаты и время отнесены соответственно к длине оболочки и времени прохождения волны деформации по длине, V — отношение скорости удара к скорости звука в оболочке; величины w, h и R также отнесены к длине оболочки.
Аппроксимация функции прогиба рядом
и применение процедуры Бубнова — Галеркина приводит к бесконечной системе независимых обыкновенных уравнений
fmn Щ тя 1 122 - 1 ill2 -г fmn 0, 8.24
где l ti27iRm — параметр, определяющий отношение размера вмятины вдоль образующей к размеру в кольцевом направлении.
Граница зон «устойчивых» и «неустойчивых» решений каждого из уравнений 24 определяется из условия
откуда следует выражение для «критической» скорости удара V:
где г mnR. Термины «устойчивость» и «неустойчивость» применены здесь в условной трактовке, см. главу VI.
8.22
ОО оо
8.23
т— 1 п—1
mVi 122 - Vm2 я2 1 ni2 -- 0, 8.25
V'
-L.mAn0 6
m2n2R2
8.26
1 Ш2
или
8.27
l 42
§ 86 ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА ПРИ ПРОДОЛЬНОМ УДАРЁ 301
В области «неустойчивых» решений темп нарастания прогибов определяется выражением
Q2 FmVl ц2_-.т4я41 22__
-L. vzHl Hi2 - -jgr г<1 i22 - l. 8.28
Большим Q2 соответствует большая скорость развития прогибов. Исследование Q2 на экстремум по z показывает, что наиболее интенсивное развитие прогибов отвечает значению
R
hl2
1671 ц£2. 8.29
Полученные результаты можно уточнить посредством учета поперечного сдвига и инерции вращения. В осесимметричном случае имеем уравнения:
i<>ddw., f d2w V w
k w-dr V-v-M-»T--w
<Э2ф 12ft2 dw,, <2b
-ЩГ-ПГХdF j -
8.30
о выборе коэффициента k2 аналогичного v на стр. 309, см. главу I. Задаваясь аппроксимацией вида
w
т1
lS Ф т C0S МП
т1
8.31
и проводя аналогичное исследование, получим «критическую» скорость удара
V — k2tn2n2, 1 о от
у, 2, 2k2 m2n2R2 9 I®
2 —
или
Г 8.33
22 12ft2 -ф-
При R -> оо получается критерий для эквивалентного стержня.
На рис. 8.10 приведена зависимость «критической» скорости V от параметра z для фиксированного значения hR в нашем случае hR 1,385 10-2 при осесимметричном выпучивании 0. На рис. 8.11 даны зависимости Vz для различных значений параметра. Характерно, что с уменьшением числа
302
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
полуволн в кольцевом направлении расширяется область «неустойчивых» решений. Из приведенных графиков видно, что
цго
V
0,15
0,10
-
Li
,
А
I
Рис. 8.10. Связь между «критической скоростью» и параметром волнообразования.
о 5 w 15 Z0 z
Рис. 8.11. Связь «критической скорости» и параметра волнообразования при различных соотношениях окружного и продольного размеров вмятин.
граница «неустойчивости»—V как функция г — имеет минимум, равный V. Исследование экстремума показало, что минимальные значения «критических» скоростей, определяемых по
формулам 27 или 33,
равны соответственно т._ h 1£»
при z2 и
Уз 1 ц2 2 Vs' R
8.34
V при
А 16
12 Rk2 12 k2R
Рис. 8.12. Прогибы оболочки в различные моменты времени.
а23 к2 - А'
8.35
Характерно, что при V < V выпучивания не происходит. В силу соотношения
dV h 1 — fx
dV RVW 1 ii22
>0
минимум «критической» скорости уменьшается с уменьшением параметра g; наименьшее значение У соответствует осесимметричному выпучиванию оболочки.
ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА ПРИ ПРОДОЛЬНОМ УДАРЕ
303
Перейдем к анализу осесимметричного выпучивания оболочки на основе более полных уравнений главы I. Интегрирование их проводилось по методу конечных разностей см. О.о.
На рис. 8.12 показаны характерные прогибы цилиндрической оболочки в различные моменты времени. Анализ результатов показал, что процесс выпучивания оболочек также распадается
Рис. 8.13. Развитие амплитуды первой полуволны.
о 1 г з 5
V-10г
Рис. 8.14. Зависимость динамического коэффициента от скорости удара.
на три характерные стадии, аналогичные описанным ранее для стержней.
Рассмотрим некоторые особенности поведения оболочек при ударе. На рис. 8.13 показано развитие амплитуды первой полуволны во времени при различных значениях R. Видно, что с увеличением радиуса оболочки темп нарастания прогибов снижается. По-видимому, существенный вклад в развитие прогибов, особенно на начальном этапе, вносит слагаемое aR дидху отвечающее осевому сжатию. С ростом R его влияние уменьшается; темп развития прогибов снижается. Если проследить за тем, как меняется величина взаимного сближения торцов оболочки Адин, при котором начинается выпучивание, в зависимости от скорости удара, то окажется, что эта величина растет при увеличении скорости. На рис. 8.14 приведена зависимость динамического коэффициента от величины относительной скорости удара V.
304
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
§ 87. Случай неосесимметричного выпучивания
В предыдущем параграфе вычисления относились к осесимметричной задаче о продольном ударе. Эта постановка приемлема лишь для относительно толстых оболочек, форма выпучивания которых близка к осесимметричной. Если же оболочка достаточно тонкая, выпучивание сопровождается образованием волн в окружном направлении.
Обратимся к неосесимметричной задаче об устойчивости упругой круговой цилиндрической оболочки при продольном ударе. Будем считать, что явление потери устойчивости можно разделить на две стадии — первую, в течение которой происходит накопление мембранных напряжений в срединной поверхности, и вторую, в процессе которой происходит выпучивание. Исходя из этого предположения, условимся при определении сжимающих усилий пренебрегать изгибом оболочки: на этом этапе основной является продольная составляющая сил инерции. На втором этапе, при интенсивном нарастании прогибов, наоборот, решающее значение имеет нормальная составляющая инерционных сил.
Для определения динамических сжимающих напряжений нужно воспользоваться уравнением 1
д2и _ 1 д2и,
дх2 — с2 dt2 9 o.ao
где теперь cYEgy 1—х2 —скорость звука в оболочке.
Уравнение 36 может быть проинтегрировано, например, по методу характеристик, после чего закон изменения сжимающих усилий по длине оболочки будет определен. Предположим, что найденный закон изменения усилий распространяется на некоторую область вблизи рассматриваемого сечения, и для каждого момента времени определим сжимающие усилия для выбранной «узкой зоны» вдоль длины 8.1.
Эти значения мембранных напряжений введем в уравнения изгиба оболочки, которые примем в виде
8.37
где по-прежнему w — полный прогиб, w0 — начальный прогиб оболочки, Ф — функция напряжений в срединной поверхности, отвечающая зоне вблизи выбранного сечения.
Подобная постановка задачи была сформулирована И. Г. Кильдибековым и автором 8.5, 1964 г.
§ 87
СЛУЧАЙ НЕОСЕСИММЕТРИЧНОГО ВЫПУЧИВАНИЯ
305
Перейдем к уравнениям, описывающим вторую стадию потери устойчивости. Предполагая, что при выпучивании оболочки вмятины имеют ромбовидный характер, примем выражение для полного и начального прогибов в виде
где а nmL, р nR. Подставляя 38 во второе уравнение 37, находим, как обычно, функцию напряжений в срединной поверхности, к которой добавим член —ру22Е, причем р pt определяется для некоторой зоны оболочки, как отмечалось выше.
Дальнейшее решение сводится к применению процедуры Бубнова — Галеркина, приводящей к обыкновенному дифференциальному уравнению относительно амплитуды заданной формы выпучивания U — скорость удара:
Для решения задачи должны быть определены параметры -ф,
I и п. Первый из них может быть выбран так же, как в статической задаче; параметр задает форму вмятины.
Это решение задачи принадлежит В. Л. Агамирову и автору 8.1; эксперименты проведены В. Л. Агамировым.
w f sin ах sin у ф sin2 ах sin2, w0 f0 sin ax sin y -ф sin2 ax sin2 py
8.38
£S - 27£« 27£ - l0£S« «Э -
где
306
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
Рассмотрим результаты численного интегрирования уравнения 39 для оболочки с геометрическими параметрами
hR -yLR 2,2B случае удара бесконечно большой массой
при амплитуде начальной погиби, составляющей 0,001г. На рис. 8.15 приведены диаграммы роста стрелы прогиба во времени. Кривые имеют три характерных участка. На начальном этапе прогибы почти не увеличиваются, что соответствует стадии
накопления мембран-
£ “
6
7
Т72
i
S
У
1,8 7J 2fl 2J 2,2 2J 2f t4
Рис. 8.15. Рост стрелы прогиба при выпучивании обо лочки.
ных напряжении; затем происходит интенсивное выпучивание.
Как видно из графиков, наиболее бурный рост имеет место для кривой, соответствующей л11. Отсюда следует вывод, что наиболее вероятным в данном примере является выпучивание оболочки по форме с числом волн по окружности, равным 11. Здесь было принято, что скорость удара составляет 0,001 от скорости звука в оболочке. Судя по результатам вычислений, изменение стрелы прогиба во времени имеет одинаковый характер для всех зон по длине оболочки; отсюда следует, что критическое значение параметра t характеризует поведение оболочки в целом.
Таким образом, здесь мы приходим к результатам, близким к описанным в предыдущей главе.
Вычисления показали, что увеличение скорости удара приводит к повышению числа окружных полуволн и критического значения параметра времени t.
Интересно проследить, какое влияние на характер потери устойчивости оказывает величина массы. При бесконечно большой массе вмятины оказываются сильно вытянутыми вдоль дуги. Если же х 5, то вмятины близки к квадратным.
§ 88. Данные опытов по ударному нагружению оболочек
Изложенное выше исследование неосесимметричного выпучивания оболочек при ударе основывалось на ряде допущений, справедливость которых может быть проверена с помощью опы¬
§ 88 ДАННЫЕ ОПЫТОВ ПО УДАРНОМУ НАГРУЖЕНИЮ ОБОЛОЧЕК 307
тов. Перейдем к результатам серии экспериментов с цилиндрическими оболочками, подверженными продольному удару падающим грузом. Деформации в оболочке в процессе удара фиксировались проволочными тензодатчиками, сигналы от которых подавались на двухлучевой катодный осциллограф и фотографировались.
В проведенных опытах вмятины располагались, как правило, у торца оболочки, испытывающего удар, и у неподвижного торца, образуя в каждой из этих зон один или два пояса.
На рис. 8.16 показаны ромбовидные вмятины, расположенные у нагруженного торца. В некоторых случаях это относится к сравнительно толстым оболочкам удар сопровождался появлением сплошной кольцевой складки, что объясняется, вероятно, переходом деформаций в упруго-пластическую область.
На рис. 8.17 приведено сопоставление экспериментальных данных критических напряжений с теоретическими результатами. Кривая на рисунке показывает зависимость параметра динамического критического напряжения, отвечающего «критическому» значению t9 и отношения массы оболочки к массе груза. Точками здесь отмечены экспериментальные величины напряжений, определенные из опытов при Rh — 180.
Параметр скорости удара был равен Uc 10“3, где И — скорость удара, с — скорость распространения продольных упругих волн в оболочке. Как видно из рисунка, все экспериментальные точки
Рис. 8.16. Форма ромбовидных вмятин, возникающих при продольном ударе.
О 0,05 0,7 О5 0,2 0,25 1х
Рис. 8.17. Зависимость критического напряжения от соотношения масс оболочки и груза.
располагаются достаточно близко к теоретической кривой, причем сверху от нее.
Зависимость параметра критической нагрузки от формы вмятины, характеризуемой величиной £, показана на рис. 8.18
308
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
сплошной кривой. Приведенная диаграмма получена при х 5 и цс 10_3 под х понимается отношение массы груза к массе оболочки. Треугольниками показаны опытные данные при динамических испытаниях, когда х 3,8—5 и Uc 0,8—1 • 10'3. Здесь же пунктиром нанесена кривая, полученная из решения соответствующей нелинейной статической задачи. Кружками
Рис. 8.18. Зависимость критического напряжения от формы вмятины.
24
к
16
180 -х—
Rh1ZO
-V
А
N
0,4 0,8
Рис. 8.19. Скорость удара, при которой происходит выпучивание оболочки.
отмечены данные экспериментов по статическому продольному нагружению. Видно, что динамичность процесса проявляется в увеличении параметра нагрузки, в данном случае почти вдвое.
Ряд опытов проведен с постепенным увеличением скорости удара с целью определить минимальное значение критической скорости. На рис. 8.19 показаны результаты испытаний. Треугольниками отмечены опытные данные, полученные на оболочках, имеющих Rh 120, кружками —для Rh 180. Кривые построены по данным экспериментов. Найденные здесь значения сжимающих напряжений удовлетворительно согласуются с результатами решения волнового уравнения.
§ 89. Упруго-пластическое выпучивание оболочек при ударе
Приведенные в § 16 уравнения используем для исследования поведения круговой цилиндрической оболочки при продольном ударе рис. 8.20. Рассмотрим случай осесимметричной
89
УПРУГО-ПЛАСТИЧЕСКОЕ ВЫПУЧИВАНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
309
деформации. Уравнения движения 1.75 — 1.78 выпишем в виде _
dNx д2й д1 дт2
d2w дт2
дМх
Л п
гу2 Ч — дт2
д а‘
Здесь введены безразмерные параметры: и
701. L ъ L
г2 1 —х л L _<> h2
8.40
и Т>
w х t Eg
w — I • г > Х lV yO-Ц2 ’
V
Qx
D-
N
x— в
уЛ
С
M ML r Eh M D I — i2 2 ’ 'w R ’ 12L2
Qx Bv '
Eh
12 1 — Ц2 В дальнейшем черту над безразмерными величинами опускаем.
Предположим, что оболочка, шарнирно опертая по торцам, в момент времени т 0 испытывает соударение с абсолютно U
Рис. 8.20. Схема нагружения оболочки.
твердым телом массы тгр, движущимся в продольном направлении со скоростью U. Решение уравнений 40 должно быть подчинено граничным и начальным условиям:
w 0, т 0, w 1, т 0,
мх0, т 0, Мх1, т 0,
т 0О, т, и1, т 0;
«I, 0 0, I, 0 F при 0, 4 0 при >0,
8.41
8.42
дх
Ю6. 0 0, 4- I, 0 о,
I, 0 0, 0 0,
Решение задачи, приведенное в §§ 89, 90, принадлежит В. А. Фельдштейну 8 14.
310
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
где, как и ранее, к — отношение массы груза к массе оболочки.
Для интегрирования уравнений 40 используем метод сеток в виде явной разностной схемы. Заменяя дифференциальные операторы симметричными разностными, получим аппроксимирующую алгебраическую систему:
и1
Wnkl
— 2uk — «Г Ат27 и,
2wl — Wk' Ат2Fk w,
<1 2--'At 2ЗД,
8.43
k 0, 1,., К — 1; п 0, 1,. ; Fk — левые части системы 40, вычисленные в узлах разностной сетки.
Для линеаризованных уравнений 40 можно получить необходимые условия устойчивости явной разностной схемы, используя критерий Лакса — Рихтмайера. На рис. 8.21 приведено семейство кривых, определяющих максимально допустимые шаги Ат в зависимости от используемых шагов по пространственной координате 8.1. Как следует из приведенных графиков, условие устойчивости сильно зависит от толщины оболочки: чем меньше отношение Rh, тем слабее ограничение, налагаемое на соотношение шагов.
Соотношение шагов, необходимое для интегрирования нелинейных уравнений, устанавливается эмпирически, а полученный критерий можно использовать в качестве первого приближения. Оказалось, что наличие нелинейных членов требует уменьшения Ат, определяемого из графиков на рис. 8.21, в 2—3 раза. Расхождение результатов при варьировании Ат в этих пределах оказывается одного порядка с погрешностью аппроксимации. Как видно, схема типа 43 требует довольно малого временного
шага, что создает известные неудобства при ее использо¬
вании.
70
10гД£
Рис. 8.21. К выбору соотношения шагов разностной сетки.
См. Р. Д. Рихтмайер, Разностные методы решения краевых задач, Изд-во иностр. лит., 1960.
§89 УПРУГО-ПЛАСТИЧЕСКОЕ ВЫПУЧИВАНИЕ ОБОЛОЧЕК ПРИ УДАРЕ 311
В работе 8.4 предложен подход, позволяющий значительно увеличить Ат. Для этого нужно ввести замену
позволяющую после подстановки в уравнения выразить значения •ф через значения функций на предыдущих временных шагах.
О 0,2 0,4 О,Б Ofi 7,0
xL
Рис. 8.22. Прогибы оболочки в различные моменты времени.
О 0,2 0,4 О,Б 0,8 О
XL
Рис. 8.23. Характерная форма динамического выпучивания за пределом упругости.
Однако указанный прием автоматически исключает из уравнений движения инерцию вращения, что, как будет показано ниже, может привести в ряде случаев к существенной погрешности.
Обратимся к результатам вычислений. Поставим цель выяснить характер изгиба оболочки при различных скоростях удара.
312
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
Серия вычислений, проведенных на ЭЦВМ, позволила выявить следующие закономерности процесса выпучивания.
О Ot2 Ot4
Рис. 8.24. Остаточные прогибы оболочки, теория и эксперимент,
ЦБ ’ 0,8 Ifl
XL
ЦОЗ
Uc
0JZ
ЩП
П> ЦБ XL
1 •
1 °
■ ▲ •
• • Вычисления оло Эксперимент
° V ■ ▲ >
■ о '
»
о
N. •
д
■ □
О
■
А '
•
■
■
10
20
JO
Рис. 8.25. Локальное выпучива- Рис. 8.26. Зависимость формы выпучивания от парание в зоне удара. метров ударного нагружения.
На начальном этапе прогибы оболочки имеют явно выраженную форму бегущей волны рис. 8.22. К моменту времени т 2,5 — 3 начинает складываться устойчивая форма изгиба, остающаяся неизменной до наступления максимальных значений деформации в случае конечной массы ударяющего тела. К ней близка и форма остаточного прогиба по окончании удара.
УП>УГО-ПЛАСТИЧЁСКОЕ ВЫПУЧИВАНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
Рис. 8.27. Деформации поперечного сдвига в оболочках различной толщины.
— Wтих'h
О 2 4 6 д 10
t
Pwc. 8.28. Влияние инерции вращения на развитие прогибов.
314
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
Оболочки, для которых были проведены вычисления, по характеру изгиба делятся на три группы. К первой группе относятся оболочки, имеющие вблизи торцов близкие по величине складки рис. 8.23, ко второй — оболочки с преобладающим изгибом у неподвижного торца рис. 8.24 и к третьей — оболочки, у которых изгиб локализован в узкой зоне, примыкающей к месту удара рис. 8.25. На рис. 8.26 в плоскости параметров, определяющих условия удара, квадратами отмечены точки,
когда остаточные прогибы относятся к первой, треугольниками— ко второй и кружками — к третьей из перечисленных групп.
Представляет интерес выяснить, насколько существенными оказываются эффекты, вносимые учетом поперечного сдвига и инерции вращения. На рис. 8.27 показано развитие во времени поперечных сдвигов в торцевом сечении оболочек различной толщины. Как видим, сдвиговые деформации достигают значительной
величины, причем с увеличением толщины их роль становится более ощутимой.
Влияние инерции вращения на
Рис. 8.29. кольцевые складки при вы- раЗВИТИв Прогибов оболочки ИЛ-
пучивании за пределом упругости. ЛЮСТрируеТСЯ графиками, ПрИВе-
денными на рис. 8.28. Здесь
показано развитие максимальных прогибов во времени при различных скоростях удара. Сплошными линиями изображены кривые, относящиеся к решениям, полученным с учетом сдвига и инерции вращения, пунктиром — без учета инерции вращения. Видим, что при малых скоростях кривые близки, однако при увеличении скорости удара пренебрежение инерцией вращения приводит к завышению максимальных и остаточных прогибов. Анализ других параметров деформации также приводит к выводу, что при скоростях удара, составляющих более 0,5 скорости звука, влияние «вторичных эффектов» является существенным.
Проведенные эксперименты подтвердили вывод об определяющем влиянии импульса на характер выпучивания. На рис. 8.26 светлыми значками отмечены параметры удара, реализованные при испытаниях. Остаточные прогибы, которые приобретали образцы после удара, имели описанную выше характерную форму. На рис. 8.24 пунктиром показана конфигурация про¬
§ 90 КОНИЧЕСКАЯ ОБОЛОЧКА ПРИ ПРОДОЛЬНОМ УДАРЕ 315
гибов, полученная экспериментально. Как видно из приведенного графика, теоретические и опытные данные находятся в хорошем соответствии. Внешний вид оболочки после испытания показан на рис. 8.29.
§ 90. Коническая оболочка при продольном ударе
Перейдем к рассмотрению поведения круговых конических оболочек при осевом ударе.
Будем рассматривать задачу в той же постановке, что и в § 89 8.14. Ввиду большой общности между исследуемыми задачами, введем геометрию конуса следующим образом: определим некоторый «основной» цилиндр длины L и радиуса R0 и будем рассматривать конические поверхности, образующие которых проходят через среднее сечение оболочки под углом а к образующей цилиндра рис. 8.30.
Ограничимся рассмотрением осесимметричного случая. Уравнения движения имеют вид 8.14:
Рис. 8.30.
Геометрия
оболочки.
конической
здесь
1 д АГ ч. xr sin а д2и 8.44
t xL, x
L V Vl-
a2
ft2
12Z.2 ’
Y1 -i2 ’ N -- О ——
« B, Чх Bv
rL ’ U T■
M,
MXL
D
w -
fe2l-n
2
причем в 44 и всюду в дальнейшем черта над безразмерными величинами опущена. Принимая, что край оболочки 1 шарнирно оперт на жесткой неподвижной опоре, а другой торец радиуса гt укреплен на жесткой диафрагме, свободно перемещающейся вдоль оси, запишем граничные условия следующим
316 ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
образом:
до 0, т ы0, ttga, ы 1, т 0, Мл0,т 0, АМ1,т 0,
ЛГ 0, т vQx 0, г tg ct Nx 0, т 0, т tg a
д2и
ГЛ. VIII
к1к
Ж’Г0, т> R0
г cos2 a ’
8.45
где х — по-прежнему отношение массы груза к массе оболочки. Начальные условия имеют вид:
и1,0 0, 0 -ycosa при £ 0
w, 0 0,, 0 sin а при £ 0
♦ 6, 0 0, -§-£, 0 0.
8.46
Для интегрирования системы 44 используем метод конечных разностей в той же форме, что и ранее, в случае цилиндрической оболочки. Опуская подробности вычислительного
-wrfi
iff
Of
-V
-v
5
R0h 75 Ш02 a ZOa VH003 х0,1
4
г
У
у
V о,
4 4ч
Г 0,L
7 xL
Рис. 8.31. Прогибы конической оболочки при ударе.
алгоритма, полностью аналогичного 43, перейдем к результатам вычислений.
Как показали вычисления, устойчивая форма изгиба стабилизируется после двух-трехкратного прохождения волн деформации по длине образующей. Изгиб характеризуется образованием
КОНИЧЕСКАЯ ОБОЛОЧКА ПРИ ПРОДОЛЬНОМ УДАРЕ
317
нескольких полуволн, наибольшей' из которых является первая, примыкающая к нагруженному торцу рис. 8.31. При весьма
Рис. 8.32. Развитие основной полуволны при различных углах конусности.
больших скоростях удара, составляющих более 3 от скорости звука в оболочке, у нагруженного торца возникает полуволна, тогда как остальная часть -шь оболочки практически не возмущена. Формирование преобладающей полуволны происходит раньше, чем волна деформации отразится от противоположного края; это объясняет независимость амплитуды прогиба от длины оболочки.
Рассмотрим подробнее процесс образования преобладающей полуволны изгиба. Обратимся к рис. 8.32, где показаны максимальные
значения прогибов w в зависимости от времени при различных углах полураствора а. Как было показано выше, на начальном этапе выпучивания цилиндрической оболочки ее прогибы состоят из одной быстро нарастающей полуэолны, обращенной выпуклостью наружу. В конической
Рис. 8.33. Развитие основной полуволны в зависимости от скорости удара.
318
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
оболочке прогибы на торце не равны нулю в силу краевого условия 45.
Как следует из рис. 8.32, в слабоконических оболочках формирование основной полуволны происходит без изменения знака прогиба, тогда как с увеличением а первая полуволна возникает в результате резкого изменения знака прогиба до. При значительных скоростях удара, даже при больших а, до не меняет знака, так что хлопок отсутствует рис. 8.33.
§ 91. Двухслойная оболочка. Общие зависимости
Многослойные конструкции типа оболочек находят широкое применение в технике. Весьма распространенным конструктивным элементом является двухслойная оболочка, внутренний слой которой является несущим, а внешний, играющий вспомогательную роль, выполнен из материала, имеющего значительно более низкие механические характеристики. Однако толщина наружного слоя может быть значительной, так что в целом необходимо учитывать его влияние на прочностные свойства пакета.
Некоторые известные теории оболочек, состоящих из двух и более разнородных слоев, используют либо модель Кирхгофа — Лява, применяемую ко всему пакету в целом
1.5, либо в отдельности к несущим слоям, связанным легким заполнителем, для которого
справедлива гипотеза прямых линий 8.7.
Рассмотрим модель оболочки из упруго-пластического материала, учитывающую поперечные сдвиги и инерцию вращения. Если исходить из непрерывности касательных перемещений на поверхности контакта и постоянства сдвигов по
толщине каждого из слоев, то получится, что касательные напряжения претерпевают разрыв при переходе через поверхность контакта. В реальных конструкциях этот скачок воспринимается весьма тонким склеивающим слоем.
Поверхность контакта между слоями 50 отнесем к ортогональным координатам ху у, совпадающим с линиями кривизны
Рис. 8.34. К выбору обобщенных координат элементарного объема.
Это решение дано В. А. Фельдштейном Изв. АН СССР, МТТ, 1972.
ДВУХСЛОЙНАЯ ОБОЛОЧКА. ОБЩИЕ ЗАВИСИМОСТИ
319
kXi ky. В качестве обобщенных координат, характеризующих положение элемента в пространстве, примем общее для обоих слоев нормальное перемещение w и касательные и0, vo в поверхности S0, а также щly Vk в поверхностях S, отстоящих от поверхности раздела на расстояния zk рис. 8.34. Индекс 1,2 обозначает номер слоя. Предположим, что к поверхностям оболочки приложены внешние нормальные напряжения р±х, руУ pzz Знаки ± относятся соответственно к поверхностям z —Л2, z hi. На торцах х ai, 2, У bit2 действуют напряжения а, Э л:, у у z.
Согласно принятым допущениям перемещения слоев распределены следующим образом:
Деформации, определяемые по теории пологих оболочек, имеют вид:
Далее получим уравнения движения оболочки, исходя из принципа Гамильтона — Остроградского:
ик и0--и0 — ик,
к
8.47
vk v0 — 7-t>o — »•
zk
8.48
где
■ф
8.49
320
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
К и П — кинетическая и потенциальная энергия, a W — работа внешних сил. Учитывая 47, запишем выражение для кинетической энергии р — плотность материала слоя:
Vk — объем, занимаемый слоями оболочки. Выражением 50 учитывается энергия вращательного движения. Координаты ги выберем таким образом, чтобы после интегрирования по г в 50 подынтегральная функция содержала только квадраты обобщенных скоростей. Легко проверить, что для этого нужно
2
принять 2ft ± -g hk. В этом случае кинетическая энергия запишется в виде
-1 V
of bzf т<> 6y£> т£> 6у£> dx dy dz. 8.52
' Vk
A1 S.
8.51
где обозначено:
ipA- 4pAk> mk
p Л
Вариация потенциальной энергии
2
sn S Ш к
Интегрируя по г и вводя обозначения
4
4
8.53
J az dz M< J т<«г dz Я«‘>,
ДВУХСЛОЙНАЯ ОБОЛОЧКА. ОБЩИЕ ЗАВИСИМОСТИ
:-2Я
Nk Ьех Гк' Ьеху NT Ьеу QT 6e'J Q™ 6е
г1;
Лк
■»<« Ал<>
получим 2
611
kl So
’ тйЬ »'М« '»’« т <»• 8-54
Элементарная работа внешних сил:
b'w S' J р - QS 6«о - rk Qw
1. ai
тг <25 К 0 о Р bw dx
k 1» 2 Ьг
j PS - ТГ Qg Pffi- b
-г Q- QSS 6y 4 dy
J Pixb“-h2dxdy JJ
Pjcjc l So
J J pyy 6v ” dx dyJrl pyy bv h>dx dy
So So
J J Pzz 6ш dx dy, 8.55
So
где 6н Aft, 6t> Л — вариации перемещений, вычисленные на поверхностях оболочки. Здесь обозначено:
JpS. « ft
Подставляя вариации 6С, 6П и 6'W в интеграл Гамильтона и провоДя обычные выкладки, получим уравнения движения:
dNx. дТ дМх
дх
dNu
ду
ду
дТ
дх
дх
pi i - -р„ 1 4г - «’<’
д2и0
dt2
dMv дН 1, 1
-т-2- — Л QI> —Q2
ду дх 1 zx г z2 У
Рву 1 - 1г руу 1 г К0 <’ 4 - 8,56>
322 ПОВЕДЕНИЕ ОЁОЛОЧЕК ПРИ УДАРЕ ГЛ. VIII
-ггзг k‘N ‘A a w« srт if
Mn’- ttt ”<m,l> >“> T'
ам'и <Я1 4 д2и.
дх d Q — Pxxi m z W > 8.56а
дМ дН1 d2v.
—и- г,— QLn - PZuK -
ду 1 дх иуу 1 1 I <2
ЗМ® дН2 д
дх ду РххК т2z2 Qt2 ’
дМ2 дН2 „ m д
” <3 Л mz> dF ' 8-56в>
Здесь и далее для краткости обозначено:
Nx Nx Nx Ny N Nf, Qx Qx Qx Qy QJ Qf,
M i;Mx M<x2 My — --My Mf,
н — я1 — я<2
Zi z2
ЯаЗ Р QapQ Q«p, а
Р у >
г.
В зависимости от условий закрепления быть сформулированы следующие варианты вий для кромки х а:
оболочки могут граничных усло-
NX Мх -f- Рхх Qxx 0
или
и0 0,
Т Н -f- Рху Qxy 0
или
t>o 0,
■М'Чргэ-о
или
Щ 0,
iM' Q2o
или
и2 0,
8.57
Hlu Q<>
или
v 0,
±h» qS_ о
или
С2
to
II
О
M,---T- Q, P„ 0
или
w 0.
Условия на краю у b получаются из 57 заменой индексов х и у.
§ 91
ДВУХСЛОЙНАЯ ОБОЛОЧКА. ОБЩИЕ ЗАВИСИМОСТИ
323
В случае физической и геометрической симметрии слоев, положив 2и0 зз ui и2у 2v0 Vi v2 и перегруппировав члены в выражении действия по Гамильтону, получим уравнения для однослойной оболочки; уменьшение числа уравнений соответствует дополнительной гипотезе об отсутствии излома нормали на поверхности контакта, что снижает число степеней свободы элемента.
Остается вывести соотношения, связывающие усилия и моменты с перемещениями. Интенсивность деформаций в каждом из слоев запишем, пользуясь выражением 1.197, где через pk9 pk и pk теперь обозначено:
Воспользуемся сделанными в § 16 предположениями о характере разгрузки с той лишь разницей, что определять состояние элемента будем не по знаку dejdt в соответствующей точке срединной поверхности, а по знаку defdt в точках Zh на поверхностях 5ft. Вычисляя при помощи соотношений деформационной теории напряжения и интегрируя по толщинам слоев, получим выражения для внутренних усилий и моментов. В области активных пластических деформаций будет см. стр. 70:
рГ
8.58
324
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ, VIII
где
Jk
Г о'-’
»’ J -щ-Znldz ral, 2, 3.
Ч 61
В области разгрузки
NТнГ1ЕА „; i.»; т £ 4,
яр - <4 в л <j й £.
г»<»• i £, а,,
«’ - <г j E»M’«Sr, q« - сГj м11м1'4- Ethi Г т I <;4-4
»»'«♦г 1 «ri
зШ '2-дГ’
Mf<• ‘ г,»2 Г т V.П1
з Т а.Г
я> „«• 4 £l« 14,ilMl.
Здесь параметры, отмеченные кружком, представляют собой разности вида ° f —, где — значения соответствующей величины в момент начала разгрузки. Подставив 58 или 59 в систему уравнений 56, можно получить уравнения движения оболочки в перемещениях. Однако мы не будем этого делать ввиду чрезвычайной громоздкости получающихся выражений. Кроме того, при численном интегрировании уравнений нет необходимости иметь их запись в перемещениях; удобнее строить вычислительный алгоритм путем последовательного определения деформаций, напряжений, внутренних усилий, моментов и последующей подстановки их в систему 56.
Полученные уравнения принадлежат к гиперболическим. Анализ коэффициентов системы показывает, что отвечающие ей решения при упругих деформациях представляют собой волны сжатия — растяжения, распространяющиеся в поверхностях Sk со скоростями
ck
- Фщ’ 8'60
§ 92 РЕШЕНИЕ ЗАДАЧИ О ПОВЕДЕНИИ ДВУХСЛОЙНОЙ ОБОЛОЧКИ 325
а в S0 — со скоростью
'•-rSrt-TTFT’ <8-6»
а также волны изгиба — сдвига, имеющие скорость
° ‘»-ПТ ТРгГ.62
где обозначено:
Р2Л2 0 _ ЯгО - 1h2 „ _ ft21 - Ц
X Р - п I 1, ' ' f
Р1Л1 1 С1 — и-г 1 2
Если деформации слоев превосходят предел текучести, формулы 60 — 62 остаются справедливыми, если заменить в них
модули упругости осредненными по толщинам слоев секущими
модулями:
§ 92. Решение задачи о поведении двухслойной оболочки
Аналитическое решение уравнений, полученных выше, весьма затруднительно. Поэтому здесь, так же как и ранее, будет использован метод конечных разностей.
Рассмотрим осесимметричную деформацию цилиндрической оболочки при продольном ударе. Уравнения движения в этом случае принимают вид
1 ON™ 1 dNf 6j дм Vj
326
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ
ГЛ. VIII
здесь введены безразмерные параметры x xL, x c0tL„ йк — UklL, w wL, Ьк hkjL, zk zkL, X LR, M'Bkt
Q <2>vftSft> Mx MLDk, причем в 63 и далее для краткости записи черта над буквой опущена.
Предположим, что торцы оболочки по всей поверхности «приклеены» к жестким диафрагмам, одна из которых неподвижна, а другая может свободно перемещаться в направлении образующих. В этом случае граничные условия запишутся следующим образом:
а» 0, т 0, щ>1, т 0,
ы,0, т и0 0, т, «,1, т 0,
и20, т ы00, т, и21, т 0,
• Ж» 0, т -7— г- М2> 0, т Щ-
х1 р ’ xl ; дх2
u0U т 0,
где к — отношение массы груза к массе оболочки. Начальные условия имеют вид
д' х. 0 0,
8.64
w х, 0 0, и0х, 0 0, «1 х, 0 0, и2х, 0 0,
дх
ди0 m U -Wx> ° 77 при 0>
ди' х, 0 — при л: 0,
дх
°>-£
при л: 0,
8.65
Разобьем область определения задачи 0 х <с; 1, т 0 прямоугольной сеткой хп пАх, Дт п 0,1,., N — 1; k 1,2,. тогда, заменяя дифференциальные операторы центрально-разностными, получим аппроксимирующую алгебраическую систему
fkl 2fk _ л-х Ax2Fk. 8.66
здесь f — определяемые функции, F — левые части уравнений 63, разрешенных относительно вторых производных по времени.
При анализе устойчивости разностной схемы в качестве первого приближения использовался критерий, полученный в 8.14. Основанием для этого служит естественный предельный переход к однослойной оболочке при весьма малых толщинах наружно го слоя. Как показал ряд примеров, указанный критерий дех удовлетворительные результаты.
§ 92 РЕШЕНИЕ ЗАДАЧИ О ПОВЕДЕНИИ ДВУХСЛОЙНОЙ ОБОЛОЧКИ 327
Обратимся к результатам вычислений. Они были проведены для оболочки, внутренний слой которой изготовлен из материала, имеющего кривую нагружения с линейным упрочнением,
-zvЛ,
о,г
0,4 '0,6 Щ 10
xL
Рис. 8.35. Прогибы двухслойной, оболочки при продольном ударе.
а внешний — из неограниченно упругого материала, модуль упругости которого принимался равным модулю упрочнения основного слоя. На рис. 8.35 показана форма прогибов оболочки при продольном ударе. Качественно кривые близки к полученным ранее см. § 89 для однослойной оболочки.
Оказалось, что добавление наружного упругого слоя сравнительно слабо влияет на форму и максимальные значения прогиба. На рис.
8.36 приведены кривые развития максимального прогиба во времени при различных соотношениях толщин слоев. Как следует из графиков, внешний слой, толщина которого в три раза превышает толщину основного слоя, снижает максимальные значения прогиба примерно на 20.
Распространение волны деформации eix9t в пластическом слое показано на рис. 8.37. В представленном случае пластические деформации развиты сильно и их фронт заметно отстает от
Рис. 8.36. Влияние соотношения толщин слоев на темп развития прогибов.
328
ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЁ
ГЛ. VIII
фронта упругой составляющей. Упругие деформации, отражаясь от противоположного края, накладываются на прямую волну и образуют волну уже пластических деформаций. Характерным
Рис. 8.37. Интенсивность деформаций внутреннего слоя в различные моменты времени.
-0,016 -Ofiiz -0,00В -0.004
Rh,100 Rhz-33 V0,01
т2 XX
у0,2
V
о,бв,з
1,0
XX N
0,2 О А- 0,6
Рис. 8.38. Продольные усилия в слоях.
ом
xL
является перераспределение сжимающих усилий в слоях при возникновении пластических деформаций рис. 8.38.
Пока оболочка деформируется в упругой области, усилия распределяются пропорционально жесткостям слоев на сжатие.
ВЫПУЧИВАНИЕ ПРИ ТЕПЛОВОМ УДАРЕ
329
После того как в несущем слое возникают пластические деформации, начинается перераспределение сжимающих усилий: снижение жесткости внутреннего слоя приводит к увеличению нагрузок на внешний.
§ 93- Выпучивание цилиндрических оболочек при тепловом ударе
В заключение рассмотрим задачу о поведении тонкой круговой цилиндрической оболочки конечной длины при действии осесимметричного теплового импульса в некоторой зоне, расположенной у одного из торцов.
При распространении теплового потока вдоль конструкции часть длины оболочки будет подвергаться динамическому сжатию. При известных условиях это приведет к появлению в сжатой зоне оболочки глубоких вмятин, весьма опасных для тонкостенных конструкций. В случае, если период времени подвода тепла значительно меньше времени распространения упругой волны вдоль длины конструкции, можно считать, что эффект продольного теплового удара аналогичен воздействию собственно ударной нагрузки.
Для описания поведения оболочки в основных уравнениях необходимо учесть силы инерции, соответствующие не только прогибу, но и перемещениям в срединной поверхности. Так как подобная задача оказывается весьма сложной, будем условно считать, что изменение термоупругой деформации по длине оболочки не зависит от прогиба и определяется из решения соответствующей одномерной задачи для упругого стержня. Что же касается явления выпучивания, то примем, что образующиеся при этом прогибы сравнимы с толщиной оболочки и находятся из решения геометрически нелинейной задачи.
Прежде чем перейти к термодинамическим соотношениям, описывающим упругое поведение оболочки во времени, выпишем основные зависимости, относящиеся к распространению температурных напряжений в стержне. Допустим, что элемент стержня нагревается от некоторой абсолютной температуры 0 до температуры 0 0, при этом в стержне возникают напряжения а. Полная упругая линейная деформация будет
в 1г Т 6<’ <8'67>
где k — коэффициент линейного расширения. Параметры Е и k зависят, вообще говоря, от температуры. Но в задаче,
Эта задача исследовалась А. Т. Пономаревым и автором, см. ДАН СССР 192, 4 1970, 757—759.
См., например, Nuclear Engineering and Design 7, 2 1968.
См. I. N. Sneddon, Proc. Roy. Soc. of Edinburgh A65, 2 I969f
330 ПОВЕДЕНИЕ ОБОЛОЧЕК ПРИ УДАРЕ ГЛ. VIII
рассмотренной ниже, и в ряде других примеров, когда элементы конструкции подвергаются резкому поверхностному нагреву, можно принять эти коэффициенты в качестве постоянных. Из зависимости 67 имеем
а £2--б. 8.68
Соотношение для энтропии на единицу объема упругого стержня, если 0 мало по сравнению с ©, имеет вид
S Cv- kEe, 8.69
где Cv — удельная теплоемкость материала.
Второй член в правой части 69 отражает влияние деформации на протекание термодинамического процесса. Тогда количество тепла, поглощаемое единицей объема, можно считать равным
h Se C0Q kEe. 8.70
С другой стороны, по закону сохранения тепловой энергии должно быть
dx dx 0, 8.71
где q — а — количество тепла, протекающего через сечение в течение одной секунды; а — коэффициент теплопроводности.
Используя выражения 70 и 71, получим следующее уравнение:
d0 d20 а, д2и Q 70ч
-жк-ш-Р-тг' <8-72>
Здесь введены обозначения
КЛ- 8-73»
Присоединяя к 68 и 72 уравнение движения элемента
§ 93
ВЫПУЧИВАНИЕ ПРИ ТЕПЛОВОМ УДАРЕ
331
и исключая из этой системы а, приходим к так называемой связанной задаче термоупругости для стержня:
где с VEgy — по-прежнему скорость распространения деформации сжатия в материале.
Далее выпишем основные динамические соотношения термоупругости теории пологих оболочек 0.6:
Через Nq и М9 здесь соответственно обозначены эквивалентное температурное усилие и температурный момент сечения оболочки, определяемые с помощью выражений
Начальный и полный прогибы по-прежнему выберем в форме 38. Подставляя выражение 38 в правую часть уравнения 78 и интегрируя его, находим функцию напряжений Ф. При этом в выражение для Ф входит член —ру22, где р pt — интенсивность сжимающих усилий в выбранном сечении оболочки, определяемая по формуле
Для нахождения зависимости между параметрами прогиба оболочки и изменяющимися во времени сжимающими усилиями воспользуемся применительно к уравнению 77 методом Бубнова— Галеркина. В результате приходим к нелинейному обыкновенному дифференциальному уравнению второго порядка относительно стрелы прогиба.
8.75
ди. дв1 д2и дх дх с2 dt2
8.76
£-V4w — w0 Lw, Ф -4
-L V4<D — 4М» — L wQ, а>о1 —
d2wd-Wo--Ne. 8.78
JVe j kzQzEzdz, Afe j kzQzEzzdz.
8.79
332 Поведение оболочек прй ударё 1гл. viii
Для примера будем исследовать случай, когда происходит резкий местный нагрев одного из торцов оболочки; остальную поверхность примем теплоизолированной. Решение задачи сводится к интегрированию следующей системы безразмерных разрешающих уравнений:
<8'80> 8-81
dxz дх2 дх
I - s р - -L л С2 - Ф -
121 — ц2 Т1 £ So р 'Ф vl С — Со 1 22 922
4Г ФС С So 1 1 2г Ф 1 22 S2 — So —
п, 6у S — Со 0- 8.82
Здесь в дополнение к обозначениям § 87 введены новые безразмерные параметры:
X d л л U
х —, X —j—, 0 fe0, и -j-,
где i IY2 —радиус инерции сечения оболочки, — общая гибкость оболочки, рассматриваемой как стержень кольцевого сечения. Значение -ф условно принимаем, исходя из решения статической задачи для идеальной оболочки. Решение уравнений 80 и 81 было получено в замкнутой форме последовательным применением к ним интегральных преобразований Фурье
по х и Лапласа по т при следующих граничных и начальных
условиях:
-L u 0 при 0; 1,
и0, е -г при т 0, х 0,
где h — количество подведенной тепловой энергии.
Уравнение 82 было проинтегрированно методом Рунге — Кутта с помощью цифровой машины БЭСМ-2М в предположен
ВЫПУЧИВАНИЕ ПРИ ТЕПЛОВОМ УДАРЕ
333
нии, что дополнительный прогиб и скорости точек оболочки в начальный момент времени равны нулю:
£ — £о t 0 при т 0.
В процессе решения задачи определялись коэффициент динамичности, представляющий собой отношение величины максимального сжимающего усилия
к верхнему критическому значению рръу и число волн, при котором наступает бурный процесс выпучивания.
Результаты вычислений представлены на рис. 8.39 в виде кривых, характеризующих темп нарастания стрелы прогиба £ в оболочке для сечения х L2, в зависимости от безразмерного времени т, при параметре теплового импульса 0 0,3. Они относятся к оболочке с отношением Rh 300, амплитудой начальной погиби £0 0,001 и параметром волнообразования 3. В качестве критического времени условно принимался момент тКр, соответствующий фронту бурного нарастания прогиба. Как видно из рис. 8.39, наиболее вероятная форма выпучивания оболочки соответствует числу волн п 27. Аналогичные результаты были получены для оболочек с различным сочетанием геометрических соотношений и параметра нагружения. Вычисления и здесь показали, что эффект динамичности проявляется тем сильнее, чем больше отношение Rh см. стр. 281.
О
60J
II
Rh 300
А 26
LR 3,75
Z3,0
1 28
1
II
1
1
1
1
1
0,3
Т Гу
кр
Ofi
Рис. 8.39. Выпучивание оболочки при тепловом ударе.
Г Л ABA IX
ПОВЕДЕНИЕ ПЛАСТИНОК И ОБОЛОЧЕК ПРИ ДЕЙСТВИИ ПОДВИЖНОЙ НАГРУЗКИ
§ 94. Общие положения. Понятие критической скорости движения нагрузки
Поведение упругих балок при действии подвижных нагрузок рассматривалось еще в начале XX века многими авторами в применении к задачам железнодорожного транспорта. Определялась такая скорость движения нагрузки вдоль балки, при которой прогибы балки резко возрастали. Эта критическая скорость для железнодорожного пути составляла около 500 мсек, что значительно превышало и до сих пор превышает скорость подвижного состава. В дальнейшем были решены более сложные задачи, связанные с движением нагрузки по мостам и другим сооружениям.
В начале 50-х годов такого же типа проблема возникла в связи с описанием поведения тонкостенных оболочек, являющихся например, элементами авиационных конструкций. В качестве подвижной нагрузки подразумевалась при этом волна давления.
В большинстве опубликованных в этой области работ подобные задачи изучались в линейной постановке. При решении линейной задачи для цилиндрических оболочек определяется несколько значений критической скорости движения нагрузки, соответствующих скоростям распространения упругих волн различной природы — продольных волн, связанных с радиальными колебаниями, собственно продольных волн и волн сдвига.
Влияние подвижной нагрузки на поведение цилиндрической оболочки конечной длины L иллюстрируется графиком, представленным на рис. 9.1 9.18. Здесь даны значения динамического коэффициента Сд, представляющего собой отношение амплитуды динамического прогиба, обусловленного набегающей на¬
См. книгу С. П. Тимошенко 0.36, стр. 341; там же приведена обширная библиография.
§ 94 ПОНЯТИЕ КРИТИЧЕСКОЙ СКОРОСТИ ДВИЖЕНИЯ НАГРУЗКИ
335
грузкой, к максимальному прогибу, возникающему при статическом приложении такой же нагрузки ко всей поверхности оболочки. По оси абсцисс отложен безразмерный параметр скорости
' 9.1
Т
£т4
Ро R2
где Уф — скорость перемещения фронта нагрузки, р0 — плотность материала оболочки.
Различные кривые относятся к оболочкам, имеющим разные параметры р L2Rh. Как видим, для оболочек с различными параметрами движение нагрузки вызывает резкое увеличение прогибов; их величина до- стигает максимума скорости, которая является критической. Значение первой критической скорости УКр, i равно здесь
при нд
W-
ЕН
1
роR 31 -ц2' 9.2
В том случае, когда на оболочку действуют до-
В 5184
Yi гт
Ж
576
278
у
ЦВ
од
Рис. 9.1. К определению динамического коэффициента при подвижной нагрузке.
полнительно статические
продольные усилия, распределенные по торцам, первая критическая скорость определяется зависимостью 9.25
Eh Ро R
Ырг-'- <9-2а>
где р pREh здесь р > 0 при сжатии.
Выписанные выше значения критических скоростей получены из решения линеаризованной задачи. Однако для тонких оболочек с относительно большими прогибами важными являются нелинейные эффекты. Для систем, имеющих мягкую характеристику, резкое возрастание прогибов может иметь место при скорости набегания фронта меньшей, чем величина, определяемая по 9.2 или 9.2а. Напротив, в случае системы, имеющей жесткую характеристику, максимальные прогибы развиваются при скорости движения нагрузки, несколько превышающей приведенные значения.
Вторая критическая скорость оказывается равной
336 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
Третья критическая скорость равна УКр, з k VGPo и отвечает волнам изгиба — сдвига, см. уравнение 1.82; в дальнейшем эту скорость мы рассматривать не будем.
Задача о нагрузке, перемещающейся с переменной скороростью, обсуждается в § 100.
Одним из видов подвижной нагрузки являются скачки уплотнения, фронт которых совершает колебания вдоль образующей оболочки; вместе с тем скачок может перемещаться по потоку с некоторой скоростью 9.22. При совпадении частоты колебаний фронта с частотами собственных колебаний оболочки могут возникнуть интенсивные вибрации конструкции; динамический коэффициент при этом достигает значительной величины.
§ 95. Решение линеаризованной задачи
Рассмотрим более подробно решение линеаризованной задачи, в общих чертах описанной в предыдущем параграфе. Исследуем поведение замкнутой круговой цилиндрической оболочки, вдоль оси которой с постоянной скоростью движется волна давления. Будем пользоваться уравнениями типа Тимошенко для осесимметричного случая; при наличии заданных продольных усилий Мх N const их можно представить в виде
Lu L2w Li3tyx — 0,
L2U L22w Lvftx —
1-Ц2
Eh
qx, t,
L:iu -f- L32w -f- зз'Фл: где L>ij — линейные операторы:
£ц l
9.4
i-n2 t, po i -ц2 a»
v; dx2 E dt2
Eh 1 — ц
'22 2,v 1 Eh
гжч
Po 1 — i2h2 d2
h2 12 R2
Po 1 — M-2 d2 E dt2>
12 dx2
L2 21 d >
L i3 L31
2
a d R dx h2 d2
12 E
dt2
PoO — M>2 h2 d2
12R dx2
12 ER
dt2
L2 3 — L39 — k2
-32
dx •
9.5
Эта задача рассмотрена в книге П. М. Огибалова и М. А. Колтунова 0.15. Здесь изложение дано по статье 9.25:
§ 95
РЕШЕНИЕ ЛИНЕАРИЗОВАННОЙ ЗАДАЧИ
337
Здесь, в отличие от 1.80 — 1.84, сохранены члены порядка
WR.
Кольцевую нагрузку q, движущуюся с постоянной скоростью с, можно представить в виде
qx, 0 <7i6 л: — с. 9.6
где бх — ct — функция Дирака, a q — интенсивность приложенной нагрузки.
Рассмотрим решение в осях, движущихся вместе с нагрузкой. Предположим, что цилиндр имеет бесконечную длину и что достигнуто установившееся состояние движения. Тогда можно ввести следующее преобразование координат:
а х — ct.
Введем безразмерные величины:
rj — JL w — - -n —— А 2 c2qqR и>2
R9 R ’ R 9 Eh ’ 8 R 9
Е0 14’ 2-L9iL>
Eh
1-И2
Eh
, N N 1 “ 1x2
Eh
9.7
9.8
d2‘фл
Тогда уравнения 4 примут вид
II КТ л 2 d2U dW 82 п л2 liV-eA,---n--1j 1-еА, rft2
“ ТЯГ « - л1 -£.' К П,
О,
d4J
dW
9.9
Для нахождения решения системы 9 воспользуемся интегральными преобразованиями Фурье типа
и s J
9.10
9.11
Умножая систему 9 на eisr, выполняя интегрирование и решая полученные уравнения относительно U, W, ф, получим
- p — l-eWs' pK
isC 5
w -g- 1 - е,2 l N - Я2 - еЛ2 s2 К 1 N-e
Чо
С s
Я»
Cs
9.12
338 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
Здесь
С 5 e2s4 6S2 е0у e2 K N-stf-l-eX2ey
е, -l-eX2E0e-n2-2KKlN-eX2JV-eX2, j 9.13
e0KE0lN-eX2-Kli2,
е1 JV-sX2--£l-еХ2.
Перемещения и, w и угол поворота нормали найдутся при переходе от выражений 12 к оригиналам по формулам типа 11. Для выполнения такого перехода необходимо найти корни характеристического уравнения
Cs 0. 9.14
Если это уравнение имеет кратные корни, лежащие на действительной оси, то интеграла обратного преобразования не существует. Поэтому возникает резонанс в том смысле, что перемещения неограниченно возрастают.
Значения безразмерного параметра скорости, при котором достигаются неограниченные значения перемещений, назовем критическими.
Выпишем выражение
А е2е0 е2е0 — -j eJ. 9.15
Условия существования кратного корня имеют вид при е2 Ф 0:
е2е0 — е 0 9.16
е0 0. 9.17
Учитывая 13, можно заметить, что уравнение 16 —восьмой степени относительно X. Если ограничиться областью реально возможных значений параметров системы, то убедимся, что силы инерции для и и х оказывают весьма слабое влияние на значения двух низших корней уравнения 16. Если этими факторами пренебречь, то уравнение 16 примет вид
еъА елХ2 е3 0, 9.18
где е3у е, е5 функции безразмерных параметров 8:
е5 К2е2у
е4 2Ке -g- 1 N - Е0 - 2ц2 2N 2 — К ы2ц,
e3 -£0liV-4--22-
- -f-K К N £0 1 N - ц2 1 N - -g.
§ 951 РЕШЕНИЕ ЛИНЕАРИЗОВАННОИ ЗАДАЧИ 339
Корни уравнения 18 равны
т -2 тГ <£° - 1 X- ЩN
— I н- 2ю, 9.19
- т 2 4Г • ■- ’>''■ 1 w -
-£0-,i 2itf. 9.20
Здесь опущены члены, имеющие порядок е2 и N по сравнению с единицей.
Выражения 19 и 20 показывают, что при уменьшении величины К значения и Я2 снижаются. Параметр С, при котором эти величины приближенно равны нулю, может быть найден из уравнения
£з 0. 9.21
Отсюда
Т5-<о-Ц
е2 у2 > 9.22
Е0-Ц2'2 Е - И2
2 77MV5 9.23
N
Здесь снова опущены члены порядка е2 и N по сравнению с единицей.
Практический интерес представляет случай, когда К > Ki выражение 20 имеет смысл лишь при К > Кг. Учитывая эти ограничения и пренебрегая членами е и N по сравнению с единицей, переписываем 19 и 20 в следующем виде:
“ 7 “ 2 ЙГ £о - И2'г N - 4к £о - ' <9-24
- т 2 4Г £о - >12 N1WE°- • 9-25>
Если в уравнении 14 также пренебречь членами порядка е по сравнению с единицей, то можно показать, что это уравнение должно иметь действительные одинаковые корни при выполнении условий Я2 Я и К > е2 12,г Е0 — к2' Поэтому параметр первой критической скорости равен
4.1 7 2 -£Vl Е0 - ц2'г N--E0-и2. 9.26
Он соответствует низшей критической скорости.
340 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
Если е0 0, т. е. выполняется равенство 17, то уравнение 14 имеет равные корни при условии 5 0. Решая уравнение е0 0, получим
где N по-прежнему считается величиной, малой по сравнению с единицей. Кратный нулевой корень лежит на действительной оси, и обратного преобразования Фурье не существует. Поэтому величина 2 отвечает критической скорости.
Возвращаясь к прежним обозначениям и, как обычно, пренебрегая величинами порядка е2 по сравнению с единицей, получим следующие значения критических скоростей:
_ Eh u J_
Скр' 1 PoR К31 -ц2 Рог ’
Таким образом, мы пришли к формулам 2а и 3 для критических скоростей, приведенным в предыдущем параграфе; напомним, что в выражении 2а усилия р считаются положительными при сжатии, и надо положить р —Nh.
Ниже излагаются результаты теоретических и экспериментальных исследований некоторых нелинейных задач о поведении оболочек при действии подвижных и пульсирующих нагрузок.
§ 96. Замкнутая цилиндрическая оболочка при действии подвижной волны давления. Применение метода Бубнова—Галеркина
Рассмотрим вначале задачу для случая замкнутой цилиндрической оболочки, нагруженной внешним равномерным давлением и подвергающейся воздействию набегающей волны давления.
Движение оболочки будем описывать обычными нелинейными уравнениями типа 1.40, 1.41, считая, что действие нагрузки может привести к возникновению больших прогибов и прощелкиванию конструкции.
Возникающее при набегании продольной волны гидродинамическое давление складывается из давления в падающей волне и давления излучения. В акустическом приближении последнее в свою очередь состоит из двух частей — давления, полученного в предположении, что каждая точка поверхности оболочки является точкой плоскости, и нагрузки, являющейся поправкой —
Эта задача рассматривалась Э. Д. Скурлатовым 9.13; см. также книгу Е. Н. Мнева и А. К. Перцева 5.14.
ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА
341
в том или ином виде — на кривизну цилиндра. Примем интенсивность нагрузки равной в общем случае
q qe <<-> ct — х — рс w, 9.28
где q — давление на фронте волны, ц — показатель экспоненты, определяющий закон изменения давления за фронтом, с — скорость распространения волны в среде, окружающей оболочку, р — плотность среды, Н — функция Хевисайда. Координата х отсчитывается от передней кромки оболочки; таким образом, давление распределяется в каждый данный момент на участок оболочки длиной ct— х. Последний член в 28 представляет собой поправку на кривизну оболочки, о которой говорилось выше 5.9.
Для случая шарнирного закрепления торцов аппроксимируем функцию прогиба оболочки в виде
W х, у у t fltsnaxsiny --f2sn2ax, 9.29
где а тлL, р nR, т — число полуволн в направлении образующей, п — число волн вдоль окружности.
Применяя процедуру метода Бубнова — Галеркина, придем к системе двух обыкновенных дифференциальных уравнений, которые после введения безразмерных параметров
>r — -£L г —h. г —А
L 9 h ' э2— h
принимают вид
dT2 dx l” а Ь а1112 а2>1>2 “Ь a3£l “Ь Ql Т £l О’
g 012 2112 20 2 Т 0»
9.30
где Яю, Ли, 12,. — некоторые коэффициенты. Численное интегрирование уравнений движения проводилось на ЭЦВМ при различных значениях параметров оболочки и волны давления. Вычисления, проведенные для оболочек при различных скоростях набегания фронта волны, позволяют сделать заключение, что каждой паре значений тип, отвечающей форме волнообразования оболочки в продольном и окружном направлениях, соответствует своя «критическая скорость»; при этом динамический прогиб имеет наибольшую величину по сравнению с прогибами, развивающимися при других скоростях.
На рис. 9.2 и 9.3 приведены кривые, характеризующие изменение составляющей динамического прогиба во времени для оболочки с параметрами LR 2, Rh 200, q 10 ат,
342 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
г 2. Рис. 9.2 относится к случаю т 3, п 20, рис. 9.3 — к случаю m 1, п 10. В первом примере критическая
Рис. 9.2. Изменение динамического прогиба оболочки во времени при т3, п 20 для различных скоростей набегания нагрузки.
Рис. 9.3. Изменение динамического прогиба оболочки прит 1, л 10 для различных скоростей набегания нагрузки.
скорость составляет 100 мсек, во втором — 700 мсек; Построив подобные зависимости для различных возможных комбинаций <7ф и г, определяем ту скорость набегания нагрузки, при которой имеет место наибольшая реакция оболочки на волну с фиксиро¬
ЗАМКНУТАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА
343
ванными т и пу а также соответствующую форму волнообразования оболочки. По-видимому, эта скорость будет наиболее опасной для рассматриваемой оболочки.
Рис. 9.4. Изменение динамического прогиба во времени для оболочки при комбинированном нагружении.
На рис. 9.4 представлены результаты для случая, когда по всей поверхности оболочки приложено равномерное давление и
вместе с тем на оболочку начинает набегать волна давления. Даже если каждая из этих нагрузок, взятая в отдельности, не является опасной, то, действуя одновременно, они могут привести к прощелкиванию оболочки.
При значительном коэффициенте демпфирования может иметь место апериодический переходный процесс; максимум
344 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
амплитуды здесь достигается позже и имеет меньшую величину, чем для системы без демпфирования.
Это иллюстрируется рис. 9.5; здесь приведены кривые «прогиб — время», с учетом демпфирования для разных сред — воздуха кривая 1 и воды кривая 2.
§ 97. Решение задачи с помощью метода 9
конечных разностей
При использовании метода Бубнова — Галеркина нам приходилось аппроксимировать прогиб оболочки рядом, причем погрешность результата зависела от того, насколько удачно выбрано выражение для прогиба. Более точное решение задачи можно получить, если представить исходные уравнения в конечных разностях. При этом удается проследить за изменением характера изогнутой поверхности оболочки при действии набегающей нагрузки.
Примем здесь, что оболочка подвергается действию сжимающих статических усилий р вдоль оси. При определении интенсивности давления введем, дополнительно к 28, член, учитывающий конструкционное демпфирование, тогда получим
q схн ct — х — рс w — p0he 4-, 9.31>
где р0 — по-прежнему плотность материала оболочки.
Воспользуемся безразмерными параметрами
d, w, х, и
т_ шт, ' т> у' у-
П Ф Etf
9.32
тогда исходные уравнения 1.40 и 1.41 можно представить
следующим образом штрихи опускаем:
d2w. dw, d4w d4w, d4w, d2w д2Ф,
dx2 dx dx1 dx2 dy2 dy4 dy2 dx2
. d2w d2Ф, d2w d2Ф д2Ф
dx2 dy2 dxdy dxdy dx2
— a7e -> т — x — asw 0, 9.33
d2Ф, о д4Ф, 1 а4Ф d2w 2
Ь dx2 dx2 dy2 bx dy4 дхду
, d2w d2w, u d2w л л 0„ч
9.34
Здесь введены в качестве коэффициентов а2,., Ьи Ь2,.
Эта задача рассматривалась Л. И. Долгих, Э. Д. Скурлатовым, В. Р. Солоненко и автором Труды VII Всесоюзной конференции по теории оболочек и пластинок, «Наука», Москва, 1970, 133—155.
§ 97 РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ МЁТОДА КОНЕЧНЫХ РАЗНОСТЕЙ 345
некоторые безразмерные величины, зависящие от размеров оболочки, коэффициента Пуассона и параметров р и q.
Отметим, что при выборе параметров по 32 развертка оболочки соответствует квадратной области с длиной стороны, равной единице.
Граничные условия будем считать неизменными во времени; начальные условия могут, например, иметь вид
dw л w w0, 0 при т 0.
Производные по пространственным координатам и времени заменим симметричными разностными операторами с погрешностью, имеющей порядок квадрата шага. Подставляя их в уравнения 33 и 34, получим в текущей точке трехмерной сеточной области пространства переменных х, у их по два уравнения в конечных разностях. Для решения больших систем линейных алгебраических уравнений применялся метод сопряженных градиентов и метод случайного поиска.
Приведем некоторые результаты решения полученных разностных уравнений с помощью ЭЦВМ при различных значениях параметра осевой нагрузки р pREh и различных величинах скорости набегающей волны давления с. Исследовался переходный процесс деформации оболочки с размерами R 50 мм, L 200 мм, h 0,8 мм, сжатой предварительно приложенными статическими осевыми усилиями 0,1 и подвергающейся воздействию набегающей в продольном направлении экспоненциальной волны давления при различных скоростях. Критическая скорость движения волны для сжатой в осевом направлении оболочки оказалась лежащей значительно ниже, чем для ненапряженной, и равной 350 мсек; критическая скорость свободной от продольных усилий оболочки такого типа составляет 500 мсек. Динамические прогибы, возникающие при скорости набегания фронта волны давления, отличной от критической величины 350 мсек, имеют меньшее значение и развиваются медленнее, чем при критической скорости. При скорости, равной критической или близкой к ней, прогиб имеет максимальную величину у задней кромки оболочки. Это иллюстрируется рис. 9.6; здесь отложены безразмерные прогибы wh для различных
05
шfy
OJO
qos
tjL
уол
xl
Рис. 9.6. Распределение приведенных прогибов по длине оболочки для различных моментов времени.
346 ПЛАСТИНКИ Й ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВЙЖН. НАГРУЗКИ ГЛ. IX
сечений оболочки с относительными координатами хL в разные моменты времени т.
Предварительное осевое растяжение приводит к повышению критической скорости; в некотором диапазоне скоростей подвижной нагрузки растянутая оболочка может иметь большие динамические прогибы, чем свободная от продольных усилий оболочка или сжатая вдоль оси.
Эти особенности поведения оболочек, подвергающихся действию продольных статических усилий и набегающих волн давления, качественно согласуются с экспериментальными данными.
Исследуем рассмотренную выше задачу о поведении замкнутой оболочки в более общем виде, учитывая влияние начальной погиби; при этом воспользуемся уравнениями в перемещениях. Как и ранее, будем предполагать, что в начальный момент в направлении образующей набегает волна давления, имеющая прямой фронт и экспоненциальное изменение давления за фронтом; оболочка может быть также нагружена статическими продольными усилиями р и равномерным внешним давлением <. Поведение оболочки будем описывать следующими уравнениями, аналогичными 1.24 — 1.26:
Ро рг Рое 4- — DV4w — w0 -Ny Nx
§ 98. Применение метода конечных разностей к уравнениям в перемещениях
и д2и _ dNx дТ и d2v дТ dNy
VbhW дх ду' й2 дх ду9
и у- ил иу ил ил иу иу
Вводя безразмерные параметры
9.36
где Со — скорость звука в материале оболочки,
См. ссылку на стр. 344.
ПРИМЕНЕНИЕ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ
347
выпишем уравнения в безразмерном виде черточки опущены:
д2и dNx I дТ
д‘г dl дв ’ d2v дТ dNy
дхГ д 56 ’
s-aWw-Wo Nll ±Nx
h ат d2w h j dNx dTdw f h j дТ dMy dw f
r Ny W T l“aF dW Hi я vaf Wj M
. 0 h d2w - d2w a — с. f ч rk 0«v R dl дв P dl2 ’ T’ 0.37
где
q g, 0, t Ц- 42 1 - H2 _11 XE Я Ц. x -, р --1-Ц2.
Представим далее эти уравнения в конечных разностях. Рассмотрим плоскость 0 с переменными 0 g v, 0 0 2я, соответствующую m — 1 временному слою. Выбрав шаг Дт вдоль координаты т, расположим следующие временные слои m, m 1, гп 2 и т. д. На плоскость g, 0 нанесем сетку с помощью прямых Д и Д0, параллельных координатным осям, которую будем в дальнейшем называть сеточной областью с шагом по координатам Д£ vN— 1 и Д0 2яМ— 1, где N — число узлов в направлении £, М — число узлов в направлении 0. Тогда для каждого внутреннего узла сеточной области операторы дифференцирования могут быть аппроксимированы разностными операторами см., например, 0.6. Таким образом, мы приходим к системе нелинейных алгебраических уравнений, которая решается совместно с зависимостями, соответствующими условию замкнутости оболочки и граничным условиям. Эти уравнения имеют рекуррентную форму, что позволяет по заданным значениям и, и и до на m — 1 и m слоях вычислить величины перемещений на m 1 слое.
Устойчивость расчетной схемы обеспечивается соответствующим выбором шага по времени Дт и шагов по пространственным координатам. В качестве первого приближения принимался критерий, полученный в одной из работ 8.14 для линеаризованных уравнений. Путем численного эксперимента было установлено, что при интегрировании нелинейной системы необходимо уменьшить шаг в 2—3 раза.
Для проверки точности полученных решений проводилось сопоставление результатов вычислений, полученных при разбиении поверхности оболочки на различное число продольны ц
348 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
окружных узлов. Например, для фиксированного времени, соответствующего моменту прохождения фронтом волны нижнего торца оболочки, для сеток, имеющих 20 X 20 и 36 X 36 узлов, прогибы различаются не более чем на 0,25.
Остановимся на некоторых результатах вычислений. На рис. 9.7 изображены кривые, характеризующие изменение формы
Рис. 9.7. Форма волнообразования оболочки для различных моментов времени.
волнообразования оболочки вдоль образующей в различные моменты времени после начала набегания фронта волны с постоянным давлением за ним. В случае экспоненциально изменяющегося давления за фронтом ц 2 для такой же оболочки переходный процесс деформаций имеет более сложный характер. Оказалось, что форма волнообразования существенно зависит от величины скорости набегания фронта волны, закона изменения давления за фронтом, а также от характера начальных несовершенств оболочки. В рассматриваемой постановке, как и ранее, удается проследить эффект возрастания динамических прогибов по длине оболочки.
§ 99. Поведение пологой цилиндрической панели при действии подвижной нагрузки
Исследуем далее поведение шарнирно опертой по кромкам пологой цилиндрической панели под воздействием волны давления, распространяющейся в продольном направлении. Будем и здесь считать, что панель подвергается одновременно действию сжимающих или растягивающих продольных усилий.
Поведение оболочек при действии боковой акустической волны давления изучалось Э. И. Григолюком и А. Г. Горшковым Научные труды Института механики Моск. гос. ун-та, 2, 1970. Здесь приведено решение задачи для случая продольной волны, полученное в статье 9.13.
§ 99 ПОЛОГАЯ ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ ПРИ ПОДВИЖН. НАГРУЗКЕ 349
Основные уравнения примем в виде 1.40, 1.41; интенсивность давления примем по формуле 28, функцию прогиба оболочки аппроксимируем выражением
w х, г, t f t sin y sin фу. 9.38
Здесь у яа, -ф я6, а и b — длина и ширина панели. Предположим, что в исходном состоянии панель имеет начальный прогиб, описываемый зависимостью, аналогичной 38. Опуская промежуточные выкладки, выпишем уравнения движения панели, полученные после применения к зависимостям 1.40, 1.41, процедуры метода Бубнова — Галеркина:
•0 8 § А3 А£2 Л3С А,£ — £о Л5 0. 9.39
Коэффициенты Л зависят от размеров панели начальных неправильностей и характеристик материала оболочки. Далее, под 0 понимается отношение ррв, где рв — верхняя критическая
Рис. 9.8. Изменение максимальных динамических прогибов в зависимости от скорости набегания нагрузки.
статическая нагрузка при сжатии, под ф — отношение qqB, где qB— верхнее критическое статическое нормальное давление для оболочки тех же размеров, см. 1.11, k b2Rh.
Вычисления проводились для квадратных панелей, имеющих различные кривизны и толщину. Варьировались также скорость движения фронта волны, давление во фронте, закон спада давления за фронтом, осевые усилия и коэффициент демпфирования.
На рис. 9.8 приведены кривые изменения динамического прогиба для частного случая совершенной оболочки £0 0 при скоростях движения короткой волны давления, изменяющихся в диапазоне 50—1500 мсек. Под скоростью движения волны давттп понимается скорость движения фронта относительно
350 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
оболочки. Значение кривизны панели и параметры, характеризующие нагрузку, выписаны на графике.
Из рис. 9.8 видно, что при увеличении скорости движения волны до некоторого значения динамические прогибы возрастают. Превышение этой скорости, которую мы и здесь назовем первой критической, ведет к снижению прогибов.
В отличие от линеаризованной задачи, приводящей к бесконечно возрастающим прогибам, при решении нелинейной задачи определяется максимальный динамический прогиб, имеющий, как и в реальной системе, ограниченную величину, а также устанавливается значение параметров системы «оболочка — ударная волна», при которой произойдет прощелкивание панели.
Анализ результатов вычислений показывает, что движение панели, подвергающейся воздействию набегающей волны давления в воздухе, имеет колебательный характер, в то время как в тяжелой жидкости движение близко к апериодическому; естественно, это объясняется значительным демпфированием в соответствующей среде.
Судя по характеру переходного процесса для оболочек в воздухе и вакууме, можно сделать вывод, что давлением излучения в воздухе можно пренебречь; погрешность при этом не превышает нескольких процентов.
Установлено, что при прочих равных условиях динамические прогибы тем выше, чем больше параметр кривизны панели. Анализ данных для различных величин давления на фронте волны показывает, что повышение давления приводит к более интенсивному росту прогибов. При параметре давления ф 200 прогиб стенок панели развивается быстрее, чем при ф 40, и переходный процесс завершается затухающими колебаниями около нового прощелкнутого положения равновесия.
§ 100. Особенности поведения нелинейной системы при подвижной нагрузке
Остановимся на некоторых особенностях поведения оболочек, определяемых как линейные либо нелинейные системы. На рис. 9.9, а, б пунктирной линией изображена резонансная кривая для линейной системы, максимальные динамические прогибы которой достигаются при некоторой скорости движения фронта, отнесенной к критической. При скорости набегания нагрузки, большей или меньшей критической, значения прогибов плавно убывают. На этих же рисунках сплошной линией нанесены резонансные кривые для нелинейных систем с мягкой рис. 9,9, а и жесткой 9.9, б упругими характеристиками см. главы II—IV. Скелетная линия, разделяющая две ветви амплитуд вынужденных колебаний, является прямой в линейном случае и изогнута — влево или вправо —для нелинейных — мягкой или
.§ 100 ОСОБЕННОСТИ ПОВЕДЕНИЯ ПРИ ПОДВИЖНОЙ НАГРУЗКЕ 351
жесткой характеристик. Можно заключить, что для конструкций, имеющих мягкую характеристику, динамические прогибы достигают максимума при скорости движения нагрузки, меньшей, чем критическая скорость VKp, определяемой из решения линейной задачи. Для системы с жесткой характеристикой наибольшие прогибы возникают при скорости, большей VKp. С увеличением давления во фронте максимальные динамические прогибы развиваются при все меньших скоростях движущейся нагрузки в случае мягкой характеристики системы и все больших скоростях
Рис. 9.9. Резонансные кривые систем с мягкой а и жесткой б характеристиками в зависимости от скорости с волны.
в случае жесткой. На рис. 9.9, а, б нанесены три резонансные кривые, соответствующие различным величинам давления во фронте <7фз > <7фг > <7ф1 при постоянном демпфировании.
При введении статических продольных осевых сжимающих или растягивающих усилий, распределенных по кромкам оболочки, резонансные кривые смещаются соответственно в сторону меньших или больших скоростей движения нагрузки. Из рис. 9.9, а, б видно, что при некоторой скорости движения фронта могут иметь место одновременно два значения £. Какое из них имеет место в действительности, зависит от предыстории движения. Рассмотрим, например, случай воздействия на оболочку такой волны, для которой характерно быстрое уменьшение скорости движения фронта по конструкции. Если принять, что скорость фронта затухает по линейному закону, то в уравнениях движения выражение для нагрузки 28 необходимо заменить следующим:
<7 — ctst2x Н ct — st2 —,
где з — ускорение фронта волны.
Проследим за изменением амплитуды колебаний оболочки в зависимости от скорости движения фронта. Если в
Аналогичный эффект для случая периодических внешних воздействий рассмотрен выше в главе III.
352 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ, подвижн. НАГРУЗКИ ГЛ. IX
начальный момент фронт движется со скоростью, превышающей VKV и соответствующей точке F на рис. 9.9,6, то по мере убывания скорости колебания оболочки происходят с плавно возрастающими амплитудами, определяемыми нижней ветвью FDE резонансной кривой. В точке Е амплитуда скачком возрастает до величины, соответствующей точке В. Если при этом не произойдет прощелкивания оболочки, то дальнейшее уменьшение скорости фронта приводит к колебаниям с плавно уменьшающимися амплитудами движение вдоль верхней ветви резонансной кривой В А.
При возрастании скорости, имеющей в начальный момент величину, меньшую FKp, происходит увеличение амплитуд колебаний линия ABC у и в момент прохождения точки С амплитуда скачком изменится до меньших значений линия CD, с последующим движением вдоль участка DF.
Отметим, что в некотором диапазоне изменения геометрических параметров цилиндрических панелей преобладает мягкая нелинейность при сравнительно малых прогибах, переходящая в жесткую при больших прогибах. Резонансные кривые для этих случаев имеют более сложный вид; при плавном изменении скорости набегания нагрузки оказывается возможным существование двух точек срыва амплитуд.
Задача об исследовании резонансных режимов при действии подвижной нагрузки для оболочек, рассматриваемых с геометрически нелинейных позиций, является еще недостаточно изученной.
§ 101. Поведение цилиндрической панели при действии подвижных пульсирующих скачков давления
Перейдем к рассмотрению поведения пологой цилиндрической панели, закрепленной в жестком цилиндрическом экране рис. 9.10, а при наличии осциллирующих скачков уплотнения. Нагрузку на внешней поверхности панели, возникающую при появлении скачков уплотнения при дозвуковом обтекании, будем в первом приближении аппроксимировать ступенчатой волной давления, фронт которой движется в направлении образующей оболочки, совершая одновременно колебания с постоянной частотой около некоторого сечения 9.22. Движение оболочки описывается системой нелинейных уравнений теории пологих оболочек 1.40, 1.41. Внешняя нагрузка при этом
принимается в виде
Я —, 9.40
Эта задача исследовалась Э. Д. Скурлатовым и В. Р. Солоненко Всесоюзный симпозиум по распространению упругих и упруго-пластических волн, Алма-Ата, 1971, «Проблемы прочности», 1972, 6, 7—11.
§ 1011 ПАНЕЛЬ ПРИ ПОДВИЖНЫХ ПУЛЬСИРУЮЩИХ СКАЧКАХ ДАВЛЕНИЯ 353
где
В ф sin at.
Здесь и со — амплйтуда и Частота колебаний фронта в сечении, определяемом координатой ф cty В — текущая координата фронта.
Аппроксимируя функцию прогиба в виде
оо оо
wx, у, 2 2 fm„ sin cursing,
m 1 n— 1
9.41
где a mna, p плb, и применяя к уравнениям движения
Ь
пЛ
а
С,
а
CUU0
Ф0,5а
1а017 к12
200 idid0
9>фа.
lаО,т к 24
d
в
Рис. 9.10. Цилиндрическая панель при наличии осциллирующих скачков давления а и динамическая реакция для панели с параметром кривизны k l2 б и As24 в.
процедуру метода Бубнова — Галеркина, получим систему нелинейных дифференциальных уравнений в обыкновенных производных, которая может быть проинтегрирована с помощью ЭЦВМ.
В первом приближении будем изучать поведение панели в предположении, что фронт волны давления совершает колебания около некоторого фиксированного сечения, определяемого координатой ф const; в разложении 41 учтем один член ряда. Тогда уравнения движения запишутся в виде
ib
4 Л, А21 Л3£2 л5,
9.42
354 ПЛАСТИНКИ И ОБОЛОЧКИ Под ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
где введены следующие безразмерные параметры:
ct Л 2 а
а '
1 2. Е
t — h ’
-е,
А2 —
а‘ сг р
121
Eh я4 1
- И2 I а2
-Г
Ая —
4Ehai
<wlr
_Т
я'
•X
X“sir B-icosl7 Bre-icosf вЧт SH’
8,- ‘-““f8
n2h2c2 ро
о а. 2я D В —— sin — В 2л а
Точками обозначены производные по времени.
Численное интегрирование системы уравнений 42 проводилось с помощью ЭЦВМ методом Рунге — Кутта с автоматически
выбираемым шагом по времени. Результаты вычислений показывают, что колебания оболочки имеют амплитуды порядка нескольких толщин стенки, причем закон изменения амплитуд во времени существенно зависит от кривизны панели k b2Rh> координаты среднего положения фронта, амплитуды колебаний фронта, частоты колебаний возмущающей силы со, величины давления во фронте q и коэффициента демпфирования е. Динамический коэффициент Сд при этом имеет большие значения; например, для панели значительной кривизны было получено значение д 13 при колебаниях фронта посередине пролета панели с относительной величиной амплитуды 1а 0,4. Напомним, что под динамическим коэффициентом здесь понимается отношение максимальной величины прогиба, возникающего при воздействии на панель нагрузки с колеблющимся фронтом, к величине прогиба, обусловленного статически приложенной нагрузкой. Таким образом, величины прогибов, определяемые с учетом и без учета подвижности нагрузки, могут сильно различаться между собой.
0,1
OtZ 0,3 1а
Рис. 9.11. Зависимость динамического коэффициента от амплитуды колебаний скачка давления.
§ 102 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ОБОЛОЧЕК 355
Решение нелинейной задачи позволяет также исследовать колебательные движения, сопровождающиеся прощелкиванием панели и представляющие собой опасность в отношении развития усталостных трещин см. ниже главу X. На рис. 9.10, б, в представлены результаты вычислений, выполненных для панелей с параметрами кривизны k 12 и k 24; другие характеристики приведены на рисунке. Под соо понимается частота собственных колебаний панели, соответствующая заданной форме волнообразования. Как видим, для пологой оболочки при рассмотренном виде нагружения оказываются возможными колебания около основного устойчивого положения и колебания, охватывающие прощелкнутое и основное положения равновесия. Динамический коэффициент в этом случае может принимать значение Сд 9. Это видно из рис. 9.11, на котором величина Сд показана в зависимости от параметра а.
§ 102. Экспериментальное исследование поведения оболочек при действии подвижных волн давления
Рассмотрим некоторые результаты опытов, проведенных с замкнутыми цилиндрическими оболочками. Образцы закреплялись с помощью специальной модели, состоящей из несущей штанги, на верхнем по потоку конце которой имеется обтекатель оживальной формы. На цилиндрической части обтекателя расположен датчик давления; второй датчик давления размещается в средней части модели. На модели могут быть размещены одновременно две оболочки, имеющие одинаковые радиусы, в то же время длины и толщины оболочек могут быть различными. Оболочка, располагаемая ниже по потоку, может нагружаться статическими осевыми силами растяжения или сжатия, создаваемыми с помощью специального устройства.
В экспериментах для каждой серии оболочек вначале выбирались заведомо безопасные величины давления во фронте <7ф и импульса, под которым понимается величина площади, заштрихованной на рис. 9.12, а. Далее оболочка подвергалась воздействию волн давления со все более возрастающими значениями q и до тех пор, пока не происходило выпучивание оболочек. Некоторые результаты опытов представлены на рис.9.12, а стальные оболочки и на рис. 9.12, б, в, г дюралюминовые оболочки. Тем значениям q и, при которых выпучивание не имело места, соответствуют светлые кружки, при наличии выпучивания—светлые треугольники. Определенная теоретическим
Эти опыты были проведены Э. Д. Скурлатовым, см. 9.13, 9.14, а также «Проблемы прочности», 1972, 9.
356 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН НАГРУЗКИ ГЛ. IX
Рис. 9.12. Границы устойчивости для а стальных, б, в, г дюралюминовых оболочек.
Рис. 9.13. Типичные формы волнообразования оболочек; в максимальные остаточные деформации достигаются у нижнего по потоку шпангоута.
§ 1021 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ОБОЛОЧЕК 357
путем граница устойчивости нанесена сплошной линией см. § 98. На этих же графиках приведена величина критического внешнего статического давления qy равномерно распределенного по боковой поверхности. Для оболочек, получивших выпучины, выписаны также данные, касающиеся формы волнообразования п — число окружных вмятин. Видно, что при давлении во фронте, слабо j превышающем критиче- дд ское статическое давление левый участок границы, и больших величинах импульсов длинная волна, оболочки те- 30 ряют устойчивость по квазистатической форме. По мере увеличения давления во фронте и уменьшения времени действия Ю нагрузки правый участок 8 границы выпучивание д происходит по все более высокой форме. При этом 4 более тонкие и более ко- л роткие оболочки имеют при прочих равных уело- виях большее количество окружных выпучин. На рис. 9.13 показаны типич- ные формы волнообра- зован ия цилиндрических оболочек, выпучившихся при продольном набегании волны давления.
Для достаточно толстых оболочек, нагружаемых волной с большим давлением на фронте и малой длительностью действия нагрузки, возникает осесимметричная деформация оболочки. При дальнейшем увеличении давления во фронте такая оболочка получает остаточные осесимметричные деформации, на которые накладываются неосесимметричные вмятины.
На рис. 9.14 сплошной линией представлена граница устойчивости для ненапряженной в осевом направлении цилиндрической оболочки, пунктирной линией с темным треугольником — граница устойчивости этой же оболочки, сжатой осевой силой, составляющей 0,278 от верхней статической критической нагрузки. Как видим, ненапряженная оболочка выпучивается при величине импульса в 1,5 раза большем, чем сжатая.
Рис. 9.14. Границы устойчивости для ненапряженной в осевом направлении оболочки сплошная линия и оболочки, сжатой осевой силой.
358 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН НАГРУЗКИ ГЛ. IX
Выпучивание оболочек, подвергающихся комбинированному нагружению, характеризуется образованием ромбовидных вмятин с плавными очертаниями. На рис. 9.15,6 приведена фотография оболочки, потерявшей устойчивость при комбинированном нагружении, для сравнения слева показана оболочка такого же типа, выпучившаяся при действии только волны давления.
Другой целью проведенных опытов было исследование резонансных явлений и переходных процессов в оболочках при одновременном действии осевых статических усилий и динамической нагрузки, создаваемой подвижной волной. Фронт волны
Рис. 9.15. Характерная форма выпучивания оболочки при: а действии только волны давления, б комбинированном нагружении.
давления набегал перпендикулярно продольной оси оболочки. На внутренней стороне оболочки вблизи торцов наклеивались тензометрические датчики на рис. 9.16 указаны номера датчиков, позволяющие с помощью катодного осциллографа производить запись динамических деформаций стенок оболочки. Измерялись также скорость набегания фронта волны давления, давление на фронте и за ним.
На рис. 9.16 представлены осциллограммы деформации оболочки е при набегании волны давления со скоростями 665 и 935 мсек и при осевых сжимающих усилиях, составляющих 0,5 и 0,94 от экспериментального значения статического критического усилия. При сопоставлении осциллограмм, записанных при различных сечениях оболочки, видно, что динамическая деформация возрастает вдоль оболочки и достигает максимальной величины у задней кромки см. § 98. Сравнивая осциллограммы, представленные на рис. 9.16, а и 9.16,6, можно заключить, что
ОБОЛОЧКИ, ОБТЕКАЕМЫЕ ПОТОКОМ ГАЗА
359
деформации оболочки, сжатой осевыми усилиями, составляющими 0,5 ркр, значительно выше, чем динамические деформации
оболочки, сжатой большими 0,94 >Кр, что свидетельствует о значительном смещении критической скорости для данной оболочки см. §§ 96, 98.
Рассматривая осциллограммы, изображенные на рис. 9.16, можно сделать вывод, что динамические деформации
.dji-w
Гг р
осевыми усилиями, равными
£,
0,05
6
0,05
—
с
ж
'5м,
to
1
Л
Ч,р-
1 1 1
Рл
'P ■
J
пи
щ
т
1
7muiH A9J _
J
d
□
□
•1
т млыш
_ >
vs.
mm
7 _
■
Р
П
г
г
и
L
г
L
С
t
L
L
t
t,cex
£,
Ц05
О
й
'0,05
t,ceH
Z0-10
-J
—
C-
5.
J5a
чсек, М,5Рнр-
wM
l l l l l
Ппгтлfs М°1 —
14
1 1
mm
4
Ш
Й
Z1 1
1.1
-j
t,cen 20-W3
Рис. 9.16. Осциллограммы динамических деформаций оболочки при различных величинах сжимающих осевых усилий и скоростей набегания фронта волны давления.
оболочки под действием ударной волны, набегающей со скоростью 935 мсек, имеют меньшую величину, чем деформации при скорости 665 мсек.
§ ПОЗ. Поведение замкнутых цилиндрических оболочек, обтекаемых кратковременным потоком газа
Ранее мы рассматривали подвижную волну давления заданного профиля, причем считалось, что давление действует нормально к поверхности оболочки и что давление на поверхности оболочки равно давлению в набегающей волне. При этом, однако, не учитывалось, что давление, передающееся поверхности деформируемой оболочки, будет некоторым образом перераспределяться в зависимости от формы волнообразования оболочки.
360 пластинки й оболочки под ДЕйстй. подвИжм Нагрузкй гл. IX
Как будет показано ниже, учет подобных сил, обусловленных набегающим потоком, приводит к возникновению динамических прогибов, значительно превышающих величины прогибов, вычисленных в предположении, что поток отсутствует. Форма волнообразования при этом также изменяется 9.13.
Рис. 9.17. Распределение во времени динамических прогибов вдоль оболочки при набегании волны давления штрих-пунктирные линии и волны давления совместно со спутным потоком сплошные линии.
Рассмотрим задачу о поведении замкнутой круговой цилиндрической оболочки при набегании на нее вдоль образующей волны экспоненциального профиля и спутно’го потока газа повышенной плотности.
Для решения этой задачи были выписаны нелинейные уравнения в перемещениях 1.27 — 1.29.
Это решение дано Э. Д. Скурлатовым и автором 9.4, см. сб. «Теория пластин и оболочек», «Наука», Москва, 1971, 29—33.
§ ЮЗ
ОБОЛОЧКИ, ОБТЕКАЕМЫЕ ПОТОКОМ ГАЗА
361
Выражение для интенсивности нагрузки должно включать давление, обусловленное подвижной волной и давление, вызываемое набегающим потоком газа, который мы будем считать сверхзвуковым. Примем здесь, что давление и скорость газа за фронтом также изменяются по экспоненциальному закону. Тогда см. 0.6
q qectxH ct — х
qctxH ct — л: 1 —
2 x
-i 9.43
где q— давление во фронте волны, г — показатель экспоненты, определяющий закон изменения давления за фронтом, к — показатель политропы, М — число Маха набегающего потока, с — скорость движения фронта волны давления.
Уравнения движения, представленные в конечных разностях, решались на ЭЦВМ; при этом прямоугольная развертка поверхности оболочки покрывалась сеткой, имеющей от 30 до 60 узлов в продольном и окружном направлениях. Опуская подробности вычислительной схемы, остановимся на некоторых результатах.
На рис. 9.17 для различных моментов времени приведены кривые, характеризующие распределение динамических прогибов вдоль оболочки, имеющей параметры L 250 мм, R 50 мм, h 0,2 мм при набегании длинной волны х 0 совместно с потоком сплошная линия и при набегании только волны давления штрих-пунктирная линия. Там же для сравнения нанесены данные, полученные для короткой волны ц 5 совместно с потоком пунктирная линия. Принималось, что давление во фронте волны составляло 10 ату скорость частиц газа за фронтом соответствовала числу М 20.
Из графиков видно, что влияние потока на переходный процесс деформаций оболочки значительно и проявляется уже в первые моменты времени после начала набегания фронта волны. С течением времени формы колебаний оболочки, полученцые при решениях задачи с учетом и без учета потока, все более
Рис. 9.18. Форма остаточных вмятин и характер разрушения панели-при обтекании сверхзвуковым потоком газа.
362 ПЛАСТИНКИ И ОБОЛОЧКИ ПОД ДЕЙСТВ. ПОДВИЖН. НАГРУЗКИ ГЛ. IX
различаются; оболочка, обтекаемая потоком, совершает интенсивные колебания с амплитудами, значительно превышающими амплитуды, обусловленные только волной давления. На графиках нанесено безразмерное время т ctL. Анализ распределения напряжений, возникающих в срединной поверхности оболочки, приводит к заключению, что в оболочке образуются зоны с напряжениями, приближающимися по величине к пределу текучести. Эти зоны расположены в шахматном порядке и перемещаются в направлении потока, непрерывно меняя свои очертания. Наличием таких подвижных зон, по-видимому, объясняются остаточные выпучины, покрывающие большую часть поверхности оболочек, совершавших в течение некоторого времени колебания типа флаттера.
На рис. 9.18 приведена фотография части боковой поверхности цилиндрической панели, испытанной при действии подобной нагрузки. Размеры вмятин возрастают к задней кромке; разрушение панели начинается также у задней кромки по граням вмятин. Подобная картина имеет место и при «импульсном» флаттере.
Сопоставляя данные см. рис. 9.17 для короткой и длинной волн при наличии нагрузки, создаваемой потоком, можно заключить, что амплитуды стенок оболочки при потоке меньшей продолжительности имеют значительно меньшую величину.
§ 104. Экспериментальное исследование поведения оболочек при подвижных пульсирующих скачках давления
Для изучения поведения гибких оболочек при наличии пульсирующих скачков давления была проведена серия опытов
с цилиндрическими оболочками. Параметры оболочек составляли LR 4 и 7,4; Rh 250.
Для измерения нормальЬ,сен ного давления, обусловленного пульсирующими скачками, использовался пьезоэлектрический датчик, располагаемый на цилиндрической части обтекателя. Измерение динамических деформаций производилось с помощью тензометрического датчика, наклеенного на внутренней поверхности оболочки. Сигналы с обоих датчиков подавались на двухлучевой электронный осциллограф. Продольные осевые усилия
Рис. 9.19. Изменение давления во времени в точке поверхности модели при трансзвуковом обтекании.
См. ссылку на стр. 352.
§ 104 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ОБОЛОЧЕК 363
оставались при эксперименте неизменными. Скорость набегающего потока изменялась от дозвуковой до сверхзвуковой.
Характер изменения давления во времени при М < 1 иллюстрируется осциллограммой, изображенной на рис. 9.19. По-видимому, испытанная оболочка подвергалась воздействию скачков давления, имеющих приблизительно постоянную частоту колебаний. Всплески давления на осциллограмме соответствуют моменту, когда фронт скачка находится посередине чувствительного элемента датчика. По мере перемещения фронта вниз по потоку давление уменьшается и затем вновь нарастает, так как на поверхность датчика набегает следующий пульсирующий скачок, имеющий такую же частоту колебаний и максимальную амплитуду.
Результаты скоростной киносъемки также свидетельствуют о том, что на оболочку непрерывно набегают серии скачков, движущихся по поверхности оболочки в направлении потока, совершая одновременно колебания около среднего положения. Наиболее бурные колебания имели место при совпадении частоты пульсаций скачков давления с одной из собственных частот оболочки; изменение частоты достигалось подбором соответствующей величины сжимающих усилий.
Разрушение стенок обычно начиналось в области поверхности, расположенной у задней кромки оболочки, с образования крестообразных трещин, причем от момента образования трещин до полного разрушения оболочки проходило 3—5 секунд.
Исследования эффекта подвижных пульсирующих скачков давления должны быть продолжены.
В заключение отметим, что поведению оболочек при действии волн давления был посвящен, преимущественно в линейной постановке, ряд работ, принадлежащих Карьеру С а г г i е г G. F., Techn. Rep. 4, Brown Un-ty, 1951, Миндлину и Блейху М i n d 1 i n R. D., В 1 е i с h Н. Н., J. Appl. Mech. 20, 2, 1953, В. В. Новожилову Прикл. матем. и механ. 23, 4, 1959, А. А. Ильюшину и П. М. Огибалову Упруго-пластическая деформация полых цилиндров, Изд-во Моск. госуд. ун-та, I960, А. П. Филиппову 0.27, Л. И. Балабуху 5.2, Н. А. Кильчевскому 5.11а, Э. И. Григолюку, Л. М. Куршину, В. Л. Присекину ДАН СССР 155, 1 1964 и другим авторам.
ГЛАВА X
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
§ 105. Характеристика задач и методов исследования
Перейдем к нелинейным задачам, для которых исследование поведения пластинок и оболочек связано с применением теории случайных функций.
Ниже основное внимание будет уделено колебаниям и устойчивости оболочек в акустическом поле. Существенно нелинейный характер поведения пластинок и оболочек при нагружении звуковым давлением обнаружен в ряде работ. Наиболее важным является изучение нелинейных колебаний элементов конструкций, склонных к потере устойчивости в большом. Акустические колебания при этом характеризуются значительными прогибами и могут сопровождаться хлопками оболочек, приводящими к быстрому разрушению конструкции см. § 41.
В настоящей главе будет рассмотрено поведение оболочек в подобных случаях нагружения с учетом случайного характера акустической нагрузки. Целью при этом является получение вероятностных характеристик движения системы, склонной к прощелкиванию. Случайный процесс изменения акустического давления будет представлен нами в виде белого шума. Установлено, что акустическое излучение двигателей характеризуется почти постоянной спектральной плотностью в широком диапазоне частот см. работы 10.27, 10.40, 10.65. Эта особенность позволяет аппроксимировать подобного типа акустическое давление белым шумом и использовать при решении задачи аппарат теории марковских процессов. Применение нелинейной теории оболочек с привлечением статистического подхода позволяет провести анализ различных типов колебаний оболочки.
Наиболее важные вероятностные характеристики поведения динамической системы могут быть получены, если известны законы распределения «выходных характеристик» — обобщенных координат. Аппарат теории марковских процессов и уравнений
См. статьи 3.Г1 а, 10.32, 10.42, 10.44.
Методы решения этих задач в детерминированной постановке для случаев, когда акустическое давление может быть представлено изменяющимся по гармоническому закону, изложены в главе III.
§ 105 ХАРАКТЕРИСТИКА ЗАДАЧ И МЕТОДОВ ИССЛЕДОВАНИЯ
365
типа Фоккера — Планка — Колмогорова уравнений ФПК позволяет определить плотности вероятности для обобщенных координат, исходя из общего вида соответствующего уравнения движения системы. Этот метод может быть приложен и в случае системы с несколькими положениями равновесия.
Рассмотрение поведения систем в акустическом поле с помощью подобных методов является важным, как было уже сказано, для расчетов на прочность и выносливость панелей обшивки летательных аппаратов. Остановимся на этих практических приложениях более подробно.
Как известно, обшивка корпуса самолета воспринимает акустические давления, создаваемые струей реактивных двигателей — источником сильного шума. Это приводит во многих случаях к усталостному разрушению таких элементов конструкции самолета, как хвостовая часть крыла, закрылки, элероны, обшивка и нервюры горизонтального оперения. При наличии пульсаций низкой частоты могут возникнуть интенсивные колебания целых агрегатов, например хвостового оперения 10.38, 10.60.
Вибрации элементов летательных аппаратов, вызываемые акустическим давлением, нередко нарушают режим работы различных приборов и систем. Возможна, например, недопустимая прецессия гироскопов и выход из строя электронного оборудования, гидравлических систем и т. д. Повреждения, связанные с акустическими нагрузками, могут быть весьма серьезными см. 10.60., 10.55; это относится, например, к панелям обшивки герметизированного фюзеляжа самолета.
Относящиеся к этой области задачи стали особенно актуальными для авиации в последние годы в связи со все более интенсивным ростом скорости полета, веса и габаритов конструкций. При этом, с одной стороны, повышается тяга двигателей, а вместе с тем и мощность струи. С другой стороны, возрастают акустические давления, не связанные непосредственно с двигателем и вызываемые пульсациями в турбулентном пограничном слое, пульсациями скачков уплотнения и т. д.
Уровень акустической нагрузки, превышающий 150 децибел сб, признан опасным для прочности панелей в имеющихся авиационных конструкциях. Между тем, судя по данным работы 10.60, эта величина была превзойдена еще в 50-х годах. В этот период появились первые сообщения о разрушениях участков обшивки под дейстием акустического давления. К 1970 г. этот уровень уже превосходит 170 дб. Более того, в ближнем акустическом поле зарегистрированы давления до 180 дб.
Первые исследования в этой области применительно к оболочкам были выполнены И И. Воровичем 10.10, В. М. Гончаренко 10.11 и М. Ф. Диментбергом 10 12.
См. «Noise of rockets» в журнале «Space Aeronautics» 44, 5, 1965
366
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
Акустические давления большой частоты, доходящей до нескольких тысяч герц, могут вызвать разрушения элементов конструкций за короткий срок. Даже в том случае, когда напряжения от акустической нагрузки сравнительно малы и лежат ниже предела выносливости для данного материала, они могут существенно сократить ресурс работы отдельных элементов конструкций — особенно, если одновременно действуют повторные усилия иного происхождения.
То обстоятельство, что акустические нагрузки имеют весьма широкий спектр частот, сильно затрудняет «отстройку» конструкции по отношению к резонансному режиму колебаний путем смещения собственных частот. Моделирование реальной системы, находящейся под действием акустической нагрузки, является весьма сложным. Нередко проводятся дорогостоящие натурные испытания конструкций летательных аппаратов на акустическую прочность; подобные эксперименты требуют длительной работы двигателей на режиме максимальной мощности и применения уникальной измерительной аппаратуры 10.39.
Другим важным фактором, вызывающим вибрации элементов обшивки летательных аппаратов, являются пульсации в турбулентном пограничном слое; соответствующие акустические воздействия достигают наибольшей интенсивности при полете в режиме максимального скоростного напора <7шах.
Следующий возможный источник значительных акустических нагрузок — турбулентная спутная струя, расположенная за движущимся летательным аппаратом. Эта струя имеет приблизительно такую же структуру, как и струя реактивного двигателя. Но у реактивной струи эпюра дополнительных скоростей имеет пик, направленный против направления полета, а у спутной струи — по полету 10.26, 10.33.
Усталостные разрушения для дозвуковых и сверхзвуковых самолетов вызываются также срывом потока, например в районе стыка крыла с фюзеляжем. Это явление может иметь место и в том случае, если струя от компрессора двигателя или пневматической системы направлена перпендикулярно скорости полета. Флуктуации давления, вызванные срывом потока, оказываются настолько большими, что могут вызвать резкие вибрации элементов, находящихся на значительном расстоянии от места срыва. Были обнаружены флуктуации давления с интенсивностью в 160 дб при относительно небольшой дозвуковой скорости полета. Характер усталостных трещин, возникающих в этих случаях, близок к тому, который отмечается при наличии акустических давлений 10.26.
См. В. С. Петровский, Гидродинамические проблемы турбулентного шума, «Судостроение», 1966.
§ 106
ПЛАСТИНКА В АКУСТИЧЕСКОМ ПОЛЕ
367
§ 106. Пластинка в акустическом поле.
Закон распределения прогиба
Перейдем к решению задач.о поведении пластинок под действием акустического излучения. Прежде всего рассмотрим случай пластинки, шарнирно опертой по контуру. Будем пред полагать, что в дополнение к акустической нагрузке пластинка испытывает действие статических усилий осевого сжатия. При мем, что пластинка имеет начальные прогибы.
Исходные уравнения теории гибких пластинок примем в виде 1.42а, 1.43а; здесь qt — случайный процесс изменения акустического давления.
Для случая шарнирного опирания краев пластинки аппроксимируем полный и дополнительный прогибы выражениями 3.2, 3.3. Используя метод Бубнова — Галеркина, придем к выражениям, полученным в § 38 при т — п 1. Уравнение движения типа 3.5 запишем в виде с учетом демпфирования
£§. 2е <Л1 -4W3-2 a£-£0co024 <70. ЮЛ
dt dt р0 р0
где параметр акустического давления в случае равномерного распределения по поверхности пластинки равен
O'W-W £’««• 10.2
Входящие в уравнение 1 величины со, р, a, р, определяются по соответствующим формулам главы III при т п 1. Исследуем колебания пластинки в предположении, что qt — белый шум с нулевым средним значением и спектральной плотностью, равной S0.
Используемый здесь и в последующих параграфах путь исследования задачи основан на представлении колебаний системы, подверженной действию белого шума, в виде некоторого сглаженного процесса марковского типа. Этим предположением мы воспользуемся ниже, определяя плотность вероятности экстремумов, исходя из двумерной функции распределения координаты и скорости на основе формулы Райса 10.54. Такой путь решения задачи был принят Лайоном 10.46 при рассмотрении узкополосного процесса колебаний системы с одним положением устойчивого равновесия. В § 110 этот метод применяется к системе с прощелкиванием, имеющей два положения устойчивого
Результаты, приведенные в §§ J0§—114, принадлежат И. Г. Кильдибе кову 10.15; см. также 10.9.
368
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
равновесия. Деформацию пластинки представляем в виде двумерного марковского процесса изменения стрелы прогиба £ и скорости £ dydt.
Приведем некоторые сведения из теории марковских процессов, необходимые в дальнейшем. Марковский процесс характеризуется тем, что его вероятностные свойства в последующий промежуток времени определяются значением функции в заданный момент времени и не зависят от ее значений в предыдущие моменты. Процесс, протекающий в физической системе, называется процессом Маркова процессом без последействия, если в случае, когда известно состояние системы в момент U> распределение вероятностей состояний системы для t > t0 не зависит от любых сведений о ходе изменения ее состояний до момента to. Таким образом, отличительной особенностью марковского процесса является то, что вероятностное суждение о состоянии системы в конце каждого интервала времени зависит только от характеристики ее состояния в начале этого интервала и не зависит от предыстории процесса.
Непрерывный процесс без последействия характеризуется функцией перехода Fx, tуу т, выражающей вероятность Ф того, что в момент t значение некоторой случайной функции £ будет ниже уровня х, если в момент т, предшествующий моменту, случайная функция имела значение у
Ф£ < xlx y Fx, ty, т.
Плотность вероятности перехода
Пусть случайная функция переходит от значения у к значению х не непосредственно, а принимая некоторое промежуточное значение г в момент s, лежащий в интервале между т и t: t < s <. Плотность вероятности перехода от у к г, а затем и к л; выражается в виде произведения плотностей для каждого перехода, т. е. fx,tz,sfz,syt. Результат интегрирования этого выражения по всем z определяет плотность вероятности перехода от значения у к значению х:
оо
fx,ty,x J fx,tz, sfz,sy,xdz. 10.3
— ОО
Исходя из этого соотношения, известного как уравнение Чепмена — Колмогорова, выводится уравнение ФПК. Для
Другой путь определения плотности вероятности координаты для системы с прощелкиванием, требующий знания трехмерной функции распределения координаты, скорости и ускорения, был дан М. Ф. Диментбергом 10.121.
См., например, книгу 0.6, стр. 898—901-
§ 106
ПЛАСТИНКА В АКУСТИЧЕСКОМ ПОЛЕ
369
одномерного процесса оно имеет вид
df д -рч. 1 д2 прч
дГ 1х Т дх
где
ОО
Лг,Пт -L Г x — zfx,t Atz,tdx,
Д<-»0 аг •<
— ОО
оо
Bz,t lim ' Г x — zffx,t Atz,tdx.
At-± О АГ J
Ю.4
10.5
Таким образом, среднее смещение точки за промежуток Дt будет равно A zyt А, а средняя дисперсия смещения равна Bztkt. Обозначим через М среднее значение и представим 5 в виде
Az, t lim —--д, Bz, t lim 10.5a
д->о Ar д-»о
Если изучается изменение состояний некоторой системы, характеризуемой несколькими случайными функциями, то исследуется я-мерный процесс. В этом случае эволюция состояний системы соответствует перемещению точки в некотором фазовом пространстве Ч;. Пусть г-мерный процесс характеризуется параметрами хи х2> •., п- Плотность вероятности f для такого процесса будет представлять собой функцию перехода f x, ty, т. Уравнение ФПК для этой функции принимает вид
К
dt
д2
ii
i111
dxt dxj
.Bt,f. 10.6
Здесь коэффициенты Ah Вц будут функциями Ах, t, Bjx, t; они определяются соотношениями типа 5
ОО
Az, t lim
Д->0 J
— оо
оо
J xt — zt fx,t At z, t dx 1 dx2. dxn,
— oo
op
Bi,z, t lim Г
д-»о j
— оо
оо
J Xi — Zi Xj — Zj f x, t -f At z, t dxi dx2. dxn.
•rep
Ю.7
370 ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ 1ГЛ. X
Выражения типа 5а запишутся в виде
Atz,t т А
д о
М ГДz, Дг,1 Btjz,t lim —
At-0 АГ
10.7а
В случае стационарного марковского процесса будет dfdt 0. Уравнение 4 запишется следующим образом:
- А х f у -JJ- В х f 0. 10.4а
Для м-мерного процесса вместо 6 получим
п п п
- 2 -FT < f 7 S 2 -аАг f W 0. 10.6а
1 1 1 1 1
Составим уравнение ФПК применительно к исследуемой
пластинке. В уравнении 6а будет £, х2 £. Найдем величины Л, для этого уравнения. Процесс qt в уравнении 1, как уже отмечалось выше, рассматривается как белый шум с нулевым средним значением и спектральной плот¬
ностью So
Mq 0, М q t q t2 2nS0 6 t - t2. 10.8
Далее находим
л, lim x2 i, 10.9
Д£->0
A2 lim Мг, 10.10
At->0 Ы
где Д2 определяется из уравнения движения оболочки 1. Тогда
М
— 2e£ — «§ — К а - PS2 л£3 -41 д<
А2— lim -I LiloJ _
Л«-ЬП iit
<Л I
J <7 и rfttj
Д-»0
М
lim
, 10.11
§ 106 ПЛАСТИНКА В АКУСТИЧЕСКОМ ПОЛЕ 371
С учетом первого из условий 8
А2 - 2et - со; 1 - -О ag - К2 л£3 £0«>о 00.12
V Ро Р о
Вц lim М д.•Уг 0, 10.13
Д-»0 АГ
В12 В21 Пт М АдАХа1 0, 10.14
д-»о АГ
В22 Пт, 10.15
м
или
В22 — lim -J--2eS«02'l -4«С-РС2 лС3
Д<-о М I UV Ро
tAt ч 2
£0®о ■л< j МdM lim М f Г— 2et 02 1 — ЛА a — Р£2 т£3 £
Д<-0 Ц Ро tAt
2 Г— 2et 02 1 — Лт a — р£2 rg3 Л- Г q ы ро po i
tAt tAt л
-irj J я'Ыя'и2<1щ<1иЛ. 10.16
t t >
Исходя из свойств нагрузки по 8 будет
В 22 — 2jT»Sq.
Далее выпишем стационарное уравнение ФПК для совместной плотности вероятности £, £ координаты £ и скорости £:
1Г5ГВЛ В,“0- <10л7
Подставляя сюда значения найденных выше коэффициентов, получим
4- nS°- 0. 10.18
ГЛ. X
32 ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
Это уравнение представим в следующей форме:
£-s,--£«-w.1n-w£f-£-£
-i2ei«fLf°- <10-19>
Потребуем, чтобы совместная плотность вероятности £,£ удовлетворяла двум уравнениям, получающимся в результате приравнивания нулю соответствующих частей 19:
к i-4«с - к2 rg3 - 0со02 -С
L Ро.
is., JtSp df __ q
2e dt
Отсюда получаем для стационарного процесса
где плотность вероятности координаты будет J_ i _ Plj а — 1 <уз _i_ J1 н
0, 10.20 10.21
10.22
Ш — exp
2 p
а закон распределения скорости
10.23
V°
10.24
В 23 и 24 принято обозначение
SS
JCSq
eco;
2
10.25
Величина So равна удвоенному значению среднего квадрата безразмерной стрелы прогиба линейной идеальной системы при отсутствии сжимающих усилий. Постоянные С и С' определяются из условия нормировки. Значение С равно
Ы
dl.
10.26
§ 10fj РАСПРЕДЕЛЕНИЕ ЭКСТРЕМУМОВ ПРОГЙБА ДЛЯ ПЛАСТИНКИ 373
Величина С' будет
С' J е V° 4 10.27
— ОО
Находим значение среднего квадрата прогиба
оо
Mi2 J42f£d£. 10.28
— оо
§ 107. Распределение экстремумов прогиба для пластинки
Перейдем к исследованию другой характеристики динамической прочности пластинки, связанной с законом распределения экстремумов прогиба. Используемый здесь метод основан на предположении, что колебательный процесс является узкополосным. В этом случае выражение для плотности вероятности максимумов и минимумов координаты можно получить, исходя из понятия средней относительной частоты пересечений процессом заданного уровня. Среднее в единицу времени число максимумов, лежащих выше некоторого уровня £, равно среднему в единицу времени числу превышений процессом заданного уровня пересечений этого уровня снизу вверх и находится по формуле Райса см. 0.6, стр. 903
оо
v jfbidt 10.29
о
где £, t —двумерная функция распределения, найденная из уравнения ФПК. С другой стороны, среднее число всевозможных максимумов равно числу vj превышений процессом исходного уровня
оГЧ
v; v jfuiidi ю.зо
о
Отношение величин v£ и vm характеризует относительную частоту превышений процессом заданного уровня
vt
л -4-. ю.зо
vm
Очевидно, значение п определяет вероятность f £max > £ того, что максимум координаты превысит уровень £:
£тах >£. Ю.32
Далее вычисляется интегральная функция распределения
374
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
максимумов
fUfUx< 01-. ю.зз
vi,
Выражение для плотности вероятности максимумов принимает вид
Г, ч 1 dvt
f Стах 10.34
к
Аналогичным путем получаем формулу для плотности вероятности минимумов
с ч 1 dvt
fUn 10.35
Ч, к
Плотность вероятности экстремумов в случае системы с одним положением равновесия будет иметь вид
1 dvt 1 dvt
f Zmax, mln -t- Z H T 10.36
Vm dl V dt
Для УЗКОПОЛОСНОГО Процесса, ВЫЧИСЛЯЯ f£max> мы должны учитывать лишь область £ > а при определении f £m1п — область
£ < в остальных областях соответствующие плотности будут
равны нулю. Заменяя в 36 числа v их значениями по формуле Райса 29 и учитывая соотношение 22, получаем
1п 7Ь-Г'- Ю-37
Подставляя сюда 23, приходим к окончательной формуле:
2> --4
f Ux. mln ± fg 7 - Р£2 л£3 - j X
х ехр i ' ■- 5 ■'- ■ i ■vi i “ •,0-38
§ 108. Акустические колебания цилиндрической, оболочки.
Модель системы со многими степенями свободы
Исследуем поведение замкнутой круговой цилиндрической оболочки, шарнирно опертой по торцам, находящейся под действием внешнего давления q, включающего воздействия типа случайных процессов и статических усилий осевого сжатия, равномерно распределенных по торцевым сечениям.
См. статью 10.15, 1971 г.
§ 108 АКУСТИЧЕСКИЕ КОЛЕБАНИЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 375
Уравнения типа 1.40, 1.41, с учетом демпфирования и внешнего давления, будут
£> v74 ч г, 1 д2Ф d2w 0 dw. q х, уу t
TVw-w0 Lw, Ф т--р--2рег,
10.39 ±У4Ф — -jLoy, w — Lw0, a0 —d ю»>. Ю.40
Величина включает статическое давление и случайные процессы <7i, <720> имеющие характер белого шума:
qx, у у t q0 q sin rx sin sy q2 t sin2rx. 10.41
Как и в § 29, задачу рассмотрим для расчетной модели в ви¬
де системы с двумя степенями свободы. Для дополнительного и начального прогибов воспользуемся выражениями 2.159, 2.160.
Система уравнений типа 2.163, 2.164 приводится к виду
dKi, 0г «1, v dUli,b_.Л nniftv
i dT vi дЪ < 10-42
d2Z,2 I о d£>2 dU t,i, £2 n t 1 n A
dt dt “W- Ю.43
Здесь v, 1, v223, qt q.tV2IEh2, V VEgy. Выражение для U будет
i---CI-CI>o oc. -C2-S2. ofe 10.44
где q0 q0V2CiEh2. Здесь приняты те же обозначения и безразмерные параметры, что и в § 29. Значения аь Р, х> 0» х, Ф> Ф определяются через соответствующие значения величин по 2.171 — 2.178 с учетом множителя а2 а2ЧУ2К2.
Функции qt, 0 в 42, 43 представим в виде случайных процессов типа белого шума со спектральными плотностями
376 ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ ГЛ X
Si, S2. Средние значения, корреляционные функции и условия взаимной корреляции
м м О,
я 1 я2
Mqt q'xtT 2nSfiT, М я 0 42 Т 2jt526 »
10.45
Исходя из принятых предположений для условий нагружения, деформацию оболочки рассматриваем как четырехмерный марковский процесс изменения параметров прогиба £2 и скоростей £1, £2.
Если конструкция сводится к расчетной модели в виде системы с п степенями свободы, исследуется 2д-мерный марковский процесс с параметрами хи 2,., хп. Система уравнений типа 42, 43 в этом случае имеет вид
d2t,m 1 ог j dU Ji, £2» • • • £m 1П IА
Ж 2гтЧГ дй — QmVh У1 °-46
т 1, 2,., г.
Для обобщенных сил
М 0,
м К 0 0 2Sm6 г, 10.47
М qm 0 < т 0, т ф к.
Пользуемся стационарным уравнением ФПК по 6а при — 2г. Параметры процесса
£m> Хтп tm 10.48
Характеристики марковского процесса по 7а с использованием 46, 48 и с учетом 47 будут
ди
Ат хтп, Атп 2етхтп vm а
илщ
втк о, Бот„.й„ 0, тФ k,
В тп mn, mn 2jlSm.
Подставляя в 6а значения величин по 49, получим
—£<к,,,
ml охтп m1
n
10.49
S <10-50>
fll
§ 108 АКУСТИЧЕСКИЕ КОЛЕБАНИЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 37
Представим это уравнение в виде V Г, д v ди f nSm df I
jLJ L дхтп m dxm 2em dxm
ml
2e dxmn дХ‘п2 dxln 0- 10-51
В результате Интегрирования находим
fxu х2,.л:2„ --ехр
1
Sm
где
s-rG- <10-53>
Повторным интегрированием исключаем скорости; тогда
f х 1, х2, яп —ехр S” 10.54
Применительно к системе 42, 43 в 6а будет 4 параметры процесса определяются в виде
lCl> 2 2> -3 S1 > 4 2 10.55
Выражения 47 переходят в 45, значения Aiy BtJ в 6а будут:
Alti А2 2»
дУ1 ь £2
10.56
Л3 — — 2в — V,
— 2е2£2 2
£2
<2
Вц — В12 — В21 — В22 — В 34 — В43 — 0, 1
B33 2nS1 В44 2я52. J 10-57
В соответствии с соотношением 53 имеем S1 S2, причем
10.58
Закон распределения параметров прогиба:
Ни У jrехР - —-,0-59
Вместо U в 59 подставляется выражение 44, величина С'
находится из условия нормировки.
378
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
Средние квадраты параметров прогиба:
с» оо
м j
10.60
— ОО —оо
— оо —оо оо оо
МШ I J СГ5,. £2<МЕ2-
10.61
— ОО —оо
§ 109. Цилиндрическая панель. Вероятностные параметры прогиба
Перейдем к исследованию случая пологой круговой цилиндрической панели, закрепленной по краям, совершающей колебания под действием акустического давления. Так же как и в предыдущих параграфах, будем учитывать действие статических усилий осевого сжатия, а акустическое воздействие представим в виде белого шума. Нелинейные акустические колебания в рассматриваемом случае будут характеризоваться скачкообразными перемещениями оболочки от одного положения устойчивого равновесия к другому хлопками оболочки, а также колебаниями вокруг новой устойчивой равновесной формы.
Основные обозначения примем по рис. 2.41. Пользуясь соотношениями 1.40, 1.41 и аппроксимируя полный и дополнительный прогиб выражениями 3.2, 3.3, придем к уравнению движения 1
здесь 9 t — по-прежнему белый шум, характеризующийся нулевым средним значением и спектральной плотностью S0. Значение qt определяется по 2.
Проводя интегрирование уравнения ФПК, придем к выражениям структуры 22—24, заменяя в них р0 на р; значения со2, а, р, т, р в формулах 23—25 для рассматриваемого случая определяются по 2.210, 2.211, 3.27, 3.28.
На рис. 10.1 —10.4 приведены данные, характеризующие влияние сжимающих осевых усилий, а также параметра начальной погиби £0 в срединной поверхности на закон распределения
Формула 66, полученная ниже, описывает поведение системы с прощелкиванием. Такого типа зависимость для совершенной системы была выведена иным путем М. Ф. Диментбергом см. сноску на стр. 368; при этом выполнялся предельный переход от экспоненциально-коррелированного возмущающего процесса к белому шуму.
§ 109
ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ
379
динамического прогиба по 23. Для примера принят случай квадратной в плане А, 1 панели с параметром кривизны
Рис. 10.1. Плотность вероятности динамического прогиба в центре цилиндрической панели при акустических нелинейных колебаниях в случае осевого сжатия усилиями, близкими к нижнему критическому значению.
k 24; зависимости построены для случаев, когда значения параметра сжимающих усилий р равны 5, 6, 9, 15. Нагрузка р 5 выбрана вблизи нижнего критического значения р 4,6.
т
Ч
н
1
РРдрзз
п
0,3
ш
4
Фх
у
°0
—и,ии
т
У
У
J
У
Г
W. „
-2 -1 01 234 5£
Рис. 10.2. Закон распределения прогиба для идеальных и несовершенных панелей при другом уровне сжимающих усилий вблизи нижнего критического значения.
Рассмотрим сначала случай идеальной панели при различных значениях сжимающих усилий сплошные кривые на графиках рис. 10.1 — 10.4. Как видим, при р 5 0,278 рис. 10.1 наибольшая доля вероятности приходится на область значений прогиба в окрестности основного устойчивого положения равновесия; при незначительном изменении нагрузки
380
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГГЛ. X
вблизи нижнего критического значения до р 6 0,333р рис. 10.2 существенно меняется характер кривой распределения; при этом растет доля вероятности интервала значений прогиба, соответствующих окрестности второго устойчивого
Рис. 10.3. Плотности вероятности прогиба для идеальных и несовершенных оболочек при сжимающих усилиях, составляющих половину верхнего критического значения.
Рис. 10.4. Закон распределения прогиба при акустических колебаниях панели в случае действия сжимающих усилий, близких к верхнему критическому значению.
состояния оболочки. С увеличением сжимающей нагрузки до значения, равного половине верхнего критического рис. 10.3, резко возрастает вероятность той области значений прогиба, которая соответствует окрестности второго положения равновесия. Наконец, при р 15 0,832 рис. 10.4 вероятность интервала значений прогиба в окрестности основного равновесного состояния оболочки пренебрежимо мала.
§ 110 ЭКСТРЕМУМЫ ПРОГИБА ДЛЯ СИСТЕМЫ С ПРОЩЕЛКИВАНИЕМ 381
Обратимся далее к влиянию начальных неправильностей в форме срединной поверхности при различных уровнях сжимающих усилий. При 6 и £о 0,25 рис. 10.2 значительно возрастает доля вероятности интервала значений прогиба вблизи второго устойчивого положения. С увеличением начального прогиба до £0 0,55 функция распределения имеет единственный экстремум в виде максимума в точке £ £3; в этом случае оболочка совершает колебания вокруг прощелкнутого положения равновесия. Влияние значений £0 0,1 и £0 0,25 при р 9 демонстрируется графиком рис. 10.3. Влияние начальных неправильностей на закон распределения динамического прогиба оказывается значительным при низком уровне сжимающих усилий: с увеличением параметра р эффект начальной погиби ослабевает.
Зависимость среднего квадрата прогиба от рассмотренных факторов демонстрируется ниже данными табл. 10.1. Для этой характеристики решающим является влияние условий нагружения; напротив, начальные несовершенства не приводят к заметному изменению значения среднего квадрата прогиба.
§ 110. Плотность вероятности экстремумов прогиба для системы с прощелкнванием
Выше был рассмотрен путь исследования плотности вероятности экстремумов прогиба при анализе узкополосного процесса колебаний системы с одним положением равновесия § 107. Применим его к системе с прощелкиванием, когда становятся возможными три вида колебаний: около основного положения равновесия около второго устойчивого положения £з и с охватом обоих этих состояний рис. 10.5. Считается, что при колебаниях оболочки реализуются движения только трех указанных типов, связанных с пересечениями трех характерных уровней прогиба.
При этом понятие узкополосности связывается с характером колебательных движений каждого типа.
Обозначим через v, v£, v средние в единицу времени числа превышений каждого из трех уровней равновесного
Указанный подход к решению задачи об определении плотности вероятности экстремумов в системе с прощелкнванием принадлежит И. Г. Кильдибеков>.
Рис. 10.5. К определению среднего в единицу времени числа экстремумов динамического прогиба для системы с прощелкнванием.
382
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
положения оболочки. Тогда с учетом принятых выше допущений о возможных движениях только трех типов, среднее в единицу времени число vm всевозможных максимумов рассматриваемого узкополосного процесса колебаний будет равно
Vm Vt;4V 10-63
Здесь величина взята с минусом, так как в циклах третьего типа с хлопками один максимум связан с пересечением обоих уровней устойчивого положения рис. 10.5, между тем число прямых хлопков прощелкиваний панели в сторону центра кривизны равно v£. Термин «цикл» по отношению к дви¬
жению того или иного типа здесь и далее связывается с однократным пересечением в процессе этого движения некоторого характерного уровня; под средней частотой циклов того или иного типа понимается среднее в единицу времени число таких пересечений. Возвращаясь к формуле 36 и заменяя в ней vm значением по 63, находим плотность вероятности экстремумов для системы с прощелкиванием
1 dvt
f £max, mln Т 7у 10.64
Значения £тах будут отличны от нуля при Ci < £ < £2 и £ > £3> значения Urn — в области £ < £1 и £2 < £ < £зИспользуя формулу Райса 29, находим
f Стах, mln f, f, - f £, ' Ю.66
Учитывая, что £ определяется по 23, окончательно находим
2Г'1-4
f Стах, mln ± «, Ь-, “ К2 ЛС® р ° X
Xexpi1 -zH2-зр'3-10-66
Определим еще одну важную характеристику оболочки — среднее число N прямых и обратных хлопков в единицу времени. Величина N определяется по формуле Райса 29 как число пересечений уровня £2
оо
W 2v 2jf£2, iidl 10.67
Этот прием относится к системе с тремя положениями равновесия. Если не исключать v£, то циклы первого типа будут учитываться дважды.
nil
ТРАКТОВКА УЗКОПОЛОСНОГО ПРОЦЕССА
383
Подставляя сюда 22 и проводя интегрирование, приходим к выражению
С»-68
§ 111. Трактовка узкополосного процесса для системы с прощелкиванием
Рассмотрим случай квадратной панели с параметром кривизны k 24. Результаты вычислений плотностей вероятности экстремумов координаты по 66 для значений параметра сжимающего усилия р, равных 5; 6; 9; 15 приведены на рис. 10.6—10.9.
Рис. 10.6. Плотности вероятности максимумов и минимумов динамического прогиба в центре цилиндрической панели при акустических колебаниях и действии сжимающих усилий, близких к нижнему критическому значению.
Эти диаграммы дают наглядное представление о распределении колебательного процесса по возможным циклам и иллюстрируют влияние сжимающих усилий и начальных неправильностей в форме оболочки на относительную частоту повторяемости циклов каждого типа. Отметим, что циклы третьего типа сопровождаются опасными прощелкиваниями оболочки.
Общая площадь под кривой распределения экстремумов состоит из трех частей. Площадь fl>i характеризует вероятностный уровень колебательных движений вокруг основного положения равновесия, а Фг — вокруг прощелкнутого состояния. Под Ф3 понимается вероятность экстремумов, соответствующих колебаниям с охватом двух положений устойчивого равновесия.
Рассмотрим вначале влияние сжимающих усилий на распределение колебаний по возможным циклам в случае идеальных
384
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
панелей. Значения Фь Ф2, Фз приведены в табл. 10.1. Очевидно, в рассматриваемом случае вероятность Ф3 относится к всевозможным пересечениям, связанным с превышением- уровня £2.
тал
min
А пп
II -
1
г- Т
Ctrs
V
1 ПК
о
0,67
h V
toL
7,25
г1иР
'4
П
1 V
Со0
ГС
II
1
1
II
л
1 П9
,
rJ,
1 У ж.
0>Z
к
' л
yf
О
3 М 4
Я С,
та, гтп
Рис. 10.7. Законы распределения максимумов и минимумов динамического прогиба для идеальных и несовершенных панелей при ином уровне сжимающих усилий вблизи нижнего критического значения.
-4-2 0 2 4 М в 8 Цтах>т1п
Рис. 10.8. Законы распределения экстремумов прогиба для идеальных и несовершенных оболочек при сжимающих усилиях, составляющих половину верхнего критического значения.
Как видим из таблицы и рис. 10.6, при р 5 0,278р значительную вероятность Ф4 0,867 имеют экстремумы колебаний вокруг основного положения равновесия. С увеличением продольной нагрузки до значения р 0,333р происходят существенные изменения в поведении оболочки; заметно падает значение Oi, а вероятность циклов колебаний второго и третьего типов
§ 111
ТРАКТОВКА УЗКОПОЛОСНОГО ПРОЦЕССА
385
растет рис. 10.7. При р 0,5р вероятность Ф2 возрастает до 0,6; значительную относительную частоту Ф3 0,37 составляют циклы третьего типа рис. 10.8, табл. 10.1. При р 15 0,83 имеет место почти нулевая вероятность экстремумов колебаний
гж, тт
4 ПС
РР0,ВЗ
S4,Z
1
1 ' тах
цб
ПЛ
0
0 ф
Ll>
uft
пп
1
ф -hi л
- о,г Ь
1 —
У
✓
1 i_
-2
0tz г
4
8 £
max,mtn
Рис. 10.9. Плотности вероятности максимумов и минимумов динамического прогиба цилиндрической панели при акустических колебаниях в случае сжатия усилиями, близкими к верхней критической нагрузке.
вокруг исходного положения равновесия и весьма малая вероятность циклов колебаний с охватом двух устойчивых положений
Т а б л и ц а 10.1
р
Р Рв
so
МП2
Ф.
Ф2
Фз
ЛГсОоНО8
5
0,28
0,603
0
2,4
0,867
0,005
0,128
27
6
0,333
0,67
0
6,6
0,55
0,25
0,2
38
0,25
7,2
0,235
0,36
0,405
60
0,55
7,1
0
1
0
0
9
0,5
3,8
• 0
16,2
0,03
0,6
0,37
85
0,1
15,4
0,01
0,6
0,39
91
0,25
14,3
0
1
0
0
15
0,83
4,2
0
32,8
0,0005
0,962
0,0375
17
0,05
31,9
0
1
0
0
386
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
равновесия рис. 10.9; колебания вокруг прощелкнутого положения реализуются со средней относительной частотой Ф2 0,962.
В табл. 10.1 приводится и среднее в единицу времени число хлопков Л 103• Vоо- Как видно, увеличение сжимающей силы до р 9 0,5 приводят к возрастанию частоты хлопков до значения N 85; при 15 0,83 среднее в единицу времени число хлопков падает: при этой нагрузке в колебательном процессе значительную долю составляют движения вокруг прощелкнутого положения.
Рассмотрим влияние начальных неправильностей на распределение колебаний по циклам и на среднее в единицу времени число хлопков. Параметр £0 оказывает значительное влияние при низких, по сравнению с верхним критическим, значениях сжимающих усилий рис. 10.7, 10.8, табл. 10.1. Из этих данных видно, насколько возрастает доля циклов второго и третьего типов с увеличением £о- Начальные неправильности, характеризующиеся величиной £0 0,25, при 0,333 приближают этот вариант нагружения к случаю идеальной оболочки при существенно большем значении, равном половине от верхнего критического: в обоих случаях циклы третьего типа имеют вероятность Ф3, близкую к 0,4. Среднее в единицу времени число хлопков достигает наибольшего значения JV 91 при £о 0,1 табл. 10.1.
§ 112. Описание напряженного состояния панели.
Плотность вероятности напряжений
Определим статистические характеристики напряженного состояния оболочки. Для системы с прощелкиванием применительно к случаю круговой цилиндрической панели, рассмотренному в предыдущих параграфах, определим плотности вероятности напряжений и их экстремумов, проведем исследование возможных циклов изменения напряжений и установим вероятность реализации циклов каждого типа. Характеристики, относящиеся к плотности вероятности напряжений, их экстремальным значениям и среднему квадрату, а также к анализу процесса изменения напряжений по возможным циклам, могут быть использованы при проведении оценок усталостной долговечности конструкций.
В рассматриваемом случае напряжения в оболочке складываются из мембранных напряжений и напряжений изгиба.
См. доклад И. Г. Кильдибекова на Каунасской Всесоюзной конференции по проблемам устойчивости в строительной механике, 1967, Тезисы докладов, Вильнюс, 1967.
§ 112 ОПИСАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ ПАНЕЛИ 387
Напряжения в срединной поверхности аХу оу действующие вдоль образующей и дуги, находятся по формулам 1.30: д2Ф д2Ф u °х'ду2 аУдхг' Напряжения изгиба аХ и, оу> и в произвольной точке у поверхности оболочки zh2 равны wi w—w0
Eh d2w. d2wA
— 21 -ц2 дх2 dy2 '
re Eh d2tt>i I n
°v-— 21 -H2 dy2 t dx2 '
Выберем для исследования значения напряжений, действующих в точке максимального прогиба — в центре панели; здесь они достигают наибольшего значения. Используя выражения 3.2, 3.3, 3.25 для прогиба и функции напряжений в срединной поверхности, получим мембранные напряжения в центре панели х а2, у Ь2 равными см. рис. 2 41
»;-v,»,£'• <Ш>
где
v _ So12 Л2 р, р'.
х Ш2 51А,22’ ф 40Х2ух ' °5ух' УМ-1
Soft2 k ТС2 Г 1 Чу— 20 51Я,22’ Уи— Щу’ 10.71
Здесь введены безразмерные параметры напряжений по формулам
ОхЬ2 _ ОуЬ2
°х 5Eh2 ’ — ЪЕк2
Напряжения изгиба в центре панели равны
а1.и Уу,£> Ю-72
где
п2. ХЯ2 Я2. ЦП2
н — ЮЛ2 1 -ц2 101 -ц2 ’ и — 101 -ц2 юл2 1 — X2 •
10.73
Полные напряжения <r, or, действующие на поверхности оболочки z h2 в центре, найдем, складывая найденные выше значения мембранных напряжений и напряжений изгиба:
л 10.74
Величины, определяющие сг>п, будут
я2 ■ ця2 ■ £0я2 kX2 пп 7«
• ЮЛ1 — ц- f 10 1 — х2 1 20Я2 51 Л22 ’
r-jSj. 10.76
388 ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
Значения уу,п и <pj,,n равны
1ГЛ. х
v — I у»'а 101-I2 10Я21 — ц2
я2£,
20
51 Л22 ’ Ъ.а —
10.77
Определим далее плотность вероятности для полных напряжений ох, п. Зависимость а£_ „ 0 по 74 для квадратной идеальной панели при уровне сжимающих усилий p 6 0,333pl приведена на рис. 10.10. Исходя из уравнения 74, находим
.nYJc.ntl 2<рЖП£. 10.78
Преобразования, обратные 74, 78, являются двузначными и
Рис. 10.10. Зависимость полных напряжений в центре квадратной идеальной панели от прогиба.
определяются следующим образом ниже индекс для полных напряжений опущен:
Ui, 2o£ £it2
1±£iw.
Ух
2фл
Vlt2Oxy Ox t,2
Ух
4рхох 1_ 4ф ХР Ух
10.79, 10.80
U и С2 отвечают соответственно левой и правой ветвям кривой рис. 10.10.
§ 112
ОПИСАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ ПАНЕЛИ
389
Исходя из выражения 22 для f£, С, определим двумерную функцию распределения fcrx, дх. При этом пользуемся известной формулой
т, o'x'2lful, vt
д Ui, Vt
д<х> дх
10.81
где
д Uj, Vi
дх> °х
dUi dUt
дах
дУ
да'
дах
dVj
до
Окончательное выражение для совместной плотности вероятности полных напряжений а,п и скорости а. „ получает вид
IK
•Г
X exp и,« exp х2 а; exp
. 2
«ж 4фхР
Ух
•
10.82
здесь
,«- Jji -4 »yf - w fi;4-м,. Ю.83
Аналогично определяется величина и2<тс заменой в выражении 83 U1 на U2. Значения £4 и U2 определяются по 79. Исключая скорости, приходим к следующей формуле для плотности вероятности:
сю
— oxdax о
сх 1
4<Рхах
Ух
-1
4фХР ехрх, оехрх2 сг. 10.84
Аналогично получаются законы распределения о£, п и напряжений в срединной поверхности о£, оу при этом преобразование закона распределения 22 проводится по 81 с учетом выражений 74 и 69 для рассматриваемых случаев.
390
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
Для напряжений изгиба <rJjH получим
f <Ух, и, 0х, и — - л-— еХР °х, И “
®oY,hV«5o L 5° РвУх,и ’
_JL а3 j I— у4 j_ JL £1. а 1 у
3 X, И 04 X и I с v °Х,И А
Ух, и Ух, и 0 Рв Ух, и J
3 YS
X ехр —
и
Se»SY. и ’
10.85
где y,„ находится по 73. Интегрируя 85 по скорости, найдем
1
к.
CY. „
2
ехр
00-86
, И Ух, И 0 Рв Ух, и J
Результаты вычислений интегральной функции распределения полных напряжений ах для идеальной квадратной в плане
Рис. 10.11. Интегральная функция распределения полных напряжений при акустических колебаниях панели с прощелкиванием.
панели с параметром кривизны k 24 при уровне сжимающих усилий р 6 0,333р приведены на рис. 10.11.
Находим средний квадрат суммарных напряжений
м аЯ j' ofo'xdo'x.
По результам вычислений для случая идеальной оболочки при ft 24, p 0,333pl значение среднего квадрата равно 6,28,
§ 113 ЭКСТРЕМУМЫ НАПРЯЖЕНИИ ДЛЯ СИСТЕМЫ С ПРОЩЕЛКИВАНИЕМ 391
§ 113. Закон распределения экстремумов напряжений для системы с прощелкиванием.
Анализ возможных циклов
Рассмотрим далее возможные циклы изменения полных напряжений ох. На рис. 10.10 точкам D, С, L отвечают прогибы £i£d> £2 £к> соответствующие трем возможным по¬
ложениям равновесия системы. Им отвечают напряжения
<х, lOx,D> 0х,2 <yxtK> °х,г <Ух,Ь-
Как видно из характера зависимости a£ рис. 10.10, максимумы прогиба в области £ > приводят к появлению максимумов ох; возможным минимумам прогиба, лежащим в этой области, соответствуют минимумы напряжений. Минимумам прогиба в интервале значений, относящихся к участку CD, отвечают экстремумы ах в виде минимумов. В области значений £min < £с экстремумам прогибов в виде минимумов соответствуют экстремумы ох в виде максимумов.
' Таким образом, в системе с прощелкиванием реализуются циклы изменения напряжений пяти типов. Они показаны на рис. 10.12. Здесь через ах>с обозначен уровень, отвечающий точке С на рис. 10.10, и нанесены значения полных напряжений Ох, ь <х, 2, ох,з в центре панели, отвечающих соответственно первому, второму и третьему равновесным положениям оболочки. Через I и II обозначены циклы изменения напряжений вокруг уровня oXt i'. в первом случае мы имеем простые циклы, во втором — составные. Циклы типа III реализуются вокруг уровня ох, з, достигающегося в прощелкнутом положении системы. Циклы типов IV и V отвечают изменениям напряжений с охватом значении oXt и ох, з: будем называть их соответственно простыми и составными циклами с прощелкиванием.
Как видим, значения экстремумов oXtfnSLX заключены в области ох, шах>ох<с и отвечают ветви Vх кривой <т£; максимумами представлены также области or D < a max < сг 2 и oXt max > oXt 3 участок U2 на рис. 10.10. Минимумы полных напряжений заключены в интервалах ох, с ох> min < ох> d, Ох, 2 < Ox, min < oXt 3, принадлежащих ветви U2. Цикл изменения прогиба с минимумом £ < £с приводит в напряжениях к циклу с двумя минимумами a min, равными сг с составные циклы типов II и V на рис. 10.12.
Здесь мы исследовали случай, относящийся к полным напряжениям а£. Аналогичные циклы относятся к напряжениям ву, а также к напряжениям в срединной поверхности.
Процесс изменения напряжений изгиба ох, «, Oyt и будет включать циклы того же типа, что и процесс изменения прогиба,
392
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
Найдем выражение для плотности вероятности экстремумов для рассматриваемой системы. Определим плотность вероятности максимумов полных напряжений о£ тах. Для экстремумов, отвечающих участкам МА и DL рис. 10.10, можно воспользоваться методом, использованным в § 10 при определении плотности вероятности экстремумов прогиба. Среднее в единицу
Рис. 10.12. Возможные циклы изменения напряжений в системе с прощелкиванием.
- времени число максимумов v напряжении, превышающих
- °тах
уровень Ох в рассматриваемом интервале значений, находим по формуле Райса
J f вх> oxexddx
10.87
Подставляя сюда выражение 82 для совместного распределения напряжений ах и скорости дх и интегрируя, приходим к соотношению для v :
max
’i.—
expx2«l
x, 2’ ■
•
, 3 J
10.88
Среднее в единицу времени число Гатахдля максимумов, отвечающих участку МС рис. 10.10, найдем как среднее в единицу времени число минимумов прогиба £ в интервале м <,
§ 113 ЭКСТРЕМУМЫ НАПРЯЖЕНИЙ ДЛЯ СИСТЕМЫ С ПРОЩЕЛКНВАНИЕМ 393
<С £min < £с. Подставляя в 29 решение 22 — 24 и выражение для Ui по 79, придем к следующему выражению:
'«1, - -5Г “Р К.; с<„ <11Ш>
Общее выражение для среднего в единицу времени числа максимумов полных напряжений, превышающих заданный уровень, определится в виде
Va Va еХРКК1>а шах max max r x > °x, С
expx2<xl. 10.90
1 V x, I <ax< ax, 2' °x>ax,3 J
Среднее в единицу времени число рассматриваемых экстремумов будет
Va 5rleXPhKl_„-
max r I ax x, С
expx2a; ехрк2а; - exp x2 a;.
°x'°x, 1 °х°х, 3 ax Jx, 2 J
10.91
Далее находим интегральный закон распределения максимумов напряжений
V.
FoXt max 1 1 — exp Xj а V
а,
exp К а; ехрк2а; - ехр х2«. I Х
°х—°хл 1 °х—°х, 3 х х, 2
xexp-i'-fK-yi£,
S0 Рв
Jx>°x,C
ехр“‘“Ж_71
-Kz0U2. 10.92
«bfl Р о I Jax,l<ax<ax. °x><’x,zi
Отсюда определяется плотность вероятности полных напряжений.
Минимумы напряжений отвечают минимумам прогиба в интервалах, соответствующих участкам CD и KL рис. 10.10.
394
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
1ГЛ. X
Минимумы вдоль участка CD реализуются в простых циклах первого и четвертого типов рис. 10.12, а вдоль участка KL — в циклах изменения напряжений третьего типа при колебаниях оболочки вокруг прощелкнутого положения. Таким образом, среднее в единицу времени число минимумов ах, лежащих ниже заданного уровня, равно среднему в единицу времени числу минимумов прогиба в интервалах значений £< < Urn < и £2 <С £min < £з; при этом необходимо учесть минимумы величиной Ох, с, реализующиеся в составных циклах второго и пятого типов рис. 10.12 при колебаниях оболочки вокруг основного положения равновесия и с охватом обоих положений устойчивого равновесия.
Используя формулу Райса, решение 22 — 24 и выражение для и2 по 79, найдем соответствующие указанным выше интервалам значения частоты повторяемости минимумов. Окончательное выражение для среднего в единицу времени числа минимумов напряжений, лежащих ниже заданного уровня а, будет
Определяем выражение для интегрального закона распределения минимумов напряжений
Да ul-jWl
2 exp х2 <т
10.93
F ox, min ехр щ а. V х °х, С
ехр и а,. ехрх2ог. —
сх ах, 1 а а,з
°х, 2<0х<0х,г
-j- 2 ехр к2 а. 10.94
§ 113 ЭКСТРЕМУМЫ НАПРЯЖЕНИЙ ДЛЯ СИСТЕМЫ С ПРОЩЕ ЛКИВ АНИ ЕМ 395
Отсюда также можно определить плотность вероятности минимумов.
Аналогичным образом получаются законы распределения экстремумов полных напряжений а и напряжений в срединной поверхности <х 0, сг 0. Соответствующие выражения для изгибных напряжений можно получить, пользуясь понятием средней относительной частоты пересечений процессом заданного уровня, исходя из формулы Райса 87 с использованием двумерного закона распределения по 85.
max min
-в
О бп
’Х2
В 6
Xf max,min
Рис. 10.13. График интегральной функции распределения экстремумов полных напряжений при акустических колебаниях квадратной идеальной цилиндрической панели с прошелкиванием.
На рис. 10.13 приведен график интегральной функции распределения экстремумов полных напряжений ст; для примера взят случай цилиндрической панели без начальной погиби, квадратной в плане, при уровне сжимающих усилий р 6 0,333 р. Параметр кривизны оболочки принят k 24.
Интегральную функцию распределения максимумов, определяющих возможные циклы изменения напряжений, находим из формулы 92:
Ф К шах 1 — ехр к2 «. X
ехр К К. -ехР Ы<. I
ах ах,3 ах ах, 2
О-0-1
Хехр
1
s:
_2_
к рв
10.95
°х, 1<ах< ах, 2’ °х > ’х, 3
396 ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ ГЛ. X
Соответствующее выражение для функции распределения минимумов будет
фК. min ехР К «. ехр х2 а;,, -
°х ах,1 ах ах,3
-ехрЬЧ;.<,Г,ехР-,-7гаУ-
ах. С<ах< °х, Г °х, 2<ах<ах,3
ехрх2 а’ 10.96
ах ах, с
Преходим к анализу распределения процесса изменения напряжений по различным циклам. Соответствующие данные приведены на рис. 10.14. Здесь принято k 24, Al, £о 0,
-4, 0 б2 Z 5 4 63 6 7 8 бтахМп
Рис. 10.14. Распределение вероятности циклов различного типа в процессе изменения напряжений при акустических колебаниях с прощелки
ванием.
рр 0,33. Точка С на этом графике определяет суммарную
вероятность реализации составных циклов CDi Ф3 Ф1 — относительная частота повторяемости составных циклов второго типа, Фз — относительная частота повторяемости составных циклов пятого типа при колебаниях с прощелкиванием системы рис. 10.12. Точкой 1 определяется общая вероятность реализации простых и составных циклов, отвечающих колебаниям, сопровождающимся хлопками оболочки. Уровень вероятности циклов первого и второго типа отвечает точке 2.
Распределение процесса изменения напряжений по возможным циклам в зависимости от уровня сжимающих усилий и на¬
§ И4
ПОЛОГАЯ ОБОЛОЧКА
397
чальных неправильностей в форме срединной поверхности_оболочки демонстрируется данными табл. 10.2. Здесь через Фь Ф3 обозначены вероятности реализации простых циклов. Как видим из таблицы, наиболее неблагоприятный для прочности оболочки режим колебаний реализуется при сжимающих усилиях, составляющих половину от верхней критической величины. При этом циклы третьего типа, связанные с колебаниями оболочки вокруг прощелкнутого положения, реализуются со средней относительной частотой повторяемости, равной 0,6; значительную вероятность составляют циклы пятого типа.
Т а б л и ц а 10.2
р
р'р'в
so
с»
Ф, Ф,
ф Фз
Ф,
Ф,
Ф2
Ф3
Фа
5
0,28
0,6
0
0,215
0,78
0,187
0,68
0,005
0,028
0,1
0
0,13
0,62
0,09
0,46
0,25
0,04
0,16
6
0,33
0,67
0,25
0,337
0,303
0,124
0,111
0,36
0,213
0,192
0,55
0,918
0,082
0
0
1
0,918
0,082
.0
0,008
0,392
0,001
0,029
0,6
0,007
0,363
9
0,5
3,8
0,1
0,0205
0,3795
0,0005
0,0095
0,6
0,02
0,37
0,25
0,654
0,346
0
0
0
0,654
0,346
15
0,83
4,2
0
0,0026
0,035
0
0,0005
0,962
0,0026
0,0345
0,05
0,965
0,035
0
0
0,965
0,035
§ 114. Пологая оболочка
Исследуем, наконец, случай пологой панели произвольного очертания, прямоугольной в плане, в предположении, что в дополнение к акустической нагрузке qt оболочка испытывает действие статического нормального внешнего давления q0. Будем считать, что панель шарнирно оперта по контуру при наличии свободного смещения точек ее краев. Здесь сохраняется направление координатных линий, принятых на рис. 2.47. Предположим, что оболочка имеет начальные отклонения в форме срединной поверхности, отвечающие форме дополнительного прогиба. Размеры сторон опорного контура равны а, Ь. Главные кривизны kXi kv принимаются постоянными.
398
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
В исходных уравнениях 1.38, 1.39 интенсивность поперечной нагрузки будет равна
где qt аппроксимируется белым шумом.
Используя для полного и начального прогибов выражения 2.234, из уравнения 1.39 определим функцию напряжений в срединной поверхности по 2.235. Уравнение колебаний оболочки произвольной формы с учетом статического равномерно распределенного давления запишем в виде
Здсь приняты те же обозначения, что и в § 34. Квадрат основной частоты собственных колебаний идеальной панели при малых прогибах со определяется по формуле 2.237, значения а, р, г находятся по 2.240 — 2.242. Через q0 обозначена величина
значение qt отвечает формуле 2. По-прежнему, примем, что qt —белый шум с нулевым средним значением и спектральной плотностью, равной SJ, а колебания оболочки представим в виде двумерного марковского процесса.
Находим величины Aiy Bijy входящие в уравнение Фоккера — Планка — Колмогорова 6а. Исходя из уравнения движения 98, с учетом характеристик акустического давления находим
Решение получается в виде 22, где закон распределения прогиба отвечает выражению
qx, у, t -ph-r — грге- q0 qt, 10.97
-g- 2е <ol 2 т3 <7осоо <7 0- 10.98
10.99
А2 - 2et - ©§ К - 2 Л£3 <7ошо, 10.100 Вц В2 :: 21 0, 22 : 2я5. 10.101
Уравнение ФПК получает вид
I 2е С, i 2et Оо2 а£ - К2 г£3 -
£ — ехр
§ И4
ПОЛОГАЯ ОБОЛОЧКА
399
а закон распределения скоростей £ определяется по 24 с соответствующим значением соо. Под So понимается величина 25; постоянная С, а также С' из 24 находятся из условий нормировки.
Рассмотрим в качестве примера случай сферической панели; примем параметр k 48, значение X 1. Законы распределения стрелы прогиба оболочки по 103 в зависимости от величины параметра равномерного давления q0 и начальных непроизвольностей в форме срединной поверхности приведены на риСс 10.15—10.19.
Рис. 10.15. Плотность вероят- Рис. 10.16. Закон распределения прогиба в случае
ности прогиба в центре по- пологой оболочки с прощелкиванием при уровне
лОгой панели при акустиче- статической внешней нагрузки, составляющим
ских колебаниях в условиях 0,78 от верхней критической величины,
отсутствия статического внешнего давления.
Обратимся к результатам вычислений в случае идеальной оболочки сплошные линии на рис. 10.15—10.19 для различных условий нагружения статическим внешним давлением. Параметр верхнего критического давления для рассматриваемой оболочки равен о, в 1,185, а нижнее критическое значение составляет величину <7о,н 0,874 см. рис. 2.48. Значения q0 выбирались равными 0,92; 1; 1,12; 1,3. Соответствующие им отношения
qolqo, в равны 0,78; 0,84; 0,95; 1,1.
При отсутствии статического давления q0 0 оболочка совершает колебания около единственного положения равновесия £i 0 рис. 10.15. В случае q0 0,92 Oy78q0j в оболочка имеет второе устойчивое состояние равновесия прй значении прогиба £з 6,6; прогибу £2 5,2 отвечает неустойчивое положение равновесия рис. 10.16. С возрастанием параметра q0 до значения qQ 1 0,84 q0t в заметно увеличивается
400
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
вероятность интервала значений £ в области значительных прогибов рис. 10.17. При параметре q0 1,12, близком к верхнему
т
—0t30 —Ц25 —0,20 —0J5 — 0,10 — 0JD5
5
и
■
. j
А>
оЧР'
А
Д
1
7' аЦ25
i
0 ‘
V
V
>
4
8
Рис. 10.17. Возрастание вероятности больших прогибов с увеличением статического внешнего давления. Влияние начальной погиби.
Рис. 10.18. Плотности вероятности прогиба в центре для идеальной и несовершенной оболочек при акустических колебаниях и наличии статического внешнего давления, близкого к верхней критической величине.
критическому, нибольшая доля вероятности приходится на область значений прогиба в окрестности второго устойчивого положения равновесия рис. 10.18. Рис. 10.19 отвечает случаю
qo 1,3, когда оболочка
имеет единственное прощелкнутое состояние равновесия: функция распределения охватывает область прогибов, в несколько раз превышающих толщину оболочки.
Влияние начальных неправильностей пунктирные линии на рис. 10.17, 10.18 оказывается более значительным при меньших значениях параметра статического давления qo. Как видно из рис. 10.17, переход от случая идеальной оболочки к варианту £0 0,25 заметно увеличивает вероятность значений прогиба в окрестности прощелкнутого положения равновесия. При значении qo 1,12 0,945 <7о, в оболочка с начальной погибью £0 0,25 совершает колебания вокруг единственного прощелкнутого
О
4
Рис. 10.19. Закон распределения динамического прогиба для пологой оболочки при акустических колебаниях вокруг прощелкнутого положения.
§ П4
ПОЛОГАЯ ОБОЛОЧКА
401
положения равновесия: функция распределения имеет один максимум отвечающий прогибу £ 6,8 рис. 10.18.
Т а б л и ц а 10.3
0
«olio, в
5о
mV
Ф,
Ф2
Ф3
N 1О3М0
0
0
0
0,4
1
0
0
0
0,92
0,78
0
10,9
0,833
0,021
0,146
22
0
20,8
0,514
0,22
0,266
34
1
0,84
0,1
21,0
0,427
0,212
0,361
41
0,25
0,67
21,0
0,265
0,195
0,54
53
0,5
20,4
0,012
0,18
0,808
69
0
39,9
0,043
0,781
0,176
25
1,12
0,95
0,1
37,7
0,012
0,776
0,212
29
0,25
34,6
0
1
0
0
1,3
1,1
0
55,6
0
1
0
0
Данные для среднего квадрата прогиба в зависимости от рассмотренных факторов приведены в табл. 10.3. Изменение условий нагружения приводит к существенному изменению этой характеристики. При отсутствии статического давления средний квадрат прогиба составляет величину, равную 0,4. С увеличением параметра q0 эта величина резко возрастает; значениям q0, равным 0,92; 1; 1,12; 1,3, соответствуют значения среднего квадрата динамического прогиба для идеальной оболочки, равные 10,9; 20,8; 39,9; 55,6. Как видно из таблицы, зависимость среднего квадрата'прогиба от начальных несовершенств в форме оболочки оказывается несущественной.
Определяя выражения для плотности вероятности экстремумов, используем формулы 64, 65. Подставляя в 65 решение для £ по 103, получим
2 SaC”1
Стах, mln £, f £„-f <£ — q0 X
х ехр “ зКа2 ” i1i4т0 • 1°-104
402
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
Законы распределения экстремумов прогиба для случая сферической оболочки при k 48, к 1 в зависимости от условий нагружения и начальных неправильностей в форме срединной поверхности приводятся на рис. 10.20—10.24. На рис. 10.20,
10.21, 10.24 сплошными-линиями нанесены плотности вероятности максимумов, пунктирными — плотности вероятности мини¬
мумов; на рис. 10.22, 10.23 сплошным линиям отвечают плотности вероятности экстремумов для идеальной оболочки; пунктирные и штрих-пунктирные — для оболочек с различными параметрами начальных неправильностей.
А
о
1
1 1 1 1
77
А
1 1
а псгт
- Р
o-L
0l
9
'§—J
п
L £min
1
1
1
1
1
1
1
4
-з -г -1 о 1 г з t
чтах,тт
Рис. 10.20. Плотности вероятности максимумов и минимумов динамического прогиба для пологой оболочки при акустических колебаниях в условиях отсутствия статического внешнего давления.
О £f 2 £2 6 в tfnaX'tnln
Рис. 10.21. Законы распределения максимумов и минимумов прогиба в случае пологой оболочки с прощелкиванием при уровне статического внешнего давления, составляющем 0,78 от верхней критической величины.
Рассмотрим вначале влияние параметра распределенного давления до- При отсутствии статического давления рис. 10.20 экстремумы охватывают область сравнительно небольших значений прогиба в окрестности равновесного положения £i 0. Рис. 10.21—10.23 относятся к случаям, когда оболочка имеет два устойчивых положения равновесия и совершает колебания трех типов.
По-прежнему обозначим через Di вероятность реализации циклов колебаний первого типа, через Фг, Фз — второго и третьего типов соответственно. Значения Ф4, Фг, Ф3 приведены в табл. 10.3. При qo 0,92 0,78 cjo, в циклы колебаний первого типа имеют вероятность Ф1 0,83; относительные частоты повторяемости циклов второго и третьего типов соответственно равны Ф2 0,021 и Фз 0,146 рис. 10.21, табл. 10.3. Увеличение статического давления до величины q0 1 0,84 q0t в
§ 114
ПОЛОГАЯ ОБОЛОЧКА
403
приводит к резкому возрастанию вероятности циклов второго типа до значения Ф2 0,22 график рис. 10.22 при £0 0, при £о 0,25 относительная частота реализации наиболее опасных
Рис. 10.22. Плотности вероятности экстремумов прогиба в центре для идеальных и несовершенных оболочек, нагруженных акустическим давлением при одновременном действии статического давления, составляющего 0,84 от верхней критической величины.
Рис. 10.23. Законы распределения максимумов и минимумов прогиба для идеальной и несовершенной оболочек при акустических колебаниях в случае действия статического внешнего давления, близкого к верхней критической величине.
для прочности оболочки циклов третьего типа возрастает до значения Ф3 0,54 рис. 10.22, табл. 10.3. Как видим, в этом варианте нагружения оболочка с параметром £о 0,5 испытывает
404
ЗАДАЧИ СТАТИСТИЧЕСКОЙ ДИНАМИКИ
ГЛ. X
наиболее тяжелый режим колебаний: циклы с прощелкиваниями реализуются с вероятностью Ф3 0,808.
Среднее число хлопков оболочки в единицу времени находится по формуле 68. Значения величины N 103 Nш0 для сферической оболочки с приведенными выше параметрами даны
в табл. 10.3. Как видим, fmax,min ДЛЯ идеальной 060Л0ЧКИ
наибольшее значение этой величины, равное 33,6, имеет место при уровне tfo — 1 — 0,844 q0> в. В этом же случае отмечается значительное влияние начальных неправильностей в форме оболочки: при значениях параметра Ь>, равных 0,1; 0,25; 0,5, реализуются колебательные режимы оболочки со средним в единицу времени числом хлопков N, равным соответственно 41; 53; 69. С увеличением
значения q0 влияние начальных несовершенства является менее существенным.
Анализ вероятностных характеристик напряженного состояния может быть проведен по методу, изложенному в предыдущем параграфе.
Рис. 10.24. Закон распределения экстремумов для пологой оболочки при акустических колебаниях вокруг прощелкнутого положения.
§ 115. Задачи для дальнейших исследований
Перечислим в заключение задачи, которые желательно рассмотреть в ближайшие годы.
Прежде всего ждет своего дальнейшего развития общая нелинейная теория динамических процессов в оболочках и пластинках. Необходимо выяснить границы применения различных вариантов основных уравнений и, в частности, вариантов теории типа Тимошенко. Должны быть составлены приемлемые для практических применений динамические уравнения, относящиеся к вязко-упругим, упруго-пластическим и вязко-пластическим оболочкам.
Особое внимание желательно уделить разработке динамических моделей для двухслойных, многослойных и подкрепленных конструкций с учетом возможных деформаций различного типа
§ 115
ЗАДАЧИ ДЛЯ ДАЛЬНЕЙШИХ ИССЛЕДОВАНИЙ
405
для чередующихся слоев. Должны быть также исследованы физические и математические модели для новых композиционных материалов той или иной структуры.
Необходима разработка конкретных задач по собственным, вынужденным и параметрическим нелинейным колебаниям цилиндрических, конических и сферических оболочек как систем с несколькими степенями свободы, с учетом возможности перескоков от одних форм колебаний к другим. Более подробно должны быть исследованы вынужденные колебания при случайных нагрузках, вызванных шумом двигателей летательных аппаратов, пульсациями в турбулентном пограничном слое, турбулентностью атмосферы, срывами потока газа, пульсациями донного давления и другими родственными явлениями.
Желательно продолжить изучение переходных процессоз в оболочках, связанных с их выпучиванием, при динамических и ударных нагрузках; это относится к оболочкам различной формы и структуры. Для сферических оболочек важен случай несимметричной деформации. Дополнительному исследованию должен быть подвергнут вопрос о критериях динамической устойчивости.
Значительное внимание необходимо уделить задачам аэрогидроупругости, включая проблему автоколебаний оболочек, обтекаемых сверхзвуковым потоком газа, задачам о поведении оболочек при воздействии подвижных и пульсирующих нагрузок и в случае теплового удара.
Малоисследованным остается вопрос о влиянии условий закрепления по краям оболочек на нелинейные колебания и на переходные процессы для оболочек различной конфигурации.
До сих пор нет надежных данных, касающихся оценки ресурса и несущей способности реальных конструкций при действии случайных нагрузок при значительных амплитудах напряжений.
Важными являются задачи оптимального проектирования оболочек при различного типа динамических нагрузках. Целесообразно исследовать разные варианты подкрепляющих элементов с учетом их различной ориентации.
В связи с развитием численных методов решения динамических задач большое значение приобретает разработка рациональных алгоритмов вычислений и их реализация на ЭЦВМ.
Наконец, должны быть найдены новые методы экспериментального исследования поведения оболочек при динамических и ударных нагрузках с применением современной измерительной аппаратуры и более тонких способов определения конфигурации оболочки в различные моменты временц,
ЛИТЕРАТУРА
Ко всей книге
0.1. Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, изд. 2-е, Физматгиз, Москва, 1959.
0.2. Бабаков И. М., Теория колебаний, изд. 3-е, «Наука», Москва, 1968.
0.3. Болотин В. В., Динамическая устойчивость упругих систем, Гостехиздат, Москва, 1956.
0.4. Болотин В. В., Неконсервативные задачи теории упругой устойчивости, Физматгиз, Москва, 1961.
0,4а. Болотин В. В., Некоторые новые задачи динамики оболочек, Доклад на Всесоюзном совещании по теории оболочек Тарту, 1957, «Расчеты на прочность» 4, Машгиз, Москва 1959, 331—365; Современные направления в области динамики пластин и оболочек, Теория пластин и оболочек, Труды II Всесоюзной конференции по теории пластин и оболочек Львов, 1961, Изд-во АН УССР, Киев, 1962, 16—32.
0.5. Бубнов И. Г., Труды по теории пластин, Гостехиздат, Москва, 1953.
0.6. В о л ь м и р А. С., Устойчивость деформируемых систем, изд. 2-е, «Наука», Москва, 1967.
0.6а. В о л ь м и р А. С., Устойчивость при ударе, сб. «Строительная механика», Стройиздат, Москва, 1966, 61—67; Актуальные задачи теории устойчивости оболочек, Механика твердого тела, Труды II Всесоюзного съезда по теоретической и прикладной механике Москва, 1964 3, «Наука», Москва, 1966, 95—115; Задачи теории устойчивости оболочек и пластинок, Труды VI Всесоюзной конференции по теории оболочек и пластинок Баку, 1966, «Наука», Москва, 1966, 977—983; Современные проблемы устойчивости и динамики оболочек, Строит, мех. и расчет coop., 2 1970, 32—37; Нелинейные задачи динамики оболочек, Расчеты на прочность 15, «Машиностроение», Москва 1971, 291—311.
0.7. В о р о в и ч И. И., Некоторые математические вопросы в теории пластин и оболочек, Механика твердого тела, Труды II Всесоюзного съезда по теоретической и прикладной механике Москва, 1964 3, «Наука», Москва, 1966, 116—136; Общие проблемы в теории пласгин и оболочек, Труды VI Всесоюзной конференции по теории оболочек Баку, 1966, «Наука», Москва, 896—903.
0.7а. Г ольденблат И. И., Нелинейные проблемы теории упругости, «Наука», Москва, 1969.
0.8. Г р и г о л ю к Э. И., Кабанов В. В., Устойчивость круговых цилиндрических оболочек, Итоги науки, Механика твердых деформированных тел 6 1967, ВИНИТИ, Москва, 1969.
0.8а. Ильгамов М. А., Колебания упругих оболочек, содержащих жидкость и газ, «Наука», Москва, 1969.
0.9. Ильюшин А. А., Механика сплошной среды, Изд-во Моск. гос. ун-та, 1971.
ЛИТЕРАТУРА
407
0.10. Кононенко В. О., Колебательные системы с ограниченным возбуждением, «Наука», Москва, 1964.
0.10а. Крылов А. Н., Вибрация судов, ОНТИ, Ленинград, 1936.
0.11. Крылов Н. М., Боголюбов Н. Н., Введение в нелинейную механику, Изд-во АН УССР, Киев, 1937.
0.12. Лурье А. И., Некоторые нелинейные задачи теории автоматического регулирования, Гостехиздат, Москва, 1951.
0.12а. Л у р ь е А. И., Теория упругости, «Наука», Москва, 1970.
0.13. Малкин И. Г., Некоторые задачи теории нелинейных колебаний, Гостехиздат, Москва, 1956.
0.13а. Митропольский Ю. А., Метод усреднения в нелинейной механике, «Наукова думка», Киев, 1971.
0.14. Новожилов В. В., Основы нелинейной теории упругости, Гостех издат, Москва, 1948.
0.15. О г и б а л о в П. М., Колтунов М. А., Оболочки и пластины, Изд-во Моск. гос. ун-та, 1969.
0.16. О ни а ш вил и О. Д., Некоторые динамические задачи теории оболочек, Изд-во АН СССР, Москва, 1957.
0.17. Пановко Я. Г., Основы прикладной теории упругих колебаний, изд. 2-е, «Машиностроение», Москва, 1967.
0.17а. Пономарев С. Д., Бидерман В. Л., Лихарев К. К., Мак уш и н В. М., Малинин Н. Н., Ф е о д о с ь е в В. И., Расчеты на прочность в машиностроении 1 1956; 2 1958; 3 1959, Машгиз, Москва.
0.18. Попов Е. П., П а л ь т о в И. П., Приближенные методы исследования нелинейных автоматических систем, Физматгиз, Москва, 1960.
0.19. Седов Л. И., Механика сплошной среды 1, 2, «Наука», Москва, 1970.
0.19а. Седов Л. И., К теории построения механических моделей сплошных
сред, Труды Всесоюзного съезда по теоретической и прикладной меха¬
нике Москва, 1960, Изд-во АН СССР, Москва, 1962, 176—212.
0.20. Труды Международного симпозиума по нелинейным колебаниям 1—3, Изд-во АН УССР, Киев, 1963; Труды V Международной конференции по нелинейным колебаниям, 1—4, Изд-во АН УССР, Киев, 1970.
0.21. Филиппов А. П., Колебания деформируемых систем, изд. 2-е, «Машиностроение», Москва, 1970.
0.22. Bland D. R., Nonlinear dynamic elasticity, Waltham, 1969.
0.22a. Cunningham W. J., Introduction to nonlinear analysis, New York, 1958.
0.23. Den H a r t о g J. P., Mechanical vibrations, 4th ed., New York, 1956 имеется руский перевод: Ден Гартог Дж., Механические колебания, Физматгиз, Москва, 1960.
0.24. Dynamic stability structures, Proc. of an Intern, confer, ed. by Herrmann G., Oxford, 1967.
0.25. Fliigge W., Statik und Dynamik der Schalen, Berlin, 1957 имеется русский перевод: Ф л ю г г e В., Статика и динамика оболочек, Госстройиздат, Москва, 1961.
0.26. Hale J. К., Oscillations in nonlinear systems, New York, 1963 имеется русский перевод: Хейл Дж., Колебания в нелинейных системах,
«Мир», Москва, 1966.
0.27. Hayashi С., Forced oscillations in nonlinear systems, Osaka, 1953 имеется русский перевод: X а я с и Т., Вынужденные колебания в нелинейных системах, Изд-во иностр. лит., Москва, 1957; Nonlinear oscillations in physical systems, New York, 1964 имеется русский перевод: Нелинейные колебания в физических системах, «Мир», Москва, 1968.
0.28. Kauderer Н., Nichtlineare Mechanik, Berlin, 1958 имеется русский перевод: Каудерер Г., Нелинейная механика, Изд-во иностр. лит., Москва, 1961.
408
ЛИТЕРАТУРА
0.29. К о i t е г W. Т., Устойчивость и закритическое поведение упругих систем, Доклад на Всесоюзном съезде по теоретической и прикладной механике Москва, 1960, сб. «Механика», 5 1960, Изд-во иностр. лит., Москва; Elastic stability and postbuckling behavior, Proc. Symp. nonlinear problems ed. by Lange r R. E., Madison, 1963; The effect of axisymmetric imperfections on the buckling of cylindrical shells under axial compression, Proc. Kon. Ned. Ak. Wet. B66, 1963; General equations of elastic stability for thin shells, Proc. Symp. in honor of L. H. Donnell ed. by Muster D., Univ. of Houston, 1966; On the nonlinear theory of thin elastic shells, Proc. Kon. Ned. Ak. Wet. B69 1966, 1—54; The nonlinear buckling problem of a complete spherical shell under uniform external pressure, I—IV, Proc. Kon. Ned. Ak. Wet. B72, 1969; On the foundations of the linear theory of thin elastic shells, I, II, Proc. Kon. Ned. Ak. Wet. B73 1970, 169—195; Error estimates for certain approximate solutions of problems in the linear theory of elasticity, J. Appl. Math. Phys. 21, 4 1970, 534—538.
0.30. N a g h d i P. М., Foundations of elastic shell theory, «Progress in solid mechanics» ed. by Sneddon I. N. and Hill R. 4, Amsterdam, 1963,
1—90.
0.31. Poincare H., Les methodes nouvelles de la mecanique celeste 1 1892;
2 1893; 3 1899, Paris.
0.32. Rayleigh, The theory of sound 1, 2, 2nd ed., London, 1929 имеется русский перевод: Рэлей Стретт Дж., Теория звука 1, 2, изд.
2-е, Гостехиздат, Москва, 1955.
0.33. Sympson A., Nonlinear structural dynamics problems in aeronautics, Aeron. Res. Council. Curr. papers, 1048, 1969.
0.34. Skudrzyk E., Simple and complex vibratory systems, Pennsylvania, 1968 имеется русский перевод: С к у ч и к Е., Простые и сложные колебательные системы, «Мир», Москва, 1971.
0.35. Stoker J. J., Nonlinear vibrations in mechanical and electrical systems, New York, 1950 имеется русский перевод: Стокер Дж., Нелинейные колебания в механических и электрических системах, Изд-во иностр. лит., Москва, 1953.
0.36. Timoshenko S. P., Y о u n g D. Н., Vibration problems in engineering, 3d ed., New York, 1955 имеется русский перевод: Тимошенко С. П., Колебания в инженерном деле, изд. 2-е, «Наука», Москва, 1967.
0.37. Z i е m b a S., Vibration analysis, Warszawa, 1970.
К главе I
1.1. А й и о л а Л. Я., Нелинейная теория типа Тимошенко для упругих оболочек, Изв. АН Эст. СССР, сер. физ.-матем. и техн. наук, 14, 3
1965, 337—344; Вариационные методы для нелинейных уравнений движения оболочек, Прикл. матем. и мех. 32, 1 1968, 154—158.
1.2. Айнола Л. Я., Нигул У. К., Волновые процессы деформации упругих плит и оболочек, Изв. АН Эст. ССР, сер. физ.-матем. и техн. наук, 14, 1 1965, 3-63. '
1.3. Алексеев С. А., Задачи статики и динамики мягких оболочек, Труды VI Всесоюзной конференции по теории оболочек Баку, 1966, «Наука», Москва, 1966, 28—37.
1.4. Алумяэ Н. А., О представлении основных соотношений нелинейной теории облочек, Прикл. матем. и мех. 20, 1 1956, 136—139.
1.5. Амбарцумян С. А., Теория анизотропных оболочек, Физматгиз, Москва, 1961.
1.5а. Амбарцумян С. А., Теория анизотропных пластин, «Наука», Москва, 1967.
ЛИТЕРАТУРА
409
1.6. Амензаде Ю. А., Теория упругости, 2-е изд., изд-во «Высшая школа», Москва, 1971.
1.7. Болотин В. В., О вариационных принципах теории упругой устойчивости, сб. «Проблемы механики твердого деформированного тела», «Судостроение», Ленинград, 1970, 83—88.
1.7а. Бондарь Н. Г., Нелинейные автономные задачи механики упругих систем, «Буд1вельник», Киев, 1971.
1.8. Век у а И. Н., Об одном методе расчета призматических оболочек, Труды Тбилисского матем. института 21 1955, 191 —195.
1.9. Власов Б. Ф., Об уравнениях теории изгиба пластинок, Изв. АН СССР, Отдел, техн. наук, 12 1957, 57—60.
1.10. Власов В. 3., Общая теория оболочек и ее приложения в технике, Гостехиздат, Москва, 1949.
1.11. Вольмир А. С., Гибкие пластинки и оболочки, Гостехиздат, Москва, 1956.
1.12. Г а леркин Б. Г., Упругие тонкие плиты, Госстройиздат, Ленинград,
1933; Собрание сочинений 1 1952; 2 1953, Изд-во АН СССР,
Москва.
1.13. Гольденвейзер А. Л., Теория тонких упругих оболочек, Гостехиздат, Москва, 1953.
1.13а. Г о л ь д е н в е й з е р А. Л., Развитие теории упругих тонких оболочек, Труды Всесоюзного съезда по теоретической и прикладной механике Москва, 1960, Изд-во АН СССР, Москва, 1962, 339—357; Асимптотические методы исследования спектра частот собственных колебаний оболочек, Механика твердого тела, Труды II Всесоюзного съезда по теоретической и прикладной механике Москва, 1964 3, «Наука», Москва, 1966; Методы обоснования и уточнения теории оболочек, Прикл. матем. и мех. 32, 4 1968, 684—695; Некоторые вопросы общей линейной теории оболочек, Труды VII Всесоюзной конференции по теории оболочек и пластинок Днепропетровск, 1969, «Наука», Москва, 1970, 749— 755; Об ортогональности форм собственных колебаний тонкой упругой оболочки, сб. «Проблемы механики твердого деформированного тела», «Судостроение», Ленинград, 1970, 121 — 129.
1.136. Кан С. Н., Строительная механика оболочек, «Машиностроение», Москва, 1966.
1.13в. Кантор Б. Я., Нелинейные задачи теории неоднородных пологих оболочек, «Наукова думка», Киев, 1971.
1.14. Карм и шин А. В., М я ч е н к о в В. И., Методы решения задач теории устойчивости оболочек, Труды VII Всесоюзной конференции по теории оболочек и пластинок Днепропетровск, 1969, «Наука», Москва,
1970, 794—807.
1.14а. К а р м и ш и н А. В., Лясковец В. А., Мяченков В. И., Репин А. А., Ф р о л о в А. Н., Единый метод решения задач прочности, устойчивости и колебаний оболочек и пластин, VIII Всесоюзная конференция по теории оболочек и пластин, Ростов-на-Дону, 1971.
1.15. Кильчевский Н. А., Основы аналитической механики оболочек, I, Изд-во АН УССР, Киев, 1963.
1.16. Кильчевский Н. А., Теория нестационарных динамических процессов в оболочках, Прикл. мех. 4, 8 1968, I —18.
1.16а. К о л к у н о в Н. В., Основы расчета упругих оболочек, изд-во «Высшая школа», Москва, 1972.
1.166. К о р н и ш и н М. С., Нелинейные задачи теории пластин и оболочек и методы их решения, «Наука», Москва, 1964.
1.17. Королев В. И., Упруго-пластические деформации оболочек, «Машиностроение», Москва, 1971.
1.18. Лурье А. И., Статика тонкостенных упругих оболочек, Гостехиздат, Москва, 1947,
410
ЛИТЕРАТУРА
1.19. Москаленко В. Н., К применению уточненных уравнений изгиба пластинок к задаче о собственных значениях, Инжен. журн., 3 1961; Об учете инерции вращения и деформации сдвига в задачах о собственных колебаниях пластин, Теория пластин и оболочек; Труды
II Всесоюзной конференции по теории пластин и оболочек, Львов, 1961, Изд-во АН УССР, Киев, 1962, 264—266.
1.20. Муштари X. М., Качественное исследование напряженного состоя¬
ния упругой оболочки при малых деформациях и произвольных смещениях, Прикл. матем. и мех. 13, 2 1949, 121—134.
1.21. Муштари X. М., Галимов К. 3., Нелинейная теория упругих
оболочек, Таткнигоиздат, Казань, 1957.
1.22. Новожилов В. В., Теория тонких оболочек, Судпромгиз, Ленинград, 1951.
1.23. П а п к о в и ч П. Ф., Труды по строительной механике корабля 3 1962,
4 1963, Судпромгиз, Ленинград.
1.23а. С е л е з о в И. Т., Об уравнениях движения гибких пластинок, Прикл. мех. 5, 4 1959, 444—448.
1.236. Уфлянд Я. С., Распространение волн при поперечных колебаниях стержней и пластин, Прикл. матем. и мех. 12, 3 1948, 287—300.
1.24. Черных К. Ф., Линейная теория оболочек 1 1962; 2 1964, Изд-во
Ленингр. ун-та.
1.24а. Ш и м а н с к и й Ю. А., Справочник по строительной механике корабля
1, 2 1958; 3 1960, Судпромгиз, Ленинград.
1.25. Bolle L., Contribution au problem lineaire de flexion d’une plaque elastique, Bulletin technique de la Suisse Romande 73, 21 1947, 281— 285; oNb 22 1947, 293—298.
1.26. Green A. E., A d k i n s J. E., Large elastique deformations and nonlinear continuum mechanics, Oxford, 1960 имеется русский перевод: Грин А., Адкинс Дж., Большие упругие деформации и нелинейная механика сплошной среды, «Мир», Москва, 1966.
1.27. Habip L. М., Theory of elastic plates in the reference state, Intern. Journ. of solids and struct. 2, 2 1966, 157—166.
1.28. Herrmann G., Mirsky J., Three dimensional and shell theory analysis of axially symmetric motions of cylinders, J. Appl. Mech. 23, 4 1956, 563—568.
1.29. Huang Т. C., Applications of variational methods to the vibration of plates including rotatory inertia and shear, Developments in mechanics 1 1961, 61—72.
1.30. Karman Th., Festigkeitsprobleme in Maschinenbau, Encykl. d. Math. Wiss. 4, No 4 1910, 311—385.
1.31. Lamb H., On waves in an elastic plate, Proc. of Royal Soc. A93, 648 1917, 114—128.
1.32. Love A., Mathematical theory of elasticity, 1927 имеется русский перевод: Ляв А., Математическая теория упругости, Москва, 1935.
1.33. Mindlin R. D., Influence of rotatory inertia, shear on flexural motions of isotropic elastic plates, J. Appl. Mech. 18 1951, 31—38.
1.34. Naghdi P. М., Cooper R. М., Propagation of elastic waves in cylindrical shells including the effects of transverse shear and rotatory inertia, J. Acoust. Soc. of Amer. 28, Nq 1 1956, 56—63.
1.34a. Nash W. A., Recent advances in the buckling of thin shells, Appl. Mech. Rev. 13, 3 1960, 161 —164 имеется русский перевод: Нэш У., Обзор новых исследований по устойчивости тонких оболочек, сб. «Механика», 5 1960, Изд-во иностр. лит., Москва, 111—119.
1.35. Rayleigh, On the free vibrations of an infinite plate of homogene isotropic elastic material, Proc. of Math. Soc. 10 1889, 225—229.
1.36. Reissner E., On transverse vibration of thin shallow shells, Quarterly of Appl. Math. 13, No 2 1955, 169—17Q.
ЛИТЕРАТУРА
411
1.37. Timoshenko S. P., On the correction for shear of the differential equation for transverse vibration of prismatic bar, Philosophical Magazin 41, JMb 6 1921, 744—746.
1.38. Timoshenko S. P., Woinowsky-Krieger S., Theory of plates and shells, 2nd ed., New York, 1959 имеется русский перевод: T имошенко С. П., Войновский-Кригер С., Пластинки и оболочки, Физматгиз, Москва, 1963.
К главе II
2.1. Ал футов Н. А., Балабух Л. И., О возможности решения задач устойчивости пластин без предварительного определения начального напряженного состояния, Прикл. матем. и мех. 31, 4 1967, 716—722.
2.2. Биргер И. А., Колебания пластинок и оболочек, сб. «Прочность и динамика авиационных двигателей», 5, «Машиностроение», Москва, 1969, 5—27.
2.3. Болотин В. В., Краевой эффект при колебаниях упругих оболочек, Прикл. матем. и мех. 24, 5 1960, 831—842; Динамический краевой эффект при упругих колебаниях пластинок, Инж. сб. 31, Изд-во АН СССР, Москва 1961, 3—14; Асимптотический метод исследования задач о собственных значениях для прямоугольных областей, сб. «Проблемы механики сплошной среды», Изд-во АН СССР, 1961, 60—72; Асимптотический метод в теории колебаний упругих пластин и оболочек, Труды конференции по теории пластин и оболочек Казань, 1960, Изд-во Казанского гос. ун-та, 1961, 21—26; Обобщение асимптотического метода решения задач о собственных значениях для прямоугольных областей, Инж. журн. 1, 3 1961, 86—92; О плотности частот собственных колебаний тонких упругих оболочек, Прикл. матем. и мех. 27, 2 1963, 362—364; Плотность собственных значений в задачах о колебаниях упругих пластин и оболочек, Труды VI Всесоюзной конференции по теории оболочек и пластинок Баку, 1966, «Наука», Москва, 1966, 161—167.
2.4. Болотин В. В., Макаров Б. П., М и ш е н к о в Г. В., Ш в е ftко Ю. Ю., Асимптотический метод исследования спектра собственных частот упругих пластинок, Расчеты на прочность 6, Машгиз, Москва, 1960, 231—253.
2.5. Болотин В. В., Москаленко В. Н., Колебания пластинок, в книге «Прочность, устойчивость, колебания» 3, «Машиностроение», Москва, 1968, 370—417; Колебания оболочек, там же, 418—467.
2.5а. Бреславский В. Е., О колебаниях цилиндрических оболочек, Инж. сб. 16, Изд-во АН СССР, Москва 1953, 109—118.
2.6. Вольмир А. С., Кильдибеков И. Г., О линейной теории устойчивости цилиндрических оболочек, Инж. журн. 4, 2 1964, 263—265.
2.7. Вольмир А. С., Кильдибеков И. Г., Изгиб пластинок, в книге «Прочность, устойчивость, колебания» 1, «Машиностроение», Москва, 1968, 526—586; Гибкие пластинки и мембраны, там же, 597—614.
2.8. Вольмир А. С., Кильдибеков И. Г., Устойчивость пластинок, в книге «Прочность, устойчивость, колебания» 3, «Машиностроение», Москва, 1968, 91 —126; Устойчивость оболочек, там же, 117—215.
2.8а. Вольмир А. С., Кильдибеков И. Г., Медведева С. В., Исследование собственных нелинейных колебаний пологих оболочек, Сборник, посвященный 100-летию со дня рождения И. Г. Бубнова, Судпромгиз, Ленинград, 1972.
2.86. Вольмир А. С., Логвинская А. А., Рогалевич В. В., Собственные нелинейные колебания оболочек, VIII Всесоюзная конференция по теории оболочек и пластинок, Ростов-на-Дону, 1971.
412
ЛИТЕРАТУРА
2.9. Г о н т к е в и ч В. С., Собственные колебания пластинок и оболочек, «Наукова думка», Киев, 1964.
2.10. Гр иго люк Э. И., Нелинейные колебания и устойчивость пологих оболочек и стержней, Изв. АН СССР, Отдел техн. наук, В 1955,
33—68; О колебаниях круговой цилиндрической панели, испытывающей конечные прогибы, Прикл. матем. и мех. 19, 3 1955, 376—382.
2.11. Калинин В. С., О расчете нелинейных колебаний гибких пластин и пологих оболочек методом малого параметра, Теория обо почек и пластин, Труды IV Всесоюзной конференции по теории оболочек и пластин Ереван, 1962, Изд-во АН Арм. ССР, Ереван, 1964, 480—488; Нелинейные колебания стержней, пластин и пологих оболочек, Тезисы докладов на совещании по' проблеме упругих колебаний механических систем Рига, 1961, Изд-во АН Латв. ССР, Рига, 1961; Вынужденные нелинейные изгибные колебания однородного призматического стержня и весьма длинной прямоугольной пластины, Всесоюзный съезд по теоретической и прикладной механике Москва, 1960, аннот. докл., Изд-во АН СССР, Москва, 1960; Вынужденные нелинейные колебания призматических стержней и вытянутых прямоугольных пластин под действием гармонической вибрации опор,'«Судостроение», 12 1959, 11 —16; Нелинейные колебания упругих тел, Третий Всесоюзный съезд по теоретической и прикладной механике, аннот. докл. «Наука», Москва, 1968.
2.12. Кильдибеков И. Г., Собственные нелинейные колебания круговой цилиндрической оболочки, VIII Всесоюзная конференция по теории оболочек и пластин, Ростов-на-Дону, 1971.
2.13. Лужин О. В., К вопросу о свободных колебаниях тонкой сферической оболочки, Строит, мех. и расчет, сооруж., 3 1961, 32—36.
2.14. Метсавеэр Я. А., Нелинейные колебания прямоугольных пластин с жестким защемлением по контуру, Труды Таллинского политехи, инта А, Ко 257 1967, 127—138.
2.15. М их лин С. П., Вариационные методы в математической физике, «Наука», Москва, 1970.
2.16. Морозов Н. Ф., Нелинейные колебания тонких пластинок с учетом инерции вращения, Дифф. уравн. 4, 5 1969, 932—937.
2.17. Пановко Я. Г., Основы теории колебаний механических систем, в книге «Прочность, устойчивость, колебания» 3, «Машиностроение», Москва, 1968, 216—284.
2.18. Пановко Я. Г., Г у б а н о в а Л. И., Устойчивость и колебания упругих систем, изд. 2-е, «Наука», Москва, 1967.
2.19. Рабинович Р. И., Динамический расчет пологих оболочек по нелинейной теории, сб. «Строительное проектирование промышленных предприятий» 5 1965, 45—50; Свободные колебания гибких прямоугольных пластинок, Изв. высш. уч. зав., Стр-во и архитект., N° 1
1966, 63—69; Свободные колебания гибких пологих оболочек, Строит, мех. и расчет сооруж., 2 1966, 38—41; О свободных колебаниях гибких пологих оболочек, Строит, мех. и расчет, сооруж., 4 1968.
2.20. Образцов И. Ф., Вариационные методы расчета тонкостенных авиационных пространственных конструкций, «Машиностроение», Москва, 1966.
2.21. Трапезин И. И., О малых колебаниях круговой тонкостенной конической оболочки, Расчеты на прочность 2, Машгиз, Москва 1958; О колебаниях круговой тонкостенной конической оболочки. Расчеты на прочность 4, Машгиз, Москва 1959, 367—373.
2.22. Ф е о д о с ь е в В. И., Об одном способе решения задач устойчивости деформируемых систем, Прикл. матем. и механ. 27, М> 2 1963; Геометрически нелинейные задачи теории пластин и оболочек, Труды
VI Всесоюзной конференции по теории оболочек и пластинок Баку, 1966, «Наука», Москва, 1966, 971—976.
ЛИТЕРАТУРА
413
2.22а. Якушев Н. 3., Влияние больших амплитуд на частоты осесимметричных собственных колебаний круговой цилиндрической оболочки, Итоговая научная конф. Казанского гос. ун-та за 1962 г. краткое содерж. докл., секция прикл. матем. и мех., Изд-во Казанского гос. ун-та,
1963.
2.23. Akkas N., В a u 1 d N. R., Buckling and initial post-buckling behavior of clamped shallow spherical sandwich shells, Intern. J. Sol. Struct. 7, 9 1971, 1237—1259.
2.24. Arnold R. N., Warburton G. B., The flexural vibrations of thin cylinders, Proc. Inst. Mech. Eng. 167, 1 1953.
2.25. Baron M. L., В 1 e i с h H. H., Tables for frequencies and modes of free vibration of infinitely long thin cylindrical shells, J. Appl. Mech. 21, 2 1954.
2.25a. В a s и 1 i S., Note on the large deflection of a circular plate under a concentrated load, Z. Angew. Math. Mech. 12 1961, 357.
2.26. Berger H. М., A new approach to the analysis of large deflections of plates, J. Appl. Mech. 22 1955, 465.
2.27. Chu H. N., Influence of large amplitudes of flexural vibrations of a thin circular cylindrical shell, J. Aerospace Sci. 28, 8, 1961.
2.28. Chu H. N., Herrmann G., Free flexural vibrations of rectangular elastic plates, J. Appl. Mech. 23, 4 1956.
2.29. С о 11 a t z L., Eigenwertaufgaben mit technischen anwendungen, Leipzig, 1963 имеется русский перевод: Коллатц JI., Задачи на собственные значения, «Наука», Москва, 1968.
2.30. Cummings В. Е., Large amplitude vibration and response of curved panels, AIAA Journ. 2, 4 1964.
2.31. Dowell E. H., On the nonlinear flexural vibrations of rings, AIAA Journ. 5 1967, 1508—1509.
2.32. Dowell E. H., V e n t r e s C. S., Modal equations for the nonlinear flexural vibrations of a cylindrical shell, Intern. J. Sol. Struct. 4, 10
1968.
2.33. Evensen D. A., Some observations on the nonlinear vibration of thin cylindrical shells, AIAA Journ. 1 1963, 2857—2858.
2.33a. Forsberg K., A review of analytical methods used to determine the modal characteristics of cylindrical shells, NASA CR-613, 1966.
2.34. Fung Y. С., В a r t о n М. V., Shock response of a nonlinear system, J. Appl. Mech. 29 1962, 465—476.
2.35. Fung Y. C., S e с h 1 e г E. E., К a p 1 a n A., On the vibration of thin cylindrical shells under internal pressure, J. Aeronaut. Sci. 24 1957, 650—660.
2.36. G a j e n d a r N., Large amplitude vibrations of plates on elastic foundations, Intern. J. Nonlinear Mech. 2, 2 1967.
2.37. Greenspon J. E., A simplified expression for the period of nonlinear oscillations of curved and flat panels, J. Aerospace Sci. 27, 2
1960.
2.37a. Hoff N. J., Thin shells in aerospace structures, Astronautics and aeronautics 5, 2 1967, 26—45.
2.38. L e i s s a A. W., Free vibrations of elastic plates, AIAA paper Nb 69— 24, New York,.1969; Vibration of plates, Washington, 1969.
2.38a. Matsuzaki Y., Influence of the in-plane boundary conditions on the nonlinear characteristics of flexural vibration of rectangular plates, Presented at 12th'Conf. Strength. Struct., Japan Soc. Aero Space Sci. 1970; Influence of the in-plane boundary conditions on the natural frequency of cylindrically curved panels with simply supported edges, Intern. J. Sol. Struct. 7, 11 1971, 1555—1571,
2.39. Mo r ley L. S., An improvement of Donnel’s approximation for thin walled circular cylinders, Quart. J. Mech. Appl. Math. 12 1959, 93.
414
ЛИТЕРАТУРА
2.40. Nash W. А., М о d е е г J. R., Certain approximate analysis of nonlinear behavior of plates and shallow shells, Proc. Symp. on the theory of thin elastic shells, Delft, 1959.
2.41. Nowinski J. L., Note on analysis of large deflections of rectangular plates, Appl. Sci. Res. All 1962, 85; Nonlinear transverse vibrations of orthotropic cylindrical shells, AIAA Journ. 1, 1964, 617—620.
2.42. Pal М. C., Large amplitude free vibrations of rectangular plates, J. Sci. and Engng Res. 11 1967, 2.
2.43. Reissner E., On transverse vibrations of thin shallow elastic shells Quart. Appl. Math. 13 1955, 169—176.
2.44. S i n h a S. N., Large deflections of plates on elastic foundation, Proc. ASCE, J. Engng Mech. Div. EMI 1963, 1—24.
2.45. Sun C. L., L u S. Y., Nonlinear dynamic behavior of heated conical and cylindrical shells, Nuclear engineering and design 7, 2 1968.
2.46. W a h Th., Large amplitude flexural vibrations of rectangular plates, Int. J. Mech. Sci. 5 1963, 425; Vibration of circular plates on large amplitudes, Proc. ASCE, J. Engng Mech. Div. 1963, 1—15.
2.47. We in gar ten V. I., Free vibration of thin cylindrical shells, AIAA Journ, 4 1964.
2.48. Yamaki N., Influence of large amplitudes on flexural vibrations of elastic plates, Zeitschr. fur angew. Math, und Mech. 41, 12 1961.
2.49. Yang T. Y., A finite element procedure for large deflection analysis of plates with initial deflections, AIAA Journ. 9, 8 1971, 1468— 1473.
К главе III
3.1. Алексеева H. К., Нелинейные колебания пластин и пологих оболочек, канд. дисс., Москва, 1967; Вынужденные и параметрические колебания пластин конечного прогиба с учетом тангенциальных сил инерции, Расчет пространственных конструкций 12, «Машиностроение», Москва,
1969, 177—185.
3.2. Амбарцумян С. А., Г н у н и В. Ц., О вынужденных колебаниях и динамической устойчивости трехслойных ортотропных пластинок, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 3 1961, 117—123.
3.3. Б а г д а с а р я н Ж. Е., Г н у н и В. Ц., Резонанс в вынужденных нелинейных колебаниях слоистых анизотропных оболочек, Изв. АН Арм. ССР, серия физ.-матем. н. 14, 1 1961, 41—49.
3.4. Б а л а б у х JI. И., М о л ч а н о в А. Г., Плоские колебания жидкости в прямоугольном упругом сосуде, Расчеты на прочность 13, «Машиностроение», Москва 1968, 231—250.
3.5. Б а л а б у х Л. И., М о л ч а н о в А. Г., Об одной краевой задаче теории колебаний с граничными условиями, зависящими от параметра, Прикл. матем. и мех. 30, 6 1966, 1098—1102; Осесимметричные колебания сферической оболочки, частично заполненной жидкостью, Инж. журн., Механ. тв. тела, 5 1967, 56—61.
3.6. Бурмистров Е. Ф., Нелинейные поперечные колебания ортотропных оболочек вращения, Инж. сб. 26, Изд-во АН СССР, Москва 1958, 5—20.
3.7. Вериженко Е. П., Варвак П. М., И т е н б е р г Б. 3., Амплитуды нелинейных колебаний прямоугольных пластинок, сб. «Сопрот. матер, и теория сооруж.» 7, «Буд1вельник», Киев 1968, 45—51.
3.8. Вольмир А. С., Кильдибеков И. Г., Нелинейные акустические колебания цилиндрической оболочки, Изв. АН Арм. ССР, серия физ.матем. н. 17, 3 1964, 65—70.
3.9. Диментберг М. Ф., Определение нелинейной диссипативной характеристики системы с одной степенью свободы на основе испытаний при
ЛИТЕРАТУРА
415
вынужденных колебаниях, Инж. журн., Механ. тв. тела, 2 1968, 32—34.
ЗЛО. Кац А. М., О вынужденных нелинейных колебаниях, Тр. Ленингр. индустр. ин-та, раздел физ.-матем. н. 3 1939, 102—120.
3.11. Кильдибеков И. Г., Исследование нелинейных колебаний пластинок, Теория пластин и оболочек, Труды Всесоюзного симпозиума по теории оболочек и пластин Казань, 1971, «Наука», Москва, 1971, 151—154.
3.11а. К и л ь д и б е к о в И. Г., М и ц ю к А. А., Исследование несущей способности подкрепленных панелей в акустическом поле, Прикладная механика 7, 12 1971, 82—86.
3.12. Лурье А. И., К задаче о вынужденных нелинейных колебаниях, Ученые зап. Ленингр. госуд. ун-та, серия матем. н., N° 8 1939, 25—33.
3.13. Мишенков Г. В., О вынужденных нелинейных колебаниях упругих
панелей, Изв. АН СССР, Отдел, технич. н., Механ. и машиностр., 4
1961, 97—103; Вынужденные колебания механической системы при наличии сухого трения и асимметричной квазиупругой характеристики, Инж. журн. 4, 4 1964, 759—764; К вопросу о взаимодействии параметрически возбуждаемых и вынужденных колебаний упругих панелей, Изв. АН Арм. ССР, серия физ.-матем. н., 18, 1 1965,
53-60.
3.14. Морозов Н. Ф., Нелинейные колебания круглой пластинки, Тр. Ленингр. технол. ин-та целлюл.-бум. пром. 17 1965.
3.15. Нестеров С. В., Нелинейные вынужденные колебания круглой пластинки, Акуст. журн. 11, 1 1965, 74—78.
3.16. Пастушихин В. И., Установившиеся колебания пластинок и пологих оболочек из сжимаемых нелинейно-упругих материалов, Труды Моск. инж.-строит. ин-та 53 1968, 185—201.
3.17. Соколова Г. А., Колебания гибких трапециевидных пластинок, Труды Моск. инж.-строит. ин-та 53 1968.
3.18. Сочинский С. В., Чувиковский В. С., О нелинейных динамических деформациях прямоугольных пластин и цилиндрических оболочек, Труды конференции по теории пластин и оболочек Казань, 1960, Изд-во Казанского гос. ун-та, 1961, 358—361.
3.19. Chobotov V. A., Nonlinear response of a circular membrane to sinusoidal acoustic excitation, J. Acoust. Soc. Amer. 36, 1 1964.
3.20. E i s 1 e y, Nonlinear vibration of beams and rectangular plates, Z. Angew. Mathem. und Phys. 15, 2 1964, 167—175.
3.21. Evensen D. A., Evan-I wanowski R. М., Dynamic response and stability of shallow spherical shells subject to time depended loading, AIAA Journ. 5, 5 1967.
3.22. Evensen D. A., F u 11 о n R. E., Some studies of the nonlinear dynamic response of shell-type structures, в книге 0.24, 237—254.
3.23. H a s s e r t J. E., N о w i n s k i J. L., Non-linear transverse vibrations of a rectangular orthotropic panel, Proc. 5th Intern. Sympos. Space Technol. and Sci., 1963, Tokyo, 1964.
3.24. Herbert R. E., Random vibrations of plates with large amplitudes, Papers Amer. Soc. Mech. Engrs, 1965.
3.25. К i г с h m a n E. J., G r e e n s p о n J. E., Nonlinear response of aircraft panels to acoustic noise, J. Acoust. Soc. Amer. 29, 7, 1957.
3.26. N о w i n s k i J. L., Nonlinear transverse vibrations of circular elastic plates built at the boundary, Proc. 4th US Nat. Congr. Appl. Mech., Berkeley, Calif., 1962 1, Pergamon Press 1962; Nonlinear vibrations of elastic circular plates exhibiting rectilinear orthotropy, Z. angew. Math, und Phys. 14, 2 1963.
3.27. Tobias S. A., Nonlinear forced vibrations of a circular discs. An experimental investigation, Engineering 186, 4818 1958.
416
ЛИТЕРАТУРА
К главе IV
4.1. Амбарцумян С. А., Гнуни В. Ц., Параметрические колебания пластинки в поле действия высоких температур, Изв. АН СССР, Отдел. техн. н., Механ. и машиностр., 6 1964.
4.2. Болотин В. В., Некоторые нелинейные задачи динамической устойчивости пластинок, Изв. АН СССР, Отд. техн. н., 10 1954, 47—59; Устойчивость тонкостенной сферической оболочки под действием периодического давления, Расчеты на прочность, Машгиз, Москва 2 1958, 284—289; Параметрические колебания упругих систем, в книге «Прочность, устойчивость, колебания» 3, «Машиностроение», Москва, 1968, 347—369.
4.3. Гнуни В. Ц., К теории динамической устойчивости слоистых анизотропных оболочек, Изв. АН Арм. ССР, серия фиа.-матем. н. 13, 1
1960, 47—58; О границах динамической неустойчивости оболочек, Труды по теории пластин и оболочек, Изд-во Казанского гос. ун-та, Казань, 1961, 117—123; О параметрически возбуждаемых колебаниях слоистых анизотропны'х гибких оболочек, Изв. АН Арм. ССР, серия физ.-матем. н. 15, 3 1962, 29—36.
4.3а. Ильгамов М. А., Сахабутдинов Ж. М., Параметрически возбуждаемые колебания цилиндрической оболочки, заполненной сжимаемой жидкостью или газом, Теория пластин и оболочек, «Наука», Москва, 1971.
4.4. М и ш е н к о в Г. В., О динамической устойчивости пологих упругих оболочек, Инж. журн. 1, 2 1961, 112—118.
4.5. М и ш е н к о в Г. В., С у д о м о е в А. Д., Е ф и м о в В. А., Электронное моделирование параметрически возбуждаемых колебаний в нелинейных системах, Сб. докл. научно-техн. конф. по итогам научно-исслед. работ за 1966—1967 гг., подсекция динамики и прочности машин, Моск. энергет. ин-т, 1967, 278—286.
4.6. Капа D. D., С г a i g R. R., Parametric oscillations of a longitudinally excited cylindrical shell containing liquid, J. Spacecraft and Rockets 5, 1 1968, 13—21.
4.7. Капа D. D., Dodge F. T., Bubble behavior in liquids contained in vertically vibrated tanks, J. Spacecraft and Rockets 3, 5 1966, 760— 763.
4.8. Капа D. D., G о r m 1 e у J. F., Longitudinal vibration of a model space vehicle propellant tank, J. Spacecraft and Rockets 4, 12 1967, 1585— 1591.
К главе V
5.1. Амбарцумян С. А., Багдасарян Ж. Е., Флаттер цилиндрической оболочки, находящейся в поле действия высоких температур, Изв. АН СССР, Отдел, техн. н., 5 1964, 77—82; Об устойчивости ортотропных пластинок, обтекаемых сверхзвуковым потоком газа, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 4 1961; Об устойчивости нелинейно-упругих трехслойных пластинок, обтекаемых сверхзвуковым потоком газа, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 5 1961.
5.1а. Багдасарян Ж. Е., Об устойчивости трехслойной ортотропной пластинки'в сверхзвуковом потоке газа, Изв. АН Арм. ССР, серия физ.матем. н., 14, 5 1961.
5.2. Б а л а б у х JI. И., Взаимодействие оболочек с жидкостью и газом, Труды VI Всесоюзной конф. по теории оболочек и пластинок Баку, J966, «Наука», Москва, 935—943
ЛИТЕРАТУРА
417
5.3. Болотин В. В., Колебания и устойчивость упругой цилиндрической оболочки в потоке сжимаемой жидкости, Инж. сб. 24 1956, 3—16; К вопросу об устойчивости пластинок в потоке сжимаемого газа, «Вопросы прочности материалов и конструкций», Изд-во АН СССР 1959, 194—204; Некоторые новые задачи теории оболочек, Расчеты на прочность 4 1959, 33Г—365; О применении метода Галеркина к задачам флаттера упругих панелей, Изв. высш. уч. зав., Машиностроение, 12
1959, 25—32; Нелинейный флаттер пластин и оболочек, Инж. сб. 28
1960, 55—75; О применении «закона плоских сечений» для определения аэродинамического давления на колеблющиеся оболочки, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 1 1961, 159—162; Нестационарный флаттер пластин и пологих оболочек в потоке газа, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 3 1962, 106—113; О поведении нагретых пластин и пологих оболочек в потоке газа, Инж. журн. 2, 3 1962, 119—125.
5.4. Болотин В. В., Гаврилов Ю. В., Макаров Б. П., Ш в е ftко Ю. Ю., Нелинейные задачи устойчивости плоских панелей при больших сверхзвуковых скоростях. Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 3 1959, 59—64.
5.5. Болотин В. В., Макаров Б. П., Мишенков Г. В., Наго рн о в J1. Н., П о м а з и Л., Некоторые задачи динамической устойчивости упругих колец при внезапном нагружении, Изв. высш. уч. зав., Машиностроение, 6 1965, 76—82.
5.6. Болотин В. В., Н о в и ч к о в Ю. Н., Выпучивание и установившийся флаттер термически сжатых панелей, находящихся в сверхзвуковом потоке, Инж. журн. 1, 2 1961, 82—96.
5.7. Болотин В. В., Новичков Ю. Н., Швей к о Ю. Ю., Теория аэрогидроупругости, в книге «Прочность, устойчивость, колебания» 3, «Машиностроение», Москва, 1968, 468—512.
5.8. Брусиловский А. Д., Мельникова Л. М., Ш в е й к о Ю. Ю., Колебания и устойчивость цилиндрической оболочки в потоке газа, Инж. журн. 6, 1 1966, 67—73.
5.8а. Вольмир А. С., С е л е з о в а Л. В., Поведение упругой цилиндрической панели в потоке проводящего газа при действии магнитного поля, Прикл. мех. 7, 5 1971, 3—8.
5.9. Г р и г о л ю к Э. И., Горшков А. Г., Взаимодействие слабых ударных волн с упругими конструкциями, Научные труды Ин-та механики Моск. гос. ун-та, 2, 1970.
5.10. Г р и г о л ю к Э. И., Л а м п е р Р. Е., Ш а н д а р о в Л. Г., Некоторые теоретические и экспериментальные исследования автоколебаний криволинейных панелей в потоке газа, Теория оболочек и пластин, Изд-во АН Арм. ССР, Ереван, 1964, 401—411; Флаттер панелей и оболочек, «Итоги науки», Механика, 1969, 34—90.
5.11. Г риг о люк Э. И., М и х а й л о в А. П., Флаттер трехслойных цилиндрических оболочек, Инж. журнал 5, 6 1965, 1087—1091.
5.11а. Кильчевский Н А. ред., Механика систем оболочка — жидкость— нагретый газ, «Наукова думка», Киев, 1970.
5.12. М а к а р о в Б. П., О нелинейном флаттере закрепленных пластин, Теория пластин и оболочек, Изд-во Казанского гос. ун-та, Казань, 1960; Амплитуда установившегося флаттера защемленных панелей, Изв. высш. уч. зав., Машиностроение, 5 1961.
5.13. Микишев Г. Н., Экспериментальное исследование автоколебаний квадратной пластинки в сверхзвуковом потоке, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 1 1959, 154—157.
5.14. Мне в Е. Н., П е р ц е в А. К., Гидроупругость оболочек, «Судостроение», Ленинград, 1970
418
ЛИТЕРАТУРА
5.15. Новичков Ю. Н., О решении уравнений установившегося флаттера цилиндрических панелей, Инж. журн. 2, 4 1962; Об устойчивости решений в задаче о флаттере панелей, Изв. АН СССР, Механ. и машиностр., 4 1962, 352—358; Устойчивость и автоколебания плоских и криволинейных панелей в потоке газа Труды III Всесоюзной конф. по теории пластин и оболочек, Киев, 1962; О применении трехмерной аэродинамической теории к задачам выпучивания и флаттера панелей, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 3
1963, 138—141; Нестационарный флаттер цилиндрических панелей, Труды IV Всесоюзной конф. по теории оболочек и пластин, Изд-во АН Арм. ССР, Ереван, 1964.
5.16. Скур латов Э. Д., Об устойчивости круговой цилиндрической оболочки в сверхзвуковом потоке газа, Сб. «Прочность и устойчивость элементов тонкостенных конструкций», 2, «Машиностроение», Москва
1967, 201—209; Поведение цилиндрических оболочек в сверхзвуковом потоке газа, Расчеты на прочность 15, «Машиностроение», Москва 1971, 356—365; Некоторые вопросы устойчивости цилиндрических оболочек в сверхзвуковом потоке, Переходные процессы деформации оболочек и пластин, Таллин, 1967, 173.
5.17. Смирнов А. И., Сверхзвуковой флаттер трехслойных пластин, ДАН СССР 183, 3 1969, 540—543.
5.18. Швейко Ю. Ю., О влиянии сверхзвукового потока газа на нижнее
критическое усилие для цилиндрических панелей, Изв. АН СССР, Отдел. техн. н., Механ. и машиностр., 4 1961, 14—19.
5.19. A n d е г s о n W. I., Experiments of the flutter of flat and slightly cur¬
ved panels at Mach number 2, Rept. Calif. Inst. Tech. 1962; Oscillatory pressures in an idealized boundary layer with application to cylinder flutter, AIAA Journ. 4, 5 1966, 865—872.
5.20. Callahan J. A., Structural dynamics aspects of the Gemini program, J. Spacecraft and Rockets 4, 1 1967, 58—64.
5.21. Dzygadlo Z., Local analysis of nonlinear forced vibration of a plate of finite length in plane supersonic flow, Proc. vibr. Problems 4, ц
1970, 353—368.
5.22. Evensen D. A. Nonlinear flexural vibrations of thin circular rings, Calif. Inst, of Techn., 1964.
5.23. F a u r e G., Flottements de panneaux en transsonique. Rech. aeronaut., 88 1962.
5.24. Fung Y. C., Flutter of curved plates with edge compression in a su¬
personic flow, Proc. 3d Midwest. Conf. Solid Mech.; Ann. Arbor, 1957, 221—245; On two-dimensional panel flutter, J. Aeronaut. Sci. 25, 3 1958, 145—160; Some recent contributions to panel flutter research, AIAA Journ. 1, 4 1963, 898—909.
5 25. G a r r i k I. E., A survey of aerothermoelasticity, Aerospace Eng. 22,
No 1 1963, 140—147.
5.26. H a r p u r N. F., Structural development of the Concorde, Aircraft Engineering 40, 3 1968, 21—25.
5.27. Harris G. Z., The problem of panel flutter with reference to the Blue Streak and Black Knight vehicles, ARC Current Papers, 848, London
1966.
5.28. Librescu L., Statica si dinamica- structurilar elastice anizotrope si
eterogene, Bucuresti, 1969.
5.29. Librescu L., M a 1 a i u E., Supersonic flutter of circular cylindrical
heterogeneous orthotropic thin panels of finite length, J. Sound Vib. 8, No 3 1968, 494—512.
5.30. Lock М. H., Fung Y. C., Comparative experimental and theoretical studies of the flutter of flat panels in a low supersonic How, Calif, Inst. Tech. No. 670 1961.
ЛИТЕРАТУРА
419
5.31. Menkes Е. G., Houbolt J. С., Evaluation of aerothermoelasticity problems for unmanned Mars-entry vehicles, AIAA paper, 68—283
1968.
5.32. Olson M. D., Fung Y. C., Supersonic flutter of circular cylindrical shells subjected to internal pressure and compression, AIAA Journ. 4, N° 5 1966, 858—864; Comparing theory and experiment for the supersonic flutter of circular cylindrical shells, AIAA Journ. 5, N° 10 1967, 1849—1856.
5.33. Rayburn L. C., Shrouds for space payloads, Space Aeronaut. 47, 2
1967, 66—73.
5.34. Runyon H. L., Some research related to the structural dynamics of launch vehicles, Proc. of the 6th Intern. Symposium on Space Technology and Science, 1966, 421—430.
5.35. Sylvester М. А., В а к e r J. E., Some experimental studies of panel flutter at Mach number 1,3; NASA TN, N° 3914 1957.
5.36. Walker R. W., Rosecrans R., Deveikis W. D., Flutter investigation of streamvise oriented arrays of curved panels under compressive loading and aerodynamic heating, NASA TN-2910 1965.
5.37. Young G., Shiokari Т., Buffeting data obtained on Mercury-Atlas, NASA Rep. TDR 594 1961.
К главе VI
6.1. Ага мир о в В. Л., Обзор исследований по устойчивости конструкций при импульсивном нагружении, Расчет пространственных конструкций 12, Стройиздат, Москва 1969, 186—200.
6.2. А л у м я э Н. А., Переходные процессы деформации упругих оболочек, Труды VI Всесоюзной конференции по теории оболочек и пластинок Баку, 1966, «Наука», Москва, 1966, 883—889.
6.3. Болотин В. В., О понятии устойчивости в строительной механике, Проблемы устойчивости в строительной механике, Труды Всесоюзной конференции по проблемам устойчивости в строительной механике Москва, 1963, Стройиздат, Москва, 1965, 6—27.
6.4. Вольмир А. С., Stability and post-buckling behavior of shells under dynamic loads, «Applied mechanics», Proc. Xth Intern. Congr. Appl. Mech., Amsterdam, 1962, 276—277.
6.5. Даревский В. М., Устойчивость оболочки при динамической нагрузке, Труды VII Всесоюзной конференции по теории оболочек и пластин, «Наука», Москва, 1970, 224—229; сб. «Проблемы механики твердого деформированного тела», «Судостроение», Ленинград, 1970, 149— 160.
6.6. Джанелидзе Г. Ю., Устойчивость упругих систем при динамических нагрузках, Проблемы устойчивости в строительной механике, Труды Всесоюзной конференции по проблемам устойчивости в строительной механике Москва, 1963, «Наука», Москва, 1965, 68—84.
6.7. Лаврентьев М. А., Ишлинский А. Ю., Динамические формы потери устойчивости упругих систем, ДАН СССР 64, N° 6 1949, 779— 782.
6.8. Budiansky В., Dynamic buckling of elastic structures: criteria and estimates, в книге 0.24, 83—106; Notes on nonlinear shell theory, J. Appl. Mech. 35 1968, 393—401.
6.9. Budiansky B., Hutchinson J. W., Dynamic buckling of imper¬
fection-sensitive structures, Proc. XI Intern. Congr. Appl. Mech., Berlin, 1964, 636—651; A survey of some buckling problems, AIAA Journ. 4,
1966, 1505—1510.
6.10. Hoff N. J., Dynamic stability of structures, в книге 0.24, 7—41.
420
ЛИТЕРАТУРА
6.11. Hutchinson J. W., Initial post-buckling behavior of toroidal shell segments, Intern. Journ. Sol. Struct. 3 1967, 97—115; Imperfectionsensitivity of externally pressurized spherical shells, J. Appl. Mech. 34
1967, 49—55; Buckling and initial post-buckling behavior of oval cylindrical shells under axial compression, J. Appl. Mech. 35 1968, 66—72.
6.12. Hutchinson J. W., Budiansky B., Dynamic buckling estimates, AIAA Journ. 4 1966, 525—530.
6.13. Hutchinson J. W., Koiter W. Т., Postbuckling theory, Applied Mechanics Reviews 23, 12 1970, 1353—1366 имеется русский перевод: Хатчинсон Дж., К о й т е р В. Т., Теория послекритического поведения конструкций, сб. «Механика», 4 1971, Изд-во иностр. лит-ры, Москва, 129—149.
6.14. Stein М., Some recent advances in the investigation of shell buckling, AIAA Journ. 6, No. 12 1968.
К главе VII
7.1. Ага миров В. Л., Вольмир А. С., Поведение цилиндрических оболочек при динамическом приложении всестороннего давления и осевого сжатия, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 3 1959, 78—83.
7.2. Биркган А. Ю., Вольмир А. С., Исследование динамической
устойчивости пластинок с помощью электронных цифровых машин, ДАН СССР 135, 5 1960, 1083—1086.
7.3. Блохина А. И., Динамическая устойчивость цилиндрической обо¬
лочки с начальным изгибом при заданной скорости сближения торцов, Инж. сб. 31 1961, 196—201.
7.4. Болотин В. В., Бойченко Г. А., Макаров Б. П., Суда-
коваН. И., Швейко Ю. Ю., О потере устойчивости тонких упругих оболочек под действием импульсивной нагрузки, Строит, мех. и расчет сооружений, 2 1959, 9—16.
7.5. Болотин В. В., Бойченко Г. А., Исследование прощелкивания тонких упругих оболочек под действием динамических нагрузок, Расчеты на прочность 5, Машгиз, Москва 1960, 259—272.
7.6. Вольмир А. С., Об устойчивости цилиндрических оболочек при динамическом нагружении, ДАН СССР, 123, 5 1958, 806—808.
7.6а. Вольмир А. С., К и л а д з е Б. А., Поведение цилиндрических оболочек при действии осевой динамической нагрузки и внутреннего давления, Сообщ. АН Груз. ССР 62, 2 1971, 373—376.
7.7. Вольмир А. С., Минеев В. Е., Экспериментальное исследование
процесса выпучивания оболочки при динамическом нагружении, ДАН СССР 125, 5 1959, 1002—1003.
7.8. Вольмир А. С., Сметанина Л. Н., Исследование динамической устойчивости стеклопластиковых оболочек, Механика полимеров, 1
1968, 109—115; Об устойчивости цилиндрической ортотропной оболочки при продольном ударе, ДАН СССР 193, 2 1970, 306—308; Поведение оболочек из композиционных материалов при динамическом приложении осевого сжатия, Строит, механ. и расчет coop., 4 1970,
34—37.
7.8а. Вольмир Е. А., Поведение упругой панели под действием ударной
волны в жидкости, Изв. АН СССР, Механ. тв. тела, 1 1969, 180—
184; Поведение круговой цилиндрической панели, подвергающейся действию осевого динамического сжатия, ДАН СССР 201, 6 1971, 46— 48; Выпучивание пластинок и цилиндрических панелей под действием осевого динамического сжатия, Изв. АН Арм. ССР 14, 4 1971, 48—50.
ЛИТЕРАТУРА
421,
7.9. В о р о в и ч И. И., 3 и п а л о в а В. Ф., М и н а к о в а Н. И., С р у б-
щ и к Л. И., Ш е п е л е в а В. Г., О результатах математического исследования и численного анализа устойчивости некоторых типов пологих и непологих оболочек, Третий Всесоюзный съезд по теоретической и прикладной механике, аннот. докл., «Наука», Москва, 1968 7.9а. Г е р ш т е й н М. С., К расчету на устойчивость пластин судового набора, Изв. высш. уч. зав., Машиностроение, 6 1966, 10—15; Выпучивание прямоугольной пластинки при динамическом сдвиге, Труды
VII Всесоюзной конференции по теории оболочек и пластинок, «Наука», Москва, 1970, 177—180.
7.10. Гр иго люк Э. И., Сребовский А. И., Тонкие круговые цилиндрические оболочки под действием импульса внешнего давления, Механ. тв. тела, 3 1968, 110—118.
7.11. К а д а ш е в и ч Ю. И., Перцев А. К., О потере устойчивости цилиндрической оболочки при динамическом нагружении, Изв. АН СССР, Отдел. техн. н., Механ. и машиностр., 3 1960, 30—33.
7.12. К а р м и ш и н А. В., К устойчивости арок на упругом основании, Инж. журн. 1, 2 1961, 168—174.
7.12а. К о л ь м а н Э. Р., Устойчивость конической оболочки при динамическом нагружении равномерным давлением, Изв. высш. уч. зав., Машиностроение, 4 1968, 60—65.
7.13. Косты л ев В. В., Устойчивость круговых конических оболочек под действием динамического внешнего давления, сб. «Исследования по теории пластин и оболочек» 5, Казань 1967, 480—493.
7.14. Мик а эл ян Г. 3., Динамическая устойчивость многослойной ортотропной круговой цилиндрической оболочки, Изв. АН Арм. ССР 21, 2 1968, 42—52.
7.15. Наумов К. А., Ш а п к и н А. С., Динамическая устойчивость ортотропной цилиндрической оболочки, Труды Моск. ин-та радиотехники, электрон, и автоматики 38 1969, 256—259.
7.16. Платонов Э. Г., С л е п о в Б. И., Воздействие динамической нагрузки на незамкнутые сферические оболочки, сб. «Исследования по теории пластин и оболочек» 5, Казань 1967, 444—453.
7.16а. Р и к а р д с Р. Б., Тетере Г. А., Формы выпучивания оболочек из композитного материала при длительном нагружении, Механика полимеров, 4 1971, 697—703.
7.17. Сальников Г. М., К з'адачам динамической устойчивости тонкой конической оболочки, сб. «Исследования по теории пластин и оболочек» 3, Казань 1965; Устойчивость и колебания конической оболочки при комбинированных нагрузках, Изв. высш. уч. зав., Авиац. техн., 4 1966, 57—62; Динамическая устойчивость цилиндрических и конических оболочек кругового и некругового сечения при различных граничных условиях, сб. «Исследования по теории пластин и оболочек» 5, Казань 1967, 469—479.
7.18. Сметанина Л. Н., Нелинейная задача динамической устойчивости ортотропных оболочек при внешнем поперечном давлении, сб. аспир. работ Воронежского лесотехн. ин-та 2 1964.
7.19. Старцева Л. П., Поведение трехслойной цилиндрической стеклопластиковой оболочки при действии осесимметричной динамической нагрузки, Труды Всесоюзного заочн. политехи, ин-та 52 1969, 68—72; Осесимметричная деформация трехслойных стеклопластиковых оболочек при динамическом нагружении, там же, 62—67.
7.20. С у р к и н Р. Г., Влияние симметричной начальной неправильности на значение критического внешнего давления равномерно нагруженной сферической оболочки, сб. «Исследования по теории пластин и оболочек» 3, Казань 1965, 18-23.
422
ЛИТЕРАТУРА
7.21. Суркин Р. Г., Зуев Б. М., Степанов С. Г., К вопросу об экспериментальном исследовании устойчивости металлических сферических сегментов при динамическом нагружении равномерным внешним давлением жидкости, Тезисы докл. юбилейной научн. конф., поев, двадцатилетию Казанского физ.-техн. ин-та АН СССР, секц. мех.-матем. н., Казань, 1966; Экспериментальное исследование динамической устойчивости сферических сегментов, Прикладная механика 3, 8 1967, 124— 132; Об устойчивости сферических сегментов при ударном нагружении всесторонним внешним давлением жидкости, сб. «Исследования по теории пластин и оболочек» 5, Казань 1967, 454—468.
7.22. Теребушко О. И., Устойчивость цилиндрической оболочки при быстром нагружении осевой силой, Строит, механ. и расчет coop., 1
1960, 10—12.
7.23. Феодосьев В. И., Осесимметричная эластика сферической оболочки, Прикл. матем. и мех. 33, 2 1969, 280—286.
7.24. Ш к у т и н Л. И., О критерии динамической устойчивости пологих оболочек вращения, Теория оболочек и пластин, Труды IV Всесоюзной конференции по теории облочек и пластин Ереван, 1962, изд-во АН Арм. ССР, Ереван, 1964, 1008—1013; Устойчивость упругих оболочек вращения при внезапно приложенном давлении, Проблемы устойчивости в строительной механике, Труды Всесоюзной конференции по проблемам устойчивости в строительной механике Москва, 1963, Стройиздат, Москва, 1965, 347—354.
7.25. Ш у м и к М. А., Устойчивость цилиндрических оболочек под действием динамического радиального давления, Труды VII Всесоюзной конференции по теории оболочек и пластин., «Наука», Москва, 1969, 625—628.
7.26. A b г a h a m s о n G. R., G о о d i е г J. N., Dynamic plastic flow buckling of a cylindrical shell from uniform radial impulse, Proc. 4th U. S. National Congr. Appl. Mech., 1962, 939—950.
7.27. Archer R. R., Lange C. G., Nonlinear dynamic behavior of shallow spherical shells, AIAA Journ 3, 12 1965, 2313—2317.
7.28. Baker W. E., H u W. C., J a с k s о n T. R., Elastic response of thin spherical shells to axisymmetric blast loading, J. Appl. Mech. 33, 4
1966, 800—806.
7.29. В i e n i e k M. P., F a n Т. C., L a с k m a n L. М., Dynamic stability of cylindrical shells, AIAA Journ. 4, 3 1966, 495—500.
7.30. Cheung М. С., В a b с о с k С. D., Stability of a clamped shallow arch subjected to impulsive loading, AIAA Journ 8, 8 1970, 1434—1439.
7.31. Budiansky B., Roth R. S., Axisymmetrical dynamic buckling of clamped shallow spherical shells, Collected papers on instability of shell structures, NASA TN D-1510 1962, 597—606.
7.32. С о 11 i s M. G., On the dynamic response of an orthotropic finite cylindrical shell to an arbitrary pressure field, Journ. of sound and vibration 7, No 1 1968, 31—38.
7.33. С о p p a A. P., On the mechanism of buckling of a circular cylindrical shell under longitudinal, impact Space sciences Laboratory, General Electric 1960.
7.34. Evensen H. A., E v a n -1 w a n о w s k i R. М., Dynamic response and stability of shallow spherical shells subject to time-dependent loading, AIAA Journ. 5, 5 1967, 969—976.
7.35. Florence A. L., Buckling of viscoplastic cylindrical shells due to impulsive loading, AIAA Journ. 6, 3 1968, 532—537.
7.36. Fulton R. E., Dynamic axisymmetric buckling of shallow conical shells subjected to impulsive loads, J. Appl. Mech. 32, 1 1965, 129— 134.
7.37. Goodier J. N., M с I v о r I. K., The elastic cylindrical shell under nearly uniform radial impulse, J. Appl. Mech. 31, 2 1964.
ЛИТЕРАТУРА
423
7.38. Humphreys J. S., On dynamic snap buckling of shallow arches,
AIAA Journ. 4, N° 5 1966, 878—886.
7.39. Humphreys J. S., В о d n e r S. R., Dynamic buckling of shallow shells under impulsive loading, Journ. Engin. Mechanics, Division Proc. American Soc. Civil Engrs. 88, N° 1 1962, 17—36.
7.40. Humphreys J. S., Roth R. S., Z a 11 e r s J., Experiments on dynamic buckling of shallow spherical shell under shock loading, AIAA
Journ. 3, N° 1 1965, 33—39.
7.41. Humphreys J. S., Sve C., Dynamic buckling of cylinders under
axial shock-tube loading, AIAA Journ. 4, < 8 1966, 1477—1480.
7.42. К a p p W. A., Lemke D. G., Electromagnetic generation of high dynamic buckling pressures, AIAA Journ. 3, 9 1965, 1777—1779.
7.43. Koiter W. I., Over de stabiliteit van het elastisch evenwicht, Amsterdam, 1945; A consistent first approximation in the general theory of thin elastic shells, The theory of thin elastic shells, Proc. of the IUTAM Symposium Delft, 1959, Amsterdam, 1960;-Foundations and basic equations of shell theory. A survey of recent progress, The 2nd IUTAM Symposium, Copenhagen, 1967.
7.44. Konrad D. W., On the dynamic stability of eccentrically reinforced circular cylindrical shells, Syracuse Univ., 1967, Dissert, abstr. 28, N° 4
1967, 1556.
7.45. Kornecki A., Dynamic stability of truncated conical shells under pulsating pressure, Journ. of Technology 4, N° 1 1966, 110—120.
7.46. L i n d b e r g H. E., Buckling of a very thin cylindrical shell due to an impulsive pressure, J. Appl. Mech. 31, N° 2 1964, 267—272.
7.47. L i n d b e r g H. E., Dynamic plastic buckling of a thin cylindrical shell containing an elastic core, J. Appl. Mech. 32, N° 4 1965, 803—812.
7.48. Lock М. H., The snapping of a shallow sinusoidal arch under a step pressure load, AIAA Journ. 4, N° 7 1966, 1249—1256.
7.49. Lock М. H., Snapping and buckling under dynamic pulse load, AIAA paper, N° 69—22 1969.
7.50. Lovell E. G., M с I v о r I. K., Effect of pressurization on the cylindrical shell under nearly uniform radial impulse, J. Appl. Mech. 33, N° 2 1966, 454—455.
7.51. Lyons W. C., Elastic and plastic buckling of cylindrical shells subjected to impulsive loads, Arch. Mech. Stosowanej 1, N° 22 1970, 111— 124.
7.52. Me Ivor I. K., The elastic cylindrical shell under radial impulse, J. Appl. Mech. 33, 4 1966, 831—837.
7.53. O’N e i 11 J. P., Dynamic loading of structural models by electrostatic forces, AIAA Journ. 3, N° 3 1965, 518—520.
7.53a. Ramsey H., Vaughan H., Dynamic elastic-plastic bucking of rectangular plates in sustained flow, Quart. Appl. Math. 28, 4 1971, 473—487.
7.54. Stephens W., Fulton R. E., Axisymmetric static and dynamic buckling of spherical caps due to centrelly distributed pressures, AIAA Paper N° 68—89 1969.
7.55. S t u i v e r W., On the buckling of rings subjected to impulsive pressures, J. Appl. Mech. 32, N° 3 1965, 511—518.
7.56. Thurston G. A., A numerical solution of the nonlinear equations for axisymmetric bending of shallow spherical shells, J. Appl. Mech. 28, N° 4
1961, 557—562.
7.57. Vaughan H., L i n d b e r g H. E., Dynamic plastic buckling of sand¬
wich shells, J. Appl. Mech. 35, N° 3 1968, 539—546.
7.58. Wilkinson J. P., К a 1 n i n s A., On nonsymmetric dynamic problems
of elastic spherical shells, J. Appl. Mecfi. 32 N° 3 1965, §25—532.
424
ЛИТЕРАТУРА
7.59. W i t m e r E. A., P i a n Т. H., Balmer H. A., Dynamic deformation
and buckling of spherical shells under blast and impact loading, Collected Papers on instability of shell structures, NASA TN D-1510, 1962.
7.60. Witmer E. A., Balmer H. A., Leech J. W., P i a n Т. H., Large
dynamic deformations of beams, rings, plates and shells, AIAA Journ.
1, 8 1963, 1848—1857.
7.61. Wood L. D., К о v a 1 L. R., On the buckling of cylindrical shells under dynamic loads, AIAA Journ. 1, 1 1963, 2576—2582.
К главе VIII
8.1. А г а м и p о в В. JL, В о л ь м и р А. С., Об устойчивости цилиндрической оболочки при продольном ударе, ДАН СССР 157, 2 1964, 307—308; Поведение цилиндрических оболочек при продольном ударе, Проблемы устойчивости в строительной механике, Труды Всесоюзной конференции по проблемам устойчивости в строительной механике Москва, 1963, Стройиздат, Москва, 1965, 143—152.
8.2. Амбарцумян С. А., Некоторые вопросы развития теории анизотропных слоистых оболочек, Изв. АН Арм. ССР, серия физ.-матем. н. 17, 3 1964, 29—48; Специфические особенности теории оболочек из современных материалов. Изв. АН Арм. ССР, серия «Механика» 21, 4 1968, 3—19.
8.3. Б а г д о е в.А. Г., М о в с и с я н J1. А., К вопросу определения ударной волны в нелинейных задачах теории упругости, Изв. АН Арм. ССР, серия «Механика» 21, 3 1968.
8.3а. Б о ж и н с к и й А. Н., В о л ь м и р А. С., Пономарев А. Т., Устойчивость упругих стержней при тепловом ударе, Изв. высш. уч. зав., Машиностроение, 4 1966, 34—38.
8.4. Борисенко В. И., К л о к о в а А. И., Закритическая деформация цилиндрической оболочки при ударе, Прикл. механ: 2, 10 1966, 29—35.
8.5. Вольмир А. С., Кильдибеков И. Г., К исследованию поведения оболочек и пластинок при ударе, Изв. высш. уч. зав., Машиностроение, 7 1964, 26—30; Исследование процесса выпучивания стержней при ударе, ДАН СССР 167, 4 1966, 775—777.
8.6. Вольмир А. С., П о н о м а р е в А. Т., Динамическая устойчивость упругих систем при тепловом ударе, Доклад на Всесоюзной конф. по проблемам устойчивости в строит, мех. Каунас, 1967; Устойчивость цилиндрических оболочек при тепловом ударе, ДАН СССР 192, 4
1970, 757—759; Поведение цилиндрических оболочек из композиционных материалов при неравномерном нагреве, Механика полимеров, 2
1971, 1289—1292; Поведение стержней и цилиндрических оболочек при распространении термоупругих волн, Доклад на V Всесоюзном симпозиуме по распространению упругих и упруго-пластических волн, АлмаАта, 1971; Динамическая устойчивость оболочек при неравномерном нагреве, Прикладная механика, 1 1972, 3—9.
8.6а. Г о р д и е н к о Б. А., Экспериментальное исследование поведения стержней и цилиндрических оболочек при ударе,г Труды VII Всесоюзной конф. по теории оболочек и пластин, «Наука», Москва, 1970, 190— 193; Поведение стержней и цилиндрических оболочек при осевом ударе, канд. дисс., Москва, 1969; Выпучивание стержней при ударном нагружении, Изв. АН СССР, Механ. тв. тела, 1 1969.
8.7. Г р и г о л ю к Э. И., Уравнения трехслойных оболочек с легким заполнителем, Изв. АН СССР, Отдел, техн. н., 1, 1957, 77—84.
8.7а. Даревский В. М., Устойчивость цилиндрической оболочки при осевой динамической нагрузке, VIII Всесоюзная конференция по теории оболочек и пластин, Ростов нД, 1971.
3.8. Ильюшин А. А., Пластичность, Изд-во АН СССР, 1963.
ЛИТЕРАТУРА
425
8.9. К а ц и т а д з е О. И., Теоретическое и экспериментальное исследование ударного продольного изгиба, Труды Кутаисского с.-х. ин-та 1 1957, 151 —168; О продольном изгибе стержней при продольном ударе, Труды Грузинского ин-та субтроп, хоз-ва 5—6 1961, 284—286; Влияние эксцентриситета и предварительного прогиба на устойчивость стержней при продольном ударе, Труды Грузинского ин-та субтроп, хоз-ва 9—10 1965, 417—423 совместно с В. Д. Гогоберидзе; Об устойчивости стержней большой гибкости при продольном ударе, Строит, механ. и расчет сооруж., 4 1969, 54—55; Об устойчивости стержней при динамическом нагружении продольной следящей силой, Строит, механ. и расчет сооруж. 2 1970, 76—77.
8.9а. К и й к о И. А., Цилиндрическая оболочка, заполненная жидкостью, под действием осевой ударной нагрузки, Научные труды ин-та механики МГУ, 8 1971, 88—92.
8.96. Корнев В. М., О формах потери устойчивости упругого стержня при ударе, Журн. прикл. матем. и техн. физики, 3 1968.
8.10. Лурье А. И., Операционное исчисление и его приложение к задачам механики, Гостехиздат, Москва, 1951.
8.11. Размадзе Г. Н., Инженерные вопросы теории удара, Тбилиси, 1959; Устойчивость простой балки при синусоидальном распределении изгибающего момента, Труды Грузинского ин-та субтропич. хоз-ва 5—6
1961, 225—230.
8.12. Размадзе Г. Н., Кацитадзе О. И., О проблеме ударной продольной устойчивости, Труды Кутаисского с.-х. ин-та 2 1958, 381 — 386.
8.13. Рахматулин X. А., Д е м ь я н о в Ю. А., Прочность при интенсивных кратковременных нагрузках, Физматгиз, Москва, 1961.
8.14. Фельдштейн В. А., Упруго-пластические деформации цилиндрической оболочки при продольном ударе, Волны в неупругих средах, Кишинев, 1970, 199—204; Поведение упруго-пластической конической оболочки при продольном ударе, Труды VII Всесоюзной конф. по теории оболочек и пластинок, «Наука», Москва, 1970, 588—591.
8.15. Gerard G., В е с k е г Н., Column behavior under conditions of impact, J. Aeron. Sci. 19, 1.1952, 58—60.
8.16. Goldsmith W., Impact, London, 1960 имеется русский перевод:
Гольдсмит В., Удар, Стройиздат, Москва, 1965.
8.17. Jones I. P., Whit ter J. S., Axially symmetric motions of a twolayred Timoshenko-type cylindrical shell, J. Appl. Mech. 33, 4 1966, 838—844.
8.18. Lindberg H. E., Impact buckling of a thin bar, J Apol. Mech. 32, 2 1965, 315—322.
К главе IX
9.1. Бивин Ю. К., Исследование поведения цилиндрических и сферических
оболочек при кратковременных нагрузках, Переходные процессы де¬
формации оболочек и пластин, Таллин, 1967, 33—39.
9.2. Вольмир А. С., Нелинейные задачи теории переходных процессов деформации оболочек и проблема устойчивости, Переходные процессы деформации оболочек и пластин, Таллин, 1967, 51—66.
9.3. Вольмир А. С, Долгих Л. Н., Скурлатов Э. Д., Солоненко В. Р., Поведение цилиндрических оболочек при действии подвижных нагрузок, Труды VII Всесоюзной конференции по теории оболочек и пластинок, «Наука», Москва, 1970, 153—155.
9.4. Вольмир А. С., С к у р л а т о в Э. Д., Флаттер оболочек в кратковременном потоке газа, Теория пластин и оболочек, «Наука», Москва,
1971.
426
ЛИТЕРАТУРА
9.5. Г р и г о л ю к Э. И., Г о р ш к о в А. Г., Ш к л я р ч у к Ф. Н., Прощелкиванке цилиндрической панели под действием ударной акустической волны давления, Инж. журн., Механ. тв. тела, 1967, 5, 50—55; О воздействии ударной акустической волны на упругую цилиндрическую оболочку, Инж. журн., Мех. тв. тела, 3 1967, 60—65.
9.6. 3 а м ы ш л я е в Б. В., Яковлев Ю. С., Динамические нагрузки при подводном взрыве, «Судостроение», Ленинград, 1967.
9.7. М н е в Е. Н., Перцев А. К., Динамическая реакция окруженной жидкостью цилиндрической оболочки при воздействии осесимметричных движущихся нагрузок, IV Всесоюзная конференция по прочности и пластичности, тезисы докл., Изд-во АН СССР, Москва, 1967.
9.8. М н е в Е. Н., Реакция погруженной оболочки на волну давления, рас¬
пространяющуюся со сверхзвуковой скоростью в направлении образующей, Инж. журн., Механ. тв. тела, N° 3 1968, 119—125.
9.9. Моргаевский А. Б., О критических скоростях и устойчивости со¬
оружений, загруженных нагрузками, движущимися с большой скоростью, Проблемы устойчивости в строительной механике, Госстройиздат, Москва, 1965.
9.10. Моргаевский А. Б., О колебаниях пластины, несущей подвижную нагрузку, Прикладная механика 2, 8 1966, 64—70.
9.11. Перцев А. К., К а д а ш е в и ч Ю. И., Устойчивость погруженных в жидкость цилиндрических оболочек при кратковременных нагрузках, Труды конференции по теории пластин и оболочек, Казань, 1961, 271— 277.
9.12. Размадзе Г. Н., О флаттере панели в кратковременном потоке
газа, Труды Груз, ин-та субтроп. хоз. 2 1967, 413—419.
9.13. Скурлатов Э. Д., О поведении цилиндрических панелей и оболо¬
чек, находящихся под воздействием набегающей волны давления, Теория пластин и оболочек, «Наука», Москва, 1971, 256—261.
9.14. Скурлатов Э. Д., Экспериментальное исследование устойчивости цилиндрических оболочек при действии подвижных нагрузок, VIII Всесоюзная конференция по теории оболочек и пластин, Ростов нД, 1971.
9.15. Слеп ян Л. И., Резонансные явления в пластинках и оболочках при бегущей нагрузке, Труды VI Всес. конференции по теории оболочек и пластинок, «Наука», Москва, 1966, 690—696.
9.16. Старцева Л. П., Расчет трехслойных стеклопластиковых цилиндрических оболочек при действии движущихся нагрузок, Сб. трудов Всесоюзного заочного полит, ин-та 52 1969, 73—78.
9.17. Anderson D. L., Lindberg Н. Е., Dynamic pulse buckling of cylindrical shells under transient lateral pressure, AIAA Journ. 6, 4
1968.
9.18. В hut a P. G., Transient response of thin elastic cylindrical shell to a moving shock wave. J. Acoustical Soc. Amer. 35, 1 1963, 25—30.
9.19. Burns I. I., Popelar I. C., Foral F. R., Experimental buckling of thin shells under transient pressure pulse loadings, Launch vehicles struct, and mater, conf., Arisona, 1962.
9.20. С h a n d i r a m a n i K. L., W i d n a 11 S. E., Lyon R. H., Franken P. A., Structural response to inflight acoustic and aerodynamic environments, NASA CR 1966.
9.21. Condos E. М., Titan aerodynamic vibration analysis, The shock and vibration bull. 35 1—7, Washington 1966.
9.22. Crocker М. I., Response of aerospace vehicle skin panels to oscillating shock waves, AIAA Paper, 68—287 1968.
9.23. Hedgepeth I, Widmayer E., Dynamic and aeroelastic problems of lifting re-entry bodies, Aerospace Eng. 22, 1 1963, 148—153.
9.24. H e n s h a 11 B. D., On some aspects of the use of shock tubes in aero dynamic research, ARS Rep. and Memor., 3044, London 1957.
ЛИТЕРАТУРА
427
9.25. Herrmann G., Baker E. H., Response of cylindrical sandwich shells to moving loads, J. Appl. Mech. 34, 1 1967, 81—86.
9.26. Rayburn L., Shrouds for space payloads, Space Aeronautics 47, Jl 2, 66—73.
9.27. Williams L., Tereniak W., Noise level measurements for improved Delta Atlas, The shock and vibration bulletin 36 1967.
К главе X
10.1. Андронов А. А., П о н т p я г и н Л. С., В и т т А. А., О статистическом рассмотрении динамических систем, Журн. эксперим. и тёорет. фи¬
зики 3, 3 1933, 165-180.
10.2. Болотин В. В., Статистические методы в строительной механике,
изд. 2-е, Стройиздат, Москва, 1965.
10.3. Болотин В. В., Применение методов теории вероятностей и теории надежности в расчетах сооружений, Стройиздат, Москва, 1971.
10.4. Болотин В. В., Статистические методы в нелинейной теории упругих оболочек, Изв. АН СССР, Отдел, техн. н., 3 1958, 33—41; Некоторые обобщения теории суммирования усталостных повреждений и их приложения к анализу долговечности при действии случайных сил, Изв. высш. уч. зав., Машиностроение, 8 1959, 27—40; Об оценке долговечности при стационарных случайных нагрузках, Изв. высш. уч. зав., Машиностроение, 9 1959, 129—134; Долговечность конструкций при квазистационарных режимах напряжений, Инж. сб. 29 1960, 30—36; «Прочность и накопление повреждений при случайных нагрузках, Расчеты на прочность» 7, Машгиз, Москва 1961, 23—49; Об упругих колебаниях, возбуждаемых случайными силами с широким спектром, Изв. высш. уч. зав., Машиностроение, 4 1963, 14—31; Об оценке ресурса конструкций при действии случайных нагрузок, Расчеты на прочность 9, Машгиз, Москва 1963, 302—326.
10.5. Болотин В. В, О стационарных распределениях вероятностей в статистической динамике упругих систем, сб. «Вопросы динамики и динамической прочности» 10, Изд-во АН Латв. ССР, Рига 1963, 57—67; Акустическая усталость и родственные вопросы, сб. «Вопросы механической усталости», «Машиностроение», Москва, 1964, 167—177; Применение методов теории вероятностей в теории пластин и оболочек, Теория оболочек и пластин, Труды IV Всесоюзной конференции по теории оболочек и пластин Ереван, 1962, Изд-во АН Арм. ССР, Ереван,
1964, 15—63; Обзор исследований по статистической динамике упругих систем, Расчеты на прочность 10, «Машиностроение», Москва 1964, 211—260.
10.6. Болотин В. В., Механика твердого тела и теория надежности, Механика твердого тела, Труды II Всесоюзного съезда по теоретической и прикладной механике Москва, 1964 3, «Наука», Москва 1966, 68— 82; Стохастические краевые задачи в теории пластин и оболочек, Труды
VI Всесоюзной конференции по теории оболочек и пластинок Баку, 1966, «Наука», Москва, 996—1007; Statistical aspects in the theory of structural stability, в книге 0.241, 67—81; Статистическая динамика и теория надежности конструкций, Третий Всесоюзный съезд по теоретической и прикладной механике, аннот. докл., «Наука», Москва, 1968; Случайные колебания в упруго-акустических системах, Расчеты на прочность 13, «Машиностроение», Москва 1968, 213—230; Планирование виброизмерений на конструкциях, испытывающих случайные колебания, Изв. АН СССР, Механ. тв. тела, 1 1970, 19—27; Стохастические краевые эффекты при докритических деформациях упругих оболочек, Изв. АН СССР, Механ. тв. тела, 2 1970, 94—99.
428
ЛИТЕРАТУРА
10.7. Болотин В. В., Диментберг М. Ф., Статистические задачи колебаний и устойчивости упругих систем, в книге «Прочность, устойчивость, колебания» 3, «Машиностроение», Москва, 1968, 513—546.
10.7а. Б о л о т и н В. В., Е л и ш а к о в И. Б., Е ф и м ц о в Б. М., Москаленко В. Н., Ш а р ы й Н. В., Методика расчета случайных акустических полей внутри подкрепленных оболочек, Сб. докл. научн.-техн. конф.-Моск. энерг. ин-та, секция энергомашиностр, подсекция динамики и прочности машин, 1969.
10.8. Болотин В. В., М а к а р о в Б. П., О приближенном решении некоторых задач статистической динамики, Изв. АН СССР, серия «Механика», 3 1965, 77—83; О корреляции перемещений в тонких упругих оболочках со случайными начальными неправильностями, Проблемы надежности в строительной механике, Материалы ко II Всесоюзной конференции по проблемам надежности в строительной механике, Вильнюс, 1968, 163—168; Корреляционная теория докритических деформаций тонких упругих оболочек, Прикл. матем. и механ. 32, 3 1968, 428—434.
10.8а. Б о л о т и н В. В., Москаленко В. Н., Случайные термоупругие напряжения в оболочках, Труды VI Всесоюзной конференции по теории оболочек, «Наука», Москва, 1966, 168—176.
10.9. Вольмир А. С., Кильдибеков И. Г., Вероятностные характеристики поведения цилиндрической оболочки при действии акустической нагрузки, Прикладная механика 1, 3 1965, 1—9; Нелинейные колебания и устойчивость пологой оболочки в акустическом поле, Проблемы надежности в строительной механике, Материалы ко II Всесоюзной конференции по проблемам надежности в строительной механике, Вильнюс, 1968, 169—174.
10.9а. Вольмир А. С., Д а н и л е н к о А. Ф., Поведение цилиндрических панелей под влиянием порывов ветра, Строит, механ. и расчет сооруж., 4 1971, 66—68; Нелинейные колебания цилиндрических панелей под действием атмосферной турбулентности, Строит, механ. и расчет сооруж., 2 1972.
10.10. Ворович И. И., Статистический метод в теории устойчивости оболо¬
чек, Прикл. матем. и мех. 23, 5 1959, 885—892; Некоторые вопросы использования статистических методов в теории устойчивости пластин и оболочек, Теория оболочек и пластин, Труды IV Всесоюзной конференции по теории облочек и пластин Ереван, 1962, Изд-во АН Арм. ССР, Ереван, 1964, 64—94. 4
10.11. Гончаренко В. М., Об одном аспекте статистического метода в теории устойчивости оболочек, Теория пластин и оболочек, Труды II Всесоюзной конференции по теории пластин и оболочек Львов, 1961, Изд-во АН УССР, Киев, 1962, 368—371; Применение марковских процессов в статистической теории устойчивости оболочек, Укр. матем. журн. 14, 2 1962, 198—202; Исследование вероятности хлопка удлиненной цилиндрической панели под действием случайного давления, Прикл. матем. и мех. 26, 4 1962, 740—744; Прощелкивание панелей при наличии случайных силовых воздействий, Теория оболочек и пластин, Труды- IV Всесоюзной конференции по теории оболочек и пластин Ереван, 1962, Изд-во АН Арм. ССР, Ереван, 1964, 383—390; О динамических задачах статистической теории устойчивости упругих систем, Проблемы устойчивости в строительной механике, Труды Всесоюзной конференции по проблемам устойчивости в строительной механике Москва, 1963, Стройиздат, 1965, 210—216; О влиянии рассеяния энергии в материале на колебания упругого элемента при случайном возбуждении. Прикладная механика 2, И 1966, 90—96; Колебания пластин из нелинейного упругого материала в однородном поле случайных давлений, Проблемы надежности в. строительной механике, Ма¬
ЛИТЕРАТУРА
429
териалы ко II Всесоюзной конференции по проблемам надежности в строительной механике, Вильнюс, 1968, 229—234.
10.11 а. Гончаренко В. М., Е г у н о в а С. П., Некоторые задачи о нелинейных колебаниях пластин при одновременном действии гармонической и случайной нагрузки, Труды VI Всесоюзной конференции по теории оболочек и пластинок Баку, 1966, «Наука», Москва, 1966, 277— 283.
10.12. Диментберг М. Ф., Вынужденные колебания пластин при нагрузке, представляющей собой пространственно-временной случайный процесс, Инж. журн. 1, 2 1961, 97—105; О нижней оценке долговечности при стационарных случайных напряжениях, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 5 1962, 167—170; Вынужденные колебания панелей при случайных нагрузках, Теория пластин и оболочек, Труды II Всесоюзной конференции по теории пластин и оболочек Львов, 1961, Изд-во АН УССР, Киев, 1962, 270—273; Нелинейные колебания упругих панелей при случайных воздействиях, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 5 1962; О нелинейных колебаниях упругих оболочек при случайных нагрузках, Теория оболочек и пластин, Труды IV Всесоюзной конференции по теории оболочек и пластин Ереван, 1962, изд-во АН Арм. ССР, Ереван, 1964, 437—444; Некоторые задачи устойчивости оболочек, находящихся под действием случайных возмущений, Проблемы устойчивости в строительной механике, Труды Всесоюзной конференции по проблемам устойчивости в строительной механике Москва, 1963, Стройиздат, Москва,
1965, 217—222; Колебания нелинейной системы с одной степенью свободы при действии периодической силы и изменении собственной частоты по периодическому закону, Инж. журн., Механ. тв. тела, 4 1966, 176—178; Исследование нелинейной стохастической системы методом регулируемых автоколебаний, Инж. журн., Механ. тв. тела, 5
1968.
10.13. Ел ишаков И. Б., О вычислении спектральных плотностей внешних сил для пластин и оболочек, Проблемы надежности в строительной механике, Материалы к III Всесоюзной конференции по проблемам надежности в строительной механике, Вильнюс, 1971, 37—44; Случайные колебания круговых цилиндрических оболочек, содержащих акустическую среду, VIII Всесоюзная конференция по теории оболочек и пластин, Ростов-на-Дону, 1971.
10.14 Е л и ш а к о в И. Б., X р о м а т о в В. Е., О колебаниях панелей в сверхзвуковом потоке при случайных воздействиях, Изв. АН СССР, Механ. тв. тела, 1 1971, 54—58; Влияние скорости набегающего сверхзвукового потока на поведение панелей, находящихся в поле случайных сил, Динамика и прочность машин, Труды Моск. энерг. ин-та 74, 1970.
10.15. Кильдибеков И. Г., Устойчивость и нелинейные колебания цилиндрической оболочки, находящейся под действием акустического давления, Всесоюзная конференция по проблемам устойчивости в строительной механике Каунас, 1967, Тезисы докл., Вильнюс, 1967; Нелинейные колебания круговой цилиндрической оболочки при действии осевого сжатия и акустического давления, Проблемы надежности в строительной механике, Материалы к III Всесоюзной конференции по проблемам надежности в строительной механике, Вильнюс, 1971, 58—63.
10.16. Колмогоров А. Н., Об аналитических методах в теории вероятностей, Успехи матем. н. 5 1938, 5—41.
10.16а. Левин Б. Р., Теоретические основы статистической радиотехники, 1,
2-е изд. 1969; 2 1968, изд-во «Советское радио», Москва.
10.17. Ломакин В. А., Статистические задачи механики твердых деформируемых тел, «Наука», Москва, 1970.
430
ЛИТЕРАТУРА
10.18. Макаров Б. П., Применение статистического метода для анализа нелинейных задач устойчивости оболочек, Теория пластин и оболочек, Труды II Всесоюзной конференции по теории пластин и оболочек Львов, 1961, Изд-во АН УССР, Киев, 1962, 363—367; Случайные несовершенства в тонких оболочках и их влияние на прочность и устойчивость, Третий Всесоюзный съезд по теоретической и прикладной механике, аннот. докл., «Наука», Москва, 1968; Статистический анализ устойчивости несовершенных цилиндрических оболочек, Труды VII Всесоюзной конференции по теории оболочек и пластинок Днепропетровск, 1969, «Наука», Москва, 1970, 387—391; Послекритические деформации неидеальных сферических оболочек, Проблемы надежности в строительной механике, Материалы к III Всесоюзной конференции по проблемам надежности в строительной механике, Вильнюс, 1971, 90—93.
10.18а. М а к а р о в Б. П., Ч е ч е н е в Н. А., О прощелкивании тонких упругих панелей при случайных импульсных нагрузках, Расчеты на прочность 11, «Машиностроение», Москва 1965, 378—384.
10.19. Николаенко Н. А., Вероятностные методы динамического расчета машиностроительных конструкций, «Машиностроение», Москва, 1967.
10.20. Пугачев В. С., Теория случайных функций и ее применение к задачам автоматического управления, Физматгиз, Москва, 1960.
10.20а. П у г а ч е в В. С., Статистические методы в технической кибернетике, изд-во «Советское радио», Москва, 1971.
10.21. Ржа ниц ын А. Р., Статистический метод определения допускаемых напряжений при продольном изгибе, Госстройиздат, Москва, 1951; Определение коэффициента безопасности при изменяющихся во времени случайных нагрузках и прочности, Проблемы надежности в строительной механике, Материалы к III Всесоюзной конференции по проблемам надежности в строительной механике, Вильнюс, 1971, 143—150.
10.22. Федоров Ю. А., Колебания замкнутой цилиндрической оболочки в поле случайных акустических давлений, Изв. АН СССР, Отдел, техн. н., Механ. и машиностр., 1 1963; О нелинейных колебаниях прямоугольной пластинки под воздействием случайных сил. Инж. журн. 4, 3 1964, 523—532.
10.23. А г i а г a t n a m S. Т., Random vibrations of nonlinear suspensions, J. Mech. Eng. Sci. 2, 3 1960.
10.24. Ballentine J. R., Sonic proof testing B-58 weapons system, SAE preprint, 355A, 1961.
10.25. Belcher P. М., Use of a high-intensity siren in fatigue testing of structures subjected to acoustic forcing, J. Acoust. Soc. Amer. 29, 1 1957, 176.
10.25a. В e 1 с h e г P. М., V a n Dyke I. D., Eshleman A. L., Development structure to withstand acoustic loads, Aero-Space engineering 18, 6 1969.
10.26. Bingman R. N., Resonant fatique failures associated with noise, SAE preprint, 164 В 1960.
10.27. Callaghan E. E., Howes W. L., Colls W. D., Near noise field of a jet engine exhaust 1 — Cross correlation of sound pressures, NASA TN 3764 1956, Appl. Mech. Rev. 10 1957, 919.
10.28. Caughey Т. K-, Derivation and application of the Focker-Planck equation to discrete nonlinear dynamic systems, subjected to white random excitation, J. Acoust. Soc. Amer. 35, 11 1963.
10.29. Clarkson B. L., Stresses produced in aircraft structures by jet engine, Journ. Roy. Aeronaut. Soc. 61, 554 1957; The effect of jet noise on aircraft structures, Aeronaut. Quart. 10, p. 2 1959; Effects of noise on structures and human beings, Techn. aspects of sounds 3, Amsterdam, 1962; The design of structures to resist jet noise fatigue, J. Roy. Aeronaut. Soc. 66, 622 1962, 603—616 имеется русский перевод;
ЛИТЕРАТУРА
431
Кларксон Б. JL, Проектирование конструкций, способных хорошо сопротивляться усталости от шума ракетных двигателей, сб. «Механика», 5 1963, Изд-во иностр. лит., Москва, 25—61.
10.30. Clarkson В. L., F о г d R. D., Random excitation of a tailplane section by jet noise, J. Roy. Aeronaut. Soc. 65, 608 1961; The response of a typical aircraft structure to jet noise, J. Roy. Aeronaut. Soc. 66, 613 1962.
10.31. Crandall S. H., Random vibration 1 1958; 2 1963; Massachusetts имеется русский перевод второго тома: Кренделл С., Случайные колебания, «Мир», Москва, 1967; Случайные колебания систем с нелинейными восстанавливающими силами, Симпозиум по нелинейным колебаниям, Ин-т матем. АН УССР, Киев, 1961; Random vibration of a nonlinear system with a set-up spring, Journ. Appl. Mech. 29, 3
1962, 477—482.
10.32. Dyer I., Estimation of sound-induced missile vibration, в книге 10.31, 9.1—9.50.
10.33. Dyer I., F r a n k e n P. A., U n g a r E. E., Noise environements of flight vehicles, Noise Control 6, 1 1960.
10.34. Franklin R. E., Space-correlations in the fluctuating pressure field near a jet engine, J. Roy. Aeron. Soc. 65, 610 1961.
10.35. Goodman L. E., Rattayya J. V., Review of panel flutter and effects of aerodynamic noise, p. II, Structural effects of aerodynamic noise, Appl. Mech. Rev. 13, 2 1960, 81—87 имеется русский перевод: Гудмэн Л., Раттайя И., Обзор литературы по флаттеру панели и влиянию аэродинамического шума, ч. И, Влияние аэродинамического шума на конструкцию, сб. «Механика», 5 1960, Изд-во иностр. лит., Москва, 135—152.
10.36. Hogan A. W., Acoustical fatigue facility, Missile design and development 5, 10 1959.
10.37. Hubbard H. H., H e s s R. W., Some comparisons of the response of simple panels to random and discrete noise, J. Acoust. Soc. Amer. 29, No 1 1957, 176.
10.38. Hubbard H. H., M a g 1 i e r i D. J., Noise considerations in the design and operation of the supersonic transport, Noise Control 7, 4
1961.
10.39. Keast D. N., Measurement of rocket engine noise, Noise Control 7, 2 1961.
10.40. Kennard D. C., Sonic vibration as exemplified by the RB-66B airplane, J. Acoust. Soc. Amer., 5 1958.
10.41. Kowalewski J., On the relation between fatigue lives under random loading and under corresponding program loading, Full-scale fatigue testing of aircraft structures, Oxford, 1961.
10.42. Lassiter L. W., Hess R. W., Hubbard H. H., An expiremental study of the response of simple panels to intense acoustic loading, J. Aeronaut. Sci. 24, 1 1957.
10.43. L i g h t h i 11 M. J., On sound generated aerodynamically, Proc. Roy. Soc. A211, 1952; A222, 1954; Jet noise, AIAA Journ. 1, 7 1963, 1507—1517; Распространение теории шума струй на струи, в том числе ракетные, при больших сверхзвуковых скоростях, Второй Всесоюзный съезд по теоретической и прикладной механике, аннот. докл., «Наука», Москва, 1964.
10.44. Lin Y. К-, Response of a nonlinear flat panel to periodic and randomlyvarying loadings, Journ. Aerospace Sci. 29, 9 1962, 1029—1033; Probability distributions of stress peaks in linear and nonlinear structures, AIAA Journ. 1, No 5 1963, 1133—1138.
10.45. Lin Y. K-, Probabilistic theory of structural dynamics, 1967.
432
ЛИТЕРАТУРА
10.46. Lyon R. H., On the vibration statistics of a randomly excited hardspring oscillator, J. Acoust. Soc. Amer. 32, 9 1960.
10.47. Lyon R. H., Random noise and vibration in space vehicles, 1967.
10.48. Maestrello L., Design criterion for minimum structure response and sound radiation of a panel excited by a turbulent boundary layer, AIAA 5th Aerospace Sciences Meeting, 1967; Radiation from and panel response to a supersonic turbulent boundary layer, J. of Sound and Vibration 10, No. 2 1969, 261—295.
10.49. Mayes W. H., Some near- and far-field noise measurements for rocket engines operating at different nozzle pressure ratios, J. Acoust. Soc. Amer. 31, 7 1959, 1013—1015.
10.50. Mead D. J., A note on the useof sandwich structures in severe acoustic environments, Univ. of Southampton, Rep. 145 1960.
10.51. Meltzer E. C., Stewart D. A., Acoustic and pverpressure design considerations as related to missile ground systems, J. Envir. Sci. 7, 6
1964.
10.52. Miles J. W., On structural fatigue under random loading, Journ. Aeronaut. Sci. 21, 11 1954; J. Acoust. Soc. Amer. 29, 1 1957, 176.
10.53. Powell A., On the fatigue failure of structures due to vibrations excited by random pressure fields, J. Acoust. Soc. Amer. 30, 12 1958, 1130—1135.
10.54. Rice S. O., Mathematical analysis of random noise, Bell system technical Journ. 23, No. 3 1944, 282—332; 24, > 1 1945, 46—156 имеется русский перевод: Райс С., Теория флуктуационных шумов, сб. «Теория передачи электрических сигналов при наличии помех», Изд-во иностр. литер., Москва, 1953, 88—238.
10.55. Richards Е. J., Mead D. J., Noise and acoustic fatigue in aeronautics, London, 1968.
10.56. Reed W. S., Laboratory to investigate sonic fatigue, Aviation Week and Space Technology 73, 1 1960.
10.57. R e g i e r A. A., H u b b a r d H. H., Response of structures to high in¬
tensity noise, Noise Control 5, 5 1959.
10.58. Schj elder up H. C., Structural acoustic proof testing, Noise Con¬
trol 5, No 6 1959.
10.59. Sobszyk K., Random vibrations in homogenous elastic systems, Proc. Vibr. Problems 4, 11 1970, 369—384.
10.60. Symposium on acoustical fatique, ASTM, Special Technical publication, No 284 1961.
10.61. Ted rick R. N., D о r 1 a n d W. D., Noise problems associated with
testing large vehicles, Aviation week 77, 19 1962.
10.62. Trapp W. J., Forney D. М., Acoustical fatigue in aerospace struc¬
tures, Proc. of the 2nd Intern. Congress, Syracuse, 1965.
10.63. Wiener F. М., Rocket noise of large space vehicles, 4th Intern. Congress on acoustics, Copenhagen, 1962.
10.64. Willmarth W. W., Wall pressure fluctuations in a turbulent boundary layer, J. Acoust. Soc. Amer. 28, 6 1956, 1048—1053.
10.65. Wolfe М., The structural aspects of jet noise, J. Roy. Aeron. Soc. 61,
554 1957.
10.66. Wolff H., Barnes L. Т., Survey of special areas of rocket testing, AIAA Paper, 65—476 1965.
10.67. Zien T. F., Reshotko E., Boundary-layer induced pressures, AIAA
Journ. 8, No 1 1970.