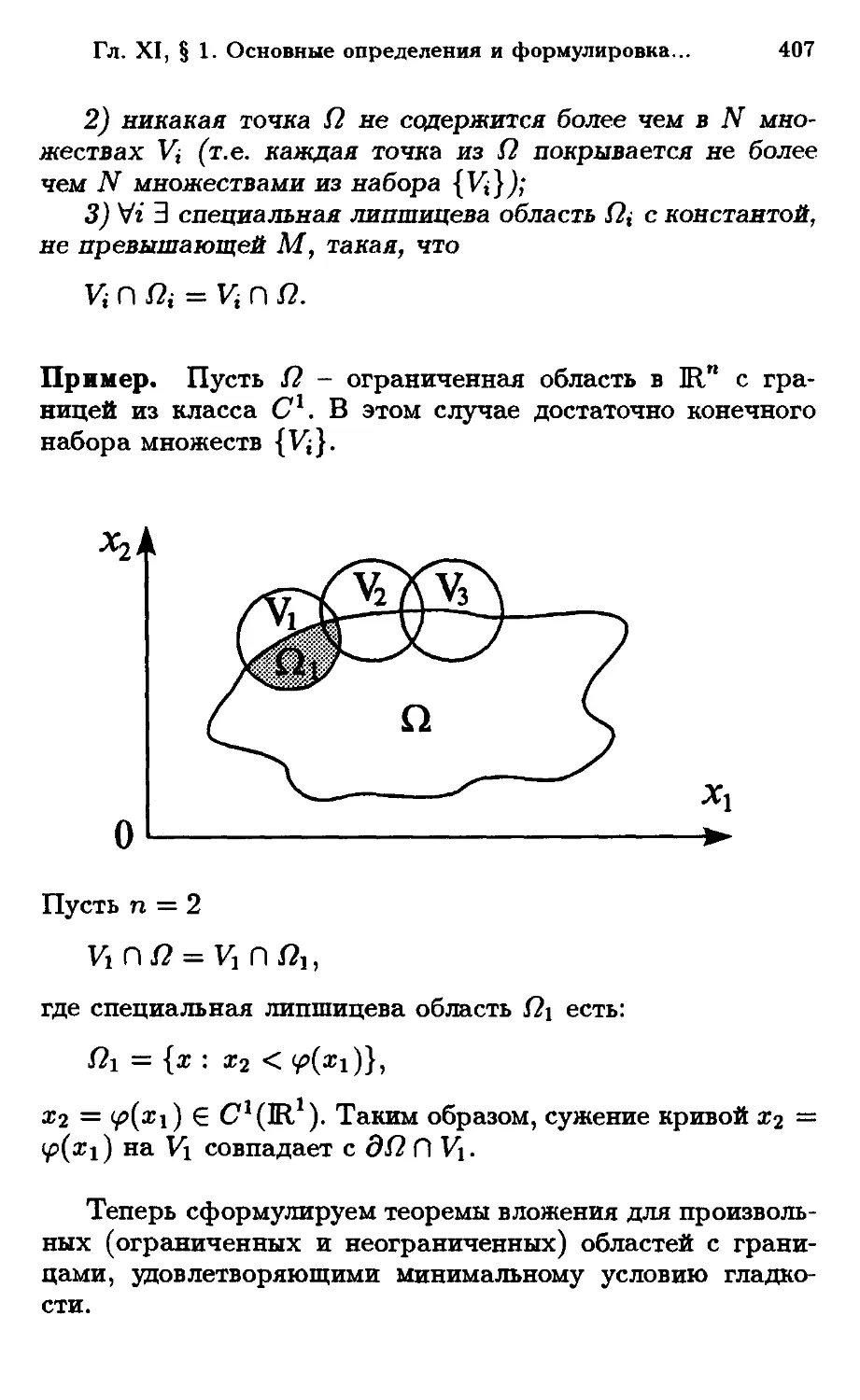
Автор: Масленникова В.Н.
Теги: математический анализ функциональный анализ высшая математика дифференциальные уравнения
ISBN: 5-209-00847-9
Год: 1997
Текст
В.Н. Масленникова
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
Рекомендовано Министерством общего и про-
профессионального образования Российской Федерации в ка-
качестве учебника для студентов высших учебных заведе-
заведений, обучающихся по направлениям "Математика",
"Прикладная математика и информатика", "Математика,
прикладная математика", специальностям "Математика",
"Прикладная математика"
Москва
Издательство Российского университета дружбы народов
1997
ББК 22.161.62 Утверждено
М 31 РИС Ученого совета
Российского университета
дружбы народов
Рецензенты:
док. физ.-мат. наук, проф. В.П.Глушко,
док. физ.-мат. наук, проф. А.А.Дезин
М 31 Масленникова В.Н.
Дифференциальные уравнения в частных производных:
Учебник. - М.: Изд-во РУДН, 1997. - 447 с.
ISBN 5-209-00847-9
Учебник написан на основе лекций, читаемых автором на факуль-
факультете физико-математических и естественных наук Российского универ-
университета дружбы народов.
В книге отражены следующие темы: выводы основных уравнений
математической физики и гидродинамики; общая теория дифферен-
дифференциальных уравнений в частных производных, включая теорему Кова-
Ковалевской, характеристики, классификацию уравнений и систем; даны
основы теории обобщенных функций и пространств Соболева, с ис-
использованием которых изучены задачи Коши, краевые и начально-
краевые задачи, в том числе задача на собственные значения для эл-
эллиптического уравнения второго порядка с переменными коэффици-
коэффициентами. Изложены приближенный метод Галеркина и свойства гармо-
гармонических функций. Последняя глава посвящена общим теоремам вло-
вложения для пространств Соболева. Книга написана на современном
уровне, сочетающимся с доступностью изложения, для студентов уни-
университетов, обучающихся по специальностям "Математика", "Прикла-
"Прикладная математика", "Информатика и прикладная математика". Учеб-
Учебник полезен также для физических специальностей.
ISBN 5-209-00847-9 ББК 22.161.62
©В.Н. Масленникова, 1997 г.
ОГЛАВЛЕНИЕ
Введение 16
ГЛАВА I. ПОСТАНОВКА КРАЕВЫХ ЗАДАЧ ДЛЯ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 1. Введение. Основные определения 19
1. Суть предмета 19
2. Основные определения в теории урав-
уравнений с частными производными ... 20
3. Примеры уравнений в частных
производных 22
4. Из истории предмета 23
§ 2. Некоторые математические модели
физических процессов 25
1. Вывод уравнения теплопроводности;
граничные и начальные условия .... 25
2. Вывод уравнения равновесия
мембраны и граничных условий .... 32
3. Вывод уравнения колебаний мембраны.
Начальные и граничные условия ... 38
4. Частная и полная производные вектора
и скаляра. Вывод уравнения
неразрывности сплошной среды .... 40
5. Уравнения движения сплошной
среды 44
6. Вывод уравнения звуковых волн
(волнового уравнения) 48
§ 3. О постановке краевых задач
математической физики 49
4
ГЛАВА II. НЕКОТОРЫЕ ВОПРОСЫ
ОБЩЕЙ ТЕОРИИ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 1. Задача Коши. Теорема Ковалевской 52
1. Определение системы типа
Ковалевской. Примеры. Постановка
задачи Коши для общей нелинейной
системы уравнений в частных
производных типа Ковалевской .... 52
2. Определение аналитической функции
многих действительных переменных.
Формулировка теоремы Ковалевской
о единственности и локальной разре-
разрешимости задачи Коши в классе
аналитических функций для нели-
нелинейных систем типа Ковалевской ... 53
3. Доказательство теоремы Ковалевской
для линейных систем первого
порядка 54
а. Доказательство единственности
аналитического решения 56
б. Мажоранты аналитической функции
и их построение 58
в. Доказательство существования ана-
аналитического решения; неравенства
между коэффициентами данной и
мажорирующей систем; построение
явного решения мажорирующей
системы С1
4. Некоторые замечания к теореме
Ковалевской 6G
г. Об области существования
аналитического решения 66
д. Пример уравнения теплопровод-
теплопроводности, для которого не существует
аналитического решения задачи
Коши в окрестности точки 66
е. Примеры локально неразрешимых
уравнений 67
§ 2. Задача Коши с начальными данными на
произвольной поверхности. Возможность ее
сведения к задаче Коши с начальными
данными на гиперплоскости 68
§ 3. Характеристики и характеристические
направления. Особенности постановки
задачи Коши с начальными данными на
характеристиках 76
1. Определение характеристической
поверхности (характеристики) для
уравнения в частных производных.
Примеры 76
2. Особенности постановки задачи
Коши с начальными данными
на'характеристиках 79
3. Характеристические направления.
Определение характеристик с помощью
характеристических направлений.
Примеры 81
4. Характеристики и характеристические
направления для линейных
систем произвольного порядка 84
§ 4. Классификация уравнений и систем уравнений
в частных производных. Определение эллипти-
эллиптических, гиперболических и параболических
по Петровскому линейных уравнений и
систем произвольного порядка. Системы
эллиптические по Дугласу - Ниренбергу.
Примеры 85
§ 5. Приведение уравнения второго порядка от
многих независимых переменных к канони-
каноническому виду в фиксированной точке.
Классификация 100
§ 6. Приведение уравнения второго порядка на
плоскости к каноническому виду. Еще раз
о типах уравнений 107
§ 7. Преобразования Фурье и Лапласа.
Определение пространства S. Преобразо-
Преобразование Фурье функций из 5 114
§ 8. Определение корректности постановки
задачи Коши 118
§ 9. Условие некорректной постановки задачи
Коши в терминах корней характеристичес-
характеристического многочлена. Лемма об эйспоненциальном
решении. Определение обобщенно однород-
однородного многочлена. Основная теорема.
Примеры 120
ГЛАВА III. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ
ТЕПЛОПРОВОДНОСТИ. ОБОБЩЕННЫЕ
ФУНКЦИИ И ИХ ПРИМЕНЕНИЕ
К ИССЛЕДОВАНИЮ РЕШЕНИЯ
7
§ 1. Решение задачи Коши для уравнения
теплопроводности методом преобразо-
преобразования Фурье с начальными данными из S.
Преобразование Фурье на L\{R )
и на Z,2(JT) 130
§ 2. Понятие обобщенной функции, ее физический
смысл. Определение ^-функции Дирака.
Пространство основных функций V и
пространство обобщенных функций ТУ .... 134
§ 3. Определение пространства обобщенных
функций S'. Преобразование Фурье
обобщенных функций из 5' 138
§ 4. Свертка двух функций: /(ж) € S, д(х) € С&.
Теорема о свертке 140
§ 5. Применение теоремы о свертке к решению
задачи Коши для уравнения теплопровод-
теплопроводности. Вычисление ядра Пуассона 142
§ 6. Свойства ядра Пуассона 146
§ 7. Решение задачи Коши для уравнения тепло-
теплопроводности с непрерывной ограниченной
начальной функцией 149
§ 8. Задача Коши для неоднородного уравнения
теплопроводности. Принцип Дюамеля 153
§ 9. Принцип максимума для решения урав-
уравнения теплопроводности 155
1. Принцип максимума для ограниченной
области. Следствия: единственность
решения первой начально-краевой
задачи и непрерывная зависимость его
от краевых и начальных значений .. 155
2. Принцип максимума для полосы.
Следствия: единственность решения
задачи Коши и непрерывная зависимость
его от начальных данных. Корректность
постановки задачи Коши для уравнения
теплопроводности 157
ГЛАВА IV. ЗАДАЧА КОШИ ДЛЯ ВОЛНОВОГО
УРАВНЕНИЯ. ПРИМЕНЕНИЕ
ОБОБЩЕННЫХ ФУНКЦИЙ
К ИССЛЕДОВАНИЮ РЕШЕНИЯ
§ 1. Вывод энергетического неравенства
для волнового уравнения. Следствия:
теорема единственности решения
задачи Коши и непрерывная зависимость
его от начальных данных; область
единственности 162
§ 2. Решение задачи Коши для волнового
уравнения при начальных данных,
принадлежащих пространству S 170
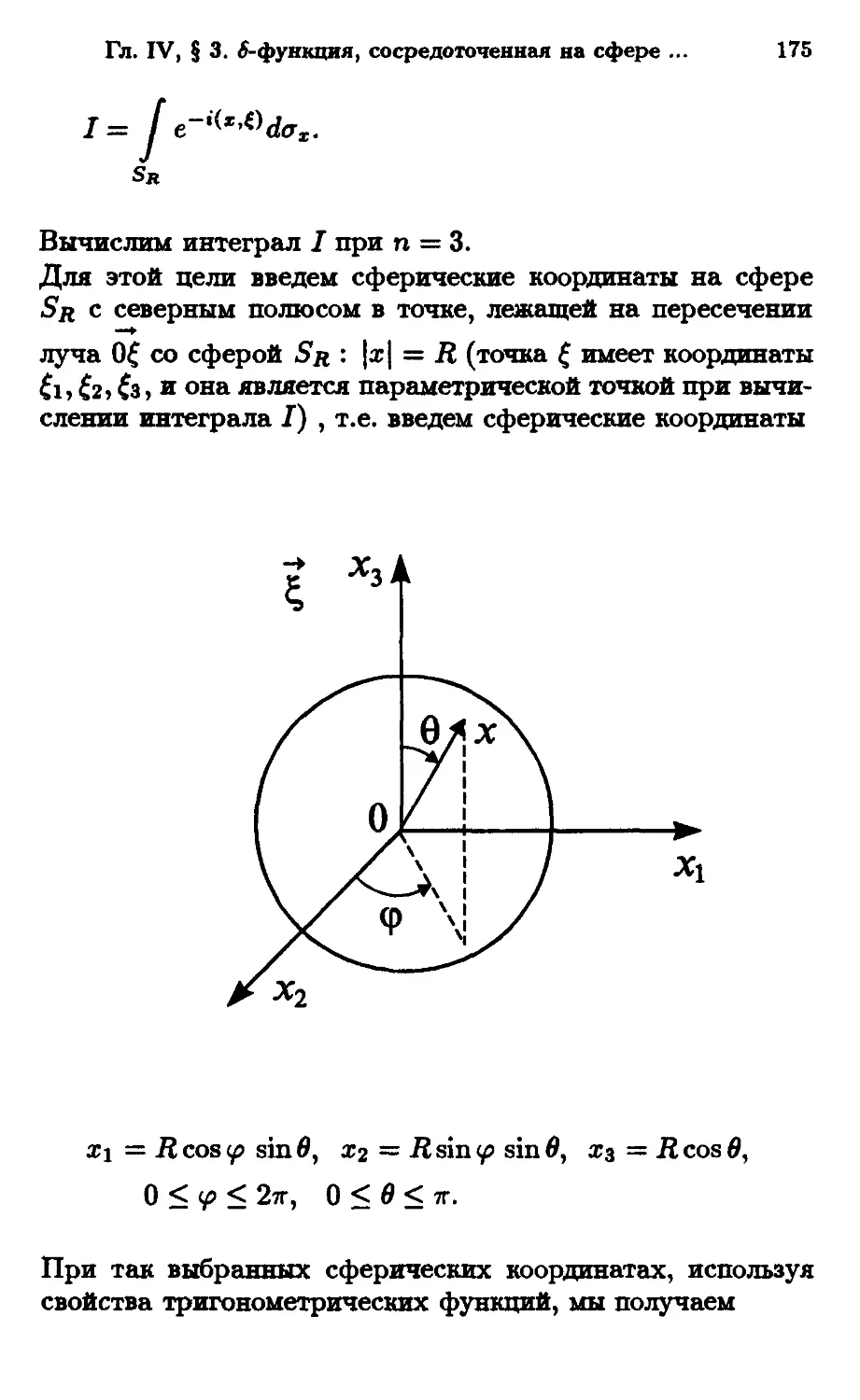
§ 3. ^-функция, сосредоточенная на сфере.
Преобразование Фурье ^-функции,
сосредоточенной на сфере. Теорема о свертке
обобщенной функции из 5" с компактным
носителем и функции из 5 173
§ 4. Вывод формулы Кирхгофа для решения
задачи Коши для волнового уравнения
в случае трех пространственных
переменных 179
§ 5. Вывод формулы Пуассона для решения задачи
Коши для волнового уравнения в случае двух
пространственных переменных. Метод спуска.
Формула Даламбера для уравнения колебания
струны 185
§ G. Корректность постановки задачи Коши
для волнового уравнения 189
§ 7. Решение задачи Коши для неоднородного
волнового уравнения 190
§ 8. Фундаментальное решение (функция Грина)
задачи Коши для волнового уравнения 192
§ 9. Качественные свойства решения задачи
Коши для волнового уравнения. Распро-
Распространение волн 197
1. Область зависимости решения
задачи Коши. Конечность скорости
распространения возмущений.
Область влияния 197
2. Распространение волн в случае трех
пространственных переменных.
Принцип Гюйгенса 198
3. Распространение волн на плоскости
и в случае одного пространственного
переменного. Диффузия волн 199
ГЛАВА V. ОСНОВНЫЕ НАЧАЛЬНО-КРАЕВЫЕ
ЗАДАЧИ ДЛЯ НЕСТАЦИОНАРНЫХ
УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ
ФИЗИКИ. МЕТОД РАЗДЕЛЕНИЯ
ПЕРЕМЕННЫХ
(предварительные рассмотрения)
Введение 201
§ 1. Начально-краевые задачи для гипер-
гиперболического уравнения второго
10
порядка. Энергетические оценки.
Интеграл энергии. Теоремы единст-
единственности и непрерывной зависимости 202
§ 2. Метод разделения переменных (метод Фурье)
для уравнения колебания струны. Сходи-
Сходимость рядов, определяющих классическое
решение 212
§ 3. Начально-краевые задачи для пара-
параболического уравнения второго порядка.
Энергетическая оценка. Теоремы единст-
единственности и непрерывной зависимости 224
§ 4. Метод разделения переменных для
решения первой начально-краевой
задачи для уравнения теплопро-
теплопроводности; сходимость рядов, опре-
определяющих классическое решение 228
§ 5. Метод Фурье для уравнений с пере-
переменными коэффициентами. Предвари-
Предварительные рассмотрения 231
§ 6. О линейных ограниченных и неогра-
неограниченных опраторах в гильбертовом
пространстве 233
ГЛАВА VI. ОБОБЩЕННЫЕ ПРОИЗВОДНЫЕ,
ПРОСТРАНСТВА СОБОЛЕВА,
ОБОБЩЕННЫЕ РЕШЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Обобщенные решения дифференциальных
уравнений. Два способа введения
обобщенного решения 239
11
§ 2. Обобщенные производные в смысле
Соболева и их основные свойства 243
§ 3. Пространство Соболева W%{ft) и
его полнота 253
§ 4. Пространство Соболева WJ,(ft) 256
о
§ 5. Пространство Соболева W\(ft) и его
эквивалентная нормировка. Неравенство
Фридрихса 257
§ 6. Средние функции, их свойства: бесконечная
дифференцируемость, сходимость в норме Lp,
перестановочность операций дифференци-
дифференцирования и усреднения. Ядро усреднения
и его свойства 263
§ 7. Граничные свойства функций из прост-
о
ранств Соболева W\(ft) и ^(/2).
Формула интегрирования по частям 270
§ 8. Основные понятия о продолжении функций
из пространств Соболева на более ши-
широкую область с сохранением класса 280
§ 9. Неравенство Пуанкаре 283
§ 10. Компактность вложения ограниченного
множества Из W% (ft) в L2(ft) 284
§ 11. Обобщенные решения основных краевых
задач для эллиптического уравнения
второго порядка 288
ГЛАВА VII. ЗАДАЧИ НА СОБСТВЕННЫЕ
ЗНАЧЕНИЯ И МЕТОД ФУРЬЕ
(продолжение)
В ПРОСТРАНСТВАХ СОБОЛЕВА
12
§ 1. Задачи на собственные значения для эллип-
эллиптического уравнения. Обобщенные собственные
функции задач Дирихле, Неймана и третьей
краевой задачи. Сведение задач на собст-
собственные значения к операторному уравнению
с самосопряженным вполне непрерывным
оператором 300
§^2. Свойства собственных значений и
обобщенных собственных функций для
эллиптического оператора. Основная
теорема , 308
§ 3. Вариационный принцип собственных
значений и собственных функций. О точной
постоянной в неравенстве Фридрихса 316
§ 4. Обоснование метода Фурье для гипер-
гиперболического уравнения в пространстве
Соболева 319
ГЛАВА VIII. МЕТОД ГАЛЕРКИНА ДЛЯ
НАХОЖДЕНИЯ
ПРИБЛИЖЕННЫХ РЕШЕНИЙ
§ 1. Метод Галеркина для приближенного
обобщенного решения задачи Дирихле
для уравнения Пуассона 330
§ 2. Метод Галеркина для приближенного ре-
решения первой начально-краевой задачи для
уравнения теплопроводности. Теорема
единственности обобщенного решения 337
13
ГЛАВА IX. ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
И ФУНКЦИЯ ГРИНА
§ 1. Определение фундаментального решения
для произвольного линейного дифферен-
дифференциального уравнения и его построение
методом преобразования Фурье. Фундамен-
Фундаментальное решение для оператора Лапласа . . 348
§ 2. Решение дифференциальных уравнений с
постоянными коэффициентами во всем
пространстве в виде свертки с помощью
фундаментального решения 352
§ 3. Формула Грина для оператора Лапласа . . . 354
§ 4. Функция Грина в задаче Дирихле для
оператора Лапласа. Представление решения
задачи Дирихле для уравнения Пуассона
через функцию Грина. Ньютонов потенциал,
потенциалы простого и двойного слоя.
Свойства функции Грина 355
ГЛАВА X. ГАРМОНИЧЕСКИЕ ФУНКЦИИ
И ИХ СВОЙСТВА
§ 1. Примеры и физический смысл
гармонических функций 362
§ 2. Слабый принцип максимума для гармо-
гармонических функций и его следствия 363
§ 3. Лемма Жиро (о знаке производной в
граничной точке для гармонической
в шаре функции) 366
§ 4. Строгий принцип максимума для гармо-
гармонических функций и его следствия 370
14
§ 5. Теорема о знаке производной в гра-
граничной точке гармонической в области
функции и ее следствия (теоремы
единственности) 372
§ б. Дальнейшие свойства гармонических функ-
функций: теорема о потоке тепла, необходимое
условие разрешимости задачи Неймана для
уравнения Лапласа и Пуассона, теоремы о
среднем по сфере и шару, бесконечная
дифференцируемость гармонических
функций внутри области 375
§ 7. Вывод формулы Пуассона для решения
задачи Дирихле для уравнения Лапласа
в шаре с непрерывной граничной
функцией 381
§ 8. Свойства гармонических функций: теорема
Гарнака о равномерно сходящейся после-
последовательности гармонических функций,
неравенства Гарнака, теорема Лиувилля и
теорема об устранимой особенности 388
§ 9. Внешние краевые задачи для уравнения
Лапласа 392
1. Постановка внешней задачи
Дирихле в случае тг > 3, теорема
единственности 393
2. Постановка внешней задачи
Дирихле в плоском случае 395
3. Сведение решения внешней зада-
задачи Дирихле к решению задачи
Дирихле для ограниченной облас-
области. Преобразование Кельвина 395
15
4. Внешняя задача Неймана 401
ГЛАВА XI. ДОПОЛНЕНИЕ. ОБЩИЕ ТЕОРЕМЫ
ВЛОЖЕНИЯ ДЛЯ КЛАССОВ
ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ
МНОГИХ ПЕРЕМЕННЫХ
§ 1. Основные определения и форму-
формулировка основных теорем вложения 404
§ 2. Вспомогательные теоремы о продолжении
функций с Q на все R и о плотности
финитных функций C°°{Rn) в WJ,(Rn) ... 411
§ 3. Теоремы вложения для дифференци-
дифференцируемых функций, заданных во всем
пространстве R 416
1. Формулировка теорем вложения .... 416
2. Бесселевы потенциалы 418
3. Доказательство теорем вложения для
функций многих переменных,
заданных во всем пространстве .... 426
§ 4. Доказательство теорем вложения для
функций, заданных в области 435
Литература 438
Предметный указатель 441
16 Предисловие
Предисловие
Книга написана на основе лекций, читаемых автором бо-
более 20 лет студентам специальностей "Математика. При-
Прикладная математика", "Прикладная математика и инфор-
информатика" в Российском университете дружбы народов. На-
Начиная с этих лекций и предлагаемой книги, студенты зна-
знакомятся с богатой идеями и важной областью математики -
дифференциальными уравнениями в частных производных,
их простейшими приложениями, с классическими и совре-
современными методами решения краевых задач.
Книга начинается с очень подробного оглавления, кото-
которое вводит читателя в круг рассматриваемых в ней задач и
методов.
Первая глава посвящена выводам основных математиче-
математических моделей физических процессов: уравнений теплопро-
теплопроводности, равновесия и колебаний мембраны, уравнений не-
неразрывности сплошной среды, звуковых волн, а также осно-
основных нелинейных систем гидродинамики.
Вся вторая глава посвящена общей теории дифферен-
дифференциальных уравнений в частных производных. Она начина-
начинается с самой классической задачи - задачи Коши для общих
систем типа Ковалевской в классе аналитических функций
(т.е. посвящена построению решения в виде ряда) с началь-
начальными данными, заданными на гиперплоскости. Рассмотре-
Рассмотрение задачи Коши с начальными данными на произвольной
поверхности естественным образом приводит к одному из
фундаментальных понятий - характеристической поверхно-
поверхности и характеристического направления.
Последнее также естественным образом приводит к кла-
классификации уравнений и систем общего вида и уравнений
второго порядка. В основном дается классификация ура-
уравнений и систем по Петровскому, но мы даем и понятие
эллиптической системы по Дуглису - Ниренбергу, сопрово-
сопровождаемое примерами. Дано определение корректной и некор-
некорректной постановки задач. Под корректностью понимается
существование решения и его единственность в одном и том
Предисловие 17
же классе функций, а также непрерывная зависимость ре-
решения от данных задачи, в том или ином функциональном
пространстве.
Доказательство корректности задачи - это математиче-
математическое обоснование правильности той или иной математиче-
математической модели: модель не противоречива (теорема существо-
существования решения), модель однозначно описывает тот или иной
процесс (теорема единственности), и модель мало чувствует
погрешности измерений (решение непрерывно зависит от за-
заданных в задаче функций). Доказывается теорема о некор-
некорректной постановке задачи Коши в терминах корней харак-
характеристического многочлена.
При решении задачи Коши широко используется преоб-
преобразование Фурье, в том числе и в классе обобщенных фун-
функций. Приводятся все необходимые сведения из теории обоб-
обобщенных функций для решения задачи Коши для уравнения
теплопроводности и волнового уравнения: физическая ин-
интерпретация обобщенной функции и ее определение в виде
функционала над пространствами D и 5, преобразование
Фурье в пространстве 5"', теоремы о свертке. С помощью
обобщенных функций наглядно интерпретируется смысл то-
точечного источника в теории теплопроводности, сферической
волны, описываемой волновым уравнением и фундаменталь-
фундаментального решения.
Пятая, шестая и седьмая главы посвящены краевым и
начально-краевым задачам для эллиптических, параболиче-
параболических и гиперболических уравнений в обобщенной постано-
постановке в пространствах Соболева. Дана достаточно полная те-
теория этих пространств для решения задач для уравнений
второго порядка, включая теоремы вложения и теоремы о
следах, компактность вложения и теорию усреднения, т.е.
регуляризацию функций из пространств Соболева.
Задачи на собственные значения для эллиптического
уравнения и обоснование метода Фурье для гиперболиче-
гиперболического уравнения рассматриваются также в пространствах
Соболева.
В восьмой главе дается обоснование применения прибли-
приближенного метода Галеркина к решению задачи Дирихле для
2 - В Н Масленникова
18 Предисловие
уравнения Пуассона и первой начально-краевой задачи для
уравнения теплопроводности в классе обобщенных решений.
Главы девятая и десятая посвящены в основном клас-
классическим вопросам: фундаментальным решениям и постро-
построению их методом преобразования Фурье, функции Грина
и свойствам гармонических функций. Для гармонических
функций доказывается принцип максимума в сильной и сла-
слабой форме, теорема Жиро о знаке производной в граничной
точке и все классические свойства. Изучаются внешние кра-
краевые задачи для уравнения Лапласа.
Последняя, одиннадцатая глава, дана как дополнение
к основному курсу. В ней доказаны все основные теоремы
вложения для классов дифференцируемых функций многих
переменных. В основе доказательств лежат бесселевы потен-
потенциалы в Ш,п и теорема о продолжении функций с области п
на все Шп.
Для упражнений по всем основным главам рекоменду-
рекомендуются: "Сборник задач по уравнениям математической фи-
физики" B.C. Владимирова, В.П. Михайлова, А.А. Вашарина,
Х.Х. Каримовой, Ю.В. Сидорова, М.И. Шабунина, На-
Наука 1982 г.; "Сборник задач по математической физике"
Б.М. Будака, А.А. Самарского, А.Н. Тихонова, все годы
издания; Методические рекомендации к изучению курса
"Дифференциальные уравнения в частных производных"
М.Е. Боговского. Москва, УДН, 1986г.
Выражаю глубокую благодарность моим коллегам Сухи-
иину М.Ф., прочитавшему книгу в рукописи и сделавшему
ряд ценных замечаний, Боговскому М.Е. за конструкти-
конструктивные и плодотворные советы при написании книги, Бурен-
кову В.И. за полезные обсуждения и Гольдману М.Л. за
рецензирование дополнения; я благодарна также официаль-
официальным рецензентам профессорам А.А. Дезину и
В.П. Глушко. Моя особая благодарность Ректорату Россий-
Российского университета дружбы народов и спонсору, кандидату
физико-математических наук, доценту Ученову В.Н., выде-
выделивших средства на издание книги.
19
Глава I. Постановка краевых задач для
дифференциальных уравнений
в частных производных
§ 1. Введение. Основные определения
1. Суть предмета
При математическом моделировании различных явлений
получаются дифференциальные уравнения, в которые вхо-
входит неизвестная функция, зависящая от многих независимых
переменных и, следовательно, уравнение, поскольку оно яв-
является дифференциальным уравнением, содержит частные
производные от неизвестной функции. Уравнения в частных
производных имеют очень широкое применение и к их изу-
изучению привлекаются многие разделы современной матема-
математики: математический анализ, алгебра, геометрия, функцио-
функциональный анализ, топология, комплексный анализ и особенно
- теория бесконечномерных функциональных пространств.
Так как почти все физические явления описываются ура-
уравнениями в частных производных, то часто в тех случаях,
когда дифференциальное уравнение описывает физический
процесс, эти уравнения в частных производных называются
уравнениями математической физики. Однако надо иметь в
виду, что уравнениями в частных производных описываются
не только физические, но и химические, биологические, эко-
экономические и многие другие явления и процессы в природе
и обществе.
Типичным примером уравнения в частных производных
является уравнение теплопроводности, которое мы ниже вы-
выведем. Неизвестной функцией в этом уравнении будет тем-
температура тела u(x,t), которая зависит от точки тела х =
(х!,Х2,хз) и времени t, т.е. температура в различных точ-
точках тела и в различные моменты времени будет определяться
как решение некоторого уравнения в частных производных.
20 Глава I. Постановка краевых задач для диф. уравн. ...
2. Основные определения в теории уравнении с частными
производными
Пусть Q есть область в IRn. Уравнение в частных про-
производных от неизвестной функции u(zi, ...,xn) или коротко
и(х), где х = (si, ...,£„) £ Q С Ип, называется уравнением
т-то порядка, если оно содержит хотя бы одну производную
ш-го порядка и не содержит производных более высокого
порядка.
Порядком системы уравнений в частных производных
называется наибольший из порядков входящих в нее ура-
уравнений.
Уравнение в частных производных называется линей-
линейным, если оно линейно относительно неизвестной функции
и ее производных. Например, уравнение
2и д2и
+К)
является линейным уравнением второго порядка относи-
относительно неизвестной функции u(xi,.t2).
Уравнение в частных производных называется квазили-
квазилинейным, если оно линейно относительно всех старших про-
производных от неизвестной функции. Например, уравнение
ди д2и ди д2и
есть квазилинейное уравнение второго порядка относительно
неизвестной функции и(ж1,хг).
Уравнение вида
является нелинейным уравнением.
Произвольное уравнение в частных производных в слу-
случае п независимых переменных имеет вид
,—,...,,_,...,
Гл. I, § 1. Введение. Основные определения 21
Сюда входят все линейные и нелинейные уравнения.
Если уравнение линейное, то его можно записать в виде
u = f(x), B)
где через £)'а1 обычно обозначается частная производная по-
порядка |а| по переменным xj,...,xn, т.е. .D'a' = ■„ *f „ ап ;
ОХ у ...ОХп
суммирование ]Г) производится по всем целочисленным
|а|<т
значениям ajt, начиная от 0 до т, причем а означает муль-
тииндекс а = ot\Q.2-.an, и принято обозначение \а\ =
а\ + ... + ап. Но обычно знак модуля в обозначении порядка
производной мы будем опускать и писать в B) Dau вместо
£>Ии.
Уравнение в частных производных рассматривается или
во всем пространстве IR" или в области п С Шп. В качестве
п в некоторых физических и математических задачах рас-
рассматривают, например, полупространство Q = IR" = {х :
х' € Ип~х, хп > 0}, где х' = (xi,X2,-..,xn-i), или неко-
некоторую ограниченную или неограниченную область, напри-
например, шар, внешность шара, прямоугольник и т.д. или общую
произвольную область Q.
Вообще говоря, уравнение в частных производных может
иметь бесчисленное множество решений. Чтобы уравнение
имело одно решение (или в некоторых более сложных слу-
случаях несколько вполне определенных решений), т.е. задача
была детерминированной, необходимо на искомое решение
дифференциального уравнения наложить дополнительные
условия, которыми могут быть начальные и граничные усло-
условия и которые, как правило, вытекают из физической (или
иной другой) постановки задачи.
Для уравнений в частных производных всегда очень
важно указать класс функций и(х), среди которых разыски-
разыскивается решение; обычно это будет то или иное функциональ-
функциональное пространство, определяемое в курсе функционального
анализа. Мы будем рассматривать так называемые класси-
классические решения и обобщенные. При изучении классических
22 Глава I. Постановка краевых задач для диф. уравн. ...
решений рассматривается пространство непрерывных фун-
функций Ck(f2), имеющих непрерывные производные до по-
порядка к (обычно этот порядок равен порядку уравнения) и
до соответствующего порядка в замкнутой области Q (поря-
(порядок непрерывных производных в замкнутой области опреде-
определяется порядком производных от неизвестной функции и(х),
входящей в граничные и начальные условия). При изучении
обобщенных решений дифференциальных уравнений будут
использоваться другие функциональные пространства, вве-
введенные С.Л. Соболевым и поэтому носящие его имя.
3. Примеры уравнений в частных производных
Большинство физических явлений описывается уравне-
уравнениями или системами уравнений в частных производных.
Приведем примеры уравнений в частных производных,
встречающихся наиболее часто.
а) Уравнение распространения тепла (коротко его назы-
называют уравнением теплопроводности).
Если среда, где изучается температура тела, трехмерна
и однородна, а температура зависит от времени, то уравне-
уравнение теплопроводности имеет вид
ди д2и д2и д2и
+ + +*{^ {3)
где обычно через t обозначают время, а через х = (xi,Х2,жз)
— точки тела, т.е. функция и есть функция t и х. Уравнением
вида C) описываются также явления диффузии, в том числе
в живом организме, и другие процессы.
б) Уравнение распространения волн (коротко волновое
уравнение) имеет вид
д2и д2и д2и д2и ,, .
+ + + «Л D)
Уравнением D) описываются, например, звуковые волны.
Гл. 1, § 1. Введение. Основные определения 23
в) Для стационарных процессов f(x,t) = /(ж),
u(x,t) = и(х), а уравнения C) и D) принимают вид
Э2и д2и д2и ,, .
Уравнение E) называется уравнением Пуассона. Сумму
вторых (несмешанных) частных производных обозначают
символом Ли, а уравнение
называют уравнением Лапласа.
Уравнением вида E) описывается также потенциальное
течение жидкости. Уравнения C) - E) имеют постоянные
(даже единичные) коэффициенты; это бывает в случаях, ко-
когда рассматривается однородная среда. Решения уравнений
C) - E) определяют при заданных начальных и граничных
условиях. Например, для решения уравнения C) можно за-
задать начальное условие
u(t,x)\t=to =u(to,s), x € О
и граничное условие
u(t,x)\dn = 4>(x,t), t>t0,
где символом дп мы будем обозначать границу области /2,
а для решения уравнения E) достаточно задать только гра-
граничное условие и(х) = vK^)-
4. Из история предмета
Теория дифференциальных уравнений в частных про-
производных имеет очень богатую историю. Большой вклад в
ее развитие внесли многие математики мира. Для решения
задач для дифференциальных уравнений в частных произ-
производных были созданы новые разделы математики такие, как
функциональный анализ, теория обобщенных функций, те-
теория новых функциональных пространств. Имена многих
24 Глава I. Постановка краевых задач для диф. уравн. ...
математиков, механиков и физиков, создавших новые мате-
математические модели и новые математические методы для их
исследования, вы встретите в курсе в названиях уравнений,
теорем и различных формул.
Я хочу здесь отметить лишь имена Ивана Георгиевича
Петровского и Сергея Львовича Соболева, с которыми свя-
связаны многие концепции этой книги. В работах И.Г. Петро-
Петровского было положено начало развития общей теории линей-
линейных систем уравнений в частных производных, в частности,
их классификация. Особенно велико влияние на предлага-
предлагаемый читателю Курс работ моего учителя Сергея Львовича
Соболева, с которым были связаны почти сорок лет моей
научной деятельности. С.Л. Соболевым было введено новое
понятие - обобщенное решение дифференциального уравне-
уравнения, на основе общей концепции обобщенных функций; им
были введены и изучены новые функциональные простран~
ства. Благодаря этому теория уравнений в частных произво-
производных развивалась особенно интенсивно, начиная с конца со-
сороковых годов. Отметим, что научно-технический прогресс
и многочисленные приложения также явились большим сти-
стимулом в развитии этой области математики.
Исследования в теории дифференциальных уравнений
в частных производных идут в двух направлениях. Созда-
Создается общая теория дифференциальных уравнений в частных
производных, т.е. для общих уравнений и граничных усло-
условий изучаются вопросы существования решений, их един-
единственности, устойчивости и т.д. Для приложений - это ра-
работа впрок; например, когда получают какую-либо мате-
математическую модель того или иного явления, то из общей
теории можно узнать, оправдана ли она с математической
точки зрения. С другой стороны, существует много уравне-
уравнений в частных производных, описывающих те или иные фи-
физические, биологические и другие явления (например, ура-
уравнение теплопроводности и диффузии, уравнения колеба-
колебаний мембраны, упругого тела, звука, уравнения гидродина-
гидродинамики и газовой динамики, уравнение Шредингера в кван-
квантовой механике и т.д.), решения которых надо изучить при
различных граничных условиях, в том числе надо изучить
Гл. I, § 2. Некоторые матем. модели физ. процессов 25
различные качественные свойства этих решений. При этом
необходимо отметить, что создаются все новые и новые ма-
математические модели.
Всеми этими вопросами и занимается теория уравнений
в частных производных.
§ 2. Некоторые математические модели
физических процессов
При построении математической модели необходимо от-
отразить существенное в явлении и отбросить второстепенное.
При этом главное и несущественное определяются научным
поиском на заданном этапе исследования.
1. Вывод уравнения теплопроводности; граничные и на-
начальные условия
Рассмотрим тело Q, температура которого в точке х =
(ж!,Х2,хз) в момент времени t определяется функцией
и(ж, t), которая имеет непрерывные производные второго по-
порядка по переменным х;, i = 1,2,3 для любого t > О и
непрерывную производную по t, т.е. u(x,t) € Сх'\. Вывод
уравнения, описывающего процесс распространения тепла,
основан на следующем экспериментальном физическом за-
законе: если различные части тела имеют различную темпе-
температуру, то в теле возникают тепловые потоки, направленные
из мест с более высокой температурой в места с более низ-
низкой температурой. Пусть поверхность S расположена вну-
внутри тела £2, и пусть на поверхности S определен непреры-
непрерывно меняющийся вектор нормали п. Тогда количество тепла,
проходящее через поверхность 5 по направлению нормали
п за промежуток времени от t\ до <2, определяется форму-
формулой:
q = - [{ f k(x)^ds\dt. A)
26 Глава I. Постановка краевых задач для диф. уравн. ...
Здесь -^=г - производная в точке х поверхности 5 по на-
д п
правлению нормали п в направлении уменьшения темпе-
температуры, т.е. -%■ < 0; внутренний интеграл берется по по-
д п
верхности S. Положительная функция к(х) называется ко-
коэффициентом внутренней теплопроводности тела в точке х
и считается известной для рассматриваемой среды. Фор-
Формула A) равносильна тому, что через бесконечно малую
площадку ds за бесконечно малый промежуток времени dt
протекает количество тепла, равное
ди
dq = -к(х)—— ds dt. B)
д п
Это есть физический закон Фурье в теории теплопроводно-
теплопроводности.
Мы будем рассматривать тело, изотропное в отношении
теплопроводности, т.е. будем предполагать, что функция
к(х) не зависит от направления нормали к поверхности 5 в
точке х. Кроме того, предположим, что к(х) G С1 по всем
переменным хг, Х2, жз.
Для вывода уравнения теплопроводности мысленно вы-
выделим внутри тела Q произвольный объем D, ограничен-
ограниченный гладкой поверхностью 5, и рассмотрим изменение ко-
количества тепла в этом объеме за промежуток времени от t\
до t2.
Через поверхность 5 входит количество тепла, опреде-
определяемое формулой A), где -%■ - производная по внутренней
8 п
нормали к поверхности 5.
С другой стороны, это количество тепла можно опреде-
определить через изменение температуры в объеме D за промежу-
промежуток времени от t\ до <2- Изменение количества тепла, как
известно, пропорционально разности температур в моменты
времени t-i и t\, т.е. оно равно
/ с(х)р(х) [u(t2, x) - u(U, x)] dx, C)
D
Гл. I, § 2. Некоторые матем. модели физ. процессов 27
где р(х) - плотность, с(х) - теплоемкость тела в точке х,
и интеграл распространен по объему D. Составив баланс
тепла, т.е. приравняв A) и C), получим
/ с(х)р(х) [u(t2, ж) — u(ti, x)] dx =
D
■-/{/
a n
и s
dt.
Пользуясь формулой Гаусса - Остроградского, имеем
J
S D '-1
и переписав интеграл в левой части D) в виде
ti D
так как
u(t2,x)-u{tux) = / -j^
h
вместо D) получаем
D
Так как функции, стоящие под знаком интеграла, непреры-
непрерывны, объем D и промежуток времени [U,t2] произвольны, то
для любой точки тела п и для любого момента времени t
должно выполняться равенство
28 Глава I. Постановка краевых задач для диф. уравн. ...
«***>!-Ё £(*>£)• E)
Это и есть уравнение теплопроводности для неоднородного,
но изотропного тела.
Если тело однородно, т.е. к,с,р = const, то уравнение
E) принимает вид:
срди
к dt
з 2
где символ Л определяется формулой Л = ]Г) ^Ц-. Заме-
няя j-t на t' и обозначая t' опять через t, мы приходим к
уравнению
Уравнения E) и F) имеют много решений.
Чтобы выделить из всей совокупности решений какое-
либо одно, надо задать дополнительные условия.
Такими дополнительными условиями являются гранич-
граничные условия, т.е. условия, задаваемые на границе области,
и начальные условия.
При математическом моделировании различных процес-
процессов эти дополнительные условия обычно задаются эмпириче-
эмпирически, но задача математика часто состоит в том, чтобы узнать,
правильно ли заданы те или иные дополнительные условия,
т.е. разрешима ли поставленная задача.
Рассмотрим граничные и начальные условия для уравне-
уравнения теплопроводности, которые возникают из физических
соображений.
Физически ясно, что знание температуры тела в некото-
некоторый момент времени и теплового режима на границе тела
определяет температуру тела в последующие моменты вре-
времени, причем тепловой режим на границе тела может быть
задан разными способами.
Гл. I, § 2. Некоторые матем. модели физ. процессов 29
Если область ft совпадает со всем пространством, то
можно доказать, и ниже мы это сделаем, что, например,
ограниченное решение уравнения теплопроводности при
t > to единственным образом определяется одними началь-
начальными условиями: значениями u(x,t) при t = to. Такая за-
задача называется задачей Коши. Если п - ограниченная
или неограниченная область, то, кроме начальных условий,
можно задать температуру в каждой граничной точке тела
при t > to-
Начальное условие
о) G)
и граничное условие
t>t0 (8)
определяют первую начально-краевую задачу.
Вместо того, чтобы задавать и(х, t) на границе тела при
t > to, можно, для определения единственного решения ура-
уравнения теплопроводности, задать на границе производную
по внутренней нормали к границе дп от искомой функции
u(.c,t). К такой задаче мы придем, если будем изучать тем-
температуру тела Q при условии, что нам известно количество
тепла, отдаваемого телом во внешнюю среду (или наобо-
наоборот - из внешней среды телу) через любую площадку ds
на границе тела. Это количество тепла (тепловой поток) по
формуле A) равно
ди
—к——ds dt.
д п
Зная закон теплоотдачи для каждой площадки ds гра-
ницы области, можно найти значения ■— на границе. В ча-
д п
стности, если нет теплообмена через границу, то на ней
f =0
R общем случае имеем
ди ,
д п
\ап
(9)
30 Глава I. Постановка краевых задач для диф. уравн. ...
Условия G) и (9) определяют вторую начально-краевую за-
задачу. Можно в качестве граничного условия при t > to за-
задать на границе дп линейную комбинацию
к(х)—— — к\(х)и,
дп
где ki(x) - коэффициент внешней теплопроводности при пе-
переходе от окружающего пространства к телу. Этот коэффи-
коэффициент считается известным. К такой математической задаче
мы придем, если будем изучать температуру u(x,t) тела п
при условии, что нам известна температура щ(х,Ь) среды,
окружающей тело, и на поверхности тела происходит тепло-
теплообмен с окружающей средой, температура которой ui(x,t)
известна.
Закон теплообмена может быть очень сложным, мы рас-
рассмотрим наиболее простой его вариант - в виде закона
Ньютона. По закону Ньютона количество тепла, проходя-
проходящего за промежуток времени t*i, *г] через площадку 5 от
окружающего пространства к телу, равно
t3
/ f
s
-u)dsdt.
Здесь щ(х, t) и и(х, t) определяются на 5 предельным пере-
переходом снаружи и изнутри тела соответственно. С другой сто-
стороны, количество тепла, переданного за это же время внутрь
тела через поверхность 5" равно
k(x)>0.
Таким образом, мы имеем два выражения для теплового
потока; это приводит к граничному условию на дп вида
-и) = -*—=г,
Гл. I, § 2. Некоторые матем. модели физ. процессов 31
где п - внутренняя нормаль к поверхности тела; обозначая
— ^- = h(x), мы получаем граничное условие для третьей
начально-краевой задачи
^ + h(x)u\ao = tpa(x,t), A0)
о п
где <ps(x,t) = ~kli'Xl(x)X'^i заметим, что h(x) < 0, так как
к и кг положительны. И в этом случае нужно задать еще
начальное условие G). Если щ = 0, то граничное условие
будет иметь вид
Пусть температура в каждой точке тела установилась, т.е.
она не меняется при изменении t. Тогда ^ = 0 и ура-
уравнение теплопроводности примет вид уравнения Лапласа:
Ли = 0. Первая краевая задача для этого уравнения, ко-
когда на границе 8Q задается функция и(х): u|ai? = ^iC^)
называется задачей Дирихле. Для определения и(х) теперь
не нужно задавать начальных условий. Достаточно задать
одни граничные условия, которые не зависят от времени.
Иногда изучают температуру стержня или пластины, при-
причем боковая поверхность стержня и верх, и низ пластины
теплоизолированы. Тогда уравнение теплопроводности для
стержня примет вид:
ди _ д2и
dt ~ Эх2'
а для пластины
dt ~ дх\ + дх\'
Эти уравнения также рассматриваются с начальным усло-
условием G) и одним из граничных условий (8), (9) или A0).
32 Глава I. Постановка краевых задач для диф. уравн. ...
Отметим, что если в среде имеются источники тепла
или поглощение тепла, то уравнение теплопроводности будет
иметь вид
-^ - Аи = f(x,t),
где f(x,t) - заданная функция.
При выводе уравнения теплопроводности мы предпола-
предполагали, что коэффициенты теплопроводности не зависят от
температуры и получили линейное уравнение. Однако, су-
существуют среды, где коэффициенты теплопроводности зави-
зависят от температуры, в этом случае мы получим квазилиней-
квазилинейное уравнение и нелинейные граничные условия.
2. Вывод уравнения равновесия мембраны и граничных
условии
Рассмотрим пленку (т.е. очень тонкое упругое тело),
натянутую равномерно по всем направлениям. Будем пред-
предполагать, что пленка столь тонка, что не сопротивляется
изгибу, т.е. изменению формы, не вызывающему изменения
площади, и сопротивляется растяжению, вызывающему из-
изменение площади. Такая пленка называется мембраной.
Работа внешней силы, вызывающей изменение площади
некоторого участка мембраны, пропорциональна этому из-
изменению. Положительный коэффициент пропорционально-
пропорциональности Г называется натяжением мембраны.
Заметим, что работа внутренних сил упругости равна
по абсолютной величине и противоположна по знаку ра-
работе внешних сил, вызывающих изменение площади. Пусть
в состоянии покоя мембрана расположена в плоскости IR и
имеет форму некоторой плоской области Q с границей dQ.
Предположим, что на мембрану действует внешняя сила,
плотность которой в точке х = (жьЖг) равна /(ж) и на-
направление этой силы перпендикулярно плоскости IR . Под
действием этой силы мембрана прогнется и примет форму
некоторой поверхности, уравнение которой запишем в виде
и = и(х\,хг). Ось и перпендикулярна плоскости Ш2. Мы
Гл. I, § 2. Некоторые матем. модели физ. процессов
33
U а
х2
an
Х\
выведем уравнение, которому удовлетворяет функция и(х)
в положении равновесия, при следующих ограничениях:
1. Предположим, что в интересующем нас положении
равновесия поверхность мембраны не сильно изогнута, т.е.
производные J^7, г = 1,2 малы, и в наших рассуждениях мы
будем пренебрегать высшими степенями этих производных.
2. Предположим, что под действием внешней силы с
плотностью f(x) точки мембраны двигаются только по пер-
перпендикулярам к плоскости IR2, так что их координаты х\, ж 2
при этом не меняются.
Вывод уравнения опирается на одно из основных положе-
положений механики - принцип возможных перемещений, который
состоит в том, что в состоянии равновесия сумма элемен-
элементарных работ всех действующих на систему сил при любом
возможном перемещении должна равняться нулю.
Для вычисления всех элементарных работ найдем ра-
работу, произведенную силами, действующими на мембрану,
при перемещении ее из первоначального плоского состояния
в положение, задаваемое функцией и(х) = u(xi,x2).
3 - В. Н. Масленникова
34
Глава I. Постановка краевых задач для диф. уравн.
Работа силы, плотность которой равна /(ж), определя-
определяется интегралом
/
п
f(x)u(x)dxi dx2,
так как на элемент мембраны dx\dx2 действует сила
f(x\, X2)dx\dx2- Изменение площади мембраны при этом пе-
перемещении равно
п
(первоначальную площадь мы взяли равной 1), а работа вну-
внутренних сил упругости при этом изменении площади равна:
Разложим подынтегральную функцию в последнем вы-
выражении в ряд по степеням ^-, -§f- и, воспользовавшись
предположением о малости этих величин, отбросим стар-
старшие члены этого разложения. Тогда для работы внутренних
сил упругости получим выражение:
Г
п
Таким образом, работа всех действующих на мембрану вну-
внутренних сил упругости и приложенных внешних сил при
перемещении мембраны из положения покоя в некоторое по-
положение и(х) равна
Гл. I, § 2. Некоторые матем. модели физ. процессов 35
А(и) =
ди\\(ди
Заметим, что интеграл A1) равен с точностью до знака по-
потенциальной энергии мембраны в положении равновесия.
Произведем теперь некоторое возможное перемещение
мембраны (чтобы воспользоваться принципом возможных пе-
перемещений), т.е. добавим к и(х) некоторую функцию 6и(х).
Работа всех действующих сил при этом перемещении равна
вариации интеграла A1), которую мы должны подсчитать.
Мы имеем
6 А = А(и + 6и) - А(и) =
= J [-Т(и'Х16и'Х1 + u'XiSu'Xj) + fSu] dXldx2.
п
Эта вариация интеграла должна быть равна нулю согласно
принципу возможных перемещений.
В формуле A2) проинтегрируем по частям в первых двух
слагаемых (считая, что Г = const).
Получим
ди с\ д
С\ д ( ди
п
/Л Л
Au8udxidx2 = — I ——6uds+
J дп
п п
+ I Au6udxidx2,
п
з*
36 Глава I. Постановка краевых задач для диф. урави. ...
где -£=? - производная по внешней нормали к границе dQ
д п
области Q.
Таким образом, мы имеем
= - I T^Suds + /(Г Аи + /Nudxxdx2 = 0. A3)
J дп J
6А
J дп
an n
У нас 8и - возможное перемещение мембраны, т.е. пере-
перемещение, допускаемое связями, наложенными на мембрану.
Эти связи накладываются обычно на край мембраны, по-
поэтому функция 8и(хх,Х2) во внутренних точках мембраны
является произвольной непрерывной функцией; следователь-
следовательно, из равенства нулю 8А можно сделать вывод, что в поло-
положении равновесия функция и{х\,Х2) в любой внутренней
точке области Q удовлетворяет уравнению Пуассона
ТАи + / = 0. A4)
Что же касается связей, то они сказываются на гранич-
граничных условиях, которые могут быть разнообразными.
Рассмотрим наиболее часто встречающиеся граничные
условия.
1. Закрепленная мембрана.
Пусть край мембраны закреплен вдоль некоторой про-
пространственной кривой, проектирующейся в dQ. Если пара-
параметрические уравнения дп заданы в виде
где з - длина дуги,
то мы требуем, чтобы мембрана проходила через некоторую
пространственную кривую
'хх =£i(e),
х2 =
Гл. I, § 2. Некоторые матем. модели физ. процессов 37
При этом единственным ограничением, наложенным на 6и,
будет 8и = О на дП.
Благодаря этому ограничению в формуле A3) исче-
исчезает криволинейный интеграл, а полученная задача - найти
u(ii,i2) - решение уравнения Пуассона A4) с граничным
условием
называется задачей Дирихле.
2. Свободная мембрана.
Можно не накладывать никаких ограничений на поло-
положение края мембраны, тогда ее край может свободно пере-
перемещаться по вертикальной боковой поверхности цилиндра с
основанием дB.
В этом случае 8и произвольно как внутри, так и на гра-
границе S2, и мы получим условие на дп вида:
дп
3. Пусть кроме внешней силы с плотностью /, действу-
действующей на внутренние точки мембраны, к ее краю приложена
вертикальная сила с линейной плотностью <pi, так что на
элемент ds границы дп действует сила
Тогда граничное условие имеет вид:
Задача с граничным условием A6) или A7) называется за-
задачей Неймана или второй краевой задачей.
4. Иногда рассматривается упругое закрепление мембра-
мембраны, т.е. случай, когда сила, действующая на край мембраны,
пропорциональна отклонению: /i(s) = ku(s).
В этом случае краевое условие для уравнения Пуассона
принимает вид:
38 Глава I. Постановка краевых задач для диф. уравн. ...
а соответствующая задача называется третьей краевой зада-
задачей.
3. Вывод уравнения колебаннМ мембраны. Начальные н
граничные условия
Выведем уравнение движения мембраны, рассматривая
только малые (т.е. с малыми значениями u, Jj-, J-^-) и только
поперечные колебания с неизменными координатами xi,x2
точки х мембраны.
Скорость точки с координатами x\,x2 равна —v 'э, ' ,
а ускорение равно ^
Чтобы получить уравнение движения мембраны, нужно
по принципу Даламбера учесть силу инерции мембраны.
Плотность этой силы равна pf^r, где р{хх,Х2) - плотность
мембраны в точке х — (х\,Х2).
Мы получим уравнение поперечных колебаний мембра-
мембраны, если в уравнение A4) добавим член — р^$- Уравнение
колебаний мембраны будет иметь вид
TAu-p-~ + f = 0. A9)
Граничные условия остаются теми же с той лишь разницей,
что теперь граничные функции могут зависеть и от времени.
Как и в случае уравнения теплопроводности из физиче-
физических соображений ясно, что одни граничные условия не мо-
могут единственным образом определять движение мембраны,
так как оно существенным образом зависит от начального
положения и начальной скорости. Поэтому для единственно-
единственности решения уравнения A9), кроме краевых, нужно задать
начальные условия
u(x,t)
Я (
dt
Гл. I, § 2. Некоторые матем. модели физ. процессов 39
Теоретически можно рассматривать неограниченную
мембрану, т.е. колебания всей плоскости, подчиненные ура-
уравнению A9). К такой задаче мы придем, если мембрана
столь велика, что влиянием границы можно пренебречь. В
этом случае для единственности решения достаточно одних
начальных условий B0). Если изучать малые колебания
струны или газа в трубке, то при определенных физических
предположениях можно показать, что функция u(t,x) удо-
удовлетворяет уравнению
которое называется уравнением колебания струны. Здесь
р(х) - линейная плотность струны в точке ж, Г - натяже-
натяжение, u(t, x) - отклонение струны от положения равновесия.
Начальные и граничные условия для уравнения B1) того
же вида, что и для колебания мембраны.
Замечание 1. Уравнения A9) и B1) получаются только
при условии, что мы пренебрегаем величинами (-§f-\ по
сравнению с (-^ J . Если же этого не сделать, т.е. не пред-
предполагать малости колебаний, то уравнения движения соот-
соответствующих упругих тел будут гораздо более сложными не-
нелинейными уравнениями.
Замечание 2. Когда мы вывели уравнение теплопроводно-
теплопроводности или уравнение колебаний, то оказалось, что в эти ура-
уравнения, если среда однородная, вошли выражения
Так бывает всегда в линейных уравнениях второго порядка,
написанных для однородной изотропной среды двух или бо-
более измерений, потому что эти выражения (лапласианы)
есть единственные (с точностью до постоянного множителя)
40 Глава I. Постановка краевых задач для диф. уравн. ...
линейные комбинации вторых частных производных от и, ко-
которые остаются инвариантными при любом ортогональном
преобразовании, т.е. при повороте ортогональных коорди-
координатных осей.
Отметим, что преобразование независимых переменных,
оставляющее инвариантным волновое уравнение D) из § 1
(которое мы выведем ниже), называется преобразованием
Лоренца. Это преобразование играет важную роль в тео-
теории относительности.
Замечание 3. Уравнению Лапласа An = 0 удовлетворяют
потенциалы поля тяготения и стационарного электрического
поля, и как мы увидим ниже, потенциальное (безвихревое)
течение жидкости также описывается решением уравнения
Лапласа.
4. Частная н полная производные вектора и скаляра. Вы-
Вывод уравнения неразрывности сплошной среди
Пусть мы имеем движение некоторой сплошной среды,
например, жидкости или газа, и пусть поле скоростей при
этом движении задается дифференцируемой по х и t вектор-
функцией v(x,t) так, что v(x,t) есть вектор скорости ча-
частицы жидкости, проходящей в момент времени t через
точку х = (жх, Х2, жз). Изменение во времени вектора v(x, t)
з фиксированной точке х характеризуется частной произ-
производной ^г. Бели мы хотим охарактеризовать изменение век-
вектора и(х, t) во времени для заданной частицы жидкости, пе-
перемещающейся в пространстве вместе со всей сплошной сре-
средой, а не для фиксированной точки пространства, то мы дол-
должны считать Ж1,Ж2,.тз функциями £, так как частица жид-
жидкости, имеющая координаты х\, Х2, хз, перемещается со ско-
скоростью v(x, t), причем проекции скорости на оси координат
определяются формулами
Ui = ^ =i г = 123
Гл. I, § 2. Некоторые матем. модели физ. процессов 41
т.е. мы должны рассматривать v(x,t) как сложную функцию
t. Поэтому полная производная по времени от поля скоро-
скоростей определяется с помощью формулы Тейлора следующим
образом:
dv ,. Аи ,. v(x(t + At),t + At)-v(x,t)
— = hm -г— = lim т— =
dt д*-»о At д<—о At
»+fe*2(t)+feiT3(t) + t
дГ^о! At ' B2)
o(At)l =
At J
где символом V обозначена операция grad,
(и, V) = ui -^ + «2 afj + V3 j^ - скалярное произведение в
И,3. Полная производная ^ есть ускорение частиц жидко-
жидкости. Как видно из формулы B2) полная производная вектор-
функции v(x,t) состоит из двух частей: производной, ха-
характеризующей изменение функции во времени в заданном
месте пространства и конвективного (второго) члена, ха-
характеризующего изменение вектор-функции из-за того, что
рассматриваемая частица переносится в пространстве. Та-
Таким образом, конвективный член появляется только при дви-
движении сплошной среды и связан с переносом (конвекцией)
частиц. Точно таким же образом вычисляется полная про-
производная от скалярной функции (p(x,t), которая рассматри-
рассматривается как сложная функция t:
dip _ д(р д(р dx\ dip dxi dip dx$
~dt ~ !Н+ d~x~^~dT + dx2 dt + dx3 dt
или >
dip dip dip dip dip
dt at ox\
dip ,
= + (
42 Глава I. Постановка краевых задач для диф. уравя. ...
Выведем уравнение неразрывности сплошной среды для
области Q С И.3. Рассмотрим произвольную подобласть
ш С Q с гладкой границей дш, произвольный интервал вре-
времени (ti, *2) С @, оо), 0 < ii < t < *2 и запишем закон
сохранения массы для ш при t € (*г ,*г)- Так как дш - ге-
геометрическая, а не физическая граница, то частицы (жи-
(жидкости или газа) могут свободно через нее перемещаться.
Плотность потока частиц через кусок поверхности в напра-
направлении внешней нормали п () п \ = 1) к границе дш обо-
обозначим через N(x,t). Он равен массе частиц, проходящих
через единицу площади поверхности в единицу времени, т.е.
по определению
N(x,t)= hm .
Рассмотрим бесконечно малый, вообще говоря, наклон-
наклонный цилиндр высоты Ah с основанием As С дш с образу-
образующими | v \At, состоящий из частиц жидкости, которые за
Гл. I, § 2. Некоторые матем. модели физ. процессов 43
время At пройдут через площадку As. За время At через
цилиндр пройдет масса жидкости, равная Am = pAsAh,
где Ah = |u|Atcos(n, v) = (u,n)Ai, так как элемент
объема (малый цилиндр), который заполнят частицы жид-
жидкости, проходящие за время At через поверхность As, ра-
равен (и, n)AtAs. Тогда Am = pAsAt(v, n)+ малые более
высокого порядка. Откуда находим N = р( v, п). Из этой
формулы виден смысл условия непротекания: ( v, n) =0.
дш
Тем же способом сосчитаем массу частиц, которые вы-
вышли из объема ш. в направлении внешней нормали за время
(*i,*г)- Она равна / J N(x,t)dsdt.
«1 дш
С другой стороны масса M(t) = f p(x,t)dx. Пусть, на-
ш
пример, M(ti) > M(ti), т.е. масса вышла из объема и>. За-
Запишем закон сохранения массы, из которого и получаем ура-
уравнение неразрывности:
*2
M(h)-M(t2)= I f N(x,t)dsdt
дш
ИЛИ
[p(x,t2) — p(x,t\)]dx + / / р • (v ,Я) ds dt = 0.
ш ti дш
Пользуясь формулой Ньютона - Лейбница и теоремой
Остроградского - Гаусса, получаем
tl U
VwC/2 и V(tbt2) С @,оо).
44 Глава I. Постановка краевых задач для диф. уравн. ...
Откуда получаем уравнение неразрывности для сжимаемой
жидкости при отсутствии источников и стоков в рассматри-
рассматриваемом объеме Q в виде:
^ + div(pU) = 0. B4)
Если плотность жидкости или газа постоянна, т.е. p(x,t) =
const, то уравнение B4) переходит в уравнение
divu = 0. B5)
Формула B5) есть уравнение неразрывности для несжима-
несжимаемой однородной жидкости. Отметим, что если поле скоро-
скоростей v потенциально и не зависит от времени, т.е. v(x) =
grades), то потенциал скорости ф(х) удовлетворяет ура-
уравнению Лапласа
div grad ф==Аф = 0. B6)
5. Уравнения движения сплошной среды
Выделим мысленно в жидкости произвольный объем и>,
ограниченный замкнутой поверхностью дш. На этот объем
действуют силы двух типов. Во-первых, это массовые силы
(например, гравитационные), действующие на каждый эле-
элемент dw объема ш. К другому классу сил, действующих в ш,
относятся силы взаимодействия между различными части-
частицами жидкости. Так как внутри Q в силу принципа равен-
равенства действия и противодействия эти силы уравновешива-
уравновешиваются, то рассматриваются только поверхностные силы. По-
Поэтому сила, действующая на частицы, заключенные в объ-
объеме w, равна J Fds, где F - поверхностная плотность силы.
дш
В гидродинамике доказывается существование матрицы Т
такой, что F = Тгг, а Т называют тензором напряже-
напряжений. Таким образом, напряжение есть поверхностная плот-
плотность силы. (Носителем напряжения является поверхность.)
Будем использовать уравнения движения в форме Коши, ко-
которые имеют вид
Гл. I, § 2. Некоторые матем. модели физ. процессов 45
p^=DivT + /(x,t), B7)
где f(x,t) есть объемная плотность внешних сил,
/divTA
DivT= divT2 ,
VdivT3/
Tj - j-я строка матрицы Г.
Сначала рассмотрим невязкую жидкость. По определе-
определению жидкость называется невязкой, если для любой повер-
поверхности S напряжение направлено по нормали к S (т.е. от-
отсутствуют касательные напряжения). В каждой точке невяз-
невязкой сплошной среды величина напряжения не зависит от
направления нормали к поверхности, т.е. величина напря-
напряжения в невязкой сплошной среде есть скаляр, Г = — Ер,
где Е - единичная матрица, а р называется давлением (ска-
(скалярная функция). Таким образом, уравнения движения не-
невязкой сплошной среды - уравнения Эйлера, исходя из ура-
уравнений движения в форме Коши B7), имеют вид
p^ + gradp = /(*,<), B8)
где ^j - полная производная по времени от вектора v.
К системе B8) присоединяется уравнение неразрывно-
неразрывности B4). Система B8), B4) содержит 4 уравнения с пятью
неизвестными v\, V2, из,р, р, если считать р(х, t) неизвестной
заранее плотностью. Для замкнутости системы задают так
называемое уравнение состояния
Р = *(Р), B9)
т.е. зависимость р от р. Уравнение B9) в общем случае имеет
очень сложный вид, но иногда ограничиваются простой ли-
линейной зависимостью р = ае р, где ае - постоянная.
Если рассматривать вязкую жидкость, то нужно учиты-
учитывать силы внутреннего трения, поэтому поверхностные силы
46 Глава I. Постановка краевых задач для диф. уравн. ...
будут иметь более сложную структуру. Для изотропной вяз-
вязкой сжимаемой жидкости тензор Т является симметричным,
а система уравнений движения имеет вид
— + (v,V)v - vAv - /ugraddivu + -gradp = F(x,t).C0)
at p
Система C0) вместе с уравнением неразрывности B4) и
уравнением состояния B9) называется системой Навье -
Стокса.
Бели жидкость несжимаема и однородна, уравнение не-
неразрывности имеет вид B5), а система C0) получит более
простой вид:
Л + (Ю| V> - uAv + Vp = F(x, t). C1)
Вместе с уравнением неразрывности B5) система C1) со-
содержит 4 уравнения и 4 неизвестных функции v\,V2,V3,p.
Эта система называется системой Навье - Стокса для нес-
несжимаемой жидкости.
Приведенные нами системы Эйлера и Навье - Стокса
являются нестационарными, поэтому для нахождения их ре-
решений задаются начальные условия
v(x,t) =u°(ar,t), ж£ Q, C2)
t=o
Q=p°(x,t), x£Q. C3)
В случае несжимаемой жидкости задается только начальное
условие C2).
Бели область /?, где изучается течение жидкости или
газа, ограничена поверхностью df2, то на этой поверхности
необходимо задать граничные условия, которые могут иметь
самый разнообразный характер. Для течения невязкой (сжи-
(сжимаемой или несжимаемой) жидкости часто используют гра-
граничное условие непротекания жидкости через поверхность
Гл. I, § 2. Некоторые матем. модели физ. процессов 47
vn(x,t) =0, C4)
Oil
где, как было отмечено выше,
vn(x,t) = (гГ,гг).
Если идет поток жидкости через границу, то условие C4)
переходит в неоднородное
vn(x,t) = <p(x,t),
Oat
где (p(x,t) - заданная функция. Если рассматривать вяз-
вязкую жидкость, т.е. системы Навье - Стокса для сжимаемой
или несжимаемой жидкости, то на границе дп можно задать
условие прилипания вида
v(x,t) =0, C5)
если дп - неподвижна и неоднородное условие прилипания
v(x,t) =a(x,t), C6)
oil
если граница тела подвижна (например, когда изучается за-
задача обтекания движущегося в жидкости твердого тела).
Граничные условия C5) и B6) обосновываются возникно-
возникновением пограничного слоя, теория которого была разрабо-
разработана Л. Прандтлем. При обтекании тел потоком вязкой или
невязкой жидкости (внешние задачи для неограниченных об-
областей) необходимо задавать те или иные условия на беско-
бесконечности (когда \х\ —* со).
Отметим, что в гидродинамике изучаются и стационар-
стационарные процессы, которые описываются функциями явно не за-
зависящими от времени, но при этом есть движение и ускоре-
ускорение частиц. В этом случае ускорение описывается конвекти-
конвективным членом (и, V)u. Например, можно рассматривать ста-
стационарное (установившееся) течение по кругу (каждая ча-
частица движется по кругу), тогда ^ = 0, а ускорение равно
{v,V)v.
48 Глава I. Постановка краевых задач для диф. уравн. ...
6. Вывод уравнения звуковых воли (волнового уравнения)
Рассмотрим систему Эйлера для сжимаемой жидкости
р4: + Pip, V)w + Vp = F(x, t),
a? C7)
и сделаем несколько упрощающих предположений. Будем
считать, что движение газа представляет собой малые от-
отклонения газа от положения равновесия. Пусть в положении
равновесия давление ро и плотность ро постоянны. При этих
предположениях можно пренебречь конвективными членами
(и, V)i> и членами -jfiv. Тогда систему уравнений движения
из C7) можно представить в виде
F(x,t). C8)
Применяя к системе C8) операцию div, получим
—div (pv) + Ар = div F(z, t).
at
Теперь, воспользовавшись уравнением неразрывности из
C7), мы получаем
Используя уравнение состояния р = Ф(р), имеем
C9)
Будем считать, что Ф'(р) в малом промежутке изменения р
является постоянной Ф(ро), а квадратичный член (f^j мал
при малом изменении давления по t. Тогда уравнение C9)
примет вид
§ 3. О постановке краевых задач матем. физики 49
1 Я2Л
где ^ = Ф'(ро), f(x, t) = divF(x,t). Уравнение D0) с хо-
хорошей точностью описывает распространение звука в газе и
им широко пользуются на практике.
В дальнейшем неизвестное давление в газе p(x,t) будем
обозначать через u(x,t).
Начальные условия, очевидно, имеют вид B0), а ти-
типичные граничные условия - задач Дирихле, Неймана или
третьей начально-краевой задачи.
§ 3. О постановке краевых задач математической
физики
Как было сказано выше, для нестационарных (зависящих
от времени) уравнений нужно задавать начальные условия
для определения решения. Если при этом рассматривается
по х все И", п = 1,2,3, то такую задачу называют задачей
Коши. При рассмотрении задачи во всем пространстве (за-
(задачи Коши) или в неограниченной области (например, на
внешности компакта) необходимо учитывать еще поведение
решения "на бесконечности" (в далеких точках изучаемой
области), и только при некоторых предположениях об этом
поведении решение может быть найдено однозначно.
Таким образом, задача математической физики ставится
как задача решения уравнения в частных производных при
некоторых дополнительных условиях, называемых началь-
начальными и краевыми, которые фиксируются часто самой физи-
физической постановкой задачи.
При постановке задач математической физики нужно
учитывать еще один важный факт. Он состоит в следующем.
Все известные функции, входящие в уравнение, а также в
начальные и граничные условия, определяются из опыта и
поэтому не могут быть найдены совершенно точно. Всегда
неизбежна некоторая погрешность в начальных и гранич-
граничных условиях. Эта, пусть и малая, погрешность будет ска-
сказываться и на решении, причем погрешность решения не
4 - В. Н. Масленникова
50 Глава I. Постановка краевых задач для диф. уравн. ...
всегда оказывается малой. Существует много примеров, ко-
когда малая погрешность в исходных данных влечет большую
ошибку в решении. Поэтому, исследуя уравнения математи-
математической физики, мы всегда должны рассматривать вопрос о
зависимости решения от исходных данных задачи.
Задача математической физики считается поставленной
корректно, если решение задачи, удовлетворяющее
требуемым условиям, существует, единственно и устойчиво.
Последнее свойство означает, что малые изменения задан-
заданных в задаче функций должны приводить к малым измене-
изменениям решения.
Требование существования и единственности означает,
что среди краевых и начальных условий нет лишних, т.е.
задача "совместна", и их достаточно, чтобы выделить среди
бесконечного множества решений дифференциального ура-
уравнения единственное. При этом задачу решают всегда в
определенном функциональном пространстве (пространстве
непрерывных функций, обобщенных функций и т.д.) и важ-
важно, чтобы в одном и том же функциональном пространстве
имела место теорема существования и единственности, а ре-
решение в норме того или иного пространства непрерывно за-
зависело от заданных в задаче функций.
Разберем пример, принадлежащий Адамару. Найдем ре-
решение уравнения Лапласа:
дх\ + дх\ ~
в области Q - полуполосе: Q = {х : xi > 0, — j < xi < j
с граничными условиями
и
Il=-f
и начальными условиями
и
где п
= е ^ cosnzi,
- нечетное
число.
ди
дх2
= 0,
12=0
§ 3. О постановке краевых задач матем. физики 51
Можно проверить, что функция
u(xi,X2) = e~v^ cos(nxi) ch(nx2) A)
удовлетворяет уравнению Лапласа и начальным, и гранич-
граничным условиям. Можно показать также, что в некотором
Классе функций решение поставленной задачи единственно.
Легко видеть, что, когда п —»• +оо, начальная функция
e~v™ cos(nx\) —► 0 равномерно по х вместе со всеми про-
производными по ij. Однако решение A) при любом х2 ф О
имеет вид косинусоиды со сколь угодно большой амплитудой.
Ясно, что в этом случае ни в какой области Q, лежащей в
полуполосе и примыкающей к оси х2 = 0, нет непрерывной
зависимости решения от начальной функции.
Таким образом, рассмотренная задача для уравнения
Лапласа поставлена некорректно. Непрерывная зависи-
зависимость от начальных данных в теории обыкновенных диф-
дифференциальных уравнений носит название "устойчивости
по Ляпунову". В теории уравнений в частных производных
вопрос корректности постановки задачи значительно более
сложен. Ниже мы дадим точное определение корректной по-
постановки задачи Коши для общих уравнений в частных про-
производных и докажем теорему, позволяющую определить, ко-
когда задача Коши не является корректно поставленной.
Надо иметь в виду, однако, что существуют реальные
физические и другие математические модели, в которых нет
непрерывной зависимости решения от изменения задавае-
задаваемых в задаче функций. Например, такие задачи возникают
в геофизике. Для решения этих задач используется так на-
называемый метод регуляризации. Мы эту тему в нашей книге
не затрагиваем, эти вопросы обычно излагаются в специ-
специальных курсах и специальной литературе. Мы рекомендуем
читателю книгу [25], где можно найти большую литературу
по этому вопросу.
52
Глава II. Некоторые вопросы общей
теории дифференциальных
уравнений в частных
производных
§ 1. Задача Коши. Теорема Ковалевской
1. Определение системы типа Ковалевской. Примеры. По-
Постановка задачи Коши для общей нелинейной системы
уравнений в частных производных типа Ковалевской
Рассмотрим систему уравнений в частных производных
с неизвестными функциями ui,v,2,...,un:
dniui(x,t) / duj \ , .
^i^x^», ) A)
где х = aji,...,a;n, a = «о + «i + ... + а„, а < rij, ао < п,-,
i,j = l,...,iV (число уравнений равно числу неизвестных).
Из написанных уравнений видно, что в них каждая из не-
неизвестных функций и,- имеет свой наивысший порядок п,
производных по i, входящих в рассматриваемую систему.
Независимая переменная t играет особую роль среди про-
прочих независимых переменных, так как:
а) среди производных наивысшего порядка гц от каждой
функции, входящей в систему, должна содержаться произво-
б) система разрешена относительно этих производных.
Обычно через t обозначают временную переменную, а
через xi,...,xn - пространственные переменные. Условиям
а) и б) удовлетворяет, например, уравнение Q^y — Аи, а
уравнение -£ = Аи и система
div ~v = О
Гл. II, § 1. Задача Коши. Теорема Ковалевской 53
не удовлетворяют им.
Систему A), удовлетворяющую условиям а) и б), будем
называть системой Ковалевской.
При некотором t = t° зададим начальные значения неиз-
неизвестных функций Ui(x,t) и их производных по t до порядка
ni — 1:
дкщ
dtk
= ¥>?(*), * = 0,1,...,гц-1. B)
Здесь <рк(х) заданы в области Go С И", лежащей на гипер-
гиперплоскости t — t°.
Задача A), B) называется задачей Коши. Нашей целью
является доказательство существования и единственности (в
окрестности рассматриваемой точки) решения задачи Коши
в классе аналитических функций при условии аналитично-
аналитичности коэффициентов уравнения и начальных данных.
2. Определение аналитической функции многих действи-
действительных переменных. Формулировка теоремы Ковалевской
о единсхвенносхи и локальной разрешимости задачи Коши
в классе аналитических функции для нелинейных систем
типа Ковалевской
Определение. Колшлексозначная функция F(x), опреде-
определенная в некоторой области Q, называется аналитической в
окрестности точки V = (ж°, ...,х°п), если она разлагается в
степенной ряд
■••£
£*!=<) £*m=0
абсолютно сходящийся при достаточно малых \х — х°
54 Глава II. Некоторые вопросы общей теории диф. уравн...
Известно, что в этом случае функция F(x) имеет в точке
х° производные всех порядков
В б
р рд
Введем сокращенное обозначение для производных от
начальных данных <р*[(х) по х:
где
а' = ах +а2 +...+«„, <*i > 0, i = l,...,JV.
Теорема Ковалевской (о единственности и локальной раз-
разрешимости задачи Коши для системы Ковалевской).
Если все функции <^*(х) аналитичны в окрестности точки
х° = (ж°,...,а;°), а функции F{ определены и аналитичны
в окрестности точки (to,x°...Xn,ui(t°,x°)...,<pl{a,(xo)...), то
задача Коши A), B) имеет аналитическое решение в неко-
некоторой окрестности точки (t°,x°) = (t°,x°, ...,x°), притом
единственное в классе аналитических функций.
3. Доказательство теоремы Ковалевской для линейних си-
систем первого порядка
Доказательство теоремы Ковалевской мы проведем для
линейных систем 1-го порядка. Можно доказать, что задачу
Коши для общих линейных систем можно свести к задаче
Коши для линейных систем первого порядка (а нелинейную
систему A) - свести к нелинейной системе 1-го порядкаI.
Итак, рассмотрим задачу Коши для следующей линей-
линейной системы 1-го порядка, разрешенной относительно про-
производных по t от всех неизвестных функций
Ч = Е Е <(*' *)тг+Е м*> *ь+/■■(*> *) (з)
01 axk
1 См.: Петровский И.Г. Лекции по уравнениям в частных произ-
производных.
Гл. II, § 1. Задача Коши. Теорема Ковалевской 55
с аналитическими коэффициентами а*Д<,ж), bij(t,x) и
fi(t,x) при произвольных аналитических начальных дан-
данных:
= 4>i(x). где i = l,N. D')
t-ta
Систему (З) коротко можно записать в операторном виде
ди _ ^ -
где м - вектор с компонентами ui,...,uyv, a A - дифферен-
дифференциальный оператор такой, что А и есть вектор со следую-
следующими N компонентами
N п г, N
где г = 1, JV.
Неоднородные начальные условия можно свести к одно-
однородным начальным условиям вида
Ui(t,x) =0, i = l,JV D)
t=t°
с помощью замены неизвестных функций. Вместо прежних
неизвестных функций и,- введем новые неизвестные функции
Vi = Ui - <fi
или в векторной форме
v = и — V .
Тогда функции и^ будут удовлетворять системе
C')
56 Глава II. Некоторые вопросы общей теории диф. уравн...
с начальными условиями
to=0. D')
Доказав существование решения для системы C') с услови-
условиями D'), мы докажем тем самым и разрешимость исходной
задачи. Будем считать, что такое преобразование сделано,
т.е. будем рассматривать задачу C), D).
а. Доказательство единственности аналитического реше-
решения
Перенесем точку V(t° ,ж°), в окрестности которой мы
будем решать задачу, в начало координат; и сначала дока-
докажем единственность решения в классе аналитических фун-
функций в окрестности точки "Р@,0), т.е. докажем, что ни в
какой окрестности этой точки не существует двух различ-
различных аналитических решений системы C), удовлетворяющих
при t = 0 одним и тем же начальным условиям D).
Итак, пусть в окрестности точки V существует аналити-
аналитическое решение задачи Коши - вектор и = (ui,...,un).
Аналитические в окрестности начала координат фун-
функции Ui(t,x) разлагаются в степенные ряды по t, x\, ...,хп.
Как известно, коэффициенты в этих разложениях вычисля-
вычисляются через производные от разлагаемой функции, взятые в
соответствующей точке (в нашем случае в начале коорди-
координат).
Обозначим через а^осц...£*„> или коРоче> через ага коэф-
коэффициент при ta°x"y ...х"п в разложении функции Ui(t,x) в
ряд в окрестности начала координат:
-""'-■■-• а„!о,!...о»!
■ hD°u<
E)
Тогда искомое решение задачи C), D), существование кото-
которого мы предположили, запишется в виде ряда:
Гл. II, § 1. Задача Коши. Теорема Ковалевской 57
-<", F)
где агаоа1 ап определяются формулами E).
Единственность решения задачи Коши будет доказана,
если мы докажем, что система C) и начальные условия D)
единственным образом определяют коэффициенты разло-
разложения функций Ui(t,x) в степенные ряды. Будем опреде-
определять эти коэффициенты, т.е. производные от Ui(t,x) в точке
"Р@,0), последовательно.
Начальные условия определяют единственным образом
все производные в точке "Р@,0) по Xi,...,xn:.
da'Ui{t,x)
t=0
1=0
и все они равны нулю в силу условия D). Так как мы предпо-
предположили, что решение задачи Коши существует, то подставим
в систему C) это решение. Получим тождества. Продиффе-
Продифференцируем все полученные тождества а\ раз по х\, а.г по х^
и т.д. Тогда в левых частях получатся производные вида
^'^~ G)
*1 я.а„ 1 VV
а в правых частях - только производные по ж* (к = 1,..., п)
отии коэффициентов, т.е. вполне определенные величины
в точке "Р@,0) (так как производные по Хк от и в *Р@,0)
мы определили); таким образом, производная G) в точке
V@,0) определяется однозначно. Продифференцировав си-
систему C) один раз по t и а\ раз по х\, сиг раз по х^ и т.д.,
мы определим однозначно в точке "Р@,0) производные вида
так как производная G) уже определена однозначно. Про-
Продолжая этот процесс дальше, мы однозначно определим ко-
коэффициенты E), которыми в свою очередь определяется
58 Глава II. Некоторые вопросы общей теории диф. уравн...
разложение F) нашего решения в степенной ряд, причем
однозначным образом (можно воспользоваться методом ин-
индукции). Таким образом, два аналитических решения за-
задачи C), D) с одними и теми же начальными условиями со-
совпадают в некоторой окрестности начала координат. Этим
доказана единственность решения задачи Коши в классе
аналитических функций.
Для доказательства существования решения задачи Ко-
Коши C), D) нам достаточно доказать, что степенные ряды F),
определенные коэффициентами E), сходятся в некоторой
окрестности начала координат.
Эти ряды будут удовлетворять нулевым начальным ус-
условиям D) и системе C), так как при построении этих ря-
рядов (при вычислении коэффициентов) мы пользовались тем,
что левые части системы C) равнялись ее правым частям в
некоторой окрестности начала координат.
Для доказательства сходимости степенных рядов исполь-
используют метод мажорантных рядов.
б. Мажоранты аналитической функции и их построение
Определение. Мажорантой (мажорантным рядом) для
функции ip(t,x), аналитической в некоторой окрестности
точки (t°,x°), называется всякая функция ф(г,х), анали-
аналитическая в этой окрестности, у которой все коэффициенты
разложения в степенной ряд Тейлора по степеням t — t°,
х\ — х°,...,х„ — ж° неотрицательны и не меньше абсолют-
абсолютных значений соответствующих коэффициентов разложения
функции <p(t, х), т.е. если <p(t, х) = £ с<*(* ~ t°)a°(x ~ х°)а' >
) = ^2Ca(t-t°)a°(x-x°)a', то \са\ < Са.
Перенесем начало координат в точку (t°,x°) и построим
для функции <p(t, ж), аналитической в окрестности этой
точки, мажоранту специального вида, которой мы будем
пользоваться в дальнейшем.
Пусть функция <p(t, x) разложена в ряд вида
...sS», (8)
Гл. II, § 1. Задача Коши. Теорема Ковалевской 59
и пусть он сходится в точке (t = bo,x = b), b = (bi,...,bn),
где все \bk\ > 0, к = 0,1, ..,п. Тогда существует постоянная
М > 0 такая, что при всех целых неотрицательных а,-
т.е.
М . .
|Caoai -ап' - M-i*ih»-iMe-'
Неравенство (9) мы получили для заданной функции (р(х),
для которой будем строить мажоранты.
Рассмотрим функцию
М
)
где |i| < |bo|> |a;jfc| < |bjfc|> ^ = l,...,n, a M взята из формулы
(9). Разложим каждый множитель вида -—Кт— в степенной
х~1*Гг
ряд по формуле
oo
**, W<i,
т.е. запишем ф(г, х) в виде
м
Очевидно, ^>(t, ж) является мажорантой для нашей <p(t, x) в
силу (9) и A1).
60 Глава II. Некоторые вопросы общей теории диф. уравн...
Мажоранты можно строить разными способами. Так, для
<p(t, x), заданной рядом (8), мажорантой будет также фун-
функция
1 _ Н-Zl+...+Zn '
1 d
где d = min(|bo|,|*i|,..,|bn|), |bfc| Ф 0, fc = 0,n, a
b = (bo,...,bn), как и прежде, некоторая точка сходимости
ряда (8) для ip(t, x).
В самом деле, при |£| + \х\\ + ... + \хп\ < d эта функция
разлагается в сходящийся ряд
Но
«! _ (a0 + a\ + ... + ап)\ >
ao\...anl ao\ai\...an\ ~
поэтому коэффициенты ряда для tf>i(t,x) положительны и
мажорируют коэффициенты ряда A1), а по доказанному
ряд A1) мажорирует ряд (8), значит и %l)i(t,x) мажорирует
ряд (8), т.е. функцию <p(t, х). Точно также для tp(t,x) мажо-
мажорантой будет функция
Гл. II, § 1. Задача Коши. Теорема Ковалевской 61
где d имеет прежнее значение, а число 7 > 1- Действи-
Действительно, если теперь разложить (tj + ац + — + ап)а в ряд
по степеням t,x\,...,xn, то получится ряд, отличающийся
от A2) только тем, что теперь коэффициенты будут больше,
так как умножаются на 7°°, где 7 > 1-
в. Доказательство существования аналитического реше—
ния; неравенства между коэффициентами данной и ма—
жорирующей систем; построение явного решения мажо-
мажорирующей системы
После того как мы научились строить мажоранты, перей-
перейдем к доказательству сходимости рядов для решения задачи
C), D).
Промажорируем коэффициенты системы C) с помощью
построенной нами функции г/*2(*>£)> подобрав при этом чи-
числа М > 0 и d > 0 так, чтобы функция
p(t)
при 7 > 1 была мажорантой для всех коэффициентов си-
системы, кроме свободных членов. Свободные же члены /,- про-
промажорируем функцией
1
1
—+х„
с другой постоянной Mi, не зависящей от М. Это можно
сделать, так как мажоранта такого вида существует у ка-
каждого коэффициента, и для построения общей мажоранты
надо числам М и М\ придать наибольшее, а числу d - наи-
наименьшее из всех значений, соответствующих различным ко-
коэффициентам.
Выбрав таким образом числа М, Mi, d, мы получим ма-
мажорирующую систему:
62 Глава II. Некоторые вопросы общей теории диф. уравн...
где A(t,x) = rp2(t,x), m = fy
Начальные условия возьмем в виде
A4)
где Uf(x) - есть мажоранты нуля (для и\ = 0), т.е. такие
функции, которые разлагаются в ряды Тейлора с неотри-
неотрицательными коэффициентами. Система A3) более простая,
чем C), и ее решение мы построим в явном виде. Как ска-
сказано выше, будем искать решение задачи C), D) в виде сте-
степенного ряда, определяя коэффициенты этого ряда из си-
системы указанным при доказательстве единственности ана-
аналитического решения способом. Этот ряд имеет вид:
Ui(t,x) = J2<°i-°r,ta°X<[l-Xnn- F)
Допустим, что решение задачи A3), A4) представляется
сходящимся рядом
Ui(t4x) = J2C-oar...aJQ°xi1-<n A5)
(ниже мы построим это решение).
Докажем, что тогда будут иметь место неравенства между
коэффициентами рядов (б) и A5):
Так как ряд A5) по предположению сходится, то неравен-
неравенства A6) доказывают сходимость ряда (б) в окрестности
точки @,0). Итак, докажем A6). По условию все С^о ап >
0. Для коэффициентов, которые определяются производ-
производными по х,-, t = 1, ...п при t = х = 0 неравенства A6)
выполняются, так как по условию W,|t_0 = U°{x), a U°(x)
является мажорантой нуля.
Для тех коэффициентов, которые определяются произ-
производными, где есть дифференцирование по tf, т.е. для с*о Ф 0,
соотношения A6) докажем по индукции по «о-
Гл. II, § 1. Задача Коши. Теорема Ковалевской 63
Допустим, что для любого а с а0 < к неравенства A6)
доказаны. Докажем A6) при ао = к + 1. Обозначим че-
через Da и, производную, соответствующую мультииндексу
а' = @,ai,...,<*„), и пусть Do = ^, D = -^. Тогда, диф-
дифференцируя систему C), получаем
Возьмем соответствующую производную и для мажорирую-
мажорирующей системы
3=1 к=1 }=\
В правых частях A7) и A8) содержатся производные от
Ui(t, x), Ui(t, x) только вида Da с <*о < к, а для коэффициен-
коэффициентов, определяемых ими, A6) выполнено по предположению
индукции.
Так как правая часть равенства A8) содержит только не-
неотрицательные члены, превосходящие модули соответствую-
соответствующих членов в A7) при х = 0, t = 0, а левые части A7) и
A8) выражаются через правые, то мы имеем
Таким образом, неравенства A6) доказаны.
Теперь докажем, что аналитические функции Ui(t,x), яв-
являющиеся решением задачи A3), A4), существуют в неко-
некоторой окрестности точки t — 0, х = 0.
Будем искать решение системы A3) в виде функции от
одного независимого переменного:
64 Глава П. Некоторые вопросы общей теории диф. уравн...
Ux{t,x) = U2{t,x) = ...=UN(t,x)=U{t,x) =
хг + ... + xn) = W(y),
где у = <7 + a?! + ... + ж„, \у\ < d.
Подставим предполагаемое решение в систему A3), то-
тогда получим, что функция U{y) должна удовлетворять ура-
уравнению
^ = A(y)(Nn^- +NU + m), A9)
ay ay
где
M
Af \
обыкновенное дифференциальное уравнение A9) с разделя-
разделяющимися переменными можно переписать в виде:
NU
G - A(y)Nn) dU = m( + l) A(y) dy
TTL
или
dU _ mA(y) dy _
ЖТТ " 7 - NnA(y) =
где
Выберем теперь положительное число 7 настолько боль-
большим, чтобы было 7~ NnA(y) > 0 в окрестности точки у = 0.
Тогда В(у) в этой окрестности будет аналитической фун-
функцией.
Интегрируя B0), мы найдем частное решение уравнения
A9):
откуда
Гл. II, § 1. Задача Коши. Теорема Ковалевской 65
се.
-
J
Докажем, что это частное решение дает нам искомую мажо-
мажоранту для решения задачи C), D).
Так как функции Ui(y) = Ui(t,x) удовлетворяют системе
A3), мажорирующей исходную систему, и так как неравен-
неравенства A6) мы уже доказали, то для доказательства того, что
B1) мажорирует решение задачи C), D), нам надо доказать,
что W(y)| 0 мажорирует тождественный нуль, т.е. U(y) при
t = 0 разлагается в ряд по xi,X2,...,xn с положительными
коэффициентами. Докажем это. Функция А(у) = 1^ljd есть
функция с положительными коэффициентами разложения
по у:
= l
1-y/d
следовательно,
Nn ., чЧ2
А(у)У +
тоже имеет положительные коэффициенты разложения по
степеням у. Этим же свойством обладает функция
т
о
Так как
5 - В. Н. Масленникова
66 Глава II. Некоторые вопросы общей теории диф. уравн...
то, очевидно, и функция U(y) тоже имеет положительные
коэффициенты при разложении по степеням у. Поэтому и
коэффициенты разложения U{t~i + хх + ... + хп) по степе-
степеням t,х\, ...,хп также положительны, т.е. 1/@,х) действи-
действительно является мажорантой нуля. Следовательно, Ы{—Ы —
U(t~( + Xi +... + a;n) действительно является решением нашей
задачи, т.е. мажорирует решение задачи C), D). Аналитич-
Аналитичность решения U(t~i + х\ + ... + хп) вытекает из того, что,
как мы показали выше, оно разлагается в ряд по степеням у,
а следовательно, и по степеням 2, х. Таким образом, сходи-
сходимость степенных рядов (б) доказана, т.е. доказана теорема
Ковалевской.
4. Некоторые замечании к теореме Ковалевской
г. Об области существования аналитического решения
При мажорировании свободных членов постоянную Mi
мы выбрали не зависящей от М для того, чтобы область, где
сходятся ряды, не зависела от начальных данных и свобо-
свободных членов уравнений. Действительно, область существо-
существования решения Ui{t,x) мажорирующей системы определя-
определяется областью аналитичности функции А(у) (т.е. коэффи-
коэффициентов a,ij(t, x) и bi(t, x)), которая зависит от чисел М и
d и не зависит от значений /j(z,t), а значит, и от началь-
начальных функций <fii(x). Таким образом, область существования
решения v,i(x,t) нашей задачи Коши C), D;) определяется
только числами Mud, т.е. не зависит от значений fi(t,x)
системы C) и начальных данных D').
д. Пример уравнения теплопроводности, для которого не
существует аналитического решения задачи Коши в
окрестности точки
Для систем, не имеющих вида A), теорема Ковалевской,
вообще говоря, неверна; об этом говорит следующий при-
пример, принадлежащий Ковалевской. Рассмотрим уравнение
теплопроводности
Гл. II, § 1. Задача Коши. Теорема Ковалевской 67
ди _ д2и
dt ~ дх2
с начальным условием
Аналитическое решение u(t, x) этой задачи, если оно су-
существует в окрестности начала координат, представляется
рядом:
^ 2n)! tn
7Г (Г^
n=0 v '
но этот ряд расходится в каждой точке при t ф 0. Ниже
мы покажем, что решение задачи Коши для уравнения те-
теплопроводности в классе неаналитических функций, напри-
например, в классе Сх\(/2х@, Т]) существует и выражается явной
формулой при t > 0.
е. Примеры локально неразрешимых уравнений
Уже из теоремы Ковалевской следует, что вопрос о раз-
разрешимости задачи Коши для уравнений в частных произво-
производных значительно сложнее, чем для обыкновенных диффе-
дифференциальных уравнений. Более того, для уравнений в ча-
частных производных вообще нет столь общих теорем о раз-
разрешимости задачи Коши, как для обыкновенных дифферен-
дифференциальных уравнений. Решение задачи Коши для уравнений
в частных производных может не существовать в классе Ст
(или в классе обобщенных решений), если даже все коэффи-
коэффициенты уравнения, правые части и начальные данные беско-
бесконечно дифференцируемы. Существуют примеры уравнений
в частных производных, которые в любой окрестности точки
(t°,x°) не имеют ни одного решения. Такие уравнения на-
называются локально неразрешимыми. Впервые пример такого
уравнения 2-го порядка с комплекснозначными коэффици-
коэффициентами был построен Г. Леви (США) в 1957 году. Он указал
множество (второй категории) функций f(x,y) € C°°(JR2),
68 Глава II. Некоторые вопросы общей теории диф. уравн...
для которых уравнение |^- + ix^- = f(x,y) не имеет реше-
решений в любой окрестности точки @, у).
Л. Хермандер [27] доказал, что можно найти такую фун-
функцию /(ж) € C°°AR-3), для которой уравнение второго по-
порядка с действительными коэффициентами вида
{х\ - xl)uXlXl + A + х1)(иХгХз - иХзХа) - xix2
a - (xix2u)XlX2 + (xix3u)XlX3 = f(x)
не имеет ни одного решения для любой окрестности 0 € IR3,
т.е. начала координат.
В настоящее время получены достаточные условия ло-
локальной неразрешимости уравнений с частными произво-
производными.
Как доказал Л. Хермандер, дифференциальное уравне-
уравнение с постоянными коэффициентами всегда разрешимо при
произвольной правой части, по крайней мере в любом ком-
компактном открытом подмножестве того открытого множества,
где задана правая часть уравнения f(x).
Отметим, что теорема Ковалевской утверждает, что вся-
всякое уравнение типа Ковалевской, в котором коэффициенты
и правая часть аналитичны, имеет решение на некотором
достаточно малом открытом множестве. Однако, для напе-
наперед заданного фиксированного множества решение, вообще
говоря,может и це существовать.
§ 2. Задача Коши с начальными данными на
произвольной поверхности. Возможность
ее сведения к задаче Коши с начальными
данными на гиперплоскости
Рассмотрим общее линейное уравнение порядка т:
aa(x)Dau = f(x), x = xo,xi,...,xn. A)
|a|<m
Пусть в окрестности Q точки V имеется п-мерная гладкая
поверхность S класса Ст и ее уравнение есть:
Гл. II, § 2. Задача Коши с нач. данными на произв. пов. ...
69
^■(хо,хь...,а:п) = 0.
Пусть п - нормаль к 5, и пусть S не имеет особых точек,
т.е. |V/"| ф 0. Пусть на поверхности 5 заданы условия:
дки
дп
к =
B)
Вместо нормали п в условии B) можно взять любое напра-
направление 7, не касательное к поверхности S.
Рассмотрим общую задачу Коши: найти функцию и (ж),
удовлетворяющую A), B) в некоторой окрестности п точки
V. Возникает вопрос: для каких уравнений, поверхностей 5
и начальных данных <£*(ж), к = 0,..., т — 1 эта задача имеет
решение в окрестности точки "Р? Сведем задачу A), B)
к задаче Коши, рассмотренной в предыдущем параграфе.
Сделаем замену независимых переменных так, чтобы повер-
поверхность Т = 0 перешла в одну из координатных гиперплоско-
гиперплоскостей. Такую замену можно сделать, например, в виде:
Уо = f{xo,...,xn),
Vj =*j, j = l,.-,n.
Эта замена не вырожденная, так как якобиан преобразова-
преобразования
70
Глава П. Некоторые вопросы общей теории диф. уравн...
3Z дТ_ д£
дхй
0
о о
Эх„
о
в виду того, что, не ограничивая общности, можно предпо-
предположить jg- ф 0.
В новых переменных у поверхность 5 задается уравне-
уравнением уо = 0. После замены независимых переменных ура-
уравнение A) примет вид:
C)
Ъа(у)В*й = /(у).
\<*\<т К
Чтобы это уравнение можно было записать в виде
необходимо, чтобы коэффициент ba(y), соответствующий
а = (т,0, ...,0), был отличен от нуля в окрестности точки
V. Если вычислить коэффициент ba(y) V« = ao...an такого,
что \а\ = т, т.е. при старшей производной, то мы увидим,
что он равен
D)
°<х\У) = X, а<*
|a|=m
Покажем это на примере уравнения 2-го порядка с двумя
независимыми переменными. В этом случае A) имеет вид:
Y^ aa(x1,x2)Dau = f(x1,x2)
или в более подробной записи (положим х\ = х, х2 = у)
Гл. II, § 2. Задача Коши с нач. данными на произв. пов. ...
71
+
+ a0Qu = /(z, y).
E)
Начальные условия зададим на кривой L:
ди
F)
Пусть уравнение кривой L имеет вид J-{x,y) — 0 и на ней
нет особых точек, т.е. |grad^F| ф 0 на L. Если мы сделаем
замену
{ = ?(*,у), ч = Ф{х,у),
где <P(z, у) - произвольная гладкая функция, для которой на
кривой якобиан преобразования
ат ат
дх ду
дФ дФ
дх ду
(можно взять Ф(х,у) = у, т.е. г) = у, тогда якобиан будет
иметь вид
ат
-аТ
0
ат
ду
1
то это преобразование "распрямит" нашу кривую X, пре-
превратив ее в кусок координатной прямой £ = 0. Ниже мы
покажем, что начальные условия теперь запишутся в виде:
ди
G)
А как при этом преобразуется уравнение A)? Имеем
72 Глава 11. Некоторые вопросы общей теории диф. уравн...
«х = Uttx+Urfx, Uy - U^ty +
«xj, =
y + (yT)x) +
+ Uttxy +
Если теперь полученные производные (8) подставить в E),
то мы получим новое уравнение вида
где через / мы обозначили сумму линейных членов, содер-
содержащих первые производные от и по f, г/, само и(£, г/), а также
свободный член. В (9) введены обозначения
Ъ\\ —
Чтобы наше новое уравнение (9) было уравнением Ковале-
Ковалевской для начальных данных G), необходимо, чтобы
Ьго = a2ofx + 2вц&£» + ао2$ ф О,
а это соответствует выражению C) для общего уравнения
порядка men независимыми переменными.
Докажем, что если на поверхности S заданы функция
и{х) и ее производные по направлению нормали до порядка
m — 1 включительно (или производные по любому не каса-
касательному направлению), то тем самым заданы все произво-
производные от и(х) до порядка m — 1 по каждому ж,.
При m — 2, п = 2, т.е. для уравнения E) этот факт
доказывается просто. Действительно, имеем
Гл. II, § 2. Задача Коши с нач. данными на произв. нов. ...
73
ди
дп
ди
ди -
ди
= — cos(r,z) + —cos(r,t/)
дх
ду
д<р0
(Ю)
где т - касательное направление к кривой L в точке (ж, у).
п
Пусть |п| = 1,|т| = 1. Обозначим направляющие ко-
косинусы этих векторов через ni,
и т\,
соответственно.
Система A0) имеет единственное решение |^, ^, так как
ее определитель
П\
т2
. —►
(отметим, что если вместо п взять любое некасательное на-
направление, то определитель будет тоже ф 0).
Покажем, каким путем можно доказать этот факт для
любых тип. Введем локальные криволинейные коорди-
координаты £о,£ъ •••,£?» в окрестности поверхности S таким обра-
образом, чтобы уравнение поверхности Т{х) — 0 приняло вид
£о = 0, а нормали к S совпадали с координатными линиями:
6
= с„.
74 Глава II. Некоторые вопросы общей теории диф. уравн...
По предположению, поверхность S гладкая, поэтому на
ней можно ввести параметры f i,..., £„ таким образом, чтобы
уравнения
задавали нашу поверхность S, и при этом ранг функцио-
функциональной матрицы ||dzj/9fjfc||, г = 0,1,...,п, к = 1,2,...,п
был равен п в каждой точке 5 и правые части в A1) были
достаточно гладкими функциями.
Пусть уравнения
х0 = -X"o(£<b£i,---»£n),
A2)
совпадают с уравнениями A1) при £о = 0, и пусть ура-
уравнения A2) определяют нормаль к поверхности S в точке
(£ь--ч£п) при изменении £о» т.е. £о - параметр вдолв нор-
нормали, a fi,...,£n - параметры точки пересечения нормали
с S, т.е. лежат на поверхности. Пусть параметр £о таков,
что хотя бы одна из производных дХ{/д£о ф 0, i = 0,1, ...п.
Тогда в точках S, т.е. при £о = 0, функциональный опреде-
определитель
эхо aXi эхп
дхй дхл дх„
дхд
Щп
Ф 0, A3)
так как последние п строк его линейно независимы потому,
что ранг матрицы
Гл. II, § 2. Задача Коши с нач. данными на произв. пов. ... 75
дх{
ее*
к = 1,2,...,п
равен п по предположению, а первая строка не может быть
линейной комбинацией остальных строк потому, что после-
последние п строк представляют собой векторы, лежащие в каса-
касательной плоскости к S, а первая строка представляет собой
вектор, ортогональный к S.
По непрерывности определитель A3) ф 0 в некото-
некоторой окрестности S. Поэтому в этой окрестности £0» Съ •••, £п
действительно можно принять за новые координаты точки
(жо,Х1,...,ж„). Тогда
A4)
дп
Эти равенства можно дифференцировать по £i, ...,£„. Тогда
получим все производные от и в координатах £ до порядка
т — 1 включительно.
Переходя к переменным zo,a;i,...,a:n согласно равен-
равенствам A2), получим на S все производные от и(х) до по-
порядка m — 1 включительно по переменным «о, ...,#„.
Согласно A0) для п = 2, т = 2 и A4) для любых пит
можно получить начальные данные на гиперплоскости, если
первоначально они заданы были на произвольной поверхно-
поверхности.
Нам надо еще ответить на вопрос, когда задачу A), B)
можно свести к задаче Коши с начальными данными на ги-
гиперплоскости, т.е. ответить на вопрос, поставленный в на-
начале § 2. Для этого мы вынуждены ввести одно из фундамен-
фундаментальных понятий в теории дифференциальных уравнений в
частных производных - определить характеристическую по-
поверхность (характеристику) для рассматриваемого уравне-
уравнения.
76 Глава II. Некоторые вопросы общей теории дйф. уравн...
§ 3. Характеристики и характеристические
направления. Особенности постановки
задачи Коши с начальными данными на
характеристиках
1. Определение характеристическое поверхности (харак-
(характеристики) для уравнения в частпнх производных. При-
Примеры
Вернемся к задаче Коши для уравнения
aa(x)Dau = /(*) A)
\a\<m
с начальными данными на произвольной гладкой поверхно-
поверхности 5, заданной уравнением 3-{х) = 0:
д*и _ . _ . . B)
Л
дп
S
т.е. к задаче, рассмотренной в § 2. Сведем задачу A), B) к
той, которую мы рассматривали в теореме Ковалевской (там
начальные данные задавались на плоскости х0 — const).
Для этого от переменных х перейдем к новым независимым
переменным
!№ = **(*), fc=0,l,...,n, C)
причем, пусть преобразование C) - невырожденное в окре-
окрестности точки V, т.е. det ||&F/9z|| ф 0 и кроме того, будем
считать, что Tq — Т, т.е. в новых координатах уравнение
Уо = 0 в окрестности точки V задает поверхность S. Было
доказано, что по заданным начальным условиям на S можно
определить все производные функции и{х) на поверхности S
до порядка т — 1 включительно по переменным ж, а значит,
и по переменным у. Эти производные в переменных у опре-
определяют данные Коши в окрестности точки V на гиперпло-
гиперплоскости уо = 0. Мы хотим применить теорему Ковалевской
Гл. II, § 3. Характеристики и характер, направления... 77
для нового уравнения. Поэтому нас интересует в новом ура-
уравнении коэффициент при старшей производной по уо. Этот
коэффициент при D™u равен
\а\=т
где Dj = g^- Пусть поверхность S, заданная уравнением
^F(x) = 0 такая, что в окрестности точки V
\а\=т
Тогда, разделив на указанный коэффициент, уравнение A)
в новых переменных можно записать в виде
дти ж—»
—- = J2 ba{y)D°u + f(y).
ар <т— 1
К этому уравнению можно применить теорему Ковалевской
в случае, если функция ^"(х), определяющая поверхность
S, коэффициенты уравнения и начальные данные - анали-
аналитические функции.
Важное значение имеет условие, что на 5
rr...(DnTr»?0. D)
Определение. Поверхность S, для которой выполняется
равенство
E)
a«(*)(grad.F)e=O, '
|a|=m
78 Глава II. Некоторые вопросы общей теории диф. уравн...
называется характеристической поверхностью или характе-
характеристикой для уравнения A).
Для рассмотренного нами уравнения второго порядка
(т = 2, п = 2) уравнение характеристики есть
(дТ\2 п
UJ °
Из определения E) видно, что уравнение характери-
характеристики определяется старшими членами дифференциального
уравнения, т.е. коэффициентами при старших производных.
Примеры:
1) Рассмотрим уравнение теплопроводности
дх\ ' дх\ '
Характеристика удовлетворяет уравнению
= 0. G)
Функция T{xq) = xq — с = 0 удовлетворяет G), поэтому
Xq = const есть характеристика для уравнения теплопрово-
теплопроводности.
2) Для волнового уравнения
= а Аи, х € JR ,
уравнение характеристик имеет вид
Гл. II, § 3. Характеристики и характер, направления... 79
Несколько позже мы проверим, что конус at — ±г, где
/~з
г = * / 23 x\i есть характеристическая поверхность для вол-
нового уравнения.
2. Особенности постановки задачи Коши с данными па ха-
характеристиках
Предположим, что поверхность S оказалась характери-
характеристической. Тогда коэффициент при дти/ду™ равен нулю и
уравнение A) превратилось на 5 в соотношение, куда входят
производные от и по уо,..., уп вида Dau, где ао < т — 1.
Так как на S заданы данные Коши
D*u
о'
»о=О
= <Рк(у'),
то уравнение на характеристической поверхности преврати-
превратилось в соотношение между начальными данными. Таким об-
образом, начальные данные на характеристической поверхно-
поверхности не могут быть заданы произвольно, они связаны между
собой соответствующим соотношением (в силу уравнения).
а) Рассмотрим задачу Коши для уравнения теплопрово-
теплопроводности F) с начальными данными
и
хо=О
xo=O
(8)
Бели решение задачи Коши F), (8) существует, то заданные
начальные функции должны удовлетворять соотношению
<pi = A<fo при xq = 0. (9)
б) Может случиться, что решение задачи Коши с началь-
начальными данными B)
может быть не единственным.
Рассмотрим уравнение колебаний струны
80 Глава II. Некоторые вопросы общей теории диф. уравн...
Соотношение E) для него есть
Прямые х\ — аха = const, x\ + ахо = const являются ха-
характеристиками уравнения A0). Замена независимых пере-
переменных
xi — ах0 = уо, *i + аж0 = у\
приводит к уравнению
Зададим для A1) начальные условия на характеристике:
ди
дуо уо=о
с такими началшяыми условиями решение задачи A1), A2)
существует только при некоторых условиях на </?i, и оно
не единственно. Покажем это. Все решения уравнения A1)
представляются в виде
«(yo,yi) = $i(yo) + $2(yi)- A3)
Функции Ф\ и #2 определим из начальных условий A2).
Имеем ч
откуда
а решение A3) примет вид
Гл. II, § 3. Характеристики и характер, направления... 81
u(yo,yi) = #i(yo)
Теперь используем второе начальное условие из A2) для
еделения #i(yo)-
Имеем
du(yo,yi)
определения
Имеем
у о=о ду0
у о=о
=ipi(yi) = const, A4)
т.е. начальная функция <fi(yi) должна быть постоянной.
Покажем, что и при этом условии задача A1), A2) имеет
бесчисленное множество решений. Действителмо, функция
^i(yo) есть произвольная функция класса С2(Ж1), удовле-
удовлетворяющая только условию A4). Такую функцию можно
представить в виде
*i(lto) = /Ы ~ /@) + УоМО) - /*@I, A5)
где /(уо) - произвольная функция из С2(Н1).
Легко видеть, что A5) удовлетворяет условию A4):
5*1 (уо)
дуо
Решение задачи A1), A2) при <^>o(yi) € С2(Н1) представля-
представляется теперь в виде
«(yo.yi) = Vo(yi) + /(Уо) ~ /@) + УоМО) - /'@)].
3. Характеристические направления. Определение харак-
характеристик с помощью характеристических направлений.
Примеры
Рассмотрим уравнение A).
Его левой части можно сопоставить многочлен от дей-
действительных переменных £ = (£о,£ъ--ч£п) вида
6 - В. Н. Масленникова
82 Глава II. Некоторые вопросы общей теории диф. уравн...
где £а = ££f1...£n"> те- ввести соответствие:
О . С > t<*Op<*l £<*„
дхк С*' дх%°дх°1...дх$п ?0 Cl ">Cn •
Многочлен A6) называется полным символом уравнения
A).
Многочлен от £ вида
|a|=m |a|=m
назовем главной частью символа уравнения A) или харак-
характеристическим многочленом.
Замечание. Иногда, в случае, когда используется преоб-
преобразование Фурье, главным символом и, соответственно, пол-
полным символом называют многочлены
\a\=m |a|<m
соответственно.
Оиределеиие. Рассмотрим вектор £ = (£0,6 > —> £п), |^| ф
О, ^ € Hn+1. Направление f называется характеристиче-
характеристический для уравнения A) в данной точке х, если
aa(x)C = О
|а|=т
или, более подробно,
eo+ori+...+an=ro
Гл. II, § 3. Характеристики и характер, направления... 83
Поверхность F{x) = О является характеристической,
если в любой ее точке направление нормали является ха-
характеристическим направлением. В самом деле, grad.F на-
направлен по нормали к поверхности Т = 0, а уравнение ха-
характеристики имеет вид
£ aa(:r)(grad:F)a=0.
а =го
Примеры:
1. Рассмотрим уравнение Лапласа
Выражение £% + £\ + £% = 0 есть уравнение характери-
характеристических направлений для оператора Лапласа. Мы имеем
из него, что все £* = 0, т.е. уравнение Лапласа не имеет
действительных характеристических направлений, а зна-
значит, не имеет и характеристик. Поэтому задачу Коши для
него можно рассматривать с начальными данными, задан-
заданными на любой поверхности.
2. Рассмотрим уравнение теплопроводности вида
ди ^-s 6Pu
2
Вектор £ = (^0,^1,^2^3M удовлетворяющий уравнению
задает характеристическое направление,
б*
84 Глава П. Некоторые вопросы общей теории диф. уравн...
Итак, £ = A,0,0,0) - характеристическое направление
для уравнения теплопроводности. Характеристическая по-
поверхность, у которой нормаль направлена параллельно оси
есть плоскость xq = const.
4. Характеристики и характеристические направления для
линейных систем произвольного иорядка
Рассмотрим систему
Здесь п j - порядок старших производных от каждой неизве-
неизвестной фуНКЦИИ Uj.
Поверхность Т{х) = 0 называется характеристической
поверхностью для системы A7), если на ней
,f^ tjK 'XdxJ \dxj \dxj ]
Аналогично определяется характеристическое направле-
направление. Вектор $ = (£(ь—,£п) G Hn+1, \Ц ф 0, имеет характе-
характеристическое направление для системы A7) в точке х, если
Поверхность, нормаль к которой в каждой точке имеет ха-
характеристическое направление, называется характеристи-
характеристической поверхностью.
Гл. II, § 4. Классификация уравнений и систем ... 85
Пример. Рассмотрим систему Копта - Римана.
дх0 + *- -°'
ди dv _
хх дх0
Найдем характеристические направления для этой системы.
Компоненты вектора £ = (£o,£i) должны удовлетворять со-
соотношению
6 -Со
т.е. а + 8 = 0.
Отсюда вытекает, что £i = fo = 0, т.е. система Коши -
Римана не имеет характеристических направлений, а зна-
значит, и характеристик.
§ 4. Классификация уравнений и систем
уравнений в частных производных.
Определение эллиптических,
гиперболических и параболических по
Петровскому линейных уравнений и
систем произвольного порядка. Системы,
эллиптические по Дуглису — Ниренбергу.
Примеры
Основные результаты по классификации уравнений вы-
высокого порядка и систем уравнений в частных производных
принадлежат И.Г. Петровскому.
Классификация имеет большое значение для теории ура-
уравнений в частных производных, так как принадлежность
уравнения к тому или иному типу говорит о многих свой-
свойствах решений этого уравнения и постановке для него кра-
, евых задач.
86 Глава II. Некоторые вопросы общей теории диф. уравн...
Отметим, однако, что при классификации выделяются
только три наиболее важных типа уравнений и систем: эл-
эллиптические, гиперболические и параболические. В то же
время значительно большая часть уравнений и систем ура-
уравнений в частных производных не принадлежат ни к одному
из этих трех типов. Таковыми, например, являются очень
важные в приложениях системы гидродинамики, приведен-
приведенные нами в § 2 главы I.
В настоящее время классификация еще продолжается.
Так, например, получили свое название и изучаются гипоэ-
ллиптические уравнения, которые характеризуются не свой-
свойствами корней характеристического уравнения, а
свойствами решений самого дифференциального уравне-
уравнения, а именно его гладкостью (см. [27]).
Классификация основана на свойствах характеристиче-
характеристической формы
|а|=т |а|=т
т.е. главной части символа уравнения
= /(.) A)
\а\<т
и, соответственно, системы уравнений.
При этом выделяются два важных класса уравнений по-
порядка т: уравнения эллиптического типа и уравнения ги-
гиперболического типа.
Определение 1. Уравнение A) называется эллиптическим
в точке х € Hn+1, если
aa(x)C ф 0 B)
при всех i € lRn+1 таких, что |£| ф 0.
Гл. II, § 4. Классификация уравнений и систем ... 87
Если условие B) выполнено во всех точках области О,
то уравнение A) называется эллиптическим в области Q.
; Таким образом, по определению эллиптическое уравне-
уравнение не имеет характеристических направлений.
Замечание. Говорят также, что уравнение A) является эл-
эллиптическим в точке х (или области Г2), если его характе-
характеристическая форма
|a|=m |a|=m
знакоопределена в точке х (или в области /2) для любого
f € Hn+1, |£| ф 0 (например, положительно определена).
Можно доказать, что для эллиптического уравнения A)
с вещественными коэффициентами m всегда четно (т = 21),
что является следствием алгебраической теоремы.
Онределеиие 2. Уравнение A) называется гиперболиче-
гиперболическим в точке х в направлении оси х0, если его характери-
характеристическое уравнение
аа(а:)^ЧГ-е"в=0 C)
|а|=го
имеет только действительные корни относительно £о
k'i' )
При этом, если все m действительных корней различны,
то уравнение называется строго гиперболическим (или ги-
гиперболическим по Петровскому) в направлении оси хо в
точке х; если же среди m действительных корней уравне-
уравнения C) есть кратные, то уравнение A) называется слабо
гиперболическим в направлении оси х0 в точке х.
Если уравнение A) гиперболично в каждой точке х € fi,
то говорят, что оно гиперболично в области /2.
Простейшим примером эллиптического уравнения явля-
является уравнение Лапласа:
88 Глава II. Некоторые вопросы общей теории диф. уравн...
так как
п
*=о
Простейшим примером строго гиперболического уравне-
уравнения в направлении оси xq является волновое уравнение
д2и
i
Действительно, его характеристическое уравнение
п
г2
имеет два действительных различных корня: £о = ||
И.Г. Петровским был выделен еще один важный класс
уравнений порядка т, которые носят название уравнений,
параболических по Петровскому.
При определении этого класса учитываются не только
члены уравнения с производными от и(х) порядка т, но и
некоторые члены с производными низшего порядка. В ура-
уравнении A) выделим особо переменную х0 и запишем A) в
виде
u(x) = f(x). (б)
Н<го
Пусть р - целое положительное число.
Многочлен вида
CUY G)
\а'\+рао=т
Гл. II, § 4. Классификация уравнений и систем ... 89
назовем обобщенной характеристической формой с весом р
для уравнения F) в точке х.
Определение 3. Уравнение F) называется параболиче-
параболическим (по Петровскому) в точке х, если для некоторого р
действительные части всех корней уравнения
aa(xQ,x'№(iaa'=0 (8)
|or'|+por0=m
относительно £о для любых действительных £' = (£i,..., £„)
таких, что |£'| = 1, имеют отрицательную действительную
часть, т.е. Re £о < —5, где £ = const > 0.
Если уравнение F) является параболическим в любой
точке х € ft, то оно называется параболическим в области
п.
Простейшим примером параболического уравнения яв-
является уравнение теплопроводности
dxQ ^ dx)
Действительно, обобщенная характеристическая форма с
весом р = 2 имеет вид
Уравнение (8) для нее
относительно £о при |£'| = 1 имеет единственный корень
90 Глава II. Некоторые вопросы общей теории диф. уравн...
т-е-
Классификация линейных систем уравнений в частных про-
производных проводится также путем выделения главной части,
но уже матричного дифференциального оператора.
Определение 4. Система уравнений
где u = (uj, г*2,..., ujv), называется эллиптической в точке х
(или в области п), если в точке а; (или лри всех х Е fi) для
любых действительных £ = fo> —,Zn, If | ^ 0 детерминант
Ея«/\ лого tori tor
|or|=n,-
A0)
представляет собой знакоопределенную форму по
fo,—,£n, т.е. он не обращается в нуль ни при каких дей-
действительных £,, j = 0, ...,п, если только не все они равны
п
нулю, т.е. если ^2 £? ф О-
i=o
Согласно определению 4 система Коши - Римана
du dv
о— + д— = О,
OXq ОХ\
du dv _
является эллиптической системой. Действительно, как мы
уже проверили выше, ее определитель
Гл. II, § 4. Классификация уравнений и систем ... 91
- -Р2 - B
— Со Ci
знакоопределен, т.е. ве обращается в воль, если |£| ^ 0.
Приведенное определение эллиптической по Петровско-
Петровскому системы достаточно просто, но оказалось недостаточно
широким.
Наиболее общее к настоящему времени определение эл-
эллиптической системы принадлежит А. Дуглису и Л. Нирен-
бергу (отметим, что есть и промежуточные определения, на-
например, сильно эллиптических систем). Мы приведем опре-
определение эллиптической по Дуглису - Ниренбергу системы,
как дополнительный материал, так как в научных и практи-
практических исследованиях это определение бывает полезно (см.
[2], [3]).
Мы видели, что для определения эллиптичности по Пе-
Петровскому системы (9) нужно выделить максимальный по-
порядок П] дифференциальных операторов в каждом столбце
матрицы (см. [10])
/lu(x,D) ... hN(x,D)\
C(x,D)=[ (И)
\lN1(x,D) ... lNN{x,D)/
(здесь линейные дифференциальные операторы Uj(x,D) яв-
являются полиномами от дифференциальной операции D =
(sir' —» af^J c переменными коэффициентами), т.е. для ка-
каждой неизвестной функции uj, j = l,...,i\T, определить чи-
число
deg 1ц(х, D), j = 1,..., N,
где символом deg обозначен порядок старшей производной,
входящей в оператор. Обозначим через Uj{x, D) главную ча-
часть порядка rij каждого оператора lij(x,D) в A1), т.е.
92 Глава П. Некоторые вопросы общей теории диф. уравн...
{О, если deg Uj(x, D) < n,,
Y^ "Tj(x)Da, если deg 1ф,D) = n,. A2)
Таким образом, главной частью по Петровскому оператора
£(z, D) является матричный оператор
/In(x,D) ... hN(x,D)\
£(*,£>)=( , A3)
\lN1(x,D) ... iNN{x,D)J
используемый в определении A0), т.е. система (9) будет эл-
эллиптической по Петровскому в точке i6fi, если
detC{x,O^0 V£eIRn\{0}.
Для определения эллиптичности по Дуглису - Нирен-
бергу главная часть оператора С(х, D) определяется другим
путем, и в нее могут входить младшие производные.
Предположим, что существуют два набора целых чисел:
Ы?=1 и {*,}?=!, A4)
удовлетворяющих условию
Si + tj A5)
для всех тех i,j, для которых оператор Uj{x,D) ф 0, при
этом hj(x, D) = 0, если st + tj < 0; очевидно, любые за-
заданные Si,tj могут быть заменены на Si + const, tj + const.
Главная часть оператора C(x,D) по Дуглису - Ниренбергу
определяется с помощью этих наперед заданных наборов це-
целых чисел A4) с условием A5). Согласно введенным набо-
наборам, определим вектора с целочисленными компонентами:
з = (si,...,sn), t = (<i,...,<jv). Главной частью оператора
C(x,D) по Дуглису - Ниренбергу, соответствующей набо-
наборам smt, назовем матричный дифференциальный оператор:
Гл. II, § 4. Классификация уравнений и систем ... 93
где дифференциальные операторы
о ecJDIdes №>
Определение 5. Система (9) называется эллиптической по
Дуглису - Ниренбергу в точке х € п, если существуют
два набора целых чисел, удовлетворяющих условию A5) и
такие, что
M(x,O^0 V£elRn\{0}. A6)
Система (9) называется эллиптической по Дуглису - Ни-
Ниренбергу в области п € Ип, если она является эллиптиче-
эллиптической по Дуглису - Ниренбергу в каждой точке х G П. Вся
трудность состоит в том, как найти наборы s и t, удовлетво-
удовлетворяющие условиям A5) и A6). Этому помогает нормировка
наборов s и t.
Из условий A5) видно, что существенно только значение
суммы si + tj. Поэтому, добавляя одно и то же число ко
всем компонентам вектора s и вычитая то же число из всех
компонент вектора t, получим новые наборы s' и t', которые
эквивалентны наборам s и t в том смысле, что
Отсюда следует, что можно считать
si<Q, i = l,...,N. A7)
Так как система (9) является системой N уравнений с N
неизвестными, то для каждого j = 1,...,N найдется хотя бы
94
Глава II. Некоторые вопросы общей теории диф. уравн...
одно значение t = 1,..., JV, для которого Uj(x,D) ф 0, т.е.
матрица A1) не имеет нулевых столбцов. А тогда из условия
A5) следует, что
j(x,D)>0. A8)
A9)
Из A7), A8) находим, что
Условия A7) и A9) называются условиями нормировки на-
наборов s и t. Условия нормировки A7) и A9) принципиаль-
принципиальной роли не играют, но они облегчают процедуру нахожде-
нахождения наборов s -a t, удовлетворяющих требованиям A5) и
A6).
Рассмотрим некоторые примеры.
1. Характерным и важным примером системы эллипти-
эллиптической по Дуглису - Ниренбергу и не эллиптической по Пе-
Петровскому, является система, описывающая установившееся,
т.е. стационарное, медленное течение вязкой несжимаемой
жидкости:
Г -&v + gradp = О,
\ div у = О,
B0)
где поле скоростей v(x) = (wi, t>2, v$), p(x) - скалярная фун-
функция, х € Ci С Ж3. Обозначив u = (vi,v2,V3,p), перепишем
B0) в виде
C(D)u(x)
где оператор
C(D) =
= 0,
/-Д
0
0
0
-А
0
0
0
-д
;
д
эХ1
a
ш;
a
9X8
0 /
B1)
Гл. II, § 4. Классификация уравнений и систем ...
95
Выделяя главную часть оператора C(D) no Петровскому,
находим п\ = П2 = пз = 2, П4 = 1- Поэтому главная часть
оператора C(D) по Петровскому есть
£(£>) =
f-A
0
0
< 0
ет, что
-lei
0
0
0
0
-л
0
0
2
0
lei
0
0
0
0
-д
0
2
Эц \
9
9X2
0/
0
0
-|£|2
0
е2
0
= 0 V£ € В3,
т.е. система B0) не является эллиптической по Петровскому.
Посмотрим, будет ли система B0) эллиптической по Ду-
глису - Ниренбергу. Для этого необходимо установить су-
существование наборов s и t с условиями A5), A6). Вопрос
решается перебором конечного числа вариантов, если вос-
воспользоваться условиями нормировки A7) и A9) и следую-
следующим правилом: значения Si выбирать максимальными, а зна-
значения tj - минимальными из всех возможных значений Si и
tj, которым соответствует главная часть оператора C(D):
... hN(D)\
Ini(D) ..
\
Ь
где Uj(D) есть обычная главная часть оператора
Удобно выписывать значения з^ в виде столбца слева от ма-
матрица C(D), а значения tj - в виде строки над матрицей
C{D). Для рассматриваемого нами примера максимальными
Si и минимальными tj, для которых выполняются условия
A5),A6), являются:
s = @,0,0,-l), * = B,2,2,1),
96
Глава II. Некоторые вопросы общей теории диф. уравн.
т.е.
2
2
0 /-Д 0
0
0
0 -Д
0 0
2
0
0
-Д
9x7
Соответствующая главная
/-Д
0
0
^ ail
а ее определитель
det£e,t(O =
ж3 \ {o}
не
0
0
fl
0
-Д
0
9
9x2
2
1
9
977
9
9хг
9
0 *
часть
0
0
-Д
9
9xs
0
-lep
0
•
/
будет]
_9_ч
9xi \
9
9X2
9
9xs
0 /
0
0
ер
ешеть вид
6
6
0
= ч
т.е. система B0) является эллиптической по Дуглису - Ни-
Ниренбергу.
2. Любая эллиптическая система или одно уравнение мо-
могут быть сведены к системе первого порядка. Но оказыва-
оказывается, что невырожденные преобразования уравнений и си-
систем не сохраняют эллиптичности по Петровскому, но со-
сохраняют эллиптичность по Дуглису - Ниренбергу. Чтобы в
этом убедиться, рассмотрим уравнение Лапласа
Дм(х) = 0, х G И2.
Как было нами установлено, оно является эллиптическим по
Петровскому. Преобразуем это уравнение второго порядка
в систему уравнений первого порядка. Обозначив
Гл. II, § 4. Классификация уравнений и систем ... 97
и(х) = Мз(ж), Uj(x) = — 7j , ^2C5) = —7ч ,
мы получаем систему первого порядка вида
«1 + т^- = О,
= 0, B2)
Система B2) с постоянными коэффициентами и ее оператор
A1) есть:
1 о ш:
C(D) = | 0 1 ^ | B3)
а а п
ЭХ! 9X2
Попытаемся найти вектора s и t с целочисленными ком-
компонентами, которые бы одновременно удовлетворяли усло-
условиям A5), A6). Бели, например, взять наборы s = @,0,0)
и t = A,1,1) или ^ = @,0,0), t = B,2,2), то они, очевидно,
удовлетворяют условию A5), но не удовлетворяют условию
A6), так как главные части оператора B3) для них есть со-
соответственно
■ °
чах!
0
0
а
дх2
_а_\
а^7 1
0 )
и /
и Са
AD) = |
/о
0
0
0
0
0
0
0
для которых условие A6) не выполняется. Но для удовлетво-
удовлетворяющих условию A5) наборов s = (—1,-1,0), t = A,1,2),
соответствующая главная часть
0
1
7 - В. Н. Масленникова
98
Глава II. Некоторые вопросы общей теории диф. уравн...
Ей соответствует определитель:
1 0 £i
О 1 £2
6 6 О
Поэтому система B2) будет эллиптической по Дуглису -
Ниренбергу.
Теперь определим главную часть по Петровскому для
системы B2Х т.е. определим матричный оператор A3) по
правилу A2). Эта главная часть имеет вид:
£(£>) =
т£- О
а ее определитель
0 0 £2
6 6 0
= 0 V£€lR2
т.е. система B2) не является эллиптической по Петровскому,
хотя она эквивалентна эллиптическому уравнению Лапласа.
Следовательно, невырожденные преобразования уравне-
уравнений и систем не сохраняют эллиптичности по Петровскому.
М.Ф. Атья и И.М. Зингер доказали, что эллиптичность
по Дуглису - Ниренбергу сохраняется при любых невыро-
невырожденных преобразованиях уравнений и систем (см. [3]).
Замечание. Отметим для сведения читателей, что порядок
полинома A6) по £ для системы эллиптической по Дуглису
- Ниренбергу с вещественными коэффициентами, как и в
случае системы Петровского, всегда четный. Но если си-
система имеет комплексные коэффициенты, то порядок по-
полинома будет четным, если число независимых переменных
Гл. II, § 4. Классификация уравнений и систем ... 99
п > 3; в случае п = 2 порядок полинома A6) может быть
как четным, так и нечетным (см. [2]).
Определение 6. Система линейных уравнений (9) назы-
называется гиперболической по переменной xq в данной точке
х (или в области О), если при любых действительных £',
£' = £ь ...,£„ таких, что |£'| ф О, определитель A0) относи-
относительно £о имеет в этой точке (или области Q) только дей-
действительные корни £о = £о(£ъ— »&>)• Вели эти корни раз-
различны, то система (9) называется гиперболической в стро-
строгом смысле.
Примером гиперболической в направлении оси хо си-
системы является система
du dv _
dxo dx\
du dv
dxi dxo '
описывающая одномерные звуковые волны и колебания стру-
струны. Характеристическая форма, т.е. определитель A0), для
этой системы есть
Корни уравнения — £jj + $ — 0 относительно £о имеют вид
£о = i^i и являются действительными и различными при
161*
161*
Рассмотрим систему уравнений, разрешенную относи-
относительно первой производной по хо, следующего вида
Онределенне 7. Система A1) называется параболической
в точке х (или в области Q), если при любых действительных
£' = £i, ...,£я таких, что |£'| = 1, все корни определителя
7*
100 Глава II. Некоторые вопросы общей теории диф. уравн.
|а|=2т
относительно £о в точке х (или в области Q) имеют отрица-
отрицательные действительные части Fij - символ Кронекера).
Для уравнений в частных производных второго порядка
можно провести более детальную классификацию, разбивая
все уравнения второго порядка на классы, инвариантные
при любой невырожденной замене независимых перемен-
переменных. Одновременно можно доказать, что уравнение второго
порядка можно привести линейной заменой независимых пе-
переменных к более простому каноническому виду в каждой
фиксированной точке х°. Если же уравнение второго по-
порядка зависит только от двух переменных, то его можно при-
привести к каноническому виду одной и той же заменой незави-
независимых переменных во всей области п, где задано уравнение.
§ 5. Приведение уравнения 2-го порядка от многих
независимых переменных к каноническому
виду в фиксированной точке. Классификация
Рассмотрим общее линейное уравнение 2-го порядка
Е в«(*) яйг- + Е wJr+<х> = я*)' w
.' . C/XtC/X] . CXi
t,j=O J 1=0
заданное в некоторой области п С И" ; пусть a,j = ац.
Зафиксируем точку х° € п. Пусть вектор $ = (£<ь—»£п)-
Рассмотрим квадратичную форму
a(x°,0 = J2 ац(х°)ЬЬ = £ a&fcO. B)
t,j=O i,j=0
соответствующую матрице А = Ца^Ц, которая является ха-
характеристической для уравнения A) в точке х°. Квадра-
Квадратичную форму B) можно привести к каноническому виду в
Гл. II, § 5. Приведение уравнения 2-го порядка... 101
каждой фиксированной точке х°. Так как мы считаем ма-
матрицу ||а°,|| симметрической, то ее собственные значения
действительны.
Пусть к\ - число положительных, &2 - число отрицатель-
отрицательных, &з - число нулевых собственных значений матрицы А.
Очевидно, к\+к2 + кз = п + 1 и числа Аг,- инвариантны отно-
относительно замены независимых переменных в квадратичной
форме B).
Тип уравнения A) в фиксированной точке х° определя-
определяется тремя числами: к\, &2> &з-
1. Бели все собственные значения матрицы А одного
знака, то уравнение называется эллиптическим.
2. Если либо
кг = п, к2 = О, к3 = 1,
либо
к\ =0, &2 = п, кз = 1,
то уравнение называется параболическим (или слабо пара-
параболическим).
3. Бели либо
fci = п, &2 = 1> &з = О,
либо
h = 1, кг = п, к3 = О,
то уравнение называется гиперболическим.
Рассмотрим примеры.
1.
Jt=O
Все собственные значения квадратичной формы равны 1,
значит, уравнение эллиптического типа.
102 Глава II. Некоторые вопросы общей теории диф. уравн...
2.
п
здесь а(х°,£) = - £ ££, fci = 0, к2 = п, fo = 1, по-
Jt=i
этому рассматриваемое уравнение принадлежит к парабо-
параболическому типу.
3.
д2и
n
здесь а°(£) = $j — ]>3 £(, &i = 1, k2 = n, &з = О, поэтому рас-
рассматриваемое уравнение принадлежит к гиперболическому
типу.
Классификация должна быть инвариантной относительно
замены независимых переменных в уравнении; докажем,
что введенная классификация действительно удовлетворяет
этому требованию.
Из алгебры известно, что линейной заменой независи-
независимых переменных квадратичную форму B) можно привести
к каноническому виду.
Канонический вид квадратичной формы есть
t=0
где 7t принимает значения 0,1 или — 1.
Уравнение 2-го порядка вида A) также можно привести
к каноническому виду в точке. Сделаем линейную замену
независимых переменных. Пусть
у = Вх
или более подробно
Гл. II, § 5. Приведение уравнения 2-го порядка... 103
п
У к =
1=0
где det(Bki) ф 0. Тогда
ди _ ^ ди д*ч _ ^ д*и
а уравнение A) примет вид:
или
где В' означает матрицу, транспонированную к В.
Так как любая постоянная матрица может быть при-
приведена к диагональному виду ортогональным преобразова-
преобразованием, то выберем это преобразование у — Вх с самого на-
начала именно таким; тогда получаем
104 Глава II. Некоторые вопросы общей теории диф. уравн...
Таким образом, наше уравнение A) примет канониче-
канонический вид, т.е. в уравнении не будет смешанных производных,
а коэффициентами будут собственные числа матрицы ||а°.-||,
т.е. уравнение A) будет иметь вид:
^~ ди .
Сделаем еще дополнительную замену вида:
1
*С ) I Т/ 4 JLJ1SL /\ 4 ^Р U ч
тогда уравнение A) в рассматриваемой фиксированной точ-
точке запишется в каноническом виде
где 7* = 0,1,-1.
Число нулевых значений 7* и разность между числом по-
положительных и отрицательных 7it являются инвариантами.
Следовательно, определенные нами выше классы инвариан-
инвариантны относительно линейного преобразования независимых
переменных.
Согласно выше приведенным определениям канониче-
канонический вид эллиптического уравнения в точке есть:
Канонический вид параболического уравнения в точке:
Канонический вид гиперболического уравнения:
Гл. II, § 5. Приведение уравнения 2-го порядка... 105
Бели т коэффициентов в квадратичной форме имеют один
знак, а п + 1 — га - противоположный, то уравнение называ-
называется ультрагиперболическим:
дги
Jk=O ^* k=m+l K
В параболическом случае может быть равен нулю больше,
чем один коэффициент при второй производной: например,
уравнение
будет также уравнением параболического типа; иногда ура-
уравнение -
называют слабо параболическим; при этом, если в F) знак
"-", то уравнение называют прямо параболическим, а если
знак "+" - обратно параболическим.
Уравнение A) называется эллиптическим (гиперболиче-
(гиперболическим, параболическим) в области fi, если оно эллиптиче-
эллиптическое (соответственно, гиперболическое, параболическое) в
каждой точке х £ Q.
Замечание. Во всей области п С Hn+1 при п > 2 уравне-
уравнение A) с переменными коэффициентами к каноническому
виду, вообще говоря, не приводится, так как число смешан-
смешанных производных в нем равно
Со Ып + 1)
Ui= V 2 У > п + 1 при п>2,
106 Глава II. Некоторые вопросы общей теории диф. уравн...
а при замене (к = (к(х) число неизвестных функций (к,
к = 0,1,...,п (с помощью которых мы могли бы привести
уравнение к каноническому виду) равно п ■+- 1, что недо-
недостаточно, чтобы уничтожить коэффициенты при смешанных
производных.
Действительно, если брать линейную замену, то из ал-
алгебры известно, что квадратичная форма только с постоян-
постоянными коэффициентами приводится такой заменой к канони-
каноническому виду; если брать нелинейную замену
С* = С*0*0, fc = 0,l,...,n,
то коэффициенты при смешанных производных в новых пе-
переменных должны удовлетворять дифференциальным соот-
соотношениям вида:
i,j=0
Число этих уравнений при к ф I равно С£+1 = п ^ ^' > п+
1, а число определяемых функций С* при п > 2 равно п +1.
При п = 2, т.е. в трехмерном пространстве, коэффициенты
при смешанных производных можно обратить в нули, но при
этом коэффициенты при несмешанных производных будут
различными.
Бели коэффициенты уравнения A) постоянны, то линей-
линейной невырожденной заменой независимых переменных ура-
уравнение A) можно привести к каноническому виду C) во всем
Hn+1 Vn. Однако, в случае двух независимых переменных
(п = 1 в наших обозначениях) уравнение с переменными
коэффициентами можно привести к каноническому виду во
всей области (или в IR2) с помощью нелинейного преобра-
преобразования, что будет доказано в следующем параграфе.
Гл. II, § 6. Приведение уравнения 2-го порядка ... 107
§ 6. Приведение уравнения 2-го порядка на
плоскости к каноническому виду. Еще раз о
типах уравнений
Рассмотрим уравнение
Lu ее а^у)— +
д2и С(
в области Q С И2, где о,-у зависят от х и у. Поставим такой
вопрос: можно ли выбрать замену независимых переменных
х и у таким образом, чтобы уравнение A) можно было при-
привести к каноническому виду в области, а не в фиксирован-
фиксированной точке, как это было сделано в предыдущем параграфе.
Ответ на этот вопрос положительный.
Рассмотрим невырожденную замену переменных:
= г](х,у) с якобианом
дх , ду
дп дг)
дх
л/г * ду
отличным от нуля. Мы подсчитали, что в новых переменных
наше уравнение будет иметь вид
Lu =
« -A&u г,» ди ди.
+ 2а12г]хг]у + а22г)у\ j-j- + /(£, 77, и, —, —) = О
ди ди.
—, —
ИЛИ
д2и OL 52« , д2и .
6n + 2bl2 + b22+ / = 0.
Приведение уравнения 2-го порядка с переменными коэф-
коэффициентами в случае двух независимых переменных вида
108 Глава II. Некоторые вопросы общей теории диф. уравн...
A) к каноническому виду, определение характеристик этого
уравнения и его типа сводится к решению пары обыкновен-
обыкновенных дифференциальных уравнений. Эта пара обыкновен-
обыкновенных дифференциальных уравнений определит 2 семейства
характеристик уравнения A).
Изучим подробно этот вопрос. Согласно выше рассмо-
рассмотренным определениям уравнение характеристик для ура-
уравнения A) имеет вид
п ЬТдТ
+ 2 ^
Имеет место следующая
Лемма. Пусть функция f(x, у) класса С1 такова, что ^- ф
0 в рассматриваемой области 17. Для того, чтобы семейство
кривых Т{х, у) = const представляло собой характеристики
уравнения A), необходимо и достаточно, чтобы выражение
Т{х,у) = с было общим интегралом обыкновенного диффе-
дифференциального уравнения
Доказательство. Необходимость.
Пусть Т{х, у) =■ с есть семейство характеристик уравне-
уравнения A), т.е. Т{х,у) удовлетворяет B). Тогда, подставив это
Т{х, у) в B) и разделив на {Т'уJ ф 0 (заметим, что условие
Ту ф 0 в Q естественно, так как иначе бы Т не зависело от
у, а значит, в силу B), и от ж), мы получаем, что равенство
является тождеством, так как оно удовлетворяется для всех
ж, у в той области, где задано решение уравнения B).
Гл. II, § 6. Приведение уравнения 2-го порядка ... 109
Рассмотрим это Р(х, у) = с и разрешим его по у: у =
/(ж, с) (пользуясь теоремой о неявной функции). Вычисляя
производную функции, заданной неявно, получаем.
dy Я,(»,у)
dx
Отсюда следует, что у = f(x,c) удовлетворяет обыкновен-
обыкновенному дифференциальному уравнению C).
Достаточность.
Пусть Р(х, у) = с есть общий интеграл обыкновенного
дифференциального уравнения C). Покажем, что он есть
частное решение уравнения B), т.е. определяет характери-
характеристику уравнения A). Для этого достаточно доказать, что
Т{х,у) удовлетворяет B) в произвольной точке (х°,у°).
Проведем через точку (х°,у°) интегральную кривую
уравнения C), полагая Т{х°, у ) = с°, т.е. рассмотрим инте-
интегральную кривую у = /(ж,с°). Для всех точек этой кривой
имеем
(dy\2 dy
1 —1 — 2ai2-j-
= o.
Полагая в последнем равенстве х = ж°, получаем, что
■^"(я»!/) удовлетворяет уравнению B) в точке (ж°,у°).
Лемма доказана.
В силу только что изложенного, обыкновенное диффе-
дифференциальное уравнение C) называется характеристическим
уравнением для уравнения в частных производных A), а
его интегралы - характеристиками уравнения A). Бели те-
теперь при замене независимых переменных в A) в качестве
£ взять f(x,y), где f(x,y) есть общий интеграл обыкно-
обыкновенного дифференциального уравнения C), то мы обра-
обратим в нуль коэффициент при и^; если, кроме того, взять
110 Глава II. Некоторые вопросы общей теории диф. уравн. .
г/ — Q(x, у), где Q(x, у) - другой общий интеграл уравне-
уравнения C), независимый от первого, то мы обратим в нуль и
коэффициент при uvv.
Бели обыкновенное дифференциальное уравнение C)
решить как квадратное уравнение, то оно распадается на
два уравнения относительно -^\
, у) ± у/а\2{х, У) - «п(^ y)«22(s, у)
dx an (ж, у) '
Это и есть 2 обыкновенных дифференциальных уравнения
для характеристических кривых для уравнения в частных
производных A) в случае двух независимых переменных.
Интегральные кривые уравнений D) зависят от знака
дискриминанта
D = о12 - Оца22,
и этот знак, оказывается, определяет тип уравнения в ча-
частных производных A) в случае двух независимых перемен-
переменных.
Определение. Уравнение A) в точке ж, у называется ги-
гиперболическим, если D > 0; эллиптическим, если D < 0;
параболическим, если D = 0.
Отсюда ясно, что в различных точках области уравне-
уравнение с переменными коэффициентами может принадлежать
различным типам. Рассмотрим область Q, во всех точках
которой уравнение A) имеет один и тот же тип.
Через каждую точку области п проходят, согласно D),
две характеристики, причем для уравнения гиперболиче-
гиперболического типа они действительны и различны, для уравнений
эллиптического типа они комплексны и различны, а для ура-
уравнений параболического типа обе характеристики действи-
действительны и совпадают между собой. Разберем каждый случай
отдельно:
Гл. II, § 6. Приведение уравнения 2-го порядка ... 111
1. Для уравнения гиперболического типа мы найдем два
общих интеграла из D): !F(x, у) = с; Q(x, у) = с. Если те-
теперь сделаем замену f = f(x, у), r\ = Q(x, у) с якобианом
ф О, так как Т и Q линейно независимы, то мы получим
уравнение A) в виде:
Это каноническая форма гиперболического уравнения от
двух независимых переменных. Если мы положим
где хо,х\ - новые переменные, т.е. сделаем еще раз замену
переменных, тогда уравнение A) примет вид:
т.е. мы получим уравнение колебаний струны в обычной
форме.
2. Для уравнения параболического типа
D = а\2 -опо22 =0,
т.е. уравнения D) совпадают, и мы получаем один общий
интеграл f(x,y) = с уравнения C). Положим £ = f(x,y),
в качестве rj возьмем любую функцию, линейно независи-
независимую от !F{x, у). Так как в этом случае из D = О =Ф- а\2 =
у/апам, то при указанном выборе новых независимых пе-
переменных коэффициент
Отсюда следует, что новый коэффициент при смешанной
производной обратится в нуль. Действительно,
112 Глава II. Некоторые вопросы общей теории диф. уравн...
= {у/ап£х
+ Verity ) (yunVx + у/аггЪ) = 0.
Поэтому канонический вид уравнения A) в параболическом
случае:
Если случится так, что в правую часть не войдет и^, то
мы получаем обыкновенное дифференциальное уравнение,
зависящее от £, как от параметра.
3. Для уравнения эллиптического типа D < 0, т.е. об-
общие интегралы обыкновенного дифференциального уравне-
уравнения комплексны.
Если f(x, у) = с есть комплексный интеграл первого
уравнения D), тогда f(x,y) — с, где Т - функция, сопря-
сопряженная с Т, будет комплексным общим интегралом второго
уравнения.
Если теперь перейти к комплексным переменным
£ = !F(x, у), г] = f(x, у), то уравнение эллиптического типа
будет иметь тот же канонический вид, что и гиперболическое
уравнение. Однако в комплексных переменных уравнение
рассматривать неудобно, поэтому вводят действительные пе-
переменные
_ f + f _ т-У
Хо ~ "Г"' Xl ~ ~2Г~'
так что £ = хо + ix\, т/ = хо — гх\.
В этих новых переменных xq, х\\ Ь\\ = 622, &12 = 0,
поэтому уравнение эллиптического типа примет вид
д2и д2и
+
Если Ф = 0, то получаем уравнение Лапласа.
Гл. II, § 6. Приведение уравнейия 2-го порядка ... 113
Замечание. Уравнение A) может иметь в одной части об-
области fl один тип, а в другой части - другой тип, все зависит
от коэффициентов ац, агг, о,\2-
Так, в газовой динамике встречается уравнение Чап-
Чаплыгина
,5,
где к(х\) - непрерывная функция, fc(O) = 0, k(xi) > О при
xi > 0, ^i(xi) < 0 при xi < 0.
Уравнение E) является эллиптическим при х\ > 0, ги-
гиперболическим при xi < 0 и параболическим на оси xi = 0.
К такому же типу относится уравнение Трикоми:
д2и д2и п
8 - В. Н. Масленникова
114 Глава П. Некоторые вопросы общей теории диф. уравн...
Уравнения (б) и F) называются уравнениями смешанного
типа; для них fi\ - область эллиптичности, i?2 - область
гиперболичности, Х\ — О - линия вырождения.
§ 7. Преобразования Фурье и Лапласа.
Определение пространства S. Преобразование
Фурье функций из S
В настоящее время одним из широко применяемых мето-
методов исследования дифференциальных уравнений в частных
производных являются метод преобразования Фурье и метод
преобразования Лапласа. Поэтому напомним коротко неко-
некоторые свойства таких преобразований.
Преобразование Фурье интегрируемых в Жп функций
определяется формулой
z— J
где скалярное произведение в Жп : (#,£) = a?i£i + ...
+ хп£п. В функциональном анализе вводится линейное про-
пространство S, состоящее из всех функций и(х) G
C°°(IEtn) и убывающих при \х\ —* оо достаточно быстро,
чтобы сходился несобственный интеграл A) и сходились все
интегралы, полученные дифференцированием A) по пара-
параметру £.
Пространство S определяется следующим образом:
S = {и(х) € C°°(lRn): A + \xf)\Dau\ < Са(} Уж € IRn
и любых мультииндексов а — ai...an, a* > 0 и для лю-
любых целых ft > 0}. Другими словами, 5 состоит из функций
и(х) G C°°(IEln) и убывающих при |ж| -+ оо вместе с про-
производными любого порядка быстрее любой функции вида
Примером функции из S может служить функция
ехр{—|х|2}. Для функций из пространства S преобразова-
преобразование Фурье A) всегда существует, при этом замечательным
Гл. II, § 7. Преобразования Фурье и Лапласа ... 115
фактом является то, что после преобразования Фурье мы по-
подучим опять функцию из 5, т.е. если и(х) G 5, то й(£) G S.
То есть имеет место
Лемма. Если функция и(х) € S, х € IFtn, то ее преобразо-
преобразование Фурье «(£) = Fx-,(u(x), как функция ( G IRn, снова
принадлежит S.
Доказательство. Преобразование Фурье «(£) функции
и(х) € S есть функция ограниченная и непрерывная в IR".
Действительно,
= KOI =
< J Hx)\dx
<oo,
из этого неравенства следует и равномерная сходимость ин-
интеграла й@ по параметру £, т.е. непрерывность й(£) по
£. Преобразование Фурье функций и(х) € 5, т.е. интеграл
A), можно дифференцировать по параметру £ любое число
раз, так как после дифференцирования мы опять получим
равномерно сходящийся по параметру £ интеграл:
Я? J <х.
= _-н/ /" -к B)
( г) J х и(х)е
откуда
< I |xau(x)|da? < сх)
в.-
(здесь ха — х ...х"п), так как и(х) убывает при \х\ —* оо
быстрее любой отрицательной степени |ж|. Следовательно,
8*
116 Глава II. Некоторые вопросы общей теории диф. уравн...
«(£) € C°°(lRn). Осталось доказать, что существуют посто-
янные C'aff: \t\»\D<*u(O\ < &afi, если \x\e\D°u(x)\ < Cafi
для любых мультииндексов а = ai...an, где целые а*, /? > 0.
Интегрированием по частям с использованием B) полу-
получаем:
/
Rn ж-
где or = «!...«„, /9 = /9i..^n, art, fa > 0, |a| = «i + ... + atn,
\0\ = 0i + ... + /?n, ^ = tf1...^" откуда
в.-
так как под интегралом стоит интегрируемая функция. Та-
Таким образом, преобразование Фурье переводит простран-
пространство S в себя. Лемма доказана.
В теории обобщенных функций доказывается, что пре-
преобразование Фурье переводит 5 на 5, притом взаимно одно-
однозначно, и операция преобразования Фурье непрерывна из S
в 5 (см. [7]).
Определим сходимость в S следующим образом: после-
последовательность {uk(x)} € S сходится к функции и(х) G S
при к —► оо, если для любых мультииндексов а, а* > О, и
любых целых 0 > 0 последовательность A + \x\P)D%Uk(x)
сходится равномерно в Жп к функции A + \x\P)D*u{x) при
к —> оо. Очевидно, S - линейное пространство.
Используя только что доказанную лемму, с помощью об-
обратного преобразования Фурье можно перейти от й(£) к
и(х), т.е. найти
R»
Гл. II, § 7. Преобразования Фурье и Лапласа ... 117
функция й(£) называется образом Фурье для и(х), а и(х)
называется прообразом Фурье для й(£). Переменные ж и £
при преобразовании Фурье называются двойственными пе-
переменными. С помощью интегрирования по частям полу-
получаем:
= f
Таким образом, преобразование Фурье производной есть по-
полином, умноженный на образ Фурье «(£) функции и(х); по
этой причине интегральное преобразование Фурье удобно
Использовать при исследовании дифференциальных уравне-
уравнений.
Кроме преобразования Фурье при решении начально-
Краевых задач математической физики часто используется
известное из комплексного анализа преобразование Лапла-
Лапласа, которое определяется формулой:
оо
u(t)e~Mdt = u(A),
где в отличие от преобразования Фурье, А - комплексный
параметр: А = а + i/?. Изучены классы функций, к которым
применимо интегральное преобразование Лапласа.
Обратное преобразование Лапласа определяется кон-
контурным интегралом в комплексной плоскости А по формуле
a+too
/ eAt-u(A)dA, где ReA = a>0.
+
J
Преобразование Лапласа для производной имеет вид:
оо оо
А
n t=o
о о
118 Глава II. Некоторые вопросы общей теории диф. уравн...
Таким образом,
оо
%x Лй(Л)-
Если функция u(t) имеет нулевое "начальное условие", т.е.
«@) = 0, тогда
^e-Xtdt = Au(A),
т.е. при преобразовании Лапласа производной дифферен-
дифференцирование заменяется умножением на параметр А также,
как и при преобразовании Фурье дифференцирование по х&
переходит в умножение на ifa. Особенно удобно использо-
использовать преобразование Фурье при решении уравнений во всем
Жп ила в IR.+ = {х : хп > 0}, а преобразование Лапласа -
при решении задачи Коши и начально-краевых задач.
§ 8. Определение корректности постановки задачи
Коши
Дадим определение корректной постановки задачи Ко-
Коши. Пусть п - область в пространстве Etn+1, может быть и
неограниченная.
Через C*(J2) обозначим пространство всех ограничен-
ограниченных непрерывных функций и(х), имеющих ограниченные и
непрерывные производные до порядка к в П.
Норма функции и(х) € C*(i7) определяется следующей
формулой:
\Datt{x)\,
где а, как обычно, - мультииндекс.
Гл. II, § 8. Определение корректности ...
119
Пусть область п частью G своей границы примыкает к
гиперплоскости х0 — 0; х — (xq,x'), х' = (xi,...,xn).
Пусть в области п задано дифференциальное уравне-
уравнение, разрешенное относительно старшей производной по Xq :
A)
DqU + 2_j aa(x)Dau = 0, x e Q,
ao<*-l
а при Xq — 0 на G задано к начальных условий
.t/ou — у>дж j, j—v,i,...,k i.
B)
м X0
0 G
х'
Определение. Задача Коти A), B) корректно поставлена
в области Q, если выполнены следующие условия:
1) Существует такое I > 0, что V<pj(x') G C[{G), j =
0, k — 1, 3 непрерывное в Q U G решение и(х) задачи A),
B), обладающее в п всеми непрерывными производными,
входящими в уравнение A), и удовлетворяющее начальным
условиям B), т.е. имеет непрерывные вплоть до границы G
производные по х0 до порядка к — 1.
2) Указанное в п. 1) решение и(х) задачи A),B) един-
единственно.
120 Глава П. Некоторые вопросы общей теории диф. уравн...
3) 3 такое г > 0 и постоянная М > 0, не зависящая от
4>j{x'), что
к-\
II II Ч
C)
Условие C) означает, что решение и(х) непрерывно зависит
от начальных условии <pj до порядка г в ворме Сь(П).
Замечание. Если выполнены условия 1), 2), 3), то говорят,
что задача Коши корректна в пространстве Сь- Если выпол-
выполнены условия 1), 2), 3) с заменой пространства Сь другими
функциональными пространствами В типа Банаха, то го-
говорят, что задача Коши корректно поставлена в этих про-
пространствах В.
§ 9. Условие некорректной постановки задачи
Коши в терминах корней характеристического
многочлена. Лемма об экспоненциальном
решении. Определение обобщенно
однородного многочлена. Основная теорема.
Примеры
Рассмотрим линейное дифференциальное уравнение в
частных производных с постоянными коэффициентами, раз-
разрешенное относительно старшей производной по одной из
переменных:
Ы<">
ао<*-1
где ос = осоос', ос' = a\...an, Dti — ■§-£, Dau =
я ^я V я ». ) aa - постоянные действительные коэффици-
axa axl ...axn
енты; через L(Dq, D) обычно обозначается дифференциаль-
дифференциальное выражение (оператор). Например, если задано линейное
уравнение
Гл. II, § 9. Условие некорректной постановки ... 121
ди д?и
C/Xq С/Хч
то для него, что уже использовалось в § 4 главы II,
дхо дх\
Бели мы сделаем в уравнении A) преобразование Фурье по
х и Лапласа по t с соответствующими нулевыми начальными
условиями, то L(Dq, D'), как легко видеть, перейдет в мно-
многочлен L(X, «£').
Иногда, когда это удобно, характеристическим многочле-
многочленом, или полным символом для уравнения A), называется
многочлен
Этот многочлен иногда мы будем записывать следующим об-
образом:
e'. B)
аО<к-1
Многочлен B) получается из левой части уравнения A),
если в ней сделать следующие подстановки:
Do -* A, Dj -4 i£j, j = 1, ...,n.
Уравнение L(A, i£') = 0 называется характеристическим для
уравнения A). Выражение L(X,i(') = А* +
+ 2 aaAa(i£')a называют главным символом уравнения
A). Нам будет полезно найти для уравнения A) решение
экспоненциального вида, т.е. вида
u(x) = e i-1 . C)
122 Глава II. Некоторые вопросы общей теории диф. уравн...
Лемма. Для того, чтобы функция C) была решением ура-
уравнения A), необходимо и достаточно, чтобы Л и £,• удовле-
удовлетворяли характеристическому уравнению.
Доказательство.
Необходимость.
Пусть функция C) есть решение уравнения A). Имеем
= Ае >-1 ,
. D)
Таким образом, дифференцирование функции и(х) вида C)
сводится к умножению на соответствующий множитель Л
или i£j. Поэтому, подставляя и(х) в виде C) в уравнение
A), получим
п п
Xxo+i ^2 XjSj \xo+i ^ £j xj
L(DQ,D')e '-1 =L(\,i(')e i-* =0.
Отсюда следует, что L(A,i£') = 0.
Достаточность.
Пусть L(X, i£') = 0. Используя D), получаем
n n
Аю+t J2 ti xi Aio+« ^2 tj xj
0 = L(A,»Oe '-1 =L(DQ,D')e *-* ,
откуда следует, что функция вида C) удовлетворяет уравне-
уравнению A).
Определение. Многочлен
Гл. II, § 9. Условие некорректной постановки ... 123
где (£')а' = £ •••££" называется обобщенно однородным по-
порядка т с весом Ь относительно А, если W > О
для любых комплексных А я £,.
Пример. Рассмотрим параболическое уравнение
Его характеристический многочлен
обобщенно однороден порядка т = 2с весом Ь = 2 относи-
относительно А:
,t i?) = *2A + f^t2^ = <2(A
Рассмотрим задачу Коши для уравнения A) с действи-
действительными постоянными коэффициентами с начальными ус-
условиями
Докажем следующую теорему.
Теорема 1. Пусть выполнены следующие условия:
1) Характеристический многочлен L(\,i£') уравнения
A) обобщенно однороден порядка т с весом Ь относительно
А, причем Ь > 1:
124 Глава II. Некоторые вопросы общей теории диф. уравн...
L(tb\,ti£') = tmL(\,i?), VA(=<D, e' = 6,-,e«6lRn. F)
2) Для некоторого £' такого, что |£'| ф О, f G И", суще-
существует корень Л = а + ът уравнения
L(<r+ гг,г£')= 0, G)
такой, что Re А = а > 0.
Тогда задача Коши для уравнения A) с начальными
данными E) не является корректно поставленной в полосе
/2+ = {х : 0 < хо < S, х' 6 Ип}, примыкающей к гипер-
гиперплоскости G = {х : хо — 0,х' 6 Шп}.
Доказательство. Докажем, что при сформулированных в
теореме условиях нарушается свойство корректности поста-
постановки задачи Коши. Допустим противное, т.е. предположим,
что при некотором г имеет место оценка
||к|| (8)
Из условий теоремы F) и G) следует, что при любом нату-
натуральном п, т.е. п 6 Z^_, имеем
L{nb{a + tV), in?) = nmL{a + ir,i?) = 0.
Следовательно, Vn € 2^., в силу леммы, функция
является решением уравнения A). Так как уравнение A)
имеет вещественные коэффициенты, то и
й„(хо,х') = Reun(x0,x') = е4""'0 соз[пьтхо + п(х',(')]
также является решением этого уравнения. Заметим, что
A) есть однородное уравнение (с правой частью равной
нулю), поэтому для него решение, умноженное на постоян-
постоянную, также будет решением, т.е. функция
Гл. II, § 9. Условие некорректной постановки ...
125
и„(х0, х') = ^е"**10 cos[n6rx0 + п(х', £')],
где N > к + г - постоянное число, также будет решением
уравнения A).
При хо = 0 для функции и„(х) справедливы следующие
оценки:
x'€G ГС"
Далее
~6~
Doun(xQ,x') =
Tt
пьт
п
bN
sin[n'
cos[nbrx0
х
sin[n
или
ь
Таким образом,
sup
x'€G
п"
где постоянные Cj зависят лишь от а, т и j. И далее, анало-
аналогичным образом получаем:
sup
x'6G
Da>Diun@,x')
= sup
x'EG
A0)
126 Глава II. Некоторые вопросы общей теории диф. уравн...
1/2
Если |а'| = ai +... + а„<г, то учитывая, что N > к + г,
j < к — 1, получаем, что правые части (9) и A0) стремятся
к нулю при п —> оо. Значит, этим же свойством обладают и
левые части этих неравенств, и мы имеем
\\Diun@,x')\\c:{G)= £ sup Da'Diun@,x') -* 0 A1)
при n —» +oo. С другой стороны, при заданных хо, 0 < хо <
S, п,£' выберем такое ж', зависящее от £' и жо, чтобы
cos[n6Tx0+n(x',^')] > -.
Тогда
при п —»■ +сх).
Из соотношений A1) и A2) видно, что неравенство (8)
для решения ип(х) не может иметь места, так как если в
него подставить u(x) = un(x), то правая часть у него будет
стремиться к нулю при п —> +оо, а левая - к бесконечности.
Получили противоречие. Теорема доказана.
Замечание. Из доказательства теоремы 1 и ее формули-
формулировки видно, что для того, чтобы получить условие некор-
некорректной постановки задачи Коши в области QJ = {х : — ё <
хо < 0, х' 6 Ип}, т.е. снизу от гиперплоскости жо = 0,
нужно в формулировке теоремы условие Re Л = а > 0 заме-
заменить на условие Re Л = а < 0. Таким образом, имеет место
Теорема 1'. Пусть выполнено условие 1) теоремы 1, и пусть
для некоторого £': |£'| ф 0, (' 6 IR", существует корень
Л = а + it уравнения L(a + гт, i£') = 0 такой, что Re A =
Гл. II, § 9. Условие некорректной постановки ... 127
а < 0. Тогда задача Коши для уравнения A) с начальными
условиями E) не является корректно поставленной в полосе
QJ = {х : -S < xQ < 0, х' € ЕГ},
примыкающей к гиперплоскости G = {х : жо = 0, х' € Ш,"}
снизу.
Примеры.
1) Рассмотрим параболическое уравнение (уравнение
теплопроводности):
L(D)u = тг У] о"Т = 0
в области
/?- = {Х: -8<хо<0, х' еШп = G}.
Соответствующее характеристическое уравнение
п
к ~
имеет относительно Л один корень: Л = — J2 (к ~ а-> причем
п
если ^ (I ф 0, то а < 0. Поэтому, так как и жо < О,
то по теореме 1' задача Коши «|Хо=о = У0(ж') некорректно
поставлена в области QJ. В области О* условия теоремы не
выполняются, поэтому задача Коши может быть поставлена
и корректно.
В дальнейшем мы докажем, что в области f2f она дей-
действительно поставлена корректно.
2) Разберем еще раз пример Адамара.
Рассмотрим уравнение Лапласа (эллиптическое уравне-
уравнение):
128 Глава II. Некоторые вопросы общей теории диф. уравн...
в области Of или О6 . Его характеристическое уравнение
/ » \i/2
имеет два корня A = ±(£I£j) =
По доказанным теоремам 1 и 1' задача Коши u|lo==o =
ди
Ш1
= <р* не поставлена корректно ни в области
io=O
Of, ни в области OJ.
3) Рассмотрим гиперболическое (волновое) уравнение:
i=i J
Характеристическое уравнение для него L(\,i(') =
Л2 + |^'|2 = 0, (' € Ип, имеет корни Л = ±i|f'| чисто мни-
мнимые, что не противоречит корректности постановки задачи
Копта. В дальнейшем мы покажем, что для волнового ура-
уравнения задача Коши поставлена корректно как в области
Of, так и в области OJ.
4) Рассмотрим еще пример:
д2и &и д*и
dt* dtdx*+ дх*~
с начальными данными
dt>
t—Q
=V(*), i = o,i.
Характеристический многочлен для этого уравнения есть
Л2 + 2А£* + £4; он является обобщенно однородным порядка
4 с весом 2 относительно А:
Гл. II, § 9. Условие некорректной постановки ... 129
L(t2X,t if) = (<2АJ + 2t2\t2t2 + t4t4 =
Найдем корни Л характеристического уравнения
А2 + 2А£2 + е4 = О,
Таким образом, Re А = а < 0 при любом действительном
t, \t\ ф 0, и поэтому задача Коши для рассматриваемого
уравнения не является корректно поставленной в области
9 • В. Н Масленникова
130
Глава III. Задача Коши для уравнения
теплопроводности. Обобщенные
функции и их применение к
исследованию решения
§ 1. Решение задачи Коши для уравнения
теплопроводности методом преобразования
Фурье с начальными данными из S.
Преобразование Фурье на Li(TRn) и на
Рассмотрим задачу Коши для уравнения теплопроводно-
теплопроводности
с начальным условием
и
t=0
B)
Сначала предположим, что <р(х) € S. Допустим, что реше-
решение u(t,x) задачи A), B) существует в таком классе фун-
функций, для которых законны применяемые ниже операции:
преобразование Фурье, дифференцирование под знаком ин-
интеграла и т.д. В дальнейшем мы все эти предположения
оправдаем, т.е. покажем, что построенное решение удовле-
удовлетворяет этим условиям. Итак, пусть преобразование Фурье
начальной функции <р(х) есть
«о = /
+00
e~tx^<f(x) dx =
и преобразование Фурье решения есть
Гл. Ill, § 1. Решение задачи Коши ...
131
+ оо
■Tilt /Л — / p~*x^ii(t -тЛ dr — F etj(i r\
— oo
9u(t,z) a«(*,e) „ &u(t,x)
D)
2
иъ иг их"
причем последняя формула есть следствие известного
свойства преобразования Фурье: операции Jj в образах
Фурье соответствует операция умножения на г|.
В результате применения преобразования Фурье к A) и
B), получим
F)
dt
«=0
G)
Решая обыкновенное дифференциальное уравнение F) с
постоянными коэффициентами с начальным условием G),
однозначно находим
Для любого t > 0 функция u(i, £), задаваемая формулой (8),
принадлежит S по £. Действительно, так как
<^(z) € S, то
и
Поэтому
Для любых о,/?
для любых at,fi € Ж+,
и, очевидно, u(t, () € С°° по переменным ^ и £. Применив
к (8) оператор Fr},x, т.е. обратное преобразование Фурье,
находим решение u(t,x) задачи A), B) в виде:
9*
132
Глава HI. Задача Коши для уравнения теплопро-ти
h
+ оо
I
(9)
Итак, если существует решение u(t,x) задачи A), B), для
которого законны приведенные выше выкладки (т.е. спра-
справедливы формулы D), E)), то оно дается формулой (9).
Докажем теперь законность формул D), E) для u(t,x), за-
задаваемой формулой (9). Законность формулы D) и второй
формулы в E) для u(t, £) вытекает из того, что й(<,£) =
е~^ V(£) € S для любого t > 0. Для того, чтобы оправдать
первую формулу в E), достаточно доказать, что (9) можно
дифференцировать по параметру t под знаком интеграла:
du(t,x)
dt
+ ОО
A0)
Для этого надо доказать, что интеграл в A0) сходится ра-
равномерно при t > 0. Так как подынтегральная функция в
(9) принадлежит С°° по £, <, ф(() € S, то Vt > 0 и Ve > 0 3
такое достаточно большое число А > 0, что
-А
J
— оо
что и доказывает равномерную сходимость интеграла в A0)
для любого t > 0. Из E), A0) следует, что функция u(t,x),
задаваемая формулой (9), удовлетворяет уравнению тепло-
теплопроводности
— ОО
+оо
~h J (-
— оо
Гл. Ill, § 1. Решение задачи Коши ... 133
и начальному условию
t=o = ± J
Таким образом, мы доказали, что функция u(t, ж), определя-
определяемая формулой (9), является решением задачи A), B). Оче-
Очевидно, что в классе функций u(t, x), для которых законны
приведенные выше выкладки, это решение единственно, так
как преобразование Фурье u(i,£) = Fe_►£«(*, х) удовлетво-
удовлетворяет соотношениям F), G), а из F), G) u(t, x) определяется
единственным образом (что следует из теории обыкновенных
дифференциальных уравнений).
Найдем теперь более удобную формулу для решения
u(£, x) задачи A), B), выражающую его непосредственно
через <р(х), т.е. вычислим обратное преобразование Фурье
для u(t,x). Для этого нам нужно изучить несколько более
полно свойства преобразования Фурье. Можно определить
преобразование Фурье не только на функциях из 5, но и на
более широких классах функций, например, на функциях
из L\ или Li и на классах обобщенных функций.
1. Пусть f{x) € £i(lRn) (т.е. / \f(x)\dx < оо и ин-
теграл понимается в смысле Лебега). Тогда для этой f(x)
преобразование Фурье вычисляется по обычной формуле:
Ff(x) = J f{x)c-^dx = /(О- (И)
Е"
Очевидно, написанный интеграл сходится, так как
/ f(x)e-ix*dx < I |/(x)| dx < оо.
В анализе доказывается, что в этом случае /(£) - непреры-
непрерывная, ограниченная функция переменной £, которая стре-
стремится к нулю при |£| —* оо.
134 Глава III. Задача Коши для уравнения теплопро-ти
2. Если f(x) € ХгAЯп), то для нее тоже определяется
преобразование Фурье по формуле A1), причем замечатель-
замечательным здесь является тот факт, что /(£) тоже будет принадле-
принадлежать Хг(lRn) по £, и будет иметь место формула, называемая
равенством Парсеваля:
Bп)" J\f(x)fdx= J\f(O\2d£, A2)
которая связывает образ и прообраз преобразования
Фурье. Равенство Парсеваля A2) имеет место и для
f{x) € S.
Для более ясного понимания физического смысла реше-
решения уравнения теплопроводности и нахождения обратного
преобразования Фурье от й(£,£) = е~^ *ф(£) приведем осно-
основные сведения из теории обобщенных функций (подробнее
см. [7)).
§ 2. Понятие обобщенной функции, ее физический
смысл. Определение О-функции Дирака.
Пространство основных функций D и
пространство обобщенных функций D'
В курсе функционального анализа дается определение
обобщенной функции / как линейного непрерывного фун-
функционала Tf = (f,<p), заданного на некотором линейном
пространстве основных функций (р. Впервые это понятие
обобщенной функции было дано СП. Соболевым в 1936
году. Понятие обобщенной функции является обобщением
классического понятия функции, которое возникло для нужд
математической физики. Это обобщение классического по-
понятия функции дает возможность выразить в математически
корректной форме такие идеализированные понятия, как
плотность материальной точки, плотность точечного заряда,
интенсивность мгновенной силы, приложенной в точке, и т.д.
Гл. III, § 2. Понятие обобщенной функции ... 135
Из теоретической физики известна ^-функция Дирака, кото-
которая определяет плотность, создаваемую материальной точ-
точкой массы т = 1.
Дадим математическое определение 6-функции как фун-
функционала (распределения).
Пусть точка массы т = 1 находится в начале коорди-
координат пространства R3. Чтобы определить плотность, созда-
создаваемую этой точкой, распределим (или, как говорят, разма-
размажем) единичную массу равномерно внутри шара радиуса е
с центром в нуле. В результате получим среднюю плотность
/е(ж), равную
О, если |ж| > е.
Нас интересует плотность при е = 0. Посмотрим, нельзя ли
принять в качестве искомой плотности (обозначим ее через
6(х)) поточечный предел средних плотностей fe(x) при е —>
+0, т.е. функцию
{+оо, если х = 0,
A)
0, если х фО.
От плотности 6(х) естественно потребовать, чтобы интеграл
от нее по всему пространству давал бы полную массу веще-
вещества, т.е.
/
6(x)dx = 1. B)
Но для функции 6(х), определенной формулой A),
(L) j 6(x)dx = 0. Это значит, что функция A) не восстана-
IR3
вливает массу (т.е. не удовлетворяет условию B)) и потому
не может быть принята в качестве искомой плотности.
136 Глава III. Задача Коши для уравнения теплопро-ти
Таким образом, поточечный предел последовательности
средних плотностей fe(x) не дает нам искомой плотности
в точке. Надо идти другим путем. Найдем слабый предел
/е(х) при е —♦ 0; т.е. для любой непрерывной функции <р(х)
(можно считать, что <р(х) € S) найдем предел числовой фун-
функции f fe(x)ip(x)dx при е —» 0. Покажем, что
lim / fe(x)<p(x)dx = <^@). C)
ю.3
Действительно, так как у(х) - непрерывная функция, то для
любого rj > 0 существует £q > 0, что \<р(х) — у@)| < т?, как
только |д;| < £q. Отсюда, при всех е < бо имеем
\ ^\ j [tp(x) - tp{O)]dx
\x\<* |*|<.
\x\<e |x|<.
Таким образом, слабым пределом f€(x) при е —» 0 является
функционал <р@) (а вовсе не функция!), сопоставляющий
каждой непрерывной функции <р(х) число ^>@) - значение
ее в точке х = 0; этот функционал можно принять за опре-
определение плотности 6(х) единичной массы, сосредоточенной
в точке х = 0. Это и есть известная функция Дирака.
Итак, мы можем написать
fe(x)^S(x\ с-» 0,
понимая под этим предельное соотношение C). Значение
функционала 6 на функции <£>(ж), т.е. число <^@), обычно
обозначают
(tf, V) = *>(()). D)
Проверим теперь, что функционал 6 восстанавливает пол-
полную массу. Действительно, как только что было доказано,
Гл. III, § 2. Понятие обобщенной функции ... 137
роль "интеграла" от 6(х) играет величина F,1), равная, в
силу D), значению функции, тождественно равной 1 в точке
х = О, т.е. F,1) = 1. Если массы /х* сосредоточены в различ-
различных точках Хк, к = 1,2,.., TV, то плотность, соответствующая
этому распределению масс, равна
N
-а;*). E)
Выражение E) есть линейный функционал, сопоставляю-
сопоставляющий каждой непрерывной функции f{x) число
N
Таким образом, ^-функция определяется с по-
*1
мощью непрерывных функций, как линейный функционал,
определенный на этих функциях.
Непрерывные функции, как говорят, являются основны-
основными функциями для определения ^-функции. Эта точка зре-
зрения и берется за основу определения произвольной обобщен-
обобщенной функции как линейного непрерывного функционала на
совокупности достаточно "хороших" основных функций.
Определение. Носителем непрерывной функции у{х) на-
называется замыкание множества тех точек, где ц>{х) ф 0; но-
носитель обозначается через supp<^>. Функция у>{х) называется
финитной, если ее носитель ограничен.
Функция (р(х) G C°°CR"), если (р(х) € C°°(lRn) и имеет
компактный носитель, т.е. <р{х) = 0 для х € Hn \ А', где К -
о
компакт в И". Аналогично определяется С°°(^) VJ2 С 1R".
Пространство основных функция D состоит из финит-
о
ных бесконечно дифференцируемых функций C°°(IRn), в
котором сходимость введена следующим образом: последо-
последовательность функций {<£>*} € D сходится к у € D, если су-
существует число R > 0 и шар Br такие, что supp^jt С Br,
и при каждом а = ai,...,an, ati > 0, Da<pk(x) сходится ра-
равномерно к Day> при к —» оо. Примером основной функции
из D является функция
138 Глава III. Задача Коши для уравнения твплопро-ти
О, |я;|>Л,
где постоянная ае h выбирается таким образом, чтобы
/ uh{x)dx = 1,
т.е.
Обобщенной функцией из D', заданной в открытом мно-
множестве B, называется всякий линейный непрерывный фун-
функционал, определенный на пространстве основных функций
D{Q).
В теории преобразований Фурье удобно использовать
преобразование Фурье так называемых обобщенных фун-
функций медленного роста, так как операция преобразования
Фурье не выводит за пределы этого класса.
В этом случае за пространство основных функций берут
пространство S.
§ 3. Определение пространства обобщенных
функций S'. Преобразование Фурье
обобщенных функций из S'
Обобщенной функцией медленного роста называется ли-
линейный непрерывный функционал над пространством S.
Пространство таких обобщенных функций обозначается
через 5'. Дадим определение преобразования Фурье обоб-
обобщенных функций из S'. Пусть f(x) - обычная функция
класса Xi(lRn). Поставим ей в соответствие обобщенную
функцию / по формуле
Гл. Ill, § 3. Определение пр-ва обобщенных функций... 139
(/(*),?(*)) = J f{x)<p{x)dx ty(*) € S. A)
Обозначим через
= J
преобразование Фурье функций /(х) € Li(IRn). Имеем для
любой <р(х) € 5:
/(/ ) B)
R» Щ
Так как подынтегральная функция в B) абсолютно интегри-
интегрируема на И" х Ш%:
1
\f(x)\dx J
< I \f(x)\dx / |<ЖМ < oo,
щ m'(i
то, по теореме Фубини, можно в B) поменять порядок инте-
интегрирования, в результате чего мы получим
ir" C)
Таким образом, если f(x) € L\ и ^(.r) € 5, то имеет место
формула C). Пусть теперь / € 5', т.е. (/, <р) - линейный не-
непрерывный функционал на S(tp € S). В этом случае правая
часть C) тоже имеет смысл, так как Fip € 5, если <р € S.
140 Глава III. Задача Коши для уравнения теплопро-ти
Можно доказать, что правая часть является линейным не-
непрерывным функционалом относительно у € S. Поэтому
корректно следующее определение преобразования Фурье
обобщенной функции:
Преобразованием Фурье обобщенной функции / € S'
называется такая обобщенная функция Ff £ S', для которой
справедливо соотношение, аналогичное C):
°=
€ s.
Пример. Найдем преобразования Фурье 6-функции Ди-
Дирака. Пусть f(x) = 6(х), т.е. F(х),(р(х)) =
Имеем:
= («(*), J
Отсюда F^ = 1.
§ 4. Свертка двух функций: f(x) e S, g(x) G С^.
Теорема о свертке
Пусть заданы две функции: f{x) € S, g(x) G C& (напом-
(напомним, что Сб есть пространство ограниченных непрерывных
функций на IRn).
Сверткой двух функций называется интеграл
J f{y)g{x -y)dy = f*g, (l)
Гл. Ill, § 4. Свертка двух функций /(ж) G 5, д(х) € Сь- 141
где справа стоит обозначение для свертки.
По своему определению свертка коммутативна, т.е.
К"
= / g(y)f(x -
Свертка двух функций связана с преобразованием Фурье
следующим образом:
Теорема о свертке. Если /(£) € S(TRn), а д({) € Ьг(Ш.п),
то
т.е. обратное преобразование Фурье произведения двух фун-
функций есть свертка их прообразов Фурье.
Замечание. Аналогичное утверждение справедливо и
для прямого преобразования Фурье: преобразование
Фурье произведения двух функций равно свертке их обра-
образов Фурье
Доказательство. Заметим, что если </(£) € Li(lRn), то
функция д(х) = F-^@ € Сь. Так как /(£И@ € Li(TRn),
то преобразование Фурье этого произведения может быть
вычислено по обычной формуле:
1 (НО
1R.n
1 г. г ' . B)
щ щ
142 Глава III. Задача Коши для уравнения теплопро-ти
Подынтегральная функция этого повторного интеграла аб-
абсолютно интегрируема по у и £; действительно,
и
< f \f(y)\dy ■ I
<oo,
так как /(у) € S, g(£) € L\. Поэтому, по теореме Фубини,
можно поменять в B) порядок интегрирования, в результате
получим:
F-1 (/(О • №) = щ; J f(y)(J
= J f(y)g(x -y)dy = f*g(x).
Теорема доказана.
§ 5. Применение теоремы о свертке к
решению задачи Коши для уравнения
теплопроводности. Вычисление ядра Пуассона
Вернемся к задаче Коши для уравнения теплопроводно-
теплопроводности. Мы получили решение этой задачи в виде:
+ ОО
u(t,x) = A- J е~^ф(Ое"^ A)
— оо
и проверили, что это решение удовлетворяет уравнению
-щ — gjf = 0 и начальному условию u\t=o = <p(x). Преобра-
Преобразуем формулу A) к более удобному виду с помощью теоремы
о свертке. Имеем
Гл. III, § 5. Применение теоремы о свертке ... 143
Обозначим обратное преобразование Фурье функции е * *
при t > 0, т.е. Fr}>xe~t ' через G(t,x); обратное преобра-
преобразование Фурье ф(£) нам известно - оно есть <р(х); поэтому
получаем u(t, x) = G(t, x) * <р(х), причем свертка берется по
х, a t входит как параметр, т.е.
+ оо
u(t,x)= / G(t,x-y)(p(y)dy.
Напомним, что в теореме о свертке предполагалось, что
один множитель принадлежит Li (ГО1), а второй из 5. Эти
условия в нашем случае выполнены, если взять д — е~^ * €
Li, t > 0, / = ф(£) € S. Остается найти функцию G(t,x),
т.е. вычислить интеграл:
G(t, х) = F"ixe-*2t = 1. J e-^'e^de. B)
—оо
Для вычисления этого интеграла используем теорию фун-
функций комплексного переменного.
Имеем
+ оо
Рассмотрим интеграл /е tv drj на комплексной плоскости
г
г] = £ + icr, где контур Г состоит из отрезка действитель-
действительной оси — N < £ < N, отрезка прямой Im7/ = а = — ^
144
Глава III. Задача Коши для уравнения теплопро-ти
-N i
1
I
i
i
'CT N
0 i ^
I
-ix/2t I
и отрезков лрямых Re 77 = £ = N и Re ту = £ = — N. Вое
пользуемся теоремой Коши, согласно которой J e~trt dr) = С
Г
Тогда получим
ЛГ N О
-ЛГ
О
21
Так как два последние интеграла стремятся к нулю пр:
ЛГ —> со, то мы получаем после замены \Д£ = б
J e
+00
+00
у
-L
Таким образом, наш интеграл B), т.е. функция G(t,x), ко
горая называется ядром Пуассона, вычислена и имеет вид:
Гл. III, § 5. Применение теоремы о свертке ... 145
Теперь наше решение можно записать в виде:
+ ОО
Г
+
1 Г
u(t,x) = —7= I
= / G(t,x-y)tp(y)dy.
Это классическая формула Пуассона для решения задачи
Коши для уравнения теплопроводности.
Если х € Нп (т.е. рассматривается уравнение теплопро-
теплопроводности с п пространственными переменными), формула
Пуассона, дающая решение задачи Коши, имеет вид
, " D)
= / G(t,x -y)<p(y)dy,
n
где \x - y\2 = Y, (xk - ykJ.
k=\
Способ ее получения тот же, что и в случае одного про-
пространственного переменного. Действительно, если мы имеем
уравнение
с начальным условием
u(t,x) =<p(x),
t=0
где <р(х) € S, то после преобразования Фурье мы получаем
уравнение
10 - В. Н Масленникова
146 Глава III. Задача Коши для уравнения теплопро-ти
к=1
Решая его с начальным условием и
и производя
t=0
обратное преобразование Фурье, мы получим решение за-
задачи Коши в виде
К"
и воспользуемся теоремой о свертке.
Для вычисления ядра Пуассона в этом случае доста-
достаточно заметить, что
Bтг)-п /
JJ
а одномерные интегралы нами вычислены.
§ 6. Свойства ядра Пуассона
Как показано выше, функция u(t, x), задаваемая форму-
формулой D) § 5 при (р(х) € 5, ж € Ш.п, удовлетворяет уравнению
теплопроводности и начальному условию.
Опишем свойства ядра Пуассона
1. Его образ Фурье
удовлетворяет следующим соотношениям:
Гл. III, § 6. Свойства ядра Пуассона 147
0, <> 0, B)
C)
Из B) следует, что при t > 0 сама функция G(t,x) удовле-
удовлетворяет уравнению теплопроводности
dG(t,x)
dt -£- дх\ ■
к=\ К
Действительно, уравнение D) получается, как следствие
B), если к обеим частям B) применить оператор F7j>x:
__, dG(t,Q dG(t,x)
*-** dt dt '
Далее
h dxl '
как следствие дифференцирования преобразования
Фурье.
2. Изучим, какому начальному условию при t = 0 удо-
удовлетворяет ядро Пуассона.
Докажем следующую лемму.
Лемма. Ядро Пуассона G(t, х) при t —> 0 стремится в
смысле обобщенных функций к ^-функции Дирака 6(х):
G(t, х) —>• 6(х), т.е. для любой <р(х) € S
E)
10*
К"
148 Глава III. Задача Коши для уравнения теплопро-ти
Доказательство. Как доказано выше, формула D) (преды-
(предыдущий параграф) при <р(х) € S дает решение задачи Коши
для уравнения теплопроводности при t > 0.
Положим в ней х = 0, получим
ti(i,0) = J G(t,-yMy)dy = У G(t,x)<p(x)dx,
К." Ж"
где мы положили у = х, a. G(t,—x) = G(t,x) в виду чет-
четности функции С? по ж. В силу условия u(t,x)\t=o = <р(х),
получаем lim u(t, 0) = <р@).
Лемма доказана.
Таким образом, ядро Пуассона G(t, x) описывает закон
распределения температуры, например, в бесконечном стер-
стержне (при х € IR1) в том случае, когда при t —+ +0 темпера-
температура и = G стремится к 6(х) в смысле обобщенных функций.
Обобщенная функция 8(х) соответствует тому, что при t = 0
в начале координат имеется сосредоточенный источник те-
тепла (в остальных точках стрежня при t = 0 температура
равна нулю), выделяющий мгновенно количество тепла, ра-
равное единице, что следует из определения ^-функции F(х)-
функция есть плотность единичной массы, сосредоточенной
в точке х = 0). Поэтому функция G(t, x) называется фун-
функцией источника. Она описывает распределение темпера-
температуры в стержне в момент времени t > 0, если при t = 0
подействовал указанный выше точечный источник. График
функции G(t,x) при разных t > 0 и х € Ж1 имеет вид,
указанный на рисунке.
3. Зная функцию источника G(t,x), по формуле Пуас-
Пуассона D) § 5 можно найти распределение температуры u(t, x)
при любых начальных условиях
р()
При этом суммарное количество тепла в теле, соответству-
соответствующее ядру Пуассона G(t, x) при любом t > 0, постоянно и
равно 1:
Гл. Ill, § 7. Решение задачи Коши для уравнения ...
149
i
lG(;,x) ,
G(tlfx)
G(t2 ,x)
JL< t2
►
0
]Rn
+00
*•»*
где ifc/2-уД =
= 1,
= 2yfidyk.
§ 7. Решение задачи Коши для уравнения
теплопроводности с непрерывной
ограниченной начальной функцией
Формула Пуассона дает решение задачи Коши для ура-
уравнения теплопроводности
ди
U
t=0
= <р(х)
A)
не только при </j(i) € 5, но и для (р(х) € Съ(Ш.п), т.е. когда
(р(х) - ограниченная непрерывная функция.
150 Глава III. Задача Коши для уравнения теплопро-ти
Теорема. Формула Пуассона
JRn
есть решение задачи Коши \/у?(х) € Сб(ГО.п).
Доказательство.
а) Проверим, что в этом случае B) удовлетворяет ура-
уравнению теплопроводности.
Действительно, ядро Пуассона G(t, х), как было дока-
доказано выше, удовлетворяет уравнению теплопроводности при
Теперь все дело в том, чтобы доказать, что можно диффе-
дифференцировать по параметрам t, x под знаком интеграла; если
это можно делать, тогда будем иметь
at
(эс(<^-у) ) - о.
Для того, чтобы доказать законность дифференцируемости
под знаком интеграла по параметрам t и х, надо доказать
равномерную сходимость (в окрестности данных значений t
и х, t > 0) интегралов, полученных в результате формаль-
формального дифференцирования not и ж при <р(х) £ Сь-
Докажем это для одной из производных (для других
производных доказательство аналогично), для простоты при
п = 1.
Пусть \ф(х)\ <М,А>0. Имеем
Гл. III, § 7. Решение задачи Коши для уравнения ... 151
-А +оо
-оо А
-А +оо
-оо
в достаточно малой окрестности точки (х,<), £ > О, если
Л = А(е) - достаточно большое число.
б) Докажем, что функция B) удовлетворяет начальному
условию, если <р(х) € СбAЯ1) (п = 1).
Нам надо оценить разность
u(t,x)~(p(x) =
+оо +оо
= J G(t,x - y)<p(y)dy - ф) J G{t,x - y)dy =
—оо
+oo
+
= J G{t,x-y){4>{y)-4>{x))dy=
—оо
-А А +оо
-оо -А А
Здесь мы воспользовались свойством ядра Пуассона
+ О0
/ G(ty х — y)dy = 1 и сделали замену *г-д = z, т.е.
—оо
у = Izy/i + х, dy = 2y/idz; тогда (х - уJ = Az2t,
+00 +00
1
—оо —оо
Докажем, что при достаточно большом А и достаточно ма-
малых t каждый из трех интегралов в C) не превосходит |.
152 Глава III. Задача Коши для уравнения теплопро-ти
Действительно,
-А
^ J e-z2[<p{2z>A + x)-<p(x)]dz
—оо
1М [ zi
< —r= I e «
утг J
—оо
по определению сходимости несобственного интеграла, где
М = sup |y(y)|; А. при этом выбрано так, чтобы имела ме-
сто оценка D). Очевидно, что при этом третий интеграл в
C) тоже будет по модулю меньше |. Зафиксируем теперь это
значение А и оценим второй интеграл в C).
Нам надо оценить его при малых t. Пусть 0 < t < 6 и
8 выбрано столь малым, что |(х + 2г\Д) — х\ < 1A\fS = Ь\;
тогда в силу непрерывности функции <р(х) отсюда следует,
что
И* + 2zy/t) - ф)\ < ei =
тогда
-А
гак как е~* < 1.
Таким образом, доказано, что Ve > О
\u(t, х) — <р(х)\ < е, как только 0 < t < 6.
Следовательно, lim u(t,x) = v?(x) для любой непрерывной
и ограниченной на всей оси функции <р(х). Таким образом,
мы доказали, что формула Пуассона есть решение задачи
Коши для уравнения теплопроводности У<р(х) €
Случай х € IRn рассматривается аналогично.
Гл. III, § 8. Задача Коши для неоднор. уравн. ... 153
§ 8. Задача Коши для неоднородного уравнения
теплопроводности. Принцип Дюамеля
Найдем решение задачи
dt
-Aui=f(x,t), Ul =0. A)
t=0
Тогда, как легко видеть, сумма решений задачи
ди2
dt
- Аи2 =0, и2 = <р{х), B)
<=о
и задачи A) (ввиду их линейности), т.е. и = щ + иг, есть
решение задачи
— -Ди = /(*,*), «|<=0 = ^)- C)
Решение задачи A) можно получить так же, как и решение
задачи B). В преобразовании Фурье мы получим неодно-
неоднородное обыкновенное дифференциальное уравнение с одно-
однородным начальным условием, решая которое и переходя за-
затем к функции u(t,x) с помощью обратного преобразования
Фурье, мы получим формулу для решения задачи A) в виде:
t
'x) = l2^Y П
от»
Однако формулу D) можно получить из формулы Пуассона,
т.е. решения задачи B), с помощью следующего приема, ко-
который называется "принципом Дюамеля".
Рассмотрим вспомогательную задачу:
dv
— - Av = 0, t>r, x € IRn,
at
154 Глава III. Задача Коши для уравнения теплопро-ти
Ее решение определяется формулой Пуассона:
Тогда, как легко проверить, решение задачи A) есть
t
щ(х,г) = / v(x,t,T)dr.
F)
Действительно,
1) для F) выполняется начальное условие из A):
<=0
= 0;
2) функция щ вида F) удовлетворяет уравнению тепло-
теплопроводности:
= v
т—t
= y xvdv.
Так как и, определяемая формулой E), есть решение одно-
однородного уравнения теплопроводности, то мы имеем:
= /ОМ) + /(%-
т.е. (б) есть решение задачи A).
Гл. III, § 9. Принцип максимума для решения ... 155
§ 9. Принцип максимума для решения уравнения
теплопроводности
1. Пршшцшп максимума для ограниченном областш.
Следствия: единственность решения нервов* начально- кра-
краевой задачи и непрерывная зависимость его от краевых и
начальных значений*
Рассмотрим первую начально-краевую задачу для ура-
уравнения . теплопроводности. Обозначим через Qt цилиндр
вида: QT = {(*, t) : х G п С Шп, О < t < Г}, через 5
- боковую поверхность цилиндра Qt, A) - основание ци-
цилиндра при t = 0, а через Г - параболическую границу
цилиндра Qt'-
Требуется найти непрерывную в Qt U Г функцию u(x,t),
удовлетворяющую уравнению теплопроводности
и принимающую на Г заданные значения ip(x,t):
u(x,t) r-(p(x,t),
при этом
Теорема 1. Всякое решение уравнения теплопроводности,
непрерывное в Qt U Г, принимает наибольшее и наимень-
наименьшее значение на Г, т.е. если М = max u(x,t), m =
min u(x,t), то
m<u(x,t)<M V(x,t)eQTur
156 Глава III. Задача Коши для уравнения теплопро-ти
Доказательство. Теорема о минимуме сводится к теореме
о максимуме переменой знака у u(x, t), поэтому мы ограни-
ограничимся доказательством только теоремы о максимуме. Пред-
Предположим, что теорема о максимуме неверна, т.е. найдется
в Qt точка (xe,tQ), в которой u(xo,to) > М. Обозначив
е = u(xo,to) — М > О, рассмотрим функцию
, . , . eT-t
v(x,t) = u(x,t) +-—р- ■
Имеем v(x,t) < u(x,t) + § V(x,<) G QT. Тогда
/Tl ±
- ° >
e T — <
= e+M>e + u(x,<) = e + u(x,<)---y- >
'>e + t;(*,t)-| = ! + »(*, t) V(*,t)er.
Отсюда следует, что u(x,t) принимает свое максимальное
значение в какой-то внутренней точке цилиндра. Обозначим
эту точку через (xi, t\) € Qy (Точка (xj, t\) может совпасть
с (хо,*о).) Тогда по теореме из математического анализа в
этой точке должно быть -щ = 0, Ди < 0, |^ > 0 (если U <
Г, то || = 0 в точке (xi,*i), если же <i = Т, то |^ > 0, т.е.
может быть граничный экстремум). Поэтому в точке (xi,ti)
имеем ^г — Аи > 0. С другой стороны,
dv . ди . е е
__д„ = __ди__ = __<0.
Получили противоречие, теорема доказана.
Замечание. Принцип максимума и соответствующие
оценки решения имеют место для параболического уравне-
уравнения второго порядка с переменными коэффициентами, как
однородного, так и неоднородного, в том числе в области,
которая является более общей, чем цилиндр.
Гл. III, § 9. Принцип максимума для решения ... 157
Подробнее об этом можно прочитать в [11] и [20].
Следствия
1. Решение первой начально-краевой задачи для ура-
уравнения теплопроводности в Qt, непрерывное в Qt U Г1,
единственно. Действительно, пусть мы имеем два решения
ui(t, x) и U2(t, x) с одними и теми же начальными и гранич-
граничными значениями на Г. Тогда их разность и\—и2 принимает
нулевые значения на Г и в силу теоремы о максимуме и ми-
минимуме эта разность есть тождественный нуль в QT:
«1 — «2 = 0 =$■ «1 = «2 в QT.
2. Решение первой начально-краевой задачи для уравне-
уравнения теплопроводности непрерывно зависит от функций, за-
заданных на боковых сторонах и нижнем основании цилиндра
Qt- Это следует из неравенства:
min u(x,t) < u(x,t) < max u(x,t).
2. Пршнцнп максимума для полосы. Следствия: единствен-
единственность решения задачи Коши и непрерывная зависимость
ею от начальных данных. Корректность постановки задачи
Коши для уравнения теплопроводности
Теперь рассмотрим задачу Коши для уравнения тепло-
теплопроводности в слое П:
-0-
V0
dt ^хдх\~ ; ={(*,*): x€TRn,0<t<T},
u(t,x) =<р(х).
tQ
t—Q
Теорема 2. Всякое решение u(t, x) уравнения теплопрово-
теплопроводности, непрерывное и ограниченное в слое
П = {(*, х) : х G IRn, 0 < t < Т},
158 Глава III. Задача Коши для уравнения теплопро-ти
т.е. u(t, х) € Съ(Н) П С^£(П) удовлетворяет в этом слое П
неравенствам
m<u(t,x)<M, B)
где М = sup u@, х), т = inf u@, x).
z€WLn *€Rn
Доказательство. Для доказательства используем уже до-
доказанную нами теорему о принципе максимума для ограни-
ограниченной области - цилиндра Qt-
Докажем, что u(t, х) < М (Доказательство второго нера-
неравенства сводится к доказательству первого переменой знака
yu(t,x)).
Пусть е > 0 - произвольное число. ^Докажем, что
u(to,xo) < М + е в любой точке (*о,яо) € П. Рассмотрим
функцию w(t,x) = 2nt + |x|2, которая является решением
уравнения теплопроводности. Положим N = swp\u(t,x)\.
П
Функция
удовлетворяет уравнению теплопроводности в круговом ци-
цилиндре Qt — {(x,t) • \х\ < R, 0 < t < Т} и неотри-
цательна на Г = {{x,t) : (x,t) € 5 U п0}, где R —
/{—-—)w(to,xo) ^_ |Жо|^ ^г _ боковая поверхность кругового
цилиндра, а /?о - его основание при t = 0.
Действительно,
= ,£.|Х| .+М-и@,х)>0.
При |ж| = R имеем
Гл. III, § 9. Принцип максимума для решения ... 159
eBnt + R2)
w(tO,Xo)
М -u{t,x)
|г|=Я
w(to,xo)
\2nt
M-u(t,x)
+M-u(t,X)
>
\z\=R
t£ik как N = sup \u(t, x)\.
П
По теореме о максимуме и минимуме для ограниченной
области функция ui(t,x) > 0 и в цилиндре Qt, в кото-
котором лежит точка (^о^о). Следовательно, в этом цилиндре
u(t, х)<М+ У/О*;*о\, т.е. u(t0, х0) < М + е. Так как точка
(<о, xq) и число е произвольны, то из последнего неравенства
вытекает, что u(t,x) < М всюду в П. Теорема доказана.
Отметим, что принцип максимума для полосы также ве-
верен для всего класса параболических уравнений второго по-
порядка.
Из теоремы 2 вытекает теорема единственности:
В классе функций, ограниченных и непрерывных в слое
П, u(t, x) € C^'J(n), задача Коши для уравнения теплопро-
теплопроводности имеет единственное решение.
Доказательство. Применим неравенство B) к разности
u\(t,x) — u2(t,x) = u(t, x) для двух решений рассматри-
рассматриваемой задачи. Тогда, так как и = 0, то и = 0 в П, т.е.
Ui =U2.
Из теоремы о максимуме и минимуме для слоя и дока-
доказанной выше теоремы о разрешимости задачи Коши в классе
ограниченных функций следует корректность постановки
задачи Коши. Действительно:
1) для любого <р(х) € Сь решение задачи Коши для ура-
уравнения теплопроводности представляется формулой
160 Глава III. Задача Коши для уравнения теплопро-ти
Пуассона, причем это решение ограничено:
\u(t,x)\< J G(t,x-y)\<p(y)\dy<
<К [ G{t,x-y)dy=K,
Rn
где К — sup |y?(z)|, так как / G(t,y)dy = 1 V* > 0;
х€Ш.п И»
2) задача Коши имеет единственное решение в классе
ограниченных непрерывных функций;
3) решение u(i, x) непрерывно зависит от начальных
условий в метрике Су.
< sup |it@,x)| = ||u@,
Замечание. Мы доказали, что решение задачи Коши в
классе ограниченных функций единственно. Возникает во-
вопрос: будет ли единственно решение задачи Коши для ура-
уравнения теплопроводности в классе растущих при
|х| —► оо функций? Ответ на этот вопрос дает теорема
А.Н. Тихонова (см. [24]), в которой решение может ра-
расти даже экспоненциально, но оно будет попадать в класс
единственности. Поясним более подробно. Пусть v(x) =
max \u(t, x)\. Если u(t, x) удовлетворяет однородному
уравнению теплопроводности при t > 0, «@, х) = 0, х €
IRn, и существует постоянная с такая, что v(x)e~~cW —* 0
при |х| —► оо, то u(t,x) = 0. Это класс единственности Ти-
Тихонова. В этом классе справедлива формула Пуассона B)
§ 7, если начальная функция (р(х) = u(t,x) растет не
1 t=0
быстрее, чем ес1*1 .
Необходимое и достаточное условие на класс растущих
функций, в котором сохраняется теорема единственности
Гл. III, § 9. Принцип максимума для решения ... 161
в задаче Коши для уравнения теплопроводности, было по-
получено Теклиндом: решение может расти при \х\ —> оо не
быстрее, чем elxlfcdxD, где неубывающая функция Теклинда
оо оо
h(s) такова, что J -Ajr = оо. При этом, если J ^т^у <
оо, то существует нетривиальное решение, для которого
«(О, ж) = 0.
11 . И Н М
162
Глава IV. Задача Коши для волнового
уравнения. Применение
теории обобщенных функций к
исследованию решения
§ 1. Вывод энергетического неравенства для
волнового уравнения. Следствия: теорема
единственности решения задачи Коши и
непрерывная зависимость его от начальных
данных; область единственности
Рассмотрим задачу Коши для волнового уравнения
dt2
2
х € Etn, t > 0,
a = const,
с начальными условиями
dt\t=o
A)
B)
C)
iiU
(xvx2)
Гл. IV, § 1. Вывод энергетического нер-ва
163
При п — 2 уравнению A) удовлетворяют любые колеба-
колебания натянутой мембраны. В этом случае u(t, x) = u(t, x\, жг)
есть отклонение точки {х\,х%) мембраны в момент времени
t от положения равновесия и = 0 (см. рисунок).
Обозначим через K{Vo) - конус с вершиной в точке
), который задается уравнением
> 0, <0 > О,
to:t>o
Очевидно, ось конуса параллельна оси Ot.
Введем еще следующие обозначения:
QT = K(Vo) n{t = Г}, где 0 < Г < t0,
Sot - боковая поверхность конуса, заключенная между ги-
гиперплоскостями t = 0 и t = Т (т.е. боковая поверхность
усеченного конуса).
t
t=T
11*
164 Глава IV. Задача Коши для волнового уравнения ...
Покажем, что поверхность 5 конуса IC(Vo):
п
F(t,Xl,x2) = a\t - toJ - J>,- - xoiJ = 0 D)
является характеристической поверхностью для волнового
уравнения A). Действительно, направление £, совпадаю-
совпадающее с направлением grad.F, т.е.
= Ba?(t - t0), -2(xt - x01),..., -2(xn - xOn))
будет характеристическим направлением, так как вектор £ с
указанными компонентами, как известно, направлен по нор-
нормали к поверхности Sot, уравнение которой для 0 < t < Т
Таким образом, компоненты вектора £ есть:
2a2(t-t0) = fo, -2(xj -xoi) = 6,...,-2(sn -xOn) = £n.
n
Тогда £q = fl2 ^2 £l в силу формулы D). А последнее озна-
*=i
чает, что вектор £ = (£о»£ъ—»£п) имеет характеристиче-
характеристическое направление для уравнения A). Итак, доказано, что
нормаль в любой точке конической поверхности 5 имеет
характеристическое направление, а следовательно, повер-
поверхность 5 является характеристической поверхностью.
Теорема (об энергетическом неравенстве).
Пусть u(t,x) - любое решение в K.(Vo) (в замкнутом ко-
конусе) уравнения A), принадлежащее классу C2(JC{Vo)). То-
Тогда имеет место следующее неравенство:
Гл. IV, § 1. Вывод энергетического нер-ва ... 165
Я0Х
E)
о
Замечание. Для колебаний мембраны неравенство E) озна-
означает, что полная энергия колеблющейся мембраны, т.е. сум-
сумма кинетической энергии (слагаемое J (^Jdx) и потенци-
потенциям
альной энергии (сумма остальных слагаемых
п
J а2 ^2 (~§jrJdx) по области Q% не возрастает с возраста-
nt к=\ *
нием времени t.
Доказательство. Имеем
Ik' a<2"~ 2~di \~dt) ' !кЩ ~ 'дх1\Ж'дх1)~
д2и ди _ Л_(дид^\ _ 1 д /ди\*
~ dtdxi) ~ 2dt \дх{) '
Для доказательства E) умножим уравнение A) на ^, про-
проинтегрируем по усеченному конусу 1Сот(Ро), получим
ди /д2и
= 1/7 /!гEг
2] J \dtl\dt*
ди
t=i
Теперь воспользуемся формулой Гаусса - Остроградского,
обозначив через N внешнюю нормаль, получим:
166 Глава IV. Задача Коши для волнового уравнения
2 У {[(л) ^Efe
!£(*.>}-о.
Выясним, чему равны направляющие косинусы. На
имеем:
cos(j?,*) = l,
На п0:
oos(N,t) = -1, cos(N,Xi) = 0.
На Sot-
n
cos2(N,t) - a2J2cos4N,xk) = 0,
k=i
что является условием на характеристическое направление.
Действительно, направляющие косинусы единичной нор-
нормали совпадают с направляющими косинусами градиента,
т.е.
|gradF|
= (
V|gradF|'|gradF|'*"'
В наших обозначениях
io = 2a2(t -10), (к = -2(хк - xo,k).
Поэтому
Гл. IV, § 1. Вывод энергетического нер-ва ... 167
хт2 2 V^ хт2 _ Л( дт а\ _ !
^Vj -а 7 ,iVfc —cos ^,1; -а
*=i *=i
п
fe=1 = о,
|gradF|2
в силу того, что на боковой поверхности конуса вьшолняется
соотношение
Левую часть формулы F) можно переписать следующим об-
образом:
5 У [Ы
От |=1
\21
'; J
г—ч ди ди -* —► I
> — -?—cos(JV^,Xi)cos(iV,t) > da = 0.
i=i ' J
Обозначим последний интеграл в G) через I и докажем, что
» —> —»
он неотрицателен. Так как а2 ^ cos2(JV,a?t) = cos2(JV,<), то
мы имеем:
168 Глава IV. Задача Коши для волнового уравнения ...
х
I €L
cost Л/
Лот
Но на Sot cos(N,t) > 0 (угол острый), отсюда следует,
что I > 0. Тогда мы имеем
/[(!)'+'£(£)>-
Отбрасывая неположительный член "—I" справа, мы полу-
получаем энергетическое неравенство.
Теорема доказана.
Следствия
1. Теорема единственности.
Пусть u(t,x) 6 C2(K(Vo)) удовлетворяет волновому ура-
уравнению A) в конусе IC(Vo) и нулевым начальным условиям
на основании по конуса:
и
—
' dt
По
= 0. (8)
Тогда u(t,x) = 0 для (*,я) €
Гл. IV, § 1. Вывод энергетического нер-ва ... 169
Доказательство. В силу энергетического неравенства E)
и начальных условий (8) для любого t, удовлетворяющего
неравенству 0 < t < to, имеем
[\/ди\ 2watM2b ^
I ( ТГ" +a 7 ("^— ) \dx <
Следовательно, |^ = 0, ^ = 0, г = 1,2, ...,п для (t,x) €
f?t- Так как t - любое из интервала @,<о)> то ^ = ^т = О
во всем конусе /С('Ро)- Отсюда вытекает, что u(t,x) = const
)
Но
u(t, x) = 0 =*► u(<, ж) = 0 в £(Vo),
t=0
а значит, и в K.{Vq) в силу непрерывности u(t,0) в
2. Пусть начальные условия <р(х) и ф(х) обращаются в
нуль в некоторой области Go С Ш,п. Тогда по доказанной
теореме единственности, решение u(t,x) задачи Коши A) -
C) обращается в нуль в области G, являющейся объедине-
объединением внутренностей конусов вида JC(Vo), основания которых
лежат в Go (см. рисунок)
Область G называется областью единственности реше-
решения задачи Коши.
3. Из энергетического неравенства следует непрерывная
зависимость решения задачи Коши от начальных данных в
интегральном смысле.
170
Глава IV. Задача Кошя для волнового уравнения ...
§ 2. Решение задачи Коши для волнового
уравнения при начальных данных,
принадлежащих пространству S
Допустим, что функции из начальных условий B), C) §
1 <р(х), ф(х) € 5(ИП). Предположим, что существует столь
гладкое и убывающее вместе с производными при х —> оо
решение u(t,x) задачи Коши для волнового уравнения в
IRJ х И" = Ип+1, что все приводимые ниже выкладки за-
законны. В дальнейшем мы оправдаем эту гипотезу.
Обозначим через u(t, £) преобразование Фурье по х фун-
функции u(t,x):
= J u(t,
A)
Тогда согласно свойствам преобразования Фурье
гласно нашей гипотезе
и со-
соГл. IV, § 2. Решение задачи Коши для волн, уравн.
_ d*u(t,x) _ fl»u(<,Q.
.2
171
B)
»=i
где |£|2 = f2 + £г + — + &•
Рассмотрим волновое уравнение вида (а = 1)
ян..
— Ли = О
с начальными условиями
и применим к нему оператор Fx-*£, тогда получим
В силу начальных условий получаем
и
*=о
дй
т
t=0
ri
а<
*=0
C)
D)
E)
F)
G)
Таким образом, исходная задача Коши C), D) перешла в
задачу E) - G) для обыкновенного дифференциального ура-
уравнения, содержащего параметр £ = (£i,£2>—>£n).
Решение задачи E) - G) дается следующей формулой:
здесь iei = v[w
Взяв обратное преобразование Фурье, получим
172 Глава IV. Задача Коши для волнового уравнения ...
^«■■*>«■ <8)
Ж"
Теорема. Если функции (р(х) и ф(х) принадлежат
S(TRn), то функция u(t,x), задаваемая формулой (8), яв-
является классическим решением задачи Коши, т.е. u(t,x) 6
С2(И ), и удовлетворяет волновому уравнению C) и на-
начальным условиям D).
Доказательство. Нам нужно убедиться в том, что если
<£(£) и г/>(£) принадлежат S, то интегралы, полученные в
результате дифференцирования по t и х решения (8), будут
равномерно сходиться относительно параметров t, x.
Рассмотрим, например,
du(t, x) _
Ы
ж»
Очевидно, полученный после дифференцирования интеграл
равномерно сходится:
-А +оо
J (\(\№)\
-оо
Ao{c) и V(*,O€R"+1, т.к.
Поэтому законно дифференцирование под знаком интегра-
интеграла. На самом деле, если <£(£), V>(£) € S, то интеграл (8)
можно дифференцировать под знаком интеграла сколько
угодно раз. Поэтому
Гл. IV, § 3. 6-функция, сосредоточенная на сфере ... 173
d2U уч d2U =
Ж"
««Ю + ЛО=§р] }'""{Ч = о.
Таким образом, u(t, x), задаваемое формулой (8), удовлетво-
удовлетворяет волновому уравнению.
Полученное решение также удовлетворяет и начальным
условиям:
U
Ж"
ди
Ы
Ж"
Теорема доказана.
Замечание. Из теоремы единственности вытекает, что ре-
решение, даваемое формулой (8), единственно.
§ 3. ^-функция, сосредоточенная на сфере.
Преобразование Фурье ^-функции,
сосредоточенной на сфере. Теорема о свертке
обобщенной функции из S' с компактным
носителем и функции из S
Нашей целью теперь будет упростить формулу (8) про-
прошлого параграфа, т.е. пользуясь теоремой о свертке, полу-
получить выражение для решения подобно тому, как мы это де-
делали при решении уравнения теплопроводности.
174 Глава IV. Задача Коши для волнового уравнения ...
Для этого введем в рассмотрение еще одну обобщенную
функцию - ^-функцию, сосредоточенную на сфере. Обозна-
/
чим через Sr = Sr(Q) = {х : |ж| = л / £ х\ — Щ сферу в
у *=1
n-мерном евклидовом пространстве.
Определение. 6-функцией, сосредоточенной на сфере
(обозначим ее через f>sR), называется обобщенная фунющя,
т.е. линейный непрерывный функционал, вида
°= J
Sr
где dax - элемент площади сферы Sr.
Найдем преобразование Фурье от 6sR. По определению
имеем
J

Sr Щ
= J (J
Щ Sr
Мы поменяли порядок интегрирования в последнем инте-
интеграле A), что законно, так как подынтегральная функция
суммируема в 1R£ x Sr. Из A) следует, что
F6Sr= [ e-i
Sr
Введем обозначение
Гл. IV, § 3. ^-функция, сосредоточенная на сфере
175
=f c-i{s
Sr
Вычислим интеграл I при п = 3.
Для этой цели введем сферические координаты на сфере
Sr с северным полюсом в точке, лежащей на пересечении
—+
луча 0£ со сферой Sr: \х\ = R (точка £ имеет координаты
£ъ £г> £з, и она является параметрической точкой при вычи-
вычислении интеграла /) , т.е. введем сферические координаты
х\ = Rco8(p sinfl, X2 = Rsin(p sin9, х$ = RcosO,
О < (р < 2тг, 0 < в < тт.
При так выбранных сферических координатах, используя
свойства тригонометрических функций, мы получаем
176 Глава IV. Задача Коши для волнового уравнения
2ir it
о о
1Г
= 2*Д2 IV
о
IT
= 2vR2 [[co8(\Z\R cos в) - i sin(|£|.R cos в)] sin вв,в =
I
cos(\i\R cos в) sin 6d6 =
0 1
= -4тгЯ2 f cos{\Z\Rz)dz = 4тгЛ2 /
т.е.
B)
Таким образом, преобразование Фурье обобщенной фун-
функции SsR согласно A), B) при п = 3 имеет вид
т.е.
Гл. IV, § 3. 6-функция, сосредоточенная на сфере ... 177
Нам нужно рассмотреть свертку обобщенной функции с
компактным носителем и функции из S. Поясним, что зна-
значит обобщенная функция с компактным носителем. Хотя
обобщенные функции, вообще говоря, не имеют значений
в отдельных точках, тем не менее имеет смысл говорить об
обращении обобщенной функции в нуль в области.
Обобщенная функция / обращается в нуль в области
п С lRn, если (/,¥>) = 0 Vy> € S{u). Этот факт записы-
записывают обычным образом: f(x) = 0 для х б Q. Если обоб-
обобщенная функция обращается в нуль в области Q С Жп,
то, очевидно, она обращается в нуль в окрестности каждой
точки этой области. Верно и обратное: если обобщенная
функция обращается в нуль в окрестности каждой точки об-
области Q С lRn, то она обращается в нуль и в области Q.
Объединение всех окрестностей, где обобщенная функция
обращается в нуль, образует открытое множество О/, кото-
которое называется нулевым множеством обобщенной функции.
Носителем обобщенной функции / называется дополнение
Of до всего Нп: supp/ = IRn \ Of. Носитель / есть зам-
замкнутое множество. Бели носитель / образует ограниченное
множество, то обобщенная функция называется финитной,
или обобщенной функцией с компактным носителем.
Примером обобщенной функции с компактным носите-
носителем является ^-функция, сосредоточенная на сфере.
Сверткой обобщенной функции / с компактным носите-
носителем и функции ф € S называется функционал:
(/ * ф)(х) = (/(у), ф(х - у)) Щ € 5. D)
Заметим, что ф(х — у) = ф\{у) € S. поэтому для любого
х € IRn выражение D) имеет смысл.
Найдем выражение для свертки 8sR и функции ф 6 5.
Согласно D) имеем
х - у)) =Р j ф(х - y)day. E)
Sr
Легко проверить, что свертка E), рассматриваемая как
функция от ж, принадлежит пространству 5, т.е. убывает
12 - В. Н. Масленникова
178 Глава IV. Задача Коши для волнового уравнения ...
быстрее, чем г, [gia , где а > 0 - любое положительное чи-
число, и имеет производные любого порядка.
Имеет место следующая теорема о свертке для обобщен-
обобщенных функций.
Теорема. Пусть / € 5"' и имеет компактный носитель. То-
Тогда Щ € S
Эта теорема доказывается в курсе функционального ана-
анализа. Нам нужен ее частный случай, который мы будем при-
применять для решения задачи Коши для волнового уравнения,
его мы и докажем.
Пусть f = SsR, <Р,Ф €5.
Имеем, пользуясь D) и E):
= ( / ф(х - y)day, I v(Oe"l(l'°^) = F)
ж; sR ж»
= J {J e-<(^ (j ф(х - y
Изменение порядка интегрирования, которое было произве-
произведено, законно, так как подынтегральная функция суммиру-
суммируема на Ш£ х Н£ X Sr. Во внутреннем интеграле по Ш£ в
Гл. IV, § 4. Вывод формулы Кирхгофа ... 179
F) можно сделать сдвиг, т.е. замену х — у = z, от этого ин-
интеграл не изменится; обозначая новую переменную z опять
через х, получим:
= J
Таким образом, мы получили
R-
или
Таким образом, теорема о свертке в частном случае / = 6sR
доказана.
§ 4. Вывод формулы Кирхгофа для решения
задачи Коши для волнового уравнения в
случае трех пространственных переменных
Вернемся к рассмотрению задачи Коши и рассмотрим ее
частный случай, когда <р(х) = 0, ф(х) € S, ф(х) ф 0, т.е.
- - Ли! = 0, хе 1R3, t > О,
at
12*
180 Глава IV. Задача Коши для волнового уравнения ...
Тогда, согласно полученной формуле (8) § 2 для решения
задачи Коши A) имеем:
к- B)
Согласно формуле, выведенной для преобразования Фурье
6sR, n = 3,
Поэтому
А по теореме о свертке преобразования Фурье обобщенных
функций имеем
Из формул B) - D) получаем, что
s.(o)
'= Ш J
Гл. IV, 5 4. Вывод формулы Кирхгофа ... 181
где
x-y = z, day- daz,
St@) = {\у\ = t},
Полученную формулу можно записать еще в следующем
виде:
«i(t, х) = t • ^-р- / ip{z)d(Tz = гМгф(х),
где через Мгф обозначено среднее арифметическое значение
функции ф на сфере St(x) = {z : \z — х\ = t}:
J
St(x)
Получим аналогично формулу для решения задачи
, t>0,
E)
=0 dt 1=0
Решение задачи E) с использованием (8) из § 2 есть
R3
Bn)*dtJ
R8
Тогда решение нашей первоначальной задачи
182 Глава IV. Задача Коши для волнового уравнения
•^■-Л« = о, хеш.3, t>o,
и
*=0
<
является суммой решений u\(t,x) и U2{t,x), т.е.
u(t,x) =
где Mtt/> = -dp J i>(z)daz.
S,(*)
Формула F) называется формулой Кирхгофа. Интеграл
в ней берется по сфере с центром в точке х радиуса t, a
(t, x) - точка, в которой мы вычисляем решение.
Отметим, что F) выведена при условии <р,ф € S, но на
самом деле она дает решение задачи Коши при tp € C3(IR3),
ф € С2(Щ,3). Для этого нужно F) подставить в волновое
уравнение и начальные условия и доказать, что интегралы
будут иметь смысл. Для простоты, проверим этот факт в слу-
случае однородности одного из начальных условий, например,
<р = 0.
Тогда
St(x)
Имеем
Airt2
\u(t,х)\ < max \ф(г)\ • —— = max\ib\-t
и, очевидно,
lim«(<, x) = 0.
Докажем, что
ди
dt
Гл. IV, $ 4. Вывод формулы Кирхгофа ... 183
= ф(х), ф е С2.
<=0
Для этого в G) сделаем замену переменных z —»/3:
Тогда сфера \z — х\ = t перейдет в единичную сферу в пе-
переменных /3 с центром в начале координат. Действительно,
Z - Х\ = v^l - *lJ + (*2 " Х2У + B3 - *зJ =
= у/р*е
т.е.
(цель нашего преобразования - замены переменных - состо-
состояла в том, чтобы область интегрирования - сфера - стала не
зависящей от х и <). Таким образом, после преобразования
переменных получаем из G)
t f
u(t,X) = -— / ф{Х\ -\-t/3i,X2 -\-tp*2,X3 +^з)<£(Тя, (8)
4тгу
Si
где d<r/j = p-
Поэтому
du_J_
dt 4тг
Si
з (9)
* дф
Очевидно, lim ^ = ^(х)? так как последний интеграл в (9)
при < —» 0 ограничен, поэтому мы получаем
184 Глава IV. Задача Коши для волнового уравнения ...
3
*=1
а предел первого интеграла при t —+ О есть ф(х). Осталось
доказать, что u(t,x) удовлетворяет волновому уравнению.
Из равенства (8) имеем
Axu{t,x) = — I Aipdap = — I
Si St(x)
если перейти к старым переменным z.
Вычислим вторую производную по t в формуле (9). Для
этого преобразуем (9) по теореме Гаусса - Остроградского.
Умножив и разделив на t первый член в (9), а во втором,
переходя к старым координатам, получим
ди _ u(t,x) 1 [ дф
dt t +4тг< J дп '~
где Vt(x) есть шар радиуса t с центром в точке х, а
/(*)= / Д^Лг. A1)
Vt(x)
Тогда, дифференцируя A0), получаем
#и u(t,x) 15« Щ
_
dt2 t2 * t dt 4тг*2 + 4тг*
0* W
Гл. IV, § 5. Вывод формулы Пуассона ... 185
Вычислим -§il{t). Переходя в A1) к сферическим коорди-
координатам (г, в, ip) и отмечая, что интегрирование в A1) прово-
проводится по шару \z — х\ < t, получаем
t я- 2п
Щ= f I I Аф(г,$,<р)г2 sin ed<pd$dr,
ооо
откуда
ir 2ir
^- = / I Аф(г,<р,0)Ь2sin$dipd$ = I Aфd<тx.
о о st(x)
Таким образом, имеем
S»(x) St(x)
т.е. волновое уравнение удовлетворяется, если ф €
C2(IR3). Аналогично доказывается этот факт при неодно-
неоднородном начальном условии и
1=0
= ф) е С3(И3).
§ 5. Вывод формулы Пуассона для решения задачи
Коши для волнового уравнения в случае двух
пространственных переменных. Метод спуска.
Формула Даламбера для уравнения колебания
струны
Рассмотрим уравнение
Э2и &и &и
dt2 6х\ Ьх\ ~
В случае п = 2 начальные условия
186 Глава IV. Задача Коши для волнового уравнения ...
ди
и
= <p(xi,x2), -57 м ^ = ф{хх,х2) B)
являются функциями двух переменных.
Адамар предложил следующий способ нахождения ре-
решения задачи Коши в этом случае, если уже построено ре-
решение при п = 3. Функции <p(xi,X2) и ф(хг,Х2) рассматри-
рассматриваются как функции, заданные в IR (х\,Х2,хз), но не за-
зависящие от хз, а двумерное волновое уравнение заменяется
трехмерным
" дх\ Т дх\ Т 0Х| V" 5x2 "
Таким образом, решение u(t, Х1,хг) задачи Коши A), B),
которое существует и единственно по доказанному нами
выше при любом п (см. метод преобразования Фурье), удо-
удовлетворяет также уравнению C) в IRj x IR^ и начальным
условиям B). Поэтому это решение можно выразить с по-
помощью формулы Кирхгофа:
где j^ /
St(x)
Так как функции <p(z\, z-i) и ф(г\, z^) не зависят от z3, то ин-
интегралы Щф и Mt<p по сфере 5«(х) можно заменить удвоен-
удвоенными интегралами по проекции St(x) на плоскость z% = х3,
т.е. по кругу Kt(x), который образуется сечением шара Vt(x)
плоскостью z% = х$.
По известной формуле из математического анализа для
поверхностных интегралов имеем:
JJf(x,y,z)da = jf f(x,у,z(x,y))^l + z'x2 + z'y2 dxdy,
так как элемент поверхности da = л/l + z'x2 + z'y2 dxdy, где
D - плоская область. В нашем случае z = Z3, и проекция
Гл. IV, § 5. Вывод формулы Пуассоца ... 187
элемента daz поверхности 5*(х), заданной уравнением z% —
хз = ±y/t2 — (z\ — xiJ — B2 — Z2J, на плоскость ^з = хз
(см. чертеж) задается формулой
- (z2 -
Поэтому формула Кирхгофа F) § 4 при п — 2 переходит в
формулу
u(t,Xl,x2) = ±j J
Kt(x)
--
2ndt
<p(zi,z2)dzidz2
Kt(x)
D)
188 Глава TV. Задача Коши для волнового уравнения ...
Формула D) называется формулой Пуассона.
Бели начальные функции <р и ф не зависят иотжг, т.е.
¥>(zi), ij>(xi), то тем же методом спуска из формулы Пуас-
Пуассона можно получить формулу Даламбера решения задачи
Коши для уравнения колебания струны:
912 ~dxV E)
ди
t=o ot
<=0
Но проще формулу Даламбера получить, используя общее
решение уравнения колебания струны. Действительно, об-
общее решение уравнения колебания струны имеет вид:
u(t,xi) = $i(xi - *) + Ф2(хг + *).
Находя Ф\ и Фг из двух начальных условий, получаем:
откуда
или
= I rf>(a)da
о
= \{Ч>{*\) + J*Ka)da] +
Тогда
Гл. IV, § 6. Корректность постановки задачи Коши ... 189
xi-t
Последняя формула F) называется формулой Даламбера.
§ 6. Корректность постановки задачи Коши для
волнового уравнения
Имеет место корректность постановки задачи Коши для
волнового уравнения в смысле данного нами ранее опреде-
определения.
Действительно:
1) Vip(x) € C3(]Rn), ф € C2(IR2) задача Коши для вол-
волнового уравнения имеет решение, определяемое формулой
Кирхгофа (п = 3), Пуассона (п = 2) и Даламбера (п = 1);
2) это решение единственно, в силу доказанной выше те-
теоремы единственности;
3) решение u(t,x) непрерывно зависит от начальных
условий в интегральном смысле в силу энергетического не-
неравенства:
fit t=1 Яо
где Qt - сечение конуса К.(Ро) плоскостью t = const. Можно
доказать, что справедлива также оценка
4) волновое уравнение не меняется при замене t на —t,
поэтому мы могли бы решать задачу Коши "вниз" по t,
190
Глава IV. Задача Коши для волнового уравнения ...
т.е. имеет место корректность постановки задачи Коши при
t < О с начальными данными при t = 0.
§ 7. Решение задачи Коши для неоднородного
волнового уравнения
Решение неоднородного волнового уравнения можно най-
найти, применяя принцип Дюамеля, также как мы это делали
для параболического уравнения. Пусть п = 3, рассмотрим
задачу:
- А ±И Л
~ + (х' ;'
, О 0,
и
*=0
ди
= ф) € C3(IR3),
A)
э = ф(х) е C2(]R3).
Решение задачи A) есть сумма решений двух задач:
= ^«ь
«1
t=o
<=о
: = * (*);
A')
«2
<=0
= 0,
A")
= 0.
Решение задачи A') мы нашли. Найдем решение задачи
Для этого рассмотрим вспомогательную задачу
= Ли, * > г, х € IR3,
dt2
V
<=г
= 0,
B)
dt
t—T
= F(x,r), x
Гл. IV, § 7. Решение задачи Коши для неоднор. волн. ур. 191
По формуле Кирхгофа решение задачи B) имеет вид
St-r(x)
Тогда искомая функция и^(х, t) может быть найдена по фор-
формуле
t
u2(x,t) = / v(x,t,
C)
Действительно, функция U2(x,t), задаваемая формулой C),
есть решение задачи A"):
1) «2
t=o
= 0;
2) ^ = чх,м
iSr**-
t
=7
dv(x,t,r)
dt
dr,
поэтому
3)
dt
= 0.
t=0
~~~di +; aP dT~
t
= F(x,t)+ I Av(x,t,T)dT =
о
t
= F(x,t) + Л I v(x,t,T)dr =
192 Глава IV. Задача Коши для волнового уравнения
т.е. неоднородное уравнение в A") удовлетворяется.
Преобразуем формулу C). Имеем
О |x-z|=t-r
t
-hl( И £?
О \x~z\=t-r
Сделаем замену
t — т = г, т —» г, dr = —dr,
тогда

О |х-г|=г
\\
\x-z\<t
Интеграл D) называется запаздывающим потенциалом.
Задача на дом. Получите решение неоднородного волно-
волнового уравнения в случае п = 2 и п = 1.
§ 8. Фундаментальное решение (функция Грина)
задачи Коши для волнового уравнения
1. Согласно доказанному нами в предыдущих лекциях
Гл. IV, § 8. Фундаментальное решение ... 193
if
Рассмотрим функцию £i(i,£) = |if > она удовлетворяет
следующему уравнению и начальным условиям:
t=0
— I/,
dt
— ■!••
t=0
Но нами было доказано, что F,_^r(l) = 6(х), где преоб-
преобразование Фурье понимается в смысле обобщенных фун-
функций. Поэтому, взяв обратное преобразование Фурье F7^x
от обеих частей формул A), мы получим:
д*1 B)
=о, ^^
at t=o
где
а формулы B) и C) следует понимать в смысле обобщенных
функций. Функция £\(x,t), задаваемая формулой C) и удо-
удовлетворяющая B), называется фундаментальным решением
задачи Коши для волнового уравнения или функцией Грина
этой задачи.
Так как мы не изучаем детально теории обобщенных
функций, то условимся понимать соотношения B) в том
смысле, что образ Фурье £\(t, £) = Fx-,.(S\(t,x) фундамен-
фундаментального решения £i(t,x) = ^i^st(o)(x) удовлетворяет со-
соотношениям A), которые имеют обычный смысл. Из формул
B) и C) вытекает следующий физический смысл фундамен-
фундаментального решения £i(i,x), задаваемого формулой C): если
13 ■ В. Н. Масленникова
194
Глава IV. Задача Коши для волнового уравнения ...
в начальный момент t = 0 в трехмерной среде появляется
единичный импульс, сосредоточенный в начале координат
t=o
= 6(х) и £\
*=0
= 0,
то в среде возникает сферическая волна вида
т.е. в момент времени t возбуждаются точки, находящиеся на
сфере |х| — t\ возмущение распространяется в виде сфери-
сферической волны |х| = t. С ростом t сферическая волна переме-
перемещается со скоростью, равной 1, причем после прохождения
волны опять наступает покой. В этом смысле говорят, что в
пространстве 3-х измерений (п = 3) имеет место принцип
Гюйгенса.
ПОКОИ
Гл. IV, § 8. Фундаментальное решение ... 195
3
Отметим, что для уравнения м« — а2 53 и**** соот~
ветствующее фундаментальное решение имеет вид сфери-
сферической волны
т.е. в момент t > О возбуждаются точки, находящиеся на
сфере \х\ = at; другими словами, возмущение распростра-
распространяется в виде сферической волны |х| = at со скоростью,
равной а. (Поэтому коэффициент а2 в волновом операторе
- это квадрат скорости.)
2. Если известно фундаментальное решение £\(t, x), то
решение задачи Коши для волнового уравнения
x € ПГ, t > О
с начальными данными
= 0,
«=о ' dt
t=o
можно представить в виде свертки фундаментального реше-
решения S\(t,x) и функции ф(х):
{х-y)da»= h J
S,@) St(r)
3. Аналогичную интерпретацию допускает функция
13*
196 Глава IV. Задача Коши для волнового уравнения
Она является решением задачи Коши
dt2
t=o
= 0.
t=o
Действительно, ее образ Фурье по х
удовлетворяет соотношениям
t=o ' dt
= 0.
Решение же задачи
= Аи, и2
t=o
= ¥>(*)>
Эй'
dt
t=o
= 0
получается в виде свертки
8t \4:TTt J
S,(r)
47Г* J
F)
Гл. IV, § 9. Качественные свойства решения ... 197
§ 9. Качественные свойства решения задачи Коши
для волнового уравнения. Распространение
волн
1. Область зависимости решения задачи Коши. Конечность
скорости распространения возмущений. Область влияния
Определение. Областью зависимости решения u(t,x) в
точке V(t, х) называется такая область, что решение в точке
V(t, x) зависит от данных задачи, заданных только в этой
области.
Данные задачи - это данные Коши и внешние силы. Фор-
Формула F) § 4 для п = 3 показывает, что решение задачи Коши
для однородного волнового уравнения, т.е. значение фун-
функции u(t, х), зависит от начальных данных, расположенных
только на границе основания характеристического конуса с
вершиной в точке V(t, х), т.е. на сфере |х — у\ = t. Формулы
Пуассона и Даламбера показывают, что решение зависит от
начальных данных на всем основании характеристического
конуса.
Свойства решений гиперболических уравнений:
1) Конечная область зависимости.
2) Конечная скорость распространения возмущений.
Назовем областью влияния ту область, в которой на ре-
решение влияют начальные данные, заданные только на осно-
основании характеристического конуса.
Графически можно изобразить область единственности
решения и область влияния, которые ограничены характе-
характеристиками, следующим образом (для простоты, рассмотрим
случай п = 1) (см. рисунок).
Теперь проанализируем, как распространяются волны в
случае п = 3, п = 2, п = 1.
Пусть начальные данные <р(х) и У>(х) - финитные фун-
функции, сосредоточенные в некоторой конечной области
198
Глава IV. Задача Коши для волнового уравнения
область влияния
Hx,i)
область
единствен
ности
2. Распространение волн в случае трех пространственных
переменных. Принцип Гюйгенса
Решение задачи
dt2
= Ли,
и
ди
dt
t=0
определяется формулой Кирхгофа, т.е. оно есть суперпози-
суперпозиция (наложение) возмущений, даваемых формулами D) и F)
§ 8. В случае п = 3 из формул Кирхгофа следует, что ре-
решение зависит от начальных данных, задаваемых только на
границе основания характеристического конуса и возмуще-
возмущения имеют резкий передний фронт и резкий задний фронт.
Поясним это подробнее. Пусть в точке х находится наблю-
наблюдатель (см. чертеж).
В точку х € IR возмущение придет (например, мы услышим
звук) в момент времени to = d (и в момент времени to = ^,
если скорость распространения возмущения равна а) и будет
действовать в этой точке в течение времени D — d (~^ - в
случае скорости, равной а), где dvi D - минимальное и мак-
максимальное расстояние от точки х до точек рассматриваемого
Гл. IV, § 9. Качественные свойства решения ...
199
задний фронт
передний фронт
компакта. При t > D — t\ в точке х снова наступит покой.
Таким образом, решение будет отличным от нуля только для
тех точек (x,t), для которых сфера |х| = t пересекает носи-
носитель начальных данных. В противном случае решение есть
тождественный нуль.
Наличие резкого переднего фронта и резкого заднего
фронта и есть математическая интерпретация принципа
Гюйгенса.
3. Распространение волн на плоскости и в случае одного
пространственною переменною. Диффузия волн
Если же п = 2, то, как следует из формулы Пуассона,
возмущение, произведенное в начальный момент в области
ft отзывается, вообще говоря, во всех точках, лежащих вну-
внутри круга радиуса t с центром в х. При этом наблюдается
передний фронт волны |х| = i, движущийся на плоскости со
скоростью, равной 1 (или со скоростью, равной а, если вол-
волновое уравнение имеет вид utt = а2 Аи). Однако, в отличие
200 Глава IV. Задача Коши для волнового уравнения ...
от пространственного случая, за передним фронтом возму-
возмущение наблюдается во все последующие моменты времени,
так что задний фронт волны отсутствует. В этом случае го-
говорят, что на плоскости имеет место диффузия волн. При
этом принцип Гюйгенса, очевидно, нарушается. При п = 3
диффузии не бывает. Доказано, что диффузии не бывает для
решений волнового уравнения при любом нечетном п > 3.
С случае колебания газа (звуковые волны) u(t,x) означает
отклонение от нормального давления газа в точке х в момент
времени t. В случае п = 3 возмущения, произведенные в ко-
конечной области U С IR3, вызывают волны, не оставляющие
после себя следа. В случае же п = 2 начальные возмущения
(при колебании континуума) вызывают волны, оставляющие
после себя след, если предположить, что эти колебания под-
подчиняются волновому уравнению. Практически эти колеба-
колебания (струны и мембраны) очень быстро затухают вследствие
наличия трения, которое не учитывается при выводе ура-
уравнения колебаний мембраны и струны. Наличие же резкого
заднего фронта волны (отсутствие диффузии) при п — 3
объясняет тот факт, что звук, издаваемый каким-то источни-
источником, не затухает постепенно в данной точке пространства,
а прекращается сразу после прохождения волны.
В случае одного пространственного переменного из фор-
формулы Даламбера
x+at
<р(х - at) + <р(х + at) [
tt(tx) = -i '-£-+
+
1 [
2а I
x-at
следует, что если ф(х) ф 0, то область зависимости решения
есть весь отрезок [х — at, x + at]. В этом случае наблюда-
наблюдаются два передних фронта х — at, x — —at, движущихся
по прямой со скоростью, равной а, направо и налево со-
соответственно. Как и в плоском случае, за фронтом волны
наблюдается возмущение, т.е. имеет место диффузия волн.
Если ф = 0, то областью зависимости решения будут концы
отрезка [х — at, х + at], т.е. получаем такую же картину, как
и в трехмерном случае: после прохождения волны |х| = at
снова наступает покой.
201
Глава V. Основные начально-краевые
задачи для нестационарных
уравнений математической
физики. Метод разделения
переменных (предварительные
рассмотрения)
Введение
В главах 1-4 мы изучили некоторые общие вопросы
теории уравнений в частных производных, такие как клас-
классификация уравнений 2-го порядка с двумя и многими не-
независимыми переменными, классификация уравнений и си-
систем высокого порядка. Изучили постановку задачи Коши,
условия ее корректности и некорректности, а также харак-
характеристики уравнений в частных производных.
Мы вывели основные уравнения математической физики
и подробно изучили задачу Коши для уравнения теплопро-
теплопроводности и волнового уравнения; изучили свойства решений
этих уравнений при условиях, когда область пространствен-
пространственных переменных х = (xi,...,xn) есть IRn, и поэтому в не-
нестационарных задачах, т.е. задачах, зависящих от времени,
мы не учитывали граничных условий.
Теперь мы будем изучать колебания ограниченных тел
(волновое уравнение с граничными условиями), распростра-
распространение тепла в ограниченных телах (параболическое уравне-
уравнение с граничными условиями), а также различные стацио-
стационарные процессы, происходящие в ограниченных и неогра-
неограниченных объемах (эллиптические уравнения и, в частно-
частности, уравнение Лапласа в ограниченных и неограниченных
областях). Таким образом, мы будем изучать различные ура-
уравнения математической физики, учитывая граничные усло-
условия, заданные на границе дП области П С Шп, в которой
мы изучаем решение.
202
Глава V. Основные начально-краевые задачи ...
§ 1. Начально-краевые задачи для
гиперболического уравнения второго
порядка. Энергетические оценки. Интеграл
энергии. Теоремы единственности и
непрерывной зависимости
Многие колебательные процессы в однородных изотроп-
изотропных средах (колебания струн, мембран, трехмерных тел,
акустические и электромагнитные колебания и т.д.) описы-
описываются решениями волнового уравнения
A)
«a
Л=1
которое рассматривается на множестве
QT = {x,t: жб/?сЕп,0<КТ
оо}.
Обозначим через QT = QrUi?oU5l цилиндр с образующими,
параллельными оси 0t, с основанием По С Ш-п при t = 0 и
боковой границей S = дB х [0,Г], где fi - ограниченная
область, Пт = {(x,t) : х €/?,< = г}.
По J
Гл. V, § 1. Начально-краевые задачи ...
203
Границу дП будем считать достаточно гладкой, например
один раз дифференцируемой, т.е. dQ € С1, хотя во многих
случаях она может быть липшицевой.
При t = 0 зададим начальные условия:
u(t,x)
= Ф{х).
B)
В первой части мы вывели три основных типа граничных
условий:
и
s
ди
дп
ди
= ipi(t,x) - первая краевая задача C');
= y><2(t,x) - вторая краевая задача C");
~ + <т(х)и = <p3(t,x) - третья краевая задача C"),
д п S
где непрерывная функция сг(ж) > 0, ~ - производная по
внешней нормали к S.
Неоднородные граничные условия C') - C"), если фун-
функции сг(х), y>i(x,t), г — 1,2,3, достаточно гладкие, можно
свести к однородным граничным условиям заменой неизве-
неизвестной функции. Поэтому в дальнейшем будем рассматривать
однородные граничные условия вида
и
или
= 0
D')
дп
= 0,
ИЛИ
ди
+
= 0.
D")
D'")
Некоторые физические задачи, например, задачи о коле-
колебаниях неоднородных упругих тел, приводят к уравнениям
с переменными коэффициентами вида
204 Глава V. Основные начально-краевые задачи ...
1=1
при тех же начальных и граничных условиях; при этом
р{х) > Ро > 0, р(х) > ро > 0, q(x) > О,
Так как волновое уравнение A) и уравнение E) не изменя-
изменяются при замене t на —t, то все рассуждения, проведенные
для этих уравнений при t > 0, будут справедливы и при
t <0.
Мы будем называть решение u(x,t) смешанных задач A),
B), D) классическим, если оно имеет непрерывные вторые
производные на множестве Qt и_ непрерывные первые про-
производные в замкнутой области QT = Qt U По U S. В этом
случае мы будем пользоваться доказываемой в анализе фор-
формулой интегрирования по частям:
f ди , f dv , [ ,-* . ,_
/ ~—vdx = — / u^—ах + / uucos(n,«i)ao,
У сю* У ах, у
я n an
где п - внешняя по отношению к П единичная нормаль к
поверхности дП, cos(n,Xi) - косинус угла между внешней
нормалью п и направлением оси Х{, г = 1,...,п.
1. Единственность решения начально-краевых задач. Ин-
Интеграл энергии
Теорема 1. Если u\(t,x), U2(t,x) два решения уравнения
A) с одинаковыми начальными условиями B) и одним из
граничных условий D), принадлежащие C2(Q) П Cl(Q), то
ui(t, x) = u2(t,x) в Qt. При этом для простоты мы предпо-
предположим, что / 6 C(Q).
Гл. V, § 1. Начально-краевые задачи ... 205
Доказательство. Для доказательства теоремы достаточно
доказать, что функция u(t, x) = ui(£, x) — u<2(t,x), удовле-
удовлетворяющая однородному уравнению A), нулевым началь-
начальным условиям и одному из однородных граничных условий
вида D), есть тождественный нуль в QT. Для доказательства
этого факта мы получим энергетическую оценку для реше-
решений начально-краевых задач A), B), D), подобную той, ко-
которую мы получили при исследовании задачи Коши, однако
не для конуса IC(V), а для цилиндра Qt-
Для получения этой оценки умножим уравнение A) на
ди
■gjr и проинтегрируем полученное равенство по цилиндру
Qr, где г - любое число из отрезка [0, Г]: г 6 [0, Г].
Затем сделаем преобразования, похожие на те, которые
мы проводили при выводе энергетического неравенства для
решения задачи Коши.
Получаем
о я о п
Так как
ди д2и _ 1 д /du\
dt ' Ik* ~ 2lk~\~di)
ди
дх\ ~ ~дх~\Ш ' дан) + Шдх~д~х~
^^^ l д /ди\*
f
~ дх{ \dtdx) + 2Ы\дх) '
то левая часть в F) (обозначим ее через J) будет равна:
206 Глава V. Основные начально-краевые задачи
_ 1 f Г д иди\2
о n I=1
dxi
о я I=1
n
^ J
n0 '-1 о an
Пользуясь начальными условиями и (б), получаем:
пт
Яо i=1
G)
Второе слагаемое слева в G) равно нулю для первой и вто-
второй начально-краевых задач и равно
о an an о
для третьей начально-краевой задачи. Поэтому, обозначив
через
Гл. V, § 1. Начально-краевые задачи ... 207
(8)
a{x)u2{r,x)dS,
получаем из G)
т
Е\т) = #2@) + 2j j f(t,x)~dxdt. (9)
о п
Величина Е2(т) называется интегралом энергии. Она
представляет собой сумму кинетической и потенциальной
энергии колеблющегося тела в момент времени т. После-
Последнее слагаемое в правой части (8) присутствует только в
третьей начально-краевой задаче.
Если f(t, x) = 0, то имеем
Е\т) = #2@), г > 0, (9')
т.е. полная энергия колеблющейся мембраны (или другого
тела) при отсутствии внешних воздействий не меняется со
временем. Равенство (9') выражает закон сохранения энер-
энергии при отсутствии внешних сил. Из (9') немедленно вы-
вытекает теорема единственности. Действительно, если / =
^ = 0 в П Vr € [0,Т], т.е.
и = const, но так как и
= 0, то и = 0 в Q. (Напом-
ним, что мы рассматриваем решение, непрерывное вплоть
до границы SU Д>.)
Теорема 1 доказана.
2. Энергетические оценки и теорема о непрерывной зави-
зависимости
Исследуем вопрос о непрерывной зависимости решений
краевых задач от начальных данных и правой части уравне-
уравнения A), для этого получим энергетические оценки.
208
Глава V. Основные начально-краевые задачи ...
Лемма. Для решения начально-краевых задач A), B), D)
имеют место следующие оценки:
tE@) + J(t -
A1)
Доказательство. Продифференцируем (9) по г и восполь-
воспользуемся неравенством Коши - Буняковского, получим
п
пт
dt
Но из (8) следует:
2
dt
< Е2(т), т.е.
\ди
\dt
<Е(т)
A2)
A3)
ввиду неотрицательности члена J a(x)u2(T,x)dS. Анало-
s
гично получаем
s||V,u||Ll(nr)<f;(r). A4)
Поэтому из A2) получаем
Гл. V, § 1. Начально-краевые задачи ... 209
или, интегрируя по г в пределах от 0 до t, получаем
t
E(t) < Е@) + J \\f\\L2(nr)dr. A5)
Из A3) - A5) и неравенства (а + Ь) < у/2~у/а? + б2 следует
оценка A0).
Теперь оценим норму ||u||L2(r?)> т.е. получим оценку
A1). Продифференцируем по t равенство
п
воспользуемся неравенством Коши - Буняковского и оцен-
оценками A3) и A5), получим
2||«||L,(o)^ll«IUa(o) = 2у u—dx <
п
t
<2\\u\\Li(n)(E@) + j\\f\\L2{n)dr),
или после сокращения на
t
< (Е@) + J \\f\\Li(n)dr) V* € [0,Т].
Интегрируя это дифференциальное неравенство, получаем
14 - В. Н. Масленникова
210
Глава V. Основные начально-краевые задачи ...
<1Ио,*)|1ыя) + <Д(о)+
t t\
+ J(j Wf\\wr)dT)dtx.
о о
Меняя порядок интегрирования в последнем интеграле сле-
следующим образом:
t t
о о
О г
f
= / (t - т)Ф(т)<1т,
где Ф(т) = ||/|и2(Ят)? мы получаем окончательную оценку
t
Лемма доказана.
Теорема 2. (о непрерывной зависимости решения от пра-
правой части и начальных данных). Пусть п - классическое
решение 1-й, 2-й или 3-й начально-краевой задачи для ура-
уравнения A) с правой частью /, начальными данными </>, ф и
однородным краевым условием D'), или D"), или D'"), а п-
решение с соответствующими f,fp,ij> и однородным краевым
условием. Пусть
II7-7IIl2(qT) <£. \\тр-
где е > 0. Тогда существует С > 0, зависящее в случае
1-й и 2-й начально-краевых задач только от Т, а в случае
Гл. V, § 1. Начально-краевые задачи ... 211
3-й начально-краевой задачи - только от Г и <г, такое, что
У<€[0,Г]
\\u(t,x) -V(t,x)\\Lt(n} < Се, ||Vxu-
дп дп
< Се.
Доказательство. Используя оценку A0) из доказанной лем-
леммы, получаем
an
г
(/Xf f\T,x)dx)dtI'2].
о n
Пусть max <r(x) = M, тогда
< VM\\<p(x)\\L3(dn)-
an
Поэтому
где d = y/2{2 + VT+ VM).
Аналогично из оценки A1) имеем
14»
212 Глава V. Основные начально-краевые задачи ...
где С2 = A + ГA + >/М + 2л/Г)).
Применяя оценки A6) и A7) к разностям u(t,x) =
u(t,x) - f(*,a:), (р(х) = ^(ж) - ^(i), ^(z) = ^(х) - ^(х),
, ж) = f(t, x) — /(*, ж), мы получаем
\\u(t,x) -S(*,
l| w> -4Ci£-
Теорема 2 доказана.
Замечание 1. Равенства (9), (9') и оценки A0) - A1), а сле-
следовательно, и теоремы единственности и непрерывной зави-
зависимости справедливы и для уравнения E) с переменными
коэффициентами. Докажите.
§ 2. Метод разделения переменных (метод Фурье)
для уравнения колебания струны. Сходимость
рядов, определяющих классическое решение
Одним из широко распространенных методов решения
краевых задач для уравнений в частных производных явля-
является метод Фурье (метод разделения переменных). Мы раз-
разберем сначала этот метод на двух простейших примерах:
первой начально-краевой задаче для уравнения колебаний
струны и уравнения теплопроводности. Затем мы дадим обо-
обоснование этого метода для гиперболических уравнений 2-го
порядка вида E) из § 1.
Пусть требуется найти классическое решение уравнения
Гл. V, § 2. Метод разделения переменных ... 213
' ={x,<: x€@,0, 0<<<oo} U
с однородными граничными условиями
u(t,0) = u(t,0 = 0 B)
и неоднородными начальными условиями
и@,х) = ?(*), %\М = Ф(*>> 0<х</. C)
Сначала мы найдем нетривиальные, т.е. не равные то-
тождественно нулю, решения уравнения A) в виде произведе-
произведения двух функций:
u(t,x) = T(t)X(x), D)
где Г зависит только от £, а X зависит только от i; причем
эти решения u(t, х) будем искать такими, чтобы они удо-
удовлетворяли однородным граничным условиям B). Подставив
правую часть из D) вместо u(£, i) в уравнение A), получим
Х"Т = Т"Х, или после деления на XT:
х(х) -
Левая часть последнего равенства не зависит от £, а правая
не зависит от х, следовательно, каждая из величин X" /X,
Т"/Т не зависит ни от х, ни от £, т.е. постоянная.
Обозначим эту постоянную через —Л, т.е.
Х»{х) T»(t)
Х(х) T{t)
у позже мы докажем, что эта постоянная Л действительна).
Тогда из последнего соотношения получаем два обыкновен-
обыкновенных дифференциальных уравнения
Х"(х) + XX (х) = 0, (б)
Г"@ + XT(t) = 0 G)
214 Глава V. Основные начально-краевые задачи ...
для определения функций Х(х) и T(t).
Граничные условия B) дают:
u(t, 0) = Х@)Г@ = О,
u@,l) = X(l)T(t) = 0.
Отсюда следует, что функция Х(х) должна удовлетворять
граничным условиям
Х@) = 0, ХA) = 0, B')
так как иначе бы мы имели T(t) = 0, т.е. u(t,x) = 0, а мы
ищем нетривиальные решения. Таким образом, мы пришли
к простейшей, так называемой, задаче о собственных зна-
значениях: требуется найти значения А, называемые собствен-
собственными значениями, при которых существуют нетривиальные
решения задачи
X"(t) + XX (х) = 0, F)
Jf(O) = X(l) = 0, B')
называемые собственными функциями, а также надо найти
эти решения. Поставленная задача называется задачей
Штурма - Лиувилля. Здесь надо рассмотреть отдельно 3
случая:
1 А<0; 2)А = 0; 3) А > 0.
1. При А < 0 задача не имеет нетривиальных решений.
Действительно, общее решение уравнения (б) имеет вид:
Х(х) = C
и граничные условия дают:
т.е.
Гл. V, § 2. Метод разделения переменных ... 215
Ci=-C2,
d = о, с2 = о,
так как еа — е~а ф 0 при любом действительном а ф 0.
Таким образом, Х(х) = 0.
2. При Л = 0 также не существует ненулевых решений.
Действительно, в этом случае общее решение (б) имеет вид
Х(х) = Cix + Ci
и граничные условия дают Х@) = Сч = 0; ХA) = С\\ =
= 0 =^ С\ = 0. Таким образом, Х(х) = 0.
3. При Л > 0 общее решение уравнения содержит мни-
мнимые показатели и поэтому может быть записано в виде
Х(х) = С\ cos у\х + Сч sin у\х.
Чтобы удовлетворить граничному условию Х(О) = 0,
получаем С\ = 0. Тогда условие Х{1) = 0 примет вид
Сч sin \\f\ = 0 или sin l\/\ = 0 (так как если положим
С2 = 0, то получим опять тривиальное решение). Уравне-
Уравнение sin/VA = 0 выполняется тогда и только тогда, когда
/\/А = птг, т.е. Л = п{* , где п - любое целое ф 0 число (так
как мы предположили, что Л ф 0).
При отрицательных значениях п величина Л принимает
те же значения, что и при положительных. Поэтому все зна-
значения Л, при которых уравнение F) имеет нетривиальные
решения, удовлетворяющие краевым условиям B'), даются
формулой
Ап — — , п —1,2,3,...
Таким образом, мы нашли собственные значения поставлен-
поставленной задачи. Этим собственным значениям соответствуют
собственные функции
■л.п\х) = Сч sin —j-x.
216 Глава V. Основные начально-краевые задачи ...
Ввиду однородности уравнения F) собственные функции
определяются с точностью до постоянного множителя Сг,
который можно положить или равным единице, или выбрать
его так, чтобы собственная функция Хп(х) удовлетворяла
дополнительному условию, так называемому условию нор-
нормировки, или, как говорят, можно пронормировать собствен-
собственную функцию.
Удобно ввести нормировку так, чтобы
2n(x)dx = 1.
Для этого должно быть Сч = л/j.
Действительно,
1 /
I X2n(x)dx= ICl{smT^x
■«/L
2 I
* ' 2
откуда С2 = у у-
Чтобы в дальнейшем не писать нормирующий множитель,
будем считать, что Сч = 1.
Вернемся теперь к первоначально поставленной задаче
A) - C). Подставив в уравнение G) (для функции T(t)) най-
найденные нами значения Л, мы получим уравнение для опре-
определения T(i) в виде:
Г: + ^Тп = 0. G')
Очевидно, теперь T(t) зависит от номера п.
Общее решение этого уравнения имеет вид:
Гл. V, § 2. Метод разделения переменных ... 217
Tn(t) = Ап cos ^-t + Bn sin ™«,
где Ап и Вп - коэффициенты, подлежащие определению.
Все функции
un{t,x)=Xn{x)Tn(t) =
. П7Г П7Г . П7Г
= &т(—х)(Ап cos —< + i?n sm -у-*)
удовлетворяют уравнению A) и граничным условиям B)
при любых постоянных Ап и Вп. В силу линейности и одно
N
родности уравнения A) сумма частных решений Y2 un(t, x)
п=1
также будет удовлетворять уравнению и граничным усло-
условиям.
Попытаемся определить постоянные Ап и Вп таким об-
образом, чтобы бесконечный ряд
u(t,x) =
оо
= У(Ап cos — t + Вп sin —r-t) sm —
""' (8)
n=l
удовлетворял уравнению A), граничным условиям B) и на-
начальным условиям C). Начнем с начальных условий. Дол-
Должно быть, во-первых,
оо
и@, х) - ^2 Ап sin — а; = <р(х). (9)
п=1
Кроме того, если бы ряд (8) можно было дифференцировать
почленно, то должно было бы быть
о
ОП
218 Глава V. Основные начально-краевые задачи ...
Допустим, что функции <р(х) и ф(х) можно разложить в ра-
равномерно и абсолютно сходящиеся ряды по sin^f-x на от-
отрезке [О, I]. Из теории тригонометрических рядов мы знаем,
что это будет так, по крайней мере, в том случае, когда
<р(х) и ф(х) непрерывны вместе с первыми производными
и ¥?@) = (p(l) = 0, и ^>@) = фA) = 0, т.е. когда на концах
отрезка функции обращаются в ноль. Пусть эти условия вы-
выполнены. Таким образом, если tp(x) и ф{х) удовлетворяют
вышеприведенным условиям разложимости в ряд Фурье, то
П=1
. тгп 2 /" П7Га.а
>п sin Т"ж' где 'Рп = 1 ^'8Ш Т"
sin Т"ж' где
п=1
2 Г
п = 1 ^)sin ~f
и ряды для (р(х) и ф(х) абсолютно и равномерно сходятся.
Если сравнить эти ряды с формулами (9) и A0), и если
ряд (8) можно дифференцировать почленно по £, то очеви-
очевидно, что для выполнения начальных условий надо положить
Ап = <рп, Вп = ^фп- Тогда решение задачи A) - C) будет
представляться формулой
оо ,
u(t, х) = у (<pncos—t-\ фп sm -т-t) sm —ж. A1)
*—' ( П7Г J /
п—1
Если ряд A1) расходится, или функция, определяемая этим
рядом не является дифференцируемой, то он, конечно, не
может представлять классического решения нашего диффе-
дифференциального уравнения.
Таким образом, нам нужно знать условия при которых
ряд A1) сходится равномерно (чтобы решение было непре-
непрерывным), и условия, при которых его можно дифференциро-
дифференцировать два раза по t и два раза по ж, если мы хотим получить
классическое решение задачи (для этого нужно, чтобы ряды
Гл. V, § 2. Метод разделения переменных ... 219
после дифференцирования сходились равномерно). Для ра-
равномерной сходимости ряда A1) достаточно, чтобы мажо-
оо
рантный для него ряд JZ (lv»»| + l^n^l) сходился, а это
п=1
зависит от начальных функций <р(х) и ф(х), так как <рп и
фп являются их коэффициентами Фурье. Чтобы сходились
равномерно ряды, полученные из A1) двукратным диффе-
дифференцированием, надо, чтобы сходился мажорантный ряд
п=1
а чтобы удовлетворялись оба начальных условия C), надо,
чтобы сходился мажорантный ряд
n=l
Таким образом, наша задача свелась к доказательству схо-
сходимости рядов
оо
]Г^п"|у?„|, I/= 0,1,2;
п=1
оо
£V|^n|, U= -1,0,1.
п=1
Из курса математического анализа известна теорема о по-
порядке убывания коэффициентов Фурье периодической с пе-
периодом 21 функции F(x) в зависимости от ее гладкости:
если F(x) имеет производные до порядка &, причем
DkF(x) кусочно-непрерывна и
то для коэффициентов Фурье а„ и Ъп функции F(x) имеют
место оценки
220 Глава V. Основные начально-краевые задачи ...
а числовые ряды
сходятся при и = 0,1,..., к — 1.
Далее, чтобы разложить функцию /(ж), заданную только
на отрезке [0,1], в ряд по sin^as, нужно, чтобы указанные
выше требования были выполнены для функции F(x), полу-
получающейся из f(x) нечетным продолжением.
В частности, для непрерывности F(x) необходимо, чтобы
/@) = 0, так как в противном случае при нечетном про-
продолжении получится разрыв в точке х = 0; аналогично, в
точке х = / должно быть /(/) = 0, так как продолженная
функция должна быть непрерывна и периодична с пери-
периодом 21. Непрерывность первой производной (при х = 0,
х — I) продолженной функции F(x) получается автоматиче-
автоматически при нечетном продолжении, так как производная нечет-
нечетной функции четна. Таким образом, для непрерывности чет-
четных производных продолженной функции надо требовать,
чтобы /B")@) = /B")(/) = 0. Непрерывность нечетных про-
производных имеет место без дополнительных требований.
оо
Таким образом, для сходимости рядов ^2 п"\<рп\, и =
п=1
0,1,2, надо требовать, чтобы <р(х) имела две непрерывных
производных, а третью кусочно-непрерывную и, кроме того,
(р@) = (р{\) = 0; (р"@) = ip"{l) = 0.
оо
Для сходимости рядов ^2 п"|^>„|, и = —1,0,1, достаточно,
чтобы ф(х) была непрерывно дифференцируема и имела
кусочно-непрерывную вторую производную и
ф@) = фA) = 0.
Гл. V, § 2. Метод разделения переменных ... 221
При этих условиях на данные задачи (т.е. начальные
данные) ряд A1) будет классическим решением поставлен-
поставленной задачи. Все полученные условия достаточны для суще-
существования классического решения.
Таким образом, имеет место
Теорема. Бели у>(х) имеет две непрерывные производные
и третью - кусочно-непрерывную, а ф(х) имеет первую не-
непрерывную, а вторую - кусочно-непрерывную производную,
и кроме того,
v(o) = v@ = о, <Ло) = <А0 = о, v(o) = v(O = o,
то существует единственное решение краевой задачи A) -
C) из класса u(t,x) G C2(Q) П CX(Q), где
Q = {x,t: 0<х <l, 0 <t <T < oo},
и оно представляется рядом A1).
Замечание 1. Каждая из функций un(t,x) - членов ряда
A1):
un(t, x) = Xn(x)Tn(t) = sin -y-x (ipn cos -т-*+
l . . ПЖ \ _ . П7Г . П7Г
Н Фп sin —r-t J = Dn sin —r-x • sin -y-it + Г),
П7Г t / t t
описывает собственные колебания струны, закрепленной на
концах. При п = 1 струна издает основной (самый низкий)
тон. При колебаниях соответствующих большим п, струна
издает более высокие тоны, "обертоны".
Замечание 2. На практике часто бывает, что начальные
функции <р(х) и ф(х) разрывны или не являются достаточно
гладкими. Тогда полученный ряд A1) не будет классическим
решением. В этом случае можно использовать его сходимость
вместе с первыми производными в норме Li к так называе-
называемому обобщенному решению, что мы докажем ниже.
222 Глава V. Основные начально-краевые задачи ...
Решение, представляемое формулой A1), определяет сво-
свободные колебания струны (они обусловлены начальными воз-
возмущениями).
Теперь рассмотрим задачу о нахождении вынужденных
колебаний струны, жестко закрепленной на концах (краевые
условия B)), под действием внешней силы, т.е. рассмотрим
неоднородное уравнение струны
^=g+F(,,<) A2)
с граничными условиями B) и начальными условиями C).
Ввиду линейности задачи A2), B), C) можно ее искать в
виде суммы u(x,t) = v(x,t) + w(x,t), где v(x,t) - решение
задачи A) - C), и оно представляется рядом A1), a w(x,t)
есть решение уравнения A2) с граничными условиями B)
и однородными начальными условиями
Решение w(x,t) определяет вынужденные колебания струны
(эти колебания происходят из-за воздействия внешней силы
при отсутствии начальных возмущений).
Решение w(x, t) ищем в виде ряда по собственным фун-
функциям задачи F), B'), т.е. в виде
?*• A4)
Подставляя A4) в A2), мы получаем
п=1
Разложим F(x, t) на интервале @, /) в ряд Фурье по синусам
„(<) sin ^, A6)
n=l
Гл. V, § 2. Метод разделения переменных ... 223
тогда из A5), A6) получаем обыкновенное дифференциаль-
дифференциальное уравнение для нахождения Tn(t):
T№)+(™JTn(t) = Fn(t), A7)
где Fn(t) = U F(U) sin
о
Известным из теории обыкновенных дифференциальных
уравнений методом, находим решение неоднородного ура-
уравнения A7) с нулевыми начальными условиями
Гп@), ВД = 0 A8)
в виде
A9)
Подставляя A9) в A4), находим w(x,t).
Каким условиям должна удовлетворять F(x, t), чтобы ряд
A4) после подстановки в него A9) давал классическое ре-
решение задачи A2), B), A3)? Очевидно, должно выполняться
условие согласования F@,t) = F(l,t) = 0. Далее, если
F(x,t) имеет непрерывную производную щ^ и кусочно-
q3 e»
непрерывную Qfidt, тогда полученное решение будет клас-
классическим. Этот факт легко доказать, используя метод инте-
интегрирования по частям. Докажите.
224
Глава V. Основные начально-краевые задачи ...
§ 3. Начально-краевые задачи для параболического
уравнения второго порядка. Энергетическая
оценка. Теорема единственности И
непрерывной зависимости
Рассмотрим уравнение, описывающее распространение
тепла в неоднородной среде при наличии источников (сто-
(стоков) тепла:
du(t,x)
х><), A)
где р(х) > ро > О, q(x) > О, р(х) € С1(П), q{x) € С(П),
f(x,t) € C(Qt), с начальным условием
u(t,x) =<p(x), хеп B)
и однородными граничными условиями всех трех типов
u(t,x)
= 0
или
ди
дп
= 0,
или
ди
— + а(х)и
дп
на множестве
= 0
C')
C")
C'")
(x,t) € Qt = {х G п С И", 0 < t < Т < оо},
5 - боковая поверхность цилиндра Qt, u(t,x) G C2(Q) П
C^Q), где n - внешняя нормаль к 5, сг(х) > 0.
Краевые условия C'), C"), C'") можно записать одной
формулой
Гл. V, § 3. Начально-краевые задачи для парабол. ... 225
ди
а(х)и+Р(х)
дп
= 0,
C)
где при Р(х) = 0, а(х) ф 0 имеем C'), при а(х) = 0 , /3 ф 0
имеем C"), при /3(х) > /30 > 0, а(х) ф 0 имеем C'"):
ди а(х)
дп
= 0.
Пусть ^ = а(х), дп € С1
Лемма 1. Пусть <т(х) > 0, и(ж,<) - классическое решение
задачи A) - C). Тогда V* G [0, Т] имеем
f(x,r)u(x,T)dx)dr. D)
0 I?
Доказательство. Умножим уравнение A) на 1и и проин-
проинтегрируем по Qt при любом < > 0. Имеем
Qt
ди
Qt
1=1
ft
}dxdT + 2I[IЛ*»r)"(a;'
о n
Пользуясь теоремой Гаусса - Остроградского и граничными
условиями C), получаем
15 - В. Н. Масленникова
226 Глава V. Основные начально-краевые задачи ...
I u2(t,x)dx= I\>2(x)dx-
П, По
t
о п l=1
г г
-If 2«2(r, x)<r(x)p(x)dTdS + 2 I ( I f(x, r)u(x, r)dx) dr
OS ОП
(предпоследнее слагаемое справа равно нулю в задаче C') и
C")), откуда отбрасывая справа отрицательные слагаемые,
получаем утверждение леммы 1.
Следствие. Если f(t, х) = О, то W G [О, Т]
F)
Обозначим E(t) = |К*, x)\\L2{n) = (/ \u{t, x)\2dx) , E{t)
- тепловая энергия, это есть средняя температура тела в п в
момент времени t при / = 0 и однородных граничных усло-
условиях C). Неравенство F) означает, что тепловая энергия не
возрастает.
Лемма 2. В предположениях леммы A) V< G [О, Г] спра-
справедливо неравенство
t
J \\f(T,x)\\LAn)dT. G)
о
Доказательство. Продифференцируем равенство E) по t,
учитывая Ju2(t,x)dx = E2(t), получаем
п
Гл. V, § 3. Начально-краевые задачи для парабол. ... 227
2E(t)E'{t) = -2 [{52р(х)(о^-J + q(x)u2\dx-
-2 I u2(t,x)a(x)p(x)dS + 2 I f(x,t)u(x,t)dx,
an n
откуда
E(t)E'(t) < f f(x,t)u(x,t)dx <
сокращая на E(t) имеем
E'(t)<\\f(x,t)\\L2{n),
и интегрированием по t получаем утверждение леммы 2.
Теорема 1. Классическое решение начально-краевых за-
задач A) - C) единственно.
Доказательство. Пусть имеется 2 решения и\ и иг. Рас-
Рассмотрим разность u(t, х) — и\ — U2.
Для нее имеем
fu2(x,t)dx = 0 V*e[0,T],
п
и так как и G C(QT), то отсюда следует, что u(x,t) = 0 в
QT, т.е. ui = и2.
Теорема 1 доказана.
Теорема 2. Классическое решение задач A) - C) непре-
непрерывно зависит от начальных данных и правой части f(x,t)
в следующем смысле:
15*
228 Глава V. Основные начально-краевые задачи ...
пусть ||7-7||l2(Qt) < c»JI^-WIU,(i7) < e, тогда, если п
- решение с правой частью / и начальной функцией Тр, а п
- решение соответственно с / и ~<р, то Vtf £ [О, Г]
||п(*,а:) -t(*,a:)||L,(fl) < Се,
где е зависит только от Т.
Доказательство. По лемме 2, используя неравенство Коши
- Буняковского в интеграле по t, имеем
\\u(t,x) -it(t,x)\\Li{n) <
t
где С = 1 + у/Т.
Теорема 2 доказана.
§ 4. Метод разделения переменных для решения
первой начально-краевой задачи для
уравнения теплопроводности; сходимость
рядов, определяющих классическое решение
К решению задачи о распространении тепла в ограни-
ограниченном стержне также можно применить метод разделения
переменных, который подробно мы разобрали на уравнении
колебания струны.
Найдем решение уравнения теплопроводности
dt Эх2' ={0<x<l,0<t<T<oo} К ]
I]]
в классе u(x,t) G CI]](Qt) с начальным условием
Гл. V, § 4. Метод разделения переменных ... 229
и@,х) = <р(х) B)
и граничным условием
u(t,0) = u(t,l) =■ 0. C)
При применении метода разделения переменных получаем:
u(t,x) = T(t)X(x\ 1?1 = ^ = -Л,
откуда
X" + XX = 0, Г' + a2 XT = 0. D)
Таким образом, опять получаем задачу на собственные зна-
значения
которая нами уже рассматривалась выше.
Получаем
/717Г\2 . . 717Г
Хп = [ -j-) ; хп(х) =
Этим значениям Лп соответствует решение второго уравне-
уравнения из D):
Tn(t) = Спе
Таким образом, мы получили частные решения уравнения
теплопроводности с нулевыми граничными условиями в виде:
un(t, х) = Спе (^} • sin —х.
Чтобы удовлетворить начальному условию, составим ряд
f u,(«, x) = f) Спе-**^2*. sin ^-x. E)
230 Глава V. Основные начально-краевые задачи ...
Из начального условия определим коэффициенты Сп через
коэффициенты Фурье начальной функции ¥>(х). Имеем
w@, x) = ip(x) = 2^Cn sin — x,
n=l
т.е. Сп являются коэффициентами Фурье функции <р(х) при
разложении ее в ряд по синусам
F)
Для окончательного решения задачи надо доказать, что
ряд E) с Сп, определяемыми по формуле F), сходится ра-
равномерно вместе со второй производной по а; и первой про-
производной по t (чтобы ряд E) удовлетворял уравнению).
Если <р(х) имеет кусочно-непрерывную первую произво-
производную и удовлетворяет условиям у?@) = <рA) = 0, то ряд E)
абсолютно и равномерно сходится в Q = {t > 0, 0 < х < /},
т.е. определяет непрерывную функцию в Q.
Остается доказать, что полученный ряд можно диффе-
дифференцировать почленно, т.е. что он удовлетворяет уравнению
теплопроводности.
Докажем, что ряд E) при t > to > 0 можно диффе-
дифференцировать почленно по t и х любое число раз каково
бы ни было to > 0; при этом все полученные ряды бу-
будут сходится равномерно. Таким образом, свойства реше-
решений уравнения теплопроводности сильно отличаются от ре-
решений волнового уравнения. Это объясняется тем, что в
решение E) входит экспонента в отрицательной степени
оо
(при t > to > 0), поэтому мажорантный ряд £) ап =
п=1
2^ Mngexp{—a2[2jL) to} всегда сходится, что легко про-
п=1
веряется по признаку Даламбера:
Гл. V, § 5. Метод Фурье для уравнений с перем. ... 231
lim
n—»oo
an+1 = lim
(
,2
n
e i
= 0.
Таким образом, мы доказали теорему: если <р(х) € C(Q), <p'
- кусочно-непрерывна в Q, у>@) = (рA) = 0, то существует
единственное решение задачи
ди од2и
20/ i0
at ox1
u@, x) = у?(ж), u(t,0) = u(t,/) = 0
непрерывное в области Q и удовлетворяющее заданному
уравнению внутри Q. Это решение представляется рядом
>„е K i > a l ■ sin— x. G)
n=l
Решение G) является бесконечно дифференцируемой
функцией по t и х при t > 0.
§ 5. Метод Фурье для уравнений с переменными
коэффициентами. Предварительные
рассмотрения
Метод Фурье применим только к определенному классу
уравнений в частных производных, для которого, как го-
говорят, "разделяются переменные", хотя задача может быть
разрешима для значительно более широкого класса уравне-
уравнений.
Метод Фурье для уравнений с постоянными коэффи-
коэффициентами в простейших областях позволяет построить яв-
явное решение (как в рассмотренных нами выше примерах) в
виде бесконечного ряда. Этот ряд образуется из собствен-
собственных функций однородной задачи, которые для постоянных
232 Глава V. Основные начально-краевые задачи ...
коэффициентов и некоторых областей часто можно вычи-
вычислить в явном виде через тригонометрические или специ-
специальные функции. Можно рассматривать гиперболические и
параболические уравнения со многими пространственными
переменными и с переменными коэффициентами, но специ-
специального вида.
Рассмотрим гиперболическое уравнение
P(x)-q^- = div * (p(*)gradxu) - q(x)u(t, x) A)
в области Q = {x,t : x € O,t > 0} (где Q - область в ГО."),
с начальными условиями
и(*„х)
t=0
«=о
и граничным условием
= 0. C)
дп
Здесь, как выше, -4г означает дифференцирование по на-
д п
правлению внешней нормали п к поверхности S - боковой
поверхности цилиндра Q. Пусть дп - кусочно-гладкая по-
поверхность, р(х), q(x), р(х), а(х), /?(х) - достаточно гладкие
функции (например, р(х) € Cl{Q), a,fl,q,p € С(П)), и
пусть р(х) > ро > 0, р(х) > ро > 0, q(x) > 0, а(х) > 0,
E{х) > 0, а2 + Р2 > 0. Мы видели, что общий вид условий
C) содержит в себе три основные краевые задачи.
Будем искать решение поставленной задачи методом раз-
разделения переменных
u(t,x) = T(t)-v(x), i6i?cE",t>0.
Обозначив правую часть A) через — Lu, мы получаем
pvT" = —TLv; разделив на p(x)v(x)T(t), имеем
T"(t) _ Lv(x)
T{t) ~ P(x)v(x) ~ C°nSt -. "Л>
Гл. V, § 6. О линейных огран. и неогран, операторах ... 233
Таким образом, мы придем к следующим уравнениям для
определения v(x) и T(t):
1) Lv = Xpv, где Lv(x) = —div (p(z)Vu) + q(x)v(x) с
граничным условием
av
дп
an
= 0; D)
2) T" + XT = 0.
Задача D) называется задачей на собственные значения
для эллиптического уравнения. Та же задача на собственные
значения получится при решении начально-краевых задач
для параболического уравнения вида
где
Lu = -divxfp(x)Vxuj +q(x)u(t,x).
Решение задачи D) уже нельзя получить явно, но можно изу-
изучить свойства собственных функций и собственных значе-
значений и доказать их существование. В ближайших лекциях мы
и займемся этими вопросами. Для этого необходимо изучить
свойства самого оператора L в гильбертовом пространстве.
§ 6. О линейных ограниченных и неограниченных
операторах в гильбертовом пространстве
Остановимся на некоторых простейших фактах из тео-
теории операторов в гильбертовом пространстве Н. Из фун-
функционального анализа известно общее определение ограни-
ограниченного оператора А, определенного на некотором множе-
множестве (области определения) D(A) гильбертова пространства
ff, который сопоставляет каждому элементу и € D(A) неко-
некоторый элемент v € Я : v = Auf т.е. А : D(A) -+ Я. Если на
D{A) справедливо равенство А(Хщ + ци2) = ХАи\ + A
234 Глава V. Основные начально-краевые задачи ...
где Л, (/, - комплексные числа, то А называется линейным
оператором, при этом предполагается, что D(A) - линей-
линейное множество, плотное в Н. Если существует постоянная
С такая, что для всех и G D(A)
||Аи||<С||и||, A)
где норма берется в Н, то А называется ограниченным опе-
оператором на D(A). Из функционального анализа известно
также, что ограниченный оператор можно распространить
на все Н с сохранением неравенства A), при этом наимень-
наименьшая С, при которой выполняется A), называется нормой
оператора А, так что
\u\
Большой интерес представляют два класса ограниченных
операторов: самосопряженные и вполне непрерывные (ком-
(компактные).
Ограниченный оператор А называется самосопряжен-
самосопряженным, если (Au,v) = (u,Av) Vu,u € Н; (•,•) означает ска-
скалярное произведение в Н. Оператор А называется вполне
непрерывным (или компактным), если он любое ограничен-
ограниченное множество переводит в предкомпактное в Н множество,
т.е. его замыкание компактно.
В теории дифференциальных уравнений мы имеем дело
с неограниченными операторами, для которых не суще-
существует постоянной С, при которой выполняется неравенство
A). Покажем это на примере оператора А, заданного диф-
дифференциальным выражением j^ с областью определения
С°°[0,1]; в качестве Н возьмем L2(f2). Покажем, что этот
оператор неограничен.
Рассмотрим последовательность sin(n7rx), n = 1,2,3...;
определяя на ней оператор А, получаем Аип =
= -п2тг2
Имеем
Гл. V, § 6. О линейных огран. и неогран, операторах ... 235
1
ж 1 /л
||«п||я = ( / sin2 rnrxdxj =
о
1
— cos2n7rar , ч1/2 /1 sin2n7r\1/2
= I I dx) = ( ) -+
\J 2 ) \2 4птг / n-o
о
Но ||Аы„|| = (п7гJ||и„||, откуда следует, что
||Ли„||н . ч2
——f— = (п7г) —>• оо при п —► оо,
11«п||Я
т.е. А - неограниченный оператор: \\A\\ = sup ^Гм = °°-
г- T~\i А\ '' М
Так как неограниченный оператор определен не на всем
Н, и его, вообще говоря, нельзя доопределить на всем Н,
то при задании неограниченного оператора нужно обяза-
обязательно указывать область его определения. Так дифферен-
дифференциальную операцию j^ можно определить на С°°[0,1] и
на С°°[0,1]. Мы получим разные операторы. Обозначим их
соответственно А и А. Так как D(A) С -О(А), то опе-
оператор А называют расширением оператора А. Очевидно,
область определения дифференциального оператора можно
выбрать бесчисленным множеством способов, и каждый раз
мы придем к другому неограниченному оператору, вообще
говоря, с другими свойствами. Например, для оператора А
~ о
с D(A) = С°°[0,1] справедливо соотношение
= f
~vdx = (u,Av) Vu,veD(A). B)
Если выполнено B), то оператор А называется симметрич-
симметричным. Для оператора А с D(A) = С°°[0,1] соотношение B)
не имеет места, так как при интегрировании по частям, мы
получим граничные члены:
236 Глава V. Основные начально-краевые задачи ...
(Аи, v) = (и, Аи) + —V
ах
х=\
— и-
х=о
х=1
х=0
В теории неограниченных операторов выделяется важный
класс самосопряженных операторов, но изучение их свойств
для нужд уравнений в частных производных довольно тру-
трудная задача. Поясним эту мысль.
Так как неограниченные операторы определены не на
всем Н, то возникает задача замыкания оператора. Пусть
оператор А задан на плотном множестве D(A), лежащем в
Н (в случае дифференциального оператора в качестве плот-
плотного множества в Н можно взять непрерывно дифференци-
дифференцируемые функции с теми или иными граничными условиями).
Определение замкнутою оператора. Оператор А называ-
называется замкнутым, если из существования пределов
lim un = u, lim Aun = f Vun
n—юо n—»oo
следует, что и € D(A) и / = Аи, т.е. lim Aun = Аи.
п—»оо
Очевидно, ограниченный, т.е. непрерывный оператор
всегда замкнут. Действительно, линейный ограниченный
оператор А с плотной в Н областью определения D(A)
всегда можно доопределить по непрерывности на все Н.
Это можно сделать следующим способом. Рассмотрим про-
произвольный элемент v € Н \ D(A). Так как D(A) = Н, то
существует и* € D(A): ujt —* v в Н. Ввиду ограниченности
и линейности оператора А, имеем
\\Аик - Аит\\ = \\А(ик - ит)\\ < С\\щ - ит\\ -> О,
к, т —* оо.
Отсюда следует, что ЦЛи* — л4ит|| -+ 0, к,т —> оо, т.е.
- фундаментальна в Н. Но Н - полное пространство, по-
поэтому существует / € Н: Аи к —» /, к —> оо. Теперь положим
Av = f, т.е. ограниченный линейный оператор аамкнут.
Гл. V, § 6. О линейных огран. и неогран, операторах ... 237
Обратное неверно. Бели оператор А не замкнут, но для
различных последовательностей {и„}, {«„} G D(A) схо-
сходящихся к одному и тому же пределу, последовательности
{i4un}, {-4vn} не могут сходится к различным пределам, то
у оператора А имеются замкнутые расширения. Среди всех
расширений выделяется минимальное замкнутое расшире-
расширение, его обозначают через А_и называют замыканием опе-
оператора А. Чтобы получить А нужно присоединить к D{A)
все те элементы и € D{A) (где D{A) - замыкание области
определения оператора А, которая плотна в Н), которые
можно аппроксимировать элементами {ип} € D(A), сходя-
сходящимися к и(х), для которых {Аи„} сходится, и положить
Аи — lim Aun.
в—»оо
Определение сопряженного оператора для неограничен-
неограниченного оператора А. Пусть А - произвольный линейный опе-
оператор, область определения D(A) которого плотна в Н.
Пусть D(A*) — {v € Н : функционал (Au,v) ограни-
ограничен на D(A)}. По теореме Рисса Vu € D(A*) существует
единственный элемент w € Н : (Au,v) = (u,w). Положим
A*v = w. Таким образом, (Au,v) = (u, A*v).
Оператор А* называется сопряженным к оператору А
Оказывается оператор А* всегда замкнут, в том числе и для
незамкнутых А.
Определение самосопряженною неограниченною опера-
оператора. Оператор А называется самосопряженным, если он
совпадает со своим сопряженным. Другими словами, А яв-
является самосопряженным, если
1) сопряженный ему оператор А* имеет ту же область
определения D{A) и
2)(Au,v) = (u,Av), C)
т.е. выполнено условие симметрии.
Для операторов А, порожденных дифференциальными
выражениями, легко проверяется справедливость (или нес-
несправедливость) C) с помощью интегрирования по частям,
238 Глава V. Основные начально-краевые задачи ...
но весьма сложно бывает эффективно описать область D(A*)
и выяснить, совпадает ли она с D(A) или нет.
Этот вопрос сегодня полностью решен только для диф-
дифференциальных операторов, порожденных обыкновенными
дифференциальными выражениями.
Для уравнений в частных производных эту задачу ино-
иногда удается решить "обходным путем", с привлечением об-
обратных операторов, если они оказываются ограниченными,
так как для ограниченных операторов, определенных уже на
всем Н, самосопряженность есть следствие их симметрии.
В дальнейшем мы будем проводить исследования не в
пространствах Ск@), а в пространствах Соболева с обоб-
обобщенными производными, к изучению которых мы и перей-
перейдем. Бели идти прямым путем, то для получения, напри-
например, самосопряженного расширения оператора, заданного
дифференциальным выражением в частных производных с
плотной в Н областью определения, который должен быть
симметричным, нужно использовать процесс замыкания опе-
оператора. В этом случае опять нужно использовать понятие
обобщенной производной, но, как было отмечено выше, этот
путь довольно труден.
239
Глава VI. Обобщенные производные,
пространства Соболева,
обобщенные решения
дифференциальных уравнений
§ 1. Обобщенные решения дифференциальных
уравнений. Два способа введения обобщенного
решения
Если начальные данные, граничные условия и правые
части уравнений в частных производных являются непре-
непрерывными функциями со своими производными до опреде-
определенного порядка, то для рассмотренных нами уравнений мы
получили непрерывное вместе с нужными производными ре-
решение, такое решение мы назвали классическим. Однако,
многие физические и другие задачи приводят нас к началь-
начальным данным, граничным условиям и т.д., не являющимися
достаточно гладкими, и мы не можем утверждать, что полу-
получим решение задачи с достаточной гладкостью, чтобы оно
могло удовлетворять уравнению в обычном смысле. Другими
словами, если, например, начальные данные не являются
непрерывными и дифференцируемыми достаточное число
раз, то может не существовать и дифференцируемое реше-
решение соответствующей краевой задачи. Поэтому вводятся так
называемые обобщенные решения дифференциальных ура-
уравнений.
Теория обобщенных решений для уравнений в частных
производных была разработана С.Л. Соболевым в 30-х го-
годах.
Такие решения могут определяться двумя способами.
1-й способ: обобщенное решение определяется как пре-
предел последовательности классических решений.
2-й способ: состоит в замене дифференциального ура-
уравнения (и граничных условий) некоторым интегральным со-
соотношением.
240 Глава VI. Обобщенные производные, пространства ...
В качестве примера, когда в задаче нет непрерывно диф-
дифференцируемых решений, рассмотрим уравнение
?! - ®! (л\
dt дх к }
с начальным условием
и@,х) = <р(х). B)
Бели <р(х) непрерывно дифференцируемая функция на от-
отрезке а < х < Ъ, то решением задачи A), B) в области
п — {x,t : а < х +1 < b} является функция
u(t,x) = <p(x + t). C)
Действительно, имеем
Ъ-& Ф + *)„-Ф)-
Пусть теперь функция <р(х) на отрезке [а, Ь] непрерывна, но
не дифференцируема. Как же теперь определить решение
задачи A), B)? Можно поступить следующим образом. Из-
Известно, что такую функцию можно представить как предел
равномерно сходящейся на отрезке [а, Ь] последовательности
функций </?*(х), имеющих непрерывные производные. При
этом соответствующие решения u*(x, t) = tpk(x +1) уравне-
уравнения A) будут равномерно в п сходится к функции C). Это
дает основание функцию tp(x +1) также считать решением
уравнения A), но уже в обобщенном смысле.
Определение 1. Функция u(x), x € О С ГО", называется
обобщенным решением дифференциального уравнения в об-
области Q, если существует бесконечная последовательность
классических решений {и*(ж)} этого уравнения для сгла-
сглаженных данных задачи, сходящаяся к и(х) в той или иной
норме. В качестве нормы можно взять норму в С (О), т.е.
когда
sup
Гл. VI, § 1. Обобщенные решения диф. уравн. ... 241
и(х) — Uk(x) —* 0 при к —► оо,
или порму в Ь2{И), т.е. когда
[и(х) — Uk(x)]2dx —* 0 при к —* оо.
я
Очевидно, обобщенные решения, в смысле предела в Ьг,
могут быть даже разрывными. Пределы можно брать и в нор-
нормах других функциональных пространств.
Расширение класса решений той или иной краевой за-
задачи представляет интерес только в том случае, когда при
этом расширении сохраняется единственность решения. При
этом, вводя обобщенные решения, нужно особо определять,
как понимать краевые условия для обобщенных решений.
Для линейных эллиптических и параболических уравне-
уравнений с достаточно гладкими коэффициентами, граничными
условиями и гладкой границей дп области п введение ука-
указанным выше способом обобщенных решений не расширяет
класса обычных решений этих уравнений. Но если в этих
уравнениях коэффициенты и другие данные задачи не явля-
являются гладкими, расширение понятия решения существенно,
ибо классическое решение может и не существовать. Рассмо-
Рассмотрение же обобщенных решений естественно, так как обычно
сама начальная функция <р(х), например, в примере A),
B) нам бывает известна приближенно (устанавливается из
опыта). Поэтому соответствующая функция «(<, х) — <p(t+.i )
в нашем примере также является только некоторым прибли-
приближением к точному решению поставленной задачи. И нам со-
совершенно безразлично, является ли это приближение клас-
классическим или только обобщенным решением уравнения.
Важно, что оно мало отличается от истинного решения
в соответствующим образом определенной норме, если фун-
функция <р(х) мало отличается от истинного начального значе-
значения.
Другой способ введения обобщенных решений, также
принадлежащий С.Л. Соболеву, состоит в использовании
16 - В. Н. Масленникова
242 Глава VI. Обобщенные производные, пространства ...
интегральных тождеств, которые для классических решений
являются следствием рассматриваемых уравнений. Этот
2-ой способ получил наибольшее распространение, и в его
основе лежит определение обобщенной функции вообще.
Определение 2. Пусть задано дифференциальное уравне-
уравнение вида
Lu= ]Г aQ{x)Dau = /(ж), х € Я, D)
|а|<т
где
aa(x) е С°°(Я), /еЛЧЯ),
т.е. / - обобщенная функция из D1.
Обобщенным решением уравнения Lu = / в области Q
можно назвать такую обобщенную функцию u € D', что
€ D выполняется равенство:
E)
|a|<m
Бели функции и(х) и f(x) являются локально сумми-
суммируемыми, то функционалы в последнем равенстве можно
представить в виде соответствующих интегралов, т.е. вме-
вместо дифференциального уравнения можно рассмотреть не-
некоторое интегральное тождество, которое получается умно-
умножением D) на <р(х) и интегрированием по частям.
Но при каждом выше данном определении обобщенного
решения перед нами стоят две трудности:
1. При решении дифференциальных уравнений нужно
учитывать краевые условия. Вопрос состоит в том, как удо-
удовлетворить краевым и начальным условиям в случае обоб-
обобщенных решений. Дело в том, что если функция только ин-
интегрируема (по Лебегу) по n-мерной области, то она может
быть не определена на многообразиях меньшей размерно-
размерности.
Гл. VI, § 2. Обобщенные производные в смысле ... 243
2. При слишком широком понимании решения краевой
задачи может нарушаться теорема единственности.
Для того, чтобы в каждой конкретной задаче разобраться
в этих вопросах, С.Л. Соболевым было введено понятие
обобщенной производной для интегрируемой по Лебегу фун-
функции, в соответствии с этим понятием определяется и обоб-
обобщенное решение. Им же были введены новые функциональ-
функциональные пространства (вместо пространств типа С), которые
теперь принято называть пространствами Соболева. Выби-
Выбирая для решения каждой конкретной задачи правильным
образом соответствующее соболевское пространство, можно
дифференциальное уравнение заменить интегральным то-
тождеством, т.е. не требовать от решения слишком большой
гладкости, не вызванной существом дела. Причем при ре-
решении соответствующей задачи обосновываются пункты 1
и 2.
В линейных задачах обычно рассматривают банаховы
пространства, т.е. полные линейные нормированные про-
пространства. Кроме того, все функциональные пространства,
которые мы будем вводить и изучать, будут сепарабельными,
т.е. будут содержать в себе всюду плотное счетное множество
элементов.
В некоторых задачах рассматривают только частные слу-
случаи банаховых пространств - вещественные гильбертовы
пространства Я, которые характеризуются наличием ска-
скалярного произведения.
Чтобы разобраться во всех этих вопросах перейдем к
фундаментальному понятию современной математики - по-
понятию обобщенной производной.
§ 2, Обобщенные производные в смысле Соболева
и их основные свойства
Рассмотрим в Шп область п (ограниченную или неогра-
о
ничейную) и функцию <р(х) € C°°(S7), т.е. <р(х) € C°°(S2),
и имеющую компактный носитель, содержащийся в Q: для
244 Глава VI. Обобщенные производные, пространства ...
х € fi\К ч>(х) = О, где К - компакт в Q. Тогда по формуле
интегрирования по частям для гладкой и(х) имеем:
п п
Эта формула интегрирования по частям берется за основу
определения обобщенной производной. Пусть и(х) и Ui(x) -
обобщенные функции типа функции, т.е.
u(x),Ui(x) € Lij,
= {v(x) : V компакта К С i?, / |u(a;)|dx < с»}.
к
Определение 1. Если для данной и(х) € Litioc(fi) суще-
о
ствует u>i(x) € ii,ioc(^) такая, что У(р(х) € С°°(B) выпол-
выполняется равенство
J Ui(xMx)dx = (-1) j u(x)^-dx,
n n
то говорят, что и(х) имеет обобщенную производную на £1
в смысле Соболева -^ € Lijoc(Q) и полагают ври этом
du
Аналогичным образом можно определить обобщенную
производную любого порядка а, где a = ati...an - муль-
тииндекс.
Определеппе 1'. Функция ша(х) € L\}ioc{^) называется
обобщенной производной на Q порядка а от функции и(х) 6
О
)> если Vy> € С °°(Л) выполняется тождество
Гл. VI, § 2. Обобщенные производные в смысле ... 245
Ju>a(x)<p(x)dx = (-l)M JuDa<pdx; A)
n n
при этом полагают wa(x) = —^—- — = Dau.
OX j ...0Xn
Очевидно, введенное понятие обобщенной производной
есть расширение понятия классической производной.
Действительно, имеет место
Лемма 1. Пусть область Q е ГО." и Dau(x) € С(п) есть
обычная производная, определенная в каждой точке области
Q. Тогда Dau является обобщенной производной от и(х) по-
порядка а на п.
Доказательство следует из интегрального тождества A),
которое получается интегрированием по частям.
Рассмотрим пример. Пусть п = (—1,1) С И1, п = 1,
и{х) = |х|. В точке х = 0 обычной производной из C(Q) не
существует, но обобщенная производная в смысле Соболева
существует на всем интервале (—1,1) и u'x(x) = sign ж. Дей-
Действительно, воспользуемся определением обобщенной произ-
производной. Имеем Vip(x) € С °°(-1,1)
1 0 1
/ \x\ip'(x)dx = ~ I xip'(x)dx + / x<p'(x)dx = —х<р(х)
о
-1
-1 -1
о
+ / <p(x)dx + х<р(х) — I ip(x)dx = — I sign x <p(x)dx,
-1 0 -1
т.е. |х|' = sign х в смысле Соболева.
Лемма 2. Обобщенная производная от и(х) определяется
образом с точностью до эквивалентности.
246 Глава VI. Обобщенные производные, пространства ...
Доказательство. Пусть область п С Ш/\ а/Ои фун-
функции и(х), vi(x), v2(x) € L\joc(Q), и пусть иг = Dau, v2 =
Dau на Q. Докажем, что v\ эквивалентно v2 на Q. Имеем
I'vx<pdx = (-l)|or| f uDaipdx,
n n
Iv2<pdx = (-1)H fuDa<pdx.
n n
Вычитая одно равенство из другого, получаем
I
— v2)ipdx — О
n
Согласно основной лемме вариационного исчисления v\ =
v2 на Q с точностью до множества меры нуль, т.е. v\ экви-
эквивалентна v2, что и требовалось доказать.
Обобщенные производные сохраняют некоторые свойства
классических производных.
Основные свойства обобщенных производных, следую-
следующие из их определения:
1) если «1 и «2 имеют обобщенную производную в J2, то
сумма с\и\ + сг«2 также имеет обобщенную производную в
/2, при этом
Da(c\U\ + с2и2) = c\Dau\ + c2Dau2,
где ci, C2 - постоянные;
2) если v есть обобщенная производная вида v = Dlu,
а а; есть обобщенная производная вида и> = Dav в 1?, то и;
есть обобщенная производная от и вида и> = Da+lu;
3) из определения обобщенной производной
Гл. VI, § 2. Обобщенные производные в смысле ... 247
видно, что она не зависит от порядка дифференцирования.
Однако, обобщенные производные сохраняют не все свой-
свойства классических.
1) Например, при дифференцировании произведения
нужно потребовать, например, чтобы ttfc, -£*■ (к = 1,2)
принадлежали L2(f2), или в общем случае: если «i, |Ц- €
LPtioc(f2), то необходимо, чтобы «2, ^. € Lpiytoc(S2), где
1/р + 1/р' = 1, что следует из неравенства Гельдера. Тогда
существует обобщенная производная дх и
д{щ • и2) _ ди2 дих _
2) Далее, из существования у и(х) обобщенной про-
производной вида „ &1Э ап f вообще говоря, не следует су-
oXj ...axn
ществование производных более низкого порядка. Условия,
при которых этот факт имеет место даются "теоремами
вложения" Соболева. Приведем пример функции, имеющей
обобщенную производную второго порядка и не имеющей
обобщенной производной первого порядка. Пусть «(х, у) =
и\(х) + «г(у), где непрерывные функции и*(я), к = 1,2,
не имеют обобщенной производной. Тогда, очевидно, «(ж, у)
не имеет обобщенной производной первого порядка. Однако,
и(х,у) имеет вторую обобщенную производную вида
9 ax a ' котоРая равна нулю.
о
Докажем это. Пусть у>(х, у) € С°°(^)- Имеем
п
п п
248 Глава VI. Обобщенные производные, пространства ...
Рассмотрим отдельно каждый интеграл справа как повтор-
повторный:
П а ■ф1{
b
a
Аналогично,
d
f d<2<f> ft
J dxoy J \
d
= / «2(У):
с
ду
с
Следовательно,
/д<р [
u{x,y)-j—r-dxdy = 0 = / 0 • tpdxdy
п п
Таким образом, производная -§щ- существует и равна нулю.
3) Другим важным отличием обобщенных производных
от классических является то, что обобщенные производные
определяются с точностью до множества меры нуль и имеют
глобальный, иначе говоря, интегральный характер. Это ви-
видно из самого определения обобщенной производной. Обоб-
Обобщенная производная является элементом функционального
пространства L\tioc (или Lp при р > 1 в более общем слу-
случае).
Гл. VI, § 2. Обобщенные производные в смысле ... 249
Отметим, однако, что функция может иметь классиче-
классическую производную почти всюду в области, и не иметь обоб-
обобщенной производной в этой области; т.е. определение обоб-
обобщенной производной не совпадает с определением произво-
производной почти всюду.
Поясним, что значит обобщенная производная имеет гло-
глобальный, а не локальный характер, т.е. зависит от области.
Пусть и(х) имеет обобщенную производную Dau в об-
области Q; тогда, очевидно, она имеет ее и в любой п' С Q.
Однако, если область п разбита на три части: две непере-
непересекающиеся подобласти Q\ и Qi и множество Г, разделяю-
разделяющее их, то из 3 обобщенной производной Dau в каждой п{
(i = 1,2), вообще говоря, не следует существование у и(х)
обобщенной производной Da во всей области п. Действи-
Действительно, рассмотрим следующий пример: пусть и{х) опреде-
определена для х € И1 и бесконечно дифференцируема всюду в
И1, кроме точки х = 0, в которой и(х) имеет разрыв первого
рода. Такая функция не имеет в И1 обобщенной произво-
производной даже первого порядка, несмотря на то, что она имеет
классическую производную почти всюду, т.е. везде, кроме
точки х = 0. На любом же интервале, не содержащем точки
х = 0, т.е. ъ п\ =■ (—оо, 0) и в пг — @, оо), рассматриваемая
функция имеет обобщенную производную любого порядка.
3 качестве и(х) можно рассмотреть ступенчатую функцию
250 Глава VI. Обобщенные производные, пространства ...
u(*)=< ' - ' B)
\0, x < 0.
В Q\ = (—oo,0) и в J?2 = @»°°) "С1) имеет обобщенную
производную равную нулю, но на (—оо, +оо) обобщенная
производная не существует. Посмотрим, чему равна произ-
производная ступенчатой функции B).
Эта функция определяет линейный функционал
оо
(u(x),<p(xj) = J<p(x)dx Уф) €
В соответствии с определением обобщенной производной,
имеем
оо
(«', V) = -(«, ?•) = -/ <p'(x)dx = „@),
о
так как <р(х) имеет компактный носитель. Но
Таким образом, «'(ж) = ^(х), т.е. производная ступенчатой
функции не является локально интегрируемой функцией, а
является функцией обобщенной. Однако, для существова-
существований обобщенной производной нет необходимости требовать,
чтобы функция и(х) была непрерывной. Действительно, так
как обобщенная производная от и(х) принадлежит L\joc{Q)
(или Lp(f2)), то функцию и(х), имеющую какую-либо обоб-
обобщенную производную в Q, можно произвольно изменить на
множестве меры нуль. С другой стороны, можно привести
примеры функций, имеющих обобщенные производные, ко-
которые никаким переопределением их на множестве меры
нуль не сделать непрерывными в п. Например, функция
двух переменных и(х\,хъ) = Дг, 0 < е < 1, в круге
Гл. VI, § 2. Обобщенные производные в смысле ... 251
К = {х : \х\ = yjx\ + х\ < R) имеет обобщенные про-
производные первого порядка, равные Jjr = —£ \x\i+* > * — 1>2,
что можно доказать интегрированием по частям:
причем интеграл справа сходится, т.е. J-*7 €. L\(K)t но
функцию тЛг нельзя сделать непрерывной, и даже ограни-
ограниченной, с помощью ее переопределения на множестве меры
нуль.
На вопрос о том, какую гладкость в классическом смысле
имеют функции и(х), имеющие те или иные обобщенные
производные, интегрируемые по Q с теми или иными сте-
степенями (принадлежащими Lp при р > 1), если их переопре-
переопределять на множестве меры нуль, отвечают теоремы вложе-
вложения; ответ зависит от размерности пространства п, порядка
обобщенных производных и степеней их интегрируемости.
Замечания
1. Можно дать другое определение обобщенной произво-
производной по Соболеву, эквивалентное определению 1.
Определение 2. Пусть область Q С Ш.п, a = t*i...an,
а ф 0, u(x),wa(x) G L\ti0C(Q). Функцию wa(x) назовем
обобщенной производной порядка а от и(х) на Q, если
Vu* G С°°(П), uk-*uB Lx,loc(Q), Dauk чУ„в L{Q)
Напомним, что ик —* v ъ L\tioc(i2)
lim llufc - и|к,(Ю — 0 \/компакта К С Q.
fc—<-оо
Эквивалентность этих двух определений можно доказать
путем сглаживания (усреднения) функций из Lp(i2). Опре-
Определение средних функций будет дано позже.
252
Глава VI. Обобщенные производные, пространства ...
Из определения 2 следует, что операция обобщенного
дифференцирования по Соболеву является минимальным
замкнутым расширением в смысле L\joc(fl) оберации обыч-
обычного дифференцирования функций, заданных на C°°(Q), о
чем шла речь в § 6 главы V.
Классические
производные
2. В теории обобщенных функций дается определение
производной как функционала: пусть Ця) € D\Q), тогда
Чу € D(Q) = С°°{П) имеем
(Рв«^) = (-1)И(и,д^), C)
где Dau - функционал.
Бели и(л), Dau(x) - регулярные обобщенные функции,
т.е. и(ж), Dau(x) 6 I-i,/ос(/?), то функционалы в C) можно
Гл. VI, § 3. Пространство Соболева W%(f2) и его полнота 253
реализовать в виде интегралов, тогда получим определение
обобщенной производной по Соболеву
/ Dau(x)ipdx = (-1)|а| / u(x)Da<pdx Чуй С
п п
Таким образом, обобщенная производная по Соболеву от
и(х) совпадает с производной в смысле обобщенных фун-
функций в предположении, что и(х) и Dau(x) являются ло-
локально интегрируемыми функциями. Мы имеем вложение
(см. рисунок).
§ 3. Пространство Соболева W^i^) и его полнота
Определение. Рассмотрим множество всех функций и(х),
х € Q С IRn, для которых выполнены условия:
1) и(х) € Ь2{П)\
2) Vi = l,2,...,n Зр-
OXi
в смысле Соболева, причем -^ € Ii2(f2) (i = 1,2, ...,n).
Введем, в этом множестве норму
A)
П t=1
Из 1) и 2) следует, что для элементов этого множества норма
A) всегда конечна. Это множество с нормой A) называется
пространством W^ift) в обозначениях Соболева, и норма в
нем записывается со значком внизу
254 Глава VI. Обобщенные производные, пространства ...
Замечание. Докажем, что Ь2{п) С bijjoc(/2). Пусть и{х) €
Ь2{0). Тогда для любого компакта К С. Q § \u(x)\dx <
к
оо. Действительно, для компакта К С п имеем, согласно
неравенству Коши - Буняковского:
J
, Г ч 1/2 / Г ч1/2
\u{x)\dx < I I 1 dx) • I I \u(x)\ dx) < oo,
к к к
так как J dx = mesK < оо в силу ограниченности К и
я-
J |«(x)|2dx < оо, так как и(х) € Li2(Q), К С Q; следова-
следовательно, u(z) € Liti
В W^(/2) можно задать гильбертову структуру, т.е. ска-
скалярное произведение: любым двум функциям «,«6 ]^)
сопоставляем число:
It
я
Тогда W2{0) становится вещественным гильбертовым про-
пространством, очевидно, B) обладает всеми свойствами ска-
скалярного произведения:
1) {и, v} = {у, и) (симметрия);
2) {u,v1 + v2) = {u,vi} + {«,Уг} (дистрибутивность);
3) {Л«,у} = Л{«,у}, где Л - вещественное число;
4) {«, и} > 0, причем {и, и} = 0 только при и = 0 (почти
всюду).
Возникает вопрос: будет ли W2(Q) полным простран-
пространством?
Теорема. Пространство W2 {Q) - полное метрическое про-
пространство относительно нормы A).
Доказательство. Рассмотрим последовательность {«*},
) € W^(i2) и предположим, что она фундаментальна
Гл. VI, § 3. Пространство Соболева W%({2) и его полнота 255
в W^(H), т.е. \\ик — ui\\wi(n) -» 0 при к,1 -+ оо. Тогда из
определения нормы A) следует, что
))Jdx-*O,
я я
при fc, / —► оо Vi = 1, п.
Но L2(f2) - полное пространство. Поэтому 3 функции
и(х) и a>i(x), (г = 1,п) такие, что и(х), а>Дх) € L-iifT) и при
этом
I (ик(х) - u(xj) dx^O, fc-юо; C)
0, Jk^oo,Vt = M. D)
я
Докажем, что шг(х) = ^- в смысле Соболева. Так как ик(х)
имеет обобщенную производную |^- € 1*2(A) С ii,jOc (в
силу того, что ик{х) € WaH^)), то Vy> € С
я я
Но из сильной сходимости в Ьг(О) (по норме), т.е. из фор-
формул C) и D) следует слабая сходимость последовательно-
последовательностей {ик}и {%%}, т.е.
im / -^—<p(x)dx = / a>i(x)y(x)rfx, F)
-с» J 0Zi ./
П Я
lim I uk(x)^-dx= I u(x)^-dx. G)
:—>oo J 0Xj J OXi
к
Я П
256 Глава VI. Обобщенные производные, пространства ...
Переходя в E) к пределу при fc-юос использованием F),
G), получаем
п п
т.е. Ш{ = J^ в смысле Соболева. Отсюда следует, что и(х) €
W^fi), так как и(х) £ 1*2@), Wi(x) € £2@). Если теперь
в D) подставить а>,(х) = -^ и сложить формулы C), D), то
мы получим
Это и доказывает полноту пространства
§ 4. Пространство Соболева p
По аналогии с пространством W\ (О) можно ввести про-
пространство Wj,(i2). Рассмотрим множество всех функций
и(х) €. Lp(f2), 1 < р < оо, имеющих все обобщенные про-
производные до целого порядка / включительно, интегрируемые
со степенью р. Мы превратим это множество в нормирован-
нормированное пространство, если на этом множестве введем норму по
формуле
где ^2 есть суммирование всех возможных произво-
дных целого порядка \а\. Рассматриваемое множество с нор-
нормой A) называется пространством Соболева W^(Q).
Пространство Wj,(i2) является банаховым. Его полнота
доказывается так же, как полнота W\
Гл. VI, § 5. Пространство Соболева w\(n) и ••• 257
Пространство W^{Q) при р = 2 является гильбертовым
со скалярным произведением
- /
/
В этом случае для W\{^i) иногда используется обозначение
Hl{Q). При / = 1 получаем введенное нами выше простран-
пространство W\{Q\ т.е. Н\П).
Пространства Соболева с различными р > 1 и I > 1
можно вводить как замыкание множества C°°(i2) в норме
A). Функции и(х), принадлежащие этому замыканию, опре-
определяют пространство Wp(i2). Очевидно, WL шире, чем Wj,.
Однако, для достаточно широкого класса областей П, с "не
очень" плохой границей, Wlp(Q) совпадает с Wp{Q). Это
имеет место, например, для так называемых звездных об-
областей и конечной суммы звездных областей.
Определение. Область Q называется областью звездного
типа, если 3 внутренняя точка хо € B, что всякий радиус-
вектор, выходящий из хо, пересекает границу области только
в одной точке; говорят также, что такая область звездна от-
относительно точки хо. Если область звездна относительно ка-
каждой точки шара Вщ. С Q, то область звездна относительно
шара
§ 5. Пространство Соболева W\(ft) и его
эквивалентная нормировка. Неравенство
Фридрихса
Определение. Замыкание множества С°°(^) в норме
W^J?) называется пространством
17 - В. Н. Масленникова
258 Глава VI. Обобщенные производные, пространства ...
Заметим, что здесь "нолик наверху" уже не будет обо-
о
значать финитность функций, входящих в W\{^)i a ПРИ
о
замыкании С°°(&) в норме W£(fi) будут удерживаться "ну-
"нулевые граничные условия" для и(х) "в среднем", т.е. в Li,
что будет нами ниже доказано.
о
Пространство W\{fi) является собственным подпрост-
подпространством пространства W\(C1). Из его определения следует,
о
что для любой и(х) € W\{&) 3 последовательность фун-
кций {ffc(x)}, vk € С°°(&) таких, что
п '-1
при к —» оо.
Опишем основные свойства пространства \()
Пусть Q - ограниченная область в Ш.п. Покажем, что
о
в W\{&) можно ввести новое скалярное произведение по
формуле
у
порождающее норму, эквивалентную исходной норме для
Замечание. Напомню, что нормы ||u||i и ||и||2 называются
эквивалентными в некотором линейном нормированном про-
пространстве X, если для всех и £ X существуют постоянные
С\,С2 > 0, для которых выполняются неравенства
Очевидно, что последовательность {«*}, сходящаяся в
одной норме сходится и в другой, эквивалентной ей. При
Гл. VI, § 5. Пространство Соболева w\(Л) и ••• 259
решении вопросов полноты, сепарабельности, компактности
и т.д. безразлично, какую из эквивалентных норм рассма-
рассматривать. Дистрибутивный оператор, ограниченных в одной
норме, является ограниченным и относительно другой эк-
эквивалентной нормы. При этом норма ограниченного опера-
оператора, вообще говоря, меняется при переходе к эквивалентной
нормировке пространства, но остается конечной.
Для доказательства того, что скалярное произведение A)
порождает норму в W\{^)i эквивалентную исходной для
W^ifl), покажем, что для любой и(х) € W\№) справедливо
так называемое неравенство Фридрихса. Именно, докажем
следующую теорему.
Теорема Фрндрнхса. Пусть Q - ограниченная область в
Ш/\ Тогда ЗС = С(П) > 0, что для любой функции и €
справедливо неравенство
2(^Jdx, B)
1
или, что эквивалентно,
п п t=1
где постоянные С(B) и C\(Q) не зависят от и(х), а опреде-
определяются только размерами области Q.
Доказательство. Неравенство B) достаточно доказать
о
лишь для и(х) € С °°(^), так как тогда оно получается "за-
О
мыканием в норме W^ifi) " для любой и € wl(&)-
Поясним, что такое "замыкание в норме W\(J2)". Пусть
О
и(х) какой-нибудь элемент из W\(Q). Аппроксимируем его
о
в норме Wl(u) функциями {vu) {k = 1,2,...) из С
Пусть B) доказано для у*. Тогда, взяв B) для г*:
17»
260
Глава VI. Обобщенные производные, пространства
п
п
i==1
C)
перейдем к пределу в нем по к при к —» оо в норме W%{)
так как пределы в левой и правой частях C) существуют, то
О
получим B) для и € W\(Q). Эта процедура и называется
"замыканием в норме W\ (■#)"•
о
Итак, пусть rfc(x) € C°°(f2). Так как носитель 1>*(я)
принадлежит Л, то ffc(x) можно продолжить нулем вне Q и
рассмотреть вместо Q параллелепипед 77, в который заклю-
заключена область Q. Не ограничивая общности (перенеся начало
координат) можно считать, что
Я = {х : 0 < х, < dj.
Пусть d\ наименьшее из всех его ребер.
о
Для
имеем
vk(xi,x2,...,xn)= /
J
Гл. VI, § 5. Пространство Соболева W\№) и ... 261
Возведем обе части этого равенства в квадрат и проинте-
проинтегрируем по Я:
fv\dX = jdXxj{f
2, ,
dX
дуг d
Я О Я' О
где
П' = {х' : 0< Xi < di, г = 2,..., п}.
Одномерный интеграл в правой части последнего равенства
оценим с помощью неравенства Конга - Буняковского. По-
Получим
0 0
Поэтому
Я 0 Я'
di f / dvk \ 2
= — I I ) dx.
2 J \dxx)
n
Или, так как и* = 0 вне 1?, то
Л Л
Пусть Vk(x) —* и(х) в норме Wl{0). Тогда Vk -* u(x) в
Ьг(п) и |^- —» J-jy в L2(S2). Переходя в D) к пределу при
к —* оо, получим неравенство Фридрихса B) или
262 Глава VI. Обобщенные производные, пространства ...
f II ди ||
Теорема доказана.
Замечание. Неравенство Фридрихса справедливо для об-
областей "конечной толщины", т.е. для областей, ограничен-
ограниченных в одном из направлений. Действительно, пусть суще-
существует ось 0£ такая, что проекция Q на 0£ ограничена. Ми-
Минимальный из диаметров этих проекций на разные напра-
направления есть "толщина" области Q. Пусть толщина равна d и
п
пусть d реализуется на оси 0£. Тогда §| = ]С ~§^ cos(£j xk)
и
d ^\
n n k~1
где Сг зависит только от п (см. [1]).
Итак, нами доказано, что в W\(ft) в случае ограничен-
ограниченной области Q вместо нормы
1/2
Л
можно рассматривать эквивалентную ей другую норму вида
п l=1
Так как пространства W\{Q) и W^ift) являются гиль-
бертовыми, то иногда их записывают Н 1(^) и Hl(Q) соот-
соответственно. Опишем, каким путем можно получать аппрок-
аппроксимацию функций из Lp гладкими функциями. Этой цели
Гл. VI, § 6. Средние функции и их свойства ... 263
служат так называемые "средние функции". Они дают ме-
метод сглаживания функций из Lp.
§ 6. Средние функции и их свойства: бесконечная
дифференцируемость, сходимость в
норме Lp, перестановочность операций
дифференцирования и усреднения. Ядро
усреднения и его свойства
Для того чтобы определить усреднение (сглаживание)
функций из LP(Q), введем в рассмотрение функцию, кото-
которую назовем ядром усреднения. Для этого рассмотрим нео-
неотрицательную функцию и)(х), обладающую свойствами:
2) suppers') С Вх = {я € IRn : |as| < 1};
3) / u)(x)dx = 1.
В качестве примера такой функции можно взять
*) = {
I 0, |х|>1,
где ае = f f exp{i i_1 }dxj . Функция и)(х), задавае-
Vl
мая формулой A), удовлетворяет условиям 1) - 3). Действи-
Действительно, условия 2) и 3) очевидны. Проверим, что она явля-
является бесконечно дифференцируемой и обращается в нуль
на сфере \х\ = 1 вместе со своими производными любого
порядка. В самом деле,
где Va(x) есть многочлен от х. Тогда, очевидно, мы имеем
=0 Va = ах...осп.
264
Глава VI. Обобщенные производные, пространства ...
Ядром усреднения с радиусом усреднения h > О назовем
функцию
B)
Из свойств 1) - 3) функции и>(ж), вытекают свойства ядра
усреднения:
2) зирри;Л(а:) С Bh(x) = {я € IRn : |*| < Л};
3) / uh(x)dx = 1.
шп
(Последнее свойство доказывается заменой f = у:
J u)h(x)dx = J u)(y)dy = 1.) При п = 1 график u>h{x)
к.» к."
имеет вид:
А Ч(х)
Определение среднеМ функции. Пусть <р С Lp(Q),
1 < р < оо. Продолжим ее нулем вне Q. Для продолжен-
продолженной функции оставим прежнее обозначение. Средней фун-
функцией для <р(х) называется <рн(х), определяемая как свертка
с ядром усреднения ии(х), по формуле
Гл. VI, § 6. Средние функции и их свойства ...
= V ♦
265
C)
где 5д(а:) - шар радиуса /i с центром в точке х.
Приведем пример. Пусть п = 1 и рассмотрим разрывную
функцию
= / Uh(x - y)ip(y)dy =
ж-
= / u)h{x - y)y>(y)dy,
0, |х| > 1.
Определим для нее усредненную (сглаженную) функцию по
формуле C). Ее график изображен ниже на рисунке.
Л Фа (*)
Л-h -I A+h О 1-Л 1 1+Л х
266 Глава VI. Обобщенные производные, пространства ...
Для гладкой tpн (х) имеем:
1) <ри(х) = 0, \х\ > 1 + Л, так как в этом случае
suppy>fc(a;)n£fc(:r) = 0;
2) <ри(х) = 1, если \х\ < 1 — h, таккак тогда
Bh(x) = Bfc(ar), и мы имеем после замены ^r^ = z
x+h +1
= Ju(z)dz =
x-h -1
Свойства средних функций.
1. Так как подынтегральная функция в C) равна нулю
вне шара Вн(х), то tph(x) = 0, если dist {x, ft} > h. Но если
<£>(■)") € C{ft), <р(х) = 0 на dft, то, вообще говоря, ул(ж) ф О
на dft: нулевое граничное значение у функции ip{x) при ее
усреднении не удерживается.
2. Функции <ри(х) непрерывны и имеют непрерывные
производные любого порядка в IRn, т.е. tph(x) € C°°(IRn).
Докажем непрерывность tph(x). Пусть х + Лж = xi,...,
Xi + Axi,..., хп, Vi = 1,..., п. Используя неравенство Гельде-
ядра усреднения, получаем:
i,, , ,, у р
ра: - + - = 1,1<р, q < оо и. равномерную непрерывность
<ph{x + Ах) - tph(x)\ < (у \y(y)\pdy) х
х П \шн(х + Ах-у)- uh(x - у)\Чу) <
< eCh\\tp\\Lp(n) < е,, где Ch -
так как <р(х) Е Lp(ft) и, следовательно, (рн{х) непрерывная
функция. При р = 1 доказательство очевидно. Непреры-
Непрерывность производных доказывается аналогично, и произво-
производные средних функций вычисляются дифференцированием
под знаком интеграла ядра усреднения в формуле C).
3. Последовательность средних функций (рн(х) сходится
к tp(х) при h —► 0 в норме Lp, т.е. Wtp € Lp(ft), I < р < оо,
Гл. VI, § 6. Средние функции и их свойства ... 267
\\v>h - <р\\ь,(П)-> 0 при h -► О,
при этом для любой (р(х) € LP{Q) и при любом h > О вы-
выполняется неравенство:
1Ы1Мл) < 1И1мп). D)
Докажем сначала неравенство D). Опять возьмем два дей-
действительных числа р и q таких, что 1/р + 1/q = 1 и пусть
1 < р, q < oo. Запишем среднюю функцию для ip(x) в виде:
В* (г)
и применим неравенство Гельдера. Получим
= ( f wfc(a:-
Возведем обе части полученного неравенства в степень р и
проинтегрируем по области Q. Получим
Так как вне Bh(x) ядро w^ равно нулю, а вне Q функция
>р(у) равна нулю, то во внутреннем интеграле область Вн(х)
можно заменить на Q и переставить порядок интегрирова-
интегрирования. Пользуясь теоремой Фубини, получаем
-y)dx)dy.
п п
268 Глава VI. Обобщенные производные, пространства ...
Так как внутренний интеграл равен 1, то мы получаем ис-
искомую оценку D), возведя в степень 1/р:
\\Vh\\ь,(П) <
При р = 1 оценка D) очевидна (она получается без исполь-
использования неравенства Гельдера). Доказательство сходимости
V?fc(:r) к <р(х) при h —» 0 в норме Lp(fi) основывается на
известном из функционального анализа свойстве непреры-
непрерывности в среднем функций из LP{Q), в силу которого для
1 <р< оо
приE->0. E)
Используя свойство 3) ядра усреднения, имеем
4>h(x) - <р(х) = / uh(x - у)[<р(у) - tp(x)]dy,
Вн(х)
откуда, для 1 < р < оо, используя неравенство Гельдера
(таким же путем, как и при доказательстве неравенства D)),
получаем
/ |^fc(s) - tp(x)\pdx <
п
р
t dx <
Вн(х)
Гл. VI, § 6. Средние функции и их свойства ... 269
<J(J uh{x-
П Bh(x)
x( / Uh(x-y)\tp(y)-<p(x)\pdy)dx =
Bh{x)
= /( / "h(x -y)\tp(y)-tp(x)\pdy)dx =
П \x-y\<h
= / ujh(z)(l1Ф + z) - y{x)\pdx}dz
\z\<h П
(y - x = z, у = x + z, dy = dz).
Оценка F) при р = 1 очевидна (без использования неравен-
неравенства Гельдера).
Из F), вынося sup \(p(x + z) — у(ж)|р за знак интеграла
1
по г и используя свойство 3) ядра усреднения, следует
\\ч>ь - И1мл) ^ sup \\ч>(х + z) - у(жIи,(я) -* °
при h —► 0 для 1 < р < оо.
4. Имеет место следующая
Теорема (о перестановочности операций обобщенного
дифференцирования и усреднения)
Если ц>[х) имеет обобщенную производную вида Datp, то
производная от средней функции равна средней функции от
обобщенной производной
Davk{x) = [D*<p(x)]k, « = «!,-,«„, G)
Va: € О: dist (x, dQ) > h, т.е. для любой строго внутренней
подобласти Q' С Q операции усреднения и дифференци-
дифференцирования перестановочны, при этом слева в G) производная
имеет классический смысл.
270 Глава VI. Обобщенные производные, пространства ...
Доказательство. Рассмотрим
(х - y)<p(y)dy.
= /
п
Ввиду свойства ядра и>н имеем
= I
п
п
Интегрируя по частям в последнем равенстве, получаем
D°uh{x) = (-IJ'*! / uk(x - y)D^{y)dy = [D°tp]h,
n
так как для dist (x, dQ) > h функция ши(х — у) вместе с
производными финитна в Q, из-за чего интегралы по дп
исчезают.
Теорема доказана.
§ 7. Граничные свойства функций из пространств
Соболева Wz(^) и ^^(^)* Формула
интегрирования по частям
Мы ввели функциональные пространства Соболева
о
W\{Ji) и W\{0). В этих пространствах обычно решают
краевые задачи для эллиптических уравнений второго по-
порядка, в частности, для уравнений Лапласа и Пуассона.
Гл. VI, § 7. Граничные свойства функций ...
271
Но встает в этом случае вопрос, в каком смысле будут
приниматься те или иные граничные условия у наших обоб-
обобщенных решений. Другими словами, нам нужно выяснить
вопрос о следах элементов и(х) € W^{O) на поверхностях
размерности п — 1. Сначала будем рассматривать случай,
когда граничное многообразие есть гиперплоскость в IR™,
затем рассмотрим случай произвольного гладкого многооб-
многообразия размерности п — 1 в IR".
Теорема 1. Пусть Q - полупространство IR" = {х £ Ип :
х' = (zi,...,zn-i) € IR", xn > 0}. Тогда любая функция
О
и(х) € W\{&) обладает следующим свойством: и(х) почти
всюду в Ш,+ совпадает с функцией u'(xl5 ...,zn), суммируе-
суммируемой в квадрате по Х\,...,zn_i = х' при всяком хп > 0, для
которой справедлива оценка
+ 0О
/
ди>
дхп
dx\...dxn—\ <
dx\...dxn < xn|lu |
т.е.
Замечавие 1. Так как функции и(х) и и\х) отличаются
лишь на множестве меры нуль, то они совпадают как эле-
0
менты пространства W \(&) (и ^гС1^))- Такие функции на-
называются эквивалентными. В дальнейшем мы будем обозна-
обозначать их через и(х).
Замечавие 2. Из A) следует, что
272 Глава VI. Обобщенные производные, пространства ...
2
/
dx' —» О при хп —+ О,
B)
т.е. функция и'(х', хп) стремится в среднем квадратичном к
нулю при хп —» 0.
о
Из теоремы 1 следует, что любая и(х) € W^^"
след на гиперплоскости Г = {хп = const}, как элемент
Ь^{Г), причем этот след непрерывно зависит от хп € [0,6]
в норме пространства £О
Доказательство теоремы 1. Для простоты проведем его
при п = 2. Пусть u(zi,z2) € C°°(IR4_). Тогда по формуле
Ньютона - Лейбница имеем
, ч [ dv(xi,y)
v(xi,x2) = J —— dy.
Используя неравенство Коши - Буняковского, имеем
Уж2 > 0:
Х2 XI
\v(xux2)\2<jl-dyj\
= х2
о о
2
ду
dy =
dy.
о
Интегрируя обе части по zj, получаем
Г 2 ГГ\
I \v(xi,x2)\ dx\ < x2 II
J ~ JJ I
дх2
dx\dx2 <
C)
Гл. VI, § 7. Граничные свойства функций ... 273
Пусть и{х\,х2) € Т^г(^-+) и имеется последовательность
vn(x\,x2) € C°°(IR.+ ) такая, что vn(x\,x2) -* u(zi,z2) в
норме И^ (IR-+)- Тогда, подставляя в C) v — vm — uU5 полу-
получаем
+ 0О
D)
При JTO, П —► ОО \/ж2 > 0.
Следовательно, функции vn{x\,x2) при любом фиксиро-
фиксированном х2 > 0 образуют фундаментальную последователь-
последовательность в L2(—oo < х\ < +оо). Из полноты пространства L2
следует существование функции u'(xi,z2) € L2(—oo < x\ <
оо) такой, что
+ оо
\и'(хг,х2) — vn(xi,x2)\2dxi —► 0 Vio > 0.
п—>оо
—оо
Докажем, что функция и'(х%,х2) совпадает почти всюду в
Ш4_ с функцией u(zi,z2).
Перейдем в D) к пределу при т —* с». Так как {vm} —*
и(х) в норме И^2(Н^.), то получаем
+ оо
12 j_ s* _ II..
/
\и\хих2) - vn{xux2)\2
— оо
Проинтегрируем E) по х2 от 0 до Л VA: 0 < А < с», полу-
получаем
А +оо
HI \u'{xux2) - vn{xux2)\2dxijdx2 <
О -оо F)
А2
»* и
18 - В. Н. Масленникова
274 Глава VI. Обобщенные производные, пространства ...
С другой стороны, так как {vn} —► и при п —► с» в норме
W2 (JR-+)j то vn(x\, х2) сходится к u(zj, х2) в L2(Si^.), а зна-
значит, ив £2 {—оо < zi < оо,0 < £2 < -А}. Отсюда и из F)
вытекает, что и(хх,х2) = u'(xi,x2) почти всюду в полосе
{—с» < х\ < +оо, 0 < Х2 < А}, а значит, и в Н+. Следова-
Следовательно, и'(х\,х2) € ЙЛ2('К'+) и совпадает как элемент этого
пространства с и{х\,х2).
Подставляя в неравенство C) вместо v{x) функции vn(x)
+oo
/ \vn(xx,x2\2dxi <x2 II | —" T' T°
dx\dx2
и переходя к пределу при п —* оо, получим неравенство A).
Теорема доказана.
Рассмотрим теперь произвольную ограниченную область
Q С И2 с границей dQ, регулярной класса С1 (т.е. фун-
функция, которая задает в локальных координатах уравнение
границы, принадлежит пространству С1).
Пусть пары функций
У\ =
осуществляют взаимнооднозначное и взаимнонепрерывное
отображение области Q на область Q\ С TR2(yi,y2), рас-
расположенную в полуплоскости у2 > 0 и примыкающую к оси
Oyi вдоль отрезка а <у\ <Ь. Пусть А = <р(а, 0), В = <р(Ь, 0),
причем при отображении у = ф{х) кусок границы АВ С dQ
переходит в отрезок [а, Ь] С dQ\.
о
Рассмотрим функции v(x) e С °°(&), их можно продол-
продолжить нулем вне Q. Продолженные функции будем опять обо-
обозначать через v(x). Очевидно, они принадлежат С°°(Ш?).
Гл. VI, § 7. Граничные свойства функций ...
275
Функции и(х) € И^гС1^) также можно продолжить нулем
вне Q; эти продолжения также будем обозначать через и(х).
И мы при этом имеем: если vn(x) —► и(х) при п —» с» в
о
)) то после продолжения нулем vn(x) —* u(x) в
норме VI
о
W^IR- )• Обозначим через Ге = (Ае,Ве) прообразы отрез-
отрезков {у2 = е} П Q\ в Q при отображении у = ф(х): Q —* Q\.
Имеет место
Теорема 2. Пусть
о
2) элементы матрицы Якоби
18*
276 Глава VI. Обобщенные производные, пространства ...
непрерывны в п\, и всюду в Q\ определитель этой матрицы
отличен от нуля. Тогда и(х) почти всюду в Q совпадает с
функцией и'(х) такой, что для любого е: 0 < е < £i, она
принадлежит Ь2(Ге)у причем
\u'(xi,x2)\2dre-*0 прие-»О. F)
Г.
Если выполнено F), то говорят, что функция и'(х) в среднем
обращается в нуль на дуге АВ.
о о
Доказательство. Пусть и(х) € W\{fl) и vn(x) € С
о
vn —» u(x) в W" г(^) или5 после продолжения функций нулем
/2
вне
Обозначим
Тогда (из-за непрерывности отображения)
Q
(УьУг) в w
П—+ОО
Действительно, если последовательность
vn(x) —> и(х) в L2(fi),
ТО
> Й(у) В X2(^l)j
Гл. VI, § 7. Граничные свойства функций ...
277
так как
/ \vn(y)-u(y)\2dyidy2 =
= j \vn{x) - u(x)
п
Р{У)
D(x)
dx\dx2 <
< С I \vn(x) — и(х)\2dxidx2 —* О при п
п
с».
Аналогичное рассуждение можно провести для произво-
производных: если *1П' —* я в L2(Q), то я ~* я в
OXi ОХ* * \ /' CtJ/i Gм:
■^2(^1), * = 1,2, так как
9zj 9j/t
dvn
дх2 dyi dxi dyi
ди
дх2
Д(у)
D(«)
дх\
/?
дх2 dyi dx2 3
dvn du * ш dvn du 2
~ Cl J \\
n
дх2 дх2
\dx\dx2 —»0
при n —♦ с».
Продолжим функции vn(y) и й(у) нулем вне i?i и будем
рассматривать их в полуплоскости Ш.+. Тогда по теореме 1
278
Глава VI. Обобщенные производные, пространства ...
й(у) почти всюду в И+ совпадает с функцией й'(у) такой,
что
J
О,
поэтому
6,
I
J \u'(y)\2dyi = I \u'{yx,y2)\2dyx -> 0 при у2 -♦ 0.
— оо а.
Обозначим и'(х1,х2) = «'(i/>i(a;i,Z2),^2(^1,3:2)). Очевидно,
и'(х\,х2) почти всюду совпадает с u(xi,x2), при этом
f
А
6.
G)
, е-0.
Теорема 2 доказана.
Таким образом, нами доказано, что любая функция
о
и(х) € W 2(Q) в среднем обращается в нуль на dQ в смысле
G) (очевидно, часть АВ границы дп можно взять любой,
т.е. дп есть объединение дуг: dQ = (J
То же доказательство проходит и в n-мерном случае.
Заметим, что и(х) = const ф 0, х € Q, не принадлежит
Для пространства Соболева W2{Q) верна аналогичная
теорема, которую можно сформулировать следующим обра-
образом:
Гл. VI, § 7. Граничные свойства функций ... 279
Теорема 3. Если dQ - кусочно-гладкая поверхность, то для
элементов и{х) € W2l(Q) определены следы на dQ как эле-
элементы L2(dQ).
Теорема 3 есть одна из простейших теорем вложения Со-
Соболева и ее можно переформулировать следующим образом:
Если дп - кусочно-гладкая граница, то W2{Q) ограни-
ограниченно вкладывается в £2(d.f2), т.е. имеет место оценка
< С\\и\\Щ{а). (8)
Отметим, что в теореме 2 (при рассмотрении простран-
о
ства W \{Q)) можно не налагать на границу dQ области Q
условия гладкости. Это объясняется тем, что любую фун-
о
кцию и[х) € W\(Q) можно продолжить нулем вне Q и счи-
о
тать элементом W2(B), гДе Я» например, - шар, заключа-
заключающий в себе Q.
Суть теорем вложения Соболева состоит в специаль-
специальном упорядочивании пространств так, что одно простран-
пространство целиком вкладывается в другое и это вложение со-
сопровождается неравенствами между нормами одной и той
же функции, рассматриваемой как элемент различных про-
пространств.
Формула интегрирования по частям. Из теорем 2 и 3 сле-
следует, что для элементов и(х) € W2l{0) справедлива осно-
основная формула теории краевых задач - формула интегри-
интегрирования по частям: для любых двух элементов u(z), и(ж),
принадлежащих Wl(Q), имеем
/ -= vdx = — / u-=—dx + / uvcos(n,Xi)dS, (9)
n n ' an
где n - внешняя по отношению к области dQ единичная
нормаль к dQ. Формула (9) известна из анализа для фун-
функций и(ж), v(x) € С1 (Q) и гладких поверхностей dQ. Из
280 Глава VI. Обобщенные производные, пространства ...
теоремы 3 о свойстве следов элементов из WK&) следует,
что формула (9) сохраняется Уг = 1,...,п и для функций
u(z), v(x) € ^2(^I если dQ - гладкая поверхность. Для
проверки этого надо аппроксимировать и(х) и v(x) глад-
гладкими элементами {«„}, {vn}, записать для них (9), а затем
перейти к пределу при п —» с».
о
В силу теоремы 2 для элементов и(х), v(x) € W\(^)
формула (9) принимает более простой вид:
[ p-vdx = - [ u^-dx Vt = l,...,n. A0)
J OX{ J OXi
n n
§ 8. Основные понятия о продолжении функций
из пространств Соболева на более широкую
область с сохранением класса
Как уже отмечалось выше, при решении краевых задач в
пространствах Wj,(O) иногда приходится продолжать фун-
функции, заданные на i?, на большую область Q Э О при-
притом так, чтобы продолженные функции были элементами из
), 1 < р < с», и чтобы выполнялось неравенство
fl) ^ C(p,l,n,n)\\u\\w,in) A)
с постоянной С, не зависящей от функции и(х). За продол-
продолженными функциями часто оставляют прежнее обозначение.
Если можно каким-либо способом продолжить и(х) с обла-
области Q на Q э О, то по этому продолжению можно построить
и такое, при котором продолженные элементы будут равны
нулю вблизи дп и вне Q. Для этого используют так называе-
называемую срезающую функцию ((х) £ С°°, равную 1 на Q, нулю
вблизи дП и вне B, и изменяющуюся от 1 до 0 в остальных
точках.
Бели й(х) - продолжение функции и(х) на 1?, тогда
Гл. VI, § 8. Основные понятия о продолжении ... 281
( ч \й(х)С(х), x€fi,
tt(x) = < _
будет продолжением функции и(х), заданной на П, на все
1R". В курсах теории функциональных пространств изу-
изучают различные способы продолжения функций и условия
на область О, допускающие продолжение функций с сохра-
сохранением класса, т.е. с выполнением неравенства A). Рассмо-
Рассмотрим два примера, иллюстрирующие это продолжение.
1. Пусть П есть шар BR@), u(x) € W}(BR@)). Рас-
Рассмотрим точку х € Br и ей сопряженную х* относительно
сферы BBr так, что |х| • \х*\ = Н2, и положим и(х*) =
и(х). Такое продолжение, очевидно, будет сохранять норму
Wp(Q\ т.е. для него будет выполняться неравенство B).
2) Из полупространства Н" = {х : х' € Нп~\хп > 0}
на все Нп функции из Wi(Hl) можно продолжать по спо-
собу Уитни. Пусть /(я) G WJAR£) или /6 С1(Щ). Тогда
продолженная на Нп функция / определяется следующим
способом:
/(*) =
Y^akf(x',-/3kxn), хп < 0, числаfik > 0.
B)
В качестве /?* удобно взять, например, числа 2~к.
Для принадлежности /(х) к Wp(IRn) достаточно, чтобы
числа «jt удовлетворяли алгебраической системе уравнений
1-х
£(-/?*)'«* = 1, J=0,l,...,/-l. C)
Jt=o
с определителем Вандермонда, при этом будут (в опреде-
определенном смысле) выполнены условия склейки на плоскости
•с„ = 0 функции и ее производных до порядка / — 1:
282 Глава VI. Обобщенные производные, пространства ...
аГ^ = 5~^ , ш = 0,...,/-1. D)
При таком продолжении функций из Wi(H") имеет место
неравенство A).
В случае пространств C'(IR") в B)-D) вместо / нужно
взять / +1. В общем случае области п с липшицевой грани-
границей дп имеет место
Теорема. Пусть дп G Lipl, I С IN, 1 < р < оо. Тогда
Vu(x) G И^(^) существует продолжение U(x) G (n)
U(x) = и(х), iGfi, при этом
где С не зависит от и(х). Отметим, что если и(х) G Wlp(Q)
продолжить нулем на все Нп, то мы получим функцию
Теоремы о продолжении дают возможность сводить ис-
исследование свойств функций из WjJ(J2) к исследованию
о
свойств функций из Wр(&), в котором плотно множество
о _ о
С°°(О). Кроме того, из неравенства A) и плотности С °°(^)
в Wlp(O) вытекает, что для тех областей п, для которых
верны теоремы о продолжении функций из И^(^), мно-
множество С°°(п) плотно в Wl(u). Вопросам продолжения
функций с сохранением класса посвящена обширная лите-
литература (см. [4], [23] и главу 11 настоящей книги).
Гл. VI, § 9. Неравенство Пуанкаре 283
§ 9. Неравенство Пуанкаре
Для функций u(x) G У/ЦМ) имеет место неравенство
Пуанкаре вида
n n n k=1
Оно доказано в книге С.Л. Соболева [22.2)]. Мы его дока-
докажем с уточненными постоянными для случая, когда П С IRn
есть параллелепипед П = {х : 0 < х,- < di), т.е. докажем
неравенства вида [17]:
I
u2dx<
-
mes#
Я n n K-x
Будем доказывать B) на гладких функциях, так как они
плотны в Wl{II). Итак, пусть u(x) G С1 (Я). Перейдем к
новым координатам гц = Xi/di, i = l,n. После умножения
на (d\...dn)~l неравенство B) перейдет в эквивалентное ему
C), но уже для куба П\ = {у : 0 < t/i < 1} и для новых фун-
функций й[у) = и(
tffl*- C)
Я! Я! Я, fc-J
Таким образом, докажем C).
Для доказательства возьмем две произвольные точки у =
(У1, •», Уп), у' = (у{,.», yj») и цепочку точек
У1 =(у1,У2,-,Уп), ~°
у2 = (у1у£уУ)
По теореме Ньютона - Лейбница имеем:
284 Глава VI. Обобщенные производные, пространства ...
~( >\ ~( \ [
«(у) - «(у) = J
91
г п
J дт2 2 '" J дтп
У2 Уп
Возведем обе части этого равенства в квадрат и оценим пра-
правую часть, используя неравенство 2аЬ < а2 + Ь2 и неравен-
неравенство Коши - Буняковского, получим
й2(у')-2й(у1)й(у) + 2
В последнем неравенстве проинтегрируем по у G Hi и у'
III, получим
откуда следует неравенство Пуанкаре C), а следовательно,
и B).
§ 10. Компактность вложения ограниченного
множества из W^(/2) в L{fi)
Предположим, что п - ограниченная область, допуска-
допускающая продолжение функций из W2{^1) на более широкую
область с сохранением класса, т.е. с выполнением неравен-
неравенства A) § 8. Тогда имеет место
Теорема 1. Всякое ограниченное множество из {
(ограниченное по норме У/Ц^)) является компактным в
Гл. VI, § 10. Компактность вложения огр. множ-ва ... 285
Замечание 1. Поясним смысл теоремы 1. Пусть множество
А С Wjifl) и пусть постоянная С > 0 такова, что Vu(z) €
А: ПиПи'Чл) < С. Теорема 1 говорит о том, что если после-
последовательность {itm} С А, тогда существует ее подпоследо-
подпоследовательность {ит,} такая, что {um,} сходится в £-2(^)> т-е-
существует и(х) G L2(fi), что lim \\ит, - u\\L^n) = 0.
♦оо
Доказательство. Продолжим функции из И^{&) вне Q на
параллелепипед П = {х : 0 < х< < в.{\ с сохранением
класса, считая Q С П. Разобьем П на элементарные парал-
параллелепипеды Л,- со сторонами dk/N, к = 1,2,..., п, и гранями,
параллельными координатным плоскостям.
Для любой функции u(x) G W^ifl) справедливо нера-
неравенство Пуанкаре B) из § 9 с заменой П на Я,, Из него
следует
п |=1 п, я
Рассмотрим множество функций {um(x)}, ограниченное по
норме W%(ft), как сказано в условии теоремы, т.е. пусть
B)
Из неравенства A) §8 следует, что B) имеет место и для
продолженных на П функций. Пространство W^II) явля-
является гильбертовым. Известно, что замкнутое ограниченное
множество в Н слабо компактно в себе. Таким образом, мно-
множество {ит} слабо компактно в I<2(#), т.е. из {ит} можно
выбрать слабо сходящуюся подпоследовательность. Предпо-
Предположим, не ограничивая общности, что сама последователь-
последовательность {ит} слабо сходится в £/2(П). Для любых Up и и,
неравенство A) дает оценку
286 Глава VI. Обобщенные производные, пространства ...
<||ир-«,|Ца(п)<
1
-1 л,
n
2N2 f^x к\\дхк дхк\\ып)
Последнее слагаемое справа в C) может быть сделано сколь
угодно малым (т.е. < |) за счет выбора достаточно большого
N, (т.е. за счет мелкости разбиения) сразу для всех р ж q.
Выберем и зафиксируем это достаточно большое N. Тогда
первое слагаемое будет стремиться к нулю при р, q —> оо за
счет слабой сходимости последовательности {ит} в 1,2(П),
т.е. оно будет меньше е/2 при достаточно больших р и q.
Тогда
при p,q —* оо, т.е. последовательность {ит} сходится в
норме L2(#), а значит и в норме ■^(•Я).
Теорема 1 доказана.
Замечание 2. Теорема 1 остается справедливой и для про-
о
странства W\{O). В этом случае для ее доказательства фун-
кции из W\(Q) можно продолжить нулем на параллеле-
параллелепипед 77, а остальные рассуждения останутся без измене-
изменений.
Замечание 3. Теорема 1 остается справедливой и для об-
— N ^~
ластей /2, где Q = U fl,-, где Д - области, допускающие
1
продолжение элементов из W^fii) на более широкие обла-
области Qim. Hi С Hi, т.е. имеет место
Гл. VI, § 10. Компактность вложения огр. множ-ва ... 287
— N — ^
Теорема 2. Если п = U J/j, где щ - подобласти и, допу-
екающие продолжение элементов W%(/?i), то любое ограни-
ограниченное множество в W2l(B) компактно в ХС^)
Замечание 4. Теорему 1 (а значит, и теорему 2) можно
переформулировать следующим образом: W} (ti) вкладыва-
вкладывается в 1<2(/2) компактно.
Замечание 5. Для неограниченных областей Q теорема 1,
вообще говоря, неверна, как показывает следующий
Пример. Рассмотрим последовательность _шаров_ Вк ра-
радиуса 1 с центром в точках ж*, таких что В к П Bj = 0 и
оо
пусть П такова, что Q Э {J Вк-
Возьмем функцию ио(ж) € С°°(-Во), где Во = {х : \х\ <
1}, щ(х) ф 0. Рассмотрим подмножество А С И^Л),
А = {uk}\*Li и пусть ufc(x) = ио(ж — Xjk). Имеем
0.
Из А нельзя выделить подпоследовательность, сходящуюся
в Li2(B). Действительно, Чх € U lim ufc(x) = 0, т.е. если
к—>оо
«it (ж) -♦ u(x) в Ьг(^)) то и(ж) эквивалентна нулю на Q.
Но
IIй*. - и\\ып) = 1КЛмя) = IKIU2(Bo) -h 0-
288 Глава VI. Обобщенные производные, пространства ...
§ 11. Обобщенные решения основных краевых
задач для эллиптического уравнения второго
порядка
Переходим к решению краевых задач для дифференци-
дифференциальных уравнений в частных производных в обобщенной по-
постановке, т.е. будем искать обобщенные решения этих задач.
Опишем подробно метод доказательства существования
обобщенного решения, основанный на теореме Рисса (пред-
(представлении линейного функционала в гильбертовом прост-
пространстве).
1. Рассмотрим первую краевую задачу для уравнения
Пуассона
-Ли = /(ж), i = ii,...)inefl, A)
где Q - ограниченная область в Кп, с однородным гранич-
граничным условием
и
дп
= 0. B)
Определение. Пусть f(x) G 1/2{п). Назовем обобщенным
о
решением задачи A), B) функцию u(x) G Wlifyi удовле-
удовлетворяющую интегральному тождеству
п '-1 п
для любой Ф{х) G W \{О).
Таким образом, равенство C) берем за основу определе-
определения обобщенного решения. Отметим, что если и(х) - класси-
классическое решение задачи A)-B), то и(х) является обобщенным
решением этой задачи.
Гл. VI, § 11. Обобщенные решения ... 289
Интегральное тождество C) получено с помощью инте-
интегрирования по частям равенства, которое получается умно-
жением A) на функцию Ф(х) € У/\(&), интегрированием
по П и интегрированием по частям в левой части равенства:
/ -Аи(х)Ф(х)<1х = f /(х
п п
о
Мы доказали, что норма в W\(Q) может быть определена
через скалярное произведение:
ди dv
J ^
п '-1
т.е.
Этой нормой мы и будем пользоваться (обозначим ее со
штрихом). Она эквивалентна обычной норме
Обозначим скалярное произведение в 'W\(fl) фигурными
скобками:
ди дФ . , _,
—dx = {и,Ф},
п t=1
тогда интегральное тождество C) можно записать в виде:
К#} = (/,#), (з')
19 • В. Н. Масленникова
290 Глава VI. Обобщенные производные, пространства ...
где круглыми скобками обозначено обычное скалярное про-
произведение в 1/2({2), т.е. (/,Ф) = / /Фс1х. Если и(х) €
п
О
W 2(^I то и(х) удовлетворяет в среднем граничному усло-
условию B). Докажем теорему единственности обобщенного ре-
решения задачи A), B) независимо от теоремы существования.
Теорема 1. Обобщенное решение задачи A), B) един-
единственно.
Доказательство. Пусть 3 два обобщенных решения ui и
и2 в смысле нашего определения:
f-f дх{ dxi J J '
t=1 n
n t=1 n
n l-1 n
Вычтем одно равенство из другого, получим
п >=]
Возьмем в качестве Ф разность и\ — иг (что мы имеем право
сделать, так как и(х) и Ф(х) принадлежат одному и тому же
о
пространству W\{&)), тогда получаем
п •=1
Уг = 1, ...,гг; т.е. и\ — U2 = const,
эта константа должна быть равна нулю на дП, следова-
следовательно, и% — U2 = 0, т.е. и\ = U2 (равенство выполняется
Гл. VI, § 11. Обобщенные решения ... 291
с точностью до множества меры нуль, т.е. решение един-
единственно с точностью до эквивалентности).
Теорема 1 доказана.
Теорема 2. (Существования и единственности обобщен-
обобщенного решения)
Пусть Q - ограниченная область в IRn и /(х) € Ьъ(П).
Тогда определенное выше обобщенное решение и(х) €
о
W\(ft) задачи A), B) в смысле интегрального тождества
C) существует и единственно для любой функции /(х) €
()
Доказательство. Для доказательства воспользуемся теоре-
теоремой Рисса об общем виде линейного функционала, задан-
заданного на гильбертовом пространстве.
Теорема Рисса. Пусть дан линейный непрерывный фун-
функционал 1(Ф) на гильбертовом пространстве Н: Ф € Н. То-
Тогда 3 и притом единственный элемент и €. Н такой, что
= {и,Ф}
где {•, •} - скалярное произведение в Н.
Применим теорему в нашем случае. При фиксированном
/ € Ьъ(П) рассмотрим линейный функционал, заданный на
п
Так как f(x) G Хг(^?), то этот функционал задан для любой
О
Ф € Хг(^), а следовательно, и для любой Ф(х) € ' W\{u) С
о
L2(f2). Докажем, что он непрерывен на ' W\{&)-
О
Пусть последовательность Фп G 'w\(Q) и Фп —> Ф в
о
норме 'w\(fi), заданной скалярным произведением {•,•},
т.е. в норме
292 Глава VI. Обобщенные производные, пространства ...
1 / Z-Л Я—/ I = Hull, ° !
о о
Тогда, в силу эквивалентности норм W\(^) и ' W\{_d\ эта
последовательнось сходится и в норме \У\№)> а следова-
следовательно, и в Ьг{О)'- Фп —* Ф ъ £г(^2), а значит,
lim (
и—►оо
Так как функционал //(^) непрерывен на гильбертовом про-
о
странстве ' W\{&), то по теореме Рисса найдется и притом
о
единственный элемент (функция) щ(х) € 'w\№) такой,
что
Отсюда и из C;) следует, что искомое решение и(х)
должно удовлетворять соотношению
Следовательно, и(х) = щ(х) - единственное решение за-
задачи A) - B).
Теорема 2 доказана.
2. Изложенный метод обобщается на случай более общих,
чем A), уравнений, например, на эллиптические уравнения
с переменными коэффициентами.
Рассмотрим эллиптическое уравнение с переменными
коэффициентами:
ди * (х)и = f(x), D)
где р(х) > ро >_0, q(x) > 0, f(x) € L2(f2). Пусть р(х), q(x)
непрерывны в I?, Q - ограниченная область.
Рассмотрим опять первую краевую задачу
и
Гл. VI, § 11. Обобщенные решения ... 293
= 0. B)
Обобщенное решение задачи D), B) определяется как выше:
о
обе части D) умножим скалярно (в Li(Q)) на Ф € W\(f})',
после интегрирования по частям приходим к интегральному
тождеству:
E)
[
п i=1 о
Определение. Обобщенным решением задачи D), B) яа-
о
зывается и(х) € W\(^)f ^ля которого выполняется инте-
тральное тождество E) УФ € И
Теорема 3. Пусть п С IR" - ограниченная область, р(х) >
ро > 0, q{x) > 0, р(х), д(х) € С(П), f e L2(f2). Тогда
существует единственное обобщенное решение задачи D),
B).
Доказательство. Рассмотрим скалярное произведение,
определяемое интегралом в E)
F)
п
Определим норму в^|(^) этим скалярным произведением.
При выше приведенных ограничениях на коэффициенты
о
р(х) и q(x) эта норма эквивалентна норме 'w\(ft), а сле-
следовательно, норме Wl{Q). Действительно, имеем
i
" 2
[p(x),q(x)\ \\и
294 Глава VI. Обобщенные производные, пространства ...
Повторяя дословно все предыдущие рассуждения с приме-
применением теоремы Рисса, мы получаем теорему существова-
существования и единственности обобщенного решения E) для и(х) €
W\(u) прш f(x) е L2(u).
3. Рассмотрим уравнение:
-Ди-А2и = / G)
с граничным условием B), где знаки оператора —Д и коэф-
коэффициента при и(х) не согласованы, поэтому оператор слева
не знакоопределен. Пусть Q - параллелепипед с ребрами
П = {х : О <Х{ < di}, г = 1,2,...,п.
Пусть d = max di.
i
Определение. Обобщенным решением задачи G), B) на-
зовем u(x) € W\(II), удовлетворяющую интегральному то-
тождеству
я *=1 я
Теорема 4. Пусть А < y^!1, f € Li(Q). Тогда существует
единственное обобщенное решение задачи G), B).
Доказательство. По неравенству Фридрихса D) § 5 гл. VI
для и(х) имеем
я i=1 я
ИЛИ
J ~ 2nJ ^\dxi
Гл. VI, § 11. Обобщенные решения ... 295
dx.
я я
Поэтому для решения рассматриваемой задачи имеем
{u,u},wx(n) - A2(u,u) > {u,u
Для положительной определенности левой части в (8) при
Ф(х) = и(х) нужно потребовать 1 — А^~ > 0, а это возможно,
когда область мала или Л мало.
В этом случае будем иметь эквивалентность нормы
и нормы
1- 2п
Отсюда следует условие на Л или на область для одно-
однозначной разрешимости задачи G), B), сформулированное
в условии теоремы.
Заметим, что при большом Л (или большой области) мо-
может не быть однозначной разрешимости рассматриваемой за-
задачи.
4. Рассмотрим теперь разрешимость 3-ей краевой задачи
для уравнения Пуассона
-Ли = /(*) A)
с граничным условием
= 0, (9)
дп -
где п - нормаль к дО, внешняя по отношению к ограничен-
ограниченной области Q. Пусть измеримая функция о{х) ограничена,
~),о(х) ><т0 >0.
296 Глава VI. Обобщенные производные, пространства ...
Определение. Обобщенным решением задачи A), (9) на-
назовем функцию и(х) € W^fi), удовлетворяющую инте-
интегральному тождеству:
{Щ
t i i
п l-1 an n
для любой Ф(х) е
Интегральное тождество A0) получено с помощью ска-
скалярного в Lzift) умножения A) на Ф{х) € Wl{O) и инте-
интегрирования по частям с использованием краевого условия
(9):
о о i=:1
n'-1 an n
= /(Vu,V^)dx+ <r(x)u(
п an
Роль основного функционального пространства здесь будет
О
играть W%(Q) (а не W\(ft), как в задаче Дирихле). Введем
в нем обычное скалярное произведение
п '=г
Можно доказать, что норма, задаваемая скалярным произ-
произведением A1), эквивалентна следующей норме
A2)
n tssl ' а'п
Гл. VI, § 11. Обобщенные решения ... 297
задаваемой скалярным произведением, участвующим в опре-
определении обобщенного решения вида A0), т.е.
A3)
где С\,С% - постоянные, зависящие от области П, но не за-
зависящие от функции и(х).
Для доказательства A3) сначала докажем, что норма,
определяемая равенством A2) эквивалентна норме, опреде-
определяемой формулой
/7 /

П l-1 дП
п ( я \2
Обозначая J3 l^') чеРез |V«|2, получаем
[\Vu\2dx + <r0 I u2ds< f\Vu\2dx+ I <r(x)u2ds <
n an n an
< f\Vu\2dx+ <ti f u2ds,
n an
где. согласно условию задачи, <Tq = inf cr(x) > 0,
х£дП
o\ = sup o{x). Или, обозначая min(l,<To) = C\,
xean
max(l,<Ti) = С2, получаем
Поэтому вместо A3) теперь достаточно доказать неравен-
неравенства
Ci\\\u\\.wi. A5)
Левое неравенство в A5) есть следствие неравенства (8) из
теоремы 3 § 7. Действительно,
Глава VI. Обобщенные производные, пространства ...
J \Vu\2dx + J u2ds < J \Vu\2dx + C\\u\\2wiin) <
< const \\u\\2wiin).
Для доказательства же правого неравенства из A5) надо ис-
использовать неравенство Фридрихса "для ненулевого гранич-
граничного значения", т.е. для функций из W%{Q). (Неравенство
о
Фридрихса было доказано нами для функций из
Это неравенство имеет вид:
ju2dx<M\\ f nds
п an
A6)
n
Его доказательство есть следствие общих теорем вложения
и эквивалентных нормировок пространств WJ,(Q) и содер-
содержится в книге С.Л. Соболева [22.2), стр. 87]. Если считать
A6) известным, то правое неравенство из A5) для ограни-
ограниченных областей доказывается следующим образом.
(\Vu\2dx + fu2dx<
n n
< f \Vu\2dx
n
= M
an
an
n
I l-uds2 +A + M) f\Vu\
n n
dx
< M(mes дП) I u2ds + A + M) I \Vu\2dx <
an а
< тах{М . mesdtf, 1 + M} IMI^
Ввиду эквивалентности норм A3) в
скалярное произведение по формуле
можно ввести
Гл. VI, § 11. Обобщенные решения ... 299

J&kf
П l-1 дП
которое порождает норму, эквивалентную обычной норме в
Wj (Л), а интегральное тождество A0) записать в виде:
Тогда опять можно применить теорему Рисса и получить
следующую теорему.
Теорема 3. Пусть О - ограниченная область с компактной
границей класса С1, / € £г(^), ^(я) > 0о > Q, ff{x) огра-
ограничена и измерима, тогда существует единственное обоб-
обобщенное решение и(х) G W\{Q) задачи A), (9) в смысле
интегрального тождества A0).
Таким же путем решается задача (9) для уравнения D).
Таким образом, методы функционального анализа, т.е.
о
введение пространств Соболева w\(Q) и W\(Q) и дока-
доказательство соотношений между нормами в этих простран-
пространствах, дают очень простой, широко применимый метод ре-
решения краевых задач математической физики.
Можно исследовать также дифференциальные свойства
обобщенных решений в пространствах Соболева.
300
Глава VII. Задачи на собственные
значения и метод Фурье
(продолжение) в пространствах
Соболева
§ 1. Задачи на собственные значения для
эллиптического уравнения. Обобщенные
собственные функции задач Дирихле,
Неймана и третьей краевой задачи.
Сведение задач на собственные значения к
операторному уравнению с самосопряженным
вполне непрерывным оператором
Вернемся к изучению задач на собственные значения для
эллиптического уравнения
Lv(x) = -div(p(x)Vv) + q(x)v(x) = Ли, х € п С Hn(l)
(I? - ограниченная область) с граничными условиями
= 0 B)
v
an
или
dv
<t(x)v(x)
где все коэффициенты в A), C) и дП удовлетворяют усло-
условиям, сформулированным в § 5 главы V, <т(х) > 0.
Нам нужно найти те значения Л, при которых задачи A),
B) и A), C) имеют нетривиальные, т.е. с нормой ||и|| ф 0,
решения. Такие значения Л называются собственными зна-
значениями, а соответствующие им нетривиальные решения за-
задач A), B) или A), C) называются собственными функци-
функциями. Число линейно-независимых собственных функций, от-
отвечающих одному и тому же значению Л, называется крат-
кратностью собственного значения. Как уже отмечалось выше,
Гл. VII, § 1. Задачи на собственные значения и ... 301
если v(x) - собственная функция, то в силу линейности
и однородности задачи функция cv(x) для любой постоян-
постоянной с ф 0 также является собственной функцией, отвеча-
отвечающей тому же собственному значению. Поэтому мы будем
рассматривать нормированные в ^2(^) собственные фун-
функции условием ||f||.L2(x2) = 1- Можно рассматривать за-
задачи A), B) и A), C) в классической постановке, т.е. ис-
искать собственные функции в пространствах соответственно
v(x) € С2{П) П С(П) или v(x) € С2{П) П С1 (Л), как мы
делали в примерах § 2 и 3 главы V. Сейчас же мы будем
рассматривать собственные функции в обобщенной поста-
о
новке, т.е. в пространстве Wl(ft) Для задачи Дирихле и
в пространстве W^(f2) в задаче Неймана и в 3-ей краевой
задаче.
Рассмотрим сначала задачу Дирихле.
Определение 1. Не равное тождественно нулю обобщен-
о ,
ное решение v(x) € W\{iT) уравнения A) называется обоб-
обобщенной собственной функцией 1-ой краевой задачи (задачи
Дирихле), если существует такое число А (собственное зна-
тение, отвечающее собственной функции v(x)), что v(x) удо-
удовлетворяет интегральному тождеству
dv дФ
р(х) 1- а(хI){х)Ф{х)\ ах =
OXh дх h *V/^/ J
D)
п
Для второй и третьей краевых задач введем
Определение 2. Не равное товдествеяяо нулю обобщен-
обобщенное решение v(x) € W^J?) уравнения (I) называется обоб-
обобщенной собственной функцией второй (при a = 0) или
третьей (при сг(х) > 0) краевой задачи, если существует
302 Глава VII. Задачи на собст. зн-я и метод Фурье...
такое число А (собственное значение, отвечающее собствен
ной функции v(x)), что v(x) удовлетворяет интегральному
тождеству
a *-*
+ [ p(x)a{x)v$ds = A I vMx \/Ф € W]{Q).
эп a
Отметим, что в главе VI мы рассматривали действитель-
действительные функции и пользовались скалярным произведением б
1/2(О) в виде (/, Ф) = J /Ф<1х. Теперь же функции могу!
п
быть, вообще говоря, комплексозначными, поэтому скаляр-
скалярные произведения мы взяли в виде (/,Ф) = J /Фс1х.
п
В дальнейшем для нахождения обобщенных собствен-
собственных функций мы будем пользоваться интегральными то-
тождествами D) и E), и нам необходимо, чтобы левые ча-
части этих интегральных тождеств порождали скалярные про-
произведения в соответствующих гильбертовых пространствах.
Легко видеть, что левая часть D):
n *=1
порождает скалярное произведение в W\{ft) при наших
условиях на коэффициенты р(х) > ро > 0, q(x) > 0, так как
из неравенства Фридрихса и из {и, v} = 0 следует v(x) = 0
(с точностью до множества меры нуль).
То же самое имеет место для левой части E):
Гл. VII, § 1. Задачи на собственные значения и ... 303
[
" *"' G)
/ р(х)а(х)ьФ<1&
эп
при v(x), Ф(х) € \¥^(О), если q(x) и <r(z) ^ 0 одновременно.
В случае же q(x) = а(х) = 0 G) не будет скалярным
произведением, так как из условия {у,у}а = 0 следует, что
v = const.
Для того чтобы левая часть интегрального тождества
в определении обобщенного решения для задачи Неймана
также порождала скалярное произведение, будем вместо ура-
уравнения A) рассматривать эквивалентное ему уравнение (во
всех трех краевых задачах для единообразия)
-div(p(x)Vt;) + e(x)t; = (A + lHx), x € п С Нп, (8)
где теперь q(x) = q(x) + 1 > 1 и соответствующие (8) ин-
интегральные тождества D) и E) с собственными значениями,
сдвинутыми на 1.
Рассмотрим сначала задачу (8), B), т.е. задачу Дирихле.
Введем скалярное произведение для рассмотрения задачи
Дирихле в виде
{у,Ф} • i = f\p{x)VvV^ + q{x)v^]dx. (9)
^2 J
n
Тогда интегральное тождество D) примет вид:
(Ю)
где справа в A0) стоит обычное скалярное произведение в
L2(Q):
= /
п
304 Глава VII. Задачи на собст. зн-я и метод Фурье...
Используя теорему Рисса докажем следующую теорему
Теорема 1. Существует линейный ограниченный оператор
А из L-iiJi) в Wl(&) (с областью определения L2(■#)), для
о
которого при всех Ф € W\(ft) имеет место равенство
Оператор А имеет обратный А".
о о
Оператор А, если его рассматривать из Wl(ft) в
о
(т.е. с областью определения D(A) = Wli^)) является са-
самосопряженным, положительным и вполне непрерывным.
Доказательство. Применим теорему Рисса об общем виде
линейного непрерывного функционала в гильбертовом про-
пространстве. Пусть v(x) € 1/2@) - фиксированная фун-
о
кция. Рассмотрим линейный по Ф, Ф € W\{m), функционал
1(Ф) = (и, Ф)ьъ(п)' Он ограничен, так как по неравенству
Фридрихса
Поэтому согласно теореме Рисса существует единственная
о
функция i»o € W\№) такая, что
о
для всех Ф € Wl(O), при этом
A2)
Вспомним, что линейным оператором А называется отобра-
отображение, которое всякому v € D(A) ставит в соответствие
Гл. VII, § 1. Задачи на собственные значения и ... 305
однозначно определенный элемент «о: Av = vo. В нашем
случае это означает, что на L^Q) задан линейный опера-
тор A: Li2(Q) —* W^fi), Av = vq, для которого выполняется
равенство A1). Из A1) и A2) следует, что
т.е. оператор А, как оператор из Li2(O) в W\№)i ограничен.
Оператор А имеет обратный А". Действительно, оператор
А определяется для любого линейного оператора А, обла-
обладающего тем свойством, что в любых двух различных точках
он принимает различные значения. Если это условие выпол-
выполнено, то по определению A~1Vq = и, если Av = vq. Обла-
Областью определения А~1 служит область значений исходного
оператора А. Необходимым и достаточным условием суще-
существования А~1 является требование тривиальности его ядра:
N(A) = 0, т.е. Аи = 0 только при и = 0. Проверим, что в
нашем случае оператор А имеет тривиальное ядро. В самом
деле, из A1) следует, что если при некотором v G L^f})
Av = 0, то (u,<P)l2(x2) = 0 УФ € W\(n), т.е. v = 0. Этим
доказано, что оператор А имеет обратный А".
о
Докажем, используя A1), что А как оператор из W\{^)
о
в W\№) является самосопряженным. Заметим, что если А
задан и ограничен на L,2(f2), то он задан и ограничен и на
Wl(^) С Li2(O). Поэтому достаточно проверить его симме-
о
тричность. Для всех v и Ф из W\(^) имеем
= &,АФ}
Вспомним из функционального анализа, что оператор А на-
называется положительным, если порожденная им квадратич-
квадратичная форма принимает только неотрицательные значения,
т.е. (Av,v) > 0 Vu € D(A). Мы имеем {Av,v}
20 - В. Н. Масленникова
306 Глава VII. Задачи на собст. зн-я и метод Фурье...
> 0, т.е. оператор А положителен. Покажем, что
о о
оператор А из W\(^) в W\№) является вполне непре-
о
рывным. Рассмотрим произвольное ограниченное в W\№)
множество функций. Согласно теореме о компактности вло-
о
жения W\{fi) в L2(fi), доказанной в § 10 главы VI, это
множество компактно в L^^Q). Значит, из любого его бес-
бесконечного подмножества можно выбрать подпоследователь-
подпоследовательность {ид. }, фундаментальную в L2(O). Но оператор А ли-
линеен и ограничен. Отсюда следует, что
Av\\ о t = ||A(u£ — и)|| о t <
— ^IU2(«) —* 0 при*а-»оо.
Следовательно, подпоследовательность {Аиь } фундамен-
о
тальна в W\(^)i T<e- оператор А всякое ограниченное в
о
W\{^) множество переводит в компактное в этом же про-
пространстве, значит, А - вполне непрерывен.
Теорема 1 доказана.
Вернемся к задаче на собственные значения.
Используя теорему 1, интегральное тождество A0) для
определения обобщенного решения можно переписать в виде
{и, Ф) о = (А + 1){Av, Ф}о УФ € W 1(П). A3)
Откуда получаем операторное уравнение
w = (A + l)Aw, vewl(n) A4)
с вполне непрерывным оператором А. Таким образом, за-
задача Дирихле на собственные значения для эллиптического
уравнения (8) (т.е. для уравнения A)) свелась к задаче на
собственные значения для вполне непрерывного положитель-
положительного самосопряженного оператора А. Аналогичным обра-
образом, можно свести задачу на собственные значения с крае-
краевым условием C) B-ю и 3-ю краевые задачи) к задаче на соб-
собственные значения для волне непрерывного положительного
Гл. VII, § 1. Задачи на собственные значения и ... 307
самосопряженного оператора А, действующего из W^i?) в
Wj (X2), т.е. имеет место
Теорема 2. Существует линейный ограниченный оператор
А из Ьъ^О) в Wlift) (с областью определения L2(O)), для
которого при всех Ф € W2l{fi) имеет место равенство
A5)
Оператор А имеет обратный А 1. Оператор А, если его
рассматривать из W£(X2) в W^Q), является самосопряжен-
самосопряженным ^положительным и вполне непрерывным. Доказательство
теоремы 2 вполне аналогично доказательству теоремы 1.
Для этого введем скалярное произведение, порожденное
уравнением (8), (согласно E)), в виде
v,$}w}(n) = J\p(x)Vv
п
г - A6)
+ / р(х)а(х)у(х)Ф(х)с1з.
an
Нами было ранее (см. § 11, гл. VI) доказано, что скалярное
произведение A6) порождает норму, эквивалентную обыч-
обычной норме W^ifl). Повторяя выше приведенные рассужде-
рассуждения, но теперь уже в пространстве W2\fi) со скалярным
произведением A6) и используя теорему о компактности
вложения Wl{O) в 1/2@), мы придем к задаче на собствен-
собственные значения для операторного уравнения
с вполне непрерывным положительным самосопряженным
оператором А, действующим из гильбертового пространства
W\ (О) в то же пространство W^ft).
Из теорем 1 и 2 мы получаем следующие утверждения.
20*
308 Глава VII. Задачи на собст. зн-я и метод Фурье...
Утверждение 1. Число Л является собственным значением
задачи Дирихле B) для эллиптического оператора, задавае-
о
мого уравнением A) с областью определения W\(^)^ а v{x)
- соответствующей обобщенной собственной функцией то-
тогда и только тогда, когда (А + 1) есть характеристическое
число самосопряженного положительного вполне непреры-
О О
вного оператора А, действующего из Wl(fy B W\№)-, а
v(x) - соответствующий этому числу собственный элемент.
Утверждение 2. Число Л является собственным значением
краевой задачи C) для эллиптического оператора A) с обла-
областью определения W\ (i?), a v{x) - соответствующая этому Л
обобщенная собственная функция, тогда и только тогда, ко-
когда Л + 1 есть характеристическое число самосопряженного
положительного вполне непрерывного оператора А, действу-
действующего из Wj A2) в W\ (i?), a v(x) - соответствующий этому
числу собственный элемент.
§ 2. Свойства собственных значений и обобщенных
собственных функций для эллиптического
оператора. Основная теорема
Для удобства ссылок мы продолжаем нумерацию формул
из § 1 главы VII.
Из теории линейных самосопряженных вполне непреры-
непрерывных операторов в гильбертовом пространстве известно:
1) Существует не более чем счетное множество собствен-
собственных значений задачи B) (задачи C)).
2) Это множество не имеет конечных предельных точек.
3) Все собственные значения действительны.
4) Каждому собственному значению соответствует конеч-
о
ное число взаимно ортогональных в Н (Н = W\(&) в за-
задаче B) и Н = Wl{&) в задаче C)) собственных функций,
т.е. конечное число линейно независимых собственных фун-
функций. Таким образом, каждое собственное значение имеет
конечную кратность.
Гл. VII, § 2. Свойства собст. значений и ... 309
5) Собственные функции, отвечающие различным соб-
о
ственным значениям, ортогональны в Н (Н = W\{&) в за-
задаче B) и Я = W%{Q) в задаче C)).
6) Собственные функции можно выбрать действитель-
действительными. Это свойство следует из того, что оператор L имеет
действительные коэффициенты и собственные значения дей-
действительны. В самом деле, пусть Ло - собственное значе-
значение и vq{x) - соответствующая ему собственная функция:
Lvq = Aouo- Отделяя в последнем равенстве действитель-
действительную и мнимую часть, полагая vq = v\ + гЧ>2, мы получаем,
что и v\, и t>2 также являются собственными функциями, со-
соответствующими собственному значению Ло'. Lvk = Аои*(:к),
к = 1,2 (т.е. кратность с. зн. удваивается).
7) Так как по доказанному в теоремах 1 и 2 операторы А
и А положительны, то все собственные значения задач A),
\2) и A), C) неотрицательны, что следует также из инте-
интегральных тождеств D), E) при Ф = и, так как ||u||l2(X2) = 1-
Действительно, подставляя в D) вместо Ф собственную фун-
функцию v(x), получаем в задаче Дирихле
n k-1 n
n *=1
+ j p(x)a(x)\v\*ds = A|H|i,(n)>0
an
в задаче (З).
Обозначим через L дифференциальный оператор, за-
заданный дифференциальным выражением из A) с областью
о
определения W\{&) в задаче Дирихле и Wjf(i?) в задаче
C). Установим, когда А = 0 будет собственным значением
оператора L. Имеет место следующая
310 Глава VII. Задачи на собст. зн-я и метод Фурье...
Теорема 3. Для того чтобы Л = 0 было собственным зна-
значением оператора L, заданного уравнением A) с областью
о
определения W\(O) в задаче B) и областью определе-
определения ]¥^(О) в задаче C) необходимо и достаточно, чтобы
q(x) = О, а{х) = 0 (т.е. когда рассматривается задача
Неймана при q(x) = 0 в уравнении A)). При этом А = 0 -
простое (однократное) собственное значение, и v(x) = const
- соответствующая ему собственная функция.
Доказательство. (Необходимость) Пусть Л = 0 - собствен-
собственное значение оператора L, a v(x) = const ф 0 - соответству-
соответствующая ему собственная функция.
Рассмотрим определение обобщенного решения в форме
E) и подставим в него вместо Ф(х) функцию v(x) € Й^(Л)
(в задаче Дирихле вместо Ф(х) подставим функцию v(x) €
о
W\№)i B этой задаче отсутствует интеграл по границе дB,
т.е. используется интегральное тождество D)). Тогда полу-
получаем
+
фОН2]<*г + I p(x)a(x)\v\2ds = О,
[
п k=l an
откуда находим, что p(z)|Vu| = 0, qv = 0, т.е. v = const,
q(x) = 0, x € 42, а из граничного интеграла получаем &(х) =
0,х€ дП.
Необходимость доказана. Одновременно доказано, что
v(x) = const - единственная собственная функция, соответ-
соответствующая собственному значению Л = 0, т.е. собственное
значение Л = 0 однократно.
(Достаточность) Пусть q(x) = 0, сг(х) = 0, и рассматри-
рассматривается задача C) (очевидно, в задаче Дирихле значению
Л = 0 соответствует v(x) = 0, т.е. Л = 0 не является соб-
собственным значением). Тогда задача A), C) имеет вид
-div(p(x)Vu) = Ли, х € Q,
dv
дп
an
= 0.
Гл. VII, § 2. Свойства собст. значений и ... 311
Используя для этой задачи интегральное тождество E) (при
q(x) = О, <т{х) = 0), получаем, что v(x) = const соответ-
соответствует собственному значению Л = 0.
Теорема доказана.
Изучим свойства обобщенных собственных функций за-
дач A), B) и A), C).
Все собственные значения рассматриваемых нами задач
можно перенумеровать в порядке возрастания их величин
0 < Ai < А2 < ... < Хк < ...,
повторяя при этом А* столько раз, какова его кратность.
Тогда каждому А* будет соответствовать только одна обоб-
обобщенная собственная функция
v2(x), ..., vk(x), ..., A8)
при этом vk(x) взаимно ортогональны в пространстве
о
W\{fi) в задаче Дирихле B) и в пространстве W
() ||||
\{) р ()
задаче C), кроме того ||г>*||£,2(я) = 1.
Теперь перед нами стоит задача о разложении в ряды
о
Фурье функций <р(х) из Z^fi), из W\(^) и из Wj (J2) и ис-
исследования сходимости этих рядов. Для этого надо узнать,
когда собственные функции образуют базис в соответствую-
соответствующих пространствах.
Рассмотрим операторные уравнения A4), A7), подста-
подставив в них Хк и Vk(x):
A9)
B0)
О
Умножим A9) скалярно в W\(Q) на vk(x), получим, ис-
используя A1):
B1)
= (л* + !)(«*» «*IЯ(Я) = Afc + 1.
Из B1) следует, что система
312 Глава VII. Задачи на собст. зн-я и метод Фурье...
B2)
является ортонормированной в \{
Аналогичная процедура умножения B0) на и* скалярно
в W^fi) приводит к соотношению
со скалярным произведением в W^O), задаваемым форму-
формулой A6) (в задаче A), C)). Из B3) следует, что система
Щ .. B4)
для задачи C) является ортонормированной в
Из курса функционального анализа известна теорема
Гильберта - Шмидта:
Для любого линейного вполне непрерывного самосопря-
самосопряженного оператора А в гильбертовом пространстве Н (А :
Н —► Н) существует ортонормированная система {е*} соб-
собственных элементов и соответствующих им собственных зна-
значений {Afc} такая, что произвольный элемент <р € Н пред-
оо
ставляется единственным образом в виде ip = ^ Vfcefc + <p't
где <р' удовлетворяет условию: А<р' = 0 (т.е. у>' - ядро опера-
оо
тора А), ряд Фурье ^ <fkek сходится в Я, А<р разлагается
в ряд Фурье вида
оо
по системе
Теорема Гильберта - Шмидта имеет важное следствие:
Гл. VII, § 2. Свойства собст. значений и ... 313
Следствие. Если у линейного вполне непрерывного само-
самосопряженного оператора А: Н —► Н ядро тривиально, то си-
система {е*} является ортонормированным базисом простран-
пространства Н.
Напомним, что ортонормированная система {ei,e2,...,
ejt,...} называется полной или ортонормированным базисом
пространства Н, если любой элемент <р € Н может быть
оо
разложен в ряд Фурье <р = J2 ¥>*е* по этой системе, схо-
дящейся в Н. Используя следствие из теоремы Гильберта
- Шмидта получаем, что полученная нами система B2),
о
(B4)) является ортонормированным базисом в W\№) (B
W2l(i2)). А так как пространство W\{i2) (и W2\i2)) бес-
бесконечномерно, то множество B2) (и B4)) бесконечно. По-
Поэтому А* —► оо при к —► оо. Покажем, что система A8) ор-
ортонормирована в Ьг(^). Действительно, если операторное
о
уравнение A9) для Vk умножить скалярно в W\{.^) на vji
j ф к и, соответственно, B0) умножить скалярно в W
на vj, j ф к, то используяA1) и A5) получим
0 = {vk,vj}wi(n) = {(А + l)Avk,Vj}wi(n) =
Таким образом, система A8) ортонормирована в Z^^)- Так
о
как система B2) есть ортонормированный базис в w\{Q),
(и соответственно, B4) в W^ift)), то линейное многообра-
многообразие натянутое на эту систему, а значит систему A8), всюду
О О
плотно в w\(Q) (и соответственно, в W^i?)). Но w\ {ts.
W%) всюду плотно в Li2{£2), следовательно, система A8) яв-
является ортонормированным базисом в L2("I?), т.е. любой эле-
элемент <р(х) € Ьъ({}) разлагается в сходящийся в Ьг(/2) ряд
Фурье
314
Глава VII. Задачи на собст. ан-я и метод Фурье...
оо
B5)
где ipk = ((f,Vk)b2(n) есть коэффициенты Фурье функции
<р(х) по системе Vk(x), и имеет место равенство Парсеваля
оо
B6)
о
Кроме того, если у>{х) G W\(f2)i то она разлагается в ряд
Фурье по ортонормированному базису B2):
liwlifi) y/Xk + 1
B7)
и имеет место равенство Парсеваля
'i(fl)
B8)
Согласно нашим определениям скалярных произведений,
ряд B7) сходится и в £г(^) к функции <р(х).
Сравним теперь ряды B5) и B7), получим
, B9)
Из равенства Парсеваля B8) и равенства B9) получаем
k=l
Гл. VII, § 2. Свойства собст. значений и ... 315
откуда следует, что
или, так как А* > О,
C0)
Аналогичное неравенство
Х>Ы2 < IMI2^) (si)
имеет место для <р(х) G W
Резюмируя все вышесказанное, мы получаем следующую
основную теорему:
Теорема 4. Решение задач на собственные значения A),
B) и A), C) обладает следующим свойствами:
1) Множество собственных значений счетно и не имеет
конечных предельных точек: А* —► +оо при к —► оо; ка-
каждое собственное значение имеет конечную кратность. Все
собственные значения неотрицательны, они являются поло-
положительными в задаче Дирихле и в третьей краевой задаче.
Задача Неймана при q(x) = 0 имеет однократное нулевое
собственное значение, которому соответствует обобщенная
собственная функция v(x) = const.
2) Обобщенные собственные функции Vi(x),V2(x),... за-
задач A), B) и A), C) образуют ортонормированный базис в
Ьг(^), т.е. любая функция <р(х) € Ьг(^) разлагается в ряд
Фурье
<Рк = (ф,Ук)ьг(П), C2)
316 Глава VII. Задачи на собст. зн-я и метод Фурье...
о
сходящийся в L2(i7). Если р(х) € W\№)-> то РЯД C2) по
обобщенным собственным функциям задачи Дирихле схо-
о
дится в W\(£l) (т.е. вместе с первыми обобщенными произ-
производными), и имеет место неравенство
Если <р(х) € W^fl), то ряд C2) по обобщенным собствен-
собственным функциям задачи A), C) сходится в W^J?), и имеет
место неравенство
§ 3. Вариационный принцип собственных
значений и собственных функций. О точной
постоянной в неравенстве Фридрихса
Оператор А, определяемый равенством A1) § 1 является
ограниченным, положительным, самосопряженным, вполне
непрерывным оператором в гильбертовом пространстве
W\(£2) (и соответственно А: в W^i?)). Из теории таких
операторбв известно, что характеристические функции и
характеристические значения могут быть получены следу-
следующим вариационным методом. Первое наименьшее харак-
характеристическое число (с использованием A3) и A1) из § 1)
равно
= mf 73 г = inf
Гл. VII, § 3. Вариационный принцип собст. значений ... 317
при этом функционал ||и||20 ^ /1М112(Л) принимает зна-
значение fii при v = г>1, где v\ - первый собственный элемент
оператора А.
Далее, (к + 1)-е характеристическое число оператора А
равно
IMI2. IMI2.
так как
Тогда, используя соответствующие скалярные произведения,
получаем, что первое наименьшее собственное значение за-
задачи Дирихле для оператора L с областью определения
о
W\(^) определяется следующим образом:
J\p(x)\Vv\2+q(x)v2]dx
п 5 A)
п
и точная нижняя грань функционала и—— на
J «2dx
п
о
пространстве W\(fi) достигается на, первой собственной
функции v\(x). Далее, (к + 1)-е собственное значение за-
дачи Дирихле для оператора L с D(L) = W\{Q) есть:
inf
J\p(x)\Vv\2+q(x)v2]dx
[vdx
1 = 1,2,...,*
318 Глава VII. Задачи на собст. зн-я и метод Фурье...
при этом точная нижняя грань функционала
f
на подпространстве пространства
тг—
а
i состоящем из всех функций v(x), ортогональных
в Ьг(/2) к предыдущим собственным функциям vi(x),V2(x),
...,Vk(x) рассматриваемой краевой задачи, достигается на
собственной функции Vk+i(x).
Аналогичные утверждения имеют место для других кра-
краевых задач.
Следствие. О точной постоянной в неравенстве Фрид-
рихса.
Рассмотрим задачу на собственные значения для опера-
оператора Лапласа в обобщенной постановке в ограниченной об-
области i?:
Ли = Ли, v = 0. B)
an v
Тогда из A) для наименьшего собственного значения имеем
оценку
ч S
J v2dx
п
откуда получаем неравенство Фридрихса
П П
- на-
нас точной (наилучшей) постоянной С* = j-, где
именьшее собственное значение задачи B). Экстремальной
же функцией, для которой неравенство C) превращается в
равенство, является собственная функция, соответствующая
собственному значению Ai.
Гл. VII, § 4. Обоснование метода Фурье для гипер. уравн.... 319
С другой стороны, знание постоянной C(i2) в неравен-
неравенстве Фридрихса
n n K-J
дает оценку снизу для первого (минимального) собственного
значения, так как С* = -ц <С(П), откуда Ai > щщ-
§ 4. Обоснование метода Фурье для
гиперболического уравнения в пространстве
Соболева
Вернемся к обоснованию метода Фурье для гиперболиче-
гиперболического уравнения. Начнем с исследования однородного ура-
уравнения
-^ - div , (p(:r)grad xu} + q(x)u(x, t) = 0 A)
в области QT = {x,t : х € п С Ип, 0 < * < Т}, (П -
ограниченная область) с начальными условиями
du(t,x)
dt t=o
и граничным условием Дирихле
и
= 0, 5 = а/2х[0,Т]. D)
Обоснование метода Фурье для уравнения A) с началь-
начальными условиями B), C) и граничными условиями вида
а(х)и +
ди
дп
= 0
320 Глава VII. Задачи на собст. зн-я и метод Фурье...
при одновременном неравенстве нулю q(x) и <т(х) прово-
проводится по ниже приведенной схеме. Бели q(x) — о{х) = 0,
необходимо только учесть, что первое собственное значение
Ai равно нулю, и ему соответствует собственная функция
i>i = const.
Пусть р(х), q(x) е С(п), р(х) > ро > 0, q(x) > 0, ф(х) €
L2(Q), y(x)ew
Определение. Обобщенным решением задачи A) - D) на-
называется функция u(t, x) € W2 х г(Ят), если она удовлетво-
удовлетворяет начальному условию B), граничному условию D) (в
обобщенном смысле) и интегральному тождеству
Qt fc=1
Qt ' ' E)
= I фФ(х,0)<1х
По
для любой Ф(г,х) € W^'xtiQT) такой, что #|s = О,
Для удовлетворения последнему условию Ф(Ь, х) можно
t 0
взять в виде: Ф^,х) = Jr)(r,x)dr, где r)(t,x) € W2'x AQt)-
т
Из энергетических оценок § 1 главы V следует единствен-
единственность введенного обобщенного решения. Перейдем к реше-
решению задачи A) - D) методом Фурье.
Итак, ищем решение u(t, x) задачи A) - D) в виде
u(t,x) = T(t)v(x).
Тогда для v(x) получаем исследованную нами выше задачу
на собственные значения для эллиптического уравнения
- div(p(x)Vvk(x)) + q(x)vk = \kvk(x), x € i?,
F)
Гл. VII, § 4. Обоснование метода Фурье для гипер. уравн.... 321
a T(t) удовлетворяет уравнению
T'k'(t) + XkTk(t) = 0. G)
для найденных в задаче F) с. зн. А*.
Нами доказано, что существует ортонормированная в 1г(^)
система обобщенных собственных функций
ui(x), v2(x), ..., ufc(x), ... (8)
задачи F), которая является ортонормированным базисом в
L2(O). Системе (8) соответствует последовательность соб-
собственных значений
0 < Aj < А2 < ... (9)
(так как мы рассматриваем задачу Дирихле, то все А* >
0), причем каждое А* повторяется в последовательности (9)
столько раз, какова его кратность, А* —♦ оо при к —► оо.
Общее решение Т*(<) уравнения G) равно
Tk(t) = ак cos(v/AT<) + Ьк sin(>/M)- A0)
Очевидно, Tk(t) - гладкая функция t, поэтому
Tk(t)ew^[o,T].
Рассмотрим ряд
оо оо
u(t,x) = 2_]uk{t, x) — 2_\Tk{t)Vk{x) =
к=1 *=1 (п)
cos(tу/Хк) + bk six
ib=i
Постоянные ак и Ь* однозначно определяются из начальных
условий
u(t, x) = 2_, akVk(x) = if(x),
t=0 k=l
21 - В. Н. Масленникова
оо
322 Глава VII. Задачи на собст. зн-я и метод Фурье...
т.е. ак = ((p,Vk)b2(t2) = <Pk, A2)
du(t,x)
dt
t=0 *=1
т.е. Ьк = -j==(^,vk) = ~р=Фк- A3)
Таким образом,
u(t,x) -
Обоснование метода Фурье состоит в исследовании сходи-
сходимости ряда A4) и проверке того, когда он дает обобщенное
решение задачи A) - D) в смысле интегрального тождества
E).
Имеет место
Теорема 1. Если п - произвольная ограниченная область,
р(х), q(x) е С(П), р(х) > ро > 0, q{x) > 0, ф) € W\(U),
ф € Ьг{п), тогда ряд A4) и ряды, полученные после одно-
однократного дифференцирования по t и х,, сходятся в норме
1*2@) равномерно по t € [О, Т]. Сумма ряда есть обобщен-
обобщенное решение задачи A) - D) в смысле интегрального то-
тождества E).
о
Доказательство. Так как у?(ж) € W\(fi), то ряд ip(x) =
оо о
Щ У*и*(ж) сходится в норме W\(O) и имеет место равен-
оо
ство Парсеваля ]£ у>\ — ||v|lx, iq\ и неравенство
ib=i n ;
• Так как ф(х) € L2(Q), то ряд
Ф(х) — Е ФкУк(х) сходится в норме Zi2(f2) и имеет место
равенство Парсеваля
Гл. VII, § 4. Обоснование метода Фурье для гипер. уравн.... 323
*=1
Рассмотрим частичные суммы ряда A4):
/ /(x). A5)
Для этих частичных суым получаем
N
так как ||«*(а;)|||2(л) = 1, (^,«1ьЬ2(Л) = £*, где ^ -символ
Кронекера.
Для оценки первых производных по х от ряда A4) ис-
используем введенное нами скалярное произведение F) из § 1
о
(которое порождает обычную норму в W\{^))i и интеграль-
интегральное тождество D) § 1, в которое вместо Ф(х) подставлено
(), т.е. тождество
/ [Е РМ
() 2 К\ j v\dx.
[
п i=1 п
Получаем
21*
324 Глава VII. Задачи на собст. зн-я и метод Фурье...
N ,
{SN, SN}. = YV ^
2< ' t=\
+q(x)vl(x)]dx =
n i=1
N .
ЛЙ ^ ^2 < A7)
Для производных по t имеем
N
Далее, существует Nq(e) такое, что ViV > JV0 и V* € [О, Г]
выполнено
N .
<2 Т (<рк + р.)<е, A9)
откуда следует, что ряд A4) сходится в ^(Л) равномерно
по t € [О, Т]. Аналогичным образом доказывается, используя
A7) и A8), что ряд для первых производных по ж,- и t от
и(х,<) сходится в 1<2(Л) равномерно по < € [0,Т]. Поэтому
можно перейти к пределу в A6) - A8) при N —»■ оо.
Таким образом, мы доказали, что ряд A4) и ряды, по-
полученные дифференцированием A4) по х^ и t, сходятся в
^(Л) равномерно по t € [О, Г], т.е. они сходятся в Ьг{С}т)-
Гл. VII, § 4. Обоснование метода Фурье для гипер. уравн.... 325
Покажем, что ряд A4) есть обобщенное решение задачи
A) - D) в смысле интегрального тождества E). Докажем
сначала, что частичная сумма ряда A4)
N
UN(t,x) = V^jfcCOS
удовлетворяет интегральному тождеству E), переходя затем
к пределу при JV —► оо, ввиду сходимости ряда A4) вместе
с его первыми производными по Xi и t, мы получим, что ряд
A4) есть обобщенное решение. Используя свойства функций
Tk(t), 4>(x,t) и уравнение G), рассмотрим
Qt П
п
= - J vk(x)TUmt, x)\*^ + JI »*(хJУ @ х С20)
п по
х Ф(г, x)dx dt = ij>k j vk(xL>@, x)dx-
i
- J J vk(x)\kTk(t№{t, x)dt dx.
n о
Тогда, используя B0) и определение обобщенной собствен-
собственной функция для задачи F), получаем для частичных сумм
326 Глава VII. Задачи на собст. зн-я и метод Фурье...
£ / [p
к=1А
•д(х)и*(х,*)-Ф(х,*)-
dt dt
N T
dukd*]dxdt = Y lTk{t)dt /[p(x)Vxv*Vx£+
vk(x№@,t)dx = "£,4>k
N , N
Переходя в B1) к пределу при JV —» оо, мы получаем, что
ряд A4) для u(t,x) удовлетворяет интегральному тождеству
E).
Теорема доказана.
Рассмотрим теперь начально-краевую задачу Для неод-
неоднородного уравнения
Lu(x,t) = f(x,t), B2)
где дифференциальное выражение Lu определено левой ча-
частью уравнения A), а начальные условия B), C) теперь
можно взять однородными
u(x,t) =0, ^ =0, B3)
t=o
t=o
граничное условие имеет вид D).
Пусть f(x,t) € Lz(Qt) и коэффициенты уравнения B2)
удовлетворяют выше указанным условиям.
Определепже. Обобщенным решением задачи B2), B3),
D) называется функция u(t,x) € W^xiQr), если она удо-
удовлетворяет граничному условию D), начальному условию
и(х,0) = 0 (в обобщенном смысле) и интегральному то-
тождеству
Гл. VII, § 4. Обоснование метода Фурье для гипер. уравн.... 327
А ди дФ(г,х) , дидФл
E')
Qt
для любой пробной функции Ф{1,,х) € W2 \ x{Qt) и такой,
что Ф
s
t=T
= 0.
Для решения в обобщенной постановке E') методом
Фурье задачи B2), B3), D) разложим f(x,t) в ряд Фурье
по обобщенным собственным функциям задачи F). Так как
по теореме Фубини для f(x,t) € Z<2(Qt) имеем f(x,t) €
L2(O) для почти всех значений t € @,Т), то f(x,t) —
оо
Е /*(*)"*(*)> гДе /*(*) = J f(x,t)vk{x)dx, k = 1,2,...,, при
fc=i п
этом имеет место равенство Парсеваля
Е/?(*)= [f4*,t)dx B4)
*=1 о
n
и равенство
~ т
= f f(x,t)dxdt. B5)
*='0 QT
Как и ранее, решение задачи B2), B3), D) ищем в виде
ряда
)> B6)
где ujt(x) - обобщенные собственные функции задачи F), а
для определения Т*(<) получаем неоднородное обыкновен-
обыкновенное дифференциальное уравнение
328 Глава VII. Задачи на собст. зн-я и метод Фурье...
TH(t) + XkTk(t) =
Его решение имеет вид
Tk(t) = -±= Jfk(r)sm((t -
о
Решение задачи B2), B3), D) получаем в виде ряда:
со <
u(t, x) = T -y^Vkix) / Д(г) sin(* - T)y/Tk)dT. B7)
По аналогии с оценками A6) - A9) для частичных сумм
ряда B7) получаем оценки
N
B8)
*=i0
N Т
- Е / /* Wd*' B9)
TV
Переходя в них к пределу при N —♦ оо получаем, что ряд
B6) сходится в Ьг{0) вместе с первыми производными по
Xj и t равномерно по t € [0, Г].
Суммируя все сказанное для решений задач A) - D) и
B2), B3), D) мы получаем для решения уравнения B2) с
начальными и граничными условиями B) - D) оценку
Гл. VII, § 4. Обоснование метода Фурье для гипер. уравн.... 329
где постоянная С(Т) зависит только от Т и не зависит от
(р{х), ф(х), f(x,t).
Она получена с помощью интегрирования оценок A6) -
A8) и B8) - C0) при N = оо по t от 0 до Г и использования
равенств Парсеваля
оо оо
*=1
неравенства ]£ А*|у>*|2 < ||у»|| о и равенства B5).
ib=i w\(n)
Тот факт, что сумма ряда B6) есть обобщенное решение
задачи B2), B3), D) в смысле интегрального тождества E')
доказывается таким же путем, как для однородного уравне-
уравнения A) в обобщенной постановке E).
Таким образом имеет место следующая
Теорема 2. Если п - произвольная ограниченная область,
р(х), q(x) е С(П), р(х) > ро > 0, q(x) > 0, f(x, t) € L2(QT),
тогда ряд B7) и ряды, полученные однократным дифферен-
дифференцированием по t и х,-, сходятся в норме 1*2(^) равномерно
по t € [0, Г]. Сумма ряда есть обобщенное решение задачи
B2), B3), D) в смысле интегрального тождества E').
о
Если (р(х) € W\(Q), ф(х) € L2(O), то обобщенное ре-
решение задачи B2), B) - D) удовлетворяет оценке C1).
330
Глава VIII. Метод Галеркина для
нахождения приближенных
решений
§ 1. Метод Галеркина для приближенного
обобщенного решения задачи Дирихле для
уравнения Пуассона
Решения краевых задач для эллиптических уравнений
могут быть найдены как пределы приближенных решений,
вычисленных до методу Галеркина. При этом указанный ме-
метод хорошо применять в пространствах Соболева.
Рассмотрим этот метод на примере задачи Дирихле для
уравнения Пуассона:
- д„ = /(х), х е п с и", п -
область, (л\
и(х) = 0.
v ' an
Идея этого метода состоит в следующем. В пространстве
о
W\{ft) берется какая-нибудь полная, линейно-независимая
система функций {/*(х)}, принадлежащих области опреде-
определения дифференциального оператора, и решение краевой
задачи ищется в виде линейной комбинации этих функций
с неизвестными коэффициентами. Неизвестные коэффици-
коэффициенты определяются как решения или алгебраической си-
системы (в стационарных задачах), или системы обыкновен-
обыкновенных дифференциальных уравнений (в нестационарных за-
задачах).
Определение. Линейно-независимая система функций
о
{/*(х)} называется полной в W\(ft), если для любой фун-
о
кции и(х) € W\(u) и для любого е > 0, найдутся такие
номер N € 2+ и постоянные Cnu € И1,
Гл. VIII, § 1. Метод Галеркина .,. 331
Это означает, что любую функцию и(х) € W 1№) можно
сколь угодно точно приблизить конечной линейной комби-
комбинацией по системе /&(х). Бели h(x) ортонормированы, то
N
J2 CNkh(x) - отрезок ряда Фурье.
Jt=i
Функции h(x), к = 1,2,..., называются линейно-незави-
линейно-независимыми, если любое конечное число из них линейно незави-
независимо.
о
Отметим, что пространство W\(fl), как гильбертово
пространство, сепарабельно, отсюда будет следовать суще-
существование полной линейно-независимой системы. Какую кон-
конкретно полную линейно-независимую систему взять для при-
приближенного решения той или иной задачи, зависит, конечно,
от конкретной задачи и вида области п.
Примеры
1) Пусть п - прямоугольник в Ш.2:
п = {х,у : 0 < х < а, 0 < у < Ь}.
О
Полную в W\{Q) систему образуют функции
. тпх . тгту
*тп(*,У) = мп sin——, п,т = 1,2,...
а о
Это вытекает из разложимости любой гладкой функции, за-
заданной в Q, обращающейся в нуль на дП, в двойной триго-
тригонометрический ряд Фурье (доказывается в анализе).
2) Пусть Q - внутренность эллипса:
Тогда полную систему в W\№) образуют функции
332 Глава VIII. Метод Галеркина для нахождения ...
Метод Галеркина состоит в следующем. Ищем приближен-
приближенное решение нашей задачи A) в виде
N
Подставим это приближенное решение в уравнение Пуас-
Пуассона, умножим его на базисную функцию lj(x), тогда после
интегрирования по Q и по частям это приближенное реше-
решение будет удовлетворять интегральному тождеству:
{«*(*),/,-(*)} = (/(*),/,•(*)), з = 1,..,N. B)
Из этого интегрального тождества и будут определяться не-
неизвестные постоянные Смк(к = 1,2,..., iV), так как B) пред-
представляют собой N линейных алгебраических уравнений, от-
относительно неизвестных С^к-
Таким образом, требуется чтобы и^(х) удовлетворяла
интегральному тождеству, которому обычно удовлетворяет
обобщенное решение задачи A):
C)
где
n *=1
не для любых Ф(х), а только для Ф{х) — lj(x), j = 1,..., N.
Бели для исходной задачи справедлива теорема един-
единственности, а в нашем случае задачи A) это имеет место, то
система B) оказывается однозначно разрешимой, и ее реше-
о
ния un(x) стремятся при N —► оо в норме W\(Q) к обоб-
обобщенному решению задачи A). Отметим, что метод Галер-
Галеркина является достаточно универсальным, т.е. применим к
Гл. VIII, § 1. Метод Гаяеркина ... 333
широким классам уравнений разных типов (эллиптических,
параболических, гиперболических) и к уравнениям, не при-
принадлежащим к определенному типу с переменными коэффи-
коэффициентами, в том числе и высокого порядка как в ограничен-
ограниченных, так и в неограниченных областях. Для решения задачи
A) докажем следующую теорему.
Теорема.
1. Для любого натурального числа N > О существует и
притом единственное решение галеркинских уравнений B).
о
2. При N —* оо un(x) —► и(х) в норме Wl(fl), где и(х)-
обобщенное решение задачи A) в смысле интегрального то-
тождества C).
Доказательство. Систему B)
N
Jt=i
можно записать в виде
N
J^CN^kj^fj, ;=l,...,iV, D)
Jt=i
где числа
n
, ={lk(x), fa)} = yg ^ ^ dx.
Определитель системы D)
совпадает с определителем Грама линейно-независимой си-
системы функций
334
Глава VIII. Метод Галеркина для нахождения ...
По определению, определителем Грама линейно-независи-
линейно-независимой системы {<Pj{x)}, j = 1,..., N, из гильбертова простран-
пространства Z-2 называется определитель из скалярных произведе-
произведений
\
= det
( f 2 , f f
I u>idx, I u>i<p2dx, ..., /
J J J
n a n
/ (pNVidx, / <pN<p2dx, ..., /
В случае линейно-независимых функций определитель от-
отличен от нуля, точнее: определитель Грама равен нулю то-
тогда и только тогда, когда элементы {<fj} линейно зависимы.
В нашем случае определитель Грама состоит из скалярных
произведений {•,•} в пространстве w\{^)'
Так как по предположению наша система {lj(x)} линей-
линейно-независима, ее определитель Грама отличен от нуля, по-
поэтому система D), как алгебраическая система относительно
неизвестных C7jvfc, к = 1,2, ...,N, однозначно разрешима.
2. Докажем, что галеркинские приближения сходятся к
о
обобщенному решению нашей задачи в норме W\(Q), опре-
определяемой формулой
= (j(Vu)*dx)
n
l/2
Обозначим через Ln конечномерное подпространство про-
о
странства W\(fl), натянутое на векторы Ii(x),l2(x),...,
In(x), т.е. Фаг € Ln = £(//)
если
N
Гл. VIII, § 1. Метод Галеркина ... 335
Умножим равенство
(x),Ii(*)} = (f,h), J = 1, -, JV, B)
на произвольные числа a^j и просуммируем по j от 1 до N,
получим
Сначала докажем, что последовательность норм ||идг|| о х
равномерно ограничена. Для этого в F) положим Фн = идг,
получим
1l{~^~) dx= I f(x)uN(x)dx.
»=1 о
п '-1 п
Правую часть оценим с помощью неравенства ab < ^а2
|Ь2 и неравенства Фридрихса, получим
J f(x)uN(x)dx <±J f\x)dx + £-J u%(x)dx <
n n n
n n
Выбрав e > 0 столь малым, чтобы 1 — |C7(/2) = С > 0, мы
получаем равномерную по N оценку
п t=1 я
а из неравенства Фридрихса и оценку
п п
336 Глава VIII. Метод Галеркина для нахождения ...
Из равномерной ограниченности последовательности
в норме W\(^) следует, что из {upj} можно выбрать слабо
сходящуюся подпоследовательность {«#*}> т.е. такую под-
подпоследовательность, что {uNk} и { д^к } слабо сходятся к
и(х) и J^r соответственно.
Тогда в F) можно перейти к пределу по выбранной под-
подпоследовательности Nk, к = ко,ко + 1,..., зафиксировав
(ж), и получить в пределе
Индекс ко здесь произволен, так что G) справедливо
Yl aNkh(x) с любым N. Но такие Флг(ж) плотны в
о
так как {/fc(a;)} полная система в W\(^), поэтому функция
о
и(х) будет удовлетворять G) УФ € W\(fl), следовательно,
предельная функция будет обобщенным решением рассма-
рассматриваемой задачи. В силу единственности обобщенного ре-
решения задачи, можно сделать заключение, что вся последо-
последовательность un(x) сходится к обобщенному решению. Пере-
Переходя в G) к пределу при Nk0 —* оо, получим
{и{х),Ф(х)}.=(/,Ф), (8)
W 2
т.е. предельная функция и(х) есть обобщенное решение за-
задачи A).
Последовательность {идг(ж)} сходится к обобщенному
о
решению в смысле (8) не только слабо, но и в норме W\(ft),
т.е. сильно.
Действительно, в силу полноты системы {fjt(z)} B гиль-
о
бертовом пространстве W\ линейная оболочка Ln: Li С
оо о
L2 С L3 С ... С ... обладает свойством (J Ln = W\(Q),
т.е. замыкание объединения всех Ln, N = 1,2,..., совпадает
Гл. VIII, § 2. Метод Галеркина для ... 337
о
с W\(ft), поэтому проекция IIpLAr и(х) = и^{х) —► и(х) в
О
норме W\(ft) при JV —»■ оо.
Теорема доказана.
§ 2. Метод Галеркина для приближенного
решения первой начально-краевой задачи
для уравнения теплопроводности. Теорема
единственности обобщенного решения
Рассмотрим решение уравнения
du(t,x)
dt
-Au = f(x,t) A)
в ограниченной области Q = п х (О, Т] - цилиндре, удовле-
удовлетворяющее начальному условию
u(t,x) =0, ieficln, B)
t=0
и граничному условию
и= 0, C)
где S - боковая поверхность цилиндра Q: S = дп х [0, Г].
Рассмотрим задачу A) - C) в обобщенной постановке. Пусть
Определение. Назовем обобщенным решением задачи A)
- C) функцию u(t,x) e W гхх,(Я) (т-е- Функцию, имеющую
первые обобщенные производные по ж, яз L2(Q)c гранячяым
условием и = 0), которая удовлетворяет интегральному
s
тождеству:
Q
22 - В. Н. Масленникова
D)
i=i '"" "■''"'
338 Глава VIII. Метод Галеркина для нахождения ...
V функции Ф{г,х) € W2^]t(Q) такой) что
Ф
t=T
= 0, Ф
= 0.
В качестве пробной функции Ф(г, х) можно брать фун-
функции вида
t
#(*,*) = JV(r,x)dT, E)
где r)(t, x)
т
о
Теорема единственности. Обобщенное решение задачи A)
- C) единственно.
Доказательство. Положим в D) / = 0, докажем, что тогда
u(t,x) = 0 в Q. Из D) имеем
- // u^-dxdt +[fy P^^L
JJ & JJ ^ дх{ dxi
Q Q t=1
y P^ = 0. F)
J ^ дх{ dxi K }
Q t=1
Мы не можем здесь положить Ф = u(t,x), как делали это в
эллиптическом случае, так как u(t,x) не имеет производной
по t и начальные условия у нее не те, что у Ф(£, х).
t
Для доказательства положим Ф{1, х) = J и(т, x)dr и под-
т
ставим ее в F). Получим
ПО 17 0 t—1
Обозначим
Гл. VIII, § 2. Метод Галеркина для ... 339
t
/ди , . dzt ди
дх{
т
и мы получаем
Q Q
или
- JJ
u2dxdt ~\
откуда следует, что u(t,x) = 0, (x,t) € Q.
Теорема единственности доказана.
Существование решения.
о
Обозначим через {1ь(х)} полную в W\{0) линейно не-
независимую систему функций, где п С Ш.п.
Приближенное решение задачи A) - C) ищем в виде:
N
». (8)
где CNk(t) — функции, зависящие от t. Подставим это
и^(г,х) в наше уравнение, умножим его на функцию lj(x),
проинтегрируем по х по области Q и по частям. Получаем
n t=1 п
Подставляя в (9) upf(t, x) из (8), получаем
340 Глава VIII. Метод Галеркина для нахождения ...
N
Nk(*) f lk(x)lj(x)dx+
fc. 3 J 3
п
(Ю)
где
™KK> dt
Зададим начальные условия для Слга-(О: пусть Сл^л-(О) =
0, тогда приближенное решение будет удовлетворять нуле-
нулевым начальным условиям. Обозначим матрицы из скалярных
произведений:
/ h{x)lj{x)dx =akj,
п
п i=1
Для определения Cjvjk(<) получаем задачу Коши для си-
системы обыкновенных дифференциальных уравнений
N
к=\
Так как постоянная матрица акз невырожденная (она есть
матрица из скалярных произведений полной линейно не-
независимой системы), правые части fj(t) - интегрируемые
на [0, Т] функции, то по известной теореме о разрешимости
таких систем обыкновенных дифференциальных уравнений
заключаем, что решение задачи A1), существует и един-
единственно, причем CNk(t) будут абсолютно непрерывными на
Гл. VIII, § 2. Метод Галеркина для ... 341
[О, Т] функциями. Напомним, что функция f(t) называется
абсолютно непрерывной на отрезке [а, Ь], если Ve > 0 36 > О,
что для любой конечной системы попарно не пересекаю-
пересекающихся интервалов (ai,bi),(a2,b2), ...,(an, Ьп), для которой
п
J2 (bfc — ait) < 6, выполняется неравенство
Wk) fM\ e.
*=i
Абсолютно непрерывная функция почти всюду имеет про-
производную, которая является интегрируемой функцией, и аб-
абсолютно непрерывная функция представима (с точностью
до постоянной) в виде интеграла Лебега с переменным вер-
верхним пределом от своей производной. Осталось доказать,
что приближенное решение (8), с коэффициентами, опреде-
определенными из A1), сходится к обобщенному решению нашей
задачи.
Для этого докажем равномерную относительно N оценку:
dx + C
о и
\ f[uN{t,x)?
о и -i A2)
<С2 I I f(t,x)dxdt.
о п
Для ее доказательства равенство (9), из которого мы нашли
наше приближенное решение, умножим на C^vj(i), проинте-
проинтегрируем по t от 0 до t < Т и просуммируем по j от 1 до JV.
Получим
on о п
t
= J J f(t,x)uN(t,x)dtdx.
п
о п
342 Глава VIII. Метод Галеркина для нахождения ...
Преобразуем первый член слева, он равен
HI m(UNJdxdt=\J
HI J
on n
кроме того, интеграл справа оценим с помощью неравенства
ab < j^a2 + |Ь2. Применяя неравенство Фридрихса, полу-
получим:
jj f(t,x)uN(t,x)dtdx <Jj[^£f2dx
on on n
n l=1 n
где е - положительное число.
Выбирая £ столь малым, чтобы было |Сл < 1, получаем
искомую оценку A2).
Заметим, что оценка A2) равномерна по N (правая ча-
часть A2) не зависит от N). Из нее следует, что норма
ограничена равномерно по iV, а из неравенства Фридрихса
следует, что норма
также ограничена равномерно относительно N.
Воспользуемся теоремой о слабой компактности огра-
ограниченного множества из гильбертова пространства, откуда
следует, что из последовательности {идг} можно выбрать
Гл. VIII, § 2. Метод Галеркина для ... 343
подпоследовательность {и^„}, слабо сходящуюся в Q, т.е.
такую, что
ел.
ди
Докажем, что слабый предел u(t, x) есть обобщенное реше-
решение нашей задачи в смысле определения D).
Мы имеем интегральное тождество (9) для идг(£,х) (за-
(запишем интегралы через скалярные произведения в L(B))
Надо освободиться от производной по t от ujv(i, x) (так
как производные по t могут не сходится слабо) для того,
чтобы перейти к пределу при N —♦ оо в равенстве A3).
Кроме того, нужно, чтобы интегральное тождество выпол-
выполнялось при любой
= о,
s
= 0,
а не только для базисных функций lj(x).
Умножим A3) на произвольную абсолютно непрерывную
функцию dNi(i) такую, что Цр- е Х2@,Т), dNj(T) = 0,
просуммируем по j от 1 до N и проинтегрируем по t от 0
до Т. Обозначив
N
*), A4)
получим
344 Глава VIII. Метод Галеркина для нахождения ...
Интегрируя по частям по t в последнем равенстве, получим
_f (* \ №n\ A/o|ujv дФм\ _
\uN[t,x), m )L^Q) + L\dx., dx.)L2{Q)-
Теперь зафиксируем Ф^и и рассмотрим подпоследователь-
подпоследовательность индексов Nu —► оо в u^v(t,x). На основании слабой
сходимости получаем при Nu —* оо
Этот предел u(f, x) - еще не обобщенное решение, так как
в A5) Флг - не любая функция из W2l^x{Q), а выражается
через базисную систему. Вспомним, что в определении обоб-
обобщенного решения "пробная" функция <P(t, x) должна прина-
принадлежать W2 t'x(Q)i $ = 0, т.е. <P(t,x) может быть пред-
представлена в виде ~~
t
Ф(г,х) = Jrj(T,x)dT, E)
Докажем, что с помощью линейной комбинации функций
(£)} можно приблизиться сколь угодно близко в норме
^ к такой ФЦ, х).
Действительно, функцию т/(<, х) G W2,t,x(.Q) (принадле-
(принадлежащую Хг@, Т) по t) на отрезке [0,Т] можно разложить в
ряд Фурье по t:
^ A6)
n=l
Гл. VIII, § 2. Метод Галеркина для ... 345
сходящийся в норме W 2 t xiQ)i где
п{х) = - / т/(г, я) si
sin
b
о
Очевидно, Хп(х) G РГ2(^M так как T](x,t) принадлежала
W\{fi) по переменной х.
о
Полную в W\(^) систему {/^(х)} ортонормируем по ме-
методу Грама - Шмидта, после чего разложим Хп(х) в ряд
Фурье по ортонормированному базису {/*(£)}:
оо
к=1
сходящийся в Wl(M), гДе апк =
Тогда Хп{х) для каждого п = 1,2,... можно аппрокси-
аппроксимировать частичной суммой ряда Фурье: Ve > О 3N такое,
что для N\ > N:
N1
\\Xn(x)-Yfaknh(x)\\^(o)<e. A7)
Используя A6), A7), для T}(x,t) e W'г£х(О) для Достаточно
больших N\, N2 имеем:
*» sin
n=lfc=l
Обозначим
riNxN2{t, x) = 2^,1^ пкп 8Ш ~r"/fc(z)'
n=l Jk=l
346 Глава VIII. Метод Галеркина для нахождения ...
t
Тогда для Ф(г,х) = J Т)(т,х)Aт имеем для достаточно боль-
т
ших N\ и iV2:
dT)NlN2(T,x)
т
Используя неравенство Фридрихса, получаем
t
Т
t
для достаточно больших Nj и iV2.
Таким образом, мы доказали, что линейной комбинацией
функций {lk(x)} можно аппроксимировать функции вида
E) в норме Wai;l(g).
Отметим, что если теперь сравнить все сказанное с фор-
формулой A4), в которой
t
= /
то мы видим, что проведена аппроксимация и функций
линейной комбинацией
. mrt
Таким образом, мы доказали, что последовательности
в норме LiiQ) при
Гл. VIII, § 2. Метод Галеркина для ... 347
NUo —* оо соответственно к ^-, Ф, ^. Поэтому в-A5) можно
перейти к пределу при NUo —* оо, и мы получаем
u ЭФ\
т.е. получаем обобщенное решение нашей задачи. Из тео-
теоремы единственности обобщенного решения следует, что не
только unv —♦ и, но и вся последовательность и# слабо схо-
сходится к и(х) вместе с первыми производными по Х{.
Таким образом, нами доказана
Теорема. Задача A) - C) имеет единственное обобщен-
обобщенное решение в смысле определения D) при любой f(t,x) €
LziQ)-, которое есть слабый предел галеркинских прибли-
приближений.
Можно было бы доказать теоремы о гладкости обобщен-
обобщенного решения D). Оказывается, если f(t,x) € L2(Q), то
можно доказать, что ^ € Li(Q), и тогда можно доказать
сильную сходимость метода Галеркина.
Более того, если /(<, х) € Хг@) И граница области i? из
класса С2, то обобщенное решение
348
Глава IX. Фундаментальные решения
дифференциальных уравнений
и функция Грина
§ 1. Определение фундаментального решения для
произвольного линейного дифференциального
уравнения и его построение методом
преобразования Фурье. Фундаментальное
решение для оператора Лапласа
При исследовании дифференциальных уравнений в ча-
частных производных большую роль играют фундаментальные
решения этих уравнений. Зная фундаментальные решения,
можно построить решение задачи Коши и функцию Грина
краевой задачи.
Для построения фундаментальных решений уравнений
с постоянными коэффициентами можно использовать метод
преобразования Фурье, что было сделано нами при построе-
построении фундаментальных решений задачи Коши для уравнения
теплопроводности и волнового уравнения.
Дадим общее определение фундаментального решения
дифференциального уравнения, заданного во всем прост-
пространстве IRn. Рассмотрим линейный дифференциальный опе-
оператор вида:
L(x,D)u=
\а\<т A)
<* = <*!...<*„, аа(х) е C°°(IRn).
Определение. Фундаментальным решением дифференци-
дифференциального оператора A) называется обобщенная функция
£(х) (Е D'(TRn), удовлетворяющая в Ш.п уравнению:
) = 6(x) B)
Гл. IX, § 1. Определение фундаментального решения ... 349
в смысле обобщенных функций.
Это означает, что V<£> (E Z)(IRn)
¥>) =(*,¥>) =¥>@). C)
и, кроме того,
где L*(x,D)<f = X) (-l)]a]Da(aa(x)<p(x)) - формально
\а\<т
сопряженный оператор к оператору L(x, D). Действительно,
-/
JR."
К." W<
\<*\<™
Здесь используется факт, что аа(х) £ Coo(IRTl), откуда сле-
следует L*(x,D)ip(x) G £)(IRn). Для оператора L с постоян-
постоянными коэффициентами L*(D) = L(—D). Очевидно, если
£(х) удовлетворяет B), то £(х — xq) удовлетворяет уравне-
уравнению Lx€(x — хо) = 6(х — хо). "'
Фундаментальное решение £(х) оператора L, вообще го-
говоря, не единственно, оно определяется с точностью до сла-
слагаемого £о(#) ~ произвольного решения уравнения LSo = 0.
Для вычисления фундаментального решения для уравне-
уравнения с постоянными коэффициентами можно применять ме-
метод преобразования Фурье, если фундаментальное решение
определить в S', когда C) выполняется для V<£> G 5'(IRn).
В некоторых случаях фундаментальным решением будет
являться обобщенная функция типа обычной функции.
Так, фундаментальным решением оператора Лапласа
является функция
350 Глава IX. Фундаментальные решения диф. уравн. ...
2) = —In |х|, п = 2,
где ц;„ - площадь поверхности единичной сферы в IRn:
Si
Г(п/2) - гамма-функция или эйлеров интеграл первого
рода:
оо
Г(г)= I t-Hz~ldt.
Бели п - целое, то JT(n) = (n — 1)! Напомним также, что
Д1/2) = ^/тг, ГC/2) = у^/2- Тогда если п = 3, тои;3 = 4тг,
а следовательно, при п = 3
Как сказано выше, для нахождения фундаментального реше-
решения уравнений с постоянными коэффициентами применим
метод преобразования Фурье в пространстве обобщенных
функций S'. Мы знаем, что Fx-+tL(D) = L(i£), где L(i£)
есть полином от £.
Теорема. Если l/L(i£) e Xi(IRn), тогда функция £(х) =
F^-Lxi^/LiiO) является фундаментальным решением опера-
оператора L(D).
Доказательство. Так как £(х) (Е Сь, следовательно,
£(х) € 5", то
Гл. IX, § 1. Определение фундаментального решения ... 351
Пример. В случае оператора Лапласа в IR3 имеем
причем — ттгт является локально интегрируемой функцией.
В этом случае можно вычислить фундаментальное решение,
как обратное преобразование Фурье следующим образом:
Л 2ir it .. .
е*\х\гсояв
= -Тт-тт lim / / / 5 г2 anBdrMdip
BтгK л-оо J J J г2 г
0 0 0
К T/-S
= — —-z lim / / cos(|a:|r cos0)sin0d0dr.
27Г я~*°°J J
о о
Сделаем замену
cos 0 = z; — sin 0d0 = dz.
Тогда
352 Глава IX. Фундаментальные решения диф. уравн. ...
Я 1
£(х) = —-—г- lim / / cos(\x\rz)dzdr —
2тг2 я-оо,/ J mi'
о о
я
=_ 1 lim ^mdr=
2тг2 R-*ooJ \x\r
о
оо
_ 1 f sm\x\r _ 1
= ~2^R У ~~^ ~ ~4ф|'
о
Таким образом,
4тг|а;|
Замечание. Если l/£(t^)e£i(IRn), то фундаментальное
решение можно вычислять, используя понятие интеграла в
смысле главного значения. В теории обобщенных функций
доказывается, что для любого оператора L(D) с постоян-
постоянными коэффициентами существует фундаментальное реше-
решение £ е D'(IRn) и даже из 5'(IR").
§ 2. Решение дифференциальных уравнений
с постоянными коэффициентами во всем
пространстве в виде свертки с помощью
фундаментального решения
Теорема. Если L(D) - дифференциальный оператор с по-
постоянными коэффициентами и 1/L(i£) G £i(IRn), то реше-
решение дифференциального уравнения в Шп
= f(x), feS(JRn) A)
Гл. IX, § 2. Решение дифф. уравн. с пост, коэфф.... 353
дается сверткой фундаментального решения оператора L(D)
и правой части A):
и(х) = В * f(x) = J £{x- y)f(y)dy. B)
К."
Доказательство. Сделаем преобразование Фурье в A), по-
получим
ШНО = /@.
Тогда
Пользуясь теоремой о свертке и тем, что F7^x Lha = S(x),
получаем
что и требовалось доказать.
Замечание. Теорема остается справедливой при значитель-
значительно меньших ограничениях на символ L(i£): для его спра-
справедливости достаточно локальной интегрируемости функции
23 - В. Н. Масленникова
354 Глава IX. Фундаментальные решения диф. уравн. ...
§ 3. Формула Грина для оператора Лапласа
Если Q С Ип и имеет кусочно-гладкую границу di2, a
и(ж), v(x) € С2A?)ПС1A?), п^ - внешняя нормаль, то имеет
место формула Грина:
s. A)
V C/T* UTl'
n an
Доказательство. Рассмотрим произвольную подобласть Q'
с кусочно-гладкой границей, лежащую строго внутри 12, т.е.
п С п. Так как и(х) € С2A7), то и(х) € С2(/2 ). Используя
формулу Гаусса - Остроградского, имеем
[ л j [\тг* д / ди\ ^ dv дил.
У Jl^dxiKdxiJ 4-^дх{дхх\
Г ди
+ I v—^ds.
J дп
У
п
^ dv ди
Устремляя в полученном равенстве Q' к Q и пользуясь тем,
что и,и € С1A?), получаем, что предел правой части суще-
существует, значит, существует и предел левой части, т.е. полу-
получаем формулу
/а . Г \-> dv ди , Г ди . ._.
J f^dxidxi J дп
Аналогично имеем
/ uAvdx = -[y P^P-dx + / u^ds. C)
J J f^dxidxi ^ J дп KJ
n n '-1 an
Интегралы слева в B) и C) будем понимать как несобствен-
несобственные. Вычитая из B) формулу C), получаем формулу Грина
(!)
Гл. IX, § 4. Функция Грива в задаче Дирихле ... 355
§ 4. Функция Грина в задаче Дирихле для
оператора Лапласа. Представление решения
задачи Дирихле для уравнения Пуассона
через функцию Грина. Ньютонов потенциал,
потенциалы простого и двойного слоя.
Свойства функции Грина
Рассмотрим классическое решение уравнения Пуассона
-Аи = /(*) A)
в ограниченной области Q С И3 с кусочно-гладкой грани-
границей.
Лемма. Пусть и(х) € С2A?) П С1A?). Для любой точки
х° Е Q имеет место представление:
4тг/ rJK ' 4тг J \ дпг rQn
п an
где п - внешняя нормаль к df2, a f(x) такова, что первый
интеграл справа в B) существует, \х — х° | = г.
Доказательство. Вырежем точку х° € О шаром Ве(х°)
достаточно малого радиуса е и рассмотрим формулу Грина
A) из § 3, где в качестве функции v(x) возьмем: v(x) = —1/г,
где г = \х — х°\. Очевидно, Д£ = 0 в п \ Ве(х°). Используя
формулу Грина, получаем
23*
356 Глава IX. Фундаментальные решения диф. уравн. ...
— / -Audx = — lim / -&udx =
J Г e—0 J Г
B П\В.(х")
= lim / (--I
e—0 J \ r
Лд 1 1 ди
dnr rQn
да
[/91 1 ди \
+ lim / [и—— ■^\dsx-
e~*° J ^ dnr г gn/
Изучим предел последнего слагаемого при £ —♦ 0. Учи-
Учитывая, что мы рассматриваем внешнюю нормаль к области
Q \ Ве(х°), имеем на сфере радиуса е:
д 1 _ _ Э 1 _ 1 _ 1
я~£г дг г г2 £2'
Таким образом,
Г д 1 _ 1 Г
J U7rzr x~£2 / u{<x)ds*-
•/ \J Iff •/
ЭВ,(х°) ЭВ«
£2 у I U I
Оценим первое слагаемое правой части в последнем выра-
выражении. Так как и(х) € СA2), то |«(х) — «(ж0)! < Е\ при
|ж — ж0 ( < е. Тогда
[u(x) - и(*
~£2
Гл. IX, § 4. Функция Грина в задаче Дирихле ... 357
Таким образом, получаем
и(х)——-dsx = 4тга(а:0).
дпг
9Bt(x')
В силу ограниченности |-%-| < М в /2, имеем
d n
— lim / z;dsx = lim -М4тге2 = 0.
«—° J rQn е~*° £
Подставляя значения рассмотренных пределов в C), полу-
получаем:
/iA , л , вч /г э 1 iaui,
J r J\-dnrrQnl
п an
п an
Откуда, заменяя —Ли на /(ж), получаем формулу B).
Лемма доказана.
Бели бы были известны одновременно и\эп и -^=г
дп
эп
для
решения уравнения A), то формула B) давала бы явное
представление решения краевой задачи для уравнения Пу-
Пуассона A) в произвольной ограниченной области. Однако,
мы не можем произвольно задать и\дп = fii^) и "^=" =
д п ЗП
(ръ(х) (в данном случае можно задать или и|эя, или — ),
и поэтому формула B) не дает решения краевой задачи;
однако, ее можно использовать для представления решения
краевой задачи через функцию Грина, что мы ниже и сде-
сделаем. Интегралы же, входящие в B), имеют прямой физи-
физический смысл. Первый интеграл справа в B) называется
ньютоновским потенциалом, a f(x) - его плотность. Инте-
Интеграл / ^:<P2(x)dsx называется потенциалом простого слоя с
эп
плотностью <^2(я)) а интеграл / ^\(x)~^d3x называется
ВП Вп
358 Глава IX. Фундаментальные решения диф. уравн. ...
потенциалом двойного слоя с плотностью ifi(x). С помощью
потенциалов простого и двойного слоя можно строить ре-
решения задач Неймана и Дирихле для уравнений Лапласа
(и Пуассона), сводя эти задачи к интегральным уравнениям
Фредгольма 2-го рода (см. [21]).
Аналогичная B) формула для представления решения
уравнения Пуассона в области Q С Шп имеет вид
x°) = -Jsn()x-x°\)f(x)dx+
f \u-^Sn(\x -x°\)- 6.A* - x°\)~]dsx.
J L dn 9nJ
n D)
ди ^ l j
Докажите!
Рассмотрим задачу Дирихле для уравнения Пуассона в
ограниченной области Q С ГОП с кусочно-гладкой границей
дП:
-Аи = /(х), хеПсШ", и = <р(х). E)
дП
Мы дадим представление решения задачи E) с помощью
функции Грина.
Определение. Функцией Грина задачи Дирихле для опе-
оператора Лапласа называется функция G(x,x°), где х,х° Е О,
удовлетворяющая следующим условиям:
1. Функция G(x,x°) есть гармоническая функция точки
х во всей области Q, исключая точку х°,
&xG(x,x°) = 6(x-x°), F)
F(х — х°) - S-функция, сосредоточенная в точке х = х°).
2. Функция G(x, x°) как функция точки х удовлетворяет
условию
G(x,xo)\dn = 0. G)
Гл. IX, § 4. Функция Грива в задаче Дирихле ... 359
3. В области п С Шп функция G(x,x°) допускает пред-
представление
G(x, х°) = Еп{х - х°) - </(*, Xе), (8)
где £п(х — х°) - фундаментальное решение оператора Лап-
Лапласа, а д(х,х°) - регулярная гармоническая функция, т.е.
Д*0 = 0.
4. Функция Грина при таком определении обладает свой-
свойством симметрии, т.е. для любых двух точек х1 их2, при-
принадлежащих области 12,
Для доказательства этого свойства применим формулу
Грина A) из § 3 к области Ое = Q \ {Be(xl) U Ве(х*)},
т.е. к области, из которой вырезаны точки х1 и х1 ша-
шарами достаточно малого радиуса е и положим в ней v(x) =
G(x,xl), u(x) = G(x,x2). Учитывая, что AxG(z,a;1) = 0,
&xG(x, x2) = 0 в Qe и G\dn — 0, получаем, что
J
d n
(9)
-G(x,xri
дп
где п - внешняя нормаль к дВе(хг) и ()
Воспользуемся представлением функции Грина, откуда
G(x,xl) = S(\x-x1\)-g(x,x1),
G(x,x2) = £(\x-x2\)-g(x,x2).
Подставляя эти представления в (9) и используя метод до-
доказательства формулы B) из § 4, получаем, что предел
интеграла (9) по сфере дВе(х1) при е —* 0 будет равен
—G(xl,х2), а предел интеграла (9) по сфере дВе(х2) при
£ —* 0 будет равен G(x2,xl), откуда получаем
360 Глава IX. Фундаментальные решения диф. уравн. ...
Теперь рассмотрим задачу E). Имеем место
Теорема. Пусть и(х) € С2{П)С\С(П), f(x) G С(П), tp(x) €
C(dQ). Тогда Vz° e Q
G(x,x°)f(x)dx + j <p(x) ~—ds
J dn
n an
где G(x,x°) - функция Грина со свойствами F) - (9).
Доказательство. Рассмотрим формулу Грина A) из § 3
для оператора Лапласа:
(vAu-uAv)dx = / (v-^-u~\ds. A1)
J J ^ дп дп'
n an
Пусть g(x,x°) € C2(l?) П C1(i?) - гармоническая функция
точки х в Q при любой х° Е 1?, принимающая на границе
6Q области Q значение, равное £п(х — х°). Применим фор-
формулу Грина (И) к этой гармонической функции д{х, х°) и к
рассматриваемому решению уравнения Пуассона, получим,
полагая в A1) v = д, —Аи = /,
0= fg(x,x°)f(x)dx+ I \g^-u%]dsx. A2)
J Jan1 dn dni
n
Складывая формулы D) и A2), получаем
Ф°) = J [g(*, *°) - £п(х - х°)] f(x)dx + J
>n ' j dn
an
Гл. IX, § 4. Функция Грина в задаче Дирихле ... 361
Так как д{х, х°)\еп = Sn(x — x°)\an, то последний интеграл
обращается в нуль и мы получаем
(»»»e)] ~ Ъ{* ~ x°))f(x)dx+
Л ragrt(xx)_ag(xxI
Используя обозначение (8), мы получаем A0).
Теорема доказана.
Как мы видим, для решения задачи Дирихле для ура-
уравнения Пуассона нам надо уметь построить гармоническую
функцию с заданным частным условием на границе, то-
тогда мы будем знать функцию Грина и представление ре-
решения в виде A0) с любой (непрерывной) граничной фун-
функцией <р(х). Построение гармонической функции с гра-
граничным условием, равным £ п(х — х°), иногда можно осу-
осуществить явно, например, для некоторых простейших об-
областей. Ниже мы построим функцию Грина для шара мето-
методом отражения, известным из комплексного анализа.
Для сложных областей функцию Грина можно строить
приближенными методами или изучать ее свойства.
362
Глава X. Гармонические функции и их
свойства
§ 1. Примеры и физический смысл гармонических
функций
Функция и(х) € С2(О) называется гармонической в об-
области Q С Жп, если она удовлетворяет уравнению Лапласа
А« = 0 в этой области. При п = 1 гармонические функции
есть линейные функции. Поэтому будем полагать п > 2.
Примером гармонической функции в Etn\{0} является фун-
фундаментальное решение уравнения Лапласа
*) = -i-ln-L п = 2;
ад = -;
ЬГ=2' П^3'
Из графика £п(х) видно, что £п(х) - монотонная функция.
о
Гл. X, § 2. Слабый принцип максимума ... 363
Мы знаем, что эллиптическими уравнениями описыва-
описываются стационарные процессы. В частности, уравнению Лап-
Лапласа удовлетворяет установившаяся в однородном теле тем-
температура и(х); решением этого уравнения при п = 2 опи-
описывается форма мембраны, натянутой на некоторую про-
пространственную кривую, находящуюся в равновесии. Потен-
Потенциалы поля тяготения и стационарного электрического поля
также удовлетворяют уравнению Лапласа. Бели рассматри-
рассматривать безвихревое стационарное течение несжимаемой жи-
жидкости, то ее скорость v(x) является потенциальным век-
вектором, т.е. v = grad<p, где <р(х) - скалярная функция,
называемая потенциалом скорости. Бели отсутствуют ис-
источники в объеме несжимаемой жидкости, то div v = 0.
Подставляя в последнее выражение v = grades, получаем
div(grady>) = 0, т.е. А<р = 0. Таким образом, потенциал
скорости течения жидкости является гармонической фун-
функцией.
§ 2. Слабый принцип максимума для
гармонических функций и его следствия
Наиболее важным свойством гармонических функций яв-
является принцип максимума.
Принцип максимума для гармонических функций имеет
место в так называемой слабой и сильной форме.
Теорема (слабый принцип максимума). Гармоническая в
ограниченной области Q функция, непрерывная вплоть до
границы dQ, нигде внутри Q не может принимать значе-
значений больших, чем наибольшее ее значение на границе, или
меньших, чем наименьшее ее значение на границе^.е. если
т = minu(x), М = maxu(x), того< и(х) < М
an v ' an v ' - \ > -
Доказательство (от противного). Обозначим через у° точ-
точку максимума на dQ: и(у°) = max u(y).
v ' yean v '
364 Глава X. Гармонические функции и их свойства
Пусть Зх° € Q: и(х°) > и(у°). Рассмотрим е =
u(z°)-u(y0) > 0 Тогда и(х»^ > u(yOj _|_ £ и для любой точки
у € дО имеем и(х°) > и(у) + е. Рассмотрим функцию
v(x) = и(х) + rj\x — х°|2, где rj - положительная постоян-
постоянная. Мы имеем
v(x°) - и(х°) > и(у) + е = v(y) - г}\у - х°\2 + е >
>u(y)-nmax|x-x°|2+e Vy e дП.
Ввиду ограниченности области max |х — х°| = d, где d -
£дП
конечная величина.
Выберем число 1} столь малым, чтобы во всей области Q
было —r\d + е > f, тогда v(x°) > v(y) — rjd + e > v(y) + f
Vy € dft. Следовательно, v(x) достигает максимума где-то
внутри Q. Пусть это будет точка х1, тогда -gz~ — О,
< 0, к = 1,...,п. Но Аи = Аи + 2г}п = 2щ > 0.
Получили противоречие. Левое неравенство m < и(х), х €
п, доказывается заменой и(х) на — и(х).
Теорема доказана.
Замечание. Для неограниченных областей Q теорема, во-
вообще говоря, неверна. Пример.
Пусть п = IR+ = {х е JRn : х„ > 0}, и(х) = х»; Аи = 0,
u|Xn=o = 0 и утверждение теоремы не имеет места.
Следствия из слабого принципа максимума:
Следствие 1. Гармоническая функция, непрерывная
вплоть до границы и равная нулю на границе ограничен-
ограниченной области {2, тождественно равна нулю во всей области.
Следствие 2. Из следствия 1 вытекает следующая теорема
единственности классического решения задачи Дирихле для
уравнения Пуассона в ограниченной области:
Гл. X, § 2. Слабый принцип максимума ... 365
решение задачи Дирихле и\ап = <р для уравнения
Аи = —/ единственно в классе C2{Q) П С{п).
Доказательство. Пусть имеется два решения и\ и u-i- То-
Тогда их разность v = и\ — U2 есть гармоническая функция с
нулевыми условиями на границе:
Аи = 0, х € Я, v\an = 0.
Следовательно, v = 0 в О, т.е. щ = ui в п.
Следствие 3. Из принципа максимума вытекает непреры-
непрерывная зависимость решения задачи Дирихле от граничных
данных для произвольной ограниченной области Q. Дей-
Действительно, пусть и\ и u<i - решения задачи Дирихле для
уравнения Лапласа в области О и ui|ал = y?i, «2|ai? = V2,
причем |у>1 — (рг\ < е, т.е. граничные значения гармони-
гармонической функции и\ — «2, равные (р\ — (р2, удовлетворяют
неравенствам — е < (р\ — <р2 < е, тогда всюду в области Q
имеем —e<u\—U2< е, т.е. |ui — иг| < £, что и требовалось
доказать.
Следствие 4. Бели последовательность функций ип(х),
гармонических в ограниченной области п и непрерывных
вплоть до границы, сходится равномерно на границе дп об-
области {2, то она сходится равномерно во всей замкнутой об-
области.
Для доказательства рассмотрим последовательность гар-
гармонических функций {ип(х)}, и пусть {<рп} - их гранич-
граничные значения на дп. По предположению последователь-
последовательность {<рп} равномерно сходится. По критерию Коши это
значит, что Ve > 0 существует номер N, что при m,n > N
всюду на dQ: \ipn — ipm\ < е. Но тогда из принципа мак-
максимума для этих пит будет следовать, что |un — um| < e
всюду в Q. Но тогда опять же по критерию Коши заключаем,
что последовательность {ип} равномерно сходится в замкну-
замкнутой области. Ниже мы докажем, что эта последовательность
сходится к гармонической функции.
366 Глава X. Гармонические функции и их свойства
§ 3. Лемма Жиро (о знаке производной в
граничной точке для гармонической в шаре
функции)
Рассмотрим шар Br, и(х) € C2(Br) П C(Sr), Аи = О
в Br. Пусть х° € QBr - точка строгого .минимума, т.е.
Vx € Br u{x) > и(х°). Пусть v - направление, образу-
образующее острый угол с внутренней нормалью п к 8Br, т.е.
соз(г/,гГ) > 0 и пусть 3-% . Тогда ^{х°) > 0. (Ана-
д v х=х°
логично в точке строгого максимума: если и(х) < и(х°),
х° € дВк, то fj;(x ) < 0).
А—0
Замечание. То, что -%(аг°) > 0 очевидно: -%(х°) =
а V д v
Доказательство. Так как при ортогональном преобразова-
преобразовании гармоническая функция переходит в гармоническую, то
сделаем такое ортогональное преобразование, чтобы точка
i° 6 dBR оказалась в начале координат, а шар был распо-
расположен так, как показано на рисунке: Br = {у € IRn; (yi —
RJ + \у'\2 = R2}, т.е. полусфера в новых координатах
у = j/i,...,уп имела бы уравнение
1=2
Тогда имеем
Рассмотрим параболоид вращения с уравнением у\ =
y'|2, где 0 < у\ < h < у, и обозначим
Гл. X, § 3. Лемма Жиро ...
367
Введем вспомогательную функцию (барьер)
Чу) = Уг exp{Ciyi} - ^
A)
где положительные постоянные С\ и Съ связаны соотноше-
соотношением
С2 = A +
> 0.
Постоянные С\ и h выберем позже.
Функция и(у) обладает следующими свойствами:
1. v(y) < 0 Vy € S = {У1 = l^f, 0 < У1 < Л}, где 5 -
поверхность рассматриваемой части параболоида. Действи-
Действительно,
368 Глава X. Гармонические функции и их свойства
ЩСг1ге <0 Vy€5.
К
2. Ли > 0 Vy € Д@, h). Действительно,
Av(y) =
> 2Сг -
Теперь VCi > 0 подберем /i(Ci) такое, чтобы 0 < C\h < 1,
тогда A + C\h)tClh < 2e. Получаем
2п
Аи > 2Ci - -^-2e.
К
Выберем теперь С\ таким образом, чтобы С\ — ^- > 0, т.е.
d > ^, тогда Аи > 0 Vy € Я@, Л).
3. Так как и(у) 0 0, то max |и(у)| = т > 0.
Введем еще одну вспомогательную функцию
w(y) = "(У) - «@) - ev(y).
По условию леммы
min[u(y) - u@)] = ^ > 0.
Выберем е столь малым, чтобы 0 < е < ^. Тогда
a) w(y) = и(у) - и@) - ev(y) > 0 Vy € S^h) = {У1 = Л}
- основание параболоида;
6)iw(y) = u(y)-u@)-eu(y) > OVy e 5, так как и(у) < 0
на S.
Таким образом, w(y) > 0 на дП@, h). Тогда w(y) > 0
Vy € П@, h). Действительно, функция iu(y) не может вну-
внутри П принимать минимальное значение, так как
Гл. X, § 3. Лемма Жиро ... 369
Ди>(у) = Ди(у) - еАи(у) = -eAv < О
ввиду того, что Ли(у) > 0 Vy € Я@, h), а в точке минимума
должны выполняться неравенства wyiy. > 0. Таким образом,
w(y)>0 Уу€Я(О,Л).
Тогда
«(у) - «@) > sv(y) = е
где у\ = |y|cosa, cos а > 0, так как 0 < |a| < j и при
|У| < hi
Сз, , С2 ,
cos a йг1у| > cos a jr"i-
it i
24 - В. Н. Масленникова
370 Глава X. Гармонические функции и их свойства
Выберем теперь h\ столь малым, чтобы
С2 cos a
cos а — ni > —-—.
К 2
Тогда
и(у) - ц@) ^ е
откуда
.. и(у)-и@) е
hm , > - cos a > О,
»-о \у\ ~ 2
что и требовалось доказать. Лемма о знаке производной в
точке строгого максимума доказывается аналогично.
§ 4. Строгий принцип максимума для
гармонических функций и его следствия
Используя лемму Жиро докажем строгий принцип мак-
максимума для гармонических функций.
Теорема. Пусть ft - область в JRn, n > 2, и пусть и(х) €
С2(О) - гармоническая в Q функция, отличная от посто-
постоянной. Тогда и(х) не может принимать в какой-нибудь вну-
внутренней точке О значение, равное своей верхней или ниж-
нижней грани.
Доказательство (от противного). Пусть и(х) ф const и
существует точка х° G О, что и(х°) = т = inf u(y). Пусть
Е = {х € ft : и(х) = т}; Е ф$ и Е - замкнутое множество
в силу непрерывности функции и(х). Так как и(х) ф const,
то существуют точки х € ft: и(х) > т, х£Е. Рассмотрим
открытое множество ft\ такое, что p(ft\,dft) > 0, х°,хг Е
ft\, хг£Е. Существует точка х2 Е fti'. х2~ЁЕ и
Р(х2,Е) < p{x\dft).
Гл. X, § 4. Строгий принцип максимума ...
371
Рассмотрим шар Вр(х2), где р = 6ist(x2,E), Вр(х2) С
Q\ и на границе шара существует точка ж3 € Е: ж3 €
дВр(х2), а все внутренние точки шара не принадлежат Е,
т.е. Уж € Вр(ж2), ж<=.Е, м(ж) > и(ж3). Теперь воспользуемся
леммой Жиро. Согласно этой лемме существует направле-
направление и (направление и не является касательным к дВр(х2))
> 0.
такое, что §^
х=х8
хх
С другой стороны, х3 - точка локального экстремума
функции и(х), т.е. ^г(ж3) = 0, т.е. для любого направления
7: %
a
=0.
х=ха
i
Получили противоречие. Полученное противоречие до-
доказывает, что гармоническая в п функция, если она не
равна постоянной, не может принимать внутри п значе-
значение m = inf u(x). Если бы и(х) принимала в Q значение
М = sup и(ж), то функция — и(х) принимала бы значение,
равное нижней грани ее значений в П, что невозможно.
Теорема доказана.
Замечание. Если Q - ограниченная область, и(х) непре-
непрерывна в Q, Ли = 0, ж € Q, то, очевидно, верхняя и нижняя
грани значений и(х) в Q совпадают соответственно с ее мак-
максимальным и минимальным значениями в Q.
24«
372 Глава X. Гармонические функции и их свойства
Следствие 1. Гармоническая в ограниченной области фун-
функция и(х), и(х) € С D2), принимает свое наибольшее и наи-
наименьшее значение на границе этой области.
Следствие 2. Бели гармоническая в ограниченной области
функция и(х), непрерывная в Q, принимает свое наиболь-
наибольшее или наименьшее значение внутри области, то она ра-
равна постоянной. Действительно, если бы она не была равна
постоянной, то по теореме о строгом принципе максимума
она не могла бы принимать свое максимальное и минималь-
минимальное значение внутри области. Таким образом, для гармо-
гармонической функции и(х) € C2(f2) П C(f2) мы имеем: пусть
m = minu(x), M — тьхи(х), тогда
an v ' an v '
1) если m > M, то m < u(x) < M, x € Q;
2) если m = M, то u(x) = m = const, x € п.
§ 5. Теорема о знаке производной в граничной
точке гармонической в области функции и ее
следствия (теоремы единственности)
С помощью леммы Жиро докажем теорему о знаке произ-
производной по внутреннему направлению в граничной точке для
гармонической функции в области, удовлетворяющей усло-
условию шара.
Определение. Будем говорить, что граница дп области Q
удовлетворяет "условию шара", если каждой точки V гра-
границы дП можно коснуться шаром В, целиком принадлежа-
принадлежащим области Q, т.е. существует шар В, который содержит
точку V е дП, и все внутренние точки которого принадле-
принадлежат Q.
Теорема 1. Пусть граница дп области Q удовлетворяет
"условию шара", и{х) - гармоническая в Q функция, не-
непрерывная в Q и не равная постоянной в Q. Тогда в точке
Гл. X, § 5. Теорема о знаке производной ... 373
V границы dQ, где и(х) принимает наименьшее (соответ-
(соответственно наибольшее) значение, производная -^=г от функции
a v
и{х) по направлению и, образующему острый угол с напра-
направлением внутренней нормали, если только она существует,
будет положительной, т.е. -^=г > 0 (соответственно отрица-
д U
тельной, т.е. -^-г < 0).
д и
Доказательство. Проведем шар (или круг при п — 2),
касающийся границы dQ в точке х°. По предположению,
все внутренние точки этого шара принадлежат Q. По усло-
условию теоремы и принципа максимума функция и(х) прини-
принимает наименьшее значение на границе dQ области Q, т.е.
и(х) > и(х°), если х € Q, х° € dQ. Мы находимся в
условиях применимости леммы Жиро, откуда следует, что
-%■ > 0. В точках dQ, где и(х) принимает наибольшее зна-
чение, функция "—и(х)" принимает наименьшее значение,
и по доказанному -4г(—и(х)) > 0, т.е. -%• < 0.
аи д v
Теорема доказана.
Замечание. "Условие шара" для границы dQ области Q
является только достаточным условием в теореме, но не яв-
является необходимым. В настоящее время получены необходи-
необходимые в определенном классе поверхностей dQ и достаточные
условия на границу области для справедливости теоремы.
Они получены в работах [13].
Рассмотрим решение второй краевой задачи для уравне-
уравнения Пуассона:
-Ли =
dn
an
=<*>, u(x)eC2(Q)nC\Q), A)
где dQ удовлетворяет условию шара, Q - ограниченная об-
область.
374 Глава X. Гармонические функции и их свойства
Теорема 2. Решение второй краевой задачи, если оно суще-
существует, определяется однозначно с точностью до аддитивной
постоянной.
Доказательство. Пусть ui(x) и иг(х) - два решения за-
задачи A). Тогда u(x) = ui — иг является гармонической в П,
непрерывной в Q и ~: = 0. Если бы и(х) отличалась
от постоянной, то по теореме о знаке производной в точке
х° € dQ, где и(х) принимает наименьшее или наибольшее
значение, производная ~z была бы отличной от нуля. Сле-
дп
довательно, и — const в П.
Теорема 3. (о единственности решения третьей краевой за-
задачи для уравнения Пуассона)
Пусть
а е, \ ^ ^ ограниченная
-Аи = f(x), х е п, п-
4 ' область,
ди
Т=: + <х)
дп
и(х) € С2(П) П
п - направление внутренней нормали к dfi, <т{х) < 0, о ф
0, dfi удовлетворяет условию шара. Если решение третьей
краевой задачи существует, то оно единственно.
Доказательство. Пусть имеется 2 решения щ и иг, тогда
и(х) = и\ — «г удовлетворяет уравнению Лапласа и одноро-
однородным граничным условиям:
а ди . .
Ли = 0, —zt + сг(ж)и
дп
ЭП
= 0.
Пусть и(г) ф 0. Тогда max|u(x)| = max \и(х)\ > 0. Откуда
q х€ЭП
следует, что 3 точка х° G .Г?, в которой u(x°) = minu(x) < 0,
п
Гл. X, § 6. Дальнейшие свойства гарм. функций ... 375
т.е. в точке х° достигается отрицательный минимум или
и(х°) — паахи(ж) > 0, т.е. в точке х° достигается поло-
п
жительный максимум.
Рассмотрим первый случай. В силу строгого принципа
максимума х° € дB и, следовательно, и(х) > и(х°) Vx° €
dft, тогда по теореме 1 имеем ■— > О, кроме того,
дп
х=х"
<ти(х°) > О, т.е. -^ёг + <т(х)и > 0. Получили противоре-
в п эп
чие, следовательно, и(х) = 0.
Аналогичным образом рассматривается случай положи-
положительного максимума.
Теорема единственности доказана.
§ 6. Дальнейшие свойства гармонических
функций: теорема о потоке тепла, необходимое
условие разрешимости задачи Неймана для
уравнений Лапласа и Пуассона, теоремы
о среднем по сфере и шару, бесконечная
дифференцируемость гармонических
функций внутри области
Теорема 1. (о потоке тепла)
Пусть и(х) € С2{п)С\Сх(п) и гармонична в ограничен-
ограниченной области О, дП - кусочно непрерывно дифференциру-
дифференцируема. Тогда
J дп
an
ds = 0, A)
где п - внешняя нормаль к dfi.
Доказательство. Рассмотрим формулу Грина для опера-
оператора Лапласа из § 3 главы 9:
376 Глава X. Гармонические функции и их свойства
(vAu-uAv)dx- (v-^-u—^)ds, B)
J v дп дп'
п an
и положим в ней v — 1, Аи = 0, тогда получим
ди
1
дп
an
-ds = 0.
Теорема доказана. Теорема 1 имеет важное следствие.
Следствие 1. (необходимое условие разрешимости задачи
Неймана для уравнения Лапласа)
Рассмотрим задачу:
Ли = 0, х е п С !Rn, # -
область,
ди
—37 = v?(z)-
Согласно теореме A) условие на граничную функцию <р(х):
I <p(x)dx = О
ал
является необходимым условием для разрешимости задачи
Неймана для уравнения Лапласа. Если это условие не вы-
выполнено, то решение задачи Неймана для уравнения Лап-
Лапласа из класса и(х) е С2(П) П С1(П) не существует.
Пример. Рассмотрим шар Br(Q) € Ш.3. Если <р(х) — 1,
т.е. ~г = 1, то f 1 • ds = 4тгД2 ^ 0; таким образом,
8п ™ авн
гармонической функции с граничным условием
ди
дп
an
= 1
не существует.
Гл. X, § 6. Дальнейшие свойства гарм. функций ... 377
Следствие 2. Теорема 1 имеет следующую физическую ин-
интерпретацию. Пусть и(х) задает стационарное распределе-
распределение температуры внутри однородного изотропного тела О,
т.е. Ли = 0 в Q. Тогда поверхностный интеграл
ди
——as
задает поток тепла через поверхность 6Q в сторону напра-
направления нормали п, и теорема 1 утверждает, что поток те-
тепла через поверхность dfi при стационарном распределе-
распределении температуры при отсутствии источников равен нулю.
Теорему 1 можно обобщить следующим образом:
Теорема 1'. Рассмотрим задачу Неймана для уравнения
Пуассона
-Ли = /(х), хеBсШ.п,
Q - ограниченная область,
ди
дп
аа
п - внешняя нормаль, и(х) € C2(Q) П Cl(Q). Тогда
-ff(x)dx= [ <p(x)ds. C)
п аа
Теорема следует из формулы Грина B), полагая в ней
t)£l, (
Теорема 1' дает необходимое условие разрешимости задачи
Неймана для уравнения Пуассона*, это условие имеет вид
C).
378 Глава X. Гармонические функции и их свойства
Теорема 1' допускает следующую физическую интер-
интерпретацию: поток тепла через поверхность dfi при стаци-
стационарном распределении температуры внутри Q равен ко-
количеству тепла, выделяемому источниками, находящимися
внутри Q.
Теорема 2. (о среднем значении по сфере)
Пусть в шаре Br(x°) задана гармоническая функция,
непрерывная в замкнутом шаре, т.е. и(х) € C2(Br(x°)) П
C(BR(x°)). Тогда
dBR(z°)
2 п/2
где о>„ = реп/2) ~ площадь поверхности единичной сферы.
2 п/2
=
Доказательство. Рассмотрим интегральное представление
D) из § 4 главы 9 для гармонической функции через сумму
потенциалов простого и двойного слоя
^}x, E)
on an
an
где £n(x, x°) - фундаментальное решение уравнения Лапла-
Лапласа в Ш,п, а точка х° лежит внутри п.
Возьмем в E) за область Q шар Вг(х°), где г < R:
п
Так как фундаментальное решение Sn(r) = ~~(rt_2)u)tlr2~ra
зависит только от радиуса шара, то на сфере дВг(х°) оно
не изменяется, поэтому ^по теореме 1 о потоке тепла
^ds = Sn(r) f
on J
on
Гл. X, § 6. Дальнейшие свойства гарм. функций ... 379
Учитывая, что на сфере дВг(х°) производная по внешней
нормали —S- = Ц?-, получаем Щ*-
—; поэтому
из E') находим
Г
u(x)ds. (б)
Переходя к пределу в последнем равенстве при г —► R
в силу непрерывности функции и(а-) в замкнутом шаре
Br(x°), получаем равенство D).
Теорема доказана.
Теорема 3. (о среднем значении по шару)
Пусть гармоническая в шаре Br(x°) функция и(х) €
C2(Br(x°)) П C{Br(x°)) . Тогда значение гармонической
функций в центре шара равно среднему арифметическому
ее значений по шару, т.е.
/ «(*)<**, G)
Br(x')
где ае п обозначает объем шара радиуса 1 в n-мерном про-
пространстве:
mesBl =
ЩТТу
Доказательство. Умножим равенство F) на шпгп~1 и про-
проинтегрируем его по г от 0 до R. Получим
R R
и(х°)и>п trn-ldr= /( / u{x)
о о авт(х»)
Так как Щ + 1) = f Щ), то
380 Глава X. Гармонические функции и их свойства
f
где sen ~ объем единичного шара, и
R
I ( I udsj = / udx.
Получаем
senRnu(x°)= I u(x)dx.
Br(x°)
Разделив на senRn получаем утверждение теоремы.
Теорема 4. (о бесконечной дифференцируемости гармони-
гармонических функций)
Гармоническая в Q функция и(х) имеет в каждой точке
внутри области Q непрерывные производные любого по-
порядка.
Доказательство следует из интегрального представления
E) гармонической функции в виде потенциалов, так как
стоящие в правой части интегралы можно дифференциро-
дифференцировать по параметру х° любое число раз во всякой подобласти
П1 С п (П' С Q), когда dist(/?',9fi) = h > h0 > 0 ввиду
бесконечной дифференцируемости в этом случае €п(х,х°).
Теорема 4 следует также из теоремы о перестановочно-
перестановочности операции дифференцирования и усреднения в строго
внутренней подобласти Q:
0 = (Ли)Л = Л(ил) в П' С Q,
а средние функции бесконечно дифференцируемы.
Гл. X, § 7. Вывод формулы Пуассона для решения ... 381
§ 7. Вывод формулы Пуассона для решения задачи
Дирихле для уравнения Лапласа в шаре с
непрерывной граничной функцией
Для доказательства дальнейших свойств гармонических
функций полезно использовать формулу Пуассона, дающую
явное представление решения задачи Дирихле для уравне-
уравнения Лапласа в шаре Br@):
Ди = 0, х€Вя(О), и =tp(x). A)
8B
Явное представление решения указанной задачи можно по-
получить или методом Фурье, или построив соответствующую
функцию Грина.
Выше было доказано (см A0) гл. IX, § 4), что решение
задачи Дирихле для уравнения Лапласа выражается фор-
формулой
«(хв) = / dG{^X\(x)dsx, B)
где G(x,x°) - функция Грина задачи Дирихле, п - внешняя
нормаль. Функция Грина всюду, кроме точки х = х° есть
гармоническая функция, имеющая представление
G(x,x°) = £n(x,x°)-g(x,x°),
где <jr(z, x°) - регулярная гармоническая функция с гранич-
граничным условием
д(х,х°) =£п(х,х°),
а £п(х, х°) есть фундаментальное решение оператора Лапла-
Лапласа, причем
382
Глава X. Гармонические функции и их свойства
Итак, пусть Вд@) - шар радиуса R с центром в начале ко-
координат. Функцию Грина в этом случае можно построить
методом отражения (методом инверсии, известным из ком-
комплексного анализа).
Рассмотрим точки х° € #я@) и ж € 8Br@) и сопряжен-
сопряженную х° точку хх вне шара такую, что рр\ = R2, где р = |ж°|,
Р\ = \хг\, г = \х - х°\, п = \х- х11.
Так как фундаментальное решение для оператора Лапла-
Лапласа есть функция расстояния, т.е.
то оказывается, что функция Грина для шара имеет вид:
О,
C)
G(x,o) = еп(\х\) -en(R), |*°| =
Действительно,
Гл. X, § 7. Вывод формулы Пуассона для решения ... 383
является гармонической функцией точки х (или х1) при х ф
хх. Проверим, что
x€dBR
= О Уж° е Бя.
Рассмотрим треугольники ж°0ж и ж*Ож; они подобны, так
как имеют общий угол при вершине О, а стороны, образую-
образующие этот угол, пропорциональны в силу выбора точки ж1:
R pi*
из подобия указанных треугольников следует, что д- = — =
£; для точек х € ЗВя получаем г = -^гь т.е. G|rg9BH = 0
согласно C).
Теперь вычислим производную по нормали к дВл от по-
построенной функции Грина, когда х € ЗВя(О), ж° € Вя@).
Имеем
дп
Так как г = д-п при ж € сШя(О), то
на сфере, поэтому
дп
дп
Далее, производная lz _f ' в точке ж на сфере равна ко-
д п
синусу угла /Зо между направлением внешней нормали п к
384
Глава X. Гармонические функции и их свойства
в точке х и направлением х°х; аналогично, произ-
производная 'z~If I равна косинусу угла 0\ между направлением
д п
внешней нормали п к 8Br@) в точке х и направлением х1х.
Действительно, имеем
= (V/,n) = |V/|.|n|cos(V/,n).
В нашем случае
\
t=l
Vr =
д\х — х°\ 1 _► _f I _f. .-*. ,-► -*ч
—^———'- = -(г, п) = -| г I • I n |cos(r, п) = cos/3o.
дп r r
Аналогично для д*х^ '• Из АОх°х и Ож!ж получаем, что
р2 = R2 + г2 - 2Rr cos j90,
Pi = R2 + r\ - 2Rri cos 0i.
Поэтому при х €
дп
9BH@)
2Rr
pR2+r2-p2-
R 2Rrx
подставляя в эту формулу гх = —, рх = ^-, получаем
Кроме того,
Гл. X, § 7. Вывод формулы Пуассона для решения ... 385
(п - 2)шп
поэтому
dG(x,x°) I R2-p2
д п
u>nR rn
Подставляя полученный результат в формулу B), получаем
явное представление решения задачи Дирихле для опера-
оператора Лапласа в шаре в виде:
dBR(O)
Если обозначить через 7 угол между направлениями 0х° и
Ох, то формулу D) можно представить в виде
l
9Вя@)
Формула D) и есть искомая формула Пуассона для реше-
решения задачи Дирихле для уравнения Лапласа. Но она выве-
выведена нами при условии, что решение задачи A) существует
и принадлежит классу:
и(х) € С2{П) П С1 (Л)
(именно при этом условии гладкости на и{х) была выведена
нами формула Грина, которую мы использовали для вывода
формулы B)).
Докажем, что функция, задаваемая формулой D), явля-
является гармонической и удовлетворяет граничному условию
для любой непрерывной функции <р(х).
Гармоничность и(х°) внутри 8Br@) следует из гармо-
гармоничности функции Грина, когда х ф х°
25 - В. Н. Масленникова
°
386 Глава X. Гармонические функции и их свойства
Докажем, что и(х°) —► <р(х) при j;°-»iG сШя(О). Оче-
Очевидно, решение задачи Дирихле при <р = 1 существует, при
этом и(х) = 1 € C2(f2), и из полученных формул имеем:
J
1 — ——
9BR{Q)
R2-p2
9Вя@)
Поэтому
Надо доказать, что \и(х°) — <р(х)\ < е, если \х° — х\ < 8, где
8 - достаточно мало. Из-за непрерывности <р(х) на сфере
имеем \<р(х) — <р(х)\ < е/2, если \х — х\ < Si. Обозначим
через (T^j пересечение сферы 8Br@) и шара \х — х\ < Si.
Тогда
дВя(О)\<тб1
Если ж € сШя(О) \ сг^, а |ж° — ж| < й и й достаточно
мало, то
г" = |ж° - х\п > а = const > 0;
кроме того, при х° —► х имеем R2 — р2 —> 0, поэтому первое
слагаемое в правой части последнего неравенства меньше
е/2. Далее, в силу первого равенства из F), получаем
Гл. X, § 7. Вывод формулы Пуассона для решения ...
Л2-/,2 Г \ф) - <f(x)\
387
l-dsr<
< max
I
unRrn
9BR@)
при достаточно малом 6г. Следовательно, Ve > О
\и(х°) - и(х)\ < е, если |ж° - х\ < S.
х°е BR(O)
Таким образом, формула D) дает решение задачи Ди-
Дирихле в шаре для уравнения Лапласа при любой непреры-
непрерывной граничной функции.
25"
388 Глава X. Гармонические функции и их свойства
§ 8. Свойства гармонических функций:
теорема Гарнака о равномерно сходящейся
последовательности гармонических функций,
теорема Лиувилля и теорема об устранимой
особенности
Теорема 5. (о равномерно сходящейся последовательности
гармонических функций - теорема Гарнака)
Если последовательность {и*(а:)}, к = 1,2,..., гармони-
гармонических внутри ограниченной области ft и непрерывных в ft
функций сходится равномерно на границе dft, то она ра-
равномерно сходится во всей области. При этом предельная
функция будет гармонической внутри ft.
Первая часть теоремы доказана нами как следствие 4 из
слабого принципа максимума (глава X, § 2): если последова-
последовательность непрерывных в ft и гармонических в ft функций
равномерно сходится на границе области, то она равномерно
сходится во всей рассматриваемой области.
Остается доказать, что предельная функция гармонична
в ft. Для доказательства этого факта возьмем произвольную
точку Q € ft и построим шар Br(Q), лежащий внутри ft. В
этом шаре каждую из функций и*(ж) представим в виде ин-
интеграла Пуассона (причем это представление единственно,
что следует из теоремы единственности решения задачи Ди-
Дирихле). Получаем
^ A)
J "xx"
9Br(Q)
"xx"
где ifk(x) - значение и*(ж) на 0Br(Q), x° e Br(Q). В
силу равномерной сходимости последовательности функций
ifk(x) и равномерной сходимости tik(x) в любой внутренней
точке х° € Br{Q) в равенстве A) можно перейти к пределу
при к —* оо.
Гл. X, § 8. Свойства гармонических функций ... 389
Обозначая предельные значения соответственно через
и(х°) и <р(х), получаем
^Дь,
9BR(Q)
откуда следует, что u(z°) гармонична в круге Br{Q), а зна-
значит, и в Q в силу произвольности выбора Br{Q).
Теорема 6. (неравенства Гарнака)
Пусть гармоническая в шаре -Вд(О) функция и(х) €
C(BR@)) и и(х) > 0 в Вя@). Тогда для любой точки
х° € Bfi@) справедливы неравенства:
где u@) - значение и(х) в центре шара, р = |ж°|.
Доказательство. В силу единственности решения задачи
Дирихле функция и{х) представляется формулой Пуассона:
^ ' ~ R / »* v,yX)asx, x fc &R\v)-
авн(о)
Из ДОх°х (см. рисунок) имеем Я — /Э<г<Я + /э, поэтому
R2 -р2 ^ R2 - р2 R2-p2
г»,.
Если и(х) > 0, то можно умножить полученные неравенства
на ~-^и{х) и проинтегрировать по сфере Э1?я@), получаем
9Вн@)
1
9Вя@)
390
Глава X. Гармонические функции и их свойства
Пользуясь теоремой о среднем по сфере: и@)
i / u(x)ds, получаем
Теорема доказана.
Теорема 7. (теорема Лиувилля)
Гармоническая во всем пространстве JRn функция не мо-
может быть ограниченной сверху или снизу, если она не по-
постоянна.
Доказательство. Пусть, например, всюду в Ш": и(х) >
М, где М - постоянная. Прибавляя в случае надобности к
функции и(х) постоянную, мы всегда можем добиться того,
чтобы было М > 0, т.е. и(х) > 0.
Принимая это предположение ограниченности снизу, по-
покажем, что значение и (ж) в любой точке Q € Ш," равно зна-
значению и(х) в начале координат, откуда будет следовать, что
Гл. X, § 8. Свойства гармонических функций ... 391
и(х) = const. Возьмем шар Br@) такого большого радиуса
R, чтобы точка Q лежала внутри него. Пользуясь неравен-
неравенствами Гарнака теоремы 6, имеем
При R —*• оо получаем и@) < u(Q) < и@), т.е. u(Q) = и@).
Так как Q - произвольная точка в IR", то это равенство
означает, что и — const в И", что и требовалось доказать.
Следствие. Гармоническая функция, ограниченная во
всем пространстве И", равна постоянной.
Изучим изолированные особенности гармонических фун-
функций. Фундаментальное решение уравнения Лапласа явля-
является примером гармонической в И" \ {х°} функции с изо-
изолированной особенностью в точке х°, при этом \£п(х,х°)\
неограниченно растет при \х — х°\ —* 0, так как £п(х^х°) =
Сп\х - х°\2~п при п > 3 и S2(x,x°) = С21п|ж - ж°| при
п = 2, где Сп = (<^пB —п)) при п > 3, Сг = 1/27Г. Оказы-
Оказывается, изолированная особенность такого типа у гармони-
гармонической функции в определенном смысле является минималь-
минимальной, а именно имеет место следующая теорема о стирании
особенностей у гармонической функции.
Теорема 8. Пусть и(х) - гармоническая функция в Q \
{ж°}, х° € /2, и удовлетворяет условию
и(х) = о(£п(ж,ж°)) при х —* ж°, C)
где £n{xi х°) - фундаментальное решение оператора Лапла-
Лапласа. Тогда особенность функции и(х) в точке х = х° устра-
устранима, т.е. в точке х° функцию и(х) можно доопределить так,
что она будет гармонической всюду в Q.
Доказательство. Воспользуемся тем, что для шара реше-
решение задачи Дирихле для оператора Лапласа существует для
любой непрерывной граничной функции. Рассмотрим шар
392 Глава X. Гармонические функции и их свойства
Br(x°) С i7, и пусть в этом шаре задана гармоническая
функция v{x) с граничным значением, равным граничному
значению рассматриваемой гармонической функции и(х) на
дВл(х°): Ли = 0 в Вд@), и|эвя(х°) = и(х). На самом деле
мы имеем, что v 6 C°°(Br). Пусть w(x) = u(x) — v(x). Тогда
w(x) = о(£„(|ж — ж°|)) при х —> ж°.
Зададим любое е > 0, тогда существует г: Уж € сШг(ж°)
имеем
\w(x)\ < е\£п(\х - х°\)\.
Согласно принципу максимума тогда можем утверждать, что
\/ж € Вд(ж°) \ Вг(ж°) выполнено неравенство
При е —» 0 ю(ж) = 0, если х ф х°, откуда следует, что t (ж) =
и(ж) при х ф х°. Теперь доопределим функцию и(х) в точке
ж°, положив и(х°) = v(x°). Таким образом, мы получили,
что
(О Л О
Ж ) Ж = Ж
является гармонической в Br(x°) функцией.
Теорема доказана.
§ 9. Внешние краевые задачи для уравнения
Лапласа
В этом параграфе мы будем рассматривать решения в
неограниченных областях - внешности компактов. Такие за-
задачи называют внешними краевыми задачами.
Пусть дана ограниченная область Q С И" такая, что
точки не принадлежащие Q и ее границе дО, образуют об-
область Q\ с границей dft\\ f2\ = Ж" \ Q. Пусть на границе
Гл. X, § 9. Внешние краевые задачи ... 393
df2\ области О\ задана непрерывная функция ц>(х). Требу-
Требуется найти гармоническую в Q\ функцию и(х) такую, что
u\xedf2i — Ц>{х)- Такую задачу будем называть внешней за-
задачей Дирихле для уравнения Лапласа. Если не наклады-
накладывать никаких условий на поведение решения внешней задачи
Дирихле на бесконечности (при |ж| —* оо), то эта задача
будет иметь много решений (не будет выполняться теорема
единственности). Для того чтобы гарантировать единствен-
единственность решения в двумерном случае требуют ограниченно-
ограниченности решения, или его рост не более логарифмического, точ-
точнее и(х) — оAп|ж|), |ж| —> оо; в многомерном случае тре-
требуют стремления этого решения к нулю при |ж| —* оо, т.е.
lim и(х) — 0: и(х) — оA), \х\ —> оо.
\х\—*оо
Решение внешней задачи Дирихле можно свести к реше-
решению внутренней задачи Дирихле с помощью преобразова-
преобразования инверсии. При этом становятся понятными условия на
оо и их различие в случаях п = 2 и п > 3.
1. Постановка внешнее задачи Дирихле в случае П > 3,
теорема единственности
Требуется найти и(х), удовлетворяющую условиям:
1) Аи = 0 в неограниченной области fi\ с границей дп\;
2) и(х) е C2{f2i) П С{ПХ U дПх);
3) u{x)\ant = р{х);
4) и(х) = оA), \х\ —у оо, т.е. lim и(х) — 0.
|z|—оо
Замечание. Последнее условие является существенным для
единственности решения, в чем можно убедиться на простом
примере:
Пусть требуется решить задачу Дирихле для внешности
шара Вд@) радиуса R с условием: и\авя ~ Vo = const.
Если не требовать стремления к нулю на оо от искомого ре-
решения, то получаем, что решениями задачи являются фун-
функции
R
394
Глава X. Гармонические функции и их свойства
а также любая линейная комбинация этих функций:
и = ащ + /3t«2, где а + 0 = 1.
Имеет место следующая теорема единственности.
Теорема 1. Решение пространственной внешней задачи
Дирихле в постановке 1 единственно.
Доказательство. Пусть имеется 2 решения щ и иг- Их
разность v = it 1 — ui удовлетворяет уравнению Ди = О,
граничному условию v\qqx = 0 и условию убывания на оо,
т.е. Ve > 0 можно указать такое i?i, что \v{x)\ < e при
Ы Д
Применим принцип максимума для области G, заклю-
заключенной между дп\ и дВцх, где 8Brx - поверхность сферы
достаточно большого радиуса R\\ из него следует, что \v\ < e
в G, т.е. v = 0 в силу произвольности £.
Гл. X, § 9. Внешние краевые задачи ... 395
2. Постановка внешней задачи Дирихле в плоском случае
Требуется найти функцию «(ж), удовлетворяющую усло-
условиям
1) Аи — 0 в рассматриваемой неограниченной области
2) и{х) € C2(f2i) П C(Ql U дПх);
3) и\аПх =ф);
4) и(х) = о (In |ж|), |ж| —> с», т.е. ы(х) может расти при
|ж| —> с» медленнее, чем In |ж|, т.е. медленнее, чем фун-
фундаментальное решение. В частности, можно потребовать,
чтобы и(х) была ограниченной при \х\ —* оо.
Замечание. Требование обращения в нуль на оо и здесь
не противоречиво для единственности, т.е. доказательство
теоремы 1 проходит, как легко видеть, и в двумерном случае,
но оно является слишком сильным, так как при нем задача
оказывается неразрешимой.
Теорема 2. Внешняя плоская задача Дирихле в постановке
2 имеет единственное решение.
Доказательство этой теоремы будет проведено ниже све-
сведением внешней задачи Дирихле к внутренней.
3. Сведение решения внешней задачи Дирихле к решению
задачи Дирихле для ограниченной области. Преобразова-
Преобразование Кельвина
Задачу Дирихле для ограниченной области называют
внутренней задачей Дирихле. При сведении внешней за-
задачи Дирихле к внутренней выявляется роль тех дополни-
дополнительных условий, которые налагаются на решение внешней
задачи Дирихле при |ж| —* оо.
Возьмем внутри ограниченной области Q точку О и
сферу 8Br@) (в двумерном случае - окружность). Сде-
Сделаем преобразование инверсии, т.е. такое преобразование,
при котором каждой точке ж, лежащей вне шара Br(O),
ставится в соответствие сопряженная точка х*, лежащая на
луче Ох, для которой
396
Глава X. Гармонические функции и их свойства
х* =
х
и, обратно, х -
х*
\x*
br(°)-
При этом преобразовании точки сферы 8Br@) остаются
неизменными, вся та часть пространства, которая лежит
вне шара Br(O) взаимно однозначно преобразуется в ту
часть пространства, которая лежит внутри 8Br@). Оче-
Очевидно, при таком преобразовании все точки пространства,
которые лежат вне ограниченной области J2, преобразуются
в точки некоторой ограниченной области 1?*, окружающей
точку О. Каждой точке из /?*, кроме О, при таком преоб-
преобразовании соответствует одна и только одна точка, лежащая
вне Q. Только самой точке О при этом преобразовании не
ставится в соответствие никакая точка пространства.
Пусть функция и(х) задана в п\ = IR" \ Q. Функция
п-2
B)
Гл. X, § 9. Внешние краевые задачи ... 397
называется преобразованием Кельвина функции и(х). Из
формул A), B) следует, что
т.е. преобразование, обратное к B), тоже является преобра-
преобразованием Кельвина.
Дальнейшее рассмотрение удобнее проводить отдельно
для п = 2 и п > 3. Для простоты будем считать R = 1, чего
можно добиться изменением масштаба.
Теорема 3. Если функция и(х) гармонична в области B\,
то ее преобразование Кельвина и*(х*) будет гармонической
в области Q*.
Доказательство.
а) Плоский случай. Перейдем к полярным координатам:
х\ — pcostp, X2 = psirnp. Пусть х = (p,ip), тогда х* =
(/э*,у>), где р = |ж|, р* = |ж*|, а преобразование инверсии
примет вид: рр* — 1.
Положим и(р,<р) = и*(р*,<р), т.е.
и{х) = «•(*•), ф) = ср*(х*).
Функция и*(х*) будет определена всюду в области 1?*, кроме
точки О, и будет принимать значение <р*(х*) на границе
дО*. Проверим, что и*(х*) будет гармонической функцией
от координат (р*,ф), если и(х) = u(p,tp) была гармониче-
гармонической по р и <р.
Уравнение Лапласа в полярных координатах имеет вид
1 д / ди\ 1 д2и .
р др V др / /э2 дер2 w ■> v /
Тогда
о
д ди д2и
+
о . д ди ди
Р Д^« = р^р^ + ^ = 0.
398 Глава X. Гармонические функции и их свойства
творяет уравнению Лапласа:
Но так как и(р, (р) — и*(-,(р), то и* по р и </? тоже удовле-
удовлеp2Ap,<fiU = p2Apvu* = p-^-p ~ 1 ■—. = 0.
Op Op O(p
Докажем, что u*(p*,<p) удовлетворяет уравнению Лапласа
по (р*, <р). Для этого перейдем к переменным р*, <р, где р* =
К Получим
(h£_ _ dvT_d£_ _ _dv*_\ _ _ тди*
dp dp* dp dp* p dp*'
т.е.
д ,. д
Тогда р^р^ = P*&P*^?, поэтому
д тди* д2и*
т.е. и*(/э*,у>) - гармоническая функция.
Если функция и(х) была ограничена на оо или и(х) =
оAп|х|) при |ж| —* оо, то и*(х*) также будет ограничена
или и(х) = о (In |ж|) при х —* 0. Тогда по теореме об устра-
устранимой особенности и*{х*) можно так доопределить в точке
О, чтобы полученная функция была гармонической всюду
внутри Q*. Из теоремы единственности решения внутрен-
внутренней задачи Дирихле будет следовать, что ограниченная фун-
функция и*(х*) единственным образом определяется в Q* сво-
своими значениями на границе. А отсюда следует единствен-
единственность решения внешней плоской задачи Дирихле в классе
функций ы(х) = о (In |ж|), |ж| —* оо, т.е. имеет место теорема
2, и если существует решение внутренней задачи Дирихле,
то существует и решение внешней задачи Дирихле.
Гл. X, § 9. Внешние краевые задачи ... 399
б) Рассмотрим п = 3 (в случае п > 3 доказательство
аналогично: оно получается переходом к сферическим коор-
координатам в n-мерном пространстве). Пусть (г, ср, в) - сфери-
сферические координаты точки х € П\. Обозначим через и(г, ср, в)
решение внешней задачи Дирихле для области п\. Преоб-
Преобразование инверсии в сферических координатах имеет вид
г*г — 1, где |х| = г, |х*| = г*, х* = (г*,р,в). Согласно
преобразованию Кельвина, положим
или, что эквивалентно, и*(х*) = ги(х). Аналогично для гра-
граничных значений: tp*(x*) — ~(р(х), или р(х) = ^(р*(х*).
Таким путем и*(х*) определяется всюду внутри 1?*, кроме
точки О. Функция и*(ж*) будет принимать значение <р*(х*)
на всей границе дп*.
Приведя уравнение Лапласа к сферическим координа-
координатам, покажем, что и*(х*) будет гармонической в области
/?*, если и(х) была гармонической в B\, т.е. докажем, что
Ar*,e,v?«* = 0> если &r,e,tfiU = 0.
Уравнение Лапласа в сферических координатах имеет
вид:
1 д -уди
г2 дг дг
8 ( . йди\ 1 д2и _
в)+ ~
Преобразуем первое слагаемое к виду:
\_д_ 2сЫ,_д^и 2ди 1д2(ги)
г2 дг дг дг2 г дг г
так что имеем
д2 , ч
+ 4|-T^r^(sing^)+ .\~ГУ\=0.
JL[_l_^(si
400 Глава X. Гармонические функции и их свойства
Но так как ы*(£,0,ц>) = ru(r,6,tp), то
lr 1 dr. ди*
2 ивШ
ав)+ sin2 вд^
Перейдем в E) к координатам r*,9,ip. Замечая, что
djS_ _ chS_dr^_ _ _}_dv*_ _ _ ш2ди*
дг ~ ~дг* дг ~ ~^'дг* ~ ~Г ~дг*'
т.е.
дг дг*' дг2 дг* дг*'
мы получаем
дг* дг*
. оди*\ 1 д2и
или
г*4Дг.)в)^и* = 0.
Таким образом, мы доказали, что ы*(г*,^,<р) - гармониче-
гармоническая функция.
Далее, если и (ж) стремилась к нулю при |ж| —* оо, то
и*(х*) будет удовлетворять условию:
К(ж*I < — \и(х)\, где \и(х)\ -» 0 при |ж*| -» 0.
Тогда по теореме об устранимой особенности, функцию и*
можно так доопределить в точке О, чтобы полученная фун-
функция была гармонической всюду внутри Q*. В силу един-
единственности решения внутренней задачи Дирихле отсюда
Гл. X, § 9. Внешние краевые задачи ... 401
будет следовать, что ограниченная функция и* единствен-
единственным образом определится в Q* своими значениями на гра-
границе. Отсюда следует единственность решения внешней за-
задачи Дирихле в классе функций, стремящихся к нулю на оо;
при этом это стремление к нулю имеет порядок ^: и(х) =
^и*(х*), так как и*(х*) - ограниченная функция внутри 42*
и порядок 1/гп~2 при п > 3. И если граница области 42* и
ц>(х*) таковы, что внутренняя задача Дирихле разрешима,
то разрешима и внешняя задача Дирихле в классе функций,
стремящихся к нулю на бесконечности.
Примеры
1. Решением внешней задачи Дирихле для области i?i в
плоском случае, когда заданная на границе функция равна
С = const, является функция равная С. Это единственное
решение в классе ограниченных функций.
2. Решением внешней задачи Дирихле в трехмерном слу-
случае, когда область есть внешность шара радиуса R с центром
в начале координат и когда на границе шара задано условие
С = const, является функция и(х) = т-4. Это единствен-
единственное решение рассматриваемой внешней задачи Дирихле в
классе функций, стремящихся к нулю на оо.
4. Внешняя задача Неймана
Постановка задачи. Пусть задана ограниченная одно-
связная область с границей дп. Пусть точки, не принадле-
принадлежащие 4? U дп образуют область Q\ с границей дп\. Требу-
Требуется найти гармоническую в Q\ функцию и{х) = C2{Q\) П
C1(i?i U 9i?i) с граничным условием f^-|ar?i = <Р, где п -
внешняя по отношению к i?i нормаль к границе дп\. При
этом мы опять будем требовать, чтобы решение и(х) внешней
задачи Неймана было ограниченным или и{х) — оAп|х'|),
|х| —* оо, в случае двух независимых переменных и стре-
стремилось к нулю на оо в случае трех и более независимых
переменных.
4°. Плоский случай.
В плоском случае внешняя задача Неймана сводится
к внутренней задаче Неймана преобразованием инверсии.
26 • В. Н. Масленникова
402 Глава X. Гармонические функции и их свойства
Путь тот же, что и в задаче Дирихле, требуется выяснить
только, как преобразуется граничное условие. Так как, как
известно из комплексного анализа, рассматриваемое преоб-
преобразование конформно, то сохраняются углы при этом пре-
преобразовании. Поэтому нормаль к границе прежней области
переходит в нормаль к границе новой области. Граничная
функция для возникающей таким образом внутренней 2-ой
краевой задачи получается в случае двумерной области сле-
следующим образом.
При тех же обозначениях, что и в задаче Дирихле, имеем
и*(х*) = и(х), pp* = R\
«/ «ч 9и* ди* dn , . dn
Здесь через s и s* обозначены соответственно границы преж-
прежней и новой областей, через пап* - нормали к их границам,
j2jt - коэффициент растяжения в точке границы по напра-
направлению нормали. Так как при конформном преобразовании
коэффициент растяжения в данной точке не зависит от на-
направления, то для вычисления jjf? можно предположить, что
направления п и п* проходят через центр преобразования
О. Тогда
dn dp R2
d~n~* ~ dp* ~ ~p*2'
Таким образом,
Чтобы внешняя задача Неймана имела решение необходимо,
чтобы соответствующая ей внутренняя задача Неймана име-
имела решение, т.е. чтобы
I ip(s)ds = 0.
an*
Гл. X, § 9. Внешние краевые задачи ... 403
Так как решение внутренней задачи определяется с точно-
точностью до постоянной, то и внешняя задача Неймана в классе
ограниченных на ос функций определяется с точностью до
постоянного слагаемого.
4б. Случай п > 3.
В случае п > 3 независимых переменных внешнюю за-
задачу Неймана нельзя свести к внутренней преобразованием
обратными радиусами-векторами, так как в этом случае
на границе выражается не только через J^, но и через зна-
значения самой неизвестной функции на дй\.
Теорема единственности внешней задачи Неймана в случае
п>3.
Пусть dQ\ удовлетворяет условию шара. Тогда решение
задачи Ли = 0; f^|ar?i = /, где и{х) —♦ 0 при \х\ —> оо,
и(х) € C2(#i) П С1 {их U ai?i), единственно.
Доказательство. Пусть и(х) такова, что Ли = 0,
0, и(х) —* 0 при \х\ —* оо. Покажем, что в этом случае
и = 0. Рассмотрим область, ограниченную дп\ и сферой
столь большого радиуса, что на этой сфере \и{х)\ < е. Так
= 0, то на дп\ гармоническая функция не может
как
Эи
принимать наибольшее или наименьшее значение, так как в
этом случае согласно теореме Жиро было бы ^~ < 0 или
|^ > 0 соответственно.
Но гармоническая функция принимает свое наибольшее
и наименьшее значение на границе, значит, она принимает
такие значения на поверхности сферы. Но на ней |г*(х)| <
е, следовательно, |г*(х)| < е во всей области, но так как е
можно взять произвольно малым, то и(х) = 0 в каждой точке
области i?i, что и требовалось доказать.
Аналогичным путем рассматривается третья краевая за-
задача.
26'
404
Глава XI. Дополнение.
Общие теоремы вложения для
классов дифференцируемых
функций многих переменных
Включение этой главы в книгу вызвано необходимостью
использования теорем вложения студентами при выполне-
выполнении ими курсовых и дипломных работ по дифференциаль-
дифференциальным уравнениям в частных производных и математической
физике. Имеющиеся источники, в особенности широко из-
известная книга СП. Соболева "Некоторые применения фун-
функционального анализа в математической физике", в кото-
которой впервые изложены его теоремы вложения, стали библи-
библиографической редкостью. Другие издания, как например,
книга И. Стейна [23] и книга [4], трудны для понимания их
студентами 3-го - 4-го курсов ввиду их большой общности.
Поэтому хотелось изложить материал достаточно кратко и
доступно студентам.
§ 1. Основные определения и формулировка
основных теорем вложения
Круг вопросов, объединенных под названием "теоремы
вложения", посвящен следующей общей проблеме: как, зная
дифференциальные свойства функций в одной норме, уста-
установить их свойства в другой норме. А сами теоремы вло-
вложения важны потому, что они дают возможность просле-
проследить, как ограничения на поведение частных производных
налагают соответствующие ограничения на поведение са-
самой функции. Первые результаты такого типа были полу-
получены, как сказано выше, С.Л. Соболевым для введенных им
пространств
Гл. XI, § 1. Основные определения и формулировка... 405
Будем рассматривать функции f(x) п вещественных пе-
переменных х = (xi,...,xn), определенные на области
Определение 1. Пусть I - натуральное число и 1 < р <
оо. Будем говорить, что измеримая функция f(x) € W^{Q),
если f(x) € Lp(B) и существуют обобщенные производные
D%f порядка \a\ < I, a = ai...an - мультииндекс, причем
D«J € L()
Введенные классы W^{O) становятся банаховыми про-
пространствами, если в них ввести следующую норму:
-E
* Ч(о)
Область О не предполагается ограниченной. В частности,
Q может совпадать со всем пространством JRn: Q = Жп.
Соболев ответил на вопрос о том, что можно сказать о не-
непрерывности и о суммируемости в Lq(Q), q > p, функций из
WJ,(Q), и какие могут иметь следы на многообразиях мень-
меньшей размерности функции из И^(/2).
Введем следующую терминологию. Пусть X и Y - неко-
некоторые нормированные пространства. Запись
X-+Y
будет означать, что
1) XCY
и
2)
где С > 0 - постоянная, не зависящая от /. Таким образом,
запись X —> Y означает, что множество X вкладывается в
множество У, и, кроме того, оператор вложения (т.е. опе-
оператор, переводящий всякий элемент / € X в тот же самый
406 Глава XI. Дополнение. Общие теоремы вложения...
элемент /, но рассматриваемый как элемент пространства
Y) - ограничен.
Следует заметить, что в ряде случаев вложение носит
несколько условный характер: например, если X = WJ,(Q),
Y = С(П), то функция / € X возможно и не принадлежит
Y, но Y принадлежит функция /, получающаяся из / после
изменения ее на множестве меры ноль. И, соответственно,
неравенство
И/Ну < №
справедливо для функции /. В подобных случаях мы также
будем использовать обозначение X —* Y без дополнительных
оговорок.
Теоремы вложения будут сформулированы для областей
с минимально гладкой границей.
Рассмотрим области вида
{*€ЛГ, х„ <¥>(xi,...)xn_i)}) A)
где функция <р(х'), х' = (xi,...,xn_i), удовлетворяет усло-
условию Липшица
\Ф') - <рЫ)\ < М\х' - у'\, х', у1 € ИГ.
Определение 2. Области вида A), а также области, полу-
получающиеся из A) путем замены знака (xn > <p(xi,..., жп-1)),
путем перестановки координат или путем поворота, будем
называть специальными липшицевыми областями.
Определение 3. Будем говорить, что граница дП области
Q удовлетворяет минимальному условию гладкости, если 3
е > 0, 3N,M, N - натуральное число и М > 0, и 3{V;}
- конечный или бесконечный набор открытых множеств V{,
i = 1,..., s (s - натуральное или s = оо) таких, что
1) если х € дП, то шар Ве(х) радиуса е с центром в
точке х содержится в некотором V): Ве(х) С V);
Гл. XI, § 1. Основные определения и формулировка...
407
2) никакая точка Q не содержится более чем в N мно-
множествах Vi (т.е. каждая точка из Q покрывается не более
чем N множествами из набора {Vi});
3) Vi 3 специальная липшицева область J2; с константой,
не превышающей М, такая, что
Vi П fli = Vi П п.
Пример. Пусть Q - ограниченная область в Ш." с гра-
границей из класса С1. В этом случае достаточно конечного
набора множеств
о
Пусть п = 2
Vi П О = Vi П Г2],
где специальная липшицева область Q\ есть:
Й1 = {х : х2 < <f(xi)},
Х2 = ф{х\) € Сг(Ш ). Таким образом, сужение кривой х-i =
() на Vi совпадает с дП П Vi.
Теперь сформулируем теоремы вложения для произволь-
произвольных (ограниченных и неограниченных) областей с грани-
границами, удовлетворяющими минимальному условию гладко-
гладкости.
408 Глава XI. Дополнение. Общие теоремы вложения...
Теорема 1. Вложение Wlp{Q) в С{П).
Пусть граница dfi области Q удовлетворяет минималь-
минимальному требованию гладкости. Тогда
1) если / > J, 1 < р < оо, то Wlp(Q) -* С(П);
2) если / = п, р = 1, то также W?(S2) -* С(П).
Важную роль в теории уравнений в частных произво-
производных, а именно, для решения краевых задач, играют тео-
теоремы вложения для следов функций из WJ,(Q) на многооб-
многообразиях размерности меньшей п. Так как функции из Wp(f2)
определены с точностью до множества меры ноль, то воз-
нинает проблема определения следа функции из WHQ) на
многообразии размерности меньшей п, поскольку это мно-
многообразие имеет меру ноль.
Корректное определение следа на многообразии Sm раз-
размерности т < п можно получать различными способами.
Один из них состоит в приближении функций из Wp(Q) с
помощью функций из C°°(i?) П Wp(Q). Такие приближения
строятся с помощью теоремы 5, приведенной ниже. Для фун-
функций из С°° П Wp(f2) следы определяются естественным об-
образом, как их сужения на многообразие Sm. Доказывается
при некоторых условиях на параметры р,1,т ограничен-
ограниченность оператора следа как оператора из C°°(i?) П Wf,(B) с
нормой Wp(f2) в то или иное пространство функций, за-
заданных на многообразии (например, в Lg(Sm)), и затем
производится расширение оператора следа по непрерывно-
непрерывности с плотного в Wp(f2) множества C°°(i?) П W^{Q) на все
Wlp{Q). Именно, если fk 6 С°°(П) П Wj(fl), / 6 Wlp(Q) и
fk —* f при к —» оо по норме Wi(f2), а оператор следа Тг:
С°°(Г2) П WlJQ) -> Lg(Sm) ограничен по норме Wj(fl), то
следы (fk = Tr fk образуют сходящуюся последовательность
по норме Lg(Sm), так как
\\<Рк ~
Гл. XI, § 1. Основные определения и формулировка... 409
при к, I —♦ оо, что в силу полноты Lq(Sm) гарантирует су-
существование предела: 3ip = lim <pk € Lq(Sm). Этот предел
it—КЭО
не зависит от выбора {/*} при условии, что fk —* f при
к —* оо. Его и называют следом для функции / € WHQ):
P f
Таким образом, необходимы теоремы об ограниченности
оператора следа Тг, которые можно трактовать как вложения
Wj(fl) в Lg(Sm).
Следующие теоремы гарантируют единственность и при-
принадлежность следа функции из Wj,(Q) пространствам
Lq(Sm), где Sm - m-мерное гладкое многообразие в Q. В
частности, может быть Sn~x = дп или Sm - внутреннее
гладкое многообразие в Q.
Теорема 2. Вложение Wlp(Q) в Lq(Sm) при 1 < т < п.
Пусть граница дП области Q удовлетворяет минималь-
минимальному требованию гладкости, и Sm - гладкое многообразие
размерности т, лежащие в Q. Тогда
1)если/< J,l<p<g<-M-,TO
Wlp{Q) -> L9(Q).
2) если / < j, 1 < р < оо, п — 1р < т < п,
а при р = 1, H^x'(/2) —> L^S1) и в случае т = п — /;
3) если / = ^, 1 < р < оо, то
Wf (П)-> LAST),
где 1<т<п, 1<р<5<оо.
В основном тексте книги было замечено, что из суще-
существования обобщенных производных порядка / не следует,
410 Глава XI. Дополнение. Общие теоремы вложения...
вообще говоря, существования производных более низкого
порядка.
Приведем теорему о том, когда такие вложения имеют
место, т.е. теорему о производных низшего порядка.
Теорема 3. Пусть граница дП области Q удовлетворяет
минимальному условию гладкости и f(x) € Wlp(Q). Тогда
функция /(ж) имеет в Q все обобщенные производные по-
порядка ниже /, при этом
1) если / > J, it 6 JV0, 0 < к < I- J, то Wj(fl) -* Ск{П)
(в качестве числа к можно взять (/ — ^), т.е. наибольшее
целое число, меньшее, чем / — **•; таким образом, к = [I — ^],
если / — — - не целое; к = I — — — 1, если I — - - целое).
2) Если/ < J, it >0, /> к >l- J,n> m >n-(l-k)p,
то на всяком сечении области Q гладким многообразием Sm
т измерений
Dkf{x) € Lg(Sm), где q < п _™?_ к)р,
и ||#fc/llMs~) < C\\f\\w,{n), т.е.
l > Wkq{Sm).
то
3) Если 1<р<9<оо, [/-J + ^]=r>0, l<m<n,
Wlp{Q) -» WgrEm).
Заметим, что ни одно из вложений теорем 1 - 3 не может
быть улучшено в терминах рассматриваемых пространств.
Теоремы вложения сначала мы будем доказывать для Шп,
и сечений Жт, 1 < т < п, и к этому случаю сведем тео-
теоремы вложения для произвольной области с помощью про-
продолжения функций с Q на все Н". Теоремы же вложения
для JEC1 доказывать значительно проще, чем для области J2,
так как в Ш.п мы можем пользоваться хорошо знакомым нам
преобразованием Фурье.
Гл. XI, § 2. Вспомогательные теоремы ... 411
§ 2. Вспомогательные теоремы о продолжении
функций с f2 на все ГО,П и о плотности
финитных функций C°°(IRn) в Wi(f2)
Мы будем рассматривать продолжения функций, задан-
заданных в области Q за пределы границы дп на все простран-
пространство Ип.
Определение 4. Если существует линейный оператор Т,
отображающий функции, заданные на J? в функции, задан-
заданные на всем пространстве Ш.п:
Т : {и(х) : х € п} -> {й(х) : х € Ип}
и обладающий свойством
(Г«)(х)
то б^ем говорить, что Г - оператор продолжения, а фун-
функцию й(х) — (Ти)(х) будем называть продолжением фун-
функции и(х) с Q на все пространство IRn.
Имеет место следующая
Теорема 4. Пусть граница dfl области J? удовлетворяет
минимальному требованию гладкости. Тогда 3 линейный не-
непрерывный оператор продолжения
Г : Wlp{Q) -+ W^(TRn)
V/ натурального и Vp, 1 < р < оо.
Замечание. Непрерывность оператора продолжения Г из
Wlp{Q) в W^(IRn) означает, что Vu € Wlp(Q) выполнено не-
неравенство
412 Глава XI. Дополнение. Общие теоремы вложения...
где С > О - постоянная, не зависящая от щ иными словами,
для продолжения й(х) — (Ти)(х) функции и(х) с i? на все
IRn выполнено неравенство
Такое продолжение называют продолжением с сохранением
класса.
Теорема 4 доказана в книге [23] довольно сложно, мы же
докажем ее более простой вариант: когда дп С С1.
Доказательство теоремы 4 в случае дп С С1.
Рассмотрим локально-конечное покрытие кратности
< N области Q. Пусть окрестность границы дО покрыта
оо
шарами Bj, j' > 1 так, что вся область П — U У;, где
Vj = Q П Bj, j > 1, Vo может быть и неограниченной.
oo
Рассмотрим разложение единицы 1 = $Z 4>}{х), гДе
j=o
о
<Pj{x) € С °°(Vj), и выберем его так, чтобы Bj П dQ, j > 1,
было графиком функции хп = rj)j{x') € С, ж' = xi, ...,xn-i.
Функции ф](х') доопределим нулем с сохранением гладко-
гладкости так, что
Qi : хп < tbi(x').
Гл. XI, § 2. Вспомогательные теоремы ...
413
**«
х„ - щ (х)
П,
Пусть и(х) € Wlp(Q) и с помощью разложения единицы
и(х) представим в виде:
оо
где Uj(x) = <pj(x)u(x), j > 0.
оо
Отметим, что ряд ^Р uj(x) в каждой точке х содержит
j=o
не более, чем N слагаемых ввиду локальной конечности по-
покрытия. Каждую uj(x) доопределим нулем вне Vy
Uj(x) € Wp(f2j),
где Qj — {х : хп < xj)j{x'), x' € Ж"}, j > 1, есть специ-
специальная литпицева область (см. определение 2). Распрямим
границу в каждой пу.
Г х1 = у1,
\ хп = Vj(y') - у„,
тогда i?j —> IR",
414 Глава XI. Дополнение. Общие теоремы вложения...
Продолжим Uj(y) с IR+ на все Нп по способу Уитни (см.
гл. VI, § 8). Тогда окончательно имеем
uj(x) = Uj(x',ф;(х') -хп) е W^JR.11) для; > 1,
при этом uj(x) имеет компактный носитель. Теорема 4 для
случая дп С С1 доказана.
Докажем еще одну важную теорему, которой в даль-
дальнейшем будем пользоваться, а именно теорему о плотности
финитных бесконечно дифференцируемых функций в про-
пространствах Соболева. Теорема эта важна тем, что она дает
возможность исследовать свойства пространств И^(ИП) на
о
функциях из C°°(IR- ), которые плотны в
Теорема 5. Пусть 1 < р < оо. Функция / € И^(НП) тогда
и только тогда, когда существует последовательность {fm}
такая, что
l)/m(*)eC°°(IRn)Vm;
2) ||/ - /m||ty;(]R») -> 0 при m -> оо.
Доказательство. Достаточность условий 1), 2) очевидна. В
самом деле, пусть Daf = lim Dafm в норме ip(IRn), a =
m—>oo
«1,..., а„, |а| < /. Тогда, используя определение обобщенной
производной
J
<pDafmdx
и переходя к пределу при т —► оо, мы получаем
J fDa<pdx = (-l)|al J <pDafdx
го." mn
что доказывает, что предельная функция / € W'(IRn).
Гл. XI, § 2. Вспомогательные теоремы ... 415
Докажем необходимость условий 1), 2).
Пусть f(x) G WJ,(JRn). Усредним ее с ядром uJh(\x — j/|).
Тогда Д(ж), как доказано в § б гл. VI, будут бесконечно
дифференцируемыми функциями и lim Dafh(x) = Daf(x)
h—►()
в норме Lp(JRn) при \а\ < l. Но функции Д(ж) не имеют
компактного носителя, поэтому требуется изменить их соот-
соответствующим образом.
Пусть т/(ж) - бесконечно дифференцируемая срезающая
функция с компактным носителем, принимающая значения
от 0 до 1, и такая, что
■п(х) —
Рассмотрим двухпараметрическое семейство t][^,
h > 0, ^ > 0. Мы выберем сначала h столь малым, чтобы
Dafh аппроксимировали функции Daf в норме Lp(TRn)
V|a| </.
Теперь докажем, что при фиксированном h > 0
V|a| < /. Действительно, для fh(x) имеем
J 1ДИA-^(^))|Р^< / \fk(x)\'dx, A)
где правая часть последнего неравенства стремится к нулю
при R —► оо ввиду сходимости интеграла. При доказа-
доказательстве сходимости производных при дифференцировании
г)( jH no Xi возникает множитель -^ в соответствующей по-
положительной степени. Так, например, для первой произво-
производной, используя неравенство Минковского, которое утвер-
утверждает, что норма от суммы не превосходит суммы норм, по-
получаем
416 Глава XI. Дополнение. Общие теоремы вложения...
Первое слагаемое справа стремится к нулю при R —> оо
ввиду A), а второе слагаемое также стремится к нулю при
R —► оо, так как стоящая при 1/R норма конечна.
Действительно,
< sup
a sup \gtb,dr](x)\ < С, так как г](х) € C°°(IR-n)-
Совершенно аналогично доказательство для любой про-
производной порядка \а\ при \а\ < I.
Теорема 5 доказана.
§ 3. Теоремы вложения для дифференцируемых
функций, заданных во всем пространстве ГО,П
В этом параграфе мы докажем теоремы вложения, когда
область Q есть все IRn.
1. Формулировка теорем вложения
Теорема 6. Вложение Wj(Etn) в С(ПГ).
1. Если 1 < р < оо, I > J, тогда Wj(Hn) -» С(ИП).
2. Если / = J, р = 1, то И?(ГС.П) -» С(ИП).
3. Если р = 1, / > п, то ^'(Ш.") -> С(Ш-П).
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 417
Теорема 7. Вложение И^(П1П) -»• Lq(TRm).
1.Если/< J,1<p<9<^5?,to
^ -+ Lq(TRn).
2. Если / < j, 1 < р < оо, п - 1р < т < п,
а при р = 1, Wl(TRn) -» Xi(IRm) и в случае т = п-1.^
3. Если Z = j, 1 < р < со, то
W/ (Ш,п) -» Ь,(Ит)
при 1<т<п,ад- любое число, удовлетворяющее нера-
неравенству 1 < р < q < схз.
Формулировку теорем вложения в IRn для различных
функциональных пространств, в том числе с нецелым поряд-
порядком дифференцирования, можно найти в обзорной статье [6,
2)]-
Поясним, что мы будем ниже понимать под следом фун-
функции на гиперплоскости IRm. Пусть f(x) € Lp(JRn) и
х = {х',х"), х' = (жь...,жт), х" = (xm+i,...,xn). Будем
говорить, что функция <р(х') = f(x)\jnm есть след фун-
функции f(x) на гиперплоскости IRm, если Э/(ж) такая, что
f(x) — f(x) п.в. в IRn, и, кроме того,
1) /(*',*") € Lp(WLm) W € Hn"m;
2)/(х',0) = ^');
3) \\f(x',x") - v»(*')IIlf(r-) - 0 при |*"| -» 0.
Вложение Wp(JRn) —» Lg(IRm) означает, что множество
следов на IRm функций из WJ,(TRn) содержится в ig(IRm) и
выполняется соответствующее неравенство.
Другими словами, если А - линейный оператор, задава-
задаваемый формулой
27 - В. Н. Масленникова
418 Глава XI. Дополнение. Общие теоремы вложения...
то вложение WjJ(IRn) —► Lq(TRm) означает, что А - ограни-
ограниченный оператор из Wj((IRn) в Х,(Ит).
Для того чтобы доказать теоремы б и 7 нам понадобится
найти подходящий способ выражения функции через ее ча-
частные производные.
В связи с этим рассмотрим так называемые бесселевы
потенциалы.
2. Бесселевы потенциалы
Пусть
/(у) = J
x = F[f](y)
- преобразование Фурье функции /(ж) € Li(TRn). Заметим,
что JF[e~'rlIl ] = е""*'"' , что доказывается тем же путем,
которым вычислялось ядро Пуассона в теории теплопрово-
теплопроводности (см. гл. III, § 5).
Аналогично находим, что
'f тде6>0.
Рассмотрим гамма-функцию
оо
о
Заменой t\ —* 8: t\ = tS, ее можно представить в виде
A)
Полагая для вещественного а > 0, а = j, t =
находим из A)
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 419
где а > 0. А тогда
F
x-*y
= 1 f F fe-"*»
D7Г)°-/2Г(|) J Xtyi
0
Dтг)°'/2Г(|) J e б
о
B)
Введем следующее
Определение 5. Функцию Ga(x), преобразование Фурье
которой есть Ga(y) = A + 47г2|у|2)~а/2 с a > 0, будем
называть ядром бесселева потенциала. Свертку f * Ga с
f € Lp(TRn), p > 1, будем называть бесселевым потенциа-
потенциалом.
Лемма 1. V<*>0h1<s<oo, 1-^<^
GQ(x) € L3(WLn).
В частности, V а > 0 Ga(x) € ii(IRn) так, что преобразо-
преобразование Фурье GQ(x) определено в обычном смысле.
Доказательство. Из определения 5 и равенства B) сле-
следует, что
О
Воспользуемся неравенством Минковского для интегралов
27*
420 Глава XI. Дополнение. Общие теоремы вложения...
\F(x,y)\°dxI/3dy,
Е" ]Rm ]Rm Ж"
где1 < s < оо,ж = (жь...,жп), у = (уь ...,ym), n,m-любые
натуральные числа. Это неравенство утверждает, что норма
от интеграла не превосходит интеграла от нормы.
Применяя неравенство Минковского к C), получаем
Ga\\ <
< L 7|le^|| е
~ Dтг)°/2 Щ) J IIе IL.(ii-)
о
Далее, вычисляя интеграл в сферических координатах, по-
получаем
* = Ип I с * А ал,
где Qn - площадь поверхности единичной сферы в IRn.
Обозначая
о
получим
ML.(]Rn)
откуда следует
А тогда
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 421
утгм f ■* V 2
О
Интеграл в правой части последнего неравенства сходится
для всех а > О и s таких, что 1 — ^ < ^.
Действительно, сходимость на бесконечности есть V а,
s > 0 за счет множителя е~**, а для сходимости в нуле
необходимо и достаточно, чтобы
п /1 \ а 1 а
2\s ~ ) 2> ~ sK n'
Лемма 1 доказана.
Лемма 2. Пусть е*>0, l<s<oo, I — j<^, тогда
dGQ+i(x)
<G*a(x), i = l,...,n,
где G* (x) e Xe(Bn).
Доказательство. Продифференцируем интеграл C), где
вместо а подставлено а + 1, по параметру х,-, получим
dGa+i(x) I
2ttxj 7 _ii|£
Вычислим норму в Ls(JRn), воспользовавшись неравенством
Минковского:
oo
1 2тг
/,| ~'l«l2 .. f -n + a + 1 dS
Переходя к сферическим координатам и обозначая, как и
при доказательстве леммы 1, через £2'п интеграл по угловым
422 Глава XI. Дополнение. Общие теоремы вложения.
координатам, делая в процессе вычислений замену
A —» Ai, получаем
= / e-^Wdx = ffn
oo
где мы ввели обозначение П'п J e~nXi A^+*~1rfA1 = (СK. То-
о
гда
Тогда
\dGQ+l(x)\
Для сходимости интеграла в нуле полагаем п+^а+1 -|- itt» _
1 > 0, откуда а > пA - i) или ^ > 1 - \.
Лемма 2 доказана.
Теперь найдем способ выражения функции через ее ча-
частные производные. Такое представление функций и(х) €
Wp(f2) в звездной области Q через интегралы, содержащие
функцию и(х) и ее частные производные, было получено
С.Л. Соболевым в его книге [22.2), формула 7.12]. Затем оно
было получено с помощью формулы Тейлора (см. [6.1)]). В
JRn такое представление получить значительно проще.
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 423
Имеет место
Лемма 3. Для V /(х) € С °°(IRn) имеем
1) в случае четного I = 2к
/(*) = J G2k(x - у)[A - Ay)kf(y)]dy-
2) в случае нечетного / = 2к + 1
/(*) = J G2k+2(x - у)[A - Д,)*/(v)]<*V-
п 2
где Ах = X) ^Т ~ оператор Лапласа, а A — Ау)к означает
формальное возведение в степень к выражения, стоящего в
скобках.
Доказательство.
Докажем сначала пункт 1). Имеем /(х) = F~*[f], где /
- преобразование Фурье функции /.
Представим / в виде
Дх) =
Вспоминая, что
= F [G2k(y)\
У-*Х
и замечая, что
A + 4тг2|х|2)*/>)= F [A -
и—*х L
424 Глава XI. Дополнение. Общие теоремы вложения.
имеем
Откуда следует, что
/(*) = / G2k(x - у)[A - Ay)kf(y)]dy.
К"
В случае нечетного / = 2А; -+-1 представим / в виде
= [A + 4тг2|х|2)*/(*)]A +4тг2|х|2)-^ • A + 4тг2|х|2) =
1=1
= F[(l-Ay)hf(y)].F[G2k+2(y)}-
откуда следует пункт 2). Таким образом, лемма 3 доказана.
Лемма 4. Для любого натурального I 3 неотрицательная
функция gi(x) € Le(IRn), где l<s<oo, I — \ < j; такая,
о
что V/(x) € C°°(IRn) выполнено неравенство
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 425
где С = тахСа, постоянные Са взяты из равенства
A-Д,)*/(у) = £ CaD"yf(y).
Н<2*
Доказательство. В случае четного I — Ik согласно лемме
3 мы можем взять в качестве д\ функцию
gi(x) = G2jt(x),
так как согласно лемме 1 G^kix) € Ls(IRn) при 1 < s < оо,
1 — j < ~, Gf2fe(x) неотрицательна.
В случае нечетного / = 2к + 1 в качестве gi мы можем
взять функцию
g,(x) = G2k+2{x)+G*k+1(x). D)
Действительно, функция G2Jt+2(a;) € L8(JRn), I < s < оо,
1 _ I < 2*+г; так как согласно лемме 1 (?2*+2 € L8(JR,n) при
2Jfc
n
n
Функцию С?2к+1(я) выберем в виде
О
Нетрудно убедиться (см. лемму 2), что Vi = 1, ...,га
dx{
F)
Применяя к E) неравенство Минковского тем же путем, что
и при доказательстве леммы 1, получим, что G1^k+X(x) €
Le(IRn), l<s<oo, 1~7< 7^L- Пользуясь леммой 3
и выбирая gi в виде D), получаем на основании (б) и того
факта, что
426 Глава XI. Дополнение. Общие теоремы вложения...
G2k+2 € La, G^k+i € La,
неравенство
/
H<*R»
для нечетных /, где неотрицательная функция
9l(x) € be(IRn), 1 < s < со, 1--<-,
s n
что завершает доказательство леммы 4.
Переходим теперь к доказательству теорем б и 7, в ко-
которые входят все основные теоремы вложения для функций,
заданных о всем пространстве.
3. Доказательство теорем вложения для функций многих
переменных, заданных во всем пространстве
Доказательство теоремы б.
1) Пусть I > -, 1 < р < со, докажем, что
WJ,(JRn) — C(IRn). A)
О
Из леммы 4 и неравенства Гельдера находим V / € С °°(IRn)
||/||с(н») = sup |/(х)| <
< С
Согласно лемме 4 gi € Xp»(lRn), если только
р1 п р п р
Обозначая
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 427
Ы\ьр. =Си
получаем
B)
V/ € C°°(IRn), причем С2 > 0 не зависит от /.
Теперь воспользуемся стандартной схемой рассуждений,
которая будет использоваться нами при доказательстве всех
теорем вложения.
Для произвольной / € Wp(TRn), согласно теореме 5, 3
о
последовательность {/m} € C°°(IRn) такая, что
II/ - /m||vyj(]R") -+ 0 при m -► оо.
Так как {/т} сходится в Wp(TRn), то {/т} фундаментальна
в Wpl(TRn). Из B) находим
||/т - fk\\c(TRn) < C\\fm - fk\\wp(Win)
о
У fimfk € C°°(IRn). Следовательно, {/m} фундаментальна
в C(IRn). В силу полноты C(IRn) последовательность {/т}
будет сходиться в С(НП) к некоторой непрерывной функции,
т.е. 3/(х) в С(Шп) такая, что
||7-/m||c(R") -► при m -юо.
Остается выяснить вопрос о том, как связаны между собой
функции / и /:
/: ||/-/m||i*r.(R«)->0 при m -» оо, / € И^(Нп);
7: 117 ~ /«llc(R-) -» 0 при m -► оо, / € С(Ш.п).
Воспользуемся следующим свойством пространств Lp(IRn),
а именно, если /т —* f в Lp(IRn), to 3 подпоследователь-
подпоследовательность {/mfc} последовательности {fm} такая, что
lim fmh =/п.в.вГ
к
к—+оо
428 Глава XI. Дополнение. Общие теоремы вложения...
Далее
H7-/mHc(R») "> 0 =» И/" /m
т.е. {/mfc} сходится в С(Нп) к /. Но предел {/TOfc} равен
/ п.в. в IRn, следовательно, равенство / = / справедливо
п.в. в IRn, т.е. функцию / можно изменить на множестве
меры ноль так, что она станет непрерывной в IRn функцией.
Таким образом, вложение A) доказано.
2) Рассмотрим теперь случай I — z, где р — \. Этот слу-
случай значительно проще. Покажем, что имеет место вложение
-> C(JRn). C)
Схема доказательства та же. Сначала получим соответству-
о
ющее неравенство для функций из С°°(Ш.п). Пусть /(ж) €
С°° ВТ), тогда
dx\ = ... =
дх\дх2
оо оо оо
f f f дп f
откуда находим
dnf(x)
дх\...дхп
dx,
т.е.
Заметим, что функции из C°°(IRn) не плотны в простран-
пространстве с полунормой
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 429
поэтому нам эту полунорму необходимо оценить через норму
/ в Wp(JRn). Имеем очевидное неравенство:
l«l<»
Таким образом, V/ е С|ОО(Е-П)
Далее, пользуясь вышеизложенной стандартной схемой, по-
получаем вложение C).
3) Наконец, если р — 1, I > п, имеем, очевидно,
ft -> W?(JRn) -> C(TRn).
Таким образом, теорема б вложения
И^(Ш.П) -> С(Ш.П)
полностью доказана.
Займемся теперь доказательством теоремы вложения 7
Wj(lRn) - L?(IRm).
Определение 6. Показатель go = ;f^~ будем называть пре-
предельным показателем.
Теоремы вложения W^(IRn) —> L?(IRm) имеют место для
показателей q: p < q < go- Случай вложения с предельным
показателем q = qo требует особого подхода. Поэтому мы
докажем теоремы вложения Wj,(JEln) —> L?(IRm) для показа-
показателей р < q < qo-
Доказательсво теоремы вложения для предельного пока-
показателя читатель может найти в книге [23].
Докажем сначала пункт 1 теоремы 7, т.е. рассмотрим
случай m = п. Докажем, что если l<^,l<p<q< ^z^>
то Wj(IRn) - L,(IRn).
430 Глава XI. Дополнение. Общие теоремы вложения...
Воспользуемся леммой 4. Согласно этой лемме V/
9i(x-y)\D°f(y)\dy,
где gi e Le(IRn), 1<«<оо, 1-±<£. Тогда
Применим к свертке, стоящей в правой части последнего
неравенства, известное неравенство Юнга для сверток:
где 1<р, g, s<coH- = -+i — 1. Неравенство Юнга спра-
справедливо для любых функций /, д таких, что / € Lp(JRn),
д € La(JRn).
Из неравенства Юнга находим
r») < с Е
где мы ввели обозначение ||fifj||L,(]Rn) = Ci» причем постоян-
постоянная Съ > 0, очевидно, не зависит от /. Неравенство Юнга,
которым мы воспользовались, справедливо при условии
Ч1
q p s
а функция (ft € Le(IRn) - при условии, что 1 — ^ < п'
поэтому
11,1/ 11/
р q s n p q n
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 431
откуда находим, что
пр
п — 1р
Поскольку s > 1, то заключаем, что
Р<Я-
Заметим, что если р = 1, то q = s, тогда 1 — ^ < £, откуда
О
q < ^37. Таким образом, мы доказали, что V/ € C°°(IRn)
выполнено неравенство
II/IIl,(ir«) < C\\f\\w,(nnh D)
если 1 < р < q < ~^f-, I < ^. Далее пользуемся вышеизло-
вышеизложенной стандартной схемой доказательства теорем вложе-
вложения.
Рассмотрим теперь случай, когда т < п, т.е. докажем
пункт 2 теоремы 7 при т < п. Пусть 1 < р < оо. Имеем
V/€C°°(IRn)
II/IIl,(»-) < С ]Г || / 91(х - y)|D-
Пусть х' = (xi,..., xm), x" = (xm+1,..., xn_i, xn), тогда
x / pj(x'-y',x"-y")|D^/(y',y")|(iy'||L4(]Rm).
lRm
Воспользуемся неравенством Минковского, тогда
М»») <
< С
432 Глава XI. Дополнение. Общие теоремы вложения...
Оценим норму свертки с помощью неравенства Юнга
И/Им»-) ^ с £ /
<' ]R,n-
где - = - + ^ — 1. Теперь воспользуемся неравенством
Гельдера с показателем р > 1
Покажем, что интеграл
_
конечен, если
— + —- + 1>п. E)
г р
Для этого достаточно показать, что конечна норма
|'"|| (б)
где Gi - ядро бесселева потенциала.
Имеем, пользуясь неравенством Минковского
Гл. XI, § 3. Теоремы вложения для дифф. функций ... 433
1 1
-D^"Д|)О
_ j_ , -n+i ч dS
x e <» oy 2 ;-—.
Тогда
oo
x
lLp,(]R"-m)
x e 4ir 8^ 2 ' —
о
Вспоминая, что
II *H"
находим условие конечности нормы (б):
т п — т I — п
Откуда следует неравенство E). Обозначим норму F) через
С, где постоянная С > 0 не зависит от функции /. При этом
получим, что V/ е C°°(IRn)
G)
V:r" G IRn~m, при условии E). Так как jr = 1 - £, то из E)
находим
-т+ + />0. (8)
г р
28 - В И Масленникова
434 Глава XI. Дополнение. Общие теоремы вложения...
Неравенство Юнга, которым мы пользовались, справедливо
при
! = !-! + !. О)
Г q p
Тогда, подставляя в (8) равенство (9), получаем
= - = + />0, A0)
q p
Откуда следует, что если / < -, то q < п™^ .
Так как 1 < г < оо, то неравенство Юнга справедливо
о
при р < q. Поэтому V/(x) € C°°(IR<n) имеет место неравен-
неравенство G), если выполнено условие 1 < р < q < ^zf~, I < ^,
при этом должно выполняться неравенство п — 1р < т < п.
Далее опять пользуемся стандартной схемой рассужде-
рассуждений, т.е. плотностью С°°(^п) в Wp(IRn). В пункте 2 тео-
теоремы 7 осталось рассмотреть случай р = 1 при / < п. В
этом случае предыдущее доказательство не годится (нельзя
использовать неравенство Гельдера), но если считать, что те-
теорема вложения верна для предельного показателя q < ^у,
то в этом случае можно положить т = п — /, откуда имеем
1 < q < 1, т.е.
Рассмотрим случай /=-и1<р<оо. Повторим схему
доказательства пункта 2 при / = -, тогда вместо A0) полу-
получим — > 0, т.е. все интегралы будут сходится для любых
q > 0. Но в неравенстве Юнга было уже использовано, что
р < q, поэтому терема 7 при /=^,1<р<оо доказана для
любого q: \<p<q<ooia. любого т: 1 < т < п.
Теорема 7 доказана.
Гл. XI, § 4. Доказательство теорем вложения ... 435
§ 4. Доказательство теорем вложения для функций,
заданных в области
Сначала докажем вложение
j > С(Л).
Согласно теореме 4 функцию /(ж), заданную в области S2,
можно продолжить на все пространство IR". Пусть /(ж) -
продолжение функции /(ж) на все IR", при этом /(ж) =
/(ж). По теореме 4, если /(ж) € И^A7), 1 < р < оо, тогда
/(ж) € Wp(IRn) и выполнено неравенство
где Ci - независимая от / постоянная.
Для функции /(ж) € И^'(Ш,П) справедлива теорема вло-
вложения
j -► С(Шп),
I > ^, 1 < р < схэ, и / > п, р = 1, поэтому /(ж) непреры-
непрерывна в IR" и, следовательно, ее сужение на 17: / = /(ж)
непрерывно в области 1?, при этом
SUp |/(ж)| < SUp |/(ж)|
т.е.
п
Н/|1с(П) < \\f\\w^n),
Теорема 1 доказана.
28*
436 Глава XI. Дополнение. Общие теоремы вложения...
Точно также доказывается вложение
Wlp{Q) -> Lq{Q%
1 < р < q < w^*j , I < ^, т.е. пункт 1 теоремы 2.
Докажем пункты 2 и 3 теоремы 2, т.е. вложение Wl,{Q) —*
Lq{Sm) для / < J, 1 < р < q < ^, п-lp <т <п,
вложение W/(Л) -► Lq(Sm), когда Z = ^, 1 < р < оо,
1 <m<mnq- любое число, удовлетворяющее неравенству
1 < р < q < оо и W}(Q) -> Ii(-Sm) при р = 1, где 5т
- пг-мерное сечение области Q гладким многообразием m
измерений.
Согласно определению 3 § 1 пусть {Vj} - локально ко-
конечное покрытие кратности N < оо многообразия Sm; пусть
Vj — Vj П Sm. Сделав замену переменных, как указано, при
доказательстве теоремы 4, превратим Vj в плоское многооб-
многообразие Vj'. Тогда получаем
fc=l
где х' = х\...хт. Пусть Хк(х) - характеристическая фун-
( 1 х € VI'
кция множества Vfc": \к(х) - ] д' ж G IR7" \ У" ' Тогда' ис~
пользуя теорему вложения для И" и теорему о продолжении,
получаем
(Е /1/(*I?^'I/9 < c(f; J Хк(хЫх
т.е.
что и требовалось доказать.
Гл. XI, § 4. Доказательство теорем вложения ... 437
Теорема 2 доказана.
Доказательство теоремы 3 следует из определения нормы
в VF'(l?) и теорем 1 и 2, так как в них есть запас гладко-
гладкости для существования промежуточных производных и их
суммируемости с определенными степенями.
Все операторы вложения, рассмотренные нами выше, яв-
являются ограниченными.
Отметим, что если область Q ограничена в Ж", то все
операторы вложения являются вполне непрерывными (ком-
(компактными) за исключением вложения Wlp{Q) в Lq(Sm) для
предельного показателя q = т^. , 1 < т < п. Доказатель-
Доказательства всех основных теорем о компактности вложения при-
принадлежат ученику С.Л. Соболева Кондрашову В.И. и их
можно найти в книге С.Л. Соболева [22. 2)].
438 Литература
ЛИТЕРАТУРА
1. Adams R. Sobolev spaces. - New York: Academic Press,
1975.
2. Agmon S. Lectures on elliptic boundary value problems.
- Princeton, 1965.
3. Agmon S., Douglis A., Nirenberg L. Estimates near the
boundary for solutions of elliptic partial differential equa-
equations satisfying general boundary conditions. II. - Com-
Communications on Pure and Applied Math. 1964, vol. 17, N
1, p. 35-92.
4. Бесов О.В., Ильин В.П., Никольский СМ. Интеграль-
Интегральные представления функций и теоремы вложения. - М.:
Наука, 1975.
5. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник
задач по математической физике. - М.: Наука, 1972.
6. Буренков В.И.
1) Интегральное представление Соболева и формула
Тейлора. Труды МИАН им. В.А. Стеклова. т. 131. -
М.: Наука, 1974.
2) Теоремы вложения и продолжения для классов диф-
дифференцируемых функций многих переменных, задан-
заданных во всем пространстве. (Обзорная статья без доказа-
доказательств). Итоги науки, серия математика. Математиче-
Математический анализ. Москва, 1966, с. 71-155.
7. Владимиров B.C.
1) Уравнения математической физики. - М.: Наука,
1981.
2) Обобщенные функции в математической физике. -
М.: Наука, 1979.
8. Владимиров B.C., Михайлов В.П., Башарин А.А., Ка-
Каримова Х.К., Сидоров Ю.В., Шабунин М.И. Сборник
задач по уравнениям математической физики. - М.: На-
Наука, 1982.
Литература 439
9. Дезия А.А. Общие вопросы теории граничных задач. -
М.: Наука, 1980.
10. Douglis A., Nirenberg L. Interior estimates for elliptic
systems of partial differential equations. Communications
on Pure and Applied Math., 1955, vol. 8, N 4, p. 503-538.
11. Ильин A.M., Калашников А.С., Олейник О.А. Линей-
Линейные уравнения второго порядка параболического типа.
Успехи математических наук, 1962, т. XVII, вып. 3, с. 3-
146.
12. Камынин Л.И. Курс математического анализа. - Изд-
во МГУ, Москва, 1993, т. 1; 1995, т. 2.
13. Камынин Л.И., Химченко Б.Н.
1H теореме типа Жиро для эллиптического уравнения
2-го порядка слабо вырождающегося вблизи границы.
ДАН СССР, 1975, т. 224, N 4, с. 752-755.
2) Теорема типа Жиро для уравнения 2-го порядка
со слабо вырождающейся характеристической формой.
Сибирский математический журнал, 1977, т. XVIII, N
1, с. 103-121.
14. Колмогоров А.Н., Фомин СВ. Элементы теории фун-
функций и функционального анализа. - М.: Наука, 1976.
15. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая ги-
гидродинамика, части I, И. - М.: Физматгиз, 1955, 1963.
16. Курант Р. Уравнения с частными производными. - М.:
Мир, 1964.
17. Ладыженская О. А. Краевые задачи математической фи-
физики. - М.: Наука, 1973.
18. Ландис Е.М. Уравнения второго порядка эллиптиче-
эллиптического и параболического типов. - М.: Наука, 1971.
19. Михайлов В.П. Дифференциальные уравнения в ча-
частных производных. - М.: Наука, 1976.
20. Олейник О.А. Лекции об уравнениях в частных произ-
производных. - М.: Изд-во МГУ, 1976.
440 Литература
21. Петровскиий И.Г. Лекции об уравнениях в частных
производных. - М.: Физматгиз, 1961.
22. 1) Соболев С. Л. Уравнения математической физики. -
М.: Наука, 1966.
2) Некоторые применения функционального анализа
в математической физике. - М.: Наука, 1988.
23. Стейн И. Сингулярные интегралы и дифференциаль-
дифференциальные свойства функций. - М.: Мир, 1973.
24. Тихонов А.Н. Теоремы единственности для уравнения
теплопроводности. Математический сборник, 1935, т.
42, N 2, с. 189-216.
25. Тихонов А.Н., Арсения В.Я. Методы решения некор-
некорректных задач. - М.: Наука, 1979.
26. Тихонов А.Н., Самарский А.А. Уравнения математиче-
математической физики. - М.: Наука, 1977.
27. Хермандер Л. Линейные дифференциальные операторы
с частными производными. - М.: Мир, 1965.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
441
Абсолютно непрерывная
функция 341
Адамара пример 50
Аналитическая функция
многих вещественных
переменных 53
Аналитическое решение 54
Базис ортонормированный 313
Банахово пространство 243,
256, 405
Весселевы потенциалы 419
Вариационный принцип соб-
собственных значений и соб-
собственных функций 316, 317
Вложения теоремы 251, 279,
404, 405, 408, 409, 410, 416,
417
Внешние краевые задачи 392,
393, 401
Волновое уравнение 22, 48, 49
Вполне непрерывный опера-
оператор 234
Вторая краевая задача 37, 203
— начально-краевая задача
203
Гамма-функция 350, 418
Гарнака неравенства 389
— теорема 388
Галеркина метод для уравне-
уравнения Пуассона 330
теплопроводности
337
Гармоническая функция 362
Гидродинамики уравнения 44,
45, 46
Гильбертово пространство 243,
254, 257
Гиперболическая система
уравнений 99
Гиперболическое уравнение 87
Главный символ уравнения 82,
86
Грама - Шмидта метод 345
Граничные условия 29, 30, 31
Грина формула 354
Грина функция 358
Гюйгенса принцип 199
Даламбера формула 189
Двойного слоя потенциал 358
Дирихле задача 31, 37, 288, 330
Дифференциальный оператор
309
Диффузия волн 199, 200
Дюамеля принцип 153, 190
Единственность классического
решения краевых и началь-
начально-краевых задач 157, 160,
168
— обобщенного решения крае-
краевых задач для уравнения
Пуассона 290
первой начально-крае-
начально-краевой задачи для уравнения
теплопроводности 338
Жиро лемма для шара 366
— теорема 372
Задача Дирихле 31, 37, 288,
330
— корректно поставленная 119
— Коши 29. 53, 162
— Неймана 37, 377
— Штурма-Лиувилля 214
Закон сохранения энергии 165,
207
Замкнутый линейный опера-
оператор 236
Замыкание линейного опера-
оператора 237
Запаздывающий потенциал 192
Звездная область 257
Инверсии преобразование 382
Интеграл энергии 165, 207
Канонический вид дифферен-
дифференциального уравнения в част-
частных производных второго
порядка 101, 104, 105,111,112
Квадратичная форма 100
442
Предметный указатель
Кельвина преобразование 397
Кирхгофа формула 182
Классификация систем урав-
уравнений произвольного поряд-
порядка 90, 91, 99
— уравнений второго порядка
101, 105, 110
Классическое решение 21, 22,
150, 170, 172, 204, 212, 239
Ковалевской пример 66
— теорема 54
Колебаний уравнение 22, 38,
39,49
Компактное множество 284,
285
Компактность вложения 284,
287, 437
Конус характеристический 164
Корректность постановки зада-
задачи Коши 50, 119, 189
Коши задача для уравнения
волнового 162
теплопроводности
130
Коэффициенты Фурье 219, 314
Кратность собственного значе-
значения 300
Лапласа уравнение 23, 40, 363
— преобразование 117
Линейная зависимость элемен-
элементов 334
Линейно независимые системы
функций 330
Линейное дифференциальное
уравнение произвольного
порядка 21
— нормированное простран-
пространство 253, 256
Линейный дифференциальный
оператор 234, 309
Лиувилля теорема 390
Локально конечное покрытие
412
— неразрешимые уравнения 67
Мажоранта 58, 230
Мажорирующая задача Коши
61
Максимума принцип для урав-
уравнения Лапласа 363, 370
Максимума принцип для урав-
уравнения теплопроводности
155, 157, 158
Метод Галеркина 330, 337
— спуска 185
— Фурье 212, 232
Минимально гладкие границы
406
Минковского неравенство 415,
419
Навье - Стокса система 46
Начально-краевая задача 29,
30, 31, 203, 224
Начальные условия 29, 38
Неймана задача 37
Непрерывность оператора
продолжения 411
— средних функций 266
Непрерывный оператор 236
Неравенства Гарнака 389
Неравенство Минковского для
интегралов 419
— сумм 415
— Пуанкаре 283
— Фридрихса 259, 262, 318
— Юнга для свертки 430
Неразрывности уравнение 44
Норма 234, 253, 256
— линейного оператора 234
— порожденная скалярным
произведением 258
Нормированное пространство
253, 256
Носитель 137, 177
Нулевое множество обобщен-
обобщенной функции 177
Ньютона закон теплообмена 30
Ньютонов потенциал 357
Область влияния 197
— зависимости 197
— звездная 257
— значений оператора 305
— определения оператора 233,
235, 304
— специальная липшицева 406
Обобщенная производная 244,
245, 251, 405
— собственная функция 301,
302
Предметный указатель
443
Обобщенная функция 134, 138
финитная 177
Обобщенно однородный много-
многочлен 89
Обобщенное решение 239, 240,
242, 288
Обоснование метода Фурье 319
Оператор вложения 405
— вполне непрерывный 234
— замкнутый 236
— линейный 234
неограниченный 234, 235
ограниченный 233, 234,
418
— положительный 305
— продолжения 411
— самосопряженный 234, 236,
237, 304
— сопряженный 237
Операторное уравнение 306,
307
Ортонормированная система
312
Ортонормированный базис 313
Основные функции 137, 138
Остроградского - Гаусса
формула 225
Параболическая система
уравнений 99
Параболическое уравнение 89
Парсеваля равенство 134, 314
Первая краевая задача 31, 37
Первая начально-краевая за-
задача для уравнения волно-
волнового 38
гиперболи-
гиперболического 203
параболи-
параболического 224, 337
— — теплопро-
теплопроводности 29, 337
Петровский И.Г. 24, 85, 87, 88,
89, 91
Поверхность характеристи-
характеристическая 77
Полная система 330
— производная вектора и ска-
скаляра 40
Полное нормированное про-
пространство 254
Полный символ уравнения 82
Порядок линейного дифферен-
дифференциального уравнения 20
— системы 20
Потенциал двойного слоя 358
— запаздывающий 192
— Ньютонов 357
— простого слоя 357
Потенциалы Бесселя 419
Предельный показатель в тео-
теоремах вложения 429, 437
Преобразование Лапласа 117
— Фурье 114
из S в 5" 115
из
S" в S' 140
Приближенное решение 330,
332, 337
Приведение уравнения к кано-
каноническому виду в области
105, 111, 112
точке 100, 101
Пример Адамара 50
— Ковалевской 66
Принцип возможных переме-
перемещений 33
— Гюйгенса 199
— максимума для уравнения
Лапласа 363, 370
теплопроводности
155, 157, 158
Продолжение функций 280,
282, 411
Продолжения оператор 411
Производная обобщенная по
Соболеву 244, 245, 249, 251
Пространство обобщенных
функций D' 138
5' 138
— основных функций 5 114
D 137
— Соболева 253, 256
Пуанкаре неравенство 283
Пуассона уравнение 23, 36
— формула 145, 188, 385
— ядро 144
Равенство Парсеваля 134, 314
444
Предметный указатель
Равновесия мембраны уравне-
уравнение 32
Разделение переменных 212,
228, 232
Разложение единицы 412
Расширение* оператора 235
Решение задачи Дирихле 288,
292
Неймана 308, 310
Решение первой начально-крае-
начально-краевой задачи для уравнения
волнового 322, 329
гиперболи-
гиперболического 319, 322, 329
параболи-
параболического 337, 347
— второй (и третьей) началь-
начально-краевой задачи для урав-
уравнения гиперболического
232
болического 233
— задачи Коши для уравне-
уравнения волнового 172
теплопроводно-
теплопроводности 149, 150, 153
Рисса теорема 291
Ряд Фурье по собственным
функциям краевой задачи
222, 313
Самосопряженный оператор
234, 236, 237, 304
Свертка 140, 177
Свойства обобщенных произ-
производных 246, 247, 252
— собственных значений 308,
310, 315
функций 309, 311, 315,
316
— функции Грина 358, 359
Система ортонормированная
312
Скалярное произведение 254,
289, 303
Слабо компактное множество
285
— сходящаяся последователь-
последовательность 136, 336
След функции 271, 408, 417
Соболев С.Л. 24, 134, 238, 241
243, 251, 256, 270, 278, 298,
404
Соболева пространства 253, 256
Собственное значение 214, 215,
300
Собственные функции 214, 215,
300
Сопряженный оператор 237
Специальная липшицева
область 406
Средние функции 264
Срезающая функция 280, 415
Сужение на подмногообразие
408, 435
Сходимость в среднем (силь-
(сильная) 255, 336
— слабая 255, 336, 347
Теорема Гарнака 388
— Гильберта - Шмидта 312
— Ковалевской 54
— Лиувилля 390
— о непрерывной зависи-
зависимости 210, 228
— об устранимой особен-
особенности 391
— Рисса 291
Теоремы о продолжении
функций 280, 282, 411
— о среднем для гармони-
гармонических функций 378, 379
Теплопроводности уравнение
22, 28, 66
Тихонов А.Н. 51, 160
Третья краевая задача 38, 295,
374
— начально-краевая задача 31
Уравнение волновое 22
— гиперболическое 87
— колебаний мембраны 38
струны 39
— Лапласа 23, 40
в полярных координа-
координатах 397
в сферических коорди-
координатах 399
— неразрывности 44
-— равновесия мембраны 36
— параболическое 89
Предметный указатель
445
Уравнение Пуассона 23, 36
— смешанного типа 113, 114
— состояния 45
— теплопроводности 22, 28
— Трикоми 113
— ультрагиперболическое 105
— Эйлера 45
— эллиптическое 86
Уравнения гидродинамики 44,
45, 46
Условие некорректной поста-
постановки задачи Коши 123,
124, 126
Условие, непротекания жид-
жидкости через границу 46
Условия граничные 29, 30, 31
— начальные 29
Усреднение функции (средние
функцииJ64
Усреднения ядро 263
Финитная функция 137
Формула Даламбера 189
— Грина 354
— Кирхгофа 182
— Пуассона для решения
уравнения Лапласа в
шаре 385
теплопровод-
теплопроводности 145
колебаний
мембраны 188
Фридрихса неравенство 259,
262, 318
— теорема 259
Фундаментальное решение
уравнения волнового 193,
195
Лапласа 349, 350
линейного дифферен-
дифференциального 348, 350
теплопроводности 148
Функционал линейный 134
Функция гармоническая 362
— Грина 358
— источника 148
Фурье закон в теории тепло-
теплопроводности 26
— коэффициенты 219, 314
— преобразование 114, 140
— ряд 218
по собственным функ-
функциям краевой задачи 218
Характеристика (характери-
(характеристическая поверхность) 77
Характеристическая поверх-
поверхность для уравнения
волнового 78, 79, 164
теплопроводности
78
Характеристический много-
многочлен 82
Характеристическое направле-
направление 82
Штурма - Лиувилля задача
214
Эйлера уравнения движения
жидкости 45
Эквивалентные нормы 258
Энергетические оценки 165, 208
Эллиптическая система по
Петровскому 90
Дуглису - Ниренбергу
93
Эллиптическое уравнение 86
Юнга неравенство 430
Ядро бесселева потенциала 419
— Пуассона 144, 147, 148
— усреднения 263
Вера Николаевна Масленникова
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
Учебник
Редактор Ж.В. Медведева
Технический редактор Ю.В. Чваяова
Компьютерная верстка Е.М. Мещерякова
Сдано в набор 19.08.96 г. Подписано в печать 23.06 97 г.
Формат 60 х 90 7i6. Печать офсетная.
Усл. печ. л. 28,0. Уч.-изд. л. 26,1- Усл.крготт. 28,25. Тираж 2000 экз.
Издательство Российского университета дружбы народов
117923, ГСП-1, Москва, ул.Орджоникидзе, 3
Заказ 805.
Московская типография № 6 Комитета РФ по печати,
109088, Москва, Ж-88, Южнопортовая ул., 24