Дифференциальные уравнения - Демидович Б.П., Моденов В.П.

Часть I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Глава II. Дифференциальные уравнения первого порядка
§ 4. Теорема существования и единственности
§ 5. Уравнения с разделяющимися переменными
§ 10. Понятие об интегрирующем множителе
§ 11. Интегрирующий множитель линейного уравнения
§ 12. Уравнение первого порядка, не разрешенные относительно производной
§ 18. Составление дифференциальных уравнений
Глава III. Дифференциальные уравнения второго порядка
§ 2. Механический смысл дифференциального уравнения второго порядка
§ 5. Линейные однородные уравнения с постоянными коэффициентами
§ 6. Физическая интерпретация линейного однородного уравнения второго порядка
§ 7. Линейные неоднородные уравнения с постоянными коэффициентами
§ 8. Физическая интерпретация линейного неоднородного уравнения второго порядка
§ 9. Нахождение частных решений неоднородного уравнения методом неопределенных коэффициентов
§ 10. О краевых задачах для уравнений второго порядка
Глава IV. Дифференциальные уравнения высших порядков
§ 2. Уравнения, допускающие понижение порядка
§ 3. Однородные линейные дифференциальные уравнения
§ 4. Неоднородные линейные дифференциальные уравнения
§ 5. Метод вариации произвольных постоянных
§ 6. Однородные линейные уравнения с постоянными коэффициентами
§ 7. Неоднородные линейные уравнения с постоянными коэффициентами
Часть II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
§ 2. Задача Коши для линейного однородного уравнения
Глава III. Классификация уравнений второго порядка
§ 2. Приведение к каноническому виду линейных относительно старших производных уравнений второго порядка с двумя независимыми переменными
Глава IV. Основные уравнения математической физики
Автор: Демидович Б.П. Моденов В.П.
Теги: математический анализ функциональный анализ математика дифференциальные уравнения
ISBN: 978-5-8114-0677-7
Год: 2008
Похожие
Дифференциальные уравнения
Составление и решение дифференциальных уравнений инженерно-технических задач
Текст
                    КЛАССИЧЕСКАЯ
ЕБНАЯ ЛИТЕРАТУРА
ПО МАТЕМАТИКЕ


Б. п. ДЕМИДОВИЧ
В. п. МОДЕНОВ


ДИФФЕРЕНUИАЛЬНЬIЕ
УРАВНЕНИЯ


УЧЕБНОЕ ПОСОБИЕ


Издание третье,
стереотипное


ь
ЛАНЬ@
Санкт
Ilетер6урr.
осква.l(раснодар
2008




ВВК 22.161.1
Д 30
Демидович Б. П., Моденов В. п.
Д 30 Дифференциальные уравнения: Учебное пособие.
3
e изд., стер.
 СПб.: Издательство «Лань», 2008.

288 с.: ил.
 (Учебники для вузов. Специальная лите..
ратура).


ISBN 978..5..8114..0677..7


Предлаl'аемая читателям КНИl'а состоит из двух частей: в первой
части рассматриваются основы теории обыкновенных дифференци

альных уравнений, во второй
 дифференциальные уравнения с част

ными производными.
Учебное пособие предназначено для студентов технических BY

зов. Написанная ясным и простым языком, КНИl'а представляется
полезной также лицам, занимающимся математикой самостоятельно.


ВВК 22.161.1


Оформление обложки с. ШАПИРО, А. ЛАПШИН


Охраняется законом рф об авторском праве.
Воспроизведение всей КНИl'и или любой ее части
запрещается без письменноl'О разрешения издателя.
Любые попытки нарушения закона
будут преследоваться в судебном порядке.


@ Издательство «Лань», 2008
@ Б. п. Демидович, В. п. Моденов,
наследники, 2008
@ Издательство «Лань»,
художественное оформление, 2008




ОТ ИЗДАТЕЛЬСТВА


Предлаrаемое читателям учебное пособие состоит из двух
частей. В первой части рассматриваются основы теории обык

новенных дифференциальных уравнений, во второй
 диф

ференциальные уравнения с частными производными.
Первая часть написана на основе курса лекций, читав

шихся Б. п. Демидовичем в Военной Артиллерийской ин

женерной академии им. Ф. э. Дзержинскоrо (ныне BoeH

ная академия ракетных войск стратеrическоrо назначения
им. Петра Великоrо). Ее содержание соответствует изложе

нию за один семестр раздела «обыкновенные дифференци

альные уравнения» курса высшей математики для техничес

ких вузов.

атериал первой части пособия представлен в четырех
rлавах. В первой rлаве даются общие понятия теории обык

новенных дифференциальных уравнений. Во второй rлаве
излаrаются сведения об уравнениях первоrо порядка. :Кроме
детальноrо разбора интеrрируемых случаев, в ней затраrива

ются элементы общей теории дифференциальных уравнений
(особые точки, особые решения и др.). Третья rлава посвя

щена подробному исследованию уравнений BToporo порядка.
В четвертой rлаве рассматриваются уравнения высших по

рядков.
Автор второй части книrи, В. п.
oдeHOB написал ее на
основе курса лекций, прочитанноrо Б. п. Демидовичем CTY

дентам химическоrо факультета
OCKoBcKoro rосударствен

Horo университета им.
. В. Ломоносова. Ее материал COOT

ветствует изложению, также в течение одноrо семестра, раз

дела «дифференциальные уравнения с частными произ

водными» из курса высшей математики для технических
вузов.
Вторая часть пособия, как и первая, содержит четыре
rлавы. В первой rлаве даются сведения об уравнениях в част

ных производных первоrо порядка. Вторая rлава посвящена




изложению необходимой далее теории рядов Фурье. В Tpe

тьей rлаве подробно рассматривается классификация линей..
ных уравнений с частными производными BToporo порядка.
В четвертой rлаве анализируются основные уравнения MaTe

матической физики.
В книrе приводится разбор характерных задач, содер..
жатся упражнения для самостоятельноrо решения, снабжен

ные необходимыми указаниями и ответами. В конце ее име

ется список дополнительной литературы.
Издательство выражает признательность В. Б. Демидо

вичу и Н. п. Осмоловскому за помощь, оказанную при под

rOToBKe настоящеrо учебноrо пособия.
:Книrа рассчитана на студентов технических вузов. Ha

писанная простым и ясным языком, она представляется
также полезной лицам, занимающимся математикой caMO

стоятельно.




ЧАСТЬ 1


ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ


Под обыкновенным дифференциальным уравнением (сокращён

но, ОДУ) понимается равенство, содержащее независимую перемен

ную, неизвестную функцию от этой переменной и её производные.
Порядком старшей производной, ВХОДЯIl
ей в состав уравнения,
задаётся порядок ОДУ. Функuией, имеющей соответствующие про

изводные и обращающей уравнение в тождество, определяется реше

ние ОДУ. Процесс нахождения решений ОДУ обычно называют ero
UHmezpupoeaHueM.
При изложении теории ОДУ основное внимание мы сосредоточим
на случаях точноrо интеrрирования таких уравнений.


rлава 1
ОБЩИЕ ПОНЯТИЯ



 1. ЗАДАЧИ, ПРИВОДЯЩИЕ к ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ


Математическое изучение закономерностей действительноrо мира
часто приводит к уравнениям, связывающим неизвестные величины и
производньrе этих величин. Такие уравнения называются дuфферен

циальнымu.
Прежде чем переходить к точным определениям основных поня

тий, рассмотрим ряд примеров.
Пример 1. Скорость распада радия в каждый текущий момент Bpe

мени t пропорциональна ero наличному количеству Q. Найти закон
распада радия, если в начальный момент t = О имелось Qo радия.
Ре Пl е н и е. Под скоростью распада радия понимается производ

ная; поэтому соrласно условию задачи имеем дифференциальное
уравнение


dQ

dt =
kQ,


(1.1)


5




rде k
 известный коэффици.ент пропорuиональности*, а знак ,,
"
указывает на то, что с увеличением времени t величина Q убывает:
dQ
dt < о. Кроме уравнения (1.1) имеем еще так называемое начальное
условие:


Q = Qo при t = О,


( 1.2)


роль KOToporo вьrяснится впоследствии.
у равнение (1.1) леrко может быть решено. А именно, разделив обе
ero части на Q, будем иметь


d(Jn Q) =
k
dt


или


d
di(InQ+kl)=O.


Отсюда


lnQ + kt = lnC,


rде lnC.......... произвольная постоянная интеrрирования в лоrарифмиче-
ском виде. Потенцируя последнее равенство, окончательно получим


Q = Ce
kt .


( 1.3)


Формула (1.3) представляет собой семейство функций от независи-
мой переменной t, зависящее от произво.пьной постоянной С, причем
каждая из этих функций удовлетворяет дифференциальному уравнению
(1.1) . Такое решение называется общим и не дает KOHKpeTHoro ответа на
вопрос задачи. Чтобы получить решение задачи, нужно определить зна-
чение постоянной С; это можно сделать, используя начальное условие
(1.2). Полаrая t = О в формуле (1.3), получим
Qo = С.l.


Отсюда


с= Qo.
Подставляя это значение в формулу (1.3), найдем так называемое
частное решение


Q = Qoe
kt ,


(1.4)


* А именно, k
 физическая ПОСТОЯННdЯ, выраженная обычно через период полу

распада 'С.


б




полностью решающее задачу. rеометрически это есть показательная
кривая (рис. 1).


Q


Qo


2


.
t


Рис. 1


Пример 2. Материальная точка массы т брошена вертикально
вверх с начальной скоростьк) vo. Найти закон движения точки, прене

бреrая сопротивлением воздуха.
Реш е н и е. Будем считать, что траектория точки есть ось Ох, Ha

правленная вертикально вверх, причем в начальный момент t = О точ

ка находилась в нача.ле координат. Единственная сила, действующая
на нашу точку, есть сила тяжести, равная тg и направленная верти-
. кально вниз. Применяя закон Ньютона, соrласно которому произведе

ние массы на ускорение равно действующей силе, по.лучим дифферен

циальное уравнение BToporo порядка
d 2 x
т2=
Пlg
dt


или


d 2 x

=
g
dt 2 .


(1.5)


Начальные условия здесь записываются следующим образом:


(х = О,
; = v о) пр и t = о.


(1.6)


Интеrрируя уравнение (1.5) последовательно два раза, будем
иметь




 = С 1
 gt


(1.7)


и


gt 2
Х = С 2 +Clt
2.


(1.8)


Функция (1.8), зависящая в этом случае от двух произвольных по

стоянных С 1 и С 2 , представляет собой так называемое общее решение


7




уравнения (1.5). Из уравнений (1.7) и
(1.8), используя начальные условия
(1.6), имеем
С 1 =ио, С 2 =0;


х


Рис. 2


отс.юда, подставляя эти значения в
t формулу (1.8), получим частное pe

шение


о


.)
gt

Х = vot
2'
представляющее искомый закон движения материальноЙ точки. reo

метрически это есть парабола с осью параллельной оси ординат, Kaca

тельная к которой в начале координат (рис. 2) образует уrол
а = arctg ио.



 2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ


Введем несколько определений.
Оп р е Д е л е н и е 1. Уравнение
F( , ( п ) )
 О
Х, у, у , ..., у
,
связывающее независимую переменную х, искомую функцию у = у(х)
и ее производные (или дифференциалы) до п
ro порядка включитель

но, называется обыкновенньrм дифференциальным уравнением п
ro
порядка.
Например:
уу' + х = О
 дифференциальное уравнение 1
ro порядка;
у" + у = о
 дифференциальное уравнение 2
ro порядка и т. д.
О п р е Д е л е н и е 2. Всякая функция у = у(х), которая при ее под

становке в дифференциальное уравнение (1.9) обращает ero в тожде

ство, называется решением этоrо уравнения, а rрафик этой функции
называется инmееральной кривой.
Уравнение


(1.9)


Ф(х, у) = о (1.10)
называется интеrралом диффереНllиальноrо уравнения (1.9), если
каждая функция у = У(Х), определяемая уrавнением (1.1 О) и имею

щая непрерывные производные у', ..., у(п до п
ro порядка включи

тельно, является решением данноrо дифференциальноrо уравнения
Обобщая понятие интеrральной кривой, линию определяемую
уравнением ( 1.1 О), будем по
прежнему называть UНПlе2ральной Kpи

вой или UНПlе2ральной линией дифференциальноrо уравнения (1.9).


8




Разрешая уравнение (1.9), если это возможно, относительно CTap

шей производной у(п), получим одно или несколько уравнений вида
у(n) == [(х, у', .... y(п
l)), (1.11)


rде f
 известная функция. В дальнейшем мы будем изучать rлавным
образом дифференциальные уравнения (1. J 1 ), разрешенные относи

тельно старшей производной.
На при мерах мы видели, что дифференциальное уравнение имеет
бесчисленное множество решений. Чтобы выделить одно вполне опре

деленное конкретное решение, кроме уравнения (1.11) нужно задать
дополнительные условия, вытекающие из условий данной задачи.
В простейшем случае ими являются так называемые начальные усло

вuя, состоящие в том, что при некотором значении х == Ха, задаются
значения искомой функции у и ее последовательных производных
у', ..., y(п
l). Тоrда мы приходиftл в задаче Коши: найти решение у диф

ференциальноrо уравнения (1.11), удовлетворяющее заданным нача

льным условиям
I
 ' /
 I ( n
 1) I
 ( п
 1) ( 12 )
у Х=Хо
 Уа, У Х=Хо
 Уа, ..., У Х=Хо
 Уа ' 1.
, (п
l) Е
rде хо, Уа, Уа, ..., Уа
 некоторые определенные числа. сли эта
задача для любой системы начальных условий имеет единственное pe

шение, то rоворят, что дифференциальное уравнение (1.11) обладает
свойством единственности. rеометрически задача Коши состоит в Ha

хождении интеrральной кривой У = у(х), проходящей через данную
точку Ма(Хо, Уа), причем так, чтобы производные у', ..., y[п
O прини-
мали заданные значения.
Если порядок уравнения первый (п = 1), то требование о производ-
ных, естественно, отпадает.
О п р е Д е л е н и е з. Решение дифференuиаЛЬНОI'О уравнения (1.11)
у = <р(Х, С 1 ' ..., Сп)' (1.13)


содержаrцее п произвольных постоянных С 1 , ..., Сп ,будем называть
общим, если путем выбора этих постоянных можно получить реше

ние, удовлетворяющее любым начальным условиям*.
Постоянные С 1 , ..., Сп' обладающие этим свойством, назовем суще

ственными Поэтому коротко можно сказать, что общим решением
диффереНllиальноrо уравнения ll
ro порядка называется ero решение,
содержащее п существенных произвольных постоянных.


* Вообще rоворя. в известнои области.


9




Если выполнено свойство единственности, то общее решение пред

ставляет собой совокупность всех решении данноrо дифференциаль

Horo уравнения, Т. е. дает полное решение задачи.
О n р е Д е л е н и е 4. Реш
ние дифференциа.пьноrо уравнения
(1.11), получающееся из общеrо (1.13) при некотором конкретном BЫ

боре произвольных постоянных С 1, ..., Сп' называется частным.
rеометрически общее решение представляет собой семейство ин

теrральных кривых, зависяшее от п парамеТРОБ (поле инmесраЛЬНblХ
кривых), а частное решение
 отдельную интеrральную кривую, BXO

дящую В это семейство.
Если известно общее решение (1.13) дифференциальноrо ypaBHe

ния (1.11), то ero частное решение, удовлетворяющее заданным Ha

чальным условиям (1.12), мы получим, определяя произвольные по

стоянные С 1 , ... , Сп из системы уравнений:


1


................ J
(п
O (п
O
уо = <р х (хо. С 1 , ..., Сп)'


УО = <Р(Хо, С 1 ' ..., Сп ),
Уа = <P
(Xo, С 1 , ..., Сп)'


(1.14)


Пример. Найти решение дифференциальноrо уравнения
у'II = 6х,


(1.15)


удовлетворяющее начальным условиям
ylx=o = о, y'l x ::: o = 1, y"lx=o =
2.
Реш е н и е. Интеrрируя обе части уравнения (1.15) последовате

льно три раза, будем иметь
у" = 3х 2 + С 1 ' 1
у' = х З + С( х + С 2 .

х 4 С х2 С С I
У = 4""" + 1"2" + 2 Х + 3.J


(1 16)


Полаrая х = О в уравнениях (1.16), получим

2 = С}, 1 = С 2 , О = С з .


Отсюда


С 1 =
2, С 2 = 1, С з = о


10




и, следовательно, искомое частное реlдение есть
у = i x4
x2 +х.


о п р е Д е л е н и е 5. Соотношение
Ф (Х, у, С 1 , ..., Сп) = о


( 1.17)


называется 06и{им uнтеералом дифференциальноrо уравнения (1.11),
если 1) при любом выборе произвольных постоянных С 1 ,..., Сп
кривая, определяемая уравнением (1.17), является интеrральной и
2) среди семейства (1.17) имеются интеrральные кривые, удовлетво

ряющие произвольным начальным условиям.
Если дифференциальное уравнение дано в общем виде,


р( I ( п ) )
 О
Х,у,у,...,у
,


(1.18)


то в простейшем случае это уравнение эквивалентно нескольким ypaB

нениям вида (1.11). т оrда соотношение (1.17) будем называть общим
интеrралом дифференииальноrо уравнения (1.18), если оно эквива

лентно совокупности общих интеrралов всех отдельных уравнений
вида (1.11).
rеометрически общий интеrрал (1.17) представляет собой n
па

раметрическое семейство интеrральных кривых дифференuиаль

Horo уравнения (1.11), или соответственно (1.18).
Обратно, имея семейство кривых


Ч'(х, у, C 1 , С 2 , ..., Сп) = О,


(1.19)


зависящее от п существенных пара метров С l' С 2 , ..., Сп' путем диффе

ренцирования получим еще n уравнений




 = О, ....
:
 = о.


(1.20 )


Исключая из n + 1 уравнений (1.19) и (1.20) п параметров С l'
С2' ..., Сп' получим, вообще rоворя*, дифференuиальное уравнение
п
ro порядка, общим интеrралом KOToporo является данное семейство
кривых (1.19).
Пример. Составить дифференциальное уравнение семейства пря

мых, проходящих через начало координат.


* Предполаrается. что исключение параметров С. ' С 2 , ... t Сп не может быть произ-
ведено из частичной системы уравнений '1'==0, ... dk'V =Опри k < n.
dx k


11




у


с=о х


Рис. 3


Реш е н и е. Имеем (рис. 3)
у = Сх.
Дифференцируя равенство
находим


( 1.21 )
(1.21),


у' = С. ( 1.22)
Исключая С из (1.21) и (1.22), полу-
чаем дифференииальное уравнение
х у' = у,
для KOToporo семейство (1.21) являет-
ся общим интеrралом.


Задания для самостоятельноrо решения
1. Проверить, что для заданных дифференциальных уравнений сле-
дующие функции являются их решениями (С, С 1, С 2
 произвольные
постоянные):
а) уу' = Х, у = j;2 + С ;
б) у"
 (k 1 + k 2 )у' + k 1 k 2 y = О, У = C1e k1X + C 2 e k2X
(k., k 2 ...... постоянные);
в) у" + 2ру' + р2 у = О, У = e
PX(Cl + С 2 Х) (р
 постоянно);
r) у" + 2ру' + (р2 + q2)y = О. у = e
PX(Cl cosqx + С 2 sinqx)
(р, q
 постоянны).
2. Составить дифференциальные уравнения заданных семейств
кривых (С, С 1 , С 2
 параметры):
а) у = х + С (параллельные прямые);
б) у = сх 2 (параболы);
в) у = х 2 + C1x + С 2 (KoHrpyeHTHbIe параболы);
r) (Х
 с 1 )2 + (у
 с 2 )2 = 1 (окружности единичноrо
радиуса).
3. Зная общие решения дифференциальных уравнений, найти их
частные решения у = у (Х), удовлетворяющие заданным начальным
условиям, если
а) у = Сх 2 , у(2) = 3;
б) х2 + 2у2 = С, У (1) = 5;
в) у = eX(C 1 + С 2 х), у (О) = 1, у'(О) = о;
r) у = eX(C 1 cosx + C 2 sinx), у (О) = О, у'(О) = 10.




r л а в а 11
ДИФФЕРЕНЦИАЛЬНblЕ УРАВНЕНИЯ ПЕРвоrо ПОРЯДКА



 1. РАЗЛИЧНЫЕ ФОРМЫ ДИФФЕРЕНЦИАЛьноrо УРАВНЕНИЯ ПЕРвоrо
ПОРЯДКА
Общий вид дифференциальноrо уравнения 1
ro порядка с неизвест"
ной функцией у = у (х), неразрешенноzо относительно производ..
ной у', следующий:


Р(х, у' у') = О,


(2.1 )


rде F
 заданная функция. Разрешая уравнение (2.1), если это воз-
можно, относительно aprYMeHTa у', получим дифференциальное урав-
нение первоrо порядка, разрешенное относительно производной:


у'=!(х,у),


(2.2)


rде t
 некоторая известная функция. В общем случае, уравнение
(2.1) эквивалентно нескольким уравнениям вида (2.2) (см. rл. 11, Э 12).
в уравнении (2.2) переменные х и у входят неравноправно: х
 яв

ляется независимой переменной, а у
 функцией от х. При решении
задач иноrда удобно для дифференциальноrо уравнения (2.2) пользо-
ваться иной записью, в которой переменные равноправны. Полаrая
, = dy и t( x ) =
 Р(х, у )
у dx ' У Q( Х t У )


(здесь учтено, что t (х, у), вообще rоворя,
 есть дробная функция, и
знак минус взят для удобства дальнейших выкладок), будем иметь
симметрическую форму дифференциальноrо уравнения l-ro порядка:


р(х, y)dx + Q(x. y)dy = о.


(2.3 )


Под решением этоrо уравнения понимается система функций


х = q>(t), у = 'I'(t)
(t
 параметр) таких, что
{Р [q>(t) , \V(t)]<p'(t) + Q [q>(t), \V(t)]\V'(t)}dt == о.


в частном случае за пара метр может быть принята переменная х
или переменная у.
Линии, соответствующие решениям уравнения (2.3), называются
интеzральными кривыми этоrо уравнения.


13





 2. ПОЛЕ НАПРАВЛЕНИЙ
Пусть в некоторой области G плоскости ОХУ задано дифференци-
альное уравнение (2.2)


.у' =.f(x, у).
Это уравнение в каждой точке М(х, у), принадлежащей области а,
определяет, с точностью до поворота на 180°, направление касатель-
ной к искомой интеrральной кривой, проходящей через точку М. reo-
метрически направление изображается небольшим отрезком прямой
(черточкой), проведенным через точку М и наклоненным к оси Ох под
уrлом а таким, что


tga = f(x, у)
(рис. 4). Совокупность таких направлений носит название поля на-
правлений дифференциальноrо уравнения (2.2).
Расширяя поле направлений, мы будем считать направление в точ-
ке Мо(хо, Уа) перпендикулярным к оси Ох, если
liт f(x, у) = 00.
Х--7 ХО
У--7 УО
. Интеrральными кривыми дифференциальноrо уравнения (2.2) яв-
ляются те и только те линии, которые в каждой своей точке касаются
соответствующеrо направления (рис. 4).
rеометрическое место точек плоскости, с одинаковым направлени-
ем поля, называется изоклиной. Очевидно, уравнение изоклины име-
ет вид


f(x,y)=k,


rде k = tg а
 заданный наклон поля.


'У


у


о


х


х


Рис. 4


Рис. 5


14




Построив достаточно rустую сеть изоклин, иноrда удается соста-
вить примерное представление о поведении интеrральных кривых
дифференциальноrо уравнения. Т ак, напр имер, для уравнения
У' =
 X 2 + У 2


изоклинами являются окружности х2 + у2 = k 2 . Приблизительное рас-
положение интеrральных кривых показано на рис. 5.


Задания для самостоятельноrо решения
Построить изоклины, поле направлений и указать примерное рас-
положение интеrральных кривых для дифференциальных уравнений:
а) у' = 1 + у 2; б) у' = х + у; в) у' = ху
 1; r) у' = ;:
 .



 3. полиrоны ЭЙЛЕРА
Для приближенноrо построения интеrральной кривой дифферен-
циальноrо уравнения


У' = f(x, у),
проходящей через данную точку Мо (хо, Уо), эту кривую заменяют ло-
маной (полиrон Эйлера), звенья которой имеют направления, принад-
лежащие полю направлений дифференциальноrо уравнения (рис. 6).
Пусть M i (Xi, Yi) (i = О, 1,2, ...)
 последовательные вершины поли-
rOHa Эйлера и


д-х. = х. 1
x. I1 У . = У . 1
 y .
t t+ t ' t t+ t

 приращения координат. Очевидно, имеем


l1 у . = д-х. t g a.
t l l
или, так как tg (X,i = t (Xi, Yi)' то

Yi =l1x i f(Xi,Yi) (i=O, 1,2, ...).


, Кроме Toro, Yi+l = Yi +
Yi.
По этим расчетным формулам, задавая
значения х l' Х2' ..., можно последовательно
определять Yl' У2, ... . На практике точки
значений Xi обычно берут равноотстоящи-
ми, считая ДХi = h = const (шаz процесса).
Тоrда


l1у i = h {(Х i, У i ).


у


о ХО Х, Х 2 Х З Х
Рис. 6
15




Недостаток этоrо метода вычисления
 систематическое накопле-
ние ошибок и вследствие этоrо
 малая точность.
Пример. Для уравнения


,
у = х+у


найти у (2), если у (1) = 1.
Реш е н и е. Положим h = О, 1. Результаты вычислений с точностью
до 0,001 даны в таблице.


i х. Yi AYi
1
О 1 1 0,2
1 1,1 1,2 0,23
2 1,2 1,43 0,263
3 1,3 1 ,693 0,299
4 1,4 1 ,992 0,339
5 J ,5 2,331 0,383
6 1,6 2,714 0,43 1
7 1,7 3,145 0,485
8 1,8 3,630 0,543
9 1,9 4,173 О!607
10 2 4.780


Для сравнения приводим точный ответ: у (2) = 5,155.
Упражнение. Методом Эйлера найти у (1), если
у'=

 и у(О) = 2.
1 + х


Улучшенный метод ломаных. Пусть
l1x i = h и fi = f(Xi' у).


Положим


Xi+l = xi +
 , Yi+l = У; +.
 ti
2 2
и


о


Х;


х о +l
h ' 2


Xi+) Х


f i + 1 = t ( Х. l' у. 1 J .
2 1+2' 1+"2
l1Yi В таком случае принимают
у i + 1 = У i + hy i t
rде д'Уi = hfi+ 1 .
2
Уточнение здесь состоит в том, что в He

которой мере учитываются последующие
значения направления поля (рис. 7).


у


M i + 1


М;


..
..I


......
,
I
I
У; Y i +l 1 Ун}
2 I
I
I


Рис. 7


16




Пример. Найти у (1), если
у'= у
 2х . у(О) = 1.
у
Реш е н и е. Примем h = 0,2. Результаты вычислений даются в таб

лице ниже.


l Х' У; hti Xi+l Yi+l ДУi
l 2 2
О 0,0 1,0 0,2 0,1 1 ,1 О, 184
1 0,2 1 , 184 0,169 0,3 1,268 0,159
2 0,4 1,343 0.149 0.5 1,417 0.142
3 0,6 1,485 0,135 0,7 1,553 0,130
4 0,8 1 ,615 0,124 0,9 1,678 0,121
5 1,0 1.736


Точное решение задачи есть у = .J 2x + 1; отсюда при х = 1 получаем
у = JЗ = 1,732.

 4. ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
Для дифференииальноrо уравнения 1
ro порядка (2.2)
у' = f(x, у)
задача Коши формулируется так: найти решение у = у (х) данноrо
уравнения (2. 2), удовлетворяющее заданному начальному условию
у(хо) = уо.
rеометрически это равносильно следующему: найти интеrральную
кривую дифференциальноrо уравнения (2.2), проходящую через дaH

ную точку Мо(хо, Уа).
Естественно возникает вопрос: при каких условиях задача Коши
имеет решение и будет ли это решение единственным? Приведем без
доказательства теорему существования и единственности решения,
дающую ответ на поставленный вопрос.
т е о р е м а. Если в некоторой окрестности точки Мо(Хо, уо)
I х
 Ха I < а, I у
 у 01 < Ь


выполнены следующие условия:
1) функция f(x, у) непрерывна по совокупности переменных х и у;
2) производная f
 (Х, у) оrраничена,
то существует решение у = у(х) дифференциальноrо уравнения (2.2),
определенное на некотором отрезке
Ix
xal
h,


17




и удовлетворяющее начальному условию у(хо) = уо, причем такое pe

шение единственно.
Из сформулированной выше теоремы вовсе не следует, что COOT

ветствующее частное решение фактически может быть найдено с по

мощью конечноrо числа математических операций. Это удается cдe

лать лишь в редких случаях. В следующих параrрафах мы рассмотрим
ряд таких интеrрируемых случаев.



 5. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Дифференциальное уравнение первоrо порядка, допускающее при

ведение к виду


X(x)Y(y)dx + X 1 (х)У} (y)dy = О, (2.4)
rде Х(Х), X1(x)
 известные функции лишь переменной х, а У(у),
Y 1 (у)
 известные функции лишь переменной у, называется ypaBHe

нием с разделяющимися переменными.
Для решения этоrо уравнения нужно произвести разделение пере

менных, т. е. преобразовать уравнение (2.4) Tak, чтобы при dx стоял
бы множитель, зависящий только от х, а при dy стоял бы множитель,
зависящий только от у. Для этоrо, очевидно, достаточно обе части
уравнения (2.4) разделить на произведение X 1 (х)У(у), после чеrо бу

дем иметь


Х(х) }'} (у)
X 1 (x) dx + У(у) dy = О.


Рассматривая для определенности в последнем равенстве у как
функцию переменной х, получим
[ Х(х) + }}(у) . ' ]d = О
х 1 (х ) у( у) ух.


Отсюда, интеrрируя по х, будем иметь
f[ х(х) + }'} (у) . ' ] dx = С
X1(x) У(у) У


или


f х(х) f }}(y) С
x 1 (x) dx + У(у) dy = ,


(2.5)


rде С
 произвольная постоянная*.


* Здесь, как и ВО мноrих местах в дальнейшем, под неопределенными интеrралами
понимаются некоторые первообраЗНbIе функции.


18




Кроме решений, даваемых формулой (2.5), уравнение (2:4) допус

кает решения, обращающие в нуль произведение Х 1 (х) У(у), т. е. явля"
ющиеся корнями уравнений X1(X) = о, или У(у) = о. в самом деле,
пусть х = а, rде X1(a) = О, тоrда dx = о. Подставляя эту функцию в
уравнение (2.4), получим
Х(а)У(у).О + X 1 (a)Y 1 (y)dy = О,
т. е. х == а
 есть решение уравн"ения (2.4). Аналоrично можно пока

зать
 что функция у = Ь, rде У(Ь) = о, является также решением ypaB

нения (2.4). rеометрически эти решения, если они существуют, пред

ставляют собой прямые, параллельные осям координат.
Пример. Пусть
xdy
 ydx = о.
Реш е н и е. Разделяя переменные, получим
dy = dx
У х


(2.6)


Интеrрируя обе части последнеrо равенства, будем иметь
lnl у I = lnl х I + ln C 1 ,
rде С 1
 положительная постоянная. Отсюда
I у I = С 1 1 х I


или


у = Сх, (2.7)
rде С = + С 1
 произвольная постоянная, которая может принимать
как положительные, так и отрицательные значения.
Решениями данноrо дифференциальноrо уравнения являются так..
же функции
х = О и у = о.
Кстати сказать, последнее решение получается из общеrо решения
(2.7) при с = о. rеометрически совокупность решений уравнения
(2.6) представляет собой пучок прямых линий, проходящих через на..
чало координат (см. рис. 3).
Задания для самостоятельноrо решения
1. sinx .dy = ycos х .dx.
2. (1+y2)dx=(1+x 2 )dy.
3. у'=е Х + У .
4. Найти интеrральную кривую уравнения у' = /у, проходящую
через точку М(2, О).


19




I б. ОДНОРОДНЫЕ УРАВНЕНИЯ
Как известно, функция f(x, у) называется однородной измерения
а, если при любом значении t выполнено тождество


f(tx, ty) == t a {(х, у).


(2.8)


в частности, мноrочлен


р(х, у) = LCijx i yi
i, j
представляет собой однородную функцию n
ro измерения, если все
члены ero имеют одно и то же измерение, равное n, т. е. если


i + j = n.


о п р е д е л е н и е. Дифференциальное уравнение первоrо порядка


р(х, y)dx + Q(x, у) dy = О


(2.9)


называется однородным, если коэффициенты Р(х, у) и Q(x, у) при
дифференциалах переменных х и у
 суть однородные функции OДHO

ro и Toro же измерения.
Пусть общее измерение однородности функций р(х, у) и Q(x, у)
равно а. Используя основное тождество (2.8), принимая t = х, будем
иметь


р(х, у) = Р(х .1, х
 ) = ха P(l,
 )


и


Q(x, у) = Q(x .}, xf) = x<XQ(l, !).
х х


Подставляя эти выражения в уравнение (2.8), после сокращения на
ха получим


Р(I, f)dx + Q(l, f)dy = О
х х


или


dy ( У )
dx =f
,


(2.10)


РО, !)
rде f(J...) = х
 однородная функция O
ro измерения Таким об

х Q(l,
)
разом, всякое однородное уравнение (2.9) может быть приведено к
нормальной форме (2.1 О).
20




Для нахождения общеrо интеrрала уравнения (2.10) положим


у

=и
х '


(2.11 )


отсюда


у=хи


(2.12)


и, следовательно,


dy = х du + и.
dx dx


Делая соответствующую подстановку" получим уравнение с разде-
ляющимися переменными


х

 = t (и)
 и.


Разделяя переменные, будем иметь
du
 dx
[(и)
и .... х.


Интеrрируя почленно последнее равенство, получим общий интеr-
рал


J H:)
и = InlCxl,


(2.13 )


rде u = JL, а произвольная постоянная взята в лоrарифмическом виде.
х
Из формулы (2.13) вытекает, что общий интеrрал однородноrо уравнения (2.10)
rеометрически представляет собой семейство подобных кривых с центром подобия
в начале координат. В самом деле, рассмотрим интеrральную кривую


J dUl = In l XI I ,
f(Ul)

U.
соответствующую С = 1. Производя В уравнении (2.14) преобразование подобия


(2.14)


х 1 = Сх, у 1 = С У


и учитывая при этом, что


U
 Yl
 У
 U
I




 ,
х. х
получим, очевидно, произвольную кривую семейства
(2.13).
Поэтому, чтобы построить поле интеrральных кри-
вых однородноrо уравнения, достаточно нарисовать
одну интеrральную кривую, соответствующую С = 1.
а затем подобно преобразовать ее в соответствующем
отношении (рис. 8).
При решении уравнения (2.1 О) нам при-
шлось делить на выражение {(и)
 и. Поэто-
му интеrральными кривыми этоrо уравнения


у


х


Рис. 8


21




будут также прямые у = kx, уrловой коэффициент которых удовлетво

ряет уравнению f(k)
 k = о. Кроме Toro, уравнение (2.9) может иметь
еще решение х = о.
3 а м е ч а н и е. Для решения однородноrо уравнения (2.9) мы пред

варительно приводили ero к нормальному виду (2.10). На практике в
этом нет необходимости. мо)Кно сразу пользоваться подстановкой
у = хи.
Пример. Решить уравнение


(х + y)dx+ (x
 y)dy=O.


(2.15 )


Реш е н и е. Уравнение однородно, так как, очевидно, Р=х+ у и Q
= х
 у
 однородные функции 1
ro измерения. Используя замеча

ние,полаrаем


у=хи и dy=xdu+udx.


Отсюда


(х + xu)dx + (х
 xu)(xdu + udx) = О


или после очевидных сокращений


(1
 u)xdu + (1 + 2и
 u 2 )dx = о.


Разделив переменные и интеrрируя последовательно, будем иметь
(l
u)du dx О
+


1+2u
u2 х



и


J I
u du + J dx = с.
1+ 2и
и2 х


Отсюда



 ln 11 + 2и
 u 21 + lnlxl = lriC


или


X2(1+2u
U2)=Cl'


rде С 1 = + С 2 . подставляя вместо u ero значение, получим общий ин..
теrрал


x2+2xy
 у2= С 1 .


(2.16)


Так как в процессе решения нам приходилось делить на выражение
1 + 2и
 u 2 , то решениями уравнения (2 15) будут так)Ке прямые у= kx,
rде 1 + 2k
 k 2 = о. в данном случае эти решения получаются из форму

лы (2.16) при С 1 = о.
22




Задания для самостоятельноrо
решения
1. (х 2 + y2)dx
 xydy = о .
2. xdx
(y+
 x2+y2)dy=0.
3. у' = r ln r.
х х


у


rеометрически общий интеrрал (2. 16)
представляет собой семейство rипербол,
включая их две асимптоты у = (1 + J2)x
(рис. 9).


Рис. 9


17. ЛИНЕЙНЫЕ УРАВНЕНИЯ
Оп Р е Д е л е н и е. Дифференциальное уравнение l-ro порядка на-
зывается линейным, если оно первой степени относительно неизвест-
ной функции у и ее производной у' (или дифференциала dy) и не со-
. держит произведения этих величин. В общем случае линейное
уравнение имеет вид


а(х)у' +
(x)y + у(х) = О,


(2.17)


rде коэффициенты а(х),
(x), у(х) .......... данные непрерывные функции в
некотором промежутке а < х < Ь.
Предполаrая, что а(х)"* О, и вводя обозначения
( ) Р(х) ( ) у(х)
р х = а(х) ' q х =
 а(х) '
уравнение (2.17) можно привести к нормальному виду
у' + р(х)у = q(x),


(2.18 )


rде функции р(х) и q(x) определены и непрерывны в интервале
а < х < Ь.
Если q(x) = O, то линейное уравнение (2.18) называется однород-
ным; в противном случае
 неоднородным.
1. Однородное линейное уравнение. Рассмотрим однородное
линейное уравнение


у' + р(х)у = о


(2.19 )


или


:
 =
p(x)y.


23




Очевидно, в этом уравнении можно разделить переменные. Пред-
полаrая у ;/:. О, будем иметь
dy =
p(x)dx.
у
Интеrрируя последнее равенство, получим
I d : =
Ip(x)dx


или


ln Iyl =
 1 p(x)dx + InC 1 .


(2.20)


rде С 1
 положительная произвольная постоянная. Потенцируя ра-
венство (2.20), находим


Iyl = С 1 е
Ip(x)dx


или


у = Се
Ip(x)dx,


(2.21 )


rде С = + C 1
 произвольная постоянная, которая может принимать
как положительные, так и отрицательные значения. Заметим, что при
С = О получается решение у = о уравнения (2.19); поэтому с может
принимать любое действительное значение и формула (2.21) дает об-
щее решение этоrо уравнения.


Обозначая через


Yl =C 1 e
Jp(x)dx
решение уравнения (2.19), соответствующее С = 1, из формулы (2.21) будем иметь
У = С Yl.
Следовательно, чтобы построить поле интеrральных кривых уравнения (2.19),
достаточно нарисовать rрафик функиии


У. = Yl (Х) (а < х < Ь).
а затем ординаты ero изменить в соответствующем отношении (рис. 10).


у


2YI


I







 YI

 O,5Yl
I
I


о


а


ь


х


Рис. 10


24




2. Неоднородное линейное уравнение. Рассмотрим неодно"
родное линейное уравнение


У' + р(х)у = q(x).


(2.23 )


Будем искать решение этоrо уравнения в форме


у = С(Х)Уl,


(2.24)


rде С(х)
 новая неизвестная функция и Уl = Уl (х)
 некоторое He

нулевое решение соответствующеrо однородноrо уравнения


У} + P(X)Yl = о.
Используя формулу (2.21), можно положить
Yl = е
fp(x)dx.


(2.25)


(2.26)


Заметим, что если в формуле (2.24) С считать постоянной, то эта
формула дает общее решение линейноrо однородноrо уравнения
(2.25). Мы же предполаrаем, что С = С(х)
 есть некоторая функция
переменной х, т. е. варьируем эту постоянную и тем самым добиваем

ся, чтобы функция У удовлетворяла неоднородному уравнению (2.23).
Поэтому этот метод называется «методом вариации произвольной
постоянной» .
Подставляя выражение (2.24) для у в исходное дифференциальное
уравнение (2.23), будем иметь
С'(Х)Уl + С(Х)Уl + Р(Х)С(Х)Уl = q(x)


или


С'(Х)Уl + С(х)[у} + р(х) Уl] = q(x). (2.27)
в силу формулы (2. 25) коэффициент при С(х) в последнем уравнении
равен о. Поэтому это уравнение принимает вид
С'(х) Yl = q(x),


отсюда


С'(х) = q(x)
Yl


и, следовательно,


С(х) = С 1 + J q(x) dx,
Yl


(2.28)


rде С 1
 произвольная постоянная.


25




На основании формулы (2.24) получаем, что общее решение неодно-
родноrо линейноrо уравнения (2.23) имеет вид


[ f Q(X) ]
у = Yl C 1 +
dx


(2.29)


или, подставляя сюда выражение (2.26) для Yl' окончательно будем
иметь


у = e
Ip(x)dX[ С1 + f q(x)elp(x)dxdx ] .


(2.30)


Таким образом, чтобы решить неоднородное линейное уравнение
(2.23), нужно сначала найти общее решение соответствующеrо OДHO

родноrо линейноrо уравнения (2.25), а затем входящую в Hero произ

вольную постоянную, положить некоторой функцией от х, которую
следует подобрать так, чтобы было удовлетворено неоднородное
уравнение.


Из формулы (2.29) следует, что


у = С IYI + У,


(2.31 )


rде V = у(х)
 некоторое частное решение неоднородноrо уравнения (2.23) (полу

чается при C 1 = О), т. е. У является линейной функцией произвольной постоянной C 1 .
Поэтому построение поля интеrральных кривых неоднородноrо линейноrо уравне-
ния будет такое же, как и в однородном случае, с той лишь разницей, что роль нуле

вой линии отсчета будет иrрать rрафик функции У = у(х) (рис. 11).


у( с 1 ,Х)


I
I
С 1 = 1
С =0:
y
)
 i
I I
Cl=
l

I I
I I


о


а


ь


х


Рис. 11


Из способа построения следует, что через каждую точку Мо(Хо, Уо) полосы
{а < х < Ь,
 00 < У < +со} проходит одна и только одна интеrральная кривая.
3 а м е ч а н и е. На практике метод вариации произвольной постоянной можно
применять сразу для линейноrо уравнения (2.17).


26




Пример. Решить уравнение
(1 + х 2) у' + ху = 1.


(2.32)


Реш е н и е. Рассмотрим сначала однородное уравнение
.(I+х 2 )у' +ху = О


или


(1+X2)
t +xy=O.
Разделяя переменные, будем иметь
dy xdx
У =
 1 + х 2 '


отсюда


f d Y =
 f

у 1 + х 2 '


то есть


lnlyl =

 lnO + х 2 ) + ln C ,


rде С
 положительная произвольная постоянная. ПотеНllИРУЯ по-
следнее равенство, получим


у= с
.Jl + х 2 '


(2.33 )


rде


с= + с.
Соrласно нашему методу в формуле (2.33) положим с = С(х) и бу-
дем искать решение данноrо неоднородноrо уравнения (2.32) в виде
у = С(х) (2.34)

 1 + х 2 .
Подставляя это выражение в уравнение (2. 32), получим

l+ х2с ,(х)
 хС(х)
(1 2 ) J 1 + х 2 хС( х)
+х . + =1
1+ х 2
 l+ х 2


или


.J 1 + х 2 С' (х) = 1.


Заметим, что члены, содержащие с(х), обязательно должны сокра-
титься. Это служит контролем правильности выкладок.
Из последнеrо уравнения получаем
С'(х) = 1

 1 + х 2


21




И,следова
ельно,
С(х) = J
 = In(x +
 1+x2) + С 1 .
I+x


rде С 1 ....... произвольная постоянная.
На основании формулы (2.34) окончате льно и меем
у =
 [ С1 + In(x +
l + х 2 )].
3 а м е ч а н и е. Из формулы (2.24) вытекает, что общий интеrрал
линейноrо неоднородноrо уравнения (2.23) можно искать в виде про

изведения двух функций


у = uv,
rде одну из них, например функцию v, следует подобрать так, чтобы
обратился в нуль коэффициент при друrой функции, в данном случае
при и, в преобразованном уравнении (сравни формулу (2.27)!). Не
проделывая выкладок в общем виде, оrраничимся рассмотрением при

мера.
Пример. Решить уравнение
(х + у) у' = 1.
Реш е н и е. По форме это уравнение не является линейным, так
как оно содержит произведение искомой функции у и ее производной.
Однако, если рассматривать х как функцию от у, то, учитывая, что


, 1
У = х' ,


будем иметь линейное уравнение
х'=х+у.


(2.35)


Положим


x=uv


(2.36)


и, следовательно,


dx = v du + U dv
dy dy dy'
Подставляя эти значения в уравнение (2.35), получим
v du + и dv = uv + у
dy dy


или


v du + ( dV
v ) u = у.
dy dy


(2.37)


28




Выберем функцию v;/:.o так, чтобы обратился в нуль коэффициент
при и; это дает


dv
 v = о.
dy ,


отсюда


dv = dy
v


и, следовательно,


lnlvl = у ln C ,


то есть


v = Се У ,
rде С = + с
 произвольная постоянная. Так как нам требуется лишь
одна конкретная функция V, то можно положить С = 1, и поэтому
v = е У . (2.38)
Подставив это выражение в формлу (2.37), получим
е У du = У
dy ,


отсюда


du = ye
Y
dy


и, следовательно,
и = Jye
Ydy =
ye
Y
 e
Y + С!.


(2.39)


rде С 1
 произвольная постоянная.
Таким образом, на основании формул (2.36), (2.38) и (2.39) общее
решение данноrо уравнения имеет вид
х = C1e Y
 (у + 1).


Задания для самостоятельноrо реmения.
1. ху' + 2у = х 2 .
2. (х 3 + y)dx
 xdy = о.
3. (х + у2) у' = 1.
4. Сила тока 1 в электрической цепи с омическим сопротивлением
R и коэффициентом самоиндукции L удовлетворяет дифференциаль

НОМУ уравнению


L d/ + R/ = V
dt '
rде V
 напряжение тока. Найти силу TOI<a через t секунд после вклю-
чения, если V

остоянно И / = /0 при t = о.


29




I 8. УРАВНЕНИЕ БЕРНУЛJlИ


к линейным уравнениям леrко сводятся уравнения Бернуллu


у' + р(х)у = Q(x)ya,


(2.40 )


rде р(х) и q(x)
 данные непрерывные функции; а
 любое действи-
тельное число.
Если а = 1 , то уравнение Верну лли (2.40) является линейным одно-
родным и леrко интеrрируется.
При <х ;/:.1, деля обе части уравнения (2.40) на уа, будем иметь
y
 у' + p(x)yl
a = q(x). (2.41)


Положим


yl
a = z,


(2.42)


тоrда


(l
 <x)y
a у' = z'


и, следовательно,


,

a' z
у у = l
a .
Подставляя выражения (2.42) и (2.43) в уравнение (2.41), получим
линейное уравнение относительно z:


(2.43)


z'

 l + p(x)z = q(x).

a


Найдя отсюда z, из формулы (2.42) определяем у.
Отметим также, что при<х > О уравнение (2.40) имеет очевидное ре-
шение у = о.
3 а м е ч а н и е. Так как уравнение Бернулли (2.40) преобразуется в
линейное, то для ero решения можно сразу использовать способы ре-
шения линейноrо уравнения, т. е. метод вариации произвольной по-
стоянной или подстановку у = uv.


Пример. Решить дифференциальное уравнение
ху'+у=х 2 у 2.


Реш е н и е. Очевидно, это уравнение Бернулли. Разделив обе час..
ти уравнения на у2, будем иметь
у' 1
x
 +
 = х 2
у2 у


30




Полаrая


,
.1 = z и

 = z',
у у
получим линейное уравнение

xz'+z = х 2 .


(2.44)


Соrласно методу вариации произвольной постоянной решаем CHa

чала однородное уравнение

x

 +z=o.
Разделяя переменные, имеем
dz = dx
z х


После интеrрирования получим
lnlzl = Inlxl + ln C


или


z=Cx
,


(2.45)


rде С = +с . Как обычно, будем считать, что С = С(х) есть некоторая
функция х. Подставляя выражение для z в уравнение (2.44), находим

x(xC' + с) + Сх = х 2


или


с' =
 1.


Поэтому


с =
 х + C 1 ,
rде C 1
 произвольная постоянная. Далее, из формулы (2.45) полу..
чаем


Z=
X2+CIX.
Так как z = .1, то окончательно имеем
у
у
 1

 Clx
x2.
Кроме Toro, наше уравнение имеет еще решение у = О, формально
соответствующее значению С 1 = 00.


Задания для самостоятельноrо решения
1. у 2 у'
 ху3 = х 3 .
2. ху'
 У = х 2 /у.
з. (ху + х 2 у З)у' = 1.


31





 9. УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ
Пусть левая часть дифференциальноrо уравнения
Р(х, y)dx + Q(x, y)dy = О (2.4б)
является полным дифференциалом некоторой функции z = z(x, у), т. е.
Р(х, y)dx + Q(x, y)dy = dz. (2.47)
Как известно, необходимым и достаточным условием этоrо служит
выполнение тождества


дР
 дQ
ду :::
.
В этом случае уравнение (2.46) называется уравнением в полных
дифференциалах и решается весьма просто. А именно: в точках интеr

ральной кривой одну из переменных х и у можно рассматривать как
функцию друrой*. Предполаrая для определенности, что у есть Функ

ция от х, уравнение (2.46), в силу формулы (2.47), можно записать в
виде равенства
dz(x, у) = О,
rде z(x, у)
 рассматривается как сложная функция от х, или
:x z(x, у)=О.
Отсюда получаем общий интеrрал уравнения
(2.46)
z(x, у) = с, (2.49)


(2.48)


rде С
 произвольная постоянная.
rеометрически общий интеrрал (2.49) представляет собой семей

ство линий уровня поверхности z = z(x, у).
Если выполнено условие полноrо дифференциала (2.48), то для Ha

хождения функции z можно поступить следующим образом: из ypaB

нения (2.47) имеем




 = Р(х, у),
: = Q(x, у).


(2.50 )


Отсюда, интеrрируя первое равенство формулы (2.50), получим
z = J Р(х, y)dx + q>(y), (2.51)
rде <р(у)
 некоторая функция от у.


* Исключение составляют лишь точки (х, у), rде выполнено условие Р(х, у) =
= Q(x, у) = о. Такие точки называются особыми для дифференциальноrо ypaBHe

ния (2.46) (подробнее СМ.
 16).


32




Используя второе равенство формулы (2.50), будем иметь
(j)'(y) = Q(x, у)
 д
 ! Р(х, y)dx == R(x. у).


При наличии равенства (2.48) функция R(x, у) не зависит от х, так
как


aR = aQ
 l... [
 J p(x Y)dX ] =
дх дх дх ду ,


= aQ
 l... [
 J p(x Y)dX ] = aQ
 дР = о.
дх ду дх' дх ду


Поэтому R(x, у) = R(y). Последнее обстоятельство может служить
контролем правильности выкладок. Следовательно,


и


<р'(у) = R(y)
(j)(Y) = J R(y)dy + С!.


Из формулы (2.51) окончательно имеем
z = J Р(х, y)dx + J R(y)dy + С!.


в последней формуле произвольная постоянная С} может быть
пропущена, так как для получения общеrо интеrрала (2 49) нам нуж

на хотя бы одна функция z, удовлетворяющая уравнению (2.47).
Пример. Решить уравнение


(2х
 y)dx
 (х
 2y)dy = о.
Реш е н и е. Здесь
р = 2х
 у, Q =
(.x
 2у),


(2.52)


причем


дР
 aQ

 1
ду
 дх

и, следовательно, левая часть уравнения (2.52) является полным диф

ференциалом некоторой функции Z, т. е.
(2х
 y)dx
 (х
 2y)dy = dz.
На основании последней формулы имеем


 = 2х
 у,
; =
(x
 2у).


(2.53)


33




Интеrрируя первое из равенств (2.53), находим
z = f (2х
 y)dx + ЧI(у) = х 2
 ху + ЧI(у).
Используя второе из равенств (2.53), будем иметь

; =
(x
 2у) =
x + ЧI'(у).


Отсюда находим


<р'(у) = 2у


и


<р(у) = у2 +С 1 .


Следовательно,


z = х 2
 ху + у2 + С 1.
Полаrая у = у(х), уравнение (2.52) можно записать в виде
dz(x, у) = о.


Отсюда, приняв для простоты С 1 = О, получаем общий интеrрал это

ro уравнения


х 2
 ху+ у2 = С,


(2.54 )


rде С
 произвольная постоянная.
rеометрически общий интеrрал (2.54) есть семейство линий уровня
эллиптическоrо параболоида z = х 2
 ху + у2 (рис. 12).


Рис. 12


З а м е ч а н и е. На практике уравнение в полных дифференциалах
часто встречается в виде


р(х, y)dx+ Q(x, y)dy=P1(x, y)dx + Ql(X, y)dy,
rде р(х, у), Q(x, У), P 1 (х, у) и Ql (х, у)
 заданные функции.
34




Если Р(х, y)dx + Q(x,y)dy = dz(x,y) и Pt(x,y)dx + Ql(x,y)dy=
= dZ 1 (х, У), то общий интеrрал этоrо уравнения имеет вид
Z(X, у) = ZI (х, у) + с.
Функции Z(X, у) и Zl(X, у) находятся способом, указанным выше.


Задания для самостоятельноrо решения
1. (х 2
 2xy)dx
 (х 2 + y4)dy = о.


xdx + ydy = dx
2.
x2+y2 .


i 10. ПОНЯТИЕ ОБ ИНТЕrРИРУЮЩЕМ МНОЖИТЕЛЕ
о n р е д е л е н и е. Интеrрирующим множителем дифференциаль

Horo уравнения
Р(х, y)dx + Q(x, y)dy = О (2.55)
называется не равная нулю функция Jl(x, у), после умножения на ко-
торую левая часть уравнения обращается в полный дифференциал,
то есть
Jl[P(x, y)dx +Q(x, y)dy] = dz, (2.56)
rде Z = х(х, у)
 некоторая функция переменных х и у.
Используя условие полноrо дифференциала, получим, что функция
Jl удовлетворяет уравнению с частными производными
a(J!Q) a(JlP)
дх = ау.
Если для уравнения (2.55) интеrрирующий множитель найден, то,
считая для определенности у = у(х) искомой функцией, получим, что
это уравнение эквивалентно уравнению
.1L z (x у) = о
dx '


и, 'следовательно, общий интеrрал ero есть
Z(X, у) = С,
rде функция Z = Z(X, у) может быть леrко определена (см. э 9). Однако
в общем случае отыскивание интеrрирующеrо множителя есть задача
столь же трудная, как и решение caMoro дифференциальноrо ypaBHe

ния (2.55). Поэтому метод интеrрирующеrо множителя не имеет
большоrо практическоrо значения.


35




3 а м е ч а н и е. Если дифференциальное уравнение задано в виде
Р(х, y)dx + Q(x, y)dy = Р 1 (х, y)dx + Ql (х, y)dy,
то, найдя общий интеrрирующий множитель f..l = Jl(x, у) для левой и
правой части этоrо уравнения, т. е. считая Jl функцией, удовлетворяю

щей условиям


Jl[P(x, у )dx + Q(x, y)d у] = dz


и


Jl[Pl (х, y)dx + Ql (х, y)dy] = dz 1 ,
rде z= Z(X, у) и Zl(X, у)
 некоторые известные функции, для общеrо
интеrрала этоrо уравнеНИ$I будем иметь следующее выражение:


z(X, у) = ZI (Х, у) + С,


rде С
 произвольная постоянная.


i 11. ИНТЕrрирующий МНОЖИТЕЛЬ пИНЕйноrо УРАВНЕНИЯ
Рассмотрим линейное уравнение
у'+ р(х)у = q(x)


или


dy + р(х)у dx = q(x)dx.


(2.57)


Общим интеrрирующим множителем для левой и правой части
уравнения, как леrко непосредственно проверить, является функция
J.1 = e}p(x)dx.


в самом деле, умножая уравнение (2.57) на Jl, очевидно, имеем
elp(x)dXdy + p(x)eIp(x)dx ydx = q(x)elp(x)dxdx;


отсюда


d(yeJp(X)dX) = q(x)eJp(x)dxdx.


Следовательно,


yeJp(X)dx = с + f q(x)eJp(x)dxdx,


rде С
 произвольная постоянная. Это наиболее практичный способ
решения линейноrо уравнения.


36




Пример. РеllIИТЬ уравнение
у'
 ау = f(x),


(2.58)


rде а
 постоянная величина.
Реш е н и е. Здесь


Jl = е
 J а dx = е
ax


или


d(ye
ax) = e
ax 1 (x)dx.


Отсюда


ye
ax = С + fe
axt(x)dx


и


у = еаХ(с + fe
axt(x)dxl


(2.59)


Этой формулой мы воспользуемся в дальнейшем.


i 12. УРАВНЕНИЯ ПЕРвоrо ПОРЯДКА, НЕ РАЗРЕШЕННЫЕ
ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ
Дифференuиальное уравнение первоrо порядка в общем случае
имеет вид


Р(х, у, у') = О,


(2.60 )


rде F
 известная функция. Уравнение (2.60) может содержать у' в
любой степени и даже ПОД знаком трансцендентной функции.
Рассмотрим сначала тот случаЙ, коrда уравнение (2.60) можно раз

решить относительно у'. Предполаrая, что число корней k конечно,
мы получим k уравнений (k
 1)


у' = 11 (х, у), ..., у' = tk (х, у).


(2.61 )


Таким образом, здесь через каждую точку области О, в которой
определены правые части уравнений (2.61), проходят, вообще rоворя,
k интеrральных кривых.
Если


Фl (х, у, С) = о, Ф2 (х, у, С) = о, ..., ф k (Х, у, С) = о

 общие интеrралы уравнений (2.61), то общий интеrрал уравнения
(2.60) в области G может быть записан в следующем виде:
Фl(Х, у, С) ХФ 2(Х, у, С)Х ... ХФk(Х, у, С) = о.


37




Пример. Решить дифференциальное уравнение
у,2
 (х + у)у' + ху = о.


(2.б2)


Реш е н и е. Решая квадратное уравнение (2.62) относительно про

изводной у', получим


, ,
у = х, у = у.


Отсюда


2
У =
 + С и у = Се Х
И, следовательно, общий интеrрал уравнения (2.62) есть
2
(у


 С) (у
 Се Х ) = о.


(2.б3)


Х


Рис. 13


rеометрически оБLЦИЙ интеrрал (2.63) представляет собой COBO

купность семейств парабол и показательных кривых (рис. 13).


113. ПАРАМЕТРИЧЕСКИЙ СПОСОБ РЕШЕНИЯ
Иноrда удается получить решение общеrо уравнения первоrо порядка
(2.60), выражая переменные х и у как функции HeKoToporo параметра р.
Рассмотрим следующие два случая.
С л у чай 1. Пусть уравнение (2.60) разрешимо относительно х.
Имеем


х = <р(у, у').


(2.64 )


Примем за параметр р величину у'. Тоrда


х = <р(у, р).


(2.65)


38




Дифференцируя это уравнение по у и учитывая, что
: = ; , бу-
дем иметь


1 = дч> + дч> dp
Р ду др dy.
Отсюда, рассматривая у как функцию пара метра р, ПРИХОДИМ к
уравнению, разрешенному относительно производной от неизвест"
ной Функuии


дч>
p

dy
 др
dp
 1
p д<р .
ду


(2.6б)


Общее решение уравнения (2.66) имеет вид
у = 8(р, С),


(2.67)


rде е
 некоторая известная функция и С
 проивольная постоян..
ная. Чтобы получить х, нужно последнее выражение подставить в
формулу (2.65).
Совокупность двух формул
х =
(8(P'C),p) }
у = 8(р, С)


(2.68)


дает общий интеrрал уравнения (2.64) в параметрической форме. При
фиксированном С получается отдельная интеrральная кривая, кот о..
рую можно построить по точкам, давая р различные значения, причем
в каждой точке этой кривой р равно уrловому коэффициенту каса- ,
тельной. Исключая параметр р из системы (2.68), получим общий ин-
теrрал уравнения (2.60) в обычном виде


Ф(х, у, С) = о.
в частном случае, если уравнение (2.б4) явным образом не зависит
от у, будем иметь


х = <р(у').
Полаrая у' =

 = р. получим


х = q>(p).


(2.69)


Очевидно,


dy = pdx = pq>'(p)dp


39




и, следовательно,


у = f pq>'(p)dp + С.


Совокупность формул для х и у дает общий интеrрал уравнения
(2.б9) в пара метрическом виде.
Пример. Решить уравнение
у,2
 х + у = о.


(2.70)


Реш е н и е. Полаrая у' = р и разрешая уравнение (2.70) относите

льна х, будем иметь


х = р2 + у.
Дифференцируя последнее уравнение по у, получим
1 = 2р dp + 1.
р dy


(2.71 )


Отсюда


dy
 2 р 2
dp
 1
p


И,следовательно,


= f 2р2 d = 2 :! 1
H
 р2 ) d =
у l
p Р l
p Р
= 2! 1

 2fO + p)dp =
2Inll
pl
 (2.72)

 (2р + р 2) + С,


rде С
 произвольная постоянная.
Подставляя это выражение в формулу (2.71), будем иметь


х =
2p
 21nll
pl + с.


(2.73)


Совокупность формул (2.73) и (2.72) дает общий интеrрал ypaBHe

ния (2.70) в параметрическом виде. Из формулы (2.71) можно Bыpa

зить р через х и у, а именно:


р = +.J x
y.


Подставляя это выражение в формулу (2.72), получим общий ИН

теrрал уравнения (2.70) в обычной форме.


40




с л у чай 2. Пусть уравнение


р(х, у, у') = о


разрешимо относительно у. В таком случае это уравнение можно за-
писать в виде


у = \II(X, у'),


(2.74)


rде '"
 не которая известная функция.
Принимая за параметр р величину у' получим


у = 'V(x,p).


(2.75)


Дифференцируя уравнение (2.75) по х, имеем

 d'V + d'V d Р .
Р
 дх др dx'


(2.76)


отсюда находим


дЧ'
dx др
dp = d'V .
p


дх


(2.77)


Мы получили разрешенное относительно производной
X уравне-
ние для неизвестной функции Х. Если это уравнение може
 быть ре-
шено (например, если оно относится к одному из известных типов), то
ero общее решение записывается в виде


Х = е(р, С),


(2.78)


rде 8
 некоторая известная функция и С
 произвольная постоян-
ная.
Подставляя последнее выражение в формулу (2.75), получим


у = 'V(8(p, С), р).


(2.79)


Совокупность формул (2.78) и (2.79) дает общий интеrрал уравне..
ния (2.74) в параметрическом виде.
В частном случае, если уравнение (2.74) явным образом не зависит
от х, будем иметь


у = 'I'(y').


(2.80)


41




Полаrая


, dy
Р = у =

dx'


получим


у = V(p).


Очевидно,


d '( )
dx =
 =
dp
р р


и, следовательно,


х = J Ijf
p) dp + С.


Совокупность формул для х и у дает общий интеrрал уравнения
(2.80) в параметрическом виде.
При нахождении общеrо интеrрала уравнения (2.80) нам приходи

лось некоторое выражение делить на р. Полаrая р = О, получим оче

видное решение у = '1'(0), которое следует включить в состав общеrо
интеrрала (если ",(О) имеет смысл).
Пример. Решить уравнение
у = у' + у,2 е у '. (2.81)


Реш е н и е. Полаrая у' = р, получим
у = р + р 2 еР.


(2.82)


Отсюда


dx = dy = 1+(р 2 +2р)е Р dp
р р


И,следовательно,


х = J ; + J(p + 2)e P dp = Inlpl + (р+Ое Р + С.
Формулы (2.83) и (2.82) дают общий интеrрал уравнения (2.81).
Кроме Toro, на основе приведенных выше соображений общий интеr

рал нужно дополнить очевидным решением у = о.
3 а м е ч а н и е. Таким образом, общим приемом решения диффе

ренциальных уравнений (2.64), (2.74), разрешенных соответственно
относительно переменNыIx х и у, является дифференцирование по дpy

rой переменной.


(2.83)


42





 14. УРДВНЕНИЕлдrРАНЖА
о п р е Д е л е н и е. Уравнением Лаzранжа называется дифферен-
циальное уравнение l-ro порядка, линейное (первой степени) относи-
тельно независимой переменной хинеизвестной функции у. Общий
вид уравнения Лаrранжа следующий:
а(у')х + Р(у')у + у(у') = о, (2.84)
rде а(у'),
(y'), у(у')
 некоторые известные функции от у' =

 . По-
лаrая у' = р, будем иметь
а(р)х + Р(р)у + у(р) = о. (2.85)
Уравнение (2.85) леrко может быть разрешено как относительно х,
так и относительно у; поэтому для нахождения ero общеrо интеrрала,
соrласно предыдущему параrрафу, можно использовать методдиффе-
ренцирования.
Рассмотрим ряд случаев, которые MorYT представиться.
С л у чай 1. Пусть Р(р)
 о. Разрешая уравнение (2.85) относите-
льно у, будем иметь


у =
(p)x +o/(p

( ) а (р ) ( ) 'у (р )
<р р =

 (р ) , '" р =

 (р ) .
Функции <р(р), ",(р) предполаrаются непрерывными и имеющими
непрерывные производные
' (р) и",' (р).
Дифференцируя уравнение (2.86) по переменной х и учитывая, что


 = р, получим
р = <р(р) + [q>'(p)x + 'JI'(p))
 . (2.87)
Рассматривая х как функцию параметра р, уравнение (2.87) можно
записать в следующем виде:
[р
 <p(p))
; = <р'(р)х + 'JI'(p). (2.88)


(2.8б)


rде


Отсюда леrко усмотреть, что это уравнение является линейным от-
носительно переменной х.
Если р
 <р(р) 1= О, то общее решение уравнения (2.88) может быть
найдено обычными методами и имеет вид
х =
l(P) + C
2(P), (2.89)
rде
 1 (р),
 2 (р)
 известные функции и С
 произвольная постоян-
ная.


43




Подставляя выражение для х в уравнение (2.86), получим
у = 11] (р) + C1l 2 (p), (2.90)
rде 111 (р) = <p(p)
 1 (р) +'I!(p) и 112 (р) = <P(P)
2 (р). Совокупность фор-
мул (2.89) и (2.90), вообще rоворя, дает общий интеrрал уравнения
Лаrранжа (2.85) в параметрической форме
Если р
 <р(р) = О, то решение уравнения (2.88) получается без вся-
ких квадратур. Этот исключительный случай мы подробно paCCMOT

рим в следующем параrрафе.
С л у чай 2. Пустьа(р)
 О, Р(р) = о.
Уравнение (2.85) имеет вид
а(р)х + у(р) = О


(2.91 )


или


х = <р(р), (2.92)
rдеq>(р) =



 . Это уравнение было рассмотрено в
 13 (см. формулу
2.69).
Так KaKdy = pdx = pq>'(p)dp, то
У = J pq>'(p)dp + с. (2.93)
Случай 3. Пустьа(р) = О, Р(р)=О, у(р)
o. Уравнение (2.85)
имеет вид


у(р) = о.
Пусть р = k
 корень уравнения (2.94), т. е.
y(k) = О.
Так как

 = k, то, интеrрируя, булем иметь


(2.94 )


(2.95)


у = kx + С,


rде С
 произвольная постоянная. Отсюда
k=1L
 С .
х


Подставляя последнее выражение в равенство (2.95), получим об-
щий интеrрал дифференциальноrо уравнения (2.94)
у( у
 С ) = о.
х


44




Пример. Решить уравнение
ху'З
 уу'
 1 = о.


(2.96 )


Реш е н и е. Полаrая у' = р и разрешая уравнение (2.96) относите

льно у, получим


y=p2X
1.
р


(2.97)


Дифференцируя по х последнее уравнение, будем иметь
р = р 2 + 2рх dp + J.... dp .
dx р2 dx'


отсюда


dx = k + 1
dp l
p p30
p).
Применяя к линейному уравнению (2.98) метод вариации произ-
вольной постоянной, последовательно находим


(2.98)


dx
 2dp
х
 l
p


и


X
 С

 (1
p)2 .


(2.99)


Варьируя произвольную постоянную С и подставляя выражение
для х и
; в уравнение (2.98), будем иметь
d С + 2С = 2С + 1 .
(I
p)2 dp (I
p)3 (I
p)2 р3О
p)'


отсюда


dC
 1
p
dp
 р3


и


с =
L + 1 + С 1
2р 2 Р 2 '


rде С 1
 произвольная постоянная. Подставляя это выражение в фор-
мулы (2.99) и (2.97), окончательно получим

l+ 2р+С 1р 2
х = 2p2(1
p)2 '

l+ 2p+C 1p 2
 1
у = 2(1
 р )2 Р


45




115. УРАВНЕНИЕ КЛЕРО


Рассмотрим тот исключительный случай уравнения Лаrранжа


у = xq>(y') + \V(y'),


(2.100)


коrда имеет место тождество


q>(y') == у'.


Этот частный вид уравнения
у = ху' + ",(у')


(2.101)


носит название уравнения Клеро. Вводя обычное обозначение у' = р,
уравнение Клеро можно записать в виде


у = рх + \V(p).


(2.102)


Относительно функции ",(р) мы будем предполаrать, что она непре

рывна вместе со своими производными '1" (р) и ",Н (р).
Для решения уравнения, как и в общем случае, применим метод
дифференцирования. Дифференцируя обе части уравнение (2 102) по
переменной х, получим
Р = Р + х dp + ",'( р ) dP .
dx 't' dx'


отсюда




 [x + 'I"(p)] = О.


(2.103)


Приравнивая нулю первый множитель в формуле (2.103), получим
dp =0
dx


и, следовательно,


р= С,


rде С
 произвольная постоянная.
Из уравнения (2.102) находим общее решение уравнения Клеро


у = Сх + \V(C),


(2.104)


rеометрически представляющее собой семейство прямых линий.
Приравняем теперь нулю второй множитель в формуле (2.103). Это
дает нам уравнение некоторой кривой (r):


х =
'V'(p), }
у =
 p'V'(p) + ",(р).


(2.105)


46




Эта кривая является интеrральной во всех точках, rде
'l'H(p) *- О,


так как


dy
Чf'(р )
РЧf"(р)+ 'I"(р)
dx =
'I'''(p) = р.
Система уравнений (2.105) дает особое решение уравнения Клеро
(подробнее об особых решениях СМ. Э 17). Так как через каждую точку
(Х, у) кривой r, отвечающую значению пара метра р = у' = С, проходит
также прямая (2.104) с уrловым коэффициентом С, то кривая r Kaca

ется всех этих прямых. Следовательно, rеометрически особое реше-
ние (2.105) представляет собой оrибающую семейства прямых
(2.1 04).
Пример. Решить уравнение Кл еро
у = ху' + a
 l + у,2 (а >0).


Реш е н и е. Полаrая у' = р, получим
у = рх + a
 l + р 2 .


(2.106)


Дифференцируя последнее уравнение, будем иметь
dp ар dp
Р
 Р + x
 +

 dx
1+p2 dx'


откуда находим



 (x+
 )=o.
Если
 = О, то р = с и, следовательно,


(2.107)


у = Сх + a
 l + с 2 .


(2.108)


Это общее решение, соrласно общей теории, мы моrли написать
сразу, заменив в уравнении (2.1 Об) р на с.
Приравнивая нулю второй множитель в формуле (2.107) и подстав-
ляя выражение для х в уравнение (2.105), получим особое решение


ар
Х =

1+p2 '
у = а

1+p2 .


(2.109)


47




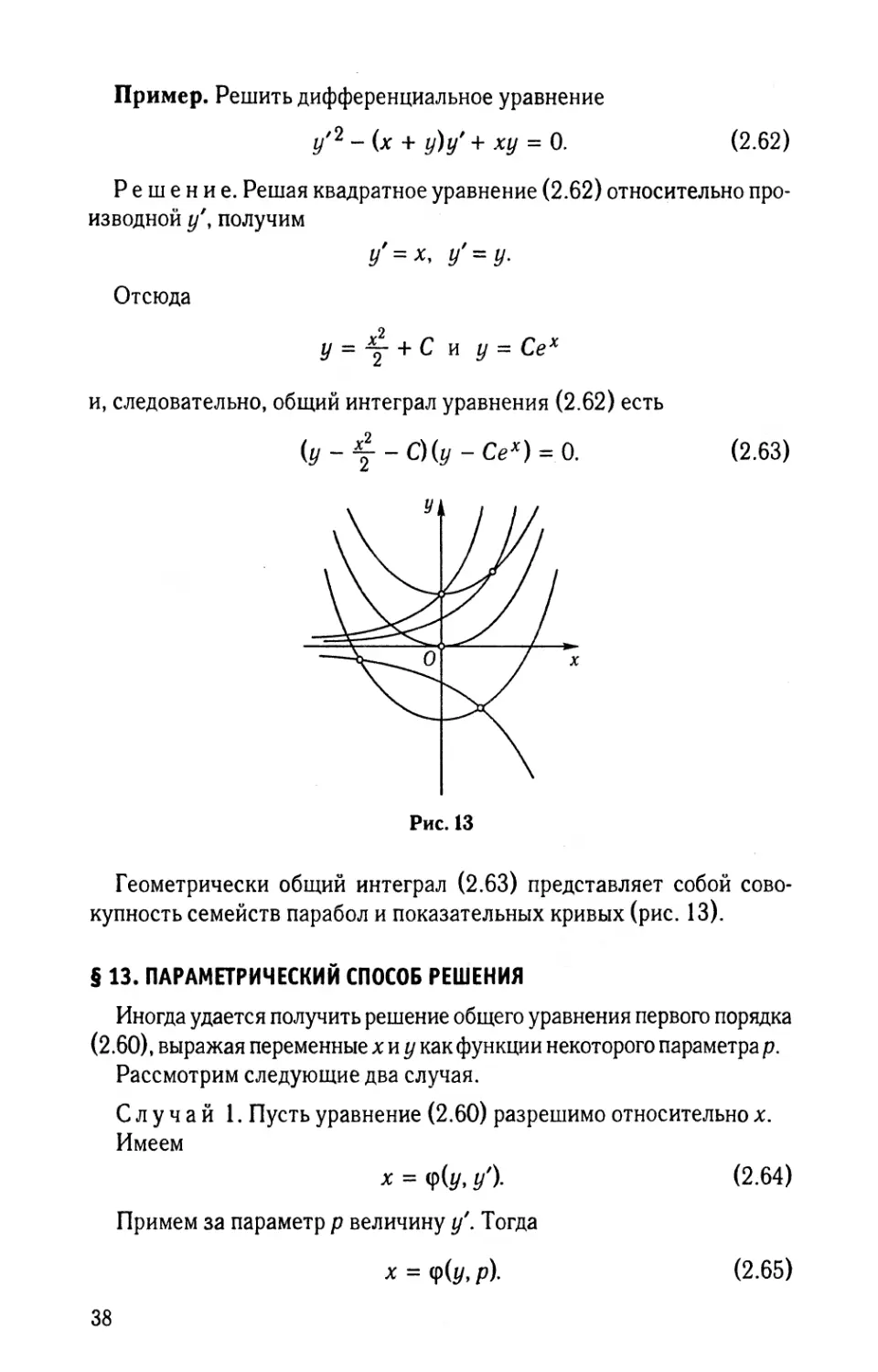
Чтобы выяснить, что это за кривая, исключим параметр р. Возво

дя уравнение (2.109) в квадрат и складывая, получим


х 2 + у2 = а2.


(2.110)


Отсюда ясно, что это окружность с центром в начале координат, pa

диуса а (точнее это верхняя часть окружности, так как из (2.109) сле

дует, что у> О). Прямые (2.108), очевидно, касаются этой окружно

сти (рис. [4).


Рис. 14
В заштрихованной части рисунка дифференциальное уравнение не
определено.


Задания для самостоятельноrо решения
1. у = ху' + cos у'. 3. 6ху,2
 6уу'
 Зу'3 = 2.
2. у = у'(х
 у' + у,2). 4. У = ху' + у'2.



 16. ОСОБЫЕ точки
Рассмотрим поле интеrрзльных кривых дифференциальноrо ypaB
 .
нения


Р (х, y)dx + Q(x, у) dy = О,


(2.111)


заполняющее некоторую область G с rраницей r (рис. 15).
Оп р е д е л е н и е. Точка М(х, у) области G называется обыкно

венной для дифференциальноrо уравнения (2.111), если через эту
точку в не которой ее окрестности и проходит одна и только одна ин

теrральная кривая (рис. 15). Всякую точку N области О, не являющу

юся обыкновенной, или принадлежзщую rранице r области О, мы бу



48




дем называть особой для дифференциальноrо уравнения (2.111).
Через особую точку или совсем не проходит ни одна интеrральная
кривая, или же проходит несколько интеrральных кривых (возможно
бесконечное множество).


Рис. 15
В частном случае, если дифференциальное уравнение имеет вид


y'=f(x,y),


(2.112)


rде функция {(х, у) определена в области О, то из теоремы существова

ния и единственности решений (э 4) получаем следующий результат:
если в некоторой окрестности точки М области G правая часть f(x, у)
уравнения (2.112) непрерьrвна и имеет оrраниченную производную
{
 (х, у), то точка М заведомо обыкновенная для этоrо уравнения.
Как следствие, имеем такое утверждение: внутренняя точка N об

ласти G может быть особой для дифференциальноrо уравнения
(2.112) только в том случае, если 1) функция [(х, у) терпит разрыв в
точке N, или в любоЙ ее окрестности; или же 2) функция {(х, у) непре

рывна в не которой окрестности точки N, но ее производная {
 (х, у)
неоrраничена в любой окрестности этой точки*.
Аналоrичные формулировки получаются для уравнения вида


х' = g(x, у).


(2.113)


Возвращаясь к уравнению (2.111), предположим, что функции
Р(х, у) и Q(x, у) непрерывны вместе со своими частными производны

ми первоrо порядка в области о. Если в некоторой точке М(х, у) обла

сти G выполнено условие Р(х, у) * о или же Q(x, у) ;/:. О, то уравнение
(2.111) в окрестности этой точки может быть приведено к виду
(2.112) (или, соответственно, к виду (2.113) и, следовательно, в Ha

ших предположениях эта точка является обыкновенной).


* Эти точки являются «подозрительными» В нашем смысле; чтобы разобраться в их
природе, требуется дополнительное исследование.


49




Таким образом, ос'обые точки дифференциальноrо уравнения
(2.111) удовлетворяют системе уравнений


Р(х, у) = о, Q(x, у) = о.


(2.114)


Пример. Определить особые. точки дифференциальноrо уравнения


2ydx
 xdy = о.


(2.115 )


Реш е н и е. Очевидно, единственной особой
точкой уравнения (2.115) может быть только
х = о, у = о.
Непосредственным интеrрированием убеж

с = о х даемся, что общее решение уравнения (2.115)
c=
 1 есть


у = Сх 2


и, следовательно, через точку 0(0, О) проходит
бесчисленное множество интеrральных кривых
[(парабол) (рис. 16)]. Такая особая точка называется узлом.


Рис. 16


в случае, если дифференциальное уравнение первоrо порядка имеет вид
Р(х, у, у')= О,
не разрешенный относительно производной у', то оно эквивалентно нескольким (дo

пустим k) уравнениям вида
у' = {. (х, у ), ..., у' = f k (х, у ),
определенных в некоторой области о.
Следовательно, здесь, как правило, через каждую точку М (х, у) области G про

ходит k интеrральных кривых, имеющих, вообще rоворя, различные направления.
В этом случае точка N области G называется особой только тоrда, коrда по одному и
тому же направлению проходит несколько интеrральных кривых.
Упражнение. Определить особые точки дифференциальноrо
уравнения


I 2х
 у
 х 2
У = x
2y+xy.



 17. ОСОБЫЕ РЕШЕНИЯ


О п р е Д е л е н и е. Решение дифференциальноrо уравнения перво

ro порядка


Р(х,у, у') = О


(2.116)


называется особым, если в любой ero точке нарушается свойство
единственности, т. е. через каждую точку М(х, у) особоrо решения по


50




не которому допустимому направлению tga = у', определяемому за

данным дифференциальным уравнением (2.116), проходит несколько
интеrральных кривых (рис. 17).


Рис. 11


Так как особое решение в каждой своей точке касается какой-то
друrой интеrральной кривой, то rеометрически оно представляет co

бой оrибающую HeKoToporo семейства интеrральных кривых. Обрат-
но, если мы имеем некоторое семейство интеrральных кривых уравне-
ний (1 .116)


ЧJ(х, у, С) = о,


(2.117)


то оrибающая К этоrо семейства обязательно является особым реше..
нием. В самом деле, оrибающая К является прежде Bcero интеrраль

ной кривой дифференциальноrо уравнения (2.116), так как в каждой
своей точке М(х, у) она касается одной из интеrральных кривых се..
мейства (2.117) и, следовательно, имеет с ней общее значение у',
удовлетворяющее дифференциальному уравнению (2.116). Кроме
Toro, в каждой точке оrибающей, очевидно, нарушено свойство един-
ственности.
Таким образом, разыскивание особых решений дифференциально-
ro уравнения (2.116) сводится к нахождению оrибающих некоторых
семейств интеrральных кривых этоrо уравнения.
Пусть известен общий интеrрал


Ф(х, у, С) = о


(2.118)


дифференциальноrо уравнения (2.116). Как известно из курса мате..
матическоrо анализа, оrибающая семейства кривых (2.118) удовлет-
воряет системе уравнений


Ф(х, У, С) = о,
 = о


(2.119)


51




и заведомо существует, еслиФ
 (х, у., C);tO дЛЯ всех значений Х, у, С,
подчиненных условиям (2.119). Исключая из системы (2.119) пара

метр С, получим уравнение некоторой линии


DC(X, у) = О,


(2.120)


носящей название С
дискриминантной кривой дифференциальноrо
уравнения (2.116). Это кривая, кроме оrибающей, если последняя cy

ществует, может содержать еще rеометрическое место особых точек
интеrральных кривых (точек возврата, двойных точек и т. п.).
Поэтому, чтобы найти особое решение дифференциальноrо ypaBHe

ния (2.116), нужно: 1) определить все однозначные ветки у = '11 (Х),
входящие в состав С
дискриминантной кривой; 2) среди них отобрать
те, которые удовлетворяют заданному дифференциальному ypaBHe

нию (2.116), что можно обнаружить непосредственной проверкой.
Кроме Toro, особыми решениями MorYT быть также участки rранич-
ной кривой r области G задания дифференциальноrо уравнения
(2.116).
Пример 1. Рассмотрим дифференциальное уравнение
2
у' = у"3 .
Общий интеrрал этоrо уравнения есть
= ( х
 С ) 3
Уз.


(2.121)


(2.122)


Составляя уравнение С-дискриминантной кривой, получим систему
= ( х
C ) 3 ( х
c ) 2 =0
У 3 '3 .


т


Рис. 18


52


n


Отсюда у = о. Непосредственно
видно, что эта функция YДOB

летвЬряет дифференциальному
уравнению (2.121) и, следова

тельно, является ero особым pe

шением. rеометрически кривая
у = о (ось Ох) представляет co

х бой оrибающую семейства куби

ческих парабол (2.122) (рис. 18).
Заметим, что через каждую точку
особоrо решения у = О проходит
б е с к о н е ч н о е множество ин

теrральных кривых; например,




через точку 0(0, О) проходят следующие интеrральные кривые: а)
прямая у = о; б) кубическая парабола у = (
 )3; в) составные кривые
( + Ь ) 3
тВАп, rде у = \ х 3 при ---00 < х <
b, у = О при .....lJ
 х
 а,
у = ( х ; а )3 при а < х < +00, причем а >0 и Ь >0
 произвольны.
Пример 2. Пусть


уу,2 = 1.


(2.123)


Тоrда


Бу' = + 1.
Интеrрируя это уравнение, получим общий интеrрал
з
у 2 = +
 (х
 С)


или


у3 = [
 (x
 С) Т .
С
дискриминантная кривая имеет вид
у3 = [
 (x
 С)] 2 , О = З(Х
 С),


(2.124)


откуда находим


у=о. (2.125)
Эта кривая, очевидно, не является интеrральной (а следовательно, не
является особым решением) и представляет собой rеометрическое
место особых точек (точек возврата) парабол (2.124) (рис. 19).
у


C=
I О


С=2 С=3


х


Ри с. 19
Укажем еще один метод разыскания особых решений. Пусть дифференциальное
уравнение имеет вид


F(x, у, р) = О,


(2.126)
53




rдер = у', причем Ру' Рр
 непрерывны. Предполаrая, что уравнение (2.126) может
быть разрешено относительно производной р, получим одно или несколько ypaBHe

ний вида


р = f(x, у),
rде функция '(х, у) непрерывна в некоторой области о. В силу теоремы существова

ния И единственности решений (э 4) в каждой точке области а, в которой сушеству

ет непрерывная производная {у(Х, у), заведомо имеет место свойство единственно

сти и, следовательно, эта точка не может принадлежать особому решению
дифференциальноrо уравнения (2.126). Таким образом, особое решение состоит
только из тех точек, rде производная fy(X, у )или терпит разры.в, или не существует.
Очевидно,
Р[х, у, /(Х, у)] == о.
Дифференцируя последнее тождество по у, получим
'i1F + 'i1F ! ' ( Х у) = о
ду др у' ,


откуда


'iJF
f , ( )
 ду
у Х, У

дF.
др
Если

 *" О, то производная [у(Х, у) непрерывна. Поэтому в точках особоrо реше

ния должны быть выполнены соотношения


(2.127)


р(х, у, р)=о,
j =o.


(2.128)


Линия, определяемая уравнениями (2. 128), называется р
дискриминантной
кривой. Исключая из системы (2.128) параметр р, получим уравнение р
дискрими

нантной кривой в обычном виде
Dp(X, у)=О. (2.129)
Из уравнений (2.128) видно, что особое решение представляет собой оrибаЮll
УЮ
семейства кривых (2.126), rде р иrрает роль параметра.
В общем случае р
дискриминантная кривая (2.129) кроме особых решений может
содержать rеометрическое место особых точек интеrральных кривых. Поэтому, OTЫC

кивая особое решение, каждый раз нужно проверять, что функции у= V(x), определя-
емые уравнением (2.129), удовлетворяют данному дифференциальному уравнению
(2.126).


Пример. Пусть дано уравнение
у 2 (l + у' 2 ) = 1.


(2.130)


Полаrая у' = р, получим


у2 (1 + р2) = 1.
Отсюда уравнения р
дискриминантной кривой есть


у2 (1 + р2) = 1, 2 у2 Р = о


или


а)у=О; б)у=:f:l.


54




Первая кривая (у = О) не является интеrральной и представляет собой rеометри

ческое место особых точек (точек прикосновений) семейства интеrральных кривых


(x
 С)2 + у2= 1


(2.131)


дифференциальноrо уравнения (2.130) (рис. 20). Прямые у =:f:l являются особыми
решениями и представляют собой ветки оrибающей семейства окружностей (2.131).


у


х


Рис. 20
Задания для самостоятельноrо решения
Найти общие интеrралы, особые решения дифференциальных
уравнений и вычертить rрафики семейств решений:
1. у,2 = у;
2. у = ху' +
, ;
3. у,2 (2
 3у)2 = 40
 у).


i 18. СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Метод дифференциальных уравнений, основы KOToporo были зало..
жены Ньютоном и Лейбницем, представляет собой один из наиболее
плодотворных методов изучения действительноrо мира. Математики
XYII
 XVIII веков, периода создания высшей математики, не без осно"
вания считали, что «язык природы
 есть язык дифференциальных
уравнений». Действительно, дифференциальные уравнения являют..
ся математическим аппаратом, позволяющим устанавливать законы
протекания физических процессов на основании изучения скоростей
изменения величин, характеризующих эти процессы. Исходными
предпосылками при этом являются физические законы, получаемые
в результате непосредственноrо изучения материальной действи..
тельности.


55




в XVII....XVIII веках при помощи дифференциальных уравнений
были сформулированы и решены мноrочисленные задачи механики,
физики, химии и т. п., недоступные прежним математическим средст-
вам. В частности, Ньютон решил знаменитую задачу о движении

ДBYX тел

 солнца и планеты. В дальнейшем особое развитие полу-
чили дифференциальные уравнения в частных производных, к кото-
рым приводят мноrочисленные задачи по теории тепла, электричест-
ва, маrнетизма, rазовой динамики и друrих разделов естествознания.
В конце прошлоrо столетия выдающийся русский ученый А. М. Ля-
пунов создал новое направление в теории дифференциальных уравне-
ний

теорию устойчивости движения», имеющую первостепенное
значение для вопросов техники.
Большой вклад в теорию дифференциальных уравнений внесли
также отечественные ученые: С. В. Ковалевская, В. А. Стеклов,
с. Н. Бернштейн, с. А. Чаплыrин, Н. М. Крылов, и. r. Петровский,
С. л. Соболев и др.
Решение задачи прикладноrо характера обычно состоит из двух ча-
стей:
1) составление дифференциальноrо уравнения;
2) решение этоrо уравнения.
Приемы решений дифференциальных уравнений первоrо порядка
были разобраны в предыдущих параrрафах. Здесь мы займемся pac

смотрением типичных rеометрических и физических задач, приводя-
щих к дифференциальным уравнениям l-ro порядка.



 19. ЗАДАЧИ rЕОМЕТРИЧЕскоrо ХАРАКТЕРА
Составление дифференциальных уравнений l-ro порядка для задач
rеометрическоrо характера основывается на том фундаментальном
факте, что уrловой коэффициент касательной МТ к данной кривой
у = у (х) в ее точке М (Х, у) равен производной у' (рис. 21), Т. е. tga= у'.


х


х


Рис. 21


56




Отсюда получаем уравнение касательной МТ
Y
y = y'(X
x),
rде Х, У
 текущие координаты точки касательной, и уравнение нор-
мали MN (перпендикуляра к касательной в точке касания)
у
y =
 ;, (Х
x),


rде Х, у
 соответственно, текущие координаты точки нормали.
Из чертежа, учитывая, что РМ = у, получаем также формулы для
длин отрезков (с учетом знаков): подкасательной St = ТР, noдHOp

мали Sn = PN, длины оmрезка касательной t = МТ , длины отрезка
нормали п = MN, а именно:
St = :, ; Sn = уу'; t = I

 l + у,2 ;
n = I у I
 1 + у,2 .


(2.132)


Задача. Найти кривую, для которой подкасательная в любой ее
точке М(х, у) равна удвоенной абсциссе точки касания.
Реш е н и е. На основании формулы для подкасательной имеем
дифференциальное уравнение

 = 2х.
у


. Отсюда


У ,
 JL.

 2х


и, следовательно,


у2 = Сх,
rде С
 произвольная постоянная.
Таким образом, искомым свойством обладают параболы с верши

ной в начале координат, осью симметрии которых является ось Ох.
Заметим, что решенная нами задача имеет качественный характер
и формулируется так: какова та кривая, которая обладает известным
свойством. Ответом служит не число, а уравнение кривой, т. е. закон
изменения ее ординаты в зависимости от изменения абсциссы. По
уравнению мы узнаем также «имя» кривой. В этом состоит сущест-
венное отличие дифференциальных уравнений от алrебраических,
rде результат решения задачи представляет собой число.
Таким образом, дифференциальные уравнения позволяют решать
задачи не только количественноrо, но также и качественноrо характе-
ра, что значительно усиливает мощь математических методов.


57




Задача об ортоrональных траекториях. Кривая у = у(х) назы

вается ортоzональной траекторией данноrо семейства кривых


F (
, 11, С) = О,


(2.133)


rде
, 11 ....... текущие координаты и С
 параметр, если в каждой своей точ

ке М(х, у) эта кривая пересекает некоторую линию семейства (2.133)
под прямым уrлом (рис. 22).


Рис. 22


Уравнение семейства кривых (2.133)
удобно записать в дифференциальной
форме. Дифференцируя уравнение
(2.133), будем иметь
дР дР dll
д
 + д11 d
 = о.


(2.134)


Исключая из уравнений (2.133) и
(2.134) параметр С, получим диффе

ренциальное уравнение вида


ф (
. 11.

 ) = О.


(2.135)


которому удовлетворяет любая кривая данноrо семейства (2.133).
Пусть через точку
(x, у) ортоrональной траектории проходит
одна из кривых семейства (2.133). в этой точке, очевидно, имеют Mec

то равенства



 = х, 11 = у.


Кроме Toro, в силу условия перпендикулярности касательных,
имеем


dll 1
d
 =
 dy .
dx


(2.136)


Подставляя эти величины в уравнение (2.135), получим дифферен

циальное уравнение


ф ( Х, у,
 :, ) = о


(2.137)


(здесь у' =

 ), которому удовлетворяют координаты точек и направ-
ление ортоrональной траектории. Интеrрируя последнее уравнение,
найдем все семейство ортоrональных траекторий.


58




З а м е ч а н и е: Записывая дифференциальное уравнение кривых
(2.135) в обычной форме


Ф(х, у, у') = О,


(2.138)


мы на основании формулы (2 137) имеем следующее простое правило:
чтобы получить дифференциальное уравнение ортоrональных траекто-
рий данноrо семейства , нужно в дифференциальном уравнении семейст-
ва заменить у' на

.
у


Пример. Найти ортоrональные траектории семейства эллипсов
(рис. 23)


х 2 + 2у2= с.


(2.139)


Реш е н и е. Дифференцируя уравнение (2.139), будем иметь
2х + 4уу' = О,


откуда


2уу' + х = о.


(2.] 40)


Это и есть дифференциальное уравнение семейства эллипсов
(2.139). Соrласно замечанию, заменяя в уравнении (2.140) у' на

,
у
получим дифференциальное уравнение ортоrональных траекторий


2у


 + х = О
у'


или


, 2у
У =
.
х


(2.141)


Интеrрируя последнее уравнение,
получим семейство ортоrональных
траекторий


у = Сх 2 ,


представляющее собой семейство па-
рабол (рис. 23).


у


х


Рис. 23


59




Задания ДЛЯ самостоятельноrо решения
1. Найти кривую, проходяu
ую через точку (О, 1), у которой подка

сательная постоянна.
2. Найти кривую, у которой поднормаль постоянна.
3. Найти кривую, у которой касательная в любой ее точке образует
постоянный уrол а с радиусом"вектором этой точки.
4. Найти кривую, для которой подкасательная равна среднему
арифметическому координат точки касания.
5. Найти КРИВУЮ, у которой ордината точки касания есть среднее
rеометрическое ее абсциссы и отрезка, oTceKaeMoro нормалью на оси
Ох.
6. Найти ортоrональные траектории семейства rипербол


ху = с.


! 20. ЗАДАЧИ ФИЗИЧЕскоrо ХАРАКТЕРА
При составлении дифференциальноrо уравнения физической зада

чи, обычно, используя известные физические законы, приходится на..
ходить соотношение между бесконечно малыми приращениями иско

мых величин.
Здесь имеет место nринциn от6расыlанияя бесконечно малых
высших порядков.
т е о р е м а. При составлении дифференциальноrо уравнения пер..
Boro порядка, связываЮlцеrо некоторые переменные х и у, можно от..
кидывать бесконечно малые высших порядков относительно прира

щений f1x и f1y этих переменных, заменяя последние при этом, COOT

ветственно, дифференциалами dx и dy.
Д о к а 3 а т е л ь с т в о. Пусть точное соотношение между перемен

ными х и У и их бесконечно малыми приращениями f1x и Ау имеет вид


А(х, y)
 + В(х, y)
y + <xLlx +
6.y = о, (2.142)
rде а = а(х, у, м" 6.у)
 о и
 =
(x, у, /h" l1y)
 О при /ll
 О и
6.у
 о.
Деля обе части равенства (2.142) на
x, получим
А(х, у) + В(х, y)
 + а +

 = О,


отсюда, переходя к пределу при f1x
 О и f1y
 О и учитывая, что
Нт h.y = dy
Ах ----+ О /).х dx


60




будем иметь


А(х, у) + B(x,y)

 = О


или


А(х, у) dx + В (х, у) dy = о.


(2.143)


Как видно, дифференциальное уравнение (2.143) формально полу

чается из уравнения (2.142) путем отбрасывания совокупности бес-
конечно малых высшеrо порядка CJJix и CJJiy относительно l1x и l1y и за-
мены I1х на dx и l1у на dy.
Таким образом, наш принцип установлен.
3 а м е ч а н и е. В дальнейшем при составлении дифференциальных
уравнений 1
ro порядка мы будем вместо бесконечно малых прираще

ний величин писать дифференциалы этих величин, иrнорируя при
этом члены высшеrо порядка малости относительно прирашений дaH

НЫХ величин.


Задача 1. В резервуар, содержащий 1 О Kr соли на 100 л смеси, каж-
дую минуту поступает 30 л воды и вытекает 20 л смеси (рис. 24). Опре-
делить, какое количество соли останется в резервуаре через t мин.,
предполаrая, что смесь MrHoBeHHo перемешивается
Реш е н и е. При составлении дифферен-
циальноrо уравнения изучаемое явление
следует расматривать в общем положении;
начальные данные определяют лишь началь-
ные условия и, как правило, не ВХОДЯТ в само
дифференциальное уравнение.
Пусть х
 количество соли в резервуаре
в момент времени t мин., ах + dx
 количе

ство соли в момент времени t + dt мин. Об-
ращаем внимание, ЧТО здесь вместо прира-
щений мы пишем дифференциалы. Таким
образом, dx есть изменение количества
соли за бесконечно малый промежуток вре-
мени dt, причем так как количество соли убывает, то dx < О при dt>O.
С друrой стороны, изменение количества соли происходит лишь по-
тому, что вытекающая смесь уносит с собой соль. Так как объем смеси
в резервуаре в момент времени t, очевидно, равен v = 100 + 30t
 20t =
= 100+ 10t, то концентрация соли (т. е. количество соли, содержащее-
ся в единице объема) в момент времени t будет равна 100: 10t .


I ЗО.....:!!.....
мин


20 M
H


Рис. 24


61




с точностью до бесконечно малой высшеrо порядка относительно
dt можем считать, что в течение бесконечно малоrо промежутка Bpe

мени (t, t+ dt) концентрация соли остается постоянной и поэтому KO

личество соли, ушедшее из резервуара за промежуток времени dt, OT

считанный от момента времени t, равно
100
 10t .20dt = 19:t dt.
Приравнивая это выражение абсолютной величине изменения KO

личества соли, Т. е. I dx 1, будем иметь дифференциальное уравнение
задачи



dx = 15
t dt.


(2.144)


Кроме Toro, имеет место начальное условие
xlt=0=10. (2.145)
Разделяя переменные в уравнении (2.144) и интеrрируя, последо-
вательно получим


dx

...14L
х
 10+t


и


ln х = ln С
 21n (1 0+ t),


откуда


Х
 с

 (10+ t )2 ·
Из начальноrо условия (2.145) находим
10 = 192 '
т. е. С = 1000. Поэтому окончательно закон изменения количества
соли х в Kr, находящейся в резервуаре, в зависимости от текущеrо
времени t в минутах дается формулой (рис. 25)
1000
х = (10+ t )2


(2.146) _


Рис. 25


3 а м е ч а н и е. Из формулы (2.146),
u
зная количество соли, находящеися в
резервуаре (последнее леrко YCTaHO

вить, измеряя объем резервуара и кон-
центрацию соли в нем), можно опреде

лить сколько времени прошло от
t мин Н u
I начала процесса. а этои идее OCHOBa

но вычисление возраста морей и OKea

нов.


5


10


о


2 4 6 8 10


62




Задача 2. На какой высоте х от поверхности земли находится лет-
чик, если давление барометра в кабине самолета равно Р Kr / см2, а на
поверхности земли РО Kr / см2.
Реш е н и е. Давление Р воздуха на площад-
куа= 1 см2. помещенную на высоте х, создается
весом бесконечноrо воздушноrо столба, опира-
ющеrося на эту площадку (рис. 2
). Поэтому,
если уровень площадки увеличится на dx, то
давление Р уменьшится на величину
dP, рав-
ную весу отпавшеrо столбика воздуха с основа-
нием (J' и высотой dx. Обозначая через у удель-
ный вес воздуха на высоте х, имеем
дифференциальное уравнение



dP= ydx.


(2.147)


I
I
I
I
I
A


/1


х
l


Рис. 26


Предположим, что температура воздуха на поверхности земли и на
высоте х одна и та же. Тоrда соrласно закону Бойля
Мариотта удель-
ный вес воздуха изменяется пропорционально давлению и мы имеем


:L
.E..
'у о
 Ро'


(2.148)


rде 10 ---- удельный вес воздуха на поверхности земли. Отсюда
y=

 P
и, следовательно, дифференциальное уравнение (2.147) принимает
вид


dP=


 Pdx.


(2.149)


Начальные условия здесь таковы: Р = РО при х = о.
Интеrрируя уравнение (2.147), получаем
dx =
 РО dP
10 Р


и


R
х = С
 .....Q..ln Р.
10


Из начальных условий находим
С = РО ln .А О .
10 '


63




поэтому окончательно имеем


х = РО ln РО
10 Р
(барометрическая формула Лапласа).
Для численных расчетов примем техническую систему мер. При
температуре 15 ос имеем


(2.150)


УО = 1 ,293 Kr / м3
 1 ,3 Kr / м3


и


Ро= 1 атм.= 1 Kr/cM2= 10000 Kr/M2.


Отсюда


х = 77001п Ь м,


rде давление Р выражено в атмосферах. В частности, при Р =
 атм.
имеем:


х = 7700 .ln 2 = 7700.0,69 = 5500 м = 5,3 км.


Формула (2.151) дает лишь приблизительные значения, так как не
учтено изменение температуры воздуха с высотой и друrие факторы.


Задания для самостоятельноrо решения
1. Соrласно закону Ньютона скорость охлаждения тела пропорци

ональна разности температур тела и среды. Через сколько минут тело,

HarpeToe до 100 ос и находящееся в воздухе температуры 20 ос, охла

дится до 30 ос, если в течение 20 минут это тело охладил ось до БО ос.
2. В какое время вода, заполняющая полусферическую чашу диа-
метра D = 2 м, вытечет через круrлое отверстие диаметра d = 0,2 м в
дне чаши?
у к а 3 а н и е. Скорость истечения воды при напоре h равна
v = c .J2gh ,


rде с = 0,6
 опытный коэффициент и g = 9,82 м/ сек2
 ускорение
силы тяжести.




r л а в а 111
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ BTOPOrO
ПОРЯДКА



 1. ОБЩИЕ ПОНЯТИЯ


Дифференциальное уравнение BToporo порядка с неизвестной Фун

кцией У = у(х) имеет вид


Р(х, у, у', у") = О,


(3.1 )


rде F
 данная функция.
Предполаrая, что уравнение (3.1) может быть однозначно разреше

u "
но относительно производнои У , получим


уН = [(х, у, у'),


rде f
 некоторая известная функция.
Общее решение этоrо уравнения


у = <р(х, с l' С 2)


содержит две произвольные постоянные
С 1 и С 2 . Поэтому через данную точку
Мо(Хо, Уо), вообще rоворя, проходит пу

чок интеrральных кривых (рис. 27), так
как одна из произвольных постоянных
остается неопределенной. Чтобы Bыдe

лить определенную интеrральную кри

вую, кроме точки Мо, достаточно задать
еще направление касательной в точке Мо
к искомой интеrральной кривой


tgao = Уа.


(3.2)


(3.3 )


Рис. 27


(3.4)


Таким образом, мы имеем следующие начальные условия:


ylx=xo = Уо, y'lx=Xo = уа. (3.5)
Основная задача, которая здесь ставится, есть следующая: найти
решение дифференциальноrо уравнения (3.2), удовлетворяющее
начальным условиям (3.5) (задача Коши). rеометрически это
значит: найти интеrральную кривую уравнения (3.2), проходящую че

рез данную точку Ма(хо, Уа) в заданном направлении tg ао = Уа.


65




Из начальных условий (3.5) вытекает, что постоянные С 1 И С 2 должны
удовлетворять системе уравнений
Уа = <Р(Хо, C 1 , С 2 ) } (3.6)
Уа = <p
 (хо ' С 1 ' С 2 ) .
в зависимости от Toro, имеет или не имеет эта система решения, за-
дача Коши разрешима или не разрешима.
Приведем без доказательства важную теорему существования и
единственности решений.
т е о р е м а. Если в некоторой области
Ix
xal<a, Iy
yol<b, Iy'
yol<c
(а, Ь, с
 положительные числа) функция f(x, у' у') непрерывна и
имеет оrраниченные частные производные
f
 (х, у' у'), f
'(x, у, у'),


то существует единственное решение
у = <р(х) (3.7)
дифференциальноrо уравнения (З.2), удовлетворяющее начальным
условиям (З.5) и определенное на некотором отрезке Ix
 xol
 h.



 2. МЕХАНИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛьноrо УРАВНЕНИЯ
BToporo ПОРЯДКА
Пусть по оси Ох движется материальная точка массы т (рис. 28),
причем действующая сила
Х = x(t, х,
; ).
в самом общем случае, зависит от времени t, координаты точки х и ее
dx
скорости di. На основании закона Ньютона имеем дифференциальное
уравнение движения


d 2 Х x(t dX )
т dt 2 = , х, cii .


(З.8)


х
""...-...............
......................" т
..........а' *' " о .
О Х


.
х


Рис. 28
Таким образом, всякое дифференциальное уравнение BToporo
порядка, разрешенное относительно старшей производной, можно


66




рассматривать как дифференциальное уравнение прямолинейноrо
движения материальной точки. Начальные условия здесь приобрета

ют следующий вид:


xl/ =/0 = хо,
; I/ =/0 = хо,


(3.9)


т. е. в начальный момент to задаются: хо
 начальное положение точ

ки и Хо
 ее начальная скорость.



 з. ИНТЕrРИРУЕМЫЕ (JIУЧАИ
с л У чай 1. Пусть правая часть дифференциальноrо уравнения
2
ro порядка (З.2) является функцией только от переменной Х, т. е.
дифференциальное уравнение имеет вид


у" = Х(Х),


(3.10)


rде Х
 известная функция.
Интеrрируя последовательно два раза обе части уравнения (З.I0),
будем иметь


. у' = JX(x)dx + С)


и


у = JdxJX(x)dx + С)х + С 2 .


. rде С 1 и С 2
 произвольные постоянные.
Пример. Решить уравнение


" 1
У =
.
х


Реш е н и е. Интеrрируя, последовательно находим
у' = J
X + С) = In/xl + С)


и


у = Jlnlxldx + С)Х + С 2 = xlnlxl
 х + C1X + С2.


Объединяя два члена, окончательно получим
у = xlnlxl + C1x + С 2 .


(З.ll )


с л у чай 2. Пусть правая часть дифференциальноrо уравнения
(3.2) явным образом зависит только от неизвестной функции у, Т. е.


у" = У(у),


(3.12)


rде У
 данная функция.


67




Примем у за независимую переменную. Тоrда, применяя правило
дифференцирования сложной функции, получим
" dy' dy' dy , dy'
У



.

 у


 dx
 dy dx
 dy .
На основании уравнения (3.12) имеем
" , d у' У( )
y=y
= у
dy


или


y'dy' = Y(y)dy.
Интеrрируя последнее равенство, находим
,2 J (;

 = Y(y)dy + f


(3.13)


И,следовательно,


у' = X
2] Y(y)dy + С 1 .


(З.14)


Разделяя переменные в уравнении (3.14) и интеrрируя, получим
общий интеrрал нашеrо дифференциальноrо уравнения:
J d у = + ( х + С 2 ) (З.15)

 2IY(y )dy + (;1
 ,
rде C 1 и С 2
 произвольные постоянные.
3 а м е ч а н и е. Не следует запоминать формулу (З.15), достаточно
усвоить соответствуюший прием.
Пример. Решить уравнение


" 1
У =3.
у


(3.16)


Реш е н и е. Полаrая


d '
уН = у'
 ,


будем иметь


, dy' 1
У dy = уз


или


y'dy' = d; .
у


Отсюда находим


J y'dy'= J d; ,
у


то есть


у,2 1 С}




 +

2
 2 у 2 2


68




И,следовательно,


,
 +
 С. у 2
 1
y

 .
у
Разделяя переменные в последнем уравнении, получим
у dy
 + d

 C.y2
1

 х.


Отсюда


J ydy = + J dx

 CI у 2
 1



или


d l
 Cly2
 1 = + (х + С 2 ).


Таким образом, общий интеrрал уравнения (3.16) имеет вид.
C 1y 2 = 1 + (С 1 Х + С 2 )2,
rде C 1 и С 2
 произвольные постоянные, причем очевидно, что С 1 > о.
с л у чай 3. Пусть правая часть дифференциальноrо уравнения
(3.2) явным образом зависит только от у', т. е. уравнение имеет вид
у" = Р(у'),


rде Р
 некоторая известная функция.
Полаrая


у' = р и у" =
 .


будем иметь




 = Р(р).


Отсюда


dp
dx = Р(р)



,следовательно,


J dp
х = Р(р) + C 1 .
Разрешив уравнение (З .18) относительно р, получим
р = <р(х, с 1).


(3.18)


* в этой формуле через С2 мы обозначили выражение С I С2.


69




Из последнеrо уравнения,
итывая, что р =

 , леrко найти у:
у = f q> (х. С 1 )dx + С 2 . (3.19)
Однако не всеrда уравнение (З.18) леrко разрешимо относительно р.
Поэтому мы укажем друrой способ нахождения функции у. Очевидно,
н dp dp dy dp
У = dx = dy . dx = Р dy .
Используя дифференциальное уравнение (3.17), получаем
p dp =p(p)
dy


и, следовательно,


f р dp ( )
у = Р(р) + С 2 . 3.20
Система уравнений (З.18), (З.20) дает общий интеrрал дифферен

циальноrо уравнения (3. 17) в параметрическом виде, rде роль пара

метра иrрает р. Исключая из этих уравнений р, получим общий интеr

рал уравнения (3.17) в обычном виде
Ф(х, у, С}, С 2 ) = о.
3 а м е ч а н и е. Так как параметрическое представление кривой He

однозначно, то в формулах (з. 18) и (з. 20) за параметр можно при

нимать любую величину е = ",(р), являющуюся известной функцией
от р.
Пример. Найти все плоские кривые, имеющие постоянный радиус
кривизны, равный R.
Реш е н и е. Вспоминая формулу радиуса кривизны, имеем диффе

ренциальное уравнение


3
(1 + у,2 )2 = R.
у"


Отсюда


3
у" = k (1 + у'2) 2 .


Полаrая


I "dp dp
У = Р и у =
 = p

dx d у ,


получим


3
d

d
 = k O + р2)2


70




и


3
d

Р d
 = k (l + р 2 ) 2 .


Следовательно,


f dp
х = R 3 + С 1
О+р2)2


(3.21 )


и


f pdp
У = R з + С 2 .
0+ р2)2
Полаrая в интеrралах (З.21), (З.22)
de
p=tg8, dp= 2е '
COS ..


(3.22)


находим


х = Rfcos8d8 + С) = Rsin8+ч


(З.2З)


и


у = Rfsin8d8 + С 2 =
Rcos8+C2' (3.24)
Формулы (З.2З), (З.24) дают параметрическое представление сис

темы интеrральных кривых. Исключая из уравнений (З.2З) и (З.24)
параметр е, получим
(х
 С 1 )2 + (у
 С 2 )2 = R2. (3.25)
Как и следовало ожидать, искомые интеrральные кривые есть
окружности радиуса R.


Задания для самостоятельноrо решения
1. у" = sin 2 х.
2. у" + 2;2 = О, если у(О) = 1 и у'(О) = 1.
3. 2у' у" = 1.
4. Материальная точка брошена вертикально вверх с начальной
скоростью vo. Найти наибольшую высоту поднятия точки, принимая
сопротивление воздуха пропорциональным квадрату скорости.



 4. (JIУЧАИ ПОНИЖЕНИЯ ПОРЯДКА
Укажем два случая, коrда дифференциальное уравнение BToporo
порядка (З.l) леrко при водится к дифференциальному уравнению
первоrо порядка.


71




с л у чай 1. Левая часть дифференциальноrо уравнения BToporo по

рядка (З.1) не содержит х, т. е. дифференциальное уравнение имеет вид
Р(у, у', у") = о. (З.2б)


Полаrая


, "dp dp dy dp
У = Р и у =
 =

 = P

dx dy dx dy'
получим дифференциальное уравнение первоrо порядка
Р(у, р, р :: ) = о,


(3.27)


rде роль независимой переменной иrрает у.
С л у чай 2. Левая часть дифференциальноrо уравнения BToporo
порядка (3.1) не содержит у, т. е. дифференциальное уравнение имеет
вид


р(х, у', уН) = о.


(3.28)


Полаrая


, "dp
У = р, У = dx '
получим дифференциальное уравнение первоrо порядка
Р( х, р.
 ) = о. (3.29)
Для решений уравнений первоrо порядка (З.27), (З.29) следует
применить разобранные ранее приемы.
3 а м е ч а н и е. При преобразовании производной у нужно доби

ваться Toro, чтобы дифференцирование функции у' = р происходило
по той переменной х или у, которая входит в правую часть дифферен

циальноrо уравнения.
Пример. Найти решение уравнения
" ,2
У = У
 у,


удовлетворяющее начальным условиям
y=
 l , у'=
 при x=l.
Реш е н и е. Полаrая


, "d p
У =р, У =P dy '


получим


dp 2
p
 = Р
 у
dy


(з. 30 )


72




или




 = р
 yp
)


(З.31 )


Очевидно, это уравнение Бернулли. Поступая соrласно общему Me

т оду , делим обе части уравнения (3.31 ) на p
 1, т. е. возв ращаемся CHO

ва к виду (з.зо). Примем теперь
Р 2 = z 2 Р dp = dz
, dy dy'


откуда находим


1 dz = z
 у
2 dy


или



;
 2z =
 2у. (3.32)
Интеrрирующий множитель для уравнения (З.32) имеет вид
fl = e
J2dy = e
2y.


Умножая обе части уравнения (3.З2) на 11, получим
..A..(e
2y z) =
2 y e
2y
dy ,


откуда


e
2yz =
2Jye
2Ydy = ye
2y +
 e
2Y + С).


Следовательно,


z = у +
 + C 1 e 2y


или


р2 = у +
 + C 1 e 2y .


Используя начальные условия, будем иметь
)
1 1 1



 =

 +
 + С } е 2
4 4 2 '


откуда


С 1 =0


и, следовательно,


( d y ) 2
р2 = dx = У + t.


(з.зз)


Заметим, что если бы мы на этом этапе решения не определили про-
извольную постоянную С l' то задача сильно усложнилась бы.


73




Из уравнения (з.зз) получаем
dy = +
 y + 1
dx
 2 .
Т u' dy
ак как в окрестности начальных значении производная у = dx поло

жительна, то перед радикалом следует взять знак плюс (+). Поэтому
dy

 = dx.
" У +"2


Интеrрируя последнее равенство, будем иметь
f R = f dx
l+

2


или


2
y+
 = х + С 2 .


(3.34 )


Для определения постоянной С 2 используем начальные условия
у =

 при х = 1.


Имеем


1 = 1 + С 2 ' т. е. С 2 = о.
Таким образом, искомая интеrральная кривая задается уравнением
2
y+
 = х


или


У =д:.
l
4 2.


(З.З5)


Задания для самостоятельноrо решения


1. уу" = у,2 + y 2 1ny.
2. (1 + х 2 )уН + (I + у' 2) = о.
3. у" + у'2 = уу', если у(О) = о и у'(о) =
 1
4. Найти кривую для любой точки, проекция радиуса кривизны KO

торой на ось Оу имеет одно и то же значение.
5. Найти форму равновесия каната с закрепленными концами,
принимаемую им под действием собственной тяжести.
6. Цепь длины [= 10 м соскальзывает вниз со стола без трения. За Ka

кое время Т соскользнет цепь, если движение начинается из положения,
коrда свисает а = 2 м цепи.


74




i 5. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ


в технических приложениях важное значение имеют линейные
дифференциальные уравнения
у" + р(х) у' + q(x) у = f(x), (3.36)
rде р(х) и q(x) (коэффициенты уравнения) и f(x) (правая часть,
или свободный член уравнения)
 некоторые данные непрерывные
функции. Если {(х) == о. то уравнение (З.З6) называется однородным
или без правой части; в противном случае оно называется неодно"
родным, или с правой частью.
Мы здесь изучим лишь линейные уравнения с постоянными коэф"
фицuенmами, причем в первую очередь рассмотрим однородное урав-
нение.
Итак, пусть


р(х) = а, q(x) = ь,


(3.37)


rде а и Ь
 постоянные действительные числа и '(х) == о.
Уравнение (З.З6) при этом принимает вид
у" + ау' + Ьу = о.


(З.38)


Наряду с дифференциальным уравнением рассмотрим соответству-
ющее алrебраическое уравнение


k 2 + ak + Ь = О,


(З.39 )


которое называется характеристическим уравнением для уравне-
ния (3.38). Формально характеристическое уравнение (З.39) получа-
ется из дифференциальноrо уравнения (3.38) путем замены производ-
ных различных порядков на соответствующие степени неизвестной k,
причем функция у, как всеrда, считается производной нулевоrо по-
рядка.
Пусть k} и k 2
 корни характеристическоrо уравнения (3.39), т. е.
k!.2 =

 +
a: Ь. (3.40)


в силу известной теоремы Виета имеем
k l + k 2 =
a, k}k 2 = Ь. (З.41)
Поэтому дифференциальное уравнение (3.З8) можно записать в
следующем виде:


у"
 (k 1 + k2) у' + k} k2 У = О


75




или


(У'
 k1y)'
 k2 (У'
 k1y) = о.
Здесь возможны следующие три случая.
С л у чай 1. Пусть


(3.42)


2
D = а4
 Ь > о.
Тоrда корни k} и k 2 (3.40) характеристическоrо уравнения (3 39) дей

ствительны и различны.
Полаrая


у'
klY = и.
из уравнения (3.42) будем иметь
и'
 k 2 u = О


(3.43)


или


duU = k 2 dx.


Отсюда


ln u = k 2 х + ln С


И,следовательно,


u=Ce
X,


(3.44 )


rде С ......... произвольная постоянная.
Подставляя это выражение в формулу (3.43), получим линейное
уравнение первоrо порядка
у'
 k 1 y = c k2X . (3.45)


Как известно, линейное уравнение (3.45) имеет интеrрирующий
множитель (см. rл. 1, Э 11)


Jl = e
klX.


Умножая обе части уравнения (3.45) на f.!, будем иметь
(ye
klX)' = Ce(k 2
kl )Х;


отсюда


ye
klX = С 1 + C2e(k2
kl )Х,
rде С I и С 2 =

kl
 произвольные постоянные. Следовательно.


У = C1e k1x + C 2 e k2X .


(3.46)


76




Заметим, что формула (3.46), как вытекает из ее вывода, дает совокупность всех
решений однородноrо дифференциальноrо уравнения (3.38). Кроме Toro, решение
(3.46) является общим, так как оно способно удовлетворить любые начальные
условия.
В самом деле, положим


У Ix=Xo = Уо, У' Ix=Xo = Уб, (3.47)
rде Уо, Уб
 какие
нибудь определенные числа. Для нахождения соответствующих
постоянных С 1 И С 2 из формулы (3.46), имеем следующую систему вравнений
С} e k1Xo + C2e
Xo = Уо } (3.48)
C}k1e kJXo + C2
e
Xo = Уб


Определитель этой системы
e k1Xo
1:1=
k} e kJ хо


e
Xo
= (

 k} )e(k, +
)Xo "* О,

ek;.xo


поэтому система (3.48) совместна и имеет единственное решение. Следовательно, cy

ществует одно и только одно частное решение уравнения (3. 38), удовлетворяющее
начальным условиям (3.47) и получающееся из формулы (3.46) соответствующим
этим условиям выбором постоянных С 1 И С 2 .
Пример. Найти решение уравнения
уН
 2у'
 15 = О,


удовлетворяющее начальным условиям


у (О) = 1, у'(О) =
2.


Реш е н и е. Составим характеристическое уравнение
k 2
 2k
 15 = о.


Решая это уравнение, получим
k = 1 +
 1 + 15 = 1 :!: 4,


. то есть


k 1 = 5, k 2 =
з.
Следовательно, обшее решение уравнения на основании формулы
(З.46) имеет вид


у = C 1 e 5x + C2e
3X.


Для определения постоянных С 1 и С 2 ' в силу начальных условий,
получаем уравнения
1 = C 1 + С 2 ,
2 = 5C 1
 ЗС 2 .


77




Решая последнюю систему, будем иметь
C 1 =
 , С 2 =
 .


Следовательно, искомое частн<?е решение таково:
у ==
 (е 5х + 7e
3X).


Случай 2. Пусть


2
D = t
 ь < о.
Тоrда корни k} и k 2 характеристическоrо уравнения (3.39) различ-
ны, но являются комплексно сопряженными, т. е.


k 1 = а + i
, k 2 = а
 iP,


(3.49)


rдеi= Д ,а a=

 и
 =
b а;
действительны.
Вычисления в случае 2 полностью аналоrичны вычислениям в слу-
чае 1, но с той только разницей, что здесь приходится иметь дело с
комплексными функциями от действительной переменной х. Поэтому
общее решение дифференциальноrо уравнения (З.З8) формально вы-
разится той же формулой (З.46)
у = C}e k1x + C 2 e k2X , (3.50)


rде С 1 и С 2 ........ произвольные постоянные, вообще rоворя, комплекс-
ные.
Справедливость этой формулы леrко проверить непосредственно.
В самом деле, подставляя эту функцию в уравнение (З.З8), получим
у" + ау' + Ьу = C 1 (kr + ak 1 + b)e ktX + С 2 (kr + ak 1 + Ь) == о,
т. е. у
 есть решение уравнения (З.З8).
Формуле (3.50) можно придать друrой вид. Подставляя значе-
ния(З.49) корней k} и k 2 в формулу (З.50), будем иметь
у = Cle(a+i
)x + C2e(a
i
)x = eax(Clei
x + C2e
i
x).


Используя формулы Эйлера
ei
x = cos
x + isin
x,


и


e
i
x = cospx
 isiпрх,


78




окончательно находим


У = eax(A 1 COSPX + А 2 sinpx),


(3.51)


rде А 1 = С 1 + С 2 ' А 2 = i (С I
 С 2 )
 произвольные постоянные.
Формулу (З.51) можно записать также в несколько ином виде. По

лаrая в формуле (З.51)
А 1 = Asin<p, А 2 = Acos<p,


rде А и q>
 новые произвольные постоянные, определяемые по фор-
мулам


1 2 2 А
А = "Аl + А 2 . tg q> = A
 '


очевидно, ПОЛУЧИМ


у = Ае ах sin(px + <р).


(3.52)


Пример. Решить уравнение
уН
 2у' + 5у = о.
Реш е н и е. Характеристическое уравнение имеет вид
k 2
 2k + 5 = о.


(3. 5З )


Отсюда


k 1 , 2 = 1 + 2i,
т. е. а = 1 и
 = 2. По формуле (з. 51) имеем общее решение уравнения
(З.53)


у = е Х (А 1 cos2x + A 2 sin2x),
rде А 1 и А 2
 произвольные постоянные.
С л уч айЗ. Пусть


2
D = Т
 ь = о.
Корни характеристическоrо уравнения (З.З9) будут кратные (совпа-
дающие)


k} = k 2 =

 .
Дифференциальное уравнение (3.42) принимает вид
(у'
 kly)'
 k 1 (у'
 k1y) = о.


(З. 54)


(З.55)


79




Отсюда, полаrая


у'
 k} у = о,


(3.5б)


получим


и'
 .k 1 u = о.
Решив последнее уравнение, будем иметь
и = C 1 e k ,x,


rде С 1
 произвольная постоянная.
Подставляя последнее выражение в формулу (З.56), будем иметь
у'
 k1y = C}e kIX .


Используя интеrрирующий множитель
Jl = e
klX,


получим


(ye
kIX)' = С 1 ,


откуда


ye
klX = С}Х + С 2


И,следовательно,


у = (С 1 х + С2) е k l Х ,


(3.57)


rде С 1 и С 2
 произвольные постоянные.
Формула (3.57), как леrко убедиться, дает общее решение линейно..
ro однородноrо дифференциальноrо уравнения (З.55).
Пример. Решить уравнение


у" + 2у' + у = о.


(З.58)


Реш е н и е. Характеристическое уравнение имеет вид
k 2 + 2k + 1 = О
,


откуда


k} = k 2 =
 1.
Поэтому общее решение уравнения (3.58), в силу формулы (3.57),
есть


у = (C 1 Х + С 2 ) е k 1 Х .


Сводка результатов случаев 1
3 дается в таблице.


80




Таблица решений уравнения)'" + а)" + Ьу= О


2


Характер корней k 1 и k 2
характеристическоrо Общее решение
авнения
Корни k} и k 2 действитель
 у = С 1 e kJx + C2ek2X
ные и азличные (k;f:. )
Корни комплексные:
k 1 =а + ёр и У = еа.х(с) cospx+ С 2 sinpx)
k =а.
 i
Корни кратные: у = ekJx(C) + С 2 х)
k) =



Случай


3


Задания для самостоятельноrо решения
Решить уравнения.
1. у" + у'
 2у = о. 2. у" + у' + у = о.
3. 4у"
 4 у ' + у = о. 4. d 2 x + 0)2 х = О (00 > О......... постоянно).
dt 2



 б. ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЛИНЕйноrо ОДНОРодноrо
УРАВНЕНИЯ Broporo ПОРЯДКА
Рассмотрим задачу о прямолинейных колебаниях материальной
точки в сопротивляющейся среде под действием центральной упруrой
'силы (zармонuческuй осцuляmор).
Пусть на материальную точку массы т в направлении оси Ох дей

ствует uентральная упруrая сила


х =
kx,
rде х
 отклонение точки от положения равновесия О (рис. 29),
k
 постоянный коэффициент пропорциональности. Кроме Toro, на
эту точку действует еще сила сопротивления среды
Х
 k dx
1

 1 dt'


которую мы принимаем пропорциональной первой степени абсолют-
ной величины скорости (k 1
 коэффициент пропорциональности).


"'....-
,.."
.".
...........о'"


х
..... ....

 ...... .... ......


.....
.......... т
. ...... .
Х X 1


..


о


х


Рис. 29


81




Соrласно закону Ньютона имеем дифференциальное уравнение
движения


т d 2 x =
kx
 k dx
dt 2 1 dt


или


d 2 x + 2а dx + А 2 Х = О
dt2 dt tJ ,


(3.59)


rде


a=
 А2=.!.
2т' tJ m .


Мы предположим, что в начальный момент t = О материальная точ

ка имела отклонение равное Ха и была отпущена без толчка. Поэтому
начальные условия имеют вид
Х It=O = Ха'
: It=o = о. (3.60)


Характеристическое уравнение в нашем случае принцмает вид*


p2+2ap+
2=o,


(З.61)


отсюда


PI, 2 =
a +
a 2

 2 .


(З.62)


Рассмотрим три случая.
С л у чай 1. Пусть


а 2

 2 = б 2 > о.


Физически это значит, что сопротивление среды велико по cpaBHe

нию с упруrой силой.
Тоrда корни характеристическоrо уравнения (З.61) в силу форму

лы (3.62) будут


Pl =
a + б, Pl =
a
 Ь
и, следовательно, общее решение имеет вид
Х = Cle(
a + o)t + C2e(
a
 o)t .


(з. 6З )


(з. 64)


Для определения произвольных постоянных С 1 и С 2 используем Ha

чальные условия (3.60). Составляя производную

: = С 1 (----а + б)е( ---<х + б)t + С 2 (
a
 б)е( ---<х
 б)t (3.65)


* Во избежание путаницы мы здесь неизвестную обозначаем через р


82




и полаrая t = О В уравнениях (3.64) и (3.65), получим
C 1 + С 2 =хо,
(а
б)Сl + (а +Ь)С 2 = о.


(3.66 )


Отсюда


С 1 =
 (1 +
 ). С 2 =
 (1

 }
Следовательно,
х
 хо e
at [ <е бt + е
бt) + а (e
t
 e

t ) ]

 2 &


(3.67)


или


х = xoe
t (СЫ5t +
 sЫ5t J (3.68)
Так как О < Ь < (1, то rрафик (3.68) имеет ВИД, указанный на рис. 30
(апериодический процесс).
х


Хо


х = х(о


о


t


Рис. 30


Случай 2. Пусть


a2
p2=b2=o.
Решение задачи можно получить из формулы (3.68) путем перехо

да к пределу при S
 о. в результате будем иметь
х = xoe
a! (1 + at). (3.69)
Явление имеет примерно тот же характер, как и В случае 1.
, С л у чай 3. Пусть
(х 2
 Р 2 =
b 2 < о.
Физически это обозначает, что упруrая сила велика по сравнению с
сопротивлением среды. Корни характеристическоrо уравнения в этом
случае комплексные
PI = ----а + ib, Р2 = ---а
 ib.
Отсюда общее решение уравнения (3.59) имеет вид
х = e
at (C 1 cosbt + С 2 siпбt). (3.70)


83




Так как; очевидно,

; =
ae
at (С} cosbt + С 2 siпбt) +
+ Se
at (
Cl siпБt + С 2 cosSt),
то, полаrая t = О, на основании начальных условий (3.60) получим
C 1 = Хо }
----аС} + БС 2 = О '


откуда


С} = Ха, С 2 =
 Ха


(3.71)


и, следовательно,


Х = xoe
at (соsбt +
 siпбt). (3.72)
rрафик решения (3.72) изображен на рис. 31 (затухающие колеба..
нuя), rде положено ХО = xo
l +
: . Период колебаний, очевидно, равен
Т
 2п

 о.


х
 --at
х=хое


о


-- -- ....
...._---_.........




t


............
",,""
,,""
"
.",



xo



 --at
x=
xe


Рис. 31
Таким образом, все случаи решений линейноrо однородноrо урав"
нения с постоянными коэффициентами допускают наrлядную физи-
ческую интерпретацию.
Задачи для самостоятельноrо решения.
1. Определить период Т свободных колебаний двухрессорноrо ва..
rOHa веса Р Kr, если под статическим действием веса BaroHa каждая из
рессор проrибается на 5 см.
2. Тело весом Р = 1 О Kr колеблется ПОД действием упруrой силы,
равной 20 Kr, при смещении в 1 м, причем сопротивление среды про

порционально скорости. Найти закон колебаний и период колебания,
если тело было выведено из положения равновесия путем сообщения
ему начальной скорости Vo = 5 м/ с и после 3
x колебаний амплитуда
уменьшилась в 10 раз.


84





 7. ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ


Рассмотрим линейное неоднородное уравнение BToporo порядка


уН + ау' + Ьу = {(х),


(3.73)


коэффициенты KOToporo а и Ь
 постоянны.
т е о р е м а. Общее решение лИ-нейноrо неоднородноrо уравнения
(3.73) есть сумма общеrо решения соответствующеrо линейноrо oд

нородноrо уравнения и какоrо
нибудь частноrо решения данноrо He

однородноrо уравнения.
Д о к а 3 а т е л ь с т в о. Пусть У = У(х)
 частное решение данноrо
линейноrо неоднородноrо уравнения (3.73), т. е.
у" + аУ' + ЬУ = f(x). (3.74)
Вычитая почленно из уравнения (3.73) уравнение (3.74), будем
иметь


(у
 У)" + а(у
 у)' + ь(у
 у) = о.


(3.75)


Таким образом, разность у
 у = Уа является решением COOTBeTCT

вующеrо линейноrо однородноrо уравнения. Отсюда


у = Уо + У,


(3.76)


. rде Уа
 есть решение уравнения
у" + ау' + Ьу = О. (3.77)
Если в формуле (3.76) считать Уа общим решением линейноrо одно-
родноrо уравнения (3.77), то эта формула t очевидно, дает общее pe

шение линейноrо неоднородноrо уравнения (3.73).
Теореме доказана.



 8. ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЛИНЕйноrо НЕОДНОРодноrо
УРАВНЕНИЯ второrо ПОРЯДКА
, Рассмотрим колебания rармоническоrо осциллятора при наличии
переменной внешней силы тf(t), rде т
 масса точки. Придержива-
ясь обозначений Э б, получаем следующее уравнение движения:


d 2 Х + 2а dx + А 2 х = f (t)
dt2 dt tJ ,


(3.78)


rде а и

 постоянны. Колебания механической системы при нали-
чии возмущающей внешней силы называются вынужденными, а при
отсутствии ее
 свободными. Таким образом, однородное линейное


85




уравнение с постоянными коэффициентами BToporo порядка описыва

ет свободные колебания rармоническоrо осциллятора, а HeOДHOpoд

ное
 вынужденные колебания. С этой точки зрения формула (3.7б)
имеет следующий смысл: общие вынужденные колебания системы
есть сумма некоторых ее вынужденных колебаний и соответствую-
щих свободных колебаний системы.


i 9. НАХОЖДЕНИЕ ЧАСТНЫХ РЕШЕНИЙ НЕОДНОРодноrо УРАВНЕНИЯ
МЕТОДОМ НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
Пусть дано линейное неоднородное уравнение


у" + ау' + Ьу = {(х),


(3.79)


коэффициенты KOToporo а и Ь
 постоянные. Как извеСТН0 9 общее pe

шение этоrо уравнения имеет вид


у = Уа + У,


(3.80)


rде Уа
 общее решение соответствующеrо однородноrо уравнения, а
у
 частное решение aaHHOZO HeoaHopoaHOZO уравнения.
В Э 5 было показано как находится функция Уа. Следовательно, OCTa

ется дать метод нахождения частноrо решения У по заданной правой ча-
сти f (х) дифференциальноrо неоднородноrо уравнения (3.79). Мы orpa-
ничимся здесь лишь рассмотрением отдельньrх частных случаев; общий
прием для уравнений любоrо порядка будет дан в следующей rлаве.
А. Правая часть есть мноrочлеН t т. е.


{(х) = ао + atX + ... + атх т .
1. Если Ь :F- О, то полаrаем
У = Аа + At X + ... + Атх т .
2. Если Ь = О и а
 О, то полаrаем
у = х(А о + A1x + ... + Атх т ),


(3.81 )


(3.82)


(3.83)


rде Аа, А l' ..., А т
 неопределенные коэффициенты.
Правильность этих рассуждений будет доказана впоследствии.
Для определения коэффициентов Ао, А 1, ..., А т подставляем выраже-
ние (3.82) [или соответственно (3.83)] в левую часть уравнения (3.79)
и приравниваем коэффициенты при одинаковых степенях перемен-
ной х. Полученная алrебраическая система линейных уравнений, как
можно доказать, является совместной и, следовательно, дает возмож

ность найти коэффициенты Ао, Al' ..., А т .


86




Пример. Решить уравнение
у" + у'
 12y = Х 2 .


Реш е н и е. Корни характеристическоrо уравнения
k 2 + k
 12 = О,


очевидно, есть k} = 3, k 2 =
4. Поэтому общее решение однородноrо
уравнения имеет вид


Уа = C 1 e 3x + C2e
4x,


rде С 1, С 2
 произвольные постоянные.
Так как Ь =
 12 *' О, то ищем частное решение неоднородноrо ура в..
нения в следующем виде:
у = Аа + A1x + А 2 х 2 .


Отсюда


2А 2 + (A 1 + 2А 2 )х
 12(А а + A1x + А2х2) = х 2


или



12A2x2 + (2А 2
 12A 1 )x + (2А 2 +Al
 12Ао) == х 2 .


Приравнивая соответствующие коэффиuиенты, получим систему:

12A2 = 1, 1
2А 2
 12А} = О,

2А 2 + А!
 12Ао = O.J


Отсюда


А
 1 А
 I А
 13
2

12' 1

 72 ' а

 864


и, следовательно,


У
 ( 13 1 1 2 )


 864 + 72 х + 12 х .


в силу формулы (3.80) общее решение данноrо уравнения есть
У = С}е ЗХ + C2e
4x
 8
4 03 + 12х + 72х 2 ).


Б. Правая часть есть rармоника, т. е.
f(x) = Msinrox + Ncosrox,
rде М, N
 постоянные.


(3.84 )


87




1. Ищем частное решение уравнения (3 79) также в виде rармоники
у = Asin(Ox + Bcos(Ox, (3.85)
rде А, В
 постоянные. Подставляя это выражение в дифференциаль

ное уравнение (3.79), будем иметь
(
Aro2 sinrox
 Вro 2 cosrox) + a(Arocosrox
 Brosinrox) +
+ b(Asinrox + Bcosrox) = Msinrox + Ncosrox,


или


A(
2 + Ь)
 Ваro = м, }
Ааro + B(---{J)2 + Ь) = N.


(3.86)


Система (3.86) заведомо совместна, если ее определитель не равен
нулю:


---{J) 2 + Ь
/).=
аro



aro = (ю2
 ь)2 + а 2 ro 2 ;f. о.
---{J)2+b


(3.87)


в этом случае коэффициенты А и В леrко MorYT быть определены.
2. Если а = О и Ь= (02, то
 =0 и система (3.8б) несовместна. В этом
исключительном случае функцию У следует брать более сложноrо
вида:


у = x(Asinrox + Bcosrox).


(З.88)


3 а м е ч а н и е. Если правая часть f (х) зависит только от sin(Ox или
только от cos(Ox, то в формуле (3.85), как и в общем случае, следует
брать и sinrox, и cOS(OX, так как при дифференцировании синус перехо

дит в косинус И обратно.
Пример. Найти вынужденные колебания системы
d:tx +
 2 х = Msinrot. (3.89)


Реш е н и е. Характеристическое уравнение здесь имеет вид


k 2 +
2 = о;


отсюда k 1 , 2 = +
i. Следовательно, общее решение однородноrо ypaB

нения таково:


хо = С 1 sinpt + С 2 cospt.


(З.90)


При нахождении частноrо решения Х неоднородноrо уравнения
(З.89) приходится различать два случая.


88




с л у чай 1. пустыl ;/:.I
 1, т. е. период внешней силы не совпада

ет с периодом свободных колебаний (3.90).
Ищем фУНКllИЮ Х в виде
Х = Asinmt + Bcosrot.
Подставляя это выражение в уравнение (3.89), будем иметь
(
Aro2 sinrot
 воо 2 cosrot) + Р 2(Asinrot + Bcosrot) = Msinmt,


отсюда


A(
2
 (02)= М,
В (Р 2
 ro 2) = о,


то есть


A=
2M 2 ' в=о

ы


И,следовательно,


х =
2 М 2 sinrot,

ы


(3.91)


х
А


2п
ro



A


Рис. 32


Таким образом, в этом случае у системы имеются вынужденные
оrраниченные колебания (3.91), период которых равен периоду внеш

ней силы (рис. 32).
с л у чай 2. Пусть 1(0 I = I Р 1, т. е. период внешней силы совпадает с
периодом свободных колебаний.
В этом случае формула (3.91), очевидно, теряет смысл. Соrласно
теории полаrаем


Х = t(Asinrot + Bcosrot).


(3.92 )


89




Подставляя это выражение в дифференциальное уравнение (3.89),
будем иметь
t(
Aro2 sinrot
 8ro 2 cosrot) + 2(Arocosrot
 8rosinrot) +
+ ro 2 t(Asinrot + 8cosrot) = Msinrot


или


2(Arocosrot
 Brosinrot) = Msinrot.


Отсюда


А = О, 8 =
.м..
2О)


И, следовательно,


х =
 Mt cosrot
2ы .


(3.93 )


Формула (3. 93) показывает, что размах колебаний Х неоrраничен-
но растет со временем t (рис. 33). Таким образом, даже малая внеш-
няя сила в случае 2 вызывает неоrраниченные колебания. Это явле-
ние носит название резонанса. Физическим последствием резонанса
является нарушение работы или даже разрушение системы. Извест-
ны случаи, коrда ритмический стук колес поезда, идущеrо по желез-
нодорожному мосту, приводил к разрушению этоrо моста. В силу тех
же обстоятельств, колонну солдат, идущих по мосту, заставляют идти
«не В Hory».


х


о


/ Mt
Х =

 cosmt
2ы


t


Рис. 33
Общие вынужденные колебания системы (3.89) даются формулой


х = C 1 sin
t + С 2 cospt + х.


(3.94 )


Для удобства запоминания рассмотренные случаи сведены в табли-
цу:
90




Таблица частных решений уравнения у" + ау' + Ьу = f(x)


Сл чай Частное р ешение
l(х) = Р п (Х) . у = Qn(X)'
1 rде Рn(Х)
 мноrочлен n
ой rде Qп(x)
 мноrочлен n
ой
степени и Ь = О степени
2 (Х) = р (х) и ь = О, а
 О У = xQ ,, (x)
!(х)= м sin(Ox+ N cosrox, у = Аsiпroх+ Bcosrox
«(02
 ь)2 + а 2 (1)2
 О
II
2 f(x)= м siп(Ох+ N cosrox, у = х(А siпroх+ Bcosrox)
а = О. Ь = ro 2


Задания для самостоятельноrо решения
1. уН + 2у' + х 2 = о.
2. Найти частное решение уравнения
у"
 2у' + у = 2x
4,
удовлеТВОРЯЮlцее начальным условиям
у(О) = О, у'(о) = 2.
3. у"
 2у' + 2у = sinx + cosx.
4. у" + lOOy = cosIOx.
5. rруз массой т = 4 Kr подвешен на пружине и увеличивает ее
длину на 1 см. Найти закон движения rруза, если верхний конец пру-
жины совершает вертикальное rармоническое колебание у = sin30t
(сопротивлением среды пренебреrаем).


110. О КРАЕВЫХ3АДАЧАХДnЯ УРАВНЕНИЙ BTOPOrO ПОРЯДКА
Для уравнений BToporo порядка можно рассматривать вопрос не
только о нахождении решения по заданным в одной точке начальным
условиям, определяющим в указанной точке значения как caMoro ре-
шения уравнения, так и ero производной (задачу Коши), но и о поис-
ке решения по zраничныМ, условиям в двух фиксированных точках,
задающих в них (как в концах соответствующеrо промежутка) инфор-
мацию о решении уравнения и (или) ero производной (краевую зада..
чу). Поясним постановку краевоЙ задачи на конкретных примерах.
Пример 1. Найти функцию у = у(х), удовлетворяющую дифферен-
циальному уравнению
у" = f(x, у, у') (3.95)
и принимающую при х = а и х = Ь (а < Ь) заданные rраничные значе

ния:


у(а) = А, у(Ь) = В.


(3.96 )


91




у


rеометрически сказанное озна-
чает, что в плоскости Ох у требует-
ся найти интеrральную кривую
дифференциальноrо уравнения
(3.95), проходящую через две за-
данные точки М(а, А) и N(b, В)
х
(см. рис. 34).
. Пример 2. Видоизменением за-
дачи, приведенной в примере 1, будет: найти такое решение у = у(х)
дифференциальноrо уравнения (3.95), для KOToporo выполнялись бы
rраничные условия
у'(а) = Al' у'(Ь) = 81. (3.97)
rеометрически это сводится к отысканию в плоскости Оху интеrраль-
ной кривой уравнения (3.95), пересекающей прямые х = а и х = Ь под
заданными соответственно уrлами а и
 такими, что tg а=А 1 , tg
= 81
(СМ. рис. 35).
Пример 3. Можно рассмотреть также следующую задачу: найти
решение у = у(х) уравнения (3.95). удовлетворяющее rраничным
условиям


о


а


N'
I
I
I
I
I
81
I
I
Ь


J\tf


Рис. 34


у(а) = А, у'(Ь) = BI.


(3.98 )


в этой ситуации в плоскости Оху требуется найти интеrральную кри-
вую дифференциальноrо уравнения (3.95), которая должна пройти
через точку М(а, А) и пере сечь прямую х= Ь под уrлом
 (см. рис. 36).
в случае линейноzо дифференциальноrо уравнения


у" + р(х)у' + q(x)y = {(х),


(3.99 )


коэффициенты KOToporo на рассматриваемом промежутке [а, Ь] не-
прерывны, линейные rраничные условия описываются равенствами


ау(а) +
Iy'(a) = А, Ру(Ь) + Ply'(b) = в,


(3.100)


у


у


м
А


о


а


ь


х


о


а


ь


х


Рис. 35


Рис. 36


92




rде 0., a.l'
'
1' А, В
 одновременно не равные нулю заданные посто

янные числа (линейная краевая задача). Линейная краевая задача
(3.99)
(З.I00) называется однородной, если, во
первых, f(x) = о
(т. е. само дифференциальное уравнение (З.99) однородно) и, BO
BTO

рых, А = В = О (т. е. rраничные условия также однородны); в против

ном случае краевая задача (3.99)
(3.100) называется неоднородной.
Краевая задача для уравнений BToporo порядка (в том числе и для
линейных однородных уравнений, и даже при наличии у них пocтo

ЯННblХ коэффициентов) может совсем не иметь решений, иметь
единственное решение или же иметь множество решений.
Пример 4. Для линейноrо однородноrо уравнения с постоянными
коэффициентами
у"+у=о, (З.I01)
общее решение KOToporo имеет вид
у = С 1 sinx + С 2 cosx (З.102)
(см. таблицу в Э 5 rлавы 111), рассмотрим три краевые задачи со следу

ющими rраничными условиями:
1) у(о)=о, y(п)=
1; (З.I0З)
2) у(О) = о, у(тс/2) = 1: (З.I04)
З) у(о)=о, у(п) =0. (3.105)
Краевая задача (З.I01), (З.I03) не имеет решения, так как из фор-
мулы (3.102), в силу (3.10З), дЛЯ Hero должны были бы выполняться
равенства 0= С 2 = 1, что невозможно.
Краевая задача (З.l 01), (З.I04) имеет единственное решение
у== sinx, поскольку из (З.I02) и (З.I04) получаем С} = 1, с 2 =о.
Краевая задача (3.101), (3.105) имеет бесконечно MHoro решений
вида у = С 1 sinx, rде С 1
 произвольная постоянная, ибо в силу перво-
ro в (З.1 05) rраничноrо условия находим С 2 = о, а второе rраничное
условие в (З.I05) тоrда будет выполняться при любом выборе кон-

станты С}.
ДЛЯ KOHKpeTHoro решения линеЙной краевой задачи сначала нужно
П9стараться найти общее решение исходноrо дифференциальноrо урав-
нения, после этоrо, используя rраничные условия, следует 8blпucamb
алzебраuческую систему уравнений относительно входящих в об

щее решение произвольных констант, а затем вычислить (если это
возможно) значения этих констант как решений выписанной сис-
темы уравнений. Частным решением дифференuиальноrо уравнения,
отвечающим найденным значениям констант, и будет определяться
решение рассматриваемой краевой задачи.


93




Пример 6. Найти решение уравнения
у"
 у = х, (З.I06)
удовлетворяющее rраничным условиям
у(о)=о, y(l)=I. (3.107)
Реш е н и е. Характеристическое уравнение k 2
 1 = О имеет корни
k 1 , 2 = + 1. Следовательно общее решение соответствующеrо OДHO

родноrо уравнения можно записать в виде Уа = С 1 е Х + C2e
X, rде С l'
С 2
 произвольные константы.
Поскольку коэффициент уравнения (3.107) при у равен
1
O, то
(соrласно э 9 rлавы 111) частное решение неоднородноrо уравнения
(З.107) будем искать в виде У = Jl + vx. Отсюда
 (Jl + vx) == х. Прирав

нивая коэффициенты при одинаковых степенях переменной х, полу

чаем Jl = О, v =
 1. и тем самым У =
x. Поэтому общее решение ypaB

нения (З.I07) есть
у = C1e x + C2e
X
 х. (З.I08)
Так как из (З.l 08) имеем
у(О) = С 1 + С 2 , у(1) = С 1 е + С 2
 11
е
то из rраничных условий (3.107) получаем систему уравнений для
определения С l' С 2 :


С 1 + С 2 = О, 1
} (З.l 09 )
еС. +
 С 2
 1 = l-J
Из первоrо уравнения системы (З.109) получаем С 2 =
Cl' а потому
второе уравнение системы приводит нас к равенству еС}
 lc} = 2.
е
Следовательно,


С 1 = е: 1 = s
 l ' С 2 =
 s
 l '
е


т. е. решение искомой краевой задачи однозначно определяется функ

цией


е Х e
X 2 sh Х
У = sh 1
 sh 1
 х = sh 1
 х.
Задачи для самостоятельноrо решения
Решить следующие краевые задачи:
1. УН
 У = о; у( О) = О. у(2п) = 1.
2. у"+у=l; у(о)=о, y(
 )=O.
3. у" + У = О; у'(О) = о, у'(п) = 1.
4. уН + У = 2х
 п; у(о) = о, у(х) = о.


(З.I10)




r л а в а IV
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

 1. ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ РЕШЕНИЙ
Рассмотрим дифференциальное уравнение n-ro порядка
у(n) = f (х, у, у', ..., у(n
 1». (4.1 )
Здесь имеет место следующая общая теорема, которую мы приве-
дем без доказательства.
Т П ' (п
O
е о р е м а. усть хо, Уа, Уо, ..., Уа
 некоторая система чи-
сел, а правая часть t уравнения (4.1) непрерывна и имеет оrраничен-
ные производные по арrументзм у, у', ..., У(п
l) в области
I х
 Ха I < а, I У
 У а I < Ь, I У'
 Уа I < Ь 1 '
. . . , f у< n
 1)
 У о
 1 « ь п
'I.


(4.2)


rде а, Ь, b 1 , ..., Ь п
 1
 положительные числа.
В таком случае существует единственное решение уравнения (4.1 )
у=<р(х) (Ix
xol<h), (4.3)


удовлетворяющее начальным условиям
<Р (Ха) = Уа, <р' (Ха) = Уо, 000' <р(n
 1) (Ха) = Ybn
!). (4.4)
Решение уравнения (4.1)
У = <р (Xl' C 1 , ..., Сп)' (4.5)
содержащее n произвольных постоянных (параметров) С 1, ..., Сп' С
помощью выбора которых можно получить решение (4.3) (частное
решение), удовлетворяющее любым начальным условиям (4.4)*, на-
зывается общим.
В частности, если условия предыдущей теоремы при некотором
Х = ха выполнены для всех значений чисел
, (п
O
Уа, Уа. ..., Уа ·


то эти числа можно рассматривать как параметры, входящие в состав
решения (4.3); чтобы получить общее решение (4.5), достаточно по-
ложить


С С ' С (п
l)
1 = УО, 2 = Уа, ..., п = Уа .


* Вообще rоворя, в известной области.


95




Если семейство этих решений заполняет область G, то в силу BЫ

полнения свойства единственности общее решение (4.5) дает COBO

купность всех решений дифференциальноrо уравнения (4.1) в об

ласти о.
О п р е Д е л е н и е. Соотношение
Ф(х, у, с 1, ... , Сп) = о (4.6)
называется общим uнmеzралом дифференциальноrо уравнения
(4.1), если при любых значениях постоянных С 1, ... , Сп определяемые
им кривые являются интеrральными, причем среди семейства кривых
(4.6) найдутся интеrральные кривые, удовлетворяющие произволь

ным начальным условиям.
Если в некоторой области G для уравнения (4.1) выполнены
условия теоремы существования и единственности решений, то
любая интеrральная кривая уравнения (4.1), расположенная в G,
может быть получена из уравнения (4.6) при соответствующем BЫ

боре постоянных С 1, С 2 ' ..., СП. В этом случае общий интеrрал дает
полное решение задачи интеrрирования дифференциальноrо ypaB

нения в данной области. В общем случае MorYT существовать реше

ния уравнения (4.1), не входящие в ero общий интеrрал.
Иноrда для уравнения (4.1) удается получить дифференциальное
уравнение более низкоrо порядка п
 k (1
 k < п):
ф k (х, у, у', ..., у< n
 k), с l' ..., С k) = О, ( 4. 7)
содержащее k произвольных постоянных С 1, ..., Сп, следствием KOTO

poro является данное дифференциальное уравнение, т. е. найти такое
уравнение (4.7), что каждое ero решение у есть также решение ypaB

нения (4.1). в таком случае соотношение (4.7) называется k
bIM пpo

межуmОЧНblМ uнmеzралом, а при k = 1
 первым uнтеzралом.
В простейших случаях процесс решения дифференциальноrо ypaBHe

ния (4.1) состоит в построении цепочки промежуточных интеrралов;
интеrрируя (п
 1 )
й промежуточный интеrрал, получим общий интеr

рал (4.6) уравнения (4.1).
Пример. Пусть имеем уравнение
у/" = 1. ( 4.8)
Реш е н и е. Последовательно интеrрируя, получаем промежуточ

ные интеrралы


y"=x+C 1


и


, х 2 С С
У = 2 + lX + 2.


96




Отсюда общий интеrрал уравнения (4.8) есть
х 3
 2 С С
У = б + Т Х + 2 Х + З,
. rде C 1 , C2
 С з
 произвольные постоянные.
Общее уравнение п
ro порядка, не разрешенное относительно CTap

шей производной Р(х, у, у', ..., у(n») = о, эквивалентно, вообще rоворя,
нескольким уравнениям вида (4.1). Соотношение, равносильное COBO

купности общих интеrралов всех этих последних уравнений, Ha3ЫBa

ется общим интеrралом данноrо уравнения (см. rл. 1,
 2).



 2. УРАВНЕНИЯ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Рассмотрим общее дифференциальное уравнение п
ro порядка


Р( , (n»
 О
Х,у,у,...,у
.


(4.9)


Укажем несколько случаев, коrда порядок этоrо уравнения леrко
может быть понижен.
С л у чай 1. Левая часть уравнения (4.9) не содержит х, т. е. ypaB

нение имеет вид


Р( ,,, (n»
 О
у, У ,у , ..., У
.


(4.10)


Примем у за новую независимую переменную, а у' = р за новую неиз

вестную функцию. Применяя правило дифференцирования сложной
функции, последовательно получаем
"
 dyl
 dy' dy
 dp
У
 dx
 dy dx
Pdy'
,,, = dy" = dy" dy = [ d2p + ( d P ) 2 ]
У dx dy dx Р Р dy2 dy


и Т. д. Подставляя эти выражения в уравнение (4.10), получимдиффе

ренциальное уравнение (п
 1 )
ro порядка следующеrо вида:
( dp dп
lp )
Fl у, р, dy ' ..., dyп
l = о.
Пример. Найти частное решение уравнения


у' у'" = 2у'З + у"2,


удовле
воряющее начальным условиям


у(О) = о, у'(О) = 1, у"(О) = о.


97




Реш е н и е. Полаrая у' = р, получим
Р [ р2 d2p + P ( d P ) 2 ] = 2 р З + ( Р dP ) 2
dy2 dy dy


или


( d2p )
р3 dy2
 2 = о.


Так как в силу начальных условий р
 О, то отсюда
d 2 p
dy2 = 2.
Интеrрируя обе части этоrо уравнения два раза по переменной у,
последовательно будем иметь
dp
dy = 2у + С 1


и


p=y2+C 1 y+C 2 .
Из начальных условий, учитывая, что d d P = 1 уН, получаем
у Р


о = о + С 1 и 1 = С 2 '


откуда


С 1 =ОиС 2 =I


и, следовательно,


р =

 = у2 + 1.


Разделяя переменные в последнем уравнении, находим
dy

 l = dx,
у +


. откуда


J Y:
l = Jdx.


то есть


аrсtgу=х+С з .
Из начальных условий имеем
0=0+С 3 '
то есть С З = о. Поэтому окончательно искомое решение таково:
у = tg х.


98




Случай 2. Левая часть уравнения (4.9) не содержит у, т. е. уравне-
ние имеет вид


F ( , 11 (n»
 О
Х,у,у ,...,у
.


(4.11)


Полаrая


У , = Р У " = Р ' У (n) = Р (n
 1)
"..., ,
получим уравнение (п
 1 )-ro порядка
Р(х, р, р', ..., p(n
 1» = о
относительно неизвестной функции р.
Если в уравнении (4.11) вместе с у отсутствуют и производные
у', ..., у (k
 1) (k < п), т. е. уравнение имеет вид
Р(х, y(k), ..., у(п» = О, (4.12)
то, применяя подстановку y(k) = z, получим дифференциальное урав-
нение


Р(х, z, ..., z(п
 k» = О,
порядок KOToporo на k единиц ниже порядка исходноrо уравнения.
Пример. Решить уравнение
х у'"
 у" = 1.


Реш е н и е. Полаrая


у" = Z,


будем иметь


xz'
 z = 1.


Отсюда


...Jk..
 dx
z+ 1
 х


и, следовательно,


ln I z + 1 I = ln С + ln х.


Таким образом,


z = y"=
l + C1X.
Интеrрируя два раза последнее уравнение, окончательно получим
у =

 x2 + C 1 x 3 + с 2 х + Сз,
rде С l' С 2 ' С 3
 произвольные постоянные.


с л у чай 3. Левая часть уравнения (4.9) однородна относительно переменных у,
у', ..., у(n), т. е. для любоrо k имеет место тождество
Р(х, ky. ky', ..., ky(п») == k a Р(х, у, у', ..., у(п»,
rде а
 некоторое постоянное число (nоказатель однородности).


99




Положим


у = eludx,


rде и
 новая неизвестная функция. Отсюда последовательно находим
у' = уи, у" = у(и' + и 2 ), ...
и т. д. Подставляя эти выражения в дифференциальное уравнение (4.9) получим
Р(х, у, уи, ...) = о,
или в силу однородности функции F будем иметь
уар(х, 1, и, ...)= О,
rде а
 показатель однородности. Отсюда получаем, что функция и удовлетворяет
некоторому дифференциальному уравнению (п
 1 )
ro порядка
F 1 (Х, и, и', ..., и(п
 1) = о.
Кроме Toro, если а > О, то у = О, очевидно, является решением данноrо уравнения.
Пример. Решить уравнение


хуу"
 ху'2 = уу'
Реш е н и е. Уравнение, очевидно, является однородным относительно у, у' и у".
Полаrая


у = е J udx,


получим


ху2 (и' + u 2 )
 ху 2 и 2 = у 2 и,


или, если у Ф. О, ТО


х

 = и.


Отсюда


u=Сх


и, следовательно,


у = eICxdx = eClx2+lnC2,


или окончательно


у = C2eClx2,
rде С 1 И С 2
 произвольные постоянные.
Решение у = о получается при С 2 = о.



 3. ОДНОРОДНЫЕ ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Общий вид линейноrо дифференциальноrо уравнения п
ro порядка
следующий:
у(п) + fl(X) y(п
 1) + ... + fп(x) У= !(х), (4.13)
rде функции fk(X) (k = 1, ..., п)
 называются коэффициентами
уравнения, а !(Х) ........ ero правой частью или свободным членом. Ec

ли f(x) == О, то линейное уравнение называется однородным, в против

ном случае........ неоднородным. Мы будем предполаrать, что функции


100




{fk (х)} k=1 и {(х) непрерывны на некотором общем (конечном или бес

конечном) интервале (а, Ь). Разрешая уравнение (4.13) относительно
. старшей производной у(n), будем иметь


у(n) = р(х, у, у', ..., у(n
 1),


(4.14)


rде


n
l
F = f(x)
 'Lf n
k (x)y(k).
k=O


(4.15)


Так как


д

) =
fn
k(x) (k = 0,1, ..., n
o


соrласно предположению непрерывны при а < х < Ь, то на основании
теоремы существования и единственности решений (
 1) для любой
( Ь) , (n
O
системы чисел Ха а < Ха < , Уа, Уо, ..., Уа существует решение


У = <р(Х)


(4.16)


и притом единственное, такое, что
(k)
 (k) ( ) (k
 О 1
 1 )
У а
 <р ХО
" ..., п .


Можно доказать, что это частное решение имеет смысл во всем ин

тервале (а, Ь).
Мы займемся сначала однородным линейным дифференциальным
уравнением


у(n) + fl(x)y(n
 1) +. .. + [n(х)у= о.
Заметим, что это уравнение имеет очевидное решение
у=О,


( 4.17)


(4.18)


однозначно определяемое нулевыми начальным условиям
У(Хо) = у'(хо) = . . . = у(n
 1 )(ХО) = о,


(4.19)


носящее название нулевоrо или тривиальноrо. В дальнейшем мы, как
правило, будем заниматься нетривиальными решениями.
Уравнение (4.17) для сокращения будем записывать в виде


L [у] = О,


(4.20)


rде


L [У] = у(n) + fl (x)(n
.l) + . . . + [n(Х) у.


(4.21 )


Выражение L[y] называется линейным дифференциальным oпe

раmором и представляет собой некоторую функцию, которая


101




получается из у в результате выполнения указанных действий (4.21).
Например. если


L [у] = у"
 2ху' + х2у,


то


L [х] = о
 2х .1 + х 2 . х = х 3
 2х.
L [х2] = 2
 2х . 2х + х2 . х 2 = х 4
 4х2 + 2 и т. д.
С этой точки зрения решениями уравнения (4.20) являются те и
только те функции у = у(х), которые обращают оператор L[y] в нуль.
Укажем два основных свойства оператора L [у].
Свойство 1. Постоянный множитель можно выносить за знак ли

нейноrо оператора.
В самом деле, если С
 постоянная, то имеем


L(Cy) = (Су)(n) + [l(X)(Cy)(n
 1) +. . . + [n(х)(Су) =
= С[у(n) + [l(Х) y(п
 1) +.. . + [n(х) У] = CL[y],


то есть


L[ Су] = CL[y].


(4.22)


С в о й с т в о 2. Линейный оператор от суммы равен сумме операто

ров от слаrаемых.
В самом деле, если Уl и У2
 функции от Х, то имеем
L[Yl + У2] = (Уl + У2){n) + fl(X)(Yl + Y2)(n
 1) +.. .
... + {n(Х)(УI + У2) = [y
n)+ Mx)y
n
1) +... fn(X)YI] +
+ [y
n) + {l (x)y
n
1) +. . · + f n(Х)У2] = L[YI] + ЦУ2],


то есть


L[Yl + У2] = L[Yl] + L[Y2].


(4.23)


Следствие. Линейный оператор от линейной комбинации не..
скольких функций равен такой же линейной комбинации операторов
этих функций.
Действительно, если С 1 и С 2
 постоянные, то последовательно
имеем
L[ С lYl + С 2 У2] = L[ С lYI] + L[ С 2 у 2 ] = С 1 L[Yl] + C 2 L[Y2],
то есть
L[C1Yl + С 2 у 2 ] = C 1 L[Yl] + C 2 L[Y2]
(свойство линейности).


( 4.24)


102




Установим некоторые важные свойства решения линеиноrо OДHO

родноrо уравнения (4.20).
т е о р е м а 1. Произведение решения линейноrо однородноrо
уравнения на постоянную есть также решение этоrо уравнения.
В самом деле, если С
 постоянная величина и Уl .......... решение ypaB

нения (4.20), т. е.


L[Yl] = о,


то в силу свойства 1 имеем


L[CYI] = CL[Yl] = о.


Следовательно, CYl
 также решение этоrо уравнения.
т е о р е м а 2. Сумма двух решений линейноrо однородноrо ypaB

нения есть также решение этоrо уравнения.
В самом деле, если Уl и У2
 решения уравнения (4.20), т. е.
L[Yl] = О и L[ У 2 ] = о,


то в силу свойства 2 имеем


L[Yl + У 2 ] = L[Yl] + L[Y2] = о.
Следовательно, Yl + У2 есть также решение уравнения (4.20).
С л е Д с т в и е. Любая линейная комбинация решений линейноrо
однородноrо уравнения есть также решение этоrо уравнения.
В самом деле, если Yl' У2, ..., Yk
 решение уравнения (4.20) и С 1,
С 2 , ..., С k
 постоянные, то
L[C1Yl + С 2 У2 +... + CkYk] =
= C 1 L[Yl] + C 2 L[Y2] +. . . + CkL[Yk] = о,


то есть


У = С 1 У 1 + С 2У 2 + . .. + С kY k
есть также решение уравнения (4.20).
( Таким образом, составляя линейные комбинации из частных реше

ний Уl' У2' ..., Yk линейноrо однородноrо уравнения, мы получаем HO

вые ero решения. Возникает вопрос, сколько частных решений и Ka

кие именно следует взять, чтобы их линейная комбинация дала все
решения данноrо дифференциальноrо уравнения? Чтобы ответить на
это, нужно ввести понятие линейно независимых решений.
Оп р е Д е л е н и е 1. Функции <1'1 (Х), <Р2(Х) , ..., <i>k(X), определенные
в общем интервале (а, Ь), называются линейно зависимыми в этом


103




интервале, если существуют постоянные С l' С 2 , ..., C k , из которых по
u
меньшеи мере одна не равна нулю, и такие, что


C1<Pl(X) + С 2 <Р2(Х) +. . . + Ckq>k(X) == О


(4.25)


при а < Х < Ь. В противном случае функции называются линейно неза

вuсимыми, т. е. для линейно независимых функций тождество (4.25)
может иметь место только в том случае, коrда


C 1 =C 2 =... =Ck=O.
Заметим, что функция, тождественно равная нулю, не может BXO

дить в совокупности линейно независимых функций, так как если, Ha

пример, <Pl(X) == о, то тождество (4.25) будет иметь место при C 1 = 1,
С 2 = . . . = C k = О и, следовательно, функции СР. (Х), <Р2(Х), ..., <Pk(X)

линейно зависимы.
Пример 1. Функции 1, Х, х2
 линейно независимы.
Реш е н и е. Из тождества


С 1 + С 2 х + С зх 2 == О


вытекает


С 1 = С 2 = С З = о.
Пример 2. Функции 1, sin 2 х, cos 2 Х
 линейно зависимы.
Реш е н и е. Действительно, полаrая


Cl=
I, С 2 =1. С з =l,


получим тождество



 1 . 1 + sin 2 Х + 1 . cos 2 Х == о.
Пусть Уl = YI (Х), У2 = У2 (Х), . . . , Уп = Уп (Х)
 функции, имеющие
непрерывные производные до (п
 1 )
ro порядка включительно
Определитель


YI У2 Уп
, У2 ,
w(x) = Yl Уп (4.26)
(п
O ( п
O ( п
O
Уl У2 .. . Уп


называется определителем ВрОНСКОсО или вронскuано.м системы
функций Yl' У2' ..., Уn.


104




Т е о р е м а 3. Если функции Yl' У2' ..., Уп
 линейно зависимы, то
их вронскиан тождественно равен нулю (на соответствующем проме

жутке).
Для простоты доказательства оrраничимся случаем трех функций,
т. е. положим п = 3.
Пусть


C1Yl + С 2 У2 + СзУз == О,


(4.27)


rде по меньшей мере одна из постоянных C 1 , С 2 , С з отлична от нуля.
Дифференцируя тождество (4.27) последовательно два раза, получим
C1Yl + С 2 У2 + Сзуз = О,


C1yi + С 2 У2 + СзУз = о.


( 4.28)


Фиксируя х = х, будем рассматривать постоянные С l' С 2 , С З как изве

стные. Т оrда уравнение (4.27), (4.28) представляют собой алrебраи

ческую линейную однородную систему, заведомо допускающую HeHY

левые решения, так как не все C k (k = 1,2, 3) равны нулю. Это, как
известно, возможно лишь в том случае, если определитель этой систе

МЫ, представляющий собой вронскиан функций Yl' У2, Уз, равен нулю,
то есть


У 1 У 2 Уз
W(i)= Уl У2 уз = о.
Yi У2 Уз


(4.29)


Так как это рассуждение справедливо для любоrо х, то W(x) == о.
Теорема доказана.
Следс твие. Если вронскиан системы функuий YI' У2' ..., Уп отличен
от нуля хотя бы в одной точке, то эти функции линейно независимы.
Предположим теперь, что Yl' У2, ..., Уп есть решения уравнения
(4.20). Тоrда справедлива обратная теорема:


, т е о р е м а 4. Если вронскиан системы решений Yl' У2' ..., Уп ли

нейноrо однородноrо уравнения (4.20) равен нулю хотя бы в одной
точке интервала (а, Ь), то эти решения линейно зависимы.
При доказательстве для простоты оrраничимся случаем п = 3.
Пусть w(xo) = О, rде а < Ха < Ь.
Рассмотрим следующее решение:


У = C1Yl (Х) + С 2 У2(Х) + Сзуз(х),


( 4.30 )


105




rде Yl = Yl (Х), У2 = У2(Х), Уз = Уз(Х)
 данные решения и C 1 , С 2 , С З

некоторые постоянные. Подберем постоянные С 1, С 2 , С з так, чтобы
были выполнены условия


У(Хо) = О, у'(Хо) = о, у"(Хо) = о.


(4.31 )


Из формулы (4.30) следует, что постоянные С 1, С 2 , С з удовлетворя

ют системе уравнений


C1Yl (хо) + С 2 У2(ХО) + СзУз (ХО)
 0,.1
C1yi(xo) + С 2 У2(ХО) + Сзуз(хо)=О,

C1yj(xo) + С 2 У2(ХО) + Сзуз(хо) = o.J


(4.32)


Так как по условию определитель этой системы равен нулю, т. е.


Yl(Xo) У2(ХО) УЗ(Хо)
W(xo) = Yl(Xo) У2(ХО) Уз (ХО) = о,
yj(xo) У2(ХО) Уз(Хо)


то система (4.32) допускает ненулевое решение






C1=C 1 , С 2 =С 2 , Сз=С з .


Тоrда решение


у = ё1Уl (Х) + ё 2У2 (Х) + ёзуз(х)


(4.33)


будет удовлетворять начальным условиям (4.31). С друrой стороны,
тривиальное решение


у=о


( 4.34)


также, очевидно, удовлетворяет начальным условиям (4.31). В силу те..
оремы единственности эти два решения должны совпадать во всем ин..
тервале (а, Ь). Следовательно,
ё1Уl (х) + ё 2 У2 (Х) + ёзуз(х) = о,


причем не все числа С 1, С 2 , С з равны нулю. Это значит, что решения
Yl' У2' Уз линейно зависимы.
Теорема доказана.
Следствие. Если решения Yl' У2' ..., Уп линейноrо однородноrо
уравнения линейно независимы, то вронскиан их не равен нулю ни в
одной точке интервала (а, Ь).


106




о п р е д е л е н и е 2. Фундаментальной системой решений ли

нейноrо однородноrо уравнения называется любая совокупность ли

нейно независимых частных решений Yl' У2, ..., Уп' число которых
равно порядку системы.
Чтобы построить фундаментальную систему решений, достаточно
взять произвольную систему п 2 чисел aij (i, j = 1, 2, ..., п), удовлетво

ряющих единственному условию


all al2 . .. al n
А= а21 а22 .. . а2п *0, (4.35)
anl а п 2 .. . а пп


и рассмотреть частные решения
Yl = Yl (Х), У2 = У2(Х), ..., Уп = Уn(Х)'


(4.36)


определяемые начальными условиями
Yk(XO)=alk.Yk(xO)=a2k. .... yin
I)(XO)=ank (k=1.2. ..., n),


rде а < Ха < Ь (эти решения существуют в силу теоремы существова

ния и единственности и определены при а < Х < Ь). Решения (4.36) об

разуют фундаментальную систему решений, так как, очевидно, BpOH

скиан их W(X) при Х = Ха отличен от нуля
W(Xa) = А :i: О
и, следовательно, в силу следствия к теореме 3 решения (4.36) линей

но независимы.
т е о р е м а 5. Общее решение линейноrо однородноrо уравнения
(4.20) представляет собой линейную комбинацию ero частных реше

ний, образующих некоторую фундаментальную систему решений,
т. е. общее решение выражается формулой
У = C1Yl + С 2 У2 + ... + СпУп' (4.37)
rfie Yl = Yl(X), У2 = У2(Х), ..., Уп = Уп(Х)
 линейно независимые част

ные решения и C 1 , С 2 , ..., Сп
 произвольные постоянные.
Требуется доказать, что формула (4.37) при некотором выборе по

стоянных C 1 , С 2 , ..., Сп дает решение У = у (х), удовлетворяющее лю

бым начальным условиям

 ( )

' ( )
'
(п
H ( )
(п
H
у Ха = Уа, У Ха = Уа, ..., У Ха = Уа '


(4.38)


rде а < Ха < Ь.


107




Для определения постоянных С l' С 2 , ... , Сп из условий (4.38) полу

чаем неоднородную систему линейных уравнений


C1Yl(Xo) + С 2 У2(ХО) + ... + СпУn(ХО) = УО,
C 1 Yl(XQ) + С 2 У2(ХО) + ... + C
Y
(Xo) = УО,


1


(4.39 )


CIY
n
O(xo) + C2y
n
1)(xo) + ... + Cпy
n
1)(xo) = yЪn
1).


Определитель этой системы есть не что иное как значение вронски

ана W(x) решений у l' У2, ..., у n при Х = Ха; поэтому этот определитель
отличен от нуля


W(XO) * о.


Следовательно, система (4.39) совместна и имеет единственное pe

шение


С 1 =C 1 , С 2 =с 2 , ..., Сп =С n .


Таким образом, получаем


у = с 1 У 1 + С 2У2 + ... + С пУп'


Т. е. у содержится в совокупности решений (4.37).
Теорема доказана.
Следствие. Если коэффициенты fk(X) (k = 1,2, ..., п) линейноrо
однородноrо уравнения непрерывны, то формула (4.37) дает все реше

ния этоrо уравнения.


Задания для самостоятелъноrо реmения
1. Исследовать на линейную зависимость следующие системы
функций:
а) х, 2х, х2;
б) sin х, cos х;
в) Х, х + 1, Х + 2;
r) ek(x, e k2X , e k3X , rде k 1 , k 2 и k3
 постоянны и k} < k 2 < k3.
2. Фундаментальная система решений есть х, х 2 , ХЗ. Найти реше

ние у, удовлетворяющее начальным условиям:


у( 1) = о, у'( 1) = о, у"( 1) = 2.


108





 4. НЕОДНОРОДНЫЕ ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ


Рассмотрим неоднородное уравнение


L[y] = [( х),


( 4.40)


rде


L[y] = у(n) + fl(x)y(n
 1) + ... + [п(Х)У.


(4.41)


т е о р е м а. Общее решение неоднородноrо линейноrо дифферен

циальноrо уравнения есть сумма общеrо решения соответствующеrо
однородноrо линеиноrо уравнения и частноrо решения данноrо Heoд

нородноrо линейноrо уравнения.
В самом деле, пусть У = У(х)
 частное решение неоднородноrо ли

нейноrо уравнения (4.40), т. е.


L[y] = {(Х).


(4.42)


Рассмотрим функцию


у = у + У,


(4.43)


rде у
 общее решение соответствующеrо однородноrо линейноrо
уравнения


L[ y ] = о.


(4.44)


Покажем, что у есть общее решение неоднородноrо линейноrо ypaB

нения (4.40). Прежде Bcero у удовлетворяет этому дифференциально

МУ уравнению, так как


L[y] = L[ y ] + L[ У] = О + [(х) = [(х).


Кроме Toro, из формулы (4.43) можно получить частное решение
у = у(х), удовлетворяющее любым начальным условиям


( )
 ' ( )
, ( n
 I) ( )
 ( n
 1) .
у Ха
 уа, У Ха
 Уа, ..., У Ха
 Уа '


(4.45)


для этоrо, очевидно, достаточно в качестве у = У (Х) взять частное реше

ние однородноrо уравнения, удовлетворяющее начальным условиям
У (Ха) = Уа
 У(Хо), у '(Хо) = Уа
 У'(Хо), ...

(n
o ( )
 (n
o
 Y (n
O ( )
..., у Хо
 У а Ха
(такое решение заведомо существует).
Таким образом, теорема доказана.


109




С л е Д с т в и е. Общее решение линейноrо неоднородноrо уравне.
ния (4.40) дается формулой


п
У = У(Х) + LCk Yk (X),
. k=1
rде У(х)
 некоторое частное решение этоrо уравнения, Уl (Х), У2 (х),
..., Уп (х)
 фундаментальная система решений соответствующеrо од.
нородноrо уравнения (4.44) и С 1 , С 2 , ..., Сп
 произвольные посто.
янные.



 5. МЕТОД ВАРИАЦИИ произвопьных ПОСТОЯННblХ
Рассмотрим способ нахождения частноrо решения У неоднородно.
ro линейноrо уравнения


L[y] = {(х),


( 4.46 )


если известно общее решение У соответствующеrо однородноrо ли

нейноrо уравнения


L[ y ] = о.


(4.47)


Для простоты выкладок оrраничимся случаем


L(y] = у'" + 11 (х)у" + 12 (х)у' + 1з (х)у,


(4.48)


коrда фундаментальная система решений
Уl = Уl (Х), У2 = У2 (х), Уз = Уз (х) (4.49)
уравнения (4.47) состоит из трех функций (общий случай вполне ана.
лоrичен) .
Пусть


у = с lУl + С 2 У2 + СзУз.


( 4.50)


Если С 1 , с 2 , с з .......... постоянные, то функция У удовлетворяет однород.
ному уравнению (4.47). Будем считать
C 1 = С 1 (х), С 2 = С 2 (х), С З = с з (х)
некоторыми функuиями от х (т. е. проварьируем эти постоянные) и
положим
У = C 1 (X)Yl + С 2 (Х)У2 + Сз(Хз)Уз, (4.51)
причем подберем функции С 1 (х), С 2 (х), Сз(х) так, чтобы функция у,
определяемая формулой (4.51), была бы решением неоднородноrо ли.
нейноrо уравнения (4.46). Так как в нашем распоряжении имеется


110




три функции C1(X), С 2 (х), Сз(х), то две из них мы можем считать про

извольными или же можно наложить на эти три функции Д в а у с л о

в и я, причем дифференциальное уравнение (4 46) будет удовлетворе

но за счет выбора третьей, оставшейся свободной функции.
Пользуясь этим обстоятельством, в дальнейшем мы потребуем, чтобы
производные у' и у" имели такой вид, как будто бы функции C1(x),
С 2 (х) и Сз(х) являются постоянными.
Дифференцируя формулу (4.51), будем иметь
у' = C 1 (Х)Уl + С 2 (Х)У2 + сз (Х)Уз +
+ [Cf(X)Yl + С 2 (Х)У2 + Сз(х)уз]. (4.52)
Наложим на функции С 1 (х), С 2 (х), Сз(х) условие
Ci(X)Yl + С 2 (Х)У2 + Сз(х)уз = о. (4.53)


Тоrда получим


у' = С] (Х)У} + С 2 (Х)У2 + С З (Х)У3.
Дифференцируя еще раз, находим
уН = C 1 (Х)Уl + С 2 (Х)У2 + сз (Х)Уз +
+ [Cf(x)Yl + С 2 (Х)У2 + СЗ(х)уз].


( 4.54)


Потребуем, чтобы
Cf(X)Yl + С 2 (Х)У2 + С з (Х)Уз = о;


(4.55 )


тоrда


У" = C 1 (Х)Уl + С 2 (Х)У2 + сз (Х)Уз. (4.56)
Дальнейшее дифференцирование дает
у'" = С 1 (x)yi" + С 2 (Х)У2 + С з (Х)Уз +
+ [C1(x)yi + С 2 (Х)У2 + Сз(х)уз]. (4.57)
Подставляя функцию у (4.51) и ее последовательные производные у'
(4.54), уН (4.56) и У'" (4.57) в неоднородное линейное уравнение
L[y] = уlII + {l (Х)У" + 12 (Х)У' + fз (Х)У = [(х), (4.58)


получим


-С 1 (x)L[Yl] + С 2 (x)L[Y2] + С з (х)L[уз] +
+ [Ci(X)Yl + С'2(Х)У2 + Сз(Х)Уз] = [(Х)


или, так как


L[Yl]=O, L[Y2]=0, L [Уз] =0,


111




то


Cf(x)y]' + С 2 (Х)У2 + СЗ(х)уз = /(Х). (4.59)
Таким образом, для определения неизвестных функций C1(X),
С 2 (Х), Сз(Х) в силу уравнений (4
53), (4.55), (4.59) имеем систему
С) (X)Yl + С 2 (Х)У2 + сз (Х)Уз = о, 1
Cl(
)YI + С 2 (Х)У2 + С з (Х)У3 = о,
 (4.60)
Ч(х)уj + Q(X)Y2 + СЗ(х)уз = f(x).J


Вид этой системы полезно запомнить. Система (4.60) представляет
собой аЛI'ебраическую линейную неоднородную систему трех ypaBHe

ний с тремя неизвестными C1(x), С 2 (х), С з (Х). Определитель этой сис

темы


Yl У2 Уз
W(X)= Уl У2 Уз
yi У2 Уз


(4.61)


есть вронскиан для системы решений Yl' У2' УЗ; поэтому W(x) -:/:. О и,
следовательно, система (4.60) совместна и имеет единственное реше

ние. Решая систему (4.60, будем иметь
r I ( ) f (х) ( )
j C 1 Х = w(х) W З1 х ,
I ( ) f (х) ( )
С 2 Х = w(x) W З2 х ,
l сз(х) =


) Wзз(х),


(4.62)


rде wзk(х) (k = 1,2, 3)
 соответствующие миноры со знаками опре

делителя W(x).
Отсюда


r х f(
)
C1(x)=A 1 + f wЮ WЗl(
)d
,
ХО
х
С 2 (х) = А 2 + f

r) WЗ2(
)d
,
Хо


( 4.63 )


J X f(
)
с з (х) = Аз + W(
) W зз (
)d
)
хо


112




rде Ха
 некоторое фиксированное значение и А l' А2' Аз
 произ

вольные постоянные. Так как мы ищем частное решение, то можно
положить


Аl =А 2 =А з =0.


( 4.64 )


Если в выражениях (4. б3) сохранить постоянные А l' А2' Аз, то фор

мула (4.51) даст общее решение неоднородноrо уравнения. Подстав

ляя функции C1(X), С 2 (х), Сз(х) в формулу (4.51) с учетом условия
(4.б4), получим частное решение
х УI (
) У2 (
) уз (
)
у = f


) YI(
) Y2(
) УЗ<
) d
. (4.65)
ХО УI (х) У2 (х) уз (х)


Заметим, что решение У (4.б5), как леfКО проверить непосредст

венно, удовлетворяет нулевым начальным условиям
у(хо) = о, У'(хо) = о, У"(хо) = о.
Пример. Решить уравнение
у'" + у' = +.
SlПХ


Реш е н и е. Однородное уравнение имеет вид
у'" + у' = о.


П ' ,,,,,
олаrая у = и и у = u , получим
иН + u = о.
Отсюда (см. rл. III,
 5)
dy С С .
и = dx = 1 cos х + 2 Sln х


и, следовательно,


У=С 1 siПХ
С2СОSХ+Сз.


Таким образом,


у 1 = sin х, У2 =
cos Х, уз = 1.
Положим С 1 = С 1 (х), С 2 = С 2 (х), С з = Сз(х). Для определения произ

водных Cf(x), С 2 (х), Сз(х) соrласно формулам (4.60) имеем следую

щую систему уравнений:
Q(x)sinx
 C 2 (x)cosx + q(x)=O.l
Ci(x) cosx + С 2 (х) sinx = О, }

Cf(x)sin(x) + C 2 (x)cosx = +. J
stnx


113




Отсюда


Cr(x) =
l, С 2 (х) = ctgx, сз (х) = Si
 х


и поэтому


C1(X) =.
 х + Al'
с 2 (х) = ln I sin х I + А2'
Cj(x) = ln I tg
 I+А з .


rде А l' А2' Аз
 произвольные постоянные.
Следовательно
у =
xsinx
 cosx-lnlsinxl + lnltg
 1 + A1sinx
 A 2 cosx + Аз.


Задания для самостоятелъноrо реmения
1. уН
 У = хе Х .
2. ху'" + уН = х 2 . Найти частное решение, удовлетворяющее Ha

чальным условиям
у( 1 ) = О, у' ( 1 ) = О, у" ( 1 ) = о.


t б. ОДНОРОДНЫЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
Рассмотрим дифференциальное уравнение


L[y] = О,


( 4.66)


rде


L[y] = у(n) + alY(n
 I) + ... + апу,


( 4.б7)


причем коэффициенты а l' а2, ..., а п
 постоянные действительные
числа.
Чтобы построить общее решение уравнения (4.66) соrласно общей
теории, достаточно найти систему п линейно независимых частных
решений этоrо уравнения (фундаментальную систему). Будем ис

кать эти решения в форме показэтельной функции
у = e kX , (4.68)


rде k
 некоторое постоянное число.
Очевидно,


у(т) = (ekx)(т) = kтe kx (т = О, 1, ..., n).


114




Подставляя эти выражения в дифференциальное уравнение (4.66),
будем иметь


L[e kx ) == e kx F(k) = о,


(4.69)


rде


F(k) = k n + al kn
l + ... + а n .
Так как ekX:I= о, ТО из уравнения (4.69) получим


(4.70)


F(k) = о.


(4.71)


Полином F(k) называется характеристическим МНО20члено.м
для дифференциальноrо уравнения (4.66), а уравнение (4.71) ........ ха-
рактеристическим уравнением. Последнее формально получается
в результате замены производных у(т) (т = о, 1, ..., п) в дифференци

альном уравнении (4, 66) на соответствующие степени величины k.
Характеристическое уравнение (4. 71) есть алrебраическое ypaBHe

ние п
й степени и, как известно из алrебры, имеет п действительных
или комплексных корней


k 1, k 2 , ..., k n .
Если k есть корень характеристическоrо уравнения, то, как следует
из формулы (4.69), функция e kx является решением дифференциаль

Horo уравнения (4.66).
Рассмотрим различные случаи, которые здесь мотут представиться.
С л у чай 1. Корни характеристическоrо уравнения действитель

ны и различны.
Имеем п частных решений
Yl =e k1x , У2 =e k2X , ..., Уn =e knx (4.72)


Леrко убедиться, что эти решения линейно независимы. В самом
деле, пусть для определенности


k 1 < k 2 < ... <k n .
Предположим, что существуют постоянные


C 1 , С 2 , ..., Сп


такие, что


C1e kJx + C 2 e k2X + ... + Cne knx = О,


(4.73)


причем С т ........ последняя в этом наборе константа, отличная от нуля.


115




Разделив обе части тождества (4.73) на e kтx , тоrда будем иметь
Cle
(kт
kl)X + C2e
(kт
k2)X + ... + С т = о.


Отсюда, переходя к пределу при х ----+ + 00, получим


С т = О,


что противоречит предположению.
Итак, тождество вида (4.73) невозможно, т. е. функции Yl' У2, ...,
Уп
 линейно независимы.
Поэтому решения (4.72) образуют фундаментальную систему pe

шений. Следовательно, общее решение дифференциальноrо ypaBHe

ния (4.66) есть


у = C1e k1x + C 2 e k2X + ... + Сп е knx ,


rде С l' С 2 , ... , Сп
 произвольные постоянные.
Пример. Пусть


у'"
 У' = о.
Реш е н и е. Характеристическое уравнение есть


k 3
 k = О.
,


отсюда корни


k 1 = о, k 2 = 1 t k3 =
 1.
Этим корням соответствуют частные решения


у 1 = 1, У2 = е Х , у = е
 Х.
Так как корни характеристическоrо уравнения действительны и
различны, то общее решение этоrо уравнения имеет вид
У = C 1 + С 2 е Х + Сзе
Х ,


rде С 1 t С 2 , С З
 произвольные постоянные.
G л у чай 2. Корни характеристическоrо уравнения различны, но
среди них есть комплексные.
В этом случае удобно рассматривать комплексные решения
у = u + iv, (4.74)
rде и и v
 действительны и i = Д
 мнимая единица. При диффе

ренцировании функции у число i рассматривается как постоянная.


116




Л е м м а 1. ЕСJIИ комплексная функция У (4.74) удовлетворяет ли-
нейному однородному уравнению (4.66) с действительными коэффи

циентами, то u
 действительная часть и v
 коэффициент мнимой
части этой функuии также удовлетворяют данному уравнению.
В самом деле, в силу линейности оператора L[y), имеем
L[u+iv] = L[u] + iL[v) == о.


Но комплексное число равно нулю тоrда и только тоrда, коrда paB

ны нулю ero действительная и мнимая части:


L[u]=O и L[v)=O,


Т. е. u и v
 являются решениями уравнения (4.66).
Переходим теперь к построению фундаментальной системы решений.
Заметим, что так как коэффициенты характеристическоrо ypaBHe

ния (4.72) действительные, то комплексные корни ero попарно сопря

женные. Пусть, например,


k 1 = а + i
, k 2 = а
 i

(а.,


 действительные)
 комплексные корни характеристическоrо
уравнения. Из свойств показательной функции следует, что функции
ek(x = е(а+ i
)x = eax(cos
x + isin
x)


и


ek2X = e(a
i
)X = eax(cos
x
 isin
x)
по
прежнему являются решениями (комплексными) дифференциаль

Horo уравнения (4.6б).
в силу леммы 1 действительная часть и коэффициент мнимой части
приведенных выше решений, а именно:
Yl = eaxcos
x, У2 = ea.xsin
x
также являются решениями уравнения (4.6б).
в случае, если некоторый корень ks
 действителен, то мы, как и
прежде, берем частное решение в форме показательной функции
У = e ksx . Можно доказать, что построенная таким образом система ча

стных решений Yl' У2' ..., у п будет фундаментальной. Общее решение
дифференциальноrо уравнения (4.66), как всеrда, выразится фор

мулой


у = C1Yl + С 2 У2 + ... + СпУп'
rде C 1 , С 2 , ..., Сп
 произвольные постоянные.


117




Пример. Пусть


у"'
 2у'
 4у = о.
Реш е н и е. Характеристическое уравнение имеет вид
kЗ
2k
 4 = о.
Отсюда подбором получаем один очевидный корень
k 1 = 2.
Деля левую часть уравнения (4.75) на бином k
 2, будем иметь
(k
 2)(k 2 + 2k + 2) = о.


(4.75)


Следовательно, два друrие корня характеристическоrо уравнения
будут


k2=
1 + i, kз=
1
i.
Фундаментальная система решений здесь такова:
Yl = е 2х , У2 = e
X cos х уз = e
X sin х.
Поэтому общее решение есть
у = C 1 e 2x + e
X(C2 cos х + сз sin х),
rде C 1t С 2 , С з
 произвольные постоянные.
Случай з. Среди корней характеристическоrо уравнения имеют-
ся действительные кратные корни.
Установим предварительно одно свойство оператора L[y].
Лемма 2. Если
L[y] = у(n) + aly(n
I) + ... + аnу,
то при постоянной k имеем
L[e kx у] = e kx { F(k) У + F'(k) у' + Fi,k) у" + ... + F(:
k) у(n) }. (4.76)
rде F(k) = k n + alkn
l + ... + а п ....... характеристический мноrочлен
оператора L[y].
Д о к а з а т е л ь с т в о. В силу формулы Лейбница имеем
ekxy = ekxy;
(ekXy)' = e kx (ky + у');


(e kx у)(n) = e kx (k n у + cAkn
1 у' + c
 kn
2 у" + ... + у(n) ).


118




Умножая эти равенства соответственно на й п ' й п
 l' ... , й l' 1 и скла-
дывая, получим
L[e kx у] = e kx {[k n + al kn
l + ... + ап]у +
+ [nkn
l + (п
 l)al kn
2 + ... + an
l] у' +
+
, [п(п
1) kn
2 + (п
l)(п
2)alkn
3 + ... + 2.1an
2]Yw +
+ ... +
[п(п
 1) ... ну(n)} =
n.
= e kX { F(k)y + F'(k)y' + Fi!k) уН + ... + F(:
k) у(n)},


что и требовалось доказать.
Пусть


k 1 = k 2 = ... = ks
(s
2)
 корень характеристическоrо уравнения (4.71), кратность
KOToporo равна s. Положим


у = ek1Xu,


(4.77)


rде u = и(х)
 новая неизвестная функция.
Подставляя это выражение в дифференциальное уравнение (4.66),
будем иметь


L[ektxu] = о


или, применяя лемму 2 и учитывая, что e k1x * О, получим
F(k\)u + F'(k l ) и' + p
() иН + ... + F(п:
kt) и(n) = о. (4.78)
Так как k 1
 корень характеристическоrо уравнения (4.71) кратно-
сти s, то


F(k l ) = F'(k 1 ) = ... = F(s
 1) (k 1 ) = О,
p(s) (k 1 ) ;i: о.
п'оэтому уравнение (4.78) принимает вид
F(S) (k l ) (s) р(n) (k l ) (п)

I U + ... + , и
 о.
s. n.


(4.79)


Ввиду Toro, что наинизший порядок производной В уравнении
(4.79) равен s, это уравнение имеет s очевидных частных решений
U
 l U
 X Us = x s
l .
1
, 2
 ,...,


119




Следовательно, исходное дифференциальное уравнение допускает
систему s частных решений вида
Yl =. ek[x, У2 =. xe k1X . ..., Ys = xs
lekIX. (4.80)


Эти решения и составляют соответствующую часть фундаменталь

ной системы решений.
Пример. Решить уравнение


yIV + 2 у'"
 2 у'
 у = о.


(4.81)


Реш е н и е. Составим характеристическое уравнение


k 4 + 2k 3
 2k
 1 = О


или, так как


k 4 + 2k 3
 2k
 1 = (k 4
 1) + 2k (k 2
 1) =
=(k 2
 1 )(k 2 + 1 + 2k) = (k 2
 1 )(k + 1)2 =
= (k
 1 )(k + 1)3,


то


(k
 1 )(k + 1)3 = о.


Отсюда


k 1 = 1, k 2 = k3 = k4 =
 1.
Поэтому фундаментальная система решений имеет вид
Уl =е Х , Y2=e
X, уз=хе
Х, Y4=x2e
X.
Следовательно, общее решение данноrо уравнения (4.81) будет
у = C1e x + (С 2 + Сзх + С 4 х 2 ) e
X,
rде С l' С 2 ' С з , С 4
 произвольные постоянные.
Сл уч ай 4. Среди корней характеристическоrо уравнения имеются
кратные комплексные.
Так как коэффициенты характеристическоrо уравнения (4.71) дей

ствительны, то комплексные корни ero попарно сопряженные, при

чем кратности сопряженных корней одинаковы. Пусть


k 1 = k 2 = ... = ks = а + i

«Х"

 действительны)
 корень характеристическоrо уравнения
(4.72) кратности s. В таком случае
k s + 1 = k s + 2 = ... = k 2s = a
 i



120




также s
кратный корень этоrо уравнения. На основании формулы
(4.80) корню k 1 соответствует 8 частных комплексных решении
e ktX = eax(cos
x + isin
x);
xe ktX = xeax(cos
x + isin
x);


xs
lektX = xs
leax(cos
x + isin
x).
Поэтому в силу леммы 1 дифференциальное уравнение (4.66) имеет
28 действительных решений вида


Yl = е Ш cos
x, у s+ 1 = е ах sin
x;
У2 = хеШ cos
x, у s+ 2 = хеШ sin
x;


Ys = xs
lea.x cos
x, Y2s = xs
leax sin
x,


которые и войдут в общую фундаментальную систему решений как со-
ответствующие кратным корням а. + i
.


Пример. Решить уравнение


yIV + 2у" + у = О.


Реш е н и е. Характеристическое уравнение имеет вид


k 4 + 2k 2 + 1 = О


или


(k 2 + 1)2 = О.


Отсюда


k 1 = k 2 = i, k3 = k4 =
i.
Фундаментальная система решений будет иметь вид:
Yl = cos х, У2 = х cosx, Уз = sin х, У4 = xsinx.
Следовательно, общее решение этоrо уравнения таково:


у = (C 1 + С 2 х) cos х + (С 2 + С 4 х) sin х
(C 1 , С 2 ' С з , С 4
 постоянные).


121




Задания для самостоятельноrо решения
1. ylV
 5у" + 4у = о.
2. у'" + у = о.
3. у'"
 3у' + 2у = о.
4. yIV + 2у'" + 3у" + 2у' + у = о.
5. Найти решение уравнения
ylV + у=О,
удовлетворяющее начальным условиям
у(О) = о, у'(О) = 1. у"(О) = о, у'''(О) = о.


17. НЕОДНОРОДНЫЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
Рассмотрим неоднородное линейное уравнение


L[y] = [(х),


(4.82)


rде


L[y] = у(n) + aly(n
l) + ... + аnу,


(4.83)


ak (k = 1, ..., п)
 постоянные, а [(х)
 некоторая данная непрерыв

ная функция. Как известно (см. э 4), общее решение уравнения (4.82)
выражается формулой


у = у + У,
rде у
 общее решение соответствующеrо однородноrо линейноrо
уравнения и У
 частное решение данноrо неоднородноrо линейноrо
уравнения (4.82). в предыдущем параrрафе указывал ось как найти
функцию у . Для нахождения частноrо решения У можно воспользова

ться методом вариации произвольных постоянных (см. э 4), однако
этот метод приводит к длинным выкладкам. Поэтому мы укажем для
некоторых простых правых частей [(Х) друrой метод нахождения фун

кции У, носящий название метода неопределенных коэффuцuен"
тО8. Рассмотрим ряд случаев.
Случай 1. (Правая часть уравнения
 полином.) Пусть
[(х) = ьох т + b1x m
l + ... + Ь т , (4.84)


rде Ь о , b 1 , ..., Ь т
 некоторые постоянные.
1. Предположим, что


а п = F(O):J: о,


122




т. е. k = О ........ не является корнем характеристическоrо уравнения
F(k) = k n +alkn
l + ... +а п = о.


Ищем частное решение в форме полинома той же (как и у правой ча-
сти) степени
У А т А т
l А т
2 А
= оХ + lX + 2 Х + ... + т'


(4.85)


с неопределенными коэффициентами Ао, А 1, ..., А т . Последовательно
дифференцируя, будем иметь
У' = тАох т
l + (т
 I)AIxт
2 + ... + 1. Aт
l;
УН = т(т
 OAoxт
2 + (т
 l)(т
 2)A 1 хт
З + ... + 2 .1. Aт
2;


.... ......... .............. ........


Подставляя эти выражения в уравнение (4.82) и делая приведение
подобных членов, получим
L[Y] = Аоапх т + (man
lAo + anAl)xт
1 +
+ [т (т
Oaп
2Ao + (т
1)an
IAl + anA2]xт
2 + ...

 Ь т Ь т
l Ь т
2 +
... == оХ + 1 х + 2 Х ...
Приравнивая коэффициенты при одинаковых степенях Х, получаем
систему уравнений:
Аоа п = Ь о , 1
A1a n + man
IAo = b l .


.2


.(
.
l
.n
I.
I.+.







.2

 . .
2'J


(4.86)


из которой, учитывая, что а п =F О, последовательно можно определить
коэффициенты Ао, А 1, Аз, ..., А т .
Итак, если р(о) =F о, то уравнение (4.82) имеет частное решение в
форме полинома, степень KOToporo равна степени полинома, стояще-
ro в правой части уравнения.
, 2. Пусть


p(r) (о)
an
, = I = О (r = о, 1, ..., s
 1)
'.


и


р (n) ( о)
an
s = , *0,
s.
т. е. k = О ....... является корнем характеристическоrо уравнения крат-
ности s.


123




Уравнение (4.82) имеет вид
у(n) + atY(n'
 I) + ... + а п
 sy(s) = [(х).


(4.87)


Полаrая


y(s) = и,


(4.88)


получим


u(n
s) + alU(n
s
l) + ... + an
sU = f(x).


(4.89)


Так как an
s ,*0, то в силу предыдущих рассуждений последнее
уравнение имеет частное решение и в форме полинома

.
 т
 m
l

и
 Аох + A1x + ... + А т '






rде Ао, А l' ..., А т
 некоторые определенные числа.
На основании формулы (4.88), интеrрируя почленно последнее pa

венство s раз, получим частное решение исходноrо уравнения (4.87)
у = СО + C1x + ... + Cs
lXs
l +
+Aox m + s + AIXm+s
l + ... +Amx S ,


rде Со' С 1 , ..., Cs
 1
 произвольные постоянные иА о , Al' н., А т
 не..
которые определенные коэффициенты. Так как мы ищем лишь част

ное решение, то можно положить


СО = С 1 = ... = CS
 1 = О


и, следовательно,


у = X S (Аох т + AIXт
l + ... + А т ).


( 4.90 )


Итак, если Р(О) = О и кратность нулевоrо корня равна 5, то диффе

ренциальное уравнение имеет частное решение в форм
 полинома,
степень KOToporo на 5 единиц выше, чем степень полинома, стоящеrо в
правой части уравнения.
Пример. Решить уравнение


уОО) + у(9) = х.
Реш е н и е. Характеристическое уравнение имеет вид
k 10 + k 9 = о.


(4.91)


Отсюда


k 1 = k2 = ... = kg = О, k 1 О =
 1.


124




Соrласно теории ищем частное решение У в такой форме:


у = х 9 (Ах + В)


или


у = Ах 1 О + Вх 9 .
Подставляя это выражение в дифференциальное уравнение (4.91),
получим


lO!A + lO!Ax + 9!В == х.


Отсюда


1 О!А = 1 }
10!А +. 9!В = О


и, следоватеЛЬНО t


А= l
! ' B=
 J! .


Таким образом, находим


Xl О х9
У = 10!
 т.


Общее решение данноrо уравнения, очевидно, таково:
9

 C m
l С
X х 9 x lO
У = LJ т х + lOe
 9т + 10! .
т=]
С л у чай 2. (Правая часть уравнения
 полином, умноженный на
показательную функцию.)
Пусть


{(х) = Р т(Х) е С1Х ,


(4.92)


rде


Рт(Х)=ЬоХт + blxт
l+ ... +Ь т


и а.
 постоянное число.
Положим


у = еаХи,
rде u
 новая неизвестная функция. Тоrда уравнение (4.82) примет
вид


е С1Х L1[u] = е С1Х р т(х)


или


L1[u] = Р т(Х),


(4.93 )


rде


LI [и] = Р(а)и + Р'(а)и' + Fi
) и'" + ... + F(п

a) и(n)


125




Мы пришли к разобранному выше случаю с той только разницей,
что коэффициент при неизвестной функции и равен Р(а).
1. Пусть Р(а) =F о, т. е. а. не является корнем характеристическоrо
уравнения. Тоrда уравнение (4.93) имеет частное решение и в форме
полинома степени т. Следовательно, данное уравнение (4.82) имеет
частное решение вида


у = е ах Qт(x), (4.94)
rде Qт(x)
 полином степени т.
Коэффициенты полинома Qт(X) находятся путем подстановки BЫ

ражения (4.94) в данное дифференциальное уравнение.
2. Пусть Р(а) = о, причем k = а
 корень характеристическоrо
уравнения кратности s.
Уравнение (4.93) допускает частное решение и в форме полинома
степени т, умноженное на XS. Следовательно, наше дифференциаль-
ное уравнение (4.82) имеет такое частное решение
у = xSe ax Qт(x), (4.95)
rде Qт(x)
 полином степени т.
Пример. Решить уравнение
у" .... у = х 2 е Х . ( 4.96 )
Реш е н и е. Составляем характеристическое уравнение
k 2
 1 = о.


Корни ero k 1 =
 1, k 2 = 1.
Так как (Х, = 1 = k 2 , то полаrаем
у = х(Ах 2 + Вх + С) е Х


или


у = (Ах 3 + вх2 + Сх)е Х .


Применяя формулу Лейбница, получаем
ун = (Ах 3 + вх2 + Сх)е Х +
+ 2(3Ах 2 + 2Вх + С)е Х + (БАх + 2В)е Х .


Отсюда, подставляя У и У" в уравнение (4.96), будем иметь
2(3Ах 2 + 2Вх + С)е Х + (6Ах + 2В)е Х == х 2 е Х


или


6Ах 2 + (6А + 4В)х + (2В + 2С) Е х 2 .


126




Следовательно,


6А = 1. 1
БА + 48 = О,

28 + 2С = о. J


Решая эту систему, находим
A =l B
 1 C
l
6'

4'
 4'


поэтому


У
 ( Х З х2 Х ) Х

 6
4+4e .
Общее решение уравнения (4.96) имеет вид
у = C1e x + C2e
X + ( х:
 х: +
 )eX.


в дальнейшем иноrда будет удобно пользоваться комплексными ре-
шениями.


Лемма. Пусть дано линейное неоднородное уравнение


L[y] = f(X)t


( 4.97)


правая часть KOToporo есть комплексная Функuия


{(х) = <Р(Х) + i'l'(x)


( 4.98 )


и L[y] есть линейный оператор (4.83) с действительными коэффици

ентами.
Если комплексная функция
у = u + iv
удовлетворяет уравнению (4.97), то действительные функции и и v
удовлетворяют соответственно уравнениям
L[u] = <Р(Х) и L[v] = 'I'(x).


в самом деле, имеем


L[u + iv] = L[u] + iL[v J = <Р(Х) + i'Jf<x).
Так как коэффициенты оператора L[y] действительные, то отсюда сле

дует, что


L[u] = <р(х) и L[v] = 'I'(Х).


Лемма доказана.


121




с л у чай 3. Правая часть уравнения
 произведение показатель

ной функции на триrонометрический полином с полиномиальными
коэффициентами.
Пусть


[(х) = еах[Р т (x)cos
x + Qm (x)sin
x],


( 4.99 )


rде а. и

 действительные числа, Р т(х) и Qт(X)
 полиномы, кото-
рые, без нарушения общности рассуждения, можно считать имеющи-
ми одинаковую степень т.
Применяя формулу Эйлера
cos
x ==
 (ei
x + e
i
x). sin
x == ii (ei
X
 e
i
x),


получим


{(х) =
 e(a+ i
)x P
 (х) +
 e(a
i
 )xQ
 (х),
rде p
 (Х), Q
 (х)
 некоторые комплексно сопряженные полиномы
степени т. Рассмотрим вспомоrательное уравнение


L[y] = е(а+ i
)x p
 (х).


(4.100).


Очевидно, что


{(Х) = Re[e(a+ i
)x P
 (х)].


Соrласно случаю 2 имеем две возможности.
1. Пусть Р(а. + i
) #; О, т. е. число k = а. + i

 не является корнем
характеристическоrо уравнения.
Уравнение (4.100) имеет частное решение вида*


л
у = е(а+ i
 )X[R m (х)
 iS m (Х)],


(4.101)


rде Rm(x) и Sm(x)
 некоторые полиномы степени т. На основании
леммы заключаем, что исходное дифференциальное уравнение (4.82)
имеет частное решение вида


у = eax[R m (x)cos
x + Sm (x)sin
xJ.


( 4.102 )


2. Пусть р«(1 + i
) = О, причем кратность корня k = (1 + ip равна s.
Вспомоrательное уравнение (4.100) имеет частное решение вида


л
у = X S е(а+ i
 )X[R т (х)
 iS m (Х)].


* Знак минус (
 ) взят для удобства выкладок.


128




Следовательно, наше дифференциальное уравнение имеет частное
решение вида


у = xSeax[R m (X)CoS
X + Sm (x)sin
x].


(4.103)


На практике можно не переходить к комплексным функциям, а cpa

зу пользоваться rотовыми видами частных решений (4.102) и (4.103).
Пример. Решить уравнение


уН
2y' +5у = е Х sin 2х.


(4.104)


Реш е н и е. Составляем характеристическое уравнение


k 2
 2k + 5 = О,


откуда


k} = 1 + 2i, k 2 = 1
 2i.


Так как число а. + i
 = 1 + 2i является простым корнем характери

стическоrо уравнения, то полаrаем


у = xex(Acos 2х + Bsin 2х).


(4.105)


Подставляя это выражение в дифференциальное уравнение (спра

ва налево), будем иметь
5xeX(Acos2x + Bsin2x)


 2[(х + l)eX(Acos2x + Bsin2x) +
+ 2xeX(
Asin2x + Bcos2x)] +
+ [(х + 2)eX(Acos2x + Bsin2x) +
+ 4(x+l)eX(
Asin2x + Bcos2x)


 4xeX(Acos2x + Bsin2x)] = e X sin2x


или, производя очевидные сокращения, получим

 4Asin 2х + 4Bcos 2х == sin2x.


в силу линейной независимости функций sin 2х и cos 2х имеем
А =
l В = О
4' ,


следовательно, частное решение будет иметь вид
Y=

 excos2x.
Отсюда общее решение уравнения (4 .104) таково:
у = еХ(С} cos2x + С 2 sin2x)

 е Х cos2x.


129




З а м е ч а н и е. Случаи 1, 2, 3 МОЖНО объединить общим правилом:
для правых частей укззанноrо вида частное решение дифференциаль

Horo уравнения, вообще rоворя, имеет тот же вид, что и ero правая
часть; при исключительных обстоятельствах нужно добавлять допол

нительный степенной множитель x S .
Принцип наложения решений. Если правая часть линейноrо
неоднородноrо уравнения (с постоянными или переменными коэффи

циентами) представляет собой сумму нескольких функций, то част

ное решение этоrо уравнения можно находить как сумму частных pe

шений соответствующих неоднородных уравнений, правыми частями
которых служат отдельные слаrаемые суммы.
т е о р е м а. Пусть


L[y] = <Pl (Х) + <Р2(Х)
и Yl' У2
 решения уравнений
L[Yl] = <1>1 (Х) и L[Y2] = <l>2(Х).


(4.105)


в таком случае


у = Уl + У2
является решением исходноrо уравнения (4.105).
в самом деле, в силу линейности оператора имеем


L[y] = L[Yl] + L[Y2] == <Pl (Х) + <l>2(Х) ,


что и требовалось доказать.
Пример. Решить уравнение
У'" +у" +У' +у = х2 +sin 2 Х.


(4.106)


Реш е н и е. Составляем характеристическое уравнение
k 3 + k 2 + k + 1 = О


или


(k 2 +l)(k+O = о.


Отсюда


k 1 =
 1, k 2 = i, k3 =
i.
Правую часть уравнения (4.106) можно представить в таком виде:


{(х) = (х 2 +
 ) + (

 cos2x).


130




Соrласно принципу наложения решений рассматриваем уравнения
yi" + yj + УI + Yl = х 2 +
 (4.107)


и


'" ", 1 2
У2 + У2 + У2 + У2 =
2cOS х.


( 4.1 08 )


Соответствующие частные решения имеют вид
Уl = Ах 2 + Вх + С


и


У 2 = Dcos2x + Esin2x.
Подставляя эти выражения соответственно в уравнения (4.107) и
(4.108), находим


А = 1- В =
2. С = 1
, , 2


и


D = J.... Е = 1
14' 7.
Отсюда частное решение уравнения (4.106) будет таково:
у = Y 1 + У2 = х 2
 2х +
 + l
 (cos2x + 2sin2x)


и, следовательно, ero общее решение имеет вид
у = Cle
x + C 2 cosx + Сзsiпх +
+ х 2
 2х +
 + l
 (cos2x + 2sin2x),
rде С l' С 2 , С З
 произвольные постоянные.


Задания для самостоятельноrо решения
1. Указать форму частных решений У, если
а) у'" + у' = 1 + cos х;
б) yIV
 у = х 2 е Х + е 2х ;
в) yIV + 2у" + у= х sin х;
, r) у" + 2у' + у = x2e
X cos х.
2. Решить уравнение
у/"
 у" = х + cos х.
3. Найти частное решение уравнения
у"' + 2у" + 2у' + у = х,
удовлетворяющее начальным условиям
у(О)::: у'(О) = у"(О) = о.


131




J 8. УРАВНЕНИЕ ЭЙЛЕРА


к линейному уравнению с постоянными коэффициентами леrко
приводится уравнение Эйлера
хпу(п) + alxп
ly(n
I) + ... + апУ= '(х), (4.109)


rде al ' а2 ' ... ,а п
 постоянные числа.
Для простоты оrраничимся рассмотрением уравнения BToporo по

рядка


х2 уН + alxy' + а2У = [(х).


(4.110)


Считая, что х > О, положим


х = е ! .


(4.111)


Используя правило дифференцирования функции, заданной пара

метрически, последовательно находим
,
 d у
 d у . dx

! d У
У
 dx
 dt . dt
 е dt '
Н
 dy'
 dy' . dx

2t ( d2y
 d Y )
у
 dx
 dt . dt
 е dt 2 dt.


Подставляя эти выражения в дифференциальное уравнение
(4.11 О), после очевидных сокращений получим линейное уравнение с
постоянными коэффициентами
( d2 у dy ) dy
 ( t ) ( )
dt 2
 dt +al dt +а2У
 f е . 4.112
Если х < О, то, полаrая х =

, МЫ приходим К уравнению Эйлера OT

носительно переменной
, rде
 > о.
Замечание. Рассмотрим однородное уравнение Эйлера
х n у(п) + alxп
1 y(п
1) + ... + апУ = о. (4.113)
Так как при замене х = e t это уравнение приводится к Jlинейному уравнению с по

стоянными коэффициентами, то оно допускает частные решения вида
у = e kt = xk,
rAe k
 постоянно. Задаваясь этой формой, ,леrко непосредственно найти эти реше

ния.
В иск,лючительном случае. коrда корни соответствующеrо характеристическоrо
уравнения кратные, частные решения у имеют более с,ложный вид
У = t' e kf = xk In' х (, = о, 1, ..., т)1


rде т
 кратность корня.


132




Пример. Решить уравнение
2" ,
х у + ху + у = х.


(4.114)


Решение. Полаrая


х = e t ,


будем иметь


d 2 . d d
2

 + ..JL + у = e t
dt 2 dt dt


или


d 2 У + у = e t .
dt 2
Характеристическое уравнение здесь имеет вид
k 2 + 1 = о.


(4.115)


Отсюда


k] -= i, k 2 =
i.
Будем искать частное решение уравнения (4.115) в виде
у = Ae t .
Подставляя У в (4.115), находим
2А е t == е t ,


следовательно,


A
l

2


и


У
 l e t

 2 ·
Так как корни характеристическоrо уравнения мнимые, то общее pe

шение уравнения (4.115) таково:
у = t et + C 1 sin t + С 2 cos t
и, следовательно, общее решения уравнения (4.114) есть
у =
 х + С 1 sin(lnx) + С 2 cos (lnx)
(С l' С 2
 произвольные постоянные).


Задания для самостоятельноrо решения
1. x2yH+xy'
p2y=0 (р
постоянно).
2. х 2 у" + 3ху' + у =
 .
3. х З у'n = б(х + у). Найти частное решение у = у(х), удовлетворя

ющее начальным условиям у( 1) = о, у'( 1) = 2, уН( 1) = 6.


133




I 9. СИСТЕМЫ ДИФФЕРЕНЦИAJ1ЬНЫХ УРАВНЕНИЙ
Если в задаче дифференциальноrо характера имеется несколько
искомых функций, то для определения этих функций, вообще rоворя,
следует составить столько дифференциальных уравнений, сколько
имеется функции. Так мы приходим к системе дифференциальных
уравнений.
Пусть, например, t
 независимая переменная их = x(t), у = y(t)

искомые функции. Допустим, что эти функции удовлетворяют систе-
ме уравнений




 = f(t, х, у), t

 = g(t, х, y),J
разрешенной относительно производных
; ,

 , rде f и g
 заданные
непрерывные функции.
Система TaKoro вида называется нормальной, а число уравнений в
нормальной системе называется ее порядком: таким образом, HOp

мальная система (4.116)
 BToporo порядка. Под решением системы
(4.11б) мы понимает любую совокупность двух функций


(4.116)


х = x(t), у = y(t),


(4.117)


которые будучи подставлены в эту систему обращают ее в тождество.
rеометрически в пространстве Otxy решение (4.117) представляет
собой некоторую линию, которая называется ин,mе
ральной кривой.
Система дифференциальных уравнений, как правило, имеет бесчис..
ленное множество решений, образующих поле инте
ральных KpU

8ЫХ. Чтобы из этоrо поля выделить одну конкретную интеrральную
кривую, в простейшем случае достаточно указать точку Мо (t о' Ха, Уа)
(рис. 37) искомой кривой, т. е. нужно задать начальное условие
х I t =t o = Х О ' У 1/ =/0 = У а .


Рис. 37


134




в приложениях к механике и физике независимую переменную t
часто рассматривают как время. В таком случае переменные х и у
можно интерпретировать как координаты некоторой точки М(х, у)
плоскости Оху. Эту плоскость обычно называют фазовой плоско

стью (в случае большоrо числа переменных фазовым пpocтpaHcт

ВОМ). Решение (4.117) носит название движения, а соотвеТСТВУЮlцая
кривая (4.117) фазовой плоскости, rде t иrрает роль параметра, назы

вается траекторией движения. Если предположить, что фазовая
плоскость заполнена непрерывно движущейся средой (поток жидко

сти), для любой точки которой проекции скорости движения в каж

дый момент времени t определяются уравнениями (4.116), то TpaeKTO

рию движения можно наrлядно представлять как траекторию
движения точки этой среды.
Если правые части системы (4.116) явным образом зависят от Bpe

мени t (нестационарный поток), то траектория, начинаЮlцаяся в
данный момент to в точке Мо(Хо, Уо), будет, вообще rоворя, зависеть
от этоrо момента. В случае же, если правые части системы (4.116) яв

ным образом не зависят от времени t (стационарный поток), то pac

пределение скоростей движения точек пространства для любоrо мо"
мента времени t одинаково и поэтому точки среды, занимающие в
какие
либо моменты времени t o и t' о положение Мо, будут иметь одну
и ту же rеометрическую траекторию движения (конечно, кинематиче

ские законы движения их будут различны).
Пример. Уравнение упруrих колебаний материальной точки в oд

ном измерении при отсутствии сопротивления среды имеет вид
d 2 x + А 2 х = О
dt 2 fJ '
rде
 > о
 постоянная величина.
Реш е н и е. Полаrая у =

 , получим систему дифференциальных
уравнений


dx dy А 2
di = у, dt =
tJ х.
( Движения этой системы имеют вид
х = Asin(
t + <р), у = A
cos(
t + <р),
rде А и <р
 произвольные постоянные.
Исключая отсюда время t, получим уравнение семейства фазовых
траекторий


х 2 у2
А2 + (
A)2 = 1.


(4.118)


135




Очевидно, что здесь траектории движения
 подобные эллипсы (рис. 38).
у


х


Рис. 38
Зная кривые на фазовой плоскости, можно составить примерное
представление о механическом движении. В нашем случае точка фа

зовой плоскости м(х, у) есть совокупность положения х и скорости у
материальной точки. Из уравнения (4.118) вытекает, что при любых
начальных условиях координата х и скорость у материальной точки
остаются оrраниченными, причем, чем больше отклонение х, тем
меньше скорость у, и наоборот. Кроме Toro, траектория замкнута и,
следовательно, механическая система через определенные проме

жутки времени возвращается к прежнему состоянию, т. е. движение
ее носит периодический характер.
З а м е ч а н и е. Систему, содержащую производные высших поряд-
ков от искомых функций и разрешенную относительно старших про-
изводных, путем введения новых неизвестных Функuий можно приве-
сти к нормальному виду. В частности, уравнение n-ro порядка,
разрешенное относительно старшей производной, можно записать в
виде нормальной системы n уравнений первоrо порядка.
Пример. Пусть


d 2
 = х 2 + у 2 + dx ,l
d:
 dt

dy ( dx )
 J
dt = ty + dt .
Решение. Полаrая


dx
 х
dt
 1,


получим нормальную систему
dx
 Х 1
"&
 l'

 = х2 + у2 + Х\.

dy 2 J
dt = ty + xl


136




Редукция нормальной системы к одному уравнению высше-
ro порядка. Одним из основных методов решения системы диффе

ренциальных уравнений является метод исключения, состоящий в
том, что при помощи дифференцирования системы получают ряд HO

вых дифференциальных уравнений, из которых, в совокупности с дaH

ными уравнениями, исключают все искомые функции, кроме одной.
Таким образом, приходят к одному уравнению, содержащему одну He

известную функцию.
Мы изложим этот метод применительно к нормальной системе BTO

poro порядка




 = f(t, х, У),

 = g(t, х, У).


(4.119)


Рассматривая х и у как ФУНКllИИ от t и дифференцируя по t, например,
первое уравнение системы (4.119). получим
d 2 x а[ д! dx д! dy

=
+

+


dt 2 dt ах dt ау dt


или


d 2 х а! а[ а[
 ( )
dt2 = дt + t ах + g ау = fI t, х, У .


(4.120)


Определяя из первоrо уравнения системы (4.119) функцию у (пред

полаrая, что это возможно), будем иметь


у = F(t, х,
; ).


(4.121)


Подставляя это выражение в уравнение (4.120), получим одно ypaB

нение 2
ro порядка относительно искомой функции x(t)
d 2 х
 t ( t dx )
dt 2
 2 ' Х, dt .


(4.122)


Если удастся найти общее решение этоrо уравнения


х = q> (t, C 1 , С 2 ),
то функцию у можно непосредственно определить по формуле (4.121 )
Очевидно, аналоrичным способом можно получить также диффе

ренциальное уравнение относительно у.
3 а м е ч а н и е. На практике часто бывает возможно произвести
исключение всех искомых функций, кроме одной, не пользуясь общей
схемой.


137




Пример. Решить систему
dx = t + Х
 2у dy 1 + + 4
dt ' dt = Х у.


(4.123)


Реш е н и е. Дифференцируя-первое уравнение, будем иметь
d 2 х = 1 + dx
 2 dy
dt 2 dt dt


или


d 2 x 1

 = t

 Х
 lO y .
dt 2


Так как


У = l ( t + Х
 dx )
2 dt '


(4.124)


то


d 2 x = t
 1
 Х
 5 ( t + х
 dx )
dt 2 dt


или


d 2 x
 5 dx + 6х =
l
 4t
dt 2 dt .
Характеристическое уравнение имеет вид
k 2
 5k + 6 = О,


(4.125)


откуда находим ero корни


k 1 = 2, k 2 = 3.


Ищем частное решение


х = А + Bt.


Получаем


о
 58 + 6(А + 8t) ==
l
 4t.


Следовательно,


А =
ы. В =
1
18' 3


и


Х = ы
 l t
18 з.


Поэтому


Х = C 1 e 2t + С 2 е 3!
 /8 03 + 12t).
Из формулы (4.124) находим
у =

 C 1 e 2t
 С 2 е зt
 3
 (1
 6t).


(4.126)


(4.127)


Совокупность формул (4.12б), (4.127), rде C 1 , С 2
 произвольные
постоянные, дает решение системы (4.123).


138




"онитие о первых интеrралах. Нетождественное соотношение


F(t,x,y)=C


(4.126)


(С
 произвольная постоянная) называется первым uнmе
ралом си

cTeMы




 = f(t, х. у).

 = g(t. х. у),


(4.119)


если оно обращается в тождество при подстановке вместо х и у KaKO

rо
нибудь решения этой системы. Зная первый интеrрал, можно одну
из искомых функций выразить через друrую и, следовательно, поря

док системы понизить на единицу.
В случае системы BToporo порядка (4.119), имея два независимые
между собой первые интеrралы


Ft(t, х, у) = C 1 , F 2 (t, х, у) = С 2


(4.127)


и разрешая полученную систему (4.127) относительно х и у, будем
иметь общее решение системы (4.119)
х = <1> 1 (t, С 1, С 2) , У = <1>2 ( t, С 1, С 2) . ( 4.128 )
Пример. Решить систему
dx = У dy
 х
dt '7ft
 .


(4.129)


Реш е н и е. Складывая уравнения почленно, будем иметь
:t (Х + у) = х + у.


Отсюда получаем первый интеrрал
х + у = С 1 et. ( 4.130 )
Умножая первое уравнение системы (4.129) на Х, а второе на у и
вычитая, будем иметь
х dx
 У dy = О или 1...4..(x2
 У 2) = О
dt dt 2 dt .
, Отсюда получаем еще один первый интеrрал
х2
 у2 = С 2. ( 4.131 )
Система уравнений (4.130) и (4.131) дает общее решение системы
(4.129) в неявном виде. Разрешая эту систему относительно х и у, Ha

ходим


Х = Ae t + Be
t, у = Ae t
 Be
t
(А, В
 произвольные постоянные).


139




Задания для самостоятеJlьноrо решения
1 dx dy
· di = Х + у, (ft = Х
 у.
Найти частное решение t удовлетворяющее начальным условиям
Х(О) = 1, У(О) = о.
d 2 x d 2 y
2. dt 2 = Yt dt 2 = Х.



 10. ОБ ОБЩИХ КРАЕВЫХ ЗАДАЧАХ
Для уравнений п
ёO порядка
F(X t у, y't ..., у(n» = О,


(4.132)


rде п > 2, постановка общей краевой задачи заключается в следую

щем: найти решение у = У(Х) уравнения (4.132), для KOToporo в фик

сированном наборе из т
 2 точек х = Х i (i = 1, ..., т) значения ero
caMoro Yi = Y(Xi) и ero производных y
S) = y(S )(Xi) (s
 1) удовлетво

ряют п независимым между собой
раНUЧНblМ условиям вида
G ( I ( (1) v ) , ( (j mv » )
 О
v Yl,Yl,...,Y] ,...,Ут,Ут,...,Ут

(v=l,...,п),


( 4.133 )


rде G v .......... заданные (вообще rоворя, нелuнейные) функции своих ap

rYMeHToB, а а 1 v' ..., а mV
 заданные порядки производных функции
у(х)*
Общая краевая задача может быть однозначно разрешимой, вовсе
не обладать решением или же иметь несколько (и даже бесконечно
MHoro) решений. Конкретный поиск решения подобной задачи следу

ет производить, по возможности, путем, аналоrичным указанному
при изложении краевых задач для уравнений BToporo порядка.
Пример 1. Найти решение у = у(х)уравнения
y]V + у" = о, (4.134)


удовлеТВОРЯЮlцее rраничным условиям
У (о) = у'(О) = 1, y(
 ) =
 , y'(
 ) = о.


(4.135)


* Так как для решения у = у(х) уравнения (4.132) ero производные порядка п и
выше выражаются (путем пос.ледовательноrо дифференцирования исходноrо
уравнения при естественном допущении о нужной 2ладкостu TaKoro решения)
через искомую функцию у и ее младшие производные у', ..., y(n
l), то можно
считать, что здесь справедливы неравенства а iv
 n
 1 (i = 1. ..., т; v = 1, ..., п).


140




Реш е н и е. Характеристическое уравнение (4.134) имеет вид
k 4 +k 2 = О, а ero корнями служат числа k 1 , 2 = о, k3,4 = Н. Поэтому
общее решение уравнения (4.134) можно записать формулой
У=С 1 + С 2 х + C 3 sinx + C 4 cosx, (4.136)
rде С 1 , С 2 , С з , С 4
 произвольные постоянные. Отсюда получаем


у(0)=С 1 + С 4 , y(
 )=Cl + С 2
 + С з .


(4.137)


Дифференцируя равенство (4.136), находим у' = С 2 +С З cos х
C4 sinx,
и потому


у'(О) = С 2 +С з , yl(
 )= С 2
C4.


(4.138)


Тем самым, из rраничных условий (4.135) приходим к системе
уравнений относительно С 1 ' С 2 ' С з , С 4 :
С 1 + С 4 = 1, 1
С 2 + G.3 = 1,

С] +
 С 2 + G.3 =
 , J
С 2
 С 4 = о.


(4.139)


Выражая из nepBoro, BToporo и четвертоrо уравнений системы
(4.139) переменные С} , С 2 ,G.3 через С 4 , получаем
С 1 = 1
 С 4 ' С 2 = С 4 , С З = 1
 С 4 . ( 4.140)
Подставляя эти представления дЛЯ С 1 ' С 2 , G.3 в третье уравнение сис

темы (4.139), приходим к равенству
(I
 С 4 ) +
 С 4 + (I
 С 4 ) =
 ,


которое можно переписать в виде
(

 2 ) С 4 =

 2.


Отсюда заключаем, что


С 4 = 1,
а тем самым, соrласно (4.140), и что
С} = О, С 2 = 1, С З = о.


Следовательно, единственным решением искомой краевой задачи
служит функция у = х + cos х.


141




Для систем уравнений общие краевые задачи также можно рас.
сматривать. Но при этом нужно иметь в виду, что разрешимость та-
кой задачи естественно ожидать лишь в случае, коrда удается пред-
ставить общее решение исходной системы дифференциальных
уравнений в виде функций от nекотОРО20 числа произвОЛЬНblХ пo

стОЯННblХ, а rраничные условия позволяют эти константы реально
определить. Приведем по этому поводу иллюстрирующие примеры.
Пример 2. В предыдущем Э 9 для системы уравнений
dx = t + х
 2u 1
dt
 '



 = 1 + х + 4у J


(4.141)


было найдено ее общее решение в виде соотношений
х = C 1 e 2t + C 2 e 3t
 1
 03 + 12t), }
у =

 Cle2!
 C 2 e 3t
 з
 (I
 6t)


(4.142)


с двумя произвольными постоянными С 1 и С 2 . Поэтому разрешимость
краевой задачи здесь можно ожидать, в частности, в двухточечной
ситуации, коrда в каждой из точек задается лишь по одному rранич-
ному условию для совокупности функций х = x(t), у = y(t): скажем, в
первой точке t 1 указывается значение для функции x(t) (или ее произ-
водной), во второй точкеt2
 для функции y(t) (или ее производной).
Например, полаrая tl = О, t2 = 1 и требуя выполнение rраничных
условий


х (t 1 ) = О, у (t 2 ) = О,


(4.143)


приходим К следующей системе уравнений относительно С l' .С 2 :
С 1 + С 2 = 1: , }
(4.144)
е 2 2 С 1 + е 3 С 2 = 3
 '
Из первоrо уравнения системы (4.144) имеем
С
 13 С
2
Т8
 1.


(4.145)


Подставляя это выражение дЛЯ С 2 во второе уравнение системы
(4.144), приходим К равенству
е 2 С 3 ( 13 С )
 5
"2 1 + е 18
 1
 36 '


142




которое можно переписать в виде
е 2 С 3 С
 5 13 3
2""" 1
 е 1
 36
 тв е .


Отсюда заключаем, что




 !lе З
С
 36 18

1
 е 2 3
T
e


1 26е З
 5
18е 2 2е
 1 '


(4.146)


а тем самым, соrласно (4.145), и что
С
 13 С
 13 1 26e3
5
 1 5
13e2 (4147)
2
 18
 1
 тв
 18е 2 2е
 1
 18е 2 2е
 1 . .


Следовательно, единственным решением краевой задачи (4.141),
(4.143) служат функции x(t), y(t), rде


x(t) = 1 26е 3
 5 e2t
 1 lЗе 2
 5 e 3t
 ..L(13 + 12t)
18е 2 2е
 1 18е 2 2е
 1 18 '


(4.148)


( ) 1 13е
 5 Зt 1 26е 3
 5 2t 1 ( )
у t = 18е 2 2е 2
 I е
 36е 2 2е
 I е
 36 1
 6t .


(4.149)


Пример 3. Рассмотрим систему уравнений


d 2 x 1
dt 2 = Y.


:
 = x.J


( 4.150 )


Для построения ее общеrо решения можно воспользоваться MeTO

дом исключения. Именно, дифференцируя дважды первое уравнение
d 2
в системе (4.150) и заменяя производную
 ее значением из BToporo
dt
уравнения данной системы, приходим к линейному однородному
уравнению четвертоrо порядка


d 4 x
 Х = о.
dt 4


(4.151)


Ero характеристическое уравнение k 4
 1 = О имеет корни
k] 2 = + 1, k3 4 = +i . Поэтому общее решение уравнения (4.151) MO

, ,
жет быть записано формулой


х = C1e t + C2e
t + сз sin t + С 4 cos [.


(4.152)


143




А так как в силу первоrо уравнения системы (4.150) должно выпол

няться равенство у = d2X 2 ' то имеем также формулу
dt


у = C}e t + C2e
t
 сз sint
 С 4 cost.


(4.153)


Тем самым, общее решение системы (4.150) описывается COOTHO

шениями


х = C1e t + C2e
t + Сзsiпt + C 4 cos.t, }
у = C1e t + C2e
t
 сз sint
 С 4 cost,


(4.154)


rде C 1 , С 2 , Сз, С 4
 произвольные постоянные.
Разрешимость краевой задачи здесь возможна не только в ДBYXTO

чечной ситуации, но и в ситуациях с заданием условий в трех или же
четырех точках: нужно лишь чтобы такие требования порождали бы
разрешимую систему уравнений относительно вышеуказанных KOH

стант. Конкретный вид rраничных условий, заключающих информа

цию о функциях x(t), y(t) и их производных В выбранных точках, MO

жет быть весьма разнообразным, но при этом естественно ожидать
«блаrополучный исход
 в отношении разрешимости получаемой для
искомых констант системы уравнений в случаях, коrда число
ранич

ных условий совпадает с числом разыскиваемых констант, т. е.
равно четырем.
В простейшей двухточечной ситуации, скажем, с точками t} = О,
t 2 =
 и rраничными условиями


х (t 1 ) = 1, у (t 1 ) =
 1, х (t 2 ) =
 1, у (t 2 ) = 1


( 4 .155 )


соответствующая система уравнений для констант С}, С 2 , С з , С 4 при

нимает вид


С 1 + С 2 + С 4 = 1, 1
С} + С 2
 С 4 =
 1, I
n n

е 2 С} + е
2 С 2 + сз =
 1' ]
n n
е 2 С 1 + е
2 С 2
 сз = 1.


( 4.156 )


Вычитая в системе (4.156) из первоrо уравнения второе уравнение,
из TpeTbero уравнения четвертое уравнение, находим, что


С 4 = 1, сз =
 1.


(4.157)


144




Подставляя найденные С з , С 4 в первое и третье уравнения системы
(4.156), для констант С 1, С 2 получаем линейную однородную систему
двух алrебраических уравнений
С} + С 2 = О, 1
1t 1t

е "2 C 1 + е
2 С 2 = O,J


....
с отличным от нуля определителем, единственныrM решением которои
будут служить числа


С} = о, С 2 = о.


(4.158)


Следовательно, краевая задача (4.150), (4.155), rде t 1 =0, t2 =
 ,
однозначно разрешима и ее решение определяется функциями
x(t) = cost
sint, y(t) = sint
cost.


Задания для самостоятельноrо решения
Решить следующие краевые задачи:


1. у'"
 5у" + 6у' = о; y(
I) = О, у'(о) = 1, у(1) = о.


 = 2х
 y.l
2. dy }; х(О) = о, y(
 ) = О.
dt = Х + 2у J




ЧАСТЬ 11


ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ С чАстныии
производныии


Под дифференциальным уравнением с частными производным'U
(сокращённо, дучп) понимается равенство, содержащее несколько
независимых переменных, неизвестную функцию от независимых пе

ременных и её частные производные по этим переменным. Порядком
старшей производной, входящей в состав уравнения. задается поря

док дучп. Функцией, имеющей соответствующие частные производ

ные и обращающей уравнение в тождество, определяется решение
дучп. Процесс нахождения решений дучп принято называть ero
интеzрированием. Дифференциальное уравнение с частными произ..
водными превращается в обыкновенное дифференциальное ypaBHe

ние, если независимая переменная одна.
В теории дучп наиболее изучены линейные и квазилинейные
уравнения первоrо и BToporo порядков. Ими мы далее и оrраничимся.


rлава 1
УРАВНЕНИЯ ПЕРвоrо ПОРЯДКА


в этой rлаве мы рассмотрим линейные однородные и квазилиней

ные дифференциальные уравнения с частными производными перво..
ro порядка. Особенностью таких уравнений служит тот факт, что Ha

хождение их решений сводится к интеrрированию обыкновенных
дифференциальных уравнении.



 1. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ
1. Определения. Линейное однородное уравнение в частных про

изводных nepeozo порядка определяется соотношением вида
n ди
LAi(Xl, ..., Х п)а;- = о, (1.1)
. 1 1
'=
rде Xl, ..., Х n
 независимые переменные, и = U(Xl, ..., Х n)....... неизве

стная функция, д ди
 ее частныle производные, A i = A i (Xl' ..., Х п)

xi


146




коэффuцuенmbl
 не зависящие от и. Будем далее полаrать, что ypaB

нение (1.1) рассматривается в некоторой области D переменных
Xl, ..., Х п' а коэффициенты уравнения:
1) непрерывно дифференцируемы в области D;
2) одновременно не обращаются в нуль ни в одной точке из D, т. е.


п
LA?(Xl, ..., Хп»О, (Xl, ..., хп)е D.
i=l


( 1.2)


Решением уравнения (1.1) будем называть любую непрерывно диф

ференцuруемую в D функцию и = U(Xl, ..., Х п)' обращающую paBeHCT

во (1.1) в тождество:


п
LA i (х\, 00., х n) ;;. = О, 'v'(x\, ..0' х n) Е D.
. 1 t
t=


rеометрически решение рассматриваемоrо уравнения можно интер

претировать как некоторую rладкую п
мерную поверхность в про


TpaHCTBe ОХ}, ..., Х п' и, называемую инте
ральной поверхностью
дляданноrоуравнения.ЗамеТИМ,чтолинейноеоднородноеуравнение
(1.1) всеrда имеет решение и = С, rде С
 любое постоянное число: Ta

кие решения называются очевидными и далее не обсуждаются.
Для соответствующеrо уравнения с двумя независимыми перемен

ными


Р(х, y)
: + Q(x, y)
; = о


( 1.1')


ero решение и = f(x, у) в пространстве Охуи представляет собой про

сто некоторую rладкую двумерную поверхность.
2. Характеристическая система и характеристики. Поста

вим в соответствие уравнению с частными производнымu (1.1) сис..
тему обыкновенных дифференциальных уравнений, в симметриче

СКой форме записываемую в виде
dXI

 dX n (1.3)
AI (XI , ..., Х п )
 ...
 An(XI, ..., Х п )'


а при ее эквивалентной записи в параметрической форме имеющей
вид

 = Ai(x\, ..., х n )' i = 1,2, о.., n (1.4)
(здесь t
 новая независимая параметрическая переменная). Ta

кую систему ОДУ называют характеристической для уравнения


147




(1.1), а ее решения (интеrральные кривые)
 характеристиками
этоrо уравнения.
В oroBopeHHbIx для уравнения (1.1) условиях ero характеристиче

ская система удовлетворяет теореме существования и единственно

сти решений. Поэтому через каждую точку области D проходит един

ственная характеристика уравнения (1.1), в параметрической
форме представимая в виде п функций
Xi = Xi(t), i = 1,2, ..., n. (1.5)
в случае уравнения с двумя независимыми переменными (1.1') ero
характеристическая система в симметрической форме вырождается
в одно ОДУ /
ZO порядка
P(

 у) = Q(

 у) или Q(x. y)dx
 Р(х. y)dy = О. (1.3/)


а в параметрической форме приобретает вид автономной системы
ОДУ 2
zo порядка



: = Р(х, у), 1


 = Q(x, y),J


( 1.4')


причем соответствующая ее характеристика может быть записана с
помощью двух функций


х = x(t), у = y(t).


( 1.5')


3. Первый интеrраn. Для системы ОДУ определено понятие
первоrо интеrрала. В соответствие с ним под первым интеzралом xa

рактеристической системы уравнения (1.1) будем понимать отлич

ную от константы непрерывно дифференцируемую в D функцию
g(Xl' ..., Х п ), которая на любой характеристике (1.5) aaHHozo урав..
нения (т. е. при подстановке в качестве aprYMeHToB Xl' ..., Х п COOTBeT

ствующих выражений Xl (t), ..., Х п (t» имеет постоянное значение:


g(Xl(t), ..., xn(t))=C \7'(Xl' ..., xn)eD, (l.б)


rде С .......... константа.
т е о р е м а 1. Если U = f(Xl' ..., Х п ).......... решение уравнения (1.1), то
функция f(Xl' ..., Х п ) является первым интеrралом для характеристи

ческой системы данноrо уравнения.
Обратно, если функция g(x 1, ..., Х n ) служит первым интеrралом xa

рактеристической системы уравнен
я (1.1), то и = g(x l' ..., Х п ) есть
решение этоrо уравнения.


148




д о к а з а т е л ь с т в о. Пусть u = f(Xl' ..., Х п) ....... решение ypaBHe

нин (1.1) t И тем самым справедливо тождество
п дf
LAi(XI, ..., Xп)
 = О V' (Xl' ..., хп)е D. (1.7)
. 1 t
1=


Подставим в (1.7) в качестве aprYMeHToB Xl' ..., Х п функции
Xl и), ..., Х п (t), определяющие какую
нибудь характеристику (1.5)
уравнения (1.1). Тоrда, дифференцируя f по t (по правилу дифферен"
цирования сложной функции) и учитывая, что всякая характеристи

ка уравнения (1.1) должна удовлетворять характеристической систе

ме данноrо уравнения, на основании (1.7) получаем:


п
df д[ dXt д{ dX n

 A ( ) д!

dt = дх!
dt + ... + dxn "dt

 i Хl' ..., Х п дх; = о.
t=l


Отсюда следует, что
[(Хl (t), ..., Х п (t» = с Vt,
rде С
 константа., А это и означает, что функция f(Xl' ..., Х п ) являет

ся первым интеrралом для характеристической системы уравнения
(1.1).
Пусть, обратно, функция g(Xl, ..., Х п) служит первым интеrралом
характеристической системы уравнения (1.1). т оrда для любоrо ре-
шения (1.5) этой системы имеет место тождество


g(Xl (t), ..., Х п (t» = с Vt,
rде С
 константа. Дифференцируя (1.8) по t, получаем
{lg dg dXl dg dX n f ( ) dg
О = dt = дх) "dt + ... + dxn "dt =
Ai Xl' ..., Х п aXi .
1=1


(1.8)


Отсюда следует, что
п dg
LA i (Xl' ..., Х п) дх. = О V (Хl' ..., Х п) е D,
. 1 t
1=


т. е. что и = g(x l' ..., Х п) является решением уравнения (1.1). Теорема
доказана.
В отношении уравнения с двумя независимыми переменными (1.1 ')
можно заметить, что ero характеристической системе будет COOTBeT

ствовать лишь один ее первый интеrрал вида g(x, у).


149




4. Общее решение. Пусть известны п
 1 первых интеrрала для
характеристическоЙ системы уравнения (1.1 ):


gl(Xl' ..., Х п ), ..., gn
l(xl' ..., Х п ),


( 1.9)


причем в области D они независим,ыl' т. е. для их якобиана имеет Mec

то невырожденность:


д( gt ' ... , g п
1 ) О \.-1 ( ) D
д{ . . )
 v Х 1, ..., Х п Е
X J1 ' ..., Х, n
!


(1.10)


по крайней мере при одном выборе п
 1 переменных X J . ,..., X J . из их
I п
1
набора х 1, ..., Х n. т оrда выражение


и = Ф(g 1 t ..., g п
 1).


(1.11)


rде Ф
 произвольная непрерывно дифференцируемая функция от
своих aprYMeHToB, будем называть общим решением линейноrо OДHO

родноrо уравнения (1.1 ).
Проверим, что формулой (1.11) при всяком выборе функции Ф за

дается решение уравнения (1.1).
в самом деле, пусть в выражении (1.11) функция Ф фиксирована.
Поскольку арrументами для Ф служат первые интеrралы характери

стической системы уравнения (1.1), то на любой характеристике это

ro уравнения функция (1.11) будет постоянной. Тем самым, paCCMaT

ривая Ф как функцию от переменных Xl, ..., Х п' заключаем, что она
сама является первым интеrралом для характеристической системы
уравнения (1.1). А тоrда из теоремы 1 следует, что выражением ( 1.11 )
задается решение для уравнения (1.1).
Отметим теперь, что если условие (1.1 О) реализуется, например, в
виде


д(gl , ..., gn
l) ..J. О \.-1 ( ) D
д( ) .,... v xl, ..., Х п Е ,
XI , ..., Xп
}


(1.12)


то любое решение


и == f(Xl' ..., Х n )


(1.13)


уравнения (1.1) может быть выражено формулой (1.11) при COOTBeT

ствующем подборе функции Ф.
Действительно, подставляя функции gi (i = 1, 2, ..., n .... 1) и f из
(1.9), (1.1 З) в уравнение (1.1), приходим К соотношениям вида
150




А dg 1 А dg l
 О 1
..: .


.
 ...... .
...
.


. .
...' l
А dgn
t А dgn
l О
1
 д + ... + п
 д = ' ]
xl Х п
д[ д[
Al
 д + ... + А п
 д = о.
xl Х п


( 1.14)


Относительно A 1 , ..., А п соотношения (1.14) представляют собой
систему однородных линейных алzебраических уравнений В силу
условия (1.2) эта система имеет нетривиальное решение, а значит, ее
определитель!!1 в области D должен быть равен нулю. Отсюда имеем
тождество


А de I d(gl, ..., gn
l ' [)
 О \.-1 ( ) D
L1 д( ) v Хl, ..., Х п Е .

 Xl , ..., Xп
1 'Х п



Тем самым, функции
gl(Xl,.'.,X n ), ..., gn
I(Xl, ...,X n ),f(Xl, ".'Х n )
в области D зависимы, т. е. существует нетривиальная непрерывно
дифференцируемая функция F от п переменных такая, что
F(gl, ..., gn
l' f) = о V(Xl, ..., хп)е D. (1.15)
А на основании (1.12) равенство (1.15) можно однозначно разре..
шить относительно переменной f и придти к выражению


t = h(gl, ..., gn
l) \/(XI, ..., хп)е D,


(1.16)


rде h
 соответствующая непрерывно дифференцируемая функция.
Поэтому решение (1.13) действительно может быть представлено в
виде и= h(gl, ..., g n
l), как и требуется в формуле (1.11). *
Для уравнения с двумя независимыми переменными (1.1 ') в слу

чае, коrда g(x, у) является первым интеrралом ero характеристиче

С,кой системы, общее решение можно записать в явном виде


u = Ф(g(х, у»,


( 1.11 ')


rде Ф
 произвольная непрерывно дифференцируемая функция


* Утверждения о зависимости функций gt, ..., gn-I, f с соблюдением равенства
(1.15), а также о возможности, 8 условиях (1.12), перейти от (1.15) к cooтHO

шенuю (] .16) требуют, вообще rоворя, более подробных обоснований, но их изло-
жение будет опираться на сведения, выходящие за рамки стандартноrо
втузовскоrо курса высшей математики.


151




I 2. ЗАДАЧА КОШИ для ЛИНЕйноrо ОДНОРодноrо УРАВНЕНИЯ
ОДНОЙ из важнейших задач, рассматриваемых в теории дифферен-
циальных уравнений, служит задача Коши, коrда решение уравне-
ния ищется удовлетворяющим заданным начальным условиям.
Для линейноrо однородноrо уравнения с частными производными
первоrо порядка


п
:LAi (Xl' ..., Х п) д ди. = О,
. x r
i=l


(2.1 )


в котором, без оrраничения общности, положим


А 1 (Xl ' ..., Х п)
 о \1' (Xl ' ..., Х п) Е D,


(2.2)


задача Коши ставится так:
среди всех решений уравнения (2.1) выделить такое ero решение


и = {(х), ..., х п ),


(2.3)


которое удовлетворяет начальному условию


ul X1 =хр = <Р(Х2, ..., Х п)' (2.4)
rде хр
 заданное число, а <Р(Х2, ..., Х n)
 заданная непрерывно диф

ференцируемая функция своих aprYMeHToB.
При данной постановке задачи Коши, естественно, полаrается, что
в (n + 1 )
MepHOM пространстве ОХ.... хпи соответствующая n-мерная
. ПЛОСКОСТЬХl =хр пересекается с областью D. Тем самым, в ней речь
идет о построении в этом пространстве п-мерной интеrральной по

верхности, описываемой уравнением (2.3), проходящей через задан

ную rладкую (n
 1 )
мерную поверхность


и = <Р(Х2,...,Х n ), Xl=Xr.


(2.5)


Если подобная задача Коши рассматривается для уравнения с дву-
мя .независимыми переменными


P(x,y)
: +Q(x,y)
; = о


(2.1')


с начальным условием


ulx=x o = <р(у),


(2.4')


152




то в ней требуется найти решение u = !(Х, у), для KOToporo изобража

ющая в пространстве Охуи интеrральная поверхность будет прохо

дить (в плоскости х = хО) через заданную кривую


и = <р(у), х = хо.


(2.5')


Пусть теперь


gt(Xl, ..., х n )' ..., gn
l(Xl, ..., Х n )


(2.б)



 независимые первые интеrралы для характеристической системы
уравнения (2.1), причем положим, что для них выполняется условие


d(gt ' 00.' gn
t) ..J- О \.-1 ( ) D
д( ) r V Х 1 ' ..., Х n Е .
Х2' о.., Х п


(2.7)


Тоrда можно сформулировать алzорuтм построения решения YKa

занной задачи Коши, состоящий из следующих трех этапов:
1) подставляя Хl =хр в первые интеrралы (2.6), составить систему
равенств


gl(XP,X2,...,X n ) = С!, 1
g 2 (х Р . х 2, .... х n) = С 2 .




:

'p :

... ".:,'
.

. . . ·
n
) J


(2.8)


с произвольными параметрами С 1, ..., С п
 1 ;
2) разрешая систему (2.8) относительно Х2, ..., х n (что возможно в
силу условия (2.7) ), найти выражения для этих переменных:


Х2 = Р2 (C 1 , ..., Cn
l ),)
хз = Рз (С). ..., Cn
),



. . . ·

 (
:.. '.:.: .


:) J


(2.9)


с соответствующими rладкими функциями;
3) подставляя выражения (2.9) в функцию <Р(Х2, ..., х n )' задающую
начальное условие (2.4), составить формулу


u = <Р(Р2 (C 1 ' ..., Cn
l), ..., Р n (С 1 , ..., Cn
l»


(2.10)


153




и положить в ней


rC 1 = gl(Xl,X2,...,Xп
1,Xп)'

 С 2 = g 2 (х 1 . х 2, ..., х n
 1, х n ) .
l


:
 .


: (


,

'''.::''
'


. х n).


(2.11 )


Такой алrоритм, действительно, приведет к решению рассматривае

мой задачи Коши, поскольку из соотношений (2.1 O)
.(2.11) дЛЯ u име

ет место: вo
пepвыx, представление (соrласно свойствам суперпози

ции rладких функций) вида (1.11), определяющеrо выражение общеrо
решения уравнения (2.1), а, вo
вmopыx, справедливость (в силу
(2.8» требования (2.4), задающеrо поставленное начальное условие.
В отношении задачи Коши для уравнения (2.1') с условием (2.4')
можно конкретизировать следующее: поскольку характеристическая
система в этом случае характеризуется лишь одним первым интеrра

лом вида g(x, у), то система (2.8) сведется к одному уравнению


g(X O , у) = С,
система (2.9) перейдет в одно равенство


(2.8')


у = р(С),


(2.9')


а из соотношений (2.10)
(2.l1) вытекает единая формула для иско

Moro решения задачи Коши


и = <p(p(g(x, у»).
i з. КВАзипИНЕЙНЫЕ УРАВНЕНИЯ
Рассмотрим теперь уравнения с частными производными первоrо
порядка вида


(2.10')


n
"LA i (Xl' ..., Х n' и) ::. = B(Xl, .... Х n' и).
. 1 t
'=


(3.1)


полаrая, что в заданной области Q переменных xl' ..., х п ' U коэффици

енты уравнения A i (Xl, ..., х n ' и) и ero правая часть B(Xl, ..., Х п ' и) есть
непрерывно дифференцируемые функции, причем, например,
A1(Xl,...,Xn,U)
 О \i(Xl,...,Xn,u)e а. (3.2)


Поясним, как решение TaKoro уравнения, называемоrо квазилuней

ным уравнением в частных производных первоrо порядка, может


154




быть сведено к решению пpиcoeдиHeHHO
O уравнения
 специально
строящеrося для Hero соответствующеrо линейно
о однородНО20
уравнения.
Пусть D
 область изменения переменных Xl' ..., Х N ' В которой pac

сматривается уравнение (3.1). Будем искать решение
и = f(xl,""x п ), (xl,...,xп)eD, (3.3)
уравнения (3.1) в неявном виде, т. е. полаrая, что должно выполнять

ся равенство


F(Xl,".'Xп,u) = О, (Xl,...,xп,u)e Q,


(3.4)


rде F
 непрерывно пифференцируемая в области Q функция, дЛЯ KO

торой

F I *0 \f(XI. .... Х п , и) Е N. (3.5)
и и = f (Хl ' ..., Х п )


т е о р е м а 2. Если выраженная из уравнения (3.4) функция (3.3)
непрерывно дифференцируема в области D и является решением для
квазилинейноrо уравнения (З.l), то функция
v=F(XI,"', Х п ' и), (Xl' ..., Х п , u)е Q, (З.6)
служит решением для присоединенноrо (к (3.1» уравнения
n
L,A j (XI..... Х п , и) :;. + В(ХI' ..., Х п . и)
 = о (3.7)
. 1 t
[=
на решении (з.з) исходноrо уравнения (З.l).
Д о к а з а т е л ь с т в о. Действительно, пусть выраженная из ypaB

нения (З.4) функция (3.3) в области D является непрерывно диффе

ренцируемой и служит решением для уравнения (З.l). Тоrда, в силу
(3.5), существуют непрерывные частные производные
dF
ди дх;
дх; =
 дР (i= 1,2, ..., n).
ди u == /(Х. ' о.., Х п )
Подставляя эти частные производные в уравнение (З.l), умножая за-
дР
тем обе части на
дii" и перенося все члены в левую часть, получаем
равенство


п
L,A j (XI. .... Х п , и) t:. + B(XI,"', Х п . и)

 = О. (3.8)
i=l t
 f( )
u
 Хl, ..., Х п


155




А равенство (3.8) и означает, что функция (3.6) служит решением
присоединенноrо уравнения (3.7) на реIllении (3.3) исходноrо ypaBHe

ния (3.1). Теорема доказана.
Данная теорема обладает тем недостатком, что для переменных
xl' ..., Х n ' и она требует реализации связи в виде формулы (3.3), rде
f(Xl' ..., Х п ), вообще rоворя, неизвестная функция. Поэтому на прак

тике поступают по"иному: считают, что функция F(Xl, ..., Х n ' и) долж

на строиться как решение присоединенноrо уравнения (3.7), в котором
все переменН,ые пОАа
аются независимыми. Тоrд
 присоединенное
уравнение (3.7) будет уже являться линейным однородным ypaвHe

нием, определенным в области Q переменных Xl"'..' Х п , и. Следова

тельно, для Hero можно будет написать соответствующую характери

стическую систему, в симметрической форме определяемую видом


dx} . dx n du
А} (XI, ..., Х п! и) = ... = Aп(Xl, ..., Х n ' и) = B(XI, ..., Х п , и)'


(3.9)


а в параметрической форме имеющей вид
dx,
 А ( ) 1
o

oo
oooloo
ol"oo::,o
o
:o
, l


п = А п (XI. 000' Х п . и),


 = B(Xl,...,Xп,u). J


(3.1 О)


Отсюда, если для такой характеристической системы известны ее n
независимых в области Q первых интеrралов


g 1 (Хl ' ..., Х n ' и), .... g п (Х 1, .... Х n ' и),


(3.11 )


то выражением


v=Ф(gI, ..., g п)'


(3.12)


rде Ф
 произвольная непрерывно дифференцируемая функция от
своих aprYMeHToB, определяется общее решение присоединенноrо
уравнения (3.7). А тоrда формулой
Ф(gI (Хl' .... Х п , и), ..., g п (Xl, ..., Х п ' и») = о (3.13)
будут задаваться (Н,еявным образом) решения искомоrо квазилиней

Horo уравнения (3.1).
Напомним, что при построении функции Ф для выражения (3.12)
мы использовали дополнительные о
ранuченuя, потребовав, чтобы


156




функция F служила бы решением присоединенноrо уравнения, в KO

тором все переменные Xl' ..., Х п ' и считались бы независимыми. Тем
самым, мы не можем, вообще rоворя, утверждать, что формулой
(3.13) описываются все решения уравнения (3.1). Решения для ypaB

нения (3.1), не определяемые формулой (3.13), называют спецuаль

ныМ,и, но их мы исключаем из рассмотрения. Поэтому соотношение
(3.13) мы будем называть просто формулой обще
о решения для ква-
зилинейноrо уравнения (3.1).
Заметим, что если u входит только в один из первых интеrралов
(3.11), например в последний из них, ТО формулу (3.13) можно запи

сать и в виде равенства


gп(Xl, ..., хп,и) = ЧJ(gl(Хl, ..., Х п ), ..., gn
I(Xl, ..., Х n »'


(3.14)


rде \}l
 произвольная непрерывно дифференцируемая функция от CBO

их aprYMeHToB. Разрешив равенство (3.14) относительно и, из Hero тоrда
получим явное представление для общеrо решения уравнения (3.1).
В случае соответствующеrо уравнения с двумя независимыми пе

ременными
Р(х. у. и)

 + Q(x. у. и)

 = R(x. у. и) (3.1')


указанный способ поиска ero решения u = {(х, у) сводится к построе

нию решения v = р(х, у, и) присоединенноrо уравнения вида
Р(х. у. и)
: + Q(x. у. и)
; + R(x. у. и)

 = О. (3.7')


чья характеристическая система может быть записана как в симмет

рической форме


dx
 dy
 du
Р(х,у ,и)
 Q(x,y ,и)
 R(x,y ,и)'
так и в параметрической форме


 = р(х, у, и), 1


 = Q(x. у. и).



 = R(x. у. и). J


( 3.9')


(3.1 о')


Такой характеристической системе будет соответствовать уже
только два независимых (в рассматриваемой области) первых интеr

рала


gl (Х, у, и), g 2 (Х, у, и),


(3.11')


157




и потому выражение (3,13) здесь перейдет в формулу общеrо решения
для уравнения (3.1') вида


Ф(gl (х, у, и), g2 (х, у, и» = О


(3.13')


с произвольной непрерывно дифференцируемой функцией Ф. В свою
очередь, коrда U входит только во второй из первых интеrралов
(3.11'), то формулу (3.13') можно переписать в виде


g2(X, у, и) = Ч'(gl (Х, у»,


(3.14')


в котором произвольной непрерывно дифференцируемой функцией
служит уже '1'. Наконец, в случае возможноrо разрешения относи-
тельно и равенства (3.14'), от Hero можно перейти к явному представ-
лению общеrо решения рассматриваемоrо уравнения (3.1').


Пример 1. Для уравнения
y

 x.Qц. = О
дх ду


найти общее решение.
Реш е н и е. Будем рассматривать данное уравнение на всей nлос

кости независимых переменныхх, у, rде только, соrласно нашим тре-
бованиям к коэффициентам линейноrо однородноrо уравнения, иск-
лючим точку (х = о, у = о).
Поскольку У уравнения лишь две независимые переменные, то ero
характеристическая система в симметрической форме определяется
одним ОДУ l-ro порядка xdx + ydy = о. Интеrрируя ero, приходим к
равенству х 2 + у2 = С, rде С
 произвольная константа (С> О). Отсю-
да заключаем, что первый интеrрал для характеристической системы
рассматриваемоrо уравнения задается функцией g(x, у) = х 2 + у2, а
ero общее решение записывается в явном виде U = ф(х 2 + у2), rде Ф

произвольная непрерывно дифференцируемая функция cBoero одноrо
aprYMeHTa.
rеометрически на плоскости Оху совокупность таких первых интеrралов пред

ставляет собой одн,оnараметрическое семейство концен,трических OKPY3iCHO

стей с центрами в н,ачале координат. При этом в пространстве Охуи функцией Ф
задается интеrральная поверхность, являющаяся поверхностью вращен,ия вокруе
оси Ои.


Пример 2. Для уравнения
y.Qц.
 xk = О
дх ду


158




решить задачу Коши с начальным условием


ul x = 1 =
 l + у2 de ! <р(у).


Реш е н и е. Прежде Bcero отметим, что в дальнейших рассуждени

ях, соrласно нашим требованиям к задаче Коши для линейноrо OДHO

родноrо уравнения, из плоскости независимых переменных Оху мы
исключим уже целую прямую у = о.
Из предыдущеrо примера следует, что общее решение уравнения
имеет вид и = Ф (х 2 + у2), rде Ф
 произвольная непрерывно диф

ференцируемая функция, а выражением g(x, у) = х 2 + у2 определя

ется первый интеrрал соответствующеrо характеристическоrо ypaB

нения. Подставляя х = 1 в первый интеrрал, на основании начальноrо
условия приходим К равенству х 2 +у21Х=1 = С, rде С
параметр.
Отсюда 1 + у2 = С и тем самым находим, что y= .JC 1 (С>I). Поэто

му, после п одста новк и найден ноrо значения у в функцию <р(у), полу

чаем и =
 l + у2 = .J l + (С
 1) = Jё. А тоrда. заменяя С выражением
для g(x, У), заключаем , что ре шением рассматриваемой задачи Коши
служит функция u =
 x2 + у2 .
rеометрически в пространстве Охуu найденной функцией и =
 х 2 + у2 задается
интеrраJ1ьная поверхность, являющаяся верхней частью прямоrо KpyroBoro конуса
(с вершиной в начале координат и осью в ращения Оu), проходящей (в плоскости
х = 1) через заданную кривую и =
 l + у2 (представляющей собой ветвь равнобоч

ной rиперболы и 2
 у2 = 1).


Пример 3. Для уравнения
ху.ш&. + (х
2и).Qц. = У и
дх ду
построить общее решение.
Реш е н и е. Соrласно нашим требованиям к коэффициентам KBa

зилинейноrо уравнения, далее будем считать, что ху '* О, т. е. из плос

кости переменных (х, у) исключим как прямую х = О, так и прямую
у = о. Кроме Toro, отметив сразу, что данное уравнение, очевидно,
допускает тривиальное решение и = О, далее будем также полаrать,
что и '* о.
Записывая характеристическую систему для присоединенноrо
(к исходному) уравнения в симметрической форме, имеем равенства
dx = d
 = du . Рассматривая в них равенство между первым и
ху x
 и уu


159




третьим членами, приходим к соотношению dx = du , которе можно
ху уи
переписать в виде дифференциальноrо уравнения du = dx . Интеrри

u х
руя ero, получаем lnl u 1= lnl Х I + C 1 , rде ё 1
 произвольная константа.
Представляя константу ё 1 в ло
арuфмuческой форме ё 1 = InlC11
(С 1 =1' О), Torдa находим lnl : 1= In1C11, а тем самым, после потенцирова-
ния приходим к равенствум. = C 1 . Поэтому выражением gl (Х, у, и) = R
х х
определяется первый интеrрал для исследуемой системы.
Рассматривая теперь в характеристической системе присоединен

Horo уравнения равенство между первым и вторым членами, получа

ем соотношение dx = d
 , которое мы перепишем в виде равенства
ху x
 u


dy
 x
2и
dx
 ху
Отсюда, используя уже имеющуюся возможность выразить u через
Х с помощью формулы и = С lX' приходим К дифференциальному ypaB

нению d d Y = 1
2Cl , которое, после разделения переменных. можно пе..
х у
реписать в виде ydy = (1 .... 2C 1 )dx. Поэтому после интеrрирования по

лучаем У2 2 = (1
 2C 1 )x + С 2 , rде С 2
 произвольная постоянная. Тем
самым, представляя константу С 2 в более удобной форме, полаrая
С 2 = 2С 2 , заключаем о справедливости равенства у2 = 2Х.... 4С l Х + С 2 .
Последним равенством еще не определяется первый интеrрал для
характеристической системы присоединенноrо (к исходному) ypaB

нения, поскольку оно содержит две произвольные постоянные. Но
в результате исключения в нем, используя связь u = C1X, константы
C 1 ' из Hero вытекает равенство с одной
произвольной постоянной
у2 + 4и.... 2х = С 2 . Поэтому выражением g2(X, у, и) = у2 + 4и.... 2х уже
задается дpy
oй первый интеrрал для этой системы.
Леrко проверить, что найденные первые интеrралы gl (Х, у, и) = R,
х
g 2 (Х, у, и) = у 2 + 4и .... 2х являются незавUСUМblМU, причем для них
невырожден якобиан вида
f
::) .
a(g g) (
...!l...
2 ) уu
В самом деле, имеем д( l' ) = det х 2 = .... 22. В силу orOBO

х, У О 2у х
ренных в начале условий, этот детерминант отличен от нуля и тем


160




самым утверждаемая независимость искомых первых интеrралов дей

ствительно имеет место.
Резюмируя все сказанное, заключаем, что для общеrо решения
рассматриваемоrо уравнения справедлива не явная формула
Ф(
 , у 2 + 4u
 2х ) = О, rде Ф
 произвольная непрерывно дифферен

цируемая функция от двух своих переменных.
Отметим, что при рассмотрении всех трех разобранных примеров мы вынужде

ны были сначала определять условия на области, делающие дальнейшие наши pac

суждения обоснованными. а лишь потом проводить непосредственные исследова

ния уравнений. В последующих упражнениях необходимые условия, при которых
предлаrается исследовать соответствующие уравнения, будут, по возможности,
конкретизироваться в формулировках самих заданий.


Задания для самостоятелъноrо реmения
1. Для уравнения
2х ди + у ди +
 ди = О (х > О)
дх ду 2 dz


построить общее решение.
2. Для уравнения


у ди + х ди = О ( У > О)
дх ду


. решить задачу Коши с начальным условием
ulx=o = 2 у 2.


3. Для уравнения
ди ( ) ди ( )
x
+ x+y
=u х>О
дх ду
построить общее решение.
4. Для уравнения


х ди + и дu = О (х > О)
дх ду


построить общее решение.
5. Для уравнения
(x+и)
: + (y+и)

 = х+у (yt;x)


построить общее решение.




r л а в а 11
РЯДbl ФУРЬЕ


Прежде чем перейти к изучению дифференциальных уравнений с
частными производными BToporo порядка, приведем необходимые
сведения из теории рядов Фурье.



 1. 0pToroHaпbHbIe системы функций и обобщенные ряды Фурье
1. Основные определения.
Оп р е д е л е н и е 1. Две действительные функuии <р (х) и 'v (Х),
определенные на интервале (а, Ь), называются на этом интервале op

тоzонаЛЬНblМU, если


ь
f q>(x)'I'<x)dx = О.
а


(1.1)


Определенная на (а, Ь) система действительных функций {<Рn (х)} Ha

зывается ортоzональной на рассматриваемом интервале, если Функ

ции этой системы на данном интервале попарно орmО20наЛЬНbl меж

ду собой:


ь
fq>n(x)q>m(x)dx = О. прип
m.
а


(1.2 )


Аналоrичные определения вводятся и для отрезка [а, Ь).
Оп р е Д е л е н и е 2. Под нормой функции <р (х) на данном проме

жутке понимается квадратный корень из соответствующеrо интеrра

ла от квадрата этой функции и обозначается 11 <р(Х) 11:
ь
Iq>(x) 11 = f[q>(x)]2 dx. (1.3)


Система функций называется нормированной, если норма каждой
функции равна единице.
О п р е Д е л е н и е з. Ортоrональная нормированная система назы

вается орmонормированной. Для нее выполняются условия


ь {
О, п * т,
f q> n (х) q> т (х )dx =

1, п
 т.
а


(1.4)


162




Введем символ Кронекера
 числовую функцию

 { О, п * т,
ь nт

1, п = m.


(1.5)


Тоrда для ортонормированной системы характеризующие ее соот-
ношения можно записать в следующем виде:


ь
J <Р п (х) <Р m (х )dx = б пт .
а


(1.6)


Комплексные функции


'(х) = а(х) + i
(x), g(x) = а} (х) + i
l (х),
(а,(х),
(x), а} (Х),
l (Х)
 действительны. i 2 =
 1), называются ор..
mО20наЛЬНblМU на промежутке (а, Ь), если
Ь
J f(x) g (x)dx = О,


а


rде


g (х) = а 1 (х)
 i
 1 (х)


........ сопряженная функция. В этом случае норма функции определяет-
ся формулой


{ Ь 1

11 {(x)
 = J I f(x)1 2 dx
 2,
а J


rде


If(x)1 =
a 2(x)+
2(x)


""'7"" модуль функuии {(х).
2. Нормирование ортоrональной системы функций.
Л е м м а. Всякую ортоrональную систему можно нормировать ум-
ножением ее членов на подходящие множители (нормирующие мно-
жители).
Д о к а з а т е л ь с т в о. Пусть в промежутке а
 х < Ь задана орто-
rональная система функций {<рn(х)}. Введем новые функции


163




( ) q> (х) }
'V п Х = 11q>:(x
l . Полученная таким образом система {\vn(x) будет op

тонормированнои.Действительно,
Ь Ь
J", п (х) '" т (x)dx = I 'Pп(x.)111 'Pт(x)I J <Р п (Х)<Р т (х) = ь пт ·
а а


3. Обобщенные ряды Фурье. Пусть некоторая функция [(х), за

данная в промежутке а
 х
 Ь, допускает разложение в ряд по opToro

нальной в этом промежутке системе функций {q>n(x)}:


со
[(х) = I,Cn<f) п (х).
n=l
Найдем численные коэффициенты Сп' предполаrая равномерную
сходимость ряда. Для этоrо умножим обе части (1.7) на <Рт(Х) (т =
= 1,2, ...) и проинтеrрируем по промежутку (а, Ь), считая, что ряд,
стоящий справа, можно интеrрировать почленно (ввиду ero paBHO

мерной сходимости):


(1.7)


ь ь со со Ь
Jt(x)<pm(x)dx = JI,cn<Pn(x)<Pm(x)dx = I,cnJ<Pn(x)<pm(x)dx.
а an=l n=l а


в силу ортоrональности системы {<Рn (х)} на (а, Ь), получаем вместо
ряда единственный член, соответствующий п = т.
Следовательно, заменяя т на n, будем иметь:
ь
J !(x)«pп(x)dx
Сп = а I 'Pп(x)1 2 (n = 1, 2, ...),


(1.8)


Коэффициенты СП' определяемые по этим формулам, -называются
коэффициентами Фурье функции [(х) относительно данной 0pToro

нальной системы функций {<Рп(Х)}.
Функциональный ряд (1.7) с коэффициентами Фурье (1.8) называет

ся рядом Фурье функций '(х) независимо от ero сходимости. Следова

тельно, функции f(x) можно поставить в соответствие ряд Фурье:


со
[(х)
 I,Cn<P п (х).
n=l
При определенных предположениях относительно функции [(х) ряд
Фурье этой функции будет сходиться и ero сумма будет равна [(Х).


164




! 2. Триrонометрические ряды Фурье
1. Триrонометрическая система функций и ее ортоrональ-
ность. Рассмотрим систему триrонометрических функций с общим
периодом т = 21:


{ nпх . nпх } (
 О 1 2 )
COS l' SlП 1 п
 , , ,....


(2.1 )


л е м м а. Система триrонометрических функций ортоrональна на
любом промежутке, длина KOToporo равна общему периоду этих
функций.
Д о к а 3 а т е л ь с т в о. Пусть С
 любое действительное число и
(С, С + 21) любой промежутокдлины 2l. В дальнейшем для определен

насти мы будем брать С =
l, т. е. роль промежутка (С, С + 2l) будет у
нас иrрать промежуток (
l, [). В силу определения ортоrональности
(1.2) мы должны убедиться, что интеrрал по этому промежутку от
произведения любых двух различных функций системы (2.1) равен
нулю, Т. е.


1
fcos n
 cos т
 dX =0. n *т.

l
1 l
f cos n
 sin т
 dx = о, f sin n
 sin т
 dx = о, n * т, (2.2)

l
l


(п = 1,2, ..., т = 0,1,2, ...).
Докажем, например, первое соотношение:
l 1
f Cos n1tx cos m1tX dx = l f [ cos (n
т)пx +cos (n+ m)1tx ] dx

l l 2 1 1


l
l


1 [ 1 . ( n
 m )пх 1 . ( n + т )хх ] 1 О
=
 SlЛ + SlЛ =
2 ( n
 т )х l ( n + m )п 1
 l


Остальные соотношения получаются аналоrично.
3 а м е ч а н и е. Вычислим квадрат нормы этих функций на проме

жутке (
l, [): .


l
111112 = f 12 dx = 21;

l


165




2 1 . 1
11 cos nr I = f cos 2 nr dx =
 f (l + cos 2
1tX )dx = 1. n = 1. 2. ... ;

l
l (2.3)
2 1 1
Ilsin nr 11 = f sin 2 nr dx =
 f o
 cos 2
1tX )dx = 1. n = 1,2. ....

l
l


Можно показать, что интеrрал от любой функции <р(х) периода т по
любому промежутку ДЛИНЫ Т не зависит от начала этоrо промежутка,
С+Т
т. е. величина интеrрала f q>(x)dx не зависит от С. Поэтому полу

с
ченные выше формулы (2.2) и (2.3) имеют место при интеrрировании
по любому промежутку (С, С + 21) длины, равной периоду функции
т = 21.
2. Триrонометрический ряд Фурье. Предположим, что некото-
рая функция {(х), определена в промежутке (
l, 1), а затем при осталь-
ных значениях х продолжена по закону периодичности с периодом
т = 21. Пусть /(х) допускает триrонометрическое разложение в ряд
Фурье:


00
( ) ао
 ( nпх . nПХ )
f х = 2 + L.J а п cos
 + Ь п Sln
 .
n=l 1 1


(2.4)


Коэффициенты Фурье ао, а п , Ь п этоrо триrонометрическоrо ряда
Фурье вычисляются по формулам (1.8) с использованием соотноше..
ний (2.3) и имеют следующий вид:
{ 1 { cos nnx
а п 1 1
= 1 f {(х) . n1tX dx. n = О, 1.2. ....
Ь п
l SlП[


(2.5)


Отметим частный случай Т = 2п (1 = п), коrда коэффиuиенты Фурье
считаются по формуле


{ 7t {
а п 1 cosnx
=
 f {(х). dx. n = О, 1,2, .., ·
Ь п 1t SlnnX

1t


(2.6)


Мы предполаrали, что заданная функция может быть разложена в
равномерно сходящийся ряд Фурье (2.4) с коэффициентами (2.5). Ka

кой должна быть функция [(х), заданная в промежутке (
 1,1), чтобы
ее триrонометрический ряд Фурье сходился и представлял функцию


166




{(х)? На этот вопрос дает ответ теорема сходимости для триrономет"
рических рядов Фурье. которую мы сейчас сформулируем
3. Теорема сходимости.
Оп р е Д е л е н и е. Функция называется кусочно"непреРЫ8НОЙ на
данном промежутке, если: 1) она оrраничена на этом промежутке;
2) имеет на нем конечное число точек разрыва, причем все точки раз

рыва 1
ro рода.
Пусть дана периодическая функция f (х) с периодом Т = 2l. Проме

жуток (
l, 1) при l =
 называется основной областью. Для этой фун

кции можно построить триrонометрический ряд Фурье:


00
{(х) -- а 2 0 + L( а п cos п7 Х + Ь п sin п7 Х ).
п=l
Т е о р е м а. Если функция [(х) кусочно
непрерывна в основной
области и имеет кусочно"непрерывную первую производную, то: 1) ее
соответствующий триrонометрический ряд Фурье сходится для любо

ro значения aprYMeHTa;
2) сумма S(x) триrонометрическоrо ряда Фурье равна функции
{(х) в точках ее непрерывности и равна среднему арифметическому
пределов функции слева и справа в точках разрыва функции, т. е.
( ) ( ) ) [(x
O)+ [(х+ О)
S х = f х ,rде х ........ точка непрерывности и S(x = 2 ' rде
х
 точка разрыва.
Так как в точках непрерывности х функции f(x) выполнены paBeH

ства


f(x
 О) = [(х + О) = [(х),
то для суммы S(x) имеем общую формулу
S(x) =
 [f(x
o) + f(x +0)].


Это одна из основных теорем теории рядов Фурье. Доказательство
этой теоремы мы здесь не приводим.
4. Лемма об интеrрале четной и нечетной функций.
О п р е Д е л е н и е. Функция называется четной, если она не меня

ет cBoero значения при изменении знака aprYMeHTa, т. е. {(
x) = [(х).
Функция называется нечетной, если при изменении знака aprYMeHTa
она меняет знак на обратный, сохраняя абсолютную величину, т. е.


[(
x) =
 !(х).


167




При вычислении коэффициентов Фурье может оказаться полезной
следующая лемма.
Л е м м а. Интеrрал в симметричных пределах от четной функции
равен удвоенному интеrралу по половине отрезка интеrрирования,
а от нечетной функции равен нулю, т.. е.
J f(x)dx = J 2!f(X)dX. если [(х)
 четная;

l l О, если [(х)
 нечетная.


(2.7)


д о к а 3 а т е л ь с т в о. Рассмотрим
l О l
J f(x)dx = J f(x)dx + J f(x)dx.

l
l О
Положим в первом интеrрале х =

, dx =
d
. Получим
1 О 1 1 l
J f{x)dx =
 J f(

)d
 + J f(x)dx = J f(

)d
 + J f(x)dx =

l 1 О О О
= J[f(
x) + f(x)]dx = J 2!f(X)dX. если [(х)
 четная функция;
О l О, если [(х)
 нечетная функция.


Лемма доказана.


5. Триrонометрические ряды Фурье четных инечетных
функций.
т е о р е м а. Триrонометрический ряд Фурье четной периодичес

кой функции содержит только косинусы кратных дуr. Триrонометри

ческий ряд Фурье нечетной функции содержит только синусы KpaT

ных дуr.
Д о к а з а т е л ь с т в о. Допустим, что функции [(х) соответствует
ряд Фурье (2.4) с коэффициентами (2.5).
Если /(х)
 четная функuия, то применяя лемму (2.7) к интеrра

лам (2.5), определяющим коэффициенты Фурье, мы получаем:
1 1
а =! J f(x)cos п1tX dx = 1 } f(x)cos п1tX dx (n
 О 1 2 ) (2 8)
п 1 1 1 1
 , , ,..., .

l О


168




1
Ь п = Н f(x)sin п7 Х dx = О (n = 0,1,2, ...), (2.9)

l


так как в первом случае под знаком интеrрала стоит произведение
четной функции на четную, т. е. четная функция, а во втором слу

чае
 произведение четной функции на нечетную, т. е. нечетная Функ

ция. Следовательно, для четной функции имеет место разложение


00
[(х) = а 2 0 + La n cos п7 Х .
п=l
Если t (х)
 нечетная функция, то в силу предыдущей леммы для
коэффициентов Фурье аналоrично имеем
1
а п = 1 f f(x)cos п7 Х dx = О, (n = 0,1, 2, ...); (2.11)

l


(2.10)


1 1
Ь п = Н f(x)sin nr;x dx =
 f f(x)sin п7 Х dx, (n = 1,2, ...).
1 о
Разложение самой функции будет иметь вид:


(2.12 )


00
[(х) = Lb n sin nr;x .
n=l
Тем самым теорема доказана.
В случае, если функция {(х) периода т = 2х (1 = х), полученные
выше формулы принимают вид:
для четной функции



(2.13)


00
[(х) = а 2 0 + La n cosпx,
n=l


(2.14)


7t
а п = ; f f(x)cosnxdx, (n = 0,1,2, ...);
о
для нечетной функции



(2.15)


00
f(x) = Lb n sinпx,
n=l


(2.16 )


1t
Ь п = ; f f(x)sinnxdx, (n = 1,2, ...).
о


(2.17)


169




6. Четное и нечетное продолжение функции. Пусть некоторая
функция !(х) задана только на участке 0< х < l. Для разложение этой
функции в ряд Фурье ее надо продолжить на промежуток
l < Х < о.
Это можно сделать различными способами. Например, эту функцию
можно разложить в промежутке (о, [) как в ряд вида (2.10) по косину

сам кратныхдуr с коэффициентами (2.11), так и ряд вида (2.13) по си

нусам кратных дуr с коэффициентами (2.12). Оба эти ряда внутри
промежутка (о, [) будут иметь суммой функцию {(х) или среднее
арифметическое в точках разрыва. Но вне промежутка они будут
представлять совершенно различные функции: ряд по косинусам даст
функцию, получающуюся из t(х) четным продолжением в соседний
промежуток (
l, О), а затем периодическим продолжением с периодом
т = 2l вне промежутка (
l, l). Ряд по синусам даст функцию, получаю

щуюся нечетным продолжением функции {(х) в соседний промежу

ток (
l, о) и затем периодическим продолжением с периодом Т = 2l
вне промежутка (
l, [).
Итак, функцию !(Х), заданную на промежутке (О, [), можно разло

жить бесчисленным множеством способов в зависимости от способа
продолжения ее в отрицательную область. В частности, ее можно раз

ложить в ряд косинусов (четное продолжение) или в ряд синусов (He

четное продолжение).
7. "опитие о разложении в ряд Фурье непериодических
функций. Функцию, заданную в основной области (
[, [), можно пе

риодически продолжить за основную область с помощью функцио

нальноrо соотношения t(х + 21) = {(х).
Для непериодической функции {(х) (
oo < х < +00) можно выделить
участок (
l < х <1), а затем взять периодическую функцию <р(х) с
периодом Т = 21, которая в промежутке (
l, [) равна [(х). Периодиче

скую функцию <р(х) можно разложить в ряд Фурье:


00
<р(х) = а 2 0 + :L( а n cos п7 Х + Ь n sin nr ).
n=l


(2.18)


Формула (2.18) верна на всей оси
oo < Х < 00. Можно написать подоб

ное разложение для функции !(х):


00
[( х) =
 +
 ( a cos nпх + Ь sin nпх )
2 k.J n 1 n l.
n=l


(2.19 )


170




Формула (2.19) будет верна только на конечном промежутке (
1, 1),
так как на этом промежутке !(х) и <р(х) совпадают.
Таким образом, непериодическую функцию можно разложить в ряд
Фурье только на конечном промежутке.
8. Комплексная форма триrонометрическоrо ряда Фурье.
Ряд Фурье (2.4) по триrонометрической системе функций с коэффи

циентами (2 5) может быть представлен в комплексной форме. Для
этоrо воспользуемся соотношениями


. nпх . nпх
е 'т = соs.!J:.'Ш. + i sin n1tx . е
'T = соs.!J:.'Ш.
 i sin nпх
l l ' l l


(2.20)


и выразим триrонометрические функции по формулам


[ . ппх . ппх ]
cos nпх = 1 elT +е
lT .
1 2 '


[ . nпх . nпх ]
'

t

sin п7 Х =
i е l
 е l .


(2.21 )


Отсюда получим


00
{( х )
 ао +
 ( a cos nпх + Ь sin nпх )

......2 LJ n 1 n 1

n=l
00 ( . . nпх . . nпх )

 ао
 an
lbn 'т а п + 'Ь n
IT

 2 +
 2 е + 2 е .
n=l


Введем обозначения:


l
СО = а 2 0 =
l f /(x)dx,

l
1 1
Сп = an;ib n = il f /(x
 cos nr
isin nr )dx = il f /(х)е
i '7 dx,

l
l


1 l
C
n = an
ibn = i/ f /(x)(cos nr +isin nr )dx = il f /(x)e i '7 dx

l
l
Здесь мы воспользовались выражением (2.5) для коэффициентов Фу-
рье и соотношениями (2.20). Отсюда окончательно получаем комп-
лексную форму ряда Фурье в следующем виде:


00 . kпх
!(х)= l:ckelT,
k=---oo


(2.22 )


171




1 . k7tX
C k = il f [(х)е
IT dx,

l


(2.23)


rде значок k принимает не только целые положительные но и отрица

тельные значения.
9. Интеrральная формула Фурье. Пусть функция f(x):
1) кусочно
непрерывна и имеет кусочно
непрерывную производ

ную !'(х) на каждом промежутке (
l, 1) с (
OO, +(0);
2) абсолютно-интеrрируема на оси (
oo, +00), т. е. существует интеr-
рал


со
fl f(x)ldx <-t«>.


(2.24 )


----со


Тоrда при
l < х < 1 эту функцию можно представить в виде ряда
Фурье:


. +00 . k1tx
{(х) = I,Cke lT ,
k=..-.oo


(2.25)


rде комплексные коэффициенты Фурье определяются по формуле
(2.23) (см. э 2, п. 8)


l . k7t

C k = il f [(
)e
IT d
,

l
(k = O,:tl, :t2, ...). Здесь, по сравнению с формулой (2.23), для удобст

ва дальнейших выкладок переменная интеrрирования х обозначена
друrой буквой
, что законно для определенноrо интеrрала.
Подставляя формулу (2.26) в формулу (2.25), будем иметь
+00 1 . k1t (х

)
[(х) = L il f [(
)e I 1 d
. (
l < х < о. (2.27)
k=---oo
l


(2.26 )


Введем обозначения


k
 =Лk' (k=0,:tI,:t2,...)


и


( k + Оп k1t 1t
М k = л k+ 1
 Л k = 1
 Т = Т,


172




откуда


1
 /:"Лk
l
 1t
Тоrда формула (2.27) примет вид
-t<ю l
[(х) = 2
 2 I1Лk J f(
)еiЛk(Х

)d
 (
l < х < Н. (2.28)
k =.....00
 1


Пусть теперь l
 00 и, следовательно,
ДЛk =

 о.
Формула (2.28) напоминает интеrральную сумму. Как известно,
если функция q> (Х) непрерывна на отрезке [а, Ь] и
а = Ха < XI < ... < Х п = Ь,
ДХk = xk + 1
 Xk (k = О, 1, 2, ..., п
 1),


то


n
l Ь
liт 2q>(Xk )I1ч = J q>(x)dx.
rnax!lx k ---7 О k=O а
Можно доказать, что при предположениях 1) и 2) для нашеrо ряда
(2.28) на промежутке (
oo, +00) при llЛk
 О будет верна аналоrичная
формула, rде Функuия q> имеет вид


(2.29 )


+00
q>(л) = J f(
)еiЛ(Х

)d



(2.30)


.....00


(в силу условия (2.24) интеrрал (2.30) абсолютно сходится).
Таким образом, переходя к пределу l
 00 в формуле (2.28) будем
иметь интеrральную формулу Фурье:


+00 +00
[(х) = 2
 f dл f f(
)еIЛ(Х

)d
 (
oo < х < +00) (2.31)


.....00
oo


или


+00
[(х) = J С(л)еIАхdл,


(2.31 а)


----со


rде


+00
с(л) = .l... J f(
)е
i'Л;d

2х


(2.316)


.....00


(спектральное разложение функции /(Х».


173




3 а м е ч а н и е. Как следует из теоремы сходимости рядов Фурье
(
 2, п. 3), в точках разрыва х функции f(x) левая часть формулы
(2.31) равна



 [f(x
 О) + {(х + О)].


10. ИнтеrраJl Фурье в действительном виде. Используя форму

лу Эйлера


e ia = cosa + i sina.,


формулу (2.31) можно записать в виде


+00 +00
{(х) = 2
 f dл f f(
)cos л(х

)d
 + (2.32)


.....00 .....00


+00 +00
+ 2i1[ f dл f f(
)siпЛ(х

)d
.


.....00 .....00


Так как мы предполаrаем, что функция {(х) действительна, то ее
мнимая часть равна нулю. Поэтому ИЗ формулы (2.32) получаем


+00 +00
{(х) = 2
 f dл f f(
)соsл(х

)d
 (....00 < х < +00). (2.33)



co ....со


11. Интеrральная формула Фурье ДЛЯ четных инечетных
функций. Так как
COSA(X

) = cosA х соsЦ + siпЛх siпЦ,
то формулу (2.33) можно переписать в виде


+00
{(х) = J[а(л)соsл.х +Ь(л)siпл.х]dл, (2.34)
.....00
rде
+со
а(л) = 2
 f f(
)cos Цd
 (2.35)
.....00
и
+00
ь{л) = 2
 J f(
)siпЦd
. (2.36)
.....00
174




Если функция {(х)
 четная, Т. е. !(
x) = {(х), то на основании
леммы (э 2, п. 4), имеем


+00
Ь('Л,) = 2
 J f(
)sin Цd
 = О.


....-00


Поэтому тоrда


+00
{(х) = J а('Л,)соs 'Лхd'Л,


(.....00 < Х < +00) t


(2.37)


....-00


т. е. справедливо так называемое «косинус
разложенuе функции
!(х)>>, rде
+00 +00
а('Л,) = 2
 J f(
)соsЦd
 =
 J f(
)соsЦd
. (2.38)
....-00 о
Если же функция f(x)
 нечетная, т. е. {(
x) =
f(x), то аналоrично
получаем


+00
а('Л,) = 2
 J f(
)cos Цd
 = О


---со


и


+00
{(х) = J Ь('Л,)siп 'Лхd'Л,


(
oo < х < +00),


(2.39)


.....()Q


«(сuнус
разложение» функции [(х)), rде


+00 +00
Ь('Л,) = 2
 J f(
)siпЦd
 =
 J f(
)siпЦd
 (2.40)
....-00 О


При мер 1. Построить интеrральное представление функции (рис 1)
f(x)= { l, Ixl<l;
о, 'х' > 1.
у


I
: 1/2 у = '(х) :
r-










i
I I



l


о


l


х


Рис. 1


175




Реш е н и е. Так как функция f(x)
 четная, то имеем


+00
f(x) = fа(л)соsл.хdл,


.....00


rде


+00 { l +00 1
а(л) =
 J f(
)соsЦd
 =
 fl.соsЦd
 + fО.соsЦd

 =
о о 1 J


. '1 j:
=l
SlП '



пА
=o


sin А!


пА


(2.41 )


На основании формулы (2.41) получаем


+00
f(x) =
 f Si
 лl cos л.хdл.


(Ixl*l).


(2.42)


.....00


в силу замечания (9.1) при х = 1 имеем
. +00 +00
f(l
 О) + (l + О) = 1 = 1. J sin лl cos лldл = ...L J sin 2лl dA.
2 2 1t Л 2п Л.


.....00


....со


Отсюда, полаrая 1 =
 , получаем замечательный uнтеzрал Дuрuхле


+00 +00
J Si
 л dл = 2 J Si
 л dл = п.
.....00 О


(2.43)


Пример 2. Разложить в ряд Фурье функцию /(х) = I
I в интервале

x < Х < х. Изобразить rрафик функции и
rрафики нескольких частич

ных сумм ряда Фурье этой функции. Пользуясь разложением, найти
сумму ряда Лейбница


00

 (
I)п
l 1 1 1
.t..J 2n
 1 = 1
 3 + 5"
 "7 + ....
п=l


Реш е н и е. Так как функция [(х)
 нечетная, то ее триrонометри

чес кий ряд Фурье (2.16) содержит только синусы кратныхдуr:


со
'(х) = I,b n sinпx,
n=l


176




rде коэффициенты Ь п вычисляются по формулам (2.17) и равны


7t
2 J . 2 [ (
 ОП 1 ]
Ь =
 slnпxdx =


 +
 .
n 7t 1t n n
О


Следовательно, в точках непрерывности


со
[ (х) = 1 = i
 sin(2n
I)x (х *0).
7t
 2n
1
n=1


Полаrая х =
 t получим


00

 (
I)n
1 = 1t
L. 2п
 1 4.
n=1


Частичные суммы данноrо триrонометрическоrо ряда равны:
81 = isin х,
7t


S2 = Sl + з
 siп3х и т. д.
На рис 2 изображены rрафики частичных сумм 81 и S2'


1t

2


8) 82
'......... ,", I
',\1


/7 О
/1
//


1t 1t Х
2


Рис. 2


Пример з. Разложить в ряд Фурье функцию [(х) = х 2 в интервале
(
п, п).
Реш е н и е. Так как данная функция
 четная, то имеет место раз..
ложение (2.14)


со
{(х) = a
 + La n cosпx,
n=l
rде коэффициенты а п вычисляются по формулам (2.15) и равны


1t 7t
ао =
 Jx2dx =
 x2, а п =
 Jx2cosnxdx = 4(:
)п .
о о


177




Следовательно,


со
2 2
 (
on
[(х) = х =
 + 4
7COSпX.
n=1


Пример 4. Разложить в ряд Фурье функцию
[(х) = Icos xl.
Реш е н и е. Данная функция
 четная и имеет период 1t (21 = п)
Следовательно, для нее имеет место разложение (2.10)


со
Icosxl = a
 + la n cos2пx,
n=1


rде коэффициенты а n вычисляются по формулам (2.8) и равны


7t
4 f 4(
oп+l
а п = 1t cos Х cos2пxdx = п(4n2
O .
О


Следовательно,


со
Icosxl = .2. + .i l (;I
п+; cos2nx.
1t 7t n

n=l


Задания для самостоятелъноrо решения
1. Разложить в ряд Фурье в указанных интервалах следующие
функции:
а) [(х) = I х I в интервале (
п, п);
б) [(х) = х в интервале (
п, п);
в) f(x) = п 2
 х 2 в интервале (
п, п);
[ А
r) {(x)=
 в:
t А;В . если x=
x. О, 1t
на cerMeHTe [
п, п], rде А и В постоянные;
д) {(х) = xcos х в интервале (

 ,
 ).
2. По казать справедливость следующих равенств:
со
)
 ( .... 1) n cos(2n+ 1) = 1t
.к < х < п .
а k.i 2п + 1 4' 2 2'
n=о


если



п<х<О,
О < х < П,


если


178




00

 п2
зх2
б)
(
l)п со: 2 пх = 12 '
п
 х
 п;
п=l


00

 1 . п 2 х х 3
в)
(
Oп+ SI

X = 1; ,
п
 х
 п.
п=l
3. Функцию /(х) = sin 4 x разложить в ряд Фурье.
4. Разложить в ряды Фурье следующие периодические функции:
а) [(х) = sign (cosx);
б) [(х) = arcsin (sinx);
в) [(х) = I sin х 1.
5. Указанные ниже функции разложить в интервале (О, п) в непол

ные ряды Фурье: а) по синусам кратных дуr, б) по косинусам кратных
дуr. Нарисовать rрафики функций и rрафики частичных сумм COOT

ветствующих рядов в области их существования.
{ l' если О < х <
 '
а) /(х) =
О, если

 х < п;
б) '(х) = х.
6. Показать справедливость следующих равенств:
00
)
 sin(2п+ ОХ
 1!. О .
а k.J 2n+l
 4' <х<п,
п=О


00
L . 1t Х
б ) sт пх =......:...... О < х < 2п.
п 2 ' ,
п=l


00
в)
 cos(2п+ ОХ = п2
2xx О
 х
 п;
LJ (2n+ 1)2 8'
п=О


00 2 2
)
 cosпx = 3х
61tX+ 2п О 2
r LJ п 2 12 '
 х
 п;
п=l


00 3 2 2
)
 sin пх = х
3пx + 2п х О 2
д k.J п 3 12 '
 х
 п.
n=l
7. Разложить в ряды Фурье в интервале (О, п) по синусам кратных
дуr функции:
а) [(х) = х(п
 х); б) [(х) = sin
 .


179




8. Разложить в рЯДЫ Фурье в интервале (О, п) по косинусам KpaT

ных дуr функции:
а) f(x) = { l
 2
 ' если 0< х '5:2h,
О,
{ 1 если
б) f(x) = О ' ,
если


если 2h < х < п;
О < х '5: h,
h < х '5: п.


9. Разложить в указанных интервалах в неполные ряды Фурье:
А) по синусам кратных дуr и Б) по косинусам кратных дуr следующие
функции:
а) f(x) = 1 в интервале О < х < 1;
б) {(х) = х в интервале О < Х < l.
10. В указанных интервалах разложить в ряды Фурье функции:
а) [(х) = Ix I в интервале
 1 < Х < 1;
б) f(x) = 10
 х в интервале 5 < Х < 15.
tl. Представить интеrралом Фурье следующие функции:
а) {(х) = { signx, если I х 1< 1,
О, если Ixl> 1;
б) {(х) = { 1' если Ixl < 1,
О, если Ixl > 1;
в) f(x) = { 1
 I х 1, если I х 1'5: 1,
О, если I х I > 1;
r) [(х) = ......L..
1+ х 2


у к а з а н и е. Воспользоваться интеrралом Лапласа


+00
J cosa.x dx = 1t e
lal;
1 + х 2 2
О


д) f(x) =
 l х 2 .
+х


у к а з а н и е. Воспользоваться интеrралом


+00
J xsinax dx = 1t signae
lal;
1 + х 2 2
О


180




е) [(х) = { sinx, если
O
 если
ж) {(х) = e
1 xl, (о: > О);
у к а з а н и е. Воспользоваться интеrралом


Ixl
1t,
Ixl>1t;


+00
J e
ax cosbxdx == а (а> О);
а 2 + ь 2
О
з) f(x) = e
x2 ;
у К а з а н и е. Воспользоваться интеrралом


+
 ь 2
J e
ax2 cosbxdx =
И е"4fi (а >0);
о
rl, если
l<x<O,
( I
, если х =
 1, О, + 1,
и)f х) =
 1
l х, если О < х < 1,
О, если Ixl > 1.
12. ФУНКЦИЮ f(x) = e
X, (О < х <;-00) представить интеrралом
Фурье, продолжая её: а) четным образом; б) нечетным образом.
у к а з а н и е. Воспользоваться интеrралами


;-со +00
J e
ax cosbxdx = а . J e
ax sinbxdx = Ь
а 2 + Ь 2 ' а 2 + ь 2
О О
(здесь а > О).




r л а в а 111
КЛАССИФИКАЦИЯ УРАВНЕНИЙ BTOPOrO ПОРЯДКА


в этой rлаве дается классификация линейных относительно CTap

ших производных уравнений BToporo порядка с двумя независимыми
переменными.


t 1. Основные определения
Мноrие задачи физики и техники приводят к дифференциальным
уравнениям в частных производных.
О п р е Д е л е н и е 1. Уравнением в частных производНbtХ назы

вается соотношение, которое связывает неизвестную функцию He

скольких переменных и (Xl, Х2, . . . ,Х п ) и ее частные производные:
Ф( ди дu дтu ) О
Хl, Х2' ..., Х п , и, дх ,..., дх ,..., тl тп ,... = ,
I n дх} ... дХ п


(1.1)


rде Ф
 заданная функция своих aprYMeHTOB.
О п р е Д е л е н и е 2. Решением уравнения в частных производных
(1.1) называется всякая функция, которая после подстановки вместо
неизвестной функции обращает это уравнение в тождество по незави

симым переменным.
О п р е Д е л е н и е 3. Порядок старшей производной, входящей в
дифференциальное уравнение, называется порядком этоrо ypaB

нения.
В математической физики наиболее часто встречаются дифферен

циальные уравнения BToporo порядка. Основными из них являются:
уравнение колебаний cтpYHbl


д 2 u 2 д 2 u .
dt 2 = а дх2 '


(1.2 )


уравнение теплопроводности
дu = а 2 д 2 и .
dt дх 2 '


(1.3 )


ураsненuеJ7аnласа


д 2 u д 2 и О
ах 2 + д у 2 = .


( 1.4)


182




t 2. Приведение к каноническому виду линейных относительно
старших проиэводных уравнений BToporo порядка с двумя
неэависимыми переменными


1. Замена переменных в уравнении. Рассмотрим линейное от-
носительно старших nроизводНbtх уравнение BToporo порядка,
определяемое видом


( ) д2 и д 2 u ) д2 и ( дu ди )
А х, у ах 2 + 2В(х, у) ах ау + С(х, у ау2 = F х, у. и, ах ' ау ,


(2.1)


rде х, у
 независимые переменные, и = и(х, у)
 неизвестн,ая фун

кция, А = А(х, у), 8 = 8(х, у), с = С(Х, у)
 коэффициенты ypaBHe

ния, не зависящие от и, F = Р( х, у, и,

 ,
; )
 ero правая часть,
причем будем считать, что уравнение (2.1) рассматривается в неко-
торой области D переменных (Х, у). Положим, что коэффициенты
данноrо уравнения непрерывно дифференцируемы в D, а ero правая
часть является непрерывно дифференцируемой функцией в заданной
области Q изменения своих aprYMeHToB. Наконец, потребуем, чтобы в
области D искомые коэффициенты одновременно не обращалuсь БЬL
в нуль.
Назовем выражение


Ll = 82
 АС
дискриминантом уравнения (2.1) и будем rоворить, что уравнение
(2.1) в области D принадлежит:
а) rиперболическому типу, если!1 > о;
б) параболическому типу, если А. = о;
в) эллиптическому типу, если 11 < о.
Введем вместо (Х, у) новые независимые переменные (
, 11) (рис. 3):


у


х


Рис. 3


183




Пусть преобразование переменных



 = <р(х, у), 11 = 'II(x, у)


(2.2)


является невырожденным, Т. е. якобиан
aq> dv
ах ах
J = dq> a'll ;t О
ау ау


в области D.
Производные в новых независимых переменных (
, 11) вычисляют

ся по формулам:
r ди = ди
 + ди dll . аи = ди д
 + ди д1l
дх д
 ах iЛ1 дх' ау д
 ду дТ) ду ,
д 2 и = д 2 и (
 ) 2 + 2 д 2 и
 ih1 + д 2 и ( iЩ ) 2 + ди д2
 + аи д 2 Т)
дх 2 д
2 ах д
дrr ах ах дтi 2 дх д
 ах 2 дч дх 2 '
а 2 и д 2 и ( д
 ) 2 д2и a
 dч д 2 и ( <Л1 ) 2 аи д2
 ди а 2 Т)
д у 2 =
2 ду + 2 д!;дq ду ду + дq2 ду + д!; д у 2 + дq д у 2 ' (2.3)
а 2 и = д 2 и д
 а; + д 2 и ( a
 iЛ1 + д
 iЩ ) +
дхду д
2 дх ау д
iЩ ах ау ау дх
+ д 2 и дтt ih1 + ди a2
 + ди д 2 11
d11 2 дх ау д
 дхду dr1 дхду .


Подставляя значения производных из (2.3) в уравнение (2.1), полу

чим:


д 2 и а 2 u д 2 u ( ди ди )
А 1
2 + 281 d1;дq + С 1 дq2 = F 1
,11, и, d1; , дq I


(2.4)


rде


r А = A ( dq» 2 + 28 aq> aq> + C ( aq» 2
j 1 ах дх ду ду'
В = А dq> д", + B ( dq> d'V + дц> d'V ) + С дц> d'V (2.5)
I I ах дх ах ду ау ах ду ау ,
С 1 = А ( a'V ) 2 + 2В a'V dv + С ( d'V ) 2
ах дх ау ау
При преобразовании (2.2) порядок дифференциальноrо уравнения
(2.1) не может увеличиться. Заметим, что в уравнении (2.4) коэффи

циенты А) = Al(
' 11), В) = Bl(
' 11) и С 1 = CI(
' 11) не MorYT OДHOBpe

менно обращаться в нуль.


184




Действительно, производя обратное преобразование
х = <1>1 (
, 11), У = Ч'1 (
, 11),
мы должны вернуться к исходному уравнению (2.1), rдеА2 + 82 + C2

;f. о. А это невозможно, если в некоторой точке (
, 11) имеем
А? +812 +С? = о.
Таким образом, уравнение (2.4) также есть уравнение BToporo по

рядка.
Леrко непосредственно убедиться, что


8[
A]Cl =J2(82
AC).


(2.б)


Отсюда следует инвариантность типа уравнения при преобразовании
переменных.
Таким образом, при невырожденной замене независимых перемен

ных в линейном дифференциальном уравнении не меняется:
1) порядок уравнения,
2) линейность,
3) тип уравнения.
2. Характеристики уравнения.
О п р е Д е л е н и е. Под характеристически.м семейством кривых
понимается однопараметрическое семейство, обладающее тем свой

ством, что если параметр семейства принять за новую криволиней

ную координату, то в преобразованном дифференциальном ypaBHe

нии будет отсутствовать член, содержащий вторую производную
неизвестной функции по этой координате.
Всякая кривая, входящая в характеристическое семейство, называ

ется характеристикой.
Например, если



 = <р(х, у)

 характеристическое семейство, то А 1 = О. то есть
A ( dq» 2 + 28 dq> dq> + C ( dq» 2 = О
дх дх ду ду
в силу соотношения (2.5).
Пусть


(2.7)


<р(х, у) =
 = const (2.8)
некоторая фиксированная характеристика. Дифференцируем (2.8):
а<р dx + а<р d у = О
дх ду


185




или


dy d
aq) =
 = к = const.
ах
 ау


Отсюда


дч>
 dy' дч> dx
дх
 К' ду =
 к .
Подставляя (2.9) в (2.7), будем иметь:
A(dy)2
 2B;
dY + C(dx)2 = О


(2.9)


или


A(dy)2
2Bdxdy + C(dx) 2 = о.


(2.10)


Полученное уравнение (2.10) называется дифференцuаЛЬНblм, ypaв

нением характеристик.
При dx
 О оно эквивалентно следующему уравнению:


( d y ) 2 dy
А

 2B
+C=0
dx dx


или


dy
 B+.JB2
AC
dx
 А


dy
 B
.JB2
AC
dx
 А


(2.11) ,


Аналоrично, если 11 = 'I1(x, у)
 характеристическое семейство, то
C 1 = о, а характеристики удовлетворяют также уравнение (2.10).
Итак, если выбрать в качестве новых независимых переменных
 и
11 характеристики, Т. е. общие интеrралы уравнения (2.10), то преоб

разованное уравнение (2.4) примет наиболее простой вид.
3. Канонический вид уравнения rиперболическоrо типа.
Для уравнения rиперболическоrо типа в области D справедливо Hepa

венствов2
AC > О, а общие интеrралы <р(х, у) = const, 'I'(x, у) = const
уравнений (2.11) действительны и различны. Поэтому уравнение rи

перболическоrо типа имеет два различныхсемействадействител ьных
характеристик.
Пусть в преобразовании (2.2)



 = 'Р(х, у), 11 = 'I'(x, у).
Тоrда в силу (2.5) в уравнении (2.4) коэффициенты
Al =C 1 =0.


(2.12 )


186




Якобиан J в рассматриваемой области предполаrается отличным ОТ
нуля. Поэтому из соотношения (2.6) следует, что
В] "# о,


и уравнение (2.4) примет вид:
а 2 u
281 а
iЩ = Fl.


Разделив на 281' получим
д 2 и t ( }:. аu аu )
d
dr1 = 1
, 11, и, д
 ' iЛ1 .


(2.13)


Это
 канонический вид уравнения
uперболическо
о типа.
Полаrая
 = а: + р. 11 = a:
 р. rде а=

 1') .
=
;1')
 новые перемен-
ные, можно получить вторую каноническую форму уравнения rипер-
болическоrо типа:


д 2 u д 2 u * ( * )
да2
 д
2 = f f =4fl .


Простейшим примером уравнения данноrо типа может служить
уравнение колебаний струны
д 2 u д 2 u
ах 2
 д у 2 = о.


4. Канонический вид уравнения параболическоrо типа. Для
уравнения параболическоrо типа в области D


B2
AC=0.


(2.14)


Следовательно, один из коэффициентов А и С отличен от НУЛЯ t так
как мы предполаrали, что коэффициенты А, В и С уравнения (2.1) не
обращаются одновременно в нуль.
Пусть, например, А #; о. т оrда уравнения (2.11) совпадают:
dy В ( )
dx = А . 2.15


Мы получаем один общий интеrрал уравнения характеристик (2.10):


<р(х, у) = const.
Следовательно, уравнение параболическоrо типа имеет одно се-
мейство действительных характеристик.


187




() .
Предполаrая, что
 *0, в уравнение (2.1) введем новые пере мен-
ные


; = <р(х, у), 11= у;


(2.16)


при этом


а<р д<р
J = дх ду =
 * о.
о 1


Тоrда в силу (2.5) в уравнении (2.4) коэффициент Al = о, а
В = А а<р dt1 + В ( д<Р iЩ + а<р dт1 ) + С д<р iЩ = в а«р + с д<р .
1 ох ах ах ау ау дх ду ау дх ду


(2.17)


Покажем, что коэффициент В} = о. Для этоrо уравнение (2.7), которо-
му удовлетворяют семейства характеристик


А ( д<р ) 2 + 2B
 а<р + с ( д«р ) 2 = О
ах дх ду ду ,


(2.18)


умножим и разделим на с. Используя соотношения (2.14) и (2.17), по-
лучим


( ()(р ) 2 ( ()(р d<p ) 2
( AC
B2 )
 + B
+C
 В 2
ах ах ду
..J...
 О
с
 с
 ,


откуда следует, что В 1 = о.
Таким образом, уравнение (2.1) параболическоrо типа в новых пе..
ременных (2.16) принимает следующий вид:


д 2 u
С 1 дтt 2 = Р 1


или


д 2 и f (
 ди ди )
iЩ2 = 1
,11, и, д
 ' iЛ1 .


(2.19 )


Это
 канонический вид уравнения nараболuческоzо типа.
Примером уравнения параболическоrо типа может быть уравнение
теплопроводности:


д 2 u
 ...L дu
дх 2
 а 2 ду


188




Заметим, что если коэффиuиент С = О. то из (2.14) получаем в = О,
т. е. тоrда уравнение (2.1 )изначально имеет канонический вид (2.19)
и преобразование (2.16) излишне.
Можно показать, что в параболическом случае любое преобразова..
ние вида:



 = <р(х. у). 11 = 'I'(X, у)


с якобианом J,* О приводит уравнение (2.1) к каноническому виду.
5. Канонический вид уравнения эллиптическоrо типа. Для
уравнения эллиптическоrо типа в области D справедливо неравен-
ство 82
 АС < О и правые части уравнений (2.11) комплексны. Пусть
<р(х, у) = const, 'I'(x, у) = const

 комплексные интеrралы этих уравнений. Переходя к комплексным
переменным



 = <р(х, у), 11 = 'J!(X, у)


(2.20)


получим, как и в случае уравнения rиперболическоrо типа, преобра

зованное уравнение (2.4) в следующем виде:


д 2 и
д
ёh1 = Л.


(2.21 )


Чтобы не иметь дела с комплексными переменными, введем новые
. переменные а. и
:


а

+11 . А =

11

 2 ,
 2i'


так что



 = а. + i
; 11 = а.
 i
.
При этом уравнение (2.21) принимает вид:
д 2 u д [ ди ] д [ ди да ди д
 ]
д
дтt = dr1
 = дтt да д
 + дi3
 =

 д [ ди 1 ди 1 ] 1 [ д2 U 1 д 2 U ( 1 )]

 ih1 да "2 +
 2i = 2 да 2 "2 + дaд

 2i +
1 [ д2и 1 д 2 и ( 1 )] 1 ( д2и д
и )
+ 2i д
 да 2 + др 2
 2i = 4" да 2 + д
 2 = 11


или


д 2 и д 2 и *
да 2 + д
 2 = f ,


(2.22)


r Д е f* = 4 f 1 .
Это
 канонический вид уравнения эллuптuчеСКО20 типа.


189




Простейшим примером уравнения эллиптическоrо типа является
уравнение Лапласа.
3 а м е ч а н и е. Может случиться, что уравнение (2.1) в разных ча

стях области D принадлежит различным типам. Примером TaKoro
уравнения смешанноrо типа может служить уравнение Трикоми
д 2 u д 2 и
У дх 2 + д у 2 = о.


При у > о оно принадлежит эллиптическому типу, .при у < о
 rипер

болическому типу, а у = О
 линия параболичности.


I З. Задачи с начальными данными
1. Задача Коши. Рассмотрим общую постановку задачи с началь

ными данными для уравнения:


L[u] = F( х, у' и,

 , :: ).


(3.1)


rде оператор
[ ] ( ) д2 и д 2 u ( ) д2 и
L u = А х, у ах2 + 2В(х, у) ахду + С х, у ау2 '


(3.2)


Пусть на плоскости Оху задается некоторая rладкая кривая К, на
которой задаются значения функции и ее производной:
1) ul K = <Р(Х, у); 1
2)

 к = v(x, Y)'J


(3.3)


Начальные условия (3.3) называются начальными данными Коши, а
кривая К
 носительницей начальных данных.
Задача Коши ставится так: требуется найти решение уравнения
(3.1), удовлетворяющее данным Коши (3.3).
З а м е ч а н и е 1. Начальные условия (3.3) позволяют найти значе

u ди u к .. 6( )
ния производнои дх на кривои ,задаваемои уравнением у = х.
Действительно,. ВДОЛЬ этой кривой


и(х, е(х)) = <р(х, е(х».
Дифференцируя соотношение (3.4) по х, получим
ди I + ди I .8'(х) = d«r> ! '
дх К ду К dx К


(3.4)


190




откуда, учитывая (3.3), будем иметь


 IK = :х <р(х, е(х»
 'I'(х, у)О'(х).


(3.5)


3 а м е ч а н и е 2. Начальные условия Коши нельзя задавать на xa

рактеристиках (задача не будет иметь решения или будет неопреде

ленной).
3 а м е ч а н и е 3. Задача Коши обычно ставится для уравнений rи-
перболическоrо и параболическоrо типов. Для уравнений эллиптиче

cKoro типа она не рассматривается, так как может быть HeKoppeKT

ной*. Например, задача Коши для уравнения Лапласа является HeKOp

ректно поставленной. Поэтому для уравнений эллиптическоrо типа
обычно ставятся краевые задачи.
Пример. Пусть требуется решить задачу Коши для уравнения
д 2 и
 д 2 и = О (3.6)
дх 2 д у 2


с начальными данными


u I к = х 2,

 I к = х,
задаваемыми на линии К:


(3.7)


у = 2х. (3.8)
Рассматриваемое уравнение (3.6)
 rиперболическоrо типа, так
как


А = 1, В = о, с =
 1
и В2
 АС = 1 > о. Для Hero уравнение характеристик (2.10) имеет вид
(dy)2
 (dx)2 = О или (dy
 dx)(dy + dx) = о. Отсюда, решая ypaBHe

иия dy
 dx = О и dy + dx = О, получаем два семейства действитель

ных характеристик
(1) у
 х = С 1 и (11) у + х = С 2 .


(1)


х


оо


Рис. 4


* СМ.
 5, п. 2.


191




Вводим координаты:
 = у
 Х, 1) = у + х.
Тоrда уравнение (3.6) приводится к виду
а 2 u
a
dт} = О
или
 ео = о. Обозначая
 =
l (
). будем иметь
u = J
l (
)d
 + ",(,,) =
(
) + ",(,,)
или, возвращаясь к старым переменным (х, у), получим решение
уравнения (3.б) в виде
u(х, у) = <р(у
 х) + v(y + Х), (3.10)


(3.9)


rде q> и 'V
 произвольные функции.
Обеспечим выполнение начальных условий (3.7):


 =

'(y
 х) + ",'(у + х)
х 2 = и I ; х = аu I
у=2х ах у=2х


или


х 2 = <р(2х
 х) + 'I'(2x + х) = <р(х) + 'I1(3x);
х =
<p'(x) + 'II'(3x).
Интеrрируя второе из уравнений системы (3.11), получим

 +с=
 J
'(x)dx + J",'(Зх)dх =

(х)+!'I'<Зх).
Складывая это выражение с первым уравнением системы (3.11), бу

дем иметь


(3.11 )



 х 2 + С = j 'V(зх).


Отсюда


w(3x) =
 x 2 +
 С


или


lJl(X)
 9 ( х ) 2 +
C = lх 2 +
C
'f'
8 3 4 8 4


и соответственно


<р(х) = х 2
 W(3x) =

 x2

 c.


Следовательно,
u =
(y
x)+",(y+x) =

 (y
x)2

 c +
 (y+x)2 +
 c =
 xy.


192




2. Задача [урса. Рассмотрим задачу с данными на характеристи

ках. Эту краевую задачу называют задачей (урса. Она встречается,
например, при изучении процессов сорбции и десорбuии rазов, про

цессов сушки воздушным потоком. проrревания трубы потоком воды
и мноrих друrих процессов.
Мы рассмотрим задачу rypca на примере простейшеrо уравнения
rиперболическоrо типа


д 2 и ( )
дхду = f Х,у .
Для Hero уравнение характеристик (2.1 О) имеет вид
dx.dy=O,


(3.12)


т. е. dx = О или dy = о. Эти уравнения имеют соответственно решения
у и х. Следовательно,
х = const, у = const

 семейства характеристик рассматриваемоrо уравнения (3.12).
Пусть дополнительные условия даны на прямых х = О и у = О, явля

ющихся характеристиками данных семейств:


и(х, О) = <1>1 (х); и(О, у) = <l>2(У).


(3.13)


Итак, требуется решить задачу rypca: найти решение уравнения
. (3.12), принимающее заданные значения (3.13) на характеристиках
х = О и у = о.
Будем считать, что функции <1'1 (х) и <l>2(У) дифференцируемы и
удовлетворяют условию сопряжения:


<1' 1 (О) = <1'2 ( О) .
Интеrрируя уравнение (3.12) последовательно по х и по у, будем
иметь


х


 (х, у) =

 (О, у) + J t(
, y)d
,
о


у х
и(х, у) = и(х, О) + и(О, у)
 и(О, О) + J dl1J t(
, l1)d

о о
или, воспользовавшись данными (3.13), окончательно получим


у х
и(х, у) = q>1 (х) + q> 2 (у)
 q> 1 (О) + J J t(
, l1)d
df\.
о о


(3.14)


193




Формула (3.14) представляет в явной аналитической форме реше

ние поставленной задачи rypca для простейшеrо уравнения (3.12). Из
нее непосредственно следует единственность и существование реше

ния этой задачи.
Пример 1. Определить тип и найти характеристики уравнения
у2 д 2 и
 х 2 д 2 и = ди (х *0, у *0).
дх 2 д у 2 ау


Реш е н и е. Так как коэффициенты этоrо уравнения


А = у2, В = О, С =
x2,


то выражение


В2
 АС = х 2 у2
 О


и, следовательно, вне осей координат данное уравнение принадлежит
rиперболическому типу. Дифференциальное уравнение характери

стик (2.10) имеет вид


y2(dy)2
 x 2 (dx)2 = О


и распадается на два уравнения


ydy
 xdx = О и ydy + xdx = о.
Интеrрируя эти уравнения, получаем два семейства действительных
характеристик


у2
 х 2 = С 1 и у2 + х 2 = С 2 '
из которых первое представляет собой семейство rипербол, а BTO

рое
 семейство окружностей.
Пример 2. Привести к каноническому виду и решить уравнение
д 2 и д 2 и аи (
х дх 2
 У дх ау = дх у * О).


Реш е н и е. Так как для всех значений у i:- О выражение
2
B2
AC= (

 ) >0,


то рассматриваемое уравнение принадлежит rиперболическомутипу.
Дифференциальное уравнение характеристик (2.10) имеет вид
x(dy)2 + y(dx.dy) = О


194




и распадается на два уравнения
dy = О и xdy + ydx = о.
Следовательно, мы получаем два различных семейства действитель

ных характеристик:


у = C 1 и ху = С 2 .
Введем вместо (х, у) новые переменные (
, 11), полаrая

 = у, 11 = ху.


Данное преобразование переменных является невырожденным, так
как якобиан


д
 дll
J дх дх

 д
 iЛ1

ду ду


о у
=
y :f:. О
1 х


в рассматриваемой области.
Вычисляя производные в новых независимых переменных
 и 11 по
формулам (2.3), перепишем исходное уравнение следующим образом:
д 2 u 2 ди О
д
 ih1 +
 dч = .


. Решим это уравнение, для чеrо введем функцию р =
 . Torдa уравне-
ние примет вид:


др 2 д (1 ) 2
д
 +
p = О или д
 пр =

.
Отсюда ln р =
21n
 + ln <р (11), rде <р (11)
 произвольная функция
. переменной 11. Потенцируя, получим
Р
 «1>( 11 ) И ди
 q>( 11 )


2 ли dч

2 .


И.нтеrрируя последнее равенство, находим
u =
12 J q>( 1»dll + Р 2 (
) = I)
;) + Р 2 (
),


rде Fl и Р 2
 две произвольные функции. Возвращаясь к первона

чальным переменным, получаем окончательный ответ:
( ) 11 (х . у ) ( )
и х, у = 2 + Р 2 у .
у


195




Пример 3. Привести к каноническому виду уравнение
2 д 2 и д 2 и 2 д 2 u 3 дu
tg х дх 2
 2ytgx дхду + у д у 2 + tg х дх = О (у
O).


Реш е н и е. Это уравнение
 параболическоrо типа, так как выра-
жение


82
 АС = о.


Дифференциальное уравнение характеристик
(tgx)dy + ydx = О
имеет один общий интеrрал


ysinx = С.
Введем вместо (Х, у) новые независимые переменные

 = ysinx, 11 = у.


Так как в рассматриваемой области у '* О, якобиан
J = ycosx '* О,
то данное преобразование переменных является невырожденным.
Используя формулы (2.3), перепишем исходное уравнение в виде
,,2 д 2 u
 2
 ди = О
дч 2 д



или


а 2 u
3. ди
dч 2
 1')2 д
 .


Это
 канонический вид рассматриваемоrо уравнения параболи-
ческоrо типа.


Пример 4. Привести к каноническому виду уравнение
д 2 u + 4 д 2 U + 5 д 2 u + дu + 2 ди = о.
дх 2 дхду д у 2 дх ду


Реш е н и е. Так как коэффициенты уравнения


A=l 8= 2 С=5
, , ,


ТО


82
AC=
1 <О


196




и, следовательно, рассматриваемое уравнение принадлежит эллипти

ческому типу. Решая дифференциальное уравнение характеристик
(dy)2
 4dxdy + 5(dx)2 = О,


получаем два комплексно
сопряженных общих интеrрала


(у
 2х) 1: ix = С 1 2.
,


Вводя новые независимые переменные



 = у
 2х, 11 = х
и вычисляя производные по формулам (2.3), исходное уравнение при

водим к следующему каноническому виду
д 2 u д 2 u ди
д
2 + дт1 2 =
 дt, "


Задания для самостоятелъноrо решения
1. Найти общее решение следующих уравнений:


а) д 2 u =0.
дх ду ,


д 2
б)
......!L = х у.
дхду ,


) д2 и х
В дх ду = у;


r) д 2 u = а дu .
дхду ду ,
) д2и
Ж ах 2 =0.


) l.:.

 х 2 дu .
Д дх ду
 ду ,


е) д 2 u + 1 дu = о.
дхду хду ,


2. Решить уравнение
д 2 u д 2 u д 2 u
A
 д 2 +2B
 д д +C
 д 2 =0,
Х Х у у


rдеА, В, С
 постоянные и В2
 АС > о, вводя новые независимые пе-
ременные



 = х + л'lУ, 11 = х + Л2У.


3. Решить уравнение


ди дu О
y

x
=
дх ду ,


вводя новые независимые переменные



 = х, 11 = х 2 + у2.


197




4. Решить уравнение
х ди + у ди
 и = О
дх ду ,


положив


; = х, 1) =

и приняв
 и 11 за новые независимые переменные.
5. Определить тип и найти характеристики уравнений:
а)х2 д2u
4y2 д2и = ди ;
дх 2 д у 2 дх
б) д2

 2 д 2 и + д 2 и + а ди +
 ди + уu = о.
дх 2 дх ду д у 2 дх ду ,
) 2 д 2 u д 2 u 2 д 2 U ди .
в х ах2 + 2ху дхау
 Зу ау2 + 9х аУ
 и = О,
) ( 2 ) д2 U ( 2 ) д2и
r 1 + х ах2 + 1 + у ау 2 = О.
6. Привести к каноническому виду следующие уравнения:
) д2и д 2 и 2 д 2 u ди
 .
а дх 2
 2х дхду + Х д у 2
 2 ду
 о,
б) (l + х 2 ) д 2 u + (l + у 2 ) д 2 u + х ди + у ди = о.
дх 2 д у 2 дх ду ,
в) у2 д 2 u + х2 д 2 и = о.
дх 2 ду 2
7. Привести к каноническому виду и решить следующие уравнения:
) д2u д 2 u д 2 u
а дх 2
 4 дх ду + 3 ду 2 = о;
б) х 2 д 2 и
 у2 д 2 u =0.
дх 2 д у 2 '
) 2 д 2 u д 2 u 2 д 2 и
в х дх 2 + 2ху дхду + у д у 2 = о.
8. Решить уравнения:
а) д 2 и
 у д 2 и = 1 дu (у > о);
дх 2 д у 2 2 ду
б) д 2 и
 4 д 2 и + 4 д 2 и = о.
дх 2 дхду д у 2 '
в) 2 д 2 u + д 2 u
 д 2 u + дu + дu = о.
дх 2 дхду д у 2 дх ду ,
r) х 2 д 2 и
 у2 д 2 u
2y ди =0.
дх 2 д у 2 ду ,
) д2и . д 2 u 2 д 2 х ди

Д дх 2
 2S1ПХ дхду
 cos х д у 2
 cosx ду
 о.


198




9. Найти области rиперболичности, эллиптичности и параболично

сти уравнений:
а) у д 2 и + д 2 и = О;
дх 2 д у 2
2 2 д
б)
 + y
 + a
 = О, а = const,
дх 2 д у 2 ду
и привести их к каноническому виду в областях эллиптичности-и rи

перболичности.
10. Переходя к полярным координатам r и <р, полаrая
х = rcos<p, у = rsinq>,


решить уравнения:
а) X
 + у ди = о.
дх ду ,
б) х 2 д 2 и + 2 xy k + у2 д 2 и = о.
дх 2 дхду д у 2 '
) 2 д 2 и 2 д2и 2 д 2 и ( ди ди ) О
в у ах 2
 ху дхду + х д у 2
 Х дх + у ду = .
11. Найти решение u(х, у) уравнения
ди = х 2 + 2 У
ду ,


удовлетворяющее начальному условию
ul y =x 2 = 1.


12. Решить задачи Коши:
r д 2 и
I д у 2 = 2,
а)
 иly=o = 1,
[ au l = Х.
ду у = о '


r д 2 и
I ду 2 = 2,
б)
 и 'у=о = Asinx,
[ au l = Вх;
ду у = о


r д 2
j ........Е.. = 2 У 3
д 2 '
В) иiy=x =х 2 (х 3 +2),
[ ди = 3х( х 3 + 1);
ду у = х


r д 2 u
 ди
I дх 2
 дх'
r)
 иlx=o = А,
l ди I = в
дх х = О .


199




13. Найти решение u(х, у) уравнения
д 2 и д 2 и д 2 и
дх 2 + 2 дхду
 3 ду2 = О,


удовлетворяющее начальным УСЛОJ3иям
и I У = О = 3х 2 ,
и I = о.
у у=о


14. Найти решение и(х, у) уравнения
4у2 д 2 и + 2 ( 1
 у2 ) д2и
 д 2 и

 ( 2 ди
 ди ) = О
ах 2 дхду д у 2 1+ у2 ах ду ,


удовлетворяющее начальным условиям


и I Y =0 = <р(х) ,
 y и = \V(x).
у=о


15. Найти решение u(х, у) уравнения
д 2 и +2cosx д 2 и
sin2x a2u
sinx du =0
дх 2 дхду д у 2 ду'


удовлетворяющее начальным условиям
иl =sinx = <р(х) ,
и I . = v(x).
у у У=SlПХ


16. Найти решение и(х, у) уравнения
х 2 д 2 и
 2xyk
 3у2 д 2 и = О
дх 2 дхау д у 2'


удовлетворяющее начальным условиям


u I У = 1 = <р(х) ,
и = \jI(X).
у y=l




r л а в а IV
ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ


Целью данной rлавы служит вывод и исследование уравнений с ча

стными производными BToporo порядка, широко применяющихся в
математической физике.



 1. Уравнение колебаний струны
1. ВЫВОД уравнения колебаний струны. Понятие о rранич-
ных и начальных условиях. Рассмотрим натянутую струну,
т. е. тонкую rибкую упруrую нить, расположенную в плоскости Охи,
которая в результате известноrо возмущения была выведена из Поло

жения равновесия Ох. 11зучим поперечные колебания струны, пола

rая, что при таком колебании струны ее точки движутся перпендику

лярно оси Ох.
Обозначим через и = и(х, t)
 смещение точки струны с абсциссой
х в момент времени t относительно Ох (рис. 5).


. u


p(x
 t )dx


I
I
I
I
I
() х x+dx х
Рис. 5


Тоrда функцией и(х, t) при О
 t < 00 опишется процесс колебаний
струны: для любоrо фиксированноrо момента времени t = t 1 выраже

нием u = и(х, [1) определяется Мёновенный профuль струны
, Сделаем следующие допущения:
1). Будем предполаrать, что струна совершает малые колебания,
т. е. ее форма в процессе колебаний незначительно отличается от пря

мой и = о. Будем предполаrать, что наклон касательной к rрафику
функции u = и(х. О. t = const. т. е. tg а =

 , есть малая по модулю Be

личина по сравнению с единицей. Отсюда получаем, что sin а.
 tg а и
cos а
 1.


201




)
,
2 . К концам любоrо участка ММ струны приложены направлен

ные по касательной упруrие силы натяжения (см. рис. 5), модули KO

( I

 )
торых равны I т (М, t) = т (М', t) = т о и являются практически по-
стоянными, т. е. Т О не зависит от х и t.
3). На струну действуют непрерывно распределенные внешние
силы, перпендикулярные оси Ох, с плотностью (наrрузкой) р(х, t),
рассчитанной на единицу длины.
Вырежем из струны бесконечно малый элемент ММ', абсциссами
KOToporo являются х и х + dx. Воздействие отброшенных левой и пра

вой частей струны заменим соответствующими силами натяжения.
,..............
Тоrда элемент ММ' можно рассматривать, как свободную материаль


 4
ную точку, находящуюся под действием упруrих сил Т(М, t), т(М', ()
и внешней силы р(х, t)dx. ё и , rде е и
 орт оси Ои.
Пусть р(х)
 линейная плотность струны в точке х. Так как в поло

жении равновесия масса элемента равна p(x)dx, то, в силу coxpaHe


,
ния массы, элемент ММ имеет ту же массу. Обозначим через а и а'
уrлы, образованные с осью Ох касательными к профилю струны в MO

мент времени t в точках М и М' соответственно. Проектируя на ось Ои
".............,
силы, приложенные к элементу ММ , в силу закона Ньютона и пред

положения 2) будем иметь
p(x)dx
;
 = Тоsiшх'
 Тоsiп<х + р(х, t)dx.
Соrласно предположению 1) уrлы а и а' малы; поэтому
. t ди
Slna.
 ga. = дх


и


(1.1)


(1.2)


. , t ' ди I
Slna
 ga = ах x+dx.
Для подсчета (1.2') используем известную формулу математическоrо
анализа
[(х + dx) = {(х) + ['(x)dx,
справедливую с точностью до бесконечно малых высших порядков.
Отсюда имеем:


sina.'
 ди + а 2 и dx.
ах дх 2
Подставляя выражение (1.2) и (1.3) в формулу (1.1), получим
) д2 U д 2 u ( )
р(х dt 2 = То дх 2 + р х, t .


202


( 1.2')


(1.3 )


( 1.4)




Мы получили искомое уравнение малых вынужденных поперечных
колебаний струны.
В случае постоянной плотности (р = const) это уравнение обычно
записывается в виде


д 2 и 2 а 2 и ( )
dt 2 = а дх 2 + Р х. t .
2 То p(x,t)
rде а =
, а Р =
 плотность силы, отнесенная к единице
р р


(1.5)


массы.
При отсутствии внешней силы (Р(х, t) = О) мы получаем уравнение
малых свободных колебаний струны:
д 2 и 2 д 2 u
at 2 = а дх2 .


( 1.6)


Уравнение (1.4), как показано выше, имеет бесчисленное множест

во решений. Поэтому для однозначной характеристики процесса KO

лебаний необходимо к уравнению при соединить некоторые дополни

тельные условия, вытекающие из физическоrо смысла данной задачи.
Эти условия MorYT быть весьма разнообразными. В простейшем слу

чае, как и в динамике точки, задается положение и скорость точек
струны в начальный момент времени:
и(х,О) = <р(х);

 (X,O) = \jI(x). 0.7),


Эти условия, которым должно удовлетворять решение и(х, t) при
t = О, называются начальными условиями.
Далее, если струна оrраничена, то необходимо задать условия на ее
концах. В частности, для струны, концы которой х = О их = lзакреплены,
и(О, t) = О; u(l, t) = о (1.8)


при всяком t
 о. Условия (1.8) называются zраничными условиями.
Возможны и друrие типы rраничных условий.
Таким образом, физическая задача о колебаниях струны, закреп

ленной на концах, свелась к следующей математической задаче: най

ти решение и(х, t) уравнения (1.4), удовлетворяющее начальным
условиям (1.7) и rраничным условиям (1.8). Это так называемая сме..
шанная краевая задача для уравнения колебаний. К ней также мож

но прийти при изучении одномерных колебаний идеальноrо rаза или
одномерных продольных колебаний стержня.
2. Замечание о «корректно поставленных) задачах. MaTeMa

тическое описание физическоrо процесса начинается с постановки


203




задачи, т. е. с ВЫВода уравнения и формулирования условии, ДOCTa

точных для однозначноrо определения этоrо процесса. Эти
дополнительные условия, называемые данными задачи, должны
обеспечить ей физическую определенность. Чаще Bcero данными за

дачи являются начальные условия, т. е. условия в некоторыЙ момент
времени, с KOToporo начинается изучение физическоrо процесса, и
rраничныe условия, т. е. УСJIОВИЯ на rранице области, в которой ищет

ся решение. В поставленной выше задаче о колебаниях струны это
условия (1.7) и (1.8).
Математическая задача, соответствующая физическому явлению,
должна удовлетворять следующим трем требованиям: 1) решение
должно существовать; 2) решение должно быть единственным; 3) pe

шение должно непрерывно зависеть от данных задачи (требование
устойчивости). То есть малым изменениям любоrо из данных задачи
должны соответствовать малые изменения решения.
Задача, удовлетворяющая всем трем требованиям, называется кор..
ректно поставленной задачей.
Первое и второе требования означают, что среди данных задачи нет
противоречащих друr друrу и их достаточно для выделения единст

BeHHoro решения.
Третье требование необходимо, чтобы математическая задача пра

вильно описывала наблюдаемые физические явления. В деиствитель

ности данные задачи нельзя считать cTporo фиксированными, т. е. они
(особенно экспериментально полученные) всеrда заданы в некоторых
пределах точности. Поэтому необходимо, чтобы малая поrрешность в
данных приводила к малой неточности в решении. Это требование
«устойчивости» имеет существенное значение также ДJIЯ приближен-
ных методов.
Л1ы будем рассматривать только классические корректно постав

ленные задачи. Однако следует заметить, что это далеко не единствен

ные задачи, правильно отражающие физические явления. Имеются
примеры задач, которые «некорректно поставлены». Их исследованию,
особенно в приближенных вычислениях, в последнее время уделяется
большое внимание.
3. Задача Коши для неоrраниченной струны. Формула Да-
ламбера. Корректность задачи. Физическая интерпретация.
Рассмотрим задачу с начальными условиями для неоrраниченной
струны: найти решение и(х, t) уравнения


д 2 и 2 д 2 и


=a

at 2 дх 2


(
OO < х < 00, t > О)


(1.9)


204




с начальными условиями:
и(х, О) = <р(х) 1
ди ( )
 ( )
 при
 00 < х < 00,
dt Х, О
 'V Х J


(1.10)


rде <р(Х), 'I'(Х)
 достаточно r ладкие заданные функции.
Эту задачу называют задачей Коши.
Приведем уравнение колебаний' струны (1.9) к виду, допускающе-
му непосредственное интеrрирование. Возьмем в качестве новых не-
зависимых переменных характеристики уравнения (1.9)

 = Х + at, 11 = Х
 at.


Вычислим производные:
ди = ди + ди д 2 и д 2 и 2 д 2 и д 2 и
дх д
 д1l ' дх 2 = д
2 + д
д1l + дТ}2 '
ди ( ди ди ) д2и = 2 ( д 2 и
 2
 + д 2 и )
дt = а д

 д1l 'at 2 а д
2 д
дТ} dт1 2 .


у равнение в новых переменных запишем в виде
д 2 и
д
дll = О


или


:
(
 ) = О.


Отсюда находим



 = f(ч),


rде /(11)
 произвольная функция только переменной 11. Интеrрируя
полученное уравнение по 11 при фиксированном
, получим:
u = J f(ч)dч + Рl (
) = Рl (
) + Р 2 (Ч),


rде F 1 (
) и F 2(11) являются функциями только переменных
 и 1}. Воз-
вращаясь к старым переменным, будем иметь


и(х, t) = F1(x + at) + Р 2 (Х
 at).


(1.11)


Непосредственной подстановкой в уравнение убеждаемся, что по

лученная функция и(х, t) является решением общеrо вида уравнения
(1.9), если Рl и Р 2
 произвольныедважды непрерывно дифференци-
руемые функции.


205




Выберем функции F 1 и F 2 так, чтобы удовлетворить начальным
условиям (1.10):


u(х, О) = Р} (х) + Р 2 (х) = <р(х),


 (х, О) = аР{(х)
aP2(X) = 'J!<X).


Отсюда, интеrрируя второе равенство, получим:
r Р} (х) + Р 2 (х) = <р(х),
1 Р 1 (х)
 Р 2 (х) =
 1 'J!<z)dz + С,
t Хо


(1.12)


rде ХО и С
 произвольные постоянные. Из равенств (1.12) находим
r х
I Рl (Х) = q>( 2 X) + 2
 J 'V(z)dz +
 ,

 хо
[ Р 2 (Х) = q>(;>
 2
 1'V(z)dz

 .
Хо


(1.13)


Эти формулы определяют функции F 1 и F 2 через заданные функции <р
и 'V, причем равенства (1.13) справедливы при любом значении apry

мента. Подставляя в (1.11) найденные значения F 1 (х) и Р 2 (х), будем
иметь


{ х+а! x
at }
( t) <Р(Х+ at) + <P(X
 at) 1 J ( )d J ( )d
u х, = 2 + 2а '1' z z
 \jI Z Z
Хо хо


или окончательно



 х+ at
( t) = <р(х+ at) + q>(x
 at) ...L J ( )d
u х, 2 + 2а '11 Z Z.
x
at


( 1.14)


Формула (1.14) дает решение задачи Коши (1.9)
(I.l0) и называ

ется формулой Даламбера.
Докажем, что задача Коши (1. 9 )
( 1.1 О) поставлена корректно.
Действительно, непосредственной проверкой леrко убедиться, что
формула (1.14) удовлетворяет (в предположении, что <р(х) имеет He

прерывные производные до BToporo порядка включительно, а "'(х)

до первоrо) уравнению и начальным условиям.


206




Далее, эта формула доказывает единственность решения. В самом
деле, если бы существовало друrое решение задачи (1.9) и (1.1 О), то
оно давалось бы формулой Даламбера (1.14) и совпадало бы с первым.
Таким образом, решение существует и единственно.
Докажем, наконец, что решение непрерывно зависит от начальных
данных, т. е. для любоrо Е > О можно указать такое 8 > О, что если за-
менить начальные значения <р (х) и '1/ (х) на <р (х)и \V (x), отличающие

ся друr от друrа меньше, чем на 8:


I <p(
)
 <p (
) I < б, I 'I/(
)
 'V (
) I < б (
 00 <
 < 00), ( 1.15 )


то новое решение u (х, t) и первоначальное и(х, t) будут различаться
между собой меньше, чем на Е:


'и(х, t)
 u (х, t)1 < Е


на любом конечном промежутке времени О
 t
 Т.
Доказательство этоrо утверждения сразу следует из формулы Дa

ламбера (1.14), которая связ.ывает функции и(х, t) и u (х, t) со своими
начальными значениями <р(х), v(x) и <р (х), 'I' (X).
Действительно


I ( [ )

 ( t ) I < I <р( х + а t )
 (р( х + а t ) I
u х, u х,
 2 +



 x+at
I
(x
 at )
 <р(х
 at ) I
 f I ( )

 ( ) I d
+ 2 + 2а 'v z 'v z Z,
x
a!


Откуда в силу неравенств (1.15) получаем:


lu(x,t>
 u {x.t>1

 +
 + 2
 8 .2at
 80 + Т),


что и доказывает наше утверждение, если положить




 Е
U
 1 + т .


Дадим физическую интерпретацию полученноrо решения (1.14) за

дачи Коши для неоrраниченной струны. Как мы видели, оно может
быть представлено в виде суммы двух слаrаемых:


и(х, t) = F1(x + at) + Р 2 (х
 at).


(1.11)


207




В каждый фиксированный момент времени t rрафик ФУНКllИИ
F 1 (х + at) получается из rрафика F 1 (х) смещением влево на величину
at, а rрафик Р 2 (х
 at)
 смещением rрафика Р 2 (х) вправо на ту же
величину. Если построены rрафики функций F 1 (х) и Р 2 (х), то для по

строения профиля струны в любой момент времени t достаточно сдви

нуть кривую F 1 (х) влево на величину at, кривую Р 2 (х)
 вправо на ту
же величину и затем для каждоrо х сложить rрафически ординаты по

лученных кривых. Полученная в результате сложения кривая даст
форму (профиль) струны в момент времени (.
Функция F 1 (х + at) описывает волну, распространяющуюся влево
со скоростью а, а функция Р 2 (х
 at)
 волну, распространяющуюся
вправо с той же скоростью а. Таким образом, профиль струны и(х, t)
есть суперпозиция двух волн.
Рассмотрим случай, коrда начальные скорости точек струны равны
нулю, Т. е. v(x) = о. Соrласно формуле Даламбера (1.14) профиль
струны определяется в этом случае rрафиком функции


и(х, t) = Fl (Х + at) + Р 2 (х
 at) =
<Р(Х + at) <р(х
 at)
2 + 2


Как уже отмечалось, он представляет собой сумму двух волн,
распространяющихся налево и направо со скоростью а. Начальная
форма обеих волн определяется функцией <Р<2 Х ) , равной половине за

данноrо начальноrо отклонения. При перемещении форма этих волн
остается неизменной.


З а м е ч а н и е. Функция и(х, t), определенная формулой (1.14),
может быть решением уравнения (1.9) только при условии дифферен

цируемости функций <р и 'V. Такое дважды непрерывно дифф€рен

цируемое решение называется классическu.:мрешением. Однако BCTpe

чаются случаи, коrда функции <р(х) и v(x) не имеют нужных
производных. Например, если струна в начальный момент имеет фор

му ломаной линии, то <р (Х) не имеет определенной производной в Bep

шине ломаной. В этих случаях считают, что формула Даламбера TaK

же дает решение задачи, хотя при этом функция и(х, t) не всюду
дважды дифференцируема. Такое решение называется обобщенным
решением задачи. Определяемое формулой (1.14), оно является пре

делом решений уравнения колебаний с HeMHoro сrлаженными началь

ными условиями.


208




4. Колебания полуоrраниченной струны. Рассмотрим задачу о
поперечных колебаниях полуоrраниченной струны х
 О с жестко за

крепленным концом. Она может быть сформулирована следующим
образом: найти решение и(х, t) уравнения колебаний
д 2 и 2 д 2 и
at 2 = а дх 2 ' О < х < 00, t > О,


(1.16)


удовлетворяющее rраничному условию
и(О, () = О


( 1 .1 7)


и начальным условиям


{ и(х, о) = q>(x) ,


 (х, О) = 'I'(x),


(1.18)


при этом <р(0) = '11(0) = о, иначе rраничные и начальные условия про

тиворечат друr друrу.
Решим вспомоrательную задачу для неоrраниченной струны, при

чем на отрицательную часть продолжим функции <р(х) и \v(x) нечет-
ным образом, т. е.


q>(
x) =
<p(x), V(
x) =
\v(x).


Следовательно, начальными данными вспомоrательной задачи явля-
. ются нечетные функции
( ) { q>(x) , х > О, ( ) { 'V(x), х > О,
Фх= и\}Jх=
. ----<р(
x), х < о,
'V(
 х), х < О,


(1.19)


а ее решение, соrласно формуле Даламбера (1.14), дается функцией


x+at
( t ) = Ф( х + а t ) + ф( х
 af) ....L J Ul ( )d
u х, 2 + 2а т z Z,
x
at


(1.20 )


определенной для всех х и для t > о.
Покажем, что полученная функция и(х, t) при t > О, х > О удовлет

воряет также дополнительным условиям (1.17) и (1.18), т. е. является
решением поставленной исходной задачи. Действительно, функция
и(х, t), определяемая формулой (1.20), при х = О равна


а!
u(О. t) =
 [Ф(аt) + Ф(
t)] + 2
 J Ч'(z)dz = О,

at


209




так как первое слаrаемое равно нулю в силу нечетности Ф(х), а BTO

рое равно нулю, поскольку интеrрал от нечетной функции в пределах,
симметричных относительно начала координат, всеrда равен нулю
(см. лемму э 2). Кроме Toro, при t = О эта функция удовлетворяет необ

ходимым начальным условиям:


{ и(х, О) = Ф(Х) = <Р(Х) ,
а при Х > о.
д
 (Х, О) = ЧJ(х) = 'J!(X) ,


Итак, решение задачи о распространении волн на полуоrраничен

ной прямой с rраничным условием и(О, t) = о сводится к задаче о коле

бании неоrраниченной струны, если начальные данные продолжить
на всю прямую нечетным образом.
5. Основная лемма метода Фурье.
Л е м м а. Если в прямоуrольнике R плоскости Оху (рис. 6):
{ а < Х < Ь,
(R)
А<у<В


для некоторых функций выполняется тождество


Х(Х) == У(у),


(1.21 )


то в этом случае


Х(Х) = У(у) = const.


у
в


у
А


о


а


Х)


Х 2


ь


х


Рис. 6


д о к а з а т е л ь с т в о. Предположим противное, т. е. что
Х(х) i:- const;
тоrда существуют значения Xl и Х2 в интервале (а, Ь) такие, что


X(Xt) i:- Х(Х2).


210




Рассмотрим точки (Х l' у) и (Х2' у) t принадлежащие прямоуrольни

ку R. На R справедливо тождество (1.21), а потому
X(Xl) = У(у),
Х(Х2) = У(у).


Сравнивая эти равенства, приходим к противоречию с нашим пред

положением. Следовательно,


Х(х) = const,


а тоrда и


У(у) = const.


6. Метод Фурье для уравнения колебаний оrраниченной
струны. Понятие о стоячих волнах. Метод Фурье (метод разделе

ния переменных) является одним из наиболее распространенных Me

тодов решения уравнений с частными производными. Изложим этот
метод на примере задачи о поперечных колебаниях струны, закреп

ленной на концах (в точках Х = О и Х = 1). Как известно (э 5, п. 1), эта
З.адача сводится к решению уравнения
д 2 и 2 д 2 и

=a

at 2 дх 2


(1.22)


с rраничными условиями


u(О, t) = О, u(l, t) = о


(1.23 )


и начальными условиями
и(х, О) = q>(x) ,

 (х, О) = 'I/(x) (О < х < п,


( 1.24)


rде <р(Х) и v(x)
 заданные функции.
Метод построения решения данной задачи заключается в том, что
сначала находятся Функции* ип(х, t) (п = 1,2, ...), удовлетворяющие
уравнению (1.22) и rраничным условиям (1.23). Затем из этих част

H
IX решений составляется линейная комбинация


00
и(х, t) = I,CпU n (х, t),
n=l


которая при любых значениях коэффициентов Сп В силу линейности и
од.нородности уравнения и однородности rраничных условий также


* Линейно независимые.


211




удовлетворяет уравнению и rраничным условиям (принцип суперпо..
зuцuu) Наконец, коэффициенты Сп составленноrо ряда выбираются
такими, чтобы выполнялись начальные условия (1.24). Тем самым,
построенная таким образом функция и(х, t) будет удовлетворять всем
условиям исходной задачи, т. е. будет являться ее решением.
Ищем частные решения уравнения (1.22), не равные тождественно
нулю и удовлетворяющие rраничным условиям (1.23), в виде произве

дения


и(х, t) = х(х) . T(t),


(1.25 )


rде Х(х)
 функция только переменной х, T(t)
 функция только пе

ременной t.
Подставляя (1.25) в уравнение (1.22), получим
X(x)T"(t) == а 2 X"(x)T(t)


или, разделив переменные:


T"(t)
 х "(х)
a 2 T(t) = Х(х).


Левая часть тождества зависит только от t, а правая
 только от х и
на основании основной леммы Фурье представляют собой одну и ту
же постоянную. Для удобства выкладок обозначим эту постоянную
через
'Л2:


T"(t) Х"(х) 2 ·


 л
a 2 T(t) = Х(х)

 .


( 1.26)


Отсюда получаем систему из двух обыкновенных дифференциальных
уравнений:


Х"(х) + 'Л 2 Х(х) = о, }
т" (t) + а 2 л 2 Т (t) = о.


( 1.27)


rраничные условия (1.23) дают:
u(О, t) = Х(О). T(t) = О, u(l, t) = X(l). T(t) = О


Так как ищутся нетривиальные решения, то T(t) i:-O.
Поэтому функция х(х) должна удовлетворять следующим допол..
нительным условиям:


Х(О) = о, X(l) = о.


(1.28 )


* Если в уравнении (1.26) обозначить постоянную через +1.-2 вместо
I.-2, то для воз

никающих далее собственных значений получим мнимые величины. Это не OTpa

зится на конечном результате.


212




Следовательно, для получения не paBHoro нулю решения вида
(1.25), удовлетворяющеrо rраничным условиям (1.23), мы приходим
К слеДУЮll
ей задаче (о собственных значениях): найти такие значе-
. ния Л, при которых существуют нетривиальные решения первоrо
уравнения из системы (1.27), удовлетворяющие rраничным условиям
(1.28).
Эти решения л называются собственными значениями (их сово-
купность
 спектром), а соответствующие решения Х ......... собствен..
нымu функциями краевой задачи (1.27) и (1.28). Найдем эти собст-
венные значения и собственные функции.
Общее решение первоrо уравнения из (1.27) имеет вид
х(х) = С1siплх + С 2 соsЛх,
rде С 1 и С 2
 произвольные постоянные. Удовлетворяя ero rранич"
ным условиям (1.28), получим
С 1 . О + С 2 . 1 = О,
С 1 siплl + С 2 соsлl = о.
Отсюда С 2 = О и С1siплl = о.
Мы должны считать С 1 :1= О, Т. К. ищутся нетривиа.льные решения.
Поэтому для определения л получаем следующее спектральное
.уравнение:


siпл.l = О,


то ест ь


А = А = llХ
n l'


rде п
 целое число.
Следовательно, нетривиальные решения задачи (1.27) и (1.28) воз-
можны лишь при значениях


А п = n
 (n = 1. 2, ...).


( 1.29)


Этим собственным значениям соответствуют собственные функ-
ции


Х п (Х) = sin nf х (п = 1. 2, ...),


( 1.30)


определяемые с точностью до постоянноrо множителя, который без
нарушения общности можно считать равным единице.


213




Значения л'п' соответствующие п = О,
 1,
2, ..., не принимаем во
внимание, так как они отвечают или нулевому решению


Хо(х) = о


или линейно зависимому решению


х
n(x) =
Xn(x).
Решение BToporo уравнения из (1.27) при л = Аn имеет вид
т (t) = А cos n1tat + В sin n1tat
n n 1 n l'


rде Аn и Вn
 коэффициенты, подлежащие определению.
Таким образом, функции
и n (х, t) = Х n (х)т n (t) =
= ( А cos n1Cat + В sin n1Cat ) sin n1tX
n 1 n 1 1
являются частными решениями уравнения (1.22), удовлетворяющи

ми rраничным условиям (1.23) при любых Аn и Вn.
В силу принципа суперпозиции решений линейноrо однородноrо
уравнения ряд


00
и(х t) =
 ( A cos n1Cat + В sin n1Cal ) sin n1tX
, k.J n 1 n 1 1
n=l
также будет ero решением, если ряд р,авномерно сходится, и ero можно
дважды почленно дифференцировать по х и t. Сумма этоrо ряда и(х, t)
удовлетворяет также и однородным rраничным условиям (1.23), так
как каждое слаrаемое в (1.31) удовлетворяет этим условиям.
Определим коэффициенты Аn и Вn так, чтобы выполнялись началь

ные условия (1.24) . Продифференцируем ряд (1.31) по t:


(1.31)


00
ди =
 n1Са (
A sin n1Cat + В cos n1Cat ) sin.mц.
дt
 1 n 1 n 1 1 .
n=l


( 1.32)


Полаrая в (1.31) и (1.32) t = О, в силу начальных условий (1.24) полу

чим:


00
<р(х) = LAn sin n
X ,
п=l


(1.33 )


00


'I1(x) = L n
a В п sin п
x .
n=1


214




Эти ряды представляют собою разложение заданных функций <р(х)
и 'I1(X) в ряд Фурье по синусам кратных ДУf. Коэффициенты разложе..
ний (1.33) вычисляются по известным формулам (см. (2.12), с. 169) и
имеют вид


1
А п = Н <p(x)sin mf dx;
о


( 1.34 )


1
В = ...1.... J \l/ (x)sl . n n1tx dx п
 1 2
n nпа "t' l'
" ....
о
Подставляя эти значения коэффициентов в (1.31), получим ряд, фор..
мально удовлетворяющий всем требованиям решаемой задачи.
Мы не останавливаемся на выяснении условии, при которых этот
ряд сходится и представляет единственное решение, непрерывно за..
висящее от начальных данных задачи.
Дадим физическую интерпретацию полученноrо решения (1.31)


00
и(х, t) = Lu n (Х, [).
n=1


(1.35 )


Слаrаемые


и n (Х, t) = <р n (t)sin n7 Х ,


(1.36 )


rде


<р ( t ) = А cos n1tat + В sin n1tat
n n 1 n l'


называются стоячuмu волнамu. Таким образом, форма струны в лю..
бои момент времени есть результат сложения бесконечноrо числа
стоячих волн (еармоник). Из формулы (1.36) видно, что стоячая вол..
на представляет собой «пульсирующую» синусоиду.
Точки


Х k = E.z (k = 1, 2, ..., п
 1), i
п


в которых


sin nпх = О
1 '


в любой момент времени остаются неподвижными и называются уз..
ламu стоячей волны иn(х, t). Точки
2т
l
Х т = 2 1 (т = 1, 2, ..., n),
n


215




в которых


sin nr = + 1,


совершают колебания с максимальной амплитудой и называются
пучностЯJrtu стоячей волны. Период ИХ колебания
't = 2п . . n1ta = 1.L (п 1 2 )
n 1 па = , ,....


Для поперечных колебаний струны а 2 = То и, следовательно,
р


1: = 11
 р
п п То.


Полученная формула объясняет законы колебания струны, откры-
тые впервые экспериментально.



 2. Уравнение теплопроводности
1. ВЫВОД уравнения теплопроводности. Постановка задачи
о распределении температуры в оrраниченном стержне. Если
температура тела неравномерна, то происходит процесс передачи
тепла от участков более HarpeTbIx к участкам менее HarpeTbIM.
Рассмотрим однородный стержень длины [, направленный по оси х.
Стержень теплоизолирован с боков и достаточно тонкий, чтобы счи-
тать температуру в каждом ero сечении постоянной. Тоrда процесс
распространения тепла в стержне может быть описан функцией
u(х, t), представляющей температуру в сечении х в момент времени t.
Для определенности предположим, что температура растет с увеличе-
нием х. Напомним некоторые закономерности, известные из физики.
Рассмотрим бесконечно малую площадку da, через которую прохо-
дит тепловой поток. Построим вектор нормали п, направленный в CTO

рону увеличения температуры. Тоrда закон теплопроводности (закон
Фурье) можно сформулировать следующим образом: количество теп-
ла dQl' проходящее через бесконечно малую площадку da за единицу
времени, пропорционально ее площади и величине rрадиента темпе-
ратуры:


dQl =
k

 dO".


rде k
 коэффициент теплопроводности.


216




Соrласно закону Фурье, количество тепла, проходящеrо через ce

чение с координатой х за промежуток времени (t, t + dt) равно
dQ =
kS дu dt (2.1)
дх '


rде S
 площадь поперечноrо сечения стержня. Для неоднородноrо
стержня k зависит от х.
Рассмотрим бесконечно малый элемент стержня [х, х + dx]
Количество тепла, которое необходимо сообщить элементу
[х, х + dx] за время dt, чтобы повысить ero температуру на
Аu ==

 dt,


равно


dQ == epSdxAu = ер

 Sdxdt,


(2.2)


rде е
 удельная теплоемкость, р
 плотность,


 скорость изме-
нения температуры.
Будем предполаrать, что в некоторых частях стержня находятся
тепловые источники. Пусть q(x, t)
 количество тепла, создаваемое
тепловым источником, помещенным в точке х в момент времени t за
единицу времени, отнесенное к единице массы стержня (интенсив

ность тепловоrо источника). Тоrда количество тепла, выделяемое на
отрезке стержня [х, х + dx] за промежуток времени [t, t + dt] будет


dQ = q(x, t)pSdxdt.


(2.3)


Выделение или поrлощение тепла может происходить, например,
вследствие химических реакций, в результате прохождения электри

ческоrо тока и т. д.
Выведем уравнение, которому должна удовлетворять функция
и(х, t). Для этоrо составим уравнение тепловоrо баланса для беско

нечно малоrо элемента стержня [х, х + dx] за промежуток времени dt.
Воспользовавшись приближенной формулой


[(х + dx)
 [(х) + {'(x)dx,


(2.4)


а также соотношениями (2.1) и (2.3), получим для количества тепла,
накопленноrо элементом стержня за время dt, следующее выражение:
dQ =
 kS дu dt + kS ( au + д 2 и dx ) dt +
дх дх дх 2
+ q(x, t)pSdxdt == [k
:
 + pq(x,O]Sdxdt.


(2.5)


217




Та же величина dQ получается на основании изменения температу

ры элемента стержня на величину

 dt и определяется формулой
(2.2). Приравнивая оба выражения, получим:
[k ::
 + pq(x,t>]Sdxdt = cp

 Sdxdt.


Отсюда, введя обозначения
c
 = а 2 , [(х, {) =
 q(x, {),


будем иметь


ди 2 д 2 U {( )
дt = а дх 2 + х, t .
Это уравнение называется уравнением теплопроводности. Оче

видно, если тепловые источники отсутствуют, то
аи = а2 д 2 и (2.7)
at дх 2 .


(2.6)


Для выделения единственноrо решения уравнения теплопроводно

сти необходимо к уравнению присоединить начальные и rраничные
условия.
Начальные условия (в отличие от уравнения колебаний) состоят
лишь в задании значений функции и(х, t) в начальный момент BpeMe

ни t = о:


u(х, о) = <р(х).


(2.8)


rраничные условия MorYT быть различны, в зависимости от темпе

paTypHoro режима на rранице. Например, если на концах стержня
поддерживается постоянная температура (в точке х = О
 температу

ра А, в точке х = 1
 температура В), то rраничные условия имеют
вид:


и(О, t) = А, u(l, t) = В.


(2.9)


Таким образом, задача о распределении температуры в однородном
оrраниченном стержне с постоянной температурой на ero концах ста-
вится так: найти решение уравнения теплопроводности (2.6), удов-
летворяющее начальному условию (2.8) и rраничным условиям (2.9).
2. ВЫВОД уравнения диффузии. Рассмотрим трубку, заполнен

ную веществом, концентрация KOToporo в каждом поперечном сече

нии одинакова и меняется от сечения к сечению. Тоrда, как известно,
имеется диффузия вещества из мест с более высокой концентрацией в
места с меньшей концентрацией.


218




Математически такой процесс диффузии может быть описан функ

цией С(Х, t), представляющей концентрацию в сечении Х в момент вре-
мени t. Получим уравнение. которому удовлетворяет эта функция,
для чеrо составим уравнение баланса массы веIцества на отрезке
[х, х + dx] за промежуток времени dt.
Пусть с(х, t) увеличивается с ростом х. Соrласно закону Нернста,
количество вещества, проходящее в единицу времени через данное
поперечное сечение, пропорционально ero площади S и rрадиенту
концентрации, т. е. за время dt оно равно
d Q =
"S dC dt (2.10)
I I дх '


rде 11
 коэффициент диффузии.
Используя формулы (2.4) и (2.1 О), получим, что количество веще

ства dQ, накопленное выделенным отрезком [х, х + dx] за время dt,
равно


dQ =
llS dC dt + ll S ( dC + (}2с dx ) dt = llS d2c dxdt. (2.11)



2
2


с друrой стороны, изменение концентрации за время dt
Ас=

 dt,


а следовательно,


dQ = 5dxAc = 5

 dxdt.


(2.12 )


Приравнивая выражения (2.11) и (2.12), получим:
115
:
 dxdt = 5

 dxdt


или


де = а 2 д 2 с
dt дх 2 '


(2.13 )


rде а 2 = 11. Это и есть искомое уравнение диффузии. Оно совершенно
аналоrично уравнению теплопроводности (2.7).
При выводе этоrо уравнения мы предполаrали, что диффузия через
стенки трубки отсутствует и внутри трубки нет источников вещества.
При наличии источников получается неоднородное уравнение, анало-
rичное уравнению (2.6). Поскольку уравнения (2.13) и (2.7) одинако

ВЫ, то краевые задачи для них ставятся также одинаковым образом.


219




3. Решение краевой задачи для уравнения теплопровод-
IIОСТИ методом Фурье. 'Семпературные волны. Пусть на отрезке
[о, 1] оси Ох раСПОJIожен тонкий однородный стержень, боковая по

верхность KOToporo теплоизолирована от окружающей среды. Поло

жим, что на концах этоrо стеРЖНfI поддерживается постоянная темпе

ратура: на левом конце
 температура А, на правом
 температура
8. Начальное распределение температуры в стержне зададим функ

цией <р(х). Найдем температуру в точке х в момент времени t > О, пред-
полаrая, что внутри стержня отсутствуют источники и поrлотители
тепла.
Эта задача, как известно (см. Э 2, п. 1), заключается в решениидиф

ференциальноrо уравнения
ди = а 2 д 2 }! (2.14a)
dt дх 2 '


при начальном условии


и(х, О) = <р(х)
и при rраничных условиях:
и(О, t) = А, u(l, t) = в.


(2.15a)


(2.16а)


Сделаем замену переменных такую, чтобы новая неизвестная функ

ция удовлетворяла однородным rраничным условиям. А именно, BBe

дем функцию v(x, t), связанную с искомой функцией и(х, t) соотноше

нием:


V(X,1) = и(х, t)
 ( B
A Х + А ).
Функция v(x, t) удовлетворяет уравнению
dV = а 2 l)2v
at дх 2 '


(2.146)


начальному условию
[ В А ]
v(x, О) = и(х, о)

 х + А =
= <Р(Х)
 [ B
A Х +А] = q>1(X)


(2.15б)


и однородным rраничным условиям:
v(O, t) = о, v(l, t) = о.


(2.166)


Однородное уравнение (2.146) с неоднородным начальным услови

ем (2.156) и однородными rраничными условиями (2.16б) можно pe

тать методом Фурье совершенно так же, как мы решали задачу о KO

лебаниях струны, закрепленной на концах.


220




Именно, будем сначала искать нетривиальные решения уравнения
(2.146), удовлетворяющие rраничным условиям (2.166), в виде про из-
ведения


v = X(x)T(t) 1= о.
Подставляя (2.1 7) в уравнение (2.146), получим
X(x)T'(t) = а 2 X"(x)T(t)


(2.1 7)


или


T'(t)
 х"(х)
 2

a 2 T(t)
 Х(х)

 л
 const


(2.18)


в силу основной леммы метода Фурье. ОТСIqда
Т'(t) + а 2 л 2 Т(t) = о,
Х"(х) + л 2 Х(х) = о.
rраничные условия (2.16б) дают
X(O)T(t) = о, X(l)T(t) = О,


(2.19 )
(2.20)


откуда


х(о) = о, X(l) = о.


(2.21 )


Следовательно, мы приходим к задаче о собственных значениях:
Х"(х) + л 2 Х(х) = о, }
Х(О) = о, X(l) = о,


уже исследованной в Э 1, п. 6 при изучении колебаний однородной
оrраниченной струны. Там 6ыло показано, что только при значениях
Л, равных


л n = n; (п = 1, 2, ...)
существуют нетривиальные решения задачи (2.20) и (2.21):
Х n (х) = sin nr (2.23)


(2.22 )


(линейно независимые).
При л = л'n уравнение (2.19) имеет решение в виде
Тn (t) = Ane
b2n2t , (2.24)


rде Аn
 подлежащие определению коэффициенты, а
Ь 2 = а 2 п 2 > О
[2 .


221




Таким образом, соrласно (2.17), каждая функция
V N (х, t) = Х n (х)т n (О = Ane
b2n2t sin nr (2.25)
будет решением уравнения (2.14б), удовлетворяющим rраничным
условиям (2.16б). Тому же самому уравнению и тем же самым rранич

ным условиям в СИЛУ принципа суперпозиции будет удовлетворять
ряд


00 00
v(x, О = LV n (х, О = LAne
b2n2t sin nr .
n=l n=l
Выберем коэффициент Аn так, чтобы выполнялось начальное условие
(2.156). Полаrая t = О, получим


(2.26)


00
<Рl(Х) = LAn sin n
X .
n=l
Написанный ряд представляет собою разложение заданной функ

ции ((>l(X) в ряд Фурье по синусам кратных дуr. Коэффициенты А п
определяются по известной формуле (см. (2.12), с. 170) простым ин

теrрированием:
1 l
Аn = Н q>l (x)sin n7 x dx = Н {q>(x)
 [ А + B
A х ]}sin nr dx =
о о (2.28)


(2.27)


1
= l J q>(x )sin n1СХ dx .... ..-L [ A + (
1) n + 1 В ] .
1 1 n1С
О
Ряд (2.26) с коэффициентами (2.28) формально будет удовлетворять
всем условиям задачи (2.14б)
(2.16б).
Слаrаемые vn(x, t) ряда (2.26) MorYT быть интерпретированы как
температурные волны. Амплитуда температурных волн ум
ньшается
со временем, т. к. В нее входит множителье
Ь2n2t.
Теперь мы можем написать окончательное решение исходной Kpae

вой задачи (2.14a)
(2.16a):


00
в
 А
 Ь 2 2 t .
и(х, t) = А +
X + LJAпe
 n Sln n
x ,
n=l
rде коэффициенты А п выражаются формулой (2.28).
Исследуем полученное решение при t ---+ 00.
Обозначим


(2.29)


и оо (Х) = Нт U(Х, t).
t ----+ 00


222




Если ряд СХОДИТСЯ равномерно, то
( ) B
A
и оо х = А +
x.


Таким образом, предельный режим
 это линейное распределение
температуры (рис. 7).


u(x.t)


в


А
О


l


х


Рис. 7
В заключение отметим, что мы оrраничились лишь формальным по

строением решения и не будем останавливаться на выяснении усло

вий, при которых ряд (2.29) представляет функцию, удовлетворяю

щую всем условиям исходной краевой задачи. Можно показать
также, что эта задача поставлена корректно для t > О инекорректно
для отрицательных t, если начальное условие дано при t = о.
4. Задача о распределении температуры в бесконечном
стержне. Интеrрал Пуассона. Пусть мы имеем бесконечный OДHO

родный стержень, теплоизолированный с боков, ось KOToporo примем
за ось Ох. Температуру стержня в точке х в момент времени t обозна

чим через u = и(х, t)
 это интересующая нас функция.
В отсутствии источников тепла функция u должна удовлетворять
уравнению теплопроводности


ди 2 д 2 u ( )
дt = а дх 2
oo < х < +00, t > О ,


(2.30)


rде а 2
 физическая константа. Поставим следующую задачу: зная
начальное распределение температуры


и(х, о) = {(х),


(2.31)


найти температуру точек стержня и(х, t) для любоrо последующеrо
момента времени t > О.
Из физических соображений будем предполаrать, что температура
стержня в бесконечно удаленных точках х = J: 00 не может быть беско

нечно большой.


223




Для нахождения частных решений уравнения (2.30), как и в п. 3,
применим метод разделения nеременных, т. е. будем искать ero pe

шенияспециальноrовида


и = XC
)T(t)
 О,


(2.32)


rде Х(х)
 функция только от х и T(t)
 функция только от t.
Подставляя выражение (2.32) в уравнение (2.30), получим
X(x)r(t) = а 2 X"(x)T(t),
или в силу основной леммы (э 1, п. 5) будем иметь
х"(х)
 T'(t)
 2

х(х) = a 2 T(t)

 л
 const.


(2.33)


Отсюда получаем систему обыкновенных дифференциальных ypaBHe

ний:


Х"(х) + л 2 Х(х) = о, }
T'(t) + а 2 л 2T(t) = о.


(2.34)


Так как характеристическое уравнение для первоrо уравнения сис

темы (2.34) имеет вид


k 2 + л 2 = О


и, следовательно,


k 1 2 = :t i Л,
,


то можно положить


Х(х) = А(л)е iлх .


(2.35)


Аналоrично получаем
T(t) = В(л)е
а2л2t .


(2.36)


Отсюда


ил = X(x)T(t) = с(л)е
а2л2t + iл.х,


(2.37)


rде


С(Л) = А(л)В(л).


Параметр л в формуле (2.37) должен быть действительным, причем
.....00 < Л < +00, так как в противном случае ил была бы бесконечно боль

той при х =
oo или при х = +00, что физически невозможно.
Положим


+со +00
u(х, t) = J u')..dл. = J с(л.)е
а2л2t + if..xdл..


(2.38)


......со ......со


Функция и(х, t) удовлетворяет уравнению теплопроводности (2.30).


224




ДействитеЛЬНО,лолаrая
L[u] = ди
a 2 д 2 и
. at дх 2


(2.39 )


и предполаrая законность дифференцирования по параметрам х и t
под знаком несобственноrо интеrрала (2.38), будем иметь:


+00 +00
L[u] =
 f с(л)е
а2л2t + iЛхdл
 а 2
 J с(л)е
а2л2t + iЛхdл =-
at дх 2










+00 +

= J
а2л.2с(л.)е
а2л.2t + iМdл. + а 2 J л.2с(л.)е
а2л.2t + iМdл. == о.


.....00






Для функции (2.38) обеспечим теперь выполнение начальноrо
условия (2.31). Полаrая t = О, получим
+00
[(х) = J с(А.)еiМdл.. (2.40)







Сравнивая интеrрал (2.40) с интеrралом Фурье (СМ. rл. 11, Э 2, п. 9, фор

мулы (2.31), (2.31а) и (2.316»
+00 +00
[(х) = 2
 f dл. J [(
)e iл.(Х

)d
,


.....00 ......(х)


. находим


+

с(л.) = 2
 J f(
)e
iЦd
.


(2.41 )







Следовательно,


+00 +

u(х, t) = 2
 J dл. J f(
)е
а2л.2t + iл.(Х

)d
. (2.42)







Изменяя в формуле (2.42) порядок интеrрирования, будем иметь


+

U(Х, t) = J f(
)G(
, х, t)d
,







rде


+

G(
; х, t) = 2
 f е
а2л.2t + iл.(Х

)dл.


(2.43)








 так называемая функция [рина.


225




Интеrрал (2.43) может быть найден в конечном виде. Из курса aHa

лиза известно значение интеrрала вероятностей:


+00
J e
x2 dx = ..fi.


(2.44 )






Можно показать, что формула (2.44) остается верной, если х на комп

лексной плоскости пробеrает прямую х = а. + iP, (
oo < а. < 00), парал

лельную действительной оси, т. е.
+00 + ip +00
J e
x2 dx = e
2 J e
(a2 + 2ia
 )da = ..fi.
....со + ip ....со


Отсюда


+00
Je
(a2+2iaf3)da = ..fie

2.


(2.45)



oo


Полаrая в формуле (2.43)
а 2 л 2 t=f.l2 (
oo<f.l< +00),


последовательно получим


л
 L dл = dJ!

 a.fi' a.fi


и с учетом (2.45)


+00 [ 2 НХ

) ]

 Jl +
J! d
a (
. х t ) = J.... J е aJt
 =

" 2п a.fi


....со


(2.46)





2

u2
= 1 ..fi е 4a 2 t = 1 е 4a 2 t.
2пa
 2a



Подставляя это выражение в формулу (2.42), получаем uнтеzрал
Пуассона


+00 (x

)2
и(х. t) = 2ak J {(
)e 4a 2 t d
,


....со


дающий распределение температуры в точках бесконечноrо стержня
для любоrо момента времени t Е (О, +00).


226




t з. Уравнение Лапласа
1. Распространение тепла в однородной пластинке. Процесс
распространения тепла в тонкой пластинке может быть описан функ

. цией и(х, у, t), характеризующей температуру пластинки в данной
точке М(х, у) в данный момент времени t.
Обозначим:
р = const
 плотность пластинки,
с
 удельная теплоемкость,
k = const
 коэффициент теплопроводности,
h
 толщина пластинки.
Предположим, что источники тепла в пластинке отсутствуют.
Найдем уравнение, которому должна удовлетворять функция
u(х, у, t). Поступим так же, как и при выводе уравнения теплопровод

ностидля стержня (см. Э 2, п. 1). Выделим в пластинке бесконечно Ma

лый элемент dS = dxdy (рис. 8) и составим для Hero уравнение тепло

Boro баланса. Для определенности предположим, что тепло растет в
положительном направлении осей х и у (заметим, что окончательный
результат не зависит от этоrо предположения).


у
N dx Р
_d Y
М(х,у) Q
о х
Рис. 8


Соrласно закону теплопроводности, количество тепла, протекающе-
ro через сечение MN площади hdy за промежуток времени dt, равно

k Ju hd y dt
дх '


а через сечение PQ. в силу формулы (2.4) для функции

 . равно

k e
 +
:
 dx )hdydt.


Аналоrично, для сечения MQ площади hdx имеем:



k ди hdxdt
ду ,


227




а для сечения N Р:



k(

 +
;
 dY)hdXdt.


Поэтому количество тепла dQ,
акопленное элементом за время dt,
равно


аu ( ди д 2 u )
dQ =
k дх hdydt + k д;" + дх 2 dx hdydt

ди ( ди д 2 u )

 k dy hdxdt + k ау + dy2 dy hdxdt.


или


( д 2 и д 2 и )
dQ = kh дх 2 + д у 2 dSdt.


(3.1)


За время dt температура повысится на величину
du =

 dt,
ди П
rде дt
 скорость возрастания температуры. ри этом количество
тепла, которое необходимо сообщить элементу массы phdS, чтобы
увеличить ero температуру на du, равно
dQ = cphdS

 dt. (3.2)


Приравнивая соотношения (3.1) и (3.2), получаем:
( д 2 u д 2 и ) дu
kh дх 2 + д у 2 dSdt = cphiitdSdt.


Отсюда имеем


ди k ( а 2 u а 2 u )
дt = ер дх 2 + ду 2 .
Введем оператор Лапласа (или лаnласuан) !1, полаrая
д 2 и д 2 и ( )
!:щ = дх 2 + д у 2 ' 3.3


Обозначая .в... = а 2 , получаем тоrда уравнение теплопроводности для
ер
однородной пластинки в виде


 = а 2 Аи. (3.4)


228




2. Стационарное распределение температуры в пластинке.
Распределение температуры называется стационарным, если оно не
зависит от времени, т. е.

 = о. Уравнение стационарноrо распреде-
Jlения температуры получается из уравнения (3.4) и имеет вид



и = о.


(3.5)


Это уравнение называется уравнением Лапласа.
Функция называется ёармонuческой в данной области, если она
имеет непрерывные производные до BToporo порядка включительно и
удовлетворяет уравнению Лапласа во внутренних точках области.
([Iримеры rармонических функций: u = ах + Ьу, и = х 2
 у2.)
Пусть С(2)
 класс функций с непрерывными вторыми производны

ми. Тоrда, со!"ласно определению, rармоническая в области G функция
удовлетворяет двум условиям:


1) u Е С(2) в о;
2) f1u(P) = О. если РЕ а.


(3.6)


Всякая rармоническая функция описывает стационарное распреде

ление температуры пластинки.
3. Необходимое условие максимума функции. Пусть в облас

ти G задана функция и(х, у) Е С(2). И пусть в точке Ро(Хо, Уо) Е G фун

кция принимает максимальное значение и(Р о ) = тахи.
G
т оrда для любой точки Р Е G t находящейся внутри Kpyra радиуса r
с центром в точке РО, справедливо неравенство


и(Ро) > и(Р), если О < Р(Ро, Р) < р,
rде Р(Р о , Р)
 расстояние между точками РО и Р (рис. 9).
у


(3.7)


Уо



iJ:'
G W


о


ХО


х


Рис. 9


229




Докажем следующую теорему.
т е о р е м а. Если функция имеет максимум во внутренней точке
области, то в этой точке ее частные производные равны нулю, а лапла

сиан не больше нуля.
Д о к а з а т е л ь с т в о. Необходимое условие эусrремума функции
дает


и
(Po) = О,
и
 (РО) = О.
Так как функция и(х, Уо) имеет максимум при х = Хо, то
и
x(Po)
 О,
Аналоrично, так как функция и(хо, у) максимальна при у = Уо, то
uZ y (РО)
 О,
Складывая неравенства, получим



и(Po) S о.


(3.8)


Теорема доказана.
4. Принцип максимума для rармонических функций. Pac

смотрим оrраниченную область G с rраницей r. Пусть функция
и(х, у) определена и непрерывна в замкн уто й области G = G + r и
удовлетворяет уравнению Лапласа внутри G .
Из курса математическоrо анализа известно, что всякая непрерыв

ная функция в замкнутой оrраниченной области достиrает cBoero
максимальноrо значения. Для rармонической функции справедлива
следующая теорема.
т е о р е м а. Функция, rармоническая вн утри оrраниченной облас

ти G и непрерывная в замкнутой области G , не может достиrать СТРО-
roro максимума внутри этой области.
Д о к а з а т е л ь с т в о. Пусть Qo Е r
 точка rраницы r, в которой
функция и(х, у) принимает максимальное rранич но е значение. ДOKa

жем, что эта функция не может внутри области G принимать значе

ния, большие чем в точке Qo Е [. Доказательство проведем от против

н О ro.
Пусть найдется такая точка РО Е а, что


U(Ро) > u(Qo),


(3.9)


причем и(Ро)
 максимальное значение функции и в области а.


230




Отсюда


и(Ро)
 u(Qo)
 а > О


или


и(Ро)
 и( Qo) + а.
Пусть Р Е G + r. Рассмотрим вспомоrательную функцию
v(P) = и(Р) + Ер2, (3.11)
I
rде р = р(Р, РО) = [(х
xo)2 + (у
 уо)2] 2, О < Е < +00.
У


(3.1 О)


о


х


Рис. 10.


Так как функция и(Р) достиrает CBoero наибольшеrо значения во
внутренней точке РО области G , то функция v(P) при достаточно Ma

лом значении Е > О также достиrает cBoero наибольшеrо значения в
некоторой внутренней точке Р6 области G .
Действительно, при Q Е r и r = p(Q, РО) имеем
v(Po)=u(Po)
u(Qo)+<x
 u(Q) + <Х. (3.12)
Отсюда на основании (3.11 ) получаем
v(P o )
 v(Q)
 Er 2 + а
 v(Q) + (а
 ER2), (3.13)
rде R = maxr.
Qer
Следовательно, выбирая


0<Е< ;2 '


из (3.13) будем иметь


Отсюда и подавно


v(Po) > v(Q).
v(P6>
 v{Po> > v(Q),


(3.14)


причем


Р6 Е r.


231




Подсчитаем#лапласиан f1v в точке РО. ИЗ (3.11) имеем


v
x(P6) = и
x(P6) + 2t


и


vZ y (РО) = uZ y (Р6) + 2t.


Отсюда



v(P6) =
и(P6) + 4€ = 4е > О,


что невозможно в силу теоремы, приведенной в Э 3, п. 3. Следователь

но, предположение (3.9) неверно.
Теорема доказана.
С л е Д с т в и е 1 (принцип минимума). Функция, rармоническая
вн утри оrраниченной области G и непрерывная в замкнутой области
G , не может достиrать cTpororo минимума внутри области.
Д о к а з а т е л ь с т в о. Предположим, что rармоническая Функ

ция u достиrает cTpororo минимума в некоторой внутренней точке
РО Е а, т. е.


и(Ро) = minu.
G
Рассмотрим функцию v =
и, которая, равно как и и, непрерывна в G и
rармоническая в а, так как f1v =
 f1u = о.
Но в точке РО, rде u принимает минимальное значение, функция v
имеет максимальное значение


v(Po) = maxv.
G
что невозможно в силу принципа максимума. Следствие доказано.
С л е Д с т в и е 2. Значения функции, rармонической вн ут ри orpa

ниченной области G и непрерывной в замкнутой области а, заклю

чены между наименьшим и наибольшим ее значениями на rранице
этой области, т. е.


f!.
 и(Р)
 и ,


(3.15)


rде: и = minu, U = тахи, РЕ а.

 r r
З а м е ч а н и е. Функция, rармоническая вн утри оrраниченной об

ласти О, непрерывная в замкнутой области G и отличная от постоян

ной, достиrает свои наибольшее и наименьшее значения лишь на rpa

нице области.


232




5. Задача Дирихле. Пусть G
 конечная область, оrраниченная
замкнутым контуром r, на котором задана непрерывная функция
{( Q) .
Требуется найти функцию и(Р) rар моническую внутри области а,
непрерывную в замкнутой области G = G + r и принимающую задан

ные значения f на rранице r, т. е.
1) L\u(p) = О, РЕ о;
2) ul r = f(Q), Q Е r.
Эта краевая задача носит название задачи Дuрuхле.
Примером задачи Дирихле может служить следующая: зная pac

пределение температуры на rранице пластинки, найти стационарное
распределение температуры по пластинке.
6. Корректность задачи Дирихле. Докажем теорему единст

венности.
т е о р е м а 1. Для оrраниченной замкнутой области задача Ди-
рихле имеет единственное решение.
Д о к а з а т е л ь с т в о. Предположим противное, т. е. что задача
имеет два решения:
функцию иl, для которой
{
Иl (Р) = о, РЕ а,
Ul(Q)=!(Q), Qer,


и функцию и2, для которой
{ L\U 2 (Р) = О, РЕ а,
U2(Q)=!(Q), QEr.


Рассмотрим разность и = и}
 и2. Она обладает следующими свойст

вами:
1) f1u(P) = О, РЕ о;
2) u непрерывна в замкнутой области G = G + r;
3) ulr = f(Q)
 f(Q) = о.
Следовательно, и = minu = О, u = тахu = о.

 r r
В силу формулы (3.15) имеем
о = ff
 и(Р)
 u = О,


откуда


и(Р) == О, т. е. ul == и2.


Теорема доказана.


2ЗЗ




о п р е Д е л е н и е. Область называется выпуклой, если любые две
ее точки можно соединить отрезком, принадлежащим этой области.
т е о р е м а 2. Для оrраниченной выпуклой области задача Дирих

ле имеет решение и это решение единственное (без доказательства).
Для доказательства корректности задачи Дирихле достаточно по

казать, что ее решение непрерывно зависит от rраничных данных.
т е о р е м а 3. Решение задачи ДИРИХJlе для замкнутой и оrрани

ченной области (в частности, выпуклой) непрерывно зависит от rpa

ничных данных.
Д о к а з а т е л ь с т в о. Допустим, что
Ut(X, у) и и2(Х, у)

 решения задачи Дирихле, соответственно принимающие на rрани-
це значения


[l(Х' у) и [2(Х, у).
Пусть всюду на rранице r выполнено неравенство
Ifl (Х, у)
 [2(Х, у)! < Е,


rде Е ....... произвольно малое положительное число.
Рассмотрим rармоническую функцию
и(х, у) = иl (Х, у)
 и2(Х, у).
На rранице r эта функция принимает значение
{(х, у) = 11 (Х, у)
 [2(Х, у).
Так как
E < {(х, у) < Е на r, то в силу принципа максимума имеем

E < u (х, у) < Е при (Х, у) Е а,


Т. е.



E < u 1 (х, у)
 и2(Х, у) < Е


или


I u 1 (х, у) .... и2 (х, у)! < Е.
Следовательно, для любоrо Е > О можно указать такое S (а именно:
8 = Е > О), что при изменении rраничных значений меньше, чем на б,
решение в области G изменяется меньше, чем на Е.
ИЗ теорем 1.....3 следует корректность задачи Дирихле для оrрани

ченной выпуклой области.
7. Оператор Лапласа в полярных координатах. Запишем опе

ратор Лапласа


д 2 u д 2 и
fJ.u = дх 2 + д у 2


234




в полярных координатах (r, <р), (,
 О,
 1t < <р < п), которые, как изве

стно, связаны с декартовыми координатами следующими соотноше

ниями (см. рис. 11):


у


х = rcos <р, }
у = rsin<p;


у


м (х, у)
--.....--......------


r =
 x2 :у2 , } *
<р = arctg
.
х


о


х х


Рис. 11


Вычислим производные:
ди
 ди д, + ди дц>
 ди х + ди (
y / х 2 )
дх
 д, дх aq> дх
 д,
 x2 + у2 dq> 1 + у2 / х 2



ди ди sin q>
=
cosq>


.
д, dq> , ,
д 2 и д ( ди ) д ( ди ди sin <Р )
............. = ..........
 =

cos<p


 cosq>

ах 2 ах ах д, д, dq> ,


д ( ди ди sin <Р ) sin q>



CoS<p



 =
д<р д, dq>"
( д 2 и д2и sin q> ди sin <Р )
=
COS<p


 +

 COSln

d,2 д, дер r дер,2 '1'


(3.16)


( д2и ди . д 2 и . sinq> ди Cosq» Sinq>

 ............... с о s <р

 s 1 n <р

 ...............

 ............... ............... =
д, дер д, дер2, dq>' ,
д 2 u 2 2 д 2 u sin q>cosq> д 2 u sin 2 q> дu sin 2 q> 2 дu sin <pcos<p
= д,2 cos <р
 д, дер , + дер2 ,2 + д, , + дер ,2 .
д 2 и
Для нахождения д у 2 заменим в формуле (3.16) q> на

q> и dq> на

 д<р:


д 2 u
 д 2 и . 2 2 12u cosepsin ер
д 2
 д 2 SIn q> + д "'\ +
У' <ро"
+ д 2 u COs 2 ер + аu cos 2 ер
 2 дu cosepsin q>
дер 2 ,2 dr, дер,2.


(3.17)


* Точнее, <р = arctg 1., еСJIИ х > о; <р = 1t + arctg!l.., еСJIИ х < о, у
 О; <р =
 1t + arctg!l..,
х х х
если х < о, у s о. Во всех случаях tgq> = 1.
х


235




Складывая вы'ражения (3.16) и (3.17), получим


f1и = д 2 u + д 2 и
 + ди 1
д,2 dq>2 ,2 д, r .


(3.18 )


Итак, оператор Лапласа в полярных координатах определяется видом
д 2 1 а 2 1 д

 = а 2 + 2" д 2 +
,"::\".
r r q> , и'


8. Фундаментальное решение уравнения Лапласа в поляр-
ных координатах. I--Iайдем решение уравнения Лапласа в полярных
координатах, зависящее только от одной переменной r и не зависящее
от <р. Соrласно формуле (3.18), оно будет определяться тоrда из обbl.К

новенноео дифференциаJIьноrо уравнения
d 2 u{,) + 1 du(,) = О
dr 2 r dr


и, как леFКО убедиться, равно
u(r) = C 1 ln r + С 2 ,


rде С 1 и С 2
 произвольные постоянные.
Полаrая С 1 =
 1, С 2 = О, получим
ио = ln';.


Функция uo(r) удовлетворяет уравнению l1и = О всюду, кроме точки
r = О, rде она обращается в бесконечность. Эту функцию называют
фундаментальным решением уравнения Лапласа на плоскости.
9. fармонические полиномы. Полиномы, удовлетворяющие
уравнению Лапласа, называются еармоническими.
Рассмотрим однородный полином степени n


Рn(х,У) = 2: С а.рх а у р.
a+
=n


(3 19)


Переходя к полярным координатам по формулам


х = rcos <р, у = rsin <р,


получим


Рn =r n 2:caJpcosaq>sin
<p = rnФп(<Р).
а+р=n


236




СJIедовательно, всякий однородный полином можно представить в
виде


Р п = ,пф n (<р), п = О, 1, 2, ....


(3.20)


Для rармонических однородных полиномов, кроме Toro,


!1Р = о
n
или В полярных координатах, соrласно формуле (3.18),
д2Рп. + 1 dP'l +
 а2Рп = о
dr 2 r dr r 2 д
2 .


(3.21 )


Подставляя (3.20) в (3.21), получим
п(п
 1), n
2ф n (<р) + п, n
2ф n (<р) + ,n
2ф
 (q» = о.


Отсюда следует. что функция Фn(<Р) определяется из уравнения
Ф
(q» + п2фn(<р) = О


и равна


ф n (<р) = Аn cosnq> + В л sinпq>,
rде А п и В п
 произвольные постоянные.
Итак, однородные rармонические полиномы степени n в полярных
координатах имеют вид


Рn = ,n (А n cosnq> + Вn sinn<p), п = О, 1, 2, ....


(3.22)


ПереЙдем к декартовым координатам. Воспользовавшись форму-
лой Муавра


(х + iy)n = ,n(cosnq> + isinnq»,


получим


,ncosnq> = Re(x + i у)n, ,nsinn<p = 1т (х + i у)n.
Следовательно, однородные rармонические полиномы степени п в де-
картовых координатах MorYT быть представлены в виде


Рn(х, у) = AnRe(x + iy)n + BnIm(x + iy)n.


(3.23)


Например, построим однородные rармонические полиномы тре-
тьей степени Рз(х, у). Имеем
(х + iу)З = х 3 + 3ix 2 y
 3 ху 2
 iy3.


237




Отсюда имеем
Re(x + iу)З = х З
 3ху2, Im(x + iy)3 = 3х 2 у
 уЗ


и


Рз(х, у) = Аз(х З
 3ху2) + В з (3х 2 у
 уЗ).


10. Решение задачи Дирихле для Kpyra. Пустьдан Kpyr радиуса
R с центром в начале координат. Решим задачу Дирихле для Kpyra:
найти функцию u(r, q» rармоническую внутри Kpyra и принимающую
На ero rранице r заданные непрерывные значения, т. е.


1)
u(r, <р) = о (О < r < R);
2) u(R, '1') = Нт u(r, q» = f(v),
r
R
O,

W
rде 1(",) ....... заданная непрерывная функция (рис. 12)


(3.24)
(3.25)


х


Рис. 12


Функцию u(r, <р), представляющую решение данной задачи Дирих-
ле, ищем в виде ряда rармонических полиномов


00
u(r,q» = L,rn(Ancosпq>+Bnsinпq». (3.26)
n=О


Таким образом,
и = о.
Выберем коэффициенты Аn и Вn такими, чтобы эта функция удов-
летворяла также заданному rраничному условию. Пусть r = R, q> = '11.
Тоrда rраничное условие (3.25) дает


00
t6v) = L,Rn(A n cosп'V + 8n sinn'V).
n=О


(3.27)


238




Напишем разложение функции 1 (\jI) , период которой Т = 2п, В ряд
Фурье:


00
1(0/) = а 2 о + 2: (ancosn'l' + Ь n sinn'l')
п=l


(3.28)


с коэффициентами, определяемыми по формуле (2.б)(см. rл. 11, Э 2)


а п } = .1 j f(\jI) { c
sn\V d'l1.
Ь n 1t slnn\V

п


(3.29)


Ряды (3.27) и (3.28) должны быть тождественны. Поэтому, сравнивая
ИХ, получаем


А ао А а п В Ь п
О = """2' n = Rn ' n = Rn .


(3.30)


Итак, мы построили формальное решение задачи Дирихле дЛЯ КРУ-
ra в виде ряда (3.26) с коэффициентами (3.30). Чтобы убедиться в том,
что функция u(r, <р), определяемая этим рядом, действительно являет-
ся решением исходной задачи, надо доказать сходимость ряда, воз-
можность ero почленноrо дифференцирования, а также доказать не-
прерывность этой функции (изнутри) в точках rраницы Kpyra.
11. fеометрическая проrрессия в комплексной области. Рас-
смотрим бесконечно убывающую rеометрическую проrрессию


00
Lq n = I
 q I I q I < 1.
n=О


(3.31 )


Пусть q
 комплексно и представлено в триrонометрической форме
q = p(cos<p + isin<p),


rде р = I q I и <р = arg q.
, Тоrда по формуле Муавра имеем
q п = р n ( cos nq> + i sin nq»


и равенство (3.31) может быть записано в следующем виде:


00
L п ( .. )
 1
 1
 Р cos <р + ip sin <р
cosn + tSlПn
 ..
 .
р <р <р 1
 pcosq>
 lpsln q> 1
 2pcosq> + р2
n=О


239




Приравнивая действительные и мнимые части, получим


00
L n 1
 Р cos ер
cosп = ,
р <р 1
 2pcosq> + р2
n=о


(3.32)


00
L n . psinq>
slnп = ,
Р <Р 1
 2pcosq> + р2
n=о
rде I р I < 1. Эти формулы мы используем ниже.
12. Интеrрал Пуассона. Решение задачи Дирихле для Kpyra, как
было показано выше, дается в виде ряда (3.26) с коэффициентами,
определяемыми по формулам (3.30) и (3.29). Пуассон нашел сумму
ряда (3.26) в конечном виде.
Подставляя выражение коэффициентов в (3.26) и меняя порядок
суммирования и интеrрирования, будем иметь
1t 00 { 1t
u(r, q» = 2
 J!('I')d'l' +

(
 ) n cosnq> J!('I')cOSn'l'd'l' +
1t 1 1t
+ sinnq> J f('I')sinn'l'd'l'
 = 2
 J f('I')d'l' +

п J
1t


(3.33)


00 1t
+
 L(
 ) n J f('I')cosn('I'
 q»d'l' =
n= 1
1t


=
 It<'I'{
 +
(
 )n Cosn('I'
q»}'I"
 < 1.
Воспользуемся формулой (3.32)


00 00
"" "" 1
 Р cos ер
L-,P n cosпq> = 1 + L-,p n cosпq> =
1 2 2 '
n=о n=l
 pcosep + р


I p'l < 1,


полаrая р =
 . Тоrда выражение, стоящее в квадратных скобках, пре-
образуется следующим образом:
[ 1 L OO ( r ) n ( )] 1

cos(\jI
ep) 1

 +
 cosп 'V
<P =

 =
2 R 1 2 , ( ) ,2 2
n=1 .
 RCOS \jI
<P + R2


R2
 r 2

 2[R2
 2Rrcos(\jI
ep) +r2]'


240




Поэтому окончательно получаем:


1t
1 J R2 ,2
и(, ) =

 ( )d .
· <р 2п R2
 2R, cos( '11
<p) + ,2 f '" '"

1t


(3.34 )


Эта формула называется интеrралом Пуассона.
13. Теорема о среднем для rаvмонических функций.
т е о р е м а. Значение rармонической функции в центре Kpyra
равно среднему арифметическому ее значений на окружности L этоrо
Kpyra.
Доказательство. Применяя формулу (3.34), полаrая r = О и
1('1/) = u(R, '1/), получаем:


1t
и(О) = 2
 J u(R. '" ы",.

п


или, переходя к интеrрированию по дуrе окружности


dl = Rd'V,


будем иметь


и(О) = 2
R fu(Q)dl. (Qe L).
L


(3.35)


что и требовалось доказать.
14. Приближенное решение задачи Дирихле методом сеток.
В тех случаях, коrда не удается получить аналитическоrо решения за

дачи, применяют приближенные методы. Эти методы наиболее широ

кое распространение получили в связи с бурным развитием вычисли

тельной техники.
Для численноrо решения задачи Дирихле


д 2 u д 2 u
дх 2 + д у 2 = О при (х. у) Е G


(3.36)


и


ul r = f(Q) при Q Е r,


rде f(Q)
 заданная непрерывная функция, часто применяют метод
сеток. Идея этоrо метода состоит в следующем:
1 ) заданная область G, в которой ищется решение, заменяется ceT

чаrой областью G h , аппроксимирующей область о;


241




2) дифференциальное уравнение Лапласа заменяется разностным;
3) из rраничноrо условия устанавливаются значения искомоrо pe

шения в rраничных узлах области G h , образующих ее rраницу r h .
При rрубой аппроксимации значение искомоЙ функции и в rранич

ных узлах сетки G h ' считают равными значению этой функции в бли-
жайших точках rраницы r, rде функция U задана.
Найдя решение разностноrо уравнения, для чеrо, вообще rоворя,
нужно решить алrебраическую систему с большим числом неизвест

ных, мы получим значения искомой функции в узлах сетки, т. е. будем
иметь численное решение нашей задачи.
Для простоты рассмотрим случай квадратной сетки. Выбрав шаr h,
построим систему узлов (рис. 13)
Xi = Ха +ih, Yj = Уа + jh, (i, j = О, :tl, + 2, ...).
Значение искомой функции U = и(х, У) в точках (Х;, Yj), обозначим
через
Uij = U(Xi, Yj).
Заменим производные их разностными отношениями:


' ( . . ) ,... ui+l,j
Ui,j .
и х Х р У}"" h '


, ( . . ) ,... Ui,j+l
Ui,i .
И у Х р у/,... h '


U
x(Xi' Yj) ". ( иt+l. i h
 Щ. i
 Щ. i
hUI
l. i ) : h ". ui+l. i
 2:j
 i + иН.1 ;


" ( ) ...., и i, j + 1
 2 и i , j + U i, j
l
И уу Xi, Yj ,.., h 2 .


i, j+ J


i
 1. j i, j i+ 1 , j


G h


i, j
l


r h


Рис. 13


242




Дифференциальное уравнение Лапласа тоrда заменится разностным:


Ui
), j
 2Ui, i + ui+l, j + и;, i
1
 2Ui, j + ui, /+)
h 2


=0


или


Uij =
 (UH,i + Ui+l,i + Ui,H + Ui,i+l).


(3.37)


rде Xi:t 1, Yj:t. 1
 расчетные точки.
В узловых точках r h rраничную функцию fh полаrаем равной значе

нию функции f в ближайших точках rраницы r.
Итак, мы приходим к следующем задаче: найти функцию, удовлет

воряющую в узловых точках внутри G h разностному уравнению Лап

ласа (3.37) и принимающую на r h значения, равные fh.
Для определения решения в каждой внутренней точке сетки необ

ходимо решить неоднородную линейную систему алrебраических
уравнений (3.37). Число неизвестных (т. е. число внутренних узлов
сетки) равно числу уравнений.
Покажем, что система (3.37) всеrда совместна и имеет единствен

ное решение. Будем опираться на следующую теорему: линейная He

однородная система совместна и имеет единственное решение тоrда и
только тоrда, коrда соответствующая линейная однородная система
имеет только нулевое решение.
Рассмотрим однородную систему

 l (


 )
Иц = "4 Иi
l, j + Ui+l, j + Иi, j
] + Иi, j+l ,


(3.38 )


rде


й. . =0
{, /
для точек (Xi' Yj) Е r h.
Пусть система (3.38) имеет некоторое решение iii, j. Обозначим че

рез Ир, q
 максимальную компоненту этоrо решения, т. е.
... <... \-.1 ( . . )
Иi,j
 Up,q V l,}.
, Из уравнения (3.38) получаем
(Ир, q
 Ир
l, q) + (Ир, q
 Ир+l. q) +
+ (Ир, q
 Ир, q
l) + (Ир, q
 Ир, q+l) = о.


(3.39)


(3.40 )


(3.41 )


Так как все скобки в равенстве (3.41) неотрицательны, то отсюда BЫ

водим


",., -- ..... -- --
Ир, q = Ир
l, q = И р +l, q = Ир, q
l = Ир, q+l.


(3.42)


243




Таким образом, при изменении на единицу одноrо из индексов рили q
решения Ир, q выполняется равенство (3.42). Повторяя это рассужде

ние достаточное число раз, мы через конечное число шаrов достиrнем
точки rраницы U s , t Е r h, причем


Up,q =Us,t =0,


т. е.



a?CUi, j = о.
t, I
Аналоrично доказывается, что

i
Ui, i = о.
l, I


Следовательно,


Ир, q = О,
а значит, система (3.37) совместна и имеет единственное решение.
Задача. Методом сеток приближенно решить задачу Дирихле для
квадрата G = {о < Х < 3; О < У < 3} при заданных rраничных условиях
ul r =x 2 +y2.


Реш е н и е. Выбираем шаr h = 1. В узлах сетки проставляем значе

ния искомой функции u (см. рис. 14). На основании схемы (3 37)
составляем систему уравнений


9 /0 13 18 а =
 (1 + Ь + d + О, 1
4 d с 13 Ь=
 (4+10+c+a), l
с =
 (Ь + 13 + 13 + d), J
1 Ь 10 d =
 (а + с + 1 О + 4)
а
или
4а
 Ь
 d = 2, 1
о / 4 9
 + 4Ь
 с = 14,
 (3.43)

 + 4с
 d = 26, J
Рис. 14
a
 с + 4d = 14.
Из BToporo и четвертоrо уравнений получаем Ь = d.
244




Следовательно. из (3.43) получим систему
4a
2b=2, 1

a + 4Ь
 с = 14,


2b + 4с = 26. J
Решая систему (3.44), будем иметь а = 4, Ь = 7, с = 10, d = 7
Следовательно, решение этой задачи можно записать в виде таб-
лицы:


(3.44 )




. I


-





I
у х О I 1 2 3 I
J
I
О О 1 4 9
'
 1 L 1 4
.. 7 10
2 4 I 7 10 lH
3

O 13 18


Для контроля заметим, QTO ДJIЯ функции tl соблюдены принцип ми-
нимума и принцип максимума.
Пример 1. Решить задачу Коши для уравнения колебаний иеоrра-
ниченной струны:
f д2и д 2 и


=

oo<x<+oo t>O
1 dt 2 дх 2 ' ,.

и(x,o) = х 2 ,
l
 (х, о) = х.
Реш е н и е. Воспользуемся формулоЙ Даламбера (1.14). Имеем:
а = 1, q>(z) = z2, O/(Z) = z. Следовательно,
х+!
(х + {)2 + (t
 t )2 1 J 2 2
и(х, t) =
 . 2
 + 2" zdz = х + t + xt.
x
t


Пример 2. Построить профиль бесконечной струны для моментов
времени: t o = О, tl = 2 <Х , t2 = а , если
а а


(О, вне (
, а):
u(х, о) = <р(х) =
 х + h,
a
 х
o,

 (х, о) = 'V<x) = о;
l
x+h, O
x
a.


245




Реш е н и-е. По формуле Даламбера:
и(х t ) = <р(х) + <р(х)
, о 2 2'


( )
 q>{x + i) <Р(Х
 i)
u х, t)
 2 + 2 '
U(X,t2) = ч><х;а> + ч><х;а> .


и(х, t o )


h

.
.
.
2


....2а


....а


о


а


2а


х


и(х, 1.)


h

.
.
.
2



2a
a О а 2а х
h
.
."2


---а


(х


х


Рис. 15


Функция и(х, t), представляющая распространение начальноrо OT

клонения <р(х) при нулевой начальной скорости 'II(X) = .0, дается в
силу формулы Даламбера:
( t)
 <р(х + at) q>(x
 at)
U Х,
 2 + 2 .


в виде суммы двух волн, распространяющихся направо и налево со
скоростью а, причем начальная форма обеих волн определяется Функ

u <р(х) u
циеи 2' равнои половине начальноrо отклонения.
Пример 3. Построить профиль бесконечной струны, если началь

ное отклонение ее равно нулю, а начальная скорость отлична от нуля
только на отрезке [х), Х2]' rде принимает постоянное значение:


246




и(х, О) = <р(х) = О,


ди ( ) ) { '11 О, если Х 1
 Х
 Х 2 '
........ х О = \V(X =
at ' О вне [Х} ,Х2],


для моментов времени
/0 = О, t 1 = 4 l a (Х2
Xl), t2 = 2 1 a (Х2
Xl).


Реш е н и е. В этом случае формула Даламбера принимает вид


x+at
U(Х, t) = 2
 J '!'<z)dz = 'Р(х+а!)
 'P(x
aп,
x
at


т. е. и в этом случае функция и(х, t) дается в виде двух волн, причем
\f(x) является интеrралом от v(z) и представляет профиль волны,
идущей налево:


х
'Р(х) = 2
 J '!'<z)dz.
хо
Нам будет удобно выбрать Хо = Xl. 8спомоrательная функция име-
. ет вид (рис. 16):


fo, X
Xl
'Р(х) =
 2
 (x
x,Mo, х,
 х'
 Х2.
l 2
 (Х2
X,Mo, х
 Х2.


'Р(х)


о х I Х 2 Х


Рис. 16
Для получения функции U(Х, t) мы должны взять разность левой и
правой волн, определяемых функцией 'Р(х).


247




Изобразим последовательные положения этих волн и их разности в
различные моменты времени t (рис. 17):
u(x,t o )


о


Х 2


х


х.


01 U
 X. t, l)

 U
X .
 2)


х.


..
х


I I I
х.


I I

' . ,
X2



..
х


Рис. 17
Пример 4. Построить профиль струны и(х, t) с закрепленным кон-
цом и(О, t) = О для моментов to = О, tl =
 , если О < Х < +00 И
и(х, О) = { AX(l
 х), о
 Х
 [, дu ( )
дix,O=O,x>O.
О, х > l;
Реш е н и е. Решение этой задачи будет получено, если начальные
данные нечетно продолжить на бесконечную прямую (рис. 18).


to=O


U(Х, t o )



21



l
\' ,/ 1 О
\ "--... ___ -' I
\ I
, /
....-"


2l


х


1
t. = .....
а


u(х, t.)


"...........
" ,

2l
l / \
...
...
.......
I--...
+-
...
, I О
" ,/
...-.....-'


Рис. 18


248




Пример 5. Найти продольное смещение и(х, t) точек стержня дли

ной 1, жестко закрепленноrо с обоих концов, если начальное смеще

ние


{ 2Х'
и(х, О) = <р(х) =
20
 х),


o<x

 ,

 <x
l,


а начальные скорости равны нулю:
Реш е н и е. Это
 первая краевая задача для уравнения колеба

u
нии:


r д 2 и 2 д 2 и
I at 2 = а дх2 ' О < х < 1, t > о,

 и(х, о) = q>(x) ,
l

 (х, о) = \jI(x) = о,
u(O,t) = u(l,t) = о.


Ее решение представляется в виде ряда Фурье (1.31) с коэффици

ентами Аn и Вn, вычисляемыми по формулам (1.34):
1 1/2
А = l ) cn(x)sin nпх dx = 2. ) 2xsin nпх dx +
n 1
 1 1 1
О О


1
+ 2. ) 2(1
 x)sin nпх dx =
sin nП В N = о.
1 1 n 2 х 2 2 '
1/2


Следовательно,


00
и ( х t ) = м "" ...Lsin nп cos n1Cat S i n n1СХ
, 2 LJ 2 2 1 1 .
1с n=l n


Задания для самостоятельноrо решения.
,1. Решить задачу Коши для уравнения колебаний неоrраниченной
струны:


r д 2 и
 а 2 и
I dt 2
 ах 2 '
а)
 и(х, о) = sinx,
l

 (х, о) = о;


r а 2 и 2 д 2 и
I at 2 = а дх 2 '
б)
 u(х, о) = о,
l

 (х. о) = Asinx;


r а 2 u = 4 д 2 u
I at 2 ах 2 '
в)
 и(х, О) = о,
l аи ( о)
 х
at х ,
 е .


249




2. Построить профиль бесконечной струны для моментов времени
t O = О t 1 =..L t 2 =..L если
, 2а ' а'
( )
 ! А cos

 , 'хl < [, ди ( )

u х, О
 dt х, О
 о.
о, Ixl > l;


з. ПОСТРQИТЬ профиль бесконечной струны для моментов времени
О 1 2 3 4
t O = t l =
 t 2 =
 t 3 =
 t 4 =
 если
, 4а ' 4а ' 4а ' 4а '


( )
 { l
 Ixl, при Ixl
 1, ди ( )

u х, О
 I I dt Х, О
 о.
О, при х > 1;
4. Построить профиль струны и(х, t) с закрепленным концом:
и(О, t) = о (o
 х < +00)
ДЛЯ моментов времени t о = О, t 1 =
 . t 2 =
 , tз = 2; , если начальные
скорости отсутствуют, а начальное отклонение имеет вид, изобра

женный на рис. 19.
у



1










:
h I
I
I
I
О С 2С


зс


х


Рис. 19
5. Построить профиль струны и(х, t) с закрепленным концом
и(О, t) = о для моментов времени t =0, t =1., если О
 х < +00, а
а
( ) = ! ASin 1t l x , О < х '5: [, аи ( О) =
u х, О dt Х, О.
О, х > l;
6. Найти профиль полубесконечной струны и(х, t) с закрепленным
концом и(О, t) = о для моментов времени t O = О, tl =
 2 1 ,t2 = 1/3 = :М,
а а а


если


{А 1t(L
x) < 1
и(х, О) = cos 21 ' х
, ди ( О) О (о )
дt х, = '5: х < +00 .
О, х > 1;


250




7. Полуоrраниченная однородная струна с закрепленным концом
Х = О возбуждена начальным отклонением
rO, о
 х < l,
и(х, о) =

sin 7 , 1
 х < 21,
l о, 21
 х <-1-00.


Определить rрафически форму струны в моменты времени
t
..1... t
.l t
М-
1
 4 ' 2
 '3
 2 '
а а а


8. Для полуоrраниченной струны с закрепленным концом х = О в
начальный момент времени выполнены следующие соотношения:


[О,
I
 (X
C),
U(Х, О) =

l

 (Х
3c),
О,


х <С,


с :5; Х :5; 2с,




 (Х, о) =0,
(h > О, с > О).


2c
x
3c
Х
 3с;


Начертить профиль струны в моменты времени
t =.f.. t = 2с t = 3с t =

1 а' 2 а' 3 а' 4 2а .


(а
 скорость распространения колебаний по струне).
9. Найти закон колебания однородной струны длины 1 = 1t С закреп

ленными концами, если начальное отклонение <р(х) = sinx, а началь

ная скорость равна нулю.
10. Заключенный в цилиндрической трубке идеальный rаз соверм
шает малые колебания, причем плоские поперечные сечения, состоя-
щие из частиц rаза, не деформируются и все частицы rаза двиrаются
параллельно оси цилиндра, а концы трубки закрыты жесткими непро

ницаемыми переrородками.
, Найти смещение и(х, t) частиц rаза при t > О, если начальное сме..
щение имеет вид


u(х, О) = Asin
X (О :5; х
 [),


а начальные скорости равны
ди ( О) В . пх
дt х, = slnT


(О
 х
 1).


251




11. Методом Фурье решить первую краевую задачу для уравнений
колебаний:


f д 2 u 2 а 2 u
I дt 2 =
 дх 2 ' О < Х < (, t > О,

 и(х, О)
 <р(х),
l

 (х, О) = 'I'(x) ,
u (О, t) = u(l, t) = О,


если:


а) <р(х) = о, ",(х) = sin
X ;
б) <р(х) = о, '(х) = 1.


12. Однородная струна, закрепленная на концах х = О и х = 1, имеет
в начальный момент времени форму параболы, симметричной относи

тельно перпендикуляра, проведенноrо через точку х =
 . Определить
смещение точек струны от прямолинейноrо положения равновесия,
предполаrая, что начальные скорости отсутствуют.
у к а 3 а н и е. Начальное отклонение точек струны равно
( ) 4hx(l
x) ( 1 )
<р х = [2 ' rде h = u 2" О .


13. КОНЦЫ С1"РУНЫ х = О и х = 1 закреплены. Начальное отклонение
задано равенством


r
 x. при O
x
xo,
и(х, О) =
 Mx
 1)
l l ' П р и Х а
 х S [.
Xo



Начальные скорости равны нулю. Найти отклонение и(х, t) при t > о.
14. Продольные колебания стержня длины l, у KOToporo один конец
(при х = о) закреплен, а друrой (при х = [) свободен, определяются
уравнением


д2

 2 д 2 u
dt2
 а дх 2 '


rде и(х, t)
 продольное смещение точки стержня с абсциссоЙ х в MO

мент времени t, rраничными условиями
U I О = О
И I = о
х= 'иХ х= 1


252




при любом t и начальными условиями при t = о:
ult=o = <р(х),

 It=o = 'J!(X).


Найти функцию и(х, t), если:
а) <р(х) = kx, 'J!(x) = о;
б) <р(х) = О, "'(х) = VO.


Пример. Трубка длиной 1 содержит растворенное вещество с на-
чальной концентрацией


{ Х'
<р(х) =
1
 х,


при О < х

 ,
при

 х < [.


Найти концентрацию С(х, t) вещества при t > О, если на концах
трубки она поддерживается равной нулю.
Реш е н и е. Мы имеем первую краевую задачу для уравнения диф-
фузии:


r дС = " д 2 С
I at '. дх 2 '

 С(х, О) = <р(х),
lC(O,t) = C(I,t)=O,


О < х < 1, t > О,
O<x<l,
t > О,


rде т}
 коэффициент диффузии.
Решение ее определяется рядом Фурье


00 ( nП ) 2 t . nпх
С(х, t) = IAn e
 т 11 StnT
n=l


с коэффициентами Фурье, вычисленными по формуле:
1/2 1 . тс
А =.2. f xsin n1СХ dx + .2. f (l
 x)sin nпх dx = Jl stn 2 .
n 1 1 1 1 х 2 п 2
О 1/2


Следовательно,


( ) 4t
 (
I)n (2n+ll
2 ,,2 111 . (2n + I)и
Ох, t = 1(2 ';-о(2n + 1)2 е sш 1


253




15. Дан тонкий однородный стержень длиной 1. боковая поверх

ность KOToporo теплоизолирована. Концы стержня поддерживаются
при температуре, равной нулю. Определить температуру стержня в
момент времени t > О, если начальная температура равна
<р(х)
 А sin 2
 х.


16. Методом Фурье решить краевую задачу:
r ди
 а 2 и
I at
 дх 2 '

 U (х, О) = sin х, О < х < п,
l и(О, t) = и(пЛ = о, t > О.


о <х < п, !->О,


17. Решить первую краевую задачу
r дu
 2 а 2 и
I dt
 а ах 2 '

 и(х, О) = q>(x),
lu(O, t) = u(l. t) = о,


0< х < 1, t > О,
0< х < 1,
t >0,


если:


а) <Р(Х) = x(l


 );
) ( ) х х 2 х 3
б q> х = 6/
 4/2 + 1213 .


18. Растворенное вещество с начальной концентрацией СО = const
диффундирует из раствора, заключенноrо между плоскостями х = О и
х = h, в растворитель, оrраниченный плоскостями х = h их = [, (1 > h).
Определить концентрацию С(Х, t) вещества в момент времени t > О,
предполаrая, что rраницы х = О и х = 1 непроницаемы для-вещества, то
есть


ас I = о ас I = о
ах х= О 'ах х = l .


19. Решить краевую задачу:
r аи = а 2 д 2 и О < х < 1, t > о,
I dt ах 2 '

 u (Х, О) = q>(x), о < х < 1,
l

 (О, t) =

 (ц) = О, t > О.


254




20. Пусть в пластине, перпендикулярной оси Ох (О
 х
 [), распро

страняющейся бесконечно в направлениях Оу и Oz и имеющей Ha

чальную температуру <р(х), стенки внезапно охладились до темпера

туры окружающей среды ио.
Найти зависимость и(х, t) между температурой и временем от нача

ла охлаждения для различных точек пластины.
Рассмотреть случай постоянной начальной температуры
<р(х) = и} = const.
21. Задача о массопроводности. Пусть сосуд с единичным попе

речным сечением и высотою 1 заполнен раствором соли. Положим,
что этот сосуд с содержимым поrружен в емкость с большим количе

ством БОДЫ, причем открытый край сосуда находится непосредствен

но под поверхностью воды. Примем, что верхний край сосуда всеrда
находится в соприкосновении с чистой водой. Тоrда в сосуде будет
протекать процесс диффузии соли в соответствии с законом Фурье:
де д 2 е
дt = 11 дх2 '
rде с = с(х, t)
 концентрация соли в растворе;
11
 коэффициент диффузии;
t
 время;
х
 высота слоя раствора в сосуде.
rраничные и начальные условия процесса таковы:


 Ix=o = О, clX=1 = О, clt=o = со.


Определить концентрацию соли с(х, t) в зависимости от времени и
от высоты слоя жидкости в сосуде.
Найти выражение для концентрации диффундирующеrо вещества
в различных частях сосуда после Toro, как процесс массопроводности
установился.
22. При рассмотрении процесса взаимной диффузии двух rазов воз

никает следующая краевая задача:
r ди д 2 и
I дt = 11 дх 2 '

 ult=o = 1.
l ulx=o = о,
: IX=1 = О t > О,
rде функция и(х ,t) определяет парциальное давление одноrо из rазов
Найти решение этой краевой задачи.


0< х < 1, t > О,


0< х < [,


255




Пример. На rранице Kpyra х 2 + у2
 R2 температура распределяет

ся по закону u = у2. Найти распределение температуры внутри Kpyra,
предполаrая, что оно стационарно.
Реш е н и е. Это задача Дирихле для Kpyra:
{ l:1U
 О,
ul r =y2,
rде r
 окружность х 2 + у2 = R2. На этой окружности
у2 = f('f) = R2 sin 2 'f =
2 (I
 cos2\v).
Решение рассматриваемой задачи представляется рядом (3.26):


00
и =
 + L(
 )n(ancosтp + bnsinтp),
n=l
с коэффициентами а n и Ь N ' определяемыми по формулам (3.29):
n n
а п =
 J f('f)cosn'fd'f =
 J
2 (I
cos2\v)cosn'fd'f. Ь п = о.

n
n
Следовательно,
а
 R 2 а
 R2
 Ь
 О
о
 'n

 2 u п2, n
 ,


rде


б n2 = { 1' п = 2,
О, п
 2,


а значит,
и =
2
 '; cos2\v =
2

 (r 2 cos 2 'f
 r 2 sin 2 'f) =
2

 (х2
 у2).
Пример. Найти значение rармонической функции в центре Kpyra
х 2 + у2
 R2, если на ero rранице u = 1 х 1.
Реш е н и е. Зная значение функции на окружности:
u = 1 х 1 = R Icos '111
и применив теорему о среднем, получим
1t 1t
u(о) = 2
 J RlcoS'fld'f =
 Jicos'fld'f =

п О
= R J J 1!. cos'fd'f
 J \OS'fd'ft = 2R .
2t l о t J 1t


256




23. Построить все однородные rармонические полиномы, степени
которых не выше второй.
24. Решить задачу Дирихле для Kpyra радиуса R с центром в начале
координат, если заданы следующие rраничные условия:
а) ulr=R = А; б) ulr=R = Acos<p;
в) ulr=R = Asinq>; r) ulr=R = А + Bsinq>;
д) ulr=R = Asin 2 <p + Bcos 2 q>; е) ulr=R = Asin 3 q> + В,
rде А и В
 постоянные, (r, <р)
 полярные координаты.
25. Найти решение уравнения Лапласа внутри Kpyra радиуса R,
если на rранице Kpyra заданы условия:
а) ulr=R = А + Ву; б) ulr=R = Аху.
26. Найти функцию u(r, <р), удовлетворяющую уравнению Лапласа
внутри Kpyra с центром в начале координат и радиуса R, если на rpa

нице этоrо Kpyra


r Asinq>, О
 <р
 п,
ul =

r=R ltAsin3q>, 1t
q> <2п.
27. Найти функцию u = и(х, у), rармоническую внутри Kpyra
х 2 + у2
 х + у


и принимающую на ero rранице значения:
а)и=х; б)u=у.
28. НаЙти функцию u = и(х, у), rармоническую внутри Kpyra
х 2 + у2
 1
и принимающую на ero rранице значение u = х з .
29. Найти значение rармонической функции u = и(х, у) в центре
Kpyra х 2 + у2
 4, если на ero rранице она принимает значение


и=ху.
30. Найти значение rармонической функции и(х,У) в центре Kpyra
х 2 + у2
 х, если на ero rранице она принимает значение
u = х + у.
31. Определить стационарное распределение температуры внутри
кольца R 1 < r < R2' если на окружности r = R 1 поддерживается темпе

ратура u = Ul' а на окружности r = R 2
 температура u = и2.




Ответы к заданиям части 1


fлава 1



2


з
2. а)у'= 1; б)ху'=2у; в)у"=2; r)y" = 0+ у'2)2.
3. а) у = ix2; б) х 2 + 2у2 = 51; В) у = хе Х ; r) у = 10e
xsinx.


fлава 11



3


y(l) = 0.95.


1. у = Csinx.



5
С+х
2. у = 1
 Сх .


3. у =
ln(C
eX)


( Х 2 ) 2
4. у = т (x
2) и у=о.


1. у2 = 2х 2l n Cx.



6
2. у = 2Ь (х 2
 с 2 ) (С > О).


3. у = xe 1 +Сх.



7


3: х = Се У
 (у2 + 2у + 2).


2. у = х; + Сх.
v ( У ) Rt
4. 1 = R + 1 о
 R е
T ·


1 х2 С
· У = 4 + х2 .


*8


{. уЗ = Се
tx2
 (х2 +
 )-
у2
з.1 = СеТ
 (у2 + 2).
х


2
2.y=(tx2+ .JCx ) ;у=о


258





 9.


3 2 у5
1.

 х у
 5 = с.


2.
 x2 + у2
 х = с.



 15.
t. У = Сх + cosC; Х = sinp, у = psinp + cosp.
2.y=Cx
C2+C3; x=2p
3p2, у=р2
2p3.
3. У = Сх

2
 3
 ; х = р
 3
2 ' У = Р;
 3
 .
4. у = Сх + с2 I У =

 .



 16


0(0, О); А(I, 1); 8(3,
3).



 17
1. У = ( х; С ) (семейство парабол), особое решение у = о;
2. у = Сх +
 (семейство ПРЯМЫХ), особое решение
 парабола
у2 = 4х;
3. у 2 (l ..... у) = (х
 с)2, особое решение у = 1.



19


х
1. у = е а .
2. Парабола у2 = 2а(х
 С).
3. Лоrарифмическая спираль r = Се q>ctga (, и <р ......... полярные коорди

наты).
4. Парабола (х
 у)2 = Су.
5.у2 = x2In C
 .
х
6. rиперболы х 2
 у2 = с.


*20


1. 60 мин. 2. 35,2 сек.


259




rлава 111



3
1. у = С 1 + С 2 х + ix2 +
 cos2x.
2
2. у = (1 +
 х у .
3
3.у = +
 (x + С 1 )"2 + С 2 .
4. 2
 lП( 1 + k;б ). rде k
 коэффициент пропорциональности, отне-
сенный к единице массы.


3. у = 1
 е Х .



4
Х I+C? ll С I С
2.y=
c+ с2 пl+ l Х + 2.
I I
4. у = а 1пl cos х : t; I + С 2 .
X
CI Н
5. Цепная линия у = ach + С 2 , rде а =
, н
 сила rоризон-
а q


1. lny = С 1 е Х + C2e
X.


тальноrо натя жения и q
 вес поrонноrо метра каната.
. 6. Т = .н ln 1 +
 12
 а 2 2

 ,3 сек.
g а


х
3.у = е 2 (С} + С 2 х).



5
2. у = е
ч Сl cos x
 + С 2 sin X
 ).
4. х = С 1 cosrot + С 2 sinrot.


1. у = Cle
2x + С 2 е Х .



6
{
 0,45 сек. 2. х = 1,21e
lt6t sin 4,13t; 1,52 сек.



9
1. у = С 1 + C2e
2x
 ( k х з

 х 2 + i х ).
2. у = 2х.
3. у = е Х (С 1 sinx + С 2 cosx)
 (sinx + cosx).
260




4. у = С 1 sinl0x + С 2 cosl0x + {O sinl0x.
5.х = 1
 0,12sin(IO.Jgt) + O,Olcos(IO.Jgt) + O,12sin30t М.



10


1 У = shx
· sh 2п .


2. у = 1
 sin х
 cos х.
3. Решений нет.


4. у = 2х
 1t + 1tCOSX + Csinx, С
 произвольное.


fлаваlV



з


1. а) линейно зависимы; б) линейно независимы; в) линейно зависи

мы; r) линейно независимы.
2. у = х
 2х 2 + х 3 .



5
1. у = С\е Х + C2e
X + ( i х 2
 i х )ех.
2
 1 2 1 4 X I
.У

4+9Х+ З6 Х
зпх.



6


1. у = С 1 е Х + C2e
X + Сзе 2х + C4e
2x.
2. у = C\e
x + еЧ С 2 cos xf + Сз sin xf ).
з. у = eX(C 1 + С 2 х) + Сзе
2х.


 [( С ) х.JЗ ( С ) х.JЗ ]
4. у = е 2 С 1 + 2 Х cosT + сз + 4 Х sinT .


х ( ) х ( )
1
 Х 1t 1

 Х 1t
5 У =
e J2 sin
 +
 +
e ..f2 sin



· 2 .J2 4 2 J2 4.


261





7
1. а) у = Ах + x(Bcosx + Csinx);
б) у = х(Ах 2 + Вх + С)е Х + Ое 2х ;
в) у = х 2 [(Ах + B)sinx + (Сх + D)cosx];
r)Y = xe
X[(Ax2 + Вх + C)COSX + (A 1 x 2 + B1x + C1)sinx).
2. у = С 1 + С 2 х + Qзе Х
 (i X3 +
 x2 ) +
 (cosx
 sinx).
3. у = e
X(
 x2 + 2х + 3) + х
 3.



8
1. у = C1xP + C2X
P, если p;f:. о; у = С} + C 2 1nx, если Р = о.
2. у = 1(С 1 + C 2 1nx) +
 2 1 In2 х.
х х


3. у = х 3
 х.



9
. 1. х = .й sh(t.J2); у = ch(t.J2)
 .й sh(t.J2).


2. х = C 1 cost + С 2 sint + Сзсht + C 4 sht;
у =
Cl cost
 С 2 sint + Qзсht + C 4 sht.


fl0
1. У = sh3 е 2х
 sh2 е3Х
 shl
2sh3
 3sh 2 2sh3
 3sh 2 2sh3
 3sh 2 .


2. x(t) = Ce 2t sint, y(t) =
Ce2tcost, С
 произвольное.




Ответы к заданиям части 11


r Jlава 1


( у 2 4 )
1. и = Ф
 L .
х ' х


2. и = 2(у2
 х 2 ).
ф ( У
 xlnx К ) = О ( У ХlПХ )
3. х ' х или же и = х'Р .... х .
4. Ф(u. у
 :Inx ) = о.
5. Ф(
;
 у+/ ' (х
 у)(х + Y
2u») = о.


fJlaBa 11


00
1. а) {(х) =


 L (2п : 1)2 cos(2n + 1)х.
n=о


00
б) '(х) = 2 L(
1)n+ 1 Si:nx .
n=l
00
2
 (....t)n+1
в) '(х) = з-1t 2 + 4
 п 2 cosnx.
n=1
00
r) '(х) = А;В + ; (B
A)L sin

п++l1)x .
n=о
00
16
 (
l )n+ I n .
д) {(х) = 1t
 (4п2
 02 SШ2nх .
n=l
3.. {(х) =


 cos2x +
 cos4x.


00
4. а) '(х) =
 L (
1)п cos

n++1 Ох .
n=о


00
4
 (
 l)n. )
б) {(х) = 7t
 (2п + 1)2 sш(2n + 1 х.
п=О


263




00
в) !(х) = .2.
 l.
 cos2nx .
1t 1t
4n2
1
n=l


00
5. 1) а) ; L (1
 с о s п; ) si Пn пх ;
n=l


00
б) 1 + .2.
 sin nп cosnx .
2 x
 2 n
п=l


00
2) а) 2 L (
I
n
l sinnx;
n=l


00
б) 1t
 l.
 cos(2n
 ОХ
2 1t
 ( 2 n
 1)2 .
n=l


00
7. а) [(х) =
 L (2n
 1)3 sin(2n
I)x.
n=l


00
8
 (
l)n
l п
б) !(х) = 1t LJ 4n 2
 1 sinnx.
n=l


8. а) {(х) = 21th [
 + f ei
:h )2 c osnx ] .
n=l


б) {(х) = 2: (
 + f Si
:h c osnx ) .
n=l


00
А) а) ..!
 sin(2п + Охх.
9. 1t LJ 2n + 1 '
n=О


б) f (х) = 1.


00
Б ) а ) 11
 (
Hn+l sin nХХ .
1t LJ п l'
n=l


00 (2n + 1 )пх
) 1 4l
 cos l
б "2
 ;2 LJ ( 2 n + 1 )2 .
п=О


264




.. 00
10. а) {(х) = !
 п 42
 (2n
 1)2 cos(2n + l)пх.


00
б) {(х) = 10
 (
l)п siп.!Ш&..
x
 n 5
п=l


+00
) ( ) 2 J 1
 cos л ·
11. а f х = 1t Л Slпл.хdл.
О


+00
б}f(х) = ; J Si
Л соsл.хdЛ.
О


+00
) ( ) 2 J 1
 cos л
в f х = 1t л 2 соs'Лхdл.
О


-f-oo
r) {(х) = Jе
лсоsл.хdл.
О


+00
д) {(х) = J е
Л siпл.хdл.
О


+00
) ( ) 2 J sin л1t ·
е f х = 1t 1
 л 2 SlпЛхdл.
О


+00
ж) {(х) = 2а J л
оSЛх2 dл.
1t +а
О
+00
л2
3) [(х) = Jп J е 4 соsл.хdл.
о
+00
)f( )
 1. J ( 2лsiпл+ соsл
l '1.. + siпл
л . '1.. )d '1
И Х
 1t л 2 COS I\,A, л 2 Sln I\,A, А.
О


+00
12. а) [(х) = ; J lC:s
 dл (о < х < +00);
О


+00
б) { (х) = .2. J лsiп 'л.х dл (О < Х < +00).
1t 1 + л 2
О


265




fлава 111


1. а) и(х, у) = Р 1 (х) + Р 2 (у);
х 2 у2
б) и(х, у) = Р] (х) + Р 2 (у) + ----т---;
2
В) и(х, у) = Р} (х) + Р 2 (у) + Х 2 lnly

r) и(х, у) = Р] (х) + Р 2 (у)е ах ;


х 3
д) и(х, у) = Р 1 (х) + Р 2 (у)е""3;
F (у)
е) и(х, у) = Р] (х) +
;
х
ж)u(х, у) = xF1(y) + Р 2 (у).
Здесь Р 1 и Р 2
 произвольные функции.


2. и(х, у) = Р 1 (х + л}у) + Р 2 (х + Л2У)' rде Лl, 2
 корни
уравнения А + 28 л + Сл 2 = о.
3. u(х, у) = р(х 2 + у2), rде F
 произвольная функция.


4. u(х,У) = хр е ). rде F
 произвольная функция.


5. а) rиперболический тип:



 = С}, ху = С2;
х + у = с;
3
Х у =с L=C.
1, у 2,
r) Эллиптический тип: Iп(х+
 1+х2) + In(y+.J1+Y2)=C 1 ,2'


б) Параболический тип:
В) rиперболический тип:


) ди д 2 u
 х 2
6. а д
 = дч 2 ; "="2 + у' 11 = х;
) д2и д 2 и
.
 (
 ) (
 )
б д
2 + дтj2
o,

 'П x+vl+x
 . ll=ln y+vl+y
 ;
В) Уравнение эллиптично всюду, кроме осей координат, состоя-
щих из точек параболичности. Оно приводится заменой

 = у2, 11 = х 2 к каноническому виду:
(}2 и (}2 и 1 (}u 1 (}u О
д
2 + dr}2 + 2
 д
 + 211 dr1 = .


266




) д2и
7. а д;дt1 = о;
 = 3Х + у, 11 = Х + у;
U(Х, у) = F 1 (3x+y) + Р 2 (х+у);
б ) д2 u 1 ди о.
 у .
д; дt1
 2; дt1 = , '" = Х у, 11 =
,
и(х, у) = РI e ) .J 2x y + Р2(ХУ);
В)

 = о;
 = : ' 11 = у; и(х, у) = УРI е ) + р 2 е ).
rде Fl и Р 2
 произвольные функции.


8. а) и(х, у) = Fl (х
 2/у) + Р 2 (х + 2/у);
б) и(х, у) = yF 1 (2x + у) + Р 2 (2х + у);
В) и(х, у) = F1(x + 2у)е
1-(x
y) + Р 2 (х
 у);
r) и(х, у) = /f Fl (ху) + Р 2 е );
д) и(х, у) = F1(x + у
 cosx) + Р 2 (х
 у + cosx);
9. а)

 +

 + 3

 = о;
 = х, 11 =
 У % (у < о);
д 2 и 1 ( ди ди ) О
d;rm
 6(;
 11) д;
 rm = ;
3 3

 = х

 (
y)2, 11 = х +
 (
y)2 (у<о);
б ) д2и + д 2 и + 2a
1 ди
 о.

 11 = 2 С У (у > 0 ), .
д; 2 дt1 2 11 дl1
 , '"
 Х, · I V У
1

2

 :=
e


 ) = о;

 = х
 2
 у ' 11 = х + 2
 у (у < О).


10. а) и(х, у) = F(arctg : );
б) и(х, у) = Fl(a rctg
)
 x2+y2 + F2(a rctg
);
в) и(х, у) = Fl (
 x2 + у2) arctg
 + Р 2 (
 x2 + у2).
11. и(х, у) = 1 + х 2 у + у2
 2х 4 .


267




12. а) и = 1 + ху + у2;
б) и = у2 + Вху + Asinx;
в) и = х 2 у3 +ху+у2;
r)u = ВеХ +А
B.
13. и(х, у) = зх 2 + у2.
У к а з а н и е. Общее решение уравнения есть
и(х, у) = Р} (х + У) + Р 2 (3х
 у),
rде Р} и Р 2
 произвольные функции.
х+2у
14. и(х, у) = q>( х

 у3) +
 J v(z)dz.
x

y3


y
sin Х+ х
15 ( )
 <p(
y + sin х + х) + <р(у
 sinx + х) 1 J ( )d
· и х, у
 2 + 2 '1' z z.

y+sinx+x
у к а 3 а н и е. Общее решение уравнения есть
U(Х,у) = F1(y
 sinx
x) + Р 2 (у
 sinx +х),
rде F 1 и Р 2
 произвольные функции.
16. и(х, у) =
 q>(xVY) +
 yq> (; ) +



 ж
у 7 У 7
+ }3 6
x3y Jq>(
)

4d


 t/x 3 y J'I'(
)

4d
.
х'(У х'(У


fлаваlV


1. а) и(х, t) = sinxcost;
б) и(х, t) = А siпхsiпаt;
а


В) и(х, t) = е; sh2t.
9. и(х, t) = sinxcosat.
10. и(х, t) = (acos 1t
t + :
 sin
)sinT'


268




11. а) U(Х, t) =
 sin
 tsin
 х.


00
б) ( ) 21
 1 . (2n+О . (2n+l)
и Х, t = х 2 а ;:о (2n + 1)2 sш 1 nat sш 1 пх.


00
12 ( ) 32h
 1 (2n+ 1) . (2n+ 1)
· и х, t = х 3 ;:о (2n + 1)3 cos 1 nat sш 1 пх.


о()
13. U(Х, t) = 2hl 2 L ....Lsin хnхо cos 1tnat sin ппх .
1t2xo(l
xo) n 2 1 1 1
n=l


00
14 а ) ( t)
 8kl
 (
I)n (2n+ l)1tat . (2n+ l)1tx .
· и Х,
 х 2 ;:О(2n + 1)2 cos 21 sш 21 '


00
б) ( t)
 8vol
 1 . (2п + l)1tat . (2п + l)1tX
и х,
 х 2 а ';;0 (2n + 1)2 sш 21 sш 21 .


15. u(х, t) = Ае
 (2п 2 а 2 / sin 2r .
16. U(Х, t) = e
t sinx.


00 ( ) 2

l n
l
 nп a 2 t
17. а) и(х, t) = 12} L ( )3 е 1 sin nr ;
1t n=l n


. 00 ( ) 2

 nп a 2 t
б) u(х, t) =
 L
e 1 sin n
X .
1t n=l п


18. с(х, t) = с о [
 + ; i
 sin mr е
 ('
 )21]/ cos nr ] .
п=l


у к а з а н и е. Задача приводится к решению уравнения
дс д 2 с (
дt = 11 дх 2 О < Х < 1, t > О)


при условиях:
( ) { СО, о < х < h,
с х,о =
О, h < х < 1;




 (О, t) =

 (1, t) = О.


269




00 ( ) 2
а nп a 2 t
19. и(х, t) = f + Lane
 т cos n
x ,
n=l


1
rде а n = Н q>(x)cos nr dx, n = О, 1, 2, ....
О


00 ( ) 2

 nп a 2 t
20. и(х, t) = ио + LAn e 1 sin n
x ,
n=l


1
rде А = l J <p(x)sin nпх dx
 2ио [ 1 + (
On+l ] .
п l 1 n1С
О
При q>(x) = Ul:
00
(2k+1)2п2а2t
( t)
 4(UI
иo)
 1 12 . (2k+ Нхх
u х,
 ио + 7t
 ( 2k + 1) е SlП 1 .
k=O


00 ( 2n+l ) 2 2
21 ( t)
 4со
 (
On+l

 1t t)t (2n+ 1)
. с х,
 1с
 2п + 1 е cos 21 пх.
n=о
При установившемся процессе
де О д2с О
дt = и дх 2 = .


Следовательно, с = Ах + В, rде А и В ........ постоянные, которые мож-
но определить экспериментально.


00 ( 2n+l ) 2 2
22 ( t)
 .i



 1t t)t . (2n+ 1)
. и х,
 1t
 2n+] е Sln 21 пх.
n=О


2
. У к а з а н и е. Воспользоваться формулой (3.23) (СМ. rл. IV,
 3)
при п = О, 1 t 2.


в) U =
 rsin<p;


б) и =
 rcos<p;
r) U = А +
 rsin<p;


24. а) U = А;


д) u =
 (1


 cos2q> ) +
 (1 +

 cos2q> );


270




е)и = в +

 rsin<p
 l A(
 )3 sin3<p.
у к а з а н и е: sin 3 <р =
 sin<p
 l sin3<p.


25. а) u = А + Ву;


б) и = Аху.


00
( ) А r. 8А
 ( , ) 2n cos2пq>
26.ur,q> = R Sln<p
1t
 R 4n2
9 .
n=1


27. а) u = х;


б) u = у.


28.и= l x3....
 xy2+
 x.


29. и(О, О) = о.
30. и(
 ' о ) =
 .


31. У к а з а н и е. Искать решение в виде:
u(r) = CJlnr + С 2 ,
rде С 1 и С 2 находятся из условий на rранице кольца.




Литература


1. В. В. Степанов. «Курсдифференциальныхуравнений».
Моск-
ва: «q)изматrиз», 1959.
2. и. Т. Петровский. «Лекции по теории обыкновенных дифферен-
циальных уравнений».
 Москва: «Наука», 1984
3. л. с. ПонтРЯ2ин. «Обыкновенные дифференциальные ура вне-
ния».
 Москва: «Наука», 1982.
4. л. э. ЭЛЬС20ЛЬЦ. «Дифференциальные уравнения и вариацион-
ное исчисление».
 Москва: «УРСС», 1998.
5. Н. М. Матвеев. «Методы интеrрирования обыкновенных диф-
ференциальных уравнений».
 Минск: «Вышейш. шк.», 1974.
6. А. п. Карташев, Б. л. Рождественский. «Обыкновенные диф-
ференциальные уравнения и основы вариационноrо исчисле-
ния».
 Москва: «Наука», 1980.
7. ю. с. БО2данов, с. А. Мазаник, ю. Б. Сыроид. «Курс дифферен-
циальных уравнений».
 Минск: «Унiверсiт
цкае», 1966.
8. В. К. Романко. «Курс дифференциальных уравнений и вариацион-
Horo исчисления».
 Москва
Санкт-Петербурr: «Изд-во ЛБЗ»,
2000.
9. А. К. Боярчук, Т. п. rоловач. «Справочное пособие по высшей
математике. Том 5: Дифференциальные уравнения в примерах и
задачах».
 Москва: «УРСС», 1999.
10. Б. п. Демидович, В. А. Кудрявцев. «Краткий курс высшей мате-
матики».
 Москва: «Астрель
АСТ», 2001.
11. А. Ф. Филиппов. «Сборник задач по дифференциальным ура вне-
ниям».
 Москва
Ижевск: «Изд-во РХД», 2000.
12. Н. М. Матвеев. «Сборник задач и упражнений по обыкновенным
дифференциальным уравнениям».
 Минск: «Вышейш. шк.»,
, 1987. ·
13. «Задачи и упражнения по математическому анализу для втузов»
/ под редакц. Б. п. Демидовича/.
 Москва: «Астрель
АСТ»,
2001.
14. и. r. Петровский. «Лекции об уравнениях с частными производ-
ными».
 Москва: «Наука», 1961.
15. В. п. Михайлов. «Дифференциальные уравнения в частных про-
изводных».
 Москва: «Наука», 1983.


272




16. Р. Курант. «Уравнения с частными производными».......... Москва:
«Мир», 1964.
17. А. Н. Тихонов, А. А. Самарский. «Уравнения математической
физики».
 Москва: «Наука», 1972.
18. с. л. Соболев. «Уравнения математической физики».......... Москва:
«Наука», 1966.
19. В. с. Владимиров. «Уравнения математической физики»
 Mo

сква: «Наука>.>, 1976.
20. и. Т. Араманович, В. и. Левин. «Уравнения математической фи

зики».......... Москва: «Наука», 1964.
21. с. К. Тодунов. «Уравнения математической физики».......... Москва:
«Наука», 1971.
22. ю. с. Очан. «Методы математической физики».......... Москва: «Высш.
шк.», 1965.
23. Б. М. Будак, А. А. Самарский, А. Н. Тихонов. «Сборник задач по
математической физике».......... Москва: «Наука», 1972.
24. Н. с. Кошляков, э. Б. rлинер, М. М. Смирнов. «Уравнения в ча

стных производных математической физики».......... Москва: «Высш.
шк.», 1970.
25. М. М. Смирнов. «Задачи по уравнениям математической физи

ки».
 Москва: «Физматrиз», 1961.
26. «Сборник задач по уравнениям математической физики» / под
редакц. В. с. Владимирова/.......... Москва: «Наука», 1974.
27. с. К. Тодунов, Е. В. 30лотарёва. «Сборник задач по уравнениям
математической физиКи».......... Москва: «Наука», 1974.
28. ю. с. Очан.
Сборник задач по методам математической физи

Ки».......... Москва: «Бысш. шк.», 1967.
29. и. В. Мисюркеев, «Сборник задач по методам математической
физики».......... Москва: «Просвещение», 1975.
30. «Сборник задач по математике для втузов. Часть 4: методы опти

мизации, уравнения в частных производных, интеrральные ypaB

нения» / под редакц. А. В. Ефимова/.......... Москва: «Наука», 1990.




Оrлавление


Часть 1
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ . . . . . . . . . . . . . . . 5
r л а в а 1. Общие понятия. . . . . . . . . .. ...... . . 5
Э 1. Задачи, приводящие к дифференциальным
уравнениям . . . . . . . . . . . . . . . . . . . .
э 2. Основные определения . . . . . . . . . . . . .


r л а в а 11.


э 1.


э 2.
Э 3.
Э 4.
Э 5.
Э 6.
Э 7.
Э 8.
Э 9.
Э 10.
Э 11.


э 12.


э 13.
Э 14.
Э 15.
Э 16.
Э 17.
Э 18.


э 19.
Э 20.


274


Дифференциальные уравнения nepBoro
пор ядка. . . . . . . . . . . . . . . . . . . . . .
Различные формы дифференциальноrо
уравнения первоrо порядка ....
Поле направлений . . . . . . . . . . . .
Полиrоны Эйлера. . . . . . . . . . . . .
Теорема существования и единственности
Уравнения с разделяющимися переменными . .
Однородные уравнени.я. .
Линейные уравнения. . . . . . . . . . .
Уравнение Бернулли . . . . . . . . . . .
Уравнения в полных дифференциалах.
Понятие об интеrрирующем множителе. . .
Интеrрирующий множитель линейноrо
уравнения . . . . . . . . . . . . . . . . . . . . . . . . 36
Уравнение первоrо порядка, не разрешенные
относительно производной . . . . . . . . . . . 37
ПараметрическиЙ способ решения . . . . . . . . . . 38
Уравнение Лаrранжа. . . . . . . . . . . . . . . 43
Уравнение Клеро . . . . . . . . . . 46
Особые точки . . . . . . . . . . . . 48
Особые решения . . . . . . . . . . 50
Составление дифференциальных
уравнений . . . . . . . . . . . . . .
Задачи rеометрическоrо характера.
Задачи физическоrо характера . . . . .


. . 5
. . 8


13


13
14
. . . . . 15
17
18
. . 20
. . . 23
. . . 30
. . . 32
. . . . 35


. 55
. . . 56
. . 60




r л а в а 111. Дифференциальные уравнения BToporo
порядка. . . . . . . . . . . . . . . . . . . . . 65
Э 1. Общие понятия . . . . . . . . . . . . . . . . . . 65
Э 2. Механический смысл дифференциальноrо
уравнения BToporo порядка . . . 66
Э 3. Интеrрируемые случаи. . . . . . . . . . . . . . 67
Э 4. Случай понижения порядка. . . . . . . . . . . 71
Э 5. Линейные однородные уравнения
с постоянными коэффициентами . . . . . . . . . . . 75
Э 6. Физическая интерпретация линейноrо
однородноrо уравнения BToporo порядка. . . . . . . 81
Э 7. Линейные неоднородные уравнения
с постоянными коэффициентами . . . . . . . . . . . 85
Э 8. Физическая интерпретация линейноrо
неоднородноrо уравнения BToporo порядка .. . 85
Э 9. Нахождение частных решений неоднородноrо
уравнения методом неопределенных
коэффициентов . . . . . . . . . . . . . . . . . 86
Э 10. О краевых задачах для уравнений BToporo
порядка. . . . . . . . . . . . . . . . . . . . . . 91


r л а в а IV.


э 1.


э 2.


э 3.


э 4.


э 5.
Э 6.


э 7.


э 8.
Э 9.

 10.


Дифференциальные уравнения высших
порядков . . . . . . . . . . . . . . . . . . .
Теорема существования и единственности
решениЙ . . . . . . . . . . . . . . . . .
Уравнения, допускающие понижение
по рядка. . . . . . . . . . . . . . . . . . . . . .
Однородные линейные дифференциальные
уравнения . . . . . . . . . . . . . . . . . . . . .
Неоднородные линейные дифференциальные
уравнения . . . . . . . . . . . . . . . . . . . . .
Метод вариации произвольных постоянных. .
Однородные линейные уравнения с постоянными
коэффициентами. . . . . . . . . . . . . . . . . . . .
Неоднородные линейные уравнения
с постоянными коэффициентами . .
Уравнение Эйлера. . . . . . . . . . .
Системы дифференциальных уравнений .
Об общих краевых задачах. . . . . . . . .


. 95


. 95


. 97


100


109
110


114


122
132
134
140


275




Часть 11
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. . . .


rлава 1.
Э 1.
Э 2.


э 3.
r л а в а п.
Э 1.


э 2.


Уравнения nepBoro порядка .
ЛинеЙные однородные уравнения . .
Задача Коши для линейноrо однородноrо
уравнения . . . . . . . . . . . . . . . .
Квазилинейные уравнения . . . . . . . . . . .


146
146
146


152
154
162


Ряды Фурье .............. . . . . .
Ортоrональные системы функций и обобщенные
ряды Фурье. . . . . . . . . . . . . . . . . . .
Триrонометрические ряды Фурье . . . . . . . . . .


162
165


r л а в а 111. Классификация уравнений BToporo
порядка . . . . . . . . . . . . . . . . . . . 182
Э 1. Основные определения . . . . . . . . . . . . .. 182
Э 2. Приведение к каноническому виду линейных
относительно старших производных уравнений
BToporo порядка с двумя независимыми
переменными. . . . . . . . . . . . . . . . . . . 183
Э 3. Задачи с начальными данными. . . . . . . . . . . . 190
r л а в а IV. Основные уравнения математической ·
Физики .. . . . . . . . . . . . . . . . . . . . 201
Э 1. Уравнение колебаний струны . . . . . . 201
Э 2. Уравнение теплопроводности . . . . . . . 21 б
Э 3. Уравнение Лапласа.. . . . . . . 227


Ответы к заданиям части 1
Ответы к заданиям части Il
Литература . . . . . . . . .


. 258
. . . 263
. . . 272




Борис Павлович ДЕМИДОВИЧ
Владимир Павлович МОДЕНОВ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Учебное пособие
Генеральный директор А. Л. Кноп
Директор издательства О. В. Смирнова
ЛР №065466 от 21.10.97
Гигиенический сертификат 78.01.07.953.П.001665.03.02
от 18.03.2002 г., выдан ЦГСЭН в СПб
Издательство «ЛАНЬ»
lan@lpbl. spb. ru
www.lanbook.com
www. lanpbl. spb. ru/price. htm
192029, Санкт-Петербург, Общественный пер., 5.
Издательство: тел./факс: (812)567-29-35, 567-05-97, 567-92-72
pbl@lpbl.spb.ru
print@lpbl. spb. ru
Бумага офсетная. Гарнитура Школьная. Формат 84x108 1/32.
Печать высокая. Уел. п. л. 15,12. Тираж 1500 экз.
Заказ №
Отпечатано с готовых диапозитивов
в ОАО «Владимирская книжная типография».
600000, г. Владимир, Октябрьский проспект, д. 7.
Качество печати соответствует качеству
предоставленных диапозитивов