Автор: Письменный Д.Т.
Теги: математика учебные пособия и учебники по математике
ISBN: 5-8112-1778-1
Год: 2006
Текст
Д.Т.Письменный - автор бестселлера I оювимся к экзамену по математике», пыпускаемого в серии «Домашний репетитор» । н к обия, по которому за последние । оды готовились к экзаменам более S00000 школьников и абитуриентов из России и других стран бывшего СССР.
Вчерашний школьник, став студентом, зачастую «почивает на лаврах» и благополучно «заваливает» первый экзамен по математике, особенно если этот предмет не является пр< 'филирующим.
Д.ИН1.1-.1 ШИ1.1 поможем ыудешам
Н У' II' 'НИЯХ Д' ФИЦИ1.1 нромопи ПОДГОТОВИТЬСЯ
I >i i.ii u'iiy И" пы< un-н м<пем<лике, чуп' иman.' "tin п<1 нем уверенно п ।. i|и и ирон, пл <('!" положи юны |ую оценку.
АЙРИС ПРЕСС
Конспект лекций по высшей математике Дмитрий Письменный
Дмитрий Письменный
Конспект______
лекций по высшей математике
Полный курс
УДК 51(075.8)
ББК 22.1я73-2
П34
Все права защищены.
Никакая часть данной книги не может переиздаваться или распространяться в любой форме и любыми средствами, электронными или механическими, включая фотокопирование, звукозапись, любые запоминающие устройства и системы поиска информации, без письменного разрешения правообладателя.
Серийное оформление А. М. Драговой
Письменный, Д. Т.
П34 Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. — 4-е изд. — М.: Айрис-пресс, 2006. — 608 с.: ил. — (Высшее образование).
ISBN 5-8112-1778-1
Настоящий курс лекций предназначен для всех категорий студентов высших учебных заведений, изучающих в том или ином объеме высшую математику.
Книга содержит необходимый материал по всем разделам курса высшей математики (линейная и векторная алгебра, аналитическая геометрия, основы математического анализа), которые обычно изучаются студентами на первом и втором курсах вуза, а также дополнительные главы, необходимые при изучении специальных курсов (двойные, тройные, криволинейные и поверхностные интегралы, дифференциальные уравнения, элементы теории поля и теории функций комплексного переменного, основы операционного исчисления).
Изложение теоретического материала по всем темам сопровождается рассмотрением большого количества примеров и задач, ведется на доступном, по возможности строгом языке.
Пособие поможет студентам освоить курс высшей математики, подготовиться к сдаче зачетов и экзаменов по математическим дисциплинам.
ББК 22.1я73-2
УДК 51(075.8)
ISBN 5-8112-1778-1
©Айрис-пресс, 2005, 2006
ОГЛАВЛЕНИЕ
Предисловие.............................................. 15
Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
'§ 1. Матрицы............................................ 16
1.1. Основные понятия............................... 16
1.2. Действия над матрицами......................... 17
^§2. Определители...................................... 20
). 2.1. Основные понятия............................. 20
2.2. Свойства определителей......................... 22
§ 3. Невырожденные матрицы............................... 24
3.1. Основные понятия............................... 24
3.2. Обратная матрица............................... 25
3-3. Ранг матрицы................................... 27
- (§ 4. Системы линейных уравнений........................ 29
‘ s 4.1. Основные понятия............................. 29
/ J 4.2. Решение систем линейных уравнений.
Д Теорема КронскераКапслли......................... 30
' 4.3. Решение невырожденных линейных систем. Формулы Крамера....................................... 32
4.4. Решение систем линейных уравнений методом Гаусса.. 34
4.5. Системы линейных однородных уравнений.......... 37
Глава П. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
§ 5. Векторы............................................. 39
5.1. Основные понятия............................... 39
5.2. Линейные операции над векторами................ 40
5.3. Проекция вектора на ось...................... 42
5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы............. 44
5.5. Действия над векторами, заданными проекциями... 45
! § 6. Скалярное произведение векторов и его свойства..... 47
6.1. Определение скалярного произведения............ 47
6.2. Свойства скалярного произведения............... 48
> 6.3. Выражение скалярного произведения
через координаты................................ 49
(. 6.4. Некоторые приложения скалярного произведения. 50
§ 7. Векторное произведение векторов и его свойства.... 51
7.1. Определение векторного произведения............ 51
3
7.2. Свойства векторного произведения.............. 52
7.3. Выражение векторного произведения через координаты................................... 53
7.4. Некоторые приложения векторного произведения.. 54
§ 8. Смешанное произведение векторов................... 55
8.1. Определение смешанного произведения, его геомет рический смысл.......................... 55
8.2. Свойства смешанного произведения.............. 55
8.3. Выражение смешанного произведения через координаты................................... 56
8.4. Некоторые приложения смешанного произведения.. 57
Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
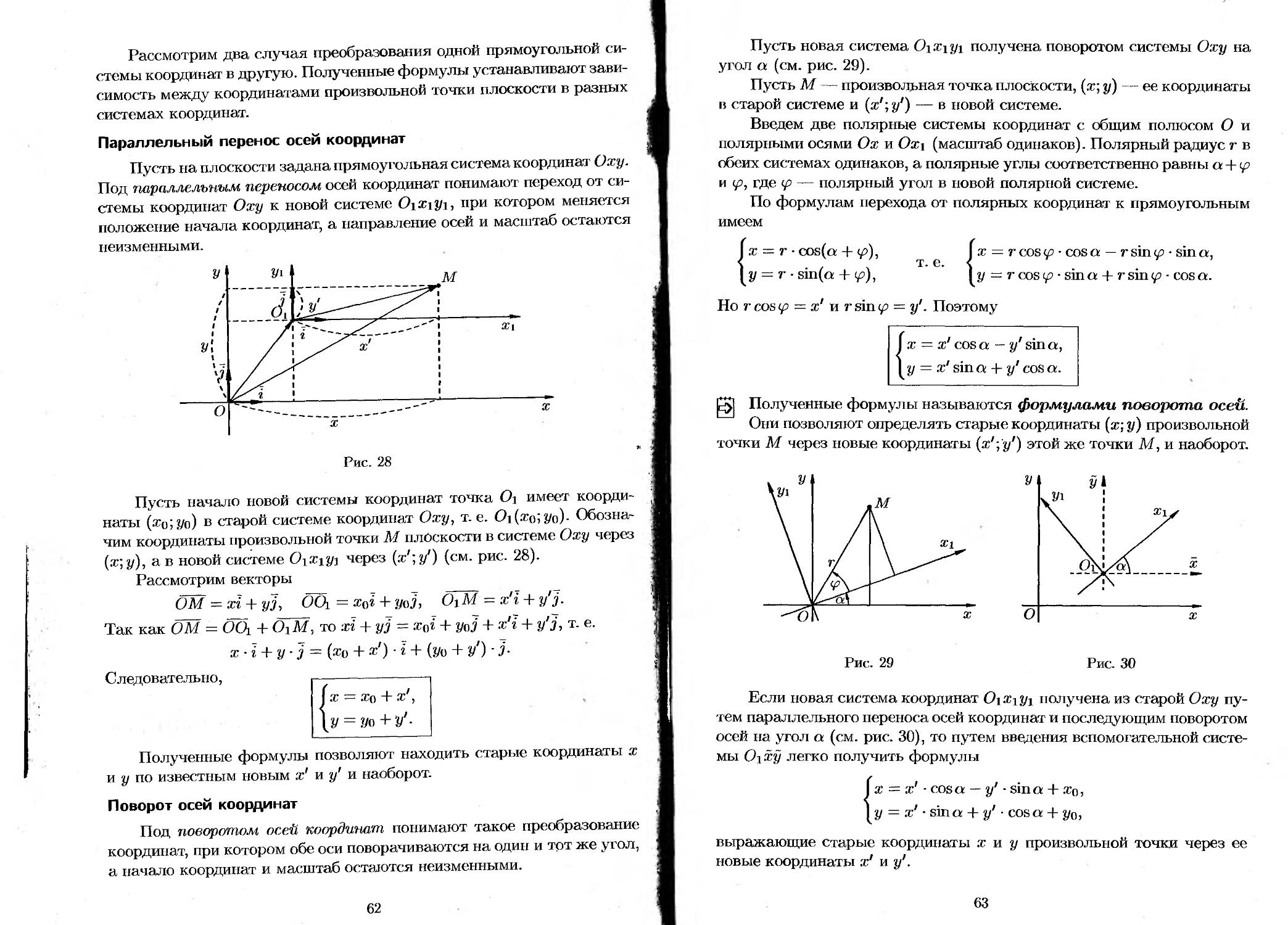
§ 9. Система координат на плоскости.................... 58
9.1. Основные понятия.............................. 58
9.2. Основные приложения метода координат на плоскости....................................... 60
9.3. Преобразование системы координат.............. 61
§ 10. Линии на плоскости............................... 64
10.1. Основные понятия............................. 64
10.2. Уравнения прямой на плоскости................ 68
\ 10.3. Прямая линия на плоскости. Основные задачи.. 73
§11. Линии второго порядка на плоскости............... 74
11.1. Основные понятия............................. 74
11.2. Окружность................................... 75
11.3. Эллипс....................................... 76
11.4. Гипербола.................................... 79
11.5. Парабола................................... 84
11.6. Общее уравнение линий второго порядка........ 86
Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
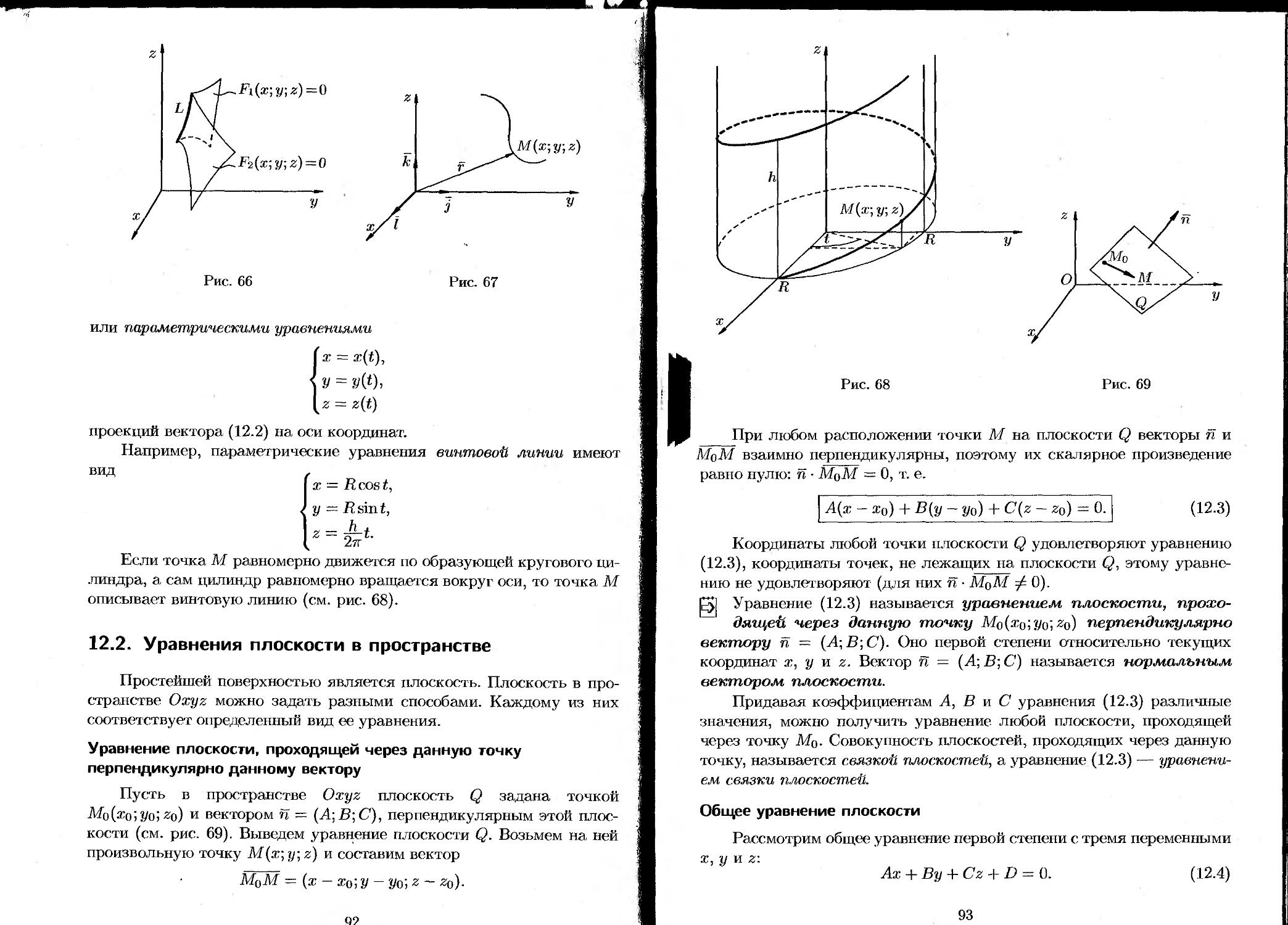
§ 12. Уравнения поверхности и линии в пространстве..... 90
12.1. Основные понятия............................. 90
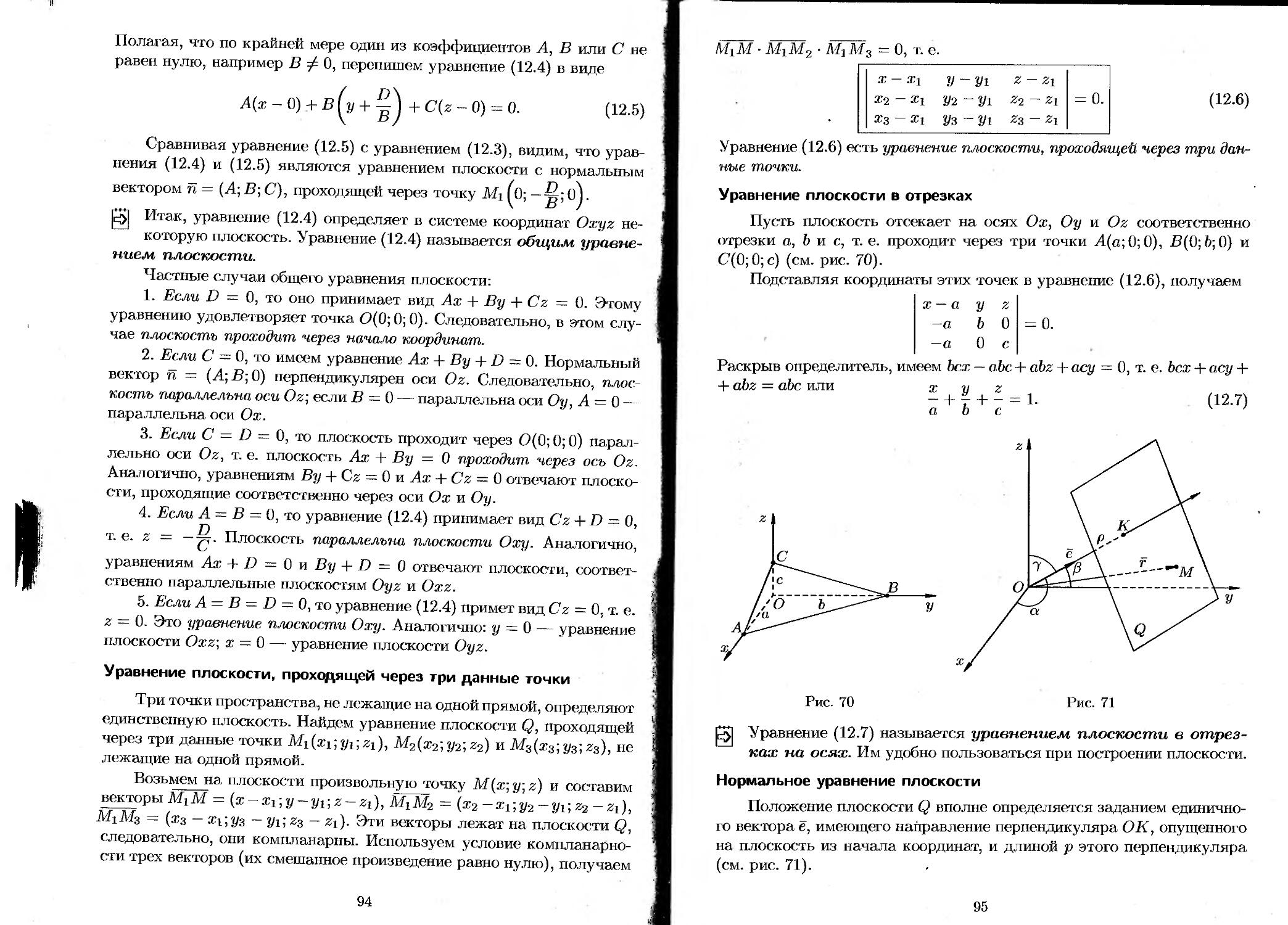
12.2. Уравнения плоскости в пространстве........... 92
12.3. Плоскость. Основные задачи................... 96
12.4. Уравнения прямой в пространстве.............. 98
12.5. Прямая линия в пространстве. Основные задачи. 101
12.6. Прямая и плоскость в пространстве. Основные задачи................................... 103
12.7. Цилиндрические поверхности.................. 104
4
12.8. Поверхности вращения. Конические поверхности. 106
12.9. Канонические уравнения поверхностей второго порядка.................................... 109
Глава V. ВВЕДЕНИЕ В АНАЛИЗ
§ 13. Множества. Действительные числа.................. 116
13.1. Основные понятия............................. 116
13.2. Числовые множества. Множество действительных чисел..................... 117
13.3. Числовые промежутки. Окрестность точки....... 119
§ 14. Функция.......................................... 120
14.1. Понятие функции............................ 120
14.2. Числовые функции. График функции. Способы задания функций............................ 120
14.3. Основные характеристики функции.............. 122
14.4. Обратная функция............................. 123
14.5. Сложная функция.............................. 124
14.6. Основные элементарные функции и их графики... 124
§ 15. Последовательности............................... 127
15.1. Числовая последовательность.................. 127
15.2. Предел числовой последовательности........... 128
15.3. Предельный переход в неравенствах............ 130
15.4. Предел монотонной ограниченной последовательности.
Число е. Натуральные логарифмы................. 130
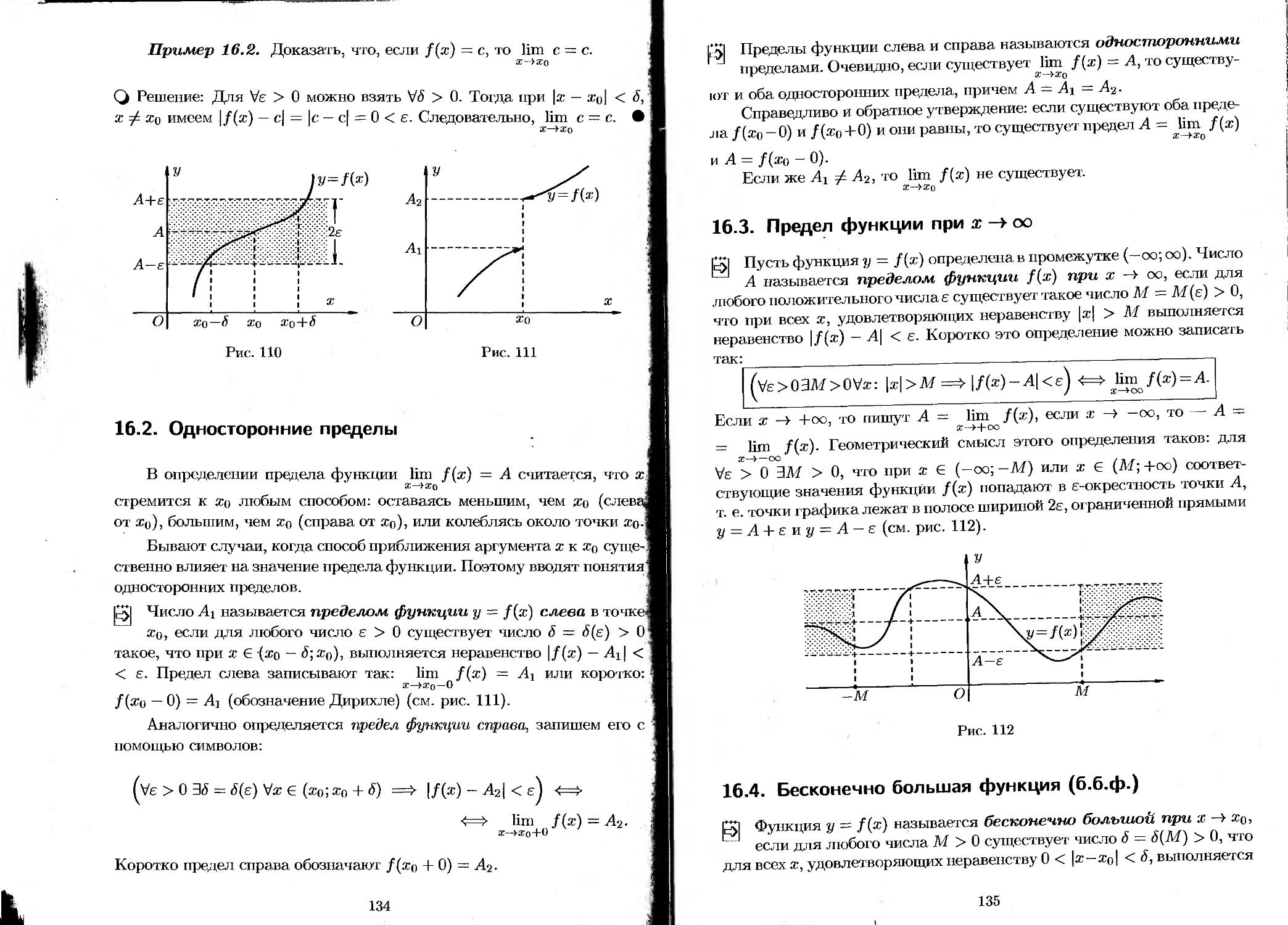
§ 16. Предел функции................................... 132
16.1. Предел функции в точке....................... 132
16.2. Односторонние пределы........................ 134
16.3. Предел функции при х —> оо................... 135
16.4. Бесконечно большая функция (б.б.ф.).......... 135
§ 17. Бесконечно малые функции (б.м.ф.)................ 136
17.1. Определения и основные теоремы............... 136
17.2. Связь между функцией, ее пределом и бесконечно малой функцией........................ 140
17.3. Основные теоремы о пределах.................. 141
17.4. Признаки существования пределов.............. 144
17.5. Первый замечательный предел.................. 145
17.6. Второй замечательный предел.................. 146
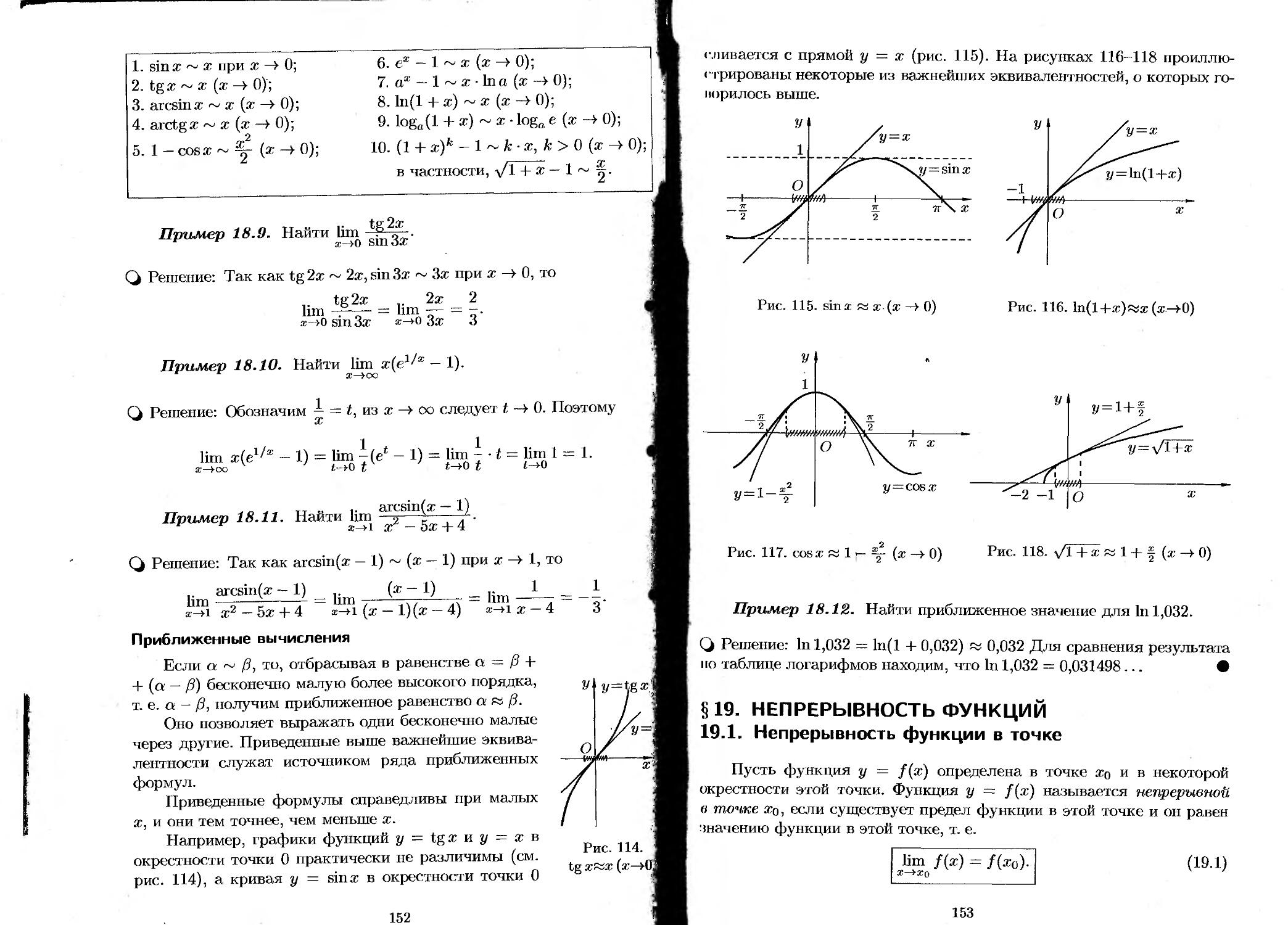
§ 18. Эквивалентные бесконечно малые функции........... 148
18.1. Сравнение бесконечно малых функций........... 148
18.2. Эквивалентные бесконечно малые и основные теоремы о них........................... 149
5
18.3. Применение эквивалентных бесконечно малых функций...................................... 151
§ 19. Непрерывность функций............................ 153
19.1. Непрерывность функции в точке................ 153
19.2. Непрерывность функции в интервале и на отрезке....................................... 155
19.3. Точки разрыва функции и их классификация..... 155
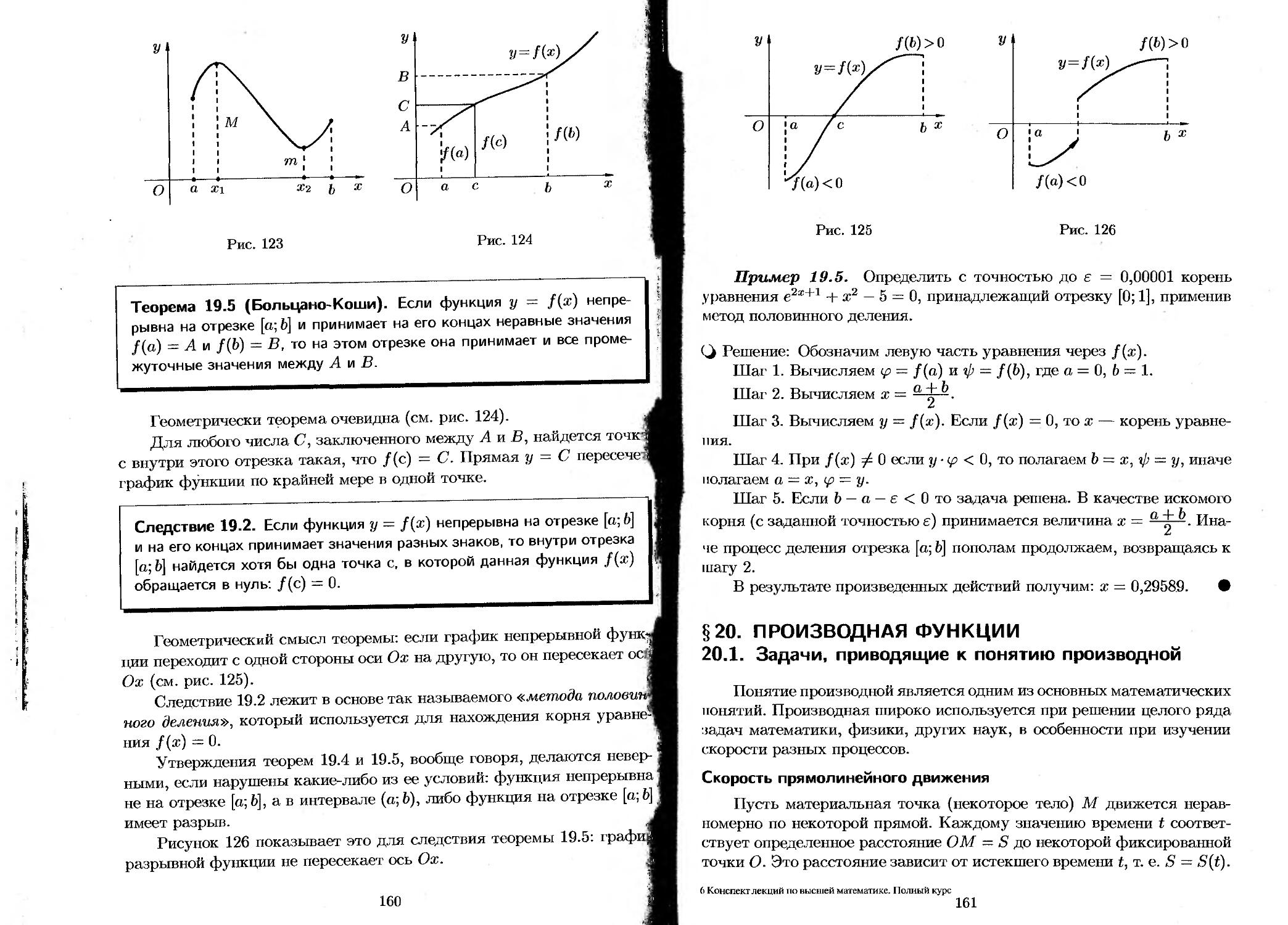
19.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций................. 158
19.5. Свойства функций, непрерывных на отрезке..... 159
§ 20. Производная функции.............................. 161
20.1. Задачи, приводящие к понятию производной..... 161
20.2. Определение производной; ее механический
и геометрический смысл. Уравнение касательной и нормали к кривой............................. 164
20.3. Связь между непрерывностью и дифференцируемостью функции............................................ 166
20.4. Производная суммы, разности, произведения и частного функций............................... 167
20.5. Производная сложной и обратной функций....... 169
20.6. Производные основных элементарных функций.... 171
20.7. Гиперболические функции и их производные..... 175
20.8. Таблица производных.......................... 177
§21. Дифференцирование неявных и параметрически заданных функций................................................ 179
21.1. Неявно заданная функция...................... 179
21.2. Функция, заданная параметрически............. 180
§22. Логарифмическое дифференцирование................ 181
§ 23. Производные высших порядков...................... 182
23.1. Производные высших порядков явно заданной функции.............................. 182
23.2. Механический смысл производной второго порядка .... 183
23.3. Производные высших порядков неявно заданной функции............................ 183
23.4. Производные высших порядков от функций, заданных параметрически..................................... 184
§ 24. Дифференциал функции............................. 185
24.1. Понятие дифференциала функции................ 185
24.2. Геометрический смысл дифференциала функции... 186
24.3. Основные теоремы о дифференциалах............ 187
24.4. Таблица дифференциалов....................... 188
6
24.5. Применение дифференциала к приближенным вычислениям....................... 189
24.6. Дифференциалы высших порядков.............. 190
§25. Исследование функций при помощи производных.....192
25.1. Некоторые теоремы о дифференцируемых функциях... 192
25.2. Правила Лопиталя........................... 196
25.3. Возрастание и убывание функций............. 200
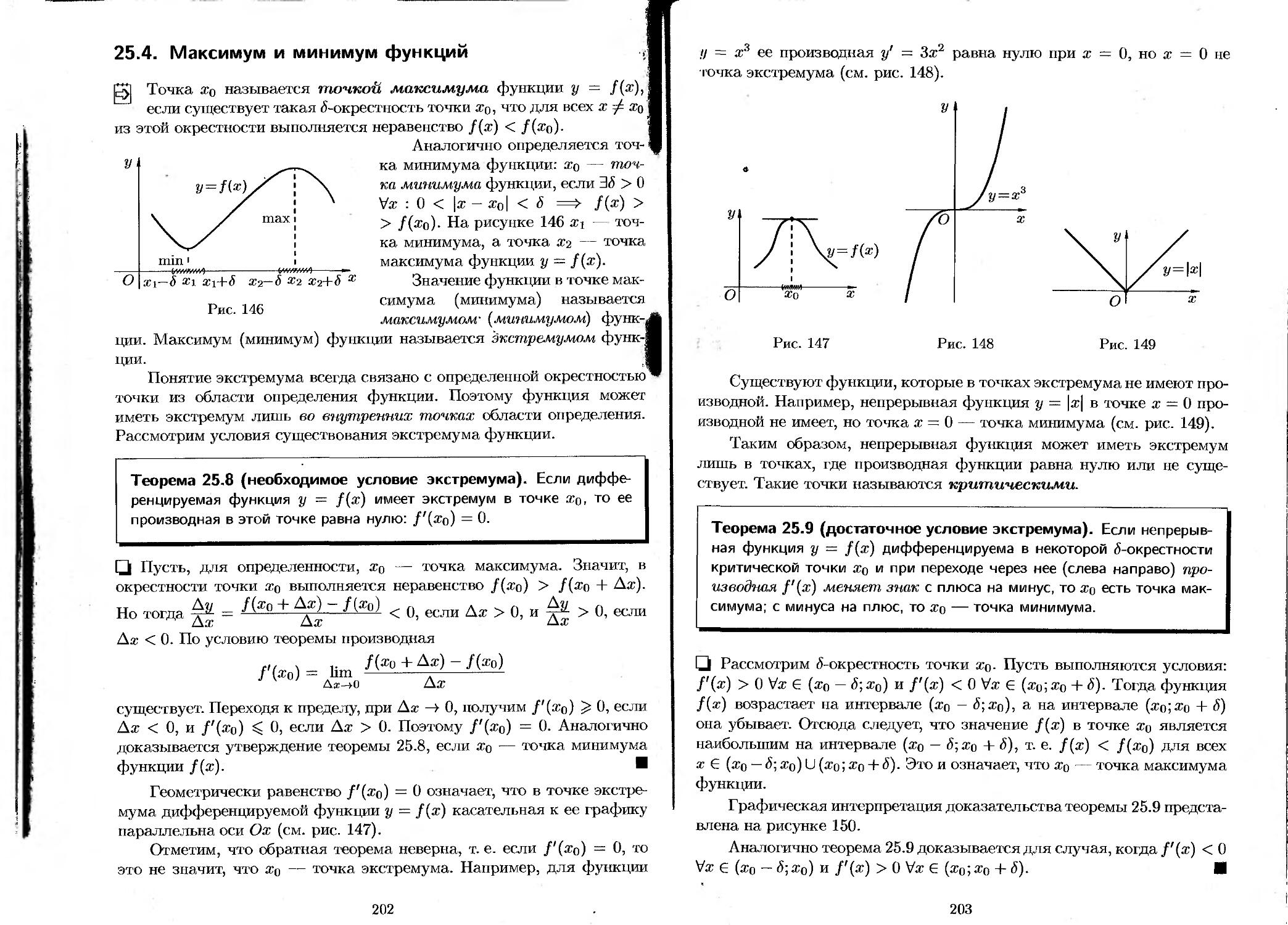
25.4. Максимум и минимум функций................. 202
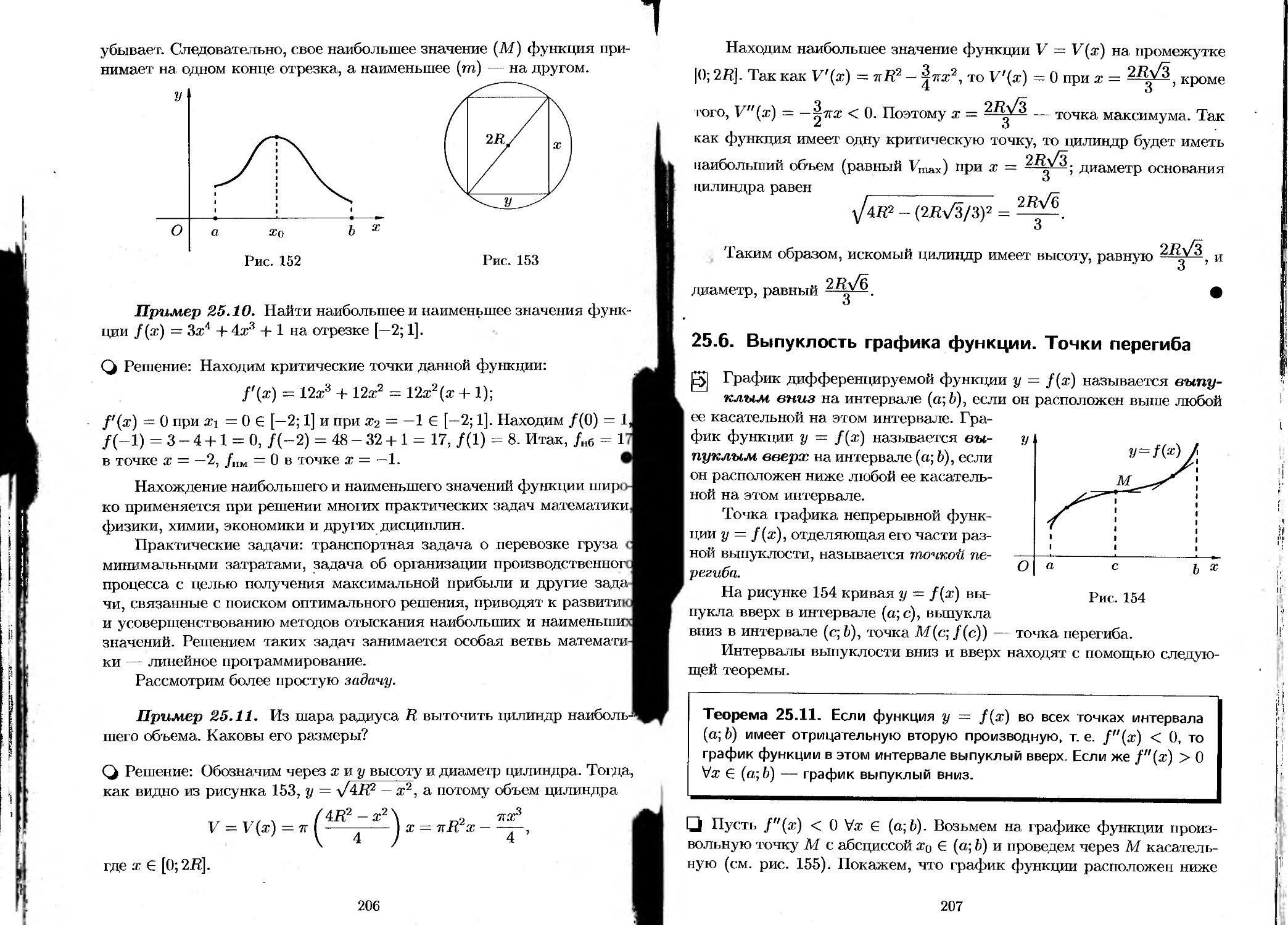
25.5. Наибольшее и наименьшее значения функции на отрезке....................................... 205
25.6. Выпуклость графика функции. Точки перегиба... 207
25.7. Асимптоты графика функции.................. 209
25.8. Общая схема исследования функции и построения графика............................. 211
§ 26. Формула Тейлора................................ 213
26.1. Формула Тейлора для многочлена............. 214
26.2. Формула Тейлора для произвольной функции... 215
Глава VI. КОМПЛЕКСНЫЕ ЧИСЛА
§ 27. Понятие и представления комплексных чисел...... 218
27.1. Основные понятия........................... 218
27.2. Геометрическое изображение комплексных чисел. 218
27.3. Формы записи комплексных чисел............. 219
§ 28. Действия над комплексными числами.............. 221
28.1. Сложение комплексных чисел................. 221
28.2. Вычитание комплексных чисел................ 221
28.3. Умножение комплексных чисел................ 222
28.4. Деление комплексных чисел.................. 223
28.5. Извлечение корней из комплексных чисел..... 224
Глава VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 29. Неопределенный интеграл........................ 226
29.1. Понятие неопределенного интеграла.......... 226
29.2. Свойства неопределенного интеграла......... 227
29.3. Таблица основных неопределенных интегралов... 230
§ 30. Основные методы интегрирования................. 232
30.1. Метод непосредственного интегрирования..... 232
30.2. Метод интегрирования подстановкой (заменой переменной)............................. 234
30.3. Метод интегрирования по частям............. 236
§ 31. Интегрирование рациональных функций............ 237
31.1. Понятия о рациональных функциях....;....... 237
7
31.2. Интегрирование простейших рациональных дробей. 244
31.3. Интегрирование рациональных дробей........... 246
§32. Интегрирование тригонометрических функций........ 248
32.1. Универсальная тригонометрическая подстановка.. 248
32.2. Интегралы типа f sin’"1 х cos” х dx........ 249
32.3. Использование тригонометрических преобразований.... 250
§ 33. Интегрирование иррациональных функций............ 251
33.1. Квадратичные иррациональности................ 251
33.2. Дробно-линейная подстановка.................. 253
33.3. Тригонометрическая подстановка............... 254
33.4. Интегралы типа f R(xj у/ах2 ft- bx + с) dx... 255
33.5. Интегрирование дифференциального бинома...... 255
§ 34. «Берущиеся» и «неберугциеся» интегралы........... 256
Глава VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 35. Определенный интеграл как предел интегральной суммы ... 259
§ 36. Геометрический и физический смысл определенного интеграла.............................................. 261
§ 37. Формула Ньютона-Лейбница......................... 263
§ 38. Основные свойства определенного интеграла........ 265
§39. Вычисления определенного интеграла............... 269
39.1. Формула Ньютона-Лейбница..................... 269
39.2. Интегрирование подстановкой (заменой переменной)... 269
39.3. Интегрирование по частям..................... 271
39.4. Интегрирование четных и нечетных функций в симметричных пределах............................ 272
§ 40. Несобственные интегралы.......................... 273
40.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода).................... 273
40.2. Интеграл от разрывной функции (несобственный интеграл II рода)................... 276
§41. Геометрические и физические приложения определенного интеграла.............................................. 278
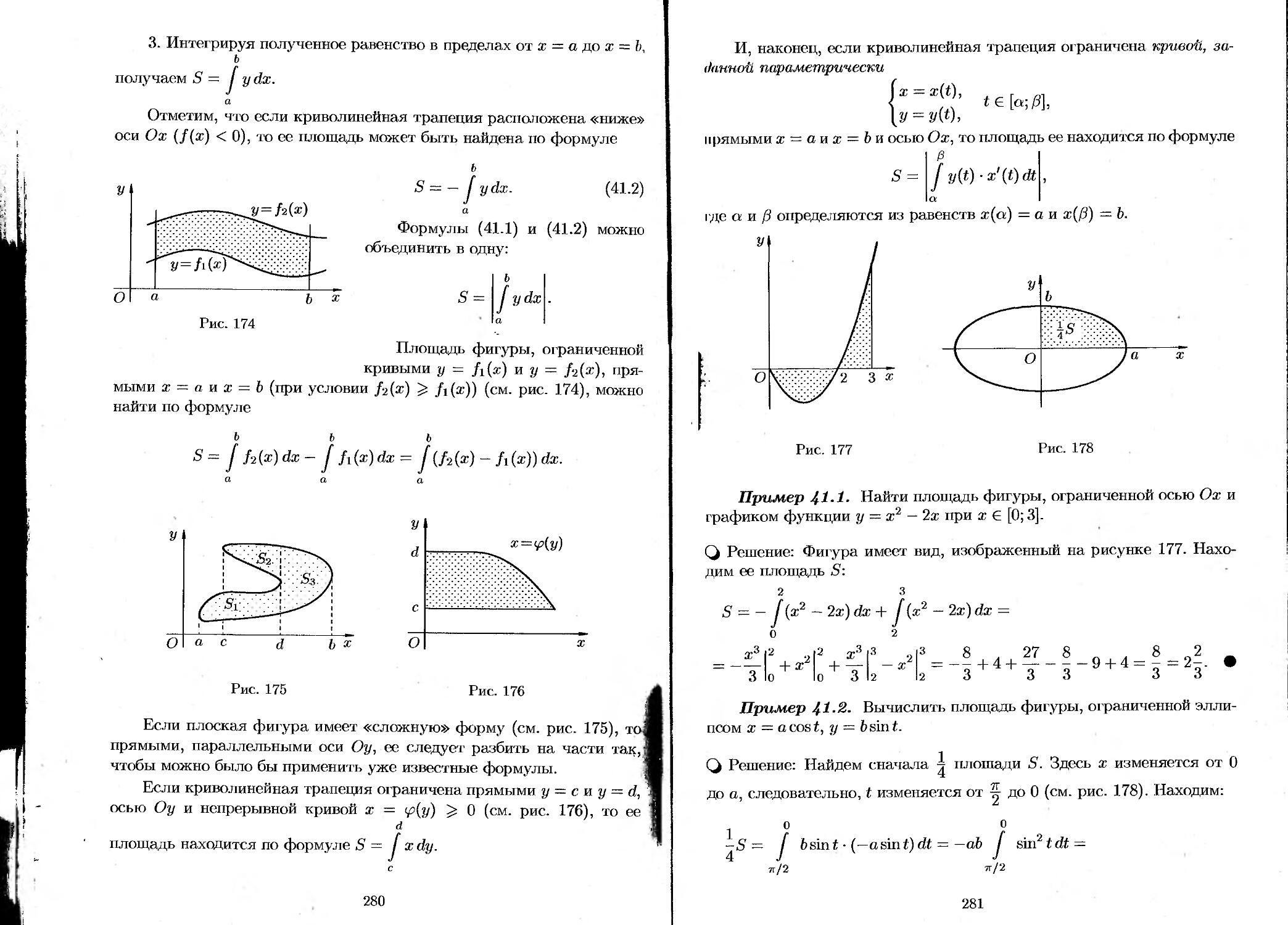
41.1. Схемы применения определенного интеграла..... 278
41.2. Вычисление площадей плоских фигур............ 279
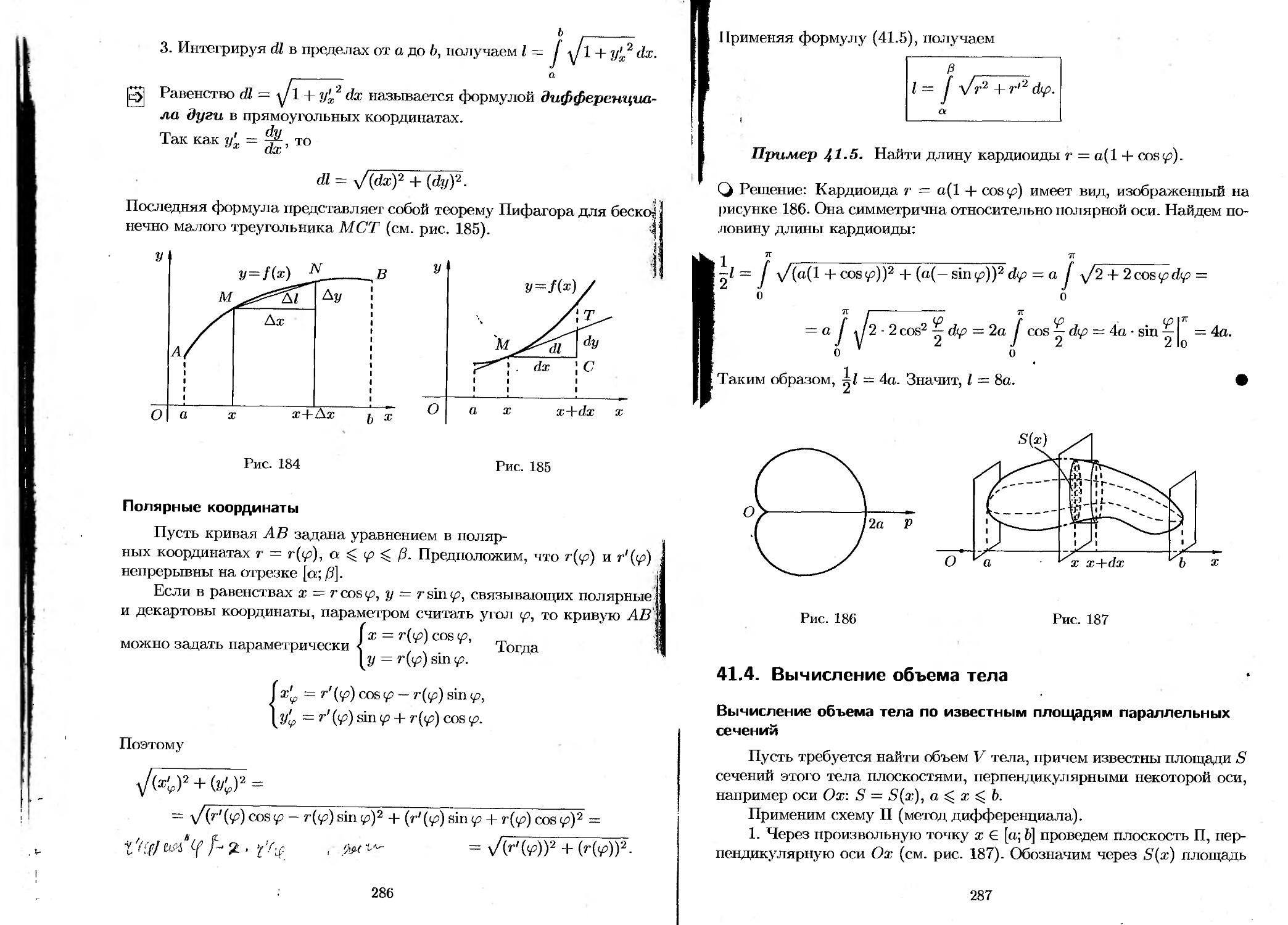
41.3. Вычисление длины дуги плоской кривой......... 283
41.4. Вычисление объема тела..................... 287
41.5. Вычисление площади поверхности вращения...... 289
41.6. Механические приложения определенного интеграла... 291
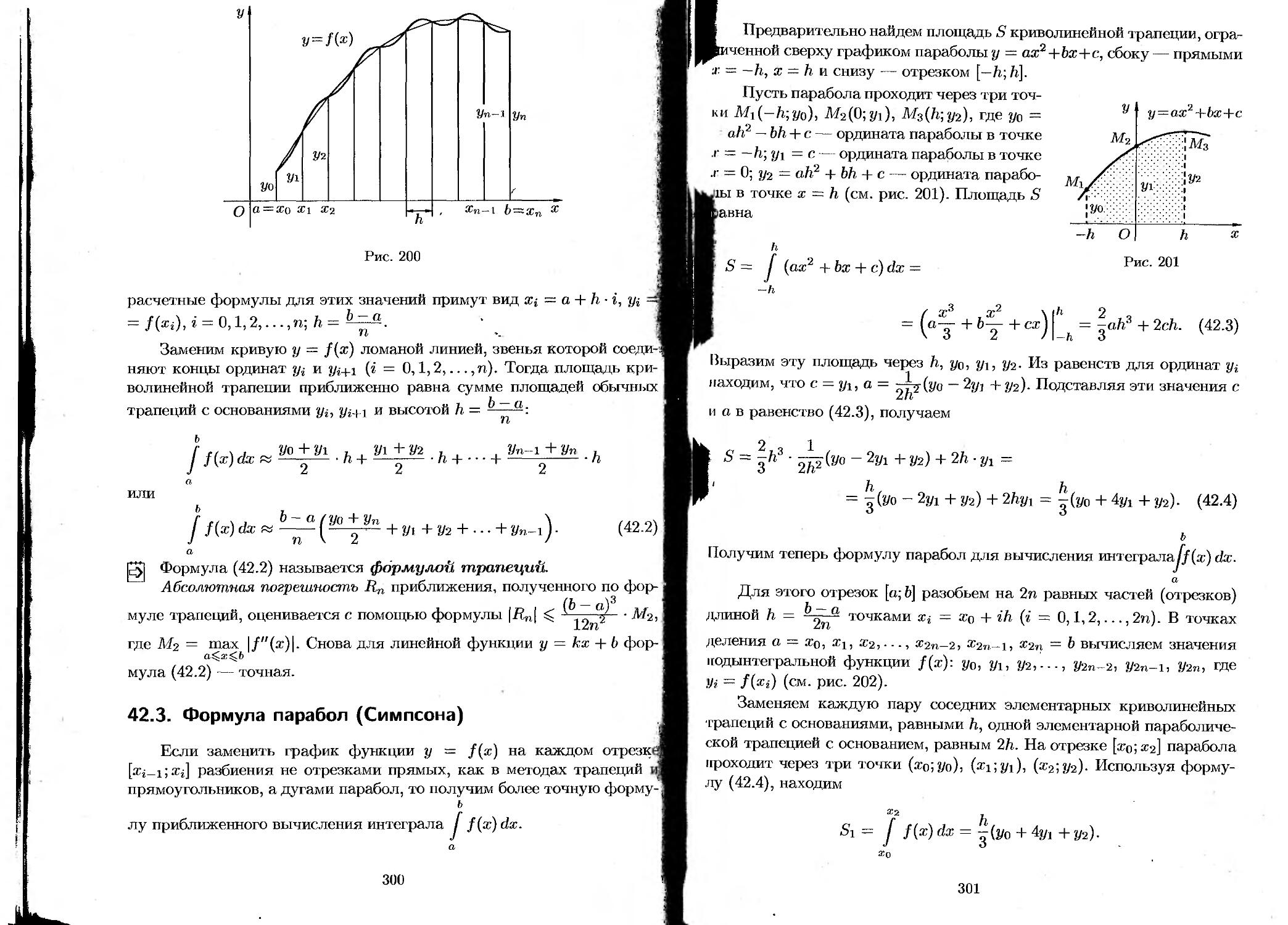
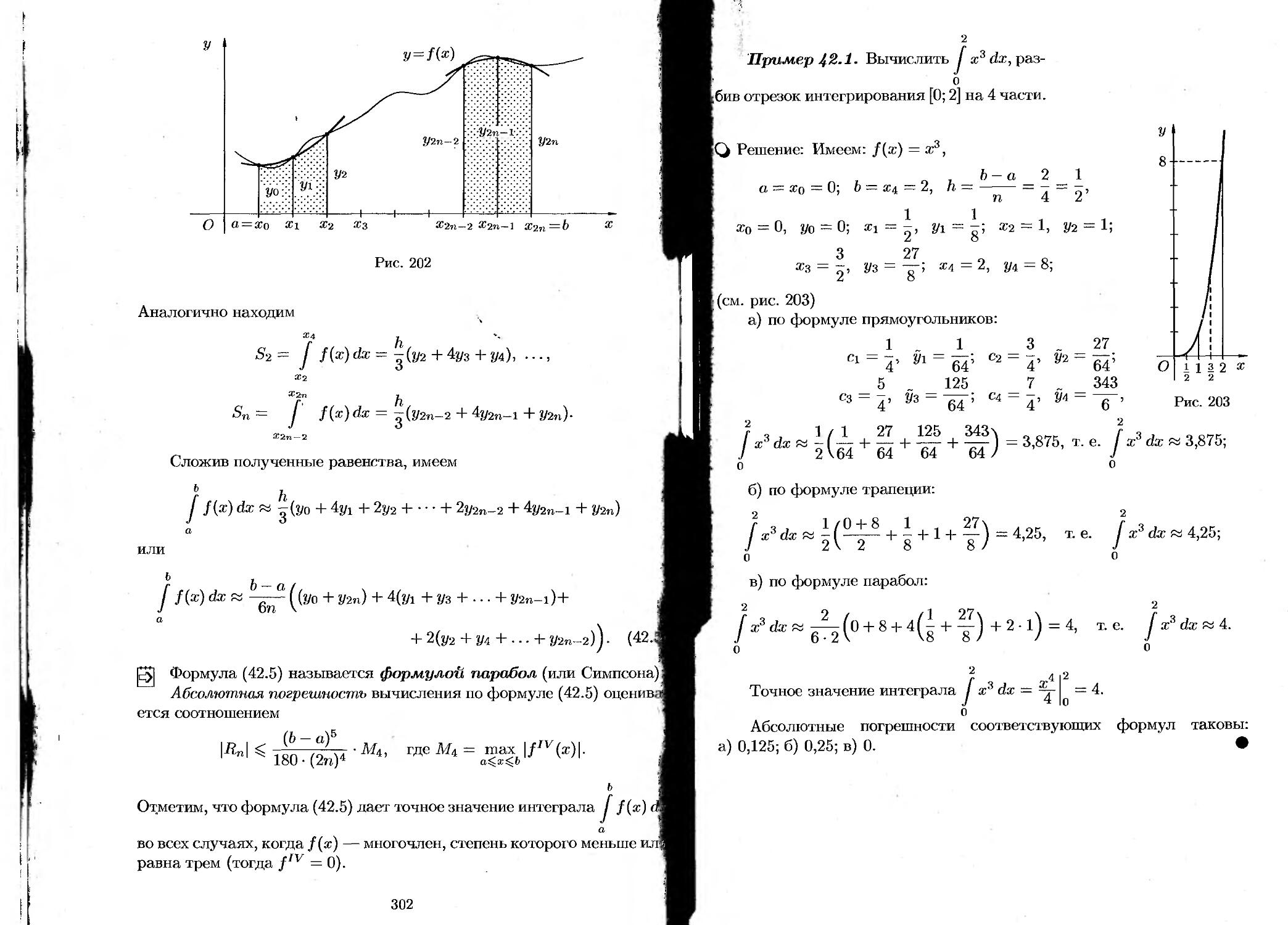
§ 42. Приближенное вычисление определенного интеграла... 298
42.1. Формула прямоугольников...................... 298
8
42.2. Формула трапеций.......................... 299
42.3. Формула парабол (Симпсона)................ 300
Глава IX. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 43. Функции двух переменных....................... 304
43.1. Основные понятия.......................... 304
43.2. Предел функции............................ 305
43.3. Непрерывность функции двух переменных..... 306
43.4. Свойства функций, непрерывных в ограниченной замкнутой области................ 307
§44. Производные и дифференциалы функции нескольких переменных............................... 308
44.1. Частные производные первого порядка и их геометрическое истолкование................ 308
44.2. Частные производные высших порядков....... 310
44.3. Дифференцируемость и полный дифференциал функции......................................... 311
; 44.4. Применение полного дифференциала к приближенным
вычислениям................................. 312
44.5. Дифференциалы высших порядков............. 313
j 44.6. Производная сложной функции. Полная производная .. 314
i 44.7. Инвариантность формы полного дифференциала... 316
44.8. Дифференцирование неявной функции......... 317
§ 45. Касательная плоскость и нормаль к поверхности. 318
§ 46. Экстремум функции двух переменных............. 320
46.1. Основные понятия.......................... 320
46.2. Необходимые и достаточные условия экстремума. 321
46.3. Наибольшее и наименьшее значения функции в замкнутой области............................. 323
Глава X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 47. Общие сведения о дифференциальных уравнениях.. 325
47.1. Основные понятия.......................... 325
47.2. Задачи, приводящие к дифференциальным уравнениям...................................... 325
§ 48. Дифференциальные уравнения первого порядка.... 327
48.1. Основные понятия.......................... 327
48.2. Уравнения с разделяющимися переменными.... 330
48.3. Однородные дифференциальные уравнения..... 332
48.4. Линейные уравнения. Уравнение Я. Бернулли. 334
48.5. Уравнение в полных дифференциалах. Интегрирующий множитель......................... 338
9
48.6. Уравнения Лагранжа и Клеро.................. 342
§ 49. Дифференциальные уравнения высших цорядков...... 344
49.1. Основные понятия.............X-............. 344
49.2. Уравнения, допускающие понижение порядка.... 346
49.3. Линейные дифференциальные уравнения высших порядков.......................................... 349
49.4. Линейные однородные ДУ второго порядка...... 350
49.5. Линейные однородные ДУ n-го порядка......... 353
§ 50. Интегрирование ДУ второго порядка с постоянными коэффициентами......................................... 354
50.1. Интегрирование ЛОДУ второго порядка
с постоянными коэффициентами.................. 354
50.2. Интегрирование ЛОДУ n-го порядка с постоянными коэффициентами...................... 357
§51. Линейные неоднородные дифференциальные уравнения (ЛИДУ)................................................. 358
51.1. Структура общего решения ЛИДУ второго порядка.... 358
51.2. Метод вариации произвольных постоянных...... 360
51.3. Интегрирование ЛИДУ второго порядка
с постоянными коэффициентами и правой частью специального вида............................. 362
51.4. Интегрирование ЛИДУ n-го порядка (п > 2) с постоянными коэффициентами и правой частью специального вида................................. 365
§ 52. Системы дифференциальных уравнений.............. 367
52.1. Основные понятия............................ 367
52.2. Интегрирование нормальных систем............ 369
52.3. Системы линейных ДУ с постоянными коэффициентами.................................... 372
Глава XI. ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ
§53. Двойной интеграл................................. 378
53.1. Основные понятия и определения.............. 378
53.2. Геометрический и физический смысл двойного интеграла......................................... 379
53.3. Основные свойства двойного интеграла........ 381
53.4. Вычисление двойного интеграла в декартовых координатах.......................... 382
53-5. Вычисление двойного интеграла в полярных координатах......................... 386
53.6. Приложения двойного интеграла............... 388
§ 54. Тройной интеграл................................ 391
10
54.1. Основные понятия............................ 391
54.2. Вычисление тройного интеграла в декартовых координатах.......................... 392
й; 54.3. Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах............................................ 395
54.4. Некоторые приложения тройного интеграла..... 398
I Глава XII. КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
-1
§ 55. Криволинейный интеграл I рода.................... 402
1 55.1. Основные понятия............................. 402
1 55.2. Вычисление криволинейного интеграла I рода... 404
55.3 . Некоторые приложения криволинейного интеграла
I рода........................................ 405
§ 56. Криволинейный интеграл II рода................... 407
56.1. Основные понятия............................ 407
56.2. Вычисление криволинейного интеграла II рода.. 410
' 56.3. Формула Остроградского-Грина................. 412
v 56.4. Условия независимости криволинейного интеграла
II рода от пути интегрирования................ 414
56.5. Некоторые приложения криволинейного интеграла II рода........................................... 418
§ 57. Поверхностный интеграл I рода.................... 420
57.1. Основные понятия............................ 420
57.2. Вычисление поверхностного интеграла I рода.. 422
57.3. Некоторые приложения поверхностного интеграла I рода............................................ 425
§ 58. Поверхностный интеграл II рода................... 427
58.1. Основные понятия............................ 427
58.2. Вычисление поверхностного интеграла II рода. 429
58.3. Формула Остроградского-Гаусса............... 431
58.4. Формула Стокса.............................. 433
58.5. Некоторые приложения поверхностного интеграла II рода........................................... 437
Глава XIII. ЧИСЛОВЫЕ РЯДЫ
§ 59. Числовые ряды.................................... 438
59.1. Основные понятия............................ 438
59.2. Ряд геометрической прогрессии............... 441
59.3. Необходимый признак сходимости числового ряда. Гармонический ряд................................. 442
11
§ 60. Достаточные признаки сходимости знакопостоянных рядов................................. 444
60.1. Признаки сравнения рядов.................... 444
60.2. Признак Даламбера........................... 446
60.3. Радикальный признак Коши.................... 448
60.4. Интегральный признак Коши.
Обобщенный гармонический ряд.................. 449
§61. Знакочередующиеся и знакопеременные ряды........ 451
61.1. Знакочередующиеся ряды. Признак Лейбница.... 451
61.2. Общий достаточный признак сходимости знакопеременных рядов............................. 453
61.3. Абсолютная и условная сходимости числовых рядов.
Свойства абсолютно сходящихся рядов........... 454
Глава XIV. СТЕПЕННЫЕ РЯДЫ
§ 62. Функциональные ряды............................. 457
62.1.Основные понятия............................. 457
§ 63. Сходимость степенных рядов...................... 458
63.1. Теорема Н. Абеля............................ 458
63.2. Интервал и радиус сходимости степенного ряда.. 459
63.3. Свойства степенных рядов.................... 462
§ 64. Разложение функций в степенные ряды............. 463
64.1. Ряды Тейлора и Маклорена.................... 463
64.2. Разложение некоторых элементарных функций
в ряд Тейлора (Маклорена)..................... 465
§ 65. Некоторые приложения степенных рядов............ 471
65.1. Приближенное вычисление значений функции.... 471
65.2. Приближенное вычисление определенных интегралов .. 473 65.3. Приближенное решение дифференциальных
уравнений..................................... 475
Глава XV. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
§ 66. Ряды Фурье...................................... 478
66.1. Периодические функции. Периодические процессы. 478
66.2. Тригонометрический ряд Фурье................ 480
§ 67. Разложение в ряд Фурье 2я-периодических функций... 483
67.1. Теорема Дирихле............................. 483
67.2. Разложение в ряд Фурье четных и нечетных функций.. 486 67.3. Разложение в ряд Фурье функций произвольного
периода....................................... 487
67.4. Представление непериодической функции
рядом Фурье................................... 489
12
67.5. Комплексная форма ряда Фурье............... 491
§ 68. Интеграл Фурье................................. 493
Глава XVI. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
§ 69. Основные понятия теории поля................... 499
§ 70. Скалярное поле................................. 501
70.1. Поверхности и линии уровня................. 501
70.2. Производная по направлению..................- 502
70.3. Градиент скалярного поля и его свойства.... 504
§ 71. Векторное поле................................. 506
71.1. Векторные линии поля....................... 506
71.2. Поток поля................................. 507
71.3. Дивергенция поля. Формула Остроградского Гаусса... 510
71.4. Циркуляция поля............................ 513
71.5. Ротор поля. Формула Стокса................. 515
§ 72. Оператор Гамильтона............................ 518
72.1. Векторные дифференциальные операции первого порядка.................................. 518
72.2. Векторные дифференциальные операции второго порядка.................................. 519
§ 73. Некоторые свойства основных классов векторных полей .... 520
73.1. Соленоидальное поле........................ 520
73.2. Потенциальное поле......................... 521
73.3. Гармоническое поле......................... 524
Глава XVII. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
§ 74. Функции комплексного переменного............... 525
74.1. Основные понятия........................... 525
74.2. Предел и непрерывность функции комплексного переменного...................................... 526
74.3. Основные элементарные функции комплексного переменного...................................... 527
74.4. Дифференцирование функции комплексного переменного. Условия ЭйлераДаламбсра............. 532
74.5. Аналитическая функция. Дифференциал........ 535
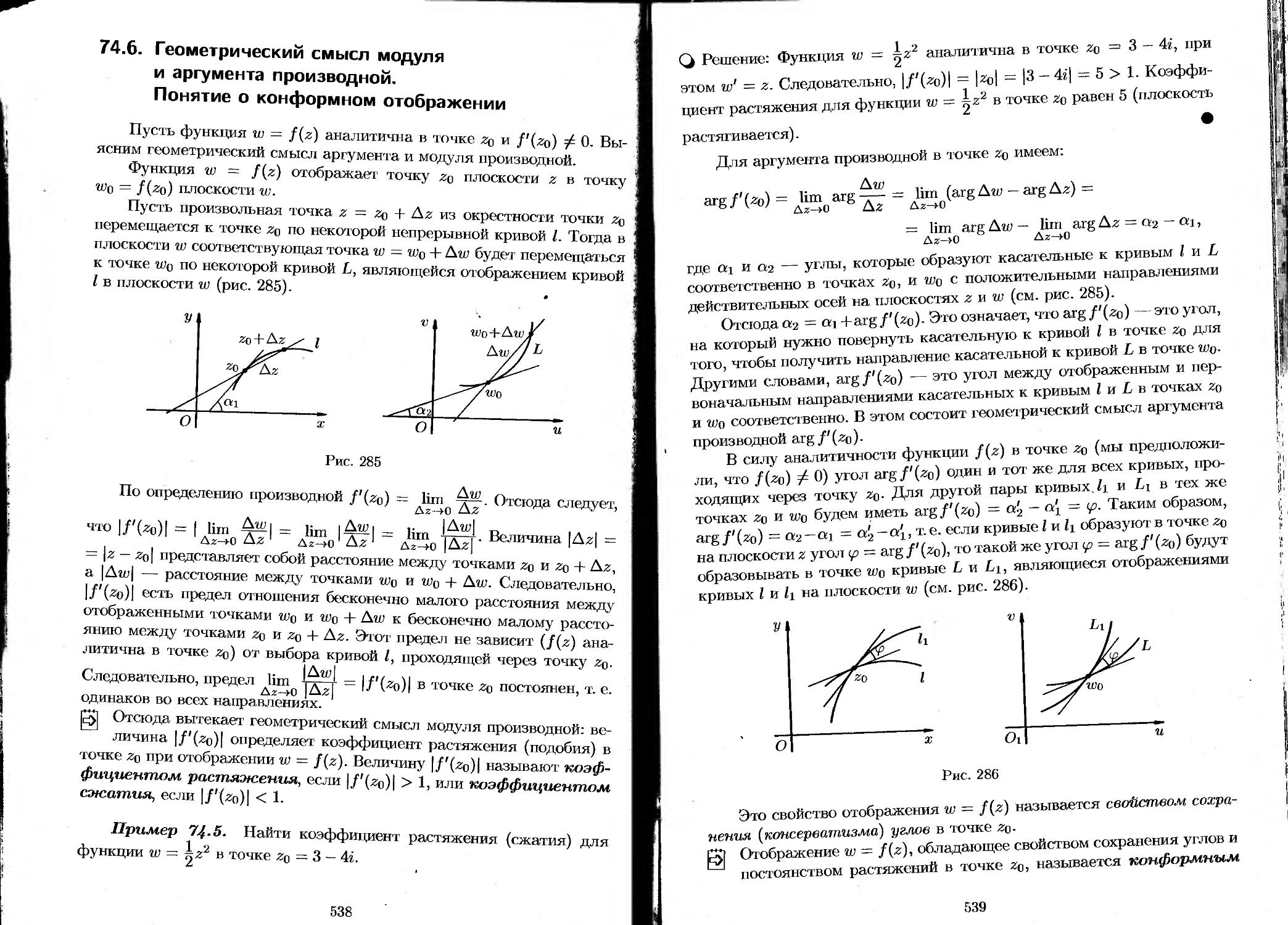
74.6. Геометрический смысл модуля и аргумента производной. Понятие о конформном отображении..... 538
§ 75. Интегрирование функции комплексного переменного. 540
75.1. Определение, свойства и правила вычисления интеграла........................................ 540
13
75.2. Теорема Коши. Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница................. 544
75.3. Интеграл Коши. Интегральная формула Коши..... 547
§ 76. Ряды в комплексной плоскости..................... 551
76.1. Числовые ряды................................ 551
76.2. Степенные ряды............................... 553
76.3. Ряд Тейлора.................................. 555
76.4. Нули аналитической функции................... 558
76.5. Ряд Лорана................................... 558
76.6. Классификация особых точек. Связь между нулем и полюсом функции.................................. 563
§ 77. Вычет функции.................................... 567
77.1. Понятие вычета и основная теорема о вычетах.. 567
77.2. Вычисление вычетов. Применение вычетов в вычислении интегралов............................ 568
Глава XVIII. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
§ 78. Преобразование Лапласа........................... 572
78.1. Оригиналы и их изображения................... 572
78.2. Свойства преобразования Лапласа.............. 576
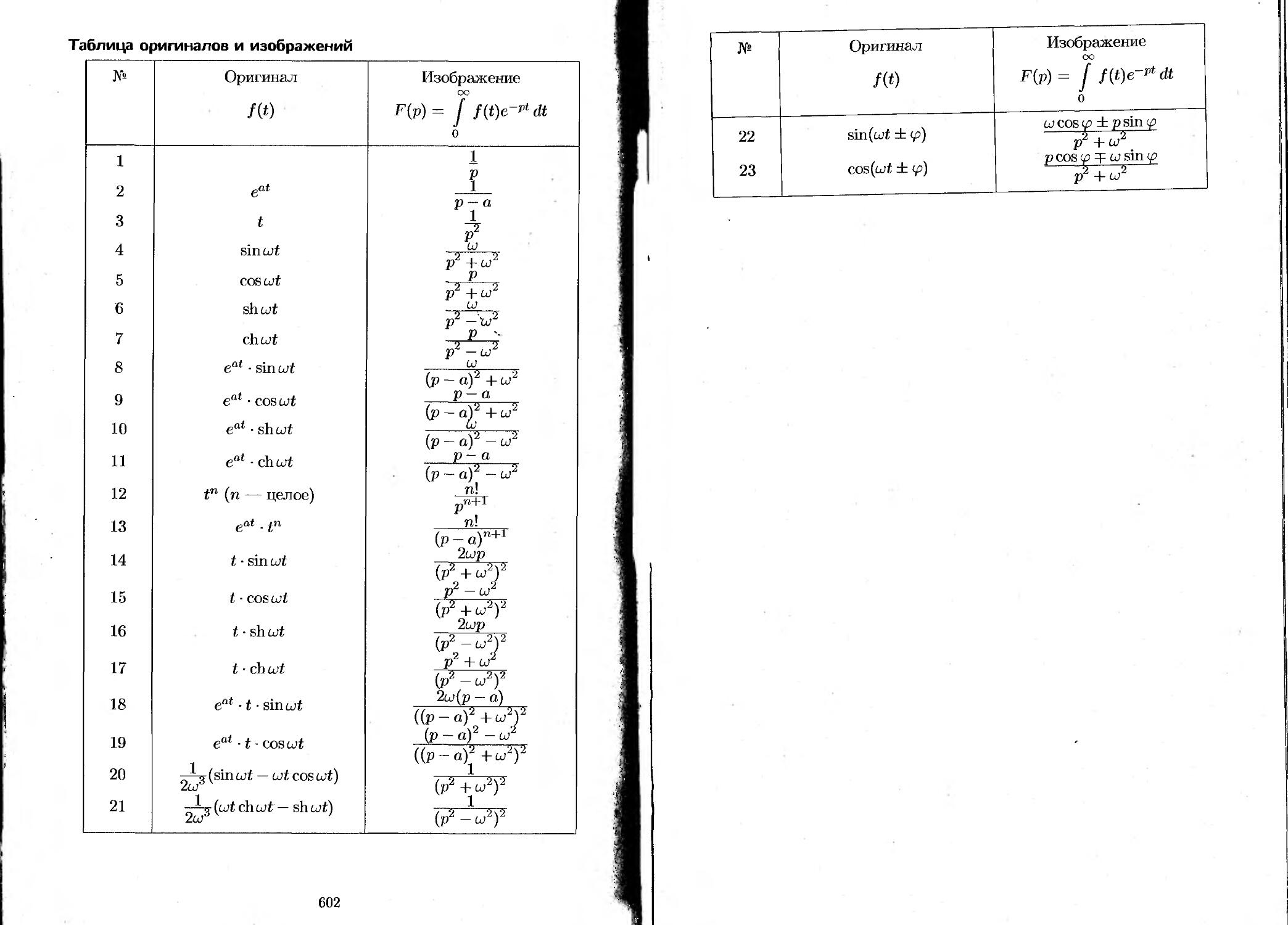
78.3. Таблица оригиналов и изображений............. 588
§ 79. Обратное преобразование Лапласа.................. 590
79.1. Теоремы разложения......................... 590
79.2. Формула Римана-Меллина.... I................. 593
§ 80. Операционный метод решения линейных дифференциальных уравнений и их систем................. 594
- Приложения............................................ 599
ПРЕДИСЛОВИЕ
Настоящее пособие предназначено, в первую очередь, для студентов инженерно-технических специальностей; может быть полезным для Йсех категорий студентов, изучающих в том или ином объеме высшую Математику. Оно представляет собой конспект лекций и адресовано, в Основном, студентам первого и второго курсов. Набор освещаемых во-„просов хорошо виден из оглавления.
Данный конспект содержит необходимый материал по всем раз-делам курса высшей математики и дополнительным главам, необходимым при изучении специальных курсов. Изложение теоретического материала по всем темам сопровождается рассмотрением большого 'количества примеров и задач, ведется на доступном, по возможности Строгом языке.
Пособие может быть использовано студентами также для самосто-’ятельного изучения соответствующего материала, является базой для < подготовки к семестровым зачетам и экзаменам по высшей математике, 'д' Кроме того, книга должна помочь студенту и в тех случаях, когда Йбн что-то не успел записать на лекции, какие-то лекции были пропу-••Щены, в чем-то трудно (или нет времени) разобраться по другим учебникам, когда некоторые вопросы «слишком длинны» в его конспектах или много фактического материала, который следует изучить за ограниченное количество недель, дней.
ч Автор надеется, что данный курс лекций будет полезен и преподавателям, а использование данного пособия будет способствовать более глубокому изучению студентами курса высшей математики и смежных дисциплин.
Список обозначений:
О ® — начало и конец решения примера или задачи;
Q — начало и конец доказательства;
р5| — важные определения;
|©| — «обратите особое внимание!»
В рамку заключены формулы, которые важно помнить.
Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Лекции 1-3
§1. МАТРИЦЫ
1.1. Основные понятия
Матрицей называется прямоугольная таблица чисел, содержащая т строк одинаковой длины (или п столбцов одинаковой длины). Ма
трица записывается в виде
«11 012 • • - «1п \
д _ 021 «22 • • • «2п I
\ Omi От2 ^тп J
или, сокращенно, А = (а^), где г = 1, т (т. е. i = 1,2,3,..., ш) — номер строки, j = 1, п (т. е. j = 1,2,3,..., п) — номер столбца.
Матрицу А называют матрицей размера тхп и пишут Л Числа atj, составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.
Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.
А -- В, если aij — bij, где i = 1, т, j = 1, п.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера п х п называют матрицей п-го порядка.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.
Пример 1.1. г /10 0
£?зхз = ( 0 1 О
\ 0 0 1
— единичная матрица 3-го порядка.
— единичная матрица n-го порядка.
16
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Матрица, все элементы которой равны нулю, называется нулевой.
Обозначается буквой О- Имеет вид
/О 0 ... О \
О 0 ... О
\ 0 0 ... О /
В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.
|ф| Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответствен-
но). Их вид:
сц > а2
А =
, В - (bl b2 • • ь„).
\ <hn /
Матрица размера 1x1, состоящая из одного числа, отождествляется с этим числом, т. е. (5)ixi есть 5.
|ф| Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается АТ.
/1 2\ - (1 3\ /1\
Так, если А= I 1,тоАт=1 I, если А= I 1, то Лг = (1 0).
\ О *) х'" */ \ U/
Транспонированная матрица обладает следующим свойством: (Ат)т = А.
1.2. Действия над матрицами
Сложение
Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц Атуп = (ау) и Втуп = (bij) называется матрица СтХп = (су) такая, что су = «у + by (i = l,m, j = l,n).
Пример 1.2.
/ 2 -3 0 \ / 3 3—1\_/5 0—1\
( 4 5 6 J + —2 -5 4 J ~ 2 0 10 J ‘
Аналогично определяется разность матриц.
17
Умножение на число
Произведением матрицы АтХп — (ciij) на число к называется матрица Втхп — такая, что bi3 = к • (г — 1,т, j = 1,п).
Пример 1.3.
А=( U
А \ 3
2
5 J
-1
4
к = 2, А к = ( 2
\ 6
—2 4 \
8 10 ) '
Матрица —А = (—1) • А называется противоположной матрице А.
Разность матриц А - В можно определить так: А - В = А + (—В).
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. А + В = В + А-
2. А + (В + С) = (А + В) -t- С-
3. А + О = А;
4. А - А = О-
5. 1-А = А;
6. а (А + В) = аА + аВ;
7. (а + /?) - А = аА + /?А;
8. а (J3A) = (а/3) • А,
где А, В, С — матрицы, а и ft — числа.
Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
• перестановка местами двух параллельных рядов матрицы;
• умножение всех элементов ряда матрицы на число, отличное от нуля;
• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Ц>| Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например
/1 0 0 0\
0 10 01
0 0 10‘
х0 0 0 0/
18
Пример 1.4. Привести к каноническому виду матрицу /2 3 1 2\
А = 10 2 -1 1 .
\4 0 5 1/
Q Решение: Выполняя элементарные преобразования, получаем
2 3 1
0 2-1
4 0 5
2\
1 I
1/
3
2
0
2
0
4
j Произведение матриц
0 0
о
О' о о
; |@| Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй
, матрицы.
Произведением матрицы Атхп = (а^) на матрицу Впур = (Ьрь) называется матрица СтХр — (cj*) такая, что
cik = ап • bik + ai2 b‘2k Ч-Ь ainbnk, где г = 1,т, к = 1,р,
Ч т. е. элемент г-й строки и к-vo столбца матрицы произведения С равен сумме произведений элементов г-й строки матрицы А на соответствующие элементы к-ro столбца матрицы В.
Получение элемента с.,к схематично изображается так:
Если матрицы Ли В квадратные одного размера, то произведения АВ и В А всегда существуют. Легко показать, что А Е = Е • А = А, где А — квадратная матрица, Е — единичная матрица того же размера.
Пример 1.5.
«п «21
012
«22
«13
«23
3x2
/ ОцЬц + ai2b2i + «13631 йцЬщ + ai2b22 + ащЬзгА \й21Ь11 + a22b2i + О2зЬз1 <121Ь12 + а22Ь22 + 0.23^32 / 2х2
19
Пример 1.6. А = [ ), В = ( „ ). Тогда произведение
А • В не определено, так как число столбцов матрицы А (3) не совпада-
ет с числом строк матрицы В (2). При этом определено произведение В х А, которое считают следующим образом:
в-л=(;
3\ /1 2 1\
2/ \3 1 О/
1 + 9 2 + 3 1 + 0\
1 + 6 2 + 2 1 + 0/
10 5 1\
7 4 1/
Матрицы А«В называются перестановочными, если АВ = В А.
Умножение матриц обладает следующими свойствами:
1. А • (В • С) = (А В) - С; 3. (А + В) С = АС + ВС;
2. А • (В + С) = АВ + АС; 4. а(АВ) = (аА)В,
если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
1. (А + В)Т = АТ + ВТ;
2. (АВ)Т = Вт Ат.
§2. ОПРЕДЕЛИТЕЛИ
2.1. Основные понятия
Квадратной матрице А порядка п можно сопоставить число det А (или |А[, или Д), называемое ее определителем, следующим образом:
1. п = 1. А = (oi); det А = О1.
2. п = 2. А = f «11 012 ; det А = Oil 012 — Ou 022 — O12 • O21
\ 021 022 021 022
/ Oil 012 О1з\ Oil 012 013
3. п = 3, А = I 021 022 023 I; det А = 021 022 023
\О31 032 Озз/ 031 O32 О33
= 011022033 + O12O23O31 + O21O32O13 — O31O22O13 — O21O12O33 — О32О23ОЦ.
Определитель матрицы А также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов
20
основан на свойстве разложения определителя по элементам некоторого ряда (с. 23, свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.
Вычисление определителя 2-го порадка иллюстрируется схемой:
у. i: :i=n-w
Пример 2.1. Найти определители матриц
•i /2 —3\ ( o&sa sinoA 1 к ю 1 и у 5 6/ у— sin Q cos а/
Q Решение: 2 —Ч 5 = 2-6-5-(-3) = 12-(-15) = 27; coso sin о 2.2^ - = cos а + sm а = 1. • — sm a cos а
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:
(основания равнобедренных треугольников параллельны главной диагонали)
(основания треугольников параллельны побочной диагонали)
Пример 2.2. Вычислить определитель матрицы
5
3
6
—2 1
1 —4
О -3
Q Решение:
det А =
= 5• Г (—3) 4-(—2) • (—4)-6 + 3-0-1 — 6-1 • 1 — 3-(—2) - (—3) —0-(—4)-5 =
= -15 + 48 - 6 - 18 = 48 - 39 = 9. •
21
2.2. Свойства определителей
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.
Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот.
Иными словами,
Оц Й21 «31
012 022 «32 .
013 «23 Озз
В дальнейшем строки и столбцы будем просто называть рядами определителя.
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен
«11 012
«21 «22
011 021
012 022
«11
021
031
012
022
«32
013 «23 Озз
нулю.
Свойство 4- Общий множитель элементов какого-либо ряда опре
делителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все. элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
□ Действительно,
Оц 012 013 Оц «12 013
к оц к а\2 к • О1з = к- Оц «12 013 = к • 0 = 0.
031 032 Озз 031 032 «33
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть
разложев на сумму двух соответствующих определителей.
Например, Оц 012 021 022
031 032
Свойство 6
013 +Ь
023 +с озз + d
Оц 021
0.31
012
022 «32
013
«23
Озз
011
«21
031
(«Элементарные
преобразования
012 b
022 с .
032 d
определителя»).
Определитель не изменится, если к элементам одного ряда прибавить
соответствующие элементы параллельного ряда, умноженные на любое число.
Пример 2.3. Доказать, что
Оц 012 «13 Оц 012 013 + к 012
021 022 «23 — «21 022 «23 + к 0,22
031 032 Озз «31 032 Озз + к 032
22
Ci Решение: Действительно, используя свойства 5, 4 и 3, получим
«11 «12 «13 + к • «12
«21 «22 «23 + к «22 =
«31 «32 «33 + к «32
«И «12 «13 «И «12 «12
= «21 «22 «23 + к «21 «22 «22 = Д + fe • 0 = Д. ®
«31 «32 «33 «31 «32 «32
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.
Минором некоторого элемента определителя n-го порядка называется определитель п — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается ту.
Так, если
Л «и «12 «13 «22 «23 «И
А = «21 «22 «23 , то Той = , т32 = «21
«32 «33
«31 «32 «33
«13
«23
Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком «плюс», если сумма г + j — четное число, и со знаком «минус», если эта сумма нечетная. Обозначается Aij-. = (—l)’+j • ntij.
Так, Дц = +тц, Д32 — -тлю-
Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.
Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что
; «и «12 «13
«21 «22 «23
«31 «32 «33
— «11 ’ Д11 + «12 ' Д12 + «13 ’ Д13-
Q В самом деле, имеем
«11 ' Д11 + «12 Д12 + «13 • Д13 —
— «И ’
«22
«32
«23
«33
+ «12 •
«21 «23
«31 «33
+ «13 •
«21 «22
«31 «32
= «11(а22«33 — «23«3г) — «12(«21«33 ~ «23«31) + «1з(«21«32 — «22«31) =
= «И«22«33 — «И«23«32 — «12«21«33 + «12«23«31 +
+ «13«21«32 ~ «13«22«31 = А- 1
23
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.
Пример 2.4- Вычислите определитель матрицы
/ 3 5 7 8\
-1 7 0 1
0 5 3 2'
\ 1 -1 7 4/
Q Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю.
;'3'1 5 7 8
!—1’ 7 0 1
; 0 : 5 3 2~
: 1; -1 7 4
= 3- 7 0 1 5 3 2 -17 4 + 1- 5 7 8 5 3 2 -17 4 + 0- 5 7 8 7 0 1 -17 4 - 1 5 7 8 7 0 1 5 3 2 =
= 3 • (7-3-4+(-1)- Э-2 + 5-7- 1-(- 1)-3-1-7 -7-2 -5-0-4)- 1-
+ (5 - 3 - 4 + (- -1)-7 -2 + 5-7-8 -(-1 ) -3-8 — 5- 7-4 — 5-7-2)—
-G 5-O-2 + 7- 1-5 + 7-3-8-5 0-8- 3-1-5 —7 -7-2) = 122. •
Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например, оц А21 + 012^-22 + О13А23 = 0.
§ 3. НЕВЫРОЖДЕННЫЕ МАТРИЦЫ
3.1. Основные понятия
Пусть А — квадратная матрица n-го порядка ^11 012 О1»Д _ 021 °22 • - О2п
\ОП1 Оп2 - - . Опп j
|ф| Квадратная матрица А называется невырожденной, если определитель Д = det А не равен нулю: Д = det Л 0. В противном
случае (Д = 0) матрица А называется вырожденной.
24
Матрицей, союзной к матрице А, называется матрица ^Ац А.21 ... А„А
_ ^12 А22 - - • АП2
\А1и А2п ... А пп/
где Aij — алгебраическое дополнение элемента данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента
, определителя).
? Матрица А-1 называется обратной матрице А, если выполняется
q условие
.. А • А1 = А1 - А = Е, (3.1)
' где Е — единичная матрица того же порядка, что и матрица А. Ма-1 трица А-1 имеет те же размеры, что и матрица А.
3.2. Обратная матрица
Теорема 3.1. Всякая невырожденная матрица имеет обратную.
Q Проведем доказательство для случая матрицы 3-го порядка. Пусть
(«И <212 «13 \
а-21 022 О2з I ; причем det А 0.
О31 Оз2 O33)
Составим союзную матрицу
/Ац А21 А3Л
А* = I А12 А22 А32 I
\А1з А23 А33/
и найдем произведение матриц А и А*:
А-А*
012
022
032
A21
А22
А23
Аз1\
А32 I =
А33/
/ Оц Ац + О12А12 + О!зА13 I О21Ац + O22AJ2 + ОгзА13 \Оз1Ац + О32А12 + O3sAj3
011А3] + П12А32 + О1зАзз\ O21А31 + О22А32 + ОгзАзз I =
О31А31 + азгАзг + 033 А33/
(det А О 0 \ /1 О 0\
О det А 0 j=detA- О 1 O|=detA-E,
О 0 det А/ \0 О 1 /
т. е.
А • А* = det А - Е. (3.2)
Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).
25
Аналогично убеждаемся, что
А* A = detA-F.
(3.3)
Равенства (3.2) и (3.3) перепишем в виде
А- -^- = Е и -^-т-А = Е. det A det А
Сравнивая полученные результаты с определением (3.1), получаем
det А’
т. е.
det А
Ац
Ai2
А1з
А21
А22
А23
А31 \
А32 I А33/
Отметим свойства обратной матрицы:
1. det(A ) = detj4;
2. (АВ)-' = В-'А~'-,
3. (А1)7’= (Л7)-1.
Пример 3.1. Найти А х, если А =
2
-1
ЗА
1/’
Q Решение: 1) Находим det A: det А —
2) Находим А*: Ац поэтому А* =
2 з
-1 1
= 2 + 3 = 5^ 0.
= 1, А-21 — —3, А12 = —( — 1) = 1, А22 = 2,
1
1 2Г
3) Находим А г: А 1
1 -3
2
Проверка:
1
5
1
.5
_з
5
2
5
А • А'1 =
2 з
-1 1
1
5
1
.5
_ з 5
2
5.
2,3 6,6
5'5 ~5 + 5
1,1 3,2
5 5 5 5
= Е. •
_ 1 , ~ з h
1 О
О 1
Пример 3.2. Определить, при каких значениях А существует матрица, обратная данной:
(1 -2 2\
А 3 0 .
2 1 1/
26
Q Решение: Всякая невырожденная матрица имеет обратную. Найдем определитель матрицы А:
1 -2 2
ДА = А 3 0 = 3 - 0 + 2А - 12 - 0 + 2А = 4А - 9.
2 1 1
Если 4А — 9 7^ 0, т. е. А |, то ДА 0, т. е. матрица А невырожденная, имеет обратную. *
Пример 3.3. Показать, что матрица А является обратной для В,
если
1 ( 3 -3 1 '
А= | 12 3 |, в= | -3 5 -2
<1 3 6> <1-21
Q Решение: Найдем произведение матриц АнВ;
/1 1 1\ / 3 -3 1 \
АВ=(1 2 3 ) 1 -3 5 —2 =
V 3 6/ \ 1 ~2 1 /
/3- 3 + 1 -3 + 5-2 1 - 2 +1\ /1 0 0\
= I 3- 6 + 3 -3 + 10-6 1 - 4 + 3 = 0 1 0 = Е.
\3 - 9 + 6 -3+15-12 1-6 + 6/ \0 0 1/
Аналогично В А = Е. Следовательно, матрица А является обратной для В. *
3.3. Ранг матрицы
Рассмотрим матрицу А размера т х п.
/|°и (I12I (113 а1п
1(121 <122' (123 й2п
А = аз1 <132 <133 а3п
^ml ®т2 &тЗ ^тп
Выделим в ней к строк и к столбцов (fc min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель fc-ro порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить штук,
где С„ — к1^— 'к)1 — число сочетаний из п элементов по fc.)
27
g Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается г, г(А) или rang А.
Очевидно, что 0 г min(m; тг), где min(m; п) — меньшее из чисел т и п.
|ф] Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.
Пример 3.J. Найти ранг матрицы: /2 0 4 0\
А= 3 О 6 0 .
\1 0 -3 О/
Q Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го
3 6
1 -3
порядка, отличный от нуля
= —15 0 0. Значит, г(А) = 2.
Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.
Отметим свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы (см. с. 18).
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
Пример 3.5. Найти ранг матрицы /2 3 1 2\
А= 0 2 -1 1 ,
\4 0 5 1/
используя результаты примера 1.4.
Q Решение: В примере 1.4 показано, что
/1 0 0 0\
А~ I 0 1 0 0 ’
\° 0 0 0/
то есть л 1 0 0 0\
А р 1 0 or
Таким образом, ранг матрицы А равен г(А) = 2.
28
§4. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИИ
4.1. Основные понятия
Системой линейных алгебраических уравнений, содержащей т уравнений и п неизвестных, называется система вида
«цац + <112^2 4- • • • + а\пхп — bi, О21®1 + 022^2 + • • + а^п^п — &2,
к От!®! 4" ат2Х2 + •••-!- атпхп — Ь?71,
где числа Оу, г = 1, т, j = 1, п называются коэффициентами системы, числа bi — свободными членами. Подлежат нахождению числа хп.
Такую систему удобно записывать в компактной матричной форме _________
|А-Х = В.
Здесь А — матрица коэффициентов системы, называемая основной
матрицей:
\Хп/ (ъД Ь2
Й12 ... 0.1п^
Й21 Й22 - - • Й2п
\o,,ti ат2 - - - атп ]
— вектор-столбец из неизвестных Xj,
— вектор-столбец из свободных членов Ь7.
\Ьт /
Произведение матриц А-Х определено, так как в матрице А столбцов столько же, сколько строк в матрице X (о штук).
Расширенной матрицей системы называется матрица А системы, дополненная столбцом свободных членов
( Oil 012 • - • ьД
А = 021 а22 • • &‘2п Ь2
O„t2 - • ®тп Ьт)
Решением системы называется п значений неизвестных Xi =ci, Х2=в2, ..., хп—сп, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в
29
виде матрицы-столбца , .
/ Cl'
\Сп/
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
011271 -I- 012^2 -I-+ ЩпХп — О,
* .............................
4“ Ощ2372 4" * * " 4" ЩппХп 0.
Однородная система всегда совместна, так как Xi = ®2 = • • • = хп = О является решением системы. Это решение называется нулевым или тривиальным.
4.2. Решение систем линейных уравнений.
Теорема Кронекера-Капелли
Пусть дана произвольная система т линейных уравнений с п неизвестными
' О11Ж1 + 012^2 4--1- «1А = А,
О21Ж1 4" 022372 4" • • ’ 4" О2п37п = Ь%, <
. 4~ 0^23-2 4* • • * 4~ О/тпХп —
30
Исчерпывающий ответ на вопрос о совместности этой системы дает теорема КронекераКапелли.
Теорема 4.1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Примем ее без доказательства.
Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема 4.2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 4.3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Правило решения произвольной системы линейных уравнений
1. Найти ранги основной и расширенной матриц системы. Если г(А) г( А), то система несовместна.
2. Если г(А) = г( А) = г, система совместна. Найти какой-либо базисный минор порядка г (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять г уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные п — г неизвестных называют свободными и переносят в правые части уравнений.
3. Найти выражения главных неизвестных через свободные. Получено общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.
Пример 4-1- Исследовать на совместность систему
X + у = 1,
Зж + Зу = —2.
31
Q Решение:
Л=(1 Г), r(A) = 1, \ О О / |
^=(3 3 Л)’ ’® = 2 (Д = |з -2р°)-
Таким образом, г (А) 0 г( А), следовательно, система несовместна. •
Пример 4-2. Решить систему Х1 - 2X2 + = 1,
< — 2х2 + Х3 — ®4 = —1,
а?! — 2х2 + + 3®4 = 3.
1
1
1
-1
А =
= -2 00,
Q Решение: г(А) = г( А) = 2. Берем два первых уравнения: J - 2X2 +;®з + Xi] = 1, I Х1 — 2X2 +l®3_—= — 1-
1
Х3 + Xi = 1 - + 2X2,
Хз — Xi = — 1 — Х1 + 2х2-
Ai =
- Ж1 + 2X2 1
-1-®1+2®2 -1
= 2®i — 4®2,
1 1 - Xi + 2X2
1 -1 - + 2X2
= 1 — общее решение. Положив,
Аг =
= —2.
Следовательно, х3 = —Xi + 2®г, например, ац = 0, <г2 = 0, получаем одно из частных решений: Xi = 0, Х2 = 0, Х3 = 0, Xi = 1. •
4.3. Решение невырожденных линейных систем. Формулы Крамера
Пусть дана система п линейных уравнений с п неизвестными 'ац®1 + ащЖг Ч---------------Ь QinXn = Ъ\,
a2i®i + а22®2 Ч-Ь а,2ПХп = Ьг,
,0/0^1 + 0/12^2 + • + Чппхп = Ьп
или в матричной форме А • X = В.
Основная матрица А такой системы квадратная. Определитель этой матрицы an • • • a>in
А = ............
<xni .. - ann
32
называется определителем системы. Если определитель системы отличен от нуля, то система называется певырождемпоб,.
Найдем решение данной системы уравнений в случае Д 0.
Умножив обе части уравнения А X = В слева на матрицу А-1, получим А“х А • X = А1 В. Поскольку А1 • А = Е и Е • X = X, то
Х = А1 В.
(4Л)
Отыскание решения системы по формуле (4А) называют матриц ным способом решения системы.
Матричное равенство (4.1) запишем в виде
Отсюда следует, что
г _ АцЬ1 + А21?>2 +------Н Anibn
~ А
„ _ Ainfei + А2та62 + • • • + Аnn^'i Хп- д
Но АцЬ1 + A2i62 +----Ь Anibn есть разложение определителя
bi 012 • a>in
Ъ-2 а-2,-2. а,2п
Ьп ®п2 • * • ^пп
по элементам первого столбца. Определитель Ai получается из определителя А путем замены первого столбца коэффициентов столбцом из свободных членов.
Итак, Xi =
Аналогично: где Аг получен из А путем замены второго
Дч
столбца коэффициентов столбцом из свободных членов; х3 = -А,...
_ А,, А
...
2 Конспект лекций По высшей математике. Полный курс
33
KI Формулы
г = l,n
(4-2)
называются формулами Крамера.
Итак, невырожденная система п линейных уравнений с п неиз
вестными имеет единственное решение, которое может быть найдено матричным способом (4.1) либо по формулам Крамера (4.2).
Пример 4-3.
J 2Ж! - х2 = О, Решить систему <
I + За.’2 = 7.
0
7
Q Решение: Д = X о
Значит, Xi = Z = 1, = у
= 7^0, Дх =
= 2.
-1
3
= 7, Д2 = 2 ° =14.
4.4. Решение систем линейных уравнений методом Гаусса
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
aii^i 4- 012^2 4- • • 4- а±пхп = bi, 021^1 + 022^2 + • - + О2пХп = Ь2,
(4.3)
4“ Om2-^2 4“ ' ' ' ~катпХп — Ь7П.
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
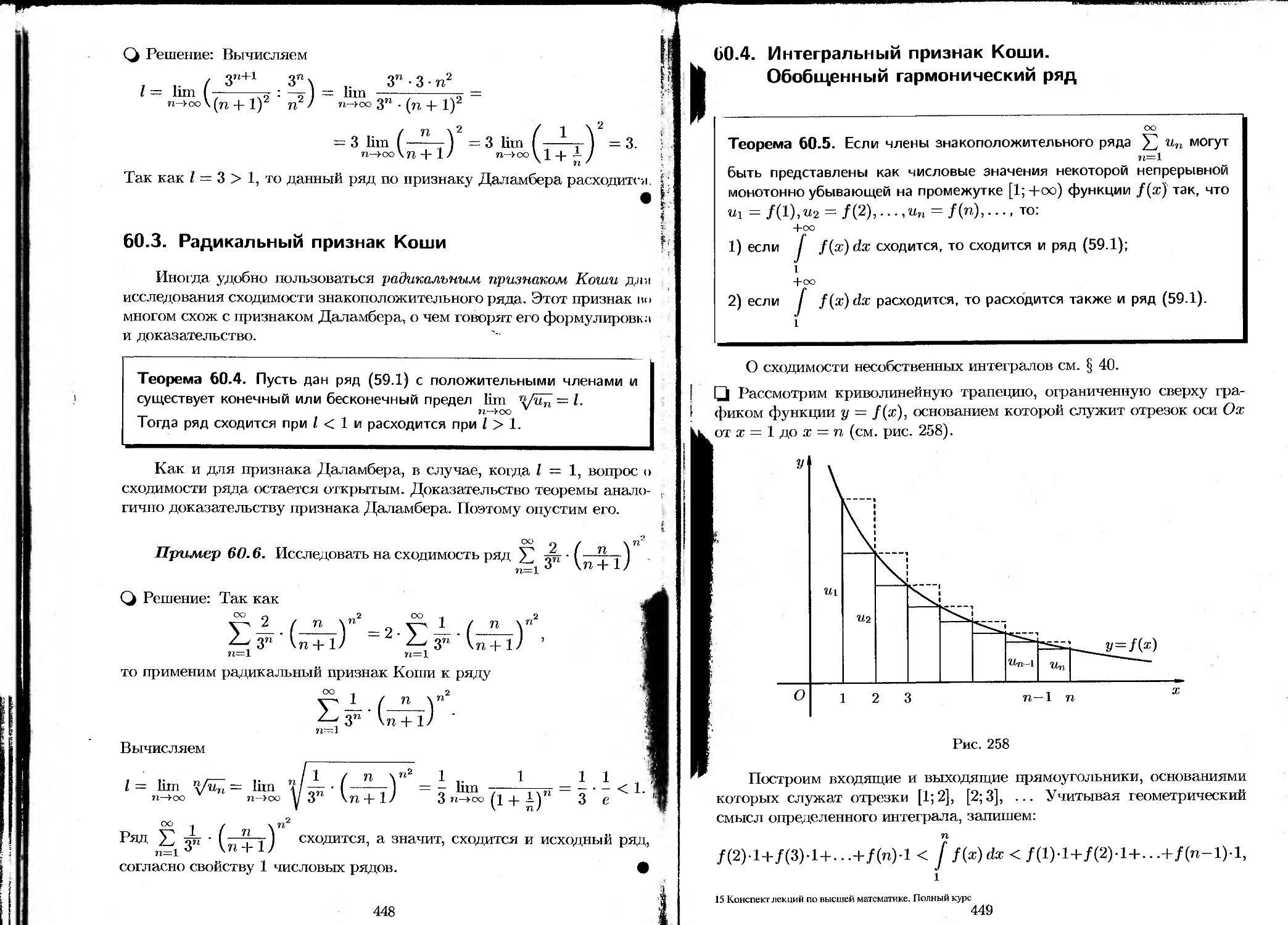
Приведенная ниже система имеет ступенчатый вид
ацЯ1 4- «12^2 4- • 4- QikXk 4- • • 4- ain%n — bi,
022^2 4- • • 4- a2k%k +--Ь а-2пХп = &2,
вкк^к 4“ * " " 4“ ОкпХп — bfc,
где к п, оц 0, г = 1, к. Коэффициенты ац называются главными элементами системы.
На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
34
Опишем метод Гаусса подробнее.
Прямой ход.
Будем считать, что элемент ап 0 (если ац = 0, то первым в системе запишем уравнение, в котором коэффициент при Xi отличен от нуля).
Преобразуем систему (4.3), исключив неизвестное ад во всех уравнениях, кроме первого (используя элементарные преобразования си-. Для этого умножим обе части первого уравнения на — и ац сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на — и сложим с третьим уравнением си-
стемы. Продолжая этот процесс, получим эквивалентную систему
ацЖ1 + ацжг 4----F ainxn = Ьг,
„(1)т . ... , „(1)г а22 а?2 -г • -t- а2п хп — а2 ,
n(i)r ... .я(1)т _АП) ^7712^2 ^тп^п — Um -
Здесь а-p, (г, j = 2,m) — новые значения коэффициентов и правых частей, которые получаются после первого шага.
Аналогичным образом, считая главным элементом a2i? 0, исключим неизвестное х% из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.
Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида 0 = 0, их отбрасывают. Если же появится уравнение вида 0 = bi, a bi А 0, то это свидетельствует о несовместности системы.
Второй этап (обратный ход) заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное Xk через остальные неизвестные (агд+1,... ,хп). Затем подставляем значение Xk в предпоследнее уравнение системы и выражаем Xk-i через (гщ,...лп); затем находим Xk^2,.. -, . Придавая свободным неизвестным (адщ, - - -, хп) произвольные значения, получим бесчисленное множество решений системы.
Замечания: 1. Если ступенчатая система оказывается треугольной, т. е. к = п, то исходная система имеет единственное решение. Из последнего уравнения находим хп, из предпоследнего уравнения xn~i, далее поднимаясь по системе вверх, найдем все остальные неизвестные (®n_2,...,a:i).
2. На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над
35
ее строками. Удобно, чтобы коэффициент ац был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на ац 1).
Пример 4-4- Решить систему методом Гаусса:
'2®! — + 3®з — 5®4 = 1,
— 5®з = 2,
<
3®i — 2®2 — 2®з — 5®4 = 3,
k 7®i — 5®2 — 9®з — 10®4 = 8.
О Решение: В результате элементарных преобразований над расши-
ренной матрицей системы
/2 -1 3 -5 1\
1-1-5 0 2
3 -2 -2 -5 3 ~
\7 -5 -9 -10 8/
/1—1—5 0 2 \
0 1 J3 -5 -3
0 1 \з -5 -3
\0 2 26 -10 -6/
/1 -1 -5 0 2\
2-13 -5 1
3 -2 -2 -5 3 ~
\7 -5 -9 -10 8/
/1—1—50 2 \
0 1 13-5 -3
0 0 0 0 0
\0 0 0 0 0 /
исходная система свелась к ступенчатой:
- Х2 — 5®3 = 2,
®2 + 13®з — 5x4 = — 3.
Поэтому общее решение системы: х2 = 5x4 ~ 13®з -3; = 5®4 — 8®з — 1.
Если положить, например, ®з = 0, Х4 = 0, то найдем одно из частных решений этой системы хА = — 1, х2 = —3, ®з = 0, Х4 = 0. •
Пример 4-5- Решить систему методом Гаусса: + ®2 + ®3 = 3, 2®i + 3®2 + 2®3 = 7, <
3®i + х2 + х3 = 5, k 5®i — х-2 — х3 = 3.
Q Решение: Произведем элементарные преобразования над строчками
расширенной матрицы системы:
Л 1
2 3
3 1
V -1
1
2
1
-1
3\
7
5
3/
о о
\0
1 1 3 \
1 0 1
—2 —2 —4
-6 -6 -12/
Л 1 1 3\
0 10 1
0 112 \0 1 1 2/
Л 1 1 3\
0 10 1
0 0 11
\о о о о/
36
Полученная матрица соответствует системе
Xi + х2 + х3 = 3, < х2 =1, Хз = 1-
Осуществляя обратный ход, находим х3 = 1, х2 = 1, Xi = 1.
4.5. Системы линейных однородных уравнений
Пусть дана система линейных однородных уравнений ап®1 + 0,12X2 + • • • + Gin®n = О, G21 Xi + G22®2 + ’ • + G2n®n = О,
',тп1Х1 4“Ош2^2 Т "ЬОгппХп — О-
Очевидно, что однородная система всегда совместна (г(А) = г( А)), она имеет нулевое (тривиальное) решение Xi = Х2 = • • = хп = 0.
При каких условиях однородная система имеет и ненулевые решения?
Теорема 4.4. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг г ее основной матрицы был меньше числа п неизвестных, т. е. г < п.
□ Необходимость.
Так как ранг не может превосходить размера матрицы, то, очевидно, г п. Пусть г = п. Тогда один из миноров размера п х п отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: хг = = 0, А; = 0, А 0. Значит, других, кро-
ме тривиальных, решений нет. Итак, если есть нетривиальное решение, то г < п.
Достаточность.
Пусть г < п. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения.
Пусть дана однородная система п линейных уравнений с п неизвестными _
Gll®i + Gi2®2 + ' ‘ + Gin®n — 0,
< ..................................
Gni®! + ап2Х2 +••-- + аппхп = 0.
37
Теорема 4.5. Для того, чтобы однородная система п линейных уравнений с п неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель Д был равен нулю, т. е. Д = 0.
□ Если система имеет ненулевые решения, то Д = 0. Ибо при Д 0 система имеет только единственное, нулевое решение. Если же Д — 0, то ранг г основной матрицы системы меньше числа неизвестных, т. е. г < п. И, значит, система имеет бесконечное множество (ненулевых) решений.
Пример 4-6. Решить систему
— 1X2 + 4жз = 0, 2®i — 3®2 + 5жз = 0.
Q Решение:
1 -2
2 -3
, г(А) = 2
1 —2
2 -3
= 10 0), 77 = 3-
Так как г < Найдем их
71,
то система имеет бесчисленное множество решений.
- 4хз
-5зг3
—2
-3
хг - 1x2 = -4ж3, 2ал — За?2 = —5®з.
1 -4ж3 2 —5®з
= 2ж3, Дг =
= З^з- Стало быть, ац =
Д1 =
= = 2ж3, Х2 = = Зж3 — общее решение.
Положив хз = 0, получаем одно частное решение: ау — 0, х3 — 0, хз = 0. Положив х3 = 1, получаем второе частное решение: ал = 2, Х2 = 3, Хз = 1 и т. д. •
А =
4
5
Д =
Глава II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Лекции 4-6
§5 . ВЕКТОРЫ
5.1. Основные понятия
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
£5] Вектор — это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А — начало вектора, а В — его конец, то вектор обозначается символом АВ или а. Вектор В А (у него начало в точке В, а конец в точке А) называется противоположным вектору АВ. Вектор, противоположный вектору а, обозначается —б.
Длиной или модулем вектора АВ называется длина отрезка и обозначается |ЛВ|. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 0. Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным вектором и обозначается через ё. Единичный вектор, направление которого совпадает с направлением вектора а, называется ортом вектора а и обозначается а°.
Векторы а и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают а || Ь. Коллинеарные векторы могут быть направлены одинаково или 11 ротивоположно.
Нулевой вектор считается коллинеарным любому вектору.
|,'5| Два вектора а нЬ называются равными (а = Ь), если они коллинеарны, одинаково направлены и имеют одинаковые длины. Из определения равенства векторов следу-
ет, что вектор можно переносить параллельно ------------
самому себе, а начало вектора помещать в лю- -
бую точку О пространства. _______________
На рисунке 1 векторы образуют прямо- j
угольник. Справедливо равенство b = d, но а
с. Векторы бис — противоположные, а = —с. ^ис’ 1
39
Равные векторы называют также свободными.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
5.2. Линейные операции над векторами
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть а и Б — два произвольных вектора. Возьмем произвольную точку О и построим вектор О А = б. От точки А отложим вектор АВ = Ь. Вектор ОБ, соединяющий начало первого вектора с концом второго, называется суммой векторов а и Ь: О В = а + Ь (см. рис. 2).
Это правило сложения векторов называют правилом треугольника.
Сумму двух векторов можно построить также по правилу параллелограмма (см. рис. 3).
Рис. 4
40
Под разностью векторов а и b понимается вектор с = а — Ь такой, что Ь + с = а (см. рис. 5).
Рис. 5
Отметим, что в параллелограмме, построенном на векторах а и Ь, одна направленная диагональ является суммой векторов а и Ь, а другая — разностью (см. рис. 6).
Рис. 6
Можно вычитать векторы по правилу: а — b = а + (—6), т. е. вычитание векторов заменить сложением вектора а с вектором, противоположным вектору Ь.
Произведением вектора а на скаляр (число) Л называется вектор Л • а (или а • Л), который имеет длину |Л| • |а|, коллинеарен вектору а, имеет направление вектора а, если А > 0 и противоположное направление, если А < 0. Например, если дан вектор —2», то векторы
За и —2а будут иметь вид » и .... ---
Из определения произведения вектора на число следуют свойства этого произведения:
1) если b = А • а, то b || а. Наоборот, если b || а, (а 0), то при некотором А верно равенство b = Аа;
2) всегда а — |а| а0, т. е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
1. а + b — b + а,
2. (а + Ь) + с = а + (Ь + с),
3. Ai • (Аг а) = А] - Аг • о,
4. (At + Аг) а — Aj а 4- Аг • а, 5. А (а 4- Ь) = А • а 4- А Ь.
Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: сла-
41
гаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
5.3. Проекция вектора на ось
Пусть в пространстве задана ось I, т. е. направленная прямая.
Проекцией точки М на ось I называется основание Mi перпендикуляра MMi, опущенного из точки на ось.
Точка Mi есть точка пересечения оси I с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).
Если точка М лежит на оси I, то проекция точки М на ось совпадает с М.
Пусть АВ — произвольный вектор (АВ 0). Обозначим через Аг и Bi проекции на ось I соответственно начала А и конца В вектора АВ и рассмотрим вектор Ai Bi.
Проекцией вектора АВ на ось I называется положительное число |Л] Bi |, если вектор AiBi и ось I одинаково направлены и отрицательное число — IXtBil, если вектор Aj Bi и ось I противоположно направлены (см. рис. 8). Если точки Аг и совпадают (AiBi = 0), то проекция вектора АВ равна 0.
Проекция вектора АВ на ось I обозначается так: прг АВ. Если 4В = 0 или АВ ± I, то прг АВ = 0.
Угол <р между вектором а и осью I (или угол между двумя векторами) изображен на рисунке 9. Очевидно, 0 тг.
О1
Рис. 9
42
Рис. 10
Рассмотрим некоторые основные свойства проекций.
Свойство 1. Проекция вектора а на ось I равна произведению модуля вектора а на косинус угла ip между вектором и осью, т. е. прг а = = |а| - cosy?.
□ Если у? = (а,Г) < то пргб =
= +|6i | = |б| • cos </?.
Если ip > (9? я), то прга =
— — |6i| = —|б| - cos(tt — 9?) = |а| - COS9?
(см. рис. 10).
Если 9?=^, то прг й=0= |сг| cos 9?.
Следствие 5.1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
□ Пусть, например, d — a+b+c. Имеем npzd = +|di| = +|6i|+|bi| —|ci|, т. е. прг(б + b + с) = прг а + прг b + прг с (см. рис. 11).
Свойство 3. При умножении вектора а на число А его проекция на ось также умножается на это число, т. е.
прг(А • а) = А прг а.
□ При А > 0 имеем прг(А-сг) = |А«| • cosy? = (свойство 1)
— А |а| - cos 9? = А • прг а.
При А < 0: прг(А а) — |Аб| • cos(tt — <р) = ~ —А • |й| (— cosy?) = А • а cos у? = А прг а. Свойство справедливо, очевидно, и при А = = 0.
Рис. 11
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
43
5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые г, j, к соответственно (см. рис. 12).
Рис. 12
Выберем произвольный вектор а пространства и совместим его начало с началом координат: а = ОМ.
Найдем проекции вектора а на координатные оси. Проведем через конец вектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через Му, М-2 и М3. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда прж а = = |(97И1|, пру а = 1ОМг[, пргб = |(97Из|. По определению суммы нескольких векторов находим а = ОМ у + MyN + NM.
А так как MN = ОМ2, NM = ОМ3, то
а = ОМу+ОМ2 + ОМ3. (5.1)
Но
ОМу = \ОМу\-г, OM2 = \OM2\-j, ОМ3 = \ОМ3\-к. (5.2)
Обозначим проекции вектора а = ОМ на оси Ох, Оу и Oz соответственно через ах, ау и az, т. е. [ОМу | = ах, |ОЛ/21 = ау, |О7И3| = az. Тогда из равенств (5.1) и (5.2) получаем
(5-3)
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных oceii.
а = ах i + ау j + az к.
44
Числа аж, ау, az называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом ви-де: а = (ax;ay-,z_z).
Равенство b = (bx;by;bz) означает, что b = Ьх • г + Ъу • j + bz • k.
Зная проекции вектора й, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать |ОЛ-/|2 = lOAfJ2 + |ОМ2|2 + |ОМ312, т. е.
|й|2 = а2 + а2 4-а2. (5.4)
|^| т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора а с осями Ох, Оу и Oz соответственно равны
а, /3, 7. По свойству проекции вектора на ось, имеем
ах = |«| • coso!, ау = |й| • cos/в, a2 = |a|-cos7. (5.5)
Или, что то же самое,
Дг п ау az
COSO = —, COSO = 7727, COS7 = —.
I«l l«l 1°1
Числа cos a, cos (3, cos 7 называются направляющими косинусами вектора а.
Подставим выражения (5.5) в равенство (5.4), получаем
|й|2 = |й|2 • cos2 а 4- |й|2 • cos2(3 4- |й|2 • cos2 7.
Сократив на |й|2 0 0, получим соотношение cos2 а 4- cos2 (3 + cos2 7 = 1,
|^| т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора ё являются числа cos a, cos (3, cos 7, т. е. ё = (cos a; cos /в; cos 7).
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т. е. сам вектор.
5.5. Действия над векторами, заданными проекциями
Пусть векторы а = (ax-,ay-,az) и b — (bx;by;bz) заданы своими проекциями на оси координат Ох, Оу, Oz или, что то же самое
а = ах i + Оу j + az k, b — bx i + by j + bz к.
45
Линейные операции над векторами
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
1. а ± b = (аж ± bx)i 4- (ау ± by)j 4- (а2 ± b2)fc, или кратко а ± b = = (ax±bx-,ay±by-,az±bz). То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).
2. Ха = Хах-i+Xay -j+Xaz-k или короче Ха = (Хах; Хау; Xaz). То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
Равенство векторов
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора a ub равны тогда и только тогда, когда выполняются равенства: ах = Ьх, ау = Ьу, az = bz, т. е.
п — А —ч. j ft® — ^х > К
ц> — и \ 7 < —
ft 2 — bz.
Коллинеарность векторов
Выясним условия коллинеарности векторов а и Ь, заданных своими координатами.
Так как а || Ь, то можно записать а = Х-Ъ, где А — некоторое число. То есть
ах • i + ау j + az k = A(6r • i + Ьу j 4- bz • k) = Xbx i 4- Xby • J 4- Xbz • k. Отсюда
az = Xbz, ах ау az
bx by bz
— Xbx,
_ д Оу _ д bx by
О'у — ^^у '
— = А или bz _ а
g Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.
т. е.
Координаты точки
Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Для любой точки М координаты вектора ОМ называются координатами точки М. Вектор ОМ называется радиус-вектором точки М, обозначается г, т. е. ОМ = г. Следовательно, координаты точки — это координаты ее радиус-вектора
г = (ж; у, z) или r = x- i + y- j + z-k. Координаты точки М записываются в виде M(x;y;z).
46
Координаты вектора
Найдем координаты вектора а = АВ, если известны координаты точек A(a?i;yi;zi) и В(х2;у2; z2)- Имеем (см. рис. 13):
АВ = ОВ — О А = (х2 i + у2 j + z2 к) — (хг - i + yi • j + zi • к) = = (ж2 - xi)i + (г/2 - Vi)j + (z2 - zi)k.
Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала: АВ = (х2 — xi',y2 — у Г, z2 — zi).
§6 . СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
6.1. Определение скалярного произведения
|^| Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается ab, а Ъ (или (а, Ь)). Итак, по определению,
а • b = |а| • |6| • cos ip,
(6-1)
где <р — (а, Ь).
Формуле (6.1) можно придать иной вид. Так как |а|cosy? — npg«, (см. рис. 14), а |Ь| сову = прг6, то получаем:
ab = |а| • npff b = |6| • пр^ а,
(6-2)
т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
47
6.2. Свойства скалярного произведения
1. Скалярное произведение обладает переместительным свойством: ab = Ьа.
□ ab = |й| |6| -cos(o, 6), а Ьа = |6| - |й| -cos (6, а). И так как |й| • |6| = |6| - |й|, как произведение чисел и cos(a, Ь) = cos (6, а), то ab = Ьа.
2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: (Ай) • Ь = А(й6).
□ (Ха)Ь = |6| • пр& Ай = А • |Ь| • пр^й = Х(аЬ).
3. Скалярное произведение обладает распределительным свойством: а(Ь + с) = ab+ ас.
□ _a(b + с) = |й| - прй-(6 + с) = |й| • (прй- Ь + прй с) = |й| прй Ъ + |й| • прйс = = ab + ас.
4. Скалярный квадрат вектора равен квадрату его длины: й2 = |й|2. □ й2 = а - а = |й| |а| cos0 = |й| • |й| = |й|2.
-2 —2 —2
В частности: г = j —к =1.
|@| Если вектор й возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль |й|, т. е.
а/й2 = |й| (^ а).
Пример 6.1. Найти длину вектора с = Зй—46, если |й| = 2, |6| = 3, (3) = J.
Q Решение:
|с| = V? = у/(За-4b)2 = \/эй2 — 24й6 + 1662 =
= ^9-4- 24-2-3-+16-9 = v/108 = 6а/3. •
5. Если векторы а и Ь (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если а ± Ь, то ab = 0. Справедливо и обратное утверждение: если ab = 0 и а 0 6, то а ± Ь.
□ Так как (р = (а.Ь) = то cosy: = cos^ = 0. Следовательно, а • Ь — |й| • |6| - 0 = 0. Если же а - Ь = 0 и |й| ^0, |Б| 0, то со8(й, 6) = 0.
Отсюда у? = (й, Ь) = 90°, т. е. й ± Ь. В частности:
г • j'• = j • к = к • г = 0.
48
6.3. Выражение скалярного произведения через координаты
Пусть заданы два вектора
а = ахг + ayj + azk и b = bxi + byj + bzk.
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, к:
a-b = (ахг 4- ayj + azk) (bxi + byj + bzk) =
— axbxii 4“ axbyij 4- axbzik 4-
4- aybxji 4- aybyjj 4- aybzjk 4-
4- azbxki 4- azbykj 4- azbzkk =
= axbx 4- 0 4- 0 4- 0 4- ttyby 4-04-04-04- <izbz,
t. e.
a ~ b — ttxbx 4“ by 4“ azbz.
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
Пример 6.2. Доказать, что диагонали четырехугольника, заданного координатами вершин Л(—4;— 4; 4), В(—3; 2; 2), (7(2; 5; 1), 0(3; —2; 2), взаимно перпендикулярны.
Q Решение: Составим вектора АС и BD, лежащие на диагоналях данного четырехугольника. Имеем: АС — (6; 9; —3) и BD = (6; —4; 0). Найдем скалярное произведение этих векторов:
АС • BD = 36 - 36 - 0 = 0.
Отсюда следует, что AC ± BD. Диагонали четырехугольника ABCD взаимно перпендикулярны. •
49
6.4. Некоторые приложения скалярного произведения
Угол между векторами
Определение угла ср между ненулевыми векторами а = (ax;ay',az) и b = (bx;by;bz):
а' b Qxbx 4- (^1/Ьу + azbz
cos ср = ———, т. е. costp = —. - — .- .. =.
1°1 ' Н ^+а2+о2 . ^+6^4-62
Отсюда следует условие перпендикулярности ненулевых векторов а и Ь: _
a -1- b 4 z ехЬх Qyby + azbz — 0.
Проекция вектора на заданное направление
Нахождение проекции вектора а на направление, заданное вектором 6, может осуществляться по формуле
______ cl * b р =- а' Ь\ _ dxbx dyby 4~ dzbz прьа = “^Г (праЬ = ЪГ)’ т-е- пРь°=--------------/---:
V ’ Jb2x + b2y+b2z
у У z
Работа постоянной силы
Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием постоянной силы F, образующей угол ср с перемещением АВ = S (см. рис. 15).
Из физики известно, что работа силы F при перемещении S равна
р A — F-S- cos ср т. е. А = F • S.
; Таким образом, работа постоянной силы
/У при прямолинейном перемещении ее точ-
ки приложения равна скалярному произ-Рис. 15 ведению вектора силы на вектор переме-
щения.
Пример 6.3. Вычислить работу, произведенную силой F=(3; 2; 4), если точка ее приложения перемещается прямолинейно из положения Л (2; 4; б) в положение 23(4; 2; 7). Под каким углом к АВ направлена сила F?
Q Решение: Находим S = АВ = (2, —2,1). Стало быть, A=FS = 3- 2 + 2- (—2) + 4-1 = 6 (ед. работы).
F • S
Угол ср между F и S находим по формуле cos</? = т. е.
l-f’l ’ Pl
6 6 2 2
V9 + 4 + 16 V4 + 4 + 1 а/29-3 а/29 а/29
50
§7. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА
7.1. Определение векторного произведения
Три некомплаиарных вектора й, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору Ъ виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).
правая тройка,
левая тройка
Рис. 16
Векторным произведением вектора а на вектор Ъ называется вектор с, который:
1) перпендикулярен векторам а и Ь, т. е. с ± а и с ± Ь;
2) имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е.
|с| = |й| • |6| sin у, где <р = (а, 6);
3) векторы а, b и с образуют правую тройку.
Рис. 18
Рис. 17
Векторное произведение обозначается а х b или [й, 6].
Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами г, j и к (см. рис. 18):
г х j = к, j х к = г, к х i = j.
Докажем, например, что г х j = к.
51
□ 1) к ± i, к _L J;
2) |fc| = 1, но |i x j| = |i| • |J| • sin90° = 1;
3) векторы i, j и к образуют правую тройку (см. рис. 16).
7.2. Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак, т. е. а х Ъ = —(Ь х а) (см. рис. 19).
□ Векторы а х Ь и b х а коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки a, b, а х Ъ и а,Ь,Ь х а противоположной ориентации). Стало быть, а х Ь = —(Ь х а).
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. А(й х 6) = = (Ай) х b = а х (А6).
□ Пусть А > 0. Вектор А(йх Ь) перпендикулярен векторам а и Ь. Вектор (Ай) х Ь также перпендикулярен векторам й и Ь (векторы й, Ай лежат в одной плоскости). Значит, векторы А(й х Ь) и (Ай) х Ь коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:
|А(а х Ь)| = А|а х Ь| = А|а| • |6| sin(a,b)
и _ _ —
|(Ай) х &| = |Ай| |Ь| • sin(Aa,Ь) = А|й| • |b|sin(a,Ь).
Поэтому А(й х Ь) = Ай х Ь. Аналогично доказывается при А < 0.
3. Два ненулевых вектора а и Ь коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а || b <==> й х Ь = 0.
□ Если а || Ь, то угол между ними равен 0° или 180°. Но тогда |й х 6| = = |й| • |6| - 8ш(й, Ь) — 0. Значит, й х Ъ = 0.
Если же й х Ь = 0, то |й| • |Ь| sin = 0. Но тогда </> = 0° или ip = 180°, т. е. а || Ь.
|@| В частности, ixi = jxj = kxk — 0.
4. Векторное произведение обладает распределительным свойством: _ _
(а + Ь) х с = а х с + b х с.
Примем без доказательства.
52
7.3. Выражение векторного произведения через координаты
Мы будем использовать таблицу векторного произведения векторов г, j и к'.
г 3 к
i 0 к 1 ^.1
3 -к 0 г
к ] —1 0
Чтобы не ошибиться со знаком, удобно пользоваться схемой:
если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».
Пусть заданы два вектора а = ахг + ayj 4- azk и b = bxi 4- byj 4- bzк. Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
а х b = (ахг 4- ayj 4- azk) х (Ьхг 4- byj 4- bzk) =
= axbx(i х г) 4- axby(i х j) 4- axbz(i x к) 4- aybx(j x i) 4 ayby(j x j)+
4- aybz(j x fc) 4- azbx(k x i) 4- azby(k x j) 4- azbz(k xk) =
= 0 4- axbyk - axbzj - aybxk 4-0 4- aybzi 4- azbxj - azbyi 4- 0 =
— (aybz c^zby'j'i ^fixbz a>zbx)j 4“ {,o>xby aybx)k —
t. e.
Полученную формулу можно записать еще короче:
3 к
ау az by bz
так как правая часть равенства (7.1) соответствует разложению определителя третьего порядка по элементам первой строки. Равенство (7.2) легко запоминается.
53
7.4. Некоторые приложения векторного произведения
Установление коллинеарности векторов
Если а || Ь, то а х Ь = 0 (и наоборот), т. е.
а х b =
i
О>х
Ьх
3 ау Ъу
к
Q>z bz
&х
О/у &Z
by bz
= О
<=> а || b.
Нахождение площади параллелограмма и
треугольника
Согласно определению векторного произведения векторов а и b |й х 6| = |й| |6| sin 99, т. е. Snap = |б х 6|. И, значит, = ^|й х Ь|.
Определение момента силы относительно точки
Пусть в точке А приложена сила F = АВ и пусть О — некоторая точка пространства (см. рис. 20).
Из физики известно, что моментом силы F относительно точки О называется вектор М, который проходит через точку О и:
1) перпендикулярен плоскости, проходящей через точки О, А, В;
2) численно равен произведению силы на плечо
\М\ = |F| • ON = |F| • |f| • sinV = |F| |63|sin(K33);
3) образует правую тройку с векторами О А и АВ.
Стало быть, М = О А х F.
Нахождение линейной скорости вращения
Скорость v точки М твердого тела, вращающегося с угловой скоростью ш вокруг неподвижной оси, определяется формулой Эйлера й = иЗ х г, где г = ОМ, где О — некоторая неподвижная точка оси (см. рис. 21).
54
§8. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
8.1. Определение смешанного произведения, его геометрический смысл
Рассмотрим произведение векторов а, b и с, составленное следующим образом: (о х 6) • с. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.
Выясним геометрический смысл выражения (ах Б)-с. Построим параллелепипед, ребрами которого являются векторы а,Ъ,стл вектор d = а х b (см. рис. 22).
Имеем: (а х Ь) • с = d - с = |d| • пр^с, |d| = |а х Б| = S, где S — площадь параллелограмма, построенного на векторах а и Б, пр^с = Н для правой тройки векторов и пр^с — —Н для левой, где Н — высота параллелепипеда. Получаем: (а х Б) • с = S - (±Н), т. е. (а х Б) • ё = = ±У, где V — объем параллелепипеда, образованного векторами а, Ъ и с.
Таким образом, смешанное произведение трех векторов равно объ
ему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
8.2. Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х Ь) - с = (Ь х с) • а = (с х а) • Ь.
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. (а х Ь) с = а - (Ь х с).
Действительно, (а х Ь) - с = ±У и а • (Ь х с) = (Б х с) - а = ±Vr. Знак в правой части этих равенств берем один и тот же, так как тройки векторов а,Ь,с и Б, с, а — одной ориентации.
55
Следовательно, (б х Ь) • с = а(Ь х с). Это позволяет записывать смешанное произведение векторов (б х Б) с в виде abc без знаков векторного, скалярного умножения.
3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. abc — —acb, abc = — bac, abc = = —cba.
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4. Смешанное произведение ненулевых векторов б, b и с равно нулю тогда и только тогда, когда они компланарны.
Q Если abc = 0, то б, Б, с — компланарны.
Допустим, что это не так. Можно было бы построить параллелепипед с объемом V 0. Но так как abc — ±Vr, то получили бы, что abc 0. Это противоречит условию: abc = 0.
Обратно, пусть векторы б, Ь, с — компланарны. Тогда вектор d = = б х Б будет перпендикулярен плоскости, в которой лежат векторы б, Б, с, и, следовательно, d _1_ с. Поэтому d • с = 0, т. е. бБс = 0. И
8.3. Выражение смешанного произведения через координаты
Пусть заданы векторы б = axi + ayj + azk, Ь = bxi + byj + bzk, с = схг + cyj + czk. Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
(а х Ь)с =
ау az b& by bz
(cxi 4- Cyj +czk) =
Полученную формулу можно записать короче:
abc =
ау Ъу Су
CLZ bz cz
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки.
Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
56
8.4. Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов а, b и с основано на следующих соображениях. Если abc > 0, то й, Ь,с — правая тройка; если abc < 0, то а, Ь, с - левая тройка.
Установление компланарности векторов
Векторы а, Ь и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю (й О, b ф 0, с 0):
abc = 0
ay az bx by bz сх Су cz
= 0 <=> векторы а, Ь, с компланарны.
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах й, b и с вычисляется как V — |й6с|, а объем треугольной пирамиды, построенной на этих же векторах, равен V = 1 |й6с|.
Пример 8.1. Вершинами пирамиды служат точки Л(1;2; 3), В(0; —1; 1), (7(2; 5; 2) и D(3; 0; —2). Найти объем пирамиды.
Q Решение: Находим векторы а, Ь, с:
а = АВ = (—1;—3;—2), Ь = ЛС = (1; 3;-1), с = AD = (2; -2; -5).
Находим abc:
-3
3
—2
—2
-1
-5
= —1-(—17) + 3-(—3) —2-(—8) = 17-9+16 = 24.
Следовательно, V = i • 24 = 4.
Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Лекции 7-9 I
§ 9. СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
9.1. Основные понятия
|ф! Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная (декартова) система координат.
Прямоугольная система координат за-
дается двумя взаимно перпендикулярными прямыми — осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей. Эти оси называют осями координат, точку их пересечения О — началом координат. Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу) (рис. 23).
На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат - вертикально и направленной снизу вверх. Оси координат делят плоскость на четыре области — четверти (или квадранты).
Единичные векторы осей обозначают i и j (|г| = |j| = 1, г _L j).
Систему координат обозначают Оху (или Oij), а плоскость, в которой расположена система координат, называют координатной плос
костью.
Рассмотрим произвольную точку М плоскости Оху. Вектор ОМ называется радиусом-вектором точки М.
|,'у] Координатами точки М в системе координат Оху (Oij) называются координаты радиуса-вектора ОМ. Если ОМ — (х\у), то координаты точки М записывают так: М(х\ у), число х называется абсциссой точки М, у — ординатой точки М.
Эти два числа хну полностью определяют положение точки на плоскости, а именно: каждой паре чисел ж и у соответствует единственная точка М плоскости, и наоборот.
58
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Ор, называемым полярной осью, и еди-
ничным' вектором ё того же направления, что и луч Ор.
Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием г от полюса О и углом <р, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24).
Числа г и <р называются полярными координатами точки М, пишут М(г;р), при этом г называют полярным радиусом, р — полярным углом.
Для получения всех точек плоскости достаточно полярный угол р ограничить промежутком (—тг;тг] (или 0 р < 2тг), а полярный радиус — [0;оо). В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел г и р, и обратно.
Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось — с положительной полуосью Ох. Пусть х и у — прямоугольные координаты точки М, а г и р — ее полярные координаты.
Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:
х = г • cos р, у — г - sin р.
Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами:
г = у/.т2 + у2,
W =
Определяя величину р, следует установить (по знакам х и у) четверть, в которой лежит искомый угол, и учитывать, что —л < р ^.тг.
59
Пример 9.1. Дана точка М(—1; —л/З). Найти полярные координаты точки М.
Q Решение: Находим г и </?:
_____ — v3 г-
т = д/3 + 1 = 2, tg <р =--— — v3.
Отсюда ip — 5 + mi, n(EZ. Но так как точка М лежит в 3-й четверти, О
то п = — 1 и^ = | - 7г = — Итак, полярные координаты точки М О о
есть г = 2, <р = — Д?, т. е. м(2; —. •
о \ о /
9.2. Основные приложения метода координат на плоскости
Расстояние между двумя точками
Требуется найти расстояние d между точками Л(.Т1; «д) и В(х2', Уъ) плоскости Оху.
Q Решение: Искомое расстояние d равно длине вектора АВ = = (х,2 - Ж];«/2 ~yi), т. е.
d = |АВ| = у/(ж2 - Xi)2 + (у2 ~У1)2- •
Деление отрезка в данном отношении
Требуется разделить отрезок АВ, соединяющий точки H(rci;j/i) и В(хг;у2) в заданном отношении А > 0, т. е. найти координаты точки М(х;у) отрезка АВ такой, что = А (см. рис. 26).
Q Решение: Введем в рассмотрение векторы AM и МВ. Точка М делит отрезок АВ в отношении А, если
AM = А МВ.
(9-1)
Но AM = (х — xi; у — j/i), т. е. AM — (х — xi)i + («/ — yi)j и МВ = = (ж2 — х-,у2 - у), т. е. МВ = (ж2 — x)i + («д - y)j- Уравнение (9.1) принимает вид
(ж - Ж1)г + (у - yi)j = А(ж2 - ж)г + А(«/2 - y)j-
Учитывая, что равные векторы имеют равные координаты, получаем
Xi + Ажг
т. е. ж = ———;—
X — Х1 = А.Т2 — Аж,
(9-2)
i i'
60
и
\ X + ^У‘2 О4
У - У1 = Лу-2 ~ лу, Т. е. у= -. (9-3)
Формулы (9.2) и (9.3) называются формулами деления отрезка в данном отношении. В частности, при А = 1, т. е. если AM = МВ, то они примут вид х = у = 2 • В этом случае точка М(х;у)
является серединой отрезка АВ. •
Замечание: Если А = 0, то это означает, что точки Л и М совпадают, если А < 0, то точка М лежит вне отрезка АВ — говорят, что точка М делит отрезок АВ внешним образом (А — 1, т. к. в противном случае — — 1, т. е. AM + МВ = 0, т. е. АВ = 0).
Площадь треугольника
Требуется найти площадь треугольника АВС с вершинами А(хг;уг), В(х2-,у2), С{х3;у3).
Q Решение: Опустим из вершин А, В, С перпендикуляры ААг, ВВ\, C’C'i на ось Ох (см. рис. 27). Очевидно, что
8АВС = SaA^BiB + Sb,BCCx — Sa,ACC,-
Поэтому
е У1 + У2 , 4 , У2 + УЗ . 4 УЛ + Уз
8АВС = -------(-Т2 - Ж1) + ----(х3 - Х2)--------
= |(Ж2У1 - ЯТ1«/1 + х2у2 - Х1У2 + х3у2 ~ Х2у2 + Х3у3~
~ х2у3 - ХзУ1 + Х1У1 - х3у3 + Ж1Уз) =
= |(жз(з/2 - У1) - XI (у2 - У1) - Ж2(?/з - У1) + хг (у3 - зл)) =
= |((«/2 - У1)(жз - ®1) - (?/3 - г/1)(Ж2 - -Т1)) = т. е.
1 ятз ~
2 Уз - У1
ж2 - Ж1
У2 - Уг
s _ 1 Х3 - X!
2 уз -уг
Х2 - «1
У2 - У1
Замечание: Если при вычислении площади треугольника получим S = 0, то это означает, что точки А, В, С лежат на одной прямой, если же получим отрицательное число, то следует взять его модуль.
9.3. Преобразование системы координат
Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.
61
Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.
Параллельный перенос осей координат
Пусть на плоскости задана прямоугольная система координат Оху. Под параллельным переносом осей координат понимают переход от системы координат Оху к новой системе Oi xi yi, при котором меняется положение начала координат, а направление осей и масштаб остаются неизменными.
Пусть начало новой системы координат точка О, имеет координаты (хо',Уо) в старой системе координат Оху, т. е. Oi(.to;?/o)- Обозначим координаты произвольной точки М плоскости в системе Оху через (х;у), а в новой системе Oixpyi через (т';г/) (см. рис. 28).
Рассмотрим векторы
ОМ — xi 4- yj, OOi=x0i+y0j, OjM = x'i + y'j.
Так как ОМ = OOi + OiM, то xi + yj = xoi + yoj + x'i + y'j, t. e.
x • l + у j - (.r0 + x') • г + (y0 + y') j.
Следовательно,
X = .To + .t', У = Уо + У'-
Полученные формулы позволяют находить старые координаты х и у по известным новым х' и у' и наоборот.
Поворот осей координат
Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.
62
Пусть новая система Oixpyi получена поворотом системы Оху на угол а (см. рис. 29).
Пусть М — произвольная точка плоскости, (ж; у) — ее координаты в старой системе и (ж';«/) — в новой системе.
Введем две полярные системы координат с общим полюсом О и полярными осями Ох и ОЖ1 (масштаб одинаков). Полярный радиус г в обеих системах одинаков, а полярные углы соответственно равны а + у? и у?, где у? — полярный угол в новой полярной системе.
По формулам перехода от полярных координат к прямоугольным имеем
{ж = т - cos(a + у>), ( ж = г cosy? • cos а — г sin у? • sin а,
у = г - sin(a + ip), = г cos ср • sin а 4-т sin ср - cos а.
Но г cos у? — х' и т sin у? = у'. Поэтому
ж = ж' cos а — у' sin а, у = ж' sin а + у' cos а.
|ф| Полученные формулы называются формулами поворота осей.
Они позволяют определять старые координаты (ж; у) произвольной точки М через новые координаты (ж'; у') этой же точки М, и наоборот.
Рис. 29
Рис. 30
Если новая система координат О1Ж1Х/1 получена из старой Оху путем параллельного переноса осей координат и последующим поворотом осей на угол а (см. рис. 30), то путем введения вспомогательной системы 01 ху легко получить формулы
ж = ж' - cosq — у' sin си + ж0, у = х' • sin а + у' • cos а + у0,
выражающие старые координаты ж и у произвольной точки через ее новые координаты ж' и у'.
63
§10. ЛИНИИ НА ПЛОСКОСТИ
10.1. Основные понятия
Линия на плоскости часто задается как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, окружность радиуса R есть множество всех точек плоскости, удаленных на расстояние R от некоторой фиксированной точки О (центра окружности).
Введение на плоскости системы координат позволяет определять положение точки плоскости заданием двух чисел — ее координат, а положение линии на плоскости определять с помощью уравнения (т. е. равенства, связывающего координаты точек линии).
Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x; у) = 0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Переменные х и у в уравнении линии называются текущими координатами точек линии.
Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием его уравнения.
Так, для того чтобы установить лежит ли точка А(а:о; уо) на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки А уравнению этой линии в выбранной системе координат.
Пример 10.1. Лежат ли точки А'(—2; 1) и L(l; 1) на линии 2.т 4- у 4- 3 = О?
Q Решение: Подставив в уравнение вместо х и у координаты точки К, получим 2 • (—2) 4-1 4- 3 = 0. Следовательно, точка К лежит на данной линии. Точка L не лежит на данной линии, т. к. 2 • 14-1 4- 3 / 0. •
Задача о нахождении точек пересечения двух линий, заданных уравнениями Fj(x; у) = 0 и F2(x-,y) = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к решению системы двух уравнений с двумя неизвестными:
ГFA (ж; у) = 0,
(F2(.t;«/) = 0.
Если эта система не имеет действительных решений, то линии не пересекаются.
Аналогичным образом вводится понятие уравнения линии в полярной системе координат.
64
Уравнение F(r-,<p) = 0 называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.
Линию на плоскости можно задать при помощи двух уравнений:
х = x(t), у = i/W,
(10.1)
где х и у — координаты произвольной точки М(ж; у), лежащей на данной линии, a t — переменная, называемая параметром-, параметр t определяет положение точки (ж; у) на плоскости.
Например, если х = t + 1, у = t2, то значению параметра t = 2 соответствует на плоскости точка (3; 4), т. к. х = 2 + 1 = 3, у = 22 = 4.
Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется параметрическим, а уравнения (10.1) — параметрическими уравнениями линии.
Чтобы перейти от параметрических уравнений линии к уравнению
вида F(.t; у) = 0, надо каким-либо способом из двух уравнений исклю-
{'£ —
’ путем подстанов-У =t,
ки t = х во второе уравнение, легко получить уравнение у = х2; или у — ж2 = 0, т. е. вида F(.r;y) — 0. Однако, заметим, такой переход не
всегда целесообразен и не всегда возможен.
Линию на плоскости можно задать векторным уравнением f = f(t), где t — скалярный переменный параметр. Каждому значению io соответствует определенный вектор го = г (to) плоскости. При изменении параметра t конец вектора г — f(t) опишет некоторую линию (см. рис. 31).
Векторному уравнению линии г = f(t) в системе координат Оху соответствуют
два скалярных уравнения (10.1), т. е. уравнения проекций на оси ко
ординат векторного уравнения линии есть ее параметрические уравне
ния.
Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениям,и движения, а линия — траекторией точки, параметр t при этом есть время.
Итак, всякой линии на плоскости соответствует некоторое уравнение вида F(.r; у) = 0.
3 Конспект лекций по высшей математике. Полный курс
65
Всякому уравнению вида F(.r; у) = 0 соответствует, вообще говоря, некоторая линия, свойства которой определяются данным уравнением (выражение «вообще говоря» означает, что сказанное допускает исключения. Так, уравнению (.т — 2)2 + (у — З)2 — 0 соответствует не линия, а точка (2; 3); уравнению х2 4- у2 + 5 = 0 на плоскости не соответствует никакой геометрический образ).
В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти ее уравнение; вторая: зная уравнение кривой, изучить ее форму и свойства.
На рисунках 32-40 приведены примеры некоторых кривых и указаны их уравнения.
Рис. 34. Трехлепестковая роза
В полярных координатах ее уравнение имеет вид г — а • cos.3^5, где а > 0.
Рис. 33. Лемниската Бернулли
Уравнение в прямоугольных координатах: (а2 + у2)2 — а2(х2 — у2) = 0, а > 0; в полярных координатах: г ~ а Vcos2^.
66
Уравнение в полярных координатах имеет вид г = b + a cos ip.
Рис. 36. Полукубическая парабола
Уравнение кривой у2 — х3 или
Рис. 37. Астроида
Уравнение в прямоугольных координатах: хз +уз = аз; параметрические уравнения:
х = а • cos31, у = а sin3 t.
Рис. 38. Кардиоида
Уравнение в полярных координатах имеет вид г = а(1 + cos <р), где а > 0. Кардиоида — частный случай улитки Паскаля (а = Ь).
Р
Рис. 39. Спираль Архимеда Уравнение кривой в полярных координатах г = ар, где а > 0 — постоянное.
67
2тга х
Рис. 40. Циклоида
х = a(t — sint),
; ' где а > 0. Ци-
у = а(1 — cost),
Параметрические уравнения циклоиды имеют вид
клоида — это кривая, которую описывает фиксированная точка окружности, катящаяся без скольжения по неподвижной прямой.
10.2. Уравнения прямой на плоскости
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.
Уравнение прямой с угловым коэффициентом
Пусть на плоскости Оху задана произвольная прямая, не параллельная оси Оу. Ее положение вполне определяется ординатой Ь точки 7V(0; Ь) пересечения с осью Оу (см. рис. 41).
и углом а между осью Ох и прямой
Под углом а (0 а < я) наклона прямой понимается наименьший угол, на который нужно повернуть вокруг точки пересечения прямой и оси Ох против часовой стрелки ось Ох до ее совпадения с прямой.
Возьмем на прямой произвольную , точку М(х\у) (см. рис. 41). Проведем ,i через точку N ось Nx', параллельную ' оси Ох и одинаково с ней направлен- 1
ную. Угол между осью Nх' и прямой равен а. В системе Nx'y точка М имеет координаты х и у — Ь. Из определения тангенса угла следует равенство tga = V ~, т. е. у = tga-ж + Ь. Введем обозначение tga = к, получаем уравнение
у = кх + b,
(Ю-2) которому удовлетворяют координаты любой точки М(х-,у) прямой. Можно убедиться, что координаты любой точки Р(х;у), лежащей вне данной прямой, уравнению (10.2) не удовлетворяют.
Число к = tga называется угловым коэффициентом прямой, а уравнение (10.2) — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то Ь — 0 и, следовательно, уравнение этой прямой будет иметь вид у — кх.
68
Если прямая параллельна оси Ох, то а = 0, следовательно, к = = tga = 0 и уравнение (10.2) примет вид у = Ь.
Если прямая параллельна оси Оу, то a = ту, уравнение (10.2) теряет смысл, т. к. для нее угловой коэффициент к — tga = tg^ не существует. В этом случае уравнение прямой будет иметь вид
х — а, (10.3)
где а — абсцисса точки пересечения прямой с осью Ох. Отметим, что уравнения (10.2) и (10.3) есть уравнения первой степени.
Общее уравнение прямой
Рассмотрим уравнение первой степени относительно х и у в общем виде
Ах + By + С = 0, (10.4)
где А, В, С — произвольные числа, причем Л и В не равны нулю одновременно.
Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая.
Если В = 0, то уравнение (10.4) имеет вид Ах + С = 0, причем
С1
А 0, т. е. х = — Ч-. Это есть уравнение прямой, параллельной оси Оу и проходящей через точку ^;0).
л
Если В ,4 0, то из уравнения (10.4) получаем у — — — jj. Это
есть уравнение прямой с угловым коэффициентом к = tga = —
Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.
Некоторые частные случаи общего уравнения прямой:
С1
1) если А = 0, то уравнение приводится к виду у — — Это есть уравнение прямой, параллельной оси Ох-,
2) если В = 0, то прямая параллельна оси Оу,
3) если С = 0, то получаем Ах+Ву = 0. Уравнению удовлетворяют координаты точки 0(0; 0), прямая проходит через начало координат.
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку М(х0;у0) и ее направление характеризуется угловым коэффициентом к. Уравнение этой прямой можно записать в виде у = кх + Ъ, где Ь — пока неизвестная величина. Так как прямая проходит через точку М(ху,уо), то координаты точки удовлетворяют уравнению прямой: </0 = кх0 + Ъ. Отсюда b = уо — кх0.
69
Подставляя значение b в уравнение у = кх + Ь, получим искомое уравнение прямой у = кх + у о — кх0, т. е.
у - Уо = к(х - я0).
(10.5)
Уравнение (10.5) с различными значениями к называют также уравнениями пучка прямых с центром в точке Л7(.т(|; у(|). Из этого пучка нельзя определить лишь прямую, параллельную оси Оу.
Уравнение прямой, проходящей через две точки
Пусть прямая проходит через точки M\(xi',yi) и M^x^yz). Уравнение прямой, проходящей через точку М\, имеет вид
у — у у = к(х — Xi),
(10.6)
где к — пока неизвестный коэффициент.
Так как прямая проходит через точку Mz^xzjyz), то координаты этой точки должны удовлетворять уравнению (10.6): уъ~У1 — k(x2—Xi). Отсюда находим к = Подставляя найденное значение к в урав-
нение (10.6), получим уравнение прямой, проходящей через точки Мг и М2:
(Ю.7)
У ~У1 _ Ж - Xj
У2 - У1 Х2 - Хг
Предполагается, что в этом уравнении xi / Х2, yi -^yz-
Если Х2 = то прямая, проходящая через точки M\(xy,yi) и М2{х2',У2), параллельна оси ординат. Ее уравнение имеет вид х = хг.
Если у2 = у г, то уравнение прямой может быть записано в виде у = У1, прямая МгМ2 параллельна оси абсцисс.
Уравнение прямой в отрезках
Пусть прямая пересекает ось Ох в точке Л1)(о;0), а ось Оу — в точке Л/2(0; 6) (см. рис. 42). В этом случае уравнение (10.7) примет вид
у — 0 _ х — а 6 — 0 0 — а’
т. е.
Это уравнение называется уравнением прямой в отрезках, так как числа а и b указывают, какие отрезки отсекает прямая на осях координат.
70
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем уравнение прямой, проходящей через заданную точку Мо(хо',Уо) перпендикулярно данному ненулевому вектору п = (А-В).
Возьмем на прямой произвольную точку М(х;у) и рассмотрим вектор М0М = (х — ха\у — у0) (см. рис. 43). Поскольку векторы п и М0М перпендикулярны, то их скалярное произведение равно нулю: п MqM = 0, то есть
А(х - .т0) + В (у - у0) = 0.
(10.8)
Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Вектор п = (Л; В), перпендикулярный прямой, называется нормальным вектором этой прямой.
Уравнение (10.8) можно переписать в виде
Ах + By + С = 0,
(10.9)
где Ан В — координаты нормального вектора, С = — Ах0 - Ву0 — свободный член. Уравнение (10.9) есть общее уравнение прямой (см. (10.4)).
Рис. 44
Полярное уравнение прямой
Найдем уравнение прямой в полярных координатах. Ее положение можно определить, указав расстояние р от полюса О до данной прямой и угол а между полярной осью ОР и осью I, проходящей через полюс О перпендикулярно данной прямой (см. рис. 44).
Для любой точки М (г; ip) на данной прямой имеем:
прг ОМ = р.
71
С другой стороны,
пр; ОМ = |ОМ| cos(a — ip) = г cos(<£ — а).
Следовательно, ----------------
r cos(</? — а) = р.
(10.10)
Полученное уравнение (10.10) и есть уравнение прямой в полярных координатах.
Нормальное уравнение прямой
Пусть прямая определяется заданием р и а (см. рис. 45). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взяв О за полюс и Ох за полярную ось. Уравнение прямой можно
записать в виде
г cos(</> — a) — р = 0, т. е. г • cos</?cosa + г sin^sina — р = 0.
Но, в силу формул, связывающих прямоугольные и полярные координаты, имеем: г cos<£> = .т, rsin</> = у. Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид
х cosa + у sina — р = 0.
(10.11)
Уравнение (10.11) называется нормальным уравнением прямой.
Покажем, как привести уравнение (10.4) прямой к виду (10.11).
Умножим все члены уравнения (10.4) на некоторый множитель А 0. Получим ХАх + ХВу + ХС = 0. Это уравнение должно обратиться в уравнение (10.11). Следовательно, должны выполняться равенства: ХА = cosa, ХВ = sina, АС = — р. Из первых двух
равенств находим
А2А? + А2В2 = cos2 a + sin2 а, т. e. A = ±—7 a/a2 + B2
Множитель А называется нормирующим множителем. Согласно третьему равенству АС = — р знак нормирующего множителя противоположен знаку свободного члена С общего уравнения прямой.
Пример 10.2. Привести уравнение — З.т + 4у + 15 = 0 к нормальному виду.
Q Решение: Находим нормирующий множитель А = —~
= — 1. Умножая данное уравнение на А, получим искомое нормальное О
уравнение прямой: ^х — ^у — 3 = 0. •
О о
72
10.3. Прямая линия на плоскости. Основные задачи
Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
Пусть прямые Li и заданы уравнениями с угловыми коэффициентами у = к]Х + by и у = fc2.r + Ь2 (см. рис. 46).
Требуетсд найти угол ip, на который
надо повернуть в положительном направлении прямую L\ вокруг точки их пересечения до совпадения с прямой Т2.
Q Решение: Имеем а2 = V + «1 (теорема о внешнем угле треугольника) или ip = = а2 — «1. Если <р А , то
te^=te(O3-Q,) =
1 + tg oj tg а2
Но tgaj = fci, tga2 = к.2, поэтому
(10.12)
откуда легко получим величину искомого угла.
Если требуется вычислить острый угол между прямыми, не учитывая, какая прямая является первой, какая — второй, то правая часть формулы (10.12) берется по модулю, т. е. tg<р = L I-
|@| Если прямые Ьг и Т2 параллельны, то tp = 0 и tg ip = 0. Из формулы (10.12) следует fc2 — кг = 0, т. е. fc2 = ki. И обратно, если прямые Li и Т2 таковы, что fci = fc2, то tgy? = 0, т. е. прямые параллельны. Следовательно, условием параллельности двух прямых является равенство их угловых коэффициентов: fci = fc2.
Если прямые Iq и Т2 перпендикулярны, то р = 5-. Следовательно, ctg</9 = + ^1^2 = 0. Отсюда 1 + ki fc2 = 0, т. е. кА к? = —1 (или к,2 = Справедливо и обратное утверждение. Таким образом, условием перпендикулярности прямых является равенство к\ -к? = —1.
Расстояние от точки до прямой
Пусть заданы прямая L уравнением Ах + By + С = 0 и точка Мо(х0',уо) (см. рис. 47). Требуется найти расстояние от точки Мо до прямой L.
73
Q Решение: Расстояние d от точки Мо др прямой L равно модулю проекции вектора М^Мц, где Mi(xi;yi) — произвольная точка прямой В,
С = — Axi — Byi. Поэтому
на направление нормального вектора п = (Л; В). Следовательно,
d - | npjjMiMol =
Mj Мо п |й|
I(.т0 - Ж!)Л + (j/p — 7/г)В|
у/А2 + В2
|Лж0 + Ву0 - Axi - Byi\
у/а2 + в2
Так как точка Mi(.ti;«/i) принадлежит прямой L, то Л.Т1 + Вух + С = 0, т. е.
_ |Лж0 + Ву0 + С| а/Л2 + В2
(10.13)
что и требовалось получить.
Пример 10.3. Найти расстояние от точки Мо(2; —1) до прямой Зх + Ау — 22 = 0.
Q Решение: По формуле (10.13) получаем
_ |3 • 2 + 4 • (—1) — 22| _ 20 _ 4 ф
( ~ 79+16 5
§ 11. ЛИНИИ ВТОРОГО ПОРЯДКА НА плоскости 11.1. Основные понятия
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат
Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0. (11.1)
Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел Л, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Ниже будет установлено, что уравнение (11-1) определяет на плоскости окружность, эллипс, гиперболу или параболу. Прежде, чем переходить к этому утверждению, изучим свойства перечисленных кривых.
74
11.2. Окружность
Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R с центром в точке Мо называется множество всех точек М плоскости, удовлетворяющих условию MqM = R. Пусть точка М(| в прямоугольной системе координат Оху имеет координаты хо,уо, а М(х-,у) — произвольная точка окружности (см. рис. 48).
Тогда из условия MqM = R получаем уравнение
V(ж - х0)2 + (у - ?/о)2 = R,
то есть
(.Т-Хо)2 + (у~уо)2 =R2. (11.2)
Уравнению (11.2) удовлетворяют координаты любой точки М(ж; у) данной окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности.
Уравнение (11-2) называется каноническим уравнением окружно
сти.
В частности, полагая х0 = 0 и у0 = 0, получим уравнение окружности с центром в начале координат х2 + у2 = R2.
Уравнение окружности (11.2) после несложных преобразований примет вид х2 + у2 — 2жож — 2уоу + Xq + у2} — R? — 0. При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:
1) коэффициенты при ж2 и у2 равны между собой;
2) отсутствует член, содержащий произведение ху текущих координат.
Рассмотрим обратную задачу. Положив в уравнении (11.1) значения В = 0иЛ = С^0, получим
Ат2 + Ay2 + 2Dx + 2Ey + F = 0. (11.3)
Преобразуем это уравнение:
2 о D Е F
х2 + У2 + 2т.т + 2-у + - = 0,
71 ТА /1
т. е.
2 2 2Г» D2 . Е Е2 F
х +у +— х+-+у +2^у+~ + --
D2 Е2 _
А2" ~ Д2 ~ °’
75
т. е.
£\2 A J
(11-4)
Е\2 Е2 D2 F
у Ч-7 — Д7Г Ч-7.Т-т-
А) А2 А2 А
Отсюда следует, что уравнение (11.3) определяет окружность при уело-F
вии “ту Ч- — т- > 0. Ее центр находится в точке А А А радиус ___________
, а
Е2 D2 F
А2 + А2~'А'
R —
тд2 т~\2
Если же “2 + лТ ~ то уравнение (11.3) имеет вид А А А
( D\2 ( Е\2 л
Ст+л) =0-
Ему удовлетворяют координаты единственной точки Oj В
этом случае говорят: «окружность выродилась в точку» (имеет нулевой
радиус).
Если
Е2 . D2 _ F
А2 А? А
< 0, то уравнение (11.4), а следовательно,
и равносильное уравнение (11.3), не определяет никакой линии, так как правая часть уравнения (11-4) отрицательна, а левая часть — не отрицательна (говорят: «окружность мнимая»).
11.3. Эллипс
Каноническое уравнение эллипса
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Рис. 49
чтобы фокусы Fi и Ег лежали дало с серединой отрезка F\F^. координаты: ЕД—с;0) и Еа(с;0)
Обозначим фокусы через Fy и Е, расстояние между ними через 2с, а сумму расстояний от произвольной точки эллипса до фокусов — через 2а (см. рис. 49). По определению 2а > 2с, т. е. а > с.
Для вывода уравнения эллипса выберем систему координат Оху так, на оси Ох, а начало координат совпа-Тогда фокусы будут иметь следующие
76
Пусть М(х:у) — произвольная точка эллипса. Тогда, согласно определению эллипса, МF} + М = 2а, т. е.
\/(ж + с)2 + у2 + \/(ж - с)2 + у2 = 2а. (11.5)
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение (11.5) к более простому виду следующим образом:
у/ (ж + с)2 + у2 = 2а — у/(х — с)2 + у2,
ж2 + 2сж + с2 + у2 = 4а2 — 4а • у/(ж — с)2 + у2 + ж2 — 2сх + с2 + у2, а^/(ж ~ с)2 + У2 = с? — сх, а2х2 — 2а2сх + а2с2 + а2у2 — а4 — 2а2 сх + с2ж2, (а2 - с2)ж2 + а2у2 — а2(а2 - с2).
Так как а > с, то а2 — с2 > 0. Положим
(U-6)
Тогда последнее уравнение примет вид Ь2ж2 + а2у2 — а2Ь2 или
а2 — с2 = Ь2.
— 4-^- = 1 а2 Ь2
(11.7)
g Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса.
Эллипс — кривая второго порядка.
Исследование формы эллипса по его уравнению
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (11.7) содержит ж и у только в четных степенях, поэтому если точка (ж; у) принадлежит эллипсу, то ему также принадлежат точки (ж;—у), (—ж;у), (—х; —у). Отсюда следует, что эллипс Симметричен относительно осей Ох и Оу, а также относительно точки 0(0; 0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат. Положив у = 0, находим две точки Л, (а; 0) и Лг(—а; 0), в которых ось
Ож пересекает эллипс (см. рис. 50). Положив в уравнении (11.7) ж = 0, находим точки пересечения эллипса с осью Оу. Bi(Q;b) и В2(0;— Ь). Точки Л1, А-2, В1; В2 называются вершинами эллипса. Отрезки AjAq и
Bi(0;5)
В2(0; -Ь)
Рис. 50
77
В1В2, а также их длины 2а и 2Ь называются соответственно большой и малой осями эллипса. Числа а и b называются соответственно большой и малой полуосями эллипса.
3. Из уравнения (11-7) следует, что каждое слагаемое в левой части 2 »,2
не превосходит единицы, т. е. имеют место неравенства < 1 и fs- < 1 а о
или —а х а и —Ь у Ь. Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми ж = ±а, у = ±Ь.
- 2 и2
4. В уравнении (11-7) сумма неотрицательных слагаемых ^7 11 ^2 равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если |ж| возрастает, то |у| уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).
Дополнительные сведения об эллипсе
Форма эллипса зависит от отношения . При Ь = а эллипс превращается в окружность, уравнение эллипса (11.7) принимает вид ж2+«/2 = = а2. В качестве характеристики формы эллипса чаще пользуются отношением —. а
Отношение ~ половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой £ («эпсилон»):
с
£ = — а
(И-8)
причем 0 < £ < 1, так как 0 < с < а. С учетом равенства (11-6) формулу (11.8) можно переписать в виде
\/а2 — Ь2 1а2 -Ь2 /~ /Ь\2
е =--------= V-----2— = \ 1 “ ( - ) >
а у а у ^а'
т. е. I-------
£=4/l-f-') и - = \/1 - е2-у \а/ а
Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить £ = 0, то эллипс превращается в окружность.
Пусть М(х;у) — произвольная точка эллипса с фокусами Fj и F2 (см. рис. 51). Длины отрезков FtM = гг и F?M = Г2 называются фокальными радиусами точки М. Очевидно,
Г] + г2 = 2а.
78
Имеют место формулы
ri = а + ех и Г2 = а — ех.
Прямые х = называются директрисами эллипса. Значение директрисы эллипса выявляется следующим утверждением.
Теорема 11.1. Если г — расстояние от произвольной точки эллипса до какого-нибудь фокуса, d — расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение есть постоянная
величина, равная эксцентриситету эллипса: = е.
Из равенства (11.6) следует, что а > Ь. Если же а < Ь, то уравнение (11.7) определяет эллипс, большая ось которого 2Ь лежит на оси Оу, а малая ось 2а — на оси Ох (см. рис. 52). Фокусы такого эллипса находятся в точках Fi(0;c) и Fa(0; — с), где с = л/Ь2 — а2.
11.4. Гипербола
Каноническое уравнение гиперболы
|ф| Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
79
В.
мс
И
н<
и
в
______хтобзначим фокусы через F\ и F-2, расстояние между ними через 2Я а модуль разности расстояний от каждой точки гоперболы до фокуса через 2а. По определению 2а < 2с, т. е. а < с. 1
Для вывода уравнения гиперболы выберем систему координат О.тж так, чтобы фокусы и F2 лежали на оси Ох, а начало координа! совпало с серединой отрезка FjF2 (см. рис. 53). Тогда фокусы буду! иметь координаты Fi(—с;0) и F2(c;0). 1
Пусть М(х‘,у) — произвольная точка гиперболы. Тогда согласи! определению гиперболы | MF) — 7tfF2| = 2a или MF\ —MF2 = ±2a| т. e. \/(x + c)2 + y2 — a/(x — c)2 + y2 — ±2a. После упрощений, было сделано при выводе уравнения эллипса, получим уравнение гиперболы
как эта ка‘аоническоЛ
где
(11.9)1
(11.10)
Гипербола есть линия второго порядка.
Исследование формы гиперболы по ее уравнению
Установим форму гиперболы, пользуясь ее каконическим уравне-5 нием. ।
1. Уравнение (П-9) содержит х и у только в четных степенях. Сле-довательно, гипербола симметрична относительно осей Ох и Оу, j а также относительно точки 0(0; 0), которую называют центром ги- ! перболы. I
2. Найдем точки пересечения гиперболы с осями координат. Поло- I жив у = 0 в уравнении (11.9), находим две точки пересечения гипербо- i лы с осью Ох-. Аг(а;0) и Аг(-а;0). Положив х — 0 в (11.9), получаем | у2 = —F2, чего быть не может. Следовательно, гипербола ось Оу не | пересекает. |
Точки Л|(«;0) и Аг(—а;0) называются вершинами гиперболы, а I отрезок А। Аг = 2а — действительной осью, отрезок OAi = I
= ОА-2 = а — действительно-li полуосью гиперболы. 1
Отрезок Bi В‘2 (В| В-2 = 2Ь), соединяющий точки В\ (0; Ь) и В2(0; -Ь) | называется мнимой осью, число Ъ — мнимой полуосью. Пря- 1 моугольник со сторонами 2а и 2Ь называется основным прямоуголъ- 1 ником гиперболы. 1
3. Из уравнения (11.9) следует, что уменьшаемое не меньше I
2 a l
единицы, т. е. что 1 или |х| а. Это означает, что точки гипербо- 1 a 1
лы расположены справа от прямой х — а (правая ветвь гиперболы) и 1 слева от прямой х = —а (левая ветвь гиперболы). I
80
4. Из уравнения (11.9) гиперболы видно, что когда |ж| возрастает, 2 2
то и |«/| возрастает. Это следует из того, что разность сохраняет постоянное значение, равное единице.
Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 54 (кривая, состоящая из двух неограниченных ветвей).
Асимптоты гиперболы
Прямая L называется асимптотой неограниченной кривой К, если расстояние d от точки М кривой К до этой прямой стремится к нулю при неограниченном удалении точки М вдоль кривой К от начала координат. На рисунке 55 приведена иллюстрация понятия асимптоты: прямая L является асимптотой для кривой К.
2
Покажем, что гипербола ~ р" ~ 1 имеет две асимптоты:
(11.11)
Ь
—х. а
Ъ
У = -а _________
Так как прямые (11.11) и гипербола (11.9) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти.
Возьмем на прямой у — -х точку N имеющей ту же абсциссу х, а
что и точка М(х-, у) на гиперболе у — — а2 (см. рис. 56), и найдем
разность MN между ординатами прямой и ветви гиперболы: MN = —х — ~-\/х2 — а2 — —(х — х2 — а2) = а а а
b (х — \/х2 — а2)(х + у/х2 — a2) _ h а2 _ а ‘ ° а х + у/х2 — а2 х + Vx‘2 — а2
и У =
ab
81
Как видно, по мере возрастания х знаменатель дроби увеличивается; числитель — есть постоянная величина. Стало быть, длина отрезка MN стремится к нулю. Так как MN больше расстояния d от точки М до прямой, то d и подавно стремится к нулю. Итак, прямые у = ±-х
|@] При построении гиперболы (11.9) целесообразно сначала построить основной прямоугольник гиперболы (см. рис. 57), провести прямые, проходящие через противоположные вершины этого прямоуголь-' ника, — асимптоты гиперболы и отметить вершины Aj и А-± гиперболы.
Уравнение равносторонней гиперболы, асимптотами которой служат оси координат
|£| Гипербола (П.9) называется равносторонней, если ее полуоси равны (а = Ь). Ее каноническое уравнение
х2-у2=а2. (11.12)
Асимптоты равносторонней гиперболы имеют уравнения у = хку=-х и, следовательно, являются биссектрисами координатных углов.
Рассмотрим уравнение этой гиперболы в новой системе координат Ох'у' (см. рис. 58), полученной из старой поворотом осей координат
на угол а = —Используем формулы поворота осей координат (их вывод показан на с. 63):
х = х' cos а — у1 sin а, у = х’ sin а + у1 cos а.
Подставляем значения х и у в уравнение (11.12):
где к =
Уравнение равносторонней гиперболы, для которой оси Ох и Оу являются асимптотами, будет иметь вид у =
Дополнительные сведения о гиперболе
Эксцентриситетом гиперболы (11-9) называется отношение расстояния между фокусами к величине действительной оси ги-
перболы, обозначается е:
с
Е = а
Так как для гиперболы с > а, то эксцентриситет гиперболы боль-
ше единицы: е > 1. Эксцентриситет характеризует форму гиперболы.
1,2 2
Действительно, из равенства (11.10) следует, что = % — 1, т. е.
- = у/е2 — 1 и е = -»/1 + (~\
а V \aj
Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение ее полуосей, а значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет равносторонней гиперболы равен д/2. Действи-
тельно,
yj а2 + а2 а
с
Е = ~ а
\/(х- с)2 + у2 для
Фокальные радиусы г\ = \/(х + с)2 + у2 и г2 =
точек правой ветви гиперболы имеют вид r\ = ех + а и г2 = ех — а, а для левой - Г1 = —(ех + а) и г2 = —(ех — а).
Прямые х = ±- называются директрисами гиперболы. Так как
для гиперболы е > 1, то < а. Это значит, что правая директриса расположена между центром и правой вершиной гиперболы, левая —
между центром и левой вершиной.
83
Директрисы гиперболы имеют то же свойство = е, что и директрисы эллипса.
2 2
Кривая, определяемая уравнением — 2L — 1 также есть гипер-Ъ а
бола, действительная ось 2Ь которой расположена на оси Оу, а мнимая ось 2а — на оси Ох. На рисунке 59 она изображена пунктиром.
Рис. 59
2 2 2 2
Очевидно, что гиперболы ~ |5- = 1и|?-^2- = 1 имеют общие асимптоты. Такие гиперболы называются сопряженными.
11.5. Парабола
Каноническое уравнение параболы
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через р (р > 0).
Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директрисой (см. рис. 60). В выбранной системе фокус F имеет координаты а уравнение директрисы имеет вид х = — ё, или х + ё = 0.
£> Li
84
Пусть М(х;у) — произвольная точка параболы. Соединим точку М с F. Проведем отрезок MN перпендикулярно директрисе. Согласно определению параболы MF = MN. По формуле расстояния между двумя точками находим:
JWF = — 2) ^2’ а + f) + ~
Следовательно, .--------------- .-----------
Возведя обе части уравнения в квадрат, получим
х2 -рх + + у2 = х2 + рх +
I у2 = 2рх. | (11.13)
Уравнение (11.13) называется каноническим уравнением параболы. Парабола есть линия второго порядка.
Рис. 61
Рис. 60
Исследование форм параболы по ее уравнению
1. В уравнении (11.13) переменная у входит в четной степени, значит, парабола симметрична относительно оси Ох; ось Ох является осью симметрии параболы.
2. Так как р > 0, то из (11.13) следует, что .г > 0. Следовательно, парабола расположена справа от оси Оу.
3. При х = 0 имеем у — 0. Следовательно, парабола проходит через начало координат.
4. При неограниченном возрастании х модуль у также неограниченно возрастает. Парабола у2 = 2рх имеет вид (форму), изображенный на рисунке 61. Точка 0(0; 0) называется вершиной параболы, отрезок FM = г называется фокальным радиусом точки М.
85
Уравнения у2 = —2рх, х2 = 2ру, х2 = ~2ру (р > 0) также определяют параболы, они изображены на рисунке 62.
Нетрудно показать, что график квадратного трехчлена у = Ах2 + + Вх + С, где А ^4 0, В и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.
11.6. Общее уравнение линий второго порядка
Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям
Найдем сначала уравнение эллипса с центром в точке О1(ж0;?/о)) оси симметрии которого параллельны координатным осям Ох и Оу и полуоси соответственно равны а и Ь. Поместим в центре эллипса Oi начало новой системы координат Oiх'у', оси которой Ojx1 и Oiy1 параллельны соответствующим осям Ох и Оу и одинаково с ними направленны (см. рис. 63).
В этой системе координат уравнение эллипса имеет вид
,2 ,2
х у'
----|- — = 1.
а2 Ь2
Так как х' = х — хд, у' = х — у0 (формулы параллельного переноса, см. с. 62), то в старой системе координат уравнение эллипса запишется в ВВДе (ж-жо)2 , (у-у0Г = .
д а2 + Ь2
Аналогично рассуждая, получим уравнение гиперболы с центром в точке О1(хо;уо) и полуосями а и b (см. рис. 64):
(ж ~ яд)2 _ (у ~ Уо)2 = а2 Ь2
И, наконец, параболы, изображенные на рисунке 65, имеют соответствующие уравнения.
(.У - Уо)2 = 2р(ж - яд)
Рис. 65
Уравнение Ах2 + Су2 + 2Dx + 2Еу + F = О
Уравнения эллипса, гиперболы, параболы и уравнение окружности (ж — .т0)2 + (г/ — ?/о)2 = R2 после преобразований (раскрыть скобки, перенести все члены уравнения в одну сторону, привести подобные члены, ввести новые обозначения для коэффициентов) можно записать с помощью единого уравнения вида
Ах2 + Су2 + 2Dx + 2Еу + F = 0, (11.14)
где коэффициенты Л и С не равны нулю одновременно.
Возникает вопрос: всякое ли уравнение вида (11.14) определяет одну из кривых (окружность, эллипс, гипербола, парабола) второго порядка? Ответ дает следующая теорема.
87
Теорема 11.2. Уравнение (11.14) всегда определяет: либо окружность (при А = С), либо эллипс (при А С > 0), либо гиперболу (при А-С < 0), либо параболу (при А С = 0). При этом возможны случаи вырождения: для эллипса (окружности) — в точку или мнимый эллипс (окружность), для гиперболы — в пару пересекающихся прямых, для параболы —- в пару параллельных прямых.
Пример 11.1. Установить вид кривой второго порядка, заданной уравнением 4а:2 + 5у2 + 20а: — ЗОу + 10 = 0.
Q Решение: Предложенное уравнение определяет эллипс (Л-С = 4-5 > > 0). Действительно, проделаем следующие преобразования:
4(аг2 + 5а: + + 5(у2 - бу + 9) - 25 - 45 +10 = 0,
4(а:+ j)2 + 5(у - З)2 = 60,
Получилось каноническое уравнение эллипса с центром в О
и
полуосями а = д/15 и b = а/12.
Пример 11.2. Установить вид кривой второго порядка, заданной уравнением а:2 + 10а: — 2у + 11 = 0.
Q Решение: Указанное уравнение определяет параболу (С = 0). Действительно,
а:2 + 10а: + 25 - 2у + 11 - 25 = 0,
(а: + 5)2 = 2у + 14, (а: + 5)2 = 2(у + 7).
Получилось каноническое уравнение параболы с вершиной в точке
ОД—5; — 7) и р = 1. •
Пример 11.3. Установить вид кривой второго порядка, заданной уравнением 4а:2 — у2 + 8а: — 8у — 12 = 0 (Л • С = -4 < 0).
Q Решение: Преобразуем уравнение:
4(а:2 + 2х + 1) - (у2 4- 8у + 16) - 4 + 16 - 12 = 0,
4(а: + I)2 - (у + 4)2 = 0,
(2(® + 1) + (у + 4)) • (2(т + 1) - (у + 4)) = 0,
(2а: + у + 6)(2а: — у — 2) = 0.
88
Это уравнение определяет две пересекающиеся прямые 2х + у + 6 = О и 2.т — у — 2 = 0. •
Общее уравнение второго порядка
Рассмотрим теперь общее уравнение второй степени с двумя неизвестными: „ „
Ах2 + 2Вху + Су2 + 2Dx + ‘2EyA-F = 0. (11.15)
Оно отличается от уравнения (11.14) наличием члена с произведением координат (В 0). Можно, путем поворота координатных осей на угол а, преобразовать это уравнение, чтобы в нем член с произведением координат отсутствовал.
Используя формулы поворота осей (с. 63)
х = х' cos а — у' sin а, у = х' sin а + у' cos а, выразим старые координаты через новые:
А(х' cosa — у1 sina)2 + 2В(а/ cosa — у' sina)(a:' sina + у1 cosa)+
+ С(х' sin a + у' cos a)2 + 2D(x' cos a — y1 sin a)+
+ 2E(x' sin a + y' cos a) + F = 0.
Выберем угол a так, чтобы коэффициент при х' у' обратился в нуль, т. е. чтобы выполнялось равенство
—2 A cos a sin a + 2B(cos2 a — sin2 a) + 2C sin a cos a = 0,
(C — A) sin 2a + 2Bcos2a = 0, (11.16)
2B cos 2a = (A — C) sin 2a.
Отсюда 2n
tg2a=-——. .(11-17)
— о
Таким образом, при повороте осей на угол а, удовлетворяющий условию (11.17), уравнение (11.15) сводится к уравнению (11.14).
Вывод: общее уравнение второго порядка (11.15) определяет на плоскости (если не считать случаев вырождения и распадения) следующие кривые: окружность, эллипс, гиперболу, параболу.
Замечание: Если А = С, то уравнение (11.17) теряет смысл. В этом случае cos2a = 0 (см. (11.16)), тогда 2a = 90°, т. е. a = 45°. Итак, при А = С систему координат следует повернуть на 45°.
Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Лекции 10-121
§12. УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ
В ПРОСТРАНСТВЕ
12.1. Основные понятия
Поверхность и ее уравнение
Поверхность в пространстве, как правило, можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке Oi есть геометрическое место всех точек пространства, находящихся от точки Oi на расстоянии R.
Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х, у и z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.
р>| Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, y,z) = 0 с тремя переменными ж, у и г, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные ж, у и z в уравнении поверхности называются текущими координатами точек поверхности.
Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка на данной поверхно-
сти, достаточно подставить координаты точки Mi в уравнение поверхности вместо переменных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.
Уравнение сферы
Найдем уравнение сферы радиуса R с центром в точке Oi (ж0; уо! ^о)-Согласно определению сферы расстояние любой ее точки М(ж; у, z) от центра С*1(ж0; у0; z0) равно радиусу К, т. е. OiM = R.HoOiM = |OiM|, где Oi М = (ж — жо; у — у о; z — zq). Следовательно,
\/(ж - ж0)2 + (у - у0)2 + (z- z0)2 = R
90
или
(ж - ж0)2 + (у- Уо)2 + (г - г0)2 = В2.
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.
Если центр сферы Ог совпадает с началом координат, то уравнение сферы принимает вид х2 + у2 + z2 = В2.
Если же дано уравнение вида F(x; у, z) = 0, то оно, вообще говоря, определяет в пространстве некоторую поверхность.
Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y;z) = 0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».
Так, уравнению 2х2 + у'2 + z'2 + 1 = 0 не удовлетворяют никакие действительные значения ж, у, z. Уравнению 0 ж2 + у2 + z2 =0 удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, ах — любое число).
Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:
1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.
2. Дано уравнение F(x;y,z) = 0. Исследовать форму поверхности, определяемой этим уравнением.
Уравнения линии в пространстве
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, общих двум поверхностям.
Если Fi(x-,y;z) = 0 и F2(x; у, z) = 0 — уравнения двух поверхностей, определяющих линию Г, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:
'№;»;«) = 0, (12])
F2(x;y,z) = 0.
Уравнения системы (12.1) называются уравнениями линии в
{У — ^7
естъ уравнения оси Ох.
z = 0
Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением
г = f(t) (12.2)
91
или параметрическими уравнениями
х = x(t), ' ?/ = ?/(<), г = z(t)
проекций вектора (12.2) на оси координат.
Например, параметрические уравнения вид
винтовой линии имеют
При любом расположении точки М на плоскости Q векторы п и МдМ взаимно перпендикулярны, поэтому их скалярное произведение
х = R cos t, у — Rsmt, z = 2тг
равно нулю: п М()М = 0, т. е.
А(х - ®0) + В(У - Уо) + C(z - z0) = 0.
Если точка М равномерно движется по образующей кругового ци-
линдра, а сам цилиндр равномерно вращается вокруг оси, то точка М описывает винтовую линию (см. рис. 68).
12.2. Уравнения плоскости в пространстве
Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
Пусть в пространстве Oxyz плоскость Q задана точкой М)(жо;?/о; zq) и вектором п = (Л; В; С), перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости Q. Возьмем на ней произвольную точку M(x;y;z) и составим вектор
М0М = (х - х0-,у - у0-, z - г0).
Q9
(12.3)
Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них п М$М ^4 0).
g Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку Mo(xo;yo-,zo) перпендикулярно вектору п = (Л; В; С). Оно первой степени относительно текущих координат х, у и z. Вектор п = (А; В; С) называется нормальным вектором плоскости.
Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей через точку Мо. Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) — уравнением связки плоскостей.
Общее уравнение плоскости
Рассмотрим общее уравнение первой степени с тремя переменными о» ?/ И 2"
Ax + By + Cz + D = 0. (12.4)
93
Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например В ф 0, перепишем уравнение (12.4) в виде
Л(х-0) + ВЬ + ^) +C(z-0) = 0. (12.5)
\ н /
Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравнения (12.4) и (12.5) являются уравнением плоскости с нормальным вектором п = (А; В; С), проходящей через точку Mi ^0; — jj;о).
Итак, уравнение (12.4) определяет в системе координат Oxyz не-
которую плоскость. Уравнение (12.4) называется общим уравнением плоскости.
Частные случаи общего уравнения плоскости:
1. Если D — 0, то оно принимает вид Ах + By + Cz — 0. Этому уравнению удовлетворяет точка 0(0; 0;0). Следовательно, в этом случае плоскость проходит через начало координат.
2. Если С = 0, то имеем уравнение Ах + By + D — 0. Нормальный вектор п = (А;/?;()) перпендикулярен оси Oz. Следовательно, плоскость параллельна оси Oz; если В = 0 — параллельна оси Оу, А = 0 -.
параллельна оси Ох.
3. Если С = D = 0, то плоскость проходит через 0(0; 0; 0) параллельно оси Oz, т. е. плоскость Ах + By = 0 проходит через ось Oz. Аналогично, уравнениям By + Cz = 0 и Ах + Cz = 0 отвечают плоскости, проходящие соответственно через оси Ох и Оу.
4. Если А = В = 0, то уравнение (12.4) принимает вид Cz + D — О, т. е. z = “О' Плоскость параллельна плоскости Оху. Аналогично, уравнениям Ах + D — 0 и By + D = 0 отвечают плоскости, соответственно параллельные плоскостям Oyz и Oxz.
5. Если А = В — D = 0, то уравнение (12.4) примет вид Cz = 0, т. е. z = 0. Это уравнение плоскости Оху. Аналогично: у — 0 — уравнение плоскости Oxz; х = 0 — уравнение плоскости Oyz.
Уравнение плоскости, проходящей через три данные точки
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки Mi(xr,yi;zi), М2(х2;у2; 2г) и M3(x3;y3;zs), не лежащие на одной прямой.
Возьмем на плоскости произвольную точку М(х; у; z) и составим векторы MiM = (х — Xi; у — yi; z — zi), MiM2 = (x2 — Xi;y2—yi;z2—zi), MiM3 = (жз — xi;y3 — yr,z3 — zi). Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем
94
М1М МгМ2 Mt M3 = О, т. е.
х — XI
Х2 - Xi
Х3 - Xi
У-У1
У2 ~ У1
Уз ~ У1
Z — Z1
Z2 - Z1
Хз - XI
= 0.
(12.6)
Уравнение (12.6) есть уравнение плоскости, проходящей через три дан
ные точки.
Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях Ох, Оу и Oz соответственно отрезки а, b и с, т. е. проходит через три точки А(а;0;0), В(0;Ь;0) и С(0; 0; с) (см. рис. 70).
Подставляя координаты этих точек в уравнение (12.6), получаем
х — а
—а
—а
У z ь о 0 с
= 0.
|ф| Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.
Нормальное уравнение плоскости
Положение плоскости Q вполне определяется заданием единичного вектора ё, имеющего направление перпендикуляра ОК, опущенного на плоскость из начала координат, и длиной р этого перпендикуляра (см. рис. 71).
95
г • е — р = 0.
х cos а + у cos р + z COS7 — р — 0.
Пусть OK = р, a a, /3, 7 — углы, образованные единичным вектором ё с осями Ох, Оу и Oz. Тогда ё = (cosa;cosр-cos7). Возьмем на плоскости произвольную точку М(х; у; z) и соединим ее с началом координат. Образуем вектор г = ОМ = (x;y,z).
При любом положении точки М на плоскости Q проекция радиус-вектора г на направление вектора ё всегда равно р: npf г — р, т. е.
(12-8)
Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов г и ё, уравнение (12.8) перепишем в виде
(12-9)
Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.
Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на нормирующий множитель Л =------, - - - ..., где знак берется
±х/Д2 + В2+С2 противоположным знаку свободного члена В общего уравнения плоскости.
12.3. Плоскость. Основные задачи
Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
Пусть заданы две плоскости Qi и Q2:
Агх + Bly + Ciz + Di =0, A2x + B2y + C2z + D2 = 0.
|ф| Под углом мемсду плоскостями Qi и Q2 понимается один из двугранных углов, образованных этими плоскостями.
Угол у? между нормальными векторами щ = (Ai;Bi;Ci) и п2 = = (А2-,В2-,С2} плоскостей Qi и Q2 равен одному из этих углов (см. рис. 72). Поэтому cosy? = или
А,А2 + В,В2 + С1С2
COSW = -7:='-:-...." ; . -г
у/А1 + В2 + С2 - /А2 + В2 + С2
Для нахождения острого угла следует взять модуль правой части.
Если плоскости Qi и Q2 перпендикулярны (см. рис. 73, о), то таковы же их нормали, т. е. П\ ± п2 (и наоборот). Но тогда ni • п2 = 0,
96
т. е. А]А2 + BiВ2 + CjC2 = 0. Полученное равенство есть условие перпендикулярности двух плоскостей Qi и Q2.
Если плоскости Qj и Q2 параллельны (см. рис. 73, б), то будут параллельны и их нормали nj и п2 (и наоборот). Но тогда, как известно, АВС
координаты векторов пропорциональны: -д1 = -g1 = gr- Это и есть условие параллельности двух плоскостей Qi и Q2.
Расстояние от точки до плоскости
Пусть задана точка Мр(хо;уо', го) и плоскость Q своим уравнением Ах + By + Cz + D = 0. Расстояние d от точки Мо до плоскости Q находится по формуле
d _ |Ае0 + Ву0 + Czp + D\ у/А2 + В2 + С2
Вывод этой формулы такой же, как вывод формулы расстояния от точки М0(х0; уо) до прямой Ах + By + С = 0 (см. с. 73).
Расстояние d от точки Мо до плоскости Q равно модулю проекции вектора MiM0, где М.у (.Г|; т/i; ) — произвольная точка плоскости Q, на направление нормального вектора п = (А-,В\С) (см. рис. 74). Следовательно,
МгМр-п _ |(ffO-a:i)A+(t/o-t/i).B + (zo-zi)C,| _ |п| ~ ^А2+В2+С2
_ lAxo + Byo + Czo-Axj-Byi-Czil х/А2+В2+С2
А так как точка Mj(xj; ур, zj) принадлежит плоскости Q, то
Axi + Byi + Czi + D = 0, т. е. D — — Axj — Byj — Czj.
Поэтому d = ^z° ^1. Отметим, что если плоскость Q
yj А2 + В2 + С2
задана уравнением я: cos а + ycos/З + г cos 7 — р = 0, то расстояние от
4 Конспект лекций по высшей математике. Полный курс
d=| прйМ1М0| =
97
точки Мо(хо;уо', zo) до плоскости Q может быть найдено по формуле d = |®о cosa + уо cos/3 + z0 COS7 — р|.
Рис. 74
Рис. 75
12.4. Уравнения прямой в пространстве
Векторное уравнение прямой
|ф| Положение прямой в пространстве вполне определено, если задать какую-либо точку Мо на прямой и вектор S, параллельный этой прямой. Вектор S называется направляющим вектором прямой. Пусть прямая L задана ее точкой Мо(жо; Уо'> £'о) и направляющим вектором S = (т; п;р). Возьмем на прямой L произвольную точку М(х; у, г). Обозначим радиус-векторы точек Мо и М соответственно через го и г. Очевидно, что три вектора fo, г и МоМ связаны соотношением
г = г0 + М0М. (12.10)
Вектор МоМ, лежащий на прямой L, параллелен направляющему вектору S, поэтому МоМ = tS, где t — скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки М на прямой (см. рис. 75).
Уравнение (12.10) можно записать в виде
(12.11)
|ф| Полученное уравнение называется векторным уравнением прямой.
Параметрические уравнения прямой
Замечая, что f = (x;y;z), го = (хо',Уо‘, zo), tS = (tm;tn-,tp), уравнение (12.11) можно записать в виде
хг + у] + zk = (ж0 + tm)i + (?/0 + tri)j + (z0 + tp)k.
г = го + tS.
98
Отсюда следуют равенства:
х — хо + mt, ' У = Уо + nt, z = Zq + pt.
(12.12)
Они называются параметрическими уравнениями прямой в пространстве.
Канонические уравнения прямой
Пусть S = (т; п; р) — направляющий вектор прямой L и Л/О(®о; У о; л)) — точка, лежащая на этой прямой. Вектор МоМ, соединяющий точку Мо с произвольной точкой М(х\ у, z) прямой L, параллелен вектору S. Поэтому координаты вектора М0М=(х—,г0; У~Уо', z~zo) и вектора S — (т;п;р) пропорциональны:
(12.13)
х-хр _ у -уо _ Z-Zp т п р
|^| Уравнения (12.13) называются каноническими уравнениями прямой в пространстве.
Замечания: 1) Уравнения (12.13) можно было бы получить сразу из параметрических уравнений прямой (12.12), исключив параметр t. Из уравнений (12.12) находим
х-хр _ у — уо _ z- Zp _ т п р
2) Обращение в нуль одного из знаменателей уравнений (12.13) означает обращение в нуль соответствующего числителя.
тт rf_о 7/ —4 р' ____- 1
Например, уравнения - — — = п задают прямую, про-
О Ха U
ходящую через точку Мо(2; —4; 1) перпендикулярно оси Oz (проекция вектора S на ось Oz равна нулю). Но это означает, что прямая лежит в плоскости z = 1, и поэтому для всех точек прямой будет z — 1 = 0.
Уравнение прямой в пространстве, проходящей через две точки
Пусть прямая L проходит через точки М^ху, у у, гх) и Л/2(ж2; у 2', ^)-В качестве направляющего вектора S можно взять вектор М^М2 = = (ж2 — Х1',у2 — уг, z2 — zx), т. е. S = М±М2 (см. рис. 76). Следовательно, т = х2 — Xi, п — У2 ~ У1, Р = z2 — zi. Поскольку прямая проходит через точку Мх(.гх; у\; гх), то, согласно уравнениям (12.13), уравнения прямой L имеют вид
Ж.-Ж] = У~У* = Z~Z1.\ (12.14)
%2 -Х1 у2~ У1 Z2 - Z!
99
К| Уравнения (12.14) называются уравнениями прямой, проходя-
Общие уравнения прямой
Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей. Рассмотрим систему уравнений
Ajx + Вру + C\z + Dr = О, + В%у + C2Z + 1?2 = 0.
(12.15)
Каждое из уравнений этой системы определяет плоскость. Если плоскости не параллельны (координаты векторов щ = (X^BijCi) и й2 — = (А2: В2; С2) не пропорциональны), то система (12.15) определяет прямую L как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы (см. рис. 77). Уравнения (12.15) называют общими уравнениями прямой.
От общих уравнений (12.15) можно перейти к каноническим уравнениям (12.13). Координаты точки Мо на прямой L получаем из системы уравнений (12.15), придав одной из координат произвольное значение (например, z = 0).
Так как прямая L перпендикулярна векторам п.\ и п2, то за направляющий вектор S прямой L можно принять векторное произведение
Пг х п2:
S = Пг X П2 =
г j к Аг Вг Сг а2 в2 с2
Замечание: Канонические уравнения прямой легко получить, взяв две какие-либо точки на ней и применив уравнения (12.14).
100
Пример 12.1. Написать канонические уравнения прямой L, заданной уравнениями
х + у — г + 1 = О, 2ж — у — 3z + 5 = 0.
Q Решение: Положим z = 0 и решим систему
х + у = —1, 2ж — у = —5.
Находим
точку Л/Д—2; 1; 0) € L. Положим у = 0 и решим систему
х — z = — 1, 2х — 3z = — 5.
Находим вторую точку М2(2;0;3) прямой L. Записываем уравнение
прямой L, проходящей через точки Mi и М2-
х + 2 _ у — 1 _ z
4 “ -1 ~ 3
12.5. Прямая линия в пространстве. Основные задачи
Угол между прямыми. Условия параллельности
и перпендикулярности прямых
Пусть прямые L] и L2 заданы уравнениями
х-xi _ у-yr _ Z-Z1
mi щ pi
И Х~Х2 __ у-У2 _ Z — Z2
т2 п2 Р2
Под углом между этими прямыми понимают угол между направляющими векторами Si = (mi;ni;pi) и S2 =
= (т2;п2;Р2) (см. рис. 78). Поэтому, по известной формуле для косинуса угла между векторами, получаем
_ mim2 + + Р1Р2___
Vm'l +nl+pl~ у/т^ + п^+р^
(12.16)
Для нахождения острого угла между прямыми Li и L2 числитель правой части формулы (12.16) следует взять по модулю.
Если прямые L\ и L® перпендикулярны, то в этом и только в этом случае имеем cos у? = 0. Следовательно, числитель дроби (12.16) равен нулю, т. е. mim2 + П1П2 +Р1Р2 = 0.
1П1
Если прямые Li и L2 параллельны, то параллельны их направляющие векторы Si и §2- Следовательно, координаты этих векторов пропорциональны, т. е. — 2к
m2 п2 р2
х у — 2 z + 2
2 = -1 “ 3 И
Пример 12.2. Найти угол между прямыми
2х + у — z — 1 = 0,
2х — у + Зх + 5 = 0.
Q Решение: Очевидно, Si = (2; —1; 3), a S2 = ni хц2, где ni = (2; 1; —1), П2 = (2; —1; 3). Отсюда следует, что 52 = (2; —8; —4). Так как Si • 52 = = 4 + 8 - 12 = 0, то v = 90°. •
Условие, при котором две прямые лежат в одной плоскости
Пусть прямые Li и Т2 заданы каноническими уравнениями
x-xt _ y-yi _ Z — Zj
mi щ Pl
и
Х-Xi _ У ~У2 _ z~ Z2
т2 П2 Р2
Их направляющие векторы соответст-венно51 = (mi;ni;pi) иУ2 = (m2;n2;p2) (см. рис. 79).
Прямая Li проходит через точку Ml (ад; yi; Zi), радиус-вектор которой обозначим через гр, прямая £2 проходит
через точку М2(а:2;«/2; z2), радиус-вектор которой обозначим через г2. Тогда
г2 - 71 = МХМ2 = (ж2 ~хр,у2~ yi;z2 - zi).
Прямые Li и Т2 лежат в одной плоскости, если векторы Si, S2 и Mi М2 = г2 —г] компланарны. Условием компланарности векторов является равенство нулю их смешанного произведения: (r2 — Г1)У|У2 = 0,
т. е.
Х2 — Xi
mi
т2
У2 - У1 ni
П2
Z2 ~ Zi
Pl
Р-2
= 0.
При выполнении этого условия прямые Li и L2 лежат в одной плоскости, то есть либо пересекаются, если S2 ф A-Si, либо параллельны, если Si || §2-
102
12.6. Прямая и плоскость в пространстве. Основные задачи
Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
Пусть плоскость Q задана уравнением Ах + By + Cz + D = О, а прямая L уравнениями ——— У -№> — -—31. т п р
pg| Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Обозначим через р угол между плоскостью Q и прямой £, а через 0 — угол между векторами п — (А; В; С) и S = (т;п;р) (см. рис. 80). Тогда cost? = .Д' . Найдем синус угла р, считая р <
|n| • |о|
sinр — sin(^ — в) = cost?. И так как sinр 0, получаем
Ат + Вп + Ср\ Sin р — , , -j^.
дЛ42 + В2 + С2 х/т2 + п2 +р2
(12.17)
Если прямая L параллельна плоскости Q, то векторы п и S перпендикулярны (см. рис. 81), а потому S п — 0, т. е.
Ат + Вп + Ср = 0
является условием параллельности прямой и плоскости.
Рис. 82
Рис. 80
Рис. 81
Если прямая L перпендикулярна плоскости Q, то векторы п и S параллельны (см. рис. 82). Поэтому равенства
А _ В _ С т п р являются условиями перпендикулярности прямой и плоскости.
103
Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости
Пусть требуется найти точку пересечения прямой
с плоскостью
Ах + By + Cz + D = 0. (12.19)
Для этого надо решить систему уравнений (12.18) и (12.19). Проще всего это сделать, записав уравнения прямой (12.18) в параметрическом виде:
х = xq + mt,
* У = Уо +nt,
Z = Z0 +pt.
Подставляя эти выражения для х, у и z в уравнение плоскости (12.19), получаем уравнение Л(ж0 + mt) + В{у$ + nt) + C(z0 + pt) + D = 0 или
t(Am + Bn T Ср) T (jAxq + By$ + Czq 4- В) — 0. (12.20)
Если прямая L не параллельна плоскости, т. е. если Ат + Вп + Ср А 0, то из равенства (12.20) находим значение t:
, _ Ахо + Вуо + Czq + В
Ат + Вп + Ср
Подставляя найденное значение t в параметрические уравнения прямой, найдем координаты точки пересечения прямой с плоскостью.
Рассмотрим теперь случай, когда Ат + Вп + Ср = 0 (L || Q):
а) если F = Axq + Вуо + С z^ + В =4 0, то прямая L параллельна плоскости и пересекать ее не будет (уравнение (12.20) решения не имеет, так как имеет вид 0 • t + F = 0, где F / 0);
б) если Ахо + Вуо + Czq + В = 0, то уравнение (12.20) имеет вид t - 0 + 0 = 0; ему удовлетворяет любое значение t, любая точка прямой является точкой пересечения прямой и плоскости. Заключаем: прямая лежит в плоскости. Таким образом, одновременное выполнение равенств ,
J Ат + Вп + Ср = 0,
+ Вуо + Czq + В = 0
|ф| является условием принадлежности прямой плоскости.
12.7. Цилиндрические поверхности
|ф] Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндрической
1ПЯ
поверхностью или цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L — его образующей (см. рис. 83).
Будем рассматривать цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой плоскости.
Пусть в плоскости Оху лежит некоторая линия К, уравнение которой
F(a;;j/) = 0. (12.21)
Построим цилиндр с образующими параллельными оси Oz и направляющей К.
Теорема 12.1. Уравнение цилиндра, образующие которого параллельны оси Oz, имеет вид (12.21), т. е. не содержит координаты z.
□ Возьмем на цилиндре любую точку М(х-, у, z) (см. рис. 84). Она лежит на какой-то образующей. Пусть N — точка пересечения этой образующей с плоскостью Оху. Следовательно, точка N лежит на кривой К и ее координаты удовлетворяют уравнению (12.21).
Но точка М имеет такие же абсциссу х и ординату у, что и точка N. Следовательно, уравнению (12.21) удовлетворяют и координаты точки М(ж; у, г), так как оно не содержит z. И так как М — это любая точка цилиндра, то уравнение (12.21) и будет уравнением этого цилиндра. .
Теперь ясно, что F(x-, z) = 0 есть уравнение цилиндра с образующими, параллельными оси Оу, a F(y; z) =0 — с образующими, параллельными оси Ох. Название цилиндра определяется названием направляющей. Если направляющей служит эллипс
|ф| в плоскости Оху, то соответствующая цилиндрическая поверхность называется эллиптическим цилиндром (см. рис. 85).
105
|ф| Частным случаем эллиптического цилиндра является круговой цилиндр, его уравнение ж2 + у2 = R2. Уравнение ж2 = 2pz определяет в пространстве параболический цилиндр (см. рис. 86). Уравнение о 9
а2 Ь2
|ф| определяет в пространстве гиперболический цилиндр (см.
Ш рис. 87).
|ф| Все эти поверхности называются цилиндрами второго порядка, так как их уравнения есть уравнения второй степени относительно текущих координат ж, у и z.
12.8. Поверхности вращения. Конические поверхности
Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнения этой кривой запишутся в виде
Г(«/;г) = О, ж = 0.
(12.22)
Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz.
Возьмем на поверхности произвольную точку M(x;y-,z) (см. рис. 88). Проведем через точку М плоскость, перпендикулярную оси Oz, и обозначим точки пересечения ее с осью Oz и кривой L соответственно через Oi и N. Обозначим координаты точки N через (0; уу, Zi). Отрезки Oi М и Oi N являются радиусами одной и той же окружности. Поэтому OiM — OiN. Но О±М = д/ж2 + у2, OiN = (g/i|. Следовательно, |a/i | = у/х2 + у2 или yi = ±у/х2 + у2. Кроме того, очевидно, z^ = z.
106
Так как точка лежит на кривой L, то ее координаты удовлетворяют уравнению (12.22). Стало быть, F(y1;z1) = 0. Исключая вспомогательные координаты у \ и Z\ точки N, приходим к уравнению
F(±x/x2 + у2; z) = 0. (12.23)
Уравнение (12.23) — искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точки М этой поверхности и не удовлетворяют координаты точек, не лежащих на поверхности вращения.
Как видно, уравнение (12.23) получается из (12.22) простой заменой у на ±у/х2 + у2, координата z сохраняется.
Понятно, что если кривая (12.22) вращается вокруг оси Оу, то уравнение поверхности вращения имеет вид
F(y, ±\/.т2 + z2) = 0;
если кривая лежит в плоскости Оху (г = 0) и ее уравнение F(.r; у) = 0, то уравнение поверхности вращения, образованной вращением кривой вокруг оси Ох, есть F(x; Fy/y2 + г2) = 0.
|ф| Так, например, вращая прямую у — z вокруг оси Oz (см. рис. 89), получим поверхность вращения (ее уравнение ±^/ж2 + у2 = z или х2 + у2 = z2). Она называется конусом второго порядка.
Поверхность, образованная прямыми линиями, проходящими через данную точку Р и пересекающими данную плоскую линию L (не проходящую через Р), называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р — ее вершиной, а прямая, описывающая поверхность, называется образующей.
107
Рис. 90
Пусть направляющая L задана уравнениями
Г1(а:;2/;г) = 0,
Fz(x;y;z) = 0,
(12.24)
а точка Р(жо;«/о;го) — вершина конуса. Найдем уравнение конуса.
Возьмем на поверхности конуса произвольную точку М (ат; у, z) (см. рис. 90). Образующая, проходящая через точки Р и М, пересечет направляющую L в некоторой точке N(xi;yx;zx). Координаты точки N удовлетворяют уравнениям (12.24) направляющей:
Fi(xi;yr,zi) = 0,
F2(xr,yr,zi) = 0.
(12.25)
Канонические уравнения образующих, проходящих через точки Р и N, имеют вид
х- х0 _ у-уо _ z- z0
Х1 - Ж0 Ух -у0 Zl-Zo'
Исключая хх, ух и zx из уравнений (12.25) и (12.26), получим уравнение конической поверхности, связывающее текущие координаты х, у и z.
Пример 12.3. Составить уравнение конуса с вершиной в точке 2
0(0; 0;0), если направляющей служит эллипс ^ + ^2=1, лежащий в плоскости z = с.
Q Решение: Пусть М (ж; у; z) — любая точка конуса. Канонические уравнения образующих, проходящих через точки (0;0;0) и точку (xx‘,yx;zx) пересечения образующей ОМ с эллипсом будут — = =
У1
108
— Исключим ЯГ1, j/i и Z[ из этих уравнений и уравнения ^•1
2 2
Э+%=1 <12-эт)
(точка (xi',yi;zi) лежит на эллипсе), z\ = с. Имеем: — =
*£1 с у\ с
Отсюда Ж1=с-^и?/1 = с-^. Подставляя значения и yi в уравнение эллипса (12.27), получим
с2 • х2 с2 - у2 х2 у2 z2
~2 2 "I 2 г2 = ИЛИ — + — —
z a z Ъ а Ъ с
Это и есть искомое уравнение конуса. •
12.9. Канонические уравнения поверхностей второго порядка
По заданному уравнению поверхности второго порядка (т. е. поверхности, уравнение которой в прямоугольной системе координат является алгебраическим уравнением второй степени) будем определять ее геометрический вид. Для этого применим так называемый метод сечений: исследование вида поверхности будем производить при помощи изучения линий пересечения данной поверхности с координатными плоскостями или плоскостями, им параллельными.
Эллипсоид
Исследуем поверхность, заданную уравнением
(12.28)
Рассмотрим сечения поверхности (12.28) с плоскостями, параллельными плоскости хОу. Уравнения таких плоскостей: z = h, где h - любое число.
Линия, получаемая в сечении, определяется двумя уравнениями
(12.29)
Исследуем уравнения (12.29):
2 „.2
а) Если |/i| > с, с > 0, то 4- <0. Точек пересечения поверх-
ности (12.28) с плоскостями z = h не существует.
109
б) Если |Л| = с, т. е. h = ±с, то =0. Линия пересече-
ния (12.29) вырождается в две точки (0; 0; с) и (0; 0; —с). Плоскости z = с и z = —с касаются данной поверхности.
в) Если |/'| < с, то уравнения (12.29) можно переписать в виде:
Как видно, линия пересечения есть эллипс с полуосями (см. рис. 91)
При этом чем меньше |Л|, тем больше полуоси и 1ц. При h = 0 они достигают своих наибольших значений: <ц = a, bi = b. Уравнения (12.29) примут вид
Аналогичные результаты получим, если рассмотрим сечения поверхности (12.28) плоскостями х = h и у = h.
р>| Таким образом, рассмотренные сечения позволяют изобразить поверхность (12.28) как замкнутую овальную поверхность. Поверхность (12.28) называется эллипсоидом. Величины а, b и с называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехосным-, если какие-либо две полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения; если а = b = с, то — в сферу х2 + у2 + z2 = а2.
Однополостный гиперболоид
Исследуем поверхность, заданную уравнением
ж2 у2 z2
-----1- --------= 1.
а2 Ъ2 с2
(12.30)
Пересекая поверхность (12.30) плоскостью z — h, получим линию пересечения, уравнения которой имеют вид
110
Как видно, этой линией является эллипс с полуосями
/ /,2 /
a1=a1/l + ^V и b, = bJl + ус V
Полуоси ai и bi достигают своего наименьшего значения при h = 0: ai = a, bi = b. При возрастании |/i| полуоси эллипса будут увеличиваться.
Если пересекать поверхность (12.30) плоскостями х = h или у = h, то в сечении получим гиперболы. Найдем, например, линию пересечения поверхности (12.30) с плоскостью Oyz, уравнение которой ж = 0. Эта линия пересече-
ния описывается уравнениями
h2
х = 0.
Как видно, эта линия есть гипербола (см. рис. 92).
Анализ этих сечений показывает, что поверхность, определяемая уравнением (12.30), имеет форму бесконечной расширяющейся трубки. Поверхность (12.30) называется однополостным гиперболоидом.
Замечание: можно доказать, что через любую точку гиперболоида (12.30) проходят две прямые, лежащие на нем.
Двухполостный гиперболоид
Пусть поверхность задана уравнением
(12.31)
Если поверхность (12.31) пересечь плоскостями z -- h, то линия пересечения определяется уравнениями /4 + й < а2 Ъ z = h.
с2
(12.32)
Отсюда следует, что:
а) если |/г| < с, то плоскости z = h не пересекают поверхности;
б) если |Л| = с, то плоскости z = ±с касаются данной поверхности соответственно в точках (0;0;с) и (0;0; —с).
в) если |/i| > с, то уравнения (12.32) могут быть переписаны так
ж2 У2 = 1
< а2(£_1)+И£-1) ’
z = h.
Ill
Эти уравнения определяют эллипс, полуоси которого возрастают с ростом |/i|.
Пересекая поверхность (12.31) координатными плоскостями Oyz (х = 0) и Oxz (у = 0), получим в сечении гиперболы, уравнения которых соответственно имеют вид
V2 z2 х2 z2
Ъ = -1 и = -1.
Ъ с а с
У обеих гипербол действительной осью является ось Oz. Метод сечения позволяет изобразить поверхность (см. рис. 93), определяемую уравнением (12.31), как поверхность, состоящую из двух полостей, имеющих форму выпуклых неограниченных чаш. Поверхность (12.31) называется двухполостным гиперболоидом.
Рис. 93
Эллиптический параболоид
Исследуем поверхность, заданную уравнением
(12.33)
где р > 0, q > 0. Рассечем поверхность (12.33) плоскостями z = h. В сечении получим линию, уравнения которой есть
^+^=2А, < р q
z = h.
Если h < 0, то плоскости z = h поверхности не пересекают; если h = 0, то плоскость z = 0 касается поверхности в точке (0; 0; 0); если h > 0,
112
то в сечении имеем эллипс, уравнение которого имеет вид
' = 1
< 2ph 2qh ' z = h.
Его полуоси возрастают с ростом h.
При пересечении поверхности (12.33) координатными плоскостями
Oxz и Oyz получатся соответственно параболы z = и z =
Таким образом, поверхность, определяемая уравнением (12.33), имеет вид выпуклой, бесконечно расширяющейся чаши (см. рис. 94). Поверхность (12.33) называется эллиптическим. параболоидом.
Гиперболический параболоид
Исследуем поверхность, определяемую уравнением
х^ Р
у2
— = 2z,
<1
(12.34)
где р > 0, q > 0. Рассечем поверхность (12.34) плоскостями z = h. Получим кривую
xL - jjL = i < 2ph 2qh ’ z — /i, которая при всех значениях h 0 является гиперболой. При h > 0 ее действительные оси параллельны оси Ох; при h < 0 — параллельны 2
оси Оу; при h — 0 линия пересечения = 0 распадается на
пару пересекающихся прямых = 0 и — 0. При
пересечении поверхности плоскостями, параллельными плоскости Oxz (у = h), будут получаться параболы
х2 = 2p(z +
У = h, ветви которых направлены вверх. При у = 0 в сечении получается парабола
, ветви которых направлены вниз.
х2 = 2pz, У = О
с вершиной в начале координат и осью симметрии Oz.
Пересекая поверхность (12.34) плоскостями х = h, получим пара-
болы у2 =
[^] Анализ линии пересечения позволяет определить вид поверхности: она имеет вид седла (см. рис. 95). Поверхность (12.34) называется гиперболическим параболоидом.
113
Рис. 95
Рис. 96
Конус второго порядка
Исследуем уравнение поверхности
ж2 у2 z2 п -------------= о
а2 Ь2 <?
(12.35)
Пересечем поверхность (12.35) плоскостями z = h. Линия пересечения 2 „.2 >2
+ — ^,z — h. При h = 0 она вырождается в точку (0; 0; 0). При
h 0 в сечении будем получать эллипсы
ж2 у2 _
, g2h2 b2h2 Х’
Z = h. к
Полуоси этих эллипсов будут возрастать при возрастании |А|.
Рассечем поверхность (12.35) плоскостью Оуz (ж = 0). Получится линия
,.2
И____z — о
ь2 ? - и’
х = О, распадающаяся на две пересекающиеся прямые у z у z
f - - = О и у + - = 0. b с Ъ с
При пересечении поверхности (12.35) плоскостью у = 0 получим линию „2 2
- К = о, ' а с
JJ = о,
114
также распадающуюся на две пересекающиеся прямые
х z х z
-----— Q и - + - = 0.
ас ас
Поверхность, определяемая уравнением (12.35), называется конусом второго порядка, имеет вид, изображенный на рисунке 96. Поверхности, составленные из прямых линий, называются линейчатыми. Такими поверхностями являются цилиндрические, конические поверхности, а также однополостный гиперболоид и гиперболический параболоид.
Глава V. ВВЕДЕНИЕ В АНАЛИЗ
Лекции 13-22
§ 13. МНОЖЕСТВА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
13.1. Основные понятия
|ф| Понятие множества является одним из основных неопределяемых понятий математики. Под множеством понимают совокупность (собрание, класс, семейство...) некоторых объектов, объединенных по какому-либо признаку. Так можно говорить о множестве студентов института, о множестве рыб в Черном море, о множестве корней уравнения х2 + 2х + 2 = 0, о множестве всех натуральных чисел и т. д.
Объекты, из которых состоит множество, называются его элементами. Множества принято обозначать заглавными буквами латинского алфавита А, В,..., X, У,..., а их элементы — малыми буквами а, Ь,..., х, у,...
Если элемент х принадлежит множеству X, то записывают х е X-запись х 6 X или х X означает, что элемент х не принадлежит множеству X.
Множество, не содержащее ни одного элемента, называется пустым, обозначается символом 0.
Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества.
Например, запись А = {1,3,15} означает, что множество А состоит из трех чисел 1, 3 и 15; запись А = {ж : 0 х 2} означает, что множество А состоит из всех действительных (если не оговорено иное) чисел, удовлетворяющих неравенству 0 х 2.
|ф| Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В.
Символически это обозначают так А с В («А включено в В») или В D А («множество В включает в себя множество Л»).
Говорят, что множества А кВ равны или совпадают, и пишут А = В, если А С В и В с А. Другими словами, множества, состоящие из одних и тех же элементов, называются равными.
|ф| Объединением (или суммой) множеств Аи В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение (сумму) множеств обозначают ЛиВ (или А + В). Кратко можно записать ЛиВ = {ж : х е А или х G В}.
116
pgj Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Пересечение (произведение) множеств обозначают АГ\В (или А-В). Кратко можно записать Ап В — {х : х £ А и х £ В}.
В дальнейшем для сокращения записей будем использовать некоторые простейшие логические символы:
а => (3 — означает «из предложения а следует предложение /?»;
а <=> /3 — «предложения а и р равносильны», т. е. из а следует Р и из (3 следует а;
V — означает «для любого», «для всякого»;
3 — «существует», «найдется»;
: — «имеет место», «такое что»;
— «соответствие».
Например-. 1) запись \/х £ А : а означает: «для всякого элемента х £ А имеет место предложение а»;
2) (х € A U В) <=> (х е А или х € В); эта запись определяет объединение множеств А и В.
13.2. Числовые множества.
Множество действительных чисел
Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:
N = {1; 2; 3; ...; п; ...} — множество натуральных чисел;
Ко = {0; 1; 2; ...; п; ...} — множество целых неотрицательных чисел;
К = {0; ±1; ±2; ...; ±п; ... } — множество целых чисел;
Q = : m € К, п £ — множество рациональных чисел.
Ж — множество действительных чисел.
Между этими множествами существует соотношение
NcZoCZcQCIR.
Множество Ж содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, i — 0,5 (= 0,500...),
= 0,333... — рациональные числа.
Действительные числа, не являющиеся рациональными, называются иррациональными.
117
Теорема 13.1. Не существует рационального числа, квадрат которого равен числу 2.
Q Допустим, что существует рациональное число, представленное несократимой дробью —, квадрат которого равен 2. Тогда имеем:
п
/ \ 2
( т \ Л 9^9
( — ) = 2, т. е. тп2 = 2п2.
\п
Отсюда следует, что т2 (а значит, и ш) — четное число, т. е. т — 2к. Подставив т = 2к в равенство т2 = 2п2, получим 4fc2 = 2п2, т. е. 2к2 — п2. Отсюда следует, что число п — четное, т. е. п = 21. Но тогда дробь — = сократима. Это противоречит допущению, что — дробь несократима. Следовательно, не существует рационального числа, квадрат которого равен числу 2.
Иррациональное число выражается бесконечной непериодической дробью. Так, л/2 = 1,4142356..., тг — 3,1415926... — иррациональные числа. Можно сказать: множество действительных чисел есть множество всех бесконечных десятичных дробей. И записать
Ж = {ж : х = а,а!а2аз ... }, где а Е Z, оц Е {0,1,... ,9}.
Множество Ж действительных чисел обладает следующими свойствами.
1. Оно упорядоченное: для любых двух различных чисел а и Ъ имеет место одно из двух соотношений а < b либо b < а.
2. Множество Ж плотное: между любыми двумя различными числами а и b содержится бесконечное множество действительных чисел х, т. е. чисел, удовлетворяющих неравенству а < х < Ъ.
Так, если а < Ь, то одним из них является число а
и
а < b => 2а < а + b
а + Ь<2Ь=>
„ , а+Ь '
2a<a+b<2b => а< <b
3. Множество Ж непрерывное. Пусть множество Ж разбито на два непустых класса А и В таких, что каждое действительное число содержится только в одном классе и для каждой пары чисел а Е А и b Е В выполнено неравенство а < Ь. Тогда (свойство непрерывности) существует единственное число с, удовлетворяющее неравенству а с С Ъ (Va Е A, Vb Е В). Оно отделяет числа класса А от чисел класса В. Число с является либо наибольшим числом в классе А (тогда в классе В нет наименьшего числа), либо наименьшим числом в классе В (тогда в классе Л нет наибольшего).
118
Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек прямой. Это означает, что каждому числу ж € Ж соответствует определенная (единственная) точка числовой оси и, наоборот, каждой точке оси соответствует определенное (единственное) действительное число. Поэтому вместо слова «число» часто говорят «точка».
13.3. Числовые промежутки. Окрестность точки
Пусть а и b — действительные числа, причем а < Ь.
Числовым,и промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:
[а; Ь] = {ж : а х 6} — отрезок (сегмент, замкнутый промежуток);
(а; Ь) = {х : а < х < Ь} — интервал (открытый промежуток);
[а; Ь) = {х : а 5$ х < Ь};
(а; 6] = {х : а < х < 6} — полуоткрытые интервалы (или полуоткрытые отрезки);
(—оо; 6] = {ж : х 6}; [а, +оо) = {ж : ж а};
(—оо; Ь) = {х : ж < 6}; (а, +оо) = {ж : ж > «};
(—оо,оо) = {ж : —оо < ж < +оо} = Ж. — бесконечные интервалы (промежутки).
Числа а и b называются соответственно левым и правым концами этих промежутков. Символы —оо и +оо не числа, это символическое обозначение процесса неограниченного удаления точек числовой оси от качала 0 влево и вправо.
|£| Пусть жо - любое действительное число (точка на числовой прямой). Окрестностью точки жо называется любой интервал (а; 6), содержащий точку жо- В частности, интервал (жо — е, ж0 + е), где е > О, называется е-окрестностъю точки хд. Число жо называется центром, а число £ — радиусом.
О
Рис. 97
Если ж G (жо — е; жо + е), то выполняется неравенство жо — е < ж < < жо+е, или, что то же, |ж—жо| < е. Выполнение последнего неравенства означает попадание точки ж в £-окрестность точки жо (см. рис. 97).
119
§14. ФУНКЦИЯ
14.1. Понятие функции
Одним из схновных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.
Пусть даны два непустых множества X и У. Соответствие /, которое каждому элементу х G X сопоставляет один и только один элемент у G У, называется функцией и записывается у = f (ж), х G X или f : X -> У. Говорят еще, что функция f отображает множество X на множество У.
Рис. 98
Например, соответствия fug, изображенные на рисунке 98 а и б, являются функциями, а на рисунке 98 в и г — нет. В случае в — не каждому элементу х G X соответствует элемент у е У. В случае г не соблюдается условие однозначности.
Множество X называется областью определения функции f и обозначается D(f). Множество всех у е У называется множеством значений функции / и обозначается E(f ).
14.2. Числовые функции. График функции.
Способы задания функций
Пусть задана функция f : X —> У.
Если элементами множеств X и У являются действительные числа
(т. е. X С R и У С К), то функцию f называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать У = /(ж).
Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от ж). От
120
носительно самих величин хну говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от .г пишут в виде у = у(х), не вводя новой буквы (/) для обозначения
зависимости.
Частное значение функции f(x) при х = а записывают так: /(а). Например, если /(а;) = 2т2 — 3, то /(0) = —3, /(2) = 5.
Графиком функции у = f(x) называется множество всех точек плоскости Оху, для каждой из которых ж является значением аргумента, а у — соответствующим значением функции.
Например, графиком функции у = х/1 — ж2 является верхняя полуокружность радиуса R = 1 с центром н 0(0; 0) (см. рис. 99).
Чтобы задать функцию у = /(.т), необходимо указать правило,
позволяющее, зная х, находить соответствующее значение у.
Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
Аналитический способ: функция задается в виде одной или нескольких формул или уравнений.
Например:
1)5 = я/?2;
2)У = <
х2 + 1
х — 4
при х < 2, при х 2;
3) у2 - 4х = 0.
Если область определения функции у = /(ж) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. Так, областью определения функции у — х/1 — ж2 является отрезок [—1; 1].
Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию у = f(x).
Графический способ: задается график функции.
Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.
Преимуществом графического задания является его наглядность, недостатком — его неточность.
Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные
121
таблицы значений тригонометрических функций, логарифмические таблицы.
На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.
14.3. Основные характеристики функции
1. Функция у = f(x), определенная на множестве D, называется четной, если Мх £ D выполняются условия —х € D и f(—x) = = f(x); нечетной, если V® G D выполняются условия —х 6 D и /(-ж) = -/(ж).
График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.
Например, у = х2, у = х/1 4- х2, у = 1п|®| — четные функции; а у = sin®, у = х3 — нечетные функции; у = х — 1, у = у/х — функции общего вида, т. е. не четные и не нечетные.
р5| 2. Пусть функция у = f(x) определена на множестве D и пусть
Г>1 С D. Если для любых значений ®i,®2 € D} аргументов из неравенства Xj < Х2 вытекает неравенство: /(®i) < /(®2), то функция называется возрастающей на множе-
,у стве Pi; /(®i) /(®2), то функция на-
зывается неубывающей на множестве .s ] £>i; /(®i) > /(®2), то функция назы-
1 х. /Г ! вается убывающей на множестве Di;
; \ _/ [ ] /(ti) /(тг), то функция называется
J / [ I невозрастающей на множестве .
—Г — —|1------------Г—— Например, функция, заданная гра-
фиком (см. рис. 100), убывает на интер-
Рис. 100 вале (—2; 1), не убывает на интервале
(1; 5), возрастает на интервале (3; 5).
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве £*i называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности. На рисунке (выше) функция строго монотонна на (—2; 1) и (3; 5); монотонна на (1; 3).
3. Функцию у = f(x), определенную на множестве D, называют ограниченной на этом множестве, если существует такое число М > 0, что для всех х G D выполняется неравенство |/(®)| М (короткая запись: у = f(x), х G D, называется ограниченной на D, если ЭМ > 0 : \/х G D => |/(ят)| М). Отсюда следует, что график
ограниченной функции лежит между прямыми у = —М и у = М (см. рис. 101).
122
р5| 4. Функция у = f(x), определенная на множестве D, называется периодической на этом множестве, если существует такое число
Т > 0, что при каждом х € D значение (х + Т) е D и f(x + Т) = f(x). При этом число Т называется периодом функции. Если Т — период функции, то ее периодами будут также числа тп Т, где m = ±1; ±2,... Так, для у = sin х периодами будут числа ±2тг; ±4тг; ±6тг,... Основной период (наименьший положительный) — это период Т — 2тг. Вообще обычно за основной период берут наименьшее положительное число Т, удовлетворяющее равенству f(x + T) = /(ж).
14.4. Обратная функция
Пусть задана функция у = /(ж) с областью определения D и множеством значений Е. Если каждому значению у € Е соответствует единственное значение х € D, то определена функция х = tp(y) с областью определения Е и множеством значений D (см. рис. 102). Такая функция <£>(?/) называется обратной к функции f(x) и записывается в следующем виде: х = ip(y) — У”1 (у). Про функции у = f(x) и х ~ ip(y) говорят, что они являются взаимно обратными. Чтобы найти функцию х = </9(у), обратную к функции у = У(.т), достаточно решить уравнение У (ж) = у относительно х (если это возможно).
Примеры-.
1. Для функции у = 2х обратной функцией является функция
Х=ЪУ'
2. Для функции у = х2, х е [0; 1], обратной функцией является х = y/у-, заметим, что для функции у = ж2, заданной на отрезке [—1; 1], обратной не существует, т. к. одному значению у соответствует два значения х (так, если у = i, то Xi = х% = — i).
123
|@| Из определения обратной функции вытекает, что функция у = /(ж) имеет обратную тогда и только тогда, когда функция f (ж) задает взаимно однозначное соответствие между множествами D и Е. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Заметим, что функция у = f(x) и обратная ей х = tp(y) изображаются одной и той же кривой, т. е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т. е. аргумент) обозначить через х, а зависимую переменную через у, то функция обратная функции у = /(ж) запишется в виде у = <р(х).
Это означает, что точка Mi (xq ; у0) кривой у = f(x) становится точкой М2(уо;®о) кривой у = ^(®)- Но
точки Mi и М2 симметричны относительно прямой у = х (см. рис. 103). Поэтому графики взаимно обратных функций у = f(x) ну = <р(х) симметричны относительно биссектрисы первого и третьего координатных углов.
14.5. Сложная функция
|^| Пусть функция у = f(u) определена на множестве D, а функция и = ip(x) на множестве Di, причем для V.t € Di соответствующее значение и = ^(х) € D. Тогда на множестве Di определена функция и = f(ip(x)), которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функций).
Переменную и = р(х) называют промежуточным аргументом сложной функции.
Например, функция у = sin2x есть суперпозиция двух функций у = sin и и и = 2х. Сложная функция может иметь несколько промежуточных аргументов.
14.6. Основные элементарные функции и их графики
Основными элементарными функциями называют следующие функции.
1) Показательная функция у = ах, а > 0, а ф 1. На рис. 104 показаны графики показательных функций, соответствующие различным основаниям степени.
124
2) Степенная функция у = ха, а € К. Примеры графиков степенных функций, соответствующих различным показателям степени, предоставлены на рис. 105.
125
3) Логарифмическая функция у = \ogax, а > 0, а ф 1; Графики логарифмических функций, соответствующие различным основаниям, показаны на рис. 106.
4) Тригонометрические функции у = sina:, у = cosa:, у — tgx, у = = ctga:; Графики тригонометрических функций имеют вид, показанный на рис. 107.
5) Обратные тригонометрические функции у = arcsina:, у = = arccosa:, у = arctgar, у = arcctga:. На рис. 108 показаны графики обратных тригонометрических функций.
|^5| Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия функции от функции, называется элементарной функцией. Примерами элементарных функций могут служить функции
y = 3cos'/®; у = arcsinl_ у = ig(2 _|_ ж3).
X
126
у = signa: —
Примерами неэлементарных функций могут служить функции
1, х > 0, ( 2 п
1 х + 1, если х < U,
О, х = 0, у = <
I х, если х > О:
-1, х < 0; '
о»3 ,v»5 ф7
+ —-------— + • I • 4- (-1)п---------------+ ...
3! 3 5! • 5 71-7 1 } (2п + 1)! • (2п + 1)
§ 15. ПОСЛЕДОВАТЕЛЬНОСТИ
15.1. Числовая последовательность
|^| Под числовой последовательностью Х1,Х2,Хз,...,хп,--- понимается функция -------------------
хп = f(n), (15-1)
заданная на множестве N натуральных чисел. Кратко последовательность обозначается в виде {жи} или хп, п G N. Число .ti называется первым членом (элементом) последовательности, х? — вторым,..., хп — общим или п-м членом последовательности.
Чаще всего последовательность задается формулой его общего члена. Формула (15.1) позволяет вычислить любой член последовательности по номеру п, по ней можно сразу вычислить любой член последовательности. Так, равенства
1 ТЬ — 1
vn = n2 + l, zn = (-1)” • п, уп = -, ип =----, п е N
п п
127
задают соответственно последовательности
vn = {2,5,10,..., п2 + 1,...}; zn = {-1,2, -3,4,, (-1)" п,... };
г 1 1 1 1 I ( 1 2 3 4 5 п-1 1
Уп — — |’ Un — ]б, >•••(•
1234 п ) 123456 п J
|^| Последовательность {хп} называется ограниченной, если суще-. ствует такое число М > 0, что для любого п е N выполняется неравенство
м.
В противном случае последовательность называется неограниченной. Легко видеть, что последовательности уп и ип ограничены, a vn и zn — неограничены.
|ф| Последовательность {ж,,} называется возрастающей (неубывающей), если для любого п выполняется неравенство «п )1 > а„
(an+i ап). Аналогично определяется убывающая (невозрастающая) последовательность.
Все эти последовательности называются монотонными последовательностями. Последовательности vn, уп и ип монотонные, а zn — не монотонная.
Если все элементы последовательности {жп} равны одному и тому же числу с, то ее называют постоянной.
Другой способ задания числовых последовательностей — рекуррентный способ. В нем задается начальный элемент xi (первый член последовательности) и правило определения к-го элемента по (п - 1)-му:
3>п = /(Жп-1).
Таким образом, х% = /(®i ), хз = /(жг) и т. д. При таком способе задания последовательности для определения 100-го члена надо сначала посчитать все 99 предыдущих.
15.2. Предел числовой последовательности
Можно заметить, что члены последовательности ип неограниченно приближаются к числу 1. В этом случае говорят, что последовательность ип, п е N стремится к пределу 1.
р5| Число а называется пределом последовательности {ж„}, если для любого положительного числа е найдется такое натуральное число N, что при всех п > N выполняется неравенство
|жп — а| < £. (15.2)
В этом случае пишут liin хп = 1ппж„ = а или хп —> а и говорят, что п—>оо
последовательность {жп} (или переменная хп, пробегающая последовательность Ж1, Я2, жз,...) имеет предел, равный числу а (или хп стремится к а). Говорят также, что последовательность {жп} сходится к а.
128
Коротко определение предела можно записать так:
(Ve > О ЭЛ;Г : \/п > N => |.т„ — «| < е)
lira хп = а. п—>оо
Пример 15.1. Доказать, что lim -—1 = 1. n—>ос П
Q Решение: По определению, число 1 будет пределом последовательности хп ~ п € N, если Ve > 0 найдется натуральное число IV, - 11 п I
Е. Оно справедливо для всех п > -, т. е. для всех п > N = £
— целая часть числа 1 (целая часть числа х, обозначаемая [яг],
такое, что для всех п > N выполняется неравенство | т. е. 1 п
Где
|есть наибольшее целое число, не превосходящее х; так [3] = 3, [5,2] — 5).
Если е > 1, то в качестве N можно взять Г-11 + 1.
Le J
Итак, Ve > 0 указано соответствующее значение N. Это и доказывает, что lim п = * = 1. •
I п—>ос 'Л
О
Заметим, что число N зависит от Е. Так, если е = то
Н1-*
26 .3.
N =
если е = 0,01, то
= [100]= 100.
’ 1 т ~ 26 J
1 ~т~ 100
Поэтому иногда записывают N = N(e).
Выясним геометрический смысл определения предела последовательности.
Неравенство (15.2) равносильно неравенствам — е < хп — а < е или а — е < хп < а + е, которые показывают, что элемент хп находится в Е-окрестности точки а.
хп
—( I +Н111ПМЖ--1- ।—)-----•»
а—е а а+е х
Рис. 109
Поэтому определение предела последовательности геометрически можно сформулировать так: число а называется пределом последовательности {.'си], если для любой Е-окрестности точки а найдется натуральное число N, что все значения хп, для которых п > N, попадут в Е-окрестность точки а (см. рис. 109).
5 Конспект лекций по высшей математике. Полный курс
129
Ясно, что чем меньше е, тем больше число N, но в любом случае внутри s-окрестности точки а находится бесконечное число членов последовательности, а вне ее может быть лишь конечное их число. |@| Отсюда следует, что сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела, называется расходящейся. Таковой является, например, последова-1 тельность vn (см. с. 128). j
Постоянная последовательность хп = с, п е N имеет предел, рав-., ный числу с, т. е. lim с — с. Действительно, для Ve > О при всех нату-j ральных п выполняется неравенство (15.2). Имеем |®п — с| — |с — с| =1 = 0 < Е. . I
15.3. Предельный переход в неравенствах ;
Рассмотрим последовательности {жп}, {уп} и {zn}.
Теорема 15.1. Если lim хп = a, lim уп = b и, начиная с некоторого 71-400 П—>ОО
номера, выполняется неравенство хп уп, то а Ь.
Q Допустим, что а > Ь. Из равенств lim хп = а и lim уп — b следует, п-4оо п—>оо
что для любого е > 0 найдется такое натуральное число N(e), что при всех п > N(s) будут выполняться неравенства |жп — а| < е и \уп — Ь| < £, т. е. а — E<xn<a+Ewb — е < уп < Ъ + е. Возьмем Е = в^. Тогда: хп>а-Е = а- т. е. хп > куп<Ь + Е = Ь+
т. е. уп < Отсюда следует, что хп > уп. Это противоречит условию
хп Уп- Следовательно, а < 6.
Теорема 15.2. Если lim хп = a, lim уп = а и справедливо нера-71-400 71-400
венство хп zn уп (начиная с некоторого номера), то lim zn — а. 72-400
(Примем без доказательства.)
15.4. Предел монотонной ограниченной последовательности. Число е. Натуральные
логарифмы
Не всякая последовательность имеет предел. Сформулируем без доказательства признак существования предела последовательное™.
130
Теорема 15.3 (Вейерштрасс). Всякая монотонная ограниченная последовательность имеет предел.
В качестве примера на применение этого признака рассмотрим последовательность хп = (1 4- — , п € N.
По формуле бинома Ньютона
(а + Ь)п = ап + ~ ап^ b + - ап~2 -Ь2 + ...
п(п - 1)(п - 2)... (п - (п - 1)) „ 1-2-3.............п
Полагая а = 1, b = i, получим
f1,1V-ij-n 1 n(n-l) 1 п(п-1)(п-2) 1
V I n 1-2 п2 1-2-3 ‘п3
п(п — 1)(и — 2)... (п — (п — 1)) 1
1-2-3.....п пп
или
Из равенства (15.3) следует, что с увеличением п число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении п число убывает, поэтому величины (1—i), (1—...возрастают. Поэтому последовательность {.т„} = { (1+} — возрастающая, при этом п
(1 + 1) > 2. (15.4)
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства (15.3) на единицу; правая часть увеличится, получим неравенство
7 1\« 11 1
(1-1— ) <1 + 1 + -—- + -—-—- 4 1- - -------------•
\ п) 1-2 1-2-3 1-2-3......п
131
Усилим полученное неравенство, заменив числа 3, 4, 5,..., стоящие в знаменателях дробей, числом 2:
/ 1\" , / 1 1 1 \
(1+гс) <1 + (1+2+?+" + F=T)-
Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:
1 1
1+2 + ^ + ‘” +
1 _1.(1-(1)")
1 - 1
< 2.
Поэтому , _. п
(14-1) <14-2 = 3. (15.5)
Итак, последовательность ограничена, при этом для Vn € N выполняются неравенства (15.4) и (15.5):
2<(1 + 1)”<3
Следовательно, на основании теоремы Вейерштрасса последовательность хп = (1 4- 1) , п € N, имеет предел, обозначаемый обычно буквой е: . 1 „
Нш (14— ) = е. (15.6)
п-кю \ п/
Число е называют неперовым числом. Число е иррациональное, его приближенное значение равно 2,72 (е = 2,718281828459045...). Число е принято за основание натуральных логарифмов: логарифм по основанию е называется натуральным логарифмом и обозначается Ins, т. е. In х = loge х.
Найдем связь между натуральным и десятичным логарифмами. По определению логарифма имеем х = е1пж. Прологарифмируем обе части равенства по основанию 10:
lgгг = lg(elnж), т. е. Igs = 1ns • Ige.
Пользуясь десятичными логарифмами, находим 1g е к. 0,4343. Значит, 1g х « 0,4343 • In х. Из этой формулы следует, что In х и 4343 т- е-Ins r; 2,3026Igs. Полученные формулы дают связь между натуральными и десятичными логарифмами.
§16. ПРЕДЕЛ ФУНКЦИИ
16.1. Предел функции в точке
Пусть функция у = /(s) определена в некоторой окрестности точки So, кроме, быть может, самой, точки xq.
132
Сформулируем два, эквивалентных между собой, определения пре-цела функции в точке.
|'5| Определение 1 (на «языке последовательностей», или по
Гейне). Число А называется пределом функции у = f(x) в точке х0 (или при х -> ж0), если для любой последовательности допустимых значений аргумента хп, п е N (хп х0), сходящейся к х0 (т. е. lim хп = жо), последовательность соответствующих значений функ-II->ос ции f (хп), п е N, сходится к числу А (т. е. lira f(xn) = А).
п—>сю
В этом случае пишут lira f(x) — А или /(ж) —> А при х —> жо-Х—УХо
Геометрический смысл предела функции: lim f(x) = А означает, что X—
для всех точек х, достаточно близких к точке ж0, соответствующие значения функции как угодно мало отличаются от числа А.
Определение 2 (на «языке Е-ё», или по Коши). Число А называется пределом функции в точке жо (или при х —> жо), если для любого положительного е найдется такое положительное число ё, что для всех х ф жо, удовлетворяющих неравенству |ж — жо| < ё, выполняется неравенство |/(ж) — А| < е.
Записывают lim /(ж) = А. Это определение коротко можно запи-
Х—>Хо сать так:
Ve > 0 3<5 > 0 Уж :
|ж — ж0| < <5, ж жо => или 0 < |ж — Жо| < ё
|/(ж) - А| < Е
<=> lim /(ж) = А.
X—
Геометрический смысл предела функции: А = lim /(ж), если для X—^Xq
любой s-окрестности точки А найдется такая ^-окрестность точки ж0, что для всех ж ж(| из этой ^-окрестности соответствующие значения функции /(ж) лежат в s-окрестности точки А. Иными словами, точки графика функции у — f(x) лежат внутри полосы шириной 2е, ограниченной прямыми у = А + е, у = А — е (см. рис. 110). Очевидно, что величина ё зависит от выбора е, поэтому пишут ё = <5(е).
Пример 16.1. Доказать, что 1пп(2ж — 1) — 5.
Q Решение: Возьмем произвольное е > 0, найдем ё — <5(е) > 0 такое, что для всех ж, удовлетворяющих неравенству |ж — 3| < ё, выполняется неравенство |(2ж—1) —5| < е, т. е. |ж—3| < Взяв ё = видим, что для всех ж, удовлетворяющих неравенству |ж — 3| <<’) (= выполняется неравенство |(2ж — 1) - 5| < е. Следовательно, 1пп(2ж — 1) = 5. •
133
Пример 16.2. Доказать, что, если /(ж) = с, то lim с = с.
Х~>Жо
Q Решение: Для Vs > О можно взять \/ё > 0. Тогда при |ж - ж0| < ё,
х хо имеем |/(ж) — с| = |с — с| = 0 < е. Следовательно, lim с = с. • х—YXq
16.2. Односторонние пределы
В определении предела функции lim fix') — А считается, что х х—1хо
стремится к жо любым способом: оставаясь меньшим, чем хо (слева, от ж0), большим, чем х0 (справа от ж0), или колеблясь около точки хо-
Бывают случаи, когда способ приближения аргумента х к х0 существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
р5| Число Л1 называется пределом функции у = /(ж) слева в точке ж0, если для любого число е > 0 существует число ё = й(е) > 0 такое, что при ж € (жо — <5; rcG), выполняется неравенство |/(ж) — Ai| < < е. Предел слева записывают так: lim /(ж) = Aj или коротко: х—>х0 — О
/(жо — 0) = А] (обозначение Дирихле) (см. рис. 111).
Аналогично определяется предел функции справа, запишем его с помощью символов:
(Vs > 0 Эй = й(е) \/ж е (ж0; ж0 + й) => |/(ж) - Л2| < е) <=>
Ит /(ж) = Л2.
ж-—>жо4-О
Коротко предел справа обозначают /(ж0 + 0) = А2.
134
|,‘5| Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует lim /(ж) = А, то существу-х—
ют и оба односторонних предела, причем А — Ai = А2.
Справедливо и обратное утверждение: если существуют оба предела f (х0 ~0) и f (х0 +0) и они равны, то существует предел А — lim /(ж) х—>2Го и А = f(x0 - 0).
Если же Ai Аг, то lim /(ж) не существует.
X—
16.3. Предел функции при х -> оо
Пусть функция у — f(x) определена в промежутке (—оо; оо). Число
А называется пределом функции f(x) при х —> оо, если для любого положительного числа е существует такое число Л/ = Л/ (е) > 0, что при всех х, удовлетворяющих неравенству |ж| > М выполняется неравенство |/(ж) — А| < е. Коротко это определение можно записать так: ________________________________________________
(Ve>03M>0\/ж: |ж|>7И => |/(я)-А|<е') <==> lim f(x) = A. \ / х—lOO
Если х —> +оо, то пишут А = lim f(x), если ж —> —оо, то — А = х—>+оо
= lim /(ж). Геометрический смысл этого определения таков: для х~->—оо
\/е > О ЗМ > 0, что при ж G (—оо; — М) или ж 6 (М;+оо) соответствующие значения функции /(ж) попадают в е-окрестность точки А, т. е. точки графика лежат в полосе шириной 2е, ограниченной прямыми у=А + еиу = А- е (см. рис. 112).
Рис. 112
16.4. Бесконечно большая функция (б.б.ф.)
|^| Функция у = /(ж) называется бесконечно большой при ж -> ж0, если для любого числа М > 0 существует число ё = ё(М) > 0, что для всех ж, удовлетворяющих неравенству 0 < |ж—ж0| < ё, выполняется
135
неравенство |f (ж)| > M. Записывают lim f(x) = oo или f{x) —> oo при X—>#0
x —> x0. Коротко:
> 0 3<5 > 0 Vx : |ж — x0| < 6, x xo => |/(ж)| > Afj <=>
<=> lim f(x) — oo.
X }XQ
Например, функция у = —есть б.б.ф. при х —> 2. Ж Li
Если /(ж) стремится к бесконечности при х —> х0 и принимает лишь положительные значения, то пишут lim f(x) — +оо; если лишь
X—>5Со отрицательные значения, то lim f(x) = —oo. x—txo
Функция у = f(x), заданная на всей числовой прямой, называется бесконечно большой при х оо, если для любого числа М > О найдется такое число N = N(M) > 0, что при всех х, удовлетворяющих неравенству |ж| > JV, выполняется неравенство \f (ж)| > М. Коротко: (VM >0 3N> 0 Ух: \х\ > N => |/(ж)| > м} <=> lim f(x) = oo. \ / х—>ос
Например, у = 2х есть б.б.ф. при х оо.
Отметим, что если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т. е. х G N, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность ип = п2 + 1, п € N, является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки ж0 является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у = х sin х.~)
Однако, если lim f(x) — А, где А — конечное число, то функция X—>Жо
/(ж) ограничена в окрестности точки xq.
Действительно, из определения предела функции следует, что при х —> ж() выполняется условие |/(ж) — А| < е. Следовательно, А — е < < f(x) < А + е при х G (жо — е; х0 + е), а это и означает, что функция /(ж) ограничена.
§17. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ (Б.М.Ф.)
17.1. Определения и основные теоремы
Функция у — f(x) называется бесконечно малой при ж —> ж(),
если
lim /(ж) = 0.
Х-^Хо
(17.1)
136
По определению предела функции равенство (17.1) означает: для любого числа £ > 0 найдется число 6 > 0 такое, что для всех х, удовлетворяющих неравенству 0 < |ж — ж0| < <5, выполняется неравенство (ж)| < Е.
Аналогично определяется б.м.ф. при х —> х0 4- 0, х —> х() — О, х +оо, х —> —оо: во всех этих случаях f(x) —> 0.
Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами а,ри т. д.
Примерами б.м.ф. служат функции у = ж2 при х —> 0; у = х — 2 при х —> 2; у = sin ж при х -4 тг/г, k € Z.
Другой пример: хп = п G N, — бесконечно малая последовательность.
Теорема 17.1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Q Пусть о-(ж) и /3(х) — две б.м. функции при х —> ж0. Это значит, что lim о (ж) = 0, т. е. для любого е > 0, а значит, и § > 0 найдет-ся число <51 > 0 такое, что для всех ж, удовлетворяющих неравенству О < |ж — ж0| < <51, выполняется неравенство £
|«(ж)| < - (17.2)
и lim /3(ж) = 0, т. е.
х—>Xq
(у| > О Э<52 > 0 Уж : 0 < |ж - ж0| < <52) => |0(*)| < |- (17-3)
Пусть <5 — наименьшее из чисел <51 и <5-2. Тогда для всех ж, удовлетворяющих неравенству 0 < |ж — жо| < <5, выполняются оба неравенства (17.2) и (17.3). Следовательно, имеет место соотношение £ £
|а(ж) 4- /?(ж)| $ |а(ж)| 4- |/3(ж)| < - 4- - = е.
Таким образом,
Уе > О Э<5 > 0 Уж : 0 < |ж — ж0| < <5 ==> |о(ж) 4- /3(ж)| < е.
Это значит, что lim (а(ж) 4- /?(ж)) = 0, т. е. а(ж) 4- Дж) — б.м.ф. при Х-УХо
X —> Жо-
Аналогично проводится доказательство для любого конечного числа б.м. функций.
Теорема 17.2. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
137
[_j Пусть функция f (ж) ограничена при х —> жо- Тогда существует такое число М >0, что
|f (ж)| М (17.4)
для всех х из «^-окрестности точки х0. И пусть а(х) — б.м.ф. при х —> хо. Тогда для любого е > 0, а значит, и -^ > 0 найдется такое число <5-2 > 0, что при всех ж, удовлетворяющих неравенству 0 < < |ж — жо| < й'2, выполняется неравенство
!«(*)! <
(17.5)
Обозначим через ё наименьшее из чисел Ф и ф Тогда для всех ж, удовлетворяющих неравенству 0 < |ж — жо| < ф выполняются оба неравенства (17.4) и (17.5). Следовательно, |/(ж)-О!(ж)| = |Дж)|-|а(ж)| < < • М = е. А это означает, что произведение /(ж) си(ж) при ж —> ж0
есть бесконечно малая функция.
Следствие 17.1. Так как всякая б.м ф. ограничена, то из теоремы (17.2) вытекает: произведение двух б.м.ф. есть функция бесконечно малая.
Следствие 17.2. Произведение б.м.ф. на число есть функция бесконечно малая.
Теорема 17.3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Q Пусть lira о(ж) = 0, a lim /(ж) — а 0. Функция -77-у может быть X—>«о Х-+Х0 J\%)
представлена в виде произведения б.м.ф. о(ж) на ограниченную функцию . Но тогда из теоремы (17.2) вытекает, что частное =
= о(ж) есть функция бесконечно малая.
Покажем, что функция ограниченная. Возьмем е < |а|. Тогда, на основании определения предела, найдется ё > 0, что для всех ж, удовлетворяющих неравенству 0 < |ж — жф < ё, выполняется неравенство |f (ж) — а| < е. А так как е > |f (ж) - а| = |а - f (ж)| > |д| — |f (ж)|,
138
то |«1 — |/(ж)1 < е> т- е- I/(ж)1 > |а| — е > 0. Следовательно,
/(ж)1 |/(ж)| < |«| - е
г. е. функция
— ограниченная.
Теорема 17.4. Если функция а(ж) — бесконечно малая (о ф 0), то функция есть бесконечно большая функция и наоборот: если функция /(ж) — бесконечно большая, то у^у — бесконечно малая.
Q Пусть а(ж) есть б.м.ф. при х —> хо, т. е. lim а(х) — 0. Тогда
Х—ЬХо
(Ve > 0 Зй > 0 \/х : 0<|ж — ж0| < <^
=> |«О)| < Е,
т. е. —I—г > i, т. е. 7—г > М, где М = i. А это означает, что функ-
| CV (57) I £7 | 157} | £7
ция —Дт есть бесконечно большая. Аналогично доказывается обратное а(х)
утверждение. И
Замечание: Доказательства теорем приводились для случая, когда х —> Хо, но они справедливы и для случая, когда х —> оо.
Пример 17.1. Показать, что функция f(x) = (х- I)2 sin3 при х —> 1 является бесконечно малой.
Q Решение: Так как lim (ж — I)2 = 0, то функция ^(х) — (х — I)2 есть х—>1 о 1
бесконечно малая при х —> 1. Функция р(ж) — sin -Д’ х 1> ограничена |sin3 — Д j | С 1.
Функция /(ж) = (х — I)2 • sin3 * представляет собой произведение ограниченной функции (р(ж)) на бесконечно малую (^(ж)). Значит, /(ж) — бесконечно малая при х —> 1. •
139
17.2. Связь между функцией, ее пределом и бесконечно малой функцией
Теорема 17.5. Если функция /(ж) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции а(ж), т. е. если lim /(ж) — А, то f (ж) = А 4- а(х).
X—^XQ
Q Пусть lim /(ж) = А. Следовательно, Х—ЬХо '
(Уе > 0 Эй > О Х/ж: 0 < |ж — ж0| < й) => |/(ж) — А| < е,
т. е. |/(ж) — А — 0| < е. Это означает, что функция f(x) — А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через а(ж): f (ж) — А = а(ж). Отсюда /(ж) = А + а(х). Ц
Теорема 17.6 (обратная). Если функцию /(ж) можно представить в виде суммы числа А и бесконечно малой функции а(ж), то число А является пределом функции /(ж), т. е. если /(ж) — А + а(ж), то lim /(ж) = А.
Х~>Жо
□ Пусть /(ж) = Л+а(ж), гдеа(ж)—б.м.ф. при ж -> жо, т. е. lim о(ж) = X—
= 0. Тогда
>0 Эй > 0 Х/ж: 0 < |ж — жо| < й) => |а(ж)| < е.
А так как по условию /(ж) = А + а(ж), то о(ж) = /(ж) — А. Получаем
(\/е > 0 Эй > 0 \/ж : 0 < |ж — Жо| < й) => |/(ж) — А\ < е.
А это и означает, что lim /(ж) = А.
х—>ЖО
Пример 17.2. Доказать, что lim (5 + ж) = 7.
х—>2
Q Решение: Функцию 5 + ж можно представить в виде суммы числа 7 и б.м.ф. ж — 2 (при ж -> 2), т. е. выполнено равенство 5 + ж = 7 + (ж — 2). Следовательно, по теореме 17.6 получаем lim (5 + ж) = 7. •
140
17.3. Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределов функции. Формулировка и доказательство теорем для случаев, когда х -» яд и х -> оо, аналогичны. В приводимых теоремах будем считать, что пределы lim /(ж), lim у>(ж) существуют.
X—X—*Xq
Теорема 17.7. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
lim (/(ж) ± у?(ж)) = lim /(ж) ± lim у?(ж).
х—>Хо х—>Ж() ж—>жо
Q Пусть lim /(ж) = A, lim <£>(ж) = В. Тогда по теореме 17.5 о свя-ж—>Жо X—>Жо
зи функции, ее предела и б.м.ф. можно записать /(ж) = А + а(ж) и у>(ж) = В + /3(ж). Следовательно, /(ж) + у>(ж) = А + В + (а(ж) + /?(ж)). Здесь а(ж) + /3(ж) — б.м.ф. как сумма б.м.ф. По теореме 17.6 о связи функции, ее предела и б.м.ф. можно записать lim (/(ж)+<р(ж)) = А + В, X—^Xq
т. е.
lim (/(ж) + 9?(ж)) — lim /(ж) + lim <^(ж).
X —>жо Х—^Хо х—
В случае разности функций доказательство аналогично.
Теорема справедлива для алгебраической суммы любого конечного числа функций.
Следствие 17.3. Функция может иметь только один предел при ж -> ж0.
Q Пусть lim /(ж) — А и lim /(ж) = В. По теореме 17.7 имеем: X—X—>Жо
О = lim (/(ж) - /(ж)) = lim /(ж) - lim /(ж) = А — В. X—^XQ X—^Xq х—>Жо
Отсюда А — В = 0, т. е. А = В.
Теорема 17.8. Предел произведения двух функций равен произведению их пределов:
lim (/(ж) 9?(ж)) = lim /(ж) lim </>(ж).
х—>Жо Х—^Хо х—>Жо
141
Ql Доказательство аналогично предыдущему, проведем его без особых пояснений. Так как lim /(ж) = A, lim <Дж) = В, то
Ж—>Ж() х—>Жо
/(ж) = А + а(ж), <Дж) = В + /?(ж),
где а(ж) и /3(ж) — б.м.ф. Следовательно,
/(ж) • <Дж) = (А + а(ж)) • (В + £(ж)),
т. е.
/(ж) • Дж) = АВ + (А • /3(ж) + В • о (ж) + а(ж)/3(ж)).
Выражение в скобках есть б.м.ф. Поэтому
lim /(ж) Дж) = А • В,
х—>жо
т. е.
lim (/(®)</’(ж)) = lim /(ж) lim Дж).
X—>Жо Ж—>Жо ж—>Жо
• Отметим, что теорема справедлива для произведения любого конечного числа функций.
Следствие 17.4. Постоянный множитель можно выносить за знак предела:
lim с - f(x) = с- lim Нж).
X—>Жо Ж—>Жо
□ lim (с-/(ж)) = lim с- lim /(ж) = с- lim /(ж), ж—>Жо Ж—>Жо ж—>Жо ж—>Жо
Следствие 17.5. Предел степени с натуральным показателем равен той же степени предела: lim (/(ж))’1 = ( lim /(ж)) В частности, Ж—>Жо \ж—>Жо /
lim хп = Xq, п € N.
Ж—>Ж0
□ lim (/(ж))” = lim (/(ж) • /(ж) ... /(ж)) = lim /(ж)-... - lim /(ж) =
Ж—>Жо Ж—>Жр^ _ у ж—>Жо ж—>Ж0
п сомножителей
= ( 1Ш1 /(ж)] .
\ж—>Жо /
Теорема 17.9. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:
Нж1 И?1 \
lim —7-т = ". -°- ( lim <р(ж) б).
X-+XQ ip(x) lim ip(x) \ж->жо /
142
:_j Доказательство аналогично предыдущему. Из равенств
lim f(x) = А и lim ip(x) = В / О
. X—>Ж() Х—^Хо
Вл ед у ют’ соотношения /(ж) = А + о(ж) и <Дж) = В + Р(х). Тогда
® /(ж) А + о(ж) _ А / А + а(ж) А \ _ А В а(ж) — А Р(х) ДД = В + /?(ж) ~ В + \В + /3(ж) “ в) ~ В + В2 + В /?(ж) '
Второе слагаемое есть б.м.ф. как частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел.
гл \ . г/ \ lim /(ж)
тт г f(X) А г JW) х->х0 _
Поэтому пm -/А — т. е. lim ) у = —р-----------т-у.
ж-лжо щж) В ж->ж0 <Дж) lim Дж)
X—^Xq
Рассмотрим пример.
Пример 17.3. Вычислить lim (Зж2 — 2ж + 7).
х—>1
Q Решение:
lim (Зж2 — 2ж + 7) = lim Зж2 — lim 2ж + lim 7 =
X—>1 х—>1 х—>1
= зГйтж^ — 2 lim ж + 7 = 3 • 1 — 2 + 7 = 8. •
\Ж->1 / X—>1
Пример 17.4- Вычислить lim х ^х—^2.
ж->2 Ж - 6ж + 8
Q Решение: Здесь применить теорему о пределе дроби нельзя, т. к. предел знаменателя, при ж —> 2, равен 0. Кроме того, предел числителя равен 0. В таких случаях говорят, что имеем неопределенность вида 2. Для ее раскрытия разложим числитель и знаменатель дроби на множители, затем сократим дробь на ж — 2 0 (ж —> 2, но ж 2):
, ж2 + 14ж —32 (ж — 2)(ж+16) 11ГП О 7.---Д- = 1]1П л- ^77------7V
®-»2 ж2 — 6ж + 8 г->2 (ж — 2)(ж — 4)
ж+ 16 lim(® + 16) 2 + 16 lim ------—--------------— = ———
х^>2 ж — 4 lim (ж — 4) 2 — 4
г->2
Пример 17.5. Вычислить lim +.3_ж + 1
г->оо 4ж + 2ж + 5
Q Решение: Здесь мы имеем дело с неопределенностью вида Для нахождения предела данной дроби разделим числитель и знаменатель
143
на х :
2ж2+Зж+1 2+1 + ^ М(2 + * + 1
ПН) ----------- ~ lim ----—----— — - —-.—------ — —.
ж->оо 4ж2 + 2х + 5 х-юо 4 + 2 + Л Пт (4 + 2 + 2'
х х ж—>оо х Х '
о 1
Функция 2 + есть сумма числа 2 и б.м.ф., поэтому
lim (2 + - 4- = 2; lim (4 + - + X) = 4.
х-гоо \ X X ' ,т->ос \ X X '
й
17.4. Признаки существования пределов
Не всякая функция, даже ограниченная, имеет предел. Например, функция у = sin® при х —> оо предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования предела.
Теорема 17.10 (о пределе промежуточной функции). Если функция /(ж) заключена между двумя функциями <д(ж) и д(ж), стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т. е. если
lim <р(х) — А, Um д(х) — А, (17.6)
х—X —>Жо
<Хж) < /(«) < р(ж), (17-7)
то
lim /(ж) — А.
X-iXQ
□ Из равенств (17.6) вытекает, что для любого е > 0 существуют две окрестности и точки жо, в одной из которых выполняется неравенство |<£>(ж) — Л| < е, т. е.
—£ < ср(ж) — А < £, (17.8)
а в другой |д(ж) - А| < е, т. е.
-е < д(х) - А < £. (17.9)
Пусть <5 — меньшее из чисел <51 и <$2- Тогда в ^-окрестности точки ®о выполняются оба неравенства (17.8) и (17.9).
Из неравенств (17.7) находим, что
д>(х) - А < /(ж) - А д(х~) - А. (17.10)
144
С учетом неравенств (17.8) и (17.9) из неравенства (17.10) следуют не-
равенства — е < f(x) — А < Мы доказали, что Ve > 0 3<5 > 0 Vж : е или | f (ж) — А| < е. 0 < |ж — Жо| < 8 => (ж) — А| < е,
то есть lim /(ж) = А.' х—
Теорему 17.10 иногда шутливо называют «принципом двух милиционеров». Роль «милиционеров» играют функции <д(ж) и <у(ж), функция /(ж) «следует за милиционерами».
Теорема 17.11 (о пределе монотонной функции). Если функция /(ж) монотонна и ограничена при х < жо или при х > жо, то существует соответственно ее левый предел lim /(ж) — — 0) или
х—>Ж()—0 ее правый предел lim /(ж) =/(жо + 0). х—>яо+0
Доказательство этой теоремы не приводим.
Следствие 17.6. Ограниченная монотонная последовательность хп, п € N, имеет предел.
17.5. Первый замечательный предел
При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел
ешж
hm ---- = 1
ж->0 X
(17.11)
|ф| называемый первым замечательным пределом. Читается: предел отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю. Докажем равенство (17.11).
□ Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х (см. рис. 113). Пусть 0 < ж < На рисунке |А7И| = вшж, дуга МВ численно равна центральному углу ж, |j3C'| = tgж. Очевидно, имеем S^mob < ^сектора мов < Влсов- На основании соответствующих формул геометрии получаем ^вшж < ^ж < itgж. Разделим неравенства на 1 sin ж > 0, получим 1 < - < —-— или cos ж < 8ШЖ < 1.
2 sm ж cos ж ж
145
Так как lim cos® = 1 и lim 1 = 1, то х—>0 х >0
по признаку (о пределе промежуточной функции) существования пределов
lim ^ = 1. (17.12)
аг-10 X (а:>0)
Пусть теперь х < 0. Имеем 8111 ж —
' ', где —х > 0. Поэтому
lim ж—>0 (Ж0)
sin#
х
(17.13)
Из равенств (17.12) и (17.13) вытекает равенство (17.11).
Пример 17.6. Найти lim :r>0 2®
Q Решение: Имеем неопределенность вида 2. Теорема о пределе дроби неприменима. Обозначим 3® = t; тогда при ® —> 0 и t -> 0, поэтому sin3® „ sint , 3 sint 3sint 3,3 '
lim ——— = Inn-----j- = lim - ----= - lim-----= -•! = -. •
ж->о 2® t->o 2 • | г-ю 2 t 2 £—>o t 2 2
Пример 17.7. Найти lim
х-Ю ®
z-. tg® sm® 1 sm® г™ , 1
(J Решение: lim---------= lim---------------= lim---------—--------- = 1- = 1.
я-Я) x ar—10 ® cos® ж->0 ® lim cos® 1
x—>0
17.6. Второй замечательный предел
/ i \n
Как известно, предел числовой последовательности хп = (J + — I п € N, имеет предел, равный е (см. (15.6)):
/ 1
lim (1 + - ) = е.
п—>00 \ Ц/
(17.14)
Докажем, что к числу е стремится и функция хп
X
при х ОО
(ж е К):
lim х—>оо К) X = е.
(17.15)
146
1. Пусть х —> 4-оо. Каждое значение х заключено между двумя
положительными целыми числами: п х < п 4- 1, где п = [ж] — это целая частью. Отсюда следует—< 1 < —,14------тт < 14-— 14-—,
п 4-1 х п 714-1 ж п
поэтому
п-Ы
Исли х —> 4-оо, то п —> оо. Поэтому, согласно (17.14), имеем:
j lim 1 + ^п-ь1 lim (1 4- -4) = \ ч
77 4-1/ hm(l 4- 41)
е
1 ~е
/ 1 \ п+] / 1V1 / 1 \
lim (14— ) = lim (14— ) - lim (14— ) = е 1 = е.
п->оо \ п/ п—юо \ п) п->оо \ п)
I Io признаку (о пределе промежуточной функции) существования пренилов
1чК
- = е.
lim
(17.16)
2. Пусть х —> — оо. Сделаем подстановку — х = t, тогда
lim
iV ..
— = Inn
- = lim
t
1
t- 1
1
1 t-1
= е • 1 = е. (17.17)
t->4-оо \ t — 1
Дз равенств (17.16) и (17.17) вытекает равенство (17.15).
Если в равенстве (17.15) положить 1 = а (а —> 0 при х —> оо), оно )апишется в виде
lim (14-a)° = e.
(17.18)
Равенства (17.15) и (17.18) называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием е. Функция у = ех называется экспоненциальной, употребляется также обозначение ех = ехр(ж).
(14-
\ х)
Пример 17.8. Найти lim
х—>00
Q Решение: Обозначим х = 2t, очевидно, t —> оо при х —> оо. Имеем
Z 2\ж / 1 \ 27
lim (1+-) = lim (14--) =
ж->оо\ х) t->oo\ t/
/ 1 \ / 1 \ л
= lim (14--) - lim (14--) =e-e = e2.
t->oo \ t/ t->oo \ Г/
147
§ 18. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
18.1. Сравнение бесконечно малых функций
Как известно, сумма, разность и произведение двух б.м.ф. ест функция бесконечно малая. Отношение же двух б.м.ф. может вести о бя различным образом: быть конечным числом, быть бесконечно бол шой функцией, бесконечно малой или вообще не стремиться ни к к: кому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть а = а(х) и /3 = /3(ж) есть б.м.ф. при х —> ®о, т. е. lira а(х)
X—УХо = 0 и lim /3(х) = 0.
1. Если lim ? = .4 О (Л £ К), то а и /3 называются бесконечч Х~>Жо Р
малыми одного порядка.
2. Если lira § = 0, то а называется бесконечно малой более выс Х~Р
кого порядка, чем /3.
3. Если lira % = оо, то а называется бесконечно малой более низ X—bXQ Р
кого порядка, чем /3.
4. Если lira не существует, то а и /3 называются несравнимым Х—^Хо Р
бесконечно малыми.
Отметим, что таковы же правила сравнения б.м.ф. при
Пример 18.1. Сравнить порядок функций а = З®2 и при X -» 00.
Q Решение: При х -> 0 это б.м.ф. одного порядка, так как
.. а г За;2 3 / п
lira — = lira----? = — / 0.
ж-»о /3 ж-»о 14аг 14
Говорят, что б.м.ф. « и Р одного порядка стремятся к нулю с одинаковой скоростью.
Пример 18.2. Являются ли функции а — З®4 и /3 = одного порядка при х —> О?
/3 = 14®
пример)
7х б.м.1
148
Q Решение: При х —> 0 функция а есть б.м.ф. более высокого порядка, чем В, так как lim % = lim = lim = 0. В этом случае б.м.ф. а ж-Ш р ж—>0 7ж ж-->0 7 J 'V
стремится к нулю быстрее, чем /3. *
Пример 18.3. Сравнить порядок функций а = tg® и fi — х2 при х -> 0.
Q Решение: Так как
a tg® sin® 1 1
lim — = lim —5- = lim------- ------- — = 00,
ж->о p ж->0 ®2 ®->o x cos x x
то а есть б.м.ф. более низкого порядка, чем /3.
Пример 18. Jt. Можно ли сравнить функции а = х sin i и /3 = х при х —> 0?
Q Решение: Функции о = ж • sin — и /3 = ж при х -> 0 являются не-
а г ж’8Й1ж г • 1
сравнимыми б.м.ф., так как предел lim = lim-------— = hm sin — не
ж—>0 р х—>0 X ж—>0 X
существует. •
18.2. Эквивалентные бесконечно малые и основные теоремы о них
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.
Р\| Если lim % = 1, то а и /3 называются эквивалентными беско-
LtJ х—>«о Р
нечно малыми (при х —> ®о); это обозначается так: а ~ р.
Например, sin® ~ х при х —> 0, т. к. lim - tg« x При
a—>0 X
x -> 0, т. к. lim = 1.
ж->0 X
Теорема 18.1. Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
□ Пусть а ~ а' и /3 ~ /3' при ж —> ®0- Тогда
lim — = lim
Х—УХо р X—^XQ
а а' Р'\
-p'oTJ')
г а г I3' с а' I . г а' lim — • lim — • lim — = 1 • 1 - hm ,
Ж—>Ж0 OLl ж->жо р ж->жо р' Ж->Жо р'
149
т. е. lim % = lim х—Иво Р Х-^Хо р
Очевидно также, что lim = lim % = lim %. Х—^Хо Р X—>Ж() Р X—НВо Р
Теорема 18.2. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.
Q Пусть а ~ Р при х -> Хо- Тогда
lim - = lim (1 - -) = 1 - lim ^ = 1-1=0,
X->XQ (У X-^XQ \ (У/ X-^XQ Ol
аналогично lim - -a =0.
X—P
Справедливо и обратное утверждение: если разность б.м.ф. а и Р есть бесконечно малая высшего порядка, чем а или р, то а и Р — эквивалентные бесконечно малые.
Действительно, так как lim ——— = 0, то lim (1—^1 = 0, т. е. ж—>жо (У х—>жо \ (У/
1 — lim = 0. Отсюда lim — = 1, т. е. а ~ р. Аналогично, если х—(У х—Ухо (У
lim — -д— = 0, то а- ~
х—>ЖО Р
Теорема 18.3. Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Q Докажем теорему для двух функций. Пусть а —> 0, /3 —> 0 при х —> хо, причем а — б.м.ф. высшего порядка, чем р, т. е. lim % = 0. ж—>Жо Р
Тогда
lim —_ цт + й = цт ^ + 1 = 0 + 1 = 1.
X->»<?. Р X-t-Хо \р / X-+XV р
Следовательно, а + Р ~ р при х —> х0.
Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой, суммы..
Замена суммы б.м.ф. ее главной частью называется отбрасыванием бесконечно малых высшего порядка.
Пример 18.5. Найти предел lim Зх Д 7х
ж—>0 S1I1ЛХ J
150
(J Решение: lim = lim 3^> = lim = 3 поскольку
ж->о sin 2x ®->o sin 2® k->o 2® 2 ’ J
3® + 7®2 ~ 3® и sin 2® ~ 2® при ж -> 0. *
18.3. Применение эквивалентных бесконечно малых функций
Вычисление пределов
Для раскрытия неопределённостей вида ~ часто бывают полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно, sin® ~ х при х -> 0, tg® ~ х при х -> 0. Приведем еще примеры эквивалентных б.м.ф.
___ 2
Пример 18.6. Покажем, что 1 — cos х ~ при х —> 0.
Q Решение:
lim х—>0
1 — COS X
2
= lim
х—>0
2sin2f _
Ж2 2
lim x—>0
sin f-
= 1-1 = 1.
(|->0)
sin |
X 2
Пример 18.7. Найдем lim ^rcsin x
Решение: Обозначим arcsin® = t. Тогда I [оэтому
x = sin t и t -> 0 при x -> 0.
,. arcsin® t „1
lim-------= lim-------= hm -r—r
ж-Ю x t->o sin t t-^o
Следовательно, arcsin x ~ x при x —> 0.
Пример 18.8. Покажем, что \/1 + x — 1 ~ при х -> 0.
Q Решение: Так как
V1 + ® — 1 ,. (л/1 + ® — 1) (х/1 + х + 1)
Li m----------= lim------------_------------- =
®-»о гс ^° | • (\/l + x +1)
x"Э-0 (\/l + x T 1) ж—>o ^/1 4- ® T 1 2
то \/l + ® — 1 ~ 2 ПрИ x —> o. •
Ниже приведены важнейшие эквивалентности, которые используются при вычислении пределов:
151
1. sin ж ~ x при x —> 0;
2. tga: ~ x (x —> 0);
3. arcsina: ~ x (x —> 0);
4. arctga: ~ x (x -> 0);
„2
5. 1 — cos a: ~ (x -> 0);
6. ex — 1 ~ x (x —> 0);
7. ax — 1 ~ x In a (x -> 0);
8. ln(l + x) ~ x {x -> 0);
9- loga(l + x) ~ x loga e (x -> 0);
10. (1 + x)k — 1 ~ к x, к > 0 (x —> 0); в частности, у/\ + х — 1 ~
Пример 18.9. Найти lim .
>о sm За:
Q Решение: Так как tg 2х ~ 2х, sin Зт ~ За: при х -» 0, то
, tg2x 2х 2
lim -—— = lim — = -
я->о sin За: ®-»о За: 3
Пример 18.10. Найти lira х(е^х — 1). х—>оо
Q Решение: Обозначим i = t, из х оо следует t —> 0. Поэтому lim xte1^ — 1) = lim i(e4 — 1) = lim - • t — lim 1 = 1. x—>oo t-->0 t t—>0 t t—>-0
Найти lim
Пример 18.11.
arcsin(a: — 1) x2 - 5x + 4
Q Решение: Так как arcsin(a: — 1) ~ (ж — 1) при x —> 1, to
arcsmfa: — 1) (x — 1) 1
lim —-------y- = lim -—-—— = lim -------
г->1 x2 — 5a: + 4 ®->i [x — l)(a: — 4) ®->i x — 4
Приближенные вычисления
Если a ~ /3, то, отбрасывая в равенстве a = /3 + + (a — /3) бесконечно малую более высокого порядка, т. е. а — /3, получим приближенное равенство о га /3.
Оно позволяет выражать одни бесконечно малые через другие. Приведенные выше важнейшие эквивалентности служат источником ряда приближенных формул.
Приведенные формулы справедливы при малых х, и они тем точнее, чем меньше х.
Например, графики функций y~tgxny = xB окрестности точки 0 практически не различимы (см. рис. 114), а кривая у = sin а: в окрестности точки 0
1
3’
Рис. 114.
tg «гая: (х—>0,
152
сливается с прямой у = х (рис. 115). На рисунках 116 118 проиллюстрированы некоторые из важнейших эквивалентностей, о которых говорилось выше.
Пример 18.12. Найти приближенное значение для In 1,032.
Q Решение: In 1,032 — 1п(1 + 0,032) ₽» 0,032 Для сравнения результата по таблице логарифмов находим, что In 1,032 = 0,031498... •
§ 19. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
19.1. Непрерывность функции в точке
Пусть функция у = f (ж) определена в точке хо и в некоторой окрестности этой точки. Функция у — /(ж) называется непрерывной в точке хо, если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.
lim f(x) = /(т0).
X—^Xq
(19.1)
153
Равенство (19.1) означает выполнение трех условий:
1) функция /(ж) определена в точке ®о и в ее окрестности;
2) функция f (т) имеет предел при х —> хщ
3) предел функции в точке хо равен значению функции в этс точке, т. е. выполняется равенство (19.1).
Так как lim х = xq, то равенство (19.1) можно записать в виде X—
lim /(ж) = /( lim х) = f(x0). (19.1
Х—ЬХо Х—ЬХо
Это означает, что при нахождении предела непрерывной функцс f(x) можно перейти к пределу под знаком функции, то есть в функци f(x) вместо аргумента х подставить его предельное значение xq.
тг 1* «in« lim s'^х ,, ,
Например, hm е ® = е®~*° = е. В первом равенстве функци
х~>0
и предел поменялись местами (см. (19.2)) в силу непрерывности фун ции ех.
Пример 19.1. Вычислить А = lim
я-Ю X
Q Решение:
1п(1+ж) 1 , ,, , ,-1/4
hm-----------= hm — • lii( 1 + х) = hm 1п(1 + x) * =
я—>0 X z—>0 X ®-»0
= ln(lim(l + a?)i) = hie = 1.
Отметим, что ln( I + ж) ~ x при x —> 0.
Можно дать еще одно определение непрерывности функции, oi
раясь на понятия приращения аргумента и функции.
Пусть функция y=f(x) опр делена в некотором интерв-.и (а;Ь). Возьмем произвольную ТО' ку Жо€(а;Ь). Для любого хе (ар разность х—хо называется прир гцением аргумента х в точке з и обозначается Дж («дельта х» Ах=х—Хо- Отсюда х=хо+Ах.
Разность соответствующе значений функций f(x)~ /(«о) н;
зывается приращением функци.
f(x) в точке х() и обозначается А
(или Af или Д/(а?о)): Ду=/(®)~ рис. 119).
/(«о) или Ду=/(ж0 + Д«)
/(ж0) (см.
Очевидно, приращения Да: и Ау могут быть как положительными,
так и отрицательными числами.
154
lim Ду = 0.
Дж-Ю
Запишем равенство (19.1) в новых обозначениях. Так как условия .с -> хо и х — хо —> 0 одинаковы, то равенство (19.1) принимает вид lim (/(яг) — /(яго)) = 0 или
.Г ->Жо
(19.3)
|>‘5| Полученное равенство (19.3) является еще одним определением непрерывности функции в точке: функция у = /(я?) называется непрерывной в точке хо, если она определена в точке яд и ее окрестности и выполняется равенство (19.3), т. е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Исследуя непрерывность функции в точке, применяют либо первое (равенство (19.1)), либо второе (равенство (19.3)) определение.
Пример 19.2. Исследовать на непрерывность функцию у = sin яг.
Q Решение: Функция у = sin х определена при всех я: € Ж.
Возьмем произвольную точку х и найдем приращение Ду:
Л . , * \ ( С±х\ . Ах
Ау = бш(я: 4- Дяг) - sin х = 2 cos I х + — 1 • sm —.
Тогда lim Ду = Бт 2cos(х + Ar I ’ sin Аг = 0, так как произ-
Дж—>0 Дж—>0 \ -^ / А
ведение ограниченной функции и б.м.ф. есть б.м.ф.
Согласно определению (19.3), функция у = sin я: непрерывна в точке х. •
Аналогично доказывается, что функция у = cos я: также непрерывна.
19.2. Непрерывность функции в интервале и на отрезке
Функция у = /(я:) называется непрерывной в интервале (а,Ь), если она непрерывна в каждой точке этого интервала.
Функция у = /(я:) называется непрерывной на отрезке [о, &], если она непрерывна в интервале (а, Ь) и в точке х = а непрерывна справа (т. е. lim f(x) — f(a)l, а в точке х = b непрерывна слева (т. е. \ ж—^о.~4~0 / \
К™ Я®) =/(*>))
а: >6—0 /
19.3. Точки разрыва функции и их классификация
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х — яд — точка разрыва функции у = f(x), то в ней не выполняется по крайней ме
155
ре одно из условий первого определения непрерывности функции, а именно:
1. Функция определена в окрестности точки хо, но не определена в самой точке «о-
Например, функция у = —Цу не определена в точке ®о = 2 (см.
ОС £
рис. 120).
Рис. 120 Рис. 121
2. Функция определена в точке «о и ее окрестности, но не сущм ствует предела /(«) при х -» Хо-
Например, функция
{х — 1, если — 1 < х < 2,
о о <- п 1
2 — х, если 2 х 5, 1
определена в точке х0 = 2 (/(2) — 0), однако в точке х0 = 2 имеете разрыв (см. рис. 121), т. к. эта функция не имеет предела при х -> 2: 1 lim f(x) = 1, a lim f(x) = 0.
s^2-0 я->2+0 v
3. Функция определена в точ
ке хо и ее окрестности, существу- v ет lim f (ж), но этот предел не ра- ?
X—
вен значению функции в точке хо'- lim f(x) £ /(«о). I
Ж—г
Например, функция (см.
рис. 122) Д
( если х ф 0; fl
д(х) = < х Я
[2, если х = 0. Я
Здесь «о=О — точка разрыва: Я
sin» л я
urn - = 1, ж
,-<->0 х Ж
lim о(ж) = г—>0
а р(ж0) = 9(0) = 2.
156
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Точка разрыва «о называется точкой разрыва первого рода функции у = f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т. е. lim /(ж) = Аз и lim /(ж) = Аг- При этом:
। О я-->ао+0
а) если At = Аг, то точка жо называется точкой устранимого разрыва-, б) если Ai Аг, то точка жо называется точкой конечного разрыва. Величину |Ai — Аг| называют скачком функции в точке разрыва первого рода.
Точка разрыва жд называется точкой разрыва второго рода функции у = f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.
1. Обратимся к функциям, рассмотренным выше (см. рис. 120). у = ^2, жо = 2 — точка разрыва второго рода.
2. Для функции
I,. , [ж—1, если — 1 < ж < 2,
f(X) = )-) о / / с
12 —ж, если 2 х 5,
.го = 2 является точкой разрыва первого рода, скачок функции равен
3. Для функции
г sin х g(x) = < х
I 2
при ж 0, при ж = 0
жо = 0 является точкой устранимого разрыва первого рода. Положив </(ж) = 1 (вместо <у(ж) • 2) при ж = 0, разрыв устранится, функция станет непрерывной.
Пример 19.3. Дана функция /(ж) = Г _ I _ Найти точки разры-
ва, выяснить их тип.
Q Решение: Функция /(ж) определена и непрерывна на всей числовой о cv j-/ \ I 1 при Z > 3,
оси, кроме точки ж = 3. Очевидно, /(ж) = < Следова-
1—1 при ж < 3.
тельно, lim о/(ж) = 1, а Пто/(ж) = —1. Поэтому в точке ж = 3 функция имеет разрыв первого рода. Скачок функции в этой точке равен 1 — (—1) = 2. •
157
19.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах.
Теорема 19.1. Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).
Q Пусть функция /(ж) и у?(ж) непрерывны на некотором множестве X и жо — любое значение из этого множества. Докажем, например, непрерывность произведения Н(ж) — /(ж) - у?(ж). Применяя теорему д| пределе произведения, получим: I
lim F(x)= lim (/(ж)-у?(ж)) = lim /(ж)- lim <^(ж) = /(жо)-<Джо) = .Т(жо)Я
X—>Xq x—X~¥Xq X~+Xq Ц
Итак, lim F(t) = Т(ж0), что и доказывает непрерывность функ-Х-+ХО
ции /(ж) • у>(ж) в точке жо- И
Теорема 19.2. Пусть функции и = <Дж) непрерывна в точке жо, а функция у = f(u) непрерывна в точке uq — <Джо). Тогда сложная функция /(<Д®)), состоящая из непрерывных функций, непрерывна в точке жо-
Q В силу непрерывности функции и = <Дж), lim <Дж) = <Джо) = и». X—>Xq
т. е. при ж -> жо имеем и -> к0. Поэтому вследствие непрерывности функции у — f(u) имеем: Я
lim /(<Дж)) = lim /(и) = /(и0) = /(</>(ж0)).
X—и—>Uo
Это и доказывает, что сложная функция у = /(<Дж)) непрерывна в точке жо.
Теорема 19.3. Если функция у = /(ж) непрерывна и строго монотонна на [а; 6] оси Ох, то обратная функция у = <Дж) также непрерывна и монотонна на соответствующем отрезке [с; d] оси Оу (без доказательства).
158
Так, например, функция tgx = —, в силу теоремы 19.1, есть COS ОС
Функция непрерывная для всех значений ж, кроме тех, для которых cos ж = 0, т. е. кроме значений х = 5- + тгп, п & Z.
Функции агент ж, arctgar, arccosx, arcctg:r, в силу теоремы 19.3, непрерывны при всех значениях х, при которых эти функции определены.
Можно доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Как известно, элементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. Поэтому из приведенных выше теорем вытекает: всякая элементарная функция непрерывна в каждой, точке, в которой она определена.
Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.
Пример 19.4- Найти lim 2ctga:.
Q Решение: Функция 2ctg® непрерывна в точке х — поэтому
lim 2ctgI = 2ctg ? - 21 = 2. •
ж—> —
X—4
19.5. Свойства функций, непрерывных на отрезке
Непрерывные на отрезке функции имеют ряд важных свойств. Сформулируем их в виде теорем, не приводя доказательств.
Теорема 19.4 (Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Изображенная на рисунке 123 функция у = /(ж) непрерывна на отрезке [а; Ь], принимает свое наибольшее значение М в точке х\, а наименьшее т — в точке Жг- Для любого ж € [а; Ь] имеет место неравенство т /(ж) М.
Следствие 19.1. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
159
Рис. 123
Теорема 19.5 (Больцано-Коши). Если функция у = /(ж) непрерывна на отрезке [а; 6] и принимает на его концах неравные значения /(а) = А и f(b) = В, то на этом отрезке она принимает и все промежуточные значения между А и В.
Геометрически теорема очевидна (см. рис. 124). >
Для любого числа С, заключенного между А и В, найдется точкч с внутри этого отрезка такая, что /(с) = С. Прямая у = С пересечет график функции по крайней мере в одной точке.
Следствие 19.2. Если функция у = /(ж) непрерывна на отрезке [а; 6] и на его концах принимает значения разных знаков, то внутри отрезка [а; 6] найдется хотя бы одна точка с, в которой данная функция /(а:) обращается в нуль: /(с) = 0.
Геометрический смысл теоремы: если график непрерывной фу ню ции переходит с одной стороны оси Ох на другую, то он пересекает ос! Ох (см. рис. 125).
Следствие 19.2 лежит в основе так называемого «метода помет ного деления», который используется для нахождения корня уравне3 ния f(x) = 0.
Утверждения теорем 19.4 и 19.5, вообще говоря, делаются неверными, если нарушены какие-либо из ее условий: функция непрерывна не на отрезке [а; 5], а в интервале (а; Ь), либо функция на отрезке [а; Ь] имеет разрыв.
Рисунок 126 показывает это для следствия теоремы 19.5: граф) разрывной функции не пересекает ось Ох.
160
Рис. 125 Рис. 126
Пример 19.5. Определить с точностью до е = 0,00001 корень уравнения е2ж+1 + х2 — 5 = 0, принадлежащий отрезку [0; 1], применив метод половинного деления.
О Решение: Обозначим левую часть уравнения через f(x).
Шаг 1. Вычисляем = /(а) и ijj = /(6), где а = 0, b = 1.
Шаг 2. Вычисляем х = Q \
Шаг 3. Вычисляем у = /(х). Если f(x) = 0, то х — корень уравнения.
Шаг 4. При f(x) 0 если у • < 0, то полагаем Ь = х, = у, иначе полагаем а = х, <р — у.
Шаг 5. Если b — а — е < 0 хо задача решена. В качестве искомого корня (с заданной точностьюе) принимается величина х = Ина-
че процесс деления отрезка [а; 5] пополам продолжаем, возвращаясь к шагу 2.
В результате произведенных действий получим: х = 0,29589. •
§20. ПРОИЗВОДНАЯ ФУНКЦИИ
20.1. Задачи, приводящие к понятию производной
Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов.
Скорость прямолинейного движения
Пусть материальная точка (некоторое тело) М движется неравномерно по некоторой прямой. Каждому значению времени t соответствует определенное расстояние ОМ = S до некоторой фиксированной точки О. Это расстояние зависит от истекшего времени t, т. е. S = S(t).
6 Конспект лекций по высшей математике. Полный курс
161
О___________М Mi I
s(t) I
Ь S(t-t-At) 4
Рис. 127
Это равенство называют законом движения точки. Требуется найти скорость движения точки.
Если в некоторый момент времени t точка занимает положение М, то в момент; времени i+At (At — приращение времени).; точка займет положение Mi, где OMi 1 = S + AS (AS приращение расстояния] (см. рис. 127). Таким образом, перемещу] ние точки М за время At будет AS =4 = S(t +At)-S(t). ‘ 1
д c 1
Отношение выражает среднюю скорость движения точки з I
время At: Л с 1
V - —
Vcp- " At ’ :
Средняя скорость зависит от значения At: чем меньше At, тела точнее средняя скорость выражает скорость движения точки в данный момент времени t. j
Предел средней скорости движения при стремлении к нулю про^ межутка времени At называется скоростью движения точки в данный момент времени (или мгновенной скоростью). Обозначив эту скорость через V, получим
IZ r Д-S г г r S(t + At) — S(t)
V = lim -т—, или V = lim —------------------
At-Ю At At-Ю
(20.1)
At
Касательная к кривой
Дадим сначала общее определение касательной к кривой.
Возьмем на непрерывной кривой L две точки М и Mi (см. рис. 128)..
Прямую MMi, проходящую через эти точки, называют секущей. 1
Пусть точка Mi, двигаясь вдоль кривой L, неограниченно приблиД жается к точке М. Тогда секущая, поворачиваясь около точки М, стр. 1 мится к некоторому предельному положению МТ. 1
Касательной к данной кривой в данной точке М называ-J ется предельное положение МТ секущей МMi, проходящей через] точку М, когда вторая точка пересечения Mi неограниченно приблиД жается по кривой к точке Mi. Я
Рассмотрим теперь график непрерывной кривой у = f(x), имен Я щий в точке М(ж; у) невертикальную касательную. Найдем ее угловоЯ коэффициент k = tga, где а — угол касательной с осью Ох. 3
Для этого проведем через точку М и точку Mi графика с абсцися сой х + Дж секущую (см. рис. 129). Обозначим через — угол меж уя секущей MMi и осью Ох. На рисунке видно, что угловой коэффициенЯ секущей равен 1
k - teю - Ау - А* + Аж) ~ № 1
Асек-tg^- Дж- . 1
162
Рис. 128
Рис. 129
При Дж —> 0 в силу непрерывности функции приращение Ду тоже стремится к нулю; поэтому точка МА неограниченно приближается по кривой к точке М, а секущая ММ\, поворачиваясь около точки М, переходит в касательную. Угол w —> а, т. е. lim <р = а.
Дж—>0
: Следовательно, lim tg <р = tg a.
' Дж—>0
-4 Поэтому угловой коэффициент касательной равен
5 k = tga= lim tg<£>= lim lim /СЕ+ДЕ)-----------(20.2)
Дж->0 Дж—>0 Дж Дж—>o Дж
К нахождению пределов вида (20.1) и (20.2) приводят решения и множества других задач. Можно показать, что:
- если Q = Q(t) — количество электричества, проходящего через
поперечное сечение проводника за время t, то сила тока в момент
времени t равна
Т г г
1 = пгп —— = Jim
Д4—>0 At Д(->0
Q(t + At) - Q(t) Дt
(20.3)
- если N = 7V(t) — количество вещества, вступающего в химиче-
скую реакцию за время t, то скорость химической реакции в момент
времени t равна
ДА
V = lim —— = lim
Д(->0 Д! Д(->0
AT(t + At) - AT(t) Дt
(20.4)
- если т = т(ж) — масса неоднородного стержня между точками 0(0; 0) и М(ж; 0), то линейная плотность стержня в точке ж есть
„ Дт т(ж + Дж) — т(ж)
S = lim —— = lim k Л 7---------------(20.5)
Дж—>0 Дж Дж—>0 Дж
Пределы (20.1) (20.5) имеют одинаковый вид; везде требуется найти предел отношения приращения функции к приращению аргумента. Этот предел называют производной. Эти пределы можно записать так:
V = S'; tga = y'; I - Q't; V = N'; S = m'x (читается «V равно S штрих no t», «тангенс а равен у штрих по ж» и т. д.).
163
20,2. Определение производной; ее механический и геометрический смысл.
Уравнение касательной и нормали к кривой
Пусть функция у — /(т) определена на некотором интервале (а; 6).
Проделаем следующие операции:
- аргументу х G (а; Ъ) дадим приращение Ат: х + Ат е (а; Ь);
- найдем соответствующее приращение функции: Ау = /(т+Ат) --/(ж);
- составим отношение приращения функции к приращению аргу-Ду
мента: д^;
- найдем предел этого отношения при Ат —> 0: Urn
Если этот предел существует, то его называют производной функции /(т) и обозначают одним из символов f'(x); у'; у'х.
g Производной функции у = f(x) в точке хо называется предел отношения прирашения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Итак, по определению
lim /(жо + Аа;) - /(^о) Дж-ю Ат
п/ ' /(я:) - /(^о)
или / (то) = Um ---------------------
х->хи Т — То
Производная функции /(т) есть некоторая функция /'(т), произ-\ веденная из данной функции.
р>| Функция у = f(x), имеющая производную в каждой точке интерва-1 ла (а; Ь), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференциро
ванием.
Значение производной функции у = /(т) в точке т = То обозначается одним из символов: /'(то), или у'(хо).
1X—XQ
Пример 20.1. Найти производную функции у — С, С = const.
Q Решение:
- Значению т даем приращение Ат;
- находим приращение функции Ду; Ду = /(т + Ат) — /(т) = С - С = 0;
Ац 0 <->
- значит, = ^ = 0;
- следовательно, у' — /Um0 — д’гп( 0 = 0, т. е. (с)' = 0.
164
Пример 20.2. Найти производную функции у = ж2.
Q Решение:
- Аргументу х даем приращение Дж;
находим Ду: Ду = (ж + Дж)2 — ж2 = 2ж • Дж + (Дж)2;
Ду Ду 2ж • Дж + (Дж)2 „ , л
- составляем отношение -г^: =------т—* — = 2ж + Дж;
Дж Дж Дж ’
- находим предел этого отношения:
Ду
lim —— = lim (2ж + Дж) = 2ж.
Дя-ю Дж д®-ю
Таким образом, (ж2)' = 2ж. •
В задаче про скорость прямолинейного движения было получено
V= lim 4т-
Д4-Ю Дг
Это равенство перепишем в виде V = S't, т.е. скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t. В этом заключается механический смысл производной.
|©| Обобщая, можно сказать, что если функция у = /(ж) описывает какой-либо физический процесс, то производная у1 есть скорость протекания этого процесса. В этом состоит физический, смысл производной.
|@| В задаче про касательную к кривой был найден угловой коэффициент касательной k = tga = lim 4^. Это равенство перепишем Дж->0 Аж
в виде /'(ж) = tga = к, т. е. производная f'(x) в точке ж равна угловому коэффициенту касательной к графику функции у — /(ж) в точке, абсцисса которой равна ж. В этом заключается
геометрический смысл производной.
|ф| Если точка касания М имеет координаты (ж0;у0) (см. рис. 130), то угловой коэффициент касательной есть к = /'(жо). Пользуясь уравнением прямой, проходящей через заданную точку в заданном направлении (у—Уо : к(х—Жо)), можно записать уравнение касательной: у — у0 = /'(жо) • (ж — жо)-
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
Так как нормаль перпендикулярна касательной, то ее угловой коэффициент
*норм-= ~кк~ = ~7Ы'
'кас.
165
Поэтому уравнение нормали имеет вид у — у о — — —v ’ ~ #о)
J \хо)
(если /'(ж0) Ф 0).
20.3. Связь между непрерывностью
и дифференцируемостью функции
Теорема 20.1. Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Q Пусть функция у = f(x) дифференцируема в некоторой точке х. Следовательно, существует предел lim
Дж—>0
Отсюда, по теореме 17.5 о связи функции, ее предела и бесконечно малой функции, имеем = /'(ж) + о, где а -> 0 при Дж —> 0, то есп Ду = /'(ж) Дж + а • Дж.
Переходя к пределу, при Дж -> 0, получаем lim Ду = 0. А это и
Д®->0 означает, что функция у = /(ж) непрерывна в точке ж.
Обратная теорема неверна: непрерывная функция может не иметь производной. Примером такой функции является функция
ж, если ж 0, <
—ж, если ж < 0.
Изображенная на рисунке 131 функция не прерывна в точке ж = 0, но не дифференцируем^ в ней.
Действительно, в точке ж = 0 имеем
Ау = /(0 + Аж)-/(0) = /(Дж) = |Дж| Дж Дж Дж Дж
1, если Дж > 0, —1, если Дж < 0.
Отсюда следует, что lim не существует, т. е. функция у — |ж| Дж->0 £аЖ
не имеет производной в точке ж = 0, график функции не имеет касательной в точке 0(0; 0).
|@1 Замечания: 1. Существуют односторонние пределы функции у = |ж| м Ди Ди
в точке ж = 0: lim = —1, lim -т-^ = 1. В таких случаях Дж—>0—0 Дж—>0-г0
говорят, что функция имеет односторонние производные (или «производные слева и справа»), и обозначают соответственно // (ж) и Д (ж).
166
Если /4 (ж) 7^ то производная в точке не существует. Не
существует производной и в точках разрыва функции.
2. Производная у' = f'(x) непрерывной функции у = f(x) сама не обязательно является непрерывной.
|@| Если функция у = /(ж) имеет непрерывную производную у' = f'(x) в некотором интервале (а; Ь), то функция называется гладкой.
20.4. Производная суммы, разности, произведения и частного функций
Нахождение производной функции непосредственно по определению часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.
Пусть функции и = и(х) и v = v(x) - две дифференцируемые в некотором интервале (а; Ъ) функции.
Теорема 20.2. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: (и ± v)' = и' ± и'.
□ Обозначим у — и ± и. По определению производной и основным теоремам о пределах получаем:
' lir (и(ж + ± + Ля)) — (и(я) ± г?(я)) _
ДаД0 дж
— lim (U^X + ~ ± V^X + Ах) ~ v(x>) А _
д.т>о у Аж Аж J
г г Л” / . I
= нгп —— ± шп —— = и ± V ,
Дж>() Дж Дж—>0 Дж
т. е. (и ± v)' = и' ± и'.
Теорема справедлива для любого конечного числа слагаемых.
Теорема 20.3. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: {u-v)'=u'v+v'u.
167
Q Пусть у — uv. Тогда
, , Ди и(х + Дж) • v(x + Дж) — и(х) и(ж)
у = lim —— = lim ---------------------т----------—------=
Дж-ю Дж Дж—>о Дж
j. (и(ж) + Ди) (и(ж) + Ди) — и(ж) - и(ж) Дж—>0 Дж
и(ж) и(ж) + и(ж) • Ди + и(ж) • Ди + Ди Ди — и(ж) и(ж) lim — ---——————------------------
Дж—>0 Дж
= lim
Дж—>0
( . . Ди . . Ди и(ж) ---1- и ж --F Ди •
\ v Дж v ' Дж
Ди\
Дж /
, - .. Ди , Ч .. 1- л 1-
= и(ж) - lim ------Ь и(ж) • hm ----------1- lim Ди • lim —— =
Дж—>0 Дж Дж—>0 Дж Дж—>0 Дж—>0 Дж
= и' - и + и • и' + 0 • и' = и' • и + и • и',
т. е. (и • и)' = и' - и + и • и'.
При доказательстве теоремы использовалась теорема о связи непрерывности и дифференцируемости: так как функции и = и (ж) и и = и(ж) дифференцируемы, то они и непрерывны, поэтому Ди -> О и Ди —> 0 при Дж -» 0.
Можно показать, что:
а) (с и)' = с • и', где с = const;
б) (и - и • w)' = и' - и • w + и • и' • w + и • и • w'.
Теорема 20.4. Производная частного двух функций . если и (ж)
0 равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: (и / 0.
XV J V2
□ Пусть у = Тогда
у' — lim
Дж—>0
ц(а?+Дж) _ и{х) г/(®-|-Д®) v(x)
Ах
lim
Да?—>0
ц(ж)+Дц _ ц(ж) я/(®)+Д«> v\x)
Ах
= lim
Дж—>0
и(ж) - и(ж) + и(ж) • Ди — и(ж) - и(ж) — и(ж) - Ди
Дж - (и (ж) + Ди) и (ж)
168
it
•г
,. v-Aa-u-Av
— |im -------------- — |1П1 -ЬДД----—
Дж->о Дж • (z?2 + v • Дг>) Дж->о v2 + v • &u
v • lim 4^ — и • lim Дх->0 Аж Д.тХ) Аж
v2 + v • lim Av
Дж—>0
и v — uv
v2
т. е.
UV — UV
V2
Следствие 20.1
= - и', с
V
(C \ 1
- ) = , где c = const.
V/ V
20.5. Производная сложной и обратной функций
Пусть у = f(u) и и — ip(x), тогда у = /(<^(т)) — сложная функция с промежуточным аргументом и и независимым аргументом х.
Теорема 20.5. Если функция и = tp(x) имеет производную и'х в точке х, а функция у = /(w) имеет производную у'и в соответствующей точке и = <£>(я), то сложная функция у = /(<^(ж)) имеет производную у'х в точке х, которая находится по формуле у'х = у'и и'х.
□ По условию lim = у'и. Отсюда, по теореме о связи функции, ее Д«—>0
предела и бесконечно малой функции, имеем = у'и + а или
Ау = у'и Ди + а Ди, (20.6)
где а —> 0 при Ди 0.
Функция и = ip(x) имеет производную в точке х: lim ^4 = и'х, Дж—>0 АЖ
поэтому
Ди = их Дх + /3 Дх, где /3 —> 0 при Дх -> 0.
Подставив значение Ди в равенство (20.6), получим
= У'и(их Дх + (3- Дх) + а(и'х Дх +/3 Дх),
&У = y{ru'z Ах + у'и- /3 Дх+ и'х-а-Дх + а- /3 Дх.
Разделив полученное равенство на Дх и перейдя к пределу при Дх —> 0, получим у'х = у'и и'х.
,1
169
g Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько. Так, если у = f(u), и = <Д'с), v = g(x), то у'х = y'u-u'v- v'x. Пусть у = f(x) и х = — взаимно обратные функции.
Теорема 20.6. Если функция у = f(x) строго монотонна на интервале (а; Ъ) и имеет неравную нулю производную f'(x) в произвольной точке этого интервала, то обратная ей функция х = ip(y) также имеет производную <Д(у) в соответствующей точке, определяемую равен-_ 1
Ух'
СТВОМ tp'(y) =
ИЛИ х'у
□ Рассмотрим обратную функцию х = Ду). Дадим аргументу у приращение Ау 7^ 0. Ему соответствует приращение Аж обратной функции, причем Аж ф 0 в силу строгой монотонности функции у = /(ж). Поэто-
му можно записать
Аж 1 Ау “ Ai" ,у Дж
Если Ду —> 0, то в силу непрерывности обратной функции приращение Аж -> 0. И так как lim = /'(ж) 0, то из (20.7) следуют]
~,т.е. ^'(у) = ?7^.
т /\т* равенства hm =
(20.7)
А^од2/ lim Д^ /'О)
Дж—>0 Д#
производная обратной функции равна обратной величине производной данной функции. * Правило дифференцирования обратной функции записывают так:
Таким образом,
,1 dy 1
у,,. = —- или — = .
ж' dx &
У «?/
Пример 20.3. Найти производную функции у = log2 tgж4.
Q Решение: Данная функция является сложной. Ее можно представить в виде цепочки «простых» функций: у = и3, где и — log2 z, где z = tg у, где q — ж4. По правилу дифференцирования сложной функции (у'х = у'и u'z z'g q'x) получаем:
Ух = 3 ‘ !og2 tg^4 •
1
tg ж4 • In 2
1
cos2 ж4
4ж3.
170
Пример 20.4- Пользуясь правилом дифференцирования обратной функции, найти производную у'х для функции у = yjx — 1.
Решение: Обратная функция х = у3 + 1 имеет производную х'у = Зу2. Следовательно,
I ,111
Ух “ х'у ~ ~ з •
20.6. Производные основных элементарных функций
Степенная функция у = хп, п € 14
Дадим аргументу х приращение Дж. Функция у = хп получит при-’ращение Ау = (ж + Дж)" — ж". По формуле бинома Ньютона имеем
Ду = ^ж" + п ж"”1 • Аж + П^2, • Дж2 -I--F (Дж)п) - ж" =
= п ж"-1 Дж + —^^ж"~ ‘2Дж2 +--ь (Дж)".
Тогда
Ду _ п ж"-1 Дж + п(п2-1}ж"-2Дж2 4—F (Дж)"
Дж Дж
= п ж"-1 + — • ж"-2 • Дж -|--F (Дж)"-1.
Находим предел составленного отношения при Дж -> 0:
lim = lim ( n-ж""1-F-zi-(zi—1)-ж"-2ДжЧ-----р(Дж)"-1^ = д-ж"-1.
Дж-шДж д®->о\ 2 v ’ J
Таким образом,
(ж”)' = п-хп~1.
Например, (ж3)' = Зж2, (ж2)' = 2ж, ж' = 1.
Ниже (см. замечание на с. 175) будет показано, что формула производной степенной функции справедлива при любом и е R (а не только натуральном).
Показательная функция у = ах, а > 0, 1
Найдем сначала производную функции у = ех. Придав аргументу ж приращение Дж, находим приращение функции Ду: Ду — еж+Лж— ех = = еа:(еЛж — 1). Стало быть, = е ^'А и
' ’ /\х Лз:
Л?/ рД® — 1 рД® — 1 Д /р
lim = lim ех----------= ех-Urn —------= ех- lim = ех-1 = ех.
Дя->0Дж Дж—>0 Дж Дж—>0 Дж Дж->оДж
171
При вычислении предела воспользовались эквивалентностью ех — 1 ~ х при х —> 0.
Итак, у' = ех, т. е.
(еж) = е .
Теперь рассмотрим функцию у = ах, х 6 К. Так как ах = ех1па, то по формуле производной сложной функции находим:
(ахУ = (еж1пй)' = еж1пй (х Ina)' = ех1па Ina = ах Ina.
Таким образом, (аж)' = аж1па.
Пример 20.5. Найти производную функции у = 7ж2-4®.
Q Решение: Используя формулу производной сложной функции и формулу производной показательной функции, находим
у' = = 7*2-4* . In 7 (ж2 - 4а:)' = 7ж2“4а: • In 7 • (2® - 4). •
Логарифмическая функция у = loga х, а > 0, а 1
Найдем сначала производную функции у = In х.
Для нее
Ду _ 1п(® + Дж) — In ж = 1п(^) = 1п(1 +
Да; Да; Да; Да;
Переходя к пределу при Да: ч 0 и воспользовавшись эквивалентностью ln(l + ~ при Да; -> 0, получаем:
Ду 1п(1 + ^) г 1 1
lim —— — hm -------—— = hm ~~ — bin - = - ,
Дж->0 Дж Дж->0 Дж Дж->0 Дж Дж—>0 ж ж
т. е. у' = — или (Ina;)' = 1. Ж ж
Теперь рассмотрим функцию у = logo х.
Так как logaa; = то
v /ТпаА' 1 . , 11
(log а;) = — = ----(Ina;) = -----.
\1па/ 1па 1па х
Таким образом, (log„®)' = Г
Пример 20.6. Найти производную функции у = In (а;4 — 2ж2 + 6).
О Решение: »' = • («4 -+ 6)' = •
Производную логарифмической функции у = loga х можно найти иначе. Так как обратной для нее функцией является х = ау, то по формуле производной обратной функции имеем:
Л У = 1 = 1 = 1
(. °Sa х) ^аУу ау -1па х Ina"
172
Тригонометрические функции у = sini, у = созж, у = tga;, у — ctga:
Для функции у = sin ж имеем:
Ду _ 8ш(ж + Дж) - sin ж _ 2 sin cos (ж + А£) sin Аг
Дж Дж
Переходя к пределу при Дж —> мечательным пределом lim ®п1Ал Дж
.. Ду sin
hm —— — hm —• cos Дж—>0 /лХ Дж ->()
т. е. у' = cos ж или (sin ж)' = cos ж.
Найдем производную функции у=cos х, воспользовавшись формулой производной сложной функции:
( Дж\ cost ж+~^-I.
Дж
О и воспользовавшись первым за-= 1, получаем
/ Аж н+т
• cos ж,
=cos
=cos
— sin ж,
т. е. (cos ж)'= —sin ж.
Для нахождения производных функций у=tg ж и у = ctga: воспользуемся формулой производной частного:
Ct. (sin ж)Х COS Ж — 8П1ж(сО8ж)' COS2 Ж-J-Sin2 Ж 1
cos2 ж cos2 ж ’
cos2 ж
т. е. (1§ж)'=—К—. cos ж
Проделав аналогичные операции, получим формулу
(ctgx) =---
sin ж
Этот результат можно получить иначе:
(<*®ж) = (tgl - - ж ) = ——------------- • (-1) = —
У \2 7/ cos2(f - ж) sin2ж
Пример 20.7. Найти производную функции у = соз2ж.
Q Решение: (со8 2ж)' = — вш2ж - (2ж)' = — 2зт2ж.
Обратные тригонометрические функции у = arcsina:, у = агссозж, у — arctgrr, у = arcctgx
У € [— На интервале ~
Пусть у = агсвтж. Обратная ей функция имеет вид ж — sin у, верно равенство ж' = cosy ф 0.
По правилу дифференцирования обратных функций , . v 1 1 1 1
(агсзшж) = ——— =-------= —===== = . ,
(sm у)' cosy \/l“sin2y Vl-ж2
173
где перед корнем взят знак плюс, так как cosy > 0 при у G (д’ 2/' Итак, (arcsin х}' = . *.—
у X Д’
Аналогично получаем, что (arccos®)' =-----.-- Эту формулу
VI — х2
можно получить проще: так как arccos® + arcsin® = А, т. е. arccos® =
= А — arcsin®, то (arccos®)' = fly - arcsin®') =-.-
2 ) \/\ — х2
Найдем производную функции у = arctg ®.
Она является обратной к функции ® = tgy, где у G i f)-
Поэтому, по правилу дифференцирования обратных функций, получаем, что
1 1 2 1 1
(arctg®) = 7---г? = —т = COS у = --- 2 — — 2-
№уУ 1 + tg2?/ 1 + я2
1 ' Замечание: Найдем производную степенной функции у = ха с лю-
бым показателем а 6 R. В этом случае функция рассматривается для ® > 0.
Можно записать ®“ = е“‘1пж. По правилу дифференцирования сложной функции находим
(®“)' = (е“1пж)' = е“-1пж (а In®)' = а еа1пж - - = а — = а ха~\ х х
г. е. (®“)' = а ж"1.
Формула остается справедливой и для ® < 0, если функция у = ха
существует: 1
(®i)' = -®-i
при всех х V 0.
2 1
Пример 20.9. Показать, что функция у = + С удовле-
2 2®
творяет уравнению ®3 • у' + 1 = ж4.
Итак, (arctg®)' —
Функции arctg ® и arcctg ® связаны отношением
7Г 7Г
arctg® + arcctg® = -, т. е. arcctg ж =--arctg ж.
Z £
Дифференцируя это равенство, находим
\' 1
(arcctg®)' = - - arctg® = -(arctg®)' = - 2,
\ z j it*
т. е. (arcctg®)' =
Q Решение: Находим у':
у' = | - 2® + J (—2)®”3 + 0, Z Z
т. е. у' = х —Подставляем значение у' в данное уравнение: ®
®3 • (х—^•')+1=®4, т. е. ж4 — 1 + 1 = ®4, 0 = 0. \ хл/
Функция удовлетворяет данному уравнению.
20.7. Гиперболические функции и их производные
Пример 20.8. Найти производные функций: 1) у = arccos ®2; 2) у = = ®-arctg®; 3) у = (1 + 5®-З®3)4; 4) y = arccosA/®5 5) у = к^2(3 + 2”ж).
1 2д’
Q Решение: 1) (arccos®2)' =----. ..-= (ж2)' =---, ..--;
VI — (ж2)2 V1- х4
2) (® - arctg®)' = ®' • arctg® + ® • (arctg®)' = arctg® + --2 ’
1 ~}~ Д’
3) ((1 + 5® - З®3)4)' = 4(1 + 5® - З®3)3 (5 - 9®2);
4) (arccos V®)' =-, == - =
' к v ’ у/1 - (у/®)2 2у/®
5)(1ое^(3 + 2-))' = 31ое2(3 + 2-Д-(Г}^у1^-2-.1п2-(-1). •
В математике, механике, электротехнике и некоторых других дисциплинах встречаются гиперболические функции, определяемые следующими формулами: ех — е~х
sh х = -—--------гиперболический синус;
„ж X
ch® = -...-------гиперболический косинус («цепная линия»);
1 О* 1 о* Р“£ -4- р
th х = = ь-—. и cth х = -т е — гиперболиче-
ch х е + е sh ® е — е
ский тангенс и котангенс, где е — неперово число.
На рисунках 132-135 показаны графики гиперболических функций.
Между гиперболическими функциями существуют следующие основные зависимости:
174
175
Рис. 132
Рис. 133
Рис. 135
ch2 х — sh2 х = 1;
sh(a: ± у) = sh х • ch у ± ch х • sh у,
ch(a: ± у) = ch а: - chy ± sha: • shy;
,, , , ч th х ± th у
(х ~ 1 ± th а: • th у ’
sh 2а: = 2 sh х • ch х; ch 2а? = ch2 х + sh2 х.
Все эти формулы вытекают из определения гиперболическ функций.
Например,
ch2 х — sh2 х =
= у(е2х + 2 + е-2х - е2х + 2 - е~2х) = А • 4 = 1. 4 ' 4
176
Геометрическая интерпретация гиперболических функций (см. рис. 137) аналогична интерпретации тригонометрических функций (см. рис. 136).
Рис. 136. Параметрические уравнения х — cos t и у — = sin t определяют окружность х2 + у2 = 1, причем О А = cost, AM = sin t
Рис. 137. Параметрические уравнения x = chtHy = sht определяют гиперболу х2 — у2 = 1, причем О А = chi, AM = sh t
Найдем производные гиперболических функций: (sha:)' = ( (cha:)' =
ш
—— т. е. (th а:)' =
_ sh х =----------1—; т. е. (ctha:)' =-Д—
----- sh х sh х sh2 х
e —e
2
e~x
' рх I р~х
= -...— = ch а:, т. е. (sha:)' = ch а:;
ех — е
2
_ (sh a:)' ch а: — sh a:(ch а:)' ch2 х
= sha:, т. е. (chа:)' = sha:;
_ ch2 х — sh2 x _
ch2 x
ch2 а:’
1 .
ch2 х ’
20.8. Таблица производных
Выведенные правила дифференцирования, формулы производных основных элементарных функций запишем в виде таблицы.
На практике чаще всего приходится находить производные от сложных функций. Поэтому в приведенной ниже таблице формул дифференцирования аргумент «а:» заменен на промежуточный аргумент «и».
Правила дифференцирования
1. (и ± v)' = и' ± г/;
2. (и • v)' = u'v + uv', в частности, (си)' = с-и'\
177
cv'. ~V^'
3. " V—2UV в частности,
\vj v \v)
4- Ух = Уи ’ «Д если У = f («)> и = <р(ж);
5- Ух = если У = /(Д и х =
*Ьу
Формулы дифференцирования
1. (с)' = 0;
2. (н“)' = а иа~4 и', в частности, (у/й)' =
3. (а“)' = аи Ina • и', в частности, (е“)' = ё
4- (logo иУ
5. (sin и)' =
7. (tg?z)' =
и;
и;
, в частности, (In г/)' = — и'-.
6. (cosh)' = — sinu - и';
8. (ctguY =-----Д— • и';
7 sin и
10. (arccosu)' = - = - и';
12. (arcctguY = — -—L . и>.
1 + w
14. (ch и)' = sh?z • и';
16. (cthuY = —-i— • и'.
v sir и
9. (arcsinw
и In а и ,
- COS и и'\ 1
n * LL COS и Y- 1 5
} а/1- / _ 1 и2 и1
1 + и4 chu • и'; —4— • и':
и';
11. (arctgu)'
13. (shu)' —
15. (th uY = ch" и
Для вычисления производных надо знать лишь правила дифференцирования и формулы производаых основных элементарных функций, строго соблюдать эти правила при выполнении упражнений.
Пример 20.10. Найти производную функции у = ж4 — Зж3+2х — 1.
Q Решение:
у1 = - Зж3 + 2ж - 1)' = (ж4)' - (Зж3)' + (2ж)' - (1)' =
= 4ж3 — З(ж3)' + 2(ж)' - 0 = 4ж3 — 9ж2 -I- 2. •
Надо стараться обходиться без лишних записей.
Пример 20.11. Найти производную функции у = tg ж
Q Решение:
' = (= 2 fo3)'~ ж3'fogs)' _ 2 3x2 'tgx ~ xJ ' 7^ •
У Vtgж7 (tgz)2 ~ (tga:)2
Производная найдена. В процессе решения использованы правила 2, 3 и формулы 2, 7.
Пример 20.12. Найти производную функции у = cos(ln12 2ж).
178
Решение: Коротко: у' = — sin(ln12
2®) • 12 Ln11 2® • J--2. ' //г
Решение с пояснениями: данную функцию можно представить следующим образом: у = cos и, и = t12, t = In г, z = 2х. Производную сложной функции найдем по правилу у'х = у'и- u't t'z • z'x (здесь промежуточных аргументов три):
у' — — sin и -12 -111 - — - 2, х z
т. е. у'х = -sint12 12 (Inz)1’ ~ -2,
т. е. у'х = — sin(lnz)12 • 12 - In11 z
т. е. у'х = — sin(ln12 2т) -12 - In11 2х -
Окончательно у'х — -12 - sin(ln12 2х) In11 2х
§21. ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ
И ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИЙ 21.1. Неявно заданная функция
Если функция задана уравнением у = f{x), разрешенным относительно у, то функция задана в явном виде (явная функция).
ЦЦ Под неявным заданием функции понимают задание функции в виде уравнения F(x; у) = 0, не разрешенного относительно у.
Всякую явно заданную функцию у = f(x) можно записать как неявно заданную уравнением f (я) - у = 0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у + 2х + cos у — 1 = 0 или 2V — х + у = 0).
Если неявная функция задана уравнением F(x\ у) = 0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по х, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
Пример 21.1. Найти производную функции у, заданную уравнением х3 + у3 — Зху = 0.
179
Q Решение: Функция у задана неявно. Дифференцируем по х равенство х3 + у3 — Зху = 0. Из полученного соотношения
Зж2 + 3 • у2 у' — 3(1 • у + х у') = 0
следует, что у2у' — ху' — у — х2, т. е. у' = ——. 9
У & 3 1
j
21.2. Функция, заданная параметрически Л
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений )
Р = (21.4
V = ?/(*), ;
где t — вспомогательная переменная, называемая параметром.
Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х = ar(t) имеет обратную t == tp(x). По правилу дифференцирования обратной функции
t'x = i- (21.2)
Функцию у = f(x), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у = y(t), где t = <р(х).
По правилу дифференцирования сложной функции имеем: у'х = = y't t'x.
С учетом равенства (21.2) получаем
, , 1 I Vt
У* =yt--y, т. е. ух = _______________________"t
Полученная формула позволяет находить производную ух от функции заданной параметрически, не находя непосредственной зависимости у от х.
Пример 21.2. Пусть < ’
\У = t •
Найти у'х.
СЪЛ.
Q Решение: Имеем x't = 3t2, у\ = 2t. Следовательно, y'x = —у, т. e.
v' = 2 •
Vx ЗГ 1
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, t = \/х. Тогда у = \х2. Отсюда у'х = sт. е.
О "у Ж
у -
180
§22. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
Пример 22.1. Найти производную функции
_ (ж2 + 2) • У(ж - 1)3 • еж
У (х + 5)3
Q Решение: Можно найти у1 с помощью правил и формул дифференцирования. Однако такой способ слишком громоздкий. Применим логарифмическое дифференцирование. Логарифмируем функцию:
1пу = 1п(ж2 + 2) + 1п(ж — 1) + х — 31п(ж + 5).
Дифференцируем это равенство по х;
1 . 1 „ 3 1 , „ 1
у х2 + 2 4 ж - 1 ж + 5
Выражаем у':
. ( 2х 3 3 \
У " У (^Ь2 + 4(ж - 1) + ~ J ’ т. е.
, _ (ж2 + 2) {/(х - I)3 • ех / 2х 3 3 \
У (х + б)3 у®2 + 2 1 4(ж — 1) х + 5/ ’
Существуют функции, производные которых находят лишь логарифмическим дифференцированием. К их числу относится так называемая степенно-показательная функция у = uv, где и = «(ж) и v — и(х) - заданные дифференцируемые функции от х. Найдем производную этой функции:
1 1
lny = v-lnw, => - у' = и' In и + и — и', =>
у и
=> у'= у( и'-1пи + и — и'],
' \ и J
т. е. / । \
у' = uv ( и' • In и + и • — • и' I,
\ и 7
ИЛИ («’')' = uv • In и • v' + v • u” 1 - и'. (22.1)
181
Сформулируем правило запоминания формулы (22.1): производная степенно-показательной функции равна сумме производной показательной функции, при условии и = const, и производной степенной функции, при условии и = const.
Пример 22.2. Найти производную функции у = (sin 2ж)'с^+1.
Q Решение: Пользуясь формулой (22.1), получаем:
у' = (вт2ж)г +1 • lnsin2x 2х + (ж2 + 1)(вт2ж)® • соз2ж • 2. •
Отметим, что запоминать формулу (22.1) необязательно, легче запомнить суть логарифмического дифференцирования.
§23. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
23.1. Производные высших порядков явно заданной функции
Производная у' — /'(ж) функции у = /(ж) есть также функция от ж и называется производной первого порядка.
Если функция /'(ж) дифференцируема, то ее производная называ-/ л2„.
у dl
ется производной второго порядка и обозначается у" ^или /"(ж),
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (i
или
Производной n-го порядка (или тг-й производной) называется производная от производной (п — 1) порядка:
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозна-’ чают римскими цифрами или числами в скобках (yv или у^ — производная пятого порядка).
Пример 23.1. Найти производную 13-го порядка функции у = = sin ж.
182
Q Решение:
/ / • \/ . i
у = (sin X) — COS Ж = Sin( X + “
у" = (у')' = (cos х)' = — sin х = sin I x + —
y'" = (— sin x)' = — cos x = sin I x + —
= (— cos x)' = sin x = sin I x + — • 4 \ Z
j/13) = sinf® + ^ • 13
23.2. Механический смысл производной второго
порядка
Пусть материальная точка М движется прямолинейно по закону S = f(t). Как уже известно, производная S} равна скорости точки в данный момент времени: S't = V.
Покажем, что вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т. е. S" = а.
Пусть в момент времени t скорость точки равна V, а в момент t + At — скорость равна V + ЛК, т. е. за промежуток времени At скорость изменилась на величину АП.
Отношение выражает среднее ускорение движения точки за /АГ
время At. Предел этого отношения при At —> О называется ускорением точки М в данный момент t и обозначается буквой a: — °;
т. е. V = а.
Но V = S't. Поэтому а = , т. е. а = S"
23.3. Производные высших порядков неявно заданной функции
Пусть функция у = f(x) задана неявно в виде уравнения F(a:;y) = 0.
Продифференцировав это уравнение по я и разрешив полученное уравнение относительно у', найдем производную первого порядка (первую производную). Продифференцировав по х первую производную, получим вторую производную от неявной функции. В нее войдут х,у и
183
у Подставляя уже найденное значение у' в выражение второй произ водной, выразим у" через ж и у.
Аналогично поступаем для нахождения производной третьего (и дальше) порядка.
Пример 23.2. Найти у'", если ж2 + у2 = 1.
Q Решение: Дифференцируем уравнение ж2 + у2 — 1 = 0 по ж: 2ж + + 2у • у1 — Q. Отсюда у' — — Далее имеем: у" = — ^'У ' У , т. е
У
• (~f) _ jt/2 +ж2
У2 У3
-1 • З?/2 • у1 3 тельно, у — —
у"
У6
—х (так как ж2 + у2 = 1), следова Ул
( х\ Зж
< у) у5
23.4. Производные высших порядков от функций, заданных параметрически
Пусть функция у = /(ж) задана параметрическими уравнениями {ж = %(t),
У = y(t\
Как известно, первая производная у'я. находится по формуле
Ух = (23.1
Найдем вторую производную от функции заданной параметриче ски.
Из определения второй производной и равенства (23.1) следует, что * = «)! = «< = Ж
т. е.
У XX
А
(23.2)
Аналогично получаем
III __ (.Ухх^1 IV _____ (yxxx)t
УхХХ I у УХХХХ I
X ~*~ cos t
Пример 23.3. Найти вторую производную функции
у — sin t.
Q Решение: По формуле (23.1)
, (sin t)'f cost у' = ±----(I- = ------ = - ctgt.
(cost)J — Sint
184
Тогда по формуле (23.2)
. „ = = =___________________1 •
хх (cos t)'( — sin t sin31'
Заметим, что найти y"x можно по преобразованной формуле (23.2):
» = Ш'1 = = У" xt ~ х" • У{
Vxx Л (,Л\3 ’
"Ч ХГЧ)
пшоминать которую вряд ли стоит.
§24. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
24.1. Понятие дифференциала функции
Пусть функция у = /(ж) имеет в точке х отличную от нуля производную д^т0 = f'(x) / 0- Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать = /'(ж) +а, где а —> 0 при Дж —> 0, или Ду = /'(ж) • Дж + а Дж.
Таким образом, приращение функции Ду представляет собой сумму двух слагаемых /'(ж) • Дж и а Дж, являющихся бесконечно малыми при Дж —> 0. При этом первое слагаемое есть бесконечно малая функ-(ос] * /\ж
ция одного порядка с Дж, так как lim -- Д-— = /'(ж) 0, а второе
Дж—>0 /АЖ
слагаемое есть бесконечно малая функция более высокого порядка, чем Дж:
lim = lim а = 0.
Джч-О Дж Дж->0
Поэтому первое слагаемое /'(£) • Дж называют главной частью приращения функции Ду.
|ф| Дифференциалом функции у = /(ж) в точке ж называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x)):
dy = /'(ж) • Дж. (24.1)
Дифференциал dy называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной ж, т. е. дифференциал функции у = ж.
Так как у1 — ж' = 1, то, согласно формуле (24.1), имеем dy = dx = = Дж, т. е. дифференциал независимой переменной равен приращению этой переменной: dx = Дж.
Поэтому формулу (24.1) можно записать так:
dy = f'(x)dx,
(24.2)
g иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (24.2) следует равенство = f'(x). Теперь обозна-
чение производной можно рассматривать как отношение дифференциалов dy и dx.
Пример 24.1. Найти дифференциал функции
/(ж) = Зж2 — sin(l + 2ж).
Q Решение: По формуле dy = f'(x) dx находим
dy = (Зж2 — sin(l + 2ж))' dx = (6ж — 2 cos(l -|- 2ж)) dx. •
Пример 24.2. Найти дифференциал функции у = 1п(1 + е10ж) + х/ж2 + 1.
Вычислить dy при ж = 0, dx = 0,1.
О Решение;
---- / 1о* \
dy = (1п(1 + е10ж) + \/ж2 + 1)' dx = ( , 75^ + ) dx.
х 1 + е у/х1 -у 1 / Подставив ж = 0 и dx = 0,1, получим
dy\ х=0, = (у+0)0,1 = 0,5. <
d#=O,l
24.2. Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала.
Для этого проведем к графику функции у = /(ж) в точке М(ж;у) касательную МТ и рассмотрим ординату этой касательной для точки ж + Дж (см. рис. 138). На рисунке |AM| = Дж, |АЛ41| = Ду. Из прямоугольного треугольника МАВ имеем:
tga = т. е. |АВ\ — tga • Дж. Дж
Но, согласно геометрическому смыслу производной, tga = /'(ж). Поэтому АВ — f'(x) Ах.
Рис. 138
186
|@j Сравнивая полученный результат с формулой (24.1), получаем dy = АВ, т. е. дифференциал функции у = f(x) в точке х ранен приращению ординаты, касательной к графику функции ч этой точке, когда х получит приращение Дх.
В этом и состоит геометрический смысл дифференциала.
24.3. Основные теоремы о дифференциалах
Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции (dy = f'(x)dx) и соответствующие теоремы о производных.
Например, так как производная функции у = с равна нулю, то дифференциал постоянной величины равен нулю: dy = c' dx = 0- dx = 0.
Теорема 24.1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:
d(u + v) = du + dv, d(uv) = v • du + u dv, , /u\ vdu — udv . , d I 7 ) = -2---- (” 0).
\ W / V
□ Докажем, например, вторую формулу. По определению дифференциала имеем:
d(uv) = (uv)'dx = (uv + uv')dx = v и dx + и v'dx = vdu + udv.
Теорема 24.2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Q Пусть у — f(u) и и = <Дт) две дифференцируемые функции, образующие сложную функцию у = f(y>(x)). По теореме о производной сложной функции можно написать
Ух =у'и-и'х-
Умножив обе части этого равенства на dx, получаем y'xdx=y'uu'xdx. Но у'х dx = dy и и'х dx = du. Следовательно, последнее равенство можно переписать так:
dy = у'и du.
187
Сравнивая формулы dy — у'х • вый дифференциал функции у =
dx и dy = уи • du, f(x) определяется
видим, что нер-
одной
и той же
формулой независимо от
того,
является ли
ее аргумент
независимой
переменной или является функцией другого аргумента.
Это свойство дифференциала называют инвариантностью (не изменностью) формы первого дифференциала.
Формула dy
Ух
dx по внешнему виду совпадает с формулой
dy = у'и du, но между ними есть принципиальное отличий: в формуле х — независимая переменная, следовательно, dx =
первой
Дж, во
второй формуле и есть функция от х, поэтому, вообще говоря, du
Д'«.
1
С помощью определения дифференциала и основных теорем о диф
ференциалах легко преобразовать таблицу производных в дифференциалов.
таблицу
Например, d(cos ы) = (cos и)'и - du = — sin и du.
24.4. Таблица дифференциалов
1. d(u ±v) = du ± dv;
2. d(u v) — vdu + u dv, в частности, d(cu) = c du;
3. d(a) = vdu-udv в частности d(c\ = _cdn \vj v \vj v
4. dy = y'x dx, если у = /(ж);
5. dy = y'u du, если у = f(u), и = </>(ж);
6. de = 0;
7. d(ua) = a u01-1 • dv,
8. d(au} = au • In a - du, в частности, d(e“) = e“ • du;
9. d(logou) = ц j-— • du, в частности, d(lnw) = du;
10. d(sinw) — cos и du; 16. d(arctgw) = du;
11. d(cosw) = — sina du;
12. d(tgw) = = —К— du; 17. d(arcctg u) = — —2 du;
13. d(ctgw) = — du; 18. d(slw) = ch и du;
sin и 19. d(cliH) = shudu;
14. d(arcsin и)- 'du; V 1 - tr 20. d(th и) = —Д— du; v 7 ch2 и
15. d(arccos «) - Д—-du; V 1 “ и 21. d(cthi«) = —-1—du. ' sir u
188
24.5. Применение дифференциала к приближенным вычислениям
Как уже известно, приращение Ду функции у = /(ж) в точке х можно представить в виде Ду = f'(x) • Дж + а Ах, где а —> 0 при Дж —> 0, или Ду = dy + а Ах. Отбрасывая бесконечно малую а Ах более высокого порядка, чем Да:, получаем приближенное равенство
Ду » dy, (24.3)
причем это равенство тем точнее, чем меньше Ах.
|@| Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (24.3) широко применяется в вычислительной практике.
Пример 2^-3. Найти приближенное значение приращения функции у = х3 — 2а: + 1 при х = 2 и Ах — 0,001.
Q Решение: Применяем формулу (24.3): Ду « dy = (ж3 — 2х-I-1)'- Ах = = (Зж2 — 2) • Ах.
dy\ ж=2 = (3-4-2)-0,001 = 10-0,001 = 0,01.
Дя=0,001
Итак, Ду « 0,01.
Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем Ду:
Ду = ((ж + Дж)3 — 2(ж + Да:) + 1) — (а:3 — 2ж + 1) =
= ж3 + Зж2 • Ах + За: • (Дж)2 + (Дж)3 - 2ж - 2 Дж + 1 - ж3 + 2ж - 1 =
= Дж(3ж2 + Зж • Дж + (Дж)2 - 2);
Ду| ж=2 = о,001(3-4 + 3-2-0,001 + 0,0012 -2) = 0,010006.
Дж=0,001
Абсолютная погрешность приближения равна
|Ду - dy| = |0,010006 - 0,011 = 0,000006. •
Подставляя в равенство (24.3) значения Ду и dy, получим
/(ж + Дж) - /(ж) » f'(x) Ах
или ---------------------------
/(ж + Ах) к /(ж) + f (ж) Ах. (24.4)
Формула (24.4) используется для вычислений приближенных значений функций.
Пример 24.4. Вычислить приближенно arctg 1,05.
189
т. е.
Q Решение: Рассмотрим функцию /(ж) = arctg ж. По формуле (24. имеем:
arctg(ar + Дж) « arctgж + (arctg ж) • Дж,
/ Л >
arctg(T + Дж) » arctgж + -
Так как ж + Дж = 1,05, то при ж = 1 и Дж = 0,05 получаем:
arctg 1,05 « arctg 1 + + 0,025 » 0,810.
Можно показать, что абсолютная погрешность формулы (24.4)
превышает величины М (Дж)2, где М — наибольшее значение | f"(x на сегменте [ж; ж + Дж] (см. с. 196).
Пример 2^-5. Какой путь пройдет тело при свободном паден на Луне за 10,04 с от начала падения. Уравнение свободного паден тела Н = 9^-- , дл = 1,6 м/с2.
Q Решение: Требуется найти Л(10,04). Воспользуемся приближенной формулой (ДЛ Pd dH)
H{t + до « л(0 + л'(t) Дб
При t = 10 с и Д1 = dt = 0,04 с, H'(t) = g^t, находим
Л(10,04) w 1,6 210° + 1,6 • 10 0,04 = 80 + 0,64 = 80,64 (м). •
Задача (для самостоятельного решения). Тело массой m = — 20 кг движется со скоростью v = 10,02 м/с. Вычислить приближенно кинетическую энергию тела (ек = Лк(10,02) и 1004 (Дж)^.
24.6. Дифференциалы высших порядков
Пусть у = /(ж) дифференцируемая функция, а ее аргумент ж -независимая переменная. Тогда ее первый дифференциал dy = /'(ж) есть также функция ж; можно найти дифференциал этой функции.
Дифференциал от дифференциала функции у = /(ж) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается (Ру или d?f(x).
Итак, по определению (Ру = d(dy). Найдем выражение второго дифференциала функции у = /(ж).
Так как dx = Дж не зависит от ж, то при дифференцировании считаем dx постоянным: J
d2y = d(dy) = с?(/'(ж) dx) = (/'(ж) dx)' dx = /"(ж) dx dx = /"(ж)(г/ж)21
190 П
d2y = f"(x) dx2. (24.5)
Здесь dx2 обозначает (dx)2.
Аналогично определяется и находится дифференциал третьего по-
рядка:
d3y = d(cPy) = d(f"(x) dx2) = f"'(x)(dx)3.
И, вообще, дифференциал n-го порядка есть дифференциал от
дифференциала (п — 1)-го порядка: dny = d(dn гу) = f^(x)(dx)n.
Отсюда находим, что f(n\x) =
dny
dx11
. В частности, при п = 1, 2, 3
соответственно получаем:
Г(Ж) = ^’ Г(Ж) =
/'"(ж) =
d3y dx31
ФЧ/ dx2 ’
т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени
дифференциала независимой переменной.
|@| Отметим, что все приведенные выше формулы справедливы только, если х — независимая переменная. Если же функцию у = f(x), где х — функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
Используя формулу дифференциала произведения (d(u v) = = v du + и dv), получаем:
(Ру = d(f'(x) dx) = d(f'(x)) dx + f'(x) d(dx) = f"(x) dx-dx + f'(x) (Px,
(Py = f"(x) dx2 + f'(x) (Px. (24.6)
Сравнивая формулы (24.5) и (24.6), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое f'(x) (Рх.
Ясно, что если х — независимая переменная, то
dPx = d(dx) = <7(1 - dx) — dx • d(l) = dx • 0 = 0 и формула (24.6) переходит в формулу (24.5).
Пример 24-6. Найти (Ру, если у — е3х иж — независимая переменная.
Q Решение: Так как у' = Зе3ж, у" = Эе3®, то по формуле (24.5) имеем
<Ру = 9е3® dx2. •
Пример 24-7. Найти (Ру, если y = x2wx = t3 + lwt — незави
симая переменная.
191
Q Решение: Используем формулу (24.6): так как
у' — 2х, у" = 2, dx — 3t2 dt, сРх — 6tdt2,
то
cPy = 2dx2 + 2x Qtdt2 = 2(3t2 dt)2 + 2(t3 + l)6tdt2 =
= 18t4 dt2 + 12t4 dt2 + 12tdt2 = (30t4 + 12t) dt2.
Другое решение: у = x2, x = t3 + 1. Следовательно, у = (t3 + I)2 Тогда по формуле (24.5)
d2y = y" • dt2,
d2y = (30t4 + 12t) dt2.
§25. ИССЛЕДОВАНИЕ ФУНКЦИЙ ПРИ ПОМОЩИ ПРОИЗВОДНЫХ
25.1. Некоторые теоремы о дифференцируемых функциях
Рассмотрим ряд теорем, имеющих большое теоретическое и при к ладное значение.
Теорема 25.1 (Ролль). Если функция f{x) непрерывна на отрезке [а; Ь], дифференцируема на интервале (а;Ь) и на концах отрезка принимает одинаковые значения f(a) = f(b), то найдется хотя бы одна точка с € (а;Ь), в которой производная f'(x) обращается в нуль, т. е. /'(с) = 0.
□ Так как функция f(x) непрерывна па отрезке [а; 6], то она достигает
на этом отрезке своего наибольшего и наименьшего значений, соответственно, Мит. Если М = т, то функция f(x) постоянна на [а; Ь] v следовательно, ее производная f'(x) = 0 в любой точке отрезка [а; 6].
Если М т, то функция достигает хотя бы одно из значений Л или т во внутренней точке с интервала (а; Ь), так как /(а) = f(b).
Пусть, например, функция принимает значение М в точке х -= с G (а; Ь), т. е. /(с) = М. Тогда для всех х G (а-,Ь) выполняете
соотношение
/(с) > f(x).
(25.1
Найдем производную f'(x) в точке х = с:
/(С+Дж)-/(С)
Inn --------------
Дж->0 Дж
192
Рис. 139 Рис. 140 Рис. 141
В силу условия (25.1) верно неравенство f(c + Дж) — /(с) 0. Если
Дж > 0 (т. е. Дж —> 0 справа от точки х = с), то
Если Дж < 0, то
/(С+2Дж ~(С) ° И //(С) °’
Таким образом, /'(с) = 0-
В случае, когда /(с) = т, доказательство аналогичное.
Геометрически теорема Ролля означает, что на графике функции у = / (ж) найдется точка, в которой касательная к графику параллельна оси Ох (см. рис. 139 и 140). На рисунке 141 таких точек две.
Теорема 25.2 (Коши). Если функции /(ж) и у?(ж) непрерывны на отрезке [а; &], дифференцируемы на интервале (а;Ь), причем у>'(х) 0
для х G (а;Ь), то найдется хотя бы одна точка с € (а; Ь) такая, что f (Ь) - f (а) /'(с)
выполняется равенство — ) < — ,; -(.
VW - ¥>(а) /(с)
Q Отметим, что у?(д) — </?(а) 0, так как в противном случае по теореме
Ролля нашлась бы точка с, такая, что ip'(c) = 0, чего не может быть по условию теоремы. Рассмотрим вспомогательную функцию
- /(«> - - »>(«»
Она удовлетворяет всем условиям теоремы Ролля: непрерывна на отрезке [a;t>] и дифференцируема на интервале (а; 6), так как является
7 Конспект лекций по высшей математике. Полный курс
193
линейной комбинацией функций f(x) и <р(х)-, на концах отрезка она принимает одинаковые значения F(a) — F(b) — 0.
На основании теоремы Ролля найдется точка х = с G («; Ъ) такая, что F'(c) = 0. Но F'(x) — f'{x) - следовательно,
Отсюда следует 1
/'(с) =
/(b) ~ /(«) ЛЬ) - Ла)
у/(с)
№ _ /(b)-/(а) Л (с) ЛЬ)-Ла)’
И
Теорема 25.3 (Лагранж). Если функция /(ж) непрерывна на отрезке [а;Ь], дифференцируема на интервале (а;Ь), то найдется хотя бы одна точка с € (а; Ь) такая, что выполняется равенство
ЛЬ)-/(о) = /'(с)(Ь-а). (25.2)
Q Решение: Теорему Лагранжа можно рассматривать как частный случай теоремы Коши. Действительно, положив tp(x) = х, находит Л&) - Ло) = Ь - а, Л (Л = 1, Л(с) = 1-
тт к /(b) - /(а) /'(с)
Подставляя эти значения в формулу _ Лд) = Л(с)’ полУча
ем = /'(с) или ЛЬ) “ Ла) = /'(С)(Ь - а). 1
Полученную формулу называют формулой Лагранжа ил) формулой о конечном приращении : приращение дифференцируемой функции на отрезке [а; 6] равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней
точке этого отрезка.
Теорема Лагранжа имеет простой геометрический смысл. Запишем формулу (25.2) в виде
о —а
где а<с<Ь. Отношение
/(b)-/(a)
Ь — а
есть угловой коэффициент секущей АВ, а величина f'(c) — угловой коэффициент касательной к кривой в точке с абсциссой х=с.
194
Следовательно, геометрический смысл теоремы Лагранжа таков: на графике функции у = /(ж) найдется точка С(с; /(c)) (см. рис. 142), в которой касательная к графику функции параллельна секущей АВ.
Следствие 25.1. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке.
Q Пусть f'{x) — 0 для Мх € (а; 6). Возьмем произвольные х.\ и ж2 из (а;Ь) и пусть Ж) < ж2. Тогда по теореме Лагранжа Зс € (Ж1;ж2) такая, что f (ж2) — f(xi) = f'{c)(x2 — Ж1). Но по условию /'(ж) = 0, стало быть, , /'(с) = 0, где Ж] < с < ж2. Поэтому имеем /(ж2) — /(жт) = 0, т. е.
/(ж2) = /(ж1). А так как Ж1 и ж2 — произвольные точки из интервала (а; Ь), то Уж £ (а; Ь) имеем /(ж) = с.
Следствие 25.2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
□ Пусть /{(ж) = f^) при х € (а;Ь). Тогда (fi(x) - /2(ж))' = f[(x) -— /2(^) = Следовательно, согласно следствию 25.1, функция fi(x) — — /2(ж) есть постоянная, т. е. Л (ж) — /2(ж) = С для \/х € («; Ь).
Пример 25.1. Доказать,чтоarcsinх+arccosх = ^,гдеж G [—1;1].
Q Решение: Пусть /(ж) = arcsin ж + arccosж. Тогда \/ж € (—1; 1) имеем /'(ж) = . * -I—. ~1 = 0. Отсюда следует, что /(ж) = С, т. е.
V1 - ж2 v 1 — ж2
arcsinж + arccosж — С. Положив ж = 0, находим 0 + ? = С, т. е. С = 5.
Поэтому arcsin ж + arccos ж = 5. Это равенство выполняется и при ж = ±1 (проверьте!). •
Аналогично доказывается, что arctg ж + arcctg ж = А.
Формуле Лагранжа можно придать другой вид. Применив теорему Лагранжа к отрезку [ж; ж + Дж] (Дж > 0), будем иметь
/(ж + Дж) - /(ж) = /'(с)Дж. (25.3)
Каждое число с G (ж; ж -I- Дж) можно записать в виде с — ж + #Дж, где 0 < 0 < 1 (действительно, ж < с < ж + Дж => 0 < с — ж < Дж ==> => 0 < Сдд5 < 1; положим = 0 => с = ж + #Дж). Формула (25.3) примет вид
/(ж + Дж) —/(ж) = f (ж + 0Дж)Дж, где 0 < в < 1.
195
Используя теорему Лагранжа, можно оценить точность приближенного равенства Ду « dy. Сделаем это, считая, что функция /(ж) имеет непрерывную вторую производную f"(x):
Ay - dy — (f(x + Дж) - /(ж)) - /'(ж)Дж = /'(с)Дж - f'(x)Ax =
- (/'(с) - /'(ж))Да; = f"(c1)(c-x)Ax,
где ci €Е (ж; с) (рис. 143).
Итак, Ду - dy = f"(ci)(c- ж)Дж. Пусть М = max |/"(ж)|. Так
[ж;ж+Дж]
как |с— ж| < Дж, a /"(cj) М, то получаем оценку |Ду — dy\ М|Дж|2.
X С1 с ж+Дж
Дж
Рис. 143
Хо с X
Рис. 144
25.2. Правила Лопиталя
Рассмотрим способ раскрытия неопределенностей вида q и к<> торый основан на применении производных.
Теорема 25.4 (Правило Лопиталя раскрытия неопределенностей вида g). Пусть функции /(ж) и уэ(ж) непрерывны и дифференцируемы в окрестности точки хо и обращаются В' нуль в этой точке: у(ж0) = у?(жо) = 0. Пусть <р'(х) 0 в окрестности точки жо- Если
fi(x} fix'} • fi(x'\
существует предел .lim A ( = I, то lim } ( = lim ---£-4- = I. x-+x0 p (ж) х->хс ‘/’(Ж) x-+x0 tp (ж)
Q Применим к функциям /(ж) и <Дж) теорему Коши для отрезка [жо; ж] m /(ж) - Джо) /'(с)
лежащего в окрестности точки жо- 1огда j' = уДс)’ ГДв *
лежит между жо и ж (рис. 144). Учитывая, что /(жо) = <Дж0) = 1 получаем ... ... .
/(^) = / (с) f25 J
<^(ж) <р'(с)'
При ж “Э жо, величина с также стремится к жо; перейдем в раве! стве (25.4) к пределу:
x-txt) <Р(Х) с-эжо </Дс)
196
'Г Г f(X) J Г /ЧС) / ГТ г /(#) 1
1 ак как lim Л- (- = L то lim —(- = L Поэтому lim —г = I.
Ж-Э-Жо (Х) С->Жо (с) ’ Х~>«о (Р\*£)
Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.
Замечания: 1. Теорема 25.4 верна и в случае, когда функции /(ж) и <р(х) не определены при х = яд, но lim /(я:) = 0 и lim </?(я:) = 0.
Ж~~>Ж(3 Ж—>ЖО
Достаточно положить f (яд) = lim f (я:) = 0 и <^(яд) = lim р(х) = 0. ж—»Жо ж—>Жо
2. Теорема 25.4 справедлива и в том случае, когда х —> оо. Действительно, положив х = 1, получим
r fM r J(|) r (/(I))' г /'(!)(-£) r m
lim —— = hm —= lim z. - hm \ \ = hm
•'<->00 <p(x) z->0 y?(ij z-Ю z->0 4j.) j-юо <p (X)
3. Если производные f'(x) и <p'(x) удовлетворяют тем же условиям, что и функции f(x) и <р(х), теорему 25.4 можно применить еще раз:
/"(*)
.. f(x) /Ч®) hm —г-г = hm — = hm
‘Р(х) (р (X) ж-»жо (р"[х)
И т. д.
Пример 25.2. Найти lim
ж->1я:1пя:
х — 1
Q Решение: lim —:— = s-л х т х
Г Г 1
= hm —--------- = hm ---------- = 1.
(я: In я:)' ж ->1 1пя: +J
Пример 25.3.
Найти lim -—cos бя: s-ю 2я:
Q Решение:
.. 1 — созбя;
hm-----—-----
®-и> 2я:2
О’ о
.. бвтбя:
= hm —-------
а:-И) 4я:
3 бсозбя;
= - hm —-------= 9.
2 ж—>о 1
0 о
о о
0
О’
Теорема 25.4 дает возможность раскрывать неопределенность вида Сформулируем без доказательства теорему о раскрытии неопреде-оо
ленности вида —. 00
197
Теорема 25.5 (Правило Лопиталя раскрытия неопределенностей вида ^).
Пусть функции f(x) и </?(ж) непрерывны и дифференцируемы в окрестности точки Хо (кроме, может быть, точки жо), в этой окрестности
lim /(ж) = lim <р(х) — оо, <р'(х) ф 0. Если существует предел х—а;—>жо
Г /Ч®) г /(ж) г /Ч®) hm то lim = lim J .
X—tXG (p \X) X-~>X() PyX) X—>Xo P (X)
Пример 25.4- Найти lim • r r ’ :r->5 tg5ж
Q Решение:
lim
x—
tgЗж _ Too
tg5ж [oo
3 • cos2 3 5ж 3 1 + cos 10ж
= hm -----5------= - lim ----------—
cos2 Зж • 5 о Т + созбж
3 —lOsinlOa: sinllte Г01 .. ЮсовЮж
— lim ----------= hm --------= — = hm --------------
5 — бвшбж sin6ж 0 бсовбж
2-й способ:
tgЗж оо ж — $ = t
11П1 --— = ----- . Л =
tg5ж [ooj [ t —> и
tg(|7T + 3f) Ctg3t tg5t 5
= hm —-(--------- = lim----— = lim ——- =
t-ю tg(|7T + 5t) / »octg5t t-rotg3t 3
Раскрытие неопределенностей различных видов
Правило Лопиталя применяется для раскрытия неопределешю-стей вида и 22, которые называют основными. Неопределенности вида 0 • оо, оо — оо, 1°°, оо°, 0° сводятся к двум основным видам путем тождественных преобразований.
1. Пусть /(ж) -> 0, </>(ж) -> оо при ж -> ж0. Тогда очевидны следующие преобразования:
hm (/(ж)у?(ж)) = [0-оо] = 1пп = - Гили hm
с-тжо L ж-тжо-1 0 \ х-ухо Л— LooJAj
v(x) J 4 5 f(x)
Например,
\ г л! i- 2 —ж ГО] —1 4
hm tg —(2 - ж) = [оо • 0] = hm = - = hm -------------т----- = -.
^2 & 4 7L x->2ctg^ [0j 71
198
2. Пусть /(а:) -> оо, <р(х) -> оо при х -> х0- Тогда можно поступить гак:
lim (f (а:) — <р(хУ) = [оо - оо] =
Х~>®о
r ( 1 lim ( —j—
X-нео \ \ f(x)
1 \ ,
—-j— ) = lim -
—j— J Ж-1Ж0 . . , у(ж)7
’ На практике бывает проще, например,
/ 1 1 \ г , а: — 1 — Ina;
lim [ ------------- = loo — ool = hm---------:------
®->i \ In x x — 1 / ‘
1
0
0
1 1 vM f(.x)
__________ Г0
ж->1 Ina: • (a: — 1) [6
1-1 X
о о
1
2
= lim — ,---------
ж->1 + Ina:
= lim —r
x-+i X 4- A x
3. Пусть или f(a:) -Ии <p(x) —> оо, или f(x) —> оо и ip(x) 0, или /(a:) —> 0 и ip(x) —> 0 при x —> a:o- Для нахождения предела вида lim /"(а:)^®) удобно сначала прологарифмировать выражение ж—>®0
А = f (а:)^.
Пример 25.5. Найти lim (cos 2а:) . а—>0
(J Решение: Имеем неопределенность вида 1°°. Логарифмируем выражение А = (cos 2т) , получим: In А — In cos 2х. Затем находим предел:
lira In А= lim х—>0 х—>0
In cos 2x x2
01 I- E^2j(-sin2a:)2 OI- *ё2ж
- = lim ® —---------— = -2hin-l;— =
0 ж->о 2a: ж-»о 2a:
= — 2, t. e. In lim A= — 2. Отсюда lim A=e 2 и lim (cos 2a:) =e 2. • «—>0 x—>0 x~>0
Решение можно оформить короче, если воспользоваться «готовой» формулой
lim /(а:)*’(ж) = =ехр( lim tp(x) In/(т))
х~>хо \ж-»а:о >
(использовано основное логарифмическое тождество: = eIn-^).
Пример 25.6. Найти lim(l)tg®. s-Ю х
Q Решение:
lim ( - । = [оо°] = expf lim tga:In —= expflim ——'j =
ж-гОуа:/ \ж—>o х/ \x-^octgx/
A. Л. /sina:\2\ 04 0 *
= exp lim-----f— = exp hm a: I-------) ) = e = e = 1. •
\ ж—>o —r-4— ) \x~>o \ x / /
x sirr X 7
199
Пример 25.7. Пусть
/(®) =
при х О, при х = О.
О
Найти f'(x). (Дополнительно: найти /^”ц0).)
Q Решение: При х 0 имеем
/'(ж) = е-®-2 • (—ж-2)' = 2е-®-2 • ж-3
При х = 0 по определению производной:
до) = ы'<0+У»» =
А-»О А А—>0 А
Делаем замену у = р- и применяем правило Лопиталя lim = lim = lim —*------------------------------= 0.
А—>о А г/-юо е» у-^оо t^jy • еу
Таким образом,
2ж-3 • е~х 2 при х О,
О при х — 0.
Аналогично можно показать, что /^"^(0) — 0.
25.3. Возрастание и убывание функций
Одним из приложений производной является ее применение к исследованию функций и построению графика функции.
Установим необходимые и достаточные условия возрастания и убывания функции.
Теорема 25.6 (необходимые условия). Если дифференцируемая на интервале (а; 6) функция /(ж) возрастает (убывает), то /'(ж) 0
(/'(ж) 0) для Уж е (а;Ь).
Q Пусть функция /(ж) возрастает на интервале (а; Ь). Возьмем произ-
вольные точки х и х + Дж на интервале (а; Ь) и рассмотрим отноше-
ние
Ду - /(ж + Дж) ~ /(ж)
Дж Дж
. Функция /(ж) возрастает, поэтому если
Дж > 0, то ж + Дж > ж и /(ж + Дж) > /(ж); если Дж < 0, то ж 4- Дж < ж и /(ж + Дж) < /(ж). В обоих случаях = -^Х > 0, так
200
как числитель и знаменатель дроби имеют одинаковые знаки. По условию теоремы функция /(ж) имеет производную в точке х и является пределом рассматриваемого отношения. Следовательно,
/'W
Um Щ + Дд) -/(») Дя-Ю Дж
Аналогично рассматривается случай, когда функция /(ж) убывает на интервале (а; 6).
Геометрически теорема 25.6 означает; что касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси Ох или в некоторых точках (на рисунке 145 в точке с абсциссой жо) параллельны оси Ох.
Теорема 25.7 (достаточные условия). Если функция /(ж) дифференцируема на интервале (о; Ь) и /'(ж) > О (/'(ж) < °) Для б (а; 6), то эта функция возрастает (убывает) на интервале (а; 6).
[_] Пусть f'(x) > 0. Возьмем точки Ж1 и Ж2 из интервала (а; Ь), причем Ж1 < Ж2- Применим к отрезку [ад;жг] теорему Лагранжа: /(жг) — /(ад) = = /'(с)(жг — хг), где с е (Ж1;жг). По условию /'(с) > 0, ж2 — Ж1 > 0. Следовательно, f(x-2) - /(ж1) > 0 или /(ж2) > /(жД т. е. функция /(ж) на интервале (а; Ь) возрастает.
Рассмотренные теоремы 25.6 и 25.7 позволяют довольно просто исследовать функцию на монотонность. Напомним, что функция возрастающая или убывающая называется монотонной (см. с. 122).
Пример 25.8. Исследовать функцию /(ж) = ж3 — Зж — 4 на возрастание и убывание.
Q Решение: Функция определена на R=(—оо;оо). Ее производная равна:
/'(ж)=3ж2 — 3 = 3(ж — 1)(ж + 1);
/'(ж)>0 при ж£ (—оо; —1) U (1; оо);
/'(ж)<0 при жб(-1;1).
Ответ: данная функция
и (1; оо); убывает на интервале (—1; 1).
возрастает' на интервалах (—оо;—1)
201
25.4. Максимум и минимум функций
Точка жр называется точкой максимума функции у = /(ж), если существует такая ^-окрестность точки Жр , что для всех х / х$ из этой окрестности выполняется неравенство /(ж) < /(жр).
Аналогично определяется точка минимума функции: жо — точка минимума функции, если 3<5 > О Уж : 0 < |ж — ж0| < 6 => /(ж) > > /(ж0). На рисунке 146 Ж1 — точка минимума, а точка жг — точка максимума функции у = /(ж).
Значение функции в точке максимума (минимума) называется максимумом- (минимумом) функ-.
Рис. 146
ции. Максимум (минимум) функции называется 'экстремумом функ-1
ции.
Понятие экстремума всегда связано с определенной окрестностью
точки из области определения функции. Поэтому функция может
иметь экстремум лишь во внутренних точках области определения. Рассмотрим условия существования экстремума функции.
Теорема 25.8 (необходимое условие экстремума). Если дифференцируемая функция у = f(x) имеет экстремум в точке ж0, то ее производная в этой точке равна нулю: /'(жр) = 0.
Q Пусть, для определенности, ж0 — точка максимума. Значит, в окрестности точки жо выполняется неравенство /(жр) > /(жр + Дж). Но тогда = ^Х° + Ах).—f(xo) < Q если Дж > 0, и > 0, если Дж Дж Дж
Дж < 0. По условию теоремы производная
/'W
Н111 /(жр + Дж) - У(ж0) Д.Ж-+0 Дж
существует. Переходя к пределу, при Дж —> 0, получим /'(ж0) 0, если
Дж < 0, и /'(жо) $ 0, если Дж > 0. Поэтому /'(жо) = 0. Аналогично доказывается утверждение теоремы 25.8, если жо — точка минимума функции /(ж).
Геометрически равенство /'(ж0) = 0 означает, что в точке экстремума дифференцируемой функции у = /(ж) касательная к ее графику параллельна оси Ох (см. рис. 147).
Отметим, что обратная теорема неверна, т. е. если /'(жр) — 0, то это не значит, что жр — точка экстремума. Например, для функции
202
у = x3 ее производная у' = Зж2 равна нулю при х = 0, но х = 0 не точка экстремума (см. рис. 148).
Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция у — |ж| в точке х = 0 производной не имеет, но точка х = 0 — точка минимума (см. рис. 149).
Таким образом, непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.
Теорема 25.9 (достаточное условие экстремума). Если непрерывная функция у = /(ж) дифференцируема в некоторой (5-окрестности критической точки хо и при переходе через нее (слева направо) производная f'(x) меняет знак с плюса на минус, то хо есть точка максимума; с минуса на плюс, то хо — точка минимума.
□ Рассмотрим ^-окрестность точки xq. Пусть выполняются условия: f'(x) > О Уж £ (ж0 — <5;®о) и /'(ж) < 0 Уж £ (ж0;ж0 + (5). Тогда функция /(ж) возрастает' на интервале (жо — 6; жо), а на интервале (жо;®о + <5) она убывает. Отсюда следует, что значение /(ж) в точке xq является наибольшим на интервале (жо — <5; Жо + S), т. е. /(ж) < /(жо) для всех х £ (®о — <5; жо) U (жо; жо + (5). Это и означает, что жо — точка максимума функции.
Графическая интерпретация доказательства теоремы 25.9 представлена на рисунке 150.
Аналогично теорема 25.9 доказывается для случая, когда /'(ж) < 0 Уж £ (ж0 — (5; ж0) и /'(ж) > 0 Уж £ (жо;жо + й).
203
Исследовать функцию на экстремум означает' найти все ее экстремумы. Из теорем 25.8 и 25.9 вытекает' следующее правило исследования функции на экстремум:
1) найти критические точки функции у = /(ж);
2) выбрать из них лишь те, которые являются внутренними точками области определения функции;
3) исследовать знак производной f'(x) слева и справа от каждой из выбранных критических точек;
4) в соответствии с теоремой 25.9 (достаточное условие экстремума) выписать точки экстремума (если они есть) и вычислить значения функции в них.
Пример 25.9. Найти экстремум функции у =
О
Q Решение: Очевидно, D(y) = Ж. Находим у' = А — т. е. у' =
*5 О * "у
_1 %/ж —2
3 ’ у/х
Производная не существует при a?i = 0 и равна нулю при ж2 = 8. Эти точки разбивают всю область определения данной функции на три интервала (—оо;0), (0;8), (8;оо). Отметим на рисунке 151 знаки производной слева и справа от каждой из критических точек.
б 8 х
Рис. 151
Следовательно, х± =0 — точка максимума, «/тах = ?/(0) = 0, и ' = 8 — точка минимума, ymin = т/(8) = — А. •
О
Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.
204
Теорема 25.10. Если в точке ®0 первая производная функции /(ж) равна нулю (/'(жо) = 0), а вторая производная в точке Жо существует и отлична от нуля (/"(ж0) 0), то при f"(#o) < 0 в точке ж0 функция
имеет максимум и минимум — при /"(жд) > 0.
□ Пусть для определенности /"(®о) > 0. Так как
ГЫ
lim /'(жо + Аж) - /'(жо) Дж-+0 Дж
,. f'(xo + Аж) п пт —-—-——- > 0,
Дж->0 Дж
/'(ж0 + Дж) „
то х ---------- > 0 в достаточно малой окрестности точки жо. Если
Дж < 0, то /'(ж0 + Дж) < 0; если Дж > 0, то /'(ж0 + Аж) > 0.
Таким образом, при переходе через точку жд первая производная меняет знак с минуса на плюс. Следовательно, по теореме 25.9, жо есть точка минимума.
Аналогично доказывается, что если /"(ж0) < 0, то в точке жд функция имеет максимум.
25.5. Наибольшее и наименьшее значения функции на отрезке
Пусть функция у = f(x) непрерывна на отрезке [а; 6]. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке жо отрезка [а; Ь], либо на границе отрезка, т. е. при жд = а или жо = Ь. Если жо € (а; Ь), то точку жо следует искать среди критических точек данной функции (см. рис. 152).
Получаем следующее правило нахождения наибольшего и наименьшего значений функции на [а; 6]:
1) найти критические точки функции на интервале (а; 5);
2) вычислить значения функции в найденных критических точках;
3) вычислить значения функции на концах отрезка, т. е. в точках ж = а и ж = Ь;
4) среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Замечания: 1. Если функция у — f(x) на отрезке [а; 5] имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение. На рисунке 152 /(жд) — /нб — /шах (нб — наибольшее, max — максимальное).
2. Если функция у — f(x) на отрезке [а; 5] не имеет критических точек, то это озачает, что на нем функция монотонно возрастает или
205
убывает. Следовательно, свое наибольшее значение (М) функция принимает на одном конце отрезка, а наименьшее (т) — на другом.
Пример 25.10. Найти наибольшее и наименьшее значения функции /(ж) = Зж4 4- 4ж3 + 1 на отрезке [—2; 1].
Q Решение: Находим критические точки данной функции:
f'(x) = 12ж3 + 12ж2 = 12ж2(ж 4- 1);
/'(ж) = 0 при Xi = 0 е [—2; 1] и при жг = —1 G [—2; 1]. Находим /(0) = 1 /(-1) = 3-44-1 = 0, /(-2) = 48 - 32 4-1 = 17, /(1) = 8. Итак, /нб = 11 в точке х = —2, = 0 в точке х = —1. •
Нахождение наибольшего и наименьшего значений функции широ-ко применяется при решении многих практических задач математики физики, химии, экономики и других дисциплин.
Практические задачи: транспортная задача о перевозке груза < минимальными затратами, задача об организации производственной процесса с целью получения максимальной прибыли и другие зада чи, связанные с поиском оптимального решения, приводят к развитии и усовершенствованию методов отыскания наибольших и наименьшие значений. Решением таких задач занимается особая ветвь математики — линейное программирование.
Рассмотрим более простую задачу.
Пример 25.11. Из шара радиуса R выточить цилиндр наибольшего объема. Каковы его размеры?
Q Решение: Обозначим через х и у высоту и диаметр цилиндра. Тогда, как видно из рисунка 153, у = y/^R? — х"2, а потому объем цилиндра
т/ ел/ \ /47?2 —ж2\ 2 яж3
V = У(ж) = я I -------) X = 7rR2X--— ,
\ 4 / 4
где х Е [0;2/?.].
206
Находим наибольшее значение функции V = Г’(.т) на промежутке |(); 2R], Так как V'(x) = тгИ2 — ?тга2, то V'(ar) = 0 при х = ^ДУ^, кроме
4 о
того, Г"(.'с) = — йтг.т < 0. Поэтому х = 2Д>/3 — точка максимума. Так как функция имеет одну критическую точку, то цилиндр будет иметь наибольший объем (равный Vmax) при х = ^Д^Д диаметр основания цилиндра равен _____________________
^4Я2 - (2/?V3/3)2 =
О
Таким образом, искомый цилиндр имеет высоту, равную -Д^, и О
диаметр, равный . •
«5
25.6. Выпуклость графика функции. Точки перегиба
График дифференцируемой функции у = /(т) называется выпуклым вниз на интервале (а; 6), если он расположен выше любой
ее касательной на этом интервале. График функции у — f(x) называется выпуклым вверх на интервале (а; Ь), если он расположен ниже любой ее касательной на этом интервале.
Точка графика непрерывной функции у = /(ж), отделяющая его части разной выпуклости, называется точкой перегиба.
На рисунке 154 кривая у = /(ж) выпукла вверх в интервале (а; с), выпукла
вниз в интервале (с; 5), точка Л£(с;/(с)) — точка перегиба.
Интервалы выпуклости вниз и вверх находят с помощью следую-
щей теоремы.
Теорема 25.11. Если функция у = f(x) во всех точках интервала (а; 6) имеет отрицательную вторую производную, т. е. f"(x) < 0, то график функции в этом интервале выпуклый вверх. Если же f"(x) > 0 V.T 6 (а; 6) — график выпуклый вниз.
□ Пусть /"(ж) < 0 Vt G («;/>). Возьмем на графике функции произвольную точку М с абсциссой xq G («; b) и проведем через М касательную (см. рис. 155). Покажем, что график функции расположен ниже
207
этой касательной. Для этого сравним в точке х е («; Ь) ординату у кривой у = f(x) с ординатой укас ее касательной. Уравнение касательной, как известно, есть
?/Кас - /(ж0) = /'(жо)(ж - х0), т. е. ук&с = /(ж0) + /'(жо)(ж-жо). Тогда у — ?/кас = f(%) — /(®о) — /'(ж0)(ж — жо). По теореме Лагранжа, /(ж) — /(жо) = Г (с) (ж — xq), где с лежит между хо и х. Поэтому
У ~ Ук&с = /'(с)(ж ~ жо) - /'(жо)(ж - хо), т. е.
У-У^с = (/'(<=) -f(xo))(x-xo). J Разность /'(с) — /'(ж0) снова преобразуем по формуле Лагранжа:
/'(с) - f'(«o) =/"(с1)(с - жо), где ci лежит между а?0 и. с. Таким образом, получаем
У -у™ = /"(С!)(с- Хо){х - То).
Исследуем это равенство:
1) если х > хо, то аг —то > 0, с—то > 0 и /"(щ) < 0. Следовательно,
У ?/кас < 0, Т. е. у <Z Укас'
2) если ж < то, то т —то
—о •----• •----—
То С1 ст т
< 0, с—то < 0 и /"(щ) < 0. Следовательно,
У ~~ Укяс < 0, Т. е. у < ?/кас: % с То ж
Итак, доказано, что во всех точках интервала (а; Ь) ордината касательной больше ординаты графика, т. е. график функции выпуклый вверх. Аналогично доказывается, что при /"(ж) > 0 график выпуклый вниз. И
Для нахождения точек перегиба графика функции используется следующая теорема.
Теорема 25.12 (достаточное условие существования точек перегиба). Если вторая производная /"(ж) при переходе через точку То, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой ж0 есть точка перегиба.
□ Пусть /"(ж) < 0 при х < хо и /"(ж) > 0 при ж > хо- Это значит, что слева от ж = жо график выпуклый вверх, а справа — выпуклый вниз. Следовательно, точка (жо;/(жо)) графика функции является точкой перегиба.
Аналогично доказывается, что если /"(ж) > 0 при ж < жо и /"(ж) < < 0 при ж > жо, то точка (жо; /(жо)) — точка перегиба графика функции У = f(x).
208
- Пример 25.12. Исследовать на выпуклость и точки перегиба график функции у = ж5 — х + 5.
Q Решение: Находим, что у' = 5ж4 - 1, у" = 20х3. Вторая производная существует1 на всей числовой оси; у" = 0 при х = 0.
Отмечаем, что у" > 0 при х > 0; у" < 0 при х < 0.
Следовательно, график функции у = ж5 — ж + 5 в интервале (—сю; 0) — выпуклый вверх, в интервале (0; оо) — выпуклый вниз. Точка (0; 5) есть точка перегиба. •
25.7. Асимптоты графика функции
Построение графика функции значительно облегчается, если знать его асимптоты. Понятие асимптоты рассматривалось при изучении формы гиперболы (см. с. 81).
Напомним, что асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис. 156).
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Говорят, что прямая ж = а является вертикальной асимптотой графика функции у = /(ж), если lim /(ж) = оо, или lim /(ж) = ж—>о,—0
= сю, или lim /(ж) = оо.
ж->а+0
Действительно, в этом случае непосредственно из рисунка 156 видно, что расстояние точки М (х; у) кривой от прямой ж = а. равно d — = |ж - а|. Если ж -> а, то d -> 0. Согласно определению асимптоты, прямая ж = а является асимптотой кривой у = f(x). Для отыскания вертикальных асимптот нужно найти те значения ж, вблизи которых функция /(ж) неограниченно возрастает по модулю. Обычно это точки
разрыва второго рода.
Например, кривая у = % , имеет вертикальную асимптоту (см.
X । 1
9 • 2
рис. 157) ж = —1, так как lim —-3- = +00, lim - — ~ = —оо.
Уравнение наклонной асимптоты будем искать в виде
у = кх + Ь.
(25.5)
Найдем к и Ь.
209
Рис. 157
Пусть М (ж; у)
По формуле расстояния от точки до прямой (d = находим расстояние от точки М до прямой (25.5): d = I
Условие d —> 0 будет выполняться лишь тогда, когда числитель
произвольная точка кривой у = f (ж) (см. рис. 158). ' Ах0 + Ву0 + С 1\ х/л2 + В2 I' кх — у + b | \/fc2 + l I
дроби стремится к нулю, т. е.
lim (кх - у + Ь) = 0. (25.6)
X—loo
Отсюда следует, что кх — у + b = а, где а — а(х) бесконечно малая: а —> 0 при х —> оо. Разделив обе части равенства у — Ь+кх — а на ж и перейдя к пределу при х —> оо, получаем:
У V (Ъ , а lim — = lim I —F к------
я—>oo £ ж—x
Так как — —> 0 и — 0, то
х х
к= lim -.
ж->оо X
(25.7)
Из условия (25.6) находим Ъ:
(25.8)
Итак, если существует наклонная асимптота у — кх + Ъ, то к и b находятся по формулам (25.7) и (25.8).
Верно и обратное утверждение: если существуют конечные пределы (25.7) и (25.8), то прямая (25.5) является наклонной асимптотой.
Если хотя бы один из пределов (25.7) или (25.8) не существует или равен бесконечности, то кривая у = f(x) наклонной асимптоты не имеет.
210
В частности, если к = 0, то b = lim f(x). Поэтому у = b — урав-. я—>оо
пение горизонтальной асимптоты.
Замечание: Асимптоты графика функции у = f(x) при х —> +оо и х —> — оо могут быть разными. Поэтому при нахождении пределов (25.7) и (25.8) следует отдельно рассматривать случай, когда х —> +оо и когда х -> —оо.
Пример 25.13. Найти асимптоты графика функции у = хех.
Q Решение: Так как lim = цт еж = +оо, то график функции х—>4-оо X х—> 4-оо
при х —-> +оо наклонной асимптоты не имеет.
При х —> —оо справедливы соотношения
ТСХ
к = lira --= lim еж = О,
х—>—оо X а—>—оо
b = lim (хех — (to) = lim хех — lim — = — = lim —— = 0. а—>—оо а—>—оо а—>—оо е х ОО а->—оо — е а
Следовательно, при х —> — оо график имеет горизонтальную асимптоту У = 0. •
25.8. Общая схема исследования функции и построения графика
Исследование функции у = f(x) целесообразно вести в определенной последовательности.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями координат.
3. Найти интервалы знакопостоянства функции (промежутки, на которых f(x) > 0 или /(ж) < 0).
4. Выяснить, является ли функция четной, нечетной или общего вида.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности функции.
7. Найти экстремумы функпии.
8. Найти интервалы выпуклости и точки перегиба графика функ-г ции.
На основании проведенного исследования построить график функции. Заметим, что приведенная схема исследования не является обязательной. В более простых случаях достаточно выполнить лишь несколько операций, например 1, 2, 7. Если же график функции не совсем
211
понятен и после выполнения всех восьми операций, то можно дополнительно исследовать функцию на периодичность, построить дополнительно несколько точек графика, выявить другие особенности функции. Иногда целесообразно выполнение операций исследования сопровождать постепенным построением графика функции.
Пример 25.14- Исследовать функцию у — - $ и построить ее 1 — х
график.
Q Решение: Выполним все восемь операций предложенной выше схемы исследования.
1. Функция не определена при ж = 1иж = —1. Область ее определения состоит из трех интервалов (—оо; —1), (—1; 1), (1; +оо), а график из трех ветвей.
2. Если х = 0, то у = 0. График пересекает ось Оу в точке 0(0; 0); если у ~ 0, то х = 0. График пересекает1 ось Ох в точке 0(0; 0).
3. Функция знакоположительна (у > 0) в интервалах (—оо;-1) и (0; 1); знакоотрицательна— в (—1; 0) и (1;+оо).
4. Функция у = -- %—-% является нечетной, т. к.
= 1 7^)2 = -^2 =
Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при ж 0.
5. Прямые ж = 1иж = —1 являются ее вертикальными асимптота-1 ми. Выясним наличие наклонной асимптоты: ’
—1
к = lim ~ж = lim --- = 0 ’
ж—>оо X 1 — хл I
(к = 0 при ж —> +оо и при ж -> —оо),
b = lim ( Ж — Ож) = lim - = 0.
ж—>оо 1 — X2, т>ос 1 — xz
Следовательно, есть горизонтальная асимптота, ее уравнение у = 0-1 Прямая у — 0 является асимптотой и при ж -> +оо, и при ж -> —оо.
6. Находим интервалы возрастания и убывания функции. Так как] ж
1 — ж2
1—ar
1(1 — ж2) - ж(—2ж) _ ж2 + 1 (1-ж2)2 = (1-ж2)2’
то у' > 0 в области определения, и функция является возрастающей на] каждом интервале области определения.
7. Исследуем функцию на экстремум. Так как у' = ~~ то
(1 — ж ) критическими точками являются точки х\ = 1 и ж2 = — 1 (у' не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
У =
212
8. Исследуем функцию на выпуклость. Находим у":
/ ж2 + 1 2ж(1 - ж2)2 - (ж2 + 1)2(1 - ж2)(-2ж) _ 2ж(ж2 + 3)
\(1— ж2)2 у (1 —ж2)4 (1 — ж2)3
»1 Вторая производная равна нулю или не существует в точках Ж] = == 0, ж-2 = —1, Жз = 1. На рисунке 159 представлена схема изменения Знаков второй производной исследуемой функции.
Точка 0(0,0) — точка перегиба графика функции.
1 График выпуклый вверх на интервалах (—1; 0) и (1; оо); выпуклый вдиз на интервалах (—оо; -1) и (0; 1).
| График функции изображен на рисунке 160. •
§ 26. ФОРМУЛА ТЕЙЛОРА
В определении функции у = /(ж) не говорится о том, при помощи каких средств находятся значения у по значениям ж. В тех случаях, ,,..з
когда функция является формулой вида у = ~— 5ж + 7, значения функции найти легко с помощью четырех арифметических действий. Но как найти значения, например, функций у = sin ж, у = 1п(14- ж) при любых (допустимых) значениях аргумента?
Для того, чтобы вычислить значения данной функции у = f(x), ее заменяют многочленом Рп(х) степени п, значения которого всегда и легко вычисляемы. Обоснование возможности представлять функцию многочленом дает формула Тейлора.
213
26.1. Формула Тейлора для многочлена
Пусть функция /(ж) есть многочлен Рп(х) степени п:
= Рп(х) = do + а^х + а2ж2 + ... + апхп.
Преобразуем этот' многочлен также в многочлен степени п относительно разности х — Хо, где жо — произвольное число, т. е. представим Рп (х) в виде
Рп(х) = Ао + АДж - ж0) + А2(ж - жо)2 + ... + А„(ж - ж0)". (26.1)
Для нахождения коэффициентов Ао, Аг,..., Ап продифференцируем п раз равенство (26.1):
-Р«(ж) = Ai + 2А2(ж - ж0) + ЗА3(ж - ж0)2 + ... + пАп(х - Жо)”-1,
Р"(х) = 2А2 + 2 • ЗА3(ж - жо) + ... + п(п - 1)Л„(ж — ж0)”~2, i
Р^'(х) = 2 ЗА3 + 2 3 • 4А4(ж - ж0) + -..
... + п(п — 1)(п — 2)Ап(ж — х0)п~3,
Р^п)(х) = п(п - 1)(п — 2)... 2 1А„.
Подставляя ж = ж0 в полученные равенства и равенство (26.1), имеем: '
т. е. Ао
^о) = А, т. е. Ai _^о) 1! ’
Р"(жо) = 2А2, т. е. а2 2! ’
Р'"(ж0) = 2 - ЗА3, т. е. Аз _ РЦ'Ы 3!
П^(жо)=п(п-1)...2-1Ап, т.е. Ап = п!
Подставляя найденные значения Ао, Ац...,Л„ в равенство (26.1), по- й лучим разложение многочлена n-й степени Рп(ж) по степеням (ж -ж0):
Р„(Х) = Р„(жо) + ^^(ж - жо) + 5^(ж - жо)2 + . . .
••-^-^^(ж-ЖоГ. (26.2)
214
’£j Формула (26.2) называется формулой Тейлора для многочлена Рп(х) степени п.
Пример 26.1. Разложить многочлен Р(х) = — 4х3 + Зя2 - 2а; + 1 по степеням х + 1.
< J Решение: Здесь xq = —1, Р'(х) = —12а;2 + 6х — 2, Р"(х) = —24а; + 6, Р"'(х) = -24. Поэтому F(—1) = 10, F'(-l) = -20, F"(-l) = 30, F"'(—1) = —24. Следовательно,
Р(х) = 10 + —(а; + 1) + ^(а; + I)2 + -^(а; + I)3,
т. е.
—4а;3 + За;2 - 2х + 1 = 10 - 20(х + 1) + 15(а; + I)2 - 4(х + I)3. •
26.2. Формула Тейлора для произвольной функции
Рассмотрим функцию у = /(а;). Формула Тейлора позволяет', при определенных условиях, приближенно представить функцию /(а;) в ви- -де многочлена и дать оценку погрешности этого приближения.
Теорема 26.1. Если функция /(а?) определена в некоторой окрестности точки а;о и имеет в ней производные до (п + 1)-го порядка включительно, то для любого х из этой окрестности найдется точка с 6 (а;о;а;) такая, что справедлива формула
/(а;) = /(а;0) + ^~-(х - аг0) + ~ жо)2 + • • •
(с = хо + 6(х — а;о), 0 < 3 < 1). (26.3)
Формула (26.3) называется формулой Тейлора для функции f(x). Эту формулу можно записать в виде f(x) = Рп(х) + F„(a;), где
Рп (х) = /(а;0) + - х0) + (а; - а;0)2 +... + ~ хоУ
|ф| называется многочленом Тейлора, а
ЛГ+1
215
|ф| называется остаточным членом формулы Тейлора, записанным в форме Лагранжа. Л„(ж) есть погрешность приближенного равенства /(ж) и Рп(ж). Таким образом, формула Тейлора дает возможность заменить функцию у = /(ж) многочленом у = Р„(ж) с соответствующей степенью точности, равной значению остаточного члена Я„(ж). '
|ф| При жо = 0 получаем частный случай формулы Тейлора — формулу Маклорена:
/« = Ж + ® ви +... + , (26.4)
где с находится между 0 и ж (с = 0х, 0 < 6 < 1).
При п = 0 формула Тейлора (26.3) имеет вид /(ж) = /(жо) + +/'(с)(ж—жо) или/(ж) — /(жо) = f'(c)(x—жо), т. е. совпадает с формулой Лагранжа конечных приращений. Рассмотренная ранее формула для приближенных вычислений /(ж) « /(жо) + /'(жо)(ж.— жо) (см. «дифференциал функции») является частным случаем более-точной формулы
/(ж) « f (ж0) + ~~(ж - ж0) + ... + ™“Г^(а; - хо)п-
Пример 26.2. Найти число е с точностью до 0,001.
Q Решение: Запишем формулу Маклорена для функции /(ж)=еж. Находим производные этой функции: f(x)=ex, f"(x)=ex, ..., f(n+1\x') = =ех. Так как /(0)=е° = 1, /'(0)=е° = 1, ..., /(")(0)=1, /(п+1)(с)=ес, то по формуле (26.4) имеем:
9 Ч «z.
e‘ = 1+i!+2!+¥
ж” есхп+1 п! + (тг+1)!
Положим ж = 1:
1, то ес < 3.
меньше 0,001. Так как 0
111 1 ес
C~1+l! + 2! + 3!+--- + M + (^W
Для нахождения е с точностью 0,001 определим п из условия, что остаточный член
\п + 1)!
Поэтому при п = 6 имеем
7! <
з
5040 = О’0006 <0’001-
Итак, получаем приближенное равенство
. 11111
+ + 2! + 3! + 4! + 5! + 6!
» 2 + 0,5 + 0,1667 + 0,0417 + 0,0083 + 0,0014 = 2,7181« 2,718, т. е. е ps 2,718.
216
Приведем разложения по формуле Маклорена некоторых других элементарных функций:
™3 ,г5 ™2п+1 ™2п+3
™2 4 ,,.2п „2п+2
" 1 - 2! + ¥ -' + (-1’" W + <~1)W
/у»2 zv»3 ntTl 1
ln(I + = , _ _ + _ +... + (-!)»- _ + (-!)' (n+ 1)(1 +c)„+,
«(lU — 1) 9 — 1)... (ju — n + 1) „
(1 + .?'' = 1 + .' x2 + ... + —-1----------------’-xn+
2! nl
p(p - 1)... (p - n)(l + c)^-1 +1
*r z _\ , ' ———
Глава VI. КОМПЛЕКСНЫЕ ЧИСЛА
Лекции 23-24
§27. ПОНЯТИЕ И ПРЕДСТАВЛЕНИЯ КОМПЛЕКСНЫХ ЧИСЕЛ
27.1. Основные понятия
|ф| Комплексным, числом z называется выражение вида z = x + iy, где х и у — действительные числа, аг — так называемая мнимая единица, i'2 = — 1.
|ф| Если х = 0, то число 0 + iy = iy называется чисто мнимым;
если у = 0, то число х + г'О — х отождествляется с действительным числом х, а это означает, что множество Ж всех действительных чисел является подмножеством множества С всех комплексных чисел, т. е. Ж С С.
|ф| Число х называется действительной частью комплексного числа z и обозначается х = Rez, ay — мнимой частью z, у = Im z.
|ф| Два комплексных числа zj = х± + iyi и z? = ®2 + гуч называются равными (zi = Z2) тогда и только тогда, когда равны их действи-1 тельные части и равны их мнимые части: хг = x^,yi = y-i- В частности, комплексное число z = х + iy равно нулю тогда и только тогда, когда х = у = 0. Понятия «больше» и «меньше» для комплексных чисел не вводятся.
|ф| Два комплексных числа z = х + iy к. z — х — iy, отличающиеся лишь знаком мнимой части, называются сопряженными.
27.2. Геометрическое изображение комплексных чисел
Всякое комплексное число z = х + iy можно изобразить точкой М{х; у) плоскости Оху такой, что х = Rez, у = Imz. И, наоборот, каждую точку М{х; у) координатной плоскости можно рассматривать как образ комплексного числа z = х + iy (см. рис. 161). |ф| Плоскость, на которой изображаются комплексные числа, называется комп
лексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа z = х + Oi = х. Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные числа z — 0 + iy.
218
|ф| Комплексное число z = х + iy можно задавать с помощью радиус-вектора г = ОМ = (х;у). Длина вектора г, изображающего комплексное число z, называется модулем этого числа и обозначается \z\ или г. Величина угла между положительным направлением действительной оси и вектором г, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Arg z или <р.
Аргумент комплексного числа z = 0 не определен. Аргумент комплексного числа z 0 — величина многозначная и определяется с точностью до слагаемого 2як (к = 0,-1,1, —2,2...): Arg г = argz+27rfc, где arg г — главное значение аргумента, заключенное в промежутке (—тг; я], т. е. —тг < argz тг (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку [0;2тг)).
27.3. Формы записи комплексных чисел
|ф| Запись числа z в виде z = х + iy называют алгебраической формой комплексного числа.
|ф| Модуль г и аргумент <р комплексного числа можно рассматривать как полярные координаты вектора г = ОМ, изображающего комплексное число z = х + iy (см. рис. 161). Тогда получаем х = rcos</?, у = г sin Следовательно, комплексное число z = х + iy можно записать в виде z = г cos <р + ir sin ip или
z = r(cos</? + zsin</?).
Такая запись комплексного числа называется тригонометрической формой.
Модуль г = \z\ однозначно определяется по формуле
г = |г| — у/х2 + у2.
Например, |г| = л/02 + I2 = 1. Аргумент <р определяется из формул
х . у у
cos<£ = —, smw=-, tgw = —.
Г Г X
Так как
<р = Arg z = arg z + 2кк,
то
cos</? = cos(argz + 2&7г) = cos(argz), sin</? = sin(argz).
Поэтому при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного числа z, т. е. считать <р = arg г.
219
Так как — тг < argz тг, то из формулы tg<^ = получаем, что
’ arctg
arg z = < arctg + тг
arctg — тг
Если точка z лежит
для внутренних точек
I, IV четвертей,
для внутренних точек
II четверти,
для внутренних точек III четверти.
, действительной или мни-
мой оси, то arg z можно найти непосредственно (см. рис. 162). Например, argzi = 0 для z\ = 2; arg zi = тг для z2 = -3; arg z3 = А для z3 = г; и
argz4 — — для Z4 = —8г.
Используя формулу Эйлера
= cos tp + i sin ip,
|^| комплексное число z = r (cos ip + i sin ср) можно записать в так называемой показательной (или экспоненциальной) форме z = гегч>, где г = |z| — модуль комплексного числа, а угол ip — Argz — = argz + 2/стг (Л = 0, —1,1, —2,2,...).
В силу формулы Эйлера, функция е1Ч> периодическая с основным периодом 2тг. Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа, т. е. считать ip = arg z.
Пример 27.1. Записать комплексные числа zj = —1+г и z2 = —1 в тригонометрической и показательной формах.
Q Решение: Для zi имеем
|Д = г = \/(-1)2 + I2 = д/2, argz = arctg(-^j-) + тг = + тг = ~,
т. е. ip = Поэтому
—1 + i = ^(cos ~ + i sin j = \/2е’^г.
Для Z2 имеем
г = у/ (—I)2 + б2 = 1, argz — arg(—1) = я,
т. е. ip = тг. Поэтому —1 = cos тг + г sin тг = ег7Г. •
220
§28. ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
28.1. Сложение комплексных чисел
|,'5| Суммой двух комплексных чисел z\ — Х\ + гу\ и z2 = х2 + iy2 называется комплексное число, определяемое равенством
zi + £2 = (®1 + ®г) + г(т/1 + у2).
(28.1)
|jg Сложение комплексных чисел обладает переместительным (коммутативным) и сочетательным (ассоциативным) свойст-
вами: . .
Zi + z2 — z2 + Zi, (zi + z2) + z3 = zi + (z2 + z3).
Из определения (28.1) следует, что геометрически комплексные числа складываются как векторы (см. рис. 163).
Непосредственно из рисунка видно, что |zi + z2| Sj |zi| + |z2|. Это соотношение
называется неравенством треугольника.
28.2. Вычитание комплексных чисел
|^| Вычитание определяется как действие, обратное сложению. Разностью двух комплексных чисел zi и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число zi, т. е. Z — Zi — Z2, если Z + Z2 = Z1-
Если zi = xj + iyi, z2 = х2 + гу2, то из этого определения легко получить z:
Z = 21 - Z2 = (®1 - Х2) + i(yi - у2).
(28.2)
Из равенства (28.2) следует, что геометрически комплексные числа вычитаются как векторы (см. рис. 164).
Непосредственно из рисунка видно, что |zi — z2| > |zi| — |z2|. Отме-
ki - z2\ = V(xi -x2y + (?/i -yiY = d, т. e. модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости. Поэтому, например, равенство \z — 2г| = 1 определяет на комплексной плоскости множество точек z, находящихся на расстоянии 1 от точки zq = 2г, т. е. окружность с центром в zq = 2i и радиусом 1.
221
28.3. Умножение комплексных чисел
Ц>| Произведением комплексных чисел z{ = хл + iy\ и z2 = ж2 + гу2 называется комплексное число, определяемое равенством
z - zAz2 = - 2/1Z/2) + г(.Х!у2 + г/]Ж2).
(28.3)
Отсюда, в частности, следует важнейшее соотношение
г2 = -1.
(28.4 Действительно, г2 = гг = (0 + 1г) (0 + 1г) = (0 — 1) + г (0 + 0) = —1| Благодаря соотношению (28.4) формула (28.3) получается формально путем перемножения двучленов Xi + iyt и ж2 + гг/2:
(Ж1 + гг/1)(ж2 + гг/2) = хгх2 + xpiy2 + iyix2 + iypiy2 =
= xi x2 + г2 г/i г/2 + г (ж, у2 + ytx2) = XiX2 - уру2 + i(xpy2 + гджД. Например,
(2 - Зг)(—5 + 4г) = -10 + 8г + 15г - 12г2 = -10 + 23г + 12 = 2 + 23г.
Заметим, что zz = (х + гу) (х — iy) = х? + у2 — действительное число.
Умножение комплексных чисел обладает переместительным, соче тательным и распределительным (дистрибутивным) свойствами:
Z1Z2 = Z2Z1,
(ziz2)z3 = Zl(z2Z3), Zi (z2 + Z3) = ZAZ2 + Z1Z3.
В этом легко убедиться, используя определение (28.3).
Найдем произведение комплексных чисел Z| = 7*1 (cos ip\ + г sin ip-j и z2 = r2(cosip2 + г sin </?2), заданных в тригонометрической форме:
ziz2 = n(cos^i + г sin 991 )r2 (cos 992 +ism<^2) =
= rir2(cos tpi eostp2 + г sin 991 coS9?2 + г COS991 sin 99-2 — sin 991 sin tp2) = = rir2((cos93i cos992 — sin^i sin992) + i(sin99j cos992 + cos991 sintp2)) = = 7*i7*2 (cOS(99i + 9?2) +7Sin(99i + 992)),
т. e.
ziz2 = 7*17*2(008(991 + ip2) + isin(<£i + ip2)).
g Мы показали, что при умножении комплексных чисел и', модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множите--лей. В частности, если есть п множителей и все они одинаковые, то
(28.5)
z" = (r(cos 99 + г sin 99))”' = rn(cos nip + i sin nip).
|ф| Формула (28.5) называется формулой Муавра.
Пример 28.1. Найти (1 + \/Зг)9.
222
Q Решение: Запишем сначала число z = 1 + yjbi в тригонометрической форме:
г = 0. + (л/3)2 = 2;
V3 arg z = arctg -у
7Г argz = -, О
/ 7Г . . 7Г
z — 2 ( cos - + г sin -' о о
По формуле Муавра имеем
z9
= (1 + х/Зг)9 = 29
cos 9— + г sin 9
О
37
— 29(cos3tt + гвтЗтг) = 29(— 1) = —512.
28.4. Деление комплексных чисел
|ф| Деление определяется как действие, обратное умножению. Част-ным двух комплексных чисел Z| и z2 0 называется комплексное число г, которое, будучи умноженным на z2, дает число zi, т. е. = г, если z2z = z^ z?.
Если положить zi = Xi + iyi, z2 = ж2 + iy2 0, z = х + гу, то из равенства (ж2 + г'у2)(ж + iy) = + iyi следует
ХХ2 - УУ2 = Хг, ХУ2 + УХ2 - У1-
Решая систему, найдем значения х и у.
Х1Х2+У!У2 У1Х2-Х1У2
X — 9 9 , У ~~ - О О
Х2 + yi Х$ + у$
Таким образом,
Z1 _ Ж1Ж2 +J/1J/2 -У\Х2 -Х1У2
9 9 ' 9
Z2 Х22 + yj Х2+ у2
На практике частное двух комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»).
Пример 28.2.
Выполнить деление
1 + Зг 2 -р i
Q Решение:
1+Зг _ (1 + Зг)(2-г) _ 2-г + 6г + 3 2 + г “ (2 + г)(2-г) ~ 4+1
5 + 5г
5
= 1 + г.
223
Для тригонометрической формы комплексного числа формула деления имеет вид
ri(cos<pi И . .
—--------——-------- = — (cos((pi - ^2) + гвпф| - <р2)).
r2(cos<p2 + *sin<p2) Г2 '
При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются.
28.5. Извлечение корней из комплексных чисел
Извлечение корня п-й степени определяется как действие, обрат-; ное возведению в натуральную степень. i
Корнем п-й степени из комплексного числа z называете^ комплексное число ш, удовлетворяющее равенству cvn = z, т. eJ
Ч/z = а>, если шп = г.
Если положить z = r(cos<p + г sin 99), а ш = p(cos0 + г sin 0), то, по определению корня и формуле Муавра, получаем
z — ivn = p”(cosn0 + zsinn#) = r(cos<p + ?sin<p).
Отсюда имеем рп = г, п0 = <р + 2-zrfc, к — 0, —1,1, —2,2,... То есть 0 = и р = у/г (арифметический корень).
Поэтому равенство y/z = w принимает вид
п/~7-----------V п/~( 4> + %лк . . <р + 2тг&\
vr(cos ip + % sin <р) — yr I COS--1- I sin--- I,
\ n n /
к = 0,1,... ,n — 1.
Получим n различных значений корня. При других значениях к, в силу периодичности косинуса и синуса, получатся значения корня, совпадающие с уже найденными. Так, при к — п имеем
Итак, для любого z 0 корень n-й степени из числа z имеет ровно п различных значений.
Пример 28.3. Найти значения a) y/i — си; б) = w-
224
Решение: а) Запишем подкоренное выражение в тригонометрической форме: i = 1 (cos 4- i sin . Стало быть,
4 + 2zrfc . £ + 2тгА;
----------+ г sin -----------
О
3 к = 0,1,2.
I [ри к = 0 имеем
7Г . 7Г \/3 1
ш0 = cos - + г sin - = — + г-;
6 6 2 2
при к = 1 имеем
§ + 2тг . . 4 + 2тг 5тг . . 5тг л/3 1
W1 = cos—-— +isin-<—— = cos— -Msrn— = —— +г-;
о о о 6 2 2
при к = 2 имеем
V , ¥ Зтг .. Зтг
ш2 — cos + г sin -4- = cos — + г sin — = -г. О О £j
б) Снова запишем подкоренное выражение в тригонометрической форме:
—1 = cos тг + i sin тг.
Поэтому
-—Г !--------------- тг + 2-zrfc . . тг + 2тг/г
— 1 = v cos тг + г sin тг = cos----------h г sin ———, к = 0,1.
£ л
При к = 0 получаем ш0 = cos ~ + i sin = г, а при к = 1 получаем
Wi = cos + i sin ~ —i. Таким образом, 1 = i и = —г.
Глава VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Лекции 25—28
§29. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
29.1. Понятие неопределенного интеграла
В дифференциальном исчислении решается задача: по данной функции f(x) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F'(x) = f(x) (или дифференциал). Искомую функцию F(x) называют первообразной функции /(ж).
|ф| Функция F(x) называется первообразной функции f(x) на интервале (а; 5), если для любого х G (а; 5) выполняется равенство
F'(x) = f(x) (или dF(x) = /(ж) dx).
Например, первообразной функции у = х2, х € К, является функция 3
F(ar) = так как
О
3 ггг) = т'=а:2=ж). ' о /
Очевидно, что.первообразными будут также любые функции
Xs F(x) = -+C, О
где С — постоянная, поскольку
з
f'(x) = (v +СУ = х2 = №) (х е ®)-X О /
Теорема 29.1. Если функция F(x) является первообразной функции f(x) на (а;Ъ), то множество всех первообразных для f(x) задается формулой F(x) + С, где С — постоянное число.
□ Функция F(x) + С является первообразной f(x). Действительно, №) + С)' = F'(x) = Ж).
Пусть Ф(ж) — некоторая другая, отличная от F(x), первообразная функции f(x), т. е. Ф'(ж) = f (ж). Тогда для любого х G (а; Ъ) имеем (Ф(ж) - F(x))' = Ф'(ж) - F'(x) = f (х) - f(x) = 0.
А это означает (см. следствие 25.1), что
Ф(ж) - F(x) = С, где С — постоянное число. Следовательно, Ф(т) = F(x) + С.
226
|,"£| Множество всех первообразных функций F(x) + С для /(ж) называется неопределенным интегралом от функции f(x) и
обозначается символом J f(z) dx.
Таким образом, по определению
У /(ж) dx = К(ж) + С.
|£| Здесь f (ж) называется подынтегральной функцией, f(x) dx — подынтегральным выражением, х — переменной интегрирования, у — знаком неопределенного интеграла.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
р>| Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых у = F(x) + С (каждому числовому значению С соответствует определенная кривая семейства) (см. рис. 165). График каждой первообразной (кривой) называется интегральной кривой.
Рис. 165
Для всякой ли функции существует неопределенный интеграл?
Имеет место теорема, утверждающая, что «всякая непрерывная на (а; Ь) функция имеет на этом промежутке первообразную», а следовательно, и неопределенный интеграл.
29.2. Свойства неопределенного интеграла
Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
<1^У f(x)dx^ = f(x)dx,
(У f(x)dxj = /(ж).
227
□ Действительно,
/(x) de) = d(F(x) + C) = dF(x) + d(C) = F\x) dx = f(x) dx
И
(У f (x) dx)' = (F(x) + C)' = F'(x) + 0 - /(x).
Благодаря этому свойству правильность интегрирования проверяется дифференцированием. Например, равенство
У (Зх2 + 4) dx = х3 + 4х + С
верно, так как (х3 + 4х + С)' = Зх2 + 4. ,
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: j
I dF(x) = F(x) + С. . j
□ Действительно, j dF(x) = J F'(x) dx = J f(x) dx = F(x) + C.
3. Постоянный множитель можно выносить за знак интеграла:
[ af(x) dx = a - j f(x) dx, a 0 — постоянная.
□ Действительно,
= a. • F(x) + Ci = a (f(x) + = a(F(x) + C) = a f f(x) dx
(C, положили —1
a
4. Неопределенный интеграл от алгебраической суммы конечного,! числа непрерывных функций равен алгебраической сумме интегралов, от слагаемых функций:
/(/(®) ± p(®)) dx
= j f (ж) dx ± у g(x)
dx.
□ Пусть F'(x) = f (x) и G'(x) = </(x). Тогда
J(f(x) ± g(x)) dx = I(F'(x) ± G'(x)) dx =
= y"(F(x) ± G(x))' dx = у d(F(x) ± G(x)) = F(x) ± G(x) + C =
= (F(x) + Ct) ± (G(x) + C2) = у /(x) dx ± у g(x) dx, гдеС1±С2 = С.
228
5. (Инвариантность формулы интегрирования). Если J f(x)dx — = F(x) + С, то и у /(«) du — F(u) + С, где и = </?(ж) — произвольная функция, имеющая непрерывную производную.
□ Пусть х — независимая переменная, f (а?) — непрерывная функция и F(x) — ее первообразная. Тогда j f(x)dx = F(x) -F С. Положим теперь и = <р(а;), где ip(x) — непрерывно-дифференцируемая функция. Рассмотрим сложную функцию F(u) = F(tp(x)). В силу инвариантности формы первого дифференциала функции (см. с. 188) имеем
dF(u) = F'(u) du = f (n) du.
Отсюда У" f (и) du = у d(F\u)) = F(u) + С.
Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.
х2 dx = д' + С путем замены х на и (и = </?(а;)) получаем j и2 du — + С. В частности,
г . о ./ • ч sin3 ж
J sin a;a(sina;) = —---FC,
Г. > ч In3а: _
/ In2 х d(ln ж) = —--F С,
J о
У tg2 х d(tg х) = + С.
Пример 29.1. Найти интеграл у(2а;4 — За;2 -Fa; — 5) da;.
Q Решение:
У (2ж4 — За;2 + х — 5) dx = 2 j х4 dx — 3 J х2 dx + J xdx — 5 J dx — ,,.5 т3 т2 2 1
= 2---F С\ — 3— -F С2 -F -F С3 — 5а; + С4 = —а:5 — a;3 -F —х2 — 5а; -F С,
5 3 2 5 2
где С = (71 + С2 + (7з + С4. ®
Пример 29.2.
/х + 1 , ---------dx.
х
Q Решение; j —-----dx = f (1 + dx = х + In |а;| + С.
229
29.3. Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул дифференциального исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла.
Например, так как
d(sin и) = cos и du,
У cos и du = j d(sin w) = sin и + С.
Вывод ряда формул таблицы будет дан при рассмотрении основных методов интегрирования.
Интегралы в приводимой ниже таблице называются табличными. Их следует знать наизусть. В интегральном исчислении нет просты: и универсальных правил отыскания первообразных от элементарны: функций, как в дифференциальном исчислении. Методы нахожденщ первообразных (т. е. интегрирования функции) сводятся к указании приемов, приводящих данный (искомый) интеграл к табличному. Сле довательно, необходимо знать табличные интегралы и уметь их узна вать.
Отметим, что в таблице основных интегралов переменная инте-: грирования и может обозначать как независимую переменную, так и функцию от независимой переменной (согласно свойству инвариантности формулы интегрирования).
В справедливости приведенных ниже формул можно убедиться, взяв дифференциал правой части, который будет равен подынтегральному выражению в левой части формулы.
Докажем, например, справедливость формулы 2. Функция i определена и непрерывна для всех значений и, отличных от нуля.
Если и > 0, то 1п|'«| = Inu, тогда dln|u| = dlnu = Поэтому I — = In и 4- С = In |н| + С при и > 0. J и
Если и < 0, то In |ti| = 1п(—и). Но <Пп(—и) = =~ = —. Значит, [ — ln(—и) 4- С = In |п| + С при и < 0.
Итак, формула 2 верна.
Аналогично, проверим формулу 15:
1 и
- arctg - 4- С а а
d
1 1 1 _ du
а 1+(^)2 а~ а2 + и2'
230
Таблица основных интегралов
1. у иа du = 1 4- С (а —1)
2. у^ = 1пМ + С;
3. f аи du = -р---1- С;
J Ina
4. у еи du = еи + С;
5. у sin и du = — cos и + С
6. у cos и du = sin и + С
7. у tgudu = —In|cosn| + С;
8. у ctgudu = In| sinw| + C;
9. f du = tg u + C
J cos и
10- f .ty = — ctg и + C
J sin и
du = и
(J shи du = ch и +
(У ch и du = shu + C1);
(/J^=th“+C);
f Г = — cth и + C);
\J sh и /
11 . /’_d^=ln|tg^|+C;
J sm и 1 ° 21
12 I _du_==ln|tg(| + £)|+C';
J cos и I ° V 2 4/|
13 . f ,<1ч-= arcsin И + C;
J у/a2 - u2 a
14 Г du = ln |u + 7^2 + o2| + C;
1 v и2 + a2
15. [ = - arctg — + C;
J a? +u? a b a
16- f -^4 = ^--lnl^J^|+C;
J a2 - и | a - и |
17. у \/a2 - u2 du = • x/a2 — u2 + arcsin + C;
18. у x/w2 ± a2 du — y/u2 ± a2 ± In |w + y/u2 ± a21 + C.
231
§30. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
30.1. Метод непосредственного интегрирования
g Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется не! посредственным интегрированием. >
При сведении данного интеграла к табличному часто используют! ся следующие преобразования дифференциала (операция «подведенил под знак дифференциала»):
du — d(u + а), а — число, ’
]
du = —d(au), а 0 — число, а
и- du = -d(u2),
cos и du = d(sin и), sinudu = — d(cosu),
— du — d(lnu), и
—-— du = d(tgu).
cos2 и
Вообще, f '(u) du = эта формула очень часто используется при
вычислении интегралов.
Примеры:
d(x + 3)
—-----— = In |ж + 3| + С (формула 2 таблицы инте-
х Ч- 3
гралов);
2) f(3x-l)24da; = |/(Зж-l)24d(3z-l) = | • + С
(формула 1);
r , rl — sin2 х , r ( 1 Л , / 1 ,
3) / ctg х dx = / -----dx = / —X------1 I dx = / —dx —
J J sin x J \sin x / J sin x
— I dx — — ctg ж — x + С (формулы 10 и 1);
r dx d(v^3 x) 1 . a/3 • x
J - Зж2 v/3-/ у(2)2_ (73.^2 x/3 2
(формула 13);
232
B5) J sin2 fix dx = | /(1 - c “ I / COS 12ard(12a:)' =
1 /* 1 г
cos 12а;) dx = - J dx— -J cos 12a; dx =
1 1
----- —x — — sin 12a; + С (формулы 1 и 6);
г dx 1 г (a; - 1) - (a; + 2) =
> J (a: - l)(a; + 2) 3 J (x- 1)(® + 2)
~з/(Г-Т)(ж + 2)^+з/
1 r d(x + 2)
3 J x + 2
-----7—7-----r dx —
(x - l)(a; + 2)
1 r d(x -1) 1 , . 1, , _
r- = --l„|3, + 2| + 51„k-1| + C;
формулы 7);
sinwdzt cosw
d(cos«) _ _ ^ । cos ы| + (7 (ВЫВОд cosw
„ r du r cos2 # + sin2 # , r cos2 Ц
8) / ~— - / л ~~ u-------------гЛ du - о и-----------й du +
J sm и J 2 sin cos | J 2 sm cos |
f sin2 2 ,
+ / O • и и du
J 2 sin cos |
с и ,/u\ г U ,/U\ , I . U I
= /CtS2‘,(2)+/tS2<,(2)=1Tr'2|-
.1 и I , smf
- In cos - + C = In -
121 cos
формулы 11);
+ C = In |tg + С (вывод
9) J x(x + 2)9 dx = j (x + 2 — 2)(.r + 2)9 dx = J (x + 2)10 dx — -2j(x + 2)9dx = J(x + 2)10d(a: + 2) - 2 (x + 2)s d(x + 2) =
(ar + 2)11 (z + 2)10
= -—jj2----2^——------+ С (формула 1);
10) f g <fe. 2 = - f(ctga;)-5d(ctga;) = -Ctg Ж + C = J ctg- x sin x J —4
= 4^+С(*ОР"УЛа
f dx — f dx — f d(x ~
J V3-2x + x2 J /2+(a:-I)2 ' +
= ln|a; — 1 + \/з — 2a: + x2 | + С (формула 14);
12>- dt+3‘"') * = 4/*s * -1 / sSs “ г 5 31-®
— / 3l- :cd(l — x) = a:4 - - tg2a:-j—— + С (формулы 1,
J Z 111 О
9, 3);
233
13) у ж3 • V1 + ж2 dx = у (1 + х2) з х • (х2 +• 1 — 1) dx =
= I У (i + z2)s d(l + ж2) - ~ /(1 + ж2)5 d(l + X2) =
= Л(1+®2)5 -|(! + a:2)s +с.
14 о
Как видно, вычисление интегралов иногда требует некоторой изобретательности, так сказать, «индивидуального подхода к каждой подынтегральной функции».
Соответствующие навыки приобретаются в результате значительного числа упражнений.
30.2. Метод интегрирования подстановкой
(заменой переменной) и
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом задана ный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл j f(x)dx. Сделаем подстановку х = 99(f), где 99(f) — функция, имеющая непрерывную производную.
Тогда dx = 9?'(t)dt и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой
У f(x)dx = у /(99(f)) V(t)dt.
(30.1)
Формула (30.1) также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Иногда целесообразно подбирать подстановку в виде t = 99(3;), тогда у/(99(3:)) ip'(x)dx = у f(t)dt, где t = ff(x). Другими словами, формулу (30.1) можно применять справа налево.
Пример 30.1. Найти dx.
Q Решение: Положим х = 4t, тогда dx = 4dt. Следовательно,
е* dx — 4 / е* dt = 4е* + С = 4е« + С.
234
Пример 30.2. Найти / х \/х — 3dx.
Q Решение: Пусть у/х — 3 = t, тогда х = t2 + 3, dx = 2t dt. Поэтому
г Г td
t4dt + d t 2 dt = 2 — + 6 ~ + C =
J 5 3
х у/х — 3 dx = J (t2 + 3) • t • 2/, dt =
= 2 y(t4 + 3t2) dt = 2
= | (x - 3)5/2 + 2(ж - З)3/2 + C. •
5
Пример 30.3. Получить формулу
f du ~ _ I ^/u2 а2 I (J
J y/u2 4- a2 1 1
□ Обозначим t = y/u2 + a2 + и (подстановка Эйлера). Тогда
, 2w
dt = —. —---du + du.
2yW + a2
„ y/u2 + a2 + и , т. e. dt —-----— du.
y/u2 + a2
°ТСЮДа du _ dt =
y/u2 + a2 y/u2 + a2 + и t
Стало быть, / du.............- = / — = In |i| + C = In + x/w,2 + a2| + C.
J y/u2 + a2 Ji
Пример 30.4- Найти / x (x + 2)100 dx.
Q Решение: Пусть x + 2 = t. Тогда x — t — 2, dx = dt. Имеем:
Jx-(x + 2)wodx = twodt = j tim dt-lf t100 dt =
i102 i101 „(z + 2)102 2(ж + 2)101
“ 102 2' 101 + - 102 101
Пример 30.5. Найти f ——~т-J ex + 1
Q Решение: Обозначим e® = t. Тогда x == Ini, dx = Следовательно,
[ dx _ / _ f dt
J ex + 1 ~ J t+1 ~ J t(t + 1) “ J t2 + t ~
- f dt _ r d(t + |) =___1 , 11 + * + 2 I , c =
/(*+|)2-| Л|)2-(^ + |)2 2-1
235
= - In
. е
In------
еж + 1
Здесь используется формула 16 таблицы основных интегралов.
30.3. Метод интегрирования по частям
Пусть и = и(х) и v = г (ж) — функции, имеющие непрерывные производные. Тогда d(uv) = и dv + v du. Интегрируя это равенство, получим
d(m>) = j Г и dv + j Г v du или udv = uv — j v du.
g Полученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интегра-, который может оказаться
к вычислению интеграла
ла существенно более простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
1. Интегралы вида где Р(х)
обозначить все остальные сомножители.
2. Интегралы вида у Р(ж) arcsin ж tfcc, J Р(х) arccos ж dx, У Р(ж)1пжйж, / Р(ж) arctg х dx, I Р(ж) arcctg ж г?ж. Удобно положить Р(ж) dx = dv, а за и обозначить остальные сомножители.
3. Интегралы вида j еах sin Ьх dx, J еах cos bx dx, где а п Ь — числа. За и можно принять функцию и = еах.
• sin кх dx, J Р(х) cos кх dx, многочлен, к — число. Удобно положить и = Р(ж), а за dv
Пример 30.6. Найти
и = 2ж + 1 => du = 2dx
dv = е3ж dx => v = J e3x dx = ^eSx
положить C — 0). Следовательно, по формуле интегрирования по частям:
Q Решение: Пусть
(можно
|е3ж- f |е3ж2йж = |(2ж+1)е3ж-|е3ж+С'. • о J о о У
236
Пример 30.7. Найти J Inxdx.
Q Решение: Пусть
и = In X
du = i dx x
. Поэтому
х In X
х • hi х — х + С.
Пример 30.8. Найти J х2ех dx.
„ „ , , и = ж2 => du = 2х dx 1 „
Q Решение: Пусть = ] Поэтому
j х2ех dx = х2ех — 2 J ех -xdx. (30.2)
Для вычисления интеграла J ехх dx снова применим метод интегрирования по частям: и = х, dv — ех dx => du = dx, v = ех. Значит,
I ех xdx = х ех — f ех dx = х ех — ех + С. (30.3)
Поэтому (см. (30.2)) f х2ех dx — х2ех — 2(ж ех — ех 4- С). 9
Пример 30.9. Найти / arctg х dx.
Решение: Пусть
it = arctg ж dv = dx
du = -—dx
1 + x2
V = X
. Поэтому
J arctg ж dx = x arctg ж — j
.2
x , 1 гб?(14-ж2)
j-j-—dx = ж arctg ж--i ---------=
= ж arctg ж — | ln(l + ж2) + C. •
§ 31. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
31.1. Понятия о рациональных функциях
Многочлен (некоторые сведения справочного характера)
Функция вида
Рп(х) = аохп + щж”-1 -I-F а„-1Ж + ап, (31-1)
где п — натуральное число, а, (г = 0,1,..., п) —- постоянные коэффициенты, называется многочленом (или целой рациональной функцией). Число п называется степенью многочлена.
237
рз] Корнем многочлена (31.1) называется такое значение хо (вообще говоря, комплексное) переменной х, при котором многочлен обращается в нуль, т. е. Рп(®о) = 0.
Теорема 31.1. Если х\ есть корень многочлена Рп(х), то многочлен делится без остатка на х — х^, т. е.
Рп(х) = (х - Ж1) • Рп^(х), (31.2)
где Pn~i(x) — многочлен степени (п-1).
Возникает' вопрос: всякий ли многочлен имеет корень? Положительный ответ на этот вопрос дает следующее утверждение.
Теорема 31.2 (основная теорема алгебры). Всякий многочлен п-й степени (п > 0) имеет по крайней мере один корень, действительный или комплексный.
Доказательство этой теоремы мы не приводим.
Пользуясь основной теоремой алгебры, докажем теорему о разложении многочлена на линейные множители.
Теорема 31.3. Всякий многочлен Рп(х) можно представить в виде
Рп(х) = а0(х - xi)(x - ж2)... (х - хп), (31.3)
где Ху, Х2, ...,хп — корни многочлена, ад — коэффициент многочлена при хп.
□ Рассмотрим многочлен (31.1). По теореме 31.2 он имеет корень. Обозначим его через х±. Тогда имеет место соотношение (31.2). А так как Pn-ifx) — также многочлен, то он имеет корень. Обозначим его через ж2. ТогдаPn-i(x) — (ж-ж2)-Гп2(а:), где Fn_2(z) — многочлен (л,-2)-й степени. Следовательно, Рп(х) = (х — xi)(x — ж2)Рп_2(ж).
Продолжая этот процесс, получим в итоге:
Рп(х) = ао(х - Xi)(x - х2) (х - хп).
ру| Множители (х — х,) в равенстве (31.3) называются линейными множителями.
Пример 31.1. Разложить многочлен Рз(х) = х3 — 2ж2 — х 4- 2 на множители.
238
Q Решение: Многочлен Рз(х) = х3 — 2а:2 — х + 2 обращается в нуль при х = —1, х = 1, х = 2. Следовательно,
х3 - 2а:2 — х 4- 2 = (х + 1)(а: - 1)(а; — 2). . •
Пример 31.2. Представить выражение х3 — х2 + 4х — 4 в виде произведения линейных множителей.
Q Решение: Легко проверить, что
х3 — х2 + 4а: — 4 = (а: — 1) (а: — 2г)(а: + 2г). •
Если в разложении многочлена (31.3) какой-либо корень встретился к раз, то он называется корнем кратности к. В случае к = 1 (т. е. корень встретился один раз) корень называется простым.
Разложение многочлена (31.3) можно записать в виде
Рп(х) = а0(х — xi)kl (х — х%)к2. - - (х — хг)к", (31-4)
если корень Xi имеет кратность fcj, корень х? — кратность &2 и так далее. При этом к\ +кз~\----Ь кг — п, а г — число различных корней.
Например, разложение
Р8(ж) = (х — 3)(а: + 1)(а: — 4}(х — 3)(а: — 3)х(х — 4)(а; — 3) можно записать так:
Р8(а?) = {х — З)4 • (а: + 1) • (а: - 4)2 - х.
Пользуясь теоремой 31.3, можно доказать следующие утверждения.
Теорема 31.4. Если многочлен Pn(a:) = аохп + aixn 1 + ••• + ап тождественно равен нулю, то все его коэффициенты равны нулю.
Теорема 31.5. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Например, если ах3 + bx2 + сх + d = х3 — За:2 4-1, то а = 1, b = —3, с = 0, d = 1.
239
Теорема 31.6. Если многочлен Рп(х) с действительными коэффициентами имеет комплексный корень a + ib, то он имеет и сопряженный корень а — ib.
В разложении многочлена (31.3) комплексные корни входят сопряженными парами. Перемножив линейные множители
(х — (а + ib)) - (ж — (а — ib)), получим трехчлен второй степени с действительными коэффициентами ж2 + px + q. В самом деле,
(ж — (а + ib))(x — (а — гб)) — ((ж — а) — гЬ)((ж — а) + ib) = = (ж — а)2 + Ь2 = ж2 — 2аж + а2 + Ь2 = ж2 + px + q, где р = —la, q = а2 +b2.
Таким образом, произведение линейных множит'елей, соответствуй ющих сопряженным корням, можно заменить квадратным трехчленом! с действительными коэффициентами.
С учетом вышеизложенного справедлив следующий факт.
Теорема 31.7. Всякий многочлен с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами, т. е. многочлен /„(ж) можно представить в виде
Рп(х) = «о(ж - Ж1)*1 (ж — ж2)*2... (ж — хг)кг х
х (ж2+р1ж + д1)Я1 ... (х2 + ртх + qm)Sm. (31.5)
При этом ki + /v2 Ч-Е kr + 2(st + s2 Н-Е sm) = п, все квадратные
трехчлены не имеют вещественных корней.
Примеры разложений (31.5):
1) ж4 - 1 = (ж - 1)(ж + 1)(ж2 + 1);
2) ж3 — 16ж = ж(ж2 — 16) = ж(ж — 4)(ж + 4);
3) ж5 — 6ж4 + 9ж3 — ж2 + 6ж - 9 = ж3 (ж2 - 6ж + 9) — (ж2 — 6ж + 9) =
= (ж2 — 6ж + 9)(ж3 — 1) = (ж — З)2 • (ж - 1)(ж2 + ж + 1).
Дробно-рациональная функция
|ф| Дробно-рациональной функцией (или рациональной дробью) называется функция, равная отношению двух многочле-Р (ж)
нов, т. е. /(ж) = гДе Рт(х) — многочлен степени т, a Qn(x) — многочлен степени п.
240
|ф| Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, т. е. т < п; в противном случае (если т п) рациональная дробь называется неправильной.
Р(х)
|@| Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена Цх) и правильной рациональной дроби т-е-
Р(Ж) -L(X\ I Д(Ж)
Например,
—---+ — неправильная рациональная дробь.
Разделим числитель на знаменатель в столбик:
ж4 — 5х +9 а: — 2________________
а;4 - 2ж3 | а;3 + 2а;2 + 4а: 4- 3
2а:3 — 5х + 9
~ 2а:3 - 4а:2__________
_ 4а:2-5а:+ 9
4а;2 — 8х ____
За: Ч- 9
За: — 6
15.
Получим частное Цх) = х3 + 2а;2 + 4а: + 3 и остаток R(x) — 15. Следовательно, х ~ &£ + 9 == х3 + 2а;2 4- 4а: Ч- 3 Ч—
’ х — 2 х — 2
Правильные рациональные дроби вида
(I). -А_;
v ’ х — а
(Щ- 2, Л 6 N);
(III). (корни знаменателя комплексные, т. е. р2 — 4г/<0);
Q
(IV). + {к 2, корни знаменателя комплексные),
\Х Ч- px Ч" Q/
[ф| где А, а, М, N, р, q — действительные числа, называются простейшими рациональными дробями I, II, III и IV типов.
241
Теорема 31.8. Всякую правильную рациональную дробь . знаменатель которой разложен на множители '
Q(x) = {х-х^кх-(х-х^ .-.{х* 1 2+pi'£ + q1')S1 ... (ж2+ртж + дто)®т, можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
Р&) = At А2 Ак1
Q{x) х — xi (х — xi)2 ’ (х — xi)kt JB2 4---------------1----_---f-... 4---—-----F ...
x - X2 (ж - ж2)2 (ж - ж2)к2
। CjX + Di 1 C2x + P2 1 1 Csix + DS1 1
ж2+р1Ж + д] (ж2 + Pjt +гд )2 (ж2+Р1Ж + gi)si
I Mix + Ni 1 M2x + 1V2 । 1 M,mx + NSm
x2+pmx + qm (ж2+ртож + дт)2 (ж2+ртж + gTO)s-’ (31.6) где Ai, A2..Bi, B2.....Ci, Di, , Mi, Ni, ... — некоторые
действительные коэффициенты.
Поясним формулировку теоремы на следующих примерах: ж2+4 _ А В С D
(ж - 2)(ж - З)3 * ~ ж - 2 + ж - 3 + (ж - З)2 + (ж - З)3 ’
. х$ 4-1 А В Сх 4~ D ж2(ж2 + 1) ж + ж2 + ж2 + 1 ’
. 7ж2 + 8ж + 9 _ А В Сх + Р
(ж — 1)(ж — 2)(ж2 + ж 4-1)2 ж — 1+ж — 2^ж2 + ж + 1^
Mx + N
(ж2 + ж + I)2
Для нахождения неопределенных коэффициентов Ai, А2,...,Вг, 1
В2,... в равенстве (31.6) можно применить метод сравнивания коэффициентов. Суть метода такова:
1. В правой части равенства (31.6) приведем к общему знаменате-Р(ж) Six')
лю Q(ж); в результате получим тождество где —
многочлен с неопределенными коэффициентами.
2. Так как в полученном тождестве знаменатели равны, то тожде-
ственно равны и числители, т. е.
Р(ж) = 5(ж).
(31-7) .
242
3. Приравнивая коэффициенты при одинаковых степенях х (по теореме 31.5 о тождестве многочленов) в обеих частях тождества (31.7), получим систему линейных уравнений, из которой и определим искомые коэффициенты Ai, А2,..., Вг,...
Огт.2 _ О
Пример 31.3. Представить дробь -— Л; „ -—гг в видесум-
(х— 1)(я? — 2ж + 5) мы простейших дробей.
Q Решение: Согласно теореме 31.8 имеем:
2ж2 - Зж - 3 _ А Вх + С
(х — 1)(ж2 — 2ж + 5) ж — 1 + ж2 — 2ж + 5’
т. е.
2ж2 - Зж - 3 _ А(ж2 - 2ж + 5) + (ж - 1)(Вж + С)
(ж - 1)(ж2 - 2ж + 5) (ж - 1)(ж2 - 2ж + 5)
Отсюда следует
2ж2 — Зж — 3 = Ах2 — 2Ах + 5А + .Вж2 — Вх + Сх — С',
т. е.
2ж2 - Зж - 3 = (А + В)х2 + (-2А - В + С)х + (5А - С).
Приравнивая коэффициенты при ж2, ж1, ж0, получаем
{2 = А + В,
-3 = -2А - В + С,
-3 = 5А - С.
Решая систему, находим, что А = —1, В = 3, С = —2. Следовательно, 2ж2 - Зж - 3 _ -1 Зж - 2
(ж — 1)(ж2 — 2ж + 5) ж — 1 + ж2 — 2ж+5
Для нахождения неопределенных коэффициентов применяют также метод отдельных значений аргумента: после получения тождества (31.7) аргументу ж придают конкретные значения столько раз, сколько неопределенных коэффициентов (обычно полагают вместо ж значения действительных корней многочлена 0(ж)).
в виде суммы
простейших дробей.
о Решение: Имеем: = 4 + + Отсюда сле.
Зж — 4 = А(ж — 2)(ж + 1) + Вх(х + 1) + Сж(ж — 2).
Представить дробь
Пример 31.4-
243
I
Положим x = 0, тогда -4 = -2А, т. е. А = 2; положим х = 2, тогда 2 = 6В, т. е. В — i; положим х = —1, тогда —7 = ЗС, т. е. С = /О
Следовательно, Зж - 4 2 1 .
ж(ж-2)(ж4-1) х ж-2 ж 4-1' J
31.2. Интегрирование простейших рациональных J дробей
Найдем интегралы от простейших рациональных дробей.
1 - I о- = [ Z = A-hi |ж — а| +С (формула (2) таблицы J &> U J Jb U
интегралов);
2 I * = А f{x - d(x ’ о) = А' + <j
(формула (1)); j
3 . Рассмотрим интеграл J = / — + N dx. 3
J х2 +рх + q j
Выделив в знаменателе полный квадрат, получим: ;
г Мх 4- TV 1
J = / —---------—dx, <
J (x+^ + q-^- 1
причем q - > 0. Сделаем подстановку х 4- = t. Тогда х = t ~
2
dx — dt. Положим <7— 4 = а2- Следовательно, используя формулы (2) ] и (15) таблицы интегралов, получаем
г г Mx + N , г м (t - 2) 4-TV I
J = / "TT--—o dt =
J x2 +px + q J t2 + a2 fl
v(z|vb x Al / J b tv --i
I /х2 , 2\ /лг Mp\ 1 t „ 1
= --Mt2 4-a2 4-(AT- - arctg - 4-С, I \ 2 / a a 1
т. e., возвращаясь к переменной ж,
_ f Mx + N 1 Мл , 2 х TV - х + %
J = J +'’:е+’> + ^тг агс,вёг^+с'
Пример 31.5. Найти f -п --------dx.
J х 4“ 2й7 4-10
244
Q Решение: x2 + 2x +10 = (x + I)2 + 9. Сделаем подстановку x + 1 = t. Тогда x = t — 1, dx = dt и
. /• Зж + 1 , /-3(t-l) + l „ г tdt dt _
J ^ + 2x+10(Lc~J t2+9 d 4 t2 + 9 J t2+9
. .= |ln(t2 +9) - |arctg| +C = 1п(ж2 + 2ж + 10) - | arctg + C.
2 3 3 2 о о
4. Вычисление интеграла вида / М?dx к^2, q — Я- > 0. н J (x2+px + q)k 4
Данный интеграл подстановкой х + = t сводится к сумме двух
интегралов:
Mf
tdt
(t2 + а2)к
N-MP\ I'____dl_
2 ) J (t2 + a?)k’
2 P2
«2=<7-T-
+
Первый интеграл легко вычисляется:
/ ТО = I/<‘! + * + “2> = + С-
Вычислим второй интеграл:
j - Г dt 1 l^+a^-t2dt-
Jk~ J (t2 + a2)k ~ a2 J (t2+a2)k
1 / r dt г t2 dt \ _ 1 / г t2 dt \
= U (t2 + a2)*”1 ~ J (t2 + a2)k ) \к^ J (t2+a2)k)'
(31.8)
К последнему интегралу применим интегрирование по частям. Положим
и = t, dv — , . du = dt,
(t2 + a2)K
v = 2 /(f2 + “2) " + = 2(1 - fc)(t2 + a2)fc-i ’
тогда
r t2 dt _ t 1 r dt
J (t2+a2)fc ~ 2(1 — fc)(t2 + a2)fc l “ 2(1 - k) J (t2 + a2)*-1 “
t______________1 j
2(1 - k)(t2 + a2)*-1 2(1 — *) k b
Подставляя найденный интеграл в равенство (31.8), получаем 1 t 1
Jk ~ ^Jk-k ~ 2(l-fc)(t2+a2)fc~1 + 2(1 - ку^
245
т. е.
1 pfc-3 t X 1
k ~ a2 \2k - 2 + 2(fc — l)(t2 + a2)fc~i) '
Полученная формула дает возможность найти интеграл J); для любого натурального числа к > 1. I
Пример 31.6. Найти интеграл J3 = J %~^з •
О Решение: Здесь а = 1, к — 3. Так как
/cZt
= arctg t + С, tS +1
то
г dt 2-2 — 3 t
2 “ J (t2 + I)2 “ 2-2-2J1 + 2 • (2 - l)(t2 + 1) ~ .
1 t
= 2arCtgf+2(^Tl)+C’
7 3 7 1 1 3 fl t X „
3 “ 4J2 + 4(t2 + I)2 ~ 4(t2 + I)2 + 4 \2arCtg<+ 2(«2 + l)7 +C' *
31.3. Интегрирование рациональных дробей
Рассмотренный в пунктах 31.1-31.2 материал позволяет сформулировать общее правило интегрирования рациональных дробей.
ЦЦ 1. Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби;
2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей;
3. Проинтегрировать многочлен и полученную сумму простейших дробей.
Пример 31.7. Найти интеграл [ % + 4^ + 4 dx.
J х 4" 2.т 4" 2х
Q Решение: Под знаком интеграла неправильная дробь; выделим ее целую часть путем деления числителя на знаменатель:
_ х5 + 2ж3 + 4ж + 4 ж4 + 2ж3 + 2ж2
х5 + 2ж4 + 2ж3 х — 2
— 2ж4 -|- 4ж 4
- 2ж4 — 4ж3 — 4ж2
4ж3 + 4ж2 + 4ж + 4 (остаток).
246
Получаем:
ж5 + 2а:3 + 4х + 4 _ 4а:3 + 4а:2 + 4ж + 4
х4 + 2а;3 + 2а:2 Х + X4 + 2а:3 + 2а:2
Разложим правильную рациональную дробь на простейшие дроби:
4а:3 + 4а:2 + 4х + 4 _ 4х3 + 4а:2 + 4х + 4 _ А В Сх + D х4 + 2х3 + 2а:2 х2(х2 + 2х + 2) х + х2 + х2 + 2х + 2 ’
4а;3 + 4а:2 + 4х + 4 = Ах(х2 + 2х + 2) + В(х2 4- 2х + 2) + (Сх + D)x2,
т. е.
4х3 + 4х2 + 4х + 4 = (А + С)х3 + (2А + В + D)x2 + (2А + 2В)х + 2В.
Отсюда следует, что
и
А + С = 4,
2А + В + D = 4, 2 А + 20 = 4, 20 = 4.
Находим: В = 2, А = О, С = 4, D = 2. Стало быть,
4х + 2
+ 2а* + 2
4а: + 2 х2+ 2x4-2'
4х3 + 4а:2 + 4а: + 4 _ 2 х4 + 2а:3 + 2а:2 х2
х5 + 2а:3 + 4а: + 4 _ а-4+2а;3 + 2а:2 ~Х~ + .
Интегрируем полученное равенство:
/ х5 + 2а:3 + 4а: + 4 , г ( 2
/ -—т—---s-----х— dx = I \ х — 2 + —~
J х4 + 2х3 + 2х2 J \ х2
х2
= —— 2х —
™2
2
4х + 2
x2 + 2x + 2J
4а: + 2 .
(а: + 1)2 + 1
Обозначим х + 1 = t, тогда х = t — 1 и dx = dt. Таким образом,
г 4х + 2 r4t-4 + 2 г tdt г dt
J (x + l)2 + ldX~ J t2+l dt~4 t2 + l 2J t2 + l
= 4 • - ln(t2 + 1) - 2 arctgt + C =
= 2 • ln(a;2 + 2x + 2) — 2 arctg(a: + 1) + C. Следовательно,
f ж5.+ 2^3 „+4^4:4 dx = ^-2a:--+21n(a:2+2a:+2)-2arctg(a: + l)+C.
J x4 + 2a:3 + 2a:2 2 x v 7
Отметим, что любая рациональная функция интегрируется в элементарных функциях.
247
§ 32. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
32.1. Универсальная тригонометрическая подстановка
Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными sina: и cosa:, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать /{(sin a; cos а:), где R — знак рациональной функции.
|ф| Вычисление неопределенных интегралов типа J /{(sin х; cos х) dx сводится к вычислению интегралов от рациональной функции подстановкой tg = t, которая называется универсальной.
‘ив 2tSf 2t
Действительно, sm х = -—~-
2
х=2 arctg t, dx = - Поэтому
. l-tg2f 1-t2
cosa:-- i+tg2|-1 + t2
f 1 + t2’
iin x; cos x
2t 1-t2
1 + t2’’1+t2
1 + t2
dt= Ri(t)dt,
где jRi(t) — рациональная функция от t. Обычно этот способ весьма громоздкий, зато он всегда приводит к результату.
На практике применяют и другие, более простые подстановки, в зависимости от свойств (и вида) подынтегральной функции. В частности, удобны следующие правила:
1) если функция /{(sin х; cos ж) нечетна относительно sin а:, т. е. /?(—sina; cosa:) = — /{(sina:; cosa:), то подстановка cosa: = t рационали
зирует интеграл;
2) если функция R(sin a:; cos х) нечетна относительно cos х, т. е. /{(sina:; — cosa:) = —//(sina; cos а1), то делается подстановка sina: = t;
3) если функция /{(sin a; cos ж) четна относительно sin х и cos х R(— sin х; — cos х) = /{(sin ж; cos х), то интеграл рационализируется подстановкой tg х = t. Такая же подстановка применяется, если интеграл имеет вид / R(tgx)dx.
Пример 32.1. Найти интеграл / . ,-----.
J 3 + sin X + COS X
Q Решение: Сделаем универсальную подстановку t = tg Тогда dx =
248
Q Л-f- П2 1 _ y.2
. 9, sina: = „ >, cosa; = 4—Ц-. Следовательно,
1+t2 1 + t2 1 + t2
dx г 2dt г dt
3 + sina; + cosa; J (1 + t2)(3 + -|-1_^) J t2 + t + 2
<i(t+|) 2 t+| 2 l + 2tgf
. 2 7 = -7= arctg -=-f- + C = -7= • arctg--
+ |)2 + £ V7 V7/2 V7 V7
Пример 32.2. Найти интеграл I = j .-2 —.
Q Решение: Так как
R(— sina;: — cosa;) = --„ = R(sinx; cosa;),
v ’ l + (—sina;)2 l + sin2a; ' ’ ’
то полагаем tg x = t. Отсюда
, dt . 2 tg2 x t2
x = arctg t, dx = -—и sin x = -----------—5— = ---
6 1 + t2 l + tg2a; 1 + t2
Поэтому
dt г dt 1 r d(V2t)
(i + t2)(i+ = ' v? +1 (V^ty + 1
= arctg V%t + C --
1
—z= arc
V2
tgfv^tga;) + C.
32.2. Интегралы типа J sin"1 x • cos” x dx
Для нахождения таких интегралов используются следующие приемы:
1) подстановка sina; = t, если п — целое положительное нечетное число;
2) подстановка cos х — t, если т — целое положительное нечетное число;
3) формулы понижения порядка: cos2 а; = ^(1 + cos 2а;), sin2 а; = = i(l — cos2а:), sina; • cosa; = sin2а;, если тип — целые неотрицательные четные числа;
4) подстановка tg х — t, если т + п — есть четное отрицательное целое число.
Пример 32.3. Найти интеграл I = / sin4 х cos5 х dx.
249
Q Решение: Применим подстановку sin х — t. Тогда х = arcsin t, dx = = ->.1-- dt, cos x — \/l — f2 и
a/1 -t2
/ = j t4 • (л/l — *2)5 t2 = 114(1 -t2)2 dt = J(t4 - 2t6 +18) dt J
= У — 2у + у + С = i sin5 x — | sin7 x+ 1 sin9 x + C. fl
Пример 32-4- Найти интеграл I = J sin4 x cos2 x dx. |
* -1
Q Решение:
г г 1 1 /I
/ = J (sin x cos ж)2 sin2 x dx = / - sin2 2x • -(1 — cos’ 2y) dx — ’
lr lr 1 f 1 .1
= - / sin2 2xdx — - sin22xc.os2xdx = - / -(1 — cos4ar)dx— |
о J о J 8 J 2 jl
1 * 1X1 J
— — j sin2 2x d(sin 2x) = —x — — sin 4x — — sin3 2rr + C. fl
Пример 32.5. Найти интеграл г dx г ___j . _о
1=1 ---------о— = / cos x • sin x dx.
J cos x sin x J
Q Решение: Здесь m + n = —4. Обозначим tga: — t. Тогда x = arctg t, dx = - , sin x — - . .-., cos a: = - . * и
1 +1 Vl + t2 y/l + t2
dt 1+t2
P
1 + i2
л/1+Н ’ (•s/i+F)3
~ +ln И + • ctg2 Ж + In I tgtf| + C.
32.3. Использование тригонометрических преобразований
Интегралы типа j sin ах cos bx dx, J cos ax cos bx dx, J sin ax sin bx dx вычисляются с помощью известных формул тригонометрии:
1 1
sin a cos ft = - (sin(o — /?) + sin(o + /?)), i
I
Л,
cos a cos /3 — -(cos(a — [3] + cos(« + /?)), sin a sin /3 = -(cos(a — /3) — cosfa + /3)).
Пример 32.6. Найти интеграл I = I sin 8a: cos 2.r dx.
Решение:
!
I = j sin &zr cos 2a: dx = - J (sin 10a: + sin 6a:) dx —
= x (— t^-cos 10a: — cos6aA + C. • 2 \ 10 6 /
§33. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
33.1. Квадратичные иррациональности
Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.
Интегралы типа
г dx г /—х— ------ , г тх + п ,
I - - - - , / у/ах2 + bx + cdx, I - . - - - dx
•' \/ах2 +bx + с J J у/ах2 + Ьх + с
называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под радикалом выделить полный квадрат
ах2 +Ьх + с =
— о(а:2 + -а:+-) \ а а)
+
4ас — Ь2 \
и сделать подстановку х + = t. При этом первые два интеграла при-
водятся к табличным, а третий — к сумме двух табличных интегралов.
Пример 33.1. Найти интегралы 1=1 - ,------
J y/^ + lx + l
О Решение: Так как 4ж2 + 2х +1 = 4 (х2 + +
то j г dx _ 1 г dx
^/4((ж +1)2 + й) 2 \/(* + |)2 + те
251
Сделаем подстановку х + | = t, х = t — i, dx = dt. Тогда
Пример 33.2. Найти интеграл I = / —. х— - dx.
> /б-2а:-а:2
Q Решение: Так как 6 — 2х — х2 = —(а;2 + 2х — 6) = — ((а: + I)2 — 7) = 7 — (ж + I)2, то подстановка имеет вид х + 1 = t, х = t ~ 1, dx — t Тогда
/= f~PL=
J у/7-t2 J у/Т^В
+ Sf
dt \/7-t2
= ~| /~(7-t2)-^(7-t2) + 3 f -dt- - =
' J у(y/7)2 - t2
= — \/7 — t2 + 3 - arcsin + C = 3 arcsin X 13 — \/б — 2a: — a:2 + C.
a/7 y/7
г P lx]
Интегралы типа / - nv ’ dx, где Pn(a:) — многочлен ci J у ax2 + bx + c
пени п, можно вычислять, пользуясь формулой
[ ~7==^=7== ~ Q*1-1 (х) ’ х/ах2 + bx + с + Л [ ———— =,
J V ах2 +Ьх + с J у/ах2 +Ьх + с
(33.1) где Qn-i(ic) — многочлен степени п — 1 с неопределенными коэффициентами, X — также неопределенный коэффициент.
Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих частей равенства (33.1):
/ = = (Qn-i(^) \/aa2 + Ьх + с)' + -.-г- Л —,
V ах2 +Ьх + с у/ах2 4- Ьх + с
после чего необходимо приравнять коэффициенты при одинаковых степенях неизвестной х.
Пример 33.3. Найти интеграл 1= , Фе.
г 1 — 2х х
Q Решение: По формуле (33.1) имеем:
I — [ -Х- - - - dx = (.4х + В) \/1 — 2х — х2 + Л [ г - —
J V1 - 2а: - a:2 J у/1-2х -
252
Дифференцируя это равенство, получаем:
. —- = А л/1-2а:-а:2 + (Ах+В) . . ------,
\/1 — 2х—х2 2у/1-2х-х2 у/1~2х-х2
г. е.
х2 = Д(1 — 2х — ж2) + (Ах + В)(—1 — х) + А, х2 = А — 2Ах — Ах2 — Ах — В — Ах2 — Вх + Л.
Сравниваем коэффициенты при одинаковых степенях х:
1 — —А — А при а:2, < 0 = — 2 А — А — В при х1, О = А — В + А при х°.
1 ч
Отсюда А — —к, В — А = 2. Следовательно,
I = (--х + -) \/1 - 2а- - х2 +2 / dx == = V 2 2/V J у/2-(х +1)2
"Т » . х + 1 . ~ _
х1 + 2 arcsin —=- + G. • х/2
33.2. Дробно-линейная подстановка
Интегралы типа \ r(x, ,..., dx, где а, Ь,
с, d — действительные числа, а,/3,..., ё, 7 — натуральные числа, сводятся к интегралам от рациональной функции путем подстановки = гДе — наименьшее общее кратное знаменателей дробей а
/З’-'-’у- *
Действительно, из подстановки следует, что х=
, -dktlc~1(etk — а) — (b — dtk')cktk~1 , ,
и dx = -------1---------р-----i-----dt, т. e. x и dx выражаются
через рациональные функции от t. При этом и каждая степень дроби выражается через рациональную функцию от t.
Пример 33.Л. Найти интеграл 7 = / ч , , —
1 J Зу/(х + 2)2 - у/^+2
2 1
Q Решение: Наименьшее общее кратное знаменателей дробей g и есть 6. Поэтому полагаем х+ 2 = t6, х = t6 — 2, dx = 6t5 dt, t = y/x + 2.
253
Следовательно,
с 6t5 dt r t2 dt г (t2 — 1) + 1
’ = / = v Г~1 = <7Чг dt =
= 6 J (t + 1 + dt = 3t2 + 6t + 6 In |t - 1| + C =
= 3- </x + 2 + 6 - Vx + 2 + 61n| Vx + 2- l| + c. •
Пример 33.5. Указать подстановку для нахождения интегралов:
г у/х — 1 г 3 /м +1 dx
h — / 777=--dx, I2 — I \ ——г - 7——Tx-
J 7,yfX — X J \ X — 1 (1 — X)2
Q Решение: Для Ц подстановкам — t2, для 12 подстановка 2LE1 — t3.
х — 1
33.3. Тригонометрическая подстановка
Интегралы типа
\/а2 + x2)dx, J R(x\ \/х2 ~ a2)dx приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок: х — a - sin t для первого интеграла; х = а - tg t для второго интеграла; х = Д;м третьего интеграла.
Пример 33.6.
Найти интеграл I
Q Решение: Положим х — 2sint, dx = 2 cost (ft, t = arcsin^. Тогда
\/4 —4sin2 t r
- • 2 cos tdt = I
dt г
— I dt = — ctg t — t + C =
. X x/^ — X2 arcsin ---
2
4 sin21 r 1 — sin21 J sin21
4 cos21 , t) dt — 4sin2t
sin21
x t
= C — arcsin — — ctg^
arcsin
х
(curt = ^1~sin2f = x/1 - (fF _ х/4-м2
V g sint f
x
254
33.4. Интегралы типа / R(x; \/ах2 +bx + c) dx
Здесь подынтегральная функция есть рациональная функция относительно х и у/ах2 + to + с. Выделив под радикалом полный квадрат и сделав подстановку х + = t, интегралы указанного типа
приводятся к интегралам уже рассмотренного типа, т. е. к интегралам чипа у R(t; х/а2 — f2) dt, J R(t\ х/а2 + I2) dt, j R(t; x/t2 — a2) dt. Эти интегралы можно вычислить с помощью соответствующих тригонометрических подстановок.
Пример 33.7. Найти интеграл I
х/х2 + 2ж - 4 (ж+1)3
dx.
Q Решение: Так как а;2 + 2х—4 = (х+1)2 — 5, то а;+1 = t, х = t— 1, dx = = dt. Поэтому I = f ч 5 dt. Положим t — , dt ~ 2COS z dz,
J t sinks’ sin2 z
.fa z ~ arcsin Тогда
dz =
- 9 sin z
cos2 z dz =
10
10
(x + I)2
1 . - sin 2z
arcsin
. х/5
arcsin-----;
1 .
arcsin------F — sin
t 2
. a/5 1 . ’
arcsin —— + — sin
'б X
arcsin x +1
Замечание: Интеграл типа / — J xx
дить с помощью подстановки х = j.
dx
целесообразно нахо-
33.5. Интегрирование дифференциального бинома
Интегралы типа j хт • (а + bxn)p dx (называемые интегралами от дифференциального бинома), где а, b — действительные числа; т, п, р — рациональные числа, берутся, как показал Чебышев П.А., лишь в
255
случае, когда хотя бы одно из чисел р, т + или ггк^ 1 + р является целым. 4
Рационализация интеграла в этих случаях осуществляется следуй
ющими подстановками:
1) если р — целое число, то подстановка х = tk, где к — наимены шее общее кратное знаменателей дробей тип; .1
2) если w + 1 — целое число, то подстановка а + bxn = ts, где s —1
знаменатель дроби р; У
3) если w + 1 + р — целое число, то подстановка а + Ьхп = хп • Я
где s — знаменатель дроби р. Я
Во всех остальных случаях интегралы типа j хт(а +
не выражаются через известные элементарные функции, т. е. «не бЛ
рутся». 1
Пример 33.8. Найти интеграл I = J
dx.
Q Решение: Так как
2 • (1 + ж«)з dx,
то m = —i,zi = pp = w + I = 2. Поэтому делаем подстановка %[х + 1 = t3, х = (t3 — I)4, dx = 4(t3 — I)3 • 3t2 dt, t = y/x + 1. Таки$ образом,
____t_________ 12/2(73
(f3 - I)2 1
§34. «БЕРУЩИЕСЯ» И «НЕБЕРУЩИЕСЯ» 3
ИНТЕГРАЛЫ 1
Как уже отмечалось выше, операция интегрирования функций знав чительно сложнее операции дифференцирования функций. Не всегФЯ выбранный путь интегрирования является наилучшим, более коров ким, простым. Интегрирование часто может быть выполнено не едияИ ственным способом. Многое зависит от знания рекомендуемых мноы™ искусственных приемов интегрирования, от сообразительности, от тренированности. Например, j —можно найти, не используя реко
256
мендуемую подстановку tg# = г, а применив искусственный прием:
dx г (cos2 х + sin2 ж)2 , —= / '----------------«--------dx
cosb х J cos” x
1 + 2 tg2a: + tg4.r A
COS2 X cos2 X COS2 X J
2 1
dx = tga; + - tg3 x + - tg5 x + C.
3 5
-ряд ли стоит вычислять интеграл
г Зж2 + 4ж + 1
J х(х> + 2ж + 1) dX'
разлагая подынтегральную функцию на простейшие дроби:
Зж2 + 4ж + 1 _ Зж2 + 4ж + 1 _ А В С
ж(ж2 + 2ж + 1) ж(ж + I)2 ж + ж + 1 + (ж + I)2 •
Заметив, что числитель Зж2 + 4ж +1 является производной знаменателя :(ж2 + 2ж + 1) = ж3 + 2ж2 + ж, легко получить:
г Зж2 + 4ж + 1 г d(pc3 + 2ж2 + ж) 3 2
/ —о------dx = / \ , о ?--------- = 1п ж + 2ж + х + С.
J х(х2 + 2ж +1) J ж3 + 2ж2 + ж 1 1
На практике при вычислении неопределенных интегралов исполь->уют различные справочники, содержащие таблицы особенно часто встречающихся интегралов. В частности, «Таблицы неопределенных интегралов» М. Л. Смолянского.
Изученные методы интегрирования позволяют во многих случаях вычислить неопределенный интеграл, т. е. найти первообразную функцию для подынтегральной функции.
Как известно, всякая непрерывная функция имеет первообразную. В том случае, когда первообразная некоторой элементарной функции /(ж) является также элементарной функцией, говорят, что J f(x) dx «берется», т. е. интеграл выражается через элементарные функции (или интеграл вычисляется). Если же интеграл не выражается через элементарные функции, то говорят, что интеграл «не берется» (или «его найти нельзя»).
Так, например, нельзя взять интеграл
существует элементарной функции, производная от которой была бы равна \/ж cos ж. Приведем еще примеры «неберущихся» интегралов, которые имеют большое значение в приложениях:
cos ж dx, так как не
е х dx — интеграл Пуассона (теория вероятностей),
— интегральный логарифм (теория чисел),
9 Конспект лекций по высшей математике. Полный курс
257
cost2 dx, j sin ж2 dx — интегралы Френеля (физика), dx, j dx — интегральные синус и косинус, — ах — интегральная показательная функция.
Первообразные от функции е , cost2, и других хорошо изучены, для них составлены подробные таблицы значений для различных значений аргумента х.
Глава VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Лекции 29-33 |
§35. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ ИНТЕГРАЛЬНОЙ СУММЫ
Пусть функция у = /(ж) определена на отрезке [а; 6], а < Ъ. Выполним следующие действия.
1. С помощью точек жо = а, Ж1, ж2,..., хп = b (жо < Ж1 < ... < хп) разобьем отрезок [а, 6] на п частичных отрезков [жо;жх], [жх;ж2], ... ,[жп-1,жп] (см. рис. 166).
Cl С2 Ci сп х
—।----1—.—।—.—।—.—।—.—।—.—।—•—।—•—।—.—।----
О а=хо Xi Х2 Xi-i Xi b=xn
Рис. 166
2. В каждом частичном отрезке [®{_х;ж<], г = 1,2, ...,п выберем произвольную точку Ci 6 [жг-1;Жг] и вычислим значение функции в ней, т. е. величину /(с^).
3. Умножим найденное значение функции f(ci) на длину Дж; = = Xi — Жг-i соответствующего частичного отрезка: f(ci) Axt-
4. Составим сумму Sn всех таких произведений: п
Sn = /(сх)Джх + /(с2)Дж2 + ... + /(с„)Джп = /(Сг)Дж». (35.1)
i=l
Сумма вида (35.1) называется интегральной суммой функции у = f (ж) на отрезке [«;/>]. Обозначим через А длину наибольшего частичного отрезка: А = max Дж^ (г = 1,2,... ,п).
5. Найдем предел интегральной суммы (35.1), когда п —> оо так, что А —> 0.
Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка [а; 6] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = f(x) на отрезке [а; 6] и обозначается 6
У /(ж) dx. Таким образом, а
Ъ п
I /(ж) dx = lim 52 /(Сг)Д^г-
(Х-Я)) г=1
(35.2)
259
Числа а и Ь называются соответственно нимсним и верхним] пределами интегрирования, f(x) — подынтегральной функцией, f(x) dx — подынтегральным выражением, х — пере-' менной интегрирования, отрезок [а;Ь] — областью (отрезком)1, интегрирования.
[ф| Функция у = f(x), для которой на отрезке [а; Ь] существует опреде-;
ленный интеграл J f(x) dx, называется интегрируемой на этом' отрезке.
Сформулируем теперь теорему существования определенного ин-' теграла.
Теорема 35.1 (Коши). Если функция у = f(x) непрерывна на отрез-ft
ке [а;Ь], то определенный интеграл j f(x)dx существует.
а
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (35.2).
1. Определенный интеграл не зависит от обозначения переменной интегрирования:
ь ь ь
I f(x)dx = J f(t)dt= J f(z)dz. a a a
Это следует из того, что интегральная сумма (35.1), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
У f (х) dx = 0. а
Ъ
3. Для любого действительного числа с: J cdx = с - (Ь — а).
а
260
§36. ГЕОМЕТРИЧЕСКИМ И ФИЗИЧЕСКИИ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Площадь криволинейной трапеции
Пусть на отрезке [а; Ь] задана непрерывная функция у = /(ж) 0.
Фигура, ограниченная сверху графиком функции у = f(x), снизу — осью Ох, сбоку — прямыми х = а и х = Ь, называется криволинейной трапецией. Найдем площадь этой трапеции.
Для этого отрезок [«; Ь] точками а = x0,Xi, ,Ь = хп (яд < < xi < ... < хп) разобьем на п частичных отрезков [x0;xj], [я?1;я:2],... ... , [хп_1;жп]. (см. рис. 167). В каждом частичном отрезке
(г = 1,2, ...,п) возьмем произвольную точку с, и вычислим значение функции в ней, т. е. f(ci).
Умножим значением функции /(с,) на длину Ах; = - Xi-i соот-
ветствующего частичного отрезка. Произведение /(g) • Дя:,- равно площади прямоугольника с основанием Ах,- и высотой Сумма всех таких произведений
/(ci)Aar! + /(с2)Дя,-2 + ... + /(сп)Дх„ = ^/(с^Дх» = Sn г=1
равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:
п
S « Sn = /(с,) • Дж,.
г=1
С уменьшением всех величин Дх-j точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда п неограниченно возрастает так, что А = max Дх, —> 0:
п Ь
S = lim Sn = lim Y'/(с^Дяч, то есть S = / /(ж) dx.
(А—>0) г=1 а.
261
Итак, определенный интеграл от неотрицательной функции чш сленно равен площади криволинейной трапеции. ||
В этом состоит геометрический смысл определенного интеграла. '
Работа переменной силы
Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х — абсцисса движущейся точки М.
Найдем работу А силы F по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (а < Ь). Для этого отрезок [а;Ь] точками а = х0, :ei, b = хп (жо < ад < ... < хп) разобьем на п частичных отрезков [жо;Ж1], [ж'1;ж2], ..., [жп_!;жп]. Сила, действующая на отрезке [ад-х; ж,], меняется от точки к точке. Но если длина отрезка Лад = Xi — жг-1 достаточно мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F — F(x) в произвольно выбранной точке х — Ci е [xi-i;xi]. Поэтому работа, совершенная этой силой на отрезке [жх-1; ад], равна произведению F(ci) Дх/. (Как работа постоянной силы F(q) на участке [ж,-1;жг].)
Приближенное значение работы А силы F на всем отрезке [а; 6]j есть j
'i
п I
А к Г(с1)Дж1 + Е(с2)Дж2 + ... + Г(с„)Дж„ = F(c,) Джд. (36.1)^
г=1
Это приближенное равенство тем точнее, чем меньше длина Джд. По-,1 этому за точное значение работы А принимается предел суммы (36.1)4 при условии, что наибольшая длина А частичных отрезков стремится® к нулю:
А = lim Е(с,)Джг- = J F(x)dx. j
«=1 _ а 9
Итак, работа переменной силы F, величина которой есть непрерывная’ функция F = Е(ж), действующей на отрезке [а;Ь], равна определенно-_• му интегралу от величины Е(ж) силы, взятому по отрезку [а; Ь]. j
В этом состоит физический смысл определенного интеграла. 1
Аналогично можно показать, что путь S, пройденный точкой за 1 промежуток времени от t = а до t = Ь, равен определенному интегралу j от скорости v{t):
S = У v(t) dt; а
масса т неоднородного стержня на отрезке [а; Ь] равна определенному ь
.интегралу от плотности 7(ж): т = j 'yfx'jdx. J
° и
262
§37. ФОРМУЛА НЬЮТОНА-ЛЕИБНИЦА
Пусть функция у = f(x) интегрируема на отрезке [а; Ь].
Теорема 37.1. Если функция у = Дх) непрерывна на отрезке [а; /;] и F(x) — какая-либо ее первообразная на [а; Ь] (F'(x) = /(ж)), то имеет место формула
J Дх) dx = F(b) - F(a). (37.1)
а
□ Разобьем отрезок [а; Ь] точками а = xq, xj,..., b = ж„ (х0 < Xi < ... ... < хп) на п частичных отрезков [x0;xi],[ж1;ж2],.-, [xn-i;xn], как это показано на рис. 168.
С1 с2 а сп х
—।----1—♦—।—•—।—•—।—»—।—•—।—•—।—•—।—•—।-----
О а = Хо Xi Х2 Хг~1 Хг Ь = Хп
Рис. 168
Рассмотрим тождество
F(b) - F(a) = F(x„) - F(x0) = (F(x„) - F(xn_1)) +
+ (F(x„_i) - F(xn_2)) + - - • + (И(ж2) - F(xi)) + (F(xi) - F(xq)). Преобразуем каждую разность в скобках по формуле Лагранжа ДЬ)-Да)=/'(с)-(Ь-а).
Получим
F(b) - F(«) = F'(cn) (жп - жп_1) + F'(cn-i) • (ж„_1 - жп_2) + ...
---hF'(c2) • (ж2 -Ж1) +Р'(с1)(ж1 -х0) = ^F'^Axi = ^/(^)Дх<, i=l г=1
т. с. п
F(b) - F(a) = (37.2)
i=l
где с, есть некоторая точка интервала (x^i;xj). Так как функция у = f^x) непрерывна на [а; Ь], то она интегрируема на [а; Ь]. Поэтому существует предел интегральной суммы, равный определенному интегралу от Дх) на [а; 6].
Переходя в равенстве (37.2) к пределу при А = max Дх, -> 0, получаем П
F(b) - F(a) = lim Y2 /(с»)Дх7,
Л—УО .
263
т. е.
ь
F(b) — F(a) = у f(x)dx.
а
g Равенство (37.1) называется формулой Ньютона-Лейбница.
Если ввести обозначение F(6) — F(а) = F(x)|^, то формулу Ньютона-Лейбница (37.1) можно переписать так:
ь
f f(x)dx = F(x)|‘.
а
Формула Ньютона-Лейбница дает удобный способ вычисления определенного интеграла. Чтобы вычислить определенный интеграл от непрерывной функции f(x) на отрезке [«; Ь], надо найти ее первообразную функцию F(x) и взять разность F(b) — F(a) значений этой первообразной на концах отрезка [а; 6].
з
Например, J х2 dx = = 9 — 0 = 9,
о
2 2
J 4 + х2 2 6 21^2 2\4 \ 4// 4
-2
Пример 37.1.
1 +
Вычислить интеграл
Q Решение:
2
У cos х dx + о
= sinx|2 + (~sinx)|^= 1 + 1=2.
Пример 37.2.
Вычислить интеграл
dx
X In X
Q Решение:
dx х In x
= In | In s| |e = In 2 — In 1 = In 2.
264
§38. ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию интегрируемой на отрезке [а;Ь]. При выводе свойств будем использовать определение интеграла и формулу Ньютона Лейбница.
1. Если с — постоянное число и функция f(x) интегрируема на |а; Ь], то
J с f(x) dx = с - У /(ж) dx, (38.1)
а а
т. е. постоянный множитель с можно выносить за знак определенного интеграла.
□ Составим интегральную сумму для функции с /(ж). Имеем:
. п п
52 С - /(С»)ДЖ4 = С • 52 /(Сг)ДаГ»-
г—1 2,=1
b п п 7.
Тогда lim 52 с ' = с • lim 52 f(ci) ~ с I f(x)dx. Отсюда
n->oo i==j п—Уоа i==1 J
а
вытекает, что функция с /(ж) интегрируема на [а; Ь] и справедлива формула (38.1).
2. Если функции /1(х) и /2(ж) интегрируемы на [а; Ь], тогда интегрируема на [а; 6] их сумма и
ь ь ь
J (fi (ж) + h (ж)) dx = f fi (®) dx + f fa (ж) dx, (38.2)
a a a
т. e. интеграл от суммы равен сумме интегралов.
b п
□ f (fa(x) + Ь(ж)) dx. = ^lirn^ ^2(fl(Ci) + /2(Сг))ДЖг = a ^”1
71 n b b
= lim У'/1(Сг)Да,'г + lim S^fa(ci)Axi = f^x)dx+ fa(x)dx.
П—yOQ 71—^00 J J
i=l a a
Свойство 2 распространяется на сумму любого конечного числа слагаемых.
3. у /(ж) dx = — у /(ж) dx. а b
265
Это свойство можно принять по определению. Это свойство также подтверждается формулой Ньютона-Лейбница.
b а
I /(ж) drr = F(b) - F(n) = -(F(a) - F(b)) = - у /(ж) dx. a b
4. Если функция f(x) интегрируема на [a; b] и a < c < b, mo b c b
I f(x) dx = у f (ж) dx + У f (ж) dx, (38.3)
a a c
t. e. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью onpened ленного интеграла (или свойством аддитивности). |
При разбиении отрезка [а; Ь] на части включим точку с в число точеи деления (это можно сделать ввиду независимости предела интеграль! ной суммы от способа разбиения отрезка [а; Ь] на части). Если с = хт 1 то интегральную сумму можно разбить на две суммы: 1
п т п ']
52 / (сг)Джг = 52 №) Дж* + 52 Лсг)ДаТ >
г=1 i=l i=m <
Каждая из написанных сумм является интегральной соответственней для отрезков [а; Ь], [а; с] и [с; Ь]. Переходя к пределу в последнем равенстве при тг —> оо (А —> 0), получим равенство (38.3).
Свойство 4 справедливо при любом расположении точек а, Ь, с (считаем, что функция /(ж) интегрируема на большем из получающихся отрезков).
Так, например, если а < b < с, то с b с ;
У /(ж) dx = у /(ж) dx + у /(ж) dx. I
а а Ь
Отсюда
Ь с с с b 1
I f(x) dx = у /(ж) dx- у /(ж) dx = у /(ж) б/ж + у /(ж) dx а а Ь а с ;
(использованы свойства 4 и 3).
5. «Теорема о среднем». Если функция f(x) непрерывна на отрезке\ [а; Ь], то существует точка с G [а;Ь] такая, что
ь
У /(ж) dx = f(c) (b - а), а
266
По формуле Ньютона-Лейбница имеем
ь
I f(x)dx = F(x)\ba = F(b) — F(a), а
где F'(x) = f(x). Применяя к разности F(b) — F(a) теорему Лагранжа (теорему о конечном приращении функции), получим
F(b) - F(a) = F'(c) • (b - a) = /(c) • (b - a).
Свойство 5 («теорема о среднем») при f(x) 0 имеет простой геометрический смысл: значение определенного интеграла равно, при некотором с G (а;Ь), площади прямоугольника с высотой /(с) и основанием b — а (см. рис. 169). Число
= //(*)*= а
называется средним значением функции f(x) на отрезке [а; Ь].
6. Если функция f(x) сохраняет знак на отрезке [а; Ь], где а < Ь, ь
то интеграл J /(.т) dx имеет тот же знак, что и функция. Так, если а
b
f(x) 0 на отрезке [а; Ь], то /(х) dx 0.
а
□ По «теореме о среднем» (свойство 5)
ь
У f(x)dx = /(с) • (Ь — а), а
где с £ [а; Ь]. А так как f{x) 0 для всех х £ [а; Ь], то и
/(с) > 0, b - а > 0.
ь
Поэтому /(с) • (Ь — а) 0, т. е. J f(x) dx 0.
a
7. Неравенство между непрерывными функциями на отрезке [а; Ь], (а < Ь) можно интегрировать. Так, если fi(x) /2(х) при х € [а;Ь], ь ь
то У /х (ж) dx. < у /2 (ж) dx. а а
267
□ Так как /2(ж) — /1 \х) 0, то при а < Ь, согласно свойству 6. имеем
ь
I (/2 (ж) - /1(®))йг > 0.
а
Или, согласно свойству 2,
ь ъ
I f2(x) dx - J fi(x) dx 0, t. e.
a a
b
j f2(x)dx.
a
Отметим, что дифференцировать неравенства нельзя.
8. Оценка интеграла. Если т и М — соответственно наименьше и наибольшее значения функции у = f(x) на отрезке [a; b], (а < b), zr
ь
m(b — a)^. f f(x) dx M(b — а). (38.^
а
□ Так как для любого х € [а; Ь] свойству 7, имеем
имеем т С -/(а,-) М, то, согласи
b ь ь
J mdx J f(x) dx С J М dx.
а а а
Применяя к крайним интеграла\ свойство 5, получаем
ь
т(Ь—а) С j f(x)dx М(Ъ—а). I
Если f(x) 0, то свойство J иллюстрируется геометрически
площадь криволинейной трапеции заключена между площадями пря моугольников, основание которых есть [а; Ь], а высоты равны т и Ad (см. рис. 170).
9. Модуль определенного интеграла не превосходит интеграла оп модуля подынтегральной функции:
b ь
У f(x)dx J |/(ж)|(£с; а < Ь. а а
Q Применяя свойство 7 к очевидным неравенствам — |/(ж)1 /(ж)
1/(ж)1> получаем ь ь ь
- J \f(x)\dx у f(x)dx^ j\f(x)\dx. i а a a
Отсюда следует, что b b
J f(x)dx J \f(x)\dx. a a
268
10. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования, заменена этим пределом, т. е.
/ X \ '
\J f(t)dt\ = f(x).
\а / х
IJ По формуле Ньютона-Лейбница имеем:
X
[ f(t)dt = F(t)\xa = F(x)-F(a). а
= №) - F(a))'x = F'(x) - 0 = /(х).
Следовательно,
X а Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.
§39. ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
39.1. Формула Ньютона-Лейбница
Простым и удобным методом вычисления определенного интегра-ь
ла f f(x) dx от непрерывной функции является формула Ньютона-а
Лейбница: ь
f f(x)dx = F(x)\ba = F(b)-F(a).
а
Применяется этот метод во всех случаях, когда может быть найдена первообразная функции F(x) для подынтегральной функции /(ж).
7Г
Например, J sinxdx = — cosx|q — —(cos-тг — cosO) = 2. о
При вычислении определенных интегралов широко используется метод замены переменной и метод интегрирования по частям.
39.2. Интегрирование подстановкой (заменой переменной)
ь
Пусть для вычисления интеграла J f(x) dx от непрерывной функ-а ции сделана подстановка х = <р(б).
269
Теорема 39.1. Если:
1) функция х = <p(t) и ее производная х1 = непрерывны при t е [а;/?];
2) множеством значений функции х = ip(t) при t G [а, (3] является отрезок [а;Ь];
3) у?(а) = а и </>(/?) = Ь,
то ь 0
f f(x)dx = f (39.1)
a a
□ Пусть F(x) есть первообразная для f(x) на отрезке [а; Ь]. Тогда по ь
формуле Ньютона-Лейбница [ f(x)dx = F(b) — F(a). Так как а
(F(<^(t))' = /(</?(/))-<p'(t), то F(</:(/,)) является первообразной для функции /(y’(t)) • <^'(£), t е [а;/3]. Поэтому по формуле Ньютона-Лейбница имеем
0
/ Ш </(*) dt = F^t))\0a = F^f})) - F(y>(a)) =
a b '
= F(b)-F(a) = J f(x)dx.
° -I
Формула (39.1) называется формулой замены переменной в опре4 деленном интеграле.
Отметим, что:
1) при вычислении определенного интеграла методом подстановки! возвращаться к старой переменной не требуется;
2) часто вместо подстановки х = y?(t) применяют подстановку t = = ff(^);
3) не следует забывать менять пределы интегрирования при замене., переменных! 1
2
Пример 39.1. Вычислить J х2х/4 — х2 dx.
о
Q Решение: Положим х = 2 sin t. тогда dx = 2 cos t dt. Если x = 0, то t = 0; если x = 2, то t = Поэтому
2 k/2
У x2 \/4 — ®2 dx = J 4 sin2 ty/4 — 4 sin21 2 cos tdt =
о о
270
п/2 тг /‘i тг/2 1
= 16 у sin21 cos21 dt = 16 У -sin22tdt = 4 J -(1 — cos4f) dt = 0 0 0
=2(е-1й„4енй-о)=-
39.3. Интегрирование по частям
Теорема 39.2. Если функции и = и(х) и v = v(x) имеют непрерывные производные на отрезке [а;д], то имеет место формула
(39.2)
□ На отрезке [а; 6] имеет место равенство (uv)' = u'v + uv'. Следовательно, функция uv есть первообразная для непрерывной функции u'v + uv'. Тогда по формуле Ньютона-Лейбница имеем:
ь
У (u'v + uv') dx = ww|a-» a
Следовательно,
Формула (39.2) называется формулой интегрирования по частям для определенного интеграла.
е
Пример 39.2. Вычислить J х In xdx.
i
Q Решение: Положим
и = In х
dv = х dx
du = — dx x
v = ^-
v 2 J
271
Применяя формулу (39.2), получаем
[xlnxdx = — • 1пж — f — dx = J 2 11 J 2 x
i i
1 X^ Iе
= T-°-rH =
Пример 39.3. Вычислить интеграл J x sin x dx. о
Q Решение: Интегрируем по частям. Положим и — х => du = dx
dv = smxdx ==? « = —cosrc
Поэтому 7Г
J = ~a;cosa:|о 4- f cosxdx = — тг • (—1) 4- 0 4- sina:)* = тг. о
39.4. Интегрирование четных и нечетных функций в симметричных пределах
а
Пусть функция f(x) непрерывна на отрезке [—а; а], симметрично! относительно точки х = 0. Докажем, что а
2 • у f(x) dx, если /(ж) — четная функция, о
,0, если /(ж) — нечетная функция.
□ Разобьем отрезок интегрирования [—а; а] на части [—а; 0] и [0; а]. То-; гда по свойству аддитивности
(39.3)
—а
а Оо,
У /(ж) dx = J f(x) dx + J f(x) dx. (39.4)
--a ~a 0
В первом интеграле сделаем подстановку ж = — t. Тогда
У f(x)dx = — J f(—t)dt = f f(-t)dt = J f(-x)dx —a ft 0 0
(согласно свойству: «определенный интеграл не зависит от обозначения переменной интегрирования»). Возвращаясь к равенству (39.4), получим
а
J f(x)dx =
—а
j f(~x)dx + J f(x)dx о о
а
- [ U(~*) + f(x))dx.
о
(39.5)
272
Лели функция f(x) четная (/(—ж) = /(ж)), то /(—ж) 4- /(ж) = 2/(ж); если функция /(ж) нечетная (/(—ж) = —/(ж)), то /(—ж) + /(ж) = 0.
Следовательно, равенство (39.5) принимает вид (39.3).
Благодаря доказанной формуле можно, например, сразу, не производя вычислений, сказать, что
7Г 3
J cos2 ж • sin3 ж dx = 0, J е~х • sin ж dx = 0.
—7Г —3
§40. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
ь
Определенный интеграл J /(ж) dx, где промежуток интегрирова-а
ния [«; 5] конечный, а подынтегральная функция /(ж) непрерывна на отрезке [а; Ь], называют еще собственным интегралом.
Рассмотрим так называемые несобственные интегралы, т. е. определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв.
40.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)
Пусть функция /(ж) непрерывна на промежутке [а; +оо). Если ь
существует конечный предел lim / /(ж) dx, то его называют несоб-Ь-^+оо J +оо
а. л
ственным интегралом первого рода и обозначают / f(x)dx.
а
Таким образом, по определению
Н-оо Ь
[ f(x) dx = lim [ /(ж) dx.
J b—>-}-oo J
a a
-boo
В этом случае говорят, что несобственный интеграл J f(x)dx сходится. Если же указанный предел не существует или он бесконечен, 4-оо
то говорят, что интеграл J /(ж) dx расходится.
а
273
Аналогично определяется несобственный интеграл на промежутке
б
ь lim / f(x) dx. —oo J
a
Несобственный интеграл с двумя бесконеч-1 ними пределами определяется формулой '
У /(ж) dx = j f(x) dx +
где с — произвольное число. В этом случае интеграл слева сходится лишь тогда, когда,
сходятся оба интеграла справа. Отметим, что если непрерывная функ-
-J-oo
ция /(ж) 0 на промежутке [а; -t-oo) и интеграл J /(ж) dx сходит-
ся, то он выражает площадь бесконечно длинной криволинейной трапеции (см. рис. 171).
Пример 40.1. Вычислить несобственные интегралы или устало-4-ос 0 оо
вить их расходимость: 1) J 2) J cosxdx; 3) J ~.
1 —оо 1
+°о b ь
Q Решение: 1) [ - lim [ х~2 dx = — lim 1| = —(0— 1) = 1,
./ X b-^+ooJ Ь-Н-ооЖ|1 '
1 I
интеграл сходится; о о
2) / cost </ж = lim / совжйж — lim sinxl = 0 — lim sin а, J а—>—co J а—>—оо 1а а->—оо
—оо а
интеграл расходится, так как при « —> — ос предел lim sin а не суще-а—>—оо
ствует. оо b
3) f dx _ Цщ f dx _ цт [пь _ интеграл расходится. • J Ж б—>оо J ж Ь-Юо
1 1
В некоторых задачах нет необходимости вычислять интеграл; достаточно лишь знать, сходится ли он или нет.
Приведем без доказательства некоторые признаки сходимости.
274
Теорема 40.1 (признак сравнения). Если на промежутке [а; +оо) непрерывные функции f (ж) и </?(ж) удовлетворяют условию 0 С /(ж) С -f-oo
<р(ж), то из сходимости интеграла J ip(x)dx следует сходимость а 4-оо 4-ос
интеграла J /(ж) dx, а из расходимости интеграла а
сле-
дует расходимость интеграла J <p(x)dx. а
Пример 40.2. Сходится ли интеграл J
1
Q Решение: При ж 1 имеем 2 - < —%. Но интеграл 1
X (14-3) Ж J
1
сходится. Следовательно, интеграл J 3^) также сходится (и его 1 ' ' '
значение меньше 1). •
Теорема 40.2. Если существует предел Игл = к, 0 < к < оо х—>оо ^\х)
оо оо
(/(ж) > 0 и (р(х) > 0), то интегралы J /(ж) dx и J </>(ж) dx одновре-а а
менно оба сходятся или оба расходятся (т. е. ведут себя одинаково в смысле сходимости).
Пример ^О-З. Исследовать сходимость интеграла j In ж2 dx.
Q Решение: Интеграл J In 2 dx сходится, так как интеграл
сходится и
1
in 4 lim
—v 4-rv>
2
lim
1п(1 4-
1
X2
lim $ = 1.
275
40.2. Интеграл от разрывной функции (несобственный интеграл II рода)
Пусть функция /(ж) непрерывна на промежутке [а; Ь) и имеет бесконечный разрыв при х = Ь. Если существует конечный предел Ь~Е
I f(x)dx, то его называют несобственным интегралом второго
lim
Е—>0
а Ъ
рода и обозначают J f(x) dx.
а
Таким образом, по определению,
Ь Ь—Е
I f(x)dx = lim / f(x)dx.
J г->0 J
а а
Если предел в правой части существует, то несобственный интеграл ь
I f(x) dx сходится. Если же указанный предел не существует или бес-CL г.
конечен, то говорят, что интеграл / /(ж) dx расходится.
Аналогично, если функция f(x) терпит бесконечный х = а, то полагают ь
I f(x)dx = lim у f(x)dx. а аЛ-Е
Если функция /(ж) терпит разрыв во внутренней точке с отрезка [а; Ь], то несобственный интеграл второго рода определяется формулой
Ь с Ь
разрыв в точке
ь
В этом случае интеграл слева называют сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.
В случае, когда /(ж) > 0, несобственный интеграл второго рода ь
I /(ж) dx (разрыв в точке х = Ь) можно истолковать геометрически как а
площадь бесконечно высокой криволинейной трапеции (см. рис. 172).
' 1
Пример 40.4- Вычислить (
J х о
276
Решение: При х = 0 функция у = терпит бесконечный разрыв;
г dx г „2 1,1 ( 1\
/ —- = lim / х dx- = — lim - , = — 1 — hm - = ос,
J X2 е-Ш J e->0 X lu+£ \ e->0 E/
0 o+e
интеграл расходится. •
Сформулируем признаки сходимости для несобственных интегралов второго рода.
Теорема 40.3. Пусть на промежутке [а; Ь) функции /(ж) и <р(х) непрерывны, при х = b терпят бесконечный разрыв и удовлетворяют ь
условию 0 < /(ж) < <Дж). l/h сходимости интеграла f ip(x)dx вытекает сходимость интеграла / f(x)dx, а из расходимости интеграла 6 { ь
У f(x)dx вытекает расходимость интеграла J <p(x)dx.
а а
Теорема 40.4. Пусть функции /(.т) и <р(х) непрерывны на промежутке [а; Ь) и в точке х = b терпят разрыв. Если существует предел
lim = fc, 0 < fc < оо, то интегралы J f(x) dx и J ip(x) dx одновременно сходятся или одновременно расходятся.
Пример 40.5.
Сходится ли интеграл
dx 9 sin х'
Q Решение: Функция /(«) = Л имеет на [0:1] единственный разрыв в точке х = 0. Рассмотрим функцию у>(х) = —. Интеграл
[ — = lim f — = lim Ins = 0 — lim Ine
J X е-УО J X e->0 ,e e->0
0 0+e /
расходится. И так как
Шп Ж , to-Л-= 1,
аг->0 <р(х) Ж-ю sms
f Нт то интеграл / также расходится.
о
277
§41. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
41.1. Схемы применения определенного интеграла
Пусть требуется найти значение какой-либо геометрической или физической величины А (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком [a; bj изменения независимой переменной х. Предполагается, что эта вели-) чина А аддитивна, т. е. такая, что при разбиении отрезка [а; Ь] точкой с 6 (а; Ь) на части [а; с] и [с; Ь] значение величины А, соответствующей всему отрезку [а;Ь], равно сумме ее значений, соответствующих [«;cf и [с; Ь].
Для нахождения этой величины А можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала).
Первая схема базируется на определении ойределенного интеграла.
1. Точками so = a, xi,..., хп = Ъ разбить отрезок [а; Ь] на п частей. В соответствии с этим, интересующая нас величина А разобьется на п «элементарных слагаемых» ДА, (г ~ 1,... ,п): А = ДА1 + ДА2 + ... - - • + ДЛП.
2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину: ДА, « /(с,)Дх,.
При нахождении приближенного значения ДА, допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д.
Получим приближенное значение величины А в виде интегральной суммы: п
А & f(ci)Ax! + ...+ f(c.,l)Axn = У" f(ci)^Xi.
г=1
3. Искомая величина А равна пределу интегральной суммы, т. е. n b
А = = / f(x)dx.
(А эО) г=1 а
Указанный «метод сумм», как видим, основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых.
Схема I была применена для выяснения геометрического и физического смысла определенного интеграла.
278
Вторая схема представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»:
1) на отрезке [а; Ь] выбираем произвольное значение х и рассматриваем переменный отрезок [а; ж]. На этом отрезке величина А становится функцией х: А = Л (я), т. е. считаем, что часть искомой величины А есть неизвестная функция А(ж), где х £ [а; Ь] — один из параметров величины А;
2) находим главную часть приращения ДЛ при изменении х на малую величину Дж — dx, т. е. находим дифференциал dA функции Л = Л(.т): dA = f(x)dx, где /(ж), определяемая из условия задачи, функция переменной ж (здесь также возможны различные упрощения);
3) считая, что dA к ДЛ при Дж —> 0, находим искомую величину путем интегрирования dA в пределах от а до Ь:
ь
А(Ь) = А = J /(ж) dx.
а
41.2. Вычисление площадей плоских фигур
Прямоугольные координаты
Как уже было установлено (см. «геометрический смысл опреде-
У
y — f(x)
S(x)
d'S. dp'.
х x+dx Ь x
Рис. 173
ленного интеграла»), площадь криволинейной трапеции, расположенной «выше» оси абсцисс (/(ж) 0), рав-
на соответствующему определенному интегралу: ь ь
s = f /(ж)dx или S = У ydx. (41.1) а а
Формула (41.1) получена путем при-
менения схемы I — метода сумм. Обоснуем формулу (41.1), используя схему II.
Пусть криволинейная трапеция ограничена линиями у = f(x) 0, х = а, х = Ь, у — 0 (см. рис. 173). Для нахождения площади S этой
а
О
трапеции проделаем следующие операции:
1. Возьмем произвольное ж £ [а; Ь] и будем считать, что S = S(x).
2. Дадим аргументу ж приращение Дж = dx (ж + Дж £ [а; Ь]). Функция S = 5(ж) получит приращение Д,8', представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).
Дифференциал площади dS есть главная часть приращения Д5 при Дж —> 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у. dS — у • dx.
279
3. Интегрируя полученное равенство в пределах от х = а до х = Ь, ь
получаем S = J ydx.
а
Отметим, что если криволинейная трапеция расположена «ниже» оси Ох (f (т) < 0), то ее площадь может быть найдена по формуле
Рис. 174
ь
S = — f ydx. (41-2)
а
Формулы (41.1) и (41.2) можно объединить в одну:
Площадь фигуры, ограниченной кривыми у — /1(ж) и у = f2(x), прямыми х = а и х = Ъ (при условии /2 (ж) Ji (ж)) (см. рис. 174), можно найти по формуле
ь ь ь
S = J fa(x)dx- у Л(х) dx = j(/2(ж) - fi (ж)) dx.
а а а
Рис. 175
Рис. 176
Если плоская фигура имеет «сложную» форму (см. рис. 175), то прямыми, параллельными оси Оу, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.
Если криволинейная трапеция ограничена прямыми у = с и у = d, осью Оу и непрерывной кривой х = <р(у) 0 (см. рис. 176), то ее
d
площадь находится по формуле S = J xdy.
С
280
II, наконец, если криволинейная трапеция ограничена кривой, за-
данной параметрически
х — x(t), <
у = y(t),
t е [се; /3],
прямыми х = аих = Ьи осью Ох, то площадь ее находится по формуле
0
f y(t)-x'(t)dt
где а и /3 определяются из равенств х(а) = а и х(/3) = Ь.
Пример 41.1. Найти площадь фигуры, ограниченной осью Ох и графиком функции у = х2 — 2х при х G [0; 3].
Q Решение: Фигура имеет вид, изображенный на рисунке 177. Находим ее площадь S:
2 з
У (ж2 — 2т) dx + J (х2 — 2т) dx =
о 2
8 л 27 8 п л ~з + 4 + Т-з~9 + 4 =
3 3
Пример 41.2. Вычислить площадь фигуры, ограниченной эллипсом х = a cost, у = bsint.
Q Решение: Найдем сначала плошади S. Здесь х изменяется от 0 до а, следовательно, t изменяется от ” до 0 (см. рис. 178). Находим:
1 ° °
-5= J bsint (—asint)dt ——ab J
7г/2 7г/2
sin2 tdt =
281
1 k/v .
ab г л ч , G'b / । £
= у J (1 - cos 2t) dt = у (t|02
0
Таким образом, 1.S = Значит, S = каЬ.
1 .
- sin
2
2t|5) =
Io / 4
Полярные координаты
Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией г = г(р) и двумя лучами у? = а и у? = /3 (о < /3), где г и р — полярные координаты (см. рис. 179). Для решения задачи используем схему II — метод дифференциала.
1. Будем считать часть искомой площади S как функцию угла pi т. е. S = S(p), где а р /3 (если р = а, то S(a) = 0, еслиу? = /3, та ЭД = S). 1
2. Если текущий полярный угол р получит приращение Ду? = dp, то приращение площади А .5’ равно площади «элементарного криволинейного сектора» О АВ.
Дифференциал dS представляет собой главную часть приращения А .5’ при dp —> 0 и равен площади кругового сектора О АС (на рисунке она заштрихована) радиуса г с центральным углом dp. Поэтому dS = dp.
3. Интегрируя полученное равенство в пределах от р = а до р — (3, получим искомую площадь
Рис. 179
Пример 41.3. Найти площадь фигуры, ограниченной «трехлепестковой розой» г = acos3y? (см. рис. 180).
282
Q Решение: Найдем сначала площадь половины одного лепестка «розы», т. е. часть всей площади фигуры:
1 1 V6
-S = - у (acos3</>)2 dip =
1 2
2°
тг/б
! -(1+cos6</?)d</7 = о
I 1 . г: р/6
+ gSm6^|0
9
t. e. ~S = Следовательно, S =
О .Ztc tc
Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке 181, имеем:
а? тг
1?6
тга2
IT’
1 /
'idV~ % f r2 dlfi'
<3
Рис. 181
о
41.3. Вычисление длины дуги плоской кривой
Прямоугольные координаты
Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у = /(ж), где а х Ь.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю.
Покажем, что если функция у = /(ж) и ее производная у' = f'(x) непрерывны на отрезке [а; 6], то кривая АВ имеет длину, равную
ь
I = / а/1 + №))2 dx.
а
(41-3)
Применим схему I (метод сумм).
1. Точками хо = a, Xi,хп = b (жо < х± < ... < хп) разобьем отрезок [а; 6] на п частей (см. рис. 182). Пусть этим точкам соответствуют точки Мо = A, Mi,..., Мп = В на кривой АВ. Проведем хорды M0Mi, М^,..., Mn- iMn, длины которых обозначим соответственно через ДТ1; ДМ,..., &Ln. Получим ломаную MqMiMz ... Мп~\Мп, п
длина которой равна Ln = Д£1 + ДТ2 + • + ДТ« = 52
г=1
283
Рис. 182
2. Длину хорды (или звена ломаной) ДД можйо найти по теореме Пифагора из треугольника с катетами Дж$ и Дуг-
ьц = 7(ДтО2 + (Д?д)2,
где Дж,- — xi — Xi-i, Д?д = /(Tj) — /(Tj-x). По теореме Лагранжа oi конечном приращении функции Д?д = &.Xi, где с, G (xi-ь
Поэтому 1
= \/(Дтх)2 + (f(Ci) Дт,)2 = д/1 + №))2 Дть ‘ а длина всей ломаной М0М\ ... М„ равна 1
п п j
Ln = £ ДЬг = £ + №))2 • А®»- (41.4)|
i=l г=1 Я
3. Длина I кривой АВ, по определению, равна
n J
I = lim Ln = lim £ j
maxAIj->0 maxAIj->0z-' .]
2=1 1
Заметим, что при ДЬ,—>0 также и Дт,—>0 (Д Д = у/(Д а;г-)2 + (Д ?/Д2 и,1 следовательно, |ДаД <Д.Д). Функция \/1 + (/'(т))2 непрерывна на от-1 резке [cz; 6], так как, по условию, непрерывна функция Следова-1 тельно, существует предел интегральной суммы (41.4), когда max Дтг—>0:
п Ъ
1= lim У у/1 + (/'(ci))2A®i = [ + (/'(ж))2 dx.
niaxAtj—>0 ' J
{п—>оо) а
Ь
Таким образом, 1=1 \/1 + (/Ч^))2 dx, или в сокращенной записи I = ь _____________ а
= / х/г + W?dx. а
284
Если уравнение кривой АВ задано в параметрической форме
х = x(t), y = y(t),
а t [3,
где x(t) и y(t) — непрерывные функции с непрерывными производными и ж (о ) = а, х(/3) = Ь, то длина I кривой АВ находится по формуле
/з
1 = f V^'(t)y + (y'(t)ydt. а
(41-5)
Формула (41.5) может быть получена из формулы (41.3) подстановкой
ж = ж(1), dx = ж'(1) dt, /'(ж) =
у'Ю x'(ty
Пример 41-4- Найти длину окружности радиуса R.
1
Q Решение: Найдем часть ее длины от точки
(0;1?) до точки (4?;0) (см. рис. 183). Так как у = / \
= VR2 -х2, то 4——-------
1 г / X2 X тг /
-1= /1/1 + -Б5-----dx = R- arcsin — =R -
4 J V R2-x2 R Io 2
о
Значит, I = 2tvR. Если уравнение окружности запи- Рис- 183 сать в параметрическом виде ж = Rcost, у = Rsint (О t 2тг), то
2тг
1= J \/(—Rsint)2 + (Rcost)2 dt = Rt\^ = 2ttR. •
о
Вычисление длины дуги может быть основано на применении метода дифференциала. Покажем, как можно получить формулу (41.3), применив схему II (метод дифференциала).
1. Возьмем произвольное значение ж € [а; Ь] и рассмотрим переменный отрезок [а; ж]. На нем величина I становится функцией от ж, т. е. I = /(ж) (1(a) = 0 и 1(b) = I).
2. Находим дифференциал dl функции I = /(ж) при изменении ж на малую величину Дж = dx: dl = l'(x)dx. Найдем l'(x), заменяя бесконечно малую дугу MN хордой Д/, стягивающей эту дугу (см. рис. 184):
П/ X 1- Ы „ У(Дж)2 + (Ау)2
I (ж) = lim -— = lim —-----------------—
Дж->0 Дж Дж—>0
Ах
= lim
Дж-Ю
Стало быть, dl = у/1 -I- (у'У)2 dx.
285
b _______
3. Интегрируя dl в пределах от а до 6, получаем I = I yj 1 + у'х2 dx.
а
Равенство dl = ^/1 + у'х2 dx называется формулой дифференциала дуги в прямоугольных координатах.
Так как у'х — то
dl = y/(dxY + (d^)2.
Последняя формула представляет собой теорему Пифагора для беско^ нечно малого треугольника МСТ (см. рис. 185).
Рис. 184
Рис. 185
Полярные координаты
Пусть кривая АВ задана уравнением в поляр-
ных координатах г = г(уз), а у? < (3. Предположим, что и г'(у?)
непрерывны на отрезке [а; /3].
Если в равенствах х = г cos у?, у = г sin уз, связывающих полярные и декартовы координаты, параметром считать угол у?, то кривую АВ
I х = r(y?) cos у?, m
можно задать параметрически < ' Тогда
I у = r(y?) sin у?.
( = г'(у?) cos у? - г (уз) sin у?,
у[р = sin V5 + r(</?)cos ¥’•
Поэтому
= \/(г'(у?) cos у? — r(y?) sin у>)2 + (? ' (у?) sin у? + r(y?) cos у?)2 =
Д = V(r'MY + И^))2-
286
Применяя формулу (41.5), получаем
Пример £1.5. Найти длину кардиоиды г = а(1 + cosy?).
Q Решение: Кардиоида г = а(1 + cosy?) имеет вид, изображенный на рисунке 186. Она симметрична относительно полярной оси. Найдем половину длины кардиоиды:
1‘
= У \/ (а(1 + cos у?))2 + (а(— sin у?))2 dy? = а J у/2 + 2cosy?dy? = о о
у? у?
cos — dip — 4а - sin у
2-2cos2^
= а
о ' о
Таким образом, = 4а. Значит, 1 = 8а.
= 4а.
2 1о
Рис. 187
Рис. 186
41.4. Вычисление объема тела
Вычисление объема тела по известным площадям параллельных сечений
Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ox: S = S(x), а х Ь.
Применим схему II (метод дифференциала).
1. Через произвольную точку х & [а; Ь] проведем плоскость П, перпендикулярную оси Ох (см. рис. 187). Обозначим через S(x) площадь
287
сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; ж] величина v есть функция от х, т. е. v = v(x) ('с(а) — 0, v(b) = V).
2. Находим дифференциал dV функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и ж + Дж, который приближенно может быть принят за цилиндр с основанием 5(ж) и высотой dx. Поэтому дифференциал объема dV = .$’(ж) dx.
3. Находим искомую величину V путем интегрирования dA в пределах от а до Ь: -------------
ь
V = J S(x)dx.
а
(41.6)
|£| Полученная формула называется формулой объема тела п<, площади параллельных сечений.
Пример б. Найти объем эллипсоида + ^ = 1.
а о с
Q Решение: Рассекая эллипсоид плоскостью, параллельной плоскости
Oyz и на расстоянии х от рис. 188):
Объем тела вращения
нее (—а х а), получим эллипс (см.
у2!________г2 _ 1
(«/'-Иг
Площадь этого эллипса равна S(x) = = тгЬс^1 — S Поэтому, по формуле (41.6), имеем
И = тгЬс J (1 — dx = ^тгаЬс. •
Пусть вокруг оси Ох вращается криволинейная трапеция, огра-
ниченная непрерывной линией у = /(ж) > 0, отрезком а х < Ъ и
прямыми х = а и х = b (см. рис. 189). Полученная от вращения фигура
называется телом вращения. Сечение этого тела плоскостью, перпен-
дикулярной оси Ох, проведенной через произвольную точку х оси Ох (ж € [а; 6]), есть круг с радиусом у = /(ж). Следовательно, 5(ж) = тгу2.
Применяя формулу (41.6) объема тела по площади параллельных
сечений, получаем
ь
У у2 dx.
(41-7)
288
Если криволинейная трапеция ограничена графиком непрерывной функции х = <р(у) 0 и прямыми х = 0, у — с, у = d (с < d), то
< >бъем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.7), равен
Рис. 189
Рис. 190
(41.8)
Пример Найти объем тела, образованного вращением фи-2 г—
гуры, ограниченной линиями у — х = 0, у = 2у2 вокруг оси Оу (см. рис. 190).
Q Решение: По формуле (41.8) находим:
2у/2
Vy = 7f J 2ydy = 7vy2\^ = 8Tr. •
О
41.5. Вычисление площади поверхности вращения
Пусть кривая АВ является графиком функции у = /(ж) 0, где
х € [a; ft], а функция у = /(а;) и ее производная у' = f'(x) непрерывны на этом отрезке.
Найдем площадь S поверхности, образованной вращением кривой АВ вокруг оси Ох.
Применим схему II (метод дифференциала).
1. Через произвольную точку х & [a; ft] проведем плоскость П, перпендикулярную оси Ох. Плоскость П пересекает поверхность вращения по окружности с радиусом у = /(ж) (см. рис. 191). Величина S поверхности части фигуры вращения, лежащей левее плоскости, является функцией от х, т. е. s = s(x) (s(a) = 0 и s(ft) = S}.
10 Конспект лекций по высшей математике. Полный курс
289
2. Дадим аргументу х приращение Дж = dx. Через точку х + dx £ [а; 6] также проведем плоскость, перпендикулярную оси Ох. Функци s = з(ж) получит приращение Де, изображенного на рисунке в вид:
«пояска».
Найдем дифференциал площади ds, з. меняя образованную между сечениями ф1 ГУРУ усеченным конусом, образующая кот рого равна dl, а радиусы оснований равны и у + dy. Площадь его боковой поверхност равна ds = 7r(y + y + dy) -dl = 2ivydl + 'ndyc Отбрасывая произведение dydl как беек нечно малую высшего порядка, чем ds, п лучаем ds = 2-irydl, или, так как dl = л/1 + (2/ж)2^ж> то = ^Уу/^ + (Ух)2 dx.
3. Интегрируя полученное равенство пределах от ж = а до ж = Ь, получаем
ь
= 2тг у у \/1 + (у02о!ж. (41.9
Если кривая АВ задана параметрическими уравнениями ж = x(t), у = = ?/(t), ti t =$ ^2, то формула (41.9) для площади поверхности вращ<
ния принимает вид
42
Sx = 2тг J y(t)- y/(x'(t))2 + (y'(t))2dt.
Пример 41-8. Найти площадь поверхности шара радиуса R.
Q Решение: Можно считать, что поверхность шара образована враще нием полуокружности у = \/R2 — ж2, —R ж sj R, вокруг оси Ох. П формуле (41.9) находим
я
S = 2тг у y/R2 - х'2
-н
Я ________________ /
= 2тг J \/н2 — ж2 + ж2 dx = 2tvR ж|^л = 4тг/?2.
-я
Пример 41-9-
Дана циклоида ж = a(t — sint), у = а(1 — cost),
О < t 2тг.
290
Найти площадь поверхности, образованной вращением ее вокруг пси Ох.
Решение: При вращении половины дуги циклоиды вокруг оси Ох площадь поверхности вращения равна
^Sx = 2тг j а(1 — cost) ^/(а(1 — cost))2 + (asint)2 dt = о
= 2^ о
= 4тга2 j о
sin2 ~ \/l - 2 cos t + cos21 + sin2 t dt =
9 t
2 - 2 sin2 - dt
С . 2 i . i м j sin ~ • sin ~ dt =
0
= — 8тга2 • 2 у ( о
1 — cos2
cos3 | 3
= —16тга2 (б — 1 ~ 0 + -) = —16тга2 =
г. e. As® = Д^тгн2. Следовательно, Sx = ^тга2.
Z о о
32тга2
41.6. Механические приложения определенного интеграла
Работа переменной силы
Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F = F(®), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (а < Ь), находится по формуле
ь
А= jF(x)dx (41.10)
(см. п. 36). “
Пример 41.10. Какую работу нужно затратить, чтобы растянуть пружину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?
Q Решение: По закону Гука упругая сила, растягивающая пружину, пропорциональна этому растяжению х, x.e.F = кх, где к — коэффициент пропорциональности. Согласно условию задачи, сила F = 100 Н растягивает пружину на® — 0,01 м; следовательно, 100 = fc-0,01, откуда к = 10000; следовательно, F = 10000®.
291
Искомая работа на основании формулы (41.10) равна 0,05
А = J lOOOOxdx = 5000ж2|°’°5 = 12,5 (Дж), о
Пример 41.11. Найти работу, которую необходимо затратить^ чтобы выкачать через край жидкость из вертикального цилиндрического резервуара высоты Н м и радиусом основания R м.
Q Решение: Работа, затрачиваемая на поднятие тела весом р на выа ту h, равна р h. Но различные слои жидкости в резервуаре находятс на различных глубинах и высота поднятия (до края резервуара) раз
Для решения поставленной задач применим схему II (метод дифференци< ла). Введем систему координат так, ка указано на рисунке 192.
1. Работа, затрачиваемая на выкач> вание из резервуара слоя жидкости то.’ щиной х (0 х Н), есть функция от а т. е. А = Л(ж), где 0 х Н (Л(0) = ( Л(я) = А)).
2. Находим главную часть приращ* ния ДЛ при изменении х на величин Дж = dx, т. е. находим дифференциал d функции Л(ж). j
личных слоев не одинакова.
Ввиду малости dx считаем, что «элементарный» слой жидш епт находится на одной глубине х (от края резервуара) (см. рис. 192), Тогда dA = dp-x, где dp — вес этого слоя; он равен g-^dv, где g — уск> рение свободного падения, 7 - плотность жидкости, dv — объем «эл ментарного» слоя жидкости (на рисунке он выделен), т. е. dp = gyd Объем указанного слоя жидкости, очевидно, равен тгЯ2 dx, где dx — в! сота цилиндра (слоя), тгЯ2 — площадь его основания, т. е. dv = ттВ? d
Таким образом, dp = <77 • тгЯ2 dx и dA — gynR? dx х.
3) Интегрируя полученное равенство в пределах от х = 0 до х — 1 находим н
Ао = J g'fivl&xdx = -gyrcR^H2 (Дж).
о
Путь, пройденный телом
Пусть материальная точка перемещается по прямой с переменю скоростью v = v(t). Найдем путь S, пройденный ею за промежуто времени от t, до В-
292
Q Решение: Из физического смысла производной известно, что при движении точки в одном направлении «скорость прямолинейного движения равна производной от пути по времени», т. е. v(t) — Отсюда следует, что dS = v(t) dt. Интегрируя полученное равенство в пределах «2 '
ют 1Л до /2, получаем S = J v(/) dt. •
tl
Отметим, что эту же формулу можно получить, пользуясь схемой I или II применения определенного интеграла.
। Пример £1.12. Найти путь, пройденный телом за 4 секунды от .начала движения, если скорость тела v(t) — 10/ + 2 (м/с).
Q Решение: Если v(t) = 10/ + 2 (м/с), то путь, пройденный телом от начала движения (/ = 0) до конца 4-й секунды, равен
4
S = У (10/+ 2) (//= 5/2|* + 2/|4 = 80 + 8 = 88 (м). •
о
Давление жидкости на вертикальную пластинку
По закону Паскаля давление жидкости на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием пластинку, а высотой — глубину ее погружения от свободной поверхности жидкости, т. е. Р = д • 7 - S • h, где д — ускорение свободного падения, 7 — плотность жидкости, S — площадь пластинки, h — глубина ее погружения.
По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.
Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = Ь, уг = fi(x) и у-2 = /2(ж); система координат выбрана так, как указано на рисунке 193. Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала).
1. Пусть часть искомой величины Р есть функция от х: р = р(ж), т. е. р = р(х) — давление на часть пластины, соответствующее отрезку [а; ж] значений переменной х, где х е [а; 6] (р(а) = 0, р(Ь) = Р).
2. Дадим аргументу х приращение Дж = dx. Функция р(х) получит приращение Др (на рисунке — полоска-слой толщины dx). Найдем дифференциал dp этой функции. Ввиду малости dx будем приближенно считать полоску прямоугольником, все точки которого находятся на одной глубине х, т. е. пластинка эта — горизонтальная.
Тогда по закону Паскаля dp = g • у (у2 — У\) • dx •
' * ' h
293
3. Интегрируя получённое равенство в пределах от х = а до х = b получим
ь ъ
Р = 9 ’7 f (У2-yi)xdx или Р = ду - fa^xY)-xdx. а а
Рис. 193 Рис. 194
Пример 41-13. Определить величину давления воды на полу круг, вертикально погруженный в жидкость, если его радиус R, а цен' О находится на свободной поверхности воды (см. рис. 194).
Q Решение: Воспользуемся полученной формулой для нахождения давления жидкости на вертикальную пластинку. В данном случае пластинка ограничена линиями yi = —y/R? — ж2, у2 = y/R2 — ж2, ж = О ж = R. Поэтому
я
Р = 97 J (VR? - х2 - (-y/R2 — x2/)xdx = о
R 1 R
= 2ду у \/й2-ж2ж</ж = 297- (--) J (В2 - ж2)1/2 d(B2 - ж2) = о о
2J(R2 - ж2)3 |Я 2 . 2 3
= -57--------о-----1 = - х57(0 - R ) = Х57-Й • •
о 10 О о
Вычисление статических моментов и координат центра тяжести плоской кривой
Пусть на плоскости Оху задана система материальных точек А41(ж1; г/i), М2(х2-,у2),..., Мп{хп\уп) соответственно с массами mi,m2, -. - ,тп.
294
Статическим моментом Sx системы материальных точек относительно оси Ох называется сумма произведений масс этих точек на п
их ординаты (т. е. на расстояния этих точек от оси Ox): Sx = ^2 т1"У1-г=1
Аналогично определяется статический момент Sy этой системы п
относительно оси Оу: Sy — ' Xi.
i=l
Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.
Пусть у = f(x) (а х Ь) — это уравнение материальной кривой А13. Будем считать ее однородной с постоянной линейной плотностью j (7 = const).
Для произвольного х € [а; 6] на кривой АВ найдется точка с координатами (ж; у). Выделим на кривой элементарный участок длины dl, содержащий точку (х;у). Тогда масса этого-участка равна ydl. Примем этот участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у. Тогда дифференциал статического момента dSx («элементарный момент») будет равен 7 dl - у, т. е. dSx = ydl • у (см. рис. 195).
Отсюда Следует, что статический момент Sx кривой АВ относительно оси Ох равен
b
У f У- a/1 + (y'xYdx.
Аналогично находим Sy: f °'
Sy J x- 0 + (y'x)2dx.
Статические моменты Sx°m Sy кривой позволяют легко установить положение ее центра тяжести (центра масс).
Центром тяжести материальной плоской кривой у = /(ж), ж g £ [а; 5] называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу т заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой у = /(ж) относительно той же оси. Обозначим через С(хс; ус) центр тяжести кривой АВ.
Из определения центра тяжести следуют равенства т - жс = Sy и
S S т ус = Sx или yl хс = Sy и yl • ус = Sx. Отсюда жс = —ус = —или
295
b
j xdl
a_____
l
b t_____________
f x-y/l + (y'x)2dx
a___________________
b _________
J V1 + (y'^2dx
a
b
fydl
„ я
Уе= —
b
/у л/1 + (Ух)2 dx
a____________________
b
f \/l + (Ух)2 dx
a
Пример 41-14- Найти центр тяжести однородной дуги окружнс сти х2 + у2 — R2, расположенной в первой координатной четверти (см рис. 196). ]
Рис. 196 Рис. 197
Q Решение: Очевидно, длина указанной дуги окружности равна ~ т. е. Z = ”. Найдем статический момент ее относительно оси Ох. Та как уравнение дуги есть у = л/R2 — ж2 и у'х = -—=, то (7 = const
V R2 - ж2
R / 2
Sx=y f VR2 - ж2 • Jl + ( Х dx =
J V V V Hr ~ X* '
0 V
R p R
= 7 I у/R2 -X2 , 2 _ 2 dx = yR J d,x~ 7^|o = 7-R2-о * x 0
Стало быть, Sx ^R2 2R
Ус Г — тгй „ • 7« 7 • %
Так как данная дуга симметрична относительно биссектрисы перво го координатного угла, то хс = ус = Итак, центр тяжести имея координаты (2/?; У
Вычисление статических моментов и координат центра тяжести плоской фигуры
Пусть дана материальная плоская фигура (пластинка), ограничен ная кривой у — /(ж) 0 и прямыми у = 0, х = а, х = b (см. рис. 197)..
296
Будем считать, что поверхностная плотность пластинки постоянна ь
(7 = const). Тогда масса всей пластинки равна y-S, т. е. m = 7 / f(x) dx.
Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоуголь
ником.
Тогда масса его равна 7 • у dx. Центр тяжести С прямоугольника лежит на пересечении диагоналей прямоугольника. Эта точка С отстоит от оси Ох на ^у, а от оси Оу на х (приближенно; точнее на расстоянии х + 1Дт). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения
dSx = 7 ydx -^у = ^7 ’ У2, dx и dSy = 7 • ydx • х = ^xydx. ь ь
Следовательно, Sx = ^7 J у2 dx, Sy = у J ху dx.
а а
По аналогии с плоской кривой получаем, обозначив координаты центра тяжести плоской фигуры (пластинки) через С(хс:ус), что hi хс = Sy, тп • ус — Sx. Отсюда
Пример Найдем координаты центра тяжести полукруга
т2 + у2 R2, у 0 (7 = const) (см. рис. 198).
Q Решение: Очевидно (ввиду симметрии фигуры относительно оси Оу), что хс = 0. е>2
Площадь полукруга равна . Находим Sxt
1 я
5ж = ~7 / (VR2~x2)2dx =
-R
1 ,„2 ж3дя 1 /„з т->з R3 R3 \ 2 3
= - у)|_я = - -у - Т) = 7
297
Стало быть,
Sx _ 2yR3 _ 4 R yS ~ 37^ ~ 3 тг '
Итак, центр тяжести имеет координаты
§42 . ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
ь
Пусть требуется найти определенный интеграл J /(ж) dx от непр а
рывной функции /(ж). Если можно найти первообразную F(x) функщ /(ж), то интеграл вычисляется по формуле Ньютона-Лейбница:
ь
J f (ж) dx = F(b) - F(a).
а
Но отыскание первообразной функции иногда весьма сложно; к
ме того, как известно, не для всякой непрерывной функции ее перв!
образная выражается через элементарные функции.
этих и други
случаях (например, функция у = f(x) задана графически или табли’ но) прибегают к приближенным формулам, с помощью которых опр< деленный интеграл находится с любой степенью точности.
В
Рассмотрим три наиболее употребительные формулы приближен ного вычисления определенного интеграла — формулу прямоуголын ков, формулу трапеций, формулу парабол (Симпсона), основанные и геометрическом смысле определенного интеграла.
42.1. Формула прямоугольников
Пусть на отрезке [а; Ь], а < Ь, задана непрерывная функция f(&} ь
Требуется вычислить интеграл J f(x) dx, численно равный площад а
соответствующей криволинейной трапеции. Разобьем основание это трапеции, т. е. отрезок [а;Ь], на п равных частей (отрезков) длин h = -^-d ~ Xi _ i (шаг разбиения) с помощью точек Хо = ( Ж], а?2,..., хп = Ь. Можно записать, что Xi = Xq + h • i, где i = 1,2,...,' (см. рис. 199).
В середине = Хг~1^ Хг каждого такого отрезка построим ордг нату у.; = f(ct) графика функции у = f(x). Приняв эту ординату з высоту, построим прямоугольник с площадью h-yi.
298
Рис. 199
Тогда сумма площадей всех п прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла
f f(x)dx » Zi(^i +у2 + ...+уп) = 12+Жг)' (42Л)
a i=l
Формула (42.1) называется формулой средних прямоугольников.
Абсолютная погрешность приближенного равенства (42.1) оценивается с помощью следующей формулы:
IKK
(6 - а)3 М2 24п2
где М2 — наибольшее значение |/"(ж)| на отрезке [а; 6],
|К| =
Отметим, что для линейной функции (/(ж) = кх + 6) формула (42.1) дает точный ответ, поскольку в этом случае /"(ж) = 0.
42.2. Формула трапеций
Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.
Разобьем отрезок [а; 6] на п равных частей длины h = и. Абсциссы точек деления а = ж0, х1,х2>. . ,Ъ = хп (рис. 200). Пусть ус, У1,... ,уп — соответствующие им ординаты графика функции. Тогда
299
Рис. 200
расчетные формулы для этих значений примут вид х^ = а + h • г, yi =4 = f(Xi),i = 0,1,2,...,п; h= |
Заменим кривую у — f(x) ломаной линией, звенья которой соеди-: няют концы ординат и ?/г+1 (г = 0,1,2,... ,п). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями yt, yi+i и высотой h = ° ~ Q:
или
ь
/ Г/ ~Уо + У1 С , 2/1 + У2 , , , Уп-1 + Уп
I f(x) dx к ——-------h + —---------h + • + ----------h
a
b ,
J fix') dx » —2-w + Щ + ?/2 + • - + 2/n-i)- (42.2)
a
Формула (42.2) называется формулой трапеций.
Абсолютная погрешность Rn приближения, полученного по формуле трапеций, оценивается с помощью формулы ^2’
где Л/г = max |/"(х)|. Снова для линейной функции у = кх + b фор-а^х^.Ь
мула (42.2) — точная.
42.3. Формула парабол (Симпсона)
Если заменить график функции у = /(ж) на каждом отрезка [xj_i;a;j] разбиения не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную форму-fc
л у приближенного вычисления интеграла J f(x) dx. а
300
Предварительно найдем площадь S криволинейной трапеции, ограненной сверху графиком параболы у = ах2 +Ьх+с, сбоку — прямыми ;< = —/г, х = h и снизу — отрезком [—7г; /г].
Пусть парабола проходит через три точки 7И1(-7г;?/о)> М2(0; «ц), M3(h;y2), где у0 = а№ — bh + c— ордината параболы в точке .г = — 7i; j/i = с — ордината параболы в точке — 0; У2 = о/г2 + bh + с — ордината парабо-1ы в точке х = h (см. рис. 201). Площадь S авна
h
~h
+ CX
h 2 ,
= o°^3 + 2c/i. (42.3)
—h <3
Выразим эту площадь через h, уо, у\, у2- Из равенств для ординат <ji находим, что с = ylt а = ^^-(«/о ~ + 2/г)- Подставляя эти значения с
и а в равенство (42.3), получаем
2 1
S = д/г3 • 2^2 (Уо - 2Ш + У2) + 2Л • У1 =
= х(?/о -2yi + у2) + 2hy} = ~(у0 +4^ +у2). (42.4) о о
b
Получим теперь формулу парабол для вычисления интеграла^ (ж) dx. а
Для этого отрезок [а; 6] разобьем на 2п равных частей (отрезков) длиной h = точками Xi = xq + ih (г = 0,1,2,..., 2п). В точках деления а = ж0, хг, х2,..., х2п-2, %2n-i, х2п = b вычисляем значения подынтегральной функции /(ж): у0, у2,..., у2п-2, y2n-i, У2п, где
= /(ж*) (см. рис. 202).
Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями, равными h, одной элементарной параболической трапецией с основанием, равным 2h. На отрезке [ал; х2] парабола проходит через три точки (жо;?/о), (^i;?/i), (х2;у2). Используя формулу (42.4), находим
Х2 h
Si= [ f(x) dx = -(г/о + 4yi + у2). J о
Хо
301
Рис. 202
Аналогично находим xr h
Sz~ f(x)dx = -(у2 +4«/3 + у4), J о
®2
Я?2тг
Sn = / f(x)dx = -(«/271-2 +4j/2n-l + У2п)-
J о
Ж2п-2
Сложив полученные равенства, имеем г h
J f(x) dx « -(«/о + 4yt + 2у2 + • • • + 2у2п-2 + 4у2п-1 + У2п) а
ИЛИ
Ь ь_
J /(») dx Ki ((«/о + У2п) + 4(«/! + у3 + . . . + ?/271-1)+ а
+ 2(«/2 + «/4 + • • + «/2тг-г)^ • (42.
Формула (42.5) называется формулой парабол (или Симпсона) Абсолютная погрешность вычисления по формуле (42.5) оцепив;
ется соотношением
|Лп|« 180Л2.,)«'"*’ ™e"‘ = a““l/'V(a:)l' I
ъ ‘
Отметим, что формула (42.5) дает точное значение интеграла J f(x)d а
во всех случаях, когда / (ж) — многочлен, степень которого меньше ил равна трем (тогда fIV = 0).
302
2
Пример 4%-1- Вычислить / х3 dx, раз-
о
бив отрезок интегрирования [0; 2] на 4 части.
Q Решение: Имеем: f(x) = х3,
Ъ — а 2 1
а = хо = 0; о = «4 = 2, А =------= - = -,
п 4 2
Хо = 0, Уо = 0; «1 = i У! = |; х2 = 1, у2 = 1; Z о
3 27 9 Я
Хз = л, Уз = -л-; ®4 =2, ?/4 = 8; Z о
(см. рис. 203)
а) по формуле прямоугольников:
1 1 3 27
С1 = 4’ У1 = 64; С2“4’ У2=64;
5 125 7 343
Сз = 4’ y3 = -64; С4 = 4’
Рис. 203
2
У х3 dx rs о
1/J_ X 125 343\ 2\64 + 64 + 64 + 64 )
= 3,875, т. е.
и 3,875;
б) по формуле трапеции:
2 2
[x3dx as | + 1 + = 4,25, т. е. [х3 dx rs 4,25;
J 2 \ 2 о 8/ J
о о
в) по формуле парабол:
Точное значение интеграла j х3 dx = 1 =4.
о
Абсолютные погрешности соответствующих формул таковы: а) 0,125; б) 0,25; в) 0. •
Глава IX. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Лекции 34-36
Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.
Будем рассматривать функции двух переменных, так как все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Эти факты обобщаются на случай большего числа переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию.
§43 . ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
43.1. Основные понятия
g Пусть задано множество D упорядоченных пар чисел (ж; у). Со-ответствие /, кцторое каждой паре чисел (ж; у) е D сопоставляв# одно и только одно число z € IK, называется функцией двух пере! менных, определенной на множестве D со значениями в R, и записы! вается в виде z = f(x~, у) или / : О -> К. При этом ж и у называются независимыми переменными (аргументами), az — зависимой переменной (функцией).
Множество D = D(J) называется областью определения функции.. Множество значений, принимаемых z в области определения, называ-, ется областью изменения этой функции, обозначается E(J) или Е.
Примером функции двух переменных может служить площадь 5? прямоугольника со сторонами, длины которых равны ж и у. S = ху] Областью определения этой функции является множество {(ж; у) | ж > 0, у > 0}. ’
р>| Функцию z = f(x;y), где (ж; у) € D можно понимать (рассматривать) как функцию точки М(х;у) координатной плоскости Оху. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается D. Примером замкнутой области является круг с окружностью.
304
Значение функции z = f(x;y) в точке Л/о(жо;«/о) обозначают zq — = /(жо;Уо) или z0 = f(Mo) и называют частным значением функции.
Функция двух независимых переменных допускает геометрическое истолкование. Каждой точке Л/о(^о;2/о) области D в системе координат Oxyz соответствует точка М(х0',уо; z0), где z$ = f(x0; уо) — аппликата точки М. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию z — f(x-y).
Например, функция z = yl — х2 — у2 имеет областью определения круг х2 + у2 1 и изображается верхней полусферой с центром в точке 0(0; 0;0) и радиусом R = 1 (см. рис. 204).
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило аналитическим способом: когда функция задается с помощью формулы.
Рис. 205
43.2. Предел функции
Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек М(х-,у) плоскости, координаты которых удовлетворяют неравенству \/(х — хо)2 + (у — ?Л))2 < Ф называется 6-окрестностью точки Мо(хо',уо)- Другими словами, (’(-окрестность точки Мо — это все внутренние точки круга с центром Мо и радиусом 6 (см. рис. 205).
|£| Пусть функция z = f(x,y) определена в некоторой окрестности точки Мо(хо',уо), кроме, быть может, самой этой точки. Число А называется пределом функции z — f(x; у) при х -> хо и у -> уо (или, что то же самое, при М(х;у) —> Мо(хо',уо)), если для любого е > 0 существует S > 0 такое, что для всех х хо и у уо и удовлетворяю-
305
щих неравенству у/(я: — жо)2 + (у — уо)'2 < 6 выполняется неравенство \f(x;y) — А| < е. Записывают:
А = xl^L или А = JinL ^М>>-
^~^хо М-+Мп
Из определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к 7И0 (число таких направлений бесконечно; для функции одной переменной х -> х0 по двум направлениям: справа и слева!)
Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число е > 0, найдется (5-окрестность точки Мо(хо;уо), что во всех ее точках М(х;у), отличных от Мо, аппликаты соответствующих точек поверхности z = f(x;y) отличаются^ от числа А по модулю меньше, чем на е.
х2 - и2
Пример 43.1. Найти предел lim —5—
ж—>0 X + 11“
У~+0 у
Q Решение: Будем приближаться к 0(0; 0) по прямой у = кх, где к — 1 некоторое число. Тогда j
х2 - у2 х2 - к2х2 1 - к2 1 - к2 j
пт —j = Inn = hm------ч =------ч. 1
х + х + у ж"+0 1 + fc2 1 + к2 х2 -у2 :
Функция z — "2 ~ 2 в точке 0(0; 0) предела не имеет, т. к. при разных 1 значениях к предел функции не одинаков (функция имеет различные ? предельные значения). • '
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной (см. п. 17.3). Это • означает, что справедливы утверждения: если функции f(M) и д(М) ! определены на множестве D и имеют в точке Мо этого множества пре- i целы А и В соответственно, то и функции f(M) ± д(М), f(M) д(М), : имеют в точке 7И0 пределы, которые соответственно j
равны А ± В, А В, (В ^4 0).
43.3. Непрерывность функции двух переменных
g Функция z = /(ж; у) (или У(М)) называется непрерывной в точке Мо(хо;уо), если она: 1
а) определена в этой точке и некоторой ее окрестности, б) имеет предел lim f(M), М-+Мо .
в) этот предел равен значению функции z в точке Л/о, т. е.
lim f (7И) = /(Мо) или lim /(ж; у) = /(ж0; у0).
М-*М0
V-tVo
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z = f (ж; у) могут образовывать целые линии разрыва. Так, О
функция z = —имеет линию разрыва у — х.
Можно дать другое, равносильное приведенному выше, определение непрерывности функции z = f (ж; у) в точке. Обозначим Аж = х—хо, /Ху = у — у0, /Xz = f(x,y) — /(жо;г/о)- Величины Дж и /Ху называются приращениями аргументов х и у, а Аг — полным приращением функции f(x;y) в точке Мо(хо',Уо)-
g Функция z = f(x-y) называется непрерывной в точке Мо(жо;?/о) €
€ D, если выполняется равенство lim Az = 0, т. е. полное прира-
Aji—>0
щение функции в этой точке стремится к нулю, когда приращения ее аргументов х и у стремятся к нулю.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям — подобные теоремы имели место для функций одной переменной (см. п. 19.4).
43.4. Свойства функций, непрерывных в ограниченной замкнутой области
Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной —см. п. 19.5). Предварительно уточним понятие области.
g Областью называется множество точек плоскости, обладающих свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.
|^| Точка No называется граничной точкой области D, если она не принадлежит В, но в любой окрестности ее лежат точки этой области (см. рис. 206). Совокупность граничных точек области D называет-
ся границей D. Область D с присоединенной к ней границей называется замкнутой областью, обозначается D . Область называется огра-
Рис. 206
ниченной, если все ее точки принадлежат некоторому кругу радиуса R. В противном случае область называется неограниченной. Примером неограниченной области может служить множество точек перво
го координатного угла, а примером ограниченной — Л-окрестность точки Mo(xq-, уо).
Теорема 43.1. Если функция z = f(N) непрерывна в ограниченной замкнутой области, то она в этой области: а) ограничена, т. е. существует такое число R > 0, что для всех точек N в этой области выполняется неравенство |/(N)| < R; б) имеет точки, в которых принимает наименьшее т и наибольшее М значения; в) принимает хотя бы в одной точке области любое численное значение, заключенное между т и М.
Теорема дается без доказательства.
§44 . ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
44.1. Частные производные первого порядка и их геометрическое истолкование
Пусть задана функция z = f(x;y). Так как а: и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Да;, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается Даг. Итак,
= f(x + Да;; у) - f (аг; у).
Аналогично получаем частное приращение z по у:
Д^х = f(x;y + Ду) - /(ж; у).
Полное приращение Дз функции z определяется равенством
/\z = f (х + Да;; у + Ду) - f(x; у).
Если существует предел
Джг f(x + Да:; у) — / (а;; у)
hm -f- = hm —--------А ,
Да:-И) Дх Да:—И) Дх
ЗЛЯ
то он называется частной производной функции z — f(x-,y) в точке М (х; у) по переменной х и обозначается одним из символов:
г' — Г
x,9x,Jx’dx’
Частные производные по х в точке Мо(хо',уо) обычно обозначают символами fx\
• Mq
Аналогично определяется и обозначается частная производная от
z — f(x-,y) по переменной у:
/ 1* !• z' -- lim ~~ = lim
& Ag/—>0 l\y Аг/—>0
/(ж; у + ^у)- f(x; у) Ду
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции /(ж; у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно ж или у считается постоянной величиной).
Пример 44-1 • Найти частные производные функции z = 2у + ех2~у + 1.
Q Решение:
г' = (2?/ + ех"~у + 1)' = (2у)'х + (е^)' + (1)' =
= 0 + е®2-®' • (ж2 - у)'х + 0 = ех2~у (2ж - 0) = 2ж • е3’2'8';
4 = 2 + ^-(-I).
Геометрический смысл частных производных функции двух переменных
Графиком функции z=f(x; у) является некоторая поверхность (см. п. 12.1). График функции = /(ж;?/о) есть линия пересечения этой поверхности с плоскостью у = уо- Исходя из геометрического смысла производной для функции одной переменной (см. п. 20.2), заключаем, что K(®o;?/o) = tga, где а — угол между осью Ох и касательной, проведенной к кривой г = /(ж;?/о) в точке Мо(жо;«/о;/(жо;уо)) (см. рис. 207).
Аналогично, /^(жо;?/о) = tg/?.
Рис. 207
309
44.2. Частные производные высших порядков
3f(x'v} с) f (х‘'ll}
Частные производные — ' и —называют настигши про-
изводными первого порядка. Их можно рассматривать как функции от (ж; у) G D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
д / dzy \ д2г ... ,
дх ^дх^ ) = = zxx = fxA^yY
9 ( 'dz\ d2z ,, ...
дх \ <ду) дудх ~ Zxy ~
9 (
ду \ ,дх ) дхду Zyx
д (дг> \ d2z ,, ... ,
ду \дУ; }^d^=Zyy =
Аналогично определяются частные производные 3-го, 4-го и т. д. поряд-1 ков Так г'" = -@- (1 д ( д3 z \ _ Э4г у _
’ хху Qy ygx2р gx удхдудх) дхдудх2 хух)х
= Zxyx^ и т- А-
|ф| Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной
производной. Таковыми являются, например, z"
д3 z „т д^ду2’ хух'
Пример Найти частные производные второго порядка
функции z — х4 — 2х2у3 + у5 + 1.
Q Решение: Так как z'x = 4а:3 - 4ггу3 и z'y — —6х2у2 + 5у4, то z"y = (4ж3 - 4жу3)^ = -12ж?Д zyx = (-бх2у2 + 5у4)^. = — \2ху2.
Оказалось, что z'' = z" •
Л,У У^
Этот результат не случаен. Имеет' место теорема, которую приведем без доказательства.
Теорема 44.1 (Шварц). Если частные производные высшего поряд-
ка непрерывны, то смешанные производные одного порядка, отлича-
ющиеся лишь порядком дифференцирования, равны между собой.
В частности, для z = f(x;y) имеем:
d2z _ d2z дх ду ду дх
310
44.3. Дифференцируемость и полный дифференциал функции
Пусть функция z f(x;y) определена в некоторой окрестности точки М(х;у). Составим полное приращение функции в точке М:
Az = /(а; + Да:; у + Ду) - f (а?; у).
g Функция z = f(x-,y) называется дифференцируемой в точке М(х',у), если ее полное приращение в этой точке можно представить в виде
Дг = А Ах + В Ау + а Ах + (3 Ау, (44.1)
где а = а(Ах, Ау) —> 0 и /3 — /3(Ах,Ау) —> 0 при Ах —> 0, Ау —> 0. Сумма первых двух слагаемых в равенстве (44.1) представляет собой главную часть приращения функции.
Главная часть приращение функции z = f(x',y), линейная относительно Да: и Ау, называется полным дифференциалом этой функции и обозначается символом dz:
dz = А • Да? + В Ау. (44.2)
Выражения Л - Да: и В -Ау называют частными дифференциалами. Для независимых переменных х и у полагают Да? = dx и Ду = dy. Поэтому равенство (44.2) можно переписать в виде
dz = А • dx + В • dy.
(44-3)
Теорема 44.2 (необходимое условие дифференцируемости функции). Если функция z = f(x-,y) дифференцируема в точке М(х;у), то она непрерывна в этой точке, имеет в ней частные производные и причем & — А, — В. дх ду дх ду
□ Так как функция дифференцируема в точке М, то имеет место равенство (44.1). Отсюда вытекает, что lim Az — 0. Это означает,
Дг/—>0
что функция непрерывна в точке М. Положив Ау = 0, Да? 0 п равенстве (44.1), получим: Axz = А Да? + а Ах. Отсюда находим
= А+а. Переходя к пределу при Ах -> 0, получим ^lim^ — А, т. е. = А. Таким образом, в точке М существует частная производная /'(а:; у) = А. Аналогично доказывается, что в точке М существует частная производная /^(а:; у) — = В. И
311
Равенство (44.1) можно записать в виде
Az = Дж + —Ду + 7, (44.4)
Ох оу .
где 7 = а • Дж + /3 Ду -> 0 при Дж -> 0, Ду -> 0.
Отметим, что обратное утверждение не верно, т. е. из непрерывности функции или существования частных производных не следует дифференцируемость функции. Так, непрерывная функция z = у/х2 +У2 не дифференцируема в точке (0; 0).
Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула (44.3) принимает вид:
, dz dz
dz = —dx+ — dy ox oy
(44.5)
или
dz = dxz + dyz,
где dxz = §^dx, dyz = z = /(ж;у).
dy dy y
— частные дифференциалы функции
Теорема 44.3 (достаточное условие дифференцируемости функции). Если функция z — f(x-,y) имеет непрерывные частные производные z'rj. и z'y в точке М(ж;у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой (44.5).
Примем теорему без доказательства.
ЦЦ Отметим, что для функции у = f(x) одной переменной существование производной /'(ж) в точке является необходимым и достаточным условием ее дифференцируемости в этой точке.
Чтобы функция z — f(x-,y) была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она имела в точке непрерывные частные производные.
Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциалов функции двух (и большего числа) переменных.
44.4. Применение полного дифференциала к приближенным вычислениям
Из определения дифференциала функции z = fix; у) следует, что при достаточно малых | Дх| и | Ду| имеет место приближенное равенство
Дг « dz. (44.6)
312
Так как полное приращение Дг = /(ж + Дж; у + Ду) — f(x;у), равенство (44.6) можно переписать в следующем виде:
f{x + Дж;у + Ду) w /(ж;у) + f'x(x;у) Ах + fy(x;у)Ду. (44.7)
Формулой (44.7) пользуются в приближенных расчетах.
Пример 44-3- Вычислить приближенно 1,О23,01.
Q Решение: Рассмотрим функцию г =ху. Тогда 1,023,01 = (х + Ах)у+Лу, где ж=1, Дж = 0,02, у = 3, Ду = 0,01. Воспользуемся формулой (44.7), предварительно найдя z'x и z'y: zx = (xy')'x = y-xy~1, zy = (xy)y = xy Лпх. Следовательно, l,023’01wl3+3-13-1-0,02 + l3-In 1-0,01, t. e. l,O23’01» RS 1,06.
Для сравнения: используя микрокалькулятор, находим:
1,О23’01 и 1,061418168. •
Отметим, что с помощью полного дифференциала можно найти: границы абсолютной и относительной погрешностей в приближенных вычислениях; приближенное значение полного приращения функции и т. д.
44.5. Дифференциалы высших порядков
Введем понятие дифференциала высшего порядка. Полный дифференциал функции (формула (44.5)) называют также дифференциалом первого порядка.
Пусть функция г = f(x;y) имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле Дг = d(dz). Найдем его:
d2z = d ( —dx + тг-dy
\ох dy
(dz dz , \, (dz dz \' ,
= I =- dx 4- — dy -dx+ \-^-dx + —dy dy =
ydx dy ) ydx dy J
d2z \
ЪэД)
( d2z d2z \
dx + dx + d'u ’ dy-у dxdy dy /
Отсюда: d2z = ^-4ydx2 4- 2 - §-5 dx dy + ^-4(Zy2. Символически это dx2 dxdy ady2
записывается так:
72 u u 1 \
d z = \ — dx + TZ~dV ‘ z-ydx dy )
313
Аналогично можно получить формулу для дифференциала третьего порядка:
,3 jz j2 \ ( d 7 ।
d z = d(dz) = I —- dx + -x~dy ) • z, \dx dy )
где
( d , d \3 s3 ,3 o 92 ,2 0 J a J d2 J 2 б3 з (—d.r+—ф/) = ~~gdx +3—-^dx -dy+3—dx-—-bdy2 + —^dy .
\dx dy J dxA dx2 dy dx dy2 dy3
Методом математической индукции можно показать, что
/ д д \п
dnz = ( — dx + у—dy ) • z, n E N.
\dx dy J
Отметим, что полученные формулы справедливы лишь в случае, когда переменные х и у функции z = f(x;y) являются независимыми.
Пример 2ДД- (Для самостоятельного решения.) Найти d?z, если Z = х3у2.
Ответ: tPz = бху2 dx2 + 12x2ydx dy + 2ж3 dy2.
44.6. Производная сложной функции. Полная производная
Пусть z = /(ж; у) — функция двух переменных х ну, каждая из которых является функцией независимой переменной t: х = x(t), у = y(t). В этом случае функция z = j (x(t\,y(t)) является сложной функцией одной независимой переменной t; переменные х и у — промежуточные переменные.
Теорема 44.4. Если z = f(x;y) — дифференцируемая в точке М(ж;у) € D функция и ж = ж(1) и у = y(t) — дифференцируемые функции независимой переменной t, то производная сложной функции z(t) = y(t)) вычисляется по формуле
dz dz dx dz dy , . 4
Д7 = о" ’ Д7 + (44.8)
dt dx dt dy dt
Q Дадим независимой переменной i приращение At. Тогда функции ж = ж(£) и у = y(t) получат приращения Дж и Ду соответственно. Они, в свою очередь, вызовут приращение Дз функции z.
Так как по условию функция z = f(x; у) дифференцируема в точке М(х', у), то ее полное приращение можно представить в виде
. dz dz
/\.z — — /\х -I- — Ду + аДж + /3/\у, dx dy
314
где а -> О, Р -> О при Дж -> 0, Ду -> О (см. п. 44.3). Разделим выражение Дх на Д? и перейдем к пределу при Д/. -» 0. Тогда Дж -» 0 и Ду -> 0 в силу непрерывности функций ж = ж(£) и у = y(t) (по условию теоремы — они дифференцируемые). Получаем:
Дз dz Дж dz Ду Ах .. „ Ду
lim —= т—• lim —— + — • lim — + lim a- lim + nm р- lim —, At—ю Д£ dx At-ю /\t dy Д£ At->o At ->о At At-ю At-ю At
dz _ dz dx dz dy n dx q dt dx dt + dx dt dt dt’
dz dz dx dz dy dt dx dt dy dt
Частный случай: z = f(x-,y), где у = у(ж), т. е. z = /(ж;у(ж)) — сложная функция одной независимой переменной ж. Этот случай сводится к предыдущему, причем роль переменной t играет ж. Согласно формуле (44.8) имеем:
dz dz dx dz dy dx dx dx dy dx
или
dz _ dz dz dy dx dx dy dx
(44.9)
Формула (44.9) носит название формулы полной производной.
Общий случай: z = J(x;y), где ж = ж(п;-с), у = y(ir,v). Тогда z = /(ж(и; v); у(«; v)) — сложная функция независимых переменных и и v. Ее частные производные и можно найти, используя фор-dz мулу (44.8) следующим образом. Зафиксировав г>, заменяем в ней
соответствующими частными производными
dz _ dz dx dz dy du dx du± dy du
(44.10)
Аналогично получаем:
Таким образом, производная сложной функции (z) по каждой независимой переменной (и и -г) равна сумме произведений частных производных этой функции (z) по ее промежуточным переменным (ж и у) на их производные по соответствующей независимой переменной (it и г>).
Пример 44-5. Найти и если z — 1п(ж2 + у2), ж = и - V,
у = --у v
315
Q Решение: Найдем (g^ — самостоятельно), используя формул; (44.10):
dz 1 1
du x. + y2 x + у
Упростим правую часть полученного равенства:
dz 2 ( у
л- ~ ~2---2 I Я • ц + ~
du х + у2 \ v
(uv)2 +
т. e.
dz = 2
du u'
2у~. v
u\ \
V J
2v2
и uv v + -—
V V
u2(v4 + 1)
n,-(-c4 + 1) _ 2
v2 и
2
/ \ 2
44.7. Инвариантность формы полного дифференциала
Используя правило дифференцирования сложной функции, можн. показать, что полный дифференциал обладает свойством инвариант ности: полный дифференциал функции z = f(x-,y) сохраняет один i тот же вид независимо от того, являются ли аргументы независимым! переменными или функциями независимых переменных. i
Q Пусть z = f(x\ у), где хну — независимые переменные. Тогда полный дифференциал (1-го порядка) функции имеет вид
, dz dz j
dz = dx + — • dy
dx dy
(формула (44.5)).
Рассмотрим сложную функцию z = f(x-,y), где х — x(u\v), у = = у(щи), т. е. функцию z — f(x(u;v);y(u;v)) = F(u;v), где и и v — независимые переменные. Тогда имеем:
J dF J dF J dz , dz ,
dz = —— du + -77— dv = — • du + —- dv =
du dv du dv / dz dx dz dy
\с?ж du + dy du
dz (dx dx \
= .. Hr ' du + IT ’ dv + ~ dx \ du dv ) <
dv
/ dz dx dz dy dv + dy dv
. \ dz (dy .
- i • л ' V ’ du + ~F~ ’ dv J • / dy \du dv )
Выражения в скобках представляют собой полные дифференциалы dx и dy функций х = x(u;v) ну = y(u;v). Следовательно, и в этом случае, dz dz
dz = у— dx + —- dy.
dx dy
du +
dv =
316
44.8. Дифференцирование неявной функции
Функция z — f(x;y) называется неявной, если она задается уравнением , ч
F(x- у, z) — 0, (44.
неразрешенным относительно z. Найдем частные производные и
неявной функции z, заданной уравнением (44.11). Для этого, подставив в уравнение вместо z функцию f(x',y), получим тождество Г(ж;у;/(ж;у)) = 0.
П)
OZ ду
Частные производные по х и по у функции, тождественно равной нулю, также равны нулю:
Q 0F д dF 9F dz dF 0Z ,, . —- = 0 (у — считаем dx dz постоянным),
8 , dz — = 0 (ж — считаем 9?/ dz F* постоянным),
х дх ~ F' и (44.12)
Замечания.
а) Уравнение вида (44.11) не всегда определяет одну переменную как неявную функцию двух других. Так, уравнение ж2 + ?/2 + z2 —4 = 0 определяет функции zi = ^/4 — ж2 — г/2 и z2 = — \/4 — ж2 — г/2, определенные в круге ж2 + у2 4, z3 = д/4 — ж2 - у2, определенную в полукруге ж2 + у2 4 при у 0 и т. д., а уравнение сок (ж + 2у + 3z) — 4 = 0 не определяет никакой функции.
|@| Имеет место теорема существования неявной функции двух переменных: если функция F(x;y,z) и ее производные F'x(x-,y,z), F&(x-,y,z), F'z(x-,y,z) определены и непрерывны в некоторой окрестности точки Мо(жо; уу, гь), причем F^o; ?/о; «о) = 0, а Д^(жо; уу, z0) J 0, то существует окрестность точки Л/о, в которой уравнение (44.11) определяет единственную функцию z = f(x;y), непрерывную и дифференцируемую в окрестности точки (жо;?/о) и такую, что /(жо;«/о) = zq-
б) Неявная функция у = f(x) одной переменной задается уравнением Т(ж;у) = 0. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле
(F' * 0).
F'
г у
Пример 44-б • Найти частные производные функции z, заданной уравнением ег + z — х2у + 1 = 0.
317
Q Решение: Здесь F(x-,y;z) ~ ez + z — x2y + 1, F'x = — 2xy, F' = —я2, F' — ez + 1. По формулам (44.12) имеем: = -f-—т.
z K J ' dx e +1 ’ dy e +1
•
Пример Ц-7. Найти если неявная функция у = f(x) задана уравнением у3 + 2у = 2х.
Q Решение: Здесь F(x-,y) = у3 +2у - 2х, F'. = -2, Fy = 3>у2 + 2. Следовательно, у' = , т. е. 4^ = . •
’ Ух Зу2 + 2 ’ dx Зу2 + 2
Рис. 208
§45. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
Рассмотрим одно из геометрических приложений частных производных функции двух переменных. Пусть функция z = f(x;y) дифференцируема в точке (хо;уо) некоторой области D G К2. Рассечем поверхность S, изображающую функцию z, плоскостями х — Хд п у = уо (см. рис. 208). Плоскость х = хо пересекает поверхность S по некоторой линии zo(y), уравнение которой получается подстановкой в выражение исходной функции z = f(x;y) вместо х числа хо- Точка М0(х0; уо; /(®о; Уо)) принадлежит кривой z0(y). В силу дифференцируемости функции z в точке Мо функция z0(y) также является дифференцируемой в точке у = = уо- Следовательно, в этой точке в плоскости х = хо к кривой zo(y) может быть проведена касательная Ц.
Проводя аналогичные рассуждения для сечения у = уо, построим касательную 12 к кривой zo(a:) в точке х = ат0. Прямые /1 и 12 определяют плоскость а, которая называется касательной плоскостью к поверхности S в точке Мо-
Составим ее уравнение. Так как плоскость а проходит через точку А4о(а:о;уо; zq), то ее уравнение может быть записано в виде
А(.т - х0) + В(у - уо) + C(z - zo) = 0, которое можно переписать так:
z - zo = Ах(х - х0) + Bi(y - уо) (45.1)
318
(разделив уравнение на —С и обозначив А? = Alt = В\). (Найдем А1 и В].
Уравнения касательных Zi и 12 имеют вид
z - z0 = fy(x0; у0) (у - уо), х = х0', z- z0 = Л (ад Уо) (х-хо), У = Уо
< •< ютветственно.
Касательная 1\ лежит в плоскости а, следовательно, координаты всех точек ZT удовлетворяют уравнению (45.1). Этот факт можно записать в виде системы
{Z - Zo = /,)(ад Уо)(у ~ Уо), х = ад
z - Zo = Ах(х - Хо) + В}(у - Уо).
Разрешая эту систему относительно В^, получим, что В\ = = fy(^o;yo)-
Проводя аналогичные рассуждения для касательной 12, легко установить, что Л1 = Ц(хо-,уо).
Подставив значения А} и В\ в уравнение (45.1), получаем искомое уравнение касательной плоскости:
z - Zo - fz(xo;yo) (х - ®о) + ?у(хо;уо) (?/ ~ Уо)- (45.2)
Прямая, проходящая через точку Мо и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью.
Используя условие перпендикулярности прямой и плоскости (см. с. 103), легко получить канонические уравнения нормали:
х-хр = У~Уо = z-zp ?х(хо’,Уо) fy(xo;yo)
Если поверхность S задана уравнением F(x; у; z) = 0, то уравнения (45.2) и (45.3), с учетом того, что частные производные могут быть найдены как производные неявной функции:
п/ Рх(х<АУо) \ Ву(хо',Уо)
fx(xp-,yo)~ F'{xo;yoy fy(xo,yo) F^xo-,yo)
(см. формулы (44.12)), примут соответственно вид
Fx(x0;y0) (х - хр) + F'y(xp-,yo) (у - Уо) + F'z(xo-,yo) - (z - z0) = 0
и ' X - Хр _ у - у о _ z - Zp
Fx(xo;yo) Ву(хО',уо) F^xo-,yo)'
319
Замечание. Формулы касательной плоскости и нормали к поверх ности получены для обыкновенных, т. е. не особых, точек поверхности Точка Мо поверхности называется особой, если в этой точке все чао ные производные равны нулю или хотя бы одна из них не существуе i Такие точки мы не рассматриваем.
Пример 45.1. Написать уравнения касательной плоскости и нормали к параболоиду вращения z — ж2 + у2 в точке Мо(1; —1; 2).
О Решение: Здесь z'x = fx(x;y) = 2ж, /^(ж;у) = 2у, /'.(1;-1) = 21 /^(1;—1) = —2. Пользуясь <}хд)мулами (45.2) и (45.3) получаем ур; нение касательной плоскости: z — 2 = 2 (ж
2х - 2у — z - 2 = 0 и уравнение нормали: ж ~
- 1) - 2 • (у + 1) ил1
- 2L+1 - z-2 (
~ -2 " - 1 ’
§46. ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
46.1. Основные понятия
Понятие максимума, минимума, экстремума функции двух пер менных аналогичны соответствующим понятиям функцйи одной нещ висимой переменной (см. п. 25.4).
Пусть функция z = f(x;y) определена в некоторой области / точка N(xo;yo) е D.
Точка (жо;уо) называется точкой максимума функции z :
= /(ж; у), если существует такая «5-окрестность точки (жо;уо)> ,,тС> для каждой точки (ж; у), отличной от (жо;уо), из этой окрестности выполняется неравенство f(x;y) < f(xo;yo).
Аналогично определяется точка минимума функции: для всех точек (ж; у), отличных от (жо; уо), из ^-окрестности точки (жо;уо) выполняется неравенство: /(ж;у) > > f(x0;y0).
На рисунке 209: Ni — точка максимума, аЛд — точка минимума функции z = f(x;y).
Значение функции в точке максимума (минимума) называется
Рис. 209
максимумом (минимумом) функции. Максимум и минимум функ-
ции называют ее экстремумами.
Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке
320
сравнивается с ее значениями в точках, достаточно близких к ' „; ?/о). В области D функция может иметь несколько экстремумов или иметь ни одного.
i6.2. Необходимые и достаточные условия экстремума
Рассмотрим условия существования экстремума функции.
Теорема 46.1 (необходимые условия экстремума). Если в точке /У(жо;уо) дифференцируемая функция z — f(x;y) имеет экстремум, ю ее частные производные в этой точке равны нулю: /'(жо;з/о) = О, Р№(хо;уо) = °-
IJ Зафиксируем одну из переменных. Положим, например, у = уо- То-। ia получим функцию /(ж; уо) = <р(х) одной переменной, которая имеет жстремум при х = жо- Следовательно, согласно необходимому условию ж стремума функции одной переменной (см. п. 25.4), уз'(ж()) = 0, т. е. /'(жо;уо) = 0.
Аналогично можно показать, что /^(жо;?/о) =0.
Геометрически равенства /Дад;?/о) = 0 и /Джо;?/о) = 0 означают, что в точке экстремума функции z = f(x',y) касательная плоскость к поверхности, изображающей функцию f(x;y), параллельна плоскости Оху, т. к. уравнение катательной плоскости есть z = zq (см. формулу (45.2)).
Замечание. Функция может иметь экстремум и точках, где хотя бы одна из частных производных не существует. Например, функция z — 1 — у/ж2 + у2 имеет максимум в точке 0(0; 0) (см. рис. 210), но не имеет в этой точке частных производных.
|ф] Точка, в которой частные производные первого порядка функции z — f(x',y) равны нулю, т. е. f'x = 0, /' = 0, называется стационарной точкой функции z.
Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию z = ху. Для нее точка 0(0; 0) является критической (в ней z'x = у и z' = х обращаются в ноль). Однако
11 Конспект лекций по высшей математике. Полный курс
321
экстремума в ней функция z = ху не имеет, т. к. в достаточно малой окрестности точки 0(0; 0) найдутся точки для которых z > 0 (точки I и ТП четвертей) и z < 0 (точки II и IV четвертей).
Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.
Теорема 46.2 (достаточное условие экстремума). Пусть в стационарной точке (жд;у0) и некоторой ее окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (жо;З/о) значения А = /"аХ^сьЗ/о), В = = f"y^o;yo), С = fyy(x0;y0). Обозначим
А = = АС-В2. и
югда: jm 1) если А > 0, то функция f(x; у) в точке (жо; З/о) имеет экстремум: максимум, если А < 0; минимум, если А > 0; 2) если А < 0, то функция /(ж; у) в точке (ж(); уо) экстремума не имеет. В случае А = 0 экстремум в точке (жо; уб) может быть, может не быть. Необходимы дополнительные исследования.
Примем без доказателг Пример 6.1. Найти Q Решение: Здесь z'x = 6ж частные производные не су Найдем стационарные >ства. i: экстремум функции z = 2>х2у — ж3 — у4. | у — Зж2, z'y = Зж2 — 4у3. Точки, в которЯ ществуют, отсутствуют. я точки, решая систему уравнений: .1 I бжу — Зж2 = 0, J Зж2-4у3=0. Ч
Отсюда получаем точки ЛЛ(6;3) и Мг(0;0).
Находим частные производные второго порядка данной функции: z"x = 6?/ - 6ж, z"y = 6ж, z'yy — -12у2.
В точке Л/|(6;3) имеем: А = —18, В = 36, С = —108, отсюда
АС - В2 = -18 (-108) - 362 = 648,
т. е. А > 0.
Так как А < 0, то в точке Mi функция имеет локальный максимум: zmax = z(6;3) = 3 • 36 3 - 63 - З4 = 324 - 216 - 81 = 27.
322
В точке ТИ2(0;0): А = О, В = О, С = 0 и, значит, А = 0. Проведем пнюлнительное исследование. Значение функции z в точке М2 равно кулю: г(0;0) = 0. Можно заметить, что z = —у4 < 0 при х = 0, у 0;
—ж3 > 0 при х < 0, у = 0. Значит, в окрестности точки АффО;!)) функция z принимает как отрицательные, так и положительные значения. Следовательно, в точке М2 функция экстремума не имеет. •
46.3. Наибольшее и наименьшее значения функции в замкнутой области
Пусть функция z = f (ж; у) определена и непрерывна в ограниченной замкнутой области D. Тогда она достигает в некоторых точках I) своего наибольшего М и наименьшего тп значений (т. н. глобальный жстремум). Эти значения достигаются функцией в точках, расположенных внутри области D, или в точках, лежащих на границе области.
Правило нахождения наибольшего и наименьшего значений дифференцируемой в области D функции z = f(x; у) состоит в следующем:
1. Найти все критические точки функции, принадлежащие D, и вычислить значения функции в них;
2. Найти наибольшее и наименьшее значения функции z = f(x;y) на границах области;
3. Сравнить все найденные значения функции и выбрать из них наибольшее М и наименьшее т.
Пример 46.2. Найти наибольшее и наименьшее значения функции z = ж2 у + ху2 + ху и замкнутой области, ограниченной линиями: у — -, ж = 1, х = 2, у = —1,5 (см. рис. 211).
(J Решение: Здесь z'x = 2ху + у2 + у, z'y = ж2 + Ь 2ху + ж.
1. Находим все критические точки:
у(2х + у + 1) = 0, ж(ж + 2у + 1) = 0.
Решением системы являются точки (0;0), (—1;0), (0;—1), у д;~зу-Ни одна из найденных точек не принадлежит области D.
2. Исследуем функцию z на границе области, состоящей из участков АВ, ВС, СЕ и ЕА (рис. 211).
323
На участке АВ: х ~ 1, z - у2 + 2у, где у е 1], 4 = %/ + 2у 4- 2 = 0, у = —1. Значения функции z(—1) = —1, ^(~к) = — z(l) = 3.
На участке ВС: у = i, z = х + 1 + 1, где х е [1; 2], z'x — 1 - -j ЖЖ д
1 — —j = О, жх = 1, жг = —1 [1;2]. Значения функции z(l) =
z(2) = 3,5.
На участке СЕ: х - 2, z = 2у2 + Gy, у € 1], z' = 4у +
L 2 ZJ &
о
4у + 6 = 0, у = — g. Значения функции z
-4,5, zQ) =3,5.
На участке АЕ: у - -|, z = 4- %х, х е [1; 2], z'x = -Зж +
-Зж 4-1 = 0, ж = i [1; 2]. Значения функции z(l) = — z(2) = -4,1 3. Сравнивая полученные результаты, имеем:
JW = +3,5 = z(2;|) -z(C);
a m = -4,5 = z^2; = z(E).
Глава X. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Лекции 37—43
547. ОБЩИЕ СВЕДЕНИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ
47.1. Основные понятия
При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде v равнений, связывающих независимую переменную, искомую функцию к се производные. Такие уравнения называются дифференциальными (термин принадлежит Г. Лейбницу, 1676 г.). Решен«ел« дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Так, решением уравнения у' = f(x) является функция у = F(x) — первообразная для функции /(ж).
Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ).
Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным-, в противном случае — ДУ в частных производных. Далее будем рассматривать только обыкновенные ДУ.
Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.
Например, уравнение у'" — Зу" +2у = 0 — обыкновенное ДУ третьего порядка, а уравнение х2у' + 5ху = у2 — первого порядка; у • z'x = — х • z'y — ДУ в частных производных первого порядка.
Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ — интегральной кривой.
Рассмотрим некоторые задачи, решение которых приводит к дифференциальным уравнениям.
47.2. Задачи, приводящие к дифференциальным уравнениям
Задача 1
Материальная точка массы m замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скоро
ОПК
сти V. Найти зависимость скорости от времени. Найти скорость точД через 3 с после начала замедления, если V(0) = 100 м/с, а V(l) = 50 мД
Q Решение: Примем за независимую переменную время t, отсчитывЯ емое от начала замедления движения материальной точки. Тогда с Л рость точки V будет функцией t, т. е. V = V(t). Для нахождения У.Я воспользуемся вторым законом Ньютона (основным законом механЯ ки): т- а = F, где а = V'(t) — есть ускорение движущегося тела, F < результирующая сила, действующая на тело в процессе движения.
В данном случае F = — kV2, к > 0 — коэффициент пропорциона Л ности (знак минус указывает на то, что скорость тела уменьшается Следовательно, функция V = V(t) является решением пиффере.шД ального уравнения т • V = — к • V2 или V' = ——V2. Здесь т — масЯ тела.
Как будет показано ниже (пример 48.5), V = -г----, где с -Я
— t + с I
m V
const. Найдя зависимость скорости от времени, легко найти скороеп точки через 3 с после начала замедления. !
Найдем сначала параметры ~ и с. Согласно условию задачи, hmi3
ем: V(0) = 1 = 100 и У(1) = -=Д- = 50. Отсюда с = 4n, ~
с 100 т Ю ]
m j
Следовательно, скорость точки изменяется по закону V = П<я этому У(3) = 25 м/с.
Задача 2 , И
Найти кривую, проходящую через точку (4; 1), зная, что отрезом любой касательной к ней, заключенный между осями координат, де-1 лится в точке касания пополам.
Q Решение: Пусть М(х\у) — произвольная точка кривой, уравнение которой у = f(x). Для опреде^ ленности предположим, что кривая расположена в первой четверти (см. рис. 212).
Для составления дифференциального уравнения воспользуемся геометрическим смыслом первой производной: tga есть угловой коэффициент касательной; в точке М(х-у) он равен у', т. е. у' — tga.
Из рисунка видно, что tg(ZMВС) = Но
tg(Z.M ВС) = tg(180° — a) = — tga,
MC = у. По условию задачи AM = MB, следовательно, ОС = СВ = х.
326
Таким образом, получаем — tga: = или у' = —Решением по-। н-много дифференциального уравнения является функция у = ....‘рбола). Решение будет приведено в п. 48.2 (пример 48.4). •
Другие задачи
Можно показать, что:
• закон изменения массы радия в зависимости от времени («радиоактивный распад») описывается дифференциальным уравнением = —к т, где к > 0 — коэффициент пропорциональности, m(t) — масса радия в момент t;
• «закон охлаждения тел», т. е. закон изменения температуры тела в зависимости от времени, описывается уравнением ~ = к(Т—to), где T(t) — температура тела в момент времени t, к - коэффициент пропорциональности, t0 — температура воздуха (среды охлаждения);
• зависимость массы х вещества, вступившего в химическую реакцию, от времени t во многих случаях описывается уравнением = к • х, где к — коэффициент пропорциональности;
• «закон размножения бактерий» (зависимость массы т бактерий от времени t) описывается уравнением m't = к • т, где к > 0;
• закон изменения давления воздуха в зависимости от высоты над уровнем моря описывается уравнением = -к-p, где p(h) — атмосферное давление воздуха на высоте h, к > 0.
Уже приведенные примеры указывают на исключительно важную роль дифференциальных уравнений при решении самых разнообразных задач.
§48. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
48.1. Основные понятия
Дифференциальное уравнение первого порядка в общем случае можно записать в виде
F{x-y,y') = 0. (48.1)
497
Уравнение связывает независимую переменную х, искомую функцию у и ее производную у'. Если уравнение (48.1) можно разрешить оти<> сителыю у', то его записывают в виде
У' = /(ж; у) (48.2)
и называют ДУ первого порядка, разрешенным относительно проил водной. Мы в основном будем рассматривать эту форму записи ДУ.
Уравнение (48.2) устанавливает связь (зависимость) между коор динатами точки (ж;?/) и угловым коэффициентом у' касательной к интегральной кривой, проходящей через эту точку. Следовательно. ДУ у' = /(ж; у) дает совокупность направлений (поле направлений) iu плоскости Оху. Таково геометрическое истолкование ДУ первого по рядка.
Кривая, во всех точках которой направление поля одинаково, на зывается изоклиной. Изоклинами можно пользоваться для приближен ного построения интегральных кривых. Уравнение изоклины можно по лучить, если положить у' = с, т. е. ф(х-,у) — с.
Пример 48.1. С помощью изоклин начертить вид интегральных
кривых уравнения у' — 2ж.
Q Решение: Уравнение изоклин этого ДУ будет 2ж — с, т. е. изоклинами здесь будут прямые, параллельные оси Оу (х = -).
В точках прямых проведем отрезки, образующие с осью Ох один и тот же угол а, тангенс которого равен с.
Так, при с — 0 имеем х = 0, t.go = О, поэтому о =0;
при с = 1 уравнение изоклины ж = А, поэтому tgo = 1 и а = 45°;
при с = —1: х = —i tgo = —1, а = = -45°;
при с = 2: х — 1, tgo = 2, а = arctg 2 ss 63° и т. д.
Построив четыре изоклины и отметив на каждой из них ряд стрелочек, наклоненных к оси Ох под определенным углом (см. рис. 213), по их направлениям строим линии. Они, как видно, представляют собой семейство парабол. •
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:
Р(х; y)dx + Q(x; у) dy — О,
(48.3)
. « ly(x\y) и Q(x;y) — известные функции. Уравнение (48.3) удобно к м, что переменные х и у в нем равноправны, т. е. любую из них мож-II.> рассматривать как функцию другой. Отметим, что от одного вида 1.ШИСИ ДУ можно перейти к другому.
Интегрирование ДУ в общем случае приводит к бесконечному мно-А1< тву решений (отличающихся друг от друга постоянными величинами). Легко догадаться, что решением уравнения у' — 2ж является функция у = ж2, а также у = ж2 + 1, у = ж2 — л/2 и вообще у = х2 + с, I и - с - - const.
Чтобы решение ДУ приобрело конкретный смысл, его надо подчини гь некоторым дополнительным условиям.
Условие, что при х — жо функция у должна быть равна заданному числу ?/о, т. е. у = уо называется начальным условием. Начальное v .новие записывается в виде
у(хо) = уо или J = уо- (48.4)
\Х—ХО
|Д| Общим решением ДУ первого порядка называется функция у = = <Дж; с), содержащая одну произвольную постоянную и удовле-шоряющая условиям:
1. Функция Дж; с) является решением ДУ при каждом фиксированном значении с.
2. Каково бы ни было начальное условие (48.4), можно найти такое шачение постоянной с = со, что функция у = Дж; сд) удовлетворяет данному начальному условию.
Частным решением ДУ первого порядка называется любая функция у — Дж;со), полученная из общего решения у = Дж; с) при конкретном значении постоянной с = со-
Если общее решение ДУ найдено в неявном виде, т. е. в виде уравнения Ф(ж; у-с) — 0, то такое решение называется общим интегралом ДУ. Уравнение Ф(ж;г/;со) = 0 в этом случае называется частным интегралом уравнения.
С геометрической точки зрения у = Дж; с) есть семейство интегральных кривых на плоскости Оху, частное решение у = Дж;со) — одна кривая из этого семейства, проходящая через точку (жо;2/о)-
Задача отыскания решения ДУ первого порядка (48.3), удовлетворяющего заданному начальному условию (48.4), называется задачей Коши.
Теорема 48.1 (существования и единственности решения задачи Коши). Если в уравнении (48.2) функция /(ж;?/) и ее частная производная fy(x-,y') непрерывны в некоторой области D, содержащей точку (хо',уо), то существует единственное решение у = Дж) этого уравнения, удовлетворяющее начальному условию (48.4).
329
(Без доказательства).
Геометрический смысл теоремы состоит в том, что при выполне ее условий существует единственная интегральная кривая ДУ, пр< дящая через точку (жо5Уо)-
Рассмотрим теперь методы интегри{)ования ДУ первого пора определенного типа.
48.2. Уравнения с разделяющимися переменными
Наиболее простым ДУ первого порядка является, уравнение в Р(х) dx + Q(y) • dy — 0. (4
В нем одно слагаемое зависит только от ж, а другое — от у. Ино: такие ДУ называют уравнениями с разделенными переменными. П интегрировав почленно это уравнение, получаем: '•
J Р(х) - dx,+ у Q(y) • dy = с
— его общий интеграл.
Пример 48.2. Найти общий интеграл уравнения х - dx + у • dy =
Q Решение: Данное уравнение есть ДУ с разделенными переменным! Поэтому Jxdx-Jydy = а или = щ. Обозначим = с
Тогда х2 — у2 — с — общий интеграл ДУ. ।
Более общий случай описывают уравнения с разделяющимися п ременными, которые имеют вид
•РДж) • Qi(y) dx + Р2(ж) • Qz(y) dy = 0. (48.1
Особенность уравнения (48.6) в том, что коэффициенты при dx dy представляют собой произведения двух функций (чисел), одна i которых зависит только от х, другая — только от у.
Уравнение (48.6) легко сводится к уравнению (48.5) путем почленного деления его на Qi(y) Р‘2(х) ф 0. Получаем:
^(®) 01 (У) j Р^х) ./ 01 (у)
— общий интеграл.
Замёчания. 1. При проведении почленного деления ДУ на 01 (з/)х хР2(х) могут быть потеряны некоторые решения. Поэтому следуе' отдельно решить уравнение Qi(y) - Pz(x) — 0 и установить те решен ДУ, которые не могут быть получены из общего решения, — особь решения.
330
2. Уравнение у' = fi(x) fa(y) также сводится к уравнению с разделенными переменными. Для этого достаточно положить у' = и рпчделить переменные.
3. Уравнение у' = f(ax + by + с), где а, Ь, с — числа, путем замены ах + by + с = и сводится к ДУ с разделяющимися переменными. Дифференцируя по ж, получаем:
dy du , .
7“’ т-е' 77 = a + 6'A«),
dx dx
du
— = а dx
откуда следует
du
-—77\ = dx. a + b- f(u)
Интегрируя это уравнение и заменяя и на ах + by + с, получим общий интеграл исходного уравнения.
Пример 48.3. Решить уравнение (у + ху) • dx + (ж — ху) • dy = 0.
Решение: Преобразуем левую часть уравнения:
у • (1 -I- ж) dx + ж • (1 — у) • dy = 0.
Оно имеет вид (48.6). Делим обе части уравнения на ху ,4 0:
1+ж j 1 - у , п
dx -I — dy = 0. ж-----------у
Решением его является общий интеграл ж + In |ж| + In |у| — у = с, т. е. In |жу| + ж — у = с.
Здесь уравнение Q\(y) Ръ(х) = 0 имеет вид ху = 0. Его решения ж = 0, у = 0 являются решениями данного ДУ, но не входят в общий интеграл. Значит, решения ж = 0, у = 0 являются особыми. •
Пример 48.4- Решить уравнение у' = удовлетворяющее условию у (4) = 1.
Q Решение: Этот пример представляет собой решение задачи 2 из п. 47.2.
Имеем: 'Р = или Проинтегрировав, получим:
ах х у х
1п |j/| = In |с| — In |ж|, т. е. у = £ — общее решение ДУ.
Оно представляет собой, геометрически, семейство равносторонних гипербол. Выделим среди них одну, проходящую через точку (4; 1). Подставим ж = 4ну - 1 в общее решение уравнения: 1 = £, с = 4.
тт 4 i Q
Получаем: у — — — частное решение уравнения у = — •
331
Пример 48.5. Найти общее решение ДУ т • V = — к • V2.
Q Решение: Этот пример демонстрирует решение задачи 1 из и. 47.2 Приведем данное уравнение к виду (48.5):
т = — kV2, т • dV + kV2 dt = 0, + — dt = 0. ’
dt V т ;
Интегрируем: J J dt = —с, т. е. — р + Д t + с = 0. Отсюда
V = -т—------общее решение уравнения. ф
& + с
48.3. Однородные дифференциальные уравнения
К уравнению с разделяющимися переменными приводятся одно родные ДУ первого порядка.
Функция /(ж; у) называется однородной функцией п-го порядка (in мерения), если при умножении каждого ее аргумента на прои < вольный множитель А вся функция умножится на А", т. е.
/(А ж; А • у) = А" •/(ж; у).
Например, функция /(ж; у) = ж2 — 2ху есть однородная функщ второго порядка, поскольку
/(А • ж; А у) = (Аж)2 - 2(Аж)(Ау) = А2 • (ж2 - 2ж?/) = А2 • f(x-,y).
Дифференциальное уравнение
y' = f(x-,y) (48.
|ф[ называется однородным,, если функция f(x;y) есть однородн функция нулевого порядка.
Покажем, что однородное ДУ (48.7) можно записать в виде
у' = v
(48
□ Если /(ж; у) - однородная функция нулевого порядка, то, по оп| делению, f (ж; у) = /(Аж; Ху). Положив Л = получаем:
х
х
х)
Однородное уравнение (48.8) преобразуется в уравнение с раздел: кицимися переменными при помощи замены переменной (подстановки
У
— — и
X
или, что то же самое, \у — и ж7|
(48.9
332
Р(х; у) dx + Q(x-, у) dy = 0.
Действительно, подставив у = их и у' = и'х + и в уравнение (48.8), п<и|учаем и'х+и = ^(w) или ^и)~иут- е- уравнение с разделяющимися переменными. Найдя его общее решение (или общий интеграл), следует заменить в нем и на Получим общее решение (интеграл) исходного уравнения.
Однородное уравнение часто задается в дифференциальной форме:
(48.10)
1У (48.10) будет однородным, если Р(х-,у) и Q(x;y) — однородные Фг акции одинакового порядка.
Переписав уравнение (48.10) в виде и применив в
правой части рассмотренное выше преобразование, получим уравнение "'МЮ-
[ф| При интегрировании уравнений вида (48.10) нет необходимости предварительно приводить их (но можно) к виду (48.8): подстановка (48.9) сразу преобразует уравнение (48.10) в уравнение с разде-||яющимися переменными.
Пример 48.6. Найти общий интеграл уравнения (ж2 — у2) dx + 2ху - dy = 0.
Q Решение: Данное уравнение однородное, т. к. функции Р(х;у) = ~х2—у2н Q(x-y) = 2ху — однородные функции второго порядка.
Положим у = и-х. Тогда dy — x-du + u-dx. Подставляем в исходное уравнение:
(ж2 — д2ж2) dx + 2ж • их • ж du + 2ж - их - и- dx, ж2(1 — и2 + 2и2) dx + 2иж3 du = 0, (1 + и2) dx -I- 2пж • du — 0,
последнее — уравнение с разделяющимися переменными. Делим переменные 2и
---1-----о • du = 0
ж 1 + и2
и интегрируем
In |ж| + 1п(1 4-и2) = ci, 1п(|ж| • (1 + и2)) = щ, |ж|(1 + и2) = еС1.
Обозначим с — еС1, с > 0. Тогда
|ж| • (1 + и2) — с.
Заменяя и на получаем: ж2 + у2 = сх — общий интеграл исходного уравнения.
333
Отметим, что данное уравнение можно было сначала привести? виду (48.8):
2 2,9 dy n dy У2-х2 , (^)2-1
х - Г + 2ху — = 0, 7-=—z-----, У = ' у •
ах ах 2ху 2 • *
Затем положить у = и х, тогда у1 = и'х + и и т. д. ;
Замечание. Уравнение вида у' = f )> гДе а> с> а
bi, ci — числа, приводится к однородному или с разделяющимися пер< менными. Для этого вводят новые переменные и и v, положив х = н4~< у = v + 0, где а и /3 — числа. Их подбирают так, чтобы уравнение ста однородным.
Пример 48.7. Найти общий интеграл уравнения
т. е. у' —
(х + 2у 4-1) dx — (2х + у — 1) -dy = О, ж + 2т/ + 1 2ж 4- у — 1'
Q Решение: Положив х = и 4- а, у = v 4- 0, получаем: ;
dx = du, dy = dv;
, _ dy _ dv _ и + a + 2v + 20 + 1 _ и + 2v 4- (a 4- 20 4-1)
У dx du 2u + 2a + v 4- 0 — 1 2u 4- v 4- (2a 4- 0 — 1) ’ i
Подберем a и 0 так, чтобы
fa 4-2^ 4-1 = 0,
[2a 4- 0 - 1 = 0.
Находим, что a = 1, 0 = -1. Заданное уравнение примет вид dv и 4- 2v du 2и 4- v
и будет являться однородным. Его решение получается, как это были показано выше, при помощи подстановки v = tu. Заметим, что, решиз его, следует заменить и и v соответственно на ж - 1 и J/ + 1. В итог получим (у—ж4-2)3 = с(ж4-у) — общий интеграл данного уравнения. <
48.4. Линейные уравнения. Уравнение Я. Бернулли
Дифференциальное уравнение первого порядка называется неиным, если его можно записать в виде
у' +р(ж) -у = д{х), (48.1
где р(х) и д(х) — заданные функции, в частности — постоянные.
Особенность ДУ (48.11): искомая функция у и ее производная ;
входят в уравнение в первой степени, не перемножаясь между собой.'
Рассмотрим два метода интегрирования ДУ (48.11) — метоЗ И. Бернулли и метод Лагранжа.
4.44
Метод И. Бернулли
Решение уравнения (48.11) ищется в виде произведения двух дру-। их функций, т. е. с помощью подстановки у = и • v, где и = п(ж) и i> = ц(ж) — неизвестные функции от х, причем одна из них произвольна (но не равна нулю — действительно любую функцию у(х) можно
ишисать как
у(х) = п(ж) = и(х) - v(x),
|.це а (ж) ф 0)- Тогда у' = и' • v 4- и V . Подставляя выражения у и у в уравнение (48.11), получаем: и' • v 4- и • v' 4- р(ж) • и - v = д(х) или
и' -v + и (у1 4- р(ж) • и) = д(х). (48.12)
Подберем функцию v — v(x) так, чтобы выражение в скобках было равно нулю, т. е. решим ДУ v' 4- р(х) • v = 0. Итак, 4-р(ж) • v = 0, т. е.
= —р(ж) • dx. Интегрируя, получаем:
Ввиду свободы выбора функции v(ж), можно принять с = 1. Отсюда v = e~fp(x)-dx_
Подставляя найденную функцию v в уравнение (48.12), получаем =д(х).
Получено уравнение с разделяющимися переменными. Решаем его:
| = д(х), du = g(x)-e+fpWdxdx,
| dx
р и = У р(ж) - e^p^'dxdx 4- с.
Возвращаясь к переменной у, получаем решение
y = uv=(j д(х) efp^ dxdx + с) е~ f P^'dx (48.13)
исходного ДУ (48.11).
Пример 48.8. Проинтегрировать уравнение у' 4- 2ху = 2ж.
Q Решение: Полагаем у = и • v. Тогда и' • v 4- и • и' 4- 2х - uv — 2ж, т. е. и' • v 4- и • (у' 4- 2жп) = 2ж. Сначала решаем уравнение v' 4- 2ж - v = 0:
Л? „ .11 2 -т2
— = -2x-dx, In Ы = —ж , п = е v
Теперь решаем уравнение и' • е~х^ 4- и 0 = 2ж, т. е.
dU п _2 Г 1 2
— = 2ж • е , du = I 2ж е • dx, и = в 4- с.
dx J
Итак, общее решение данного уравнения есть у = и • v = (еж 4- с) • е~х , т. е. у = 1 + с е . •
Метод Лагранжа (метод вариации произвольной постоянной)
!
Уравнение (48.11) интегрируется следующим образом. j
Рассмотрим соответствующее уравнение без правой части, т. i уравнение у' + р(ж) - у = 0. Оно называется линейным однородным ДУ первого порядка. В этом уравнении переменные делятся: J
— = — р(х) dx и In |р| — — J р(ж) • dx + In |ci|. J;
Таким образом, |^| — e~^p^'dx, т. е. Ц,
у = ±С1е~ S p(x)dx или y = c-e~J^x>dx, где с = ±С1. J
Метод вариации произвольной постоянной состоит в том, что по* стоянную с в полученном решении заменяем функцией с(ж), т. е. полагаем с = с (ж). Решение уравнения (48.11) ищем в виде
у = с(х) e-fp(x)dx, (48.14)
Находим производную1:
у' = с'(ж) ехр(- у р(ж) dxj + с(ж) exp^- J р(х) dxj (-р(ж)).
Подставляем значения у и у' в уравнение (48.11): |
с'(ж) ехр у р(ж) dx) — с(х)р(х) exp Г р(х) dx) +
+ с(ж)р(ж) ехр у р(ж) dx) = g(x).
Второе и третье слагаемые взаимно уничтожаются, и уравнение приме! вид / Г X
с'(ж)ехр(— / p(x)dx) = р(ж).
Следовательно, 4
</с(ж) = р(ж) ехр(У Р(ж) dx'j • dx. Интегрируя, находим:
dx + с.
Подставляя выражение с(ж) в равенство (48.14), получим общее jxune-ние ДУ (48.11): <
с
Естественно, та же формула была получена методом Бернулли (ср с (48.13)).
Пример 48.9. Решить пример 48.8 методом Лагранжа.
1 Для удобства записи пользуемся обозначением e.F^ = exp(F(x)).
336
1 j Решение: Решаем уравнение у' + 2ху = 0. Имеем
dy _ У
—2ж dx, или
у = с-е ®2. Заменяем с на с(ж), т. е. решение ДУ у' + 2ху — 2х ищем в виде у = с(х) е~х . Имеем
2 2
у' — с'(х) е~х + с(х) - е~х (—2х).
Тогда
с'(ж) • е-®2 - 2хс(х) е~х + 2хс(х) -е~х — 2х, т.е. с'(ж) • е~х — 2ж, или с(ж) = J 2х • е®2 - dx, или с(ж) = ех'2 + с. Поэтому у = (е* + с) • е'х , или у — 1 + с ё~х2 — общее решение данного уравнения. •
Замечание. Уравнение вида (ж Р(у) + Q(y)) • у' — R(y), где Р(у), Q{y), R(y) 0 — заданные функции, можно свести к линейному, если х считать функцией, а у — аргументом: ж = ж (у). Тогда, пользуясь ра-, 1 ж РМ + QM г>/ \ z Р(у)
венством ух = -^г, получаем---= R(y), т. е. ж — 'х =
= — линейное относительно ж уравнение. Его решение ищем в
R(3P
виде ж = и • v, где и — и(у), v = v(y) — две неизвестные функции.
Пример 48.10. Найти общее решение уравнения (ж +?/)•?/ = 1.
Решение: Учитывая, что у' = от исходного уравнения переходим к линейному уравнению ж' = ж + у.
Применим подстановку ж — и v. Тогда ж' = и' • v + и • v'. Получаем: и' v + и v' — и v + у, или и' • v + д(н' — v) = у.
Находим функцию щ v' — v = 0, = dy, v = еу.
Находим функцию и: и' • еу + и • 0 = у, т. е. и' = у е~у, или и — fy-е~у dy. Интегрируя по частям, находим: и = —у е~у ~е~у + с.
Значит, общее решение данного уравнения:
х — и • v = (—у е~у — е~у + с) • еу, или ж = — у — 1 + с- еу. •
Уравнение Я. Бернулли
Уравнение вида
у' +р(.х) ’ У = д(х) ‘ УП1 п 6 Я п 0, п 1 (48.15)
|ф| называется уравнением Бернулли. Покажем, что его можно привести к линейному.
Если п = 0, то ДУ (48.15) — линейное, а при п — 1 — с разделяющимися переменными.
337
В общем случае, разделив уравнение (48.15) на уп 0, получим: 2/-п • у' + р(ж) - = е(ж). (48.16)
Обозначим ?Дп+1 = z. Тогда z' = = (1 - п) у~п у1. Отсюда находим
у~п ' У1 — у £; п Уравнение (48.16) принимает вид
• z' +р(ж) • Z = <;(ж).
Последнее уравнение является линейным относительно z. Решение его известно. Таким образом, подстановка z — y~n+1 сводит уравнение (48.15) к линейному. На практике ДУ (48.15) удобнее искать методом И. Бернулли в виде у = и • v (не сводя его к линейному).
48.5. Уравнение в полных дифференциалах.
Интегрирующий множитель
Уравнение
Р(ж; у) dx + Q(x; у) dy = 0 (48.17)
называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции и(х;у), т. е.
Р(ж; у) dx + Q(x; у) dy — du(x; у).
В этом случае ДУ (48.17) можно записать в виде du(x; у) = 0, а его общий интеграл будет:
и(х;у) — с. (48.18)
Приведем условие, по которому можно судить, что выражение
Д = Р(х; у) dx + Q(x; у) dy есть полный дифференциал.
Теорема 48.2. Для того чтобы выражение Д = Р(х; у) dx+Q(x; у) dy,
где функции Р(х-у) и Q(x;y) и их частные производные
дР
м дх.
непрерывны в некоторой области D плоскости Оху, было полным
дифференциалом, необходимо и достаточно выполнение условия
дР _ 8Q ду дх
(48.19)
Необходимость
Q Пусть Д есть полный дифференциал, т. е.
Р(х-, у) dx + (Дж; у) dy — du(x; у).
Учитывая, что du(x;y) = dx + dy (см. п. 44.3), имеем:
. ди
Дифференцируя эти равенства по у
дР д2и ~ —------— и
ду дх • ду
и по ж соответственно, получаем dQ _ д?и дх ду дх
д2и д2и
А так как смешанные частные производные и равны
между собой (см. п. 44.2), получаем (48.19).
Достаточность
Пусть в области D выполняется условие (48.19). Покажем, что существует функция и(х', у) в области D такая, что
du(x; у) — Р(х; у) dx + Q(x-, у) dy.
Найдем эту функцию. Искомая функция должна удовлетворять требованиям: л„, я,.
^ = P(x-,y)v^- = Q(x-,y). дх ду
Если в первом уравнении (48.20) зафиксировать у и проинтегрировать его по х, то получим:
и(х;у) = У P(x;y)dx + (р(у). (48.21)
Здесь произвольная постоянная с = <р(у) зависит от у (либо является числом). В решении (48.21) не известна лишь </>(?/)- Для ее нахождения продифференцируем функцию (48.21) по у:
^= ([ Р(х; у) dx) + <р'(у). ду \J 'у
Используя второе равенство (48.20), можно записать: О(ж;у) = (У P(x;y)dx)^ + <р'(у).
Отсюда .
<р'(у) = Q(^;y) - (у P(x;y)dx)y (48.22)
В равенстве (48.22) левая часть зависит от у. Покажем, что и правая часть равенства зависит только от у.
ЧЧО
Для этого продифференцируем правую часть по х и убедимся, что' производная равна, нулю. Действительно,
?®_l.(P) = ?Q_dP дх ду' ' дх ду
с, с — const.
в силу условия (48.19).
Из равенства (48.22) находим ср(у):
V>(y) = J (Q(x; у) - (J P(x; y) <
Подставляя найденное значение для ср(у) в равенство (48.21), находим функцию н(ж; у) такую, что du(x; у) — Р(х; у) dx + Q(t; у) dy.
Таким образом, при решении ДУ вида (48.17)-сначала, проверяем выполнение условия (48.19). Затем, используя равенства (48.20), находим функцию и(х,у). Решение записываем в виде (48.18).
5 — 2жн
Пример 48-11. Решить уравнение у' = —5-------Чу.
лу + ж
Q Решение: Запишем уравнение в дифференциальной форме: (2ху — 5) dx + (3j/2 + ж2) dy — 0.
Здесь Р(х',у) = 2ху — 5, Q(xyy) — З//2 + ж2. Проверяем выполнение условия (48.19):
^ = 2т. ^ = 2з,. d_L = dQ ду ’ дх ’ ду дх Следовательно, данное уравнение есть уравнение в полных дифференциалах. Условия (48.20) будут здесь выглядеть как
c)w _ ди „ 2 2
•— = 2ху - 5, —- = З?/2 + х2. дх ду
Отсюда имеем
«(ж; у) = у [2ху — 5) dx = х2у — 5х + <^(?/); — = (х2у - 5ж + <р(у))'у = х2 + ср'(у).
Далее
З?;2 + х2 = х2 + <р'(у), р'(у) — З?/2, ‘/’(г/) — у3 + о, ы(ж; у) = х2у ~ 5х + у3 + ci.
Общим интегралом является х2у— 5x+y3+ci = C2, или х2у — 5х+у3 = с, где с = сг - Ci. •
340
Если условие (48.19) не выполняется, то ДУ (48.17) не является уравнением в полных дифференциалах.
Однако это уравнение иногда можно привести к уравнению в полных дифференциалах умножением его на некоторую функцию Л(ж; //), называемую интегрирующим множителем.
Чтобы уравнение £(ж; у) Р(х; у) dx + t(x; у) Q(x; у) dy = 0 было уравнением в полных дифференциалах, должно выполняться условие
В д
-^(t(x-,y) р(х-,у)) = ‘
Выполнив дифференцирование -F + 4^ t = + и пРивеДя
подобные слагаемые, получим
at р _ . о = t(9(2 _
ду дх V дх ду)
(48.23)
Для нахождения Дж; у) надо проинтегрировать полученное ДУ в частных производных. Решение этой задачи не простое. Нахождение интегрирующего множителя может быть упрощено, если допустить существование t как функции только одного аргумента х либо только у. Пусть, например, t = 1(ж). Тогда уравнение (48.23) принимает вид
(BQ _ дР\ dx'^ \дх. дуР
U QP _ 52 dt Q-u ИЛИ — = ——
t
дх 1
— dx.
Отсюда
дР 8Q
&- 8Р dx
(48.24)
дР _
тт dii дх
При этом выражение - ----должно зависеть только от ж.
Аналогично получаем, что если t — t(y) (t не зависит от ж), то
/ 82 ар \
t(x/) = exp f у -8х--р 8у- dy),
а подынтегральное выражение должно зависеть только от у.
Пример 48-12. Решить уравнение (ж2 — у)-dx+ (ж2?/2 + ж)-dy = 0.
Q Решение: Здесь = — 1; = 2ху2 + 1, т. е. Однако
дР _ 8Q 2 1 о
ду дх _ -1 ~ 2жг/ - 1 _ —2
ж2 у2 + ж
зависит только от ж.
341
Следовательно, уравнение имеет интегрирующий множитель, зависящий только от х, выражение которого может быть получено при помощи формулы (48.24). В нашем случае получим, что
1
?'
Умножая исходное уравнение на t = , получаем:
/(.т) = exp
,2
т. е. уравнение в полных дифференциалах! Решив его, найдем, что общий интеграл заданного уравнения имеет вид
Z/
х
48.6. Уравнения Лагранжа и Клеро
Рассмотрим дифференциальные уравнения, неразрешенные относительно производной. К ним, в частности, относятся уравнения Лагранжа и Клеро.
Уравнение Лагранжа
Уравнение вида
у = х р(у ) + ф(у ), (48.25)
оде и — известные функции от у' = называется уравнением Лагранжа.
Введем вспомогательный параметр, положив у' — р. Тогда уравнение (48.25) примет вид
У = х- <р(р) + V’(p)-
Дифференцируя по х, получим:
g=V(p) + *V(p)-g +«'(₽) g,
т. е. р - <р(р) = (х + V>'(p)) • или
(р - <р(р)) — - X • <р'(р) =
Уравнение (48.27) есть линейное уравнение относительно неизвестной функции х = т(р). Решив его, найдем:
ж = Л(р;с).
(48.26)
(48.27)
(48.28)
342
Исключая параметрр из уравнений (48.26) и (48.28), получаем общий интеграл уравнения (48.25) в виде у = 7(ж;с).
Отметим, что, переходя к уравнению (48.27), мы делили на
При этом могли быть потеряны решения, для которых = 0, т. е. р = р0 = const. Это значение ро является корнем уравнения р—<р(р) = О (см. (48.27)).
Решение у = х-1р(ри)+'Ф(Ро) является особым для уравнения (48.25) (см. понятие особого решения в п. 48.2).
Уравнение Клеро
Рассмотрим частный случай уравнения Лагранжа при <р(т/') = у'-Уравнение (48.25) принимает вид
(48.29)
|ф| и называется уравнением Клеро.
Положив у' — р, получаем:
у = хр + V’(p)- (48.30)
у = х у' + V’(p')
Дифференцируя по х, имеем:
р = р + х- ~ +^'(р) • или (а; + ^'(р)) ~ = 0. ах ах ах
Если = 0, то р = с. Поэтому, с учетом (48.30), ДУ (48.29) имеет общее решение
у = хс + V’(c)- (48.31)
Если х + -ф'(р) ~ 0, то получаем частное решение уравнения в параметрической форме:
х = — у = хр + V>(p). (48.32)
Это решение — особое решение уравнения Клеро: оно не содержится в формуле общего решения уравнения.
Пример 48-13. Решить уравнение Клеро у — ху' + у'2.
Q Решение: Общее решение, согласно формуле (48.31), имеет вид у = = сх + с2. Особое решение уравнения получаем согласно формулам (48.32) в виде х = -2р, у = агр + р2. Отсюда следует: у = т. е.
»=-< •
343
§49. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
49.1. Основные понятия
Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записыва-
ется в виде
/Дж; у; у'\ у") = О
(49-1)
или, если это возможно, в виде, разрешенном относительно старшей производной:
у" = f(x-,y,y'). (49.2)
Будем в основном рассматривать уравнение вида (49.2): от него всегда можно перейти к (49.1).
Решением ДУ (49.2) называется всякая функция у — 'Дх), которая при подстановке в уравнение обращает его в тождество.
р>| Общим решением ДУ (49.2) называется функция у — <р(х~, щ; с^), где cj и С2 — не зависящие от х произвольные постоянные, удовлетворяющая условиям:
1. (Дх; Cj; С2) является решением ДУ для каждого фиксированного значения щ и с%.
2. Каковы бы ни были начальные условия
У = Уо, ?/ = у'о,
1ж=х®0 1ж=Я'о
(49.3)
i i
существуют единственные значения постоянных щ = с° и сг = с° такие, что функция у — (Дх;cj; с°) является решением уравнения (49.2) и удовлетворяет начальным условиям (49.3).
Всякое решение у — 99(2;с°; с°) уравнения (49.2), получающееся из общего решения у = у?(ж;С1;С2) при конкретных значениях постоянных Cj = с°, сг = t‘2, называется частным решением.
Решения ДУ (49.2), записанные в виде
Ф(ж; у; cj; сг) = 0, Ф(ж; у;с°; Cg) = О,
называются общим и частным интегралом соответственно.
График всякого решения ДУ второго порядка называется инте-
гральной кривой. Общее решение ДУ (49.2) представляет собой мно
жество интегральных кривых; частное решение — одна интегральная кривая этого множества, проходящая через точку (жо; ус) и имеющая в ней касательную с заданным угловым коэффициентом ?;'(жо) = у'.
Переписав ДУ (49.1) в виде
344
Видим, что ДУ второго порядка устанавливает связь между координатами точки (ж; у) интегральной кривой, угловым коэффициентом к = у' касательной к ней и кривизной К — в точке (ж; ;</). В этом
состоит геометрическое истолкование ДУ второго порядка.
Как и в случае уравнения первого порядка, задача нахождения решения ДУ (49.2), удовлетворяющего -заданным начальным условиям (49.3), называется задачей Коши.
Теорема 49.1 (существования и единственности задачи Коши). Если в уравнении (49.2) функция f(x-,y,y') и ее частные производные /' и непрерывны в некоторой области D изменения переменных ж. у и у', то для всякой точки (жо; ;</o;z/o) G D существует единственное решение у = Дж) уравнения (49.2), удовлетворяющее начальным условиям (49.3).
Примем теорему без доказательства.
Аналогичные понятия и определения имеют место для ДУ п-го порядка, которое в общем виде записывается ка
/^(ж; г/; з/'; ;?/г0) = 0,
ИЛИ , . / чч
у(п} = f («; у-, у'-, у"; - •; у{ = О, (49.4)
если его можно разрешить относительно старшей производной.
Начальные условия для ДУ (49.4) имеют вид
И = ?Л>, ?/| = у'о, у"1 = rf, Z/(n-1)| =:</о”-1)- (49.5)
1ж=Ж0 1ж=®0 1ж=Жо 1Ж=Жо
Общее решение ДУ n-го порядка является функцией вида
у = у?(ж;С1;с2;...;сп), содержащей п произвольных, не зависящих от ж постоянных.
Решение ДУ (49.4), получающееся из общего решения при конкретных значениях постоянных q — cj, с2 = с^, ..., с„ = с°, называется частным решением.
Задача Коши для ДУ n-го порядка: найти решение ДУ (49.4), удовлетворяющее начальным условиям (49.5).
Проинтегрировать (решить) ДУ n-го порядка означает следующее: найти его общее или частное решение (интеграл) в зависимости от того, заданы начальные условия или нет.
Задача нахождения решения ДУ n-го порядка сложнее, чем первого. Поэтому рассмотрим лишь отдельные виды ДУ высших порядков.
345
49.2. Уравнения, допускающие понижение порядка
Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной (подстановки) данное ДУ сводится к уравнению, порядок которого ниже.
Рассмотрим три типа уравнений, допускающих понижение порядка.
I. Пусть дано уравнение
У" = f (®)-
(49.6)
Порядок можно понизить, введя новую функцию р(ж), положив у' = = р(.с). Тогда у" = р'(х) и получаем ДУ первого порядка: р' = f (ж). Решив его, т. е. найдя функцию р = р(ж), решим уравнение у' = р(х). Получим общее решение заданного уравнения (49.-6).
На практике поступают иначе: порядок понижается непосредственно путем последовательного интегрирования уравнения.
Так как у" = (у')' = уравнение (49.6) можно записать в виде dy' = /(ж) dx. Тогда, интегрируя уравнение у" = f (ж), получаем: у' = [ f(x) dx, или у' = <рх(ж) + С1. Далее, интегрируя полученное уравнение по ж, находим: у = f(<Р1(ж) + щ) dx, т. е. у = </>2(ж) + Cix + с2 — общее решение данного уравнения.
Если дано уравнение
У(п} = №),
то, проинтегрировав его последовательно п раз, найдем общее решение . . тп-1 „п-2
уравнения: у = <рп(х) + а + с2 + • - + с„.
Пример 4&-1- Решить уравнение уп = зш2ж.
1
- СО8'2ж + С1,
Ci dx = — sin 2ж + сух + c2,
Q Решение: Последовательно интегрируя четыре раза данное уравнение, получим
у'" — I sin 2ж dx — —
у" = I — - cos 2ж dx + I
, 1 ж2
У — О cos 2ж + Cl — + с2ж + с3, Р 2
X- 1
У = Тс sin2a: + С1 + С2“Т + £“3® + С4. 16 6 2
346
II. Пусть дано уравнение
у" = !Ш
(49.7)
не. содержащее явно искомой функции у.
Обозначим у' = р, где р = р(х) — новая неизвестная функция. Тогда у" — р' и уравнение (49.7) принимает вид р' — f(x-p). Пусть Р = <р(х-, щ) — общее решение полученного ДУ первого порядка. Заменяя функцию р на у', получаем ДУ: у' = tp(x-,ci). Оно имеет вид (49.6). Для отыскания у достаточно проинтегрировать последнее уравнение. ()бщее решение уравнения (49.7) будет иметь вид У — [ ci) дх + с^.
Частным случаем уравнения (49.7) является уравнение
У" = /У), | (49.8)
не содержащее также и независимую переменную х. Оно интегрируется гем же способом: у’ = р(х), у" = р' — Получаем уравнение р' — f(p) с разделяющимися переменными.
Если задано уравнение вида
F(®;^fc);y(fc+1);...;p(n)) = 0?| (49.9)
которое также не содержит явно искомой функции, то его порядок можно понизить на к единиц, положив у№ = р(®). Тогда у(к+1> = р'; ...; p(n) = p(n-fc) и уравнение (49.9) примет вид F(®;p;p';... ;p(”_ft)) = 0.
Частным случаем уравнения (49.9) является уравнение
F(x-,y<n-l\y&>) = 0,
ИЛИ ----------------
у(п) = f^y(n~l)Y
С помощью замены = р(х), у^ — р' это уравнение сводится к ДУ первого порядка.
Пример 49.2. Решить уравнение у" — = 0.
Q Решение: Полагаем у' — р, где р = р(.т), у" = р'.
Тогда р' — = 0. Это уравнение с разделяющимися переменны-
ми: Интегрируя, получим In |р| = 1п|®| + In |cj|,
€lX х р 3’
In |р| = In |ci®|, p = Ci®. Возвращаясь к исходной переменной, получим г 2
у' = ci®, у = Ci + С2 — общее решение уравнения. •
347
III. Рассмотрим уравнение
у" = f(y; у'),
(49.10)
которое не содержит явно независимой переменной х.
Для понижения порядка уравнения введем новую функцию р = — р(у), зависящую от переменной у, полагая у' = р. Дифференцируем это равенство по х, учитывая, что р = р(у(х)):
п = d(y') _ dp(y) _ dp(y) dy _ dp(y) dx dx dy dx dy ’
t. e. у"=Р'(^- Теперь уравнение (49.10) запишется в видер-^ = /(р;р). Пусть р = <р(р;сх) является общим решением этого ДУ первого порядка. Заменяя функцию р(р) на у', получаем у' — щ) — ДУ с разделяющимися переменными. Интегрируя его, находим общий интеграл уравнения (49.10):
= х + с2.
Частным случаем уравнения (49.10) является ДУ
Такс» уравнение решается при помощи аналогичной подстановки: у' = = р(?/)> у” = р-
Так же поступаем при решении уравнения F(p; р'; у";...; у^) = 0. Его порядок можно понизить на единицу, положив у' = р, где р = р(р). По правилу дифференцирования сложной функции находим у" =Р^~-Затем найдем у'" = ^(Р' Ру) = -^(Р' Ру)' = Р((РУ)2 + Р ’ Руу) и т. д.
Замечание. Уравнение (49.8) также можно решать, применяя подстановку у' = р, где р = р(р).
Пример 49.3. Найти частное решение уравнения ?/'-(?/)2+р'(р-1) = о, удовлетворяющее начальным условиям: р(0) = 2, у'(0) — 2.
Q Решение: Уравнение имеет вид (49.10). Положив у' = р(у), у‘ dp
= р- получаем:
р- -р2+р(р - 1) = 0.
348
Гак как р 0 (иначе у' = 0, что противоречит начальному условию у1 = 2), то — р+у— 1 = 0 - получили линейное ДУ первого порядка.
Проведем решение полученного линейного ДУ методом Бернулли (п. 48.4). Полагаем р — и и. Имеем: u'v + uv' — uv + у — 1 = О, или u'v + u(v' — v) = 1 — у.
Подберем функцию и так, чтобы v' — v = 0. Тогда ~ = dy, v = еу. Получаем:
и' • еу + и 0 = 1 — у, т. е. du = (1 — у) е~у dy.
Интегрируя это равенство, находим, что и = —(1 — у) - еу + е~у + ci. Следовательно,
р = Uv = ((— 1 + y)e~v + e~v + cj • е+у, или р — + у.
Заменяя р на у', получаем: у' = сг еу + у. Подставляя у' — 2 и у = 2 в это равенство, находим ci:
2 = С1е2+2, п=0.
Имеем у' = у. Отсюда у = С2вж. Находим сг из начальных условий: 2 = С2в°, с-2 = 2. Таким образом, у = 2еж — частное решение данного ДУ. •
49.3. Линейные дифференциальные уравнения высших порядков
Основные понятия
Многие задачи математики, механики, электротехники и других технических наук приводят к линейным дифференциальным уравнениям.
Уравнение вида,
Ьо(ж)?/(п) + 61 Ш''1 + - • + Ьп(х)у = д(х), (49.11)
где Ьо(ж) Д 0, bi(х),...,Ъп(ж),д(х) — заданные функции (от ж), называется линейным ДУ п-го порядка.
Оно содержит искомую функцию у и все ее производные лишь в первой степени. Функции Ьо(ж), bi (ж),..., Ьп(ж) называются коэффициентами уравнения (49.11), а функция д(х) — его свободным членом. М Если свободный член д(х) = 0, то уравнение (49.11) называется линейным однородным уравнением; если д(х) Д 0, то уравнение (49.11) называется неоднородным.
Разделив уравнение (49.11) на Ьд(ж) Д) и обозначив bi (ж) _ с 1 Ъп(х) _ д(х) _ ,
Ь0(Ж) й1(ж)’--”Ьо(ж) "а’г(ж)’Ь0(ж)
349
запишем уравнение (49.11) в виде приведенного-.
у^ + а1(х)у(п~г> + о.2(ж)Д”-2) + - • + ап(х)у = /(ж). (49.12)
Далее будем рассматривать линейные ДУ вида (49.12) и считать, что коэффициенты и свободный член уравнения (49.12) являются непрерывными функциями (на некотором интервале (а; Ь)). При этих условиях справедлива теорема существования и единственности решения ДУ (49.12) (см. теорему 49.1).
49.4. Линейные однородные ДУ второго порядка
Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка:
(49.13)
и установим некоторые свойства его решений.
у" + аДж)Д + а2(ж)?/ = О
Теорема 49.2. Если функции yi = ?д(ж) и у2 — уъ^х) являются частными решениями уравнения (49.13), то решением этого уравнения является также функция
У = ci yi (ж) + с2у2 (ж), (49.14)
где ci и с2 — произвольные постоянные.
□ Подставим функцию у = cpyi +с2у2 и ее производные в левую часть ЛОДУ (49.13). Получаем:
(С1У1 + С2У2)" + аДж) (ci»/i + с2у2)’ + а2(х) (сруу + С2У2) = = Сру" + С2У2 + (ж) • (ciy{ + с2у2) + а2(ж) • (сруг + с2у2) = = С1(у" + аДж) -у\ +а2(ж) - у) +с2(у" + аДж)Д> + а2(ж)г/2) =
= cj 0 + е2 • 0 = О, так как функции yi и у2 — решения уравнения (49.13) и, значит, выражения в скобках тождественно равны нулю.
Таким образом, функция у = суу^ -\-с2у2 также является решением уравнения (49.13).
Из теоремы 49.2, как следствие, вытекает, что если у\ и у2 — решения уравнения (49.13), то решениями его будут также функции У = 1/1 +У2 и у = с-у1.
Функция (49.14) содержит две произвольные постоянные и является решением уравнения (49.13). Может ли она являться общим решением уравнения (49.13)?
350
Для ответа на вопрос введем понятие линейной зависимости и линейной независимости функций.
Функции yi = 2/1(ж) и ;</2 = У2('х) называются линейно независимыми на интервале (о; 6), если равенство
aiv/i + «2Z/2 = 0, (49.15)
где 01,02 € К, выполняется тогда и только тогда, когда О] = аг = 0.
Если хотя бы одно из чисел oi или а2 отлично от нуля и выполняется равенство (49.15), то функции уг и т/2 называются линейно зависимыми на (а; Ь).
Очевидно, что функции у\ и у2 линейно зависимы тогда и только тогда, когда они пропорциональны, т. е. для всех х € (а; Ъ) выполняется равенство ^- = А, или у\ = Ат/2, А = const.
Z/2
Например, функции ?д = Зеж и ;т/2 = ех линейно зависимы: = = 3 = const; функции тд и уз = е2ж — линейно независимы: =
— Зе-Ж const; функции 3/4 = sina; и 7/5 = cosa; являются линейно независимыми: равенство сц sina; + «2cosх = 0 выполняется для всех а: € Ж лишь при сц =«2 = 0 (или = tga; const).
Средством изучения линейной зависимости системы функций является так называемый определитель Вронского или вронскиан (Ю. Вронский — польский математик).
Для двух дифференцируемых функций ух = yi(x) и у 2 = yi{x) вронскиан имеет вид —-------------------
ИДа;) =
У1 У2
У1 У2
Имеют место следующие теоремы.
Теорема 49.3. Если дифференцируемые функции yi(x) и 7/2(ж) линейно зависимы на (а;Ь), то определитель Вронского на этом интервале тождественно равен нулю.
□ Так как функции у\ и у2 линейно зависимы, то в равенстве (49.15) значение сд или а2 отлично от нуля. Пусть 0, тогда у\ = ——у2, поэтому для любого х 6 (о; Ь)
ТУ(а;) =
-^2
-^2
У2
У2
= 0.
Теорема 49.4. Если функции тд(а;) и т/2(а;) — линейно независимые решения уравнения (49.13) на (а;Ь), то определитель Вронского на этом интервале нигде не обращается в нуль.
351
Доказательство теоремы опустим.
Из теорем 49.3 и 49.4 следует, что вронскиан не равен нулю ни в
одной точке интервала Ь) тогда и только тогда, когда частные
решения линейно независимы.
Совокупность любых двух линейно независимых на интервале
(а; Ъ) частных решений у\(х) и 2/2 (ж) ЛОДУ второго порядка опре
деляет фундаментальную систему решении этого уравнения:
любое произвольное решение может быть получено как комбинация, у = 012/1 (ж) +«2 2/2 (ж).
Пример 49-4- Частные решения 2/1 = sin ж и у2 = cosx, уз — 2ишж и 1/4 = 5 cos ж (их бесчисленное множество!) уравнения у" + у = О образуют фундаментальную систему решений; решения же 2/5 = 0 и 2/6 = cos ж — не образуют.
Теперь можно сказать, при каких условиях функция (49.14) будет, общим решением уравнения (49.13). 1
Теорема 49.5 (структура общего решения ЛОДУ второго порядка). Если два частных решения уг = yi(x) и 2/2 = ’/2 (ж) ЛОДУ (49.13) образуют на интервале (а; Ь) фундаментальную систему, то общим решением этого уравнения является функция
У = 02/1 + С22/2, (49.16)
где С] и С2 — произвольные постоянные.
□ Согласно теореме 49.2, функция (49.16) является решением уравнения (49.13). Остается доказать, что это решение общее, т. е. что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
2/| = 2/о, 2/1 =2/о, (49.17)
I X~Xq I X—Xq
где ж0 е (а; Ъ).
Подставив начальные условия (49.17) в решение (49.14), получим систему уравнений
( 2/о = С12/1(ж0) + с2?/2(жо),
У о = <аУ1(хо) + С2У'2(ХО),
где r/о = 2/(жо), у'о = у'(хо), с неизвестными сг и с2. Определитель этой системы
2/1 (жо) 2/2 (ж0)
2/10о) 2/2^0)
равен значению вронскиана W (ж) при ж = Жо.
= ИДжо)
352
Уо У2(хо) __ о 1 У1(хо) уо
Уо У'Лхо) ' 2 2 Ж(ж0) У'х Оо) Уо
Так как решения уг (ж) и y^ix) образуют фундаментальную систему решений на (а;Ь) и Жо С (а;Ь), то, согласно теореме 49.4, 1У(жо) 0. Поэтому система уравнений имеет единственное решение:
_ о 1
'' 1 ИДж0) ’
Решение у = Cj.vi (ж) + <^?/2(ж) является частным решением (единствен-.... в силу теоремы единственности) уравнения (49.13), удовлетворяющим начальным условиям (49.17). Теорема доказана. И
Пример 49.5. На основании теоремы 49.5 общим решением уравнения у" +?/=0 (см. пример 49.4) является функция у=Сх siii.'c+c2 созж.
49.5. Линейные однородные ДУ n-го порядка
Полученные результаты можно распространить на линейные однородные дифференциальные уравнения n-го порядка, имеющие вид
у^ + аДж) + а2(ж) • y(n~V +...+ ап(ж) • у = о. (49.18)
1. Если функции У1 = Ух(х),У2 = 35/2(ж), - - . , z/n = Уп(х) являются частными решениями уравнения (49.18), то его решением является и функция у = С1У1 + с2;</2 + - • • + спуп-
2. Функции ух, У2, • • • ,уп называются линейно независимыми на (а; Ь), если равенство ахУх + 01.2У2 + . - + оспУп — 0 выполняется лишь в случае, когда все числа о; = 0 (г = 1,2, ...,п); в противном случае (если хотя бы одно из чисел сц не равно нулю) функции ух, У2, • • •, Уп ~ линейно зависимы.
3. Определитель Вронского имеет вид
У1 У2 Уп
У2 У'п
Ж(ж) = у" У 2 Уп
(п—1) У1 (п—1) У 2 Уп
4. Частные решения ?/i,?/2, • • • ,.%> уравнения (49.18) образуют фундаментальную систему решений на (а; Ь), если ни в одной точке этого интервала вронскиан не обращается в нуль, т. е. W (ж) 0 для всех ж 6 (а; Ь).
5. Общее решение ЛОДУ (49.18) имеет вид у ~ СхУх+с2У2+-. -+спуп, где Ci (i = 1,..., п) — произвольные постоянные, гц — частные решения уравнения (49.18), образующие фундаментальную систему.
12 Конспект лекций по высшей математике. Полный курс
353
Пример 49.6. Показать, что функции у1=ех, у2=х-ех, у3=х2 г' образуют фундаментальную систему решений некоторого ЛОДУ три тьего порядка (дополнительно: составить это уравнение).
Q Решение: Найдем Ж (ж):
ех хех х2ех
W(x) = ех (х + 1)еж (х2 + 2ж)еа! =
(х + 2)ех (ж2 + 4ж + 2)ех
1 X X2 1 Ж X2
= е3х 1 х + 1 х2 + 2х = е Зж 0 1 2ж
1 х + 2 х2 -J- 4х -J- 2 0 2 4х + 2
= е3х (4ж + 2 - 4ж) = 2е3ж.
Ясно, что И'(ж) =4 0 для всех х € R. Следовательно, данные функции образуют фундаментальную систему решений ЛОДУ третьего порял ка. В общем виде ЛОДУ третьего порядка выглядит так:
у'" + аДх)у" + аг (х)у' + «Дж)?/ = 0.
Подставив функции уг, у2, уз в это уравнение, получим систему из трех уравнений относительно функций нДж), «2 (ж), а3(х). Решая ее, получим ЛОДУ у'" — Зу" + Зу' — у = 0; его общее решение:
у = ще® + С2«еж + с3х2ех. •
§50 . ИНТЕГРИРОВАНИЕ ДУ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
50.1. Интегрирование ЛОДУ второго порядка с постоянными коэффициентами
Частным случаем рассмотренных выше линейных однородные ? дифференциальных уравнений являются ЛОДУ с постоянными коэф»*, фициентами.
Пусть дано ЛОДУ второго порядка
(50.1) где р и q постоянны.
Для нахождения общего решения уравнения (50.1) достаточно найти два его частных решения, образующих фундаментальную систему (см. теорему 49.5).
Будем искать частные решения уравнения (50.1) в виде
У = екх,
у" +ру' +qy = O,
354
пн; к — некоторое число (предложено Л. Эйлером). Дифференцируя । гу функцию два раза и подставляя выражения для у, у' и у" в урав-.... (50.1), получим: к2 • екх + р - к • екх + q екх = 0, т. е.
екх • (fc2 + рк + q) = 0, или к2 +рк + q = 0 (екх 0). (50.2)
)'i>| Уравнение (50.2) называется характеристическим уравнением ДУ (50.1) (для его составления достаточно в уравнении (50.1)
•аменить у", у' и у соответственно на fc2, fc и 1).
При решении характеристического уравнения (50.2) возможны следующие три случая.
Случай 1. Корни fcj и fc2 уравнения (50.2) действительные и различные: fci У k2 — q > о).
В этом случае частными решениями уравнения (50.1) являются функции у1 = ек1Х и у2 = ек2Х. Они образуют фундаментальную систему решений (линейно независимы), т. к. их вронскиан
W(x) =
„klX „k2X
с К-
kieklX к2ек2Х
= к2е(к1+к2',х - k!e(kl+k2)x =
= е(Л1+Л2)Ж . 0
Следовательно, общее решение уравнения (50.1), согласно формуле
(49.16), имеет вид
у = С1ек1Х + c2ekzX.
(50.3)
Пример 50.1. Решить уравнение у" — 5у' + бу = 0.
Q Решение: Составим характеристическое уравнение: к2 — 5fc + 6 = 0. Решаем его: fci = 2, fc2 = 3. Записываем общее решение данного уравнения: у — cie2x + с2е3х, где ci и с2 — произвольные постоянные (формула (50.3)). •
Случай 2. Корни fci и fc2 характеристического уравнения (50.2) действительные и равные: к\ = к2 (d = — q = 0, fci = fc2 = —
В этом случае имеем лишь одно частное решение yi = ек1Х.
Покажем, что наряду с yi решением уравнения (50.1) будет и у2 =
Действительно, подставим функцию у2 в уравнение (50.1). Имеем:
+РУ’2 + да = (^)" + р(хек’х)' + q(xe*1X) =
= (2kreklX + хк%ек1Х) + р(ек1Х + xkieklX) + q(xek*x) =
= efcl3:(2fci + k3x +p+pxki +qx) = ekiX(x[k\ +pki +q) + (p + 2fci)).
355
Ho ki +pki +q = 0, т. к. kt есть корень уравнения (50.2); p+2fci = т. к. по условию кх = fc2 — — 2’
Поэтому ;</2 + Р?/-2 + <71/2 = 0, т. е. функция у2 = хек1Х являет» решением уравнения (50.1).
Частные решения ух — ек1Х и у2 = хек1Х образуют фундаментал ную систему решений: W(:с) = e2fcl® 0. Следовательно, в этом случ! общее решение ЛОДУ (50.1) имеет вид
у = дек'х +с2хекгЯС.\ (50.
Случай 3. Корни кх и к2 уравнения (50.2) комплексные: кх = а+/:
к2 = а - /Зг (D = - q < 0, а = /3 = > 0).
В этом случае частными решениями уравнения (50.1) являют» функции уг = е(а+«/3).т и у2 _ е(а-г/3)х цо фОрМуЛам Эйлера (см. П. 27.
etv = cos <р + i sin <p, е~г<р = eosip — issup
имеем
yi = eax ei0x = eax cos /Зх + ieax sin /Зх, y2 — eax • е~г13х = eax cos/3x — ieax sin/te.
Найдем два действительных частных решения уравнения (50.1).
Для этого составим две линейные комбинации решений ух и у2:
?/1 + ?/2 о,ж а ~ У1 ~ У2 ат о ~
—-— = е cos/Зх = ух и ——— = е sm/Зх = у2. 2 2г
Функции ух и у2 являются решениями уравнения (50.1), что следуе из свойств решений ЛОДУ второго порядка (см. теорему 49.2).Эти ре шения ух и у2 образуют фундаментальную систему решений, так кал И'(:с) 0 (убедитесь самостоятельно!). Поэтому общее решение уран
нения (50.1) запишется в виде у = схеах cos^x + с2еах sin/Зх, или
(50.5);
у = eax (ci cos /Зх + c2 sin /Зх).
Пример 50.2. Решить уравнение у" — Су' + 25»/ = 0.
Q Решение: Имеем: к? — 6к + 25 = 0, кх = 3 + 4г, к2 = 3 — 4г. По формуле (50.5) получаем общее решение уравнения:
у = е3х (ci cos 4т + с2 sin 4х). •
Таким образом, нахождение общего решения ЛОДУ второго порядка с гоютоянными коэффициентами (50.1) сводится к нахождению корней характеристического уравнения (50.2) и использованию формул (50.3)-(50.5) общего решения уравнения (не прибегая к вычислению интегралов).
356
50.2. Интегрирование ЛОДУ n-го порядка с постоянными коэффициентами
Задача нахождения общего решения ЛОДУ n-го порядка (п > 2) с постоянными коэффициентами
у{п} + я у^ + Wn-2) + . • • + РпУ = о, (50.6) где pi, г — 1,п, — числа, решается аналогично случаю уравнения второго порядка с постоянными коэффициентами.
Сформулируем необходимые утверждения и рассмотрим примеры. Частные решения уравнения (50.6) также ищем в виде у = екх, где к — постоянное число.
Характеристическим для уравнения (50.6) является алгебраическое уравнение n-го порядка вида
кп +р1кп~г + р2кп~2 + ... +pn-ik + рп = 0- (50.7)
Уравнение (50.7) имеет, как известно, п корней (в их числе могут быть и комплексные). Обозначим их через к\, к2, •, кп.
|@| Замечание. Не все из корней уравнения (50.7) обязаны быть различными. Так, в частности, уравнение (к — З)2 = 0 имеет два равных корня: kt = к2 = 3. В этом случае говорят, что корень один (к = 3) и имеет кратность ть = 2. Если кратность корня равна единице: mk — 1, его называют простым.
Случай 1. Все корни уравнения (50.7) действительны и просты (различны). Тогда функции = ек1Х, у2 = ек2Х, ... ,уп = екпХ являются частными решениями уравнения (50.6) и образуют фундаментальную систему решений (линейно независимы). Поэтому общее решение уравнения (50.6) записывается в виде
у = схек1Х + с2е*2Ж + ... + спекпХ.
Пример 50.3. Найти общее решение уравнения
у'" - 2у" -у'+ 2у = 0.
Q Решение: Характеристическое уравнение к3 — 2к2 — к + 2 = 0 имеет корни ki = — 1, к2 = 1 ,кз = 2. Следовательно, у — С!е~х + с2ех+с3е2х — общее решение данного уравнения. •
Случай 2. Все корни характеристического уравнения действительные, но не все простые (есть корни, имеющие кратность т > 1). Тогда каждому простому корню к ссютветствует одно частное решение вида екх, а каждому корню к кратности т > 1 соответствует т частных решений: екх, хекх, х2екх ..., хгп~1екх.
Пример 50.4- Решить уравнение yIV — у"' — Зу" + 5у' — 2у — 0.
357
Q Решение: Характеристическое уравнение
к4 - к3 - 3fc2 + 5к - 2 = (fc + 2)(fc - I)3 = О
имеет корни ki = —2, fc2 = 1, fc3 = 1, fc4 = 1. Следовательно, у = Cie~2x + с2ех 4- сзхех + с4аг2еж
— общее решение уравнения.
Случай 3. Среди корней уравнения (50.7) есть комплексно-сопр женные корни. Тогда каждой паре а ± /Зг простых комплексно-с пряженных корней соответствует два частных решения еах cos /Зх еах sin /Зх, а каждой паре а ± /Зг корней кратности т > 1 соответствуй 2m частных решений вида
еах cos /Зх, х еах cos /Зх,..., ж”1"1 -еах cos /Зх;
еах sin/Зх, х еах sin /Зх,..., хт~г еах sin /Зх.
Эти решения, как можно доказать, образуют фундаментальную сист му решений. ।
Пример 50.5. Решить уравнение yv + yIV + 2у"' + 2у" + у' +у = J
Q Решение: Характеристическое уравнение
fc5 + fc4 + 2fc3 + 2fc2 + fc + 1 = (fc + l)(fc4 + 2fc2 + 1) = 0 имеет корни fci = — 1, fc2 = г, кз = —i, k^ = i, кз = —г. Следовательно, у = c\e~~x + c2 - cosx + c3 sin® + c4.r - cos a; + c$x sin a;
— общее решение уравнения. (
§51 . ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (ЛНДУ) 51.1. Структура общего решения ЛНДУ второго
порядка
Рассмотрим ЛНДУ второго порядка у
у” + а^х^у' + а2/х)у = f(x), (51.1)
где «1 (х), а2 (ar), f (а?) — заданные, непрерывные на (а; Ь) функции. У равнение
у" + oi (х)у' + а2(х)у = 0, (51.2)
g левая часть которого совпадает с левой частью ЛНДУ (51.1), называется соответствующим ему однородным уравнением.
358
Теорема 51.1 (структура общего решения ЛНДУ). Общим решением у уравнения (51.1) является сумма его произвольного частного решения у* и общего решения у = ciyi + C2Z/2 соответствующего однородного уравнения (51.2), т. е.
У = У*+У- (51.3)
IJ Убедимся, что функция (51.3) — решение уравнения (51.1). Так как у* есть решение уравнения (51.1), а у— решение уравнения (51.2), то
(;</*)" + щ (ж) (:</*)' + 02 (х)у* = /(ж) и (у)" + а1(х)(уУ + а2(х)у = 0.
I $ таком случае имеем:
(У* + У)" + ai (х)(у* + у)' + аг («)(?/* + У) =
= ((»/*)" + О1(ж)(г/*)' +о2(«):/) + ((у)" + oi(a;)(y)' + а2(х)у) = = f (ж) + 0 = /(ж).
Это означает, что функция (;</*+«/) является решением уравнения (51.1). Покажем теперь, что функция
У = У* + С1У1 + с2'У2 (51-4)
является общим решением уравнения (51.1). Для этого надо доказать, что из решения (51.4) можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
;</(а;о) = уо, у'(х0) = у'о- (51.5)
Продифференцировав функцию (51.4) и подставив начальные условия (51.5) в функцию (51.4) и ее производную, получим систему уравнений:
J С1щ(ж0) + с2г/2(жо) = Уо - У*(жо), (С134(жО) + С2У2(х0) - Уо- (у*У(х0), где уо = у(хоУ у'о = у'(хо), с неизвестными щ и с2. Определителем этой системы является определитель Вронского ИДжо) для функции ?/1(ж) и ;</2(ж) в точке х = ж0- Функции щ(ж) и 3/2 (ж) линейно независимы (образуют фундаментальную систему решений), т. е. W(.z?o) У 0. Следовательно, система имеет единственное решение: щ = cj и сг = с°.
Решение у = у* + <цй(ж) + <2//2 (ж) является частным решением уравнения (51.1), удовлетворяющим заданным начальным условиям (51.5). Теорема доказана. И
359
51.2. Метод вариации произвольных постоянных J
Рассмотрим ЛНДУ (51.1). Его общим решением является фут ция (51.3), т. е.
У = У* + У- ’
Частное решение у* уравнения (51.1) можно найти, если известно оС щее решение у соответствующего однородного уравнения (51.2), меть дом вариации произвольных постоянных (метод Лагранжа), состоя щим в следующем. Пусть у = сру^ (x'j+cpyvtx) — общее решение уравне-' ния (51.2). Заменим в общем решении постоянные cj и с2 неизвестными функциями сДж) и с2(ж) и подберем их так, чтобы функция
У* = ci(x) - yL(x) + с2(ж) у2(ж) (51.6)
была решением уравнения (51.1). Найдем производную
(У*)' = Citxjyitx) + С1(ж)у((ж) + d2(x)y2(x'f+ с2(х)у2(х).
Подберем функции ci (ж) и с2 (х) так, чтобы
с'1(ж) • У1(ж) + с2(ж) ’ У^х) = 0. (51.7)
Тогда
(?/*)' = с1(ж) • у\ (х) + с2(х) • у'2(х),
(у*)" = ci (ж) • у[ (ж) + а (ж) • у" (х) + 4 (ж) • у2 (ж) + с2 (ж) у2 (х).
Подставляя выражение для у*, (у*)1 и (у*)" в уравнение (51.1), полу< чим: '
ci (ж) • у'1 (ж) + ci (х) у" (ж) + с'2 (ж) - у2 (ж) + с2 (ж) у" (ж)+ +а1(ж)[с1(ж)уДж)+с2(ж)у2(ж)]+а2(ж)[с1(ж)у1(ж)+с2(ж)у2(ж)] = /(ж), -j
или
С1(ж) • [у"(ж) + (11(х) у((ж) + «2(ж) У1(ж)] + +С2(ж)[у2(ж)+а1(ж)у2(ж)+а2(ж)у2(ж)] +с'1(ж)у((ж)+с2(ж)у2(ж) = /(ж). > Поскольку-yi(ж) и у2(ж) — решения уравнения (51.2), то выражения в квадратных скобках равны нулю, а потому
с'1 (ж) • У1 (ж) + с^(ж) - у2(ж) = /(ж). (51.8)
Таким образом, функция (51.6) будет частным решением у* уравнения (51.1), если функции сДж) и с2(ж) удовлетворяют системе уравнений (51.7) и (51.8):
с((ж) -у](ж) +4(ж) -у2(ж) =0, c'i(ж) • У1 (ж) + с'2(х) у^(ж) = /(ж).
360
Определитель системы
У1(х) у2(х)
У1(х) у'2(х)
± 0, так как это определитель
Вронского для фундаментальной системы частных решений yi(x) и
ц2(х) уравнения (51.2). Поэтому система (51.9) имеет единственное решение: сДа:) = <р1(я:) и с!2(х) = </>2(а:), гДе </?1(ж) и учДа:) — некоторые функции от х. Интегрируя эти функции, находим сДа?) и с2(а:), а затем ш> формуле (51.6) составляем частное решение уравнения (51.1).
Пример 51.1. Найти общее решение уравнения у" 4- у —
Q Решение: Найдем общее решение у соответствующего однородного уравнения у"+у = 0. Имеем: к2 4-1 = 0, ki = i, к2 = —г. Следовательно, // = ci • cos а: 4- с2 • sin ж. Найдем теперь частное решение у* исходного уравнения. Оно ищется в виде (51.6): у* = ci(a:) • cos а: 4-с Да:) - sinж. Для нахождения сДа:) и сДа:) составляем систему уравнений вида (51.9):
с{(х) • cos а: + с2(х) • sina: = 0, с'Дж) • (-sina:) + с'2(х) • cosx =
Решаем ее:
Д =
cos х sin х — sin x cos x
= cos2 х 4- sin2 х = 1,
0 i
COS Ж
/ / X Д1 Cl (ж) = -д-
Д1 =
cos x 0
— sin x (
= — tga:, ci (ж) = j (— tga:) dx = In | cosa:|;
sina: cos а:
= — tga:, Д2 —
= 1;
2X2 f
c2(x) ~ ЛГ = 1’ c2(a:) = / 1 • dx = x.
Запишем частное решение данного уравнения: у* = In | cos х | cos а; 4-+ х sina:. Следовательно, общее решение данного уравнения имеет вид
у — (у + у*') = щ cos а: + с2 • sina: 4- cos а: - In | cosa:| + х sina:. •
При нахождении частных решений ЛНДУ может быть полезной следующая теорема.
Теорема 51.2 (о наложении решений). Если правая часть уравнения (51.1) представляет собой сумму двух функций: /(а:) = /Да:) + + /2(а:), a «/j и 7/2 — частные решения уравнений у" 4- а Да:) • у' 4-+ а2(х) у = /Да:) и у" + аДа:) • у' 4- а2(х)у = f2(x) соответственно, то функция у* = т/j + у2 является решением данного уравнения.
361
□ Действительно,
(у? + У2)" + «1(ж) (У1* + УгУ + «2(х-) • (уГ +у^ =
- ((уГ)" + <ч(ж) • (У1У + а2(ж) • У1) + ((7/2)" + «1U') • (.У2У + а2(а:) у^) = /1(ж) + h{x) = /(ж).
51.3. Интегрирование ЛНДУ второго порядка с постоянными коэффициентами и правой частью специального вида
у" +р-у' +<Г У = f(x),
Рассмотрим ЛНДУ второго порядка с постоянными коэффицт тами, т. е. уравнение
(51.10)
где р и q — некоторые числа.
Согласно теореме 51.1, общее решение уравнения (51.10) представляет собой сумму общего решения у соответствующего однородного уравнения и частного решения у* неоднородного уравнения. Частное решение уравнения (51.10) может быть найдено методом вариации произвольных постоянных (и. 51.2).
Для уравнений с постоянными коэффициентами (51.10) существует более простой способ нахождения у*, если правая часть /(ж) уравнения (51.10) имеет так называемый «специальный вид»:
I. /(ж) = Рп(ж) еах или
II. /(ж) = еах (Рп(ж) • cos/Зж 4- <2то(ж) • sin/Зж).
Суть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части /(ж) уравнения (51.10) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в уравнение (51.10) и из полученного тождества находят значения коэффициентов.
Случаи 1. Правая часть (51.10) имеет вид /(ж) = Рп(.%) • е“ж, где а 6 R, Рп(х) — многочлен степени п. Уравнение (51.10) запишется в
(51.11)
В этом случае частное решение у* ищем в виде:
(51.12)
у" +р-у' + g-y = РДх) еах.
у* = хг • Qn(x) еах,
где г — число, равное кратности а как корня характеристического уравнения fc2 + pk + q = 0 (т. е. г — число, показывающее, сколько раз а является корнем уравнения k2 + pk + q = 0), a Qn(x) — Аож" + + А1Ж”-1 + ... + Ап — многочлен степени п, записанный с неопределенными коэффициентами А, (г = 1,2,... ,п).
362
I Jl а) Пусть а не является корнем характерист ического уравнения к2 + pk + q = О,
г. с. а У Ацд. Следовательно,
г = 0, у* = Q„(x) еах, (у*)' = Q'n(x) еах + Qn(x) • еах • а, (у*)" = Q'^x) • еах + 2Q'n(x) еох а + Qn(x) - еах - а2.
После подстановки функции у* и ее производных в уравнение (51.11), сокращения на еах, получим:
Q"(x) + (2о + Р)С?п(ж) + (°2 +pa + q) Qn(x) = Рп(х). (51.13) Слева — многочлен степени п с неопределенными коэффициентами, справа — многочлен степени п, но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях х, получим систему (п + 1) алгебраических уравнений для определения коэффициентов A), Al, Ап.
б) Пусть а является однократным (простым) корнем характеристического уравнения к2 +рк + q = 0, т. е. а = к\ к%.
В этом случае искать решение в форме у* = Qn(x)eax нельзя, т. к. о2 + pa + q = 0, и уравнение (51.13) принимает вид
0"(ж) + (2а + р) Q’n(x) = Рп(х).
В левой части — многочлен степени (п — 1), в правой части — многочлен степени п. Чтобы получить тождество многочленов в решении у*, нужно иметь многочлен степени (п + 1). Поэтому частное решение у* следует искать в виде у* = х • Qn(x)ea:r' (в равенстве (51.12) положить г = 1).
в) Пусть а является двукратным корнем характеристического уравнения к2+pk+q = 0, т. е. а = к] = к%. В этом случае a2+pa+q = О и 2а+р = 0, а поэтому уравнение (51.13) принимает вид Q"(x) = Рп(х).
Слева стоит многочлен степени п — 2. Понятно, чтобы иметь слева многочлен степени п, частное решение у* следует искать в виде
У* = x2Qn(x)eax
(в равенстве (51.12) положить т = 2).
Случай 2. Правая часть (51.10) имеет вид
Дх) = еах - (Рп(х) cos/Зх + Qm(x) sin/Зх), где Рп(х) и Qm(x) — многочлены степени п и m соответственно, а и /9 — действительные числа. Уравнение (51.10) запишется в виде
у" +ру' + qy = еах (Рп(х) cos/Зх + Qm(x) sin/Зх). (51.14)
363
Можно показать, что в этом случае частное решение у* уравнения (51.14) следует искать в виде
у* = хг еах (Mi(x) cos/Зх 4- ЛДж) • sin/?®), (51.15)
где г — число, равное кратности a+/3i как корня характеристического уравнения к"2 + рк + q = 0, Л1/(ж) и Ni(x) — многочлены степени I с неопределенными коэффициентами, I — наивысшая степень многочленов Рп(х) и Qm(®), т. е. Z = тах(тг,г/г).
Замечания.
1. После подстановки функции (51.15) в (51.14) приравнивают многочлены, стояшие перед одноименными тригонометрическими функциями в левой и правой частях уравнения.
2. Форма (51.15) сохраняется и в случаях, когда Рп(х) = 0 или Qm(a:) = 0.
3. Если правая часть уравнения (51.10) есть.сумма функций вида I или II, то для нахождения у* следует использовать теорему 51.2 о наложении решений.
Пример 51.2. Найти общее решение уравнения у" — ly'+y = х—4.
О Решение: Найдем общее решение у ЛОДУ у" — 2у' + у — 0. Характеристическое уравнение к2 — 2fc +1 = 0 имеет корень ki = 1 кратности 2. Значит, у = ci ех + С‘2 х ех. Находим частное решение исходного уравнения. В нем правая часть х — 4 = (х — 4) еО ж есть формула вида Ру\х) е°'х, причем а = 0, не является корнем характеристического уравнения: а / ку. Поэтому, согласно формуле (51.12), частное решение у* ищем в виде у* = Qi(x) е°'х, т. е. у* = Ах + В, где А и В — неопределенные коэффициенты. Тогда (у*)' = А, (у*)" = 0. Подставив у*, (.У*)', (У*)" в исходное уравнение, получим — 2А+Ах + В = х — 4, или Ах + (—2А + В) = х — 4. Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
(А = 1,
(-2А + В = -4.
Отсюда А = 1, В = — 2. Поэтому частное решение данного уравнения имеет виду* = х—2. Следовательно, у = (у+у*) = ciex+съхех+х—2 — искомое общее решение уравнения. •
Пример 51.3. Решить уравнение у" — 4у' + 13у = 40 • cos3®.
Q Решение: Общее решение ЛНДУ имеет вид у = у + у*. Находим решение однородного уравнения у: у" — 4у' + 13у = 0. Характеристическое уравнение к'2 — 4к + 13 = 0 имеет корни Aj = 2 + Зг, к% = 2 — Зг. Следовательно, у = е2х (щ • cos За: + сг • sin За:).
364
Находим частное решение у*. Правая часть ЛНДУ в нашем случае имеет вид /(я) = еО ж • (40 cos Зя + 0 • sin Зя). Так как а = 0, /3 = 3, <(+/?« = Зг не совпадает с корнем характеристического уравнения, го г — 0. Согласно формуле (51.15), частное решение ищем в виде //’ = A cos Зя + В sin Зя. Подставляем г/* в исходное уравнение. Имеем: (//*)' = -ЗА sin Зя + ЗВ cos Зя, (г/*)" = -ЭАсозЗя - 9Bsin3.r. Получаем:
- 9 A cos Зя — 9В sin Зя — 4(—ЗА sin Зя -I- ЗВ cos Зя)+
+ 13(А cos Зя + В sin Зя) = 40 cos Зя, или
(- 9 А - 12В + 13А) cos Зя + (-9В + 12А + 13В) sin Зя = 40 cos Зя + 0 - sin Зя.
()тсюда имеем: ,
4А - 12В = 40, ' 12А + 4В = П.
Следовательно, А = 1, В = —3. Поэтому у* = cos Зя - 3 sin Зя. И наконец, у = е2ж(с1 cos Зя + с2 • sin Зя) + cos Зя - 3 sin Зя — общее решение уравнения. •
Пример 51-4- {Для самостоятельного решения.} Для предложенных дифференциальных уравнений получить вид частного решения:
а) у" — Зг/' + 2г/ = 5 + еж;
б) у” -2у' + у = 2;
в) у" + 4у — sin 2я + cos 7я;
г) у" + у = 5 cos 2я — я sin 2я;
д) у" — Зу' = я2 — 1 + cos я.
Ответы: а) А + х • В еж; б) А; в) я( A cos 2я + В sin 2я) + С cos 7я + + Dsin7x; г) (Ая + В) сов2я + (Ся + В) зт2я; д) я(Ая2 + Вя + С) + + D cos х + В sin я.
51.4. Интегрирование ЛНДУ n-го порядка (п > 2) с постоянными коэффициентами и правой частью специального вида
Рассмотрим линейное неоднородное ДУ тг-го (п > 2) порядка г/(п) + сц(я) - з/(п-1) + а2(я) у(п~2) + + ап(х) -у - f(x), где й1(я),а2(я),... ,а„(я), /(я) — заданные непрерывные функции на {а; Ь).
Соответствующее ему однородное уравнение имеет вид г/(7,) + щ(я) • у(п_1) + - - • + ап(я) • у = 0.
365
Теорема 51.3 (о структуре общего решения ЛНДУ n-го порядка). Общее решение у ЛНДУ n-го порядка равно сумме частного решения у* неоднородного уравнения и общего решения у соответствующего ему однородного уравнения, т. е. у = у* + у.
Частное решение у* ЛНДУ zi-го порядка может быть найдено, если известно общее решение у однородного уравнения, методом вариации произвольных постоянных. Оно ищется в виде
У* = сДж) • щ (ж) + с2(ж) • у2 (ж) + ... + сДж) • уп(х),
где у^х), г = 1,п, — частные решения, образующие фундаментальну, систему, однородного уравнения.
Система уравнений для нахождения неизвестных щ(ж) имеет вщ
С1У1 + С2У2 + с'3у3 + ...+ с'пуп = О,
С1У1 + С2У2 + С3У3 + • • + спУп = °, '
< с'1У? + с'.2у'4 + с'зу'1 + ... + с'пу” = О,
е' а- с' п(п~^ 4- 4- 4- г' Д’1-1) - Г ЩЛ
+ С2У2 +сзУз +--- + СпУп —
Однако для ЛНДУ zi-го порядка с постоянными коэффициентами, правая часть, которого имеет специальный вид, частное решение у* может быть найдено методом неопределенных коэффициентов.
Метод подбора частного решения у* уравнения
у(О + р1У(п1} + ...+рпу = f(x),
где pt — числа, а правая часть f (ж) имеет специальный вид, описанный в п. 51.3 для случая п = 2, переносится без всякого изменения и на случай уравнения, имеющего порядок п > 2.
Пример 51.5. Решить уравнение yIV — у' = 2ж.
Q Решение: Находим у:
k4 — k = 0, к(к — 1) • (/г2 + k + 1) = О,
кг-0, к2 = 1, fc3>4 =-| ±
х \
у = ci + с2е + е 2 ^с3 cos —ж + с4 sin •
Находим у*: f(x) = 2ж (= еО ж-Р1(ж)^, г = 1, у* — х(Ах+В') = Дж2+Рж, отсюда
(У*)' = 2Аж + В, (у*)" = 2Л, (?/*)'"= О, (2/*/V=0.
.466
Тогда —(2Ах + В) = 2®. Отсюда А = —1, В = 0 и получаем у* = —ж2. Следовательно, функция
-о®/ >/3 . \/3 \ о
у = \у + у ) = С1 + с2е +е 2 ^с3 cos — х + с4 sin — xj - х является общим решением уравнения. •
§ 52. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
52.1. Основные понятия
Для решения многих задач математики, физики, техники (задач динамики криволинейного движения; задач электротехники для нескольких электрических цепей; определения состава системы, в которой протекают несколько последовательных химических реакций I порядка; отыскания векторных линий поля и других) нередко требуется несколько функций. Нахождение этих функций может привести к нескольким ДУ, образующим систему.
Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.
Общий вид системы ДУ первого порядка, содержащей п искомых функций т/i, у2,..., уп, следующий:
-Fi (ж; уг, уу, - •; Уп, у'су'-а , у'Д = О, < ...............................
Fn(x-, уууу, • • ; Уп', у'ву'у, ', Уп) = 0.
Система ДУ первого порядка, разрешенных относительно производной, т. е. система вида
= fi(.x-,yi;yy...-,yn),
< ^ = f^ycyy,...-,yn), (52Л)
= !п(х-,ууу-2-,...-,уД),
pgj называется нормальной системой ДУ. При этом предполагается, что число уравнений равно числу искомых функций.
Замечание. Во многих случаях системы уравнений и уравнения высших порядков можно привести к нормальной системе вида (52.1).
.367
Так, система трех ДУ второго порядка
= Д (а:; у, z\ х'-, у'; z'),
< = У’Z; *'Х>' У'; Z'^
- F3(x-, у, z\ t\ х'-, у'; z'),
описывающая движение точки в пространстве, путем введения новых переменных: = к, = V, = ш, приводится к нормальной систе-
ме ДУ:
dx _ dt ' %L=V dt v’ &=w, at
— Fi(x;y; z;t;u;v;w),
~ = F2(a:;7/;z;i;«z;n;w),
— F3{x\ y\ z\ t\ w, v; w).
Уравнение третьего порядка у'" = f(x;y,y'',y") путем замены у' = = Pi у" — Р1 = Q сводится к нормальной системе ДУ
У1 ~Р, < р' = q, q' = f(x-,y;p-,q).
Из сказанного выше следует полезность изучения именно нормальных систем.
Решением системы (52.1) называется совокупность из п функций yi,y-2, • • , Уп, удовлетворяющих каждому из уравнений этой системы.
Начальные условия для системы (52.1) имеют вид
1/1 (хо) = у°, У2(жо) = У2, -,Уп(х0) = у%. (52.2)
Задача Коши для системы (52.1) ставится следующим образом: найти решение системы (52.1), удовлетворяющее начальным условиям (52.2).
Условия существования и единственности решения задачи Коши описывает следующая теорема, приводимая здесь без доказательства.
Теорема 52.1 (Коши). Если в системе (52.1) все функции непрерывны вместе со всеми своими частными производными по у^ в некоторой области D ((л + 1)-мерного пространства), то в каждой точке Мо{хо;у1;у2', -,Уп) этой области существует, и притом единственное, решение yi — 9?1(ж), у2 — Ч>Ах), .... уп = ч>п(х) системы, удовлетворяющее начальным условиям (52.2).
Меняя в области D точку Мо (т. е. начальные условия), получим бесчисленное множество решений, которое можно записать в виде решения, зависящего от п произвольных постоянных:
У1 = SP1 (ж;Ci;c2;..-;Cn),•••,?/« = <рп(х;с1;с2;...;сп).
Это решение является общим, если по заданным начальным условиям (52.2) можно однозначно определить постоянные щ, с2,..., сп из системы уравнений
(99i(a:;ci;c2;...;cn) = у?, ' < .................................................
* (у>п(а:;сг,С2;...;с„) =2/°.
Решение, получающееся из общего при конкретных значениях постоянных щ, с-2, .., сп, называется частным решением системы (52.1).
52.2. Интегрирование нормальных систем
Одним из основных методов интегрирования нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. (Обратная задача — переход от ДУ к системе — рассмотрена выше на примере.) Техника этого метода основана на следующих соображениях.
Пусть задана нормальная система (52.1). Продифференцируем по х любое, например первое, уравнение:
(5^1 = 54 + 54 ./El + 54 .+ ।
dx2 дх дуг dx ду2 dx дуп dx
Подставив в это равенство значения производных
dyi d^ d^n из dx ’ dx' ’ dx
системы (52.1), получим
d?yi = дД дД dfi dx2 дх дуг 1 dy2
54.f
дуп /п'
или, коротко,
= Г2(ж;у1;у2;...;уп).
Продифференцировав полученное равенство еще раз и заменив знач, ния производных ..., из системы (52.1), получим d3yi р i \
~Гз“ ~ ^з(ж;у1;у2;...;уп). ах
Продолжая этот процесс (дифференцируем — подставляем ем), находим: d yi
(b’,- = *п(ж;у1;у2;...;уп).
Соберем полученные уравнения в систему:
— получ;
Г^ = Л(ж;у1;у2;.. > Уп),
=-f2(a:;yi;y2;. ,Уп),
<1ЛУ1 с’ / ^-=F3(x-,yi-,y.2-,. ;Уп),
~ F^y^y^’- ',Уп)-
(52.3
Из первых (n — 1) уравнений системы (52.3) выразим функции у2,у3,..
... ,уп через х, функцию уг и ее производные у'},у",...,у^п-1\ Полу чим: _ , ,,
У2 = ‘ф2(х;у1;у'1;...;у{
t Уз = фз(х-,у1\у{-,...-,у(^}У
(52.4)
{уп = ‘фп(х;уг,у'1;...;у[п °).
Найденные значения у2,Уз, • • ,уп подставим в последнее уравнение си стемы (52.3). Получим одно ДУ n-го порядка относительно искомо! функции yi: — Ф(ж;У1;у5; • ;У1" ^)- Пусть его общее решени
есть
У1 = (ж; сх;с2; ...;сп).
Продифференцировав его (п — 1) раз и подставив значения произ водных у\,у”,... ,у[п в уравнения системы (52.4), найдем функции
У‘2, Уз, ,У,г-
У-2 = <Р2 (ж; С1; с2;...; с„),..., = У>П(Ж; С1; с2;...; сп).
Пример 52.1. Решить систему уравнений
Г^=4«-Зг, It'2»-3*-
370
г
(52.5)
< J Решение: Продифференцируем первое уравнение: у" = 4у' - 3z'. 11одставляем z' = 2у — 3z в полученное равенство: у” = 4у' — 3(2у — Зг), (/" — 4у' + бу = 9г. Составляем систему уравнений:
У' = 4у - 3z, у" - 4у' + бу = 9z.
Из первого уравнения системы выражаем z через у и у':
_ 4у - у
Z 3
11одставляем значение z во второе уравнение последней системы:
„ /I 9(4у —у')
у' - 4у + бу =--------,
О
т. е. у" — у' — бу = 0. Получили одно ЛОДУ второго порядка. Решаем его: к2-к-6 — 0, = -2, к2 = 3 и у = cie~2x + с2е3ж — общее решение
уравнения. Находим функцию z. Значения у и у' = (ще-2® + с2е3ж)' = = —2cie'“2® + Зс2е3ж подставляем в выражение z через у и у' (формула (52.5)). Получим: 1
z = 2С1е-2ж + |с2е3ж.
Таким образом, общее решение данной системы уравнений имеет вид у = ще-2® + с2е3ж, z = 2cie^2® + 1с2е3г. •
О
Замечание. Систему уравнений (52.1) можно решать методом интегрируемых комбинаций. Суть метода состоит в том, что посредством арифметических операций из уравнений данной системы образуют так называемые интегрируемые комбинации, т. е. легко интегрируемые уравнения относительно новой неизвестной функции.
Проиллюстрируем технику этого метода на следующем примере.
Пример 52.2. Решить систему уравнений: dr , г dt у+ ’
. dt
Q Решение: Сложим почленно данные уравнения: х'+у' = х+у+2, или (т+у)' = (а:+у)+2. Обозначим х+у = z. Тогда имеем z' = г+2. Решаем полученное уравнение: = dt, 1п(г + 2) — Inci = t, z — et_
Z ~r Z Cj
г + 2 = ще*, или x + у = ще* - 2.
Получили так называемый первый интеграл системы. Из него можно выразить одну из искомых функций через другую, тем самым
371
уменьшить на единицу число искомых функций. Например, у — ще4 — — 2 — х. Тогда первое уравнение системы примет вид
х' = ще4 — 2 - х + 1, т.е. xl+x = c1et-l.
Найдя из него х (например, с помощью подстановки х = iw), найдем и у.
Замечание. Данная система «позволяет» образовать еще одну интегрируемую комбинацию: х' — у' — у — х, т. е. (ж — у)' — —{х — у). Положив х — у = р, имеем: р' = —р, или = —dt, 1пр - 1пс2 — —t, p = С2в~1, или x — у = сге~4. Имея два первых интеграла системы, т. е. а: + у = ще4 — 2 и х — у = с2е4, легко найти (складывая и вычитая первые интегралы), что х = 4- ^с2е~4 — 1, у = ^ще4 — ^с2е~4 — 1. •
52.3. Системы линейных ДУ с постоянными коэффициентами
Рассмотрим еще один метод интегрирования нормальной системы уравнений (52.1) в случае, когда она представляет собой систему линейных однородных ДУ с постоянными коэффициентами, т. е. систему
вида
(йл . . .
— ащц 4- 0121/2 4-... 4- ainyn,
< ................................
— ап1У1 + «я21/2 + . . + йппУп-
Для простоты ограничимся рассмотрением системы трех уравнений с тремя неизвестными функциями Щ, уг и у3:
= 0111/1 + 0121/2 + «131/3,
' = °21^1 + °221/2 + 0231/3, (52.6)
= «311/1 + «321/2 + ОззУз, где все коэффициенты (i,j = 1,2,3) — постоянные.
Будем искать частное решение системы (52.6) в виде
У1 = a- ekx, у2 = Р • екх, у3 екх, (52.7)
где а, Р,^,к — постоянные, которые надо подобрать (найти) так, чтобы функции (52.7) удовлетворяли системе (52.6).
Подставив эти функции в систему (52.6) и сократив на множитель екх 0, получим:
ак = ацо + 012/3 + О1з7, < Рк — a2ia + 022/3 + О2з7, ук = а31а 4- а32р 4- а3з7,
372
(ац - к)а + а12/3 + 0137 = О,
< а21О + (а22 - к) fl + а237 = О, (52.8)
a3io: + а32/? + (а33 - fe)7 = О.
< Систему (52.8) можно рассматривать как однородную систему трех алгебраических уравнений с тремя неизвестными а, /3, 7. Чтобы эта chi’ гема имела ненулевое решение, необходимо и достаточно, чтобы опре-пдлитель системы был равен нулю:
ац - к ai2 ахз a2i а22 — к а23 a3i аз2 аз3 — к
(52.9)
Уравнение (52.9) называется характеристическим уравнением системы (52.6). Раскрыв определитель, получим уравнение третьей степени относительно к. Рассмотрим возможные случаи.
Случай 1. Корни характеристического уравнения действительны и различны: к\, к-2, &з- Для каждого корня к, (г = 1,2,3) напишем систему (52.8) и определим коэффициенты а,, Д, 7, (один из коэффициентов можно считать равным единице). Таким образом, получаем:
для корня ki частное решение системы (52.6): = aieklX, —
= flieklX, — 7iefcl3:;
для корня /г2 — у^ = a2eft2®, у^ = у^ = 'У‘2^х
для корня к3 — у^ — а3екзХ, у^ — /33екзХ, уд3) = 73еАзЖ.
Можно показать, что эти функции образуют фундаментальную систему, общее решение системы (52.6) записывается в виде
У1 = ciaieklX -Р С2а2екгХ + с3а3екзХ,
Уг = c.iffleklX + с2Р2екзХ + с3@3екзХ, (52.10)
З/з = с^ек1Х + с2'у2екзХ + с3^3екзХ.
Пример 52.3. Решить систему уравнений:
^=У'~У2’
^ = ~4у1+у2-
Q Решение: Характеристическое уравнение (52.9) данной системы имеет вид
-1
1-к
1-к
-4
= 0,
или 1 — 2к+к2-4 — 0, к2 — 2к — 3 = 0, ki = —1, А;2 = 3. Частные решения данной системы ищем в виде yj1’ = aieklX, у^ = /3ieklX и у*2’ = а2екзх, = /?2е*2Ж. Найдем а, и Д (г = 1,2).
373
При ki — — 1 система (52.8) имеет вид
((1-(-!))«! - ft = О, те (2ai~ft=0,
[-4ai + (1 - (-l))ft =0, Т‘е' [-401+2/31=0.
Эта система имеет бесчисленное множество решений. Положим сц = 1, тогда ft — 2. Получаем частные решения
у^ = е~х и у^ = 2е~х.
При ft = 3 система (52.8) имеет вид
(-202-/02=0, [-402 - 2ft = 0.
Положим аг = 1, тогда ft = —2. Значит, корню ft. = 3 соответствую! частные решения:
у^ = е3х и = -2е3х.
Общее решение исходной системы, согласно формуле (52.10), запишется в виде: yi = cie~x + С2в3х, у2 = 2с^е~х — 2c-ze3x. •
Случай 2. Корни характеристического уравнения различные, но среди них есть комплексные: к\ = а + ib, к? = а — ib, к%. Вид частных решений в этой ситуации определяют так же, как и в случае 1.
Замечания. Вместо полученных частных решений можно взять их линейные комбинации (и. 50.1, случай 3), применяя формулы Эйлера; в результате получим два действительных решения, содержащих функции вида еах cosbx, еах - sin ba:. Или, выделяя действительные и мнимые части в найденных комплексных частных решениях, получим два действительных частных решения (можно показать, что они тоже являются решениями уравнения). При этом понятно, что комплексносопряженный корень к-2 = а — ib не даст новых линейно независимых действительных решений.
Пример 52.4- Найти частное решение системы ^-=У1+?/2, < ^ = -Ш+У2-?/з>
удовлетворяющее начальным условиям: щ(0) = 7, уг(О) = 2, уз(0) — 1.
374
। J Решение: Составляем и решаем характеристическое уравнение:
1-к 1 0
-1 1-к -1 =0,
0 3 1-к
-1 -1 -1
(* ^к'>' 3 1 - к ~ 1 ’ 0 1-к ~ ’
(1 - fc)(fe2 - 2fc + 4) - (fc - 1) = О, (1 - fc)(fc2 - 2fc + 5) = 0, A*( — 1, k2 = 1 + 2г, кз = 1 — 2г.
Для fei = 1 получаем:
0 - Gi + /?i + 0 yi = 0, < —ai + 0 • /31 — 7i = О, О о, + 3/31 + 0 • 71 = О
(см. (52.8)). Отсюда находим: /31 = 0, о, = 1 (положили), 71 = —1.
Частное решение системы: = ех, у^ = 0, = —ех.
Для к2 — 1 + 2г получаем (см. (52.8)):
—2го2 + /32 = О,
< -а2 - 2ifa - 72 = О, З/З2 - 2г72 = 0.
Отсюда находим: о2 = 1 (положили), /32 = 2г, 72 — 3. Частное комплексное решение системы:
у(2) = е(1+2г)Ж) у(2) = 2,e(l+2i> yf = Зе(1+2<)а.
В найденных решениях выделим действительную (Re) и мнимую (Im) части:
у^ = е(1+2«> — ex/COs2x + г sin 2х),
Re г^2) = ех cos 2ж, Im у*21 = е® sin 2ж;
у^ = 2ге<1+2*>® = e®(2icos2a: - 2sin2ar),
Rey^ — — 2exsin2x, Imy.^ = 2e®cos2a:;
y^ = 3e(1+2t)® = e®(3cos2a: + i3sin2a:), Rey^2) = 3e® cos 2a:, Imy^2) = 3e® sin 2a:.
Как уже отмечено, корень кз = 1 — 2г’ приведет к этим же самым решениям.
375
Таким образом, общее решение системы имеет вид
yi = сгех + с2ех cos2а: + с3ех sin2х, у2 = ci - 0 — 2с2ех sin 2х + 2с3ех cos 2х, Уз = — с\ех + Зс2еж cos2a:'+ Зс3еж sin 2а:.
Выделим частное решение системы. При заданных начальных услови ях получаем систему уравнений для определения постоянных щ, с2, с3:
7 = ci 4- с2 + О,
2 = 0 —0 + 2с3,
1 — —ci + Зс2 + О,
ci =5, с2 = 2, сз = 1.
Следовательно, искомое частное решение имеет вид
= 5ех + 2ех cos 2ж + ех sin 2а:, у2 — — 4ех sin 2а: 4- 2ех cos 2а:,
Уз = —5ех + бе3 cos 2а: + Зеж sin 2а:. •
Случай 3. Характеристическое уравнение имеет корень fc кратности т (т = 2,3). Решение системы, соответствующее кратному корню, следует искать в виде:
а) если т = 2, то yi = (Л + Вх)екх, у2 = (С + Dx)ekx, у3 = = (E + Fx)ekx;
б) если m = 3, то yi = (А + Вх + Сх2)екх, у2 = (D + Ex + Fx2)ekx, Уз = (G + Нх + Nx2)ekx.
Это решение зависит от т произвольных постоянных. Постоянные А, В, С,..., N определяются методом неопределенных коэффициентов. Выразив все коэффициенты через т из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим т линейно независимых частных решений системы (52.6).
Пример 52.5. Решить систему уравнений:
-^=У1-У2+УЗ,
<^=У1+У2-УЗ, ^ = -У2 + 2У-
Q Решение: Составляем и решаем характеристическое уравнение
1-fc
1
О
-1
1-fc
-1
1
-1 2-fc
= 0,
376
А =0, «1 — 71 = 0.
11 - k)(2-2k-k + k2 — 1) — l(-2 + fc + l) = 0, ki = 2, k2 = k3 = 1. Корню /. i = 2 соответствует система (см. (52.8)):
' -О] - /?i + 7i = 0, < «1 — /?1 — 7х = 0, .-Д1 =0,
Полагая 71 = 1, находим Qi = 1. Получаем одно частное решение исходной системы: = е2ж, = 0, у^ = е2ж.
Двукратному корню к = к2 — к3 = 1 (т — 2) соответствует решение вида з/12’3) = (А + Вх)ех, у22,3^ = (С + Dx)ex, у32,3^ = (Е + Fx)ex. 11одставляем эти выражения (решения) в уравнения исходной системы:
В • еж + (А + Вх)ех = (А + Вх)ех — (С + Еж)еж + (Е + Fx)ex, - D - еж + (С + Dx)ex = (А + Вх)ех + (С + Dx)ex - (Е + Fx)ex,
Е • еж + (Е + Fx)ex = -(С + Ех)ех + 2(Е + Fx)ex, или, после сокращения на еж 0 и группировки,
' (D-F)x + B + C -Е = 0, - (В - F)x + А - D - Е = 0, (D — F)x + С + F — Е — 0. Эти равенства тождественно выполняются лишь в случае, когда £)-Е=0, В - Е = 0,
< В + С - Е = 0, А - D - Е = 0, С + Е-Е = 0.
Выразим все коэффициенты через два из них (т — 2), например через А и В. Из второго уравнения имеем Е = В. Тогда, с учетом первого уравнения, получаем D — В. Из четвертого уравнения находим Е = А — D, т. е. Е = А — В. Из третьего уравнения: С = Е — В, т. е. С = А — В—В, или С = А—2В. Коэффициенты А и В — произвольные.
Полагая А = 1, В — 0, находим: С = 1, D --- 0, Е = 1, Е = 0.
Полагая А - 0, В — 1, находим: С = —2, £> = 1, Е = —1,Е=1.
Получаем два линейно независимых частных решения, соответствующих двукратному корню к = 1:
(2) _ „X _.(2) _ х (2) _ х VI — е > У2 — е ; Уз ~ с и
у,(3) = хех, у(3} - (-2 + а:)еж, ^3) = (-1 + а:)еж. Записываем общее решение исходной системы:
yi = С1б2ж + с2еж + с3хех, у2 = с2еж + с3(х — 2)еж,
Уз = cie2x + с2еж + с3(х - 1)еж. •
Глава XI. ДВОЙНЫЕ 1/1 ТРОЙНЫЕ ИНТЕГРАЛЫ
Лекции 44-46
§53. ДВОЙНОЙ ИНТЕГРАЛ
53.1. Основные понятия и определения
Обобщением определенного интеграла на случай функций двух nd ременных является так называемый двойной интеграл.
У Пусть в замкнутой области D плсЛ
кости Оху задана непрерывная функцЛ z = f(x;y). Разобьем область D на I /ХА/Х! «элементарных областей» Di (г = 1,п1 площади которых обозначим через A SB
V D а диаметры (наибольшее расстояние м!
жду точками области) — через ф (сЛ
—-----------------------рис. 214). J
В каждой области Di выберем прЛ
Рис 214 извольную точку Аф(а^;?д), умножи!
значение f(xi\ у>) функции в этой точк! на A,S’; и составим сумму всех таких произведений:
/(®i;yi)ASi + f(x2;y2)^S2 +--Ь f(xn;yn)ASn = ^2 |
»=i j
(53.1)1
Эта сумма называется интегральной суммой функции f(x;y) в обла-1 сти D. J
Рассмотрим предел интегральной суммы (53.1), когда п стремит-1 ся к бесконечности таким образом, что тахф -> 0. Если этот предел! существует и не зависит ни от способа разбиения области D на ча-1 сти, ни от выбора точек в них, то он называется двойным интегралом» от функции f(x; у) по области D и обозначается [j f(x; у) dx dy (или 1 ff f(x;y)ds). ° I
D I
Таким образом, двойной интеграл определяется равенством п I
Ц f(x;y)dxdy= ^lin^ J2/(Жг;^) AS;. (53.2) '/j (maxdi—>0) i~]
|3| В этом случае функция f(x;y) называется интегрируемой в !
области D; D — область интегрирования-, х и у — пере- « менные интегрирования; dx dy (или dS) — элемент площади.
.Ч7Я
Для всякой ли функции /(ж; у) существует двойной интеграл? На нот вопрос отвечает следующая теорема, которую мы приведем здесь 1к'з доказательства.
Теорема 53.1 (достаточное условие интегрируемости функции). Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания.
I. Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
2. Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки
прямыми, параллельными координатным осям (см. рис. 215). При этом AS, = Аж, • A?/i, равенство (53.2) можно записать в виде
Ц f(x;y)dxdy = ?lirn
'jj (maxdi->0) 3=1
/(а:»;?/;) • Дж, • Д«/ц
53.2. Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу.
Объем цилиндрического тела
Рассмотрим тело, ограниченное сверху поверхностью z = /(ж; у)
О, снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = /(ж; у) на плоскость Оху) произвольным образом на п областей Di, площади которых равны AS) (г = = 1,тг). Рассмотрим цилиндрические столбики с основаниями Di, ограниченные сверху кусками поверхности z = /(ж; у) (на рис. 216 один из
470
них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием Di через АЦ, получим
ц = 52дц.
г=1
Возьмем на каждой площадке Л, произ вольную точку Мг(хцу{) и заменим ка ждый столбик прямым цилиндром с тем же основанием Di и высотой г, = ф(хр, у,). Объем этого цилиндра приближенно ра вен объему АЦ цилиндрического столби ка, т. е. ДЦ ps f(xi;yi) ASi- Тогда полу чаем:
91 П
ц = 52 дц « у^- <53-3)
i=l г=1
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей» Di. Естественно принят!.
предел суммы (53.3) при условии, что число площадок Di неограниченно увеличивается (п —> оо), а каждая площадка стягивается в точку (maxdj —> 0), за объем V цилиндрического тела, т. е.
п
v= -М (тах<2г—>0)
или, согласно равенству (53.2),
Ц = I/ f(x;y)dxdy.
D
(53.4)
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу т плоской пластинки D, зная, что ее поверхностная плотность д = 7(ж; у) есть непрерывная функция координат точки (ж; у). Разобьем пластинку D на п элементарных частей Di (?' = 1,п), площади которых обозначим через ДЦ. В каждой области Di возьмем произвольную точку ЛЦ(ж,-; yi) и вычислим плотность в ней: 7^6 Уг)-
Если области Di достаточно малы, то плотность в каждой точке (ж; у) G Di мало отличается от значения 7(ж<;у,). Считая приближенно плотность в каждой точке области Di постоянной, равной 7(ж;;уг),
380
можно найти ее массу m,-: mi к 7(07; у.,) • AS). Так как масса т воей ила-п
тинки D равна т — ^2mi, то для ее вычисления имеем приближенное равенство ?=1
' п
т ' ASi- (53.5)
г=1
Точное значение массы получим как предел суммы (53.5) при условии и -> оо и maxdj —> 0:
п
т= Ли
(maxdi—>0) i=l
или, согласно равенству (53.2),
m = y(x;y)dxdy. (53.6)
D
Итак, двойной интеграл от функции у(х; у) численно равен массе; пластинки, если подынтегральную функцию 7(ж; у) считать плотностью этой пластинки в точке (х;у). В этом состоит физический смысл двойного интеграла.
53.3. Основные свойства двойного интеграла
] Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения инте-ЧРграла функции одной переменной на отрезке (см. п. 35). Аналогичны и свойства этих интегралов и их доказательства. Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функ-
ции интегрируемыми.
jJ /(х; у) dx dy, с — const. D
с •
1. УУ c- f(x;y)dxdy =
D
2- УУ (/1 (ж; у) ± А (ж; уУ) dx dy fi(x; у) dx dy ± Ц f2(x\ y) dx dy.
D D D
3. Если область D разбить линией на две области Di и D2 такие, что Di (J D2 = D, а пересечение Di и D2 состоит лишь из линии, их разделяющей (см. рис. 217), то
Рис. 217
/ / у) dx dy = II f(x; y)dxdy + Ц f(x\ у) dx dy.
D Dl D2
381
4. Если в области D имеет место неравенство f (ж; у) 0, то и УУ f(x;y)dxdy 0. Если в области D функции f(x;y) и у? (ж; у) удо D влетворяют неравенству f(xjy) ip(x-,y), то и
УУ /(ж; у) dx dy^ II <р(х; у) dx dy.
D D
Г г
5. dS = S, так как £ Д£ = S.
d i=1
6. Если функция f(x;y) непрерывна в замкнутой области D, пло щадь которой S, то mS II f(x-,y)dxdy < MS, где тп и М — соотвеч
D
ственно наименьшее и наибольшее значения подынтегральной функции в области D.
7. Если функция /(ж; у) непрерывна в замкнутой области D, пло щадь которой S, то в этой области существует такая точка (жо; уо), что IУ /(^5 У) dx dy = f(x0- уо) • S. Величину
I? Iff
f(xo;yo) =g- JJ f(x;y)dxdy
D
называют средним значением функции f(x\y) в области D.
53.4. Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл Ц f(x;y) dxdy, где D
функция fix-, у) 0 непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = fix; у). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
ь
V = у S(x) dx, а
где 5(ж) — площадь сечения плоскостью, перпендикулярной оси Ох, а< ж = а, ж = b — уравнения плоскостей, ограничивающих данное тело. '
382
Положим сначала, что область D представляет собой криволиней-и vio трапецию, ограниченную прямыми х = а и х = b и кривыми у =
<Д| (ж) и у — «/’г (ж), причем функции <pi (ж) и ^(ж) непрерывны и ыковы, что <Д| (ж) для всех х G [а; 6] (см. рис. 218). Такая
|>| шасть называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух । очках.
Построим сечение цилиндрического тела плоскостью, перпендику-иярной оси Ох: х = const, где х G [а; Ь].
В сечении получим криволинейную трапецию ABCD, ограниченную линиями z = f(x;y), где х = const, z = 0, у = <pi(x) и у = <^(ж) (см. рис. 219).
Площадь S(x) этой трапеции находим с помощью определенного интеграла
S(x) = у f(x;y)dy.
V1 (®)
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
ь
V = у S(x) dx
а
V2(®) \
У f(x',y)dy \dx.
vi (®) '
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции f(x;y) О
383
по области D. Следовательно,
Это равенство обычно записывается в виде
Ъ V2<®)
f I f(x; у) dx dy = J vlx J f(x; y) dy.
D a V1(®)
(53.7)
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) назы вают двукратным (или повторным) интегралом от функции f(x;y) во
V2(»)
области D. При этом /(ж; у) dy называется внутренним интегра
Vl(®) лом.
Для вычисления двукратного интеграла сначала берем внутрел ний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до Ь.
Если же область D ограничена прямыми у = с и у — d (с < d), кривыми х = ipi(y) и х = ih,(y), причем ipi(y) < ’<h(y) для всех у € [с; d], т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
d тМу)
j[ f(x-, у) dx dy = I dy J f(x; y) dx.
D c V’lfo)
(53.8)
Здесь, при вычислении внутреннего интеграла, считаем у постоянным. Замечания.
1. Формулы (53.7) и (53.8) справедливы и в случае, когда f(x;y) < < 0, (ж; у) е D.
2. Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
3. Если область D не является правильной ни «по ж», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу.
4. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
384
Пример 53.1. Вычислить Ц (х + 2у) dxdy, где область D огра-
D нпчена линиями у = ж2, у = 0, х + у — 2 = 0.
< j Решение: На рисунке 220 изображена область интегрирования D. Она правильная и направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
Ц(х + 2у) dx dy = j D О
1 2-у
У
у = 2-х
У = х"!
2
О
1
1
Рис. 220
3\
1 Z ,«2
'у
}(&-у?
о
о
2 +4y-2y2 -
(Z/-2)3 6
7'У2 2 у^_2 2 2/2
2-2 3 5
18 7 2
—---_|_ — — -— — -
6 6 4 3
1
io
4 29 , лг
5 = 20 = W5'
Отметим, что для вычисления данного двойного интеграла мож-
но воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: /ф и /Д- Получаем:
Ц (х + 2у) dxdy — II (ж + 2у) dx dy + // (ж + 2у) dx dy =
r>2
2-ж
Dl
1 x2
2
О о
1
1
:2 2
О
2—х
о
1
о
2
О
О
1
1 .
/ Io \
8
ж3 (ж - 2)3
У+ 3
2
/ 11
9
- + 3 - 2 = 1,45.
Ответ, разумеется, один и тот же.
13 Конспект лекций по высшей математике. Полный курс
385
53.5. Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
x = ip(u-,v) и у=-ф{и-,и). (53.9)
Если функции (53.9) имеют в некоторой области Р* плоскости Ouv не прерывные частные производные первого порядка и отличный от нуля определитель
I(u;v) =
(53.10;
dx dx du dv 8^ ’
du dv
а функция f(x; у) непрерывна в области D, то справедлива формул замены переменных в двойном интеграле-. . у
Ц f(x;y)dxdy = /(<Дщг>);?Дг!;г>)) \I(u;v)\dudv. (53.11
b D* j
Функциональный определитель (53.10) называется определителе! Якоби или якобианом (Г. Якоби — немецкий математик). Доказатель ство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используй мый при вычислении двойного интеграла, а именно замену декартовы координат х и у полярными координатами г и tp. 3
В качестве ими возьмем полярные координаты г nip. Они связан! с декартовыми координатами формулами х = г cosip, у = rsin</> (см п. 9.1). '
Правые части в этих равенствах — непрерывно дифференцируй^ мые функции. Якобиан преобразования определяется из (53.10) как 1
dx Or
dy dr
dx dip dy dip
cos ip —r sin ip sin ip r cos ip
Формула замены переменных (53.11) принимает вид:
j f(xiy)dxdy = уу f (г cos ip; г sin ip) г dr dip,
(53.12);
где D* — область в полярной системе координат, соответствующая! области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах при-1 меняют то же правило сведения его к двукратному интегралу. Так, если J
386
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами tp = а и tp = fl, где а < fl, и кривыми г = ri(tp) и г = r2(</j), где / | (<р) rzftp), т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
/3 »'2(у)
Ц г • f (г cos tp; г sin tp) dr dtp = dtp г f (г cos tp; г sin tp) dr. (53.13)
/>* a n(v)
Внутренний интеграл берется при постоянном <р.
L Замечания.
1. Переход к полярным координатам полезен, когда подынтегральная функция имеет вид /(ж2 + у2); область D есть круг, кольцо или часть таковых.
2. На практике переход к полярным координатам осуществляется путем замены х — г cos tp, у = rsintp, dxdy — г dr dtp; уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по г и tp (исследуя закон изменения г и tp точки (г;</>) при ее отождествлении с точкой (ж; у) области D).
Пример 53.2. Вычислить / / \/9 — ,т2 - у2 dx dy, где область D —
2 । 2 с\ J J
круг х* + у* 9. D
Q Решение: Применив формулу (53.12), перейдем к полярным координатам:
11 \/9 — х2 — у2 dx dy = И \/9 — (г cos tp)2 — (г sin tp)2 г dr dtp = D D .
2 dr dtp.
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 0 С tp 2тг, 0 г С 3. Заметим: область D —
387
круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
______ 2л 3
Л г - у/9 — г2 dr dip — у dip у г - у/9 — г2 dr = D 0 0
1 2?г 3 1 -| 2?г 2\9 о ч
= = / dy(( ~Г3 ' )| =
0 0 о
1 2?Г 2тг
= —- У (0 — 27) dip = 9</?| = 18тг.
о
53.6. Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находите: по формуле
-h D f f(x-,y)dxdy,
где z — f(x: у) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
S = уу dxdy,
или, в полярных координатах,
S = уу г • dr dip.
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 7 = 7'(;с; у) находится по формуле
т = // V) d®'
388
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
Sx = Ц у у(х',у) dx dy и Sy = II х 'Y(x;y>)dxdy;
D D
а координаты центра масс фигуры — по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы т относительно оси I называется произведение массы т на квадрат расстояния d точки до оси, т. е. Mi = m-d?. Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
ЛД = IIу2 y(x;y)dxdy, Му = Ц х2 -у(х;у) dxdy.
D D
Момент инерции фигуры относительно начала координат — по формуле Мо = Мх + Му.
Замечание. Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример 53.3. Найти объем тела, ограниченного поверхностями ;с2 + у2 — z + 1 = 0 и х2 + у2 + Зг - 7 = 0.
Q Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
{X2 + у2 = z - 1,
х2 + у2 = -Зг + 7, находим уравнение линии их пересечения: х2 + у2 = 1, z = 2.
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием
(круг х2 + у2 1) и ограниченных сверху соответственно поверхностями z = |(7 - х2 - у2) и z = 1 + х2 + у2. Используя формулу (53.4), О
имеем
V = V1 - v2
= //l^7 ~ х2 ~у2^dxdy ~ /Л1+х2+у2^dxdy*
Переходя к полярным координатам, находим:
V =
| (7 — г2)?- • dr dip — УУ(1 + г2)?* ’ dr dtp —
D D
1 2тг 1 2тг 1
= 3 / d(fi/(7r~ dr ~ f
0 0 о
3 \2 4/ 1о \2 4/ 1о
о
13 „ з Л 2
15 2-г-Г2« = ^
Пример 53.4- Найти массу, статические моменты Sx и Sy и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эл-2
липсом + у = 1 и координатными осями (сМ: рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
Рис. 224
Q Решение: По формуле (53.6) находим массу пластинки. По условию, 7 = 7(;с; у) = к ху, где к — коэффициент пропорциональности.
2
т = уу кху dxdy = к Jх dx D о
Находим статические моменты пластинки:
2
Sx = jl у • кху dx dy = к j х dx D О
Sv = уу х • кху dx dy = к у ж2 dx [ у dy = D 0 0
Находим координаты центра тяжести пластинки, используя формулы
Sy Sy 16 8 ж
Хс = —И ус = Хс = Ус = TF- •
т Jc т 15’ J 15
390
5 54. ТРОЙНОЙ ИНТЕГРАЛ
54.1. Основные понятия
Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».
Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция и = f(x;y,z). Разбив область V сеткой поверхностей на п частей Vi (г = 1,п) и выбрав в каждой из них произвольную точ-п
ку Mi(xi',yi;zi), составим интегральную сумму Z) / (жб Уб ^г)ДИ для г=1
функции /(ж; у, z) по области V (здесь Д V — объем элементарной области Vi).
Если предел интегральной суммы существует при неограниченном увеличении числа п таким образом, что каждая «элементарная область» V. стягивается в точку (т. е. диаметр области d, стремится к нулю, т. е. dj -> 0), то его называют тройным интегралом от функции и = /(яг; у, z) по области V и обозначают
УУУ f(x;y;z) dx dy dz ( или /// ^x’y'z^dv)-
Таким образом, по определению, имеем:
п
[[[ f(x;y;z)-dxdydz= ^lim, /(ж;; ^)ДЦ'= у (max di-Ю) j=l
= fff f(x; y, z) dv.
(54.1)
Здесь dv — dx dy dz — элемент объема.
Теорема 54.1 (существования). Если функция и = /(ж; у; z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (54.1) при л -> оо и шахф -> 0 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек МДж,;^;^) в них.
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
1. f с f(x; у; z) dv = с jj/(ж; у, z) dv, с — const.
V V
•«11
чу
2- fff (Ji&;y;z) ± f2(x;y;z))dv = v
= I1.1 ^x' y’z)dv± III Ых’> У’dv-
V V
3. Ill f(x;y;z)dv = Щ f(x;y;z)dv + Щ f(x-,y,z)dv, если V V Vi v2
= Vi U V2, а пересечение Vi и V2 состоит из границы, их разделяющей
4‘ III^x>y''z^dv > 0, если в области V функция /(ж; у; z) (I. V
Если в области интегрирования f(x;y;z) ip(x;y;z), то и
HI f(x; y,z)dv> Щ <р(х; у, z) dv.
5. J J J dv = V, так как в случае f(x;y;z) = 1 любая интегральная V п
сумма имеет вид ^2 А К = V и численно равна объему тела.
4=1
6. Оценка тройного интеграла:
т • V HI f(x-yz)dv М-V, v
где т и М — соответственно наименьшее и наибольшее значения функции /(ж; у, г) в области V.
7. Теорема о среднем значении: если функция /(ж; у, г) непрерьп^ на в замкнутой области V, то в этой области существует такая точЯ Mo(xo;yo',zo), что Я
Щ у’dv = ^Х°’Уо’ Z°^ ’ V’ Я
и
где V — объем тела.
54.2. Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Пусть областью интегрирования V является тело, ограниченное снизу поверхностью z = zi(x;y), сверху — поверхностью z — z2(x;y), причем ai(ж; у) и z2(x; у) (zi(x; у) z2(x; j/)) — непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху
309
(см. рис. 225). Будем считать область V — правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в-области V функции f(x;y;z) имеет место формула
[ f(x;y;z)dz}ds, (54.2)
V и z\(x-,y)
' водящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство формулы (54.2) не приводим). 11 ри этом сначала вычисляется внутренний интеграл по переменной z при постоянных х и у в пределах изменения z. Нижней границей интеграла является аппликата точки А — точки входа прямой, параллельной оси Oz в область V, т. е. z = zi (ж; у); верхней границей — аппликата точки В — точки выхода прямой из области V, т. е. z — zy\x-,y). Результат вычисления этого интеграла есть функция двух переменных: .г. и у.
Рис. 225
Рис. 226
Если область D ограничена линиями х = а, х = Ь (а < Ь), у = (ж)
и у = tpzix), где (ж) и <р2(х) — непрерывные на отрезке [а, 6] функции, причем <^>1 (ж) ^(ж) (см. рис. 226), то, переходя от двойного интеграла по области D к повторному, получаем формулу
b Vz(®)
УУУ f(x;y-,z)dxdydz— j dx j dy V a.
f(x~, у; z) dz,
(54.3)
zi(x;y)
по которой вычисляется тройной интеграл в декартовых координатах.
393
Замечания.
1. Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).
2. Порядок интегрирования в формуле
(54.3), при определенных условиях, может быть иным.
Пример 54-1. Вычислить ffj
где V ограничена плоскостями х = 0, у — О 2=1, х + у + z = 2 (рис. 227).
Q Решение: Область V является правильной в направлении оси Oz (как, заметим, и в направлении осей Ох и Оу). Ее проекция на плоскость Оху является правильной в направлении оси Оу (и оси Ох). Согласно формуле (54.3), имеем:
2-х—у
1
УУУ (ж + z) dx dydz = У dx у dy [ (ж + z) dz = v ' ' ’
о
1
О
1
1—:
XZ +
о
1—ж
о
z2
~2
Г1
2ж — ж2 — ху — х +
о
1
о
(2 - ж - у)2 2
6 2У
2 У2 (2-х- у)3
ху - х£у - X— -
о
1о
.2 _ ж2 + х3 _ -4х
,2
о
3 ж2 ж3 ж4
_ ------2------1----
2 2 3 4
1 . (2 — ж)3 1 1
6 6 2 2
.2
ж3 ж4 \ 2 (2 — ж)4
¥ + Т / ” 3 ’Х 24
3 2 1 1 2 1 16 _ 1
4~3 + 4~24~3~ 24 + 24 ~ 4'
1
о
394
54.3. Замена переменных в тройном интеграле.
Вычисление тройного интеграла в цилиндрических и сферических координатах
При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.
Пусть совершена подстановка х — <p(u;v;w), у = 4p(u:,v;w), z = - y('w.; v; w). Если эти функции имеют в некоторой области V* пространства Ouvw непрерывные частные производные и отличный от ну-
ия определитель дх дх dx
ди dv dw
w) = dy ди ду dv dy dw
dz dz dz
ди dv dw
то справедлива формула замены переменных в тройном интеграле:
/// dX dy dZ =
= JJJf(<p(u;w,w);4p(u-,v;w);x(u-,w,w)>)-\I(u;v;w)\dudvdw. (54.4)
Здесь I(u;v;w) — определитель Якоби, или якобиан преобразования (примем без доказательства).
Для вычисления тройного интеграла
часто используют так называемые цилиндрические координаты.
Положение точки М(х; у, z) в пространстве Oxyz можно определить заданием трех чисел г, ip, z, где г — длина радиуса-вектора проекции точки М на плоскость Оху, у — угол, образованный этим радиусом-вектором с осью Ox, z — аппликата точки М (см. рис. 228).
Эти три числа (г, <р, z) называются цилиндрическими координатами точки М.
Цилиндрические координаты точки связаны с ее декартовыми ко
ординатами следующими соотношениями:
х = г cos <р, у = г • sin у, z = z
(г > О, у & [0; 2тг], z £ К).
395
Возьмем в качестве и, v, w цилиндрические координаты г, tp, z и
вычислим якобиан преобразования:
дх дх дх dr dip dz cosip — г simp 0
I(r; tp-, z) = ду dy ду dr dip dz = sin tp r cos tp 0
dz dz dz 0 0 1
dr dip dz
Формула замены переменных (54.4) принимает вид
УУУ f(x-,y;z)dxdydz = Щ f(r cos tp-, г sin tp-,z)r dr dtp dz.
v
(54.5)
Таким образом, вычисление тройного интеграла приводится к интегрированию по г, по <р и по z аналогично тому, как это делается в декартовых координатах.
Замечание. К цилиндрическим координатам бывает удобно перей ти в случае, если область интегрирования образована цилиндрически
поверхностью.
Пример 54-2. Вычислить JJJ z dx dy dz, где V — область, огре V
ниченная верхней частью конуса х2 + у2 = z2 и плоскостью z = 1.
Q Решение: На рис. 229 изображена область интегрирования V. Вы числим интеграл путем перехода к цилиндрическим координатам: х -= г cosip, у = г simp, z = z. Здесь dxdydz = r- drdtpdz. Уравнени, конуса примет вид г2 cos2 tp+r2 sin2 tp = z2, т. е. z = г. Уравнение окруж ности х2 + у2 = 1 (границы области D) запишется так: г = 1. Новьи переменные изменяются в следующих пределах: г — от 0 до 1, <р — о-О до 2тг, az — от г до 1 (прямая, параллельная оси Oz, пересекающая область D, входит в конус z = г и выходит из него на высоте z — 1).
' Таким образом, согласно формуле (54.5), получаем:
2тг 1 1
/ dtp I г dr I z dz —
о
о
Заметим, что, не переходя к цилиндрическим координатам, полу
чим:
1 fffz-dxdydz= J
396
Рис. 230
Сферическими координатами точки М(ж;2/;г) пространства Oxyz называется тройка чисел р, <р, в, где р — длина радиуса-вектора точки М, <р — угол, образованный проекцией радиуса-вектора ОМ на плоскость Оху и осью Ох, 6 — угол отклонения радиуса-вектора ОМ от оси Oz (см. рис. 230).
Сферические координаты р, <р, 0 связаны с декартовыми координатами х, у, z соотношениями:
ж = р cos <р • sin 0, у = psintp sin0, z = pcos0
(p 0, 0 <p 2tt,
0^0 0)-
В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования
/(г;<р;г) =
cos <р sin в sin <р sin в COS0
—р simp sin 0 р cos <р sin 0 О
р cos <р cos 0 р sin <р cos 0
—psin0
= psin<psin0
sin <p sin 0 p sin <p cos 0
cos 0 —p sin 0
+ pcos<psin0
cos <p sin 0 p cos <p cos 0 cos0 —psin0
= p sin <p sin 0(—p simp sin2 0 — psin<pcos2 0)+
+ p cos tp sin 0(—p cos <p sin2 0 — p cos tp cos2 0) =
= —p2 sin2 tp sin 0 1 — p2 cos2 tp sin 0 -1 = —p2 sin 0 • 1 = —p2 sin 0,
TO
IЦ y, z) dx dy dz =
307
= yyy f(p cos ip sin в-, p sin tp sin в; p cos в) • p2 sin в dp dtp df). (54.6
Замечание. Переходить к сферическим координатам удобно, когд] область интегрирования V есть шар (уравнение его границы х2 + у2) + z2 = R2 в сферических координатах имеет вид р = R) или его чаете а также если подынтегральная функция имеет вид f(x2 +у2 + z2).
Пример 54-3. Вычислить г гг dx- dy dz
J J J _• ./о. о , о \
где V — шар х2 + у2 + z2, 1.
Решение: Вычислим интеграл путем перехода к сферическим kooi динатам: х = р cos 7 sin 0, у = р sin 7 sin (9, z = р cos19. Тогда I
d,V = dx dy dz = p2 sin f) dp dtp df). 1
Граница области V — сфера и ее уравнение имеет вид р = 1, подынт тральная функция после замены переменных примет вид -—
т. е. Новые переменные изменяются в следующих пределах: р от 0 до 1, tp — от 0 до 2тг, в — от 0 до тг. Таким образом, согласно фо] муле (54.6),
7Г 27Г
p2 sin 0 dp dip df) = у sin 0 d0 J dip j о
27Г
ffrb
7Г
= У sin0d0 J ^(3 In |1 + p'
0
1 2
7-7—3 dp =
1 + p
2% .
0
7Г
In 2 У sin 0d0 ip
0
2?T
0
0
У sin 0 df) =
0
0 0
0
2тг I тг 4тг
= — ln2(— cos (9) =— In 2.
3 Io 3
54.4. Некоторые приложения тройного интеграла
Объем тела
Объем области V выражается формулой V = ))) dv или v
V = JI! dxdy dz — в декартовых координатах,
V = f f f r dr d ip dz в цилиндрических координатах,
v
V = fffp2 sin () dp dip dO — в сферических координатах.
Масса тела
Масса тела т при заданной объемной плотности 7 вычисляется с помощью тройного интеграла как
т = fff 7(ж; у, z) dx dy dz,
где 7'(;c; у; z) — объемная плотность распределения массы в точке М(ж;у;г).
Статические моменты
Моменты Sxy, Sxz, Syz тела относительно координатных плоскостей Оху, Oxz, Oyz вычисляются по формулам
Sxy ~ !!! Z У'dv’ Syz = f/f х' v’dv'
V V
Sxz = fff У у, z) dv.
Центр тяжести тела
Координаты центра тяжести тела V находятся по формулам Sxy т
Sxz
Ус = ---,
т
lyz = УУУ х2 7(ж; у, z) dv,
Syz
Хс = —— т
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
Ixy = fff z2 7(т; у, z) dv,
V
Ixz- fff У2 • 7(ж; yiz) dv, V
а моменты инерции относительно координатных осей:
1Х = fff (у2 + *2) • 7(®; yiz)d'o Iy = ///+ z^' ^x’y; dv’
V V
!z = fff (x2 + y2) 7(ж; у, z) dv.
Пример 54.4. Найти объем тела, ограниченного поверхностями Z = X2 + у2 И Z = 1.
300
Q Решение: Данное тело ограничено сверху плоскостью г — 1, снизу — параболоидом z = ж2+у2 (см. рис. 231). Объем тела находим, используй цилиндрические координаты:
2тг 1 I
= ууу г • dr dp dz — J dip J г dr f dz = V 0 0 ,-2
Рис. 231
Рис. 232
Пример 5^.5. Найти массу шара ж2 + у2 4- z2 2Rz, если плоп| ность в каждой точке шара обратно пропорциональна расстоянию отв нее до начала координат (дополнительно: найти координаты центра тяжести).
Решение: Уравнение сферы ж2 + у2 + z2 = 2/?.z можно записать так: ж2 + у2 + (г — 7?)2 = R2. Центр шара расположен в точке ОДО; 0; 7?) (см. рис. 232). Пусть Л-7 (ж; у; z) — произвольная точка шара. Тогда, по условию, плотность 7 определяется формулой
•уж2 + у2 + z2
где к — коэффициент пропорциональности, уСс2 + у2 + z2 — расстоя! ние от точки М до начала координат.
Итак, т = / [/ 7(ж; y;z)dv = III r--dv.
JJJ n ,У’ JJJ y/x2+y2 + z2
Вычислять интеграл будем в сферических координатах. Уравнение сферы ж2 + у2 + z2 — 2Rz примет вид р2 — 2Rp cosO, т.е.р= 22? cos 0.
4Г)П
11<>этому сферические координаты будут изменяться в следующих пределах: р — от 0 до 2R cos 6; в — от 0 до <р — от 0 до 2тг. Подынте-
t' к к тт
тральная функция примет вид Поэтому
2тг 2 2 Л cos О
f ff — р2 sinOdpdipdff = к f dip J sinOdd / pdp —
I' P ООО
7Г
2тг 2
dip J sin 6 d6 -
о 0
2тг 2
4R2 cos2 e = -2R2k dip J cos2 0 (/(cos в) = о о
2?r 3 л
r t COS# = —2R2k I dip------—
о
9 / 1 \ 2r 2 |2тг 4 „
= -2R2k- (-1) dp= Z-kR2ip\ = -M2.
\ 3' / 3 IО о
о о
Из соображений симметрии следует, что хс — 0, ус — 0, вычислив интеграл -1 [[[ z , к9 -dv, найдем гс = Итак, координа-н т JJJ ^x2+y2 + z2 а
ты центра тяжести (0; 0; §R)-
Глава XII. КРИВОЛИНЕЙНЫЕ
И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
Лекции 47-50
Обобщением определенного интеграла на случай, когда область ин тегрирования есть некоторая кривая, является так называемый криво линейный интеграл.
§55. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ I РОДА
55.1. Основные понятия
Пусть на плоскости Оху задана непрерывная кривая АВ (или L) длины I. Рассмотрим непрерывную функцию f(x',y), определенную н точках дуги АВ. Разобьем кривую АВ точками Мо — A,Mi,M2,.. ... ,Мп = В на п произвольных дуг Mi-iMi с длинами Д/?- (г = 1, 2,..., п)(см. рис. 233). Выберем на каждой дуге произвольную
точку (хр, yi} и составим сумму j
'^f{xpyi)/Ali. (55.11
г=1 j1
Рис. 233
Ее называют интегральной суммой для функции f(x;y) ио кривой АВ.
Пусть А — max Д/, — наибольшая из длин дуг деления. Если
при А —> 0 (тогда п оо) существует конечный предел интегральных
402
vmm (55.1), то его называют криволинейным интегралом от функции I (х; у) по длине кривой АВ (или I рода) и обозначают / /(ж; у) dl (или г Ав
I f&y)dl).
I
Таким образом, по определению,
(55.2)
I f(x;y)dl = lim ^/(xijyJAZi. / /<,—rCXJ *
AB (*->0) »=1
Условие существования криволинейного интеграла 1 рода (существования предела интегральной суммы (55.1) при п —> оо (А —> 0)) представляет следующая теорема, которую мы приводим здесь без доказательства.
Теорема 55.1. Если функция f(x-,y) непрерывна в каждой точке гладкой кривой (в каждой точке (ж; у) G L существует касательная к данной кривой и положение ее непрерывно меняется при перемещении точки по кривой), то криволинейный интеграл I рода существует и его величина не зависит ни от способа разбиения кривой на части, ни от выбора точек в них.
Аналогичным образом вводится понятие криволинейного интегра-К ла от функции /(ж; у; z) по пространственной кривой L.
Приведем основные свойства криволинейного интеграла по длине дуги (I рода).
1. J f(x; y)dl = j f(x; у) dl, т. e. криволинейный интеграл I ро-АВ ВА
да не зависит от направления пути интегрирования.
2. у с • /(ж; y)dl = с - J f(x-, у) dl, с = const. L L
3. у (fi(ж;у) ±f2(a:;y))<fl = j fi(x;y)dl± J f2(x;y)dl. L L L
4. J f(x-,y)dl = J f(x;y)dl+ J f (ж; y)dl, если путь интегрирова-L Li I/?
ния L разбит на части L± и L2 такие, что L — L\ (J L2 и L\ и L2 имеют единственную общую точку.
403
5. Если для точек кривой L выполнено неравенство Л(ж;у) ^/г(ж;у), то J fa(x;у) dl [ fa(x-,y)dl.
L L
Г . n
6. I dl — lim Ah = гДе I — длина кривой AB.
ab (X4o) ’=i
7. Если функция /(ж; у) непрерывна на кривой АВ, то на этой кр: вой найдется точка (жс;ус) такая, что / f(x;y)dl = f(xc;yc) I (те рема о среднем). АВ
55.2. Вычисление криволинейного интеграла I рода
Вычисление криволинейного интеграла I рода может быть сведе! к вычислению определенного интеграла. Приведем без доказательст! правила вычисления криволинейного интеграла I рода в случаях, ecj кривая L задана параметрическим, полярным и явным образом.
Параметрическое представление кривой интегрирования
Если кривая АВ задана параметрическими уравнениями х = x(t У = y(t), t G [«;/?], где x(t) и y(t) — непрерывно дифференцируемь функции параметра t, причем точке А соответствует t = а, точке В -значение t = /3, то
0
У f(x; y)dl = J f (x(t);y(t)) у/x2t' + yf dt. (55.3
AB ot
Аналогичная формула имеет место для криволинейного интеграла от функции /(ж; у, z) по пространственной кривой АВ, задаваемой' уравнениями х — x(t), у — y(t), z — zlt), a^t р:
0 __________
I f(x; у; z) dl = J f(x(t);y(t); z(tj) yj x2t' + y? + zf' dt. (55.4)
AB a
Явное представление кривой интегрирования
Если кривая АВ задана уравнением у = <р(х), х G [а; Ь], где <д(ж) — непрерывно дифференцируемая функция, то
У f(x;y)dl = у / (ж; ^(ж)) • yjl + y2x' dx. (55.5)
АВ а
Подынтегральное выражение в правой части формулы (55.5) получается заменой в левой части у = у(х) a dl = yJ\-\-y2' dx (дифференциал дуги кривой — см. п. 41.3).
404
Пример 55.1. Вычислить
У ху2 dl, где L — отрезок прямой ме-L
жду точками <9(0; 0) и Л(4;3). ,
Q Решение: Уравнение прямой О А есть £/=^ж,0^.т^4. Согласно формуле (55.5), имеем:
, 45 г 3
dx = —- х dx =
64 J о
Полярное представление кривой интегрирования
Если плоская кривая L задана уравнением г = г(р), а
полярных координатах, то dl = , /г2 + (г' )2dp и
/з
I f(r cos р; г sin
(55.6)
Подчеркнем, что нижний предел определенного интеграла в формулах (55.3)-(55.6) должен быть меньше верхнего.
Пример 55.2. Вычислить J (х + y)dl, где L — ________________________£
лепесток лемнискаты г = y^sin 2р, расположенной в I координатном углу.
Q Решение: Кривая интегрирования изображена на рисунке 234. Воспользуемся формулой как
(55.6). Так
dl =
cos2 2р dp
sin 2р -I-;—-—dp = —=
sin 2р л/sin:
dtp
то, заметив, что 0 < р < получаем:
2
о
2
. dp г
г sin р) — = / (cos р +
о
sin р) dp = 2.
55.3. Некоторые приложения криволинейного интеграла I рода
Криволинейный интеграл I рода имеет разнообразные приложения в математике и механике.
405
Длина кривой
Длина I кривой АВ плоской или пространственной линии вычп сляется по формуле I = J dl.
лв
Площадь цилиндрической поверхности
Если направляющей цилиндрической поверхности служит кривая АВ, лежащая в плоскости Оху, а образующая параллельна оси Oz (см. рис. 235), то площадь поверхности, задаваемой функцией z = — f&y'h находится по формуле Q — = J f(я;у) сП-ав
Масса кривой
Масса материальной кривой АВ (провод, цепь, трос,...) определяется формулой т = у 7(M)dZ, где 7 = 'у(М) — 7(ж;у) — плотность АВ
кривой в точке М.
□ Разобьем кривую АВ на п элементарных дуг (г = 1,п).
Пусть (xi;yi) — произвольная точка дуги Считая прибли-
женно участок дуги однородным, т. е. считая, что плотность в каждой точке дуги такая же, как и в точке (^;у,), найдем приближенное значение массы mi дуги М^М^:
mi « 7(®г;уг)Д/г>
Суммируя, находим приближенное значение массы т: п
т & ^7(х{;уг)А1г. (55.7)
г=1
За массу кривой АВ примем предел суммы (55.7) при условии, что шах Д/, —> 0 (п —> оо), т. е.
т = п1^о
(maxAZj~>0) 7—1
или, согласно формуле (55.2),
т = у 7(3;; у) dl. АВ
(Заметим, что предел существует, если кривая АВ гладкая, а плотность задана непрерывной в каждой точке АВ функцией.)
406
Статические моменты, центр тяжести
Статические моменты относительно осей Ох и Оу и координаты центра тяжести материальной кривой АВ определяются по формулам Sy Sx
Жс = —, Ус~— т т
АВ
Sx = J У- у) dl, АВ
Моменты инерции
Для материальной кривой АВ моменты Ix, Iy, Iq инерции относительно осей Ож, Оу и начала координат соответственно равны:
4= J y2-7(x;y)dl, Iy= f x2-y(x;y)dl, Io = f (x2+y2)-y(x;y)dl. AB AB AB
Пример 55.3. Найти центр тяжести полуокружности х2 +у2 = R2, лежащей в верхней полуплоскости. Плотность считать равной единице в каждой точке кривой (7 = 1).
Q Решение: Из соображений симметрии ясно, что центр тяжести находится на оси Оу (см. рис. 236). Поэтому хс = 0. Ордината центра тя-жести Jy-dl
АВ
Ус~ Jdl • АВ
Знаменатель дроби — длина полуокружности. Поэтому у dl = ttR. АВ
Для вычисления числителя воспользуемся параметрическими уравнениями окружности х = Rcost, у = Rsint, 0 С t я. Имеем:
J у dl = J R sin t VR2 sin2t + R2 cos21 dt = R2 J sin t dt = 2R2. ab о о
Следовательно, yc — Итак, xc =0,yc~
§56. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ II РОДА
56.1. Основные понятия
Решение задачи о вычислении работы переменной силы при перемещении материальной точки вдоль некоторой кривой (и других) приводит к понятию криволинейного интеграла II рода.
Криволинейный интеграл II рода определяется почти так же, как и интеграл I рода.
407
Пусть в плоскости Оху задана непрерывная кривая АВ (или L) и функция Р(х-,у), определенная в каждой точке кривой. Разобьем кривую АВ точками Мо = A, Mi,..., Мп — В в направлении от точки А к; точке В на п дуг Afj-iAf j с длинами /М, (г = 1,2,..., п).
На каждой «элементарной дуге»' Mi-iMi возьмем точку (хр,у,) и составим сумму вида
;Уг) • Д®г,
(56.1
где Дж,' = x.i — Xi-i — проекция дуп Mi-iMi на ось Ох (см. рис. 237).
Сумму (56.1) называют интеграль ной суммой для функции Р(х; у) по пе ременной х. Таких сумм можно соста
вить бесчисленное множество. (Отличие сумм (55.1) и (56.1) очевидно.)
Если при А = max Д/j 0 интегральная сумма (56.1) имеет ко 1^7^72
нечный предел, не зависящий ни от способа разбиения кривой АВ, ни от выбора точек (хр,у,), то его называют криволинейным интегралом по координате х (или II рода) от функции Р(х;у) по кривой АВ и обозначают J АВ
Итак,
или J Р(х; у) dx. L
I P(x}y)dx = Um У2Р(хр,у^^Х1. J П—гОО и*
АВ (А—>0) j=l
Аналогично вводится криволинейный интеграл от функции Q(x; у) по координате у:
I Q(x;у) dy = Jim, Q^y^Kyi АВ (Х->0) j—1
где Ду,- — проекция дуги M,-iMi на ось Оу.
Криволинейный интеграл II рода общего вида
/
АВ
Р(х; y)dx + Q(x;y)dy
определяется равенством
У P(x-,y)dx + Q(x-,y)dy = J P(x;y)dx+ [ Q(x;y)dx. AB AB AB
408
Криволинейный интеграл j Q(x;y; z) dx+Q(x;y; z) cly+R(x;y; z) dz L
но пространственной кривой L определяется аналогично.
Теорема 56.1. Если кривая АВ гладкая, а функции Р(х-,у) и Q(x’,y) непрерывные на кривой АВ, то криволинейный интеграл II рода существует.
Отметим лишь некоторые свойства криволинейного интеграла II рода.
1. При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т. е.
/=-/
АВ ВА
(проекция дуги M^Mi на оси Ох и Оу меняют знаки с изменением направления).
2. Если кривая АВ точкой С разбита на две части АС и СВ, то интеграл по всей кривой равен сумме интегралов по ее частям, т. е.
/ = /-/
АВ АС СВ
3- Если кривая АВ лежит в плоскости, перпендикулярной оси Ох, то
I P(x;y)dx = 0 (все Дж, — 0);
L аналогично для кривой, лежащей в плоскости, перпендикулярной оси Оу:
j С?(ж; y)dy = 0 (все Ду, = 0).
L
4. Криволинейный интеграл по замкнутой кривой (обозначается не зависит от выбора начальной точки (зависит только от направления обхода кривой).
Q Действительно,
Рис. 238
АтпСпА АтС СпА (см. рис. 238). С другой стороны,
409
СпАтС
СпА
АтС
Таким образом,
/ = /
АтС'пА СпАтС
56.2. Вычисление криволинейного интеграла II рода
Вычисление криволинейного интеграла II рода, как и I рода, может, быть сведено к вычислению определенного интеграла.
Параметрическое представление кривой интегрирования
Пусть кривая АВ задана параметрическими уравнениями х = ж(£)1 и У = y(t), где функции x(t) и y(t) непрерывны вместе со своими npjj изводными x'(t) и y'(t) на отрезке [а;/3], причем-начальной точке I кривой соответствует значение параметра t = а, а конечной точке В I значение t = /3. И пусть функция Р(ж; у) непрерывна на кривой А Л Тогда, по определению, Я
72
/ P(x;y)dx = lim V Р(ж^;у;)Джц Ч
I ГЪ~~тСХ? *
АВ (А *°) 4=1 7
Преобразуем интегральную сумму к переменной t. Так как 3 Дж» = Xi - Х,л = x(ti) - X^ti-i), J
то по формуле Лагранжа (см. (25.2)) имеем: Дж,- = x'(ci)Ad,, где с; Я С (tj—l,i«), Д3,‘ — tf ti~\. II
Выберем точку (x^yi) так, чтобы ж, = ж(с,), у.) = y{ci). Тогда пр-Я n fl
образованная интегральная сумма 52 Р(ж(с,);у(с?)) • ж'(сг) - Дб; будеЯ г=1 11
интегральной суммой для функции одной переменной Р(ж(1); y(t)) -ж'(Л на промежутке [о; /3]. Поэтому Я
? 1
У P{x;y)dx = j P(x(t);y(tY)x'(t)dt. (56.21
АВ а Я
Аналогично получаем: 3
У Q(x;y)dy= J Q(x(t);y(t))y'(f)dt. (56.3);
АВ а
Складывая почленно полученные равенства (56.2) и (56.3), no.nyJ чаем: S
Р 1
У Р(ж; у) dx + <Э(ж; у) dy = J (P(x(t); у(£))ж'(1) + Q(x(t\, y(i))y'(/)) (й| АВ a J
(56.4)1
410
Явное представление кривой интегрирования
Если кривая АВ задана уравнением у = </>(ж), х G [а; 6], где функция <р(х) и ее производная у'(х) непрерывны на отрезке [а; 6], то из формулы (56.4), приняв х за параметр, имеем параметрические уравнения кривой АВ: х — х, у = <fi(x), х & [а; 6], откуда получим:
ь
У P(x-,y)dx + Q(x-,y)dy = j |р(ж;9г(ж)) 4-<2(ж; <£>(ж))<//(rc)j[ dx. (56.5) IB а
В частности,
ь
I P(x;y)dx = у Р(ж;у>(ж)) efa. (56.6)
АВ а
Если АВ — гладкая пространственная кривая, которая описывается непрерывными на отрезке [а;/3] функциями х = x{t), у = y(t) и г = z(t), то криволинейный интеграл
I Р{х\ y;z)dx + Q(x\ у, z)dy + R(x; у; z) dz
AB
вычисляется по формуле
/3
I Pdx + Qdy+Rdz = J [P(x(t)-y(t);z(t))x'(t)+
AB a
+Q(x(t);y(t);z(t))y'(t) + R(x(t)-,y(t);z(t))z'(t)]dt. (56.7)
Замечание. Криволинейные интегралы I и II рода связаны соотношением / Pdx + Qdy = / (Pcosa + Qcos/?) ей, где о и/?— углы, АВ АВ
образованные касательной к кривой АВ в точке М (ж; у) с осями Ох и Оу соответственно.
Пример 56.1. Вычислить I = J (ж — у)2 dx + (х + у)2 dy, L —
ломаная О АВ, где 0(0; 0), Д(2;0), В(4;2).
Q Решение: Так как L = О АВ — О А + АВ (см. рис. 239), то I = f — [ + У -
L ОА АВ
Уравнение стрелка О А есть у = 0, 0 ж < 2; уравнение отрезка АВ: у — х — 2, ж G [2; 4]. Со
411
гласно формуле (56.5), имеем:
2 4
1 = 1 [(ж - О)2 + 0] dx + Д22 + (2ж - 2)2 • 1] dx =
О 2 '
= <С+Ч + 5&Уа£1М + (16-8’ + в«216-8> = Т •
Пример 56.2. Вычислить I = J у2 dx + (x2+z)dy + (x+y + z2)dz, l 1
L — отрезок прямой в пространстве от точки А(1;0;2) до точки® 2?(3;1;4). I
Q Решение: Составим уравнение прямой, проходящей через точки А и | В: —~ 2 или в параметрической форме: х = 2t + 1, у = t, | z = 2t + 2. При перемещении от точки А к точке В параметр t меняется от 0 до 1. По формуле (56.7) находим, что
1 = j\t2 • 2 + ((2f + I)2 + 2t + 2) 1 + (2t + 1 +1 + (2t + 2)2) 2] dt Щ
95
= у (14t2 + 28* + 13) dt = у. Ш
0 W
56.3. Формула Остроградского-Грина S
Связь между двойным интегралом по области D и криволиней-^ ным интегралом по границе L этой области устанавливает формула Остроградского Трина, которая широко применяется в математическом анализе.
Пусть на плоскости Оху задана область D, ограниченная кривой, пересекающейся с прямыми, параллельными координатным осям не более чем в двух точках, т. е. область D — правильная.
Теорема 56.2. Если функции Р(х;у) и Q(x-,y) непрерывны вместе со своими частными производными и в области D, то имеет место формула
././ (Й ' * dy = f Pdx+Qdy- <56-8) где L — гранив области D и интегрирование вдоль кривой L производится в положительном направлении (при движении вдоль кривой, область D остается слева).
Формула (56.8) называется формулой Остроградского-Грина.
IJ Пусть у — <pi(x) — уравнение дуги АпВ, а у = (ж)
|уги АтВ (см. рис. 240). Найдем сначала dxdy.
— уравнение По правилу
вычисления двойного интеграла, имеем:
ПО Ь V2<'X'1 яе>
//а?''3’''’ = /* ! atdy = D b a ^i(a:)
r , , pMO
= dx- Р(ж;у) = J
Или, согласно формуле (56.6),
f[~n~dxdy= j P(x;y)dx — J P(x;y)dx =
I D Am В AnB
= — f P(x-,y)dx— J P(x\y)dx — — £ P(x;y)dx. (56.9)
! Вт A AnB L
Аналогично доказывается, что
Jf = f Q{x;y)dx. (56.10)
i D L
Если из равенства (56.10) вычесть равенство (56.9), то получим формулу (56.8).
Замечание. Формула (56.8) справедлива и для произвольной области, которую можно разбить на конечное число правильных областей.
Пример 56.3. С помощью формулы Остроградского-Грина вычислить
I — £ Vх2 + У2 dx + y • {ху + In (ж + \/х2 +г/2)) dy,
L
где L — контур прямоугольника с вершинами /1(3; 2), В(6; 2), С(6; 4), Р>(3;4).
Q Решение: На рисунке 241 изображен контур интегрирования. Поскольку = у • (У ' = У- по форму-
ох \ у/%2 + У2 / иУ ух/ + у2
ле (56.8) имеем:
413
D
yi.V'/x2 +y2 +1)
Рис. 242
Рис. 241
56.4. Условия независимости криволинейного интеграла II рода от пути интегрирования
Пусть А(ж1;у1) и В(ж2;?/2) — две произвольные точки односвяз ной области D плоскости Оху (область D называется односвяз ноИ, если для любого замкнутого контура, лежащего в этой области ограниченная им часть плоскости целиком принадлежит D (области без «дыр»)). Точки А и В можно соединить различными линиями (на рис. 242 это Li, Ьг и L3). По каждой из этих кривых интеграл
I- J P(x;y)dx + Q(x;y)dy
АВ
имеет, вообще говоря, свое значение.
Если же его значения по всевозможным кривым АВ одинаковы, то говорят, что интеграл I не зависит от вида пути интегрирования. Ь этом случае для интеграла I достаточно отметить лишь его начальную, точку А(ж1;у!) и его конечную точку В(ж2;?/2) пути. Записывают:
1 = I Р(х;у) dx + Q(x;y) dy. (56.11)
Каковы же условия, при которых криволинейный интеграл П рода не зависел от вида пути интегрирования?
414
Теорема 56.3. Для того чтобы криволинейный интеграл
1 = J Pdx + Qdy
L
не зависел от пути интегрирования в односвязной области D, в которой функции Р(х;у), Q(x;y) непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие
dP__dQ ду дх
(56.12)
IJ Докажем достаточность условия (56.12). Рассмотрим произвольный замкнутый контур АтВпА (или L) в области D (см. рис. 243). Для пего имеет место формула Остроградского Грина (56.8). В силу условия (56.12) имеем:
<l> Р dx + Q dy = 0, или у Р dx + Q dy = 0. L АтВпА
Учитывая свойства криволинейного интеграла, имеем:
У Р dx + Qdy =
АтВпА
= j Pdx + Qdy + j Pdx + Qdy = AmB ~
= I Pdx + Qdy— у Pdx + Qdy = AmB
t. e.
ВпА
о,
АпВ
I Pdx + Qdy = j Pdx + Qdy.
AnB
Полученное равенство означает, что криволинейный интеграл не зависит от пути интегрирования. И
ЛтВ
|(@)| В ходе доказатепьства теоремы получено, что если выполняется
М дР dQ
условие то интеграл по замкнутому контуру равен нулю: г
ф Pdx + Qdy = 0.
L
Верно и обратное утверждение.
415
Следствие 56.1. Если выполнено условие (56.12), то подынтеграль ное выражение P(x;y)dx + Q(x;y)dy является полным дифференци алом некоторой функции и = и(х;у) (см. (44.5)), т. е.
Р(ж; у) dx + Q(x; у) dy = dU(x; у). (56.13)
Тогда (см. (56.11)):
(«2:3/2) («2:3/2)
1= j P(x,y)dx + Q(x,y)dy = J dU(x;y) =
(«i;s/i) (®i;j/i)
i («2:3/2)
= Р(ж;у) = U(x2;y2) - U^yr),
T‘ e’ («2:3/2)
I F(s; у) dx + Q(x-, y)dy = U(®2; y2) - U(xr, j/i). (56.14)
(«1:3/1)
Формула (56.14) называется обобщенной формулой Ньютона Лейбница для криволинейного интеграла от полного дифференциала.
Следствие 56.2. Если подынтегральное выражение Pdx. + Qdy есть полный дифференциал и путь интегрирования L замкнутый, то
<j> Р dx + Q dy = Q. г,
Замечания.
1. Чтобы не спутать переменную интегрирования х с верхним пределом х, переменную интегрирования обозначают другой буквой (например, t, £, и т.д.).
2. Функцию U = U(x;y), удовлетворяющую условию (56.12), можно найти, используя формулу
х у
и{х-,у)= j P(x;y0)dx+ у О(ж;С)^ + С. (56.15)
Уо
В качестве начальной точки (жо; уо) обычно берут точку (0; 0) — начало координат (см. пример 56.5).
3. Аналогичные результаты справедливы для криволинейного интеграла
j Р dx + Q dy + Rdz
L
416
ч<> пространственной кривой. Условие (56.12), равенство (56.13), формулы (56.14) и (56.15) имеют соответственно вид:
др _ ЭД эд __ ан ак ар
ду дх' dz ду" дх dz ’
Pdx + Qdy + Rdz = dU{x-,y\ z),
(®2;3/2;22)
I Pdx + Qdy + Rdz = U(x2-,y2;z2) - Щх-^у^гУ), (®i;vi;«i)
a: у z
U(x;y;z) = I P(x;y0-, z0) d\. + j Q(x;Q, z0) tZ£ + j R(x;y;Q) < + C Хо У0 Zq
(cm. пример 73.1).
(i;i)
Пример 56.4- Найти 1 = J ydx+xdy.
(0;0)
Q Решение: Здесь P = у, Q = x,
QP = ЭД dy dx
— 1. Согласно вышепри-
веденной теореме, интеграл не зависит от пути интегрирования. В ка-
честве пути интегрирования можно взять отрезок прямой у = х, дугу параболы у = х2 и т. д. или воспользоваться формулой (56.14). Так как ydx + xdy = d(xy), то
(i;i)
(0;0)
= 1-0 = 1.
Пример 56.5. Убедиться, что выражение е~у dx — (2у + xe~v) dy представляет собой полный дифференциал некоторой функции (7(ж; у) и- найти ее.
Q Решение: Для того чтобы указанное выражение являлось полным дифференциалом, необходимо выполнение условий (56.12): о о
SL(e-y) = -е-У- — (—(2у + хе-У)) = -е^ dy dx
условия выполнены, следовательно, е уdx, — (2у + xe~y)dy = dU(ж; у).
А так как полный дифференциал имеет вид д д
dU(x;y) = — U(x;y)dx+ -^-U(х;у) dy ох оу
(см. п. 44.3), то верны соотношения
-^-U(x;y) = ^-Р(ж; у) = ~(2у + хеу).
ох оу
14 Конспект лекций по высшей математике. Полный курс
417
(56.16)
Интегрируем по х первое из уравнений, считая у постоянным, при этс вместо постоянной интегрирования следует поставить Ду) — неизвес ную функцию, зависящую только от у:
U(x-,y) = j e~~v dx = хе~у + <р(у).
Подставляя полученное выражение во второе из уравнений (56.16), на: дем <р(у):
д I
-у
+ <Ху))=~же У + <р'(у) = — (2у + хе у);
9?'(у) = -2у, <р(у) = -у2 + с.
Таким образом, П(ж; у) = хе у — у2 + с.
Отметим, что функцию U проще найти, используя формулу (56.15)
П(ж;у) = j е °d\ + J (—2% + хе ^)d^ + C —
о о — х — у2 + хе~у — х + С = хе~у —у2+С.
56.5. Некоторые приложения криволинейного интеграла II рода
Площадь плоской фигуры
Площадь S плоской фигуры, расположенной в плоскости Оху ограниченной замкнутой линией L, можно найти по формуле
(56.1’
при этом кривая L обходится против часовой стрелки.
Q Действительно, положив в формуле Остроградского-Грина (56.8) Р(х-,у) = 0, Q(x;y) = х, получим:
или г
S = <j> xdy. (56.18)
L
Аналогично, полагая Р = —у, Q = 0, найдем еще одну формулу для вычисления площади фигуры с помошью криволинейного интеграла: .
S = -aydx. (56.19)
L
418
Сложив почленно равенства (56.18) и (56.19) и разделив на два, получим: 1
S = - <j> xdy — уdx.
(56.20)
Формула (56.17) используется чаще, чем формулы (56.18) и (56.19).
Работа переменной силы
Переменная сила F(P(z; у); <Э(ж; у)) на криволинейном участке АВ производит работу, которая находится по формуле
А = J Pdx + Qdy. АВ
l_j Действительно, пусть материальная точка (ж; у) под действием переменной силы F перемещается в плоскости Оху по некоторой кривой АВ (от точки А до точки В).
Разобьем кривую АВ точками Мо = A, Mi, М2,..., Мп — В на п «элементарных» дуг Mj-iMj длины Д/г: и н каждой из них возьмем произвольную точку Сг(жг;уг), i = 1;2;...;п (см. рис. 244). Заменим каждую дугу Mi lMi вектором Мг-1Мг = (ДЖг; Дуг), а силу F будем считать постоянной на векторе перемещения АЦ-уМ; и равной заданной силе в точке Q дуги М^М^:
Fi = (P(xi;yi);Q(xi;yi)Y _ ______
Тогда скалярное произведение Ft - М,-__|ЛД можно рассматривать как приближенное значение работы Ft вдоль дуги
Ai^Fi- Mt-iMi = P(xi; у^ • Джг-_+ Q(^; yi) • Ду,-Приближенное значение работы А силы F на всей кривой составит величину п п п
А = 52 А« ~ 52' Лж* + 52
За точное значение работы А примем предел полученной суммы при А = max AZj -> 0 (тогда, очевидно, Дж, -> 0 и Ду» -> 0):
п
А = lim У^Р(жг;уг)-Дх^ + (Э(жг;уг)-Дуг = [ Р(х;у) dx + Q(x;y) dy.
А>0 J Ш
(п—>оо) 1 АВ
Замечание. В случае пространственной кривой АВ имеем:
А= J P(x-,y;z)dx + Q(x-,y;z)dy + R(x;y;z)dz.
АВ
419
Пример 56.6. Найти площадь фигуры, ограниченной астроидой х = а • cos3t, у — а sin31.
Q Решение: При обхождении астроиды в положительном направлении параметр t изменяется от 0 до 2тг (см. рис. 245).
Применяя формулы (56.17) и (56.4), получим:
1
S=- J (acos31 • 3asin21 cost + asin31 • 3acos2 tsint) dt =
° 1 о 2 3a2 /“l-cos4t 3a2 я
2 J 4 8 J 2 8
о о
Пример 56.7. Найти работу силы F — 4®6г + xyj вдоль кривой у = х3 от точки 0(0;0) до точки 13(1; 1).
Q Решение: По формуле (56.20) находим:
1 1
А = J 4ж6 dx + xydy = J(4ж6 + х • х3 З®2) dx = J 7х6 dx = 1. • L 0 0
§57. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ I РОДА 57.1. Основные понятия
Обобщением двойного интеграла является так называемый поверхностный интеграл.
Пусть в точках некоторой поверхности S, с площадью S, пространства Oxyz определена непрерывная функция f(x;y;z). Разобьем поверхность S'на п частей Si, площади которых обозначим через AS,-(см. рис. 246), а диаметры — через di, i — 1;п. В каждой части S,
420
возьмем произвольную точку М^х^ус, zt) и составим сумму
п
i=l
(57.1)
Она называется интегральной для функции /(ж; у, z) по поверхности S.
Г<| Если при А — max di —> 0 интегральная сумма (57.1) имеет пре-дел, то он называется поверхностным интегралом I рода от функции f{x-,y,z) по поверхности S и обозначается jj f(x; у, z) ds.
s
Таким образом, по определению,
U f(x; У, z) ds = lim /(ж4; ?ц; z^ ASi S (n—loo) 4=1
(57.2)
|@| Отметим, что «если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция /(ж; у, z) непрерывна на этой поверхности, то поверхностный интеграл существует» (теорема существования).
Поверхностный интеграл I рода обладает следующими свойствами:
' 1 11С ^Х’ = с 11 ^х’где с — число-
i S S
2. JJ(fa (х; у; z) ± /2(ж; у; z)) ds = J J fa (ж; у; z) ds ± s s
3. Если поверхность S разбить на части Si и S? такие, что S = = Si (J S2, а пересечение Si и S2 состоит лишь из границы, их разделяющей, то
Jf f(x; у, z) ds
s
J J f2(x; у; z)ds. s
= ff f(x;y;z)ds + IJ f(x;y;z)ds. 51 «2
4. Если на поверхности S выполнено неравенство fa(x-,y,z) /г(®;?/;г), то уу fa(x;y;z)ds JJ fa(x; у, z) ds.
s s
5. JУ ds ~ S, где S s
площадь поверхности S.
6.
УУ f (x; y, z) ds s
ff \f(x;y;z)\ds. s
421
7. Если f(x;y; z) непрерывна на поверхности S, то на этой поверхности существует точка (xc\yc\zc) такая, что
JJ f(x; у; z) ds = f(xc-, yc; zc) - S
s
(теорема о среднем значении).
57.2. Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S н; плоскость Оху.
Разобьем поверхность S на части Si, г = 1;п. Обозначим через <т проекцию Si на плоскость Оху. При этом область D окажется разбито на п частей ..., ап. Возьмем в сц произвольную точку Pi(xi;yi) восстановим перпендикуляр к плоскости Оху до пересечения с поверх ностью S. Получим точку на поверхности Si. Проведем
точке Mi касательную плоскость и рассмотрим ту ее часть '1\, котора на плоскость Оху проектируется в область (см. рис. 247). Площад элементарных частей Si, Ti и ai обозначим как Д.8), Д7',- и Да,- соо-ветственно. Будем приближенно считать, что
Д7) « ASi. (57.J
Следовательно,
COS 7г =
Обозначив через острый угол между осы Oz и нормалью П, к поверхности в точке Mi, п< лучаем:
Д7) • cos 7i = До£ (57.4
(область <п есть проекция 7) на плоскость Оху).
Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке Mi есть
z'x(xi-,yi)-(x-Xi) + z'y(xi-,yi)-(y-yi)-(z-Zi) = О, где z'x(xi;yi), z'y(xi\yi), -1 —- координаты нормального вектора к плоскости. Острый угол есть угол между векторами к = (0; 0; 1) и
Hi = (,-z'x[xi-,yi);-z'y(xi;yi)-l).
кпг
|&| ’ l«i|
_________________1__________________ ^/1 + z,3.2(xi;yi) + z'y2(Xi;yi)
422
I Равенство (57.4) принимает вид
[ ЛГг = +
В правой части формулы (57.2) заменим Д,8) (учитывая (57.3)) на полученное выражение для Д7), a Zj заменим на z{xp,yi). Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра Si (а следовательно, и <Tj), получаем формулу
JJ f(x; у; z) ds = J J f(x; у- z(x; у))- y/l + z'2 + zj/ dx dy, (57.5) S D
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.
Отметим, что если поверхность S задана уравнением вида у = = у(х-, z) или х = х{у, z), то аналогично получим:
JJ f(x;y;z)ds= Ц f(x; у(х- z)-,z) yj 1 + у'2 + у'2 dxdz
S Di
И
II f(x; y, z) ds = J J f(x{y,z)\ y; z) yj 1 + x'2 x'2 dy dz, (57.6) s d2
где Д] и Л — проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.
Пример 57.1. Вычислить I = JJ (ж — Зу + 2z) ds, где S — часть s
плоскости 4.т + 3?/+ 2z — 4 = 0, расположенной в I октанте (см. рис. 248).
Q Решение: Запишем уравнение плоскости в виде z = 2
2ж
2у-
Находим zx'
— По формуле (57.5) имеем:
-2, zy>
j! (4 — Зж — 6?/) dxdy —
D
|(1^)
J (4 — Зж - бу) dy —
О
dx\ky — Зху — Зу2)
о
423
где S — часть цилиндрической поверхности х = д/1 - у2, отсеченной плоскостями z = 0, z = 2 (см. рис. 249).
□ Решение: Воспользуемся формулой (57.6). Поскольку ху' =----, xz' = 0, то
V1 -у
dydz = JJ (у + z) dy dz =
Dl
т)1о^У= / =
-1
где £>i — прямоугольник AAiB^B.
Л9Л
57.3. Некоторые приложения поверхностного интеграла I Рода
Приведем некоторые примеры применения поверхностного интеграла I рода..
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx{x\y) и Zy(x,‘,y) — непрерывные функции, то ее площадь S вычисляется по формуле
S
или S'= уу ^/1 + zx'2 + zy'2 dx dy.
D
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы 7 = 7(®;?/;z). Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть 7 = 7(ж; z). Для нахождения массы поверхности:
1. Разбиваем поверхность S на п частей Si, г — 1,2,... ,п, площадь которой обозначим AS;.
2. Берем произвольную точку Mi(xi',yi',zi) в каждой области Si. Предполагаем, что в пределах области Si плотность постоянна и равна значению ее в точке
3. Масса т, области Si мало отличается от массы 7(.т,-; ?/;; z,-)AS? фиктивной однородной области с постоянной плотностью
7 = l^yi-Zi).
п
4. Суммируя mi по всей области, получаем: т &
i=l
5. За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение
ЛОЯ
при стремлении к нулю диаметров областей Si, т. е.
п
т= lim y^^Xi-y^Zi^Si,
max di—>0 *—y
i=l
m = JJ y(x;y, z)ds. (57.'
s
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, момент инерции материальной поверхности S находятся по соответствующе формулам:
SXy= J J Z- y(x; y, z) ds, Mx = fj\y2 + Z2) y(x; y, z) ds,
s s
Syz = JJ x'^x:>y'z^ds' My = J J (x2 + z2) y(x; y; z) ds,
s S
Sxz = J J у 7(ж; у, z) ds, Mz = /J+ ' ^X’У’dS’
s s
$1JZ $xz , Ус = , ZC = m m m Mo = J J{x2 + y2 + z2) • 7(ж; у, z) ds. s
Пример 57.3. Найти массу полусферы радиуса R, если в кажд точке поверхности плотность численно равна расстоянию этой точки радиуса, перпендикулярного основанию полусферы.
Q Решение: На рисунке 250 изображена полусфера радиуса R. 1 уравнение z = y/R2 — х2 — у2-, 'у = у/х2 + у2 — поверхностная пло
ность полусферы.
По формуле (57.7) находим:
Переходим к полярным координатам:
2тг и 2 2 т
ГГ Г Г Г Г 7Г /
m = R —j== - г dr dip = R I dip- / —. dr = —-
y/R? — r2 ' vR2 — r2
49C
Внутренний интеграл вычислен с помощью подстановки г = Rsint:
г /?2sm2l
/ —--------- R cos tat =
J R cos t
о
о
1
- sm
2
2
r 1 — cos 2t ,
I —2—»=
.2
§58. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ II РОДА
58.1. Основные понятия
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет. |,'5| Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z — f(x:y), где f(x-,y), fx' и fy' — функции, непрерывные в некоторой области D плоскости Оху и т. д.). После обхода такой поверхности, не пересекая ее границы, направление нормали к ней не меняется. Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что точка А совмещается с точкой С, а В — с D (см. рис. 251).
Рис. 251
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части Si, где i = 1,2,.. .,п, и проектируем их на координатные плоскости. При этом площадь проекции До-j берем со знаком «плюс», если выбрана верхняя сторона поверхности, или, что то же самое, если нормаль п к выбранной стороне поверхности составляет с осью Oz острый угол (см. рис. 252, а), т. е. cos7$ > 0; со знаком «минус», если выбрана нижняя сторона поверхности (или cos7; < 0) (см. рис. 252, б). В этом случае интегральная сумма имеет вид п
52 f(Xi’ У” z№ai’' (58.i)
i=l
497
где Act.; = (Si)oxy — площадь проекции Si на плоскость Оху. Ее отличие от интегральной суммы (57.1) очевидно.
Рис. 252
Предел интегральной суммы (58.1) при А = тахф —> 0, если он существует и не зависит от способа разбиения поверхности S на части Si и от выбора точек Mi е Si, называется поверхностным интегралом II рода (по координатам) от функции /(х; у, z) по переменным х и у по выбранной стороне поверхности и обозначается
УI f(x;y;z)dxdy.
s
Итак,
71
f [ f(x; у, z)dxdy = lim /(жб Уи S (n-»oo) «=1
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:
п
/У /(^; у; z) dy dz = lim f(xf, ур, Zi) (Si)Oyz,
S (n—>оо) г=1
п
JJ f(x\y,z)dxdz = lim У" /(a*; щ-, Zj) • (Sj)oxz.
S (п—>00)
Общим видом поверхностного интеграла II рода служит интеграл
УУ Р(х; у; z) dy dz + Q(x; у, z) dz dx + 7?(x; y, z) dx dy s
(= Pdydz + Ц Qdzdx + Ц Rdxdy\, ' s s s'
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.
428
' V1 Отметим, что если S — замкнутая поверхность, то поверхностный Интеграл по внешней стороне ее обозначается по внутренней $ .
S -S
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
1. Поверхностный интеграл II рода изменяет знак при перемене «тороны поверхности.
2. Постоянный множитель можно выносить за знак поверхностного интеграла.
3. Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
4. Поверхностный интеграл II рода по всей поверхности S = Si+S-2 равен сумме интегралов по ее частям Si и S2 (аддитивное свойство), если Si и S2 пересекаются лишь по границе, их разделяющей.
5. Если Si, S-2, S3 — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
JJ R(x;y;z)dxdy = P(x;y;z)dydz = Q(x;y; z) dxdz = St s2 s3
0.
58.2. Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция R(x; у; z) непрерывна во всех точках поверхности S, заданной уравнением z = z(x-,y), где z(x-,y) — непрерывная функция в замкнутой области D (или Dxy) — проекции поверхности S на плоскость Оху.
Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда Д<т4 > 0 (г = 1,2,..., п).
Так как zi — г(хцуд, то интегральная сумма (58.1) может быть записана в виде
п п
^R(xi-,yi-,zi')^(ji = ^R(xi-,yi;z{xi-,yi))^(ji. (58.2)
i=l i=l
Правая часть этого равенства есть интегральная сумма для функции R(x-,y,z(x-,yy), непрерывной в области D. Переходя к пределу в равенстве (58.2) при А —> 0, получаем формулу
JJ R(x;y,z)dxdy = ffR(x;y;z(x;y))dxdy, (58.3)
S D
выражающую поверхностный интеграл II рода по переменным х и у через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю,
429
поверхности S, то полученный двойной интеграл берут со знаком «мп нус». Поэтому
JJ R(x-,y;z)dxdy = ± R(x-,y;z(x;y)) dxdy. (58.4'
S D
Аналогично
JJ Q(x-,y; z) dxdz = ± Q(x;y(x;z);z) dxdz, (58.5)
S D„
P(x', y, z) dy dz = ± Ц P(x(y;z)-,y;z)dydz, (58.d S Dyz I
где Dxz и Dyz — проекции поверхности S на плоскости Oxz и Oyl соответственно (замкнутые области). I
В формуле (58.5) поверхность S задана уравнением у = y(x;z), I в формуле (58.6) — уравнением х = x(y;z). Знаки, перед интегралам! выбираются в зависимости от ориентации поверхности S (так, в фоп муле (58.5) берем знак «плюс», если нормаль к поверхности образуя с осью Оу острый угол, а знак «минус» — если тупой угол). !
Для вычисления общего поверхностного интеграла II рода исполУ зуют формулы (58.4) (58.6), проектируя поверхность S на все три kJ ординатные плоскости:
Ц Р{х\ у, z) dy dz + Q(x-, у; z) dx dz + R(x;y, z) dxdy = fl
s I
= ±УУ P(x(y,z);y;z)dydz±
Dy*
± Q(x-,y(x;z);z) dxdz ± JJ R(x;y; z(x;y)) dxdy. 1
Замечание. Можно показать справедливость равенств I
dxdy = cos 7 • ds, dxdz = cos ft • ds, dy dz = cos a ds, (58.7| где ds — элемент площади поверхности S; cos a, cos ft, cos 7 — направляющие косинусы нормали n к выбранной стороне поверхности S.
Поверхностные интегралы I и II рода связаны соотношением
JJ Pdydz + Qdxdz + Rdxdy = JJ(Pcosa + Qcosft+Rcosry)ds. (58.8) s s
Пример 58.1. Вычислить
Ii = J J — x dy dz + z dzdx + 5 dxdy s
по верхней стороне части плоскости 2® — Зу + z = 6, лежащей в IV
октанте.
Q Решение: На рисунке 253 изображена заданная часть плоскости. Нормаль л, соответствующая укачанной стороне поверхности, образует с осью Оу тупой угол, а с осями Ох и Oz — острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора п = (2; —3; 1) плоскости:
Рис. 253
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
Dyz
О Зг/4-6
f dy J (~3~2y+2Z.
—2 О
) dydz — JI zdzdx + 5 J J dx dy = Dasz Dg-y
3 6-2ж 1
J zdz + 5- --2-3 = —9. о
о
58.3. Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема 58.1. Если функции P(x;y;z), Q(x;y,z), R(x-,y;z) непрерывны вместе со своими частными производными первого порядка в пространственной области V, то имеет место формула
— JJ> Р dy dz+Q dx dz+Rdx dy, (58.9) У Z s
где S — граница области V и интегрирование по S производится по ее внешней стороне.
Ж
V
Формула (58.9) называется формулой Остроградского Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
Q Пусть область V ограничена снизу поверхностью Si, уравнение которой z — zi(x;y)-, сверху — поверхностью S-2, уравнение которой
4Q1
z — Z2(x-y) (функции z\ (ж; у) и х2(ж;?/) непрерывны в «замкнутой обла сти D — проекции V на плоскость Оху, Z\(x\y) < z2(t;t/)); сбоку — цилиндрической поверхностью S3, образующие которой параллелыц оси Oz (см. рис. 254). ,
Рассмотрим тройной интеграл
zz(x;y) л о
= f/^ J =
= JJ R^y'’Z2^x'y'>)dxdy~
D
- JJ R(x;y, Zi(x;y))dx dy.
D
Двойные интегралы в правой части ранен-? ства заменим поверхностными интегралами II рода по внешней стороне поверхностей Si и S2 соответственно (см. (58.3)).’ Получаем:
JJ/ ^/dx dz = 1.1 dx + v
JJ Rdxdy.
S2 Si
Добавляя равный нулю интеграл JJ R dx dy по внешней стороне S3 (см. свойство 5 п. 58.1), получим: s3
JJJ dy dz = JJ Rdxdy +
J J Rdxdy + J J Rdxdy, St s3
J JI j/~dx dydz = JJ R(x\ y, z) dx dy, v J s
где S — поверхность, ограничивающая область V.
Аналогично доказываются формулы
JJJ ~^d-7: dydz = JJ Q(x\ у; z} dx dz, v s
JJJ ~Q^dx dydz = JJ P(x-, y, z) dy dz. v s
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем’
формулу (58.9) Остроградского-Гаусса.
или
S2
(58.10)'
(58.11)
(58.12)
432
Замечания.
1. Формула (58.9) остается справедливой для любой области V, которую можно разбить на конечное число областей рассмотренного вида.
2. Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
Пример 58.2. Вычислить I = —xdydz + zdzdx + 5dxdy, +s
где S — внешняя сторона пирамиды, ограниченной плоскостями 2х — Зу + z = 6, х = 0, у = 0, z - 0.
Q Решение: По формуле (58.9) находим:
I = JJJ(—1 + 0 + 0) dxdy dz = — ууу dv ~ — - • 3 • 6 = —6. v v
Заметим, что интеграл Д (см. пример 58.1) мож-
но вычислить иначе:
S2 S3 Sa
где поверхности Sy., S3, S4 есть соответственно треугольники ОАС, АОВ, СОВ (см. рис. 255).
Имеем:
^=-6+ JJ
(ОАС)
з
JJ z dz dx+ (AOB)
4- yy (—0) dydz — — 6 + 5 • — • 2 • 3
(COB) 6 0
1 3
= +9 - - у (6 - 2т)2 dx = 9 -
0
6-2®
/ zdz =
(6 - 2т)3 |3 3 Io
58.4. Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
433
Теорема 58.2. Если функции P(®;«/;z), Q(x;y;z) и Я(ж; ?/;.?) непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S, то имеет место формула
I/(£ - + & - £)* 4. + (”>42 =
J J \ ох оу / \ оу oz ) \dz ох /
= Р dx + Q dy + Rdz, (58.13)
L
где L — граница поверхности S и интегрирование вдоль кривой L производится в положительном направлении (т. е. при обходе границы L поверхность S должна оставаться все время слева).
Формула (58.13) называется формулой Стокса' (Д. Г. Стокс — английский математик, физик).
□ Пусть z = /(ж; у) — уравнение поверхности S, функции f(x:y), fy'(x-,y) непрерывны в замкнутой области D (проекции поверхности S на плоскость Оху), L\ — граница области D (см. рис. 256). Будем считать, что поверхность S пересекается с любой прямой, параллельной оси Oz, не более чем в одной точке. Выберем верхнюю сторону поверхности S. Рассмотрим сначала интеграл вида <f> P(x-,y,z) dx.
L
Значения функции Р(х; у; z) на L равны значениям функции Р(х;у; z(x;y)) на
Интегральные суммы для криволинейных интегралов II рода по контурам L и Lj совпадают. Поэтому
<£> P(x;y;z)dx = <j> Р(х;у, z(x;y))dx.
Применим к этому интегралу формулу Остроградского-Грин< (см. п. 56.3). Тогда получим:
У P(x-,y,z{x-,y))dx = -^(P(x;y,z(x;y))^dxdy =
L’ ° /"/Y— dP dz
JJ \ dy + dz dy
434
dz\ , — 1 cos yds 041/
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. п. 58.2). Для этого последнее равенство перепишем в виде
г , rrtdP dP dz\
У P(x-,v-,z{xMdx=-
Li S’
(cm. 58.7) и используем уравнение нормали к поверхности S (см. (45.3)). 'Гак как выбрана верхняя сторона поверхности S, т. е. cos7 > 0 (7 — острый угол между нормалью п к поверхности S и осью Oz), то нормаль п имеет проекции 1- Направляющие косинусы пропорцио-
нальны соответствующим проекциям:
п &Z d
cosa : cosfi : COS7 = — — : — 77- : 1.
dx dy
Отсюда — ~ = cos^ . Тогда dy cos 7 dz\ , dP cos/?
— I cosyds = - / / 1-д-д--------
dy/ \dy dz COS7
л дР «л ffdP,i л дРи xl cos у ds —— cos fids = / / ~^-dx dz —^dx dy.
dz JJ dz dy
s
) cosyds =
ЖдР dP dz
dy dz dy
s =-//%
Следовательно, С г г dP dP
P(ar; y; z) dx = J J dz — ~Q~dx dy. L S
Аналогично получаются при соответствующих условиях еще два равенства:
Ф Q(x;y;z)dy = J J —dxdy~—dydz,
L S
r ,, ffdP, , dR ,
<t> R(x-, y; z)dz = I -fi-dy dz - —— dx dz.
J J J UU (J JU
L S
Складывая почленно три последних равенства, получаем формулу
Стокса (58.13). И
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
435
Из формулы Стокса вытекает, что если выполняются условия j = 8R_dQ 9P_dR
дх ду ' dy dz’ dz dx й
(см. п. 56.4), то криволинейный интеграл по произвольному простриги ственному замкнутому контуру L равен нулю: Pdx + Q dy + Pdz = Oi
Следовательно, в данном случае криволинейный интеграл не зависти от вида пути интегрирования. I
Пример 58.3. Вычислить 7 = / х2у3 dx + dy + zdz, где кон-L
тур L — окружность X2 + у2 = R2; z = 0: а) непосредственно, б) используя формулу Стокса, взяв в качестве поверхности полусферу
= +y/R2 -х2- у2.
27Г
Q Решение: Поверхность интегрирования изображена на рисунке 257.
а) Запишем уравнение окружности в! параметрической форме:
х = Rcost, у — Rsint, z = 0, t е [0; 2тг].'
По формуле (56.7) имеем:
2тг
I = I R2 cos21 R3 sin3 t(-7?sin t) dt+ о
2тг
I sin41cos2tdt + 0 =
о о
= -R6 I sin 2i) i (1 - cos 2t)dt - sin2 21 dt+
о 0
27 /?<’ 2* Об T-,6
/ sin2 21 cos 21 dl = / (l-cos4t)dt+0 =---------2?r =-------
J 16 ./ 16 8
R6
8 __ ..
о о
б) По формуле Стокса (58.13) находим:
Г = Ij (о - 0) dydz + (0 - 0) dxdz + (0 - Зж2?/2) dxdy =
S = —3II x2y2dxdy = —3II x2y2 dxdy.
s
Переходя к полярным координатам, получаем:
2тг
• 2 9
sm 9? cos
б
J — — 3 Ц r5 sin2 ip cos2 ip dr dip = — 3 I si D
R
J r5 dr —
0
436
Ч 2/ 1 1
= —-7?6 [ --sin22tpdip =—-R6
6 J 4 8
о
1 2гг
- J (1 — cos 4^) dip = о
R6 |2^ „ ttR6
ТбЧ +0=—8"
58.5. Некоторые приложения поверхностного интеграла II рода
С помощью поверхностного интеграла II рода можно найти объем тела, ограниченного сверху поверхностью S2 (z = z2(a:;?/)), снизу — поверхностью Si (z — гДж;?/)), сбоку — цилиндрической поверхностью 8з, образующие которой параллельны оси Oz-.
| JJ xdydz + у dzdx + zdx dy, (58.14)
s
где S = Si + S2 + S3.
Действительно, положив в формуле Остроградского-Гаусса (58.9) Р(х; у, z) = х, Q(x; у; z) = 0, Я(ж; у; z) — 0, находим:
Л xdydz = JJJ dxdy dz, т. e. V = JJxdydz. (58.15)
SV s
Аналогично, полагая P — 0, Q = y, R = 0, находим еще одну формулу для нахождения объема тела с помощью поверхностного интеграла II рода: сг
V = JI ydxdz. (58.16)
s
Наконец, положив Р — 0, Q — 0, R = z, по формуле (58.9) находим третью формулу гг
V — Л zdxdy, (58-17)
s
выражающую объем тела через поверхностный интеграл II рода.
Сложив почленно равенства (58.15) (58.17) и разделив на три, получим формулу (58.14).
Другие применения поверхностного интеграла II рода рассмотрим в главе XVI «Элементы теории поля».
Глава XIII. ЧИСЛОВЫЕ РЯДЫ
Лекции 51-52
§59. ЧИСЛОВЫЕ РЯДЫ
59.1. Основные понятия
Бесконечные ряды широко используются в теоретических исследованиях математического анализа, имеют разнообразные практические применения.
Числовым рядом (или просто рядом) называется выражение вида . а
оо - а
5? ип = щ + и2 + •.. + ип + ..., (59.И
П=1
где щ, и-2,..., ип,... — действительные или комплексные числа, называемые членами ряда, ип — общим членом ряда.
Ряд (59.1) считается заданным, если известен общий член ряда ип, выраженный как функция его номера п: ип = f(n).
ру| Сумма первых п членов ряда (59.1) называется n-й частичной суммой ряда и обозначается через Sn, т. е. Sn = щ + и2 -I-Ьип.
Рассмотрим частичные суммы
Si=Uj, S2=u1+ii2, S3 = щ + и2 + и3,...
К1 Если существует конечный предел S = lim Sn последователь»
L—1 n-->oo
сти частичных сумм ряда (59.1), то этот предел называют сумм>
ОО ряда (59.1) и говорят, что ряд сходится. Записывают: S = ип-п=1
Если lim Sn не существует или lim S„ = 00, то ряд (59.1) паз п—loo п—>оо
вают расходящимся. Такой ряд суммы не имеет.
Рассмотрим примеры.
1. Ряд 2 + 17 — 3^ + 196 + ... нельзя считать заданным, а р. 2 + 5 + 8 +... — можно: его общий член задается формулой ип = Зп —I
2. Ряд 0 + 0+ 0 + ... + 0 + ... сходится, его сумма равна 0.
3. Ряд 1 + 1 + 1 + ... +1 + ... расходится, Sn = п —> оо при п —> оо.
4. Ряд 1—1+1—1+1—1+-.. расходится, так как последовательность частичных сумм 1,0,1,0,1,0,... (Si = 1, S2 = 0, S3 = 1,...) не имеет предела.
438
5. Ряд £ +3) СХ°ДИТСЯ- Действительно,
«=Г2=14
& = Ь2 + F3
1
1-3’
Sn 1 • 2 + 2 • 3 + 3 4 + ‘ ’ + п(п + 1)
Следовательно,
lim Sn = lim (1------—) = 1,
n- >oo n—>OO X Tl 4" 1
т. e. ряд сходится, его сумма равна 1.
Рассмотрим некоторые важные свойства рядов.
Свойство 1. Если ряд (59.1) сходится и его сумма равна 5, то рад
СЮ сип = сщ + си-2 4-... + сип +..., (59.2)
72=1
где с — произвольное число, также сходится и его сумма равна cS. Если же ряд (59.1) расходится и (Д 0, то и рад (59.2) расходится.
□ Обозначим тг-ю частичную сумму ряда (59.2)через S^. Тогда
= СЩ + СМ2 + - • • + сип = С^Щ +и2 + ... + Un) = с • Sn.
Следовательно,
lim S^ = lim cSn = с - lim Sn = c • S,
n~>OQ n—^CO 72-4-00
т. e. ряд (59.2) сходится и имеет сумму cS.
Покажем теперь, что если рад (59.1) расходится, с 0, то и ряд (59.2) расходится. Допустим противное: ряд (59.2) сходится и имеет сумму Si. Тогда
Si = lim — lim cSn = c lim Sn.
n~»<5O 72—>OO n—>OO
Отсюда получаем:
lim Sn = —, n—>oc c
t. e. ряд (59.1) сходится, что противоречит условию о расходимости ряда (59.1).
439
Свойство 2. Если сходится ряд (59.1) и сходится ряд
оо
5ZX (59.3)
п— 1
а их суммы равны Si и S2 соответственно, то сходятся и ряды
ОО
52^* (59.4)
П=1
причем сумма каждого равна соответственно Si ± S2-
□ Обозначим n-е частичные суммы рядов (59.1), (59.3) и (59.4) через Sn ) } Sn и S,, соответственно. Тогда
lim Sn = lim (S.^> ± S^) = lim S<u) ± lim = Si ± S2, n—>oc n—>oo n—>oo n—>oo
т. e. каждый из рядов (59.4) сходится, и сумма его равна Si ± S2 соот-ветственно.
|@| Из свойства 2 вытекает, что сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд.
В справедливости этого утверждения можно убедиться методом o-i противного.
Заметим, что сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом.
Свойство 3. Если к ряду (59.1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (59.1) сходятся или расходятся одновременно.
□ Обозначим через S сумму отброшенных членов, через к — наибольший из номеров этих членов. Чтобы не менять нумерацию оставшихся членов ряда (59.1), будем считать, что на месте отброшенных членов поставили нули. Тогда при п > к будет выполняться равенство Sn — S', — S, где S', — это п-я частичная сумма ряда, полученного из ряда (59.1) путем отбрасывания конечного числа членов. Поэтому lim Sn = S + lim S'. Отсюда следует, что пределы в левой и правой п-юо п~нх
частях одновременно существуют или не существуют, т. е. ряд (59.1) сходится (расходится) тогда и только тогда, когда сходятся (расходятся) ряды без конечного числа его членов.
Аналогично рассуждаем в случае приписывания к ряду конечного числа членов.
Ряд ~
^п+1 + 4“ — Uk (59.5)
называется n-м остатком ряда (59.1). Он получается из ряда (59.1) отбрасыванием п первых его членов. Ряд (59.1) получается из остатка
440
добавлением конечного числа членов. Поэтому, согласно свойству 3, ряд (59.1) и его остаток (59.5) одновременно сходятся или расходятся. |(Ц Из свойства 3 также следует, что если ряд (59.1) сходится, то его остаток rn = S - Sn = wn+i + ип+2 + ... стремится к нулю при п —> оо, т. е. lim гп = 0.
п—>оо
59.2. Ряд геометрической прогрессии
а 1-Q’
Исследуем сходимость ряда
а + aq + ад2 + ... + адп~} + ... («^ 0), (59.6)
который называется рядом геометрической прогрессии. Ряд (59.6) часто используется при исследовании рядов на сходимость.
Как известно, сумма первых п членов прогрессии находится по формуле Sn = — q Зайдем предел этой суммы:
о «(1 - 9") а г чп
lim Sn = шп ——-------= —--------a lim ----.
n—>oo n—>oo 1 — q 1 — q n~>oo 1 — q
Рассмотрим следующие случаи в зависимости от величины q:
1. Если Iql < 1, то qn —> 0 при п —> оо. Поэтому lim Sn
п—>оэ ряд (59.6) сходится, его сумма равна ° ;
2. Если |q| > 1, то qn -> оо при п —> оо.
ряд (59.6) расходится;
3. Если |q| = 1, то при q = 1 ряд а + а + а -I-Fа4----, для него Sn = п-а и lim
п—>сх расходится; при q = -1 ряд (59.6) принимает вид а — а + а — а+ ... — в этом случае Sn = 0 при четном п и Sn — а при нечетном п. Следовательно, lim Sn не существует, ряд (59.6) расходится.
п~>оо
Итак, ряд геометрической прогрессии сходится при |q| < 1 и расходится при |q| 1.
Поэтому lim Sn
= оо,
(59.6) принимает вид Sn = оо, т. е. ряд (59.6)
Пример 59.1. Показать, что ряд 23 + 22+ 2+ ± +... + Lg- +...
сходится.
Q Решение: Данный ряд можно переписать так:
23.1 + 23-|+23 ^+... + 23-^+...
Как видно, он представляет собой ряд геометрической прогрессии с а — 23ид = ^<1. Этот ряд сходится согласно свойству 1 числовых рядов. •
441
59.3. Необходимый признак сходимости числового ряда. Гармонический ряд
Нахождение п-й частичной суммы Sn и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них, как правило, является необходимый признак сходимости.
Теорема 59.1. Если ряд (59.1) сходится, то его общий член ип стремится к нулю, т. е. lim ип = 0.
п—>оо
Q Пусть ряд (59.1) сходится и lim Sn = S. Тогда и lim Sn-i = б' П—400 __ ? 1—4 оо
(при п -> оо и (п — 1) -> оо). Учитывая, что ип = Sn — Sn-i при п > 1, получаем:
lim ип = lim (S„ - S„-i) = lim Sn - lim Sn-i = S - S = 0. 77—400 П—>OO 77—400 71—400
Следствие 59.1 (достаточное условие расходимости ряда). Если lim ип 0 или этот предел не существует, то ряд расходится.
п—>оо
□ Действительно, если бы ряд сходился, то (по теореме) lim ип — 0.
77—400
Но это противоречит условию. Значит, ряд расходится.
Ч — 9
Пример 59.2. Исследовать сходимость ряда 52 /
п=1 п + °
Q Решение: Ряд V - ?-„=1 п+5 lim ип
расходится, т. к.
= lim ^ = 3/0,
т. е. выполняется достаточное условие расходимости ряда.
Пример 59.3. Исследовать сходимость ряда
(1 V1
1 + —) = П/
— е 0. 41
442
Теорема 59.1 дает необходимое условие сходимости ряда, но не к (Статочное: из условия lim ип = 0 не следует, что ряд сходит-п—>оо
• я. Это означает, что существуют расходящиеся ряды, для которых lim ип = 0.
и >сю
В качестве примера рассмотрим так называемый гармонический
(59.7)
Очевидно, что lim ип = 0. Однако ряд (59.7) расходится. Покажем п—>оо
ЭТО.
(1 \ П
1 + - ) - е. Отсюда следует, что
при любом п € N имеет место неравенство + < е. Логарифмируя
это неравенство по основанию е, получим:
' ’ 1 , 77 + 1 1 . . , п .
— > In--------, — > lll(77 + 1) — Ill 77.
77 77 77
Подставляя в полученное неравенство поочередно п — 1,2,..., п — 1, п, получим:
1 >1п2,
- >1пЗ —1п2, 2
i > In 4 — In 3, 3
— > 111 (77 + 1) — 111 77. 77
Сложив почленно эти неравенства, получим Sn > 1п(тг + 1). Поскольку lim ln(rz + 1) = оо, получаем lim Sn = оо, т. е. гармонический п—>оо п—>оо
ряд (59.7) расходится.
В качестве второго примера можно взять ряд
111 1
Здесь lim = lim -4= = 0. Однако этот ряд расходится, п—>оо п—>ОО 71,
443
[_j Действительно,
т. е. Sn > у/п. Следовательно, Sn —> оо при п -> оо, ряд расходится. I
§60. ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ ЗНАКОПОСТОЯННЫХ РЯДОВ
Необходимый признак сходимости не дает, вообще говоря, возмог ности судить о том, сходится ли данный ряд или нет. Сходимость j расходимость ряда во многих случаях можно установить с помощы так называемых достаточных признаков. .(
Рассмотрим некоторые из них для знакоположительных pji дов, т. е. рядов с неотрицательными членами (.знакоотрицательны ряд переходит в знакоположительный путем умножения его на (—1) что, как известно, не влияет на сходимость ряда).
60.1. Признаки сравнения рядов
Сходимость или расходимость знакоположительного ряда частя устанавливается путем сравнения его с другим («эталонным») рядом о котором известно, сходится он или нет. В основе такого сравнени, лежат следующие теоремы.
Теорема 60.1. Пусть даны два знакоположительных ряда
52 и» (60.1)
оо
(60.2)
п=1
Если для всех п выполняется неравенство
< vn, (60.3)
то из сходимости ряда (60.2) следует сходимость ряда (60.1), из расходимости ряда (60.1) следует расходимость ряда (60.2).
□ Обозначим п-е частичные суммы рядов (60.1) и (60.2) соответственно через и Sn'). Из неравенства (60.3) следует, что
(60.
Пусть ряд (60.2) сходится и его сумма равна S2. Тогда lim Sn — 82-п—>оо
11лены ряда (60.2) положительны, поэтому S,^ < S2 и, следовательно, <• учетом неравенства (60.4), С S-2- Таким образом, последовательность S^\ ... монотонно возрастает (ип > 0) и ограниче-
на сверху числом S-2- По признаку существования предела (см. теорема 15.3) последовательность имеет предел lim Sn^ — Si, т. е. п->оо
ряд (60.1) сходится.
Пусть теперь ряд (60.1) расходится. Так как члены ряда неотрицательны, в этом случае имеем lim S,^ = 00. Тогда, с учетом нера-п—>оо
венства (60.4), получаем lim S„= оо, т. е. ряд (60.2) расходится. п—>оо
Замечание. Теорема 60.1 справедлива и в том случае, когда неравенство (60.3) выполняется не для всех членов рядов (60.1) и (60.2), a начиная с некоторого номера N. Это вытекает из свойства 3 числовых рядов (см. п. 59.1).
Теорема 60.2 (предельный признак сравнения). Пусть даны два знакоположительных ряда (60.1) и (60.2). Если существует конечный, отличный от 0, предел lim = А (0 < А < оо), то ряды (60.1) п—>00 Vn
и (60.2) сходятся или расходятся одновременно.
Q По определению предела последовательности (см. п. 15.2) для всех п, кроме, возможно, конечного числа их, для любого е > 0 выполняется неравенство — А < е, или
I Vn I
(А - е) • vn < ип <(А + е)- vn. (60.5)
Если ряд (60.1) сходится, то из левого неравенства (60.5) и тео-ОО
ремы 60.1 вытекает, что ряд (А — e)vn также сходится. Но тогда,
П=1
согласно свойству 1 числовых рядов (см. и. 59.1), ряд (60.2) сходится.
Если ряд (60.1) расходится, то из правого неравенства (60.5), теоремы 60.1, свойства 1 вытекает, что и ряд (60.2) расходится.
Аналогично, если ряд (60.2) сходится (расходится), то сходящимся (расходящимся) будет и ряд (60.1).
слл -
Пример 60.1. Исследовать на сходимость ряд о 2l ч» • п=1 Л + 2
445
Q Решение: Сравним данный ряд с рядом геометрической прогреса У? 2", который сходится (g = ~ < 1). Имеем yyyr < у'- Следов тельно, данный ряд сходится.
Пример 60.2. Исследовать сходимость ряда V Д=-
П=1 V'«
Q Решение: Здесь ип = Возьмем ряд с общим членом vn = — х/n п
1 1
который расходится (гармонический ряд). Имеем Следов:
тельно, данный ряд расходится. I
ОО
Пример 60.3. Исследовать сходимость ряда )Г tg^H.
>i=i
Q Решение: Применим предельный признак сравнения. Так как lim —0 (см. пример 17.7), то по теореме 60.2 исходный сю — О
п
ряд расходится, как сравнимый с гармоническим рядом. •
60.2. Признак Даламбера
В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера, (1717-1783, французский математик) позволяет часто решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом.
Теорема 60.3. Пусть дан ряд (59.1) с положительными членами и существует конечный или бесконечный предел lim —-НТ = I, п—^сю
Тогда ряд сходится при I < 1 и расходится при I > 1.
□ Так как lim Un+1 — Ц то по определению предела для любого е > 0 п—>оо Un
найдется натуральное число N такое, что при n > N выполняется неравенство
wn+l «
ип
< £ ИЛИ I — £ < ------- <1-4-6.
(60.6)
Пусть I < 1. Можно подобрать е так, что число /+е < 1. Обозначим I + е = q, q < 1. Тогда из правой части неравенства (60.6) получаем "п|1 < q, или un+i < q un, n > N. В силу свойства 3 числовых рядов ип
446
можно считать, что un+i < q - ип для всех п = 1,2,3,... Давая номеру и эти значения, получим серию неравенств:
и2 <д-щ,
и3 <q-u2 < qI 2Ui,
и4 <q-u3 < q3ui, ............3
т/п < q' un < q wi,
t. e. члены ряда м2 + из + ш + ••• + «„ + ... меньше соответствующих членов ряда qu\ +g2wi +g3iti +... + g,l+1u1 +..., который сходится как ряд геометрической прогрессии со знаменателем 0 < q < 1. Но тогда, на основании признака сравнения, сходится ряд гд2 + и3 +... + ип +..., следовательно, сходится и исходный ряд (59.1).
Пусть I > 1. В этом случае lim = I > 1. Отсюда следует, что, n—>оо Un
начиная с некоторого номера N, выполняется неравенство Ц)‘+1 > 1, или ип+1 > ип, т. е. члены ряда возрастают с увеличением номера п. Поэтому lim ип 0. На основании следствия из необходимого призна-п- >оо
ка (см. п. 59.3) ряд (59.1) расходится.
Замечания.
I. Если I = 1, то ряд (59.1) может быть как сходящимся, так и расходящимся.
2. Признак Даламбера целесообразно применять, когда общий член ряда содержит выражение вида п! или ап.
ОО
Пример 60-4- Исследовать на сходимость ряд
Q Решение: Находим
I = lim —— lim = lim -—= lim —— = 0. n->oo un П-ЮО i n->oo (n + 1)! n-»oo 71+1
Так как I = 0 < 1, то данный ряд по признаку Даламбера сходится. •
“ on
Пример 60.5. Исследовать сходимость ряда ^7-п=1 'а
447
Q Решение: Вычисляем ||
3n+i Зп 3п-3п2
I = hm I ------s ; 1 = hm —— -----= г
n->oo \ (п + I)2 п2 ) П.-+СО Зп - (п + I)2
/ 1 \ 2
(fl \ А I 1 \ (.
----- ) = 3 lim ( -г )=3. ;
П.4* 1 / п—>оо \ 1 -4- — / ir
х п' •;
Так как I = 3 > 1, то данный ряд по признаку Даламбера расходится. Г
• Г
I
60.3. Радикальный признак Коши
Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости знакоположительного ряда. Этот признак в<> многом схож с признаком Даламбера, о чем говорят его формул ировк а и доказательство.
Теорема 60.4. Пусть дан ряд (59.1) с положительными членами и существует конечный или бесконечный предел lim ’i/u^ = I.
п—>оо v
Тогда ряд сходится при I < 1 и расходится при I > 1.
Как и для признака Даламбера, в случае, когда I = 1, вопрос о сходимости ряда остается открытым. Доказательство теоремы аналогично доказательству признака Даламбера. Поэтому опустим его.
ОО q / \ п
Пример 60.6. Исследовать на сходимость ряд 52 w' (—)
П=1 6 \п+и
Q Решение: Так как
то применим радикальный признак Коши к ряду
Вычисляем
ОО । Z \ п2
Ряд 52 ^ ' ( —т~г ) сходится, а значит, сходится и исходный ряд,
п=1 ,5 \п+1/
согласно свойству 1 числовых рядов. •
448
60.4. Интегральный признак Коши.
II .............................____________________________
оо
Теорема 60.5. Если члены знакоположительного ряда ип могут
быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке [1; +оо) функции /(гс) так, что «1 = /(l),w2 = /(2),...,wn = /(п),..., то:
+оо
1) если J f(x)dx сходится, то сходится и ряд (59.1); 1 4-оо
2) если j f(x)dx расходится, то расходится также и ряд (59.1). 1
О сходимости несобственных интегралов см. § 40.
* Q Рассмотрим криволинейную трапецию, ограниченную сверху гра-1 фиком функции у = f(x), основанием которой служит отрезок оси Ох кк от х = 1 до х = п (см. рис. 258).
Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки [1; 2], [2; 3], ... Учитывая геометрический смысл определенного интеграла, запишем:
п
f (2)-1+/(3)4 + ..-+/(п)4 < у /(ж) dx < /(1)4+/(2)4+. • -+/(п-1)4, 1
15 Конспект лекций по высшей математике. Полный курс
449
или п
и2 + и$ + ... + ип < J f(x) dx <Ui + W2 + • • • + Un-1, 1
1 I
ИЛИ n 1
Sn - Ui < J f(x) dx < Sn - Un. (60.7)1
1 I
+oo |
Случай 1. Несобственный интеграл j f[x) dx сходится, т. ej i •
l~oo n 4-oo
j f(x)dx = А. Поскольку j f(x)dx < J f(x)dx = А, то с учс-i i i
том неравенства (60.7) имеем: Sn - ur < A, t. e. Sn < щ + Л. Так как
последовательность частичных сумм монотонно возрастает и ограни чена сверху (числом щ + А), то, по признаку существования предела, имеет предел. Следовательно, ряд (59.1) сходится.'
4-оо
Случай 2. Несобственный интеграл J f(x) dx расходится. Тогда 1
+ сс п
J f (ж) dx = +оо и интегралы J f (ж) dx неограниченно возрастают 1 1
п
при я -> оо. Учитывая, что Sn > J f (ж) dx + ип (см. (60.7)), получаем, L
что Sn -> оо при п -> оо. Следовательно, данный ряд (59.1) расходится.
4-оо
Замечание. Вместо интеграла J f (ж) dx можно брать интеграл
J f(x)dx, где к € N, к > 1. Отбрасывание к первых членов ряда к
в ряде (59.1), как известно, не влияет на сходимость (расходимость) ряда.
ОС |
Пример 60.7. Исследовать на сходимость ряд V —±—.
п=2 П ‘ 1П П
Q Решение: Воспользуемся интегральным признаком Коши. Функция f (ж) = .,-ь,удовлетворяет условиям теоремы 60.5. Находим
X 111 X
dx
ж In ж
= In 11пж|
Значит, ряд с общим членом ип = - расходится.
(60.8)
где р > 0 — действительное число, называется обобщенным гармоническим рядом. Для исследования ряда (60.8) на сходимость применим интегральный признак Коши (признаки Даламбера и Коши ответа о сходимости не дают).
Рассмотрим функцию /(ж) = Эта функция непрерывна, моно-
тонно убывает на промежутке [1; +оо) и /(я) = = ип. При р 1
имеем:
оо , а 1—п 1Л
f dx [ х р р
= |im / х dx ~ пт --- —
J ж" «-ТОО J «->оо 1 — р 11
I 1 1
, А?1 1 ч (—если р > 1,
= Ит(т------Р-1’
«->оо\1— р \—pJ (оо, если р < 1.
; 1
При р = 1 имеем гармонический ряд ип = —, который расходится (второй способ: f ~ = °0)- Итак, ряд (60.8) сходится при р > 1, 1 111 расходится при р 1. В частности, ряд 1+^2+д2+.-. + ^2+-.-сходится (полезно знать).
Рассмотренные признаки сходимости (есть и другие) знакоположительных рядов позволяют судить о сходимости практически любого положительного ряда. Необходимые навыки приобретаются на практике.
§61. ЗНАКОЧЕРЕДУЮЩИЕСЯ
И ЗНАКОПЕРЕМЕННЫЕ РЯДЫ'
61.1. Знакочередующиеся ряды. Признак Лейбница
Рассмотрим важный класс рядов, называемых знакочередующимися. Знакочередующимся рядом называется ряд вида
ОО
Ui - U2 + и3 - U4 + - - - + (-1)’1+1Н11 + • • = 52(-1)"+1М„, (61.1) •
п—1
где ип > 0 для всех п & N (т. е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).
Для знакочередующихся рядов имеет место достаточный признак сходимости (установленный в 1714 г. Лейбницем в письме к И. Бернулли) .
450
451
Теорема 61.1 (признак Лейбница). Знакочередующийся ряд (61.1) сходится, если:
1. Последовательность абсолютных величин членов ряда монотонно убывает, т. е. и4 > U2 > и3 > • • • > ип > ...;
2. Общий член ряда стремится к нулю: lim ип = 0. п—>оо
При этом сумма S ряда (61.1) удовлетворяет неравенствам
0<5<«!. (61.2)
Q Рассмотрим сначала частичную сумму четного числа (2m) членов ряда (61.1). Имеем
S-Zm = Ui — U2 + U3 — U4 + ... + U2m—1 — U2m = |
= («1 - U2) + (w3 - и4) + . + (u2m-l - и2т).
Выражение в каждой скобке, согласно первому условию теоремы, положительно. Следовательно, сумма S2m > 0 и возрастает с возрастанием номера 2m. .
С другой стороны, S2m можно переписать так:
82т — Ui (w2 tl3) (U4 iig) • • (U2m—2 U2m—1) T ^2m- 1
Легко видеть, что S2m < ui- Таким образом, последовательность S2, S4} Se, , S2m-, возрастает и ограничена сверху. Следовательно, она имеет предел lim 82т = S, причем 0 < S < щ. п—too
Рассмотрим теперь частичные суммы нечетного числа (2т+1) членов ряда (61.1). Очевидно, что Svm+i = 82т + «2т+1- Отсюда следует, что
lim S2m+i = lim {S2m + M2m+i) = lim 82m + 0 = S, m—>oa т-Лоо m—xx:
т. к. lim U2m+i = 0 в силу второго условия теоремы. Итак, lim Sn ~ S т—Уоо п—>оо
как при четном п, так и при нечетном п. Следовательно, ряд (61.1) сходится, причем 0 < S < и4.
Замечания.
1. Исследование знакочередующегося ряда вида
-щ + и2 - и3 + и4 ~ ... (61.3)
(с отрицательным первым членом) сводится путем умножения всех его членов на (—1) к исследованию ряда (61.1).
Ряды (61.1) и (61.3), для которых выполняются условия теоремы: Лейбница, называются лейбницевскими (или рядами Лейбница).
j@| 2. Соотношение (61.2) позволяет получить простую и удобную: оценку ошибки, которую мы допускаем, заменяя сумму S данного:
452
ряда его частичной суммой Sn. Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд (—l)n+1 ('«„-и — ип+2 + •••), сумма которого по модулю меньше первого члена этого ряда, т. е. Sn < «п+i Поэтому ошибка меньше модуля первого из отброшенных членов.
Пример 61.1. Вычислить приблизительно сумму ряда
Q Решение: Данный ряд лейбницевского типа. Он сходится. Можно
1 4- 1
= S. Взяв пять членов, т. е. заменив S на
1 J__2 2.-3 1 1 1
:? + F~44+5B'~4 + 27- 256 + 3125
« 0,7834,
1 1
сделаем ошибку, меньшую, чем < 0,00003. Итак, S ~ 0,7834.
61.2. Общий достаточный признак сходимости знакопеременных рядов
pg| Знакочередующийся ряд является частным случаем знакопеременного ряда. Числовой ряд ип, содержащий бесконечное мно-П—1
жество положительных и бесконечное множество отрицательных членов, называется знакопеременным.
Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.
Теорема 61.2. Пусть дан знакопеременный ряд
Щ + и2 + • • • + ип + ... (61.4)
Если сходится ряд
|wi| + |г«2| + • • • + |wn| + ..., (61.5)
составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (61.4).
453
Ч
Q| Рассмотрим вспомогательный ряд, составленный из членов радон (61.4) и (61.5):
ОО
(М1 + |г«1|) + («2 + |«21) + - • - + (ип + |«„|) + - = 2Q(wn + |мп|).
п~1
оо
Очевидно, что 0 < ип + |un| < 2|un| для всех п е N. Но рад £ 2|u„|
п~1
сходится в силу условия теоремы и свойства L числовых рядов (и. 59.1)
. Следовательно, на основании признака сравнения (п. 59.3) сходится ОО
и ряд (ип + |гщ|). Поскольку данный знакопеременный ряд (61.4) п=1
представляет собой разность двух сходящихся рядов
ОО ОО ОО
' ип — ^,(.ип + |^п|) ' |^п|,
п=1 п=1 п=1
то, на основании свойства 2 числовых рядов, он (ряд (61.4)) сходится.
Отметим, что обратное утверждение несправедливо: если сходится ряд (61.4), то это не означает, что будет сходиться ряд (61.5).
ОО 1
Пример 61.2. Исследовать сходимость ряда (—1)”+1 - — • п=1 П
О Решение: Это знакочередующийся ряд, для которого выполнены условия признака Лейбница. Следовательно, указанный ряд сходится. Однако ряд, составленный из модулей членов данного ряда, т. е.
ряд
расходится (гармонический ряд).
61.3. Абсолютная и условная сходимости числовых рядов. Свойства абсолютно сходящихся рядов
Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Так, ряд, показанный в примере (61.2), условно сходящийся. Ряд
ОО .
п!
п=1
454
нбсолютно сходится, т. к. ряд, составленный из модулей его членов, < ходится (см. пример 60.4).
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм (переместительность, сочетательность, распределительность).
Основные свойства абсолютно сходящихся рядов приводим без доказательства.
1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (теорема Дирихле).
2. Абсолютно сходящиеся ряды с суммами Si и S2 можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна Si + S2 (или соответственно Si — S2).
3. Под произведением двух рядов гц + и2 + - • • и щ 4- г>2 + - - • понимают ряд вида
(midi) + (щг>2 + и2гд) + (и^з + '«2'с2 + «3^1) + ...
• + (ui vn + д2г>„-1 + ... + wnt>i) + .
Произведение двух абсолютно сходящихся рядов с суммами Si и S2 [есть абсолютно сходящийся ряд, сумма которого равна Si S2.
; Таким образом, абсолютно сходящиеся ряды суммируются, вычи-। таются, перемножаются как обычные ряды. Суммы таких рядов не за-[ висят от порядка записи членов.
J В случае условно сходящихся рядов соответствующие утвержде-; ния (свойства), вообще говоря, не имеют места.
Так, переставляя члены условно сходящегося ряда, можно добиться того, что сумма ряда изменится. Например, ряд 1 — 5 -
условно сходится по признаку Лейбница. Пусть его сумма равна S. Перепишем его члены так, что после одного положительного члена будут идти два отрицательных. Получим ряд
1 11 1 1,1 1 1
2~4 + 3- 6~8 + 5 10 12 + ”
Сумма уменьшилась вдвое!
Более того, путем перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее заданной суммой или расходящийся ряд (теорема Римана).
455
Поэтому действия над рядами нельзя производить, не убедившись в их абсолютной сходимости. Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.
Глава XIV. СТЕПЕННЫЕ РЯДЫ
Лекции 53-55 I
§62 . ФУНКЦИОНАЛЬНЫЕ РЯДЫ
62.1. Основные понятия
Ряд, членами которого являются функции от х, называется функ-ционамным:
оо
У" Un(x) = U1(X1) + W2(®) + • • + u„(rc) + . . . (62.1)
n=l
Придавая x определенное значение tq, мы получим числовой ряд Н1(ад) + ц2(ж0) + - • + ип(х0) + ,
который может быть как сходящимся, так и расходящимся.
|ф| Если полученный числовой ряд сходится, то точка Xq называется точкой сходимости ряда (62.1); если же ряд расходится
точкой расходимости функционального ряда.
Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется его областью сходимости.
В области сходимости функционального ряда его сумма является некоторой функцией от х: S = S(x). Определяется она в области сходимости равенством
S(x) = lim Sn(rc), где Sn(x) = ui(x) + u-2(x) + ... + un(x) — n—>oo
частичная сумма ряда.
oo
Пример 62.1. Найти область сходимости ряда )Г ж"-
п=0
(Д Решение: Данный ряд является рядом геометрической прогрессии со знаменателем q = х. Следовательно, этот ряд сходится при |ж| < 1, т. е. при всех х G (—1; 1); сумма ряда равна pj; :
5(т) =
ОО
п=0
L
-----, при
1 — X
Пример 62.2. Исследовать сходимость функционального ряда
. 9
Sinn X
457
Q Решение: Составим ряд из абсолютных величин членов исходного
ряда:
sina;
--+
I2
Так как при любом х 6
1
вшп2ж
sin 22х ‘i2
R имеет место соотношение
п2
(62.2)
. о sin П X п2
1
а ряд с общим членом -4^ сходится (обобщенный гармонический ряд,
п
р = 2 > 1, см. п. 60.4), то по признаку сравнения ряд (62.2) сходится при х € R. Следовательно, исходный ряд абсолютно сходится при всех х € R = (—оо; +оо). •
t
Среди функциональных рядов в математике и ее приложениях осо бую роль играет ряд, членами которого являются степенные функ ции аргумента х, т. е. так называемый степенной ряд-.
ОО
апхп = ао + а\Х + а2ж2 + ... + апхп + ... (62.3)
п=0
Действительные (или комплексные) числа ао, ai, а2,..., ап,... называются коэффициентами ряда (62.3), а; € К — действительная переменная.
Ряд (62.3) расположен по степеням х. Рассматривают также степенной ряд, расположенный по степеням (х — жо), т. е. ряд вида
ОО
У7 “п(ж — жо)" = ао + ах(ж - ж0) Ч-+ а„(ж - Жо)” + ..., (62.4)
п=0
где Жо — некоторое постоянное число.
Ряд (62.4) легко приводится к виду (62.3), если положить ж—ж0 = z. Поэтому при изучении степенных рядов можем ограничиться степенными рядами вида (62.3).
§63 . СХОДИМОСТЬ СТЕПЕННЫХ РЯДОВ
Выясним вопрос о сходимости степенного ряда (62.3). а
Область сходимости степенного ряда (62.3) содержит по крайней мере одну точку: ж = 0 (ряд (62.4) сходится в точке ж = жр).
63.1. Теорема Н. Абеля
Об области сходимости степенного ряда можно судить, исходя из следующей теоремы.
Теорема 63.1 (Абель). Если степенной ряд (62.3) сходится при ж = Жо 0, то он абсолютно сходится при всех значениях ж, удовлетворяющих неравенству |ж| < |жо|-
458
сю
□ По условию ряд 52 апжо сходится. Следовательно, по необходимо-п=0
му признаку сходимости lim апХп — 0. Отсюда следует, что величина п—>оо
апх’д ограничена, т. е. найдется такое число М > 0, что для всех п выполняется неравенство 1апХд | С М, п = 0,1,2,...
Пусть ].т| < |.то|, тогда величина q = |^-| < 1 и, следовательно,
|апжп| = |а„Жо| •
хп
•t0
< М -qn,
п = 0,1,2,...,
т. е. модуль каждого члена ряда (62.3) не превосходит соответствующего члена сходящегося (q < 1) ряда геометрической прогрессии. Поэтому по признаку сравнения при |ж| < |жо| ряд (62.3) абсолютно сходящийся.
Следствие 63.1. Если ряд (62.3) расходится при х = Xi, то он расходится и при всех х, удовлетворяющих неравенству |ж| > |Ж1|.
[_j Действительно, если допустить сходимость ряда в точке #2, для которой |®21 > |ж1|, то по теореме Абеля ряд сходится при всех х, для которых |т| < |ж-21, и, в частности, в точке Х\, что противоречит условию.
63.2. Интервал и радиус сходимости степенного ряда
Из теоремы Абеля следует, что если хо 0 есть точка сходимости степенного ряда, то интервал (—|гсо|; |ж0|) весь состоит из точек сходимости данного ряда; при всех значениях х вне этого интервала ряд (62.3) расходится.
-R ряд сходится R
ряд расходится _|Жо| ’ О |ж0| 1>ЯД расходится
Рис. 259
|ф| Интервал (—|жо|;|®о|) и называют интервалом сходимости степенного ряда. Положив |®о| = R, интервал сходимости можно записать в виде (—R-,R). Число R называют радиусом сходимости степенного ряда, т. е. R > 0 — это такое число, что при всех х, для которых |а;| < R, ряд (62.3) абсолютно сходится, а при |.т| > R ряд расходится (см. рис. 259).
459
В частности, когда ряд (62.3) сходится лишь в одной точке хо = О, то считаем, что R — 0. Если же ряд (62.3) сходится при всех значениях х € К (т. е. во всех точках числовой оси), то считаем, что R = оо.
Отметим, что на концах интервала сходимости (т. е. при х = R и при х = —R) сходимость ряда проверяется в каждом случае отдельно.
Для нахождения радиуса сходимости степенного ряда (62.3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда
|°о| + + И2-г’2| + •. + |апж”| 4-...
и применим к нему признак Даламбера. Допустим, что существует пр< дел
lim
71-
lim
71—>ОС
®п+1& йпт”
= |ж| • lim
п—>оо
О, X 0.
^п+1
По признаку Даламбера ряд сходится, если |ж| • lim ап+1 < 1, т. е> п—>сю| (Ln I
ряд сходится при тех значениях ж, для которых
lim
п—»оо
ряд, составленный из модулей членов ряда (62.3), расходится при тех
значениях х, для которых |ж| > lim . Таким образом, для ря-п- >ос| On+1 I
да (62.3) радиус абсолютной сходимости
R = lim
n->co an+i
(63.1)
= 0, то можно убедиться, что ряд (62.3) аб- i I ton I
Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что
R---------1 ____ (63.2)
lim у/|щ, |
71->ОС
Замечания.
1. Если lim
п—>оо
солютно сходится на всей числовой оси. В этом случае R = оо. Если lim I I = оо, то R = 0.
п—>ОО I dn I
2. Интервал сходимости степенного ряда (62.4) находят из неравенства |ж — Жо| < R; имеет вид (жо — R- ж0 + R). t
- 3. Если степенной ряд содержит не все степени х, т. е. задан непол-
ный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (63.1) и (63.2)), а непосредственно
460
применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда.
~ „п
Пример 63.1. Найти область сходимости ряда 22 “Г-п=0 П‘
Q Решение: Воспользуемся формулой (63.1):
R - lim —у— = lim llhzLlL = цт (n _р i) — qq П-+ОО 72->OO п\ П->ОО
(п+1!)
Следовательно, данный ряд абсолютно сходится на всей числовой оси.
Пример 63.2. Найти область сходимости ряда
„,2п-1
(-D"+1f—т
2п — 1
(J Решение: Заданный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем:
। . k2n-1l , ._k2n+1|
|Wni~2n-l’ |Ип+1,-2п + 1’
Un+1 |«2n+1| • (2n — 1) .211- 2n — 1 2
lim = lim 2-----------' \ = ж2 • hm -------- = x2.
n-^oo un n-»oo (2n + 1) I#2 11 п-юо 2'П. + 1
Ряд абсолютно сходится, если х2 < 1 или — 1 < х < 1. Исследуем поведение ряда на концах интервала сходимости.
При х = — 1 имеем ряд — 1 + А — А + 1 — ..., который сходится по признаку Лейбница.
При х = 1 имеем ряд 4-1 — 1 + 1 — = + ... — это тоже сходящий-о О ।
ся лейбницевский ряд. Следовательно, областью сходимости исходного ряда является отрезок [—1; 1]. •
Пример 63.3. Найти область сходимости ряда
ОО
Е
п—1
(х + 2)” п-2"-1’
Q Решение: Находим радиус сходимости ряда по формуле (63.1):
R = lim
П“»ОО
1
тг-2’
1
(л + 1) - 2”
,. (п + 1)-2”
= 11ГП --------j—
п-»оо 71-2” 1
= 2.
461
Следовательно, ряд сходится при —2 < х + 2 < 2, т. е. при —4 < х < 0.
При х = — 4 имеем ряд
V- (-2)”
оо
П=1 П=1
который сходится по признаку Лейбница.
При х = 0 имеем расходящийся ряд оо 2?г 00
п 2п1 п
П=1 п=1
Следовательно, областью сходимости исходного ряда является полуотрезок [—4; 0). •
63.3. Свойства степенных рядов
Сформулируем без доказательства основные свойства степенных рядов.
1. Сумма S(x) степенного ряда (62.3) является непрерывной функцией в интервале сходимости (—/?;/?).
оо оо
1@| 2. Степенные ряды апХп и )Р Ъпхп, имеющие радиусы сходи-L—। п=О п=0
мости соответственно Ri и J?2, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел Ri и R2.
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда
S(x) = «с + ai х + а2ж2 + аз®3 + ... + апхп + ...-. (63.3)
при —R < х < R выполняется равенство
S'(x) — ai + 2а2х + За3я;2 + ... + п апхп~} + ... (63.4)
4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда (63.3) при — R < а < х < R выполняется равенство (см. замечание 1, с. 416)
У S(t)dt= J aodt+ J aitdt + J a2t2dt + ... + J antndt + ... (63.5) a a a a a
Ряды (63.4) и (63.5) имеют тот же радиус сходимости, что и исходный степенной ряд.
Перечисленные свойства 1 4 остаются справедливыми и для степенных рядов вида (62.4).
Свойства степенных рядов широко используются в теоретических исследованиях и в приближенных вычислениях.
462
§64. РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ
64.1. Ряды Тейлора и Маклорена
Для приложений важно уметь данную функцию f(x) разлагать в степенной ряд, т. е. функцию f(x) представлять в виде суммы степенного ряда.
Как известно (см. теорема 26.1), для любой функции /(ж), определенной в окрестности точки хо и имеющей в ней производные до (п + 1)-го порядка включительно, справедлива формула Тейлора:
/(«) = f(x0) + f ipfo - ®о) + {х - жо)2 + • •
•••+J \ 0Дж-ж0)и + Дп(ж), (64.1) пл
|©| где Rn(x) =
- zo)’l+1
, с G (жо,ж), — остаточный член в
форме Лагранжа. Число с можно записать в виде с = жЬ + #(ж —Жо),
где 0 < в < 1. Формулу (64.1) кратко можно записать в виде
/(ж) = Рп(ж) + Д„(ж),
где Рп(ж) = /(ж0) + (ар) (ж _ Жо) +... + f ^\°\х - хо)п — многочлен Тейлора.
Если функция /(ж) имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки жо и остаточный член Я„(ж) стремится к нулю при п -> оо ( lim Дп(ж) = 0), то из формулы п—>оо
Тейлора получается разложение функции /(ж) по степеням (ж — жд), называемое рядом Тейлора:
/(ж) = /(ж0) + ^(ж - жд) + • • = £ ~f^(* -п=0
(64.2)
Если в ряде Тейлора положить жд = 0, то получим разложение функции по степеням ж в так называемый ряд Маклорена:
/(ж) = /(0)+^фж +
/"(0)^2
/(п)(0) п! а •
(64.3)
Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в
463
) J
окрестности точки xq. Но отсюда еще не следует, что он будет схем! i диться к данной функции /(ж); он может оказаться расходящимся ил(Ц сходиться, но не к функции /(ж). Так, например, функция Ш
д.г.) _ , е х , если ж 0,
О, если ж = О
имеет в точке ж = 0 производные всех порядков, причем /1п1(0) = 0 ’ при всяком п (см. пример 19.5). Ряд Маклорена имеет виц;
а 0 ° 2 0 „ ?
° + ^Ж + -Ж + ... + —Ж +... !•
Он сходится, но его сумма 5(ж) в любой точке ж равна нулю, а не /(ж).
Пусть для функции J (ж) составлен соответствующий ей ряд Тей- ;
лора.
Теорема 64.1. Для того чтобы ряд Тейлора (64.2) функции /(ж) сходился к /(ж) в точке ж, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (64.1) стремился к нулю при п —г оо, т. е. чтобы lim Rn(x) = 0. п—>оо
l_j Пусть ряд Тейлора (64.2) сходится к функции /(ж) в некоторой i окрестности точки жд, т. е. /(ж) = lim >$'„ (ж). Так как п-я частичная | п—>оо S
сумма 5п(ж) ряда (64.2) совпадает с многочленом Тейлора 1 „(ж), т. е. |
5п(ж) = Т’п(ж), находим: }
lim 7?„(ж) = lim (/(ж) - Тп(ж)) = lim (/(ж) - 5п(ж)) = ?
п—>ос п—>оо п—>ос
= У(®) - Пт б'п(ж) = /(ж) - /(ж) = 0. j
П-4-ОО £
Обратно, пусть lim Rn(x) = 0. Тогда 4
п—>оо jg
lim 5п(ж) = lim Рп(х) = lim (/(ж) - _й,г(ж)) =
п—>оо п—>оо п—>оо '|gsv
= /(ж) - lim Яп(ж) = /(ж) - 0 = /(ж). ЯЧК п—усо
Замечание. Если ряд Тейлора (64.2) сходится к порождающей Я функции /(ж), то остаточный член формулы Тейлора равен остатку ря- Я да Тейлора, т. е. Rn(x) = г„(ж). (Напомним, что Т„(ж) = /(ж) - Sn(x), Я а гп(ж) = S(x) — 5„(ж), где S(x) — сумма ряда Тейлора.) ’я
Таким образом, задача разложения функции /(ж) в степенной V ряд сведена по существу к определению значений ж, при которых Я
464
Rn{x) -» 0 (при п -> оо). Если сделать это не просто, то следует каким-нибудь иным способом убедиться, что написанный ряд Тейлора сходится к данной функции.
На практике часто пользуются следующей теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора.
Теорема 64.2. Если модули всех производных функций /(ж) ограничены в окрестности точки жд одним и тем же числом М > 0, то для любого х из этой окрестности ряд Тейлора функции f(x) сходится к функции /(ж), т. е. имеет место разложение (64.2).
□ Согласно теореме 64.1, достаточно показать, что lim Л„(ж) = 0. п—>оо
По условию теоремы 64.2 для любого п имеет место неравенство |/^(ж)| М. Тогда имеем:
lim \Rt, (ж) I = lim
(п + 1)!
(ж - ж0)п+1
(ж - ж0)и+1 (п + 1)!
= М lim
(ж - ж0)п+1 (п +1)!
Осталось показать, что ряд
Так как
I (ж — Жп)М-^”2 1
lim jv — | — 0- Для этого рассмотрим
^|(ж-жоГ+1|
ип+1 Ж-ЖО ”+2 (п+1)! 1
lim —— = lim -----гд-,--~—дггг - ж - ж0 hm ——- = 0 < 1
— ж0 +1 п-юоп + 2
то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости,
г г l*-*o|n+1 л
lim ип = hm -------—— = 0.
П—>ОО п—>00 (п 4" 1)’
Следовательно, lim Rn(x) — 0. п—>оо
64.2. Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)
Для разложения функции /(ж) в ряд Маклорена (64.3) нужно: а) найти производные /'(ж), /"(ж),-.., /м(ж),...;
б) вычислить значения производных в точке жд = 0;
465
в) написать ряд (64.3) для заданной функции и найти его интервал сходимости;
г) найти интервал (—Я; В), в котором остаточный член ряда Маклорена Rn(x) —> 0 при тг —> оо. Если такой интервал существует, то в нем функция /(ж) и сумма ряда Маклорена совпадают.
Замечание. В интервале сходимости степенного ряда остаточный член стремится к нулю при тг —> оо.
Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций (эти разложения следует запомнить):
х , х х2 хп „
е—1 + т^ + -гг + ...-1---г + ..., х б (—оо; оо),
1! 2! тг! 4
(64.4) ж3 ж5 ж2п+1
SinI = I-3! + 5F-'- + <-1>”(Smj! + -’
(64.5)
х2 хл х2п
СО8Ж = 1~ 2Г+4! '•• + (~1)n(2^j!+-"’ жб(—оо;оо),
(64.6)
(1 + х)° = 1 + +... + + +
1! 2! тг!
если а О,
если — 1 < а < 0, (64.7)
если а С — 1,
х €(-!;!), (64.8)
1п(1 + ж) = х л.2 3 п-|-1 2 3 тг + 1 ж3 ж5 . ж2п+1 + ..., ж е (-1; 1], (64.9)
arctg ж = ж — 3 + 5 — +<-‘> 2п+Г 1 ж3 1 - 3 ж5 1 • 3 • 5 • - ? ж7 ж€[-1;1], (64.10)
arcsin ж = ж + 1-3 2 3'2-4 5 1 2-4-6 • 5... (2тг - 1) ж2п+1 Т + " (64.11) жё[-1;1], (64.12)
' 2-ж3 4-6...(2п) 2тг+1 1 ' ’ ж5 ж2п+1
8ПЖ = Ж + — -|— —-4— 5! (2тг + 1)! ’ ж G (—оо; оо), (64.13)
466
т2 хл т6 х2п
Ла: = 1+2| + 4!+Й + '-+(2ф + --’ «е(-оо;«).
(64.14)
Докажем формулу (64.4). Пусть /(s) = ех.
Q Имеем:
a) f'(x) = ех, f"(x) = ех,..., /(п>(х) = ех,
б) /(0) = 1,/'(0) = 1, •••>/(п)(0) = 1, •••;
в) ех ~ 1+т) + ^г + - - -+^-г+. •; R = lim I - ап I = lim I +.I =
' 1! 2! п! п—->оо| ttn+1 I п-»оо| 71: |
= lim (n + 1) = оо, т. е. ряд сходится в интервале (—оо;оо);
г) для всех х G (—R;R) имеем |/^п^(ж)| = ех < eR = М, т. е. все производные в этом интервале ограничены одним и тем же числом М — eR. Следовательно, по теореме 64.2 lim 7?„(s) = 0. Таким обра-п—>оо
зом, еж = 1 + р + т^- + ...
Докажем формулу (64.5). Пусть /(s) = sins.
□ Имеем:
а) f'(x) = coss = sin(s + тр, /"(s) = -sins = sin(s + 2 ^), /"'(s) = — coss = sin(s -f- 3 • /бг)(.г) = sin(s + n ?p ...;
0, n = 0, 2, 4, 6, ...,
6) /<”> (0) = sin = -1, n = 3, 7, 11, ...,
+1, n = l, 5, 9, ...;
в) sms ~ s - - ... + (-1)” • + 1)!
+ ... Легко прове-
рить, что полученный ряд сходится на всей числовой оси, т. е. при всех
s € (—оо; оо);
г) любая производная функции /(s) = sins по модулю не превосходит единицы, |/<”>(ж)| — |sin(s + п С 1. Следовательно, по теореме 64.2 имеет место разложение (64.5).
Докажем формулу (64.6). Пусть /(s) = coss.
Q Формулу (64.6) можно доказать так же, как и формулу (64.5). Однако проще получить разложение функции cos s, воспользовавшись свойством 3 степенных рядов. Продифференцировав почленно ряд (64.5), получим: 2 4
coss = 1— — + — — , sG(-oo;oo).
*)l /II ' '
Докажем формулы (64.13), (64.14). Пусть /(s) = chs (или /(s) = shs).
467
Q Заменив в формуле (64.4) х на —ж, получим разложение функции с3':
_ , х я-'2 а-’3 а'4 / ж"
6 =1“Й+ 2! “ 3! + 4! + (64Л5>
справедливое для всех х € (—оо; оо).
Суммируя (и вычитая) почленно равенства (64.4) и (64.15), получим разложение гиперболического косинуса (синуса):
е» , -х 2 4
chs =--------= 1+ 2?+ 4?+ ”‘’ Х 6 (-°°;°0)’
рх _ р~х 7*3 /у®
вЬж =---------=ж + —+ ±- + ..., же (-оо;оо).
I 3! 5!
Формулы (64.13) и (64.14) доказаны. ’
Докажем формулу (64.7). Пусть /(ж) = (1 + ж)“, где а € EL
□ Имеем: '
а) /'(ж) — «(1 + ж)"-1, /"(ж) = а(а — 1)(1 + ж)"-2, ...,. /(”)(ж) = а(а - 1)... (а — (п - 1))(1 + х)а~п, ..., п € N;
б) /(0) = 1, /'(0) = а, /"(0) = а(а - 1), ..., /(”)(0) = а(а — 1)... (а — п + 1), ...;
в) (1 + ж)“ ~ 1 + ах + 1).г2 + ...
+ «(а-1)(«-2)...(а-п + 1)а;„ .
п! .......’
г) R = lim I1 = lim I «(«"^(а-2) ••• («~(^~1))-(та+1)! I = ' п-»оо|ап+11 п-юо|п!-а(а— 1)(а — 2)... (а — (п— 1))(а-п) |
= lim =1, т. е. составленный для функции (Ц-ж)а ряд сходится п—>оо| (У. — TL |
в интервале (—1; 1).
Можно показать, что и в данном случае, т. е. при ж С (—1; 1), остаточный член Лп(ж) стремится к нулю при п -> оо.
Ряд (64.7) называется биномиальным. Если а = п € N, то все члены ряда с (п + 1)-го номера равны 0, так как содержат множитель а — п = п — н = 0. В этом случае ряд (64.7) представляет собой известную формулу бинома Ньютона:
,, „ п п(п -1) о п(п — 1)... 1 „
(1 + ж)” = 1 + -ж + -Ц-, 7ж2 + ... + /----ж".
1! 2! н!
Докажем формулу (64.8). Пусть /(ж) = у 1 .
Q Формула (64.8) может быть получена разными способами: 1) пользуясь правилом разложения функции в ряд;
468
2) рассматривая ряд 1 + х + х2 + хл + ... + хп + ... как ряд геометрической прогрессии, первый член которой равен единице и знаменатель q = х; известно (см. пример 62.1), что данный ряд сходится при х 6 (—1; 1) и его сумма равна 2.
3) воспользовавшись формулой (64.7): положив в ней а = —1 и заменив х на —х, получим формулу (64.8). И
Докажем формулу (64.9). Пусть /(ж) = 1п(1 + х).
Формула (64.9) также может быть доказана разными способами. Приведем один из них.
[_} Рассмотрим равенство
—= 1-® + ®2-®3 + ... + (-1)п®п + ...,
1 + х
справедливое для всех х G (—1; 1). Используя свойство 4 степенных рядов, проинтегрируем данный ряд на отрезке [0; ж], х € (—1; 1):
г dt
J 1 +1 о
J dt — J tdt + j t2 dt — j t3 dt. + ... + (— l)’1 J tn dt +..
0 0 0 0 0
ln(l + ®)=®--- + —-... + (-l)n-—+ ... Z О fl “Г" J-
Можно показать, что это равенство справедливо и для х = 1.
Докажем формулу (64.10). Пусть /(ж) = arctg®.
Q Положив в формуле (64.7) а = —1 и заменив х на х2, получим равенство
—7 = 1 - х2 + х4 - ... + (-1)” х2п + ..., ® € (-1; 1).
1 + х
Тогда
аК*8а, = х-у + --... + (-1) 5ГП+...
Можно показать, что равенство справедливо и при х = ±1, т. е. при всех х £ [—1; 1]. И
Докажем формулу (64.12). Пусть /(®) = arcsin®.
469
□ Положив в формуле (64.7) а = — и заменив х на (—ж2), получи! равенство
1
\/1 — ж2
Г2 1-3
T + F4
1-3-5
2-4-6
ж G [—1; 1].
ж6 4-...,
Тогда
1.е л .7 «С . _
г г г 1 Ч
г~ -dt = dt + [ —dt + —-t'' dt+
,/i _ /2 J J 2 J 2-4
v1 1 о о о
или
1 ж3 1-3 ж5
агсвшж = ж 4— • — 4--т --1-...
2 3 2-4 5
Можно показать, что 'полученное равенство справедливо при всех ж G [—1; 1].
Ряды (64.4)-(64.14) в комбинации с правилами сложения, вычита ния, умножения, дифференцирования, интегрирования степенных рядов (см. свойства степенных рядов) могут быть использованы при разложении (некоторых) других функций в ряд Маклорена (Тейлора).
Пример 64-1. Разложить в ряд Маклорена функцию /(ж) = Зж.
Q Решение: Так как Зж = е’п3* = еж1п3, то, заменяя ж на жТпЗ в разложении (64.4), получим:
3*
1пЗ 1п23 2 1п33
-1ГЖ+-2ГЖ+-ЗГ
1п”3 nl
Пример 64.2. Выписать ряд Маклорена функции/(ж) = 1п(4—ж
Решение: Так как
/(ж) = 1п(4 - ж) = 1п4^ 1 - j = 1п4 4- In 1 4-
ж \ Ч
4/J’ I
то, воспользовавшись формулой (64.9), в которой заменим ж на (—^) получим:
1п(4-ж)=1п44-(-^)-Ц^ + Ц^-..
или
1 1 ж2
1п(4 — ж) — In 4 — -ж-----• —
' 4 42 2
1 жп+1 4"+1 ’ п 4-1
если -1 < -=£ < 1, т. е. -4 < ж < 4. 4 ’
470
Пример 64.3. Разложить в ряд Маклорена функцию
/(Ж) =
Q Решение: Воспользуемся формулой (64.8). Так как
„ ч 2 2 _ 2 1
3 —ж~3(1 —|) 3 1-|’
то, заменив x на в формуле (64.8), получим:
или
2 _ 2 2 .г- 2 ж2 2 ж2 2 ж3 2 ж"
'з + з'з + з7 + з 7 + з¥+- + зУ+-’
где — 1 < Ш < 1, т. е. —3 < ж < 3.
О
§65. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ
65.1. Приближенное вычисление значений функции
Пусть требуется вычислить значение функции /(ж) при ж = Ж1 с заданной точностью е > 0.
Если функцию /(ж) в интервале (—R; R) можно разложить в степенной ряд
/ (ж) = ао + в] ж + о2ж2 + ... + апхп + .. -
и Ж1 G (—/?;/?), то точное значение /(Ж1) равно сумме этого ряда при ж - Ж1, т.е.
/(Ж1) = ао + О1Я-Т + а2ж2 + ... + опж" + ...,
а приближенное — частичной сумме Sn(xi), т.е.
/(т'1) ~ Sn(%i) ~ оо + ai^i + о2ж2 + ... + апж".
Точность этого равенства увеличивается с ростом п. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.
|/(х1)-5п(ж1)| = |г„(ж1)|,
Гп(Ж1) — On-ЦЖ^ Т <2П4-2Ж^ + . . .
471
Таким образом, ошибку |/(®i) — Sn(X!)| можно найти, оценив остаток rn(xi) рада.
Для рядов лейбницевского типа
|Лг(.Т1)| = |Un+l(.T!) + Ц„+2(.Т1) + ц,ц-з(я:1) + ... | < |u„+i(.Ti)| (см. п. 61.1).
В остальных случаях (ряд знакопеременный или зиакоположи тельный) составляют рад из модулей членов ряда и для него стирают ся найти (подобрать) положительный ряд с большими членами (обычно это сходящийся рад геометрической прогрессии), который легко бы суммировался. И в качестве оценки |r„(si)| берут величину остатка этого нового ряда.
Пример 65.1. Найти sin 1 с точностью до 0,001.
Q Решение: Согласно формуле (64.5), sinl = l-ll3 + ^-l5------------------
3! 5!
,71.+1 1
(2n —1)!’
Стоящий справа ряд сходится абсолютно (проверить самостоятельно). Так как Jy rj 0,008(3) > 0,001, а rs 0,0002 < 0,001, то для нахождения sin 1 с точностью до 0,001 достаточно первых трех слагаемых:
sin 1 и 1 - -т + ^ = 0,842. 3! 5!
Допускаемая при этом ошибка меньше, чем первый отброшенный член (т. е. меньше, чем 0,0002). Вычисленное микрокалькулятором значение sin 1 примерно равно 0,84147. 4
Пример 65.2. Вычислить число е с точностью до 0,001.
Q Решение: Подставляя х = 1 в формулу (64.4), получим:
Возьмем
Справа стоит знакоположительный ряд. ним ошибку г„(ж):
п слагаемых и оце-
Гп^ (п + 1)! + (п + 2)! + (n + З)!+ "’ 1______________А 1 1
(п + 1)! \ + п + 2 + (п + 2)(п + 3) + " ’
1 Л 1 1 \ _ 1 / 1 _ -
(п + 1)! \ + п + 1 + (п + I)2 +’ ’') (п + 1)!\1-^т/ п!-п’ J
472
•г. е. гп(ж) < . Остается подобрать наименьшее натуральное число
а., чтобы выполнялось неравенство —Д— < 0,001.
п\ - п ’
Нетрудно вычислить, что это неравенство выполняется при п 6. Поэтому имеем:
1 1 1 1 1 „517
2! + 3! + 4! + 5! + 6! ~ 2720 ~ ’
Замечание. Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена
|/(Ж1)-5п(.т1)| = |7?„(Ж1)| =
f<’l+I>(c) (п+1)!
где с находится между Ои ij. В последнем примере 7?п(1) = -г—
W' “Г 1J'
О < с < 1. Так как ес < е1 < 3, то 7?п(1) <
Яб(1) < < 0,001, eRil + 1 + ^j + ... + gj
О
7—r-rvT- При п — 6 имеем: (п + 1)!
w 2,718.
65.2. Приближенное вычисление определенных интегралов
Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции (см. § 34) либо нахождение первообразной сложно.
ь
Пусть требуется вычислить J /(.г) dx с точностью до е > 0. Если а
подынтегральную функцию /(яг) можно разложить в ряд по степеням х и интервал сходимости (—R; R) включит в себя отрезок [а; 6], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.
Пример 65.3.
£ = 0,001.
Вычислить интеграл
с точностью до
Q Решение: Разложим подынтегральную функцию в ряд Маклорена, заменяя х на (—ж2) в формуле (64.4):
2 т2 т4 хе
е- =1-^г + --_ + ..., же(-оо;оо). (65.1)
473
Интегрируя обе части равенства (65.1) на отрезке jO; , лежащем вну три интервала сходимости (—оо;оо), получим:
4 1! 3 • 43 + 2! • 5 • 45 3! • 7 • 47 + ’ ’ ’
0,0052...
Получили ряд лейбницевского типа. Так как =
> 0,001, a - 1 < 0,001, то с точностью до 0,001 имеем:
1
4
/ е-’Лс « А
О
= 0,245.
192
Замечание. Первообразную F(x) для функции /(ж) = ех^ легко найти в виде степенного ряда, проинтегрировав равенство (65.1) в пределах от 0 до х:
х х / j2 лА \
FM = = /(1 - - + ...)Л =
О 0 х '
х3 х5 х7
= -г’1Гз + 2Г5“зГт + '-’
2 X
1 Г
Функции f(x) = —т=е 2 и F(x) = / f(t)dt играют очень важ-
V 2к J
о ную роль в теории вероятностей. Первая — плотность стандартного распределения вероятностей, вторая — функция Лапласа F(x) = х t2
= ~^= J е 2 dt (или интеграл вероятностей). Мы получили, что я о
функция Лапласа представляется рядом
1 / X3 X5 X7
~ у/Ъ: V 2 • 3 + 222! -5 23 • 3! 7 + ' ’ ’
который сходится на всей числовой оси.
474
65.3. Приближенное решение дифференциальных уравнений
Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора.
Познакомимся с двумя способами решения дифференциальных уравнений с помощью степенных рядов.
Пусть, например, требуется решить уравнение
У” = f(x;y;y'), (65.2)
удовлетворяющее начальным условиям
= Уо, У |®=жо = Уо- (65.3)
Способ последовательного дифференцирования
Решение у = у(х) уравнения (65.2) ищем в виде ряда Тейлора:
У = У(хо) + У ц°) (х - х0) + У ^°\ж - жо)2 + ...
... + ^)(ж-ж0Г + ..., (65.4)
при этом первые два коэффициента находим из начальных условий (65.3). Подставив в уравнение (65.2) значения ж = ж0, У = Уо, у' = у'о, находим третий коэффициент: у"(хо) — f (жо; уо’, Уо) Значения у"'(х0),у^(х0),. -. находим путем последовательного дифференцирования уравнения (65.2) по ж и вычисления производных при ж = жд. Найденные значения производных (коэффициентов) подставляем в равенство (65.4). Ряд (65.4) представляет искомое частное решение уравнения (65.2) для тех значений ж, при которых он сходится. Частичная сумма этого ряда будет приближенным решением дифференциального уравнения (65.2).
Рассмотренный способ применим и для построения общего решения уравнения (65.2), если уо и у'о рассматривать как произвольные постоянные.
Способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.
Пример 65.4. Методом последовательного дифференцирования найти пять первых членов (отличных от нуля) разложения в ряд решения уравнения у" = ж2 + у2, у(— 1) = 2, у'(—1) = i.
475
Q Решение: Будем искать решение уравнения в виде
У = у(-1) + + 1) + У + I)2 + + I)3 + • •
Здесь у(—1) = 2,у'(—1) = i. Находим у"(—1), подставив х = — 1 в исходное уравнение: у"(—1) = (—I)2 + 22 = 5. Для нахождения последующих коэффициентов дифференцируем заданное дифференциальное уравнение:
у1" = 2ж + 2уу',
у^ = 2 + 2(у')2 + 2уу",
У(Б) = 4у'у" + 2у'у" + 2уу"' = бу'у" + 2уу"',...
При х = — 1 имеем:
у"'(-1) =-2 + 2-2-= 0, у(4)(-1)= 2 + 2-1 + 2 • 2 • 5 = 22,5, у(5)(-1) = 6- -- 5 + 2- 2- 0 = 15,...
Подставляя найденные значения производных в искомый ряд, полу-чим:
1 5 15 1
у = 2 +-(ж + 1) + —(ж + I)2 + —(ж + I)4 + —(ж + I)5 + ... •
Z Z 10 О
Способ неопределенных коэффициентов
Этот способ приближенного решения наиболее удобен для интегрирования линейных дифференциальных уравнений с переменными коэффициентами.
Пусть, например, требуется решить уравнение
у" + Р1(ж)у' + р2(ж)у = /(ж) (65.5)
с начальными условиями у(ж0) = уо, у'(%о) = у'о.
Предполагая, что коэффициенты рДж), ръ(х) и свободный член f (ж) разлагаются в ряды по степеням х — Xq, сходящиеся в некотором интервале (ж0 — R', Хо + /?), искомое решение у — у(х) ищем в виде степенного ряда
у = Со + С1(ж - Жо) + с2(ж - ж0)2 + ... + сп(ж - Жо)” + ... (65.6)
с неопределенными коэффициентами.
Коэффициенты Со и щ определяются при помощи начальных условий Со = Уо, С1 = Уд.
476
Для нахождения последующих коэффициентов дифференцируем ряд (65.6) два раза (каков порядок уравнения) и подставляем выражения для функции у и ее производных в уравнение (65.5), заменив в нем Р1(ж), р2(ж), /(ж) их разложениями. В результате получаем тождество, из которого методом неопределенных коэффициентов находим недостающие коэффициенты. Построенный ряд (65.6) сходится в том же интервале (жо — R; жд + R) и служит решением уравнения (65.5).
Пример 65.5. Найти решение уравнения
у" + ху' + у = жсовж, у(0) = 0, у'(0) = 1, используя метод неопределенных коэффициентов.
Q Решение: Разложим коэффициенты уравнения в степенные ряды: Р1(ж) = ж, Р2 = 1, / ж2 ж4
/(ж) = жсовж = ж(1 - — + — .
Ищем решение уравнения в виде ряда
У = Со + С1Ж + с2ж2 + с3ж3 + ...
Тогда
у' = щ + 2с2ж + Зс3ж2 + 4с4Ж3 + ..., у" — 2с2 + 2 • 3 • с3ж + 3 - 4 С4Ж2 + ...
Из начальных условий находим: Со = О, С] = 1. Подставляем полученные ряды в дифференциальное уравнение:
(2с2 + 2 • 3 • с3ж + 3 • 4 • с4ж2 + ...)+ ж(с1 + 2с2ж + Зс3ж2 + 4с4х3 + ...)+ / 2 3 , А ж2 я-'4 ж6 \
+ (со + С1Ж + с2ж^ + с3ж +...) = ж|1- — + — - — + ...I.
Приравниваем коэффициенты при одинаковых степенях ж:
ж0 : 2с2 = О,
ж1 : 2 - 3 • с3 + 2 = 1,
ж2 : 3 • 4 • с4 + 2с2 + с2 = О,
ж3: 4 - 5 - сБ-Ь Зс3 + с3 =
ж4 : 5 • 6 • со + 4с4 + с4 — О,
Отсюда находим, что с2 = С4 = Со = . - - = 0, с3 = — gy, сБ = gy, с7 = —уу,... Таким образом, получаем решение уравнения в виде
т. е. у = sin ж.
Глава XV. РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
Лекции 56-58
§66. РЯДЫ ФУРЬЕ
66.1. Периодические функции.
Периодические процессы
При изучении разнообразных периодических процессов, т. е. пр< цессов, которые через определенный промежуток времени повторяются (встречаются в радиотехнике, электронике, теории упругости, теории и практике автоматического регулирования и т. д.), целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд.
Напомним, что функция у = f(x), определенная на множестве D, называется периодической (см. п. 14.3) с периодом Т > 0, есл| при каждом х € D значение (х + Т) € D и выполняется равенств f(x + T) = f(x).
Для построения графика периодической функции периода Т достг: точно построить его на любом отрезке длины Т и периодически пр: должить его во всю область определения.
Отметим основные свойства периодической функции.
1. Алгебраическая сумма периодических функций, имеющих оди, и тот же период Т, есть периодическая функция с периодом Т.
2. Если функция /(ж) имеет период Т, то функция f(ax) имеет
период
= f(ax +Т) = f(ax).
3. Если функция /(ж) имеет период Т и интегрируема на отрезке а+Т Ы-Т
[жо; жД £ R, то у f(x)dx = J /(ж) dx при любых а и Ь £ [яд; ®1]. а Ь
□ Пусть, например, 0 < а < b < Т, тогда
а-\-Т b tz-J-jT
j f(x)dx = у f(x)dx + I f(x)dx. a a b
С другой стороны,
Ь+Т а+т b+т
I f(x) dx = J f(x) dx 4- у /(ж) dx.
b b €l-\-T
(66.1)
(66.2'
478
b+т b b
Но у f(s) dx = (подстановка x = и + T) = J f(u + T) du = J f(x)dx. a+T &
Подставляем полученный результат в (66.2) и, сравнивая с (66.1), име-а+Т Ъ+Т
ем J f(x)dx= I f(x)dx.
а Ь
т ь+т
В частности, j f[x)dx = J f(x)dx. о ь
Простейшими периодическими функциями являются тригонометрические функции sins и coss. Период этих функций равен 2тг, т. е. Т = 2тг.
Простейшим периодическим процессом (движением) является простое гармоническое колебание (движение), описываемое функцией
у = т1 sin(cjf 4- </?о), (66.3)
/, 0, где Л — амплитуда колебания, со — частота, <ро — начальная
фаза.
Функцию такого вида (и ее график) называют простой гармоникой. Основным периодом функции (66.3) является Т = —, т. е. одно 2тг
полное колебание совершается за промежуток времени ~ показывает, сколько колебаний совершает точка в течение 2тг единиц времени).
Проведем преобразование функции (66.3):
у = Л sin(wt + <д;) = Asinwtcos^o + Л cos wt sin = acoswt + bsinwf,
(66.4) где a = Asinipo, b = Acos^o- Отсюда видно, что простое гармоническое колебание описывается периодическими функциями sinwt и coswt.
Сложное гармоническое колебание, возникающее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями вида sin ait и cos cat. Так, функция
<p(t) = Ло + Л1 sin(t + </>i) + Л2 sin(2t + <^2) + • + Л30 sin(30t + узо) = 30
= Ло + А.„ sin(nf + <рп)
71=1
30
или, что равносильно, функция 93(f) = Ло + 22 (ап cos nt + 6nsinnf) 71=1
задает сложное гармоническое колебание. Так как период первой гармоники есть 7\ — 2тг, второй З2 = лу , третьей 7з — ..., тридцатой
479
Тзо = з§> а период функции у = Л() («пулевая гармоника») есть любое число, то функция имеет период, равный 2тг, т. е. Т — 2тг.
Понятно, что при наложении простых гармоник получаем перио дическую функцию, описывающую сложное периодическое колебание (периодический процесс).
Возникает вопрос: всякую ли периодическую функцию, описываю щую периодический процесс, можно представить в виде суммы простых гармоник вида (66.3) или (66.4)? Если да, то как найти неизвестные па раметры (коэффициенты) каждой из этих гармоник? Ответим сначала на второй вопрос, а потом и на первый.
66.2. Тригонометрический ряд Фурье
С помощью так называемого тригонометрического ряда любую (практически) периодическую функцию можно представить в виде рР да, членами которого являются простые гармоники.
Тригонометрическим рядом называется функциональный pj вида
— + a,] cos х + щ sin х + ... + ап cos пх + bn sm пх + • • • =
оо
= — + ап cos пх + Ьп sin пх, (66.
П=1
где действительные числа а^, ап, Ъп (п = 1,2,...) называются коэфф} цшттами ряда.
Ряд (66.5) можно записать в виде
у + 5Z Ап sin(na: + 4>п)-
(66.1
Действительно, положив ап = Ansin^>n, bn = Ап costpn, получи! ап cos пх + bn sin пх = Ап sin (па: + у?п); ряд (66.5) принимает вид (66.6 при этом Ап = и t,g<^n =
Свободный член ряда записан в виде для единообразия пол; чающихся в дальнейшем формул.
Приведем формулы, которые понадобятся нам в,дальнейшем.
('читая т и п целыми положительными, находим:
sin пх п агГ = 2я I—7Г
I = 0 (n и 0)
I- 7Г
cos nxdx =
(66.
f sinnxdx — О при любом n,
(66.
480
У cos тх cos пх dx =
т — п)х) dx =
0 (т ф тг), я (тп = тг),
(66.9)
У sin тх cos пх dx =
-7Г 1 ?
= - J (sin(m + тг)х + sin(m — тг)х) dx = 0,
(66.10)
У sinтх sinnxdx =
1 Г
= - / (cos(m — тг)х — cos(m + тг)х) dx —
0 (ттг ri), я (ттг = п).
(66.11)
Замечания.
1. Формулы (66.7) (66.11) показывают, что семейство функций
l,cosx, sin х, cos 2х, sin 2х, cosЗх, sin3x,...,cosnx, sin nx,...
обладает свойством ортогональности: интеграл от произведения любых двух функций этого семейства на интервале, имеющем длину 2я, равен нулю.
2. Формулы (66.7)-(66.11) справедливы и в случае, когда область интегрирования есть отрезок [0; 2я] (см. свойство 3 периодических функций, п. 66.1).
Пусть /(х) — произвольная периодическая функция с периодом 2я. Предположим, что функция /(х) разлагается в тригонометрический ряд, т. е. /(х) является суммой ряда (66.5):
ап cos пх + bn sin пх.
(66.12)
Так как функция f(x) (и сумма ряда) имеет период 2тг, то ее можно рассматривать в любом промежутке длины 2я. В качестве основного промежутка возьмем отрезок [—я; я] (также удобно взять отрезок [0; 2я]) и предположим, что ряд (66.12) на этом отрезке можно почленно интегрировать. Вычислим коэффициенты ап и Ьп. Для этого проинтегрируем обе части равенства (66.12) в пределах от —я до я:
cosnx
sin nxdx
= J ~^dx = ttoq.
16 Конспект лекций по высшей математике. Полный курс
481
Интегралы от всех, кроме нулевого, членов ряда равны нулю в силу формул (66.7) и (66.8).
Отсюда
(66.13)
Умножив обе части равенства (66.12) на cos та; и проинтегрировав полученный ряд в пределах от —я до я, получим:
f (a:) cos mxdx =
cos тх dx+
cos тх • cos nx dx +
cos mx sin nx dx I.
В силу формул (66.7), (66.9) и (66.10) из последнего равенства при т = п получаем:
7Г
j f(x) cos nxdx — anir.
— 7T
Отсюда
(66.14)
Аналогично, умножив равенство (66.12) на sin та; и проинтегрировав почленно на отрезке [—я; я], найдем:
(66.15)
Числа а(), ап, Ьп, определяемые по формулам (66.13)-(66.15), называются коэффициентами Фурье функции f(x), а тригонометрический ряд (66.5) с такими коэффициентами — рядом Фурье функции /(а;).
Для интегрируемой на отрезке [—я; я] функции /(а:) записывают
оо
/(*) ~ V + ап cos пх + Ьп sin пх
п-1
и говорят: функции /(а:) соответствует (поставлен в соответствие) ее ряд Фурье. Если ряд Фурье сходится, то его сумму обозначим S(x).
482
67. РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ 27Г-ПЕРИОДИЧЕСКИХ ФУНКЦИЙ 67.1. Теорема Дирихле
Выясним условия, при которых знак соответствия (~) можно заменить знаком равенства (=), т. с. условия, при которых ряд Фурье функции /(а:) сходится и имеет своей суммой как раз функцию /(а:).
Будем рассматривать функции /(ат), имеющие период Т = 2л. Такие функции называют 2ir-периодическими.
Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.
Теорема 67.1 (Дирихле). Пусть 2л-периодическая функция /(а:) на отрезке [—тг; тг] удовлетворяет двум условиям:
1. /(ат) кусочно-непрерывна, т. е. непрерывна или имеет конечное число точек разрыва I рода;
2. f (а:) кусочно-монотонна, т. е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.
Тогда соответствующий функции /(а:) ряд Фурье сходится на этом отрезке и при этом:
1. В точках непрерывности функции сумма ряда S(x) совпадает с самой функцией: S(x) — f(x);
2. В каждой точке ад разрыва функции сумма ряда равна /(ад - 0) + /(ад + 0)
2
т. е. равна среднему арифметическому пределов функции /(а:) справа и слева;
3. В точках х = —тг и х = тг (на концах отрезка) сумма ряда равна
5(-тг) = 6 (л) - ------------------.
|@| Таким образом, если функция /(ат) удовлетворяет условиям 1 и 2 теоремы (условия Дирихле), то на отрезке [—тг; л] имеет место разложение (66.12):
ОО
/(а:) ~ ап cosпх + Ьп sinпх,
2 П=1
причем коэффициенты вычисляются по формулам (66.13)-(66.15). Это
483
равенство может нарушиться только в точках разрыва функции /(.г) и на концах отрезка [—зг; тг].
В силу периодичности исходной функции и суммы ряда Фурье мо жет быть получено указанное разложение во всей области определения функции.
Замечания.
1. Если функция /(ж) с периодом 2тг на отрезке [0; 2тг] удовлетворяет условиям Дирихле, то для нее имеет место разложение (66.12), где коэффициенты вычисляются по формулам
1 2" do = - / f (ж) dx, ТГ J
О
1 27Г
ап = — / f(x) cosnxdx, п = 1,2,3,...,
7Г J
0
1 2,Г
Ьп = — / f (х) sinnxdx, п = 1,2,3,...
' тг J
о
тг 2тг
(Интегралы J f(x)dx к J f (a:) dx равны в силу свойства 3 периода-—тг О
ческой функции — см. п. 66.1.)
2. Условиям Дирихле удовлетворяют большинство функций, которые встречаются в математике и ее приложениях. Существуют функции, не удовлетворяющие условиям Дирихле, но при этом разложимые в ряд Фурье, т. е. теорема Дирихле дает лишь достаточное условие разложимости, но не необходимое.
Пример 67.1. Разложить в ряд Фурье функцию /(а:) периода 2тг, ;i заданную на отрезке [—тг; -тг] формулой 1
2а: при 0 х тг, ;
—х при — тг < х < 0.
/ (я) = -
Q Решение: На рисунке 260 изображен график функции f(x). Эта функция удовлетворяет условиям Дирихле, значит, она разложима в ряд Фурье. Находим коэффициенты ряда:
If If If Зтг
(i0 = — / f(x)dx= — / (—x)dx-\— I 2xdx =—.
тг J тг J тг J 2 '
— 7Г ~7Г 0
1 w 1 0 1 w
an = — / fix) cosnxdx = — / (—x) cosnxdx 4— / 2x cos nx dx =
ТГ J ТГ J ТГ J
— 7Г —7Г 0
484
и = х
dv = cos nx dx
du — dx
v = — sin nx n
интегрируем по частям:
12 3
=--Д1 — COSTm) ч-q(cOS7T71 — 1) =-о (1 - ( —1)").
m m тгп
Аналогично находим
1 w 1
bn = — I f(x) sin nxdx = ••• = —(—l)n+1. тг ./ n
7Г
Исходной функции f(x) соответствует ряд Фурье
О О 1
f(x) ~ 5(ж) = --^2 (г - cosnx + sinra-
n=l
Функция f(x) непрерывна во всех внутренних точкой отрезка [—тг; тг], поэтому, согласно теореме Дирихле, для всех этих точек имеем равенство f(x) = S(x), т. е.
, , , , Зтг 6 (cos х cos За: cos 5а: \
/(a:)=S(a:) = T--^ + ^- + -^- + ... J +
( sin a: sin 2а: cos За:
+ (л ТГ+ 3
В точках х = ±7г сумма S(x) ряда равна
/(—тг + 0) + /(тг — 0) _ тт + 2тг _ 3
2 ~ ~ 2 ~ 2^’
Графики функций /(а:) и S(x) показаны на рис. 260.
485
67.2. Разложение в ряд Фурье четных и нечетных функций
Если разлагаемая на отрезке [—я; я] в ряд Фурье функция f(x) является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится так называемым неполным).
Если функция f (а:) четная, то ее ряд Фурье имеет вид
ОО
f(x) = + У^апсо8пж, (67.1)
п—1
где
2 г 2 г
«о = — / _f(x)dx, ап = — I f(x) cosnxdx, п € N. (67.2) Я J Я J
о о
Если функция f(x) нечетная, то ее ряд Фурье имеет вид
оо
f (х) = 5? bn sin па:, (67.3)
п=1
где „
2 г
bn — — f(x) sin пх dx, п € N. (67.4)
я J
о
□ Как известно (см. п. 39.4), если функция /(ж) интегрируема на симметричном отрезке [—а; а], то
{а
2 • / f(x)dx, если f(x) — четная функция,
J (67.5)
О, если /(ж) — нечетная функция.
Если функция f(x) — четная, то /(a:) cosnx — четная функция (/(—х) cos(—пх) = f(x) cos пх), a f(x) sin пх — нечетная функция (/(— х) sin(—пх) = —/(a:) sinпх).
Если же /(а:) — нечетная функция, то, очевидно, функция /(a:) cos па: — нечетная, a /(a:) sin па: — четная.
С учетом формулы (67.5) из формул (66.13)-(66.15) получаем формулы (67.1)-(67.4).
Ряды (67-1) и (67.3) называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.
Пример 67.2. Разложить в ряд Фурье функцию /(а:) = х, х £ (—я;я), Т = 2я.
486
Q Решение: На рисунке 261 изображен график заданной функции. Условиям Дирихле функция у = х удовлетворяет. Эта функция — нечетная. Следовательно, ап = 0, п = 0,1,..., а
т. е. Ьп — • (—l)’i+1 (п € N). Ряд Фурье содержит только синусы:
Е°° 2 , „/sina: sin 2а: sin За: \
- -1 "+1-sinna: = 2 —-------— + —-------... .
71 X 1 Z О /
71=1 4
При этом 5(±я) = —^2^ = О (см- Рис- 261). •
67.3. Разложение в ряд Фурье функций произвольного периода
Разлагать в ряд Фурье можно и периодические функции с периодом, отличным от 2я.
Пусть функция /(а:), определенная на отрезке [—/; /], имеет период 2/ (/(а: + 21) = f(x), где I — произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле.
Сделав подстановку х = данную функцию f(x) преобразуем в функцию ip(t) =/(—<), которая определена на отрезке [—я; я] и имеет
период Т = 2я. Действительно, если t = — —я < t < я имеем — 1 < х < /; + 2я) = f(—(t + 2я) \я т. е. + 2я) = <^(t). я, то х = — 1, если t = я, то х = 1 и при ) =f(-t + 2l \ =f(-\ =9?(i), / \7Г J \^)
487
Разложение функции <p(t) в ряд Фурье на отрезке [—тг; тг] имеет ви, 1
ОО
/ \ а0 \
<р(t) = — + у ап cos nt + bn sin nt, где
1
On = — (p(t) cos nt dt (71 = 0,1,2,...),
— 71
1 71 bn = — I ip(t) sin nt dt (n = 1,2,...).
7Г J —tv
Возвращаясь к переменной x и заметив, что t ~ dt = ydsc,
(67.6)
оо
г/ \ а0 Х-' япх
J W = у + > , ап cos + bn sm
(67.7)
Ряд (67.6) с коэффициентами, вычисляемыми по формулам (67.7), называется рядом Фуръе для функции f(x) с периодом Т = 21.
Замечание. Все теоремы, имеющие место для рядов Фурье 2тг-пе-риодических функций, остаются в силе и для рядов Фурье функций, период которых Т = 21. В частности, если /(а:) на отрезке [—1; I] четная, то ее ряд Фурье имеет вид
OO
Г/ X ^0 ^ПХ
f(x) = у + a„ cos —, (67.8)
72=1
где
2 ‘ 2 1 ттх
ao = - j f(x)dx, an = - J /(.r) cos —j— dx, n=l,2,...; (67.9)
о 0
если f(x) — нечетная функция, то
OO г/ X . ЯПХ
= 7 . bn sm -7-, (67.10)
72=1
где z
bn — J j f(x) sin dx, n = l,2,... (67.11)
0
488
Пример 67.3. Разложить функцию f(x) — х на интервале (—4; 4) и ряд Фурье.
Q Решение: Данная функция нечетная, удовлетворяет условиям Дирихле. По формулам (67.10) и (67.11), при I = 4, имеем:
ОО
Е_ . ТШХ
Ьп Sin-у,
г=1
где Ьп = | f х sin dx, п— 1,2,3,...
о
Вычисляем Ьп:
1/ 4 тта;|4 4 4 . тта:|4\
Ьп = - —х— cos —— -I------------sm —— =
2 \ тт 4 Io 7m тт 4 1о/
= — — COSTm = — • ( —1)”+1, 71=1,2,3,... TT'/Z тт
Таким образом,
8 (sin sin sin \
2' = я 2 + 3 ’ ’ J
для — 4 < х < 4.
67.4. Представление непериодической функции рядом Фурье
Пусть у = f(x) — непериодическая функция, заданная на всей числовой оси (—оо < х < оо).
Такая функция не может быть разложена в ряд Фурье, т. к. сумма
ряда Фурье есть функция периодическая и, следовательно, не может
быть равна f(x) для всех х.
Рис. 262
Однако непериодическая функция f(x) может быть представлена в виде ряда Фурье на любом конечном промежутке [а; 6], на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину отрезка [a; i>] и построить функцию /Да?) периода Т = 21 = |Ь — а| такую, что fi(x) = f(x) при — I х I. На рисунке 262 приведена иллюстрация построения функции /Дж).
4RQ
Разлагаем функцию /i (ж) в ряд Фурье. Сумма этого ряда во вод точках отрезка [а; 6] (кроме точек разрыва) совпадает с заданной функ цией /(ж). Вне этого промежутка сумма ряда и /(ж) являются север шенно различными функциями.
Пусть теперь непериодическую функцию f(x) требуется разл жить в ряд Фурье на отрезке [();/]. (Это частный случай: начало к ординат перенесено в точку х = а отрезка [а; Ь]; область определен! функции /(х) будет иметь вид [0; I], где I = |Ь - а|.)
Такую функцию можно произвольным образом доопределить а отрезке [—/;()], а затем осуществить ее периодическое продолжение периодом Т = 21. Разложив в ряд Фурье на отрезке [—/;/] полученну таким образом периодическую функцию /i(ar), получим искомый ря для функции f(a:) при х £ [();/].
В частности,-функцию f(x) можно доопределить на отрезке [—I; ( четным образом (т. е. чтобы при — I si х 0 было /(т) = /(—х)) -см. рис. 263. В этом случае функция /(ж) разлагается в ряд Фуры который содержит только косинусы (см. формулы (67.8) и (67.9)).
Рис. 263 Рис. 264
Если же функцию f(x) продолжить на отрезок [ Z; 0] нечетны* образом (см. рис. 264), то она разлагается в ряд, состоящий только и: синусов (см. формулы (67.10) и (67.11)).
Ряд косинусов и ряд синусов для функции /(т), заданной на отрез ке [0; Z], имеют одну и ту же сумму. Если хо — точка разрыва функцш /(т), то сумма как одного, так и другого ряда равна одному и тому ж( числу: S(x0) = ^Х° ~ °^ КХ° + °).
Замечание. Все, что было сказано о разложении в ряд Фурье функции f(x) на отрезке [();/], переносится практически без изменения н« случай, когда функция задана на отрезке [0; я]; такую функцию можно разложить как в ряд косинусов, так и в ряд синусов (формулы (67.1) и (67.3)).
Пример 67.4- Разложить в ряд косинусов функцию f(x) = 71 ^х, 0 < х < я.
490
Q Решение: Продолжим функцию /(а:) на отрезок [—тг; 0] четным образом (см. рис. 265). Разлагаем в ряд функцию
Л(ж) = -
0 < X < Я,
—я < х < 0
с периодом Т = 2я. Условиям теоремы
Дирихле функция /Д.т) удовлетворяет. Используя формулы (67.1) и (67.2), нахо
Рис. 265
дим:
j-. 7Г ТГ
2 /* 7Г — 37 , 7Г 2 /* 7Г — X , .
оо = - / —-—dx - —, ап = - —-—cosnxdx =—И1-совяп).
я ./ 2 2 я J 2 тт
о о
Таким образом, ,, , 77 — X 77 2 (cos х cos Зх cos 5х \
Лх) = -2~=4+^{~^ + ^ + ~^~+--)’
где 0 < х < 77 (при этом 5(0) = - 2 2 = 5, S(±77) = = 0
\ Z £ А
67.5. Комплексная форма ряда Фурье
Ряды Фурье часто применяются в комплексной форме записи. Преобразуем ряд (66.12) и его коэффициенты (66.13)-(66.15) к комплексной форме. Для этого используем формулы Эйлера, выражающие косинус и синус через показательную функцию:
Лпх । — гпх inx —гпх
С т Р . С С
cos па: =-------------, srnna; =------—-------
Zj ZI
(из формулы Эйлера ег(р = cos 99 4- i sin 99 и вытекающего из нее равенства е г1р — cos 99 — г 8:0199 находим, что cos 99 = -—, sin ip = — ~.6—-). Подставив эти выражения в ряд (66.12), находим:
ZI
/(^) = у + 52 °"
71=1
^inx । g—inx
Лпх .—гпх
с — е
2i
2
—гпх
гпх _ —гпх
~ ^п------ТГ-----
п 2
(ап~И>п)е*пх (an^ibn)e-inx
2 оо 2
= у + ^cneinx+c-ne~ п=1
где обозначено сп = °п г-д, с_п = а" .
(67.12)
491
Найдем выражения для комплексных коэффициентов сп и с_п. Ися пользуя выражения для ап и Ьп (формулы (66.14) и (66.15)), получим.!
i / -« тг л тг х
1 / -1 Г 1 Г \
cn=ol“ / cosnx dx — i~ / f(x}sinnxdx ) =
2 \TV J 7Г J J
— 7Г — 7Г
1 ТГ 1 тг
= — / f (a:)(cosna; — isinna;) dx = — / f(x)e~*nxdx, 2тг J 2тг J
—7Г —7Г
t. e.
1
c-n=~~ [ f(x)e~inxdx (n = 1,2,3,...), (67.13)
ZTT J
— 7Г
co = V = TZ / f(x)dx’' (67.14)
2 ZlT J
— 7Г
1/17 17 \
c-n = - I — / J(x) cosnxdx + i— / f (x) sinnxdx I =
2 \7T J тг J 1
— 7Г — 7Г
f (x) (cos nx 4- i sin nx) dx —
2- I f(x)einxdx (n = 1,2,3...). 2tt J
(67.15)
Таким образом, формулу (67.12) можно записать в виде
оо оо
f(х) = Со + 57 сп€гпх + с_пе~тх, или /(х) = 57 епегп:с. (67.16)
71=1 71= —ОО
Коэффициенты этого ряда, согласно формулам (67.13) -(67.15), можно записать в виде
сп = — / f(x)e~mxdx (п = 0,±1,±2,...). (67.17)
Z7T J
—7Г
Равенство (67.16) называется комплексной формой ряда Фурье функции f(x), а числа сп, найденные по формуле (67.17), — комплексными коэффициентами ряда Фурье.
Если функция /(х) задается на отрезке [—Z; /], то комплексная форма ее ряда Фурье имеет вид
in-nx 1 / — innx
f(x)= 57 Спв 1 ’ Cn~~2i J 1 dx («=
n= —OO _l
(67.18)
Как видим, комплексная форма ряда Фурье (и коэффициентов) более компактна, чем обыкновенный ряд Фурье.
492
^7ГПХ
В электротехнике и радиотехнике члены ряда спе 1 называются гармониками, коэффициенты сп — комплексными амплитудами гармоник, а числа юп — уу- (п = 0, ±1, ±2,...) — волновыми числами
ОО
функции /(а;) = спеШпХ.
П-—— ОО
Совокупность величин {щ, сг, • •, сп, - - -} называется амплитудным спектром.
Графически амплитудный спектр изображается в виде вертикальных отрезков длиной сп, расположенных в точках ujn = ™ числовой оси.
Пример 67.5. Построить ряд Фурье в комплексной форме для 2-периоди-ческой функции
У
-- 1 -- --- ---
II 1111
il 1111
—с-— --—о ' -—о——
-2-1 0 1 2 3 4 ®
Рис. 266
/(®) =
а: € [—1; 0), а: е [0; 1],
7 = 2.
Q Решение: На рисунке 266 изображен
график функции /(ж). По формулам (67.18) находим (/ = 1):
1 г р—гттх 1 _i / \
Р — Z Р~^пх(]Т — __________— = ------I е-”т -11 =
" 2 J 2ттг 0 2тгт \ /
о ”
j 1 J 1
=-----(совтт — г sin тт — 1) — — ------г, п / 0; со = — / dx = —.
2тгп 2тт 2 J 2
о
Следовательно, для всех точек непрерывности функции У (аг) справедливо равенство
П=~гОО
(п4о)
1 /^гтгж £>~пх ^Згтгя —Згтгя
-L . / С- С- С-
2 1 \ 7Г + 7Г + Зтг + Зтг
^S(o) = 0 + 1 = i, 5(±1) = 1 2 = 1> на гРаФике ые отмечена).
§ 68. ИНТЕГРАЛ ФУРЬЕ
Как известно, всякую (периодическую или непериодическую) функцию /(а:), удовлетворяющую на отрезке [—/;/] условиям теоремы
40.4
Дирихле, можно разложить в ряд Фурье
ос
/(я) = V + У? an cos ипх + ьп sin юпх, n=l
(68.1
где wn
_ тт
~ I
ап = - у f(t) coscjntdt (n = 0,1,2,...),
г (68.2
bn = j J /(t)sinwntdt (n = 1,2,...).
-i
Это разложение будет справедливым на всей числовой оси Ох том случае, когда /(а:) — периодическая функция-с периодом Т = 2/, Рассмотрим случай, когда f(x) — непериодическая функция, за данная на бесконечном промежутке (—оо;оо) (т. е. I = +оо).
Будем предполагать, что на любом конечном промежутке [—Z; функция f(x) удовлетворяет условиям теоремы Дирихле и что сходи! ся следующий несобственный интеграл:
У |/(з:)|бД = М < оо.
— сю
Говорят: /(а:) абсолютно интегрируема на всей числовой оси.
Подставляя в ряд (68.1) -значения коэффициентов ап и Ьп
(68.2)
получим:
1 I | оо I
/(ж) = 57 I [ /(0(cOSWnt
jul J I J
—I n=l
cos ivnx + sinwnt
sin ujnx) dt
У
т. e.
1 l J oo I
= oi [ dt + 7 52 ( cosa}n(t -
Xjfc J I J
-I n=l
re) dt. (68.3)
Будем теперь неограниченно увеличивать I. Первое слагаемое в части равенства (68.3) при I —> +оо стремится к нулю, т. к.
правой
1 1 1 оо . .
f ^^2, J f
—I —I — oo
Рассмотрим второе слагаемое в равенстве (68.3). Величина ™ принимает значения u>i = j, oj2 = ^, = ^, ..., образую-
щие бесконечную арифметическую прогрессию с разностью =
I
/IO/I
(Awn = wn+i — n = 0,1,2,...), при этом Дшп -> 0 при I -> +оо. Итак,
\ 7 71
х) at • — =
I
где<Дш„) = J f(t)-coswn(t-x)dt,wn = ^,^-,...,^,...
Полученная сумма напоминает интегральную сумму для функции i
<Ди) = у f(t) cosw(t — х) dt, u>e(0;+oo)
-i
(доказывается, что так оно и есть), поэтому, переходя в равенстве (68.3) к пределу при I -> +оо, получаем
1 °° j °?
/(а:) — — lim V' w(wn)Awn = — / ^(u>)dw, 7Г 1ЭОО ' ТГ J
71=1 О
ИЛИ сю сю
f(x) — —J dw J f (t) cos w(t — x)dt. (68.4)
0 —oo
Формула (68.4) называется формулой Фурье, а интеграл в правой части формулы — интегралом Фурье для функции f(x).
Формула Фурье имеет место в точках непрерывности функции /(.т); в точках разрыва данной функции интеграл Фурье равен среднему арифметическому ее односторонних пределов:
1 7 А 7 U > и /(х-0) + /(х + 0)
— / dw / f(t) cosw(t — х) dt =—---------—------.
О —oo
Формулу (68.4) можно переписать в другом виде (в виде однократного интеграла):
ОО оо
/(х) - - у dw у f(t) cosu>(t — х) dt =
О —оо
1 оо оо
= — у dw у f(t)(coswt • coswx + sinwt • sinwx)dt = 0 —oo
°° / £ °C 1 °°
= У dw(— I f(t) cos (jjtdt • cos wx 4— J f (t) sin wtdt- sin wx 0 —oo — oo
4Q5
т. е.
оо
/(а;) = I (A(w) coscjs + B(w) sin шт) du, о
(68.5)
где
Как видно, есть аналогия между рядом Фурье, и интегралом Фу-
рье: в обоих случаях функция f(x) раскладывается на сумму гармонических составляющих. Однако, ряд Фурье суммируется по индексу п,
принимающему дискретные значения п = 1,2,3,...в интеграле Фурье производится интегрирование по непрерывной переменной ш.
Некоторые сведения, связанные с интегралом Фурье, изложим в виде замечаний.
Замечания.
1. Если функция f(x) — четная, то формула Фурье (68.5) принимает вид
/(ж) = у A(w) coswtcZcj, где о
в случае нечетной функции —
ОО
f (т) = J B(w) sin wx du, где о
2 г
А(ш) = — / f (/) coswttft; тг J
о
2 г3
B(w) = — / f(t) sinotdt.
7Г J о
(68.6)
(68.7)
2. Если функция f(x) задана лишь на промежутке (0; +оо), то ее можно продолжить на промежуток (—оо; 0) разными способами, в частности — четным или нечетным образом: в первом случае она будет представлена формулой (68.6), во втором — формулой (68.7).
3. Формулу Фурье (68.5) можно представить в симметричной форме записи, если положить в формулах (68.6) и (68.7) А(о>) =
В(ы) — В случае четной функции
/(т) = 1/— J A(uj) cosujxdiv, V о
в случае нечетной функции
f(x) = j — J B(w) sinwxdw,
~ Г? °г
где A(w) = x/— / f (t) cos cut dt-, V о
где B(cu) = * — / f(t) sin cutdt.
V о
496
Kl Функции Л(ш) и В(ш) называются соответственно косинус-пре-образованием и синус-преобразованием Фуръе для функции /(ж).
4. Интеграл Фуръе (68.4) в комплексной форме имеет вид
e~iutdt;
интеграл Фурье (68.5) имеет вид
1 00
Ж = / с(ш)е^<Ь,
Z7T J
ОО
где c(w) = у /(^е-^^; или в симметричной форме записи — ОО
оо
Z7T J
—оо
где 4 оо
с(ш) = f f^e-^dt
— ОС
(c(w) = -Л=с(ш)).
Пример 68.1. Представить интегралом Фурье функцию {е-®, а: € (0;+оо), О, х = О, ех, ж € (—оо;0).
О Решение: Функция удовлетворяет условиям представимости интегралом Фурье, абсолютно интегрируема на промежутке (—оо; +оо):
У |/(a:)|da:= J exdx + j e~xdx = 2.
—оо —оо О
Функция нечетная, применим формулу (68.7):
2 7° . ,2 ш
B(oj) = — / е sin wt dt — — --------к.
' ' 7Г J 7Г 1 + W2
О
Следовательно,
f(x)=— f ———7 - sin WTcfcv', х € (—оо;0) U (0;+оо).
' тг J 1+oj2
о
497
Замечание. Интересно отметить, что если х = 1, то
2 r’wsinw j(l) = — / ——„aw.
V ' 7T J 1+W.
0 •
С другой стороны, /(1) = e-1 = Таким образом,
ОО
J 1 +у2 V 2 2e о a
Иными словами, при помощи представления функций интегралом Фурье иногда можно вычислить величины несобственных интегралов.
Глава XVI. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
Лекции 59—62
§ 69. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ПОЛЯ
Теория поля — крупный раздел физики, механики, математики, в котором изучаются скалярные, векторные, тензорные поля.
К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы — все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т. д.
Математическим ядром теории поля являются такие понятия, как
градиент, поток, потенциал, дивергенция, ротор, циркуляция и другие.
Эти понятия важны и в усвоении основных идей математического ана-
лиза функций многих переменных.
Полем называется область V пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке М этой области соответствует определенное число U = U(M), говорят, что в области определено (задано) скалярное поле (или функция точки). Иначе говоря, скалярное поле — это скалярная функция U(М) вместе с ее областью определения. Если же каждой точке М области пространства соответствует некоторый вектор а = й(М), то говорят, что задано векторное поле (или векторная функция точки).
Примерами скалярных полей могут быть поля температуры (воздуха, тела, ...), атмосферного давления, плотности (массы, воздуха, ...), электрического потенциала и т. д. Примерами векторных полей являются поле силы тяжести, поле скоростей частиц текущей жидко-
сти (ветра), магнитное поле, поле плотности электрического тока и т. д.
Если функция U(M) (а(М)) не зависит от времени, то скалярное (векторное) поле называется стационарным (или установившимся); поле, которое меняется с течением времени (меняется, например, скалярное поле температуры при охлаждении тела), называется нестационарным (или неустановившимся).
Далее будем рассматривать только стационарные поля.
Если V — область трехмерного пространства, то скалярное поле U можно рассматривать как функцию трех переменных х, у, z (координат
точки М):
U = U(x;y;z).
(69.1)
4Q0
(Наряду с обозначениями U = U(M), U = U(x; у- z), используют запись U = U(f), где г — радиус-вектор точки Л/.)
Если скалярная функция С7(Л7) зависит только т двух переменных, например х и у, то соответствующее скалярное поле U(ж; у) называют плоским.
Аналогично: вектор а = а(М), определяющий векторное поле, можно рассматривать как векторную функцию трех скалярных аргументов х, у и z: а = а(ж; у; z) (или а = б(г)).
Вектор а = б(Л7) можно представить (разложив его по ортам координатных осей) в виде
а — Р(х-, у, z)i + Q(x; у; z)j + i?(s; у, z)k,
где Р(ж;у; z), Q(x,y,z), R(x;y;z) — проекции вектора а(М} на оси координат. Если в выбранной системе координат Oxyz одна из проекций вектора а = а(М) равна нулю, а две другие зависят только от двух переменных, то векторное поле называется плоским. Например, а = Р(х,у)г +Q(x;y)j.
Векторное поле называется однородным, если а(7И) — постоянный вектор, т. е. Р, R и Q — постоянные величины. Таким полем является поле тяжести. Здесь Р — О, Q О, R = —mg, g — ускорение силы тяжести, т — масса точки.
В дальнейшем будем предполагать, что скалярные функции (U(x-,y,z') — определяющая скалярное поле, P(x;y;z), Q(x;y;z) и R(x; у, z) — задающие векторное поле) непрерывны вместе со своими частными производными.
Пример 69.1. Функция U — ^/1 — x2—y2—z2 определяет скалярное поле в точках пространства, ограниченного сферой с центром в начале координат и радиусом R. = 1; скалярное поле U — 7
х +у определено во всем пространстве, за исключением точек оси Oz (на ней х2 4- у2 = 0).
Пример 69.2. Найти поле линейной скорости V материальной точки М, вращающейся против часовой стрелки с угловой скоростью О вокруг оси Oz (см. п. 7.4).
Q Решение: Угловую скорость представим в виде вектора ш, лежащего на оси Oz, направленного вверх. Имеем:
w=(0;0;w) (w — cjfc).
Построим радиус-вектор 7 = (x;y;z) точки М (см. рис. 267).
Численное значение линейной скорости V (модуль), как известно из курса физики, равно шр, где р — расстояние вращающейся точки
500
M(x;y;z) от оси вращения (оси Ог).Но р = г sin уз (99 •— угол между вектором г и осью Oz). Следовательно, V = сир = w • г sin tp, т. е. V —
Вектор скорости V направлен в сторону вращения, совпадает с направлением векторного произведения w х г (V ± г, V ± ш, векторы w, f, V образуют правую тройку). Следовательно, V = w х г, т. е.
к
Ш
z
i
О
х
j О
У
V =
= — wyi + Ldxj + 0 - к
или V = (—ху;хх;0).
Поле линейных скоростей V тела, вращающегося вокруг неподвижной оси, есть плоское векторное поле. •
§70. СКАЛЯРНОЕ ПОЛЕ
70.1. Поверхности и линии уровня
Рассмотрим скалярное поле, задаваемое функцией V — U(x-,y,z). Для наглядного представления скалярного поля используют поверхно
сти и линии уровня.
Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U(M) принимает’ постоян-
ное значение, т. е.
U(x;y, z) — с.
(70.1)
Давая в уравнении (70.1) величине с различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают' поле. Через каждую точку поля проходит только одна поверхность уровня. Ее уравнение можно найти путем подстановки координат точки в уравнение (70.1).
Для скалярного поля, образованного функцией
U = \/1 — ж2 — у2 — z2,
поверхностями уровня является множество концентрических сфер с центрами в начале координат: у! — х2 — у2 — г2 = с. В частности, при с — 1 получим ж2 + у2 + z2 = 0, т. е. сфера стягивается в точку.
Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой, круговые цилиндры, общей осью которых служит нить.
В случае плоского поля U = U(x; у) равенство U (х; у) = с представляет собой уравнение линии уровня поля, т. е. линия .уровня —
501
это линия на плоскости Оху, в точках которой функция [7(а;; у) сохра-' няет постоянное значение.
В метеорологии, например, сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат' точек местности.
Линии уровня применяются в математике при исследовании по-! верхностей методом сечений (см. п. 12.9).
I
70.2. Производная по направлению .
Для характеристики скорости изменения поля U = U(М) в заданном направлении введем понятие «производной по направлению».
Возьмем в пространстве, где задано поле UU(x-,y, z), некоторую точку М и найдем скорость изменения функций U при движении точки М в произвольном направлении А. Пусть вектор А имеет начало в точке М и направляющие косинусы сова, cos/З, сов 7.
Приращение функции U, возникающее при переходе от точки М к некоторой точке Mi в направлении вектора А определяется как
ДП = U(Mi) - [7(М),
или
Д[7 = U(x + Да:; у + Ду; z + Дх) — U (а:; у; z) (см. рис. 268). Тогда
ДА = \MMi\ = у/(Дт)2 + (Ду)2 + (Д^2.
g Производной от функции U = U(M) в точке М по направлению А называется предел
9U ДП U(Mi) - U(M)
— = lim = lim ’—- -----------—~
дХ дх-щ ДА м^м
Производная по направлению А и характеризует скорость изменения функции (поля) в точке М по этому направлению. Если > 0, _____________________________________ ftfj ОХ то функция U возрастает в направлении А, если '/Е- < 0, то функция
U в направлении А убывает. Кроме того, величина | 1
собой мгновенную скорость изменения функции U в направлении А в точке М: чем больше | ^ |, тем быстрее изменяется функция U. В этом состоит физический смысл производной по направлению.
представляет
502
Выведем формулу для вычисления производной по направлению, считая, что функция U(xyy,z') дифференцируема в точке М. Тогда ее полное приращение в этой точке М можно записать так:
ДИ = ~ • Дх + • Ду + • Дг + & Дх + 6 Ду + СзДг,
дх ду dz
где £i, ^2, £з — бесконечно малые функции при ДЛ —> 0 (см. п. 44.3).
Поскольку Дх = ДА cos а, Ду = ДЛ cos /3, tXz — Д Л cos у, то
Д(/ dU 8U о dU г . а , .
- = —- cosa + -—cosр + cosy + A coso! + 4гcosp + C3cosy.
ДЛ dx dy dz
Переходя к пределу при ДЛ —> 0, получим формулу для вычисления производной по направлению:
ди ди ди п ди
—- = -7—cosa + — cos/3 + -—cosy. дХ дх ду dz
(70.2)
5-“
В случае плоского поля U = U(x\ у) имеем: cos ft — cos =5 sina:, cosy — 0. Формула (70.2) принимает вид: dU dU dU . 5? -дт ~ -д— cos о + sin a.
ч дХ дх ду
Замечание. Понятие производной по направлению является обобщением понятия частных производных Их можно рассма-
тривать как производные от' функции и по направлению координатных осей Ох, Оу и Oz. Так, если направление Л совпадает с положительным направлением оси Ох, то, положив в формуле (70.2) о; = 0, /? = 5, 7=5, получим ' 2 ’ дХ дх
Пример 70.1. Найти производную функции U = х2 + у2 — 4yz в точке Л4(0; 1; 2) в направлении от этой точки к точке Mi(2;3;3).
О Решение: Находим вектор ММ] и его направляющие косинусы: ______ 2 2 2 1
ММХ = (2;2;1), cosa = -==-==_= = -, cos/З = -, cosy=-.
V4+4+1 333
' Находим частные производные функции и вычисляем их значения в точке М:
dU п dU п л dU
— = 2х, — = 2у - 4г, — = -4у, дх ду dz
=2-4-2=-6, ду \м
dU\
уг — 4-dz \м
=2-°=0’
Следовательно, по формуле (70.2) имеем:
ЭС1 2 2 1 _ 16
axL ° з 6 з 4' з з ’
Поскольку
8U дХ
< 0, го заданная функция в данном направлении убы-
вает.
70.3. Градиент скалярного поля и его свойства
В каком направлении А производная имеет наибольшее значение? Это направление указывает вектор, называемый градиентом скалярного поля.
Можно заметить, что правая часть равенства (70.2) представляет собой скалярное произведение единичного вектора
ё = (cos a; cos ft; cos 7) )
____ -= (dU.dU.dU\
V дх ' ду ’ dz ) '
и некоторого вектора g — 7$z) ’
|ф| Вектор, координатами которого являются значения частных производных функции 1/(х; у, г) в точке M(x\y\z), называют гради-
ентом функции и обозначают grad 17, т. е. grad U =
или --------------------------
dU. dU. dU-gcadU = —г + — j + —fc. дх ду dz
Отметим, что grad U есть векторная величина. Говорят: скалярное поле U порождает векторное поле градиента U. Теперь равенство (70.2) можно записать в
виде
grad U
Me 6LL ax
Рис. 269
или
А
dU -
— = е - gradU,
dU
— = I grad U\ cos ip, (70.3)
ОЛ
где tp — угол между вектором grad U и направлением А (см. рис. 269).
|@| Из формулы (70.3) сразу следует, что производная по направлению достигает наибольшего значения, когда cos 93 = 1, т. е. при ip — 0. Таким образо.м, направление градиента совпадает с направлением А, вдоль которого функция (поле) меняется быстрее всего, т. е. градиент функции указывает направление наибыстрейшего возрастания функции. Наибольшая скорость изменения функции U в точке М равна
I gradt/| =
ЗИЛ2 dz )
504
В этом состоит физический смысл градиента. На указанном свойстве градиента основано его широкое применение в математике и других дисциплинах.
Приведем важные свойства градиента функции.
1. Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
Ц| Действительно, по любому направлению вдоль поверхности уровня (U - с) — 0. Но тогда из (70.3) следует, что cosy? = 0, т. е. у? = 5.
2. grad (L? + V) = grad 17 + grad V,
3. grad(c • U) = с grad U, с = const,
4. grad(77 V) = U grad V + V grad 77,
5. = VgradC-C/gradV
6. grad F(U) = grad U.
Q Доказываются эти свойства на основании определения градиента. Докажем, например, последнее свойство. Имеем:
grad/(И) = ^(/(77))i + =
(JIJ (JZ
df dU. df dU df dU T df
= aFf 7Гг + яГг'7Г':1 + ятт'7Г'к=ятт'grad U‘ И
dU dx dU dy dU dz du
Замечание. Приведенные свойства градиента функции остаются справедливыми и для плоского поля.
Пример 70.2. Найти наибольшую скорость возрастания функции
U = — + ^ + — в точке А(—1; 1; —1). у z х ' '
Q Решение: Имеем:
gradt/(-l; 1; -1) = 2i + 0j -2к= 2i - 2к.
Наибольшая скорость возрастания функции равна
| grad С7(А)| = V4 + 0 + 4 = 2ч/2.
Отметим, что функция U будет убывать с наибольшей скоростью (2а/2), если точка А движется в направлении — grad 17(A) = —2г + 2fc (антиградиентное направление). •
505
§ 71. ВЕКТОРНОЕ ПОЛЕ
71.1. Векторные линии поля
Рассмотрим векторное поле, задаваемое вектором а = а(М). Изучение поля удобно начинать с понятия векторных линий; они являются простейшими геометрическими характеристиками поля.
|3| Векторной линией поля а называется линия, касательная к ко-, торой в каждой ее точке М имеет направление соответствующего ей вектора а(М'). 1
Это понятие для конкретных полей имеет ясный физический смысл. Например, в поле скоростей текущей жидкости векторными ли-1 ниями будут линии, по которым движутся частицы жидкости (линии тока); для магнитного поля векторными (силовыми) линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.
Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Изучение векторного поля обычно начинают с изучения расположения его векторных линий. Векторные линии поля
а = Р(х; у; z)i + Q(x; у; z)j + R(t; у; z)k
(71-1)
описываются системой дифференциальных уравнений вида
dx _ dy dz
P(x;y;z) Q(xyy,z) R(x;y;z)' (71-2)
□ Действительно, пусть PQ — векторная линия поля, г = xi + yj + zk — ее радиус-вектор. Тогда вектор dr = dx i + + dy - j + dz • k направлен по касательной к линии PQ в точке М (см. рис. 270).
В силу коллинеарности векторов а и dr следует пропорциональ-
ность их проекций, т. е. равенства (71.2).
Пример 71.1. Найти векторные линии поля линейных скоростей тела, вращающегося с постоянной угловой скоростью ш вокруг оси Oz.
Q Решение: Это поле определено вектором V = —ojyi + uxj (см. пример 69.2). Согласно (71.2), имеем:
dx dy dz I ojx dx = —Ljy dy,
---- = — — — или <
— ujy сих 0 I 0 • dy = ujx dz.
506
I T — Cl, Интегрируя, получим: < ’ т. e. векторные линии данного
I Z = С‘2, поля представляют собой окружности с центрами на оси Oz, лежащие в плоскостях, перпендикулярных к этой оси. •
71.2. Поток поля
Пусть векторное поле образовано вектором (71.1). Для наглядности будем считать «(Л7) вектором скорости некоторого потока жидкости, движущейся стационарно. Представим, что некоторая поверхность S находится в этом потоке и пропускает жидкость. Подсчитаем, какое количество жидкости протекает’ через поверхность S.
Выберем определенную сторону поверхности S. Пусть п = (cos a; cos/3; cos 7) — единичный вектор нормали к рассматриваемой стороне поверхности S. Разобьем поверхность на элементарные площадки Si, S2, , S„. Выберем в каждой площадке точку Mi (г = 1,2,..., тг) (см. рис. 271) и вычислим значения вектора скорости а(М) в каждой точке: а(Л/|), я(Л/2), • -- ,а(Мп).
Будем приближенно считать каждую площадку плоской, а вектор а постоянным
по модулю и одинаково направленным в каждой точке площадки. Тогда за единицу времени через Si протекает количество жидкости, приближенно равное Ki т Hi KSi, где — площадь т-й площадки, Нг — высота т-го цилиндра с образующей а(7И;). Но Hi является проекцией вектора «(АТ,) на нормаль п,-: Н, = npnt. a(A/,) = a(Mi) щ, где щ — единичный вектор нормали к поверхности в точке Mi. Следовательно, общее; количество жидкости, протекающее через всю поверхность S за единицу времени, найдем, вычислив сумму
п
К « йС^г) •
г=1
Точное значение искомого количества жидкости получим, взяв предел найденной суммы при неограниченном увеличении числа элементарных площадок и стремлении к нулю их размеров (диаметров (Ц площадок):
п
К = JllSo 53 = [/ Й(А1) -п - ds.
(maxdf->0) i=l g
507
Независимо от физического смысла поля й(М) полученный интеграл называют потоком векторного поля.
|ф| Потоком вектора а через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т. е.
К = an ds. (71.3)
s
Рассмотрим различные формы записи потока вектора. Так как а • п = |п| прйа = прйб = ап
(см. (6.2)), то
К = JJ ands, (71.4)
s
где ап — проекция вектора а на направление норма л и п, ds — дифференциал (элемент) плошади поверхности.
Иногда формулу (71.3) записывают в виде
К = ЦаИ, S
где вектор ds направлен по нормали к поверхности, причем |ds| — ds.
Так как п = (cos а; cos/З; cos 7), а = (F;Q;I?), где Р = P(x;y;z), Q = Q(x;y; z), В = В(х\ у, z) — проекции вектора а на соответствующие координатные оси, то поток (71.3) вектора а, можно записать в виде
К = уу (Р cos а + Q cos /3 + В, cos 7) ds.
s
Используя взаимосвязь поверхностных интегралов I и II рода (см. формулу (58.8)), поток вектора можно записать как
(71-5)
Отметим, что поток К вектора а есть скалярная величина. Величина К равна объему жидкости, которая протекает через поверхность S за единицу времени. В этом состоит физический смысл потока (независимо от физического смысла поля).
Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объем V. Тогда поток вектора записывается в виде К = ands (иногда j> ands или £ ап ds,...j.
S ' S S _ '
В этом случае за направление вектора п обычно берут направление внешней нормали и говорят о потоке изнутри поверхности S (см. рис. 272).
508
Если векторное поле а = а(М) есть поле скоростей текущей жидкости, то величина потока К через замкнутую поверхность дает’ разнос ть между количеством жидкости, вытекающей из области V (объема V) и втекающей в нее за единицу времени (в точках поверхности S, где векторные линии выходят из объема V, внешняя нормаль образует’ с вектором а острый угол и а п > 0; в точках, где векторные линии входят в объем, а п < 0).
При этом если К > 0, то из области V вытекает больше жидкости, чем в нее втекает. Это означает', что внутри области имеются дополнительные источники.
Если К < 0, то внутри области V имеются стоки, поглощающие избыток жидкости.
Можно сказать, что источники — точки, откуда векторные линии начинаются, а стоки — точки, где векторные линии кончаются. Так, в электростатическом поле источником является положительный заряд, стоком — отрицательный заряд магнита (см. рис. 273).
Если К = 0, то из области V вытекает’ столько же жидкости, сколько в нее втекает в единицу времени; внутри области либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется.
Рис. 272
Рис. 273
У
Рис. 274
Пример 71.2. Найти поток вектора а = z • i — х j + у - к через верхнюю сторону треугольника, полученного при пересечении плоскости Зх + Gy — 2z — 6 = 0 с координатными плоскостями (см. рис. 274).
Q Решение: Поток найдем методом проектирования на три координатные плоскости. Для этого воспользуемся формулой (71.5). В нашем случае Р = z, Q = —х, R = y. Имеем:
JJ zdydz — xdxdz + у dx dy. s
509
Расчленим этот поверхностный интеграл на три слагаемых, затем сведем их вычисление к вычислению двойных интегралов. Нормаль к верхней стороне треугольника образует с осью Ох тупой угол, с осью Оу — тупой, а с осью Oz — острый угол. (Единичный вектор данной (О £? _ (Л
yi + — yfcl; на верхней стороне cos7 > О,
поэтому надо выбрать знак «минус»; получим: cosa = —у, cosft = — cos 7 = у.)
Итак, К = Ki + + К2. Находим К[, К2. К2:
1 О
j dy J zdz — 0 3y-‘3
2 0
I xdx 4 dz —
1 Зж—6 2
6—Зж 6
_ 3
~ 2’
s
ВОС
АОС
S
О
2
Кз = JJуdxdy = JJ ydxdy = Jdx J ydy S AOB 0 0
В результате имеем: A'=§ + 2+ X = 3§. Z о О
1
3
Пример 71.3. Найти поток радиус-вектора г через внешнюю сторону поверхности прямого конуса, вершина которого совпадает с точкой 62(0; 0; 0), если известны радиус основания R и высота конуса Н (см. рис. 275).
Q Решение:
h = ff rnds = J J rnds + J J rnds = Ai
S бок.нов. осн.
Очевидно, что Ai = 0, т. к. прйг = 0;
К2 = JJ rnds = Н J J ds — H -kR2, ОСН. осн.
т. к. нрйт = Н. Итак, К = тт///?2.
= 2,
Рис. 275
71.3. Дивергенция поля. Формула Остроградского-Г аусса
Важной характеристикой векторного поля (71.1) является так называемая дивергенция, характеризующая распределение и интенсивность источников и стоков поля.
510
|3| Дивергенцией (или расходимостью) векторного поли а(М) = Р(х; у, z)i + <2(х; у; z)j + 7?(ж; у, z)k
в точке М называется скаляр вида и обозначается
символом diva(M), т. е.
,, дР 8Q 8В
div а(М) = — + — + —. ох оу oz
(71.6)
Отметим некоторые свойства дивергенции.
1. Если а — постоянный вектор, то diva = 0.
2. div(c • a) = с • div а, где с = const.
3. div(a + 6) = div a + div b, т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
4. Если U — скалярная функция, а — вектор, то
div(l7 • a) = U • div а + a grad U.
Эти свойства легко проверить, используя формулу (71.6). Докажем, например, справедливость свойства 4.
Q Так как U • а = U Р г + U Q j + U В. • к, то
.liv(U S) = А(1/. Р) + А(Г <2) + Л) =
ГГДР — и ——Ь ох
=и(а£ \ ох
TT8Q 8U TTdB 8U
+ U-~ + Q— + u-— T B~—
dx dy dy dz dz
8Q dB\ 8U du du
+ “b B,~—
dy dz J dx dy dz
(71-7)
= U div а + а grad U.
Используя понятия потока и дивергенции векторного поля, запишем известную в анализе (см. (58.9)) формулу Остроградского-Гаусса
г г ГГГ(8Р dQ 8В
ffPdldz + Q<h^ + R<h<lll = + _ + —
в так называемой векторной форме.
Рассматривая область V, ограниченную замкнутой поверхностью S, в векторном поле (71.1), можно утверждать, что левая часть формулы (71.7) есть поток вектора а через поверхность S; подынтегральная функция правой части формулы есть дивергенция вектора а. Следовательно, формулу (71.7) можно записать в виде
Ц ап ds = III div а dv
(71-8)
s v
(в котором она чаще всего и встречается).
511
|@j Формула Остроградского -Гаусса означает, что поток векторного поля через замкнутую поверхность S (в направлении внешней нормали, т. е. изнутри) равен тройному интегралу от дивергенции эт« го поля по обвему V, ограниченному данной поверхностью.
Используя формулу (71.8), можно дать другое определение диве^ генции векторного поля а(М) в точке М (не связанное с выбором кс ординатных осей).
По теореме о среднем для тройного интеграла (см. п. 54.1) имеем III diva(Af) dv = V • diva(Mo),
где Mq — некоторая (средняя) точка области V. Тогда формулу (71.8 можно переписать в виде $ andS = V • diva(Afo). Отсюда
s
(71.9
diva(Mo) = — ап ds. s
Пусть поверхность S стягивается в точку. Тогда V —> 0, Мо —> и мы получаем выражение для div а(М) в точке М: diva(M) = lim J- <11 an ds. v->o V Jj s
Дивергенцией векторного поля в точке М называется преде;
отношения потока поля через (замкнутую) поверхность S, окружа ющую точку М, к объему тела, ограниченного этой поверхностью, npi условии, что вся поверхность стягивается в точку М (V —> 0).
Определение (71.9) дивергенции эквивалентно (можно показать' определению (71.6). !,
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном
векторном поле.
Исходя из физического смысла потока (обычно условно считают', что а(М) есть поле скоростей фиктивного стационарного потока несжимаемой жидкости), можно сказать, что: при diva(M) > 0 точка М представляет собой источник, откуда жидкость вытекает; при div а(М) < 0 точка М есть сток, поглощающий жидкость. Как следует из равенства (71.9), величина div а(М) характеризует’ мощность (интенсивность, плотность) источника или стока в точке М. В этом состоит физический смысл дивергенции.
Понятно, что если в объеме V, ограниченном замкнутой поверхностью S, нет ни источников, ни стоков, то diva = 0.
Векторное поле, в каждой точке которого дивергенция поля равна нулю, т. е. diva(M) = 0, называется соленоидальным (или трубчатым).
512
Пример 71.4- Найти дивергенцию поля линейных скоростей V жидкости, вращающейся как твердое тело вокруг неподвижной оси с постоянной угловой скоростью ш.
Q Решение: Примем ось вращения жидкости за ось Oz. Тогда, как показано ранее (см. пример 69.2), V = —wyi + wxj + 0 • к. Имеем:
divV(M) = ^(-wy) + + ^(°) = О-
Cjaj Оу (JZ
Поле V — соленоидальное.
71.4. Циркуляция поля
Пусть векторное поле образовано вектором (71.1). Возьмем в этом поле некоторую замкнутую кривую L и выберем на ней определенное направление.
Пусть г = xi + yj + zk — радиус-вектор точки М на контуре L. Известно, что вектор di' = dx-i+dy -j + dz -к направлен по касательной к кривой в направлении ее обхода (см. рис. 276) и |dr| = = dl, где dl — дифференциал дуги кривой (dl = y/(dx)2 + (dy)2 + (dz)2).
Криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора а на вектор dr, касательный к контуру L,
называется циркуляцией вектора а вдоль L, т. е.
(71.10)
Рассмотрим различные формы записи циркуляции. Так как а dr = \dr| npd~a = aT dl = Pdx + Qdy + Rdz,
где aT — проекция вектора а на касательную т, проведенную в направлении обхода кривой L, то равенство (71.10) можно записать в виде
L
(71.11)
или
Р dx + Q dy + Rdz.
(71.12)
17 Конспект лекций по высшей математике. Полный курс
513
£5| Циркуляция С, записанная в виде (71.12) имеет простой физический смысл: если кривая L расположена в силовом поле, то циркуляция — это работа силы а(М) поля при перемещении материальной точки вдоль L (п.56.5).
Отметим, что вдоль замкнутых векторных линий циркуляция отлична от нуля, потому что в каждой точке векторной линии скалярное произведение adr сохраняет знак: положительный, если направление вектора а совпадает с направлением обхода векторной линии; отрицательный — в противном случае.
Пример 71.5. Найти циркуляцию вектора поля линейных скоростей вращающегося тела (см. пример 69.2) V = —шуг + wxj вдоль замкнутой кривой L, лежащей в плоскости а, перпендикулярной оси вращения.
Q Решение: Будем считать, что направление нормали к плоскости а совпадает с направлением оси Oz. Согласно формуле (71.12), имеем:
С = —ivy dx + wxdy = w —у dx + xdy =
L L \
= 2w I - у —ydx + xdy) = 2w • S', x l '
где S — площадь поверхности, ограниченной кривой L (см. 56.17).
Заметим, что если нормаль к поверхности S образует угол 7 с осью Oz, то циркуляция будет равна С = 2w - S cos 7; с изменением угла 7 величина С изменяется. •
Пример 71.6. Вычислить циркуляцию векторного поля
а = (х - 2х)г + (ж + Зу + z)j 4- (5ж + у)к
вдоль периметра треугольника с вершинами Д(1;0;0), В(0;1;0), <7(0; 0; 1) (см. рис. 277).
Q Решение: Согласно формуле (73.12), имеем:
С = j> (ж — 2z) dx + (ж + 3«/ + z) dy + (5ж + y)dz = L
На отрезке АВ: ж + у = 1, z = 0, следовательно,
с г 3
I = / (ж — 0) dx + (ж + 3 — Зж + 0) • (—dx) + 0 = -.
АВ 1
514
На отрезке ВС: у + z = 1, х = 0, следовательно,
° 3
I = У (0 - 2 + 2у) • 0 + (0 + 2>у + 1 - у) dy + (О + у) {-dy) = вс 1
На отрезке С А: х + z = 1, у = 0, следовательно,
1
У = у {х — 2 + 2т) dx + 0 — 1 (5а; + 0) • {—dx) = —3. са о
Следовательно,
С= f = / + / + / = 1 + (~1) + (~3) = *
АВСА АВ ВС СА
71.5. Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поли
а = Р{х- у; z)i + Q{x; у, z)j + В,{х-, у, z)k
называется вектор, обозначаемый rot d{M) и определяемый формулой
Так dQY Tap дв\.=, (bq дР\=-
rota(M) = —г 4- д-“ Р + Нг " ТГ Г’ (71ЛЗ) уду dz J ydz дх J удх ду J
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
rot а{М) —
г j к а а а дх ду dz Р Q В
Отметим некоторые свойства ротора.
1. Если а — постоянный вектор, то rota = 0.
2. rot(c -а) = с- rot б, где с = const.
3. rot (а + Ь) = rota + rot b, т. е. ротор суммы двух векторов равен сумме роторов слагаемых.
4. Если U — скалярная функция, а а{М) — векторная, то
rot(U a) = U rot а + grad U х а.
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
515
Q rot(a + b) — (—(Rj + Я2) — +Q2) )i+
\dy dz )
+ (P, +P2) - ^(R, +R2)) J+ (+«
_ /dRi dQ1 \ T
\ dy dz J1
dP\ dRi
dz dx
VQ2)-~(Px+P2)\k = ду J
dQi
~д л— I fc +...
ОХ Оу )
.. . = rota + rotb.
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
0Q\ , . ~~d^)dydz+' ...
dP\
-7— ]dxdy. (71.14) dy J
dxdz +
j> Рdx + Qdy + Rdz = ~
l s ' '
(dip _ OIL + \ dz dx
Левая часть формулы (71.14) представляет собой циркуляцию вектора
а по контуру L, т. е. Pdx+Qdy+Rdz = j> aTdl (см. (71.11)). Интеграл L L
в правой части формулы (71.14) представляет собой поток вектора rota.
через поверхность S, ограниченную контуром L (см. (71.3)), т. е.
dQ\ , (dP dR — \dydz + -------—
dz J \ dz dx
s
z
Рис. 278
. . J9Q dP\ , . dxdz + —------— dx dy =
\ dx oy J
= уJ rotn a. ds. s
Следовательно, формулу Стокса можно записать в виде
(71.15)
У
f =J J rotn a ds.
L S
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре L и вы
бор стороны у поверхности S согласованы между собой так же, как в теореме Стокса.
Формула (71.15) показывает, что циркуляция вектора а вдоль замкнутого контура L равна потоку ротора этого вектора а через поверхность S, лежащую в поле вектора а и ограниченную контуром L (натянутую на контур) (см. рис. 278).
516
Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки S с контуром L, содержащей точку М.
По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
У/ rotn ads = rot,, a(Afo) • S,
s
где Mq — некоторая (средняя) точка площадки S (см. рис. 279).
Тогда формулу (71.15) можно записать в виде
У aTdl = rot„ «(F) S. L
Отсюда:
rot„ a(F) = -g j aT dl.
L
Пусть контур) L стягивается в точку М. Тогда Мо -> Л7, a S -> О. Перейдя к пределу, получаем:
rot„ а(М) = lim — J>
S—>0 /j J L
aT dl.
Ротором вектора а в точке М называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора а гщ контуру L плоской площадки перпендикулярной этому направленрпо, к площади этой площадки.
Как видно из определения, ротор вектора й(А7) есть векторная величина, образующая собственное векторное поле.
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор по.дя линейных скоростей твердого тела, вращающегося вокруг оси Oz постоянной угловой скоростью (пример 69.2) ш, т. е. ротор вектора V ~ щ у • г + щ • х • j.
По определению ротора
rot а(М) =
г j fc
а а дх ду dz
—fjliJ ЖШ О
_ Э(-;/щ) V / д(хш) _ д(—уш)\ dz )3 \ дх ду )
= 0 — 0 + 2w-fc = 2ш.
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
517
С точностью до числового множителя ротор поля скоростей V представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке S.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
§72. ОПЕРАТОР ГАМИЛЬТОНА
72.1. Векторные дифференциальные операции первого порядка
Основными дифференциальными операциями ’(действиями) над скалярным полем U и векторным полем а являются grad [7, diva, rota. Действия взятия градиента, дивергенции и ротора называются векторными операциями первого порядка (в них участвуют только первые производные).
Эти операции удобно записывать с помощью так называемого оператора Гамильтона
9 - 9 - 9 г
V = 7Гг + +
ох ду oz
Этот символический вектор называют также оператором V (читается «набла»); он приобретает определенный смысл лишь в комбинации со скалярными или векторными функциями. Символическое «умножение» вектора V на скаляр U или вектор а производится по обычным правилам векторной алгебры, а «умножение» символов на
величины U, Р, Q, R, понимают как взятие соответствующей частной производной от этих величин.
Применяя оператор Гамильтона, получим дифференциальные опе-
рации первого порядка:
Йг+ ^ + йг‘+^'+й
2. Va
.U=^-i+^j+^-k = ^U.
ох дуJ dz b
'i-kQ'j-kR'k) — 9J>-Г a— diva.
3. V х а =
3 8 ду
i д дх
Р Q
к 8 dz R
= rot а.
Оператор Гамильтона применяется для записи и других операций
и для вывода различных формул в теории поля. При действиях с ним
1. V17
/
518
надо пользоваться правилами векторной алгебры и правилами дифференцирования.
В частности, производная по направлению (70.2) может быть записана в виде „у
дл
где ё = (cos a; cos /?; cos 7).
72.2. Векторные дифференциальные операции второго порядка
После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно снова применить этот оператор. В результате получаются дифференциальные операции второго порядка. Нетрудно убедиться, что имеется лишь пять дифференциальных операций второго порядка: div grad U, rot grad U, grad diva, div rot a, rot rot a.
(Понятно, что операция div div a, например, не имеет смысла: div а — скаляр, говорить о дивергенции скаляра, т. е. о div div а, бессмысленно.)
Запишем явные выражения для дифференциальных операций второго порядка, используя оператор Гамильтона. Заметим при этом, что, оператор действует' только на множитель, расположенный непосред
ственно за оператором.
1 1. divgradt/ = V(VH) = (V - V)H = • U =
F&tj pPij
= + —V + —-у-. Правая часть этого равенства называется
дх ду dz
оператором Лапласа скалярной функции U и обозначается Д(7. Таким
°браз°м, 2 2
divgrad U = (72.1)
дх ду dz
Дифференциальное уравнение Лапласа ДС,Т = 0 играет’ важную роль в различных разделах математической физики. Решениями уравнения Лапласа являются так называемые гармонические функции.
Замечание. К равенству (72.1) можно прийти, введя в рассмотрение скалярный оператор дельта:
„ д2 д2 д2
Д = V • V — ——у + ., + -я
дх2 ду2 dz2
(который тоже называют оператором Лапласа).
|@| 2. rot grad U = V х (VJ7) = (V х V)C7 = 0, так как векторное произведение двух одинаковых векторов равно нулю (нуль-вектор). Это означает, что поле градиента есть поле безвихревое.
519
3. grad div a =
= V(V • a) = J|(diva) • г + J^(diva) j + J|(diva) к =
(d2P d2Q 92Ry / 92P d2Q ^Ry
\ дх2 + 9y9x + 9z9xP kdxdy dy2 9y9zP+
/9'2P 92Q d2R\-
+ ( 7ГЛ---1" я я' ~pT2 )&
V oxdz oyoz dz >
4. div rot a = V • (V x a) = 0, так как смешанное произведение трех, векторов, из которых два одинаковые, равно нулю. Это означает, что поле вихря — соленоидальное.
5. rot rot a = V х (V х й) = V(V • a) — (V • V)a = grad div a — Да, так как двойное векторное произведение обладает свойством
ах (Ьх с) = Ь-ас — с-а-Ь.
Здесь До. — iXPi + AQ j + tXRk — векторная величина, полученная j
результате применения оператора Лапласа к вектору а.
§ 73. НЕКОТОРЫЕ СВОЙСТВА ОСНОВНЫХ КЛАССОВ ВЕКТОРНЫХ ПОЛЕЙ
73.1. Соленоидальное поле
Напомним, что векторное поле а называется соленоидалъным, если во всех точках его дивергенция поля равна нулю, т. е. div а = 0.
Примерами соленоидальных полей являются: поле линейных скоростей вращающегося твердого тела (см. пример 71.4); магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток,и другие.
Приведем некоторые свойства соленоидального поля.
1. В соленоидальном поле а поток вектора через любую замкнутую поверхность равен нулю. Это свойство непосредственно вытекает из формулы (71.8). Таким образом, соленоидальное поле не имеет источников и стоков.
2. Соленоидальное поле является полем ротора некоторого векторного поля, т. е. если div а = 0, то существует такое поле Ь, что а = rot b. Вектор Ь называется векторным потенциалом поля а.
Любое из свойств 1-2 можно было бы взять в качестве определения соленоидального поля.
Доказывать свойство 2 не будем. Отметим лишь, что обратное утверждение — поле ротора векторного поля есть соленоидальное — нами доказано (выше мы показали, что div rot a = 0).
520
3. В соленоидальном поле а поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение (называемое интенсивностью трубки).
Q Рассмотрим векторную трубку между двумя ее произвольными сечениями Si и S-2', боковую поверхность трубки обозначим через S (см. рис. 280). Поток вектора через замкнутую поверхность, состоящую из Si, S2 и S, равен нулю. Следовательно,
Ц ап ds + Ц ап ds + Ц ап ds = Щ div adv = 0,
s Si s2 v
где п — внешняя нормаль.
Рис. 280
Так как на боковой поверхности векторной трубки нормаль п перпендикулярна к векторам поля, то Ц ап ds = 0 и, следовательно, s
Ц ands = — Ц ands.
Si s2
Переменив направление нормали на площадке Si, т. е. взяв внутреннюю нормаль ni, получим:
Ц an,ds = II ands.
Si s2
В поле скоростей текущей жидкости полученный результат означает, что количество жидкости, втекающей в трубку за единицу времени, равно количеству жидкости, вытекающей из нее.
73.2. Потенциальное поле
Векторное поле а называется потенциальным (или безвихревым, или градиентным), если во всех точках поля ротор равен нулю, т. е.
521
rota — 0. Примером потенциального поля является электрическое поле] напряженности точечного заряда (и другие). ’
Приведем основные свойства потенциального поля. j
Свойство 1. Циркуляция потенциального поля а по любому заг] мкнутому контуру в этом поле равна нулю.
Q Это непосредственно вытекает из формулы (71.14). Следовательно,
С — £ aTdl = 0.
L
В частности, для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю; в поле скоростей текущей жидкости равенство С = 0 означает, что в потоке нет
замкнутых струек, т. е. нет водоворотов.
Свойство 2. В потенциальном поле а криволинейный интеграл У Р dx + Q dy + Rdz вдоль любой кривой L с началом в точке Му ь Ч
и концом в точке М-2 зависит только от поло-жения точек М\ и М-2 и не зависит от формы ., ( \
jVl\\ \ Я т
Кривой. \
□ Это свойство вытекает из свойства 1. Дей- р
ствительно, взяв в поле две точки Mi и М-2, Рис. 281
соединим их двумя кривыми MipM% и MiqM-2 так, чтобы контур MipM-2qMi лежал внутри поля (см. рис. 281). Тогда, в силу свойства 1, имеем г
<Ь Pdx + Q dy + Rdz = 0.
MipMzqMi
Учитывая свойства криволинейного интеграла, получаем:
у Р dx + Q dy + Rdz =
MlpM‘2<]Mi
= У Р dx + Q dy + Rdz + J P dx + Q dy + Rdz =
МгрМъ
= /-/=«
M^pM? MiqM2
t. e.
У P dx + Q dy + Rdz = J Pdx + Qdy + Rdz. MipMa MiqM-2
Свойство 3. Потенциальное поле является полем градиента некоторой скалярной функции U(x;y;z), т. е. если rota = 0, то существует функция U(x;y,z) такая, что а — grad [7.
\
522
Q Из равенства rote = 0 вытекает, что =
= т. е. выражение Pdx + Qdy + Rdz является полным дифференциалом некоторой функции U — U(x',y,z) (следствие 56.1). Эту функцию называют потенциалом векторного поля а = Pi + Qj + /?£; dU = = Pdx + Qdy + Rdz.
Отсюда: P = Q = R = Следовательно, dx dy dz
- nT dU - dU — dU y a = P г + Qj + Rk = г + j + к = grad U,
dx dy dz
т. e. вектор поля а является градиентом скалярного поля.
Замечание. Из равенства rot grad U = 0 следует обратное утверждение — поле градиента скалярной функции U = U{x-, у, z) является потенциальным.
Из равенства а = grad U следует, что потенциальное поле определяется заданием одной скалярной функции U = U(x; у, z) — его потенциала. Потенциал векторного поля может быть найден по формуле
U {х\ y;z) = f Р dx + Q dy + Rdz =
(®o;«o;zo)
x у z
= j P(.X',yo',zo)dx+ J Q(x;Q,zo)d£+ [ R(x; y; 0 d< + c, (73.1) xo ya Zo
где (xo-,yo;zo) — координаты фиксированной точки, (x-,y;z) — координаты произвольной точки. Потенциал определяется с точностью до произвольного постоянного слагаемого (из-за того, что grad([7 + а) = grad U).
Произвольное же векторное поле требует задания трех скалярных функций (P(x;y;z), Q(x-,y,z}, R(x-,y,z) — проекции вектора поля на оси координат).
Замечание. Определение потенциального поля может быть дано иначе — векторное поле а называется потенциальным, если оно является градиентом некоторого скалярного поля, т. е. а = grad U. (Иногда пишут а = —gradJ7; знак «минус» пишут для удобства, обычно векторные линии направлены в сторону убывания U: поток жидкости направлен туда, где давление меньше; теплота перемещается от более нагретого места к менее нагретому и т. д.)
Пример 73.1. Установить потенциальность поля б(М) = (yz — 2х)г + (xz — 2y)j + хук и найти его потенциал.
523
О Решение: Имеем:
rota =
i
д дх
yz — 2х
3 д ду XZ — 2у
к 8 дх ху
= (х- х)г - (у- y)j + (г - z)k = 0.
Следовательно, поле вектора а потенциальное.
Найдем потенциал U по формуле (73.1), выбирая в качестве фиксированной точки начало координат, т. е. хо = = zQ — 0. Так как
Р(х;«/о,'-го) — ~2х, Q(x;y-,z0) = -2у, R(x-,y;z) = ху, то
U(x;y;z) = J (~2x)dx + J (-2£)d£+ ] xyd£+c = -x2-у2+xyz + c. • ooo
73.3. Гармоническое поле ’’
Векторное поле а называется гармоническим (или лапласовым}, если оно одновременно является потенциальным и соленоидальным, т. е. если rot а = 0 и div а = 0.
Примером гармонического поля является поле линейных скоростей стационарного безвихревого потока жидкости при отсутствии в нем источников и стоков.
Так как поле а потенциально, то его можно записать в виде а = grad U, где U = U(x-, у, z) — потенциал поля.
Но так как поле одновременно и соленоидальное, то
div а = div grad U = 0,
или, что то же самое,
Лтт д2и &2и д2и п
+ ’ТГТ + 'Х~2 - °
ох ду дх
т. е. потенциальная функция U гармонического поля а является решением дифференциального уравнения Лапласа. Такая функция называется, как уже упоминали, гармонической.
Глава XVII. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Лекции 63-68
§74. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
74.1. Основные понятия
Пусть даны два множества D и Е, элементами которых являются комплексные числа (см. гл. VI). Числа z = х + iy множества D будем изображать точками комплексной плоскости z, а числа w — и + iv множества Е — точками комплексной плоскости ш.
р5| Если каждому числу (точке) z € D по некоторому правилу поставлено в соответствие определенное число (точка) w € Е, то говорят, что на множестве определена однозначная функция комплексного переменного w = f(z), отображающая множество D в множество Е (см. рис. 282).
Если каждому z 6 D соответствует несколько значений w, то функция w = = f(z) называется многозначной.
Множество D называется областью определения функции w = f{z)\ множество Ej всех значений w, которые f(z) принимает на Е, называется областью значений этой функции (если же каждая
точка множества Е является значением функции, то Е — область значений функции; в этом случае функция f отображает D на Е).
Далее, как правило, будем рассматривать такие функции w = f(z), !•
для которых множества D и Et являются областями. Областью комплексной плоскости называется множество точек плоскости, обладающих свойствами открытости и связности (см. п. 43.1).
Функцию w = f(z) можно записать в виде и
и + iv = f(x + iy), I
т. е.
f(x + iy) = и(х; у) + iv(x; у), где
и = и(х; у) = Ref(z), v = v(x; у) = Imf(z), (x;y) 6 D.
Функцию u(x;y) при этом называют действительной частью функции < /(2), а v(x;y) — мнимой.
Таким образом, задание функции комплексного переменного рав- j посильно заданию двух функций двух действительных переменных. И
Рис. 282
Пример 74.1. Найти действительную и мнимую части функции W = Z2.
Q Решение: Функцию w — z2 можно записать в виде и + iv = (х + iy)2, т. е. 22
и + iv = х — у + г2ху.
Отсюда следует: и = х2 — у2, v = 2ху. •
74.2. Предел и непрерывность функции комплексного 1 переменного j
Пусть однозначная функция w = f(z) определена в некоторой окрестности точки zq, исключая, может быть, саму точку z0. Под 6-окрестностпъю точки z0 комплексной плоскости понимают внутрен- | ность круга радиуса 6 с центром в точке z0. '
Число wo называется пределом функции w = f(z) в точке zo
(или при z -» z0), если для любого положительного е найдется) такое положительное число 6, что для всех z zo, удовлетворяющих неравенству \z — zo| < 6, выполняется неравенство |f (г) — w0| < е.
Записывают: lim f(z) = wq- Это определение коротко можно за- Z~+Z() писать так:
(Ve>0 3<5>0 Vz:0< \z —zo\ <S=>\f(z) — w0| <e) lim f (z) = w0.
Z~^Zo
Из определения следует, что если предел wo существует, то существуют и пределы
lim и(х- у) = и0 и lim v(x; у) = v0. х->х0 ' х->хо ' ' '
У~*уо у-+уо
Верно и обратное утверждение.
Теоремы об арифметических свойствах пределов для функции од- , ного (или нескольких) действительного переменного остаются справедливыми и для функции комплексного переменного. Так, если функции । fi(z) и f2(z) имеют пределы в точке zo € D, то
lim (cifj.(z) ±c2f2(z)) =а lim /i(z)±c2 lim f2(z), z—>Zo z-»zo Z-+ZO
где cj, С2 — постоянные;
lim fi(z) f2(z) = lim ft(z) • lim f2(z) .
Z—tZo Z-+ZQ 2->Zo
и г / \ lim fi(z)
fi(z) = z-+z0JlK ’ z^zo f2(z) lim f2(z)’ Z~^Zq
если lim /2^) 7^ 0.
Z-+ZQ
pg| Пусть функция w = f(z) определена в точке z — zq и в некоторой ее окрестности. Функция w = f(z) называется •непрерывной в точке zo, если Гии /(г) = /(zo).
г—>zo
Определение непрерывности можно сформулировать и так: функция f(x) непрерывна в точке zo, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
lim &f(z) ~ 0.
Az—>0 '
Функция f(z} непрерывна в области D, если она непрерывна в каждой точке этой области.
Модуль непрерывной функции комплексного переменного обладает теми же свойствами, что и непрерывная функция действительного переменного (см. теорема 43.1).
74.3. Основные элементарные функции комплексного переменного
Определим основные элементарные функции комплексного переменного z = х + iy.
Показательная функция
p^j Показательная функция w = ez определяется формулой w = ez = ex(cosy + г siny). (74.1)
Положив в этом равенстве у = 0, устанавливаем, что для действительных значений z = х показательная функция ez совпадает с показательной функцией действительного переменного: ez = ех.
Показательная функция w = ez обладает «известным» свойством: ezi . ez2 _ ezi+z2_ Действительно, по правилу умножения комплексных чисел («модули перемножаются, а аргументы складываются», п. 28.3), имеем:
ezi . gZ2 _ gSi . -I- j/2) i sin(i/i + y2)) =
= еЖ1+ж2 (cos^ + y2) + zsinG/i +.%)) = eX1+x2+i(vi+V2} = eZ1+z*. Аналогично можно убедиться в справедливости свойств: eZl: eZ2 = eZ1~Z2, (gZ)n = gnz
Учитывая, что |ez| — ex, a ex 0, утверждаем, что показательная функция ег нигде в нуль не обращается, т. е. ег 0.
Исходя из определения (74.1), легко убедиться, что
lim ez = 0, lim ег = оо, Re*->—оо Re*—Н-оо
(ж—>—оо) (ж-у+оо)
выражение ez при z —> оо не имеет смысла.
597
Положив в равенстве (74.1) х = 0, у = ср, получим классическую формулу Эйлера eiv = cos ср + г sin ср. С ее помощью, в частности, можно представить тригонометрическую форму комплексного числа z ~ г (cos ср + i sin ср) в более компактной форме z = г-ег^(— |z| -eiarg2), называемой показательной формой комплексного числа (см. п. 27.3) |@| Показательная функция комплексного переменного обладает и специфическим свойством: она является периодической с мнимым основным периодом 2 ттг.
Q Действительно, ez+2^i = ег . е2™ = ег . + =
т. е. ег+'27гг = ez. Отметим, что е2 не всегда больше нуля. Например, е” = -1 < 0.
Логарифмическая функция
Эта функция определяется как функция, обратная показательной: число w называется логарифмом числа z 0, если ew = z. обозначается w = Ln z. Так как значения показательной функции ew = z всегда отличны от нуля, то логарифмическая функция w = Ln z определена на всей плоскости z, кроме точки z = 0 (стало быть, имеет смысл и выражение Ln(—2)).
Положив z = г - elv ,w = tz + iv, получим, согласно определению логарифмической функции, eu+w = г -e,v, или еи - ею =-r -eiv. Отсюда имеем:
еи = г, v = ср + 2fcvr, т. е. и = In г, v = ср + 2кл (fc = 0, ±1, ±2,...).
Следовательно,
w = Lnz = и + iv = In г + i(cp + 2ктс) = In \z\ + i(argz + 2/гтг), (74.2)
т. e. Ln z = In\z\ + i(argz + 2fczr) или, Lnz = In |z| + iArgz, где Arg z = arg z + 2/гтг.
Формула (74.2) показывает, что логарифмическая функция комплексного переменного имеет бесчисленное множество значений, т. е. w = Ln z — многозначная функция.
Однозначную ветвь этой функции можно выделить, подставив в формулу (74.2) определенное значение к. Положив к = 0, получим однозначную функцию, которую называют главным значением логарифма Lnz и обозначают символом lnz:
lnz = In \z\ + i argz, где - тг < argz я. (74.3) Если z — действительное положительное число, то arg z = 0 и In z = — ln|z|, т. e. главное значение логарифма действительного положительного числа совпадает с обычным натуральным логарифмом этого числа.
59«
Д Формулу (74.2) можно переписать так: Ln г = lnz + 2/гяг.
•?' Из формулы (74.2) следует, что логарифмическая функция w = Ln z обладает известными свойствами логарифма действительного переменного:
Ln(zj Z2) = Lnzi + Lnz2,
Ln( — I = Lnzj — Lnz2, ‘ \z2j
Ln zn = n • Ln z,
, Ln Vz = — • Lnz.
'1 n
Q Докажем, например, первое свойство:
Ln(zi-z2) = ln|zi z2|+?Arg(z1 -z2) =ln(|zi|-|z2|) + «(Argz1+Argz2) = = (In |zi I + zArgzi) + (In |z2| + z‘Argz2) = Ln zi + Ln z2.
Пример 7-1-2. Вычислить Ln(—1) и ln(—1); In 2г.
Q Решение: Для числа z = — 1 имеем |z| = l,argz = я. Следовательно, Ln(—1) = Ini +г(я + 2/гя) — гя(2/г + 1), ln(-l) = яг (формулы (74.2) и (74.3)); In 2г' = In |2г| + /arg2z = In 2 + г'5. •
Степенная функция w = zn
Если п — натуральное число, то степенная функция определяется равенством w = zn — rn (cos 7/95 + г sin тир). Функция w — zn — однозначная. Если п = (q е N), то в этом случае
1 п argz + 2fc7T . . argz + 2ArA
w — z 9 = \Jz = V г 006 —2 * * * *———" +г sm —~-----/>
\ q q J
где к = 0,1,2,.. - ,q— 1. 1
Здесь функция w = z9 есть многозначная («у-значная) функция. Однозначную ветвь этой функции можно получить, придав к определенное значение, например к — 0.
Если п = где р, q € N, то степенная функция определяется q
равенством
2 / „ /гт-/ p(a.rgz + 2/ся) . . p(argz + 2/гя)\
w = z9 = (z9 )р = Vlzlp ( cos -- +гsin ----------- ) •
2
Функция w = z 9 — многозначная.
Степенная функция w ~ za с произвольным комплексным показа-
телем а = a + i/З определяется равенством
w = za = eaLnz.
529
Функция w = za определена для всех z 0, является многозначной
Л. « гг i itni »»(£+2jr*) -f-2Trfc
функцией. Так, гг = е’ъпг — е 2 =е 2 , где к — 0, ±1, ±2,...
_ 7Г
При к = 0 имеем: гг = е 2 .
Tригонометрические функции
Тригонометрические функции комплексного аргумента z — х + гу определяются равенствами eiz - e-iz eiz + e-iz
sinz —----—----, cos г = -- - .-
sniz cos г
tgz = —, ctgz=-7—.
cos z sin z
При действительных z эти определения приводят к тригонометрическим функциям действительного переменного. Так, при z — х (у = 0) £ix _ e-ix j I
sin 2 =---—----= — (coss+zsinx— (cosx —z'sinx)} = —2zsinx = sinx.
2z 2z !' 2z
Тригонометрические функции комплексного переменного сохраняют многие свойства тригонометрических функций действительного переменного. В частности, sin2 z + cos2 z = 1, sin 2z = 2 sin z cos z, cos(zi + z-i) — COS Zj COS Z2 — sin 2г sin ^2, sin(z + 2тг) = sin z, cos(—z) = cos z, sin(—z) = — sin z, tg(z + zr) = tgz, 7Г cosz = 0 при z = — + fczr (fc = 0,±1,±2,...), . o 2tgz tg2z = -——2~, 1 - tg z . , Я. sin(z + —) — cos z,
/ Зтг. sin(z + —) = — COSZ,
и т. д. Докажем, например, первое свойство:
(eiz + е + \ 2~
e2iz + 2 + e"2iz ~4 “
'2iz + 2 + e~2iz
Q sin2 z + cos2 z —
giz _ e IZ 2^ e2iz - 2 + e^2iz — 4
_ -e2iz + 2 - e~2iz 4 4
2
—iz
2
530
ЦЦ Отметим, что тригонометрические функции si их и cosx в комплексной плоскости z неограничены:
lim sinz = oo, lim cosz = оо.
Im z~>rLoo Imz4±oo
Так, например, cos? = ~ 1,54 > 1, cos3г > 10-
Гиперболические функции
Эти функции определяются равенствами
е2 — e~z , ez + e~z , shz , chz shz=—-------, chz=--------, thz = ——, cthz= ——.
2 2 ch z sh z
Легко заметить связь между гиперболическими и тригонометрическими функциями. Заменяя в указанных функциях z на iz, получим:
sh iz = i sin z, или sin z = — i sh iz, ch?z = cosz
(а также tgiz = itgz, ctgzz = —zctgz).
Пользуясь этими равенствами, можно получить ряд формул, связывающих гиперболические функции. Так, заменяя в формуле sin2 z + cos2 z — 1 тригонометрические функции гиперболическими, получим
(—2sh«z)2 + (chiz)2 = 1,
|йли — sh2 zz+ch2 iz = 1. Так как здесь z — любое комплексное число, то ;^z можно заменить на z; получим формулу ch2 z — sh2 z — 1. Приведем J еще ряд формул:
I.
ch 2z = ch2 z + sh2 z, ch(—z) = ch z,
sh2z = 2shzchz, sh(—z) = —shz,
ch(zi + z2) = chzi chZ2 + shzi sh z2, sh z + ch z = ez,
% И т.д.
Из определения гиперболических функций следует, что функции
' shz и chz периодические с периодом 2тп; функции thz и cthz имеют период т.
Обратные тригонометрические и гиперболические функции
|^| Число w называется арксинусом числа z, если sin w = z, и обозначается w — Arcsin z.
Piw _
Используя определение синуса, имеем z = sinw = ---------, или
е2"" —2zze*w —1 — 0. Отсюда eiw = iz+y/(iz)2 + 1, т. е. elw = iz+^/l — z2 (перед корнем можно не писать знак ±, так как V1 - г2 имеет два
531
значения). Тогда iw = Ln(iz + д/l - z2), или w = 1Lii(«z + \/l — z2). Таким образом,
w = Arcsin z = —i Ln(«z + vl — z2).
Функция w = Arcsin z многозначна (бесконечнозначна). Аналогично определяются другие обратные тригонометрические функции. Можно показать, что
Arccosz = —iLn(z + \/z2 — 1),
Arctgz = -~ Ln г~~ (z ±г), z z j- z
. r z ~ i , ,
Arcctg z = - Ln — _ (z ф ±г).
Функции, обратные гиперболическим, обозначаются-соответственно w = Arshz (ареасинус), w — Archz (ареакосинус), w = Arthz (ареа-тангепс), w = Arcthz (ареакотангенс).
Обратные гиперболические функции имеют следующие выражения:
Arshz = Ln(z + \/z2 + 1), Archz = Ln(z + \/z2 — 1), . ., 1, 1 + z 1_ z +1
Arthz = - Ln-----, Arcthz = - Ln -----.
2 1-z’ 2 z-1
Все эти функции бесконечнозначны.
74.4. Дифференцирование функции комплексного переменного. Условия Эйлера-Даламбера
Пусть однозначная функция w = f(z) определена в некоторой окрестности точки z, включая и саму точку. Тогда предел
I- 1- /(z + Az) — f(z) .... ,
lim —- = lim —ALT = f^z\ (74.4)
&2->0 Az Az ' '
если он существует, называется производной функции f(z) в точке z, а функция f(z) называется дифференцируемой, в
точке z.
Рис. 283
Подчеркнем, что в равенстве (74.4) Az любым образом стремится к нулю, т. е. точка z + Az может приближаться к точке z по любому из бесконечного множества различных направлений (см. рис. 283) (в аналогичной ситуации для функции одного действительного переменного точка х 4- Аа: приближается к точке х лишь по двум направлениям: слева и справа).
К.Ч9
Из дифференцируемости функции /(г) в некоторой точке z следует ее непрерывность в этой точке (отношение при Az —> 0 может стремиться к конечному пределу f'(z) лишь при условии, что и Aw -> 0). Обратное утверждение не имеет места.
, При каких условиях функция w = f(z) будет дифференцируемой в данной точке?
Теорема 74.1. Если функция w = и(х\у) + w(x;y) определена в некоторой окрестности точки z ~ х + iy, причем в этой точке действительные функции и(х-,у) и и{х-,у) дифференцируемы, то для дифференцируемости функции w = /(z) в точке z необходимо и достаточно, чтобы в этой точке выполнялись равенства
ди _ ди ди _ ди дх ду' ду дх'
(74-5)
Равенства (74.5) называются условиями Эйлера-Даламбера (или условиями Коши-Римана) .
□ Необходимость
Пусть функция /(z) дифференцируема в точке z, тогда предел (74.4) существует и не зависит от пути, по которому Az — Дж+г Ду -> 0. Можно считать, что точка z + Az приближается к точке z по прямой, параллельной действительной оси (оси Ох), т. е. Az — Дж -> 0, Ду = 0 (рис. 284). Тогда
. .. (и(ж + Дж;у) +ги(х + Дж;у))
f (z) = Inn-------------------------------
7 Дж->о Дж
У
z+Az
Az=г Ду
2 Az = Ax z+Az
О х
Рис. 284
(и(х-,у) + iv(x-,y)} _
, (п(ж + Дж; у) - н(ж; у)) + г (а(ж + Дж; у) - п(ж; у)) — lim д_------------------------------------------- =
Д«-ю Дж
.. Дж'и + гДжц Джп . .. Д3;н ди , .ди = пт —— ----------= пт ——1-7, пт -т— = 77- + г-^~.
Дж->о Да Дж—»о Дж Да—ю Дж дх дх
Если же точка z + Дг приближается к точке z по прямой, параллельной мнимой оси (оси Оу), то Дг = гДу —> 0, Дж = 0. В этом случае
(п(ж;у + Ду) + то(ж;у + Ду)) - (и(х;у) + w(x',y)) f (z) = hm —— ——---------------—----------—------------—
lim
Д#—>0
г Ду
ДиЛ + гДгЩ .ди ди ди .ди
-- -------— — —2 _|_ — — 1 «
г Ду ду ду ду ду'
533
I
Сравнив найденные пределы, получим = f'(z).
Отсюда следует: = Ф^, Ф- — — Ф^. дх ду ’ ду дх
Достаточность
Пусть теперь условия (74.5) выполняются. Докажем, что функция f(z) дифференцируема.
Так как функции и(х;у) и и(х;у) дифференцируемы в точке z — х + iy, то их полные приращения можно представить (см. (44.4)) в виде Au = Ф^Дж + Ф^Ду + ai, Ди = Ф^Дж + Ф^Ду + а2, дх ду дх ду
где «1 и 02 — бесконечно малые более высокого порядка, чем |Дг| = У (Дж)2 + (Ду)2. Тогда
Дш (и(ж + Дж; у + Ду) + iv(x + Дж; у + Ду)) — (и(х; у) + ги(ж; у))
Д-г Дж + гДу
_ Ди + гДи _ (57^+ |^Ду + <*i) + a2) _
Дж + г Ду Дж + г Ду
= ^Дх + ^Ду + г^Дж+г^Ду + Q1 +ia.2 &х + г Ду Дж + г Ду
Заменяя в числителе правой части Ф^ на — Ф^-, Ф^ на Ф^, согласно ду дх' ду дх
условиям (74.5), получаем:
_ В.
__—. — —-_----------Раз,
Дх Дж 4- гДу
где , .
ai + га2 аз — —————, Дж + г Ду
т. е.
^(Дж + гДу) +г|^(Дж + гДу) ди .ди
Az Ах + гДу + °3 дх +г дх + 031
а а3 — бесконечно малая высшего порядка относительно |Дг|. Отсюда следует, что ^imo = f'(z>) существует. При этом f'(z) =
С учетом условий Эйлера-Даламбера (74.5) производную дифференцируемой функции /(z) можно находить по формулам
f'(^) =
/'(г) =
ди .ди ди .ди
дх + дх /'(-г) = 9у + дх
ди ,ди ди .ди
дх г ду' /'(^) = ду гду'
(74-6)
534
Правила дифференцирования функций действителх^ного переменного справедливы и для функций комплексного переменного, дифференцируемых в точке z. Это означает, что если /x(z) и /2(z) дифференцируемы в некоторой точке z комплексной плоскости, то верно следующее:
1. {h{z)±h{z})' =
2. (A(z) - /2(z))' = f{(z) - /2(z) + A(z) • £(z),
з. (Ш)' = о).
/2(Z)
4. Если 93 (z) дифференцируема в точке z, a f(w) дифференцируема в точке w = ip(z), то (/(^(z)))' = <p'z(z)-
5. Если в некоторой точке z функция /(z) дифференцируема и существует функция дифференцируемая в точке w = f(z),
причем # °> то /'(г) = / где _TJ(w) — функция,
(/ И)
обратная функции /(z).
ЦЦ Приведем без доказателхютва теорему о дифференцируемости основных элементарных функций комплексного переменного'. функции w = ег, w = sinz, w = cosz, w = shz, w = chz, w = zn (n 6 N) дифференцируемы в любой точке комплексной плоскости; функции w = tgz и w = thz также дифференцируемы в любой точке плоскости, кроме точек z = + кк и z = г
(к — 0,±1,±2,...) соответственно; для функций w = Lnz,w = z° в окрестности каждой точки z 0 можно выделтъ однозначную ветвь, которая является дифференцируемой в точке z функцией.
74.5. Аналитическая функция. Дифференциал
Фундаментальным понятием в теории функций комплексного переменного является понятие аналитической функции.
Однозначная функхщя /(z) называется аналитической, (голоморфной) в точке z, если она дифференцируема (выполнены условия Эйлера-Даламбера) в некоторой окрестности этой точки. Функция f(z) называется аналитической в области D, если она дифференцируема в каждой точке z G D.
Как видно из этого определения, условие аналитичности в точке не совпадает с условием дифференцируемости функции в этой же точке (первое условие — более сильное).
535
Точки плоскости z, в которых однозначная функция /(z) аналитична, называются правильными точками /(z). Точки, в кото-рых функция f (z) не является аналитической, называются особыми точками этой функции.
Пусть функция w = f(z) аналитична в точке z. Тогда lim = А#—>0 l^Z
= /'(z). Отсюда следует, что = /'(z) + о, где а -> 0 при Az -> 0.
Тогда приращение функции можно записать так: Aw = /'(z) Az + oAz. Если f'(z) 0, то первое слагаемое f'(z)Az является при Az -> 0
бесконечно малой того же порядка, что и Az; второе слагаемое oAz есть бесконечно малая более высокого порядка, чем Az. Следовательно, первое слагаемое составляет главную часть приращения функции W = f(z).
Дифференциалом dw аналитической функции w = f (z) в точке z называется главная часть ее приращения, т. е. dw = f(z)Az, или dw = f'(z)dz (так как при w = z будет dz = z'Az = Az). Отсюда следует, что f'(z) — т. е. производная функции равна отношению дифференциала функции к дифференциалу независимого переменного.
Замечание. Если функция ,f(z) = и(х- у) + w(x; у) аналитична в некоторой области D, то функции и(х; у) и и(х; у) удовлетворяют диф-о2 о2
ференциальному уравнению Лапласа (-—£ + = 0, см. п. 72.2).
ох ду
□ Действительно, дифференцируя первое из равенств Эйлера-Далам-бера по у, а второе по ж, получаем:
д2и д2и д2и д2и
дхду ду2' дх2 дудх'
откуда + ^4 = °-
дх ду
Функции и(х-,у) и и(х-,у) являются гармоническими функциями.
Пример Ц. 3. Проверить, является ли функция w = z2 аналитической. Найти ее производную.
Q Решение: Находим действительную Rew = и и мнимую Imw = v части функции:
w = z2 = (х + гу)2 — ж2 — у2 + 2гху.
Таким образом, и = ж2 — у2, v = 2ху. Проверяем условия Эйлера-Да-ламбера (74.5): „
ди _ ди _
дх ~2Ж’ ду - ’
дн ди
536
Условия (74.5) выполняются во всех точках комплексной плоскости z. Функция w — z2 дифференцируема, следовательно, аналитична во всех точках этой плоскости. Ее производную найдем по одной из формул (74.6), например по первой:
(я2)' = ^(«2 ~ У2) + = 2ж + i2y = 2<'Х + iy^ = 2z'
т. е. (z2)' = 2z.
Заметим, что производную функции w = z2 можно найти, воспользовавшись определением производной (74.4):
ф , Aw (-г + АД2 - z1 2zAz + (Az)2
= hm - = hm -----------—~--------= Inn ---------------=
;( Дг-»О Az Az-»O Az Az—>0 Az
= lim (2z 4- Az) = 2z. •
Az->0
Пример 74-4- Найти аналитическую функцию w = и + iv по ее заданной действительной части и = ж3 — Зху2 + 2.
Q Решение: Отметим, что функция и является гармонической функцией (и"х — 6ж, иуу = -6ж, следовательно, и"х + иуу = 0).
Для определения мнимой части v воспользуемся условиями Эйлера-Даламбера (74.5). Так как = (ж3 - Зху2 + 2)'а, = Зж2 — Зу2,
то, согласно первому условию, у, находим:
dv ду
= Зж2 — Зу2. Отсюда, интегрируя по
i v - I --dy - [(Зж2 - Зу2)dy = Зж2у -у3 + у>(х).
J ду J
Для определения функции <f(x) воспользуемся вторым условием Эйлера-Даламбера. Так как
= (ж3 — Зжу2 + 2)^ = —бжу,
а
~ = (Зж2у - у3 + у’(ж))^. = бжу + Д(ж), ох
то —бжу = —(бжу + Д(ж)). Отсюда Д(х) = 0 и ^(х) = С, где С = const.
Поэтому v = Зх2у — у3 + С. Находим функцию w = и + iv:
w = u + iv = х3 — Зжу2 + 2 + i(3x2y — у3 + С) =
= х3 +i3x2y-3xy2-iy3 +2 + Ci = (ж + гу)3 + 2 + iC = z3 + 2 + iC. •
537
74.6. Геометрический смысл модуля и аргумента производной.
Понятие о конформном отображении
Пусть функция w = f(z) аналитична в точке zo и f'(z0) 0. Вы-
ясним геометрический смысл аргумента и модуля производной.
Функция w = f(z) отображает точку zq плоскости z в точку Wo = /(го) плоскости w.
Пусть произвольная точка z = zo + Az из окрестности точки zq перемещается к точке Zq по некоторой непрерывной кривой I. Тогда в плоскости w соответствующая точка w = w0 + Aw будет перемещаться к точке Wo по некоторой кривой L, являющейся отображением кривой I в плоскости w (рис. 285).
Рис. 285
По определению производной /'(zq) = lim Отсюда следует, Az-Ю AZ
что |/'(z0)| = | lim = lim = lim ! . Величина IAz| =
1 V 71 'Az-HjAz1 Az-Hl'Az1 Az—>0 |Az| 1 1
= \z — zo| представляет собой расстояние между точками zq и zq + Az, a |Aw| — расстояние между точками wo и Wo + Aw. Следовательно, |/'(z0)| есть предел отношения бесконечно малого расстояния между отображенными точками u>q и Wq + Aw к бесконечно малому расстоянию между точками zq и zq + Az. Этот предел не зависит (/(z) аналитична в точке zo) от выбора кривой I, проходящей через точку z0. Следовательно, предел 2*т0 = 1/,(го)| в точке zq постоянен, т. е.
одинаков во всех направлениях.
Отсюда вытекает геометрический смысл модуля производной: величина |/'(z0)| определяет коэффициент растяжения (подобия) в точке zo при отображении w = f(z). Величину |/z(^o)| называют коэффициентом растяжения, если |/'(zo)| > 1, или коэффициентом сжатия, если |/'(zo)| < 1-
Пример Ц.5. Найти коэффициент растяжения (сжатия) для функции w = Az2 в точке Zo = 3 — 4г.
538
Q Решение: Функция w = ^z2 аналитична в точке zq = 3 — 4г, при этом ио' = z. Следовательно, |/'(zo)| = |^о| = |3 — 4г| = 5 > 1. Коэффициент растяжения для функции w — ^z2 в точке zq равен 5 (плоскость растягивается). •
Для аргумента производной в точке zq имеем:
arg/'(z0) = lim arg —--~ lim (arg Aw — arg Az) =
Az-»O Az Az-+O
= lim arg Aw — lim arg Az = a-2 — Oj, Az-»O Д«—>0
где о, и П2 — углы, которые образуют касательные к кривым I и L соответственно в точках zo, и Wo с положительными направлениями действительных осей на плоскостях z и w (см. рис. 285).
Отсюда а2 = »i +arg/'(zo). Это означает, что arg/'(z0) — это угол, на который нужно повернуть касательную к кривой I в точке zq для того, чтобы получить направление касательной к кривой L в точке wq. Другими словами, arg/'(zo) — это угол между отображенным и первоначальным направлениями касательных к кривым I и L в точках zo и wo соответственно. В этом состоит геометрический смысл аргумента производной arg/'(z0).
В силу аналитичности функции /(z) в точке zo (мы предположили, что /(z0) 0) угол arg/'(z0) один и тот же для всех кривых, про-
ходящих через точку z0. Для другой пары кривых. Zi и Lj в тех же точках zo и wo будем иметь arg/'(zo) = а!2 — а[ = ip. Таким образом, arg/'(zo) = «2—0] = т.е. если кривые I и Zj образуют в точке zo на плоскости z угол <р — arg/'(z0), то такой же угол <р — arg/'(^o) будут образовывать в точке wo кривые L и Lj, являющиеся отображениями кривых I и li на плоскости w (см. рис. 286).
Рис. 286
Это свойство отображения w = f(z) называется свойством сохранения (консерватизма) углов в точке zq-
Отображение w = /(z), обладающее свойством сохранения углов и
постоянством растяжений в точке zo, называется конформным
539
(т. е. отображением, сохраняющим форму). Если при этом сохраняется и направление отсчета углов, то такое отображение называется конформным отображением, 1-го рода-, если направление отсчета углов изменяется на противоположное — конформным отображением 2-го рода.
|@| Таким образом, если функция /(я) является аналитической в некоторой точке z0 комплексной плоскости z и в этой точке ее производная отлична от нуля, то отображение w = f(z) конформно в этой точке.
Отображение w = /(z) называется конформным в области D, если оно конформно в каждой точке этой области.
Справедливо следующее утверждение: если функция w = f(z) аналитична в области D, причем во всех точках области f'(z) 0, то
отображение конформно в D; если отображение w = f(z) конформно в области D, то функция w = f(z) аналитична в D и вр всех точках этой области f(z) 0.
Пример Ц.6. Выяснить геометрическую картину отображения, осуществляемого функцией w = 2z.
Q Решение: Отображение w = 2z конформно во всех точках плоскости z, т. к. w' = 2 0.
Коэффициент растяжения в любой точке плоскости z равен 2. Так как arg те' = arg 2 = 0, то направление при отображении не меняется. Таким образом, отображение w = 2z есть преобразование гомотетии с центром в нулевой точке (w = 0 при z = 0) и коэффициентом гомотетии, равным 2. •
§75. ИНТЕГРИРОВАНИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
75.1. Определение, свойства и правила вычисления интеграла
Пусть в каждой точке некоторой гладкой кривой L с началом в точке z0 и концом в точке Z определена непрерывная функция f(z).
Разобьем кривую L на п частей (элементарных дуг) в направлении от z0 к z точками z\, z2,..., zn_t (см. рис. 287).
В каждой «элементарной дуге» z^-iZk (fc = 1,2, выберем п
произвольную точку Ck и составим интегральную сумму 2Z /(Cfc)A^fc, где -Zfc-i. fc=1
Предел такой интегральной суммы при стремлении к нулю длины наибольшей из элементарных дуг, если он существует, называется
Рис. 287
интегралом от функции f(z) по кривой (по контуру) L и обозначается символом У f{z)dz.
L
Таким образом,
(75.1)
Покажем, что если L — гладкая кривая, а /(г) — непрерывная и однозначная функция, то интеграл (75.1) существует.
Действительно, пусть /(z) = и(х-у) + w(.t;j/), z = х + iy, Ck = = Xk + iyk- Тогда
/(Cfc) = и(хк; ук) + iv(xk; yk), Д*л = (хк + iyk) ~ (xk-i + гук-i) = &хк + iAyk.
Поэтому
п П
52 f{Ck)^Zk = 52 (и(®*5 Ук) + iv(xk-, ук)) (Д.г> + iAyk) = к=1 к=1
п п
= '^(у{хк-,Ук)^хк-у(хк-,Ук)^Ук) + i'^2(v(xk;yk)Axk+u(xk;yk)Ayk). к=1 к=1
Обе суммы, находящиеся в правой части последнего равенства, являются интегральными суммами для соответствующих криволинейных интегралов (см. п. 56.1).
При сделанных предположениях о кривой L и функции f(z) пределы этих сумм существуют. Поэтому после перехода к пределу (в последнем равенстве) при тах|Дх^| —> 0 получим:
L ( f(z) dz= j £ u, dx — vdy + i £ Г vdx + udy. (75.2)
541
Формула (75.2) показывает, что вычисление интеграла от функций комплексного переменного сводится к вычислению криволинейных инч тегралов от действительных функций действительных переменных.
Формулу (75.2) можно записать в удобном для запоминания виде:
J f(z)dz — J (w + iv)(dx + idy). (75.3)
L L
Если x = x(t),y = y(t), где ti t < t2 — параметрические уравнения кривой L, то z = z(t) = x(t) + iy(t) называют комплексным параметрическим уравнением кривой L; формула (75.3) преобразуется в формулу
*2
J f(z)dz = у f(z(t))z'(t)dt. (75.4)
l ь
Q Действительно, считая z(t) непрерывной и дифференцируемой функцией, получаем
<2
У f(z) dz = у (и + iv)(dx + г dy) = f (w + iv)(x't + iy't) dt =
L L ti
У f(z(t))z'(t)dt.
Приведем основные свойства интеграла от функции комплексного переменного.
1. У dz — z — zq. l
□ 52 ^zk = Дг:1 + - - + Azn = Z1-ZO + Z2 — Zj+. . , + Zn — Zn-! — Z— Zq. fe=l |
2- У (fi(z) ±/2(^)) dz = у f!(z)dz± у h(z)dz. j
L L L 1
3. у af(z) dz = a J f(z) dz, a — комплексное число. L L
4. у f(z)d.z = — у f(z)dz, t. e. при перемене направления пути L l-
интегрирования интеграл изменяет свой знак на противоположный (в других обозначениях кривой: j = — ).
АВ ВА
542
5. I f(z) dz = У f(z)dz+ j f(z) dz, где L — L\ +L2, т. e. интеграл L Ij2
по всему пути L равен сумме интегралов по его частям Li и L2.
6. Оценка модуля интеграла. Если |/(г)| М во всех точках кри-
вой L, то
J f(z) dz
Ml, где I — длина кривой L.
□ Действительно,
f>(Cfc)A^
Л=1
п п
£ |f(C*)Azfc| < М £ |Azft| < Ml, k=i fc=i
n
где 22 — длина ломаной Zo-?1Z2 .- - zn, вписанной в кривую L.
k=l
Все приведенные свойства интеграла функции комплексного переменного непосредственно вытекают из его определения (75.1) и представления (75.2).
Пример 75.1. Вычислить
где L — полуокружность |г| = 1, 0 $
arg г тг (см. рис. 288).
Рис. 288
Q Решение: Используя формулу (75.3), имеем:
TV
2
Используя формулу (75.4), имеем (г = cosZ + isinZ):
71 а
1= f sinZ(— sinZ + г cost) dt = J —2^ о о
— cos2t)dt + i J sintcostdt = о
1 . „ \ Г .1 . ? ,Г Л -sm2Z| -f-T-sm Z — ——.
4 Ло 2 Io 2
543
75.2. Теорема Коши. Первообразная и неопределенный ) интеграл. Формула Ньютона-Лейбница
т. к. каждый из разрезов (дуг) 71 и 72 при интегрировании проходится дважды в противоположных направлениях. Поэтому получаем:
7 г/ \ д_ / f (dz 4- f(z) dz = 0,
Теорема 75.1 (Коши). Если функция /(z) аналитична в односвязной области D, то интеграл от этой функции по любому замкнутому контуру L, лежащему в области D. равен нулю, т. е. j> f(z)dz = 0.
L
J ' J
V Г L Lx L2
т. е. интеграл от аналитической в замкнутой многосвязной области D функции f (z) по границе области D, проходимой в положительном направлении, равен нулю.
Q Докажем теорему, предполагая непрерывность производной f'(z) (это упрощает доказательство). По формуле (75.2) имеем:
•№
и dx — vdy + i
В силу аналитичности /(z) = и + iv и непрерывности f(z) в одно- ! связной области D, функции и = и(х;у) и v = v(x;y) непрерывны и i дифференцируемы в этой области и удовлетворяют условиям Эйлера-Даламбера: = —^q~ и Эти условия означают равенство 1
нулю интегралов j> иdx — vdy и <j> v dx + иdy (см. теорему 56.3). Сле- ;
довательно, j> f(z)dz = 0.
L
Теорема Коши допускает распространение на случай многосвязной области.
Рассмотрим для определенности трехсвязную область D, ограниченную внешним контуром L и внутренними контурами £] иД- Выберем положительное направление обхода контуров: при обходе область D остается слева (см. рис. 289).
Пусть функция /(z) аналитична в области D и на контурах L, L\ и £2 (т. е. в замкнутой области D; функция называется аналитической в замкнутой области D, если она аналитична в некоторой области, содержащей внутри себя область D и ее границу £).
Проведя два разреза (две дуги) 71 и 72 области D (см. рис. 289), получим новую односвязную область /Д, ограниченную замкнутым ориентированным контуром Г, состоящим из контуров L, Li, L2 и разрезов 71 и 72: Г = L + 7j+ + £х 4- 7^ + £2 + 7Г + 7Г- По теореме Коши для односвязной области j> f(z) dz = 0, но
= 0,
71- +^2 +72 +71 ~tt 71
72 72
Рис. 290
Рис. 289
Замечание. Изменив направление обхода внутренних контуров £1 и £2, будем иметь <f> f(z) dz = <f> f(z) dz+ <j> f(z) dz, где все контуры
L Li L2
(L, Li и L2) обходятся в одном направлении: против часовой стрелки (или по часовой стрелке). В частности, если /(z) аналитична в двусвязной области, ограниченной контурами Lulu на самих этих контурах (см. рис. 290), то <£ f(z) dz — j> f(z) dz, т. е. «интеграл от функции /(z)
L I
по внешнему контуру £ равен интегралу от функции /(z) по внутреннему контуру I» (контуры £ и I обходят в одном направлении).
--------— --------—,
Следствие 75.1. Если /(z) — аналитическая функция в односвязной области D, то интеграл от нее не зависит от формы пути интегрирования, а зависит лишь от начальной точки zq и конечной точки z пути интегрирования.
[_} Действительно, пусть £1 и £2 — две кривые в области D, соединяющие точки z0 и z (рис. 291).
По теореме Коши § f(z)dz = 0, т. е.
ИЛИ j
Ll
У /(z)dz+ J f(z)dz = 0,
L1
I f(z) dz = 0, откуда j f(z) dz —
L2 Ll
L2
18 Конспект лекций по высшей математике. Полный курс^
544
В таких случаях, когда интеграл зависит только от начальной точ-
Pi
ки и конечной точки пути интегрирования, пользуются обозначением J f(.z) dz — J f(z) dz. Если здесь зафиксиро-i 20 5
вать точку zq, а точку z изменять, то / f (z) dz
20
будет функцией от z. Обозначим эту функцию Z
Рис. 291 через F(z): F(z) = J f(z) dz. Можно доказать,
20
что если функция /(z) аналитична в односвязной области D, то функция F(z) также аналитична в D, причем
20
р$| Функция F(z~) называется первообразной для функции /(z) в области D, если F'(z) = f(z).
Можно показать, что если F(z) есть некоторая первообразная для f(z), то совокупность всех первообразных /(z) определяется формулой F(z) + С, где С = const.
Совокупность всех первообразных функций /(z) называется неопределенным интегралом от функции /(z) и обозначается символом J f(z) dz, т. е.
/(z) dz - F(z) + С, где F'(z) = /(z).
z
Пусть функция F(z) = J f(z) dz есть первообразная функция для 2 Z0
f(z). Следовательно, J f(z) dz — F(z) + С. Положив здесь z — zq, no-20
лучим 0 = F(zo) + C (контур замкнется, интеграл равен нулю). Отсюда С — —F(zo), а значит,
Z
f f{z)dz = F(z')-F{zG). 20
Полученная формула называется формулой Ньютона-Лейбница.
Интегралы от элементарных функций комплексного переменного в области их аналитичности вычисляются с помощью тех же формул и методов, что и в действительном анализе.
Так, у ez dz = ez+C; [ sinzdz = — cosz+C; J 3z2 dz ~ 3-^-| = — i
0 °
и т. д.
546
Пример 75.2. Вычислить интегралы: a) ; 6) $ (z — zo)ndz
L L
(п — 1), где L есть окружность радиуса R с центром в точке го, обходимая против часовой стрелки (см. рис- 292).
Q Решение: а) Теорема Коши неприменима, т. к. функция ——— не аналитична в точке го- Пара-г — го метрические уравнения окружности L есть х — = хо + R cos t, у — уо + R sin t, где 0 < t < 2тг. Следовательно,
г = х + iy = хо + R cos t+iyo + iRsin t =
2тг
J dt — 2m.
о
2r i -R- еа
J R-eu
О
Рис. 292
= (.To + iyo) + R(cost + i sin t) = zq + R elt.
Таким образом, мы получили, что комплексно-параметрическое уравнение данной окружности есть z — zo + R • elt, 0 C t 2тг. Поэтому по формуле (75.4) получим: /-*_= J Z — Zo
б) При п — 1 имеем:
27Г
j> (z — го)’1 dz = У (R
L ° 25 , рг(«+1)* |2тт
= iR"+1 у dt = Rn+l
• i elt dt =
о
pn+l 0 pn-l 1
------ (сов2тг(тг +1) + г sin2Tr(w + 1) — e°) = ---(1 — 1) = 0.
Итак,
/ -——— = 2тгг, j> (z — z0)ndz = 0, n — целое, n —1.
L Z° L
75.3. Интеграл Коши. Интегральная формула Коши
Теорема 75.2. Пусть функция /(г) аналитична в замкнутой односвязной области D и L — граница области D. Тогда имеет место формула 1г /(z)
f(z0) = д-r Ф -----dz,
2т J г — го L
где го € D — любая точка внутри области D, а интегрирование по контуру L производится в положительном направлении (т. е. против часовой стрелки).
(75.5)
547
Интеграл, находящийся в правой части равенства (75.5), называется интегралом Коши, а сама эта формула называется интегральной формулой Коши.
Формула Коши (75.5) является одной из важнейших в теории функций комплексного переменного. Она позволяет находить значения аналитической функции /(z) в любой точке z0, лежащей внутри области D через ее значения на границе этой области.
Q Построим окружность 1Г с центром в точке z0, взяв радиус г столь малым, чтобы данная окружность была расположена внутри области (чтобы 1Г не пересекала L).
Получим двусвязную область (заштрихованную на рис. 293), ограниченную контурами L и 1Г, в которой функция —аналитична. z — Zo
Тогда, согласно замечанию к теореме Коши (с. 545), имеем:
Рис. 293
f(z) dz z-z0
/(г) dz z-zq'
Отсюда следует:
1 Г f(z) dz 1 г f(z) dz _ 1 r f(zp) -1- /(z) - /(z0)
2яг J z — zq 2тгг J z — z0 2тгг / z — zo L lr lr
1 ,, . / dz 1 r = ^-л/(^о) Ф ------ + f
2m J z — zo 2m J lr lr
f(z) - /(го) -------------az
Z - Zo
Ио/
dz
Z - Zo
— 2m (см. пример 75.2). Следовательно,
1 с f(z) dz 1 . If
— 4 ---------- —f(z0) -2m + —
/яг J z — Zq 2тгг 2тгг J
L lr
Z ~ Z0
t. e.
2m J z — zo 2m J z— z0
(75.6)
Оценим разность в левой части равенства (75.6). Так как аналитическая функция /(z) непрерывна в точке z0 € D, то для любого числа £ > 0 найдется число г > 0 такое, что при |z — z0| < г (на окружности 1Г имеем |z — zq| = г) справедливо неравенство |/(z) — /(z0)| < е.
548
Применяя свойство 6 об оценке модуля интеграла (п. 75.1), имеем:
f(z) dz
Z-Zo
- Л^о)
_!г№)-/Ы|Ь
2тгг J z — zq lr
I/U) ~ Л*о)1 dz < 1 £
\z - 2п| 2тг г
Так как е может быть выбран сколь угодно малым, а левая часть последнего неравенства не зависит от е, то она равна нулю:
1 ГЙ>±_Лго) = 0,
2тгг J Z — Zq
L
откуда следует формула (75.5).
Отметим, что интегральная формула Коши (75.5) справедлива и для многосвязной области: каждый из контуров обходится так, чтобы область D оставалась слева.
Применяя интегральную формулу Коши, можно доказать следующие теоремы-следствия.
Теорема 75.3. Для всякой дифференцируемой в точке zo функции f (к) существуют производные всех порядков, причем п-я производная
имеет вид:
/(п)Ло) = ~ / 7 --L+fdz-2т J [z — к0)
(75.7)
Теорема 75.4. В окрестности каждой точки zo. где существует производная f'(z0), функция /(к) может быть представлена сходящимся рядом:
/(к) = /Ло) + /'(z0)(z - к0) + ^~~^(z ~z0)2 + ...
... + ^^-(z-z0)n + ... (75.8)
|@| Таким образом, производная аналитической функции также является аналитической функцией.
Напомним, что из дифференцируемости действительной функции не следует даже существования второй производной (функция у = у/х
1 1
3 у/х^
имеет производную в точке х = 0, а производная этой функции
при х = 0 не существует).
Ряд (75.8) называется рядом Тейлора функции /(z) в точке zq.
Ряд Тейлора дифференцируемой в точке zo функции существует и
сходится к самой функции. Ряд же Тейлора для действительной функции /(ж) может сходиться к другой функции или быть расходящимся. Замечание. Формула n-й производной функции f (z) может быть получена из формулы Коши
(75-9)
L
(в формуле (75.5) заменено z на £, zb на z) путем последовательного дифференцирования равенства (75.9) по z:
(75Л0)
Формулы (75.5) и (75.7) можно использовать для вычисления интегралов по замкнутым контурам.
Пример 75.3. Вычислить <j> , L
|z] — 1, б) L — окружность |z — г| = 2.
где a) L — окружность
Q Решение: а) функция /(z) = а - - является аналитической в обла-z +4
сти |z| С 1. В силу теоремы Коши имеем j> ~^z = 0.
б) На рисунке*-294 представлена область, ограниченная контуром интегрирования.
В этой области |z — г| 2 находится точка z = 2г, в которой знаменатель подынтегральной функции равен нулю. Перепишем интеграл в виде / = 4 -^~dz.
J z2 + 4 J z — 2г
L L
Функция /(z) = —j-a- является аналитиче-Z “I z/l
ской в данной области. Применяя интегральную формулу Коши (75.5), находим:
dz _ .
2—; =
z2 + 4
1
z 4- 2г
0-1 7Г
= 2тп— = — 4г 2
L
Пример 75.2^. Вычислить
^dz z
550
Q Решение: Внутри круга и на его границе |z| = 1 функция /(z) = cosz аналитична. Поэтому, в силу формулы (75.7), имеем
/cosz , с cosz
~^~dZ~ J (z —0)2+1 dZ~ |z|=l |z|=l
=-^~(cosz)"l = 7T«( — cosz)l = — тг?'. •
2! lz=O lz=D
§ 76. РЯДЫ В КОМПЛЕКСНОЙ плоскости
76.1. Числовые ряды
Рад оо
2 ип — Н-1 + U-2 + • - • + ип + • • , (76.1)
п=1
|ф| членами которого являются комплексные числа, называется числовым рядом (в комплексной области). Ряд (76.1) с комплексными членами ип — ап + ibn можно записать в виде
ОО оо
2 ' ип = 2 ^(о?г + ibn) = (ai + ibi) + (02 + ib-z) + ... + (ап + ibn) + • • •, П=1 п=1
где ап и Ьп (п = 1,2,3,...) — действительные числа.
Сумма Sn = 22 Uk = 22 (°* + ibk) = 22 ak + i 22 bk первых n k=i k=i fe=i fc=i
членов ряда (76.1) называется n-й частичной суммой ряда.
Если существует конечный предел S последовательности частич-п п
пых сумм Sn ряда: S = lim Sn = lim 22 °fe+« lim 22 bk, то ряд (76.1) n—>OO n—>OO П~ЮО
называется сходящимся,aS — суммой ряда; если lim Sn не существу-п—>оо
ет, то ряд (76.1) называется расходящимся.
Очевидно, что ряд (76.1) сходится тогда и только тогда, когда сходится каждый из рядов
ОО
2 ak = °i + °2 + • • • + ап + • • (76.2)
fc=i
И оо
2д Ьк = 5] + 1>2 + • • + Ъп + ... (76.3)
fc=i
При этом S = Si + iSz, где Si — сумма ряда (76.2), а S2 — сумма ряда (76.3). Это означает, что исследование сходимости ряда с комплексными членами сводится к исследованию сходимости рядов (76.2) и (76.3) с действительными членами.
551
В теории рядов с комплексными членами основные определения, многие теоремы и их доказательства аналогичны соответствующим определениям и теоремам из теории рядов с действительными членами.
Приведем некоторые из них.
Остатком ряда (76.1) называется разность
ОО ОО оо
t'n = Un+1 + Мп+2 + • - • = ^2 Uk ~ Ofc + г У2 bk'
/г=п+1 fc=n-H
Теорема 76.1 (необходимый признак сходимости ряда). Если ряд (76.1) сходится, то его общий член ип при п —> оо стремится к нулю: lim ип = 0. п—>оо
Ряд (76.1) называется абсолютно сходящимся, если сходится ряд
У" |Дп| = lMi| + |^2| + • • + |г»„| + ... (76.4)
71=1
Теорема 76.2. Если сходится ряд (76.4), то абсолютно сходится ряд (76.1).
□ По условию ряд с общим членом |г/,„| = у/о% + сходится. Тогда в силу очевидных неравенств |а„| + Ь‘„ и |Ь„| \/о^ + Ь% и на
оо
основании признака сравнения (теорема 60.1) сходятся ряды 52 |°п| и 71=1 оо
52 |ЬЯ|. Отсюда следует сходимость рядов (76.2) и (76.3), а значит, и п=1
абсолютная сходимость ряда (76.1).
Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд.
Абсолютно сходящиеся ряды можно почленно складывать и перемножать.
При исследовании на сходимость рядов с комплексными членами применимы все известные из действительного анализа признаки сходимости знакопостоянных рядов, в частности признак Даламбера: если существует lim _ I, то при I < 1 ряд (76.4) абсолютно 71—>Оо| Un I
сходится, а при I > 1 — расходится.
552
76.2. Степенные ряды
Степенным рядом в комплексной области называют ряд вида
cnzn = со + eiz + с2г2 + ... + cnzn + ..., (76.5)
71=0
где с„ — комплексные числа (коэффициенты ряда), z = х + гу — комплексная переменная.
Рассматривают также и степенной ряд вида
ОО
^cn(z - z0)n, (76.6)
77=0
который называют рядом по степеням разности z — zq, zq — комплексное число. Подстановкой z — zq = t ряд (76.6) сводится к ряду (76.5).
Ряд (76.5) при одних значениях аргумента z может сходиться, при других — расходиться.
[ф| Совокупность всех значений z, при которых ряд (76.5) сходится, называется областью -сходимости этого ряда.
Основной теоремой теории степенных рядов является теорема Абеля, устанавливающая область сходимости степенного ряда.
Теорема 76.3 (Абель). Если степенной ряд (76.5) сходится при z = z0 0 (в точке zq), то он абсолютно сходится при всех значениях z, удовлетворяющих условию |г| < |z0|.
Доказательство теоремы аналогично доказательству теоремы Абе-,ля в действительном анализе (теорема 63.1).
Следствие 76.1. Если ряд (76.5) расходится при z = z0, то он расходится при всех значениях z, удовлетворяющих условию |.гj > |го| (т. е. вне круга радиуса |z0| с центром в начале координат).
Из теоремы Абеля следует существование числа R = |^о| такого, что при всех значениях z, удовлетворяющих неравенству ]z| < R, степенной ряд (76.5) абсолютно сходится. Неравенству \z\ < R удовлетворяют точки комплексной области, лежащие внутри круга радиуса R с центром в точке z — 0.
Величина |г0| — R называется радиусом сходимости ряда (76.5), а круг |zo| < R — кругом сходимости ряда. В круге |zo| < R ряд (76.5) сходится, вне этого круга — расходится; на окружности |z(i | — R могут располагаться как точки сходимости, так и точки расходимости ряда.
553
Принято считать, что R = 0, когда ряд (76.5) сходится в одной точке z ~ 0; R = оо, когда ряд сходится на всей комплексной плоскости. Кругом сходимости ряда (76.6) является круг \z - z0| < R с центром в точке z = zo-
Радиус сходимости ряда (76.5) можно вычислить по формуле R = lim |(/га.| | (или R = —--—), получаемой после примене-
п—>ОС П
ния признака Даламбера (или Коши) к ряду из модулей его членов исходного ряда.
Приведем (без доказательств) некоторые свойства степенного ряда.
1. Сумма степенного ряда внутри круга его сходимости есть аналитическая функция.
2. Степенной ряд внутри круга сходимости можно почленно дифференцировать и почленно интегрировать любое число раз. Полученный при этом ряд имеет тот же радиус сходимости, что и исходный ряд.
Пример 76.1. Найти область сходимости ряда уу. п=0 П-
О Решение: Здесь с« = £„+1 =
R= lim —--
Cn+1
.. (п +1)! .. .
= lim --------— = lim (zi + 1) = co,
n—too n' П—ЮО
t. e. R = оо. Следовательно, областью сходимости является вся плоскость Z. •
00 (z — i)n
Пример 76.2. Найти область сходимости ряда г ",
п=0 (П +
Cj Решение: Здесь R = lim
п—>оо
области \z — z| < 2.
2”+1(n + 2) (n +1)2”
= 2. Данный ряд сходится в
Пример 76.3. Определить радиус сходимости ряда
оо
£(-1)"+1
п=0
и исследовать сходимость ряда в точках z-\ = 0, = i, z% = 3 — 2г.
554
Q Решение: Воспользуемся признаком Даламбера. Здесь
. , 1-Л , . |г2п+2| .. ип+1 ,. |г2"+2|^ . ,2
К+х -— = 11,11 -/=тгзп, =\z\
\/п Vn + 1 п-+о° ип «~>оо Vn + l|z I
Ряд сходится при всех z, удовлетворяющих неравенству |г|2 < 1, т. е. |г| < 1. Кругом сходимости является круг с центром в точке z = 0 и радиусом 1.
Точка zj = 0 лежит внутри круга сходимости, в этой точке ряд сходится абсолютно. Точка z2 = i лежит на границе круга сходимости, в этой точке ряд может сходиться (абсолютно или условно) и расходиться. Подставляя значение z2 = i в выражение общего члена ряда, получим (-1)"+^ = = -4=- Числовой
у/П у/П у/П у/П
ряд с общим членом ип = -Д= расходится согласно интегральному при-V71
знаку Коши (теорема 60.5). Следовательно, в точке z2 — i степенной
РЯД 52 (-1)”+14= расходится.
п=0 у/Т1
Точка гз = 3 — 2г лежит вне круга сходимости, ряд в этой точке , расходится. •
76.3. Ряд Тейлора
Теорема 76.4. Всякая аналитическая в круге |z — zo| < R функция f(z) может быть единственным образом разложена в этом круге в степенной ряд
/(z) = J^z-zo)", (76.7)
коэффициенты которого определяются формулами
Сп = - , - Т"7 У ------wT+T®£ (те = 0,1,2,3,...), (76.8)
п! 2т J (£ - zo)
где 1Г — произвольная окружность с центром в точке zq, лежащая внутри круга.
Степенной ряд (76.7) называется рядом Тейлора j для функции f(z) в рассматриваемом круге.
' □ Возьмем произвольную точку z внутри данного круга и проведем окружность с центром в точке zq и радиусом г < R так, чтобы точка z находилась внутри круга \z — zo\ < г (см. рис. 295).
Рис. 295
555
Так как функция f(z) аналитична в круге \z — zo| < г и на его границе 1Г, то ее значение в точке z можно найти по формуле Коши (75.9): /(z) = где £ — точка на окружности lr. Имеем:
1 = 1 = 1 =
£~z (£ - z0) - (z - z0) (£-z0)(l-|5^) 1-f^’
Так как \z — zo| < — z0|, то - ~ < 1, следовательно, выражение
I S I
1
i £~z-sq можно рассматривать как сумму членов бесконечно убываю-1 ~ С-20
щей геометрической прогрессии с первым членом с- - - - и знаменате-
S — z0
лем f—Таким образом,
? — zo
1 _ 1 , Z-ZQ (z - Zp)2 (z - Zp)n
e-z £-z0 (£-z0)2 (£-zo)3 (£-zo)n+1
Умножим обе части этого равенства на величину и проинте-
грируем его почленно по контуру 1Г. Получим:
' /ж= ’ /+2о)л /_ж_^+
2т Т £ — z^ 2т J £, — Zq 2mJ (£ —zo)2
т. е. /(z) = Д (z - 2о)П2^ / или /(*) = Дс"(2 ~ z°)"’
где с - _1_ X
Д п~ 2т f (f-z0)n-
(п = 0,1,2,...). Используя формулу (75.10),
получим представление коэффициентов ряда через п-е. производные функции /(z) в точке z0: сп = -- -^-z-(п = 0,1,2,...).
Таким образом, мы получили разложение функции /(z) в степенной ряд (76.7), коэффициенты которого определяются по формулам (76.8).
Докажем единственность этого разложения.
Допустим, что функция /(z) в круге |z — z0| < R представлена
другим степенным рядом
f(z) — bo + b| (z — z0) + b?(z — z0)2 + ... + bn(z — Zo)n + ...
556
Последовательно дифференцируя почленно этот ряд бесконечное число раз, будем иметь:
/'(z) = Ь] + 2Ь2(г - z0) + 3b3(z - z0)2 + ... + nbn(z - z0),i-' + ..., f"(z) = 2Ьг + 3 263(z — Zo) + ... + п(гг — l)fcri(z — z0)n 2 + ..., $ . f"'(z) = 3 • 2b3 + ... + n(n - l)(n - 2)6n(z - z0)n-3 + • -., Г j .......................J
. f(n)(z) = n- bn + (n + 1)! • bn+l - (z - z0) + ...,
z7 .
7! '
z6 .
6! ’
z3 ln(l + z) = z- — + — -о
сфо - 1) 2 а(а - l)(a - 2) 3
Полагая в этих равенствах, а также в исходном ряде z = z0, получаем: bo = f(z0), bx = f(zo), b2 = - -., bn = I* , - - - Сравни-
вая найденные коэффициенты bn ряда с коэффициентами ряда (76.7), устанавливаем, что Ьп = сп (п = 0,1,2,...), а это означает, что указанные ряды совпадают.
Функция /(z) разлагается в степенной ряд единственным образом.
Приведем разложения некоторых элементарных функций в ряд Тейлора (Маклорена):
г z z2 Z3
е ~1+П + 2! + 3! +-”’
z3 Z5 sinz = z- — + — -^+...,
z2 z4
cosz = l-- + --- + ...,
М(1 ; „ 2
(1 + z)“ = 1 + -Z , 2! Z. , з! ~
Первые три разложения справедливы во всех точках комплексной плоскости, последние два — в круге |z| <1.
Заменив z на iz в разложении функции ег, получим:
iz i (iz)2 i (iz)3 i _
1! ’
eiz
2! 3!
/24
7' Z Z
“ I1- 2! + 4!
з ~5
3! 5!
t. e. формулу Эйлера eiz = cos г + г sin г.
557
76.4. Нули аналитической функции
Как показано выше, всякая функция f(z), аналитическая в окрестности точки zq, разлагается в этой окрестности в степенной ряд (76.7): коэффициенты которого определяются по формулам (76.8).
£5] Точка zq называется нулем функции f(z), если /(z0) = 0. В этом случае разложение функции /(z) в окрестности точки zq в степенной ряд не содержит нулевого члена, т. к. cq = /(zq) = 0. Если не только со = 0, но и С] = С2 — = cm-i = 0, а ст 0, то разложение
функции /(z) в окрестности точки z0 имеет вид
/(z) = cTO(z - z0)m + cm+i(z - z0)m+1 + ... + c„(z - z0)” + ..., (76.9)
а точка zq называется нулем кратности m (или нулем m-го порядка). Если т, = 1, то zq называется простым нулем.
Из формул (76.8) для коэффициентов ряда Тейлора следует, что если zq является нулем кратности т функции f(z), то /(zo) = = /42o) = ... — f^m~1Kz0) = 0, но /(™)(z0) 0. В этом случае пред-
ставление функции степенным рядом (76.9) можно переписать в виде /(z) = (z - z0)mip(z), где
¥>(%) — Ст + C'm l 1 (z Z(j) -f- . . . (76.10)
Для функции <p(z) точка z = zq уже не является нулем, так как ^(z0) = — 0.
|@| Справедливо и обратное утверждение: если функция f (z) имеет вид (76.10), где т — натуральное число, a y?(z) аналитична в точке z0, причем y?(z0) 0, то точка z0 есть нуль кратности т функции f(z).
76.5. Ряд Лорана
Теорема 76.5. Всякая аналитическая в кольце г < |z — z0| < R (0 г < R оо) функция /(z) может быть разложена в этом кольце в РЯД +ОО
/(z)= £ cn(z-z0)n, (76.11)
п=—оо
коэффициенты которого определяются формулой
Cn=^/«^rde ("=°-±1-±2-(™-12)
где L — произвольная окружность с центром в точке zq, лежащая внутри данного кольца.
558
Рад (76.11) называется рядом Лорана для функции /(г) в рассматриваемом кольце.
□ Возьмем произвольную точку z внутри кольца г < |z — zo\ < R и проведем две окружности Li и L2 с центрами в точке zq так, чтобы точка z была между ними и каждая окружность находилась внутри данного кольца (см. рис. 296).
Функция /(z) аналитична в кольце между окружностями Li и Ь2 и на самих окружностях. Поэтому по формуле Коши для многосвязной области имеем:
\ 1 z IE
Лг>=й т Lr+L2
= ~ (76.13)
2тгг J E — z 2т J Е — z L2 Li
где обе окружности £1 и L2 обходятся против часовой стрелки.
Преобразуем слагаемые, стоящие в правой части равенства (76.13), рассуждая, как и при выводе формулы Тейлора.
На окружности Ь2 выполняется неравенство \z — zo| < |£ ~ zq|, или If ~-й| < 1. Поэтому дробь 14 — zo I
т-1— можно представить в виде S —z
1 ___________1__________________1 _
C-z ~ (С - го) - (г - z0) (£ - z0)(l - |5g)
1 z-zp (z - г0)и
^-zo (С-zo)2 ” (e-z0)"+1
Тогда
i /(e) = 1 /(e) , 1 . . ш ,
2m — z 2m — z0 2m' (£ — zo)2
1
2m
,n /(e) , (e-z0)"+1 -
Проинтегрируем это равенство по контуру L2:
_L / Ж= ' г/«Lde + (г 1 г +...
2т J — z 2т J — го 7 2т J (£ — zo)2
L2 L2 L2
<7614>
i2
559
T- e- 2J7 / = S СпЛ - «о)"> где
^2
^2
(здесь сп ± J , так как функция /(г), возможно, не аналитична в точке 2ь).
На окружности Li имеем |£ - г0| < \z - z0|, т. е. I & ~ г° I < 1. Тогда I z — Zo I
1 ______1 _____________1 _ 1
£ ~ z z~k~ (г - zo) - (е - г0) ~ (z-zo)(l-§fj “
_ f 1 е-го te-zo)"0 А
\z-zo (г-г0)2 (z - z0)n+1
Значит,
1 1 Ш . 1 Ьго , 1 (bzof
2ттг £—2 2тгг (г-г0) 2ттг (г-20)2 J 2т (z-z0)n+1
Проинтегрируем это равенство почленно по контуру Li:
1 Г
'йГ ~^ =
L1
= (2-2о)-1~ у /(£)< +(2-2ь)~2^т f f (£)(£-z0)d£+ ... Li Li
• • • + (Z - *o)-(n+1)^ f f Ш - zo)n dC + .. . =
XzTTZ J
bl
= ^(г - го)-п~ f - zoy-1^, (76.15) _____1 ^i7l i J
т. e.
2ттг J £ — z bl
bl
ОО
У. с_п(г - го)-”, где п—1
Подставив разложения (76.14) и (76.15) в равенство (76.13), получим
оо оо 4-оо
л*) = 12 с«л _ + 52 с-«л ~ г°)-п = 52 Спл - z^n-
п=0 п~1 П=—ОО
560
госвязной области): сп
Формулы для коэффициентов сп и с_п можно объединить, взяв вместо контура Lj и любую окружность L с центром в точке zy, лежащую в кольце между Lj и L? (следует из теоремы Коши для мно-
2m j
L
Можно доказать, что функция /(z), аналитическая в данном коль-це г < |z — zy| < R, разлагается в ряд Лорана (76.11) единственным образом.
Ряд Лорана для функции
4-оо
/(«) = 52 ~ z°yi
п=—00
(^J^„+idg(n = 0,±l>±2,...).
ОО оо
- 52 Cn^z ~ г°)п + 52 7 ~~y
состоит из двух частей. Первая часть ряда Лорана, т. е. ряд
ОО
/1 w = 52 Сп& ~
п=0
называется правильной частью ряда Лорана-, этот ряд сходится к аналитической функции /i(z) внутри круга |z — zy| < R.
Вторая часть ряда Лорана, т. е. ряд
AW = £
П—1
п
(г-zo)"’
называется главной частью ряда Лорана-, этот ряд сходится к аналитической функции /2^) вне круга |z — z0| > г.
4-ос
Внутри кольца г < |z — zy| < R ряд ^2 c-n^z — zo)n сходится к п=—оо
аналитической функции /(z) = fi(z) + /2(2)-
В частности, если функция f (z) не имеет особых точек внутри круга |z — zo\ < R, то ее разложение в ряд Лорана обращается в ряд Тей
лора.
Замечание. На практике при разложении функции в ряд Лорана используют известные разложения основных элементарных функций; дробь вида —-— разлагается в ряд, являющийся рядом геометриче-Z — Zq
ской прогрессии; дробь вида ——* , где к > 1 — целое, разлагается
в ряд, который получается из ряда геометрической прогрессии последовательным дифференцированием (fc — 1) раз; сложная дробь представляется в виде суммы простейших дробей.
1
Пример 16.4. Разложить в ряд Лорана функцию f(z) = ez в окрестности точки zy = 0.
561
Решение: Воспользуемся известным разложением „ „ и и2 ип
е =1+п + й + -'+ы+-'
справедливым на всей комплексной плоскости. Положив и =
чим 111 1
z = 1 + у;—Ь тг-2 4-... 4---г-77 4- .., Z
llz 2!z nlz
полу-
А
Пример 76.5. Разложить в ряд Лорана функцию
в окрестности точки zq = 0.
Q Решение: Функция имеет две особые точки: Zi 2 и z2 = 3. Она аналитична в областях: а) 0 \z| < 2; б) 2 < \z\ < 3; в) \z\ > 3.
Представим функцию f(z) в виде f(z) = |( —----"Го )
а) В круге |z| < 2 (рис. 297) имеем:
1 11 1Д z z2 \ ( izt
Ц^ = “зГЛ = “з(.1 + 3 + ? + - ) (здесь |-|<1,т.е.|г|<3),
1 11 1/ z z2 \ / I z\ л , , \
’‘S5 = ~2Sj=-2(1-2 + ?—) (Здесь |--|<l,T.e.H<2).
Следовательно,
____ 1
z2 — z — 6
1 1
~ 6 + 3бг~
7 27-8
z2 4-.-.,
ряд Лорана функции /(z) обращается в ряд Тейлора.
б) В кольце 2 < |z| < 3 (рис. 298) имеем:
1 1 ( z z2 \ , .
+ _ + _ + (W<3)?
1 11 1Д 2 22 \
z 4- 2 z 1 +1 zV % z2 )
1 2 22
= + (М>2).
Z Z Z
Следовательно,
УД)-
1
Z2 - Z - 6
2П z«+i
562
Рис. 298
Вис. 299
Рис. 297
в) В области |z| > 3 (рис. 299) имеем:
Следовательно,
76.6. Классификация особых точек.
Связь между нулем и полюсом функции
Как уже знаем, особой точкой функции /(z) называется точка, в которой функция не является аналитической.
g Особая точка z = z0 функции /(г) называется изолированной, если в некоторой окрестности ее функция /(z) не имеет других особых точек.
Если zo — изолированная особая точка функции /(z), то существует такое число R > 0, что в кольце 0 < |z — zo| < R функция /(z) будет аналитической и, следовательно, разлагается в ряд Лора-
ОО ОО _
на (76.11): /(z) = £ c„(z - z0)n + £ _T”nV'
п=0 п=1
При этом возможны следующие случаи:
1) Ряд Лорана не содержит главной части, т. е. в ряде нет членов с отрицательными показателями. В этом случае точка zq называется устранимой особой точкой функции /(z).
563
2) Разложение Лорана содержит в своей главной части конечное число членов, т. е. в ряде есть конечное число членов с отрицательными показателями. В этом случае точка zq называется полюсом функции /(z).
3) Разложение Лорана содержит в своей главной части бесконечное множество членов, т. е. в ряде есть бесконечно много членов с отрицательными показателями. В этом случае точка zq называется существенно особой точкой функции f(z).
Укажем особенности поведения аналитической функции /(z) в окрестности особой точки каждого типа.
Устранимые особые точки
Если zo — устранимая особая точка, то в окрестности точки zo
ОО
разложение (76.11) имеет вид f (z) = У) cn(z — zb)". Это разложение п=0
справедливо во всех точках круга |z — zq\ < R, кроме точки z = zq. Если положить f (zq) — со, где с0 = lim f (z) (т. е. определить функ-Z—VZq
цию J(z) в точке z0), то функция f (z) станет аналитической во всем круге |z — zo| < R (включая его центр z = z0); особенность точки zo устраняется, точка z0 становится правильной точкой функции f (z)).
Из равенства lim f (z) = с0 (с0 оо) следует, что в достаточно Maz-эго
лой окрестности устраняемой особой точки zo функция /(z) является ограниченной.
Справедливо и обратное утверждение: изолированная особая точка z = zq является устранимой, если существует конечный предел lim /(z) = А.
z->z0
Полюсы
Если zo — полюс, то в окрестности точки zo разложение (76.11) ОС ю
имеет вид ДЦ = £е„(г - «)» + +...+
где с_то 0. В этом случае полюс zo называется полюсом т-го порядка функции f (z); если т = 1, то полюс zo называется простым.
Запишем последнее равенство в виде
, ОС
/(*) = 7--yn(SZ - ~ *>)” + c-i(z - ^)ГО-Ч
- ^о) V
+ c_2(z - z0)m-2 + ... + c_m)
-ИЛИ , к
564
где g(z) — аналитическая функция, причем g(zo) = с-т 0. Отсюда следует, что f(z) —> оо при z —> го, т. е. в достаточно малой окрестности полюса функция /(г) бесконечно велика.
Справедливо и обратное утверждение: изолированная особая точка г = го является полюсом, если lim /(г) = оо.
z—>го
Из равенства (76.16) имеем (г — z0)mf(z) = g(z). Отсюда получаем удобный способ определения порядка полюса го: если
lim (г - г0)™У(г) = с_т (с-т 0, с_т оо), (76.17)
z->zo
то точка го есть полюс m-ro порядка.
Имеется связь между нулем и полюсом функции.
Теорема 76.6. Если точка го — нуль m-ro порядка функции f^z), то го является полюсом т-го порядка функции у^; если точка го — полюс т-го порядка функции f(z), то г0 является нулем т-го порядка ФУНКЦИИ уХу.
Q Докажем первую, часть теоремы. Пусть г = г0 есть нуль т-го порядка для . функции f(z). Тогда имеет место равенство /(г) = (г — zo)m(p(z), где Дг) аналитична в точке г0, причем g>(zo) 0. Тогда (г - г„Г у-^у = и Пт ((г - ^Гу^у) = 0 (^ оо).
Это означает (см. (76.17)), что для функции ууту точка г = го является полюсом т-го порядка. Вторая часть теоремы (обратной) доказывается аналогично.
Существенно особая точка
Если го — существенно особая точка, то, как доказывается (теорема Сохоцкого-Вейерштрасса), в достаточно малой окрестности точки го функция У (г) становится неопределенной. В такой точке аналитическая функция не имеет ни конечного, ни бесконечного предела. Выбирая различные последовательности точек {znj, сходящихся к существенно особой точке го, можно получать различные последовательности соответствующих значений функций, сходящиеся к различным пределам.
1
Пример 76.6. Определить тип особенности функции У (г) = ez в точке г = 0.
565
1
Q Решение: Функция f (z) = ez в окрестности точки z = 0 имеет следу-
1 ОО |
ющее лорановское разложение: е2 = ; ул (см. пример 76.4). Точка
n=0 n'Z
z = 0 является существенно особой точкой. Если z -> 0 вдоль положи-
1 д
тельной части действительной оси, то lime2 = lim ех = +оо: если z—>0 ж—>0+0
1 z -> 0 вдоль отрицательной части действительной оси, то lim е 2 = z—>0
1
= lim ех = 0. •
к-тО-О
Замечание. Классификацию изолированных особых точек можно распространить на случай, когда особой точкой функции f (z) является бесконечно удаленная точка, z = оо.
Окрестностью точки z = оо называют внешности какого-либо круга с центром в точке z = 0 и достаточно большим радиусом R (чем больше R, тем меньше окрестность точки z = оо).
Точку z = оо называют изолированной особой точкой, если в некоторой окрестности ее нет других особых точек функции f(z).
Бесконечно удаленная изолированная особая точка может оказаться устранимой особой точкой, полюсом порядка т или существенно особой точкой. В первом случае лорановское разложение функции /(z) в окрестности точки z = оо не имеет членов с положительными показателями, во втором — имеет их лишь конечное число, в третьем случае в разложении имеется бесконечно много членов с положительными показателями.
Изучение функции f (z) в окрестности точки z = оо можно свести путем подстановки z = 1 к изучению функции в окрестности точки z = 0.
Пример 76.7. Найти особые точки функции f(z) =
Q Решение: Особой точкой функции f (z) является z — 0. Найдем предел функции при z -> 0: lim = lim = оо. Следовательно,
z-M) Z z-+0 Z z
точка z = 0 является полюсом. Можно убедиться, что lim z2 = оо, z-тО z
lim z3^S^ = 1^0. Следовательно (см. (76.17)), точка z = 0 — полюс
третьего порядка. *
Пример 76.8. Исследовать особенности функции
z + 3 z(z 4- 2)(z — I)2
566
Q Решение: Для данной функции точки zi = 0 и z2 — — 2 — простые полюсы, z3 — 1 — полюс второго порядка. •
Пример 76.9. Выяснить поведение функций /(z) = --х, g(z) =
Z <5
z2
—j в окрестности точки z — оо.
' О Решение: Сделаем подстановку z — —. Тогда функция f (z) = —— примет вид ^Ри Условии |3w] < 1 имеет место разло-
жение = w(l + 3ш+ (3w)2 + --.)- Возвращаясь к старой переменной, имеем
/<г) = тЪ
3 з2
—
Z У
‘УП
= 52 рйд’ и >3-----п "
1
Поэтому точка z = оо является устранимой особой точкой (см. послед-
нее замечание). 2
Можно убедиться, что z = оо для функции </(z) = -% является
правильной точкой. ' •
§77. ВЫЧЕТ ФУНКЦИИ
77.1. Понятие вычета и основная теорема о вычетах
|ф| Вычетом аналитической функции /(z) в изолированной особой точке zo называется комплексное число, равное значению интеграла 2^ j> /(г) dz, взятого в положительном направлении по окружно-L
сти L с центром в точке zo, лежащей в области аналитичности функции /(z) (т. е. в кольце 0 < |z — z0| < R).
Обозначается вычет функции /(z) в изолированной особой точке zo символом Res/(zo) или Res(/(z);zo)- Таким образом,
(77.1)
Res/(z0) = ~ <[> f(z)dz.
Z7TI J L
Если в формуле (76.12) положить п = — 1, то получим
с-i = тД / f(z)dz или Res/(z0) = c_i,
2тгг J
L
j@| т. е. вычет функции /(z) относительно особой точки zo равен коэффициенту при первом члене с отрицательным показателем в разложении функции /(z) в ряд Лорана (76.11).
567
Теорема 77.1 (Коши). Если функция J(z) является аналитической в замкнутой области D, ограниченной контуром L, за исключением конечного числа особых точек zk (к — 1,2,лежащих внутри области D, то п
f(z) dz = 2m ^2 Res /(**)- (77-2)
k=i
□ Вокруг каждой особой точки zk опишем окружность 1к так, чтобы она целиком содержалась в области D, не содержала внутри других особых точек и чтобы никакие две из этих окружностей не имели общих точек (см. рис. 300).
Тогда на основании теоремы Коши для многосвязиой области (см. замечание на с. 545) имеем:
j f(z) dz= j f(z) dz+ j> f (z) dz + ... + j, f(z) dz,
Ь h /2 In
где при интегрировании все контуры обходятся против часовой стрелки. Но, согласно формуле (77.1), имеем:
У f(z)dz = 2m'Resf(zi), h
j> f{z) dz = 2 m Ros/(z2), ^2
j f{z) dz = 2mResf(z„).
Следовательно,
j> f(z) dz = 2m Res f (zi) + ... + 2m Res f (zn),
L
t. e. / f(z) dz = 2m Res/(zfc).
l k=1
77.2. Вычисление вычетов. Применение вычетов в вычислении интегралов
Правильные или устранимые особые точки. Очевидно, если z = zo есть правильная или устранимая особая точка функции f(z),
568
Resf(zp) = с-i — lim (z - z0)/(z). z-^-ZQ
то Res /(zo) = 0 (в разложении Лорана (76.11) в этих случаях отсутствует главная часть, поэтому c_i = 0).
Полюс. Пусть точка zq является простым полюсом функции f{z). Тогда ряд Лорана для функции f (z) в окрестности точки zo имеет вид ОО
Л*) = Е с«(г - zo)n + Отсюда n=0 z
оо
- *о)Л*) = с-1 + 52 c«(z “ *o)”+1-
n=0
Поэтому, переходя в этом равенстве к пределу при z —> z0, полу-
(77.3)
Замечание. Формуле (77.3) для вычисления вычета функции /(z) в простом полюсе можно придать другой вид, если функция /(z) является частным двух функций, аналитических в окрестностях точки Zq.
Пусть /(z) = 1де Л^о) 7^ 0, a g(z) имеет простой нуль при z = z0 (т.е. g(z0) = 0,g'(zo) 0). Тогда, применяя формулу (77.3),
имеем: Res/(zo) = lim (z — zp)= lim , \, ?• e.
' g(z) z->«o a(z)~aRo) g (z0) ’
г—zo
Res Uw J = У’(^о) 5'(«о)’
Пусть точка zp является полюсом m-го порядка функции f(z). Тогда лорановское разложение функции /(z) в окрестности точки zp имеет вид /(z) = Д c„(z-zo)"+^ + ^J^ + . - •+ (г^ут. Отсюда (z-z0)m/(z) = £ crl(z-zp)n+m4-c_TO+c_m+i(z-z0)+. .+e-i(z-zp)'m’1. n=0
Дифференцируя последнее равенство (m - 1) раз, получим:
дт-1
= (m-l)!c-i + 52 Сп(п+т)(п+т—1)(п+т-2)... (n+2)(z-z0)"+1. п=0
Переходя здесь к пределу при z —> zp, получаем
1 лт-\
(77.5)
Существенно особая точка. Если точка zp — существенно особая точка функции f(z), то для вычисления вычета функции в этой точке
569
обычно непосредственно определяют коэффициент c_i в разложении функции в ряд Лорана.
Пример 77.1. Найти вычеты функции f(z) — — 24 в ее особых
точках.
Q Решение: Особыми точками функции f(z) являются: Zi = 1 — про-
стой полюс, z2 = О полюс третьего порядка (т = 3). Следовательно,
z + 2
- 1 + 2 _
~ 3-4 ~
по формуле (77.4) имеем Res(/(z); 1) =
Z=1
-3.
Используя формулу (77.5), находим:
Res(/(z);0) = lim f(z-O)
3 z + 2 \" 1 Zz + 2\" 1 „ ж
i -»---J = - 11m --------- = --6 = 3. •
z3 — z4 / 2 z->o \1 — z.) 2
1
Пример 77.2. Найти вычет функции /(z) = ez в особой точке z = 0.
Q Решение: Лорановское разложение данной функции в окрестности точки z ~ 0 было найдено в примере 76.4. Из него находим c~i = 1, т. е. Res(/(z);0) = 1. •
Теорема о вычетах часто используется для вычисления интеграла от функции комплексного переменного по замкнутому контуру.
Пример 77.3. Вычислить у д
1 - i| = л/2.
(z - l)2(z2 + 1) ’Где L ~ ОКРУЖНОС'ГЬ
О Решение: Функция /(z) =
—— имеет (z-l)2(z2 + l)
б круге |z — 1 — г| < \/2 (см. рис. 301) простой полюс Zi = г и полюс второго порядка z2 = 1. Применяя формулы (77.2), (77.3) и (77.5), получаем:
dz
(z — I)2 (z2 4-1) = 27™(Res(/(X);«) +Res(/(z); 1)) =
Рис. 301
„ .Г.. z —г 1 ,. // „г 1 V
= 2тгг hm --------—5-----——----------у — lim I (z — 1)------------5—---------|
z-H (z — l)2(z + i)(z — г) 1! г-»1 \ (z - l.)2(z2 + 1) /
о -Л- 1 с —2z \ ./1 1\ ттг
(z — l)2(z + г) Z-+1 (г2 + I)2) \4 2/ 2
57(1
2тг
Определенный интеграл вида J 7?(sin х; cos х) dx с помощью заме-о
ны z = е“ в некоторых случаях удается преобразовать в интеграл по замкнутому контуру |z| = 1 от функции комплексного переменного, к которому уже применима основная теорема о вычетах.
Пример 77.-4- Вычислить с помощью вычетов интеграл
2тг ।
/= [________.
J (3 + 2 cos ж)2
Решение: Произведем замену переменного, положив z = е“. Тогда । р—гх Z + т ~2 . ।
dz = iewdx = izdx, cosa: = s----= - = -a При изменении
z 2 zz
x от 0 до 2тг точка z опишет в положительном направлении окружность
|z| = 1. Следовательно,
dx г dz _ 1 г zdz
(3 + 2 cos a:)2 ~ г>(3 + 2^)2 ~ * |гД + I)2
В круге |z| < 1 функция f(z) = . % * - i имеет полюс второго
“Ь tjZ “Г J-J
порядка zi = ~~3 + V5- По формуле (77.5) находим
г_Х^(. + ^)3 5>/5
Следовательно, I —
1.2„: з =<а£ г 5л/5 25
Глава XVIII. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
Лекции 69-71
Операционное исчисление играет важную.роль при решении прикладных задач, особенно в современной автоматике и телемеханике.
Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений, содержащих эти операторы, к рассмотрению более простых алгебраических задач.
Методы операционного исчисления предполагают реализацию следующей условной схемы решения задачи.
1. От искомых функций переходят к некоторым другим функциям — их изображениям.
2. Над изображениями производят операции, соответствующие заданным операциям над самими функциями.
3. Получив некоторый результат при действиях над изображениями, возвращаются к самим функциям.
В качестве преобразования, позволяющего перейти от функции к их изображениям, будем применять так называемое преобразование Ламаса.
§ 78. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
78.1. Оригиналы и их изображения
Основными первоначальными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть f(t) — действительная функция действительного переменного t (под t будем понимать время или координату).
Функция /(f) называется оригиналом, если она удовлетворяет следующим условиям:
1. /(f) = 0 при t < 0.
2. /(f) — кусочно-непрерывная при t 0, т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
|ц>| 3. Существуют такие числа М > 0 и so 0, что для всех t выполняется неравенство |/(t)| М-eSoiт. е. при возрастании t функция /(f) может возрастать не быстрее некоторой показательной функции. Число §о называется показателем роста f(t).
572
-S’i Условия 1-3 выполняются для большинства функций, описывающих различные физические процессы.
Первое условие означает, что процесс начинается с некоторого момента времени; удобнее считать, что в момент I = 0. Третьему условию удовлетворяют ограниченные функции (для них можно положить So =0), степенные tn (п > 0) и другие (для функций вида f(t) = ае* ^словно 3 не выполняется). Не является оригиналом, например, функция f (t) = ~ (не удовлетворяет второму условию).
Замечание. Функция f(t) может быть и комплексной функцией действительно переменного, т. е. иметь вид /(<) = У1(<)+г/г(0; она считается оригиналом, если действительные функции /i(t) и /г(0 явля-
ются оригиналами.
Изображением оригинала f(t) называется функция F(p) комплексного переменного р = в + га, определяемая интегралом
(78.1)
Операцию перехода от оригинала /(t) к изображению F(р) называют преобразованием Лапласа. Соответствие между оригина-
лом /(t) и изображением F(p) записывается в виде f (т) = F(p) или F(p) = /(т) (принято оригиналы обозначать малыми буквами, а их изображения — соответствующими большими буквами).
Теорема 78.1 (существование изображения). Для всякого оригинала f(t) изображение F(p) существует (определено) в полуплоскости , Rep = s > з01 где sq — показатель роста функции /(i), причем функ-1 ция F(p) является аналитической в этой полуплоскости (s > so).
[_J Докажем первую часть теоремы. Пусть р = = s 4- га произвольная точка полуплоскости Rep = s > s0 (см. рис. 302). Учитывая, что |/(£)| < М eSot, находим:
Re р > so
e~pt\dt
ОО
У f^-e^dt
О
у* esGte st __ м
О
О so s
Рис. 302
ОО , г
f e^-^ dt^-----,
I s-Sq
573
так как s — s0 > 0 и |е pt| = \е st-e “^1 = е st |cosoi — zsincrt| = е st. Таким образом,
|F(p)| = J ftf)
О
e^pl dt
М
S - So’
(78.2)
Отсюда вытекает абсолютная сходимость интеграла (78.1), т. е. изображение F(p) существует и однозначно в полуплоскости Rep — s > sq.
Следствие 78.1 (необходимый признак существования изображения). Если функция F(p) является изображением функции f(t), то
lim F(p) = 0. р—>оо
Это утверждение непосредственно вытекает из неравенства (78.2), когда Rep = s —> +оо.
Так как F(p) — аналитическая функция в полуплоскости Rep > so, то F(p) -> 0 при р —> оо по любому направлению. Отсюда, в частности, следует, что функции F(p) = 5, F(p) = р2 не могут быть изображениями.
Отметим, что из аналитичности функции F(p) следует, что все ее особые точки должны лежать левее прямой Rep = s = so или на самой этой прямой. Функция F(p), не удовлетворяющая этому условию, не является изображением функции f(t). Не является изображением, например, функция F(p) = tgp (ее особые точки расположены на всей оси s).
Теорема 78.2 (о единственности оригинала). Если функция F(p) служит изображением двух оригиналов fi(t) и /2(0’ то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.
(Примем без доказательства.)
Пример 78.1. Найти изображение единичной функции Хевисайда
1(0 1
о t
Рис. 303
1
о
1(0 =
при t 0, при t < 0
(см. рис. 303).
574
Q Решение: По формуле (78.1) при s = Rep > 0 (so = 0) находим:
°? г 1 J6 1
Ftp) = / 1-е pt dt — lim / е ptdt = lim — • e p = -, ' ' J 6-4oo J Ь—Уоо p iO p
0 0
t. e. F(p) = i, или, в символической записи, l(t) = i, или 1 = •
Замечание. В дальнейшем функцию-оригинал будем кратко записывать в виде /(t), подразумевая, что
fft\ = f /<*) п₽и f °’
10 при t < 0.
Пример 78.2. Найти изображение функции /(t) = eatr где а — любое число.
Q Решение: Данная функция является оригиналом. По формуле (78.1) имеем
Ftp) = 7 eate~pt dt= lim / e-(p~a)t dt = - lim —— • е~<р~с*\Ь=
' J 6-400 J ъ-нхр — а Io
о 0
/ 1 1
= lim ( ------------------- ) =-----,
б-чоо \p — a p — a ) p — a
если Re(p - a) > 0. Таким образом,
eat = —(Rep > Rea). (78.3)
p — a
Пример 78.3. Найти изображение функции /(t) = t.
и = t
dv = e~pt dt
ь
• e~pt dt — lim f te7pl dt — b-±oo J
Q Решение: В этом случае преобразование Лапласа имеет вид
du — dt v =—-e~pt =
Р J
/ + ь 1 |б\ 1
= lim [-- e~pt -4e-₽t ) =
6-400 \ р о Р 1о/ Р
т. к. lim |1 - b • е_рЬ| = . * - lim b • e~sb — о\ т. е.
6-400 \р I yS2+(72 6-400 /
t = (78-4)
Р
575
Замечание. Функция F(p)
—-— является аналитической ие р — а
только в полуплоскости Rep > Rea, 171,0 интеграл (78.1) сходится,
а на всей комплексной плоскости р, кроме точки р = а. Такая особенность наблюдается и для многих других изображений. Далее для нас будет более важным, как правило, само изображение функции, а не область, в которой оно выражается интегралом (78.1).
78.2. Свойства преобразования Лапласа
Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. «Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
Линейность
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т. е. если Д(1) = Д(р), /2(t) = F2(p), щ и сг — постоянные числа, то щ • Д(1) + с2 • /2(t) = cj • F, (р) + с2 • F2(p). Q Используя свойства интеграла, находим
СЮ
f (щ - f^t) + с2 /2(t)) e-pt dt =
0
00 сю
= Cl • J fi(t) • e~pt dt + c2 J-f2(t)-e~pt dt = Cl-Fi(p)+C2-F2(p).
о 0
Пример 78.4. Найти изображения функций since!, coscet (ce — любое число), c (const), chcet, sheet.
Q Решение: Пользуясь свойством линейности, формулой (78.3), находим:
eia,t _ e-iwt 1/1 1 \ w
since! =------—-----= 7- ------;---------— = ..-------
2г 2г \p — гш p + zee) p + ce
t. e. w
sin cet ==—?——5-. (78.5)
p + ce
Аналогично получаем формулу
cos cet = 9^6- (78.6)
p + ce
Далее, с = c • 1 = с - т. e. c
C ’ P
576
Наконец, ch cut = е -----ф • — ------1- i • —1— = г т- е-
2 2 р - w 2 р + ш р — ш
ch cut ф
Р
2 2 ’
р — CU
(78.7)
Аналогично получаем формулу
sh cut ф
cu
—2 2’
р — CU
(78.8)
Подобие
Если f(t) = F(p), Л
> 0, то /(At)
W)-
т. е. умножение
аргумента оригинала на положительное число А приводит к делению
изображения и его аргумента на это число.
□ По формуле (78.1) имеем
/(At) = у /(At) • е pt - dt = [положив At = tj] = о
о о
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть cost = 2-^
Тогда
coscut
1 5
«7+1
р
2 . 2 ’
р +ш
Смещение (затухание)
Если /(t) Ф F(p), а = const, то еа* fit) = F(p—a), т. е. умножение оригинала на функцию eat влечет за собой смещение переменной р.
□ В силу формулы (78.1) имеем
eat f(t) = J eat
О
/(i)e-₽t dt= j dt = F(p - a)
0
(Re(p-a) > s0).
19 Конспект лекций по высшей математике. Полный курс
577
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:
eat sinwt = --™-----х-, (78.9)
(р-а)2+ш2
еа1 cos wt = -—Р (78.10)
(р - а)2 + ш2
Пример 78.5. Найти оригинал по его изображению
F(p) =..g ?Р~5—.
р2 - 6р + 11
Q Решение: Преобразуем данную дробь так, чтобы можно было воспользоваться свойством смещения:
F(P) = 2Р~5 = 2(Р-3) + 1 = р2-6р+11 (р-3)2+2
= 2_______________+ — _______
(р-3)2 + (%/2)2 У2 (p-3)2 + (v/2)2
= 2 • e3t • cos V2t + —= • e3t sin V%t = /(t).
(См. формулы (78.9), (78.10) и свойство линейности.) •
Запаздывание
Если /(t) = F(p), т > 0, то f(t — т) == e-pTF(p), т. е. запаздывание оригинала на положительную величину т приводит к умножению изображения оригинала без запаздывания на е-г>т.
□ Положив t — T = t,, получим
/(t - т) = j f(t-r)- e~pt dt= f dt, =
0 -T
= f f(ti)e~pT - e-ptl dt, = e~PT J f(t)e~pt dt = e“₽TF(p).
о о
Поясним термин «запаздывание». Графики функции /(1) и f(t—r) имеют одинаковый вид, но график функции f(t.-r) сдвинут на т единиц
578
Рис. 305
Рис. 304
вправо (см. рис. 304). Следовательно, функции /(f) и f(t—т) описывают один и тот же процесс, но процесс, описываемый функцией f(t — т), начинается с опозданием на время т.
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные
процессы.
{1 при t г, _
называется обобщенной единич-
0 при t < т
ной функцией (см. рис 305).
Так как 1(f) = то l(t — т) = • е~рт.
Запаздывающую функцию
.«>= "р"'
0 при t
можно записать так: g(t) = f(t — т) l(t — т).
Пример 78.6. Найти изображение /(f) = t - 1.
Q Решение: Для того чтобы быть оригиналом, функция f(t) должна удовлетворять условиям 1-3 (см. п. 78.1). В этом смысле исходную задачу можно понимать двояко.
Если понимать функцию /(f) как
f№ =
t — 1 при t 0, 0 при t < 0,
т. е. f(t) = (f — 1) • 1(f) (см. рис. 306, а), то, зная, что t = (см.
формулу (78.4)), 1= - и, используя свойство линейности, находим р
579
/(*) =
Если же понимать функцию /(f) как
t — 1 при t 1,
О при t < 1,
т. е. f(t) = (t — 1) • l(t — 1) (см. рис. 306, б), то, используя свойство запаздывания, находим /(f) = (t — 1) • l(f — 1) = • е_р = F(p). •
Пример 78.7. Найти изображение функции
/(*) = 1
0
при t < 0, при 0 < t $ 3, при t > 3.
Q Решение: Данная функция описывает единичный импульс (см. рис. 307), который можно рассматривать как разность двух оригиналов: единичной функции 1(f) и обобщенной единичной функции l(t—3). Поэтому /(t) = 1(f) - l(t - 3) = | | • e-3p = F(p). •
Пример 78.8. Найти изображение функции
'о
/(*) = t
4 — t
при t < 0, t 4, при 0 t $ 2, при 2 < t < 4.
Q Решение: Функция-оригинал изображена на рис. 308. Запишем ее одним ана-
литическим выражением, используя функции Хевисайда 1(f) и l(t —т):
/(t) = t 1(f) - t - l(t - 2) + (4 - f) • l(f - 2) - (4 - f) • l(f - 4),
t. e.
/(t) = t • 1(f) - (t - 2 + 2) • l(f - 2) - (f - 2 - 2) • l(t - 2) + (t - 4) l(t - 4).
580
Раскроем скобки и приведем подобные слагаемые:
/(t) = t l(t) - 2(t - 2) - l(t - 2) + (t - 4) • l(t - 4).
Изображение функции /(t) будет равно
/(О = 1 - 2 - le-2₽ + le-4* = F(p). •
p p p
Замечания.
1. Изображение периодического оригинала с периодом, равным Т, т
есть F(jj) = t у f(t)e~pt dt.
2. Свойство опережения f(t + т) = ерт ^F(p) — j f(t)e~pt dt) применяется значительно реже. о
Дифференцирование оригинала
|@| Если f(t) == F(p) и функции f'(t), f"(t),..., f(n\t) являются оригиналами, то
/'(i)=p-F(p)-/(0), (78.11)
/"(O^^-F^-p/W-rCO), (78.12)
= р3 F(p) - р2 • /(0) - р • /'(0) - /"(0), (78.13)
y(n) (t) ф рП . F{p) _ pn-i . /(0) _ _ _ (0) (78 14)
□ По определению изображения находим
f'(t}^ Т f'(t}e~pt dt — [ U = e Pt du = -peptdt'
.t (t) - J f [t)e at- dv = f^t)dt v = f(t) о
|OO “
= /(i)e-₽t|o +P J f(t)e-ptdt = -f(Q)+pF(p). о
Итак, f'(t) = p-F(p)—f(O). Пользуясь полученным результатом, найдем изображение второй производной f"(t\.
f"(t) = (/'(*))' = Р(Р • F(p) - /(0)) - /'(0) = р2 F(p) - р • /(0) - /'(0).
Аналогично найдем изображение третьей производной f"'(t):
= Р(Р2 • F(p) - р - /(0) - /'(0)) - /"(0) =
= р3 • F(p) - р2 /(0) - р - /'(0) - /"(0).
Применяя формулу (78.11) (п — 1) раз, получим формулу (78.14).
581
Замечание. Формулы (78.11) (78.14) просто выглядят при нулевых начальных условиях: если /(0) = 0, то /'(t) = р F(p); если /(0) = = /'(0) = 0, то f"(t) = р2 • F(p), и, наконец, если /(0) = /'(0) = ... ... = /(п-1)(0) = 0, то = рп F(p), т. е. дифференцированию оригинала соответствует умножение его изображения на р.
Рассмотренное свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Пример 78.9. Найти изображение выражения x"'(t) - 2x"(t) - 3x'(i) + 2x(t) + 2, если x(Q) = 3, х'(0) = 0, т"(0) = —2.
Q Решение: Пусть x(t) = Х(р) = X. Тогда, согласно формулам (78.11)-(78.13), имеем
ar'(t) = Р • X — 3,
x"(t) = р2 • X — р 3 — 0,
ar"'(t) = р3 • X — р2 • 3 — р • 0 + 2,
2 2 = 21 = -.
Р
Следовательно,
x"'(t) - 2x"(t) - 3x'(t) + 2x(t) + 2 = о
= р3 • X — Зр2 + 2 — 2(р2 - — Зр) — 3(р • X — 3) + 2А'+-. •
Дифференцирование изображения
|@| Если /(i) = F(p), то
F"(p) = (-l)2-t2/(t),
F^(p) = (-l)ntn-f(t),
т. e. дифференцированию изображения соответствует умножение его оригинала на (—t).
□ Согласно теореме 78.1 существования изображения, F(p) является аналитической функцией в полуплоскости Rep = s > «о- Следовательно, у нее существует производная любого порядка. Дифференцируя интеграл (78.1) по параметру р (обоснование законности этой операции
582
опустим), получим
F'(p) = = I (f(t)-e~^'pdt =
'О ' P О
• = J/(t).(-t)e-ptdi= j (-t-f(t))e~ptdt = -t-f(t),
•' t. e. F'(p) = -t • /(t). Тогда F"(p) = (F'(p))' = -t(-t /(f)) = i2 /(t), F'"(p) = -t(t2 • /(t)) = -t3 fit) и вообще F^ip) = (-1)” • tn fit).
Пример 78.10. Найти изображения функций tn (n £ Nj, eat tn, t sinwt, t coswt, t shut, t chwt, eat • t sinwt, eat t • coswt.
Q Решение: Так как 1 = i, то, в силу свойства дифференцирования ( изображения, имеем — t • 1 = —т. е.
1
г. ~ ”2 ’
pz
Продолжая диффе-P
ц Далее находим — t2 = , ренцирование, получим
tn
р я!
Рп+1
.> С учетом свойства смещения получаем
I i „at ±п _i_ __
Л • (р-«)п+1’
Согласно формуле (78.5), smut = s Следовательно,
й ( и \' .
( -о---5- ) — — tsmut,
| \p2+u2Jp
? 2wp - . • .
^:т. е. — уз— —tsmwt, или
2шр tsmut = ----77,. (
(р + и )
Аналогично, используя формулы (78.6), (78.7) и (78.8), находим
р2 — ш2
tcoswt = —-----5-5-, I
(р2+ш2)2
, 2рш I
tsnut = ----575-,
(р2 - ш2)2
2 . 2
Fl F * Р +U tcncvt = —75--579-
(р2 - ш2)2
(78.15)
(78.16)
583
С учетом свойства смещения и формул (78.15) и (78.16), получаем
eat • t sinwt =
2w(p — a) ((p — a)2 + w2)2 ’
at . . . (p - a)2 - w2
e t • coswt = ------%----
((p — a)2 + w2)2
Интегрирование оригинала
' f F(p)
Если /(£) = F(p), to I /(t) dr = ——, т. e. интегрированию ори-o
гинала от 0 до t соответствует деление его изображения на р.
t
Q Функция <р(£) = у /(т) dr является оригиналом (можно проверить), о
Пусть <p(t) = Ф(р). Тогда по свойству дифференцирования оригинала имеем
= р Ф(р) - <р(0) = р Ф(р)
(так как <р(0) = 0). А.так как
</(*) = ( [ f(-r)dA =f(t),
Vo 7 4
то F(p) = р Ф(р). Отсюда Ф(р) = , т. е. J f(r) dr = ——).
о
Интегрирование изображения
ОО оо
Если /(£) = F(p) и интеграл J F(p) dp сходится, то f F(p) dp = V V
й
= ) 7, т. е. интегрированию изображения от р до оо соответствует
деление его оригинала на t.
Q Используя формулу (78.1) и изменяя порядок интегрирования (обоснование законности этой операции опускаем), получаем
оо оо z оо
/ F(p)dp= у Г у f^e-P^t
р р о
f(t)dt =
0 х ' о
584
Пример 78.11. Найти изображение функции ^1; найти изобра-t
жение интегрального синуса j - dr.
о
Q Решение: Так как sint = ,, то
р + 1 t
тг _ arctg р
2р р
21, 1 dp = arctg р, р + 1 4
р
т. е. = ту — arctg р = arcctgp. Применяя свойство интегрирования
t
оригинала, получаем J о
Умножение изображений
Если /i (t) = Fi(p), /2(t) = F2(p), то
t
Fi (р) F2(p) = у fi (г) • f2(t- т) dr.
О
(78.17)
t
□ Можно показать, что функция J Д (т) - f2(t — т) dr является ориги-о
налом.
Используя преобразование Лапласа (78.1), можно записать
У /1(т) f2(t-r)dr =
О
оо z I
/ (//>«•««
О Т)
-r)dr)e-ptdt =
Л(т) -f2(t-T)dr.
Область D интегрирования полученного двукратного интеграла определяется условиями 0 t < < оо, 0 т < t (см. рис. 309).
Изменяя порядок интегрирования и полагая t — т = ti, получим
У /1(т) /2(t - г) dr = У Л(т) dr J /2(t -r)dt =
О От
= / Ше~^ dr J dti = Fi(p) • F2(p).
о о
585
|ф| Интеграл в правой части формулы (78.17) называется сверткой функции и /2(t) и обозначается символом ,/i(t) * /2(t), т. е.
t
fi(t) * /2(t) = У /1(т) f2(t- г) dr.
о
Можно убедиться (положив t — т = и), что свертывание обладает свойством переместительности, т. е. /i(t) * f2(t) = f2(t) * /1(t).
Итак, умножение оригиналов равносильно их свертыванию, т. е.
Fi(p) F2(p) = /i(t) * /2(t).
Пример 78.12. Найти оригинал функций
FCp) = / 2 д1 2x2 И FW = / 2 / '2^2 ‘ (р + W ) (р + W ) ,
Q Решение: Так как F(p) ~ • 7- л ——и —7 = — - sin wt,
(р+ ш2) (p2+w2) p2+w2 ш ’
то
F(p) / — * smcjT — • sincj(t — r)dr = J cv
0
= —2 ’ / (cosw(2t — t) — cos wt) dr =
2w 1 0
1 / 1 , .1* |i\
= —5- — • suiw2t — t) — coswt-r =
2w2 \2w 'Io loy
1 /1 . \ 1 , .
= —— sinwt — tcoswt) = —j smut — wt coswt), 2w2\w ) 2w3V ’
T- e- 11
= —7(sinwt — wt • coswt).
(p2+w2)2 2w3 ’
Аналогично получаем
1
= — • t sin wt. 2w
Следствие 78.2. Если /1 * f2 = Fi(p) F2(p) и /{(t) также является оригиналом, то
t
P-F^p)-F2(p-)^ / f^-f^t-TydT + f^-hit). (78.18) 0
5Я6
□ Запишем произведение р • Ftp) F2(p) в виде
Р Ft (р) - F2(p) = р • ЕДр) - F2(p) - /ДО) • F2(p) + /ДО) F2(p),
или
р • ЕДр) • F2(p) = (р • F! (р) - /ДО)) • F2(p) + /ДО) • F2(p).
Первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам /(Д) (/{Д) = p-Fi(p) — /1(0)) и /2(t). Поэтому на основании свойства умножения изображений и линейности можно записать р - Fi (р) • F2(p) = /{(t) * /2 Д) + Д (0) • /2 Д) или
t
P-F!(p)-F2(p) = у /{(т)-/2Д-т)йт + Д(0)/2Д).
о
Формула (78.18) называется формулой Дюамеля.
На основании свойства переместительности свертки формулу Дюамеля можно записать в виде
t
Р Fi(p) F2(p) = у /2(т) • /{ Д - т) dr + /2 Д) /ДО).
о
Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
F(p) =
Пример 78.13. Найти оригинал, соответствующий изображению 2р2
(р2 + 1)2‘
Q Решение: Так как
2?Д = 2р.Д-0? + i)a p2 +1
то на основании формулы Дюамеля (78.18) имеем
t
p p2 +1
1
и -------= sm t,
р2 + 1
P - 4
-s----= COS t,
p2 + l
2₽. 1 . ?
Р + 1 Р + 1 [
Умножение оригиналов
Если ДД) = ЕДр) и /2Д) = F2(p), то
7-Ноо
fl Д) • ЬД) = 5-7 I Fi(z) F2(p - z)dz,
. i 7—ioo
’где путь интегрирования — вертикальная пря-.’мая Re^ = 7 > «о (см- рис. 310) (примем без доказательства).
— т) dr + 0 = t • cos t + sin t. •
Д+гоо
so
— гос • <<:А'
Рис. 310
О
587
Резюме
Рассмотренные свойства преобразования Лапласа представляют собой основные правила (аппарат) операционного исчисления. Для удобства пользования перечислим эти свойства.
1. Линейность: щ • /1 (i) + с2 • f2(£) = Ci Fj (p) + c2 F2(p).
2. Подобие: f(Xt) = j F^), A > 0.
3. Смещение: eat f(t) = F(p — a).
4. Запаздывание: f(t — r) == e~pT F(p),r > 0.
5. Дифференцирование оригинала:
/'(*) = P- F(p) - /(0),
/"(t)=P2-F(p)-p-/(0)-f(0),
/"'(*) = p3 . F(p) _ p2 . /(0) _ p. f,(0) _ y„(0)>
6. Дифференцирование изображения
F'(p) = -tf(t), F"(p) = (-l)2-t2-/(f),
p
t •
t
t
7. Интегрирование оригинала: j f(r) dr = -0
00
8. Интегрирование изображения: J F(p) dp p
9. Умножение изображений: F,(p) • F2(p) = Д (r) f2(t-r)dr = ~fi* fi- 0
7+гоо
10. Умножение оригиналов: Ji (t)-/2(t) = J F1(z')-F2(p—z) dz.
7—ioo
78.3. Таблица оригиналов и изображений
Составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А.Диткин и П. И. Кузнецов).
588
Таблица оригиналов и изображений,
№ Оригинал /W Изображение oo F(p)= f f(t)e~^dt 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 eat t smut cos ut short chort eat smut eat cos ut eat short eat chut tn (n — целое) eat tn t sin ut t cos ut t shut t chut eat - t sinort eat • t - cos ut —ig- (sin ut — ut cos ut) 2a) (ut ch ut — sh ut) 1 p 1 p — a 1 7? tv’ 2 . 2 p + U P 2 . 2 p + ar cv 2 2 p — 0) Л P , p2 -u2 (p — a)2 + w2 p — a (p — + u2 (p — a)2 — aj2 p — a (p — a)2 — u2 n! pn+1 n\ (p-a)n+r 2ajp p — gj (Г+Г)2 2up (p2-ry p2 +u2 (p2-ry 2u(p — a) ((p - a)'2 + u2)2 (p - a)2 - u2 ((p-a)2+w2)2 (p2 + u'2)'2 (p2 - W2)2
КОП
№ Оригинал /(*) Изображение ОО F(p)= f f(t)e-^dt 0
22 23 sin(wi ± р) cos(wt ± </>) и cos у ± р sin 9? р% + ш2 р cos т n; sin р2 + ш2
§79. ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
79.1. Теоремы разложения
Рассмотрим две теоремы, называемые теоремами разложения, позволяющие по заданному изображению F\p) находйть соответствующий ему оригинал f(t).
Теорема 79.1. Если функция F(p) в окрестности точки р = оо может быть представлена в виде ряда Лорана
гп/ 1 сп с0 . С1 . с2
(р)=2?да=₽+?+?+-’
то функция
/(£) = 52 е» ' ~7 = co + cit + ... (t>0)
71=0
является оригиналом, имеющим изображение F(p), т. е.
у. 71
^(р) = 52 Зыл 52 Сп ~
П—0 “ 71=0
Примем эту теорему без доказательства.
Пример 79.1. Найти оригинал /(t), если
F(p) = - • sin F(p) = .
Р Р р2 + 1
Q Решение: Имеем
1.1 1/1 11 11 \ 1 11 11
Р Р Р \Р 3! р3 5! р5 ) р2 3! р4 5! р6
1 Следовательно, на основании теоремы 79.1 /(£) = t — gj t >0.
Запишем лорановское разложение функции F(p) окрестности точки р = оо:
_ 5! 5!
Р „
9
р +1
\ - Р - Р - 1 1 =
{р} р2 + 1 Р2(1 + ^) Г1-НМ
_ 1 / 1 j_ \ 1 _ 1 _L _
р \ р2 + р4 ) р р3 + р5
где ру < 1, т. е. |р| > 1. Следовательно, /(t) = 1 — т. е.
f(t) = cost, t > 0. •
A(»)
Теорема 79,2. Если F(p) = — правильная рациональная
дробь, знаменатель которой В(р) имеет лишь простые корни (нули) Р1,Р2,---,Рп, ТО функция
ePkt
(79.1)
f<t) = у A(PkL B'(pk)
л=1
является оригиналом, имеющим изображение F(p).
Q Отметим, что дробь должна быть правильной (степень многочлена А(р) ниже степени многочлена В(р)); в противном случае не выполняется необходимый признак существования изображения А(»)
lim F(p) = 0 (п. 78.1), т. е. F(p) = рУ\- не МОжет быть изображением. р—^оо &\Р)
_ , А(р)
Разложим правильную рациональную дробь на простейшие:
В(р) Р~Р1 Р-Р2 Р~Рп
где ск (к = 1,2,— неопределенные коэффициенты. Для определения коэффициента щ этого разложения умножим обе части этого равенства почленно на р — р\:
А(р) / х / х / С2 (Р ~ Pi) = ci + (Р ~ Р^\----
В(р) \P-P2 P~Ps Р-Рп
Переходя в этом равенстве к пределу при р -> pi, получаем
О’ 0
С2
(79.2)
с3
г \
Q = 11т УР ~ Р1) =
Р-+Р1 J3(p)
= г = А(7>1)
Р-А-Р! p~pi
А(р)
Итак & = итак, ci в,^
(79.2) на р — pi) найдем с, =
Подставляя найденные
получим
. Аналогичным путем (умножая обе части равенства
значения ci,C2,--.,Cn в равенство (79.2),
F( } - _ ACpi) . 1 , л(Рз) 1 A(pn) 1
В(р) B'(pi) p-pi В'(р2) р~Р2 " В'(рп) р-рп'
Так как по формуле (78.3)
i gPl* gP2t ' ePnt
Р~Р1 ’ ’ Р~Р2 ' ’ Р~Рп '
то на основании свойства линейности имеем
[Р) В(р) ^В'(рк)
1 = V А(рк) Р-Рк ’ ^В\рк)
ePkt = f{t).
Замечание. Легко заметить, что коэффициенты ск (к = 1,2,... ,п) определяются как вычеты комплексной функции F(p) в простых полюсах (формула (77.4)): ск = = Res(^^!P*)-
Можно показать, что если F(p) = — правильная дробь,
но корни (нули) pi,P2, ,рп знаменателя В(р) имеют кратности mi,m2,.--,mn соответственно, то в этом случае оригинал изображения F{p) определяется формулой
п 1 / Д( \ \ (mfc—1)
Л*) = Ет-----7Т7 Um _^е^.(р-р,П . (79.3)
(тк - 1)! p-ypk\В(р) /
Теорему 79.2 можно сформулировать следующим образом:
Теорема 79.3. Если изображение F(p) = является дробнорациональной функцией от р и Р1,рг, • • ,Рп ~~ простые или кратные полюсы этой функции, то оригинал f(t), соответствующий изображению F(p), определяется формулой
F(P) = ВД Ф Е МШ) epkt) = f(t). (79.4)
79.2. Формула Римана-Меллина
(79.5)
Общий способ определения оригинала по изображению дает обратное преобразование Лапласа (формула обращения Римана-Меллина), имеющее вид
7-Ноо = f F(p) ept dt, Z7T7 J
7—гос
где интеграл берется вдоль любой прямой Rep = 7 > So.
При определенных условиях интеграл (79.5) вычисляется по фор-7-Моо п
муле/(1) = ^ у F(p)-eptdt = £Res(F(p) ept-,pk).
7—гос
Замечание. На практике отыскание функции-оригинала обычно проводят по следующему плану: прежде всего следует по таблице оригиналов и изображений попытаться отыскать для заданного изображения F(p) соответствующий ему оригинал; второй путь состоит в том, что функцию F(p) стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.
ц—3
Пример 79.2. Найти оригинал по его изображению F(p)= 27^-
3
= cos 2t — — sin 2t = f(t)
2
Q Решение: Проще всего поступить так:
р/ х _ Р- з _ р___________з =
W р2 + 4 р2 + 4 р2 + 4
_ Р __ 3 ____________
р2 +22 2 р2 + 22
(использовали свойство линейности и формулы (78.5) и (78.6)).
Если же использовать теорему 79-2 разложения, то будем иметь: А(р) = р — 3, В(р) — р2 + 4, В'(р) = 2р, корни знаменателя pi = 2i и р2 = —2г и, согласно формуле (79.1),
Л‘)= + = l(2i(e2i* + e^“)^3(e»^e-2")) =
( ^11 x-L
— (2i(cos 2t + i sin 2t + cos 2t — i sin 2t) —
4г’'
— 3(cos 2t + г sin 2t — cos 2t + i sin 2i)) =
1 3
— — (4icos2t — 6isin2i) = cos2i — - sin2Z = f(t). •
4г 2
593
Пример 79.3. Найти функцию-оригинал, если ее изображение задано как F(p) — - 1—
РЧР-1)
Q Решение: Здесь А(р) = 1, В(р) = р3(р-1), В'(р) — 4p3-3p2,pi = 1 — простой корень знаменателя, р-2 = 0 — 3-кратный корень (т = 3). Используя формулы (79.1) и (79.3), имеем:
___1____е1
е”4
/(f) — - • е1'4 + — lim . ,
4 — 3 2! р-+о \р3(р — 1)
= el + - lim |
2 r>o \p - 1
/2
.2
T. e. /(f) = e4 - у - t - 1. 4
Приведем другой способ нахождения f (t). Разобьем дробь -a?--—-
Р(Р - 1) на сумму простейших дробей: F(p) = —- = — i —ly —-L 4---1—.
p3(p-l) P p p3 P-1 ,2
Следовательно, /(t) = — 1 — t — C. + e4.
Приведем третий способ нахождения /(f). Представим F(p) как произведение *. 1 = X —Х^, и так как X = X и —X- = е* то,
р3(р-1) р3 р—1 р3 2 р-1 ’ ’
пользуясь свойством умножения изображений, имеем:
4 1
F(p) = f Tdr =
о
и = т2
dv = el~T dr
du = It dr v = —e4-'r
= _1е*-тт2|4 1.2. [Tet-rdT_ U = T du=dT ’ =
2 Io 2 J dv = e4 T dr v = -e* T
0 J
= -^f2 + 0 + (-7 e4-r)f -е4~т Г = -if2 - t + 0 - 1 + el =
2 Io Io 2 2
= e4-^--t-l = /(t). •
§80. ОПЕРАЦИОННЫЙ МЕТОД РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ИХ СИСТЕМ
Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами
г/(п) + + ... + апу = f(t), (80.1)
594
удовлетворяющее начальным условиям 2/(0) = со, р'(°) = ci, где со, ci,..., с„_1 — заданные числа.
Будем считать, что искомая функция y(t) вместе с ее рассматриваемыми производными и функция f(t) являются оригиналами.
Пусть y(t) = У (р) = У и /(/) = F(p) = F. Пользуясь свойствами дифференцирования оригинала и линейности, перейдем в уравнении (80.1) от оригиналов к изображениям:
(р’1У-рп~1со-р"-2С1-.. .-с„_1)+а1(р?1”1У-р?г-2со-. - .-с„_2) + . -. ... + an~i (рУ — Со) + anY = F.
Полученное уравнение называют операторным (или уравнением в изображениях). Разрешим его относительно У:
У(р” Teip”-1 + - •. + On-iP +On) = У + со(р” 1+aip” 2 + -.. + an-i)+ + Cj (р” 2 + aipn 3 + ... + 2) + • - • + сп_1,
т. е. Y(p)-Qn(p) = F(p)+Rn^1(p), где Qn(p) и Rn-i(p) - алгебраические многочлены от р степени п и п — 1 соответственно.
Из последнего уравнения находим
Qn\P)
Полученное равенство называют операторным решением дифференциального уравнения (80.1). Оно имеет более: простой вид, если все начальные условия равны нулю, т. е. «/(О) = р'(0) = ... = з/"-1)(0) = 0. В этом случае У(р) = ф^у-
Находя оригинал y (t), соответствующий найденному изображению (80.2), получаем, в силу теоремы единственности, частное решение дифференциального уравнения (80.1).
Замечание. Полученное решение y(t) во многих случаях оказывается справедливым при всех значениях t (а не только при 1^0).
(80.2)
Пример 80.1. Решить операционным методом дифференциальное уравнение у" — Зу1 +2у = 12е3/ при условиях р(0) = 2, у' (0) = 6.
Q Решение: Пусть y(t) = У(р) = Y. Тогда
2/'(1)=рУ-р(О)=рУ-2, y"{t) = р2У - ру(О) - у'(О) = р2У - 2р - 6, 3t - 1
и e3i =----.
р-з
595
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение: р2У — 2р — 6 — 3(рУ — 2) + 2У = 12—L Отсю-2 Р — 4
да 1 (р) = —?)(р -^2^(р- 3)' Находим т/(1). Можно разбить дробь на
сумму простейших (У(р) = —9 + - —q), но так как корни зна-Р A Р Z Р О
менателя (pj = 1, р2 = 2, рз = 3) простые, то удобно воспользоваться второй теоремой разложения (формула (79.1)), в которой
А(р) = 2р2 — 6р + 12,
В'(р) = (р - 2)(р - 3) + (р - 1)(р - 3) + (р - 1)(р - 2).
Получаем:
= Fife)6''*
Пример 80.2.
нения
е2 ‘ + Дг™ = 4е‘ - 8е2‘ + 6е3‘-
1 ( 1) 2-1
Найти решение урав-
S*’ у" + 4т/ = < з _ t,
О,
f(t)
Рис. 311
если 0 t < 2,
если 2 t < 3, если t < 0, 1^3
t
при условии 7/(0) = 0, 7/'(0) = 0.
Q Решение: График данной функции имеет вид, изображенный на рисунке 311. С помощью единичной функции правую часть данного дифференциального уравнения можно записать одним аналитическим выражением:
f (0 = • 1(0 - |1 - l(t - 2) + (3 -1) • l(i - 2) - (3 - l)l(t - 3) =
= |1 • 1(1)-|(t-2 + 2)-1(1-2)-(1-2-1)-1(1-2) +(1-3)-1(1-3) = Z Z
= 1(0 - |(t - 2) • 1(1 - 2) - 1(1 - 2) - (1 - 2) • 1(1 - 2)+
1 3
+ 1(1 —2) + (t-3)-l(t — 3) = -1-1(1) —-(t — 2)-l(t — 2) + (t — 3)-l(t — 3).
Z Z
Таким образом, имеем 1 3
у" + 4т/ = -1 1(1) - -(t - 2) • l(t - 2) + (1 - 3) • l(t - 3).
Операторное уравнение, при нулевых начальных условиях имеет вид 1131 1
р2У + 4У=^±-|4е^ + 4е^.
2 р* 2 р р2
596
Отсюда
Y(n} — i • 1_____- ______-___e~2p + -_i---e~3p
[P)~2 p2(p2+4) 2 p2(/+4) pV+4) ’
Так как
_ 1 _ 1Л1 _ 1 A _ If± _ 1. 2 \ =1^1- 2Л
p2(p2+4) 4 \p2 p2+4/ 4\p2 2 p2+22J 4\ 2 /’
то по теореме запаздывания находим:
3/(0 = |sin2/) - ~(t-2-|sin2(t-2))l(t-2)+
o\Z / о \ 4 J
+ l(t-3- isin2(£ —3))l(t —Э). •
Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами.
Покажем это на конкретном примере.
Пример 80.3. Решить систему дифференциальных уравнений
х' = у — Z,
< у' = х + у, т(0) = 1, у(0) = 2, z(0) = 3-z' — X + Z-,
Q Решение: Пусть
х = x(t) = Х(р) = X; y = y(t) = Y(p) = Y; z = z(t) = Z(p) - Z. Находим, что
ж'фрХ-1; у'=рУ-2; z'=pZ-^.
Система операторных уравнений принимает вид
'pX~Y + Z= 1,
* X- (р- 1)У = -2,
X + (l-p)Z = -3.
Решая эту систему алгебраических уравнений, находим:
Р-2
Р(Р - 1) ’
2р2 - р - 2
ад =
У(р) =
Z(p) =
р(р - I)2 Зр2 — 2р — 2 р(р - I)2
597
Переходя от изображений к оригиналам, получаем искомые решения:
у/ ч Р-2
"
_ 2р —2 —р _ 2(р—1)Р = 2_l^2_et = р(р-1) р(р-1) р(р-1) Р Р-1
у(р) = =--+А - Ф ~2+4е* -tet=
р(р-1) Р р-1 (р-1)2
. Зр2 - 2р - 2 2 5 1 t .
Z(p) = = — +----7 - т---7 = -2 + 5е* - te‘ = z(t .
р(р - I)2 р р - 1 (р - I)2
Ответ: x(t) = 2 — е*, y(t) — — 2 + 4е* — te*, z(t) = —2 + 5е* — te*. •
С помощью операционного исчисления можно также находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнений в частных производных, уравнений в конечных разностях (разностных уравнений); производить суммирование рядов; вычислять интегралы. При этом решение этих и других задач значительно упрощается.
ПРИЛОЖЕНИЯ
Правила дифференцирования
1. (и ± v)' = и' ± v'\
2. (и v)' = u'v + uv', в частности, (си)' = с и';
3. (10 = и в частности,
4- у'х = у'и • и'х, если у = f(u), и = ip(x);
5. у'х - 4~, если у = f(x) их = <р(у).
Ху
Формулы дифференцирования
1- (с)'=0;
2. (иа)' = а иа~г и', в частности, (\/и)' = • и'-,
3. (аи)' = аи • In а и', в частности, (еи)' = еи и'-,
4 (log и)' — —т— и', в частности, (Init)' = — •«';
\ оа > и . In а и
5. (sin u)' = cos и - и';
6. (cos u)' = — sin и и'-,
7. (tgu)' = —
v cos2и
8. (ctg и)' =--— и';
' 7 sin и
9. (arcsin и)' = - и'-,
10. (arccosu)' =---, 1----• и'\
V1 — и2
11. (arctg и)' = г • и';
12. (arcctgw)' =
13. (shu)' = ch и • и';
14. (chit)' = shit • w';
15-<th“)'=
w.(ca,uy = -^-»'.
599
Таблица основных интегралов
I- fu“du=^+C (а/-1)
2. f ^=1п\и\ + С-,
(J du = it 4- (S');
3. f аи du = + С; I
J In а ’
4. у е“ du = е“ 4- С;
5. у sin и du = — cos и + С
6. у cos и du = sin и + С
7. J tg и du — - In | cos u| + C;
8. у ctgitdw = In | sinit| + C;
9. f -du_ = tgu + C J cos и
10. f -ty- = -ctgit + C J sin и
11. f _^_=In|tg^|+C; J sin и । ° 2 । ’
12. f =ln|tg(ll + яЛ|+С; J cosit | b\2 4/| ’
13. [ . du = arcsin — 4- C;
I \/a2 - u2 a
14. [ du = In |it + y/u2 + a21 + C;
' у/ u2 + a2
(J sh и du = ch и + c); ch и du = sh и + c);
=thu + cY, ch2 it /
= -cthu + cV
15. f ^du- л = -1 arctg- + C: J a2 + u a a ’
17. у у/a2 - и2 du = y/a2 — u2 + arcsin + C;
18. У у/и2 ± a2 du = - y/u2 ± a2 ± In |it 4- y/u2 ± a2| 4- C.
600
Таблица разложений в ряд Маклорена некоторых элементарных функций
х ч х х2 хп
е “ 1+ 1! + 2! +‘”+ п! +"’’
„3 „5 „2п+1
впш = 1“У+5! - + (-1) (2,. И
х2 х4 / х2п cosa: - 1 - — + — + (- ) +
(1+^ = 1 + ^ • i-
х G (—оо; оо),
х G (—оо; оо),
2!
л!
ar G < (-!;!],
если a 0,
если —1 < a < 0, если a — 1,
—— = 1+ж + а:24----t-xn+..., a: G (—1; 1),
1 — x
„2 3 n+1
ln(l 4-я) = x-- + + (-ip *e(-l;l],
Z «j fl r 1
„3 5 2n+l
arctgar-ar-y + y-.-. + Fir^y..., x G [-1; 1], lx3 1-3 x5 1-3-5 x1
^0^ = 3; + -.- + —-y + r^-y + ...
l-3-5...(2n-l) x2n+1
’ ‘ ’ + 2-4-6...(2n) ’ 2n + 1 + ‘ ’ x3 x5 x2n+1
shx-x + y 1- 5, +••+ (2n + i)! +
, , x2 x4 x6 x2n
cbar-H- 2! + 4! + 6! +”’+ (2n)! +"’’
x G [—1; 1],
x G (-oo; oo), x G (-oo;oo).
601
Таблица оригиналов и изображений
№ Оригинал /(*) Изображение oo F(p) = 1 f(t)e~ptdt 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 eat t sinwt cos ut shut chut eat sin ut eat • cos ut eat sh ut eat ch ut tn (n — целое) eat - tn t sin ut t cos ut t-shut t- chut eat t sin ut eat t- cos ut -lg-(sin ut — ut cos ut) ZCO (ut ch ut — sh ut) 1 1 p — a 7 CJ p>2 + u2 p + lJ Cd 2 „2 p —bj P j 2 2 p — co (p ~ a)2 4- ^2 p— Ji (p — + u2 (p ~ a)2 — co2 p~o> (p — a)2 — u2 n! ^+r n! (p-a)n+1 2up Ср2, + u2)'2 p2 - u2 (p2 + u2)'2 2up p2 + u2 (p2 -CJ2)2 2u(p — a) ((p-а)2 +u2)2 (p — a)'2 —u2 ((p-a)^ +u2)'2 (p2 +u2)'2 (p2-u2)'2
602
№ Оригинал f(t) Изображение oo F(p) = 1 f^e^dt 0
22 23 sin(u>t ± <p) cos(wt ± <p) w cos <p ± p sin p2 + w2 p cos <рт ^sin <p p2 + w2
По вопросам оптовых закупок обращаться: тел./факс: (495) 785-15-30, e-mail: trade@airis.ru Адрес: Москва, пр. Мира, 106
Наш сайт: www.airis.ru
Вы можете приобрести наши книги с II00 до 1730, кроме субботы, воскресенья, в киоске по адресу: пр. Мира, д. 106, тел.: 785-15-30
Адрес редакции: 129626, Москва, а/я 66
Издательство «Айрис-пресс» приглашает к сотрудничеству авторов образовательной и развивающей литературы.
По всем вопросам обращаться по тел.: (495) 785-15-33, e-mail: editor@airis.ru
Учебное издание
Письменный Дмитрий Трофимович
КОНСПЕКТ ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Полный курс
Ведущий редактор В. В. Черноруцкий.
Редактор Л. В. Абламская Художественный редактор А. М. Кузнецов Обложка А. М.Драговой Иллюстрации Е. В. Панкратьев, А Ю. Терская Технический редактор С. С. Коломеец Компьютерная верстка Е. Г. Иванов Корректоры И. С. Калашникова, 3. А. Тихонова
Подписано в печать 19.12.05. Формат 60x90/16. Гарнитура «Компьютер Модерн». Печать офсетная. Печ. л. 38.
Усл.-печ. л. 38. Тираж 5000 экз. Заказ № 52.
ООО «Издательство “Айрис-пресс”»
113184, Москва, ул. Б. Полянка, д. 50, стр. 3.
ОАО «Тверской ордена Трудового Красного Знамени полиграфкомбинат детской литературы им. 50-летия СССР».
170040, г. Тверь, пр. 50 лет Октября, 46.
£
В СЕРИИ ВЫШЛИ КНИГИ:
Высшее образование
Ш Письменный Д. Т. Конспект лекций по высшей математике.
1 часть. Тридцать шесть лекций
Обложка, 288 с.
Ш Письменный Д.Т.
Конспект лекций по высшей математике.
2 часть. Тридцать пять лекций
Обложка, 256 с.
Ш Письменный Д. Т.
Конспект лекций по высшей математике.
Полный курс
Переплет, 608 с.
Ш Письменный Д., Федин С., Шевченко Ю., Лунту К
Сборник задач по высшей математике.
1 курс
Переплет, 576 с.
Ш Лунгу К Н., Норин В. И, Письменный Д. Т, Шевченко Ю. А.
Сборник задач по высшей математике.
2 курс
Переплет, 592 с.
Ш Письменный Д. Т.
Конспект лекций по теории вероятностей и математической статистике
Обложка, 256 с.
Ш Розен В. В.
Концепции современного естествознания.
Конспект лекций
Обложка, 240 с.
£Й Любецкий В. А.
Основные понятия элементарной математики. Учебное пособие для вузов
Переплет, 624 с.
Ш Гусев Д. А.
Логика. Конспект лекций с задачами
Обложка, 240 с.
£В Платонова Э. Е.
Конспект лекций по культурологии
Обложка, 304 с
£3 ЛевяшИ.Я.
Культурология. Учебное пособие для вузов
Переплет, 576 с.
Ш Малышева Е М.
Культурология. История мировой культуры
Обложка, 288 а
£3 Семенникова Л. И., Головкина Н. Л, Сдобнина Т. В., Черкасова Н.
Отечественная история.
Конспект лекций
Обложка, 320 с.
£3 Пушкарева Г. В.
Политология.
Конспект лекций
Обложка, 208 с.
ИЗДАТЕЛЬСТВО АЙРИС-ПРЕСС