Дмитрий Письменный
КОНСПЕКТ
ЛЕКЦИИ
ПО ВЫСШЕЙ
МАТЕМАТИКЕ
1 часть
АИРИС Ш ПРЕСС

Дмитрий Письменный
КОНСПЕКТ
ЛЕКЦИИ
ПО ВЫСШЕЙ
МАТЕМАТИКЕ
1 часть
11-е издание
МОСКВА
АЙРИС ПРЕСС
2011

УДК 517(075.8)
ББК 22.1я73-2
П35
Все права защищены.
Никакая часть данной книги не может переиздаваться
или распространяться в любой форме и любыми средствами,
электронными или механическими, включая фотокопирование,
звукозапись, любые запоминающие устройства
и системы поиска информации,
без письменного разрешения правообладателя.
Серийное оформление А. М. Драговой
Письменный, Д. Т.
П35 Конспект лекций по высшей математике: [в 2 ч.]. Ч. 1 /Дмитрий Пись-
менный. — 11-е изд. — М.: Айрис-пресс, 2011. — 288 с: ил. — (Высшее
образование).
ISBN 978-5-8112-4375-4 (Ч. 1)
ISBN 978-5-8112-4000-5
Настоящий курс лекций предназначен для студентов вузов, изучающих высшую мате-
матику в различных вузах.
Первая часть содержит необходимый материал по девяти разделам курса высшей
математики, что изучаются студентами на первом курсе вуза (техникума) — линейная и
векторная алгебра, аналитическая геометрия на плоскости и в пространстве, комплексные
числа и основы математического анализа (функции, пределы, производная, определенный
и неопределенный интеграл, функции нескольких переменных).
Изложение теоретического материала по всем темам сопровождается рассмотрением
большого количества примеров и задач.
ББК22.1я73-2
УДК 517(075.8)
ISBN 978-5-8112-4375-4 (Ч. 1) © ООО «Издательство
ISBN 978-5-8112-4000-5 «АЙРИС-пресс», 2002

Предисловие 9
Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
§ 1. Матрицы 10
1.1. Основные понятия 10
1.2. Действия над матрицами 11
§ 2. Определители 14
2.1. Основные понятия 14
2.2. Свойства определителей 15
§ 3. Невырожденные матрицы 18
3.1. Основные понятия 18
3.2. Обратная матрица 18
3.3. Ранг матрицы 20
§ 4. Системы линейных уравнений 22
4.1. Основные понятия 22
4.2. Решение систем линейных уравнений. Теорема Кронеке-
ра-Капелли 23
4.3. Решение невырожденных линейных систем. Формулы Кра-
мера 25
4.4. Решение систем линейных уравнений методом Гаусса 26
4.5. Системы линейных однородных уравнений 29
Глава П. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
§ 5. Векторы 31
5.1. Основные понятия 31
5.2. Линейные операции над векторами 32
5.3. Проекция вектора на ось 33
5.4. Разложение вектора по ортам координатных осей. Модуль
вектора. Направляющие косинусы 35
5.5. Действия над векторами, заданными проекциями 37
§ 6. Скалярное произведение векторов и его свойства 38
6.1. Определение скалярного произведения 38
6.2. Свойства скалярного произведения 38
6.3. Выражение скалярного произведения через координаты ... 39
6.4. Некоторые приложения скалярного произведения 40
§ 7. Векторное произведение векторов и его свойства 41
7.1. Определение векторного произведения 41
7.2. Свойства векторного произведения 42
7.3. Выражение векторного произведения через координаты ... 43
7.4. Некоторые приложения векторного произведения 44
§ 8. Смешанное произведение векторов 45
з
ОГЛАВЛЕНИЕ

8.1. Определение смешанного произведения, его геометриче-
ский смысл 45
8.2. Свойства смешанного произведения 45
8.3. Выражение смешанного произведения через координаты .. 46
8.4. Некоторые приложения смешанного произведения 47
Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
§ 9. Система координат на плоскости 48
9.1. Основные понятия 48
9.2. Основные приложения метода координат на плоскости 49
9.3. Преобразование системы координат 51
§ 10. Линии на плоскости 53
10.1. Основные понятия 53
10.2. Уравнения прямой на плоскости 56
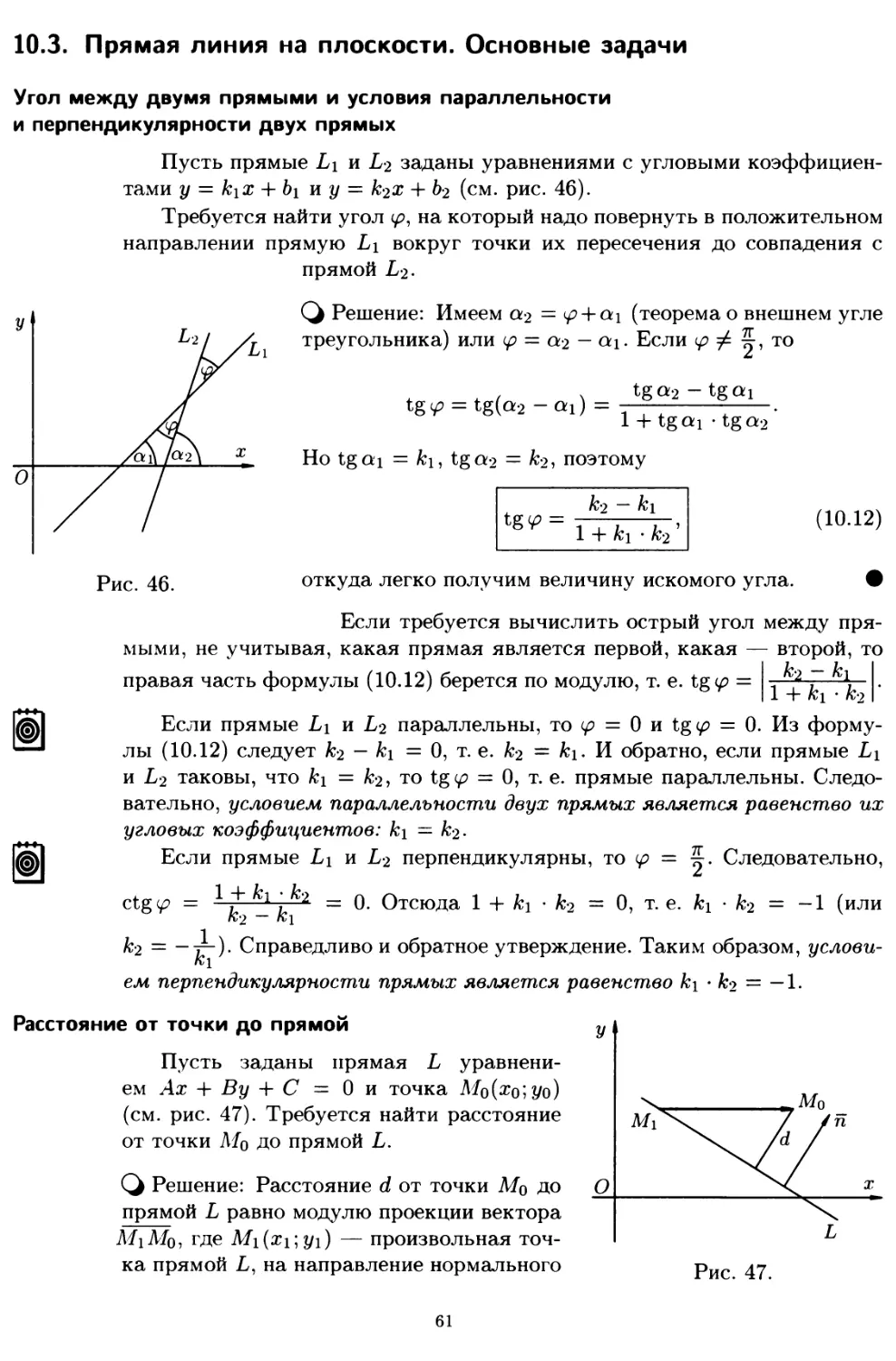
10.3. Прямая линия на плоскости. Основные задачи 61
§11. Линии второго порядка на плоскости 62
11.1. Основные понятия 62
11.2. Окружность 62
11.3. Эллипс 64
11.4. Гипербола 66
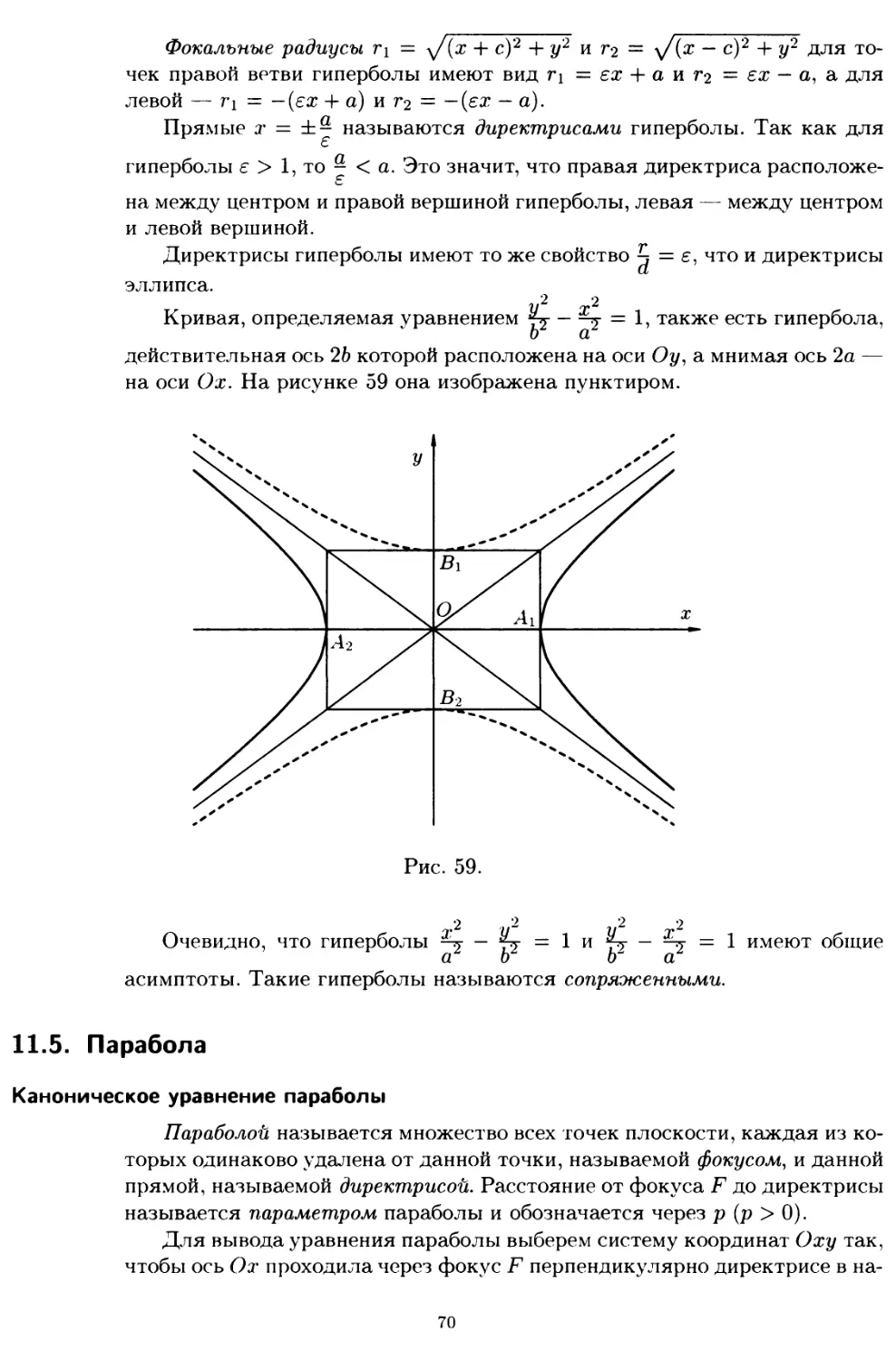
11.5. Парабола 70
11.6. Общее уравнение линий второго порядка 72
Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
В ПРОСТРАНСТВЕ
§ 12. Уравнения поверхности и линии в пространстве 76
12.1. Основные понятия 76
12.2. Уравнения плоскости в пространстве 78
12.3. Плоскость. Основные задачи 81
12.4. Уравнения прямой в пространстве 82
12.5. Прямая линия в пространстве. Основные задачи 85
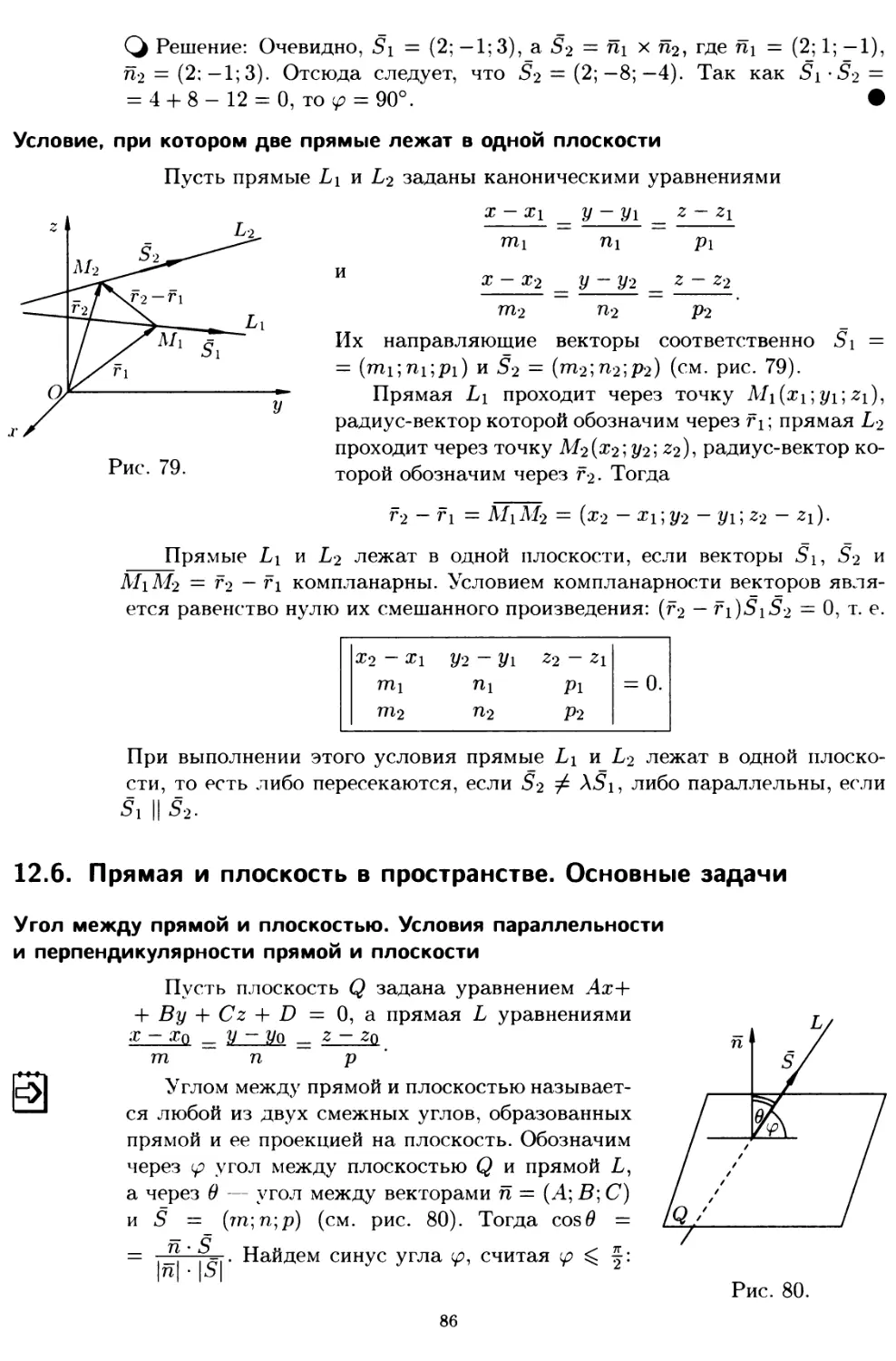
12.6. Прямая и плоскость в пространстве. Основные задачи 86
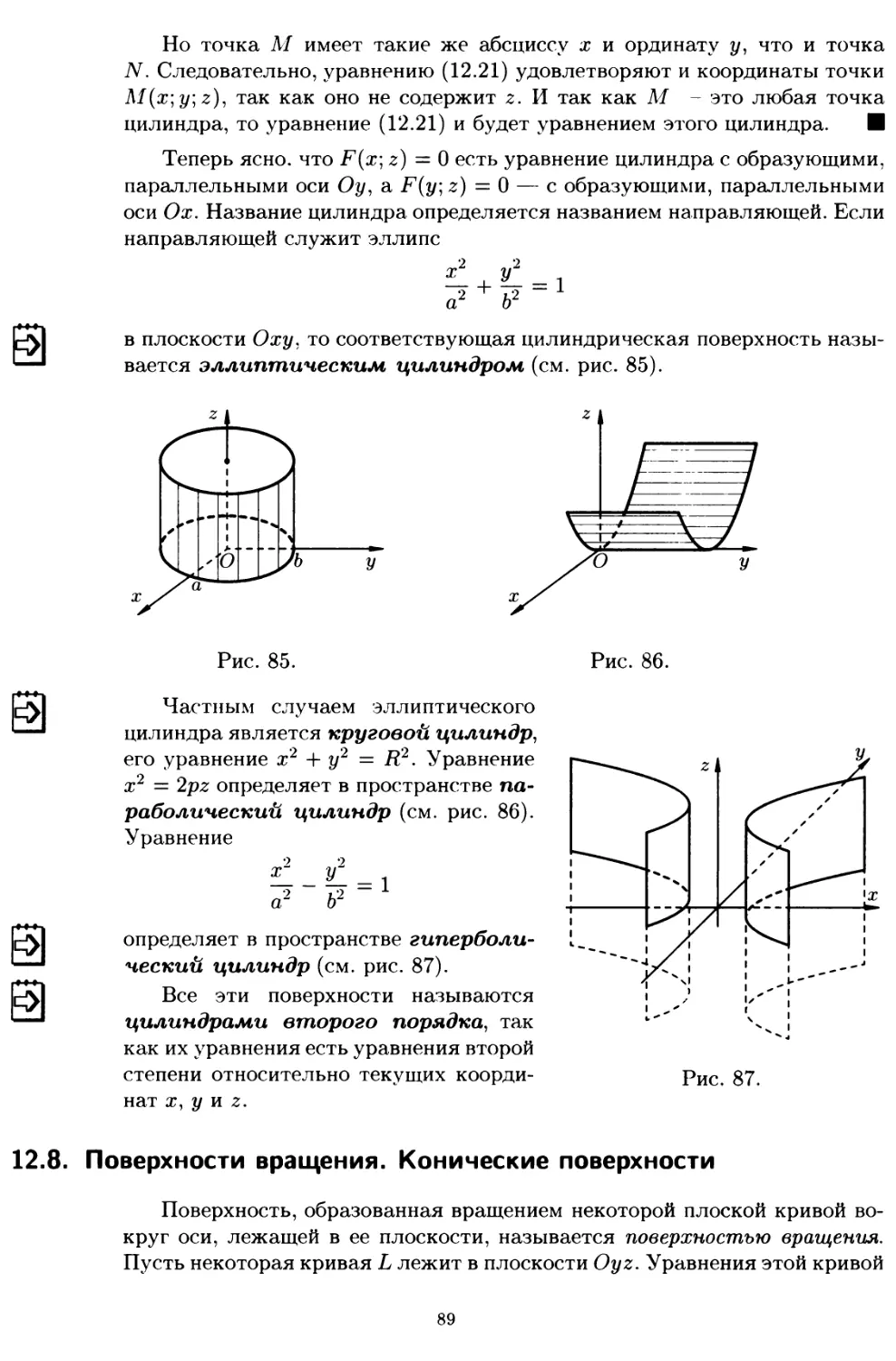
12.7. Цилиндрические поверхности 88
12.8. Поверхности вращения. Конические поверхности 89
12.9.Канонические уравнения поверхностей второго порядка... 91
Глава V. ВВЕДЕНИЕ В АНАЛИЗ
§ 13. Множества. Действительные числа 97
13.1. Основные понятия 97
13.2. Числовые множества. Множество действительных чисел .. 98
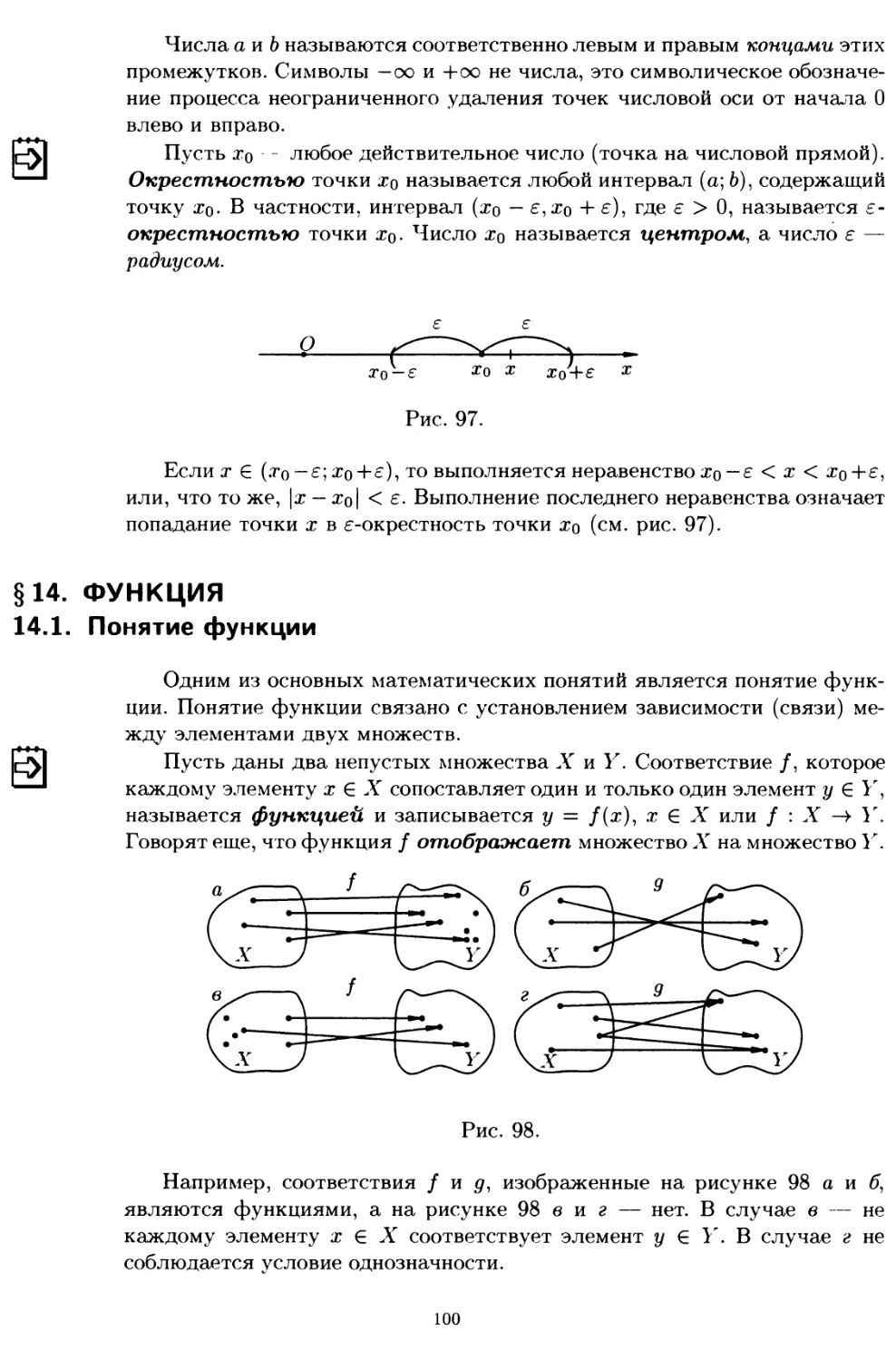
13.3. Числовые промежутки. Окрестность точки 99
§ 14. Функция 100
14.1. Понятие функции 100
14.2. Числовые функции. График функции. Способы задания
функций 101
4

14.3. Основные характеристики функции 102
14.4. Обратная функция 103
14.5. Сложная функция 104
14.6. Основные элементарные функции и их графики 104
§ 15. Последовательности 107
15.1. Числовая последовательность 107
15.2. Предел числовой последовательности 108
15.3. Предельный переход в неравенствах 109
15.4. Предел монотонной ограниченной последовательности.
Число е. Натуральные логарифмы 110
§ 16. Предел функции 112
16.1. Предел функции в точке 112
16.2. Односторонние пределы 113
16.3. Предел функции при х -> оо 114
16.4. Бесконечно большая функция (б.б.ф.) 114
§ 17. Бесконечно малые функции (б.м.ф.) 115
17.1. Определения и основные теоремы 115
17.2. Связь между функцией, ее пределом и бесконечно малой
функцией 118
17.3. Основные теоремы о пределах 119
17.4. Признаки существования пределов 121
17.5. Первый замечательный предел 123
17.6. Второй замечательный предел 124
§ 18. Эквивалентные бесконечно малые функции 125
18.1. Сравнение бесконечно малых функций 125
18.2. Эквивалентные бесконечно малые и основные теоремы
о них 126
18.3.Применение эквивалентных бесконечно малых функций... 127
§ 19. Непрерывность функций 130
19.1. Непрерывность функции в точке 130
19.2. Непрерывность функции в интервале и на отрезке 132
19.3. Точки разрыва функции и их классификация 132
19.4. Основные теоремы о непрерывных функциях. Непрерыв-
ность элементарных функций 134
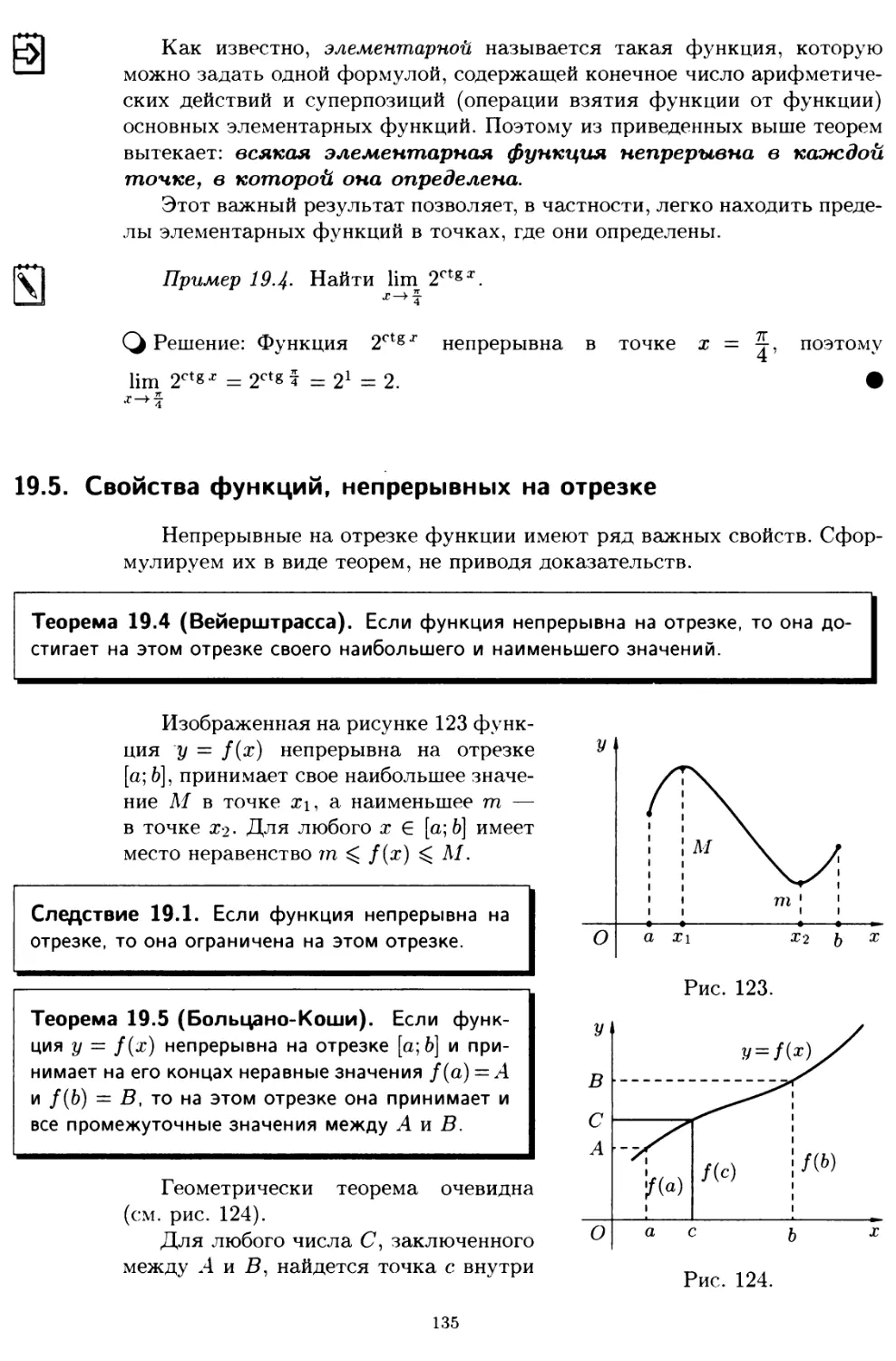
19.5. Свойства функций, непрерывных на отрезке 135
§ 20. Производная функции 137
20.1. Задачи, приводящие к понятию производной 137
20.2. Определение производной; ее механический и геометричес-
кий смысл. Уравнение касательной и нормали к кривой ... 139
20.3. Связь между непрерывностью и дифференцируемостью
функции 141
20.4. Производная суммы, разности, произведения и частного
функций 142
20.5. Производная сложной и обратной функций 143
20.6. Производные основных элементарных функций 145
20.7. Гиперболические функции и их производные 149
20.8. Таблица производных 151
5

§ 21. Дифференцирование неявных и параметрически заданных
функций 152
21.1. Неявно заданная функция 152
21.2. Функция, заданная параметрически 153
§ 22. Логарифмическое дифференцирование 154
§ 23. Производные высших порядков 155
23.1. Производные высших порядков явно заданной функции ... 155
23.2. Механический смысл производной второго порядка 156
23.3.Производные высших порядков неявно заданной функции. 156
23.4. Производные высших порядков от функций, заданных па-
раметрически 156
§ 24. Дифференциал функции 157
24.1. Понятие дифференциала функции 157
24.2. Геометрический смысл дифференциала функции 159
24.3. Основные теоремы о дифференциалах 159
24.4. Таблица дифференциалов 160
24.5. Применение дифференциала к приближенным вычислени-
ям 161
24.6. Дифференциалы высших порядков 162
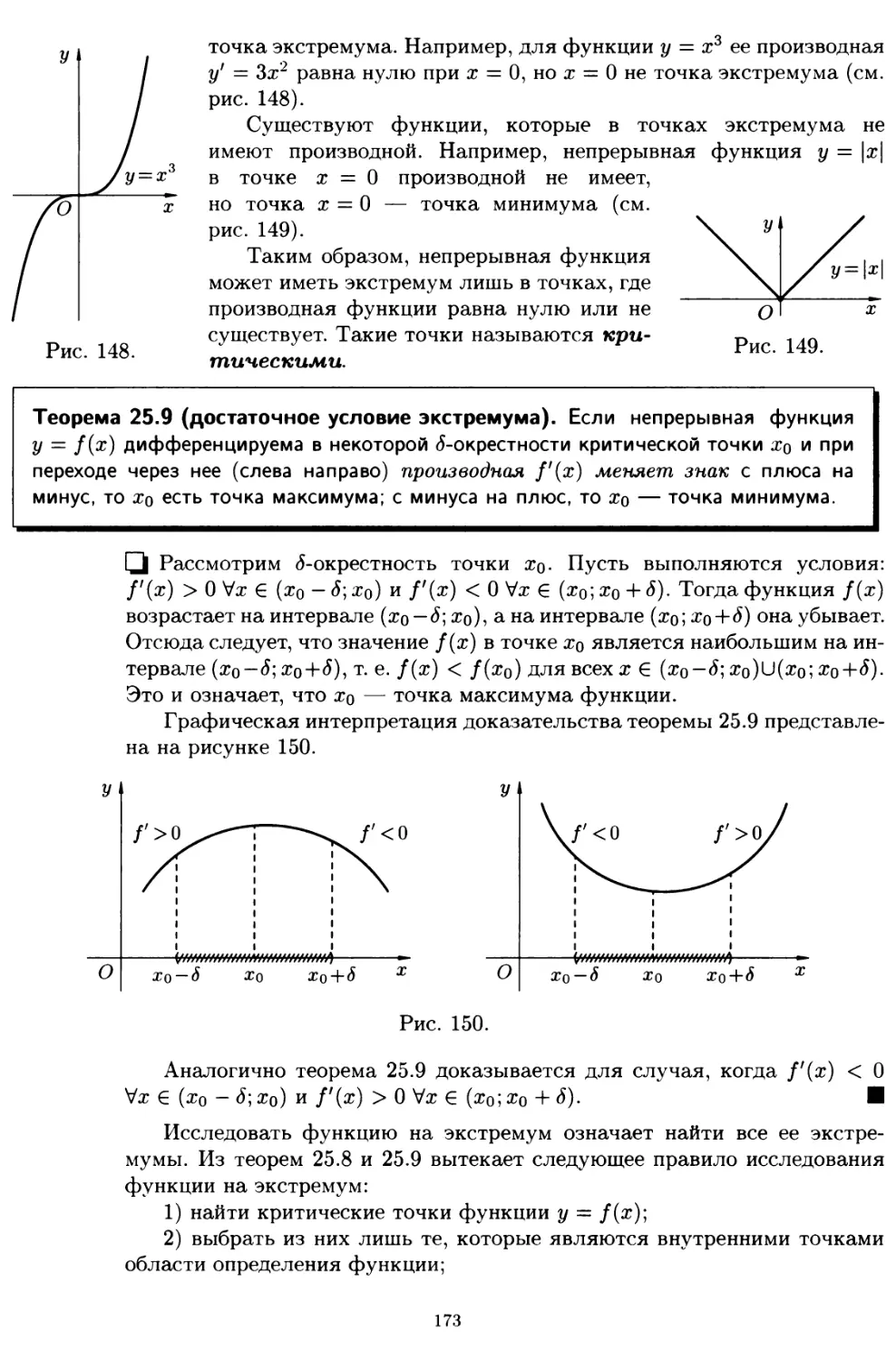
§ 25. Исследование функций при помощи производных 164
25.1. Некоторые теоремы о дифференцируемых функциях 164
25.2. Правила Лопиталя 167
25.3. Возрастание и убывание функций 171
25.4. Максимум и минимум функций 172
25.5.Наибольшее и наименьшее значения функции на отрезке.. 175
25.6. Выпуклость графика функции. Точки перегиба 176
25.7. Асимптоты графика функции 178
25.8. Общая схема исследования функции и построения графи-
ка 180
§ 26. Формула Тейлора 181
26.1. Формула Тейлора для многочлена 182
26.2. Формула Тейлора для произвольной функции 183
Глава VI. КОМПЛЕКСНЫЕ ЧИСЛА
§ 27. Понятие и представления комплексных чисел 186
27.1. Основные понятия 186
27.2. Геометрическое изображение комплексных чисел 186
27.3. Формы записи комплексных чисел 187
§ 28. Действия над комплексными числами 188
28.1. Сложение комплексных чисел 188
28.2. Вычитание комплексных чисел 189
28.3. Умножение комплексных чисел 189
28.4. Деление комплексных чисел 190
28.5. Извлечение корней из комплексных чисел 191
6

Глава VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 29. Неопределенный интеграл 193
29.1. Понятие неопределенного интеграла 193
29.2. Свойства неопределенного интеграла 194
29.3. Таблица основных неопределенных интегралов 196
§ 30. Основные методы интегрирования 198
30.1. Метод непосредственного интегрирования 198
30.2. Метод интегрирования подстановкой (заменой перемен-
ной) 200
30.3. Метод интегрирования по частям 202
§31. Интегрирование рациональных функций 203
31.1. Понятия о рациональных функциях 203
31.2. Интегрирование простейших рациональных дробей 208
31.3. Интегрирование рациональных дробей 210
§ 32. Интегрирование тригонометрических функций 212
32.1. Универсальная тригонометрическая подстановка 212
32.2. Интегралы типа / sinm x • cosn xdx 213
32.3. Использование тригонометрических преобразований 214
§ 33. Интегрирование иррациональных функций 214
33.1. Квадратичные иррациональности 214
33.2. Дробно-линейная подстановка 216
33.3. Тригонометрическая подстановка 217
33.4. Интегралы типа / R(x; \Jax2 + Ъх + с) dx 218
33.5. Интегрирование дифференциального бинома 218
§ 34. «Берущиеся» и «неберущиеся» интегралы 219
Глава VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 35. Определенный интеграл как предел интегральной суммы 221
§ 36. Геометрический и физический смысл определенного интеграла 222
§ 37. Формула Ньютона-Лейбница 224
§ 38. Основные свойства определенного интеграла 226
§ 39. Вычисления определенного интеграла 230
39.1. Формула Ньютона-Лейбница 230
39.2. Интегрирование подстановкой (заменой переменной) 230
39.3. Интегрирование по частям 231
39.4. Интегрирование четных и нечетных функций в симметрич-
ных пределах 233
§ 40. Несобственные интегралы 233
40.1. Интеграл с бесконечным промежутком интегрирования
(несобственный интеграл I рода) 234
40.2. Интеграл от разрывной функции (несобственный интеграл
II рода) 236
§41. Геометрические и физические приложения определенного ин-
теграла 237
41.1. Схемы применения определенного интеграла 237
7

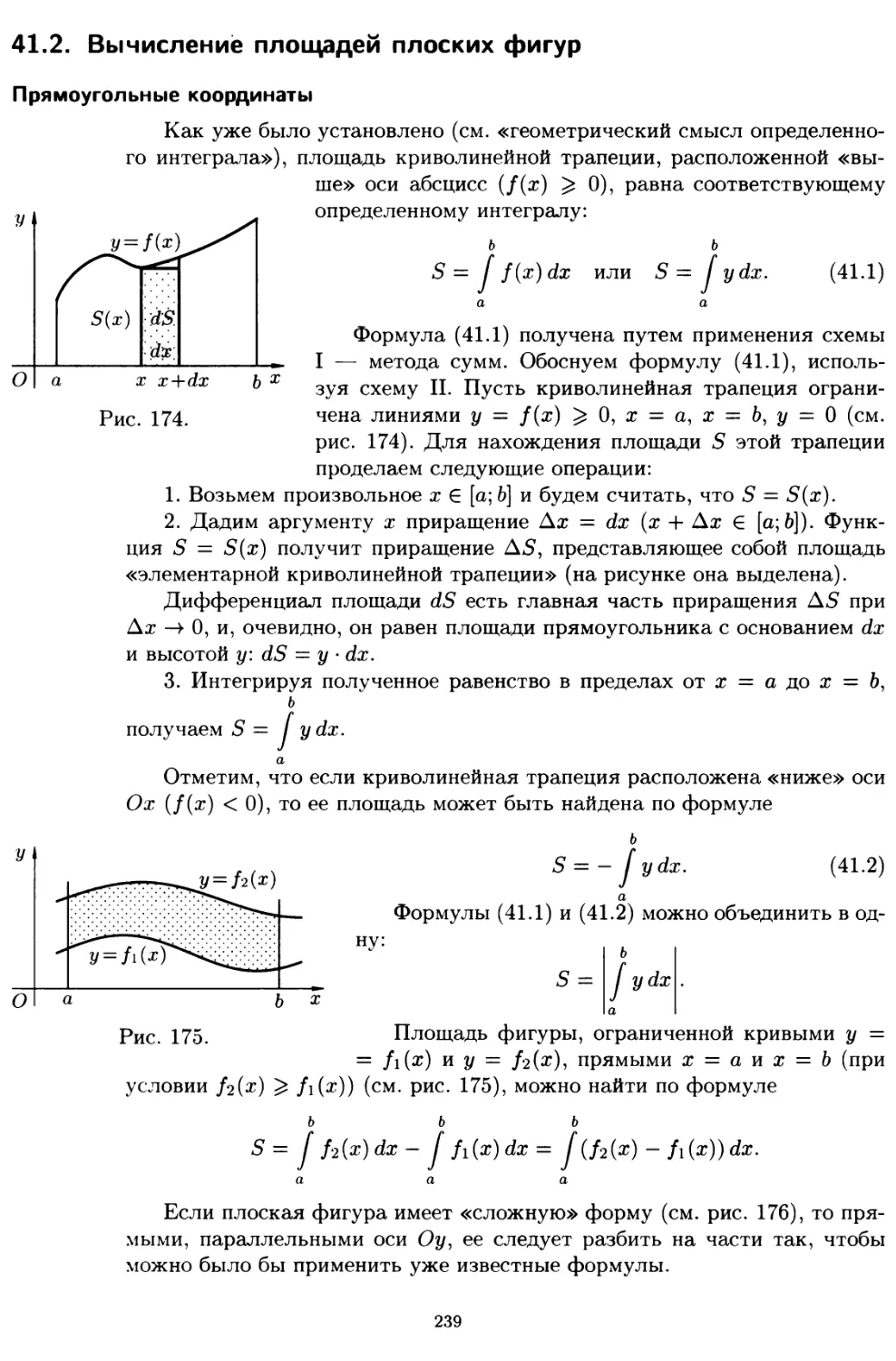
41.2. Вычисление площадей плоских фигур 239
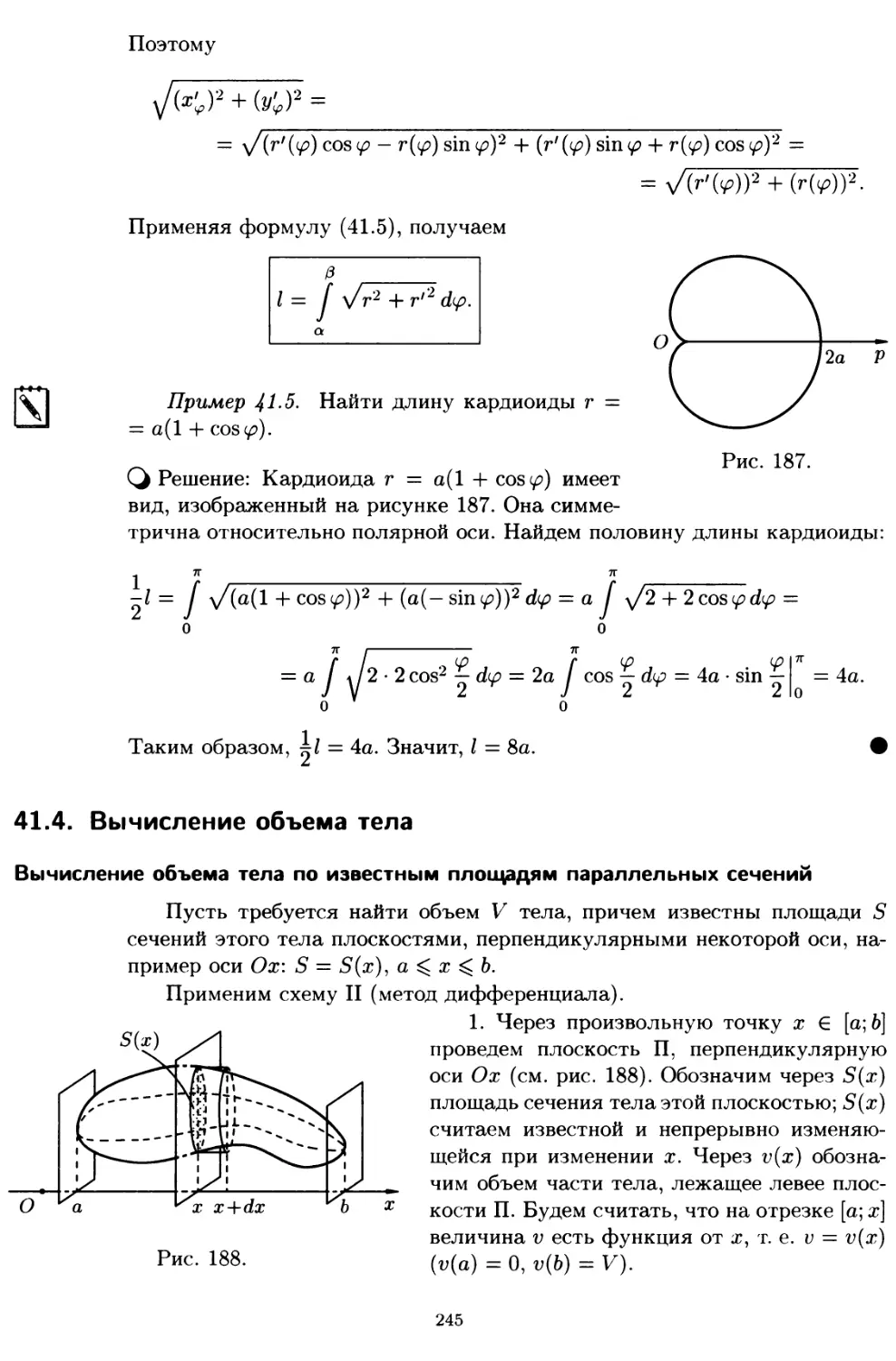
41.3. Вычисление длины дуги плоской кривой 242
41.4. Вычисление объема тела 245
41.5. Вычисление площади поверхности вращения 247
41.6. Механические приложения определенного интеграла 249
§ 42. Приближенное вычисление определенного интеграла 254
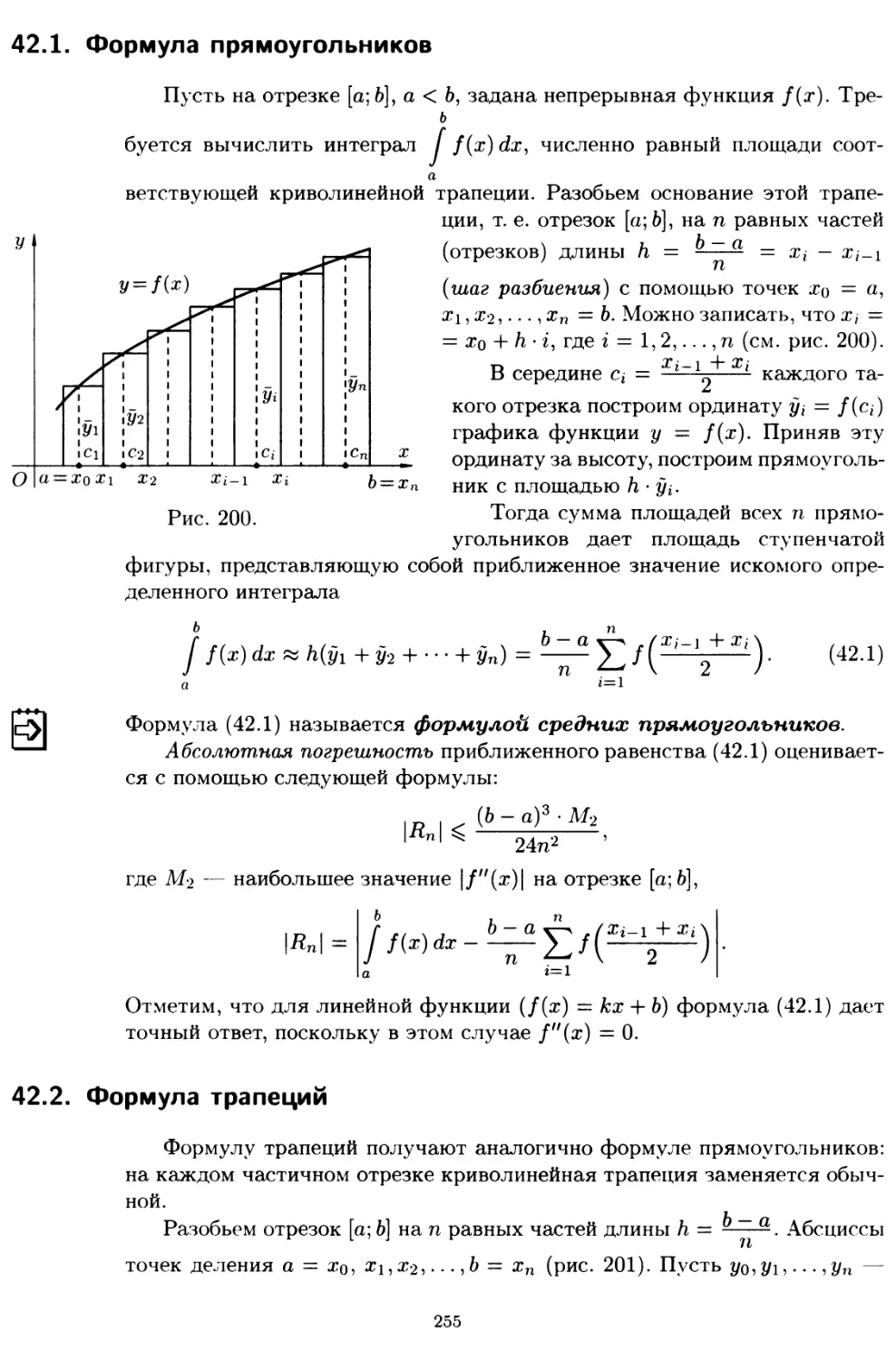
42.1. Формула прямоугольников 255
42.2. Формула трапеций 255
42.3. Формула парабол (Симпсона) 256
Глава IX. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 43. Функции двух переменных 260
43.1. Основные понятия 260
43.2. Предел функции 261
43.3. Непрерывность функции двух переменных 262
43.4. Свойства функций, непрерывных в ограниченной замкну-
той области 263
§ 44. Производные и дифференциалы функции нескольких перемен-
ных 263
44.1. Частные производные первого порядка и их геометриче-
ский смысл 263
44.2. Частные производные высших порядков 265
44.3.Дифференцируемость и полный дифференциал функции.. 266
44.4. Применение полного дифференциала к приближенным
вычислениям 268
44.5. Дифференциалы высших порядков 268
44.6. Производная сложной функции. Полная производная 269
44.7. Инвариантность формы полного дифференциала 271
44.8. Дифференцирование неявной функции 271
§ 45. Касательная плоскость и нормаль к поверхности 273
§ 46. Экстремум функции двух переменных 274
46.1. Основные понятия 274
46.2. Необходимые и достаточные условия экстремума 275
46.3. Наибольшее и наименьшее значения функции в замкнутой
области 277
Справочные материалы 279

ПРЕДИСЛОВИЕ
Настоящее пособие предназначено, в первую очередь, для студентов
инженерно-технических специальностей; может быть полезным для всех
категорий студентов, изучающих в том или ином объеме высшую матема-
тику. Оно представляет собой конспект лекций в 2 частях. Первая часть
адресована, в основном, первокурсникам. Набор освещаемых вопросов хо-
рошо виден из оглавления.
Данный конспект содержит необходимый материал по девяти разде-
лам курса высшей математики. Изложение теоретического материала по
всем темам сопровождается рассмотрением большого количества приме-
ров и задач, ведется на доступном, по возможности строгом языке.
Пособие может быть использовано студентами также для самостоя-
тельного изучения соответствующего материала, является базой для под-
готовки к семестровым экзаменам по высшей математике на 1-м курсе.
Кроме того, книга должна помочь студенту и в тех случаях, когда он
что-то не успел записать на лекции, какие-то лекции были пропущены, в
чем-то трудно (или нет времени) разобраться по другим учебникам, когда
некоторые вопросы «слишком длинны» в его конспектах или много факти-
ческого материала, который следует изучить за ограниченное количество
недель, дней.
Автор надеется, что данное пособие будет способствовать более глубо-
кому изучению студентами курса высшей математики.
Список обозначений:
— начало и конец решения примера или задачи;
— начало и конец доказательства;
— важные определения
— «обратите особое внимание!»
В рамку заключены формулы, которые важно помнить.

Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Лекции 1-3 I
§1. МАТРИЦЫ
1.1. Основные понятия
Матрицей называется прямоугольная таблица чисел, содержащая га
строк одинаковой длины (или п столбцов одинаковой длины). Матрица
записывается в виде
или, сокращенно, А = (а^), где г = 1,ш (т. е. г = 1,2,3,... ,га) — номер
строки, j = 1, п (т. е. j = 1,2,3,..., п) — номер столбца.
Матрицу А называют матрицей размера т х п и пишут Атхп. Числа
dij, составляющие матрицу, называются ее элементами. Элементы, сто-
ящие на диагонали, идущей из верхнего левого угла, образуют главную
диагональ.
Матрицы равны меэюду собой, если равны все соответствующие эле-
менты этих матриц, т. е.
А — В, если aij = bij, где г = 1, m, j = 1, п.
Матрица, у которой число строк равно числу столбцов, называется
квадратной. Квадратную матрицу размера п х п называют матрицей
п-го порядка.
Квадратная матрица, у которой все элементы, кроме элементов глав-
ной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали
равен единице, называется единичной. Обозначается буквой Е.
Пример 1.1. Единичная матрица 3-го порядка
Единичная матрица п-го порядка
Квадратная матрица называется треугольной, если все элементы,
расположенные по одну сторону от главной диагонали, равны нулю.
ю

Матрица, все элементы которой равны нулю, называется нулевой.
Обозначается буквой О. Имеет вид
Матрица размера 1x1, состоящая из одного числа, отождествляется
с этим числом, т. е. (5)ixi есть 5.
Матрица, полученная из данной заменой каждой ее строки столбцом
с тем же номером, называется матрицей транспонированной к данной.
Обозначается АТ.
Так, если А = I « 1, то Ат = I 9 . 1, если А — ( п 1, то Ат = (1 0).
Транспонированная матрица обладает следующим свойством:
(Ат)т = А.
1.2. Действия над матрицами
Сложение
Операция сложения матриц вводится только для матриц одинаковых
размеров.
Суммой двух матриц Атхп = (а^) и ВтХп = (bij) называется матри-
ца Стхп = {cij) такая, что Cij = а^ + Ь^ (г = 1,га, j = 1,п). Записывают
С = А + В.
Пример 1.2.
Аналогично определяется разность матриц.
Умножение на число
Произведением матрицы Атх?г = (a>ij) wa число к называется матрица
Втхп = {bij) такая, что Ь^ = к • а^ (г = l,m, j = l,n). Записывают
В = к-А.
и
В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в
арифметике.
Матрица, содержащая один столбец или одну строку, называется век-
тором (или вектор-столбец, или вектор-строка соответственно). Их вид:

Пример 1.3.
Матрица —А = (-1) • Л называется противоположной матрице А.
Разность матриц А — В можно определить так: А — В = А+ (—В).
Операции сложения матриц и умножения матрицы на число обладают
следующими свойствами:
1. А + В = В + А; 5. \А = А;
2. А + (В + С) = (А + В) + С; 6. а • {А + Б) = аА + а£;
3. Л + О = Л; 7. (а + /3) • А = аА + /L4;
4. Л - Л = О; 8. а • (/?Л) = (а/3) • Л,
где Л, В, С — матрицы, а и /3 — числа.
Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
• перестановка местами двух параллельных рядов матрицы;
• умножение всех элементов ряда матрицы на число, отличное от нуля;
• прибавление ко всем элементам ряда матрицы соответствующих эле-
ментов параллельного ряда, умноженных на одно и то же число.
Две матрицы Л и В называются эквивалентными, если одна из них
получается из другой с помощью элементарных преобразований. Записы-
вается А ~ В.
При помощи элементарных преобразований любую матрицу можно
привести к матрице, у которой в начале главной диагонали стоят подряд
несколько единиц, а все остальные элементы равны нулю. Такую матрицу
называют канонической, например
1 0 0 0>
0 10 0
0 0 10
0 0 0 0у
Пример 1.4- Привести к каноническому виду матрицу
2
0
4
3
2
0
1
-1
5
2
1
1
12

Операция умножения двух матриц вводится только для случая, когда
число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы Атхп = (а^) на матрицу Впхр = (bjk) на-
зывается матрица Сшхр — (с^) такая, что
Cik = an • bik + ai2 -Ь2к Н Ь a>inbnk, где г = 1,га, к - 1,р,
т. е. элемент г-й строки и fc-ro столбца матрицы произведения С равен
сумме произведений элементов г-й строки матрицы А на соответствующие
элементы к-vo столбца матрицы В.
Получение элемента с^ схематично изображается так:
Если матрицы А и В квадратные одного размера, то произведения АВ
и В А всегда существуют. Легко показать, что А • Е = Е • А = А, где А —
квадратная матрица, Е — единичная матрица того же размера.
13
О Решение: Выполняя элементарные преобразования, получаем
Пример 1.6. А= 1~ 1 л )' "^ = ( 1 9)' Тогда произведение А • В не
определено, так как число столбцов матрицы А (3) не совпадает с числом
строк матрицы В (2). При этом определено произведение В х А, которое
считают следующим образом:
R 4_/1 3\ /1 2 1\ _ /1 + 9 2 + 3 1 + 0\ _ /10 5 1\
Vi 2/ дз 1 о) \1 + б 2 + 2 1 + о; V7 4 V "

Матрицы А и В называются перестановочными, если АВ = В А.
Умножение матриц обладает следующими свойствами:
1. А-(В-С) = (А-В)-С;
2. А • (В + С) = АВ + АС;
3. (А + В) • С = АС + ВС;
4. а(ЛВ) = (аЛ)Я,
если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
§2. ОПРЕДЕЛИТЕЛИ
2.1. Основные понятия
Квадратной матрице А порядка п можно сопоставить число det А (или
\А\, или Д), называемое ее определителем, следующим образом:
Пример 2.1. Найти определители матриц
/2 -3\ / cos a sina^
V 5 6 / V — sin a cos a,
14
Определитель матрицы А также называют ее детерминантом. Прави-
ло вычисления детерминанта для матрицы порядка N является довольно
сложным для восприятия и применения. Однако известны методы, по-
зволяющие реализовать вычисление определителей высоких порядков на
основе определителей низших порядков. Один из методов основан на свой-
стве разложения определителя по элементам некоторого ряда (с. 17, свой-
ство 7). При этом заметим, что определители невысоких порядков (1, 2, 3)
желательно уметь вычислять согласно определению.
Вычисление определителя 2-го порядка иллюстрируется схемой:

О Решение:
При вычислении определителя 3-го порядка удобно пользоваться пра-
вилом треугольников (или Саррюса), которое символически можно запи-
сать так:
(основания
равнобедренных
треугольников
параллельны
главной
диагонали)
(основания
треугольников
параллельны
побочной
диагонали)
Пример 2.2. Вычислить определитель матрицы
О Решение:
detA =
= 5 • 1 • (-3) + (-2) • (-4) -6 + 3-0-1-6-1-1-3- (-2) • (-3) - 0 • (-4) • 5
= -15 + 48 - 6 - 18 = 48 - 39 = 9.
2.2. Свойства определителей
Сформулируем основные свойства определителей, присущие опреде-
лителям всех порядков. Некоторые из этих свойств поясним на определи-
телях 3-го порядка.
Свойство 1 («Равноправность строк и столбцов»). Определитель не
изменится, если его строки заменить столбцами, и наоборот.
Иными словами,
В дальнейшем строки и столбцы будем просто называть рядами определи-
теля.
Свойство 2. При перестановке двух параллельных рядов определи-
тель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен ну-
лю.
15

Свойство 4- Общий множитель элементов какого-либо ряда определи-
теля можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда про-
порциональны соответствующим элементам параллельного ряда, то та-
кой определитель равен нулю.
Q Действительно,
О Решение: Действительно, используя свойства 5, 4 и 3, получим
16
Свойство 5. Если элементы какого-либо ряда определителя предста-
вляют собой суммы двух слагаемых, то определитель может быть разло-
жен на сумму двух соответствующих определителей.
Например,
Свойство 6 («Элементарные преобразования определителя»). Опре-
делитель не изменится, если к элементам одного ряда прибавить соответ-
ствующие элементы параллельного ряда, умноженные на любое число.
Дальнейшие свойства определителей связаны с понятиями минора и
алгебраического дополнения.
Минором некоторого элемента а^ определителя n-го порядка назы-
вается определитель п — 1-го порядка, полученный из исходного путем
вычеркивания строки и столбца, на пересечении которых находится вы-
бранный элемент. Обозначается га^.
Алгебраическим дополнением элемента а%$ определителя называ-
ется его минор, взятый со знаком «плюс», если сумма i + j — четное
Так, если Д:

17
число, и со знаком «минус», если эта сумма нечетная. Обозначается А^:
Лу = (-1)*+''-ту.
Так, An = +тц, Аз2 = -т32.
Свойство 7 («Разложение определителя по элементам некоторого ря-
да»). Определитель равен сумме произведений элементов некоторого ряда
на соответствующие им алгебраические дополнения.
Проиллюстрируем и одновременно докажем свойство 7 на примере
определителя 3-его порядка. В этом случае свойство 7 означает, что
В самом деле, имеем
Свойство 7 содержит в себе способ вычисления определителей высоких
порядков.
Пример 2.4- Вычислите определитель матрицы
Q Решение: Для разложения определителя обычно выбирают тот ряд, где
есть нулевые элементы, т. к. соответствующие им слагаемые в разложении
будут равны нулю.
Свойство 8. Сумма произведений элементов какого-либо ряда опре-
делителя на алгебраические дополнения соответствующих элементов па-
раллельного ряда равна нулю.
Так, например, ацА2\ + а^А-п + «13^23 = 0.

§3. НЕВЫРОЖДЕННЫЕ МАТРИЦЫ
3.1. Основные понятия
Пусть А — квадратная матрица гг-го порядка
Квадратная матрица А называется невыроэюденной, если определи-
тель Д = det А не равен нулю: Д = det А ф 0. В противном случае (Д = 0)
матрица А называется выроэюденной.
Матрицей, союзной к матрице А, называется матрица
где Aij — алгебраическое дополнение элемента а^ данной матрицы А (оно
определяется так же, как и алгебраическое дополнение элемента опреде-
лителя).
Матрица А~1 называется обратной матрице А, если выполняется
условие
A A-1 =A~XA = E, (3.1)
где Е — единичная матрица того же порядка, что и матрица А. Матрица
А~1 имеет те же размеры, что и матрица А.
3.2. Обратная матрица
Теорема 3.1. Всякая невырожденная матрица имеет обратную.
Q Проведем доказательство для случая матрицы 3-го порядка. Пусть
Составим союзную матрицу
18
причем det А ф 0.

и найдем произведение матриц А и А*:
т. е.
19
Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).
Аналогично убеждаемся, что
Равенства (3.2) и (3.3) перепишем в виде
Сравнивая полученные результаты с определением (3.1), получаем
Отметим свойства обратной матрицы:
Пример ЗЛ. Найти А *, если А = I 1 1 ).

Пример 3.2. Определить, при каких значениях А существует матрица,
обратная данной:
О Решение: Найдем произведение матриц А и В:
Ранг матрицы
Рассмотрим матрицу А размера га х п.
Выделим в ней к строк и к столбцов (к ^ min(m;n)). Из элементов,
стоящих на пересечении выделенных строк и столбцов, составим опреде-
литель А;-го порядка. Все такие определители называются минорами этой
матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим,
что таких миноров можно составить С^ • С* штук, где С* = ,,, П'_ и\\ —
число сочетаний из п элементов по к.)
20
О Решение: Всякая невырожденная матрица имеет обратную. Найдем
определитель матрицы А:
Если 4Л - 9 ф 0, т. е. А ф т, то А А ф 0, т. е. матрица А невырожденная,
имеет обратную. •
Пример 3.3. Показать, что матрица А является обратной для В, если
Аналогично В • А = Е. Следовательно, матрица А является обратной
для В. •

Наибольший из порядков миноров данной матрицы, отличных от нуля,
называется рангом матрицы. Обозначается г, г(А) или rang Л.
Очевидно, что 0 ^ г ^ min(m; п), где min(m; п) — меньшее из чисел т
и п.
Минор, порядок которого определяет ранг матрицы, называется ба-
зисным. У матрицы может быть несколько базисных миноров.
Пример 3.4- Найти ранг матрицы:
/2 0 4 0\
Л= 3 0 б 0 .
\1 0 -3 О/
О Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го по-
рядка, отличный от нуля = —15 ^ 0. Значит, г (А) = 2. Базисный
минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами. •
Отметим свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не из-
менится.
3. Ранг матрицы не изменяется при элементарных преобразованиях ма-
трицы (см. с. 12).
Ранг канонической матрицы равен числу единиц на главной диагона-
ли. На этом основан один из способов вычисления ранга матрицы.
Пример 3.5. Найти ранг матрицы
/2 3 1 2>
А= 0 2 -1 1
\4 0 5 1,
используя результаты примера 1.4.
О Решение: В примере 1.4 показано, что
/1 О О (Л
А ~ О 1 О О
\0 О О О)
то есть
A~(l ° ° °)
\0 1 О О)
Таким образом, ранг матрицы А равен г(А) = 2.
21

§4. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИИ
4.1. Основные понятия
Системой линейных алгебраических уравнений, содержащей т урав-
нений и п неизвестных, называется система вида
где числа а^, г = l,m, j = 1,тг называются коэффициентами системы,
числа Ьг — свободными членами. Подлежат нахождению числа хп.
Такую систему удобно записывать в компактной матричной форме
Здесь А — матрица коэффициентов системы, называемая основной
матрицей:
X =
в =
— вектор-столбец из неизвестных Xj,
— вектор-столбец из свободных членов Ь{.
Произведение матриц А • X определено, так как в матрице А столбцов
столько же, сколько строк в матрице X (п штук).
Расширенной матрицей системы называется матрица А системы, до-
полненная столбцом свободных членов
/ап ai2... ain h \
-j- _ CL21 a22 • • • 0>-2п Ь-2
\Clmi 0-771,2 • • • Qmn Um/
Решением системы называется п значений неизвестных х\ = ci,
х2 — с-2, •.., хп = Стг, при подстановке которых все уравнения системы
обращаются в верные равенства. Всякое решение системы можно записать
в виде матрицы-столбца С =
22

ич| Система уравнений называется совместной, если она имеет хотя бы
*—* одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет един-
ственное решение, и неопределенной, если она имеет более одного решения.
В последнем случае каждое ее решение называется частным решением си-
стемы. Совокупность всех частных решений называется общим решением.
Решить систему — это значит выяснить, совместна она или несо-
вместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они
имеют одно и то же общее решение. Другими словами, системы эквива-
лентны, если каждое решение одной из них является решением другой, и
наоборот.
[Ж| Эквивалентные системы получаются, в частности, при элементарных
*—' преобразованиях системы при условии, что преобразования выполняются
лишь над строками матрицы.
Система линейных уравнений называется однородной, если все свобод-
ные члены равны нулю:
Теорема 4.1. Система линейных алгебраических уравнений совместна тогда и толь-
ко тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Примем ее без доказательства.
Правила практического разыскания всех решений совместной системы
линейных уравнений вытекают из следующих теорем.
23
Однородная система всегда совместна, так как х\ = x<i — • • • = хп = О
является решением системы. Это решение называется нулевым или три-
виальным.
4.2. Решение систем линейных уравнений. Теорема
Кронекера-Капелли
Пусть дана произвольная система т линейных уравнений с п неиз-
вестными
Исчерпывающий ответ на вопрос о совместности этой системы дает тео-
рема Кронекера-Капелли.

Теорема 4.2. Если ранг совместной системы равен числу неизвестных, то система
имеет единственное решение.
Теорема 4.3. Если ранг совместной системы меньше числа неизвестных, то система
имеет бесчисленное множество решений.
Правило решения произвольной системы
линейных уравнений
1. Найти ранги основной и расширенной матриц системы. Если
г (А) ф г(А), то система несовместна.
2. Если г (А) = г(А) = г, система совместна. Найти какой-либо базис-
ный микор порядка г (напоминание: минор, порядок которого определяет
ранг матрицы, называется базисным). Взять г уравнений, из коэффициен-
тов которых составлен базисный минор (остальные уравнения отбросить).
Неизвестные, коэффициенты которых входят в базисный минор, называ-
ют главными и оставляют слева, а остальные п — г неизвестных называют
свободными и переносят в правые части уравнений.
3. Найти выражения главных неизвестных через свободные. Получено
общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим
соответствующие значения главных неизвестных. Таким образом можно
найти частные решения исходной системы уравнений.
pkj Пример 4-1- Исследовать на совместность систему
х+ у = 1,
Зх + Зу = -2.
О Решение:
Пример 4-2. Решить систему
Х\ — 2^2 + #3 + #4 = 1?
xi - 2х2 + х3 - х4 = -1,
Х\ — 2х-2 + #з + 3#4 = 3.
24

О Решение: r(A) = r( A) = 2. Берем два первых уравнения:
xi - 2х2 +\хз~+~Х4\ = 1,
.Ti - 2х2 +lXZSlXj} = —1-
#3 + #4 = 1 - #1 + 2х2,
Хз — Х\ — — 1 — Х\ + 2х-2-
или в матричной форме А • X = В.
Основная матрица А такой системы квадратная. Определитель этой
матрицы
называется определителем системы. Если определитель системы отличен
от нуля, то система называется невырожденной.
Найдем решение данной системы уравнений в случае Л ф 0.
Умножив обе части уравнения А • X = В слева на матрицу А-1, полу-
чим А"1 АХ = А-1 • В. Поскольку А'1 • А = Е и Е • X = X, то
X = А-1 -В.
25
Следовательно, #з = ~х\ + 2#2, #4 = 1 — общее решение. Положив, на-
пример, х\ = 0, Х2 — 0, получаем одно из частных решений: х\ = 0, х-2 = 0,
хз = 0, х\ — 1. •
4.3. Решение невырожденных линейных систем. Формулы Крамера
Пусть дана система п линейных уравнений с п неизвестными
Отыскание решения системы по формуле (4.1) называют матричным
способом решения системы.
Матричное равенство (4.1) запишем в виде

Отсюда следует, что
Аналогично: Х2 = -т£, где Д2 получен из Д путем замены второго
столбца коэффициентов столбцом из свободных членов; хз = -г2-, ...
А ^
. . . , ХП д .
Формулы
(4.2)
называются формулами Крамера.
Итак, невырожденная система п линейных уравнений с п неизвестны-
ми имеет единственное решение, которое может быть найдено матричным
способом (4.1) либо по формулам Крамера (4.2).
Пример Ь.З. Решить систему
4.4. Решение систем линейных уравнений методом Гаусса
Одним из наиболее универсальных и эффективных методов решений
линейных алгебраических систем является метод Гаусса, состоящий в по-
следовательном исключении неизвестных.
Пусть дана система уравнений
26
Но АцЬ\ 4- А-2\Ь2 4- • • • 4- ^ni^n есть разложение определителя
по элементам первого столбца. Определитель А\ получается из определи-
теля А путем замены первого столбца коэффициентов столбцом из сво-
бодных членов.

Процесс решения по методу Гаусса состоит из двух этапов. На первом
этапе (прямой ход) система приводится к ступенчатому (в частности,
треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
где к ^ п, ац ф О, г = 1,/с. Коэффициенты ац называются главными
элементами системы.
На втором этапе (обратный ход) идет последовательное определение
неизвестных из этой ступенчатой системы.
Опишем метод Гаусса подробнее.
Прямой ход.
Будем считать, что элемент ац ф О (если ац =0, то первым в системе
запишем уравнение, в котором коэффициент при х\ отличен от нуля).
Преобразуем систему (4.3), исключив неизвестное х\ во всех уравне-
ниях, кроме первого (используя элементарные преобразования системы).
Для этого умножим обе части первого уравнения на — а-21 и сложим по-
ац
членно со вторым уравнением системы. Затем умножим обе части первого
уравнения на —^ и сложим с третьим уравнением системы. Продолжая
ац
этот процесс, получим эквивалентную систему
Здесь a\j , b\ (i,j = 2,m) — новые значения коэффициентов и правых
частей, которые получаются после первого шага.
Аналогичным образом, считая главным элементом а22 Ф 0> исключим
неизвестное Х2 из всех уравнений системы, кроме первого и второго, и так
далее. Продолжаем этот процесс, пока это возможно.
Если в процессе приведения системы (4.3) к ступенчатому виду по-
явятся нулевые уравнения, т. е. равенства вида 0 = 0, их отбрасывают.
Если же появится уравнение вида 0 = ftj, a bi ф 0, то это свидетельствует
о несовместности системы.
Второй этап (обратный ход) заключается в решении ступенчатой си-
стемы. Ступенчатая система уравнений, вообще говоря, имеет бесчислен-
ное множество решений. В последнем уравнении этой системы выражаем
первое неизвестное Xk через остальные неизвестные (x^+i, ...,xn). Затем
подставляем значение Xk в предпоследнее уравнение системы и выражаем
Xk-\ через (rr/fe+i,.. .,жп); затем находим Xk-2, • • • ,xi- Придавая свобод-
ным неизвестным (x^+i,... ,жп) произвольные значения, получим бесчи-
сленное множество решений системы.
27

28

Очевидно, что однородная система всегда совместна {г(А) = г(Л)),
она имеет пулевое (тривиальное) решение Х\ = х-2 = • • • = хп = 0.
При каких условиях однородная система имеет и ненулевые решения?
Теорема 4.4. Для того, чтобы система однородных уравнений имела ненулевые
решения, необходимо и достаточно, чтобы ранг г ее основной матрицы был меньше
числа п неизвестных, т. е. г < п.
Q Необходимость.
Так как ранг не может превосходить размера матрицы, то, очевид-
но, г ^ п. Пусть г — п. Тогда один из миноров размера п х п отличен
от нуля. Поэтому соответствующая система линейных уравнений имеет
единственное решение: Х{ — -А = О, А7; = О, А ф 0. Значит, других, кро-
ме тривиальных, решений нет. Итак, если есть нетривиальное решение, то
г < п.
Достаточность.
Пусть г < п. Тогда однородная система, будучи совместной, является
неопределенной. Значит, она имеет бесчисленное множество решений, т. е.
имеет и ненулевые решения. ■
Пусть дана однородная система п линейных уравнений с п неизвест-
ными
Теорема 4.5. Для того, чтобы однородная система п линейных уравнений с п не-
известными имела ненулевые решения, необходимо и достаточно, чтобы ее опреде-
литель Д был равен нулю, т. е. Д = 0.
29
Полученная матрица соответствует системе
Осуществляя обратный ход, находим жз = 1, #2 = 1, £i = 1.
4.5. Системы линейных однородных уравнений
Пусть дана система линейных однородных уравнений

Q Если система имеет ненулевые решения, то Д = 0. Ибо при А ф 0
система имеет только единственное, нулевое решение. Если же Д = 0, то
ранг г основной матрицы системы меньше числа неизвестных, т. е. г < п.
И, значит, система имеет бесконечное множество (ненулевых) решений.
Пример 4-6- Решить систему
\ / \ I I /
Так как г < n, то система имеет бесчисленное множество решений. Найдем
Положив #з = 0, получаем одно частное решение: х\ — 0, хч — О,
#3 = 0- Положив хз = 1, получаем второе частное решение: х\ = 2, х-2 = 3,
хз = 1 и т. д. •

Глава II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Лекции 4-6 I
§5. ВЕКТОРЫ
5.1. Основные понятия
Величины, которые полностью определяются своим численным значе-
нием, называются скалярными. Примерами скалярных величин являются:
площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются
не только своим числовым значением, но и направлением. Такие величины
называют векторными. Векторная величина геометрически изображается
с помощью вектора.
Вектор — это направленный прямолинейный отрезок, т. е. отрезок,
имеющий определенную длину и определенное направление. Если А —
начало вектора, а В — его конец, то вектор обозначается символом АВ
или а. Вектор В А (у него начало в точке В, а конец в точке А) называется
противополсписным вектору АВ. Вектор, противоположный вектору а,
обозначается —а.
Длиной или модулем вектора АВ называется длина отрезка и обо-
значается \АВ\. Вектор, длина которого равна нулю, называется нулевым
вектором и обозначается 0. Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным век-
тором и обозначается через ё. Единичный вектор, направление которого
совпадает с направлением вектора а, называется ортом вектора а и обо-
значается а0.
Векторы а и Ь называются коллинеарными, если они лежат на одной
прямой или на параллельных прямых; записывают а \\Ь.
Коллинеарные векторы могут быть направлены одинаково или проти-
воположно.
Нулевой вектор считается коллинеарным любому вектору.
Два вектора а и Ь называются равными (а = Ь), если они коллинеар-
ны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что
вектор можно переносить параллельно самому се-
бе, а начало вектора помещать в любую точку О
пространства.
На рисунке 1 векторы образуют прямоугольник.
Справедливо равенство Ь — d, но а ф с. Векторы а рис ^
и с — противоположные, а— —с.
Равные векторы называют также свободными.
Три вектора в пространстве называются компланарными, если они
лежат в одной плоскости или в параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие
векторы компланарны.
31

5.2. Линейные операции над векторами
Под линейными операциями над векторами понимают операции сло-
жения и вычитания векторов, а также умножение вектора на число.
Пусть аиЬ — два произвольных вектора. Возьмем произвольную точ-
ку О и построим вектор О А = а. От точки А отложим вектор АВ = Ь.
Вектор ОВ, соединяющий начало первого вектора с концом второго, на-
зывается суммой векторов а и Ь: О В = а + Ь (см. рис. 2).
Это правило сложения векторов называют правилом треугольника.
Сумму двух векторов можно построить также по правилу параллело-
грамма (см. рис. 3).
Рис. 3.
На рисунке 4 показано сложение трех векторов a, b и с.
В
Рис. 4.
Под разностью векторов а и Ь понимается вектор с—а — Ь такой, что
Ъ + с = а (см. рис. 5).
Рис. 5.
Отметим, что в параллелограмме, построенном на векторах а и 6,
одна направленная диагональ является суммой векторов а и 6,
а другая — разностью (см. рис. 6).
32

Рис. 6.
Можно вычитать векторы по правилу: а — Ь = а 4- (—5), т. е. вычитание
векторов заменить сложением вектора а с вектором, противоположным
вектору Ь.
Произведением вектора а на скаляр (число) А называется вектор
Х-а (или а-Л), который имеет длину |Л| • |а|, коллинеарен вектору а, имеет
направление вектора а, если А > 0 и противоположное направление, если
А < 0. Например, если дан вектор —2^., то векторы За и —2а будут иметь
вид ■ За .—^ и - ~ffi
Из определения произведения вектора на число следуют свойства это-
го произведения:
1) если Ь = А а, то Ь || а. Наоборот, если b || а, (а ф 0), то при некотором
А верно равенство Ь = Аа;
2) всегда а = \а\ • а0, т. е. каждый вектор равен произведению его мо-
дуля на орт.
Линейные операции над векторами обладают следующими свойства-
ми:
1. а + Ь = b + а, 4. (Ai + А2) • а = Ai • а + А2 • а,
2. (а + Ь) Н- с = а Н- (Ь 4- с), 5. А • (а + Ь) = А • а + А • Ь.
3. Ai • (А2 • а) = Ai • А2 • а,
Эти свойства позволяют проводить преобразования в линейных опе-
рациях с вектором так, как это делается в обычной алгебре: слагаемые
менять местами, вводить скобки, группировать, выносить за скобки как
скалярные, так и векторные общие множители.
5.3. Проекция вектора на ось
Пусть в пространстве задана ось /, т. е. на-
правленная прямая.
Проекцией точки М на ось / называется ос-
нование Mi перпендикуляра MMi, опущенного
из точки на ось.
Точка Mi есть точка пересечения оси /
с плоскостью, проходящей через точку М пер-
пендикулярно оси (см. рис. 7).
33
Рис. 7.

Если точка М лежит на оси /, то проекция точки М на ось совпадает
с Л/.
Пусть АВ — произвольный вектор {АВ ф 0). Обозначим через А\ и
В\ проекции на ось I соответственно начала А и конца В вектора АВ и
рассмотрим вектор А\В\.
Проекцией вектора АВ на ось I называет-
ся положительное число |Aii?i|, если вектор
А\В\ и ось / одинаково направлены и отрица-
тельное число — |i4iBi|, если вектор А\В\ и
ось / противоположно направлены (см. рис. 8).
Если точки А\ и В\ совпадают {А\В\ = 0), то
проекция вектора АВ равна 0.
Проекция вектора АВ на ось / обозначает-
ся так: пр/ АВ. Если АВ = 0 или АВ _L /, то
Рис. 8. пр, АВ = 0.
Угол р между вектором а и осью / (или
угол между двумя векторами) изображен на рисунке 9. Очевидно,
0 ^ р ^ 7Г.
Рассмотрим некоторые основные свойства проекций.
Свойство 1. Проекция вектора а на ось / равна произведению модуля
вектора а на косинус угла р между вектором и осью, т. е. пр; а = \а\ • cos р.
Q Если р = (aJ) < 77, то пр1 а = +\а\\ =
= \а\ - cos р.
Если р>т; (^^7г), то пр/а = — |ai| =
= -\а\ • cos(7r — р) — \а\ • cosр (см. рис. 10).
Если р — 5, то пр/ а = 0 = |a|cos</>.
Следствие 5.1. Проекция вектора на ось положительна (отрицательна), если вектор
образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.
34

Свойство 2. Проекция суммы нескольких векторов на одну и ту же
ось равна сумме их проекций на эту ось.
Q Пусть, например, d = a + b+_c. Имеем пр; d = +|di| = +|ai| + |6i| - |ci|,
т. е. пр/(а -f b + с) = пр, а + пр, Ъ + пр, с (см. рис. 11). ■
Свойство 3. При умножении вектора а на число Л его проекция на ось
также умножается на это число, т. е.
Q При Л > 0 имеем прДА-а) = \\а\ • cosc^ =
(свойство 1)
= Л • \а\ • cos ^ = А • пр, а.
При Л < 0: пр/(А • а) = |Аа| • cos(7r — у?) =
= —А • \а\ • (— cosф) = А • а • cos </? = А • пр; а.
Свойство справедливо, очевидно, и при А = 0.
Рис. 11.
Таким образом, линейные операции над
векторами приводят к соответствующим линейным операциям над проек-
циями этих векторов.
5.4. Разложение вектора по ортам координатных осей.
Модуль вектора. Направляющие косинусы
Рассмотрим в пространстве прямоугольную систему координат Oxyz.
Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты),
обозначаемые г, j, к соответственно
(см. рис. 12).
Выберем произвольный вектор а
пространства и совместим его начало
с началом координат: а — ОМ.
Найдем проекции вектора а на ко-
ординатные оси. Проведем через ко-
нец вектора ОМ плоскости, парал-
лельные координатным плоскостям.
Точки пересечения этих плоскостей с
осями обозначим соответственно че-
рез Mi, Л/2 и А/з- Получим прямо-
угольный параллелепипед, одной из
диагоналей которого является вектор
ОМ. Тогда прха = |OMi|, npy a =
— |ОЛ/2|, прс а — |ОЛ/з|. По определению суммы нескольких векторов
находим а = OMj + M^Nj- NM.
А так как MXN = 0М2, NM = ОМ3, то
а = ОМ1 + ОМ2 + ОМ3. (5.1)
Рис. 12.
35

Но _ _
О Mi = \ОМг\ • г, ОМ2 = \ОМ2\ • j, OM3 = \ОМ3\ • к. (5.2)
Обозначим проекции вектора а = ОМ на оси Ох, Оу и Oz соответственно
через ах, ау и ас, т.е. |OMi| = ах, |ОЛ/г| = ау, \ОМ$\ = az. Тогда из
равенств (5.1) и (5.2) получаем
(5-3)
Эта формула является основной в векторном исчислении и называется
разлоэюением вектора по ортам координатных осей. Числа ах,
ау, az называются координатами вектора а, т. е. координаты вектора
есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде:
а = (ax\ay',zz).
Зная проекции вектора а, можно легко найти выражение для модуля
вектора. На основании теоремы о длине диагонали прямоугольного парал-
лелепипеда можно написать |0М|2 = |OMi|2 + \ОМ2\2 + |ОА/з|2, т. е.
(5.4)
Отсюда
т. е. модуль вектора равен квадратному корню из суммы квадра-
тов его проекций на оси координат.
Пусть углы вектора а с осями Ох, Оу и Oz соответственно равны а,
/?, 7- По свойству проекции вектора на ось, имеем
ах = \а\ • cos а, ау = \а\ • cos/?, az = \a\ • cos7-
Или, что то же самое,
(5.5)
Числа cos a, cos^, cos 7 называются направляющими косинусами вектора
а.
Подставим выражения (5.5) в равенство (5.4), получаем
\а\2 = \а\2 • cos2 а + \а\2 • cos2 0 + \а\2 • cos2 7-
Сократив на \а\2 ф 0, получим соотношение
cos2 а + cos2 0 + cos2 7 = 1?
т. е. сумма квадратов направляющих косинусов ненулевого век-
тора равна единице.
Легко заметить, что координатами единичного вектора ё являются чи-
сла cos а, cos/3, cos7, т. е. ё = (cosа;cos/3;cos7).
Итак, задав координаты вектора, всегда можно определить его модуль
и направление, т. е. сам вектор.
36

5.5. Действия над векторами, заданными проекциями
Пусть векторы а = (ax;ay;az) и Ь = (bx;by;bz) заданы своими проек-
циями на оси координат Ox, Оу, Oz или, что то же самое
а = ах • г + ау • j + az • к, b = bx • i + by • j + bz - к.
Линейные операции над векторами
Так как линейные операции над векторами сводятся к соответствую-
щим линейным операциям над проекциями этих векторов, то можно запи-
сать:
1. а ± b = (ах ± bx)i + (ау ± by)j + (az ± bz)k, или кратко а ± b =
= (ах ±bx-,ay ±by;az ± bz). To есть при сложении (вычитании) векторов
их одноименные координаты складываются (вычитаются).
2. \а = \ах • г 4- \ау • j + \az • к или короче \а = (\ах\\ау\ \az). To
есть при умножении вектора на скаляр координаты вектора умножа-
ются на этот скаляр.
Равенство векторов
Из определения вектора как направленного отрезка, который можно
передвигать в пространстве параллельно самому себе, следует, что два
вектора а и b равны тогда и только тогда, когда выполняются равенства:
а<х = Ьх, ау = Ьу, az = bz, т. е.
Коллинеарность векторов
Выясним условия коллинеарности векторов а и Ъ, заданных своими
координатами.
Так как а || 6, то можно записать а = А • б, где Л — некоторое число.
То есть
Отсюда
т. е.
37
|/gj\| Таким образом, проекции коллинеарных векторов пропорциональны. Вер-
1—' но и обратное утверждение: векторы, имеющие пропорциональные коор-
динаты, коллинеарны.
Координаты точки
Пусть в пространстве задана прямоугольная декартова система коор-
динат Oxyz. Для любой точки М координаты вектора ОМ называются
координатами точки М. Вектор ОМ называется радиус-вектором точки

Рис. 13.
§6. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
И ЕГО СВОЙСТВА
6.1. Определение скалярного произведения
Скалярным произведением двух ненулевых векторов а и b называется
число, равное произведению длин этих векторов на косинус угла между
ними.
Обозначается аЬ,а-Ъ (или (а,Ь)). Итак, по определению,
(ел)
где if — (a,b).
Формуле (6.1) можно придать иной вид. Так как
|a|cos</? = пр^а, (см. рис. 14), a |6|cos(^ = пр^5, то получаем:
(6.2)
т. е. скалярное произведение двух векторов равно модулю одного из них,
умноженному на проекцию другого на ось, сонаправленную с первым век-
тором.
6.2. Свойства скалярного произведения
1. Скалярное произведение обладает переместительным свойством:
ab = Ьа.
Q ab — \а\ ■ \Ь\ • cos(a,b), а Ьа = \Ь\ • \а\ • cos(6,a). И так как \а\ • \Ь\ = |6| • |а|,
как произведение чисел и cos(a, b) = cos(5, a), то ab = ba. Ш
38
М, обозначается г, т. е. ОМ = г. Следовательно, координаты точки — это
координаты ее радиус-вектора
Координаты точки М записываются в виде M(x;y;z).
Координаты вектора
Найдем координаты вектора а = АВ, если
известны координаты точек A(x\;y\\z\) и
В{х2',У2',22)- Имеем (см. рис. 13):
Следовательно, координаты вектора равны
разностям соответствующих координат его
конца и начала: АВ = (х-2 — Х\; yi —y\\Z2 — Z\).

г
3
к
г
1
0
0
3
0
1
0
к
0
0
1
39
2. Скалярное произведение обладает сочетательным свойством отно-
сительно скалярного множителя: (Ла) • b = X(ab).
Щ (Ха)Ь — |6| • пр^ Ха = X • \Ь\ • пр^ а = X(ab). ■
3. Скалярное произведение обладает распределительным свойством:
а(Ь + с) = аб 4- ас.
4. Скалярный квадрат вектора равен квадрату его длины: а2 = |а|2.
о "2 ~2 Е2 1
В частности: г = j = к = 1.
Если вектор а возвести скалярно в квадрат и затем извлечь корень,
то получим не первоначальный вектор, а его модуль \а\, т. е. w = \a\
Пример 6.1. Найти длину вектора с = За — 4Ь, если \а\ = 2, |6| = 3,
О Решение:
5. Если векторы а и о (ненулевые) взаимно перпендикулярны, то их
скалярное произведение равно нулю, т. е. если a _L 5, то ab — 0. Справед-
ливо и обратное утверждение: если ab = 0 и а ф 0 ф 5, то а _1_ Ь.
Если же а • Ъ = 0 и \а\ ф 0, |Ь| ф 0, то cos(a, b) = 0. Отсюда
6.3. Выражение скалярного произведения через координаты
Пусть заданы два вектора
Найдем скалярное произведение векторов, перемножая их как много-
члены (что законно в силу свойств линейности скалярного произведения)
и пользуясь таблицей скалярного произведения векторов г, j, к:

40
т. е.
Итак, скалярное произведение векторов равно сумме произведений их од-
ноименных координат.
Пример 6.2. Доказать, что диагонали четырехугольника, заданного
координатами вершин Л(-4;-4;4), В(-3;2;2), C(2;5;l), D(3;-2;2), вза-
имно перпендикулярны.
О Решение: Составим вектора АС и BD, лежащие на диагоналях данно-
го четырехугольника. Имеем: АС = (6;9;-3) и BD = (б;-4;0). Найдем
скалярное произведение этих векторов:
Отсюда следует, что AC _L BD. Диагонали четырехугольника ABCD вза-
имно перпендикулярны. •
6.4. Некоторые приложения скалярного произведения
Угол между векторами
Определение угла ip между ненулевыми векторами а — (ax;ay;az) и
Ь = (bx;by;bz):
Отсюда следует условие перпендикулярности ненулевых векторов а и Ъ:
Проекция вектора на заданное направление
Нахождение проекции вектора а на направление, заданное вектором
6, может осуществляться по формуле

Работа постоянной силы
Пусть материальная точка перемещается прямолинейно из положения
А в положение В под действием постоянной силы F, образующей угол ц>
с перемещением АВ — S (см. рис. 15).
Из физики известно, что работа силы F при пере-
мещении 5 равна
Таким образом, работа постоянной силы при прямоли-
нейном перемещении ее точки приложения равна ска-
лярному произведению вектора силы на вектор пере-
мещения.
Пример 6.3. Вычислить работу, произведенную силой F = (3;2;4),
если точка ее приложения перемещается прямолинейно из положения
Л(2;4;6) в положение В(4; 2; 7). Под каким углом к АВ направлена си-
ла F?
О Решение: Находим S = А В = (2, —2,1). Стало быть,
§7. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
И ЕГО СВОЙСТВА
7.1. Определение векторного произведения
Три некомпланарных вектора о, б и с, взятые в указанном порядке,
образуют правую тройку, если с конца третьего вектора с кратчайший
поворот от первого вектора а ко второму вектору Ь виден совершающимся
против часовой стрелки, и левую, если по часовой (см. рис. 16).
41
Рис. 15.
Угол ip между F и 5 находим по формуле cos у?
Рис. 16.

Векторным произведением вектора а на вектор В называется век-
тор с, который:
1) перпендикулярен векторам а и Ь, т. е. с _1_ а и с _1_ Ь;
2) имеет длину, численно равную площади параллелограмма, постро-
енного на векторах а и b как на сторонах (см. рис. 17), т. е.
Рис. 17.
Рис. 18.
Векторное произведение обозначается а х b или [а, б].
Из определения векторного произведения непосредственно вытекают
следующие соотношения между ортами г, j и к (см. рис. 18):
7.2. Свойства векторного произведения
1. При перестановке сомножителей век-
торное произведение меняет знак, т. е. а х b =
= —(b х а) (см. рис. 19).
Q Векторы а х b и b x а коллинеарны, име-
ют одинаковые модули (площадь параллело-
грамма остается неизменной), но противопо-
ложно направлены (тройки а, 6, ах b и а, 6, bxa
противоположной ориентации). Стало быть,
а х b = -(b х а). Ш
2. Векторное произведение обладает соче-
тательным свойством относительно скалярно-
го множителя, т. е. \(axb) = (\а) xb = ах (ХЬ).
Рис. 19.
42
3) векторы a, b и с образуют правую тройку.
Докажем, например, что г х j = к.
1) к JL г, к JL J;
2) |jfc| = 1, но \г х]\ = \г\ • |J| • sin90° = 1;
3) векторы г, j и А- образуют правую тройку (см. рис. 16).

Q Пусть Л > 0. Вектор Л(а х Ь) перпендикулярен векторам а и Ь. Вектор
(Ла) х Ь также перпендикулярен векторам а и b (векторы а, Ла лежат
в одной плоскости). Значит, векторы Л(а х Ь) и (Ла) х Ъ коллинеарны.
Очевидно, что и направления их совпадают. Имеют одинаковую длину:
Поэтому Л (а х Ъ) — Ха х Ь. Аналогично доказывается при Л < 0. В
3. Два ненулевых вектора а и b коллинеарны тогда и только тогда,
когда их векторное произведение равно нулевому вектору, т. е. а || b <<=>
<$=> axb = 0.
Q Если а || 6, то угол между ними равен 0° или 180°. Но тогда \а х Ь\ =
= \а\ • \Ь\ • sin(a, b) = 0. Значит, а х b = 0.
Если же а х Ь = 0, то |а| • \b\ sin</? = 0. Но тогда <р = 0° или <^ = 180°,
т. е. а || 6. ■
В частности, ixi = jxj = kxk = 0.
4. Векторное произведение обладает распределительным свойством:
7.3. Выражение векторного произведения через координаты
Мы будем использовать таблицу векторного произведения векторов г,
j и к:
г
J
к
г
0
-к
J
j
к
0
—г
*
-J
г
0
Чтобы не ошибиться со
знаком, удобно пользо-
ваться схемой:
если направление кратчайшего пути от первого вектора к второму совпа-
дает с направлением стрелки, то произведение равно третьему вектору,
если не совпадает — третий вектор берется со знаком «минус».
Пусть заданы два вектора а = axi-\-ayj-\-azkn b = bxi+byj+bzk. Найдем
векторное произведение этих векторов, перемножая их как многочлены
(согласно свойств векторного произведения):
43
и
Примем без доказательства.

Полученную формулу можно записать еще короче:
(7.1)
(7.2)
так как правая часть равенства (7.1) соответствует разложению определи-
теля третьего порядка по элементам первой строки. Равенство (7.2) легко
запоминается.
7.4. Некоторые приложения векторного произведения
а х b =
г
ах
ьх
3
ау
by
к
az
bz
5
Установление коллинеарности векторов
Если а || 6, то а х b = 0 (и наоборот), т. е.
Нахождение площади параллелограмма и треугольника
Согласно определению векторного произведения векторов а и b \axb\ =
= |а| • |6| simp, т. е. 5пар = \а х Ь\. И, значит, 5д = i|a x Ь|.
Определение момента силы относительно точки
Пусть в точке А приложена сила F =
— АВ и пусть О — некоторая точка про-
странства (см. рис. 20).
Из физики известно, что моментом си-
лы F относительно точки О называется
вектор М, который проходит через точ-
ку О и:
1) перпендикулярен плоскости, прохо-
дящей через точки О, А, В;
Рис. 20.
44
т. е.

2) численно равен произведению силы на плечо
3) образует правую тройку с векторами
04иЖ _ *
Стало быть, М = 0.4 х F.
Нахождение линейной скорости вращения
Скорость v точки А/ твердого тела,
вращающегося с угловой скоростью й во-
круг неподвижной оси, определяется фор-
мулой Эйлера v — й х г, где f = ОМ,
где О — некоторая неподвижная точка оси
(см. рис. 21).
Рис. 21.
§8. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
8.1. Определение смешанного произведения, его геометрический
смысл
Рассмотрим произведение векторов а, Ь и с, составленное следующим
образом: (а х Ь) • с. Здесь первые два вектора перемножаются векторно,
а их результат скалярно на третий вектор. Такое произведение называ-
ется векторно-скалярным, или смешанным, произведением трех векторов.
Смешанное произведение представляет собой некоторое число.
Выясним геометрический смысл выражения (axb)-c.
Построим параллелепипед, ребрами которого являются
векторы а, 6, с и вектор d = а х Ь (см. рис. 22).
Имеем: (а х Ь) • с = d • с = \d\ • пр^ с, \d\ — \а х Ь\ = 5,
где S — площадь параллелограмма, построенного на
векторах а и 6, пр^ с = Н для правой тройки векторов и
пр^с = — Н для левой, где Н — высота параллелепипе-
да. Получаем: (axb)-c = S-(±H), т. е. (axb)-c = ±V, где
V — объем параллелепипеда, образованного векторами
а, Ь и с.
Таким образом, смешанное произведение трех век-
Рис. 22. торов равно объему параллелепипеда, построенного на
этих векторах, взятому со знаком «плюс», если эти векторы образуют
правую тройку, и со знаком «минус», если они образуют левую тройку.
8.2. Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестанов-
ке его сомножителей, т. е. (а х Ь) • с = (Ь х с) • а = (с х а) • Ь.
Действительно, в этом случае не изменяется ни объем параллелепи-
педа, ни ориентация его ребер.
45

2. Смешанное произведение не меняется при перемене местами знаков
векторного и скалярного умножения, т. е. (а х Ь) • с = а • (b x с).
Действительно, (а х Ь) • с = ±V и а • (Ь х с) = (6 х с) • а = ±V. Знак в
правой части этих равенств берем один и тот же, так как тройки векторов
а, 6, с и 6, с, а — одной ориентации.
Следовательно, (а х Ь) - с = a(b x с). Это позволяет записывать сме-
шанное произведение векторов (а х Ь)с в виде abc без знаков векторного,
скалярного умножения.
3. Смешанное произведение меняет свой знак при перемене мест любых
двух векторов-сомножителей, т. е. abc = —acb, abc = —bac, abc = —cba.
Действительно, такая перестановка равносильна перестановке сомно-
жителей в векторном произведении, меняющей у произведения знак.
4. Смешанное произведение ненулевых векторов a, hi с равно нулю
тогда и только тогда, когда они компланарны.
Q Если abc = 0, то а, 6, с — компланарны.
Допустим, что это не так. Можно было бы построить параллелепипед
с объемом V ф 0. Но так как abc = ±V", то получили бы, что abc ф 0. Это
противоречит условию: abc = 0.
Обратно, пусть векторы а, 6, с — компланарны. Тогда вектор d = axb
будет перпендикулярен плоскости, в которой лежат векторы а, 6, с, и,
следовательно, d _L с. Поэтому d • с = 0, т. е. abc = 0. В
8.3. Выражение смешанного произведения через координаты
Пусть заданы векторы а = ахг + ayj + azk, b = bxi + 6yj + &Д, с =
= cxi + cyj + czk. Найдем их смешанное произведение, используя выраже-
ния в координатах для векторного и скалярного произведений:
Полученную формулу можно записать короче:
так как правая часть равенства (8.1) представляет собой разложение опре-
делителя третьего порядка по элементам третьей строки.
Итак, смешанное произведение векторов равно определителю третьего
порядка, составленному из координат перемножаемых векторов.
46

8.4. Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов о, бис основано на следу-
ющих соображениях. Если abc > О, то а, 6, с — правая тройка; если abc < О,
то а,Ь,с - левая тройка.
Установление компланарности векторов
Векторы a, b и с компланарны тогда и только тогда, когда их смешан-
ное произведение равно нулю (а ф О, Ь ф О, с ф 0):
векторы а, о, с компланарны.
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на век-
торах о, 6и с вычисляется как V — \аЪс\, а объем треугольной пирамиды,
построенной на этих же векторах, равен V = i|abc|.
Пример 8.1. Вершинами пирамиды служат точки А(1; 2; 3), £?(0; — 1; 1),
С(2;5;2) и D(3;0; —2). Найти объем пирамиды.
О Решение: Находим векторы а, Ь, с:
Следовательно, V = ^ • 24 = 4.
Находим abc:

Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
Лекции 7-9
§9. СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
9.1. Основные понятия
|н\| Под системой координат на плоскости понимают способ, позво-
*-■ ляющий численно описать положение точки плоскости. Одной из таких
систем является прямоугольная (декартова) система координат.
Прямоугольная система координат задается двумя взаимно перпенди-
кулярными прямыми — осями, на каждой из которых выбрано положи-
тельное направление и задан единичный (масштабный) отрезок. Единицу
масштаба обычно берут одинаковой для обеих осей. Эти оси называют ося-
ми координат, точку их пересечения О — началом координат. Одну из
осей называют осью абсцисс (осью Ох), другую — осью ординат (осью
Оу) (рис. 23). Ось абсцисс обычно рисуют горизонтально и направленной
слева направо, а ось ординат — вертикально и направленной снизу вверх.
Оси координат делят плоскость на четыре области — четверти (или ква-
дранты). Единичные векторы осей обозначают г и j (\i\ = \j\ = 1, г _L j).
Систему координат обозначают Оху (или Oij), а плоскость, в которой
расположена система координат, называют координатной плоскостью.
Рассмотрим произвольную точку М плоскости Оху. Вектор ОМ на-
_ зывается радиусом-вектором точки М.
Рч| Координатами точки М в системе координат Оху (Oij) называ-
1—■ ются координаты радиуса-вектора ОМ. Если ОМ = (ж; у), то координаты
точки М записывают так: М(х;у), число х называется абсциссой точки
М, у — ординатой точки М.
Эти два числа х и у полностью определяют положение точки на плос-
кости, а именно: каждой паре чисел х и у соответствует единственная
точка М плоскости, и наоборот.
Способ определения положения точек с помощью чисел (координат)
называется методом координат. Сущность метода координат на плоско-
сти состоит в том, что всякой линии на ней, как правило, сопоставляется
ее уравнение. Свойства этой линии изучаются путем исследования урав-
нения линии.
Другой практически важной системой координат является полярная
система координат. Полярная система координат задается точкой О, на-
зываемой полюсом, лучом Ор, называемым полярной осью, и единичным
вектором ё того же направления, что и луч Ор.
Возьмем на плоскости точку М, не совпадающую с О. Положение точ-
ки М определяется двумя числами: ее расстоянием г от полюса О и углом
</?, образованным отрезком ОМ с полярной осью (отсчет углов ведется в
направлении, противоположном движению часовой стрелки) (см. рис. 24).
48

Рис. 23.
Рис. 25.
9.2. Основные приложения метода координат на плоскости
Расстояние между двумя точками
Требуется найти расстояние d между точками А{х\\у\) и В(х2',У2)
плоскости Оху.
Q Решение: Искомое расстояние d равно длине вектора АВ =
= (х-2 -х\;у2 -Уг), т. е.
49
Рис. 24.
Числа г и (р называются полярными координатами точки М, пи-
шут М (г;</?), при этом г называют полярным радиусом, <р — полярным
углом.
Для получения всех точек плоскости достаточно полярный угол </?
ограничить промежутком (—7г;7г] (или 0 ^ ip < 27г), а полярный радиус —
[0;оо). В этом случае каждой точке плоскости (кроме О) соответствует
единственная пара чисел г и ip, и обратно.
Установим связь между прямоугольными и полярными координатами.
Для этого совместим полюс О с началом координат системы Оху, а поляр-
ную ось — с положительной полуосью Ох. Пусть хну — прямоугольные
координаты точки М, а г и ip — ее полярные координаты.
Из рисунка 25 видно, что прямоугольные и полярные координаты точ-
ки М выражаются следующим образом:
Определяя величину (р, следует установить (по знакам х и у) четверть,
В КОТОРОЙ ЛеЖИТ ИСКОМЫЙ УГОЛ, И уЧИТЫВаТЬ, ЧТО — 7Г < <£> $С 7Г.
Пример 9.1. Найти полярные координаты точки М( — 1; — л/3).
О Решение: Находим г и <р: г = у/3 + 1 = 2, tg <р = "^У-i = ^- Отсюда
(р = 5 -f 7га, и Е Z. Но так как точка М лежит в 3-й четверти, то п = — 1
и <р = ^ — ж = — -4?. Итак, полярные координаты точки М есть г = 2,
¥,= -^,т.е.м(2;=|2г). •

50
Деление отрезка в данном отношении
Требуется разделить отрезок АВ, соединяющий точки А{х\\у\) и
В(х2;у2) в заданном отношении Л > 0, т.е. найти координаты точки
М(х;у) отрезка АВ такой, что ^L = А (см. рис. 26).
О Решение: Введем в рассмотрение векторы AM и MB. Точка М делит
отрезок АВ в отношении Л, если
Но АМ = (х-х1;у-у1), т. е. AM = (x-xi)i + (y-yi)j и МВ = (х2-х;у2-у),
т. е. MB = (х-2 — х)г + (у2 — у)з- Уравнение (9.1) принимает вид
Учитывая, что равные векторы имеют равные координа-
ты, получаем
Рис. 26. Формулы (9.2) и (9.3) называются формулами деления от-
резка в данном отношении. В частности, при Л = 1, т. е.
если AM = MB, то они примут вид х = Xl "I х%, у = У1 У2. В этом
случае точка М(х;у) является серединой отрезка АВ. •
Замечание: Если Л = 0, то это означает, что точки А и М совпадают,
если Л < 0, то точка М лежит вне отрезка АВ — говорят, что точка М
делит отрезок АВ внешним образом (Л ф —1, т. к. в противном случае
^ = -1, т. е. АМ + МВ = 0, т. е. АВ = 0).
Площадь треугольника
Требуется найти площадь треугольника
ABC с вершинами А{х\; j/i), B(x2; у2), С(х3;уз)-
О Решение: Опустим из вершин А, В, С пер-
пендикуляры АА\, ВВ\, СС\ на ось Ох (см.
рис. 27). Очевидно, что
Поэтому

Замечание: Если при вычислении площади треугольника получим
5 = 0, то это означает, что точки Л, £?, С лежат на одной прямой, если
же получим отрицательное число, то следует взять его модуль.
9.3. Преобразование системы координат
Переход от одной системы координат в какую-либо другую называется
преобразованием системы координат.
Рассмотрим два случая преобразования одной прямоугольной системы
координат в другую. Полученные формулы устанавливают зависимость
между координатами произвольной точки плоскости в разных системах
координат.
Параллельный перенос осей координат
Пусть на плоскости задана прямоугольная система координат Оху.
Под параллельным переносом осей координат понимают переход от систе-
мы координат Оху к новой системе 0\Х\у\, при котором меняется поло-
жение начала координат, а направление осей и масштаб остаются неиз-
менными.
Рис. 28.
Пусть начало новой системы координат точка 0\ имеет координаты
(хо;2/о) в старой системе координат Оху, т. е. 0i(#o;2/o)- Обозначим коор-
динаты произвольной точки М плоскости в системе Оху через (х;у), а в
новой системе OiXiyi через (х'\у') (см. рис. 28).
Рассмотрим векторы
51

Следовательно,
Полученные формулы позволяют находить старые координаты х и у
по известным новым х' и у' и наоборот.
Поворот осей координат
Под поворотом осей координат понимают такое преобразование ко-
ординат, при котором обе оси поворачиваются на один и тот же угол, а
начало координат и масштаб остаются неизменными.
Пусть новая система 0\Х\у\ получена поворотом
системы Оху на угол а.
Пусть М — произвольная точка плоскости,
(х] у) — ее координаты в старой системе и (#'; у') — в
новой системе.
Введем две полярные системы координат с общим
полюсом О и полярными осями Ох и Ох\ (масштаб
одинаков). Полярный радиус г в обеих системах оди-
наков, а полярные углы соответственно равны а + </? и
<р, где if — полярный угол в новой полярной системе.
Рис. 29.
По формулам перехода от полярных координат к прямоугольным име-
ем
Ho rcostp = x' и rsimp = у'. Поэтому
Полученные формулы называются формулами поворота осей. Они по-
зволяют определять старые координаты (х; у) произвольной точки М че-
рез новые координаты (х';у') этой же точки М, и наоборот.
Если новая система координат 0\Х\у\ получена из ста-
рой Оху путем параллельного переноса осей координат и
последующим поворотом осей на угол а (см. рис. 30), то
путем введения вспомогательной системы 0\ху легко по-
лучить формулы
выражающие старые координаты х и у произвольной точ-
ки через ее новые координаты х' и у'.
Рис. 30.
52

§10. ЛИНИИ НА ПЛОСКОСТИ
10.1. Основные понятия
Линия на плоскости часто задается как множество точек, обладаю-
щих некоторым только им присущим геометрическим свойством. Напри-
мер, окружность радиуса R есть множество всех точек плоскости, уда-
ленных на расстояние R от некоторой фиксированной точки О (центра
окружности).
Введение на плоскости системы координат позволяет определять по-
ложение точки плоскости заданием двух чисел — ее координат, а положе-
ние линии на плоскости определять с помощью уравнения (т. е. равенства,
связывающего координаты точек линии).
Уравнением линии (или кривой) на плоскости Оху называется такое
уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют
координаты х и у каждой точки линии и не удовлетворяют координаты
любой точки, не лежащей на этой линии.
Переменные х и у в уравнении линии называются текущими коорди-
натами точек линии.
Уравнение линии позволяет изучение геометрических свойств линии
заменить исследованием его уравнения.
Так, для того чтобы установить лежит ли точка А(хо;уо) на данной ли-
нии, достаточно проверить (не прибегая к геометрическим построениям),
удовлетворяют ли координаты точки А уравнению этой линии в выбран-
ной системе координат.
Пример 10.1. Лежат ли точки К(—2; 1) и L(l; 1) на линии 2х+?/+3=0?
О Решение: Подставив в уравнение вместо х и у координаты точки К,
получим 2 • (—2) + 1 + 3 = 0. Следовательно, точка К лежит на данной
линии. Точка L не лежит на данной линии, т. к. 2 • 1 + 1 + 3 ф 0. •
Задача о нахождении точек пересечения двух линий, заданных урав-
нениями F\(x;y) = 0 и F2(x;y) = 0, сводится к отысканию точек, коор-
динаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к
решению системы двух уравнений с двумя неизвестными:
Если эта система не имеет действительных решений, то линии не пересе-
каются.
Аналогичным образом вводится понятие уравнения линии в полярной
системе координат.
Уравнение F(r\ ф) = 0 называется уравнением данной линии в поляр-
ной системе координат, если координаты любой точки, лежащей на этой
линии, и только они, удовлетворяют этому уравнению.
53

Линию на плоскости можно задать при помощи двух уравнений:
(10.1)
где х и у — координаты произвольной точки М(х\у), лежащей на данной
линии, a t — переменная, называемая параметром; параметр t определяет
положение точки (х\ у) на плоскости.
Например, если х = t + 1, у = t2, то значению параметра t = 2 соот-
ветствует на плоскости точка (3; 4), т. к. х = 2 + 1 = 3, у = 22 = 4.
Если параметр t изменяется, то точка на плоскости перемещается,
описывая данную линию. Такой способ задания линии называется пара-
метрическим, а уравнения (10.1) — параметрическими уравнениями ли-
нии.
Чтобы перейти от параметрических уравнений линии к уравнению ви-
да F(x;y) = 0, надо каким-либо способом из двух уравнений исключить
параметр t. Например, от уравнений
путем подстановки t = х
Рис. 31
во второе уравнение, легко получить уравнение у = х2; или у — х2 = 0, т. е.
вида F(x; у) = 0. Однако, заметим, такой переход не всегда целесообразен
и не всегда возможен.
Линию на плоскости можно задать векторным уравне-
нием г — f(t), где t — скалярный переменный параметр.
Каждому значению £о соответствует определенный вектор
f0 = r(to) плоскости. При изменении параметра t конец
вектора г = f(t) опишет некоторую линию (см. рис. 31).
Векторному уравнению линии г = f(t) в системе коор-
динат Оху соответствуют два скалярных уравнения
(10.1), т. е. уравнения проекций на оси координат вектор-
ного уравнения линии есть ее параметрические уравнения.
Векторное уравнение и параметрические уравнения
линии имеют механический смысл. Если точка перемеща-
ется на плоскости, то указанные уравнения называются уравнениями дви-
жения, а линия — траекторией точки, параметр t при этом есть время.
Итак, всякой линии на плоскости соответствует некоторое уравнение
вида F(x; у) = 0.
Всякому уравнению вида F(x; у) — 0 соответствует, вообще говоря, не-
которая линия, свойства которой определяются данным уравнением (вы-
ражение «вообще говоря» означает, что сказанное допускает исключения.
Так, уравнению (х — 2)2 + (у — З)2 = 0 соответствует не линия, а точка
(2;3); уравнению х2 + у2 + 5 = 0 на плоскости не соответствует никакой
геометрический образ).
В аналитической геометрии на плоскости возникают две основные за-
дачи. Первая: зная геометрические свойства кривой, найти ее уравнение;
вторая: зная уравнение кривой, изучить ее форму и свойства.
54

На рисунках 32-40 приведены примеры некоторых кривых и указаны
их уравнения.
Рис. 32. Окружность радиуса R
Рис. 33. Лемниската Бернулли
Уравнение в прямоугольных координатах:
(х~ + у2)2 — а2(х2 — у2) — 0, а > 0; в полярных
координатах: г — а • у/со^Ър.
Рис. 34. Трехлепестковая роза
В полярных координатах ее уравнение имеет
вид г — а • cos 3<£, где а > 0.
Рис. 35. Улгсшка Паскаля
Уравнение в полярных координатах имеет вид г — b -\- acosip.
55

Рис. 36. Полукубическая парабола
Уравнение кривой у2 = х3 или
Рис. 37. Астроида
Уравнение в прямоугольных координатах:
2 2 2
13 +2/з =аз; параметрические уравнения:
Рис. 38. Кардиоида
Уравнение в полярных координатах имеет вид
г — а(1 + cos;/?), где а > 0. Кардиоида — част-
ный случай улитки Паскаля (а — Ь).
Рис. 39. Спираль Архимеда
Уравнение кривой в полярных координатах
г — а^р, где а > 0 — постоянное.
Параметрические уравнения циклоиды имеют вид
где а > 0. Циклоида — это
10.2. Уравнения прямой на плоскости
Простейшей из линий является прямая. Разным способам задания пря-
мой соответствуют в прямоугольной системе координат разные виды ее
уравнений.
56
Рис. 40. Циклоида
кривая, которую описывает фиксированная точка окружности, катящаяся без скольжения по непо-
движной прямой.

Уравнение прямой с угловым коэффициентом
Пусть на плоскости Оху задана произвольная прямая, не параллель-
ная оси Оу. Ее положение вполне определяется ординатой Ъ точки N(0;b)
пересечения с осью Оу и углом а между осью Ох и прямой (см. рис. 41).
Под углом а (О ^ а < 7г) наклона прямой понима-
ется наименьший угол, на который нужно повернуть
вокруг точки пересечения прямой и оси Ох против
часовой стрелки ось Ох до ее совпадения с прямой.
Возьмем на прямой произвольную точку М(х;у)
(см. рис. 41). Проведем через точку N ось Nx1, па-
раллельную оси Ох и одинаково с ней направлен-
ную. Угол между осью Nx' и прямой равен а. В си-
стеме Nx'y точка М имеет координаты х и у — Ь.
Из определения тангенса угла следует равенство
= tga • х + b. Введем обозначение tga = к, получаем
Рис. 41.
у = кх + Ь,
которому удовлетворяют координаты любой точки М(х;у) прямой. Мож-
но убедиться, что координаты любой точки Р(х;у), лежащей вне данной
прямой, уравнению (10.2) не удовлетворяют.
Число к = tga называется угловым коэффициентом прямой, а
уравнение (10.2) — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то b = 0 и, следова-
тельно, уравнение этой прямой будет иметь вид у = кх.
Если прямая параллельна оси Ох, то а = 0, следовательно, fc = tga = 0
и уравнение (10.2) примет вид у = Ь.
Если прямая параллельна оси Оу, то a = 5, уравнение (10.2) теряет
смысл, т. к. для нее угловой коэффициент к — tga = tg ^ не существует.
В этом случае уравнение прямой будет иметь вид
х — а,
(10.3)
где а — абсцисса точки пересечения прямой с осью Ох. Отметим, что
уравнения (10.2) и (10.3) есть уравнения первой степени.
Общее уравнение прямой
Рассмотрим уравнение первой степени относительно х и у в общем
виде
Ах + Ву + С = 0, (10.4)
где Л, В, С — произвольные числа, причем А и В не равны нулю одно-
временно.
Покажем, что уравнение (10.4) есть уравнение прямой линии. Возмож-
ны два случая.
57
уравнение

Если В — О, то уравнение (10.4) имеет вид Ах + С = 0, причем А ф 0,
/Or
т. е. х = — Ц-. Это есть уравнение прямой, параллельной оси Оу и прохо-
дящей через точку (— %■; 01.
Если В ф 0, то из уравнения (10.4) получаем у = — %х — ^. Это есть
уравнение прямой с угловым коэффициентом к = tga = — ^.
Итак, уравнение (10.4) есть уравнение прямой линии, оно называется
общим уравнением прямой.
Некоторые частные случаи общего уравнения прямой:
С1
1) если А — 0, то уравнение приводится к виду у = — %. Это есть
уравнение прямой, параллельной оси Ох;
2) если В = 0, то прямая параллельна оси Оу;
3) если С = 0, то получаем Ах + By = 0. Уравнению удовлетворяют
координаты точки О(0; 0), прямая проходит через начало координат.
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку М(хо;уо) и ее направление ха-
рактеризуется угловым коэффициентом к. Уравнение этой прямой можно
записать в виде у = кх + Ь, где Ь — пока неизвестная величина. Так как
прямая проходит через точку М(хо;уо), то координаты точки удовлетво-
ряют уравнению прямой: у0 = кх0 + Ъ. Отсюда b = у0 — кх0. Подставляя
значение Ь в уравнение у = кх + Ь, получим искомое уравнение прямой
у = кх 4- уо - кхо, т. е.
у - у0 = к(х -х0).\ (10.5)
Уравнение (10.5) с различными значениями к называют также уравне-
ниями пучка прямых с центром в точке М(хо',Уо)- Из этого пучка нельзя
определить лишь прямую, параллельную оси Оу.
Уравнение прямой, проходящей через две точки
Пусть прямая проходит через точки M\(xi\yi) и Л/2 (#2 5 2/2)- Уравнение
прямой, проходящей через точку ЛД, имеет вид
(10.7)
Предполагается, что в этом уравнении х\ ф #2, у\ Ф 2/2-
58
где к — пока неизвестный коэффициент.
Так как прямая проходит через точку Мо{х2\У2), то координаты этой
точки должны удовлетворять уравнению (10.6): У2 — У\ — к(х>2 — х\). От-
сюда находим к — №—&L. Подставляя найденное значение А: в уравне-
Х'2 — Х\
ние (10.6), получим уравнение прямой, проходящей через точки М\ и Л^:

Если Х'2 = a?i, то прямая, проходящая через точки М\(х\\у\) и
^2(^252/2)5 параллельна оси ординат. Ее уравнение имеет вид х = х\.
Если ?/2 — l/i ^ то уравнение прямой может быть записано в виде у = у\,
прямая MiM-2 параллельна оси абсцисс.
Уравнение прямой в отрезках
Пусть прямая пересекает ось Ох в точ-
ке Mi(a;0), а ось Оу — в точке М2(0;6)
(см. рис. 42). В этом случае уравнение (10.7)
примет вид
Рис. 42.
А(х - х0) + В(у - уо) = 0.
Уравнение (10.8) называется уравнением прямой, про-
ходящей через заданную точку перпендикулярно задан-
ному вектору.
Вектор п = (А; В), перпендикулярный прямой, на-
зывается нормальным вектором этой прямой.
(10.9)
где А и В — координаты нормального вектора, С = —Ахо — Вуо — сво-
бодный член. Уравнение (10.9) есть общее уравнение прямой (см. (10.4)).
Полярное уравнение прямой
Найдем уравнение прямой в полярных
координатах. Ее положение можно опреде-
лить, указав расстояние р от полюса О до
данной прямой и угол а между полярной
осью ОР и осью /, проходящей через полюс
О перпендикулярно данной прямой (см.
рис. 44).
Рис. 44.
59
Это уравнение называется уравнением пря-
мой в отрезках, так как числа а и & указы-
вают, какие отрезки отсекает прямая на осях координат
Уравнение прямой, проходящей через данную точку перпендикулярно данному
вектору
Найдем уравнение прямой, проходящей через заданную точку
Мо(хо\уо) перпендикулярно данному ненулевому вектору п = (А,В).
Возьмем на прямой произвольную точку М(х;у) и
рассмотрим вектор MqM = (х — хо; у — уо) (см. рис. 43).
Поскольку векторы п и MqM перпендикулярны, то их
скалярное произведение равно нулю: п • MqM — 0, то
есть , ,
Уравнение (10.8) можно переписать в виде

(10.10)
Полученное уравнение (10.10) и есть уравнение прямой в полярных коор-
динатах.
Нормальное уравнение прямой
Пусть прямая определяется заданием р и а (см. рис. 45). Рассмотрим
прямоугольную систему координат Оху. Введем полярную систему, взяв
О за полюс и Ох за полярную ось. Уравнение прямой можно записать в
виде
г • cos(<^ — а) — р = 0, т.е. г • cos ^> cos a + г simp sin a — р = 0.
Но, в силу формул, связывающих прямоугольные и полярные координаты,
имеем: г cos if = х, г simp = у. Следовательно, уравнение (10.10) прямой в
прямоугольной системе координат примет вид
х • cos a + у • sin a - р = 0.
(10.11)
Уравнение (10.11) называется нормальным уравнением прямой.
Покажем, как привести уравнение
(10.4) прямой к виду (10.11).
Умножим все члены уравнения (10.4)
на некоторый множитель Л ф 0. Получим
ХАх + ХВу + АС = 0. Это уравнение долж-
но обратиться в уравнение (10.11). Следо-
вательно, должны выполняться равенства:
ХА = cos а, ХВ = sin а, ХС = -р. Из пер-
вых двух равенств находим Х2А2 + Х2В2 =
= cos2 a+sin2 а, т. е. А = ± / Мно-
у/А2 + В2
рис 45 житель А называется нормирующим мно-
жителем. Согласно третьему равенству
АС = — р знак нормирующего множителя противоположен знаку свобод-
ного члена С общего уравнения прямой.
Пример 10.2. Привести уравнение — Зх + 4у + 15 = 0к нормальному
виду.
О Решение: Находим нормирующий множитель А= , = —?•
^ F -У("3)2 + 42 ^
Умножая данное уравнение на А, получим искомое нормальное уравнение
прямой: ^х — ^у — 3 = 0. •
60
Для любой точки М(г;ф) на данной прямой имеем:
С другой стороны,
Следовательно,

10.3. Прямая линия на плоскости. Основные задачи
Угол между двумя прямыми и условия параллельности
и перпендикулярности двух прямых
Пусть прямые L\ и L2 заданы уравнениями с угловыми коэффициен-
тами у = к\х + Ь\ и у = к2х + Ь2 (см. рис. 46).
Требуется найти угол </?, на который надо повернуть в положительном
направлении прямую L\ вокруг точки их пересечения до совпадения с
прямой L2.
О Решение: Имеем а2 = ip + a\ (теорема о внешнем угле
треугольника) или <р = а2 — ol\. Если (р ф ^, то
(10.12)
Рис. 46.
откуда легко получим величину искомого угла.
61
Но tgai = fei, tga-2 = ко, поэтому
Если требуется вычислить острый угол между пря-
мыми, не учитывая, какая прямая является первой, какая — второй, то
\ к- — к I
правая часть формулы (10.12) берется по модулю, т. е. tgip = L Jj,—V- .
Если прямые L\ и L2 параллельны, то (р = 0 и tgip = 0. Из форму-
лы (10.12) следует к2 — к\ =0, т. е. к2 = к\. И обратно, если прямые Li
и L2 таковы, что к\ = k2l то tgtp = 0, т. е. прямые параллельны. Следо-
вательно, условием параллельности двух прямых является равенство их
угловых коэффициентов: к\ — к2.
Если прямые L\ и L2 перпендикулярны, то ip = ^. Следовательно,
ctgV? = ltkl'JZ2 = °- 0тсюДа 1 + fa - к2 = 0, т. е. к\ • к2 = -1 (или
К2 К\
к2 — —тг)- Справедливо и обратное утверждение. Таким образом, услови-
ях
ем перпендикулярности прямых является равенство к\ • k2 = — 1.
Расстояние от точки до прямой
Пусть заданы прямая L уравнени-
ем Ах + By + С = 0 и точка Мо(хо;уо)
(см. рис. 47). Требуется найти расстояние
от точки Afo до прямой L.
О Решение: Расстояние d от точки М$ до
прямой L равно модулю проекции вектора
Mi Л/о, где М\{х\\у\) — произвольная точ-
ка прямой L, на направление нормального

вектора п = (А; В). Следовательно,
что и требовалось получить.
(10.13)
Пример 10.3. Найти расстояние от точки Л/0(2;-1) до прямой
Зх + Ау - 22 = 0.
Q Решение: По формуле (10.13) получаем
§11. ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
11.1. Основные понятия
Рассмотрим линии, определяемые уравнениями второй степени отно-
сительно текущих координат
11.2. Окружность
Простейшей кривой второго поряд-
ка является окружность. Напомним,
что окруэюностъю радиуса R с цен-
тром в точке Л/о называется множе-
ство всех точек М плоскости, удовле-
творяющих условию Л/о Л/ = R. Пусть
точка Л/о в прямоугольной системе
координат Оху имеет координаты
хо, 2Аь а М(х: у) — произвольная точка
окружности (см. рис. 48).
Рис. 48.
62
Так как точка М\(х\;у\) принадлежит прямой L, то Ах\ + Ву\ + С = 0,
т. е. С = —Ах\ — Ву\. Поэтому
Коэффициенты уравнения — действительные числа, но по крайней ме-
ре одно из чисел А, В или С отлично от нуля. Такие линии называются
линиями (кривыми) второго порядка. Ниже будет установлено, что урав-
нение (11.1) определяет на плоскости окружность, эллипс, гиперболу или
параболу. Прежде, чем переходить к этому утверждению, изучим свойства
перечисленных кривых.

Уравнению (11.2) удовлетворяют координаты любой точки М(х;у)
данной окружности и не удовлетворяют координаты никакой точки, не
лежащей на окружности.
Уравнение (11.2) называется каноническим уравнением окружности.
В частности, полагая хо = 0 и уо = 0, получим уравнение окружности
с центром в начале координат х2 + у2 = К2.
Уравнение окружности (11.2) после несложных преобразований при-
мет вид х2 + у'2 — 2яо£ — 2уо2/ + хо + Уо ~~ ^2 = 0. ^ри сравнении этого
уравнения с общим уравнением (11.1) кривой второго порядка легко заме-
тить, что для уравнения окружности выполнены два условия:
1) коэффициенты при х2 и у2 равны между собой;
2) отсутствует член, содержащий произведение ху текущих координат.
Рассмотрим обратную задачу. Положив в уравнении (11.1) значения
В = 0иА = С^0, получим
Ему удовлетворяют координаты единственной точки 0\[ — ^т',—*=т\. В
этом случае говорят: «окружность выродилась в точку» (имеет нулевой
радиус).
Ф2 Г)2 F1
Если ^рт + ^т — "т < 0, то уравнение (11.4), а следовательно, и равно-
А А Л
сильное уравнение (11.3), не определяет никакой линии, так как правая
часть уравнения (11.4) отрицательна, а левая часть — не отрицательна
(говорят: «окружность мнимая»).
63
Преобразуем это уравнение:
т. е.
т. е.
Отсюда следует, что уравнение (11.3) определяет окружность при условии
гр'2 тг\'2 т? / г\ гр\
^j + ^jj — ^т > 0. Ее центр находится в точке 0\ ( — ^f; — Ч), а радиус
гр'2 rV2 7^
Если же ±fe + ^j2~ — т = 0, то уравнение (11.3) имеет вид
то есть
Тогда из условия MqM = R получаем уравнение

11.3. Эллипс
Каноническое уравнение эллипса
|н\| Эллипсом называется множество всех точек плоскости, сумма рассто-
"—' яний от каждой из которых до двух данных точек этой плоскости, назы-
ваемых фокусами, есть величина постоянная, большая, чем расстояние
между фокусами.
Обозначим фокусы через F\ и F-2, расстояние
между ними через 2с, а сумму расстояний от произ-
вольной точки эллипса до фокусов — через 2а (см.
рис. 49). По определению 2а > 2с, т. е. а > с.
Для вывода уравнения эллипса выберем систему
координат Оху так, чтобы фокусы Fi и F-2 лежали на
оси Ох, а начало координат совпадало с серединой
отрезка FiF-2. Тогда фокусы будут иметь следующие
координаты: Fi(-c;0) и F2(c;0).
Пусть М(х;у) — произвольная точка эллипса. Тогда, согласно опре-
делению эллипса, MF\ + MF2 — 2а, т. е.
(11.5)
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение (11.5) к более простому виду следующим
образом:
Так как а > с, то а2 — с2 > 0. Положим
Тогда последнее уравнение примет вид Ь2х2 + а2у2 — а2Ь2 или
(11.7)
|нч| Можно доказать, что уравнение (11.7) равносильно исходному уравнению.
'—' Оно называется каноническим уравнением эллипса.
Эллипс — кривая второго порядка.
Исследование формы эллипса по его уравнению
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (11.7) содержит х и у только в четных степенях, поэто-
му если точка (х;у) принадлежит эллипсу, то ему также принадлежат
точки (я; —у), (—х;у), (—х; —у). Отсюда следует, что эллипс симметричен
относительно осей Ох и Оу, а также относительно точки (9(0; 0), которую
называют центром эллипса.
64

Рис. 50.
2. Найдем точки пересечения эллипса с осями координат. Положив
у = О, находим две точки А\ (а; 0) и А2(—a; 0), в которых ось Ох пересекает
эллипс (см. рис. 50). Положив в уравнении (11.7) х — 0, находим точки пе-
ресечения эллипса с осью Оу: В\ (0; Ь)
и £2(0; -Ъ). Точки Аи А2, Ви В2 на-
зываются вершинами эллипса. Отрез-
ки А\А2 и B\B'2, а также их длины 2а
и 26 называются соответственно боль-
шой и малой осями эллипса. Числа а
и Ь называются соответственно боль-
шой и малой полуосями эллипса.
3. Из уравнения (11.7) следует,
что каждое слагаемое в левой части
не превосходит единицы, т. е. имеют место неравенства \ ^ 1 и ^ ^ 1
а о
или —а ^ х ^ а и — Ь ^ у ^ Ь. Следовательно, все точки эллипса лежат
внутри прямоугольника, образованного прямыми х — ±а, у — ±Ь.
2 2
4. В уравнении (11.7) сумма неотрицательных слагаемых ^ и Tj Равна
единице. Следовательно, при возрастании одного слагаемого другое будет
уменьшаться, т. е. если \х\ возрастает, то |у| уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму, изображенную на
рис. 50 (овальная замкнутая кривая).
Дополнительные сведения об эллипсе
Форма эллипса зависит от отношения -. При b — а эллипс превраща-
ется в окружность, уравнение эллипса (11.7) принимает вид х2 +у2 = а2. В
качестве характеристики формы эллипса чаще пользуются отношением -.
Отношение - половины расстояния между фокусами к большой полу-
оси эллипса называется эксцентриситетом эллипса и обозначается
буквой е («эпсилон»):
причем 0 < е < 1, так как 0 < с < а. С учетом равенства (11.6) формулу (11.8)
можно переписать в виде
т. е.
Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс бу-
дет менее сплющенным; если положить е = 0, то эллипс превращается в
окружность.
65

Прямые х — ±- называются директрисами эллипса. Значение дирек-
трисы эллипса выявляется следующим утверждением.
Рис. 51.
Теорема 11.1. Если г — расстояние от произвольной точки эллипса до какого-
нибудь фокуса, d — расстояние от этой же точки до соответствующей этому фокусу
директрисы, то отношение ^ есть постоянная величина, равная эксцентриситету
эллипса: ^ — е.
Из равенства (11.6) следует, что а > Ь. Если
же а < Ь, то уравнение (11.7) определяет эл-
липс, большая ось которого 26 лежит на оси
Оу, а малая ось 2а — на оси Ох (см. рис. 52).
Фокусы такого эллипса находятся в точках
Fi(0; с) и F2(0; -с), где с = у/Ь2- а'2.
11.4. Гипербола
Каноническое уравнение гиперболы
Гиперболой называется множество всех
точек плоскости, модуль разности расстояний
от каждой из которых до двух данных точек
этой плоскости, называемых фокусами, есть
величина постоянная, меньшая, чем расстояние между фокусами.
Обозначим фокусы через F\ и F2, расстояние
между ними через 2с, а модуль разности расстоя-
ний от каждой точки гиперболы до фокусов через
2а. По определению 2а < 2с, т. е. а < с.
Для вывода уравнения гиперболы выберем си-
стему координат Оху так, чтобы фокусы F\ и F2
лежали на оси Ох, а начало координат совпало с
серединой отрезка F1F2 (см. рис. 53). Тогда фокусы
будут иметь координаты i*\(—c;0) и i<2(c;0).
Пусть М(х\ у) — произвольная точка гиперболы. Тогда согласно опре-
делению гиперболы \MF\ — MF^l = 2а или MF\ — NIF2 = ±2а. т. е.
Рис. 53.
66
Имеют место формулы
Пусть М(х;у) — произвольная точка
эллипса с фокусами Fi и F-2 (см. рис. 51).
Длины отрезков F\M — г\ и F2M = г2
называются фокальными радиусами точ-
ки М. Очевидно,
Рис. 52.

y/(x + с)2 + у2 — у/(х — с)2 + у2 = ±2а. После упрощений, как это было
сделано при выводе уравнения эллипса, получим каноническое уравне-
ние гиперболы
где
(11.9)
(11.10)
Гипербола есть линия второго порядка.
Исследование формы гиперболы по ее уравнению
Установим форму гиперболы, пользуясь ее каноническим уравнением.
1. Уравнение (11.9) содержит х и у только в четных степенях. Сле-
довательно, гипербола симметрична относительно осей Ох и Оу, а также
относительно точки О(0; 0), которую называют центром гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив
у = 0 в уравнении (11.9), находим две точки пересечения гиперболы с осью
Ox: А\(а;0) и Аг(—а;0). Положив ж = 0в (11.9), получаем у'2 = —б2, чего
быть не может. Следовательно, гипербола ось Оу не пересекает.
Точки .4i(a;0) и Лг(—а;0) называются вершинами гиперболы, а от-
резок A\A-2 — 2а — действительной осью, отрезок ОА\ — ОА2 —а —
действительной полуосью гиперболы.
Отрезок В1В2 (BiB2 = 26), соединяющий точки Bi(0; 6) и £?2(0; —Ь) на-
зывается мнимой осью, число b — мнимой полуосью. Прямоугольник
со сторонами 2а и 26 называется основным прямоугольником гипер-
болы.
2
3. Из уравнения (11.9) следует, что уменьшаемое ^ не меньше еди-
г2 " а
ницы, т. е. что ^j ^ 1 или |х| ^ а. Это означает, что точки гиперболы
расположены справа от прямой х — а (правая ветвь гиперболы) и слева
от прямой х — — а (левая ветвь гиперболы).
4. Из уравнения (11.9)
гиперболы видно, что когда
\х\ возрастает, то и \у\ воз-
растает. Это следует из того,
х2 " V2
что разность ^ — *V сохра-
няет постоянное значение,
равное единице.
Из сказанного следует,
что гипербола имеет форму,
изображенную на рисунке 54
(кривая, состоящая из двух
неограниченных ветвей).
Рис. 54.
67

Асимптоты гиперболы
Прямая L называется асимптотой неограниченной кривой К, если
расстояние d от точки М кривой К до этой прямой стремится к ну-
лю при неограниченном удалении точки М
вдоль кривой К от начала координат. На
рисунке 55 приведена иллюстрация понятия
асимптоты: прямая L является асимптотой
для кривой К.
Рис. 55.
Покажем, что гипербола ^ — т? = 1 имеет две асимптоты:
У
—
ъ
-х
а
и
У
—
Ъ
—х.
а
(11.11)
Так как прямые (11.11) и гипербола (11.9) симметричны относительно
координатных осей, то достаточно рассмотреть только те точки указанных
линий, которые расположены в первой четверти.
Возьмем на прямой у = -х точку 7V имеющей ту же абсциссу х, что и
точка М(х;у) на гиперболе у = -у/х2 — а2 (см.
рис. 56), и найдем разность MN между ордина-
тами прямой и ветви гиперболы:
Как видно, по мере возрастания х знаменатель дроби увеличивается; чи-
слитель — есть постоянная величина. Стало быть, длина отрезка MN
стремится к нулю. Так как MN боль-
ше расстояния d от точки М до пря-
мой, то d и подавно стремится к ну-
лю. Итак, прямые у — ±-х являются
асимптотами гиперболы (11.9).
При построении гиперболы (11.9)
целесообразно сначала построить ос-
новной прямоугольник гиперболы (см.
рис. 57), провести прямые, проходя-
щие через противоположные вершины
этого прямоугольника, — асимптоты
гиперболы и отметить вершины А\ и
А-2 гиперболы.
Рис. 57.
68

Уравнение равносторонней гиперболы,
асимптотами которой служат оси координат
Гипербола (11.9) называется равносторонней, если ее полуоси рав-
ны (а = Ь). Ее каноническое уравнение
(11.12)
Рис. 58.
Асимптоты равносторонней гиперболы имеют уравне-
ния у = х и у = —х и, следовательно, являются бис-
сектрисами координатных углов.
Рассмотрим уравнение этой гиперболы в новой си-
стеме координат Ох'у' (см. рис. 58), полученной из
старой поворотом осей координат на угол а = — А. Ис-
пользуем формулы поворота осей координат (их вы-
вод показан на с. 52):
х — х' cos a — у' sin а,
у = х' sin а + у' cos а.
Подставляем значения х и у в уравнение (11.12):
Уравнение равносторонней гиперболы, для которой оси Ох и Оу явля-
ются асимптотами, будет иметь вид у = —.
Дополнительные сведения о гиперболе
Эксцентриситетом гиперболы (11.9) называется отношение рас-
стояния между фокусами к величине действительной оси гиперболы, обо-
значается е:
Так как для гиперболы с > а, то эксцентриситет гиперболы больше
единицы: е > 1. Эксцентриситет характеризует форму гиперболы. Дей-
L 2 2 l
ствительно, из равенства (11.10) следует, что ^ — % — 1, т. е. - = у/е2 — 1
и е
Отсюда видно, что чем меньше эксцентриситет гиперболы, тем мень-
ше отношение - ее полуосей, а значит, тем более вытянут ее основной
прямоугольник.
Эксцентриситет равносторонней гиперболы равен у/2. Действительно,
69

Фокальные радиусы г\ = у/(х + с)2 + ?/2 и Г2 = ^/(# — с)2 + у2 для то-
чек правой ветви гиперболы имеют вид г\ = ех + а и т^ — ех — а, а для
левой — т\ = —(ех 4- а) и г 2 = — (ех — а).
Прямые х = ±- называются директрисами гиперболы. Так как для
гиперболы в > 1, то ^ < а. Это значит, что правая директриса расположе-
на между центром и правой вершиной гиперболы, левая — между центром
и левой вершиной.
Директрисы гиперболы имеют то же свойство ^ = е, что и директрисы
эллипса.
Кривая, определяемая уравнением yj — ^j = 1, также есть гипербола,
действительная ось 2Ь которой расположена на оси Оу, а мнимая ось 2а —
на оси Ох. На рисунке 59 она изображена пунктиром.
Рис. 59.
2,2 2 2
Очевидно, что гиперболы ^-^- = 1и^--^ = 1 имеют общие
а о о" а
асимптоты. Такие гиперболы называются сопряженными.
11.5. Парабола
Каноническое уравнение параболы
Параболой называется множество всех точек плоскости, каждая из ко-
торых одинаково удалена от данной точки, называемой фокусом, и данной
прямой, называемой директрисой. Расстояние от фокуса F до директрисы
называется параметром параболы и обозначается через р (р > 0).
Для вывода уравнения параболы выберем систему координат Оху так,
чтобы ось Ох проходила через фокус F перпендикулярно директрисе в на-
70

правлении от директрисы к F, а начало координат О
расположим посередине между фокусом и директри-
сой (см. рис. 60). В выбранной системе фокус F име-
ет координаты ( ^; 0 J, а уравнение директрисы имеет
вид х = — 2 или х + 2 — 0.
Пусть М(х;у) — произвольная точка параболы.
Соединим точку Л/ с F. Проведем отрезок MN пер-
пендикулярно директрисе. Согласно определению
параболы MF = MN. По формуле расстояния между двумя точками на-
ходим:
Рис. 60.
Следовательно,
Возведя обе части уравнения в квадрат, получим
т. е.
(11.13)
Уравнение (11.13) называется каноническим уравнением параболы. Пара-
бола есть линия второго порядка.
Исследование форм параболы по ее уравнению
1. В уравнении (11.13) переменная у входит в четной степени, значит,
парабола симметрична относительно оси Ох: ось Ох является осью сим-
метрии параболы.
2. Так как р > 0, то из (11.13) следует,
что х ^ 0. Следовательно, парабола рас-
положена справа от оси Оу.
3. При х = 0 имеем у = 0. Следователь-
но, парабола проходит через начало коор-
динат.
4. При неограниченном возрастании х
модуль у также неограниченно возраста-
ет. Парабола у2 — 2рх имеет вид (фор-
му), изображенный на рисунке 61. Точ-
ка О(0; 0) называется вершиной параболы,
отрезок FM = г называется фокальным
радиусом точки М.
Рис. 61.
71

Уравнения у2 = —2рх, х2 = 2ру, х2 — —2ру (р > 0) также определяют
параболы, они изображены на рисунке 62.
Нетрудно показать, что график квадратного трехчлена у = Ах2 +
+ Вх + С, где А ф 0, В и С любые действительные числа, представляет
собой параболу в смысле приведенного выше ее определения.
11.6. Общее уравнение линий второго порядка
Уравнения кривых второго порядка с осями симметрии,
параллельными координатным осям
Найдем сначала уравнение эллипса с центром в точке О\(хо;уо), оси
симметрии которого параллельны координатным осям Ох и Оу и полуоси
соответственно равны а и Ь. Поместим в центре эллипса 0\ начало новой
системы координат 0\х'у', оси которой 0\х' и 0\у' параллельны соответ-
ствующим осям Ох и Оу и одинаково с ними
направленны (см. рис. 63).
В этой системе координат уравнение эл-
липса имеет вид
Так как х' = х — хо, у' = х — уо (формулы па-
раллельного переноса, см. с. 52), то в старой
системе координат уравнение эллипса запи-
шется в виде
Рис. 63.
Рис. 64.
72
Аналогично рассуждая, получим уравне-
ние гиперболы с центром в точке 0\(xq; у о) и
полуосями а и Ь (см. рис. 64):

И, наконец, параболы, изображенные на рисунке 65, имеют соответству-
ющие уравнения.
Уравнение Ах2 + Су2 + 2Dx + 2Еу 4- F = О
Уравнения эллипса, гиперболы, параболы и уравнение окружности
(х — хо)2 + (у — уо)2 = R2 после преобразований (раскрыть скобки, пе-
ренести все члены уравнения в одну сторону, привести подобные члены,
ввести новые обозначения для коэффициентов) можно записать с помо-
щью единого уравнения вида
(11.14)
где коэффициенты Л и С не равны нулю одновременно.
Возникает вопрос: всякое ли уравнение вида (11.14) определяет одну
из кривых (окружность, эллипс, гипербола, парабола) второго порядка?
Ответ дает следующая теорема.
Теорема 11.2. Уравнение (11.14) всегда определяет: либо окружность (при А —С),
либо эллипс (при А - С > 0), либо гиперболу (при А • С < 0), либо параболу (при
АС = 0). При этом возможны случаи вырождения: для эллипса (окружности) — в
точку или мнимый эллипс (окружность), для гиперболы — в пару пересекающихся
прямых, для параболы — в пару параллельных прямых.
Пример 11.1. Установить вид кривой второго порядка, заданной урав-
нением Ах2 + by'2 + 20* - ЗОу + 10 = 0.
73

Q Решение: Предложенное уравнение определяет эллипс (А-С — 4-5 > 0).
Действительно, проделаем следующие преобразования:
Получилось каноническое уравнение эллипса с центром в СМ— й;3] и
полуосями а =
Пример 11.2. Установить вид кривой второго порядка, заданной урав-
нением х2 + 10х - 2у + 11 = 0.
О Решение: Указанное уравнение определяет параболу (С = 0). Действи-
тельно,
74
Получилось каноническое уравнение параболы с вершиной в точке
Oi(-5;-7) ир= 1. •
Пример 11.3. Установить вид кривой второго порядка, заданной урав-
нением 4а-2 - у2 + 8х - 8у - 12 = 0 (.4 • С = -4 < 0).
О Решение: Преобразуем уравнение:
Это уравнение определяет две пересекающиеся прямые 2х + у + 6 = 0и
2х-у-2 = 0. •
Общее уравнение второго порядка
Рассмотрим теперь общее уравнение второй степени с двумя неизвест-
ными:
Оно отличается от уравнения (11.14) наличием члена с произведением
координат (В ^ 0). Можно, путем поворота координатных осей на угол а,
преобразовать это уравнение, чтобы в нем член с произведением координат
отсутствовал.
Используя формулы поворота осей (с. 52)

Таким образом, при повороте осей на угол а, удовлетворяющий усло-
вию (11.17), уравнение (11.15) сводится к уравнению (11.14).
Вывод: общее уравнение второго порядка (11.15) определяет на плос-
кости (если не считать случаев вырождения и распадения) следующие
кривые: окружность, эллипс, гиперболу, параболу.
Замечание: Если Л = С, то уравнение (11.17) теряет смысл. В этом
случае cos2а = 0 (см. (11.16)), тогда 2а = 90°, т. е. а = 45°. Итак, при
А — С систему координат следует повернуть на 45°.
т. е.
т. е.
Отсюда
Выберем угол а так, чтобы коэффициент при х' • у' обратился в нуль,
т. е. чтобы выполнялось равенство
выразим старые координаты через новые:

Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
В ПРОСТРАНСТВЕ
Лекции 10-12 I
§12. УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
12.1. Основные понятия
Поверхность и ее уравнение
Поверхность в пространстве, как правило, можно рассматривать как
геометрическое место точек, удовлетворяющих какому-либо условию. На-
пример, сфера радиуса R с центром в точке 0\ есть геометрическое место
всех точек пространства, находящихся от точки 0\ на расстоянии R.
Прямоугольная система координат Oxyz в пространстве позволяет
установить взаимно однозначное соответствие между точками простран-
ства и тройками чисел х, у и z — их координатами. Свойство, общее всем
точкам поверхности, можно записать в виде уравнения, связывающего ко-
ординаты всех точек поверхности.
Уравнением данной поверхности в прямоугольной системе коор-
динат Oxyz называется такое уравнение F(x, у, z) — 0 с тремя переменны-
ми х, у и г, которому удовлетворяют координаты каждой точки, лежащей
на поверхности, и не удовлетворяют координаты точек, не лежащих на
этой поверхности. Переменные х, у и z в уравнении поверхности называ-
ются текущими координатами точек поверхности.
Уравнение поверхности позволяет изучение геометрических свойств
поверхности заменить исследованием его уравнения. Так, для того, чтобы
узнать, лежит ли точка M\(x\\y\\z\) на данной поверхности, достаточно
подставить координаты точки М\ в уравнение поверхности вместо пере-
менных: если эти координаты удовлетворяют уравнению, то точка лежит
на поверхности, если не удовлетворяют — не лежит.
Уравнение сферы
Найдем уравнение сферы радиуса R с центром в точке Oi(^o;2/o;^o)-
Согласно определению сферы расстояние любой ее точки М(х; у; z) от цен-
тра Oi(xo;yo;zo) равно радиусу R, т. е. 0\М = R. Но 0\М — |OiM|, где
0\М — (х — xq\ у — уо] z — zq). Следовательно,
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты лю-
бой ее точки и не удовлетворяют координаты точек, не лежащих на данной
сфере.
Если центр сферы 0\ совпадает с началом координат, то уравнение
сферы принимает вид х2 4- у2 + z2 = К2.
76
или

Если же дано уравнение вида F{x\ у; z) = О, то оно, вообще говоря,
определяет в пространстве некоторую поверхность.
Выражение «вообще говоря» означает, что в отдельных случаях урав-
нение F(x; у; z) = 0 может определять не поверхность, а точку, линию или
вовсе не определять никакой геометрический образ. Говорят, «поверхность
вырождается».
Так, уравнению 2х2 + у2 + z2 + 1 = 0 не удовлетворяют никакие дей-
ствительные значения х, у, z. Уравнению 0-х2 + у2 + z2 = 0 удовлетворяют
лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0,
z = 0, а х — любое число).
Итак, поверхность в пространстве можно задать геометрически и ана-
литически. Отсюда вытекает постановка двух основных задач:
1. Дана поверхность как геометрическое место точек. Найти уравнение
этой поверхности.
2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности,
определяемой этим уравнением.
Уравнения линии в пространстве
Линию в пространстве можно рассматривать как линию пересечения
двух поверхностей (см. рис. 66) или как геометрическое место точек, об-
щих двум поверхностям.
Если Fi(x;y;z) = 0 и F2(x;y; z) =0 — уравнения двух поверхностей,
определяющих линию L, то координаты точек этой линии удовлетворяют
системе двух уравнений с тремя неизвестными:
(12.1)
Рис. 66.
Рис. 67.
Линию в пространстве можно рассматривать как траекторию движе-
ния точки (см. рис. 67). В этом случае ее задают векторным уравнением
г = f(t) (12.2)
77
Уравнения системы (12.1) называются уравнениями линии в про-
страпстве. Например, [У = °' есть уравнения оси Ох.
I z = 0

Рис. 68.
или параметрическими уравнениями
проекций вектора (12.2) на оси коорди-
нат.
Например, параметрические уравне-
ния винтовой линии имеют вид
Если точка М равномерно движет-
ся по образующей кругового цилиндра, а
сам цилиндр равномерно вращается во-
круг оси, то точка М описывает винто-
вую линию (см. рис. 68).
12.2. Уравнения плоскости в пространстве
Простейшей поверхностью является плоскость. Плоскость в простран-
стве Oxyz можно задать разными способами. Каждому из них соответству-
ет определенный вид ее уравнения.
Уравнение плоскости, проходящей через данную точку
перпендикулярно данному вектору
Пусть в пространстве Oxyz плоскость Q задана точкой Мо(хо; Vo\zo) и
вектором п = (А\В;С), перпендикулярным этой плоскости (см. рис. 69).
Выведем уравнение плоскости Q. Возьмем на ней произвольную точку
M(x;y;z) и составим вектор MqM = (х — хо; у — уо- z — zo).
При любом расположении точки М на плоскости Q
векторы п и MqM взаимно перпендикулярны, поэтому
их скалярное произведение равно нулю: п • MqM = О,
т. е.
(12.3)
Рис. 69.^
Координаты любой точки плоскости Q удовлетворя-
ют уравнению (12.3), координаты точек, не лежащих на
плоскости Q, этому уравнению не удовлетворяют (для
них п ■ MqM ф 0).
Уравнение (12.3) называется уравнением плоскости, проходя-
щей через данную точку М0(х0;уо;^о) перпендикулярно вектору
п = (А; В; С). Оно первой степени относительно текущих координат х, у
и z. Вектор п = (А; В, С) называется нормальным вектором плоско-
сти.
78

Придавая коэффициентам А, В и С уравнения (12.3) различные зна-
чения, можно получить уравнение любой плоскости, проходящей через
точку Л/о- Совокупность плоскостей, проходящих через данную точку, на-
зывается связкой плоскостей, а уравнение (12.3) — уравнением связки
плоскостей.
Общее уравнение плоскости
Рассмотрим общее уравнение первой степени с тремя переменными х,
у и z:
79
Полагая, что по крайней мере один из коэффициентов Л, В или С не равен
нулю, например В ф 0, перепишем уравнение (12.4) в виде
Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравне-
ния (12.4) и (12.5) являются уравнением плоскости с нормальным векто-
ром п = (А; В; С), проходящей через точку М\ ( 0; — 44; 0).
Итак, уравнение (12.4) определяет в системе координат Oxyz некото-
рую плоскость. Уравнение (12.4) называется общим уравнением плос-
кости.
Частные случаи общего уравнения плоскости:
1. Если D = 0, то оно принимает вид Ах + By + Cz = 0. Этому урав-
нению удовлетворяет точка О(0; 0; 0). Следовательно, в этом случае плос-
кость проходит через начало координат.
2. Если С = 0, то имеем уравнение Ах + By + D — 0. Нормальный
вектор п = (А;В]0) перпендикулярен оси Oz. Следовательно, плоскость
параллельна оси Oz; если В = 0 — параллельна оси Оу, .4 = 0 — парал-
лельна оси Ох.
3. Если С = D = 0, то плоскость проходит через О(0; 0; 0) параллельно
оси Oz, т. е. плоскость Ах И- By = 0 проходит через ось Oz. Аналогично,
уравнениям By + Cz = 0 и Ах + Cz = 0 отвечают плоскости, проходящие
соответственно через оси Ох и Оу.
4. Если А = В — 0, то уравнение (12.4) принимает вид Cz Л- D = 0,
т. е. z = —J4- Плоскость параллельна плоскости Оху. Аналогично, урав-
нениям Ах + D — 0 и By + D — 0 отвечают плоскости, соответственно
параллельные плоскостям Oyz и Oxz.
5. Если А = В = D = 0, то уравнение (12.4) примет вид Cz — 0, т. е.
z = 0. Это уравнение плоскости Оху. Аналогично: у = 0 — уравнение
плоскости Oxz\ х — 0 — уравнение плоскости Oyz.
Уравнение плоскости, проходящей через три данные точки
Три точки пространства, не лежащие на одной прямой, определяют
единственную плоскость. Найдем уравнение плоскости Q, проходящей че-
рез три данные точки M\(x\\y\;z\), ^/2(^2; 2/2; ^2) и А/з(^з;Уз; ^з), не ле-
жащие на одной прямой.

Возьмем на плоскости произвольную точку M(x;y;z) и составим век-
торы MYM = (х - xi,y - yi-z - zi), МХМ2 = (x2 - xi\y2 - y\\z2 - zi),
Mi Ms = (xs — x\\ уз — 2/i ;гз — z\). Эти векторы лежат на плоскости Q,
следовательно, они компланарны. Используем условие компланарнос-
ти трех векторов (их смешанное произведение равно нулю), получаем
М^М ■ ЩМ2 ■ ЩМз = 0, т. е.
(12.6)
Уравнение (12.6) есть уравнение плоскости, проходящей через три данные
точки.
Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях Ох, Оу и Oz соответственно отрезки
а, Ь и с, т. е. проходит через три точки А(а;0;0), В(0;Ь;0) и С(0;0;с) (см.
рис. 70).
Подставляя координаты этих точек в уравнение
(12.6), получаем
Раскрыв определитель, имеем bcx — abc+abz + асу = 0,
т. е. bcx + асу + abz = abc или
Рис. 70.
(12.7)
Уравнение (12.7) называется уравнением плоскости в отрезках на
осях. Им удобно пользоваться при построении плоскости.
Нормальное уравнение плоскости
Положение плоскости Q вполне определяется заданием единичного
вектора ё, имеющего направление перпендикуляра ОК, опущенного на
плоскость из начала координат, и длиной
р этого перпендикуляра (см. рис. 71).
Пусть ОК = р, a a, j3, 7 — углы, обра-
зованные единичным вектором ё с осями
Ох, Оу и Oz. Тогда ё = (cos a; cos /?; cos 7).
Возьмем на плоскости произвольную точ-
ку М(х; у; z) и соединим ее с началом коор-
динат. Образуем вектор г = ОМ = (x;y;z).
При любом положении точки М на
плоскости Q проекция радиус-вектора г
на направление вектора ё всегда равно р:
пРё г = р,т.е. г -ё = р или
Рис. 71.
(12.8)
80

Уравнение (12.9) называется нормальным уравнением плоскости в
координатной форме.
Отметим, что общее уравнение плоскости (12.4) можно привести к нор-
мальному уравнению (12.9) так, как это делалось для уравнения прямой
на плоскости. А именно: умножить обе части уравнения (12.4) на норми-
= , где знак берется противопо-
рующий множитель Л = ,
± у/ А2 + В2 + С2
ложным знаку свободного члена D общего уравнения плоскости.
12.3. Плоскость. Основные задачи
Угол между двумя плоскостями. Условия параллельности
и перпендикулярности двух плоскостей
Пусть заданы две плоскости Q\ и Q-2-
Под углом меэюду плоскостями Q\ и Q<i понимается один из двугран-
ных углов, образованных этими плоскостями.
Угол <р между нормальными векторами ri\ = (А\;В\;С\) и П2 =
= (Аг; Дг; С2) плоскостей Q\ и Q2 равен одному из этих углов (см. рис. 72).
Поэтому cos (р = {1}\' V*! | или
Рис. 72.
Рис. 73.
Если плоскости Q\ и Q2 перпендикулярны (см. рис. 73, а), то тако-
вы же их нормали, т. е. й\ _L п2 (и наоборот). Но тогда й\ • п2 = 0, т. е.
А\ А2 + В\В2 + С\С2 = 0. Полученное равенство есть условие перпендику-
лярности двух плоскостей Q\ и Q2.
81
Уравнение (12.8) называется нормальным уравнением плоскости в
векторной форме. Зная координаты векторов f и ё, уравнение (12.8) пере-
пишем в виде i ,
Для нахождения острого угла следует взять модуль правой части.

Если плоскости Qi и Qi параллельны (см. рис. 73, б), то будут па-
раллельны и их нормали й\ и п~2 (и наоборот). Но тогда, как известно,
ARC
координаты векторов пропорциональны: -г1 = W- = -^. Это и есть усло-
вие параллельности двух плоскостей Q\ и Q-2-
Расстояние от точки до плоскости
Пусть задана точка Мо(хо;уо; Zq) и плоскость Q своим уравнением
Ax + By + Cz + D = 0. Расстояние d от точки Mq до плоскости Q находится
по формуле
Вывод этой формулы такой же, как вывод формулы расстояния от
точки А/о(хо; уо) до прямой Ах + By + С = 0 (см. с. 61).
Расстояние d от точки Mq до плоскости Q равно модулю проекции
вектора М\М$, где M\(x\\y\\zi) — произвольная точка плоскости <3, на
направление нормального вектора п = (А; В; С) (см.
рис. 74). Следовательно,
Рис. 74.
^ , \Axo + Byo + Czo + D\ ~ ~
Поэтому a — J , * —L. Отметим, что если плоскость и за-
у/А* + В'2 + С2
дана уравнением х cos a + у cos /? 4- z cos 7 — Р = 0, то расстояние от точки
Мо(хо; уо; zq) до плоскости Q может быть найдено по формуле
d — |xq cos а + уо cos 0 + zq cos 7 — р| •
12.4. Уравнения прямой в пространстве
Векторное уравнение прямой
Рч| Положение прямой в пространстве вполне определено, если задать
'—* какую-либо точку А/о на прямой и вектор 5, параллельный этой пря-
мой. Вектор S называется направляющим вектором прямой. Пусть
прямая L задана ее точкой Mo(xo;yo;zo) и направляющим вектором
S = (га;гс;р). Возьмем на прямой L произвольную точку M(x;y;z). Обо-
82
А так как точка M\{x\\yi\zi) принадлежит плоскости Q, то

значим радиус-векторы точек Mq и М соответственно
через fo и F. Очевидно, что три вектора fo, r и MqM
связаны соотношением
(12.10)
Вектор Л/оМ, лежащий на прямой L, паралле-
лен направляющему вектору S, поэтому MqM = tS,
где £ — скалярный множитель, называемый параме-
тром, может принимать различные значения в за-
висимости от положения точки М на прямой (см.
рис. 75).
Рис. 75.
Уравнение (12.10) можно записать в виде
(12.11)
Полученное уравнение называется векторным уравнением прямой.
Параметрические уравнения прямой
Замечая, что f = (x;y;z), f0 = (хо',Уо', zq), tS = (tm;tn;tp), уравне-
ние (12.11) можно записать в виде
(12.12)
Они называются параметрическими уравнениями прямой в пространстве.
Канонические уравнения прямой
Пусть S=(m; п;р) — направляющий вектор прямой L и Мо(хо; уо; zq) —
точка, лежащая на этой прямой. Вектор МоМ, соединяющий точку М$ с
произвольной точкой М(х; у; z) прямой L, параллелен вектору 5. Поэтому
координаты вектора М0М = (х - xq; у — уо; z — zq) и вектора S = (т; п;р)
пропорциональны:
Уравнения (12.13) называются каноническими уравнениями прямой
в пространстве.
Замечания: 1) Уравнения (12.13) можно было бы получить сразу из па-
раметрических уравнений прямой (12.12), исключив параметр t. Из урав-
нений (12.12) находим
2) Обращение в нуль одного из знаменателей уравнений (12.13) озна-
чает обращение в нуль соответствующего числителя.
83
Отсюда следуют равенства:

Например, уравнения
задают прямую, проходя-
щую через точку Мо(2; —4; 1) перпендикулярно оси Oz (проекция вектора
5 на ось Oz равна нулю). Но это означает, что прямая лежит в плоскости
z = 1, и поэтому для всех точек прямой будет 2 — 1 = 0.
Уравнение прямой в пространстве, проходящей
через две точки
Пусть прямая L проходит через точки
Mi(xi;yi;zi) и М2(х2',У2\ 2-2 )• В качестве направ-
ляющего вектора 5 можно взять вектор MiM-2 =
= (х2 - хх;у2 - 2/i; *2 - *i), т. е. 5 = МХМ2 (см,
рис. 76). Следовательно, т = х2 — х\, п = у2 — у\, Рис. 76.
р = z2 — z\. Поскольку прямая проходит через точ-
ку M\{x\;y\\z\), то, согласно уравнениям (12.13), уравнения прямой L
имеют вид
Уравнения (12.14) называются уравнениями прямой, проходящей че-
рез две данные точки.
Общие уравнения прямой
Прямую в пространстве можно задать как линию пересечения двух
непараллельных плоскостей. Рассмотрим систему уравнений
(12.15)
Каждое из уравнений этой системы определяет плоскость.
Если плоскости не параллельны (координаты векторов
п\ = (Ai\Bi\C\) и п2 = (А2;В2;С2) не пропорциональны),
то система (12.15) определяет прямую L как геометрическое
место точек пространства, координаты которых удовлетво-
ряют каждому из уравнений системы (см. рис. 77). Уравне-
ния (12.15) называют общими уравнениями прямой.
От общих уравнений (12.15) можно перейти к канониче-
ским уравнениям (12.13). Координаты точки Mq на прямой
Рис. 77. L получаем из системы уравнений (12.15), придав одной из
координат произвольное значение (например, z = 0).
Так как прямая L перпендикулярна векторам щ и п2, то за направля-
ющий вектор S прямой L можно принять векторное произведение п\ x п2:
Замечание: Канонические уравнения прямой легко получить, взяв две
какие-либо точки на ней и применив уравнения (12.14).
84

a
Пример 12.1. Написать канонические уравнения прямой L, заданной
уравнениями
12.5. Прямая линия в пространстве. Основные задачи
Угол между прямыми. Условия параллельности и перпендикулярности прямых
Пусть прямые L\ и Li заданы уравнениями
га2 п2 pi
Под углом между этими прямыми понимают угол
между направляющими векторами S\ — {т\\п\\р\)
и S-2 = {гп2\П2\Р2) (см. рис. 78). Поэтому, по извест-
ной формуле для косинуса угла между векторами,
(12.16)
Для нахождения острого угла между прямыми L\ и L2 числитель правой
части формулы (12.16) следует взять по модулю.
Если прямые L\ u L2 перпендикулярны, то в этом и только в этом
случае имеем cosy? = 0. Следовательно, числитель дроби (12.16) равен
нулю, т. е. mim-2 + п\П2 + Р\Р2 = 0.
Если прямые L\ и L,2 параллельны, то параллельны их направляющие
векторы S\ и S2- Следовательно, координаты этих векторов пропорцио-
нальны, т. е. ^ = ^- = 2L.
га-2 П2 Р2
85
/-ч I х + у = —1,
Q} Решение: Положим z = 0 и решим систему < Находим
I 2х - у — -5.
{х — z = —1,
2х - 3z = -5.
Находим вторую точку М2(2;0;3) прямой L. Записываем уравнение пря-
мой L, проходящей через точки М\ и А^:
Пример 12.2. Найти угол между прямыми
получаем cosy?
или

О Решение: Очевидно, S\ = (2; —1;3), а 5-2 = п\ х П2, где п\ — (2; 1; —1),
п-2 = (2; —1; 3). Отсюда следует, что 52 = (2;—8;—4). Так как Si-So =
= 4 + 8-12 = 0, то v? = 90°. •
Условие, при котором две прямые лежат в одной плоскости
Пусть прямые L\ и L-2 заданы каноническими уравнениями
Рис. 79.
Их направляющие векторы соответственно 5i =
= (mi;ni;pi) и 52 = (га2;п2;р2) (см. рис. 79).
Прямая L\ проходит через точку M\{x\\y\\z\),
радиус-вектор которой обозначим через ?\; прямая L2
проходит через точку Мг^гг; 2/2 5 ^), радиус-вектор ко-
торой обозначим через f2. Тогда
Прямые L\ и L-2 лежат в одной плоскости, если векторы Si, S2 и
М\М-2 = f2 — П компланарны. Условием компланарности векторов явля-
ется равенство нулю их смешанного произведения: (г2 — n)SiS2 = 0, т. е.
При выполнении этого условия прямые Li и L2 лежат в одной плоско-
сти, то есть либо пересекаются, если 52 Ф ASi, либо параллельны, если
Si II 52.
12.6. Прямая и плоскость в пространстве. Основные задачи
Угол между прямой и плоскостью. Условия параллельности
и перпендикулярности прямой и плоскости
Пусть плоскость Q задана уравнением Ах+
+ By + Cz + D — 0, а прямая L уравнениями
х - .то _ у - у о _ z - zp
т п Р
Углом между прямой и плоскостью называет-
ся любой из двух смежных углов, образованных
прямой и ее проекцией на плоскость. Обозначим
через if угол между плоскостью Q и прямой L,
а через в — угол между векторами п = (А; В; С)
и S = (т;п;р) (см. рис. 80). Тогда cos# = j
= -, ' Л^| • Найдем синус угла </?, считая ip ^ ^:
Рис. 80.
86
и

sin c^ = sin(f — в) = cos#. И так как sin c^ ^ 0, получаем
(12.17)
Если прямая L параллельна плоскости Q, то векторы п и 5 перпенди-
кулярны (см. рис. 81), а потому S • п = 0, т. е.
Лга + Вп + Ср = О
является условием параллельности прямой и плоскости.
Рис. 81.
Рис. 82.
являются условиями перпендикулярности прямой и плоскости.
Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости
Пусть требуется найти точку пересечения прямой
(12.18)
с плоскостью
Для этого надо решить систему уравнений (12.18) и (12.19). Проще всего
это сделать, записав уравнения прямой (12.18) в параметрическом виде:
Подставляя эти выражения для х, у и z в уравнение плоскости (12.19),
получаем уравнение A(xq + mt) + В(уо + nt) + C(zq + pt) + D = 0 или
87
Если прямая L перпендикулярна плоскости Q, то векторы п и 5 па-
раллельны (см. рис. 82). Поэтому равенства
Если прямая L не параллельна плоскости, т. е. если Am + Вп + Ср Ф О,

то из равенства (12.20) находим значение t:
12.7. Цилиндрические поверхности
Рис. 83.
Поверхность, образованная движением прямой L, которая перемеща-
ется в пространстве, сохраняя постоянное направление и пересекая ка-
ждый раз некоторую кривую К, называется цилиндрической поверх-
ностью или цилиндром. При этом кривая К называется направляю-
щей цилиндра, а прямая L — его образующей (см. рис. 83).
Будем рассматривать цилиндрические поверхности, на-
правляющие которых лежат в одной из координатных плос-
костей, а образующие параллельны координатной оси, пер-
пендикулярной этой плоскости.
Пусть в плоскости Оху лежит некоторая линия А', урав-
нение которой
Теорема 12.1. Уравнение цилиндра, образующие которого параллельны оси Oz,
имеет вид (12.21), т. е. не содержит координаты z.
Рис. 84.
Q Возьмем на цилиндре любую точку М(х',у; z)
(см. рис. 84). Она лежит на какой-то образующей.
Пусть N ■— точка пересечения этой образующей
с плоскостью Оху. Следовательно, точка Лг ле-
жит на кривой К и ее координаты удовлетворяют
уравнению (12.21).
88
Подставляя найденное значение t в параметрические уравнения прямой,
найдем координаты точки пересечения прямой с плоскостью.
Рассмотрим теперь случай, когда Am + Вп + Ср — 0 (L || Q):
а) если F = Axq + Вуо + Czq + D ф 0, то прямая L параллельна
плоскости и пересекать ее не будет (уравнение (12.20) решения не имеет,
так как имеет вид 0 • £ + F = 0, где F ф 0);
б) если Ахо + Вуо + Cz$ + D = 0, то уравнение (12.20) имеет вид
t • 0 + 0 = 0; ему удовлетворяет любое значение t, любая точка прямой
является точкой пересечения прямой и плоскости. Заключаем: прямая
лежит в плоскости. Таким образом, одновременное выполнение равенств
является условием принадлежности прямой плоскости.
Построим цилиндр с образующими параллельными оси Oz
и направляющей А\

Но точка М имеет такие же абсциссу х и ординату у, что и точка
N. Следовательно, уравнению (12.21) удовлетворяют и координаты точки
M(x;y;z), так как оно не содержит z. И так как М -— это любая точка
цилиндра, то уравнение (12.21) и будет уравнением этого цилиндра. В
Теперь ясно, что F(x; z) = 0 есть уравнение цилиндра с образующими,
параллельными оси Оу, a F(y; z) — 0 — с образующими, параллельными
оси Ох. Название цилиндра определяется названием направляющей. Если
направляющей служит эллипс
Рис. 85.
Рис. 86.
Частным случаем эллиптического
цилиндра является круговой цилиндр,
его уравнение х2 + у2 = R2. Уравнение
х2 = 2pz определяет в пространстве па-
раболический цилиндр (см. рис. 86).
Уравнение
определяет в пространстве гиперболи-
ческий цилиндр (см. рис. 87).
Все эти поверхности называются
цилиндрами второго порядка, так
как их уравнения есть уравнения второй
степени относительно текущих коорди-
нат х, у и z.
Рис. 87.
12.8. Поверхности вращения. Конические поверхности
Поверхность, образованная вращением некоторой плоской кривой во-
круг оси, лежащей в ее плоскости, называется поверхностью вращения.
Пусть некоторая кривая L лежит в плоскости Oyz. Уравнения этой кривой
в плоскости Оху. то соответствующая цилиндрическая поверхность назы-
вается эллиптическим цилиндром (см. рис. 85).

запишутся в виде
(12.22)
Найдем уравнение поверхности, образованной вра-
щением кривой L вокруг оси Oz.
Возьмем на поверхности произвольную точку
M(x;y;z) (см. рис. 88). Проведем через точку М
плоскость, перпендикулярную оси Oz, и обозначим
точки пересечения ее с осью Oz и кривой L соответ-
ственно через 0\ и N. Обозначим координаты точ-
ки N через (0;yi;zi). Отрезки 0\М \\0\N являют-
ся радиусами одной и той же окружности. Поэто-
му ОхМ = OiN. Но ОхМ = \/х2+у2, OxN = \У1\.
Следовательно, \у\\ = \Jx2 + у2 или у\ = ±у/х2 + у2. Кроме того, очевид-
но, Z\ — Z.
Так как точка N лежит на кривой L, то ее координаты удовлетворяют
уравнению (12.22). Стало быть, F(y\\z\) = 0. Исключая вспомогательные
координаты у\ и z\ точки N, приходим к уравнению
Рис. 88.
(12.23)
Уравнение (12.23) — искомое уравнение поверхности вращения, ему удо-
влетворяют координаты любой точки М этой поверхности и не удовлетво-
ряют координаты точек, не лежащих на поверхности вращения.
Как видно, уравнение (12.23) получается
из (12.22) простой заменой у на ±у/х2 + у2,
координата z сохраняется.
Понятно, что если кривая (12.22) враща-
ется вокруг оси Оу, то уравнение поверхно-
сти вращения имеет вид
Рис. 89.
если кривая лежит в плоскости Оху (z = 0)
и ее уравнение F(x\y) = 0, то уравнение
поверхности вращения, образованной вра-
щением кривой вокруг оси Ох, есть
F(x;±y/y* + z2) = 0.
Так. например, вращая прямую у — z во-
круг оси Oz (см. рис. 89), получим поверх-
ность вращения (ее уравнение ± \Jx2 + у2 — z
или х2 4- у2 = z2). Она называется конусом второго порядка.
Поверхность, образованная прямыми линиями, проходящими через
данную точку Р и пересекающими данную плоскую линию L (не прохо-
дящую через Р), называется конической поверхностью или конусом.
При этом линия L называется направляющей конуса, точка Р — ее вер-
шиной, а прямая, описывающая поверхность, называется образующей.
90

(12.24)
Исключая х\, у\ и z\ из уравнений (12.25) и (12.26), получим уравнение
конической поверхности, связывающее текущие координаты х, у и z.
Пример 12.3. Составить уравнение конуса с вершиной в точке О(0; 0; 0),
г2 у2
если направляющей служит эллипс ^ + 77 = 1, лежащий в плоскости
а о
z — с.
Q Решение: Пусть М(х; t/; z) — любая точка конуса. Канонические урав-
нения образующих, проходящих через точки (0; 0; 0) и точку [x\\y\\z\)
пересечения образующей ОМ с эллипсом будут — = ->*- = —. Исключим
#i ? 2/1 и zi из этих уравнений и уравнения
(12.27)
(точка (x\]yi;zi) лежит на эллипсе), z\ — с. Имеем: -£- = £,-*- = £.
Х\ С У\ С
Отсюда х\ = с • — и ?/1 — с^-. Подставляя значения х\ и у\ в уравнение
эллипса (12.27), получим
Это и есть искомое уравнение конуса.
12.9. Канонические уравнения поверхностей второго порядка
По заданному уравнению поверхности второго порядка (т. е. поверх-
ности, уравнение которой в прямоугольной системе координат является
алгебраическим уравнением второй степени) будем определять ее геоме-
91
а точка Р(хо;2/о; го) — вершина конуса. Найдем
уравнение конуса.
Возьмем на поверхности конуса произвольную
точку M{x\y\z) (см. рис. 90). Образующая, прохо-
дящая через точки РиМ, пересечет направляю-
щую L в некоторой точке N(x\\y\; z\). Координаты
точки N удовлетворяют уравнениям (12.24) напра-
вляющей: ,
Пусть направляющая L задана уравнениями
гис. JU. Канонические уравнения образующих, проходящих
через точки Р и 7V, имеют вид

трический вид. Для этого применим так называемый метод сечений: ис-
следование вида поверхности будем производить при помощи изучения ли-
ний пересечения данной поверхности с координатными плоскостями или
плоскостями, им параллельными.
Эллипсоид
Исследуем поверхность, заданную уравнением
(12.28)
Рассмотрим сечения поверхности (12.28) с плоскостями, параллельными
плоскости хОу. Уравнения таких плоскостей: z = h, где h — любое число.
Линия, получаемая в сечении, определяется двумя уравнениями
(12.29)
Исследуем уравнения (12.29):
2 у2
а) Если |/i|>c, c>0, то^ + ^з" < 0. Точек пересечения поверхно-
сти (12.28) с плоскостями z = h не существует.
б) Если |/i| = с, т. е. h = ±с, то ^ + ^ = 0. Линия пересечения (12.29)
вырождается в две точки (0;0;с) и (0;0;— с). Плоскости z = с и z = —с
касаются данной поверхности.
в) Если |ft| < с, то уравнения (12.29) можно переписать в виде:
Как видно, линия пересечения есть эллипс с полу-
осями (см. рис. 91)
Рис. 91.
При этом чем меньше |Л|, тем больше полуоси а\
и Ь\. При h = 0 они достигают своих наибольших
значений: а\ = а, Ь\ = Ъ. Уравнения (12.29) примут вид
Аналогичные результаты получим, если рассмотрим сечения поверхности
(12.28) плоскостями х — h и у — h.
Таким образом, рассмотренные сечения позволяют изобразить поверх-
ность (12.28) как замкнутую овальную поверхность. Поверхность (12.28)
называется эллипсоидом. Величины а, Ь и с называются полуосями эл-
92

липсоида. Если все они различны, то эллипсоид называется трехосным;
если какие-либо две полуоси равны, трехосный эллипсоид превращается
в эллипсоид вращения; если а = Ъ — с, то — в сферу х2 + у2 + z2 = а2.
Однополостный гиперболоид
Исследуем поверхность, заданную уравнением
(12.30)
Пересекая поверхность (12.30) плоскостью г = h, получим линию пересе-
чения, уравнения которой имеют вид
Как видно, этой линией является эллипс с полуосями
Рис. 92.
Полуоси а\ и Ь\ достигают своего наименьшего значения при
h — 0: а\ = a, bi = Ь. При возрастании |Л| полуоси эллипса
будут увеличиваться.
Если пересекать поверхность (12.30) плоскостями х — h
или у = h, то в сечении получим гиперболы. Найдем, напри-
мер, линию пересечения поверхности (12.30) с плоскостью Оуz,
уравнение которой х = 0. Эта линия пересечения описывается
УПЯЙНРНИЯММ
Как видно, эта линия есть гипербола (см. рис. 92).
Анализ этих сечений показывает, что поверхность, определяемая урав-
нением (12.30), имеет форму бесконечной расширяющейся трубки. Поверх-
ность (12.30) называется однополостпным гиперболоидом.
Замечание: можно доказать, что через любую точку гиперболоида
(12.30) проходят две прямые, лежащие на нем.
Двухполостный гиперболоид
Пусть поверхность задана уравнением
(12.31)
(12.32)
93
Если поверхность (12.31) пересечь плоскостями z — h, то линия пересече-
ния определяется уравнениями

Отсюда следует, что:
а) если |Л| < с, то плоскости z = h не пересекают поверхности;
б) если \h\ = с, то плоскости z — ±с касаются данной поверхности
соответственно в точках (0;0;с) и (0;0; —с).
в) если |Л| > с, то уравнения (12.32) могут
быть переписаны так
Рис. 93.
У обеих гипербол действительной осью является ось Oz. Метод сечения
позволяет изобразить поверхность (см. рис. 93), определяемую уравнени-
ем (12.31), как поверхность, состоящую из двух полостей, имеющих форму
выпуклых неограниченных чаш. Поверхность (12.31) называется двухпо-
лостным гиперболоидом.
Эллиптический параболоид
Исследуем поверхность, заданную уравнением
(12.33)
Рис. 94
94
Эти уравнения определяют эллипс, полуоси ко-
торого возрастают с ростом \h\.
Пересекая поверхность (12.31) координат-
ными плоскостями Oyz (х — 0) и Oxz (у = 0),
получим в сечении гиперболы, уравнения кото-
рых соответственно имеют вид
гдер > 0, q > 0. Рассечем поверхность (12.33) плоскостями
z = h. В сечении получим линию, уравнения которой есть
V
Если h < 0, то плоскости z — h поверхности не пересека-
ют; если h — 0, то плоскость z — 0 касается поверхности
в точке (0;0;0); если h > 0, то в сечении имеем эллипс,
уравнение которого имеет вид
Его полуоси возрастают с ростом h.
При пересечении поверхности (12.33) координатными плоскостями
2 -2
Oxz и Oyz получатся соответственно параболы z = Ц- и z = ^-. Таким
образом, поверхность, определяемая уравнением (12.33), имеет вид выпук-
лой, бесконечно расширяющейся чаши (см. рис. 94). Поверхность (12.33)
называется эллиптическим параболоидом.

Гиперболический параболоид
Исследуем поверхность, определяемую уравнением
(12.34)
где р > 0, q > 0. Рассечем поверхность (12.34) плоскостями z = h. Получим
кривую
Рис. 95.
Нч| Анализ линии пересечения позволяет определить вид поверхности: она
'—■ имеет вид седла (см. рис. 95). Поверхность (12.34) называется гипербо-
лическим параболоидом.
Конус второго порядка
Исследуем уравнение поверхности
(12.35)
Пересечем поверхность (12.35) плоскостями z = h. Линия пересечения
2 2 l 2
^2 + Нт — ^i-> z — h- При /i = 0 она вырождается в точку (0;0;0). При
ft/Ов сечении будем получать эллипсы
95
которая при всех значениях h ф О является гиперболой. При h > 0 ее
действительные оси параллельны оси Ох; при h < 0 — параллельны оси
2 ^2
Cty; при h = 0 линия пересечения - *- = О распадается на пару пе-
ресекающихся прямых -у= 4= = 0 и -у= + -^= = 0. При пересечении
поверхности плоскостями, параллельными плоскости Oxz (у = /г), будут
получаться параболы е
ветви которых направлены вверх. При у = 0
в сечении получается парабола
с вершиной в начале координат и осью сим-
метрии Oz.
Пересекая поверхность (12.34) плос-
костями х = /г, получим параболы у2 —
= — 2q(z — тр ), ветви которых направлены
вниз.

также распадающуюся на две пересе-
кающиеся прямые
Рис. 96.
Поверхность, определяемая уравнени-
ем (12.35), называется конусом второго порядка, имеет вид, изобра-
женный на рисунке 96.
Поверхности, составленные из прямых линий, называются линейча-
тыми. Такими поверхностями являются цилиндрические, конические по-
верхности, а также однополостный гиперболоид и гиперболический пара-
болоид.
Полуоси этих эллипсов будут возрастать при возрастании \h\.
Рассечем поверхность (12.35) плос-
костью Oyz (х — 0). Получится линия
распадающаяся на две пересекающие-
ся прямые
При пересечении поверхности (12.35)
плоскостью у — 0 получим линию

Глава V. ВВЕДЕНИЕ В АНАЛИЗ
Лекции 13-22 I
§13. МНОЖЕСТВА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
13.1. Основные понятия
К| Понятие множества является одним из основных неопределяемых по-
*—* нятий математики. Под множеством понимают совокупность (собра-
ние, класс, семейство...) некоторых объектов, объединенных по какому-
либо признаку. Так можно говорить о множестве студентов института, о
множестве рыб в Черном море, о множестве корней уравнения х2 +2x-f 2 =
= 0, о множестве всех натуральных чисел и т. д.
Объекты, из которых состоит множество, называются его элемен-
тами. Множества принято обозначать заглавными буквами латинского
алфавита А, В,..., X, У,..., а их элементы — малыми буквами а, 6,...
...,£,?/,...
Если элемент х принадлежит множеству X, то записывают х Е Л";
запись хёХ или х £ X означает, что элемент х не принадлежит множеству
X.
Множество, не содержащее ни одного элемента, называется пустым,
обозначается символом 0.
Элементы множества записывают в фигурных скобках, внутри кото-
рых они перечислены (если это возможно), либо указано общее свойство,
которым обладают все элементы данного множества.
Например, запись А = {1,3,15} означает, что множество А состоит из
трех чисел 1, 3 и 15; запись А = {х : 0 ^ х ^ 2} означает, что множе-
ство А состоит из всех действительных (если не оговорено иное) чисел,
удовлетворяющих неравенству 0 ^ х ^ 2.
К| Множество А называется подмножеством множества В, если ка-
*—■ ждый элемент множества А является элементом множества В. Символи-
чески это обозначают так А С В («А включено в В») или В D А («мно-
жество В включает в себя множество А»).
Говорят, что множества А и В равны или совпадают, и пишут А=В,
если А С В и В С А. Другими словами, множества, состоящие из одних и
тех же элементов, называются равными.
нч| Объединением (или суммой) множеств А и В называется множество,
*—' состоящее из элементов, каждый из которых принадлежит хотя бы одному
из этих множеств. Объединение (сумму) множеств обозначают АиВ (или
Ал- В). Кратко можно записать AU В = {х : х Е А или х Е В}.
н\| Пересечением (или произведением) множеств А и В называется мно-
'—' жество, состоящее из элементов, каждый из которых принадлежит множе-
ству А и множеству В. Пересечение (произведение) множеств обозначают
АПВ (или А-В). Кратко можно записать АПВ = {х : х € А и я Е В}.
В дальнейшем для сокращения записей будем использовать некоторые
простейшие логические символы:
97

Множество Е содержит рациональные и иррациональные числа. Вся-
кое рациональное число выражается или конечной десятичной дробью
или бесконечной периодической дробью. Так, ^ = 0,5 (= 0,500...), А =
= 0,333 ... — рациональные числа.
Действительные числа, не являющиеся рациональными, называются
иррациональными.
Теорема 13.1. Не существует рационального числа, квадрат которого равен
числу 2.
Q Допустим, что существует рациональное число, представленное несо-
кратимой дробью —, квадрат которого равен 2. Тогда имеем:
98
Отсюда следует, что т2 (а значит, и т) — четное число, т. е. т = 2к. Под-
ставив га — 2к в равенство га2 = 2п2, получим 4к2 = 2п2, т. е. 2к2 = п2.
Отсюда следует, что число п — четное, т. е. п = 21. Но тогда дробь — = Щ
сократима. Это противоречит допущению, что — дробь несократима. Сле-
довательно, не существует рационального числа, квадрат которого равен
числу 2. И
а => 3 — означает «из предложения а следует предложение /?»;
а <£=> /3 — «предложения а и /3 равносильны», т. е. из а следует 3 и
из в следует а;
V — означает «для любого», «для всякого»;
3 — «существует», «найдется»;
: — «имеет место», «такое что»;
I-» — «соответствие».
Например: 1) запись Vx G А : а означает: «для всякого элемента х € А
имеет место предложение а»:
2) (х £ A U В) <=> (х е А или х е В); эта запись определяет
объединение множеств А и В.
13.2. Числовые множества. Множество действительных чисел
Множества, элементами которых являются числа, называются число-
выми. Примерами числовых множеств являются:
N = {1; 2; 3; ...; п; ...} — множество натуральных чисел;
Zq = {0; 1; 2; ...; /г; ... } — множество целых неотрицательных чисел;
Ъ — {0; ±1; ±2; ...; ±п; ... } — множество целых чисел;
Q= < — : m£Z,n(zN> — множество рациональных чисел.
Е — множество действительных чисел.
Между этими множествами существует соотношение

3. Множество R непрерывное. Пусть множество Ш разбито на два непу-
стых класса А и В таких, что каждое действительное число содержится
только в одном классе и для каждой пары чисел a Е А и Ь Е В выполнено
неравенство а < Ь. Тогда (свойство непрерывности) существует единствен-
ное число с, удовлетворяющее неравенству а ^ с ^ Ь (Va Е A, Vb E В).
Оно отделяет числа класса А от чисел класса В. Число с является либо
наибольшим числом в классе А (тогда в классе В нет наименьшего числа),
либо наименьшим числом в классе В (тогда в классе А нет наибольшего).
Свойство непрерывности позволяет установить взаимно-однозначное
соответствие между множеством всех действительных чисел и множеством
всех точек прямой. Это означает, что каждому числу xGl соответствует
определенная (единственная) точка числовой оси и, наоборот, каждой точ-
ке оси соответствует определенное (единственное) действительное число.
Поэтому вместо слова «число» часто говорят «точка».
13.3. Числовые промежутки. Окрестность точки
Пусть а и b — действительные числа, причем а <Ь.
Числовыми промежутками (интервалами) называют подмножества
всех действительных чисел, имеющих следующий вид:
[а;Ь] — {х : а ^ х ^ 6} — отрезок (сегмент, замкнутый промежуток);
(а; Ь) = {х : а < х < Ь} — интервал (открытый промежуток);
[а;Ь) = {х : а ^ х < Ь};
(а; Ь] = {х : а < х ^ Ь} — полуоткрытые интервалы (или полуоткры-
тые отрезки);
(—сю; Ь] = {х : х ^ Ь}; [а, +со) = {х : х ^ а};
(-оо; Ь) = {х : х < Ь}; (а, +оо) = {х : х > а};
(—оо, ос) = {х : —оо < х < +оо} = Е — бесконечные интервалы
(промежутки).
99
Множество Ш действительных чисел обладает следующими свойства-
ми.
1. Оно упорядоченное: для любых двух различных чисел а и Ь имеет
место одно из двух соотношений а < b либо b < а.
2. Множество Ш плотное: между любыми двумя различными числами
а и b содержится бесконечное множество действительных чисел х, т. е.
чисел, удовлетворяющих неравенству а < х < Ь.
Так, если а < 6, то одним из них является число а'Т
Иррациональное число выражается бесконечной непериодической дро-
бью. Так, уД = 1,4142356 ..., тг = 3,1415926... — иррациональные числа.
Можно сказать: множество действительных чисел есть множество всех
бесконечных десятичных дробей. И записать

Числа а и b называются соответственно левым и правым концами этих
промежутков. Символы —ос и +оо не числа, это символическое обозначе-
ние процесса неограниченного удаления точек числовой оси от начала О
влево и вправо.
Пусть хо -- любое действительное число (точка на числовой прямой).
Окрестностью точки хо называется любой интервал (а; 6), содержащий
точку хо- В частности, интервал (хо — £,#о + £)> где е > О, называется г-
окрестностью точки хо. Число хо называется центром, а число е —
радиусом.
Рис. 97.
Если х £ (хо—£;хо + е), то выполняется неравенствохо — £ < х < £о+£,
или, что то же, \х — Хо\ < е. Выполнение последнего неравенства означает
попадание точки х в ^-окрестность точки xq (см. рис. 97).
§14. ФУНКЦИЯ
14.1. Понятие функции
Одним из основных математических понятий является понятие функ-
ции. Понятие функции связано с установлением зависимости (связи) ме-
жду элементами двух множеств.
Пусть даны два непустых множества X и Y. Соответствие /, которое
каждому элементу х G X сопоставляет один и только один элемент у G У,
называется функцией и записывается у = f(x), x G X или / : X -> Y.
Говорят еще, что функция / отобраэюает множество Аг на множество Y.
Рис. 98.
Например, соответствия fug, изображенные на рисунке 98 а и б,
являются функциями, а на рисунке 98 в и г — нет. В случае в — не
каждому элементу х € X соответствует элемент у Е Y. В случае г не
соблюдается условие однозначности.
100

Множество X называется областью определения функции / и обозна-
чается D(f). Множество всех у £ Y называется множеством значений
функции / и обозначается E(f).
Числовые функции. График функции.
Способы задания функций
Пусть задана функция / : X —> Y.
Если элементами множеств X и Y являются действительные числа
(т. е. X С R и Y С R), то функцию / называют числовой функцией. В
дальнейшем будем изучать (как правило) числовые функции, для крат-
кости будем именовать их просто функциями и записывать у = f(x).
Переменная х называется при этом аргументом или независимой пе-
ременной, а у — функцией или зависимой переменной (от х). Относитель-
но самих величин хну говорят, что они находятся в функциональной
зависимости. Иногда функциональную зависимость у от х пишут в виде
у = у(х), не вводя новой буквы (/) для обозначения зависимости.
Частное значение функции f(x) при х — а записывают так: f(a). На-
пример, если f(x) = 2х2 - 3, то /(0) = -3, /(2) = 5.
Графиком функции у = f(x) называется мно-
жество всех точек плоскости Оху, для каждой из
которых х является значением аргумента, а у —
соответствующим значением функции.
ччМ(а;;у) Например, графиком функции у = у/1 — х2 яв-
ляется верхняя полуокружность радиуса R = 1 с
центром в О(0; 0) (см. рис. 99).
Чтобы задать функцию у = /(х), необходимо
указать правило, позволяющее, зная х, находить со-
ответствующее значение у.
Наиболее часто встречаются три способа зада-
ния функции: аналитический, табличный, графический.
Аналитический способ: функция задается в виде одной или несколь-
ких формул или уравнений.
Например:
Если область определения функции у = f(x) не указана, то предпо-
лагается, что она совпадает с множеством всех значений аргумента, при
которых соответствующая формула имеет смысл. Так, областью опреде-
ления функции у = у/1 — х2 является отрезок [—1; 1].
Аналитический способ задания функции является наиболее совершен-
ным, так как к нему приложены методы математического анализа, позво-
ляющие полностью исследовать функцию у = f(x).
Графический способ: задается график функции.
101

Часто графики вычерчиваются автоматически самопишущими прибо-
рами или изображаются на экране дисплея. Значения функции т/, соот-
ветствующие тем или иным значениям аргумента х, непосредственно на-
ходятся из этого графика.
Преимуществом графического задания является его наглядность, не-
достатком — его неточность.
Табличный способ: функция задается таблицей ряда значений аргу-
мента и соответствующих значений функции. Например, известные табли-
цы значений тригонометрических функций, логарифмические таблицы.
На практике часто приходится пользоваться таблицами значений
функций, полученных опытным путем или в результате наблюдений.
14.3. Основные характеристики функции
1. Функция у = f(x), определенная на множестве £>, называется чет-
ной, если \ix £ D выполняются условия — х G D и f(—x) = /(x); нечет-
ной, если Vx Е £> выполняются условия —х Е -D и f(—x) = —f(x).
График четной функции симметричен относительно оси Оу, а нечет-
ной — относительно начала координат.
Например, у = х2, у = у/1 + х2, 2/ = In jx| — четные функции; а
2/ = sinx, t/ = х3 — нечетные функции; 2/ = х — 1, ?/ = у/х — функции
общего вида, т. е. не четные и не нечетные.
2. Пусть функция y = f(x) определена на множестве D и пусть D\ С D.
Если для любых значений х\,х-2 £ D\ аргументов из неравенства Xi < х-2
вытекает неравенство: f(x\) < /(#2)? то
функция называется возрастающей на
множестве D\\ f(x\) ^ /(хг), то функ-
ция называется неубывающей на мно-
жестве D\\ f{x\) > /(#2)» то функция на-
зывается убывающей на множестве D\\
/(#1) ^ /(^г), то функция называется
невозрастающей на множестве £>i.
Например, функция, заданная графи-
ком (см. рис. 100), убывает на интерва-
ле (—2; 1), не убывает на интервале (1; 5),
возрастает на интервале (3;5).
Возрастающие, невозрастающие, убывающие и неубывающие функции
на множестве D\ называются монотонными на этом множестве, а воз-
растающие и убывающие — строго монотонными. Интервалы, в кото-
рых функция монотонна, называются интервалами монотонности.
На рисунке (выше) функция строго монотонна на (—2; 1) и (3; 5); монотон-
на на (1;3).
3. Функцию у = /(х), определенную на множестве D, называют огра-
ниченной на этом множестве, если существует такое число М > 0, что
для всех х Е D выполняется неравенство |/(х)| ^ М (короткая запись:
у = /(х), х £ D, называется ограниченной на D, если ЗМ >0 : VxE D =>
102

=^ 1/(^)1 ^ hf). Отсюда следует, что график ограниченной функции
лежит между прямыми у = —М и у = М (см. рис. 101).
4. Функция у — f{x), определенная
на множестве Z), называется перио-
дической на этом множестве, если су-
ществует такое число Т > 0, что при
каждом х € D значение (х + Т) £ D
и /(.г + Т) = /(ж). При этом число Т
называется периодом функции. Если
Т — период функции, то ее периода-
ми будут также числа га • Т, где га =
= ±1; ±2,... Так, для у = sin а: пери-
одами будут числа ±27г; ±47г; ±67Г,...
Основной период (наименьший поло-
жительный) — это период Т = 27г. Во-
обще обычно за основной период берут наименьшее положительное число
Г, удовлетворяющее равенству f(x + T) = f(x).
Рис. 101.
Рис. 102.
14.4. Обратная функция
Пусть задана функция у = f(x) с областью определения D и множе-
ством значений Е. Если каждому значению у £ Е соответствует един-
ственное значение х £ D, то определена функ-
ция х = (р(у) с областью определения Е и мно-
жеством значений D (см. рис. 102). Такая функ-
ция if {у) называется обратной к функции
f(x) и записывается в следующем виде: х =
= ф(у) = f~l(y)- Про функции у = f(x) и х =
= tp(y) говорят, что они являются взаимно об-
ратными. Чтобы найти функцию х = ip(y), об-
ратную к функции у = f(x), достаточно решить
уравнение f(x) = y относительно х (если это возможно).
Примеры:
1. Для функции у — 2х обратной функцией является функция х = ky:
2. Для функции у = х2, х £ [0; 1], обратной функцией является х = у/у;
заметим, что для функции у = я2, заданной на отрезке [—1; 1], обратной
не существует, т. к. одному значению у соответствует два значения х (так,
если у = 1, то хх = i, Х'2 = -^).
Из определения обратной функции вытекает, что функция у = f(x)
имеет обратную тогда и только тогда, когда функция f(x) задает взаимно
однозначное соответствие между множествами D и Е. Отсюда следует, что
любая строго монотонная функция имеет обратную. При этом
если функция возрастает (убывает), то обратная функция также возра-
стает (убывает).
Заметим, что функция у = f(x) и обратная ей х = <р(у) изображаются
одной и той же кривой, т. е. графики их совпадают. Если же условить-
103

ся, что, как обычно, независимую пере-
менную (т. е. аргумент) обозначить через
х, а зависимую переменную через у, то
функция обратная функции у = f(x) за-
пишется в виде у = ip(x).
Это означает, что точка Mi(xo',yo)
кривой у = f(x) становится точкой
М2{уо',х$) кривой у — (р(х). Но точки Mi
и М'2 симметричны относительно прямой
у — х (см. рис. 103). Поэтому графики
взаимно обратных функций у = f(x)
и у = <р(х) симметричны относи-
тельно биссектрисы первого и тре-
тьего координатных углов.
Рис. 103.
14.5. Сложная функция
Пусть функция у = f(u) определена на множестве D, а функция
и = ip(x) на множестве D\, причем для \/х € D\ соответствующее значение
и — (р(х) Е D. Тогда на множестве D\ определена функция у = f((p(x)),
которая называется слоэюной функцией от х (или суперпозицией за-
данных функций, или функцией от функции).
Переменную и = <р(х) называют промежуточным аргументом слож-
ной функции.
Например, функция у = sin 2x есть суперпозиция двух функций у —
— sin г/ и и — 2х. Сложная функция может иметь несколько промежуточ-
ных аргументов.
14.6. Основные элементарные функции и их графики
Основными элементарными функциями называют следующие функ-
ции.
1) Показательная функция у = ах, а > 0, а ф \. На рис. 104 показаны
графики показательных функций, соответствующие различным основани-
ям степени.
Рис. 104.
104

Рис. 105.
3) Логарифмическая функция у = logftx, а > 0, а ф 1; Графики лога-
рифмических функций, соответствующие различным основаниям, показа-
ны на рис. 106.
Рис. 106.
105
2) Степенная функция у — ха, а Е Е. Примеры графиков степен-
ных функций, соответствующих различным показателям степени, предо-
ставлены на рис. 105.

4) Тригонометрические функции у = sinx, у = cosx, у = tgx,
у = ctgx; Графики тригонометрических функций имеют вид, показанный
на рис. 107.
Рис. 107.
5) Обратные тригонометрические функции у = arcsinx, у = arccosx,
у = arctgx, у = arcctgx. На рис. 108 показаны графики обратных триго-
нометрических функций.
Рис. 108.
Функция, задаваемая одной формулой, составленной из основных эле-
ментарных функций и постоянных с помощью конечного числа арифме-
тических операций (сложения, вычитания, умножения, деления) и опера-
ций взятия функции от функции, называется элементарной функцией.
106

§15. ПОСЛЕДОВАТЕЛЬНОСТИ
15.1. Числовая последовательность
Под числовой последовательностью х\, я*2, х%,..., хп,... понима-
ется функция
заданная на множестве N натуральных чисел. Кратко последовательность
обозначается в виде {хп} или хп, п Е N. Число х\ называется первым
членом (элементом) последовательности, Х2 — вторым,..., хп — общим
или п-м членом последовательности.
Чаще всего последовательность задается формулой его общего члена.
Формула (15.1) позволяет вычислить любой член последовательности по
номеру п, по ней можно сразу вычислить любой член последовательности.
Так, равенства
В противном случае последовательность называется неограниченной. Лег-
ко видеть, что последовательности уп и ип ограничены, a vn и zn — не-
ограничены.
Последовательность {хп} называется возрастающей (неубываю-
щей), если для любого п выполняется неравенство хп+\ > хп (хп+\ ^ х,г).
Аналогично определяется убывающая (невозрастающая) последователь-
ность.
107
задают соответственно последовательности
Последовательность {хп} называется ограниченной, если существу-
ет такое число М > 0, что для любого п Е N выполняется неравенство
Примерами элементарных функций могут служить функции
Примерами неэлементарных функций могут служить функции

Все эти последовательности называются монотонными последова-
тельностями. Последовательности vn, уп и ип монотонные, a zn — не мо-
нотонная.
Если все элементы последовательности {хп} равны одному и тому же
числу с, то ее называют постоянной.
Другой способ задания числовых последовательностей — рекуррент-
ный способ. В нем задается начальный элемент х\ (первый член последо-
вательности) и правило определения тг-го элемента по (п — 1)-му:
Пример 15.1. Доказать, что lim ^1 = 1.
п—>оо 71
О Решение: По определению, число 1 будет пределом последовательности
хп = п ~ , п € N, если Ve > О найдется натуральное число 7V, такое, что
для всех п > N выполняется неравенство \п ~ — 1 < е, т. е. — < е. Оно
\ п \ п
справедливо для всех п > -, т. е. для всех п > N = - , где - — целая
часть числа - (целая часть числа х, обозначаемая [х], есть наибольшее
целое число, не превосходящее х; так [3] = 3, [5,2] = 5).
Если е > 1, то в качестве N можно взять - -hi.
Итак, Ve > 0 указано соответствующее значение N. Это и доказывает,
что lim ^=-± = 1. •
71—►ОС 71
108
Таким образом, х-2 = f(xi), хз = f(x-2) и т. д. При таком способе задания
последовательности для определения 100-го члена надо сначала посчитать
все 99 предыдущих.
15.2. Предел числовой последовательности
Можно заметить, что члены последовательности ип неограниченно
приближаются к числу 1. В этом случае говорят, что последовательность
ип, п G N стремится к пределу 1.
Число а называется пределом последовательности {хп}, если для
любого положительного числа е найдется такое натуральное число iV, что
при всех п > N выполняется неравенство
В этом случае пишут lim хп = \imxn = а или хп —У а и говорят, что по-
п—юо
следовательность {хп} (или переменная хп, пробегающая последователь-
ность х\, #2, хз,...) имеет предел, равный числу а (или хп стремится к а).
Говорят также, что последовательность {хп} сходится к а.
Коротко определение предела можно записать так:

Заметим, что число N зависит от е. Так, если е
если е — 0,01, то
Поэтому иногда записывают N = N(e).
Выясним геометрический смысл определения предела последователь-
ности.
Неравенство (15.2) равносильно неравенствам — а < хп — а < е или
а — г < хп < а + е, которые показывают, что элемент хп находится в
^-окрестности точки а.
Рис. 109.
Поэтому определение предела последовательности геометрически
можно сформулировать так: число а называется пределом последователь-
ности {хп}, если для любой ^-окрестности точки а найдется натуральное
число N. что все значения жп, для которых п > N, попадут в е-окрестность
точки а (см. рис. 109).
Ясно, что чем меньше г, тем больше число N, но в любом случае
внутри ^-окрестности точки а находится бесконечное число членов после-
довательности, а вне ее может быть лишь конечное их число.
Отсюда следует, что сходящаяся последовательность имеет
только один предел. Последовательность, не имеющая предела, назы-
вается расходящейся. Таковой является, например, последовательность
vn (см. с. 107).
Постоянная последовательность хп — с, п £ N имеет предел, равный
числу с, т. е. lim с — с. Действительно, для \/е > 0 при всех натуральных
п выполняется неравенство (15.2). Имеем \хп — с\ = \с — с\ = 0 < е.
15.3. Предельный переход в неравенствах
Рассмотрим последовательности {хп}, {уп} и {zn}.
Теорема 15.1. Если lim xn = a, lim yn = b и, начиная с некоторого номера,
п—юо п—юо
выполняется неравенство хп ^ уп, то а ^ Ь.
Q Допустим, что а > Ь. Из равенств lim xn = а и lim yn = b следует,
п—юо п—уос
что для любого е > 0 найдется такое натуральное число N(e), что при
109

всех п > N(e) будут выполняться неравенства \хп — а\ < е и \уп — Ь\ < е,
т. е. а — е < хп < а + е и b — е < уп < Ъ + е. Возьмем е — д^-. Тогда:
хп > а - е = а - *=*■ = *±*, т. е. хп > ^ и уп <Ъ + е = Ъ+<^ = *±*,
т. е. уп < д^. Отсюда следует, что хп > уп. Это противоречит условию
д:п ^ Уп- Следовательно, а ^ Ь. В
Теорема 15.2. Если lim хп = a, lim уп = а и справедливо неравенство хп ^
п—юс п—юо
^ ~« ^ Уп (начиная с некоторого номера), то lim zn = a.
(Примем без доказательства.)
15.4. Предел монотонной ограниченной последовательности.
Число е. Натуральные логарифмы
Не всякая последовательность имеет предел. Сформулируем без дока-
зательства признак существования предела последовательности.
Теорема 15.3 (Вейерштрасс). Всякая монотонная ограниченная последователь-
ность имеет предел.
В качестве примера на применение этого признака рассмотрим после-
довательность хп = м + — J , n E N.
По формуле бинома Ньютона
Полагая а = 1. Ъ — —, получим
ПО
или

ill
Из равенства (15.3) следует, что с увеличением п число положительных
слагаемых в правой части увеличивается. Кроме того, при увеличении п
число — убывает, поэтому величины (1 — — J, (1 — — J, ... возрастают.
Поэтому последовательность {хп} = < (1 + - 1 > — возрастающая, при
этом / * \п
Покажем, что она ограничена. Заменим каждую скобку в правой части
равенства (15.3) на единицу; правая часть увеличится, получим неравен-
ство 1 V J! 1 1 1
Усилим полученное неравенство, заменив числа 3, 4, 5,..., стоящие в зна-
менателях дробей, числом 2:
Сумму в скобке найдем по формуле суммы членов геометрической про-
грессии:
Поэтому
Итак, последовательность ограничена, при этом для Vn Е N выполняются
неравенства (15.4) и (15.5):
Следовательно, на основании теоремы Вейерштрасса последовательность
хп = (l + —1 , n E N, имеет предел, обозначаемый обычно буквой е:
Число е называют неперовым числом. Число е иррациональное, его при-
ближенное значение равно 2,72 (е = 2,718281828459045...). Число е при-
нято за основание натуральных логарифмов: логарифм по основанию е на-
зывается натуральным логарифмом и обозначается \пх, т. е. lnx = loge x.
Найдем связь между натуральным и десятичным логарифмами. По
определению логарифма имеем х — е1пх. Прологарифмируем обе части
равенства по основанию 10:
Пользуясь десятичными логарифмами, находим lge «0,4343. Значит,
\gx « 0,4343 • \пх. Из этой формулы следует, что \пх « п лчач ^х' т* е*
\пх « 2,3026 lg я. Полученные формулы дают связь между натуральными
и десятичными логарифмами.

ПРЕДЕЛ ФУНКЦИИ
Предел функции в точке
Пусть функция у — /(х) определена в некоторой окрестности точки
х$, кроме, быть может, самой точки Xq.
Сформулируем два, эквивалентных между собой, определения преде-
ла функции в точке.
Определение 1 (на «языке последовательностей», или по Гей-
не). Число А называется пределом функции у = /(х) в точке х0 (или
при х —> хо), если для любой последовательности допустимых значений
аргумента хп, п £ N (хп ф хо), сходящейся к хо (т. е. lim хп = хо), после-
п—уос
довательность соответствующих значений функции /(xn), n € N, сходится
к числу А (т. е. lim f(xn) — A).
?i—юо
В этом случае пишут lim f(x) — А или f(x) —> А при х —> xq. Гео-
Х—УХо
метрический смысл предела функции: lim f(x) — А означает, что для
х—ухо
всех точек х, достаточно близких к точке хо, соответствующие значения
функции как угодно мало отличаются от числа А.
Определение 2 (на «языке £-<5», или по Коши). Число А на-
зывается пределом функции в точке хо (или при х —> хо), если для
любого положительного е найдется такое положительное число (5, что для
всех х ф хо, удовлетворяющих неравенству \х — Хо| < (S, выполняется не-
равенство \f(x) — А\ < е.
Записывают lim f(x) = А. Это определение коротко можно записать
X—УХО
так:
Геометрический смысл предела
функции: А = lim /(x), если для лю-
Х—УХо
бой ^-окрестности точки А найдется та-
кая (5-окрестность точки хо, что для
всех х ф хо из этой J-окрестности соот-
ветствующие значения функции /(х)
лежат в е-окрестности точки А. Ины-
ми словами, точки графика функции
у = /(ж) лежат внутри полосы шириной
2е, ограниченной прямыми у = А + е,
у — А — е (см. рис. 110). Очевидно, что
величина 8 зависит от выбора £, поэто-
му пишут 8 = 8(e).
Рис. 110.
Пример 16.1. Доказать, что lim(2x — 1) = 5.
х—уЗ
112

О Решение: Возьмем произвольное е > О, найдем 6 — 6(e) > 0 такое,
что для всех х, удовлетворяющих неравенству |х — 3| < 6, выполняется
неравенство |(2х — 1) — 5| < £, т. е. |х — 3| < £. Взяв (5 = ^, видим, что
для всех х, удовлетворяющих неравенству |х — 3| < б( = ^ 1, выполняется
неравенство |(2х — 1) — 5| < е. Следовательно, lim(2x — 1) = 5. •
X —УЗ
Пример 16.2. Доказать, что, если f(x) = с, то lim с — с.
х—ухо
О Решение: Для Ve > 0 можно взять V<5 > 0. Тогда при \х — Xq\ < <5, х ф хо
имеем |/(х) — с\ — \с — с\ = 0 < е. Следовательно, lim с — с. •
X—УХо
Рис. 111.
16.2. Односторонние пределы
В определении предела функции
lim /(х) = А считается, что х стремит-
X—УХо
ся к хо любым способом: оставаясь мень-
шим, чем хо (слева от хо), большим, чем
хо (справа от хо), или колеблясь около
точки хо-
Бывают случаи, когда способ при-
ближения аргумента х к хо существен-
но влияет на значение предела функции.
Поэтому вводят понятия односторонних
пределов.
Число А\ называется пределом функции у = /(х) слева в точке
хо, если для любого число е > О существует число S = 6(e) > 0 такое,
что при х € (хо — S;xo), выполняется неравенство |/(х) — А\\ < е. Предел
слева записывают так: lim /(х) = А\ или коротко: /(хо — 0) = А\
х—>хо—О
(обозначение Дирихле) (см. рис. 111).
Аналогично определяется предел функции справа, запишем его с по-
мощью символов:
113
Коротко предел справа обозначают /(хо + 0) = Ai-
Пределы функции слева и справа называются односторонними пре-
делами. Очевидно, если существует lim /(x) = .4, то существуют и оба
х—>хо
односторонних предела, причем А = А\ = А}.
Справедливо и обратное утверждение: если существуют оба предела
/(хо - 0) и /(хо + 0) и они равны, то существует предел А — lim /(x) и
х—>хо
A = f(xo-0).
Если же А\ ф А-2, то lim /(x) не существует.
х—ухо

16.3. Предел функции при х —► оо
Пусть функция у = f(x) определена в промежутке (—ос; сю). Число
Л называется пределом функции f(x) при х -> ос, если для любого
положительного числа е существует такое число М = М(е) > О, что при
всех х, удовлетворяющих неравенству \х\ > М выполняется неравенство
\f(x) — А\ < е. Коротко это определение можно записать так:
Если #—>+оо, то пишут А= lim /(ж), если х—>— ос, то — Л= lim f(x).
х—>-+оо я—> —оо
Геометрический смысл этого определения таков: для Ve > О ЗА/ > 0, что
при х £ (—ос; — М) или х Е (М; +оо) соответствующие значения функции
f(x) попадают в е-окрестность точки А, т. е. точки графика лежат в полосе
шириной 2е, ограниченной прямыми у=А+еиу=А— е (см. рис. 112).
Рис. 112.
16.4. Бесконечно большая функция (б.б.ф.)
Функция у = f(x) называется бесконечно большой при х —> х0,
если для любого числа М > 0 существует число S = 5(М) > О, что для
всех х. удовлетворяющих неравенству 0 < \х — хо\ < 6, выполняется нера-
венство \f(x)\ > М. Записывают lim f(x) — ос или f(x)—>oo при х —>• хо-
Коротко:
Например, функция у = -—^-~ есть б.б.ф. при х —> 2.
Если /(х) стремится к бесконечности при х -> хо и принимает лишь
положительные значения, то пишут lim /(x) = +оо; если лишь отрица-
X—>Хо
тельные значения, то lim f(x) = — оо.
Х->Хо
Функция у = /(#), заданная на всей числовой прямой, называется бес-
конечно большой при х -» ос, если для любого числа А/ > 0 найдется
114

Например, у = 2х есть б.б.ф. при х -> ос.
Отметим, что если аргумент х, стремясь к бесконечности, принима-
ет лишь натуральные значения, т. е. х Е N, то соответствующая б.б.ф.
становится бесконечно большой последовательностью. Например, после-
довательность vn = ri2 + 1, п Е N, является бесконечно большой последо-
вательностью. Очевидно, всякая б.б.ф. в окрестности точки хо является
неограниченной в этой окрестности. Обратное утверждение неверно: не-
ограниченная функция может и не быть б.б.ф. (Например, у = #sin:r.)
Однако, если lim f(x) = А, где А — конечное число, то функция f(x)
ограничена в окрестности точки х$.
Действительно, из определения предела функции следует, что при
х —> хо выполняется условие \f(x) — А\ < е. Следовательно, А — е < f(x) <
< А + е при х Е (хо — е; хо + е), а это и означает, что функция f(x) огра-
ничена.
§17. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ (Б.М.Ф.)
17.1. Определения и основные теоремы
12^1 Функция у = f(x) называется бесконечно малой при х —>• хо, если
(17.1)
По определению предела функции равенство (17.1) означает: для любого
числа е > 0 найдется число 6 > 0 такое, что для всех х, удовлетворяющих
неравенству 0 < \х — хо\ < S, выполняется неравенство \f(x)\ < е.
Аналогично определяется б.м.ф. при х -» х$ + 0, х —>• хо — 0, х —> +оо,
х —>• —ос: во всех этих случаях f(x) -> 0.
Бесконечно малые функции часто называют бесконечно малыми вели-
чинами или бесконечно малыми; обозначают обычно греческими буквами
а, 3 и т. д.
Примерами б.м.ф. служат функции у — х2 при х —> 0; у = х — 2 при
х —> 2; у — sinx при # —> тгк, к Е Z.
Другой пример: xn = J, n 6 N, — бесконечно малая последователь-
ность.
Теорема 17.1. Алгебраическая сумма конечного числа бесконечно малых функций
есть бесконечно малая функция.
Q Пусть а(х) и /3(х) — две б.м. функции при х -+ Xq. Это значит, что
lim а(х) = 0, т. е. для любого € > 0, а значит, и § > 0 найдется число
х->хо 6
115
такое число N = N(M) > О, что при всех х, удовлетворяющих неравенству
|.г| > Лг, выполняется неравенство |/(х)| > А/. Коротко:

Аналогично проводится доказательство для любого конечного числа
б.м. функций.
Теорема 17.2. Произведение ограниченной функции на бесконечно малую функ-
цию есть функция бесконечно малая.
Обозначим через 8 наименьшее из чисел Si и 82- Тогда для всех я\
удовлетворяющих неравенству 0 < \х — xq\ < 8, выполняются оба неравен-
ства (17.4) и (17.5). Следовательно, \f(x)-a(x)\ = \f(x)\-\a(x)\ < jj-M = £.
А это означает, что произведение f(x) • а(х) при х -» .то есть бесконечно
малая функция. В
Следствие 17.1. Так как всякая б.м.ф. ограничена, то из теоремы (17.2) вытекает:
произведение двух б.м.ф. есть функция бесконечно малая.
пб
6\ >0 такое, что для всех х, удовлетворяющих неравенству 0<\x — xo\<8i,
выполняется неравенство
Пусть 8 — наименьшее из чисел 8\ и ($2. Тогда для всех х, удовлетво-
ряющих неравенству 0 < \х — хо\ < 8, выполняются оба неравенства (17.2)
и (17.3). Следовательно, имеет место соотношение
Таким образом,
Это значит, что lim (а(х) + (3(х)) = 0, т. е. а(х)Л-/5{х) —б.м.ф. при х —> xq.
X—*Xq
для всех х из 8\-окрестности точки xq. И пусть а(х) — б.м.ф. при х —> xq.
Тогда для любого е > О, а значит, и -jj > О найдется такое число #2 > О,
что при всех х, удовлетворяющих неравенству 0 < \х — хо\ < 8-2, выполня-
ется неравенство
Q Пусть функция f(x) ограничена при х —> хо. Тогда существует такое
число М > О, что

Следствие 17.2. Произведение б.м.ф. на число есть функция бесконечно малая.
Теорема 17.3. Частное от деления бесконечно малой функции на функцию, име-
ющую отличный от нуля предел, есть функция бесконечно малая.
[J Пусть lim а(х) = О, a lim /(х) = а ф 0. Функция Л '{ может быть
х—>xq х—ухо v J\x)
представлена в виде произведения б.м.ф. а(х) на ограниченную функцию
1 q(x) 1
л/ ч . Но тогда из теоремы (17.2) вытекает, что частное Л ( = ос(х) • утЦ-
есть функция бесконечно малая.
Покажем, что функция ,, ч ограниченная. Возьмем е < \а\. Тогда,
J\x)
на основании определения предела, найдется 6 > 0, что для всех х, удо-
влетворяющих неравенству 0 < \х — хо\ < S, выполняется неравенство
\f{x) - а\ < е. А так как е > \f{x) — а\ = \а — f{x)\ ^ \а\ - |/(х)|, то
И ~ \f(x)\ < ei т- е- 1/0*01 > |а| — е > 0. Следовательно,
т. е. функция А ч — ограниченная.
Теорема 17.4. Если функция а(х) — бесконечно малая (а ф 0), то функция \ .
ос(х)
есть бесконечно большая функция и наоборот: если функция f(x) — бесконечно
большая, то -rr^r — бесконечно малая.
/0*0
Q Пусть a(x) есть б.м.ф. при х —>• хо, т. е. lim а(х) = 0. Тогда
т. е. / ч > -, т. е. / ч > М, где М = -. А это означает, что функ-
|а(х)| £' |а(ж)| £ ' ^J
ция 7 ч есть бесконечно большая. Аналогично доказывается обратное
а(аг)
утверждение. ■
Замечание: Доказательства теорем приводились для случая, когда
х —¥ хо, но они справедливы и для случая, когда х —> оо.
Пример 17.1. Показать, что функция
при х —> 1 является бесконечно малой.
117

Q Решение: Так как lim(x — I)2 = О, то функция ^р(х) = (х — I)2 есть
х—>1
бесконечно малая при х —> 1. Функция д(х) = sin3 —^-j, х ф 1, ограничена
Функция f(x) = (х — I)2 • sin3 -——г представляет собой произведение
ограниченной функции (д(х)) на бесконечно малую (tp(x)). Значит, f(x) —
бесконечно малая при х —> 1. •
17.2. Связь между функцией, ее пределом и бесконечно малой
функцией
Теорема 17.5. Если функция f(x) имеем предел, равный А, то ее можно предста-
вить как сумму числа А и бесконечно малой функции а(х), т. е. если lim f(x) = A,
X—tTo.
то f(x) = А + а(:г).
т. е. !/(./•) — Л — 0\ < е. Это означает, что функция f(x) — А имеет пре-
дел, равный нулю, т. е. является б.м.ф., которую обозначим через а(х):
f(x) — А — а(х). Отсюда f(x) = A + а(х). Ш
Теорема 17.6 (обратная). Если функцию f(x) можно представить в виде суммы
числа А и бесконечно малой функции а(х), то число А является пределом функции
/(.г), т. е. если f{x) = А + а(х), то lim f(x) = A.
X-+XQ
А это и означает, что lim f(x) = А. Ш
Пример 17.2. Доказать, что lim (5 + х) = 7.
х—у 2
Q Решение: Функцию 5 + х можно представить в виде суммы числа 7 и
б.м.ф. х — 2 (при х —> 2), т. е. выполнено равенство 5 + х = 7 + (х — 2).
Следовательно, по теореме 17.6 получаем lim (5 + х) = 7. •
х—v2
118
Пусть lim f(x) = А. Следовательно,
.г—кг п
А так как по условию f(x) = А + а{х), то а(х) = f(x) — А. Получаем
Q Пусть f(x) = А + а(х), где а(х) ■—■■ б.м.ф. при х —> Хо, т. е. lim а(х) = 0.
Тогда

17.3. Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределов функ-
ции. Формулировка и доказательство теорем для случаев, когда х —> xq и
х -> ос, аналогичны. В приводимых теоремах будем считать, что пределы
lim f(x). lim <р(х) существуют.
X—>Xq .L'—tXQ
Теорема 17.7. Предел суммы (разности) двух функций равен сумме (разности) их
пределов:
lim {f{x) ±#(х)) = lim f(x) ± lim <p(x).
,Г->.Г0 X-*Xq X—*Xq
Q Пусть lim f(x) — A, lim ip(x) = В. Тогда по теореме 17.5 о связи
функции, ее предела и б.м.ф. можно записать f(x) -■ А + а(х) и <р(х) =
= Б + ,3(.г). Следовательно. f(x) + р(:г) = Л + В + (а(дг) + #(я)). Здесь
а(х) + /?(.f) -— б.м.ф. как сумма б.м.ф. По теореме 17.6 о связи функции,
ее предела и б.м.ф. можно записать lim (f(x) + if{x)) = А + В, т. е.
.г—кго
lim (f(x) +<p(x)) = lim f{x)+ lim ^(x). ■
X-+XO X-^X(j X—*Xq
В случае разности функций доказательство аналогично.
Теорема справедлива для алгебраической суммы любого конечного чи-
сла функций.
Следствие 17.3. Функция может иметь только один предел при х -» х0-
Q Пусть lim f(x) = А и lim f(x) = В. По теореме 17.7 имеем:
X—УХО Х-+ХО
О = lim (f(x) - f(x)) = lim f(x) - lim /(*) = .4 - R
.r->j-o x-+x0 x->x0
Отсюда А-В = 0, т. е. Л = Б.
Теорема 17.8. Предел произведения двух функций равен произведению их преде-
лов:
lim (f(x) • у(х)) = lim f(x) • lim ip(x).
Q Доказательство аналогично предыдущему, проведем его без особых по-
яснений. Так как lim f(x) — A, lim ip(x) = В, то
119
где а(х) и д(х) — б.м.ф. Следовательно,
т. е.

Выражение в скобках есть б.м.ф. Поэтому
Следствие 17.5. Предел степени с натуральным показателем равен той же степени
предела: lim (f(x))n = ( lim f(x)) . В частности, lim xn = xfi, п G N.
.г—кго \х—>хо / х—>хо
Теорема 17.9. Предел дроби равен пределу числителя, деленному на предел зна-
менателя, если предел знаменателя не равен нулю:
Второе слагаемое есть б.м.ф. как частное от деления б.м.ф. на функцию,
имеющую отличный от нуля предел.
120
Следствие 17.4. Постоянный множитель можно выносить за знак предела:
т. е.
Отметим, что теорема справедлива для произведения любого конечно-
го числа функций.
Доказательство аналогично предыдущему. Из равенств
следуюг соотношения f(x) = А + а(х) и р(х) = В + в(х). Тогда

Рассмотрим пример.
Пример 17.3. Вычислить lim(3x2 — 2х + 7).
х—>1
О Решение:
О Решение: Здесь применить теорему о пределе дроби нельзя, т. к. предел
знаменателя, при х —> 2, равен 0. Кроме того, предел числителя равен
0. В таких случаях говорят, что имеем неопределенность вида ^. Для
ее раскрытия разложим числитель и знаменатель дроби на множители,
затем сократим дробь на х — 2 ф 0 (х —У 2, но х ф 2):
Пример 17.5. Вычислить lim 2х + Зх + 1
•г-юс 4х2 + 2х + 5
О Решение: Здесь мы имеем дело с неопределенностью вида —. Для
нахождения предела данной дроби разделим числитель и знаменатель
на х2:
17.4. Признаки существования пределов
Не всякая функция, даже ограниченная, имеет предел. Напри-
мер, функция у — sin х при х —> ос предела не имеет. Во многих вопросах
анализа бывает достаточно только убедиться в существовании предела
функции. В таких случаях пользуются признаками существования преде-
ла.
121
О I
Функция 2 + — + -tj есть сумма числа 2 и б.м.ф., поэтому

Q Из равенств (17.6) вытекает, что для любого е > 0 существуют две
окрестности 6] и S-> точки л*о< R одной из которых выполняется неравенство
\Ых) - Л\ < е. т. е.
Доказательство этой теоремы не приводим.
Следствие 17.6. Ограниченная монотонная последовательность хп, п £ N, имеет
предел.
122
Теорема 17.10 (о пределе промежуточной функции). Если функция f(x) за-
ключена между двумя функциями <р(х) и д(х), стремящимися к одному и тому же
пределу, то она также стремится к этому пределу, т. е. если
то
а в другой \д(х) — Л| < £\ т. е.
Пусть 6 меньшее из чисел S\ и ($•>■ Тогда в ^-окрестности точки хо вы-
полняются оба неравенства (17.8) и (17.9).
Из неравенств (17.7) находим, что
С учетом нефавенств (17.8) и (17.9) из неравенства (17.10) следуют нера-
венства -с < f{x) - Л < е или |/(.т) - Л| < с.
Мы доказали, что
то есть lirn f(x) = А. Ш
.г-кг о
Теорему 17.10 иногда шутливо называют «принципом двух милицио-
неров». Роль «милиционеров» играют функции >р(х) и д(х), функция f(x)
«следует за милиционерами».
Теорема 17.11 (о пределе монотонной функции). Если функция f(x) монотонна
и ограничена при х < хо или при х > х0, то существует соответственно ее левый
предел lim /(.г) = f(xo - 0) или ее правый предел lim f(x) = f(x0 + 0).
х—>xq— 0 x—кх'о+0

17.5. Первый замечательный предел
При вычислении пределов выражений, содержащих тригонометриче-
ские функции, часто используют предел
(17.11)
называемый первым замечательным пределом. Читается: предел от-
ношения синуса к его аргументу равен единице, когда аргумент стремится
к нулю. Докажем равенство (17.11).
Q Возьмем круг радиуса 1, обозначим радианную меру угла MOB че-
рез х (см. рис. 113). Пусть 0 < х < т£. На рисунке \ЛМ\ = sinx, дуга
MB численно равна центральному углу я, \ВС\ = tgx. Очевидно, име-
ем Samob < ^сектора мов < S&cob- На основании соответствующих
формул геометрии получаем ^sinx < ^х < Atgx. Разделим неравен-
1 г
ства на ^sinx > 0, получим 1 < —^— <
COSX
или
COS X <
sin a:
< 1. Так как lim cosx = 1 и lim 1 = 1,
то по признаку (о пределе промежуточной функции)
существования пределов
Пусть теперь х < 0. Имеем
—х > 0. Поэтому
Рис. 113.
(17.13)
Из равенств (17.12) и (17.13) вытекает равенство (17.11). ■
Пример 17.7. Найти lim ^.
123
О Решение: Имеем неопределенность вида У. Теорема о пределе дроби
неприменима. Обозначим Зх = t: тогда при х —> 0 и t —> 0, поэтому

1. Пусть х —> Ч-оо. Каждое значение х заключено между двумя поло-
жительными целыми числами: п ^ х < п + 1, где п = [х] — это целая часть
х. Отсюда следует —Цг < - < —, 1 Н Цг <1 + -<1 + -, поэтому
J п +1 х ^ п' п + 1 я ^ п' J
По признаку (о пределе промежуточной функции) существования преде-
лов , 1 v П.
(17.18)
Равенства (17.15) и (17.18) называются вторым замечательным пре-
делом. Они широко используются при вычислении пределов. В приложе-
ниях анализа большую роль играет показательная функция с основанием
е. Функция у = ех называется экспоненциальной, употребляется также
обозначение ех = ехр(х).
124
17.6. Второй замечательный предел
Как известно, предел числовой последовательности хп = (1 + — ] ,
п Е N, имеет предел, равный е (см. (15.6)):
Докажем, что к числу е стремится и функция хп = (1 + — ] при х -> оо
(хешу. , , v XJ
Если х —> +оо, топ-> оо. Поэтому, согласно (17.14), имеем:
2. Пусть х —> — оо. Сделаем подстановку —x = t, тогда
Из равенств (17.16) и (17.17) вытекает равенство (17.15).
Если в равенстве (17.15) положить — = а (а —> О при х —> оо), оно
запишется в виде , .

О Решение: Обозначим х = 2t, очевидно, t —>■ оо при х —>• оо. Имеем
§18. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
18.1. Сравнение бесконечно малых функций
Как известно, сумма, разность и произведение двух б.м.ф. есть функ-
ция бесконечно малая. Отношение же двух б.м.ф. может вести себя раз-
личным образом: быть конечным числом, быть бесконечно большой функ-
цией, бесконечно малой или вообще не стремиться ни к какому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть а = а(х) и 0 = /?(х) есть б.м.ф. при х —> хо, т. е. lim а(х) — 0 и
X—>Хо
lim (3(х) = 0.
Х—>Хо
1. Если lim % = А ф 0 (A G М), то а и /3 называются бесконечно
х—txo Р
малыми одного порядка.
2. Если lim % = 0, то а называется бесконечно малой более высокого
х—*хо Р
порядка, чем /?.
3. Если lim % = оо, то а называется бесконечно малой более низкого
х—ухо Р
порядка, чем /3.
4. Если lim % не существует, то а и /3 называются несравнимыми бес-
X—>Хо Р
конечно малыми.
Отметим, что таковы же правила сравнения б.м.ф. при х —> ±оо,
х —> хо ± 0.
[яГ| Пример 18.1. Сравнить порядок функций а = Зх2 и /3 — 14х2 при
*■—' х —> оо.
О Решение: При х —> 0 это б.м.ф. одного порядка, так как
125
Говорят, что б.м.ф. а и /3 одного порядка стремятся к нулю с примерно
одинаковой скоростью. •
Пример 18.2. Являются ли функции а = Зх4 и /3 = 7х б.м.ф. одного
порядка при х —> О?

то а есть б.м.ф. более низкого порядка, чем /?. •
Пример 18.4- Можно ли сравнить функции а = х • sin — и & — х при
х-» О?
О Решение: Функции а — х • sin — и /3 = х при х —> О являются не-
х • sin 1
сравнимыми б.м.ф.. так как предел lim % = lirn — = lim sin — не
.r-Ю Р х^О X х^О X
существует. •
18.2. Эквивалентные бесконечно малые и основные теоремы о них
Среди бесконечно малых функций одного порядка особую роль играют
так называемые эквивалентные бесконечно малые.
Если lim % = 1, то а и fj называются эквивалентными бесконеч-
X —УХо >
но малыми (при ./; —> хо); это обозначается так: а ~ /3.
Например, sin .с ~ х при х —>• 0, т. к. lim sm,T = 1; tgx ~ х при х —> О,
х—>0 X
,, к. lim I££ = 1.
х->0 .Т
Теорема 18.1. Предел отношения двух бесконечно малых функций не изменится,
если каждую или одну из них заменить эквивалентной ей бесконечно малой.
Теорема 18.2. Разность двух эквивалентных бесконечно малых функций есть бес-
конечно малая более высокого порядка, чем каждая из них.
126
О Решение: При х —> 0 функция а есть б.м.ф. более высокого порядка,
о, 4 о 3
чем В, так как lim % = lim Ц^- = lim ^- = 0. В этом случае б.м.ф. а
х^о о х^о 7х х-+о 7 '
стремится к нулю быстрее, чем /?. •
Пример 18.S. Сравнить порядок функций а — tgx w В — х2 при х -> 0.
О Решение: Так как

Q Пусть а ~ 0 при х —¥ xo- Тогда
аналогично lim —3-^- =0. В
x-+xo P
Справедливо и обратное утверждение: если разность б.м.ф. а и /3 есть
бесконечно малая высшего порядка, чем а или /?, то а и /? — эквивалент-
ные бесконечно малые.
Действительно, так как lim — = 0, то lim (1 — &-) = 0, т. е.
X—УХо OL X-^Xq\ О. /
о о
1 — lim — = 0. Отсюда lim — = 1, т. е. a ~ /3. Аналогично, если
Х—>Хо OL X-+XQ, Ot
lim —тг^- = 0, то a ~ /3.
X^-Xq Р
Теорема 18.3. Сумма конечного числа бесконечно малых функций разных поряд-
ков эквивалентна слагаемому низшего порядка.
Q Докажем теорему для двух функций. Пусть a —» 0, /3 —> 0 при х —> х0,
причем a — б.м.ф. высшего порядка, чем /?, т. е. lim % = 0. Тогда
X—►.Го #
Следовательно, а + /3 ~ в при х —> хо. Ш
Слагаемое, эквивалентное сумме бесконечно малых, называется глав-
ной частью этой суммы.
Замена суммы б.м.ф. ее главной частью называется отбрасыванием
бесконечно малых высшего порядка.
Пример 18.5. Найти предел lim *X + 7X .
^ х-ю sin2x
О Решение: lim ^х.+ Jx - lim ?\ - lim j^ = 3 поскольку
х-+о sin2x x-уо sin2.x x^q2x 2
Зх + 7х2 ~ Зх и sin 2х ~ 2х при х —> 0. •
18.3. Применение эквивалентных бесконечно малых функций
Вычисление пределов
Для раскрытия неопределённостей вида Ч часто бывают полезным
применять принцип замены бесконечно малых эквивалентными и дру-
гие свойства эквивалентных бесконечно малых функций. Как известно,
sin .г ~ х при х —> 0, tgx ~ х при х —> 0. Приведем еще примеры эквива-
лентных б.м.ф.
127

Пример 18.6. Покажем, что 1 — cos я ~ Щ^ при х —> 0.
Пример 18.7. Найдем lim arcsina:.
О Решение: Обозначим arcsinx = t. Тогда х = sint и t —> 0 при я —> 0.
Поэтому
Следовательно, arcsin x ~ x при x -» 0.
Пример 18.8. Покажем, что \/1 + х — 1 ~ ^ при х —> 0.
Q Решение: Так как
Пример 18.9. Найти lim -&%-.
z-ю sin За:
О Решение: Так как tg2x ~ 2a:,sin3a: ~ Зх при а: —>• 0, то
128
Ниже приведены важнейшие эквивалентности, которые используют-
ся при вычислении пределов:

Пример 18.10. Найти lim х(е^х - 1).
х—>оо
О Решение: Обозначим - = t, из х -» оо следует £ -> 0. Поэтому
Пример 18.11. Найти lim —* tr г-
x->i х2 - Ъх + 4
О Решение: Так как arcsin(x — 1) ~ (х — 1) при х —> 1, то
Приближенные вычисления
Если а ~ /?, то, отбрасывая в равенстве а =
= /? + (а — /?) бесконечно малую более высокого по-
рядка, т. е. а — /3, получим приближенное равенство
а « /3.
Оно позволяет выражать одни бесконечно ма-
лые через другие. Приведенные выше важнейшие
эквивалентности служат источником ряда прибли-
женных формул.
Приведенные формулы справедливы при ма-
лых х, и они тем точнее, чем меньше х.
Например, графики функций y = tgxny = x
в окрестности точки 0 практически не различимы
(см. рис. 114), а кривая у = sin а: в окрестности
точки 0 сливается с прямой у — х (рис. 115). На
рисунках 116-118 проиллюстрированы некоторые
из важнейших эквивалентностей, о которых гово-
рилось выше.
Рис. 114.
tgx « х (х -> 0)
Рис. 115. sin х « х (х —> 0)
Рис. 116. 1п(1 + х) « х (х -> 0)
129

Рис. 117. cos x « 1 - 2j- (х -» 0)
Рис. 118. >ДТж « 1 + f (х -> 0)
Пример 18.12. Найти приближенное значение для In 1,032.
Q Решение: In 1,032 = 1п(1 + 0,032) « 0,032 Для сравнения результата по
таблице логарифмов находим, что In 1,032 = 0,031498 ... •
§19. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
19.1. Непрерывность функции в точке
Пример 19.1. Вычислить А = lim —- *■.
х-Ю X
130
Пусть функция у = f(x) определена в точке х$ и в некоторой окрест-
ности этой точки. Функция у = f(x) называется непрерывной в точке хо,
если существует предел функции в этой точке и он равен значению функ-
ции в этой точке, т. е.
Равенство (19.1) означает выполнение трех условий:
1) функция f(x) определена в точке хо и в ее окрестности;
2) функция f(x) имеет предел при х —> xq]
3) предел функции в точке хо равен значению функции в этой точке,
т. е. выполняется равенство (19.1).
Так как lim x = хо, то равенство (19.1) можно записать в виде
Это означает, что при нахождении предела непрерывной функции f(x)
можно перейти к пределу под знаком функции, то есть в функцию f(x)
вместо аргумента х подставить его предельное значение xq.
si„* lim sifp- _ .
Например, lim e * = ex^° = е. В первом равенстве функция и
х—>0
предел поменялись местами (см. (19.2)) в силу непрерывности функции ех.

Q Решение:
Отметим, что 1п(1 + х) ~ х при х -> 0.
Можно дать еще одно определение непрерывности функции, опираясь
на понятия приращения аргумента и функции.
Пусть функция у = f(x) определена в некотором интервале (а;Ь).
Возьмем произвольную точку хо G (а; Ь). Для любого х Е (а;Ь) разность
х — хо называется приращением аргумента х в точке хо и обозначается
Ах («дельта х»): Ах = х — xq. Отсюда х = хо + Дх.
Разность соответствующих значений функций
f(x) — f(xo) называется приращением функции
/(х) в точке хо и обозначается Ау (или Д/ или
Д/(х0)): Ay = /(х) -/(х0) или Ду = /(х0 +Дх)-
—f(xo) (см. рис. 119).
Очевидно, приращения Ах и Ау могут быть
как положительными, так и отрицательными чи-
слами.
Запишем равенство (19.1) в новых обозначе-
ниях. Так как условия хчхоих-хо-^О оди-
наковы, то равенство (19.1) принимает вид
lim (/(х) - f{xo)) = 0 или
X—*Хо
(19.3)
Полученное равенство (19.3) является еще одним определением непре-
рывности функции в точке: функция у = f(x) называется непрерывной
в точке хо, если она определена в точке xq и ее окрестности и выпол-
няется равенство (19.3), т. е. бесконечно малому приращению аргумента
соответствует бесконечно малое приращение функции.
Исследуя непрерывность функции в точке, применяют либо первое
(равенство (19.1)), либо второе (равенство (19.3)) определение.
Пример 19.2. Исследовать на непрерывность функцию у = sin я.
О Решение: Функция у = sin я определена при всех х Е Ш.
Возьмем произвольную точку х и найдем приращение Ау:
Тогда lim Ау = lim 2 cos(х+ %^-) -sin Щ^- = 0, так как произведение
Дл--)-0 Дх->0 \ ^ / *
ограниченной функции и б.м.ф. есть б.м.ф.
Согласно определению (19.3), функция у = sinx непрерывна в точке х.
Аналогично доказывается, что функция у — cosx также непрерывна.
131

19.2. Непрерывность функции в интервале и на отрезке
Функция у = /(х) называется непрерывной в интервале (а, 6), если
она непрерывна в каждой точке этого интервала.
Функция у = /(х) называется непрерывной на отрезке [а, 6], если она
непрерывна в интервале (а,6) и в точке х — а непрерывна справа (т.е.
lim f(x) = f(a)). a в точке х = Ь непрерывна слева (т. е. lim f(x) = f(b)).
х^а+О / V .Г-+6-0 /
19.3. Точки разрыва функции и их классификация
|нч| Точки, в которых нарушается непрерывность функции, называются
^—' точками разрыва этой функции. Если ж = хо — точка разрыва функ-
ции у = /(х), то в ней не выполняется по крайней мере одно из условий
первого определения непрерывности функции, а именно:
1. Функция определена в окрестности точки хо, но не определена в
самой точке Хо.
Например, функция у = —~о не опРеДелена в точке хо — 2 (см.
рис. 120).
Рис. 120.
Рис. 121.
2. Функция определена в точке хо и ее окрестности, но не существует
предела f(x) при х —> xq.
Например, функция
определена в точке хо = 2 (/(2) = 0), однако в точке хо — 2 имеет разрыв
(см. рис. 121), т. к. эта функция не имеет предела при х —> 2:
132
3. Функция определена в точке xq и ее окрестности, существует
lim /(x), но этот предел не равен значению функции в точке х$\
X—t-Xo
lim f(x) ф f(x0).
X-+XQ

Рис. 122.
Пример 19.3. Дана функция /(х)
выяснить их тип.
\SLzA
х-3 '
Найти точки разрыва,
О Решение: Функция /(х) определена и непрерывна на всей числовой оси,
кроме точки х = 3. Очевидно, /(х) =
Следовательно,
lim fix) = 1, a lim fix) = — 1. Поэтому в точке х = 3 функция имеет
£-►3+0 а:-^3-0
разрыв первого рода. Скачок функции в этой точке равен 1 — (—1) = 2. •
133
Например, функция (см. рис. 122)
Здесь #о = 0 — точка разрыва:
а д(х0) = д(0) = 2.
Все точки разрыва функции раз-
деляются на точки разрыва первого и
второго рода. Точка разрыва Хо назы-
вается точкой разрыва первого ро-
да функции у = /(х), если в этой точ-
ке существуют конечные пределы функции слева и справа (односторонние
пределы), т. е. lim f(x) = А\ и lim f(x) = A2. При этом:
х—>хо— 0 х—►хо+О
а) если А\ = А2, то точка хо называется точкой устранимого разры-
ва; б) если А\ Ф Аъ, то точка хо называется точкой конечного разрыва.
Величину \А\ — А2\ называют скачком функции в точке разрыва первого
рода.
Точка разрыва х$ называется точкой разрыва второго рода функ-
ции у = /(х), если по крайней мере один из односторонних пределов (слева
или справа) не существует или равен бесконечности.
1. Обратимся к функциям, рассмотренным выше (см. рис. 120). у = -^2 >
хо = 2 — точка разрыва второго рода.
2. Для функции
хо = 2 является точкой разрыва первого рода, скачок функции равен
|1-0| = 1.
3. Для функции
хо = 0 является точкой устранимого разрыва первого рода. Положив
д(х) = 1 (вместо д(х) = 2) при х = 0, разрыв устранится, функция станет
непрерывной.

19.4. Основные теоремы о непрерывных функциях.
Непрерывность элементарных функций
Теоремы о непрерывности функций следуют непосредственно из соот-
ветствующих теорем о пределах.
Теорема 19.1. Сумма, произведение и частное двух непрерывных функций есть
функция непрерывная (для частного за исключением тех значений аргумента, в
которых делитель равен нулю).
Q Пусть функция f(x) и (р(х) непрерывны на некотором множестве Лг
и хо — любое значение из этого множества. Докажем, например, непре-
рывность произведения F(x) = f(x) • ip(x). Применяя теорему о пределе
произведения, получим:
lim F(x) = lim (f(x)-(p(x)) = lim f(x)- lim ф(х) = /(х0)чр(х0) - F(x0).
Х—УХо X—>Xq X-^-Xq X-+XQ
Итак, lim F(x) = F(xo), что и доказывает непрерывность функции
х-ьхо
f(x) • ip(x) в точке Хо- Ш
Теорема 19.2. Пусть функции и = <р(х) непрерывна в точке хо, а функция у = f(u)
непрерывна в точке щ = у?(#о)- Тогда сложная функция f(ip(x)), состоящая из
непрерывных функций, непрерывна в точке хо-
Q В силу непрерывности функции и = ip(x), Hm ф(х) = ^(хо) = Мо< т. е.
при х —> хо имеем w —>> Mo- Поэтому вследствие непрерывности функции
у = f(u) имеем:
Теорема 19.3. Если функция у = f(x) непрерывна и строго монотонна на [а; Ь] оси
Ох, то обратная функция у = <р(х) также непрерывна и монотонна на соответству-
ющем отрезке [c:d] оси Оу (без доказательства).
Так, например, функция tgx = smx , в силу теоремы 19.1, есть функ-
ция непрерывная для всех значений х, кроме тех, для которых cos а? = О,
т. е. кроме значений х = Ц + 7ггс, п £ Z.
Функции arcsinx, arctgx, arccosx, arcctgx, в силу теоремы 19.3, непре-
рывны при всех значениях х, при которых эти функции определены.
Можно доказать, что все основные элементарные функции не-
прерывны при всех значениях х, для которых они определены.
134
Это и доказывает, что сложная функция у = f(tp(x)) непрерывна в
точке xq. Ш

Как известно, элементарной называется такая функция, которую
можно задать одной формулой, содержащей конечное число арифметиче-
ских действий и суперпозиций (операции взятия функции от функции)
основных элементарных функций. Поэтому из приведенных выше теорем
вытекает: всякая элементарная функция непрерывна в каэюдой
точке, в которой она определена.
Этот важный результат позволяет, в частности, легко находить преде-
лы элементарных функций в точках, где они определены.
Пример 19.4- Найти lim 2сХ*х.
Q Решение: Функция 2ctgx непрерывна в точке х =
lim 2ct«* =2ct6T = 2* =2.
поэтому
19.5. Свойства функций, непрерывных на отрезке
Непрерывные на отрезке функции имеют ряд важных свойств. Сфор-
мулируем их в виде теорем, не приводя доказательств.
Теорема 19.4 (Вейерштрасса). Если функция непрерывна на отрезке, то она до-
стигает на этом отрезке своего наибольшего и наименьшего значений.
Изображенная на рисунке 123 функ-
ция у = f(x) непрерывна на отрезке
[а; Ь], принимает свое наибольшее значе-
ние М в точке #1, а наименьшее т —
в точке х-2- Для любого х £ [а;Ь] имеет
место неравенство т ^ f(x) ^ М.
Следствие 19.1. Если функция непрерывна на
отрезке, то она ограничена на этом отрезке.
Теорема 19.5 (Больцано-Коши). Если функ-
ция у = f(x) непрерывна на отрезке [а;Ь] и при-
нимает на его концах неравные значения f(a) = А
и f(b) = В, то на этом отрезке она принимает и
все промежуточные значения между А и В.
Геометрически теорема очевидна
(см. рис. 124).
Для любого числа С, заключенного
между А и В, найдется точка с внутри
Рис. 124.
135
Рис. 123.

этого отрезка такая, что /(с) = С. Прямая у — С пересечет график функ-
ции по крайней мере в одной точке.
Следствие 19.2. Если функция у — f(x) непрерывна на отрезке [а; Ь] и на его
концах принимает значения разных знаков, то внутри отрезка [а; Ь] найдется хотя
бы одна точка с, в которой данная функция f(x) обращается в нуль: /(с) = 0.
Геометрический смысл теоремы: если график непрерывной функции
переходит с одной стороны оси Ох на другую, то он пересекает ось Ох
(см. рис. 125).
Следствие 19.2 лежит в основе так называемого «.метода половин-
ного деления», который используется для нахождения корня уравнения
/(*) = 0.
Рис. 125.
Рис. 126.
Утверждения теорем 19.4 и 19.5, вообще говоря, делаются неверны-
ми, если нарушены какие-либо из ее условий: функция непрерывна не на
отрезке [а; Ь], а в интервале (а;&), либо функция на отрезке [а; Ь] имеет
разрыв.
Рисунок 126 показывает это для следствия теоремы 19.5: график раз-
рывной функции не пересекает ось Ох.
Пример 19.5. Определить с точностью до е = 0,00001 корень урав-
нения е2х+1 + х2 — 5 = 0, принадлежащий отрезку [0; 1], применив метод
половинного деления.
О Решение: Обозначим левую часть уравнения через f(x).
Шаг 1. Вычисляем (р = f(a) и ф = f(b), где а = 0, Ъ = 1.
Шаг 2. Вычисляем х = at •
Шаг 3. Вычисляем у = f{x). Если f(x) = 0, то х — корень уравнения.
Шаг 4. При f(x) ф 0 если у • (р < 0, то полагаем b = х, ф = у, иначе
полагаем а = х, ip = у.
Шаг 5. Если Ь — а — е < Ото задача решена. В качестве искомого корня
(с заданной точностью е) принимается величина х = а 1" . Иначе процесс
деления отрезка [а; Ь] пополам продолжаем, возвращаясь к шагу 2.
В результате произведенных действий получим: х = 0,29589. •
136

137
§20. ПРОИЗВОДНАЯ ФУНКЦИИ
20.1. Задачи, приводящие к понятию производной
Понятие производной является одним из основных математических по-
нятий. Производная широко используется при решении целого ряда задач
математики, физики, других наук, в особенности при изучении скорости
разных процессов.
Скорость прямолинейного движения
Пусть материальная точка (некоторое тело) М движется неравномер-
но по некоторой прямой. Каждому значению времени t соответствует опре-
деленное расстояние ОМ = S до некоторой фиксированной точки О. Это
расстояние зависит от истекшего времени t, т. е. S = S(t).
Это равенство называют законом движения точки.
Требуется найти скорость движения точки.
Если в некоторый момент времени t точка занима-
ет положение М, то в момент времени t + At (At —
приращение времени) точка займет положение Мь где
О Mi = S + AS (AS — приращение расстояния) (см.
рис. 127). Таким образом, перемещение точки М за время
At будет AS = S(t + At) - S(t).
Отношение 4j выражает среднюю скорость движения точки за вре-
мя At:
Средняя скорость зависит от значения At: чем меньше At, тем точнее
средняя скорость выражает скорость движения точки в данный момент
времени t.
Предел средней скорости движения при стремлении к нулю промежут-
ка времени At называется скоростью движения точки в данный момент
времени (или мгновенной скоростью). Обозначив эту скорость через V,
получим
Касательная к кривой
Дадим сначала общее определение касательной к кривой.
Возьмем на непрерывной кривой L две точки М и М\ (см. рис. 128).
Прямую ММ\, проходящую через эти точки, называют секущей.
Пусть точка A/i, двигаясь вдоль кривой L, неограниченно приближа-
ется к точке М. Тогда секущая, поворачиваясь около точки М, стремится
к некоторому предельному положению МТ.

Касательной к данной кривой в данной точке М называется
предельное положение МТ секущей ММ\, проходящей через точку А/, ко-
гда вторая точка пересечения М\ неограниченно приближается по кривой
к точке М\.
Рис. 128.
Рис. 129.
Рассмотрим теперь график непрерывной кривой у = f(x), имеющий в
точке М(х;у) невертикальную касательную. Найдем ее угловой коэффи-
циент к = tga, где а — угол касательной с осью Ох.
Для этого проведем через точку М и точку М\ графика с абсциссой
х + Ах секущую (см. рис. 129). Обозначим через ф — угол между секущей
ММ\ и осью Ох. На рисунке видно, что угловой коэффициент секущей
равен
При Ах —> 0 в силу непрерывности функции приращение Ау тоже стре-
мится к нулю; поэтому точка Afi неограниченно приближается по кривой
к точке А/, а секущая ММ\, поворачиваясь около точки А/, переходит в
касательную. Угол ip -> а, т. е. lim <p = а.
Дх->>0
Следовательно, lim tg(p = tga.
Дя-*0
Поэтому угловой коэффициент касательной равен
(20.2)
К нахождению пределов вида (20.1) и (20.2) приводят решения и мно-
жества других задач. Можно показать, что:
- если Q = Q(t) — количество электричества, проходящего через по-
перечное сечение проводника за время t, то сила тока в момент времени
t равна
- если N — N(t) — количество вещества, вступающего в химическую
реакцию за время t, то скорость химической реакции в момент времени
t равна
138

- если т = т(х) — масса неоднородного стержня между точками
О(0;0) и М(х,0), то линейная плотность стержня в точке х есть
Производная функции /(х) есть некоторая функция /;(х), произведен-
ная из данной функции.
Функция у = /(х), имеющая производную в каждой точке интервала
(а; 6), называется дифференцируемой в этом интервале; операция нахо-
ждения производной функции называется дифференцированием.
Значение производной функции у = /(х) в точке х = хо обозначается
одним из символов: /'(хо), у'\ _ или у'(хо).
Пример 20.1. Найти производную функции у = С\ С — const.
О Решение:
Значению х даем приращение Ах;
139
Пределы (20.1)-(20.5) имеют одинаковый вид; везде требуется найти
предел отношения приращения функции к приращению аргумента. Этот
предел называют производной. Эти пределы можно записать так:
V = S't; tga = y'x; I = Q't; V = N[; S = m'x
(читается «V равно S штрих по Ь>, «тангенс а равен у штрих по х» и т. д.).
20.2. Определение производной; ее механический
и геометрический смысл.
Уравнение касательной и нормали к кривой
Пусть функция у = f(x) определена на некотором интервале (а; Ь).
Проделаем следующие операции:
аргументу х Е (а; Ь) дадим приращение Ах: х + Ах Е (а: Ь);
- найдем соответствующее приращение функции: Ay = f(x + Ах) — f(x);
- составим отношение приращения функции к приращению аргумента:
- найдем предел этого отношения при Дх —> 0: lim -г-^.
Если этот предел существует, то его называют производной функции
f(x) и обозначают одним из символов f'x. /'(#); у'; -#; у'х.
Производной функции у = f(x) в точке хо называется предел
отношения приращения функции к приращению аргумента, когда прира-
щение аргумента стремится к нулю.
Итак, по определению

- находим приращение функции Ay: Ay = f(x+Ax) — f(x) = С — С = 0;
-значит, д£ = д-=0;
- следовательно, у' = lim -т-^ = Hni 0 = 0, т. е. (сУ = 0. •
Пример 20.2. Найти производную функции у = х2.
О Решение:
- Аргументу х даем приращение Дх;
- находим Ау: Ау = (х + Дх)2 - х2 = 2х • Дх + (Дх)2;
Таким образом, (х2)' = 2х. •
В задаче про скорость прямолинейного движения было получено
V= lim 4f-
Это равенство перепишем в виде V = 5J, т. е. скорость прямолинейно-
го движения материальной точки в момент времени t есть производная
от пути S по времени t. В этом заключается механический смысл произ-
водной.
Обобщая, можно сказать, что если функция у = f(x) описывает какой-
либо физический процесс, то производная у' есть скорость проте-
кания этого процесса. В этом состоит физический смысл производ-
ной.
В задаче про касательную к кривой был найден угловой коэффици-
ент касательной k = tga = lim -д^. Это равенство перепишем в виде
f'(x) = tga = fc, т.е. производная f'{x) в точке х равна угловому
коэффициенту касательной к графику функции у = f(x) в точ-
ке, абсцисса которой равна х. В этом заключается геометрический
смысл производной.
Если точка касания М имеет координаты (#о;2/о) (см- Рис- 130), то
угловой коэффициент касательной есть k = f'(xo). Пользуясь уравнени-
ем прямой, проходящей через заданную точку в заданном направлении
(У - 2/о = к(х — жо)), можно записать уравнение
касательной: у — Уо = /'(^о) • {х - х0).
Прямая, перпендикулярная касательной в
точке касания, называется нормалью к кривой.
Так как нормаль перпендикулярна касатель-
ной, то ее угловой коэффициент
140
- составляем отношение
- находим предел этого отношения:
Поэтому уравнение нормали имеет вид у — уо =
Рис. 130.

20.3. Связь между непрерывностью и дифференцируемостью
функции
Теорема 20.1. Если функция дифференцируема в некоторой точке, то она непре-
рывна в ней.
Q Пусть функция у = f(x) дифференцируема в некоторой точке х. Сле-
довательно, существует предел lim -r-^ = f'(x)-
Отсюда, по теореме 17.5 о связи функции, ее предела и бесконечно
малой функции, имеем -^ = f'(x) + а> гДе а ~> 0 ПРИ ^х ~^ 0> то есть
Ау = f'(x) • Ах + а ■ Ах.
Переходя к пределу, при Да: -» 0, получаем lim Ay = 0. А это и
Ax-fO
означает, что функция у = f(x) непрерывна в точке х. Ш
Обратная теорема неверна: непрерывная функция может
не иметь производной. Примером такой функции является
функция
х, если х ^ 0,
—х, если х < 0.
Изображенная на рисунке 131 функция непрерывна в точ-
ке х = 0, но не дифференцируема в ней.
Действительно, в точке х = 0 имеем
1, если Ах > 0,
— 1, если Ах < 0.
141
Отсюда следует, что lim -г-^ не существует, т. е. функция у — \х\ не
Дх—►() ^\Х
имеет производной в точке х = О, график функции не имеет касательной
в точке О(0; 0).
Замечания: 1. Существуют односторонние пределы функции у = \х\ в
точке х — 0: lim -г-^ — — 1, lim -г^- = 1. В таких случаях говорят,
что функция имеет односторонние производные (или «производные
слева и справа»), и обозначают соответственно f'_{x) и f'+(x).
Если f+{x) ф /!_(#), то производная в точке не существует. Не суще-
ствует производной и в точках разрыва функции.
2. Производная у' = f'{x) непрерывной функции у = f(x) сама не
обязательно является непрерывной.
Если функция у = f(x) имеет непрерывную производную у' = f'(x) в
некотором интервале (а; 6), то функция называется гладкой.
Рис. 131.

20.4. Производная суммы, разности, произведения и частного
функций
Нахождение производной функции непосредственно по определению
часто связано с определенными трудностями. На практике функции диф-
ференцируют с помощью ряда правил и формул.
Пусть функции и = и(х) и v = v(x) - две дифференцируемые в неко-
тором интервале (а; Ь) функции.
Теорема 20.2. Производная суммы (разности) двух функций равна сумме (разно-
сти) производных этих функций: (и ± v)1 = и' ± г/.
Теорема 20.3. Производная произведения двух функций равна произведению про-
изводной первого сомножителя на второй плюс произведение первого сомножителя
на производную второго: (и • v)' — u'v -h v'u.
142
Q Обозначим у = u±v. По определению производной и основным теоре-
мам о пределах получаем:
т. е. [и ± V) = и ± v .
Теорема справедлива для любого конечного числа слагаемых.
Пусть у — uv. Тогда

При доказательстве теоремы использовалась теорема о связи непре-
рывности и дифференцируемости: так как функции и = и(х) и v = v(x)
дифференцируемы, то они и непрерывны, поэтому Av —> 0 и Аи —> О при
Ах -> 0.
Можно показать, что:
а) (с • и)' — с • и\ где с = const;
б) (и • v • w)' = и' - v • w + и- v' • w + и • v • w'.
U\ X)
Теорема 20.4. Производная частного двух функций ; V, если v(x) ф 0 равна
v\x)
дроби, числитель которой есть разность произведений знаменателя дроби на про-
изводную числителя и числителя дроби на производную знаменателя, а знаменатель
-) = и ' v ~2U ' v , v ф 0.
20.5. Производная сложной и обратной функций
Пусть у = /(и) и гг = <р(х), тогда у = /(<£>(х)) — сложная функция с
промежуточным аргументом ix и независимым аргументом з*.
143

Теорема 20.5. Если функция и = (р(х) имеет производную и'х в точке х, а функ-
ция у = f(u) имеет производную у'и в соответствующей точке и = <р(х), то сложная
функция у — f(ip(x)) имеет производную ух в точке х, которая находится по фор-
муле у'х = у'и -и'х.
Разделив полученное равенство на Ах и перейдя к пределу при Ах —> О,
получим у'х =у'и-и'х. Ш
Итак, для нахождения производной сложной функции надо произ-
водную данной функции по промеэюуточному аргументу умно-
эюить на производную промежуточного аргумента по незави-
симому аргументу.
Это правило остается в силе, если промежуточных аргументов не-
сколько. Так, если у = f(u), и = ip(v), v = #(х), то у'х = у'и • u'v • v'x.
Пусть у = /(х) и х — р(у) — взаимно обратные функции.
Теорема 20.6. Если функция у = f(x) строго монотонна на интервале (а; Ь) и
имеет неравную нулю производную f'(x) в произвольной точке этого интервала, то
обратная ей функция х = р(у) также имеет производную ц>'(у) в соответствующей
точке, определяемую равенством ф'(у) — е\\ ч или х' — Ц-.
/ (х) у ух
Если Ау -» 0, то в силу непрерывности обратной функции приращение
Ах -> 0. И так как lim -д-^ = f'{x) ф 0, то из (20.7) следуют равенства
Дя->0 1\Х
lim 4^ = л- = л/7 ч, т. е. ф'(у) = ттЬт- И
дх-ю Ах
144
Q Рассмотрим обратную функцию х = (р{у). Дадим аргументу у прираще-
ние Ау ф 0. Ему соответствует приращение Ах обратной функции, причем
Ах /Ов силу строгой монотонности функции у — /(х). Поэтому можно
записать д л
т. е.
Подставив значение Аи в равенство (20.6), получим
где а —>• 0 при Аи —>• 0.
Функция и = <р(х) имеет производную в точке х: lim Q^ = и'х, по-
Ах —уО ^АХ
этому
Q По условию lim -т-^ = v!,- Отсюда, по теореме о связи функции, ее
" Аи-Ю Аи "и ^ >
предела и бесконечно малой функции, имеем -г^- = у'и + а или

\
Таким образом, производная обратной функции равна обрат-
ной величине производной данной функции.
Правило дифференцирования обратной функции записывают так:
Таким образом, _.
(хп) = п - хп \
Например, (х3)' = Зх2, (х2)' = 2х, я' = 1.
Ниже (см. замечание на с. 148) будет показано, что формула произ-
водной степенной функции справедлива при любом п Е R (а не только
натуральном).
145
Пример 20.3. Найти производную функции у — logi> tgx4.
О Решение: Данная функция является сложной. Ее можно представить в
виде цепочки «простых» функций: у = и3, где и = log2 z, где z = tg(/,
где q = х4. По правилу дифференцирования сложной функции (у'х —
= 2/и * *4 * гд ' ?i) получаем:
Пример 20.4- Пользуясь правилом дифференцирования обратной
функции, найти производную у'х для функции у = Ух — 1.
О Решение: Обратная функция х = у3 + 1 имеет производную х*^ = Зу2.
20.6. Производные основных элементарных функций
Степенная функция j/ = xn,nGN
Дадим аргументу х приращение Ах. Функция у = хп получит прира-
щение Ау = (х + Ах)п — хп. По формуле бинома Ньютона имеем
Находим предел составленного отношения при Ах -> 0:

Показательная функция у = ах,а>0, a^l
Найдем сначала производную функции у = ех. Придав аргументу х
приращение Ах, находим приращение функции Ay: Ау = ех+Ах - ех —
= е*(еАх - 1). Стало быть, ^ = е*(ед*~1} и
146
При вычислении предела воспользовались эквивалентностью ех — 1~х
при х —> 0.
Итак, у' — ех, т. е.
, %7 / /Т»\/ '7»
Теперь рассмотрим функцию у = ах, iGl. Так как а* = е*та^ то п0
формуле производной сложной функции находим:
Таким образом, (а*)' = ах In а.
Пример 20.5. Найти производную функции у — Iх ~4х.
О Решение: Используя формулу производной сложной функции и фор-
мулу производной показательной функции, находим
Логарифмическая функция у = logfl х, а > 0, а ф 1
Найдем сначала производную функции у = In я.
Для нее
Переходя к пределу при Ах —У 0 и воспользовавшись эквивалентно-
стью lnf 1 + ^Ч ~ ^- при Дх ->• 0, получаем:
т. е. у' = — или (lnx)' = —.
Теперь рассмотрим функцию у = loga x.
Так как 1ое;л х = т^, то
oa In a
Таким образом, (logax)' = х я\па-
Пример 20.6. Найти производную функции у = 1п(х4 — 2х2 + 6).

Производную логарифмической функции у = loga х можно найти ина-
че. Так как обратной для нее функцией является х = ау, то по формуле
производной обратной функции имеем:
Переходя к пределу при Дх —>> 0 и воспользовавшись первым замеча-
тельным пределом lim Б1д = 1, получаем
RT1 Пример 20.7. Найти производную функции у = cos2x.
О Решение: (cos2x)' = -sin2x • (2х)' = -2sin2x. •
Обратные тригонометрические функции у = arcsinx, у = arccosx,
у = arctgx, J/ = arcctgx
Пусть у — arcsinx. Обратная ей функция имеет вид х = sin?/, у Е
Е — ^; тт . На интервале (_ ?; ?) верно равенство х' = cos у ф 0.
147
Тригонометрические функции j/ = sinx, у = cosx, j/ = tgx, у = ctgx
Для функции у — sinx имеем:
Этот результат можно получить иначе:
Проделав аналогичные операции, получим формулу
т. е. (cosx)' = -sinx.
Для нахождения производных функций у — tgx и у — ctgx восполь-
зуемся формулой производной частного:
т. е. у' = cosx или (sinx)' = cosx.
Найдем производную функции у = cosx, воспользовавшись формулой
производной сложной функции:

148
По правилу дифференцирования обратных функций
где перед корнем взят знак плюс, так как cos у > О при у £ (— ?; 5ч.
Итак, (arcsin #)' = ,
у/Т^х^
Аналогично получаем, что (arccos я)' = , Эту формулу
V1 - х2
можно получить проще: так как arccosх + arcsinх = Ц, т.е. arccos я —
= Ц - arcsinх, то (arccosх)' = (тт — arcsinх) — .
г ^z ' v 1 - х1
Найдем производную функции у — arctg#.
Она является обратной к функции х = tgу, где у £ -?;1 .
Поэтому, по правилу дифференцирования обратных функций, получа-
ем, что
Итак, (arctgx)' = -—^-у.
Функции arctgx и arcctgx связаны отношением
Дифференцируя это равенство, находим
Пример 20.8. Найти производные функций: 1) у = arccosx2; 2) у —
= х • arctg.x; 3) у = (1 + Ъх - 3#3)4; 4) у = arccosу/х; 5) у = logi^ + 2~х).
Замечание: Найдем производную степенной функции у = ха с любым
показателем а £ Е. В этом случае функция рассматривается для х > 0.

20.7. Гиперболические функции и их производные
В математике, механике, электротехнике и некоторых других дисци-
плинах встречаются гиперболические функции, определяемые следующи-
ми формулами:
Рис. 132.
149
shx = -—ф гиперболический синус;
X | —X
chx = е ~*1е гиперболический косинус («цепная линия»);
thz = -%£- = ех ~ е_х и cthx = -Цт^- = ех +е_т — гиперболический
сп х е + е sh х е — е
тангенс и котангенс, где е — неперово число.
па рисунках lol-loo показаны графики гипер-
болических функций.
Между гиперболическими функциями сущест-
вуют следующие основные зависимости:
ch2 х — sh2 x = 1;
sh(x ± у) = sh x • ch у ± ch x • sh у;
ch(x ± у) = ch х • ch у ± sh x • sh у;
tn^±t/j- 1±tha..thy,
sh 2x = 2 sh x • ch x; ch 2x = ch2 x + sh2 x.
Все эти формулы вытекают из определения
гиперболических функций.
Функция удовлетворяет данному уравнению.
Подставляем значение у' в данное уравнение:
при всех х/0.
Пример 20.9. Показать, что функция у = Щ^- + -^Ц- + С удовлетворяет
* 2#
уравнению х3 • у' + 1 = я4.
О Решение: Находим у':
Формула остается справедливой и для х < 0, если функция у = ха
существует: л
Можно записать ха = еа1пх. По правилу дифференцирования сложной
функции находим

Рис. 133.
Рис. 134.
Рис. 135.
Геометрическая интерпретация гиперболических функций (см.
рис. 137) аналогична интерпретации тригонометрических функций
(см. рис. 136).
Рис. 136. Параметрические уравне- Рис. 137. Параметрические уравнения
ния х = cos£ и у = s'mt определя- х = cht и у = sht определяют гипер-
ют окружность х2 + у2 = 1, причем болу х2 — у2 = 1, причем О А = cht,
О А = cos t, AM = sin t AM = sh t
Найдем производные гиперболических функций:
150
Например,

20.8. Таблица производных
Выведенные правила дифференцирования, формулы производных ос-
новных элементарных функций запишем в виде таблицы.
На практике чаще всего приходится находить производные от сложных
функций. Поэтому в приведенной ниже таблице формул дифференциро-
вания аргумент «х» заменен на промежуточный аргумент «и».
Правила дифференцирования
1. (u±v)' = u'±v';
2. (и • v)' = u'v + ш/, в частности, {си)' = с • и';
3. (j)' = мЧ-ш/, в частностИ) (£)' = _^;
4- у'х = Уи ' <, если у = /(и), и = <р(х);
5- у'х = 3"' если у = f№ И х = v(y)-
ху
Формулы дифференцирования
1. (с)' = 0;
2. (иа)' = а • иа~1 • и', в частности, {у/й~У = 7гт= * и'\
2 Vи
3. (а4)' = аи • In а • гх', в частности, (еиУ = е" • и';
4. (1ое:л гг)' = —т— • и' в частности, (In и)' = — • и':
5. (sinu)' = cosu • и'; 6. (cos и)' = — sin и • и';
7. (tgii)' = —±r--u'; 8. (ctgu)' = Jj-'«';
cos a sin и
9. (arcsinu)' = , • u'\ 10. (arccosu)' = , • u'\
Vl - и'2 } ^T^
11. (arete;г*У = -—^т • и': 12. (arcctgi/У = — -——7 • it';
v ь y 1+ u2 v ь у 1 + u2
13. (shu)' — chг/ • г/'; 14. (ch г*)' = shи • и';
15. (thu)' = -Д— -w'; 16. (cthu)' = —А— -и',
ch и sh гг
Для вычисления производных надо знать лишь правила дифференци-
рования и формулы производных основных элементарных функций, стро-
го соблюдать эти правила при выполнении упражнений.
[яГ1 Пример 20.10. Найти производную функции у = х4 - Зх3 + 2х - 1.
О Решение:
151

Надо стараться обходиться без лишних записей.
Пример 20.11. Найти производную функции у — -f^—.
щх
О Решение:
Производная найдена. В процессе решения использованы правила 2, 3
и формулы 2, 7.
Пример 20.12. Найти производную функции у = cos(ln 2х).
О Решение: Коротко: у' = - sin(ln12 2х) • 12 In11 2х • ^- • 2.
Решение с пояснениями: данную функцию можно представить следу-
ющим образом: у = cos и, и = t1'2, t = \nz, z = 2x. Производную сложной
функции найдем по правилу у'х = у'и • и\ • t'z • z'x (здесь промежуточных
аргументов три):
т. е.
т. е.
т. е.
Окончательно
§21. ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ
И ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИЙ
21.1. Неявно заданная функция
Если функция задана уравнением у = /(х), разрешенным относитель-
но у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде
уравнения F(x;y) = 0, не разрешенного относительно у.
Всякую явно заданную функцию у = f(x) можно записать как неявно
заданную уравнением f(x) — у — 0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относи-
тельно // (например, у + 2х + cosy — 1=0 или 2У — х + у = 0).
Если неявная функция задана уравнением F(x;y) — 0, то для нахо-
ждения производной от у по х нет необходимости разрешать уравнение
относительно у: достаточно продифференцировать это уравнение
152

Функцию у = /(х), определяемую параметрическими уравнениями
(21.1), можно рассматривать как сложную функцию у = y(t), где t = <р(х).
По правилу дифференцирования сложной функции имеем: у'х — у\ -t'x.
С учетом равенства (21.2) получаем
Полученная формула позволяет находить производную у'х от функции
заданной параметрически, не находя непосредственной зависимости у от
х.
153
пример 21.2. Пусть
О Решение: Имеем х[ = St2, y't = 2t. Следовательно,
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, t= Ух. Тогда у— ух?. Отсюда у'х = $,-, т. е. у = тН-
3 v х от
где t — вспомогательная переменная, называемая параметром.
Найдем производную у'х, считая, что функции (21.1) имеют производ-
ные и что функция х = x(t) имеет обратную t = <p(x). По правилу диффе-
ренцирования обратной функции
21.2. Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параме-
трически в виде двух уравнений
О Решение: Функция у задана неявно. Дифференцируем по х равенство
х3 + у3 — Зху = 0. Из полученного соотношения
по х, рассматривая при этом у как функцию х, и полученное затем
уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функ-
цию у.
Пример 21.1. Найти производную функции t/, заданную уравнением
следует, что

§22. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
В ряде случаев для нахождения производной целесообразно заданную
функцию сначала прологарифмировать. А затем результат продифферен-
цировать. Такую операцию называют логарифмическим дифференцирова-
нием.
О Решение: Можно найти у' с помощью правил и формул дифференци-
рования. Однако такой способ слишком громоздкий. Применим логариф-
мическое дифференцирование. Логарифмируем функцию:
Существуют функции, производные которых находят лишь логариф-
мическим дифференцированием. К их числу относится так называемая
степенно-показательная функция у = uv, где и = и(х) и v = v(x)
- заданные дифференцируемые функции от х. Найдем производную этой
функции:
т. е.
или
Сформулируем правило запоминания формулы (22.1): производная
степенно-показательной функции равна сумме производной показатель-
ной функции, при условии и = const, и производной степенной функции,
при условии v — const.
154
Дифференцируем это равенство по х:
Выражаем у':
т. е.
Пример 22.1. Найти производную функции у

|Vj Пример 22.2. Найти производную функции у = (sin2a:)*c +1.
О Решение: Пользуясь формулой (22.1), получаем:
у' = (sin2x)x2+1 • In sin 2х • 2х + (х2 + 1) (sin га;)*2 -cos 2х-2. •
Отметим, что запоминать формулу (22.1) необязательно, легче запо-
мнить суть логарифмического дифференцирования.
§23. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
23.1. Производные высших порядков явно заданной функции
Производная у' = f'(x) функции у = f(x) есть также функция от х и
называется производной первого порядка.
Если функция f'(x) дифференцируема, то ее производная называется
производной второго порядка и обозначается у" (или f"(x), -тЦ, Т~ (7/ )'
$£). Итак,!/" = (»')'•
Производная от производной второго порядка, если она существует,
называется производной третьего порядка и обозначается у'" (или /'"(.х),
0,...). Итак, у'" = (»")'■
Производной п-го порядка (или n-й производной) называется произ-
водная от производной (п — 1) порядка:
Производные порядка выше первого называются производными выс-
ших порядков.
Начиная с производной четвертого порядка, производные обозначают
римскими цифрами или числами в скобках (yv или т/о) — производная
пятого порядка).
Пример 23.1. Найти производную 13-го порядка функции у — sin .г.
О Решение:
155

23.2. Механический смысл производной второго порядка
Пусть материальная точка М движется прямолинейно по закону
S — /М- Как уже известно, производная S't равна скорости точки в дан-
ный момент времени: S't = V.
Покажем, что вторая производная от пути по времени есть величина
ускорения прямолинейного движения точки, т. е. S" = а.
Пусть в момент времени t скорость точки равна V, а в момент t + At —
скорость равна V + Д V, т. е. за промежуток времени At скорость измени-
лась на величину AV.
Отношение =¥г- выражает среднее ускорение движения точки за время
At. Предел этого отношения при At —> О называется ускорением точки М
в данный момент t и обозначается буквой a: lim Щ^г- = а, т. е. V = а.
Д£->0 &t
Но V = S't. Поэтому а = (S't)', т. е. а = S'/.
23.3. Производные высших порядков неявно заданной функции
Пусть функция у = f(x) задана неявно в виде уравнения F{x\ у) = 0.
Продифференцировав это уравнение по х и разрешив полученное урав-
нение относительно у', найдем производную первого порядка (первую про-
изводную). Продифференцировав по х первую производную, получим вто-
рую производную от неявной функции. В нее войдут ж, у и у'. Подставляя
уже найденное значение у' в выражение второй производной, выразим у"
через х и у.
Аналогично поступаем для нахождения производной третьего (и даль-
ше) порядка.
Пример 23.2. Найти у'", если х2 + у2 = 1.
О Решение: Дифференцируем уравнение х2+у2-1 = 0 по х: 2х+2у-у' = 0.
r\ i х тт // 1-y — x-v' ,, У~х'\~й)
Отсюда у' = --. Далее имеем: у — iL-*—2-, т.е. у — —— =
У У У2
У2 + х* 1 / 2 , 2 14 /// -1-3!/2-!/'
= ^— — —* (так как ж +2/ =1)? следовательно, 2/ = « =
_ 3 / £\ _ 3# Л
у4 \ у) уъ'
23.4. Производные высших порядков от функций, заданных
параметрически
Пусть функция у = f(x) задана параметрическими уравнениями
156

Как известно, первая производная у'х находится по формуле
Найдем вторую производную от функции заданной параметрически.
Из определения второй производной и равенства (23.1) следует, что
т. е.
(23.2)
Аналогично получаем
Пример 23.3. Найти вторую производную функции
Q Решение: По формуле (23.1)
Тогда по формуле (23.2)
157
Заметим, что найти у"х можно по преобразованной формуле (23.2):
запоминать которую вряд ли стоит.
§24. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
24.1. Понятие дифференциала функции
Пусть функция у — f(x) имеет в точке х отличную от нуля производ-
ную lim -гУ- = f'{x) ф 0. Тогда, по теореме о связи функции, ее предела
Ах—>0 &X
и бесконечно малой функции, можно записать -г-^ = /'(х) + а-> гДе а ~* 0
при Ах —> 0, или Ay = f'(x) • Ах + а • Ах.
Таким образом, приращение функции Ау представляет собой сумму
двух слагаемых f'(x) • Ах и а • Дх, являющихся бесконечно малыми при

Дифференциал dy называют также дифференциалом первого по-
рядка. Найдем дифференциал независимой переменной я, т. е. дифферен-
циал функции у = х.
Так как у' = х' = 1, то, согласно формуле (24.1), имеем dy = dx = Дх,
т. е. дифференциал независимой переменной равен приращению этой пе-
ременной: dx = Ах.
Поэтому формулу (24.1) можно записать так:
иными словами, дифференциал функции равен произведению про-
изводной этой функции на дифференциал независимой перемен-
ной.
Из формулы (24.2) следует равенство -Я- = f'{x). Теперь обозначение
производной -Я можно рассматривать как отношение дифференциалов dy
и dx.
Пример 24-1. Найти дифференциал функции
158
О Решение: По формуле dy = f'(x) dx находим
Пример 24-2. Найти дифференциал функции
Вычислить dy при х = 0, dx = 0,1.
) Решение:
Подставив х = 0 и dx = 0,1, получим
Поэтому первое слагаемое f'(x)-Ax называют главной частью при-
ращения функции Ау.
Дифференциалом функции у = f(x) в точке х называется глав-
ная часть ее приращения, равная произведению производной функции на
приращение аргумента, и обозначается dy (или df(x)):
Ах —>• 0. При этом первое слагаемое есть бесконечно малая функция одно-
го порядка с Дат, так как lim I = f'{x) ф 0, а второе слагаемое
Дг-+0 LXX
есть бесконечно малая функция более высокого порядка, чем Ах:

24.2. Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала.
Для этого проведем к графику функ-
ции у = f(x) в точке М(х;у) касатель-
ную МТ и рассмотрим ординату этой ка-
сательной для точки х + Ах (см. рис. 138).
На рисунке \АМ\ = Ах, \AMi\ - Ay. Из
прямоугольного треугольника МАВ име-
ем:
\АВ\
tga = ——, т. е. \АВ\ = tga • Ах.
Ах
Но, согласно геометрическому смыслу
производной, tga = f'(x). Поэтому АВ =
= Г(х).Ах.
Сравнивая полученный результат с
формулой (24.1), получаем dy = АВ, т. е.
дифференциал функции у = f(x) e точке х равен приращению
ординаты касательной к графику функции е этой точке, когда
х получит приращение Ах.
В этом и состоит геометрический смысл дифференциала.
24.3. Основные теоремы о дифференциалах
Основные теоремы о дифференциалах легко получить, используя
связь дифференциала и производной функции (dy = f'(x)dx) и соответ-
ствующие теоремы о производных.
Например, так как производная функции у — с равна нулю, то диф-
ференциал постоянной величины равен нулю: dy = с' dx = 0 • dx — 0.
Теорема 24.1. Дифференциал суммы, произведения и частного двух дифференци-
руемых функций определяются следующими формулами:
Q Докажем, например, вторую формулу. По определению дифференциа-
ла имеем:
d(uv) — (uv)'dx = (u'v + uv')dx = v • v!dx + и • v'dx — v du + и dv. Ш
Теорема 24.2. Дифференциал сложной функции равен произведению производной
этой функции по промежуточному аргументу на дифференциал этого промежуточ-
ного аргумента.
159

Сравнивая формулы dy = у'х • dx и dy = у'и • du, видим, что первый
дифференциал функции у = f(x) определяется одной и той же формулой
независимо от того, является ли ее аргумент независимой переменной или
является функцией другого аргумента.
Рч| Это свойство дифференциала называют инвариантностью (неиз-
^—* менностью) формы первого дифференциала.
Формула dy — у'х • dx по внешнему виду совпадает с формулой dy =
= у'и - du, но между ними есть принципиальное отличие: в первой формуле
х — независимая переменная, следовательно, dx = Ах, во второй формуле
и есть функция от х, поэтому, вообще говоря, du ф Аи.
С помощью определения дифференциала и основных теорем о диффе-
ренциалах легко преобразовать таблицу производных в таблицу диффе-
ренциалов.
Например, d(cosn) = {cosu)'u • du — — sinw • du.
24.4. Таблица дифференциалов
160
Умножив обе части этого равенства на dx, получаем ух dx — y'u- u'x dx.
Ho y'x dx — dy и u'x dx = du. Следовательно, последнее равенство можно
переписать так:
Q Пусть у = f(u) и и = (р(х) две дифференцируемые функции, образую-
щие сложную функцию у = f((p(x)). По теореме о производной сложной
функции можно написать

Формула (24.4) используется для вычислений приближенных значе-
ний функций.
Пример 24-4- Вычислить приближенно arctg 1,05.
О Решение: Рассмотрим функцию /(х) = arctg x. По формуле (24.4) име-
ем:
161
24.5. Применение дифференциала к приближенным вычислениям
Как уже известно, приращение Ау функции у = f(x) в точке х можно
представить в виде Ay = f'{x) • Ах + а • Ах, где а —> 0 при Ах —> 0, или
Ay = dy + a • Ах. Отбрасывая бесконечно малую а • Ах более высокого
порядка, чем Ах, получаем приближенное равенство
причем это равенство тем точнее, чем меньше Ах.
Это равенство позволяет с большой точностью вычислить
приблиэюенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем прираще-
ние функции, поэтому формула (24.3) широко применяется в вычисли-
тельной практике.
Пример 24-3. Найти приближенное значение приращения функции
у = х3 - 2х + 1 при х = 2 и Ах = 0,001.
О Решение: Применяем формулу (24.3): Ay « dy = (х3 — 2х + 1)' • Ах =
= (Зх2 - 2) • Ах.
Итак, Ау « 0,01.
Посмотрим, какую погрешность допустили, вычислив дифференциал
функции вместо ее приращения. Для этого найдем Ау:
Абсолютная погрешность приближения равна
Подставляя в равенство (24.3) значения Ау и dy, получим
или

162
т. е.
Так как х + Ах = 1,05, то при х = 1и Ах = 0,05 получаем:
Можно показать, что абсолютная погрешность формулы (24.4) не пре-
вышает величины М • (Дх)2, где М — наибольшее значение |/"(х)| на
сегменте [х\х + Ах] (см. с. 167).
Пример 24-5. Какой путь пройдет тело при свободном падении на
Луне за 10,04 с от начала падения. Уравнение свободного падения тела
Я = 2л_^,(/л = 1,6м/с2.
О Решение: Требуется найти //(10,04). Воспользуемся приближенной
формулой (АН « dH)
При t = 10 с и At = dt = 0,04 с, H'(t) = g^t, находим
Задача (для самостоятельного решения). Тело массой т = 20 кг
движется со скоростью v = 10,02 м/с. Вычислить приближенно кинетиче-
скую энергию тела (ек = т^-\ £к(10,02) « 1004 (Дж)У
24.6. Дифференциалы высших порядков
Пусть у — f(x) дифференцируемая функция, а ее аргумент х — не-
зависимая переменная. Тогда ее первый дифференциал dy = f'(x) dx есть
также функция х; можно найти дифференциал этой функции.
Дифференциал от дифференциала функции у = f(x) называется ее
вторым дифференциалом (или дифференциалом второго порядка) и обо-
значается d2y или d2f(x).
Итак, по определению d2у = d(dy). Найдем выражение второго диф-
ференциала функции у = f(x).
Так как dx — Ах не зависит от ж, то при дифференцировании считаем
dx постоянным:
т. е.
Здесь dx1 обозначает \dxy.
Аналогично определяется и находится дифференциал третьего поряд-
ка* .О . . _rt . ........ rt. О

т. е. производную функции можно рассматривать как отношение ее диф-
ференциала соответствующего порядка к соответствующей степени диф-
ференциала независимой переменной.
Отметим, что все приведенные выше формулы справедливы только,
если х — независимая переменная. Если же функцию у = /(х), где х —
функция от какой-то другой независимой переменной, то диффе-
ренциалы второго и выше порядков не обладают свойством инвариантно-
сти формы и вычисляются по другим формулам. Покажем это на примере
дифференциала второго порядка.
Используя формулу дифференциала произведения (d(u-v)=v du+u dv),
получаем:
163
И, вообще, дифференциал n-го порядка есть дифференциал от диф-
ференциала (п — 1)-го порядка: dny = d(dn~1y) = f^(x)(dx)n.
Отсюда находим, что f^(x) = гг%- В частности, при п = 1, 2, 3
соответственно получаем:
т. е.
Сравнивая формулы (24.5) и (24.6), убеждаемся, что в случае сложной
функции формула дифференциала второго порядка изменяется: появля-
ется второе слагаемое f'(x) • dPx.
Ясно, что если х — независимая переменная, то
и формула (24.6) переходит в формулу (24.5).
Пример 24-6. Найти d?y, если у = е3х их — независимая переменная.
О Решение: Так как у' = Зе3х, у" — 9е3х, то по формуле (24.5) имеем
Пример 24-7. Найти d?y, если у = х2 и х = t3 + 1 и t — независимая
переменная.
Решение: Используем формулу (24.6): так как
Другое решение: у = х2, х = t3 + 1. Следовательно, у = (t3 + I)2. Тогда
по формуле (24.5) „ ..

§25. ИССЛЕДОВАНИЕ ФУНКЦИИ ПРИ ПОМОЩИ
ПРОИЗВОДНЫХ
25.1. Некоторые теоремы о дифференцируемых функциях
Рассмотрим ряд теорем, имеющих большое теоретическое и приклад-
ное значение.
Теорема 25.1 (Рояль). Если функция f(x) непрерывна на отрезке [а; Ь], диффе-
ренцируема на интервале (а; Ь) и на концах отрезка принимает одинаковые значения
f(a) = f{b), то найдется хотя бы одна точка с Е (а; Ь), в которой производная f'(x)
обращается в нуль, т. е. /'(с) = 0.
Q| Так как функция f(x) непрерывна на отрезке [а; 6], то она достигает
на этом отрезке своего наибольшего и наименьшего значений (по теоре-
ме 19.4), соответственно, М и га. Если М = га, то функция f(x) постоянна
на [а; Ь] и, следовательно, ее производная f'{x) = 0 в любой точке отрезка
[а;Ь].
Если М ф га, то функция достигает хотя бы одно из значений М или
га во внутренней точке с интервала (а; Ь), так как /(а) = f(b).
Рис. 139.
Рис. 140.
Рис. 141.
Пусть, например, функция принимает значение М в точке х = се(а;Ь),
т. е. /(с) = М. Тогда для всех х £ (а; Ь) выполняется соотношение
В силу условия (25.1) верно неравенство f(c + &x) — f(c) ^ 0. Если Ах > 0
(т. е. Ах —> 0 справа от точки х = с), то
^ 0 и поэтому /'(с) ^ 0.
Если Ах < 0, то
Таким образом, /'(с) = 0.
В случае, когда /(с) = га, доказательство аналогичное.
164
Найдем производную f'(x) в точке х — с:

Геометрически теорема Ролля означает, что на графике функции
у — f(x) найдется точка, в которой касательная к графику параллельна
оси Ох (см. рис. 139 и 140). На рисунке 141 таких точек две.
Теорема 25.2 (Коши). Если функции f(x) и ip(x) непрерывны на отрезке [а; Ь],
дифференцируемы на интервале (а;6), причем <р'(х) ф 0 для х Е (а;Ь), то найдется
/ ,л fib) - f(a) f'(c)
хотя бы одна точка с Е (а: о) такая, что выполняется равенство jL-tt{— ) ( = /; (.
Она удовлетворяет всем условиям теоремы Рол ля: непрерывна на отрезке
[а; 6] и дифференцируема на интервале (а; 6), так как является линейной
комбинацией функций f(x) и (р(х); на концах отрезка она принимает оди-
наковые значения F(a) = F(b) = 0.
На основании теоремы Ролля найдется точка х — с £ (а; Ь) такая, что
F'(c) = 0. Но F'(x) = f'{x) - ffglSJ^fr), следовательно,
Отсюда следует
О Решение: Теорему Лагранжа можно рассматривать как частный
случай теоремы Коши. Действительно, положив <р(х) = х, находим
(fib) - (fia) = b — a, <р'(х) = 1, ip'(c) = 1.
Подставляя эти значения в формулу )гл _ \ { = /) {, получаем
fib)bZfaia) = /'(с) или /(b) - /(a) = f'(c)(b - а). •
Полученную формулу называют формулой Лагранэюа или форму-
лой о конечном приращении: приращение дифференцируемой функ-
ции на отрезке [a; b] равно приращению аргумента, умноженному на зна-
чение производной функции в некоторой внутренней точке этого отрезка.
165
Теорема 25.3 (Лагранж). Если функция /(ж) непрерывна на отрезке [а; Ь], диф-
ференцируема на интервале (а; Ь), то найдется хотя бы одна точка с € (а; Ь) такая,
что выполняется равенство
Q Отметим, что <р(Ь) — ip(a) ф 0, так как в противном случае по теореме
Ролля нашлась бы точка с, такая, что ^р'(с) = 0, чего не может быть по
условию теоремы. Рассмотрим вспомогательную функцию

Рис. 142.
Теорема Лагранжа имеет простой геометриче-
ский смысл. Запишем формулу (25.2) в виде
^4—*-±-L = /'(с), где а < с < Ъ. Отношение
h — есть Угловои коэффициент секущей
АВ, а величина f'(c) — угловой коэффициент ка-
сательной к кривой в точке с абсциссой х = с.
Следовательно, геометрический смысл теоре-
мы Лагранжа таков: на графике функции y = f(x)
найдется точка С{с; /(c)) (см. рис. 142), в которой
касательная к графику функции параллельна се-
кущей АВ.
Следствие 25.1. Если производная функции равна нулю на некотором промежутке,
то функция постоянна на этом промежутке.
Q Пусть f'(x) = 0 для Ух Е (а; Ь). Возьмем произвольные х\ и х? из
(а;Ь) и пусть х\ < Х2- Тогда по теореме Лагранжа Зс Е (х\\Х2) такая,
что /(2Г2) — f(x\) = f'(c)(x2 — х\). Но по условию f'(x) = О, стало быть,
/'(с) = 0, где х\ < с < Х2- Поэтому имеем /(#2) — f(x\) = 0, т. е. /fe) =
= f(x\). А так как х\ и Х2 — произвольные точки из интервала (а; 6), то
Ух Е (а;Ь) имеем f(x) — с. Ш
Следствие 25.2. Если две функции имеют равные производные на некотором про-
межутке, то они отличаются друг от друга на постоянное слагаемое.
□ Пусть fi(x) = ft(x) при хе(а;Ъ). Тогда (fi(x)-f2(x)Y = f[(x)-f^x) = 0.
Следовательно, согласно следствию 25.1, функция fi{x) — /2(2) есть по-
стоянная, т. е. fi(x) — /2{х) = С для Уж Е (а; Ь). Ш
Пример 25.1. Доказать, что arcsinx + arccosx = ^, где х Е [—1; 1].
О Решение: Пусть /(ж) = arcsinx + arccos#. Тогда \/х Е (—1; 1) имеем
/'(*) =
= 0. Отсюда следует, что f(x) = С, т. е.
arcsinx + arccosx = С. Положив х = О, находим 0 + 5 = С, т. е. С — Ц.
Поэтому arcsinrr + arccosx = 5. Это равенство выполняется и при
х = ±1 (проверьте!). •
Аналогично доказывается, что arctgx + arcctgx = ^.
Формуле Лагранжа можно придать другой вид. Применив теорему Ла-
гранжа к отрезку [ж; х + Дх] (Да: > 0), будем иметь
f(x + Да?) - /(ж) = f'(c)Ax. (25.3)
166

25.2. Правила Лопиталя
Рассмотрим способ раскрытия неопределенностей вида ^ и —, кото-
рый основан на применении производных.
Теорема 25.4 (Правило Лопиталя раскрытия неопределенностей вида У).
Пусть функции /(х) и <р{х) непрерывны и дифференцируемы в окрестности точки хо
и обращаются в нуль в этой точке: /(хо) = <^(хо) = 0. Пусть (f'(x) ф 0 в окрестности
fix) fix) fix)
точки хо- Если существует предел lim ,) { = I, то lim J) I = lim J Л { = I.
x^xq <f (X) x^xq (p{X) x-+x0 If (XJ
Каждое число с Е (х; х + Да:) можно записать в виде с = х + 0Дх,
где 0 < в < 1 (действительно, а: < с < х + Дх =>> 0 < с — х < Ах =>
=> 0 < ^-^ < 1; положим £^£ = б => с = х + 0Дх). Формула (25.3)
примет вид
где 0 < в < 1.
Используя теорему Лагранжа, можно оценить точность приближен-
ного равенства Ау « ей/. Сделаем это, считая, что функция /(х) имеет
непрерывную вторую производную /"(х):
где с\ е (х;с) (рис. 143).
Итак, Ay - dy = f"(c\)(c - х)Дх. Пусть М =
= max \f"(x)\. Так как \с - х\ < Ах, a f"(ci) ^ М,
[х;х+Ах]
то получаем оценку |Д?/ — dy\ ^ М|Дх|2.
Q Применим к функциям /(х) и <р(х) теорему Коши для отрезка [х0;х],
™ /(х) - /(хр) f'(c)
лежащего в окрестности точки хо. Гогда jL-f—{—J) { = J,) (, где с лежит
<Р{х) ~ <Р(*о) V? (с)
между хо и х (рис. 144). Учитывая, что /(хо) = р(хо) = О, получаем
При х -> хо, величина с также стремится к
хо; перейдем в равенстве (25.4) к пределу:
167
Рис. 144.
Рис. 143.

Так как lim ,) ( — I, то lim ,, ( = /. Поэтому lim ) I = L Ш
x-+xq if (x) c^xo if (C) " x->x0 4>\X)
Коротко полученную формулу читают так: предел отношения двух
бесконечно малых равен пределу отношения их производных, если послед-
ний существует.
Замечания: 1. Теорема 25.4 верна и в случае, когда функции f(x) и
<р(х) не определены при х — хо, но lim f(x) = 0 и lim ip(x) = 0. Доста-
X—>Хо X—^Xq
точно положить f{xo) — lim f(x) = 0 и ip(xo) = lim <p(x) = 0.
x—>xo x—*xo
2. Теорема 25.4 справедлива и в том случае, когда х —> ос. Действи-
тельно, положив х = -, получим
3. Если производные f'(x) и ip'(x) удовлетворяют тем же условиям,
что и функции f(x) и (f{x), теорему 25.4 можно применить еще раз:
и т. д.
Пример 25.2. Найти
О Решение: lim
Пример 25.3. Найти lim 1~C(f6x.
О Решение:
Теорема 25.4 дает возможность раскрывать неопределенность вида -.
Сформулируем без доказательства теорему о раскрытии неопределенно-
00
сти вида —.
00
Теорема 25.5 (Правило Лопиталя раскрытия неопределенностей вида —).
Пусть функции f(x) и <р(х) непрерывны и дифференцируемы в окрестности точки
хо (кроме, может быть, точки хо), в этой окрестности lim f(x) = lim <р(х) = оо,
X—¥Xq X—¥Xq
fix) fix) fix)
u>'(x) Ф 0. Если существует предел lim J,, l, то lim *Ц—е = lim ,) {.
^ V ' ^ J J Г x->x0 <f (x) x^xo ip(x) x-^xq ip (x)
168

a
Пример 25.1 Найти lim -^||.
так:
На практике бывает проще, например,
lim
Xq
1
1
fix)
_j i_
<p(x) fix)
3. Пусть или /(x) —> 1 и v?(x) —► oo, или /(x) -> oo и (f(x) —»- 0,
или /(x) —> 0 и </?(x) -> 0 при x —У хо. Для нахождения предела вида
lim /(x)^(x) удобно сначала прологарифмировать выражение A=f(x)^xK
169
Решение:
2-й способ:
Раскрытие неопределенностей различных видов
Правило Лопиталя применяется для раскрытия неопределенностей
вида ^ и —, которые называют основными. Неопределенности вида 0 • оо,
ос — оо, 1°°, ос0, 0° сводятся к двум основным видам путем тождественных
преобразований.
1. Пусть f(x) —> 0, (р(х) —> оо при х —» хо- Тогда очевидны следующие
преобразования:
Например,
Тогда можно поступить

Пример 25.5. Найти lim (cos 2x) ^.
О Решение: Имеем неопределенность вида 1°°. Логарифмируем выраже-
ние А = (cos2x)^, получим: In Л = -\ In cos 2x. Затем находим предел:
т. е. In lim A = -2. Отсюда lim А = е 2, и lim (cos2x)^ = е 2. •
х-+0 х->0 х-+0
Решение можно оформить короче, если воспользоваться «готовой»
формулой
170
(использовано основное логарифмическое тождество: /^ = еХп**).
Пример 25.6. Найти
Решение:
Пример 25.7. Пусть
Найти f'(x). (Дополнительно: найти /^(0).)
О Решение: При х ф 0 имеем
При х = 0 по определению производной:
Делаем замену у = ^ и применяем правило Лопиталя
Таким образом,
Аналогично можно показать, что /^п^(0) = 0.
при х ф 0,
при х — 0.
при ж/0,
при х = 0.

25.3. Возрастание и убывание функций
Одним из приложений производной является ее применение к иссле-
дованию функций и построению графика функции.
Установим необходимые и достаточные условия возрастания и убыва-
ния функции.
Теорема 25.6 (необходимые условия). Если дифференцируемая на интервале
(а; Ь) функция /(х) возрастает (убывает), то /'(х) ^ 0 (f'{x) ^ 0) для Vx £ (а;Ь).
Q Пусть функция /(х) возрастает на интервале (а; Ь).
Возьмем произвольные точки х и х + Ах на интервале
/ 1Л Av f(x + Ax) - fix)
(а; о) и рассмотрим отношение -г^1 = — -г-1—J v '.
Функция /(х) возрастает, поэтому если Ах > 0, то
х + Ах > х и /(х + Ах) > /(х); если Ах < 0, то
х + Ах < х и /(х + Ах) < /(х). В обоих случаях
Aw fix + Ах) - /(х) ^ п
-г^- = lLA т-^—J N f > О, так как числитель и
Дх Дх
Рис. 145. знаменатель дроби имеют одинаковые знаки. По усло-
вию теоремы функция /(х) имеет производную в точ-
ке х и является пределом рассматриваемого отношения. Следовательно,
Пх) = Ит /(^Ах)-/(х) и
Аналогично рассматривается случай, когда функция /(х) убывает на
интервале (а;Ь).
Геометрически теорема 25.6 означает, что касательные к графику воз-
растающей дифференцируемой функции образуют острые углы с положи-
тельным направлением оси Ох или в некоторых точках (на рисунке 145 в
точке с абсциссой хо) параллельны оси Ох.
Теорема 25.7 (достаточные условия). Если функция /(х) дифференцируема на
интервале (а;6) и /'(х) > 0 (/'(х) < 0) для Vx £ (a;b), то эта функция возрастает
(убывает) на интервале (а;Ь).
Q Пусть f'{x) > 0. Возьмем точки х\ и х-2 из интервала (а; 6), причем
xi < #2. Применим к отрезку [xi;^] теорему Лагранжа: /(х?) — f(xi) —
= ff(c)(x-2 - £1), где с G {х\\Х2). По условию /'(с) > 0, х2 - х\ > 0.
Следовательно, /(#2) — /(#i) > 0 или /(#2) > f(x\)-> T- е- функция /(ж) на
интервале (а; 6) возрастает. В
Рассмотренные теоремы 25.6 и 25.7 позволяют довольно просто иссле-
довать функцию на монотонность. Напомним, что функция возрастающая
или убывающая называется монотонной (см. с. 102).
Пример 25.8. Исследовать функцию f(x) = х3 — Зх — 4 на возрастание
и убывание.
171

О Решение: Функция определена на Ш — (—оо; оо). Ее производная равна:
f'(x) = Зх2 - 3 = 3(х - 1)(х + 1); /'(х) > О при х G (-оо;-1) U (1;оо);
f'(x) <0прихе (-1;1).
Ответ: данная функция возрастает на интервалах (—оо; — 1) и (1;оо);
убывает на интервале ( —1; 1). •
25.4. Максимум и минимум функций
Точка хо называется точкой максимума функции у = /(х), если
существует такая (5-окрестность точки хо, что для всех х ф хо из этой
окрестности выполняется неравенство f(x) < f(xo).
Аналогично определяется точка минимума
функции: хо — точка минимума функции, если
36 >0Vx :0 <\х-х0\ <6 => /(х) > f(x0). На
рисунке 146 Х\ — точка минимума, а точка Х2 —
точка максимума функции у — f{x).
Значение функции в точке максимума (мини-
мума) называется максимумом (минимумом)
функции. Максимум (минимум) функции называ-
ется экстремумом функции.
Понятие экстремума всегда связано с опреде-
ленной окрестностью точки из области определе-
ния функции. Поэтому функция может иметь экстремум лишь во вну-
тренних точках области определения. Рассмотрим условия существова-
ния экстремума функции.
Теорема 25.8 (необходимое условие экстремума). Если дифференцируемая
функция у — f(x) имеет экстремум в точке хо, то ее производная в этой точке равна
нулю: /'(х0) = 0.
Q Пусть, для определенности, хо — точка максимума. Значит, в окрест-
ности точки хо выполняется неравенство /(хо) > f(xo + Дх). Но тогда
Д^ = f(x0 + A£-f(x0) < 0, если Ах > 0, и %£ > 0, если Ах < 0.
По условию теоремы производная /'(хо) = lim J ^ ° д-*—LLJ11 суще-
Дх—*0 ^Х
ствует. Переходя к пределу, при Ах —> 0, получим /'(хо) ^ 0, если Дх < 0,
и /'(хо) ^ 0, если Дх > 0. Поэтому /'(хо) = 0. Аналогично доказывается
утверждение теоремы 25.8, если хо — точка минимума функции /(х). Н
Рис. 147.
Геометрически равенство f'(xo) = 0 озна-
чает, что в точке экстремума дифференцируе-
мой функции у = f(x) касательная к ее графи-
ку параллельна оси Ох (см. рис. 147).
Отметим, что обратная теорема неверна,
т. е. если /'(xq) = 0, то это не значит, что хо —
172
Рис. 146.

Рис. 148.
точка экстремума. Например, для функции у = х3 ее производная
у' = Зх2 равна нулю при х = О, но х = 0 не точка экстремума (см.
рис. 148).
Существуют функции, которые в точках экстремума не
имеют производной. Например, непрерывная функция у = \х\
в точке х = 0 производной не имеет,
но точка х = 0 — точка минимума (см.
рис. 149).
Таким образом, непрерывная функция
может иметь экстремум лишь в точках, где
производная функции равна нулю или не
существует. Такие точки называются кри-
тическими.
Теорема 25.9 (достаточное условие экстремума). Если непрерывная функция
у = f[x) дифференцируема в некоторой (J-окрестности критической точки хо и при
переходе через нее (слева направо) производная f'(x) меняет знак с плюса на
минус, то хо есть точка максимума; с минуса на плюс, то xq — точка минимума.
Q Рассмотрим ^-окрестность точки хо- Пусть выполняются условия:
f'(x) > 0 Vx € (хо —6;хо) и f'{x) < 0 Vx E (хо; Хо + 6). Тогда функция f(x)
возрастает на интервале (хо — S; хо), а на интервале (хо; xq+S) она убывает.
Отсюда следует, что значение /(х) в точке xq является наибольшим на ин-
тервале (хо-8;хо+д), т. е. f(x) < f(xo) для всех х G (xo-6;xo)U(xo;xo+S).
Это и означает, что хо — точка максимума функции.
Графическая интерпретация доказательства теоремы 25.9 представле-
на на рисунке 150.
Рис. 150.
Аналогично теорема 25.9 доказывается для случая, когда f'{x) < 0
Ух е (х0 - S;x0) и f'(x) > 0 Vx G {х0;х0 + S). ■
Исследовать функцию на экстремум означает найти все ее экстре-
мумы. Из теорем 25.8 и 25.9 вытекает следующее правило исследования
функции на экстремум:
1) найти критические точки функции у = f(x);
2) выбрать из них лишь те, которые являются внутренними точками
области определения функции;
173
Рис. 149.

3) исследовать знак производной f'{x) слева и справа от каждой из
выбранных критических точек;
4) в соответствии с теоремой 25.9 (достаточное условие экстремума)
выписать точки экстремума (если они есть) и вычислить значения функ-
ции в них.
Пример 25.9. Найти экстремум функции у =
Рис. 151.
Следовательно, х\=0 — точка максимума, 2/тах=2/(0)=0, и #2 = 8 —
точка минимума, утт = у(8) = -i. •
Иногда бывает удобным использовать другой достаточный признак су-
ществования экстремума, основанный на определении знака второй про-
изводной.
Теорема 25.10. Если в точке хо первая производная функции f(x) равна нулю
(f'(xo) = 0), а вторая производная в точке xq существует и отлична от нуля
(/"(хо) Ф 0), то при f"(xo) < 0 в точке хо функция имеет максимум и минимум —
при /"(хо) > 0.
f'(xr\ + Ах)
то —-—д L > 0 в достаточно малой окрестности точки xq. Если Ах < О,
то f'(x0 + Ах) < 0; если Ах > 0, то f'(x0 + Ах) > 0.
Таким образом, при переходе через точку хо первая производная ме-
няет знак с минуса на плюс. Следовательно, по теореме 25.9, xq есть точка
минимума.
Аналогично доказывается, что если f"(xo) < 0, то в точке хо функция
имеет максимум. ■
174
О Решение: Очевидно, D(y) = R Находим у'
Производная не существует при х\ = 0 и равна нулю при х^ = 8. Эти
точки разбивают всю область определения данной функции на три интер-
вала (-оо;0), (0;8), (8;оо). Отметим на рисунке 151 знаки производной
слева и справа от каждой из критических точек.
Пусть для определенности /"(#о) > 0. Так как

25.5. Наибольшее и наименьшее значения функции на отрезке
Пусть функция у = /(х) непрерывна на отрезке [а; Ь]. Как известно,
такая функция достигает своих наибольшего и наименьшего значений. Эти
значения функция может принять либо во внутренней точке хо отрезка
[а; Ь], либо на границе отрезка, т. е. при хо = а или хо = Ь. Если хо Е (а; Ь),
то точку хо следует искать среди критических точек
данной функции (см. рис. 152).
Получаем следующее правило нахождения наи-
большего и наименьшего значений функции на [а; Ь]:
1) найти критические точки функции на интер-
вале (а; Ь);
2) вычислить значения функции в найденных
— критических точках;
3) вычислить значения функции на концах от-
резка, т. е. в точках х = а и х = 6;
4) среди всех вычисленных значений функции
выбрать наибольшее и наименьшее.
Замечания: 1. Если функция у = /(х) на отрезке [а; Ь] имеет лишь одну
критическую точку и она является точкой максимума (минимума), то в
этой точке функция принимает наибольшее (наименьшее) значение. На
рисунке 152 /(хо) = /нб = /max (нб — наибольшее, max — максимальное).
2. Если функция у = /(х) на отрезке [а; Ь] не имеет критических то-
чек, то это озачает, что на нем функция монотонно возрастает или убы-
вает. Следовательно, свое наибольшее значение (А/) функция принимает
на одном конце отрезка, а наименьшее (га) — на другом.
Рис. 152.
f'(x) = О при xi = 0 € [-2; 1] и при х2 = -1 G [-2; 1]. Находим /(0) = 1,
/(-1) = 3-4+1=0, /(-2) = 48 - 32 + 1 = 17, /(1) = 8. Итак, /нб = 17 в
точке х = —2, /нм = 0 в точке х = — 1. •
Нахождение наибольшего и наименьшего значений функции широко
применяется при решении многих практических задач математики, физи-
ки, химии, экономики и других дисциплин.
Практические задачи: транспортная задача о перевозке груза с мини-
мальными затратами, задача об организации производственного процесса
с целью получения максимальной прибыли и другие задачи, связанные с
поиском оптимального решения, приводят к развитию и усовершенствова-
нию методов отыскания наибольших и наименьших значений. Решением
таких задач занимается особая ветвь математики — линейное программи-
рование.
175
Пример 25.10. Найти наибольшее и наименьшее значения функции
f(x) = Зх4 + 4х3 + 1 на отрезке [-2; 1].
О Решение: Находим критические точки данной функции:

Рассмотрим более простую задачу.
Пример 25.11. Из шара радиуса R выточить цилиндр наибольшего
объема. Каковы его размеры?
О Решение: Обозначим через х и у высоту и диаметр цилиндра.
Тогда, как видно из рисунка 153, у = л/4 В? — х2, а потому объем
цилиндра
где я € [0;2Д].
Рис. 153. Находим наибольшее значение функции V = V(x) на про-
межутке [0;2Д]. Так как V'{x) = тгй2 - |тгх2, то V'(x) = 0 при
х = 2 д V 3 кроме того? у" (ж) = — ^тгх < 0. Поэтому х = 2ДуЗ _
точка максимума. Так как функция имеет одну критическую точку, то
цилиндр будет иметь наибольший объем (равный Vmax) при х = У ;
диаметр основания цилиндра равен
Таким образом, искомый цилиндр имеет высоту, равную У , и диа-
метр, равный
25.6. Выпуклость графика функции. Точки перегиба
График дифференцируемой функции у = f(x) называется выпуклым
вниз на интервале (а; 6), если он расположен выше любой ее касатель-
ной на этом интервале. График функции
у = /(х) называется выпуклым вверх на
интервале (а; 6), если он расположен ниже
любой ее касательной на этом интервале.
Точка графика непрерывной функции
у = /(я), отделяющая его части разной вы-
пуклости, называется точкой перегиба.
На рисунке 154 кривая у = f(x) выпу-
кла вверх в интервале (а; с), выпукла вниз
в интервале (с; 6), точка М(с; /(c)) — точка
перегиба.
Рис. 154.
176

Интервалы выпуклости вниз и вверх находят с помощью следующей
теоремы.
Теорема 25.11. Если функция у = f(x) во всех точках интервала (а; Ь) имеет
отрицательную вторую производную, т. е. f"(x) < О, то график функции в этом
интервале выпуклый вверх. Если же f"(x) > 0 Vx G (ci',b) — график выпуклый
вниз.
Q Пусть f"(x) < 0 Vx E (а; Ь). Возьмем на графике функции произволь-
ную точку М с абсциссой хо Е (а; Ь) и проведем через М касательную (см.
рис. 155). Покажем, что график функции расположен ниже этой касатель-
ной. Для этого сравним в точке х Е (а\Ь) ординату у кривой у = f(x) с
ординатой ?/кас ее касательной. Уравнение касательной, как известно, есть
т. е.
Теорема 25.12 (достаточное условие существования точек перегиба). Если
вторая производная /"(#) при переходе через точку х0, в которой она равна ну-
лю или не существует, меняет знак, то точка графика с абсциссой хо есть точка
перегиба.
177
Тогда у - укас
По теореме Лагранжа,
где с лежит между xq и х. Поэтому
т. е.
Разность /'(с) — f'(xo) снова преобразуем по формуле Ла-
гранжа:
где с\ лежит между xq и с. Таким образом, получаем
Рис. 155.
Исследуем это равенство:
Итак, доказано, что во всех точках интервала (а; о) ордината касатель-
ной больше ординаты графика, т. е. график функции выпуклый вверх.
Аналогично доказывается, что при f"(x) > 0 график выпуклый вниз. ■
Для нахождения точек перегиба графика функции используется сле-
дующая теорема.

Q Пусть /"(x) < О при х < Хо и f"(x) > О при х > xq. Это значит, что
слева от х = хо график выпуклый вверх, а справа — выпуклый вниз. Сле-
довательно, точка (хо; /(#о)) графика функции является точкой перегиба.
Аналогично доказывается, что если f"(x) > О при х < хо и /"(х) < О
при х > хо, то точка (хо;/(хо)) — точка перегиба графика функции
У = fix). ■
Пример 25.12. Исследовать на выпуклость и точки перегиба график
функции у = хъ — х + 5.
О Решение: Находим, что у' = 5х4 — 1, у" = 20х3. Вторая производная
существует на всей числовой оси; у" = О при х = 0.
Отмечаем, что у" > 0 при х > 0; у" < 0 при х < 0.
Следовательно, график функции у = х5 — х + 5 в интервале (—оо; 0) —
выпуклый вверх, в интервале (0; оо) — выпуклый вниз. Точка (0; 5) есть
точка перегиба. •
Рис. 156.
25.7. Асимптоты графика функции
Построение графика функции значительно
облегчается, если знать его асимптоты. Понятие
асимптоты рассматривалось при изучении фор-
мы гиперболы (см. с. 68).
Напомним, что асимптотой кривой называ-
ется прямая, расстояние до которой от точки, ле-
жащей на кривой, стремится к нулю при неогра-
ниченном удалении от начала координат этой
точки по кривой (рис. 156).
Асимптоты могут быть вертикальными, на-
клонными и горизонтальными.
Говорят, что прямая х — а является вертикальной асим-
птотой графика функции у = f(x), если lim f(x) = оо, или
х—Уа
lim f(x) = оо, или lim f(x) = оо.
х—>а—0 х—>-а+0
Действительно, в этом случае непосредственно из рисун-
ка 156 видно, что расстояние точки М{х-,у) кривой от пря-
мой х — а равно d = \х — а\. Если х -> а, то d —> 0. Согласно
определению асимптоты, прямая х — а является асимпто-
той кривой у = f(x). Для отыскания вертикальных асим-
птот нужно найти те значения х, вблизи которых функция
f(x) неограниченно возрастает по модулю. Обычно это точ-
ки разрыва второго рода.
Например, кривая у= * имеет вертикальную асимп-
lim —=^ = —00.
*-i-o х+\
О
Рис. 157.
тоту (см. рис. 157) х = — 1, так как
Уравнение наклонной асимптоты будем искать в виде
у = кх + Ь.
Найдем к и Ь.
(25.5)
178

Рис. 158.
Отсюда следует, что кх — у + Ь = а, где а = а(х) бесконечно
малая: а —> О при х —> ос. Разделив обе части равенства у = Ь + /сх — а на
х и перейдя к пределу при х -> оо, получаем:
Так как —
Из условия (25.6) находим b:
(25.7)
(25.8)
Итак, если существует наклонная асимптота ?/ = Ь + 6, то fc и Ь
находятся по формулам (25.7) и (25.8).
Верно и обратное утверждение: если существуют конечные пределы
(25.7) и (25.8), то прямая (25.5) является наклонной асимптотой.
Если хотя бы один из пределов (25.7) или (25.8) не существует или
равен бесконечности, то кривая у = f(x) наклонной асимптоты не имеет.
В частности, если к = 0, то b = lim f(x). Поэтому у = b — уравнение
горизонтальной асимптоты.
Замечание: Асимптоты графика функции у = f(x) при х —> +оо и
х -> -оо могут быть разными. Поэтому при нахождении пределов (25.7)
и (25.8) следует отдельно рассматривать случай, когда х —> -1-ое и когда
х —> —оо.
Пример 25.13. Найти асимптоты графика функции у = хех.
Q Решение: Так как lim ^— = lim ex = +оо, то график функции
х—► Ч-оо X х—у +оо
при х —> +оо наклонной асимптоты не имеет.
При х —у —оо справедливы соотношения
Следовательно, при я —>• — оо график имеет горизонтальную асимптоту
!/ = 0. •
179
Пусть М(х;2/) — произвольная точка кривой у = f(x)
(см. рис. 158). По формуле расстояния от точки до прямой
/, I Ахп + Вуо + С\\ ,,
[а = \ —v> уи ' ' находим расстояние от точки М до
v I лЛ42 + В2 \'
прямой (25.5): d= \kx~V + b\.
Условие d —> 0 будет выполняться лишь тогда, когда чис-
литель дроби стремится к нулю, т. е.

25.8. Общая схема исследования функции и построения графика
Исследование функции у = f(x) целесообразно вести в определенной
последовательности.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями коор-
динат.
3. Найти интервалы знакопостоянства функции (промежутки, на ко-
торых f(x) > 0 или f(x) < 0).
4. Выяснить, является ли функция четной, нечетной или общего вида.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности функции.
7. Найти экстремумы функции.
8. Найти интервалы выпуклости и точки перегиба графика функции.
На основании проведенного исследования построить график функции.
Заметим, что приведенная схема исследования не является обязательной.
В более простых случаях достаточно выполнить лишь несколько опера-
ций, например 1, 2, 7. Если же график функции не совсем понятен и после
выполнения всех восьми операций, то можно дополнительно исследовать
функцию на периодичность, построить дополнительно несколько точек
графика, выявить другие особенности функции. Иногда целесообразно вы-
полнение операций исследования сопровождать постепенным построением
графика функции.
Пример 25.Ц- Исследовать функцию у — х * и построить ее гра-
1 — х
фик.
О Решение: Выполним все восемь операций предложенной выше схемы
исследования.
1. Функция не определена при ж = 1их=—1. Область ее определения
состоит из трех интервалов (—оо; — 1), (—1;1), (1;+оо), а график из трех
ветвей.
2. Если х = 0, то у = 0. График пересекает ось Оу в точке (9(0; 0); если
у = 0, то х = 0. График пересекает ось Ох в точке О(0; 0).
3. Функция знакоположительна (у > 0) в интервалах (—оо; — 1) и (0; 1);
знакоотрицательна— в ( —1;0) и (1;+оо).
4. Функция у = -—^—j является нечетной, т. к.
Следовательно, график ее симметричен относительно начала координат.
Для построения графика достаточно исследовать ее при х ^ 0.
5. Прямые ж=1их=-1 являются ее вертикальными асимптотами.
Выясним наличие наклонной асимптоты:
180

(к = 0 при х —> + оо и при х —> — оо),
Рис. 159.
Вторая производная равна нулю
или не существует в точках х\ = О,
Х2 = — 1, хз = 1. На рисунке 159 пред-
ставлена схема изменения знаков вто-
рой производной исследуемой функ-
ции.
Точка 0(0,0) — точка перегиба
графика функции.
График выпуклый вверх на интер-
валах (—1;0) и (1;оо); выпуклый вниз
на интервалах (—оо; —1) и (0; 1).
График функции изображен на ри-
сунке 160. •
Рис. 160.
§26. ФОРМУЛА ТЕЙЛОРА
В определении функции у = /(х) не говорится о том, при помощи ка-
ких средств находятся значения у по значениям х. В тех случаях, когда
з
функция является формулой вида у — % 5х + 7, значения функции
181
Следовательно, есть горизонтальная асимптота, ее уравнение у = 0. Пря-
мая у = 0 является асимптотой и при х -» +оо, и при я -> — оо.
6. Находим интервалы возрастания и убывания функции. Так как
то у' > 0 в области определения, и функция является возрастающей на
каждом интервале области определения.
2,-1
7. Исследуем функцию на экстремум. Так как у' = -~г— 2V2' то КРИ~
(1 -х )
тическими точками являются точки х\ = 1 и х-2 = — 1 {у* не существует),
но они не принадлежат области определения функции. Функция экстре-
мумов не имеет.
8. Исследуем функцию на выпуклость. Находим у":

182
найти легко с помощью четырех арифметических действий. Но как найти
значения, например, функций у — sin я, у = 1п(1 + х) при любых (допусти-
мых) значениях аргумента?
Для того, чтобы вычислить значения данной функции у = /(х), ее за-
меняют многочленом Рп(х) степени п, значения которого всегда и легко
вычисляемы. Обоснование возможности представлять функцию многочле-
ном дает формула Тейлора.
26.1. Формула Тейлора для многочлена
Пусть функция /(#) есть многочлен Рп(х) степени п:
Преобразуем этот многочлен также в многочлен степени п относительно
разности х — хо, где хо — произвольное число, т. е. представим Рп(х) в
виде
Для нахождения коэффициентов Ao,Ai,...,An продифференцируем п раз
равенство (26.1):
Подставляя х — xq в полученные равенства и равенство (26.1), имеем:

Теорема 26.1. Если функция f(x) определена в некоторой окрестности точки хо и
имеет в ней производные до (п 4- 1)-го порядка включительно, то для любого х из
этой окрестности найдется точка с £ (xq;x) такая, что справедлива формула
Формула (26.3) называется формулой Тейлора для функции f(x).
Эту формулу можно записать в виде f(x) = Рп(х) + Rn(x), где
называется остаточным членом формулы Тейлора, записанным в
форме Лагранжа. Rn(x) есть погрешность приближенного равенства
183
называется многочленом Тейлора, а
26.2. Формула Тейлора для произвольной функции
Рассмотрим функцию у = f{x). Формула Тейлора позволяет, при опре-
деленных условиях, приближенно представить функцию f(x) в виде мно-
гочлена и дать оценку погрешности этого приближения.
Формула (26.2) называется формулой Тейлора для многочлена
Рп(х) степени п.
Пример 26.1. Разложить многочлен Р(х) = —4х3 + Зх2 — 2х + 1 по
степеням х + 1.
Подставляя найденные значения Ао,А\,...,Ап в равенство (26.1), полу-
чим разложение многочлена гг-й степени Рп(х) по степеням (х — хо):

f(x) « Pn(x)- Таким образом, формула Тейлора дает возможность за-
менить функцию у — f(x) многочленом у = Рп(х) с соответствующей
степенью точности, равной значению остаточного члена Rn{x).
При хо = 0 получаем частный случай формулы Тейлора — формулу
Маклорена:
184
где с находится между 0 и х (с = Ох, 0 < в < 1).
При п = 0 формула Тейлора (26.3) имеет вид/(х) = f(xo)+f'(c)(x—хо)
или f(x) — f{xo) = f'(c)(x — хо), т. е. совпадает с формулой Лагранжа
конечных приращений. Рассмотренная ранее формула для приближенных
вычислений f(x) « /(#о) + /'(хо)(# - хо) (см. «дифференциал функции»)
является частным случаем более точной формулы
Пример 26.2. Найти число е с точностью до 0,001.
О Решение: Запишем формулу Маклорена для функции f(x) = ех. Нахо-
дим производные этой функции: f'(x) = ех, f"(x) = ех, ..., /(п+1)(х) = ех.
Так как /(0) = е° = 1, /'(0) = е° = 1, ..., /<п)(0) = 1, /<п+1)(с) = ес, то по
формуле (26.4) имеем:
Положим х = 1:
Для нахождения е с точностью 0,001 определим п из условия, что
с
остаточный член 7—е, -im меньше 0,001. Так как 0 < с < 1, то ес < 3.
(п + 1)!
Поэтому при п — б имеем
Итак, получаем приближенное равенство
w 2 + 0,5 + 0,1667 + 0,0417 + 0,0083 + 0,0014 = 2,7181 « 2,718,
т. е. е « 2,718.

Приведем разложения по формуле Маклорена некоторых других эле-
ментарных функций:

Глава VI. КОМПЛЕКСНЫЕ ЧИСЛА
Лекции 23-24 I
§27. ПОНЯТИЕ И ПРЕДСТАВЛЕНИЯ КОМПЛЕКСНЫХ ЧИСЕЛ
27.1. Основные понятия
Комплексным числом z называется выражение вида z — хЛ-iy, где
х и у — действительные числа, а г — так называемая мнимая единица,
г2 = -1.
Если х = О, то число 0 + iy = iy называется чисто мнимым; если
у = О, то число х + г О = х отождествляется с действительным числом
х, а это означает, что множество К всех действительных чисел является
подмножеством множества С всех комплексных чисел, т. е. RcC
Число х называется действительной частью комплексного числа
z и обозначается х = Re г, а у — мнимой частью z, у = lm z.
Два комплексных числа z\ — х\ + гу\ и z-2 = X2 + iyi называются рав-
ными [z\ — 22) тогда и только тогда, когда равны их действительные
части и равны их мнимые части: х\ — x-i, у\ =2/2- В частности, комплекс-
ное число z = х + iy равно нулю тогда и только тогда, когда х = у = 0.
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Два комплексных числа z = х + iy и z — х — iy, отличающиеся лишь
знаком мнимой части, называются сопржнсенными.
27.2. Геометрическое изображение комплексных чисел
Всякое комплексное число z = x + iy можно изобразить точкой М(х; у)
плоскости Оху такой, что х = Re г, у = lm z. И, наоборот, каждую точку
М{х;у) координатной плоскости можно рассма-
тривать как образ комплексного числа z — хЛ-гу
(см. рис. 161).
Плоскость, на которой изображаются комп-
лексные числа, называется комплексной плос-
костью. Ось абсцисс называется действи-
тельной осью, так как на ней лежат действи-
тельные числа z — х + 0г = х. Ось ординат назы-
вается мнимой осью, на ней лежат чисто мни- Рис. 161.
мые комплексные числа z = 0 + iy.
Комплексное число z = х -\- iy можно задавать с помощью радиус-
вектора f = ОМ = (х',у). Длина вектора г, изображающего комплексное
число z, называется модулем этого числа и обозначается \z\ или г. Ве-
личина угла между положительным направлением действительной оси и
вектором г, изображающим комплексное число, называется аргументом
этого комплексного числа, обозначается Arg z или (р.
Аргумент комплексного числа z = 0 не определен. Аргумент комплекс-
ного числа z ф 0 — величина многозначная и определяется с точностью
186

до слагаемого 27гк (к = 0, — 1,1, —2,2 ...): Argz = argz + 2жк, где argz —
главное значение аргумента, заключенное в промежутке (—7г; 7г], т. е.
—7г < argz ^ 7Г (иногда в качестве главного значения аргумента берут
величину, принадлежащую промежутку [0;27г)).
Рис. 162.
Например, |г|
Так как
то
1. Аргумент <р определяется из формул
Поэтому при переходе от алгебраической формы комплексного числа
к тригонометрической достаточно определить лишь главное значение ар-
гумента комплексного числа г, т. е. считать ip = argz.
Так как -7Г < arg z ^ 7г, то из формулы tg (р = ^~
получаем, что
для внутренних точек
I, IV четвертей,
для внутренних точек
II четверти,
для внутренних точек
III четверти.
Если точка z лежит на действительной или мни-
мой оси, то argz можно найти непосредственно (см.
рис. 163). Например, argzi = 0 для z\ = 2; argz-2 = 7Г
187
Такая запись комплексного числа называется тригонометрической
формой.
Модуль г = \z\ однозначно определяется по формуле
27.3. Формы записи комплексных чисел
Запись числа z в виде z = х + iy называют алгебраической формой
комплексного числа.
Модуль г и аргумент р комплексного числа
можно рассматривать как полярные координаты
вектора f = О А/, изображающего комплексное
число z = х + iy (см. рис. 162). Тогда получа-
ем х = г cos (р, у = г sirup. Следовательно, ком-
плексное число z — х + iy можно записать в виде
z — г cos ip + ir sin p или
Рис. 163.

для z2 = -3; argz3 = ^ для z3 = г; и argz4 = -5- для г4 = -8г.
Используя формулу Эйлера
комплексное число z — r(cos(p + isimp) можно записать в так назы-
ваемой показательной (или экспоненциальной) форме z = гегур, где
г = \z\ — модуль комплексного числа, а угол ip = Argz = argz 4- 2kir
(£ = 0,-1,1,-2,2...).
В силу формулы Эйлера, функция elif периодическая с основным пери-
одом 2тг. Для записи комплексного числа z в показательной форме, доста-
точно найти главное значение аргумента комплексного числа, т. е. считать
<р = argz.
Пример 27.1. Записать комплексные числа z\ = — 1 + г и 22 = — 1 в
тригонометрической и показательной формах.
О Решение: Для z\ имеем
Для z-2 имеем
т. е. р = 7г. Поэтому — 1 = cos7r + zsin7r = ег7Г.
§28.
28.1.
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
Сложение комплексных чисел
Суммой двух комплексных чисел z\ = х\ + iyi и z2 = х2 + iy2 назы-
вается комплексное число, определяемое равенством
Рис. 164.
188
т. е. <р — ^j-. Поэтому
Сложение комплексных чисел обладает переме-
стипьельным (коммутативным) и сочетатель-
ным (ассоциативным) свойствами:
Из определения (28.1) следует, что геометрически
комплексные числа складываются как векторы
(см. рис. 164).
Непосредственно из рисунка видно, что \z\ + z<i\ ^ \z\\ + \Z2\- Это соот-
ношение называется неравенством треугольника.

28.2. Вычитание комплексных чисел
Вычитание определяется как действие, обратное сложению. Разно-
стью двух комплексных чисел z\ и z2 называется такое комплексное
число z, которое, будучи сложенным с z2, дает число z\, т. е. z = z\ — z2,
если z 4 z-2 = z\.
Если z\ = x\ 4- ij/i, z2 = x2 4 it/2, то из этого определения легко полу-
чить Z\ | 1
(28.2)
Из равенства (28.2) следует, что геометрически комплексные числа вычи-
таются как векторы (см. рис. 165).
Рис. 165.
Непосредственно из рисунка видно, что \z\ — z2\ ^ \z\\ — \z2\. Отметим,
что
т. е. модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости.
Поэтому, например, равенство \z — 2г| = 1 определяет на комплекс-
ной плоскости множество точек г, находящихся на расстоянии 1 от точки
zq = 2г, т. е. окружность с центром в zq = 2г и радиусом 1.
28.3. Умножение комплексных чисел
Произведением комплексных чисел z\ — х\ 4 гу\ и z2 — х2 4 iy2
называется комплексное число, определяемое равенством
Отсюда, в частности, следует важнейшее соотношение
(28.3)
(28.4)
Действительно, г2 = гг = (0 4- 1г)(0 + 1г) = (0 - 1) 4- г(0 + 0) = -1. Бла-
годаря соотношению (28.4) формула (28.3) получается формально путем
перемножения двучленов х\ + гу\ и х>2 + гу2'
189
Например,

Мы показали, что при умноэюении комплексных чисел их модули
перемноэюаются, а аргументы складываются.
Это правило распространяется на любое конечное число множителей.
В частности, если есть п множителей и все они одинаковые, то
28.4. Деление комплексных чисел
Деление определяется как действие, обратное умножению. Частным
двух комплексных чисел z\ и 22 ф 0 называется комплексное число
г, которое, будучи умноженным на 22, дает число 2i, т. е. ^1. = 2, если
22
Z2Z = Z\.
190
Заметим, что zz — (х + гу)(х — гу) = х2 + j/2 — действительное число.
Умножение комплексных чисел обладает переместительным, сочета-
тельным и распределительным (дистрибутивным) свойствами:
В этом легко убедиться, используя определение (28.3).
Найдем произведение комплексных чисел z\ — ri(cos<^i + isin<£i) и
z2 = r2(cosif2 + is'm(p2), заданных в тригонометрической форме:
т. е.
Формула (28.5) называется формулой Муавра.
Q Решение: Запишем сначала число z = 1 + %/Зг в тригонометрической
форме:
По формуле Муавра имеем

Если положить z\ = х\ + iy\, Z2 = Х2 + гуч ф О, z — х + г?/, то из
равенства (х-2 + iy2)(x + *2/) = #i + г^/i следует
Таким образом,
На практике частное двух комплексных чисел находят путем умноже-
ния числителя и знаменателя на число, сопряженное знаменателю («из-
бавляются от мнимости в знаменателе»).
Цргх делении комплексных чисел их модули, соответствен-
но, делятся, а аргументы, соответственно, вычитаются.
28.5. Извлечение корней из комплексных чисел
Извлечение корня n-й степени определяется как действие, обратное
возведению в натуральную степень.
Корнем П'й степени из комплексного числа z называется ком-
плексное число cj, удовлетворяющее равенству иоп — г, т. е. 1\fz — cj, если
UJn = Z.
Если положить z = r(cos(р + ismip), а и = p(cosO + isin#), то, по
определению корня и формуле Муавра, получаем
191
Решая систему, найдем значения х и у:
Пример 28.2. Выполнить деление
) Решение:
Для тригонометрической формы комплексного числа формула деле-
ния имеет вид
Отсюда имеем i
и р — у г (арифметический корень).
Поэтому равенство 7\J~z — и принимает вид
То есть

Получим п различных значений корня. При других значениях к, в силу
периодичности косинуса и синуса, получатся значения корня, совпадаю-
щие с уже найденными. Так, при к = п имеем
Итак, для любого z ф 0 корень n-й степени из числа z имеет ровно п
различных значений.
Пример 28.3. Найти значения a) y/i = w, б) \ГЛ = и.
О Решение: а) Запишем подкоренное выражение в тригонометрической
форме: г — 1 (cos 77 + г sin Ц ). Стало быть,
При к = 0 имеем
при к = 1 имеем
при к — 2 имеем
б) Снова запишем подкоренное выражение в тригонометрической фор-
ме:
Поэтому

Глава VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Лекции 25-28
§29. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
29.1. Понятие неопределенного интеграла
В дифференциальном исчислении решается задача: по данной функ-
ции f{x) найти ее производную (или дифференциал). Интегральное исчи-
сление решает обратную задачу: найти функцию F(x), зная ее производ-
ную F'(x) = f(x) (или дифференциал). Искомую функцию F(x) называют
первообразной функции f(x).
Функция F(x) называется первообразной функции f(x) на интервале
(а; 6), если для любого х Е (а; Ь) выполняется равенство
Теорема 29.1. Если функция F(x) является первообразной функции f(x) на (а; Ь),
то множество всех первообразных для f(x) задается формулой F(x) + С, где С —
постоянное число.
193
Q Функция F(x) + С является первообразной f(x). Действительно,
№) +су = *"(*) = /(*).
Пусть Ф(х) — некоторая другая, отличная от F(x), первообразная
функции /(х), т. е. Ф'(х) = f(x). Тогда для любого х Е (а; Ь) имеем
А это означает (см. следствие 25.1), что
где С — постоянное число. Следовательно, Ф(х) = F(x) + С.
где С — постоянная, поскольку
Например, первообразной функции у = х2, х Е Ш, является функция
F(x) = %-, так как
Очевидно, что первообразными будут также любые функции

Множество всех первообразных
функций F(x) + С для f(x) называ-
ется неопределенным интегра-
лом от функции f(x) и обознача-
ется символом / f(x) dx.
Таким образом, по определению
Здесь f(x) называется подынте-
гральной функцией, f(x) dx — Рис. 166.
подынтегральным выраоюением, х — переменной интегрирова-
ния, / — знаком неопределенного интеграла.
Операция нахождения неопределенного интеграла от функции назы-
вается интегрированием этой функции.
Геометрически неопределенный интеграл представляет собой семей-
ство «параллельных» кривых у — F(x) + C (каждому числовому значению
С соответствует определенная кривая семейства) (см. рис. 166). График
каждой первообразной (кривой) называется интегральной кривой.
Для всякой ли функции существует неопределенный интеграл?
Имеет место теорема, утверждающая, что «всякая непрерывная на
(а; Ь) функция имеет на этом промежутке первообразную», а следователь-
но, и неопределенный интеграл.
Свойства неопределенного интеграла
Отметим ряд свойств неопределенного интеграла, вытекающих из его
определения.
1. Дифференциал от неопределенного интеграла равен подынтеграль-
ному выражению, а производная неопределенного интеграла равна подын-
тегральной функции:
194
Действительно,
и
Благодаря этому свойству правильность интегрирования проверяется
дифференцированием. Например, равенство
верно, так как (х3 + 4х + С)' = Зх2 + 4.
2. Неопределенный интеграл от дифференциала некоторой функции
равен сумме этой функции и произвольной постоянной:

□ Действительно, / dF(x) = f F'(x) dx = f f(x) dx = F(x) + C.
3. Постоянный множитель можно выносить за знак интеграла:
(положили —'
4. Неопределенный интеграл от алгебраической суммы конечного чи-
сла непрерывных функций равен алгебраической сумме интегралов от
слагаемых функций:
195
постоянная.
Действительно,
5. (Инвариантность формулы интегрирования). Если
функция, имеющая непрерывную производную.
Q Пусть х — независимая переменная, f(x) — непрерывная функция и
F(x) — ее первообразная. Тогда / f(x) dx = F(x) + С. Положим теперь
и = ip(x), где <р(х) — непрерывно-дифференцируемая функция. Рассмо-
трим сложную функцию F(u) = F((p(x)). В силу инвариантности формы
первого дифференциала функции (см. с. 160) имеем
произвольная
Таким образом, формула для неопределенного интеграла оста-
ется справедливой независимо от того, является ли переменная интегри-
рования независимой переменной или любой функцией от нее, имеющей
непрерывную производную.
Отсюда
Тогда
Пусть

Вывод ряда формул таблицы будет дан при рассмотрении основных мето-
дов интегрирования.
Интегралы в приводимой ниже таблице называются табличными. Их
следует знать наизусть. В интегральном исчислении нет простых и уни-
версальных правил отыскания первообразных от элементарных функций,
как в дифференциальном исчислении. Методы нахождения первообраз-
ных (т. е. интегрирования функции) сводятся к указанию приемов, приво-
дящих данный (искомый) интеграл к табличному. Следовательно, необхо-
димо знать табличные интегралы и уметь их узнавать.
196
то
29.3. Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть действие, обратное дифферен-
цированию, можно получить таблицу основных интегралов путем обраще-
ния соответствующих формул дифференциального исчисления (таблица
дифференциалов) и использования свойств неопределенного интеграла.
Например, так как
Пример 29.2. Найти интеграл
Пример 29.1. Найти интеграл
Решение:
Так, из формулы
путем замены х на и
получаем
В частности,

Отметим, что в таблице основных интегралов переменная интегриро-
вания и может обозначать как независимую переменную, так и функцию
от независимой переменной (согласно свойству инвариантности формулы
интегрирования).
В справедливости приведенных ниже формул можно убедиться, взяв
дифференциал правой части, который будет равен подынтегральному вы-
ражению в левой части формулы.
Докажем, например, справедливость формулы 2. Функция — опреде-
лена и непрерывна для всех значений и, отличных от нуля.
Если и > О, то \n\u\ = lnu, тогда dln|u| = dlnu = —. Поэтому
/ ^ = \пи + С = In \и\ + С при и > 0.
Если и < 0, то \n\u\ = 1п(-и). Но d\n(-u) = :^а- = ^а-. Значит,
Г <J = Щ-и) + С = In \и\ + С при и < 0.
Итак, формула 2 верна.
Аналогично, проверим формулу 15:
Таблица основных интегралов

§30. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
30.1. Метод непосредственного интегрирования
|нч| Метод интегрирования, при котором данный интеграл путем тожде-
*—-* ственных преобразований подынтегральной функции (или выражения) и
применения свойств неопределенного интеграла приводится к одному или
нескольким табличным интегралам, называется непосредственным
интегрированием.
При сведении данного интеграла к табличному часто используются
следующие преобразования дифференциала (операция «подведения под
знак дифференциала»):
Вообще, f'(u)du — d(/(u)), эта формула очень часто используется при
вычислении интегралов.
Примеры:
198
(формула 2 таблицы интегра-
лов);

199

Как видно, вычисление интегралов иногда требует некоторой изобре-
тательности, так сказать, «индивидуального подхода к каждой подынте-
гральной функции».
Соответствующие навыки приобретаются в результате значительного
числа упражнений.
30.2. Метод интегрирования подстановкой (заменой переменной)
Метод интегрирования подстановкой заключается во введении новой
переменной интегрирования (т. е. подстановки). При этом заданный инте-
грал приводится к новому интегралу, который является табличным или
к нему сводящимся (в случае «удачной» подстановки). Общих методов
подбора подстановок не существует. Умение правильно определить под-
становку приобретается практикой.
Пусть требуется вычислить интеграл / f(x) dx. Сделаем подстановку
х — (p(t), где ip(t) — функция, имеющая непрерывную производную.
Тогда dx = tp'(t) dt и на основании свойства инвариантности формулы
интегрирования неопределенного интеграла получаем формулу интегри-
рования подстановкой
(ЗОЛ)
Формула (30.1) также называется формулой замены переменных в неопре-
деленном интеграле. После нахождения интеграла правой части этого ра-
венства следует перейти от новой переменной интегрирования t назад к
переменной х.
Иногда целесообразно подбирать подстановку в виде t — tp(x), тогда
/ f(ip(x)) - ip'(x)dx = / f(t)dt, где t = <p(x). Другими словами, форму-
лу (30.1) можно применять справа налево.
Пример 30.1. Найти j e^ dx.
О Решение: Положим х = At, тогда dx = 4 dt. Следовательно,
200
Пример 30.2. Найти

О Решение: Пусть у/х — 3 = £, тогда х = t2 + 3, dx = 2tdt. Поэтому
, = = In m + y/u2 + a2 + С
V u2 + a2
Стало быть,
ex + 1
О Решение: Обозначим ех = t. Тогда х — ln£, dx — Щ-. Следовательно,
Здесь используется формула 16 таблицы основных интегралов.
201
Обозначим t = у/и2 + а2 Н- и (подстановка Эйлера). Тогда
Отсюда
Пример 30.4- Найти
i Решение: Пусть х + 2 = t. Тогда х = t — 2, dx = dt. Имеем:

30.3. Метод интегрирования по частям
Пусть и = и(х) и v = v{x) — функции, имеющие непрерывные произ-
водные. Тогда d(uv) = и • dv + v • du. Интегрируя это равенство, получим
(можно по-
С
202
Полученная формула называется формулой интегрирования по ча-
стям. Она дает возможность свести вычисление интеграла / и dv к вы-
числению интеграла vdu, который может оказаться существенно более
простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное вы-
ражение заданного интеграла представляется каким-либо образом в виде
произведения двух сомножителей и и dv (это, как правило, можно осуще-
ствить несколькими способами); затем, после нахождения v и du, исполь-
зуется формула интегрирования по частям. Иногда эту формулу прихо-
дится использовать несколько раз.
Укажем некоторые типы интегралов, которые удобно вычислять ме-
тодом интегрирования по частям.
1. Интегралы вида / Р(х)екх dx, / Р(х) • sin kx dx, / P(x) cos kx dx, где
Р(х) — многочлен, к — число. Удобно положить и = Р(х), а за dv обозна-
чить все остальные сомножители.
2. Интегралы вида / Р(х) arcsinxcte, / P(x) aiccosxdx, / P(x)lnxdx,
I Р(х) arctgxdx, / Р(х) diTcctgxdx. Удобно положить Р(х) dx = dv, а за и
обозначить остальные сомножители.
3. Интегралы вида / еах • sinbxdx, / еах • cosbxdx, где а и Ь — числа.
За и можно принять функцию и = еах.
Решение: Пусть
ложить С = 0). Следовательно, по формуле интегрирования по частям:
Пример 30.7. Найти
Решение: Пусть
Поэтому

Пример 30.8. Найти х2ех dx.
Поэтому
О Решение: Пусть
. Поэтому
§31. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
31.1. Понятия о рациональных функциях
Многочлен (некоторые сведения справочного характера)
Функция вида
203
Для вычисления интеграла / exxdx снова применим метод интегрирова-
ния по частям: и = х, dv — ex dx => du — dx, v = ex. Значит,
Поэтому (см. (30.2))
Пример 30.9. Найти / arctgxdx,
где п — натуральное число, аг-{г = 0,1,..., п) — постоянные коэффициен-
ты, называется многочленом (или целой рациональной функцией).
Число /i называется степенью многочлена.
Корнем многочлена (31.1) называется такое значение xq (вообще
говоря, комплексное) переменной х, при котором многочлен обращается в
нуль, т. е. Рп(хо) = 0.
Теорема 31.1. Если х\ есть корень многочлена Р,г(#), то многочлен делится без
остатка на х — х\, т. е.
где Рп-\{х) — многочлен степени (п — 1).
) Решение: Пусть

Возникает вопрос: всякий ли многочлен имеет корень? Положитель-
ный ответ на этот вопрос дает следующее утверждение.
Теорема 31.2 (основная теорема алгебры). Всякий многочлен n-й степени
(п > 0) имеет по крайней мере один корень, действительный или комплексный.
Доказательство этой теоремы мы не приводим.
Пользуясь основной теоремой алгебры, докажем теорему о разложе-
нии многочлена на линейные множители.
Q Рассмотрим многочлен (31.1). По теореме 31.2 он имеет корень. Обо-
значим его через х\. Тогда имеет место соотношение (31.2). А так как
Pn_i(x) — также многочлен, то он имеет корень. Обозначим его через х-2-
Тогда Pn_i(x) = (х — Х2) • Рп-2{х), где Рп-2{х) — многочлен (п — 2)-й
степени. Следовательно, Рп{х) = (х — х\){х — Х2)Рп-2(х)-
Поололжая этот пооиесс. получим в итоге:
204
Теорема 31.3. Всякий многочлен Рп(х) можно представить в виде
где х\, Х2,... ,хп — корни многочлена, а$ — коэффициент многочлена при хп.
Множители (x — Xi) в равенстве (31.3) называются линейными мно-
эюителями.
Пример 31.1. Разложить многочлен
множители.
на
Решение: Многочлен 1
обращается в нуль при
Пример 31.2. Представить выражение х3 — х2 + 4х — 4 в виде произве-
дения линейных множителей.
Решение: Легко проверить, что
Если в разложении многочлена (31.3) какой-либо корень встретился
к раз, то он называется корнем кратности к. В случае к = 1 (т. е. корень
встретился один раз) корень называется простым.
Разложение многочлена (31.3) можно записать в виде
если корень х\ имеет кратность к\, корень х<ь — кратность fe-2 и так далее.
При этом к\ + fc-2 + • • • + kr = n, a r — число различных корней.

Например, разложение
Теорема 31.4. Если многочлен Рп(х) = а^хп + а\хп 1 + • • • + ап тождественно
равен нулю, то все его коэффициенты равны нулю.
Теорема 31.5. Если два многочлена тождественно равны друг другу, то коэффи-
циенты одного многочлена равны соответствующим коэффициентам другого.
Теорема 31.6. Если многочлен Рп(х) с действительными коэффициентами имеет
комплексный корень а + ib, то он имеет и сопряженный корень а — гЬ.
где р = -2а, q — а2 + 6 .
Таким образом, произведение линейных множителей, соответствую-
щих сопряженным корням, можно заменить квадратным трехчленом с
действительными коэффициентами.
С учетом вышеизложенного справедлив следующий факт.
Теорема 31.7. Всякий многочлен с действительными коэффициентами разлагается
на линейные и квадратные множители с действительными коэффициентами, т. е.
многочлен Рп(х) можно представить в виде
205
можно записать так:
Пользуясь теоремой 31.3, можно доказать следующие утверждения.
получим трехчлен второй степени с действительными коэффициентами
х2 + рх + q. В самом деле,
В разложении многочлена (31.3) комплексные корни входят сопряжен-
ными парами. Перемножив линейные множители
При этом к\ + к-2 + • • • + kr + 2(si + S2 + • • • + sm) = n, все квадратные трехчлены
не имеют вещественных корней.

Получим частное L(x) = x3 + 2х2 + 4х + 3 и остаток Д(х) = 15. Следова-
тельно, х -$х + 9 _ хз + 2х2 + 4х + 3 + -^Ц.
ж - 2 х - 2
Правильные рациональные дроби вида
(I)- -^-;
v ' х - а
(II). —-^ (fc ^ 2. * € N);
[х — а)
(III). 2 Х (корни знаменателя комплексные, т. е. р2 — Aq < 0);
х + рх + q
(IV). о^Дх + 1\ (fc ^ 2, корни знаменателя комплексные),
[х" +рх + q)K
где Л, а, М, 7V, р, g — действительные числа, называются простейшими
рациональными дробями I, II, III и IV типов.
206
Примеры разложений (31.5):
Дробно-рациональная функция
Дробно-рациональной функцией (или рациональной дробью)
называется функция, равная отношению двух многочленов, т. е. f(x) =
= nm) с , где Рт(х) — многочлен степени га, a Qn(x) — многочлен сте-
пени п.
Рациональная дробь называется правильной, если степень числите-
ля меньше степени знаменателя, т. е. т < щ в противном случае (если
га ^ п) рациональная дробь называется неправильной.
Всякую неправильную рациональную дробь -ту\ можно, пу-
тем деления числителя на знаменатель, представить в виде
суммы многочлена L(x) и правильной рациональной дроби ~\ (,
Например, п\ 1 — - 0"*" — неправильная рациональная дробь. Раз-
делим числитель на знаменатель в столбик:

P(x)
Теорема 31.8. Всякую правильную рациональную дробь ~) (, знаменатель кото-
рой разложен на множители
Поясним формулировку теоремы на следующих примерах:
Для нахождения неопределенных коэффициентов Ль Л-2, ...,£ь#27 •••
в равенстве (31.6) можно применить метод сравнивания коэффициентов.
Суть метода такова:
1. В правой части равенства (31.6) приведем к общему знаменателю
Q(x); в результате получим тождество ~S I = ^S I, где S(x) — много-
член с неопределенными коэффициентами.
2. Так как в полученном тождестве знаменатели равны, то тождествен-
но равны и числители, т. е.
207
можно представить (и притом единственным образом) в виде следующей суммы
простейших дробей:
где Ль Ао, ..., В\, В-2, ..., С\, D\, ..., Mi, N±t ... — некоторые действительные
коэффициенты.
3. Приравнивая коэффициенты при одинаковых степенях х (по теоре-
ме 31.5 о тождестве многочленов) в обеих частях тождества (31.7), полу-
чим систему линейных уравнений, из которой и определим искомые коэф-
фициенты Ль Аг,..., В\,...
в виде суммы
Пример 31.3. Представить дробь
простейших дробей.

О Решение: Согласно теореме 31.8 имеем:
Для нахождения неопределенных коэффициентов применяют также
метод отдельных значений аргумента: после получения тождества (31.7)
аргументу х придают конкретные значения столько раз, сколько неопре-
деленных коэффициентов (обычно полагают вместо х значения действи-
тельных корней многочлена Q{x)).
Пример 31.4- Представить дробь —-?—_<уГ( . -л в виде суммы про-
стейших дробей.
О Решение: Имеем:
31.2. Интегрирование простейших рациональных дробей
Найдем интегралы от простейших рациональных дробей.
208
Отсюда следует
Приравнивая коэффициенты при х2, ж1, х°, получаем
Решая систему, находим, что А = — 1, # = 3, С — —2. Следовательно,
Отсюда следует
Положим х = 0, тогда —4 = —2Л, т. е. А — 2; положим х — 2, тогда 2 = 6В,

3. Рассмотрим интеграл J = Мх + Jy дх
J x + рх + q
Выделив в знаменателе полный квадрат, получим:
причем 9 — д > 0. Сделаем подстановку х + ^ — t. Тогда х — t — ^
dx — dt. Положим q — *j- = а2. Следовательно, используя формулы (2)
и (15) таблицы интегралов, получаем
209
т. е., возвращаясь к переменной х,
Пример 31.5. Найти
О Решение: х2 + 2х + 10 = (х + I)2 + 9. Сделаем подстановку х + 1 = t.
Тогда х = t — 1, dx = dt и
4. Вычисление интеграла вида
Данный интеграл подстановкой х + ^ = t сводится к сумме двух ин-
гегралов:
Первый интеграл легко вычисляется:
Вычислим второй интеграл:

К последнему интегралу применим интегрирование по частям. Положим
Полученная формула дает возможность найти интеграл Jk для любого
натурального числа к > 1.
31.3. Интегрирование рациональных дробей
Рассмотренный в пунктах 31.1-31.2 материал позволяет сформулиро-
вать общее правило интегрирования рациональных дробей.
1. Если дробь неправильна, то представить ее в виде суммы многочле-
на и правильной дроби;
2. Разложив знаменатель правильной рациональной дроби на множи-
тели, представить ее в виде суммы простейших рациональных дробей;
3. Проинтегрировать многочлен и полученную сумму простейших дро-
бей.
210
тогда
Подставляя найденный интеграл в равенство (31.8), получаем
Пример 31.6. Найти интеграл ,
Решение: Здесь а = 1, к = 3. Так как
то
Пример 31.7. Найти интеграл

О Решение: Под знаком интеграла неправильная дробь; выделим ее це-
лую часть путем деления числителя на знаменатель:
Отметим, что любая рациональная функция интегрируется в элемен-
тарных функциях.
211
Разложим правильную рациональную дробь на простейшие дроби:
Получаем:
Отсюда следует, что
Находим: В = 2, А = О, С = 4, D = 2. Стало быть,
Интегрируем полученное равенство:
Обозначим х + 1 = £, тогда х = t — 1 и dx = dt. Таким образом,
Следовательно,

§32. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
32.1. Универсальная тригонометрическая подстановка
Рассмотрим некоторые случаи нахождения интеграла от тригономе-
трических функций. Функцию с переменными sin а: и cos#, над которыми
выполняются рациональные действия (сложения, вычитание, умножение
и деление) принято обозначать R(sinx;cosx), где R — знак рациональной
функции.
Вычисление неопределенных интегралов типа / R(sin x; cos x) dx сво-
дится к вычислению интегралов от рациональной функции подстановкой
tg Щ = t, которая называется универсальной.
где R\(t) — рациональная функция от t. Обычно этот способ весьма гро-
моздкий, зато он всегда приводит к результату.
На практике применяют и другие, более простые подстановки, в за-
висимости от свойств (и вида) подынтегральной функции. В частности,
удобны следующие правила:
1) если функция i?(sinx;cosx) нечетна относительно sinx, т.е.
R(— sin x; cos ж) = — #(sinx;cos:r), то подстановка cosx = t рационализи-
рует интеграл;
2) если функция i?(sinx;cosx) нечетна относительно cosx, т.е.
R(sin х\ — cosx) = — i?(sina;; cos х), то делается подстановка sin я = £;
3) если функция R(s'mx; cos ж) четна относительно sinx и cos#
R(— sin я; — cosx) = R(s'mx; cosx), то интеграл рационализируется подста-
новкой tgx = t. Такая же подстановка применяется, если интеграл имеет
вид / jR(tgx) dx.
Пример 32.1. Найти интеграл
212
i Решение: Сделаем универсальную подстановку t = tg :
Действительно, sin £

Пример 32.2. Найти интеграл I = f z—d? 2 •
О Решение: Так как
32.2. Интегралы типа /sinm x • cosn xdx
Для нахождения таких интегралов используются следующие приемы:
1) подстановка smx = £, если п — целое положительное нечетное
число;
2) подстановка cos a; = t, если т — целое положительное нечетное
число;
3) формулы понижения порядка: cos2 х = ^(1 H-cos2x), sin2 x =
= н(1—cos2x), sinz-cosx = ^ sin 2х, если m и n — целые неотрицательные
четные числа;
4) подстановка tgx = t, если т + п — есть четное отрицательное целое
число.
Пример 32.3. Найти интеграл
) Решение: Применим подстановку sinx = t. Тогда х = arcsin£, dx —
i
Пример 32.4- Найти интеграл

Пример 32.5. Найти интеграл
Q Решение: Здесь т + n — —4. Обозначим tgx = t. Тогда х = arctgf,
dx = , ^ .>, sin x = , * , cos x = —r=i и
1 + *" y/l + t2 y/l + t2
214
32.3. Использование тригонометрических преобразований
Интегралы типа / sin ах-cos bx dx, I cos ax• cos bx dx, / sin ax• sin bx dx
вычисляются с помощью известных формул тригонометрии:
Пример 32.6. Найти интеграл
Решение:
§33. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
33.1. Квадратичные иррациональности
Рассмотрим некоторые типы интегралов, содержащих иррациональ-
ные функции.
Интегралы типа I > ^х ■., / \/ax2 + bx + cdx, I тх + п— ^х
J yax2 + bx + c J J \/ax2 + bx + c
называют неопределенными интегралами от квадратичных иррациональ-

Пример 33.1. Найти интегралы I
Пример 33.2. Найти интеграл I = / , х "*" dx.
J у/б-2х- х2
О Решение: Так как 6-2ж-ж2 = -(ж2 + 2ж-6) = -((ж + 1)2-7) = 7-(ж + 1)2,
то подстановка имеет вид х + 1 = t, х = t — 1, dx = dt. Тогда
/ £ ж -Ь 1 /
= - V 7 - t2 + 3 • arcsin -= + С = 3 arcsin —;=- - \/6 - 2x - x2 + C. •
y/7 V7
Интегралы типа / . n^ ' dx, где Pn(x) — многочлен степени n,
J у ax2 + bx + с
можно вычислять, пользуясь формулой
/ fw(^ dx = Qn^(x)Wax2+bx + c + \f . /*=, (33.1)
J vaxz +bx + с J yjax1 + bx + с
где <2n-i(#) — многочлен степени n — 1 с неопределенными коэффициен-
тами, Л — также неопределенный коэффициент.
215
ностей. Их можно найти следующим образом: под радикалом выделить
полный квадрат
ах2 + Ьх 4- с =
и сделать подстановку х + ■£- = t. При этом первые два интеграла приво-
дятся к табличным, а третий — к сумме двух табличных интегралов.
О Решение: Так как Ах2 + 2х + 1 = 4
Сделаем подстановку

Все неопределенные коэффициенты находятся из тождества, получа-
емого дифференцированием обеих частей равенства (33.1):
Сравниваем коэффициенты при одинаковых степенях х:
1 = —А — А при х2,
0=-2А-А-В прих1,
0 = А-В + \ при я0.
1 О
Отсюда Д = —i,i? = S,A = 2. Следовательно,
33.2. Дробно-линейная подстановка
Интегралы типа Г r(x, (™ +^) ,..., (^Фд) ) dx, где а, 6, с,
d — действительные числа, а,/?,..., <5, 7 ~~ натуральные числа, сводятся
к интегралам от рациональной функции путем подстановки ах "^ = tk,
где /с — наименьшее общее кратное знаменателей дробей %,...,—.
Действительно, из подстановки ах "^ = £Л следует, что х — д и
, -dktk-4ctk -a)-(b- dtk)cktk~x ,t ,
dx = i —jf г"2 dt, т. е. х и dx выражаются через
216
после чего необходимо приравнять коэффициенты при одинаковых степе-
нях неизвестной х.
Пример 33.3. Найти интеграл /
Решение: По формуле (33.1) имеем:
Дифференцируя это равенство, получаем:

\\ I Пример 33.6. Найти интеграл I = / -^—^- dx.
О Решение: Положим х = 2 sin*, dx = 2cos*d*, t = arcsin ^. Тогда
217
рациональные функции от t. При этом и каждая степень дроби
выражается через рациональную функцию от t.
Пример 33.4- Найти интеграл /
О Решение: Наименьшее общее кратное знаменателей дробей 4и^ есть 6.
Поэтому полагаем х + 2 = t6, х = t6 - 2, dx = 6£5 dt, t = Ух + 2. Следова-
тельно,
Пример 33.5. Указать подстановку для нахождения интегралов:
О Решение: Для 1\ подстановкам = i2, для 1-2 подстановка х + ~ = t3. •
33.3. Тригонометрическая подстановка
Интегралы типа /R(x; \/a2—x2)dx, R(x; \/a2+x2)dx, R(x; y/x2—a2)dx
приводятся к интегралам от функций, рационально зависящих от три-
гонометрических функций, с помощью следующих тригонометрических
подстановок: х = а • sin t для первого интеграла; х = а • tg t для второго
интеграла; х = .Q для третьего интеграла.

33.4. Интегралы типа / R(x; у/ах2 + bx + c)dx
Здесь подынтегральная функция есть рациональная функция относи-
тельно х и у/ах2 + Ьх + с. Выделив под радикалом полный квадрат и сде-
лав подстановку х+-£- = t, интегралы указанного типа приводятся к инте-
гралам уже рассмотренного типа, т. е. к интегралам типа / R(t', \Ja2 — t2) dt,
/ R(t; \Jd2 + t2) dt, / R(t; \/t2 — a2) dt. Эти интегралы можно вычислить с
помощью соответствующих тригонометрических подстановок.
Пример 33.7. Найти интеграл 1=1 -*—, ^гтз— dx.
О Решение: Так как х2 + 2х - 4 = (х + I)2 - 5, то х + 1 = t, х = £ - 1,
ofo = Л. Поэтому 7 = / V *2 ~ 5 dt. Положим t = -Д-, dt = -v5-cosz d
J J t3 sins' sin2 г
z — arcsin ^. Тогда
Замечание: Интеграл типа / —, целесообразно находить
^ хуах2 + Ьх + с
с помощью подстановки ж = у.
33.5. Интегрирование дифференциального бинома
Интегралы типа / хт • (a + bxn)p dx (называемые интегралами от диф-
ференциального бинома), где а, Ь — действительные числа; т, п, р —
рациональные числа, берутся, как показал Чебышев П.А., лишь в случае,
когда хотя бы одно из чисел о, т ~*~ или m ~*~ +р является целым.
п п
Рационализация интеграла в этих случаях осуществляется следующи-
ми подстановками:
1) если р — целое число, то подстановка х = tk, где к — наименьшее
общее кратное знаменателей дробей тип;
218

2) если т + 1 — целое число, то подстановка а + Ьхп = ts, где s —
знаменатель дроби р;
3) если т ~*~ +р — целое число, то подстановка а + Ьхп = хп • ts, где
s — знаменатель дроби р.
Во всех остальных случаях интегралы типа / хт(а + Ъхп)р dx не вы-
ражаются через известные элементарные функции, т. е. «не берутся».
219
§34. «БЕРУЩИЕСЯ» И «НЕБЕРУЩИЕСЯ» ИНТЕГРАЛЫ
Как уже отмечалось выше, операция интегрирования функций зна-
чительно сложнее операции дифференцирования функций. Не всегда вы-
бранный путь интегрирования является наилучшим, более коротким, про-
стым. Интегрирование часто может быть выполнено не единственным спо-
собом. Многое зависит от знания рекомендуемых многих искусственных
приемов интегрирования, от сообразительности, от тренированности. На-
/Нт
—Щ,— можно найти, не используя рекомендуемую подстановку
cos х
tga; = t, а применив искусственный прием:
Вряд ли стоит вычислять интеграл
разлагая подынтегральную функцию на простейшие дроби:
Поэтому делаем подстановку
Гак им
обпазом.
Пример 33.8. Найти интеграл /
Решение: Так как

На практике при вычислении неопределенных интегралов используют
различные справочники, содержащие таблицы особенно часто встречаю-
щихся интегралов. В частности, «Таблицы неопределенных интегралов»
М. Л. Смолянского.
Изученные методы интегрирования позволяют во многих случаях вы-
числить неопределенный интеграл, т. е. найти первообразную функцию
для подынтегральной функции.
Как известно, всякая непрерывная функция имеет первообразную. В
том случае, когда первообразная некоторой элементарной функции f(x)
является также элементарной функцией, говорят, что / f(x) dx «берет-
ся», т. е. интеграл выражается через элементарные функции (или инте-
грал вычисляется). Если же интеграл не выражается через элементарные
функции, то говорят, что интеграл «we берется» (или «его найти нельзя»).
Так, например, нельзя взять интеграл / у/х • cosxdx, так как не су-
ществует элементарной функции, производная от которой была бы равна
v/Jcosx. Приведем еще примеры «неберущихся» интегралов, которые име-
ют большое значение в приложениях:
e~x dx — интеграл Пуассона (теория вероятностей),
/ у^ интегральный логарифм (теория чисел),
/ cosx2 dx, I sinx2 dx — интегралы Френеля (физика),
/ sin_x ^x I cos a: ^x — интегральные синус и косинус,
/ — dx — интегральная показательная функция.
Первообразные от функции е~х , cos я2, -н^— и других хорошо изучены,
для них составлены подробные таблицы значений для различных значе-
ний аргумента х.
Заметив, что числитель Зх2 + 4х + 1 является производной знаменателя
х(х2 + 2х + 1) = х3 + 2х2 + х, легко получить:

Глава VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Лекции 29-33 I
§35. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ
ИНТЕГРАЛЬНОЙ СУММЫ
Пусть функция у = f(x) определена на отрезке [а; Ь], а < Ь. Выполним
следующие действия.
1. С помощью точек хо = а, х\, х-2,..., хп = b (хо < Х\ < • • • < хп) разо-
бьем отрезок [а, Ъ] на п частичных отрезков [xq\x\\, [xi;^], . •., [xn_i,xn]
(см. рис. 167).
221
2. В каждом частичном отрезке [a;,_i;:r;], г — 1,2, ...,п выберем про-
извольную точку с, G [xi_i;Xi] и вычислим значение функции в ней, т. е.
величину f(c-i).
3. Умножим найденное значение функции f(ci) на длину Axi = X{ — Xi-i
соответствующего частичного отрезка: f(ci) • Ах^.
4. Составим сумму 5П всех таких произведений:
Сумма вида (35.1) называется интегральной суммой функции у =
= f(x) на отрезке [а; 6]. Обозначим через Л длину наибольшего частичного
отрезка: Л = max Дх/ (г = 1,2,... ,п).
5. Найдем предел интегральной суммы (35.1), когда п —> оо так, что
Если при этом интегральная сумма Sn имеет предел /, который не
зависит ни от способа разбиения отрезка [а; Ь] на частичные отрезки, ни от
выбора точек в них, то число / называется определенным, интегралом
ь
от функции у = f(x) на отрезке [а; Ь] и обозначается / f(x) dx. Таким
а
образом,
i—: 1

Числа аиЬ называются соответственно ниэюним и верхним пределами
интегрирования, f(x) — подынтегральной функцией, f(x) dx — по-
дынтегральным выражением, х — переменной интегрирования,
отрезок [а; Ь] — областью {отрезком) интегрирования.
Функция у = f(x), для которой на отрезке [а; Ь] существует определен-
ь
ный интеграл / f(x) dx, называется интегрируемой на этом отрезке.
а
Сформулируем теперь теорему существования определенного интегра-
ла.
Теорема 35.1 (Коши). Если функция у = f(x) непрерывна на отрезке [а; Ь], то
б
определенный интеграл / f(x) dx существует.
Отметим, что непрерывность функции является достаточным услови-
ем ее интегрируемости. Однако определенный интеграл может существо-
вать и для некоторых разрывных функций, в частности для всякой огра-
ниченной на отрезке функции, имеющей на нем конечное число точек раз-
рыва.
Укажем некоторые свойства определенного интеграла, непосредствен-
но вытекающие из его определения (35.2).
1. Определенный интеграл не зависит от обозначения переменной ин-
тегрирования:
§36. ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Площадь криволинейной трапеции
Пусть на отрезке [а;Ь] задана непрерывная функция у = f(x) ^ 0.
Фигура, ограниченная сверху графиком функции у = f(x), снизу — осью
Ох, сбоку — прямыми х = а и х = Ь, называется криволинейной тра-
пецией. Найдем площадь этой трапеции.
222
Это следует из того, что интегральная сумма (35.1), а следовательно,
и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент
данной функции.
2. Определенный интеграл с одинаковыми пределами интегрирования
равен нулю:
3. Для любого действительного числа с:

Для этого отрезок [а; Ь] точками а—х^,
х\, ..., Ь = хп (хо < х\ < ••• < хп) ра-
зобьем на п частичных отрезков [:ro;xi],
[xi;x2],...,[xn_i;xn]. (см. рис. 168). В
каждом частичном отрезке [xi_i;xj] (г =
= 1, 2,..., п) возьмем произвольную точ-
ку С{ и вычислим значение функции в ней,
т.е. f(a).
Умножим значением функции f{ci) на
длину Axi = Х{ — Xj-i соответствующего
частичного отрезка. Произведение f(c{) • Axi равно площади прямоуголь-
ника с основанием Да;.; и высотой /(с,). Сумма всех таких произведений
Итак, определенный интеграл от неотрицательной функции численно
равен площади криволинейной трапеции.
В этом состоит геометрический смысл определенного интеграла.
Работа переменной силы
Пусть материальная точка М перемещается под действием силы F,
направленной вдоль оси Ох и имеющей переменную величину F = F(x),
где х — абсцисса движущейся точки М.
Найдем работу А силы F по перемещению точки М вдоль оси Ох из
точки х = а в точку х = b (а < Ь). Для этого отрезок [а; Ь] точками а = хо,
х\, ..., b = хп (хо < х\ < • • • < хп) разобьем на п частичных отрезков
[хо; х\], [х\; х%], ..., [хп-\; хп]. Сила, действующая на отрезке [xj-i; xj, ме-
няется от точки к точке. Но если длина отрезка Ax-i — xt — х\-\ достаточ-
но мала, то сила F на этом отрезке изменяется незначительно. Ее можно
приближенно считать постоянной и равной значению функции F — F(x)
в произвольно выбранной точке х = С{ G [xi-\\Xi]. Поэтому работа, совер-
шенная этой силой на отрезке [х^—i;х/], равна произведению F(ci) • Лх?.
(Как работа постоянной силы F(ci) на участке [ajj-i;#$].)
223
С уменьшением всех величин Axi точность приближения криволинейной
трапеции ступенчатой фигурой и точность полученной формулы увеличи-
ваются. Поэтому за точное значение площади S криволинейной трапеции
принимается предел 5, к которому стремится площадь ступенчатой фигу-
ры 5„, когда п неограниченно возрастает так, что Л = max Ax-i —> 0:
равна площади ступенчатой фигуры и приближенно равна площади S кри-
волинейной трапеции:

Приближенное значение работы А силы F на всем отрезке [а; Ь] есть
Это приближенное равенство тем точнее, чем меньше длина Ах{. Поэто-
му за точное значение работы А принимается предел суммы (36.1) при
условии, что наибольшая длина Л частичных отрезков стремится к нулю:
Итак, работа переменной силы F, величина которой есть непрерывная
функция F = F(x), действующей на отрезке [а\Ь], равна определенному
интегралу от величины F{x) силы, взятому по отрезку [а;Ь].
В этом состоит физический смысл определенного интеграла.
Аналогично можно показать, что путь 5, пройденный точкой за про-
межуток времени от t = а до t = 6, равен определенному интегралу от
скорости v(t):
§37. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
Пусть функция у = f(x) интегрируема на отрезке [а; Ь].
Теорема 37.1. Если функция у = f(x) непрерывна на отрезке [а; Ь] и F(x) —
какая-либо ее первообразная на [a; b] (F'(x) — f(x)), то имеет место формула
Q Разобьем отрезок [а; Ь] точками а = хо, х\,..., Ь = хп (хо < х\ < • • •
■ • • < хп) на п частичных отрезков [xo;a:i], [xi;^],. • •, [хп-\\хп], как это
показано на рис. 169.
224
масса т неоднородного стержня на отрезке [а; Ь] равна определенному ин-
тегралу от плотности j(x): m -
Рис. 169.

Рассмотрим тождество
(37.2)
где С{ есть некоторая точка интервала (хг~\; Xi). Так как функция у = f(x)
непрерывна на [а; ft], то она интегрируема на [a; ft]. Поэтому существует
предел интегральной суммы, равный определенному интегралу от f(x) на
[а;Ь].
Переходя в равенстве (37.2) к пределу при А = max Axi -¥ О, получаем
Т. е.
Равенство (37.1) называется формулой Ньютона-Лейбница.
Если ввести обозначение F(ft) - F(a) = F(x)\ , то формулу Ньютона-
Лейбница (37.1) можно переписать так:
Пример 37.1. Вычислить интеграл
225
Преобразуем каждую разность в скобках по формуле Лагранжа
Получим
Формула Ньютона-Лейбница дает удобный способ вычисления определен-
ного интеграла. Чтобы вычислить определенный интеграл от непрерывной
функции f(x) на отрезке [a; ft], надо найти ее первообразную функцию F(x)
и взять разность F(ft) — F(a) значений этой первообразной на концах от-
резка [a; ft].
Например,

О Решение:
Пример 37.2. Вычислить интеграл
Решение:
§38. ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Рассмотрим основные свойства определенного интеграла, считая
подынтегральную функцию интегрируемой на отрезке [а; Ь]. При выводе
свойств будем использовать определение интеграла и формулу Ньютона-
Лейбница.
1. Если с — постоянное число и функция f(x) интегрируема на [а;Ь],
то
т. е. постоянный множитель с можно выносить за знак определенного ин-
теграла.
Q Составим интегральную сумму для функции с- f(x). Имеем:
Тогда lim J2 c-f(x)Ax{ = с- lim ]£ f(ci) = с' f(x) ^x- Отсюда вытекает,
а
что функция с • f(x) интегрируема на [а; Ь] и справедлива формула (38.1).
■
2. Если функции fi(x) и f-zix) интегрируемы на [а\Ь\, тогда интегри-
руема на [а; Ь] их сумма и
т. е. интеграл от суммы равен сумме интегралов.
226

227
Свойство 2 распространяется на сумму любого конечного числа сла-
гаемых.
Это свойство можно принять по определению. Это свойство также под-
тверждается формулой Ньютона-Лейбница.
4. Если функция f(x) интегрируема на [а; Ь] и а < с <Ъ, то
т. е. интеграл по всему отрезку равен сумме интегралов по частям этого
отрезка. Это свойство называют аддитивностью определенного инте-
грала (или свойством аддитивности).
Q При разбиении отрезка [а; Ь] на части включим точку с в число точек
деления (это можно сделать ввиду независимости предела интегральной
суммы от способа разбиения отрезка [а; Ь] на части). Если с = хт, то
интегральную сумму можно разбить на две суммы:
Каждая из написанных сумм является интегральной соответственно для
отрезков [а; 6], [а; с] и [с; Ь]. Переходя к пределу в последнем равенстве при
п —> оо (А -> 0), получим равенство (38.3). ■
Свойство 4 справедливо при любом расположении точек а, 6, с (счита-
ем, что функция f(x) интегрируема на большем из получающихся отрез-
ков).
Так, например, если а < Ь < с, то
Отсюда
(использованы свойства 4 и 3).

5. «Теорема о среднем». Если функция f(x) непрерывна на отрезке
[а;Ь], то существует точка с € [а; Ь] такая, что
Q По формуле Ньютона-Лейбница имеем
где F'(x) = f(x). Применяя к разности F(b) - F(a) теорему Лагранжа
(теорему о конечном приращении функции), получим
F(b) - F(a) = F'(c) -(Ь-а) = f(c) • (b - а). Ш
Свойство 5 («теорема о среднем») при /(#) ^ 0 име-
ет простой геометрический смысл: значение определен-
ного интеграла равно, при некотором с Е (а; 6), площа-
ди прямоугольника с высотой /(с) и основанием b — а
(см. рис. 170). Число
называется средним значением функции f(x) на отрезке [а;Ь].
6. Если функция f(x) сохраняет знак на отрезке [а; Ь], где а < Ь, то ин-
ь
т,еграл I f(x) dx имеет тот же знак, что и функция. Так, если f(x) ^ О
а
Ь
на отрезке [а; Ь], то / f(x) dx ^ 0.
а
□ По «теореме о среднем» (свойство 5)
228
Рис. 170.
где с £ [а; Ь]. А так как f(x) ^ 0 для всех х Е [а; Ь], то и
Поэтому
7. Неравенство между непрерывными функциями на отрезке [а;Ь],
(а < Ь) можно интегрировать. Так, если fi(x) ^ /2(2) при х Е [а;Ь],

Q Так как /2(2) — fi(x) ^ 0, то при а <Ь, согласно свойству 6, имеем
229
Q Применяя свойство 7 к очевидным неравенствам
получаем L
Отсюда следует, что
10. Производная определенного интеграла по переменному верхнему
пределу равна подынтегральной функции, в которой переменная инте-
грирования заменена этим пределом, т. е.
Или, согласно свойству 2,
Отметим, что дифференцировать неравенства нельзя.
8. Оценка интеграла. Если т и М — соответственно наименьшее и
наибольшее значения функции у = f(x) на отрезке [a;b], (a < b), то
(38.4)
□ Так как для любого х Е [а; Ь] имеем га ^ f(x) ^ M, то, согласно
свойству 7, имеем
а а а
Применяя к крайним интегралам свойство 5, по-
лучаем
Рис. 171. Если f(x) ^ 0, *то свойство 8 иллюстрирует-
ся геометрически: площадь криволинейной трапе-
ции заключена между площадями прямоугольников, основание которых
есть [а; 6], а высоты равны га и М (см. рис. 171).
9. Модуль определенного интеграла не превосходит интеграла от мо-
дуля подынтегральной функции:

Теорема 39.1. Если:
1) функция х = (f(t) и ее производная х' = v'(t) непрерывны при t E [а;/?];
2) множеством значений функции х = (f(t) при t e [а,/?] является отрезок [а; 6];
3) ip(a) = а и (/?(/?) = Ь,
то . д
230
39.2. Интегрирование подстановкой (заменой переменной)
ь
Пусть для вычисления интеграла / f(x)dx от непрерывной функции
а
сделана подстановка х = ip(t).
Применяется этот метод во всех случаях, когда может быть найдена
первообразная функции F(x) для подынтегральной функции f(x).
При вычислении определенных интегралов широко используется ме-
тод замены переменной и метод интегрирования по частям.
Это означает, что определенный интеграл с переменным верхним пре-
делом есть одна из первообразных подынтегральной функции.
§39. ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
39.1. Формула Ньютона-Лейбница
Простым и удобным методом вычисления определенного интеграла
ь
/ f(x) dx от непрерывной функции является формула Ньютона-Лейбница:
Следовательно,
\ По формуле Ньютона-Лейбница имеем:

Q Пусть F(x) есть первообразная для f(x) на отрезке [а; Ь]. Тогда по
6
формуле Ньютона-Лейбница / f(x) dx — F(b) - F(a). Так как (F((p(t)Y =
а
— /(^(0) * ^'W> T0 ^O^W) является первообразной для функции
f{ip(t)) • </>'(£), * € [<*;/?]• Поэтому по формуле Ньютона-Лейбница имеем
Теорема 39.2. Если функции и = и(х) и v — v(x) имеют непрерывные производные
на отрезке [а; 6], то имеет место формула
231
Формула (39.1) называется формулой замены переменной в определен-
ном интеграле.
Отметим, что:
1) при вычислении определенного интеграла методом подстановки воз-
вращаться к старой переменной не требуется;
2) часто вместо подстановки х = ip(t) применяют подстановку t = g(x);
3) не следует забывать менять пределы интегрирования при замене
переменных!
Пример 39.1. Вычислить
Q Решение: Положим х = 2 sin £, тогда dx = 2 cos t dt. Если х = 0, то t = 0;
если х = 2, то t = |£. Поэтому
39.3. Интегрирование по частям

□ На отрезке [а; Ь] имеет место равенство (uv)' = u'v+uv'. Следовательно,
функция uv есть первообразная для непрерывной функции u'v + uv'. Тогда
по формуле Ньютона-Лейбница имеем:
Следовательно,
ь
Формула (39.2) называется формулой интегрирования по частям для
определенного интеграла.
Пример 39.2. Вычислить xlnxdx.
1
О Решение: Положим
/i
Пример 39.3. Вычислить интеграл x sin xdx.
О Решение: Интегрируем по частям. Положим
Поэтому
232
Применяя формулу (39.2), получаем

39.4. Интегрирование четных и нечетных функций
в симметричных пределах
Пусть функция f(x) непрерывна на отрезке [—а; а], симметричном от-
носительно точки х = 0. Докажем, что
Q Разобьем отрезок интегрирования [—а; а] на части [—а;0] и [0;а]. Тогда
по свойству аддитивности
§40. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
ь
Определенный интеграл / f(x)dx, где промежуток интегрирования
а
[а; Ь] конечный, а подынтегральная функция f(x) непрерывна на отрез-
ке [а; Ь], называют еще собственным интегралом.
Рассмотрим так называемые несобственные интегралы, т. е. оп-
ределенный интеграл от непрерывной функции, но с бесконечным проме-
жутком интегрирования или определенный интеграл с конечным проме-
жутком интегрирования, но от функции, имеющей на нем бесконечный
разрыв.
233
если f(x) — четная функция,
если f(x) — нечетная функция.
В первом интеграле сделаем подстановку х = — t. Тогда
(согласно свойству: «определенный интеграл не зависит от обозначения
переменной интегрирования»). Возвращаясь к равенству (39.4), получим
Если функция f(x) четная (f(-x) — f(x)), то f(-x) + f(x) = 2/(х); если
функция f(x) нечетная (f(—x) = -/(х)), то f(—x) -+■ f(x) = 0.
Следовательно, равенство (39.5) принимает вид (39.3). В
Благодаря доказанной формуле можно, например, сразу, не производя
вычислений, сказать, что

40.1. Интеграл с бесконечным промежутком интегрирования
(несобственный интеграл I рода)
В этом случае говорят, что несобственный интеграл / f(x) dx сходится.
а
Если же указанный предел не существует или он бесконечен, то говорят,
+оо
что интеграл / f(x) dx расходится.
а
Аналогично определяется несобственный
интеграл на промежутке (—оо;Ь]:
Несобственный интеграл с двумя бесконечны-
ми пределами определяется формулой
Рис. 172.
В этом случае интеграл слева сходится лишь тогда, когда сходятся оба
интеграла справа. Отметим, что если непрерывная функция f(x) J> 0 на
+оо
промежутке [а; +оо) и интеграл / f(x) dx сходится, то он выражает пло-
а
щадь бесконечно длинной криволинейной трапеции (см. рис. 172).
Пример 40-1. Вычислить несобственные интегралы или установить их
4-оо 0 оо
расходимость: 1) I ^§; 2) / cosxdz; 3) / ^.
О Решение: 1) / Щ = lim f x~2 dx = - lim Ц = -(0 - 1) = 1,
J X2, 6->+ооУ 6-^+ooX|i
интеграл сходится;
234
Пусть функция f(x) непрерывна на промежутке [а;+оо). Если суще-
ствует конечный предел
dx, то его называют несобственным
и,
интегралом первого рода и обозначают
Таким образом, по определению

Теорема 40.1 (признак сравнения). Если на промежутке [а;+оо) непрерывные
функции f(x) и ip(x) удовлетворяют условию 0 ^ f(x) ^ Ц>(х), то из сходимости ин-
+оо + оо
теграла / <р{х) dx следует сходимость интеграла / f(x) dx, а из расходимости
интеграла / f(x) dx следует расходимость интеграла / ц>(х) dx.
Пример 40.2. Сходится ли интеграл
сходится. Следовательно, интеграл / 2 также сходится (и его
У X \ 1 i О )
значение меньше 1). •
Теорема 40.2. Если существует предел lim Д^т = к, 0 < к < ос (f(x) > 0 и
х—юс ^\х>
оо оо
ip(x) > 0), то интегралы / f(x)dx и / tp(x)dx одновременно оба сходятся или
a a
оба расходятся (т. е. ведут себя одинаково в смысле сходимости).
Пример 40.3. Исследовать сходимость интеграла / In ъ л dx.
J х + 1
i
Q Решение: Интеграл / In х* "*" ~ dx сходится, так как интеграл / Щ
J х + 1 J х
i i
сходится и
235
теграл расходится, так как при а —> — оо предел lim sin а не существует.
а—У — оо
В некоторых задачах нет необходимости вычислять интеграл; доста-
точно лишь знать, сходится ли он или нет.
Приведем без доказательства некоторые признаки сходимости.
О Решение: При х ^ 1 имеем
Но интеграл

40.2. Интеграл от разрывной функции
(несобственный интеграл II рода)
Пусть функция f(x) непрерывна на промежутке [а;Ь) и имеет
бесконечный разрыв при х = Ь. Если существует конечный предел
Ь-е
lim / f(x) dx, то его называют несобственным интегралом второго рода
a b
и обозначают / f(x)dx.
а
Таким образом, по определению,
Рис. 173.
Ь-еЬ х
В этом случае интеграл слева называют сходящимся,
если оба несобственных интеграла, стоящих справа,
сходятся.
В случае, когда f(x) > 0, несобственный интеграл второго рода
6
/ f(x) dx (разрыв в точке х = Ь) можно истолковать геометрически как
а
площадь бесконечно высокой криволинейной трапеции (см. рис. 173).
1
Пример 40-4- Вычислить /
О Решение: При х = 0 функция у = \ терпит бесконечный разрыв;
х
интеграл расходится.
236
Если предел в правой части существует, то несобственный интеграл
ь
/ f(x) dx сходится. Если же указанный предел не существует или беско-
{ ь
нечен, то говорят, что интеграл / f(x) dx расходится.
Аналогично, если функция f(x) терпит бесконеч-
ный разрыв в точке х = а, то полагают
14 1Х-ГС
Если функция f(x) терпит разрыв во внутренней
точке с отрезка [а; 6], то несобственный интеграл вто-
рого рода определяется формулой

Сформулируем признаки сходимости для несобственных интегралов
второго рода.
Теорема 40.3. Пусть на промежутке [а;Ь) функции f(x) и ip(x) непрерывны, при
х = b терпят бесконечный разрыв и удовлетворяют условию 0 ^ f(x) ^ р(х).
ъ ъ
Из сходимости интеграла / <р(х) dx вытекает сходимость интеграла / f(x) dx, а из
а а
Ъ Ь
расходимости интеграла / f(x)dx вытекает расходимость интеграла / tp(x)dx.
Теорема 40.4. Пусть функции /(#) и ф(х) непрерывны на промежутке [а; Ь) и в
fix)
точке х — b терпят разрыв. Если существует предел lim J ) \ — к, 0 < к < оо, то
ь ь х~+ь V\x)
интегралы / f(x) dx и / tp(x) dx одновременно сходятся или одновременно расхо-
ft a
дятся.
1
[яГ1 Пример 40.5. Сходится ли интеграл / . ?
Q Решение: Функция f(x) = —r=— имеет на [0; 1] единственный разрыв в
точке х — 0. Рассмотрим функцию ^р(х) = —. Интеграл
§41. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
41.1. Схемы применения определенного интеграла
Пусть требуется найти значение какой-либо геометрической или фи-
зической величины А (площадь фигуры, объем тела, давление жидкости
на вертикальную пластину и т. д.), связанной с отрезком [а; Ь] изменения
независимой переменной х. Предполагается, что эта величина А аддитив-
на, т. е. такая, что при разбиении отрезка [а; Ь] точкой с € (а; Ь) на части
237
расходится. И так как
то интеграл
также расходится.

[а\с] и [c\b] значение величины А, соответствующее всему отрезку [а; Ь],
равно сумме ее значений, соответствующих [а; с] и [с; Ь].
Для нахождения этой величины А можно руководствоваться одной из
двух схем: I схема (или метод интегральных сумм) и II схема (или метод
дифференциала).
Первая схема базируется на определении определенного интеграла.
1. Точками xq = a, #i,..., хп = Ь разбить отрезок [а; Ь] на п частей.
В соответствии с этим, интересующая нас величина А разобьется на п
«элементарных слагаемых» AAi (г = 1,..., п): А = АА\ + АА-2 Н Ь ААп.
2. Представить каждое «элементарное слагаемое» в виде произве-
дения некоторой функции (определяемой из условия задачи), вычислен-
ной в произвольной точке соответствующего отрезка на его длину:
AAi « f(ci)Axi.
При нахождении приближенного значения AAi допустимы некоторые
упрощения: дугу на малом участке можно заменить хордой* стягивающей
ее концы; переменную скорость на малом участке можно приближенно
считать постоянной и т. д.
Получим приближенное значение величины А в виде интегральной
суммы:
238
3. Искомая величина А равна пределу интегральной суммы, т. е.
Указанный «метод сумм», как видим, основан на представлении интегра-
ла как о сумме бесконечно большого числа бесконечно малых слагаемых.
Схема I была применена для выяснения геометрического и физическо-
го смысла определенного интеграла.
Вторая схема представляет собой несколько видоизмененную схему
I и называется «метод дифференциала» или «метод отбрасывания беско-
нечно малых высших порядков»:
1) на отрезке [а; Ь] выбираем произвольное значение х и рассматри-
ваем переменный отрезок [а\х]. На этом отрезке величина А становится
функцией х: А = А(х), т. е. считаем, что часть искомой величины А есть
неизвестная функция А(х), где х Е [а;Ь] — один из параметров величи-
ны А]
2) находим главную часть приращения АА при изменении х на малую
величину Ах = dx, т. е. находим дифференциал dA функции А — А(х):
dA = f(x)dx, где f(x), определяемая из условия задачи, функция пере-
менной х (здесь также возможны различные упрощения);
3) считая, что dA « АЛ при Ах —>• 0, находим искомую величину
путем интегрирования dA в пределах от а до Ь:

41.2. Вычисление площадей плоских фигур
Прямоугольные координаты
Как уже было установлено (см. «геометрический смысл определенно-
го интеграла»), площадь криволинейной трапеции, расположенной «вы-
ше» оси абсцисс (f(x) ^ 0), равна соответствующему
определенному интегралу:
Формула (41.1) получена путем применения схемы
I — метода сумм. Обоснуем формулу (41.1), исполь-
зуя схему П. Пусть криволинейная трапеция ограни-
Рис. 174. чена линиями у = f(x) ^ 0, х = а, х = Ь, у = 0 (см.
рис. 174). Для нахождения площади S этой трапеции
проделаем следующие операции:
1. Возьмем произвольное х £ [а; Ъ] и будем считать, что 5 = 5(х).
2. Дадим аргументу х приращение Ах = dx (х -Ь Ах G [а; Ь]). Функ-
ция 5 = S(x) получит приращение Д5, представляющее собой площадь
«элементарной криволинейной трапеции» (на рисунке она выделена).
Дифференциал площади dS есть главная часть приращения AS при
Ах —> 0, и, очевидно, он равен площади прямоугольника с основанием dx
и высотой у: dS = у • dx.
3. Интегрируя полученное равенство в пределах от х = а до х = Ь,
Отметим, что если криволинейная трапеция расположена «ниже» оси
Ox (fix) < 0), то ее площадь может быть найдена по формуле
(41.2)
Формулы (41.1) и (41.2) можно объединить в од-
ну:
Рис. 175.
Площадь фигуры, ограниченной кривыми у =
= f\(x) и у = fzix), прямыми х = а и х = Ъ (при
условии $2{х) ^ fi(x)) (см. рис. 175), можно найти по формуле
Если плоская фигура имеет «сложную» форму (см. рис. 176), то пря-
мыми, параллельными оси Оу, ее следует разбить на части так, чтобы
можно было бы применить уже известные формулы.
239

Если криволинейная трапеция ограничена прямыми у — с и у — d,
осью Оу и непрерывной кривой х = <£(?/) ^ 0 (см. рис. 177), то ее площадь
d
находится по формуле S = xdy.
с
И, наконец, если криволинейная трапеция огра-
ничена кривой, заданной параметрически
прямыми х = аих = Ьи осью 0#, то площадь ее
находится по формуле
где а и /3 определяются из равенств х(а) = а и х(/?) = Ь.
Рис. 178.
Пример J^l.l. Найти площадь фигуры, ограниченной осью Ох и гра-
фиком функции у = х2 — 2х при х Е [0; 3].
О Решение: Фигура имеет вид, изображенный на рисунке 178. Находим
ее площадь 5:
Пример 1^1.2. Вычислить площадь фигуры, ограниченной эллипсом
х — a cost, у = bsint.
О Решение: Найдем сначала \ площади 5. Здесь х изменяется от 0 до а,
следовательно, t изменяется от ? до 0 (см. рис. 179). Находим:
240

Рис. 179.
Таким образом, -
Полярные координаты
Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ог-
раниченной непрерывной линией г = r(ip) и двумя лучами </? = а и ip = /?
(а < /3), где г и (р — полярные координаты (см. рис. 180). Для решения
задачи используем схему II — метод дифференциала.
1. Будем считать часть искомой площади S
как функцию угла </?, т. е. 5 = S(<^), где а ^ ^ ^ /?
(если у? = а, то S(a) = 0, если<£> = /3, то S(/J) = 5).
2. Если текущий полярный угол ip получит
приращение Aip = d</?, то приращение площади
AS равно площади «элементарного криволиней-
ного сектора» ОАВ.
Дифференциал dS представляет собой глав-
ную часть приращения AS при dp -> 0 и равен
площади кругового сектора О АС (на рисунке она
заштрихована) радиуса г с центральным углом
dip. Поэтому dS = А г2 dip.
3. Интегрируя полученное равенство в пределах от ip = а до <р = /?,
получим искомую площадь
Рис. 180.
Пример 1^1.3. Найти площадь фигуры, ограниченной «трехлепестко-
вой розой» г = acos3</? (см. рис. 181).
О Решение: Найдем сначала площадь половины одного лепестка «розы»,
т. е. ^ часть всей площади фигуры:
1 2 2
т. е. ^5 = 2^-. Следовательно, 5 = ^j-.
241

Рис. 181.
Рис. 182.
Если плоская фигура имеет «сложную» форму, то лучами, выходящи-
ми из полюса, ее следует разбить на криволинейные секторы, к которым
применить полученную формулу для нахождения площади. Так, для фи-
гуры, изображенной на рисунке 182, имеем:
41.3. Вычисление длины дуги плоской кривой
Прямоугольные координаты
Пусть в прямоугольных координатах дана плоская кривая АВ, урав-
нение которой у — f(x), где а ^ х $С Ъ.
Под длиной дуги АВ понимается предел, к которому стремится дли-
на ломаной линии, вписанной в эту дугу, когда число звеньев ломаной не-
ограниченно возрастает, а длина наи-
большего звена ее стремится к нулю.
Покажем, что если функция у =
= f(x) и ее производная у' = f'(x)
непрерывны на отрезке [а; Ь], то кри-
вая АВ имеет длину, равную
(41.3)
Применим схему I (метод сумм).
1. Точками хо = а, х\,..., хп = b
(хо < х\ < • — < хп) разобьем отре-
зок [a; b] на п частей (см. рис. 183).
Рис. 183. Пусть этим точкам соответствуют
точки М0 - A, Mi,..., Мп = В на
кривой АВ. Проведем хорды М$М\, MiM-2,..., Мп-\Мп, длины которых
обозначим соответственно через AL\, AL2,..., ALn. Получим ломаную
MqM\M2 ... Mn-iMn, длина которой равна Ln = AL\ + AL2 H Ь ALn =
= t Aii-
242

2. Длину хорды (или звена ломаной) ALi можно найти по теореме
Пифагора из треугольника с катетами Axi и Ayf.
ALi = \/{Axi)2 + (Д?/г)2, где Axt = х{ - ж»_ь Ау{ = f(x{) - Дхг-i).
По теореме Лагранжа о конечном приращении функции Ayi = f'(ci) • Axi,
где Ci G (xi-i;xi). Поэтому
ALi = х/(Д*г)2 + (/'(Сг)-Д*г)2 = \Л + (/'fe))2 ' Д*г,
а длина всей ломаной MqMi ... Мп равна
(41.4)
3. Длина / кривой АВ, по определению, равна / = lim Ln =
max ALi—>Q
n
= lim ^2 A£*- Заметим, что при ALi —)• 0 также и Дя; -> О (ДЬ* =
max ALi—>0 j_i
= y/(Axi)2 + (Ayi)2 и, следовательно, |Дх*|<Д£г). Функция y/l + (f'(x))2
непрерывна на отрезке [а; 6], так как, по условию, непрерывна функция
/'(#)• Следовательно, существует предел интегральной суммы (41.4), ко-
гда max Axi -> 0:
(41.5)
Формула (41.5) может быть получена из формулы (41.3) подстановкой
х = x(t), dx = x'(t) dt, f'(x) = *Ш.
X (t)
Пример 41-4- Найти длину окружности радиуса R.
О Решение: Найдем 4 часть ее длины от точки (0; R)
до точки (i?;0) (см. рис. 184). Так как у = у/К2 - х2,
то
Рис. 184.
243
Таким образом,
1 dx, или в сокращенной записи I =
Если уравнение кривой АВ задано в параметрической форме
где x(t) и y(t) — непрерывные функции с непрерывными производными и
х(а) = а, х(0) — 6, то длина / кривой АВ находится по формуле

Вычисление длины дуги может быть основано на применении метода
дифференциала. Покажем, как можно получить формулу (41.3), применив
схему II (метод дифференциала).
1. Возьмем произвольное значение х Е [а;Ь] и рассмотрим переменный
отрезок [а;х]. На нем величина / становится функцией от х, т. е. / = 1(х)
(1(a) = 0 и 1(b) =1).
малую дугу МN хордой Д/, стягивающей эту ду-
гу (см. рис. 185):
Стало быть, dl = у/1 + (y'x)2dx.
3. Интегрируя dl в пределах от а до 6, получаем / = / л/l + у'х2 dx.
Равенство dl = л/l + у'х2 dx называется а
формулой дифференциала дуги в прямо-
угольных координатах.
Рис. 186.
Последняя формула представляет собой те-
орему Пифагора для бесконечно малого
треугольника МСТ (см. рис. 186).
Полярные координаты
Пусть кривая АВ задана уравнением в
полярных координатах г = г((f), а ^ ip ^ /3. Предположим, что г(ф) и
г'((f) непрерывны на отрезке [а;/?].
Если в равенствах х = rcos</?, у = г sirup, связывающих полярные и
декартовы координаты, параметром считать угол </?, то кривую А В можно
Тогда
244
Значит, / = 2ttR. Если уравнение окружности записать в параметрическом
виде х = Я cost, у = Rsint (О ^ t ^ 27г), то
Так как

Поэтому
Пример j[1.5. Найти длину кардиоиды г =
= а(1 + cosy?).
Рис. 188.
245
Применяя формулу (41.5), получаем
_ Рис. 187.
\J Решение: Кардиоида г = а(1 + cosy?) имеет
вид, изображенный на рисунке 187. Она симме-
трична относительно полярной оси. Найдем половину длины кардиоиды:
Таким образом,
Значит, I = 8а.
41.4. Вычисление объема тела
Вычисление объема тела по известным площадям параллельных сечений
Пусть требуется найти объем V тела, причем известны площади S
сечений этого тела плоскостями, перпендикулярными некоторой оси, на-
пример оси Ox: S = S(x), а ^ х ^.Ь.
Применим схему II (метод дифференциала).
1. Через произвольную точку х Е [а; Ь]
проведем плоскость П, перпендикулярную
оси Ох (см. рис. 188). Обозначим через S(x)
площадь сечения тела этой плоскостью; 5(я)
считаем известной и непрерывно изменяю-
щейся при изменении х. Через v(x) обозна-
чим объем части тела, лежащее левее плос-
кости П. Будем считать, что на отрезке [а; х]
величина v есть функция от х, т. е. v — v(x)
(v(a) = 0, v(b) = V).

2. Находим дифференциал dV функции v = v(x). Он представляет
собой «элементарный слой» тела, заключенный между параллельными
плоскостями, пересекающими ось Ох в точках х и х + Дх, который при-
ближенно может быть принят за цилиндр с основанием S(x) и высотой dx.
Поэтому дифференциал объема dV = S(x) dx.
3. Находим искомую величину V путем интегрирования dA в пределах
от а до Ъ:
(41.6)
Полученная формула называется формулой объема тела по площади
параллельных сечений.
г2 У2 т2
Пример ^1.6. Найти объем эллипсоида ^ + 72" + ^1 — 1-
О Решение: Рассекая эллипсоид плоскостью, параллельной плоскости
Oyz и на расстоянии х от нее (—а ^ х ^ а), получим эллипс (см.
рис. 189):
Рис. 189.
Площадь этого эллипса равна S(x) =7r6c(l-%). По-
этому, по формуле (41.6), имеем
Объем тела вращения
Пусть вокруг оси Ох вращается криволинейная трапеция, ограничен-
ная непрерывной линией у = f(x) ^ О, отрезком а ^ х ^ Ь и прямыми
х — a w х — Ь (см. рис. 190). Полученная от вращения фигура называет-
ся телом вращения. Сечение этого тела плоскостью, перпендикулярной
оси Ох, проведенной через произвольную точку х оси Ох
(х £ [а;Ь]), есть круг с радиусом у = f(x). Следовательно,
S(x) = тиД
Применяя формулу (41.6) объема тела по площади па-
раллельных сечений, получаем
Рис 190.
(41.7)
Если криволинейная трапеция ограничена графиком не-
прерывной функции х = (f(y) ^ 0 и прямыми х = 0, у = с,
246

у = d (с < d), то объем тела, образованного вращением этой трапеции
вокруг оси Оу, по аналогии с формулой (41.7), равен
Пример J^l.l. Найти объем тела, образован-
ного вращением фигуры, ограниченной линия-
ми 2/=^-, х — О, у — 2\/2 вокруг оси Оу (см.
рис. 191).
Q Решение: По формуле (41.8) находим:
(41.8)
Рис. 191.
41.5. Вычисление площади поверхности вращения
Пусть кривая АВ является графиком функции у = f(x) ^ 0, где
х £ [а; Ь], а функция ?/ = /(ж) и ее производная у' = f'{x) непрерывны
на этом отрезке.
Найдем площадь 5 поверхности, образованной вращением кривой АВ
вокруг оси Ох.
Применим схему II (метод дифференциала).
1. Через произвольную точку х е [а; Ь] проведем плос-
кость П, перпендикулярную оси Ох. Плоскость П пере-
секает поверхность вращения по окружности с радиусом
у = f(x) (см. рис. 192). Величина 5 поверхности части фи-
гуры вращения, лежащей левее плоскости, является функ-
цией от х, т. е. s = s(x) (s(a) = 0 и s(b) = S).
2. Дадим аргументу х приращение Ах = dx. Через точ-
ку х + dx £ [а; Ь] также проведем плоскость, перпендику-
лярную оси Ох. Функция s = s(x) получит приращение
As, изображенного на рисунке в виде «пояска».
Найдем дифференциал площади ds, заменяя образо-
ванную между сечениями фигуру усеченным конусом, об-
разующая которого равна d/, а радиусы оснований рав-
ны у и у Л- dy. Площадь его боковой поверхности равна
ds = тг(у + у + dy) • dl = 2тгу dl + ndydl. Отбрасывая произведение dy dl как
бесконечно малую высшего порядка, чем ds, получаем ds = 2nydl, или,
так как dl = у/1 + (у'х)2 dx, то ds — 2пуу/1 + (у'х)'2 dx.
3. Интегрируя полученное равенство в пределах от х = а до х = Ь,
получаем
Рис. 192
(41.9)
247

Если кривая АВ задана параметрическими уравнениями х = x(t), у = y(t),
t\ ^ t ^ t2, то формула (41.9) для площади поверхности вращения прини-
мает вид
Пример J^l.S. Найти площадь поверхности шара радиуса R.
Q Решение: Можно считать, что поверхность шара образована вращением
полуокружности у = \JR2 — х2, — R ^ х ^ Я, вокруг оси Ох. По форму-
ле (41.9) находим
dx =
Пример J^1.9. Дана циклоида
Найти площадь поверхности, образованной вращением ее вокруг оси Ох.
О Решение: При вращении половины дуги циклоиды, вокруг оси Ох пло-
щадь поверхности вращения равна
248

41.6. Механические приложения определенного интеграла
Работа переменной силы
Пусть материальная точка М перемещается вдоль оси Ох под дей-
ствием переменной силы F = F(x), направленной параллельно этой оси.
Работа, произведенная силой при перемещении точки М из положения
х — а ъ положение х = b (a < Ь), находится по формуле
Пример 41-11- Найти работу, которую необходимо затратить, чтобы
выкачать через край жидкость из вертикального цилиндрического резер-
вуара высоты Н м и радиусом основания R м.
О Решение: Работа, затрачиваемая на поднятие тела весом р на высоту
Л, равна р • h. Но различные слои жидкости в резервуаре находятся на
различных глубинах и высота поднятия (до края резервуара) различных
слоев не одинакова.
Для решения поставленной задачи применим схему
II (метод дифференциала). Введем систему координат
так, как указано на рисунке 193.
1. Работа, затрачиваемая на выкачивание из резер-
вуара слоя жидкости толщиной х (0 ^ х ^ Я), есть
функция от х, т. е. А — А(х), где 0 ^ х ^ Н (А(0) = 0,
А(Н) = Ао).
2. Находим главную часть приращения А А при из-
менении х на величину Ах = dx, т. е. находим диффе-
ренциал dA функции А(х).
Ввиду малости dx считаем, что «элементарный»
слой жидкости находится на одной глубине х (от края
резервуара) (см. рис. 193). Тогда dA = dpx, где dp — вес
этого слоя; он равен g-'ydv, где g — ускорение свободного
Рис. 193.
249
(см. п. 36).
Пример ^1.10. Какую работу нужно затратить, чтобы растянуть пру-
жину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?
О Решение: По закону Гука упругая сила, растягивающая пружину, про-
порциональна этому растяжению х, т. е. F = fcx, где к — коэффициент
пропорциональности. Согласно условию задачи, сила F = 100 Н растяги-
вает пружину на х = 0,01 м; следовательно, 100 = А*-0,01, откуда к = 10000;
следовательно, F = 10000а:.
Искомая работа на основании формулы (41.10) равна

падения, у — плотность жидкости, dv — объем «элементарного» слоя
жидкости (на рисунке он выделен), т.е. dp = gydv. Объем указанного
слоя жидкости, очевидно, равен ттИ2 dx, где dx — высота цилиндра (слоя),
7гЛ2 — площадь его основания, т. е. dv = 7гД2 dx.
Таким образом, dp — <п * к К2 dx и dA = дукК2 dx x.
3) Интегрируя полученное равенство в пределах от х = О до х = Н,
находим
250
Путь, пройденный телом
Пусть материальная точка перемещается по прямой с переменной ско-
ростью v = v(t). Найдем путь 5, пройденный ею за промежуток времени
от ti до t2.
О Решение: Из физического смысла производной известно, что при дви-
жении точки в одном направлении «скорость прямолинейного движения
равна производной от пути по времени», т. е. v(t) = Щ-. Отсюда следует,
что dS — v(t) dt. Интегрируя полученное равенство в пределах от t\ до t2,
получаем 5 = / v(t)dt. •
/1
Отметим, что эту же формулу можно получить, пользуясь схемой I
или II применения определенного интеграла.
[яГ1 Пример ^1.12. Найти путь, пройденный телом за 4 секунды от начала
—■ движения, если скорость тела v(t) = Wt + 2 (м/с).
О Решение: Если v(t) — 10£ 4- 2 (м/с), то путь, пройденный телом от на-
чала движения (t = 0) до конца 4-й секунды, равен
Давление жидкости на вертикальную пластинку
По закону Паскаля давление жидкости на горизонтальную пластину
равно весу столба этой жидкости, имеющего основанием пластинку, а вы-
сотой — глубину ее погружения от свободной поверхности жидкости, т. е.
Р = д • 7 • 5 • /г, где д — ускорение свободного падения, 7 — плотность
жидкости, 5 — площадь пластинки, h — глубина ее погружения.
По этой формуле нельзя искать давление жидкости на вертикально
погруженную пластинку, так как ее разные точки лежат на разных глу-
бинах.
Пусть в жидкость погружена вертикально пластина, ограниченная ли-
ниями х — а, х = b, 2/i = f\{x) и t/2 = /г(я); система координат выбрана
так, как указано на рисунке 194. Для нахождения давления Р жидкости
на эту пластину применим схему II (метод дифференциала).

Рис. 194.
1. Пусть часть искомой величины Р есть
функция от х: р = р(х), т. е. р = р(х) — да-
вление на часть пластины, соответствующее от-
резку [а; х] значений переменной х, где х Е [а; Ь]
(р(а) = 0, р(Ь) = Р).
2. Дадим аргументу х приращение Ах — dx.
Функция р(х) получит приращение Ар (на рисун-
ке — полоска-слой толщины dx). Найдем диффе-
ренциал dp этой функции. Ввиду малости dx бу-
дем приближенно считать полоску прямоуголь-
ником, все точки которого находятся на одной
глубине х, т. е. пластинка эта — горизонталь-
ная.
Тогда по закону Паскаля dp = g • 7 (2/2 — У\) ' dx • х .
у—*—' "т"
5 h
3. Интегрируя полученное равенство в пределах от х = а до х — Ь,
получим
Рис. 195.
Вычисление статических моментов и координат центра тяжести плоской кривой
Пусть на плоскости Оху задана система материальных точек
Mi(#i;i/i), М2(х2;у2), • • •, Мп(хп;уп) соответственное массами mb га2,...
Статическим моментом Sx системы материальных точек относи-
тельно оси Ох называется сумма произведений масс этих точек на их ор-
п
динаты (т. е. на расстояния этих точек от оси Ox): Sx — Y^ mi ' Vi-
i=\
251
Пример J^l.lS. Определить величину давле-
ния воды на полукруг, вертикально погружен-
ный в жидкость, если его радиус Д, а центр О
находится на свободной поверхности воды (см.
рис. 195).
О Решение: Воспользуемся полученной форму-
лой для нахождения давления жидкости на вер-
тикальную пластинку. В данном случае пластин-
ка ограничена линиями у\ = —\/В? — я2, у2 =
= у/К2 — х2, х = 0, х = R. Поэтому

Аналогично определяется статический момент Sy этой системы от-
п
носительно оси Оу: Sy = ^ га* • Х{.
г=1
Если массы распределены непрерывным образом вдоль некоторой кри-
вой, то для выражения статического момента понадобится интегрирова-
ние.
Пусть у = f(x) (а ^ х ^ Ъ) — это уравнение материальной кривой
А В. Будем считать ее однородной с постоянной линейной плотностью 7
(7 = const).
Для произвольного х Е [а; Ь] на кривой АВ найдется точка с коорди-
натами (х; у). Выделим на кривой элементарный участок длины dl, содер-
жащий точку (х;у). Тогда масса этого участка равна jdl. Примем этот
участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у.
Тогда дифференциал статического момента dSx («элементарный момент»)
будет равен jdl • у, т. е. dSx = jdl у (см. рис. 196).
Отсюда следует, что статический момент Sx кри-
вой АВ относительно оси Ох равен
Аналогично находим Sy:
Рис. 196
Статические моменты Sx и Sy кривой позволя-
ют легко установить положение ее центра тяжести
(центра масс).
Центром тяжести материальной плоской кривой у = f(x), х Е [а; Ъ]
называется точка плоскости, обладающая следующим свойством: если в
этой точке сосредоточить всю массу га заданной кривой, то статический
момент этой точки относительно любой координатной оси будет равен ста-
тическому моменту всей кривой у = f(x) относительно той же оси. Обо-
значим через С(хс;ус) центр тяжести кривой АВ.
Из определения центра тяжести следуют равенства т • хс = Sy и
С п
т • ус = Sx или yl • хс = Sy и *yl
или
Пример 41-Ц- Найти центр тяжести однородной дуги окружности
х2 +y2 = R2, расположенной в первой координатной четверти (см. рис. 197).
252

Q Решение: Очевидно, длина указанной дуги окруж-
_ ГУ _ О
ности равна ^^, т. е. / = 2i~. Найдем статический мо-
мент ее относительно оси Ох. Так как уравнение дуги
есть у = VК2 — х2 и у'х = i ~х , то (7 = const)
V Я2 - х2
Рис. 197.
Стало быть,
Так как данная дуга симметрична относительно биссектрисы первого ко-
ординатного угла, то хс — ус — ^*. Итак, центр тяжести имеет координа-
ты
V 7Г ' 7Г /'
Вычисление статических моментов и координат центра тяжести плоской фигуры
Пусть дана материальная плоская фигура (пластинка), ограниченная
кривой у = f(x) ^ 0 и прямыми у = 0, х = а, х = b (см. рис. 198).
Будем считать, что поверхностная плотность пла-
стинки постоянна (7 = const). Тогда масса всей пла-
6
стинки равна 7 • 5, т. е. т = 7 / f(x)dx. Выделим эле-
Рис. 198.
ментарный участок пластинки в виде бесконечно узкой
вертикальной полосы и будем приближенно считать его
прямоугольником.
Тогда масса его равна j-y dx. Центр тяжести С пря-
моугольника лежит г а пересечении диагоналей прямо-
угольника. Эта точка С отстоит от оси Ох на ky, а от
оси Оу на х (приближенно; точнее на расстоянии х+ А Ах). Тогда для эле-
ментарных статических моментов относительно осей Ох и Оу выполнены
соотношения
253
Следовательно,
По аналогии с плоской кривой получаем, обозначив координаты цен-
тра тяжести плоской фигуры (пластинки) через С(хс; ус), что га • хс = 5У,
т • ус = Sx. Отсюда

Пример ^1.15. Найдем координаты цен-
тра тяжести полукруга х2 + у2 ^ Я2, у ^ О
(у = const) (см. рис. 199).
Рис. 199.
О Решение: Очевидно (ввиду симметрии фигуры относительно оси Оу),
что хс = 0. Площадь полукруга равна ZL#^. Находим Sx:
Стало быть,
Итак, центр тяжести имеет координаты С( 0; 4^ 1.
§42. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
ь
Пусть требуется найти определенный интеграл / f(x) dx от непрерыв-
о
ной функции f(x). Если можно найти первообразную F(x) функции /(#),
то интеграл вычисляется по формуле Ньютона-Лейбница:
254
или
Но отыскание первообразной функции иногда весьма сложно; кроме
того, как известно, не для всякой непрерывной функции ее первообразная
выражается через элементарные функции. В этих и других случаях (на-
пример, функция у = /(#) задана графически или таблично) прибегают
к приближенным формулам, с помощью которых определенный интеграл
находится с любой степенью точности.
Рассмотрим три наиболее употребительные формулы приближенного
вычисления определенного интеграла — формулу прямоугольников, фор-
мулу трапеций, формулу парабол (Симпсона), основанные на геометриче-
ском смысле определенного интеграла.

42.1. Формула прямоугольников
Пусть на отрезке [а; 6], а < Ь, задана непрерывная функция f(x). Тре-
ъ
буется вычислить интеграл / f(x) dx, численно равный площади соот-
а
ветствующей криволинейной трапеции. Разобьем основание этой трапе-
ции, т. е. отрезок [а; 6], на п равных частей
(отрезков) длины h = = xi — Xj-i
(таг разбиения) с помощью точек xq = а,
х\, х-2, . • •, хп = Ь. Можно записать, что х\ —
— хо + h - i, где г = 1,2,..., п (см. рис. 200).
В середине с\ — г~1г> 1- каждого та-
кого отрезка построим ординату у* = /(с,)
графика функции у = f(x). Приняв эту
ординату за высоту, построим прямоуголь-
ник с площадью h- yi.
Тогда сумма площадей всех п прямо-
угольников дает площадь ступенчатой
фигуры, представляющую собой приближенное значение искомого опре-
деленного интеграла
|а = Хо^1 Х2 Xi-l Xi
Рис. 200.
(42.1)
Отметим, что для линейной функции (f(x) = kx + Ъ) формула (42.1) дает
точный ответ, поскольку в этом случае f"(x) = 0.
42.2. Формула трапеций
Формулу трапеций получают аналогично формуле прямоугольников:
на каждом частичном отрезке криволинейная трапеция заменяется обыч-
ной.
Разобьем отрезок [а; Ь] на п равных частей длины h = . Абсциссы
точек деления а = хо, х\,х-2,... ,Ь — хп (рис. 201). Пусть 2/о?2/ь • • • ?Уп —
255
Формула (42.1) называется формулой средних прямоугольников.
Абсолютная погрешность приближенного равенства (42.1) оценивает-
ся с помощью следующей формулы:
где М2 — наибольшее значение \f"(x)\ на отрезке [а; Ь],

Рис. 201.
соответствующие им ординаты графика функции. Тогда расчетные фор-
мулы для этих значений примут вид Xj = a+h-i, yi = f{xi),i = 0,1,2,..., n;
n
Заменим кривую у = f(x) ломаной линией, звенья которой соединяют
концы ординат у\ и yi+i (г = 0,1,2,.. .,п). Тогда площадь криволиней-
ной трапеции приближенно равна сумме площадей обычных трапеций с
основаниями yi, yi+\ и высотой h = :
(42.2)
Формула (42.2) называется формулой трапеций.
Абсолютная погрешность Rn приближения, полученного по форму-
ле трапеций, оценивается с помощью формулы |i?n| ^ ,0 2 ' ^2> гДе
12п
М-2 = max \f"(x)\. Снова для линейной функции у = кх + b форму-
ла (42.2) — точная.
42.3. Формула парабол (Симпсона)
Если заменить график функции у = f(x) на каждом отрезке [атг-ь^г]
разбиения не отрезками прямых, как в методах трапеций и прямоугольни-
ков, а дугами парабол, то получим более точную формулу приближенного
вычисления интеграла
//(х)
dx.
256
или

Рис. 202.
6
Получим теперь формулу парабол для вычисления интеграла / f(x) dx.
а
Для этого отрезок [а; Ь] разобьем на 2п равных частей (отрезков) дли-
ной h = °~ а точками Х{ = Хо + ih (i = 0,1,2,..., 2п). В точках деления
а — хо, xi, X2,..., Х2п-2, X'2n-i, %2п — Ь вычисляем значения подынте-
гральной функции f(x): 2/о, У\, 2/2, • • •, 2/2п-2, 2/2n-i, У2п, где yi = f(xi) (см.
рис. 203).
Заменяем каждую пару соседних элементарных криволинейных трапе-
ций с основаниями, равными h, одной элементарной параболической тра-
пецией с основанием, равным 2/г. На отрезке [хо;#2] парабола проходит
257
Рис. 203.
Подставляя эти значения с и а в равенство (42.3), получаем
Выразим эту площадь через /i, 2/0, у\, 2/2- Из равенств для
ординат yi находим, что с - 2/ъ а = -zj^iyo ~ tyi + Уг).
In
Пусть парабола проходит через три точки М\{—/i;2/o),
М2(0;yi), Ms(h] 1/2), где у0 = ah2 -bh + c — ордината пара-
болы в точке х — —h\y\ —с — ордината параболы в точке
х = 0; 2/2 = ah2 + bh + c — ордината параболы в точке х = h
(см. рис. 202). Площадь 5 равна
Предварительно найдем площадь 5 криволинейной трапеции, ограни-
ченной сверху графиком параболы у = ах2 + Ъх + с, сбоку — прямыми
х — — /г, х = h и снизу — отрезком [—/г; h].

через три точки (хо;уо), (xi;2/i), (#2;2/2)- Используя формулу (42.4), нахо-
дим
Аналогично находим
Сложив полученные равенства, имеем
или
Формула (42.5) называется формулой парабол (или Симпсона).
Абсолютная погрешность вычисления по формуле (42.5) оценивается
соотношением
(см. рис. 204)
Рис. 204.
258
Отметим, что формула (42.5) дает точное значение интеграла
пень которого меньше или равна трем (тогда
f(x) dx во всех случаях, когда f(x) — многочлен, сте-
Пример 42.1. Вычислить / хг dx, разбив отрезок инте-
о
грирования [0; 2] на 4 части.
О Решение: Имеем: f(x) = х3,

Точное значение интеграла
Абсолютные погрешности соответствующих формул таковы: а) 0,125;
б) 0,25; в) 0. •
в) по формуле парабол:
б) по формуле трапеции:
а) по формуле прямоугольников:

Глава IX. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Лекции 34-36 I
Функции одной независимой переменной не охватывают все зависимо-
сти, существующие в природе. Поэтому естественно расширить известное
понятие функциональной зависимости и ввести понятие функции несколь-
ких переменных.
Будем рассматривать функции двух переменных, так как все важней-
шие факты теории функций нескольких переменных наблюдаются уже на
функциях двух переменных. Эти факты обобщаются на случай больше-
го числа переменных. Кроме того, для функций двух переменных можно
дать наглядную геометрическую интерпретацию.
§43. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
43.1. Основные понятия
Пусть задано множество D упорядоченных пар чисел (х;у). Соответ-
ствие /, которое каждой паре чисел (х; у) Е D сопоставляет одно и только
одно число zGl, называется функцией двух переменных, определен-
ной на множестве D со значениями в IR, и записывается в виде z = f(x; у)
или / : D -» Ш. При этом х и у называются независимыми переменными
(аргументами), a z — зависимой переменной (функцией).
Множество D = D(f) называется областью определения функции.
Множество значений, принимаемых z в области определения, называет-
ся областью изменения этой функции, обозначается E(f) или Е.
Примером функции двух переменных может служить площадь 5 пря-
моугольника со сторонами, длины которых равны х и у: S = ху. Областью
определения этой функции является множество {(х;у) \ х > 0, у > 0}.
Функцию z — f(x;y), где (х;у) Е D можно понимать (рассматривать)
как функцию точки М(х;у) координатной плоскости Оху. В частности,
областью определения может быть вся плоскость или ее часть, ограничен-
ная некоторыми линиями. Линию, ограничивающую область, называют
границей области. Точки области, не лежащие на границе, называются
внутренними. Область, состоящая из одних внутренних точек, называ-
ется открытой. Область с присоединенной к ней границей называется
замкнутой, обозначается D. Примером замкнутой области является
круг с окружностью.
Значение функции z = f(x;y) в точке Мо(^о5 2/о) обозначают zq —
— f(xo'iVo) или zo = /(A^o) и называют частным значением функции.
Функция двух независимых переменных допускает геометрическое ис-
толкование. Каждой точке Мо(хо; уо) области D в системе координат Охуz
соответствует точка М(хо;уо', ^о)7 ГДО ^о = f(xo'iVo) — аппликата точ-
ки М. Совокупность всех таких точек представляет собой некоторую по-
верхность, которая и будет геометрически изображать данную функцию
z = f{x\y).
260

Например, функция z — y/l — х2 — у2 име-
ет областью определения круг х2 + у2 ^ 1
и изображается верхней полусферой с цент-
ром в точке (9(0; 0;0) и радиусом R = 1 (см.
рис. 205).
Функция двух переменных, как и функция
одной переменной, может быть задана разны-
ми способами: таблицей, аналитически, гра-
фиком. Будем пользоваться, как правило,
аналитическим способом: когда функция за-
дается с помощью формулы.
Рис. 205.
43.2. Предел функции
Рис. 206.
Для функции двух (и большего числа) переменных
вводится понятие предела функции и непрерывности, ана-
логично случаю функции одной переменной. Введем по-
нятие окрестности точки. Множество всех точек М(х;у)
плоскости, координаты которых удовлетворяют нера-
венству у/(х — хо)2 + (у — уо)2 < S, называется 6-окрест-
ностью точки Мо(хо;уо)- Другими словами, с$-окрест-
ность точки Мо — это все внутренние точки круга с цен-
тром Мо и радиусом S (см. рис. 206).
Пусть функция z = f(x;y) определена в некоторой окрестности точ-
ки Мо(хо;уо), кроме, быть может, самой этой точки. Число А называется
пределом функции z = f(x;y) при х -> х0 и у -> у0 (или, что то же
самое, при М(х;у) —> Мо(хо;уо)), если для любого е > 0 существует 6 > 0
такое, что для всех х ф хо и у ф уо и удовлетворяющих неравенству
\/(х — Хо)2 + (у — уо)2 < S выполняется неравенство \f(x;y) — А\ < е. За-
писывают:
Из определения следует, что если предел существует, то он не зависит от
пути, по которому М стремится к Mq (число таких направлений бесконеч-
но; для функции одной переменной х —> хо по двум направлениям: справа
и слева!)
Геометрический смысл предела функции двух переменных состоит в
следующем. Каково бы ни было число е > 0, найдется <5-окрестность точки
Мо(хо;уо), что во всех ее точках М(х;у), отличных от М0, аппликаты
соответствующих точек поверхности z = f{x\y) отличаются от числа А по
модулю меньше, чем на е.
261
Пример J^S.l. Найти предел

2 _ 2
Функция z — —%—У-j в точке О(0; 0) предела не имеет, т. к. при разных
х +у
значениях к предел функции не одинаков (функция имеет различные пре-
дельные значения). •
Предел функции двух переменных обладает свойствами, аналогичны-
ми свойствам предела функции одной переменной (см. п. 17.3). Это означа-
ет, что справедливы утверждения: если функции /(М) и д(М) определены
на множестве D и имеют в точке А/о этого множества пределы А и В со-
ответственно, то и функции /(М) ± д(М), /(М) • д(М), \*A {я{Щ Ф 0)
имеют в точке Mq пределы, которые соответственно равны А ± В, А В,
43.3. Непрерывность функции двух переменных
Функция z = f(x;y) (или f(M)) называется непрерывной в точке
М0(х0;уо), если она:
а) определена в этой точке и некоторой ее окрестности,
б) имеет предел lim /(M),
М—>Mq
в) этот предел равен значению функции z в точке Мо, т. е.
JinL f№> = ^М°) или J3£n f(x> W) = /0*о; l/o).
M—tMn x—txo
У-+У0
Функция, непрерывная в каждой точке некоторой области, называет-
ся непрерывной в этой области. Точки, в которых непрерывность нару-
шается (не выполняется хотя бы одно из условий непрерывности функ-
ции в точке), называются точками разрыва этой функции. Точки разры-
ва z = f(x;y) могут образовывать целые линии разрыва. Так, функция
2
z = —-^— имеет линию разрыва у = х.
Можно дать другое, равносильное приведенному выше, определение
непрерывности функции z = f(x;y) в точке. Обозначим Ах = х — хо,
Ау = у — 2/о, Az = f{x\y) — f(xo;yo). Величины Ах и Ау называются
приращениями аргументов х и у, a Az — полным приращением функции
f(x;y) в точке М0(х0;2/о).
Функция z = f(x;y) называется непрерывной в точке Мо(хо;уо) £ D,
если выполняется равенство lim Az = О, т. е. полное приращение функ-
Дя->>0
Ау->0
ции в этой точке стремится к нулю, когда приращения ее аргументов х и
у стремятся к нулю.
Пользуясь определением непрерывности и теоремами о пределах, мож-
но доказать, что арифметические операции над непрерывными функция-
ми и построение сложной функции из непрерывных функций приводит к
262
Q Решение: Будем приближаться к О(0; 0) по прямой у = кх, где к —
некоторое число. Тогда

непрерывным функциям — подобные теоремы имели место для функций
одной переменной (см. п. 19.4).
43.4. Свойства функций, непрерывных в ограниченной замкнутой
области
Приведем свойства функций, непрерывных в ограниченной замкнутой
области (они аналогичны свойствам непрерывных на отрезке функций од-
ной переменной — см. п. 19.5). Предварительно уточним понятие области.
Областью называется множество точек плоскости, обладающих
свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с неко-
торой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить не-
прерывной линией, целиком лежащей в этой области.
Точка No называется граничной точкой области
D, если она не принадлежит D, но в любой окрестности
ее лежат точки этой области. Совокупность граничных
точек области D называется границей D. Область D
с присоединенной к ней границей называется замкну-
той областью, обозначается D. Область называется р 207
ограниченной, если все ее точки принадлежат неко-
торому кругу радиуса R. В противном случае область
называется неограниченной. Примером неограниченной области может
служить множество точек первого координатного угла, а примером огра-
ниченной — ^-окрестность точки Мо(хо;уо)-
Теорема 43.1. Если функция z = f(N) непрерывна в ограниченной замкнутой
области, то она в этой области: а) ограничена, т. е. существует такое число R > О,
что для всех точек N в этой области выполняется неравенство \f(N)\ < R; б) имеет
точки, в которых принимает наименьшее т и наибольшее М значения; в) принимает
хотя бы в одной точке области любое численное значение, заключенное между т
и М.
Теорема дается без доказательства.
§44. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
44.1. Частные производные первого порядка и их геометрический
смысл
Пусть задана функция z = f(x; у). Так как х и у — независимые пере-
менные, то одна из них может изменяться, а другая сохранять свое значе-
ние. Дадим независимой переменной х приращение Ах, сохраняя значение
263

Таким образом, частная производная функции нескольких (двух, трех и
больше) переменных определяется как производная функции одной из
этих переменных при условии постоянства значений остальных незави-
симых переменных. Поэтому частные производные функции f(x;y) нахо-
дят по формулам и правилам вычисления производных функции одной
переменной (при этом соответственно х или у считается постоянной вели-
чиной).
2
Пример 44-1- Найти частные производные функции z — 2уЛ-ех ~у + 1.
О Решение:
264
Частные производные по х в точке A/o(#o;2/o) обычно обозначают симво-
лами /£(а?0;2/о), Гх\ •
IMo
Аналогично определяется и обозначается частная производная от
z = f(x;y) по переменной у:
то он называется частной производной функции z = f(x; у) в точке М(х; у)
по переменной х и обозначается одним из символов:
Если существует предел
Полное приращение Дг функции z определяется равенством
Аналогично получаем частное приращение z по у:
у неизменным. Тогда z получит приращение, которое называется частным
приращением z по х и обозначается Axz. Итак,

Геометрический смысл частных
производных функции двух переменных
Графиком функции z — f(x; у) явля-
ется некоторая поверхность (см. п. 12.1).
График функции z = f(x; yo) есть линия
пересечения этой поверхности с плоско-
стью у = уо. Исходя из геометрическо-
го смысла производной для функции од-
ной переменной (см. п. 20.2), заключа-
ем, что fx(x0;yo) = tga, где а — угол
между осью Ох и касательной, прове-
денной к кривой z = f(x;yo) в точке
М0(хо1Уо',/(хо',Уо)) (см. рис. 208).
Аналогично, fy(x0;yo) = tg/J.
Рис. 208.
44.2. Частные производные высших порядков
dfix'ij} dfix'v}
Частные производные л и я называют частными про-
изводными первого порядка. Их можно рассматривать как функции от
(х;у) Е D. Эти функции могут иметь частные производные, которые на-
зываются частными производными второго порядка. Они определяются и
обозначаются следующим образом:
Аналогично определяются частные производные 3-го, 4-го и т. д. порядков.
Пример 44-2- Найти частные производные второго порядка функции
= х4 -2х2у3 +уг° + 1.
265
и т. д.
Частная производная второго или более высокого порядка, взятая по
различным переменным, называется смешанной частной производ-
ной. Таковыми являются, например, z"y, % > z"yx-

О Решение: Так как z'x = 4х3 — 4хуг и z'y = — 6х'2у2 + 5у4, то
Теорема 44.1 (Шварц). Если частные производные высшего порядка непрерывны,
то смешанные производные одного порядка, отличающиеся лишь порядком диффе-
ренцирования, равны между собой.
В частности, для z = f(x;y) имеем: ,gj- = ^Ц^.
44.3. Дифференцируемость и полный дифференциал функции
Пусть функция z = f(x;y) определена в некоторой окрестности точки
М(х\у). Составим полное приращение функции в точке М:
Теорема 44.2 (необходимое условие дифференцируемое™ функции). Если
функция z = f(x;y) дифференцируема в точке М(х;у), то она непрерывна в этой
точке, имеет в ней частные производные §р и §р, причем ^- = А, ^- = В.
266
Оказалось, что z"y = zyx. •
Этот результат не случаен. Имеет место теорема, которую приведем
без доказательства.
Функция z = /(#; у) называется дифференцируемой в точке М(х; у),
если ее полное приращение в этой точке можно представить в виде
где а = а(&х, Ау) ->> 0 и /3 = /3(Ах, Ау) -> 0 при Ах -> 0, Ау -> 0. Сумма
первых двух слагаемых в равенстве (44.1) представляет собой главную
часть приращения функции.
Главная часть приращение функции z = f{x\ у), линейная относитель-
но Ах и Ау, называется полным дифференциалом этой функции и обозна-
чается символом dz:
Выражения А • Ах и В • Ау называют частными дифференциалами.
Для независимых переменных х и у полагают Ах = dx и Ay — dy. Поэтому
равенство (44.2) можно переписать в виде

Q Так как функция дифференцируема в точке М, то имеет место равен-
ство (44.1). Отсюда вытекает, что lim Az = 0. Это означает, что функция
Дя->-0
Ду->0
непрерывна в точке М. Положив Ау = 0, Ах /Ов равенстве (44.1), по-
д ~
лучим: Axz = А • Ах + а • Ах. Отсюда находим —^— = A + а. Переходя
к пределу при Ах —> 0, получим lim —^- = А, т. е. §р = А. Таким
образом, в точке М существует частная производная f'x(x;y) = А. Ана-
логично доказывается, что в точке М существует частная производная
№у) = % = в- ■
Равенство (44.1) можно записать в виде
где dxz — %r-dx, dyz = §р dy — частные дифференциалы функции z =
= f{x;y).
Теорема 44.3 (достаточное условие дифференцируемое™ функции). Если
функция z = f(x;y) имеет непрерывные частные производные z'x и z'y в точке
М(х;у), то она дифференцируема в этой точке и ее полный дифференциал выра-
жается формулой (44.5).
Примем теорему без доказательства.
Отметим, что для функции у = f(x) одной переменной существование
производной f'(x) в точке является необходимым и достаточным условием
ее дифференцируемости в этой точке.
Чтобы функция z = f(x\y) была дифференцируема в точке, необхо-
димо, чтобы она имела в ней частные производные, и достаточно, чтобы
она имела в точке непрерывные частные производные.
Арифметические свойства и правила исчисления дифференциалов
функции одной переменной сохраняются и для дифференциалов функции
двух (и большего числа) переменных.
267
где 7 = ct • Ах + /3 • At/ -> 0 при Ах -► 0, Ду -> 0.
Отметим, что обратное утверждение не верно, т. е. из непрерывности
функции или существования частных производных не следует дифферен-
цируемость функции. Так, непрерывная функция z = \/х2 + у2 не диф-
ференцируема в точке (0;0).
Как следствие теоремы получаем формулу для вычисления полного
дифференциала. Формула (44.3) принимает вид:
или
(44.5)
(44.4)

44.4. Применение полного дифференциала к приближенным
вычислениям
Из определения дифференциала функции z — f(x;y) следует, что при
достаточно малых |Ах| и \Ау\ имеет место приближенное равенство
Az « dz. (44.6)
Так как полное приращение Az = f(x + Ах;у + Ay) — f(x;y), равен-
ство (44.6) можно переписать в следующем виде:
Формулой (44.7) пользуются в приближенных расчетах.
Пример 44-3- Вычислить приближенно 1,023'01.
О Решение: Рассмотрим функцию z = ху. Тогда 1,023'01 = (х + Дх)2/+Ау,
где х = 1, Ах = 0,02, у = 3, Ау = 0,01. Воспользуемся формулой (44.7),
предварительно найдя zx и z'y: z'x = (ху)'х = у • ху~1, ^ = (ху)у = ху • \пх.
Следовательно, 1,023'01 « 13+313"1 -0,02 +13 -In 1-0,01, т. е. 1,023'01 « 1,06.
Для сравнения: используя микрокалькулятор, находим:
1,023'01 « 1,061418168. •
Отметим, что с помощью полного дифференциала можно найти: гра-
ницы абсолютной и относительной погрешностей в приближенных вычи-
слениях; приближенное значение полного приращения функции и т. д.
44.5. Дифференциалы высших порядков
Введем понятие дифференциала высшего порядка. Полный дифферен-
циал функции (формула (44.5)) называют также дифференциалом первого
порядка.
Пусть функция z = f{x]y) имеет непрерывные частные производные
второго порядка. Дифференциал второго порядка определяется по форму-
ле d2z = d(dz). Найдем его:
г\'2 о2 о2
Отсюда: d2z = Ц-^dx2 + 2 • Р £ dx • dy + ¥-%dy2. Символически это запи-
дх2 дхду * ду2
сывается так:
268

Теорема 44.4. Если z — f{x;y) — дифференцируемая в точке М(х;у) € D функ-
ция и х — x(t) и у — y(t) — дифференцируемые функции независимой переменной
t, то производная сложной функции z(t) = f(x(t);y(t)) вычисляется по формуле
Q Дадим независимой переменной t приращение At. Тогда функции х =
= x(t) и у = y(t) получат приращения Ах и Ау соответственно. Они, в
свою очередь, вызовут приращение Az функции z.
Так как по условию функция z = f(x;y) дифференцируема в точке
Mix-у), то ее полное приращение можно представить в виде
269
Аналогично можно получить формулу для дифференциала третьего по-
рядка:
где
Методом математической индукции можно показать, что
Отметим, что полученные формулы справедливы лишь в случае, когда
переменные х иу функции z = f(x;y) являются независимыми.
Пример 44-4- (Для самостоятельного решения.) Найти d2z, если z =
= х3у2.
Ответ: d2z = бху2 dx2 + 12х2у dx dy + 2х3 dy2.
44.6. Производная сложной функции. Полная производная
Пусть z = f(x;y) — функция двух переменных х и у, каждая из ко-
торых является функцией независимой переменной t: х = x(t), у = y(t). В
этом случае функция z = f(x(t);y(t)) является сложной функцией одной
независимой переменной t; переменные х иу — промежуточные перемен-
ные.
(44.8)
где а —> 0, (5 —> 0 при Ах —> 0, Ау —> 0 (см. п. 44.3). Разделим выражение
Az на At и перейдем к пределу при At —> 0. Тогда Ах —> 0 и Ау —> 0 в
силу непрерывности функций х = x(t) и у = y(t) (по условию теоремы —

они дифференцируемые). Получаем:
т. e.
или
Частный случай: z = /(х;з/), где у = y(x), т. е. z = f(x\y(x)) —
сложная функция одной независимой переменной х. Этот случай сводит-
ся к предыдущему, причем роль переменной t играет х. Согласно форму-
ле (44.8) имеем:
(44.9)
Формула (44.9) носит название формулы полной производной.
Общий случай: z = f(x\y), где х = x(u;v), у = y(u;v). Тогда z =
= f(x{u\v)',y{w,v)) — сложная функция независимых переменных и и v.
Ее частные производные §р и §р можно найти, используя формулу (44.8)
следующим образом. Зафиксировав v, заменяем в ней Ц|, Щ, -^ соответ-
ствующими частными производными §р, §р, тД:
(44.10)
Аналогично получаем: Ш = & • §^ + & • Ф^-.
ov ox ov ay dv
Таким образом, производная сложной функции (г) по каждой незави-
симой переменной (и и v) равна сумме произведений частных производных
этой функции (z) по ее промежуточным переменным (х и у) на их произ-
водные по соответствующей независимой переменной (и и v).
Пример 44-^- Найти тр и §^, если z = ln(x2 + у2), х = и • v, у = -
270
О Решение: Найдем
(44.10):
самостоятельно), используя формулу

Упростим правую часть полученного равенства:
44.7. Инвариантность формы полного дифференциала
Используя правило дифференцирования сложной функции, можно по-
казать, что полный дифференциал обладает свойством инвариантности:
полный дифференциал функции z = f(x;y) сохраняет один и тот же вид
независимо от того, являются ли аргументы независимыми переменными
или функциями независимых переменных.
Q| Пусть z = f(x; у), где х и у — независимые переменные. Тогда полный
дифференциал (1-го порядка) функции имеет вид dz — §p • dx + §p • dy
(формула (44.5)).
Рассмотрим сложную функцию z = f(x;y), где х = x(u;v), у — y(u;v),
т.е. функцию z = f(x(u;v);y(u;v)) = F{u\v), где и и v — независимые
переменные. Тогда имеем:
44.8. Дифференцирование неявной функции
Функция z = f{x;y) называется неявной, если она задается уравнени-
ем
F(xwz) = 0, (44.11)
неразрешенным относительно z. Найдем частные производные $р и ?р
неявной функции г, заданной уравнением (44.11). Для этого, подставив в
271
Выражения в скобках представляют собой полные дифференциалы dx и
dy функций х = х(щу) и у = y(u;v). Следовательно, и в этом случае,

Пример 44-6> Найти частные производные функции 2, заданной урав-
нением ez + z — х2у + 1 = 0.
О Решение: Здесь F(x;y;z) = ez + z - х2у + 1, F'x = -2ху, F'y = -х2,
Fl = ez + 1. По формулам (44.12) имеем:
Пример 441- Найти -#, если неявная функция у — f(x) задана урав-
нением у3 + 2у = 2х.
Q Решение: Здесь F(x; у) = у3 + 2у - 2х, Fx = -2, F'y = Зу2 + 2. Следова-
тельно,
272
Замечания.
а) Уравнение вида (44.11) не всегда определяет одну переменную как
неявную функцию двух других. Так, уравнение х2 + у2 + z'2 — 4 = 0 опре-
деляет функции z\ = \/4 — х'2 — у2 и Z2 = — \/4 — х2 — у2, определенные в
круге х2-\-у2 ^ 4, zs = \/4 — х2 — у2, определенную в полукруге х2 -\-у2 ^4
при у ^ 0 и т. д., а уравнение cos(x + 2y + 3z) — 4 = 0 не определяет никакой
функции.
Имеет место теорема существования неявной функции двух пе-
ременных: если функция F(x; у; z) и ее производные F'x(x\ у; «г), Fy(x; у; г),
F'z(x;y;z) определены и непрерывны в некоторой окрестности точки
M0(x0;yo;z0), причем F(x0;yo;z0) = О, a Fz(x0;yo;z0) ф О, то существует
окрестность точки Мо, в которой уравнение (44.11) определяет единствен-
ную функцию z — f(x;y), непрерывную и дифференцируемую в окрестно-
сти точки (х0;уо) и такую, что f(x0;yo) = *о-
б) Неявная функция у = f(x) одной переменной задается уравнением
F(x; у) = 0. Можно показать, что в случае, если удовлетворены условия
существования неявной функции одной переменной (имеется теорема, ана-
логичная вышеуказанной), то производная неявной функции находится по
формуле . .
откуда
(у — считаем постоянным),
(х — считаем постоянным),
уравнение вместо z функцию f(x; у), получим тождествоF(x; у; f(x; y))=0.
Частные производные по х и по у функции, тождественно равной нулю,
также равны нулю:

КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ
К ПОВЕРХНОСТИ
Рассмотрим одно из геометрических приложений частных производ-
ных функции двух переменных. Пусть функция z — f(x;y) дифференци-
руема в точке (#о; Уо) некоторой области D еШ2. Рассечем поверхность 5,
изображающую функцию z, плоскостями х = хо и у = уо (см. рис. 209).
Плоскость х = хо пересекает поверхность 5 по не-
которой линии Zo(y), уравнение которой получается
подстановкой в выражение исходной функции z =
=f(x] у) вместо х числа хо- Точка Мо(хо; уо', /(#о; Уо))
принадлежит кривой Zo(y). В силу дифференциру-
емое™ функции z в точке М$ функция zq (у) также
является дифференцируемой в точке у = уо. Следо-
вательно, в этой точке в плоскости х = хо к кривой
zo(y) может быть проведена касательная 1\.
Проводя аналогичные рассуждения для сечения
у = Уо-, построим касательную 1-2 к кривой zo(x) в
точке х = хо. Прямые 1\ и 1-2 определяют плоскость
а, которая называется касательной плоскостью к
поверхности S в точке Мо-
Составим ее уравнение. Так как плоскость а
проходит через точку Мо{хо\ уо', ^о)» то ее уравнение может быть записано
в виде
Рис. 209.
A R
(разделив уравнение на —С и обозначив _п = А\, _^ — В\).
(45.1)
Найдем А\ и В\.
Уравнения касательных 1\ и /2 имеют вид
z- zo = f'x(xo\yo) • (х -хо) + /'(ж0;уо) * (у~Уо)-
(45.2)
273
которое можно переписать так:
соответственно.
Касательная 1\ лежит в плоскости а, следовательно, координаты всех
точек 1\ удовлетворяют уравнению (45.1). Этот факт можно записать в
виде системы ,
Разрешая эту систему относительно В\, получим, что В\ = f'y{xo',yo)-
Проводя аналогичные рассуждения для касательной h, легко устано-
вить, что Аг = f'x{xo;yo)-
Подставив значения А\ и В\ в уравнение (45.1), получаем искомое
уравнение касательной плоскости:

Прямая, проходящая через точку Мо и перпендикулярная касательной
плоскости, построенной в этой точке поверхности, называется ее норма-
лью.
Используя условие перпендикулярности прямой и плоскости (см.
с. 87), легко получить канонические уравнения нормали:
(45.3)
Если поверхность 5 задана уравнением F(x; у; z) = О, то уравнения
(45.2) и (45.3), с учетом того, что частные производные могут быть найде-
ны как производные неявной функции:
Замечание. Формулы касательной плоскости и нормали к поверхности
получены для обыкновенных, т. е. не особых, точек поверхности. Точка Mq
поверхности называется особой, если в этой точке все частные производ-
ные равны нулю или хотя бы одна из них не существует. Такие точки мы
не рассматриваем.
Пример 45-1- Написать уравнения касательной плоскости и нормали
к параболоиду вращения z = х2 4- у2 в точке Мо(1; —1; 2).
О Решение: Здесь z'x = fx(x;y) = 2х, ?у{х\у) = 2у, /£(1;-1) = 2,
/^(1; — 1) = —2. Пользуясь формулами (45.2) и (45.3) получаем уравнение
касательной плоскости: z — 2 = 2 • (х — 1) — 2 • (у + 1) или 2x — 2y — z — 2 = 0
и уравнение нормали: х ~ = У_ ~ = z ~-, ■ •
§46. ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
46.1. Основные понятия
Понятие максимума, минимума, экстремума функции двух перемен-
ных аналогичны соответствующим понятиям функции одной независимой
переменной (см. п. 25.4).
Пусть функция z = f(x;y) определена в некоторой области Z), точка
N(x0;yo) €D.
Точка (хо;уо) называется точкой максимума функции z = f(x;y),
если существует такая (J-окрестность точки (xq; yo), что для каждой точки
(х',у), отличной от (хо;уо), из этой окрестности выполняется неравенство
ffay) < f(xo;yo)-
274
(см. формулы (44.12)), примут соответственно вид
и

Аналогично определяется точка
минимума функции: для всех точек
(х;у), отличных от (#о;2/о)> из (5-окрест-
ности точки (хо',Уо) выполняется нера-
венство: f(x;y) > f(x0;yo).
На рисунке 210: N\ — точка макси-
мума, a N-2 — точка минимума функции
z = f(x;y).
Значение функции в точке макси-
мума (минимума) называется мак-
симумом (минимумом) функции.
Максимум и минимум функции назы-
вают ее экстремумами.
Отметим, что, в силу определения, точка экстремума функции лежит
внутри области определения функции; максимум и минимум имеют ло-
кальный (местный) характер: значение функции в точке (хо;уо) сравни-
вается с ее значениями в точках, достаточно близких к (#о; Уо)- В области
D функция может иметь несколько экстремумов или не иметь ни одного.
Рис. 210.
46.2. Необходимые и достаточные условия экстремума
Рассмотрим условия существования экстремума функции.
Теорема 46.1 (необходимые условия экстремума). Если в точке N(x0;yo) диф-
ференцируемая функция z — f(x;y) имеет экстремум, то ее частные производные в
этой точке равны нулю: f'x(x0;y0) - 0, Гу(х0;уо) = 0.
Q Зафиксируем одну из переменных. Положим, например, у = уо- То-
гда получим функцию f(x;yo) = ip(x) одной переменной, которая име-
ет экстремум при х — х$. Следовательно, согласно необходимому усло-
вию экстремума функции одной переменной (см. п. 25.4), ip'(xo) = 0, т. е.
f'x(xo;yo) =0.
Аналогично можно показать, что fy(xo;yo) = 0. В
Геометрически равенства f'x(xo;yo) = 0 и fy(xo;yo) = 0 означают, что
в точке экстремума функции z = f(x; у) касательная плоскость к поверх-
ности, изображающей функцию f{x;y), параллельна
плоскости Оху, т. к. уравнение касательной плоско-
сти есть z = zo (см. формулу (45.2)).
Замечание. Функция может иметь экстремум в
точках, где хотя бы одна из частных производных
не существует. Например, функция z — \ — у/х2 + у2
имеет максимум в точке О(0; 0) (см. рис. 211), но не
имеет в этой точке частных производных.
Точка, в которой частные производные первого
порядка функции z = f(x; у) равны нулю, т. е. f'x = 0,
f'y = 0, называется стационарной точкой функ-
ции z.
Рис. 211.
275

Стационарные точки и точки, в которых хотя бы одна частная произ-
водная не существует, называются критическими точками.
В критических точках функция может иметь экстремум, а может и не
иметь. Равенство нулю частных производных является необходимым, но
не достаточным условием существования экстремума. Рассмотрим, напри-
мер, функцию z = ху. Для нее точка О(0; 0) является критической (в ней
z'x = у и z'y = х обращаются в ноль). Однако экстремума в ней функция
z — ху не имеет, т. к. в достаточно малой окрестности точки О(0; 0) най-
дутся точки для которых z > 0 (точки I и III четвертей) и z < 0 (точки II
и IV четвертей).
Таким образом, для нахождения экстремумов функции в данной обла-
сти необходимо каждую критическую точку функции подвергнуть допол-
нительному исследованию.
Теорема 46.2 (достаточное условие экстремума). Пусть в стационарной точке
(#о;2/о) и некоторой ее окрестности функция f(x;y) имеет непрерывные частные
производные до второго порядка включительно. Вычислим в точке (хо; уо) значения
А = 1"х(хо',Уо), В = /ху(х0;уо), С = fyy(x0;y0). Обозначим
Тогда:
1. если Д > 0, то функция f{x;y) в точке (х0;уо) имеет экстремум: мак-
симум, если А < 0; минимум, если А > 0;
2. если Д < 0, то функция f{x;y) в точке (хо;уо) экстремума не имеет.
В случае Д = 0 экстремум в точке (хо;уо) может быть, может не быть. Необходимы
дополнительные исследования.
Примем без доказательства.
Пример \6.1. Найти экстремум функции z = Зх2у — х3 — у4.
О Решение: Здесь z'x — 6ху-3х2, z'y = Зх2-4у3. Точки, в которых частные
производные не существуют, отсутствуют.
Найдем стационарные точки, решая систему уравнений:
276
Отсюда получаем точки Mi(6;3) и А/2(0;0).
Находим частные производные второго порядка данной функции:
4'* = 6у-6х, г%у = 6х, г';у = -12у2.
В точке Mi (6; 3) имеем: А = -18, В = 36, С = -108, отсюда
АС - В2 = -18 • (-108) - 362 = 648,

Так как А < О, то в точке Mi функция имеет локальный максимум:
Zmax = *(6; 3) = 3 • 36 • 3 - б3 - З4 = 324 - 216 - 81 = 27.
В точке М2(0;0): А = О, В = О, С = 0 и, значит, Д = 0. Проведем до-
полнительное исследование. Значение функции z в точке М2 равно нулю:
г(0; 0) = 0. Можно заметить, что z = — £/4 < 0 при я = 0, у ф 0; г = — х3 > 0
при х < 0, ?/ = 0. Значит, в окрестности точки М2(0;0) функция г прини-
мает как отрицательные, так и положительные значения. Следовательно,
в точке М-2 функция экстремума не имеет. •
46.3. Наибольшее и наименьшее значения функции в замкнутой
области
Пусть функция z — f(x',y) определена и непрерывна в ограничен-
ной замкнутой области D. Тогда она достигает в некоторых точках D
своего наибольшего М и наименьшего га значений (т. н. глобальный экс-
тремум). Эти значения достигаются функцией в точках, расположенных
внутри области D , или в точках, лежащих на границе области.
Правило нахождения наибольшего и наименьшего значений диффе-
ренцируемой в области D функции z = f(x;y) состоит в следующем:
1. Найти все критические точки функции, принадлежащие D , и вычи-
слить значения функции в них;
2. Найти наибольшее и наименьшее значения функции z = f(x;y) на
границах области;
3. Сравнить все найденные значения функции и выбрать из них наи-
большее М и наименьшее т.
Пример 46.2. Найти наибольшее и наимень-
шее значения функции z = х2у + ху2 + ху в за-
мкнутой области, ограниченной линиями: у — —,
я; = 1, а; = 2, t/ = —1,5 (см. рис. 212).
О Решение: Здесь z'x = 2ху + у2 + у, z'y = х2 +
+2ху + х.
1. Находим все критические точки:
Рис. 212.
Решением системы являются точки (0;0), (—1;0), (0;—1), ( — ^;~^)-
Ни одна из найденных точек не принадлежит области D.
2. Исследуем функцию z на границе области, состоящей из участков
АВ, ВС, СЕ и ЕА (рис. 212).
277

На участке АВ: х = 1, z = у2 + 2у, где у е -4; 1 ,
z'y = 2у + 2, 2у + 2 = О, у — — 1. Значения функции г(-1) = — 1,
*(-§) =-J,*(l) = 3.
На участке ВС: у = —, z = х + — + 1, где х £ [1; 2],
z'x = 1 —4j, 1 —ту = 0, xi = 1, ^2 = — 1 ф [1;2]. Значения функции
г(1) = 3, г(2) = 3,5.
На участке СЕ: х = 2, z = 2у2+6у, у е [-|; i],
z.^ = 4у + б, 4у + б = О, у = -4- Значения функции г( —й) = -4,5,
г(±)=3,5.
На участке АЕ: у = -|, г = -Щ- + |х, ж G [1;2],
г£. = -Зх + 4, -За: + 4=0, х=4^ [1'»2]. Значения функции
2(1) = -2,2(2) = -4,5.
3. Сравнивая полученные результаты, имеем: М = +3,5 = z\2;k\ =
= 2(C); a m = -4,5 = 2(2; -|) = г(Е).

СПРАВОЧНЫЕ МАТЕРИАЛЫ
Правила дифференцирования
279
Формулы дифференцирования

Таблица основных интегралов

По вопросам оптовых закупок обращаться:
тел./факс: (495) 785-15-30, e-mail: trade@airis.ru
Адрес: Москва, пр. Мира, д. 104
Наш сайт: www.airis.ru
Книги издательства «АЙРИС-пресс» можно приобрести в магазине
Дом книги на Ладожской
по адресу: г. Москва, ул. Ладожская, д. 8 (м. «Бауманская»).
Тел.(499)221-77-33
Интернет-магазин: www.dom-knigi.ru
доставка по почте во все уголки России и зарубежья.
Режим работы: понедельник — суббота с 9 до 21 часа,
воскресенье с 10 до 20 часов, без перерыва
Издательство «АЙРИС-пресс» приглашает к сотрудничеству
авторов образовательной и развивающей литературы.
По всем вопросам обращаться
по тел.: (495) 785-15-33, e-mail: editor@airis.ru
Адрес редакции: 129626, Москва, а/я 66
Учебное издание
Письменный Дмитрий Трофимович
КОНСПЕКТ ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
1 часть
Ведущий редактор Е. Н. Куликова
Редактор Л. В. Абламская
Художественный редактор А. М. Драговои
Обложка А. М. Кузнецов
Иллюстрации Е. В. Панкратьев, А. Ю. Терская
Технический редактор В. А. Артемов
Компьютерная верстка К. Е. Панкратьев
Корректоры Н. С. Калашникова, 3. А. Тихонова
Подписано в печать 18.08.11. Бумага офсетная.
Формат 70x100 '/i6. Гарнитура «Тайме». Печать офсетная.
Печ. л. 18,0. Усл. печ. л. 23,4. Тираж 10 000 экз. Заказ № 6510.
ООО «Издательство «АЙРИС-пресс»
129626, г. Москва, проспект Мира, д. 104.
Отпечатано в ОАО «Можайский полиграфический комбинат»
143200, г. Можайск, ул. Мира, 93.
Сайт: www.oaompk.ru, www.oaoMnK^ тел.: (495) 745-84-28, (49638) 20-685

ДЛЯ ЗАМЕТОК