55 коп.
il
Д.В. КЛЕТЕНИК
адгп
ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Д. В. КЛЕТЕНИК
СБОРНИК ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Под редакцией проф. Н. В. ЕФИМОВА
ИЗДАНИЕ ТРИНАДЦАТОЕ, СТЕРЕОТИПНОЕ
Допущено
Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов высших учебных заведений
МОСКВА «НАУКА» ГЛАВНАЯ РЕДАКЦИЯ ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1980
22.151.5 К 48
УДК 516
От издательства
Настоящее (тринадцатое) издание книги не отличается от предыдущего (1975 г.)
Давид Викторович Клетеник
Сборник задач по аналитической геометрии
М., 1980 г., 240 стр. с илл.
Редакторы Ф. И. Кизнер, В. В. Донченко Техн, редактор В. Н. Кондакова Корректоры Т. С. Плетнева, И. Д. Дорохова
ИБ № 11596
Печать с матриц. Подписано к печати 06.03.80. Бумага 84X108732, тип. № 3. Литературная гарнитура. Высокая печать. Условн, печ. л. 12,6. Уч.-изд. л. 14,73. Тираж 200 000 экз. (1-й завод 1—100 000-экз.). Заказ № 2899.
Цена книги 55 коп.
Издательство «Наука»
Главная редакция физико-математической литературы 117071, Москва, В-71, Ленинский проспект, 15
Отпечатано с матриц Ордена Трудового Красного Знамени Ленинградской типографии № 2 имени Евгении Соколовой «Союзполиграфпрома» при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли. Измайловский проспект, 29 в типографии № 2 изд-ва «Наука», Москва, Г-99, Шубинский пер., 10
ОГЛАВЛЕНИЕ
ЧАСТЬ ПЕРВАЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Глава 1, Простейшие задачи аналитической геометрии на плоскости «............................................  5
§ 1. Ось и отрезки оси. Координаты на прямой (5). § 2, Декартовы прямоугольные координаты иа плоскости (7). § 3. Полярные координаты (9). § 4. Направленный отрезок. Проекция отрезка на произвольную ось. Проекция отрезка на оси координат. Длина и полярный угол отрезка. Расстояние между двумя точками (12). § 5. Деление отрезка в данном отношении (16). § 6. Площадь треугольника (20). §7. Преобразование координат (21).
Глава 2. Уравнение линии , . •	25
§ 8. Функция двух переменных (25). § 9. Понятие уравнения линии. Задание линии при помощи уравнения (27). § 10. Вывод уравнений заранее данных линий (29). § 11. Параметрические уравнения линии (33).
Глава 3. Линии первого порядка ...,«,,,,..35
§ 12, Общее уравнение прямой. Уравнение прямой с угловым коэффициентом, Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых (35). § 13. Неполные уравнения прямой. Совместное исследование уравнений двух и трех прямых. Уравнение прямой «в отрезках» (43). § 14. Нормальное уравнение прямой. Задача определения расстояния от точки до прямой (47). § 15. Уравнение пучка прямых (53), § 16. Полярное уравнение прямой (56).
Глава 4. Геометрические свойства линий второго порядка 58
§ 17. Окружность (58). § 18. Эллипс (64). § 19. Гипербола (75).
§ 20. Парабола (85). § 21. Полярное уравнение эллипса, гиперболы и параболы (90). § 22. Диаметры линий второго порядка (92).
Глава 5 Упрощение общего уравнения линии второго порядка. Уравнения некоторых кривых, встречающихся в математике и ее приложениях . . . . 9G
§ 23. Центр линии второго порядка (96). § 24. Приведение к простейшему виду уравнения центральной линнн второго порядка (98). § 25.' Приведение к простейшему виду параболического уравнения (103). § 26. Уравнения некоторых кривых, встречающихся в математике и ее приложениях (105).
I’	3
ЧАСТЬ ВТОРАЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Глава 6. Некоторые простейшие задачи аналитической геометрии в пространстве......................................  112
§ 27. Декартовы прямоугольные координаты в пространстве (112). § 28. Расстояние между двумя точками. Деление отрезка в данном отношении (113).
Глава 7. Векторная алгебра...................................116
§ 29. Понятие вектора. Проекции вектора (116), § 30. Линейные операции над векторами (118) § 31. Скалярное произведение векторов (124). § 32. Векторное произведение векторов (123). § 33. Смешанное произведение трех векторов (131). § 34. Двойное векторное произведение (133.)
Глава 8. Уравнение поверхности и уравнения линии . . . 135
§ 35. Уравнение поверхности (135). § 36. Уравнения линии. Задача о пересечении трех поверхностей (138). § 37. Уравнение цилиндрической поверхности с образующими, параллельными одной из координатных осей (139).
Глава 9. Уравнение плоскости. Уравнения прямой. Уравнения поверхностей второго порядка ........................... 141
§ 38. Общее уравнение плоскости. Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор (141). § 39. Неполные уравнения плоскостей, Уравнение плоскости <в отрезках» (145). § 40. Нормальное уравнение плоскости. Расстояние от точки до плоскости (147). § 41. Уравнения прямой (151). § 42. Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой (154). § 43. Смешанные задачи, относящиеся к уравнению плоскости н уравнениям прямой (159). § 44. Сфера (165). § 45. Уравнения плоскости, прямой .и сферы в векторной символике (170). § 46. Поверхности второго порядка (174).
Приложение. Элементы теории определителей....................185
§ 1. Определители второго порядка и система двух уравнений первой степени с двумя неизвестными (185). § 2. Однородная система двух уравнений первой степени с тремя неизвестными (187). § 3. Определители третьего порядка (188). § 4. Свойства определителей (190). § 5. Решение и исследование системы трех уравнений первой степени с тремя неизвестными (194). § 6. Определители четвертого порядка (196).
Ответы и указания к задачам
198
ЧАСТЬ ПЕРВАЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
ГЛАВА 1
ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
§ 1.	Ось и отрезок оси. Координаты на прямой
Прямая, на которой выбрано положительное направление, называется осью. Отрезок оси, ограниченный какими-нибудь точками/1 и В, называется направленным, если сказано, какая из этих точек считается началом отрезка, какая — концом. Направленный отрезок с началом А и концом В обозначается символом АВ. Величиной направленного отрезка оси называется его длина, взятая со знаком плюс, если направление отрезка (т. е. направление от начала к концу) совпадает с положительным направлением оси, и со знаком минус, если это направление противоположно положительному направлению оси. Величина отрезка АВ обозначается символом АВ, его длина — символом | А В |. Если точки А и В совпадают, то, опрс-дечяемый ими отрезок называется нулевым; очевидно, в этом случае АВ = ВА = О (направление нулевого отрезка следует считать неопределенным).
Пусть дана произвольная прямая а. Выберем некоторый отрезок в качестве единицы измерения длин, ’назначим на прямой а положительное направление (после чего она становится осью) *) и отметим на этой прямой буквой О какую нибудь точку. Тем самым на прямой а будет введена система координат.
Координатой любой точки М прямой а (в установленной системе координат) называется число х, равное величине отрезка ОМ:
х = ОМ.
Точка О называется началом координат; ее собственная координата равна пулю. В дальнейшем символ М(х) означает, что точка М имеет координату х.
Если Л11(Х[) и М2(х2)—Две произвольные точки прямой а, ю формула
Л1|Л12 = х2 — Х|
выражает величину отрезка ЛГМг, формула
|M(M2| == |хг-х.,| выражает его длину.
*) Обычно на чертежах у горизонтальных осей положительным назначается направление слева направо.
о
1.	Построить точки А (3), В (5), С (— 1), D , Е (~у)> F (/2), Я(-/5).
2.	Построить точки, координаты которых удовлетворяют уравнениям: 1) |х|=2;2) |х—1|==3;3) |1—х| = = 2; 4) |2 + х| = 2.
3.	Охарактеризовать геометрически расположение точек, координаты которых удовлетворяют неравенствами 1) х > 2; 2) х — 3<0; 3) 12 — х < 0; 4) 2х—3<0; 5) Зх- 5 > 0; 6) 1 < х < 3; 7) —2<х<3;8)|^> > 0; 9)	10)	< 0; И) -2^=1 < 1;
’ х — 2	’ х —1	7 х—2
112) х2 —8xr-F15<0; 13) я2 - 8х‘-р 15 > 0; 14) х2-|-, + х— 12 >0; 15) х2-рх— 12^0.
4.	Определить величину АВ и длину |45| отрезка, заданного точками: 1) 4(3) и 5(11)? 2) 4(5) и В (2); 3) 4(—1) и 5(3)? 4) 4(—5) и В(-3); 5) 4(-1) и 5(-3); 6) А (-7) и В (-5).
5.	Вычислить координату точки А, если известны: 1) 5(3) и 45 = 5; 2) 5(2) и АВ = -3; 3) 5(-1) и 54=2; 4) В (-5) и ВА = -3; 5) 5(0) и |45|=2; 6) 5(2) и |45| =3; 7) 5(-1) и [45| =5; 8) В(-5) и |451 =2.
6.	Охарактеризовать геометрически расположение точек, координаты которых удовлетворяют следующим неравенствам:
1) |х|<1; 2) |х|>2; 3) |х|<2; 4) |х|>3; 5) |х-2|<3; 6) | х- 5 |<1; 7) ] х- 1 |>2; 8) | х- 3 |>1; 9) | x-f- 11 < 3; 10) |х + 2|> 1; II) |х + 5|<1; 12) |х+ 11>2.
4С
7,	Определить отношение	в котором точ-
ка С делит отрезок 45 при следующих данных: 1) 4(2), 5(6) и С(4); 2) 4(2), 5(4) и С(7); 3) 4(—1), 5(5) и С(3); 4) 4(1), 5(13) и 0(5); 5) 4(5), 5(-2) и С(-5).
,	8. Даны три точки 4 (—7), 5(—1) и С(1), Опреде-
лить отношение %, в котором каждая из них делит отрезок, ограниченный двумя другими.
,	М\М
9.	Определить отношение X =	, в котором дан-
ная точка Af(x) делит отрезок MiMz, ограниченный данными точками Mi(xi) и Л1г(Х2).
10.	Определить координату х точки М, делящей отрезок Л41Л12, ограниченный данными точками Mi(xi) и Л42(*2) в данном отношении л = -мм ).
11.	Определить координату х середины отрезка, ограниченного двумя данными точками Mi(xi) и М2(*2).
12.	Определить координату х середины отрезка, ограниченного двумя данными точками, в каждом из следующих случаев: 1) /4(3) и В (5); 2) С(—1) и D (5); 3) MJ-!) и М2(-3); 4) Pi(-5) и Р2(1)’> 5) Qi(3) и <?г(—4).
13.	Определить координату точки М, если известны:
1) ЛМЗ), М2(7)	и	А —М1М мм2	= 2;
2) 4(2), В (-5)		л __ AM	— 3*
		~мв	
3) С(—I), 0(3)	и	А	СМ MD	1 — 2 »
4) Л(—1), В(3)	и	а _ AM МВ	= —2;
5) 4(1), В (—3)	и	. — вм Л — МА	= — 3;
6) Л(-2), В(-1) и х = -^-=—Г.
14.	Даны две точки /4(5) и В(— 3). Определить:
1)	координату точки М, симметричной точке А относительно точки В\
2)	координату точки Л/, симметричной точке В относительно точки А.
15.	Отрезок, ограниченный точками 4 (—2) и В (19), разделен на три равные части. Определить координаты точек деления.
16.	Определить координаты концов 4 и В отрезка, который точками В(—25) и Q(— 9) разделен на три равные части.
§ 2.	Декартовы прямоугольные координаты на плоскости
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке.
7
Точка пересечения осей называется началом координат, а сами оси — координатными осями. Первая из координатных осей называется осью абсцисс, at вторая — осью ординат.
Начало координат” обозначается буквой О, ось абсцисс — символом Ох, ось ординат — символом Оу.
Координатами произвольной точки Л1 в заданной системе называют числа
х = ОМХ, у = ОМУ
(рис. 1), где Мх и Му суть проекции точки М на оси Ох и Оу, ОМХ обозначает величину отрезка ОМХ оси абсцисс, ОМУ — величину отрезка ОМУ оси ординат. Число х называется абсциссой точки М, число у называется ординатой этой же точки. Символ	обозначает, что
точка М имеет абсциссой число х, а ординатой число у.
Ось Оу разделяет всю плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Ох, называется правой, другая— левой. Точно так же ось Ох раз-"х деляет плоскость на две полуплоскости;; та из них, которая расположена в положительном направлении оси Оу, называется верхней, другая нижней.
Обе координатные оси вместе разделяют плоскость на четыре четверти,
которые нумеруют по следующему правилу: первой координатной четвертью называется та, которая лежит одновременно в правой и в верхней полуплоскости, второй — лежащая в левой и в верхней полуплоскости, третьей — лежащая в левой и в нижней полуплоскости, четвертой — лежащая в правой и в нижней полуплоскости.
17.	Построить точки 4(2; 3), В(—5; 1), С (—2; —3), £>(0; 3), Е (-5; 0),
18.	Найти координаты проекций на ось абсцисс точек Л(2; -3), В(3; -1), С(-5; 1), П(-3; -2), Я(-5; -1).
19.	Найти координаты проекций на ось ординат точек А (-3; 2), В(-5; 1), С(3; -2), D(-l; 1), Е(-6; —2).
20.	Найти координаты точек, симметричных относительно оси Ох точкам: 1) А (2; 3); 2)В(—3; 2); 3) C(-l? -1); 4) D(-3; -5); 5) Е(-4; 6); 6) F(a; Ь).
21.	Найти координаты точек, симметричных относительно оси Оу точкам: 1) Д(—1; 2); 2) В(3; —1)? 3) С(—2; -2); 4) П(—2; 5); 5) Е(3; -5); 6) F(a; Ь).
22.	Найти координаты точек, симметричных относительно начала координат точкам: 1) 4(3; 3); 2) В(2; -4); 3) С(-2; 1); 4) D(5; -3); 5) Е(-5; -4); 6) Е(а; Ь),
Рис. 1
23.	Найти координаты точек, симметричных относительно биссектрисы первого координатного угла точкам: 1) А (2; 3); 2) В(5; -2); 3) С(—3; 4).
24.	Найти координаты точек, симметричных относительно биссектрисы второго координатного угла точкам: 1) 4(3; 5), 2) В(-4; 3); 3) С(7; -2).
25.	Определить, в каких четвертях может быть расположена точка М(х\у). если: 1) ху > 0; 2) ху < 0; 3) х — у = 0; 4) х + у = 0; 5) х + у > 0, 6) х + у < 0; 7) х— г/> 0; 8) х — у СО.
§ 3. Полярные координаты
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, луча ОА, исходящего из этой точки, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положитель-ними (на чертежах обычно положитель-	р
ными считаются повороты против часо-вой стрелки).
Полярными координатами произ- &С--__________—J
вольной точки М (относительно задан- О	А
пой системы) называются числа р = 0Л1 и 0 = <£4ОЛ1 (рис. 2). Угол 0 при	Рис>
этом следует понимать так, как принято в тригонометрии. Число р называется первой координатой, или полярным радиусом, число 0—второй координатой, или полярным углом точки М (0 называют также амплитудой) *).
Символ М(р;0) обозначает, что точка М имеет полярные' координаты р и 0.
Полярный угол 0 имеет бесконечно много возможных значений (отличающихся друг от друга на величину вида ±2пл, где п. — целое положительное число). Значение полярного угла, удовлетворяющее неравенствам —л < 0	называется главным.
В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1) пользоваться одним и тем же масштабом, 2) при определении полярных углов считать положительными повороты в том направлении, в каком следует вращать положительную полуось абсцисс, чтобы кратчайшим путем совместить ее с положительной полуосью ординат (таким образом, если оси декартовой системы находятся в обычном расположении, т. е. ось Ох направлена вправо, а ось Оу — вверх, то и отсчет полярных
*) Здесь ОМ обозначает длину отрезка, понимаемую как в элементарной геометрии (т. е. абсолютно, без учета знака).'Употреблять более громоздкий символ | ОМ| в данном случае нет надобности, поскольку точки О и М рассматриваются как произвольные точки плоскости, , а не как точки некоторой оси. Подобное упрощение символики в аналогичных случаях часто делается и Дальни*
9
углов должен быть обычным, т. е. положительными следует считать те углы, которые отсчитываются против часовой стрелки).
При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки к декартовым координатам той же точки осуществляется по формулам
х = р cos 6, у = р sin 0.
В этом же случае формулы
р = V х2 + У2, tg 0 = —
являются формулами перехода от декартовых координат к полярным.
При одновременном рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштаб для обеих систем одинаковыми.
26.	Построить точки, заданные полярными координа-тами: л(3; -у), в (2; я). с(3; -7-), D U; Зу), £(5; 2) и Г(1; —1) (для точек D, Е и F выполнить построение приближенно, пользуясь транспортиром).
27.	Определить полярные координаты точек, симметричных относительно полярной оси точкам Mi (3; М2(2; -у). М3(3; —М4(1; 2) и М5(5; -1), задан-ным в полярной системе координат.
28.	Определить полярные координаты точек, симметричных относительно полюса точкам -j-), М2(б; у), М3(2;-~), М4(4;|п) и М,(3;-2), за-данным в полярной системе координат.
29.	В полярной системе координат даны две вершины А ^3; — ~л) и В ^5; ~ л) параллелограмма ABCD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма.
30.	В полярной системе координат даны точки А ^8; —л) и В (б; Вычислить полярные координаты середины отрезка, соединяющего точки А и В.
31.	В полярной системе координат даны точки Д(3;у),в(21 -£), C(ljn), 0(5;	2) и
10
F(2;> ~ 1). Положительное направление полярной оси изменено на противоположное. Определить полярные координаты заданных точек в новой системе.
32.	В полярной системе координат даны точки ЛГ,(3; ^), М2(1; |я), М3(2; 0), М4(б; £), М5(3; -|я) и М6(1; "ргя)* Полярная ось повернута так, что в но-вом положении она проходит через точку М(. Определить координаты заданных точек в новой (полярной) системе.
33.	В полярной системе координат даны точки Mj(12; у л) и М2(12; — у л), Вычислить полярные координаты середины отрезка, соединяющего точки Mt и М2.
34.	В полярной системе координат даны точки Mi(pi; 0i) и М2(р2; 02). Вычислить расстояние d между ними.
35.	В полярной системе координат даны точки Mt (б; у) и М2(8; —jyj. Вычислить расстояние d между ними.
36.	В полярной системе координат даны две смежные вершины квадрата Mt (12; —и М2 (з;	. Определить его площадь.	г
37.	В полярной системе координат даны две противоположные вершины квадрата р(б; —у л^ и Q (4; |jij. Определить его площадь.
38.	В полярной системе координат даны две вершины правильного треугольника А 14; —у л1 и BI8; -у л). Определить его площадь.
39.	Одна из вершин треугольника ОАВ находится в полюсе, две другие суть точки A (pi; 9i) и В (р2; 02). Вычислить площадь этого треугольника.
40.	Одна из вершин треугольника 04В находится в полюсе О, две другие суть точки А (б; у) и В (4; -у). Вычислить площадь этого треугольника.
41.	Вычислить площадь треугольника, вершины которого А (3; у л), В (в; у- л) и С (б; у л) заданы в полярных координатах.
И
42.	Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В полярной системе координат даны точки 6; ~ , М2(б;0),	М4(10;	М5(в; |я), М6(12;
— Определить декартовы координаты этих точек.
43.	Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В декартовой прямоугольной системе координат даны точки Л/1(0; 5)±М2(—3; 0), М3(/3; 1), М4 (— У 2 ; — У 2), М5 (1; — У 3). Определить полярные координаты этих точек.
§ 4.	Направленный отрезок. Проекция отрезка на произвольную ось. Проекции отрезка на оси координат. Длина и полярный угол отрезка.
Расстояние между двумя точками
Прямолинейный отрезок называется направленным, если указано, какая из ограничивающих его точек считается началом, какая — концом, Направленный отрезок, имеющий точку А своим началом и точку В концом (рис. 3), обозначается символом АВ (т. е. так же, как отрезок оси; см. § 1). Длина направленного отрезка АВ (при заданном масштабе) обозначается символом |ЛВ] (или Л В; см. сноску на стр. 13). 
s'	Проекцией отрезка АВ на ось и назы-
вается число, равное величине отрезка A]Bi оси и, где точка Л] является проек-'	цией на ось и точки Л, а В}~ проекцией
на эту же ось точки В. _
Рис. 3.	Проекция отрезка АВ на ось и обозна-
чается символом при АВ. Если на плоскости задана система декартовых прямоугольных координат, то про-г екция отрезка на ось Ох обозначается символом X, его проекция на ось Оу — символом У.
Если известны координаты точек Mj(xr, yi) и ^2(^2; У2), то проекции X и У на оси координат направленного отрезка М]Мг могут быть вычислены по формулам
Х = х2. — х1, У = у2 — ух
Таким образом, чтобы найти проекции направленного отрезка на оси координат нужно от координат его конца отнять соответствующие координаты начала.
12
Угол 9, на который нужно повернуть положительную полуось Ох так, чтобы ее направление совпало с направлением отрезка называется полярным углом отрезка М^Мг.
Угол 9 понимается, как в тригонометрии. Соответственно этому 6 имеет бесконечно много возможных значений, которые отличаются друг от друга на величину вида ±2ял (где п — целое положительное число). Главным значением полярного угла называется то из его значений, которое удовлетворяет неравенствам —л < 9 гС 4-я.
Формулы
X = d • cos 9, У = d • sin 9 выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Отсюда же вытекают формулы d = ] X2 + У2, COS 9 = у-Ду;;-, S i П 9 = 	,
+ у2 Кх -И2 которые выражают длину и полярный угол отрезка через его проекции на оси координат.
Если на плоскости даны две точки Mi(xi; У\) и М2(х2', у2), то расстояние d между ними определяется формулой
d = V (х2 — Xi)2 + (у2 — yi)2.
44.	Вычислить проекцию отрезка на ось и, если даны его длина d и угол ср наклона к оси: 1) с? = 6, ф = -|-; 2) d = 6, <р = -у-; 3) d = 7, <р = 4’> 4) d = 5, <р = 0) 5) d = 5, ф = зт; 6) d = 4, ср = —тр
45.	Построить на чертеже отрезки, исходящие из начала координат, зная их проекции на координатные оси: ]) Х=3, У = 2; 2) Х = 2, У =-5; 3) X = -5, У = 0; 4) Х=-2, У = 3; 5) X = О, У = 3; 6) X = -5, У == = — 1.
46.	Построить на чертеже отрезки, имеющие началом точку Л4(2; —1), зная их проекции на координатные оси: 1)Х = 4, У=3;2)Х = 2, У = 0;3)1 = -3, У = = 1; 4) X = -4, У = -2; 5) X = О, У = -3; 6) X == 1, У= -3.
47.	Даны точки ЛЛ(1; —2), Л42(2; 1), Л1з(5; 0), /ИД—1; 4) и Л45(0; —3). Найти проекции на координатные оси следующих отрезков: 1) Л11Л12, 2) /И3Л11, 3) МьМ$, 4) М5М3.	_____
48.	Даны проекции отрезка MiM2 на оси координат X = 5, У = —4; зная, что его начало в точке Alt (—2; 3), найти координаты его конца.
13
49.	Даны проек'ции отрезка АВ на оси координат X = 4, Y — —5; зная, что его конец в точке — 3), найти координаты его начала.
50.	‘Построить на чертеже отрезки, исходящие из начала координат, зная длину d и полярный угол 0 каждого из них: 1) d = 5, 0 = у’, 2) d = 3, 0 =-^-л; 3) d = 4, е—4; 4) d=3, 0 = -4я.
О	О
51.	Построить на чертеже отрезки, имеющие началом точку M(2f 3), зная длину и полярный угол каждо-го из них: 1) d = 2, 0 = --^; 2) d=l, 6=-|-, 3) d = 5, 0= —4 (координаты точки М— декартовы).
52.	Вычислить проекции на координатные оси отрезков, зная длину d и полярный угол 0 каждого из них! J)d=12, 0=4я; 2) d = 6, 0 = -#;	3) d = 2,
о	о
0=--^.
53.	Даны проекции отрезков на координатные оси: ]) Х==3, У=-4; 2) X — 12, У = 5; 3) X = -8, У = = 6. Вычислить длину каждого из них.
54.	Даны проекции отрезков, на координатные оси: 1) х = 1, У = ]/3; 2) Х = 3/2, У=-3/2; 3) Х = = — 2VT\ У = 2. Вычислить длину d и полярный угол 9 каждого из них.
55.	Даны точки ЛД(2; —3), М2(1; —4), Л43(—1; —7) и МД—4; 8). Вычислить длину и полярный угол следующих отрезков: 1) ЛДЛ42> 2) MtM3, 3) ММ, 4) ММ
56.	Длина d отрезка равна 5, его проекция на ось абсцисс равна 4. Наити проекцию этого отрезка на ось ординат при условии, что он образует с осью ординат: 1) острый угол, 2) тупой угол.
57.	Длица отрезка MN равна 13; его начало в точке М(3; —2), проекция на ось абсцисс равна —12. Найти координаты конца этого отрезка при условии, что он образует с осью ординат: 1) острый угол, 2) тупой угол.
14
58.	Длина отрезка МАГ равна 17, его конец в точке А7(—7; 3), проекция на ось ординат равна 15. Найти координаты начала этого отрезка при условии, что он образует с осью абсцисс: 1) острый угол, 2) тупой угол.
59.	Зная проекции отрезка на координатные оси X = 1, 7= — ]/3 , найти его проекцию на ось, которая 2
составляет с осью Ох угол 0 = у л.
60.	Даны две точки МД1; —5) и М2(4; —1). Найти проекцию отрезка MtM2 на ось, которая составляет с осью Ох угол 0 — —.
61.	Даны две точки Р(—5; 2) и Q(3; 1). Найти проекцию отрезка PQ на ось, которая составляет с осью Ох угол 0 = arctgy.
62.	Даны две точки Afi(2; —2) и М2(7; —3). Найти проекцию отрезка МЛ на ось, проходящую через точки Л(5; —4), В(—7; 1) и направленную: 1) от Л к В, 2) от В к Л.
63.	Даны точки Л(0; 0), В(3; —4), С(—3; 4), £>(—2; 2) и £(10; —3). Определить расстояние d между точками: 1)Л и 5; 2) В и С; 3) Л и С; 4) С и Z); 5) А и D; 6) D и Е.	\ J
64.	Даны две смежные вершины квадрата Л(3; —7) и В(—1; 4). Вычислить его площадь.
65.	Даны две противоположные вершины квадрата Р(3; 5) и <2(1; —3). Вычислить его площадь.
66.	Вычислить площадь правильного треугольника, две вершины которого суть Л(—3; 2) и В(1; 6).
67.	Даны три вершины Л(3; —7), В (5; —7), С(—2; 5) параллелограмма ABCD, четвертая вершина которого D противоположна В. Определить длину диагоналей этого параллелограмма.
68.	Сторона ромба равна 5]/10, две его противоположные вершины суть точки Р(4; 9) и Q(—2; 1). Вычислить площадь этого ромба.
69.	Сторона ромба равна 5 ]/2 , две его противоположные вершины суть точки Р(3; —4) и Q (1; 2). Вычислить длину высоты этого ромба.
70.	Доказать, что точки Л(3; —5), В (—2; —7) и С(18; 1) лежат на одной прямой.
15
71.	Доказать, что треугольник с вершинами /41(1; 1), А2 (2; 3) и А3(5; —1) прямоугольный.
72.	Доказать, что точки Д(2; 2), В(— 1; 6), С(—5; 3) и Д(—2; —1) являются вершинами квадрата.
73.	Определить, есть ли среди внутренних углов треугольника с вершинами Л4Д1; 1), М2(0; 2) и М3(2; —1) тупой угол.
74.	Доказать, что все внутренние углы треугольника с вершинами М(—1; 3), ЛД1; 2) и Р(0; 4) острые.
75.	Вершины треугольника суть точки 4(5; 0), В(0; 1) и 0(3; 3). Вычислить его внутренние углы.
76.	Вершины треугольника суть точки 4(—УЗ; 1), В (0; 2) и С(—2]/3; 2). Вычислить его внешний угол при вершине Л.
77.	На оси абсцисс найти такую точку М, расстояние которой до точки ЛД2; —3) равнялось бы 5.
78.	На оси ординат найти такую точку М, расстояние которой до точки ЛЦ—8; 13) равнялось бы 17.
79.	Даны две точки Л4(2; 2) и Лг(5; —2); на оси абсцисс найти такую точку Р, чтобы угол MPN был прямым.
80.	Через точку /1(4; 2) проведена окружность, касающаяся обеих координатных осей. Определить ее центр С и радиус R.
81.	Через точку Mi (1; —2) проведена окружность радиуса 5, касающаяся оси Ох. Определить центр С окружности.
82.	Определить координаты точки М2, симметричной точке Л11(1; 2) относительно прямой, проходящей через точки 4(1; 0) и В(— 1; —2).
83.	Даны две противоположные вершины квадрата 4(3; 0) и С(—4; 1). Найти две его другие вершины.
84.	Даны две смежные вершины квадрата 4(2; —1) и В( — 1; 3). Определить две его другие вершины.
85.	Даны вершины треугольника МД—3; 6), M2(9; —10) и М3(—5; 4). Определить центр С и радиус R описанного около этого треугольника круга.
§ 5.	Деление отрезка в данном отношении
Если точка Л4(х;г/) лежит на прямой, проходящей через две данные точки t/i), Л42(Х2’, уг), и дано отношение Л = в котором точка М делит отрезок ЛЦМг, то координаты точки М
16
определяются по формулам
_ х, + Лх2 _ tji + 1у2 х~~ 1 К ’ J 1 + X *
Если точка Л1 является серединой отрезка МгМэ» то ее координаты определяются по формулам
Xi + х2 ___У1+ Уг
х~~	2	’ У 2	’
86.	Даны концы 4(3; —5) и В(— 1; 1) однородного стержня. Определить координаты его центра тяжести.
87.	Центр тяжести однородного стержня находится в точке /VI (1; 4), один из его концов в точке Р(—2; 2). Определить координаты точки Q другого конца этого стержня.
88.	Даны вершины треугольника 4(1; —3), В(3; —5) и С(—5; 7). Определить середины его сторон.
89.	Даны две точки 4(3; —1) и В(2; 1). Определить:
1)	координаты точки Л4, симметричной точке 4 относительно точки В;
2)	координаты точки JV, симметричной точке В относительно точки А.
90.	Точки Л4(2; —1), N (— 1; 4) и Р (—2; 2) являются серединами сторон треугольника. Определить его вершины.
91.	Даны три вершины параллелограмма 4(3; —5), В (5; —3), С(—I; 3) Определить четвертую вершину D, противоположную В.
92.	Даны две смежные вершины параллелограмма 4(—3; 5), В(1; 7) и точка пересечения его диагоналей ЛЦ1; 1). Определить две другие вершины.
93.	Даны три вершины 4(2, 3), В(4; -—1) и С(0; 5) параллелограмма ABCD. Найти его четвертую вершину D.
94.	Даны вершины треугольника 4(1; 4), В(3; —9), С(—5; 2). Определить длину его медианы, проведенной из вершины В.
95.	Отрезок, ограниченный точками 4(1; —3) и В (4; 3), разделен на три равные части. Определить координаты точек деления.
96.	Даны вершины треугольника 4(2; —5), В(1; —2), 0(4; 7). Найти точку пересечения со стороной АС биссектрисы его внутреннего угла при вершине В.
17
97.	Даны вершины треугольника Л(3, —5), В(—3; 3) и С(—1; —2). Определить длину биссектрисы его внутреннего угла при вершине А.
98.	Даны вершины треугольника Л(—1; —1), 5(3; 5), С(—4; 1). Найти точку пересечения с продолжением стороны ВС биссектрисы его внешнего угла при вершине А.
99.	Даны вершины треугольника Л(3; —5), 5(1; —3), С(2; —2). Определить длину биссектрисы его внешнего угла при вершине В.
100.	Даны три точки Л(1; —1), В(3; 3) и С(4; 5), лежащие на одной прямой. Определить отношение X, в котором каждая из них делит отрезок, ограниченный двумя другими.
101.	Определить координаты концов Л и 5 отрезка, который точками 5(2; 2) и Q(l; 5) разделен на три равные части.
102.	Прямая проходит через точки МД—12; —13) и М2(—2; —5). На этой прямой найти точку, абсцисса которой равна 3.
103.	Прямая проходит через точки М(2; —3) и N{—6; 5). На этой прямой найти точку, ордината которой равна —5.
104.	Прямая проходит через точки Л (7; —3) и 5(23; —6). Найти точку пересечения этой прямой с осью абсцисс.
105.	Прямая проходит через точки Л (5; 2) и 5 (—4; —7). Найти точку пересечения этой прямой с осью ординат.
106.	Даны вершины четырехугольника Л(—3; 12), 5(3; —4), С(5; —4) и 5(5; 8). Определить, в каком отношении его диагональ АС делит диагональ BD.
107.	Даны вершины четырехугольника Л (—2; 14), 5(4; —2), С(6; —2) и 5(6; 10). Определить точку пересечения его диагоналей АС и BD.
108.	Даны вершины однородной треугольной пластинки A (xi; ух), 5(х2; уг) и С(х3; г/з). Определить координаты ее центра тяжести.
Указание. Центр тяжести находится в точке пересечения медиан.
109.	Точка М пересечения медиан треугольника лежит на оси абсцисс, две вершины его — точки Л (2; —3) и В(—5; 1), третья вершина С лежит на оси ординат. Определить координаты точек М и С.
18
110.	Даны вершины однородной треугольной пластинки A(Xi‘, 1/1), В(х2; у2) и С(х3; уз). Если соединить середины ее сторон, то образуется новая однородная треугольная пластинка. Доказать, что центры тяжести обеих пластинок совпадают.
Указание. Воспользоваться результатом задачи 108.
111.	Однородная пластинка имеет форму квадрата со стороной, равной 12, в которой сделан квадратный вырез, прямые разреза проходят через центр квадрата, оси
Рис. 4.
Рис. 5.
координат направлены -по Определить центр тяжести
в
котором сделан
ребрам пластинки (рис. 4). этой пластинки.
112.	Однородная пластинка имеет форму прямоугольника со сторонами, равными а и Ь, прямоугольный вырез; прямые разреза проходят через центр, оси координат направлены по ребрам пластинки (рис. 5). Определить центр тяжести этой пластинки.
113.	Однородная пластинка имеет форму квадрата со стороной, равной 2а, от которого отрезан треугольник; прямая разреза соединяет середины двух смежных сторон, оси координат направлены по ребрам пластинки (рис. 6). Определить центр тяжести
пластинки.
114. В следующих точках /4(xi; yi), В(х2; Уъ) н С (Хз', Уз) сосредоточены массы т, п и р. Определить координаты центра тяжести этой системы трех масс.
115. Точки А (4; 2), В(7; —2) и 0(1; 6) являются вершинами треугольника, сделанного из однородной проволоки. Определить центр тяжести этого треугольника.
19
§ 6- Площадь треугольника
Каковы бы ни были три точки X(xi; у\), В(х2; У2), С(х3; y3)t площадь S треугольника АВС дается формулой
± S = — I Xz ~ Х} У2 ~~Ух I “	2 I х3 — х. Уз — У] \
Правая часть этой формулы равна +S в том случае, когда крат* чайший поворот отрезка АВ к отрезку АС положителен, и —5 в том случае, когда такой поворот отрицателен.
116.	Вычислить площадь треугольника, вершинами которого являются точки: 1) А (2; —3), В(3; 2) и С(-2; 5); 2) МД-З; 2), Л12(5; -2) и М3(1; 3); 3) М(3; -4), АД—2; 3) и Р(4; 5).
117.	Вершины треугольника суть точки 4(3; 6), В(—1; 3) и С(2; —1). Вычислить длину его высоты, проведенной из вершины С.
118.	Определить площадь параллелограмма, три вершины которого суть точки А (—2; 3), В (4; —5) и С(-3; 1).
119.	Три вершины параллелограмма суть точки А (3; 7), В (2; —3) и С(— 1, 4). Вычислить длину его высоты, опущенной из вершины В на сторону АС.
120.	Даны последовательные вершины однородной четырехугольной пластинки А (2; 1), В (5; 3), С(—1; 7) и £>(—7; 5). Определить координаты ее центра тяжести.
121.	Даны последовательные вершины однородной пятиугольной пластинки А (2; 3), В (Oj 6), С(— 1; 5), Z)(0; 1) и Е(1; 1). Определить координаты ее центра тя* жести.
122.	Площадь треугольника 5 = 3, две его вершины суть точки А (3; 1) и В(1; —3), а третья вершина С лежит на оси Оу. Определить координаты вершины С.
123.	Площадь треугольника 5 = 4, две его вершины суть точки А (2; 1) и В(3; —2), а третья вершина С лежит на оси Ох. Определить координаты вершины С.
124.	Площадь треугольника 5 = 3, две его вершины суть точки А(3; 1) и В(1; —3), центр тяжести этого треугольника лежит на оси Ох. Определить координаты третьей вершины С.
125.	Площадь параллелограмма 5 = 12 кв. ед.; две его вершины суть точки А(—1; 3) и В (—2; 4). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси абсцисс.
20
126.	Площадь параллелограмма S — 17 кв. ед.; две его вершины суть точки 4(2; 1) и В (5; —3). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси ординат.
§ 7.	Преобразование координат
Преобразование декартовых прямоугольных координат при параллельном сдвиге осей определяется формулами
х = х' 4- а,
У = у' + ъ.
Здесь х, у суть координаты произвольной точки М плоскости относительно старых осей, х', у' — координаты той же точки относительно новых осей, а, Ь — координаты нового начала О' относительно старых осей (говорят также, что а есть величина сдвига в направлении оси абсцисс, b — величина сдвига в направлении оси ординат).
Преобразование декартовых прямоугольных координат при повороте осей на угол а. (который надо понимать, как в тригонометрии) определяется формулами
х = х' cos а — у' sin а, у = х' sin а + у' cos а.
Здесь х, у суть координаты произвольной точки М плоскости относительно старых осей, х', у' — координаты той же точки относительно новых осей.
Формулы
х — х cos а — у' sin а + а, у = х' sin а + у' cos а + b
спредепяют преобразование координат при параллельном сдвиге системы осей на величину а в направлении Ох, на величину b в направлении Оу и последующем повороте осей на угол а. Все указанные формулы соответствуют преобразованию координат при неизменном масштабе. Неизменность масштаба предполагается также в нижеприводимых задачах.
127,	Написать формулы преобразования координат, если начало координат (без изменения направления осей) перенесено в точку: 1) 4(3; 4); 2) В(—2; 1), 3) С(—3; 5).
128.	Начало координат перенесено (без изменения направления осей) в точку О'(3; —4). Координаты точек 4(1; 3), В (—3; 0) и С(—1; 4) определены в новой системе. Вычислить координаты этих же точек в старой системе координат.
21
129.	Даны точки А (2; 1), £(—1; 3) и С(—2; 5)^ Найти их координаты в новой системе, если начало координат перенесено (без изменения направления осей): 1) в точку Д; 2) в точку В; 3) в точку С.
130.	Определить старые координаты начала О' новой системы, если формулы преобразования координат заданы следующими равенствами: 1) х = х' + 3, у = у'Аг 4-5; 2) х = х' — 2, г/ = /Д-1; 3) х = х', у = у'—{\ 4) / = /-5, у~у'-
131.	Написать формулы преобразования координат, если оси координат повернуты на один из следующих углов: 1) 60°; 2) -45°; 3) 90°; 4) -90°; 5) 180°.
132.	Оси координат повернуты на угол а == 60°. Координаты точек Д(2 /3~; —4), В(/3 ; 0) и. С(0; — 2 /3 ) определены в новой системе. Вычислить координаты этих же точек в старой системе координат.
133.	Даны точки М(3; 1), ЛГ(-1; 5) и Р(—3; -1); Найти их координаты в новой системе, если оси координат повернуты на угол: 1) —45°; 2) 90°; 3) —90°; 4) 180°.
134.	Определить угол а, на который повернуты оси, если формулы Преобразования координат заданы еле-
1	Г 3	3*
дующими равенствами: 1)х = у/------“У~~
+	2) х==^~х'4-у/, У = — ^х' + ^~УГ>
135.	Определить координаты точки О' нового начала координат, если точка А (3; —4) лежит на новой оси абсцисс, а точка В (2; 3) лежит на новой оси ординат, причем оси старой и новой систем координат имеют соответственно одинаковые направления.
136.	Написать формулы преобразования координат, если точка Afi(2; —3) лежит на новой оси абсцисс, а точка Л4г(1? —7) лежит на новой оси ординат, причем оси старой и новой систем координат имеют соответственно одинаковые направления.
137.	Две системы координатных осей Ох, Оу и Ох', Оу' имеют общее начало О и преобразуются одна в другую поворотом на некоторый угол. Координаты точки Д (3; —4) определены относительно первой из них. Вывести формулы преобразования координат, зная, что положительное направление оси Ох' определено отрезком О А,
22
138.	Начало координат перенесено в точку О'(~ Ь 2),
5
оси координат повернуты на угол а = arctg-yTp. Координаты точек ЛД(3; 2), М2(2; —3) и М3(13; —13) определены в новой системе. Вычислить координаты этих же точек в старой системе координат.
139.	Даны три точки: А (5; 5), В (2; —1) и С(12; —6). Найти их координаты в новой системе, если начало координат перенесено в точку В, а оси координат повернуты на угол а = arctg-|-.
140.	Определить старые координаты нового начала и угол а, на который повернуты оси, если формулы преобразования координат заданы следующими равенствами: 1) х=— / + 3, у — х'— 2; 2) х — — х'— 1, у — -=-у' + 3;3) x = J^-x' + ^-y' + 5, у = -^-х' +
141.	Даны две точки: Л41(9; —3) и Мг(—6; 5). Начало координат перенесено в точку Mi, а оси координат повернуты так, что положительное направление новой оси абсцисс совпадает с направлением отрезка М1М2. Вывести формулы преобразования координат.
142.	Полярная ось полярной системы координат параллельна оси абсцисс декартовой прямоугольной системы и направлена одинаково с нею. Даны декартовы прямоугольные координаты полюса 0(1; 2) и полярные координаты точек ^7; у), М2(3; 0), М3 (б;
М4 ^2;	йМ5(2; Определить координаты этих
точек в декартовой прямоугольной системе.
143.	Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось направлена по биссектрисе первого координатного угла. Даны полярные координаты точек лЦ5;-£), Л12(3;-|), Л43(1;-|чг), лЦб;-{л) и М5 ^2; —. Определить декартовы прямоугольные ординаты этих точек.
144.	Полярная ось полярной системы координат параллельна оси абсцисс декартовой прямоугольной си
23
стемы и Одинаково с нею направлена. Даны декартовы прямоугольные координаты полюса 0(3; 2) и точек ЛЛ(5; 2), Л^(3; 1), М3(3; 5), М4(3 + ]/Г; 2 -/Г) и М5(3+ /3 ; 3). Определить полярные координаты этих точек.
145.	Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, полярная ось направлена по биссектрисе первого координатного угла. Даны декартовы прямоугольные координаты точек Я1(-12_1),М2(/Г; - /2), М3(1; /з), Л14(- /3; 1) и М5 (2 ]/3 ; -—2). Определить полярные координаты этих точек.
ГЛАВА 2
УРАВНЕНИЕ ЛИНИИ
§ 8.	Функция двух переменных
Если указано правило, согласно которому с каждой точкой М плоскости (или какой-нибудь части плоскости) сопоставляется некоторое число и, то говорят, что на плоскости (или на части плоскости, «задана функция точки»; задание функции символически выражают равенством вида и = f(M). Число и, сопоставляемое с точкой М, называется значением данной функции в точке М Например, если А — фиксированная точка плоскости, М — произвольная точка, то расстояние от А до М есть функция точки М. В данном случае f(M) = AM.
Пусть дана некоторая функция и == f(M) и вместе с тем введена система координат. Тогда произвольная точка М определяется координатами х, у. Соответственно этому и значение данной функции в точке М определяется координатами х, у, или, как еще говорят, u=f(M) есть функция двух переменных х и у. Функция двух переменных х, у обозначается символом f(x, у); если f(Af) = =f(x, У), то формула u = f(x, у) называется выражением данной функции в выбранной системе координат. Так, в предыдущем примере f(M)=<4Af; если ввести декартову прямоугольную систему координат с началом в точке А, то получим выражение этой функции:
и = V Xs + у2.
146.	Даны две точки Р и Q, расстояние между которыми равно а, и функция f(M) = d\ — где d\ — MP и = AfQ. Определить выражение этой функции, если в качестве начала координат принята точка Р, а ось Ох направлена по отрезку PQ.
147.	При условиях задачи 146 определить выражение функции f (А4) (непосредственно и при помощи преобразования координат, используя результат задачи 146), если:
25
___1) начало координат выбрано в середине отрезка PQ, ось Ох направлена по отрезку PQ.
2) начало координат выбрано в точке Р, а ось Ох направлена по отрезку QP.
148.	Даны: квадрат ABCD со стороной а и функция f (/VI) = di + dl + dl + d., где dl = MA, d2 = MB, d3 = — MC и ^4 == MD. Определить выражение этой функции, если за оси координат приняты диагонали квадрата (причем ось Ох направлена по отрезку АС, ось Оу — по отрезку BD).
149.	При условиях задачи 148 определить выражение для [(М) (непосредственно и при помощи преобразования координат, используя результат задачи 148), если начало координат выбрано в точке А, а оси координат направлены по его сторонам (ось Ох — по отрезку АВ, ось Оу — по отрезку AD).
150.	Дана функция f(x, у) = х2 -ф у2 — 6х -}- 8f/. Определить выражение этой функции в новой координатной системе, если начало координат перенесено (без изменения направления осей) в точку О'(3; —4).
151.	Дана функция f(x, у) = х2 — у2 — 16. Определить выражение этой функции в новой координатной системе, если оси координат повернуты на угол —45°.
152.	Дана функция ?(х, у) = х24-//2. Определить выражение этой функции в новой координатной системе, если оси координат повернуты на некоторый угол а.
153.	Найти такую точку, чтобы при переносе в нее начала координат выражение функции f(x,y)—x2 — — 4 г/2 — 6х + $>У + 3 после преобразования не содержало членов первой степени относительно новых переменных.
154.	Найти такую точку, чтобы при переносе в нее начала координат выражение функции f(x,y)=x2 — — 4ху + 4г/2 4- 2х Д- у — 7 не содержало членов первой степени относительно новых переменных.
155.	На какой угол нужно повернуть оси координат, чтобы выражение функции f (х, у) = х2 — 2ху 4- у2 — — 6х + 3 после преобразования не содержало члена с произведением новых переменных?
156.	На какой угол нужно повернуть оси координат, чтобы выражение функции /(х, у) = Зх2 + 2 ]/3 ху А-У2 после Преобразования не содержало члена с произведением новых переменйых?
26
§ 9.	Понятие уравнения линии. Задание линии при помощи уравнения
Равенство вида F(x, у) — о называется уравнением с двумя переменными х, у, если оно справедливо не для всяких пар чисел х у. Говорят, что два числа х = х$, у — Уо удовлетворяют некоторому уравнению вида F(x, t/)=0, если при подстановке этих чисел вместо переменных х и у в уравнение его левая часть обращается в нуль.
'Уравнением данной линии (в назначенной системе координат) называется такое уравнение с двумя переменными, которому удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты каждой точки, не лежащей на ней.
В дальнейшем вместо выражения «дано уравнение линии f(x, у) = 0» мы часто будем говорить короче: дана линия F(x, г/)=0.
Если даны уравнения двух линий F(x, у) — 0 и Ф(х, у} = 0, то совместное решение системы
F(x, #)=0, Ф(х, у) = 0
дает все точки их пересечения. Точнее, каждая пара чисел, являющаяся совместным решением этой системы, определяет одну из точек пересечения,
157.	Даны точки*) ЛД(2; -2), М2(2; 2), М3(2; -1), М4(3; —3), Л15(5; —5), М6(3; —2), Установить, какие из данных точек лежат на линии, определенной уравнением х + # = 0, и какие не лежат на ней. Какая линия определена данным уравнением? (Изобразить ее на чертеже.)
158.	На линии, определенной уравнением х24~//2 = = 25, найти точки, абсциссы которых равны следующим числам: 1) 0, 2) —3, 3) 5, 4) 7; на этой же линии найти точки, ординаты которых равны следующим числам: 5) 3, 6) —5, 7) —8. Какая линия определена данным уравнением? (Изобразить ее на чертеже.)
159.	Установить, какие линии определяются следующими уравнениями (построить их на чертеже): 1) х — #=0; 2) x4-t/ = 0; 3)х-2 = 0; 4)х4-3 = 0; 5) #-5 = 0; 6) #-(-2 = 0; 7) х = 0, 8) # = 0; 9) х2 — ху = 0; 10) ху 4-+ #2 = 0; И) х2 —#2 = 0; 12) х# = 0; 13) #2-9 = 0; 14) х2-8x4- 15 = 0; 15) г/2 4-5# 4- 4 = 0; 16) х #-7х#4-4- Ю# = 0; 17) # = |х|/ 18) х = |#|; 19) #+|х| = 0; 20) х + |#| = 0;	21) # = |х-1|;	22) # = |х4~2|;
23) х24-У2 = 16; 24) (х —2)24~(у—1)2 = 16; 25 (х + 5)2Д-
*) В гех случаях, когда система координат пе зумевается, что она —декартова прямоугольная.
названа, подра-
27
+ [у - I)2 - 9; 26) (х - I)2 + t/2 = 4; 27) x2 + (у + 3)2 = 1; 28) (x - 3)2 + y* = 0; 29) x2 + 2tf = 0; 30) 2x2 + 3г/2 + + 5 = 0; 31) (x - 2)2 + (г/ + 3)2 + 1 = 0.
160.	Даны линии: 1) x + г/ = 0; 2) x — г/ = 0; 3) x2 + + 1/2-36 = 0; 4) x2+г/2 — 2x+г/ = 0; 5) х2+г/2 + 4х--6г/-1=0.
Определить, какие из них проходят через начало координат.
161.	Даны линии: 1) х2 + г/2 = 49; 2) (х — З)2 + + (У 4- 4)2 = 25; 3) (х 4- 6)2 + (у - З)2 = 25; 4) (х + 5)2 + + 0/-4)2 = 9; 5) х2 + г/2 — 12х + 16г/= 0; 6)x2 + z/2-— 2x4-8г/+7 = 0; 7) х2 + у* - 6х + 4г/ + 12 = 0.
Найти точки их пересечения: а) с осью Ох; б) с осью Оу.
162.	Найти точки пересечения двух линий:
1)	х* + г/2 = 8; х — у =0;
2)	х2 + г/2 — 16х + 4^/+ 18 = 0; х+г/ = О;
3)	х2 + г/2 — 2х + 4г/— 3 = 0; х2+г/2 = 25;
4)	х2 + г/2 — 8х + Юг/ + 40 = 0; х2 + г/2 = 4.
163.	В полярной системе координат даны точки М,(1; |),М2(2; 0),Л13(2; i), мД/Г; |)имД1; |я). Установить, какие из этих точек лежат на линии, определенной в полярных координатах уравнением р = = 2 cos 9, и какие не лежат на ней. Какая линия определяется данным уравнением? (Изобразить ее на чертеже.)
164.	На линии, определенной уравнением Р = cos g > найти точки, полярные углы которых равны следующим числам: а) у, б) — у, в) 0, г) Какая линия определена данным уравнением? (Построить ее на чертеже.)
165.	На линии, определенной уравнением р = 	,
найти точки, полярные радиусы_которых равны следующим числам: а) 1, б) 2, в) ]/2 . Какая линия определена данным уравнением? (Построить ее на чертеже.)
166.	Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже): 1) р = 5; 2) 6 = у'> 3) 9 = —-у; 4) р cos 9 = 2; 5) р sin 9 = 1; 6.) р = 6 cos 9; 7) р = 10 sin 9; 8) sin 9 = ^-; 9) sin p = j.	Л
28
167.	Построить на чертеже следующие спирали Архи-меда: 1) р = 20; 2) р = 5в; 3) р = |; 4) р =----|.
168.	Построить на чертеже следующие гиперболические спирали: 1) Р==-§-; 2) р==-|-; 3) р = ^-; 4) р= —
169.	Построить на чертеже следующие логарифмические спирали: 1) р = 2е; 2) Р=(4) •
170.	Определить длины отрезков, на которые рассекает спираль Архимеда р = 39 луч, выходящий из полюса и наклоненный к полярной оси под углом 9=-^-. Сделать чертеж.
171.	На спирали Архимеда р=-^9 взята точка С, полярный радиус которой равен 47. Определить, на сколько частей эта спираль рассекает полярный радиус точки С Сделать чертеж.
172.	На гиперболической спирали р = -|- найти точку Р, полярный радиус которой равен 12. Сделать чертеж.
173.	На логарифмической спирали р = 3е найти точку Q, полярный радиус которой равен 81. Сделать чертеж.
§ 10.	Вывод уравнений заранее данных линий
В задачах предыдущего параграфа линия определялась при помощи данного уравнения. Здесь мы будем иметь задачи противоположного характера: в каждой из них линия определяется чисто геометрически, а уравнение ее требуется найти.
Пример 1. В декартовой прямоугольной системе координат вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух данных точек ДД—а; 0) и Л2(а;0) есть величина постоянная, равная 4а2.
Решение. Обозначим буквой М произвольную точку линии, буквами х и у обозначим координаты этой точки. Так как точка М. может занимать на линии любое положение, то х и у являются переменными величинами; их называют текущими координатами.
Запишем геометрическое свойство линии символически:
(МД i)2 + (Л1Д2)2 = 4а2.	(I)
В этом соотношении при движении тачки М могут меняться длины Л4Д] и МЛ2. Выразим их через текущие координаты точки М:
Л1Д| = У(х +а)2 + у2, Л4Д2 — У(х — а)2 + у2.
29
Подставив полученные выражения в равенство (1), найдем уравпе-ние, связывающее координаты х, у точки М:
(х + а)2 4- У2 + (х — с)2 + У2 — 4а2.	(2)
Это и есть уравнение данной линии.
Действительно, для каждой точки М, лежащей на этой линии, выполняется условие (1) и, следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на линии, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).
Таким образом, задача решена. Однако уравнение (2) можно упростить; раскрывая скобки и приводя подобные члены, получим уравнение данной линии в виде
х2 + у2 — а2.
// г\ \ Теперь легко понять, что данная ли-_	\р \ ния есть окружность с центром в на-
'/	I чале координат и радиусом, равным а.
/\J Пример 2. В полярной системе /	координат вывести уравнение окруж-
ности, которая имеет центр С(р0‘, 0О) °1—J--------------*- и радиус г (рис. 7).
О	4 Решение. Обозначим буквой
М произвольную точку окружности, Рис- '•	буквами р и 0 — ее полярные коор-
динаты. Так как точка М может занимать на окружности любое положение, то р и 0 являются переменными величинами. Как и в случае декартовой системы, их называют текущими координатами.
Все точки окружности отстоят от центра на расстоянии г; запишем это условие символически:
CM=r.	(1)
Выразим СМ через текущие координаты точки М (воспользуемся теоремой косинусов; рис. 7):
СМ = Vp2 + р2 — 2р0р cos (0 — 0О) .
Подставив полученное выражение в равенство (1), найдем уравнение, связывающее координаты р, 0 точки М:
VV + Ро — 2рор cos (0 — 0О) = г.	(2)
Это и есть уравнение данной окружности.
Действительно, для каждой точки М, лежащей на данной окружности, выполняется условие (1) и, следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на данной окружности, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).
Таким образом, задача решена. Можно лишь несколько упростить полученное уравнение и представить его в виде, свободном от радикала;
р2 - 2р0р cos (0 - 60) === г2 - р§.
174.	Вывести уравнение геометрического места точек, одинаково удаленных от координатных осей.
175.	Вывести уравнение геометрического места точек, находящихся на расстоянии а от оси Оу.
176.	Вывести уравнение геометрического места точек, находящихся на расстоянии b от оси Ох.
177.	Из точки Р(6; —8) проведены всевозможные лучи до пересечения с осью абсцисс. Составить уравнение геометрического места их середин.
178.	Из точки С(10; —3) проведены всевозможные лучи до пересечения с осью ординат. Составить уравнение геометрического места их середин.
179.	Вывести уравнение траектории точки, которая в каждый момент движения одинаково удалена от точек: 1) 4(3; 2) и В(2; 3); 2) 4(5; -1) и В(1; -5); 3) 4(5; -2) и В(—-3; -2); 4) 4(3; -1) и В (3; 5).
180.	Составить уравнение геометрического места точек, разность квадратов расстояний которых до точек 4 (—с; 0) и В (о; 0) равна с.
181.	Вывести уравнение окружности, имеющей центр в начале координат и радиус г.
182.	Вывести уравнение окружности, имеющей центр С (а; р) и радиус г.
183.	Дано уравнение окружности х24-г/2 = 25. Составить уравнение геометрического места середин тех хорд этой окружности, длина которых равна 8.
184.	Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек 4(—3; 0) и В(3; 0) равна 50.
185.	Вершины квадрата суть точки 4 (а; а), В( —а; а), О (—а; —а) и D(a\ —а). Составить уравнение геометрического места точек, сумма квадратов расстояний которых до сторон этого квадрата есть величина постоянная, равная 6а2.
186.	Через начало координат проведены всевозможные хорды окружности (х —- 8)2 4- у2 — 64. Составить уравнение геометрического места середин этих хорд.
187.	Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек /?1(—3; 0) и В2(3; 0) есть величина постоянная, равная 10.
188.	Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек ^i(—5; 0) и F2(5; 0) есть величина постоянная, равная 6.
31
30
189.	Вывести уравнение геометрического места точек, для которых расстояние до данной точки F(3; 0) равно расстоянию до данной прямой x-j-3 = 0.
190.	Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек Fi(—-с? 0) и Г2(с; 0) есть величина постоянная, равная 2а. Это геометрическое место называется эллипсом, точки Т7! и F2 — фокусами эллипса.
Доказать, что уравнение эллипса имеет вил у 2	«*2
^2-+б2-а=1> где Ь2 = а2 — с2.
191.	Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек Л(—Ц 0) и /*2(с; 0) есть величина постоянная, равная 2а. Это геометрическое место называется гиперболой, точки Fi и F2 — фокусами гиперболы.
Доказать, что уравнение гиперболы имеет вид у 2
— 1> где Ь2 = с2 — а2.
192.	Вывести уравнение геометрического места точек, для которых расстояние до данной точки о) равно расстоянию до данной прямой х = -— у. Это геометрическое место называется параболой, точка F — фокусом параболы, данная прямая — ее директрисой.
193.	Вывести уравнение геометрического места точек, для которых отношение расстояния до данной точки Г(—4; 0) к расстоянию до данной прямой 4x4-25 = 0
4 равно у.
194.	Вывести уравнение геометрического места точек, для которых отношение расстояния до данной точки F(—5; 0) к расстоянию до данной прямой 5х+ 16 = 0 5 равно
195.	Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до двух данных окружностей (x + 3)24-t/2= 1, (х — З)2 4~z/2 = 81 равны между собой.
196.	Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до двух данных окружностей (х + 10)2 + у2 = 289, (х—10)24-#2=1 равны между собой.
32
197-	Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до данной окружности (х — 5)2 + */2 = 9 и до данной прямой х-}-2 = 0 равны между собой.
198.	Прямая перпендикулярна полярной оси и отсекает на ней отрезок, равный 3. Составить уравнение этой прямой в полярных координатах.
199.	Луч выходит из полюса и наклонен к полярной оси под углом -у. Составить уравнение этого луча в полярных координатах.
200.	Прямая проходит через полюс и наклонена к полярной оси под углом 45е. Составить уравнение этой прямой в полярных координатах.
201.	В полярных координатах составить уравнение геометрического места точек, расстояния которых от полярной оси равны 5.
202.	Окружность радиуса /? = 5 проходит через полюс, ее центр лежит на полярной оси. Составить уравнение этой окружности в полярной системе координат.
203.	Окружность радиуса R — 3 касается полярной оси в полюсе. Составить уравнение этой окружности в полярной системе координат.
(1)
ме-
(1)
§ 11.	Параметрические уравнения линии
Обозначим буквами х и у координаты некоторой точки М; рассмотрим две функции аргумента t:	t
При изменении t величины х и у будут, вообще говоря, няться, следовательно, точка М. будет перемещаться. Равенства называются параметрическими уравнениями линии, которая является траекторией точки М; аргумент i носит название параметра. Если из равенств (I) можно исключить параметр /, то получим уравнение траектории точки М в виде
F (х, ?/) =0.
204.	Стержень АВ скользит своими концами А и В по координат-стержень ВМ = Ь.
ным осям. Точка М делит на две части AM = а и ____________
Вывести параметрические уравнения М, приняв в качестве параметра (рис. 8). Исключить затем параметр t траектории точки М в виде F(x,y) = 0.
параметра
траектории точки угол t =
и найти уравнение
2 Д. В. Клетеник
33
205.	Траекторией точки М является эллипс, уравнение которого ~ +	(см. задачу 190). Вывести
параметрические уравнения траектории точки М, прини-мая в качестве параметра t угол наклона отрезка ОМ к оси Ох.
206.	Траекторией точки М является гипербола, уравнение которой	(см< задачу 191). Вывести
параметрические уравнения траектории точки М, прини-мая в качестве параметра t угол наклона отрезка ОМ к оси Ох.
207.	Траекторией точки М является парабола, уравнение которой у2 = 2рх (см. задачу 192). Вывести параметрические уравнения траектории точки Л1, принимая в качестве параметра t\
1)	ординату точки Л1;
2)	угол наклона отрезка ОЛ1 к оси Ох;
3)	угол наклона отрезка FM к оси Ох, где точка F — фокус параболы.
208.	Даны полярные уравнения следующих линий:
1)	P = 27?cos9; 2) р = 2Яsin0; 3) p = 2p-^g-.
Составить параметрические уравнения этих линий в декартовых прямоугольных координатах, совмещая положительную полуось абсцисс с полярной осью и выбирая в качестве параметра полярный угол.
209.	Даны параметрические уравнения линий:
1) x = t2-2t+ 1,
2) x = acos/, z/ = asin/;
5) х = 27? cos21,
z/ = 7?sin27;
7) x==2pctg2/, # = 2pctg t;
3) x = asecf,
6) x = 7?sin2f,
у = 27? sin21;
исключив параметр /, найти уравнения этих линий в виде
Г(х, £/) = 0.
ГЛ AB A 3
ЛИНИИ ПЕРВОГО ПОРЯДКА
§ 12. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми.
Условие параллельности и перпендикулярности двух прямых
В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.
Уравнение вида
Лх- + £г/ + С = 0	(1)
называется общим уравнением прямой.
Угол а, определяемый, как показано на рис, 9, называется углом наклона прямой к оси Ох. Тангенс угла йаклонгГ прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:	,
k — tg а.	»
Уравнение у — kx + b называется уравнением прямой с угловым
коэффициентом; k — угловой коэффициент, b — величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.
Если прямая задана общим уравнением
Ах + By + С ~ О,
то ее угловой по формуле
коэффициент определяется
Уравнение y — y0 = k(x — х0) является уравнением прямой, которая проходит через точку Л10(х0; уо) и имеет угловой коэффициент k.
Если прямая проходит через точки yi) и -Мгрга; у2), то ее угловой коэффициент определяется по формуле
h . У2—У1 Х2 — Х1 ‘
а*
35
X — У; _ у —У1
*2 — Xi у2 — У!
является уравнением прямой, проходящей через две точки Afifxf.yJ и М2(х2,у2).
Если известны угловые коэффициенты двух прямых k\ и k2, то один из углов <р между этими прямыми определяется по формуле
+_ __ k2 — kj
\+k.k2'
Признаком параллельности двух прямых является равенство их угловых коэффициентов
ki = k2.
Признаком перпендикулярности двух прямых является соотношение
k\k2 = — 1 или k2 —---
«1
Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.
210.	Определить, какие из точек Aft(3; 1), М2(2; 3), Af3(6; 3), Mi(—3; —3), Л45(3; —1), Л16(—2; 1) лежат на прямой 2х— Зу— 3 = 0 и какие не лежат на ней.
211.	Точки Pt, Р2, Рз, Pi и Р5 расположены на прямой Зх — 2у — 6 = 0; их абсциссы соответственно равны числам; 4, 0, 2, —2 и —6. Определить ординаты этих точек.
212.	Точки Qi, Q2, Qs, Qi и Qs расположены на прямой х — Зг/4-2 = 0; их ординаты соответственно равны числам: 1, 0, 2, —1, 3. Определить абсциссы этих точек.
213.	Определить точки пересечения прямой 2х — Зу— — 12 = 0 с координатными осями и построить эту прямую на чертеже.
214.	Найти точку пересечения двух прямых Зх— 4у — — 29 = 0, 2х + Зу + 19 = 0.
215.	Стороны АВ, ВС и АС треугольника АВС даны соответственно уравнениями *) 4х 4- Зу — 5 = 0, х — Зу + 4- Ю = 0, х —2 = 0. Определить координаты его вершин.
216.	Даны уравнения двух сторон параллелограмма 8х 4- Зу + 1 = 0, 2х + у — 1 = 0 и уравнение одной из
*) Здесь и везде в дальнейшем под уравнением сторон мы будем понимать уравнения прямых, йа которых лежат стороны.
36
его диагоналей Зх 4-2у3 = 0. Определить координаты вершин этого параллелограмма. •
217.	Стороны треугольника лежат на прямых х 4-
5^ _ 7 = 0, Зх — 2г/ — 4 = 0, 7х 4- у 4- 19 = 0. Вычислить его площадь S.
218.	Площадь треугольника S — 8 кв. ед.; две его вершины суть точки А(1; —2) и В(2;3), а третья вершина С лежит на прямой 2х4~г/ — 2 = 0. Определить координаты вершины С.
219.	Площадь треугольника S = 1,5 кв. ед., две его вершины суть точки /1(2; —3) и В(3; —2); центр тяжести этого треугольника лежит на прямой Зх — у — 8=0. Определить координаты третьей вершины С.
220.	Составить уравнение прямой и построить прямую на чертеже, зная ее угловой коэффициент k и отрезок Ь, отсекаемый ею на оси Оу.
1) £ = -(-. 6=3; 2) 6 = 3, 6 = 0; 3) 6 = 0, b=- 2;
О
4) 6 = -|, b = 3\ 5) k = — 2, 6 = -5; 1	2
6) A = -|, /> = {
221. Определить угловой коэффициент k и отрезок/?, отсекаемый на оси Оу, для каждой из прямых:
1) 5х —г/4~3 = 0;	2) 2х4-3г/ —6 = 0;
3) 5x + 3z/ + 2 = 0; 4) 3x4-2г/= 0; 5) у — 3 = 0.
222.	Дана прямая 5х 4- Зу — 3 = 0. Определить угловой коэффициент k прямой:
1)	параллельной данной прямой;
2)	перпендикулярной к данной прямой.
223.	Дана прямая 2х 4-Зг/4-4 = 0. Составить уравнение прямой, проходящей через точку Мо(2; 1):
1)	параллельно данной прямой;
2)	перпендикулярно к данной прямой;
224.	Даны уравнения двух сторон прямоугольника 2х — 3//4-5==0, Зх-f-2г/ — 7 = 0 и одна из его вершин А (2; —3). Составить уравнения двух других сторон этого прямоугольника.
225.	Даны уравнения двух сторон прямоугольника х — 2г/= 0, х —2г/4-15 = 0 и уравнение одной из его диагоналей 7x4-// —15 = 0. Найти вершины прямоугольника.
226.	Найти проекцию точки Р(—6; 4) на прямую 4х — 5г/ -j- 3 = 0.
37
227.	Найти точку Q, симметричную точке Р(—5; 13) относительно прямой 2х — Зу — 3 = 0,
228.	В каждом из следующих случаев составить уравнение прямой, параллельной двум данным прямым и проходящей посередине между ними:
1) Зх-2//-1=0,	2) 5х4-г/4-3 = 0,
Зх-2у- 13 = 0;	5х+ // — 17 = 0;
3) 2х-\- Зу-6 = 0, 4x4-6//+17 = 0;
4) 5х + 7//+15 = 0,	5) Зх—15//—1=0,
5х + 7// + 3 = 0; х — Зу — 2 = 0.
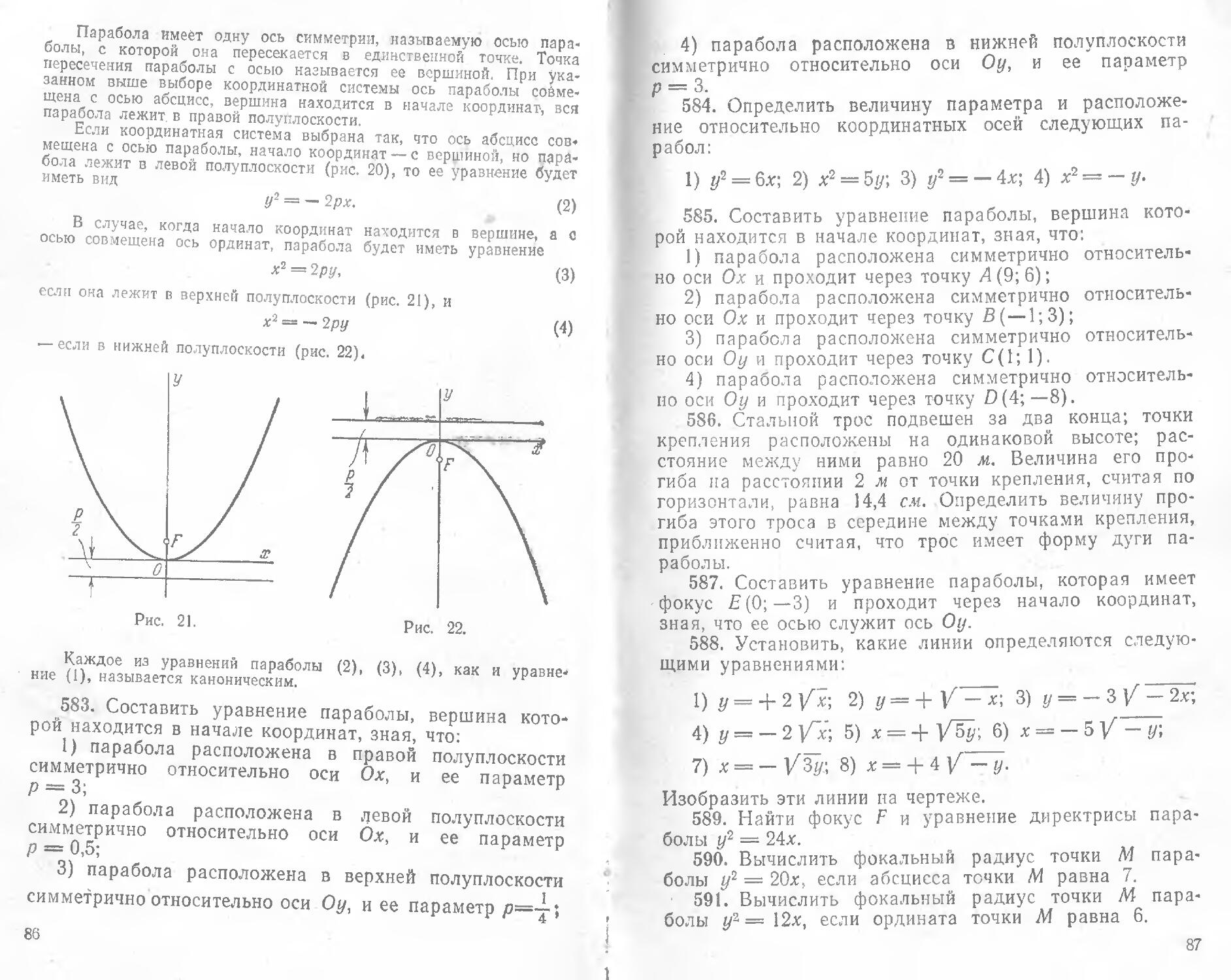
229.	Вычислить угловой коэффициент k прямой, проходящей через две данные точки: а) Л41(2;—5), Л1о(3;2); б) Р(—3; 1), Q (7; 8); в) Д(5; -3), В(-1; 6).
230.	Составить уравнения прямых, проходящих через вершины треугольника Л (5; —4), В(—1; 3), С(—3; —2) параллельно противоположным сторонам.
231.	Даны середины сторон треугольника: (2; 1), Л42(5? 3) и Л43(3; —4). Составить уравнение его сторон.
232.	Даны две точки: Р(2; 3) и Q(—1; 0). Составить уравнение прямой, проходящей через точку Q перпендикулярно к отрезку PQ.
233.	Составить уравнение прямой, если точка Р(2;3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.
234.	Даны вершины треугольника М((2; 1); Л42(—1; —1) и АТ3(3; 2). Составить уравнения его высоту
235.	Стороны треугольника даны уравнениями 4х — •— у — 7 = 0, х-\-Зу — 31=0, х-\-Зу — 7 = 0. Определить точку пересечения его высот.
236.	Даны вершины треугольника А (1; —1), В (—2; 1) и С(3; 5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану, проведенную из верщины В.
237.	Даны вершины треугольника А (2; —2), В (3; —5) и С(5; 7). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине Д.
238.	Составить уравнения сторон и медиан треугольника с вершинами Д(3: 2), В (5; —2), С (1; 0) *
38
239.	Через точки МД—1; 2) и Л12 (2; 3) проведена прямая. Определить точки пересечения этой прямой с осями координат.
240.	Доказать, что условие, при котором три точки Mi(xr, yi), М2(х2; Уъ) и Л13(х3; у.з) лежат на одной прямой, может быть записано в следующем виде:
Х1	У\	1.	
Х2	У2	1	= 0.
Хз	Уз	1	
241.	Доказать, что уравнение прямой, проходящей через две данные точки Mi(xi; у\) и М2(х2; у2), может быть записано в следующем виде:
х у
*1 У[
х2 У2
1
1
1
= 0.
242.	Даны • последовательные вершины выпуклого четырехугольника 4(—3; 1),	В(3; 9), С (7; 6) и
£)(—2; —6). Определить точку пересечения его диагоналей.
243.	Даны две смежные вершины 4(—3; —1) и В (2; 2) параллелограмма ABCD и точка Q(3; 0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма.
244.	Даны уравнения двух сторон прямоугольника 5х + 2у — 7 = 0, 5%4-2г/ — 36 = 0 и уравнение его диагонали Зх-f- 7у—10 = 0. Составить уравнения остальных сторон и второй диагонали этого прямоугольника.
245.	Даны вершины треугольника 4(1; —2), В (5; 4) и С(—2; 0). Составить уравнения биссектрис его внутреннего и внешнего углов при вершине А.
246.	Составить уравнение прямой, проходящей через точку Р(3; 5) на одинаковых расстояниях от точек А(~7; 3) и В(11; —15).
247.	Найти проекцию точки Р(—8; 12) на прямую, проходящую через точки 4(2; —3) и В(—5; 1).
248.	Найти точку Mi, симметричную точке М2(8;—9) относительно прямой, проходящей через точки 4(3;—4) и5(-1;-2).
39
249.	На оси абсцисс найти такую точку Р, чтобы сумма ее расстояний до точек Л4(1; 2) и /V(3; 4) была наименьшей.
250.	На оси ординат найти такую точку Р, чтобы, разность расстояний ее до точек М(—3; 2) и .V(2; 5) была наибольшей.
251.	На прямой 2х— у — 5 = 0 найти такую точку Р, сумма расстояний которой до точек Л(—7; 1), В(—5; 5) была бы наименьшей. -
252.	На прямой Зх— у—1=0 найти такую точку Р, разность расстояний которой до точек Д(4; 1) и В(0; 4) была бы наибольшей.
253.	Определить угол ср между двумя прямыми:
1) 5х —г/ + 7 = 0, 2) Зх — 2г/+ 7 = 0, 3) х — 2у — 4 = 0, 4) Зх + 2у- 1 =0,
Зх + 2у — 0;
2х + Зу — 3 = 0; 2х-4г/ + 3 = 0; 5х — 2у + 3 = 0.
254.	Дана прямая 2х + Зу + 4 = 0. Составить уравнение прямой, проходящей через точку ЛТ0(2; 1) под углом 45° к данной прямой.
255.	Точка А(—4; 5) является вершиной квадрата, диагональ которого лежит на прямой 7х — у + 8 = 0. Составить уравнения сторон и второй диагонали этого квадрата.
256.	Даны две противоположные вершины квадрата Д(—1; 3) и С(6; 2). Составить уравнения его сторон.
257.	Точка £(1; —1) является центром квадрата, одна из сторон которого лежит на прямой х — 2у +, + 12 = 0. Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.
258.	Из точки Мо(—2; 3) под углом а к оси Ох направлен луч света. Известно, что tg а = 3. Дойдя до оси Ох, луч от нее отразился. Составить уравнения прямых, на которых лежат лучи падающий и отраженный.
259.	Луч света направлен по прямой х — 2г/ + 5 = 0. Дойдя до прямой Зх — 2г/+ 7 = 0, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
260.	Даны уравнения сторон треугольника Зх + 4г/ — — 1=0, х —7г/—17 = 0, 7х + г/ + 31=0. Доказать, что этот треугольник равнобедренный. Решить задачу при помощи сравнения углов треугольника,
40
261.	Доказать, что уравнение прямой, проходящей через точку Afj(Xi; уА параллельно прямой Ах А-By+ + С — 0, может быть записано в виде А(х — xt) + Аг В (У ~ О-
262.	Составить уравнение прямой, проходящей через точку Л11(2; —3) параллельно прямой: 1) Зх— 7у + 3 = = 0; 2) х + 9у — 11 = 0; 3) 1бх —24у —7 = 0; 4) 2х + + 3 = 0; 5) Зу— 1 =0.
Решись задачу, не вычисляя угловых коэффициентов данных прямых.
Указание. Воспользоваться результатом предыдущей задачи.
263.	Доказать, что условие перпендикулярности прямых AiX + Вху + Ci = 0, Л2х + В2у + С2 = 0 может быть записано в следующем виде: Д1Д2 + В]В2 = 0.
264.	Установить, какие из следующих пар прямых перпендикулярны:
1) Зх —у + 5 = 0,	2) Зх —4у + 1 =0,
х + Зу — 1=0; 4х — 3у 4-7 = 0;
3) 6х— 15г/ + 7 = 0,	4) 9х — 12г/+ 5 = 0,
10х + 4у—3 = 0;	8x4- бу— 13 = 0;
5) 7х — 2у + 1 = 0,	6) 5х - 7у + 3 = 0,
’ 4х + бу +17 = 0; Зх + 2у~5 = 0.
Решить задачу, не вычисляя угловых коэффициентов данных прямых.
Указание. Воспользоваться условием перпендикулярности прямых, выведенных в задаче 263.
265. Доказать, что формула для определения угла (р между прямыми А}х + В}у + (4=0, Д2х + В2у + С2= 0 может быть записана в следующем виде:
266. Определить угол <р, образованный двумя прямыми:
1)	Зх-у + 5 = 0,
2х 4- у — 7 = 0;
2)	х V2-J/V"3-5=0,
(3 +_/2)х + (]/6 - VS)y + 7 = 0;
3)	x/3 + jj/2-2 = 0, х/б—3# + 3 = 0.
41
Решить задачу, не вычисляя угловых коэффициентов данных прямых.
Указание. Воспользоваться формулой для определения угла между двумя прямыми, полученной в задаче 265.
267, Даны две вершины треугольника A4i(—10; 2) и Afs(6; 4); его высоты пересекаются в точке Л/(5; 2). Определить координаты третьей вершины
268.	Даны две вершины 4(3; — 1) и В (5; 7) треугольника АВС и точка N(4; —1) пересечения его высот. Составить уравнения сторон этого треугольника.
269.	В треугольнике АВС даны: уравнение стороны АВ 5х— 3# + 2 = 0, уравнения высот AM 4х— ЗуЦ-'. '4-1=0 и BN 7х-\~2у— 22 =з 0. Составить уравнения двух других сторон и третьей высоты этого треугольника.
270.	Составить уравнения сторон треугольника АВС, если даны одна из его вершин 4(1; 3) и уравнения двух медиан х — 2у 4- 1 = 0 и у — 1 = 0.
271.	Составить уравнения сторон треугольника, если даны одна из его вершин В(—4; —5) и уравнения двух высот 5х + 3z/ — 4 = 0 и Зх 4*. 8(/ + 13 = 0.
272.	Составить уравнения сторон треугольника, зная одну из его вершин 4(4; —1) и уравнения двух биссектрис х— 1 s= 0 и Х‘—у—1=0.
273.	Составить уравнения сторон треугольника, зная одну его вершину 5(2; 6), а также уравнения высоты х~ 7//+ДЗ = 0 и биссектрисы 7x4-. ^4: 5 = 0, проведенных и? одной вершины.
274.	Составить уравнения сторон треугольника, зная одну его вершину В (2; —1), а также уравнения высоты Зх — 4у 27 = 0 и биссектрисы х^2у— 5 = 0, проведенных из различных вершин.
275.	Составить уравнения сторон треугольника, зная одну его вершину С(4; —1), а также уравнения высоты 2х — Зу 4- 12 = 0 и медианы 2xL+3z/ = 0, проведенных из одной вершины.
276.	Составить уравнения сторон треугольника, зная одну его вершину В (2: —7), а также уравнения высоты 3x-j-*/+11 = 0 и медианы х J-2yJ-7 = 0, проведенных из различных вершин.
277.	Составить уравнения сторон треугольника, зная одну его вершину С(4; 3), а также уравнения биссек-42
трисы х-\-2у — 5 = 0 и медианы 4x4-13//—10 = 0, проведенных из одной вершины.
278.	Составить уравнения сторон треугольника, зная одну его вершину Л (3; —1), а также уравнения биссектрисы х — 4// + Ю = 0 и медианы 6x4-10// — 59 = 0, проведенных из различных вершин.
279.	Составить уравнение прямой, которая проходит через начало координат и вместе с прямыми х— у 4*-4-12 = 0, 2x4-//4'9 = 0 образует треугольник с площадью, равной 1,5 кв. ед.
280.	Среди прямых, проходящих через точку Р(3; 0), найти такую, отрезок которой, заключенный между прямыми 2х — у — 2 = 0, х-|-г/4-3 = 0, делится в точке Р пополам.
281.	Через точку Р(—3; —1) проведены всевозможные прямые. Доказать, что отрезок каждой из них, заключенный между прямыми х— 2у— 3 = 0, х — 2//4-[4-5 = 0, делится в точке Р пополам.
282.	Через точку Р(0; 1) проведены всевозможные прямые. Доказать, что среди них нет прямой, отрезок которой, заключенный между прямыми х — 2у— 3 = 0, х — 2у 4-17 = 0, делился бы в точке Р пополам.
283.	Составить уравнение прямой, проходящей через начало координат, зная, что длина ее отрезка, заключенного между прямыми 2х — г/-|-5 = 0, 2х — у 4- 10 = и= 0, равна /10.
284.	Составить уравнение прямой, проходящей через точку С(—5; 4), зная что длина ее отрезка, заключенного между прямыми х 2у 4- 1 = 0, х4-2//—1=0, равна 5.
§ 13. Неполные уравнения прямой. Совместное исследование уравнений двух и трех прямых. Уравнение прямой «в отрезках»
Если в общем уравнении прямой
Лх+В// + С = 0	(I)
один или два из трех коэффициентов (считая и свободный член) обращаются в нуль, то уравнение называется неполным. Возможны следующие случаи:
1)	С = 0; уравнение имеет вид Ах + By = 0 и определяет прямую, проходящую через начало координат.
2)	В = 0 (Д 0); уравнение имеет вид Дх-|- С = 0 и определяет прямую, перпендикулярную к оси Ох. Это уравнение может
43
быть записано в виде х = а, где а — — -д- является величиной отрезка, который отсекает прямая на оси Ох, считая от начала координат.
3)	В = О, С — О (Л ф 0); уравнение может быть записано в виде х — 0 и определяет ось ординат.
4)	А — 0 (В 0); уравнение имеет вид By 4- С = 0 и определяет прямую, перпендикулярную к оси Оу. Это уравнение может
С
быть записано в виде у — Ь, где b = —g- является величиной отрезка, который отсекает прямая на оси Оу, считая от начала координат.
5)	А — 0, С = 0 (В^=0); уравнение может быть записано в виде у = 0 и определяет ось абсцисс.
Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к виду
f+f-1-	<2>
с с
где а— —— и b = —— суть величины отрезков, которые отсекает прямая на координатных осях.
Уравнение (2) называется уравнением прямой «в отрезках».
Если две прямые даны уравнениями
А\Х + В\у С! — 0 и А2х 4* В2у 4- С2 = 0,
то могут представиться три случая:
. Aj , В\
а)	-г- Ф	— прямые имеют одну общую точку;
А 2	&2
Л,	В]	С\
б)	-А- =	--прямые параллельны;
Л2	В2	с 2
.	А\	В-[	С\
в)	~ = -^- = —----прямые сливаются, т. е. оба уравнения
Л2	с2 определяют одну и ту же прямую.
285.	Определить, при каком значении а прямая
(а + 2) х 4- (а2 — 9) у + За2 — 8а + 5 == 0
1)	параллельна оси абсцисс;
2)	параллельна оси ординат;
3)	проходит через начало координат. .
В каждом случае написать уравнение прямой.
286.	Определить, при каких значениях тип прямая (т + 2п — 3) х + (2m — ft+l)#-)-6m + 9 = 0
параллельна оси абсцисс и отсекает на оси ординат отрезок, равный —3 (считая от начала координат). Написать уравнение этой прямой.
44
287.	Определить, при каких значениях тип прямая (2т — п + 5) х + (т + 3/г — 2) у 4- 2т 4- 7п 4- 19 = 0
параллельна оси ординат и отсекает на оси абсцисс отрезок, равный +5 (считая от начала координат). Написать уравнение этой прямой.
288.	Доказать, что в следующих случаях две данные прямые пересекаются, и найти точку их пересечения!
1) х + 5у - 35 = 0, 2) 14х —90 —24 = 0, 3) 12x4- 150-8 = 0, 4) 8х — 330— 19 = 0,
5) Зх +5 = 0,
Зх 4~ 20 — 27 = 0; 7х — 2у — 17 = 0; 16х 4-90 — 7 — 0; 12x4-550- 19 = 0; 0-2 = 0.
289.	Доказать, что в следующих случаях две данные прямые параллельны:
1)	3x4-50-4 = 0,	6x4- 1004-7 = 0;
2)	2х — 40 4- 3 = 0, х — 20 = 0;
3)	2х - 1 = 0,	х 4- 3 = 0;
4)	0 4-3 = 0,	50 — 7 = 0.
,290. Доказать, что в следующих случаях две данные прямые совпадают:
1) Зх 4- 50 — 4 = 0, 6х 4- 100 - 8 = 0;
2)х-у/2=0,	х/2 —2</ = 0;
3)х/3 —1=0,	Зх— /3=0.
291. Определить, при каких значениях а и b две прямые
ах — 2у — 1=0, 6х — 40 — 6=0
1) имеют одну общую точку; 2) параллельны; 3) совпадают.
292. Определить/ при каких значениях тип две прямые
тх 4- 80 4- ft = 0, . 2х 4- W — 1 = 0
1) параллельны; 2) совпадают; 3) перпендикулярны, 293. Определить, при каком значении т две прямые (т — 1) х 4- ту — 5 = 0,	тх 4-(2m — 1)у 4-7 »= 0
пересекаются в точке, лежащей на оси абсцисс,
43
294. Определить, при каком значении т две прямые тх 4- (2m + 3)# + т + 6 = 0,
(2m + 1) х + (m — 1)# + т — 2 = 0 пересекаются в точке, лежащей на оси ординат.
295. Установить, пересекаются ли в одной точке три прямые в следующих случаях:
1)	2х + Зу— 1 =0, 4х — Ъу + 5 = 0, 3/ —# + 2 = 0;
2)	Зх — # + 3 = 0, 5х + 3# — 7 = 0, х — 2у — 4 = 0;
3)	2х — #+1=0, х + 2# —17 = 0, х + 2# —3 = 0.
296. Доказать, что если три прямые Ах+А^/А [+ Ci = 0, А2Х + В2у + С2 = 0, A3X + B3# + Сз= 0 пересекаются в одной точке, то
А	Bi	Cl	
А	в2	с2	= 0.
А	Вз	Сз	
297. Доказать, что если
А а2 А
Bi с1
В2 С2
В% С3
то три прямые /liX+ В1#+Сг = 0, А2х + В2# + С2 = 0, АзХ + В3# 4* Оз = 0 пересекаются в одной точке или параллельны,
V 298. Определит^, при каком значении а три прямые 2х — # + 3far0, Л'+# + 3 = 0, ах + #— 13 = 0 будут пересекаться в одной точке.
299.	Даны прямые: 1) 2х+~3# —6 = 0; 2) 4х —3#+ [+24 = 0; 3) 2х+3# — 9 = 0; 4) Зх —5# —2 = 0? 5) 5х+Д#—1 =0. Составить для них уравнения «в отрезках» и построить эти прямые на чертеже.
300.	Вычислить рлощадь треугольника, отсекаемого прямой Зх —4#— 12 = 0 от координатного угла.
301.	Составить уравнение прямой, которая проходит через точку М[ (3; —7) и отсекает на координатных осях отличные от нуля отрезки одинаковой величины (считая каждый отрезок направленным от начала координат).
302.	Составить уравнение прямой, которая проходит через точку Р(2; 3) и отсекает на координатных осях 46
отрезки равной длины, считая каждый отрезок от начала координат.
303.	Составить уравнение прямой, которая проходит через точку С(1; 1) и отсекает от координатного угла треугольник с площадью, равной 2 кв ед.
V 304. Составить уравнение прямой, которая проходит через точку В (5; —5) и отсекает от координатного угла треугольник с площадью, равной 50 кв. ед.
305.	Составить уравнение прямой, -которая проходит через точку Р(8; 6) и отсекает от координатного угла треугольник с площадью, равной 12 кв. ед.
306.	Составить уравнение прямой, которая проходит через точку Р(12; 6) и отсекает от координатного угла треугольник с площадью, равной 150 кв. ед.
307.	Через точку Л4(4; 3) проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3 кв. ед. Определить точки пересечения этой прямой с осями координат.
308.	Через точку Mi (хг; f/i), где Xit/i >0, проведена прямая
а о отсекающая от координатного угла треугольник, площадь которого равна S. Определить, при каком соотношении между величинами Xi, у\ и S отрезки а и b будут иметь одинаковые знаки.
§ 14. Нормальное уравнение прямой. Задача определения расстояния от точки до прямой
Пусть на плоскости хОу дана прямая. Проведем через начало координат перпендикуляр к данной прямой и назовем его нормалью, Обозначим через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р.
Если а есть полярный угол нормали, р — длина отрезка ОР (рис. 10), то уравнение данной прямой может быть записано в виде
х • cos а + у • sin а — р = 0;
I
уравнение этого вида называется нормальным.
Пусть дана какая-нибудь прямая и произвольная точка Л1*, обозначим через d расстояние точки М* от данной прямой. Отклонением 6 точки М* от прямой называется число 4-а, если данная точка и начало координат лежат по разные стороны от данной прямой, и — d, если данная точка и начало координат расположены
47
по одну сторону от данной прямой. (Для точек, лежащих на самой прямой, б = 0.) Если даны координаты х*, у* точки М* и нормальное уравнение прямой х cos а + у sin а — р = 0, то отклонение б точки М* от этой прямой может быть вычислено по формуле
б = х* cos а + у* sin а — р.
Таким образом, чтобы найти отклонение какой-нибудь точки М* от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих коорди-
V К	нат подставить координаты точки М*.
N. р /	Полученное число будет равно искомо-
X/	му отклонению.
Чтобы найти расстояние d от точки
P'yf	до прямой, достаточно вычислить от-
// Л. клонение и взять его модуль:
.	\	d = |d|.
Если дано общее уравнение прямой р	Ах + By + С = 0, то, чтобы привести
1 ис-	его к нормальному виду, нужно все чле-
ны этого уравнения умножить на нормирующий множитель ц, определяемый формулой
1 ,	/д1 2 + в2
Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.
309. Определить, какие из следующих уравнений прямых являются нормальными:
1) |*-|г,-3 = 0;	2)|х-{«/-1=0!
3) 4*-4г' + 2 = °!	4) -4^ + -г|</-2 = 0;
5) — х 4- 2 = 0;	6) х — 2 = 0;
7) у + 2 = 0;	8) — # — 2 = 0.
310. Привести общее уравнение прямой к нормальному виду в каждом из следующих случаев:
1) 4х —3# — 10 = 0;
3) 12х —5#+13 = 0;
5) 2х — у — У5 = 0,
2) ±х-|г/+10 = 0!
4)	х + 2 = 0;
48
311.	Даны уравнения прямых:
1)	х - 2 = 0;	2) х 4- 2 = 0;	3) у - 3 = 0;
4)	У + 3 = О; 5) х/3+у-6 = 0; 6) х — г/+ 2 == 0;
7)	x + j/]/3 + 2 = 0;
8)	xcosp — ysinp — q =0,	q>Q; (J —острый угол;
9)	x cos pH- у sin 0 4-У = 0, q>Q; p — острый угол.
Определить полярный угол нормали а и отрезок р для каждой из данных прямых; по полученным значениям параметров аир построить эти прямые на чертеже (в последних двух случаях построение прямой выполнить, считая р = 30° и q = 2).
312.	Вычислить величину отклонения 6 и расстояние d точки от прямой в каждом из следующих случаев: 1) /1(2; —1), 4х 4- Зу 4-10 = 0; 2) В (0; — 3), 5х—12у —23 = 0; 3) Р(—2; 3), Зх —4у —2 = 0; 4) Q(l; —2), х —2у —5 = 0.
313.	Установить, лежат ли точка М (1; —3) и начало координат по одну или по разные стороны каждой из следующих прямых: 1) 2х — у 4- 5 = 0; 2) х — Зу — 5 = = 0 3) ЗхН-2у—1=0; 4) х —Зу4~2 = 0; 5) 10x4-Н-24у4-15 = 0.
314.	Точка /1(2; —5) является вершиной квадрата, одна из сторон которого лежит на прямой х — 2у — 7 = = 0. Вычислить площадь этого квадрата.
315.	Даны уравнения двух сторон прямоугольника Зх — 2у — 5 = 0, 2х4-Зу4-7 = 0 и одна из его вершин Л (—2; 1). Вычислить площадь этого прямоугольника.
316.	Доказать, что прямая 2х4-у-|-3 = 0 пересекает отрезок, ограниченный точками Л(—5; 1) иВ(3;7).
317.	Доказать, что прямая 2х — Зу 4- 6 = 0 не пересекает отрезка, ограниченного точками Afi(—2; —3) и Ж2(1; -2).
318.	Последовательные вершины четырехугольника суть точки А (—3; 5), В(—1; —4), С(7; —1) и /9(2; 9). Установить, является ли этот четырехугольник выпуклым.
319.	Последовательные вершины четырехугольника суть точки А(—1; 6), В(1; —3), С(4; 10) и £>(9; 0). Установить, является ли этот четырехугольник выпуклым.
49
320,	Даны вершины треугольника: Л(—10; —13), В(—2; 3) и С (2; 1). Вычислить длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершцны С.
321.	Стороны АВ, ВС и СА треугольника АВС соответственно даны уравнениями *4-211/— 22 = 0, 5л: — — \2у + 7 = 0, 4х — 331/4-146 = 0. Вычислить расстояние от центра тяжести этого треугольника до стороны ВС.
322.	Вычислить расстояние d между параллельными прямыми в каждом из следующих случаев:
1) Ъх-4у- 10 = 0,	2) 5*-121/4-26 = 0,
6х —81/4- 5 = 0;	5* — 121/— 13 = 0;
3) 4х —31/4-15 = 0, V4) 24*- 101/4-39 = 0, 8* — 61/4-25 = 0;	12* — 51/ —26 = 0.
323.	Две стороны квадрата лежат на прямых 5* — >— 121/— 65 = 0, 5* — 121/ 4- 26 = 0. Вычислить его площадь.
324.	Доказать, что прямая 5* — 2у—1=0 параллельна прямым 5* — 21/4-7 = 0, 5х— 2у — 9 = 0 и делит расстояние между ними пополам.
325.	Даны три параллельные прямые: 10*4-151/ — .— 3 = 0, 2* 4- 31/ 4- 5 = 0, 2л: 4- 31/ — 9 = 0. Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними.
326.	Доказать, что через точку Р(2; 7) можно провести Две прямые так, чтобы их расстояния от точки Q (1; 2) были равны 5. Составить уравнения этих прямых.
327.	Доказать, что через точку Р(2; 5) можно провести две прямые так, чтобы их расстояния от точки Q(5; 1) были равны 3. Составить уравнения этих прямых.
328.	Доказать, что через точку С (7; —2) можно провести только одну прямую так, чтобы расстояние ее от точки А (4; —6) было равно 5. Составить ее уравнение^
329.	Доказать, что через точку В (4; —5) невозможно провести прямую так, чтобы расстояние ее от точки С (—2; 3) было равно 12.
330.	Вывести уравнение геометрического места точек, отклонение которых от прямой 8*—151/— 25 = 0 рав-< но —2,
50
331.	Составить уравнение прямых, параллельных прямой Зх — 4#—10 = 0 и отстоящих от нее на расстоянии d = 3.
332.	Даны две смежные вершины квадрата А (2; 0) и В(—1; 4). Составить уравнения его сторон.
333.	Точка Л (5; —1) является вершиной квадрата, одна из сторон которого лежит на прямой 4х— Зу — — 7 = 0. Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.
334.	Даны уравнения двух сторон квадрата 4х— <—Зу + 3 = 0, 4х — Зу—17 = 0 и одна из его вершин Л (2; —3). Составить уравнения двух других сторон этого квадрата.
335.	Даны уравнения двух сторон квадрата 5x4-' [4-12#—10=0, Ъх + 12# + 29 = 0. Составить уравнения двух других его сторон при условии, что точка МД—3; 5) лежит на стороне этого квадрата.
336.	Отклонения точки от прямых 5х—12#—13 = = 0 и Зх— 4у— 19 = 0 равны соответственно —3 и —5. Определить координаты точки Л1.
337.	Составить уравнение прямой, проходящей через точку Р(—2; 3) на одинаковых расстояниях от точек Л(5; —1) и В(3; 7).
338.	Составить уравнение геометрического места то-:к, равноудаленных от двух параллельных прямых:
1) Зх —#4-7 = 0,	2)х-2#4-3 = 0,
Зх — # — 3 = 0; х — 2# 4" 7 = 0;
3) 5х — 2# — 6 = 0, 10х — 4# 4-3 = 0.
339. Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми:
1) х— 3#4"5 = 0, 2) х —2# —3 = 0, Зх — у — 2 = 0; 2х 4- 4у 4~ 7 = 0}
3) 3x4- 4#-1=0, 5х 4- 12# — 2 = 0.
340. Составить уравнения прямых, которые проходят через точку Р(2; —1) и вместе с прямыми 2х —#4-4~ 5 = 0, 3xJ-6# —1_=0 образуют равнобедренные треугольники.
51
841. Определить, лежат ли точка Л4(1; —2) и начало координат в одном, в смежных или вертикальных уг* лах, образованных при пересечении двух прямых:
1) 2х- у— 5 = 0,-2) 4x4-3# —10 = 0, 3x4“ #4-10 = 0;	12х — 5# — 5 = 0;
8) х — 2у — 1=0, Зх — у — 2 = 0.
342. Определить, лежат ли точки Л4(2;3) и Ат(5;—1) в одном, в смежных или вертикальных углах, образо-ванных при пересечении двух прямых.
1)	х-3#-5 = 0, 2) 2x4-7# —5 = 0,
2х 4“ 9# — 2 = 0; х 4* 3# 4" 7 = 0;
3) 12x4- #- 1 =0, 13х 4- 2# — 5 = 0.
343.	Определить, лежит ли начало координат внутри или вне треугольника, стороны которого даны уравнениями 7х — 5#—11=0, 8х 4“ 3# 4* 31 = 0, х4-3# — — 19 = 0
344.	Определить, лежит ли точка Л1(—3; 2) внутри или вне треугольника, стороны которого даны уравнениями х 4- у — 4 = 0, Зх — 7# 4* 8 = 0, 4х — у — 31 = = 0.
345.	Определить, какой из углов, острый или тупой, образованных двумя прямыми Зх — 2# 4-5 = 0 и 2x4--4- у — 3 = 0, содержит начало координат.
346.	Определить, какой из углов, острый или тупой, образованных двумя прямыми Зх — 5# — 4 = 0 и х4~> 4“ 2# 4- 3 = 0, содержит точку М (2; —5).
347.	Составить уравнение биссектрисы угла между прямыми Зх — у — 4 = 0 и 2x4-6# 4*3 = 0, в котором лежит начало координат.
348.	Составить уравнение биссектрисы угла между прямыми х — 7# 4- 5 = 0, 5x4-5# —3 = 0, смежного с углом, содержащим начало координат.
349.	Составить уравнение биссектрисы угла между прямыми х4“2#—11=0 и Зх — 6# — 5 = 0, в котором лежит точка М (1; —3).
350.	Составить уравнение биссектрисы угла между прямыми 2х — 3# — 5 = 0, 6х — 4# 4- 7 = 0, смежного с углом, содержащим точку С (2; —1),
52
351.	Составить уравнение биссектрисы острого угла, образованного двумя прямыми Зх 4-4р— 5 = 0, 5х— — 12г/4-3 = 0
352.	Составить уравнение биссектрисы тупого угла, образованного двумя прямыми х — Зг/+ 5 = 0, Зх — •— г/ + 15 = 0.
§ 15.	Уравнение пучка прямых
Совокупность прямых, проходящих через некоторую точку S, называется пучком прямых с центром S.
Если -Л1Х + Biy + Ci = 0 и А2х 4- В?у 4- Ci — 0 — уравнения двух прямых, пересекающихся в точке S, то уравнение
а(Л1х4-£1*/4'С1)4‘₽ (А2х 4- В2у 4- С2) = 0,	(1)
где а, р — какие угодно числа, не равные одновременно нулю, определяет прямую, также проходящую через точку S.
Более того, в уравнении (1) числа а, (3 всегда возможно подобрать так, чтобы оно определило любую (заранее назначенную) прямую, проходящую через точку S, иначе говоря, любую прямую пучка с центром S. Поэтому уравнение вида (1) называется уравнением пучка (с центром S).
Если а #= 0, то, деля обе части уравнения (1) на а и полагая ₽ а
— = Л, получим:
Л1х4-В1г/4-С14-Х(Л2х4-В2у4-С2) = 0.	(2)
Этим уравнением можно определить любую прямую пучка с центром S, кроме той, которая соответствует а = 0, т. е. кроме прямой ЛгХ 4* В2у 4- С2 = 0.
353.	.Найти центр пучка прямых, данного уравнением сс (2х 4-Зг/— 1) 4- Р (х — 2г/— 4) = 0.
354.	Найти уравнение прямой, принадлежащей пучку прямых а(х 4- 2г/ — 5) 4- ₽ (Зх — 2г/ 4- 1) = 0 и
1)	проходящей через точку /4(3; —1);
2)	проходящей через начало координат;
3)	параллельной оси Ох;
4)	параллельной оси Оу,
5)	параллельной прямой 4х 4-Зг/4-5 = 0;
6)	перпендикулярной к прямой 2х 4-Зг/4-7 = 0.
355. Составить уравнение прямой, проходящей через точку пересечения прямых Зх — 2г/ 4- 5 = 0, 4х4-3р — — 1 = 0 и отсекающей на оси ординат отрезок b = —3. Решить задачу, не определяя координат точки пересечения данных прямых.
356. Составить уравнение прямой, которая проходит .через точку пересечения прямых 2x4-г/ —2 = 0,
53
х — 5у — 23 = 0 и делит пополам отрезок, ограниченный точками Л11 (5; —6) и М2(—1; —4). Решить задачу, не вычисляя координат точки пересечения данных прямых, 357. Дано уравнение пучка прямых а(3х — 4у — 3)4-4-р(2х4-Зу—1) = 0. Написать уравнение прямой этого пучка, проходящей через центр тяжести однородной треугольной пластинки, вершины которой суть точки Л(—1; 2), В(4; —4) и С(6; — 1).
358.	Дано уравнение пучка прямых а(Зх — 2у~ 1)4-> 4-Р(4х — 5у4~3) = 0. Найти прямую этого пучка, проходящую через середину отрезка прямой х 4- 2у + 4 = О, заключенного между прямыми 2х4-Зу4-5 = 0, х .-Ь ,-^-1=0.
359.	Даны уравнения сторон треугольника х + 2у —> — 1=0, 5х + 4у—17 = 0, х — 4у 4-11=0. Не определяя координат его вершин, составить уравнения высот этого треугольника.
360.	Составить уравнение прямой, проходящей через точку пересечения прямых 2х 4- 7у— 8 = 0, Зх4-2у4?' 4-5 = 0 под углом в 45° к прямой 2х 4- Зу-— 7 = 0. Решить задачу, не вычисляя координат точки пересечения данных прямых.
361.	В треугольнике АВС даны уравнения высоты. AN: х4-5у— 3 = 0, высоты BN: х'-\-у—1 = 0 и стороны АВ: х'4“3у— 1 =0. Не определяя координат вершин и точки пересечения высот треугольника, составить уравнение двух других сторон и третьей высоты.
362.	Составить уравнения сторон треугольника АВС, зная одну его вершину Л (2; —1), а также уравнения высоты 7х — 10у 4- 1 = 0 и биссектрисы Зх — 2у 4- 5=0t проведенных из одной вершины. Решить задачу, не вы-, числяя координат вершин В и С.
363.	Дано уравнение пучка прямых а(2х 4- у 4- 8) 4-Щх 4~У 4-3) = 0. Найти прямые этого пучка, отрезки которых, заключенные между прямыми х — у — 5 = 0, х — у — 2 = 0, равны 1/5.
364.	Дано уравнение пучка прямых а(3х4-у—1)4? 4-^(2х —у — 9) = 0. Доказать, что прямая х4-Зу-Н 4- 13 = 0 принадлежит этому пучку.
365.	Дано уравнение пучка прямых а(5х4~3у4~6) 4-' 4-Р(3х —4у — 37) = 0. Доказать, что прямая 7х4-2у — — 15 = 0 не принадлежит этому пучку.
366.	Дано уравнение пучка прямых а(3х‘4- 2у — 9) 4-* 4-p(2xj-5у 4-5) = 0. Найти, при каком значении С 54
прямая 4х— Зу -f- С = 0 будет принадлежать этому пучку.
367.	Дано уравнение пучка прямых а (5x4- %У— 7)4* 4-0(3x4-10# 4-4) — 0. Найти, при каких значениях а прямая" а<4д 5# 4-9 = 0 не будет принадлежать этому пучку.
368.	Центр пучка прямых а(2х— 3#4-20)4-4-0(3х 4-5# — 27) = 0 является вершиной квадрата, диагональ которого лежит на прямой х 4- 7# — 16 = 0. Составить уравнения сторон и второй диагонали этого квадрата.
369.	Дано уравнение пучка прямых а(2х 4- 5# 4-4)4-4-0(Зх— 2#4~25) = 0. Найти прямую этого пучка, отсекающую на координатных осях отличные от нуля отрезки равной величины (считая от начала координат).
370.	Дано уравнение пучка прямых а(2х 4-# 4“ 1) 4-4-0(х —3#—10) = 0. Найти прямые этого пучка, отсекающие на Координатных осях отрезки равной длины [(считая от начала координат).
371.	Дано уравнение пучка прямых се (21x4-. 8#— — 18)4-Р(11-^ + 3# 4-12) — 0. Найти прямые этого пучка, отсекающие от координатных углов треугольники с площадью, равной 9 кв. ед.
372.	Дано уравнение пучка прямых а (2х4- У 4- 4) 4-Ц-0(х —2#— 3) = 0. Доказать, что среди прямых этого пучка существует только одна прямая, отстоящая от точки Р(2; —3) на расстоянии d = ]/10 • Написать уравнение этой прямой.
373.	Дано уравнение пучка прямых а(2х— у — 6)4-4-0(х— У — 4) = 0. Доказать, что среди прямых этого пучка нет прямой, отстоящей от точки Р(3; —1) на расстоянии d = 3.
374.	Составить уравнение прямой, проходящей через точку пересечения прямых 3x4-# — 5 = 0, х — .— 2# 4-Ю = 0 и отстоящей от точки С(—1; —2) на расстоянии d — 5. Решить задачу, не вычисляя координат точки пересечения данных прямых.
375.	Дано уравнение пучка прямых а (5x4-2# 4-4- 4) 4-р (х 4-9# — 25) =0. Написать уравнения прямых этого пучка, которые вместе с прямыми 2х —3#4-4-5 = 0, 12x4-8# —7 = 0 образуют равнобедренные треугольники.
376.	Составить уравнение прямой, которая проходит через точку пересечения прямых llxJ-3# — 7 = 0,
55
12x-f-г/— 19 = 0 на одинаковых расстояниях от точек Л (3; —2) и В(— 1; 6). Решить задачу, не вычисляя координат точки пересечения данных прямых.
377.	Даны уравнения двух пучков прямых
Q] (5х + Зу — 2) 4- р! (Зх — у — 4) = О,
«2 (* ~ У 4- 1) + 02 (2х — у — 2) = 0.
Не определяя их центров, составить уравнение прямой, принадлежащей обоим пучкам.
378.	Стороны АВ, ВС, CD и DA четырехугольника ABCD заданы соответственно уравнениями 5x4“ #4“ - 4-13 = 0, 2х — 1у— 17 = 0, Зх 4-2z/— 13 = 0, Зх — 4z/4“ 17 = 0. Не определяя координат вершин этого четырехугольника, составить уравнения его диагоналей АС и BD.
379.	Центр пучка прямых а(2х 4“ Зг/ ‘4“ 5) 4“ Р(3х —< — у 4- 2) = 0 является одной из вершин треугольника, две высоты которого даны уравнениями х — 4у А~ 1 = 0, 2х + #4-1=0- Составить уравнения .сторон этого треугольника.
§ 16.	Полярное уравнение прямой
Прямая, проведенная через полюс перпендикулярно к данной прямой, называется ее нормалью. Обозначим буквой Р точку, в которой нормаль пересекает прямую; установим на нормали положительное направление от точки О к точке Р. Угол, на который нуж* но повернуть полярную ось до наложения ее на отрезок ОР, будем называть полярным углом нормали.
380.	Вывести полярное уравнение прямой, зная ее расстояние от полюса р и полярный угол нормали а.
Решение. 1-й способ. На данной прямой s (рис. 11) возьмем произвольную точку М с полярными координатами р и 0. Точку пересечения прямой s с ее нормалью обозначим буквой Р. Из прямоугольного треугольника ОРМ находим:
р “ cos (6 - а) *
Мы получили уравнение с двумя переменными р и 0, которому удовлетворяют координаты всякой точки М, лежащей на прямой s, 56
и не удовлетворяют координаты никакой точки, не лежащей на этой прямой. Следовательно, уравнение (1) является уравнением прямой s. Таким образом, задача решена.
2-й способ. Будем рассматривать декартову прямоугольную систему координат,’ положительная полуось абсцисс которой совпадает с полярной осью заданной полярной системы. В этой декартовой системе имеем нормальное уравнение прямой $:
г cos а + У sin а — р = 0.	(2)
Воспользуемся формулами преобразования полярных координат в декартовы:
х = pease, у = р sin 9.
Подставляя в уравнение (2) вместо х и у выражения (3), получим: р (cos 6 cos a + sin 9 sin a) = p или n _ P p cos (9 — a)
381.	Вывести полярное уравнение прямой, если даны:
1)	угол р наклона прямой к полярной оси и длина перпендикуляра р, опущенного из полюса на эту прямую. Написать уравнение этой прямой в случае р = -у, Р = 3;
2)	отрезок а, который отсекает прямая на полярной оси, считая от полюса, и полярный угол а нормали этой прямой. Написать уравнение этой прямой '	2
в случае а = 2, a = - j л;
3)	угол р наклона прямой к полярной оси и отрезок а, который отсекает прямая на полярной оси, считая от полюса. Написать уравнение этой прямой в случае р = -?г, а = 6.
’ о
382.	Вывести полярное уравнение прямой, проходящей через точку Mi(pi;0i) и наклоненной к полярной оси под углом р.
383.	Вывести полярное уравнение прямой, проходящей через точку MJpuOi), полярный угол нормали которой равен а.
384.	Составить уравнение прямой, проходящей через точки Afi(pi; 0i) и Л12(р2;02)<
Г Л AB A 4 ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА ЛИНИЙ ВТОРОГО ПОРЯДКА
§ 17. Окружность
Уравнение
(х-а)2 + (г/-0)2 = Я2	(1)
определяет окружность радиуса R с центром С (а; 0).
Если центр окружности совпадает с началом координат, т. е. если а = 0, 0 = 0, то уравнение (1) принимает вид
х2 + у2 = Я2.	(2)
385.	Составить уравнение окружности в каждом из следующих случаев:
1)	центр окружности совпадает с началом координат и ее радиус R = 3;
2)	центр окружности совпадает с точкой С(2; —3) и ее радиус R = 7;
3)	окружность проходит через начало координат и ее центр совпадает с точкой С (6; —8);
4)	окружность проходит через точку А (2; 6) и ее центр совпадает с точкой С(—1; 2);
5)	точки Л(3; 2) и В(—1; 6) являются концами одного из диаметров окружности;
6)	центр окружности совпадает с началом координат и прямая Зх —	-f- 20 = 0 является касательной к
окружности;
7)	центр окружности совпадает с точкой С(1; —1) и прямая 5х — 12г/4-9 = 0 является касательной к окружности;
8)	окружность проходит через точки Л(3; 1) и В(—1; 3), а ее центр лежит на прямой Зх — у — 2 = 0;
9)	окружность проходит через три точки 4(1; 1), В(1;-1) и С(2; 0);
10)	окружность проходит через три точки; МД— 1; 5). М2(-2; -2) и М3(5; 5).	"
58
386.	Точка С(3; —1) является центром окружности, отсекающей на прямой 2х— 5г/4-18 = 0 хорду, длина которой равна 6. Составить уравнение этой окружности.
387.	_Написать уравнения окружностей радиуса
= У Б, касающихся прямой х~ 2у — 1=0 в точке Л11(3; 1).
388.	Составить уравнение окружности, касающейся двух параллельных прямых: 2х-}-у — 5 = 0, 2х А~ у А~ 4- 15 = 0, причем одной из них — в точке А (2; 1).
389.	Составить уравнения окружностей, которые проходят через точку А (1; 0) и касаются двух параллельных прямых: 2х 4- у + 2 = 0, 2х 4- у — 18 = 0.
390.	Составить уравнение окружности, которая, имея центр на прямой 2х4-г/ = 0, касается прямых 4х — — Зу 4- 10 = 0, 4х - Зу - 30 = 0.
391.	Составить уравнения окружностей, касающихся двух пересекающихся прямых: 7х — у — 5 = 0, х У 4- 13 = 0, причем одной из них — в точке Mi(l; 2).
392.	Составить уравнения окружностей, проходящих через начало координат и касающихся двух пересекающихся прямых: х + 2у — 9 = 0, 2х — у 4- 2 = 0.
393.	Составить уравнения окружностей, которые, имея центры на прямой 4х — Бу — 3 = 0, касаются прямых 2х — Бу — 10 = 0, Зх — 2у 4- 5 = 0.
394.	Написать уравнения окружностей, проходящих через точку А(—1; 5) и касающихся двух пересекающихся прямых: Зх 4- 4у — 35 = 0, 4х 4- Бу 4- 14 = 0.
395.	Написать уравнения окружностей, касающихся трех прямых: 4х — Бу — 10 = 0, Зх — 4у — 5 = 0 и Зх — — 4у — 15 = 0.
396.	Написать уравнения окружностей, касающихся трех прямых: Зх 4s- 4г/ — 35 = 0, Зх — 4у — 35 = 0 их — -1=0.
397.	Какие из нижеприводимых уравнений определяют окружности? Найти центр С и радиус R каждой из них:
1) (х- 5)1 2 + 0/4- 2)2 = 25;	2) (х4- 2)2 4- У2 = 64;
3) (х - 5)2 4- (У 4- 2)2 = 0;	4) х2 4- (у - 5)2 = 5;
5) х24-*/2 — 2х 4" 4г/— 20 = 0;
6) х24- У2 - 2х 4- 4у 4- 14 = 0;
7) х24-*/24-4х-2г/4-5 = 0;	8) х2 4~ г/2 4~ X = 0;
9) х24-^Чбх-4г/4-14 = 0; 10) х2 + г/2 4- у = 0.
59
398.	Установить, какие линии определяются следующими уравнениями:
1)	у =	]/9 — х2;	6)	у = 15 — ]/б4 — х2;
2)	у = - /25 - х2;	7)	x = -2-/9^V;
3)х = -/Г=ТГ;	8) x = -2+/9-/;
4)	х = + /16-/;	9)	</ = — 3 —/21-4х-х2.
5)	у = 15 + /64-х2•	10)	х = - 5 + /40-6у- й2’
Изобразить эти линии на чертеже.
399. Установить, как расположена точка Л (1; —2) относительно каждой из следующих окружностей — внутри, вне или на контуре: 1) х2 4- у2 = 1; 2) х24-у2 = 5; 3) х24-у2 = 9; 4) х24-у2-8х-4у-5 = 0; 5) х24-Н- у2 - 10х 4- 8у = 0.
400. Определить уравнение линии центров двух окружностей, заданных уравнениями:
1)	(х-*3)24-у2 = 9 и (х4-2)2 + (у — 1)2 = 1;
2)	(х4-2)24 (у- 1)2=16 и (х 4-2)2 4- (д+ 5)2 = 25;
3)	х2 4- У2 — 4х 4- Оу = 0 и х2 4- У2 — 6х = 0;'
4)	х2 4- У2 — х 4- 2у = 0 и х2 4- У2 4- 5х 4~ 2у—1 = 0.
401.	Составить уравнение диаметра окружности х24~ 4->24-4х — бу— 17 — 0, перпендикулярного к прямой 5х 4- 2у — 13 == 0.
402.	Вычислить кратчайшее расстояние от точки до окружности в каждом из следующих.случаев:
а)	Л (6; -8), х24-у2 = 9;
б)	В(3; 9), х2 4-У2 — 26х 4-ЗОу 4-313 = 0;
в)	С(—7; 2), х24-у2-10х<- 14у-151 =0.
403.	Определить координаты точек пересечения прямой 7х — у 4- 12 — 0 и окружности (х — 2)2 4- (у — I)2 = = 25.
404.	Определить, как расположена прямая относительно окружности (пересекает ли, касается или проходит вне ее), если прямая и окружность заданы следующими уравнениями:
1) у — 2х — 3 и х2 + У2 — Зх 4- 2у — 3 = 0;
2)у=уХ — у и х24-У2 —8х4-2у 4-12 = 0; •
3) у==х4- Ю и х24-У2~ 1=0.
60
405.	Определить, при каких значениях углового коэффициента k прямая у = kx
1)	пересекает окружность х2 4- у2 — 10х 4- 16 = 0;
2)	касается этой окружности;
3)	проходит вне этой окружности.
406.	Вывести условие, при котором прямая у = kx 4-4- b касается окружности х2 4- у2 — R2,
407.	Составить уравнение диаметра окружности (х — 2)2 + (у + I)2 = 16, проходящего через середину хорды, отсекаемой на прямой х — 2у — 3 = 0.
408.	Составить уравнение хорды окружности (х — З)2 4- (у — 7)2 = 169, делящейся в точке М (8,5; 3,5) пополам.
409.	Определить длину хорды окружности (х —2)24-+ (У ~ 4)2 = 10, делящейся в точке Д(1; 2) пополам.
410.	Дано уравнение пучка прямых а(х — 8у 4~ 30) 4-Ч-р(х-{-5г/ — 22) = 0 Найти прямые этого пучка, на которых окружность^ х2 + у2 — 2х 4- 2у — 14=0 отсекает хорды длиною 2 УЗ.
411.	Даны две окружности (х — т^2 4~ (*/ —
(х — т у 4- (у — /г,)2 = пересекающиеся в точках Mi(xi; z/i) и М2(х2; г/г). Доказать, что любая окружность, проходящая через точки Mi, М2, а также прямая MiM2, могут быть определены уравнением вида а [(X-	+(у - га,)2 - «?] + ₽[(*- т2) +(? - п2)2 -
= 0 при надлежащем выборе чисел аир.
412.	Составить уравнение окружности, проходящей через точку Л(1; —1) и точки пересечения двух окружностей: х2 4- У2 4- 2х — 2у — 23 = 0, х2 4- у2 — 6х 4- 12// — - 35 = 0.
413.	Составить уравнение окружности, проходящей через начало координат и точки пересечения двух окружностей: (х 4-З)2 4- (г/4-1)2 = 25, (х-2)24-(г/4-4)2 = = 9.
414.	Составить уравнение прямой, проходящей через точки пересечения двух окружностей: х2 4- У2 4- Зх — у = = 0, Зх2 4- 3//2 4- 2х 4- у = 0.
415.	Вычислить расстояние от центра окружности х2-{-у2 — 2х до прямой, проходящей через точки пересечения двух окружностей: х2 4- У2 + 5х — 8у 4- 1 = 0, х2 4-4- у2 — Зх 4~ 7// — 25 = 0.
416.	Определить длину общей хорды двух окружностей: х24- Z/2 — 1 Ох —-10// == 0, х2 J- у2 J- 6х 4- 2у — 40 = 0.
61
417.	Центр окружности лежит на прямой х-\-у = 0< Составить уравнение этой окружности, если известно, что она проходит через точки пересечения двух окружностей: (х — I)2 4- (у 4- 5)2 — 50, (х 4- 02+ (У 4- О2 = = 10.
418.	Составить уравнение касательной к окружности х2 4- у2 5 в точке А (— 1; 2).
419.	Составить уравнение касательной к окружности (х 4-2)2 4-Q/— З)2 == 25 в точке Д (—5; 7),
420.	На окружности 16х2 4- 16г/2 4- 48х — 8у — 43 = 0 найти точку Л11, ближайшую к прямой 8х — 4у 4- 73 = 0, и вычислить расстояние d от точки Mi до этой прямой.
421.	Точка Mi (хг, уА лежит на окружности х2 4- У2 — = R2. Составить уравнение касательной к этой окружности в точке Mi.
422.	Точка Mi(xi; у А лежит на окружности (х —• а)2 4* (У ~ ₽)2 =*= Я2. Составить уравнение касательной к этой окружности в точке Aft.
423.	Определить острый угол, образованный при пересечении прямой Зх — у — 1=0 и окружности (х-2)24-г/2 = 5 (углом между прямой и окружностью называется угол между прямой и касательной к окружности, проведенной в точке их пересечения).
424.	Определить, под каким углом пересекаются две окружности:	(х — З)24- (у — I)2 = 8, (х — 2)24-J
гЬ(#4-2)2==2 (углом между двумя окружностями называется угол между их касательными в точке пересечения).
425.	Вывести условие, при котором две окружности (х — at)2 4- [у — ^)2 = R2, (х — а,)2 4- (у — |32)2 = R2 пересекаются под прямым углом.
426.	Доказать, что две окружности
х2 4- У2 —' 2тх — 2пу — т2 4- п2 = 0,
х2 4- У2 — 2пх 4- 2/ш/ 4~	— /г2 = 0
пересекаются под прямым углом. /5	5 \
427.	Из точки Д(-д-; —з ) проведены касательные к окружности х24-'у2 — 5. Составить их уравнения.
428.	Из точки 4(1; 6) проведены касательные к окружности х24~ У2,4~ 2х — 19 — 0. Составить их урав^ нения,
62
429.	Дано уравнение пучка прямых а(3х4-4г/ — *“• 10) 4-р(3х — у — 5) = 0. Найти прямые этого пучка, которые касаются окружности х2 4- у2 4- 2х — 4у = 0.
430.	Из точки Л (4; 2) проведены касательные к окружности х24-У2=Ю. Определить угол, образованный этими касательными.
431.	Из точки Р(2; —3) проведены касательные к окружности (х—1)24~ (у 4~5)2 = 4. Составить уравнение хорды, соединяющей точки касания.
432.	Из точки С(6; —8) проведены касательные к окружности х2 + у2 = 25. Вычислить расстояние d от точки С до хорды, соединяющей точки касания.
433.	Из точки Р(— 9; 3) проведены касательные к окружности х2 4- У2 — 6х 4- 4г/ — 78 = 0. Вычислить расстояние d от центра окружности до хорды, соединяющей точки касания.
434.	Из точки Л1(4;—4) проведены касательные к окружности х2 4- г/2 — 6х 4- 2г/ 4- 5 = 0. Вычислить длину d хорды, соединяющей точки касания.
435.	Вычислить длину касательной, проведенной из точки Л(1; —2) к окружности х2 4- у2 4- х — Зу — 3 = 0.
436.	Составить уравнения касательных к окружности х2 4" У2 + — 2У + 6 = 0, параллельных прямой 2х4-и 4- у — 1 == 0.
437.	Составить уравнения касательных к окружности х2 + у2— 2x4- 4у = 0, перпендикулярных к прямой х — — 2у 4- 9 = 0.
438.	Составить уравнение окружности в полярных координатах по данному радиусу R и полярным координа-' там центра C(R-, 0О)«
439.	Составить уравнение окружности в полярных координатах по данному радиусу R и полярным координатам центра окружности: I) С(/?; 0); 2) C(R\ л); 3) с(/г; 4); 4) с(я: -4).
440.	Определить полярные координаты центра и радиус каждой из следующих окружностей: 1) p = 4cos0? 2) p = 3sin0; 3) р, = — 2 cos 6; 4) р = —-5sin0; 5) p = 6cos(4-e); 6) p = 8sin(e-4): 7) P — — 8 sin (4 — 1.
441.	Окружности заданы уравнениями в полярных координатах: 1) p = 3cos9; 2), р =.—4 sin 0;
63
3)' р == cos 0 — sin 0. Составить их уравнения в декартовых прямоугольных координатах при условии, что полярная ось совпадает с положительной полуосью Ох, а полюс — с началом координат.
442.	Окружности заданы уравнениями в декартовых прямоугольных координатах: 1) №-|-г/2 = х; 2) 4-//2 = -Зх; 3) х2 + </2 = 5^ 4) х2 + у2 = -у, 5) х2 + + у2 = х + у. Составить уравнения этих окружностей в полярных координатах при условии, что полярная ось совпадает с положительной полуосью Ох, а полюс — с началом координат.
443.	Составить полярное уравнение касательной к окружности р = R в точке 0о).
§ 18. Эллипс
Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами Fj, и Ft, расстояние между ними—* .через 2с. По определению эллипса 2а > 2с или а > с.
Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид
у2 у2
^2" + V=l’
где b = Vа2 — с2 ; очевидно, а > Ь. Уравнение вида (1) называется каноническим уравнением эллипса.
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат — его центром симметрии (рис, 12). Оси симметрии эллипса называются
64
просто его осями, центр симметрии — просто центром. Толки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. 12 вершины эллипса суть точки А', А, В' и В. Часто осями эллипса называются также отрезки А'А = 2а и В'В = 2Ь; вместе с тем отрезок ОА = а называют большой полуосью эллипса, отрезок OB = Ь — малой полуосью.
Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае b > а; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и Ь поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, бу к I ой b — полуось, расположенную на оси Оу, независимо от того, что больше, а или b Если а = Ь, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса,
Число
где а — большая полуось, называется эксцентриситетом эллипса. Очевидно, 8<1 (для окружности 8 = 0). Если Л4(х; у)—произвольная точка эллипса, то отрезки == и и ЕгМ = гг (рис. 12) называются фокальными радиусами точки М. Фокальные радиусы
могут быть вычислены по формулам
rt = а + ex, г2~а — &х.
Если эллипс определен уравнением (1) и а > Ь, то прямые
(рис. 12) называются директрисами эллипса (если Ь > а, то директрисы определяются уравнениями
Рис. 13.
Каждая директриса обладает следующим свойством: если г — расстояние произвольной точки эллипса до некоторого фокуса, d — расстояние от той же точки до односторонней с этим фокусом
г
директрисы, то отношение есть постоянная величина, равная эксцентриситету эллипса
г
d в8.
Если две плоскости аир образуют острый угол <р, то проекцией -на плоскость ₽ окружности радиуса а, лежащей на плоскости а, является эллипс с большой полуосью а; малая полуось b
3 Д. В. Клетеник	65
этогэ эллипса определяется по формуле b = a cos ф
Если круглый цилиндр имеет в качестве направляющей окруж-“ ”.	\	» сечении этого цилиндра плоскостью, накло-
под острым углом ф, будет эллипс, малая полуось которого равна Ь; большая полуось а этого формуле
(рис. 13).
Г.	‘ .
ность радиуса Ь, то в ненной к оси цилиндра
Рис. 14.
эллипса определяется по
ь а = _— Sin ф
(рис.. 14).
444. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что:
1) его полуоси равны 5 и 2;
2) его большая ось равна 10, а расстояние между фокусами 2с = 8;
равна 24, а расстояние между фоку-
3) сами
4)	.
3 триситет s = —;
5)	его большая ось равна 20, а эксцентриситет е = -=;
12
6)	его малая ось равна 10, а эксцентриситет е = -^;
7)	расстояние между его директрисами равно 5 и расстояние между фокусами 2с = 4;
8)	его большая ось равна 8, а расстояние между директрисами равно 16;
9)	его малая ось равна 6, а расстояние между дирек-* трисами равно 13;
10)	расстояние между его директрисами равно 32 и е==4-
445. Составить уравнение эллипса, фокусы которого лежат на оси ординат, симметрично относительно начала координат, зная, кроме того, что:
1)	его полуоси равны соответственно 7 и 2;
2)	его большая ось равна 10, а расстояние между фокусами 2с = 8;
его малая ось 2с = 10;
расстояние между его фокусами 2с = 6 и эксцен-
66
3)	расстояние между его фокусами 2с = 24 и экспен-12 триситет в == — ;
1 о
3
4)	его малая ось равна 16, а эксцентриситет 8 = -g-;
5)	расстояние между его фокусами 2с = 6 и расстоя-ние между директрисами равно 16 у*,
2
6)	расстояние между его директрисами равно 10
3
и эксцентриситет е =
446. Определить полуоси каждого из следующих эллипсов:
l)4 + 4 = Ii 2> -т + ^=1; 3) -v2 + 25v2 = 25; 1м г?	т
4) л:2 + 5г/2 == 15; 5) 4х2 + 9г/2 = 25; 6) 9х2 + 25г/2 = 1;
7) х2 + 4г/2=1; 8) 16х2 +г/2== 16; 9) 25+ + 9z/2 = 1Г
10)	9х2 + г/2==1.
447.	Дан эллипс 9х2 + 25г/2 = 225. Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
448.	Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса х2 4- 5г/2 = 20, а две другие совпадают с концами его малой оси.
449.	Дан эллипс 9х2 4- 5г/2 = 45. Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
450.	Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса 9х2+(5г/2 = 1, две другие совпадают с концами его малой оси.
451.	Вычислить расстояние от фокуса Г(с; 0) эллипса
4 + 4=1 а2 Ь2
до односторонней с этим фокусом директрисы.
452.	Пользуясь одним циркулем, построить фокусы эллипса —г +	= 1 (считая, что изображены оси коор-
динат и задана масштабная единица).
453.	На эллипсе-^-+-^-= 1 найти точки, абсцисса которых равна — 3.
3*	67
454.	Определить, какие из точек /IJ—2; 3), Л2(2; —2), гДз(2; -4), Л4(-1; 3), Л5(—4; -3), Д6(3;-1), Д7(3; —2), Л8(2; 1), Л9(0; 15) и Лю(0; — 16) лежат на эллипсе 8х2 + &У2 — 77, какие внутри и какие вне его.
455.	Установить, какие линии определяются следующими уравнениями: 1) у = + -т V16 — х2; 2) у — = _|/9=У; 3)х = -|]/9^7;4)х=+41/4УУ. Изобразить эти линии на чертеже.
2
456.	Эксцентриситет эллипса е = у, фокальный радиус точки М эллипса равен 10. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
457.	Эксцентриситет эллипса е = -^, расстояние от точки М эллипса до директрисы равно 20. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.
(5 \	х2 и2
2; — у I на эллипсе -^ + Л- = Г, составить уравнения прямых, на которых лежат фокальные радиусы точки Mi.
459.	Убедившись, что точка	—4; 2,4) лежит на
^2
эллипсе 16 = Ь определить фокальные радиусы точки М(.
460.	Эксцентриситет эллипса 8 = у, центр его совпадает с началом координат, один из фокусов (—2; 0), Вычислить расстояние от точки М1 эллипса с абсциссой, равной 2, до директрисы, односторонней с данным фокусом.
461.	Эксцентриситет эллипса s = -|-, центр его совпадает с началом координат, одна из директрис дана уравнением .v=16, Вычислить расстояние от точки Mi эллипса с абсциссой, равной —4, до фокуса, одностороннего с данной директрисой.
462.	Определить точки эллипса	> рас-
стояние которых до правого фокуса равно 14.
463.	Определить точки эллипса jg + -у=1, расстояние которых до левого фокуса равно 2,5.
68
464.	Через фокус эллипса ~ 4-	= 1 проведен пер-
пендикуляр к его большой оси. Определить расстояния от точек пересечения этого перпендикуляра с эллипсом до фокусов.
465.	Составить уравнение эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если_даны:
1)	точка МД— 2 |/5; 2) эллипса и его малая полуось b = 3;
2)	точка Mi (2; —2) эллипса и его большая полуось а = 4;
3)	точки Mi (4; — j/З) и М2(2 /2; 3) эллипса;
4)	точка М^/Тб; — 1) эллипса и расстояние между его фокусами 2с = 8;
(5 \
2; —т- эллипса и его эксцентриситет О /
6) точка Mi (8; 12) эллипса и расстояние п = 20 от нее до левого фокуса;_
7) точка М[ (-/5; 2) эллипса и расстояние между его директрисами равно 10.
466. Определить эксцентриситет 8 эллипса, -если:
I)	его малая ось видна из фокусов под углом D 60°;
2)	отрезок между фокусами виден из вершин малой оси под прямым углом;
3)	расстояние между директрисами в три раза больше расстояния между фокусами;
4)	отрезок перпендикуляра, опущенного из центра эллипса на его директрису, делится вершиной эллипса пополам.
467.	Через фокус F эллипса проведен перпендикуляр к его большой оси (рис. 15). Определить, при каком значении эксцентриситета эллипса отрезки АВ и ОС будут параллельны,
69
468.	Составить уравнение эллипса с полуосями а, b и центром С(х0; #о), если известно, что оси симметрии эллипса параллельны осям координат.
469.	Эллипс касается оси абсцисс в точке А (3; 0) и оси ординат в точке В(0; —4). Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
470.	Точка С(—3; 2) является центром эллипса, касающегося обеих координатных осей. Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
471.	Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет и уравнения директоис:
1)	5x2 -р 9^2 _ 30х	18//	9 = о-
2)	16х2 4-25#2 4~ 32х —• 100# — 284 = 0;
3)	4х24-3#2 —8x4-12# —32 = 0.
472.	Установить, какие линии определяются следующими уравнениями:
1)	У = ~ 7 4- т /16 4-бх-х2';
2)	у — 1 - 4 V - - X2;
3)	X = - 2 ]/-5-б0-г/2;
4)	х = -5 + | V& + 2y-y2.
Изобразить эти линии на чертеже.
473.	Составить уравнение эллипса, зная, что:
1)	его большая ось равна 26 и фокусы суть 7’i( —10; 0), F2(14; 0);
F ^2) его малая ось равна 2 и фокусы суть Л(—1; — 1),
3)	его фокусы суть F} (— 2;	, F2 (2; — и эксцен-
триситет g = ——;
4)	его фокусы суть Л(1; 3), F2(3; 1) и расстояние между директрисами равно 12
474.	Составить уравнение эллипса, если известны его
2
эксцентриситет е =-д , фокус 77(2; 1) и уравнение соответствующей директрисы х — 5 = 0.
70
475.	Составить уравнение эллипса, если известны его эксцентриситет 8=у, фокус F(—4; 1) и уравнение соответствующей директрисы уЦ- 3 = 0.
476.	Точка 4(—3; —5) лежит на эллипсе, фокус которого F(— 1; —4), а соответствующая директриса дана уравнением х — 2 = 0. Составить уравнение этого эллипса.
477.	Составить уравнение эллипса, если известны его эксцентриситет е==-^-, фокус F(3; 0) и уравнение соответствующей директрисы х-^у — 1 =0.
478.	Точка Л11 (2; — 1) лежит на эллипсе, фокус которого 0), а соответствующая директриса дана уравнением 2х— у—10 = 0. Составить уравнение этого эллипса.
479.	Точка Л11(3; —1) является концом малой оси эллипса, фокусы которого лежат на прямой у 4~ 6 = 0-Составить уравнение этого эллипса, зная его эксцентрика ситет е = —— •
480.	Найти точки пересечения прямой х 4-2# —7 = 0 и эллипса х2 + 4у2 = 25.
481.	Найти точки пересечения прямой 3x4-10#—25=0 и эллипса 4- -4- = 1.
25	4
482.	Найти точки пересечения прямой Зх—4#—40=0
X2 I у2 ,
и эллипса тт- + ~7г = Ь
16 1 9
483.	Определить, как расположена прямая относительно эллипса; пересекает ли, касается или проходит вне его, если прямая и эллипс заданы следующими уравнениями:
1) 2х-#-3 = 0,	2) 2х-[-у- 10 = 0,
16	9 ~	9*4
3) Зх + 2у -20 = 0, £ + £«1.
40	10
484. Определить, при каких значениях т прямая у = = — х 4- т
1)	пересекает эллипс 20"+ 5	2) касается его;
3) проходит вне этого эллипса.
71
485.	Вывести условие, при котором прямая у = kx-\-m касается эллипса -т + -тт = 1.
а2 о2
486.	Составить уравнение касательной к эллипсу 72-4-77 = 1 в его точке МДхк ух).
487.	Доказать, что касательные к эллипсу 7г 4" 77 = = 1, проведенные в концах одного и того же диаметра, параллельны. (Диаметром эллипса называется его хорда, проходящая через центр.)
488.	Составить уравнения касательных к эллипсу — 4—у-=1, параллельных прямой Зх + 2z/4-7 = 0.
489.	Составить уравнения касательных к эллипсу х2 4- 4у2 — 20, перпендикулярных к прямой 2х—2у—13 = = 0.
490.	Провести касательные к эллипсу -уу 4" ту = I параллельно прямой 4х —2у4-23 = 0 и вычислить расстояние d между ними.
491.	На эллипсе уу4--|-=1 найти точку ближайшую к прямой 2х— 3# 4-25 = 0, и вычислить расстояние d от точки Mi до этой прямой.
/10	5 \
492.	Из точки Д Н-; -5- проведены касательные к эллипсу ту 4“-^-= 1. Составить их уравнения.
493.	Из точки С(10; —8) проведены касательные к 11%
эллипсу 25	= Составить уравнение хорды, со-
единяющей точки касания.
494.	Из точки Р(—16; 9) проведены касательные к эллипсу 7- 4“ -7- — 1- Вычислить расстояние d от точки Р до хорды эллипса, соединяющей точки касания.
495.	Эллипс проходит через точку 4(4; —1) и касается прямой х 4- 4у—10 = 0. Составить уравнение этого эллипса при условии, что его оси совпадают с осями координат.
496.	Составить уравнение эллипса, касающегося двух прямых Зх — 2г/ — 20 = 0, х 4- бу — 20 = 0, при условии, что его оси совпадают с осями координат.
497.	Доказать, что произведение расстояний от центра эллипса до точки пересечения любой его касательной 72
с фокальной осью и до основания перпендикуляра, опущенного из точки касания на фокальную ось, есть величина постоянная, равная квадрату большой полуоси эллипса.
498.	Доказать, что произведение расстояний от фокусов до любой касательной к эллипсу равно квадрату малой полуоси.
499.	Прямая х — у — 5 = 0 касается эллипса, фокусы которого находятся в точках ЛД—3; 0) и /^(З; 0). Составить уравнение этого эллипса.
500.	Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к эллипсу Зх + Юг/ — 25 = 0 и его малая полуось b = 2.
501.	Доказать, что прямая, касающаяся эллипса в некоторой точке Л1, составляет равные углы с фокальными радиусами ЛЛ'1, F2M и проходит вне угла
502.	Из левого фокуса эллипса -45 +эд — 1 П°Д ТУ* пым углом а к оси Ох направлен луч света. Известно, что tga =—2. Дойдя до эллипса, луч от него отразился. Составить уравнение прямой, на которой лежит отраженный луч.
503.	Определить точки пересечения двух эллипсов: х2 4- 9г/2 — 45 = 0, х2 + 9г/2 — 6х — 27 = 0
504.	Убедившись, что два эллипса п2х2+т2у2—т2п2— = 0, т2х2 + п2у2— т2п2 = 0 (tn Ф п) пересекаются в четырех точках, лежащих на окружности с центром в начале координат, определить радиус R этой окружности^
505.	Две плоскости а и р образуют угол ф = 30°. Определить полуоси эллипса, полученного проектированием на плоскость р окружности радиуса R = 10, лежащей на плоскости а.
506.	Эллипс, малая полуось которого равна 6, является проекцией окружности радиуса R = 12. Определить угол ф между плоскостями, в которых лежат эллипс и окружность.
507.	Направляющей круглого цилиндра является окружность радиуса R — 8. Определить полуоси эллипса, полученного в сечении этого цилиндра плоскостью, наклоненной к его оси под углом ф = 30°.
508.	Направляющей круглого цилиндра является окружность радиуса /?=]/3. Определить, под каким углом к оси цилиндра нужно его пересечь плоскостью,
73
чтобы в сечении получить эллипс с большой полуосью а =’2.
509.	Равномерным сжатием (или равномерным растяжением) плоскости к оси абсцисс называется такое преобразование точек плоскости, при котором произвольная точка М у} перемещается в точку М'{х'\ у') (рис. 16) так, что х' = х, у' = qy, где q > 0 — постоян-
।
। ।
।
пая, называемая коэффициентом равномерного сжатия.
Аналогично определяется равномерное сжатие плоскости
। । ।
Рис. 16.
Рис. 17.
к оси Оу при помощи уравнений х' = qx, у' = у (рис. 17).
Определить, в какую линию преобразуется окружность у2 «= 25, если коэффициент равномерного сжа-4 тия плоскости к оси абсцисс q = -=-.
510.	Коэффициент равномерного сжатия плоскости к оси Оу равен Определить уравнение линии, в кото-у 2	112
рую при таком сжатии преобразуется эллипс -jj + -у == = 1.
511.	Найти уравнение линии, в которую преобра-11%
зуется эллипс 4g-+= 1 при двух последовательных равномерных сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ох и Оу равны соответственно 4- и 4-.
О	/
512.	Определить коэффициент q равномерного сжатия плоскости к оси Ох, при котором эллипс	1
преобразуется в эллипс ~ ф- -рг = !•
74
513.	Определить коэффициент q равномерного сжатия JT2 । у2 . плоскости к оси Оу, при котором ЭЛЛИПС	= I
о 1	^0
ft	X2 I У2 1
преобразуется в эллипс ’35+'25'~1*
514.	Определить коэффициенты qt и q% двух последовательных равномерных сжатий плоскости к осям Ох и х2 у2
Оу, при которых эллипс	1 преобразуется в
окружность х2 + У2 = 16.
§ 19. Гипербола
Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается обычно через 2а. Фокусы гиперболы обозначают буквами /ч и F?, расстояние между ними — через 2с. По определению гиперболы 2а < 2с, или а < с.
Пусть дана гипербола. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид
где Ъ = Ус2 — а2. Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат —ее центром симметрии (рис. 18). Оси симметрии гиперболы называются просто ее осями, центр симметрии — центром гиперболы. Гипербола пересекает одну из своих осей, точки
75
пересечения называются вершинами гиперболы. На рис. 18 вершины гиперболы суть точки А' и <4.
Прямоугольник со сторонами 2а и 2d, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.
Отрезки длиной 2а и 2Ь, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженные) являются асимптотами гиперболы; их уравнения суть:
b	b
Уравнение
-•£+£-• <2>
определяет гиперболу, симметричную относительно координатных осей с фокусами на оси ординат; уравнение (2),как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.
Две гиперболы, которые определяются уравнениями
У^__ .
а2 d2 ’ о2 + б2 “
в одной и той же системе координат, называются сопряженными. Гипербола с равными полуоясми (а — Ь) называется равносторонней,; ее каноническое уравнение имеет вид
х2 — у2 = а2 или — х2 + У2 = а2.
Число
с е =—, а
где а — расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы е > 1. Если А1(х; у) — произвольная точка гиперболы, то отрезки FiM и (см. рис. 18) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам
И = ex + a, r2 = ех — а, фокальные радиусы точек левой ветви — по формулам
Г1 = — ех — а,	г 2 = — ех + а.
Если гипербола задана уравнением (1), то прямые, определяемые уравнениями
называются ее директрисами (см. рис. 18). Если гипербола задана уравнением (2), то директрисы определяются уравнениями
76
Каждая директриса обладает следующим свойством: если г—расстояние от произвольной точки гиперболы до некоторого фокуса, d — расстояние от той же точки до односторонней с этим .	г
фокусом директрисы, то отношение есть постоянная величина, равная эксцентриситету гиперболы:
г ~d~S'
515.	Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:
1)	ее оси 2а = 10 и 2Ь = 8;
2)	расстояние между фокусами 2с = 10 и ось 2Ь — 8;
3)	расстояние между фокусами 2с = 6 и эксцентри-3
ситет е = —;
5
4)	ось 2а = 16 и эксцентриситет 8 = -^;
4
5)	уравнения асимптот у = ±-д х и расстояние между фокусами 2с = 20;
2
6)	расстояние между директрисами равно 22-^- и расстояние между фокусами 2с = 26;
39
7)	расстояние между директрисами равно и ось 26 = 6;
8)	расстояние между директрисами равно -х- и экс-
3 центриситет е = —;
з
9)	уравнения асимптот у = ± — х и расстояние между директрисами равно 12 у.
516. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что:
1)	ее полуоси а = 6, b = 18 (буквой а мы обозначаем полуось гиперболы, расположенную на оси абсцисс);
2)	расстояние между фокусами 2с = 10 и эксцентри-5 .
ситет е = зг,
О.	,	12
3)	уравнения асимптот у=±—х и расстояние между вершинами равно 48;
77
4)	расстояние между директрисами равно 7 -~ и экс-
7 центриситет е = у;
5)	уравнения асимптот у—± и расстояние ме-
9 жду директрисами равно 6-g-.
517. Определить полуоси а и b каждой из следующих гипербол:
1) v~V=1: 2)-^--г/а=1; 3) ^-4^ = 16;
4) х2-г/2=1; 5) 4Х2-9^=25; 6) 25х2-16^ = 1!
7)	9х2 —64z/2= 1.
518.	Дана гипербола 16х2 — 9//2 = 144. Найти: 1) полуоси а и Ь\ 2) фокусы; 3) эксцентриситету 4) уравнения асимптот; 5) уравнения директрис.
519.	Дана гипербола 16№9z/2 — —-144. Найти: 1) полуоси а и Ь* 2) фокусыj 3) эксцентриситету 4) уравнения асимптот; 5) уравнения директрис.
520.	Вычислить площадь треугольника, образованного асимптотами гиперболы -у- —	= 1 и прямой 9х-ф-
Н- 2/7 - 24 = 0.
521.	Установить, какие линии определяются следующими уравнениями:
1) = + |2) г/ = -3/^+Т;
3) x = -|VT+9; 4) У = +{/?+25.
Изобразить эти линии на чертеже.
522.	Дана точка МД10; — на гиперболе — «2
— 20" == 1. Составить уравнения прямых, на которых лежат фокальные радиусы точки Aft.
523.	Убедившись, что точка Afi (— 5; лежит на ги-\	4 /
11^
перболе -j-Q--д- = 1> определить фокальные радиусы
точки Mi.
78
524.	Эксцентриситет гиперболы 8=2, фокальный ра-диус ее точки М, проведенный из некоторого фокуса, равен 16. Вычислить расстояние от точки Л1 до односторонней с этим фокусом директрисы.
525.	Эксцентриситет гиперболы 8 = 3, расстояние от точки. М гиперболы до директрисы-равно 4. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.
526.	Эксцентриситет гиперболы е =2, центр ее лежит в начале координат, один из фокусов F(12; 0). Вычислить расстояние от точки М[ гиперболы с абсциссой, равной 13, до директрисы, соответствующей заданному фокусу.
527.	Эксцентриситет гиперболы s = -|-, центр ее лежит в начале координат, одна из директрис дана уравнением х — — 8. Вычислить расстояние от точки Mj гиперболы с абсциссой, равной 10, до фокуса, соответствующего заданной директрисе.
528.	Определить точки гиперболы — -|_=1, расстояние которых до правого фокуса равно 4,5.
529.	Определить точки гиперболы -----~ = 1, рас-
стояние которых до левого фокуса равно 7,
530.	Через левый фокус гиперболы	= 1 про-
веден перпендикуляр к ее оси, содержащей вершины. Определить расстояния от фокусов до точек пересечения этого перпендикуляра с гиперболой.
531.	Пользуясь одним циркулем, построить фокусы гиперболы -jg—(считая, что оси координат изображены и масштабная единица задана).
532.	Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны:
1)	точки Mj(6; —1) и М2(—8; 2 ]/~2) гиперболы;
2)	точка Afj (—5; 3) гиперболы и эксцентриситет е = ]/'2-
3)	точка Л4]	—1) гиперболы и уравнения асим-
птот у — ± у х\
79
г 5 \
4)	точка Mi 1 — 3; -у) гиперболы и уравнения дирек-, 4 трис х — ± -у
з
5)	уравнения асимптот у=-±-тХ и уравнения ди-ректрис х = ± —.
533.	Определить эксцентриситет равносторонней гиперболы.
534.	Определить эксцентриситет гиперболы, если отрезок между ее вершинами виден из фокусов сопряженной гиперболы под углом в 60°.
535.	Фокусы гиперболы совпадают с фокусами эл-1!^
липса 25*"^- д=1. Составить уравнение гиперболы, если ее эксцентриситет 8 = 2.
536.	Составить уравнение гиперболы, фокусы кото-рой лежат в вершинах эллипса -род Ч--^ = 1, а ди‘ ректрисы проходят через фокусы этого эллипса.
537.	Доказать, что расстояние от фокуса гиперболы X2 у2 1	,
у—ф- = 1 до ее асимптоты равно о.
538.	Доказать что произведение расстояний от любой точки гиперболы у-— до &ВУХ ее асимптот а2Ь2 есть величина постоянная, равная >
539.	Доказать, что площадь параллелограмма, ограниченного асимптотами гиперболы у—-fr = 1 и прямыми, проведенными через любую ее точку параллель-ab но асимптотам, есть величина постоянная, равная —.
540.	Составить уравнение гиперболы, если известны ее полуоси а и Ь, центр С(х0;г/0) и фокусы расположены на прямой: 1) параллельной оси Ох; 2) параллельной оси Оу.
541.	Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис:
1)	16х2—9г/2 —64х —54г/— 161 =0;
2)	9х2 - 16г/2 + 90х + 32г/ - 367 = 0;
3)	16х2-9г/2-64х-18г/+ 199 = 0.
80
v 542. Установить, какие линии определяются еле-дующими уравнениями:
1)	w = - 1 +4/х2-4х-5; о
2)	у = 7 -1 /х2 - 6л: + 13;
3)	х = 9 - 2 1Л/2 + 4(/ + 8;
4)	х = 5 - { /y2 + 4j- 12.
Изобразить эти линии на чертеже.
543.	Составить уравнение гиперболы, зная, что:
1)	расстояние между ее вершинами равно 24 и фокусы суть Fi(—10; 2), F2(I6; 2);
2)	фокусы суть Fj(3;4), F2(—3; — 4) и расстояние между директрисами равно 3,6;
3)	угол между асимптотами равен 90° и фокусы суть F, (4; —4), Л2( —2; 2).
544.	Составить уравнение гиперболы, если известны
5
ее эксцентриситет е = -^-, фокус F(5;0) и уравнение соответствующей директрисы 5х — 16 = 0.
545.	Составить уравнение гиперболы, если известны
13
ее эксцентриситет б —тГ’ фокус Г(0; 13) и уравнение соответствующей директрисы 13г/— 144 = 0.
546.	Точка А (—3; — 5) лежит на гиперболе, фокус которой F(—2;—3), а соответствующая директриса дана уравнением х-|-1=0. Составить уравнение этой гиперболы.
547.	Составить уравнение гиперболы, если известны ее эксцентриситет 8 = ^5, фокус F(2;—3) и уравнение соответствующей директрисы Зх — у 3 = 0.
548.	Точка Ah(l;—2) лежит на гиперболе, фокус которой F(—2;2), а соответствующая директриса дана уравнением 2х — у—1=0. Составить уравнение этой гиперболы.
549.	Дано уравнение равносторонней гиперболы х2 — у2 = а2. Найти ее уравнение в новой системе, приняв за оси координат ее асимптоты.
550.	Установив, что каждое из следующих уравнений определяет гиперболу, найти для каждой из них центр, полуоси, уравнения асимптот и построить их на чертеже: 1) ху = 18; 2) 2ху— 9 = 0; 3) 2ху + 25 = 0.
81
551.	Найти точки пересечения прямой 2х — у^ -10 = 0 и гиперболы — —	— 1.
552.	Найти точки пересечения прямой 4х — 3// — — 16 = 0 и гиперболы ^5 ““ ‘Тб == Ь
553.	Найти точки пересечения прямой 2х —//4~j В- 1 = 0 и гиперболы -----~ = 1.
554.	В следующих случаях определить, как расположена прямая относительно гиперболы: пересекает ли, касается или проходит вне ее:
1)Г-?-3 = 0,	£.--£=lj
2)х-2г/+1 = 0, 4~4 = 1!
3)7л-5, = 0,	£-£-1.
555.	Определить, при каких значениях т прямая у =ух + т
1) пересекает гиперболу ----= 1; 2) касается ее;
3)	проходит вне этой гиперболы.
556.	Вывести условие, при котором прямая у — kx-\-m касается гиперболы —2—-^-==1.
557.	Составить уравнение касательной к гиперболе р- —-^-=1 в ее точке М} (х^ у{).
558.	Доказать, что касательные к гиперболе, проведенные в концах одного и того же диаметра, параллельны.
559.	Составить уравнения касательных к гиперболе "2Q-----Г’==> пеРпенДикулярных к прямой 4x4-3//—•
— 7 = 0.
560.	Составить уравнения касательных к гиперболе -------~ =1, параллельных прямой 10х — 3//4-9 = 0.
561.	Провести касательные к гиперболе -jg-y® = — 1 параллельно прямой 2x4^4//— 5 = 0 и вычислить расстояние d между ними.
82
562.	На гиперболе j|-=l найти точку Мь ближайшую к прямой Зх2г/-|-1 = О, и вычислить расстояние d от точки Mi до этой прямой.
563.	Составить уравнение касательных к гиперболе х2 — г/2 =16, проведенных из точки 4(—1;— 7).
564.	Из точки С(1; —-10) проведены касательные у 2	2
к гиперболе —-----^-=1. Составить уравнение хорды,
соединяющей точки касания.
565.	Из точки Р(1;—5) проведены касательные к гиперболе ------5=*' Вычислить расстояние а
от точки Р до хорды гиперболы, соединяющей точки
касания.
566. Гипербола проходит через точку	3) и
касается прямой 9х2г/— 15 = 0. Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат.
567. Составить уравнение гиперболы, касающейся двух прямых: 5х — 6г/ — 16 = 0, 13х — Юг/— 48 = 0, при условии, что ее оси совпадают с осями ко-
ординат.
X2
20
568.	Убедившись, что точки пересечения эллипса п2	^i2
+ 4-=1 и гиперболы-пт —	1 являются вер-
О	12 о
шинами прямоугольника, составить уравнения его
сторон.
X2 У2
569.	Даны гиперболы —— р’= 1 и какая-нибудь ее касательная: Р— точка пересечения касательной с осью Ox, Q — проекция точки касания на ту же ось. Доказать, что ОР • OQ = а2.
570.	Доказать, что фокусы гиперболы расположены по разные стороны от любой ее касательной.
571.	Доказать, что произведение расстояний от фокусов до любой касательной к гиперболе 4?— -fr == 1 есть величина постоянная, равная Ь2.
572.	Прямая 2х—г/ —4 = 0 касается гиперболы, фокусы которой находятся в точках ГД—3; 0) и Г2(3;0). Составить уравнение этой гиперболы.
573.	Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение
83
касательной к гиперболе 15х’+ 16г/ — 36 = 0 и расстояние между ее вершинами 2а = 8.
574.	Доказать, что прямая, касающаяся гиперболы в некоторой точке М, составляет равные углы с фокальными радиусами FiAf, • F2M и проходит внутри угла FiMF2.
575.	Из правого фокуса гиперболы --------у- = 1
под углом сил < а < у rr 1 к оси Ох направлен луч света. Известно, что tga = 2. Дойдя до гиперболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
567. Доказать, что эллипс и гипербола, имеющие общие фокусы, пересекаются под прямым углом.
577.	Коэффициент равномерного сжатия плоскости к оси Ох равен у . Определить уравнение линии, в которую при этом сжатии преобразуется гипербола j/2 _ I 16	9 ~
Указание. См. задачу 509.
578.	Коэффициент равномерного сжатия плоскости к оси Оу равен у. Определить уравнение линии, в которую при этом сжатии преобразуется гипербола х2 г/2 ... !
25	9	1 *
579.	Найти уравнение линии, в которую преобразуется гипербола х2 — у2 = 9 при двух последовательных равномерных сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ох и Оу соответственно равны | и у.
580.	Определить коэффициент q равномерного ежа-
х2
тия плоскости к оси Ох, при котором гипербола —
у2	х^
— yr = 1 преобразуется в гиперболу уг — у = 1.
581.	Определить коэффициент q равномерного ежа-
у2
тия плоскости к оси Оу, при котором гипербола у------
^2	х^
—- -у = I преобразуется в гиперболу у — у = 1.
84
582.	Определить коэффициенты q\ и q^ двух последовательных равномерных сжатий плоскости к осям Ох и Оу, при которых гипербола-^- — уу — 1 преобразу-11% ется в гиперболу — — — 1.
1 J 25	64
§ 20. Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через
Рис. 19.
фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посредине между фокусом и директрисой (рис. 19). В этой системе координат данная парабола будет определяться уравнением
у2 = 2рх. (1)
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет
уравнение
Р
2
х =
Фокальный радиус произвольной точки Л4(х; у) параболы (т. е. длина отрезка FM} может быть вычислен по формуле
85
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параболы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис. 20), то ее уравнение будет иметь вид
У2 = — 2рх.	(2)
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
№ = 2ру,	(3)
если она лежит в верхней полуплоскости (рис. 21), и
х2 == — <2ру	(4)
— если в нижней полуплоскости (рис. 22)*
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
583.	Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
1)	парабола расположена в правой полуплоскости симметрично относительно оси Ох, и ее параметр Р = 3;
2)	парабола расположена в левой полуплоскости симметрично относительно оси Ох, и ее параметр Р = 0,5;
3)	парабола расположена в верхней полуплоскости симметрично относительно оси Оу, и ее параметр
4)	парабола расположена в нижней полуплоскости симметрично относительно оси Оу, и ее параметр р = 3.
584.	Определить величину параметра и расположение относительно координатных осей следующих парабол:
1) f/2 = 6x; 2) х2 = 5//; 3) у2 = — 4х; 4) х2— — у.
585.	Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
1)	парабола расположена симметрично относительно оси Ох и проходит через точку А (9; 6);
2)	парабола расположена симметрично относительно оси Ох и проходит через точку В(—-1; 3);
3)	парабола расположена симметрично относительно оси Оу и проходит через точку С(1; 1).
4)	парабола расположена симметрично относительно оси Оу и проходит через точку D(4;— 8).
586.	Стальной трос подвешен за два конца; точки крепления расположены на одинаковой высоте; расстояние между ними равно 20 м. Величина его прогиба на расстоянии 2 м от точки крепления, считая по горизонтали, равна 14,4 см. Определить величину прогиба этого троса в середине между точками крепления, приближенно считая, что трос имеет форму дуги параболы.
587.	Составить уравнение параболы, которая имеет фокус £(0;—3) и проходит через начало координат, зная, что ее осью служит ось Оу.
588.	Установить, какие линии определяются следующими уравнениями:
1)г/ = + 2/х; 2) у = +У~; 3) у = -3/-2г, 4) у = — 2 Ух; 5) х = + У5р; 6) х = — 5 У — у;
7) х = -УЗр-, 8) х =
Изобразить эти линии на чертеже.
589.	Найти фокус F и уравнение директрисы параболы у2 = 24х.
590.	Вычислить фокальный радиус точки М параболы у2 = 20х, если абсцисса точки М равна 7.
591.	Вычислить фокальный радиус точки М параболы у2 = 12х, если ордината точки М равна 6.
87
592.	На параболе г/2=16х найти точки, фокальный радиус которых равен 13.
593.	Составить уравнение параболы, если дан фокус F(—7;0) и уравнение директрисы х — 7 = 0.
594.	Составить уравнение параболы, зная, что ее вершина совпадает с точкой (ос,; р), параметр равен р, ось параллельна оси Ох и парабола простирается в бесконечность:
1) в положительном направлении оси Ох;
2) в отрицательном направлении оси Ох.
595. Составить уравнение параболы, зная, что ее вершина совпадает с точкой (а;р), параметр равен р, ось параллельна оси Оу и парабола простирается в бесконечность:
1) в положительном направлении оси Оу (т. е. парабола является восходящей);
2) в отрицательном направлении оси Оу (т. е. парабола является нисходящей).
596. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины А, величину параметра р и уравнение директрисы: 1) р2 = 4х —8; 2) р2 = 4 — 6х; 3) х2 = бу + 2; 4) х2 = 2 — у.
597. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины А и величину параметра р: 1) у = ~ х2 4* х + 2;
2) у = 4х2 -8x4-7; 3) у = - х2 + 2х - 7.
598. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершина А и величину параметра р:1) х = 2г/2—12г/4-14; 2) х = “ 4	3) х== ~~у2 + 2г/ — 1.
599. Установить, какие линии определяются следующими уравнениями:
1) у-3-4/Г=Т; 2) х = -4 + 3/7+5;
3)	X = 2- /6 - 2у; 4) у = -5 + / —Зх-21.
Изобразить эти линии на чертеже.
600.	Составить уравнение параболы, если даны ее фокус F(7; 2) и директриса х — 5 » 0.
601.	Составить уравнение параболы, если даны ее фокус F(4;3) и директриса =0.
88
602.	Составить уравнение параболы, если даны ее фокус F(2; —1) и директриса х —-у — 1 = 0.
603.	Даны вершина параболы А (6; — 3) и уравнение ее директрисы Зх — 5z/ + 1 = 0. Найти фокус F этой параболы.
604.	Даны вершина параболы Д (—2;—1) и уравнение ее директрисы х + 2//—1=0 Составить уравнение этой параболы.
605.	Определить точки пересечения прямой хУ— —• 3 = 0 и параболы х2 = 4у.
606.	Определить точки пересечения прямой Зх + [+ 4у —- 12 = 0 и параболы у2 — —9х.
607.	Определить точки пересечения прямой Зх — — 2у + 6 = 0 и параболы у2 — 6х.
608.	В следующих случаях определить, как расположена данная прямая относительно данной параболы — пересекает ли, касается или проходит вне ее: 1) х —// + 2 = 0, //2 = 8х; 2) 8х + 3//— 15 = 0, х2 = = —3//; 3) 5х —у — ] 5 = 0, у2 = —5х.
609.	Определить, при каких значениях углового коэффициента k прямая у — kx + 2 1) пересекает параболу у2 = 4х; 2) касается ее; 3) проходит вне этой параболы.
610.	Вывести условие, при котором прямая у — = kx + b касается параболы у2 — 2рх.
611.	Доказать, что к параболе у2 = 2рх можно провести одну и только одну касательную с угловым коэффициентом k =+ 0.
612.	Составить уравнение касательной к параболе у2 — 2рх в ее точке Mi (хг, у\).
613.	Составить уравнение прямой, которая касается параболы у2 = 8х и параллельна прямой 2х + 2// — —3 = 0.
614.	Составить уравнение прямой, которая касается параболы х2=16// и перпендикулярна к прямой 2х + + 4// + 7 = 0.
615.	Провести касательную к параболе у2 — 12х параллельно прямой Зх — 2//+ 30 = 0 и вычислить расстояние d между этой касательной и данной прямой.
616.	На параболе у2 ~ 64х найти точку ближайшую к прямой 4х + 3//—14 = 0, и вычислить расстояние d от точки Mi до этой прямой.
617.	Составить уравнения касательных к параболе //2 — збх> проведенных из точки А (2; 9).
89
618.	К параболе у2 = 2рх проведена касательная^ 'Доказать, что вершина этой параболы лежит посредине между точкой пересечения касательной с осью Ох и проекцией точки касания на ось Ох.
619.	Из точки А (5; 9) проведены касательные к параболе у2 = 5х. Составить уравнение хорды, соединяющей точки касания.
620.	Из точки Р(—-3; 12) проведены касательные к параболе у2 — 10х. Вычислить расстояние d от точки Р до хорды параболы, соединяющей точки касания.
621.	Определить точки пересечения эллипса + у2
+ "225 ~ 1 И параболы у2 = 24х.
622.	Определить точки пересечения гиперболы —
---£- = — I и параболы у2 = Зх
623.	Определить точки пересечения двух парабол: У == х2 — 2х ~|~ 1, х = у2 — бу 7.
624.	Доказать, что прямая, касающаяся параболы в некоторой точке М, составляет равные углы с фокальным радиусом точки М и с лучом, который, исходя из М, идет параллельно оси параболы в ту сторону, куда парабола бесконечно простирается.
625.	Из фокуса параболы #2=12х под острым углом а к оси Ох направлен луч света. Известно, что
= Дойдя до параболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
626.	Доказать, что две параболы, имеющие общую ось и общий фокус, расположенный между их вершинами, пересекаются под прямым углом.
627.	Доказать, что если две параболы со взаимно перпендикулярными осями пересекаются в четырех точках, то эти точки лежат на одной окружности,
§ 21. Полярное уравнение эллипса, гиперболы и параболы
Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы, имеет вид
.	Р = Л-----а>	(О
*•	1 — е cos 0
90
где р, 0 — полярные координаты произвольной точки линии, р — фокальный параметр (половина фокальной хорды линии, перпендикулярной к ее оси), е — эксцентриситет (в случае параболы е= 1). Полярная система координат при этом выбрана так, что полюс находится в фокусе, а полярная ось направлена по оси линии в сторону, противоположную ближайшей к этому фокуёу директрисы.
у 2	^*2
628. Дано уравнение эллипса -^Ч- -^ = 1- Составить его полярное уравнение, считая, что направление полярной ос?г совпадает с положительным направлением оси абсцисс, а полюс находится:
1) в левом фокусе эллипса; 2) в правом фокусе, у 2
629. Дано уравнение гиперболы — —= 1 - Составить полярное уравнение ее правой ветви, считая, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится:
1) в правом фокусе гиперболы; 2) в левом фокусе.
X2 U“	л-
630.’Дано уравнение гиперболы -£—fa = 1. Составить полярное уравнение ее левой ветви, считая, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится:
1) в левом фокусе гиперболы; 2) в правом фокусе.
631.	Дано уравнение параболы у2 == 6х. Составить ее полярное уравнение, считая, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в фокусе параболы.
632.	Определить, какие линии даны следующими уравнениями в полярных координатах:
1)	5	. п\	6 Р	1	0*	) Р 1 — cos 9 ’ 1 — — cos 9
3)	Р .	3 й’	Р 2 — cos 9 * 1 —— cos 9
5)	—	5	. fVi —	1 Р 3-4cos9 ’	Р 3 —3cos9 '
633.	Установить, что уравнение р = 13 —5cSs6 0ПРе* деляет эллипс, и найти его полуоси.
18
634.	Установить, что уравнение р =»	5’osg опре-
деляет правую ветвь гиперболы, и найти ее полуоси^
91
635.	Установить, что уравнение р= g-o^osT опРе* деляет эллипс, и составить полярные уравнения его директрис.
1g
636.	Установить, что уравнение р= 3—~VCo's~6 0ПРе’ деляет правую ветвь гиперболы, и составить полярные уравнения директрис и асимптот этой гиперболы.
637.	На эллипсе р =------- найти точки, по-
3-/2 cos 9
лярный радиус которых равен 6.
638.	На гиперболе р = -%—найти точки, по-1 г	3 — 4 cos 0
лярный радиус которых равен 3.
639.	На параболе р=п—-—найти точки: '	1 — cos 0
1)	с наименьшим полярным радиусом;
2)	с полярным радиусом, равным параметру параболы.
640.	Дано уравнение эллипса	== 1. Соста-
вить его полярное уравнение при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в центре эллипса.
641.	Дано уравнение гиперболы —-р-^1. Составить ее полярное уравнение при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в центре гиперболы.
642.	Дано уравнение параболы у2 = 2рх. Составить ее полярное уравнение при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в вершине параболы.
§ 22.	Диаметры линий второго порядка
В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, которые ей параллельны). Все диаметры эллипса и гиперболы прохо-92
дят через центр. Если эллипс задан уравнением
+^.= 1 а2 + &2
(1)
то его диаметр, сопряженный хордам с определяется уравнением
угловым коэффициентом kt
Если гипербола задана уравнением
а2 62
(2>
то ее диаметр, сопряженный хордам с угловым коэффициентом k, определяется уравнением
Ь2
У = ~~~г х.
v a2k
Все диаметры параболы параллельны ее уравнением
оси. Если парабола задана
у2 = 2рх, то ее диаметр, сопряженный хордам с опредепяется уравнением
угловым коэффициентом k,
y-i-
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.
Если k и k' — угловые коэффициенты двух взаимно сопряженных диаметров гиперболы (2), то
kk' = -~.	(3)
а2
Если k и k' — угловые коэффициенты двух взаимно сопряженных диаметров гиперболы (2), то
kk' = -^.	(4)
а*
Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.
Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.
643.	Составить уравнение диаметра эллипса +
4-== 1, проходящего через середину его хорды, отсекаемой на прямой 2х — у — 3 = 0.
93
644.	Составить уравнение хорды эллипса ‘ig+v’33 — 1, проходящей через точку Д(1;~2) и делящейся ею пополам.
645.	Составить уравнения двух взаимно сопряженных диаметров эллипса x2-]-4z/2=l, из которых один образует с осью Ох угол в 45°.
646.	Составить уравнения двух взаимно сопряженных диаметров эллипса 4х2 + 9z/2 = 1, из которых один параллелен прямой х + 2у — 5 = 0.
647.	Составить уравнения двух взаимно сопряженных диаметров эллипса х24-Зг/2=1, из которых один перпендикулярен к прямой Зх + 2у — 7 = 0.
648.	На чертеже изображен эллипс. Пользуясь циркулем и линейкой, построить его центр.
649.	Доказать, что оси эллипса являются единственной парой его главных диаметров.
650.	Пользуясь свойствами сопряженных диаметров, доказать, что каждый диаметр окружности является главным.
651.	а) В эллипс вписан равнобедренный треугольник так, что его вершина совпадает с одной из вершин эллипса. Доказать, что основание этого треугольника параллельно одной из осей эллипса.
б)	Доказать, что стороны прямоугольника, вписанного в эллипс, параллельны осям этого эллипса.
в)	На чертеже изображен эллипс. Пользуясь циркулем и линейкой, построить его главные диаметры
652.	Доказать, что хорды эллипса, соединяющие его произвольную точку с концами любого диаметра этого эллипса, параллельны паре его сопряженных диаметров.
653.	а) Доказать, что сумма квадратов двух сопряженных полудиаметров эллипса есть величина постоянная (равная сумме квадратов его полуосей).
б) Доказать, что площадь параллелограмма, построенного на двух сопряженных полудиаметрах эллипса, есть величина постоянная (равная площади прямоугольника, построенного на его полуосях).
654.	Составить уравнение диаметра гиперболы --
— ^-=1, проходящего через середину ее хорды, отсекаемой на прямой 2х — р 3 = 0.
94
655.	Дана гипербола •-—-^-=1. Составить уравнение, ее хорды, которая проходит через точку Д (3; —-1) и делится точкой А пополам.
656.	Составить уравнения двух сопряженных диаметров гиперболы х2 — 4у2 == 4, из которых один проходит через точку А (8; 1).
657.	Составить уравнения сопряженных диаметров у 2	«у 2
гиперболы -------^-=1, угол между которыми ра-
вен 45°.
658.	На чертеже изображена гипербола. Пользуясь циркулем и линейкой, построить ее центр.
659.	Доказать, что оси гиперболы являются единственной парой ее главных диаметров.
660.	На чертеже изображена гипербола. Пользуясь циркулем и линейкой, построить ее главные диаметры.
661.	Составить уравнение диаметра параболы у2 — = 12х, проходящего через середину ее хорды, отсекаемой на прямой Зх + у — 5 = 0.
662.	Дана парабола у2 — 20х. Составить уравнение ее хорды, которая проходит через точку А (2;5) и делится точкой А пополам.
663.	Доказать, что ось параболы является единственным ее главным диаметром.
664.	На чертеже изображена парабола. Пользуясь циркулем и линейкой, построить ее главный диаметр.
ГЛАВА 5
УПРОЩЕНИЕ ОБЩЕГО УРАВНЕНИЯ ЛИНИИ ВТОРОГО ПОРЯДКА. УРАВНЕНИЯ НЕКОТОРЫХ КРИВЫХ, ВСТРЕЧАЮЩИХСЯ В МАТЕМАТИКЕ И ЕЕ ПРИЛОЖЕНИЯХ
§ 23.	Центр линии второго порядка
Линия, которая в некоторой декартовой системе координат определяется уравнением второй степени, называется линией второго порядка. Общее уравнение второй степени (с двумя переменными) принято записывать в виде:
Ах2 + 2Вху + Су2 + 2Dx 4- 2Еу + F == 0.	(1)
Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами. Линии второго порядка, обладающие единственным центром, называются центральными.
Точка S(xo; Уо) является центром линии, определяемой уравнением (I), в том и только в том случае, когда ее координаты удовлетворяют уравнениям:
Ах0 4- Вуо 4- D — 0, |
Вх0 4- Су 0 4- Е == 0. J	?
Обозначим через 6 определитель этой системы:
Величина 6 составляется из коэффициентов при старших членах уравнения (1) и называется дискриминантом старших членов этого уравнения.
Если б Ф 0, то система (2) является совместной и определенной, т. е. имеет решение и притом единственное. В этом случае координаты центра могут быть определены по формулам:
	В D С Е		D А Е В
Xfl =в 	А В	Уо	А В
	В С		В С
Неравенство 6^0 служит признаком центральной линии второго порядка.
96
Если S(x0; Уо} — центр линии второго порядка, то в результате преобразования координат по формулам
X = X + Хо, у = У + УО
(что соответствует переносу начала координат в центр линии) ее уравнение примет вид
Ах2 4- 2Вху 4- Су2 4- F = О,
где А, В, С — те же, что в данном уравнении (1), a F определяется формулой
F = Dxq 4~ Еуо 4- F.
В случае 6 =# О имеет место также следующая формула:
д ’
где
А В D ВСЕ D Е F
Определитель Л называется дискриминантом левой части общего уравнения второй степени.
665.	Установить, какие из следующих линий являются центральными (т. е. имеют единственный центр), какие не имеют центра, какие имеют бесконечно много центров:
1)	Зх2 - Аху - 2у2 + Зх - 12г/ - 7 = 0;
2)	4х2 4- 5хг/ 4- Зг/2 — х 4- 9г/ — 12 = 0;
3)	4х2 — 4ху 4- г/2 — 6х 4~ 8г/ 4~ 13 = 0;
4)	4х2 — 4хг/ + У2 — 12х -j- 6г/ — 11=0;
5)	х2 — 2хг/ 4- 4г/2 + 5х — 7г/ 4- 12 = 0;
6)	х2 — 2хг/ 4~ г/2 — 6х 4- 6г/ — 3 = 0;
7)	4х2 — 20хг/ 4- 25г/2 — 14х 4- 2г/ — 15=0;
8)	4х2 - бхг/ - 9г/2 + Зх - 7г/ + 12 = 0
666.	Установить, что следующие линии явпяются центральными, и для каждой из них найти координаты центра:
1)	Зх2 4~ бхг/ 4" У2 — 8х — 11 у — 7 = 0;
2)	5х2 4- 4хг/ + 2г/2 4- 20х 4- 20г/ - 18 = 0;
3)	9х2 — 4хг/— 7г/2 — 12 = 0;
4)	2х2 - бхг/ 4- бг/2 4- 22х - 36г/ 4- 11 = 0.
667.	Установить, что каждая из следующих линий имеет бесконечно много центров; для каждой их них
4 Д, В. Клетеник	97
составить уравнение геометрического места центров:
1)	х2 - бху 4- 9г/2 — 12х+36г/+ 20 = 0;
2)	4х2 + 4ху + у2 — 8х —• 4г/ — 21 =0;
3)	25х2- Юхг/ + у2 + 40х-8г/ + 7 = 0.
668. Установить, что следующие уравнения определяют центральные линии; преобразовать каждое из них путем переноса начала координат в центр:
1)	Зх2 — бхг/ 4- 2г/2 — 4х + 2г/ + 1 — 0;
2)	бх2 + 4ху + г/2 + 4х — 2г/ + 2 = 0;
3)	4х2 + бхг/ + г/2 — 10х — 10 = 0;
4)	4х2 + 2хг/ + 6г/2 + 6х — Юг/ + 9 = 0.
669. При каких значениях тип уравнение тх2 + 12хг/ + 9г/2 + 4х + пу — 13 = 0 определяет:
1)	центральную линию;
2)	линию без центра;
3)	линию, имеющую бесконечно много центров.
670.	Дано уравнение линии 4х2-—4хг/+ г/2 + 6х + + 1 = 0. Определить, при каких значениях углового коэффициента k прямая у — kx: 1) пересекает эту линию в одной точке; 2) касается этой линии; 3) пересекает эту линию в двух точках; 4) не имеет общих точек с этой линией.
671.	Составить уравнение линии второго порядка, которая, имея центр в начале координат, проходит через точку Л4(6;—2) и касается прямой х —2 = 0 в точке ЛД2;0).
672.	Точка Р(1;—• 2) является центром линии второго порядка, которая проходит через точку Q(0; —-3) и касается оси Ох в начале координат. Составить уравнение этой линии.
§ 24. Приведение к простейшему виду уравнения центральной линии второго порядка
Пусть дано уравнение
Ах2 4- 2Вху 4- Су2 4- 2/?х 4- 2Еу 4- F ~ 0,	(1)
определяющее центральную линию второго порядка (6=ДС—В2^=0). Перенося начало координат в центр S(x0; у0) этой линии и 98
преобразуя уравнение (1) по формулам
X — X + Хо, у = у + Уо, получим:
Ах2 + 2В ху + Су2 + Р = Ъ.	(2)
Для вычисления F можно пользоваться формулой
F — Dx0 + Еуо + F или f s= А.
Дальнейшее упрощение уравнения (2) достигается при помощи преобразования координат
х — х cos а — у' sin а, 1
у — х sin а + У' cos а, ) соответствующего повороту осей на угол а.
Если угол а выбран так, что
Btg2a-(C~4)tga-B==0,	(4)
то в новых координатах уравнение линии примет вид
/ГУ2+ <?'/ + £ = О,	(5)
где Л'#=0, C'^Q.
Замечание. Уравнение (4) позволяет определить tg ос, тогда как в формулах (3) участвуют sin а и cos а. Зная tg а, можно найти sin а и cos a по формулам тригонометрии
tg a	1
sin a ==---r. -z—,	cos a = —-y— —	.
± pl + tg2 a	± у 1 + tg2 a
Между коэффициентами уравнений (1) и (5) существуют важные соотношения:
А'С' — АС — В2, А' + С' = А + С, которые позволяют определить коэффициенты А' и С', не проводя преобразования координат.
Уравнение второй степени называется эллиптическим, если 6 > 0, гиперболическим, если 6 < О, и параболическим, если 6 = 0.
Уравнение центральной линии может быть, только эллиптическим или гиперболическим.
Ках<дое эллиптическое уравнеиие является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (т. е. определяет единственную точку), либо мнимого эллипса (в этом случае уравнение не определяет никакого геометрического образа).
Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную гиперболу (т. е. пару пересекающихся прямых).
673.	Определить тип каждого из следующих уравнений*); каждое из них путем параллельного переноса
*) То есть установить, какие из них являются эллиптическими, какие гиперболическими и какие параболическими.
4*	99
осей координат привести к простейшему виду; установить, какие геометрические образы они определяют, и изобразить на чертеже расположение этих образов относительно старых и новых осей координат:
1)	4х2 4- 9у2 — 40х + 36f/ 4- 100 = 0;
2)	9х2 - 16г/2 — 54х - 64г/ — 127 = 0;
3)	9х2 + 4г/2 4- 18х — Зу 4- 49 = 0;
4)	4х2 —г/24-8х —2г/4-3 = 0;
5)	2х2 4- Зг/2 4- 8х — 6г/ 4- 11 == 0.
674. Каждое из следующих уравнений привести к простейшему виду? определить тип каждого из них; установить, какие геометрические образы они определяют, и изобразить на чертеже расположение этих образов относительно старых и новых осей координат:
1)	32х2 4- 52хг/ — 7г/2 4- 180 = 0;
2)	5х2 - Зху 4- 5г/2 — 32 = 0;
3)	17х2—12хг/4-8г/2 = 0;
4)	5х24-24хг/ — 5г/2 = 0;
5)	5х2 — бхг/ 4- 5г/2 4~ 8 = 0.
675. Определить тип каждого из следующих уравнений при помощи вычисления дискриминанта старших членов:
1)	2х2 4- Юхг/ 4- 12г/2 — 7х 4-' 18г/ — 15 == 0;
2)	Зх2 — Зху 4- 7г/2 4- 8х — 15г/ 4- 20 = 0;
3)	25х2 — 20хг/ 4- 4г/2 — 12х 4- 20у — 17 = 0;
4)	5х24-14хг/4-11г/24-12х —7г/4-19 = 0;
5)	х2 — 4хг/ 4- 4г/2 4- 7х - 12 = 0;
6)	Зх2 —2хг/— Зу24-12г/—15 = 0.
676.	Каждое из следующих уравнений привести к каноническому виду; определить тип каждого из них; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной координатной системы, оси других координатных систем, которые вводятся по ходу решения, и геометрический образ, определяемый данным 100
уравнением: 
,	1) Зх24- 1 Ox# 4-З#2 — 2х — 14г/— 13 = 0;
2)	25х2 — \4ху 4- 25г/2 4- 64х - 64# — 224 = 0;
3)	4х# 4-З#2 4-16x4-12# —36 = 0;
4)	7х2 + Qxy — г/2 4- 28х 4- 12у 4- 28 = 0;
5)	19х24-6хг/4- 11г/2 4-38x4-6г/4-29 = 0;
' 6) 5х2 — 2хг/ 4- 5г/2 — 4х 4- 20# 4- 20 = 0.
677.	То же задание, что и в предыдущей задаче, выполнить для уравнений:
1)	14х24- 24хг/ 4-,21г/2 —4x4- 18г/ — 139 = 0;
2)	Их2 — 20х# — 4г/2 — 20х — 8у + \ = 0;
3)	7х2 4- бОхг/ 4- 32г/2 — 14х — 60г/ 4- 7 = 0;
4)	50х2 —8хг/4-35г/24-ЮОх —8г/4-67 = 0;
5)	41х2 4- 24хг/ 4- 34г/2 4- 34х — 112г/ 4- 129 = 0;
6)	29х2 — 24хг/ 4- 36г/2 4- 82х - 96# — 91 = 0;
7)	4х2 4- 24хг/ 4- 11г/2 4- 64х 4- 42# 4- 51 = 0;
8)	41х2 + 24хг/4-9г/24-24х4- 18г/ — 36 = 0.
678.	Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет эллипс, и найти величины его полуосей:
1)	41х24-24хг/4-9г/2 4- 24х-|-18# —36 = 0;
2)	8х2 4- 4х# 4- 5#2 4- 16х 4- 4# — 28 = 0;
3)	13х2 4-18х#4-37#2 — 26х—18# 4-3 = 0;
4)	13х2 4- 10х# 4- 13#2 4- 46х 4- 62# 4- 13 = 0.
679. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет единственную точку (вырожденный эллипс), и найти ее координаты:
1)	5х2 — 6х# 4- 2#2 — 2х 4- 2 = 0;
2)	х24-2х#4-2#24-6#4-9 = 0;
3)	5х24-4х#4-#2-6х-2#4-2 = 0;
4)	х2 — 6х# 4- 10#2 4- 10х — 32# 4- 26 = 0.
680. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет
101
гиперболу, и найти величины ее полуосей:
1)	4х2 4-24х//4“ 11//2 4-64х 4-42//4-51 =0;
2)	12x2 + 26хг/ 4- 12у2 — 52х - 48у 4- 73 = 0=
3)	Зх2 4-4х//— 12х 4- 16 = 0;
4)	х2 — бху — 7 г/2 + 10х — 30// + 23 = 0.
681. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет пару пересекающихся прямых (вырожденную гипер-. болу), и найти их уравнения:
1)	3x2	4х// + //2 - 2х — 1 = 0;
2)	х2 — 6х// + 8у2 — 4у — 4 = 0;
3)	х2 — 4ху 4- З//2 = 0;
4)	х2 4- 4ху 4- З//2 — 6х — 12// 4- 9 = 0.
682. Не проводя преобразования координат, установить, какие геометрические образы определяются следующими уравнениями;
' 1) 8х2—12хг/4-I?//2 + 16х—12//4-3 = 0;
2)	17х2— 18х// — 7//24- 34^— 18//4-7 = 0;
3)	2х2 + 2ху — 2у2 4- 5х 4- 10// = 0;
4)	6х2 —6х//4-9//2-4х4-18//4-14 = 0;
z 5) 5х2 — 2ху 4- 8у2 — 4х 4- 20// 4- 20 = 0.
683.	Для любого эллиптического уравнения доказать, что ни один из • коэффициентов А и С не может обращаться в нуль и что они суть числа одного знака.
684.	Доказать, что эллиптическое уравнение второй степени (б > 0) определяет эллипс в том и только в том случае, когда А и А суть числа разных знаков.
685.	Доказать, что эллиптическое уравнение второй степени (6 > 0) является уравнением мнимого эллипса в том и только в том случае, когда А и А суть числа одинаковых знаков.
686.	Доказать, что' эллиптическое уравнение второй степени (6 > 0) определяет вырожденный эллипс (точку) в том и только в том случае, когда А = 0.
687.	Доказать, что гиперболическое уравнение второй степени (6 < 0) определяет гиперболу в том и только в том случае, когда А 0<
102
688.	Доказать, что гиперболическое уравнение второй степени (б < 0) определяет вырожденную гиперболу (пару пересекающихся прямых) в том и только в том случае, когда Д = 0.
§ 25.	Приведение к простейшему виду параболического уравнения
Пусть уравнение
Лх2 + 25ry + Q2 + 2Dx + 2£# + Г = 0	(1)
является параболическим, т. е. удовлетворяет условию
В этом случае линия, определяемая уравнением (1), либо не имеет центра, либо имеет бесконечно много центров. Упрощение параболического уравнения целесообразно начать с поворота координатных осей, т. е. сначала преобразовать уравнение (I) при помощи формул
х = х' cos а — у' sin а, ) у = х' sin а + у cos а. J
Угол а следует найти из уравнения
В tg2 а — (С — Л) tg а — В = 0;	(3)
тогда в новых координатах уравнение (1) приводится либо к виду
Ах2 4- 2D'x + 2EV + F == 0,	(4)
где А Ф 0, либо к виду
Сул + 2D'x' + 2Е'у + F = 0,	(5)
где С' ф 0.
Дальнейшее упрощение уравнений (4) и (5) достигается путем параллельного перенесения (повернутых) осей.
689.	Установить, что каждое из следующих уравнений является параболическим; каждое из них привести к простейшему виду; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной координатной системы, оси других координатных систем, которые вводятся по ходу решения, и геометрический образ, определяемый данным уравнением:
1)	9х2 — 24ху +' 16г/2 — 20х	110г/ — 50 = 0;
2)	9х2+12хг/4-4г/2 — 24х — 16г/4-3 = 0;
3)	16х2 - 24хг/ 4- 9г/2 — 160х & 1	± 425 = б.
103
690. То же задание, что и в предыдущей задаче, выполнить для уравнений:
1)	9x2 + 24хг/ -|- 16г/2 - 18х 4- 226^’4- 209 = 0;
2)	х2 — 2ху + у2 — 12х + 12г/ - 14 « 0|
3)	4х2 -J- 12хг/ 4- 9//2 — 4х — Gy +' 1 » 0.
691.	Для любого параболического уравнения доказать, что коэффициенты Л и С не могут быть числами разных знаков и что они одновременно не могут обращаться в нуль.
692.	Доказать, что любое параболическое уравнение может быть написано в виде:
(ах4~ Р^/)2 И- 2Dx 2Еу 4- F == 0.
Доказать также, что эллиптические и гиперболические уравнения в таком виде не могут быть написаны.
693.	Установить, что следующие уравнения являются параболическими, и записать каждое из них в виде, указанном в задаче 692:
1)	х2 4-4хг/4-4#2 4-4x4-# —15 = 0;
2)	9х2 — Gxy 4- г/2 — х 4- 2г/ — 14 = 0;
3)	25х2 — 20хг/ 4- 4у* 4- Зх — у 4- 11 = 0;
4)	16х24-16ху4-4г/2 — 5х’4-’7у = 0;
5)	9х2 — 42хг/ 4- 49г/2 4- Зх - 2у — 24 « 0.
694.	Доказать, что если уравнение второй степени является параболическим и написано в виде
(ах ’+ рг/)2 4-2Z)x 4-2£г/4-= 0»
то дискриминант его левой части определяется формулой
Д = — (Dp — £а)2.
695.	Доказать, что параболическое уравнение
(ах 4- рг/)2 4-2Dx 4-2£у + F = 0
при помощи преобразования
x = x'cos0 — w'sinQ,
у	tg 6 = — Л
у — х' sin 0 4- г/соэб,	Р
приводится к виду
Су’2 + 2D'x' + 2Е'у' 4- F' = 0,
104
где
С' = а’ + ^, D' = ±1/^,
а Д— дискриминант левой части данного уравнения.
696.	Доказать, что параболическое уравнение определяет параболу в том и только в том случае, когда Д =/= 0. Доказать, что в этом случае параметр параболы определяется формулой
/- А
(4 + С)3 *
697.	Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет параболу, и найти параметр этой параболы:
1)	9х2 + 24хг/ + 16г/2 - 120х + 90г/ = 0;
2)	9х2 - 24хг/ 4- 16г/2 - 54х - 178г/ 4- 181 = 0;
3)	х2 - 2ху + У' 4- 6х - 14г/ + 29 = 0;
4)	9х2 — бхг/ + г/2 — 50х 4- 50г/ — 275 = 0.
698. Доказать, что уравнение второй степени является уравнением вырожденной линии в том и только в том случае, когда Д = 0.
699. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет пару параллельных прямых, и найти их уравнения:
1)	4х2 4- 4хг/ + у2 — 12х — 6г/ + 5 = 0;
2)	4х2 - 12хг/ + 9г/2 + 20х - 30г/ - 11 = 0;
3)	25х2 — 1 Охг/ 4- У2 4- 1 Ох — 2г/ — 15 = 0.
700. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет одну прямую (пару слившихся прямых), и найти уравнение этой прямой:
1)	х2-6хг/4-9г/2+4х-12г/ + 4 = 0;-
2)	9х2 4- ЗОхг/ 4- 25г/2 4- 42х -J- 70г/	49 = 0;
3)	16x2 - 16хг/ + 4г/2 — 72х 4- 36г/ 4-81=0.
§ 26. Уравнения некоторых кривых, встречающихся в математике и ее приложениях
701.	Составить уравнение геометрического места точек, произведение расстояний которых до двух данных точек Fi(— с\ 0) и F2(c; 0) есть постоянная величина а2.
105
Такое геометрическое место точек называется овалом Кассини (рис. 23).
702.	Составить уравнение геометрического места точек, произведение расстояний которых до двух данных точек Л(— а\ 0) и F2(a; 0) есть постоянная величина о2. Такое геометрическое место точек называется лемнискатой (рис. 24). (Уравнение лемнискаты сначала найти непосредственно, потом — рассматривая ее как частный вид овала Кассини.) Составить также уравнение
лемнискаты в полярных координатах, совмещая полярную ось с положительной полуосью Ох и полюс с началом координат.
703.	Составить уравнение геометрического места оснований перпендикуляров, опущенных из начала координат на прямые, отсекающие от координатного угла треугольники постоянной площади S.
Указание. Составить уравнение сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох.
704.	Доказать, что геометрическое место точек задачи 703 есть лемниската (см. задачу 702).
Указание. Повернуть координаты оси на угол в 45°.
705.	Луч а, в начальном положении совпадающий с полярной осью, вращается вокруг полюса О с постоянной угловой скоростью (0.
Составить в данной системе полярных координат уравнение траектории точки М, которая, имея начальное положение в О, движется по лучу а равномерно со скоростью v (спираль Архимеда, рис. 25).
706.	Даны прямая х = 2г и окружность радиуса г, которая проходит через начало координат О и касается данной прямой. Из точки О проведен луч, пересекающий 106
данную окружность в точке В и данную прямую в точке С, на котором отложен отрезок ОМ = ВС (рис. 26). При вращении’ луча длина отрезка ОМ меняется и точка Л1 описывает кривую, называемую циссоидой- Составить уравнение циссоиды.
707.	Даны прямая х = а (а > 0) и окружность диаметра а, проходящая через начало координат О и касающаяся данной прямой. Из точки О проведен луч, пересекающий окружность в точке А и данную прямую в точке В. Из точек А и В проведены прямые, параллельные соответственно осям Оу и Ох (рис. 27). Точка М
пересечения этих прямых при вращении луча описывает кривую, называемую верзьерой. Составить ее уравнение.
708.	Из точки А (—а; 0), где а > 0, проведен луч АВ (рис. 28), на котором по обе стороны от точки В отложены отрезки BMnBN одинаковой длины b (b = const)« При вращении луча точки М и N описывают кривую, называемую конхоидой. Составить ее уравнение сначала в полярных координатах, помещая полюс в точку А и направляя полярную ось в положительном направлении оси Ох, а затем перейти к данной системе декартовых прямоугольных координат.
709.	Из точки А (—• а\ 0), где а > 0, проведен луч АВ (рис. 29), на котором по обе стороны от точки В отложены отрезки ВМ и BN, равные ОВ, При вращении луча
107
точки М и N описывают кривую, называемую строфоидой. Составить ее уравнение сначала в полярных координатах, помещая полюс в точке А и направляя полярную ось в положительном направлении оси Ох, а затем перейти к данной системе декартовых прямоугольных координат.
Рис. 28.
Рис. 29.
Рис. 30.
710.	Из начала координат проведен луч, пересекающий данную окружность х2 + у2 = 2ах (о > 0) в точке В (рис. 30); на луче по обе стороны от точки В отложены равные между собой отрезки ВМ и BN постоянной длины Ь. При вращении луча точки М и N описывают кривую, называемую улиткой Паскаля (рис. 30). Составить ее уравнение сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат.
711.	Отрезок длины 2а движется так, что его концы все время находятся на координатных осях. Составить уравнение траектории основания М перпендикуляра, опущенного из начала координат на отрезок (рис. 31), сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат. Точка М описывает кривую, называемую ч ет ы р е х л е п е с т ко в о й розой.
712.	Отрезок длины а движется так, что его концы все время находятся на координатных осях (рис. 32). Через концы отрезка проведены прямые, параллельные координатным осям, до их взаимного пересечения в точ-108
ке Р. Составить уравнение траектории основания М перпендикуляра, опущенного из точки Р на отрезок. Эта траектория называется астроидой.
Указание Составить сначала параметрические уравнения астроиды, выбирая параметр t, как указано на рис. 32 (затем исклю чить параметр t)
713.	Из точки В пересечения луча ОВ с окружностью х2 + «/2 = ах опущен перпендикуляр ВС на ось Ох. Из точки С на луч ОВ опущен перпендикуляр СМ. Вы
вести уравнение траектории точки М сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с
положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат.
714.	Нить, намотанная на окружность х2 у2 = у2, разматывается так, что в точке В, где нить отделяется от окружноси, она остается касательной к ней (рис. 33).
109
круга называется
Рис. 35.
Найти параметрические уравнения линии, описываемой концом нити, если начальным положением конца является точка Л (о? 0), где а > 0. Линия, о которой идет речь, называется эвольвентой круга.
715.	Круг радиуса а катится без скольжения по оси Ох. Траектория некоторой точки Л4 окружности этого циклоидой (рис. 34). Вывести параметрические уравнения циклоиды, принимая в качестве параметра t угол, на который поворачивается катящаяся окружность вокруг своего центра; считать при этом, что в начальный момент (t == 0) точка М находится в начале координат. Исключить параметр t из полученных уравнений.
716. Круг радиуса а катится без скольжения по окружности х2 + у2 = а2, оставаясь вне ее.
Траектория некоторой точки М окружности катящегося круга называется кардиоидой (рис. 35). Вывести параметрические уравнения кардиоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведенного в точку касания с подвижной. Считать при этом, что в начальный момент ;(/==0) точка М находится справа на оси Ох. Перейти к полярным координатам при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в точке А. Доказать, что кардиоида есть частный вид улитки Паскаля (см, задачу 710).
717.	Круг радиуса а катится без скольжения по окружности х2 + У2 — Ь2, оставаясь вне ее. Траектория некоторой точки М окружности катящегося круга называется эпициклоидой (рис. 36). Вывести параметрические уравнения эпициклоиды, выбирая в качестве параметра 1 угол наклона к оси Ох радиуса неподвижной окружности, проведенного в точку касания с подвижной; считать при этом, что в начальный момент (/ — 0) точка М находится справа на оси Ох. Доказать, что кардиоида (см. задачу 716) есть частный вид эпициклоиды.
718.	Круг радиуса а катится без скольжения по окружности х^ ^у2 = Ь2, оставаясь внутри нее. Траектория НО
некоторой точки М окружности катящегося круга называется гипоциклоидой (рис. 37). Вывести параметрические уравнения гипоциклоиды, выбирая в качестве
параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведенного в точку касания с подвижной; считать при этом, что в начальный момент (/ = 0) точка М находится справа на оси Ох. Доказать, что астроида (см. задачу 712) есть частный вид гипоциклоиды.
ЧАСТЬ ВТОРАЯ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
ГЛАВА 6
НЕКОТОРЫЕ ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В ПРОСТРАНСТВЕ
§ 27.	Декартовы прямоугольные координаты в пространстве
Декартова прямоугольная система координат в пространстве определяется заданием линейной единицы для измерения длин и трех пересекающихся в одной точке взаимно перпендикулярных осей, занумерованных в каком-либо порядке.
Точка пересечения оси — осями координат.
осей называется началом координат, а сами Первая координатная ось называется осью абсцисс, вторая — осью ординат, третья — осью апликат.
Начало координат обозначается буквой О, оси координат обозначаются соответственно символами Ох, Оу, Oz.
Пусть М — произвольная точка пространства, Л1Х, Му и Mz — ее проекции на координатные оси (рис. 38).
Координатами точки М в заданной системе называются числа:
х — ОМХ, у = ОМУ, z = OMZ
(рис. 38), где ОМХ есть величина отрезка ОМХ оси абсцисс, ОЛ1У — величина отрезка ОМУ оси ординат, ОМг — величи
на отрезка ОМг оси апликат. Число х называется абсциссой, у — ординатой, z— апликатой точки Л1. Символ M(x\y\z) обозначает, что точка М имеет координаты х, у, г.
Плоскость Оуг разделяет все пространство на два полупро-
странства; то из них, которое расположено ь положительном направлении оси Ох, называется ближним, другое — дальним. Плоскость Oxz также разделяет пространство на два полупространства; то из них, которое расположено в положительном направлении оси Оу, называется правым, другое — левым. Наконец, и плоскость Оху разделяет пространство на два полупространства; то из них, которое расположено в положительном направлении оси Oz, называется верхним, другое — нижним.
112
Три плоскости Оху, Oxz и Оуг вместе разделяют пространство на восемь частей; их называют координатными октантами и нумеруют так, как показано на рис. 39.
719.	Построить (в аксонометрической проекции) следующие точки по их декартовым координатам: А (3;4;6), В(-5; 3; 1), С(1; -3; -5), £>(0; -3; 5), Е(-3; -5; 0)
и F(—1; -5; -3).
720.	Найти координаты проекций точек 4(4; 3; 5), В(-3; 2; 1), С(2; —3; 0) и £>(0; 0; —3): 1) на плоскость Оху, 2) на плоскость Oxz\ 3) на плоскость Oyz\ 4) на ось абсцисс; 5) на ось ординат; 6) на ось апликат.
721.	Найти координаты точек, симметричных точкам 4 (2; 3; 1), В(5; -3; 2), С(—3; 2; -1) и D(a; b\ с) относительно: 1) плоскости
Рис. 39.
Оху, 2) плоскости Oxz',
3) плоскости Oyz\ 4) оси абсцисс; 5) оси ординат;
6) оси апликат; 7) начала координат.
722. Даны четыре вершины куба: 4(—о; — а\ —а),
В(а\ —ст, —а); С(—а; а; —а) и D(а; а\ а). Определить
его остальные вершины.
723.	В каких октантах могут быть расположены точки, координаты которых удовлетворяют одному из следующих условий: 1) х — у = 0; 2) х + У — 0; 3) х — z = = 0; 4) х 4- z = 0; 5) у — z = 0; 6) у 4- z = 0.
724.	В каких октантах могут быть расположены точки, если: 1) хг/ > 0; 2) xz < 0; 3) yz > 0; 4) xyz > 0; 5) xyz < 0.
725.	Найти центр шара радиуса R = 3, который касается всех трех координатных плоскостей и расположен: 1) во втором октанте; 2) в пятом октанте; 3) в шестом октанте; 4) в седьмом октанте; 5) в восьмом октанте.
§ 28.	Расстояние между двумя точками.
Деление отрезка в данном отношении
Расстояние d между двумя точками ЛЬ (хц гд; zj) и Ad2(X2i Уг\ г2)) в пространстве определяется формулой
d =	Х1)2 4- U/2 - УхУ1 + (г2 - Z02.
113
Координаты х, у, г точки М, которая делит отрезок MiM2t ограниченный точками г/г, zj и М2(Х2’> Уъ' z2), в отношении X, определяются по формулам:
.. _ *1 + Лх2 ___У\ + Хг/Я _ _ Z1 + 2v?2
1 + Л ’ у Ц-Л *	г~~ 1+Л •
В частности, при X — 1 имеем координаты середины данного отрезка:
_ Xi + х2	У\ + У2 „ zj + г2
х	2	’ У	2	’ г-------2 *
726.	Даны точки: Д(1; —2; —3), 5(2; —3; 0), 0(3; 1; —9), D(— 1; 1; 12). Вычислить расстояние между 1) А и С; 2) В и D-, 3) С и D.
727.	Вычислить расстояния от начала координат О до точек: Д(4; —2; —4), 5( —4; 12? 6), С(12; —4; 3), £>(12; 16; -15).
728.	Доказать, что треугольник с вершинами /1(3; —1; 2), 5(0; —4; 2) и С(—3; 2; 1) равнобедренный.
729.	Доказать, что треугольник с вершинами Zh(3; -1; 6), Л2(-1, 7; -2) и Д3(1; -3; 2) прямоугольный.
730.	Определить, есть ли тупой угол среди внутренних углов треугольника /4,(4; —1; 4), Л12(0; 7; —4), Мз(3; 1; -2).
731.	Доказать, что внутренние углы треугольника Л4(3; -2; 5), ЛЦ—2; 1; -3), 5(5; 1? —1) острые.
732.	На оси абсцисс найти точку, расстояние которой от точки А (—3; 4; 8) равно 12.
733.	На оси ординат найти точку, равноудаленную от точек 4(1; —3; 7) и 5(5; 7; —5).
734.	Найти центр С и радиус R шаровой поверхности, которая проходит через точку Р(4; —I; —1) и касается всех трех координатных плоскостей.
735.	Даны вершины МДЗ; 2; —5), М2(1; —4; 3) и Л43(—3; 0; 1) треугольника. Найти середины его сторон.
736.	Даны вершины А (2; —1; 4), 5(3; 2; —6), С (—5; 0; 2) треугольника. Вычислить длину его медианы, проведенной из вершины А.
737.	Центр тяжести однородного стержня находится в точке С(1; —1; 5), один из его концов есть точка А (—2; —1; 7). Определить координаты другого конца стержня.
738.	Даны две вершины А (2; —3; —5), 5(—1; 3; 2) параллелограмма ABCD и точка пересечения его диаго-114
-
налей £(4; — 1; 7). Определить две другие вершины этого параллелограмма.
739.	Даны три вершины А (3; —4; 7), В (—5; 3; —2) и С(1; 2; —3) параллелограмма ABCD. Найти его четвертую вершину D, противоположную В,
740.	Даны три вершины 4(3; —1? 2), В(1; 2; —4) и С(—1; If 2) параллелограмма ABCD. Найти его четвертую вершину D.
741.	Отрезок прямой, ограниченный точками 71 (— 1; 8; 3) и В (9; —7; —2), разделен точками С, D, В, F на пять равных частей. Найти координаты этих точек.
742.	Определить координаты концов отрезка, который точками 0(2; 0$ 2) и D(5; — 2; 0) разделен на три равные части.
743.	Даны вершины треугольника 4(1; 2; — 1), В (2; —1; 3) и С (—4; 7; 5). Вычислить длину биссектрисы его внутреннего угла при вершине В.
744.	Даны вершины треугольника 4(1; — 1; — 3), В (2; 1; —2) и С(—5; 2; —6). Вычислить длину биссектрисы его внутреннего угла при вершине А.
745.	В вершинах тетраэдра 4(хг, t/i; zj, B(x2; z/2; <z2), С(х3; уз\ z3), О(хе, у&; z4) сосредоточены равные массы. Найти координаты центра тяжести системы этих масс.
746.	В вершинах тетраэдра 4i(xi; yi\ Zi), 42(х2; г/2; z2), 43(.r3; z/з; г3), 44(а; уе, сосредоточены массы т2, т3 и т4. Найти координаты центра тяжести системы этих масс.
747.	Прямая проходит через две точки МД—1; 6; 6) и М2(3; —6; —2). Найти точки ее пересечения с координатными плоскостями,
Г Л А В A 7
ВЕКТОРНАЯ АЛГЕБРА
§ 29.	Понятие вектора. Проекции вектора
Направленные отрезки принято называть также геометрическими векТорами или просто векторами. Вектор как направленный отрезок мы будем по-прежнему записывать в тексте двумя большими латинскими буквами с общей чертой наверху при условии, что первая из них обозначает начало, вторая — конец вектора. Наряду с этим мы будем также обозначать вектор одной малой латинской буквой полужирного шрифта, которая на чертежах ставится у конца В стрелки, изображающей вектор (см, ^иИ<*****^	рис. 40, где изображен вектор а с нача-
лом А и концом В). Начало вектора часто будет называться также его точкой прило-
Рис. 40.	жен”я-
Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону.
Число, равное длине вектора (при заданном масштабе), называется его модулем. Модуль вектора а обозначается символом |а| или а. Если |а| — 1, то вектор а называется единичным.
Единичный вектор, имеющий одинаковое направление с данным вектором а, называется ортом вектора а и обозначается обычно символом аа
Проекцией вектора АВ на ось и называется число, равное величине отрезка AiB] оси и, где точка Ai является проекцией на ось и точки А, а В\ — проекцией на эту ось точки В.
Проекция вектора АВ на ось и обозначается символом: приДЖ Если вектор обозначен символом а, то его проекцию на ось и принято обозначать: приа
Проекция вектора а на ось и выражается через его модуль и угол <р наклона к оси и формулой
прйа = | а |  cos <р.	(!)
Проекции произвольного вектора а на оси некоторой заданной системы координат в дальнейшем обозначаются буквами X, У, Z. Равенство
а = {Х; У; Z}
116
означает, что числа X, У, Z являются проекциями вектора на координатные оси.
Проекции вектора на координатные оси называют также его (декартовыми) координатами. Если даны две точки Mj(xr, yr, 2j) и Л12(х2; У2', Z2), являющиеся соответственно началом и концом вектора а, то его координаты X, У, Z определяются по формулам
Х = х2 — Y = y2 — у}, Z = z2 — zv
Формула
| а | = V X2 + Y2 + Z2	(2)
позволяет по координатам вектора определить его модуль.
Если а, р, у — углы, которые составляет вектор а с координатными осями (рис. 41), то cos a, cos 0, cosy называются направляю-
щими косинусами вектора а.
Вследствие формулы (1)
X = |a|cosa, y==|a|cosp, Z=|a]cosy.
Отсюда и из формулы (2) следует, что cos2 a + cos2 Р + cos2 у = 1.
Последнее равенство позволяет определить один из углов a, р, у, если известны два Других.
748.	Вычислить модуль вектора а = {6; 3; —2}.
749.	Даны две координаты вектора X — 4, ¥ = —12. Определить его третью координату Z при условии, что | а| = 13.
750.	Даны точки Д(3; —1; 2) и
В(-1; 2; 1). Найти
координаты векторов АВ и В А.
751.	Определить точку /V, с которой совпадает конец вектора а = {3; — 1; 4), если его начало совпадает с точкой М(1; 2; -3).
752.	Определить начало вектора а — {2; —3; — 1}, если его конец совпадает, с точкой (1; —1; 2).
753.	Дан модуль вектора |а| =2 и углы а = 45°, р = 60°, у = 120°. Вычислить проекции вектора а на ко
ординатные оси.
754.	Вычислить направляющие косинусы вектора а = == {12;—15;-16}.
755.	Вычислить направляющие косинусы вектораа — ==JA.	J21
(13’ 13’ 13J*
756.	Может ли вектор составлять с координатными осями следующие углы: 1) а = 45°, р = 60°, у = 120е; 2) a = 45°, {3=135°, у = 60°; 3) a = 90°, р == 150°; у = 60°?
117
757.	Может ли вектор составлять с двумя координатными осями следующие углы: 1) а = 30°, (3 = 45°; 2) р = = 60°, у = 60°; 3) а = 150°, у = 30°?
758.	Вектор составляет с осями Ох и Oz углы а=120° и у — 45°. Какой угол он составляет с осью Оу>
759.	Вектор а составляет с координатными осями Ох и Оу углы а = 60°, р = 120°. Вычислить его координаты при условии, что |а| =2.
760.	Определить координаты точки /И, если ее радиус-вектор составляет с координатными осями одинаковые углы и его модуль равен 3.
§ 30. Линейные операции над векторами
Суммой а + b двух векторов а и b называется вектор, который идет из начала вектора а в конец вектора b при условии, что вектор b приложен к концу вектора а (правило треугольника). Построение суммы а + b изображено на рис. 42.
Рис. 43.
Наряду с правилом треугольника часто пользуются (равносильным ему) . п р а в и л о м параллелограмма: если векторы а и b приведены к общему началу и на них построен параллелограмм, то сумма а + Ь есть вектор, совпадающий с диагональю этого параллелограмма, идущей из общего начала а и b (рис. 43). Отсюда сразу следует, что а -г b — о + а.
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 44, где изображено построение суммы четырех векторов a, 6, с, d).
Разностью а — b двух векторов а и b называется вектор, который в сумме с вектором Ъ составляет вектор а. Если два вектора а и Ъ приведены к общему началу, то разность их а — Ъ есть вектор, идущий из конца Ь («вычи-шьшаемого»). Два вектора равной дли
ны, лежащие на одной прямой и направленные в противоположные стороны, называются взаимнообратными: если один • из них обозначен символом а, то другой обозначается символом —а. Легко
118
видеть, что а — Ъ-а-}-(—Ь}. Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемому».
Произведением аа (или также аа) вектора а на число а называется вектор, модуль которого равен произведению модуля вектора а на модуль числа а; он параллелен вектору а или лежит с ним на одной прямой и направлен так же, как вектор а, если а — число положительное, и противоположно вектору а, если а — число отрицательное.
Сложение векторов и умножение вектора на число называются линейными операциями над векторами.
Имеют место следующие две основные теоремы о проекциях векторов:
1.	Проекция суммы векторов на какую-нибудь ось равна сумме их проекций на эту же ось:
nPa (at] 4- а2 4" • • • 4“ fln) — nputii 4* праа2 4* • • • 4“ прйа^.
2.	При умножении вектора на число его проекция умножается на то же число;
при (аа) — а np«a.
В частности, если
а = {Х1; Г,; ZJ, &=№; У2; Z2)3 то
а 4- Ь = {JV| 4- Я2; ^14*^21 ZiH~Z2}
и
а _ ь = (X, - Х2; Ki - У2; Z. - Z2}.
Если a=={Z; У; Z}, то для любого числа а
аа == {а.¥; аУ; aZ}.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов
а = {Х,; У(; ZJ, & = {Х2; У2; Z2}
является пропорциональность их координат:
Хг У2 Z2
= У, “ Z, '
Тройка векторов I, /, ft называется координатным базисом, если эти векторы удовлетворяют следующим условиям:
1)	вектор i лежит на оси Ох, вектор / — на оси О у, вектор fe — на оси Oz;
2)	каждый из векторов I, }, k направлен на своей оси в положительную сторону;
3)	векторы f, /, k — единичные, т. е. 1 i | = 1, | j | = 1, | k | = 1.
Каким бы ни был вектор а, он всегда может быть разложен по базису i, i, k, т. е. может быть представлен в виде:
а = Xi + Yj + Zk\
коэффициенты этого разложения являются координатами вектора а (т. е. X, Y, Z суть проекции вектора а на координатные оси).
761.	По данным векторам а и Ь построить каждый из следующих векторов: 1) а + 6; 2) а — Ъ; 3) b -—а; 4) —а — Ъ.
762.	Даны: |а| = 13, |6|=19 и |а4~^| = 24. Вычислить | а — Ъ |.
763.	Даны: |а| = 11, | b | = 23 и |а —6| = 30. Определить | а + b |.
764.	Векторы а и b взаимно перпендикулярны, причем |а| = 5 и | b | = 12. Определить | а 4- b | и |а —6|.
765.	Векторы а и Ъ образуют угол ф = 60°, причем | а | = 5 и |&| = 8. Определить | а 4- Ь I и |а —&|.
766.	Векторы а и b образуют угол ф=120°, причем |а| = 3 и |6| =5. Определить |а 4- b| и |а — ft|.
767.	Какому условию должны удовлетворять векторы а и Ь, чтобы имели место следующие соотношения: 1) | а-\-Ъ | = | а—Ь |; 2) | а-\-Ь | > | а-b |; 3) |	| <| а-b |.
768.	Какому условию должны удовлетворять векторы а и Ь, чтобы вектор а 4- Ъ делил пополам угол между векторами а и Ъ.
769.	По данным векторам а и Ь построить каждый из следующих векторов: 1) За; 2) — 4-6; 3) 2а 4-4- 6;
о
4) у а-36.
770.	В треугольнике АВС вектор АВ — т и вектор АС — п. Построить каждый из следующих векторов:
т + п ,	т-~ п га — m. .v т + п гт
I) —2—’ —2—’ —2—’ -------------------2—' ПРинимая
в качестве масштабной единицы у | п |, построить также векторы: 5) | п | т 4-1 т |и; 6) | и \ т 1 т \ п.
771.	Точка О является центром тяжести треугольника АВС. Доказать, что О А 4- ОВ 4- ОС — 0.
772.	В правильном пятиугольнике ABCDE заданы векторы, совпадающие с его сторонами: АВ — т, ВС—п, CD — р, DE — q и ЕА = г. Построить векторы: 1) т—п 4~ + р~0+ п 2) m4-2p4-~-r; 3) 2т4- у и — Зр — q 4- 2г.
120
773.	В параллелепипеде ABCDA'B'C'D’ (рис. 45) заданы векторы, совпадающие с его AD*=n и АА' — р. Построить каждый из следующих векторов:
1) m + n + p; 2) m + n + ^-p;
3) |m+|n + p;	4) m + n —р;
5)	— m — я + ур.
774.	Три силы М, N и Р, приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их
равнодействующей Р, если известно, что | М. | = 2 кГ, |Ж|«10 кГ и |Р| = Н кГ.
775.	Даны два вектора а = {3; —2; 6} и & = {—2; 1; 0}. Определить проекции на координатные оси следующих векторов: 1) а + 6; 2) а — Ь\ 3) 2а; 4) — ?>&; 5) 2а4~3&; 6) le-J.
776.	Проверить коллинеарность векторов а== = {2; —1; 3} и Ь — {—6; 3; —9}. Установить, какой из них длиннее другого и во сколько раз, как они направлены — в одну или в противоположные стороны.
777.	Определить, при каких значениях а, р векторы а = — 2i + 3/+ Р& и b = ai — 6/4-2fc коллинеарны.
778.	Проверить, что четыре точки А (3; —1; 2), В(1; 2; —1), С(—1; 1; —3), D(3; —5; 3) служат вершинами трапеции.
779.	Даны точки Л(—1; 5; —10) В (5; —7; 8), С(2; 2; —7) и D(5; —4; 2). Проверить, что векторы ~АВ и CD коллинеарны; установить, какой из них длиннее другого и во сколько раз, как они направлены — в одну или в противоположные стороны.
780, Найти орт вектора а=={6; —2; —3}.
781.	Найти орт вектора а = {3; 4; —12}.
782.	Определить модули суммы и разности векторов а = {3; -5; 8} и &«={-!; 1; -4}.
783.	Дано разложение вектора с по базису г, /, k\ с — = 16г — 15/ 4- 12й. Определить разложение по этому же базису вектора параллельного вектору с и
121
противоположного с ним направления, при условии, что |d| = 75.
784.	Два вектора а = {2; —3; 6} и & = (—1; 2; —2} приложены к одной точке. Определить координаты вектора с, направленного по биссектрисе угла между векторами а и Ь, при условии, что |с| = 3]/42\
785.	Векторы ЛВ = {2; 6; —4} и ЛС = {4; 2; —2} совпадают со сторонами треугольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающих с его медианами AM, BN, СР.
786*). Доказать, что если р и q — какие угодно неколлинеарные векторы, то всякий вектор, лежащий в их плоскости, может быть представлен в виде: а=ар+р0.
Доказать, что числа аир век-торами а, р и q определяются однозначно. (Представление век-s'	тора а в виде а = ар + назы-
вается разложением его по ба-—----зису р, q; числа аир называют-
0"	ся коэффициентами этого разло-
q*- жения.)
р 4R	Доказательство. Приведем
FHC	векторы а, р и q к общему началу,
которое обозначим буквой О (рис. 46). Конец вектора а обозначим буквой А. Через точку А проведем прямую, параллельную вектору q. Точку пересечения этой прямой с линией действия вектора р обозначим через Ар. Аналогично, проводя через точку А прямую, параллельную вектору р, получим в пересечении с линией действия вектора q точку Ад.
По правилу параллелограмма получим:
а ==01 = 04^4-04^.	(1)
Так как векторы ОАр и р лежат на одной прямой, то вектор ОАр может быть получен умножением вектора р на некоторое число а
ОАр = ар.	(2)
Аналогично
=	(3)
Из равенств (1). (2) и (3) получаем: а = ар + ₽?• Тем самым возможность требуемого разложения доказана. Остается доказать, что коэффициенты а и 3 этого разложения определяются однозначно.
*) Задачи 786 и 792 существенны для правильного понимания остальных задач. Решение первой из них здесь приводится полностью.
122
Предположим, что вектор а имеет два разложения:
а ~ ар 4- Pg, а = а'р + Р'д,
и, например, а' =/= а. Вычитая почленно одно из другого, получаем:
(а'-а)р + (р'-р)д = О или Р = СЬ “ €Z
Но это равенство означает коллинеарность векторов р и q, которые, однако, по условию являются неколлинеарными. Следовательно, неравенство а а невозможно. Аналогично доказывается, что невозможно неравенство PVP. Таким образом, а'г=а, Р' — р, т. е. двух различных разложений один и тот же вектор иметь не может.
787.	На плоскости даны два вектора р — {2; —3}, д = {1; 2}. Найти разложение вектора а = {9; 4} по базису р, q.
788.	На плоскости даны три вектора « = {3; —2}, Ъ = {—2; 1} и с = {7; —4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других.
789.	Даны три вектора а = {3; —1}, & = {1; —2}, с = {—1; 7}. Определить разложение вектора р = а-р по базису а, Ь.
790.	Принимая в качестве базиса векторы АВ~Ь и АС = с, совпадающие со сторонами треугольника АВС, определите разложение векторов, приложенных в вершинах треугольника и совпадающих с его медианами.
791.	На плоскости даны четыре точки 71(1; —2), В (2; 1), С(3; 2) и £>(—2; 3). Определить разложение векторов AD, BD, CD и 71Z) + BD + CD, принимая в качестве базиса векторы АВ и АС.
792.	Доказать, что если р, q и г — какие угодно некомпланарные векторы *), то всякий вектор а пространства может быть представлен в виде: а — ар 4-+ ₽? + уг. Доказать, что числа а, 0, у векторами а, р, q и г определяются однозначно. (Представление вектора а в виде a — ap + fty + yr называется разложением его по базису р, q, г. Числа а, $ и у называются коэффициентами этого разложения.)
793.	Даны три вектора р = {3; —2; 1}, q = {— 1; 1; —2}, г = {2; 1; —3}. Найти разложение вектора с = {11; —6; 5} по базису р, q, г.
*) Три вектора называются некомпланарными, если после приведения к общему началу они не лежат в одной плоскости.
123
794.	Даны четыре вектора а = {2; 1; 0}, Ь — {!; —1; 2}, с = {2; 2; —1} и d = {3; 7; —7}. Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных.
§ 31.	Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение векторов а, b обозначается символом ab (порядок записи сомножителей безразличен, т. е. ab — Ьа).
Если угол между векторами а, Ь обозначить через <р, то их скалярное произведение можно выразить формулой
аЬ = | а | • | Ь | «cos ф	(I)
Скалярное произведение векторов а, Ь можно выразить также формулой
аЬ = | а | • про Ь, или ab = | Ь | • прй а.
Из формулы (1) следует, что а&>0, если ф —острый угол, аЬ < 0, если угол ф — тупой; аЬ = 0 в том и только в том случае, когда векторы а и Ъ перпендикулярны (в частности, ab = 0, если а — 0 или Ь = 0).
Скалярное произведение аа называется скалярным квадратом вектора и обозначается символом а2. Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
а2 = | а |2
Если векторы а и b заданы своими координатами:
a = {Xf) Ур, ZJ, & = {Х2; У2; Z2}, то их скалярное произведение может быть вычислено по формуле a& = X1X2 + r1r2 + ZiZ2.
Отсюда следует необходимое и достаточное условие перпендикулярности векторов:
^1^2 + y1y2 + z1z2 = o.
Угол ф между векторами
a = {^1;y1;Z1} и & = {X2;y2;Z2)
ab
дается формулой со5ф = -т—;—т-р или в координатах
COS ф

Проекция произвольного вектора S = {X; У; Z} на какую-нибудь ось и определяется формулой
nPzjS = Se,
124
где « — единичный вектор, направленный по оси и. Если даны углы а, р, у, которые ось и составляет с координатными осями, то е = {cos a; cos Р; cos у} и для вычисления проекции вектора S может служить формула
прм S = X cos а 4- Y cos р 4- Z cos у.
2
795.	Векторы а и Ъ образуют угол ф = ул; зная, что | а | == 3, |&| —4, вычислить: 1) аЬ', 2) а2; 3) Ь2; 4) (а4-6)2; 5) (За-26) (а 4-26); 6) (а-6)2; 7) (За4-26)2.
796.	Векторы а и b взаимно перпендикулярны; вектор с образует с ними углы, равные у; зная, что | а |= = 3, |б| = 5, |с| = 8, вычислить: 1) (За — 26) (6 4- За); 2) (а 4- 6 4- с)2; 3) (а + 26 - За)2.
797.	Доказать справедливость тождества (а 4~ 6)2 4-4- (а — 6)2 = 2 (а2 4- 62) и выяснить его геометрический смысл.
798.	Доказать, что — аб^аб^аб; в каких случаях здесь может иметь место знак равенства?
799.	Считая, что каждый из векторов а, 6, с отличен от нуля, установить, при каком их взаимном расположении справедливо равенство: (а6)с = а(6с).
800.	Даны единичные векторы а, 6 и с, удовлетворяющие условию а 4~ 6 4-а = 0. Вычислить ab-^-bc-^ca.
801.	Даны три вектора а, Ъ и с, удовлетворяющие условию а4-64-с = 0- Зная, что | а | = 3, |6| = 1 и | с | = 4, вычислить аб 4- 6с 4- са.
802.	Векторы а, 6, с попарно образуют друг с другом углы, каждый из которых равен 60°. Зная, что |а| = 4, |6| = 2 и [с 1=6, определить модуль вектора р — а 4- 6 4- с.
803.	Дано, что |а| = 3, |6| = 5. Определить, при каком значении а векторы а 4- аб, а — аб будут взаимно перпендикулярны.
804.	Какому условию должны удовлетворять векторы а и 6, чтобы вектор а 4- 6 был перпендикулярен к вектору а — 6.
805.	Доказать, что вектор р — 6 (ас) — с (аЬ) перпендикулярен к вектору а.
806.	Доказать, что вектор р — Ь—перпендикулярен к вектору а.
807.	Даны векторы АВ — Ь и АС —с, совпадающие со сторонами треугольника АВС. Найти разложение по
125
базису by с вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD.
808.	Векторы а и Ь образуют угол Ф = ^; зная, что |a!=V3, |6|=1, вычислить угол а между векторами p—-a-t~b и q — a — b.
809.	Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.
810.	Определить геометрическое место концов переменного вектора х, если его начало находится в данной точке Д и вектор х удовлетворяет условию ха=а, где а —данный вектор и а —данное число.
811.	Определить геометрическое место концов переменного вектора х, если его начало находится в данной точке А и вектор х удовлетворяет условиям ха—а, xb = р, где а, b — данные неколлинеарные векторы и а, р —данные числа.
812.	Даны векторы о_={4; —2; —4}, Ь — {6; -—3; 2}. Вычислить: 1) ab, 2) У а2; 3) У Ъ2\ 4) (2а — 3&)(аД-2&); 5) (а 4- Ь)2; 6) (а - &)2.
813.	Вычислить, какую работу производит сила f = {3; —5; 2}, когда ее точка приложения перемещается из начала в конец вектора $(2; —5; —7)*).
814.	Даны точки Л(—1; 3; —7), В (2; —1; 5) и С(0, 1; -5). Вычислить: 1) (2ЛВ - СВ) (2ВС + ВЛ); 2) /ЛВ2; 3) У~ЛС2; 4) найти координаты векторов (АВ АС) ВС и АВ(ДСВС).
815.	Вычислить, какую работу производит сила ^ = {3; —2, —5}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения Д(2; —3; 5) в положение В(3; —2; —1).
816.	Даны три силы 2И = {3; —4; 2}, N = {2; 3; —5} и р = {— 3; —2; 4}, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения Mj (5; 3; —7) в положение М2(4; —1; -—4).
*) Если вектор f изображает силу, точка приложения которой перемещается из начала в конец вектора $, то работа w этой силы определяется равенством
w — fs.
126
817.	Даны вершины четырехугольника Л (1; —2; 2), В(1; 4; 0), С (—4; 1; 1) и Z) (—5; —5; 3). Доказать, что его диагонали АС и BD взаимно перпендикулярны.
818.	Определить, при каком значении а векторы а — аг — 3/4-2& и Ь — г 4-2/ — ak взаимно перпендикулярны.
819.	Вычислить косинус угла, образованного векторами а = {2; —4; 4} и & = {—3; 2; 6}.
820.	Даны вершины треугольника Л(—1; —2; 4), В(—4; —2; 0) и С(3; —2; 1). Определить его внутренний угол при вершине В.
821.	Даны вершины треугольника Л(3; 2; —3), В(5; I; —1) и С(1; —2; 1). Определить его внешний угол при вершине А.
822.	Вычислив внутренние углы треугольника Л(1; 2; 1), В(3; —1; 7), С (7; 4; —2), убедиться, что этот треугольник равнобедренный.
823.	Вектор х, коллинеарный вектору а={6; —8; —7,5}, образует острый угол с осью Oz. Зная, что | х | = 50, найти его координаты.
824.	Найти вектор х, коллинеарный вектору а — = {2; 1; —1} и удовлетворяющий условию ха — 3.
825.	Вектор х, перпендикулярный к векторам а~ = Зг + 2/ + 2k и b — 18г — 22/ — 5k, образует с осью Оу тупой угол. Найти его координаты, зная, что |х|=14.
826.	Найти вектор х, зная, что он перпендикулярен к векторам а — {2‘, 3; —1} и & = {1; —2; 3} и удовлетворяет условию х (2г — / + k) — — 6.
827.	Даны два вектора: а = {3; —1; 5} и & — {1; 2; —3}. Найти вектор х шри условии, что он перпендикулярен к оси Oz и удовлетворяет условиям: ха = 9,	= —4.
828.	Даны три вектора: а = 2г —/4-3&, b — i — — 3/	26 и с = Зг 4- 2/ — 4£. Найти вектор х, удовле-
творяющий условиям: ха— — 5, хЬ~ — 11, хс = 20.
829.	Найти проекцию вектора S = {4; —3; 2} на ось, составляющую с координатными осями равные острые углы.	_
830.	Найти проекцию вектора S={]/2; —3; —5) на ось, составляющую с координатными осями Ox, Oz углы а = 45°, у = 60°, а с осью Оу — острый угол р.
831.	Даны две точки Л (3; —4; —2), В (2; 5; —2). Найти проекцию вектора АВ на ось, составляющую с координатными осями Ох, Оу углы а = 60°, $=120°, а с осью Oz —тупой угол у*
127
832.	Вычислить проекцию вектора в = {5; 2; 5} на ось вектора Ь = {2; —1; 2}.
833.	Даны три вектора: a = 3i — Sj — k, b = i-{-4- 4/ — 5k и с = 3i — + 12k. Вычислить npe (a 4- b).
834.	Даны три вектора: а = {1; —3; 4}, Z> = {3; —4; 2} и с = {—1; 1; 4}. Вычислить пр&+са.
835.	Даны три вектора: а = — 2/4-7 +Л, b — i-^- 5j и с = 4/4-4/ — 2k. Вычислить прс(За — 2&).
836.	Сила, определяемая вектором # = {1; —8; —7}, разложена по трем направлениям, одно из которых задано вектором a — 2i-\-2j-\-k. Найти составляющую силы R в направлении вектора а.
837.	Даны две точки М(—5; 7; —6) и ЛД7; —9; 9). Вычислить проекцию вектора а = {1; —3; 1} на ось вектора MN.
838.	Даны точки Л(—2; 3; —4), В(3; 2; 5), С(1; —1; 2), D (3; 2; —4). Вычислить пр^ДВ.
§ 32.	Векторное произведение векторов
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [aft] и определяемый следующими тремя условиями:
1)	модуль вектора [aft] равен | а | • | 6 [ sin ф, где ф —угол между векторами а и 6;
2)	вектор [aft] перпендикулярен к каждому из векторов а и &;
3)	направление вектора [aft] соответствует «правилу правой руки». Это означает, что если векторы a, ft и [aft] приведены к общему началу, то вектор [aft] должен быть направлен так, как направлен средний палец правой руки, большой палец которой направлен по первому сомножителю (т. е. по вектору а), а указательный — по второму (т. е. по вектору ft).
Векторное произведение зависит от порядка сомножителей, именно:
[aft] — — [6a]
Модуль векторного произведения [aft] равен площади S параллелограмма, построенного на векторах а и ft
|[aft]|=S.
Само векторное произведение может быть выражено формулой [aft] = Se, где е — орт векторного произведения.
Векторное произведение [aft] обращается в нуль тогда и только тогда, когда векторы а и 6 коллинеарны. В частности [аа] =я 0.
128
Ерли система коордйнатных осей правая и векторы а и 6 заданы в этой системе своими координатами:
«=={*1; К15 ZJ, 6={Х2; У2; Z2},
то векторное произведение вектора а на вектор Ь определяется формулой
М] =
или
ад ад
X2Z2
ад
I i k
[aft] == Xi У, Zt
Х2 Y3 Z2
839.	Векторы а и Ь образуют угол Ф = р Зная, что |а| = 6, | ft 1 = 5, вычислить | [aft] |.
840.	Даны: |а|=10, |6| = 2 и aft =12. Вычислить ][«*]
841.	Даны: | а | = 3, |ft| = 26 и | [aft] | — 72. Вычислить ab.
842.	Векторы а иЬ взаимно перпендикулярны. Зная, что | а ] = 3, | b | — 4, вычислить:
1) | [(а + 6)(а — 6)] |; 2) | [(За - Ь) (а - 26)] |.
2
843.	Векторы а и Ъ образуют угол <р = —л. Зная, что |а|=1, |ft| = 2, вычислить:
1) [aft]2; 2) [(2а + Ь) (а + 2ft)]2; 3) [(а + 3ft) (За - ft)]2.
844.	Какому условию должны удовлетворять векторы а, Ь, чтобы векторы а + ft и а — 6 были коллинеарны?
845.	Доказать тождество [aft]2 + (aft)2 — a2b2.
846.	Доказать, что [aft]2<a2ft2; в каком случае здесь будет знак равенства?
847.	Даны произвольные векторы: р, q, г, п. Доказать, что векторы a = [pn], b = [qn], c = [rn] компланарны (т. е., будучи приведены к общему началу, располагаются в одной плоскости).
848.	Векторы а, b н с удовлетворяют условию a + ft + c = 0. Доказать, что [aft] = [6с] — [са].
849.	Векторы a, ft, с и d связаны соотношениями [aft] = [cd], [ac] = [ft<Z]. Доказать коллинеарность векторов a — d и ft — р.
850.	Даны векторы a = {3; —1; —2} и 6 = {1; 2; — 1}. Найти координаты векторных произведений: 1) [aft]; 2) [(2a+ ft) ft]; 3) [(2a - ft) (2a + ft)].
5 Д. В. Клетеник
129
851.	Даны точки 4(2; —1; 2), 5(1; 2; —1) и С(3; 2; 1). Найти координаты векторных произведений 1) [455С]; 2) [(5С-2С4)С5].
852.	Сила / = {3; 2; —4} приложена к точке А (2; —1; 1). Определить момент этой силы относительно начала координат *).
853.	Сила Р = {2; —4; 5} приложена к точке Л10(4; —2; 3). Определить момент этой силы относительно точки 4(3; 2; —1).
854.	Сила <? = {3; 4; —2} приложена к точке С (2; —1; —2). Определить величину и направляющие косинусы момента этой силы относительно начала координат.
855.	Сила Р — {2; 2; 9} приложена к точке 4(4; 2; —3). Определить величину и направляющие косинусы момента этой силы относительно точки С (2; 4; 0).
856.	Даны три силы 2И = {2; —1; —3}, Л7 = {3; 2; — 1} и Р = {—4; 1; 3}, приложенные к точке С(— 1; 4; —2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки 4(2; 3; -1).
857.	Даны точки 4(1; 2; 0), 5(3; 0; —3) и С(5;2;6). Вычислить площадь треугольника АВС.
858.	Даны вершины треугольника 4(1; —1; 2), 5(5; —6; 2) и С(1; 3; —1). Вычислить длину его высоты, опущенной из вершины 5 на сторону АС.
859.	Вычислить синус угла, образованного векторами а = {2; -2; 1} и & = {2; 3; 6}.
860.	Вектор х, перпендикулярный к векторам й = = {4; —2; — 3} и б=={0; 1; 3}, образует с осью Оу тупой угол. Зная, что | х | = 26, найти его координаты.
861.	Вектор т, перпендикулярный к оси Os и к вектору а = {8; —15; 3}, образует острый угол с осью Ох. Зная, что |т| = 51, найти его координаты.
862.	Найти вектор х, зная, что он перпендикулярен к векторам а = {2; —3; 1} и & = {1; —2; 3} и удовлетворяет условию: х (г + 2/ — 7k) = 10.
*) Если вектор f изображает силу, приложенную к какой-нибудь точке М, а вектор а идет из некоторой точки О в точку М, то вектор fafj представляет собой момент силы f относительно точки О.
130
863.	Доказать тождество
(/{+ т\ + nf) (Z| + ml + п%) — (//2 + mim2 + п\п2^ =* = (m{n2 — т2пО2 + (Z2«i “ Zi^)2 + (А^г —
Указание. Воспользоваться тождеством задачи 845.
864.	Даны векторы а = {2; —3; 1}, & = {—3; 1; 2} и с = {1; 2; 3). Вычислить [[а&] с] и [а [6с]].
§ 33. Смешанное произведение трех векторов
Тройкой векторов называются три вектора, если указано, какой из них считается"первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись а, Ь, с означает, что вектор а считается первым, b — вторым, с — третьим.
Тройка некомпланарных векторов а, Ъ, с называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы а, Ь, с расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.
Смешанным произведением трех векторов а, Ь, о называется число, равное векторному произведению [аб], умноженному ска-лярно на вектор с, т. е.	г
Имеет место тождество: [ab] с — а [6с], ввиду чего для обозначения смешанного произведения [об] с употребляется более простой символ: abc. Таким образом,
аЬс—[аЬ]с, а6с = а[6с].
Смешанное произведение abc равно объему параллелепипеда, построенного на векторах а, 6, с, взятому со знаком плюс, если тройка abc правая, со знаком минус, если эта тройка левая. Если векторы а, Ь, с компланарны (и только в этом случае), смешанное произведение abc равно нулю; иначе говоря, равенство
abc = О
есть необходимое и достаточное условие компланарности векторов а, 6, с.
Если векторы а, Ь, с заданы своими координатами:
a = {Xi; Fi; ZJ, 6 = {Х2; У2; Z2}, с = {Х3; Y3; Z3},
то смешанное произведение abc определяется формулой
abc =
х2
Хз
Г1 X,
У2 Х2
Гз Х3
Напомним, что система координатных осей предполагается правой (вместе с тем является правой и тройка векторов i, /, fe).
5*	131
865. Определить, какой (правой или левой), если
1) a = k, b = i, c — j;
3) a — j, b — i, c — k\
5) a — i + /, b = i — j,
6) a — i + j, b = i — j,
является тройка a, b, с
2) a — i, b = k, c = j;
4) a = f + /, b = j, c = k\ c = j;
c—k.
866.	Векторы a, b, с, образующие правую тройку, взаимно перпендикулярны. Зная, что |aj = 4, |6| = 2, |с| = 3, вычислить abc.
867.	Вектор с перпендикулярен к векторам а и Ь, угол между а и b равен 30°. Зная, что | а 1 = 6, | b 1 = 3, | с | = 3, вычислить abc.
868.	Доказать, что | abc | а || Ь || с |; в каком случае здесь может иметь место знак равенства?
869.	Доказать тождество (а+ &)(& +с) (с + а) = 2abc.
870.	Доказать тождество ab (с + Ла + цй) = а&с, где Лиц — какие угодно числа.
871.	Доказать, что векторы а, Ь, с, удовлетворяющие условию [аб] + [&£.] + [са] = 0, компланарны.
872.	Доказать, что необходимым и достаточным условием компланарности векторов а, Ь, с является зависимость аа + рб + ус = 0, где по крайней мере одно из чисел а, р, у не равно нулю.
873.	Даны три вектора: а = {1; —1; 3}, & = {—2; 2; 1}, с = {3; —2; 5}. Вычислить abc.
874.	Установить, компланарны ли векторы а, Ь, с, если:
1)	а = {2; 3; -1},
2)	а = {3; -2; 1},
3)	а = {2; -1; 2},
6 = {1; -1; 3}, b = {2', 1; 2},
& = {1; 2; -3},
с = {1; 9; -11};
с = {3; -1; -2}:
с = {3; —4; 7}.
875.	Доказать, что четыре точки Л(1; 2; — 1), В(0; 1; 5), С(— 1; 2; 1), D(2; 1; 3) лежат в одной плоскости.
876.	Вычислить объем тетраэдра, вершины которого находятся в точках А (2; —1; 1), В (5; 5; 4), С(3; 2; — 1) и Z)(4; 1; 3).
877.	Даны вершины тетраэдра: А (2; 3; 1), В(4; 1; —2), С (6; 3; 7), D (—5; —4; 8). Найти длину его высоты, опущенной из вершины D.
132
878.	Объем тетраэдра о = 5, три его вершины находятся в точках Л (2; 1; — 1), В(3; 0; 1), С (2; —1; 3). Найти координаты четвертой вершины D, если известно, что она лежит на оси Оу.
§ 34.	Двойное векторное произведение
Пусть вектор а умножается векторно и а вектор Ь, после чего полученный вектор [а&] умножается снова векторно на вектор с. В результате получается так называемое двойное векторное произведение [[а&] с] (ясно, что [[аб] с] — вектор). Умножая вектор а векторно на [&с], получим двойное векторное произведение [a [6c]L
Вообще говоря,
[[а6]с]¥=[а(М1.
Докажем, что имеет место тождество
[[ab] с] = Ь (ас) — а (Ьс).
Доказательство. Введем (декартову прямоугольную) систему координат. Чтобы облегчить выкладки, расположим оси координат специальным образом, а именно: ось Ох направим по вектору а, ось Оу поместим в плоскости векторов а и Ь (считая, что векторы а, Ь приведены к общему началу), В таком случае будем иметь:
а = {Х1; 0; 0), & = {Х2; Г2; 0), с=={Х3; Г3; 23).
Теперь находим:
[а&} = {0;0;Х1У2),	1
[[а&] cj = {- XtY2Y3} Хад-, 0). J
С другой стороны,
ас = ад; Ь (ас) = {Х}Х2Хц Х}У2Х3- 0),
Ьс = ад + ад, а (Ьс) == {Х^Хз + XJJ3, 0; 0},
Следовательно,
Ь (ас) - а (Ьс) => {- XxY2Y3. XxY2X3. 0).	(2)
Сравнивая правые части формул (1) и (2), получаем:
[[а&] с]=Ь (ас) — а (Ьс). что и требовалось.
879.	Доказать тождество [а [&с]] = Ъ (ас) — с (ab).
880.	Решить задачу 864, используя тождества, данные в начале этого параграфа, и тождество задачи 879.
881.	Даны вершины треугольника Д(2; —1; — 3), В(1; 2; —4) и С(3; — 1; —2), Вычислить координаты вектора h, коллинеарного с его высотой, опущенной из вершины А на противоположную сторону, при
133
условйи, что вдабр' Л образует с осью Оу т^й'&й угол ft что его модуль равен 2 ]/ЗТ.
882.	Считая, Что каждый из векторов а, й, с отличен от нуля, установить, при каком их взаимном располо* женин справедливо равенство [а [М = [[eft] с].
883.	Доказать тождества:
I)	[й[И] + [&М] + кМ = 0;
2)	[ай] [cd] « (ас) [bd) — (ad) [be);
3)	[ай] [cd] + [ас] [db] + [ad] [йс] = 0;
4)	{[«й] [cd]] = c [abd) — d (айс);
5)	[ай] [йс] [ca] = (айс)2;
6)	[а [а [а [ай]]]] = а4й при условии, что векторы а и й взаимно перпендикулярны;
7)	[а [й [cd]]] = [ас] [bd) — [ad] (йс);
8)	[а [й [cd]]] = (acd) й — (ай) [cd];
9)	[ай]2 [ас]2 - ([ай] [ас] )2 == а2 (айс)2;
10)	[[ай] [йс]] [[йс] [са]] [[са] [ай]] = (айс)4;
11)	(ай) [cd] + (ас) [db] + (ad) [йс] = a [bed);
12)	(abc) (ade) = I аЬ‘ .
I acd асе
884.	Три некомпланарных вектора а, й и с приведены к общему началу. Доказать, что плоскость, проходящая через концы этих векторов, перпендикулярна к вектору [ай] + [йс] 4- [са].
ГЛАВА 8
УРАВНЕНИЕ ПОВЕРХНОСТИ И УРАВНЕНИЯ ЛИНИИ
§ 35.	Уравнение поверхности
Уравнением данной поверхности (в выбранной системе координат) называется такое уравнение с тремя переменными
f (х, у, z) = 0, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты никакой точки не лежащей на ней.
885.	Даны точки Mj (2; -3; 6), М2(0; 7; 0), М3(3; 2; -4), М4(2 /2 ; 4; -5), М5(1; -4; -5), М6(2; 6; - ]/5). Уста-новить, какие из них лежат на поверхности, определенной уравнением х2 + у2 4- z2 — 49, и какие не лежат на ней? Какая поверхность определена данным уравнением?
886.	На поверхности х2 4- У2 + 22 = 9 найти точку, для которой: 1) абсцисса равна 1, ордината равна 2; 2) абсцисса равна 2, ордината равна 5; 3) абсцисса равна 2, апликата равна 2; 4) ордината равна 2, апли-ката равна 4.
887.	Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:
1) х = 0; 2)^ = 0; 3) 2 = 0; 4)х-2=0;
5) ^ + 2 = 0; 6)? + 5 = 0; 7) х2 + У2 + & = 25;
8) (х - 2)2 + (у 4- З)2 + (z - 5)2 = 49;
9) x24-2^24-3z2 = 0; 10) х2 4- 2/ 4- 3z2 4- 5 = 0;
11) х — у —О', 12) х + г = 0; 13) у — z=0; 14) х#=0; 15) xz = 0; 16) yz = 0', 17) xyz = 0\ 18) х2-4х = 0; 19) ху — у2 = 0; 20) ^ + г2 = 0.
135
888.	Даны две точки ?|(—с; 0; 0) и F2(c', 0; 0). Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек есть величина постоянная, равная 2а при условии а > 0, с > 0; а > с.
Решение. Обозначим буквой М произвольную точку пространства, буквами х, у, z — ее координаты. Так как точка М может занимать любое положение, то х, у и z являются переменными величинами; их называют текущими координатами.
Точка М лежит на данной поверхности в том и только в том случае, когда
MFt + MF2 = 2a	(I)
Это есть определение поверхности, выраженное символически.
Выразим MF\ и Л4Г2 через текущие координаты точки М:
MF} = /(х + с)2 + у2 + г2 , MF2 = lF(x-c)2 + y2 + z2'.
Подставим полученные выражения в равенство (1). Тем самым мы найдем уравнение
/(х + c)2 + y2 + z2 +/(r-e)2+ y2 + z2 = 2а,	(2)
которое связывает текущие координаты х, у, z. Это и есть уравнение данной поверхности.
Действительно, для каждой точки М, лежащей на данной поверхности, выполняется условие (1) и, следовательно, координаты такой точки будут удовлетворять уравнению (2); для каждой точки, не лежащей на поверхности, условие (1) не будет выполняться и, следовательно, ее координаты не будут удовлетворять уравнению (2) Таким образом, задача решена; дальнейшие выкладки имеют целью представить уравнение поверхности в более простом виде
Уединим в уравнении (2) первый радикал:
V~(x + с)2 + г/2 + 22 = 2а — У(х — е); 4- £/2 4- z2,
возведем обе части этого равенства в квадрат и раскроем скобки мы получим:
х2 4- 2сх + с2 + у2 + z2 —
4а2 — 4а V(х — с)2 4- у2 4- z2 4- х2 — 2сх 4- с2 4- у2 4- г2,
или
а У (х — с)2 4- у2 + z2 = а2 — сх.
Снова, освобождаясь от радикала, найдем;
а2х2 — 2а2сх 4- а2с2 4- а?у2 + a2z3 — а4 — 2а2сх 4- с2х2,
или
(а2 - с2) х2 4- а2у2 4- a2z2 = а2 (а2 - с2).	(3)
136
Так как а > с, то а2—с2 > 0; положительное 4йёло а5—с3 обозначим через д2. Тогда уравнение (3) примет Ьид
W + aV4-a222 = a263 или
а3 Т Т
(4)
Рассматриваемая поверхность называется эллипсоидом вращения. Уравнение (4) называется каноническим уравнением этого эллипсоида.
889.	Вывести уравнение сферы, центр которой находится в начале координат и радиус которой равен г.
890.	Вывести уравнение сферы, центр которой С (а; р; у) и радиус которой равен г.
891.	Из точки Р (2; 6; —5) проведены всевозможные лучи до пересечения с плоскостью Oxz. Составить уравнение геометрического места их середин.
892.	Из точки А (3; —5; 7) проведены всевозможные лучи до пересечения с плоскостью Оху. Составить уравнение геометрического места их середин.
893.	Из точки С(—3; —5; 9) проведены всевозможные лучи до пересечения с плоскостью Оуг. Составить уравнение геометрического места их середин.
894.	Вывести уравнение геометрического места точек, разность квадратов расстояний которых до точек (2; 3; —5) и F2(2‘, —7; —5) есть величина постоянная, равная 13.
895.	Вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух точек F\ (— а\ 0; 0) и F2 (а; 0; 0) равна постоянной величине 4а2.
896.	Вершины куба суть точки Д(—а; —а; —а), В (а; —а; —а), С(—а; а; —а) и £)(а; а; а). Составить уравнение геометрического места точек, сумма квадратов расстояний которых до граней этого куба есть величина постоянная, равная 8а2.
897.	Вывести уравнение геометрического места точек, равноудаленных от двух точек (1; 2; —3) и М2 (3; 2; 1).
898.	Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек F\ (0; 0; —4) и F2 (0, 0; 4) есть величина постоянная, равная 10.
899.	Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек 7^(0; —5; 0) и F2 (0; 5; 0) есть величина постоянная, равная 6.
137
§ 36.	Уравнения линии. Задача о пересечении трех поверхностей
Линия в пространстве определяется совместным заданием двух уравнений
F (х, у, г) = О, Ф (х, у, z) = О
как пересечение двух поверхностей F (х, у, г) == 0 и Ф(х, у, г)«0, Есйи F (х, у, г) = О, Ф (х, у, г) = О, Т (х, у, г) = 0 суть уравнения трех поверхностей, то для разыскания точек их пересечения нужно совместно решить систему:
F (х, у, г) <= О,  Ф (х, у, г) = О, I Т(х,^, г)=0.
Каждое решение х, у, z этой системы представляет собой координаты одной из точек пересечения данных поверхностей.
900.	Даны точки Л1| (3; 4; —4), М2 (—3; 2; 4), Л13(—1; —4; 4) и М<(2; 3; —3). Определить, какие из них лежат на линии
Г (х- 1)2 + ^24-22==36,
I //4-2 = 0
и какие не лежат на ней.
901.	Определить, какие из следующих линий проходят через начало координат:
f х2 4- г/2 4“ 22 — 2z = 0,
1)L = 0;
Г(х - З)2 + (у + I)2 + (г - 2)2 - 25,
’ I х + ^ = 0;
J (x-l)2 + (</ + 2)2 + (z + 2)2 = 9,
°’ t х - z = 0.
f x2 4" У2 4“ z2 — 49,
902.	На линии s 2 , й	л- п наити
I х + 1Г 4- z — 4z — 25 = 0
точку:
1)	абсцисса которой равна 3;
2)	ордината которой равна 2;
3)	апликата которой равна 8.
138
903.	Установить, какие линии определяются следующими уравнениями:
р + 2 = 0,	р-5 = 0, р + 2 = 0,
Ь)[у-3 = 0; b)U + 2 = 0; z'lz-5 = 0;
( х2 + У2 + z2 = 9,	( х2 + у2 + z2 = 49,
Ч г = 0;	9)Ь = 0;
• Mf-2=v=20,
904.	Составить уравнения линии пересечения плоскости Oxz и сферы с центром в начале координат и радиусом, равным 3.
905.	Составить уравнения линии пересечения сферы, центр которой находится в начале координат и радиус равен 5, с плоскостью, параллельной плоскости Oxz и лежащей в левом полупространстве на расстоянии двух единиц от нее.
906.	Составить уравнения линии пересечения плоскости Oyz и сферы, центр которой находится в точке С (5; —2; 1) и радиус равен 13.
907.	Составить уравнения линии пересечения двух сфер, одна из которых имеет радиус, равный 6, и центр в начале координат, другая имеет радиус, равный 5, и центр С(1; —2; 2).
908.	Найти точки пересечения трех поверхностей: х2 + z/2 + г2 = 49, у-3 = 0, z + 6 = 0.
909.	Найти точки пересечения трех поверхностей: х2 + у2 + z2 = 9, х2 + у2 + (z — 2)2 = 5, у — 2 = 0.
§ 37. Уравнение цилиндрической поверхности с образующими, параллельными одной из координатных осей
Уравнение с двумя переменными вида
F (х, у) = 0
в пространственной системе координат определяет цилиндрическую поверхность с образующими, параллельными оси Oz. На плоскости в системе координат с осями Ох и Оу уравнение F(x,t/)=0
139
определяет линию, именно, направляющую линию рассматривав' мого цилиндра. Но эта же линия в пространственной системе коор-динат должна быть задана двумя уравнениями:
F(x, у) = 0,
2 = 0.
Аналогично: уравнение F (х, z) = 0 (в пространстве) определяет цилиндрическую поверхность с образующими, параллельными оси Оу; уравнение F(y,z)=*Q определяет цилиндрическую поверхность с образующими, параллельными оси Ох.
910. Установить, какие геометрические образы опре* деляются в пространственной системе координат следующими уравнениями:
1)^ + Z’ = 25; 2) £ + 4=-1; 3)4~4=1;
4) x2 = 6z; 5) х2 —х// = 0; 6) х2— z2 = 0;
7) z/24-z2==0; 8) х2 + 4z/2 + 4 = 0; 9)x24-z2«2z;
10) г/2-f- z2 = — z.
911.	Найти уравнение цилиндра, проектирующего окружность
p2 + (z/4-2)2 + (z-l)2 = 25,
I	х2 + f/2 + г2 = 16
на плоскость: 1) Оху; 2) Oxz; 3) Oyz.
912.	Найти уравнение проекции окружности f (х 4- I)2 4- [у 4- 2)2 -j- (z - 2)2 = 36, I x24-(r/4-2)24-(z-l)2 = 25
на плоскости 1) Оху; 2) Oxz; 3) Oyz.
ГЛАВА 9
УРАВНЕНИЕ ПЛОСКОСТИ.УРАВНЕНИЯ ПРЯМОЙ. УРАВНЕНИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
§ 38. Общее уравнение плоскости. Уравнение плоскости, проходящей через данную точку й имеющей данный нормальный вектор
В декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение Первой СТёпенй определяет плоскость.
Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение
А (х — х0)4-В(у — г/0) 4-G (ж — 20) = 0	(1)
определяет плоскость, проходящую через точку Af0 (хо; Уо‘> 2о) и имеющую нормальный вектор п = {А; В; С}.
Раскрывая в уравнении (1) скобки и обозначая число — Ахо — — Ву0 — Сг0 буквой D, представим его в виде:
Ах + By + Cz + D = 0.
Это уравнение называется общим уравнением плоскости.
913.	Составить уравнение плоскости, которая проходит через точку МД2; 1; —1) и имеет нормальный вектор я = {1; —2; 3}.
914.	Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор я=={5; 0; —3}.
915.	Точка Р(2; —1; —1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.
916.	Даны две точки (3; —1; 2) и М2(4; —2; — 1). Составить уравнение плоскости, проходящей через точку перпендикулярно вектору
141
917.	Составить уравнение плоскости, проходящей че' рез точку MJ3; 4; —5) параллельно двум векторам Л1={3; 1; —1} и а2 = {1; —2; 1}.
918.	Доказать, что уравнение плоскости, проходящей через точку Л10(х0; #0; z0) параллельно двум векторам Л] ={/[•, т/, и а2 = {!2; w2; п2}} может быть представлено в следующем виде:
X —Хо
ц
У~Уо тх т2
Z —ZO
«2
= 0.
919.	Составить уравнение плоскости, проходящей через точки Мх (2; —1; 3) и Л42(3; 1; 2) параллельно вектору а = {3; —1; 4},
920.	Доказать, что уравнение плоскости, проходящей через точки МДхр, ух\ gj) и М2(х2; у2\ z2) параллельно вектору а~{1\ т\ п}> может быть представлено в следующем виде:
X — Х1
X2 — Xj
I
у — У\ У2-У1 т
z — Zx z2-zl п
= 0
921.	Составить уравнение плоскости, проходящей через три точки: МДЗ; —1; 2), М2(4; —1; —1) и М3(2; 0; 2).
922.	Доказать, что уравнение плоскости, проходящей через три точки: Mj (хв ух\zx), М2(х2; у2; z2) и М3(х3; у3; z3), может быть представлено в следующем виде:
х —у — ух Z — Zi Х2 —Xj	У2~ У\ 22 — 2! =0,
*з“*1 Уз — У1 z3 — 2j
У — У\
2 — 2t
Уз — У\

923.	Определить координаты какого-нибудь нормального вектора каждой из следующих плоскостей. В каждом случае написать общее выражение координат произвольного нормального вектора:
1) 2х — у — 22 + 5 = 0; 2) х + Ъу — z = 0;
3) Зх — 2у — 7 == 0; 4) 5у — 32 = 0; 5) х + 2 = 0;
6) г/-3 = 0.
.142
924. Установить, какие из следующих пар уравнений определяют параллельные плоскости;
1)	2х — Зу 4- 5г — 7 = О, 2х — Зу 4- 5г 4~ 3 = 0;
2)	4х 4- 2у — 4г 4- 5 = О, 2х 4- у 4- 2г — 1 = 0;
3)	х — 3z + 2 — 0, 2х — 6г — 7 = 0.
925. Установить, какие из следующих пар уравнений определяют перпендикулярные плоскости:
1)	Зх — у — 2г — 5 = О, х 4- 9у — Зг 4- 2 = 0;
2)	2х + Зу — г — 3 = 0, х — у — z + 5 = 0;
3)	2х — 5у4-2 = 0,	х 4~ 2г— 3 = 0.
926. Определить, при каких значениях I и т следующие пары уравнений будут определять параллельные плоскости:
1)	2х 4- 1у 4- Зг — 5 = 0, тх — бу — 6г 4- 2 = 0;
2)	Зх — у 4- /г — 9 = 0, 2х 4- ту 4- 2г — 3 = 0;
3)	тх 4- Зу — 2г — 1 = 0, 2х — 5у — lz = 0.
927. Определить, при каком значении I следующие пары уравнений будут определять перпендикулярные плоскости:
плоскостей:
1)	Зх — 5у 4- /г — 3 = 0, х 4- Зу 4- 2г 4- 5 = 0;
2)	5х4-у —Зг —3 = 0, 2х4-/У“Зг4-1=0;
3)	7х — 2у — г = О, 1х 4- у — Зг — 1 = 0.
928. Определить двугранные углы, образованные пересечением следующих пар
1)	х-у/2"4-2- 1=0,
2)
3)
4)
929.
ходит через начало координат параллельно плоскости 5х — Зу 4- 2г — 3 = 0.
х 4- у V2 — г 4- 3 = 0;
2у 4- 2 = 0;
х 4-2у 4-6г- 12 = 0;
16x4-12у-15г-1=0.
Зу — г = 0, 6х 4“ Зу — 2г = 0, х 4- 2у 4- 2г - 3 = 0, Составить уравнение
плоскости, которая про
143
930. Составить уравнение плоскости, которая проходит через точку (3; —2; —7) параллельно плоскости 2х — Зг 4- 5 = 0.
931, Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостями 2х — у + Зг — 1 = 0, х 4- 2у 4- г = 0.
932.	Составить уравнение плоскости, которая проводит через точку (2; — 1; 1) перпендикулярно к двум плоскостям! 2х — г 4- 1 = 0, у = 0.
933.	Доказать, что уравнение плоскости, проходящей через точку М (х0; у0; г0) перпендикулярно к плоскостям А[Х + В^у + C\Z -j- Di — 0, А2х + В2у 4~ С2х 4- D2 = 0, может быть представлено в следующем виде:
х — х0	У~~Уо	z — Zq	
Ах	Вх	Сх	= 0.
As	В2	с2	
934.	Составить уравнение плоскости, которая проходит через две точки Mt(l; —1; —2) и Л12(3; 1; 1) перпендикулярно к плоскости х — 2у 4- Зг — 5 ==0.
935.	Доказать, что уравнение плоскости, проходящей через две точки (х^ у у, г^ и М2(х2; у2; г2) перпендикулярно к плоскости Ах 4- By 4- Сг + D = 0, может быть представлено в следующем виде:
х — Xi у —Ух Z — г, х2 — Xi у2~ Ух г2 — Zx
АВС
936.	Установить, что три плоскости х — 2# + г — 7=0, 2х У — г-f-2 = 0, х — Зг/4~ 2г — 11 = 0 имеют одну общую точку, и вычислить ее координаты.
937.	Доказать, что три плоскости 7х4-4//4-7х4“ 1 =0, 2х — у — г 4- 2 = 0, х 4~ 2г/ 4~ Зг — 1=0 проходят через одну прямую.
938.	Доказать, что три плоскости 2х — у 4- Зг —5=0, Зх 4- у 4- 2г — 1 = 0, 4х 4~ 3# 4-4-2 = 0 пересекаются по трем различным параллельным прямым.
939.	Определить, при каких значениях а и b плоскости 2х — г/ 4- Зг — 1=0, х-{-2у — г 4- 6 = 0, х-\-ау — — 6г 4- 10 = 0: 1) имеют одну общую точку; 2) проходят через одну прямую; 3) пересекаются по трем различным параллельным прямым.
144
§ 39.	Неполные уравнения плоскостей^ Уравнение плоскости «в отрезках»
Каждое уравнение первой степени
Ах ~|~ By 4* Сх -j- D = О
(в декартовых координатах) определяет плоскость. Если в этом уравнении отсутствует свободный член (D = 0), то плоскость проходит через начало координат. Если отсутствует член с одной из текущих координат (т. е. какой-либо из коэффициентов А, В, С равен нулю), то плоскость параллельна одной из координатных осей, именно той, которая одноименна с отсутствующей координатой; если, кроме того, отсутствует свободный член, то плоскость проходит через эту ось. Если в уравнении отсутствуют два члена с текущими координатами (какие-либо два из коэффициентов А, В, С равны нулю), то плоскость параллельна одной из координатных плоскостей, именно той, которая проходит через оси, одноименные С отсутствующими координатами; если, кроме того, отсутствует свободный член, то плоскость совпадает с этой координатной плоскостью.
Если в уравнении плоскости
Ах + By 4- Cz + D = 0
ни один из коэффициентов А, В, С, D не равен нулю, то это уравнение может быть преобразовано к виду
где
суть величины отрезков, которые плоскость отсекает на координатных осях (считая каждый от начала координат). Уравнение (1) называется уравнением плоскости «в отрезках».
940.	Составить уравнение плоскости, которая проходит;
1)	через точку (2; —3; 3) параллельно плоскости Оху,
2)	через точку М2(1; —2; 4) параллельно плоскости Oxz\
3)	через точку Л43(—5; 2; —1) параллельно плоскости Oyz.
941.	Составить уравнение плоскости, которая проходит:
1)	через	ось	Ох	и	точку	МД4;	—1; 2);
2)	через	ось	Оу	и	точку	М2(Г,	4; —3);
3)	через	ось	Oz	и	точку	М3(3;	—4; 7).
145
942.	Составить уравнение плоскости, которая проходит:
1)	через точки МД7; 2; —3) и М2(3; 6; —4) параллельно оси Ох;
2)	через точки -Pi (2; —1; 1) и Р2(3; 1; 2) параллельно оси Оу;
3)	через точки Q](3; —2; 5) и Q2(2; 3; 1) параллельно оси Oz.
943.	Найти точки пересечения плоскости 2х — Зу — — 42 — 24 = 0 с осями координат.
944.	Дано уравнение плоскости х 4- 2г/ — 32 — 6 = 0. Написать для нее уравнение «в отрезках».
945.	Найти отрезки, отсекаемые плоскостью Зх — — 4г/— 242 4- 12 = 0 на координатных осях.
946.	Вычислить площадь треугольника, который отсекает плоскость 5х — Зу 4-Зг 4- 120 = 0 от координатного угла Оху.
947.	Вычислить объем пирамиды, ограниченной плоскостью 2х — Зу 4- 62 — 12 = 0 и координатными плоскостями.
948.	Плоскость проходит через точку МД6; —10; 1) и отсекает на оси абсцисс отрезок а — — 3 и на оси апликат отрезок с —2. Составить для этой плоскости уравнение «в отрезках».
949.	Плоскость проходит через точки МДГ, 2; —1) и Л12(—3; 2; 1) и отсекает на оси ординат отрезок Ь — 3. Составить для этой плоскости уравнение «в отрезках».
950.	Составить уравнение плоскости, которая проходит через точку МД2; —3; —4) и отсекает на координатных осях отличные от нуля отрезки одинаковой величины (считая каждый отрезок направленным из начала координат).
951.	Составить уравнение плоскости, которая проходит через точки МД—1; 4; —1), МД—13; 2; —10) и отсекает на осях абсцисс и апликат отличные от нуля отрезки одинаковой длины.
952.	Составить уравнения плоскостей, которые проходят через точку М3 (4; 3; 2) и отсекают на координатных осях отличные от нуля отрезки одинаковой длины.
953.	Составить уравнение плоскости, отсекающей на оси Oz отрезок с = —5 и перпендикулярной к вектору п =={—2; 1; 3}.
146
954.	Составить уравнение плоскости, параллельной вектору / = {2; 1; —1} и отсекающей на координатных осях Ох и Оу отрезки а = 3, Ь = — 2.
955.	Составить уравнение плоскости, перпендикулярной к плоскости 2х — 2у + 4г — 5 = 0 и отсекающей на координатных осях Ох и Оу отрезки а — — 2, 6= у.
§ 40.	Нормальное уравнение плоскости. Расстояние от точки до плоскости
Нормальным уравнением плоскости называется ее уравнение, написанное в виде
xcos а + у cos р + z cos у — р = 0,	(1)
где cos а, cos р, cosy суть направляющие косинусы нормали плоскости, р — расстояние до плоскости от начала координат. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости (если же плоскость проходит через начало координат, то выбор положительного направления нормали безразличен).
Пусть М* — какая угодно точка пространства, d — расстояние от нее до данной плоскости. Отклонением б точки М* от данной плоскости называется число -f- d, если точка Л1* и начало координат лежат по разные стороны от данной плоскости, и число — d, если они лежат по одну сторону от данной плоскости (если М* лежит на самой плоскости, то отклонение равно нулю).
Если точка Л1* имеет координаты х*, у*, д*, а плоскость задана нормальным уравнением
х cos а + у cos р + д cos у — р = 0,
то отклонение точки М* от этой плоскости дается формулой
б = х* cos а 4- у* cos р + z* cos у — р.
Очевидно, d = | б |
Общее уравнение плоскости
Ах + By 4” Сд Ц- D = 0
приводится к нормальному виду (1) умножением на нормирующий множитель, определяемый формулой
= _________1_______
И “ “ /Д2 4- В2 4- С2~ ’
знак нормирующего множителя берется противоположным знаку свободного члена нормируемого уравнения.
147
956.	Определить, какие из следующих уравнений плоскостей являются нормальными:
1)±Х—2-5=0; 2) f.r+4y-y?-3 = 0;
3)	2+5=0; 4) -|х+|г/-|2-5 = 0;
5)|х-|г-3 = 0;	6) - -^у + г + I =0;
г-1=0; 8)4x-{j/ + 3 = 0;
9) х- 1 = 0;	10) у + 2 = 0;
[1) -£-2 = 0;	12) г-5 = 0.
957. Привести каждое из следующих уравнений плоскостей к нормальному виду:
1) 2х-2// +2-18 = 0;	2) |х -|г/+ -уг + 3 = 0;
3) 4х-бу- 12г— 11=0; 4) - 4х - 4у + 2г + 1 = 0;
5) бу- 12г + 26 = 0;	6) Зх-4у- 1=0;
7) у + 2 = 0;	8) - х + 5 = 0;
9) -г+ 3 = 0;	10) 2г—1=0.
958. Для каждой из следующих плоскостей вычислить углы а, р и у, образуемые нормалью с осями координат, и расстояние р от начала координат:
1) х + У + г—10 = 0; 2) х — у — г ]/2 + 16 = 0;
3) х + г — 6 = 0;	4) г/ — г + 2 = 0;
5) х /3‘+у+ 10 = 0; 6) г —2 = 0; 7) 2х + 1 = 0;
8) 2//+ 1=0;	9) х-2г/+ 2г-6 = 0;
10) 2х + Зг/— 6г + 4 = 0.
959. Вычислить величину отклонения 6 и расстояние d точки от плоскости в каждом из следующих случаев;
1)	МД-2; -4; 3),	2х-^ + 2г + 3 = 0;
2)	М2(2; -1; -1),	16х- 12г/ + 15г-4 = 0;
3)	М3(1; 2; -3),	5х - Зу + г + 4 = 0;
4)	М4 (3; -6; 7),	4х - Зг - 1 = 0;
5)	М5 (9; 2; -2),	12г/ - 5г + 5 = 0.
148
960. Вычислить расстояние d от точки Р(—1; 1; —2) до плоскости, проходящей через три точки Alj (1; — 1; 1), М2(-2; 1; 3) и М3(4; -5; -2).
961. Определить, лежат ли точка Q (2; —1; 1) и начало координат по одну или по разные стороны относительно каждой из следующих плоскостей!
1) 5x-3//-f-z- 18 = 0;	2)	2х + 7у + За + 1 =0;
3) x + 5z/4-12z-l=0;	4)	2х- у + z 4- 11 =0;
5) 2х 4-3//— 6z 4-2 = 0;	6)	Зх - 2у 4- 2z - 7 =0.
962, Доказать, что плоскость Зх —• 4у — 2г + 5 = 0 пересекает отрезок, ограниченный точками (3; —2; I) и Л42(—2; 5; 2).
963. Доказать, что плоскость 5х — 2у 4- z — 1=0 не пересекает отрезка, ограниченного точками (1; 4; —3) и М2(2; 5; 0).
964. В каждом из следующих случаев вычислить расстояние между параллельными плоскостями:
1) х-2у — 2г- 12 = 0, v2) 2х — 3//+ 6z—14 = 0»
х - 2у - 2z - 6 = 0;	4x-6z/+ 12z+21 = 0;
' 3) 2x-#4-2z + 9 = 0,	4) 16х+12//-15г4-50=0,
4х — 2//+ 4z — 21 = 0;	16x4-12у—15г 4-25=0;
5) 30x-32z/+24z —75 = 0, 6) 6х — 18z/ —9z-28 = 0, 15x— 16//+12z — 25 = 0; 4x—12y —6г —7 = 0.
965.	Две грани куба лежат на плоскостях 2х — 2у + 4- z — 1 = 0, 2х — 2у + z + 5 = 0. Вычислить объем этого куба.
966.	На оси Оу найти точку, отстоящую от плоскости х4- 2# —2z — 2 = 0 на расстоянии d = 4.
967.	На оси Oz найти точку, равноудаленную от точки М (1; —2; 0) и от плоскости Зх — 2у 4- 6г — 9 = 0.
968.	На оси Ох найти точку, равноудаленную от двух плоскостей: 12х — 16г/ -J- 15z + 1 = 0, 2х + 2//—z—1 =0.
969.	Вывести уравнение геометрического места точек, отклонение которых от плоскости 4х — 4у —- 2z 4- 3 = 0 равно 2.
970.	Вывести уравнение геометрического места точек, отклонение которых от плоскости 6х 4- Зу + 2z — 10 = 0 равно —3.
149
971.	Составить уравнения плоскостей, параллельных плоскости 2х — 2y — z — 3 — 0 и отстоящих от нее на расстоянии d = 5.
972.	В каждом из следующих случаев составить уравнение геометрического места точек, равноудаленных от двух параллельных плоскостей:
1) 4х - у - 2г - 3 = 0,	2) Зх + 2у - z + 3 = О,
4х — у — 2г — 5 = 0; Зх + 2у — г — 1 == 0;
3) 5х-3у + г+ 3 = 0, 10х — бу + 2г+ 7 = 0.
973. В каждом из следующих случаев составить уравнения плоскостей, которые делят пополам двугранные углы, образованные двумя пересекающимися плоскостями:
1) х — Зу + 2г — 5 = 0,	2) 5х — 5у — 2г — 3 — 0,
Зх — 2у - г + 3 = 0; х + 7у - 2г + I = 0;
3) 2х — у + 5г + 3 — 0,
2х — 1 Оу + 4г — 2 — 0.
974. В каждом из следующих случаев определить, лежат ли точка М (2; —1; 3) и начало координат в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей:
1) 2х - у + Зг - 5 = 0,	2) 2х + Зу — 5г — 15 = 0,
Зх+2у-г + 3 = 0; 5х - у-Зг- 7 = 0;
3) х+ 5у-г+ 1 =0, 2х+ 17у + г + 2 = 0.
975.	В каждом из следующих случаев определить, лежат ли точки Л1.(2; —I; I) и ЛГ(1; 2; —3) в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей:
1) Зх — у + 2г — 3 = 0,	2) 2х — у + 5г— 1=0,
х — 2у — г + 4 = 0; Зх — 2у + 6г — 1 = 0.
976.	Определить, лежит ли начало координат внутри острого или тупого угла, образованного двумя плоскостями: х — 2у + Зг — 5 = 0, 2х — у — г + 3 = 0.
977.	Определить, лежит ли точка М (3; 2; —1) внутри острого или тупого угла, образованного двумя плоскостями: 5х — у + г + 3 = 0, 4х — Зу + 2г + 5 = 0.
150
978.	Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 2х — 14г/ 4* 6г — 1 = О, Зх 4“ 5г/ — 5г 4- 3 = О, в котором лежит начало координат.
979.	Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 2х — у 4- 2г — 3 = 0, 3x4" 2г/ — 6г— 1 = 0, в котором лежит точка М(1; 2; —3).
980.	Составить уравнение плоскости, которая делит пополам острый двугранный угол, образованный двумя плоскостями: 2х — Зу — 4г — 3 = 0, 4х — Зу — 2г—3 = 0.
981.	Составить уравнение плоскости, которая делит пополам тупой двугранный угол, образованный двумя плоскостями: Зх — 4г/— г 4" 5 = 0, 4х — Зг/4" z 4" 5 = 0.
§ 41. Уравнения прямой
Прямая как пересечение двух плоскостей определяется совместным заданием двух уравнений первой степени:
А[Х + В^у + С\2 4- Di =0,	.
А2х + В2у 4- C2z + D2 = 0
при условии, что коэффициенты Д1, Ви первого из них не про» порциональны коэффициентам А2, В2, С2 второго (в противном случае эти уравнения будут определять параллельные или слившиеся плоскости).
Пусть некоторая прямая а определена уравнениями (1) и а ир — какие угодно числа, одновременно не равные нулю; тогда уравнение
а (Д]Х 4" В1У 4- Cxz 4-	4* Р (А2х 4- В2у 4- С2з 4- D2) = 0 (2)
определяет плоскость, проходящую через прямую а.
Уравнением вида (2) (при соответствующем выборе чисел а, р) можно определить любую плоскость, проходящую через прямую а.
Совокупность всех плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей. Уравнение вида (2) называется уравнением пучка плоскостей.
Если а 0, то, полагая «= %, уравнение (2) можно привести к виду
Д1Х 4" В\у 4» CfZ 4~	4- Л (ДгХ 4* By 4~ C2z 4“ ^2)в 0»	(3)
В таком виде уравнение пучка плоскостей более употребительно, чем уравнение (2), однако уравнением J3) можно определить все плоскости пучка, за исключением той, которой соответствует а==0, т. е. за исключением плоскости А2х 4- В2у 4- C2z 4* 4-£2 = О.
151
982.	Составить уравнения прямых, образованных пересечением плоскости 5х — 7у 4- 2z — 3 = 0 с координатными плоскостями.
983.	Составить уравнения прямой, образованной пересечением плоскости 3x—y—7z 4- 9 = 0 с плоскостью, проходящей через ось Ох и точки 5(3; 2; —5).
984.	Найти точки пересечения прямой
| 2% + // — z — 3 = 0,
I х + +	1=0
с координатными плоскостями.
985.	Доказать, что прямая
| 2х — Зу + 5г — 6 = 0,
I x4-5z/-7z4-Ю = 0
пересекает ось Оу.
986.	Определить, при каком значении D прямая
( 2xA'3y — zA~ D = 0,
1 Зх — 2у 4- 2z — 6 = 0
пересекает: 1) ось Ох; 2) ось Оу, 3) ось Oz.
987.	Найти соотношения, которым должны удовлетворять коэффициенты уравнений прямой
J А^х + В{у + C]Z 4- 5| = 0,
I А2х 4~ В2у 4~ C2z 4“ D2 = 0
для того, чтобы эта прямая была параллельна: 1) оси Ох; 2) оси Оу; 3) оси Oz.
988.	Найти соотношения, которым должны удовлетворять коэффициенты уравнений прямой
f А^х 4“ BLy 4~ O[Z 4"	= 0,
I А2х + B2y 4- C2z 4- D2 = 0
для того, чтобы эта прямая пересекала: 1) ось абсцисс; 2) ось ординат; 3) ось апликат; 4) совпадала с осью абсцисс; 5) совпадала с осью ординат; 6) совпадала с осью апликат.
989.	В пучке плоскостей 2х — 3$ 4- z — 3 + Л(х 4-3^4-4-2z4-l) = 0 найти плоскость, которая: 1) проходит через точку (1; —2; 3); 2) параллельна оси Ох; 3) параллельна оси Оу; 4) параллельна оси Oz, 152
990.	Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей Зх — у + + 2г+9 = 0, х+г—3=0: 1) и через точку Л41 (4; —2; —3); 2) параллельно оси Ох\ 3) параллельно оси Оу, 4) параллельно оси Oz.
991.	Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 2х —у + Зг—5=0, х + 2у — z + 2 — 0 параллельно вектору l—{2\ —1; —2}.
992.	Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 5х — 2у—z—З = 0, х + 3# — 2г+ 5 = 0 параллельно вектору Z = {7; 9; 17}.
993.	Составить уравнение плоскости, проходящей через прямую пересечения плоскостей Зх—2у + z—3 = 0, х — 2z = 0 перпендикулярно плоскости х—2#+г + 5 = 0.
994.	Составить уравнение плоскости, проходящей через прямую
5х — у — 2z — 3 = 0,
Зх — 2у — 5z + 2 = 0
перпендикулярно плоскости х + 19# — 12 — 11 = 0.
995.	Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей 2х + у — z + + 1=0, x + # + 2z+l=0 параллельно отрезку, ограниченному точками Af] (2; 5; —3) и М2(3; —2; 2).
996.	Написать уравнение плоскости, принадлежащей пучку плоскостей а (Зх—4# + г+6) + 3 (2х—3#+г+2) = 0 и равноудаленной от точек М{ (3; —4, —6), М2(1; 2; 2).
997.	Определить, принадлежит ли плоскость 4х—8#+ + 17г —8 = 0 пучку плоскостей а(5х — у + 4г — Г) + + 3(2х + 2# — Зг + 2) = 0.
998.	Определить, принадлежит ли плоскость 5х — — 9# — 2z + 12 = 0 пучку плоскостей а (2х—Зу + г—5) + + 3 (х — 2у — z — 7) = 0.
999.	Определить, при каких значениях I и т плоскость 5х + ly + 4z + т = 0 принадлежит пучку плоскостей а (Зх — 7 у + z — 3) + р (х — 9# — 2г + 5) = 0.
1000.	Написать уравнение плоскости, которая принадлежит пучку плоскостей а(х — 3# + 7г + 36) + + 3(2х + # — г — 15) = 0 и отстоит от начала координат на расстоянии р = 3.
1001.	Написать уравнение плоскости, которая принадлежит пучку плоскостей а(10х — 8# — 15г + 56) + + 3 (4х + у + Зг — 1) = 0 и отстоит от точки С (3; —2; —3) на расстоянии d = 7.
153
1002.	Найти уравнение плоскости, которая принадлежит пучку плоскостей а (4х + 13г/ — 2г — 60) + 0 (4х 4* 4- Зг/ + Зг—30) = 0и отсекает от координатного угла Оху треугольник с площадью, равной 6 кв. ед.
1003.	Составить уравнения плоскостей, проектирующих прямую
I 2х — у + 2г — 3 = 0,
( х 4~ 2у — г—1=0
на координатные плоскости.
1004.	Составить уравнения проекций прямой
( х 4- 2у — Зг — 5 = 0,
I 2х — z/4" г 4" 2 = 0
на координатные плоскости.
1003. Составить уравнение плоскости, проектирующей прямую
| Зх 4- 2у — г — 1 = 0,
( 2х — Зу 4- 2г — 2 = 0
на плоскость х 4- 2у 4- Зг — 5 = 0.
1006. Составить уравнения проекции прямой
( 5х — 4у — 2г — 5 = 0,
( х 4- 2г — 2 = 0
на плоскость 2х — у 4- 2 — 1 = 0.
§ 42. Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.
Направляющий вектор произвольной прямой в дальнейшем обозначается буквой а, его координаты — буквами /, /п, п\
а — {1\ т\ п}.
Если известна одна точка Мо (х0; t/oJ го) прямой и направляющий вектор а = {/; т', п}, то прямая может быть определена (двумя) уравнениями вида:
х — х0 у — уь = г — г0	,
I = т	п *
В таком виде уравнения прямой называются каноническими. 154
Канонические уравнения прямой, проходящей через две данные точки All (хв Уй zi) и М2 (х2; Уъ ?2), имеют вид:
X — Х[ = У — У\ __ 2 — Z1 х2 — Х1 У2 - У1 ?2 ~ 2! ’
Обозначим буквой t каждое из равных отношений в канонических уравнениях (1); мы получим:
х — хр _ у — Уо _ z — 2о _ t 1\ т п
Отсюда
| х = Хо + И,
{ У = Уо + mt,	(3)
| Z = 20 + nt.
Это — параметрические уравнения прямой, проходящей через точку Л10 (хо; Уо', 20) в направлении вектора а — {1; т; п}. В уравнениях (3) t рассматривается как произвольно изменяющийся параметр, х, у, з —как функции от /; при изменении t величины х, у, z меняются так, что точка М (х; у; z) движется по дайной прямой.
Если параметр t рассматривать как переменное время, а уравнения (3) как уравнения движения точки Л/, то эти уравнения будут определять прямолинейное и равномерное движение точки М. При t — 0 точка М совпадает с точкой Mq. Скорость v точки Л1 постоянна и определяется формулой
и = VI2 + т2 + п2.
1007.	Составить канонические уравнения прямой, проходящей через точку Afj(2; 0; —3) параллельно: 1) вектору а = {2; —3; 5}; 2) прямой ~ 1 =
3) оси Ох; 4) оси Оу; 5) оси Ох.
1008.	Составить канонические уравнения прямой, проходящей через две данные точки: 1) (1; —2; 1), (3; 1; -1); 2) (3; -1; 0), (1; 0, -3); 3) (0; -2; 3), (3; -2; 1); 4) (1; 2; -4), (-1; 2; -4).
1009.	Составить параметрические уравнения прямой, проходящей через точку (1; —1; —3) параллельно: 1) вектору а = {2; —3; 4}; 2) прямой = —= 3) прямой x — 3t — 1, //= — 2/4-3, 2 = 5/4-2.
1010.	Составить параметрические уравнения прямой, проходящей через две данные точки: 1) (3; —1; 2), (2; 1; 1); 2) (1; 1; -2), (3; -1; 0); 3) (0; 0; 1), (0; 1; -2), 1011. Через точки Л14 (—-6; 6; —5) и Л12(12; —6; 1) проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.
155
1012.	Даны вершины треугольника А (3; 6; —7), В (—5; 2; 3) и С (4; —7; —2). Составить параметрические уравнения его медианы, проведенной из вершины С.
1013.	Даны вершины треугольника 4(3; —1; — 1), В (1; 2; —7) и С (—5; 14; —3). Составить канонические уравнения биссектрисы его внутреннего угла при вершине С.
1014.	Даны вершины треугольника 4(2; —1; —3), В (5; 2; —7) и С (—7; 11; 6). Составить канонические уравнения биссектрисы его внешнего угла при вершине 4.
1015.	Даны вершины треугольника 4(1; —2; —4), В (3; 1; —3) и С (5; 1; —7). Составить параметрические уравнения его высоты, опущенной из вершины В на противоположную сторону.
1016.	Дана прямая
2х — 5у + 2 — 3 = 0, х-\-2у — z-l-2 = 0.
Вычислить проекции на оси координат какого-нибудь ее направляющего вектора а. Найти общее выражение проекций на оси координат произвольного направляющего вектора этой прямой.
1017.	Дана прямая
( 2х — у + Зг + 1 = 0,
( Зх + у — г — 2 = 0.
Найти разложение по базису i, j, k какого-нибудь ее направляющего вектора а. Выразить в общем виде разложение по базису i, /, k произвольного направляющего вектора этой прямой.
1018.	Составить канонические уравнения прямой, проходящей через точку (2; 3; —5) параллельно прямой
1 Зх — у + 2г — 7 = 0,
( х 4~ Зу — 2г 4~ 3 = 0.
1019.	Составить канонические уравнения следующих прямых:
1)	(	х	— 2у	+ Зг — 4 = 0, 2) (	5х +	//4-^ = 0,
(	Зх	+ 2у	— 5г — 4 = 0;	(2х -\-Зу — 2г +	5 = 0;
3)	J	х	— 2у	-j- Зг 4" 1 ==
[	2х	4- у	— 4г — 8 = 0.
156
1020. Составить параметрические уравнения следующих прямых:
1)	| 2х + 3г/ — г — 4 = 0, 2) [ x + 2z/-2-6 = 0, I Зх — Зу + 2г + 1 = 0;	( 2х — у + z + 1 = 0.
1021. Доказать параллельность прямых:
п х + 2 у— 1 z ( х Н" У z 0» з	~ -2 “	1 и	I	х	— // — 5г —8 = 0;
2)	х	= 2/ + 5, у = — t + 2,	z = t —	7	и
(	х	+ Зу + z +	2 = 0,
(	х	— у — Зг —	2 = 0;
3)	( х	+ У — Зг + 1	= 0,	|	х +	2у — 5г	— 1=0,
1 х	— г/ + г + 3	= О	И (	х —	2х + Зг	— 9 = 0.
1022. Доказать перпендикулярность прямых:
.ч	х_____у — 1  2 I	Зх -f-	у	5г д- 1	О,
’	т~ ^2~~У	н (	2х + 3//-8г + 3 = 0;
2)	x = 2t+ 1, // = 3^ — 2, г=-6*+ 1
| 2х + У — 4г + 2 = О, И I 4х —//— 5г + 4 = 0;
( х + у — Зг — 1 = 0, f 2х + у + 2г + 5 = О, 3 I 2х — у — 9г — 2 = О И I 2х — 2у — г + 2 = 0.
1023.	Найти острый угол между прямыми:
х — 3_ у + 2__ z х + 2 ___ у — 3 _ г + 5
1 —	! ”/2 ’ I	~'	I V2
1024.	Найти тупой угол между прямыми x = 3t — 2, У = 0, г = — / + 3 и х = 2t — 1, // = 0, z = t — 3.
1025.	Определить косинус угла между прямыми: f х — у — 4г — 5 = 0, | х —6// —6г+ 2 = 0, I 2х + у — 2г — 4 = 0; { 2х + 2у + 9г — 1 = 0.
1026.	Доказать, что прямые, заданные параметрическими уравнениями х = 2t — 3, у = 3t — 2, г = — 4^+6 и х = / + 5, г/ = —4Z —1, г = / —4, пересекаются.
157
1027.	Даны прямые
х + 2  у   z — 1 х — 3  у — 1  г — 7 ,
2	—3	4	’ I ~	4	~~	2	’
при каком значении Z они пересекаются?
1028.	Доказать, что условие, при котором две прямые
х — а\ __ z/ — &1 _ г — Ci и х — а2 У— Ь2 __ г — сг
1\	т\	П[	12	пг2 п2
лежат в одной плоскости, может быть представлено в следующем виде:
С/2	^2	С% — Cj
Zi
/722	^2
1029.	Составить уравнения прямой, которая проходит через точку М](— 1; 2; —3) перпендикулярно к вектору а = {6; —2; —3} и пересекает прямую
х — 1 __ у + 1 _ г — 3
3	“	2	“ -5 ’
1030.	Составить уравнения прямой, которая проходит через точку Л4] (—4; —5; 3) и пересекает две прямые
х + 1	_у + 3 г — 2	х —- 2__ # + 1 _ г — 1
3	“ -2	“ -1 ’	2	—	3 “ -5	•
1031.	Составить параметрические уравнения общего перпендикуляра двух прямых, заданных уравнениями х = 3/-7, у = — 2t + 4, 2 = 3/+ 4 и
х = t + 1, у = 2t — 8,	2 = — t — 12.
1032.	Даны уравнения движения точки М (х; у\ 2) х = 3 — 4/, // = 5 + 3/, 2 = — 2+12/.
Определить ее скорость v.
1033.	Даны уравнения движения точки Л4(х; //; z) х = 5 —2/, // = — 3 + 2/, 2 = 5 — /.
Определить расстояние d, которое пройдет эта точка за промежуток времени от ^=0 до /2 = 7.
1034.	Составить уравнения движения точки М (х; //; г), которая, имея начальное положение М0(3; — 1; —5), 158
движется прямолинейно и равномерно в направлении вектора $ = {—2; 6; 3} со скоростью и = 21.
1035.	Составить уравнения движения точки М (х; у\ г), которая, двигаясь прямолинейно и равномерно, прошла расстояние от точки Mj (—7; 12; 5) до точки Af2(9j —4; —3) за промежуток времени от /t = 0 до /2 = 4.
1036.	Точка М (х; //; г) движется прямолинейно и равномерно из начального положения Мо(2О; —18; —32) в направлении, противоположном вектору s = (3; —4; —12}; со скоростью и = 26. Составить уравнения движения точки М и определить точку, с которой она совпадает в момент времени / = 3.
1037.	Точки Л1(х; //; г) и N (х; //; г) движутся прямолинейно и равномерно: первая из начального положения Мо(—-5; 4; —5) со скоростью и^=14 в направлении вектора s = {3; —6; 2}, вторая из начального положения jyo(_5; 16; —6) со скоростью 1^=13 в направлении, противоположном вектору г = {—4; 12; —3}. Составить уравнения движения каждой из точек и, убедившись, что их траектории пересекаются, найти:
1)	точку Р пересечения их траекторий;
2)	время, затраченное на движение точки М отЛ!0до Р',
3)	время, затраченное на движение точки JV отЛ^0 до Р', 4) длины отрезков MGP и NQP.
§ 43. Смешанные задачи, относящиеся к уравнению плоскости и уравнениям прямой
1038.	Доказать, что прямая х = 3/ — 2, у = — 4/ + 1, z = 4/ — 5 параллельна плоскости 4х — Зу — 62 — 5 = 0.
1039.	Доказать, что прямая
Г 5х — Зу + 22 — 5 = О,
1 2х — у— 2—1=0
лежит в плоскости 4х — Зу + 72 — 7 = 0.
1040.	Найти точку пересечения прямой и плоскости:
1)	=	2л: + Зу + г — 1 =0;
2)	i±l = iz_2. = £+J-, х-2у + г - 15 = 0; О	' 1	о
3)	x + 2//-2Z + 6 = 0.
159
1041, Составить канонические уравнения прямой, проходящей через точку М0(2; —4; —1) и середину отрезка прямой
f Зх 4~ 4# 4- 5г — 26 = 0,
1 Зх — Зу — 2s — 5 = (\
заключенного между плоскостями 5х 4- Зу — 4х 4- 11 = 0, 5х 4- Зу — 4z — 41 = 0.
1042.	Составить уравнения прямой, проходящей через точку М0(2; —3; —5) перпендикулярнб К йлоскости 6х — Зу — 5z 4- 2 = 0.
1043.	Составить уравнение плоскости, проходящей через точку Мо(1; —1; —1) перпендикулярно к прямой х + 3 у- 1 _ г + 2
2 -з ~	4
1044.	Составить уравнение плоскости, проходящей через точку Л40(1; —2; I) перпендикулярно к прямой
| х — 2</ + г — 3 = 0, 1x4“ У — г + 2 = 0.
х j_ । ц___2
1045.	При каком значении tn прямая —= -------=
z -4- 3
= —_2 параллельна плоскости х — Зу + 6г 4~ 7 — 0?
1046.	При каком значении С прямая
f Зх — 2у 4- г 4~ 3 — 0,
I 4х — Зу 4- 4г 4- 1 = 0
параллельна плоскости 2х — у 4“ Сг — 2 = 0?
1047.	При каких значениях А и D прямая х = 3 + 4/, у =1—4/, г= — 3 4“ / лежит в плоскости 4x4-2// — - 4г + D = 0?
1048.	При каких значениях А и В плоскость 4x4-4- By 4- Зг — 5 = 0 перпендикулярна к прямой х — 3 4" 2/, //= 5 — 3/, г = — 2 — 2/?
х 2
1049.	При каких значениях I и С прямая —— = у + l z — 5	о п ।
=	— — _3 перпендикулярна к плоскости Зх — 2z/+
4~ Сг 4~ 1 — 0?
1050.	Найти проекцию точки Р(2; —1; 3) на прямую х = 3/, y — 3t — 7, г = 2/4~ 2.
160
1051.	Найти точку Q, симметричную точке Р (4; 1; 6) относительно прямой
х — у — 4г + 12 = 0, 2x4-// — 2г 4- 3 = 0.
1052.	Найти точку Q, симметричную точке Р(2; —5; 7) относительно прямой, проходящей через точки (5; 4; 6) и М,(-2; -17, -8).
1053.	Найти проекцию точки Р(5; 2; —1) на плоскость 2х — у 4“ Зг -j- 23 — 0.
1054.	Найти точку Q, симметричную точке Р(1; 3; —4) относительно плоскости Зх 4- У — 2г — 0.
1055.	На плоскости Оху найти такую точку Р, сумма расстояний которой до точек Д(— 1; 2; 5) и В (11; —16; 10) была бы наименьшей.
1056.	На плоскости Oxz найти такую точку Р, разность расстояний которой до точек М.{ (3; 2; —5) и М2(8; —4; —13) была бы наибольшей.
1057.	На плоскости 2х — Зу 4- Зг — 17 = 0 найти такую точку Р, сумма расстояний которой до точек Д(3; —4; 7) и В(—5; —14; 17) была бы наименьшей.
1058.	На плоскости 2х 4- 3// — 4г — 15=0 найти такую точку Р, разность расстояний которой до точек Mi (5; 2; —7) и М2(7; —25; 10) была бы наибольшей.
1059.	Точка Л4(х; у; г) движется прямолинейно и равномерно из начального положения Л40(15; —24; —16) со скоростью v = 12 в направлении вектора s = {—2; 2; 1}. Убедившись, что траектория точки М пересекает плоскость Зх 4~ 4//4-7г — 17 = 0, найти:
1)	точку Р их пересечения;
2)	время, затраченное на движение точки М от MQ ДО Р;
3)	длину отрезка М^Р.
1060. Точка М (х; у; г) движется прямолинейно и равномеоно из начального положения М0(28;—30; —27) со скоростью у =12,5 по перпендикуляру, опущенному из точки Мо на плоскость 15х— 16// — 12г 4-26 = 0. Составить уравнения движения точки М и определить:
1) точку Р пересечения ее траектории с этой плоскостью;
2) время, затраченное на движение точки М от MQ до Р;
• 3) длину отрезка М0Р.
6 Д. В. Клетеиик	161
1061. Точка Af(x; у\ г) движется прямолинейно и равномерно из начального положения Л40(11; —21; 20) в направлении вектора s = {— 1; 2; —2} со скоростью и=12. Определить, за какое время она пройдет отрезок своей траектории, заключенный между параллельными плоскостями: 2х + Зу +	— 41 = О,
2х + Зу + 5z + 31 = 0.
1062. Вычислить расстояние d точки Р(1; —1; —2) от прямой
х -|- 3 _ у + 2 _ 2 — 8
3	“	2	“ -2 *
1063. Вычислить расстояние d от точки Р(2; 3; — 1) до следующих прямых:
1	ч х — 5_ у _ 2 + 25 ф
"	3 “ 2	-2 ’
2	) x = ^ + 1, y = t + 2, z = 4t+ 13;
Г 2х — 2у +- z + 3 = 0, 3Ч Зх-2у + 2г + 17 = 0.
1064.	Убедившись, что прямые
f 2х +- 2у — z — 10 = 0,	х + 7 _ г/ — 5 _ 2-9
( х — у — z — 22 = 0,	3	4
параллельны, вычислить расстояние d между ними.
1065.	Составить уравнение плоскости, проходящей через точку М[ (1; 2; —3) параллельно прямым
л — 1 У + 1	_2 — 7 х + 5___у — 2__2 + 3
2 “ —3	“	3	’	3	-2	—1	•
1066.	Доказать, что уравнение плоскости, проходящей через точку М$(х0; у0; z0) параллельно прямым
х — сц _ у — Ь\ _ г — Ci х — а2 _ y — bi __ с2
mt «1	’	tn2 n2 *
может быть представлено в следующем виде:
X —х0	У — Уо	2 —20
	т{	
	т2	п2
162
1067.	Доказать, что уравнение плоскости, проходящей через точки Af](Xi У\\ 2j) и	У 2* ^2) парал-
лельно прямой
х — а _ у — b __ z — с
I	т	п *
может быть представлено в следующем виде:
X —Xi	У —У\	Z — Z\	
X2 — Xi	У2~У\	^2-^1	= 0.
I	т	п	
1068.	Составить уравнение плоскости, проходящей через прямую х==2/+Ь У—~ 3/+ 2, z = 2t — 3 и точку 2И] (2; —2; 1).
1069.	Доказать, что уравнение плоскости, проходящей через прямую х = х0 + /Л У =	z = z04-nf
и точку ЛМ*ь Уъ Zi), может быть представлено в сле-
дующем виде:
X — У —У\ z —z}
Л4-Х0 ?1-Уо г!-г0
I т п
1070. Доказать, что прямые
х — 1 __у + 2__2 — 5
2	“ -3 —	4 *
х = 3^ + 7, t/ = 2/4-2, 2 = -2/ + 1 лежат в одной плоскости, и составить уравнение этой плоскости.
1071.	Доказать, что если две прямые
х — Д)_____У — Ь\ _____ z — С\
Л	’
х — а2 __ у — ______ z — с2
4	т2	«2
пересекаются, то уравнение плоскости, в которой они лежат, может быть представлено в следующем виде:
х — flj	у	— bi	z	—	Ci
li	гщ	tii
/2	t^2	^2
1072.	Составить уравнение плоскости, проходящей через две параллельные прямые
х — 2	^4-1	‘2 — 3	х— 1	_ V — 2	_ z + 3
3	~	2	“ -2 ’	3	~	2	“ -2 *
6*
163
1073.	Доказать, что уравнение плоскости, проходя-щей через две параллельные прямые x^=a}-\-lt, y = bx + mt, z — C[ + ni и x — a2-}-lt, y~b2 + mt, г — с2 + nt, может быть представлено в следующем виде:
х —di у ~ z —с{
а2 — at b2 — b{ с2 — с} =0.
I т п
1074.	Найти проекцию точки С(3; —4; —2) на плоскость, проходящую через параллельные прямые
х — 5 у — 6 __ 2 + 3 х — 2 у — 3 _____ 2 + 3
13 —	1	“ — 4 ’	13 ~	1	“ — 4 ’
1075.	Найти точку Q, симметричную точке Р(3;— 4; —6) относительно плоскости, проходящей через М{ (—6; 1; -5), М2(7; -2; -1) и М3(10; -7; 1).
1076.	Найти точку Q, симметричную точке Р (—3; 2; 5) относительно плоскости, проходящей через прямые
| х — 2у + 3z — 5 = 0,	( Зх + у + Зг + 7 = 0,
I х — 2у — 4г + 3 = 0;	( 5х — Зу + 2г + 5 = 0.
1077.	Составить уравнение плоскости, проходящей через прямую х = 3/ + 1, // = 2/ + 3, г = ~ - 2 параллельно прямой
( 2х — // + г — 3 = 0,
I х + 2// — г — 5 = 0.
1078.	Доказать, что уравнение плоскости, проходящей
X — X] и —	Z — Z,
через прямую —у— =	— — — параллельно пря-
мой х — Хъ + lt, y = yQ+mt, z — zQ-^nt, может быть представлено в следующем виде:
х — хх	У — У\	2 — 2{	
1	т	п	= 0.
h		Щ	
1079.	Составить уравнение плоскости, проходящей х—1 у + 2 г — 2
через прямую —?—==-^—^-==—-— перпендикулярно к плоскости Зх + 2у — z — 5 = 0.
164
1080.	Доказать, что уравнение плоскости, проходящей через прямую х«дс04-//, у — + mt, z = zn-\-nt перпендикулярно к плоскости Ах 4- By 4- Cz 4- D =» 0, может быть представлено в следующем виде:
X — х0	У-Уо	2 — Z0	
1	иг	п	= 0.
А	В ’	С	
1081.	Составить канонические уравнения прямой, которая проходит через точку М0(3; —2; —4) параллельно плоскости Зх — 2у — Зг — 7 = 0 и пересекает х — 2 у + 4 _ _ г—1
Прямую —2— = —Z2~ = —2—*
1082.	Составить параметрические уравнения прямой, которая проходит параллельно плоскостям 3x4-12z/ — — Зг — 5 =« 0, Зх — 4zy + 9г 4~ 7 == 0 и пересекает пря-лг + 5______ у — 3 _ z +	1	х-3 __ у + 1 _>2 — 2
мне 2	“	—4	3	’	—2	3	4	
1083.	Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:
х + 7_ у + 4__ г + 3	, х — 21	_ у + 5 _ 2 — 2 е
^	3	“	4	—2	’	6	~ -4 “	-1 *
2) х = 2/ —4, z/=-J4-4, г = —2/—1;
x = 4f-5, г/= -3/4-5, г = -5/4-5;
ох х + 5_ у + 5__ г - 1 ,
3	~~	2 — -2 ’
х = 6/4-Э> у — — 2/, г = — / 4-2.
§ 44.	Сфера
В декартовых прямоугольных координатах сфера, имеющая центр С (а; Р; у) и радиус г, определяется уравнением (х — а)2 +• + (у — Р)2 4* (г — у)2 =® г2. Сфера радиуса г, центр которой находится в начале координат, имеет уравнение х2 4* У2 + г2 = г2.
1084.	Составить уравнение сферы в каждом из еле-дующих случаев:
1)	сфера имеет центр С(0; 0; 0) и радиус г = 9;
2)	сфера имеет центр С (5; —3; 7) и радиус г = 2;
3)	сфера проходит через начало координат и имеет центр С (4; —4; —2);
4)	сфера проходит через точку А (2; —1; —3) и имеет центр х С (3; —2; 1);
5)	точки А (2; —3; 5) и В (4; 1; —3) являются концами одного из диаметров сферы;
1.65
6)	центром сферы является начало координат, ц плоскость 16х — 15//—12г+ 75 = 0 является касатель* ной к сфере;
7)	сфера имеет центр С(3; — 5; —2) и плоскость 2х — у — Зг + 11 = 0 является касательной к сфере;
8)	сфера проходит через три точки Mj (3; 1; —3), М2(—2; 4; 1) и Af3(—5; 0; 0), а ее центр лежит на плоскости 2х + у — г + 3 — 0;
9)	сфера проходит через четыре точки; М,(1; -2; -1), Л12(—5; 10; -1), М3(4; 1; И), МД-8; -2, 2).
1085.	Составить уравнение сферы радиуса г = 3, касающейся плоскости х + 2г/ + 2г + 3 = 0 в точке Afi (1; 1; -3).
1086.	Вычислить радиус R сферы, которая касается плоскостей Зх + 2у — 6г — 15 = 0, Зх + 2г/ — 6г + 55 = 0.
1087.	Сфера, центр которой лежит на прямой | 2х + 4у — г — 7 = 0, [ 4х + 5г/ + г — 14 = 0,
касается плоскостей х + 2у — 2г — 2 = 0, х + 2г/ — — 2г+ 4 = 0. Составить уравнение этой сферы.
1088.	Составить уравнение сферы, касающейся двух параллельных плоскостей 6х — Зу — 2г — 35 = 0, 6х — — Зу — 2г + 63 = 0, причем одной из них в точке Afj (5; -1; -1).
1089.	Составить уравнение сферы с центром С (2, 3; —1), которая отсекает от прямой
( 5х — 4у + Зг + 20 — 0,
(, Зх — 4у + г — *-8 — 0
хорду, имеющую длину, равную 16.
1090.	Определить координаты центра С и радиус г сферы, заданной одним из следующих уравнений:
1)	(х-3)2 + 0/ + 2)2 + (г-5)2 = 16;
2)	(х+ \Y + [y-3f + z2 = &,
3)	x2 + y2 + z2-4x-2y + 2z- 19 = 0;
4)	х2 + у2 + г2 — 6г = 0;
5)	х2 + у2 + г2 + 20г/ = 0.
1091.	Составить параметрические уравнения диаметра сферы х2 + г/2 + г2 + 2х — 6г/+ г — 11 = 0, перпендикулярного к плоскости Зх — у + 2г — 17 = 0.
166
1092.	Составить канонические уравнения диаметра сферы х2 + + з2 “ * + 3# + z — 13 = 0, параллельного прямой х=2/ — 1, г/= —3/4" 5, 2 = 4/ 4-7.
1093.	Установить, как расположена точка Л (2; — 1;3) относительно каждой из следующих сфер — внутри, вне или на поверхности:
1)	(х - З)2 4- (У 4- I)2 4- (г - l)2=s4;
2)	(х 4-14)2 4- (У - 11)2 4- {z 4- 12)2 = 625;
3)	(х - 6)2 4- (У “ 1 )2 + (г - 2)2 = 25;
4)	х2 4- 4- *2 “ 4х 4- 6z/ - 8г 4- 22 = 0;
5)	х2 4- У2 4“ z2 — х 4- Зу — 2г — 3 = 0.
1094, Вычислить кратчайшее расстояние от точки А до данной сферы в следующих случаях:
а) А (-2; 6; -3), х2 4- У2 4- г2 = 4;
б)	Л (9; —4; -3),
х24-г/24-г2 4- Их- 16г/-24г 4-241 =0;
в)	Д(1; -1; 3), х24-^24-<г2 —6х4-4г/—Юг —62=0.
1095. Определить, как расположена плоскость относительно сферы — пересекает ли, касается или проходит вне ее; плоскость и сфера заданы следующими уравнениями:
1)	2 = 3,	х24-^4-22-6х4-2г/-10г4-22 = 0;
2)	у = 1, х2 4- У2 4“ z2 4- 4х — 2у — 6г 4- 14 = 0;
3)	х = 5, х2 4- У2 4- г2 — 2х -h 4z/ — 2г — 4 = 0.
1096.	Определить, как расположена прямая относительно сферы — пересекает ли, касается или проходит вне ее; прямая и сфера заданы следующими уравнениями:
1) х== — 2/4-2, г/=т=3/ —у, г = / —2,
х2 4- у2 4- z2 4- х — 4у — Зг 4- у = °;
л\ Х~~Г> _ У__ < + 26
'	3 ~ 2 *“ -2 ’
х2 4- У2 4- Z2 - 4х - Зу 4- 2г - 67 = 0;
~ ( 2*“ {/4-2г—12 = 0,
I 2x-4z/ — 2 4- 6 = 0,
х2 4- У2 4- Z2 - 2х 4- 2у 4- 4г - 43 = 0.
167
1097.	На сфере (х-1)24~(у + 2)24~(z-3)2 = 23 найти точку Мь ближайшую к плоскости Зх—4«4-19=0, и вычислить расстояние d от точки Mj до этой плоскости.
1098.	Определить центр С и радиус R окружности (х - З)2 + (у + 2)2 + (а - I)2 «= 100,
/	2х — 2у — z + 9 « 0.
1099.	Точки Л(3; —2; 5) и В(—1; 6; —3) являются концами диаметра окружности, проходящей через точку С(1; —4; 1). Составить уравнения этой окружности.
1100.	Точка С(1; —1; —2) является центром окружности, отсекающей от прямой
2х — г/-|-2s — 12 = 0, 4х — 7у — г 4- 6 = 0
хорду, длина которой равна 8. Составить уравнения этой окружности.
1101.	Составить уравнения окружности, проходящей через три точки /И] (3; — 1; —2), М2(1; 1; —2) и Л43(—1; 3; 0).
1102.	Даны две сферы
(х — т()2 4- {у — «1)2 4- (z — Р1)2 =	*
(х — т2)2 4- {у — я2)2 + (z — р2)2 = Д2,
которые пересекаются по окружности, лежащей в некоторой плоскости т. Доказать, что любая сфера, проходящая через окружность пересечения данных сфер, а также плоскость т могут быть представлены уравнением вида
а |(х — от;)2 + (у —	4- (z — а)2 — Я?] 4-
4-	М(* ~	+ (У~ я2)2 + (z — р2)2 — Я2] = 0
при надлежащем выборе чисел а и р.
1103.	Составить уравнение плоскости, проходящей через линию пересечения двух сфер:
2х2 4- 2у2 + 2z2 + Зх - 2у 4- z - 5 = 0, X2 4- уЧ 22 — X 4“ Зу — 2z 4- 1=0.
1104.	Составить уравнение сферы, проходящей через начало координат и окружность
х2 4- У2 + г2 = 25,
2х — Зу 4- 5z — 5 = 0.
168
1105.	Составить уравнение сферы, проходящей через окружность
| х2 + у2 + 22 — 2х + Зу — 6г — 5 = 0,
(	5x4-2// — z — 3 = 0
и точку А (2; —1; 1).
1106.	Составить уравнение сферы, проходящей через две окружности:
г х24-г2 = 25,	| х24-22= 16,
I i/ = 2,	1 у = з.
1107.	Составить уравнение касательной плоскости к сфере х2 4- У14- z2 = 49 в точке (6; —3; —2).
1108.	Доказать, что плоскость 2х — 6//4* Зг — 49 = 0 касается сферы х2 4- У2 4- z2 == 49. Вычислить координаты точки касания.
1109.	При каких значениях а плоскость х 4- У 4- z = а касается сферы х2 4- У2 4- z2 = 12.
1110.	Составить уравнение касательной плоскости к сфере (х—3)24-(i/—1)24-(<г4-2)2=24 в точке (—1; 3; 0>.
1111.	Точка (xf,/л; г4 лежит на сфере х24-//24~г2=г . Составить уравнение касательной плоскости к этой сфере в точке Мр
1112.	Вывести условие, при котором плоскость Дх4-4-Вг/ 4-Сг 4- D = 0 касается сферы х2 4- У2 4- z2 = R2.
1113.	Точка Mt (Xi; z/f, г4 лежит на сфере (х — а)2 4-4- {у — Р)2 4- (z — Y)2 — г2- Составить уравнение касательной плоскости к этой сфере в точке Мр
1114.	Через точки пересечения прямой x = 3t — 5, у = Ы— П, г—— 4/4-9 и сферы (х4-2)24-(*/ — 1)24-4-(z 4-5)2 = 49 проведены касательные плоскости к этой сфере. Составить их уравнения.
1115.	Составить уравнения плоскостей,-касательных к сфере х2 4- У2 4- z2 = 9 и параллельных плоскости х4-4-2//- 2г 4- 15 = 0.
1116.	Составить уравнения плоскостей, касательных к сфере (х — З)2 4- (// 4- 2)2 4- (г — I)2 = 25 и параллельных плоскости 4х4-Зг—17 = 0.
1117.	Составить уравнения плоскостей, касательных к сфере x24-z/24-22—10x4-2z/4-26z—113=0 и параллельных ппяммм х + 5_г/-1__24-13 х + 7__г/+1__г-8 нь1Х прямым " п 1	" 3	2*3 ”* _ 2	0 *
169
1118.	Доказать, что через прямую
8х — 1 \у + 8z — 30 = 0, х — у —- 2z — О
можно провести две плоскости, касательные к сфере х2 + у2 + z2 + 2х — бу +	— 15 == 0, и составить их
уравнения.
1119.	Доказать, что через прямую -~^-==у4-3 в z4-l нельзя провести плоскость, касательную к сфере х2+у2+ 4-z2 — 4х + 2у — 4z 4- 4 = 0.
1120.	Доказать, что через прямую х ===4/4-4, у== =3/4- 1, z =/4-1 можно провести только одну плоскость, касательную к сфере х2 4- У2 4- z2 — 2х 4- бу 4* 4- 2z 4- 8 = 0, и составить ее уравнение.
§ 45.	Уравнения плоскости, прямой и сферы в векторной символике
В дальнейшем символ М (г) означает, что г есть радиус-вектор точки М.
1121.	Составить уравнение плоскости а, которая проходит через точку М0(г0)и имеет нормальный вектор п.
Решение *). Пусть М (г) — произвольная точка. Она лежит в плоскости а в том и только в том случае, когда вектор Л40Л1 перпендикулярен к п. Признаком перпендикулярности векторов является равенство нулю их скалярного произведения. Таким образом, М0М 1 л в том и только в том случае, когда
—	ЛМТ«П = О.	(1)
Выразим вектор М0М через радиусы-векторы его конца и начала:
М0М = г — го.
Отсюда и из (1) находим:
(г — Го) п — 0.	(2)
Это есть уравнение плоскости а в векторной символике; ему удовлетворяет радиус-вектор г точки М в том и только в том случае, когда М лежит на плоскости а [г называется текущим радиусом-вектором уравнения (2)].
1122.	Доказать, что уравнение гп 4- В == 0 определяет плоскость, перпендикулярную к вектору л. Написать
*) Задачи 1121 и 1129 существенны для правильного понимания задач этого параграфа. Их решения приводятся в тексте.
170
уравнение этой плоскости в координатах при условии, что п = {А, В, С}.
1123.	Даны единичный вектор л° и число р > 0. Доказать, что уравнение гл° — /7 = 0 определяет плоскость, перпендикулярную к вектору л°, и что р есть расстояние от начала координат до плоскости. Написать уравнение этой плоскости в координатах при условии, что вектор л° образует с координатными осями углы а, Р и у.
1124.	Вычислить расстояние d от точки М, (rj до плоскости гл0 — /7 = 0. Выразить расстояние d также в координатах при условии, что ri = {^; r/i; zj, л° = = {cosa; cosp; cosy}.
1125.	Даны две точки (г,) и М2(г2). Составить уравнение плоскости, которая проходит через точку перпендикулярно к вектору М\М2> Написать уравнение этой плоскости также в координатах при условии, что ri = {xt; ус, zj, r2 — {x2, у2, z2}/
1126.	Составить уравнение плоскости, которая проходит через точку М0(г0) параллельно векторам и а2. Написать уравнение этой плоскости также в координатах при условии, что го = {х0; yG; z0}, «! = {/,; т{; nJ, д2 == |/2; т2, п2}.
1127.	Составить уравнение плоскости, проходящей через три точки МДгО, М2(г2) и М3(г3). Написать уравнение этой плоскости также в координатах при условии, что ri = {*i; //в zj, r2 = fe y2; z2}, r3 = {x3; y3', z3}.
1128.	Составить уравнение плоскости, которая проходит через точку М0(г0) перпендикулярно к плоскостям: rni + A —гп2-\-Г)2 = 0. Написать уравнение этой плоскости также в координатах при условии, что г0 = ={*о; f/o; z0},	=	В{; С J, л2 = {Д2; В2; С2}.
1129.	Доказать, что уравнение [(г — r0)a] = O определяет прямую, которая проходит через точку М0(г0) параллельно вектору а, т. е. что этому уравнению удовлетворяет радиус-вектор г точки М (г) в том и только в том случае, когда М лежит на указанной прямой.
Доказательство. Рассмотрим произвольную точку М (г). Пусть г удовлетворяет данному уравнению; по правилу вычитания векторов г — г0— Af0M; так как [(г — r0) а] = 0, то (Л10Л1а] = 0; следовательно, вектор М0М коллинеарен вектору а. Значит, точка М действительно лежит на прямой, которая проходит через Мо в направлении вектора а. Обратно, пусть М лежит на этой прямой. Тогда МоМ коллинеарен а. Следовательно, [М0Ма] == 0; но ЛГб'М = c==r Го; отсюда [(г — го) а] = 0. Итак, заданному уравнению
171
удовлетворяет радиус-вектор г точки М в том и только в том слу. чае, когда М лежит на указанной прямой (г называется текущим радиус-вектором уравнения).
ИЗО. Доказать, что уравнение [га] = т определяет прямую, параллельную вектору а.
1131.	Доказать, что параметрическое уравнение г= =r0 +	переменный параметр, определяет пря-
мую, которая проходит через точку М0(г0) (т. е. при изменении t точка М (г) движется по указанной прямой). Написать в координатах канонические уравнения этой прямой при условии, что r0=={x0; W, 2о}> <* = {/; w; п}.
1132.	Прямая проходит через две точки: AJj (rj иМ2 (г2). Составить ее уравнения в виде, указанном в задачах 1129, ИЗО, 1131.
1133.	Составить уравнение плоскости, проходящей через точку (rj перпендикулярно к прямой г = rQ — at. Написать уравнение этой плоскости также в координатах при условии, что г1={х1; ух\ zj, а = {1\ т\ п}.
1134.	Составить уравнение плоскости, проходящей через точку М0(г0) параллельно прямым [raj==/ni, [га2] = т2.	4
1135.	Составить уравнение плоскости, проходящей через точку М0(г0) перпендикулярно к плоскостям rn{ +	= 0, rn2 4- В2 = 0.
1136.	Прямая проходит через точку Л10(г0) перпендикулярно к плоскости гп + D «=0. Составить ее уравнение в параметрическом виде. Написать каноническое уравнение этой прямой в координатах при условии, что го = {*о; Уь го)> п=={4; В; С}.
1137.	Прямая проходит через точку М0(г0) параллельно плоскостям гщ + D{ — 0, rn2 4~ Dz ® 0. Составить ее уравнение в параметрическом виде. Написать каноническое уравнение этой прямой в координатах при условии, что г0={х0; Уо; £0}> П1={Дь Bt; CJ, п2*=*{А2\ В2;С2}.
1138.	Вывести условие, при котором прямая г — ==г04-я/ лежит на плоскости гп 4- D = 0. Написать это условие также в координатах при условии, что г0 = «{х0;-//0; Zo)« « = {/;	п}, п = {Л; В; С}.
1139.	Составить уравнение плоскости, проходящей через прямую г — r0 4- arf параллельно прямой [га2]=т.
1140.	Вывести условие, при котором две прямые г = г14-а./ и г —г2 + а2^ лежат в одной плоскости.
1141.	Найти радиус-вектор точки пересечения прямой г = г0+ в/ и плоскости гп 4- D = 0. Вычислить также
172
координаты х, у, z точки пересечения при условии, что r0 = {x0; yQ-, z0}, т\ п}, п = {А\ В- С}.
1142.	Найти радиус-вектор проекции М, (rj на плоскость гп + D = 0. Вычислить также координаты х, у, z этой проекции при условии, что г 1=(jv1; ух\zj, п={Л; В; С}.
1143.	Найти радиус-вектор проекции точки М] (rj на прямую г == г0 + at. Вычислить также координаты х, у, z этой проекции при условии, что	у{; zj, rQ =
₽={*о; //о‘> *оЬ т; п}.
1144.	Вычислить расстояние d точки Мх (rj от прямой г ==r0 + at. Выразить расстояние d также в координатах при условии, что Г1 = {Xf, ух\ zj, г0={х0; у05 *оЬ а~{1\ т\ п}.
1145.	Вычислить кратчайшее расстояние d между двумя скрещивающимися прямыми: г a\t и г~ = г24-а2/. Выразить расстояние d также в координатах при условии, что
fi={xi; у{; zj, r2 = te Уъ г2}, mt; nJ, <z2 = {Z2; тА а2}.
1146.	Доказать, что уравнение (г —г0)2 — /?2 определяет сферу с центром С(г0) и радиусом, равным R (т. е. что этому уравнению удовлетворяет радиус-вектор г точки М в том и только в том случае, когда М лежит на указанной сфере).
1147.	Найти радиус-векторы точек пересечения прямой r = at и сферы г2«В2. Вычислить также координаты точек пересечения при условии, что а = {1; т‘, п}.
1148.	Найти радиусы-векторы точек пересечения прямой г = rQ-sr at и сферы (г — г0)2 == В2. Вычислить также координаты точек пересечения при условии, что г0 = = {х0; у0; г0}, а = {/; т; п}.
1149.	Точка М] (rj лежит на сфере (г —г0)2 = /?2. Составить уравнение касательной плоскости к этой сфере в точке
1150.	Составить уравнение сферы, которая имеет центр C(rJ и касается плоскости гп + D = 0. Написать уравнение этой сферы также в координатах при условии, что ri={xf, У\\ zj, п = {Л; В\ С].
1151.	Составить уравнения плоскостей, касательных к сфере г2 == 7?2 и параллельных плоскости гп + Ь — 0. Написать уравнения этих плоскостей также в координатах при условии, что п = {А; В; С}.
173
1152.	Через точки пересечения прямой г = г0-|-а/ и сферы (г — г0)2 *= R2 проведены касательные плоскости к этой сфере. Составить их уравнения. Написать уравнения этих плоскостей также в координатах при условии, что г0«{х0; у0; z0}, л=={/; /и; п}.
§ 46. Поверхности второго порядка
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравне-
Уравнение (1) называется каноническим уравнением эллипсоида.
Величины а, Ь, с суть полуоси эллипсоида (рис. 47). Если все они
Рис. 47.
различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид является поверхностью вращения. Если, например, а = &, то осью вращения будет Oz, При а — b < с эллипсоид вращения называется вытянутым, при а==Ь > с~ сжатым. В случае, когда а = b = с, эллипсоид представляет собой сферу.
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются урав-
нениями:
х2 , у2	&
а2 + Ь2	с2
X2 , у2 
о2‘ + Тг I5" —
(2)
(3)
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 48); гиперболоид, определяемый уравнением (3), —• двухполостным (рис. 49); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины а, Ь, с .174
называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и Ь) показаны на рис. 48. В случае двухполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 49. Гиперболоиды, определяемые уравне-
Рис. 49.
Рис. 48.
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются урав* нениями:
— 4-	= 2з,	(4)
р ч	4
где р и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 50); параболоид, определяемый уравнением (5),— гиперболическим (рис. 51). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. Ё случае, когда P = q, параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Ог).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой а. Зададим, кроме того, некоторое положительное число q. Пусть М—
175
произвольная точка пространства, не лежащая на плоскости а, Мо— основание перпендикуляра, опущенного на плоскость а из точки М. Переместим точку М по прямой ММ0 в новое положение М' так, чтобы имело место равенство
Л10ЛГ = 7-М0Л1
и чтобы после перемещения точка осталась с той же стороны от плоскости а, где она была первоначально (рис. 52). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости а; точки, которые расположены на плоскости а, оставим на
своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости а, переместятся; при этом расстояние каждой точки от плоскости а изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас пе
ремещение точек пространства называется его равномерным сжатием к плоскости а; число q носит название коэффициента сжатия.
Пусть дана некоторая поверхность F; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях составят поверхность F'. Будем говорить, что поверхность F' получена из F
в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия
из поверхностей вращения.
Пример. Доказать, что произвольный трехосный эллипсоид
х2 . у2 . г2
может быть получен из ' сферы
х2 4- У2 + z2 — а2
176
результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Оху с коэффициентом сжатия qi=-~ и к плоскости Oxz с коэффициентом сжатия
b а*
Доказательство. Пусть производится равномерное сжатие пространства к плоскости Оху с коэффициентом ?i — и пусть М' (/; /)—точка, в которую переходит при этом точка М (х; у, z). Выразим координаты х', у', z точки М' через координаты х, у, z точки М. Так как прямая ММ' перпендикулярна к плоскости Оху, т0 х' = х, у' — у. С другой стороны, так как расстояние от точки М' до плоскости Оху равно расстоянию от точки М до этой плоскости, помноженному на число <?] = —, то 2< = -^-г.
Таким образом, мы получаем искомые выражения:
х' = х, у' = у, z' — Z,	(6)
или
х = х', У — У>
Предположим, что М (х; у; г)—произвольная точка сферы х2 + у2 + г2 = а2.
Заменим здесь х, у, z их выражениями (7); мы получим:
,2 .	,2 , а2 ,2	,
х + у + ~Z =а’
Следовательно, точка М' (х'; у'", z') лежит на эллипсо'иде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам:
х' — х", у' = -^- у", z' = z"\
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостиый гиперболоид и гиперболический параболоид суть линейчатые поверхности, т. е. они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
Однополостиый гиперболоид
X2 .у1 z2
J77
имеет две системы прямолинейных образующих, которые определяются уравнениями:
где а и Р — некоторые числа, не перболический параболоид
равные одновременно нулю. Гн-
х2
Р
^- = <2z q
также имеет две системы прямолинейных образующих, которые
определяются уравнениями:
а,
а
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L. Точка S называется вершиной конуса; линия L — направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
1153.	Установить, что плоскость .г - 2 = 0 пересекает
х2 , у2 , z2 *	*
эллипсоид "Уб" г-j2 +-j-== 1 по эллипсу; наити его полуоси и вершины.
1154.	Установить, что плоскость 2 4-1=0 пересекает
tp 2%
однополостный гиперболоид	+ — == 1 по гипер-
боле; найти ее полуоси и вершины.
1155.	Установить, что плоскость у 4- 6 = 0 пересекает v-2	it 2
гиперболический параболоид у — ^ = 6з по параболе; найти ее параметр и вершину.
1156.	Найти уравнения проекций на координатные плоскости сечения эллиптического параболоида у2 + z2=x плоскостью х 4- 2у — z = 0.
1157.	Установить, какая линия является сечением
j^2	^2	*#2
эллипсоида т?+4+'з = 1 плоскостью 2х — 3y-{-4z-~ — 11=0, и найти ее центр.
178
1158.	Установить, какая линия является сечением гиперболического параболоида -------з"в0 плоскостью
Зх — Зг/ 4- 4г 4- 2 = 0, и найти ее центр.
1159.	Установить, какие линии определяются следующими уравнениями:
1) ( £ + 11 = 22 J 3 + 6	.
I Зх — у 4- 6г — 14 = 0;
2)
-£_ll = 2z
4	3
. х — 2у 4- 2 = 0;
3)
х2 । у2	z2  .
«4 + 9	36“ ’
9х — 6г/ 4 2г — 28 = 0,
и найти центр каждой из них.
1160.	Установить, при каких значениях т плоскость X 4- mz — 1 = О пересекает двухполостный гиперболоид х2 4 У2 — z2 = — 1 а) по эллипсу, б) по гиперболе.
1161.	Установить, при каких значениях т плоскость X 4 W” 2 = 0 пересекает эллиптический параболоид Л-4 — = у а) по эллипсу, б) по параболе.
1162.	Доказать, что эллиптический параболоид
у 2	о,2
J~- + —s=s2y имеет одну общую точку с плоскостью 2х — 2г/ — г — 10 = О, и найти ее координаты.
1163. Доказать, что двухполостный гиперболоид •^-4-^---1 имеет °ДНУ общую точку с пло-
скостью 6x4-2г4-5«О, и найти ее координаты.
1164, Доказать, что эллипсоид тр 4-4--§-= 1
имеет одну общую точку с плоскостью 4х—Зу 412г—54=0, и найти ее координаты.
1165. Определить, при каком значении т плоскость у2 <»2
х — 2у — 2г 4- = 0 касается эллипсоида -щ- 4	4
5^2
+v=1-
1166. Составить уравнение плоскости, перпендикулярной к вектору п = {2; —1; —2} и касающейся эллиптического параболоида -у 4“	= 2г.
1167, Провести касательные плоскости к эллипсоиду 4х2 4- 16у2 -f- 8г2 = 1 параллельно плоскости х — 2у 4
179
4-2z 4- 17 = 0; вычислить расстояние между найденными плоскостями.
1168.	Коэффициент равномерного сжатия простран-з
ства к плоскости Oyz равен . Составить уравнение поверхности, в которую при таком сжатии преобразуется сфера х2 + У2 + z2 = 25.
1169.	Составить уравнение поверхности, в которую у 2
преобразуется эллипсоид ~ + — = 1 при трех последовательных равномерных сжатиях пространства к координатным плоскостям, если коэффициент сжатия к плоскости Оху равен 4, к плоскости Oxz равен 4 т:	О
„ з
и к плоскости Oyz равен -р
1170.	Определить коэффициенты q{ и q? двух последовательных равномерных сжатий пространства к координатным плоскостям Оху, Oxz, которые преобразуют сферу х2 + у2 + г2 == 25 в 'эллипсоид +	+-^ = 1.
1171.	Составить уравнение поверхности, образован-ной вращением эллипса —= 1» х = 0 вокруг оси Оу.
Решение*). Пусть М (х; у, z) — произвольная точка пространства, С — основание перпендикуляра, опущенного из точки М
на ось Оу (рис. 53). Вращением этого перпендикуляра вокруг оси Оу точка М может быть, переведен а в плоскость Oyz-, вхэтом расположении обозначим ее N (0; Y-, Z). Так как СМ — CN к СМ — У~х2 + z2,
*) Задача 1171 решена здесь как типовая.
180
CN “ I Z ], to
(1)
Кооме того, очевидно, что
К = у.	(2)
Точка М лежит на рассматриваемой поверхности вращения в том и только в том случае, когда N лежит на данном эллипсе, т. е.
югда	г х v
Ь2 + с2
принимая во внимание равенства (1) и (2), отсюда получаем уравнение для координат точки М:
У2
Л2
(3)
(4)
c2
Из предыдущего ясно, что оно удовлетворяется в том и только в том случае, когда точка М лежит на рассматриваемой поверхности вращения. Следовательно, уравнение (4) и есть искомое уравнение этой поверхности.
1172.	Составить уравнение поверхности, образован-ной вращением эллипса -^4-ф-8=1, z = 0 вокруг оси Ох.
1173.	Составить уравнение поверхности, образован-ной вращением гиперболы	г/ = 0 вокруг
оси Ох.
1174.	Доказать, что трехосный эллипсоид, опреде-ляемый уравнением ++ 77 е может быть по-лучен в результате вращения эллипса— + —==: 1,2=0 вокруг оси Ох и последующего равномерного сжатия пространства к плоскости Оху.
1175.	Доказать, что однополостиый гиперболоид, определяемый уравнением + ф-----------~ может
быть получен в результате вращения гиперболы 8=8 Ь У == 0 вокруг оси Ох и последующего равномерного сжатия пространства к плоскости Охх.
1176.	Доказать, что двухполостный гиперболоид, X2 У2 22	,
определяемый уравнением	~ ~	— 1 > может
быть получен в результате вращения гиперболы ~— ~- = 1, у*=0 вокруг оси Ох и последующего равномерного сжатия пространства к плоскости Охх.
181
1177.	Доказать, что эллиптический параболоид, опре-деляемый уравнением —+ — = 2г, может быть получен в результате вращения параболы x2 = 2pz, z/ = 0 вокруг оси Oz и последующего равномерного сжатия пространства к плоскости Oxz.
1178.	Составить уравнение поверхности, образованной движением параболы, при условии, что эта парабола все время остается в плоскости, перпендикулярной к оси Оу, причем ось параболы не меняет своего направления, а вершина скользит по другой параболе, заданной уравнениями у2 =—2qz, х = 0. Подвижная парабола в одном из своих положений дана уравнениями х2 = 2pz, ?/ = 0.
1179.	Доказать, что уравнение z = xy определяет гиперболический параболоид.
1180.	Найти точки пересечения поверхности и прямой:
» 81 +	У2	о<2 4- — = 1 9	и	х — з 	 у	— 4 _ г + 2 .
	36			3 “	-6	4	’
Л*2 2)7ё +	У2	-4=>	и	X _ у __	z + 2 ,
	9			4	-3	4 ’
3)< +	У2	= Z	и	х+ 1 _ у-	-2 г+З,
	3			2	-1	-2 *
4) 4-	У2 4	— Z	и	х _ у — 2 3	-2 '	2 + 1 2 ‘
1181.	Доказать, что плоскость 2х — \2у — z + 16 = О пересекает гиперболический параболоид х2 — 4y2 = 2z по прямолинейным образующим. Составить уравнения этих прямолинейных образующих.
1182.	Доказать, что плоскость 4х — 5у — 10г — 20 = О пересекает однополостныи гиперболоид	? = 1
по прямолинейным образующим. Составить уравнения этих прямолинейных образующих.
1183.	Убедившись, что точка М (1; 3; —1) лежит на гиперболическом параболоиде 4х2 — г2 —у, составить уравнения его прямолинейных образующих, проходящих ч?рез М.
1184.	Составить уравнения прямолинейных образую-щих однополостного гиперболоида — 4"4j------^=1,
параллельных плоскости 6х 4- 4т/ 3z — 17 == 0.
182
1185.	Убедившись, что точка А (—2; 0; 1) лежит на гиперболическом параболоиде —--определить
острый угол, образованный его прямолинейными образующими, проходящими через А.
1186.	Составить уравнение конуса, вершина которого находится в начале координат, а направляющая дана уравнениями:
а2 -1- Ь2 — Ь	а2 т
z = c\ I У = Ь'>
1187.	Доказать, что уравнение z- — xy определяет конус с вершиной в начале координат.
1188.	Составить уравнение конуса с вершиной в начале координат, направляющая которого дана уравнениями х2 — 2г + 1 == 0, у — 2+1 = 0.
1189.	Составить уравнение конуса с вершиной в точке (0; 0; с), направляющая которого дана уравнениями </2
2 = 0. а2 1 b2
1190.	Составить уравнение конуса, вершина которого находится в точке (3; —1; —2), а направляющая дана уравнениями х2 + #2 — z2= 1, x — «/ + z = 0.
4191. Ось Oz является осью круглого конуса с вершиной в начале координат, точка Mt(3; ~4; 7) лежит на его поверхности. Составить уравнение этого конуса.
1192. Ось Оу является осью круглого конуса с вершиной в начале координат; его образующие наклонены под углом в 60 к оси Оу. Составить уравнение этого конуса.
.. пп т-r	х 2 у 4- 1 з 4“ 1
♦ 1193. Прямая —g— = +z— ~ _ i 1 является осью круглого конуса, вершина которого лежит на плоскости Oyz. Составить уравнение этого конуса, зная, что точка Afl(1; 1; —у) лежит на его поверхности.
1194.	Составить уравнение круглого конуса, для которого оси координат являются образующими.
183
1195.	Составить уравнение конуса с вершиной в точке S (5; 0; 0), образующие которого касаются сферы х2 + у2 4- z2 = 9.
1196.	Составить уравнение конуса с вершиной в начале координат, образующие которого касаются сферы (х 4* 2)2 + (У - О2 + (* - 3)2 = 9.
1197.	Составить уравнение конуса с вершиной в точке S (3; 0; —1), образующие которого касаются х2 I у2 I г2 , эллипсоида -у +	= 1.
1198.	Составить уравнение цилиндра, образующие которого параллельны вектору Z = {2; —3; 4}, а направляющая дана уравнениями х24-г/2 = 9, 2=1.
1199.	Составить уравнение цилиндра, направляющая которого дана уравнениями х2 — y2~z, x + y-j-z — O, а образующие перпендикулярны к плоскости направляющей.
1200.	Цилиндр, образующие которого перпендикулярны к плоскости х-\-у — 2г — 5 = 0, описан около сферы х2 + у2-j-z2 = 1. Составить уравнение этого цилиндра.
1201.	Цилиндр, образующие которого параллельны прямой x — 2t — 3, //= — / + 7, г = -2/4-5, описан около сферы х2 4- £/2 4- z2 —• 2х 4- 4# 4- 2г — 3 = 0. Составить уравнение этого цилиндра.
1202.	Составить уравнение круглого цилиндра, проходящего через точку S (2; —1; 1), если его осью служит прямая х = 3t 4~ 1, У — — — 2, г = Z 4~ 2.
1203.	Составить уравнение цилиндра, описанного около двух сфер: (х — 2)2 4- (У — О2 4" = 25, х2 4- У1 4" 4-г2 = 25.
ПРИЛОЖЕНИЕ
ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
§ 1. Определители второго порядка и система двух уравнений первой степени с двумя неизвестными
Пусть дана квадратная таблица из четырех чисел alt а2) Ьь Ь2:
/01 &i
\ #2
(D
Число а}Ь2 — a2bt называется определителем второго порядка, соответствующим таблице (1). Этот определитель обозначается сим-
О] &>
Я 2	^2
волом
соответственно имеем:
Д1 bi
а2 Ь2
= ciib2 — o2&i.
(2)
Числа аь а2, Ъь Ъ2 называются элементами определителя. Говорят, что элементы Ь2 лежат на главной диагонали определителя, а2> Ъ\ — на побочной. Таким образом, определитель второго порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях. Например,
= —3.4 _	1). 2 = —10.
| -3 2
I -1 4
Рассмотрим систему двух уравнений
1 a2x-\-b2y^h2
с двумя неизвестными х, у. (Коэффициенты аь Ь\, а2, Ь2 и свободные члены hi, h2 предположим данными.) Введем обозначения
a, &j
а2 Ь2
&х —
h2 b2
&у —
01 hi
h2
Определитель Д, составленный из коэффициентов при неизвестных системы (3), называется определителем этой системы. Определитель А* получается путем замены элементов первого столбца
185
определителя Л свободными членами системы (3); определитель Ау получается из определителя А при помощи замены свободными членами системы (3) элементов его второго столбца.
Если	то система (3) имеет единственное решение; оно
определяется формулами

&У
*=—
(5)
Если А = 0 и при этом хотя бы один из определителей ДХ1 Ду отличен от нуля, то система (3) совсем не имеет решений (как го-ворят, уравнения этой системы несовместимы).
Если же Д = 0, но также ДХ = АУ = О, то система (3) имеет бесконечно много решений (в этом случае одно из уравнений системы есть следствие другого).
Пусть в уравнениях системы (3) hi = h2 — 0; тогда система (3) будет иметь вид:
(М + М = 0. а2х + Ь2у—0.	(6)
Система уравнений вида (6) называется однородной; она всегда имеет нулевое решение: х — 0, у — 0. Если А =# 0, то это решение является единственным; если же А==0, то система (6), кроме ну-левого, имеет бесконечно много других решений.
1204. Вычислить определители:
1)	-1 4		2)		3 -	•4	3)	3 6	
	1 сл to		9		1	2	9	5 10	У
4)	3 16		5)	б	1		6)	1 1	
	5 10			6	.2 а	J		Xi х2	9
7)	а+ 1		b — с				8)	cos а -	- sin а
	а2 + а		ab — ас		9			sin а	cos а
1205. Решить уравнения:	
1)	2 х — 4 1	4	-0;
3)	1 * я Ч—Ь * ►—* о
5)	х + 1	—5
	1	1=0; 1 х — 1
7)	4sinx 1 1	< =0; b cos х
2) 1	4
Зх х 4- 22
4)	Зх -1 х 2х — 3	_3 . — 2 ’		
6)	х2 —4	-1 х — 4 х + 2			= 0;
8)	cos 8х — sin 5х sin 8х cos 5х			в0.
185
1206. Решить неравенства!
1)	Зх — 3	2	>0;	2)	1	х + 5		<0;
	X	1			2	X		
3)	2х — 2	1	>5;	4)	X	Зх		
	7х	2			4	2х		14.
1207. Найти все систем уравнений:
1) ( Зх — 5z/ = 13,
I 2х +7^ = 81;
3) | 2х — Зу = 6, [ 4х — 6# == 5;
5) | ах + by = с, [ bx — ay — d\
решения каждой из следующих
2) ( 3// — 4х=1,
1 Зх + 4#= 18;
4) х-уУз = 1, . хУЗ — Зу=УЗ;
6) | х]/5 — 5у = У 5, I х-уУ5 =5.
1208.	Определить, при каких значениях о и система уравнений Зх — ау=1, 6x + 4y—b 1) имеет единственное решение; 2) не имеет решений; 3) имеет бесконечно много решений.
1209.	Определить, при каком значении а система однородных уравнений 13х + 2^ = 0, 5х 4- ау = 0 имеет ненулевое решение.
§ 2. Однородная система двух уравнений первой степени с тремя неизвестными
Пусть дана система двух однородных уравнений «1* + byj + с1а = 0, а2х + b2y + c2z = О
(О
с тремя неизвестными х, у, г. Введем обозначения:
Д1 —
bi
Ьз
Ci
Сз
д2 —
(Il Cl
а2
Д3 ==
Я] bi
а2 Ь2
Если хотя бы один из определителей Дь Д2, Дз не равен нулю, то все решения системы (1) будут определяться по формулам
х=Д^, у — — Z — &2t,
где t — произвольное число. Каждое отдельное решение получается при каком-либо определенном значении t.
187
Для практики вычислений полезно заметить, что определители »ДЬ Д2, Дз получаются при помощи поочередного вычеркивания столбцов таблицы:
aj bi Ci
а2 b2 с2
Если все три определителя Дь Д2, Дз равны нулю, то коэффициенты уравнений системы (1) пропорциональны. В этом случае одно из уравнений системы есть следствие другого и система фактически сводится к одному уравнению. Такая система, естественно, имеет бесконечно много решений; чтобы получить какое-нибудь из них, следует двум неизвестным придать произвольно численные значения, а третье найти из уравнения.
1210.	Найти все решения стем уравнений:
1)	Г Зх — 2у + 5г = 0, \ х + 2г/ — Зг — 0;
3) Г х — Зу + г = 0,
I 2х — 9г/ + Зг — 0;
5)	( Зх — 2у + г — 0,
[ х 2у — Зг = 0;
7)	( х + 2г/ — г = 0,
( Зх — Зу 4- 2г = 0;
9)	f х 4- 3# — г = 0,
( 5х —- Зу 4- г = 0;
1Г) ( ах + 2у — г = 0,
t 2х 4" by — Зг = 0;
каждой из следующих си-
2)( Зх — 2г/ 4~ г = 0, | 6х — 4г/ 4- Зг = 0;
4) ( Зх — 2у 4- z — 0,
I х 4- 2г/ — 2 = 0;
6) 1 2х — у — 2г = 0, | х — Зу 4- 2г = 0;
8) I Зх — Зу 4- г — 0, 1 х 4- 2у — г =•: 0;
10) Г ах 4- у 4- г = 0,
I х — у 4- az — 0;
12) J х — Зу 4- az = 0, I Ьх 4- Зу — г = 0.
§ 3. Определители третьего порядка
Пусть дана квадратная таблица из девяти чисел аь а2, а3, Ьг,			
b2, b3, Ci, с2, Сз	U1	bt	Cl \
	о2	ь2	с2 .	(1)
	а3	ь$	Сз 1
Определителем третьего порядка, соответствующим таблице (1), называется число, обозначаемое символом
	Ь\	С\
о2	ь2	с2
Оз	Ьз	сг
188
и определяемое равенством
ai b\ Ci a2 b2 c2 a3 b3 c3
= O] b2C3 -f- &1C2O3 Ч- C\a2b3 —- С[&20з “• Ь\Я2С3	tt] c2b3. (2)
Числа Oi, 02, o3, 6t, b2, b3, c1( c2, c3 называются элементами определителя Элементы оь b2, сэ расположены на диагонали определителя, называемой главной; элементы Оз, Ь2, ct составляют его побочную диагональ. Для практики вычислений полезно заметить, чтд первые три слагаемые в правой части равенства (2) представляют собой произведения элементов определителя, взятых по три так, как показано различными пунктирами на нижеприводимой схеме слева.
Чтобы получить следующие три члена правой части равенства (2), нужно перемножить элементы определителя по три так, как
показано различными пунктирами на той же схеме справа, после чего у каждого из найденных произведений изменить знак.
В задачах 1211 — 1216 требуется вычислить определители третьего порядка.
1211.	1 to to со	-2 1 0	1 3 -2	1212. «	I 0 5	2 1 0	0 3 -1	•
1213.	2	0 £		1214.	2		-1	3
	1	3 16			-2		3	2 .
	0 -	1 10			0		2	5
1215.	2 1	0		1216. 0 а	а			
	1 0	3	•	а 0	а			
	0 5	-1		а а	0			
189
§ 4. Свойства определителей
Свойство 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, т. е.
а, а2 «з
Ь\	Ci	Д]	С2	Дз
62	с2	==	6]	&2	&з
&з	Сз	С1	02	Сз
Свойство 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на —1. Например,
Qi bi Ci		Cl bl
я2 b2 с2	= —	О2 02 Ь3
а3 Ьэ сз		a3 Сз b3
Свойство 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
Свойство 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,
kai bi Cj		ai bt Cj
ka.2 ^2 02	—'k	a2 b2 c2
ka3 b3 c3		Оз b3 Сз
Свойство 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случай предыдущего (при 6 = 0).
Свойство 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
Двойство 7. Если каждый элемент гс-го столбца или л-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце, или соответственно в n-й строке, имеет первые из упомянутых слагаемых, а другой — вторые; элементы, стоящие на остальных местах, у всех трех определителей одни и те же. Например,
г ।	//	.
aj + fli
&2
г I н .
а3 I °3	“3
с2
с3
а[
Й2
а3
*1
Ь2
с3
а2 гг
Ь\
&2 С2
h Сз

+
Свойство 8. Если § элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множи-190
тель, то величина определителя при этом не изменится. Например,
ai 4- kbi b} с}		at bi С)
Я2 4" ^^2 ^2 С2	=	Яг Ь3 с3
а3 4- kb3 b3 Сз		Яз Ь3 Сз
Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркивания строки и столбца, на пересечении которых расположен этот элемент.
Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.
Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, которой обозначен сам элемент.
Свойство 9. Определитель
«1 6,
Яг ^2
я3 Ь3
Cl
Ci
Сз
равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.
Иначе говоря, имеют место следующие равенства:
Д — fljAl +	+	Я3А3,	Д	=	Я1Аj + b\B\ 4- CiOi,
Д = b[Bi 4“ &2В2 4- Ь3В3, Л = я2А2 4" ЬгВ3 4“ с3С3, Д — CiCi 4“ С2С2 4“ С3С3, Д = Я3А3 + Ь3В3 4“ С3С3.
В задачах 1217—1222 требуется, не раскрывая определителей, доказать справедливость равенств.
1217.	3 2 1		2	2	7	
	о» со СМ 1	=	-2	сч 1 со	•
	4 5 3		4	5	11	
Указание. Воспользоваться свойством					8.
1218.	1 -2	3		1	0	0
	-2	1	-5	=	СО 1 см 1	1
	3	2	7		3	8	-2
191
Указание. Воспользоваться свойством &
1219.	«1	bi	С1	
	а2	^2	с2	= 0.
	щ + аа2	bl + ab2	С[ + ас2	
Указание. Воспользоваться свойствами 7, 3, 6.
1220.
4- YC!
Р&2 + УС2
Р^з + ус3
bl Cl b2 с2 b3 с3
= 0.
Указание. Воспользоваться свойствами 7 и 6.
1221.
sin2 а	cos2 а	cos 2а	
sin2 р	cos23	cos2p	= 0
sin2 у	cos2 у	cos 2у	
1222.	0 a	—a 0	-b —c	= 0.
	b	c	0	
В задачах 1223—1227
делители, пользуясь одним
требуется вычислить опре свойством 9.
1223.
1 1 -1
1 -1 1
-1 1 1
1224.	1	17	-7
	-1	13	1
	1	7	1
1225.	2	0	5	1226.	1	2	4
	1	3	16	♦	-2	1	-3
	0	-1	10		3	-4	2
1227.
1 1 1
X у 2
X2 У2 Z2
192
1228. Определители, данные в задачах 1223—1227, пользуясь свойством 8, преобразовать так, чтобы в каком-либо столбце (или строке) определителя два элемента стали равными нулю, а затем вычислить каждый из них, воспользовавшись свойством 9.
В задачах 1229—1232 требуется вычислить опре-
делители.					
1229.	0 а b		1230.	0 sin a ctg a	
	а 0 а	9		sin a	0 sin a
	b а 0			ctg a sin a 0	
1231.	х у 2		1232.	a b c	
	X2 у2 2	2	•	cab	•
	X3 у3 2	3		b c a"	
1233. Доказать справедливость равенств:
1)
1	sin а
1	sin Р
1	sin у
sin2 а sin2 р sin2 у
— (sin а — sin p) (sin p — sin y) (sin у — sin a);
2)
1 1 1 tga tgp tgy tg2a tg2p tg2y
_ sin (a — fl) sin.(fl — y) sin (y — a) cos2 a cos2 fl cos2 у
1234..Решить уравнения:						
1)	.1	3 x	2)	3	X	-4	
	4	5-1	= 0;	2	-1	3	= 0.
	2-1	5		10	1	1	
1235. Решить неравенства:
1)	3	—2 1	2)	2. x + 2 -1	
	1	x —2	<1;	1	1 ' -2	>0.
	-1	2 -1		5	—3 x	
7 Д. В. Клетеник
193
§ 5. Решение и исследование системы трех уравнений первой степени с тремя неизвестными
Рассмотрим систему уравнений
-j- Ь-^у C-\Z = а2х+М+с2г = Л2,	(!)
. а3х + &3у+с3г = Лз
с неизвестными х, у, г (коэффициенты alt bi..с3 и свободные
члены й1( /г2, /г3 предположим данными).
Введем обозначения:
01
А = а2 &2
Оз &э
С1
Сз
Л3
а2 =
а2
аз
&i
^2
Ь.
^2
^3
С1 С2
Сз /гг ^2 Л3
Ду —
«1
а2 аз
hy ct
С-2 ^3 с3 |
. А.
Определитель Д, составленный из коэффициентов при неизвестных системы (1), называется определителем данной системы.
Полезно заметить, что определители Дх, Д!7, Дг пол\чаются из определителя Д при помощи замены соответственно его первого, второго и, наконец, третьего столбца — столбцом свободных членов данной системы.
Если А Ф 0, то система (1) имеет единственное решение: оно определяется формулами
Ах
Х Д ’
А у у—~Л, г = ~тг • * Д Д
Предположим теперь, что определитель системы равен нулю: Д = 0. Если в случае Д = 0 хотя бы один из определителей Дх, Ду, Дг отличен от нуля, то система (1) совсем не имеет решений.
В случае, когда Д = 0 и одновременно Дд. = О, Ду^0, Дг = 0, система (1) также может совсем не иметь решений; но если система (1) при этих условиях имеет хотя бы одно решение, то она имеет бесконечно много различных решений. Однородной системой трех уравнений первой степени с тремя неизвестными называется система вида’
aix + M~HiZ = 0, а^Ч-М+с22 = 0, а$х Н” ЬзУ Ч- сз2 ~
(2)
т. е. система уравнений, свободные члены которых равны нулю. Очевидно, что такая система всегда имеет решение: х = 0, y = Qt г=0; оно называется нулевым. Если А й О, то это решение является единственным. Если же Д=гО, то однородная система (2) имеет бесконечно много ненулевых решений,
194
В задачах 1236—1243 требуется установить, что системы уравнений имеют единственное решение, и найти его.
1236.
1238.
1237.
1239.
1240.
1242.
X + у— 2 — 36, X + 2 — у — 13, у + z — х== 7. 2х — 4у + 92 = 28, 7х + Зу — 6г — — 1, 7х + 9у — 9г = 5.
х 4-г/4-2 = 36,	1241.” [
2х — Зг = —17, 6х — 5г = 7.
х + у + z — a, 1243. х — у + z = Ь, х + у — z — с. >
х + 2у + 2 — 4 Зх — Зу 4* Зг = 1, 2x4-7г/ — 2 — 8.
2х 4* У== 5,  х4-3г=16,
Зу — г= 10. 7x4- 2// 4-Зг = 15, 5х — 3//4~2г=15, 1 Ох—11г/4-5г = 36. ' х — у 4- 2 = а, X 4- у — 2 = Ь, . У 4- 2 — X — C.
1244.	Найти все решения системы х4-2г/ — 4г =1, 2x4- У~ 32 — — 1, . х — у — 2= —2.
1245.	Найти все решения системы 2х — у 4- 2 = —2, х 4- 2г/ 4- Зг = — 1, . х — Зу — 2г = 3.
1246.	Найти все решения системы Зх — у 4- 2г = 5, • 2х — у— г = 2, . 4х — 2у — 2г = —3.
1247.	Определить, при каких значениях а и b система уравнений
Зх — 2у 4- 2 == Ь,
Зх — Зу 4- 9г — 3, . 2х 4- Нй2 = “1
7*
195
1)	имеет единственное решение;
2)	не^имеет решений;
3)	имеет бесконечно много решений.
1248.	Доказать, что если система уравнений
Ь[у = с{, а2х 4- Ь2у = с2г а3х 4- Ь3у = с3
совместна, то
oil
#2	^2
а3 &з
С1 с2
Сз
= 0.
1249.	Найти все решения системы
2x4- У~ 2 = 0,
х4-2#4- 2 = 0, 2х — у 4- Зг = О’
1250.	Найти все решения системы
X — у — 2 = 0, х 4- 4# 4- 2-г = О, Зх 4” 7у 4" Зг == 0.
1251.	Определить, при каком значении а система однородных уравнений
Зх— 2z/4- 2 = 0, ах — 14у 4- 15г = О,
х 4- 2у — Зг = О
имеет ненулевое решение.
§ 6. Определители четвертого порядка
Все свойства определителей, перечисленные в § 4, относятся к определителям любого порядка. В настоящем параграфе следует применить эти свойства для вычисления определителей четвертого порядка.
196
В задачах	1252—1260 требуется вычислить опре-				
делители четвертого порядка.					
1252. —3	0	0 0			1253. 2 -1 3	4	
2	2	0 0			0-15-3	
1	3-10			0	0 5 —3	•
-1	5	3 5			0	0 0	2	
1254. 2 -	1 1	0			1255. 2 3 -3	4	
0	1 2 -1			2 1-1	2	
3 -	12	3			6 2	10	•
3	1 6	1			2 3	0 -5	
1256.	8	7	2	0			1257. 0 b с d	
-8	2	7 10			b 0 d с	
4	4	4	5		•	с d 0 b *	
0	4—3	2			d с b 0	
1258. а b	с d			1259. а b с d	
b а	d с			d а b с	
с d	а b			с d а b	
d с	b а			b с d а	
1260. 0 -	-а — Ь —	d			
, а	0 —с —	е			
Ъ	с 0	0			
d	е 0	0			
1261. Доказать, что если система уравнений
совместна, то
Л1Х 4- В{у + Ciz + А а0» А2х 4- В2у 4* Сз? 4* -^2= О» Л3х 4- В3у 4- C3z 4- £>3 = О, А4х 4- В4у 4- C4z 4- D4 == О
4*	СО tO to Со со to OJ ю *— о о о о rfb . СО to •— t» Ь со to	= 0.
197
ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
ЧАСТЬ ПЕРВАЯ
1. С'л. рис. 54.	2. Указание. Уравнение |х| = 2 экви-
валентно двум уравнениям: х— — 2 и х = 2; соответственно имеем две точки: Л (—2) и А2 (2) (рис 55) Уравнение |х — 1|=3 экви-
валентно двум уравнениям: х — 1 = — 3 их—1=3, откуда находим ,г= —2 и х — 4 и соответствующие им точки В[ и В2 (рис. 55). В остальных случаях решения аналогичны. 3. Точки расположены: 1) справа от точки ЛТ, (2); 2) слева f	от точки М2 (3); включая точку М2;
1	1	3) справа от точки М3 (12); 4) сле-
°	%	&>	/3\
—I—О—I—&— I, /оХ-----ва от точки М4 — , включая
В,	\ 2 /
•	точку Л44; 5) справа от точки
Рис 55.	.. / 5 \
/И51у1; 6) внутри отрезка, ограниченного точками Л40(1) и М2 (3); 7) внутри отрезка, ограниченного точками Л47(—2) и М2 (3), включая точки М7 и М2‘, 8) внутри отрезка, ограниченного точками А(1) и В (2); 9) вне отрезка, ограниченного точками Р( —1) и Q (2); 10) вне отрезка, ограниченного точками Л(1) и В (2); 11) внутри отрезка, ограниченного точками Р(— 1) и Q (2); 12) внутри отрезка, ограниченного
198
точками М (3) и ЛЧ5), включая точки М п V; 13) вне отрезка, ограниченного точками М (3) и W (5); 14) вне отрезка, ограниченного точками Pi(— 4) и Qi (3); 15) внутри отрезка, ограниченного точками Pi(—4) и Qi (3), включая точки Р, и Q,. 4. 1) АВ —8, \АВ\ — 8; 2) АВ = -3, | АВ I = 3; 3) АВ = 4, | АВ | = 4; 4) ДР ~
ДР = 2; 5) ДР = —2, | ДР |=2; 6) ДР = 2, | АВ | = 2. 5. 1) 2) 5; 3) 1; 4) —8; 5) —2 и 2; 6) —1 и 5; 7) —6 и 4; 8) —7 и 6, 1) Внутри отрезка, ограниченного точками Д( — 1) и Р(1); 2) вне отрезка, ограниченного точками Д(—2) и Р (2); 3) внутри отрезка, ограниченного точками Д(— 2) и В (2), включая точки 4 и Р; 4 вне отрезка, ограниченного точками А (—3) и В (3), включая точки 4 и Р; 5) внутри отрезка, ограниченного точками Д( — 1) и В (5); 6) внутри отрезка, ограниченного точками А (4) и Р (6), включая точки 4 и Р; 7) вне отрезка, ограниченного точками 4 ( —1) и В (3), включая точки 4 и Р; 8) вне отрезка, ограниченного точками 4 (2) и В (4), включая точки 4 и Р, 9) внутри отрезка, ограниченного точками Д(— 4) и В (2); 10) вне отрезка, ограниченного точками 4(— 3) и Р( —I); 11) внутри отрезка, ограниченного точками 4 (—6) и Р (—4), включая точки А и Р; 12) вне отрезка, ограниченного точками 4 (—3) и Р (1), включая точки А и Р.
=& 3; 
РД______з.
~ АС	4 ’
Ю _____*1	^*2
4; 4) АВ = 2, - -	2;
-3.
X =
__ 5_, 3 ;
Лз =
_ СА
Аб— АВ 3*
11. x==2L±i
5) -4- «•
1) М (—11);
7. 1) 1; 2)
. -СВ- 1 .
3) 2; 4)
4С св = “4;
4
5) -4-, _вс_ 1 .
“ СД 4 ’
9.	.
х2 — х
. 12 1) 4;	2) 2;
4) -2;
3; 6) 0. 14. 1) М (- 11);
15. (5) и (12). 16. 4(7) и 17. См рис. 56. 18. Av(2; 0), СЛ-5; 0), • Dx(-3; 0), “	19. 4^(0; 2), Ву(0-, 1),
•2)< 2); 6); •i); 5); 3);
2
3) -2;
4) 7; 5) 2) N (13) В(-41) Вх(3; 0), £х(-5; 0). Су(0-, -2), 20. 1) (2, 3) (-1; 1);
6) (a; '-*). 3) (2; -2);
6) (- а; &). 2) (-2; 4);
5) (5; 4); 6) (- а;
2) (-2; 5); 3) (4; -2) (—3; 4); 3) (2; - , и третьей; 2) во второй и четвертой;
4) во второй и четвертой; 5) в первой,
6) во второй, третьей и четвертой; 7) в первой, третьей и
8) в первой, второй и третьей. 26. См. рис. 57. 27.
Dy(0; 1), 5^(0;
-3);	2) (-3;
4) (-3; 5); 5) (-4;
21.	1) (1; 2); 2) (-3;
4) (2; 5); 5) (-3;
22.	1) (-3;
3) (2; -1); 4) (-5; 3);
-	6). 23. 1)(3;2);
•	3). 24. 1)(—5; -3);
-	7) 25. 1) В первой
3)
в первой второй и
и третьей; четвертой; четвертой;
, (1; -2), (5;1).
л \
2
199
2;	л), (4; “431)’ (3;я-2). 29. С (з; |я) и D (б; - Н л).
30.(1;-^). 31. Л (з; - у), 5^2; -^nj, С (1; 0), D (б;
Е (3; 2 - л), Г(2;л—1). 32. Af, (3; 0), М2 (1; у), А43 | лл(б:	Мв(3; я)> А1б(1; Кя)‘ 33‘
34.4/ = /р? + p^-2p1p2cos(e2-GJ). 35. rf=7. 36. 9 (17-4/3 ) кв. ед.
Рис. 57.
37. 2 (13+6/2) кв. ед. 38.28/3 кв. ед.
39. S = у pip2 [sin (01 — 02)]. 40. 5 кв. ед.
41. 3(4/3"- 1) кв. ед. 42. М, (0; 6), М2 (5; 0), М3 (V2; /2), Л14 (б; -б/Т), Л15(-4; 4 /з),	Л46(б/3; -б).
43. М{ (б; 4)’ ЛГ2 (3; л), А13 (% -jV М4 (2;-4 л), М5 (2;-£). 44 1)3; 2) -3;	3) 0;	4) 5;	5) -5;	6) 2.
47. 1) X = 1, Y = 3; 2) X = - 4. Y = - 2; 3) X = 1, Y = - 7;	4) X = 5, Y = 3.
48. (3; -J,). 49. (-3; 2). 5_2. 1) X = - 6, Г = б/3;	2) Х = 3/3, У = -3;
3) Х = /2, У» —/2. 53. I) 5; 2) 13; 3) 10. 54. 1) d = 2, 6 = 4;
3
2) d = 6, 0 = - 4; 3) d = 4, 0 = 4 л. 55. I) d = /2, 0 = - 4 л;
'	4	о	4
2)	d — 5, 0 = arctg — л; 3) d = 13, 0= л—arctg	; 4) d = /234,
6 =-arctg 5.'	56. 1) 3; 2) -3.	57. 1) (-9; 3); _2) (-9; -7).
58.	1) (-15; -12); 2) (1; -12).	59. -2.	60.	4 . 61. 4.
62.	1) -5; 2) 5. 63. 1) 5; 2) 10; _3) 5; 4) /б"; 5) 2/2"; 6) 13. 64 137 j£B. ед. 65. 34 кв. ед. 66. в/з кв. ед. 67. 13,15. 68. 150 кв. ед. 69. 4/2. 73 # Л^ЛЛМз - тупой. 75. # ВЛС = 45°, АВС = 45°, АС В — 90°. 76.60°. Указание. Вычислить длины сторон треугольника, азатем применить теорему косинусов. 77. Л1[(6;0) и М2(—2; 0). 78.	(0; 28) и ЛГ2 (0; -2). 79. Р, (1; 0) и Р2 (6; 0). 80. Cj (2; 2),
= 2; С2 (10; 10), Я2= Ю. 81. С} (-3; -5), С2(б;*-б). 82. М2(3; 0).
83.	В (0; 4) и £>(—1; —3). 84. Условию’ задачи удовлетворяют два квадрата, симметрично расположенных относительно стороны АВ. Вершины одного квадрата суть точки С] (—5; 0), £>](—2; —4), вершины другого — С2 (3; 6), О2(6;2).	85. С (3; — 2), /?=10.
86.	(1; —2). 87. Q (4; 6). 88. Середины сторон АВ, ВС, АС соответственно суть (2; —4), (—1; 1), (—2; 2). 89. 1) М (1; 3); 2) /V (4;—3). 90. (1; -3), (3; 1) и (-5; 7).* 91. D (-3; 1). 92. (5; -3), (1; -5). 93. £>i (2; 1), Ь2(—2; 9), D3 (6; — 3). Указание. Четвертая вершина параллелограмма может быть противоположной любой из дан-
200
них. Таким образом, условию задачи удовлетворяют три параллелограмма. 94. 13. 95. (2;-1) и (3; 1). 96. (4? “2^ 97’ “Т’/з'. 98, (-11; -з).	99. 4.	100. Al=^- = 2;	=
DU	U£>
RA	2
Лз =	= - 4. 101. A (3; -1) и В (0; 8). 102. (3; -1). 103. (4; -5).
/1U	о
104. (—9;0). 105. (0; —3). 106. 1 :3, считая от точки В. 107. ^4 — ; 1 j, 108. х= + *2у —	, Ю9. М (-1; 0), С (0; 2).
О	о
Ш. (5;5).	44	m (#« 1т4
U4 x_~El+^±£2.,	у_.?У.+»»»+РУ»,	115. (4; 2).
т + п + р	т 4-я 4- р
Указание. Вес однородной проволоки пропорционален ее длине. 116. 1) 14 кв> ед.; 2) 12 кв. ед.; 3) 25 кв. ед. 117. 5. 118. 20 кв. ед. 119.7,4.	120. х=-4-, ^ — 4-4-.	121. х = 2~, у=3~,
122. (0; -8) или (0; -2).	123. (5; 0) или (—у5 °)*	121 (5; 2)
или (2; 2).	125. Cj (-7; -3),	£), (—6; -4)	или	С2 (17; -3),
£>2 (18; -4).	126. Ci (-2; 12),	(-5; 16)	или	С2(-2;-|-),
О2 I —5; -g-J.	127. 1) x = Z4-3, у — у-\-^\ 2) х — х — 2,
„ = /4-1; 3) х — х' -3, z/ = / + 5.	128. Л (4;-1), В (0; — 4),
С (2; 0). 129.	1) Л (0; 0), В (-3; 2),	С (-4; 4); 2)	Л (3;	-2), В (0; 0),
С (-1; 2); 3) Л (4; -4), В (1; -2), С (0; 0). 130^1) (3; 5); 2) £-2; 1); 3) (0; -1); 4) (—5;0). 131. 1)	, у= х'^+у' ;
2) * — у=а—^f~~} 3> * = -/. У — х'\ 4) х = /, z/ = -x'; 5)х = -/, y — — tf. 132. Л(з/3; 1), в{^~; у), С(3; -_/з). _	133. 1) Л1(УТ; 2/2), JV (-3/2; 2/2 ),
р(-/2; -2/2); 2) М (1; -3), V (5; 1), Р(-1; 3); 3) М (-1; 3), N (-5; -1), Р (1; -3); 4) М (-3; -1), N (1; -5), Р (3; I). 134. 1) 60°; 2) -30°.	135. О' (2; -4).	136.. х= /4-1, ^ = /-3.
137. х--|-/4--|/, ^ = --|/4--|/ 138. Af,(l; 5), ,Л12(2; 0), Af3 (16; -5). 139. Л (6; 3), В (0; 0), С (5; -10). 140, 1) О' (3; -2), а =90°;	2) О'(-1; 3), а =180°;	3) О'(5; —3), а = —45°.
141._х = --1|/--^-/+'9, уев А/--1|/-3. 142. ЛМ1; 9), М2 (4; 2), М3 (1; -3), М4 (0; 2 + /з), М5 (1 4-/Т; 1). 143. М{ (0; 5), М2(3; -0), Л43(-1; 0), Af4(0; -6), Л15(/3; 1).	144.	(2; 0),
Ms(l;-y),M3(3;|),	145. Mt я),
201
М, (2; -i),	IM4(2;
146. f(x, y) = 2ax — a2. 147. 1) f (x, y) = 2 ax; 2) f (x, y) — — 2ax— a2, 148. f (x, y) — 4x2 + 4y2 + 2a2.	149. f (x, y) = 4x2 4- 4y2 — 4ax —
— 4ay + 4a2.	150. f (x, y) — x2 + y2 — 25.	151. f (x, y) =* 2xy — 16.
152. При повороте координатных осей выражение функции не меняется. 153. (3; 1). 154. Такой точки не существует. 155. ± 45° или ± 135°. 156. 30°, 120°, -60°, - 150°. 157. Точки Afj, Af4 и Мъ лежат на линии; точки М2, Af3 и AfB не лежат на ней. Уравнение определяет биссектрису второго и четвертого координатных углов
(рис. 58). 158. 1) (0; -5), (0; 5); 2) (-3; -4), (-3; 4); 3) (5; 0); 4 на данной линии такой точки нет; 5) (—4; 3), (4; 3); 6) (0; —5); 7) на данной линии такой точки нет. Уравнение определяет окружность с центром 0(0; 0) и радиусом 5 (рис. 59). 159. 1) Биссектриса первого и третьего координатных углов; 2) биссектриса вто-
рого и четвертого координатных углов; 3) прямая, параллельная оси Оу, отсекающая на положительной полуоси Ох, считая от начала координат, отрезок, равный 2 (рис. 60); 4) прямая, параллельная оси Оу, отсекающая на отри-, цательной полуоси Ох, считая от начала координат, отрезок, равный 3 (рис. 60); 5) прямая, параллельная оси Ох, отсекающая на положительной полуоси Оу, считая от начала координат, отрезок, равный 5 (рис. 60); 6) прямая, параллельная оси Ох, отсекающая на отрицательной полуоси Оу,
считая от начала координат, отрезок, равный 2 (рис. 60); 7) прямая, совпадающая с осью ординат; 8) прямая, совпадающая с осью абсцисс; 9) линия состоит из двух прямых: биссектрисы первого и третьего координатных углов и прямой, совпадающей с осью ординат; 10) линия состоит из двух прямых: биссектрисы второго
202
и четвертого координатных углов и прямой, совпадающей с осью абсцисс; 11) линия состоит из двух биссектрис координатных углов (рис. 61); 12) линия состоит из двух прямых: прямой, совпадающей
Рис. 63.	Рис. 64.
с осью абсцисс, и прямой, совпадающей с осью рдинат; 13) линия состоит из двух прямых, параллельных оси абсцисс, которые.отсе
кают на оси ординат, считая от на1 и — 3 (рис. 62); 14) линия состоит из двух прямых, параллельных оси 'Оу, которые отсекают на положительной полуоси Ох, считая от начала координат, отрезки, равные 3 и 5 (рис. 63); 15) линия состоит из двух прямых, параллельных оси Ох, которые отсекают на отрицательной полуоси Оу, считая от начала координат, отрезки, равные 1 и 4 (рис. 64); 16) линия состоит из трех прямых: прямой, совпадающей с осью абсцисс, и
координат, отрезки, равные
Рис. 65.
двух прямых, параллельных оси
ординат, которые отсекают на положительной полуоси абсцисс, считая от начала координат, отрезки, равные 2 и 5; 17) линия состоит из двух лучей: биссектрис первого и второго координатных углов (рис. 65); 18) линия состоит из двух лучей: биссектрис
203
первого и четвертого координатных углов (рис. 66, а); 19) линия со* стоит из двух лучей: биссектрис третьего и четвертого коо{ * динатных углов (рис. 66, б); 20) линия состоит из двух лучей: биссектрис второго и третьего координатных углов (рис. 66, в);
двух лучей, расположенных в верхней полу-
из
21) линия состоит I И„_ плоскости, выходящих из точки (1; 0) и направленных параллельно биссектрисам координатных углов (рис. 65); 22) линия состоит из двух лучей, расположенных в верхней полуплоскости, выходящих из точки (--2; 0) и направленных параллельно биссектрисам координатных углов (рис. 65); 23) окружность с центром в начале координат и -радиусом 4 (рис. 67); 24) окружность с центром Ог (2; 1) и радиусом 4 (рис. 67); 25) окружность с центром (—5; 1) и радиусом 3; 26) окружность с центром (1; 0) и радиусом 2; 27) окружность с центром (0; —3) и радиусом 1; 28) линия состоит из одной точки (3; 0) — вырожденная линия; 29) линия состоит из одной точки (0; 0) — вырожденная линия; 30) нет ни одной точки, координаты которой удовлетворяли бы данному уравнению («мнимая линия»); 31) нет ни одной точки, координаты которой удовлетворяли бы данному уравнению («мнимая линия»). 160. Линии 1); 2) и 4) проходят через начало координат. 161. 1) а) (7; 0), (—7; 0); б) (0; 7), (0; -7); 2) а) (0; 0), (6; 0); б) (0; 0), (0; -8); 3) а) (-10; 0), (—2; 0); б) линия с осью Оу не пересекается; 4) линия с координатными осями не пересекается; 5) а) (0; 0), (12; 0); б) (0; 0), £0; —16); 6) а) линия с осью Ох не пересекается; б) (0; — 1), (0; —7); ) линия с координатными осями не пересекается. 162. 1) (2; 2), (“2; —2); 2) (1; —1), (9; —9); 3) (3; —4),	—4-^Ц; 4) линии
не пересекаются. 163 Точки М},' М2 и лежат на данной линии;
204
точки Мз и М5 не лежат на ней. Уравнение определяет окружность (рис. 68). 164. а) (б; б) (б; в) (3; 0); г) (з/з-; -|j; прямая, перпендикулярная к полярной оси и отсекающая на ней, считая от полюса, отрезок, равный 3 (рис. 69). 165. а) ^1;
б) ^2; и ^2; — nj; в) ^2; и	nj; прямая, рас-
положенная в верхней полуплоскости, параллельная полярной оси
и отстоящая от нее на расстоянии 1 (рис. 69). 166. I) Окружность с центром в полюсе и радиусом 5; 2) луч, выходящий из полюса, наклоненный к полярной оси под углом *- (рис. 70); 3) луч, выходящий из полюса, наклоненный к полярной оси под углом — — (рис. 70); 4) прямая, перпендикулярная к полярной оси, отсекающая на ней, считая от полюса, отрезок а = 2; 5) прямая, расположенная в верхней полуплоскости, параллельная полярной оси, отстоящая от нее на расстоянии, равном 1; 6) окружность с центром (3; 0) и радиусом 3 (рис. 71); 7) окружность с центром С2^5; и радиусом 5 (рис. 71); 8) линия состоит из двух лучей, выходящих из
205
полюса, один из "которых наклонен к полярной 5
а другой —под углом -^-л (рис. 71); 9) линия трических окружностей с центром в полюсе,
оси под углом Л, состоит из концен-радиусы которых г
JC
определяются по формуле г = (•—1)п-^-+ лл, где п — любое целое
положительное число или нуль. 167. Рис. 72 и рис. 73 168 Рис. 74 и рис. 75. 169. Рис. 76. 170. Отрезок, примыкающий к полюсу, имеет л
длину, равную каждый из остальных отрезков имеет длину, равную 6л (рис. 77). 171. На пять частей (рис. 78). 172. Р (12; yj (рис. 79). 173. Q (81; 4) (рис. 80). 174. Прямые х ±# = 0. 175. Прямые х ± а = 0. 176. Прямые у ± Ь — 0. 177. #4-4 = 0. 178 х—5=0. 179. 1) Прямая х — у = 0; 2) прямая х + У — 0: 3) прямая х — 1=0; 4) прямая # — 2 = 0. 180. Прямые 4ах±с = 0. 181. х2 + у2 = г2. 182. (х - а)2 4- {у - 0)2 = г2. 183. х2 + у2 = 9. 184. х2 + у2 = 16.
н2
185.	х2 + #2 = «2. 186. (х - 4)2 4- у2 = 16. 187. -^4-4-=1. zO lb
г 2
188.	—-----jg-=l. I89, У2=12х-	Ю2. #2 = 2рх — парабола.
х2	у2	х2	у2
193.	4- -7- = 1 — эллипс. 194. -77------------- — 1 — гипербола.
20	У	1Ь	У
195.	^-4-4- = 1 — эллипс. 196. Правая ветвь гиперболы 25 1о
~	= 1. 197. у2 = 20х - парабола. 198. р cos 0 = 3. 199. 0 =
64	06	3
200.	t£0=l. 201. р sin 0 4-5 = 0, р sin 0 — 5 = 0. 202. р = 10cos 0. 203. Условию задачи удовлетворяют две окружности, уравнения которых в полярных координатах р 4- 6 sin 0 = 0, р — 6 sin 0 = 0. 204. X“f“S4 — + •&=!.	abU>S‘
* у = b sin t’, J, a2 b2	ш у a2sin21 4- b2 cos21
ab sin t
У — ' -'r- r 	' I. I I ... -	*
Va2sin2t	b2 cos21
ab sin t
Yb2 cos21 — a2 sin21
ab cos t
207.
206. x = --------- -  ,
У b2 cos21 — a2 sin21
t2
1) x=—# = /; 2) x = 2pctg2f, 2p
У = 2p ctg t-, 3) x = у ctg2 # = p ctg y. 208. 1) x ~ R sin 20, 1 x = 2p ctg 0, 1
2} #=2/?sin20;J	’ # = 2pctg0. f
X2 U2	X2
2) x24-^~a2 = 0; 3) A—A--l=0; 4)
x = 2R cos2 0,) у = R sin 20; J
1) x-#2 = 0;
5) x2 4-#2 - 2flx = 0; 6) x2 4- У1 - 2Ry = 0; 7) 2px-#2 = 0 210. Точки Aflt M3 и Mi лежат на данной прямой; точки М2, М-, и Мв не лежат на ней. 211. 3, -3,0, - би - 12. 212. 1р — 2, 4, т-5 и 7. 213. (6; 0), (0; -4). 214. (3; -5). 215. А (2; -1), В (-1; 3), С (2; 4). 216. (1; -3), (-2; 5), (б; -9) и (8; -17). 217. S= 17 кв. ед
! 206
p-59
218. С, (-1; 4) или С8(-^; -у-).	219. С{ (1; -I) ИЛа
С2(-2; -10). 220. 1) 2х-Зу + 9=0; 2) Зх-0=О; 3)Н2 = 0; 4) Зх + 4у- 12 = 0; 5) 2х +0 + 5 = 0; 6) х + Зу - 2 = о.
221. 1) 6 = 5, В = 3; 2) £ = --|-, & = 2;3)fe = --|-,
3	з з3
3	5 О
4) k = --, & = 0; 5) /г = 0, &=3.	222. 1)	2)
223. I) 2х + 30 — 7 = 0; 2) Зх-20-4 = О. 224. Зх+20 = О, 2х-3у- 13 = 0. 225.	(2;	!), (4; 2), (-1; 7),	(1;	8). 226. (-2; -1).
227. Q(ll; -11).	228. 1) Зх-2у-7 = 0;	2)5х + 0-7 = О;
ЗУ 8х + 12г/+ 5 = 0;	4)	5х + 7у + 9 = 0;	5)	6х-30г/-7 = 0.
229. a) k = 7; б) k =	в) k = -	230.	5х - 2у - 33 = Q,
х +40-11=0, 7х + 60 + 33 = 0.	231. 7х —20-12 = 0.
5х + 0-28 = 0, 2х-30 - 18 = 0. 232. х+ 0+1=0. 233. 2х + + 30 - 13 = 0. 234. 4х + 30 - 11 = 0, х + 0 + 2 = 0, Зх + 20-13=0. 235. (3; 4). 236. 4х + у — 3 = 0. 237. х - 5 = 0.	238. Уравнение
стороны АВ: 2х + у — 8 = 0; ВС: х + 2у — 1 = 0; С А: х — у — 1 = 0. Уравнение медианы, проведенной из вершины А: х —3 = 0; из вершины В: х +0 — 3=0; из вершины С: 0 = 0.	239. (—7; 0);
(0;+2уУ	242. (1; 3).	243. З'х - 50 + 4 = 0, х + 70 - 16 = 0,
Зх —50 — 22 =0, х+ 70 +10 = 0. 244. Уравнения сторон прямоугольника: 2х —50 + 3 = 0, 2х — 50 — 26 = 0; уравнение его диагонали: 7х — Зу — 33 = 0. 245. 5х + 0 — 3 = 0 — биссектриса внутреннего угла; х — 50 — 11 = 0 — биссектриса внешнего угла. 246. х+у— — 8 = 0; Их — 0 — 28 = 0. Указание. Условйю задачи удовлетворяют две прямые: одна из них проходит через точку Р и середину отрезка, соединяющего точки Л и В; другая проходит через точку Р параллельно отрезку АВ. 247. (—12; 5).	248. Afj (10; —5).
(5	\
у; 01. Указание. Задача может быть решена по следующей схеме: 1) устанавливаем, что точки М и N расположены по одну сторону оси абсцисс; 2) находим точку, симметричную одной из данных точек относительно оси абсцисс, например точку симметричную точке V; 3) составляем уравнение прямой, проходящей через точки М и 4) решая совместно найденное уравнение с уравнением оси абсцисс, получим координаты искомой точки. 250. Р(0; 11).	251. Р (2; -1)>	252. Р (2; 5).	253. 1) <р = у;
2) Ф = у; 3) qp = O—прямые параллельные; 4) ф — arctg
254. х —50 + 3 = 0 или 5х + 0 — 11 =0. 255. Уравнения сторон квадрата: 4х + 30+1=0, Зх —40+ 32 = 0, 4х + 30 — 24 = 0, Зх — 40*+ 7 = 0; уравнение его второй диагонали: х + 7у — 31 = 0. 256. Зх - 40 + 15 = 0, 4х + Зу — 30 = 0, Зх - 40 - 10 = 0, 4х + Зу— — 5 = 0. 257. 2х + 0—16 = 0, 2х +0+14 = 0, х — 20—18 = 0. 258. Зх — 0 + 9 = 0, Зх + 0 + 9 = 0.	259, 29х — 2у + 33 = 0.
262. 1) Зх-70-27 = 0; 2) х +90 + 25 = 0; 3) 2х - Зу -13 = 0; 4) х—2=0; 5) 0+3=0. 264. Перпендикулярны 1), 3) и 4). 266.' 1) ф = 45°; 2) ф = 60°; 3) ф = 90°. 267.	(б; -6). 268. 4х - у - 13=0, х-5=0,
208
М — середину отрезка AD
х 4- ЗУ + 5 = 0-	269. ВС: Зх 4- 4у — 22 = 0; С А: 2х - 7у -5 = 0
CN: Зх 4- 5у—23 = 0. 270. х 4- 2у—7 = 0, х—4у —1=0, х— у4-2=0. Указание. Задача может быть решена по следующей схеме: 1. Устанавливаем, что вершина А не лежит ни на одной из данных прямых. 2. Находим точку пересечения медиан и обозначаем ее какой-нибудь буквой, например М. 3. На прямой, проходящей через точки А и М, строим отрезок MD — AM (рис. 81). Затем определяем координаты точки D, зная точку и один из его концов А. 4. Устанавливаем, что четырехугольник BDCM —параллелограмм (его диагонали взаимно делятся пополам), составляем уравнения прямых DB и DC. 5. Вычисляем координаты точек В и С. 6. Зная координаты всех вершин треугольника, мы можем составить уравнения его сторон. 271. Зх — 5у — 13 = 0, 8х—3у 4-17 = 0, 5х 4- 2у — 1 = 0. 272. 2х-у 4- 3 = 0, 2х 4- у-7 = 0, х — 2у — 6 = 0. Указание. Если на одной из сторон угла дана
точка А, то точка, симметричная точке А относительно биссектрисы этого угла, будет лежать на другой его стороне. 273. 4х—Зу 4- 10=0, 7х -f- у - 20 = 0, Зх 4- 4у - 5 = 0. 274. 4х 4- 7у - 1 = 0, у - 3 = 0, 4х 4- Зу—5 = 0. 275. Зх 4- 7у-5 = 0, Зх 4- 2у-10=0, 9х 4- 11у4~5=0. 276. х— Зу —23 = 0, 7х 4-9у 4- 19 = 0, 4х 4-Зу 4-13 = 0, 277. х 4- у-7 = 0, х + 7у 4- 5=0, х-8у 4- 20=0. 278. 2х 4- 9у—65=0, Gx—7у—25 = 0, 18x4- 13у - 41=0. 279. х 4- 2у = 0, 23х 4- 25у = 0. --- ~	24 = 0. 283. Зх4-У = 0, х—Зу = О. 284. 3x4-4у—1=0,
'	*	285. 1) а = —2, 5у —33 = 0: 2) а1 =-3,
„	5.
.................. “	“	3’
289. 8х — у
7x4- 24у -61=0.
х —56 = 0; а2 — 3, 5х 4-8 = 0; 3)	— 1, Зх — 8у = 0; а2 = 4г
ЗЗх — 56у = 0. 286. т = 7, п = — 2, у + 3= 0, 287. т = -4, п = 2, х —5 = 0. 288. 1) (5; 6); 2) (3; 2); 3)	1); 4) ^2; “ур);
5) (——; 2 . 291 1) При а ¥=3; 2) при а = 3 и b Ф 2; 3) при а-=3 и b = 2. 292. 1) т'=—4, п 2 или т = 4, п^= — 2; 2) т = —4, п = 2 или т = 4, п — —2; 3) т = 0, п — любое значе-7
ние. 293. m = -jy. 294. Условию задачи удовлетворяют два значения т: /И1=0, т2 — 6. 295. 1) Пересекаются; 2) не пересекаются;
3) не пересекаются. 298. а = —7. 299 1) у 4- -у = 1: 2)	4" 'о‘==^
3)4r+f=1 <рис82)-390. 6 кв. ед. 301. х 4- У 4- 4 = 0. 302. х 4- У — 5 = 0, х — у 4- 1 = 0, Зх — 2у = 0. 303, Решение. Напишем уравнение искомой прямой «в отрезках»:
4 + f = i а о
(1)
209
Наша задача — определить значения параметров а и Ь. Точка С (I; 1) лежит на искомой прямой, следовательно, ее координаты должны удовлетворять уравнению (1). Подставим в уравнение (1) вместо текущих координат координаты точки С; после приведения к общему знаменателю получим:
а + b = ab.	(2)
Теперь заметим, что площадь треугольника S, отсекаемого прямой от координатного угла, определяется формулой ±5=»-^-; + S в том случае, когда отрезки а и & одного знака, и -5 в том случае, когда эти отрезки разных знаков. Согласно условию нашей задачи будем иметь:
ab == ± 4.
(3)
+* b —— 4, 1 у + Z? — ~“4 1
Решим систему уравнений (2) и (3):	)	’ I
ab — 4; ) ab = —4; )
тогда получим:_дг] =2, 6] =2: а^ — — 2 + 2/Т, Ь2 = — 2 — 2/Г; Лз = —2 — 2/2, Ьъ — — 2 + 2/2. Таким образом, условию задачи удовлетворяют трй прямые. Подставим в уравнение (!) полученные
значения параметров а и 6: ~ 4--
2
X
У
-2+2/2	-2-2/2 Ь
2
X
Рис. 82.
-2-2/2	—2 + 2 /Т
После упрощения этих уравнений получим: х + «/ — 2 = 0, (1 + /Т) х+ + (1 -/2) г/-2 = 0, (1 —/2)х + + (1 + /Г) у -2 = 0.' 304. Условию задачи удовлетворяют следующие три прямые: (/2_+ 1) х + (V2_— 1) у — - 10 = 0, (/2- 1)х + (/2 + 1)у + + 10 = 0, х—г/—10 = 0.	305. Зх —
— 2у—12=0,	Зх - Sy + 24 = 0.
306. х + Зг/—30 = 0, Зх + 4#—60 = 0, Зх — у — 30 = 0,	х — 12 г/ + 60 = 0.
307. Условию задачи удовлетворяют две прямые, пересекающие соответственно оси координат в точках (2; 0), (0; -3) и (*-4; 0), (о; у). 308. S >
>2x^1. 309. Прямые 1), 4), 6) и 8) заданы нормальными уравнениями, зю. I)4^-4-v”2=o; 2) -4х+4^”1О=°; 3)	+
0	0	О О	1О
к	2	1
+ _+ у-1=0;	4) — х —2 = 0;	5) х - у - 1 = 0.
13	/б	/б
811. I) а = 0, р = 2; 2) а = я, р = 2; 3) а«у, р = 3; 4) а = — -у, р = 3; 5) a = -J, P — S\ 6) а = —р = У2; 7) а = —-|-л,
р = 1; 8) a = — ft, p = q\ 9) а=0 — n, p — q. 312. 1) 5 = — 3, j = 3; 2) 6=1, d=\\ 3) 6 = —4, d = 4; 4) 6 = 0, d — 0 — точка Q лежит на прямой. 313. 1) По одну сторону; 2) по разные стороны; 3) по одну сторону; 4) по одну сторону; 5) по разные стороны. 314. 5 кв. ед. 315. 6 кв. ед. 318. Является выпуклым. 319. Не является выпуклым. 320. 4. 321. 3. 322. 1) d = 2,5; 2) d = 3; 3) d = 0,5; 4) d = 3,5. 323. 49 кв. 'ед. 325. В отношении 2 : 3, считая от второй прямой. 326. Решение. Задача о проведении прямых через точку Р на расстоянии, равном 5 от точки Q, равносильна задаче о проведении из точки Р касательных к окружности радиуса 5, с центром в Q. Вычислим расстояние QP: QP — ]^(2 — I)2 + (7 — 2)2 = V 26. Мы видим, что расстояние QP больше радиуса окружности; следовательно, из точки Р можно провести две касательные к этой окружности. Теперь перейдем к составлению их уравнений. Уравнение всякой прямой, проходящей через точку Р, имеет вид
у-7 = А(^-2)	(1)
или kx — у + 7 — 2k = 0, где k — пока неопределенный угловой коэффициент. Приведем это уравнение к нормальному виду. С этой целью находим нормирующий множитель ц = ± ———j—-. Умножая уравнение (1) на р, получим искомое нормальное уравнение
^fex-У 4-_7.Т1Л « о.	(2)
± V& + 1
Подставляя в левую часть уравнения (2) координаты точки Q, имеем: --------------“ = 5- Решая это уравнение, найдем два
5
значения А] ------&2 = 0. Подставляя найденные значения
углового коэффициента в уравнение (1), получаем искомые уравнения: 5x4- 12у—94 = 0 и у—7 = 0. Задача решена. 327. 7х 4-24у—134=0, х — 2 = 0.	328. Зх+4у—13 = 0.	330. 8х — 15у + 9 = 0.
331. Зх —4у—25 = 0, Зх — 4у-f- 5 = 0. 332. Условию задачи удовлетворяют два квадрата, симметрично расположенных относительно стороны ЛВ. Уравнения сторон одного из них: 4х + Зу — 8 = 0, 4х + Зг/ + 17 = 0, Зх — 4у — 6 = 0, Зх — 4у + 19 = 0. Уравнения «торон другого: 4х4-3у—8 = 0, 4х 4- Зу — 33 = 0, Зх — 4у — 6 = 0, Зх— 4у + 19 = 0. 333. Условию задачи удовлетворяют два квадрата; остальные стороны одного из них лежат на прямых: Зх + 4у — 11 = 0, 4х — Зу — 23 = 0,. Зх + 4г/ — 27 = 0; остальные стороны другого — на прямых: Зх + 4у —• 11 = 0, 4х — Зг/ — 23 = 0, Зх + 4у + 5 = 0.	334. Зх + 4у 4-6 = 0, 3x-j-4y — 14 = 0 или
Зх 4- 4у 4- 6 = 0, Зх 4-4у 4-26 = 0.	335. 12х - 5у 4-61 = 0,
12х — 5г/4-22 = 0 или 12х — 5у 4-61 = 0,	12х—5у4-Ю0 = 0.
336. М (2; 3). 337. 4x 4- У + 5 = 0, у — 3 = 0. 338. 1) Зх - у 4-2 = 0; 2) х-2г/4-5 = 0; 3) 20х - 8у - 9 = 0.	339. 1) 4х - 4у + 3 = 0,
2x4-2г/-7 = 0; 2)4х4-1*=0, 8г/4-13 = 0; 3) 14х - 8у - 3 = 0, 64х 4- Н2у — 23 = 0. 340. х — Зу — 5 = 0, Зх 4- У — 5 = 0. У к a sail и е. Искомые прямые проходят через точку Р перпендикулярно к биссектрисам углов, образованных двумя данными прямыми. 341. 1) В одном углу; 2) в смежных углах; 3) в вертикальных
211
углах. 342. 1) В вертикальных углах; 2) в смежных углах; 3) в одном углу. 343. Внутри треугольника. 344 Вне треугольника. 345. Острый угол. 346. Тупой угол. 347. 8х + 4?/ — 5 — ()' 348. х + Зу —2 = 0. 349. Зх— 19 = 0. 350. 10,; - Юг/— 3 = 0* 351.7x4-56^- 40 — 0.	352. х + у + 5 = 0.	353. S (2; -1).
354. 1> Зх + 2г/ - 7 = 0; 2) 2х - у = 0; 3) у - 2 = 0; 4) х - 1 = 0; 5) 4х 4- Зг/ - Ю = 0; 6) Зх - 2у 4- 1 = 0. 355. 74х 4- 1 Зг/ 4- 39 = 0 356. х — у — 7 = 0.	357. 7x4-19г/ — 2 = 0.	358. х — у 4- 1=0.
359. 4х — 5г/ + 22 = 0, 4х + ^ — 18 = 0, 2х — у 4- 1 = 0. 360. х—5г/4-4-13 = 0, 5х + г/+13 = 0.	361. 5х — г/— 5 = 0 (ВС), х — у 4-
4-3 = 0 (ЛС), Зх — г/ —1 = О (CN). 362. х - 5г/ - 7 = 0, 5х 4- у + 4-17 = 0, Юх+7у — 13 = 0, 363. 2x 4-^+ 8 = 0, х + 2г/ 4- 1=0. 366. С = —29.	367. а =/= — 2.	368. Уравнения сторон квадрата:
4х + Зг/ - 14 = 0, Зх—4г/ + 27 = 0, Зх-4г/ + 2 = 0, 4х + Зу 4- 11=0; уравнение его второй диагонали: 7х—у + 13 = 0. 369. х + у + 5 = 0. 370. х + у + 2 = 0, х — у — 4 = 0, Зх + г/ = 0. 371. 2х + у — 6 = 0, 9х + 2г/+ 18 = 0.	372. Зх — г/+ 1 = 0.	374. Зх — 4г/+ 20 = О,
4х + Зг/ — 15 = 0. 375. х + 5г/ — 13 = 0, 5х — у + 13 = 0. 376. Условию-задачи удовлетворяют две прямые: 7х + у—9=0, 2х + у + 1=0. 377. 5х — 2у — 7 = 0. 378. ДС: Зх + 8г/ — 7 = О, BD: 8х—3у 4-7 = 0. 379. 4х + г/ + 5 = 0, х—2г/—1=0, 2х + 5г/— 11 = 0.	381.
1)	р sin (Р — 0) = р, psin^r—б\ = 3;	2) р cos (0 — а) = a cos а,
р cos I 0 +-д =-И; 3) р sin (Р-—0) = а sin p, р sin I — —. 0 I = 3. 382. р sin (Р — 0) = pi sin (Р — 0j). 383. р cos (0 — а) = р^ cos (0, — а). 384. psin^-Op /Рг + Р?-2РР1^(»-»,) 385 „ х2+у!=д.
р2 sin (02 - 0j) VР2+Р1-2p2Pi cos (O2-0i)
2)	(х - 2)2 + (у + 3)2 = 49; 3) (х-6)2 + (у+8)2 = 100; 4) (х + 1)2 4-4-(г/— 2)2 = 25;	5) (х - 1)г 4- (у - 4)2 = 8;	6) х2 + у2=16;
7)	(х - I)2 + (У + I)2 = 4; 8) (х - 2)2 + (г/-4)2 =10; 9) (х-1)2 + 4-г/2 = 1; Ю) (х - г)2 + (г/ - 1)2 = 25. 386. (х - З)2 + (г/+ I)2 = 38. 387. (х - 4)2 + (г/ + I)2 = 5 и (х - 2)2 + (г/ - З)2 = 5. 388. (х + 2)24-/	9 \2
+ (у 4- 1)2 = 20.	389. (х - Б)2 4- (у 4- 2)2 = 20 и х--£- +
\	О /
4-(г/--у)2 = 20. 390. (х — I)2 + (г/+ 2)2 = 16. 391. (х + 6)2 + ц_А_3)2 = 50 и (х — 29)2 + (г/+ 2)2 = 800. 392. (х-2)2 4- (у-1)2=5
22 V , { . 31 \2	289	.	о.2 , ,	1Ч2	81
и (х--Н +^ + ~ j “V 393-	D	=73- и
(х + 8)2 + (г/ + 7)2 = у|. 394. (х -2)2 + {у- 1 )2 = 25 и (х +	+
/	349V	/185\2	,	10\2 , / ,25V	. {	30V .
+ Н" 49)	•395, г+7) +Н?)==1 ИГ"Т) +
+ L_iy = l. 396. (х-5)2 + г/2=16, (х+15)2+ ^2 = 256, ( ' 35 \2 , /	40 V / 32 \2 /	35Д2 , ( , 40 V / 32 V
+н”"з") em иг~"т) +и+’т)	•
397. Уравнения 1), 2), 4), 5), 8) и (10) определяют окружности;
- 1) с (5; —2), R — 5; 2) С (—2; 0), Я = 8; 3) уравнение определяет
212
единственную точку (5; —2); 4) С (0;5), /? = /5; 5) С (1; —2), R = 5;
6) уравнение не определяет никакого геометрического образа на плоскость; 7) уравнение определяет единственную точку (—2, I).
8) С oj, 2?==-^-; 9) уравнение не определяет никакого геометрического образа на плоскости; 10) ' С ^0; ““тт),
398. 1) Полуокружность радиуса 1? = 3 с центром в начале координат, расположенная в верхней полуплоскости (рис. 83); 2) полуокружность радиуса = 5 с центром в начале координат, расположенная в нижней полуплоскости (рис. 84); 3) полуокружность радиуса R — 2 с центром в начале координат, расположенная в левой Полуплоскости (рис. 85); 4) полуокружность радиуса R — 4 с центром
213
в начале координат, расположенная в правой полуплоскости (рис. 86)-5) полуокружность радиуса Л? = 8 с центром С (0; 15), расположенная над прямой у —15 = 0 (рис. 87); 6) полуокружность радиуса J? = 8c центром С (0; 15), расположенная под прямой у — 15== о (рис. 88); 7) полуокружность радиуса Я = 3 с центром С (—2; 0 , расположенная влево от прямой х + 2 = 0 (рис. 89); 8) полуокружность радиуса R = 3 с центром С (—2; 0), расположенная вправо от прямой х + 2 = 0 (рис. 90); 9) полуокружность радиуса R = 5 с центром С (f-2; —3), расположенная под прямой у + 3 = 0 (рис. 91); 10) полуокружйость радиуса R — 7 с центром С (—5; —3), расположенная вправо от прямой х 4-5 = 0 (рис. 92). 399. 1) Вне окружности; 2) на окружности; 3) внутри окружности; 4) на окружности; 5) внутри окружности. 400. 1) л:-f- 5г/— 3 = 0; 2) х + 2 = о’ 3) Зх — г/ —9 = 0; 4) у 4- 1=0. 401. 2х-5^+19 = 0. 402. а) 7; б) 17; в) 2. 403.	(-1; 5) и Af2 (—2; —2). 404. 1) Пересекает
окружность; 2) касается окружности; 3) проходит вне окружности. 405.-1) |4|< 4; 2)* = ±4; 3)
Д	4	4	1 4* К"
407. 2x4- у “3 = 0 408. Их -7у -69 = 0. 409. 2/б. 410. 2х — 3п + + 8 = 0, Зх + 2г/-14 = 0	412. х2 + у2 + 6х - 9у - 17 = 0.
413. 13х2 + 13z/2 + Зх + 71г/= 0. 414. 7х — 4^ = 0. 415.2. 416.10. 417. (х + З)2 + (у - З)2 = 10. 418. х —2г/+ 5 = 0. 419. Зх - 4у + + 43 = 0.	420.	М, (-у;	. rf = 2/Г. 421. XjX + У1у = R2.
422. (Xi - а) (х - а) + (г/д - р) {у - ₽) = R2. 423. 45°. 424. 90°. 425.	(а1-а2)2+(₽1-р2)2	=	^+/?2	427. х- 2у -5 = 0 и
2х — у — 5 — 0. 428. 2х + у — 8 = 0 и х — 2у + 11 = 0. 429. 2х + у— -5 = 0, х - 2у = 0. 430. 90°. 431. х + 2у + 5 = 0. 432. d = 7,5. 433. d = 7. 434. rf = /10. 435. 3. 436. 2х + г/- 1 = 0 и 2х + у + + 19 = 0. 437. 2х + у- 5 = 0 и 2х+у+5 = 0. 438. р = 2R cos (0 -(рис. 93). 439. 1) p = 27?cos0 (рис. 94); 2) р = —2/?cos0 (рис. 95); 3) p = 2J?sin0 (рис. 96); 4) р = —2£sin0 (рис. 97). 440. 1) (2; 0) и Л-2; 2) (А; -£) и Л = -|; 3) (I; п) и Л-1; 4) £;	»
Л = 4; 5) (3; у) и * = 3; 6) (« и Л-4; 7) (4; —£) в л=4. 441. 1) х2 + у2 —Зх = 0; 2) х2 + у2 + 4 ц — 0; 3) хг + у2 -— х + У = 0. 442. 1) р = cos 0, 2) р = — 3 cos 0; 3) р = 5 sin 0; 4) р = — sin 0;	5) р = cos 0 + sin 0.	443. р = R sec (0 — 0О).
D 4 + 4 = 1; 2) 4 + 4=1; 3) ^ + -4=1; 4>< + тТ“|;5)^ + 4“1’6’|Й + Й-“1’7)4 + ^=|: 8)Гб+й-“1:9>п+т=1ми<+^=1> 10> <+<-'• 445. 1) 4 + 4=1; 2) 4 + 4=1: 3) 4 + ^=1;
у 2	/12	у2 fj2	у 2	у2
4) 64 + КЮ = 1; 5) Тб+>“1; 6>+ + -re=’1- ««• ‘НиЗ;
2) 2 и 1; 3) 5 в I; 4) И5 н ТТ; 5) и -г! 6) -i- и 4-1 7) 1 и I; л О	0	0	Z
214
8) 1 и 4; 9) - и 1; Ю) Vй1’ 447‘ 0 5 и 3’ 2) ^(“4: 0), *	ООО
Г2(4; 0); 3) е = -|-; 4) х=±-~•. 448. 16 кв. ед. 449. 1) /В" и 3;
2	9	4 у 5
2) Л(0; -2), Л(0;2); 3) е = |; 4)	450. —кв ед.
451. *!., 452. См. рис. 98. 453. (-3; - -I), (-3;	454. Точки
Д] и Л3 лежат на эллипсе; Д2, Л4 и Ла - внутри эллипса; Д3, Л5| Ац Л9 и Лю — вне эллипса, 455. 1) Половина эллипса jg- + ’^“ия 1*
213
расположенная в верхней полуплоскости (рис. 99); 2) половина эл-х2 । у'2	,	.	,
липса
9’+25= ’ расположенная в нижней полуплоскости (рис. 100); х2 и2
3) половина эллипса—+ -—= 1, расположенная в левой полу-
^2
плоскости (рис. 101); 4) половина эллипса х2 + •—==!, располо
женная в правой полуплоскости (рис. 102). 456. 15. 457. 8. 458. 5х Н- 12у4-10 = 0, х — 2 = 0. 459. г, =2,6, г2 = 7,4. 460. 20. 461. 10. 462. (-5; з/з) и (-5; -ЗУз). 463. (-2; XrQ и
’ 16	,6/3	’ ' 20	15	’	; 20 Т ’
466. I)	2)	8)	4) 1.
467. е = -^~-.	468	г*о)2 +-^~Уо)г д1
2	а2	Ь2
469	. (у + 4У 470	_(х+3)--	(у-2)>
9 Т 16	ч<«.	9	-f-	4	— 1.
471.	1) С (3; —1), полуоси 3 и Уб, 8 =_|"» уравнения
директрис: 2х—15 = 0, 2x4- 3 = 0; 2) С (—-J; 2), полуоси 5 п 4, 3
8 — —, уравнения директрис: Зх — 22 = 0, Зх 4- 28 = 0; 3) С (1; —2), О
полуоси 2 Уз" и 4, е = у, уравнения директрис: у—6=0, г/4~Ю=0. (я _ 3)2 (у 4- 7)2
472. 1) Половина эллипса -—--------Ь .	= 1, расположенная
т:
(х 1
над прямой у 4- 7 = 0 (рис. 103); 2) половина эллипса - ~1  4-
216
(у — 1)8
4-	^ - = 1. расположенная под прямой у—1=0 (рис. 104);
ov	‘ х2 , (у 4- 3)г
3) половина эллипса -т^-+ ~—й--------= 1, расположенная в левой
1о 4
/ in-ч ич	(х4-5)2 , (у— I)2	,
полуплоскости (рис. 105); 4) половина эллипса -—4- ——=1, расположенная вправо от прямой х 4- 5 = 0 (рис. 106),
Рис. 106.
473. 1) (Xl69^- + -fr=1; 2) 2х2 — 2хг/4-2г/2 — 3 = 0; 3)68х24-+ 48ху 4-82z/2 - 625 = 0; 4) 11х2 4- 2ху 4- 11г/2 - 48х-48у - 24 = 0. 474. 5х2 4- 9г/2 4- 4х - 18г/ - 55 = 0. 475. 4х24-Зг/24-32х - 14г/4-59=0. 476. 4х2 4- 5г/2 4- 14х 4- 40г/ 4- 81 = 0. 477. 7х2 - 2ху 4- 7 г/2 - 46х 4-4-‘2г/ + 71 =0.	478. 17х2 4-8хг/4-23У2 4-ЗОх - 40г/- 175 = 0.
479. хг 4- 2г/2 - 6г 4- 24//4-31 = 0. 480. 4; AV (3; 2). 481. (з;	~
прямая касается эллипса. 482. Прямая проходит вне эллипса. 483. 1) Прямая пересекает эллипс; 2) проходит вне эллипса; 3) касается эллипса. 484. 1) При | tn J < 5 — пересекает эллипс; 2) при т = ± 5 — касается эллипса; 3) при | т | > 5 — проходит вне эллипса. 485. k^+b^m2. 486. т + ^-1’ 488. 3x4-2//-10=0 а2
п Зх 4- 2у 4- Ю = 0. 489. х 4- г/ — 5 = 0 и х 4- г/ 4- 5 = 0. 490. 2х — 94 1/V	._.
-г/ - 12 = 0, 2x-j/4-12 = 0; d =	491. ЛМ-3; 2); </ = /13.
492. х4-?/““5 = 0 и х + 4у— 10 = 0.	493. 4х —5у—10 = 0.
494. d - 18. 495.	+	- I „ли £ +	- 1. 496. g + g -1.
217
499.^4
yL
8
1.Указание. Воспользоваться свойством эллипса
х2 и2
сформулированным в задаче 498. 500. ^- +	-1. Указание.
Воспользоваться свойством эллипса, сформулированным в задаче 498. 502. 2х + 11 г/ — 10 = 0. Указание. Воспользоваться свойством эллипса, сформулированным в задаче 501. 503. (3; 2) и (3; —2), 504. /? =	505. 10,5/Г. 506. <р = 60°. 507. 16,8. 508. 60е.
/т2 + п2
№	у2
509. В эллипс, уравнение которого	= 1. 510. х2+^/2 = 9.
ZO	IО
X2  У2
36 "*
- -€ = 11 5)
□о
X2	У2
4	5
х2	у2
16	9
517-
511.
515.
8)
2)
5)
15-1. 512. , = А. 513. „-I. 514. 4,-1, 4, = |
Л1_^==1. 4)
7)
; 16	9	1
х2 у2
36	324
х2 у2
24	25
а = 3, 6 = 2; 2) а = 4, Ь = \\ 3) а = 4,
16 *“ 1; 2)
X2	у2
36	64
.1;9) 64
1; 3)
9	16 “
1,5 6)ж .£=1
36 u
х2	у2
100	576
I)
X2
U3)
^yL—
25
516.
= — 1;
1)
4)
1;
6	6	11
6 = 2; 4) а=1, 6 = 1; 5) а = ^-, 6=4; 6) а = 4, & = 4 £•	о	О	4
7) а = 4-, Ь=—.	518. 1) а = 3, 6 = 4; 2) F, (-5; 0), F2(5; 0);
О	о
Ц	4	Q
3) е = -х*; 4) у = ± -т- х; 5) х = ±	519. 1) а = 3, 6 = 4;
л	о	о
ная в верхней полуплоскости (рис. 107); 2) ветвь гиперболы х2—— =я—1, расположенная в нижней полуплоскости (рис. 108);
3) ветвь гиперболы	расположенная в левой полупло-
10 У
218
-у 2
скости (рис. 109); 4) веть гиперболы уг— у- = —1, расположенная в верхней полуплоскости (рис. ПО). 522. х —4рг5'#+ 10 = 0 я х-Ю = 0. 523. п=2—, г2=10у. 524. 8, 525. 12. 526. 10. 527. 27. 528. (10; у) и (10, -у). 529. (-6; 4/У) и (-6;- 4/з).
539. 2-^ и 26-^-.	531. См. рис. 111.	532. 1)	= 1;
12	12	о 2 о
jf2	у2	о2	у2
2) х2 — г/2 =16; 3) -у 8”=1’’ 4) “4 5~sssl или 'ёГГ ~
Рис. НО.
Рис. 111.
асимптот: 4х — Зу — 17 = 0, 4х + Зу 4- 1 — 0; 2) С (—5; 1), а = 8, Ь = 6, 8 = 1,25, уравнения директрис: х = — 11,4 и х= 1,4, уравнения асимптот: Зх + 4г/4-11==0 и Зх — 4# 4-19 = 0; 3) С (2; — 1), а = 3, Ь = 4, е=1,25, уравнения директрис: у = — 4,2, у = 2,2, уравнения асимптот: 4х + Зу — 5 = 0, 4х — Зу — 11 = 0, 542. 1) Часть
219
гиперболы -—  — ~ 4 - = 1, расположенная нал прямой //+1=0 (рис. 112); 2) ветвь гиперболы -* —- —	= — i
Рис. 112.
16	4
(рис. 114); 4) часть гиперболы
расположенная под прямой у — 7 = 0 (рис. 113); 3) ветвь гиперболы (х-9)г	(г/+ 2)2
------------:------— 1. расположенная влево от прямой х — 9 = 0
(х - 5)2 {у + 2)г
16
1, распило-
9
(х __ Q\3
женная влево от прямой х — 5 = 0 (рис. 115).	543, 1) -—---------
(и — 2)2	z
-	0-.-- = 1; 2) 24хг/ + 7у2 - 144 = 0; 3) 2ху + 2х - 2у + 7 = 0.
х2	м2
544. — - 4- = 1. 545.
16	9
х2	у2
25	144
1.
546. х2 — 4г/2 — 6х —
-24г/-47 = 0. 547. 7х2 - бхг/ - у2 + 26х - 18г/-17 = 0. 548. 91xz-д|2
— ЮОху + 16г/2 — 136х + 86г/ — 47 = 0. 549. ху — при повороте
а2
старых осей на угол —45е; x//j=---при повороте на угол +45°.
550. 1) С (0; 0). а=Ь = 6, уравнения асимптот: х = 0 и у = 0; 2) С (0; 0), а = b = 3, уравнения асимптот: х =0 и у = 0, 3) С (0; 0),
а = b = 5, уравнения асимптот: х — 0 и у — 0. 551,
№ 2) и (+
2\
3?
220
прямая касается гиперболы. 553. Прямая проходит
552.
вне гиперболы. 554. 1) Касается гиперболы; 2) пересекает гиперболу в двух точках; 3) проходит вне гиперболы. 555. 1) При I т | > 4,5 — пересекает гиперболу; 2) при m = ± 4,5 — касается гиперболы; 3) при | т | < 4,5—проходит вне гиперболы. 556. k2cr—b2=m2. g57. 212.2.212-«1.	* 559. Зх-4у-10=0, Зх-4у 4-10 = 0.
560. 10х —Зу —32 = 0, 1_0х — Зу 4-32 = 0.	561. х + 2у — 4 = 0,
х + 2у 4- 4 = 0; d — — |3х + 5у + 48 = 0.
565. с? = -^/Ю.
Зх 4у2	.
45
х — — 4,	х = 4,
х2 У2	. .
5	4
2х + 11 у + 6 = 0.
8/5
5 ’
563.
564.
566. —=-о
и7-4
У = - 1 X2
573 Тб-Т 
Указание. Восполь-
562. /И, (-6; 3);
5х — Зг/ — 16 = 0, 2х + 5у — 16 = 0.
*2	У——\
45
-4->-и У = 1. -€=i.
10
568
572
575	.	_
зеваться свойством гиперболы, сформулиро' ванным
578
580.
в задаче х2	У2 .
16	9
9
Q =4 581.
О
I) 1/2 = 6х;
574. 577. х2 - г/2 = 16.
579 21 _ 21-1
5791 25	4	‘
5
q — 2 582, <71 = 2, у2 = -у,
2) у? = —х. 3) х2 = уу;
584. 1). р = 3; в пра-
Рис. 115.
у+2-0
583.
4) х2 = — бу. 584 1). р = 3; в правой полуплоскости симметрично оси Ох; 2) полуплоскости симметрично оси Оу, 3) р — 2; в
симметрично оси Ох, 4) р = -1; в нижней полуплоскости симме-
р = 2,5; в верхней левой полуплоскости
Рис. 118.
I трично оси Оу. 585 1) у2 = 4х; 2) у2 = — 9х; 3) х2 — у, 4) х2 = —2у. 586 40 см 587. х2 = —12у. 588. 1. Часть параболы у2 — 4х, расположенная в первом координатном углу (рис. 116); 2) часть пара-1 болы у2 — — х, расположенная во втором координатном углу (рис. 117); 3) часть параболы у2 = —18х, расположенная в третьем
221
координатном углу (рис. 118); 4) часть параболы у2 == 4х,_ расположенная в четвертом координатном углу (рис. 119); 5) часть параболы х2 = 5у, расположенная в первом координатном углу (рис. 120); 6) 'часть параболы х2 = — 25г/, расположенная в третьем координатном
углу (рис. 121); 7) часть параболы х2 — Зу, расположенная во втором координатном углу (рис. 122); 8) часть параболы х2= —16у, расположенная в четвертом координатном углу (рис. 123). 589. F (6; 0),
У
х + 6 —0. 590. 12. 591. 6. 592. (9; 12). (9; - 12). 593. у2 = -28х. 594.1) (у— Р)2 = 2р (х — а); 2) (у — 0)2 = — 2р (х—а). 595. 1)(х—а)2= == 2р (у — Р); 2) (х - а)2 = -2р (у - р). 596. I) 4(2; 0), р=2, х- 1=0; 2) oV р = 3, 6х - 13 = 0; 3) А (о; р = 3, бу-Ь 1’1 =0; 4) 4(0; 2), p = v> 4у-9 = 0. 597. 1)4(-2; 1),р-2;
222
2) Л (1; 3), р = 1; 3) А (6; -1), р = 3. 598. 1) Л (—4; 3), р = 1;
2) А (1; 2), р = 2; 3) Л (0; 1), р = -~. 599. 1) Часть параболы
(у—3)2 = 16(х—1), расположенная под прямой 9—3 = 0 (рис. 124);
2) часть параболы (х4-4)2 = 9 (94-5), расположенная вправо от прямой х 4-4 = 0 (рис. 125); 3) часть параболы (х—2)2 = —2 {у—3), расположенная влево от прямой х—2 = 0 (рис. 126); 4) часть параболы (94-5)2 = —3(х4-7), расположенная под прямой 94-5 = 0
(рис. 127). 600. х = ~^У2~ У~\~7‘ 601. 9 = А-х2-х-4-3. 602. х2 +
-f- 2ху 4- у — 6х -J- 2t/ 4— 9 = 0. 603. Р(9; —8)., 604. 4х2 —4ху4-4- f/2 4-32x4- 34t/4-89 = 0.	605.
(2; I), (—6; 9). 606. (—4; 6) —прямая касается параболы. 607. Прямая и парабола не пересекаются. 608. 1) Касается параболы; 2) пересекает параболу в двух точках;
3) проходит вне параболы. 609. 1) k <	; 2) fe = -y; 3) k>~.
610. p = 2bk. 612. улу = р(х-}-х1у 613. х4-94-2 = 0. 614, 2х — — 9—16 = 0. 615. d = 2K13. 616. Al, (9; —24); d=10. 617.3х — -^4-3 = 0 и Зх—294-12 = 0. 619. 5х—1894-25 = 0 620. d=13^.
621. (6; 12) и (6; —12). 622. (10; j/30), (10; — /30), (2; ИГ), (2; -]<б). 623. (2; 1), (—1; 4). (.HJCll; It 13 й /3— |/73 7— И13 \	л
( ---------------- ]. 625. у—18 = 0. Указание. Вос-
пользоваться свойством параболы, сформулированным в задаче 624. 628. 1) р = —----ff; 2) р =	-х. 629. 1) р=------2--3;
5—3cos0 54-3 cos 0	4—5cos0
9	144	144
2> ₽=-4=5^ё-	*> ₽=5+1з^= 2> р— 13cose •
з
631. р = j'_2'co's'0 ♦ 632. 1) Эллипс; 2) парабола; 3) ветвь гиперболы; 4) эллипс; 5) ветвь гиперболы; 6) парабола. 633. 13, 12. 634. 8, 6. 21	29
1635. Р = —2cos0* P = 2cose- 636‘ уРавнения Директрис: р = 34	16	20
= —г-.—х, р =— х------х ; уравнения асимптот: р = п . ъ3
5 sin 0	5 cos 0	r 3sin0—4 cos 0
р==_. .....-_^Q -637. f6; %), (б; — -J), 638. (з?-|-л\,
г	3 sin 0 4-4 cos 0	\ 4 J \	4 /	\ 3 /
73;	639? 1) (-g-; я\ 2) (р; fp; 640‘ Р2=
223
_______"_____ 641 n2 =____________-______ 642 о-----------
~ l - 82 cos2 0 ’	P e2 cos2 e - I •	0 F sin2 0 '
643. 8x 4- 25y = 0. 644. 9x — 32y — 73 = 0. 645. x — у =-0, x 4- 4z/ = Q. 646. x + 2y — 0, 8x — 9y — 0. 647. x + 2y = 0, 2x — 3y = 0. 654. 2x — 5y = 0.	655. lx + у — 20 = 0.	656. x — 8y = 0,
2x — у = 0. 657. x — 2y — 0, Зх — у = 0 x 4* 2y = 0, 3x 4- у = 0. 661. у + 2 = 0. 662. 2x — у + 1 = 0. 665. Линии 1), 2), 5) и 8) имеют единственный центр, 3), 7) — не имеют центра, 4, 6) — имеют бесконечно много центров. 666. I) (3; —2); 2) (0; —5); 3) (0; 0); 4) (-1; 3). 667. 1) х-Зу-6=0; 2) 2х + у-2 = 0; 3)5х-у4-4-4 = 0. 668. 1) 9х2 — 18ху 4- 6z/2 4- 2 = 0; 2) 6х2 4- 4ху + у2 — 7 = 0; 3) 4х2 4- бху 4- у2 — 5 = 0, 4) 4х2 + 2ху 4- бу2 4- 1 = 0. 669. 1) щ^=4, п — любое значение; 2) т = 4, n#=6; 3) т — 4, п = 6, 670. 1) k — 2; 2) £] = —!, k2 — 5; 3) при всех k^=2 и удовлетворяющих неравенствам —1<^<5; 4) прий< —1 и при й> 5. 671. х2 — 8у2 — — 4 = 0. 672. х2 4- ху + у2 4- Зу = 0. 673. 1) Эллиптическое уравне-
Х^^	у'2	,
ние; определяет эллипс -д- 4* "4 е	—2) —новое начало;
/2 У*
2)	гиперболическое уравнение; определяет гиперболу — —	= 1;
/2 у'2
О' (3; —2) — новое начало; 3) эллиптическое уравнение 4“ g =““U не определяет никакого геометрического образа (является уравнением «мнимого эллипса»); 4) гиперболическое уравнение; определяет вырожденную гиперболу — пару пересекающихся прямых 4х/2 — у 2 = 0; О'(—1; —1) —новое начало; 5) эллиптическое уравнение; определяет вырожденный эллипс (единственную точку) 2х'2 4-Зу'2 = 0. 674 *). 4) Гиперболическое уравнение; определяет х'2	U'2	1	2
гиперболу -д-----4 = 1; а = —2> cosa = ~уг=^ , sin а = —
х'2	у'2
2)	эллиптическое уравнение; определяет эллипс — 4- — = 1; а = 45°;
3)	эллиптическое уравнение; определяет вырожденный эллипс — /2/2	12
единственную точку х + 4у = 0; tg а = 2, cos а = -7= , sin а =-7=;
У 5 У 5
4)	гиперболическое уравнение; определяет вырожденную гипер-2	2	2
болу — пару пересекающихся прямых х' —у' = 0; tg а = 4-,
3	2
cos а =	, sin а = —?=•; 5) эллиптическое уравнение; не опре-
У13 У 13
деляет никакого геометрического образа (является уравнением «мнимого эллипса»); в новых координатах его уравнение имеет вУд /2
Л—[_ у'2 = — 1; а = 45°. 675. 1) Гиперболическое; 2) эллиптическое, 3) параболическое; 4) эллиптическое; 5) параболическое; 6) гиперболическое. 676. 1) Гиперболическое уравнение; определяет
*) В задачах 674 1) —5) а есть угол от положительного направления старой оси абсцисс до новой,
224
гиперболу, уравнение которой приводится к виду х —= I. путем двух последовательных преобразований координат: х — х + 2, у —у — 1 и — -~1У-*	(Рис< I28)’ %) эллиптическое
уравнение; определяет эллипс, уравнение которого приводится
%'	у'%
к виду -гх- +	= 1 путем двух последовательных преобразований
1о	У
Рис. 130.
координат: х = х — 1, у — у + 1 и
(рис. 129);- 8) гиперболическое уравнение; определяет гиперболу, х'^	у'2
уравнение которой приводится к виду ----------= 1 путем двух
последовательных
2х -р У' i
-yf-
преобразований координат: х = х + 3, у — у — 4
х ~ 2у
и х =
У
130); 4) гиперболическое урав-
8 Д. В. Клетеник
225
пение; определяет вырожденную гиперболу — пару пересекающихся прямых, уравнение которых приводится к виду х' — 4у'2 = 0 путем двух последовательных преобразований координат: х = х-— 2, х'4-Зг// _	— Зх'4~/ .	-а
у = й и х =----г=-, У =-------г—  (рис. 131); 5) эллиптическое
/10 И	/10
уравнение; не определяет никакого геометрического образа — «мнимый эллипс»; его уравнение приводится к виду х'2 4-2/2 =*= — 1 путем двух последовательных преобразований координат: х = х — 1, х' + Зу' _	— Зх' 4-/ е.
---!—,,-------------!__z_ . 6) эллиптическое уравне-
У = У И х
/10
У
Рис. 131.

> У =-----г=
/10
ние; определяет вырожденный эллипс — единственную точку; его уравнение приводится к виду 2х,24-4-Зг/'2 = 0 путем двух последовательных’ преобразований коорди-п ~ х' ~ У' нат; х=х, у = у — 2пх = —
У 2
> — х' + у' .
У / 2 ‘ 677’	30 + 5
= I — эллипс; 2) 9х2 — 16/ = 5 —-гипербола; 3) х2 — 4/ = 0 — вырожденная гипербола — пара пересекающихся прямых, уравнения которых х — 2у = 0, х + 2г/ = 0;
4)	2х2 + Зг/2 = — 1 — «мнимый
эллипс»; уравнение не определяет никакого геометрического образа; 5) х2 4~ 2/ = 0 — вырожденный
эллипс; уравнение определяет единственную точку — начало коор-и*
динат; 6) — 4- ~ = 1 — эллипс; 7)	----/= I — гипербола;
х2	1
8) -%- -Г / = I - эллипс 678 1) 3 к 1; 2) 3 к 2; 3> 1 и 4 > <) 3л ?.
У	Zr
(J73. 1) х = 2, у — 3: 2) х == 3, $=» —3; 3) х = 1, {'=« — 1; 4) х *=» — 2, у~ 4 680. 1) 2 и 1; 2) 5 и I; 3) 4 и 2; 4) 1 и 68* I) х 4-^ - I = 0,
Зх + у 4- 1 == 0: 2) х — 4г/ — 2 = 0, х - 2у + 2 = 0; 3) х - у = 0, х —Зг/==0, 4) х 4- у — 3 — 0, х 4- 3^4" 3 = 0.	682. 1) Эллипс;
2) гипербола; 3) пара пересекающихся прямых (вырожденная гипербола); ;) уравнение не определяет никакого геометрического образа («мнимый эллипс»); 5) точка (вырожденный эллипс). 689. 1) Параболическое приводится образований х' = х" -3,
уравнение; определяет параболу, уравнение которой к вид}7 у"2 = 2х" путем двух последовательных пре-— 4х' 4- 3/	— Зх' —- 4у'
координат; х =--------=--—, у —-------------— и
□	о
у' = у" 4" 2 (рис. 132); 2) параболическое уравнение; определяет вырожденную параболу — пару параллельных прямых, уравнение которых приводится к виду х"2 = 1 путем двух последо-Зх" — 2у'	2х' 4- Зу'
нательных преооразовании координат: х = —/у^'"'1	—/ТЗ “*
4
и	t/e=yN (рис. 133); 3) параболическое уравнение;
не определяет никакого геометрического образа; приводится к виду у"2 4-1=0 путем двух последовательных преобразований координат! Х = 3*'~.4у'., у = 1Х'+3»' „ х- _ v- = у« _ 4. 6М. I) у2 = 6х_, О	U
парабола; 2) у2 — 25 — вырожденная парабола — пара параллельных
прямых, уравнения которых у — 5 = 0, </4-5 = 0; 3) </2 = 0 — вырожденная парабола — пара слившихся прямых, совпадающих с осью абсцисс. 693. 1) (х4-2</)2 4-4х4-«/— 15 = 0; 2) (Зх—</)2 —х4--4- 2г/ — 14 = 0; 3) (5х - 2у)2 4- Зх - у 4- 11 = 0; 4) (4х 4-2//)2 - 5x4-4- 7г/ = 0; 5) (Зх - 7г/)2 4- Зх - 2у - 24 = 0. 697. 1) 3; 2) 3; 3) /2; 4) “VTO. 699. 1) 2x4- У-5 = 0, 2х 4-^-1 = 0; 2) 2х-3#-1 =0, 2х - Зг/ 4- П =0; 3) 5х — у — 3 = 0, ох — у 4- 5 = 0. 700., 1) х —3^4-4-2 = 0; 2) Зх 4- 5</ 4- 7 = 0; 3) 4х - 2у - 9 = 0. 701. (х2 4- У2)2 -— 2с2(х2 — у2) = а* — с1. 702. (х2 + г/2)2 = 2а2 (х2-г/2); p2 = 2a2cos20. 703, p2 = Ssin20; (х2 4- У2)2 = 2Sxy. 705. р=-^9 и р = ~^-0. 706. (2г — х) у2 = х3.	707. х (а2 4- У2) = а3.	708. р = cos q~ ± Ь;
х2у2+(х+а)2 (х2-Ь2) = 0. 709. р = ±а tg 0; х2 [(х4-а)24-у2]=ау. 710. р = 2а cos 0 ± Ь\ (х2 4- У2 — 2ах)2 = Ъ2 (х2 4“ У2)- 711. р = а sin 201;
2_	2)	2
(х2 4- У2У = 4а2х2г/2.	712. x = acos3/; у = a sin3 (; х 4-у3=а3,
713. p = acos30; (х2 4- У2)2 = ах3. 714. х = a (cos t 4-1 sin /); у = a (sin t — t sin t).	715. x = a(f—sin/), у = a (1 — cos /);
x 4- У г/ (2a — г/) = a arccos •	716. x = a (2 cos t — cos 2/),
у = a (2 sin t — sin 2/); p = 2a (I — cos 6).	717. x = (a 4- b) cos t —
a b .	, , ,, . ,	. a 4- b , _. _	.	, ,
— a cos —-— /, у = (a 4- b) sin t — a sm —-— t. 718. x = (b—a) cos/4-. b — a .	\ x i b — a *
4- a cos —-— t, у = (b — a) sin / — a sin-------1.
8*
227
ЧАСТЬ ВТОРАЯ
720. 1) (4; 3; 0), (—3; 2; 0), точка С лежит па плоскости Оху, следовательно, ее проекция на эту Плоскость с ней совпадает, (0; 0; 0)* 2) (4; 0; 5), (—3; 0; 1), (2; 0; 0), точка D лежит на плоскости Oxz, следдвательцо, ее проекция на эту плоскость с ней совпадает; 3) (0; 3; 5), (0; 2; 1), (б; —3; 0), точка О лежит на плоскости Oyz, ее проекция на эту плоскость с ней совпадает; 4) (4; 0; 0), (—3; 0; Oh (2; 0; 0), (0; 0; 0); 5) (0; б; 0), (0; 2; 0), (0; -3; 0), (0; 0; 0); 6) (0; 0; 5), (0; 0; 1), (0; 0; 0), точка D лежит на оси апликат, следовательно, ее проекция на эту ось с ней совпадает. 721. 1) (2; 3; —1)’ (5; -3; -2), (-3; 2; 1), (а; Ь\ - а); 2) (2;	1), (5; 3; 2), (-3; -2; -1)
(а;	3) (-2‘ 3; 1), (-5; -3; 2), (3; 2; -1), (- а; й; с)
4) (2; -3; -I), (5; 3; -2), (-3; -2; 1), (а; - й; - с); 5) (-2; 3; -1), (_5; -3;-2), (3;2;1), (- а; Ь; с); 6) (-2;-3; 1), (-5; 3; 2), (3; -2; -I), (- а; - Ь‘, с); 7) (-2; -3; -1), (-5; 3; -2), (3; -2; 1), (— а-, — Ь',	г). 722. (а; й; — а), (а; — а; а), (—а; а', а), (— а; — а; а),
723. 1) В первом, третьем, пятом и седьмом; 2) во втором, четвертом, шестом и восьмом; 3) в первом, четвертом, шестом и седьмом; 4) Во втором, третьем, пятом и восьмом; 5) в первом, втором, седьмом и восьмом; 6) в третьем, четвертом, пятом и шестом. 724. 1) В первом, третьем, пятом и седьмом; 2) во втором, третьем, йятом и восьмом; 3) в первом, втором, седьмом и восьмом; 4) в первом, третьем, шестом и восьмом; 5) во втором, четвертом, пятом и седьмом. 725. 1) (—3; 3; 3); 2) (3; 3; —3); 3) (-3; 3; -3); 4) (-3; -3; -3); 5) (3; -3; -3). 726. 1) 7; 2) 13; 3) 5. 727. ОА = 6, ОВ = 14, ОС = 13, OD = 25. 730. MiM3M2 — тупой. 732. (5; 0; 0) и (-11; 0; 0). 733. (0; 2; 0). 734. С (3; -3; -3), 5 = 3. 735. (2; — I; — 1), (—1; —-2; 2), (0; 1;-2).	736. 7.	737.	х = 4, у = -1, 2 = 3.
738. С (6; 1; 19) и D (9; -5; 12). 739. D (9; -5; 6). 740. Четвертая вершина параллелограмма может совпадать с одной из точек: О\ (-3; 4; -4), D2 (1; -2; 8), D3 (5; 0; -4). 741. С (1; 5; 2), D (3; 2; 1), £(5; — 1; 0), 5(7; —4; —1). 742. А (-1; 2; 4), В (8; -4; -2). 743.4/74.
О
744. 4/ТО.	745. х = 2Е1+	*з.+ *4	= У1 + Уг + Уз +
4	zi	7 u
4
4
~ - г1 +?г.Н-£з + ?4 74fi . m\Xi + т2х2 + пг3х3 + т4х< 4	’	’	mi + т2 + т3 + т4 ’
= ^1У1 + т2у2 + т3у3 + m4y4 z __	+ т2г2 + т3г3 + /л124
у /И] 4- т2 4- т3 4- У?4	’	тх 4- т2 4- т3 4- т4
747. J2; -3; 0), (1; 0; 2К_(0; 3; 4).	748. | а | = 7.	749. z = ± 3.
759. АВ = {-4; 3;-1}, 5/1={4; -3; 1}. 751. N (4; 1; 1). 752. (—1; 2; 3). 753. JV = / 2*, У = 1, Z = -l.	754. cosa = 4L cos|3 = -A
25 r 5 16	3	4	12
cosy= ——.	755. cosa=—, cos₽ = —, cosy = —.
756. 1) Может; 2) не может; 3) может. 757. 1) Не может; 2) может; 3) не может. 758. 60° или 120°. 759. a = {l;— 1; /2} или a = {1; -1; -/2}. 760. Мх (/З; /3; /з), М2 (- /3; - /з; -
761. См. рис. 134.	762. | а — Ь | = 22. _ 763. | а 4- b | = 20.
764. |a4-&|==|e-‘6| = 13. 765. |а4-&|=/129 « 11,4, |a - й[ = 7.
766. | а 4- b | =/19 «в 4,4, |а — & | = 7.	767. 1) Векторы а и Ь
228
должны быть взаимно перпендикулярны; 2) угол между векторами а и b должен быть острым; 3) угол между векторами а и Ь должен быть тупым. 768. [ а | — | b |. 769. См. рис. 135. 774. |₽| = 15. 775. 1) {1; -И б}; 2) {5; -3; 6}; 3) {6; -4; 12}; 4) { 1; -у; о|;
г к »
5) {0; —2; 12); 6) < 3; —	2 >. 776. Вектор Ь длиннее вектора а
в три раза; они направлены в противоположные стороны.
Рис. 134.
777, а = 4 R = -l. 779. Вектор АВ в два раза длиннее вектора CD\ они направлены в одну сторону. 780, а° = | у; ~~у'> ””7'/’ 781. а° = {-Ь 4s “41}’ 782, 1а + 61=6, | а — & | = 14. 783. d = — 48i + 45/ — 36fc. 784. с = {-3; 15; 12}. 785. Ж={3; 4; -3}, BV = {0; -5; 3}, СР = {-3; 1; 0}. 787. а = 2р + 5</. 788. а = 26 + с, b——a — ~c, с = а — <2Ь. 789. р-=2а-3&. 790. АЙ + у я,
Л Л	л л
BN = у с — СР = ~ 6 — с, где М, N и Р — середины сторон треугольника АВС.____791. AD = 11 АВ — 7 AC, BD = 10ЛВ — 7 АС,
С® = 11ЛВ-8ЛС, AD + BD + CD = 32ЛВ - 22ДС. 793. с = 2р-2	1	1
—Зя+г. 794. rf = 2# — 36 + с, с — — 2<х+3&+<Z, Ь — -х- а.	-х- с— — d,
о	О	о
795. 1) -6; 2) 9; 3) 16; 4) 13; 5) —61; 6) 37; 7) 73.
796. 1) —62; 2) 162; 3) 373. 797. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. 798. — ab — ab,
229
когда векторы а и & коллинеарны и имеют противоположные па* правления; ab—ab, когда векторы'а и Ь коллинеарны и имеют одинаковые направления. 799. При условии, что Ь перпендикулярен к векторам а и с, и также в тбм случае, когда векторы а и с кол-
линеарны. 800. аЬ + Ьс 4- са — — ***.	801. аЬ 4- Ьс + са — — 13.
802. I р = 10. 803. а = ± 4. 804. | а | = | Ь |. 807. BD = с - Ь. о	с
2	!	4 \
808. а = arccos —809. ср = arccos I-----.
/7	\ -б/
Пендикулярная к оси вектора а и отсекающая
810. Плоскость, пер-на ней отрезок, ве-
личина которого, считая от точки А, равна	811. Прямая
Пересечения плоскостей, перпендикулярных к осям векторов а и Ь и отсекающих на этих осях отрезки, величины которых, считая от точки А, равны у-у и у|у, 812. 1) 22; 2) 6; 3) 7; 4) —200; б) 129; 6) 41. 813. 17. 814. 1)_-б24; 2) 13; 3)’ 3; 4) (АВ-АС)-ВС = ₽={-70; 70; -350} и АВ (АС • ВС) = {-78; 104; -312}.	815. 31.
5	/	4 \
816. 13. 818. а = —6. 819. со5ф=>-у. 820. 45°. 821. arccos — -g- .
823. л: = {-24; 32; 30}.	824. x ={ 1; у; — у }. 825. x = - 4i -
6/ 4- 12Л. 826. x = {-3; 3; 3}. 827. x = {2; -3; 0}. 828. x = 2i 4-Ч-3/-2Л. 829. /з. 830. —3. 831.-5. 832.6. 833.-4. 834. 5.
14	14	7
835. -11.	836. Z = --^, y==-J±, Z = -4.	837. 3.
о	о	3
R
838. - 6 у. 839. | [aft] j = 15. 840. j [aft] ] = 16.	841. aft = ± 30.
1) 24; 2)
60.	843. 1) 3; 2) 27; 3) 300.	844. Векторы а и ft
коллинеарны. 846. В случае перпендикулярности век-и ft. 850, 1) {5; 1; 7}; 2) {10; 2; 14};	3) {20; 4; 28}.
-4; -6}; 2) {-12; 8; 12}. 852. {2; И; 7}. 853. {-4; 3; 4}.
2	2	11	3
у, cosp =--cosy = 7z. 855. 28; cosa=—
о	1о	Ю	7
cosp — ——, cos у = —-. 856. /бб; cos a =—7=-, cosB =-7—.
7	7	/бб	/бб
842.
должны быть торов a 851. 1) {6;
854. 15; cos a =cos 6 =-------£=-, cosy =
3	15
cosy = —. 856. /бб; cos a = Д— > cos В 7	/бб '
7	5V17
cosy = —,	857. 14 кв. ед. 858. 5.	859. sin <р == _L__.
/66	21
860. {-6; -24; 8}.	861. m = {45; 24; p}.	862. x = {7; 5; 1},
864. [[aft]c]={-7; 14; -7}; fa [ftcj] = {10; 13; 19}. 865. 1) Правая; 2) левая; 3) левая; 4) правая; 5) Векторы компланарны; 6) левая. 866. abc — 24	867. dbc = ± 27; знак плюс в том случае, когда
тройка векторов a, ft, с правая, и Минус -* когда эта тройка левая. 868. В том случае, когда векторы a, ft, с взаимно перпендикулярны. 873. abc = — 7. 874. 1) Компланарны; 2) нй компланарны; 3) компланарны. 876. 3 куб. ед. 877. 11, 878.	(0; 8; 0), D2 (0; — 7;0)£
881. X = — 6, У — — 8, У = — 6, §82, Векторы а и с должны быть коллинеарны или декТор ft - должен быть перпендикулярен к векторам а и с, 885. Точки М1} M2t 'М4 лежат на Поверхности, точки
230
М3, М5, М6 не лежат на ней. Уравнение определяет сферу с центров в начале координат и радиусом, равным 7. 886. 1) (1; 2;2) и 1; 2; —2k 2) на данной поверхности нет та^ой точки; 3) (2; 1; 2) Й (2; —1; 2); 4) на данной поверхности нет такой-точки, 887. 1) Плоскость Oyz; 2) плоскость 0x2; 3) плоскость Оху; 4) плоскость, параллельная плоскости Oyz и лежащая в ближнем полупространстве на расстоянии двух единиц от нее; 5) плоскость, параллельная плоскости Oxz и лежащая в левом полупространстве на расстоянии двух единиц от нее; 6) плоскость, параллельная плоскости Оху и лежащая в нижнем полупространстве на расстоянии пяти единиц от нее; 7) сфера с центром в начале координат и радиусом, равным 5; 8) сфера с центром (2; —3; 5) и радиусом, равным 7; 9 уравнение определяет единственную точку — начало координат; 10) уравнение никакого геометрического образа в пространстве не определяет) 11) плоскость, которая делит пополам двугранный угол между плоскостями Oxz, Oyz и проходит в 1, 3, 5 и 7 октантах; 12) плоскость, которая делит пополам двугранный угол между плоскостями Оху, Oyz и проходит во 2, 3, 5 и 8 октантах; 13) плоскость, которая делит пополам двугранный угол между плоскостями Оху, Oxz н проходит в 1, 2, 7 и 8 октантах; 14) плоскости Oxz и Оуг; 15) плоскости Оху и Oyz; 16) плоскости Оху и Охг; 17) совокупность всех трех координатных плоскостей; 18) плоскость Оyz и плоскость, параллельная плоскости Oyz и лежащая в ближнем полупространстве на расстоянии четырех единиц от нее; 19) плоскость Oxz и плоскость, которая делит пополам двугранный угол между плоскостями Oxz, Oyz и проходит в 1, 3, 5 и 7 октантах; 20) плоскость Оху и плоскость, которая делит пополам двугранный угол между плоскостями Оху, Oxz и проходит в 3, 4, 5 и 6 октантах. 889. х24- t/24- z2—r2, 890. (x-0t)2 + (r/-p)2 + (2-Y)2 = r2. 891. у-3 = 0. 892. 2г-7 = 0. 893. 2x4- 3 = 0.	894. 20г/4-53 = 0.	895. х2 + у2 + г2 = а2.
896. х2 + г/2 + ^ = а2. 897 х + 2г=0. 898.	~ « 1.
У У 2-0
X2	И2	Z2
899. -гт- — ~ 4- -тх-= — 1.	900. Точки ЛГЬ М3 лежат на данной
1о	9	1b
линии; точки М2, М4 не лежат на ней. 901. Линии 1) и 3) проходят через начало координат. 902. 1) (3; 2; 6) и (3; —2; 6) (3; 2; 6) и (—3; 2; 6); 3) на данной линии нет такой точки. 903. 1) Ось апликат; 2) ось ординат; 3) ось абсцисс; 4) прямая, проходящая через точку. (2; 0; 0) параллельно оси Oz; 5) прямая, проходящая через точку. (—2; 3; 0) параллельно оси Oz; 6) прямая, проходящая через точку. (5; 0; —2) параллельно оси Оу; 7) прямая, проходящая через точку (0; —2; 5) параллельно оси Ох; 8) окружность, лежащая па плоскости Оху, с центром в начале координат и радиусом, равным 3; 9) окружность, лежащая на плоскости Oxz, с центром в начале координат и радиусом, равным 7; 10) окружность, лежащая на пло* скости Oyz, с центром в начале координат и радиусом, равным 5j 11) окружность, лежащая на плоскости z — 2 = 0, с центром в точке (0; 0; 2) и радиусом, равным 4. 904. х2 4- У2 4- z2 — 9, у — 0. 905. х2 4-г/2 +-г2 = 25, у 4- 2 = 0.	906. (х - 5)2 + (у 4- 2)2 4-
+ (2—1)2 = 169, х = 0. 907. х2 + у2 4- г2 = 36, (х— 1)2 + {У 4-2)24-4- (z- 2)2 = 25. 908. (2; 3; -6), (-2; 3; -6). 909. (1; 2; 2), (-1;2;2). 910, 1) Цилиндрическая поверхность с образующими, параллельными оси Оу, имеющая направляющей окружность, которая на плоскости Охг определяется уравнением х2 + z2 = 25; 2) цилиндри
231
ческая поверхность с образующими, параллельными оси Ох, имеющая направляющей эллипс, который на плоскости Oyz определяется ^2
уравнением + ттг = 1; 3) цилиндрическая поверхность с обра-25 1о
зующими, параллельными оси Oz, имеющая направляющей гиперболу, у2
которая на плоскости Оху определяется уравнением ------у= 1;
4) цилиндрическая поверхность с образующими, параллельными оси Оу, имеющая направляющей параболу, которая на плоскости Oxz определяется уравнением х2 — 6г; 5) цилиндрическая поверхность с образующими, параллельными оси Oz, имеющая направляющей пару прямых, которые на плоскости Оху определяются уравнениями х = 0, х — у = 0; эта цилиндрическая поверхность состоит из двух плоскостей; 6) цилиндрическая поверхность с образующими, параллельными оси Оу, имеющая направляющей пару прямых, которые на плоскости Oxz определяются уравнениями х — г = 0, х + г = 0; эта цилиндрическая поверхность состоит из двух плоскостей; 7) ось абсцисс; 8) уравнение никакого геометрического образа в пространстве не определяет; 9) цилиндрическая поверхность с образующими, параллельными оси Оу, имеющая направляющей окружность; направляющая на плоскости Oxz определяется уравнением х2 + (г—1)2=1; 10) цилиндрическая поверхность с образующими, параллельными оси Ох; направляющая на плоскости Oyz опреде-/ 1 \2 1
ляется уравнением у2 -J- 1г4-\ = ^~. 9U-О x2 + 5f/2—8#—12 = 0;
2) 4х2 + 5г2 + 4г - 60 = 0; 3) 2у - г — 2 = 0. 912. 1) 8х2 + 4г/2 — — 36х + 16у -3 = 0, г = 0; 2) 2х- 2г —7 = 0, у =0; 3) 4у2 + 8г2 + + 16г/ + 20г —31 =0, х = 0. 913. х —2^ + Зг + 3 = 0. 914. 5х — Зг=0. 115. 2х — у	—	z — 6	= 0. 916. х	— у —	Зг + 2 — 0. 917. х	+ 4у + 7г +
^-16 = 0.	919.	х — у — г = 0.	921. Зх + Зу	4-г — 8 = 0.
923. 1) п = {2;-1;-2}, п = {2А; - X; - 2А,}; 2) п = {1;5;-1), п = {X; 5А;	-	А}: 3)	п = {3; -2;	0}, п = {ЗА; - 2А; 0}; 4) п	= {0; 5; -3},
п = {0: 5Х;	-	ЗА};	5)л = {1;0;0},	п = {А; 0; 0}; 6)	л = {0,1,0},
,ч = {0; А; 0}, где А — любое число, не равное нулю. 924. 1) и 3) определяют параллельные плоскости. 925. 1) и 2) определяют перпенди-2
кулярные плоскости. 926. 1) 1 — 3, т = — 4; 2) I = 3, т ——
3) /=-3± m = - 1-L 927- 0 6: 2) -19> 3)-• 928- !) 4я
□	О	/о
2 ох 1	3	л ..	2	2
и—л; 2) — л и —л; 3) —; 4) arccos-r=- и л — arccos -т=-.
3	4	4	2	15	15
929/ 4х — Зу + 2г = 0. 930. 2х — Зг — 27 = 0. 931. 7х — у — 5г = 0. 932. х + 2г — 4 = 0. 934. 4х — у — 2г — 9 = 0. 936. х = 1, у = — 2, г = 2. 939. 1) аУ=7; 2) а =* 7, Ь = 3; 3) а = 7, &=И=3. 940. 1) г-3 = 0; 2) у 4-2 = 0;	3)	х + 5 = 0.	941.	1) 2у + г = 0;	2) Зх + г = 0;
3) 4х.+ Зу = 0.	942. 1) у + 4г+10 = 0;	2) х — г — 1 = 0;
3^ 5х + у - 13 = 0.	943. (12; 0; 0),	(0; -8; 0),	(0; 0; -6).
944, £. + -L +	= 1. 945. а = —4, b = 3, e = Jr. 946. 240 кв. ед.
О О	Z	4
947. 8 куб. ед. 948. -X- +	+ у = 1. 949. Х+|+* = I.
950. х + у + г + 5 = 0. 951. 2х — 21у + 2г + 88 = 0, 2х — Зу — 2г+ + 12 = 0. 952. х + у + г — 9 = 0, х — у—г +1=0, х—у + г—3=0,
232
х4-У““^"”5 = 0. 953. 2x — у — Зг — 15 — 0. 954. 2x—Зу + г—6=0. 955. х — Зу — 2г 4“ 2 = 0. 956. Плоскости 1), 4), 5), 7), 9), 11) и 12) 2	2	1
заданы нормальными уравнениями. 957. 1) -%-х-— у 4-гт 2—6=0;
ООО
Я 6	9	9 Ч A I I
2) -у-х + уу-уг-3 = 0;	3) ~х - у у -	- ^- = 0}
9911	^19	Q
4) 4х + ту-тг-4 = 0; 5) -	+ -£г-2 = 0; 6) 4-*-
О О О О	13	13	о
4	1
- Т-У - Т = °!	7) — у — 2 = 0;	8) х —5 = 0;	9) г-3=0;
о	о
Ю) 2-у = 0. 958. 1) а = 60°, 0 = 45°, у = 60°, р = 5; 2) а =120°, Р = 60°, у = 45°, р = 8; 3) а = 45°, 3 = 90°, у = 45°, р = 3/2} 4) а = 90°, ₽ = 135°, у =45°, р = /2‘; 5) а =150°, 3=120°, у = 90°, р = 5; 6) а = 90°, 3 = 90°, у = 0°, р = 2; 7) а = 180°, 3 = 90°, у = 90°, р = 1; 8) а = 90°, 3=180°, у = 90°, p=-U 9) а = arccos 4» Л	А	о
2	2	2
3 = л — arccos, y = arccos-x-, р = 2;	10) а = гс — arccos
О	О	/
3	6	4
3 = л— arccosy, у = arccog— , р = —.	959. 1) б = — 3, rf = 3j
2) 6=1, d=l; 3) 6 = 0, d = 0 —точка Мз лежит на плоскости} 4) б = - 2, d = 2; 5) б = - 3, d = 3. 960. d = 4. 961. 1) По одну сторону; 2) по одну сторону; 3) по разные стороны; 4) по одну сто» рону; 5) по разные стороны; 6) по разные стороны. 964. 1) d=*2\ г;
2) d = 3,5; 3) rf = 6,5; 4) d= 1; 5) rf = 0,5; 6) rf = y. 965. 8 куб. ед. 966. Условию задачи удовлетворяют две точки: (0; 7; 0) и (0; —5; 0). 967. Условию задачи удовлетворяют две точки: (0; 0; —2) и 10; 0;
4 \
—6— .	968. Условию задачи удовлетворяют две точки: (2; 0; 0)
1 о /
и 0; о). 969. 4х — 4у — 2z + 15 = 0. 970. 6х 4-Зу4-2г 4- 11=0.
971. 2х — 2у — z — 18 = 0, 2х — 2у — z + 12 = 0.	972. 1) 4х — у --
- 2г — 4 = 0; 2) Зх + 2у - z + 1 = 0; 3) 20х - 12у + 4г + 13 = 0. 973. 1) 4х — 5у + г — 2 = 0, 2х + у — Зг + 8 = 0; 2) х — Зу — 1 = 0, Зх + У — 2г — 1 = 0; 3) Зх — бу 4~ lz 4- 2 = 0, х + 4у 4- Зг + 4 = 0. 974. 1) Точка М и начало координат лежат в смежных углах; 2) точка М и начало координат лежат в одном углу; 3) точка М и начало координат лежат в вертикальных углах. 975. 1) Точки М и N расположены в смежных углах; 2) точки М и N расположены' в вертикальных углах. 976. Начало координат лежит внутри острого угла. 977. Точка М лежит внутри тупого угла. 978. 8х—4у—4.г4-5=0. 979. 23х — у — 4г — 24 = 0. 980. х — у — г—1 = 0. 981. х4-у4-2г=0. 982. 5х - 7у - 3 = 0, г = 0; 5х 4- 2г - 3 = 0, у = 0; 7у-2г 4-3 = 0, х= 0.	983. Зх-у-7г 4-9 = 0 5у 4-2г = 0.	984. (2;—1; 0),
(1 4; 0;	(°; 2; -1).	986. 1) D = - 4; 2) D = 9; 3) D = 3.
\ О	о J
987. 1) Л1 = А2 = 0, и хотя бы одно из чисел Dlt D2 отлично от нуля; 2)	= В2 = 0, и хотя бы одно из чисел D2 отлично от
233
нуля; 3) C1 = C2i= 0, и хотя бы одно из чисел D{. D? отлично от нуля. 988. 1) "д~ —2)	~ГГ~’еГ'’ 4) 71 ’*’
J	/12	Z>2	£>2	*-^2	^2	^2
— D, = 0, Ло — D% — 0; 5) 5, = Dy — 0, 52 = 52 = 0; 6) Cj = 51—0, С, = О2 = °'	989. О 2х + 15у + 7г + 7 = 0; 2) 9у + 3z + 5 = 0;
3) Зх + 3z - 2 = 0; 4) Зх - 9у - 7 = 0. 990. 1) 23х-2у+21г-33=0; 2\ у + г _ 18 = 0; 3) х + z - 3 = 0; 4) 4) х - у + 15 = 0. 991. 5х + _|_ 52 — 8 = 0.	992. а (5х — 2у — г — 3) + 0 (х + Зу — 2г + 5) = О,
Указание. Прямая пересечения плоскостей 5х — 2у — г — 3 = 0, х 3^ — 2г 4-5 = 0 параллельна вектору Z = {7;9;27); следовательно, условию задачи будут удовлетворять все плоскости, при* надлежащие пучку плоскостей, проходящих через эту прямую, 993. 11х — 2у — 15г — 3 = 0. 994. а (5* — у — 2г — 3) + р (Зх — 2у— _ 5^ + 2) = 0. Указание. Прямая пересечения плоскостей 5х — у — 2г — 3 = 0. Зх — 2у — 5г + 2 = 0 перпендикулярна к плоскости х + 19у — 7г — 11 = 3; следовательно, условию задачи будут удовлетворять все плоскости, принадлежащие пучку плоскостей, проходящих через эту прямую. 995. 9х + 7у 4- 8z 4- 7 = 0. 996. х — 2у 4- z — 2 = 0, х — 5у + 4г — 20 = 0.	997. Принадлежит.
998. Не принадлежит. ’999. / = —5, т = — 11.	1000. Зх — 2у +
+ 6г+21=0, 189х + 28у + 48г — 591 =0. 1001. 2х - Зу - 6г + + 19 = 0, 6х — 2у — Зг + 18 = 0.	1002. 4х — Зу + 6г — 12 = О,
12х — 49у 4- 38г 4- 84 = 0.	1003. 4х + Зу — 5 = 0, 5х 4- Зг — 7 — 0.
1004. 7х — у + 1 = 0, г = 0; 5х — г — 1=0, у = 0; 5у — 7х — 12=0, х = 0. 1005. х —8у + 5г- 3 = 0.	1006.	2х	-	4у	-	8г	+	1 = О,
,	. п	.ч х — 2 у г + 3 х — 2
2х —у+г— 1 =0.	1007. 1)—g—=ТГз" = —5—> 2) —§— =
у г + 3 х —2 у г + 3, = у- _1 ,	3)	!	-	-
х — 2 у _ г + 3
0	~ 0 I
х — 3 у + 1  г
.х-2_у_г+3
0 “	0 ’	’	0	“ 1	0 ’
1008. 1) л+-_^±2. = +±| X у + 2 _ г — 3	X + 1
3	0	—2!	}	1
х = 2/ + 1, у = — 3/ — 1, г = 4/ — 3;
= —3; 3) x = 3f+l, у = — 41— 1, 2/+ 1, г = /+ I; 2) х = /+3, ~	' ЮН. (9;-4; 0),
1012. х = 5^ + 4, у = -11/-7, г = -2. "Ь 1014 —~ - ___ У * _ 2 + 3
1	-3 “ -8 •	6	-1 ~	7 ’
х = 3/ + 3, у =151+1, г=19/-3.	1016. а = {1;1;3}1
— любое число, не равное нулю. 1017. а = — 21 + 22J + 1IX/ + ZA, где Л — любое число, не равное х-2	у-3  г + 5 iniQ 1Ч х-2	у+1 г
3)
3 ’
1009. 1) 1» г =
-3.' 10107 1) х = 1 + 2, у
t — 1, г = t\ 3) х = 0, у = t, 2 = — 3t + 1.
-2), (0; 2; —3).	'
v — 1  У — 2
2	— 1
у — 2 г + 4
“0	0
2) х = 2^ + 1, у = 4t — 1
Z = 5t
U — —
(3; 0; -
1313. -
1015. .	. . „
а = {Л; Л: ЗЛ}, где Л + 11/ + 5й; а — — !
пулю. 1018. +^-=+4 =+f-. 1019. 1)-5---у-=т.
Решение. Полагая, например, г0 = 0, находим из данной системы: х0 = 2, Уо = — 1; таким образом, мы уже знаем одну точку прямой: Л10(2; —1; 0). Теперь найдем направляющий вектор. Имеем гч={1;—2;3}, п2 = {3; 2; —5); отсюда а = [П1П2] = {4; 14; 8}, т. е. / — 4, т = 14, п = 8. Подставляя найденные значения х0, у0, г0 и
X — Хо У — Уо 2 — 2п
I, т, т в равенства —-г—2- =	- =——получим канони-
231
L J, „ X — 2 у 4- 1	2	X—2
ческие уравнения данной прямой: —-— =  —£~ = у или ——— =
У + 1 _ 2 .	* у + 1г — 1_ х — 3 _ у-2' z
7	4 ’ Z *- 5 = 12	13 ’	1	2	1 ’
1020. 1) х = t + 1, у — — 7i, z = — 19/ — 3; 2) х = — t + 1, у=3/+2, 4
z=5/- 1. 1023.60°. 1024. 135°. 1025. cos ср = ±	1027. 1 = 3.
1029. A±L==^z2 = ±±2. юзо. =
1031. х = 2/ —5, у = — 3/ + 1, « = — 4/. 1032. v = 13. 1033. rf = 21. 1034. х = 3 — 6/, у = — 1 + 18/, г = — 5 + 9/.	1035. х = - 7 + 4/,
у = 12 - 4/, 2 = 5 — 2/. 1036. х=20—6/, у = - 18+8/, z=— 32+24/; (2; 6; 40).	1037. Уравнения движения точки М: х— — 5 + 6/,
у = 4— 12/, z = — 5 + 4/; уравнения движения точки М х=—5+4/, у = 16 — 12/, г = — 6 + 3/; 1) Р (7; —20; 3); 2) за промежуток вре-мени, равный 2; 3) за промежуток времени, равный 3; 4) Л10Р = 28, ДГ0Р = 39.	1040. 1) (2; —3; 6); 2) прямая, параллельная плоскости;
х ~ 2 у + 4 г + 1
8 прямая лежит на плоскости. 1041. —-— =	i,
2	5	3
1042.	=	Ю43. 2х — Зу + 4г — 1 =0.
6	— 3	— 5
1044. х + 2у + Зг = 0. 1045. т = — 3. 1046. С = — 2. 1047. А = 3, 1	3
7) = — 23.	1048. А = -3, 5 = 4-^.	1049. / = - 6, С = ^-.
1050. (3; —2; 4). Решение. Искомую точку найдем, решая совместно уравнения данной прямой с уравнением плоскости, проведенной из точки Р перпендикулярно к этой прямой. Прежде всего заметим, что направляющий вектор данной прямой {3; 5; 2} будет являться нормальным вектором искомой плоскости. Уравнение плоскости, которая проходит через точку Р (2; — 1; 3) и имеет нормальный вектор л = {3;5;2), будет иметь вид 3 (х — 2) + 5 {у + 1) + + 2 (г — 3) = 0 или Зх + 5у + 2г — 7 = 0. Решая совместно уравнения х = 3/, у = 5/ — 7, z = 2/ + 2, Зх + 5у + 2г — 7 = 0, найдем координаты искомой проекции: х=3, у = —2, г=4. 1051. Q (2; — 3;2). 1052. Q (4; 1; —3).	1053. (1; 4; — 7). Решение. Искомую точку
найдем, решая совместно уравнение данной плоскости с уравнениями прямой, проведенной' из точки Р перпендикулярно к этой плоскости. Прежде всего заметим, что нормальный вектор данной плоскости {2; —1; 3} будет являться направляющим вектором искомой прямой. Параметрические уравнения прямой, которая проходит через точку Р (5; 2; —1) и имеет направляющий вектор а = {2; —1; 3}, будут иметь вид х = 2/ + 5, у = — / + 2, г = 3/ — 1. Решая совместно уравнения 2х — у + Зг + 23 = 0, х = 2/ + 5, у = — / + 2, 2 = 3/—1, найдем координаты искомой проекции: х = 1, у = 4, 2 = — 7. 1054. Q (—5; 1; 0). 1055. Р (3; —4; 0). Указание. Задача может быть решена по следующей схеме: 1) устанавливаем, что точки А и В расположены по одну сторону от плоскости Оху; 2) паходим точку, симметричную одной из данных точек относительно плоскости Оху, например точку Вь симметричную точке В; 3) составляем уравнение прямой, проходящей через точки А и В^; 4 решая совместно найденные уравнения прямой с уравнением Плоскости Оху, получим координаты искомой точки. 1056. Р (—2; 0;3). 1057, Р (—2; —2; 5). 1058, Р (-1; 3; -2). 1059. 1) Р (-25; 16; 4);
2) за промежуток времени, равный 5; 3) МоР = 6О. 1060. ^«28—7,56 У = - 30 + 8t, 2= -27 + 6/; 1) Р(-2;2;-3); 2) от /, =0 до /2= 41 3) м0Р =я 50. 1061. За промежуток времени, равный 3, 1062. d = 7. 	п	чх + Зу + 2	2 — 8
Р е ш е и и е. Выберем на прямой —— = "2—   какУю'
нибудь точку, например Mi (—3; —2; 8); будем считать, что направляющий Вектор прямой а = {3; 2;—2} приложен в точке Модуль векторного произведения векторов $ и М.Р определит площадь йараллелограмма, построенного на $тнх векторах; высота этого параллелограмма, проведенная из верщинь) Р, будет являться искомым расстоянием d. Следовательно, для вычисления расстоя-
...	| ГалТТр] | „ п
ния а имеем формулу d = -!-!—:—т-2-1-. Теперь вычислим координаты ____________	Iа ।	____
вектора МгР, зная координаты его конца и начала: М\Р = {4; 1; —10}.
Найдем векторное произведение векторов а и М^Р: [аМ1Р} =»
I j k
3 2 —2	= — 18t + 22/ — 5fe. Определим его модуль:
4 1 -10_______________________
| [q/ИiP] [ = /182 + 222 + 52 == /833 = 7/17. Вычислим модуль вектора <?: |а|=/9 + 4 + 4 «/17. Найдем искомое расстояние: d= 4^-==7. 1063. 1) 21; 2) 6; 3) 15. 1064. d=25. 1065. 9х + 1 \у + + 5г-16 = 0. 1068. 4х + бу + 5г—1 = 0. 1070. 2х-16у- 13г + 31 = 0. 1072. 6х —20у — 11г + 1 =0. 1074. (2; -3; -б). 1075. Q (1; -2; 2). 1076. Q(l;-6; 3). 1077. 13х - 14у + 11г + 51 « 0. 1079. X — 8у --13г+ 9 = 0. 1081.	= £±±,	1082. х = 8/- 3,
о —о у
М = -3/-1, г = - 4/ + 2. 1083. 1) 13; 2) 3; 3) 7. 1084. 1) х2 + + у2 + 22 = 81; 2) (х — 5)2 + (у + З)2 + (г — 7)2 = 4; 3) (х - 4)2 + + (у + 4)2 + (г + 2)2 = 36;	4)	(х - З)2 + (у + 2)2 + (г - I)2 = 18;
5) (х—З)2 + (у + I)2 + (г—I)2 = 21; 6) х2 + у2 + г2 = 9; 7) (х-З)2 + + (у + 5)2 + (г + 2)2 = 56;	8)	(х - I)2 + (у + 2)2 + (г - З)2 = 49;
9) (х + 2)2 + (у - 4)2 + (г - 5)2 = 81.	1085. (х - 2)2 + (у - З)2 +
+ (г+1)2 = 9 и х2 + (у + I)2 + (г + 5)2 = 9.	1086. Р = 5.
1087. (х + I)2 + (у - З)2 + (г - З)2 = 1-. 1088. (х + I)2 + (у - 2)2 + + (г- 1)2 = 49.	1089. (х - 2)2 + (у - З)2 + (г + I)2 = 289.
1090. 1) С (3; —2; 5), г = 4; 2) С(—1; 3; 0), г = 3; 3) С (2; 1; -1), г = 5; 4) С (0; 0; 3), г = 3; 5) С (0; -10; 0), г = 10. 1091. х=5/- 1, 1	.3	,1
%	2	2	' ~	2
у = — / + 3, г — 2t — 0,5.	1092. —„—=---------д-=------А—.
»	1 ’	2	— 3	4
1093. 1) Вне сферы; 2) и 5) на поверхности сферы; 3) и 4) внутри сферы. 1094. а) 5; б) 21; в) 7. 1095. 1) Плоскость пересекает сферу; 2) плоскость касается сферы; 3) плоскость проходит вне сферы. 1096. 1) Прямая пересекает сферу; 2) прямая проходит вне сферы; 3) прямая касается сферы.	1097, Мг (— 2; — 2; 7), d = 3.
1098. С (-1; 2; 3), £=8. 1099. (х — Г)2 + (у — 2)2 + (г — I)2 = 36, 2х - г - 1 = 0. 1100. (х - I)2 + (у + I)2 + (г + 2)2 = 65, 18х-22у + + 5г - 30 = 0.	1101. (х - 2)2 + у2 + (г - З)2 = 27, х + у - 2 = 0
1103. 5х — 8у + 5г-7 = 0. 1104. х2 + у2 + г2 - 10х + 15у-25г = 0
236
1105. X24"#54-’*64-1 Зх 4* 9//** — 14 = 0. 1106. хг4-(// + 2)2+’г2 = 41. 1107. 6х-3^2г^49«О.	1108. (2; -6; 3).	1109. a=±6.
1110, 2x — U — г4~5«=±0. 1111. Xix4-*/iI/ + z{z = r2. 1112.42£24-। B2^2 + ^2==n2i	1113. (Xi-a)(.r~a)4-(z/1-p)(f/_p) +
4. (2 — у) (г — Y) “= r2.	1114. 3x — 2y + 6s— 11 = 0, 6x4-3z/4-
12z-30 = 0.	1П5. X 4-2z/— 2г — 9 = 0, x + 2z/ - 2z + 9 = 0.
1116. 4x4-32—40 = 0, 4x4-3г 4- 10 = 0. 1117. 4x + By 4- 5г-103 = 0, 4X j_ 6z + 5z + 205 = 0.	1118. 2x — By 4- 4z — 10 = 0, 3x — 4/4-
4- 2г — 10 = 0. 1120. x — z/ —z—2 = 0. 1122. Ax 4- By 4- Cz 4- D = 0. 1123. x cos a 4~ У cos0 4“ г cos у — p = 0.	1124, ^ = 1^71° — p\>
d = | X] cos a 4- У\ cos ₽ 4- Si cos у — p |. ‘ 1125. (r2 — rj (r — n) = 0; (x2 — xi) (x — xj) 4- (z/2 — у{) (у — У1) 4- (z2 — Si) (г — z{) = 0.
x — x0 у — Уо z — г0
1126. afa2 (r — ro) = 0;
h h
nx — 0. 1127. (r2 —rJX
ш2 zt2
x (>*з — n)(r - ri) = °;
1128. П1«2 (r — r0) =0;
x — x0
Ai
A2
	X — Xi у	— ух г —Zj	
	х2 — Xi у2	— У\ z2 — zi	= 0.
	х3 — Xi уг	— Уг г3 — Zi	
У -	-Уо Z — Zp		
В1	С,		= 0. 1131. ~	_£о =
в2 с2			
^L£2==±—2". 1132. [(r-ri)(r2-rI)] = 0, [r(r2-r1)] = [r1r2J,
1133. a (r — rj — 0; I (x — x^ 4- m (y — z/J 4-1134. a2 (r — r0) = 0.	1135. n,n2 (r — r0) = 0.
^ = U» = £Z^. 1137. r = r0+
m n
r = r{ 4- (r2 — ri) t. 4-я (2 — 24=0.
1136. г = го 4- nt> —д--
У Уо z —
X — Xq Bl c, B2 C2
.Cl A.
C 2 A2
Ai BL ’
A2 B2
C
1138. ron 4- D = 0, an = 0;
Лх0 4- Вуо 4~ Сг0 4- В — О, А1 4- Вт 4- Сп = 0. 1139. aYa2 (г — г0) = 0. 1140. а^г (r2 — ri) = 0.
__ Ахр 4~ Вуд 4~ Сг0 4~ В , А1 4- Вт 4- Сп ’ Лхо 4~ Вур 4- Сг0 4~ D г~г() А1 + Вт + Сп
Axj 4~ Byt 4- Cz\ 4- D .	_
А2 4- В2 4- С2 ’ У~У1
Axi 4“ Br/i 4- Czi 4~ D
А2 + В2 + С2
X = Xi
z = Zi
11Л1	*,0»4-Р
1141.	г0-----—— а;	х — х0 —
ап
Ахр 4~ Вур 4~ Czp 4~ В
Al + Вт + Сп т>
1142.	„-Z!i+£-n; п2
Axi 4- Ву\ 4- Сг1 + В п дг 4- В2 4- С2
1143.	,о + <11^! а-, а£
У — Уо
n.
..	.. , (xi - х0) I 4- (z/i — Уо) т 4- («i — z0) п ,	..	. ,
Х-Хо4-	/2 + т2 + П2----------У = Уо +
. (Х1 -.Хо) / + (^1 — Уо) m4-(zi TZ0)n _
+	гг+и! + ^-----------^т’	г~г° +
, ( Г1 — Хо) I + (у, — Уо) m + (г; г. z„) п Щ4, а ~	.
I2 4- т2 4- п2	Vа2
2В7
У1 — Уо Z1 — з0 т	п	4-	г, — г0 Xj — хо п	2 4-	Х1— Хо У1 — Уо 1	т
Vl2 4-	4- И2			Л ^2 Л-’s ““ Xj	
1
абс. вел.
«1 гп2 у2 — уг
1145 d= I«1«i('-2-=£1LL	, (1-			П1 «2	22 Т ?1.
И«1«2]2	Шу Л]	2 - Z1 4-	2 I Hi 2 4“ <
	т2 п2	Л2 «2	1 «2 tn2
R	R		Rl
			
1 а |	1 а |	х Кв	4- т2 4* п2 ’
		Rn	
VI2 + т2 4- Л2	Л]	К в 4- W2	4- л2
х — — ..	у	Rm		Rn
К/2 4* 4- п2	VI2 4- т2 4- я2 *	1		//2	^2_|_П2*
1148. Го + у^та и г0--Д-а; Xi = х0 4-гт===, Уi = Уо 4-I й I	I а I	У /2 т2 Ц_ п2
I ,. -Rn	-	₽Л	И х, = х„-
К В + т2 + пг	VI2 4- гп2 + «2
Rl	Rm	Rn
КВ4-т24-л2	//2 + /n2 + n2 VI2 + т2-у п2‘
1149.	(Г1-г0)(г-г0) = ^.	1150.	(r-r^^t-^2;
(х - X])2 4- (у - У1)2 4- (г — Z])2 =
1151. J1L—/^='0,	^4.^ = 0;
(Лх, 4- By, + CZl + В)2
Л2 4- В2 4- С2
Ах + By + Cz /-• .." — • •— — д = и,
1152.
я = о,
/? = 0,
Лх4-Ву4-Сг_ . p__Q
Кл24-В24-С2	’	, ,
а (г — Го) , „ _ п, / (х — х0) 4- лг (у — уо) + л (г - z0)
| а |	’	К/2 + т2 + П2
I (х — х0) ч- m (у — у£ 4- п (г — Zq) 0> л 153 3( з; (2; з; о), /г2 4- т24-«2
(2; — 3; 0), (2; 0; КЗ), (2; 0; -Кз). 1154. 4,3; (4; 0; - 1), (—4; 0; —1). 1155. 15; ^0; —6;—j-j. 1156. Уравнения проекции а) на плоскость Оху: f х2+4ху4-5у2—х=0, б) на плос-
(	z—0",
кость Oxz: (х2 — 2xz4-5z2 — 4х = 0, в) на плоскость Oyz: (	у = 0;
j у2 г2 _|_ 2у — z — 0, 1157. Эллипс; (2; — 1; 1) —центр этого (	х = 0.
эллипса. Указание. Центр сечения проектируется в центр проекции. 1158. Гипербола; (1; —1; —2) — центр этой гиперболы. 1159. 1) Эллипс; (—3/2; I; 13/4) — центр этого эллипса; 2) пара-
238
бола: не имеет центра; 3) гипербола; (2; —3; —4) — центр этой (гиперболы. 1160. а) 1 < | т | < V 2; б) | т. |< 1. 1161. а) г?г=/=0 и т > — 1/4, причем в случае т — — 1/4 — вырожденный эллипс — точка; б) т = 0. 1162. (9; 5; -2). 1163. (3; 0; —10). 1164. (6; -2; 2). 1165. т = ±18. 1166. 2х — у — 2г — 4 = 0. 1167. х — 2у 4* 2г — 1 = 0, 9	X2 7/2 J- г2 '	у2 ,,2
х — 2//+ 2г + 1 =0; f. 1168. -5- +	_ 1. И69. ^- + ^ +
О	□	ZiO	ои ю
1 %2	।	2	4	%2 у2 4-г2 .
+ 9—1.	1170. q{— 5, ?2— 5 • Н72. а2 4	-	— 1.
1173.	+2-у2 - -^- = 1. Ц78. —--^- = 2г 1180. 1) (3; 4; -2)
а2 с2	р q
и (6; —2; 2); 2) (4; —3; 2) — прямая касается поверхности; 3) прямая и. поверхность не имеют общих точек; 4) прямая лежит на поверхности. 1181. J 2х — 12г/ — г 4* 16 = 0, f 2х — 12г/ — г 4- 16 = 0, ( х — 2г/4-4 = 0; ( х + 2у — 8 = 0-
11 во	fy+2z — 0, f2x —5г = 0,	х , I г — I
н8г- b-5=0; l г/+4 = 0.	U83‘ T----Г~ ~=T’
х . г/ 4- 9 г 4- 3	11R4 х у — 3 г х —2_ у__ _z_
1 ” 12 ~	2	’	1 =	0	” -2’	0	3-4’
1185. arccos . 1186. 1) — 4-	= 0; 2)
у2	о»2	ij2
3’--^ + ^ + -?=0- 1188. х’ + у’-гг = 0. 1189. -jr + ф--
-	— = 0. 1190. Зх2 — air + 7гг — бет + 1О.гг - 2»г-4х +-!//-
X2 У2 «»2
_ 4г 4-4 = 0. 1191. ±. + ^--=-0. 1192. х2 - Зу2 4- г2>= 0. 1193.	35х2 4“ 35г/2 — 52г2 — 232хг/ — 116хг 4-116уг 4- 232х — 70г/ —
— 116г 4- 35 = 0. 1194. хг/4-хг 4-1/z == 0 — ось конуса проходит в первом и седьмом октантах; ху 4* хг — yz = 0 — ось конуса проходит во втором и восьмом октантах; хг/ — хг — г/г = 0 — ось конуса проходит в третьем и пятом октантах; ху — хг 4- yz — 0 — ось конуса проходит в четвертом и шестом октантах. 1195. 9х2— 16г/2— 16г2 — -90x4-225 = 0.	1196. х2 4-4г/2 — 4г2 4-4хг/4-12хг — 6г/г = 0.
1197. 4х2 — 15г/2 — 6г2 — 12хг — 36х 4-24г 4-66 = 0. 1198. 16х24-4- 16г/2 4- 13г2 - 16хг 4- 24г/г 4- 16х - 24^ - 26г - 1$1 = 0.1199. х2 — — у2 — 2хг 4- 2yz 4- х 4- </ — 2г = 0. 1200. 5х2 4- 5г/2 4" 2г2 — 2ху 4* 4- 4хг 4- 4г/г — 6 = 0.	1201. 5х2 4- 8г/2 4- 5г2 4- 4хг/ 4- 8хг — 4г/г 4*
4- 6х 4- 24^ - 6г - 63 = 0. 1202. 5х2 4- Юг/2 4- 13г2 4- 12хг/ - бхг 4* 4- 4г/г 4- 26х 4- 20г/ - 38г 4- 3 = 0.	1203.	х2 4- 4г/2 4- 5г2 - 4хг/ —
- 125 = 0. 1204. 1) 18; 2) 10; 3) 0; 4) —50; 5) 0; 6) х, - хв 7) 0; 8) 1. 1205. 1)х= 12; 2) х = 2; 3) х, = — 1, х2 = -4; 4) хх = -1/6, хг = 3/2; 5) хЬ2 = ±2г; 6) Xj=2, х2,3 = —2±г; 7) х = (—1)"^4-
4- ~2 п> Где я —целое число; 8) х = я (2/г 4-1)/6, где п —любое целое число. 1206. 1) х>3; 2) х>—10; 3) х<—3; 4) — 1<х<7, 1207. 1) х=16, у = 7; 2) х = 2, г/ = 3; 3) система не имеет решений; 4) система имеет бесконечно много различных решений, каж-л	л.	Х — 1
дое из которых может быть вычислено по формуле у = —у=-
239
где численные значения х задаются произвольно и вычисляются ac+bd be —ad соответствующие значения у, 5) х =	, у = --2	;
6) система не имеет решений. 1208. 1) а Ф — 2; 2) а — — 2, 6^2; 3)й = -2, Ь = 2. 1209. а = 10/13. 1210. I) х = —2/, у =7/, Z = 4£ 2) x — 2t, y — 3t, z — 0; 3) х — 0, y — tt z = 3t; 4) x — Q, y — t, z — 2t\ 5) x — 2t, y — 5t, z=4t; 6) x = 4t, y = 2t, z — 3t\ 7) x = t, y — 5l, z=llf; 8) x — 3t, y — 4t, z=ll/; 9) x — 0, y — t, z = 3t; 10) x — (a 4- 1) t, у ~ (1 — a2) t, z — — (a+l)t при условии, что
— I (если a — —1, то любое решение системы состоит из трек чисел х, у, z, где х, у — какие угодно, a z = х — у); 11) х = (6 — 6) t, у = (За — 2) t, z — (ab — 4)t при условии, что а =# 2/3 или 6 =£6 1если а — 2/3 и &=6, то х, у произвольны, a z = -x-\-2yy, 12) х — 3 (1 — 2а) t, у — (ab + 1) t, z — 3 (b 4- 2) t при условии, что а =^= 1 /2 или b =?= — 2 (если а = 1/2 и b = —2, то х, у произвольны, а г = 2(3у —х)). 1211. —12. 1212. 29. 1213. 87. 1214. 0. 1215. -29. 1216. 2а3. 1223. —4. 1224. 180. 1225.87. 1226.0. 1227. (х-у) (y-z) X X (г —х). 1229. 2а2Ь. 1230. sin 2а. 1231. xyz (х — у) (у — г) (г — х). 1232. (а + b 4- а) (а2 4- Ь2 + с2 — ab — ас — be). 1234. 1) х = — 3; 2) Xi = -10, х2 = 2. 1235. 1) х>7/2;2) -6<х<-4. 1236. х = 24у, у = 21 у, г= 10. 1237. х = 1, у = 1, г = 1. 1238. х = 2, г/== 3, г = 4. 1239. х=1, у = 3, г = 5. 1240. х=13-^-, у — 8~, г =14-^-. 1241. х = 2, у — — 1, z — 1. 1242. х = - ^~ С , у = — z =	.
1243. х== - у = — у-- , г = —у— • 1244. Система имеет бесконечно много решений, каждое4,из которых может быть вычислено по формулам x — 2z— 1, у = 2+ 1, где численные значения z задаются произвольно и вычисляются соответствующие значения х, у. 1245. Система не имеет решений. 1246. Система не имеет решений. 1247. I) а #= — 3; 2) а — —3, b 1/3; 3) -а = —3, Ь = 1/3. 1249. Система имеет единственное решение: х — у = z — 0. 1250. Система имеет бесконечно много решений, каждое из которых может быть вычислено по формулам х — 2t, у = —3t, z = 5/, где численные значения t задаются произвольно и вычисляются соответствующие значения х, у, Z. 1251. а = 5. 1252. 30. 1253. —20. 1254. 0. 1255. 48. 1256. 1800. 1257. (& + с + d) (b - с - d) (b - с + d) (Ь + с - d). 1258. (а 4- b + с 4- d) (а + b — с — d) (а — b + с — d) (а — Ь — с + d). 1259. (а + b 4- с + d) (а - b 4- с - d) [(а - с)24- (& - d)2]. 1260. (be-cd)2.