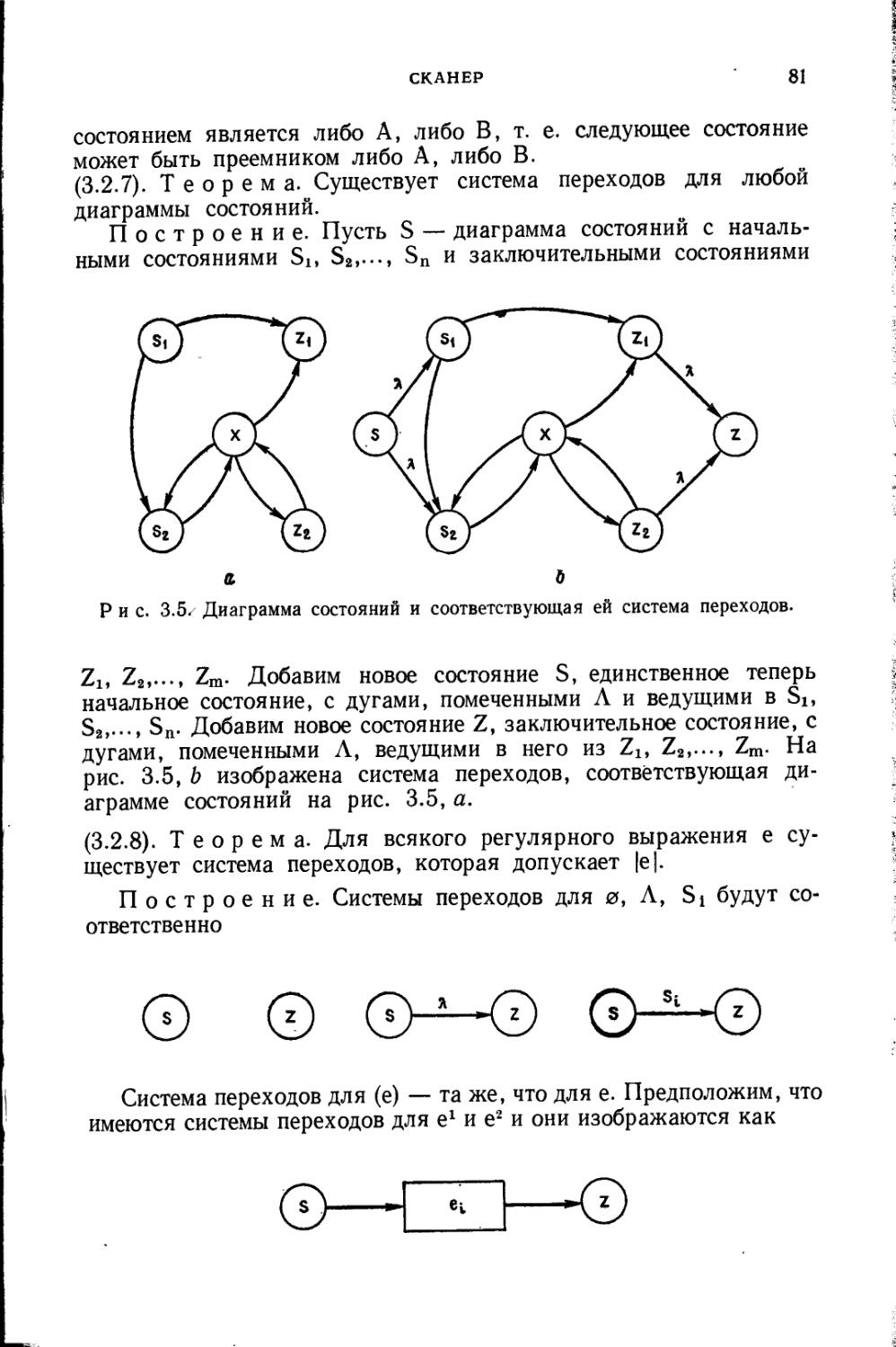
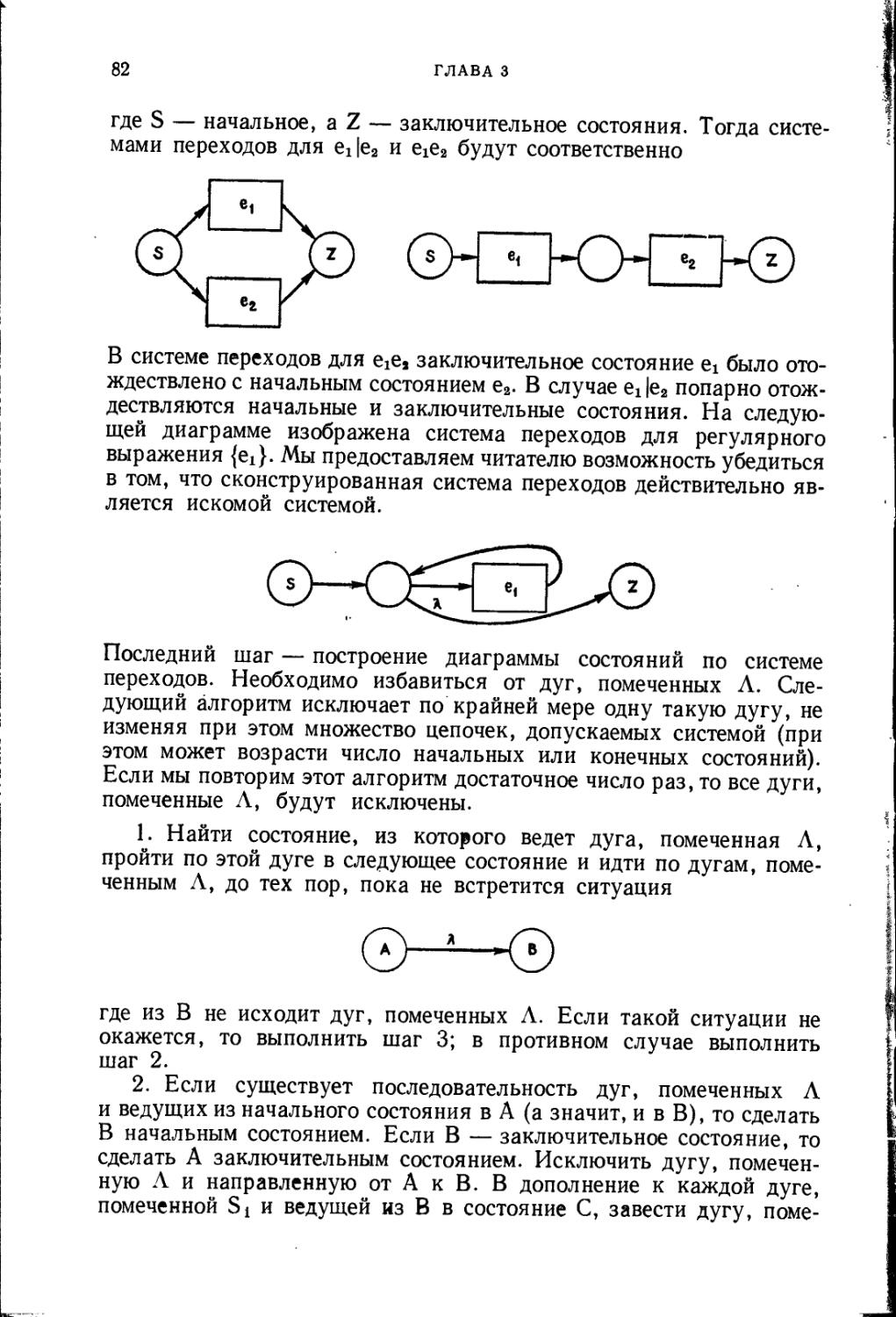
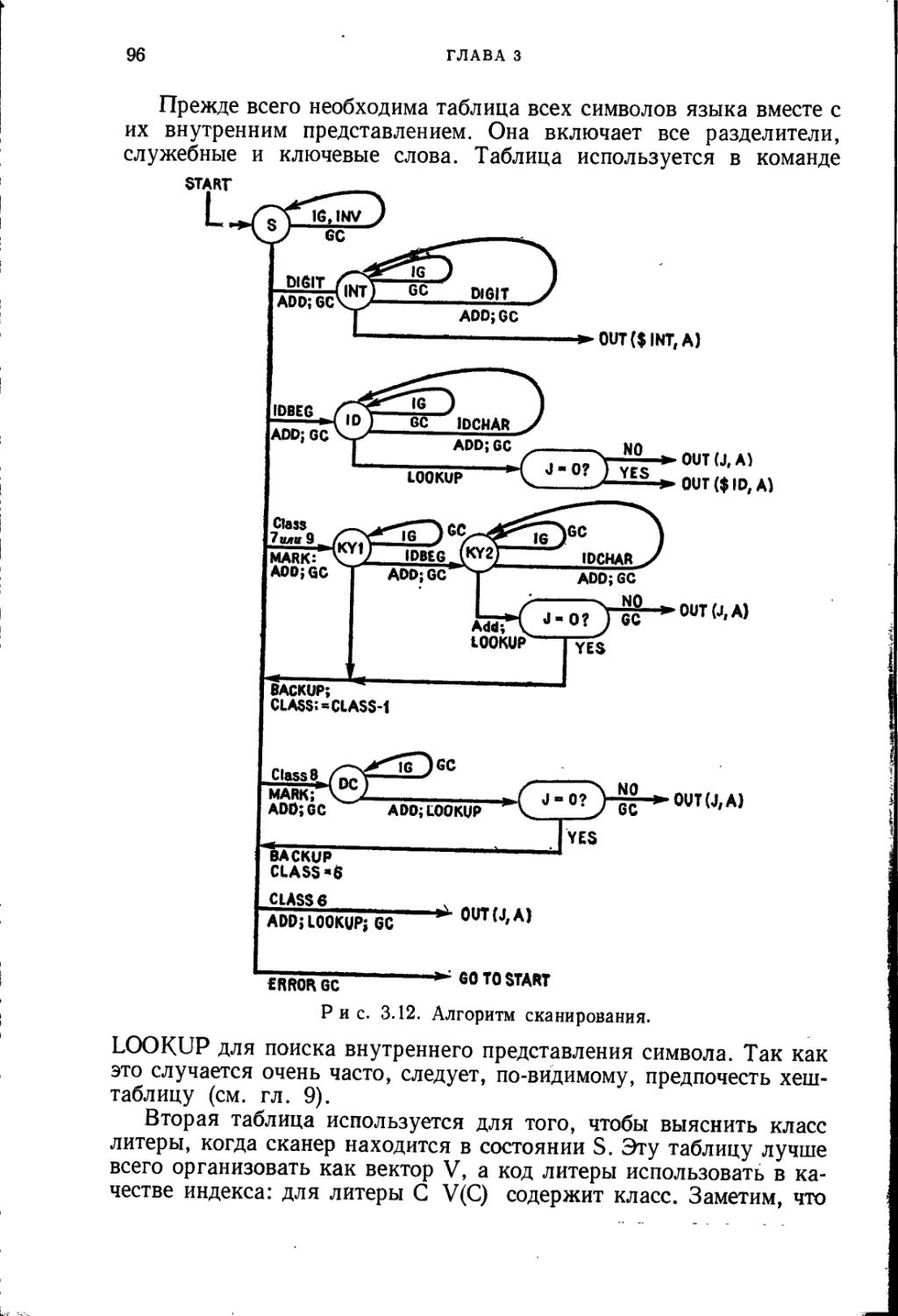
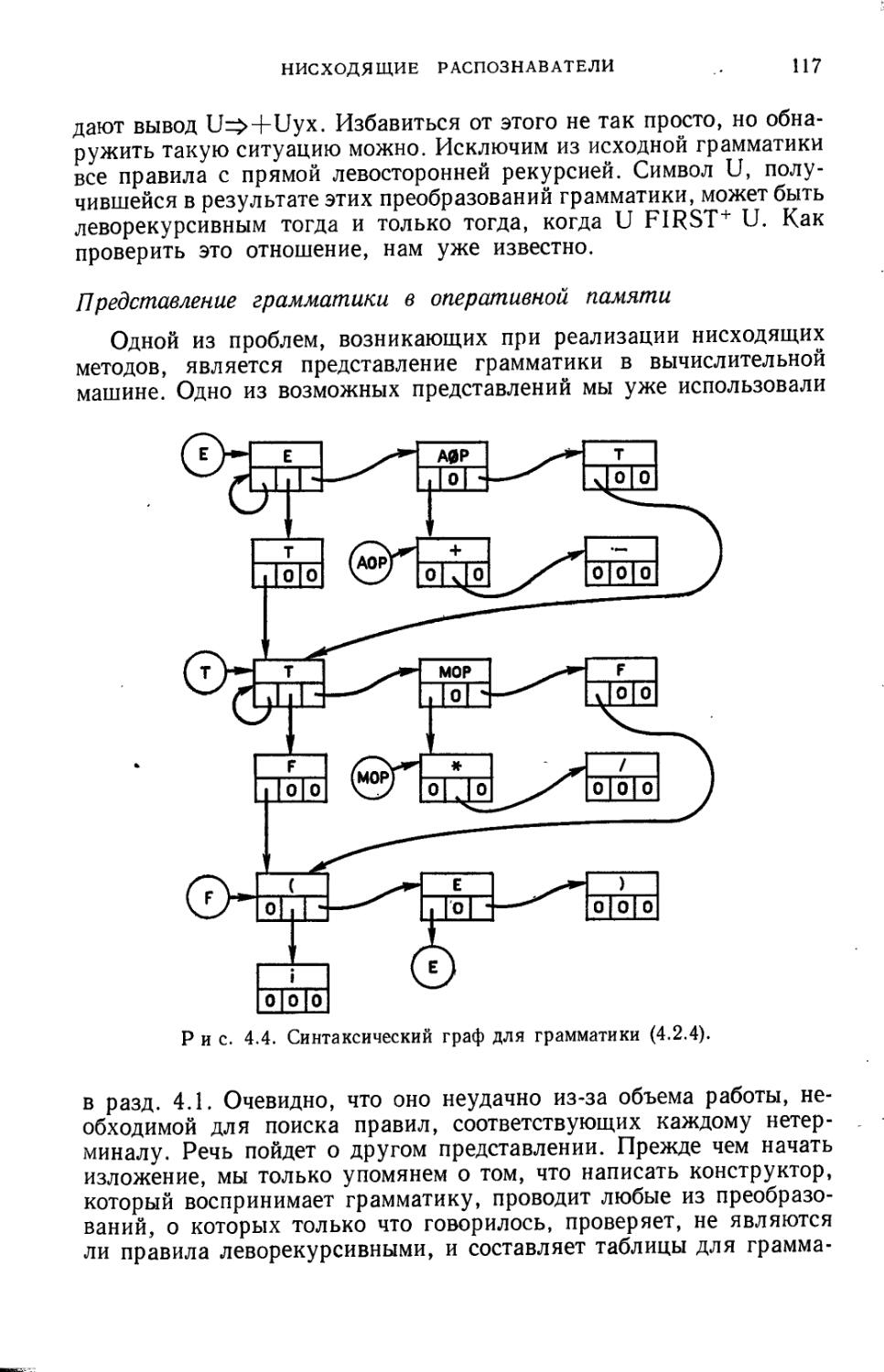
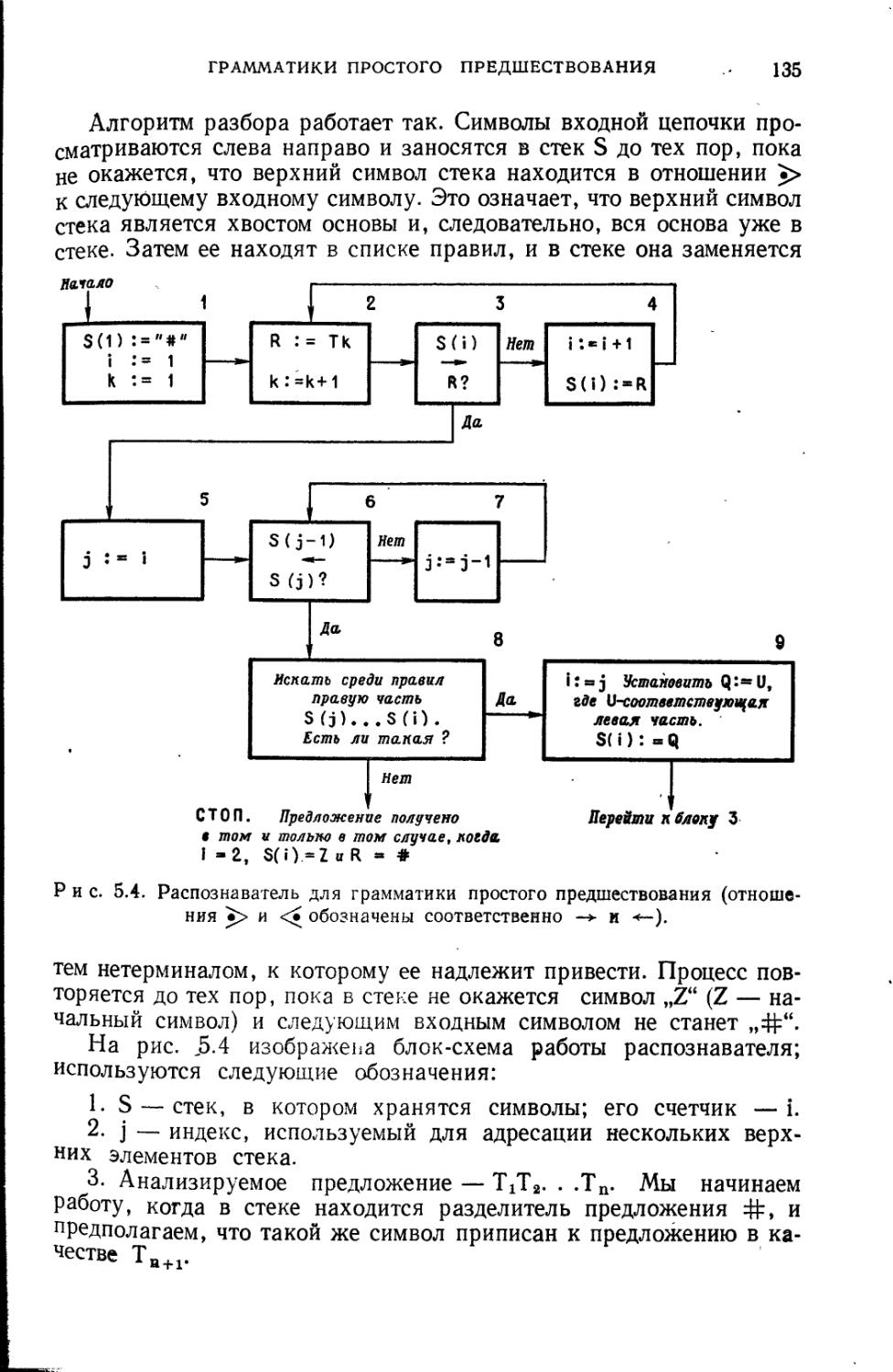
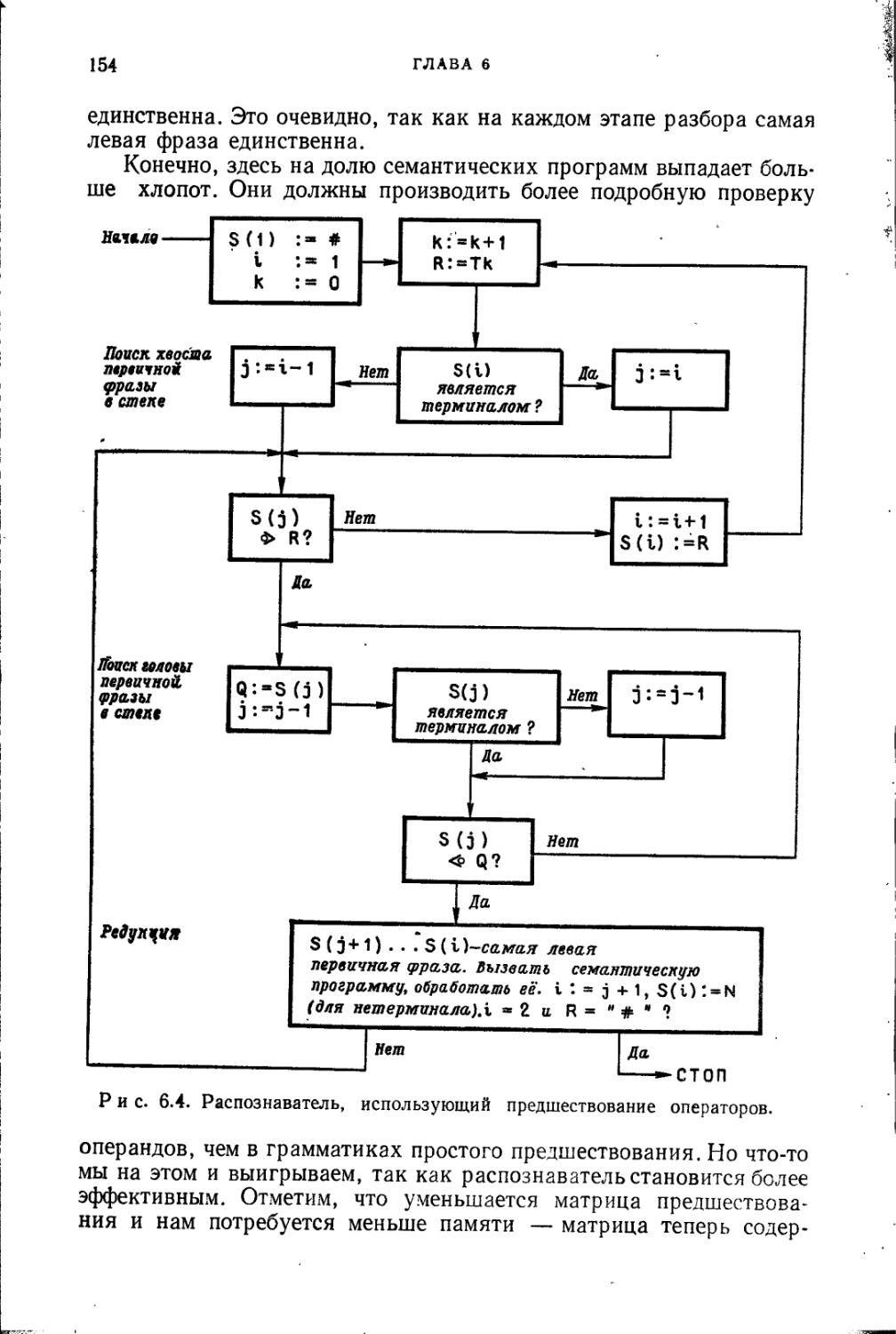
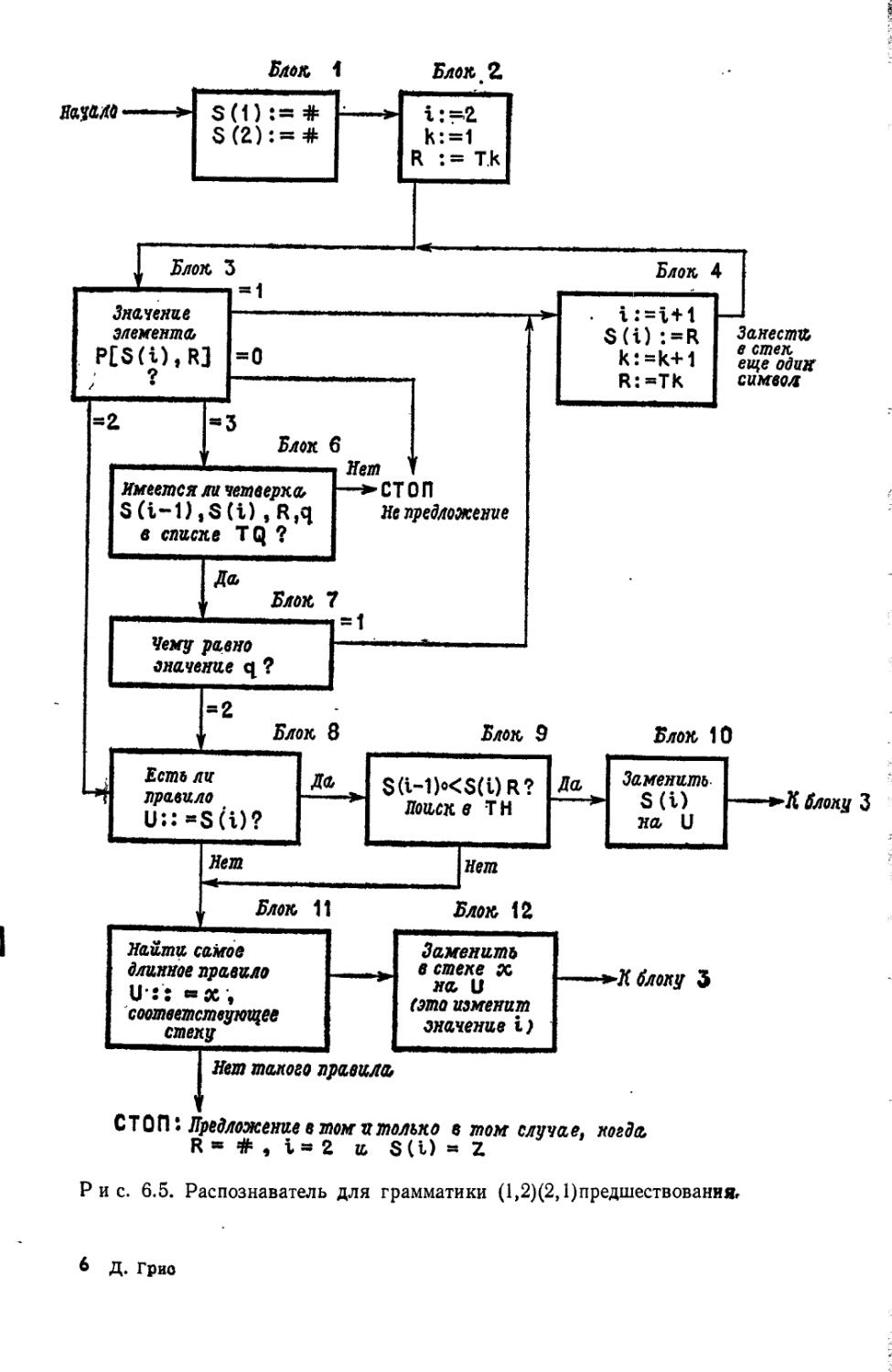
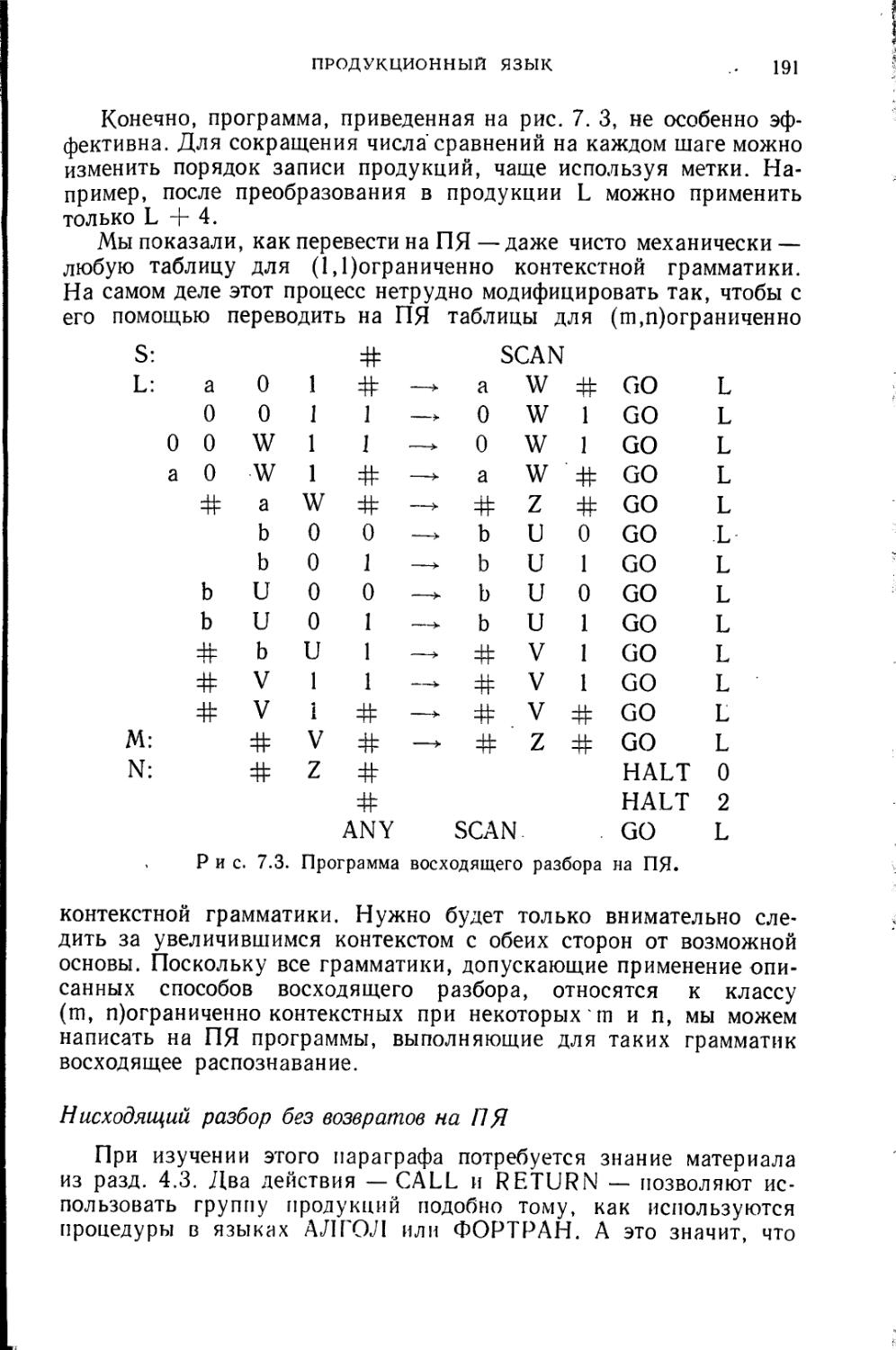
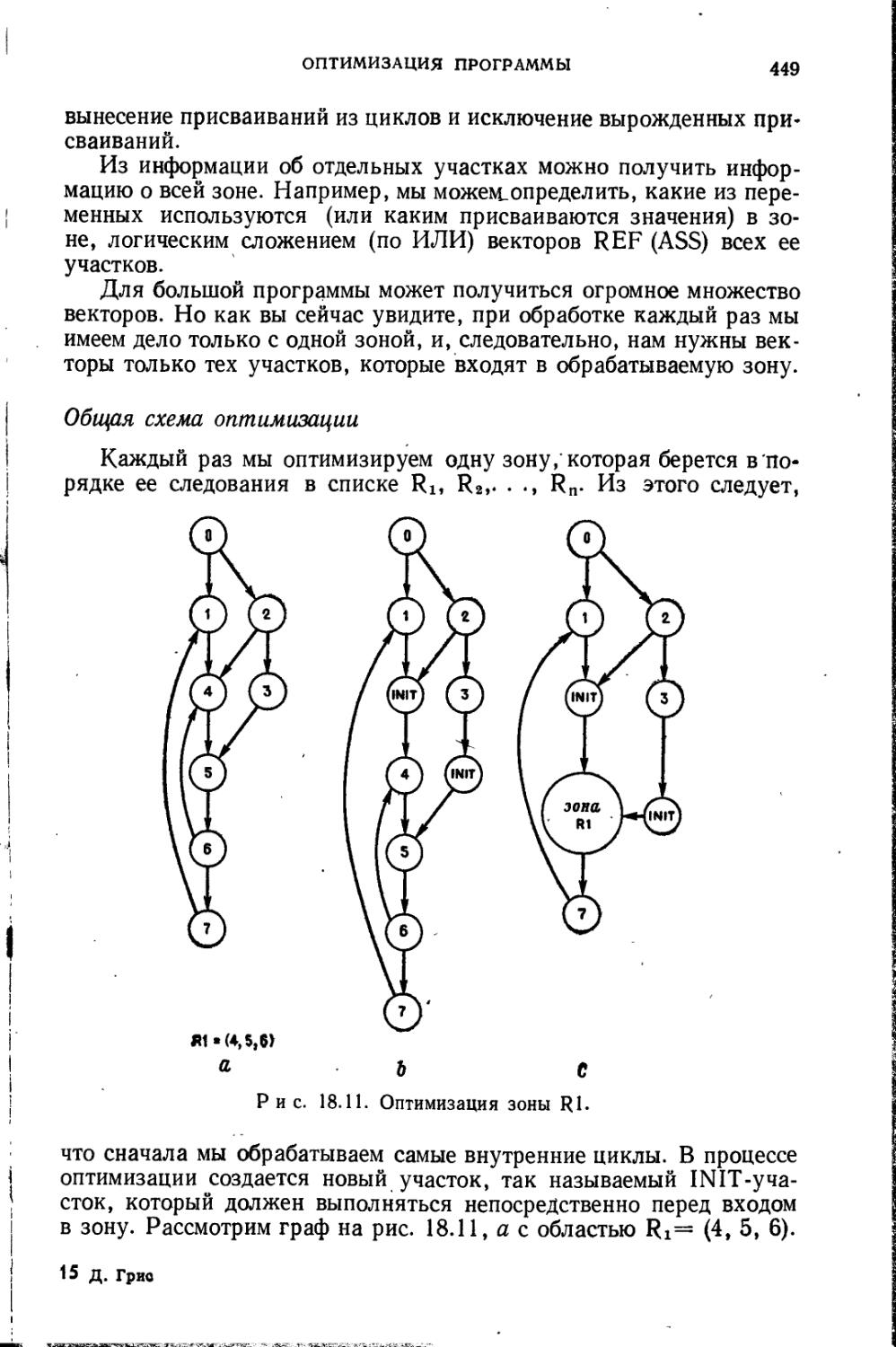
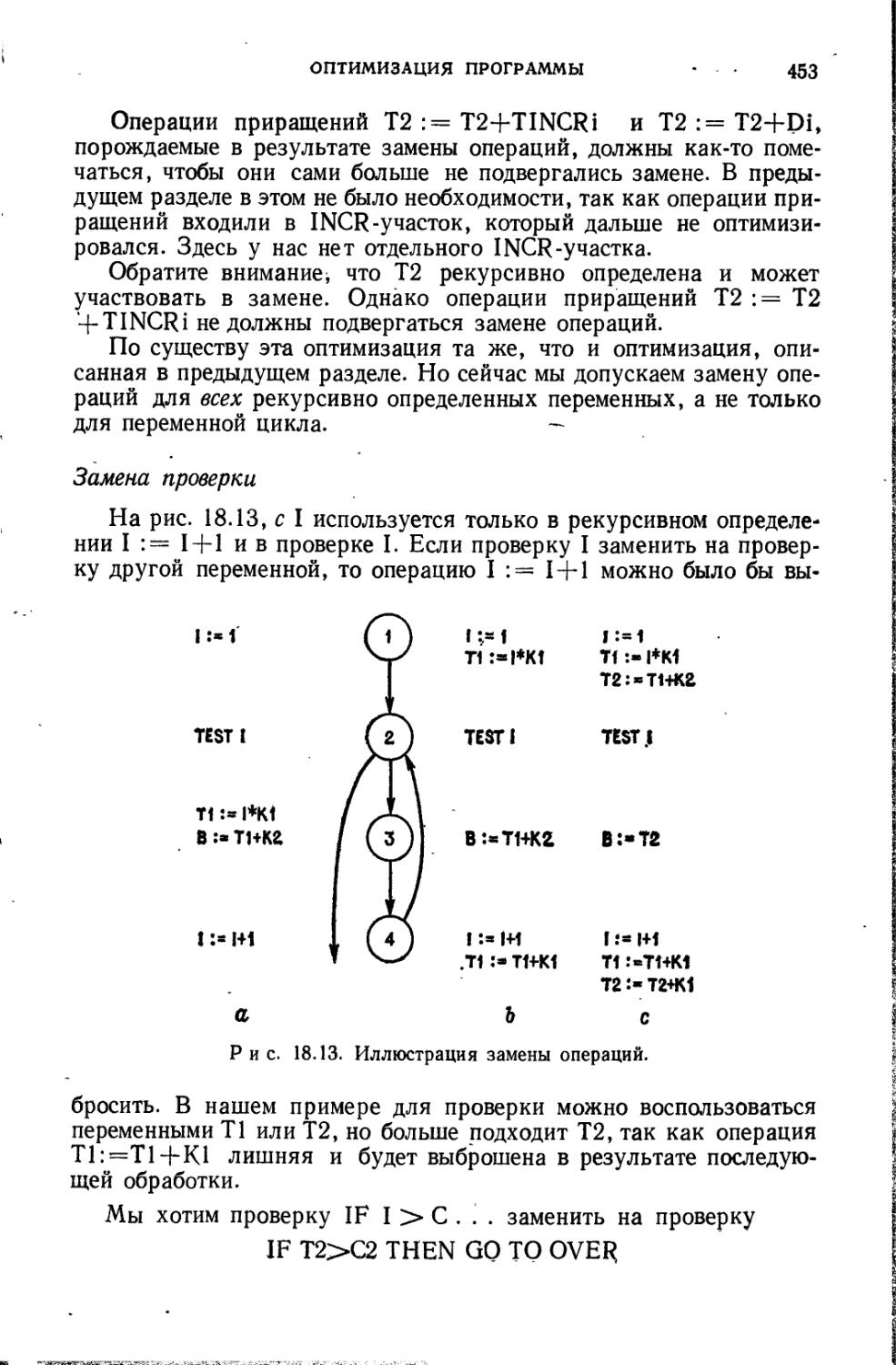
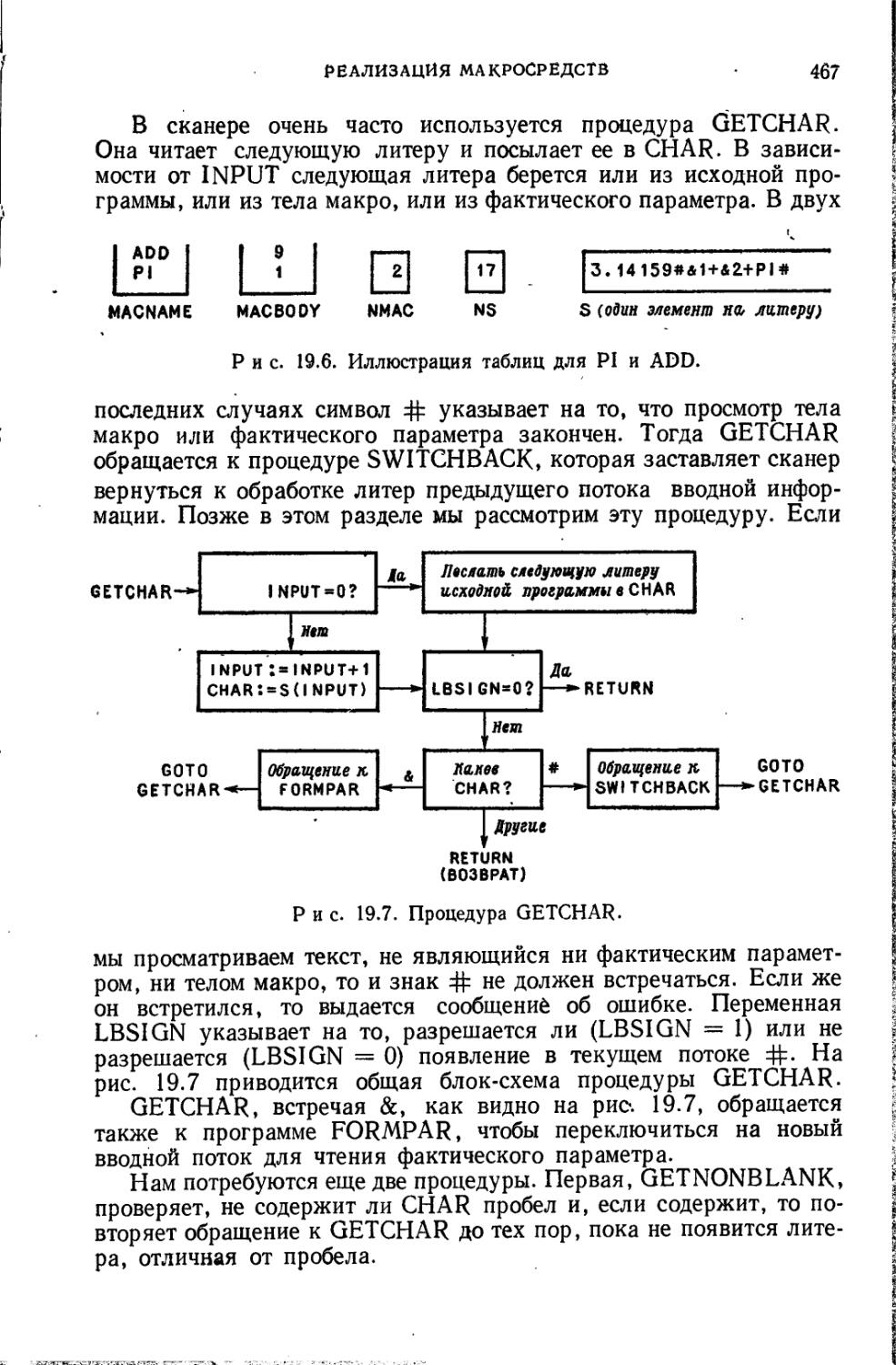
Текст
Д.Грис
КОНСТРУИРОВАНИЕ КОМПИЛЯТОРОВ ДЛЯ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
Compiler Construction for Digital Computers
David Gries Cornell University
JOHN WILEY & SONS, INC.
NEW YORK • LONDON • SYDNEY • TORONTO ♦ 1971
Д. Грис
Конструи рова н ие компиляторов для цифровых вычислительных машин
ПЕРЕВОД С АНГЛИЙСКОГО
Е. Б. ДОКШИЦКОЙ, Л. А. ЗЕЛЕНИНОЙ, Л. Б. МОРОЗОВОЙ, В. С. ШТАРКМАНА
ПОД РЕДАКЦИЕЙ
Ю. М. БАНКОВСКОГО, Вс. С. ШТАРКМАНА
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА 1975
УДК 681.142.2
В книге крупнейшего американского специалиста в области компиляторов Д. Гриса нашел отражение богатый опыт разработки и использования трансляторов для ЭВМ третьего поколения. Подробно рассмотрены как теоретические основы разработки компиляторов (теория формальных языков и грамматик), так и практические вопросы их реализации (лексический и синтаксический анализ, организация памяти и таблиц, оптимизация программ).
Книга1 может служить учебником для тех, кто впервые сталкивается с разработкой компиляторов, и справочным пособием для опытных специалистов в этой области. Книга окажет большую помощь при подготовке в университетах и институтах квалифицированных кадров по системному программированию.
Редакция литературы по математическим наукам
20204-019
Г ~Q4i joi),75 19-75 © Перевод на русский язык, «Мир», 1975
ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
Советский читатель уже имел возможность познакомиться с автором этой книги, профессором Корнельского университета Дэвидом Грисом по превосходному обзору «Системы построения трансляторов», написанному им совместно с Дж. Фелдманом. Перевод обзора был опубликован в 1971 году в сборнике «Алгоритмы и алгоритмические языки», вып. 5. И хотя зйачительная часть обзора в переработанном виде вошла в книгу, книга построена в совершенно ином плане. Она, по существу, представляет собой систематическое изложение методов конструирования компиляторов. В ее основу положено несколько курсов-лекций, прочитанных автором в ряде американских университетов и в нескольких международных школах. Поэтому неудивительно, что книге свойственна хорошая дидактическая форма, отражающая тщательно продуманную .методику изложения предмета.
Автор в своем предисловии говорит о том, что книга содержит весь необходимый материал по курсу 15 «Конструирование компиляторов», рекомендованному Комитетом университетских программ при АСМ. (Мы сочли целесообразным поместить вслед за нашим предисловием программу этого курса.) В настоящее время книга широко используется при изучении курса «Конструирование компиляторов» во многих зарубежных (не только американских) университетах. Редакторы перевода могут также отметить свой положительный опыт использования этой книги (еще в оригинале) при работе со студентами механико-математического факультета МГУ.
Не следует, однако, думать, что это всего лишь учебное пособие. В книге систематизирован и прекрасно изложен многолетний коллективный опыт разработки компиляторов. Заметим, что в список литературы вошло около 200 работ, на которые автор ссылается, иллю
6
ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
стрируя как интуитивные приемы, так и формализованные методы, применяющиеся при конструировании компиляторов. Поэтому книгу с интересом прочтут и те, у кого уже есть немалый собственный опыт в создании трансляторов. Вероятно, многие обнаружат в книге и «свои изобретения», которые, оказывается, уже давно известны и широко применяются.
Время не внесло кардинальных изменений в концепции и точки зрения, изложенные в книге. Поэтому мы лишь в отдельных местах добавили ссылки на работы, появившиеся после ее выхода.
Видимо, нет особой необходимости говорить подробнее о том, что содержится в книге и как ее следует читать. Этому вопросу уделено большое внимание в предисловии автора. Заметим лишь, что это первая, и, насколько нам известно, пока единственная в мировой литературе книга, содержащая систематическое изложение методов компиляции, не привязанное к какому-либо одному конкретному языку или тем более к одной конкретной реализации языка.
Стало уже правилом, что при переводе литературы по программированию переводчики и редакторы испытывают серьезные терминологические затруднения. Не была исключением и работа над этой книгой. Можно отметить два типа затруднений: во-первых, иногда соответствующие русские термины вообще отсутствуют, и, во-вторых, для некоторых понятий существует множество (как правило, одинаково неудачных) терминов. Несмотря на то что этой стороне работы над переводом уделялось много внимания, ни переводчики, ни редакторы не удовлетворены в полной мере ее результатами.
По поводу некоторых терминов стоит сказать отдельно. Мы приняли встречавшийся уже в литературе по программированию термин «литера» как «алфавитно-цифровой знак» (character), оставив за термином «символ» (symbol) более общий смысл. Менее последовательны мы были в отношении перевода слова string. В разделах, связанных с математической лингвистикой, используется термин «цепочка», применительно к языкам программирования сохранен термин «строка». Слово operator переводится как «оператор», и поэтому statement переводится как «инструкция» (исходя, в частности, из рекомендации IFIP, см. Гоулд [71]). Мы отважились на введение терминов «хеширование», «хеш-адресация», «хеш-функция» и т. п., происходящих от английского слова hash, понимая, что на первых порах это слово будет резать слух. Но нам представлялось
ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
7
неразумным обходиться без одинакового корня для всей совокупности терминов, связанных с данным кругом понятий, причем хотелось иметь корень, не загруженный другими значениями и дающий минимальную свободу для образования производных слов. Все попытки воспользоваться известными терминами типа «перемешанные таблицы», «рандомизация», «функция расстановки» приводили к длинным и тяжеловесным словосочетаниям.
Необходимо отметить, что английский оригинал этой книги издан не типографским способом и содержит довольно много опечаток и неточностей. При переводе многие из них были исправлены без специальных оговорок, номы, разумеется, не можем гарантировать, что не осталось незамеченных или привнесенных ошибок. Наверное, нам не удалось в полной мере сохранить стиль автора, точность и лаконичность его языка. Можно лишь сказать, что от чтения оригинала мы получили удовольствие и надеемся, что читателю перевода достанется хоть некоторая его часть.
Над переводом работали: Е. Б. Докшицкая (гл. 4—7), Л. А. Зеленина (предисловие, гл. 1—3, 20), Л. Б. Морозова (гл. 8—10,17 и приложение), В. С. Штаркман (гл. 11—16, 18, 19, 21 и дополнение).
Ю. М. Баяковский Вс. С. Штаркман
Программа курса 15 «Конструирование компиляторов»
(Из журнала „Communication of the ACM", 11, N 3, 1968, 181)
Этот курс посвящается главным образом изучению методов анализа исходного языка и генерации эффективной объектной программы. Конечно, в нем следует рассмотреть некоторые теоретические вопросы, но он должен иметь практическую направленность, т. е. в результате изучения этого курса студенты должны научиться конструировать компиляторы. Поэтому в задание по программированию необходимо включить реализацию компонент компилятора и, возможно, проектирование простого компилятора целиком (групповое задание).
Приводимый здесь перечень тем по объему, по-видимому, превышает разумные размеры курса. Поэтому преподаватель должен сделать некоторый отбор материала.
1. Обзор методов ассемблирования, техники работы с таблицей символов и методов макрогенерации. Обзор методов синтаксического анализа и других способов распознавания различных конструкций программы. Обзор методов компиляции, загрузки и выполнения готовой программы, выделение среди прочих представлений скомпилированной программы представления на языке загрузки.
2. Методы однопроходной компиляции. Перевод арифметических выражений из постфиксной формы на язык машины. Эффективное использование регистров и временных переменных.
3. Распределение памяти для констант, простых переменных, массивов и временных переменных. Функции и процедуры, структура независимых блоков, структура вложенных блоков и динамическое распределение памяти.
4. Объектный код для переменных с индексами, функции отображения и информационные векторы. Компиляция инструкций переходов. ..
5. Подробное рассмотрение общей организации простого компилятора. Таблицы символов. Лексический анализатор (сканер), синтаксический анализатор, генератор объектного кода, стеки операторов и операндов, подпрограммы вывода и диагностика ошибок.
9
6. Типы данных, функции преобразования данных из одного типа в другой, выражения и инструкции смешанного типа.
7. Компиляция подпрограмм и функций. Вызов параметров по адресу, по наименованию и по значению. Побочный эффект в подпрограммах. Ограничения, налагаемые при однопроходном выполнении. Объектный код для передачи параметров. Объектный код для тела подпрограммы.
8. Языки, предназначенные для написания компиляторов: TMG (Макклюр), COGENT (Рейнольдс), GARGOYLE (Гарвик), МЕТА II (Шорр) и TGS — II (Читэм).
9. Техника раскрутки. Обсуждение метакомпилятора, написанного на своем собственном языке.
10. Методы оптимизации. Анализ частоты использования конструкций программы с целью определения наиболее важных сторон оптимизации.
11. Локальная оптимизация, проводимая в целях более эффективного использования специальных команд, таких, как загрузка в регистр постоянного значения, запись нуля в память, замена знака на противоположный, прибавление к содержимому памяти, умножение или деление на два, возведение в квадрат, возведение в степень с целочисленным показателем степени и сравнение с нулем. Оптимизация вычисления индекса.
12. Оптимизация выражений. Вычисление общих подвыражений и другие методы. Минимизация числа используемых временных переменных и арифметических регистров в машинах с несколькими регистрами.
13. Оптимизация циклов. Несколько способов программирования типичных циклов. Использование индекс-регистра для самого внутреннего цикла. Классификация циклов в зависимости от целей оптимизации.
14. Проблемы глобальной оптимизации. Построение и анализ графа программы. Изменение последовательности вычислений для максимальной «разгрузки» самого внутреннего цикла. Вынесение инвариантных подвыражений.
ПРЕДИСЛОВИЕ
Компиляторы и интерпретаторы являются неотъемлемой частью любой вычислительной системы — без них нам пришлось бы все программировать на автокоде или даже в машинных командах! Поэтому компиляторы стали важной практической областью научных исследований, связанных с вычислительными машинами. Цель данной книги состоит в том, чтобы ясно и последовательно изложить основные методы, используемые при написании компиляторов, что позволит новичку легче освоить эту область, а специалисту ориентироваться в литературе.
В книге рассматриваются так называемые синтаксически-уп-равляемые методы компиляции. В самом деле, свыше одной трети книги посвящено теории формальных языков и автоматическому распознаванию синтаксиса. Я убежден, что любой, кто занимается составлением компиляторов, должен знать основы этого предмета. Это не означает, что каждый компилятор должен быть написан с использованием методов автоматического распознавания синтаксиса. Существует много языков программирования, для которых эти методы не пригодны. Но знание основ теории формальных языков позволит разработчику глубже понять то, что происходит в компиляторе, поможет ему более систематически и эффективно провести проектирование и программирование компилятора.
Однако синтаксический анализ составляет лишь небольшую часть компилятора, и поэтому я включил главы по таким разделам, как организация таблиц символов, нейтрализация ошибок, генерация готовой программы, оптимизация программы и т. д. Некоторые разделы (преобразование констант, шаговые компиляторы) были опущены, чтобы сохранить разумный размер книги.
Имеется в виду, что книга послужит двум целям: с одной сто
12
' ПРЕДИСЛОВИЕ
роны, она может быть использована профессиональными программистами, интересующимися или занимающимися составлением компиляторов, в качестве самоучителя или справочника, с другой стороны, она содержит материал односеместрового курса «Конструирование компиляторов».
Фактически книга покрывает (и перекрывает) все разделы, которые перечислены в программе курса 15 (конструирование компиляторов), рекомендованном Комитетом университетских программ при АСМ и опубликованном в мартовском номере журнала Communications of the АСМ за 1968 год.
Читатель должен иметь по крайней мере годичный опыт программирования на языке высокого уровня (например, на АЛГОЛе ФОРТРАНе или PL/1) и на автокоде, он также должен уметь читать и понимать программы на АЛГОЛе. В некоторых разделах книги встречаются ссылки на элементарную теорию булевых матриц (в книге содержится краткое введение в эту теорию). Предполагается, что читатель знаком с такими понятиями, как множество, объединение двух множеств и т. д. Кроме того, читатель должен иметь математические знания, скажем, на уровне младших курсов ВУЗов с математическим уклоном.
Необходимость в опыте работы с языком высокого уровня очевидна, поскольку эта книга о транслирующих программах, написанных на подобных языках. Также необходим опыт работы с автокодом. Однако опыт программирования на автокоде более важен для полного понимания работы вычислительных машин. Фактически нам почти не придется иметь дело с каким-либо конкретным автокодом. Несколько программ на языке ассемблера IBM 360, рассеянных по книге, могут быть опущены без ущерба для понимания остального материала.
Компилятор — это тоже программа, написанная на некотором языке. Следовательно, примеры частей компилятора должны быть даны на некотором языке программирования и для этой цели я выбрал язык, подобный АЛГОЛу, так как он наиболее удобен для чтения. Примеры, которые приводятся в книге, как правило, весьма коротки и в них довольно легко разобраться. Там, где многочисленные детали приводят к потере ясности рассматриваемой проблемы, я оставлял за собой право пользоваться словесным описанием вместо АЛГОЛа. Я очень тщательно проверил эти программы вручную,
ПРЕДИСЛОВИЕ
13
но хочу предупредить читателя, что не все они были отлажены на машине!
Краткое * описание используемого в книге нестандартного АЛГОЛа приводится в приложении. Это описание очень конспективное и предполагает предварительное знание АЛГОЛа. Если читатель не знаком с АЛГОЛом и синтаксическим описанием языков, ему следует читать это приложение не ранее, чем он изучит вторую главу.
Книга содержит гораздо больше материала, чем можно охватить в односеместровом курсе. Поэтому приведем рекомендуемый минимум:
Глава 1. Введение.
Глава 2. Грамматики и языки; опустить разд. 7.
Глава 3. Сканеры (программы лексического анализа); опустить разд. 4, 5, 6.
Глава 4. Методы нисходящего разбора; главным образом разд. 3. Глава 5. Грамматики простого предшествования.
Глава 8. Организация памяти в готовой программе; опустить разд. 6 и 9.
Глава 9. Организация таблиц символов.
Глава 10. Информация в таблице, символов; опустить разд. 2.
Глава 11. Внутренние формы исходной программы; опустить разд. 4 и 5.
Глава 12.' Введение в семантические программы.
Глава 13. Семантические программы для конструкций языка, подобного АЛГОЛу; опустить разд. 6.
Глава 14. Отведение памяти переменным в готовой программе; опустить разд. 3.
Глава 16. Интерпретаторы.
Глава 21. Советы разработчику компилятора.
Вы далее заметите, что из методов синтаксического анализа я придаю особое значение методу простого предшествования. И совсем не потому, что он считается наилучшим (наверное, это наихудший метод), а потому, что он самый легкий для изучения. Если на чтение курса будет отведено больше времени, то желательно, чтобы лектор добавил свои любимые методы восходящего синтаксического разбора: предшествование операторов (разд. 6.1); предшествование более высокого порядка (разд. 6.2); матрицы переходов
14
ПРЕДИСЛОВИЕ
(разд. 6.4); продукционный язык (гл. 7) и др. из числа тех, что не вошли,в минимум.
Можно также изменить порядок изучения материала. В самом деле, во время чтения курса лучше всего объединить изучение отдельных теоретических разделов с разделами более практического плана. Глава 8 об управлении памятью при работе готовой программы является совершенно независимой, тогда как гл. 9, 10, 11 и 16 по организации таблиц символов, внутреннему представлению исходной программы и интерпретаторам могут быть изучены в указанном порядке в любой момент времени.
Глава 21 заслуживает особого внимания. Она представляет собой подборку разнородных фактов и соображений, которые разработчик компиляторов должен непременно знать. Эти сведения собраны вместе по той причине, что они либо по тематике не подходят ни к одной из имеющихся глав, либо слишком важны, чтобы быть затерянными среди другого материала. Читателю следует время от времени просматривать эту главу и читать разделы, интересующие его в текущий момент.
Курс «Конструирование компиляторов» должен сопровождаться практическими занятиями. Студенты (группами от одного до трех человек) должны написать и отладить компилятор или интерпретатор для некоторого простого языка. Только в этом случае они действительно поймут, как работают компиляторы. С учебной точки зрения, интерпретаторы лучше, так как при этом студентам не надо заботиться о массе мелочей, связанных с машинным языком; идеи, несомненно, важнее мелочей. Именно поэтому транслятор следует программировать на языке высокого уровня. Мой опыт говорит, что язык PL/1 и язык, подобный АЛГОЛу, лучше отвечает этой цели, чем ФОРТРАН. Компиляторы, написанные на ФОРТРАНе, получаются более длинными и менее обозримыми. В тех случаях, когда в распоряжении студентов оказывается система построения трансляторов, ею следует обязательно воспользоваться. Чтобы работа проходила более разнообразно и творчески, нужно начать с базового простого языка, содержащего целые переменные, присваивания, выражения, метки и переходы, условные инструкции и, наконец, простые инструкции ввода и вывода. Затем в каждой группе язык расширяется путем добавления одной или двух новых возможностей. Например, можно добавить массивы, структуры, различ
ПРЕДИСЛОВИЕ
15
ные типы данных, блочную структуру, процедуры, макрокоманды, циклы.
Компилятор можно писать и отлаживать постепенно в процессе прослушивания курса. Сначала разрабатывается сканер, затем-синтаксический анализатор, далее программы для работы с таблицами символов и, наконец, программы семантической обработки. Интерпретатор можно разрабатывать и писать сразу после того, как будут пройдены относящиеся к нему главы. Таким образом, работа равномерно распределяется в течение семестра, а не концентрируется в конце.
Большинство ссылок на публикации собраны в последнем разделе каждой главы, хотя некоторые ссылки встречаются и в других разделах. Появление имени автора автоматически является ссылкой на публикацию, включенную в библиографию. Литература в библиографии приведена в алфавитном порядке по фамилиям авторов; причем работы каждого автора располагаются в хронологическом порядке. Если у автора более одной публикации, то ссылка представляется как <имя автора > [ <год >], где год — ссылка на год публикации. Например, Грис [68]. Если автор имеет более одной публикации в каком-то году, то первой будет приведена публикация с ссылкой [ <год > а], второй — [ <год > Ы и т. д. Таким образом, ссылка Флойд [64b] относится к статье Флойда о синтаксисе языков программирования.
За исключением заголовков и некоторых рисунков эта книга была отпечатана на IBM 360/65 с использованием программы ФОРМАТ, написанной Джеральдом М. Бернсом [69].
Автор также в долгу перед Джоном Эрманом, который внес несколько важных изменений и добавлений в программу. Использование программы ФОРМАТ облегчило редактирование оригинала и дало возможность снабжать слушателей материалами на различных этапах прохождения курса. Однако это заставило меня отклониться от принятых обозначений. Печатающее устройство, на котором была подготовлена книга, не имеет верхних и нижних индексов (кроме как от 0 до 9). Отсутствие индексов заставило меня писать последовательность из п символов как S[l], S[2]...Sin]1).
Когда смысл очевиден, мы просто записываем это как51,52, ...,Sn.
*) В переводе некоторые обозначения оригинала заменены на более традиционные— Прим. ред.
16
ПРЕДИСЛОВИЕ
Разделы этой книги возникли как конспекты курсов лекций, посвященных проектированию компиляторов и прочитанных в Стенфорде и Корнелле. Я воспользовался этим материалом в переработанном виде в сокращенных курсах в Мичиганской летней школе, в Анн-Арборе, в Корнелле и в 1970 году на Международном семинаре по системам программирования в Израиле. Я благодарен слушателям этих курсов за их критические замечания. Работая над книгой, я получал полезные советы от многих лиц; среди них Рихард Конвей, Джерри Фелдман, Джон Рейнолдс, Боб Роузин и Алан Шоу. Приношу мою искреннюю признательность Стиву Брауну, который внимательно прочитал рукопись, выявил много ошибок и сделал ценные пометки и критические замечания. В заключение, хочу поблагодарить мою жену, которая проявила поразительное терпение, выдержку и понимание в то время, когда я писал эту книгу.
Д. Грис
Глава 1
Введение
1.1. КОМПИЛЯТОРЫ, АССЕМБЛЕРЫ, ИНТЕРПРЕТАТОРЫ
Транслятор — это программа, которая переводит исходную программу в эквивалентную ей объектную программу. Исходная программа пишется на некотором исходном языке, объектная программа формируется на объектном языке. Выполнение программы самого транслятора происходит во время трансляции.
Если исходный язык является языком высокого уровня, например таким, как ФОРТРАН, АЛГОЛ и КОБОЛ, и если объектный язык — автокод или некоторый машинный язык, то транслятор называется компилятором. Машинный язык иногда называют кодом машины, поэтому и объектная программа иногда называется объектным кодом. Трансляция исходной программы в объектную происходит во время компиляции, а фактическое выполнение объектной программы происходит во время выполнения готовой программы.
Ассемблер — это программа, которая переводит исходную программу, написанную на автокоде, или на языке ассемблера, на язык вычислительной машины. Автокод очень близок к машинному языку; действительно, большинство автокодных инструкций является точным символическим представлением команд машины. Более того, автокодные инструкции обычно имеют фиксированный формат, что позволяет легко их анализировать. В автокоде, как правило, отсутствуют вложенные инструкции, блоки и т. п.
Интерпретатор для некоторого исходного языка принимает исходную программу, написанную на этом языке, как входную информацию и выполняет ее. Различие между компилятором и интерпретатором состоит в том, что интерпретатор не порождает объектную программу, которая затем должна выполняться, а непосредственно выполняет ее сам.
Для того чтобы выяснить, как осуществить выполнение инструкций исходной программы, чистый интерпретатор анализирует ее всякий раз, когда она должна быть выполнена. Конечно же, это не эффективно и используется не очень часто. При программировании интерпретатор обычно разделяют на две фазы. На первой фазе интерпретатор анализирует всю исходную программу, почти так же, как это делает компилятор, и транслирует ее в некоторое внутреннее представление. На второй фазе это внутреннее представление
18
ГЛАВА I
исходной программы интерпретируется или ^выполняется. Внутреннее представление исходной программы разрабатывается для того, чтобы свести к минимуму время, необходимое для расшифровки или анализа каждой инструкции при ее выполнении.
Как указывалось выше, сам компилятор — это не что иное, как программа, написанная на некотором языке, для которой входной информацией служит исходная программа, а результатом является эквивалентная ей объектная программа. Исторически сложилось так, что компиляторы писались на автокоде вручную. Во многих случаях это был единственный доступный язык! Однако существует тенденция писать компиляторы на языках высокого уровня, поскольку при этом уменьшается время, затрачиваемое на программирование и отладку, а также обеспечивается удобочитаемость программы компилятора, когда работа завершена. Кроме того, теперь мы имеем много языков, разработанных специально для составления компиляторов. Эти так называемые «компиляторы компиляторов» являются некоторым подмножеством в «системах построения трансляторов» (СПТ). Мы обсудим их кратко в гл. 20.
Эта книга познакомит вас с конструированием компиляторов. В ней также найдут отражение вопросы, связанные с интерпретаторами, хотя им будет уделено сравнительно немного места, так как большинство методов, используемых при конструировании компиляторов, применимы также и при составлении интерпретаторов. Мы не будем обсуждать ассемблеры, но любой, кто понимает, как конструировать компиляторы, без труда поймет, что делает ассемблер, и как он это делает.
Вам не удастся найти в книге полного описания какого-либо компилятора. Идея заключается не в том, чтобы показать, как я пишу один конкретный компилятор, а в том, чтобы научить вас писать свой собственный компилятор. В книге вы, конечно, встретите примеры и объяснения многих (но далеко не всех, и я даже не позволил себе сказать — большинства) приемов и методов, используемых при конструировании компилятора. Примеры будут запрограммированы на нестандартном АЛГОЛе, краткое описание которого приводится в приложении. Если вы используете эту книгу в качестве учебного пособия, то вы, несомненно, напишете свой собственный компилятор или интерпретатор на АЛГОЛе, ФОРТРАНе, PL/1 или другом языке высокого уровня; и это — наилучший способ научиться конструировать компиляторы.
1.2. КРАТКИЙ ОБЗОР ПРОЦЕССА КОМПИЛЯЦИИ
Компилятор должен выполнить анализ исходной программы, а затем синтез объектной программы. Сначала исходная программа разлагается на ее составные части; затем из них строятся части эк-
ВВЕДЕНИЕ
19
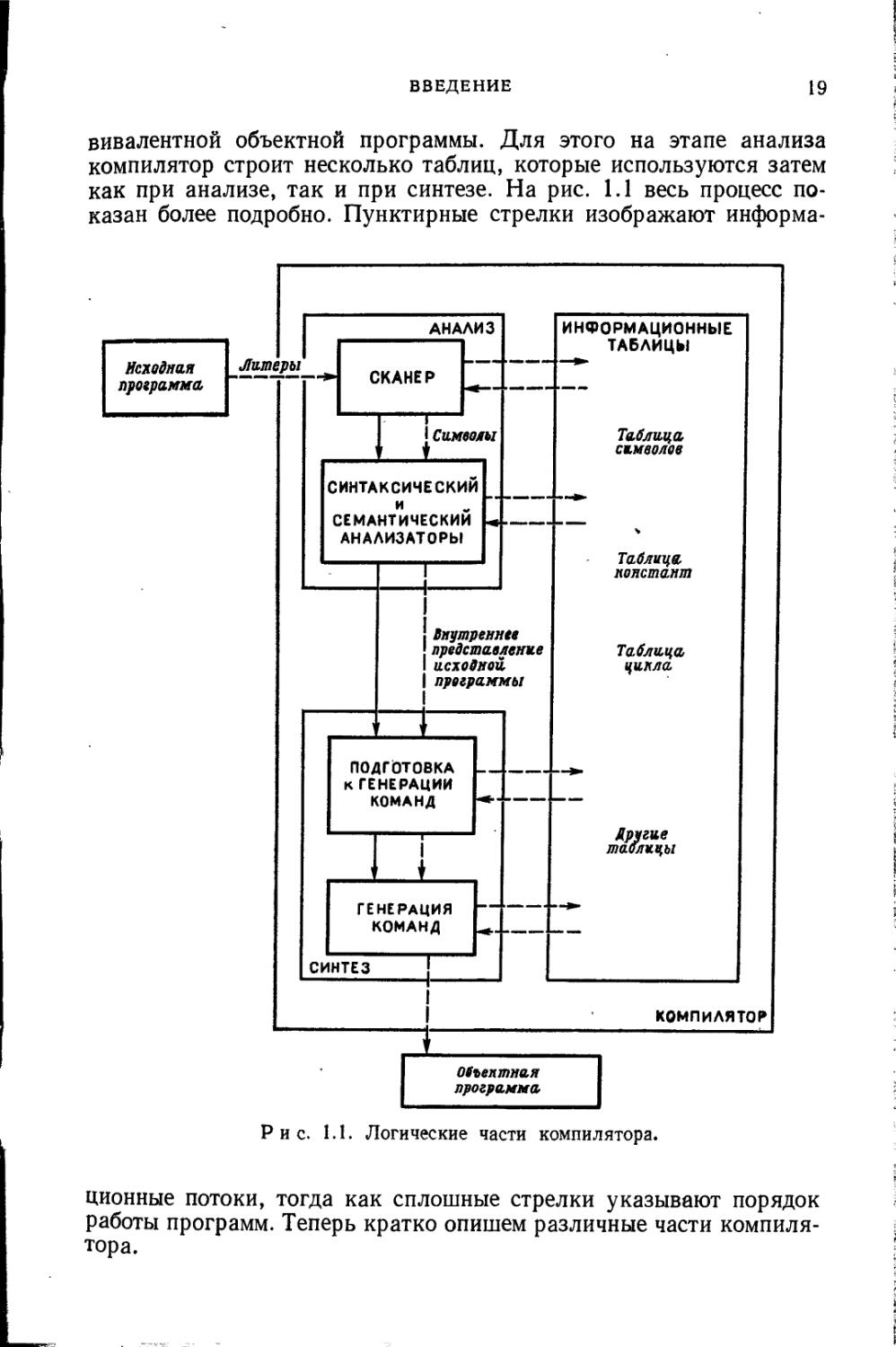
Бивалентной объектной программы. Для этого на этапе анализа компилятор строит несколько таблиц, которые используются затем как при анализе, так и при синтезе. На рис. 1.1 весь процесс показан более подробно. Пунктирные стрелки изображают информа-
Р и с. 1.1. Логические части компилятора.
ционные потоки, тогда как сплошные стрелки указывают порядок работы программ. Теперь кратко опишем различные части компилятора.
20
ГЛАВА 1
Информационные таблицы
При анализе программы из описаний, заголовков процедур, заголовков циклов и т. д. извлекается информация и сохраняется для последующего использования. Эта информация обнаруживается в отдельных точках программы и организуется так, чтобы к ней можно было обратиться из любой части компилятора. Например, при каждом использовании идентификатора необходимо знать, как был описан этот идентификатор и как он использовался в других местах программы. Что конкретно следует хранить, зависит, конечно, от исходного языка, объектного языка и сложности компилятора. Но в каждом компиляторе в той или иной форме используется таблица символов (иногда ее называют списком идентификаторов или таблицей имен). Это таблица идентификаторов, встречающихся в исходной программе, вместе с их атрибутами. К атрибутам относятся тип идентификатора, его адрес в объектной программе и любая другая информация о нем, которая может понадобиться при генерации объектной программы.
Какую еще другую информацию следует собирать? Нам наверняка потребуется таблица констант, используемых в исходной программе. В эту таблицу будет включена сама константа и соответствующий ей адрес в объектной программе. Нам также может понадобиться таблица заголовков for-циклов, отображающая структуру вложений циклов и хранящая переменные циклов; понадобится информация об инструкциях EQUIVALENCE для языков, подобных ФОРТРАНу, и размеры объектных программ для каждой компилируемой процедуры. При разработке компилятора невозможно определить вид и содержание информации, которую следует собирать до тех пор, пока не будут достаточно обстоятельно продуманы команды объектной программы для каждой инструкции исходной программы и сама синтезирующая часть компилятора. Многое зависит от глубины задуманной оптимизации программы.
Сканер
Сканер — самая простая часть компилятора, иногда также называемая лексическим анализатором. Сканер просматривает литеры исходной программы слева направо и строит символы программы — целые числа, идентификаторы, служебные слова, двухлитерные символы, такие, как ** и // и т. д. (В литературе иногда вместо термина символ используют термины элемент и атом.) Символы передаются затем на обработку фактическому анализатору. На этой стадии может быть исключен комментарий. Сканер также может заносить идентификаторы в таблицу символов и выполнять другую простую работу, которая фактически не требует анализа исходной программы. Он может выполнить большую часть работы по макро
введение
21
генерации в тех случаях, когда требуется только текстовая подстановка.
Обычно сканер передает символы анализатору во внутренней форме. Каждый разделитель (служебное слово, знак операции или знак пунктуации) будет представлен целым числом. Идентификаторы или константы можно представить парой чисел. Первое число, отличное от любого целого числа, использующегося для представления разделителя, характеризует сам «идентификатор» или «константу»; второе число является адресом или индексом идентификатора или константы в некоторой таблице. Это позволяет в остальных частях компилятора работать эффективно, оперируя с символами фиксированной длины, а не с цепочками литер переменной длины.
Синтаксический и семантический анализаторы
Анализаторы выполняют действительно сложную работу по расчленению исходной программы на составные части, формированию ее внутреннего представления и занесению информации в таблицу символов и другие таблицы. При этом также выполняется полный синтаксический и семантический контроль программы.
Обычный анализатор представляет собой синтаксически управляемую программу. В действительности стремятся отделить синтаксис от семантики настолько, насколько это возможно. Когда синтаксический анализатор (распознаватель) узнает конструкцию исходного языка, он вызывает соответствующую семантическую процедуру. или семантическую программу, которая контролирует данную конструкцию с точки зрения семантики и затем запоминает информацию о ней в таблице символов или во внутреннем представлении программы. Например, когда распознается описание переменных, семантическая программа проверяет идентификаторы, указанные в этом описании, чтобы убедиться в том, что они не были описаны дважды, и заносит их вместе с атрибутами в таблицу символов.
Когда встречается инструкция присваивания вида (переменная >: = (выражение >
семантическая программа проверяет переменную и выражение на соответствие типов и затем заносит инструкцию присваивания в программу во внутреннем представлении.
Внутреннее представление исходной программы
Внутреннее представление исходной программы в значительной степени зависит от его дальнейшего использования. Это может быть дерево, отражающее синтаксис исходной программы. Это может быть исходная программа, в так называемой польской записи. Используется еще одна форма — список тетрад (оператор, операнд, one-
22
ГЛАВА 1
ранд, результат) в порядке их выполнения. Например, присваивание «А=В+С* D» будет представлено как
с, D, Т1 + , в, Tl, Т2 = ,Т2, А,
где Т1 и Т2 — временные переменные, образованные компилятором. Операндами в приведенном примере будут не сами символические имена, а указатели на те элементы (или их индексы) в таблице символов, в которых описаны эти операнды.
Подготовка к генерации команд
Перед генерацией команд обычно необходимо некоторым образом обработать и изменить внутреннюю программу. Кроме того, должна быть распределена память под переменные готовой программы. Если мы имеем дело с компилятором с ФОРТРАНа, то должны быть обработаны инструкции EQUIVALENCE и COMMON. Одним из важных моментов на этом этапе является оптимизация программы с целью уменьшения времени ее работы.
Генерация команд
По существу, на этом этапе происходит перевод внутреннего представления исходной программы на автокод или на машинный язык. Это, по-видимому, наиболее хлопотная и кропотливая часть компилятора, хотя и наиболее понятная. Предположим, что внутреннее представление имеет вид тетрад, какописано выше, и мы генерируем команды для каждой тетрады по порядку. На языке ассемблера IBM 360х) для трех приведенных выше тетрад можно сгенерировать следующие команды:
L 5, С Загрузить С в регистр 5.
М 4, D Результат умножения в регистрах 4, 5.
А 5, В Прибавить В к результату умножения.
ST 5, А Запомнить результат.
В интерпретаторе эта часть компилятора заменяется программой, которая фактически выполняет (или интерпретирует) внутреннее представление исходной программы. Причем само внутреннее представление в этом случае мало чем отличается от того, которое получается при компиляции.
На рис. 1.1 показаны скорее логические связи между отдельными частями компилятора, чем последовательность их работы. Все четы
х) Необходимые сведения о системе команд и языке ассемблера для машин IBM 360 читатель может найти в книге Джермейна [71].— Прим. ред.
ВВЕДЕНИЕ
23
ре логически последовательных процесса: сканирование, анализ, подготовку к генерации и генерацию команд — можно выполнять в том порядке, который показан на рис. 1.1, или их можно выполнять параллельно, с определенной взаимной синхронизацией. Одним из критериев, определяющих выбор в данном случае, является объем доступной памяти. Часто выгодно или даже необходимо иметь
Рис. 1.2. Однопроходный КО?> п [ЛЯТСр.
несколько проходов (т. е. несколько раз вводить информацию в память машины). К счастью, при этом «другую информацию» удается хранить в памяти и тем самым экономить время на ввод-вывод. Другие критерии определяются целями, которые преследуются при разработке компилятора. Насколько быстрым должен быть сам компилятор? Насколько быстрой должна быть готовая программа? Какие средства отладки должны быть предусмотрены в готовой программе? Еще одним фактором является количество людей, занятых в разработке. Чем больше людей, тем больше, по-видимому, будет проходов, чтобы каждый мог отвечать за отдельную и самостоятельную часть компилятора.
Справедливым является и то, что не все этапы должны быть обязательно осуществлены. В однопроходном компиляторе нет необходимости во внутреннем представлении программы, в то время как этапы подготовки и генерации команд растворяются в семантических программах. На рис. 1.2 представлена типичная однопроходная схема. Синтаксический анализатор вызывает сканер, когда необходим новый символ, и вызывает процедуру, когда конструкция распознана. Эта процедура осуществляет семантическую проверку, распределение памяти и генерирует команды, перед тем как возвратиться к разбору.
24
ГЛАВА 1
Однако не все языки имеют такую структуру, которая допускает однопроходную трансляцию.
Естественно, возникает вопрос: в чем заключаются главные трудности реализации компилятора? Сканер — весьма прост и хорошо изучен. Синтаксические анализаторы, если речь идет о простых формальных языках, также довольно хорошо изучены. В действительности эту часть можно в значительной степени автоматизировать. (С тех пор, как синтаксис был формализован, большинство исследований по созданию компиляторов касалось именно синтаксиса, а не семантики.) Наиболее трудными и запутанными частями компилятора являются семантический анализ, программы подготовки генерации и программы генерации команд. Эти три части взаимозависимы, должны в значительной степени разрабатываться совместно и могут коренным образом измениться при переходе с одного объектного языка на другой или с одной машины на другую.
После этого краткого введения мы готовы приступить к изложению нашей первой темы «Теория формальных языков и ее применение к конструированию компиляторов». Если у вас есть желание (это не является необходимым), вы можете просмотреть следующий раздел, в котором приведены несколько примеров существующих компиляторов, для того чтобы закрепить представленный в этой главе материал.
1.3. ПРИМЕРЫ СТРУКТУР КОМПИЛЯТОРОВ
Мы приводим здесь четыре примера существующих компиляторов. Мы выбрали два компилятора с языка АЛГОЛ, чтобы показать, насколько радикально может повлиять на проект вычислительная машина, для которой создается компилятор. Затем мы описываем два различных компилятора с ФОРТРАНа для одной и той же вычислительной машины, чтобы показать, как влияют на проект цели, преследуемые при создании компилятора.
Компилятор ALCOR Illinois 7090
Это четырехпроходный компилятор, созданный для машин IBM 7090-7040 (см. Грис [68]); исходный язык компилятора—АЛГОЛ 60, из которого исключены собственные значения.
Компилятор тщательно оптимизирует вычисление индексов в циклах (описанный ниже компилятор с ФОРТРАНа выполняет гораздо более полную оптимизацию программы). Результатом трансляции является программа на языке машины 7090 в виде двоичной колоды, загружаемой в машину системным загрузчиком.
ВВЕДЕНИЕ
25
Проход Работа
1 Лексический и частичный синтаксический анализ с целью получения таблицы символов для всех идентификаторов с учетом блочной структуры. Каждый символ заменяется целым числом фиксированной длины.
2 Полный синтаксический и семантический анализ. Подготовка для оптимизации переменных с индексами. Распределение памяти в готовой программе (это, по существу, уже синтез).
3 Оптимизация переменных с индексами и генерация команд.
4 Получение двоичной колоды и вывод сообщений об ошибках, если они есть.
Компилятор для машины Gier с АЛГОЛа
Компилятор создан для машины, располагающей памятью лишь в 1024 42-разрядных слова и магнитным барабаном на 128 000 слов (см. Наур [63 b]). Несмотря на малый размер машины, компилятор транслирует по существу полный АЛГОЛ. Легко понять, почему компилятор пришлось расчленить на 9 проходов, приведенных ниже. Проходы 1 и 2 осуществляют лексический анализ, проход 3 — синтаксический аналйз, проходы 4, 5 и 6 выполняют семантический анализ (надо заметить, что здесь же осуществляется часть синтеза — распределение памяти в готовой программе). Проходы 7 и 8 представляют синтезирующую часть компилятора. Проход 9 является специфической частью этого компилятора, он необходим для получения эффективной объектной программы.
Проход Работа
1 Сканер, который переводит разделители (все символы, кроме констант и идентификаторов) в их внутреннее представление.
2 Замена всех идентификаторов в исходной программе целыми числами фиксированной длины.
3 Синтаксический анализ. Введение дополнительных разделителей и замена существующих для облегчения последующей обработки.
4 Построение таблицы символов. Для каждого блока идентификаторы, описанные или специфицированные в блоке, запоминаются в таблице вместе со своими атрибутами.
5 Распределение памяти для переменных в готовой программе. Кроме того, каждый идентификатор исходной
26
ГЛАВА 1
программы (представленный целым числом) заменяется четырьмя байтами, которые соответственно представляют тип и вид, номер блока, адрес в готовой программе, число параметров или индексов (если требуется).
6 Контроль типа и вида всех идентификаторов и других операндов. Преобразование исходной программы в польскую запись.
7 Генерация программы.
8 Заключительная работа по формированию адресов
в некоторых командах. Сегментация по трактам магнитного барабана. Получение окончательной программы.
9 Компоновка программных сегментов на магнитном барабане.
Компиляпгор/3&) WATFOR
WATFOR представляет собой некоторую систему, состоящую из подмонитора и компилятора, реализованную на машине IBM 360, для организации пакетной обработки программ, написанных на языке ФОРТРАН IV (см. Кресс и др.). Цель системы — обеспечить быстрый пропуск программ, написанных на ФОРТРАНе и имеющих относительно небольшой размер и малое время выполнения — такие программы характерны для учебных институтов. Поэтому система целиком размещается в оперативной памяти, и единственными операциями ввода-вывода являются ввод исходной программы и вывод результата компиляции. Минимум памяти, необходимый системе, составляет 128 000 байтов (32 000 слов).
Компилятор не проводит оптимизации и получает относительно неэффективную объектную программу на языке машины в абсолютных адресах, которую система тотчас выполняет. Именно в этом источник экономии — не теряется время на редактирование связей и загрузку.
Компилятор является по существу однопроходным. Сканер переводит одну инструкцию ФОРТРАНа во внутреннее представление, определяет тип инструкции и вызывает соответствующую семантическую программу для ее обработки. Эта программа анализирует синтаксис и семантику инструкции и сразу же генерирует для нее команды, т. е. анализ и синтез выполняются вместе. Для ФОРТРАНа окончательное распределение памяти в готовой программе не может быть осуществлено до тех пор, пока не будут обработаны инструкции COMMON и EQUIVALENCE. Поэтому адреса в командах программы не являются адресами памяти, а указывают на элементы таблицы символов для соответствующих переменных, описанных в
ВВЕДЕНИЕ
27
программе, или временных переменных. После того как завершится главный проход, вызывается второй, небольшой проход, который распределяет память для всех переменных и затем заменяет в объектной программе каждый указатель в таблицу символов на соответствующий адрес памяти.
Компилятор уровня Н для ФОРТРАНа IV на IBM 360
Задача компилятора (см. IBM (а)) состоит в получении максимально эффективной объектной программы, и с этой задачей он справляется блестяще. В связи с оптимизацией программы сам компилятор работает очень медленно. Компилятор имеет следующие проходы.
Проход * Работа
1 Сканирование и синтаксический анализ, формирование таблицы символов и внутреннего представления исходной программы в виде пар (оператор—операнд).
2 (Фактически три отдельных прохода.)
а) Обработка инструкций COMMON и EQUIVALENCE, b) Замена внутреннего представления исходной программы на тетрады (оператор, операнд, операнд, результат).
с) Распределение памяти в готовой программе.
3 Оптимизация программы.
а) Удаление лишних операций, вынесение, где возможно, операций из циклов и т. д.
Ь) Оптимизация переходов.
4 Окончательная генерация объектной программы.
Глава 2
Г рамматики и языки
Для читателя, не знакомого с теорией формальных языков, эта глава может оказаться самой трудной в книге. Свыше сорока терминов, таких, как «фраза», «предложение», «язык» и «неоднозначность», которые мы часто употребляем неформально, приобретают точный смысл. Список терминов в порядке их определения приводится в конце книги. Когда вы прочтете всю главу, непременно просмотрите этот список и вернитесь к определениям, которыми вы недостаточно овладели. Полное понимание этой главы значительно упростит чтение последующего материала книги и позволит прочесть книгу с большей пользой.
2.1. ОБСУЖДЕНИЕ ГРАММАТИК
Рассмотрим предложение «The big elephant ate the peanut»1). Если мы знаем английский, то поймем, что это предложение английского языка. Его можно изобразить в виде схемы, которая представлена на рис. 2.1.
Схема предложения, такая, например, как на рис. 2.1, называется синтаксическим деревом. Оно описывает синтаксис, или структуру, предложения, разлагая его на составные части. Таким образом, мы видим, что <предложение> состоит из (подлежащее), за которым следует (сказуемое); (подлежащее) состоит из (артикль), за которым следует (прилагательное), за которым в свою очередь следует (существительное) и т. д.
Для того чтобы описать структуру, мы использовали новые символы — «синтаксические единицы» или «синтаксические классы», такие, как (предложение). Эти символы заключаются в угловые скобки ( и ), чтобы отличить их от слов самого языка.
Мы узнаем, что «The big elephant ate the peanut» является предложением, либо основываясь на интуиции, либо применяя соответст- I вующие правила грамматики, выученные в школе; конечно, каждый
х) «Большой слон съел орех».
ГРАММАТИКИ И ЯЗЫКИ
29
из нас мог бы составить неформальное синтаксическое дерево для любого простого английского предложения. Однако для того, чтобы иметь возможность механически разбирать предложения, мы должны дать точные формальные правила, которые описывают структуру предложений. Для этой цели мы создадим метаязык, т. е. некий язык, на котором можно описывать другие языки. В английских школах в курсе французского языка английский язык использует-
<предложение>
<подлежаш,ее>
<артиклъ> <прилагате льное) ^уществительноО
the big elephant
(большой) (слон)
<спазуемое>
---------.------------1
Спрямое дополнение>
<глагол> <артикль> <суцес!пеи)пелъное>
ate the peanut
(съел) (орех)
Рис. 2.1. Синтаксическое дерево.
ся при описании французского языка. Следовательно, английский играет роль метаязыка. В учебниках английского языка английский язык используется как метаязык для описания самого себя.
В настоящий момент нас в основном интересует описание синтаксиса (структуры) языков программирования, а не их семантики (смысла); схемы, такие, как на рис. 2.1, не передают смысла предложения. Такое синтаксическое описание мы называем грамматикой языка.
Метаязык, который мы будем использовать, впервые был предложен Хомским [561 для описания естественных языков. Конкретная система записи, которой мы воспользуемся, принадлежит Бэ-кусу [59]. По мнению Хомского, этот метаязык полезен лишь для описания небольших подмножеств, состоящих из простых предложений, и поэтому лингвисты обратились к более мощным метаязыкам. Он не совсем удовлетворителен даже для описания структуры довольно простых формальных языков, таких, как АЛГОЛ или ФОРТРАН. Однако мы все же воспользуемся им, поскольку в нем наилучшим образом сочетается мощность и целесообразность практического использования.
Еще раз рассмотрим предложение «The big elephant ate the peanut». Как мы отмечали, рис. 2.1 показывает, что (предложение> состоит из (подлежащее), за которым следует (сказуемое). Если сократить фразу «может состоять из», заменив ее символом :: —, то наша грамматика могла бы содержать, например, такие правила: (предложение) (подлежащее) <сказуемое>
(подлежащее) :: — (артикль) (прилагательное) (суще-
ствительное)
30
ГЛАВА 2
<артикль>
<прилагательное>
<сказуемое>
<глагол>
<прямое дополнение>
<существительное>
<существительное>
= the
= big
= <глагол> <прямое дополнение>
= ate
= <артикль> <существительное>
= peanut
= elephant
Заметим, что грамматика может содержать более одного правила, в котором описывается образование конкретной синтаксической единицы. Например, на рис. 2.1 есть два правила, которые показывают, из чего может состоять <существительное>.
Если имеется множество правил, то ими можно воспользоваться для того, чтобы вывести, или породить, предложение по следующей схеме. (По этой причине такие правила часто называют правилами вывода, или продукциями.) Начнем с синтаксической единицы <пред-ложение>, найдем правило, в котором <предложение> слева от : : = , и подставим вместо <предложение> цепочку, которая расположена справа от : : = , т. е.
<предложение> => <подлежащее> <сказуемое>
Таким образом, мы заменяем синтаксическую единицу на одну из цепочек, из которых она может состоять. Повторим процесс. Возьмем одну из синтаксических единиц в цепочке <подлежащее> <сказуемое>, например <подлежащее>; найдем правило, где <под-лежащее> находится слева от : : = , и заменим <подлежащее> в исходной цепочке на соответствующую цепочку, которая находится справа от : :=. Это дает
<подлежащее> <сказуемое> => <артикль> <прилагательное>
<существительное> <сказуемое>
Символ “=>” означает, что один символ слева от => в соответствии с правилом грамматики заменяется цепочкой, находящейся справа от =>. Полный вывод предложения будет таким:
<предложение> => <подлежащее> <сказуемое>
=> <артикль> <прилагательное> <существи-тельное> <сказуемое>
=> the <прилагательное> <существительное>
<сказуемое>
=> the big <существительное> <сказуемое>
=> the big elephant <сказуемое>
=> the big elephant <глагол> <прямое дополнен ие>
ГРАММАТИКИ И ЯЗЫКИ
31
=> the big elephant ate <прямое дополнение> => the big elephant ate <артикль> <существи-тельное>
=> the big elephant ate the <существительное> the big elephant ate the peanut
Этот вывод предложения запишем сокращенно, используя новый сим-ВОЛ —I
<предложение> =>+ the big elephant ate the peanut
На каждом шаге можно заменить любую синтаксическую единицу. В приведенном выше выводе мы всегда заменяли самую левую из них. Обратите также внимание на то, что такое правило, как <пред-ложение> : : = <подлежащее> <сказуемое>, можно использовать для описания многих различных предложений; для этого необходимо только иметь различные способы образования синтаксических единиц <подлежащее> и <сказуемое>.
Из семи правил
<предложение> : <подлежащее> <подлежащее> : <подлежащее> : <сказуемое> : <сказуемое> : <сказуемое> : : = <подлежащее> <сказуемое> : =We : =Не : =1 : =гап : =sat : =ate
мы можем образовать целых девять предложений!
We ran Не ran I ran We ate He ate I ate We sat He sat I sat
Одно из назначений грамматики как раз и состоит в том, чтобы описать все предложения языка с помощью приемлемого числа правил. Это важно, если учесть тот факт, что обычно количество предложений в языке бесконечно.
После такого введения мы почти готовы описать формальные понятия грамматик и языков, но в следующем разделе нам все-таки придется прежде определить некоторые термины, которыми мы пока пользовались неформально.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.1
1. Найдите слова «язык», «мета», «метаязык», «синтаксис» и «семантика» в хорошем словаре.
32
ГЛАВА 2
2. Нарисуйте синтаксические деревья для предложений “John ate the big peanut” (Джон съел большой орех) “John ate the big brown peanut” (Джон съел большой коричневый орех) “John ate the salted big brown roasted peanut” (Джон съел соленый большой коричневый жареный орех). В английском языке любое существительное может быть определено любым числом прилагательных. Теперь попытайтесь дать только два правила для нового синтаксического класса, скажем <группа существительного>, позволяющих вывести <существитель-ное>, которому предшествует любое количество прилагательных (в том числе ни одного).
2.2. СИМВОЛЫ И ЦЕПОЧКИ
Мы неформально определяем язык как подмножество множества всех предложений из «слов» или символов некоторого основного словаря. И опять-таки нас не интересует смысл этих предложений. Например, английский язык состоит из предложений, которые являются последовательностями, составленными из слов (if, he, is и т. д.), и знаков пунктуации (например, запятые, точки, скобки). Язык программирования АЛГОЛ состоит из программ, которые являются последовательностями, составленными из таких символов, как if, begin, end, знаков пунктуации, букв и цифр. Язык четных целых чисел состоит из последовательностей, составленных из цифр О, 1....9, в которых последней цифрой должны быть 0, 2, 4, 6 или 8.
Алфавит — это непустое конечное множество элементов. Назовем элементы алфавита символами. Всякая конечная последовательность символов алфавита А называется цепочкой1). Вот несколько цепочек «в алфавите» А={а, b, с}: a, b, с, ab и ааса. Мы также допускаем существование пустой цепочки Л, т. е. цепочки, не содержащей ни одного символа. Важен порядок символов в цепочке; так, цепочка ab не то же самое, что Ьа, и abca отличается от aabc. Длина цепочки х (записывается как |х|) равна числу символов в цепочке. Таким образом,
|Л|=0, |а|=1, |abb|=3.
Заглавные буквы М, N, S, Т, U, ... используются как переменные или имена символов алфавита, в то время как строчные буквы t, u, v, w ... используются для обозначения цепочек символов. Таким образом, можно написать
x=STV, и это означает, что х является цепочкой, состоящей из символов S, Т и V именно в таком порядке.
*) Вместо термина цепочка (в английском языке — string) некоторые авторы используют термины строка или строчка.— Прим. ред.
ГРАММАТИКИ И ЯЗЫКИ
33
Если х и у — цепочки, то их катенацией1) ху является цепочка, полученная путем дописывания символов цепочки у вслед за символами цепочки X. Например, если x=XY, y=YZ, то xy=XYYZ и yx=YZXY. Поскольку Л — цепочка, не содержащая символов, в соответствии с правилом катенации для любой цепочки х мы можем написать
Лх=хЛ=х.
Если z=xy — цепочка, то х — голова, а у — хвост цепочки z. И, наконец, х — правильная голова, если у — не пустая цепочка (у не Л), у — правильный хвост, если х — не пустая цепочка. Таким образом, если x=abc, то Л, a, ab и abc суть головы х, и к тому же все они, кроме abc,— правильные головы.
Множества цепочек в алфавите обычно обозначаются заглавными буквами А, В....Произведение АВ двух множеств цепочек А и В
определяется как
АВ={ху|х€А, а у£В}
и читается как «множество цепочек ху, такое, что х из А, а у из В». Например, если А={а, Ь} и В={с, d}, то множество АВ={ас, ad, be, bd}. Поскольку Лх=хЛ=х справедливо для любой цепочки х, мы имеем
{Л}А=А{Л}=А.
Заметьте, что здесь символ Л заключен в фигурные скобки. Произведение определено для множеств, тогда как Л является символом, а не множеством. {Л} — это множество, состоящее из пустого символа Л.
Мы можем теперь определить степени цепочек. Если х — цепочка, то х° — пустая цепочка Л, х1=х, хг=хх, х3=ххх, и в общем случае хп определяется как
хххх ... хх
п раз
Для п>-0 имеем хп=ххп-1=(хп-1)х.
Так же можно определить степени алфавита А:
А°={Л}, А1=А, АП=ААП-1 для п>0.
Используя это, определим две последние операции в этом разделе — итерацию А* множества А и усеченную итерацию А+ множества А:
А+=А! U А8 и . . . и A11 U . . .,
А*=А° U А+.
*) Говорят также конкатенация.— Прим. ред.
2 д. Грио
34
ГЛАВА 2
Таким образом, если А={а, Ь), то А* включает цепочки
A, a, b, аа, ab, ba, bb, ааа, aab ....
Заметим, что А+=АА* = (А*)А.
Примеры:
Пусть z=abb. Тогда |z|=3. Головы z есть A, a, ab, abb. Правильные головы z есть A, a, ab. Хвосты z — это A, b, bb, abb. Правильные хвосты z — это A, b, bb.
Пусть х=а, z=abb. Тогда
zx=abba, xz—aabb,
z°=A, г1=аЬЬ, z1 2=abbabb, z3 4=abbabbabb,
|z°|=0, |z1|=3, |z2|=6, |z»|==9.
Пусть S={a, b, с}. Тогда
S+ = {a, b, c, aa, ab, ac, ba, bb, be, ca, cb, cc, aaa, . . .}.
S* = {A, a, b, c, aa, ab, ac, . . .}.
Иногда удобнее и, как правило, нагляднее писать х. . . вместо ху,
если нас не интересует у — остальная часть цепочки. Таким образом, три точки «. . .» обозначают любую возможную цепочку, включая и пустую. Наиболее часто встречаются следующие обозначения:
Обозначение Смысл
Z — X... x—голова цепочки z. Нам безразличен хвост.
z= .. .X х — хвост цепочки z. Нам безразлична голова.
z= .. .х... z = S... z = .. .S z = .. .S... х встречается где-то в цепочке z. Символ S—первый символ цепочки z. Символ S — последний символ цепочки z. Символ S встречается где-то в цепочке z.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.2
1. Дайте определения терминов «цепочка» и «катенация».
2. Пусть А={$}. Пусть z=$. Выпишите следующие цепочки и их длины: z, zz, z2, z5, z°. Каким будет множество А*?
3. Пусть А={0, 1, 2}. Пусть х=01, у=2 и z=011. Выпишите следующие цепочки, их длины, головы и хвосты: ху, yz, xyz, х*, (х3)(у2), (ху)2, (ухх)3.
4. Пусть А={0, 1,2}. Напишите 7 самых коротких цепочек мно-
жества А+ и множества А*.
ГРАММАТИКИ И ЯЗЫКИ
35
2.3. ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ ГРАММАТИКИ И ЯЗЫКА
Теперь мы в состоянии формализовать понятие правила, или, как иногда говорят, продукции, и абстрактно определить грамматику и язык, используя эти правила.
(2.3.1). Определение. Продукцией или правилом подстановки называется упорядоченная пара (U, х), которая обычно записывается так:
U : :==х,
где U — символ, ах — непустая конечная цепочка символов.
U называется левой частью, ах — правой частью продукции. Вместо термина продукция в дальнейшем мы чаще будем пользоваться .более коротким термином — правило.
(2.3.2.). Определение. Грамматикой G [Z] называется конечное, непустое множество правил; Z — это символ, который должен встретиться в левой части по крайней мере одного правила. Он называется начальным символом х). Все символы, которые встречаются в левых и правых частях правил, образуют словарь N.
Если из контекста ясно, какой символ является начальным символом Z, мы будем писать G вместо G [Z].
(2.3.3). Пример. Грамматика G1 [<число>] содержит следующие 13 правил:
(1) <число> : : = <чс>
(2) <чс> : : = <чс> <цифра>
(3) <чс> : :=<цифра>
(4) <цифра> : =0
(5) <цифра> : =1
(6) <цифра> : : =2
(7) <цифра> : : =3
(8) <цифра> : : =4
(9) <цифра> : : =5
(10) <цифра> : : =6
(11) <цифра> : : =7
(12) <цифра> : : =8
(13) <цифра> : : =9
V = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, <цифра>, <чс>, <число>}.
(2.3.4). Определение. В заданной грамматике Q символы, которые встречаются в левой части, правил, называются нетерми
х) Начальный символ называют также аксиомой или помеченным символом.— Прим. ред.
36
ГЛАВА 2
налами или синтаксическими единицами языка. Они образуют множество нетерминальных символов VN. Символы, которые не входят в множество VN, называются терминальными символами (или терминалами). Они образуют множество VT.
Таким образом, V=VN(jVT. Как правило, нетерминалы мы будем заключать в угловые скобки < и >, чтобы отличить их от терминалов. В грамматике G1 (пример 2.3.3) символы 0, 1,2, 3, 4, 5, 6, 7, 8, 9 — терминальные, а <число>, <чс> и <цифра> — нетерминальные. Мы будем пользоваться надстрочными литерами в том случае, когда нам надо отличить различные вхождения одного и того же нетерминала. Так, можно написать <чсх>: : = <чс2> <цифра> вместо <чс>: :=<чс><цифра>.
Множество правил U : :=х, U : :=у, . . ., U : :=z с одинаковыми левыми частями будем записывать сокращенно как
U : :=х|у|. . .|z
Например, грамматику G1 можно записать следующим образом:
<число> : :=<чс>
<чс> : :=<чс> <цифра> | <цифра>
<цифра> : :=0|1[2|3|4|5|6|7|8|9
Эта форма записи называется нормальной формой Бэкуса (сокращенно НФБ) или формой Бэкуса — Наура. Впервые она была разработана Бэкусом [59] для описания АЛГОЛа в сообщении о языке АЛГОЛ 60 (см. Наур [63а]). Наур был редактором этого сообщения. Существует несколько других способов записи для описания формальных языков. Мы их обсудим позднее.
Теперь, когда есть грамматика, как определить язык, соответствующий этой грамматике? Что является предложением этого языка? Для того чтобы ответить на эти вопросы, нам надо определить символы “=>” и “=>+”, которыми мы интуитивно пользовались в разд. 2.1 при выводе предложений. Неформально мы пишем v=>w, если можно вывести w из v, заменив нетерминальный символ в v на соответствующую правую часть некоторого правила.
(2.3.5). Определение. Пусть G — грамматика. Мы говорим, что цепочка v непосредственно порождает цепочку w, и обозначаем это как
v w,
если для некоторых цепочек х и у можно написать v=xUy, w=xuy,
где U : :=и — правило грамматики G. Мы также говорим, что w непосредственно выводима из v или что w непосредственно приводится (редуцируется) к v.
ГРАММАТИКИ И ЯЗЫКИ
37
Цепочки х и у могут, конечно, быть пустыми. Следовательно, для любого правила U :: —и грамматики G имеет место U и. В следующей таблице даны некоторые примеры непосредственных выводов, при этом используется грамматика G1 (пример 2.3.3) и обозначения из предыдущего определения.
V W Использованные правила X У
<число> => <ЧС> 1 А А
<чс> => <чс> <цифра> 2 А А
<чс> <цифра> => <цифра> <цифра> 3 А <цифра>
<цифра> <цифра> => 2 <цифра> 6 А <цифра>
2 <цифра> => 22 6 2 А
Рис. 2.2. Примеры непосредственных выводов.
(2.3.6). Определение. Говорят, v порождает w или w приводится к v, что записывается как v=>+ w, если существует последовательность непосредственных выводов
v=uO => ul => u2z>. . . => u[n]=w,
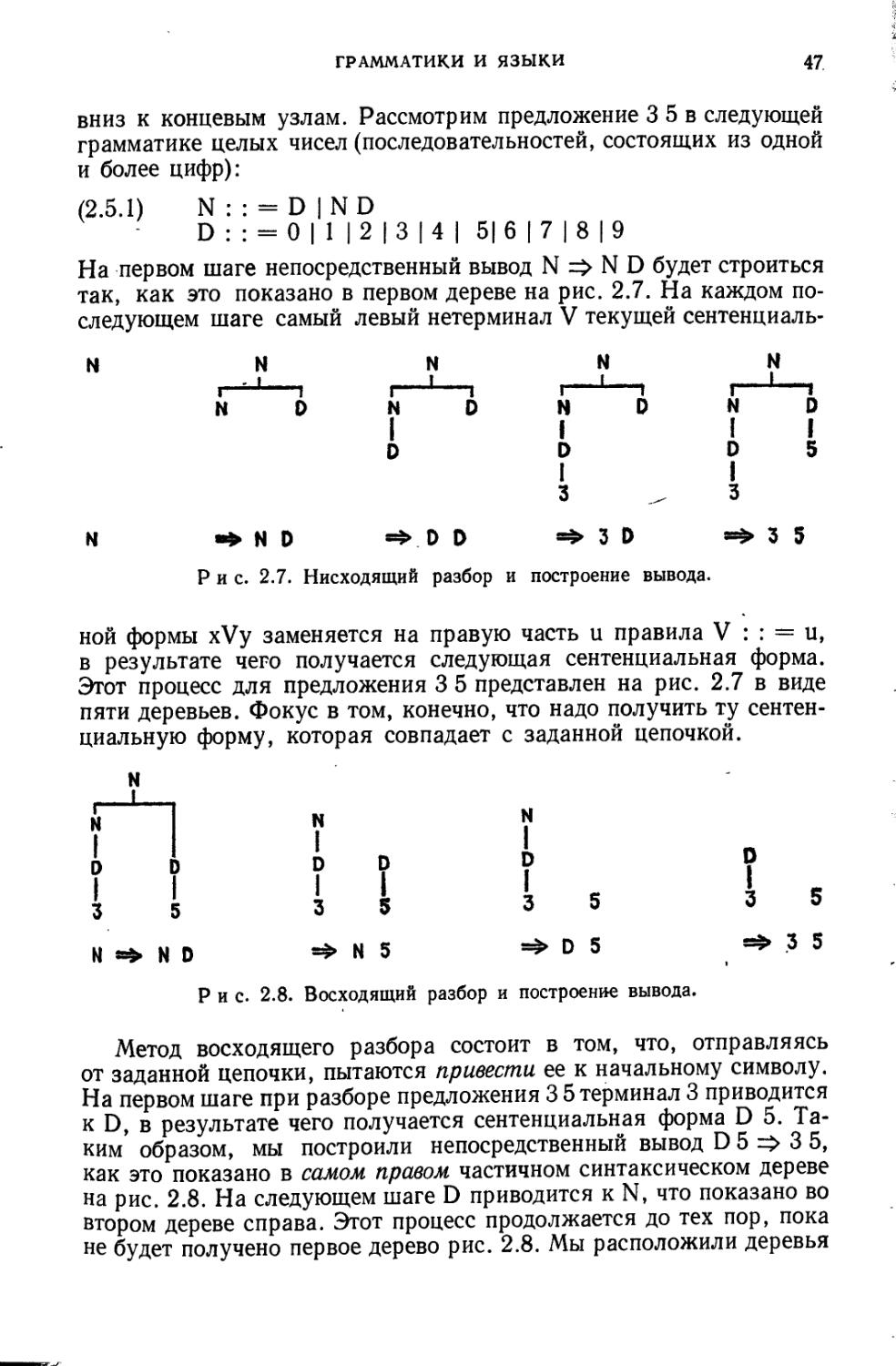
где n>0. Эта последовательность называется выводом длины п. Говорят также, что цепочка w является словом для v. И, наконец, пишут v=>* w, если v=>+ w или v=w.
Приведем пример вывода. Взгляните на первую строку рис. 2.2. Из нее видно, что <число>=>+ <чс>; длина вывода равна 1. Используя еще и строку 2 этой таблицы, получаем: <число> =>+<чс> <цифра>; длина вывода равна 2. Если мы просмотрим вниз все строки рис. 2.2, то увидим, что
<число> => <чс> => <чс> <цифра> => <цифра> <цифра> 2<цифра> ^22
Таким образом, <число> =>+ 22 и длина вывода равна 5.
Заметьте, что пока в цепочке есть хотя бы один нетерминал, из -нее можно вывести новую цепочку. Однако если нетерминальные символы отсутствуют, то вывод надо закончить. Поэтому называют «терминалом» (terminal — заключительный, конечный) символ, который не встречается в левой части ни одного из правил.
Каким будет язык, описанный грамматикой О[<число>]? В следующем определении утверждается, что этим конкретным языком является множество последовательностей из одной и более цифр.
(2.3.7). Определение. Пусть G [Z] — грамматика. Цепочка х называется сентенциальной формой, если х выводима из начального символа Z, т. е. если Z=>*x. Предложение — это сентенциальная форма, состоящая только из терминальных символов. Язык
38
ГЛАВА 2
L (G[Z]) — это множество предложений:
L(G)={x|Z=>*x и x£VT+}.
Таким образом, язык — это просто подмножество множества всех терминальных цепочек, т. е. цепочек в VT. Структура предложения задается грамматикой. Несколько различных грамматик могут, однако, порождать один и тот же язык. Мы будем часто говорить «предложение грамматики» вместо «предложение языка, определенного грамматикой».
(2.3.8). Пример. Определим грамматику для языка, содержащего вариации уже знакомого нам предложения “the big elephant ate the peanut”. Эта грамматика G2 1<предложение>) имеет вид
<предложение> :: = <подлежащее> <сказуемое>
<подлежащее> :: = <артикль> <прилагательное>
<существительное> | <местоимение>
<сказуемое> ::— <глагол> <прямое дополнение>
<прямое дополнение> :: — <артикль> <существительное> <местоимение> :: = he
<артикль> :: = the
<прилагательное> :: = big
<глагол> :: = ate
<существительное> :: = elephant | peanut
Множество терминальных символов есть {he, the, big, ate, elephant, peanut}. Язык L (G2) является множеством последовательностей этих терминальных символов, выводимых из начального символа <предложение>. Вот некоторые из таких предложений:
he ate the peanut
he ate the elephant
the big elephant ate the elephant
Ниже следует важное определение, и читатель не должен переходить к изучению дальнейшего материала до тех пор, пока смысл этого определения не будет ему полностью ясен.
(2.3.9). Определение. Пусть G[Z1 — грамматика. И пусть w=xuy — сентенциальная форма. Тогда и называется фразой сентенциальной формы w для нетерминального символа U, если Z=>* xUy и U =>+ и; и далее, и называется простой фразой, если Z =>* xUy и U=>u.
Следует быть осторожным с термином фраза. Тотфакт, что U => + и, вовсе не означает, что и является фразой сентенциальной формы хиу; необходимо также иметь Z =>* xUy. В качестве иллюстрации
ГРАММАТИКИ И ЯЗЫКИ
39
рассмотрим сентенциальную форму <чс>1 грамматики G1 (пример 2.3.3). Значит ли, что <чс> является фразой, если существует правило <число>: :=<чс>? Конечно, нет, поскольку не возможен вывод цепочки <число> 1 из начального символа <число>. Каковы же фразы сентенциальной формы <чс>1? Имеет место вывод
<число> => <чс> => <чс><цифра> => <чс>1
Таким образом,
(1) <число>=>* <чс> и <ЧС> =>+ <ЧС>1
(2) <число> <чс><цифра> и <цифра> =>+ 1
Следовательно, <чс>1 и 1 — фразы. Простой же фразой будет только 1. В дальнейшем мы часто будем говорить о самой левой простой фразе сентенциальной формы. Поэтому введем
(2.3.10). Определение. Основой всякой сентенциальной формы называется самая левая простая фраза.
Грамматика G1 примера 2.3.3 описывает бесконечный язык, т. е. язык, состоящий из бесконечного числа предложений. Это обусловлено тем, что правило <чс>: :=<чс><цифра> содержит <чс> и в левой, и в правой частях, т. е. в некотором смысле символ <чс> сам себя определяет. В общем случае, если U=>+. . .U. . ., мы говорим, что грамматика рекурсивна по отношению к U. Если U=>+U..., то имеет место левая рекурсия, если U=>+. . .U, то имеет место правая рекурсия. Правило называется лево (право) рекурсивным, если оно имеет вид U: :=U. . . (U: : = . . .U). Если язык бесконечен, то определяющая его грамматика должна быть рекурсивной.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.3
1. Пусть 0[<ид>] состоит из правил
<ид>:: =а | ы с I <ид> а |<ид>с|<ид>01 <ид> 1
Выпишите VT и VN. Выведите в тех случаях, когда это возможно, цепочки a, abO, aOcOl, 0а, 11, ааа.
2. Каковы предложения языка L(G1) для G1 из примера 2.3.3?
3. Опишите грамматику, язык которой состоит из множества четных целых чисел.
4. Опишите грамматику, язык которой состоит из множества четных целых чисел, исключая числа с нулем вначале.
5. Пусть G состоит из правил <А>: :=Ь<А>|сс. Докажите, что ее, bcc, bbbcc, ... принадлежат L(G).
6. Постройте грамматику для языка
{abna|n=0, 1, 2, 3, . . .}.
40
ГЛАВА 2
7. Постройте грамматику для языка
{апЬп|п=1, 2, 3,
8. Следующая грамматика 03(<врж>] часто используется для описания арифметических выражении, в которых встречаются бинарные операторы (под i подразумевается «идентификатор»):
<врж> : :=<терм>|<врж>+<терм>|<врж> — <терм>
<терм> : :=<множ>|<терм>*<множ>|<терм>/<множ>
<множ>_: :=(<врж>)Ц
Выведите следующие арифметические выражения: i, (i), i*i, ,i*(i+i).
9. Перечислите все фразы и простые фразы сентенциальной формы <врж>+<терм>*<множ> грамматики G3 (упражнение 8).
2.4. СИНТАКСИЧЕСКИЕ ДЕРЕВЬЯ И НЕОДНОЗНАЧНОСТЬ
Синтаксические деревья помогают понять синтаксис предложений. На рис. 2.1 показано то, что мы называем синтаксическим деревом. В качестве иллюстрации построим дерево для следующего вывода предложения 22 грамматики G1 (пример 2.3.3):
(2.4.1) <число> <чс> => <чс> <цифра>
=><цифра> <цифра>=>2 <цифра>=>22
Отправляясь от начального символа <число>, нарисуем его куст для того, чтобы указать первый непосредственный вывод (рис. 2.3, а). Куст узла — это множество подчиненных ему узлов (символов). Символы куста образуют цепочку, которая заменяет имя куста в первом непосредственном выводе <число>=><чс>.
<число>
<чс>
<шло>
<чс>
5зел
<чс> <цифро>
а Ъ
Рис. 2.3. Синтаксические деревья для двух выводов.
Чтобы показать второй вывод, из узла, представляющего заменяемый символ, рисуется куст, узлы которого образуют цепочку, заменяющую этот символ (рис. 2.3, Ь). Поступая таким же образом, мы построим одну за другой три синтаксические диаграммы, показанные на рис. 2.4.
ГРАММАТИКИ И ЯЗЫКИ
41
Концевые (висячие) узлы синтаксического дерева — это узлы, не имеющие подчиненного куста. При чтении слева направо концевые узлы образуют цепочку, вывод которой представлен деревом. Таким образом, после третьего непосредственного вывода в (2.4.1) цепочка концевых узлов — суть <цифра> <цифра> (см. рис. 2.4, а).
Концевой куст — это куст, все узлы которого концевые. На рис. 2.3, b один концевой куст; его узлы <чс> и <цифра>. На рис. 2.4, с два концевых куста с узлами 2 и 2.
<число>
<чс>
, 1----1——1 к
<чс> <цифро>
<цифра>
а
<чисяо>
<чс>
1------1-----1
<чс> <цифра>
<цифра>
2
<число>
<ЧС> F-----1-----1
<чс> <цифра>
<цифра> г
2
Р и е. 2.4. Синтаксические деревья для вывода (2.4.1).
Когда речь идет о деревьях, часто используется следующая терминология. Пусть N — узел дерева. Сыновьями N называются узлы куста, подчиненного N. N — их отец. Сыновья называются братьями > самым младшим считается самый левый из них. На рис. 2.4, b <чс> является единственным сыном узла <число>. Тот же самый <чс> имеет двух сыновей: <чс> и <цифра>. Отцом узла 2 является <цифра>.
Поддерево синтаксического дерева состоит из узла дерева (называемого корнем поддерева) вместе с той частью дерева (если она имеется), которая исходит из него. Поддеревья тесно связаны с фразами; концевые узлы образуют фразу для корня данного поддерева. Проследим это более подробно. Если U — корень поддерева и если и — цепочка из концевых узлов поддерева, то U г>+ и. Пусть х — цепочка концевых узлов слева от и, а у — цепочка концевых узлов справа от и, т. е., хиу — сентенциальная форма, заданная деревом. Тогда Z=>*xUy, а это означает, что и есть фраза для U в хиу.
Построение вывода по дереву
Можно восстановить вывод по синтаксическому дереву при помощи обратного процесса. Из рис. 2.4, с видно, что концевые узлы образуют цепочку 22. Самый правый концевой куст указывает не-, посредственный вывод:
2 <цифра> => 2g
42
ГЛАВА 2
Чтобы пройти по синтаксическому дереву до 2 <цифра>, мы отсекаем куст от дерева — удаляем его. Например, отсекание этого куста (на рис. 2.4, с) дает нам дерево на рис. 2.4, Ь. Этот процесс часто называют непосредственной редукцией.
Рассматривая рис. 2.4, Ь, мы видим, что последним здесь должен быть вывод <цифра> <цифра>=>2 <цифра>. Это нам дает
<цифра> <цифра> => 2 <цифра> => 22
Продолжаем процесс, всегда восстанавливая последний непосредственный вывод, на который указывает концевой куст синтаксического дерева, и затем отсекая этот куст.
Подводя итог, сформулируем следующие положения о синтаксических деревьях:
для каждого синтаксического дерева существует по крайней мере один вывод;
для каждого вывода есть соответствующее синтаксическое дерево (но несколько разных выводов могут иметь одно и то же дерево);
куст дерева указывает на непосредственный вывод, в котором имя куста заменяется узлами куста. Следовательно, в грамматике существует правило, левой частью которого является имя куста, а правой частью — цепочка из узлов куста;
концевые узлы дерева образуют выводимую сентенциальную форму;
пусть U — корень поддерева для сентенциальной формы w= = xuy, где и образует цепочку концевых узлов этого поддерева. Тогда и—фраза сентенциальной формы w для U. Она является простой фразой, если поддерево представлено единственным кустом.
Кроме вывода (2.4.1), есть другой вывод предложения 22 в G1:
(2.4.2) <число> => <чс> =$> <чс> <цифра>
=> <цифра> <цифра> => <цифра> 2 => 22
у него то же самое синтаксическое дерево, что и у вывода (2.4.1). В действительности есть еще и третий вывод 22:,
(2.4.3) <число>. => <чс> => <чс> <цифра> => <чс>2 => <цифра>2 => 22
Заметьте, что эти выводы отличаются лишь порядком применения правил и что синтаксическое дерево не определяет точный порядок, в соответствии с которым осуществляется вывод. На данном этапе это различие порядка в выводах для нас несущественно, и мы считаем, что выводы эквивалентны, если им соответствует одно и то же дерево.
ГРАММАТИКИ И ЯЗЫКИ
43
Неоднозначность
Гораздо более важным является вопрос неединственности синтаксического дерева. Рассмотрим грамматику, содержащую среди прочих правила:
<предложение> :: = <подлежащее> <сказуемое>
<предложение> :: = <сказуемое> <прямое дополнение>
<подлежащее> :: = <существительное>
<прямое дополнение> :: = <существительное>
<сказуемое> ::= <глагол>
<существительное> :: = time | flies
<глагол> :: = time | flies
По этим правилам мы могли бы образовать предложение “time flies” двумя различными способами с различными синтаксическими деревьями (рис. 2.5).
<предложение>
<подлежацее> <сказуемое> х I I
<суи|ествительное> <глаеол>
. I I
time flies
<предложение>
<спазуемое> <прямое йополненце>
<глагол> <су(цестеительное>
time flies
Рис. 2.5. Синтаксические деревья для неоднозначного предложения.
В английском языке каждое из этих предложений имеет смысл— либо “time flies by very quickly” (время летит очень быстро), либо “go find out how fast flies fly” (выясните, как быстро летают мухи). Дело в том, что без контекста мы не можем понять предложение, поскольку не можем его правильно разобрать; мы не можем однозначно разделить его на составные части. Поэтому, если компилятор должен уметь транслировать все правильные исходные программы, резонно потребовать, чтобы язык был однозначно определен. Теперь введем следующее
(2.4.4). Определение. Предложение грамматики неоднозначно, если для его вывода существуют два синтаксических дерева. Грамматика неоднозначна, если она допускает неоднозначные предложения, в противном случае она однозначна.
Заметим, что мы называем неоднозначной грамматику, а не сам язык. Изменяя неоднозначную грамматику, но, конечно, не изменяя ее предложения, можно иногда получить однозначную грамматику для того же самого множества предложений. Однако есть языки,
44
ГЛАВА 2
для которых не существует однозначной грамматики. Такие языки называются существенно неоднозначными (разд. 2.10).
Не надо забывать, что в данный момент речь идет лишь о синтаксисе. Согласно определению выше, предложение может быть однозначным, но мы можем все же не понять, что оно означает из-за неоднозначного смысла слов.
К сожалению, было доказано, что проблема распознавания неоднозначности алгоритмически неразрешима. Это означает, что не существует алгоритма (т. е. нельзя составить такой алгоритм), который воспримет любую НФБ-грамматику и заведомо определит за конечное число шагов, является она однозначной или нет. Можно, однако, разработать (гл. 5 и 6) достаточно простые, но нетривиальные условия, такие, что если грамматика им удовлетворяет, то можно утверждать, что она однозначна. Эти условия являются достаточными, но не необходимыми.
Однозначная грамматика для арифметических выражений
Если сентенциальная форма неоднозначна, то она имеет более чем одно синтаксическое дерево и поэтому в общем случае более чем одну основу. Покажем это на примере, который в то же время предоставит нам очень полезную грамматику для арифметических вы-
<Е>
I---------1-----Г
<Е> + <£>
I----1----1
<Е> * <Е>
а
<Е>
<Е> * <Е>
I------1-------1
<Е> + <Е>
б
Рис. 2.6. Два синтаксических дерева для <Е> 4- <Е> * <Е>.
ражений. Рассмотрим следующую грамматику арифметических выражений, в которой используются единственный операнд (в качестве идентификатора), круглые скобки и бинарные операторы 4- и *: (2.4.5) <Е> : :=<Е>+<Е>|<ЕЖЕ>|«Е» | i.
Сентенциальная форма <Е> + <Е>*<Е> имеет два синтаксических дерева (рис. 2.6) и две основы: <Е>4-<Е> и <Е>*<Е>. Если мы хотим разобрать эту сентенциальную форму, то с какой основы мы должны начать? Грамматика неоднозначна, и можно выбрать любую из основ. Таким образом, мы не можем сказать, что выполняется раньше: умножение или сложение.
ГРАММАТИКИ И ЯЗЫКИ
45
Рассмотрим теперь грамматику 03[<врж>] из упражнения 2.3.8:
(2.4.6) <врж> : : = <терм>|<врж>+<терм>|<врж>—<терм> <терм> : : = <множ>|<терм>»<множ>|<терм>/<множ> <множ> : : = (<врж»Ц
Единственное дерево для выражения i+i*i показано ниже, и, таким образом, в соответствии с этой грамматикой предложение однозначно. В действительности все предложения G3 однозначны. Теперь определим, согласно G3, что в выражении i+i*i должно выполняться раньше: умножение или сложение. Операндами для +, согласно дереву, являются <врж>, из которого получается i, и <терм>, из которого в свою очередь получается i#i. Это означает, что умножение должно быть выполнено первым для того, чтобы образовать <терм> для сложения; следовательно, умножение предшествует сложению.
(врж)
I-----------1------------, -
(врж) + (терм)
I I—----------1
(терм) (терм) * (множ)
I I I
(МНОЖ) (МНОЖ) i
i i
Грамматику G3 следует предпочесть грамматике (2.4.5) по двум причинам: она однозначна и указывает, что умножение предшествует сложению.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.4
1. Нарисуйте синтаксические деревья-для следующих выводов:
а) <число> => <чс> => <чс> <цифра> => <чс> 3 => <чс> <цифра> 3 => <чс> 2 3 => <цифра> 2 3 => 1 2 3
Ь) <число> => <чс> => <чс> <цифра> => <чс> 3
=> <чс> <цифра> 3 => <цифра> <цифра> 3
<цифра> 3^-123
Совпадают ли их синтаксические деревья?
2. Нарисуйте синтаксические деревья для следующих выводов:
а) <врж> => <терм> => <множ> =>i
b) <врж> =><терм>^> <множ>=>(<врж>)=>(<терм>)=^(<множ>)=^(1) с) <врж> + <терм> => + <множ> -f-i
46
ГЛАВА 2
3. Постройте выводы (врЖ)
(терм) I " —4--------1
(терм) * (множ)
I >
(МНОЖ) 1>
I
по следующим синтаксическим деревьям ' (врж)
(терм)
। " 1 I " ।
(терм) * (множ)
(множ) ।........ I — ।
| ( (врж) )
I ।I।
(врж) + (терм)
I I
(терм) (множ)
I !
(МНОЖ) I
4. Покажите, что следующая грамматика 0[<врж>] неоднозначна, построив 2 синтаксических дерева для каждого из предложений i+i*i и i~M+i:
<врж> : : =1|«врж>)|<врж> <оп> <врж>
<оп> : : =+|—1*|/
5. Покажите, что предложения i-H*i и i+i-f-i грамматики G3 (2.4.6) однозначны. Какой оператор старше в предложении i+i*i? В предложении
2.5. ЗАДАЧА РАЗБОРА
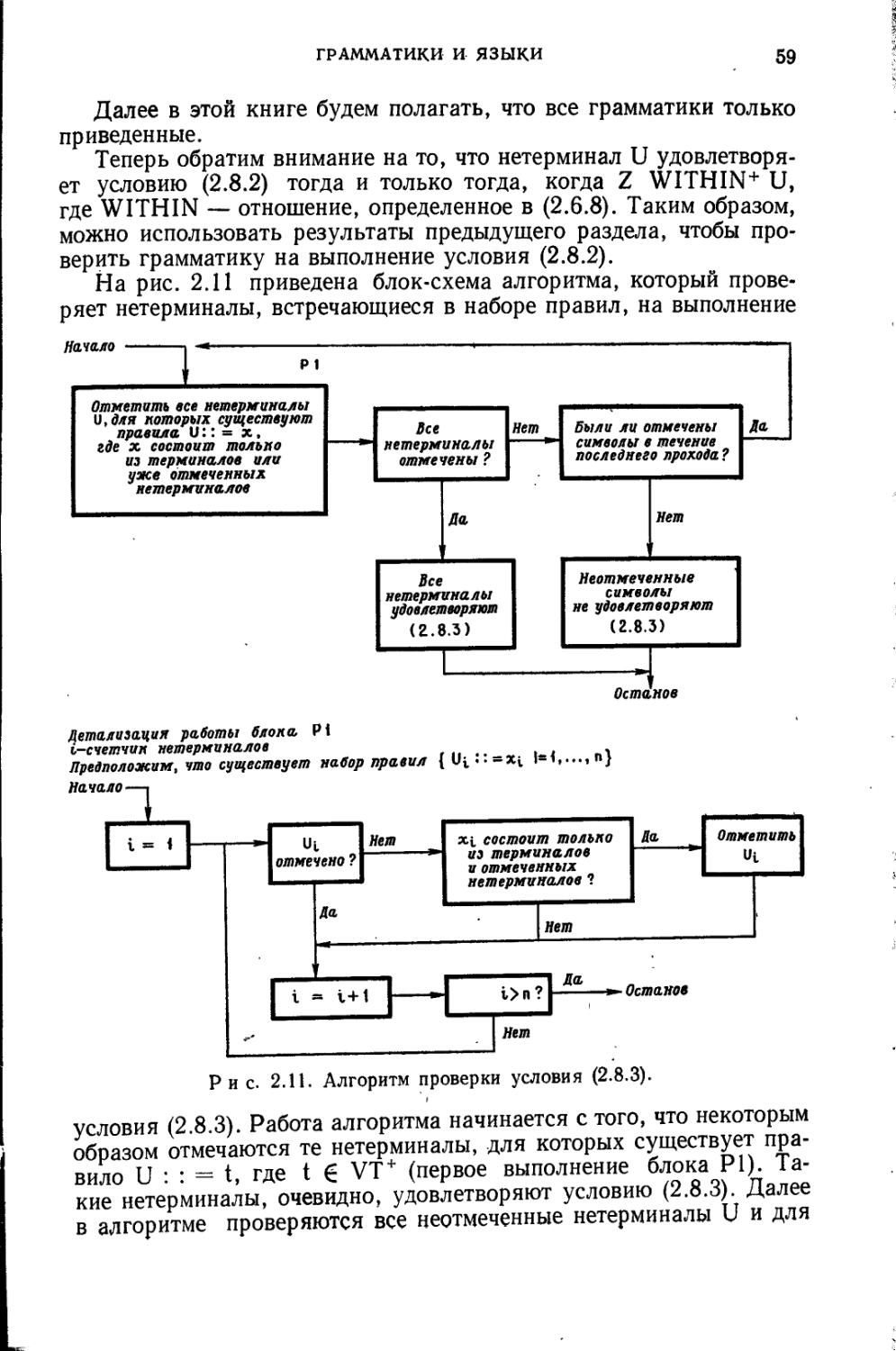
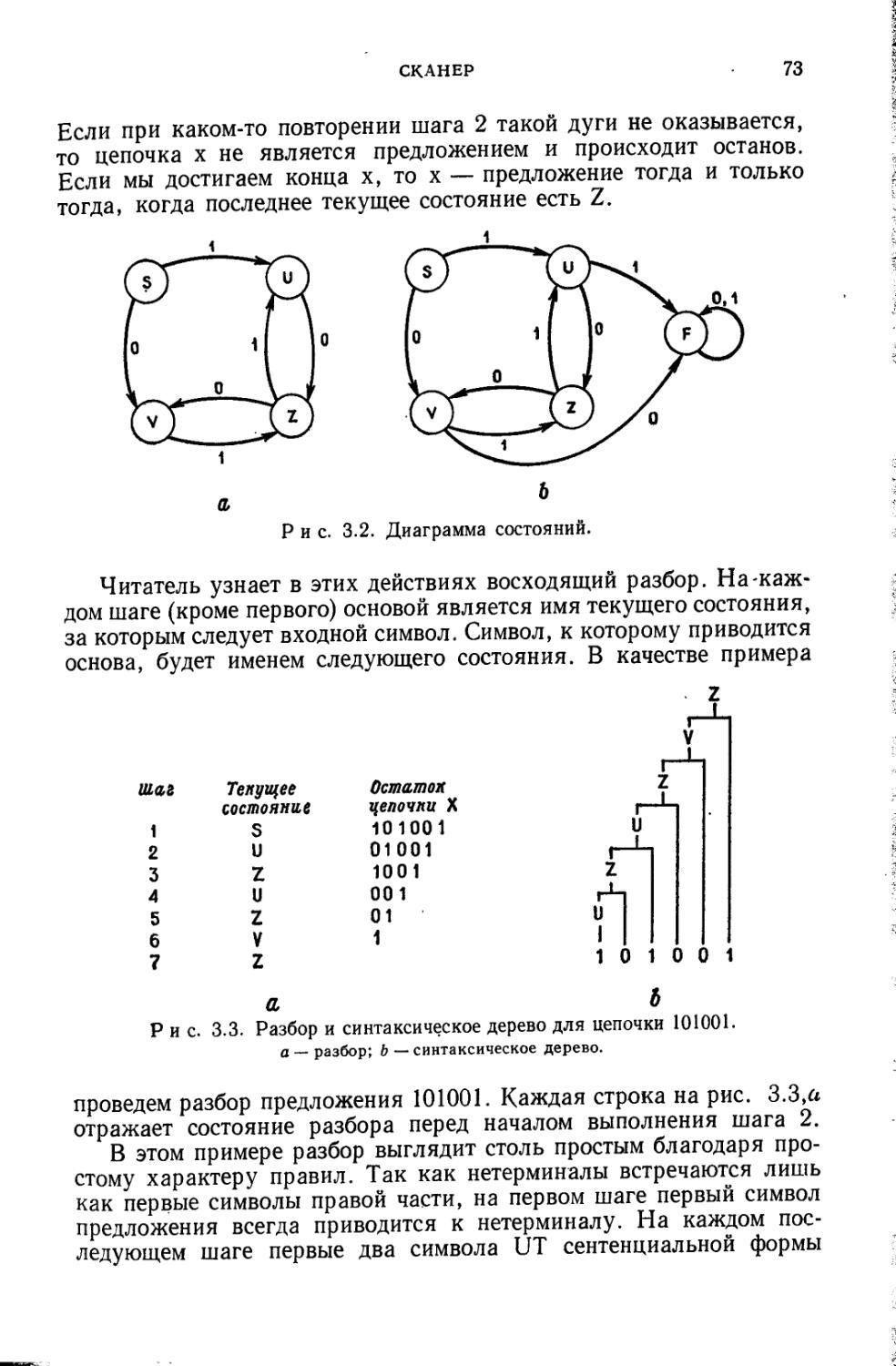
Разбор сентенциальной формы означает построение вывода и, возможно, синтаксического дерева для нее. Программу разбора называют также распознавателем, так как она распознает только предложения рассматриваемой грамматики. Именно это и является нашей задачей в данный момент, поскольку мы хотим распознавать программы, написанные на языке программирования.
Все алгоритмы разбора, которые мы описываем, называются алгоритмами разбора слева направо ввиду того, что они обрабатывают сначала самые левые символы рассматриваемой цепочки и продвигаются по цепочке вправо только тогда, кбгда это необходимо. Мы могли бы подобным же образом определить разбор справа налево, но он менее естествен. Инструкции в программе выполняются слева направо, да и мы читаем тоже слева направо.
Различают две категории алгоритмов разбора: нисходящий (сверху вниз) и восходящий (снизу вверх) J). Эти термины соответствуют способу построения синтаксических деревьев. При нисходящем разборе дерево строится от корня (начального символа)
х) Нисходящий (top-down) и восходящий (bottom-up) разбор называют также соответственно разверткой и сверткой.— Прим. ред.
ГРАММАТИКИ И ЯЗЫКИ
47
вниз к концевым узлам. Рассмотрим предложение 3 5 в следующей грамматике целых чисел (последовательностей, состоящих из одной и более цифр):
(2.5.1) N : : = D | N D
D:: = 0|l|2|3|4| 5| 6 | 7 | 8 | 9
На первом шаге непосредственный вывод N => N D будет строиться так, как это показано в первом дереве на рис. 2.7. На каждом последующем шаге самый левый нетерминал V текущей сентенциаль-
N
N N N N
I—' ’ i Г— 1 "I г—-1 "*Л Г~~
ND ND ND ND
I I II
D D D 5
I I
3 3
N D =>D D => 3 D =» 3 5
Рис. 2.7. Нисходящий разбор и построение вывода.
ной формы xVy заменяется на правую часть и правила V : : = и, в результате чего получается следующая сентенциальная форма. Этот процесс для предложения 3 5 представлен на рис. 2.7 в виде пяти деревьев. Фокус в том, конечно, что надо получить ту сентенциальную форму, которая совпадает с заданной цепочкой.
N
N * N N
D D D D D О
’I 1 I Ic I е
35 35 35 35
N =» N 0 => N 5 => D 5 =>.3 5
Рис. 2.8. Восходящий разбор и построение вывода.
Метод восходящего разбора состоит в том, что, отправляясь от заданной цепочки, пытаются привести ее к начальному символу. На первом шаге при разборе предложения 3 5 терминал 3 приводится к D, в результате чего получается сентенциальная форма D 5. Таким образом, мы построили непосредственный вывод D 5 => 3 5, как это показано в самом правом частичном синтаксическом дереве на рис. 2.8. На следующем шаге D приводится к N, что показано во втором дереве справа. Этот процесс продолжается до тех пор, пока не будет получено первое дерево рис. 2.8. Мы расположили деревья
48
ГЛАВА 2
на рисунке справа налево, потому что такое расположение лучше иллюстрирует построенный вывод, который теперь читаем, как обычно, слева направо. Заметим, что выводы, произведенные двумя различными распознавателями, различны, но имеют одно и то же синтаксическое дерево.
Поскольку мы будем часто ссылаться на тип вывода, который получается при восходящем разборе слева направо, введем еще один новый термин. Заметим, что в таком разборе на каждом шаге редуцируется основа (самая левая простая фраза) текущей сентенциальной формы и поэтому цепочка справа от основы всегда содержит только терминальные символы.
(2.5.2). Определение. Непосредственный вывод xUy => х и у называется каноническим и записывается xUy => х и у, если у содержит только терминалы. Вывод w =>+ v называется каноническим и записывается w =>+ v, если каждый непосредственный вывод в нем является каноническим.
Каждое предложение, но не каждая сентенциальная форма имеет канонический вывод. Рассмотрим в качестве примера сентенциальную форму 3D грамматики (2.5.1). Ее единственным выводом является
<число >=>ND=>DD=>3D
И второй, и третий непосредственные выводы не являются каноническими, но это не должно нас смущать, поскольку мы в основном интересуемся разбором (анализ) программ, которые являются предложениями языка программирования. Сентенциальная форма, которая имеет канонический вывод, называется канонической сентенциальной формой.
Мы, конечно, еще не касались главных проблем разбора.
1. Предположим, что при нисходящем разборе надо заменить самый левый нетерминал V, и пусть имеется п правил:
V : : = х, | х2 | . . . | хп.
Как узнать, какой цепочкой х, следует заменить V?
2. При восходящем разборе на каждом шаге редуцируется основа. Как найти основу и то, к чему она должна приводиться?
На эти вопросы не всегда легко ответить. Это будет хорошо видно при выполнении упражнения 2. В гл. 4 проблема рассматривается применительно к нисходящему разбору, тогда как в гл. 5 и 6 обсуждаются различные приемы, позволяющие решить проблему восходящего разбора.
Одним из решений является выбор некоторого из возможных вариантов наугад в предположении, что он верен. Если позднее обнаружится ошибка, то мы должны вернуться назад и попытаться применить другой вариант, Этот прием называется возвратом.
ГРАММАТИКИ И ЯЗЫКИ
49
Очевидно, что возвраты могут привести к чрезмерному расходу времени.
Другим решением является просмотр контекста вокруг обрабатываемой в данный момент подцепочки. Именно так мы поступаем, когда вычисляем выражение, подобное А + В * С. Мы задаем себе вопрос, „можно ли вначале вычислить А 4- В“, и отвечаем на него отрицательно, замечая, что за А + В следует * .
Один из первых алгоритмов разбора, который действительно использовался в компиляторе, был описан Айронсом (61а]. Алгоритм применялся в синтаксически ориентированном трансляторе Ингермана [66].
Метод, положенный в основу этого алгоритма, является смесью нисходящего и восходящего методов, и мы не будем обсуждать его подробнее.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.5
1. Найдите канонический разбор предложений 561, 0 и 0012 грамматики G1 (пример 2.3.3).
2. Проведите разбор предложений (,) (*, i (, (+(, (+(i (и (+) (i (* i( грамматики
<цель>: : = VI
VI : : = V2 | VI i V2
V2 : : = V3 | V2 + V3 | i V3
V3 : : = ) VI * | (
3. Дайте характеристику языка, порождаемого грамматикой V : : = aaV | Ьс.
2.6. НЕКОТОРЫЕ ОТНОШЕНИЯ ПРИМЕНИТЕЛЬНО К ГРАММАТИКАМ
Отношения
Символы “=>” и “=>+”, определенные в разд. 2.3, являются примерами отношений между цепочками. Вообще говоря, (бинарным) отношением на множестве является любое свойство, которым обладают (или не обладают) любые два упорядоченных символа этого множества.
Другим примером является отношение МЕНЬШЕ ЧЕМ (<), определенное на множестве целых чисел: i С j тогда и только тогда, когда j — i является положительным ненулевым целым числом. Нематематическим является отношение РЕБЕНОК, определенное на множестве людей. Некто А либо является ребенком В; либо нет,
50
ГЛАВА 2
Мы используем инфиксные обозначения для отношений: если между элементами с и d некоторого множества имеет место отношение, то мы пишем cRd. (Заметим также, что важен порядок двух объектов: из eRd автоматически не следует dRc.) Можно также рассматривать отношение как множество упорядоченных пар, для которых данное отношение справедливо: (с, d) £ R тогда и только тогда, когда cRd.
Мы говорим, 5J0 отношение Р включает другое отношение R, если из (с, d) £ R следует (с, d) £ Р.
Отношение, обратное отношению R, записывается как R-1 и определяется следующим образом: с R-1 d тогда и только тогда, когда dRc.
Отношение, обратное отношению БОЛЬШЕ ЧЕМ, есть МЕНЬШЕ ЧЕМ. Отношение, обратное отношению РЕБЕНОК, есть РОДИТЕЛЬ.
Отношение R называется рефлексивным, если cRc справедливо для всех элементов с, принадлежащих множеству. Например, отношение МЕНЬШЕ ЧЕМ ИЛИ РАВНО (^) является рефлексивным (i i для всех действительных чисел i), тогда как отношение МЕНЬШЕ ЧЕМ таковым не является.
Отношение R называется транзитивным, если aRb и bRc влечет за собой a R с. Отношение МЕНЬШЕ ЧЕМ над целыми числами является транзитивным. Отношение РЕБЕНОК не является транзитивным; если Джон сын Джека и Джек сын Джила, то, очевидно, Джон не является сыном Джила.
Для любого отношения R определим новое отношение R+ и назовем его транзитивным замыканием R. Оно называется так потому, что включается в любое транзитивное отношение, которое включает в себя R. Другими словами, предположим, что Р — транзитивное отношение, которое включает в себя R : из (с, d) С R следует (с, d) С Р. Тогда Р также включает в себя R+.
Прежде всего для двух заданных отношений R и Р, определенных на одном и том же множестве, введем новое отношение RP, названное произведением R и Р : cRPd тогда и только тогда, когда существует такое е, что cRe иеРб. Умножение бинарных отношений ассоциативно: R (PQ) = (RP) Q для любых отношений R, Р и Q.
В качестве примера рассмотрим отношения R и Р над целыми числами, определенные следующим образом:
aRb тогда и только тогда, когда b = а + 1,
аРЬ тогда и только тогда, когда b = а + 2.
Очевидно, что aRPb, тогда и только тогда, когда есть такое с, что aRc и сРЬ, т.е. тогда и только тогда, когда b = а + 3.
Используя произведение, определим теперь степени отношения R следующим образом:
ГРАММАТИКИ И ЯЗЫКИ
51
R1 = R, R2 = RR, Rn = Rn-1 R = RRn-1 для n > 1. Определим R° как единичное отношение:
aR°b тогда и только тогда, когда а = Ь.
И, наконец, транзитивное замыкание R+ отношения R определяется следующим образом:
(2.6.1). aR+b тогда и только тогда, когда aRnb для некоторого п > 0.
Очевидно, если aRb, то aR+b. Доказательство того, что R + действительно является транзитивным, предоставляется читателю в качестве упражнения. Ясно, почему для транзитивного замыкания выбрано обозначение R + ; когда отношения рассматриваются как множества упорядоченных пар, мы имеем
R + =RiU R2 U R3 • • • •
Определим рефлексивное транзитивное замыкание R* отношения R как
aR*b тогда и только тогда, когда а=Ь или aR+b.
Таким образом, R* = R° U R1 U R2 . . . .
Отношения применительно к грамматикам
Чем же вызван такой интерес к отношениям? Во-первых, теперь должно быть очевидно, что символ =>-Т (см. 2.3.6) обозначает не что иное, как транзитивное замыкание отношения =>, определенного в (2.3.5)! И, во-вторых, с грамматиками связано несколько важных символьных множеств, которые в дальнейшем нам придется построить. Эти множества легко определяются в терминах совсем простых отношений и их транзитивных замыканий. В разд. 2.7 мы дадим один несложный алгоритм, который позволит нам построить все необходимые множества из простых отношений. Единственное требование заключается в том, чтобы отношения были определены на конечном множестве элементов. Перед тем как приступить к этому алгоритму, рассмотрим те множества, которые нам будут необходимы.
Если задана грамматика и нетерминальный символ U, то нам необходимо знать множество головных символов в цепочках, выводимых из U. Таким образом, если U =>+ Sx, то цепочка Sx выводима из U и S принадлежит множеству. Назовем это множество голова (U) и определим его формально следующим образом:
(2.6.2). голова(и) : : = {S | U =>+ S . . .}.
(Напомним, что тремя точками «. . .» обозначается цепочка (возможно, пустая), которая в данный момент нас не интересует.)
52
ГЛАВА 2
В большинстве случаев такое определение могло бы быть удовлетворительным. Заметим, однако, что в определении используется отношение заданное на бесконечном множестве цепочек в словаре V, и хотя само множество голова(11) конечно, при его построении могут возникнуть трудности. Поэтому мы переопределим множество голова(Ц), используя другое отношение, заданное на конечном множестве следующим образом. Определим отношение FIRST (первый) в конечном словаре V грамматики следующим образом:
(2.6.3). U FIRST S тогда и только тогда, когда существует правило U : : = S . . . .
Затем, согласно определению транзитивного замыкания, имеем
(2.6.4). U FIRST* S тогда и только тогда, когда существует непустая последовательность правил U : : = S1 , . ., S1 : : = S2 . . ., . . Sn : : = S . . . .
Из этого, очевидно, вытекает, что
U FIRST* S тогда и только тогда, когда U =>+ S . . . .
Заметим, что если отношение FIRST* рассматривать как множество, то оно полностью определяет множество голова(Ц) из (2.6.2) для всех символов U словаря V : голова (U) — ]S | (U, S)b FIRST*}. (2.6.5). Пример. Чтобы проиллюстрировать оба отношения FIRST и FIRST*, выпишем несколько правил и справа от каждого из них укажем отношение FIRST, выведенное из этого правила.
Правило A:: =Af А:: =В В:: =DdC Отношение A FIRST А A FIRST В В FIRST D
(2.6.6) В:: =De В FIRST D
С::=е С FIRST е
D:: =Bf D FIRST В
Таким образом, мы имеем следующие пары в FIRST* :
(А, А) (А, В) (A, D) (В, В) (В, D) (D, В) (D, D) (С, е)
Следовательно, головными символами цепочек, выводимых из А, будут А, В и D, из В — В и D, из С — е.
Есть еще три других множества, которые мы хотим здесь определить. Они могут быть определены тем же путем, что и FIRST*. Первое из них — это множество символов, которыми оканчиваются цепочки, выводимые из некоторого символа U. Оно определяется для всех символов U через отношение LAST*, являющееся транзитивным замыканием отношения LAST (последний):
ГРАММАТИКИ и языки 53
(2.6.7). U LAST S тогда и только тогда, когда существует правило U S.
Второе множество — это множество внутренних символов цепочек, выводимых из нетерминала U. Оно определяется через отношение WITHIN+, являющееся транзитивным замыканием отношения WITHIN (внутри).
(2.6.8). U WITHIN S тогда и только тогда, когда существует правило U :: = ... S .. . .
И, наконец, определим множество символов S, которые выводимы из нетерминала U. Оно определяется через отношение SYMB + , являющееся транзитивным замыканием отношения SYMB (симв):
(2.6.9). U SYMB S тогда и только тогда, когда существует правило U : : = S .
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.6
1. Являются ли следующие отношения рефлексивными? Как выглядит транзитивное и рефлексивно-транзитивное замыкание каждого из них?
а) НИЖЕ ЧЕМ (на множестве людей).
Ь) > (БОЛЬШЕ ЧЕМ) на множестве действительных чисел.
с) отношение R на множестве действительных чисел, определенное следующим образом: aRb тогда и только тогда, когда а = — Ь.
2. Выпишите множества FIRST*, LAST* и SYMB* для грамматики G1 примера (2.3.3).
3. Докажите, что умножение бинарных отношений ассоциативно.
4. Покажите, что R* является транзитивным для любого отношения R.
5. Пусть Р — любое транзитивное отношение, такое, что если cRb, то сРЬ. Доказать, что если cR*b, то сРЬ. (То есть R* является наименьшим транзитивным отношением, включающим R.)
6. Каков смысл произведения отношения ОТЕЦ на самого себя?
2.7. ПОСТРОЕНИЕ ТРАНЗИТИВНОГО ЗАМЫКАНИЯ ОТНОШЕНИЙ
Мы только что определили четыре важных множества, использовав при этом транзитивные замыкания для четырех очень простых отношений. Теперь вернемся к задаче построения транзитивного
54
ГЛАВА 2
замыкания для отношений, заданных в конечных множествах элементов.
Предположим, что для некоторого отношения R в множестве А и некоторого элемента U мы хотим построить множество
B = {S|UR+S},
где R+—транзитивное замыкание R. Если множество А бесконечно, то это может оказаться делом трудным (если вообще возможным), даже если множество В конечно. Трудность возникает из-за того, что нельзя ограничить число п так, чтобы отношение aRnb включало в себя отношение aR + b. Но если А конечно, то можно ограничить длину требуемой последовательности, что и показывает следующая теорема.
(2.7.1). Теорема. Пусть в алфавите А имеется п символов, и пусть R — произвольное отношение в А. Если для двух символов Si и b мы имеем SjR + b, то существует положительное целое k п, такое, что SxRkb.
Доказательство. Так как S^R+ Ь, то существует целое р >• 0, такое, что Sx R₽b. Это означает, что существуют символы S2, Sa...Sp в А, такие, что
Si R S,. S2 R Sa, ..., Sp_x R Sp и Sp R b
(по определению Rp). Предположим, что наименьшее из р больше, чем п. Тогда для этого наименьшего р и двух целых чисел i и j, для которых справедливо i < j р, мы должны иметь Sj = Sj( так как в А только п символов. Но тогда отношения
Si R S2, . . ., Sj_i R Si,
Sj R Sj+1, . . ., Sp_x R Sp, Sp R b
показывают, что S2 Rk b, где k = p — (j — i), а это противоречит тому, что р было наименьшим. Таким образом, наше предположение, что р > п, ошибочно и теорема доказана.
Булевы матрицы и отношения
Теперь мы хотим представить отношения в алфавите в виде, удобном для машинной обработки. Для такого представления больше всего подходит булева матрица В. Это матрица, элементы которой В [i, j] могут принимать только значения 0 или 1 (ложь или истина). «Сложение» булевых матриц n-го порядка сводится к выполнению операции ИЛИ над соответствующими элементами матриц; элемент D [i, j] матрицы
D = В 4- С
определяется как
D [i, j]: = if В [i, j]=l then 1 else C £i, j]
ГРАММАТИКИ И ЯЗЫКИ
55
«Умножение» булевых матриц n-го порядка выполняется так же, как умножение над числовыми матрицами, за исключением того, что умножение заменяется операцией И, а сложение — операцией ИЛИ.
Таким образом, если В и С — две матрицы n-го порядка и D=BC, то элемент D [i, jl определяется как
D [i, j] : = В [l,j]4-B[i, 2]»С [2, j] + . . .+ В [i, nkC [n,j],
где » имеет тот же смысл, что и в следующем соотношении: а*Ь :: = if а=0 then 0 else b
Например, если то
R-Г00! и
В= 11 и
С=
1 01 10’
D1=B+C=[}°] и D2=BC= [?§].
Обратите, пожалуйста, внимание на то, что в этом контексте + и » имеют другой смысл.
Операция сложения булевых матриц ассоциативна (А+(В+С)= = (А + В) + С) и коммутативна (А+В — В+А), в то время как операция умножения только ассоциативна (А (ВС)=(АВ) С). Обе операции удовлетворяют также дистрибутивному закону (А (В + С) = АВ 4-АС).
Предположим, что отношение R определено на множестве S из и символов Sj..Sn. Для того чтобы представить это отношение,
построим булеву матрицу В n-го порядка с элементами В [i, j], равными 1 тогда и только тогда, когда Sj R Sj. Например, возьмем отношение FIRST, заданное в множестве {А, В, С, D, е, f) в (2.6.6). Матрица В для этого отношения изображена на рис. 2.9.
S1=A S2 = B S3 = C S4 = D S5 = e S6 = d S7 = f
S1=A 1 1 0 0 0 0 0
S2 = B 0 0 0 1 0 0 0
S3=C 0 0 0 0 1 0 0
S4 = D 0 1 0 0 0 0 0
S5 =e 0 0 0 0 0 0 0
S6 = d 0 0 0 0 0 0 0
S7 = f 0 0 0 0 0 0 0
Рис. 2.9. Матрица для отношения FIRST.
Теперь мы можем сделать следующее очевидное утверждение. (2.7.2). Матрица для отношения R-1 получается путем транспонирования булевой матрицы, представляющей R.
56
ГЛАВА 2
Рассмотрим произведение D = ВС двух матриц В и С, которые представляют два отношения Р и Q в алфавите S. Если D [i, jl= 1, то из определения D [i, j] мы должны иметь для некоторого к
В П, к] = 1 и С [к, j] — 1,
т. е. S! Р Sk и Sk Q Sj, а это означает, что (Sb Sj) принадлежит произведению PQ двух отношений Р и Q.
Наоборот, если (S1( Sj) € PQ, то существует к, такое, что SjPSk и SkQSj, hD [i, j] должно быть равно 1. Это означает, что матрица D представляет отношение PQ. Следовательно, доказана следующая
(2.7.3). Теорема. Произведение двух отношений, заданных в одном и том же алфавите, представляется произведением булевых матриц этих отношений.
Поскольку в общем случае Rn определяется рекурсивно как R Rn-1 для n> 1, то из этого по индукции следует, что матрица Bn = ВВВ . . . В (п раз) представляет отношение Rn. Из определения R* и теорем 2.7.1 и 2.7.3 мы сразу выводим следующую теорему.
(2.7.4). Теорема. Пусть В — булева матрица n-го порядка, представляющая отношение R, заданное в алфавите S из п символов. Тогда матрица В+, определенная как
В+ = В + ВВ + ВВВ 4- . . . + Вп, представляет транзитивное замыкание R+ отношения R.
Например, на рис. 2.10 показаны матрицы В, В2, .... В’ и В + для матрицы В, представленной на рис. 2.9 (отношение FIRST грамматики (2.6.6)). Из В+ мы вновь получаем следующие пары в FIRST* :
(А, А) (А, В) (A, D) (В, В) (В, D) (D, В) (D, D) (С, е).
Использование отношений и теории булевых матриц обеспечило нас единым алгоритмом для получения ряда различных важных множеств. Эти множества в дальнейшем будут применяться при построении алгоритмов грамматического разбора. Замечательно то, что используемые принципы являются прстыми и легкими для понимания.
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.7
1. Воршалл [62] разработал следующий эффективный алгоритм для вычисления матрицы В+ =В+ВВ + . . . + Вп отматрицыВ. Докажите, что его алгоритм работает правильно,
ГРАММАТИКИ И ЯЗЫКИ
57
1. Завести новую матрицу А — В.
2. Установить i : = 1.
3. Для всех j, если A [j, i] = 1, то для к — 1, п установить A [j, к] : = A [j, к] + А [i, к].
4. Увеличить i на 1.
5. Если i п, то перейти к шагу 3; в противном случае «останов».
2.8. ПРАКТИЧЕСКИЕ ОГРАНИЧЕНИЯ, НАЛАГАЕМЫЕ
НА ГРАММАТИКИ
В этом разделе мы снова рассмотрим грамматики, чтобы выявить некоторые ограничения, которые налагаются на них при их практическом использовании. Фактически эти условия не ограничивают множество языков, которые можно описать с помощью грамматик.
"1 1 0 0 0 0 О' ~1 1 0 1 0 0 on
0 0 0 1 0 0 0 В2 = 0 1 0 0 0- 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0 0
в = 0 1 0 0 0 0 0 В4 = 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 в* = 0 0 0 0 0 0 0
_0 0 0 0 0 0 0_ 1 _0 0 0 0 0 0 0j
“1 1 0 1 0 0 0~ Г1 1 0 1 0 0 0“1
В3 = 0 0 0 1 0 0 0 0 1 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 0 0
В5 = 0 1 0 0 0 0 0 в+ 0 1 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0
В’ = 0 0 0 0 0 0 0 0 0 0 0 0 0 0
। [_о 0 0 0 0 0 0 1 1 l0 0 0 0 0 0 0
Рис. 2.10. Вычисление В+ от В.
Алгоритмы, осуществляющие контроль выполнения этих условий для грамматик, описаны в общих чертах. Этот раздел должен также помочь читателю еще лучше освоить технику манипулирования грамматиками до того, как мы перейдем к задаче грамматического разбора.
Правило, подобное U : : = U, очевидно, не является необходимым для грамматики; более того, оно приводит к неоднозначности грамматики. Поэтому далее в этой книге мы полагаем, что
(2.8.1) грамматика не содержит правил вида U : : = U.
Грамматики могут также содержать лишние правила, которые невозможно использовать в выводе хотя бы одного предложения. Например, в следующей ниже грамматике G4 [Z] нетерминал
58
ГЛАВА 2
<d> не может быть использован в выводе какого-либо предложения, так как он не встречается ни в одной из правых частей правил:
Z : : = <Ь> е
<а> : : = <а> е |е
<Ь> : : = <с> е | <а> f
<с> : : == <с> f
<d> : : = f
Разбор предложений грамматики выполняется проще, если грамматика не содержит лишних правил. Можно с достаточным основанием утверждать, что если грамматика языка программирования содержит лишние правила, то она ошибочна. Следовательно, алгоритм, который обнаруживает лишние правила в грамматике, может оказаться полезным при проектировании языка.
Чтобы появиться в выводе какого-либо предложения, нетерминал U должен удовлетворять двум условиям. Во-первых, символ U должен встречаться в некоторой сентенциальной форме: _
(2.8.2) Z =>* xUy для некоторых цепочек х и у,
где Z — начальный символ грамматики. Во-вторых, из U должна выводиться цепочка t, состоящая из терминальных символов:
(2.8.3) U ^>+ t для некоторой t g VT+. ,
Совершенно ясно, что если нетерминальный символ U не удовлетворяет обоим этим условиям, то правила, содержащие U в левой части, не могут быть использованы ни в каком выводе. С другой стороны, если все нетерминалы удовлетворяют этим условиям, то грамматика не содержит лишних правил. Так, если U : : = и — правило, то, во-первых, Z =>* xUy => х и у. Во-вторых, так как мы можем вывести цепочку терминальных символов для каждого нетерминала, содержащегося в цепочке х и у, то
х и у =>* t для некоторой t g VT+.
В конечном итоге получаем Z =>+ t, т. е. вывод, в котором было использовано правило U : : = и.
В описанной выше грамматике G4 нетерминальный символ <с> не удовлетворяет условию (2.8.3), так как при непосредственном выводе он должен быть заменен на <с> f. Очевидно, что такая замена не может привести к цепочке из терминальных символов. Если отбросить все правила, которые нельзя использовать при порождении хотя бы одного предложения, то останутся правила
Z : : = <Ь> е, <а> : : = <а> е, <а> : : = е и <Ь> : : = <a>f.
(2.8.4). Определение. Грамматика G называется приведенной, если каждый нетерминал U удовлетворяет условиям (2.8.2) и (2.8.3).
ГРАММАТИКИ и языки
59
Далее в этой книге будем полагать, что все грамматики только приведенные.
Теперь обратим внимание на то, что нетерминал U удовлетворяет условию (2.8.2) тогда и только тогда, когда Z WITHIN* U, где WITHIN — отношение, определенное в (2.6.8). Таким образом, можно использовать результаты предыдущего раздела, чтобы проверить грамматику на выполнение условия (2.8.2).
На рис. 2.11 приведена блок-схема алгоритма, который проверяет нетерминалы, встречающиеся в наборе правил, на выполнение
Детализация работы блока Pi i-счетчик нетерминалов
Предположим^ что существует набор правил { Щ » п}
Рис. 2.11. Алгоритм проверки условия (2.8.3).
условия (2.8.3). Работа алгоритма начинается с того, что некоторым образом отмечаются те нетерминалы, для которых существует пра-вило и : : = t, где t € VT+ (первое выполнение блока Р1). Такие нетерминалы, очевидно, удовлетворяют условию (2.8.3). Далее в алгоритме проверяются все неотмеченные нетерминалы U и для
60
ГЛАВА 2
каждого из них делается попытка найти правило U : : = х, где х состоит только из терминальных символов или ранее отмеченных нетерминалов (повторное выполнение блока Р1). Символы, для которых такое правило существует, также, очевидно, удовлетворяют условию (2.8.3). Этот процесс продолжается до тех пор, пока либо все нетерминалы не будут отмечены, либо пока при выполнении блока Р1 не будет отмечено ни одного символа. Работа алгоритма завершена. Неотмеченные нетерминалы не удовлетворяют условию (2.8.3).
УПРАЖНЕНИЯ К РАЗДЕЛУ 2.8
1. Рассматривается грамматика
Z : : = Е + Т
Е : : = Е | S + F | Т
F : : = F J FP | Р
Р : : = G
G : : = G | GG | F
Т : : = T*i | i
Q : : = Е | Е + F | Т | S
S : : = i
Выполните следующие операции над этой грамматикой:
А. а) Постройте отношение WITHIN + .
b) Исключите все правила, содержащие (в левой или правой частях) нетерминалы, которые не удовлетворяют условию (2.8.2). В. а) Выполните алгоритм, показанный на рис. 2.11.
Ь) Исключите все правила, которые содержат нетерминалы, не удовлетворяющие условию (2.8.3).
с) Составьте список символов, которые до выполнения шага В считались нетерминальными, а теперь стали терминальными, d) Исключите все правила, содержащие символы, из списка, составленного в шаге с).
е) Повторяйте шаги с) и d) до тех пор, пока есть правила, которые следует исключить.
С. Повторяйте шаги А и В до тех пор, пока есть правила, которые следует исключить.
D. Грамматику, полученную в результате выполнения шага С, измените таким образом, чтобы она удовлетворяла условию (2.8.1). Опишите язык L(G) полученной грамматики.
2.9. ДРУГИЕ СПОСОБЫ ПРЕДСТАВЛЕНИЯ СИНТАКСИСА
В литературе для описания синтаксиса различных языков используются и некоторые другие способы записи. Мы хотели бы вкратце рассмотреть их. Эти способы обладают такой же мощно
ГРАММАТИКИ И ЯЗЫКИ
61
стью, что и НФБ, т. е. то, что может быть описано каким-либо из этих способов, может быть также описано и в НФБ. Но во многих отношениях они более наглядны, чем НФБ в чистом виде, и поэтому далее мы будем часто ими пользоваться.
Фигурные скобки
В НФБ только с помощью рекурсии можно задать список произвольного числа элементов. Таким образом, мы пишем
(2.9.1) <спис ид> : : = <ид> | <спис ид>, <ид> и
(2.9.2) <целое> : : = <цифра> | <целое> <цифра>
Предположим, что фигурные скобки { и } являются метасимволами и используются там, где необходимо указать, что цепочка, заключенная в фигурные скобки, может либо отсутствовать, либо повторяться любое число раз. Можно теперь переписать (2.9.1) и (2.9.2) как
(2.9.3) <спис ид> : : = <ид> {, <ид>}
<целое> : : =<цифра> {<цифра>}
Оба способа записи считаются эквивалентными. Для того чтобы задать минимальное или максимальное число возможных повторений цепочки, после фигурных скобок используются надстрочные и/или подстрочные индексы. Например, в языке ФОРТРАН идентификаторы состоят не более чем из 6 буквенно-цифровых литер. Они могут быть описаны следующим образом:
(2.9.4) <ид ФОРТРАНа> : : = <буква> { <бц»50
<бц> : : = <буква> | <цифра>
Эта же запись в НФБ выглядит неуклюже:
<ид ФОРТРАНа> : : = <буква> | <буква> <бц спис>
<бц спис> : : = <бц> | <бц> <бц>
| <бц> <бц> <бц>
| <бц> <бц> <бц> <бц>
| <бц> <бц> <бц> <бц> <бц>
Чтобы запись была линейной (без надстрочных или подстрочных индексов), примем соглашение, что минимальное число вхождений цепочки, заключенной в фигурные скобки, равно 0, а максимальное число будет записываться сразу вслед за закрывающей фигурной скобкой — без пробела между ними. Следовательно, (2.9.4) мы можем написать в виде
<ид ФОРТРАН а > : : = <буква> { <бц>}5
62
ГЛАВА 2
Заметим, что эта запись отличается от
(ид ФОРТРАНа> : : = (буква > {<бц>}5 поскольку во втором случае есть пробел между фигурной скобкой и 5.
Фигурные скобки позволяют нам использовать метасимвол | внутри них для указания на возможный выбор: так, {х | у | z) означает, что каждая из цепочек х, у или z может входить в последовательность нуль или более раз. Воспользуемся этой возможностью и перепишем синтаксис идентификаторов ФОРТРАНа таким образом:
<ид ФОРТРАНа>:: = (буква> {(буква> | (цифра>}5
Квадратные скобки
Квадратные скобки [ и ] часто используют для того, чтобы указать факультативную цепочку. Следовательно, квадратные скобки эквивалентны фигурным скобкам, за которыми непосредственно следует 1. Предположим, что требуется описать простую инструкцию цикла в языке, подобном АЛГОЛу, в которой либо начальное значение, либо величина шага (либо и то и другое одновременно) могут быть опущены. Это можно сделать так:
(1ог-цикл> :: = FOR <переменная> [: = (выражение» [STEP (выражение»
UNTIL (выражение> DO (инструкция>
Круглые скобки как метасимволы
В правых частях правил оператор конкатенации предшествует оператору выбора. Поэтому АВ | С означает либо АВ, либо С. Когда необходимо отказаться от нормального предшествования, круглые скобки используются почти так же, как это делается в арифметических выражениях. Таким образом, А (В | С) означает либо АВ, либо АС. Круглые скобки как метасимволы будут полезны, как мы сейчас увидим, при факторизации в правых частях. Однако возникает проблема, когда круглые скобки используются как терминальные символы языка. В дальнейшем мы будем использовать круглые скобки как обычные терминальные символы, если не будет оговорено противное.
Факторизация
Если круглые скобки используются в качестве метасимволов, мы можем записать правила
U : : = ху | xw | .. . | xz
ГРАММАТИКИ И ЯЗЫКИ
63
как
U : : = х (у | w | ... | z), где общая для всех альтернатив голова х вынесена за скобки. Скобки могут быть вложенными на какую угодно глубину, точно так же как в арифметических выражениях. Например, пусть У = У1У2 и w = уху8. Тогда приведенное выше правило можно переписать как
U : : = х (у! (у. | у8) |. . . I z) .
Позднее мы увидим, что в некоторых случаях благодаря факторизации облегчается разбор.
Правила Е : : = Т | Е + Т, обозначающие по крайней мере одно вхождение Т, за которым следует сколько угодно (в том числе нуль) вхождений + Т, можно переписать как
Е : : = Т {+ Т).
Более того, Е :: = Т | Е + Т | Е — Т можно записать как
Е : : = Т {(+ | - ) Т}.
Такое преобразование, которое позволяет избавиться от левой рекурсии в правиле, будет удобным при нисходящем разборе.
Метасимволы как терминальные символы
Иногда нам придется описывать язык, содержащий терминалы, такие, как : : = , | или {, которые одновременно являются метасимволами. В этом случае терминал заключается в кавычки, чтобы отличить его от метасимвола. Например, правила НФБ могут быть частично описаны так:
<правило> : : = <лев. часть> ' : : = ' <прав. часть>
Ясно, что это условие ставит кавычки в положение метасимвола. Кавычку, если она используется как терминальный символ, следует представлять двумя кавычками, заключая их в кавычки. Следовательно, соотношение <кавычка) описывает нетерми-
нальный символ <кавычка>; единственная цепочка, выводимая из него, состоит из одиночной кавычки.
2.10. КРАТКИЙ ОБЗОР ТЕОРИИ ФОРМАЛЬНЫХ ЯЗЫКОВ
Теория формальных языков быстро прогрессировала с тех пор, как Хомский впервые описал формальный язык. Однако большинство из опубликованных работ не имеет непосредственного отношения к интересующей нас проблеме разбора предложений языка
64
ГЛАВА 2
программирования; эти работы скорее касаются вопросов математической теории языков и грамматик. В них определяются различные классы языков с теми или иными свойствами. Языки характеризуются в терминах грамматик, которые порождают языки лишь из некоторого определенного класса, и в терминах автоматов (машин), которые распознают языки лишь из определенного класса. Вот несколько типичных вопросов, которые рассматриваются в таких работах: если L1 и L2 — два языка из класса Т, то является ли объединение (пересечение) двух языков также языком из класса Т? Однозначна ли грамматика? Существует ли алгоритм, определяющий однозначность любой грамматики из класса Т? Эквивалентны ли две грамматики в некотором смысле? Хорошей работой на эту тему можно считать публикацию Хопкрофта и Уллмана 169]. Монография Гинзбурга [66] содержит больше материала, но весьма лаконична и трудна для чтения *). Много статей на эту тему публикуется в двух периодических журналах Information and Control и Journal of the ACM.
Хомский [56] определил четыре основных класса языков в терминах грамматик, являющихся упорядоченной четверкой (V, Т, Р, Z), где
1. V — алфавит;
2. Т = V — алфавит терминальных символов;
3. Р — конечный набор правил подстановки;
4. Z — начальный символ, принадлежащий множеству V — Т.
Язык, порождаемый грамматикой, — это множество терминальных цепочек, которые можно вывести из Z. Различие четырех типов грамматик заключается в форме правил подстановки, допустимых в Р. Говорят, что G — это (по Хомскому) грамматика типа 0 или грамматика с фразовой структурой, если правила имеют вид
(2 .10.1) и : : = v, где u € V+ и v £ V*.
То есть левая часть ц может быть тоже последовательностью символов, а правая часть может быть пустой. Грамматикам с фразовой структурой посвящено сравнительно немного работ. Если ввести ограничение на правила подстановки, то получится более интересный класс языков типа 1, называемых также контекстно-чувствительными или контекстно-зависимыми языками* 2). В этом случае правила подстановки имеют следующий вид:
*) Рекомендуем также читателю монографию Гладкого [73].— Прим. ред.
2) В отечественной литературе чаще используется термин грамматика непосредственно составляющих, или НС-грамматика, и соответственно НС-язык (см. Гладкий [73]).— Прим. ред.
ГРАММАТИКИ И ЯЗЫКИ
65
(2 .10.2) xUy : : = xuy, где U С V — Т, u € V+ и х, у Е V*.
Термин «контекстно-чувствительная» отражает тот факт, что можно заменить U на и лишь в контексте х . . . у. Дальнейшее ограничение дает класс грамматик, полностью подобный классу, который мы используем; грамматика называется контекстно-свободной1), если все ее правила имеют вид
(2 .10.3) U : : - и, где U С V — Т и u € V*.
Этот класс назван контекстно-свободным потому, что символ U можно заменить цепочкой и, не обращая внимания на контекст, в котором он встретился. В КС-грамматике может появиться правило вида U : = Л, где Л — пустая цепочка. Однако, чтобы не усложнять терминологию и доказательства, мы не допускаем таких правил в наших грамматиках. По заданной КС-грамматике G можно сконструировать К-свободную (или неукорачивающую) грамматику G1 (наш тип), такую, что L (Gl) = L (G) — {Л}. Более того, если G однозначна, то G1 также однозначна, поэтому фактически мы не вносим ограничений.
Если мы ограничим правила еще раз, приведя их к виду
(2 .10.4) U : : = N или U : : - WN, где N € Т, а и и W е V - т,
то получим грамматику типа 3, или регулярную грамматику 2). Регулярные грамматики играют основную роль как в теории языков, так и в теории автоматов. Множество цепочек, порождаемых регулярной грамматикой, «допускается» машиной, называемой автоматом с конечным числом состояний (которую мы определим в следующей главе), и наоборот. Таким образом, мы имеем характеристику этого класса грамматик в терминах автомата. Регулярные языки (те, что порождаются регулярными грамматиками), кроме того, называются регулярными множествами. Известно, что если Lt и Ь2 — регулярные множества, то таковыми же являются Lx и U L2, Lx П L2, Lx L2, Ll • L2 = {xy | x £ Lx и у £ L2) и Lx* ={Л} U Lx U L/ U Lx3 U .... 4
Вводя все большие ограничения, мы определили четыре класса грамматик. Таким образом, есть языки с фразовой структурой, которые не являются контекстно-чувствительными, контекстночувствительные языки, которые не являются контекстно-свободными, и контекстно-свободные, которые не являются регулярными.
2) А также бесконтекстной грамматикой, или КС-грамматикой.— Прим, ред.
2) Ее называют также автоматной грамматикой, или А-грамматикой.— Прим. ред.
3 д. Грис
66
ГЛАВА 2
В большинстве работ по теории формальных языков изучаются контекстно-свободные или регулярные языки, или их подмножества. Поэтому мы также ограничимся этими классами.
Один из основных вопросов, который возникает при рассмотрении грамматики, — это вопрос ее однозначности. К сожалению (или к счастью, в зависимости от того, как вы на это смотрите), было доказано, что эта проблема алгоритмически неразрешима для класса КС-грамматик. Это означает, что нельзя построить эффективный алгоритм (написать программу), который для любой заданной грамматики за конечное число шагов мог бы решить, является она однозначной или нет. Оказываются алгоритмически неразрешимыми и многие другие интересные вопросы, касающиеся контекстно-свободных языков (например, совпадают ли два языка, пересекаются ли два языка). В этом случае ищут интересные подклассы языков, для которых этот вопрос алгоритмически разрешим. Большинство доказательств теорем алгоритмической неразрешимости в теории формальных языков прямо или косвенно зависит от результатов теоремы Поста [46].
Доказано, что проблема однозначности для произвольной КС-грамматики алгоритмически неразрешима. Следующий вопрос, который может возникнуть: всегда ли существует однозначная грамматика для произвольного контекстно-свободного языка? Ответ отрицательный. Есть языки, для которых не существуют однозначные грамматики; первым это показал Парик [61]. Такие языки называются существенно-неоднозначными. Пример такого языка:
{а* b* d | i, j > 1} U {a1 bj cj | i, j 1).
Обширная литература посвящена интересующей нас задаче разбора предложений языка. Решение этой проблемы будет обсуждаться в последующих главах.
2.11. РЕЗЮМЕ
Эта глава содержит базисный материал, необходимый для понимания следующих пяти глав, и читатель должен хорошо усвоить его, прежде чем продолжить чтение. Для того чтобы помочь читателю охватить материал, в конце главы приведен список терминов с указанием номеров страниц, где они определены.
метаязык (metalanguage) 29
алфавит (alphabet) 32
символ (symbol) 32
цепочка (string) 32
пустая цепочка (empty string) 32
ГРАММАТИКИ И ЯЗЫКИ
67
длина цепочки (length of a string) 32
катенация (catenation) 33
голова, хвост цепочки (head, tail, of a string) 33
правильная голова, хвост (proper head, tail) 33
произведение двух множеств (product of two sets) 33
степень цепочек (power of strings) 33
итерация множества (closure of a set) 33
усеченная итерация (positive closure) 33
продукция (production) 35
правило (rule) 35
левая часть правила (left part of a rule) 35
правая часть правила (right part of a rule) 35
грамматика (grammar) 35
начальный символ (distinguished symbol) 35
словарь (vocabulary) 35
нетерминал (nonterminal) 35
терминал (terminal) 36
НФБ (BNF) 36
непосредственный вывод => (direct derivation) 36
вывод =>+ (derivation) 36
длина вывода (length of a derivation) 37
сентенциальная форма (sentential form) 37
предложение (sentence) 37
язык (language) 37
фраза (phrase) 38
простая фраза (simple phrase) 38
основа (handle) 39
рекурсивная грамматика (recursive grammar) 39
рекурсивное правило (recursive rule) 39
правило с левой (правой) рекурсией [left (right) recursive rule] 39 синтаксическое дерево (syntax tree) 40
куст, узел (branch, node) 40
концевой узел (end node) ' 40
концевой куст (end branch) 41
узел — брат (brother of a node) 41
узел — отец (father of a node) 41
узел — сын (son of a node) 41
поддерево (subtree) 41
неоднозначное предложение (ambiguous sentence) . 43
неоднозначная грамматика (ambiguous grammar) 43
существенная неоднозначность (inherently ambiguous) 44
разбор сентенциальной формы (parse of a sentential form) 46
нисходящий разбор (top-down parse) 46
восходящий разбор (bottom-up parse) 46
канонический разбор (canonical parse) 48
отношение (relation) 49
3*
68 ГЛАВА 2
рефлексивное отношение (reflexive relation) 50
транзитивное отношение (transitive relation) 50
транзитивное замыкание (transitive closure) 50
произведение двух отношений (product of two relations) 50
единичное отношение (identity relation) 51
приведенная грамматика (reduced grammar)- 58
Глава 3
Сканер
3.1. ВВЕДЕНИЕ
Сканер представляет собой ту часть компилятора, которая читает литеры первоначальной исходной программы и строит слова, или иначе символы, исходной программы (идентификаторы, служебные слова, целые числа, одно- или двулитерные разделители, такие, как *, +, **,/*). Иногда символы называют атомами или лексемами. В чистом виде сканер выполняет простой лексический анализ исходной программы в отличие от синтаксического анализа, и поэтому сканер называют также лексическим анализатором.
Сразу же возникает вопрос, почему лексический анализ нельзя объединить с синтаксическим анализом. В конце концов для описания синтаксиса символов можно воспользоваться НФБ. Например, в ФОРТРАНе идентификатор можно описать следующим образом:
(3.1.1) <идентификатор> : : = буква {буква | цифра}5
Однако есть несколько серьезных доводов в пользу отделения лексического анализа от синтаксического.
1. Значительная часть времени компиляции тратится на сканирование литер. Выделение же позволяет нам сконцентрировать внимание на сокращении этого времени. Одним из способов сокращения времени является программирование части или всего сканера на автокоде, а это сделать легче, если сканер выделен. (Например, в IBM 360 для поиска литеры, отличной от пробела, в последовательности, содержащей от 1 до 256 литер, достаточно выполнить единственную команду TRT.) Конечно же, мы не рекомендуем пользоваться автокодом, если не предполагается широкое и массовое применение компилятора.
2. Синтаксис символов можно описать в рамках очень простых грамматик. Если отделить сканирование от синтаксического распознавания, то можно разработать эффективную технику разбора, которая наилучшим образом учитывает особенности этих грамматик. Более того, тогда для конструирования сканеров можно разработать автоматические методы, в которых используется эта эффективная техника.
70
ГЛАВА 3
3. Так как сканер выдает символы вместо литер, синтаксический анализ на каждом шаге получает больше информации о том, что надо делать. Более того, некоторые специфические проверки контекста, необходимые при разборе символов, проще и уместнее выполнить в сканере, чем в формальном синтаксическом анализаторе. Например, легко выяснить, что означает в ФОРТРАНе инструкция DO 101 = ... , установив, какой из символов или “(“ встречается раньше после знака равенства.
4. Развитие языков высокого уровня требует внимательного отношения как к лексическим, так и к синтаксическим свойствам языка. Разделение этих двух свойств позволит нам исследовать их независимо друг от друга.
5. Часто для одного и того же языка существует несколько различных внешних представлений. Например, в некоторых реализациях АЛГОЛа служебные слова заключены в кавычки и пробелы не играют никакой роли — они попросту игнорируются. В других же компиляторах служебные слова не могут использоваться как идентификаторы и смежные служебные слова и идентификаторы должны отделяться друг от друга по крайней мере одним пробелом. Внешние представления на перфоленте, картах и на телетайпе могут быть совершенно различными.
Выделение сканера позволит написать один синтаксический анализатор и несколько сканеров (которые написать проще и легче) по одному на каждое представление исходной программы и/или устройство ввода. При этом каждый сканер переводит символы в одинаковую внутреннюю форму, используемую синтаксическим анализатором.
Сканер можно запрограммировать как отдельный проход, на котором выполняется полный лексический анализ исходной программы и который выдает синтаксическому анализатору таблицу, содержащую исходную программу в форме внутренних символов. В другом варианте это может быть подпрограмма SCAN, к которой обращается синтаксический анализатор всякий раз, когда ему необходим новый символ (рис. 3.1). В ответ на каждый вызов SCAN распознает следующий символ исходной программы и отсылает его синтаксическому анализатору. Последний вариант, вообще говоря, лучше, поскольку нет необходимости конструировать целиком всю внутреннюю исходную программу и хранить ее в таком виде в памяти. В остальной части этой главы мы будем предполагать, что сканер должен быть реализован именно таким способом.
Повсюду в этой главе мы будем считать, что исходная программа пишется в формате, в котором границы полей не фиксируются, т. е. в виде непрерывной последовательности литер. Изменения и добавления, связанные с обработкой формата с фиксированными полями, а также случаи, когда конец карты означает конец инструкции (как в ФОРТРАНе), будут обсуждаться в конце разд. 3.3.
СКАНЕР
71
Иногда остается неясным различие между символами и конструкциями более высокого уровня. Например, можно рассматривать в качестве символов как целое, так и вещественное число вида
<целое). <целое>
или же можно рассматривать целое число как символ, а веществен-
Обращение
Рис. 3.1. Сканер как подпрограмма синтаксического анализа.
ное — как конструкцию более высокого уровня. В таких случаях мы будем делать произвольный выбор главным образом в интересах простоты изложения.
Использование регулярных грамматик
Большинство символов в языках программирования попадают в один из следующих классов:
идентификаторы;
служебные слова (которые являются подмножеством идентификаторов);
целые числа;
однолитерные разделители (+, —, (,),/ и т. д.);
двулитерные разделители (//, /*, : = и т. д.).
Эти символы могут быть описаны следующими простыми правилами:
<идентификатор> : : = буква | Идентификатор > буква | <иденти-фикатор> цифра
<целое> : <разделитель> : <разделитель> : : = цифра | <целое> цифра := +1-1(|)|/|... : = <SLASH>/I <SLASH> * 1 <AST> * I <COLON> =
<SLASH> : <AST> <COLON> : * .. II .11 II
Конечно, правила могли бы быть еще проще, но мы записываем их так, чтобы каждое правило имело вид
U :: = Т или U :: = VT
72
ГЛАВА 3
где Т — терминал, а V — нетерминал. Как было отмечено в разд. 2.10, грамматика с такими правилами — это грамматика типа 3, или регулярная грамматика. Синтаксис символов большинства языков программирования можно задать в этой форме. Следовательно, целесообразно найти эффективный способ разбора предложений регулярной грамматики. Поэтому мы начнем с разработки эффективной схемы разбора.
3.2. РЕГУЛЯРНЫЕ ВЫРАЖЕНИЯ И КОНЕЧНЫЕ
АВТОМАТЫ
Этот раздел содержит некоторые результаты, которые мы не будем формально доказывать. Нас главным образом интересует вопрос, как программировать сканеры, а для этого доказательства не потребуются. Подробные доказательства можно найти в книгах, на которые есть ссылки в разд. 3.6.
Диаграммы состояний
Рассмотрим регулярную грамматику GIZ]
Z : : = U0 | VI
U : : = Z1 | 1
V : : = Z0 | 0
Легко видеть, что порождаемый ею язык состоит из последовательностей, образуемых парами 01 или 10, т. е.
L (G) = {В" | п > 0}, где В = {01, 10}.
Чтобы облегчить распознавание предложений грамматики G, нарисуем диаграмму состояний (рис. 3.2, а). В этой диаграмме каждый нетерминал грамматики G представлен узлом или состоянием; кроме того, есть начальное состояние S (предполагается, что грамматика не содержит нетерминала S). Каждому правилу Q: Т в G соответствует дуга с пометкой Т, направленная от начального состояния S к состоянию Q. Каждому правилу Q: : = RT соответствует дуга с пометкой Т, направленная от состояния R к состоянию Q.
Мы используем диаграммы состояний, чтобы распознать или разобрать цепочку х следующим образом:
1. Первым текущим состоянием считать начальное состояние S. Начать с самой левой литеры в цепочке х и повторять шаг 2 до тех пор, пока не будет достигнут правый конец х.
2. Сканировать следующую литеру х, продвинуться по дуге, помеченной этой литерой, переходя к следующему текущему состоянию.
СКАНЕР
73
Если при каком-то повторении шага 2 такой дуги не оказывается, то цепочка х не является предложением и происходит останов. Если мы достигаем конца х, то х — предложение тогда и только тогда, когда последнее текущее состояние есть Z.
Рис. 3.2. Диаграмма состояний.
Читатель узнает в этих действиях восходящий разбор. На-каждом шаге (кроме первого) основой является имя текущего состояния, за которым следует входной символ. Символ, к которому приводится основа, будет именем следующего состояния. В качестве примера
шаа Текущее Остаток
состояние цепочки X
1 S 101001
2 и 01 001
3 Z 1001
4 и 001
5 Z 01
6 V 1
7 Z
а Ъ
Рис. 3.3. Разбор и синтаксическое дерево для цепочки 101001.
а — разбор; b — синтаксическое дерево.
проведем разбор предложения 101001. Каждая строка на рис. 3.3,а отражает состояние разбора перед началом выполнения шага 2.
В этом примере разбор выглядит столь простым благодаря простому характеру правил. Так как нетерминалы встречаются лишь как первые символы правой части, на первом шаге первый символ предложения всегда приводится к нетерминалу. На каждом последующем шаге первые два символа UT сентенциальной формы
74
ГЛАВА 3
UTt приводятся к нетерминалу V, при этом используется правило V: :=ит. При выполнении этой редукции имя текущего состояния— U, а имя следующего текущего состояния — V. Так как каждая правая часть единственна, то единственным оказывается и символ, к которому она приводится. Синтаксические деревья для предложений регулярных грамматик всегда имеют вид, подобный изображенному на рис. 3.3,Ь.
Чтобы избавиться от проверки на каждом шаге, есть ли дуга с соответствующей пометкой, можно добавить еще одно состояние, называемое F (НЕУДАЧА), и добавить все необходимые дуги от всех состояний к F. Добавляется также дуга, помеченная всеми возможными литерами и ведущая из F обратно в F. В результате диаграмма, показанная на рис. 3.2,а изменится и станет такой, как на рис. 3.2, Ь.
Детерминированный конечный автомат
Чтобы иметь возможность легко манипулировать с диаграммами состояний, нам необходима дальнейшая формализация концепции в терминах состояний, входных литер, начального состояния S, «отображения» М, которое по заданному текущему состоянию Q и входной литере Т указывает следующее текущее состояние, и заключительных состояний, аналогичных состоянию Z в приведенном выше примере.
(3.2.1). Определение. (Детерминированный) автомат с конечным числом состояний (КА) — это пятерка (К, VT, М, S, Z), где
1) К — алфавит элементов, называемых состояниями;
2) VT — алфавит, называемый входным алфавитом (литеры, которые могут встретиться в цепочке или предложении);
3) М — отображение (или функция) множества KxVT во множество К (если М (Q, T)=R, то это означает, что из состояния Q при входной литере Т происходит переключение в состояние R);
4) S (£ К) — начальное состояние;
5) Z — непустое множество заключительных состояний, каждое из которых принадлежит К.
Мы можем также формально определить, как работает КА (или диаграмма состояний) с входной цепочкой t. Сделаем это, расширив понятие отображения, которое указывает нам, как переключаются состояния в зависимости от входной литеры.
Определим
М (Q, A)=Q при любом состоянии Q;
М (Q, Tt)=M (М (Q, Т), t) для любых t£VT* и TgVT.
СКАНЕР
75
Первая строка означает, что если на входе пустой символ, то состояние остается прежним. Вторая строка показывает, что в состоянии Q и при входной цепочке Tt мы применяем М, чтобы перейти в состояние P=M(Q, Т) с входной цепочкой t, и затем применяем отображение М (Р, t). Наконец, говорят, что КА допускает цепочку t (цепочка t считается допускаемой), если М (S, t)=P, где состояние Р принадлежит множеству заключительных состояний Z.
Такие автоматы называются детерминированными, так как на каждом шаге входная литера однозначно определяет следующее текущее состояние.
(3.2.2). Пример. Диаграмме состояний, показанной на рис. 3.2, соответствует КА ({S, Z, U, V, F}, {0, 1}, М, S, {Z}), где
м (S, 0)=V М (S, 1)=и
М (V, 0)=F М (V, 1)=Z
М (U, 0)=Z M(U, 1)=F
М (Z, 0)=V M(Z, 1)=U
М (F, 0)=F M(F, 1)=F
Теперь остановимся на некоторое время и посмотрим, чего же мы достигли. Мы начали с рассмотрения регулярной грамматики, которая имела единственные правые части. Для нее мы смогли построить диаграмму состояний. Эта диаграмма фактически была неформальным представлением КА. Легко видеть, что если предложение х принадлежит грамматике G, то оно также допускается КА, соответствующим грамматике G. Несколько труднее показать, что для' любого КА существует грамматика G, порождающая только те предложения, которые являются цепочками, допускаемыми КА. Мы не будем здесь приводить доказательство этого утверждения, поскольку результат доказательства далее нам не потребуется.
Представление в ЭВМ
КА с состояниями Sx,..., Sn и входными литерами Тх,. . . , Тт можно представить матрицей В, состоящей из nxm элементов. Элемент В [i, j] содержит число к — номер состояния Sk, такого, что М {Sb Tj]=Sk. Можно условиться, что состояние Si — начальное, а список заключительных состояний представлен вектором. Такая матрица иногда называется матрицей переходов, поскольку она указывает, каким образом происходит переключение из одного состояния в другое.
Другим способом представления может быть списочная структура. Представление каждого состояния с к дугами, исходящими из него, занимает 2*к+2 слов. Первое слово — имя состояния, вто
76
ГЛАВА 3
рое — значение к. Каждая последующая пара слов содержит терминальный символ из входного алфавита и указатель на начало представления состояния, в которое надо перейти по этому символу.
Недетерминированный КА
Мы попадаем в затруднительное положение при построении КА, если G содержит два правила
V : :=UT и W : :=UT
с одинаковыми правыми частями. Это означает, что в диаграмме состояний есть две дуги, помеченные Т и исходящие из U, и отображение М оказывается неоднозначным! Автомат, построенный по такой диаграмме, называется недетерминировайным КА и определяется следующим образом:
(3.2.3). Определение. Недетерминированным КА или НКА называется пятерка (К, VT, М, S, Z) где
1) К — алфавит состояний;
2) VT — входной алфавит;
3) М — отображение множества KxVT в подмножества множества К;
4) SsK — множество начальных состояний;
5) Z=K — множество заключительных состояний.
И опять важным отличием является то, что отображение М дает не единственное состояние, а. (возможно, пустое) множество состояний.
Второе отличие состоит в том, что может быть несколько начальных состояний. Как и ранее, расширим отображение М до KxVT*, определяя
M(Q, A) = {Q) и
М (Q, Tt) — как объединение множеств М (Р, t), где P€M(Q, Т)
для каждого Т € VT и t С VT+. Продолжим расширение, определяя М ({Pi, Р2). . ., Pn}, t) как объединение множеств М (Pb t) для i = l....п.
Цепочка t допускается автоматом, если найдется состояние Р, которое принадлежит одновременно М (S, t) и множеству заключительных состояний Z.
В качестве примера рассмотрим регулярную грамматику G [Z1:
Z U1 | V0 | Z0 | Z1
U Q1 | 1
V ::= Q0 | О
Q ::= Q0 | Q1 | 0 | 1
СКАНЕР
77
Краткое рассмотрение показывает, что язык L (G) представляет собой множество последовательностей из 0 и 1, содержащих по крайней мере два смежных 0 или две смежные 1. (Чтобы убедиться в этом, начните вывод предложений из Z.) На рис. 3.4,а приводится
а
FA = ({S, Q, V, U, Z}, Ю, 1}, М ф, {Z})
M(S, 0) = {V, Q}
M(S, 1) = {U, Q}
M(V, 0) = {Z}
M(V, 1) = 0
M(Q, 0) = {V, Q}
M(Q, 1) = {U, Q}
M(U, O) = 0
M(U, 1) = {Z}
M(Z, 0) = {Z}
M(Z, 1) = {Z} b
Рис. 3.4. Диаграмма состояний и ее НКА.
соответствующая диаграмма состояний, а на рис. 3.4,b — НКА. Состояние НЕУДАЧА представлено здесь подмножеством 0, не содержащим символов.
Проблема состоит в том, что теперь на каждом шаге может быть более одной дуги, помеченной следующей входной литерой, так что мы не знаем, какой путь выбрать. На каждом шаге известна основа текущей сентенциальной формы, но не известно, к чему она приводится. Можно показать, что цепочка 01001 допускается определенной выше машиной, если на каждом шаге выбирается правильный путь. Вначале мы находимся в состоянии S. Прочитав первый 0, мы можем переключиться либо в состояние V, либо в Q; выберем Q. Так как следующий символ 1, то третье состояние либо U, либо Q; вновь выберем Q. На следующей схеме показан полный разбор:
Шаг Текущее состояние Остаток входной цепочки Возможные приемники Наш выбор
1 S 01001 V, Q Q
2 Q 1001 U, Q Q
3 Q 001 V, Q V
4 V 01 Z Z
5 Z 1 Z Z
Теперь заметим, что для любой регулярной грамматики G можно построить диаграмму состояний и, следовательно, НКА. Диаграмма состояний может иметь любое число начальных состояний. Совер
78
Глава а
шенно очевидно, что любое предложение грамматики G допускается этим НКА; говоря иначе, при работе НКА выполняется восходящий разбор. Как и в случае детерминированного автомата, для любого НКА можно найти регулярную грамматику G, предложения которой будут именно теми цепочками, которые допускаются НКА. Доказывать это мы не будем.
Построение К.А из НК.А
Итак, при работе НКА возникает проблема, которая заключается в следующем: мы не знаем какую выбрать дугу на каждом шаге, если существует несколько дуг с одинаковой пометкой. Теперь покажем, как из НКА построить КА, который как бы параллельно проверяет все возможные пути разбора и отбрасывает тупиковые. То есть если в НКА имеется, к примеру, выбор из трех состояний X, Y и Z, то в КА будет одно состояние [XYZ], которое представляет все три. Напомним, что возможные состояния на каждом шаге работы НКА — это подмножество полного множества состояний и что число различных подмножеств конечно.
(3.2.4). Теорема. Пусть НКА F=(K, VT, М, S, Z) допускает множество цепочек L. Определим КА F'=(K', VT, М', S', Z') следующим образом:
1. Алфавит состояний К' состоит из всех подмножеств множества К. Обозначим элемент множества К' через [S^ S2........ SJ, где
Si, S2,.. Sj — состояния из К. (Допустим впредь, что состояния
Si, S2,...,Siрасположены в некотором каноническом порядке таким образом, что, например, состояние из К' для подмножества {Si, S2}={S2, SJ — суть [Si, SJ.)
2. Множество входных литер VT для F и F' одно и то же.
3. Отображение М' определим как
М' ([Si, S2.. SJ, T)=[Rlt R2,..., RJ,
где M ({Sn S2... SJ, T)={Ri, R2,..., RJ.
4. Пусть S={Si,..., Sn). Тогда S'=lSi,..., SJ.
5. Пусть Z={Sj, Sk,..., SJ. Тогда Z'=[Si,Sk,..., SJ.
Утверждается, что F и F'допускают одно и то же множество цепочек. Доказательство этой теоремы предоставляется читателю.
(3.2.5). Пример. На следующем рисунке слева приводится диаграмма состояний НКА с начальными состояниями S и Р и одним заключительным состоянием Z. Справа показана диаграмма состояний соответствующего КА, у которого начальное состояние [S, Р], а множество заключительных состояний |[Z], [S, Z], [Р, Z], [S, Р, Z]}.
СКАНЕР
79
Заметим, что состояния [S] и [Р, Z] можно исключить, так как нет путей, ведущих к ним. Таким образом, построенный КА не
является минимальным — возможен автомат с меньшим числом со-
стояний. Существует алгоритм, позволяющий сконструировать минимальный КА; ссылки на литературу по этому вопросу см. в разд. 3.6.
Нам состояния: S.P Закл. состояние; Z
Регулярные выражения
Оставшаяся часть этого раздела потребуется лишь для понимания разд. 3.5, в котором описывается система AED RWORD.
В разд. 2.9 речь шла о применении символов и метасимволов |, (,), { и } в правых частях правил, соответствующих одному нетерминалу. Существует тесная связь между записанными таким образом правыми частями правил и регулярными выражениями.
Пусть S={Si..... Sn}, тогда
1) 0, Л, Si,..., Sn — регулярные выражения в множестве S;
2) если е1 и е2 — регулярные выражения в S, то
(е1), {е1}, {e^n, eJe2 и е1! е2 также регулярные выражения.
Как и ранее, А — пустой символ, а 0 — пустое множество. Регулярное выражение {е)п для некоторого целого числа п эквивалентно выражению
Л|е|(е)(е)|. . . |(е) . . . (е)
где в последнем выборе (е) повторяется п раз. Мы не будем обсуждать это в дальнейшем.
Значение регулярного выражения е (обозначим его через |е[) — это некоторое множество над S, определенное следующим образом:
1. |0|=0, пустое множество
2. |А|={Л} (множество, состоящее из пустого символа)
80
ГЛАВА 3
3. |SiH{Si} для i=l,. . ., n
4. |(e)Hie|
5. |eTe21= le11 |e21={xy |x |ex | и у |e2|}
6. |ex|e2|= le1! u |e2|
7. |{е}|=итерация |e|==|e|*
Если исключить символ 0, то по смыслу регулярное выражение очень напоминает множество правых частей правил для некоторого нетерминала. Например, мы пишем Е :: =0 { + 1}, чтобы указать, что синтаксическая единица Е производит символ 0, за которым следует произвольное количество цепочек +1. Регулярное выражение 0 { + 1} определяет то же самое множество цепочек. Регулярное выражение 0 можно задать с помощью грамматики, состоящей из единственного правила V ::=V, так как нет ни одной цепочки, которая принадлежала бы соответствующему языку.
Регулярные выражения оказываются удобным инструментом для описания лексических символов. Превосходной иллюстрацией этому может служить (3.1.1). Кроме того, мы покажем, как построить КА, который допускает множество |е|, соответствующее некоторому регулярному выражению е. Это означает, что язык, порождаемый любой регулярной грамматикой, можно определить с помощью одного регулярного выражения, и наоборот. Более важным, однако, является тот факт, что КА можно применить для разбора любой цепочки из множества |е|.
Построение КА по регулярному выражению
Можно построить КА по регулярному выражению за 4 шага: 1. Построить систему переходов (определяется ниже) для е. 2. Построить диаграмму состояний по системе переходов.
3. Построить НКА по диаграмме состояний.
4. Построить КА по НКА.
Шаги 3 и 4 уже были описаны, пояснения необходимы лишь к шагам 1 и 2. Использование системы переходов упрощает процесс комбинирования в одно целое диаграмм, представляющих несколько регулярных выражений.
(3.2.6). Определение. Система переходов — это диаграмма с одним начальным состоянием S и одним заключительным состоянием Z. Состояние S не имеет входящих дуг, a Z — исходящих. Кроме того, дуга может быть помечена пустым символом А.
На рис. 3.5, Ь изображена система переходов. Она допускает то же самое множество цепочек, что и соответствующая диаграмма на рис. 3.5, а. Общий принцип «работы» в системе переходов тот же, что и в диаграмме состояний. Нам необходимо только объяснить смысл дуг, помеченных А. Если А — текущее состояние и дуга, помеченная Л, ведет в состояние В, то мы полагаем, что текущим
СКАНЕР
81
состоянием является либо А, либо В, т. е. следующее состояние может быть преемником либо А, либо В.
(3.2.7). Теорема. Существует система переходов для любой диаграммы состояний.
Построение. Пусть S — диаграмма состояний с начальными состояниями Si, S2,..., Sn и заключительными состояниями
а ъ
Рис. 3.5/ Диаграмма состояний и соответствующая ей система переходов.
Zn Z2,..., Zm- Добавим новое состояние S, единственное теперь начальное состояние, с дугами, помеченными Л и ведущими в Si, S2,..., Sn. Добавим новое состояние Z, заключительное состояние, с дугами, помеченными Л, ведущими в него из Zlt Z2,..., Zm- На рис. 3.5, b изображена система переходов, соответствующая диаграмме состояний на рис. 3.5, а.
(3.2.8). Теорема. Для всякого регулярного выражения е существует система переходов, которая допускает |е|.
Построение. Системы переходов для 0, Л, Sj будут соответственно
Система переходов для (е) — та же, что для е. Предположим, что имеются системы переходов для е1 и е2 и они изображаются как
82
ГЛАВА 3
где S — начальное, a Z — заключительное состояния. Тогда системами переходов для ех |е2 и еге2 будут соответственно
В системе переходов для заключительное состояние ег было отождествлено с начальным состоянием е2. В случае ег |е2 попарно отождествляются начальные и заключительные состояния. На следующей диаграмме изображена система переходов для регулярного выражения {ех}. Мы предоставляем читателю возможность убедиться в том, что сконструированная система переходов действительно является искомой системой.
Последний шаг — построение диаграммы состояний по системе переходов. Необходимо избавиться от дуг, помеченных А. Следующий алгоритм исключает по крайней мере одну такую дугу, не изменяя при этом множество цепочек, допускаемых системой (при этом может возрасти число начальных или конечных состояний). Если мы повторим этот алгоритм достаточное число раз, то все дуги, помеченные А, будут исключены.
1. Найти состояние, из которого ведет дуга, помеченная А, пройти по этой дуге в следующее состояние и идти по дугам, помеченным А, до тех пор, пока не встретится ситуация
где из В не исходит дуг, помеченных А. Если такой ситуации не окажется, то выполнить шаг 3; в противном случае выполнить шаг 2.
2. Если существует последовательность дуг, помеченных А и ведущих из начального состояния в А (а значит, и в В), то сделать В начальным состоянием. Если В — заключительное состояние, то сделать А заключительным состоянием. Исключить дугу, помеченную А и направленную от А к В. В дополнение к каждой дуге, помеченной St и ведущей из В в состояние С, завести дугу, поме
СКАНЕР
83
ченную S1 и ведущую из А в С. Действия этого шага иллюстрируются на рис. 3.6.
3. Если не оказалось ситуации, описанной в шаге 1, то должна существовать последовательность состояний А1( Аа,..., Ап, Аь такая, что есть дуга с пометкой Л, ведущая из каждого Aj в Ai+, для i = l,..., п — 1, и, кроме того, есть дуга с пометкой Л, ведущая
а ь с
Рис. 3.6. Исключение дуг, с пометкой X (шаг 2).
а — нач. состояние S, закл. состояние Z;
Ъ — нач. состояния S,Z, закл. состояния Z.X; с—нач. состояния S,Z,X, закл. состояния Z,X,S.
из Апв At. (Доказательство предоставляется читателю.) Отождествить все эти состояния, т. е. заменить их одним состоянием. Исключить все упомянутые дуги с пометкой Л.
а, Ъ
Рис. 3.7. Исключение дуг, с пометкой Л (шаг 3). а—нач. состояние S, закл. состояние Z; b — нач. состояние S', закл. состояние Z.
Если какое-либо из состояний A t было начальным (заключительным) состоянием, то новое состояние сделать начальным (заключительным). Действия этого шага иллюстрируются на рис. 3.7.
84
ГЛАВА 3
УПРАЖНЕНИЯ К РАЗДЕЛУ 3.2
1. Постройте автомат для следующей грамматики G [ZJ. Детерминированный ли этот автомат? Какой язык ему соответствует?
Z ::=А0 A ::=AO|Z1|O
2. Постройте КА, который допускает все цепочки из 0 и 1, такие, что за каждой 1 непосредственно следует 0. Постройте регулярную грамматику для этого языка.
3. Постройте КА из НКА, представленного на рис. 3.4.
4. Постройте КА из НКА ({X, Y, Z}, {0, 1}, М, {X}, {Z}), где
М (X, 0)= {Z} М (Y, 0)={Х, Y} М (Z, 0)={Х, Z),
М(Х, 1)={Х} М (Y, 1)=0 M(Z, 1)={Y}.
5. Постройте НКА для следующих регулярных выражений:
a) ((A|B)|{A|C})|DEM; b) {{0|1}|(1 1)}
6. Докажите теорему (3.2.4).
3.3. ПРОГРАММИРОВАНИЕ СКАНЕРА
Покажем, как программируется сканер для небольшого и простого языка. Собственно, нас интересуют лишь символы языка, поскольку именно их построение является целью лексического анализа. Мы не будем формально применять ранее изложенный теоретический материал, но именно теория служит основой для понимания интересующей нас проблемы и будет направлять нас в работе над ней.
Символы исходного языка
Символами в языке являются разделители или операторы (/, + ,—>*,(,) и //), служебные слова (BEGIN, ABS и END), идентификаторы (которые не могут быть служебными словами) и целые числа. По крайней мере один пробел должен отделять смежные идентификаторы, целые числа и/или служебные слова. Ни одного пробела не должно появляться между литерами в слове. Идентификаторы и целые числа имеют вид
буква {буква|цифра} и цифра {цифра}
В добавление ко всему сканер должен распознавать и исключать комментарий. Комментарий начинается с двулитерного символа /* и заканчивается при первом появлении двулитерного символа */. Следующая строка является примером одного комментария:
/» Это * / / один комментарий */
СКАНЕР
85
Результат работы сканера
Сканер строит внутреннее представление для каждого символа. В большинстве случаев это целое число фиксированной длины (байт, полуслово, слово и т. д.). В других частях компилятора гораздо эффективнее обрабатываются эти целые числа, чем цепочки переменной длины, которыми фактически представляются символы.
Во внутреннем представлении некоторый номер обозначает «идентификатор», другой номер — «целое». Таким образом, во
Внутреннее представление Символ Мнемоническое имя
0 Не определен SUND
1 Идентификатор SID
2 Целое SINT
3 BEGIN SBEGIN
4 ABS SABS
5 END SEND
6 / SSLASH
7 + SPLUS
8 — SMINUS
9 * SSTAR
10 ( SLPAR
11 ) SR PAR
12 // SSLSL
Рис. 3.8. Внутреннее представление символов.
внутреннем представлении все идентификаторы обозначаются одним и тем же числом. Это естественно, поскольку «идентификатор» для синтаксического анализатора является терминальным символом, и поэтому безразлично, какой идентификатор встречается в каждом конкретном случае. Однако при семантическом анализе приходится иметь дело с самим идентификатором, поэтому его необходимо сохранить. Вопрос исчерпан, если сканером выдается две величины: первая — внутреннее представление, вторая — фактический символ или ссылка на него. (Иногда проще, если сканер содержит таблицу всех различных символов и в качестве второй величины выдает целое число фиксированной длины — индекс позиции в этой таблице.)
Для остальной части этой главы договоримся о внутреннем представлении символов (рис. 3.8). Заметим, что всем символам при
86
ГЛАВА 3
писываются мнемонические имена; с ними нам и придется оперировать. В том языке программирования, на котором пишется сам сканер, знак $ относится к буквам и может быть использован в идентификаторах. Имя можно связать с числом либо через макроопределение, либо используя переменную, которой присваивается это число при инициализации. В программировании этот прием имеет особую ценность. Благодаря ему облегчается внесение изменений в программу; программа становится более наглядной.
Рассмотрим, например, сегмент программы
BEGIN А+/ВС// /* COMMENT ++*/END 11
Сканер передаст вызывающей его программе следующее:
Шаг Результат Смысл
1 3, 'BEGIN' BEGIN
2 1, 'А' Идентификатор А
3 7, ' + ' +
4 6, 'Г /
5 1, 'ВС' Идентификатор ВС
6 12, '//' И
7 5, 'END' END
8 2, '11' Целое 11
Диаграмма состояний
Начнем реализацию сканера с того, что нарисуем диаграмму состояний, показывающую, как ведется разбор символа (рис. 3.9). Здесь есть несколько моментов, которые стоит обсудить.
Метка D используется вместо любой из меток 0, 1, 2,..., 9, т. е. D представляет класс цифр. Это делается для упрощения диаграммы. Аналогично метка L представляет класс буквы А, В,..., Z, а DELIM представляет класс разделителей, состоящих из одной литеры + , —,*, (и ). Заметим, что литера / не принадлежит классу разделителей, так как она должна обрабатываться особым образом.
Некоторые дуги не помечены. Эти дуги будут выбраны, если сканируемая (обозреваемая) литера не совпадает ни с одной из литер, которыми помечены другие дуги. Например, если мы находимся в состоянии INT, то будем оставаться в этом состоянии до тех пор, пока сканируются цифры. Если же сканируется не цифра, то проходим по дуге, ведущей в OUT.
Дуги, ведущиев OUT и ERROR, являются еще одной особенностью диаграммы состояний. Они говорят лишь о том, что обнаружен кэнец символа и необходимо покинуть сканер. Одна из проблем, которая возникает при переходе в OUT, состоит в том, что в этот момент не всегда сканируется литера, следующая за распознанным
СКАНЕР
87
символом. Так, литера выбрана при переходе в OUT из INT, но она еще не выбрана, если только что распознан разделитель (DELIM). Когда потребуется следующий символ, необходимо знать, сканировалась уже его первая литера или нет. Это можно сделать, используя, например, переключатель. Мы же в дальнейшем будем считать, что перед выходом из сканера следующая литера всегда выбрана.
Еще один момент. Мы составили детерминированную диаграмму. Таким образом, мы позаботились о проблеме детерминированности,
Рис. 3.9. Диаграмма состояний для сканирования символов.
т. е. мы сами определяем,— что начинается с литеры “/”:$SLASH, $SLSL или комментарий,— поскольку всегда идем в общее для них состояние SLA.
Эта неформальная диаграмма состояний помогла нам составить представление о том, как выполняется разбор символов. Теперь посмотрим, как добавить «семантику», т. е. добавить информацию, которая скажет нам, что надо делать с тем или иным символом в процессе его построения.
Глобальные переменные и необходимые подпрограммы
Для работы сканера требуются следующие переменные и подпрограммы:
1. CHARACTER CHAR, где CHAR — глобальная переменная, значением которой всегда будет сканируемая литера исходной программы.
2. INTEGER CLASS, где CLASS содержит целое число, которое характеризует класс литеры, находящейся в CHAR. Будем считать,
88
ГЛАВА 3
что D (цифра)=1, L (буква)=2, класс, содержащий литеру /, =3 и класс DELIM=4.
3. STRING А — ячейка, которая будет содержать цепочку (строку) литер, составляющих символ.
4. GETCHAR — процедура, задача которой состоит в том, чтобы выбрать следующую литеру исходной программы и поместить ее в CHAR, а класс литеры — в CLASS. Кроме того, GETCHAR, когда это необходимо, будет читать и печатать следующую строку исходной программы и выполнять другие подобные мелочи.
Гораздо предпочтительнее использовать для таких целей отдельную подпрограмму, чем повторять группу команд в тех местах, где необходимо сканировать следующую литеру.
5. GETNONBLANK. Эта программа проверяет содержимое CHAR, и если там пробел, то повторно вызывается GETCHAR до тех пор, пока в CHAR не окажется литера, отличная от пробела.
Добавление семантики в диаграмму состояний
Теперь, когда мы имеем общее представление о разборе символов, добавим команды, которые обеспечат построение символов. Как это сделать, показано на рис. 3.10. По существу диаграмма осталась той же, что и на рис. 3.9, но под каждой дугой появились команды, которые надлежит выполнить. К тому же мы явно ввели команду GC, сокращенно обозначив таким образом GETCHAR. Неявно это было сделано и на рис. 3.9. Мы также вынуждены были несколько расширить блок-схему в той части, где распознается конец идентификатора, чтобы проверить, не является ли набранный идентификатор служебным словом. Выражение OUT (С, D) означает возврат к программе, которая вызывала сканер, с двумя величинами С и D в качестве результата.
Под первой дугой, ведущей к состоянию S, записана команда INIT, которая указывает на необходимость выполнения подготовительных действий и начальных установок (инициализации). В данном случае выполняются команды
GETNONBLANK; А:='
Тем самым в CHAR заносится литера, отличная от пробела, и производится начальная установка ячейки А, в которой будет храниться символ. Команда ADD означает, что литера из CHAR добавляется к символу в А следующим образом:
А : =А CAT CHAR;
Команда LOOKUP осуществляет поиск символа, набранного в А, по таблице служебных слов. Если символ является служебным словом, то соответствующий индекс заносится в глобальную переменную J, в противном случае туда записывается 0.
СКАНЕР
89
Обратите внимание на тот факт, что при обнаружении комментария или ошибки мы не выходим из сканера, а начинаем сканировать следующий символ.
Проследим за разбором символа //. Начнем с инициализации (INIT). Затем переходим в состояние S. Проверяем CHAR, находим,
Рис. 3.10. Диаграмма состояний с семантическими процедурами.
что там /, и по соответствующей дуге переходим в состояние SLA. В момент перехода добавляем / в А (команда ADD) и вызываем GETCHAR, чтобы сканировать следующую литеру. В состоянии SLA мы проверяем новую литеру в CHAR и выбираем дугу, помеченную /. В момент перехода по дуге добавляем литеру из CHAR к цепочке в А и сканируем следующую литеру (GC). Заканчиваем работу возвратом к программе, которая вызвала сканер, с парой величин (SSLSL, 0). Заметим, что к моменту выхода литера следующего символа находится в CHAR.
Рекомендуем читателю самостоятельно проследить разбор следующих символов: +, 235, BEGIM, BEGIN, /«-COMMENT*/ и /.
Программа
Ниже приводится процедура, запрограммированная непосредственно по диаграмме состояний, которая изображена на рис. 3.10. Процедура имеет два параметра: первый параметр — внутреннее
90
ГЛАВА 3
представление получаемого символа; второй — цепочка литер, составляющих символ. В другом варианте SYN и SEM могли бы быть глобальными ячейками для сканера и для всех тех мест компилятора, в которых вызывается сканер. Этот вариант, вообще говоря, обеспечивает более высокую эффективность, и его следует рекомендовать.
В процедуре используется инструкция CASE, которая по номеру класса литеры, содержащейся в CHAR, определяет, какую надо выбрать дугу, ведущую из начального состояния S.
PROCEDURE SCAN (INTEGER SYN; STRING SEM)
START:GETNONBLANK; A:=' CASE CLASS OF
BEGIN
BEGIN WHILE CL ASS =1 DO BEGIN A:-A CAT CHAR;
GETCHAR;
END; SYN:=§INT;
END;
BEGIN WHILE CLASS <2 DO
BEGIN A: =A CAT CHAR; GETCHAR;
END; SYN:~$ID; LOOKUP(A);
IF J * 0 THEN SYN: = J;
END;
BEGIN A : =CHAR; GETCHAR; IF CHAR ='*' THEN
BEGIN B: GETCHAR;
C:IF CHAR # V THEN GOTO B;
GETCHAR;
IF CHAR # ,/t THEN GOTO C;
GETCHAR; GO TO START END;
Строка инициализации.
Инструкция CASE используется для перехода по дуге из состояния S в INT, ID, SLA и т. д.
CLASS=1 означает цифру. Состояние INT. Сканировать литеры и добавлять их в А до тех пор, пока будет обнаружена не цифра. Затем сформировать параметр SYN.
Состояние ID — в него приходят, если в CHAR — буква.
Сканировать литеры до тех пор, пока не будут обнаружены L или D.
Проверить, является ли идентификатор служебным словом.
Если это так, то сформировать SYN.
Состояние SLA.
Если следующая литера *, то — комментарий. Сканировать до тех пор, пока не встретится другая *.
Следующая литера может быть / (конец комментария).
Следующая литера / — комментарий кончился. Сканировать следующую литеру и начать формирование нового символа.
СКАНЕР
91
IF CHAR ='/' THEN
BEGIN А : = A CAT CHAR; GETCHAR; SYN := $SLST; END; ELSE SYN := «SLASH END; Дуга помечена / — выход из состояния SLA. Это непомеченная дуга из состояния SLA.
BEGIN LOOKUP(A); SYN : = J; GETCHAR; END; Найти номер разделителя и занести его в SYN.
BEGIN ERROR; GETCHAR; GO TO START; END Встретилась недопустимая литера. Исключить ее и продолжить работу. Конец инструкции CASE.
END; SEM A; Конец работы сканера.
Обсуждение
Есть несколько моментов, которые стоит обсудить. Прежде всего заметим, что сканер всегда строит по возможности наиболее длинный символ. Следовательно, АВС12 — это простой идентификатор, а не идентификатор, за которым следует целое число. Такой принцип вполне оправдан в большинстве случаев, но не во всех. Известным примером является инструкция ФОРТРАНа DO10I = 1,20, где DO10I — не идентификатор, а ключевое слово DO, за которым следует номер инструкции 10, за которым в свою очередь следует идентификатор I. Очевидно, что для ФОРТРАНа наш метод не будет идеальным. Обычно в таких случаях довольно легко написать небольшую программу, которая «просмотрит вперед» исходную программу и вынесет для таких случаев соответствующее решение.
Язык ФОРТРАН к тому же имеет фиксированные поля, т. е. для поля метки отводятся колонки 1—5, а для поля инструкции — колонки 7—72. Изменения, которые необходимы для представления языков с фиксированными полями, весьма просты, и мы не будем здесь о них говорить.
ФОРТРАН и многие другие языки допускают только одну инструкцию на карте. Сканер для ФОРТРАНа должен также следить за картами продолжения, которые отмечены в шестой колонке литерой, отличной от пробела. Проще всего эту проблему решить в программе GETCHAR. Когда GETCHAR достигает конца карты, читается следующая карта и проверяется литера в шестой колонке. Если там не пробел, то программа продолжает пересылать литеры из колонок 7, 8...; если пробел, то в сканер отсылается специальная литера «конец карты», которая затем передается синтаксическому анализатору как специальный внутренний символ. Эти проблемы удобно выделить и решать в одном наиболее подходящем мес
92
ГЛАВА 3
те, а не предусматривать их проверку на протяжении всей программы.
В некоторых представлениях исходных языков пробелы полностью игнорируются (исключение составляют строки). Эта возможность легко реализуется, если подпрограмма GETCHAR пропускает «игнорируемые» литеры. Другой вариант — при каждом состоянии иметь дугу (помеченную пробелом), которая ведет из этого состояния обратно в это же состояние. Подобное решение можно предпочесть в том случае, когда программа GETCHAR используется несколькими различными сканерами. Это и будет нашей следующей темой.
Некоторые языки программирования могут быть разбиты на несколько частей, каждая из которых имеет совершенно различные правила для образования символов. Так, в ФОРТРАНе обычные инструкции отличаются от инструкции FORMAT. В АЛГОЛе пробелы имеют смысл внутри строк, тогда как вне строк они полностью игнорируются. Некоторые языки позволяют включать в программу автокодные команды.
В таких случаях целесообразно иметь разные сканеры для каждой части языка и иметь команды (вызовы процедур), которые позволяют переключиться с одного сканера на другой. Осуществление этого — довольно простая задача, и она не нуждается в дальнейших обсуждениях.
Класс (CLASS) литеры в программе GETCHAR вычисляется совсем просто и эффективно, если имеется вектор С. Тогда, используя код литеры (EBCDIC, ASCII или BCD) как целочисленный индекс i, находим элемент С (i), который содержит номер класса литеры i. При этом, конечно, предполагается, что каждая литера принадлежит только одному классу. Чтобы просмотреть текст вперед до первой литеры, отличной от пробела, и занести ее класс в регистр, можно воспользоваться командами, такими, например, как команда TRT в IBM 360.
УПРАЖНЕНИЯ К РАЗДЕЛУ 3.3
1. Напишите процедуры GETCHAR и GETNONBLANK на нестандартном АЛГОЛе.
2. Составьте программу полного сканера на некотором языке высокого уровня и отладьте ее.
3.4. КОНСТРУИРОВАНИЕ СКАНЕРОВ
В большинстве языков программирования общая структура символов достаточно одинакова, и поэтому можно иметь один общий алгоритм сканирования для всех языков. Алгоритм сканирования
СКАНЕР
93
будет использовать несколько таблиц, и именно эти таблицы будут изменяться в зависимости от языка. Следовательно, можно составить программу-конструктор, которая по описанию символов языка программирования готовит таблицы, соответствующие этому языку (рис. 3.11). Как только конструктор построил таблицы, сам он
Рис. 3.11. Конструктор и сканер.
становится ненужным. Поэтому можно отбросить все, что на рисунке расположено слева от двойной линии.
Мы начнем с описания общей структуры символов (3.4.1). Затем (3.4.2) нарисуем диаграмму состояний алгоритма сканирования, а также опишем таблицы, необходимые для этого алгоритма. И, наконец, покажем, как будет выглядеть входная информация для конструктора.
3.4.1. Структура символов
Нам необходимо разбирать следующие типы символов:
1. Идентификаторы и служебные слова вида «(начальная литера) {<другие литеры)}.
В общем случае начальная литера должна быть буквой, в то время как другие литеры могут быть либо буквами, либо цифрами. Некоторые языки допускают присутствие в идентификаторах $,__, —
и других литер. Кроме того, иногда ограничивается максимальное число литер в идентификаторах.
2. Целые числа вида <цифра> {<цифра>}.
Цифры вообще — это 0,1,..., 9, но для восьмеричной системы счисления — это лишь 0, 1, ..., 7, а для шестнадцатеричной 0, 1, ..., 9, А, ..., F.
3. Однолитерные разделители, такие, как /, —, +.
4. Двулитерные разделители //, /*.
94
ГЛАВА 3
5. «Ключевые слова», такие, как 'BEGIN' в АЛГОЛе или .EQ. и .AND. в некоторых реализациях ФОРТРАНа IV. В некоторых реализациях «ключевые слова» не могут использоваться как идентификаторы, что намного упрощает сканирование и грамматический разбор.
Помимо этого, мы должны лишь определить значение, которое имеют пробелы и литеры, подобные им. Игнорируются ли они полностью или указывают на окончание других символов, или же они относятся к обычным литерам? В нашем сканере не будет реализован разбор комментария, так как допускается возможность переключения между различными сканерами. Таким образом, когда обнаруживается символ начала комментария, можно переключиться для его обработки на другой сканер.
3.4.2. Алгоритм сканирования
Классы литер
Исследование типов символов, которые будут подвергаться разбору, указывает на необходимость выделения следующих классов литер:
1. DIGIT (цифра) —литеры, которые могут появиться в символе «целое» (INTEGER).
2. IDBEG (иднач) — литеры, которые могут появиться в качестве первой литеры «идентификатора».
3. IDCHAR (идлит) —литеры, которые могут появиться на месте второй, третьей, четвертой, ..., литеры «идентификатора».
4. IGNORE (игнор) —литеры, которые сканер полностью игнорирует или исключает (такие, как пробел в некоторых реализациях АЛГОЛа).
5. INVTERMIN (консим) —литеры, которые сигнализируют о конце формируемого символа, но которые во всех других случаях игнорируются, и сканер должен их исключать (подобно пробелу в некоторых реализациях АЛГОЛа).
6. DELIM (разд) —литеры, которые сами являются символами, такие, как +, —, /, ( и ). Они, конечно, могут затем использоваться для образования двулитерных разделителей или для выделения ключевых слов.
СКАНЕР
95
Большинство этих классов не должны пересекаться, т. е. никакая литера не может принадлежать двум классам. Перекрытие допустимо только для классов DIGIT и IDCHAR. В нашем случае, исходя из целей эффективности, мы фактически разобьем разделители DELIM на четыре следующих класса:
6. Те разделители, с которых не начинаются двулитерные символы или ключевые слова.
7. Те разделители, с которых начинается по крайней мере одно ключевое слово, но ни один двулитерный символ.
8. Те разделители, с которых начинается по крайней мере один двулитерный символ, но ни одно ключевое слово.
9. Те разделители, с которых начинаются и ключевое слово, и двулитерный символ.
Диаграмма состояний
Используя эти классы, мы теперь можем нарисовать диаграмму состояний, как на рис. 3.12. Эта диаграмма имеет одну дополнительную особенность — возврат, которую нам до этого не приходилось использовать. Предположим, что на вход поступают литеры .ED., причем с начинается по крайней мере одно ключевое слово. Возникает вопрос, является ли .ED. одним символом или это три символа ., ED и .. Мы не узнаем этого до тех пор, пока не просмотрим список символов. Если .ED. не является символом, мы попросим программу GETCHAR «взять назад» литеры с тем, чтобы мы могли начать сканирование сначала. С этой целью позиция начальной литеры некоторым образом отмечается (MARK), и затем, когда возникает необходимость, происходит возврат (BACKUP) и программа GETCHAR начинает снова с последней отмеченной литеры. Заметим, что мы возвращаемся назад также и через игнорируемые литеры. И дело не только в том, что пришлось бы копировать «хорошие» литеры, которые должны повторно «сканироваться». Обусловлено это тем, что при распознавании символа в любое время может произойти переключение на другой сканер и, таким образом, изменится смысл литер.
Поскольку в нашем случае характер возврата строго определен, необходимо помнить лишь о последней отмеченной литере в течение ограниченного промежутка времени. Как только мы выдаем символ, нам не нужно дальше хранить отметку.
Таблицы для алгоритма сканирования
Конкретное представление необходимой информации может очень сильно зависеть от машины и языка, на которых реализуется алгоритм сканирования. Тем не менее можно дать некоторые общие рекомендации.
96
ГЛАВА 3
Прежде всего необходима таблица всех символов языка вместе с их внутренним представлением. Она включает все разделители, служебные и ключевые слова. Таблица используется в команде
Рис. 3.12. Алгоритм сканирования.
LOOKUP для поиска внутреннего представления символа. Так как это случается очень часто, следует, по-видимому, предпочесть хеш-таблицу (см. гл. 9).
Вторая таблица используется для того, чтобы выяснить класс литеры, когда сканер находится в состоянии S. Эту таблицу лучше всего организовать как вектор V, а код литеры использовать в качестве индекса: для литеры С V(C) содержит класс. Заметим, что
СКАНЕР
97
в данном случае не важно, принадлежит литера классу IDCHAR или нет. Здесь нас интересуют только классы IGNORE, INV-TERMIN, DIGIT, IDBEG и DELIM.
Нам потребуется и третья таблица, которая используется в состояниях ID и KY2 для того, чтобы различать классы IG, IDCHAR и другие.
3.4.3. Входная информация для конструктора таблиц
Конструктору надо задать только распределение литер по классам и все служебные слова вместе с их внутренним представлением. Работа самого конструктора заключается в том, чтобы прочитать
определение сканера и построить внутренние таблицы, которые
использует алгоритм сканера следующий: сканирования. Синтаксис для определения
<сканер> :: = - BEGIN Идентификатор г> [Идентификатор 2>] {<опр. класса>} {<опр. символа>} END
<опр. класса> <имя класса> :: = = Имя класса> <список литер> = DIGIT | IDBEG | IDCHAR | IGNORE | INVTERMIN | DELIM
<список литер> <опр. символа> :: = <символ> :: — [ALLBUT] <литера> |<литера>} = RES <целое> <символ> {<символ>} = <литера> <литера>}| “последовательность литер EBCDIC, отличных от пробела”
<литера> :: = = “EBCDIC литера, отличная от пробела” |<16-теричная цифра> <16-теричная цифра>
<16-теричная цифра> :: = 0|l|2|3|4|5|6|7|8|9|A|B|C|D]E|F
Определяемый сканер получит имя <идентификатор 1>. Это имя программист будет использовать в тех местах системы, где есть обращение к сканеру. <Идентификатор2> — имя подпрограммы, назначение которой будет объяснено позднее.
Л итеры
Чтобы можно было использовать любые внутренние литеры, мы разрешаем задавать <литера>либо как литеру в коде EBCDIC, либо как ее шестнадцатеричное представление. Пробел должен всегда задаваться шестнадцатеричным представлением в коде EBCDIC: Х'40'.
Определение классов
В Определение класса) указывается имя класса и описываются литеры этого класса. Каждая <литера) должна отделяться по крайней мере одним пробелом от других литер. Использование ALLBUT (все, кроме) указывает на то, что классу принадлежат все литеры, кроме тех, что перечислены в списке, и тех, которых нет в
Д. Грис
98
ГЛАВА 3
других классах. ALLBUT можно использовать только однажды в определении сканера.
Вот какими должны быть, например, определения классов для языка, описанного в разд.
DIGIT IDBEG
3.3:
0123456789
ABC DEFGH I JKLM NOPQRSTUVWXYZ ABCDEFGHIJKLM NOPQRSTUVWXYZ 0123456789 40
*/ + 0 ( )
IDCHAR
INVTERMIN DELIM
Предположим, что мы хотим определить сканер для комментария, который будет использоваться всякий раз, когда другой сканер распознает символ начала комментария. Таким образом, нам необходимо сканировать лишь до тех пор, пока не будет обнаружен символ конца. Предположим, что это Определения классов такие:
IGNORE ALLBUT; DELIM;
Определение символов
Определение символа имеет следующий формат:
RES (целое) (символ) {(символ)}
В этом определении (целое) соответствует внутреннему представлению первого (символ) в списке; с каждым последующим (символ) сопоставляется следующее большее целое число. Могут встретиться несколько определений символов. По крайней мере один пробел должен отделять RES от (целое), (целое) от первого (символ) и каждый (символ) от соседнего. Различным символам могут соответствовать одинаковые внутренние представления.
Любой (символ) может быть представлен последовательностью литер в коде EBCDIC, кроме пробела (исключение составляют “RES”, и “END”), или последовательностью пар шестнадцатеричных цифр. Для того чтобы использовать последние в качестве символов, мы применяем “|” как знак катенации или используем последовательность из двух (16-теричное число) для того, чтобы обозначить внутреннее представление. Например, мы можем определить символ “RES” как 40 | R | Е | S, а символ “ ’” — как 7D.
Необходимо добавить, что каждый символ должен иметь один из следующих форматов:
DELIM [DELIM]
DIGIT {DIGIT} IDBEG {IDCHAR}
DELIM IDBEG {IDCHAR} DELIM
СКАНЕР
99
Ниже мы приводим определения символов для простого языка, описанного в разд. 3.3:
RES 3 BEGIN ABS Е |N|D
RES 6 /4-----* ( )
RES 12 //
Вызов подпрограммы
Для того чтобы сделать всю систему более гибкой, мы разрешаем указать имя подпрограммы ^идентификатор 2», которая вызывается всякий раз, когда прочитана новая строка исходной программы. Цель состоит в том, чтобы допустить предварительный просмотр строки и внесение в нее любых необходимых изменений. Этим можно воспользоваться для перехода от формата с фиксированными полями к свободным полям с включением в строку некоторых внутренних символов или для обнаружения карты продолжения или карты комментария. Конечно, на такую подпрограмму не должна возлагаться слишком большая обработка; это свело бы на нет все усилия, направленные на создание быстрого, автоматического сканера.
Сама программа имеет два строковых параметра. Первый указывает входную строку, второй — имя переменной, содержащей фактическую (выходную) строку, которую должен обрабатывать сканер. Подпрограмма, если она вызывается, должна присвоить строку, которую надлежит сканировать, переменной, обозначенной вторым параметром.
Приведем пример подпрограммы предварительной обработки для ФОРТРАНа. Если карта не является ни картой комментария, ни картой продолжения, то первой в выходную строку помещается внутренняя литера Х'ОЗ'. Она определяется как разделитель и используется в качестве признака конца инструкции на предыдущей карте. Затем содержимое 6-й колонки заменяется литерой Х'04', которая будет служить признаком конца поля метки. Комментарий (Св 1-й колонке) исключается, и, таким образом, не требуется его сканирование. На картах продолжения используются только колонки с 7-й по 72-ю.
PROCEDURE FORT (STRING IN, OUT);
BEGIN
IF SUBSTR (IN, 0, 1) = 'C' THEN OUT ;= X'03'
ELSE IF SUBSTR (IN, 5, 1) # " THEN OUT := SUBSTR (IN, 6, 66)
ELSE BEGIN OUT :=X'O3'
Процедура предпроцессора для карты ФОРТРАНа.
Если на карте комментарий, то конец предыдущей карты.
Если карта продолжения, выбираем колонки 7—72, в противном случае завершаем предыдущую инструкцию.
4*
100
ГЛАВА 3
CAT SUBSTR (IN, 0, 72); SUBSTR (OUT, 5, 1)
X'04';
END
END
Передаем на обработку колонки 1—72 и записываем признак конца поля метки.
УПРАЖНЕНИЕ К РАЗДЕЛУ 3.4
1. Запрограммируйте и отладьте общий алгоритм сканирования на некотором удобном для вас языке.
3.5. СИСТЕМА AED1) RWORD
В предыдущем разделе был рассмотрен сканер и конструктор для сканирования символов, структура которых ограничена четырьмя форматами:
DIGIT {DIGIT}
IDBEG {IDCHAR}
DELIM [DELIM]
DELIM IDBEG {IDCHAR} DELIM
Синтаксис символов был ограничен так, чтобы алгоритм сканирования был простым и допускал быструю и эффективную реализацию.
В системе AED RWORD (см. Джонсон и др. [68]), которая является существенной частью системы AED-1, предназначенной для генерации компиляторов, интерпретаторов, операционных систем и т. д., принят другой подход. Система конструирует сканер, подобно тому как это делает предшествующая система, но она является гораздо более общей. В ней может быть определено любое число классов и в терминах этих классов можно описать любую структуру символов, которая поддается разбору с помощью КА. Кроме того, к программе, составленной пользователем, можно обращаться не только в момент, когда считана новая карта, а всякий раз, когда построен символ определенного типа. Эта общность позволяет использовать систему и для многих других целей, помимо конструирования сканеров.
Не следует думать, что из-за универсальности система непременно будет неэффективной. Согласно Джонсону, сканер, сконструированный с помощью RWORD на IBM 7094, обрабатывал 3000 литер
l) AED расшифровывают как Automated Engineering Design (автоматизированное инженерное проектирование) или как ALGOL Extended for Design (расширенный АЛГОЛ для проектирования).— Прим. ред.
СКАНЕР
101
в секунду, в то время как программа анализатора для той же самой цели, тщательно составленная вручную, работала со скоростью 8000 литер в секунду. В настоящий момент к системе добавляются новые методы обработки наиболее общих часто встречающихся символов (таких, как идентификаторы), чтобы еще более сократить расход времени на сканирование.
Обсуждение RWORD мы начнем с рассмотрения входной информации для конструктора. Примите к сведению, что в интересах однородности изложения мы внесли некоторые изменения в систему RWORD, касающиеся исключительно обозначений.
Синтаксис для определения сканера
Определение сканера имеет вид
BEGIN {(описание классов литер>} END
BEGIN {(описание символов)} END
FINI
Эта форма очень похожа на форму, которая использовалась в системе, описанной в разд. 3.4. Общность достигается главным образом за счет описаний символов и классов литер.
Описание классов литер
Класс можно описать двумя способами. Первый способ позволяет указать лишь литеры в коде EBCDIC, которые принадлежат классу. Второй используется тогда, когда хотят показать фактическое внутреннее представление литеры. Приведем два примера первого способа описания класса:
LET=/ABCDEFGHIJKLMNOPQRSTUVWXYZ/ и
PUNCTUATION=A.,;+ — =() $ /А
Первый пример говорит о том, что класс LET состоит из всех букв (латинского алфавита) во втором примере в класс PUNCTUATION (знаки пунктуации) включены литеры: . ,; +—— ( ) $ и /.
В обоих примерах первая отличная от пробела литера, которая следует за знаком играет роль разделителя для литер этого класса. Каждая следующая литера (включая пробел) вплоть до нового появления первой литеры принадлежит классу. В первом примере в качестве разделителя используется /; во втором — А. Ясно, что сам разделитель не может принадлежать классу. Этот прием не лишен остроумия.
Пример второго способа описания класса:
XX = $ 21,22,25 $
102
ГЛАВА 3
Пример показывает, что класс XX состоит из таких литер, внутреннее представление которых есть 21, 22 и 25. Использование разделителя $ всегда означает задание внутреннего представления литер. Таким образом, знак доллара нельзя использовать в качестве разделителя в первом способе.
Имя класса может быть любой последовательностью букв, кроме BEGIN, END и FINI. Представляет интерес класс литер со специальным именем IGNORE. Он состоит из всех литер, которые должны пропускаться или игнорироваться сканером, в том случае если они встречаются во входной информации. Этот класс соответствует классу IGnore из предыдущего раздела.
Описания символов
Любое описание класса символов имеет вид
<идентификатор> (<целое»= регулярное выражение> $
где регулярное выражение определяется, как в разд. 3.2. Переменными в выражении могут быть:
1) любая литера в коде EBCDIC, кроме |, (,$ и пробела;
2) пустая цепочка Л;
3) имя класса литер;
4) апостроф ', за которым следует любая литера в коде EBCDIC, кроме пробела. (Это механизм авторегистра, который позволяет использовать литеры, запрещенные в п. 1. За апострофом следует требуемая литера.)
Приведем три примера:
PUNCT (5)=PUNCTUATION $
BEG (3)="В Е G I N" $
ID (1)=LET {LET | DIG}5 $
Первый пример говорит о том, что символы в PUNCT, внутреннее представление которых 5, являются литерами из класса PUNCTUATION. Второй пример показывает, что символ 'BEGIN' имеет внутреннее представление 3, а третий — что символы, состоящие из буквы, за которой следуют от 0 до 5 букв или цифр, имеют внутреннее представление 1. Любой символ, который принадлежит специальному классу IGNORE, никогда не передается пользователю, а полностью игнорируется. Поскольку нет необходимости во внутреннем представлении, определение для такого класса имеет вид
IGNORE= регулярное выражение> $
Обратите внимание на различие между классом литер IGNORE и классом символов IGNORE. Предположим, что входная инфор
СКАНЕР
103
мация такова:
BEGIN IGNORE-// LET—/АВ/ END
BEGIN ID (l)-LET {LET}$ END FINI
Тогда входная цепочка “AB А” будет разобрана, как один идентификатор АВА, поскольку пробелы игнорируются. Предположим теперь, что входная информация задана по-другому:
BEGIN SPACE-// LET-/AB/END
BEGIN IGNORE—SPACER ID (l)-LET {LET} $ END FINI Тогда цепочка “AB А” будет разобрана, как два идентификатора АВ и А, так как пробел — символ, который в действительности будет сконструирован, но не будет передан пользователю.
Осталось обсудить возможность вызова подпрограммы, когда в процессе сканирования построен символ. Если мы описываем класс символов, используя формат (идентификатор) ((целое), (имя подпр.»= (регулярное выражение) $
то всякий раз, когда будет сформирован символ класса (идентификатор), произойдет вызов подпрограммы (имя подпр.). Эта подпрограмма позволяет выполнить вообще любую обработку. Например, подпрограмма, связанная с идентификаторами, будет выяснять, является идентификатор служебным словом или нет; это уже не делается автоматически, как в ранее описанной системе.
Во многих случаях разбор входной цепочки можно выполнить несколькими различными спосрбами. RWORD всегда пытается сопоставить символу самую длинную цепочку литер; так, цепочка Х123 будет идентификатором; она не будет разбита на идентификатор X, за которым следует целое 123. Есть случаи, когда система RWORD не может разрешить неоднозначность. Когда это происходит, система печатает сообщение и прекращает работу.
Примеры определений сканеров
Первый пример иллюстрирует, как определяется сканер, описанный в разд. 3.3:
BEGIN SPACE = //
LET = /ABCDEFGHIJKLMNOPQRSTUVWXYZ/
DIG = /0 12345678 9/
END
BEGIN ID (1, CHECKRES) = LET {LET | DIG} $
INT (2) = DIG {DIG} $
SSL (6) = /$ SPLUS(7)=+$ SMINUS (8)=$
SSTAR (9) = *$ SLPAR (№) = ($ SRPAR(11) = )$ SSLSL (12) = / /$ SSLST (13, COMMENT) = M IGNORE = SPACE $ END FINI
104
ГЛАВА 3
Предположим, что CHECKRES проверяет идентификатор на совпадение со служебными словами ABS, BEGIN или END и выполняет некоторые сопутствующие действия. Процедура COMMENT вызывает SCAN, используя другой сканер (он определяется ниже) для того, чтобы пропустить комментарий, и затем возвращает управление. Можно было иначе определить класс литер PUNC=A/+ —*() А и затем класс символов PUNCT (6)=PUNC $. Но тогда у всех разделителей было бы одинаковое внутреннее представление и пользователю пришлось бы самому разбираться в том, какой это разделитель.
Сканер для комментария определяется следующим образом:
BEGIN IGNCHAR = $00, 01, 02, 03, ... , АО, Al, ... , FF$ END BEGIN IGNORE = IGNCHAR $
NOEND (1)= *|/$
TERMIN (2)= */$
END FINI
Конструктор
Система RWORD интересна потому, что в ней непосредственно применяется теория конечных автоматов, изложенная в разд. 3.2. Мы не будем разбираться во всех деталях конструктора. В некотором смысле, конструктор — это тот же компилятор, который переводит входную информацию, содержащую описания классов литер и символов, в программу для распознавания символов.
Конструктор выполняет работу в два этапа, названных RWORD ЧАСТЬ I и RWORD ЧАСТЬ II. Общая блок-схема RWORD ЧАСТЬ I приведена на рис. 3.13 На первой фазе переводятся во
Рис. 3.13. Часть I системы RWORD.
внутреннюю форму и запоминаются классы литер, а затем осуществляется разбор регулярных выражений и строится НКА для каждого класса символов. На второй фазе объединяются все НКА и строится один детерминированный КА. Детерминированный КА выдается в виде программы, записанной на языке AED-0. Программа состоит из таблиц и обращений к подпрограммам (с соответствующими аргументами). На каждое состояние КА приходится одно обращение;
СКАНЕР
105
аргументы, по существу, описывают отображение данного состояния на другие в зависимости от литер во входной цепочке.
После компиляции и связывания с подпрограммами полученную программу можно выполнить, и она будет сканировать и строить символы определённого языка. Но она окажется неэффективной из-за обращений к многочисленным подпрограммам, а таблицы займут значительное место в памяти. Поэтому программа проходит дополнительную обработку в RWORD ЧАСТЬ II.
Если говорить коротко, RWORD ЧАСТЬ II необходима для того, чтобы получить эффективный сканер' как в отношении времени его работы, так и в отношении занимаемой памяти. Мы, однако, не будем останавливаться на том, какая оптимизация в данном случае применяется. Кроме того, на этом этапе можно связать вместе несколько сканеров (если они используются в одной и той же работе) и получить один большой объединенный сканер. Результатом работы RWORD ЧАСТЬ II являются таблицы в виде автокодных макровызовов, т. е. полученную программу необходимо еще транслировать, используя библиотеку предварительно написанных макроопределений. Это создает относительную независимость от машины, так как макроопределения в любое время можно переписать, чтобы получить таблицы для другой машины.
3.6. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Само понятие устройства, с конечным числом состояний связано с именами Маккалока и Питтса [43]. Формализацию мы использовали аналогичную той, что предложена Муром^ [56]. Регулярные выражения и их связь с автоматом были описаны Клини [56]. Мы лишь слегка коснулись теории автоматов, поэтому заинтересованного читателя отсылаем к работам Гилла [62], Гинзбурга [62] и Хопкрофта и Улмана [69] х).
Рассмотренный в разд. 3.4 конструктор следует рассматривать как развитие конструктора, использованного в FSL (система построения компиляторов) Фелдманом [66]. Система AED RWORD, функционирующая с 1966 г. (см. Джонсон и др. [68]), является первой, в которой формальная теория конечных автоматов была применена к задаче лексического анализа.
г) Рекомендуем также монографии Глушкова [62] и Трахтенброта и Бард-зиня [70].— Прим. ред.
Глава 4
Нисходящие распознаватели
Обсуждение методов разбора для контекстно-свободных грамматик мы начнем со знакомства с нисходящими распознавателями или, как их иногда называют, прогнозирующими или целенаправленными распознавателями. В этих названиях нашел отражение способ работы таких распознавателей и способ построения синтаксического дерева. В разд. 4.1 рассматривается в самом общем виде метод, приводящий в результате к схеме, которая в принципе не эффективна из-за неизбежных и многочисленных возвратов. Затем приводится другой алгоритм, позволяющий сократить количество возвратов для некоторых грамматик. В разд. 4.2 говорится о проблемах, свойственных нисходящим методам, и рассматривается вопрос о том, как можно реорганизовать правила и как использовать другие способы записи правил, чтобы обойти трудности. Там же обсуждается представление грамматик в машине. Наконец, в разд. 4.3 говорится об использовании рекурсивных процедур при программировании нисходящего метода.
4.1. НИСХОДЯЩИЙ РАЗБОР С ВОЗВРАТАМИ
Алгоритм нисходящего разбора строит синтаксическое дерево, начиная с корня, постепенно спускаясь до уровня предложения, как было показано на рис. 2.7 в разд. 2.5. Этот пример демонстрирует простоту и наглядность основной идеи. Описание усложняется главным образом из-за вспомогательных операций, которые необходимы для того, чтобы выполнять возвраты с твердой уверенностью, что все возможные попытки построения дерева были предприняты. Чтобы свести осложнения к минимуму, опишем этот алгоритм образно. Вообразим, что на любом этапе разбора, в каждом узле уже построенной части дерева, находится по одному человеку. Люди, находящиеся в терминальных узлах, занимают места, соответствующие символам предложения.
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
107
Некоему человеку предстоит провести разбор предложения х. Прежде всего ему необходимо отыскать вывод Z=>+x, где Z — начальный символ; следовательно, первым непосредственным выводом должен быть вывод Z=>y, где Z: :=у — правило. Пусть для Z существуют правила
Z : : = ХД2. . . Xn | YXY2. . . Ym | ZXZ2. . . Z.
Сначала человек пытается применить правило Z : : = ХхХ2. . . Хп. Если нельзя построить дерево, используя это правило, он делает попытку применить второе правило Z : :=YXY2. . . Ym. В случае неудачи он переходит к следующему правилу и т. д.
Как ему определить, правильно ли он выбрал непосредственный вывод Z => ХхХ2. . . Хп? Заметим, что если вывод правилен, то для некоторых цепочек хх будет иметь место х=ххх2. . . хп, где Xj=>*Xi для i = l,. . п. Прежде всего человек, выполняющий разбор, возьмет себе приемного сынах) Мх, который должен найти вывод Хх=>*хх для любого хх, такого, что х^=хх....Если сыну Мх уда-
лось найти такой вывод, он (и любой из его сыновей, внуков и т. д.) закрывает цепочку хх в предложении х и сообщает своему отцу об успехе. Тогда его отец усыновит М2, чтобы тот нашел вывод Х2=>*х2, где х=ххх2. . . , и ждет ответа от него и т. д. Как только сообщил об успехе сын М^, он усыновит еще и Мь чтобы тот нашел вывод X 1=>*хь Сообщение об успехе, пришедшее от сына Мп, означает, что разбор предложения закончен.
Как быть, если сыну Mt не удается найти вывод X 1=>*хр В этом случае Mi сообщает о неудаче своему отцу; тот от.него отрекается и дает старшему братуМь Mi;_x такое распоряжение: «Ты уже нашел вывод, но этот вывод неверен. Найди-ка мне другой». Если Mj„x сумеет найти другой вывод, он вновь сообщит об успехе, и все продолжится по-прежнему. Если же сообщит о неудаче, отец отречется и от него,* и тогда уже его старшего брата, Mj_2, попросят предпринять еще одну попытку. Если придется отречься даже отМь значит непосредственный вывод Z=>XxX2. . . Хп был неверен, и человек, начинавший разбор, попытается воспользоваться другим выводом Z=>YX. . . Ym.
Как же действует каждый из Положим, его целью является терминал ХР Входная цепочка имеет вид х=ххх2. . . Xi_xT. . ., где символы в хх, х2, . . . , xt_x уже закрыты другими людьми. Mj проверяет, совпадает ли очередной незакрытый символ Т с его целью Хь Если это так, он закрывает этот символ и сообщает об успехе. Если нет, сообщает о неудаче.
Если цель Mj — нетерминал X ь то Mi поступает точно так же, как и его отец. Он начинает проверять правые части правил, относящихся к нетерминалу, и, если необходимо, тоже усыновляет или
1} См. определения терминов в разд. 2.4.— Прим. ред.
108
ГЛАВА 4
отрекается от сыновей. Если все его сыновья сообщают об успехе, то Mi в свою очередь сообщает об успехе своему отцу. Если отец просит Mi найти другой вывод, а целью является терминальный символ, то Mj сообщает о неудаче, так как другого такого вывода не существует. В противном случае М} просит своего младшего сына найти другой вывод и реагирует на его ответ так же, как и раньше. Если все сыновья сообщат о неудаче, он сообщит о неудаче своему отцу.
Теперь уже вам, наверное, понятно, почему этот метод называется прогнозирующим или целенаправленным. Используется и название «нисходящий» из-за способа построения синтаксического
z
т I F
i + l * г
Рис. 4.1. Частичный нисходящий разбор предложения i+i*i.
дерева. При разборе отправляются от начального символа и нисходят к предложению (рис. 4.1).
Привлекательность этого метода (и его представления) в том и состоит, что каждый человек должен помнить лишь о своей цели, о своем отце, о своих сыновьях, а также о своем месте в грамматике и во входной цепочке. И никому не нужны точные сведения о том, что происходит в других местах. Это как раз и есть то, к чему мы вообще стремимся в программировании: в каждом сегменте программы или в подпрограмме необходимо заботиться о собственной входной и выходной информации и ни о чем более.
Для имитации усыновления и отречения от сыновей в программе используется стек типа LIFO (последний — в — первый — из), или, как его иногда называют, «магазин». Стек—основной механизм, используемый почти во всех типах распознавателей. Действительно, всякий раз, когда говорят о рекурсии, говорят о стеках. Стек — запоминающее устройство, в котором хранятся данные. Однако новые данные можно занести в стек только «сверху», проталкивая при этом вниз данные, уже находящиеся в нем. Соответственно можно ссылаться только на верхний или на несколько верхних элементов, и только их можно изменять. Если верхние элементы больше не нужны, их исключают, «поднимая» при этом вверх элементы, находившиеся ниже.
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
109
Пример стека из повседневной жизни — монетодержатель. Когда вкладывается новая монета, те, что уже были внутри, проталкиваются вниз; достать можно только верхнюю монету.
Обычно для реализации стека используются массив S и счетчик v. При v=0 стек пуст. При v=n, где п>0, в стеке находятся элементы S (1), S (2),. . ., S (п), где S (п) — верхний элемент стека.
Мы можем описать алгоритм в более явном виде, воспользовавшись нестандартным вариантом АЛГОЛа. Положим, во-первых, что грамматика задана списком в одномерном массиве GRAMMAR таким образом, что каждое множество правил U : :=х | у | . . * |z представлено как Ux|y|...|z|$. То есть каждый символ занимает одну ячейку, за каждой правой частью U следует вертикальная черта “I”, а за последней правой частью U следует Таким образом, грамматика
Z:: = E#
(4.1.1) Е : : = Т+Е | Т
Т : :=F#T ( F
F : :=(Е) | i
будет выглядеть как
(4.1.2) ZE# | $ET+E|T|$TF*T|F|$F (E)|i|$
Каждый элемент стека соответствует одному человеку и состоит из пяти компонент
(GOAL, i, FAT, SON, BRO)
которые означают следующее:
1. GOAL — цель, т. е. символ, который человек ищет. Таким образом, в незакрытой в данный момент части предложения ему предстоит найти такую голову, которая приводится к GOAL, и закрыть ее. GOAL передается ему отцом.
2. i — индекс в массиве GRAMMAR, указывающий на тот символ в правой части правила для GOAL, с которым человек работает в данный момент.
3. FAT — имя отца (номер элемента стека, соответствующего отцу).
по
ГЛАВА 4
4. SON — имя самого последнего (младшего) из сыновей.
5. BRO — имя его старшего брата.
Нуль в любом из полей означает, что данная величина отсутствует. В программе значение переменной v равно количеству участвующих в разборе людей (количеству элементов в стеке в текущий момент), с — имя (номер элемента в стеке) человека, работающего в данный момент. Остальные ожидают конца его работы. Индекс j
СТЕК ЦЕЛЬ г FAT SON BRO
Z 1 Z 4 0 15 0
1 1 г 2 Е 10 1 7 0
Е * 3 Т 20 2 4 0
।—f . 4 F 28 3 5 0
т 1 Е 5 i 0 4 0 0
1+1 6 + 0 2 0 3
F Т 7 Е 12 2 8 6
1 Н—1 8 Т 18 7 12 0
i F * Т 9 F 28 8 10 0
1 | 10 г 0 9 0 0
IF 11 * 0 8 0 9
I 12 Т 20 8 13 11
1 13 F 28 12 14 0
14 г 0 13 0 0
15 # 0 1 0 2
а. Ь
ZE#|$ET+E|T|$TF*T) F|$F(E) |i,|$
Рис. 4.2. Стек после нисходящего разбора i+i*i. а—синтаксическое дерево; стек после разбора.
относится к самому левому (незакрытому) символу входной цепочки INPUT (1), . . . , INPUT (n).
Если в программе встречаются обозначения GOAL, i, FAT, SON, BRO и нет других спецификаций, то считается, что они ссылаются на компоненты, относящиеся к тому человеку, который в данный момент работает (его имя с). Об этом следует помнить при чтении программы. Например, чтобы обратиться к полю GOAL элемента S (с), мы должны вместо GOAL написать S (с).GOAL. Такая сокращенная запись вводится, чтобы не загромождать программу.
Ранее упоминалось о том, что каждый человек должен хранить информацию о своих сыновьях. Можно хранить имена всех своих сыновей в собственном элементе стека, но в таком случае число полей элемента станет переменным. Мы поступим иначе и будем использовать поле SON для хранения ссылки на последнего (младшего) сына. Тогда поле BRO элемента, соответствующего этому сыну, укажет на его старшего брата и т. д.
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
111
В качестве иллюстрации рассмотрим изображенное на рис. 4.2, а синтаксическое дерево для предложения i+i*i грамматики (4.1.1). Состояние стека после окончания работы алгоритма разбора показано на рис. 4.2, &. Теперь у человека 2 (S (2)) есть цельЕ; предполагается, что он в соответствии с синтаксическим деревом использует правило Е : :=Т+Е. Таким образом, ему для того, чтобы найти символы Т, + и Е, потребуются три сына. Значение поля S (2) . SON=7, так что его младшим сыном является человек с номером 7, цель которого Е. Имя среднего сына — число 6, определяется значением поля S (7). BRO; цель этого сына — символ +. Имя старшего сына находится в поле BRO человека 6 и равно 3.
Вы видите, что у нас имеется список сыновей каждого человека и элементы этого списка в стеке «связаны» между собой. Использование таких связанных списков широко распространено в программировании, и читатель, который еще не вполне разобрался в этом примере, должен изучать его до тех пор, пока не почувствует, что понял все досконально. Должно стать ясным, что стек в его окончательном виде не что иное, как внутренняя форма синтаксического дерева.
Отметим, как в конце каждого предложения в соответствии с грамматикой (4.1.1) используется разделитель. По нему можно судить о том, что окончен разбор всего предложения, а не только какой-то из его голов.
Далее следует алгоритм нисходящего разбора. Он разбит на шесть частей для того, чтобы выделить разные функции. Там, где второстепенные детали могут затенить смысл алгоритма, мы даем некоторые пояснения.
НАЧАЛЬНАЯ УСТАНОВКА
S(l) :== (Z, 0, 0, 0, 0); с:=1;
v:=l; 1; GO ТО НОВЫЙ
ЧЕЛОВЕК
НОВЫЙ ЧЕЛОВЕК
IF GOAL терминал THEN
IF INPUT (j) = GOAL THEN BEGIN j:=j+l; GO TO УСПЕХ
EISE GO TO НЕУДАЧА i:= индекс в GRAMMAR правой части для GOAL;
GO TO ЦИКЛ
ЦИКЛ
IF GRAMMAR (i)=“|”
THEN IF FAT # 0
Первое усыновление. Цель усыновленного — начальный символ Z.
Новый человек изучает свою цель. Цель — терминал.
Если GOAL совпадает с символом из предложения, человек закрывает этот символ и сообщает об успехе.
Не совпадает — сообщает о неудаче. Цель нового человека — нетерминал. Подготовка к просмотру правых частей в правилах для GOAL.
Просмотр правой части.
112
ГЛАВА 4
THEN GO TO УСПЕХ
ELSE STOP — предложение;
IF GRAMMAR (i)=±=“F
THEN IF FAT #0
THEN GO TO НЕУДАЧА ELSE STOP —не предложение;
v:=v+ 1:
S(v) := (GRAMMAR (i), 0, c, 0, SON);
SON :=v; c:=v;
GO TO НОВЫЙ ЧЕЛОВЕК
УСПЕХ
c:—FAT;
i: =i+ 1; GO TO ЦИКЛ;
НЕУДАЧА
c: = FAT;
v: = v— 1;
SON := S (SON)-BRO;
GO TO ЕЩЕ РАЗ
ЕЩЕ РАЗ
IF SON = 0 THEN
BEGIN WHILE GRAMMAR
(i) + “I”
DO i:= i + 1;
i:= i+1; GO TO ЦИКЛ END;
i:— i — 1; c: = SON;
IF GOAL нетерминал
THEN GO TO ЕЩЕ РАЗ
j:= j —1;
GO TO НЕУДАЧА
Вы достигли конца правой части, поэтому сообщите об успехе. Если нет отца, то останов — окончен разбор предложения.
Нет больше правых частей, которые можно было бы попробовать, поэтому сообщите о неудаче или, если нет отца, остановитесь, не распознав предложения.
GRAMMAR (i) — другая цель, которую можно попытаться найти. Возьмите сына. Вы его отец, а его старший брат — тот, который до этого был вашим младшим сыном.
Переключить внимание на нового сына и ждать от него ответа.
Сообщить об успехе своему отцу; он предпримет следующий шаг.
Сообщить о неудаче своему отцу. Он от вас отречется и попросит вашего старшего брата предпринять еще одну попытку.
Есть у вас сын, который может предпринять еще одну попытку? Нет. Тогда пропустите эту правую часть — это не та, которая нужна — перейдите к следующей.
У вас есть сын. Попросите его повторить попытку. Его цель — нетерминал, так что он попытается еще раз добиться успеха.
Его цель — терминал. Попытка не приведет к успеху. Поэтому он открывает свой символ и сообщает о неудаче.
Несмотря на то что этот алгоритм может показаться удачным, в нем есть серьезный недостаток, смысл которого будет разъяснен в следующем разделе. Во-первых, давайте так модифицируем алгоритм, чтобы во время его работы было поменьше возвратов. Заметьте, что когда кто-либо сообщает о своей неудаче, мы отрека
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
113
емся от него и просим его старшего брата «попытаться еще раз», т. е. поискать другую подцепочку, которая приводится к желаемой цели. Поступая таким образом, мы показываем, как мало полагаемся мы на своего сына. Если бы прежде чем его усыновлять, мы делали тщательную проверку и указывали ему правильный путь, можно было бы доверять ему в гораздо большей степени. Будем теперь считать, что он сразу делает все верно. Тогда не придется просить его повторить попытку. Если кого-нибудь постигнет неудача, останется только предположить, что мы на ложном пути, и поискать совсем другую альтернативу (правую часть правила).
Для этого необходимо упорядочить правила, относящиеся к каждому нетерминалу, чтобы сразу находить верное правило. Такую операцию удается произвести с большинством языков программирования, но способа, позволяющего сделать это автоматически, нет. Можно помещать первой самую длинную из альтернатив. Грамматика (4.1.1) уже задана в такой форме. Таким образом, если у человека есть цель Е, он первым делом ищет Т+Е. Если есть Т, а символа + нет, он не просит своего первого сына найти другое Т, а отказывается от всех сыновей и переходит к следующему правилу Е : :=Т.
После таких изменений становится ненужной компонента стека BRO, зато приходится внимательнее следить за тем, какая часть цепочки уже закрыта. Теперь элемент стека выглядит так:
(GOAL, i, FAT, SON, j)
где GOAL, i, FAT и SON имеют прежний смысл, a j содержит индекс, указывающий то место во входной цепочке INPUT, которое мы в данный момент йзучаем или о котором ждем сообщения. Поскольку вся задача в целом стала проще, мы можем, находясь в данном месте, сами проверить терминальные символы в правых частях; при этом отпадает необходимость в усыновлении человека, которому пришлось бы выполнять это задание.
Еще раз заметим, что алгоритм работает правильно только при условии, что правила упорядочены так, что сразу же делается попытка применить верное правило.
НАЧАЛЬНАЯ УСТАНОВКА
S(l) := (Z, 0, 0, 0, 1); с:= 1; v:= 1; GO ТО НОВЫЙ ЧЕЛОВЕК
НОВЫЙ ЧЕЛОВЕК
i:= индекс, указывающий на первую правую часть для GOAL в грамматике;
GO ТО ЦИКЛ
Поставить перед новым человеком цель Z и начать с первого символа.
Усыновление происходит лишь в случае нетерминала. Сын находит относящиеся к нему правила и начинает работать.
114
ГЛАВА 4
ЦИКЛ
IF GRAMMAR (i) = „|“
THEN IF FAT # 0
THEN GO TO УСПЕХ ELSE STOP — предложение;
IF GRAMMAR =
THEN IF FAT 0
THEN GO TO НЕУДАЧА
ELSE STOP — не предложение
IF GRAMMAR (i) терминал
THEN IF INPUT(j) = GRAMMAR (i) THEN
BEGIN ]:==] +1;
GO TO ЦИКЛ
END
ELSE GO TO РАССМОТРИ АЛЬТЕРНАТИВУ
v:= v + 1;
S (v) : = (GRAMMAR (i), 0, c, 0, j);
SON := v; c:=v;
GO TO НОВЫЙ ЧЕЛОВЕК
УСПЕХ
c:—FAT; j:=S(SON)*j;
i:=i+1; j:=j + l;
GO TO ЦИКЛ
НЕУДАЧА
c:—FAT;
v:=c; SON:=0;
GO TO РАССМОТРИ АЛЬТЕРНАТИВУ
РАССМОТРИ АЛЬТЕРНАТИВУ
IF FAT ф 0
THEN j: =S(FAT).j ELSE j : = 1;
WHILE i:=i + l;
i: = i+1; GO TO ЦИКЛ
Просмотр правой части.
Вы достигли ее конца, так что сообщите об успехе, или, если отца нет, закончите работу; предложение распознано.
Нет больше правых частей, которые можно было бы рассмотреть, так что сообщите о неудаче, или, если отца нет, остановитесь.
Предложение не распознано.
Если терминал подходит, мы закрываем его и переходим к следующему символу.
Терминал не подходит, поэтому перейдите к правой части.
Возьмите еще одного сына, укажите ему цель — нетерминал.
Его отец — вы. Переключитесь на него и ожидайте от него сообщения.
Сообщите отцу, какая часть цепочки закрыта. Тогда он продолжит свою работу.
Сообщите о неудаче своему отцу.
Он отречется от вас и от всех остальных сыновей, а после этого рассмотрит другую альтернативу.
Узнайте у отца, с какого места продолжить обработку.
Найдите начало следующей альтернативы, если такая есть, и начните все снова.
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
115
4.2. ПРОБЛЕМЫ НИСХОДЯЩЕГО РАЗБОРА И ИХ РЕШЕНИЕ
Прямая левосторонняя рекурсия
В алгоритме, описанном в разд. 4.1, есть серьезный недостаток, который проявляется, когда цель определена с использованием левосторонней рекурсии. Если X — наша цель, а первое же правило для X имеет вид X : :=Х. . . , то мы незамедлительно усыновляем того, кто будет искать X. Он в свою очередь немедленно «заведет» себе сына, чтобы тот искал X. Таким образом, каждый будет сваливать на своего сына ответственность, и для решения этой задачи не хватит всего населения Китая.
По этой причине правила грамматики (4.1.1) написаны с применением правосторонней рекурсии вместо более привычной левосторонней. Лучший способ избавиться от прямой левосторонней рекурсии — записывать правила, используя итеративные и факультативные обозначения, которые обсуждались в разд. 2.9. Запишем правила
(4.2.1) Е : :=Е+Т | Т как Е : :=Т {+Т}
и
Т: :=T*F|T/F|F как Т: :=F { *F|/F}
Сейчас будут сформулированы два принципа, на основании которых правила языка, включающие прямую левостороннюю рекурсию, преобразуются в эквивалентные правила, использующие итерацию.
(4.2.2) Факторизация. Если существуют правила вида U : :=ху | xw | . . . | xz, то их надо заменить на U: :=x(y|w|. . . |z), где скобки являются метасимволами.
Допустима факторизация и в более общей форме, такая, как в арифметических выражениях. Например, если в (4.2.2) y=yiy2 и w=y!W2, мы могли бы заменить U : :=х (y|w|. . . |z) на
U : :=х (у! (y2|w2)|. . . |z).
Заметьте, что исходные правила U : :=х | ху мы преобразуем к виду U ::=х (у|А), где Л — пустая цепочка. Когда бы ни использовалось подобное преобразование, Л всегда помещается как последняя альтернатива, так как мы принимаем условие, что если цель — Л, то эта цель всегда сопоставляется.
Помимо того что факторизация позволяет нам исключить прямую рекурсию, использование этого приема сокращает размеры грамматики и позволяет проводить разбор более эффективно. В этом мы убедимся позже.
После факторизации (4.2.2) в грамматике останется не более одной правой части с прямой левосторонней рекурсией для каждого
116
ГЛАВА 4
из нетерминалов. Если такая правая часть есть, мы делаем следующее:
(4.2.3) Пусть U ::=х|у|. . . |z]Uv — правила, у которых осталась леворекурсивная правая часть. Эти правила означают, что членом синтаксического класса U является х, у или z, за которыми либо ничего не следует, либо следует сколько-то v. Тогда преобразуем эти правила к виду U :: = (х|у| . . . |z) {v}.
Мы использовали (4.2.3), чтобы сделать преобразование в (4.2.1), позволяющее избавиться от ненужных скобок, заключающих Т. В качестве другого примера преобразуем A ::=BC|BCD|Axz|Axy.
z
Ь
Рис. 4.3. Деревья, использующие рекурсию и итерацию.
Применив правило (4.2.2), получим А ::=ВС (D|A)|Ax (z|y); применив (4.2.3), получим А :: = (ВС (D|A)){x(z|y)}. Можно избавиться от одной пары скобок, после чего получим A ::=BC(D|A){x(z|y)}.
После таких изменений мы, конечно, должны изменить и наш алгоритм нисходящего разбора. Теперь алгоритм должен уметь обрабатывать альтернативы не только во всей правой части, но и в ее подцепочках, должен учитывать в своей работе существование пустой цепочки А, должен уметь обрабатывать итерацию. Внесение этих изменений в алгоритм предоставляется читателю.
Использование итерации вместо рекурсии отчасти меняет и структуру деревьев. Таким образом, рис. 4.3, а должен был бы походить на рис. 4.3, Ь. Мы утверждаем, что эти два дерева следует рассматривать как эквивалентные; операторы «плюс» должны выполняться слева направо.
Общая левосторонняя рекурсия
Мы не решили всей проблемы левосторонней рекурсии: с прямой левосторонней рекурсией покончено, но общая левосторонняя рекурсия еще осталась. Таким образом, правила
U ::=Vx и V ::=Uy|v
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
117
дают вывод U=>+Uyx. Избавиться от этого не так просто, но обнаружить такую ситуацию можно. Исключим из исходной грамматики все правила с прямой левосторонней рекурсией. Символ U, получившейся в результате этих преобразований грамматики, может быть леворекурсивным тогда и только тогда, когда U FIRST4" U. Как проверить это отношение, нам уже известно.
Представление грамматики в оперативной памяти
Одной из проблем, возникающих при реализации нисходящих методов, является представление грамматики в вычислительной машине. Одно из возможных представлений мы уже использовали
Рис. 4.4. Синтаксический граф для грамматики (4.2.4).
в разд. 4.1. Очевидно, что оно неудачно из-за объема работы, необходимой для поиска правил, соответствующих каждому нетерминалу. Речь пойдет о другом представлении. Прежде чем начать изложение, мы только упомянем о том, что написать конструктор, который воспринимает грамматику, проводит любые из преобразований, о которых только что говорилось, проверяет, не являются ли правила леворекурсивными, и составляет таблицы для грамма
118
ГЛАВА 4
тики в одной из описываемых далее форм — довольно легко, и мы опять предоставляем это читателю.
Для представления грамматики используется списочная структура, называемая синтаксическим графом. Каждый узел представляет символ S из правой части и состоит из четырех компонент: ИМЯ, ОПРЕДЕЛЕНИЕ (ОПР), АЛЬТЕРНАТИВА (АЛТ) и ПРЕЕМНИК (ПРЕМ), где
1. ИМЯ — это сам символ S в некоторой внутренней форме.
2. ОПРЕДЕЛЕНИЕ равно 0, если S — терминал; в противном случае эта компонента указывает на узел, соответствующий первому символу в первой правой части для S.
3. АЛЬТЕРНАТИВА указывает на первый символ той альтернативы правой части, которая следует за правой частью, содержащей данный узел (0, если такой правой части нет). Это только для первых символов в правых частях.
4. ПРЕЕМНИК указывает на следующий символ правой части (О, если такого символа нет).
Кроме того, каждый нетерминальный символ представлен узлом, состоящим из одной компоненты, которая указывает на первый символ в первой правой части, относящейся к этому символу. Примером может служить рис. 4.4, на котором изображен синтаксический граф грамматики (4.2.4). Компоненты каждого узла располагаются так:
ИМЯ
ОПР АЛТ ПРЕМ
(4.2.4) Е ::=Е<аоп>Т| Т <аоп> : :=+ | — Т ::~T<Mon>F|F <моп> : :=* |/ F ::=(E)|i
Синтаксический граф — удобная форма записи для проведения преобразований (4.2.2) и (4.2.3). На рис. 4.5 изображен модифицированный синтаксический граф грамматики (4.2.4). Для указания на итерацию в узлах имеются дополнительные символы. ST в узле означает, что данный символ начинает цепочку, заключенную в фигурные скобки, в то время как звездочка указывает на то, что символ оканчивает такую строку.
Будьте здесь внимательны. В зависимости от того, как работает анализатор, для правой части вида {{X, Y}Z} может получиться так, что в узел X нужно занести ST2, чтобы указать, что X начинает две вложенные друг в друга итерации.
Мы также можем отождествлять между собой узлы графа с идентичными компонентами. Например, на рис. 4.4 два узла с именем F
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
119
одинаковы. Если алгоритм продолжает работать и после того, как мы провели отождествление, исходная грамматика все более утрачивает свой первоначальный вид, и поэтому по семантическим соображениям (которые будут понятны гораздо позже) эта идея неудачна.
Рис. 4.5. Модифицированный синтаксический граф.
Если программирование ведется на языке, не допускающем указательных переменных, можно пользоваться одномерными массивами; указателям будут соответствовать индексы массива.
Разбор без возвратов
Программа разбора в компиляторе ни в коем случае не должна прибегать к возвратам. Мы должны иметь уверенность в том, что каждая предполагаемая цель верна. Это необходимо потому, что
120
ГЛАВА 4
нам предстоит связать семантику с синтаксисом, и по мере того, как мы будем прогнозировать и находить цели, эти символы будут обрабатываться семантически. Вот некоторые примеры «обработки»: 1) при обработке описаний переменных идентификаторы помещаются в таблицу символов; 2) при обработке арифметических выражений проверяют, совместимы ли типы операндов.
Если возврат произошел из-за того, что прогнозируемая цель неверна, придется уничтожить результаты семантической обработки, проделанной во время поисков этой цели. Сделать это не так-то просто, поэтому постараемся провести грамматический разбор без возвратов.
Для того чтобы избавиться от возвратов, в компиляторах в качестве контекста обычно используется следующий «незакрытый» символ исходной программы. Тогда на грамматику налагается следующее требование: если есть альтернативы х | у | . . . |z, то множества символов, которыми могут начинаться выводимые из х, у, . . . , z слова, должны быть попарно различны. То есть если xz>*Au и y=>*Bv, то А=#В. Если это требование выполнено, можно довольно просто определить, какая из альтернатив х, у или z — наша цель. Заметим, что факторизация оказывает здесь большую помощь. Если есть правило U : :=ху | xz, то преобразование этого правила к виду U :~х (у | z) помогает сделать множества первых символов для разных альтернатив непересекающимися.
Здесь не приводится более подробного описания этого метода, хотя в следующем разделе мы вновь встретимся с его применением.
4.3. РЕКУРСИВНЫЙ СПУСК
В некоторых компиляторах синтаксический анализатор содержит по одной рекурсивной процедуре для каждого нетерминала U. Каждая такая процедура осуществляет разбор фраз, выводимых из U. Процедуре сообщается, с какого места данной программы следует начинать поиск фразы, выводимой из U. Следовательно, такая процедура — целенаправленная, или прогнозирующая. Мы предполагаем, что сможем найти такую фразу. Процедура ищет эту фразу, сравнивая программу в указанном месте с правыми частями правил для U и вызывая по мере необходимости другие процедуры для распознавания промежуточных целей.
В действительности во время этого разбора дерево строится точно так же, как в алгоритме разбора, описанном в разд. 4.1 (без возвратов). Отличается только форма записи самого алгоритма.
Чтобы проиллюстрировать этот способ, запишем процедуры для
НИСХОДЯ ЩИЕ РАСПОЗНАВАТЕЛИ
121
нетерминальных символов такой грамматики:
<инстр>
(4.3.1)
<перем>
<выр>
<терм>
<множ>
<перем>: = <выр>
| IF <выр> THEN <инстр>
| IF <выр> THEN <инстр> ELSE <инстр> i |i «выр»
<терм> | <выр> 4- <терм>
<множ> | <терм> * <множ>
<перем> | «выр»
Чтобы удобнее было работать, перепишем грамматику так:
< инстр>:: = <перем>: = <выр>
| IF <выр> THEN <инстр> [ELSE <инстр>] (4.3.2) <перем>:: =i [«выр»]
< выр> ::=<терм> { + <терм»
< терм> :: =<множ> {*<множ>}
< множ> :: =<перем> | «выр»
Мы полагаем, что сможем провести разбор без возвратов. Для того чтобы возвратов не было, в качестве контекста используется единственный символ, следующий за уже разобранной частью фразы. Мы записываем процедуры на нестандартном АЛГОЛе с соблюдением следующих условий:
1. Глобальная переменная NXTSYMB всегда содержит тот символ исходной программы, который будет обрабатываться следующим. При вызове процедуры для поиска новой цели первый символ, который она должна исследовать, уже находится в NXTSYMB.
2. Подобно этому, перед тем как выйти из процедуры с сообщением об успехе, символ, следующий за уже разработанной подцепочкой, помещается в NXTSYMB.
3. Процедура SCAN готовит очередной символ исходной программы и помещает его в NXTSYMB.
4. Программа ERROR вызывается в тех случаях, когда обнаружена ошибка. Она печатает сообщение и передает управление обратно. После возврата мы продолжим работу так, как будто бы никакой ошибки не было (см. соображения, следующие за описанием процедур).
5. Для того чтобы начать синтаксический анализ инструкции, мы обращаемся к программе SCAN, которая поместит первый символ в NXTSYMB, а затем вызываем процедуру STATE.
122
ГЛАВА 4
PROCEDURE STATE;
IF NXTSYMB = “IF”
THEN
BEGIN SCAN; EXPR;
IF NXTSYMB # “THEN” THEN ERROR ELSE
BEGIN SCAN; STATE;
IF NXTSYMB / “ELSE” THEN
BEGIN SCAN;
STATE END
END
END
ELSE
BEGIN VAR;
IF NXTSYMB / THEN ERROR ELSE BEGIN SCAN; EXPR END
END;
PROCEDURE VAR;
IF NXTSYMB #“i”THEN ERROR
ELSE BEGIN SCAN;
IF NXTSYMB = “(” THEN BEGIN SCAN; EXPR;
IF NXTSYMB “)”
THEN ERROR
ELSE SCAN END
END;
Подпрограмма для <инстр>. Мы обычно полагаем, что можно определить вид инструкции по первому символу-
Взять первый символ выражения и вызвать процедуру для обработки вы. ражения. Следующим символом должен быть «THEN», затем — инструкция. Рекурсивный вызов. Если встретится символ «ELSE», произвести его анализ.
Это не условная инструкция. Должна быть инструкция присваивания. Перейти к разбору переменной, проверить, есть ли символ : = , и затем анализировать выражение.
Конец процедуры <инстр>.
Подпрограмма для <перем>.
Переменная должна начинаться с i.
Взять символ, следующий за 1. В том и только в том случае, когда это открывающая скобка, перейти к разбору выражения и проверить, следует ли за выражением закрывающая скобка. Занести в NXTSYMB символ, следующий за обработанной конструкцией.
PROCEDURE EXPR;
BEGIN TERM;
WHILE NXTSYMB = “+” DO
BEGIN SCAN ;TERM END
END
Подпрограмма для <выр>.
Выражение должно начинаться термом. После этого ожидается любое количество конструкций вида «+<терм>». Возврат, если следующий символ не «+».
НИСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
123
PROCEDURE TERM;
Подпрограмма для <терм>.
BEGIN FACTOR;
WHILE NXTSYMB—DO BEGIN SCAN; FACTOR END
END
PROCEDURE FACTOR;
IF NXTSYMB = “(” THEN BEGIN SCAN; EXPR;
IF NXTSYMB “)”
THEN ERROR;
ELSE SCAN END
ELSE VAR;
Процедура аналогична процедуре для <выр> и не требует объяснений.
Подпрограмма для <множ>.
По первому символу выбирается альтернатива. Это выражение, заключенное в скобки. Проверить наличие закрывающей скобки и сканировать следующий символ.
Это переменная.
Во всех этих процедурах необычно то, что они не требуют локальных переменных. Фактически единственная используемая переменная— это NXTSYMB. По существу, мы просто используем обычный стековый механизм, связывающий процедуры во время счета для того, чтобы имитировать стек, используемый в разд. 4.1.
Преимущества этого метода совершенно очевидны. Программируя, можно реорганизовать правила так, чтобы они согласовывались с процедурами. Предполагается, что автор компилятора настолько хорошо знаком с исходным языком, что может произвести реорганизацию, которая избавляет от возвратов. Метод сохраняет свою гибкость и по отношению к семантической обработке. С этой целью в любое место процедуры можно включить группу команд, не откладывая семантическую обработку до тех пор, пока будет обнаружена вся фраза. Мы познакомимся с этим подробнее, когда речь пойдет о семантике.
Основной недостаток состоит в том, что на программирование и отладку затрачивается больше усилий, чем в частично автоматизированных системах. Тем не менее это разумный метод и используется он во многих компиляторах.
Большинство компиляторов после обнаружения ошибки просто исключают весь путь вплоть до уровня инструкции. На этом уровне пропускается участок исходной программы до ближайшего символа BEGIN, END или до точки с запятой и лишь затем возобновляется обработка. Такой подход, конечно, довольно примитивен. К этой теме мы еще вернемся в гл. 15.
Несложные размышления, несомненно, убедят читателя в том, что можно написать такую программу, которая воспринимала бы правила подходящей грамматики и порождала бы рекурсивные
124
ГЛАВА 4
процедуры (написанные на каком-нибудь языке) для этой грамматики. Конечно, на грамматику пришлось бы наложить некоторые ограничения.
УПРАЖНЕНИЯ К РАЗДЕЛУ 4.3
1. Выполните вручную написанные выше процедуры для проведения синтаксического анализа следующих инструкций:
a) i: = i; b) i:=i (i); c) IF i THEN i:~i. Начните с выполнения инструкций SCAN; STATE.
4.4. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Одна из первых статей, в которых рассматривался фиксированный алгоритм разбора с описывающими язык таблицами, принадлежит Айронсу [61а]. Его метод — это не нисходящий разбор в чистом виде, как описано здесь, а некоторое смешение нисходящих и восходящих методов. Второй метод будет описан дальше. Куно и Уттингер использовали нисходящий способ в исследованиях, касающихся естественных языков. Алгоритм, приведенный в разд. 4.1, взят из обзора Флойда [64Ь]. Способ изложения принципа нисходящего разбора на примере людей позаимствован из этой же работы.
Обстоятельный доклад об использовании прогнозирующих методов при компилировании был сделан на весенней конференции (SJCC) Читэмом и Сэттли [64]. Гро [61] также описывает компилятор, в котором используются рекурсивные процедуры.
Способы, позволяющие избавиться от возвратов, описаны Унгером [68], в то время как Льюис и Стирнз [68] и Розенкранц и Стирнз [69] исследовали LL (к) грамматики и языки, в которых для проведения нисходящего разбора без возвратов достаточно на каждом шаге анализировать все уже обработанные символы и еще к символов справа.
В языке символьной обработки COGENT (Рейнольдс [65]) используется нисходящая схема разбора, причем разбор альтернатив производится параллельно и всякий раз исключаются те из них, которые оказались полностью неподходящими. Таким образом, можно обработать неоднозначные языки; при этом для неоднозначного предложения порождаются все возможные варианты разбора. Нисходящий разбор — излюбленный метод в системе написания компиляторов МЕТА (см. Шорр [64]) и используется в самом старом компиляторе компиляторов (Брукер и др. [63]). Его описание приводится в работе Розена [64]. Среди компиляторов, в которых используется рекурсивный спуск,— компилятор с расширенного языка АЛГОЛ фирмы Burroughs и компилятор с АЛГОЛа для машины 7090, разработанный группой SHARE.11 *
См. также статью Вирта [71].— Прим, ред.
Глава 5
Грамматики простого предшествования
5.1. ОТНОШЕНИЯ ПРЕДШЕСТВОВАНИЯ
И ИХ ИСПОЛЬЗОВАНИЕ
В этой главе описывается схема разбора, в которой применяется восходящий метод. Напомним, что при использовании этого метода в текущей сентенциальной форме повторяется поиск основы (самой левой простой фразы и), которая в соответствии с правилом U : :=и приводится к нетерминалу U. При применении любого из методов нисходящего разбора возникает вопрос — как найти основу и выяснить, к какому нетерминалу нужно ее приводить. В настоящей главе этот вопрос решается для определенного класса грамматик, называемых грамматиками (простого) предшествования. Для всех грамматик это, конечно, проблемы не решает. Поскольку мы будем двигаться слева направо и снизу вверх, то все сентенциальные формы и весь вывод будут каноническими. В этой главе термин «сентенциальная форма» означает «каноническая сентенциальная форма».
Как же найти основу, если задана сентенциальная форма х? Хотелось бы, двигаясь слева направо и рассматривая только два соседних символа одновременно, суметь определить, нашли ли мы хвост основы. А затем, продвигаясь назад к левому концу сентенциальной формы, найти голову основы, опять-таки принимая каждый раз решение только по двум соседним символам. То есть мы сталкиваемся с такой проблемой: если задана цепочка . . .RS. . . , то всегда ли R является хвостом основы, или RS вместе могут встретиться в основе, или возможны другие варианты? Хотелось бы, не приступая еще к разбору, исследовать грамматику и принять решение относительно каждой пары символов R и S.
Рассмотрим теперь два символа R и S из словаря V грамматики G. Предположим, что существует (каноническая) сентенциальная форма . . .RS. ... На некотором этапе канонического разбора либо R, либо S (или оба символа одновременно) должны войти в основу. При этом возникают следующие три возможности:
1. R — часть основы, a S нет (рис. 5.1, а). Эту ситуацию мы записываем как R *>S и говорим, что R больше S или что R предшествует S, поскольку символ R будет редуцирован раньше, чем S.
126
ГЛАВА 5
Заметим, что R должен быть последним (хвостовым) символом в правой части некоторого правила U . . .R. Заметим еще, что, поскольку основа находится слева otS, S должен быть терминалом.
2. Оба символа R и S входят в основу (рис. 5.1, Ь). Запишем это как R=LS. У них одинаковое значение предшествования, и они
Рис. 5.1. Примеры отношений предшествования.
должны редуцироваться одновременно. Очевидно, в грамматике должно быть правило U . . .RS. . . .
3. S — часть основы, a R нет (рис. 5.1, с). Отношение между ними записывается как R<£S; можно говорить, что R меньше, чем S. Символ S должен быть первым (головным) в правой части некоторого правила U ::=S. . . .
Если (канонической) сентенциальной формы . . .RS. . . не существует, мы считаем, что между упорядоченной парой символов (R, S) не определено никакое отношение. Заметим, что ни одно из трех определенных выше отношений предшествования <•,= и •> не является симметричным. Например, из R<»S вовсе не следует S<R
Рассмотрим в качестве примера грамматику G5 (Z)
(5.1.1) Z :: =ЬМЬ
М :: =(L|a L=Ма)
Языку L (G5) принадлежат такие цепочки, как bab, b (аа)Ь, b ((аа)а) b и b (((аа)а)а)Ь. В каждом столбце приведенной ниже таблицы показана сентенциальная форма, ее синтаксическое дерево, основа дерева и отношения, которые можно из него получить.
На рис. 5.2 представлена матрица предшествования для грамматики G5 — матрица, в которой указываются все отношения предшествования. Элемент этой матрицы В [i, j] содержит отношение между парой символов (Sb Sj). Пустой элемент матрицы свидетельствует о том, что между соответствующими двумя символами отношение предшествования не определено.
ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВОВАНИЯ
127
b ( М а ) Ь
Сентенциальная b а Ь
форма,: Синтаксическое Z
дерево: ।-----1----1
b М b
I а
b ( L b
1—I—-I М а )
Основа!. а
Отношения» b <• а
определяемые а •> Ь
деревом:
( U
Ь <• (
( = L
L •> Ь
М ) а
( <• М М ± а а = ) ) •> b
Z .—I—, ь м ь
На первый взгляд может показаться, что трудно найти все отношения предшествования между символами грамматики. Складывается впечатление, что придется просмотреть довольно много синтаксических деревьев, чтобы найти все отношения. Да и как гарантировать, что все отношения найдены? В следующем разделе мы переопределим отношения так, что их можно будет без особого труда построить для любой грамматики.
Рис. 5.2. Матрица предшествования для грамматики G5.
Как же воспользоваться отношениями предшествования при разборе предложений? Если между какой-либо парой символов (R, S) определено более чем одно отношение, они бесполезны. Если же между любой парой символов определено не более одного отношения, отношения предшествования позволят найти основу любой сентенциальной формы. Тогда можно сказать, что основой любой сентенциальной формы Si . . . Sn является самая левая подцепочка Sj . . . Sb такая, что
Sj-t^Sj
(5.1.2) S3iSJ+1iSJ+2=r. .
Si Л> SU1
128
ГЛАВА 5
(Чтобы учесть и тот случай, когда символ Sj (Si) основы является самым первым (последним) символом сентенциальной формы, последнее утверждение придется слегка изменить; мы это сделаем позже.) Из определения отношений с очевидностью вытекает, что основа Sj ... Sj удовлетворяет (5.1.2). Не столь очевидным пред-
Шаг Сентенциальная форма Основа Привести основу к Построенный непосредственный вывод
1 b ( а а ) b а М b (Ma) b b (aa) b
2 b ( М а ) b М а) L b (Lb b (Ma) b
3 b ( L b (L М bMb => b (Lb
4 b М b ьмь Z Zz>bMb
Рис. 5.3. Разбор сентенциальной формы b (аа) Ь.
ставляется тот факт, что самая левая подцепочка, удовлетворяющая (5.1.2), является основой. Это мы докажем в следующем разделе. А пока примем это на веру и завершим раздел примером канонического разбора предложения b (аа)Ь грамматики G5 с использованием матрицы предшествования, изображенной на рис. 5.2. Рисунок 5.3 иллюстрирует разбор. На каждом шаге показаны сентенциальная форма и отношения, определенные между символами в соответствии с рис. 5.2.
УПРАЖНЕНИЯ К РАЗДЕЛУ 5.1
1. По заданным синтаксическим деревьям определите все отношения предшествования. (После того как определение отношений
<блок>
BEGIN /список V ^описании/
<01шсание>
у список хинстр^кции/ <инструкция>
।-----------1 I--------1
REAL / список .(переменная):
Хибеишифцкаторов^
по данной основе будет закончено, отсеките ее от дерева; получится другое дерево. Затем определите отношения, исходя из нового дерева.)
ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВОВАНИЯ
129
2. Используя для нахождения основ матрицу предшествования, заданную на рис. 5.2, проведите разбор следующих предложений грамматики G5: b a b, b (aa)b, b (((а а) а)а) Ь.
3. Попытайтесь найти все отношения предшествования для грамматики (4.1.1).
5.2. ОПРЕДЕЛЕНИЕ И ПОСТРОЕНИЕ ОТНОШЕНИЙ
В разд. 5.1 мы определили три отношения предшествования в терминах синтаксических деревьев сентенциальных форм. Теперь мы хотим определить их заново, основываясь только на правилах грамматики, так, чтобы можно было построить отношения предшествования и доказать утверждение из предыдущего раздела. Эти определения выглядят довольно громоздкими, но для доказательства интересующих нас положений они необходимы.
(5.2.1). Определение. Если задана грамматика G, то отношения предшествования между символами из словаря V определяются следующим образом:
1. RjlS тогда и только тогда, когда в G есть правило U: :=. . .RS. . . .
2. R<«S тогда и только тогда, когда существует правило U: :=. . .RV. . . , такое, что справедливо отношение V FIRST+ S [см. (2.6.4)1.
3. R »>S тогда и только тогда, когда S — терминал и существует правило U: . .VW. . . , такое, что справедливы соотноше-
ния V LAST+ R и W FIRST* S [см. (2.6.7) и (2.6.4)].
Далее нам потребуются еще два отношения:
R<«=S тогда и только тогда, когда R^S или R<»S.
R^=S тогда и только тогда, когда R=S или R«>S.
Мы должны доказать, что отношения, определенные таким необычным путем, эквивалентны тем, более понятным, отношениям, которые описаны в разд. 5.1. Покажем это для отношений и •>, а аналогичное доказательство для отношения <• предоставим читателю (упражнение 1).
(5.2.2). Теорема. R^S тогда и только тогда, когда основа некоторой сентенциальной формы содержит подцепочку RS.
Доказательство. Пусть R=S. Мы должны построить такое синтаксическое дерево, чтобы цепочка RS содержалась в основе. По определению, для некоторых и и v существует правило U: :=uRSv. Так как каждое правило используется в выводе по меньшей мере одного предложения (предполагается, что грамматика
5 д. Грис
130
ГЛАВА S
приведенная), имеем Z=>* хПудля некоторых х и у, где Z — начальный символ. Строим искомое синтаксическое дерево в три этапа:
1. Строим дерево вывода xUy.
2. Редуцируем дерево, построенное на 1-м этапе (отсекаем основы), до тех пор, пока U не станет частью основы. Это возможно, потому что каждый символ в некоторый момент является частью основы.
3. Добавляем к дереву, полученному в результате выполнения 2-го этапа, еще один куст для правила U: :=uRSv. Так как символ U входил в основу, новой основой станет uRSv, т. е. дерево построено.
Обратно, если RS — часть основы, то по определению основы должно существовать правило U: : = . . .RS. . . .
(5.2.3). Теорема. R«>S тогда и только тогда, когда существует каноническая сентенциальная форма . . .RS. . . , где R — последний символ основы.
Доказательство. Предположим, что R*>S. Покажем, как построить синтаксическое дерево, обладающее требуемым свойством. Во-первых, так как R«>S, то имеется правило U: :~uVWv, где V LAST* R и W FIRST* S. Что это означает? Так как грамматика приведенная, мы знаем, что Z=>«xUy=>xuVWvy (Z — начальный символ). Во-вторых, отношение V LAST+ R означает, что V z>+ . . .R, а из этого следует, что
(5.2.4) Z =>+ xuVWvy =>+ xu. . .RWvy.
Строим искомое дерево следующим образом:
1. Рисуем синтаксическое дерево вывода (5.2.4).
2. Последовательно производим в основе ряд редукций до тех пор, пока R не станет частью основы. Заметим, что, так как V =>+ . . .R, символ R должен быть в основе последним.
3. Из определения W FIRST* S нам известно, что W =>#S. . . Добавим к синтаксическому дереву, полученному после 2-го этапа, кусты, соответствующие этому выводу. Очевидно, что основа при этом не меняется, так как она содержит R, а кусты добавляются справа от R. Таким образом, символ R — хвост основы и за ним следует S.
Обратно, предположим, что есть такое дерево, в котором R — хвост основы и за R следует S. Во-первых, проведем ряд редукций канонического разбора до тех пор, пока символ S не окажется в основе. При этом будет построено дерево сентенциальной формы . . .VS. . . для некоторого V, такого, что V =>+ . . .R. Возможны два случая:
ГРАММАТИКИ ПРОСТОГО ПР Е Д ШЕ СТ ВОВ АНИЯ
131
1. Если в основу входят и V, и S, заканчиваем работу, так как в этом случае должно существовать правило U: . .VS. . . ,
и мы получаем, что U: : = . . .VW. .. , где V =>+ . . .R и W=S.
2. Если S — голова основы, проводим ряд редукций до тех пор, пока не получим для некоторого W сентенциальную форму . . . . . .VW. . . , где V входит в основу. Заметьте, что W=>+S. . . . Более того, символ W должен тоже входить в основу, так как если бы последним в основе был символ V, он, начиная с первого этапа, был бы последним символом и в основе цепочки, а это противоречит тому, что в основу входит символ S.
Таким образом, существует правило U: . .VW. . . , где
V =>+ . . .R и W =>+ S. .. , и теорема доказана.
(5.2.5.). Т е о р е м a. R<£S тогда и только тогда, когда существует сентенциальная форма . . .RS. . . , где S — голова основы.
Доказательство. Доказательство этой теоремы предоставляется читателю (упражнение 1).
Мы видим, что формальные определения (5.2.1) эквивалентны неформальным, описанным в разд. 5.1 в терминах синтаксических деревьев. Важно, чтобы читатель изучил эти неформальные определения. Без их полного понимания не следует двигаться дальше. Теперь можно определить грамматику простого предшествования. (5.2.6.). Определение. Грамматику G называют грамматикой (простого) предшествования или грамматикой (1,1) предшествования, если
1) между любыми двумя символами из словаря определено не более чем одно отношение;
2) ни у каких двух продукций нет одинаковых правых частей.
Запись (1,1) означает, что для принятия решения о том, действительно ли предполагаемая основа является основой, мы используем по одному символу слева и справа от нее. То есть, если в основу входит символ R, мы по одному только следующему за ним символу S определяем, является ли R хвостом основы; аналогично решается вопрос о голове основы. Если G — грамматика предшествования, то отношения позволяют найти основу любой сентенциальной формы; при этом соблюдение второго условия [см. (5.2.6)] гарантирует нам то, что основу можно привести к единственному нетерминалу. Это будет доказано в сформулированной ниже теореме.
Прежде чем перейти к ней, остановимся еще на одной проблеме. Необходимо показать, что основа — это самая левая цепочка Sj . .. •. .Si, удовлетворяющая (5.2.9.). Однако следует не упустить из виду случай, когда в основу входит символ Si — первый символ сентенциальной формы, так как в этом случае символа So, такого, что 5*
132
ГЛАВА 6
S0<Sb нет. Попытаемся решить эту проблему, предположив следующее:
(5.2.7) Каждая сентенциальная форма заключена между символами и (при этом предполагается, что не есть символ из данной грамматики). Более того, будем считать, что # <• S и S •> # для любого символа S из грамматики.
Теперь перейдем к теореме.
(5.2.8). Теорема. Грамматика предшествования однозначна. Более того, единственная основа любой сентенциальной формы Sv .. Sn — это самая левая подцепочка Sj. . -Si, такая, что
(5.2.9) .iS,<S1+r
Доказательство. Во-первых, покажем, что основа х любой сентенциальной формы единственна. Будем считать очевидным, что если Sk. . .Sp — основа, то
Sk-i <t Sk ... .1.Sp •>Sp+1
Это следует из определения отношений <•, X и •>. Предположим, что найдется синтаксическое дерево, у которого нет самой левой подцепочки Sj. . .Sb удовлетворяющей (5.2.9) и являющейся основой. Тогда, сколько бы мы кустов ни отсекали, подцепочка не станет основой, так как если основа в какой-то момент образует самый левый полный куст, то она образует его всегда.
Во время канонического разбора каждый из символов Sj_1( Sj, . . . , Sj+i должен в какой-то момент стать частью основы. Пусть St — первый из таких символов. Так как эта основа не может совпадать с Sj. . .Si, должно выполняться одно из следующих соотношений:
1. t=j — 1, в этом случае Sj_1=±=Sj или Sj_j»>Sj.
2. t=j+l, в этом случае Sj^Sj или St <• Sj+1.
3. j<t<i
a) Sj_x входит в основу, в этом случае Sj_1=^Sj;
b) S1+1 входит в основу, в этом случае S1=^S1+];
с) для некоторого k, j<k^t, Sk — голова основы, в этом случае Sk-!<»Sk;
d) для некоторого k, t^k<i, Sk — хвост основы, в этом случае Sk*>Sk+1.
Мы видим, что в каждом из этих случаев между двумя символами из числа символов Sj_....Si+1 существует еще одно отношение,
что противоречит определению грамматики предшествования. Следовательно, Sj. . .Sj — единственная основа.
ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВОВАНИЯ
133
Таким образом, на каждом шаге разбора любой сентенциальной формы х основа определяется единственным образом. Так как основа может быть правой частью только одного правила [условие 2 из (5.2.6)], ее можно привести; следовательно, единственна и непосредственная редукция, производимая на каждом шаге. Это означает, что для любого предложения существует только одно синтаксическое дерево, т. е. грамматика является однозначной.
Мы видим, что после того, как определены отношения между символами, разбор предложений, соответствующих грамматикам предшествования, становится простым. По-видимому, это самый простой класс нетривиальных грамматик, который может иметь практическое применение. Сами отношения, если вводить их так, как описано в разд. 5.1, довольно легко воспринимаются, несмотря на то что последние определения выглядят весьма беспорядочными. Далее мы перейдем к другим классам грамматик, которые более сложны для определения, но чаще используются на практике. Тем не менее мы еще поговорим о грамматиках предшествования и составим алгоритмы для построения отношений и для реального распознавателя или анализатора предложений таких грамматик.
Построение отношений предшествования
Построение отношения простого предшествования JL не требует практически никаких объяснений. Нужно только просмотреть правые части правил и установить отношение R—S для всех R и S, таких, что . . .RS. . .— правая часть.
Установление отношений <• и •> — дело более трудоемкое, но и их вычислить несложно; необходимо только воспользоваться теорией булевых матриц, изложенной в разд. 2.7.
(5.2.10). Теорема. Отношение <• равно произведению отношений А. и FIRST*, т. е.
<• = (=^=) (FIRST+)
Доказательство. Это следует непосредственно из определения произведения отношений и из определения <£ (5.2.1).
(5.2.11). Теорема. Пусть I — единичное отношение. R«>S тогда и только тогда, когда S — терминал и
R ((LAST+)-1) (=) (I + FIRST + ) S
Доказательство. Доказательство этой теоремы предоставляется читателю (упражнение 4).
Теорема (5.2.10) показывает, что можно вычислить отношение <Ъ если 1) построить булеву матрицу F для отношения FIRST,
134
ГЛАВА S
2) построить матрицу F+, используя для этого, например, алгоритм Воршалла, 3) построить матрицу EQ для отношения = и 4) умножить EQ на F+. Процесс вычисления отношения •> почти столь же прост.
УПРАЖНЕНИЯ К РАЗДЕЛУ 5.2
1. Докажите, что R<»S тогда и только тогда, когда существует сентенциальная форма . . .RS. . . , где S — голова основы.
2. Покажите, что следующая грамматика не является грамматикой предшествования:
Z: :=ЬЕЬ, Е: : = Е+Т |Т
3. Покажите, что следующая грамматика не является грамматикой предшествования:
Z: :=b Elb, El: :=Е | Е+Т | Т | i, Т: : = i | (Е1)
4. Докажите теорему (5.2.11).
5. Постройте отношения для грамматики (5.1.1), используя теоремы (5.2.10) и (5.2.11).
6. Напишите на каком-нибудь языке высокого уровня и отладьте программу для построения и вывода отношений на печать. Входной информацией для программы должна быть заданная в удобной форме грамматика.
5.3. АЛГОРИТМ РАЗБОРА
При практическом применении отношений предшествования для распознавания предложений нам потребуется способ их компактного представления. Обычно этой цели служит матрица Р, элементы которой имеют значения:
P1j=0, если Sj и Sj несравнимы
Pi, 1=1, если Si<«Sj
Pi’j=2, если Si^Sj
Pi’j=3, если Sj *>Sj
Для грамматики предшествования такое представление возможно, так как известно, что между любыми двумя символами определено не более одного отношения.
Сами правила должны находиться в таблице, имеющей такую структуру, которая позволяет по заданной правой части найти содержащие ее правила, а затем указать соответствующую левую часть.
ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВОВАНИЯ
135
Алгоритм разбора работает так. Символы входной цепочки просматриваются слева направо и заносятся в стек S до тех пор, пока не окажется, что верхний символ стека находится в отношении •> к следующему входному символу. Это означает, что верхний символ стека является хвостом основы и, следовательно, вся основа уже в стеке. Затем ее находят в списке правил, и в стеке она заменяется
< том и только в том случае, когда, I ’2, S(i)=ZuR » #
Рис. 5.4. Распознаватель для грамматики простого предшествования (отношения •> и <• обозначены соответственно и «-).
тем нетерминалом, к которому ее надлежит привести. Процесс повторяется до тех пор, пока в стеке не окажется символ ,,Z“ (Z — начальный символ) и следующим входным символом не станет
На рис. 5.4 изображена блок-схема работы распознавателя; используются следующие обозначения:
1. S — стек, в котором хранятся символы; его счетчик —i.
2. j — индекс, используемый для адресации нескольких верхних элементов стека.
3. Анализируемое предложение — TiT2. . .Тп. Мы начинаем работу, когда в стеке находится разделитель предложения #, и предполагаем, что такой же символ приписан к предложению в качестве Та+1.
136
ГЛАВА 5
4. Q и R — переменные, принимающие значения символов; они используются для хранения некоторых символов во время работы.
Заметим, что, если цепочка ТР . .Тп не является предложением, алгоритм остановится и сообщит об этом. Далее приводятся пояснения к каждому из элементов блок-схемы.
Блок 1. Прежде всего в стек S занести разделитель предложения. Установить значение индекса, указывающее на первый символ.
Блок 2. «Сканировать» следующий символ — поместить его в R и увеличить значение к.
Блок 3. Если (S(i), R) не находятся в отношении •>, значит еще не вся основа в стеке, поэтому занести R в стек и перейти к сканированию следующего символа.
Блоки 5—7. S(i)»>R. Значит, основа находится в стеке. Теперь ведется поиск головы основы, т. е. такого j, когда S (j — 1) <• S(j).
Блоки 8—9. Проверить цепочку S (j). . .S (i). Если она не является правой частью никакого правила, то работа закончена. Эта цепочка является предложением в том и только в том случае, когда i=2, S (i)=Z и Z — начальный символ. Если цепочка — правая
Шаги S1 S2 Отношение R Tk ...
0 < ь ( а а ) b #
1 b <• ( а а ) b #
2 b ( < а а ) b #
3 b (а •> а ) ь #
4 b ( М а ) ь #
5 b ( М а ) ь #
6 ь ( М а ) > b
7 ь ( L > b
8 ъ М b
9 ь Mb > #
10 Z
Рис. 5.5. Разбор цепочки b (а а) Ь.
часть некоторого правила, то-исключить основу из стека (блок 9), поместить в стек символ, к которому эта основа приводится, и перейти к блоку 3, т. е. к поиску очередной основы.
В этом и в других подобных распознавателях очень привлекательно то свойство, что не нужно одновременно хранить в памяти всю цепочку входных символов (если только грамматика не из ряда вон выходящая). Символы считываются с входного носителя по одно
ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВОВАНИЯ
137
му и заносятся в стек, но после редукции основы те символы, которые входили в нее, исчезают. Всю цепочку приходится хранить в памяти только в том случае, если основа находится в правом конце цепочки; но грамматики языков программирования никогда не строятся подобным образом.
Используя описанную блок-схему, проведем еще раз разбор предложения b (аа)Ь грамматики (5.1.1). На рис. 5.5 для каждого шага разбора показано содержимое стека S, сканируемый символ R, отношение между верхним символом стека S (i) и символом R и та часть сентенциальной формы, которая еще не сканировалась; все это — перед выполнением блока 3.
УПРАЖНЕНИЯ К РАЗДЕЛУ 5.3
1. Используя алгоритм, изображенный на рис. 5.3, и матрицу предшествования грамматики G5 [пример (5.1.1)], попытайтесь разобрать следующие цепочки (не все они являются предложениями): #аа#, #((аа)а)#, #()#, #((((аа)а)а)а)#.
2. Запрограммируйте и отладьте алгоритм разбора, изображенный на рис. 5.4. Для этого необходимо определить вид матрицы предшествования (это результат работы программы из упражнения 5.2.6). Далее, входной информацией для программы разбора может служить результат работы какого-нибудь сканера, например запрограммированного в упражнении 3.3.2. В любом случае внутреннее представление любого символа должно быть номером строки или номером столбца в матрице предшествования.
5.4. ФУНКЦИИ ПРЕДШЕСТВОВАНИЯ
Матрица предшествования может занимать слишком большой участок памяти. Если в языке 160 символов, нам понадобится матрица, состоящая из 160x160 элементов, каждый длиной не менее двух битов. Однако во многих случаях информация, задаваемая в матрице, может быть представлена двумя функциями f и g, такими, что
из R=S следует f(R)=g(S)
(5.4.1) из R<»S следует f (R)<g (S) из R >S следует f (R)>g (S)
Для всех символов грамматики. Это называется линеаризацией матрицы. Таким образом, мы можем уменьшить объем требуемой памяти с пхп ячеек до 2хп ячеек. Для матрицы предшествования,
138
ГЛАВА S
изображенной на рис. 5.2, функции f и g таковы:
(5.4.2)
Z ЬМ L а ( ) f 1 4 7 8 9 2 8 g 1 7 4 2 7 5 9
Следует отметить, что эти функции неединственны — если для данной матрицы найдется хотя бы одна пара функций f и g, то для той же матрицы существует бесконечное количество таких функций. Но есть много матриц предшествования, для которых эти функции не существуют. Нельзя линеаризовать, например, даже такую матрицу предшествования размером 2x2 для символов Sx и S2:
Почему же? Если бы функции существовали, то из (5.4.1) следовало бы
f (Sj)>g (S2), g (S2)=f (S2), f (S«)=g (SJ, g (SO=f (Sx),
что ведет к противоречивому утверждению f (Si)>f (Si).
Функции предшествования (если они существуют) строятся следующим образом:
(5.4.3). Теорема. Построение функций предшествования производится в несколько шагов.
1. Начертить ориентированный граф с 2хп узлами, помеченными G,. . . , fn и gi, . . . , gn. Если S j«>=Sj, провести дугу от ft к gj. Если Si<^=Sj, провести дугу от gj к ft.
2. Каждому узлу поставить в соответствие число, равное числу узлов, в которые можно попасть из данного узла (включая и этот узел). Число, поставленное в соответствие fи есть f (Sj); число, поставленное в соответствие g1( и есть g (Sj).
3. Проверить, не противоречат ли значения построенных функций f и g исходным отношениям (по 5.4.1). Если нет противоречий, то функции f и g построены правильно. Если противоречие есть, то функций предшествования не существует.
Доказательство. Мы должны показать, что Sj ASj влечет за собой равенство f(Sj)=g(Sj), Sj<Sj влечет f(S4)<g (Sj), и Sj«>Sj влечет f (Si)>g (Sj). Первое непосредственно следует из построения, ибо SjstsSj означает, что есть дуга от fj к gj и дуга от gj
ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВОВАНИЯ
139
к fP Следовательно, любой узел, который достижим из одного такого узла, достижим и из другого.
Другие два условия симметричны, и мы докажем только, что из Si»>Sj следует f (Si)>g (Sj). Из отношения St»>Sj следует, что есть дуга от f1 к gj. Поэтому любой узел, достижимый из gj, достижим и из fi, следовательно, и f (S,)^g (Sj). Осталось только показать, что в случае равенства (если f (St)=g (Sj)) функций предшествования вообще не существует.
Пусть f (St)=g (Sj). Тогда должен быть путь, ведущий из ft В gj, из gj в fk, из fk в g,, ... , из gm в fj. Следовательно,
Sj»>Sj, Sk<»=Sj, Sk*> = S]..Sl< = SB1.
Из этого ясно, что для любых функций f и g должно выполняться отношение f (Sf)>f (S^, т. е. мы пришли к противоречию.
Ориентированный граф описывает отношение R, заданное в множестве узлов; xRy тогда и только тогда, когда существует дуга из узла х в узел у. Следовательно, такой граф можно представить в виде булевой матрицы В размерностью 2хп таким образом:
(5.4.4)
В :
О GE
LET О
где GE — матрица размерностью n х п для отношения •>= и LET — транспонированная матрица для отношения Таким образом, для i, j = l, ... , п имеем
В [i, j]—В [n+i, n+j]=O;
(5.4.5) ' В [i, n+j]=l тогда и только тогда, когда SiV>==Sj
(в верхней правой четверти);
В [n+j, i]=l тогда и только тогда, когда Si<»=Sj (в нижней левой четверти).
Строки 1, ... , п относятся к fx, ... , fn, тогда как строки п+1, ... , 2хп относятся Kgo... , gB. Предоставим читателю Доказать следующую теорему:
(5.4.6). Теорема. Если функции предшествования существуют, их можно построить следующим образом:
1. Построить матрицу В, как в (5.4.4).
2. Построить рефлексивное транзитивное замыкание В* для матрицы В.
3. f [5}]:=число к, такое, что В* [j, k]=l.
g [Sj]:=число k, такое, что В* [n+j, k]=l.
140
ГЛАВА 5
Для матрицы предшествования на рис. 5.2, например, получится
Г 0 0 0 0 0 0 0 0 0 0 0 0 0 0 и
0 0 1 0 0 0 0 0 0 1 0 0 0 0
0 1 0 0 1 0 0 0 1 0 0 0 1 0
GE- 0 1 0 0 1 0 0 LET- 0 0 0 0 0 1 0
0 1 0 0 1 0 1 0 1 1 0 0 1 0
0 0 0 1 0 0 0 0 1 0 0 0 1 0
1 __ 0 1 0 0 1 0 0 J 1 I 0 0 0 0 1 0 0 J
Таким образом:
~о ооооооооооооо-00000000010000 00000000100100 00000000100100 00000 0-0 0100101 00000000001000 00000000100100 00000000000000 001 00000000000 01000100000000 0 0 0 0 0 1 ооооооо» 01 100100000000 01000100000000
1_0 000100000000 0_
Г 1 000000000000 0"1 0100010001 1000 01100100111100 01110100111100 01101100111101 00000100001000 01100110111100 00000001000000 01100100111100 0100010001 1000 000 0.0 100001000 0110010011 1100 0100010001 1010
1_о 1 1 О 1 1 О О 1 1 1 1 О 1_
Подсчет числа единиц в каждой i-й строке матрицы В* дает нам значение f (Sj) для i=l, ... , п, а подсчет числа единиц в каждой строке n+j, j = l, . . . , п дает нам значение g (S^, как в (5.4.2).
Когда компилятор обнаруживает в программе ошибку, он должен попытаться нейтрализовать ее и продолжать разбор, чтобы найти другие ошибки. Поэтому иногда важно обнаружить ошибку как можно раньше, чтобы можно было ее нейтрализовать. Из-за применения функций процесс обнаружения ошибок может затянуться. Линеаризация ведет к потере информации, потому что неизвестно, существует ли в действительности между двумя символами отношение. Для иллюстрации попробуем в соответствии с грамматикой G5 провести разбор цепочки ba)))))b, используя сначала полную матрицу, а затем функции.
1) Разбор с использованием матрицы
Шаг S1S2... Отношение RTk...
0 <• b a ) ) ) ) ) b #
1 #ь <• a ) ) ) ) ) b#
2 #ba • ) ) ) ) ) b #
3 #ba) Нет отношения ) ) ) ) b#
ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВОВАНИЯ
141
2) Разбор с использованием функций f и g
Шаг SjS2... f Отношение g RTk...
0 1 < 7 ba ) ) ) ) ) b #
1 #ь 4<7 a) ) ) ) ) b #
2 #ba 9 = 9 )) ) ) ) b #
3 #ba) 8<9 )) ) ) b #
4 #ba)) 8<9 )) ) b #
5 #ba))) 8<9 )) b #
6 #ba)))) 8<9 ) b #
7 #ba))))) 8> 7 b#
При использовании функций до обнаружения ошибки было выполнено на четыре шага больше, чем в первом случае.
УПРАЖНЕНИЯ К РАЗДЕЛУ 5.4.
1. Постройте функции предшествования f и g для следующей матрицы:
2. Докажите теорему (5.4.6).
3. Измените программу из упражнения 5.2.6 так, чтобы среди результатов были значения функций предшествования.
4. Измените алгоритм разбора из упражнения 5.3.2 так, чтобы вместо отношений предшествования использовались функции.
5.5. ТРУДНОСТИ, ВОЗНИКАЮЩИЕ ПРИ ПОСТРОЕНИИ ГРАММАТИК ПРЕДШЕСТВОВАНИЯ
Мы начали с описания метода простого предшествования, как с самого простого, но иллюстрирующего многие приемы синтаксического анализа, с которыми нам еще предстоит встретиться. С теоретической точки зрения этот метод кажется безупречным и эффективным. Однако на практике он не всегда хорош. И действительно, почти любая другая техника оказывается лучше простого предшествования. Очень часто между двумя символами определено более чем одно отношение. Единственное, что мы можем тогда сделать,— это обработать и изменить грамматику так, чтобы обойти конфликт. Но в результате может измениться вся структура языка, не говоря о том, что грамматика станет неудобочитаемой.
142
ГЛАВА 6
Одна из таких проблем может возникнуть как следствие левосторонней рекурсии. Предположим, что существует некоторое правило U: :=U. . . . Если есть другое правило вида V: :=. . .SU. . получается, что одновременно SaU и S<* U. Иногда можно избавиться от такого конфликта, вводя еще один нетерминал W и промежуточное правило; заменим
V: :=. . .SU. . .
на
V: :=. . .SW. . . , W: :=U,
где W — новый символ; при этом получим, что S^W и S<»U. Такой прием иногда называют стратификацией или разделением. Однако это довольно искусственный прием, и нам придется разработать для распознавателя другие методы, при использовании которых такие конфликты встречаются реже. При правосторонней рекурсии те же проблемы возникают с отношениями •> и =L. Стратификация не всегда спасает, так как она часто приводит к конфликтам иного рода. Если одновременно R<»S и R»>S, то лучший выход— применить другую технику.
Чтобы показать, как делается стратификация, воспользуемся привычной уже грамматикой для арифметических выражений:
Е ::=Е+Т |Т
(5.5.1) Т ::=T*F | F F ::=(Е) | i
Из первого правила следует, что + = Т, а так как символ Т леворекурсивен, получаем также и 4- <• Т. Та же самая проблема возникает и с символами “)” и “Е”. Без ущерба для структуры предложений и не меняя языка, можно заменить эту грамматику такую:
Е ::=Ех
Ех и^Ех+Тх | Т»
Тх ::=Т
Т ::=T*F | F
F ::=(Е) | i
Тогда отношения FIRST* и LAST* задаются следующим
образом:
и S—такой символ, S—такой символ, что
что (U, S) € FIRST+ (U, S}£LAST+
Е Е1( Т, Тх, F, (, i Ex, Tx, T, F, ), i
Ех Ex, Т, Тх, F, .(, i T„ T, F, ),. i
Тх T, F, (, i T, F, ), i
т T, F, (, i F, ), i
F (. i ). i
ГРАММАТИКИ ПРОСТОГО ПРЕДШЕСТВОВАНИЯ
143
Отсюда получаются матрица и функции предшествования:
Е Ех Tf Т F i ( + * ) f g
Е
Et Т, T F i
> 4 3
>54 >65 > 7 6
>77 2 7
4 4
6 6
>72
Этот пример может создать впечатление, что изменения не столь значительны, однако если в грамматике 100 правил и около 100 с лишним символов (а так оно и есть в языках типа АЛГОЛ), то даже искушенный человек затратит немало времени на то, чтобы переделать такую грамматику в грамматику предшествования.
Тут читатель может задать вопрос, в чем же заключаются преимущества того или иного метода, с которыми мы собираемся его познакомить. Заметьте, что в методе предшествования решение принимается с учетом весьма ограниченного контекста возможной основы. В сущности, в каждом случае во внимание принимаются только два соседних символа. Если же рассматривать и другие символы или большее количество символов, то можно надеяться, что конфликтных ситуаций станет меньше. Таким образом, не ограничиваясь только Sj и Sj+1, для обнаружения хвоста основы рассмотрим символы
Sj_1( Sj и S1 + 1 или S1( S1 + 1 и Sj+,
Проиллюстрируем это на примере сентенциальной формы E-f-T*F грамматики (5.5.1). Поскольку отношения 4-<»Т и + 2= Т противоречивы, мы не можем всего по двум символам, + и Т, сделать вывод о том, является ли Т головой основы, т. е. нужно ли выполнять сложение. Если же известно два символа + и * или же три символа +Т*, то интуиция нам подскажет, что складывать нельзя, из чего следует, что символ + в основу не входит.
144
ГЛАВА 5
УПРАЖНЕНИЯ К РАЗДЕЛУ 5.5
1. Не меняя язык, измените заданную грамматику так, чтобы она стала грамматикой предшествования. Найдите все отношения.
<описание>
<тип>
<список ид>
=<тип> <список ид>
=REAL | INTEGER |BOOLEAN =i | <список ид>, i
2. Не меняя язык, измените заданную грамматику так, чтобы она стала грамматикой предшествования. Найдите все отношения.
Р : :=<лв>
< лв> : :=л : =<лв> | <ав>=<ав>
< ав> : :=а : =<ав> | <ат>
< ат> : :=<ат>—<ап> | <ап>
< ап> : :=а | «ав» | @(<лв»
<лв> означает логическое выражение, <ав> — арифметическое выражение, <ат> — арифметический терм и <ап> — арифметическое первичное выражение; “л” (“а”) — логический (арифметический) идентификатор. (Чтобы вычислить логическое выражение л:=<лв>, вычисляется значение <лв> и присваивается л. Тогда значение выражения становится значением л. Аналогично делается для арифметического выражения а:=<ав>. Значение «лв» равно 1, когда <лв> истина, и равно 0 в противном случае.)
5.6. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Первая формальная трактовка отношений предшествования и функции предшествования принадлежит Флойду [63]. Формализация, предложенная Флойдом, будет обсуждаться в следующей главе. Описанная здесь форма отношений была введена Виртом и Вебером [66J. Специфический метод вычисления отношений появился в статье Мартина [68]. Метод, использованный для вычисления функций предшествования, обязан своим появлением Беллу [691. В компиляторе с ALGOL W (см. Бауэр, Беккер и Грехем [68]) используется автоматически построенная матрица предшествования. Кроме того, есть несколько статей, расширяющих понятие простого предшествования. Ссылки на них см. в конце гл. 6.
Глава 6
Другие восходящие распознаватели
В гл. 5 изложены методы простого предшествования для восходящего разбора. В этой главе мы обсудим несколько других алгоритмов разбора того же типа. Сходство всех этих алгоритмов состоит в том, что до тех пор, пока предложение не будет приведено к начальному символу, выполняется следующая последовательность шагов:
1. Найти основу х (или некоторую ее разновидность).
2. Найти правило U : : = х с х в правой части.
3. Привести х к U и таким образом построить один куст синтаксического дерева.
Различия в таких распознавателях сводятся к двум моментам: к числу и расположению символов, по которым определяется основа, и к структуре задания таблиц и правил в самом распознавателе. Реализация любого распознавателя распадается на такие этапы:
1. Программируется общая часть распознавателя, которая пользуется таблицами. В таблицах описывается грамматика.
2. Программируется конструктор, который проверяет, приемлема ли заданная грамматика, и строит необходимые для распознавателя таблицы.
3. Наконец, программа-конструктор выполняется (исходными данными для нее будет грамматика), а результат ее работы объединяется с общей частью распознавателя. Таким образом получается распознаватель для заданной грамматики.
Теперь, когда есть распознаватель предложений данной грамматики, его можно использовать по мере необходимости, не выполняя всякий раз программу-конструктор. В случае простого предшествования получается такой распознаватель, как на блок-схеме, изображенной на рис. 5.4, а таблица — это матрица предшествования и правила.
Некоторые методы восходящего разбора являются формализацией методов, использовавшихся в ранних компиляторах; в ту пору требования к грамматикам определялись по большей части тем,
146
ГЛАВА б
как работали распознаватели, построенные по интуитивным соображениям. Это касается предшествования операторов и матриц переходов. Другие грамматики с (ш, п) ограниченным контекстом и типа LR (к) первоначально были получены теоретически и на практике пока не применялись
Каждый из следующих разделов посвящен определенному типу распознавателей. Изложение будет полным, но кратким. Доказательства теорем предоставляются читателю в качестве упражнений. Напомним, что все излагаемые методы схожи между собой в том, что при решении проблемы поиска основы и символа, к которому надлежит ее привести, рассматривается контекст, в котором эта основа встречается.
6.1. ПРЕДШЕСТВОВАНИЕ ОПЕРАТОРОВ
Операторные грамматики
Кто бы ни вычислял выражение 2 + 3*5, результатом всегда будет 17. На вопрос, почему сначала выполняется умножение, вам ответят, что умножение всегда выполняется раньше сложения, что оператор * предшествует оператору +. Важно отметить, что операнды 2, 3 и 5 никоим образом не влияют на последовательность выполнения операций; принимаются во внимание только сами операторы. Напомним, что при использовании техники простого предшествования определялись отношения предшествования между всеми символами — как операторами, так и операндами, что вызывало некоторые трудности. Техника предшествования операторов формализует понятие предшествования только между операторами, причем операторами могут быть лишь терминальные символы грамматики.
Начнем изложение с краткой иллюстрации того, как на практике применяется эта техника в некоторых компиляторах, обычно для анализа арифметических выражений. Программа разбора использует два стека вместо одного: стек операторов OPTOR и стек операндов OPAND. В первом хранятся бинарные и унарные операторы, круглые скобки и ограничитель #, которым начинается и заканчивается каждое выражение. В стек OPAND заносятся идентификаторы и другие операнды по мере их получения. Кроме этих двух стеков, есть еще два целочисленных вектора f и g, аналогичных функциям простого предшествования из разд. 5.4.
Шаг работы общего алгоритма разбора выполняется следующим образом (Si — верхний символ в стеке операторов, S2 — входной символ):
1. Если Si — идентификатор, то поместить его в стек операндов и пропустить шаги 2 и 3.
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
147
2. Если f (S^ g (S2), поместить Sa в стек операторов и взять следующий входной символ.
3. Если f (Si) > g (S2), вызвать (семантическую) подпрограмму, определяемую символом Si. Эта подпрограмма выполнит семантическую обработку, исключит из стека операторов St и, возможно, другие символы, исключит из OPAND связанные с этими символами операнды и занесет в OPAND нечто, являющееся результатом работы оператора Si. Это соответствует редукции основы сентенциальной формы.
Чтобы проиллюстрировать это на примере разбора арифметических выражений, проведем разбор выражения # А + В + С #; одновременно будем присваивать компонентам векторов f и g надлежащие значения. Когда начинается разбор, в стеке OPTOR находится #, а стек OPAND пуст. На первом шаге идентификатор А помещается в OPAND. На втором + следует поместить в OPTOR (мы не можем ни редуцировать, ни обрабатывать +, пока не получим сведений от обоих его операндах). А это значит, что f (#) < g(+), поэтому положим, например, f (#) = 1 и g (+) = 4.
На третьем шаге в OPAND помещается В, и теперь
оставшаяся часть f (*) = 1
цепочки,: +C# 9 С+)
Заметьте, что + есть верхний элемент стека OPTOR, а его операнды А и В — верхние в стеке OPAND. Теперь необходимо обработать + семантически, возможно, порождая при этом внутреннюю форму операции наподобие (+ А, В, Т1), а затем сделать следующее: исключить + из OPTOR, исключить А и В из OPAND и поместить в OPAND имя временной переменной Т1, представляющей результат выполнения операции А + В. Тогда получим
OPTOR
OPAND:
оставшаяся часть f (#)я1 цепочки,: +C# Т(+)в5 д(+)“4
Следовательно, должно выполняться неравенство f (+) > g (+), поэтому положим значение f (+) равным 5. Заметьте, что все это соответствует редукции с использованием правила Е : : = Е + Т.
На следующем шаге в OPAND помещается символ С
OPTOR
OPAND:
оставшаяся часть цепочки : #
f(#)= 1
f(+)=5 д(+)=4
Заметьте опять, что + находится в OPTOR, а его операнды — верхние в OPAND, так что вновь необходимо обработать либо ре
148
ГЛАВА 6
дуцировать операцию +. Следовательно, нужно, чтобы f (+) > g(#). Выполнив этот шаг, заканчиваем работу, имея
optor:
OPAND:|T2 I оставшаяся чает f (#) = 1 д (#) = 1
I I цеаотхв: * f(+)=4 9(+)“5
Таким образом, изучая, как поступить с каждой парой символов (верхний элемент в OPTOR, входной символ), и устанавливая соответствующие значения функций, мы строим функции f и g. Обратите внимание, что. из выражения # А + В * С # непосредственно следует соотношение f (+) < g (*), поскольку входной символ * заносится в стек, если символ + уже находится в OPTOR. Это можно сделать, если положить g (*) = 6. Для более систематического построения функций сначала определяются все нужные отношения, а затем используется либо метод графа, либо метод булевой матрицы (см. разд. 5.4).
Чтобы выявить ошибки и установить, какой операцией является минус — бинарной или унарной, необходимо тщательно проверить, действительно ли за каждым оператором или круглой скобкой следует операнд. Для этого в каждом элементе стека OPTOR отводится один бит, первоначально равный нулю. Всякий раз, когда в OPAND заносится операнд, в верхнем элементе стека OPTOR значение этого бита заменяется на 1, чтобы показать, что за данным символом следует операнд.
Этот метод известен так же как метод двойного приоритета, поскольку для определения того, какой из операторов предшествует, или имеет приоритет, используются две функции. Может показаться, что удалось бы обойтись и одной функцией h; если h (SJ > h (S2), в стеке выполняется редукция, а в противном случае в стек заносится символ S2. Однако обычное употребление круглых скобок в выражении делает это невозможным. Судя по выражению #(А) * В #, нам нужно, чтобы h ())>h(*); в то же время из # (А * В) # следует h (*) > h ()), а это невозможно.
Заметьте, что, когда в OPTOR производится «редукция», верхний символ некоторым образом определяет подпрограмму, которая будет выполняться. Символ S в OPTOR можно представить так:
f (S) ' адрес подпрограммы^поторую нужно выполнить 1
Компиляторы до сих пор пишут на языке ассемблера еще и потому, что обычные языки высокого уровня не позволяют использовать многие эффективные представления такого рода.
Приводя здесь краткое описание процесса, мы стремились показать, с чем обычно сталкиваются при написании компилятора. Остановимся теперь более детально на формализации этой техники.
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
149
Здесь вместо двух стеков будет использоваться один; правда, читатель дальше убедится в том, что один или два стека — это исключительно дело вкуса.
Мы накладываем на грамматики такое ограничение, что в сентенциальной форме между операторами не может быть неограниченного числа операндов (нетерминалов). Другими словами, операции должны быть записаны в инфиксной форме.
(6.1.1). Определение. Грамматика G называется операторной грамматикой (ОГ), если ни одно из ее правил не имеет вида U :: = ... VW . . . , где V и W — нетерминалы.
Таким образом, в ОГ никакая правая часть не содержит двух соседних нетерминальных символов. Это сказывается на сентенциальных формах; можно доказать (упражнение 1), что никакая
операнды (нетерминалы)
(вызов процедуры) :: = (идентификатор) «список факт, параметров))
7
операторы (терминалы)
(список факт.параметров)'.*. = (список факт.параметров), (факт.параметры)\(фаха.паражтры)
(список идентификитород)*.*^(список буке) |
.......Л,, ., операнды
(нетерминалы)
Рис. 6.1. Операторы и операнды.
сентенциальная форма в ОГ не содержит двух соседних нетерминальных символов. Большинство тех грамматик, с которыми мы работаем, можно без особого труда превратить в операторные грамматики.
Слова оператор и терминал мы будем употреблять как взаимозаменяемые. То же относится и к словам операнд и нетерминал. На рис. 6.1 показаны операнды и операторы в нескольких правилах.
Грамматики предшествования операторов
Описанные далее отношения полностью аналогичны отношениям простого предшествования. Единственное различие опять-таки состоит в том, что мы определяем эти отношения только для операторов.
(6.1.2). Определение. Пусть G — операторная грамматика, a R и S — любые два оператора (терминалы). Тогда для некоторых нетерминалов V и W
150
ГЛАВА в
1. R _£= S тогда и только тогда, когда существует правило вида U : : = . . . RS . . . или вида U : : = ... RVS ....
2. R <5 S тогда и только тогда, когда существует правило вида
U : : = . . . RW . . ., где W =>+ S . . . или W =>+ VS . . . .
3. R S тогда и только тогда, когда существует правило вида
U :: = ... WS .... где W=>+ ... R или W=>+ . . .RV.
(6.1.3). Определение. ОГ называется грамматикой предшествования операторов (ОПГ), если между любыми двумя терминалами определено не более, чем одно из отношений <5, 2> или °*.
(6.1.4). Пример. Рассмотрим опять грамматику G [Е]:
Е : : = Е 4- Т | Т Т : : = Т * F |F F :: = ( Е ) |i -
Из последнего правила мы получаем отношение (.°.). Это отно-
шение встречается в грамматике только однажды, так как лишь в
4-* ( )
Рис. 6.2. Матрица предшествования для грамматики (6.1.4).
этой правой части имеются два терминальных символа. Так как E=>E + T=>T + T=>T*F4~T=>F*F + T=^i*F + T, то из правила F : : — (Е) следует, что (<+,(<* и (<5 i. Из того же правила и из последовательностей непосредственных выводов получаем 4- §>).
Полная матрица предшествования операторов показана на рис. 6.2. Так как любые два терминала находятся не более чем в одном отношении, это ОПГ.
Построение отношений
Построение отношений SL не требует детальных объяснений: нужно просмотреть правые части правил в поисках конфигурации RVS или RS. Чтобы построить отношение <5, необходим способ, который позволяет для каждого W находить множество терминальных символов S, таких, что W=>4- S . . . или же W =>4- VS . . ., где V —нетерминал. (Аналогичное утверждение справедливо также
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
151
при построении отношения с>.) С этой целью определим два новых отношения:
(6.1.5). О п р е д е л е н и е. Пусть G — ОГ, a S — терминал.
U FIRSTTERM S тогда и только тогда, когда существует правило U : : = S . . . или U : : = VS . . . .
U LASTTERM S тогда и только тогда, когда существует правило U ::=... S или U : : — . . . SV, где V — любой нетерминальный символ.
Сокращения «FIRSTTERM» («LASTTERM») означают, что речь идет о первом (последнем) терминале в правой части правила. Очевидно, что эти отношения легко получить непосредственно из правил. Теперь можно построить отношения <5 и с>, используя отношения (отношение простого предшествования), FIRST, FIRSTTERM, LAST и LASTTERM, которые мы уже умеем строить в виде булевых матриц.
(6.1.6). Теорема. Отношение <5 есть произведение трех отношений =Г, FIRST* и FIRSTTERM: < = ( ^ ) (FIRST*) (FIRSTTERM). Аналогично > = ((LAST* ) (LASTTERM))-1 (i). (Несложное доказательство этой теоремы предоставляется читателю в качестве упражнения 3.) Следовательно,( теперь мы располагаем простыми средствами для вычисления отношений <5 (а также $>). Достаточно, исходя из правил, построить булевы матрицы для трех отношений, вычислить рефлексивное, транзитивное замыкание одного из них и затем перемножить все три матрицы.
Первичные фразы — их обнаружение и редукция
Для нахождения основ, состоящих из одного нетерминала, отношения, о которых сейчас идет речь, применять нельзя, так как для них нетерминальные символы просто не существуют. Рассмотрим, например, сентенциальную форму F + Т из арифметической грамматики примера (6.1.4). Основой является F, а отношения есть только такие: # <j * и + §> # (как и прежде, предполагаем, что сентенциальная форма заключена между ограничителями # и что # <5 S и S с> # для всех терминальных символов S). Тогда техника предшествования операторов не позволит провести канонический разбор так, как мы его определяли, а тот разбор, который можно провести с помощью этих методов, будет только отчасти напоминать канонический. Разбор здесь по-прежнему восходящий, но не строго слева направо. На каждом шаге разбора мы будем распознавать и редуцировать некую цепочку, которая будет называться самой левой первичной фразой.
(6.1.7). Определение. Пусть G — грамматика с начальным символом Z. Первичной фразой (сентенциальной формы) считается
152
ГЛАВА 6
такая, в которую входит по крайней мере один терминал, а сама она не содержит других первичных фраз.
Рассмотрим сентенциальную форму (с ограничителями #) #T + T*F + i# грамматики (6.1.4). Ее фразами являются Т + Т * F 4- i, Т + Т * F, i, самый левый символ Т и Т » F (их легко найти, просматривая единственное синтаксическое дерево сентенциальной формы (рис. 6.3)). Какие из этих фраз первичные?
Е
♦ F
Рис. 6.3. Синтаксическое дерево для T+T*F+i.
Первичная фраза не должна содержать другую фразу с терминальным символом, поэтому исключается фраза Т + T»F + i, содержащая i. Аналогично, в Т + T*F содержится фраза Т * F. Остаются Т, Т * F и i. Т не может быть первичной фразой, так как не содержит ни одного терминала. (Обратите внимание на то, что Т — основа сентенциальной формы, но не является первичной фразой.) Следовательно, первичные фразы — это Т * F и i.
Запишем теперь общий вид сентенциальной формы, заключенной между ограничителями # и #, так:
#N1T1N2T2...NnTnNn+1#
где N i — нетерминальные символы, которые могут и отсутствовать, a Ti — терминальные символы. Иначе говоря, сентенциальная форма состоит из п терминалов, причем между каждыми двумя соседними терминалами находится не более чем один нетерминал. Напомним, что в ОГ любая сентенциальная форма подчиняется этому требованию. В упражнениях 6—8 требуется доказать такую теорему:
(6.1.8). Теорема. Самой левой первичной фразой сентенциальной формы в ОПГ является такая самая левая подцепочка N <Т;. . . . . . NJt Ni+1, что
(6.1.9) ТЬ1 <5 Ть Tj Д Tj+1, . . ., Tb Ti > Т1+1
Эта теорема кажется необычайно похожей на соответствующую теорему для простого предшествования. Основное различие состоит в том, что здесь из отношений исключены нетерминальные символы. Заметим, что нетерминал, находящийся слева от Tj или справа от Tj, всегда принадлежит первичной фразе,
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
153
Чтобы проиллюстрировать теорему, проведем разбор сентенциальной формы Т + Т *F+ i, используя матрицу предшествования, изображенную на рис. 6.2. Читатель должен тщательно изучить и этот разбор, и синтаксическое дерево на рис. 6.3. В таблице даны символы, к которым приводятся первичные фразы; правда, мы еще не объяснили, как определить этот символ. Речь об этом пойдет дальше.
Шаг Сентенциальная форма Отношения Первичная фраза Привести к
1 #T + T*F + i# 4- 4- T*F Т
2 #T+T+i# # 4- + Т4-Т Е
, 3 #E + i# . i F
4 #E + F# E + F Е
При проведении этого разбора указываются нетерминалы, к которым приводится каждая из первичных фраз. Отметим, что при поиске самой левой первичной фразы, которую нужно редуцировать, нетерминальные символы вообще не принимаются во внимание. Поэтому совершенно безразлично, какой нетерминальный символ будет занесен в стек — правильный или нет. Их вообще можно было опустить!
В компиляторах с каждым нетерминалом или операндом связано много семантической информации — тип операнда, его адрес, является ли операнд формальным параметром. В гл. 1 уже кратко описывалось, что для обработки первичных фраз будут использованы семантические программы. Эти программы нуждаются только в семантической информации, связанной с символами, а не в самих символах. Например, для семантической программы, которая редуцирует Т * F, безразлично, какая это фраза: Т * F, F * Т или F * F. Она использует только семантику каждого из рассматриваемых нетерминалов — его тип, адрес и т. д. То есть для семантических программ несущественны фактические имена нетерминалов. Следует помнить (см. разд. 2.4), что появление в грамматике нетерминалов Т и F не связано с какими-либо семантическими целями; но они позволили сделать грамматику однозначной и определить предшествование операторов.
Обратите, пожалуйства, внимание на то, что если бы нам был нужен формальный алгоритм разбора, нам пришлось бы указать нетерминал, к которому следует привести первичную фразу. Мы, однако, не ставим себе формальных целей — только практические. Заметьте, что ничего не было сказано о том, что синтаксическое дерево для каждой сентенциальной формы единственно. Это и не обязательно. Но можно сказать, что структура дерева, если не принимать во внимание имен в узлах, соответствующих нетерминалам,
154
ГЛАВА 6
единственна. Это очевидно, так как на каждом этапе разбора самая левая фраза единственна.
Конечно, здесь на долю семантических программ выпадает больше хлопот. Они должны производить более подробную проверку
Рис. 6.4. Распознаватель, использующий предшествование операторов.
операндов, чем в грамматиках простого предшествования. Но что-то мы на этом и выигрываем, так как распознаватель становится более эффективным. Отметим, что уменьшается матрица предшествования и нам потребуется меньше памяти — матрица теперь содер
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
155
жит только те столбцы и строки, которые относятся к терминалам. Более того, распознаватель не выполняет в явном виде таких редукций, как Е => Т или Т => F, поскольку Т и F не первичные фразы. И это хорошо, так как такого рода редукции не несут никакой семантики.
На рис. 6.4 показана блок-схема распознавателя ОПГ, в котором, как обычно, используется стек S со счетчиком i, входная цепочка 7\ . . . Тп со счетчиком к, целочисленная переменная j и две переменные R и Q, принимающие значения символов.
По отношениям предшествования операторов можно построить функции предшествования и использовать их так же, как мы это делали в разд. 5.4. Тогда мы формально проделаем то, что объяснялось в начале раздела применительно к конкретному случаю.
Проведем в качестве примера разбор предложения i * (i + i) грамматики из примера (6.1.4):
Шаг S(l)... Отношение R Tk...
0 <5 i «0 + 0#
1 (i + i)#
2 (i + 0#
3 # N » ( i + i)#
4 # N* ( <5 i + D#
5 # N * (i + i)#
6 #N»(N <9 + 0#
7 #N»(N + <5 i )#
8 #N*(N + i . ' ) #
9 #N»(N + N ) 4t
10 #N*(N о )
11 # N * (N ) #
12 #N*N
13 #N СТОП
УПРАЖНЕНИЯ К РАЗДЕЛУ 6.1
1. Докажите, что в ОГ ни в какой сентенциальной форме не могут встретиться рядом два нетерминала. Указание: при доказательстве воспользуйтесь индукцией по числу непосредственных выводов в выводе сентенциальных форм.
2. Пусть G — грамматика. Докажите, что если в какой-то правой части содержатся рядом два нетерминала, то по крайней мере в одной сентенциальной форме содержатся рядом два нетерминала. Указание: помните, что все грамматики приведенные [см. определение (2.8.4)].
156
ГЛАВА 6
3. Докажите теорему (6.1.6).
4. Постройте булевы матрицы для отношений =°_, =, FIRST, FIRSTTERM, LAST и LASTTERM для грамматики из примера (6.1.4). Затем, исходя из FIRST и LAST, вычислите FIRST* и LAST*. Наконец, используя теорему (6.1.6), вычислите отношения <§ и £>.
5. Составьте список фраз и первичных фраз следующих сентенциальных форм грамматики из примера (6.1.4) : Е, Т, i, Т * F, F * F, i * F, F * i, F 4- F + F.
6. Докажите, что если Т входит во фразу некоторой сентенциальной формы, то это относится и к любому нетерминалу U, непосредственно предшествующему (или следующему за) Т. Указание: предположив, что это не так, постройте сентенциальную форму с двумя соседними нетерминалами.
7. Докажите, что любая первичная фраза удовлетворяет (6.1.9) (учитывая, что сентенциальная форма всегда ограничена символом # и что # <§ S, S <> # для любого терминала S).
8. Докажите, что любая подцепочка 14/14 . . . NjTjNJ+i из сентенциальной формы, удовлетворяющая (6.1.9), является первичной фразой. Указание: в качестве примера возьмите доказательство теоремы (5.2.8).
9. Проведите разбор предложений i, i + i, i * i 4- i, i * (i * i) и i * (i 4~ i * i) + ((i + i)*i) грамматики (6.1.4), пользуясь матрицей на рис. 6.2 и распознавателем, изображенным на рис. 6.4.
6.2. ПРЕДШЕСТВОВАНИЕ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
(1,2)^.,\)предшествование
Этот метод позволяет продвинуться на два шага от простого предшествования в сторону более практичного распознавателя, т. е. такого распознавателя, который годился бы для большего числа грамматик. Во-первых, разделяются задачи поиска хвоста и головы основы. Когда ведется поиск хвоста, нас интересует выполнение отношения •> . И совсем не важно, выполняются ли отношения R <• S или R = S, поскольку нас интересует один-единственный вопрос, является ли R хвостом основы или нет. Следовательно, здесь мы пользуемся только отношениями •> и <•= . Аналогично при поиске головы основы используются только отношения <• и •> =. Во-вторых, для обнаружения головы и хвоста основы используются три символа вместо двух. Определим следующие отношения:
(6.2.1). Определение. Пусть G — грамматика. R, S и Т — три символа. Тогда
RS о> Т, если есть каноническая сентенциальная форма ... RST ... , такая, что S — хвост основы;
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
157
RS о<= Т,
R O<ST,
R 0>=ST,
если есть каноническая сентенциальная форма .. . RST ... , такая, что Т входит в основу; если есть каноническая сентенциальная форма . . . RST . . . , такая, что S — голова основы; если есть каноническая сентенциальная форма . . . RST . . . , такая, что S входит в основу.
Термин (1,2) (2,^предшествование указывает на число символов, используемых для обнаружения головы и хвоста основы. Для обнаружения хвоста проверяем, находятся ли три символа R, S и Т в отношении RS о> Т или RS о<= Т, отсюда в термине — (2,1). Как только найден последний символ, мы, чтобы найти голову, начинаем двигаться от него влево, проверяя, не выполняется ли одно из отношений R о< ST или R о>= ST. Отсюда в термине—(1,2).
. Теперь возникает меньше конфликтных ситуаций, чем в случае простого предшествования. Для выражений в грамматике (6.2.2) получается, что + X Т и + <• Т. Теперь это противоречие устранено, поскольку' используется символ, следующий за Т. В самом деле, + о> Т+ и + о < Т*,
(6.2.2) Е : : = Т | Е Ч- Т Т : : ~ F | Т * F F : : = i | (Е)
Отношения, заданные в (6.2.1), можно переопределить в терминах выводов следующим образом (здесь Z — начальный символ, а подцепочка, заключенная в квадратные скобки, может и отсутствовать):
RS о> Т, если существует вывод Z =>* . . . [R] UTx
=> . . . RSTx
RS о<= Т, если существует вывод Z =>* . . . [R] [S]Ux
=> . . . RST ... х
R о< ST, если существует вывод Z =>* xRU [Т] . . . => xRST . . .
R о>= ST, если существует вывод Z =>* xU [S] [Т]. . . =► xRST ....
Определения, позволяющие построить алгоритмы для вычисления отношений по грамматике, см. в упражнениях 1—5. Приведем некоторые отношения предшествования для грамматики (6.2.2):
+т О- >) (( °< := т
(F о> >) (( о< := f
+F >) (( °< := (
*F >) (( о< ; = 1
(i >) (Е о< := )
+ 1 >) (Е о< :=+
Е) о- >) (Е о< := )
Т о > + +Т о< с =*
( ( О< о< : е + : f + ( Т О> >= Е) >= +т
( о < : i + F О/ >= +F
( о < ; т* i О / >= +F
( о < : F* Т О/ >= *F
( о< ; i * F О/ >= *F
+ о < : (Е i > = » F
+ о< ; Т* >= т +
158
ГЛАВА в
Теперь мы можем определить грамматику (1,2)(2,1)предшество-вания.
(6.2.3). Определение. Грамматикой (1,2)(2,^предшествования называется грамматика, удовлетворяющая следующим условиям.-
1. Все правые части правил единственны.
2. Ни для каких символов R, S и Т не допускается, чтобы одновременно выполнялись отношения RSo>T и RSo<=T.
3. Ни для каких символов R, S и Т не допускается, чтобы одновременно выполнялись отношения R о< ST и R о>= ST.
Можно доказать (см. упр. 6), что грамматика (1,2)(2,^предшествования однозначна и что основа любой канонической сентенциальной формы SiS2 . . . Sn является самой левой последовательностью Sj ... St, удовлетворяющей таким соотношениям:
Sj-i о< SjSj+1,
Sj о>= Sj+1Sj+2, . . . , Sj_j о>= SjSj+1,
Sj-jSj o> Sj+1.
Как и в грамматиках простого предшествования, разбор начала и конца цепочки требует осторожности. Так как отношения определены для трех символов, необходимо поместить в начало и в конец каждой разбираемой цепочки по два символа # и условиться, что для любых символов грамматики Sx и S2
(6.2.4) SxS2 о> #, #SX о> #, # о< SjSt, # о< Sx#.
Распознаватель для грамматики (1,2)(2,1)предшествования совершенно аналогичен распознавателю для грамматики простого предшествования, и его блок-схема совпадает с блок-схемой на рис. 5.4. Придется несколько изменить блок 1, так как только что описанные ограничители предложений отличаются от применявшихся ранее. В блоке 3 с помощью, скажем, трехмерной матрицы РТ, задающей отношения о> и о<=, будет проверяться выполнение отношения Si-iSj о >R, а в блоке 6 с помощью трехмерной матрицы PH, задающей отношения о< и о>=, будет проверяться, выполняется ли отношение Sj_j о< SjSJ+1. (Заметьте, что в блоке 3 мы предполагаем, что Si+1 является значением переменной R.)
Грамматики большинства используемых формальных языков весьма близки к грамматикам (1,2)(2,1)предшествования, и чтобы свести их к тому же классу, почти не требуется изменений. Однако с практической точки зрения эта техника бесполезна, так как требуются две трехмерные матрицы. Это означает, что для грамматики, в которой используется 100 символов, необходимо иметь две матрицы размерностью 100 х 100 х 100! Так как это обычно разреженные
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
159
матрицы, то можно для экономии памяти хранить список только тех троек элементов R,S и Т,для которых действительно определено отношение; но даже и этот список может иметь недопустимо большие размеры. Оставшаяся часть данного раздела посвящена тому, каким образом можно переработать грамматику и алгоритм, чтобы сделать его приемлемым для практического использования. Мы рассмотрим не все приемы, разработанные Маккиманом и др. [70]. Однако и этого будет достаточно, чтобы составить представление об имеющихся возможностях.
Как сделать (1,2)(2^предшествование пригодным для практического использования
Шаг 1. Отказаться от матрицы PH, задающей отношения о< и о>=. Матрица PH используется при поиске головы основы, когда хвост уже найден. Для большинства основ эта матрица не нужна, так как мы можем просто сопоставить верхние символы стека с правыми частями правил. Проблема возникает только в том случае, когда одна из правых частей — правильный хвост другой правой части; если есть два правила U:: = uxhV:: = xhb стеке находится их, то какую редукцию следует применить? Для правых частей, состоящих из 2 и более элементов, на этот вопрос отвечает следующая теорема (доказательство предоставляется читателю):
(6.2.5). Теорема. Пусть G — грамматика (1,2)(2,1)предшест-вования. И пусть символ Si — хвост основы, содержащей не менее двух символов. Тогда окончательной основой будет самая длинная подцепочка Sj . . . Sb которая является правой частью некоторого правила.
Следовательно,,нужно рассмотреть только случай, когда имеются два правила: U : : = иХ и U : : = X. Для каждого такого случая можно составить список тех троек (R, X, Т), для которых R о< XT. Когда во время разбора RX о> Т, мы проверяем, есть ли в списке тройка (R, X, Т). Если она есть, то применяется правило U : : =Х; в противном случае применяем то единственное правило с самой длинной правой частью, которое соответствует вэршине стека.
Таким образом удалось избавиться от матрицы PH; взамен мы просто ищем самую длинную из подходящих правых частей, не упуская, конечно, из виду проблему, о которой только что шла речь.
Шаг. 2. Исключить ненужную часть матрицы РТ. Матрица РТ используется для обнаружения хвоста основы. Поскольку мы проводим канонический разбор предложения, справа от любой основы всегда находится терминальный символ. Поэтому из матрицы РТ
160
ГЛАВА 6
можно исключить все столбцы, относящиеся к нетерминальным символам. Матрица уменьшается приблизительно вдвое.
Шаг. 3. Использовать там, где можно, отношения простого предшествования. Для реализации таких отношений (2, ^предшествования, как о> и о<=, требуется слишком много памяти, в то время как бинарные (1,1)отношения •> и <•= либо просто неадекватны, либо недостаточно гибки для обычных языков программирования. Мы идем на компромисс, т. е. там, где можно, применяем отношения простого предшествования, но если возникают конфликтные ситуации, то переключаемся к отношениям (2, ^предшествования. Для реализации используем двумерную матрицу Р, значениями элементов которой могут быть: 0 (отношение не определено), 1 (<•=), 2 (•>) и 3 (одновременно <£= и £>). При Р [i, j) = 3 мы обращаемся к списку TQ, содержащему четверки (Sk, Sb Sj, q), где q = 1, если SkSt o> Sj, и q = 2, если SrSj o<= Sj.
Пересмотренный алгоритм (1,2)(2,1) разбора
На рис. 6.5 показан пересмотренный распознаватель, в котором используются следующие переменные и таблицы. Таблицы Р, TQ, TH и PROD строит конструктор.
1. S — стек, его счетчик—i.
2. Ti . . . Tn — входная цепочка; к используется для индексирования символов в цепочке.
3. Р — матрица размером n х т, где п — число символов, ат — число терминальных символов.
Р li, j] = 0, если между символами St и Sj отношение не определено;
Р В, jl = 1, если Si <•_= Sj-,
Р В, j) = 2, если Sj •> Sj;
P [i, jl = 3, если Si <•= Sj и St •> Sj.
4. TQ — список четверок (R, S, T, q), где R и S — символы, T — терминальный символ, a q — это 1 или 2. Четверка (R, S, T, 1) находится в списке, если S <£= Т, S £> Т и RS о<= Т. Четверка (R, S,T, 2) находится в списке, если S <•= Т, S •> Т и RS о> Т.
5. PROD — список правил. Для быстрЬты доступа список следует упорядочить по последнему символу правой части.
6. TH — список троек, по которым принимается. решение об использовании правила, правая часть которого состоит из одного символа. Тройка (R, X, Т) входит в список, если Т — терминал, если существует правило U : : = X и есть хотя бы еще одно правило V X и если R о< XT.
Блок, 1
СТОП 5 Предложение 8 w и только о том случае, когда R = #, 1= 2 ic S(t) » Z
Рис. 6.5. Распознаватель для грамматики (1,2)(2,1)предшествованиЯг
6 д. грис
162
ГЛАВА 6
Верхний символ стека: Т
Список TQ пуст
тов •>, <•=)
тн (#, т, #)
(#, т, +)
(( . т, +)
((, т. ))
(#> F, #)
(-н F, #)
(нет конфлик-
(#, F, +) (( , F, +) (+, F, +) (( . F. )) (+, F, )) (#, F, *) (( , F, *) (+, F, *)
F ) i
Правила, которые мож- Е ::= Т Т ::= F F ::= (Е) F :: = i
но было бы применить: Е :: = Е + Т Т :: = Т * F
Рис. 6.6. Таблицы (1,2) (2,1) для грамматики (6.2.2).
На рис. 6.6 в качестве примера изображены таблицы, необходимые для грамматики (6.2.2).
(ш, ^предшествование
Можно предполагать, что если для какой-то грамматики не подходит ни (1, 1)предшествование, ни (1,2)(2,1)предшествование, то для получения однозначных отношений можно использовать больший контекст. Для многих грамматик это действительно так, и в настоящем разделе мы хотим в общих чертах описать такой метод. Однако необходимо отметить, что эта схема непригодна для практического использования из-за размера матриц предшествования. Можно было бы пуститься на всякого рода хитрости — как в случае (1,2)(2,1)предшествования, но не стоит этого делать.
Определим (т,п)предшествование для грамматик в терминах синтаксических деревьев так: пусть ш > 0, п > 0 — целые числа. Пусть хиу — произвольные цепочки, причем |х| = m и |у| = п. Тогда
х <• у, если существует каноническая сентенциальная форма . . . ху . . . , такая, что первый символ цепочки у является головой основы;
х JL у, если существует каноническая сентенциальная форма . . . ху . . . , такая, что первый символ цепочки у и последний символ цепочки х входят в основу;
х •> у, если существует каноническая сентенциальная "форма . . . ху . . . , такая, что последний символ цепочки х является хвостом основы.
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
163
Тогда грамматика (ш, п)предшествования — это такая грамматика, которая удовлетворяет следующим условиям:
1. Все правые части правил единственны.
2. Для любой пары цепочек х, у, таких, что |х| = m и |у| = п, выполняется не более одного из трех отношений (т, ^предшествования.
Простое предшествование — это не что иное, как (1,^предшествование. Можно было бы также показать, что грамматика (т.п) предшествования однозначна, что основа канонической сентенциальной формы определяется отношениями единственным образом и т. д. Мы предоставляем это читателю. Конечно, труднее всего определить отношения так, чтобы можно было их построить. Один способ построения отношений — это просмотр достаточно большого количества синтаксических деревьев и построение отношений по каждому из них до тех пор, пока не будет уверенности, что все отношения найдены. Именно так поступил Маккиман и др. 170] в случае (1, 2)(2,1 предшествования.
УПРАЖНЕНИЯ К РАЗДЕЛУ 6.2
В некоторых упражнениях используются следующие определения:
S — допустимый предшественник U, что обозначается как U АР S, если есть правило Ui :: = ... SV .. . , такое, что V FIRST* U.
S — допустимый преемник U, что обозначается как U AS S, если есть правило Ui: : = . . . VW . . . , такое, что V LAST* U и W FIRST* S.
1. Докажите, что отношение АР определяется как АР = (л=) (FIRST*).
2. Покажите, что RS о> Т тогда и только тогда, когда имеет место один из следующих случаев:
а) существует правило U : : = VW ... , где U АР R, V SS+ S и W FIRST* Т;
Ь) существует правило U : : = VW .... где V =>+ . . . RS и W FIRST* Т;
с) существует правило U : : = . . . RVW . . . , где V SS+ S и W FIRST* Т.
.3. Покажите, что RS о<= Т тогда и только тогда, когда имеет место один из следующих случаев:
а) есть правило U : : = SW ... , где U АР R и W FIRST* Т;
6*
164
ГЛАВА 6
Ь) есть правило U : : = . . . RSW .... где W FIRST* Т.
4. Покажите, что R о< ST тогда и только тогда, когда имеет место один из следующих случаев:
а) есть правило U : : — . . . RW, где W SS+ S и U AS Т;
Ь) есть правило U : : = . . . RW . . . , где W =►+ ST . . . ;
с) есть правило U : : = . . . RWV .... где W SS+ S и V FIRST* Т.
5. Покажите, что R о>= ST тогда и только тогда, когда имеет место один из следующих случаев:
а) есть правило U : : = . . . RS, где U AS Т;
Ь) есть правило U : : = . . . RSV. . . , где V FIRST* Т.
6. Докажите, что если выполняются отношения (6.2.4), то в грамматике (1,2)(2,1)предшествования основа любой канонической сентенциальной формы Sx . . . Sn является самой левой последовательностью узлов Sj . . . St, удовлетворяющих отношениям Sj_i О< SjSj+1, SkSk+1 о<= Sk+2 для k = j, • . ., i — 2, Si—i Si O> si+1.
7. Докажите теорему (6.2.5).
8. Используя программу (рис. 6.5) и таблицы (рис. 6.6), разберите следующие предложения грамматики (6.2.2): i + i + i, i * i + i, i + i * i, (i + i) * i. Попытайтесь разобрать цепочки ii, i + * i, не являющиеся предложениями.
9. Постройте все необходимые таблицы для описываемой ниже грамматики. Эта грамматика аналогична (6.2.2); отличие состоит в том, что операторы выполняются справа налево, а не слева направо: Е : : = Т | Т + Е, Т : : = F | F + Т, F : : = (Е) | i.
10. Используя грамматику и таблицы из упражнения 9, разберите следующие предложения: i + i + i, i * i + i.
11. Объясните, почему грамматика A : : — (В ) | dBe, В : : = с | с В не является грамматикой простого предшествования, хотя грамматика А : : = ( В ) ] d В е, В : : = с | В с, порождающая тот же язык, является грамматикой простого предшествования.
6.3. ОГРАНИЧЕННЫЙ КОНТЕКСТ
Одна из проблем, связанных с техникой простого предшествования, состоит в том, что не допускается существования двух или более правил с одинаковыми правыми частями. В качестве примера рассмотрим грамматику
(6.3.1) Z:: = aUa|bVb U::=c V : : = с.
Она не является грамматикой простого предшествования, но по контексту с можно легко установить, к U или к V следует приво
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ .. 165
дить с. Так, в предложении аса с следует привести к U, а в bcb — к V. Схемы разбора, в которых используется ограниченный контекст, позволяют нам для решения вопроса о том, к чему приводится основа, употребить фактические символы с любой стороны от обнаруженной основы (а не только отношения предшествования между символами). Заметим, что переход к технике (1,2)(2, 1)предшествования также до некоторой степени позволял нам это.
Определение (1 ^ограниченного контекста
Предположим, что Z =>+ х TURy, где U : : = и — одно из правил грамматики. Тогда если во время разбора канонической сентенциальной формы в стеке окажется хТи, а входным символом будет R, то и следует привести к U. Хотелось бы уметь по TuR составлять суждение о том, является ли и простой фразой для U в любой канонической сентенциальной форме . . . TuR . . . .То есть мы хотим, используя только контекст Т . . . R возможной основы, определять, во-первых, является ли она действительно основой, и, во-вторых, к чему следует ее приводить. Какие новые возможности возникают для основы, если Z =>+ . . . TuR . . . ?
Так как выполняется каноническая редукция, то если в стеке находится . . . Ти, мы знаем, что основа не может оказаться целиком слева от хвостового символа цепочки и. Это вытекает из сущности нашего разбора; как только в стек помещается хвостовой символ основы, мы ее редуцируем.
Теперь можно перечислить следующие возможные основы:
1. . . . Ти
2. и; но эта основа будет приведена к V, где V ф U
3. и2, где и = ихи2
(6.3.2) 4. . . . TuR . . .
5. uR . . .
6. u2R . . .
7. Полностью справа от и
В каждом из этих случаев мы можем показать, какие каноничес-
кие выводы порождают перечисленные основы:
1. Z =>+ . . . VR . . . , где V :: = ... Ти
2. Z =>+ . . . TVR . . . , где V : : = и и V ф U
3. Z =>+ . . . TuxVR .... где V : : = и2 и и = ихи2 (6.3.3) 4. Z ... V ... , где V :: = ... TuR .. .
5. Z =>+ ... TV ... , где V : : = uR . . .
6. Z =>+ . . . TuiV . . . , где V : : = u2R и и = ихи2
7. Z =>+ . . . TuV, где V . . . =»+ R
166
ГЛАВА б
Если ни один из этих семи случаев не имеет места, мы знаем, что единственное, что можно сделать в случае . . . TuR .... — это привести и к U.
(6.3.4). Определение. Правило вида U : : — и является (слева направо) (I,^ограниченно контекстным правилом, если для каждой пары символов Т и R, таких, что Z =>+ ... TuR ... , не имеет места ни один из семи случаев (6.3.3).
(6.3.5). Определение. Грамматика G является (слева направо) (1 ,\)ограниченно контекстной грамматикой, если все ее правила (слева направо) (1,1)ограниченно контекстны.
Дополнительный термин «слева направо» используется потому, что мы могли бы также определить (1,1 Ограниченный контекст для разбора, проводимого справа налево. Можно было бы даже ввести такое определение, чтобы проводить разбор в любом направлении или же с середины, т. е. можно было бы обнаружить не только основу, но и любую простую фразу.
Заданная ниже грамматика не является (1,1 Ограниченно контекстной, так как правила U : : = с и V : : = с не являются (1,1)ограниченно контекстными; в цепочке abc # по контексту Ьс # невозможно определить, какое из правил, U : : = с или V : : = с, следует применить для редукции самого правого с:
Z:: = abU|cbV U : : = с V : : = с.
,\)ограниченно контекстный распознаватель
Этот распознаватель пользуется единственной таблицей; в каждой строке таблицы три столбца. В первом столбце находится содержимое стека в форме Ти, где Т — любой символ или ограничитель # (который помещается на обоих концах разбираемого предложения), а и — правая часть правила. Во втором столбце находятся соответствующие правые контексты, каждый из которых либо одиночный терминал, либо ограничитель #. В третьем столбце записывается номер правила. Этой таблицей распознаватель пользуется следующим образом. На каждом шаге работы распознаватель среди строк таблицы ищет ту, в которой содержимое первого столбца совпадает с верхней частью стека, а содержимое второго столбца совпадает с последним сканированным символом предложения. Если такая строка найдена, выполняется редукция: основа в стеке заменяется в соответствии с правилом, указанным в третьем столбце. Если такой строки нет, то редукция невозможна; тогда последний сканированный символ помещается в стек и сканируется следующий символ предложения.
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
167
Таблица содержит все возможные конфигурации вида (Tu, R, i), такие, где и в контексте TuR можно редуцировать, используя правило с номером i. Если в любой момент можно найти совпадение не более чем с одной строкой, то всякую редукцию можно выполнить, зная только контекст Т . . . R, т. е. грамматика (^^ограниченно контекстная. На рис. 6.7 показана таблица для такой грамматики:
(6.3.6) (1) Z : : = V (4) V : : = b U (7) W : : = О W 1
(2) Z : : - a W (5) U : : = U 0 (8) W : : = 0 1
(3) V : : - V 1 (6) U : : = О
Язык, порождаемый этой грамматикой, является объединением двух множеств {aOnln | п > 0} и {bOnlm| п > 0, m 0}. Просматривая таблицу, обратите внимание, что там перечислены все
Рис. 6.7. Таблица ограниченного контекста для грамматики (6.3.6).
возможные комбинации Tu и входных символов R, вызывающие редукцию.
Сам распознаватель изображен на рис. 6.8. В нем, как обычно, используется стек со счетчиком i. Нам предстоит разобрать предложение Ti . . . Тп. Добавим символ Тп+1 = #, ограничитель предложения, и начнем работать, имея в стеке символ #. Для сканирования символов предложения применяется счетчик к.
168
ГЛАВА 6
1. Установить i : = 1, к : = 1 и S (1): = #.
2. Если верхние символы стека соответствуют содержимому стека в таблице и если Тk совпадает с правым контекстом, то номер этой строки занести в j и перейти к шагу 3; в противном случае перейти к шагу 4.
3. В стеке содержится Ти, где Ти задается в первом столбце (содержимое стека) строки j. Привести и к U, используя правило, определяемое третьим столбцом строки j. Перейти к шагу 2.
4. Если Тк равно #, перейти к шагу 6.
5. i: = i + 1; S (i) — Tk; k : = k 4- 1; перейти к шагу 2.
6. Стоп. Предложение правильное тогда и только тогда, когда i: = 2 и S (i) = Z.
Рис. 6.8. (1,1)ограниченно контекстный распознаватель.
Определение (ш, ^ограниченного контекста
Также как мы расширяли (1,1 (предшествование до (ш,^предшествования, можно расширить (1,1 (ограниченный контекст до (т, ^ограниченного контекста. В действительности ни один компилятор не пользуется (ш, п)ограниченным контекстом, хотя в некоторых случаях это было бы возможно. Поэтому при изложении мы останавливаемся только на основных моментах. Описание этого метода включено потому, что грамматики, приемлемые для всех уже описанных распознавателей, равно как и для тех, о которых будет говориться позже, являются (т, п)ограниченно контекстными при некоторых тип.
(6.3.7). Определение. Рассмотрим правило U : : = и. Для каждой пары цепочек v, w, где |v| = m, |w| = п и Z =>* xvUwy при некоторых хиу, предположим, что и является основой всякой канонической сентенциальной формы . . . vuw ... и что и нужно привести к одному символу U. Тогда такое правило (т ^ограниченно контекстное.
Это означает следующее. Предположим, что U : : = и — ограниченно контекстное правило, и предположим далее, что существует вывод Z =>* xvUwy => xvuwy. Тогда всякий раз, когда при разборе слева направо и снизу вверх в стеке оказывается . . . vu, а в оставшейся части входной цепочки — w . . ., и можно привести к U. Заметьте, что мы не перечисляли случаи, которые не должны иметь места, как это делалось в (6.3.3) для (1, ^ограниченного контекста. Предоставляем это4 читателю.
(6.3.8). Определение. Грамматика (т,п)ограниченно кон~ текстная, если каждое правило ограниченно контекстное,
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
169
(гл, ^ограниченно контекстный распознаватель и конструктор
Как и в случае (1,1 Ограниченного контекста, в таблице будет три столбца. В первом столбце находится содержимое стека tu, во втором — соответствующий правый контекст v, а в третьем — номер правила, при помощи которого . . . tuv . . . приводится к . . . tUv .... Сам распознаватель, в сущности, остается прежним, но теперь на каждом шаге приходится сравнивать большее число символов.
Как и следовало ожидать, конструктор таблиц довольно сложен. На первом шаге строятся таблицы для (1,^ограниченного контекста. То есть для каждого канонического вывода Z =>* . . . VUW . . . => VuW ... к таблице добавляется строка (если ее раньше не было), в первом столбце которой Vu, во втором столбце — W, а в третьем столбце — номер правила U : : = и. (Напоминаем читателю, что нельзя исследовать все такие выводы, так как их бесконечное количество. Но можно исследовать грамматику для того, чтобы установить, существует ли такой вывод для каждого правила U : : = и и символов V и W.)
Когда таблица уже построена, исследуются все строки для того, чтобы найти пару строк
V, И, W п
V2U2 W тп
где V2u2 является хвостом ViUi (не обязательно правильным).Если таких пар строк нет/ грамматика (1,1)ограниченно контекстная и таблица уже построена. Она (1, 1)ограниченно контекстная потому, что на каждом шаге с верхней частью стека сопоставляется не более чем одна строка.
Однако предположим, что существуют две (или более) такие строки. Тогда, если в стеке находится ViUi, a W — входной символ, для редукции можно использовать любую из этих строк. Нужно изменить таблицу так, чтобы она включала больший контекст справа от W или слева от V2u2. Предположим, например, что мы хотим добавить контекст слева и что все канонические выводы, включающие . . . V2u2W ... и использующие правило ш, имеют вид Z =>* . . . XV2UW . . . => XV2u2W или Z =>* . . . YV2UW . . . => YV2u2W .... Тогда мы можем заменить упомянутые выше строки на следующие:
Vf u( w n
XV2u2 w ТП
VV2u2 w ТП
170
ГЛАВА 6
Возможно, что такая замена позволит избавиться от неоднозначности. Если нет, придется опять добавить контекст слева или справа. Заметьте, что на каждом шаге следует проверять и менять только те строки, которые вызывают неоднозначность. С остальными все в порядке. Одна из проблем заключается в том, как решить, с какой стороны расширять контекст. На этот счет нет твердых и быстро приводящих к результату рекомендаций. Другая проблема состоит в том, что до тех пор, пока не будет получена непротиворечивая таблица, неизвестно, является грамматика ограниченно контекстной или нет.
6.4. МАТРИЦЫ ПЕРЕХОДОВ
Одна из проблем, связанных с большинством изложенных методов, состоит в том, что при выборе нужной редукции всегда необходим поиск правила или просмотр таблицы. Конечно, таблицу можно организовать таким образом, чтобы минимизировать время поиска.
* IF
IF <выр>
<перем> ; =
<выр> + ъ
THEN
а
Рис. 6.9. Частично заполненные матрицы переходов.
В описываемом здесь способе работы с этой целью используется большая матрица, иногда называемая таблицей решений или матрицей переходов. Предполагается, что мы имеем дело с операторной грамматикой (ОГ), поскольку именно эта формализация соответствует тому, как, исходя из интуитивных предположений, применялись матрицы переходов. Проиллюстрируем этот способ на примере такой грамматики.
<прог> : : = <инстр>
<инстр> : : = IF <выр> THEN <инстр>
(6.4.1) <инстр> : : = <перем> : = <выр>
<выр> : : — <выр> + <перем> | <перем>
<перем> : : = i
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
171
Составляем матрицу переходов М; ее строки соотносятся с теми головами (оканчивающимися терминальными символами) правых частей правил, которые могут появиться в стеке, а столбцы соотносятся с терминальными символами, включая и ограничитель предложений # (рис. 6.9, а). Элементами матрицы будут номера или адреса подпрограмм.
Распознаватель пользуется обычным стеком S и переменной R, принимающей значение входных символов. Однако структура стека несколько отличается от привычной. Элементами стека являются не символы, а цепочки символов. Появляющиеся здесь цепочки — это головы (оканчивающиеся терминальным символом) правых частей правил. Например, если в обычном стеке в какой-то момент содержится
# IF <выр> THEN IF <выр> THEN <перем> :== то этот стек будет выглядеть так:
<перем> : = 1F <выр> THEN IF <выр> THEN
Заметьте, что все сводится к совместному хранению тех символов, о которых известно, что они должны редуцироваться одновременно. И, наконец, нам понадобится третья переменная U. Она либо будет пуста, либо будет содержать тот символ, к которому была приведена последняя первичная фраза. Следовательно, если частичная цепочка, еще не разобранная до конца, выглядит так:
# IF <выр> THEN IF <выр> THEN <перем> : = <выр>, то стек будет таким, каким он изображен выше, а в U будет <выр>.
Распознаватель использует матрицу следующим образом. На каждом шаге работы верхний элемент стека соответствует некоторой строке матрицы, так как в обоих случаях речь идет о голове (заканчивающейся терминальным символом) некоторой правой части. По входному терминальному символу R определяется элемент матрицы, являющийся номером подпрограммы, которую нужно выполнить. Эта подпрограмма произведет необходимую редукцию или занесет R в стек и будет сканировать очередной исходный символ.
Например, в самом начале в стеке находится # и U пусто. В соответствии с грамматикой (6.4.1) входным символом должен быть либо IF, либо i. Поскольку с них начинаются правые части, необходимо занести их в стек и продолжить работу. Тогда первой подпрограммой (рис. 6.9, а) будет такая:
1: IF U =/= ' ' THEN ERROR; i : = i + 1; S (i) = R ; SCAN, где SCAN означает «поместить очередной символ из входной цепочки в R». Смысл сравнения U с пробелом сейчас будет пояснен.
172
ГЛАВА 6
Предположим, что i — верхний элемент стека. Какие символы из тех, которые могут оказаться' в R, считаются допустимыми? За i может следовать один из символов: #, THEN, : = или +. В любом из этих случаев необходимо заменить i на <перем>, т. е. выполнить редукцию . . . <перем> i .. . . В подпро-
грамме 2 (рис. 6.9,Ь) именно это и делается: .
2: IF U ' ' THEN ERROR; i : = i — 1; U : = '<перем>' .
Тогда каждый элемент матрицы является номером подпрограммы, которая либо заносит входной символ в стек, либо выполняет редукцию. В связи с тем что изменился вид элемента стека, операция занесения в стек стала несколько более сложной. Полная матрица и подпрограммы для грамматики 6.4.1 приведены на рис. 6.10. Читателю предлагается, используя матрицу и подпрограммы, провести разбор предложения: # IF i + i THEN i : = i #.
Преимущества и неудобства матриц переходов
Этот метод использовался в нескольких ранних компиляторах с АЛГОЛа, причем все матрицы были построены вручную в основном тем же способом, которым мы только что пользовались. Элементы матрицы заполнялись так: по структуре языка делался вывод о том, каким может быть следующий входной символ и какое действие следует в соответствии с этим предпринять. Используя матрицу, автор транслятора мог концентрировать свое внимание только на одной конструкции одновременно. Это позволяло разделить одну большую задачу на ряд мелких подзадач.
Способ этот гарантирует быструю работу, так как полностью исключается поиск; каждой подпрограмме точно известно, что она должна делать. Другим удобством является легкость в нейтрализации ошибок. Каждый нуль в матрице соответствует синтаксической ошибке, и так как обычно больше половины элементов — нулевые, можно написать много подпрограмм для обработки этих ошибок и допустить несколько способов нейтрализации. Ни для каких других методов хороших способов нейтрализации ошибок не найдено, потому что при нейтрализации совсем не просто выделить частные случаи. Одно из неудобств, связанных с использованием матриц переходов, — большой объем требуемой памяти. Например, в типичном компиляторе с АЛГОЛа для IBM 7090 используется матрица 100 x 45 и приблизительно 250 подпрограмм.
Построение аугментной операторной грамматики
До сих пор обсуждалось, как работает построенная по интуитивным соображениям матрица переходов. Теперь остановимся на основных особенностях построения матрицы. Все доказательства
Т Н IE : # FN=+i
5 1 0 6 0 1
IF 0 0 9 0 3 1
IF <выр> THEN 7 1 0 6 0 1
<перем>: = 8 0 0 0 3 1
<выр>+ 4 0 4 0 4 1
i 2 0 2 2 2 0
1: IF U=#" THEN ERROR;
i := i + 1; S(i):=R; SCAN.
2: IF U#=''THEN ERROR;
i:=i — 1; U :='<перем>
3: IF U =/= '<выр>' OR
U#= '<перем>' THEN ERROR;
i := i + 1; S(i) :='<выр> + ';
U:=''; SCAN.
4: IF U^='<перем>'THEN ERROR; i:=i — 1; U:='<Bbip>'.
5: IF U =#='<npor>'OR
U #='<инстр>'THEN ERROR; STOP.
6: IF U#= '<перем>' THEN ERROR; U:=' '; i: = i + l;
S (i) :='<перем> :='; SCAN.
7: IF и#='<инстр>'
THEN ERROR;
i:=i — 1; U: = '<инстр>'.
8: IF '<перем>'OR
и#='<выр>'
THEN ERROR;
i:=i—1; U:= '<инстр>'.
9: IF U#='<перем>'OR и=#'<выр>'
THEN ERROR;
S (i) :='IF <выр> THEN';
U:="; SCAN.
0: ERROR; STOP.
Рис. 6.10. Матрица и подпрограмма для грамматики (6.4.1).
174
ГЛАВА 6
предоставляются читателю в качестве упражнений. Помните, что формальный подход очень близок к интуитивному.
Как и в случае предшествования операторов, возьмем вначале ОГ. Предположим далее, что любой вывод одного нетерминального символа из другого является единственным. Таким образом, если Ui =>+ Uj, то такой вывод — единственный.
Первый шаг — замена грамматики другой, эквивалентной ей грамматикой, в которой в правой части каждого правила содержится не более трех символов. Для этого введем новые нетерминальные символы, которые будем называть выделенными нетерминальными символами (ВНТС); предполагается, что их можно отличить от первоначальных невыделенных нетерминальных символов (ННТС). Для этого ВНТС будем подчеркивать. Далее, каждый ВНТС построен так, что он является головой (оканчивающейся терминальным символом) правой части некоторого правила исходной ОГ и таким образом соотносится с одной из строк описанной ранее матрицы переходов. Эту новую грамматику назовем аугментной операторной грамматикой (АОГ). Она необязательно должна быть ОГ.
Построение происходит следующим образом: шаг 1 выполняется столько раз, сколько возможно; то же самое относится и к шагу 2. Наконец, до тех пор, пока это возможно, попеременно повторяются шаг 3 (а) и шаг 3 (Ь). Здесь Т — терминальный символ, U — нетерминальный и U — ВНТС.
1. Если есть правило Ui : : = Tyi (цепочка yi может быть пустой) и если уже существует к —- 1 ВНТС U1} . . . , Uk~i, образовать новый BHTCUk, заменить все правила Uf. : = Tyj (т. е. все правила, начинающиеся с одного и того же Т) правилами Up : = Ukyi и добавить правило Uk :: = Т.
2. Если есть правило Ui :: = UTyi и уже существует к — 1 ВНТС, то образовать новый ВНТС Uk, заменить каждое правило Ui :: = UTyi (т. е. все правила, начинающиеся одной и той же последовательностью символов UT) правилами Ui :: = Ukyi и добавить правило Uk :: = UT.
3. (а). Если есть правило Ui : : = UTyi и уже существует к —- 1 ВНТС, то образовать новый ВНТС Uk, заменить каждое правило U4 :: — UTyi правилом Ui :: = Ukyi и добавить новое правило Uk :: — UT.
(Ь) Если есть правило Ui ::=UUTyi и уже существует к — 1 ВНТС, то образовать еще один ВНТС Uk, заменить каждое правило Ui= UUTyi правилом Ui:: — Ukyi и включить новое правило Uk = UUT.
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
175
Заметив, какую форму принимают правила после выполнения каждого шага, читатель должен доказать такую лемму (упражнение 1).
(6.4.2). Лемма. Любое правило в АОГ представлено в одной из следующих семи форм:
U1::=U2, U/.^U, U(::=UU2,
U::=T, U::=UT, U^^U/T, U^^UjUT.
Кроме того, читателю предлагается выполнить описанное построение для грамматики (6.4.1) (упражнение 2). И, наконец, читатель должен доказать две следующие леммы и теорему.
(6.4.3). Лемма. Для каждого правила грамматики ОГ U : : = у, где у не является нетерминалом, существует такое единственное множество правил Ui: : = у0, U2: : = Uiyi. . . , Un: : = Un-iYn-i, U : : = Unyn “грамматики’ АОГ, “что у = уоух. . .уп.
(6.4.4). Лемма. Для каждого из отличающихся друг от друга синтаксических деревьев сентенциальной формы s ОГ можно построить другое синтаксическое дерево для s согласно АОГ следующим образом: заменить каждый куст, соотносящийся с применением правила Uj:: = у, множеством кустов, соотносящихся с правилами, описанными в лемме (6.4.3).
(6.4.5). Теорема. Если АОГ однозначна, то таким же свойством обладает и соответствующая ей ОГ.
<инсшр>
<if -lhen>
<инсшр> f..............
<и> :
Г-----j----1---1-------| j I
IF <ewp> THEN <UHCinp> IF <выр> THEN <инстр> a b
Рис. 6.11. Кусты для ОГ и соответствующей ей АОГ.
В качестве иллюстрации к построению, о котором говорилось в лемме (6.4.4), заменим куст дерева (рис. 6.11, а) на поддерево (рис. 6.11 ,Ь). Речь идет о грамматике (6.4.1). На рисунке <if> и <if-then> — ВНТС. Читатель должен сам убедиться в том, что восходящий разбор, проведенный в соответствии с АОГ, по своей сути не отличается/от разбора, проводимого в соответствии с ОГ; появляются, правда, некоторые дополнительные промежуточные редукции.
176
ГЛАВА 6
Разбор в АО Г
При восходящем разборе на каждом шаге распознается самая левая первичная фраза АОГ, где первичная фраза АОГ определяется как фраза, которая не содержит никакой другой первичной фразы АОГ, но содержит по крайней мере один терминал или ВНТС. Читатель должен сравнить это определение с определением (6.1.7). Можно сказать и так, что у является первичной фразой некоторой сентенциальной формы xyz в АОГ, если существует такая сентенциальная форма xVz (где V — ВНТС или ННТС), что V : : = у или V : : = У1, yi =>* у и все непосредственные выводы в последовательности yi =>* у следуют из правил Up : = U< для ННТС Ut и Uj.
Из леммы (6.4.2) следует, что первичная фраза АОГ должна иметь одну из следующих шести форм:
(6.4.6) U UT Т UU UT UUT
Теперь читателю предстоит доказать следующее (упражнение 6):
(6.4.7). Теорема. При разборе предложения из АОГ каждая редукция, которая редуцирует самую левую первичную фразу АОГ, имеет одну из следующих шести форм:
uUt => uUt иСЦ => uU2Tt uUtt => uTt
uUjt=>uUU2t uUjt=>uU2UTt uUt=>uUTt
где u — (возможно, пустая) цепочка ВНТС, t — цепочка терминальных символов, U, Ui, U2 — ННТС, a U, Ui и U2 — ВНТС. Следовательно, при разборе любая сентенциальная форма имеет вид ut или uUt.
В алгоритме разбора используется стек S, в котором находится подцепочка и сентенциальной формы u[U]t. Если есть символ U, он будет значением переменной U; в противном случае значением переменной будет пустой символ. Матрица содержит по одной строке для каждого ВНТС и по одному столбцу для каждого терминала. Заметим, что так как каждый ВНТС соответствует некоторой строке, в стеке он может быть представлен номером этой строки.
На каждом шаге разбора верхний символ стека (ВНТС) и очередной входной символ определяют элемент матрицы. Там записан номер подпрограммы, которую нужно выполнить. Подпрограмма проверяет значение переменной U и предпринимает соответствующее действие, выполняя одну из шести возможных редукций. Сейчас мы перечислим достаточные условия, выполнение которых позволяет только по верхнему элементу стека, входному терминалу и переменной U определить, какую именно редукцию производить на каждом шаге.
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
177
Достаточные условия для однозначной АО Г
Определим некоторые условия, из которых следует однозначность АОГ. Более того, эти условия позволяют нам на каждом шаге разбора находить самую левую первичную фразу АОГ и тот символ, к которому она должна быть приведена. Известно, что все сентенциальные формы имеют вид u_ [U] t (квадратные скобки означают, что символ U может и отсутствовать). Условия позволят нам, судя только по хвостовому символу цепочки и, головному символу цепочки t и переменной U, определять, какую сделать редукцию, если она возможна.
(6.4.8). Определение. АР (S) — это множество допустимых предшественников символа S: АР (S) : = {Si | . . . SiS ... — сентенциальная форма}.
Условие 1. Для каждой пары U, Т, где U — ВНТС, а Т — терминал, справедливо не более чем одно из следующих утверждений: (6.4.9) Есть правило U : : = U и U £ АР (Т).
(6.4.10) Есть правило Ui: : = UT.
(6.4.11) Есть правило Ui: : = Т, и U € АР (Ui).
Более того, если имеет место (6.4.9), существует только один
такой ННТС U.
Условие 2. Для каждой тройки U, U и Т, где U — ВНТС, U — ННТС, а Т — терминал, справедливо не более чем одно из следующих утверждений:
(6.4.12) Есть правило U,: : = UU2, где Ui € АР (Т) и U2=>*U.
(6.4.13) Есть правило Ui: : = UU2T, где U2=>*U.
(6.4.14) Есть правило Uj: : = U2T, где U ё АР (Ux) и U2=>*U.
Более того, если имеет место (6.4.12), Ui и U2 единственны, а в остальных двух случаях единствен символ U2.
Предоставляем читателю доказательство следующей теоремы (упражнение 7):
(6.4.15). Теорема. Грамматика АОГ, удовлетворяющая условиям 1 и 2, однозначна.
УПРАЖНЕНИЯ К РАЗДЕЛУ 6.4
1. Докажите лемму (6.4.2).
2. Постройте АОГ для грамматики (6.4.1). Вначале, на первом шаге, второе правило заменяется двумя правилами: Ux: : = IF и
178
ГЛАВА 6
<инстр> : : == Ui <выр> THEN <инстр>, а последнее правило заменяется на Ъ2: : = i, <перем> : : — U2.
3. Докажите лемму (6.4.3). (Доказательство леммы легко следует из построения.)
4. Докажите лемму (6.4.4).
5. Докажите теорему (6.4.5). Указание-, покажите, что если синтаксическое дерево некоторой сентенциальной формы единственно в АОГ, это же свойство сохраняется у соответствующего дерева в ОГ.
6. Докажите теорему (6.4.7). Указание: обратите внимание на шесть возможных форм первичной фразы АОГ и соответствующие им редукции.
7. Докажите теорему (6.4.15).
6.5. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Идея предшествования операторов была формализована Флойдом [63], но методы, основанные на этой идее, интуитивно использовались уже в ранних компиляторах. Соответствующие ссылки можно найти в работах Алларда и др. [64], Галлера и Перлиса [67] и Гриса [65]. Простое предшествование, предложенное Виртом и Вебером, использовалось в компиляторе с языка АЛГОЛ W (см. Бауэр, Беккер и Грехем [68]). Вирт и Вебер также предложили (т, п)предшествование, но их определения неверны. Маккиману [66] принадлежит идея расширения обычного предшествования до (1,2)(2,1)предшествования. Позднее эта идея была уточнена и использовалась в разработанной Маккиманом и др. [70] системе написания компиляторов. Колмерор [70] определил технику предшествования, включающую в себя как частные случаи простое и операторное предшествования. Здесь, говоря кратко, разработчик компилятора сам выбирает операторы. Имеются некоторые ограничения, так, например, все терминалы должны быть операторами. Если остановить выбор на терминальных символах, случай сводится к предшествованию операторов, если же отнести к операторам все символы, получается простое предшествование.
Некоторые исследователи пытались расширить простое предшествование так, чтобы повысить его практическую ценность. Например, Ихбия и Морз [70] определили отношения «слабого предшествования», чтобы для поиска головы основы в стеке вместо отношений использовать сопоставление с образцом. Это очень походит на то, что мы делали в случае (1, 2)(2, 1)предшествования. Циммер [70] в своей работе смягчает требование единственности правых частей, а для того, чтобы установить, какое из правил употребить при редукции, разрешает использовать контекст. Это уже походит на (1,1)ограниченный контекст.
ДРУГИЕ ВОСХОДЯЩИЕ РАСПОЗНАВАТЕЛИ
179
Идея об ограниченном контексте уровня (1,1) имеет корни в работе Пола [62] и впервые упоминалась Эйкелом и др. [63]. Расширение до (т, ^ограниченного контекста встречается у Флойда [64] и Айронса [64]; однако они ввели разные определения. Мы следовали формализации Флойда. Две последние работы были представлены на Конференции по структурам формализованных языков, состоявшейся в августе 1963 года. Материалы этой конференции помещены в февральском номере САСМ за 1964 г. и стоят того, чтобы с ними познакомиться. Реальный способ построения таблиц для (т, п) контекстно ограниченного распознавателя, работающего слева направо, был впервые предложен Эйкелом [64]. Эту статью не только трудно читать, но ее нелегко и найти. Лёкс [69] предложил для построения таблиц новый, гораздо более понятный алгоритм.
Окончательным результатом, к которому привели все исследования по распознаванию слева направо и снизу вверх, явились LR (к)грамматики и языки, введенные Кнутом [65]. Кнут показывает, как построить для LR (к)грамматики распознаватель, которому при выборе редукции доступны все символы в стеке и к символов справа. Конечно, в действительности не нужно просматривать весь стек на каждом шаге работы. Вместе с каждым символом стека хранится «состояние», содержащее информацию об остальных элементах стека, достаточную для того, чтобы принять решение.
Следует упомянуть о том, что LR (к)грамматика или по крайней мере ее слегка ограниченный вариант, предложенный Деремером [70], может быть достаточно эффективным для практического использования в компиляторах. Хорнинг [701 отмечает, что при хорошей реализации распознаватель для LR (к)грамматики может работать быстрее и занимать меньше места в памяти, чем эквивалентный (1, 2)(2, ^распознаватель.
Матрицы переходов, впервые описанные Замельзоном и Бауэром [60], использовались в нескольких компиляторах с языка АЛГОЛ, написанных группой АЛГОЛ (см. Грис [65]). Сотрудники NELIAC (см. Халстед) также применяли матрицы переходов под названием СО-NO таблиц (текущий оператор и следующий оператор), но без стеков. Эта техника была формализована Грисом [68].
Здесь необходимо упомянуть о других формализациях процесса синтаксического распознавания, хотя и не все перечисляемые работы используют восхождение. Линч [68] определил грамматики типа ICOR и дал для них алгоритм распознавания. Алгоритм До-мелки описывается в статье Хекста и Робертса [70]. Джилберт добавляет к контекстно зависимым грамматикам функцию выбора, указывающую (для текущей сентенциальной формы), какое правило употребить при редукции. Таким образом, эта грамматика скорее является синтетической, чем аналитической, ее можно использовать как алгоритм разбора без предварительной обработки конструктором.
180
ГЛАВА 6
Тиксир [67] рассматривает множество правил для любого нетерминала как регулярное выражение, определяющее для этого нетерминала множество цепочек. Можно построить конечный автомат для того, чтобы распознавать цепочки, относящиеся к каждому нетерминальному символу. Задача состоит в том, чтобы установить, во-первых, в какой момент можно переключаться с одного конечного автомата на другой, и, во-вторых, на какой из них переключиться. Например, если есть правило V : : = Ах | By, на что следует переключаться — на автомат, распознающий цепочку из множества А, или на автомат для множества В? Тиксир некоторым образом ограничивает допустимые в его конструкторе грамматики для того, чтобы решать такие проблемы, используя ограниченный контекст.
У всех описанных до сих пор распознавателей не было выходной информации, т. е. они распознавали предложения некоторой грамматики, но не переводили их ни в какую другую форму. Эта работа выполняется так называемыми семантическими программами, о которых речь пойдет в гл. 12. Льюис и Стирнз [68] определяют синтаксически ориентированные трансляторы, которые не только распознают предложения, но и переводят их в некоторую другую форму.'Эта формальная модель не является настолько общей, чтобы ее можно было действительно использовать при конструировании компиляторов.
Стирнз и Льюис [68] и независимо от них Витни расширяют контекстно свободные грамматики таким образом, чтобы на каждом шаге разбора был возможен доступ к таблице. Это делается для того, чтобы формализовать просмотр идентификаторов в таблице, а также их проверку и изменение их атрибутов. Таким образом, возможна дальнейшая формализация определения языка и как следствие облегчение процесса разработки компиляторов.
Глава 7
Продукционный язык
Продукционный язык (ПЯ) — это язык программирования, предназначенный для написания синтаксических распознавателей. Программа в основном состоит из последовательности продукций. Употребление здесь этого слова надо считать довольно неудачным, так как обычно с этим словом связывают другой смысл, обозначая им правила подстановки в грамматике. Эти новые продукции лучше было бы называть редукциями, так как они (обычно, но не всегда) используются для приведения предложений к начальному символу грамматики. Не станем, однако, изобретать новый термин и будем придерживаться слова «продукция», которое постоянно употребляется в литературе.
ПЯ обычно входит в состав системы построения трансляторов (т. е. системы, предназначенной для реализации таких программ, как ассемблеры или компиляторы), и любой программе на ПЯ предшествует определение сканера, во многом похожего на сканер, описанный в разд. 3.4. Таким образом, программа на ПЯ будет иметь дело с внутренним представлением символов исходного языка — служебными словами, идентификаторами и т. п., а не с настоящими литерами.
Обозначения, принятые в ПЯ, неодинаковы в разных реализациях. Поэтому не следует думать, что те обозначения, которые встретятся здесь, единственны или наиболее удачны. Нас главным образом интересует, что может делать написанная на ПЯ программа, а не то, как пробить ее на перфокартах.
7.1. ЯЗЫК
Продукции
Программа, написанная на ПЯ, автоматически использует стек, называемый SYN, в точности такой же, как во всех других распознавателях, рассмотренных ранее. В стеке могут содержаться символы исходного языка или объекты, подобные нетерминалам. Сама
182
ГЛАВА 7
программа в основном состоит из каждая из которых имеет вид
[(метка> :] (символ) {(символ)} i-левая часть________________I
последовательности продукций, [-► {(символ)}] {(действие)} L-правая часть—j
В данном определении (символ) — это символ исходного языка или идентификатор (возможно, заключенный в угловые скобки (и», называемые нетерминалами, в то время как (метка) — это любой обычный идентификатор. Как мы уже видели, все символы, непосредственно следующие за (метка), если она есть, образуют левую часть продукции, в то время как правая часть состоит из стрелки и любых следующих за ней символов.
Продукция задает сопоставление с образцом и преобразование стека. При выполнении программы, написанной на ПЯ, всегда есть текущая продукция. Когда продукция становится текущей, (символ) ее левой части сравниваются с верхними символами, находящимися в стеке SYN. Если полного соответствия нет, текущей становится следующая продукция из последовательности, и вновь производится сравнение. Это продолжается до тех пор, пока не произойдет совпадения. Когда же это случится, совпавшие символы стека будут заменены символами из правой части текущей продукции. (Если в этой продукции отсутствует правая часть, в стеке не произойдет никаких изменений.) Затем, если есть (действие), они выполняются в заданном порядке. В частности, такие действия могут вызвать сканирование и занесение в стек символов исходной программы, а также могут указать, какая из продукций будет следующей текущей продукцией.
(7.1.1). Пример. Предположим, что продукция
УСЛ: IF (Е) THEN-> (ICL) SCAN GO THENPART текущая. Если верхним, вторым и третьим элементами стека являются соответственно символы THEN, (Е) и IF, произойдет следующее:
1. Из SYN исключаются три верхних элемента.
2. В стек помещается символ (ICL).
3. Выполняются два действия:
a) SCAN — сканируется и помещается в стек очередной символ исходной программы;
b) GO THENPART — текущей становится продукция с меткой THENPART.
Переходя к терминам правил подстановки, можно сказать, что мы привели IF (Е) THEN к (ICL), используя правило (ICL) : : = IF (Е) THEN.
ПРОДУКЦИОННЫЙ ЯЗЫК
183
На рис. 7.1 изображены другие примеры продукций, которые мы рассмотрим позже. Это распознаватель арифметических выражений, построенных в соответствии с синтаксисом (7.1.2)
ST: # SCAN Поместить первый сим-
LF: I F SCAN GO LT вол в стек. Проверить
' N F SCAN GOLT 1-й символ F (I,N или ()
( SCAN GO LF и выбрать соответству-
ющее продолжение.
ANY HALT 2 Ошибка — стоп.
LT: Т * F ANY->T ANY GO LT1 Редукция Т: :=T*F.
F ANY T ANY Редукция T::=F.
LT1: T * SCAN GO LF Проверка, * ли. Если
да, набор последую-
щего F.
LE: E 4- T ANY E ANY GO LEI Эти три продукции соот-
E — T ANY E ANY GO LEI ветствуют редукциям:
T ANY -> E ANY Е:Е+Т, Е:Е—Т
и Е::=Т.
LEI: E + SCAN GO LF Решить, что же делать
E — SCAN GO LF с Е.
( E ) F SCAN GO LT Редукция F::=(E).
# E # -> # Z # HALT 0 Редукция Z:: = Е, стоп.
ANY HALT 3 Ошибка — стоп.
Рис. 7.1. Программа на ПЯ для грамматики 7.1.2.
Метасимволы
Метасимвол ANY часто встречается в продукциях в качестве (символ >. По смыслу, однако, он отличается от обычного нетерминала; когда символ ANY встречается в левой части, он всегда совпадает с соответствующим символом стека.
В левой части символов ANY должно быть не меньше, чем в правой. Не упуская из виду то обстоятельство, что любой (символ) из правой части помещается в стек, мы приписываем символу ANY из правой части следующий смысл: i-й (считая справа налево) символ ANY в правой части и есть тот находящийся в данный момент в стеке символ, который сопоставляется с i-м символом ANY из левой части. Поясним это двумя примерами.
Пусть текущая продукция
Т * F ANY Т ANY GO LE
и в стеке содержится Т « F + . Тогда содержимое стека сопоставляется с символами в левой части продукции. Символом ANY в правой части стал символ + , совпавший с символом ANY из ле
184
ГЛАВА 7
вой части; содержимое стека заменится на Т+. Текущей станет продукция с меткой LE.
Если в стеке содержится W X Y Z, а текущей является продукция ANY Y ANY -> ANY U ANY V, то содержимое стека будет заменено на W X U Z V.
Есть еще два метасимвола — I, который совпадает с любым полученным от сканера идентификатором, и N, который совпадает с любым целым числом.
Действия
После того как левая часть совпала с символами стека и содержимое стека было преобразовано, выполняются действия. Два наиболее важных — SCAN и GO — нам уже встречались. Выполнение действия SCAN требует вызова сканера. Он сканирует следующий исходный символ, помещает его в качестве верхнего символа в синтаксический стек и возвращается. Выполнение действия GO (метка) приводит к тому, что помеченная меткой продукция становится текущей и начинается сравнение с содержимым стека.
Позднее, в подходящий момент, мы объясним действия CALL, RETURN и EXEC. К другим общепринятым действиям относятся: ERROR (целое) и HALT (целое). Первое из них вызывает печать сообщения «ERROR (целое)», где (целое) — это целое число на стандартном устройстве вывода. Второе вызывает печать сообщения «HALT (целое)», после чего прекращается синтаксический разбор.
Пример
На рис. 7.1 представлены продукции, которые позволяют распознать предложения грамматики (7.1.2). Мы здесь опять предполагаем, что сканер распознает идентификаторы I и целые числа N. Мы предполагаем также, что к началу работы программы система поместила в стек ограничитель # и что ограничитель # встретится также и в конце предложения.
Z :: = Е
Е::=Т|Е4-Т|Е—Т
T::=F|T*F
(7.1.2) F::=I|N|(E)
1::=буква {буква | цифра)
N цифра {цифра}
Прежде чем мы воспользуемся рис. 7.1 для разбора предложения, рассмотрим его несколько подробнее. Заметим, что продукция LF + 2 не имеет правой части. Это означает, что в случае совпаде
ПРОДУКЦИОННЫЙ язык
185
ния содержимое стека не изменяется. Заметим также, что в продукции LT + 1 вообще не производится никаких действий. Если в продукции нет действия GO, то после выполнения всех действий текущей становится следующая продукция (в данном случае LT1).
Смысл программы можно описать следующим образом. В продукции ST всегда происходит совпадение, после чего сканируется
Текущая Содержимое Совпадение Очередная
продукция стека в продукции продукция
ST ST LF
LF # ( LF + 2 LF
LF # (I LF LT
LT # (F + LT+1 LT1
LT1 # (T + LE+2 LEI
LEI # (E + LEI LF
LF # (E + I LF LT
LT # (E + F) LT 4-1 LT1
LT1 # (E + T) LE LEI
LEI # (E ) LE14-2 LT
LT # F* LT + 1 LT1
LT1 LT1 LF
LF #T*I LF LT
LT #T*F# LT LT1
LT1 LE + 2 LEI
LEI #E# LE1+3 HALT 0
Рис. 7.2. Разбор предложения (A-f-B)*C, согласно рис. 7.1.
первый символ предложения. Продукции от LF до LF + 2 проверяют, может ли этим символом начинаться множитель F; если нет, то продукция LF + 3 выдает сообщение об ошибке. Если множителем оказывается I или N, то они приводятся к F, затем сканируется следующий символ и текущей становится продукция LT. Если множитель начинается с левой круглой скобки, продукция LF + 2 сканирует первый символ выражения внутри скобок и вновь переходит к LF.
Важен порядок продукций LT и LT + 1.В этот момент в стеке обязательно содержится F ANY, так что продукция LT + 1 обязательно заменит F на Т (правило подстановки Т : : = F). Однако, прежде чем это произойдет, надо проверить, не применимо ли правило Т ::= Т * F. После того как выполнена одна из этих редукций, мы смотрим, не находится ли в стеке *. Если да, то мы готовимся в дальнейшем выполнить редукцию Т : : = Т * F и с этой
186
ГЛАВА 7
целью сканируем следующий символ, а затем возвращаемся к LF, чтобы найти фразу для F. Если * в стеке нет, мы находим подходящую редукцию для Е и выполняем ее. Здесь также важен порядок расположения продукций от LE до LE + 2.
Последней выполняется продукция LE1 +3, в которой проверяется наличие завершающего ограничителя # и Е приводится к Z.
На рис. 7.2 показан разбор предложения (А + В) * С. В каждой строке указаны первая продукция, ставшая текущей после последнего совпадения, содержимое стека в этот момент, продукция, в которой происходит следующее совпадение, и, наконец, очередная текущая продукция.
Названия классов .
Продукции LE и LE + 1 на рис. 7.1 отличаются только тем, что в одной из них написан +, а в другой —- . Чтобы сократить такую запись, мы.предваряем все продукции описанием
CLASS ПМ + -
и заменяем две продукции одной
LE: Е ПМ Т ANY -> Е ANY GO LEI
Вообще говоря, описание вида
CLASS (название класса) (символ) {(символ)} ставит в соответствие символам (название класса), которое может быть любым удобным идентификатором. Если название класса встречается в левой части, оно совпадает с любым из символов, соответствующих ему по описанию.
Если название класса встречается в правой части продукции, то оно должно встречаться в левой части по меньшей мере столько же раз, сколько в правой. Смысл (название класса) в правой части аналогичен смыслу метасимвола ANY в правой части. Название класса, встречающееся в правой части i-й раз (считая справа налево), — это тот, находящийся в данный1! момент в стеке символ, который совпал с i-м вхождением данного названия класса в левой части. Например, для уже упоминавшегося описания: если в стеке содержится Н---А + , а текущая продукция
ПМ А ПМ -> В С ПМ ПМ
содержимое стека изменится на + В С — +. Заметьте, что эта продукция эквивалентна четырем продукциям:
+ А + -> В С + +
+ А — —> В С + —
_ А + В С — +
— А — —+ В С — —
ПРОДУКЦИОННЫЙ язык
187
В разд. 7.3 мы обсудим, какие преимущества дает установление соответствия между так называемыми номерами семантических подпрограмм и символами в классе. Чтобы связать подпрограмму номер 20 с символом + , а подпрограмму номер 2 с символом —, перепишем описание ПМ так:
CLASSNO ПМ +20 -2
Такое название класса можно употреблять так же, как и прежнее; об использовании дополнительных возможностей речь пойдет в разд. 7.3. Вот формат этого нового описания:
CLASSNO <название класса) <символ> (целое> {(символ) (целое)}
Использование названий классов не делает ПЯ более мощным языком, т. е. не появляется никаких принципиально новых возможностей. Однако применение названий классов упрощает программирование на ПЯ и позволяет сократить размеры программ.
Противоречия между исходным языком и символами ПЯ
Если -> является символом исходного языка, то как тогда понимать продукцию
(7.1.3) ANY ANY -> В
Ясно, что она неоднозначна. Для решения проблемы неоднозначности (и других проблем) мы условимся, что любому символу исходного языка, содержащему одну из литер -> $ ; или #, или являющемуся одним из таких символов ПЯ, как CLASS, CLASSNO, I, N, ANY, CALL, ERROR, EXEC и GO, должен предшествовать знак доллара $. Таким образом, знак доллара является специальным символом (авторегистром), обозначающим, что следующие за ним литеры (вплоть до ближайшего пробела) составляют один символ исходного яыка.
Используя это обозначение, выпишем три разные возможные интерпретации продукции (7.1.3):
ANY -+ ANY > В
ANY ANY S— В
ANY ANY —> В
Еще одйн пример: в продукции
LABE: I $: $$ -> (метка)
произойдет совпадение, если первым (верхним) элементом стека является символ «$», вторым — символ « : », а третьим — некий идентификатор; эти элементы будут заменены одним элементом (метка).
188
ГЛАВА 7
Краткое изложение синтаксиса языка
Программа на ПЯ <программа> <описание> имеет следующий синтаксис: {(описание)} {(продукция)} :: = CLASS (название класса> (символ) {(символ)} | CLASSNO (название класса) (символ) (целое) {(символ) (целое)}
<продукция> {(метка):] (левая часть) [(правая часть)] {(действие)}
<левая часть> <правая часть> :: = (символ) {(символ)} :: = —>(символ)
где
1. Каждая <метка> и каждое <название класса > —это несовпадающий с другими обычный идентификатор, который не является ни символом исходного языка, ни символом ПЯ.
2. Каждый <символ> — это либо
а) один из метасимволов I, N или ANY, либо
Ь) несовпадающий с другими обычный идентификатор, возможно, заключенный в угловые скобки < и > и не являющийся ни символом ПЯ, ни символом исходного языка, либо
с) символ исходного языка, не содержащий литер : -> ; $ или # и не являющийся символом ПЯ, либо
d) любая последовательность отличных от пробела литер, которой предшествует $.
3. Любое <целое> — это непустая последовательность из цифр от 0 до 9.
4. Символами ПЯ являются ANY, CALL, CLASS, CLASSNO, EXEC, GO, I и N.
5. (Действия) и их смысл таковы:
a) CALL (метка>. Выполнять продукции, начиная с помеченной (метка) и продолжая до тех пор, пока не будет выполнено действие RETURN. Затем продолжить выполнение со следующего действия или со следующей продукции. Таким образом, это просто вызов подпрограммы; пример приводится в разд. 7.2.
b) ERROR (целое). Напечатать “ERROR (целое)”.
с) ЕХЕС (целое). Выполнить семантическую подпрограмму с меткой (целое). Закончив, перейти к следующему действию. (Более подробное объяснение мы дадим в разд. 7.3.)
d) EXEC (название класса). Это (название класса) должно присутствовать в левой части данной продукции. Его описание должно связывать семантические подпрограммы с сим
ПРОДУКЦИОННЫЙ язык
189
волами. Выполняется семантическая подпрограмма, связанная с символом, находящимся в стеке и совпавшим с Название класса) в левой части. (Подробное объяснение см. в разд. 7.3.)
е) GO <метка>. Сделать текущей продукцию, помеченную меткой, и вновь приступить к проверке на совпадение. Любые другие действия, следующие за данным, никогда выполнены не будут.
f) HALT <целое>. Напечатать сообщение “HALT <целое>” и прекратить выполнение программы.
g) RETURN. Вернуться в точку программы, расположенную непосредственно вслед за последним выполненным действием CALL [см. п. а)].
h) SCAN. Вызвать сканер, который построит очередной символ исходного языка, и поместить этот символ в стек. Если больше символов нет, в стек помещается ограничитель #.
УПРАЖНЕНИЯ К РАЗДЕЛУ 7.1
I. Проведите разбор следующих предложений грамматики (7.1.2), выполняя (вручную) программу на ПЯ, приведенную на рис. 7.1. Считайте, что сканер строит идентификаторы и целые числа:
(а) А*В, (b) (А), (с)А+В+1, (d)A*B*l, (е) А+(В+1), (f)A*(B+l).
2. Используя (название класса), перепишите следующие шесть продукций так, чтобы число их сократилось до двух:
X Y —> Y X Z —>Z XANY Y
W Y —* Y W Z —>'L WANY —•> W
3. Что неверйо в каждой из следующих продукций?
a) E+T-*ANY
b) L: LI: Е+Т-*Е SCAN GO Y
с) L: (метка) SCAN GO STATE
4. Напишите программу на ПЯ для распознавания предложений грамматики G (Z): Z : : = + I Z+ I Z —.
7.2. ИСПОЛЬЗОВАНИЕ ПЯ
Поскольку ПЯ — язык программирования, а не механический конструктор распознавателей, как большинство других, изученных нами программ разбора, он более гибок. При разборе необяза
190
ГЛАВА 7
тельно слепо следовать формальной грамматике там, где можно постараться программировать эффективно. Большая свобода предоставляется и при согласовании синтаксиса с семантикой. Этот вопрос обсуждается в гл. 12 и 13. В данном разделе мы хотим дать некоторые советы по программированию на ПЯ. Мы покажем вначале, как можно запрограммировать на ПЯ (ш,п)ограниченно контекстный распознаватель; затем рассмотрим, как программируется метод рекурсивного спуска, изложенный в разд. 4.3. Наконец, перейдем к простому примеру, чтобы проиллюстрировать несколько приемов программирования.
Восходящий разбор на ПЯ
При изучении этого параграфа потребуется знание материала из разд. 6.3. В гл. 6 на рис. 6.7 представлена таблица для (1,1 Ограниченно контекстного распознавателя грамматики (6.3.6). В каждой строке таблицы указан образец для сопоставления и задано преобразование стека. Например, первая строка указывает, что если в стеке находится “а 0 Г, а входной символ то содержимое стека нужно заменить на “a W”.
Главное различие между программой на ПЯ и этой таблицей состоит не в форме записи, а в том, что таблица ни программой, ни алгоритмом не является; таблица — это лишь данные для алгоритма, описанного на рис. 6.8. Продукция ПЯ указывает, что нужно делать после того, как выполнено заданное в ней преобразование; строка таблицы на рис. 6. 7 таких указаний не содержит.
Можно построить на ПЯ программу, являющуюся по сути дела тем же распознавателем, который получается при объединении таблицы (рис. 6.7) и алгоритма (рис. 6.8). Именно это и сделано на рис. 7.3. В программе правый контекст R всегда оказывается верхним в стеке, поскольку лишь при таком расположении символов исходного языка ПЯ допускает обращение к ним.
Программа на рис. 7.3, как обычно, начинается с продукции, которая сканирует первый символ предложения. Затем продукции от L до М выполняют шаг 2 алгоритма, представленного на рис. 6.8. Каждая продукция соответствует одной строке таблицы на рис. 6.7. Если в некоторой продукции имеет место совпадение, то содержимое стека преобразуется так, как это задано в шаге 3 на рис. 6.8, а затем программа возвращается к продукции L, чтобы продолжить сравнение. Если совпадений не было, то продукции от N до N+2 выполняют шаги с 4-го по 6-й: работа прекращается и печатается сообщение “HALT 0”, если входная цепочка оказалась предложением, либо печатается сообщение “HALT 2”, если она предложением не является, либо сканируется следующий символ и выполняется переход к метке L, чтобы продолжать проверки на совпадение.
продукционный язык
191
Конечно, программа, приведенная на рис. 7. 3, не особенно эффективна. Для сокращения числа сравнений на каждом шаге можно изменить порядок записи продукций, чаще используя метки. Например, после преобразования в продукции L можно применить только L + 4.
Мы показали, как перевести на ПЯ—даже чисто механически — любую таблицу для (1,1)ограниченно контекстной грамматики. На самом деле этот процесс нетрудно модифицировать так, чтобы с его помощью переводить на ПЯ таблицы для (ш,п)ограниченно
S: # SCAN
L: а 0 1 # —* a W # GO L
0 0 1 1 —> 0 W 1 GO L
0 0 W 1 1 —* 0 W 1 GO L
а 0 W 1 # a W # GO L
# а b b W # 0 0 0 1 —> # Z # GO L —> b (J 0 GO L b U 1 GO L
ь и 0 0 —> b U 0 GO L
ь и 0 1 —* b U 1 GO L
# ь и 1 —-> # V 1 GO L
# V 1 1 — # V 1 GO L
# V 1 # — # V # GO L
М: # N: # V # Z # ANY —> # Z # GO L HALT 0 HALT 2 SCAN GO L
Рис. 7.3. Программа восходящего разбора на ПЯ.
контекстной грамматики. Нужно будет только внимательно следить за увеличившимся контекстом с обеих сторон от возможной основы. Поскольку все грамматики, допускающие применение описанных способов восходящего разбора, относятся к классу (гл, п)ограниченно контекстных при некоторых ш и п, мы можем написать на ПЯ программы, выполняющие для таких грамматик восходящее распознавание.
Нисходящий разбор без возвратов на ПН
При изучении этого параграфа потребуется знание материала из разд. 4.3. Два действия — CALL и RETURN — позволяют использовать группу продукций подобно тому, как используются процедуры в языках АЛГОЛ или ФОРТРАН. А это значит, что
192
ГЛАВА 7
можно запрограммировать на ПЯ нисходящий разбор, применяя описанный в разд. 4.3 метод рекурсивного спуска. И в самом деле, поскольку ПЯ разработан для преобразования символьной информации, запрограммировать рекурсивный спуск здесь намного легче.
S: SO: # <инстр> # ANY SCAN CALL ИНСТР HALT 0 HALT 2
ИНСТР: IF ANY <перем> <выр> ANY ИН1: IF <выр> THEN ANY ИН2: <инстр> ELSE <инстр> ANY ANY —> —► <инстр> ANY SCAN CALL BMP GO ИН1 CALL ПЕРЕМ SCAN CALL ВЫР RETURN SCAN CALL ИНСТР GO ИН2 HALT 2 SCAN CALL ИНСТР RETURN HALT 2
ПЕРЕМ: ПЕРЕМ 1: I I ( I ANY I (<выр>) ANY —-> <перем> <перем> SCAN SCAN CALL ВЫРООПЕРЕМ1 RETURN SCAN RETURN HALT 2
ВНР: ANY <терм> + <терм> ANY ANY —> —> <выр> ANY CALL ТЕРМ SCAN GO ВЫР RETURN HALT 2
ТЕРМ: ANY <множ> * <множ> ANY ANY —> <терм> ANY CALL МНОЖ SCAN GO ТЕРМ RETURN HALT 2
МНОЖ: МН1: ( ANY <перем> ANY (<выр>) ANY —> —> <множ> ANY <множ> SCAN CALL ВЫP GO MH 1 CALL ПЕРЕМ RETURN SCAN RETURN HALT 2
Рис. 7.4. Программа нисходящего разбора на ПЯ.
На рис. 7.4 показан пример программы на ПЯ, которая распознает предложения грамматики (4.3.2). На рисунке каждому правилу этой грамматики соответствует набор продукций. Первая продукция выполняет начальную установку, заносит в стек первый символ предложения и вызывает продукции, соответствующие <инстр>. Если программа останавливается и печатает сообщение
ПРОДУКЦИОННЫЙ ЯЗЫК
193
“HALT 2”, то это означает, что входная цепочка не является предложением.
При работе с продукциями следуют тем же соглашениям, что и при работе с рекурсивными процедурами. При вызове набора продукций в стеке находится первый символ искомой фразы, а по возвращении в стеке уже будет находиться символ, следующий за этой фразой. Если читатель сравнит каждый из наборов продукций с соответствующей процедурой из разд. 4.3, он обнаружит их поразительное сходство; изменилась только форма записи.
Программирование на ПЯ
Если, программируя распознаватель, строго придерживаться только восходящего или только нисходящего (без возвратов) метода, то ни одна из программ не достигнет предела эффективности. Как мы уже видели, восходящий распознаватель неэффективен в силу того, что на каждом шаге приходится проводить сравнение с-большим числом продукций. (Это утверждение справедливо даже в том случае, когда продукции располагают в другом порядке и изменяют действия GO, стремясь уменьшить число сравнений.) С другой стороны, строго нисходящий распознаватель слишком часто пользуется действиями CALL и RETURN, а они гораздо медленнее простых переходов.
Обычно наилучшие результаты дает объединение обоих методов. Напишите подпрограмму (т. е. набор продукций, используемый как подпрограмма) для основных единиц исходного языка. Например, для языка АЛГОЛ напишите по одной подпрограмме для инструкций, для описаний и для выражений. (Заметьте, что такое разделение позволяет разным людям писать части программы почти совершенно независимо.) Каждая из подпрограмм может из разных мест обращаться к другим подпрограммам. Подпрограмма для инструкции вызывает подпрограмму для выражения и даже обращается сама к себе всякий раз, когда нужно разобрать подинструкцию.
Как уже говорилось раньше и как было показано на примере (рис. 7.1), не представляет особого труда написать отдельную подпрограмму, применяя восходящий метод. Суть состоит в использовании контекста и переходов для сокращения числа продукций, которые приходится сравнивать на каждом шаге.
Подпрограммы, соответствующие набору правил подстановки с одинаковыми левыми частями, обычно начинаются с нескольких продукций, в которых по первому символу выбирается альтернатива и происходит переход к поднабору продукций, выполняющих разбор этой альтернативы. Хорошим примером здесь может служить подпрограмма для инструкции. Рассмотрим усеченную грамматику:
7 д. грио
194
ГЛАВА 7
<инструкция>
= IF <выр> THEN <инструкция>
|<перем>: =<выр>
|FOR <перем>: = <список элементов цикла> DO <инструкция> |READ (<перем>)
Программа на ПЯ для такой грамматики приводится ниже. Заметим, что <перем> рассматривается как одна из основных синтаксических единиц и распознается при помощи подпрограммы. Сделано так потому, что <перем> многократно встречается в разных местах. Если бы мы использовали обычное действие GO ПЕРЕМ, нам после распознавания <перем> пришлось бы пройти длинную последовательность продукций, чтобы по контексту установить, куда именно нам нужно вернуться.
ИНСТРУКЦИЯ: IF SCAN CALL ВЫР GO CONDL
FOR SCAN CALL ПЕРЕМ GO FORL
READ SCAN GO READL
ANY CALL ПЕРЕМ GO ASSL
CONDL: (продукции, распознающие усл. инструкцию)
FORL: (продукции, распознающие цикл типа FOR)
READL: (продукции, распознающие READ)
ASSL: (продукции, распознающие присваивание)
Опять-таки, используя названия классов, мы можем сэкономить усилия, затрачиваемые на программирование, и время, необходимое для выполнения программы. Сравните
READ EXEC 1 SCAN GO IDLIST
INTEGER EXEC 2 SCAN GO IDLIST
BOOLEAN EXEC 3 SCAN GO IDLIST
STRING — EXEC 4 SCAN GO IDLIST
COMPLEX EXEC 5 SCAN GO IDLIST
и
CLASSNO TYPE REAL 1 INTEGER 2
BOOLEAN 3 STRING 4 COMPLEX 5;
TYPE —> EXEC TYPE SCAN GO IDLIST
Последнее гораздо проще написать и проще прочесть.
ПРОДУКЦИОННЫЙ язык
195
УПРАЖНЕНИЯ К РАЗДЕЛУ 7.2
1. Сделайте более эффективной программу, представленную на рис. 7.3, переупорядочив продукции и изменив действия GO.
2. Напишите на ПЯ программу, распознающую предложения следующей грамматики, используя (1) нисходящий и (2) восходящий методы:
Z : : = ЬМЬ | Me, М : : = (La, L : : = Ма)
7.3. ВЫЗОВ СЕМАНТИЧЕСКИХ ПОДПРОГРАММ
Теперь мы объясним, как используются действия ЕХЕС. Может быть, на этом этапе изложенное не будет совершенно понятным, поскольку речи о семантических подпрограммах еще не было. Поэтому, изучив гл. 12 и 13, стоит вернуться к этому разделу.
В любой реализации ПЯ используются по меньшей мере два параллельно работающих стека. Об одном из них, синтаксическом стеке SYN, мы уже говорили. Во втором, который называется семантическим стеком SEM, содержится «смысл» символов, находящихся в первом стеке. То есть элемент SEM (i) содержит «смысл» или «семантику» символа, находящегося в SYN (i). В гл. 12 и 13 будет объяснено, что имеется в виду, когда речь идет о смысле.
Семантика большинства терминальных символов первоначально не определена. Это означает, что сканер помещает в стек SYN некоторый символ, а в соответствующую ячейку стека SEM никакое новое значение не заносится. Однако для терминальных символов I и N дело обстоит иначе. Когда сканер находит идентификатор (целое число) и помещает I (N) в синтаксический стек SYN, он помещает тот же идентификатор (целое число) в SEM. (Возможно, туда будет помещен указатель на данный идентификатор или целое число, но в рамках нашего изложения это безразлично.) Таким образом, семантикой I (N) является идентификатор (целое число), к которому I (N) относится.
В любой реализации ПЯ предполагается некоторый связанный с ПЯ семантический язык, на котором пишутся семантические подпрограммы. Им может быть язык ассемблера, ФОРТРАН, ПЛ/1, АЛГОЛ — все равно. Под семантической подпрограммой мы подразумеваем не что иное, как такой набор инструкций семантического языка, который можно как-то идентифицировать. Каждый такой набор может быть либо отдельной процедурой, либо одной подинструкцией в инструкции выбора (case statement), либо в семантическом языке могут быть предусмотрены специальные «семантические метки», по которым определяется начало семантической подпрограммы.
?*
196
ГЛАВА 7
В семантическом языке имеется также доступ к семантическому стеку SEM. Когда в продукции встречается, например, действие ЕХЕС5, то в семантической программе выполняется семантическая подпрограмма с номером 5. Она производит необходимые вычисления, используя верхние элементы стека SEM, переменные, описанные на семантическом языке, а затем происходит возврат.
Предположим, например, что текущей является продукция
I -> F ЕХЕС 5 SCAN GO LT
а содержимое стеков выглядит так:
SYN I АВ SEM
♦ смысл ♦
т * смысл Т
Следовательно, левая часть совпадает с содержимым стека и верхний элемент SYN заменяется на F. Затем вызывается подпрограмма 5. Она может взять из верхней позиции стека SEM идентификатор АВ, найти его в таблице символов и поместить в качестве верхнего элемента стека SEM номер позиции идентификатора АВ в таблице, равный, например, 3. В результате получим
SYN
SEM
Затем происходит возврат из семантической подпрограммы 5, сканируется следующий символ и текущей становится продукция LT.
Нам осталось только сказать о применении действия ЕХЕС «(название класса). Напомним, что это название класса должно обязательно встретиться в левой части данной продукции. Выполнение такого действия приводит к выполнению семантической подпрограммы, которая в описании данного названия класса связана с тем находящимся сейчас в стеке символом, который совпал с названием класса в левой части текущей продукции. Это проще пояснить на примере. Рассмотрим описание
CLASSNO OPER * 1 +2 — 3 /4
ПРОДУКЦИОННЫЙ язык
197
и текущую продукцию Е OPER Е -► Е EXEC OTER. Если в стеке содержится Е — Е, будет выполнена подпрограмма 3.
7.4. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Впервые продукционный язык был описан Флойдом [61Ь]. Предложенный им язык предназначался для обработки символьной информации и, помимо формы записи, во многом напоминает ПЯ. Идея такого языка получила дальнейшее развитие в работе Эванса [64]. ПЯ в качестве синтаксического метода применяется в системе построения трансляторов FSL, разработанной и реализованной Фелдманом [66]. Он также используется в некоторых других системах построения трансляторов. Было разработано несколько конструкторов (автор одного из них — Эрли), которые для заданной грамматики с подходящими свойствами пишут программу на ПЯ, являющуюся синтаксическим распознавателем для этой грамматики. Ихбия и Морз [70] описывают алгоритм, с помощью которого по грамматикам предшествования генерируются «оптимальные» продукции. В их методе семантические действия CALL и RETURN не используются.
Глава 8
Организация памяти во время выполнения программы
В этой главе описывается организация памяти во время выполнения программы, написанной на одном из трех хорошо известных языков высокого уровня. Будут объяснены многие понятия, относящиеся к языкам программирования. Можно отметить простую организацию в языках, подобных ФОРТРАНу, более сложную для языков, подобных АЛГОЛу, и самую сложную организацию для языков, подобных PL/1 со структурами, указателями и инструкциями ALLOCATE и FREE.
Конечно, у нас нет возможности описать подробно все эти языки. Нашей целью является описание основных деталей управления памятью и представление некоторых общих концепций. После усвоения материала, изложенного в этой главе, читатель должен быть в состоянии создать свою собственную программу управления памятью для любого языка. Чтение этой главы поможет уяснить, что существует много тонкостей, которые можно понять лишь при детальном знании исходного языка.
Некоторые языки требуют схемы динамического распределения памяти, когда блоки оперативной памяти произвольным образом выделяются, затем освобождаются и снова занимаются для других целей. Исчерпывающее рассмотрение таких схем выходит за рамки данной книги. Для полноты мы представим один такой метод распределения памяти в разд. 8.10, но для изучения этих методов читателю рекомендуется книга Кнута [68]. Теперь предположим, что имеются две программы
GETAREA (ADDRESS, SIZE) и FREEAREA (ADDRESS, SIZE) Первая из них выделяет для вызывающей программы последовательность, содержащую SIZE ячеек, передавая начальный адрес последовательности через выходной параметр ADDRESS. Программа FREEAREA освобождает SIZE ячеек, начиная с адреса ADDRESS.
В некоторых системах память выделяется, но никогда явно не освобождается. Если память исчерпана, то система запускает про
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 199
грамму «мусорщик», которая находит и освобождает фактически не используемые ячейки. Может оказаться также необходимым объединить всю используемую память — поместить все данные в последовательные ячейки — так, чтобы освободился большой блок последовательных ячеек вместо нескольких небольших блоков. Эта проблема кратко рассматривается в разд. 8.10; мы предполагаем также, что существует программа FREEGARBAGE, выполняющая эту работу.
Глава строится следующим образом. С целью унификации всего описания в разд. 8.1 вводится понятие области данных. В разд. 8.2 рассматриваются описатели, тогда как разд, с 8.3 по 8.6 посвящены задачам, возникающим в связи с реализацией структур данных в порядке возрастания их сложности. В разд. 8.7 рассматриваются вызовы процедур и соответствие формальных и фактических параметров. Затем мы возвращаемся к проблемам, связанным с ФОРТРАНОМ и АЛГОЛом. Глава оканчивается разд. 8.10, в котором описывается динамическое распределение памяти и сбор мусора.
8.1. ОБЛАСТИ ДАННЫХ И ДИСПЛЕИ
Областью данных является ряд последовательных ячеек — блок оперативной памяти,— выделенный для данных, каким-то образом объединенных логически. Часто (но не всегда) все ячейки области данных принадлежат одной и той же области действия в программе на исходном языке; к ним может обращаться один и тот же набор инструкций (т. е. этой областью действия может быть блок или тело процедуры). Вегнер [68] использует для аналогичного понятия термин запись активации; мы предпочитаем другой термин — область данных.
Для переменных, описываемых инструкцией COMMON на ФОР-ТРАНе, должна быть выделена память в одной области данных, в области данных непомеченного блока COMMON. В АЛГОЛе область данных времени счета может формироваться из ячеек для простых переменных, описанных в главной программе, и из необходимых ячеек для временных переменных.
Во время компиляции ячейка для любой переменной времени счета может быть представлена упорядоченной парой чисел (номер области данных, смещение), где номер области данных — это некоторый единственный номер, присвоенный области данных, а смещение — это адрес леременной относительно начала области данных. (Так, первая ячейка области данных 3 представляется парой (3,0), вторая — (3,1) и т. д.) Когда мы генерируем команды обращения к переменной, эта пара переводится в действительный адрес переменной. Это обычно выполняется установкой адреса базы (машинного адреса' первой ячейки) области данных на регистр и
200
ГЛАВА 8
обращению к переменной по адресу, равному смещению плюс содержимое регистра. Пара (номер области данных, смещение) таким образом переводится в пару (адрес базы, смещение).
Области данных делятся на два класса — статический и динамический. Статическая область данных имеет постоянное число ячеек, выделенных ей перед началом счета. Эти ячейки выделяются на все время счета. Следовательно, на переменную в статистической области данных возможна ссылка по ее абсолютному адресу вместо пары (адрес базы, смещение).
BEGIN PROCEDURE А;
BEGIN PROCEDURE В; BEGIN...END;
PROCEDURE C; BEGIN...END;
END;
PROCEDURE D; BEGIN...END;
END;
Рис. 8.1. Структура программы с процедурами на АЛГОЛе.
Динамическая область данных не всегда присутствует во время счета. Она появляется и исчезает, и всякий раз, когда она исчезает, теряются все величины, хранящиеся в ней, Примером может служить область данных, содержащая переменные процедуры в АЛГОЛе. Процедура, к которой обратились, вызывает программу QETA. REA, чтобы выделить память для своей области данных постоянной длины. Непосредственно перед возвратом в вызывающую программу процедура вызывает программу FREEAREA для освобождения памяти. Заметим, что, возможно, процедуре выделяются не одни и те же ячейки памяти для ее области данных. Однако GETAREA всегда выдает адрес базы выделенной области данных и процедура всегда хранит его в одной и той же ячейке, например, ВА. Таким образом, адресом любой переменной в области данных всегда является CONTENTS(BA)+OFFSET.
Если вызов процедуры происходит рекурсивно, то имеется несколько областей данных в оперативной памяти, каждая для отдельного вызова процедуры. Это именно то, что мы хотим; каждый раз при сбращении к процедуре она должна иметь новую область действия. Такая область данных принадлежит не собственно процедуре, а выполнению процедуры. В любой момент выполнения процедуры возможны обращения к переменным из нескольких областей данных. Рассмотрим, например, программу на АЛГОЛе, содержащую процедуры (рис. 8.1). Если для главной программы и для каждой из процедур существуют различные области данных, то при выполнении процедуры В возможно обращение к областям данных для процедур А, В и главной программы. Чтобы иметь
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 201
возможность ссылаться на них, мы собираем адреса этих областей данных в таблицу, которую назовем дисплеем. Для этого частного примера при выполнении процедуры В дисплей будет иметь вид
Адрес области. данных главней, программы
Дисплей
Адрес области данных процедуры А
Адрес области данных процедуры В
Таким образом, когда мы создаем области данных (получаем для них память), мы имеем постоянное место для запоминания их адресов. Нам нужно ответить на несколько вопросов: где должен помещаться сам дисплей? В каком порядке мы заносим в дисплей адреса? На эти вопросы мы ответим, когда будем рассматривать реализацию отдельных языков.
Вообще при счете должно быть несколько дисплеев, используемых при выполнении различных частей программы. Предположим, что в вышеприведенном примере в процедуре В есть вызов процедуры D. Здесь мы должны создать дисплей, содержащий только адреса областей данных для D и главной программы, используемых в D. Мы должны сохранить нетронутым предыдущий дисплей; он будет нужен снова, когда выполнение D завершится и выполнится возврат в В. В любой момент выполнения программы активным дисплеем является тот, который в настоящее время используется для обращений к областям данных.
УПРАЖНЕНИЯ К РАЗДЕЛУ 8.1
1. Как должен выглядеть текущий дисплей при выполнении процедуры С на рис. 8.1? При выполнении процедуры А? Какой вид будет иметь дисплей при выполнении процедуры D на рис. 8.5? При выполнении процедуры В?
8.2. ОПИСАТЕЛИ1)
Если компилятор знает все характеристики переменных во время компиляции, то он может сгенерировать полностью команды обращения к переменным, основываясь на этих характеристиках. Но во многих случаях информация может задаваться динамически
х) В оригинале употребляется термин TEMPLATE. Однако автор отмечает, что, например, Стендиш вместо TEMPLATE использует термин DISCRIPTOR.— Прим, перев,
202
глава 8
во время счета. Например, в АЛГОЛе не известны нижняя и верхняя границы размерностей массивов, а в некоторых языках тип фактических параметров не соответствует точно типу формальных параметров. В таких случаях компилятор не может сгенерировать простые и эффективные команды, так как он должен учитывать все возможные варианты характеристик.
Чтобы решить эту задачу, компилятор выделяет память не только для переменных, но и для их описателей, которые содержат атрибуты (характеристики), определяемые во время счета. Этот описатель заполняется и изменяется по мере того, как становятся известными и меняются характеристики при счете.
Возьмем простой пример: если формальный параметр является простой переменной и тип соответствующего фактического параметра может меняться, фактический параметр, передаваемый процедуре, может выглядеть, например, так:
Описатель 0 = действительный, 1»целый, 2=6улевый и т.д. Адрес значения (или само значение)
Если в процедуре есть обращение к формальному параметру, процедура должна запрашивать или интерпретировать этот описатель и затем выполнить любое необходимое преобразование типа. Эти действия можно, конечно, выполнить, обращаясь к другой программе.
Во многих случаях компилятор не может выделить память для значений переменных, так как неизвестны атрибуты размерности. Так происходит с массивами в АЛГОЛе. Все, что компилятор может сделать,— это выделить память в области данных для описателя фиксированной длины, описывающего переменную. Во время выполнения программы, когда станут известны размерности, будет вызвана программа GETAREA, которая выделит память и занесет в описатель адрес этой памяти. При этом ссылка на значение всегда выполняется с помощью такого описателя.
Для структур или записей требуются более сложные описатели, в которых указывается, как связаны между собой компоненты и подкомпоненты. Мы рассмотрим это в разд. 8.6.
Чем больше атрибутов могут меняться при счете, тем больше приходится выполнять работы во время счета. Причина, по которой для ФОРТРАНа можно скомпилировать более эффективную программу, чем для АЛГОЛа или PL/1, заключается именно в том, что для ФОРТРАНа практически все характеристики известны во время компиляции и не нужны ни описатели, ни их интерпретация.
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 203
8.3. ПАМЯТЬ ДЛЯ ДАННЫХ ЭЛЕМЕНТАРНЫХ ТИПОВ
Типы данных исходной программы должны быть отображены на типы данных машины. Для некоторых типов это будет соответствием один к одному (целые, вещественные и т. д.), для других могут понадобиться несколько машинных слов. Коротко мы отметим следующее:
1. Целые переменные обычно содержатся в одном слове или ячейке области данных; значение хранится в виде стандартного внутреннего изображения.целого числа в машине.
2. Вещественные переменные обычно содержатся в одном слове. Если желательна большая точность, чем возможно представить в одном слове, то может быть употреблен машинный формат двойного слова с плавающей запятой. В машинах, где отсутствует формат с плавающей запятой, могут быть употреблены два слова — одно для показателя степени, второе для (нормализованной) мантиссы. Операции с плавающей запятой в этом случае должны выполняться с помощью подпрограмм.
3. Булевы или логические переменные могут содержаться в одном слове, причем нуль изображает значение FALSE, а не нуль или 1 — значение TRUE. Конкретное представление для TRUE и FALSE определяется командами машины, осуществляющими логические операции. Для каждой булевой переменной можно также использовать один бит и разместить в одном слове несколько булевых переменных или констант.
4. Указатель — это адрес другого значения (или ссылка на него). В некоторых случаях бывает необходимо представлять указатель в двух последовательных ячейках; одна ячейка содержит ссылку на описатель или является описателем текущей величины, на которую ссылается указатель, в то время как другая указывает собственно на значение величины. Это бывает необходимо в случае, когда во время компиляции невозможно определить для каждого использования указателя тип величины, на которую он ссылается
8.4. ПАМЯТЬ ДЛЯ МАССИВОВ
Мы предполагаем, что каждый элемент массива или вектора занимает в памяти одну'ячейку. Обобщение на случай большого числа ячеек предоставляется читателю.
Векторы
Элементы векторов (одномерных массивов) обычно помещаются в последовательных ячейках области данных в порядке возрастания или убывания адресов. Порядок зависит от машины и ее системы команд. Например, на машине IBM 7090 для получения исполни
204
ГЛАВА 8
тельного адреса содержимое индекс-регистра вычитается из базового адреса; поэтому элементы массива хранятся обычно в порядке убывания индексов.
Мы предполагаем, что используется более стандартный возрастающий порядок, т. е. элементы массива, определенного описанием ARRAY А [1 : 101, размещаются в порядке А [11, А [21, ..., А [101.
Матрицы
Существует несколько способов размещения двумерных массивов. Обычный способ состоит в хранении их в области данных по строкам в порядке возрастания, т. е. (для массива, описанного как ARRAY All : М, 1 : N1) в порядке
All, 1], АН, 21, •••, АН, N1, А[2, 1], •••, А[2, N1, •••, А[М, 11, • ••, А[М, NI.
Вид последовательности показывает, что элемент АН, jl находится в ячейке с адресом ADDRESS (АН, ll) + (i—l)*N+(j—1), который мы запишем в виде
(8.4.1) (ADDRESS (АН, 1 ])—N—1 )+(i*N+j).
Первое слагаемое является константой, и его требуется вычислить только один раз. Таким образом, для определения адреса A[i, jl необходимо выполнить одно умножение и два сложения. Язык ФОРТРАН IV фирмы IBM требует размещения массивов по столбцам.
Второй метод состоит в том, что выделяется отдельная область данных для каждой строки и имеется вектор указателей для этих областей данных. Элементы каждой строки размещаются в соседних ячейках в порядке возрастания. Так, описание ARRAY All : М, 1 : N1 порождает
Вектор указателей строк хранится в той области данных, с которой ассоциируется массив, в то время как собственно массив хранится в отдельной области данных. Адрес элемента массива Ali, j] есть CONTENTS (адрес вектора+i—l)+(j—1).
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 205
Первое преимущество этого метода состоит в том, что при вычислении адреса не нужно выполнять операцию умножения. Другим является то, что не все строки могут находиться в оперативной памяти одновременно. Указатель строки может содержать некоторое значение, которое вызовет аппаратное или программное прерывание в случае, если строка в памяти отсутствует. Когда возникает прерывание, строка вводится в оперативную память на место другой строки. Этот метод применен в компиляторе с расширенного АЛГОЛа на машине В 55ЭЭ фирмы Burroughs. Если все строки находятся в оперативной памяти, то массив требует больше места, поскольку место нужно и для вектора указателей.
Когда известно, что матрицы разреженные (большинство элементов нули), используются другие методы. Может быть применена схема хеш-адресации, которая базируется на значениях i и j элемента массива АН, j] и ссылается по хеш-адресу на относительно короткую таблицу элементов массива (гл. 9). В таблице хранятся только ненулевые элементы матрицы.
Многомерные массивы
Мы рассмотрим размещение в памяти и обращение к многомерным массивам, описанным, например, на АЛГОЛе следующим образом:
ARRAY A[Lx : Ux, L2 : U2, •••, Ln : Unl
Метод, который мы рассмотрим, заключается в обобщении первого метода, предложенного для двумерного случая; он также применим и в случае одномерного массива.
Подмассив А[i, #, •••,#] содержит последовательность АЩ, *, • • •, *], A[Li+1, *, •••,*] и т. д. до A[Ui, •», • • •, *]. Внутри подмассива АП, *, • • •, %] находятся подподмассивы Ali, L2, • • •, d,
АН, L2+l, *, •••,*!, • • • и A[i, U2, *, • • •, d. Это повторяется для каждого измерения. Так, если мы продвигаемся в порядке возрастания по элементам массива, быстрее изменяются последние индексы:
под массив А[ L1 ]
A[L1,L2] A[L1,L2+1] A[L1,U2]
A[U1]
Вопрос заключается в том, как обратиться к элементу АП, j, к, •••, 1, ml. Обозначим
•••,da-Ua-Ln+l.
206
ГЛАВА 8
То есть di есть число различных значений индексов в i-м измерении. Следуя логике двумерного случая, мы находим начало подмассива A[i, *, •••,*]
BASELOC+(i—L1)*d2*d3*- • -*dn
где BASELOC — адрес первого элемента A[Li, L2, •••, LJ, a d2*d3*- • -«dn — размер каждого подмассива A[i, *, •••,*]. Начало подподмассива A[i, j, *, • ••, *1 находится затем добавлением
(j—L2)*d3*- • -*dn
к полученному значению.
Действуя и дальше таким же образом, мы окончательно получим
(8.4.2) BASELOC+(i—L4)*d2*d3*- • • *dn+(j—L2)*d3*- • • *dn
+(k—L3)*d4*- • -*dn4-+(1—Ln-i)*dn+m—Ln.
Выполняя умножения, получаем
(8.4.3) CONSPART+VARPART
где
(8.4.4) CONSPART=BASELOC—((• • • ((L1*d2+L2)*d3+L3)*d4+
+ • • • +Ln-i)*dn+Ln)
и
(8.4.5) VARPART=(- • • ((i*d2)+j)*d3+ • • • +l)*dn+m.
Значение CONSPART необходимо' вычислить только один раз и запомнить, так как оно зависит лишь от нижних и верхних границ индексов и месторасположения массива в памяти. VARPART зависит от значений индексов i, j, • • •, m и от размеров измерений d2, d3, • • •, dn- Вычисление выглядит довольно громоздким только потому, что оно представлено в таком виде. В действительности вычисление можно упростить, выполнив последовательность таких действий:
VARPART: = первый индекс (i)
VARPART: = VARPART*d2 + второй индекс (j) VARPART: = VARPART»dgH-третий индекс (k)
VARPART: = VARPART*dn4-n-fl индекс (m)
Таким образом, метод борьбы со сложностями существует; он позволяет очень просто запрограммировать адреса величин с индексами или сгенерировать команды вычисления этих адресов по опи
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 207
санной схеме. В действительности вследствие итеративного характера вычислений сформировать любые ссылки на многомерный массив так же легко, как и ссылки на дву- или трехмерный массив.
В некоторых случаях, когда нужно осуществить оптимизацию программы, лучше использовать (8.4.2) (отделив, конечно, постоянную и переменную часть), где dj не будут перемножаться, так как при этом вычисление распадается на несколько независимых частей. Мы увидим это в гл. 18.
Информационные векторы
В ФОРТРАНе верхняя и нижняя границы массивов известны во время трансляции. Поэтому компилятор может выделить память для массивов и сформировать команды, ссылающиеся на элементы
L1 U1 di
L2. d U2 If di
п C0NSPART
BASE ЮС
Описате гмссива
Рис. 8.2. Информационный вектор для массива.
массива, используя верхние и нижние границы и постоянные значения dlt d2, • • •, dn. В АЛГОЛе и PL/1 это невозможно, так как границы могут вычисляться во время счета. Таким образом, нам нужен описатель для массива, содержащий необходимую информацию. Этот описатель для массива называется допвектор (dope vector), или информационный вектор. Информационный вектор имеет фиксированный размер, который известен при компиляции, следовательно, память для него может быть отведена во время компиляции в области данных, с которой ассоциируется массив. Память для самого массива не может быть отведена до тех пор, пока во время счета не выполнится вход в блок, в котором описан массив. При входе в блок вычисляются границы массива и производится обращение к программе распределения памяти для массивов. Эта программа вычисляет число необходимых ячеек, вызывает GETAREA, чтобы выделить область данных нужного объема, и вносит в информационный вектор необходимую информацию. На рис. 8.3 представлена схема работы программы распределения памяти для массива.
Какая информация заносится в информационный вектор? Для предложенной выше n-мерной схемы нам как минимум нужны зна
208
ГЛАВА 8
чения d2, • ••, dn и CONSPART. Если перед обращением к массиву нужно проверять правильность задания индексов, то следует также занести в информационный вектор значения верхних и нижних границ. Необходимая информация показана на рис. 8.2.
УПРАЖНЕНИЯ К РАЗДЕЛУ 8.4
1. Выделите в (8.4.2) постоянную часть и переменную часть, которая зависит от индексов, но без перемножения dj. Предположим, что мы пользуемся новой формулой для ссылки на элементы
Рис. 8.3. Программа распределения памяти для массивов.
Параметры программы: п (число индексов), нижние и верхние границы Llt Ut, . . . . . . , Ln Un и адрес информационного вектора.
массива. Какие значения должны быть в информационном векторе, чтобы вычисления были эффективными? Переделайте блок-схему программы распределения памяти для массива так, чтоэы она заносила эти значения в информационный вектор.
2. Напишите и отладьте программу распределения памяти для массивов на каком-либо языке. Для ее отладки напишите фиктивную процедуру GETAREA.
3. Предположим, что массив хранится не по строкам, а по столбцам. Преобразуйте формулы вычисления элемента массива A[i, j, •••, ml. Составьте блок-схему программы распределения памяти для массива и формат информационного вектора.
8.5. ПАМЯТЬ ДЛЯ СТРОК
Строка есть последовательность литер. Если длина строки (число литер) не изменяется во время выполнения программы и известна при компиляции, то строку можно разместите в некотором коли
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 209
честве подряд расположенных слов, зависящем от числа символов в слове [например, на IBM 7090 в одном слове помещается6 литер, на IBM 360—4 литеры (одна литера в байте)]. Однако длина строки не всегда известна. Если известна максимальная’ длина, то можно выделить столько слов, сколько нужно для строки максимальной длины, и перед этими словами поместить слово, содержащее текущее число литер:
Текущая длина
Текущая строка
Неиспользованные слова
Место для максимального числа литер
Слово, содержащее текущее значение длины,— это своего рода описатель. Иногда бывает необходимо добавить слово, содержащее максимальную длину.
Наиболее сложный случай встречается тогда, когда значение максимальной длины не известно при компиляции. Его реализацию наиболее трудно осуществить. Выполнение присваивания значений для строк А :=В сталкивается с трудностями, если значение В, стоящее справа, содержит больше литер, чем область, занимаемая А. Одно решение, используемое в XPL и SPL (см. Маккиман и др. [70]) на IBM 360, состоит в том, что в статической области данных отводится большая область строк, способная вместить все строки. Каждая строка-переменная имеет описатель, состоящий из двух последовательных слов, содержащих текущую длину строки, и указатель-ссылку на саму строку в области строк. Этот тип описателя мы назовем указателем строки. Если мы выполним присваивания SI := 'АВ', S2 : = 'QED' и S3:= 'F', мы будем иметь
Указатель на строку
Например, выполнение присваивания SI := S2 не изменит строку, а изменит только указатель строки. Присваивание S3 :== SUBSTR (S2, 1,1) можно выполнить аналогичным образом. Например, вы.
210
ГЛАВА 8
полнение этих двух присваиваний преобразует приведенную выше схему следующим образом:
Заметьте, что все три указателя строк указывают на части той же самой строки. Простые присваивания выполняются эффективно, так как изменяются только указатели строк, но не сами строки. Сцепление строк (скажем, SI := S2 CAT S3) выполняется медленнее, так как целая строка должна быть составлена на свободном месте. Выполнение этого присваивания привело бы к схеме
В некоторый момент область строк может переполниться. Но большая ее часть при этом может оказаться «мусором», а именно символами, на которые не указывает ни один указатель строки. Символы АВ в изображенной выше области являются мусором. Когда подобное происходит, вызывается программа FREEGARBAGE, чтобы обнаружить мусор, выбросить его и перенести полезную информацию в начало области строк.
8.6. ПАМЯТЬ ДЛЯ СТРУКТУР
Существует несколько альтернатив для определения новых типов данных как структур, составленных из типов данных, определенных ранее. Величины такого типа мы называем структурными величинами. В языках КОБОЛ, PL/1, АЛГОЛ W, АЛГОЛ 68 и СНОБОЛ имеются средства определения структур в том или ином виде. Они отличаются по предоставляемым возможностям и по эффективности, с которой они могут быть реализованы. Мы опишем
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 211
три из них и коротко рассмотрим их реализацию. Здесь необходимо ответить на четыре вопроса:
Как выделять память для структурных величин?
Как строить структурные величины?
Как ссылаться на компоненту структурной величины?
Как освобождать память?
Записи по Хоору (Вирт и Хоор [66])
Определение нового типа данных имеет вид
RECORD «(идентификатору («(компонента)», <компонента>,..., «(компонента»
где каждая компонента имеет вид
Спростой тип> <идентификатор>
причем Спростой тип> является одним из основных типов языка —REAL, INTEGER, POINTER и т. д. (АЛГОЛ W использует вместо POINTER термин REFERENCE). Например,
RECORD COMPLEX (INTEGER REALPART, INTEGER IMAGPART)
определяет новый тип COMPLEX, состоящий из двух компонент типа INTEGER, названных REALPART и IMAGPART. Во время компиляции известны все характеристики всех компонент, включая тип данных, на которые могут ссылаться указатели. Во время счета не нужны описатели ни для самой структуры, ни для ее компонент, причем может быть сгенерирована эффективная программа.
Любая^структурная величина с п компонентами может храниться в памяти в виде
. компонента, 1 компонента, 2 • • • компонента, л
Поскольку при компиляции известны все характеристики, то известен также объем памяти, необходимый для каждой компоненты, и, следовательно, компилятор знает смещение каждой компоненты относительно начала структурной величины. Для упрощения сбора мусора лучше всего присвоить номер каждому типу данных (включая типы, определенные программистом) и иметь описатель для каждого указателя. Описатель будет содержать номер, описывающий тип величины, на которую в данный момент ссылается указатель.
Память для указателей и их описателей может быть выделена компилятором в области данных, с которой они связаны; это не
ГЛАВА 8
212
трудно, так как они имеют фиксированную длину. Для хранения текущих значений структурных величин может быть использована отдельная статическая область данных и специальная программа GETAREA для выделения памяти в этой области. В языке АЛГОЛ W нет явного оператора для освобождения памяти, так что, когда память исчерпана, система обращается к программе FREEGARBAGE. Заметим, что для того, чтобы иметь возможность обнаружить мусор, нужно знать, где расположены все указатели, включая те, которые являются компонентами структурных величин.
Новое значение типа COMPLEX с компонентами S1 и S2 может быть получено при выполнении инструкции
Р := COMPLEX(S1, S2)
где Р описан как указатель величин типа COMPLEX. Выполнение этой инструкции сводится к обращению к GETAREA за областью нужного размера, к запоминанию в этой области вычисленных значений S1 и S2 и к занесению в Р их адреса.
На структурные величины ссылаются только описанные указатели. Если выполняются инструкции присваивания
Р1 :== Р; Р COMPLEX (S3, S4)
первоначальная величина, связанная с Р, не теряется, так как Р1 указывает на нее. Заметим, что сразу после выполнения Р1 : = Р величины Р1 и Р указывают на одну и ту же величину.
Ссылка на компоненту имеет вид
<имя компонентьО («указатель на структурную величину») Таким образом, при выполнении
IMAGPART(P) := IMAGPART(P)+1
ко второй компоненте структурной величины с указателем Р прибавляется 1. Для этого случая можно сгенерировать эффективную программу. Например, команды для вышеприведенной инструкции на IBM 360 могли бы выглядеть так:
L 1,Р
L 2,4(1)
А 2, —F'lz
ST 2,4(1)
Загрузить значение Р в регистр 1. Загрузить IMAGPART в регистр 2. Заметим, что смещение 4 известно во время компиляции.
Прибавите 1 к содержимому регистра 2. Запомнить результат в IMAGPART.
Структуры PL/1
Структуры PL/1 являются более сложными, чем записи по Хоору. Их компоненты сами могут иметь подкомпоненты. Например:
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 213
DEGLARE 1 PERSON,
2 NAME CHARACTER (20),
2 FATHER POINTER,
2 MOTHER POINTER,
2 CHILDREN,
3 OLDEST 1 POINTER,
3 OLDEST2 POINTER,
3 OLDEST3 POINTER,
2 AGE FIXED;
Эта структура есть дерево, узлы которого связаны с именами и концевые узлы которого имеют значения данных. Корень PERSON имеет уровень I, а узлы, до которых можно дойти от корня по пути длиною i—1, находятся на уровне i.
Если бы возможность иметь подкомпоненты была бы единственным различием между записями по Хоору и структурами PL/1, не было бы существенной разницы во время выполнения программы; можно было бы спокойно разместить все компоненты и подкомпоненты так, чтобы каждая имела фиксированное смещение относительно начала структуры и это смещение было бы известно во время компиляции. Однако в языке PL/I существует еще два расширения.
С целью экономии памяти атрибут CELL для компоненты требует, чтобы все ее подкомпоненты непременно занимали одно и то же место в памяти. В любое заданное время только одна из нескольких переменных может иметь значение. Присваивание значения подкомпоненте приводит к тому, что подкомпонента, к которой обращались ранее, утрачивает свое значение. Например, в случае
DECLARE 1 DATE CELL, 2 A FLOAT, 2 В FIXED;
обе компоненты А и В используют одну и ту же память. Это вызывает осложнения во время компиляции, но в действительности не очень изменяет код готовой программы, если только объектная программа не должна проверять при каждом обращении к подкомпоненте, что значение подкомпоненты действительно существует.
Для другого расширения требуются более сложные административные функции во время выполнения программы. В PL/1 корневой узел структурного дерева или любая из подкомпонент могут быть снабжены размерностями. Например, мы могли бы переписать первую инструкцию DECLARE так:
DECLARE 1 PERSON,
2 NAME CHARACTERS (20),
2 FATHER POINTER,
2 MOTHER POINTER,
2 CHILDREN (3) POINTER,
2 AGE FIXED;
214
ГЛАВА 8
чтобы получить в основном тот же результат; одна компонента, CHILDREN, состоит из трех указателей (обращаются к ним иначе). В качестве другого примера рассмотрим определение структуры
DECLARE 1 А, 2 В (2), 3 X (М, N), 3 Y (М, N), 3 Z, 2 С LIKE В,
2 N (2);
Это приводит к структуре
X (1,N),
X(M,N) Y(M,N)
С(2)
N( t)
N (2)
Так как выражения, которые определяют границы изменения индексов, должны быть вычислены при выполнении программы, для них, как и в случае массивов, следует употреблять описатели, или информационные векторы. В предыдущей инструкции DECLARE нам необходимы информационные векторы для всех компонент, исключая само А и Z.
В PL/1 используется три различных метода распределения памяти — статическое (STATIC), автоматическое (AUTOMATIC) и управляемое (CONTROLLED) распределение.
В отличие от АЛГОЛа W нет различия в методах распределения памяти для структурных и других величин. Следует отметить, что PL/1 требует от программиста, чтобы он освобождал память, отведенную для величин CONTROLLED. Сбор мусора для них не производится.
Ссылка на компоненту состоит из последовательности имен узлов, которые ведут к ней, разделенных точками. Так, в первом примере этого раздела можно ссылаться на компоненту OLDEST1 посредством PERSON.CHILDREN.OLDEST1.
Когда компоненты являются массивами, нужно задавать требуемые индексы. В последнем примере, для того чтобы сослаться на компоненту Х(1, 2) структуры С(1), пишем А.С(1).Х(1, 2). Возможны и некоторые другие варианты. Чем больше массивов
ОРГАНИЗАЦИЯ ПАМЯТИ ВО =ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ' 215
появляется в определении структуры, тем больше работы приходится выполнять во время компиляции, чтобы создать, обратиться и уничтожить величины этого структурного типа.
Структуры данных по Стендишу (Стендиш [68])
Мы продвигаемся от простого к сложному — от структур данных, которые могут быть реализованы эффективно, к таким, для которых это невозможно, но которые богаче и мощнее. В своей диссертации Стендиш предлагает систему записи для структур, встроенную в АЛГОЛ 60, которая предусматривает, что структуры изменяются во время работы программы. Динамически могут изменяться не только размерности компонент, но и число компонент и их типы. Обычно во время компиляции ничего не известно, и все делается во время выполнения программы на основе описателей, которые сами строятся в это же время. Например, при выполнении процедуры TEMPLATE PROCEDURE
TEMPLATE PROCEDURE SEQ (n, t); INTEGER n;
TEMPLATE t; SEQ := n*[t];
создается описатель, описывающий структуру, состоящую из п компонент типа t. Выполняя
DI : = SEQ(2, REAL); D2 := SEQ(k, DI),
заносим в описательную переменную D1 описатель структурной величины, имеющий две компоненты REAL, и в D2 — описатель структурной величины, состоящий из к компонент, каждая типа D1. Имеется множество других способов построения описателей во время счета, кроме методов распределения памяти для структурных величин и создания величин. Мы не будем их здесь рассматривать; единственное, что нам хотелось отметить,— это то, что во время выполнения программы мы должны хранить описатель для каждой структурной величины. Действительно, этот описатель аналогичен набору элементов таблицы символов, используемому компилятором при компиляции, скажем, структур PL/1! Как мы увидим в гл. 10, такие описания структур лучше всего реализуются в виде дерева, где для каждого узла должно быть по крайней мере известно:
1) концевой ли это узел или нет;
2) если узел концевой, то каков его тип;
3) если узел концевой, то указатель на значение, если таковое существует;
4) если узел не концевой, то указатели на узлы для подкомпонент;
5) размерности подкомпонент.
216
ГЛАВА S
Всякий раз при обращении к значению компоненты должен быть проинтерпретирован описатель. Начиная с корневого узла, находится путь к узлу, к которому обращаются, проверяется тип этого узла и, наконец, используется или изменяется его значение.
8.7. СООТВЕТСТВИЕ ФАКТИЧЕСКИХ И ФОРМАЛЬНЫХ ПАРАМЕТРОВ
Рассмотрим различные типы формальных параметров и их соответствие фактическим параметрам и покажем, как каждый из них может быть реализован. Под формальным параметром мы понимаем идентификатор в процедуре, который заменяется другим идентификатором или выражением при вызове процедуры. В подпрограмме на ФОРТРАНе, начинающейся с
SUBROUTINE А(Х, Y)
X и Y являются формальными параметрами. Эквивалентная процедура на АЛГОЛе имеет заголовок PROCEDURE А(Х, Y). При обращении к процедуре, скажем, А(В, C*D) устанавливается некоторым образом связь между формальными параметрами и фактическими параметрами В и C*D.
Когда в каком-нибудь языке происходит обращение к процедуре, ей передается список адресов аргументов. Процедура переписывает эти адреса в свою собственную область данных и использует их для установления соответствия фактических и формальных параметров. Кроме фактических параметров, часто имеется несколько неявных параметров, о которых программист не знает. Один из них это, конечно, адрес возврата. (Мы могли бы также включить в этот список все индекс-регистры, которые нужно сохранить; однако такие вопросы зависят от специфики машины, и мы не будем их касаться.) Мы увидим, какие необходимы другие, зависящие от языка параметры, когда будем исследовать различные типы параметров в различных языках.
Следовательно, вызываемой процедуре передается список такого вида:
неявный параметр 1
неявный параметр m
адрес фактического параметра 1
адрес фактического параметра п
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 217
Обратите, пожалуйста, внимание на то, что на самом деле не все параметры могут передаваться в таком списке; мы примем такую форму для удобства изложения. Например, адрес возврата обычно передается в каком-либо регистре.
Что представляют собой адреса в списке? Это зависит от языка и от типа параметра, и мы обсудим это позднее. Ниже перечислены типы параметров, которые мы будем рассматривать:
1) вызов по ссылке;
2) вызов по значению;
3) вызов по результату;
4) фиктивные аргументы;
5) вызов по имени;
6) имена массивов в качестве фактических параметров;
7) имена процедур в качестве фактических параметров.
(Упражнения 2 и 3 предназначены для того, чтобы убедить читателя в том, что первые пять типов параметров различны в определенных контекстах.)
Вызов по ссылке (by reference)
Этот тип параметра самый простой для реализации. Фактический параметр обрабатывается во время выполнения программы перед вызовом; если он не является переменной или константой, оц вычисляется и запоминается во временной ячейке. Затем вычисляется адрес (переменной, константы или временной ячейки), И этот адрес передается вызываемой процедуре. Вызываемая процедура использует его для ссылки на ячейку (ячейки), содержащую значение. Например, предположим, что мы вызываем процедуру Р, определенную так:
(8.7.1) PROCEDURE Р(Х); BEGIN...X := Х+5; ...END
с помощью вызова Р(А[11), где А — массив. Перед вызовом процедуры вычисляется адрес А{1] и заносится в список, который должен быть передан процедуре. Выполнение присваивания X := Х+5 внутри процедуры приводит к добавлению 5 к элементу АП1. Команды для этого присваивания могли бы выглядеть так:
1. Загрузить в регистр 1 (например) адрес фактического параметра.
2. Загрузить в регистр 2 (например) значение из 0(1);
3. Прибавить 5 к регистру 2;
4. Запомнить содержимое регистра 2 в ячейке 0(1), где 0(1) означает адрес ячейки 0+CONTENTS (регистр 1).
218
ГЛАВА 8
Вызов по значению (by value)
При этом типе соответствия формального и фактического параметров вызываемая процедура имеет ячейку, выделенную в ее области данных для значения формального параметра этого типа. Как и при вызове по ссылке, адрес фактического параметра вычисляется перед вызовом и передается вызываемой процедуре в списке параметров. Однако перед фактическим началом выполнения процедура выбирает значение по адресу и заносит его в свою собственную ячейку. Эта ячейка затем используется как ячейка для величины точно так же, как любая переменная, локализованная в процедуре. Таким образом, нет никакого способа изменить в процедуре значение фактического параметра.
Другими словами, параметр, вызываемый по значению, является локализованной в процедуре переменной, которая при входе в процедуру принимает значение соответствующего фактического параметра.
Предположим, что параметр X процедуры (8.7.1) вызывается по значению. Тогда соответствующая объектная программа могла бы выглядеть так:
загрузить в регистр 1 адрес фактического параметра
загрузить в регистр 2 значение из 0(1)
запомнить содержимое регистра 2 в X (в области данных этой процедуры)
г...
загрузить в регистр содержимое X; прибавить 5; запомнить в X
Начало процедуры:
Вызов по результату (by result)
В языке АЛГОЛ W (см. Бауэр и др. [68]) для любого формального параметра X, объявленного параметром RESULT, справедливо следующее:
1. Для параметра X отводится ячейка в области данных процедуры. Эта ячейка используется в процедуре как локализованная ячейка для переменной X.
2. Как и в случае параметра VALUE, при вызове процедуры вычисляется и передается адрес фактического параметра.
3. Когда выполнение процедуры заканчивается, полученное значение X запоминается по адресу, описанному в п. 2.
ОРГАНИЗАЦИЯ ПАМЯТИ ВО бР'ЁМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 219
Другими словами, параметр RESULT есть переменная, локализованная в процедуре, значение которой при выходе запоминается в соответствующем фактическом параметре (который должен быть, конечно, переменной). Понятие RESULT было предназначено для того, чтобы дополнить в АЛГОЛе вызов по имени (который будет описан позднее), так как последний весьма неэффективен и обладает большими возможностями, чем это необходимо в большинстве случаев.
Параметр X в АЛГОЛ W может быть описан и как VALUE, и как RESULT; в этом случае локализованная переменная X возникает при входе в процедуру, а конечное значение X запоминается снова в фактическом параметре. В ФОРТРАН II все аргументы вызываются, по ссылкам; в ФОРТРАН IV формальный параметр вызывается как VALUE RESULT, но программист может указать, чтобы вызов осуществлялся по ссылке.
Фиктивные аргументы
В языке ФОРТРАН II обращение Р(3) к процедуре Р (8.7.1) приводит к необнаруживаемой ошибке. Так как ФОРТРАН передает адрес ячейки, которая содержит константу 3, выполнение присваивания Х = Х+5 изменяет саму константу на 8! С этого момента значение 8 используется вместо константы, значение которой должнр быть равно 3. PL/1 решает эту проблему, по-разному обрабатывая следующие фактические параметры:
1) константы;
2) выражения, которые не являются переменными;
3) переменные, чьи характеристики отличаются от характеристик, указанных для соответствующих формальных параметров.
Для такого фактического параметра в вызывающей процедуре заводится временная переменная. Фактический параметр вычисляется и запоминается во временной переменной, и адрес этой ячейки передается в списке параметров. Таким образом, в приведенном выше примере константа 3 не изменится.
Такая временная переменная называется фиктивным аргументом. За исключением того, что временная переменная заводится процедурой вызова, фиктивный аргумент в PL/1 аналогичен параметру, вызываемому по значению в АЛГОЛе.
И есть еще одно различие в вызовах. В АЛГОЛе формальный параметр объявляется VALUE. В PL/1 вызывающая процедура выбирает, использовать ли фактический параметр как VALUE или как в ФОРТРАНе применить вызов по ссылке. Например, если написать P(J), фактический параметр J вызывается по ссылке; если написать P((J)), он вызывается по значению, или как фиктивный аргумент.
220
ГЛАВА 8
Вызов по имени
Согласно сообщению о языке АЛГОЛ, использование вызова параметра по имени означает буквальную замену имени формального параметра фактическим параметром. Так, если для процедуры
PROCEDURE R(X, I);
BEGIN I := 2; X := 5; I := 3; X := 1 END
задано обращение
(8.7.2) R(B[J*2], J),
это должно было бы привести к изменению ее тела на BEGIN J := 2; B[J»2] := 5; J := 3; B[J*2] := 1 END
как раз перед ее выполнением.
Получить эффективную реализацию с помощью такой текстовой замены, конечно, нельзя, и мы должны разработать соответствующий эквивалентный способ. Заметим, что фактический параметр, соответствующий X, изменяется всякий раз, когда изменяется значение J, так что мы не можем просто вычислить адрес фактического параметра и использовать его; мы должны пересчитывать его каждый раз, когда мы обращаемся к формальному параметру внутри процедуры.
Обычный способ реализации вызова параметров по имени состоит в том, чтобы иметь отдельную программу или процедуру в объектном коде для каждого такого параметра. Для такой программы был введен Ингерманом [61 а] термин «санк» (thunk), и этот термин прижился. Когда происходит вызов санка, он вычисляет значение фактического параметра (если этот параметр не переменная) и передает адрес этого значения. В теле процедуры при каждой ссылке на формальный параметр происходит вызов санка, после чего для обращения к нужному значению используется переданный санком адрес.
Ниже поясняется программа для вызова (8.7.2). Следует упомянуть, что для правильной работы санка необходимо еще несколько неявных параметров; они будут описаны в разд. 8.9.
А1:
А2:
L: RET
Переход к L
санк, дня вычисления адреса B[3*2J
санк для вычисления адреса J
вызов R с этим списком
Список параметров для вызова из L
RET (адрес возврата) А1 (адрес первого санка) А 2. (адрес второго санка)
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 221
Различие между вызовом по ссылке и вызовом по имени заключается в следующем: адрес фактического параметра, вызываемого по ссылке, вычисляется только один раз, перед фактическим входом в процедуру, в то время как для вызова по имени адрес вычисляется всякий раз, когда в теле процедуры есть обращение к формальному параметру.
Имя массива в качестве фактического параметра
В этом случае и фактический, и формальный параметр должны быть массивами. Процедуре передается адрес первого элемента массива (для языков, которые не требуют информационных векторов) или адрес информационного вектора, и этот адрес используется процедурой для ссылки на элементы массива.
Имя процедуры в качестве фактического параметра
Передаваемый адрес — это адрес первой команды процедуры, которая встретилась в качестве фактического параметра.. Если это имя само является формальным параметром, то адрес был передан вызывающей процедуре, когда она вызывалась.
Это вся необходимая информация для вызовов в ФОРТРАНе. Вызовы в АЛГОЛе и PL/1 реализуются сложнее, и мы отложим их рассмотрение до разд. 9.8 об управлении памятью при выполнении программы на АЛГОЛе.
УПРАЖНЕНИЯ К РАЗДЕЛУ 8.7
1. Напишите процедуру EXCHANGE(X, У) на языке высокого уровня для того, чтобы обменять значения фактических параметров X и Y (которые должны быть переменными). Какой тип должен быть у параметров X и У? Можно ли написать такую процедуру на АЛГОЛе? Указание: рассмотрите два вызова EXCHANGE(A[I], I) и EXCHANGER, А[11).
2. Рассмотрите следующую программу на языке типа АЛГОЛ:
BEGIN INTEGER I; INTEGER ARRAY В [1:2];
PROCEDURE Q(X); INTEGER X;
BEGIN I : = 1; X :=X-f-2; В [I] : = 10;
I : =2; X : = X 4-2
END;
B[l] : = 1; В [2] : =1; I: = 1; Q (В [I])
END
222
ГЛАВА 8
Выполните программу 5 раз (и укажите, какие окончательные значения получат ВЦ] и BI2]), рассматривая формальный параметр X как параметр, вызываемый (1) по ссылке, (2) по значению, (3) как VALUE RESULT, (4) как RESULT и (5) по имени. Указание: в результате одного из вызовов получится неопределенное значение; во всех других случаях результаты различны!
3. Выполните программу из упражнения 2, предполагая, что X — аргумент типа PL/1. Затем замените вызов процедуры Q(B[I]) на Q((B[I])) и снова выполните программу. Отличаются ли конечные значения I, ВЦ] и В[2]?
8.8. УПРАВЛЕНИЕ ПАМЯТЬЮ ДЛЯ ФОРТРАНа
Язык ФОРТРАН не допускает вложенных подпрограмм, рекурсивных подпрограмм или динамических массивов. Так как вложенные подпрограммы отсутствуют, единственные переменные, к которым можно обращаться,— это переменные, локализованные в программе (в ее области данных) и переменные в области COMMON. Область COMMON статическая, ей отводится фиксированная последовательность ячеек перед выполнением программы; следовательно, ссылки на переменные в области COMMON могут быть абсолютными ссылками на машинные ячейки.
Каким же образом обращаться к локализованным переменным? Отсутствие рекурсивных подпрограмм означает, что каждая подпрограмма должна быть завершена перед тем, как она может быть снова вызвана. Поэтому ее область данных тоже может быть статической. Таким образом, все адреса переменных в ФОРТРАНе могут быть абсолютными адресами машинных ячеек.
Так как динамическое распределение памяти для массивов не допускается (все границы, указанные в инструкции DIMENSION, должны быть константами), нет необходимости в управлении памятью при выполнении программы. Компилятор может разместить массивы в области данных фиксированной длины.
Из всего этого следует, что дисплеи фактически не нужны. Вспомним, что дисплеи необходимы, чтобы сохранить адреса областей данных, на которые могут быть ссылки в любой точке программы. Но мы только что увидели, что в ФОРТРАНе все ссылки — абсолютные.
Рисунок 8.4 иллюстрирует типичную статическую область данных в ФОРТРАНе. Неявные параметры включают в себя адрес возврата и то, что диктуется конструкцией машины (регистры, сумматоры и т. д.). Вызов подпрограммы состоит из следующих действий:
1. Вычислить адреса фактических параметров и запомнить их в списке параметров (в области данных вызывающей подпрограммы).
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 223
2. Передать адрес списка параметров в некоторой согласованной глобальной ячейке (например, в регистре).
3. Занести адрес возврата в список и передать управление.
Перед выполнением подпрограмма должна:
1. Перенести неявные параметры в свою область данных.
Неявные параметры
Фактические параметры
Простые переменные, массивы, временные переменные
Рис. 8.4. Типичная область данных подпрограммы на ФОРТРАНе.
2. Перенести адреса фактических параметров в свою область данных.
Возврат из подпрограммы состоит в восстановлении сохраненных значений неявных параметров и переходе по адресу возврата.
8.9. УПРАВЛЕНИЕ ПАМЯТЬЮ ДЛЯ АЛГОЛа
АЛГОЛ имеет блочную и процедурную структуру, которая требует управления памятью при счете. Однако оно может быть реализовано с помощью довольно простой схемы. АЛГОЛ не допускает указателей в качестве переменных, что является одной из главных причин возрастания сложности распределения памяти. Кроме того, вложенные блоки и процедурная структура позволяют использовать простой механизм для распределения памяти — хорошо знакомый нам стек.
В общих чертах работа ведется так. В качестве стека используется последовательность смежных ячеек, которые вначале пусты. С каждым выполнением процедуры связана одна динамическая область данных фиксированной длины для ее переменных, информационных векторов и т. д. (Мы рассматриваем главную программу как процедуру без параметров, вызываемую системой.) Когда процедура вызвана, она забирает под свою область данных необходимый объем памяти в текущей вершине стека; когда выполняется возврат из процедуры в место вызова, все использованные ячейки «выталкиваются» из стека- Блоки работают таким же образом, так как они вложены друг в друга и в процедуры. При входе в блок выделяется память из вершины стека для области данных, чтобы разместить элементы каждого массива; при выходе из блока ис
224
ГЛАВА 8
пользованные ячейки освобождаются. Ввиду простоты этой схемы нам в действительности не нужны программы GETAREA и FR EEAREA; выделение и освобождение памяти может быть выполнено с помощью нескольких команд, без обращения к подпрограмме.
Нам необходимо обеспечить, чтобы связь между процедурами и обращения к глобальным переменным выполнялись правильно; именно это мы рассмотрим в данном разделе. Описываемый метод,
BEGIN...
PROCEDURE А (X, Y); PROCEDURE X; INTEGER Y; BEGIN PROCEDURE В (Z); PROCEDURE Z;
BEGIN ARRAY F [1:10];
L4: Z(F[1]+Y);
END;
L3: В (X);
END;
PROCEDURE C;
BEGIN ARRAY G [1:10];
PROCEDURE D (W); INTEGER W;
BEGIN
L5: G[1]:=W;
END;
L2: A (D, 1);
END;
LI: C;
END;
Рис. 8.5. Структура вложенных и параллельных процедур.
возможно, более сложен, чем другие, встречающиеся в литературе методы. Оправданием этому является наше желание сделать входы в блок и выходы из блока по возможности более эффективными. В упражнениях в конце раздела мы затронем другие схемы.
Чтобы проиллюстрировать работу стека, предположим, что у нас имеется программа, структура которой изображена на рис. 8.5. Сначала выделяется память для области данных главной программы. Предположим, что выполняется вызов процедуры С (метка L1). Тогда выделяется область данных для С, за которой следует область для массива G. При вызове процедуры А (метка L2) мы выделяем память для области данных процедуры А. К моменту, когда про-
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 225
грамма доходит до метки L3 складывается следующее распределение памяти:
Область данных процедуры А Вершина стека
Область данных для массива G
Область данных процедуры С
Область данных главной программы Дно стена
В этом разделе мы рассмотрим по порядку следующие вопросы:
1) связь между активным дисплеем и областью данных;
2) формат областей данных процедуры;
(8.9.1) 3) вход в блок, описания массивов и выход из блока;
4) вызов процедуры, имя которой не является формальным параметром;
5) инициализация процедуры и выход из нее;
6) санки и как их вызывать;
7) вызов процедуры, являющейся формальным параметром;
8) фактические параметры — имена процедуры;
9) передачи управления.
Связь между активным дисплеем и областью данных
В реализации АЛГОЛа для каждого выполнения процедуры выделяется динамическая область данных (главную программу мы также называем процедурой). В любой момент времени в процессе
Адрес области, данных главной, программы (уровень 0)
Адрес области данных для процедуры уровня 1
Адрес области данных для процедуры уровня t
Рис. 8.6. Активный дисплей при выполнении процедуры уровня i.
выполнения могут быть несколько процедур, но только одна будет действительно активной; остальные будут ожидать ее завершения и возврата. Дисплей и область данных, связанные с активной процедурой, также называются активными. Если активная процедура имеет уровень вложения i, она может обращаться, кроме своих
8 Д. Грис
226
ГЛАВА 8
собственных, к переменным в процедурах уровней 1,2, ..., i—1 и в главной программе. Активный дисплеибудет следовательно иметь вид, приведенный на рис. 8.6.
Где должны находиться сами дисплеи? Часто принято иметь для них отдельный стек. Мы выберем другой вариант: так как с каждой областью данных связан дисплей, мы помещаем его в первые несколько ячеек этой области. Таким образом, адрес активного дисплея всегда является адресом активной области данных, и наоборот. Кроме того, мы предположим, что глобальная ячейка (например, индексный регистр), называемая ACTIVE AREA, всегда содержит адрес активного дисплея (и области данных) для выполняемой в настоящее время процедуры.
Все обращения к данным из активной процедуры выполняются с использованием ячейки ACTIVE ARE А и дисплея, на который она ссылается.
Области данных процедуры
Каждая область данных процедуры имеет фиксированную длину, определяемую во время компиляции. Ниже мы приводим список данных в каждой области в порядке расположения. Смысл некоторых элементов списка пока не ясен, в свое время мы их рассмотрим.
L Дисплей для процедуры.
2. Ячейка, называемая STACKTOP. Она содержит адрес вершины стека, который получается, сразу после выделения области для данной процедуры, т. е. содержит адрес последней ячейки в этой области данных.
3. Четыре неявных параметра процедуры:
а) адрес возврата;
Ь) адрес дисплея фактических параметров;
с) адрес глобального дисплея;
d) адрес вершины стека в момент вызова.
4: Собственно фактические параметры (или их адреса).
5. Для каждого блока в процедуре:
а) ячейка STACKTOP, которая должна содержать адрес вершины стека во время работы блока;
Ь) ячейки для простых переменных;
с) ячейки информационных векторов для массивов, описан-ч ных в; блоке;
d) ячейки для необходимых в блоке временных переменных.
Порядок ячеек для простых переменных, информационных векторов и временных переменных в блоке не имеет значения.* Самый легкий способ — это распределить память, следуя порядку описаний в блоке. Так как нельзя обращаться к переменным из
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 227
параллельных блоков в одно и то же время, параллельные блоки могут использовать одни и те же ячейки, но это не обязательно. Рассмотрим процедуру на рис. 8.7 с внутренними блоками и с нумерацией для этих блоков, приведенной справа. Ниже дается
ДИСПЛЕЙ (адреса, областей, данных главной программы а процедуры А)
STACKTOP для процедуры к (адрес последнего слова в области данных процедуры К )
Неявные параметры
Фактические параметры X u Y
STACKT0P блока 1, переменная Z t информационный вектор для В
STACKTOP блока, 2, переменные D и Е • STACKTOP блока 3, информационный вектор для А
STACKTOP блока 4 t переменная Е
PROCEDURE А( X, Y) ; INTEGER X, Y; Lit BEGIN REAL Z; ARRAY B[X:Y];
L2: BEGIN REAL D, E ;
L3: : .
END;
L4: BEGIN ARRAY A[ 1 : X];
L5: BEGIN REAL E;
L6: :
END;
L7: END;
L8: END;
Рис. 8.7; Программа на АЛГОЛе, имеющая блочную структуру.
область данных для нее. Ячейки для переменных в блоке 2 совмещены с ячейками для переменных в блоке 3 и 4.
А дресац ия переменной
Предположим, что в процедуре уровня i встречается обращение к переменной или формальному параметру. Если это обращение к локализованной переменной или параметру, описанному в процедуре, их адрес во время выполнения программы есть
(смещение в области данных)+ACTIVE ARE А
Если переменная или параметр описаны в процедуре уровня к, содержащей данную процедуру, их адрес будет
(смещение в области данных)+CONTENTS( ACT IVEAR ЕА+к)
8*
228
ГЛАВА 8
Мы часто можем использовать номер уровня к вместо номера области данных в описании каждого идентификатора. Процедуры одного и того же уровня будут иметь один и тот же номер, но они никогда не будут обрабатываться компилятором одновременно. .
Вход в блок, описания массивов, выход из блока
Для каждого блока выделяется последовательность ячеек для простых переменных, информационных векторов и временных ячеек, используемых в блоке. Память для массивов должна быть выделена при входе в блок и освобождена при выходе из него» Рассматриваемая схема предназначена для минимизации работы при входе в блок и выходе из него. Действительно, вход в блок состоит из двух команд, в то время как выход из блока не требует абсолютно никаких команд!
Как упоминалось ранее, память для массивов при счете следует размещать в вершине стека. Мы устанавливаем следующее правило: когда выполняется блок, ячейка STACKTOP блока содержит адрес вершины стека для этого, блока. Это означает:
(8.9.2) Вершина стека во время выполнения программы всегда определяется ячейкой STACKTQP активного блока — блока, который выполняется в настоящее время.
Напомним, что в каждой области данных процедуры имеется ячейка STACKTOP, которая содержит адрес вершины стека после размещения этой области данных. Эту ячейку можно считать ячейкой STACKTOP для фиктивного блока, объемлющего тело процедуры.
Чтобы следовать правилу (8.9.2), мы должны, входя в блок, скопировать ячейку STACKTOP объемлющего блока (фиктивного блока при входе в главный блок процедуры) в ячейку STACKTOP блока, в который мы входим. Это делает вход в блок весьма эффективным.
Следующий шаг состоит в распределении памяти для массивов, описанных в блоке. Для каждого массива выполняется следующее:
1) вычисляются нижняя и верхняя границы;
2) вызывается программа размещения массива; ее параметры:
а) нижняя и верхняя границы;
Ь) адрес информационного вектора;
с) адрес ячейки STACKTOP для блока.
Программа размещения массива вычисляет всю необходимую информацию и заносит ее в информационный вектор. Затем она занимает в стеке нужное число ячеек, используя третий параметр, указывающий текущую вершину стека. Наконец, она заносит в третий параметр новый адрес вершины стека.
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 229
Здесь может возникнуть вопрос, почему для каждого блока необходима отдельная ячейка STACKTOP. Это становится ясным при рассмотрении выходов из блоков. Если была бы лишь одна глобальная ячейка STACKTOP, то каждый раз, когда происходил бы выход из блока, эта ячейка должна была изменяться, чтобы вытолкнуть из стека память для описанных в этом блоке переменных. Это вызывает осложнения при переходах через границы нескольких блоков и т. д. Для используемой нами схемы в этом нет необходимости, потому что справедливо (8.9.2); для обычного выхода из блока ничего не нужно делать.
Приведем пример работы этого механизма блочной структуры. На рис. 8.8, а показано состояние стека вто время, когда произошел вызов и инициализация процедуры А (рис. 8.7), а выполнение еще не началось (в метке L1). На рис. 8.8, b показано состояние стека после входа в главный блок, но перед размещением каких-либо массивов. Обе ячейки STACKTOP указывают на вершину стека. Затем (рис. 8.8, с) размещается массив и изменяется ячейка STACK-TOP для блока 1, в нее заносится адрес последней ячейки стека, которая является последней ячейкой массива В. Заметим, что ячейка STACKTOP для процедуры А не изменяется. Когда происходит вход в блок 2 (рис. 8.8, d), STACKTOP для блока 1 копируется в STACKTOP для блока 2. Поскольку в блоке 2 нет описания массивов, то, кроме этого, ничего не надо делать.
Теперь выходим из блока 2. Мы вернемся снова к рис. 8.8, с, так как переменные из блока 2 больше не являются активными. Заметим, что для этого выхода из блока на самом деле никакие команды не выполняются. Значения D, Е и STACKTOP блока Ь2 все еще в области данных, но к ним больше не будет обращейий.
При входе в блок 3 мы копируем ячейку STACKTOP и выделяем память для массива А, как это изображено на рис. 8.8, е. Теперь существуют три ячейки STACKTOP, указывающие на вершины стека: в блоке 3 (активном блоке), в блоке 1 и в блоке 0 — в самой процедуре. При входе в блок 4 мы снова копируем STACKTOP (рис. 8.8, f). Затем мы выходим последовательно из нескольких блоков; из блока 4 (рис. 8.8, е), из блока 3 (рис. 8,8, с) и из блока 1 (рис. 8.8, а).
Вызов процедуры
Код вызова процедуры состоит из санков для параметров, вызываемых по имени, команд, которые формируют список параметров и команд фактического перехода к процедуре. Формат санков мы опишем позднее. Как упоминалось ранее, когда рассматривался дисплей, список параметров состоит из фактических параметров и следующих четырех неявных параметров:
230
Массив В
-
Z ,инф.векторм. В Z; инф. вектор м. В
STACKTOP бл. 1 - STACKTOP Лт.1 -
параметры Параметры Параметры
STACKTOP пр. А STACKTOP пр. А STACKTOP лдА
ДИСПЛЕЙ ДИСПЛЕЙ ДИСПЛЕЙ
• ‘ *
<ь И 6 С L2,L4,L8
Рис. 8.8. Механизм блочной структуры.
Е
Массив А
Массив В
STACKTOP Л7.4-
Инф. вектор м. А
STACKTOP Л?.3
Z , инф.векторм. В
STACKTOP 67.1
Параметры
STACKTOP пр. А
. ДИСПЛЕЙ
е L5, L7
f L6
Рис. 8.8. Механизм блочной структуры (продолжение).
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 23! *
£
1) адрес возврата; J
2) адрес дисплея фактических параметров; ?
3) адрес глобального дисплея;
4) текущее значение STACKTOP. ' j
Второй неявный параметр — это значение ACTIVEAREA в j
момент обращения к процедуре. Он определяет область, в которой J
находятся фактические параметры. Это значение сохраняется и \ используется в санках для обращения к нужным переменным. Это I PROCEDURE В; PROCEDURE A; j
BEGIN PROCEDURE A; BEGIN...END; -
BEGIN...END; PROCEDURE B;
LI: A; , BEGIN...LI: A; ...END; I
‘END; ' . • : I
a > b
Рис. 8.9. Процедура В, вызывающая процедуру А. ।
I
же значение используется для восстановления ACTIVE AREA S
при выходе из процедуры для того, чтобы вернуться *к работе с тем же дисплеем, который был в точке вызова.
Пока мы будем считать, что в данном обращении к процедуре ;
имя ее не является формальным параметром. При этом ограни- ;
чении второй и третий параметры совпадают. Третий параметр — |
адрес глобального дисплея используется при формировании дисплея §
для вызываемой процедуры. Поясним это. [
Предположим, что мы вызываем процедуру А из процедуры В J (или из главной программы). Здесь возникают два случая. Прежде всего процедура А может быть описана внутри процедуры В (рис. | 8.9, а). Предположим, что уровень В равен i. Тогда уровень про- I цедуры А равен i+1. Она может обращаться к любой переменной, J
глобальной по отношению к В, и к любой переменной, описанной S
в блоке процедуры В, объемлющем описание А. Таким образом, первые i+1 ячейки дисплея для процедуры А те же, что и для процедуры В. При построении дисплея для процедуры А следует только переписать эти i+1 ячейки, начинающиеся с адреса, заданного в третьем параметре, т. е. адреса глобального дисплея.
Во втором случае (рис. 8.9, Ь) А описана вне В, но возможно - обращение из В к А; следовательно, А описана в блоке, объемлющем и В. Если А имеет уровень i+1, то и из А, и из В возможны обращения к переменным в процедурах уровня 0, 1, ..., i. Как и в первом случае, для построение дисплея процедуры А требуется только переписать первые i+1 ячеек, начиная с адреса глобального дис- ; плея. . I
232
ГЛАВА 8
Четвертый неявный параметр — текущее значение STACKTOP — является* текущим адресом вершины стека, начиная с которого вызванной процедуре будет выделена память. В предположении, что данный вызов процедуры произошел не из санка, это значение совпадает со значением STACKTOP для блока, в котором возникло обращение к процедуре.
Инициализация процедуры и выход из нее
Когда происходит вызов процедуры, должна быть выделена память для ее области данных, инициализирован ее дисплей и неявные и фактические параметры должны быть перенесены в ее область данных. Точнее, для процедуры i+1-го уровня вложения нужно выполнить следующие действия:
1. Продвинуть стек на величину области данных процедуры (четвертый неявный параметр указывает текущую вершину стека). Запомнить адрес области данных в ячейке i+1 области данных (в дисплее) и в глобальной ячейке ACTIVEAREA. Запомнить адрес новой вершины стека в STACKTOP для процедуры.
2. Перенести четыре неявных параметра в эту область данных.
3. Скопировать i+1 ячейку, начиная с адреса, указанного в третьем неявном параметре, в ячейки.О, 1, ..., i этой новой области данных.
4. Перенести фактические параметры следующим образом:
а) для имен массивов: скопировать информационный вектор;
Ь) для имен процедур: скопировать_ адрес фактического параметра (для чего это делается, будет объяснено позднее);
с) для параметров, вызываемых по имени: скопировать адрес санка;
d) для параметров, вызываемых по значению: записать значение Но адресу фактического параметра в новую область данных.
При выходе из процедуры следует восстановить состояние, которое было при вызове, и затем осуществить возврат. Кроме того, если процедура является функцией, значение функции должно быть передано при помощи регистра. Восстановить состояние легко; нужно просто переслать в глобальную ячейку ACTIVE AREA второй неявный параметр процедуры. Отметим снова, что ничего не нужно делать для перенастройки указаний на вершину стека. Казалось, что перенастройка нужна, поскольку область данных процедуры больше не используется, но ячейка STACKTOP, содержащая адрес вершины стека (по правилу (8.9.2)), определена активным блоком, а он изменен.
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 233
Санки и как их вызывать
Как описывалось в разд. 8.7, санк — это программа, которая вычисляет и передает адрес фактического параметра для соответствующего формального параметра, вызываемого по имени. Так как фактический параметр — это выражение, санк не содержит ни описаний, ни блоков. Следовательно, он может использовать для своих временных переменных ячейки в том блоке, где появилось обращение к процедуре. Особое внимание следует обратить на вызовы функций, появляющиеся в санке (в выражении, которое представляет собой фактический параметр), и на этом мы остановимся. Но вначале давайте рассмотрим вызов санка и собственно санк. • v. _
Для каждого обращения к формальному параметру X, вызываемому по имени, порождается вызов санка со следующим списком параметров:
1) адрес возврата;
2) текущее значение в ACTIVEAREA;
3) значение второго неявного параметра процедуры с формальным параметром X;
4) текущий адрес вершины стека.
Как вы_ можете видеть, это очень похоже на вызов процедуры без параметров. Санк. фактически не использует второй параметр; он просто запоминается и затем восстанавливается при возврата. Третий параметр используется сайком для настройки на то окружение, в котором предстоит работать. Если вы взглянете на список параметров для обычного вызова процедуры, ’ вы заметите, что третий параметр—это адрес дисплея процедуры, из которой произошел вызов. Четвертый параметр санк использует в качестве неявного параметра при вызове любой функции, чтобы сообщить этой функции, где находится вершина стека.
Сам санк выполняет следующие действия:
1) заносит третий параметр в ACTIVE ARE А;
2) запоминает" все четыре . параметра во временных ячейках (в области данных, на которую ссылается ACTIVEAREA);
3) вычисляет адрес фактического параметра (это. как раз и является телом санка);
4) заносит второй неявный параметр из обращения к сайку в ACTIVEAREA;
5) заносит адрес, вычисляемый в п. 3, в специальный регистр и передает управление по адресу возврата.
Адрес в специальном регистре используется затем процедурой, которая вызвала санк для обращения к фактическому параметру.
234
ГЛАВА 8
Вызовы функции в санке выполняются как обычно; исключение' составляет четвертый неявный параметр вызова, который является текущей вершиной стека. Если вызов функции возник не в санке, этот адрес содержится в ячейке STACKTOP для блока, в котором произошел вызов функции. Когда же выполняется вызов функции из санка, текущая вершина стека находится в ячейке STACKTOP блока, из которого произошло обращение к санку. Этот адрес является четвертым неявным параметром при обращении к санку.
Имена процедур в качестве фактических параметров
Сложные ситуации в связи с этими параметрами возникают только в очень необычных случаях, редко возникающих в реальных программах. Тем не менее нам нужно уметь их -обрабатывать. Рассмотрим программу на рис. 8.5. Она состоит из двух параллельных наборов вложенных процедур. Проследим внимательно за их выполнением. Во-первых, вызывается процедура' С (метка L1). В теле процедуры С (метка L2) вызывается процедура А, причем в качестве фактического параметра задается имя процедуры D. Затем из процедуры А (метка L3) вызывается процедура В. Фактический параметр X {имя процедуры) в этом обращении является формальным параметром процедуры А. Наконец (метка L4), вызывается процедура Z, причем Z — это формальный параметр процедуры В. Так как при вызове В фактическим параметром является X, который в свою очередь есть D, вызывается процедура D. Теперь процедуре D необходимо знать две вещи.,
1. Адрес активного дисплея в точке программы с меткой L4, с тем чтобы можно было передать его санку для вычисления фактического параметра в вызове в L4. Мы называем его адресом дисплея фактических параметров.
2. Адрес дисплея для процедуры С, в теле которой описана процедура D, с тем чтобы из D можно было обращаться к глобальным переменным. Мы называем его адресом глобального дисплея.
Это соответственно второй и третий неявные параметры для D. В случае обычного вызова процедуры оба эти параметра совпадают и равны'значению ACTIVEAREA в момент вызова.
Если имя процедуры встречается в качестве фактического параметра, адрес, пересылаемый в списке параметров, есть адрес двух ячеек, содержащих следующее:
Адрес процедуры
Значение ACTIVEAREA в момент вызова, •
Величина во второй ячейке используется как третий неявный параметр — адрес глобального дисплея при вызове процедуры, имя которой является формальным параметром. Фактический параметр,
Организация памяти во время выполнения программы 235 который сам является формальным параметром — именем процедуры, представляется адресом фактического параметра, который передается процедуре.
Чтобы это проиллюстрировать, мы приведем ниже списки параметров для вызовов в точках LI, L2, L3 и для программы на рис. 8.5 (стр. 224)’ Заметим, что в L2 адрес DAC описывает фактический параметр D. Этот адрес заносится в список для вызова в L3. Он используется процедурой В при вызове в L4, чтобы передать адрес глобального дисплея для этого вызова.
L1: вызывается процедура С
1) адрес возврата;
2) адрес области данных главной программы;
3) адрес области данных главной программы;
4) STACKTOP при вызове.
L2: вызывается процедура А
1) адрес возврата;
2) адрес области данных процедуры С;
3) адрес области данных процедуры С;
4) STACKTOP при вызове;
5) адрес DAC (см. ниже);
6) адрес санка для 1.
L3: вызывается процедура В
1) адрес возврата;
2) адрес области данных процедуры А;
3) адрес области данных процедуры А;
4) STACKTOP при вызове;
5) адрес DAC (см. ниже).
L4: вызывается процедура Z (D)
1) адрес возврата;
2) адрес области данных процедуры В;
3) адрес области данных процедуры С;
4) STACKTOP при вызове;
5) адрес санка для F[1 J+Y.
DAC,
Адрес процедуры D
Адрес области, данных С
Переходы
Переход GOTO L, который не приводит к выходу из процедуры, не требует ничего, кроме команды передачи управления. Предположим, однако, что L оказывается во внешней процедуре уровня
236
ГЛАВА 8
i. Тогда адрес области данных для этой процедуры должен быть занесен в ACTIVEAREA перед передачей управления. Так как этот адрес находится в активном дисплее, это можно выполнить с помощью инструкций
ACTIVEAREA := CONTENTS(ACTIVEAREA+i)
Предположим, что L — формальный параметр. Соответствующий адрес в списке параметров является адресом санка, и вызов этого санка выполняется обычным способом. Из санка для фактического параметра, являющегося меткой (или любым именующим выражением), нет возврата; вместо возврата происходит переход на метку.
Еще раз заметим, что при данной схеме нет необходимости заботиться об освобождении памяти при выходе из процедуры или блока; адрес вершины стека всегда содержится в ячейке STACKTOP активного блока.
УПРАЖНЕНИЯ К РАЗДЕЛУ 8.9.
1. Рассмотрите возможность трактовки каждого фактического параметра, вызываемого по имени, как функции (процедуры POINTER) без параметров, описанной в блоке, из которого происходит вызов. Она выдает адрес значения фактического параметра. Фактические и формальные параметры тогда станут именами процедур, и обращение к формальному параметру в теле процедуры станет вызовом функции. Насколько этот метод сходен с нашим? Нужны ли по-прежнему все неявные параметры?
2. Предположим, что используется более общая схема распределения памяти. Для выделения области данных размера SIZE нужно вызвать программу GETAREA(ADDRESS, SIZE) и для освобождения области данных размера SIZE, начинающейся с ячейки ADDRESS,— программу FREEAREA(ADDRESS, SIZE). Никакие ячейки STACKTOP не нужны, так как GETAREA и FREEAREA выполняют всю необходимую работу; следовательно, нужны только три неявных параметра процедуры. Рассмотрите подробно вход в блок, выход из блока, вход в процедуру, выход из процедуры и переходы. Будьте внимательны при выходе из блока, выходе из процедуры и особенно при переходах через границы блока и/или процедуры; может оказаться необходимым освободить несколько областей данных.
3. Найдите некоторые ограничения на порядок, в котором могут освобождаться области данных для массивов и процедур (в упражнении 2), так, чтобы GETAREA и FREEAREA могли бы использовать механизм стека для распределения памяти.
4. Разработайте другую схему управления памятью в АЛГОЛе, при которой для выполнения каждого блока и процедуры выделя
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 237
ется одна область данных. При этом дисплей для каждой области данных должен содержать адрес областей данных объемлющего блока и процедуры. '
5. Разработайте схему управления памятью, использующую единственный глобальный дисплей, содержащий всегда адреса областей данных, к которым возможно обращение. (Решите сами, определены ли области данных только в процедурах или в блоках и в процедурах; и то и другое хорошо.) Следует обратить внимание на вызов процедуры; может быть, необходимо сохранить часть глобального дисплея в области данных процедуры, чтобы восстановить его при возврате. Вызов сайков будет также более трудоемким.
8.10. ДИНАМИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ПАМЯТИ
Как мы видели, для некоторых языков требуется схема динамического распределения памяти во время выполнения программы, когда блоки внутренней памяти выделяются, используются и затем освобождаются для последующего использования. В реализации АЛГОЛа, описанной в разд. 8.9, аппаратом распределения памяти был единственный стек. В других приложениях стек использовать не удается из-за нестандартности и непредсказуемости порядка, в котором блоки памяти запрашиваются и освобождаются. В этой главе были показаны два таких примера: выделение памяти для строк в XPL (разд. 8.5) и выделение памяти для структур в языке АЛГОЛ W (разд. 8.6). Аналогичная ситуация возникает в языке PL/1, когда программист с помощью инструкций ALLOCATE и FREE сам резервирует или освобождает память.
Существуют два основных метода общего распределения памяти. В обоих методах вызывается некоторая программа GETAREA (ADDRESS, SIZE) для того, чтобы выделить область из SIZE ячеек; программа записывает в ячейку ADDRESS адрес этой области. В первом методе память должна освобождаться «явно» посредством вызова программы FREEAREA (ADDRESS, SIZE). Во втором методе память «явно» не освобождается. Вместо этого в тех случаях, когда GETAREA не может найти область необходимого размера, она вызывает программу FREEGARBAGE для того, чтобы найти те области во внутренней памяти, которые не используются программой, и вернуть их системе. Кроме того, она может уплотнить используемые области — сдвинуть их вместе, так чтобы все свободные ячейки были в одном блоке.
Опишем один из способов реализации первого метода.
238
ГЛАВА 8
Метод помеченных границ для распределения памяти
Распределение памяти происходит следующим образом. Когда начинает выполняться программа, в качестве свободной памяти используется один большой блок ячеек. При выполнении программы может несколько раз вызываться GETAREA. Каждый раз она выделяет необходимые ячейки, начиная от начала свободного блока памяти, и блок приобретает следующий вид:
занято занято
занято
свободно
Заметим, что размеры занятых областей могут быть разными. В некоторый момент будет вызвана FREAREA, чтобы освободить одну из использованных областей, вообще говоря, не последнюю. После нескольких вызовов GETAREA и FREEAREA блок может выглядеть так:
занято
занято свободно занято
занято свободно свободно занято свободно
где по-прежнему размеры областей различны. Система должна помнить расположение всех, свободных областей, с тем чтобы они могли быть снова использованы. Более того, смежные свободные области следует сливать в одну свободную область так, чтобы память не оказалась разбитой на области, слишком малые для использования. В приведенной выше схеме можно слить две свободные области.
Описываемый нами метод помеченных границ принадлежит Кнуту [68]. Метод требует резервирования для системных нужд двух ячеек на границах каждой области (одной в начале и одной в конце). Это приемлемая плата, так как в случаях, в которых применяется этот метод, требуются довольно большие области, например области данных процедур и память для массивов. Преимущество этого метода в том, что необходимо по существу фиксированное время, чтобы освободить область и объединить ее со смежными свободными областями, если это возможно. В других методах для этой цели требуется просмотр некоторого списка.
Ниже приводится формат каждой занятой и свободной области. Первое слово содержит поле TAG, которое указывает, свободна ли область или нет; в поле SIZE содержится число слов в области. Свободные области связываются вместе в двусвязанный список. Поле FLINK (ссылка вперед) указывает на следующую область списка, в то время как поле BLINK (ссылка назад) указывает на предыдущую область.
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 239
ТА£
TAG
TAG SIZE BLINK FLINK
TAG SIZE
Свободная область
Резервированная область
Кроме того, существует одна переменная FREE следующего вида:
TAG SIZE BLINK
FLINK
FREE
0 на последнюю область в списке на первую область в списке
Поле BLINK первой области в списке указывает на ячейку FREE, так же, как и поде FLINK последней области. Наконец, мы предположим, что блоку, используемому для распределения памяти, предшествует слово, а за блоком следует слово, содержащее в поле TAG для указания о том, что «окружающие» области заняты. Такое соглашение упрощает процесс объединения смежных областей.
Теперь мы готова представить программу GETAREA. В программе используется метод «первый подходящий»; просматривается список свободных областей и выбирается первая из них, которая является достаточно большой. Несмотря на то что выбор «наиболее подходящей» области кажется на первый взгляд лучше, на самом деле это не так (см. Кнут [68]), и, кроме того, на это затрачивается, очевидно, больше t времени. Если в программе требуется SIZE слов, а свободный блок содержит до SIZE+10 слов, программа не разбивает его на две области, оставляя одну из них в списке свободных. Это могло бы привести к тому, что память оказалась бы разбитой на очень малые практически бесполезные области. Число 10 выбрано довольно произвольно.
PROCEDURE GETAREA (ADDRESS, SIZE);
BEGIN POINTER P, Q, QI;
INTEGER S, SI;
P : —FREE.FLINK;
S :=SIZE + 2; SI :=SIZE+10;
WHILE P# ADDRESS (FREE) DO BEGIN IF P.SIZE^Sl THEN
BEGIN SL: = P.S1ZE —S;
Q: = P+S: QI : = Q + Sl — 1;
P указывает на текущую область.
S — это минимальный необходимый размер области.
Любая область , размер которой меньше S1, не делится на две области.
Просмотр областей по порядку.
Разбиение большой области на две области, размерами S и S1.
240 ГЛАВА 8
CONTENTS(Q): = CONTENTS(P);
Q.SIZE:=Q1.SIZE:=S1;
Q.TAG:=‘—’;
P.FLINK.BLINK:-
P. BLINK. FLINK:=Q;
q:—q_ 1; p.siZE :=S;
GOTO FOUND;
END;
IF P.SIZE S AND P.SIZE SI
THEN
BEGIN
P. BLINK. FLINK:-P.FLINK;
P.FLINK.BLINK:=P.BLINK;
Q—P4-P.SIZE-I; GOTO FOUND
END; P P.FLINK
END;
WRlTEfERRORNO BLOCK.’);
STOP;
FOUND: P.TAG := Q.TAG := ‘+’;
ADDRESS := P+1;
END
Перенос полного слова по указателю Р в слово по указателю Q.
Занесение в список верхней области.
Формирование SIZE для нижней области и выход.
Если область достаточно велика, выбрасывание ее из списка.
Размер области недостаточен; нужно проверять следующую область.
Нет достаточно большого блока.
Область размещена в ячейках от Р до Q.
Программа FREEAREA освобождает область и объединяет ее; если это возможно, со смежными свободными областями. Заметим, что в данном методе не используется параметр SIZE, так как необходимая информация находится в области.
PROCEDURE FREEAREA (ADDRESS, SIZE) BEGIN POINTER L,M,U,Q;
Misaddress—i; U: = m + m.size;
L:=M~1;
IF U.TAG —THEN
BEGIN M.SIZE: sM.SIZE+U.SIZE;
U.BLINK.FLINK:=U.FLINK;
U.FLINK.BL1NK:=U.BLINK; _
END;
Q : = M+M.SIZE—1;
IF L.TAG == ’ THEN
BEGIN L := M—L.SIZE;
L.SIZE L.SIZE+M.SIZE; '
Q.SIZE:=L.SIZE; Q.TAG:=<—’ END ,
Установка, указателя М на данную область, U — на соседнюю, ниже расположенную область, L — на конец выше расположенной.
Если ниже расположена свободная область, то присоединяем ее к средней области и уничтожаем ее в списке.
Q указывает на конец области, начало -ее определяет М. Если свободна область выше, то эта область просто добавляется к освобождаемой.
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 241
ELSE BEGIN Q.S1ZE: = M.SIZE;
M.TAG := Q.TAG :
M. FLINK FREE.FLINK;
M.BLINK: = ADDRESS(FREE);
FREE.FLINK. BLINK:=M;
FREE.FLINK:= M
END END
В противном случае область добавляется в начало списка свободных областей.
Сбор мусора
При втором методе распределения памяти, когда GETAREA не может найти подходящую область, вызывается программа FREEGARBAGE, цель которой — найти неиспользуемые области и за-, нести их в некоторый спйсок свободных областей. Для этого FREEGARBAGE должна быть в состоянии определить следующее:
1) расположение в памяти каждого описанного указателя;
2) точные сведения о величине, на которую ссылается каждый указатель,— длина величины и содержит ли она какие-нибудь указатели;
{ 3) для каждого указателя, содержащегося в величине, на которую ссылается другой указатель, длину указателя и его расположение в величине.
Как легко видеть, это довольно сильное требование, и поэтому, используя указатели, нужно придерживаться строгих правил. Поэтому обычно «сбор мусора» используется в тех случаях, когда система имеет определенную уверенность в том, что указатели употребляются правильно, и когда число различных форматов для величин невелико. Хорошим примером такой системы является LISP. Другой пример — это система обработки строк, преимущество которой состоите том, что величины, на которые ссылаются указатели строк, являются только строками литер, так что величина, на которую ссылается указатель, никогда не содержит других указателей.
Другая проблема состоит в трудности точного определения, какие области на любом этапе свободны. Это хорошо иллюстрирует пример на АЛГОЛе W. Рассмотрим фрагмент программы:
RECORD LISTOFREAL(REAL A; POINTER NEXT);
Р LISTOFREAL(2.0, LISTOFREAL(3.0, 0));
Чтобы выполнить последнюю инструкцию, сперва выделяется память для величины LISTOFREAL и в нее заносится (3.0, 0). Затем
242
ГЛАВА 8
выделяется память для другой величины LISTOFREAL, в которую заносится (2.0, Q), где Q — указатель на первое значение (3.0, 0). Предположим теперь, что не хватает памяти для второй величины. Тогда вызывается программа FREEGARBAGE. Заметим, что указатель с адресом Q в этот момент еще не сформирован, так что ячейки, содержащие (3.0, 0), оказываются как бы неиспользуемыми.
Это не означает, что из такой ситуации нет выхода, но нужно быть внимательным, чтобы она не оказалась неожиданностью.
Обычно сбор мусора проходит в две фазы. Во время первой фазы некоторым образом маркируются все используемые величины. Общепринятый метод состоит в том, чтобы иметь в каждой величине дополнительный бит специально для маркировки, хотя в некоторых случаях это неудобно. Другой метод заключается в том, что все биты маркировки собираются в отдельную таблицу с определенным соответствием между ячейками и битами маркировки. Однако при этом требуется специальная таблица для битов маркировки, а по-видимому, когда вызывается сборщик мусора, объем свободной памяти очень мал!
Во второй фазе мы просматриваем последовательно всю память, занося непомеченные области в список свободных областей и гася биты маркировки. Последнее делается для того, чтобы при следующем вызове сборщика мусора можно было бы правильно сформировать биты маркировки.
Иногда используется третья фаза, которая собирает свободные области вместе, так чтобы они образовывали один большой блок. Для этого требуется, чтобы программа сбора мусора изменяла значения указателей при перемещении данных.
Для рассмотрения существующих алгоритмов сбора мусора отсылаем читателя к гл. 2 книги Кнута [681.
Системы с двухуровневым распределением памяти
В некоторых системах имеются два уровня распределения памяти; большие блоки внутренней памяти резервируются и освобождаются согласно одному методу, в то время как каждый большой блок может быть подразделен с помощью другого метода. Такой прием используется в АЛГОЛе W. Каждому типу структуры присваивается целочисленный номер, и в таблице для каждого типа хранится описатель. Этот описатель содержит число ячеек, используемых величиной, и расположение всех указателей в данной структуре. Фактическая структурная величина содержит один дополнительный байт (в машине IBM 360); семь его битов образуют номер для типа структуры, последний бит используется для маркировки при сборе мусора.
Для каждого типа структуры выделяется большой блок внутренней памяти всякий раз, когда это необходимо. Все хранящиеся
ОРГАНИЗАЦИЯ ПАМЯТИ ВО ВРЕМЯ ВЫПОЛНЕНИЯ ПРОГРАММЫ 243
в нем величины принадлежат этому структурному типу, а свободные области объединены в один список свободных областей. Это позволяет эффективно выполнять выделение памяти для величины, беря очередную, свободную область в списке свободных для этого типа. Это не трудно, так как все свободные области в списке содержат одно и то же число ячеек. -
Если в списке для структурного типа не существует свободных областей, система запрашивает другой большой блок. Если Дольше нет больших блоков, выполняется сбор мусора, причем неиспользованные области заносятся в список свободных для каждого типа и пустые большие блоки передаются главной программе распределения памяти.
8.11. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Два коротких обзора методов хранения массивов и обращения к их элементам принадлежат’ Геллерману [621 и Гауэру [621. Действительно, эти,методы были независимо открыты многими программистами и трудно приписать их какому-либо одному человеку. Кнут [681 предлагает несколько других методов для хранения массивов, особенно интересных для треугольных и разреженных матриц.
Вопросы реализации различных типов структур рассматриваются в работах Вирта и Хоора166], Стендиша [68], Бауэра, Беккера и Грехема 1681 и в руководстве фирмы IBM по программированию-на^РЬ/Е Хоор [681 дает более полное рассмотрение структур и их реализации.
Выпуск САСМ за январь 1961 г. полезен тем, кто интересуется историей реализации АЛГОЛа, хотя многие описанные там приемы устарели. Ренделл и Рассел [64] описывают метод, реализации АЛГОЛа, при котором область данных выделяется при каждом выполнении блока с использованием глобального дисплея. Метод, подробно описанный в разд. 8.9, был использован в компиляторе ALGOR ILLINOIS для машины 7090 (см. Грис, Пол и Вил [65]).
Как уже неоднократно упоминалось, глава 2 книги Кнута [68] содержит превосходное описание нескольких методов распределения памяти, причем большее число.методов приведено в упражнениях. Там также дан анализ эффективности некоторых методов. Росс [67Ы рассматривает пакет программ для управления свободной памятью AED, представляющий собой хороший пример универсальной двухуровневой схемы распределения памяти.
Глава 9
Организация таблиц символов
Проверка правильности семантики и генерация кода требуют знания характеристик идентификаторов, используемых в программе на исходном языке. Эти характеристики выясняются из описаний и из того, как идентификаторы используются в программе, и накапливаются в. таблице символов или в списке идентификаторов. В данной главе рассматриваются способы организации, построения и поиска в таблице символов. Останавливаясь на организации таблиц вообще, мы обратим особое внимание на нашу конкретную проблему — проблему организации таблиц символов.
9.1. ВВЕДЕНИЕ В ОРГАНИЗАЦИЮ ТАБЛИЦ
Таблицы всех типов имеют общий вид
где слева перечисляются аргументы, а справа — соответствующие значения. Каждый элемент обычно занимает в машине более одного слова. Если элемент занимает к слов и нужно хранить N элементов, то необходимо иметь k*N слов памяти. Расположить информацию можно двумя способами:
1. Каждый элемент поместить в к последовательных слов и иметь таблицу из k*N слов.
2. Иметь к таблиц, скажем, Tl, Т2, . . . , Тк, каждая из N слов. Весь i-й элемент при этом будет находиться в словах Tlj, . . . , Тк».
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
245
Вопрос выбора между этими двумя методами — это только вопрос удобства программирования.
В нашем частном случае аргументами таблицы являются символы или идентификаторы, а значениями — их характеристики. Так как число литер в идентификаторе непостоянно, в аргументе часто помещают вместо самого идентификатора указатель на идентификатор. Это сохраняет фиксированным размер аргумента.
а Ь
Рис. 9.1. Два способа запоминания аргументов.
Идентификаторы хранятся в специальном списке строк. Число литер в каждом идентификаторе может храниться как часть аргумента или в списке идентификаторов прямо перед идентификатором. На рис. 9.1 показаны оба способа на примере таблицы, содержащей элементы для идентификаторов I, МАХ и J.
Когда компилятор начинает трансляцию исходной программы, таблица символов пуста или содержит только несколько элементов для служебных слов и стандартных функций. В процессе компиляции для каждого нового идентификатора элемент добавляется только один раз,'но поиск ведется всякий 'раз, когда встречается этот идентификатор. Так как на этот процесс уходит много времени при компиляции, важно выбрать такую организацию таблиц, которая допускала бы эффективный поиск.
Желательно сравнить различные методы работы с таблицами по времени поиска. Мы будем проводить сравнение в терминах ожидаемого числа Е сравнений аргументов, которые нужно выполнить, чтобы найти данный символ. Это число, зависящее от коэф* фициента загрузки If (load factor) таблицы в данный момент, представляет собой отношение текущего цисла элементов п к максимально возможному числу элементов N :
lf=n/N.
246
ГЛАВА 9
Мы выпишем уравнения для ожидаемого числа сравнений, но не дадим их решения — полный анализ этого вопроса читатель сможет найти в работах, перечисленных в разд. 9.6.
9.2. НЕУПОРЯДОЧЕННЫЕ И УПОРЯДОЧЕННЫЕ ТАБЛИЦЫ
Простейший способ организации таблицы состоит в том, чтобы добавлять элементы для аргументов в порядке их поступления, без каких-либо попыток упорядочения. Поиск в этом случае требует сравнения с каждым элементом таблицы, пока не будет найден подходящий. *Для таблицы, содержащей п элементов, в среднем будет выполнено п/2 сравнений. Если п велико (20 или более), этот способ неэффективен.
Поиск может быть выполнен более эффективно, если элементы таблицы упорядочены (отсортированы) согласно некоторому естественному порядку аргументов. В нашем случае, где аргументами являются строки литер, наиболее естественным является упорядочение, порождаемое внутренним представлением строк литер. Обычно оно совпадает с лексикографическим порядком. Так, строки А, АВ, АВС. АС, ВВ расположены в возрастающем порядке. Эффективным методом поиска в упорядоченном списке из п элементов является так называемый бинарный или логарифмический поиск. Символ S, который следует найти, сравнивается с аргументом элемента (n + 1 )/2 в середине таблицы. Если этот элемент не является требуемым, мы должны просмотреть только блок элементов, пронумерованных от 1 до (п + 1)/2—1, или блок элементов от (n+1)/2+1 до п в зависимости от того, меньше искомый элемент S или больше элемента, с которым его сравнивали. Затем мы повторяем процесс над блоком меньшего размера. Так как на каждом шаге число элементов, которые могут содержать S, сокращается наполовину, максимальное число сравнений равно l+log2n.
Если п=2, нам необходимо самое большее 2 сравнения; если п=4, то 3; если п=8, то 4. Для п= 128 бинарный поиск требует самое большее 8 сравнений, в то время как для поиска в неупорядоченной таблице требуется в среднем 64 сравнения.
Приведем программу бинарного поиска.'
PROCEDURE binsearch (Т, n, ARG, к); Поиск в массиве Т строки, равной ARG. STRING ARRAY Т; STRING ARG; Если строка найдена, занести в к
INTEGER п, к; индекс элемента; в противном случае
BEGIN INTEGER i, j; занести 0, п>0.
i :==x 1; j := n; Первый блок — весь массив.
LOOPfk (i + j)//2; к указывает на средний элемент в
блоке.
IF ARG T |k| IHEN Проверка- равен ли ARG элементу к? /
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
247
BEGIN IF ARG < 1 [к] Проверка: в верхнем или нижнем блоке
нужно искать ARG?
THEN j : = k— 1 ELSE i :=k + l; Затем проверка: существует ли еще IF j^i THEN GOTO LOOP; блок?
k := 0; Аргумент не найден, так как блоков
END больше нет.
END
Для бинарного поиска элементы должны быть упорядочены. Этого можно добиться с помощью метода упорядоченных вставок. Он применяется^ тех случаях, когда таблица часто просматривается до того, как она полностью заполнена, и, следовательно, должна быть упорядоченной на всех этапах. Элемент для символа S вставляется следующим образом:
1. Используется процедура binsearch, чтобы найти к, такое, что Sk<S<Sk+1.
2. Элемент п сдвигается в позицию n+1; элемент п—1 — в позицию п, . . . ; элемент к+1 — в позицию к+2.
3. S заносится в элемент к+1 (который освободился на шаге 2).
Если заполнение таблицы предшествует поискам, то упорядочение можно выполнить после заполнения. Здесь мы не будем рассматривать этот случай. Библиография по этому вопросу приводится в разд. 9.6. ' ' -
9.3. ХЕШ-АДРЕСАЦИЯ1)
Это метод преобразования символа в индекс элемента в таблице (элементам присваиваются номера 0,1,2 .. . , N — 1, если таблица состоит из N элементов). Индекс получается «хешированием» символа — выполнением над символом (и, возможно, над его длиной) некоторых простых арифметических или логических операций. Простой хеш-функцией является внутреннее представление первой литеры символа. Так, если двоичное представление А есть 11000001, то результатом хеширования символа АВЕ будет код 11000001 (С1 в шестнадцатеричной системе счисления). Начальным индексом, с которого начинается поиск элемента для аргумента АВЕ, будет 11000001. На рис. 9.2 это показано для идентификаторов АВЕ, В и I.
Пока для двух различных символов результаты хеширования различны, время поиска совпадает с временем, затраченным на хе-
х) Принятые в этой книге термины «хеш-адресация» и «хеширование» соответствуют английским терминам hash addressing и hashing. В других книгах для аналогичных понятий читатель может встретить термины: «работа с перемешанными таблицами», «функции расстановки», «рандомизация» и т. п.— Прим. ред.
248
ГЛАВА 9
ширование. Так мы получаем огромную экономию по сравнению с временем поиска по неупорядоченной таблице из п позиций (в среднем п/2 сравнений) или даже по сравнению с временем поиска по упорядоченной таблице. Однако возникает затруднение, если результаты хеширования двух разных символов совпадают. Это называется коллизией. Очевидно, в данной позиции таблицы может быть помещен только один из этих символов, так что мы должны
Идентификатор Двоичное представление первой литеры । 40 г < <Л ПП 1 . Таблих 1 1 СПМвЫ Г "'! ТОв : Элемент. 0 Элемент 11000001 Элемент 11000010 Элемент 1 1001001
Ad и 1 1 Uu U U U 1 । АВЕ
I 11001001 1 В
-
il 1
Рис. 9.2. Хеш-адресация.
найти другое место для второго. Хорошая хеш-функция распределяет вычисляемые адреса равномерно на все имеющиеся в распоряжении адреса, так что коллизии не возникают слишком часто. Хеш-функция, описанная выше, очевидно, плоха, так как все идентификаторы, начинающиеся с одной и той же буквы, ссылаются на один и тот же адрес. Мы сейчас рассмотрим различные хеш-функции, но сначала давайте обсудим два способа решения задачи коллизии — рехеширование и метод цепочек.
Мы предположим, что каждый табличный элемент занимает одно слово. Тогда для таблицы с N элементами значениями функции хеширования h являются целые числа 0,1,2, . . . , N—1. Если табличный элемент состоит из к слов, то для вычисления его адреса необходимо к базовому адресу таблицы добавить произведение значения хеш-функции h на к.
9.3.1. Рехеширование
Предположим, что мы хешируем символ S и обнаруживаем, что другой символ уже занял элемент h. Возникает коллизия. Тогда сравниваем S с элементом h+px (по модулю N, где N — длина таблицы) для некоторого целого рь Если снова возникает коллизия, сравниваем S с элементом h+p2 (по модулю N) для некоторого целого р2. Это продолжается до тех пор, пока не встретится какой-нибудь элемент h+pi (по модулю N), который либо пуст, либо содержит S, либо снова является элементом h (р i=0). В последнем
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
249
случае мы прекращаем выполнение программы, поскольку таблица полна.
Таким'образом, если возникло i коллизий, будет выполнено i + 1 сравнение с элементами h^h+pi (по модулю N). Величины Pi должны выбираться так, чтобы ожидаемое число сравнений Е было невелико и чтобы по возможности было рассмотрено большее
Рис. 9.3. Пример линейного рехеширования.
число элементов. В идеальном случае pj должны охватывать целые числа 0,1, . . . , N—1. Мы рассмотрим четыре возможных способа определения рь
Рехеширование обычно связывается с термином рассеянной памяти, так как заполненные позиции оказываются рассеянными по всей таблице. Заметим, что для того, чтобы отличать пустые элементы от заполненных, все элементы таблицы должны быть первоначально заполнены каким-либо значением, которое не может встречаться как символ. Кроме того, таблица должна быть сразу рассчитана на максимальное число элементов, поскольку нет простого способа расширить таблицу, если она заполнится, без перевычисления хеш-адресов для всех записанных символов и занесения их в соответствующие новые позиции.
Линейное рехеширование
Старейший известный метод рехеширования (и, вероятно, наименее эффективный) состоит в том, чтобы положить pt = 1, р2 = 2, Рз—3 и т. д. Таким образом сравниваются последовательные эле-ментьТ Предположим, например, что символы S1 и, S2 были хешированы и записаны в элементы 2 и 4 соответственно (рис. 9.3,а).
Теперь предположим, что символ S3 также ссылается на элемент 2. Вследствие коллизии он будет занесен в элемент 3 (рис. 9.3, Ь). Наконец, предположим, что следующий символ S4 также ссылается на элемент 2. Возникают последовательно три коллизии — с
.250
ГЛАВА 9
SI, S3 и S2 — прежде, чем S4,* наконец, заносится в элемент 5 (рис. 9.3, с).
Причина низкой эффективности этого метода становится достаточно ясной из этого примера; после нескольких коллизий, разрешенных таким образом, элементы скапливаются вместе, образуя длинные цепочки заполненных элементов. Оценка среднего числа сравнений Е для поиска одного элемента есть
Е - (.1—lf/2)(l—If),
где If — коэффициент загрузки. Таким образом, если таблица заполнена на 10%, мы можем ожидать 1,06 сравнений; если она заполнена наполовину,—1,5 сравнений, и если таблица заполнена на 90%,—5,5 сравнений. Заметим, что Е зависит не от размера таблицы, а только от степени ее заполнения.
Мы можем найти лучшие значения рь р2, . . г , но даже с рассмотренными значениями этот метод все же быстрее поиска методом бинарного дерева. Предположим, что таблица из 1024 элементов заполнена наполовину. Следовательно, заполнены 512 элементов. При бинарном поиске мы ож даем от 9 до 10 сравнений, в то время как здесь только 1,5. Время поиска для упорядоченных и неупорядоченных таблиц зависит не от максимального размера таблицы, а от текущего числа элементов.
Случайное рехеширование
Этот метод снимает проблему скопления, которая свойственна линейному рехешированию, за счет выбора в качестве pi псевдослучайных чисел. Если размер таблицы представляется степенью двойки (N=2k для произвольного к), то хорошие результаты дает следующий способ вычисления pi (см. Моррис):
1. При вызове программы положить целое R равным 1.
2. Вычислять каждое pi следующим образом:
а) установить R = R*5;
в) выделить младшие к+2 разряда R и поместить результат в R;
с) взять величину из R, сдвинуть ее вправо на 2 разряда и результат назвать pj.
Важнейшее свойство этого метода, предотвращающего скопление, состоит в том, что все числа pi+k—Pi различны. Хорошее приближение ожидаемого числа сравнений Е дает формула
Е =- (1/lf) log (1—If),
где If — это коэффициент загрузки. Так, если таблица заполнена на 10%, ожидается 1,05 сравнений; если она заполнена наполовину,— 1,39 сравнений, и если она заполнена на 90%,— 2,56 сравнений.
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
251
Рехеширование сложением
Примем рj=ih, где h — исходный хеш-индекс. Таким образом мы будем пробовать элементы h, 2h, 3h, 4h, . . . (все значения вычисляются по модулю, равному размеру таблицы). Этбт метод хорош, когда размер таблицы N является простым числом, так как все последовательности покрывают полностью -все возможные индексы 1, : . . , N—1. Новый хеш-индекс очень просто вычислить. Однако мы должны,брать в качестве h целые числа 1,2,3, . . . .. ., N — 1 вместо 0,1; .. . , N—1, с тем чтобы исключить значение h, равное 0.
Квадратичное рехеширование .
Этот частный метод использует pi=ai2+bi+c для некоторых величин а, b и с, которые могут иметь любые значения. Главная проблема, однако, состоит в том, чтобы обеспечить покрытие значениями pt достаточно большого числа элементов таблицы. Например, если окажется р^б, р2= 10, р3==5, р4= 10, рб^5, р6= 10, . . . , то мы сможем проверить самое большее три элемента: h, h+5 и h+10.
Если размер таблицы является степенью 2, оказывается, что число элементов, просматриваемых при квадратичном поиске, слишком мало. Однако, когда размер Таблицы — простое число, квадратичный поиск охватывает точно половину таблицы. Этот методу конечно, не так хорош, как метод случайного рехеширования, но здесь и число ожидаемых коллизий, и время, требуемое для вычисления рь меньше, чем при случайном рехешировании.
Выбор величин а, b и с может зависеть от машины — некоторые машинные команды могут сделать более эффективным использование определенных значений для а, b и с. ДаЬайте разберем пример квадратичного рехеширования на IBM 360, чтобы показать, как можно выбрать коэффициенты для построения эффективной программы. Мы предположим, что таблица, состоящая из 787 элементов, начинается в ячейке HTBL.
Положим с — 0; при этом, если предположить, что первый проверяемый элемент определяется индексом h+p0, мы будем иметь р0—0. Далее, pi+1—Pi=2ai+a+b. Чтобы получить коэффициент — 1 прил, мы полагаем а=—что дает
Pi+i—Pi = — i—1/2+b.
Следовательно, если i увеличивается на 1, приращение уменьшается на 1. Если мы вначале зашлем в регистр INC значение — Уа+Ь, чтобы получить следующее приращение, мы должны только уменьшить INC на 1. Мы можем также использовать INC для того, чтобы останавливаться после того, как просмотрена половина таблицы. Мы должны остановиться после 393 проверок, так что, если мы положим Ь=392+1/а, мы остановимся при INC —— 1. Окончательная
252
ГЛАВА 9
формула в этом случае имеет вид
Р1=— (1/2) i2+ (392+1/2) i.
Читатель должен теперь заметить, что, так как каждый элемент таблицы имеет длину ,4 байта, мы должны при обычной работе умножать приращение на 4: Это делает приведенная ниже программа на языке ассемблера IBM 360. Для простоты программа отыскивает в таблице свободный (равный нулю) элемент, а не заданный.
* Используемые регистры
HASH EQU 2 Текущий индекс h+Pi; первоначально
FR EQU 3
INC EQU 4
KN 'EQU 5
Z0 EQU 6
INIT L HASH,H
LA INC, 1568
LA KN,3148
SR ZO.ZO
В COMP
COLIS EXLE INC,FR,FULL
BXH HASH,INC,COMP
SR HASH,KN
COMP’ C ZO.HTBL(HASH)
BNE COLIS
Сюда попадаем, когда HTBL (HASH)
9.3.2. Метод цепочек
он равен h.
Содержит —4 (4 байта на элемент).
Содержит pi+1— pi.
Общее число байтов в таблице: 787*4. Содержит 0.
Загрузка в регистр начального значения хеш-функции (0, 4, 8, . . .). Начальное приращение (Ь—%)*4.
Размер таблицы=787*4.
Очистка регистра для сравнений. Переход к первому сравнению.
Вычитаем 4 из приращения. Если результат =—4, слишком много коллизий; тогда выходим из программы на метку FULL (в программе ее нет). Добавляем приращение к значению хеш-функции, чтобы получить h+рр Если результат < KN (в регистре 5), пропускаем следующую команду.
Берем h+pi по модулю, равному раз- . меру таблицы.
Равен ли элемент 0? Если нет, переход к COLIS, чтобы установить INC и проверить следующий элемент, содержит 0.
Метод цепочек использует хеш-таблицу, элементы которой, называемые указателями, первоначально равны 0, собственно таблицу символов, вначале пустую, и указатель POINTFREE, который указывает на текущее положение последнего элемента в таблице символов. Первоначально POINTFREE указывает на ячейку перед началом таблицы. Элементы таблицы символов имеют дополнительное поле CHAIN, которое может содержать нуль или адрес другого элемента таблицы символов. Начальное состояние выглядит так;.
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
253
Хеш-таблица указатель
1 О
2 О
Таблица символ об
АРГ значение CHAIN
Хеш-функция, примененная к символу, дает индекс указателя в хеш-таблице. Указатель либо равен нулю, либо указывает на первый Элемент таблицы Символов с данным значением хеш-функции. Поле CHAIN каждого элемента используется для того, чтобы связать в цепочку элементы, для которых хеширование символа приводит к тому же самому указателю. Рассмотрим процесс шаг за шагом. Мы начинаем с пустой таблицы символов, как было описано выше. Предположим, что символ, например S1, должен быть записан в таблицу символов. Функция хеширования вырабатывает адрес элемента хеш-таблицы, например указателя 4, который равен нулю. Тогда выполняется следующее:
1. Прибавляем 1 к POINTFREE.
2. Вносим элемент (S1, значение, 0) в позицию таблицы символов, на которую указывает POINTFREE.
3. Заносим содержимое POINTFREE в указатель 4.
Это дает
Хеш-таблица
Таблица символов
1 2
3 4
5
0 0 о
POINTFREE
Пока поступают символы, хеширование которых дает индексы разных указателей, они .вставляются так, как это описывалось выше. Так, если мы записываем символы.82, S3 и S4, хеширование которых дает ссылки на указатели 1,3 и 6 соответственно, то таблицы будут выглядеть так:
Хеш,'таблица
Таблица символов
254
ГЛАВА 9
В конце концов поступит символ S5, который ссылается на указатель, использовавшийся ранее. Вот здесь и начинает действовать ноле CHAIN. Символ S5 записывается в таблицу символов и добавляется в конец цепочки для этого указателя. Таким образом, если S5 ссылается на указатель 6, мы получаем следующую структуру:
Хеш-таблица
Таблица символов
После вставки символов S6, S7 и S8, которые ссылаются, скажем, на указатели 4,3 и 3 соответственно, мы в конце получили бы следующую структуру:
Хеш-таблица
Таблица символов
Ниже приводится блок-схема процедуры, которая ищет в таблице символ S и, если он отсутствует, заносит его в таблицу. В этой схеме PJ и Р2 являются временными переменными типа указатель. HASH — это функция хеширования, которая дает адрес указателя из хеш-таблицы для ее аргумента, символа S. В конце работы Р2 содержит адрес элемента.
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
255
Если таблица символов заполнилась, можно всегда добавить к ней новый блбк элементов (если язык или система допускает динамическое распределение памяти), так как функция хеширования дает индекс в хеш-таблице, а ссылки на таблицу символов выполняются только при помощи указателей. Таким образом, максимальное число элементов в таблице символов, в отличие от метода рехеширования, не ограничено (однако ограничено максимальное число указателей). Заметим также, что только указатели требуют начальной установки, но не сами элементы таблицы символов. Число указателей находится в пределах от 100 до 300, в то время как элементов в таблице символов намного больше. Как только все символы внесены в таблицу, хеш-таблицу можно уничтожить и ее место использовать для других целей (мы предполагаем, что все идентификаторы заменены в таблице символов номерами элементов или чем-нибудь подобным). Для метода цепочек требуется одно дополнительное слово для каждого элемента, и в большинстве случаев это окупается.
9.3.3. Хеш-функции
Если символ S, являющийся аргументом хеширования, занимает более одного машинного слова, то на первом шаге хеширования по S формируется одно машинное слово S\ (Например, в IBM 360 в одном слове размещается 4 литеры.) Как правило, S' вычисляется суммированием всех слов при помощи обычного сложения или при помощи поразрядного сложения по модулю 2 (т; е. по операции EXOR — исключающее ИЛИ, которая определяется следующим образом: 1 EXOR 1=0, 0EXOR 0=0, 1 EXOR 0=1,0 EXOR 1 = 1).
На втором шаге из S' вычисляется окончательный индекс, причем это можно сделать несколькими способами:
256
ГЛАВА 9
1. Умножить S' на себя и использовать п средних битов в качестве значения функции хеширования (если таблица имеет 2П элементов). Поскольку п средних битов зависят от каждого бита S', этот метод дает хорошие результаты.
2. Использовать какую-нибудь логическую операцию, например EXOR, над некоторыми частями S'.
3. Если в таблице имеется 2П элементов, расщепить S' на п частей и просуммировать их. Использовать п крайних правых битов результата.
4. Разделить S' на длину таблицы и остаток использовать в качестве хеш-индекса.
Все эти методы применялись и давали удовлетворительные результаты. Можно было бы разработать и другие методы. Нужно только быть уверенным, что на множестве аргументов, к которому будет применяться функция хеширования, она дает достаточно случайные адреса. В нашем случае, когда начальное формирование таблицы состоит в занесении в нее всех резервируемых слов и стандартных идентификаторов языка, стоит проверить первоначальную таблицу и посмотреть, каково число возникших коллизий. Хеш-функция может быть достаточно хорошей с точки зрения статистики, но может как раз случиться, что 10 резервируемых слов ссылаются на один и тот же адрес!
Следует также упомянуть, что два крайних левых бита в коде EBCDIC для всех прописных букв и чисел совпадают (11), а в коде ASCII совпадают два крайних .левых бита для прописных-букв (10). Так что будьте осторожны при построении хеш-функций.
В компиляторе с языка PL/1 уровня F (см. IBM (b)) используется следующая хеш-функция:
1. Суммируются последовательные части идентификатора, содержащие по четыре литеры, в один 4-байтовый регистр. .
2. Результат делится на 211 и получается остаток R.
3. Берется значение 2*R в качестве индекса для ссылки на. хеш-таблицу из 211 указателей (каждый указатель имеет длину 2 байта).
Каждый идентификатор и константа в исходной программе заменяется ссылкой на ее элемент в таблице символов. После заполнения таблицы символов хеш-таблица отбрасывается. Элементы таблицы символов имеют переменную длину (минимум 4 байта плюс имя в коде EBCDIC).
9.4. ТАБЛИЦЫ СИМВОЛОВ, ИМЕЮЩИЕ СТРУКТУРУ ДЕРЕВА
В этом методе для упорядочения элементов используется бинарное дерево, в котором к каждому узлу может быть «подвешено» не более двух поддеревьев. Каждый узел дерева представляет собой
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
257
заполненный элемент таблицы, причем корневой узел является первым элементом. На рис. 9.4, а показана таблица с одним элементом для идентификатора G. Предположим теперь, что надо записать идентификатор D. Для него выбирается левое поддерево, так как D < G (рис. 9.4,ft). Теперь запишем идентификатор М. Так как G <М, для М выбирается правое поддерево G (рис. 9.4, с). Наконец, запишем идентификатор Е. Так как E<G, идем по левой дуге от G
Рис. 9.4. Пример бинарного дерева.
и попадаем в D. D<E, поэтому мы выбираем дугу, ведущую вправо от D (рис. 9.4, d). На рис. 9.4, е изображено дерево после того, как последовательно добавлены идентификаторы А, В и F.
Для реализации метода можно в каждом элементе выделить два поля указателей, одно поле для левой, а другое — для правой ветви. Число требуемых сравнений во многом зависит от порядка, в котором поступают идентификаторы. Например, если они поступают в таком порядке: А, В, С, D, Е, F, то, чтобы найти F, нужно 6 сравнений. Можно перестраивать дерево на определенных этапах работы для того, чтобы сбалансировать его и уменьшить максимальный поиск. Описанным бинарным деревом можно воспользоваться для печати списка идентификаторов в алфавитном порядке (см. упражнение 1).
Компилятор FORTRAN Н (см. IBM (а)) работает с шестью такими деревьями, по одному дереву для идентификаторов, состоящих из 1,2,3,4,5 и 6 литер соответственно. Имеется также по одному дереву для констант, занимающих 4,8 и 16 байтов, дерево для меток инструкций и несколько других. Все элементы содержатся в одной И той же таблице; каждый элемент занимает 52 байта (13 слов).
УПРАЖНЕНИЯ К РАЗДЕЛУ 9.4
1. Построить алгоритм печати в алфавитном порядке имен, хранящихся в узлах бинарного дерева. Указание: нужно воспользоваться стеком для хранения точки дерева, в которой мы находимся в любой момент времени и пути, по которому мы в нее попали.
Д- Грис
258
ГЛАВА 9
9.5. ТАБЛИЦЫ СИМВОЛОВ, ИМЕЮЩИЕ БЛОЧНУЮ
СТРУКТУРУ
Языки типа АЛГОЛ имеют структуру вложенных блоков и процедур. Один и тот же идентификатор может быть описан и использован много раз в различных блоках и процедурах, и каждое такое описание должно иметь единственный, связанный с ним элемент в таблице символов. При использовании идентификатора возникает проблема, как найти соответствующий ему элемент в таблице символов.
BEGIN REAL a, b , с, d;
BEGIN REAL e,f;
Li:
END;
BEGIN REAL g, h;
L2:begin real a;
end;
L3:
end;
end;
L3
Рис. 9.5. Блочная структура.
Пронумеруем блоки в исходной программе в том порядке, в каком они открываются (в порядке появления символа begin). Это естественный порядок, так как именно в этом порядке блоки будут встречаться при грамматическом разборе слева направо.
Правило нахождения соответствующего идентификатору описания состоит в том, чтобы сначала просмотреть текущий блок (в котором идентификатор используется), затем оэъемлющий блок и т. д. до тех пор, пока не будет найдено описание данного идентификатора. Мы можем осуществить такой поиск, храня все элементы таблицы для каждого блока в смежных ячейках и используя список блоков. Мы можем пока считать, что элементы для каждого блока не упорядочены. Элемент i списка блоков содержит номер блока, объемлющего блок i (SURRNO), число элементов в таблице символов для блока i (NOENT) и указатель на эти элементы (POINT). То есть каждый элемент списка блоков имеет три поля:
(SURRNO, NOENT, POINT).
На рис. 9.6 изображена таблица символов для программы, приведенной на рис. 9.5. Такая таблица символов с «блочной структурой» может быть использована всякий раз, когда мы сталкиваемся с вложениями блоков, где к символу, описанному в блоке, можно обращаться только в этом блоке. Например, мы можем создать
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
259
внутренний блок для каждого цикла for, так как циклы for вкладываются друг в друга так же, как и блоки. Тогда переходы извне внутрь тела цикла будут обнаруживаться автоматически, так как описания меток, определенных внутри цикла, будут найдены только в том случае, когда процедура поиска начнет работать для метки,
Спасал блоков
Таблица, символов
Рис. 9.6. Список блоков и таблица символов.
используемой также внутри цикла. Можно создать дополнительный блок для формальных параметров и тела процедуры, входящих в описание процедуры или функции. Это не позволит обращаться к формальным параметрам вне тела процедуры. (Само имя процедуры, конечно, не принадлежит этому внутреннему блоку.)
Открытие и закрытие блоков
В таблице символов на рис. 9.6 блоки расположены в порядке 2, 4, 3, 1. Фактически это порядок, в котором блоки закрывались (порядок, в котором встречались в программе символы end). Это диктуется необходимостью располагать элементы одного блока в смежных позициях таблицы. В процессе построения таблицы мы используем нижнюю часть таблицы (последние несколько ячеек) как стек. Этот стек S (N), S (N — 1).будет содержать элементы
всех блоков, для которых слово begin уже встретилось (блоки были открыты) в процессе грамматического разбора, но до end грамматический разбор еще не дошел. После того как обработан весь блок, его элементы переносятся в верхнюю часть таблицы. Если мы представим синтаксис блока в виде
(1 ) (начало блока} : := BEGIN
(2 ) (блок} : := (начало блока} (список описаний}; (список инструкций} END
то «открывать» блок мы будем при выполнении семантической программы для правила (1) и «закрывать» при выполнении программы Для правила (2). Ниже приведены три состояния, которые возника
9*
260
ГЛАВА 9
ют при грамматическом разборе программы на рис. 9.5 в моменты анализа меток LI, L2 и L3. Необходимы следующие переменные:
S (1:N)
В(1:М)
INTEGER CURRBL
INTEGER LASTBL
INTEGER TOPEL
INTEGER LASTEL
Таблица символов из N элементов. S(N), S(N—1), . . . используются как стек. Все элементы в конце концов попадают в S(l), S(2), . . .
Список блоков. Каждый элемент имеет три поля для целых чисел SURRNO, NOENT и POINT.
Номер текущего блока; первоначально 0.
Наибольший из присвоенных номеров блоков; первоначально 0.
Индекс элемента вершины стека; первоначально N+1.
Индекс последнего элемента в верхней части таблицы символов; первоначально 0.
Список блоков
Таблица символов в момент появления
L1
Список блоков
Таблица символов в момент появления
L2
Список блоков
Таблица символов в момент появления
L3
Приведем программные сегменты, выполняющие открытие и закрытие блока;
ОРГАНИЗАЦИЯ ТАБЛИЦ СИМВОЛОВ
• 261
1. ОТКРЫТЬ БЛОК. Добавить элемент в список блоков и сделать его текущим блоком:
LASTBL := LASTBL+1;
В (LASTBL) := (CURRBL, О, TOPEL);
CURRBL := LASTBL;
2. ЗАКРЫТЬ БЛОК. Перенести элементы для переменных блока в верхнюю часть таблицы:
B(CURRBL).POINT := LASTEL+1;
FOR i : = 1 STEP 1 UNTIL B(CURRBL).NOENT DO
BEGIN LASTEL := LASTEL+1;
S(LASTEL) : = S(TOPEL);
TOPEL := TOPEL+1
END;
Сделать объемлющий блок текущим:
CURRBL := В (CURRBL).SURRNO;
Заведение и поиск идентификатора
Проблема заведения идентификатора в текущем блоке сводится просто к добавлению этого идентификатора к верхнему в стеке блоку идентификаторов в таблице и к продвижению счетчика идентификаторов этого блока. Для поиска нужны две процедуры: одна, просматривающая только текущий блок (например, при обработке описаний), и другая — просматривающая текущий и все объемлющие блоки. Эти процедуры написать несложно, и мы предоставляем это читателю.
Обсуждение
Если язык допускает использование переменной до ее описания, то ссылки на переменные не могут быть связаны с позициями в таблице символов до тех пор, пока не будет закончено построение таблицы символов. Следовательно, необходим первый проход, целью которого и является построение таблицы символов. Он может использовать очень простую грамматику для языка, так чтобы большинство инструкций просто пропускалось. Этот проход должен принимать во внимание описания, определения меток, структуру блоков и процедур и, может быть, циклы. На следующем проходе можно выполнить полный анализ программы, используя таблицу символов, построенную ранее.
Некоторые языки не допускают использование переменной до ее определения. Это ограничение обычно налагается только для того,
262
ГЛАВА 9
чтобы облегчить компиляцию. Однако почти всегда на метки ссылаются до их определения, и не желательно требовать от программиста, чтобы он описывал метки до их использования. В гл. 13 рассматриваются способы обработки таких меток в однопроходном компиляторе.
Для того чтобы обработка была более единообразной, можно перед началом собственно трансляции сформировать псевдоблок, объемлющий всю исходную программу, и занести в таблицу элементы для стандартных функций и переменных.
В однопроходном компиляторе, как только блок закроется, его идентификаторы больше не нужны. Поэтому можно просто исключить их элементы из стека таблицы символов вместо того, чтобы переносить их на постоянное место. Такая таблица называется стековой таблицей символов.
Блочная структура с хешированием
Использование хеширования не позволяет легко сгруппировать элементы таблицы ‘символов по блокам. Метод решения проблемы, который первым приходит в голову, состоит в том, чтобы аргумент хеширования получать в результате приписывания к идентификатору номера блока. Все аргументы при этом будут различны. Для того чтобы отыскать в таблице элемент для используемого идентификатора В, нужно провести поиск, сначала приписав к В номер текущего блока, а затем объемлющих блоков и т. д.
Другой возможный путь — это завести в каждом элементе поле для второго указателя и с его помощью связывать в цепочку одинаковые идентификаторы, определенные в разных блоках. После того, как будет найден первый элемент, для нахождения нужного останется только просмотреть эту цепочку. К сожалению, обработка описания в блоке далеко не всегда завершается до того, как открывается новый блок (так случается, например, когда в описании встречается процедура). Поэтому элемент для идентификатора В из блока 3 может попасть в таблицу раньше, чем элемент для такого же идентификатора В из блока 1. Следовательно, мы не можем гарантировать, что элементы в цепочке будут упорядочены. Для повышения эффективности поиска может оказаться желательным упорядочивать элементы цепочки при поступлении нового элемента или в момент закрытия блока.
9.6. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Познакомиться с методами упорядочения (сортировки) и поиска можно у Флореса [69] или Кнута [70]. Многие книги по программированию вводного характера также содержат разделы о простейших методах сортировки.
ОРГАНИЗАЦИ Я ТАБЛИЦ СИМВОЛОВ
263
Хеш-адресация — это еще один метод в программировании из числа тех, которые изобретаются и развиваются многими людьми на протяжении ряда лет. Петерсон [57] первым опубликовал статью на эту тему; в ней он рассматривает метод линейного рехеширования. Метод случайного рехеширования (и его анализ) описывается в обзорной статье Морриса [68]; он является вариантом метода, предложенного Висотски (см. Макилрой [63]). Метод квадратичного рехеширования предложен Маурером [68]. Недавно он был расширен в двух направлениях. Радке [70] решил проблему исследования другой половины таблицы, которая не просматривается при методе квадратичного рехеширования. В том же выпуске САСМ Белл [70] расширяет его, используя формулу p1=a(h) i2+bi вместо pi=ai2+bi. Это означает, что коэффициент при i2 является функцией начального хеш-адреса h. Белл показывает аналитически и экспериментально, что это уменьшает число ожидаемых коллизий.
Батсон [65] описывает использование метода линейного рехеширования в компиляторе с АЛГОЛа.
Моррис [68] также приводит анализ решения проблемы коллизий методом цепочек; впервые этот анализ встречается у Джонсона.
Более подробное рассмотрение бинарных деревьев встречается в томе 1 у Кнута [68]. Оба рассматриваемых метода организации таблиц символов с блочной структурой используются во многих компиляторах, и авторов установить трудно.
Глава 10
Информация в таблице символов
10.1. ОПИСАТЕЛЬ
Вся информация об идентификаторе хранится в той части элемента таблицы символов, которую мы назвали «значением» (см. разд. 9.1). Для каждого вхождения идентификатора в исходной программе осуществляется поиск соответствующего элемента в таблице символов, информация, полученная при данном вхождении, сопоставляется с ранее полученной информацией, выполняется необходимый контроль и регистрация новой информации. Таким образом, таблица символов является очень важной частью компилятора и в некотором смысле узловой точкой всей трансляции. Ее структура должна допускать эффективный поиск и внесение информации. (В то же время каждый элемент должен занимать как можно меньше места, для того чтобы хватало места на большие программы с большим числом идентификаторов. Это обычная проблема времени и пространства.) Вообще говоря, желательно, чтобы возможно меньшее число программ транслятора непосредственно работало с таблицей символов. Это позволит достаточно легко вносить необходимые изменения. Особенно важно тщательно согласовать формат описателя до того, как начнется программирование транслятора.
Часть элемента «значение» мы называем описателем, так как в этой части описывается идентификатор. Для обозначения ее существует другой термин, введенный Фелдманом [66J, — семантическое слово.
Количество информации, которое нужно хранить в описателе, зависит оттого, чем является фактически идентификатор—простой переменной, массивом, функцией и т. д. Поэтому в некоторых реализациях описатели имеют переменную длину. Это допустимо не при любой организации таблицы символов. Иногда в целях экономии памяти выбирают элемент таблицы малого размера, а для идентификаторов, требующих больше места, отводят по несколько соседних элементов. Другая возможность открывается, если в нужных случаях отводить часть описателя под указатель, ссылающийся на дополнительную таблицу. Это несколько осложняет программирование, поскольку поле описателя может менять свой смысл в зависимости от типа элемента.
ИНФОРМАЦИЯ в ТАБЛИЦЕ СИМВОЛОВ
265
Для переменных и процедур в описателе, видимо, нужна следующая информация:
Переменная: Тип (вещественный, целый, строка, комплексный, метка и т. д.). Точность, масштаб, длина. Вид (простая переменная, массив, структура ит. д.). Адрес во время выполнения программы. Если массив, то число измерений. Если граничные пары—константы, то их значения. Если структура или компонента структуры, то связь данной компоненты с другими компонентами. Формальный параметр или нет; если да, то тип соответствия параметров. Описана ли переменная в инструкции COMMON или EQUIVALENCE (ФОРТРАН)? Если да, то связь с соответствующими идентификаторами. Обрабатывалось ли уже ее описание? Существует ли инструкция, присваивающая ей значение?
Процедура: Является ли она внешней по отношению к программе? Является ли она функцией? Каков ее тип? Обрабатывалось ли уже ее описание? Является ли она рекурсивной? Каковы ее формальные параметры? Их описатели должны быть связаны с именем функции, для того чтобы можно было проверить их соответствие фактическим параметрам.
Показать, что содержит описатель, видимо, лучше всего на примерах существующих компиляторов. Мы рассмотрим два примера компиляторов для разных языков на разных машинах. Мы отступим от обозначений и форматов, принятых в описаниях этих компиляторов, и опустим информацию, не относящуюся к данному рассмотрению. Таким образом наши описания не будут точными.
Компилятор ALCOR Illinois для машины IBM 7090
(Грис, Пол и Вил)
Это четырехпроходный компилятор с АЛГОЛа для машины IBM 7090. При первом проходе просматриваются описания и метки и выясняется структура блоков, процедур и циклов. При этом строится
266
ГЛАВА 10
неупорядоченная таблица символов с блочной структурой и список блоков. В это время атрибуты еще не заполняются. На втором проходе с помощью метода матриц перехода осуществляется грамматический разбор программы и заполняется описатель каждого идентификатора. На этом проходе распределяется память для времени выполнения программы и выполняется некоторая предварительная работа по оптимизации циклов. На третьем проходе генерируется код, а на четвертом печатаются сообщения и программа приводится к виду, необходимому для загрузки.
В машине IBM 7090 слово состоит из 36, а адрес из 15 битов. В некоторых командах можно обращаться к отдельным полям слова, занимающим разряды 0—2, 3—17, 18—20 и 21—35. Каждый описатель сначала занимает два слова, как показано ниже. После завершения второго прохода сохраняется только первое из двух слов, а освободившаяся память используется для других целей.
0-5 6-7
8
9-13 14-20 21-35
тип класс формальный, параметр обработана ли описание ? номер иерархии число индексов или параметров адрес объектной программы
0-2 3-17
18-20 21-35
использование номер элемента указатель для оптимизации циклов
Слово Биты Значение
1 0-5 Эти биты определяют тип (2 бита) и класс (4 бита) переменной. Например, 000000 = неопределенный (пока) 010001 = целый простая переменная 010010 = целый массив 100001 — вещественный простая переменная 100100 = вещественный функция 100101 = вещественный константа 001111= метка
1 6—7 Если переменная—формальный параметр, бит 6 равен Г, если этот параметр вызывается по
значению, бит 7 равен 1.
1 8 Первоначально 0. Устанавливается 1, когда на
2-м проходе обрабатывается описание.
1 9—13 Номер иерархии (уровня вложения) процедуры,
в которой описана переменная.
ИНФОРМАЦИЯ В ТАБЛИЦЕ СИМВОЛОВ
267
1
1
2
2
2
14—20 Для имени массива (процедуры) число индексов (параметров); в противном случае 0.
21—35 Смещение в области данных процедуры, в которой описана переменная.
0—2 Используются для формальных параметров, вызываемых по имени. Первоначально эти разряды содержат 0. Если формальному параметру присваивается значение внутри процедуры, устанавливается 1. Если соответствующий фактический параметр—константа, устанавливается 2. Заметим, что эти два случая несовместимы, так как нельзя присвоить значение константе. Это позволяет обнаруживать большинство подобных ошибок.
3—17 Номер данного элемента в таблице.
21—35 Используется для оптимизации циклов. См. гл. 18. Используется также для нейтрализации ошибок. См. гл. 15.
В главе 8 говорилось о том, что каждый адрес во время выполнения программы определяется парой чисел (номером области данных и смещением). В рассмотренном компиляторе нет номера области данных; вместо него используется номер иерархии (уровень вложения). Это вполне допустимо, так как те процедуры, которые имеют один и тот же номер иерархии, находятся в параллельных блоках; следовательно, компилятор никогда не обрабатывает их одновременно. Заметим (см. разд. 8.9), что если В, например, описано в процедуре с номером иерархии i и к В есть обращение в процедуре с номером иерархии k (i^k), то i-я ячейка k-й области данных дает адрес i-й области данных, что нам и нужно для обращения к В.
Компилятор /360 WATFOR (Кресс и др. [68])
Как упоминалось в гл. 1, /360 WATFOR это по существу однопроходный компилятор с языка ФОРТРАН IV для машин IBM/360.
Таблица символов состоит из пяти разных списков: список меток, список арифметических констант, список имен общих блоков, имен подпрограмм и имен переменных, список общих блоков и список имен подпрограмм (таким образом некоторые элементы оказываются в двух списках). Элементы всех списков помещаются в одной и той же таблице; первые два байта каждого элемента используются для ссылки на следующий элемент в этом же списке. Следовательно, поиск отдельного элемента сводится к линейному просмотру по ссылкам.
268
ГЛАВА 10
Элементы различных типов имеют различные длины в пределах от 8 до 20 байтов. Например, элемент для переменной, имеющий длину 16 байтов, содержит следующую информацию (первые два байта на рисунке опущены):
Лайты 3-4 5-10 11-12 13-14 15-16
В2 идентификатор размерность COMMON EQUIVALENCE
В полях COMMON и EQUIVALENCE помещаются указатели на элементы других переменных, связанных с данной при помощи инструкций COMMON и EQUIVALENCE. Подробно это описывается в гл. 14. В поле «размерность» содержится 0, если переменная не является массивом; в противном случае оно указывает на отдельный элемент, содержащий всю информацию о размерности: величины dn. . dn и общую длину di*. . .*dn.
Два байта, обозначенные В2, содержат остальную информацию, как показано на схеме ниже. Первоначально все поля содержат нули, и в них заносится информация по мере обработки программы. Единица в каждом однобитовом поле на схеме говорит о наличии соответствующего факта.
0—1 2—4 5—6 7 8 9 10 11 12 13 14 15
1—Встречается в EQUIVALENCE
—Встречается в COMMON
—Имеет начальное значение
—Присваивается значение по ASSIGN
----Текущий параметр цикла
— Формальный параметр программы
— Использование сформировано
---- Тип сформирован
— Длина задается програм мистом
-----Тип (00 = логический, 01= целый, 10 = вещественный,
11 = комплексный)
----Число индексов в случае массива
----10 = простая переменная, Н=массив.
10.2. ОПИСАТЕЛИ ДЛЯ КОМПОНЕНТ СТРУКТУР
Элементы таблицы символов для компонент структур должны быть связаны друг с другом, чтобы представлять полную структуру. Это можно реализовать многими способами. Наша цель — полу
ИНФОРМАЦИЯ В ТАБЛИЦЕ СИМВОЛОВ
269
чить представление, которое позволит эффективно обращаться к структурам и их компонентам. Примерами структур, с которыми мы будем иметь дело, являются:
1 А 1 L
2 В 2 М
(10.2.1) 3 С и 4 С
3D 4 D
2 Е 2 В
2 F 5 С
5 D
Они подсбны структурам в языках КОБОЛ или PL/1. Структура, изображенная слева, имеет имя А; она состоит из трех компонент: В, Е и F. Здесь Е и F — элементарные компоненты, так как они сами не содержат подкомпонент. Элементарные компоненты обладают типом, и им могут присваиваться значения, хотя мы не будем это рассматривать, так как нас в данный момент интересует только связь между компонентами. В не является элементарной компонентой; эго имя группы (под)компонент С и D, причем С и D — элементарные компоненты. Имена структур А и L также являются именами группы.
Правила описания структур следующие:
1. Каждому имени предшествует положительное целое число, называемое его номером уровня.
2. Имя структуры является первой компонентой в описании структуры; ее номер уровня должен быть меньше номеров уровня других компонент.
3. За каждым именем группы следуют ее подкомпоненты. Все подкомпоненты должны иметь один и тот же номер уровня, который должен быть больше, чем номер уровня группы.
Мы не затрагиваем здесь правил относительно однозначности имен.
Каждая структура может быть представлена в виде дерева. Корневой узел дерева — это имя структуры. Каждое групповое имя — это имя куста, чьи узлы являются компонентами группы. Конечными узлами дерева являются элементарные компоненты.
Компоненты группы (все они имеют один и тот же номер уровня) часто называются братьями. Компонента, дающая имя группе, является их отцом, в то время как компоненты группы являются его сыновьями. Например, в приведенной выше структуре сыновьями А являются В, Е и F; они — братья. Компонента В также имеет Двух сыновей С и D; их отцом является В.
270
ГЛАВА 10
Ссылка на компоненту имеет вид
An*. . .’Ai.A0,
где п^О и где для i=0>. . п—1 каждая At должна быть именем некоторой компоненты (но не обязательно ближайшего уровня) в группе с именем Ai+1. Только одна компонента должна удовлетворять этому условию.
Заметим, что вовсе не обязательно всегда задавать имя компоненты с полной «спецификацией». Если предположить, что в программе определены только две описанные выше структуры, то окажется, что и А.В.С, и А.С ссылаются на компоненту С группы В в структуре А, в то время как и M.D, и L.M.D ссылаются на компоненту D группы М в структуре L. В то же время ссылка L.C является двусмысленной, так как это может означать L.M.C или L.B.C. Точно так же двусмысленна ссылка В.С, так как она может означать А.В.С или L.B.C.
Если простое (не составное) имя появляется в качестве ссылки, то это имя должно быть однозначно определено. М ссылается однозначно на компоненту М структуры L, в то время как В двусмысленно.
Эквивалентными системами обозначений для ссылки Ап. . . . . . . .Ax.Aq являются Ао (Aj (. . . (Ап) . . . )) и Ао OF Ах OF . . . .. . OF An.
Эти различия в обозначениях не влияют на способы представления и обработки структур.
Представление структур в таблице символов
Мы можем представлять структуру, отводя по одному элементу для каждой компоненты. Кроме обычных полей (которые мы не будем рассматривать), каждый элемент имеет три дополнительных поля: FATHER, SON и BROTHER. Поле FATHER указывает на отца, поле SON — на первого сына компоненты, а поле BROTHER — на ее следующего брата в последовательности братьев группы. Поле содержит 0, если данный элемент не имеет отца, сына или следующего брата соответственно.
На рис. 10.1 показаны элементы для двух структур, приведенных в (10.2.1). Этой информации может хватить с избытком (а может оказаться и недостаточно) для эффективной работы со структурами. Эти вопросы мы рассмотрим по ходу дальнейшего изложения.
Поскольку могут существовать элементы, имена которых совпадают, вводится еще один указатель SAME, связывающий такие элементы между собой. Первый из этих элементов содержит в этом поле 0. Таким образом, имеются пять полей:
1. ID — имя компоненты;
ИНФОРМАЦИЯ В ТАБЛИЦЕ СИМВОЛОВ
271
2. SAME — указатель на предыдущий элемент с тем же именем (О, если его нет);
3. FATHER — указатель на элемент для имени группы, непосредственно содержащей данную компоненту;
4. SON — указатель на элемент для первой подкомпоненты данной компоненты (следовательно, данная компонента должна быть именем группы или это поле содержит 0);
5. BROTHER. Указатель на следующую компоненту в группе, к которой принадлежит данная компонента (0, если следующая компонента отсутствует).
ID SAME FATHER SON BROTHER
А1 А 0 0 Bl 0
В1 В 0 Al Cl El
С1 С • 0 Bl 0 DI
D1 D 0 • Bl 0 0
Е1 Е 0 Al 0 Fl *
F1 F 0 Al 0 0
L1 L 0 0 Ml 0
Ml М 0 LI C2 B2
С2 С Cl Ml 0 D2
D2 D DI Ml 0 0
В2 В Bl LI C3 0
СЗ С C2 B2 0 D3
D3 D D2 B2 0 0
Рис. 10.1. Структуры в таблице символов.
Построение таблицы символов
Программа, изображенная на рис. 10.2, строит таблицу символов для структуры, представленной последовательностью пар (номер уровня, идентификатор). Предположим, что эта информация задана в двух массивах LEVEL и ID и что п — целая переменная, определяющая число пар. Предположим также, что существует программа ADDENTRY (Р, NAME), которая заводит новый элемент для идентификатора NAME, заносит нули во все его компоненты, заполняет поля ID и SAME и осуществляет возврат с адресом элемента в указателе Р. Наконец, мы отведем еще одно поле LEV в каждом элементе, чтобы поместить в него номер уровня компоненты..
272
ГЛАВА 10
После того как построение таблицы окончено, это поле не нужно и может быть использовано для других целей. При некотором усложнении программы можно обойтись без поля LEV (см. упражнения 1 и 2).
BEGIN POINTER РО, Р, Q;
ADDENTRY (РО, ID [1]); Р := РО;
P0.LEV := LEVEL [1];
FOR i := 2 STEP 1 UNTIL n DO BEGIN ADDENTRY (Q, IDJiJ);
Q. LEV: =LEVEL [i];
TESTRELATION:
CASE SIGN (P. LEV —
Q. LEV) + 2 OF
BEGIN
BEGIN IF P.SON # 0 THEN STOP;
Q. FATHER :=P;
P. SON:=Q
END;
BEGIN
Q. FATHER: = P. FATHER;
P. BROTHER : =Q
END;
BEGIN P: -P. FATHER;
IF P = 0 THEN ERROR;
GOTO TESTRELATION;
END;
END;
P:=Q;
END;
IF PO. SON г 0 THEN ERROR;
END
РО указывает на элемент для имени структуры, Q — на обрабатываемую компоненту, а Р — на возможных братьев или отца Q.
Внесение элемента для 1-й компоненты.
Цикл по компонентам.
Внесение элемента для i-й компоненты.
Инструкция CASE решает, является ли Q братом Р, сыном Р, или Q не связано непосредственно с Р.
Сын. Если Р уже имеет сына, то это ошибка. В противном случае заполняем информацию в полях FATHER и SON.
Брат. Он имеет того же отца, и Q является следующим братом Р.
Не связан непосредственно. Если у Р нет отца, это ошибка. В противном случае проверить, не связан ли Q с отцом Р.
Конец инструкции CASE.
Далее фиксируется Р и процесс повторяется со следующей компонентой. Работа завершена. Нужно проверить, что 1-я компонента не имеет брата.
Рис. 10.2. Программа построения таблицы для структуры.
Обработка ссылки Ап........Ai.A0
Идентификатору Ао могут соответствовать несколько элементов таблицы; задача состоит в том, чтобы найти тот элемент, который однозначно определен цепочкой Аъ А2,. . ., Ап. Проверяются все элементы Ао. На каждом i-м шаге проверки, выполняемой для данного Ао, по Aj.j с помощью ссылки FATHER определяется имя отца АР Если этот путь приводит нас к Ап, то Ао, с которого началась
ИНФОРМАЦИЯ В ТАБЛИЦЕ СИМВОЛОВ
273
проверка, является искомым. Заметим, что для того, чтобы удостовериться в том, что ссылка однозначна, должны быть проверены все Ао.
В приводимой ниже программе предполагается, что имена Aj содержатся в массиве А типа STRING с нижней границей, равной 0; переменная п указывает, из скольких простых имен состоит ссылка. В результате работы Q будет содержать адрес компоненты, на которую ссылаются, или нуль, если такой компоненты не существует. Ниже приводится программа поиска компоненты по ссылке
Ап......АХ.АО
BEGIN POINTER Р, Q, S;
INTEGER i;
р : = «адрес первого элемента с именем АО»; Q : = 0;
WHILE Р ^0 DO
BEGIN S: = Р;
FOR i: =1 STEP 1 UNTIL n DO BEGIN LOOP: S: = S. FATHER;
IF S-0 THEN GOTO TRYNEWP;
IF S.ID A [i]
THEN GO TO LOOP;
END;
IF Q 0 THEN ERROR;
Q := P;
TRYNEWP: P :=P. SAME;
END
END
P указывает на элемент для Ао, Q будет содержать адрес компоненты, на которую ссылаются, S — временная переменная, i принимает значения от 0 (Ао) до п (Ап).
Выполнить цикл один раз для каждого элемента с именем Ао.
Просмотр цепочки FATHER для Аь А2, . . ., Ап.
Достигли корня дерева.
Если найденный элемент не тот, переход к проверке следующего отца.
Элемент найден. Если Q не 0, то он не единственный (ошибка).
Занесение адреса другого элемента с.именем Ао в Р и повторение просмотра.
В программе по существу выполняется восходящий просмотр, который начинается с каждого Ао и движется вверх по направлению к корню дерева. В программе используются только поля-FATHER и SAME, так что поля SON и BROTHER могут быть опущены, если они не нужны для других целей (см. упражнение 3).
В некоторых языках имя структуры воспринимается как новый тип данных, и переменные такого типа можно описывать и создавать. Например, в АЛГОЛе W мы можем написать
RECORD COMPLEX (REAL REALPART; REAL IMAGPART);
COMPLEX В
и тем самым создать переменную В с двумя действительными компонентами. В любой ссылке Ап.........АХ.АО (например,
B.REALPART) Ап должно быть именем структурной величины (или указателем на нее) и тип этой структурной величины известен из Ац.
274
ГЛАВА 10
Для таких случаев можно использовать нисходящий просмотр, который начинается от единственного элемента, определяемого Ап, и проходит вниз по дереву к Ап_п. . ., Ах, Ао, используя поля SON и BROTHER. (Мы предоставляем читателю составление программы такого просмотра.)
Хотя в этом случае нужно исследовать только одно дерево, нельзя утверждать, что просмотр сверху вниз будет выполняться быстрее просмотра снизу вверх. Это связано с необходимостью просматривать на каждом уровне всех братьев. При просмотре снизу вверх приходится обрабатывать только цепочку отца; здесь же должны быть просмотрены все сыновья и братья. Заметим также, что просмотр снизу вверх можно было бы ускорить, если бы в каждом элементе имелось поле, которое указывало бы на само имя структуры.
Покомпонентный перенос
В языке КОБОЛ можно написать инструкцию
MOVE CORRESPONDING А ТО L
для того, чтобы перенести в L значения всех элементарных компонент А, которые имеют соответствующие имена в L. Например, в предположении, что А и L являются структурами, описанными в начале этого раздела, эта инструкция эквивалентна двум:
MOVE А.В.С ТО L.B.C
MOVE A.B.D ТО L.B.D
в то время как инструкция
MOVE CORRESPONDING А.В ТО L.M
эквивалентна
MOVE А.В.С TOL.M.C
MOVE A.B.D ТО L.M.D
В языке PL/1 имеется аналогичная инструкция присваивания “BY NAME”. Ее выполнение определяется следующим правилом: MOVE CORRESPONDING X ТО Y (где X и Y могут быть составными именами) является сокращенной записью последовательности всех возможных инструкций MOVE Xi ТО Yn таких, что
Xi=X.An........АХ.АО
Yx=Y.An........АьАо
где Xi или Yx (или оба) — элементарные компоненты. Более того, цепочка компонент Ап. ; . . .АХ.АО должна быть полной в каждом случае; At должно быть прямым отцом А^х для i = 1, . . ., п.
Один из способов преобразования инструкции MOVE CORRESPONDING в последовательность простых инструкций
ИНФОРМАЦИЯ в ТАБЛИЦЕ СИМВОЛОВ
275
MOVE состоит в следующем: на любом шаге преобразования имеется последовательность инструкций
MOVE CORRESPONDING Xi ТО Yi
MOVE CORRESPONDING Xn TO Yn
Сначала n = l. Каждая компонента Xi и Y4 в действительности представляется указателем на соответствующий элемент таблицы символов, т.е. фактически нам нужен массив пар указателей (Хь Yi). Следующий процесс повторяется до тех пор, пока последовательность инструкций не опустеет. Процесс состоит в том, что первая инструкция частично преобразуется и затем исключается из последовательности.
1. Если либо Xi, либо Yi в первой инструкции последовательности являются элементарными компонентами, то в качестве выходного результата выдать оператор MOVE Хх ТО Yi и перейти к п. 3.
2. Для каждого сына А из Хъ если Yi имеет сына с тем же именем А, к последовательности добавить инструкцию
MOVE CORRESPONDING XVA ТО YrA
3. Исключить первую инструкцию (включающую Xi и Yx) из последовательности.
Описанный способ преобразования прост и естествен, однако для его выполнения нужна таблица, содержащая пары (Xh Yj). Ниже приводится другая программа, в которой узлы поддеревьев структур для X и Y проходятся другим способом. Указатели Р и Q используются для хождения по поддеревьям X и Y соответственно.
Программа базируется на предположении, что правило об однозначности ссылки не имеет силы. В языке КОБОЛ утверждается, что каждая ссылка на компоненту должна допускать однозначное толкование (см. упражнение 4). В этом случае, как только какая-либо пара (Р, Q) определена, не нужно проверять, имеется ли еще брат с тем же именем, что и Р. Следовательно, программу можно несколько изменить, сделав ее более эффективной (см. упражнение 6).
Обработка MOVE CORRESPONDING
BEGIN POINTER P, Q, PO; P(Q) проходит поддерево X (Q). PO
P:=P0: = „адрес элемента дляХ“; все время указывает на узел X.
Q: = „адрес элемента для Y“;
ELEM:
IF Р. SON = 0 OR Q. SON = 0 THEN Если либо P, либо Q — элементарные, BEGIN output (P,Q); выдаем пару указателей и переходим
GOTO NEXT; к следующей паре.
END;
276
ГЛАВА 10
P:=P.SON; Q:=Q.SON;
TESTEQ:
IF P.ID = Q.ID THEN GOTO ELEM;
NEXT:
IF Q.BROTHER # 0 THEN BEGIN Q:-Q.BROTHER;
GOTO TESTEQ
END;
BROTHERP:
IF P.BROTHER # 0 THEN BEGIN P: =P.BROTHER;
Q :== Q.FATHER.SON;
GO TO TESTEQ
END;
P: =P.FATHER; Q : — Q.FATHER;
IF P P0 THEN
GOTO BROTHER P;
END
Движение по ссылкам SON.
Проверить, совпадает ли хоть один брат Q с Р. Если да, переход к ELEM.
Проверка брата Q.
Ни один брат Q не соответствует Р, поэтому сравниваем братьев Р с Q и его братьями.
Р не имеет больше братьев.
Поэтому переходим к отцам.
Если мы вернулись к РО, то останавливаемся.
УПРАЖНЕНИЯ К РАЗДЕЛУ 10.2
1. Измените программу, которая строит таблицу символов, так, чтобы она не использовала поле LEV. Указание: поле LEV используется только для установления родственных отношений между Р и Q. В любой момент необходимы номера уровней только для Р и для компонент, связанных с Р по цепочке FATHER. Используйте для их хранения стек.
2. Измените программу, которая строит таблицу символов, так, чтобы она не использовала поле LEV, и при этом обойдитесь без стека для хранения номеров уровня. Указание: номера уровней необходимы только для Р и для компонент, связанных с ним по цепочке FATHER. Эти компоненты пока не имеют братьев, так что используйте поле BROTHER для хранения номеров уровня. Не забудьте своевременно сформировать поле BROTHER.
3. Измените программу, которая строит таблицу символов, исключив поля SON и BROTHER. Помните о том, что нужно контролировать ошибки, подобные 1 А 3 В 2 С. Контроль сведется теперь к тому, чтобы в момент обработки 2 С проверить, нетли уже сыновей у А. Другой способ — это использовать сами номера уровней.
4. В языке КОБОЛ требуется, чтобы каждая ссылка однозначно определяла компоненту. Например, в структуре
, IX 2Y 3Z 2Z
невозможно сослаться на компоненту Z структуры X, так как X.Z
ИНФОРМАЦИЯ В ТАБЛИЦЕ СИМВОЛОВ • 277
определено неоднозначно. Измените программу, которая строит таблицу символов, чтобы она обнаруживала такого рода ошибки.
5. Предполагая, что имя Ап в ссылке Ап...АХ.АО является
именем единственного элемента, составьте программу нахождения этого элемента, используя нисходящий просмотр.
6. Предполагая, что правило языка КОБОЛ, изложенное в упражнении 4, имеет силу, измените программу, преобразующую любую инструкцию MOVE CORRESPONDING так, чтобы проверялись только те компоненты Р и Q, которые могут иметь одно и то же имя.
Глава 11
Внутренние формы исходной программы
В тех случаях, когда не хватает памяти либо когда исходный язык достаточно сложен или к компилятору предъявляются повышенные требования, первоначальная исходная программа переводится в некоторую внутреннюю форму, более удобную для простой машинной обработки. В большинстве внутренних представлений операторы располагаются в том порядке, в котором они должны выполняться. Это существенно облегчает последующий анализ и генерацию объектного кода. В действительности эти внутренние представления можно было бы также использовать для интерпретации. То есть мы могли бы написать программу, которая выполняла бы исходную программу, представленную во внутренней форме.
В этой главе мы познакомимся с несколькими наиболее часто используемыми внутренними формами. В каждом случае в качестве
BEGIN INTEGER К;
ARRAY А [1:1 — J];
К : =0;
L: IF I > J
THEN K: =-K + A [I —J]*6
ELSE BEGIN I: =1 + 1; I: - I + 1; GO TO L END
END
Рис. 11.1. Сегмент программы на АЛГОЛе.
примера нам будет служить сегмент программы на АЛГОЛе (рис. 11.1). Конечно, следует помнить, что каждое частное представление зависит от исходного языка и от назначения компилятора. Например, в языке ФОРТРАН нет необходимости включать во внутреннюю исходную программу инструкцию DIMENSION, так как вся информация, содержащаяся в ней, попадет в таблицу символов и никакие команды генерироваться не будут. Вы увидите, что описание INTEGER К (см. рис. 11.1) не встретится ни в одном извнут-
ВНУТРЕННИЕ ФОРМЫ ИСХОДНОЙ ПРОГРАММЫ
279
ренних представлений, так как для него также не требуется генерация команд.
Следует также решить, насколько подробным должно быть начальное внутреннее представление. Включать ли во внутреннее представление операции преобразования значений из одного типа в другой или это делать позже? Например, цикл можно представлять эквивалентной группой присваиваний, переходов и условных инструкций, или его можно задавать с меньшей степенью детализации и транслировать позже. Вообще говоря, первоначальная форма программы лаконичнее и короче, но более подробное представление открывает новые возможности для оптимизации и в общем случае многое облегчает.
Мы начнем обсуждение с раздела об операторах и операндах и о способах их представления. В разд. 11.2 мы опишем первое внутреннее представление — польскую запись. Затем рассмотрим тетрады (разд. 11.3), триады, деревья, косвенные триады (разд. 11.4) и представление программы в виде графа (разд. 11.5).
Читатель должен понимать, что в очень немногих компиляторах применяется одно из этих представлений в чистом виде. Обычно используется некоторое смешанное представление, зависящее от личных желаний и склонностей разработчика компилятора.
11. 1. ОПЕРАТОРЫ И ОПЕРАНДЫ
Все внутренние представления обычно содержат в себе две вещи— операторы и операнды. Различия лишь в том, как эти операторы и операнды соединяются. В дальнейшем мы будем использовать такие операторы, как +, —, /, *, BR (Branch — переход) и т. д. Внутри компилятора они, конечно, представлены целыми числами. Таким образом, мы могли бы использовать число 4 вместо +, 5 вместо —, 6 вместо / и т. д.
Возможно, нам потребуется отличать операторы от операндов, если они могут встречаться в любом порядке. В таком случае операнд будет занимать две ячейки; в первой содержится целое число, не совпадающее ни с одним из чисел, представляющих операторы, а во второй — собственно операнд. (Иногда эти две компоненты упаковываются в одну ячейку.)
Операндами, с которыми мы имеем дело, являются простые имена (переменных, процедур и т.д.), константы, временные переменные, генерируемые самим компилятором, и переменные с индексами. Если все идентификаторы и константы хранить в одной общей таблице, то, за исключением переменных с индексами, каждый операнд может представляться указателем на соответствующий элемент в таблице символов. Если описания операндов находятся в не
280
ГЛАВА 11
скольких таблицах, то в первой ячейке необходимо иметь различные целые числа для разных типов операндов (см. рис. 11.2).
В поле операнда можно предусмотреть признак косвенной адресации и не заводить для этой цели отдельный оператор. То есть операнд может указывать, что данное значение есть адрес того значения, которое на самом деле требуется.
Это позволяет нам следующим образом описывать переменные с индексами. Последовательность операций описывает вычисление VARPART (см. 8.4.5)для переменной с индексами: A [i, j, . . ., к].
простая переменная
указатель на элемент таблицы символов
константа
2 1 "' —' ' 1' ч W Т» указатель на элемент таблицы констант
временная переменная
3 I | указатель на элемент таблицы временных переменных
I-единица в этом разряде указывает па косвенную адресацию
описание индексов
х=1 - указатель в таблицу символов
2- указатель в таблицу констант Ъ- указатель в таблицу временных, переменных
переменная с индексами
4 I указатель на элемент для имени массива X I указатель на элемент для индекса
Рис. 11.2. Возможные форматы операндов.
Затем идет специальная операция индексирования SUBS (subscript — индекс). Ее операндами являются имя массива, VARPART и временная переменная (назовем ее Т), в которой запоминается полученный в результате вычислений адрес элемента массива. Тогда A [i, j, . . ., к] представляется косвенной ссылкой на Т.
Другой способ обработки переменных с индексами основан на том, что в качестве операнда задается одновременно и имя массива, и значение VARPART, как это показано на рис. 11.2. Операнд теперь занимает больше места, но такое внутреннее представление может быть лучше, так как позволяет генерировать более эффективную объектную программу. Это замечание станет более понятным в последующих главах.
В дальнейшем операнд A li, j,. . ., к] мы будем изображать, как А [Т], где А — имя массива, а Т — переменная, содержащая значение VARPART.
Возможны, конечно, и другие способы, о которых читатель непременно узнает, когда будет разрабатывать компилятор.
ВНУТРЕННИЕ ФОРМЫ ИСХОДНОЙ ПРОГРАММЫ
281
11 .2. ПОЛЬСКАЯ ЗАПИСЬ
Арифметические выражения
Для представления арифметических и логических выражений часто используется польская запись, которая просто и точно указывает порядок выполнения операций. Кроме того, она не требует скобок. В этой записи, впервые примененной польским логиком Я. Лукашевичем, операторы следуют непосредственно за операндами. Поэтому ее иногда называют суффиксной, или постфиксной записью. Например, А*В записывается как АВ*, А*В+С — как АВ*С+, A* (B+C/D) — как ABCD/+*, a A*B+C*D — как AB*CD*-|--
В гл. 12 мы расскажем, как переводить выражения из инфиксной записи в польскую, используя синтаксический распознаватель и семантические программы. Тем не менее следующие правила, касающиеся польской записи, помогут нам это делать вручную.
1. Идентификаторы в польской записи следуют в том же порядке, что и в инфиксной записи.
2. Операторы в польской записи следуют в том порядке, в каком они должны вычисляться (слева направо).
3. Операторы располагаются непосредственно за своими операндами. Таким образом, мы могли бы записать следующие синтаксические правила:
<операнд> : := идентификатор | <операнд> <операнд> (оператор)
(оператор) : :== + I — I / I * I . . .
Унарный минус и другие унарные операторы можно представлять двумя способами: либо записывать их как бинарные операторы, т. е. вместо —В писать 0 — В, либо для унарного минуса можно ввести новый символ, например @, и использовать еще одно синтаксическое правило (операнд) : : = (операнд) @. Таким образом, А+ (—B+C*D) мы могли бы записать, как AB@CD*H—К
С равным успехом мы могли бы ввести и префиксную запись, в которой операторы стоят перед операндами. Таким образом, мы имеем три формы записи выражений — префиксную, инфиксную (обычная запись, когда операторы располагаются между операндами) и постфиксную. Сами мы используем инфиксную запись, в то время как для автоматического вычисления выражений самой удобной является постфиксная запись. Давайте посмотрим, как эти вычисления производятся.
Вычисление арифметических выражений
С помощью стека арифметические выражения в польской записи можно вычислить за один просмотр слева направо. В стеке будут находиться все операнды, которые встретились при просмотре
282
ГЛАВА И
выражения или получились в результате выполнения некоторых операций, но еще не использовались в вычислениях. Мы начинаем с самого левого символа, обрабатываем его, переходим к символу справа от него, обрабатываем его и т. д. Обработка состоите следующем:
1. Если сканируемый символ является идентификатором или константой, то его значение заносится в стек и осуществляется переход к следующему символу. Это соответствует использованию правила (операнд) : := идентификатор.
Шаг Цепочка и сканируемый символ Старое состояние стека Исполь- Новое состояние зуемое стека правило
1 2 3 4 V AB@CDw+ -j-* V AB@CD*+ + V AB@CD*+ + V AB@CD* -f- V А А|В А|—В 1 А 1 А|В 3 А| —В 1 А|—В|С
5 AB@CD* -j- Ч- V А|—В | С 1 А|—B|C|D
6 AB@CD* “4~ V А|—В | С| D 2 А|—B|C#D
7 AB@CD*+ + V А|—В | C*D 2 А|—B4-C«D
8 AB @CD*+ + Рис. 11.3. А| —В+ C*D 2 АВ 4-C*D) Вычисление выражения AB@CD«4—Н
2. Если сканируемый символ — бинарный оператор, то он применяется к двум верхним операндам в стеке, и затем они заменяются на полученный результат. С точки зрения семантики это эквивалентно использованию правила (операнд> : := (операнд) (операнд) (оператор).
3. Если сканируемый символ — унарный оператор, то он применяется к верхнему операнду в стеке, который затем заменяется на полученный результат. Это соответствует использованию правила: (операнд) : := (операнд) (оператор).
На рис. 11.3 этот алгоритм иллюстрируется на примере вычисления выражения AB@CD* + + (в инфиксной записи (А+ (—B+OD)). (На рис. 11.3 значения в стеке отделены друг от друга вертикальными черточками.)
ВНУТРЕННИЕ ФОРМЫ ИСХОДНОЙ ПРОГРАММЫ
283
Включение в польскую запись других операторов
Польскую запись очень просто расширять. Нужно только придерживаться правила, что за операндами должен следовать соответствующий им оператор. Так, присваивание <пер> :== <выр> в польской записи будет иметь следующий вид: <пер> <выр> := . Например, присваивание А := B*C+D записывается в виде АВС* D+ :== • Однако необходимо соблюдать осторожность при выполнении оператора . После его выполнения и <пер>, и <выр> должны быть исключены из стека, так как оператор := не имеет результирующего значения. В этом состоит его отличие от бинарных арифметических операторов. Кроме того, в стеке должно находиться не значение <пер>, а ее адрес, так как значение <выр> должно запоминаться по адресу <пер>. Мы встретимся и с другими операторами, которым свойственны аналогичные проблемы.
Давайте рассмотрим, как в польской записи представляются инструкции перехода, условные инструкции, описания массивов и индексирование. Этого будет достаточно, чтобы научиться пополнять польскую запись новыми операторами.
Переход GOTO А будем записывать как “A BRL”, где метка А представлена адресом соответствующего ей элемента таблицы символов, а оператор BRL (Branch to label) означает переход на метку.
Условные переходы будут иметь следующий вид:
<операндх> <операнд2> ВР1), где первый операнд является значением арифметического выражения, а второй указывает номер или место символа в цепочке польской записи. Если первый операнд положительный, то в качестве следующего символа берется символ, на который указывает второй операнд, в противном случае работа продолжается, как обычно. Мы также допускаем операторы переходов: по минусу — ВМ (Branch on minus), по нулю — BZ (Branch on zero), по минусу или нулю — BMZ, по положительному значению или нулю — BPZ и т. д.
Условная инструкция
IF <выр> THEN <инстр!> ELSE (инстр2>
в польской записи будет иметь следующий вид:
<выр> <Cj>BZ <инстр1> <с2> BR <инстр2>
где мы предполагаем, что для любого выражения 0 означает ложь, а =7^0— истину. Другие обозначения имеют следующий смысл:
х) BP (Branch on positive) — переход по положительному значению.— Прим, перев.
284
ГЛАВА 11
1- <Ci> — номер (или место) символа, с которого начинается <инстр2>.
2. BZ — оператор с двумя операндами: <выр> и <сх>. Смысл оператора таков: если (и только если) <выр> равно нулю, то изменяется обычный порядок вычислении и осуществляется переход на символ с номером <сх>.
3. <с2 > — номер (или место) символа, следующего за <инстр2>.
4. BR (Branch — переход) — оператор с одним операндом <с2>. Он изменяет обычный порядок вычислений, осуществляя переход на символ с номером <с2>.
Заметим, что бинарный оператор BZ не порождает результирующего значения. При его выполнении верхними элементами стека будут <выр> и <сх>; следовательно, часть работы состоите исключении из стека этих двух элементов. То же можно сказать и о безусловном переходе BR1). Заметим также, что у нас теперь два оператора безусловного перехода. Один из них — (метка> BRL — используется в тех случаях, когда в исходной программе встречается GOTO, причем (метка > есть адрес элемента таблицы символов; другой оператор — (с2> BR — используется для внутренних генерируемых переходов.
Могут сказать, что (выр>, (инстр!> и <инстр2> являются операндами условной инструкции, а значит, и польская запись условной инструкции должна быть такой:
<выр> <инстр!> (инстр2> IF
Рассмотрим, однако, что произойдет при вычислении польской записи такой инструкции. К моменту выполнения оператора IF все три операнда будут уже вычислены или выполнены. Не забудьте, что мы вычисляем слева направо, кроме тех случаев, когда операторы перехода изменяют порядок вычислений. Поэтому-то мы и стремились выбрать такую структуру условной инструкции, чтобы при вычислении слева направо получился желаемый результат.
В языке АЛГОЛ описание массива ARRAY A [Li : Un . . . ... , Ln : Unl можно представить в виде . . LnUn AADEC, где ADEC — единственный оператор. Он имеет переменное число операндов, зависящее от числа индексов. Операнд А, очевидно, будет адресом элемента таблицы символов для А. При вычислении ADEC из этого элемента таблицы извлекается информация о размерности массива А и, следовательно, о количестве операндов ADEC.
Обратите внимание на то, что порядок следования идентификаторов изменен. ADEC имеет переменное количество параметров, но поскольку последним параметром является А, в каждом конк-
х) С той лишь разницей, что из стека исключается один элемент, а не два.—-Прим, перев.
ВНУТРЕННИЕ ФОРМЫ ИСХОДНОЙ ПРОГРАММЫ ' 285 I
ретном случае ADEC может из элемента А таблицы символов опре- J делить общее количество параметров. Если бы мы пользовались записью ALiUi* . . LnUn ADEC, то невозможно было бы определить количество параметров и размерность пришлось бы задавать, на- | пример, дополнительным параметром перед оператором ADEC. ?
Аналогично переменная с индексами А [<выр>, . . ., <выр>] представляется в виде <выр> . . . <выр> A SUBS. Оператор SUBS, * используя элемент А таблицы символов и индексные выражения, . вычисляет адрес элемента массива. Затем операнды исключаются i из стека и на их место заносится новый операнд, специфицирующий J тип элемента массива и его адрес.
Рассмотрим сегмент программы на рис. 11.1. Польская запись этого сегмента представлена на рис. 11.4. На этом рисунке добавле- * ны еще два оператора без операндов — BLOCK („начало блока”) и BLCKEND („конец блока”).
Заметим, что для индексирования мы использовали оператор I SUBS. Он больше подходит для польской записи. В следующем *
разделе вы увидите пример другого способа описания индексирова- J
ния. i
S £
(1) BLOCK 1 I J — A ADEC К 0 : = j
(11) I J — 29 BMZ - j
(16) К К I J — A SUBS 6 * + : = 41 BR j
(29) III + : = I I 1 + : = L BRL j
(41) BLCKEND j
Рис. 11.4. Польская запись сегмента программы, изображенного на рис. 11.1. «
Полезно, вероятно, рассмотреть, как польскую запись можно |
представить в машине или на некотором языке высокого уровня. 1
Это показано на рис. 11.5. Для каждого символа польской записи I (см. также рис. 11.4) отводится одна строка. Операторы занимают по одной ячейке и представлены числами: 6 = SUBS, 7 = := , 8—BMZ,9—BR, 10—BRL, 11 -BLOCK, 12—BLCKEND, 13-ADEC, ?
14— +, 15— *, 16— —.Если символ является константой, то он занимает две ячейки (или два слова). Первая ячейка содержит чис- *
ло «1», обозначающее, что это константа, вторая — собственно кон- I
станту. Аналогично для идентификатора первая ячейка содержит 5 число «2», обозначающее, что данный символ — идентификатор, вторая — адрес или индекс элемента таблицы символов для этого идентификатора. Обратите также внимание на особенности нумера- | ции; нумеруются ячейки, а не символы. t
286
ГЛАВА II
Номер Содержимое Символ слова, слов
1 11 BLOCK
2 1 1 1
4 2 1 J
6 2 2 а
8 16
9 2 3 А
1 1 13 ADEC
12 2 4 К
14 1 0 0
16 7 * =
17 2 1 I
19 2 2 J
21 16 —
22 1 45 45
24 8 BMZ
25 2 4 К
27 2 4 К
29 2 1 1
31 2 2 3
33 16 —
34 2 3 А
Номер Содержимое слова, слов
36 6
37 1 6
39 15
40 14
41 7
42 1 64
44 9
45 2 1
47 2 1
49 1 1
51 14
52 7
53 2 1
55 2 1
57 1 1
59 14
60 7
61 1 5
63 10
64 12
Рис. 11.5. Внутреннее представление польской записи на рис. 11.4.
УПРАЖНЕНИЯ К РАЗДЕЛУ 11.2
1. Представьте следующие арифметические выражения в польской записи: 1+5» (6+8/4), — 3+6* (—5+6), 25/(5/1+6—5).
2. Проведите вычисление полученных в упражнении 1 цепочек польской записи, используя описанный выше метод.
3. Представьте следующие инструкции в польской записи:
(1) FOR I := 1 STEP 1 UNTIL 10 DO A [I] := 1;
(2) CASE (выражение) OF BEGIN Sx; S2; . . . ; Sn END;
(3) IF (выражение > THEN Si;
(4) DO (номер инстр> (nepi) = (пер2), (пер3> (цикл DO в ФОРТРАНе)
11.3. ТЕТРАДЫ
Тетрады для арифметических выражений
Для бинарной операции удобной формой представления является тетрада
((оператор), (операндх>, (операнд2>, (результат»
где (операнД1> и (операнд2> специфицируют аргументы, а (ре
ВНУТРЕННИЕ ФОРМЫ ИСХОДНОЙ ПРОГРАММЫ
287
зультат> — результат. Таким образом, А*В мы могли бы представить, как
*, А, В, Т
где Т — некоторая переменная, которой присваивается результат вычисления А*В. Аналогично A*B+C*D представляется в виде последовательности следующих тетрад:
*, А, В, Т1
*, С, D, Т2 + , Tl, Т2, ТЗ
Очень важно отметить, что в отличие от обычной записи А*В+ 4-C*D тетрады располагаются в том порядке, в котором они должны выполняться. Унарные операторы также оформляются в виде тетрад, но <операнд2> остается пустым. Так, вместо — А появится тетрада “—, А, ,Т”, что означает “присвоить Т значение —А”. Унарный минус в некоторых случаях мы могли бы заменить другим оператором, чтобы отличать его от бинарного минуса, что и делали в польской записи.
Тетрады для других операторов
Добавление тетрад с другими операторами не вызывает затруднений, и мы ограничимся тем, что объединим в один список операторы, которые нам в дальнейшем понадобятся. На стр. 288 приводится таблица, в которой Р, Pl, Р2 и РЗ обозначают операнды в виде, указанном на рис. 11.2. На рис. 11.6 показан сегмент программы рис. 11.1, записанный в форме тетрад.
(1) BLOCK (Ю) + К, Т4, Т5
(2) —I. J, Т1 (Н) : = Т5, , К
(3) BOUNDS I, Т1 (12) BR 18
(4) ADEC А (13) + L 1. Тб
(5) :=0,,К (14) :=Т6, , I
(6) — I, J, Т2 (15) + L 1, Т7
(7) BMZ 13, Т2 (16) : = Т7, ,1
(8) — I, J, ТЗ (17) BRL L
(9) *А [ТЗ], 6, Т4 (18) BLCKEND
Рис. 11.6. Тетрады для сегмента программы, изображенного на рис. 11.1.
Чтобы продемонстрировать, как выглядит индексирование для двумерной матрицы, рассмотрим инструкцию С := A [i, В [j]]. Если dl описывает диапазон изменения второго индекса массива
288
ГЛАВА 11
А, то получится следующее:
*, i, dl, Т1
+ , Tl, B[j], Т2 : =, А[Т2], , С
Оператор
1. BR
2. BZ[BP, ВМ]
3. BG[BL, BE]
4. BRL
5. +[*> / >— ]
6. : =
7. CVRI
8. CVIR
9. BLOCK
10. BLCKEND
11. BOUNDS
12. ADEC
Операнды
i i, P
i, Pl, P2
P
Pl, P2, P3
Pl, , P3
Pl, , P3
Pl, , P3
Pl, P2
Pl
Комментарий
Переход на i-ю тетраду.
Переход на i-ю тетраду, если значение, описанное в Р, равно нулю [положительное, отрицательное].
Переход на i-ю тетраду, если значение, описанное в Р1, больше [меньше, равно] значения, описанного в Р2. Переход на тетраду, номер которой задан в Р-м элементе таблицы символов.
Сложение [умножение, деление, вычитание] значений, описанных в Р1 и Р2, и запоминание результата по адресу, описанному в РЗ. Запоминание значения, описанного в Р1, в ячейке, описанной в РЗ.
Преобразование значения, описанного в Р1, из типа REAL в тип INTEGER и запоминание результата в ячейке, описанной в РЗ.
Преобразование значения, описанного в Р1, из типа INTEGER в тип REAL.
Начало блока.
Конец блока.
Р1 и Р2 описывают граничную пару массива.
Массив описан в Р1. Если размерность массива п, то этой тетраде предшествуют п операторов BOUNDS, задающих п граничных пар.
ВНУТРЕННИЕ ФОРМЫ ИСХОДНОЙ ПРОГРАММЫ '
289
УПРАЖНЕНИЯ К РАЗДЕЛУ 11.3
1. Запишите инструкции из упражнения 3 к разд. 11.2 в форме тетрад.
2. Предложите запись в форме тетрад для вызова процедуры А (X, Y,. . ., Z). Параметрами процедуры могут быть имена массивов, константы, переменные, выражения и т. д. Будьте внимательны. Помните, что параметр сам может содержать вызов процедуры (функции).
11.4. ТРИАДЫ, ДЕРЕВЬЯ И КОСВЕННЫЕ ТРИАДЫ
Триады
К недостаткам тетрад следует отнести большое количество временных переменных, которые приходится описывать. Эта пробле-
(1) BLOCK (2) — I, J (3) BOUNDS 1, (2) (4) ADEC А (5) := 0, К (6) - I, J (7) BMZ (13), (6) (8) - I, J (9) * А[(8)1, (6) (Ю) + К, (9) (11) := (10), К (12) BR (18) (13) 4-1,1 (14) := (13), I (15) + I, 1 (16) := (15), I (17) BRL L (18) BLCKEND
Р и с. 11.7. Триады для сегмента программы, изображенного на рис. 11.1.
ма полностью отпадает при использовании триад. Триада имеет следующую форму:
<оператор> <операнД1> <операнд2>
В триаде нет поля для результата. Если позднее какой-то операнд окажется результатом данной операции, то он будет непосредственно на нее ссылаться. Например, выражение А+В*С будет представлено следующим образом:
(1)* В, С
(2)+А, (1)
Здесь (1) —ссылка на результат первой триады, а не константа, равная 1. Выражение 1+В * С будет записано так:
(1)*В, С
<2)4-1, (1)
Ю Д. Грио
290
ГЛАВА И
Конечно, в компиляторе мы должны отличать этот тип операнда, используя новый код в первой ячейке операнда.
Пользуясь обозначениями операторов, введенных в предыдущем разделе, запишем сегмент программы (рис. 11.1) так, как на рис. 11.7. Заметим, что для этого нам потребовалось столько же триад, сколько было тетрад в предыдущем представлении. Но теперь нам не нужны временные переменные, и, кроме того, триада занимает меньше места, чем тетрада. Конечно, при работе с триадами нам придется хранить описания результатов, значения которых в дальнейшем еще потребуются. Например, при обработке триады (2) на рис. 11.7 мы генерируем описание ее результата. Но после того, как триада (4) обработана, это описание становится ненужным и его можно ликвидировать.
Деревья
Для обычных арифметических выражений деревья определяются следующим образом. Дерево для простой переменной или константы есть простая переменная или константа. Если выражениям е! и е2 соответствуют деревья Тх и Т2, то выражениям ei+e2, ех — е2, Ci*e2, ei/e2 и —ех будут соответствовать такие деревья:
е< +е2
z
е1 *е2
г
Например, выражению А*В+С—D*E соответствует дерево, изображенное на следующей диаграмме слева:
(1) (* А, В)
(2) (+ (1), С)
(5) (* 0, Е)
(4) (- (2), (3))
в
Триады любого арифметического выражения можно также рассматривать как прямое представление дерева, что и показано на предыдущей диаграмме справа от дерева. Последняя, 4-я триада соответствует корню дерева. Каждая i-я триада соответствует поддереву, оператор триады является корнем поддерева, а каждый операнд — либо именем переменной, которая соответствует концевому узлу, либо номером триады, описывающей под-поддерево.
От того, как рассматриваются триады (как последовательность операций в порядке их выполнения или как дерево), существенным
ВНУТРЕННИЕ ФОРМЫ ИСХОДНОЙ ПРОГРАММЫ
291
образом зависит генерируемый объектный код. К этому вопросу мы вернемся в гл. 17.
При представлении инструкций, блоков, описаний и т. д. триады уже не образуют полного дерева, так как связи между различными инструкциями и описаниями явно не заданы. Например, для составной инструкции
BEGIN А := В; В := С; D := С; END
дерево и триады имеют следующий вид:
«(составная инсшрукция>
BEGIN <cmicon инсгор >
<инстр> <UHcmp> <uwcmp>
END
<uHcmp >
(1) 8,A)
(21) (:= С, B) ft) (:» Cf D)
В дереве отражены прямые связи (указатели) с инструкциями, в то время как в триадах эти связи подразумеваются.
Косвенные триады
Во время оптимизации объектного кода (гл. 18) обычно требуется какие-то операции исходной программы исключить, какие-то переставить на другое место. С тетрадами это делается легко, а с триадами сложнее, так как они часто ссылаются друг на друга. Для решения этой проблемы заведем две таблицы. В одной таблице (ТРИАДЫ) будем хранить триады, а в другой таблице (ОПЕР) — последовательность ссылок на триады в том порядке, в каком они должны выполняться. Например, операторы А := В#С и В := В*С представляются в следующем виде:
ОПЕР ТРИАДЫ
1. (1) (1)* В, С
2. (2) (2) := (1), А
3. (1) (3) := (1), В
4. (3)
Теперь мы можем переставлять или исключать операции в ОПЕР, не изменяя сами триады и ссылки на них.
Заметим, что одинаковые триады в таблице ТРИАДЫ не повторяются. Две триады считаются одинаковыми, если у них совпадают все три компоненты. Операнды, соответствующие двум разным переменным В, описанным в разных блоках, конечно, будут разными.
Обычно в исходной программе много одинаковых триад, особенно если встречаются переменные с индексами, и поэтому общее ко-
ю*
292
ГЛАВА 11
личество триад меньше количества операций в ОПЕР. Это, очевидно, означает, что при добавлении каждой новой триады приходится просматривать всю таблицу триад на тот счет, нет ли уже такой триады в таблице, а это требует времени. Здесь можно с успехом применить методы хеширования.
На рис. 11.8 представлен сегмент программы (рис. 11.1) в виде косвенных триад.
Надо быть внимательным, если операнд является ссылкой на триаду. Триада может выполняться в нескольких местах, и ссылка на ее результат должна быть связана с правильным выполнением триады. Например, триада (+ I, 1), согласно ОПЕР, выполняется дважды в 13-й и 15-й операциях. Вторая ссылка на 11-ю триаду
ОПЕР ТРИАДЫ
1. (1) 10. (8) (1) BLOCK (8) + К, (7)
2. (2) 11. (9) (2) — I, J (9) := (8), К
3. (3) 12. (Ю) (3) BOUNDS 1, (2) (Ю) BR 18
4. (4) 13. (Н) (4) ADEC А (И) + I, 1
5. (5) 14. (12) (5) := 0, К (12) := (И), I
6. (2) 15. (Н) (6) BMZ 13, (2) (13) BRL L
7. (6) 16. (12) (7) * А [(2)], 6 (14) BLCKEND
8. (2) 17. (13)
9. (7) 18. (14)
Рис. 11.8. Косвенные триады для сегмента программы, изображенного на рис. 11.1.
встречается в 15-й операции после вычисления 12-й триады и, следовательно, зависит от результата вычисления в 14-й операции. Это вносит некоторые трудности при перестановках операций во время оптимизации объектного кода.
11.5. ЛИНЕЙНЫЕ УЧАСТКИ
Для оптимизации часто бывает удобно разбить программу на «линейные участки» и отдельно иметь «граф программы», описывающий, как эти участки связаны между собой. Линейный участок— это последовательность операций с одним входом и одним выходом (им соответствуют первая и последняя операции). Более того, все операции выполняются последовательно и внутри участка нет переходов. На рис. 11.9, а в качестве примера приведены линейные участки сегмента программы (рис. 11.1) в виде тетрад (с тем же ус-
ВНУТРЕННИЕ ФОРМЫ ИСХОДНОЙ ПРОГРАММЫ
293
пехом можно было использовать косвенные триады). Заметим, что в операциях переходов в качестве операндов указываются номера линейных участков, а не номера тетрад. Тетрада BMZ во 2-м линейном участке означает следующее: если значение Т2 меньше или равно нулю, то происходит переход на 4-й линейный участок, в противном случае — переход на 3-й участок. В общем случае последняя операция может быть переходом на любой линейный участок. Заметим также, если участок имеет один преемник, то в
1. BLOCK
!• о, Т1 BOUNDS 1, Т1 ADEC А : = 0,, к
2. - I, 3, Т2. BMZ 4, 3, Т2
3. - I, 3, ТЗ
* А[ТЗ], 6, Т4 + К, Т4, Т5 := Т5, , К
4. + I, 1, Тб
: = Тб,, I + I, 1, Т7
:» Т7,, I
5. BLCKEND
0 10 0 0
0 0 110
0 0 0 0 1
0 10 0 0
0 0 0 0 0
ъ
Рис. 11.9. Линейные участки и граф программы для сегмента, изображенного на рис. 11.1. *
а—линейные участки; 6—граф программы.
конце нет необходимости явно указывать переход на него, так как этот переход неявно указан в графе программы.
Граф программы содержит для каждого линейного участка список непосредственных преемников (к которым от него есть переход) и непосредственных предшественников (от которых к нему есть переход). На рис. 11.9 граф программы изображен в виде матрицы М, для которой М [i, j] = 1 в том и только том случае, если j-й линейный участок является преемником i-ro линейного участка. На практике для представления графа программы лучше подходит списочная структура, так как, возможно, потребуется хранить больше информации о каждом линейном участке, а также создавать или уничтожать участки в процессе оптимизации.
Такое представление программы позволяет нам в пределах каждого участка производить экономию команд. Мы можем также, анализируя граф программы, находить циклы и переносить операции из одних участков в другие. Об этом речь пойдет в гл. 18.
Возможны и другие варианты. Например, если в первоначальной исходной программе оптимизируются только for-циклы, то для облегчения обработки операции в них придется сгруппировать в некоторого рода линейные участки.
294 ГЛАВА 11
11.6. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Польская запись, тетрады и триады использовались в качестве внутренних представлений во многих компиляторах. Для облегчения оптимизации объектного кода были предложены линейные участки и графы программы. Аллен [69] использует похожую схему с косвенными триадами, а в’ ФОРТРАНе Н для IBM 360 используется такая же схема, но с тетрадами (см. Лоури и Медлок [69]).
Синтаксические деревья, оформленные в виде списка, используются в некоторых системах построения трансляторов. Наиболее известны среди них компилятор компиляторов Брукера и Морриса и COGENT Рейнольдса. Используются они и в компиляторе АЛГОЛа W (см. Бауэр, Беккер и Грехем [681).
Глава 12
Введение в семантические программы
В этой главе мы рассматриваем идею сопоставления семантической программы с каждым правилом грамматики. Такая программа осуществляет семантическую обработку, когда связанное с ней правило вызывает синтаксическую редукцию. В разд. 12.1 мы познакомимся с этой идеей на примере перевода арифметических выражений из инфиксной записи в польскую с помощью восходящего грамматического разбора. В разд. 12.2 рассмотрим, как генерируются тетрады для арифметических выражений, и обнаружим, что нам требуется дополнительная семантическая информация к синтаксическому дереву. В разд. 12.3 речь пойдет о том, как представлять эту семантическую информацию и как могли бы выглядеть семантические программы в компиляторе. Наконец в разд. 12.4 мы познакомимся с семантической обработкой при нисходящем разборе.
Задача этой главы состоит в том, чтобы показать, как осуществляется перевод арифметических выражений с указанным ниже синтаксисом в различные внутренние формы. При этом нас не интересуют таблицы символов, атрибуты и т. д.
(12.0.1) Z : := Е
Е : := Т | Е+Т | Е—Т | —Т
Т : := F | T*F | T/F
F : :== I | (Е)
12.1. ПЕРЕВОД ИНФИКСНОЙ ЗАПИСИ В ПОЛЬСКУЮ
Мы предполагаем, что всякий раз, когда в сентенциальной форме основа х найдена и ее можно привести к нетерминалу U, синтаксический распознаватель вызывает программу, связанную с правилом U : х. Программа осуществляет семантическую обработку символов в х и выдает ту часть польской цепочки, которая имеет непосредственное отношение к х. Заметим, что нам абсолютно безразлично, какой распознаватель используется в данный момент.
296
ГЛАВА 12
Важно лишь то, что
(1 2.1.1) основа редуцируется при каждой редукции.
То есть редуцируется самая левая простая фраза (в случае предшествования операторов необходимо сделать оговорку, но в данный момент она не имеет значения). А поскольку основа редуцируется, мы можем сделать следующее важное допущение:
(1 2.1.2) Если в основе встречается нетерминал V, то часть польской цепочки, включающая подцепочку, которая приводится к V, уже была сгенерирована.
Будем предполагать, что генерируемая польская цепочка хранится в одномерном массиве Р. Целая переменная р (вначале она имеет значение 1) содержит индекс, указывающий на первый свободный элемент массива. Каждый элемент массива может содержать один символ (идентификатор или оператор). Предположим также, что вызванная семантическая программа имеет доступ к символам основы S (1) . . . S (i), находящимся в синтаксическом стеке S, который используется распознавателем.
Семантические программы
Рассмотрим программу, связанную с правилом Ех: : = Е2+Т. Если она вызвана, то мы можем считать, что польская запись для Еа и Т уже получена. При этом массив Р содержит
. . . <код для Е2> <код для Т>
поскольку Е2 расположено левее Т. Заметим также, что правее Т код еще не генерировался. Справа от Т в исходной программе находятся только терминалы, так как разбор производится слева направо. Следовательно, все, что требуется от программы,— это занести знак «+» в польскую цепочку. При этом инфиксная запись Е2+Т переводится в суффиксную запись Е2 Т +. Следовательно, семантическая программа имеет вид Р (р) := '+'; р :== р+1.
Рассмотрим семантическую программу для F : := I, где I обозначает произвольный идентификатор. В соответствии с правилами польской записи (см. гл. 11) идентификаторы предшествуют своим операторам; более того, они встречаются в том же порядке, что и в инфиксной записи. Все, что нам необходимо сделать,— это занести идентификатор в массив Р. Поэтому программа имеет следующий вид:
Р (р) := S (i); р := р+1
где S (i) — верхний символ стека.
ВВЕДЕНИЕ В СЕМАНТИЧЕСКИЕ ПРОГРАММЫ
297
Семантическая программа, связанная правилом F : := (Е), ничего не делает, так как в польской записи скобок нет, а для Е польская запись уже сгенерирована.
Тем же способом можно построить и другие программы; они перечислены на рис. 12.1. Когда это возможно, одну и ту же про-
Правило Семантическая программа
(1) Z :: := Е нет
(2) Е : := Т нет
(3) Е : := Е + Т Р(р) := '+'; Р := р + 1
(4) Е : := Е —Т Р(р) := р := р + 1
(5) Е : := — Т Р(р) := р : = р+1
(6) Т :: := F нет
(7) Т : := T*F Р(р) := ' * р := р+1
(8) Т : := T/F Р(р) := р : = р + 1
(9) F : := I Р(р) := S (i); р := Р+-1
(Ю) F :: ;= (Е) нет
Рис. 12.1. Семантические программы для генерации польской записи.
грамму следует использовать для нескольких схожих по смыслу правил. Например, для правил 3,4,7 и 8 семантические программы можно заменить одной-единственной программой:
Р (р) := S (i-1); р:== р+1
Разбор предложения
На рис. 12.2 показан разбор предложения А * (В+С). Мы предполагаем, что в распознавателе используется стек S, входной символ R и оставшаяся часть предложения Тк. . . . На рисунке перечислены шаги грамматического разбора, каждый из которых либо является редукцией, либо содержит занесение в стек символа R и сканирование следующего символа. Непосредственно перед редукцией и вызывается семантическая программа. Эта программа либо выдает, либо не выдает следующую часть польской цепочки, которая содержится в последней колонке на рис. 12.2.
Обсуждение
У читателя может возникнуть ощущение, что мы доставляем себе массу хлопот только ради того, чтобы получить
АВС+* из А* (В+С).
Что и говорить, нам пришлось обратиться к 12 семантическим
298
ГЛАВА 12
Стек S R Тк... Номер исполь- Семантиче- Полученная к данному
зуемого ская моменту
пра- про- польская
вила грамма цепочка
А *(В+С)#
#А * (В+С) # 9 9 А
#F * (В+С)# 6 6 А
#Т * (В+С) # А
#т* ( В+С)# А
#т*( в +Q# А
#Т*(В + С)# 9 9 АВ
# Т * (F + С)# 6 6 АВ
#Т»(Т + С)# 2 2 АВ
#Т*(Е + С)# АВ
#Т*(Е + с )# АВ
#Т*(Е+С ) 9 9 АВС
#T*(E + F ) 6 6 АВС
#Т*(Е + Т ) # 3 3 АВС +
#Т*(Е ) АВС +
#Т*(Е) # 10 10 АВС +
#T*F # 7 7 АВС + #
#т # 2 2 АВС + *
# Е 1 1 АВС + *
#z STOP АВС + *
Рис. 12.2. Разбор выражения А*(В+С).
программам, многие из которых ничего не делают! И действительно, для частного случая арифметических выражений мы, вероятно, могли бы найти и запрограммировать более короткий метод. Но мы рассматриваем общий случай, когда приходится разбирать предложения любой подходящей грамматики и извлекать некоторый смысл из предложения. Поэтому нам необходим некоторый систематический подход, чтобы для нового языка не начинать все сначала.
Мы разделим задачу на две части — на синтаксис и семантику. Задача, естественно, упростилась, так как, во-первых, из грамматики нам известно, каким образом будет происходить разбор предложения (в каком порядке будут выполняться редукции), и это позволяет нам не программировать каждый раз заново. Мы пользуемся один раз запрограммированным конструктором и рас
ВВЕДЕНИЕ В СЕМАНТИЧЕСКИЕ ПРОГРАММЫ
299
познавателем. Во-вторых, для каждой продукции мы пишем одну семантическую программу. Это помогает нам поделить обработку на мелкие независимые части, каждую из которых можно запрограммировать отдельно, что позволяет нам не думать обо всем сразу.
Наконец, небольшие изменения в синтаксисе или семантике требуют лишь незначительных изменений в соответствующих правилах грамматики или семантических программах. Различные части анализа отделены друг от друга, поэтому внесение изменений не представляет особых затруднений.
УПРАЖНЕНИЯ К РАЗДЕЛУ 12.1
1. Проведите разбор предложений А,- А+В, (А+В), (((А))), ((А+В)«С+В)*С, пользуясь семантическими программами на рис. 12.1 и грамматикой (12.0.1).
2. Добавьте к грамматике (12.0.1) правила, соответствующие инструкции присваивания S : := I := Е и инструкции чтения S : := READ I. Определите польскую запись для этих инструкций и напишите семантические программы для перевода их в польскую форму.
3. Проведите разбор инструкций А:= А+В и READ С (см. упражнение 2).
4. К грамматике (12.0.1) добавьте правила для переменных с индексами и напишите для них семантические программы.
12.2. ПРЕОБРАЗОВАНИЕ ИНФИКСНОЙ ЗАПИСИ В ТЕТРАДЫ
Давайте попытаемся провести разбор выражения А* (В+С) и сгенерируем тетрады
+ , В, С, Т1
*, A, Tl, Т2
по ходу дела составляя семантические программы. Логичнее всего генерировать первую тетраду в семантической программе для правила Е : :== Е+Т. Итак, будем выполнять восходящий разбор до того момента, пока не возникнет необходимость в применении этого правила. Ниже приводятся сентенциальные формы, порождаемые на каждом шаге (подчеркнута основа), а на рис. 12.3, а показано частичное синтаксическое дерево, построенное к этому моменту.
А * (В + С) Т * (Т + С)
F»(B + C) Т*(Ё+С)
Т*(в + С) T*(E + F)
T*(F + C) Т»(Е + Т)
300
ГЛАВА 12
На следующем шаге Е+Т приводится к Е; одновременно с этим семантическая программа должна выдать тетраду. К сожалению, мы не можем ее построить, так как сентенциальная форма не содержит информации об именах операндов Е и Т. Эта информация была потеряна, когда выполнялись редукции F В и F ::= С.
При получении польской записи у нас не возникало подобного рода затруднения, так как во время выполнения редукций F::=B и F :: — С имена В и С заносились в выходную цепочку. Очевидна,
Е
А * ( В + С )
Е,В
Т,А Т,В Т,с
г,A F,B F,c
А * ( В + С )
Ъ
а
Рис. 12.3. Частичные синтаксические деревья без семантики и с семантикой.
при генерировании тетрад необходимо где-то хранить имена до момента их использования, а сохранять их должна программа для F I.
Подобного рода информация почти всегда связывается с нетерминалом. Таким образом, по-видимому, разумно привязывать семантическую информацию к узлам синтаксического дерева в процессе грамматического разбора, как это показано на рис. 12.3, Ь. Заметим, что и идентификаторы тогда будут представлены более корректно, чем раньше. Напомним, что сканер распознает идентификаторы и выдает два аргумента — символ I, означающий, что это идентификатор, и сам идентификатор. Символ I относится к синтаксическим символам, в то время как сам идентификатор является связанной с I семантической информацией,что и показано на рис. 12.3, Ь.
Ниже, ссылаясь на семантическую информацию, связанную с нетерминалом U в дереве, мы будем писать U.SEM. Кроме того, нам придется генерировать имена Тп Т2, ..., обозначая таким образом подвыражения. Для этого мы используем счетчик i, который вначале равен нулю. На нашем семантическом языке для генерации нового идентификатора и привязки его к U используются инструкции ,,i := i+1; U.SEM := Tf’.
Наконец, для генерации тетрады, содержащей четыре параметра, используется процедура ENTER(W, X, Y, Z).
А теперь проведем разбор цепочки А*(В+С) и по ходу дела составим семантические программы. Первой основой является I, и ей соответствует семантическая информация А. Эта основа приводится к F. С новым нетерминалом следует связать имя А. Таким
ВВЕДЕНИЕ в СЕМАНТИЧЕСКИЕ ПРОГРАММЫ 301
образом, семантическая программа для F :: = I имеет вид F.SEM := I.SEM
На рис. 12.4, а показана часть синтаксического дерева, образованного пссле этого шага. Следующей основой будет F, и она должна приводиться к Т. И вновь с Т нужно связать имя, в настоящий момент связанное с F, как показано на рис. 12.4, Ь. После того
F, А
I I, А *
Т,А
F,A I I, А *
Т, А
Г
ПА F,B
I I
I, А * ( I.B *
ад с
Е,В I
Т,А Т,В Т,С
I г г
F,Z * F.B F.C
1*1 I
I, А * ( I , В + I, С )
Т,А Г F, А I 1, А *
т,с I ПС I + ЬС )
Рис. 12.4. Некоторые частичные деревья с семантикой.
как рассмотрены эти два случая, мы могли бы обобщить их и сказать, что семантическая программа для правила U ::= V будет следующей:
U.SEM := V.SEM
Вот и все, что нам нужно для этой простой грамматики. На рис. 12.4, с — 12.4, е показано несколько частичных деревьев, полученных в процессе разбора. На рис. 12.4, е показано дерево в тот момент, когда основой является Е+Т. Теперь с помощью правила Ех Е2+Т выражение Е2+Т необходимо привести к Ex. Семантической программе предстоит, во-первых, сгенерировать новый идентификатор Т i и привязать его к новому нетерминалу Ev Во-вторых, она должна сгенерировать тетраду для оператора «+». Имена операндов находятся в E2.SEM и в T.SEM, а имя результатов Ei.SEM. Таким образом, мы выполняем программу
i: = i+ 1; Er.SEM: = Tf,
ENTER (“ + ”, E2.SEM, T.SEM, ErSEM)
и получаем синтаксическое дерево, изображенное на рис. 12.4, Д
302
ГЛАВА 12
Продолжение разбора и построение остальных программ предоставляем читателю. Читатель может сравнить результаты своей работы с программами, приведенными на рис. 12.5.
Правило
(1) Z ::=Ё
(2) Е :: — Т
(3) Et::=Ea + T
(4) Ei:;=E2-T
(5) Е :: =— Т
(6) Т :: = F
(7) ТХ:: = Т2*Р
(8) !,:•.= !,/ F
(9) F ::=Г
(10) F ::=(Е)
Семантическая программа
Z.SEM := E.SEM.
E.SEM := T.SEM.
i := i+1; EVSEM := Tf,
ENTER („ + “, E2.SEM, T.SEM, EVSEM).
i := i + 1; EX.SEM := Tjj
ENTER („—“, E2.SEM, T.SEM, EX.SEM).
i := i + 1; E.SEM := Tf
ENTER 0, T.SEM, E.SEM).
T.SEM := F.SEM.
i := i+1; TrSEM := TP
ENTER („*“, T2.SEM, F.SEM, TVSEM).
i : = i+1; TrSEM := Tf,
ENTER („/“, T2.SEM, F.SEM, TX.SEM).
F.SEM : = I.SEM.
F.SEM := E.SEM.
Рис. 12.5. Семантические программы для генерации тетрад.
УПРАЖНЕНИЯ К РАЗДЕЛУ 12.2
1. Проведите разбор выражений А, (А+В), (((А))) и ((А+В)* С+В)*С, используя программы на рис. 12.5.
2. Добавьте к грамматике (12.0.1) правила S ::= I := Е и S ::= READ I, определите для этих новых инструкций форму тетрады и напишите семантические программы для их генерации.
3. Проведите разбор инструкций А := В+С и READ С.
12.3. РЕАЛИЗАЦИЯ СЕМАНТИЧЕСКИХ ПРОГРАММ И СТЕКОВ
Вообще говоря, с каждым нетерминалом может быть связано несколько семантических атрибутов. Однако заметим, что после редукции с применением, например, такого правила, как Ех — Е2+ Т, информация, связанная с Е2 и Т, становится ненужной. Обычно нужна только та семантическая информация, которая связана с нетерминалами, входящими в текущую сентенциальную форму.
ВВЕДЕНИЕ В СЕМАНТИЧЕСКИЕ ПРОГРАММЫ
303
Давайте определим способ для ее хранения. Так как текущая сентенциальная форма находится в стеке S, то можно завести еще несколько семантических стеков SI, S2, ..., в которых хранится соответствующая семантическая информация. Эти стеки работают параллельно с синтаксическим стеком S. Семантическая программа
REAL
INTEGER
20
40
$1(mufi)
S 2 (адрес)
имеет доступ ко всем стекам S, SI, S2, ... . Если, например, S(i) содержит символ Е, то Sl(i), S2(i), ... могут содержать тип выражения Е, адрес результата выражения во время выполнения программы и т. д., как это показано выше. В действительности не имеет значения, используем ли мы несколько стеков или один стек с отдельными полями для хранения синтаксического символа и его семантических атрибутов.
PROCEDURE SEMANTICS (г); VALUE г; INTEGER г; CASE г OF BEGIN Р(р) : = „ + р:=р+1 Аргументом является но-
мер применяемого правила. Выбрать программу, которой соответствует правило 1 правило 2 END; правило 3
BEGIN Р(р) : = р:=р + 1 END; правило 4
BEGIN Р(р) : = „@“; р:=р+1 END; правило 5
BEGIN Р(р) : = р: = р + 1 правило 6 END; правило 7
BEGIN Р(р) : = р : = р + 1 END; правило 8
BEGIN Р(р) : = Sl(i); р :=р + 1 END; правило 9
ENDCASE правило 10
Рис. 12.6. Семантическая процедура для грамматики (12.0.1).
304
ГЛАВА 12
Способы связи с семантическими программами
Каждую семантическую программу можно оформить в виде отдельной процедуры на некотором языке. Но тогда синтаксический распознаватель должен знать имя каждой процедуры, что ведет ко многим трудностям технического характера. Проще перенумеровать правила грамматики и написать одну-единственную процедуру, скажем SEMANTICS, при вызове которой номер правила передается в качестве аргумента. Когда синтаксический распознаватель обращается к SEMANTICS, аргументом может быть номер правила,
Р и с. 12.7. Конструктор, порождающий сегмент программы.
определяющего редукцию. На рис. 12.6 это иллюстрируется на примере программ, которые генерируют польскую запись, такую, как в разд. 11.2.
Если компилятор программируется на ФОРТРАНе или АЛГОЛе, то вместо инструкции CASE можно пользоваться вычисляемым GO ТО или переключателем.
Синтаксические и семантические стеки можно поместить в COMMON-область или, в случае АЛГОЛа, они могут быть глобальными параметрами. Кроме того, их можно передавать семантической программе как аргумент.
Вероятно, лучший результат (с точки зрения времени компиляции) достигается в том случае, когда имеется синтаксический конструктор и синтаксический распознаватель строится в виде сегмента программы на том языке, на котором программируется компилятор. Этот сегмент будет содержать в себе все необходимые описания стеков и других переменных, сам распознаватель и даже сканер. В компилятор этот сегмент включается так, как показано да рис» 12.7. При этом должны соблюдаться некоторые соглашения
ВВЕДЕНИЕ В СЕМАНТИЧЕСКИЕ ПРОГРАММЫ
305
о метке SEM для семантических программ, об имени стека, о метке возврата из семантических программ и т. д. Заметим, что при обращении к семантической программе нет вызова процедуры —-используется обычный переход к метке. Этот метод применяется в системе построения компиляторов, известной под названием XPL (см. Маккиман и др. [70]).
12.4. СЕМАНТИЧЕСКАЯ ОБРАБОТКА ПРИ НИСХОДЯЩЕМ РАЗБОРЕ
Чтобы использовать рекурсивные процедуры для грамматического разбора и трансляции предложений грамматики (12.0.1), нам прежде всего придется переписать грамматику следующим образом:
Z — Е
Е :: = [—]Т{(+ I —) Т}
Т F{(* | /)F}
F I | (Е)
Затем, как это делалось в разд. 4.3, напишем следующие четыре рекурсивные процедуры:
PROCEDURE Z; Е
PROCEDURE Е;
BEGIN
IF NXTSYMB = '—'THEN SCAN; T;
WHILE NXTSYMB = '+'OR
NXTSYMB-' —'DO
BEGIN SCAN; T END END
PROCEDURE T;
BEGIN F;
WHILE NXTSYMB =='*' OR
NXTSYMBDO BEGIN SCAN; F END END
PROCEDURE F;
BEGIN
IF NXTSYMB —'Г THEN SCAN ELSE
IF NXTSYMB#'(' THEN ERROR
ELSE BEGIN SCAN; E;
IF NXTSYMB
THEN ERROR ELSE SCAN £ND ENp
Для правила Z::—E
Для правил E::=[—]T{(+ | — )T}. Вначале проверка на первый унарный минус. Получение терма. Итеративный поиск вхождений +Т или —Т.
Для правил T::=F{(* |/)F}. Сначала разбор множителя. Затем итеративный поиск вхождений * F и /F.
Для правил F::—I | (Е)
Проверка на идентификатор.
Если не I, то множитель должен начинаться с открывающей скобки; после нее должно следовать Е и закрывающая скобка.
306
ГЛАВА 12
Теперь дополним каждую процедуру инструкциями для семантической обработки символов. Будем генерировать тетрады. Проиллюстрируем эту обработку на примере процедур Т и F, оставив возможность читателю сделать то же самое для двух оставшихся процедур.
Заметим, что синтаксическое дерево и семантический стек явно не заданы. Мы могли бы вставить инструкции для их задания, но в этом нет необходимости. Вместо этого в каждой процедуре используются локальные переменные, а формальные параметры позволяют передавать семантичёскую информацию.
Семантикой любого нетерминала Z, Е, Т или F является имя переменной из исходной программы или имя временной переменной. Это имя необходимо связать с нетерминалом, как только закончен разбор фразы для этого нетерминала. Поэтому в каждой из процедур предусматривается параметр X типа STRING. После выполнения процедуры имя соответствующей переменной возвращается в X.
Ниже, в качестве примера, приводится измененная процедура F(X). Программируя ее, мы исходили из предложения, что процедура SCAN, если встретился идентификатор, поместит 'Г в NXTSYMB, а сам идентификатор в NXTSEM. Заметим, что в процедуре имеется обращение к Е(Х), которая в X вернет имя переменной для фразы Е. То же самое имя используется и для F.
PROCEDURE F (X); STRING X;
BEGIN
IF NXTSYMB = T THEN
BEGIN X: = NXTSEM; SCAN END
ELSE
IF NEXTSYMB THEN
ERROR ELSE
BEGIN SCAN; E (X);
IF NEXTSYMB #')'
THEN ERROR ELSE SCAN
END END
Семантика F (имя переменной) возвращается в X.
Если идентификатор, то его имя SCAN поместит в NXTSEM.
Если (Е), то проверка скобок и затем разбор Е. Имя, связанное с Е, будет также именем, связанным с F!
Рассмотрим теперь процедуру Т, в которой генерируются тетрады для * и /. Сначала делается разбор множителя и его имя заносится в локальную переменную Y. Затем мы сканируем операцию * (или /) и второй операнд, после чего для нее генерируется тетрада. Заметим, что после каждой генерации тетрады в Y заносится имя переменной, содержащей результат операции. Этот процесс повторяется до тех пор, пока не будут обработаны все операции * и /.
ВВЕДЕНИЕ В СЕМАНТИЧЕСКИЕ ПРОГРАММЫ
307
PROCEDURE Т (X); STRING X;
BEGIN STRING Y, Z, OP;
F(Y); OP := NXTSYMB;
WHILE OP = 4' OR OP —7'DO
BEGIN SCAN; F (Z); j: =j + l;
ENTER (OP, Y, Z, Tj);
Y : = Tj; OP NXTSYMB;
END
X := Y
END
В X возвращается имя переменной для фразы Т.
Разбор первого множителя; его имя заносится в локальную переменную Y. На каждой операции вызывается F для разбора следующего множителя, генерируется имя временной переменной, генерируется тетрада. Имя результата есть Tj .
Пересылка имени результата из Y в возвращаемый параметр X.
Раньше мы говорили, что почти в любом алгоритме грамматического разбора используется стек. Здесь стек явно не выражен, а неявно содержится в стековом механизме, предназначенном для запоминания информации о вызове процедуры во время выполнения программы (см. разд. 8.8 и 8.9). В каждой процедуре используются локальные переменные, и, заметьте, они локальны по отношению к каждому конкретному выполнению процедуры, что, собственно, нам и требовалось. Семантическая информация передается как параметры процедур, а не так как ранее в явном виде через семантический стек.
В разд. 13.6 приводится еще один пример использования нисходящего грамматического разбора при компиляции.
12.5. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Один из первых методов перевода инфиксных выражений в другую форму был предложен Рутисхаузером [52]. Его метод заключался в многократном просмотре всего выражения, выявлении на каждом шаге самой внутренней простой операции, генерации для нее внутреннего представления и замены ее одним операндом. В первом компиляторе с ФОРТРАНа также требовалось несколько просмотров выражения, для того чтобы перевести его во внутреннее представление (см. Бэкус и др. [57]). Замельзон и Бауэр [60] впервые описали то, что можно было бы назвать эффективным алгоритмом восходящего разбора (использовались матрицы переходов), в который были включены программы для семантической обработки. Они рассмотрели трансляцию большинства конструкций языка АЛГОЛ 60. Дейкстра [63] применил технику предшествования операторов для перевода выражений в польскую запись. Большинство этих интересных в историческом плане методов кратко описано Шоу [66].
Методы, о которых говорилось в разд. 12.1 и 12.2, хороши тем, что они зависят только от факта использования алгоритма восходящего разбора, а не от частных способов реализации.
308
ГЛАВА 12
В райних компиляторах не было четкого разделения между синтаксисом и семантикой, что и до сих пор характерно для многих существующих компиляторов. Разделение синтаксиса и семантики позволяет формализовать и автоматизировать синтаксическую обработку и использовать более систематический подход при ее реализации. Такое разделение имело место в ранних системах построения синтаксически управляемых компиляторов Айронса [61] и Брукера и др. Последний использует схему нисходящего разбора, при котором, по существу, строится синтаксическое дерево. Программист затем может работать с этим деревом в семантических программах, названных в этой системе программами «FORMAT». Термин «семантические» программы предложен Фелдманом [66]. Вирт и Вебер [66] называют их «правилами интерпретации».
Глава 13
Семантические программы для конструкций языка, подобного АЛГОЛу
Мы рассмотрим семантические программы, генерирующие тетрады для переменных, выражений, условных инструкций, меток, переходов и for-циклов. Эти знания позволят читателю без труда справиться с семантическими программами для других конструкций. В этой главе мы не касаемся распределения памяти во время выполнения программы; необходимые сведения по этому вопросу читатель найдет в гл. 14. Язык, с которым нам придется иметь дело, похож на АЛГОЛ, но в нем отсутствует блочная структура и переменные должны быть описаны раньше, чем они используются. Там, где это уместно, мы будем дополнять изложение замечаниями, касающимися особенностей ФОРТРАНа и языков с блочной структурой.
Семантические программы будут генерировать тетрады в формате, описанном в разд. 11.3, но (и на это следует обратить внимание) операнды мы будем задавать иначе, чем в разд. 11.2. Преж* ний способ формирования операндов вынудил бы нас заняться излишне подробным программированием и не позволил бы достичь той ясности изложения, к которой мы стремимся. Далее каждый операнд будет указателем на элемент таблицы символов, содержащей описания всех переменных, встречающихся в исходной программе, описания временных переменных, констант и т. д. Почти всюду в этой главе используется восходящий разбор, и только в последнем разделе для логических выражений применяется нисходящий разбор.
В этой главе мы не ставим своей целью написать компилятор, но хотим показать, как поступает разработчик компилятора в тех или иных случаях. Читатель должен постараться понять, почему некоторые вещи делаются именно так, а не иначе. Далее вы увидите, что мы нередко реорганизуем синтаксис, согласуй его с семантикой, но не обсуждаем возникающую как следствие дополнительную проблему о приемлемости нового синтаксиса для того типа распознавателя, которым пользуемся.
310
ГЛАВА 13
Многие описанные здесь приемы перевода в тетрады будут также применимы для перевода в другие внутренние формы и для перевода на машинный язык.
13.1. ОБОЗНАЧЕНИЯ, ПРИНЯТЫЕ В СЕМАНТИЧЕСКИХ ПРОГРАММАХ
Для работы с таблицей символов, где хранятся все идентификаторы программы, мы пользуемся следующими процедурами LOOKUP, LOOKUPDEC и INSERT:
1. LOOKUP(NAME, Р). В таблице символов ищется элемент с именем NAME (идентификатор). Адрес найденного элемента заносится в Р. Если такого элемента нет, то в Р заносится 0.
2. LOOKUPDEC(NAME, Р). Работает так же, как LOOKUP, но используется для описаний. В языке с блочной структурой эта программа просматривает только идентификаторы текущего блока.
3. INSERT(NAME, Р). Новый элемент с именем NAME заносится в таблицу символов. Адрес этого элемента заносится в Р.
Такие обращения к процедурам можно использовать также при компиляции с ФОРТРАНа и почти с любого другого языка. Различия в реализации этих процедур определяются различиями в организации таблицы символов.
Из атрибутов, имеющихся в элементах таблицы символов, нас будут интересовать только следующие пять целочисленных компонент:
1. TYPE. Атрибут, указывающий тип: 0=UNDEFIND (неопределенный), ISREAL (вещественный), 2=INTEGER (целый), 3=BOOLEAN (логический), 4=LABEL (метка);
2. TYPE1. 1=простая переменная, 2=имя массива, 3=пере-менная с индексами;
3. TEMPORARY. 1= временная переменная, 0=нет;
4. DECLARED. 0=не определена, 1 = определена;
5. ADDRESS. Номер помеченной тетрады или адрес другого элемента таблицы символов;
6. NUMBER. Размерность массива.
Следует помнить, что UNDEFIND, REAL, INTEGER, BOOLEAN и LABEL в нашем компиляторе понимаются как переменные с перечисленными выше постоянными целыми значениями. Так как все описания операндов хранятся в одной таблице, операнд во внутренней форме может быть просто указателем на соответствующий ему элемент таблицы символов. Мы выбрали простое представление и можем сосредоточить внимание на других проблемах. Если Р — указатель на элемент таблицы символов, то, чтобы сослаться на атрибуты, достаточно написать Р. TYPE, Р. TYPE1 и т. д.
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 311
Если метка определена, то в соответствующем ей элементе компонента таблицы символов ADDRESS содержит номер тетрады, помеченной этой меткой.
Переменной с индексами соответствует позиция таблицы, в которой TYPE 1=3. В этом случае TYPE содержит тип элемента массива, NUMBER — адрес элемента таблицы символов с описанием массива, a ADDRESS — адрес элемента таблицы символов, описывающего VARPART для переменной с индексами.
Доступ к семантическим стекам
Если основа х рассматриваемой сентенциальной формы должна быть приведена с помощью правила U ::= х к нетерминалу U, то для работы с семантикой символов используется программа, которая:
1) заносит информацию в таблицу символов или проверяет ее;
2) проверяет семантическую информацию, связанную с х;
3) генерирует тетрады;
4) связывает семантическую информацию с нетерминалом U.
Так же как в гл. 12, для обращения за информацией S, связанной с символом U, будет применяться обозначение U.S. Например, с символом <выр> связан указатель ENTRY, содержащий адрес элемента таблицы символов, в котором описано выражение. Чтобы получить доступ к этой информации, достаточно написать
<выр>.ENTRY.
Мы знаем, что, независимо от реализации, сам символ <выр>, вероятно, должен быть где-то в синтаксическом стеке, а значение <выр>.ENTRY в соответствующем элементе семантического стека. Ниже приводится неполный перечень символов, которые мы будем использовать, и соответствующая этим символам семантика:
1. I.NAME, где NAME — цепочка, содержащая литеры идентификатора.
2. <пер>.ENTRY, где ENTRY содержит указатель на элемент таблицы символов для переменной.
3. <выр>.ENTRY. Имеет тот же смысл, что и <пер>.ENTRY.
4. <условие>.ЛиМР. Правой частью правила для символа <условие> является IF <выр> THEN. Во время разбора генерируется тетрада с операцией BZ, но мы еще не знаем, куда должен быть совершен переход. Поэтому JUMP содержит номер BZ-тет-рады, в которую позднее будет добавлен адрес перехода.
Используемые подпрограммы и переменные
Семантические программы программируются на нестандартном АЛГОЛе с использованием следующих переменных и подпрограмм:
312 ГЛАВА 13 ,f
1. Подпрограмма ENTER (+, Pl, P2, РЗ) добавляет очередную тетраду во внутреннюю исходную программу; компонентами тет-рады будут четыре аргумента.
2. Подпрограмма ERROR(i) печатает сообщение об ошибке с номером i и прекращает трансляцию.
3. Переменная NEXTQUAD типа INTEGER своим значением будет иметь номер следующей генерируемой тетрады. Первоначально ее значение равно 1.
4. Подпрограмма QUAD(i, j) формирует ссылку на j-ю компоненту i-й тетрады, которая была сгенерирована ранее. Может использоваться, когда нужно получить адрес соответствующей компоненты или изменить ее.
5. Подпрограмма GENERATETEMP(P) заносит в таблицу символов элемент для временной переменной, а адрес этого нового элемента в указательную переменную Р.
6. Подпрограмма CHECKTYPE(P, N) сравнивает тип элемента таблицы символов, на который указывает Р, с N (например, CHECK-TYPE^, BOOLEAN)). Печатает сообщение об ошибке и прекращает трансляцию в случае несовпадения.
7. Подпрограмма CONVERTRI(P) проверяет тип Р-го элемента таблицы символов. Если тип — INTEGER, то ничего не делается, если REAL, то с помощью GENERATETEMP заводится новая временная переменная типа INTEGER и генерируется CVRI-тетрада для преобразования заданной переменной в тип INTEGER и занесения результата в новую временную переменную. Указатель на временную переменную в таблице символов остается в Р. Если тип Р-го элемента не INTEGER и не REAL, то выдается сообщение об ошибке.
8. Подпрограмма CONVERTIR(P) работает аналогично CON-VERTRI, с той лишь разницей, что требуется преобразование из INTEGER в REAL.
9. Другие переменные (например, Р, Pl, Р2) используются в процессе компиляции в качестве временных переменных. Их типы и назначение будут ясны из контекста.
13.2. УСЛОВНЫЕ ИНСТРУКЦИИ
Мы начнем с программ семантической обработки условных инструкций, так как, с одной стороны, они достаточно просты, а с другой — все же иллюстрируют некоторые из обсуждаемых здесь проблем. Обычно условная инструкция определяется следующим образом:
<инстр!> :: = <условие><инстр2>ЕЕ5Е<инстр3>|<условие><инстрг> <усл<?вие> ;:= IF<Bbip>THEN
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 313
где <выр> должно иметь тип BOOLEAN. Исходя из предположения, что нуль означает FALSE (ложь), а не нуль — TRUE (истина) и что значение вычисленного выражения присваивается временной переменной Т, мы должны сгенерировать одну из следующих последовательностей :
(1) Тетрады для Т := <выр> (1) Тетрады для Т := <Ьыр>
(р) BZq + 1, Т, 0 (р) BZq, Т, О
<инстр2> <инстр2>
(q) BR г (q)
(q + 1) <инстр3> (г)
BZ-тетрада генерируется программой, связанной с правилом <ус-ловие> ::= IF<Bbip>THEN. Так как пока неизвестно, куда будет переход, мы запоминаем номер тетрады в качестве семантической информации к символу <условие>, чтобы позднее воспользоваться этой информацией. Заметим, что, каким бы сложным ни было выражение, код для него уже сгенерирован. При этом с <выр> связан указатель ENTRY, значением которого является адрес элемента таблицы символов, описывающего данное выражение.
Программа имеет следующий вид:
<условие> ;: = IF <выр> THEN
Р : = <выр>. ENTRY; Занести в Р адрес элемента таблицы
CHECKTYPE (Р, BOOLEAN); символов для <выр>.
<условие>. JUMP := NEXTQUAD; Запомнить номер следующей тетрады, которая будет BZ-переходом через оператор, следующий за THEN.
ENTER (BZ, О, Р, 0); Генерация BZ-тетрады.
Заметим, что подпрограмма CHECKTYPE контролирует, чтобы выражение было типа BOOLEAN.
Теперь позаботимся о генерации адреса перехода в том случае, когда значением выражения будет FALSE. Рассмотрим вначале программу обработки условной инструкции без ELSE. Если <ус-ловие> <инстр2> приводится к <инстр1>, мы можем считать, что все тетрады для <инстр2> уже сгенерированы. Очевидно, они следуют за BZ, так как никакая часть <инстр2> не будет анализироваться, пока цепочка IF <выр> THEN не редуцирована. Поэтому нам остается только вставить в BZ-тетраду адрес перехода через <инстр2>. Если вы помните, номер этой тетрады мы сохранили в <условие>.ЛиМР. Семантическая программа, следовательно, имеет следующий вид:
314
ГЛАВА 13
<HHCTpj> : : = <условие> <инстр2>
I <условие>. JUMP; Занести номер следующей тетрады во
QUAD (I, 2) NEXTQUAD вторую компоненту BZ-тетрады (с но-
мером I).
При генерации кода для условной инструкции с ELSE с использованием упомянутых выше правил грамматики непременно возникает следующая проблема. Нам нужно, чтобы между <инстр2> и <инстр3> была вставлена команда перехода. Но, если действовать в соответствии с прежним синтаксисом, разбор <инстр2> и <инстрз> будет закончен прежде, чем такая возможность представится. Чтобы привести синтаксис в соответствие с желаемой семантикой, мы изменим его таким образом:
<инстр1> <ист. часть><инстр3>
<ист. часть> :: = <условие> <инстр2>ЕЬ5Е
Теперь мы можем написать следующие две семантические программы:
< ист. часть>::~<условие> <hhctp2>ELSE
< ист. часть>. JUMP : = NEXTQUAD; Запомнить номер следующей тетрады, ENTER (BR, 0, 0, 0); чтобы позднее можно было вставить в
нее адрес перехода.
I := <условие>. JUMP; Занести в BZ адрес перехода через
QUAD(I, 2) NEXTQUAD; <инстр!>, как это делалось выше.
< инстр!>: : = <ист. часть> <инстр3>
I := <ист. часть>. JUMP Вставить адрес перехода через
QUAD (I, 2) := NEXTQUAD; <инстр2>.
Эта совокупность семантических программ позволяет нам еще раз обратить ваше внимание на два основных момента. Во-первых, когда основа XY ... Z редуцируется, тетрады для тех нетерминалов, которые есть в основе, уже сгенерированы. И если потребуется вставить дополнительные тетрады между теми, которые уже были сгенерированы, то следует изменить синтаксис таким образом, чтобы он соответствовал семантике.
Во-вторых, в программах показано, как используется семантика, связанная с символом, для запоминания информации, которая потребуется позже. Заметим, что можно было бы допустить любое количество вложенных друг в друга условных операторов, если на некоторых стадиях разбора иметь произвольное число символов <условие>. С каждым из них будет связана своя JUMP-компо-нента (адрес перехода в BZ-тетраде), а стековый механизм обеспечивает автоматическое сохранение каждой такой компоненты отдельно.
В дальнейшем мы еще не раз будем обращать внимание на эти два момента.
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 3)5
УПРАЖНЕНИЯ К РАЗДЕЛУ 13.2
1. Для инструкции вида IF А^В THEN <инстр2> получается довольно плохая программа. Сначала мы вычитаем А из В и получаем TRUE или FALSE в зависимости от знака результата, после чего выполняем BZ-переход через <инстр2>. Измените синтаксическое определение символа <условие> так, чтобы распознавался специальный случай IF <выр1>^<выр2> THEN и для этого случая генерировалась одна тетрада (BG, 0, <выр!>, <выр2>).
2. Измените также синтаксис и семантику так, чтобы выделять IF <выр!>^<выр2> и генерировать тетраду (BG, 0, <выр2>, <выр!>).
13.3. МЕТКИ И ПЕРЕХОДЫ
Метка определяется следующим образом:
<инстр!> I : <инстр2>
где I — нетерминал, обозначающий идентификатор. И опять возникает та же проблема, что и в условных инструкциях. Метке I нужно присвоить адрес начала <инстр2>, а это невозможно сделать, так как код <инстр2> был уже сгенерирован, прежде чем мы приступили к анализу идентификатора. Внесем изменения в синтаксис:
<инстрх> ::== Определение метки> <инстр2>
Определение метки> ::= I :
Имея в виду, что в программе ссылаться на метки можно раньше, чем они фактически определяются, напишем следующую семантическую программу:
определение метки> : : = I: LOOKUPDEC (I. NAME, Р); IF Р —0 THEN BEGIN INSERT (I. NAME, P); Поиск идентификатора в таблице. Если его нет, то занести его в таблицу с типом LABEL
P. TYPE : = LABEL END ELSE BEGIN CHECKTYPE (P, LABEL); IF P. DECLARED - 1 THEN ERROR (3) END; P. DECLARED :== 1; P. ADDRESS : = NEXTQUAD; Если он есть, то проверить, метка ли это? Если да, то проверить, не повторное ли это определение? Если повторное, то напечатать сообщение об ошибке (номер 3). Если нет, то установить признак, что метка определена, и занести значение в поле ADDRESS,
316
ГЛАВА 13
С правилом <инстрх> = Определение метки><инстр2> нет необходимости связывать какую-либо дополнительную семантику.
В ФОРТРАНе инструкция GO ТО не вызывает никаких затруднений, так как номера (метки) инструкций не должны повторяться. Семантическая программа для перехода GO ТО I следующая:
<инстр> = GO ТО I
LOOKUP (I.NAME, Р);
IF Р=0 THEN
BEGIN
INSERT (I. NAME, P);
P. TYPE := LABEL;
P. DECLARED := 0;
END
ELSE CHECKTYPE (P, LABEL);
ENTER (BRL, P, 0, 0);
Поиск идентификатора в таблице.
Если его нет, то занести его в таблицу с типом LABEL и признаком «не определен».
Если он есть, то проверить тип. Генерировать тетраду перехода.
Образование списка из операций переходов
Иногда появляется желание для переходов к метке вместо BRL использовать BR, т. е. в поле операндов задавать номер тетрады, а не адрес элемента таблицы символов. Это необходимо, в част-
GO ТО L; (10) BR 0,0,0 NAME ADDRESS DECLARED
GO ТО L; (20) BR 10,0,0 L 40 0
GO ТО L; (40) BR 20,0,0
некоторые поля в элементе
исходная про&р&Мма, тетрады таблицы символов
Р и с. 13.1. Организация списка переходов на еще неопределенную метку.
ности, когда генерируются машинные команды и в команде перехода нам нужно сформировать адрес команды, на которую передается управление.
Но инструкция GO ТО L может встретиться раньше, чем будет определена метка L, и, следовательно, мы не можем вставить номер тетрады до тех пор, пока не будет обработано определение метки. К одной метке может быть несколько переходов, а это еще больше усложняет задачу.
Простой способ обработки переходов вперед состоит в следующем. Все тетрады для GO ТО L связываются в один список, а указатель на начало списка помещается в поле ADDRESS элемента таблицы символов для L. На рис. 13.1 это демонстрируется на примере трех переходов к L в тетрадах с номерами 10, 20, 40. Совсем необязательно хранить связи между элементами списка в от
семантические программы для ЯЗЫКА, ПОДОБНОГО АЛГОЛу 3\Т
дельном стеке или таблице; в данном случае мы можем воспользоваться полем первого операнда в тетрадах переходов.
Как только завершен анализ определения метки L, семантическая программа может пройти по списку и вставить соответствующий номер во все тетрады переходов. Это очень простой и эффективный способ решения проблемы переходов вперед. Его можно иногда использовать для обработки ссылок вперед на переменные процедуры и т. д. Все зависит от конкретного исходного языка.
Переходы вперед для языков с блочной структурой
При обработке переходов вперед для языка с блочной структурой возникают дополнительные трудности. Если встречается переход на метку, которая еще не определена в данном блоке, но уже определена в каком-либо объемлющем его блоке, то возникает вопрос: появится ли определение этой метки в данном блоке или нет? Так, при анализе последней инструкции в цепочке
BEGIN L : BEGIN GO ТО L
совершенно не ясно, куда будет переход по GO ТО L: к ранее определенной метке или к метке, определение которой встретится позднее? Одно из очевидных решений состоит в том, что на первом проходе просматривается только структура блоков, описания и определения меток, а также полностью строится таблица символов. Тогда на втором проходе будет известно, где определяется каждая метка. Если требуется действительно однопроходный компилятор, то можно было бы потребовать от пользователя дополнительное описание для меток, используемых в блоке, например такое — LABEL L. С точки зрения программиста, этб, конечно, ужасное решение, и прибегать к нему можно лишь в исключительных случаях, так как это потребует от пользователя слишком много усилий при программировании. Третье решение, на котором мы кратко остановимся, требует больших усилий от разработчика компилятора.
Если встречается переход к метке, которая в блоке еще не определена, то в этом блоке для нее заводится элемент таблицы символов. Для каждого открытого блока и каждой такой метки внутри блока организуется список тетрад, в которых есть ссылка на эту метку. Если метка действительно описана в этом блоке, то все хорошо, т. е. ссылки на эту метку сформированы правильно. Если же метка не описана в блоке (это известно, когда закончен анализ блока), то мы должны исключить этот элемент из таблицы символов и добавить элемент для этой метки в ближайший объемлющий блок (если ее там не было), а весь список ссылок только что закрытого блока присоединить к списку ссылок этой метки в объемлющем блоке.
318
ГЛАВА 13
Очевидно, остается еще проблема, связанная с переходом за пределы блока, в тех реализациях, когда при выходе из блока необходимо обращаться к специальной подпрограмме. Как и прежде, можно объединить в список все команды, в которых требуется переход из блока к метке L, и дополнить их правильными адресами в тот момент, когда станет наконец известен номер блока, где определена метка L.
УПРАЖНЕНИЯ К РАЗДЕЛУ 13.3
1. Измените семантические программы для переходов и меток, чтобы вместо команды BRL генерировать команду BR.
2. Напишите семантические программы, реализующие предложенную схему обработки переходов вперед в языках с блочной структурой.
13.4. ПЕРЕМЕННЫЕ И ВЫРАЖЕНИЯ
Переменные в языках типа АЛГОЛ определяются следующим образом:
<пер> I |1(<список выр»
<список выр> := <выр>|<список выр>, <выр>
Правило <пер> :: = I не требует генерации тетрад. Мы должны только найти идентификатор в таблице символов и адрес соответствующего ему элемента связать с <пер>. Таким образом, получается следующая семантическая программа:
<пер> I
LOOKUP (I. NAME, Р);
IF Р = 0 THEN ERROR (4);
<пер>. ENTRY := Р;
Поиск идентификатора.
Если Р=0, то он не найден; выдается сообщение об ошибке.
С <пер> связывается адрес найденного элемента в таблице.
При компиляции с ФОРТРАНа тот факт, что идентификатор не был найден, не следует воспринимать как ошибку. Все, что мы должны сделать,— это с помощью процедуры INSERT занести идентификатор в таблицу и установить TYPE равным REAL или INTEGER в зависимости от первой буквы идентификатора.
Анализ переменной с индексами I «список выр>) требует больше усилий с нашей стороны. Мы должны сформулировать тетрады для вычисления всех индексных выражений и для вычисления адреса элемента массива, используя метод, описанный в разд. 8.4. ;
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 319
Необходимо также подсчитать количество индексов и проверить, совпадает ли оно с размерностью массива.
Можно было бы воспользоваться прежним синтаксисом, но, чтобы вычислять VARPART с помощью (8.4.5), нам придется заменить его на следующий:
<инд> ::= I «выр> I <инд>,<выр>
<пер> ::= <инд»
Атрибуты в элементе таблицы символов для идентификатора массива будут иметь следующие значения: TIPE1=2, TYPE — тип каждого элемента массива!, NUMBER — размерность массива. Для простоты предположим, что в таблице символов в подряд стоящих ячейках содержатся также адреса элементов таблицы символов для di, d2, d3, .... dn (см. 8.4.5). Это требует дополнительной памяти,, но зато упрощает само описание. При обычном способе работы в поле ADDRESS имеется адрес информационного вектора, что дает возможность узнать, где находятся dj, d2 и т. д.
Теперь вернемся к программе для правила <инд> :.= I (<выр>. Нам необходимо найти идентификатор массива, сгенерировать тетрады для VARPART := <выр> и связать с <инд> адрес элемента таблицы символов для dx.
<инд> :: = I ( <выр>
LOOKUP (I.NAME, Р);
IF Р = 0 OR Р. TYPE / 2
THEN ERROR (5);
<инд>.СОиыТ = Р.NUMBER —1;
<HHfl>.ARR := Р;
<инд>.ENTRY := Р+1;
GENERATETEMP(P);
P.TYPE := INTEGER;
OiHzi>.ENTRY2 ;= P;
CONVERTRI (<выр>. ENTRY);
P := <выр>.ENTRY;
ENTER (: = , P, , <инд>. ENTRY2);
Поиск идентификатора.
Он должен быть описан и иметь тип ARRAY.
Одно индексное выражение мы уже имеем. Для подсчета количества индексов используется счетчик COUNT. Запомнить адрес описателя массива. Занести в ENTRY адрес описателя dx-Генерация временной переменной типа INTEGER для VARPART.
Запомнить ее адрес.
Эта процедура генерирует команды преобразования типа, если они нужны. Генерация тетрады занесения первого индекса в VARPART.
Перечислим семантическую информацию, связанную с <инд>:
1. <инд>.ENTRY Адрес элемента таблицы символов для ф, если сгенерирован код для i-ro индексного выражения.
2. <инд>.ЕЫТЕУ2 Адрес элемента таблицы символов для VARPART.
320
ГЛАВА 13
3. <инд> .COUNT
4. <hha>.ARR
(размерность) —i, если сгенерирован код для i-ro индексного выражения.
Адрес описателя имени массива в таблице символов.
Теперь нам нужно составить программу для правила <индх> : = <инд2>, <выр>. Мы должны сгенерировать код для VARPART : — VARPART*di+<Bbip>, если это i-e по счету индексное выражение.
<инД1> :: = <инд2> , <выр>
<инд!>. COUNT
:= <инд2> .COUNT— 1;
<HHAi>.ARR := <hha2>.ARR;
<hhA1>.ENTRY
<hh42>.ENTRY+ 1;
Pl := <инд2>. ENTRY2;
<hha1>.ENTRY2 := Pl;
ENTER (*, Pl, <индх>.ENTRY, Pl);
P := <выр>.ENTRY;
CONVERTRI (P);
ENTER ( + , Pl, P, Pl);
Подсчет индексов.
Запомнить тип элемента массива.
<hha1>:ENTRY в данный момент указывает на элемент таблицы для dp Заполнить в Р1 и ENTRY2 адрес элемента таблицы символов для VARPART.
Получение тетрады для
VARPART : = VARPART*di.
Генерирование тетрады преобразования в INTEGER, если, конечно, это необходимо.
Получение тетрады для
VARPART : -VARPART+индекс.
Заметим, что нам не важно, насколько сложным является индексное выражение. В нем могут быть ссылки на элементы других массивов и функции — словом, все, что вообще может быть в выражении, так как мы здесь имеем дело всего лишь с указателем на элемент таблицы символов, описывающий результат. Нам осталось написать программу для правила <пер> <инд». В этой программе мы можем проверить количество индексных выражений и построить элемент таблицы символов с описанием элемента массива.
<пер> :: = <инд> )
IF <инд>.COUNT #0
THEN ERROR (6);
GENERATETEMP (P);
P.TYPE1 := 3;
P.TYPE <hha>.ARR.TYPE;
P.ADDRESS := <hha>.ENTRY2;
P.NUMBER := <hha>.ARR;
Нуль в COUNT означает, что количество индексов было правильным. Генерирование временной переменной для описателя элемента массива. Занести тип, адрес элемента таблицы для VARPART и адрес описателя элемента таблицы, содержащего имя
массива.
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 321
Арифметические и логические операции
Бинарные операторы обрабатываются в основном так, как об этом говорилось в гл. 12, и нам нет необходимости снова подробно останавливаться на этом. Для правил вида <выр!> <выр2>+ +<терм>; <выр2> и <терм> проверяются на соответствие типов и, если необходимо, генерируются тетрады преобразования того или иного операнда в требуемый тип. Генерируются новая временная переменная для запоминания результата и тетрада с соответствующим оператором. Подобным же образом обрабатываются унарные операторы.
УПРАЖНЕНИЯ К РАЗДЕЛУ 13.4
1. Напишите семантическую программу для правила <выр!>::= <выр2>+<терм>.
2. Напишите семантическую программу для правила
<множ>:: =—<первичное выр>.
13.5. FOR-ЦИКЛЫ
Рассмотрим семантические программы для for-циклов, которые определяются следующим образом:
<инстр> :: = FOR <пер> <!ог-список> DO <инстр>
<1ог-список> <вырх> STEP <выр2> UNTIL <выр3>
в предположении, что шаг <выр2> всегда положительный. При таком предположении for-цикл можно переписать в следующей эквивалентной форме:
<пер> := <выр!>;
GO ТО OVER;
AGAIN : <пер> :== <пер>+<выр2>;
OVER:
IF <пер>^<выр3>
THEN BEGIN <инстр>; GO ТО AGAIN END
Заметим, что переменная цикла используется в нескольких местах. Следовательно, при разборе цикла мы должны где-то хранить указатель на ее элемент таблицы символов. Теперь, очевидно, нужно изменить правила таким образом, чтобы генерировать тетрады в правильном порядке. Мы будем использовать следующие правила:
11 Д. Грис
322
ГЛАВА 13
< forl> ::= FOR <пер> := <вырх>
< for2> <forl> STEP <выр2>
< for3> <for2> UNTIL <выр3>
< инстр1> <for3> DO <инстр2>
Теперь мы можем написать следующие семантические программы. Для большей ясности в этих программах сознательно опущены проверки типов операндов и генерация тетрад для преобразования типов.
<forl> FOR <пер> := <выр!>
LOOKUP (<nep>.NAME, P);
IF P = 0 THEN ERROR (7);
Pl <вырг>.ENTRY;
ENTER (:=, Pl, , P);
<forl>.ENTRY := P;
<for 1>. JUMP NEXTQUAD;
ENTER (BR, 0, 0, 0);
<forl>. JUMP2 := NEXTQUAD;
Занести адрес элемента таблицы символов в Р.
Генерация тетрады для начальной установки переменной цикла.
Запомнить адрес элемента таблицы символов для переменной цикла и номер BR-перехода к OVER.
Генерация BR-тетрады для перехода к OVER.
Нам также понадобится номер тетрады с меткой AGAIN.
<for2> <forl> STEP <выр2>
<for2>.JUMP2 := <forl>7JUMP2;
<for2>.ENTRY := <forl>.ENTRY;
P := <выр2>.ENTRY;
ENTER ( + , <forb.ENTRY, P, <forl>.ENTRY);
I := <forl>.JUMP;
QUAD (I, 2) := NEXTQUAD;
<for3> <for2> UNTIL <выр3>
<for3>.JUMP2 := <for2>.JUMP2;
<for3>.JUMP NEXTQUAD;
Запомнить адрес метки AGAIN и адрес переменной цикла.
Генерация тетрады прибавления шага к переменной цикла.
Сформировать адрес перехода к OVER.
ENTER (BG, 0, <for2>.ENTRY, <выр3>. ENTRY);
<HHCTpx> ::= <for3> DO <инстр2>
ENTER (BR, <for3>.JUMP2, 0, 0);
I := <for3>.JUMP;
QUAD (I, 2) := NEXTQUAD;
Запомнить адрес метки AGAIN.
Сейчас мы собираемся сгенерировать условный переход для IF и запомнить его номер.
Это тетрада IF <пер><:<выр3>.
Это тетрада GO ТО AGAIN, номер этой тетрады сохраняется в JUMP2. Формируется адрес перехода в тетраде BG <пер>, <выр>.
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 323
УПРАЖНЕНИЯ К РАЗДЕЛУ 13.5
1. Для тех же циклов напишите семантические программы, не делая предположения, что значение шага всегда положительно.
2. Для тех же циклов напишите семантические программы так, чтобы шаг и граничное значение цикла вычислялись один раз.
3. Напишите семантические программы для инструкции WHILE, имеющей следующую структуру: <инстр> WHILE<Bbip>DO <инстр>.
4. Для рассмотренных циклов перепишите семантические программы так, чтобы генерировать оптимальный код в случае, когда <пер> — целая и все выражения — константы, предполагая, что существует тетрада (TEST, <пер>, <kohcti>, <конст2>), которая делает следующее: 1) добавляет <констх> к <пер>, 2) если результат больше Осонст2>, то выполняет следующую за ней тетраду, в противном случае пропускает ее.
13.6. ОПТИМИЗАЦИЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
В этом разделе мы хотим показать два разных способа генерации кода для логических выражений, которые определяются так:
Z ::= Е
(13.6.1) Е :: = Т | Е OR Т Т ::- F | Т AND F F ::= I |(Е) | NOT F
В этом разделе все идентификаторы — это переменные типа BOOLEAN, которые принимают значения TRUE (истина) или FALSE (ложь). Для них определены три операции: OR, AND и NOT, смысл которых ясен из таблиц:
OR TRUE FALSE TRUE TRUE TRUE FALSE TRUE FALSE
AND TRUE FALSE NOT|TRUE FALSE
TRUE FALSE TRUE FALSE FALSE FALSE |FALSE TRUE
Из синтаксиса видно, что AND имеет более высокий приоритет, чем OR, а у NOT из этих трех операций самый высокий приоритет. Заметим, что NOT NOT А эквивалентно А. Обычный способ вычисления таких выражений тот же, что и для арифметических выражений, т. е. операции выполняются слева направо с учетом их приоритетов и скобок. Польская запись для A AND (В OR NOT С) будет следующей: ABC NOT OR AND. Таким образом можно было бы легко написать семантические программы для перевода логических выражений из инфиксной записи в польскую или в тетрады. Однако существует более эффективный способ вычисления таких выражений.
И*
324
ГЛАВА 13
Оптимальный способ вычисления логических выражений
Рассмотрим выражение A AND (В OR NOT С). Если переменная А имеет значение FALSE, то нет необходимости вычислять остальную часть выражения, так как результат всегда будет FALSE. Аналогично если А и В имеют значение TRUE, то не нужно вычислять NOT С. Поэтому мы хотим вычислять выражения слева направо, прекращая вычисление сразу, как только становится известным окончательный результат. Для предыдущего выражения можно считать эквивалентной следующую запись:
IF А
THEN IF В
THEN TRUE ELSE NOT C ELSE FALSE
Переопределим синтаксис и семантику логических выражений следующим образом:
Z = Е
(13.6.2) E::=T|TORE
Т ::= F | F AND Т
F ::= I | (Е) | NOT F
где
с OR d определяется, как IF с THEN TRUE ELSE d c AND d определяется, как IF c THEN d ELSE FALSE NOT с определяется, как IF c THEN FALSE ELSE TRUE.
Мы будем генерировать тетрады, используя идентификаторы, константы 0 и 1 и два типа тетрад (: = , I, ,Т) и (В, I, i, j), где I — идентификатор. Последняя тетрада имеет следующий смысл: если I имеет значение TRUE, то осуществляется переход на i-ю тетраду, в противном случае — переход на j-ю тетраду.
На рис. 13.2 приводится несколько примеров. При разборе этих примеров нужно учитывать следующее. Во-первых, результат всегда остается в X. В первой тетраде в X заносится 1, т. е. вначале значение выражения предполагается равным TRUE. Если обнаруживается, что выражение и в самом деле имеет значение TRUE, то выполняется переход с пропуском оставшихся тетрад, в том числе и последней; если значение выражения FALSE, то происходит переход на последнюю тетраду, в которой в X заносится 0.
Во-вторых, идентификаторы в тетрадах располагаются в том же порядке, что и в исходном выражении. И наконец, для оператора NOT тетрады не генерируются. Если А представляется, как (В, A, i, j), то NOT А представляется, как (В, A, j, i), т. е. меняются местами адреса переходов по TRUE и FALSE.
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 325
В конце этого раздела будет ясно, что с равным успехом мы могли бы генерировать польскую запись, а в случае однопроходного компилятора даже команды машины. Придется, правда, иметь в
виду множество мелких подробностей, но техника останется прежней.
(1)(: = , 1. - X) (!)(: = , 1, , X) (1)С=, 1, , X)
(2) (В, А, 5, 3) (2)(В, А, 3, 5) (2) (В, А, 3, 4)
(3)(В, В, 5, 4) (3) (В, В, 5, 4) (3)(В, В, 5, 4)
(4)(: = , 0, , X) A OR В (4)(:==, 0, , X) NOT A OR В (4)(: = , А 0, , AND В X)
(1)(: = . 1, . X) (1)(: = . 1. . X) (1)С=. 1, , X)
(2) (В, А, 6, 3) (2)(В, А, 6, 3) (2) (В, А, 3, 5)
(3)(В, В, 6, 4) (3)(В, В, 4, 6) (3)(В, В, 6, 4)
(4) (В, С, 5, 6) (4) (В, С, 6, 5) (4) (В, С, 6, 5)
(5)(: = , 0, , X) (5)(: = ,0, , X) (5)(: = , 0, , X)
A OR В OR NOT С A OR NOT В OR С A AND (В OR С)
(1)(: = , 1, , X) (1)(: = , 1, , X) (1) (: = , 1, , X)
(2) (В, А, 4, 3) (2) (В, А, 3, 4) (2) (В, А, 3, 6)
(3)(В, В, 6, 4) (3)(В, В, 4, 7) (3) (В, В, 5, 4)
(4) (В, С, 5, 7) (4) (В, С, 6, 5) (4) (В, С, 7, 5)
(5) (В, D, 7, 6) (5) (В, D, 7, 6) (5) (В, D, 7, 6)
(6)(:=, 0, , X) (6)(: = , 0, , X) (6) (:=, 0, , X)
(A OR NOT В) (A AND NOT В) (A AND (NOT (В
AND (NOT С OR D) Рис. 13.2. OR (NOT С AND D) OR NOT C) OR D)) Булевы выражения в форме тетрад.
В основном нам важно показать, как обеспечивается правильное заполнение адресов, так как в этом и состоит главная проблема. Поэтому мы здесь не будем обращать внимание на типы, таблицу символов и тому подобные вещи.
13.6.1 . Восходящий метод
Реорганизация продукций
Если используется грамматика (13.6.2), то при вызове, например, программы для Е ::= Т OR Е тетрады для Т и Е уже будут сгенерированы. А нам нужно, чтобы код выглядел так:
326 ГЛАВА 13
(1) (В, Т, 3, 2)
(2) <тетрады для Е>
То есть если Т имеет значение TRUE, то необходимо пропустить вычисление Е. Этого можно добиться, если разбить правила так, чтобы Т и Е не встречались одновременно в правой части одного и того же правила. Заменим грамматику на следующую:
Z ::= Е
Е ::= Т | TOR Е
(13.6.3) TOR ::= Т OR
Т F | FAND Т .
FAND ::= F AND
F ::= I | (Е) | NOT Е
Семантическая информация
Всякий раз, когда в процессе разбора логического выражения основой оказывается идентификатор, например А, мы генерируем тетраду (В, А, 0, 0). В этот момент еще неизвестны адреса переходов по TRUE и FALSE. Поэтому с F (для правила F ::= I) связывается информация, которая позволит позднее сформировать адрес перехода по TRUE (из TCHAIN), адрес перехода по FALSE (из FCHAIN). Чтобы различать ссылки на 3-ю и 4-ю компоненты к-й тетрады, мы будем обозначать 3-ю компоненту числом к, а 4-ю компоненту — числом —к. Таким образом, после разбора первого идентификатора в выражении получим F.TCHAIN=2, F.FCHAIN= —2 и тетрады
(1) С = , 1. , Т)
(2) (В, А, 0, 0)
Рассмотрим какой-либо из нетерминалов Е, TOR, T.FAND илиР. За каждым из них может скрываться сложное логическое выражение, содержащее много идентификаторов. Для каждого, следовательно, может быть длинный список переходов по TRUE или FALSE, в которых еще неизвестны адреса переходов. Мы организуем список всех переходов по TRUE, а ссылку на первый элемент списка запомним в TCHAIN (в информации к нетерминалу). Те же действия проделаем для FALSE и соответственно для FCHAIN. Таким образом, мы строим списки так же, как это делалось для переходов вперед в разд. 13.3.
Рассмотрим к примеру подвыражение (A OR В AND С). Предположим, что мы привели его к F. Тогда тетрады для него будут следующими:
(1) С = . 1, , Т)
(2) (В, А, 0, 3)
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 327
(3) (В, В, 4, 0)
(4) (В, С, 0, 0)
где нулевые компоненты обозначают еще неизвестные адреса. Но если их использовать для внутренних ссылок в списке, мы будем иметь следующие тетрады:
F.TCHAIN=4, F.FCHAIN=—4
и
(1) С = . 1, , Т)
(2) (В, А, 0, 3)
(3) (В, В, 4, 0)
(4) (В, С, 2, —3)
Для образования списков и работы с ними в семантических программах используются процедуры MERGE и FILLIN. При написании семантических программ мы исходим из предположения, что генерация тетрад уже началась и в списке тетрад содержится первая тетрада (: = , 1, , Т). Ознакомьтесь вначале с этими двумя программами, затем перейдите к программе для нетерминала F, которая будет основой для изучения всех остальных программ. Это облегчит понимание всего процесса обработки.
PROCEDURE FILLIN (К);
VALUE К; INTEGER К;
BEGIN INTEGER SAVE;
WHILE К * 0 DO
BEGIN I := IF К > 0
THEN 3 ELSE 4;
SAVE := ABS (K);
К := QUAD (SAVE, I);
QUAD (SAVE, I) := NEXTQUAD
END END
PROCEDURE MERGE (KI, K2);
INTEGER KI, K2;
BEGIN INTEGER K;
IF Kl=0 THEN KI := K2 ELSE
BEGIN К := KI;
LOOP: I := IF К > 0
THEN 3 ELSE 4;
К ;= ABS (K);
FILLIN заносит в список, начинающийся с К-й тетрады, номер следующей тетрады.
Если К=0, то работа выполнена.
Какую компоненту нужно заполнить, 3-ю или 4-ю?
Получение номера тетрады.
Перейти к следующему элементу в списке.
Заполнить соответствующую компоненту номером следующей тетрады.
К1 и К2 содержат начальные номера списков.
Подключить список К2 в конец списка К1.
Если К1—0, то просто К2 пересылается в KL
Далее идем по цепочке ссылок до конца списка К1.
328
ГЛАВА 13
IF QUAD (К, I) F 0 THEN BEGIN К := QUAD (К, I); GO TO LOOP;
END; QUAD (К, I) := K2; END; END Подсоединить список K2 к концу списка К1.
Z E FILLIN (E.FCHAIN); ENTER (:=, 0, , X); FILLIN (E.TCHAIN); Все сделано. Занести все адреса переходов по FALSE и сгенерировать последнюю тетраду. Занести переходы по TRUE.
E ::= T E.TCHAIN := T.TCHAIN; E.FCHAIN := T.FCHAIN; Е и Т семантически идентичны. Поэтому только копирование цепочек.
Ex ::z= TOR E2 EpFCHAIN := E2.FCHAIN; Для TOR FALSE-переходы были за-
EpTCHAIN :== TOR.TCHAIN; полнены раньше, поэтому только копирование из Е2.
MERGE (EPTCHAIN, E2.TCHAIN); Слияние двух списков TRUE-переходов в один список Ег
TOR ::z= T OR FILLIN (T.FCHAIN); TOR.FCHAIN := 0; TOR.TCHAIN := T.TCHAIN; Заполнение всех FALSE-переходов в Т номером следующей тетрады. Запомнить список TRUE-переходов.
FAND F AND FILLIN (F.TCHAIN); FAND.TCHAIN : = 0; FAND.FCHAIN := F.FCHAIN; Заполнение всех TRUE-переходов в F номером следующей тетрады. Адреса FALSE-переходов еще не известны.
T F T.TCHAIN := F.TCHAIN; T.FCHAIN := F.FCHAIN; Комментарии излишни.
Tx ::== FAND T2 TPTCHAIN := T2.TCHAIN; Tx.FCHAIN := FAND.FCHAIN; Для FAND TRUE-переходы уже заполнены, поэтому только копирование из Т2.
MERGE (TpFCHAIN, T2.FCHAIN); Слияние двух списков FALSE-nepe-ходов в один список для Тг
F (E) F.TCHAIN := E.TCHAIN; Все TRUE- и FALSE-переходы для
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 329
F.FCHAIN := E.FCHAIN;
F1 NOT F2
Fi.TCHAIN := F2.FCHAIN;
FpFCHAIN := F2.TCHAIN;
F те же самые, что и для Е.
Для NOT Fj—TRUE, если F2== =FALSE. Переключение цепочек.
F ::= I
F.TCHAIN := NEXTQUAD;
F.FCHAIN :=—NEXTQUAD;
ENTER (B, l.SEM, 0, 0)
Фиксация цепочек в месте, соответствующем номеру следующей тетрады. Затем генерация тетрады.
УПРАЖНЕНИЯ К РАЗДЕЛУ 13.6.1
1. Сделайте разбор выражений, данных на рис. 13.2, используя приведенные выше семантические программы для генерации тетрад.
2. Определите польскую запись для тех же выражений и измените семантические программы для ее генерирования.
13.6.2. Метод нисходящего разбора
Для сравнения покажем, как те же самые вещи можно было бы сделать, пользуясь методом рекурсивного спуска. Так как мы идем сверху вниз и пишем нашу собственную синтаксическую схему, мы получаем дополнительную гибкость. Приводимые ниже процедуры программируются аналогично тому, как это описывалось в разд. 12.4, но требуют некоторого обсуждения. Они программируются с использованием грамматики (13.6.4) с применением итераций. В действительности легче использовать грамматику (13.6.2), в основе которой лежит правая рекурсия, а не итерации (см. упражнение 4).
Семантическая информация FCHAIN и TCHAIN передается в программы в качестве параметров.
Z ::= Е (13.6.4) Е T{OR Т}
Т ::= F{AND F}
F ;;= I | NOT F|(E)
PROCEDURE Z;
BEGIN INTEGER FCHAIN,TCHAIN;
Процедура для правила Z ::=E.
END
ENTER (:=, 1, , X);
E (FCHAIN, TCHAIN);
FILLIN (FCHAIN);
ENTER (: = , 0, , X);
FILLIN (TCHAIN)
Генерация первой тетрады.
Разбор Е.
После возврата заполнение адресов для FALSE-переходов и генерация тетрады для занесения нуля в X. Затем заполнение адресов для TRUE-nepe-ХОДОВ.
330
ГЛАВА 13
PROCEDURE E(TCHAIN, FCHAIN); INTEGER TCHAIN, FCHAIN; BEGIN INTEGER TC;
TCHAIN :=0; FCHAIN :=0;
LOOP: T(TC, FCHAIN);
MERGE(TCHAIN, TC);
IF NXTSYMB=“OR” THEN BEGIN FILLIN (FCHAIN);
FCHAIN := 0;
SCAN; GO TO LOOP
END END
PROCEDURE T (TCHAIN, FCHAIN);
INTEGER TCHAIN, FCHAIN;
BEGIN INTEGER FC;
TCHAIN :=0; FCHAIN :=0;
LOOP: F (TCHAIN, FC);
MERGE (FCHAIN, FC);
IF NXTSYMB =“AND” THEN
BEGIN FILLIN(TCHAIN);
TCHAIN : = 0;
SCAN; GO TO LOOP; END
END
PROCEDURE F(TCHAIN, FCHAIN);
INTEGER TCHAIN, FCHAIN;
BEGIN INTEGER K;
L: IF NXTSYMB = “(’’THEN BEGIN SCAN; E(TCHA1N, FCHAIN);
IF NXTSYMB = “)” THEN SCAN ELSE ERROR;
GO TO ENDF
END;
IF NXTSYMB = “NOT” THEN BEGIN SCAN; F (TCHAIN, FCHAIN);
К := TCHAIN;
TCHAIN := FCHAIN;
FCHAIN := K;
GO TO ENDF;
END;
IF NXTSYMB = “I” THEN
BEGIN TCHAIN : = NEXTQUAD;
Процедура для E : := T{OR T}
Вначале списки TCHAIN и FCHAIN пустые. Разбор терма.
Добавить переходы по TRUE к списку TCHAIN. Если есть еще OR, мы во всех FALSE-переходах устанавливаем номер следующей тетрады.
Сканируется следующий терминал и повторяется обработка.
Процедура для Т ::= F{AND F}.
Вначале списки пустые.
Разбор множителя.
Добавить новый переход по FALSE. Есть ли еще AND?
Да. Запомнить TRUE-переходы.
Искать следующий множитель.
Процедура для F : := I |(Е) |NOT F.
Если первый символ ( , то разбор выражения и проверка наличия закрывающей скобки.
Если NOT, то разбор следующего множителя. Затем «переключение» цепочек (то, что было TRUE, становится FALSE, и наоборот).
Если идентификатор, то оформление переходов, как указывалось выше.
СЕМАНТИЧЕСКИЕ ПРОГРАММЫ ДЛЯ ЯЗЫКА, ПОДОБНОГО АЛГОЛу 331
FCHAIN := —NEXTQUAD;
ENTER (В, NXTSEM, 0, 0); Генерация тетрады.
END
ELSE ERROR;
ENDF: END
УПРАЖНЕНИЯ К РАЗДЕЛУ 13.6.2
1. Проведите разбор выражений, приведенных на рис. 13.2, используя программы нисходящего разбора.
2. Определите польскую запись для логических выражений и измените процедуры этого раздела, чтобы генерировать польскую запись.
3. Заметим, что если AND идет за идентификатором, перед которым нет NOT, то мы можем генерировать тетраду (BZ, i, А, 0) для перехода на i-ю тетраду, если A=FALSE. Если A=TRUE, то программа перейдет к выполнению следующей тетрады. В польской записи или на языке машины это приведет к более эффективной программе. Аналогичный прием можно использовать при обработке идентификаторов, за которым следует OR. Измените рассмотренные выше процедуры так, чтобы генерировать более эффективный код.
4. Перепишите приведенные выше рекурсивные процедуры так, чтобы следовать грамматике (13.6.2).
Глава 14
Отведение памяти переменным в готовой программе
Поскольку схема распределения памяти и форматы областей данных готовой программы уже известны (см. гл. 8), осуществление распределения памяти во время компиляции становится довольно простой задачей. В разд. 14.1 мы очертим общую схему, не рассматривая пока областей COMMON и эквивалентности, и поясним, когда такое распределение памяти могло бы иметь место. В разд. 14.2 мы рассмотрим распределение памяти для временных переменных. Наконец, в разд. 14.3 мы обсудим проблемы распределения памяти, связанные с областями COMMON и эквивалентностью.
Некоторые машины имеют несколько быстрых регистров, которые могут использоваться для хранения промежуточных результатов. Хотя задачу эффективного использования этих регистров можно рассматривать как задачу распределения памяти, но мы все же рассмотрим ее в разд. 17.5 в связи с оптимизацией программ.
14.1. ПРИСВАИВАНИЕ АДРЕСОВ ПЕРЕМЕННЫМ
Мы исходим из того, что для каждой компилируемой процедуры компилятор отводит одну область данных. В эту область входят все неявные параметры, фактические параметры, переменные, определяемые программистом (или их описатели), и временные переменные, используемые процедурой.
Так как в ФОРТРАНе одновременно может компилироваться только одна подпрограмма, то работа ведется только с одной областью данных. В противоположность этому в АЛГОЛе или PL/1 одновременно может компилироваться любое количество процедур и каждая со своей областью данных.
В общем случае компилятор имеет таблицу D, где перечислены все области данных объектной программы. Элемент таблицы D для каждой области данных содержит поле, в котором помечено, статическая эта область или динамическая, поле LENGTH, указывающее на число ячеек, занимаемых областью, и т. д. Сначала LENGTH-0.
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ 333
Программа, осуществляющая присвоение переменным адресов, каждый раз имеет дело с одной процедурой. Ее первая задача — отвести в начале области место для дисплея (если он используется) и для неявных параметров. В поле LENGTH устанавливается количество ячеек, используемых этими стандартными объектами фиксированного размера.
Вторая задача состоит в том, чтобы обработать элементы таблицы символов, соответствующие формальным параметрам, а также переменным, описанным в этой процедуре, и присвоить им адреса. Для каждого элемента таблицы символов делается следующее:
1. Элементу таблицы символов присваивается смещение, равное значению LENGTH, т. е. ему присваивается адрес первой свободной ячейки области данных.
2. LENGTH увеличивается на число ячеек, отводимых под формальный параметр или переменную, описываемую этим элементом таблицы символов.
Это простая и очевидная обработка, и нет необходимости давать дополнительные пояснения. Нужно только, чтобы из таблицы символов можно было узнать количество ячеек, требуемых для каждой переменной. В некоторых языках (например, в ФОРТРАНе IV) эта информация не известна до окончания просмотра всей исходной программы. Поэтому для присваивания адресов после обычного анализа необходим второй просмотр.
В компиляторе WATFOR 360 с ФОРТРАНа IV (см. Кресс и др.) используется следующая схема. Во время первого, главного просмотра компилятор генерирует команды машины непосредственно с исходного языка. Ссылки на переменные в командах машины представляются указателями на соответствующие им элементы таблицы символов. Во время второго, малого просмотра переменным присваиваются адреса, которые запоминаются в элементах таблицы символов. Затем просматриваются команды машины и каждая ссылка в таблицу символов заменяется на соответствующее значение адреса, взятое из элемента, на который ссылается команда.
В языках, которые требуют описания переменных до их использования, распределение памяти может выполняться семантическими программами, предназначенными для обработки описателей. В этом случае действительно возможен однопроходный компилятор.
Переменные с начальными значениями
До сих лор мы полагали, что на этапе компиляции нам не нужна область данных процедуры. Как правило, это действительно так; нам нужен только счетчик LENGTH, указывающий на размер области данных. В некоторых языках имеется возможность задавать переменным начальные значения, которые устанавливаются
334
ГЛАВА 14
во время компиляции. Самый легкий способ осуществить это — создать область данных с начальными значениями в виде части объектной программы и занести в нее начальные значения. Другое решение (вероятно, не столь хорошее) — сгенерировать последовательность операторов присваивания для установки начальных значений.
Проблемы выравнивания
Для IBM 360 требуется, чтобы некоторые величины начинались с границы двойного слова, слова или полуслова. Предположим, нам нужно отвести память переменным Bl, Fl, Н1 и D1 в том порядке, как они написаны (с выравниванием, если это необходимо), причем каждая из этих переменных занимает соответственно 1,4, 2 и 8 байтов, и их адреса должны быть кратны соответственно 1, 4, 2 и 8. Тогда получится следующее распределение памяти:
байт 0 В1 байты 8—9 Н1
байты 1—3 не используются байты 10—15 не используются
байты 4—7 F1 байты 16—23 D1
Здесь плохо то, что многие байты совсем не используются. Чтобы избежать этого, можно распределять память сначала для переменных, которые должны начинаться с границы двойного слова, затем с границы слова, полуслова и байта.
Использование блочной структуры для экономного распределения памяти
Предположим, что в языке с блочной структурой каждой процедуре отводится одна область данных. Область содержит ячейки всех переменных для всех блоков процедуры. Таким образом, для программы, приведенной на рис. 14.1, потребовалось бы 7 ячеек.
Однако, используя блочную структуру, мы можем сэкономить часть памяти. Например, АЗ и А4 (см. рис. 14.1) можно расположить в одной ячейке. То же самое можно сказать о А2 и А5. Тогда потребуется только 5 ячеек.
При реализации такой схемы область данных процедуры можно мысленно себе представить в виде стека. Во время счета при входе в блок в стек заносятся ячейки для переменных этого блока, имеющих фиксированную длину, а при выходе из блока они выталкиваются из стека.
Алгоритм, присваивающий адреса во время компиляции, распределяет память для блоков в порядке их появления. Он исполь
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ
335
зует две переменные и стек. Переменная CURRENTLENGTH содержит число ячеек, выделенных для блоков, которые открыты в данный момент и еще находятся в обработке. LENGTH содержит максимальное число ячеек в области данных. Вначале обе переменные имеют нулевое значение. Стек S используется для хранения
BEGIN REAL Al, Bl; ячейка значение
BEGIN REAL A2, B2; 0 Al
BEGIN REAL АЗ; ... END; 1 Bl
BEGIN REAL A4; ... END; 2 A2, A5
END; 3 B2
BEGIN REAL A5; ... END; 4 АЗ, A4
END
Рис. 14.1. Распределение памяти для бло той структуры.
начальных адресов ячеек, выделенных для блоков, все еще находящихся в обработке. Алгоритм следующий:
1. НАЧАЛО БЛОКА. Значение CURRENTLENGTH засылается в вершину стека S. Это значение снова будет восстановлено в CURRENTLENGTH после выхода из блока, для того чтобы параллельные блоки использовали то же самое место памяти. Затем для каждой переменной, описанной в блоке, например К, делается следующее:
Переменной К присваивается адрес, равный значению CURRENTLENGTH;
CURRENTLENGTH увеличивается на число ячеек, отведенных для К-
В заключение отводится память для временных переменных, используемых в данном блоке (см. разд. 14.2).
2. КОНЕЦ БЛОКА. LENGTH := MAXIMUM (LENGTH, CURRENTLENGTH);
Значение, хранящееся на вершине стека S, выталкивается из стека и переносится в CURRENTLENGTH.
Для иллюстрации алгоритма покажем, как он работает на примере программы, изображенной на рис. 14.1. Для каждого шага приводятся значения переменных и стека перед тем, как этот шаг выполняется.
336
ГЛАВА 14
Шаг CURRENT LENGTH LENGTH Стек S Адреса След. шаг
Al Bl A2 B2 A3 A4 A5
I 0 0 Нач. бл.
2 2 0 0 0 I Нач. бл.
3 4 0 0 2 0 I 2 3 Нач. бл.
4 5 0 0 2 4 0 l 2 3 4 Кон. бл.
5 4 5 0 2 0 I 2 3 4 Нач. бл.
6 5 5 0 2 4 0 I 2 3 4 4 Кон. бл.
7 4 5 0 2 0 I 2 3 4 4 Кон. бл.
8 2 5 0 0 I 2 3 4 4 Нач. бл.
9 3 5 0 2 0 I 2 3 4 4 2 Кон. бл.
Ю 2 5 0 0 I 2 3 4 4 2 Кон. бл.
0 5 0 0 I 2 3 4 4 2
14.2. ОТВЕДЕНИЕ ПАМЯТИ ВРЕМЕННЫМ ПЕРЕМЕННЫМ
Временные переменные нужны главным образом для хранения промежуточных результатов вычисления выражений. Они нужны также для хранения адресов переменных с индексами, значений фактических параметров и списков параметров при обращении к функциям. Обычно для временных переменных отводятся ячейки в той области данных процедуры (или блока), в которой встретилось выражение. Мы могли бы для каждой временной переменной выделить отдельную ячейку, но это было бы неэкономно. Поэтому нам хотелось бы иметь такой алгоритм распределения памяти, который бы минимизировал количество используемых ячеек. Для начала мы будем рассматривать только линейные участки, т. е. последовательность команд, выполняемых по порядку и не имеющих переходов ни внутрь, ни наружу.
Рассмотрим последовательность тетрад для следующих инструкций: Е А* В-f-C*D; F:=A»B-|-1; G:=C*D;
(14.2.1) (I) * А, В, Т1 (2) * С, D, Т2 (3) +Tl, Т2, ТЗ (4) := ТЗ, , Е (5) * А, В, Т4 (6) + Т4, I, Т5 (7) := Т5, , F (8) * С, D, Тб (9) := Тб, , G
Поскольку нас интересуют одни только ЗАПиси и ЧТения
временных переменных Т1, Т2, .. ., это можно записать как
(I) ЗАП Т1 (5) ЗАП ТЗ (9) ЗАП Т5
(14.2.2) (2) ЗАП Т2 (б) ЧТ ТЗ (Ю) ЧТ Т5
(3) ЧТ Т2 (7) ЗАП Т4 (Н) ЗАП Тб
(4) ЧТ Т1 (8) ЧТ Т4 (12) ЧТ Тб
Зоной существования временной переменной Т i мы назовем
последовательность операций от начальной установки до ее послед-
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ- 337 него использования. Очевидно, временные переменные с непересе-кающимися зонами могут располагаться в одних и тех же ячейках. В приведенном примере Т1, ТЗ, Т4, Т5 и Тб все можно расположить в одной ячейке.
Часто алгоритм распределения памяти для временных переменных работает после того, как команды машины уже сгенерированы. Он имеет дело с командами машины, а не с внутренним представлением. Это делается по той причине, что не для всех временных переменных требуются ячейки памяти. Например, значение Т5 в командах машины для (14.2.1), вероятно, будет оставаться на сумматоре или в быстром регистре на протяжении всей своей зоны и не потребует никакой ячейки памяти. Но об этом известно только тогда, когда команды уже сгенерированы.
Ниже приводится алгоритм распределения памяти в виде отдельного прохода в терминах последовательности ЗАПисей и ЧТений. Сам алгоритм может быть включен в фазу генерации программы или работать как отдельный проход после генерации программы.
Использование стека во время счета для временных переменных
Предположим, что во время счета ячейки а, а+1, а+2, ... могут использоваться под временные переменные. Прежде всего давайте рассмотрим арифметические выражения с простыми переменными или константами в качестве операндов. Далее предположим, что выражения вычисляются согласно следующей грамматике:
Е ::= Е+Т | Е—Т | Т
Т :: = T*F | T/F | F
F :: = (Е) | I
При вычислении выражения Е+Т сначала вычисляется Е, затем Т и наконец Е+Т. Это означает, что все временные переменные, которые использовались при вычислении Е, уже больше не нужны, как только получен его результат. То же можно сказать и о Т. Кроме того, после вычисления выражения Е+Т временные переменные, содержащие Е и Т, также не нужны.
Здесь важно то, что зоны Ti и Tj либо не пересекаются, либо одна из них целиком лежит в другой. Например, последовательность ЗАПисей и ЧТений временных переменных выражения (A+B)*(C+(D*E)) следующая:
(1) ЗАП Т1
(2) ЗАП Т2
(3) ЧТ Т2
(4) ЗАП ТЗ
(Т1 := А + В)
(Т2 := D*E) (вычисление С+Т2) (ТЗ := С+Т2)
338
ГЛАВА 14
(5) ЧТ ТЗ
(6) ЧТ Т1
(7) ЗАП Т4
(вычисление Т1 * ТЗ) (вычисление Т1 * ТЗ) (Т4 Т1*ТЗ)
(В действительности можно написать ЧТ Т1, ТЗ, так как чтения ТЗ и Т1 идут подряд.) Такая вложенность зон временных переменных позволяет нам использовать а, а+1, а+2, ... во время счета как стек, точно так же, как мы это делали при вычислении выражений в польской записи. Вовремя компиляции это осуществляется следующим образом. Заводится ячейка L, которая вначале содержит 0, а затем указывает на текущий размер стека. Для отведения памяти под временные переменные мы просматриваем последовательность операций. При каждой ЗАПиси во временную переменную Tj, открывающей ее зону, переменной отводится ячейка a+L и L увеличивается на 1. При последнем ЧТении временной переменной Tj содержимое ячейки L уменьшается на 1.
В последнем примере Т1 присваивается адрес а, Т2 — адрес а+1, ТЗ — адрес а+1, Т4 — адрес а, т. е. используется только две ячейки.
Заметим, что, как определено выше, для временных переменных в выражениях допустимы лишь одна ЗАПись и одно ЧТение, и, следовательно, их зоны легко определяются.
Более общая схема распределения памяти
Если программа на внутреннем языке изменяется так, что зоны временных переменных Ti и Tj могут пересекаться частично, то предыдущая схема уже становится неприемлемой. Например, оптимизирующий проход мог определить, что А*В и OD в (14.2.1) должны вычисляться только по одному разу, и (14.2.1), следовательно, примет вид
(1) * А, В, Т1 (2) * С, D, Т2 (3) + Т1, Т2, ТЗ (5)+ (6): = (7) : = Т1, 1, Т5
Т5, Т2, , F , G
(4) := ТЗ, , Е
Здесь зоны Т1 и Т2 пересекаются частично:
(1) ЗАП Т1 (6) ЧТ ТЗ
(2) ЗАП Т2 . (7) ЧТ Т1
(14.2.3) (3) ЧТ Т2 (8) ЗАП Т5
(4) ЧТ Т1 (9) ЧТ Т5
(5) ЗАП ТЗ (Ю) ЧТ Т2
Мы должны, следовательно, рассматривать произвольные после-
довательности операций ЗАП Ti и [ ЧТ Ti. Данциг и Рейнольдс
[66] доказали, что следующий алгоритм минимизирует число ис-
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ 339
пользуемых ячеек. Заводится стек времени компиляции S, который вначале содержит адреса а+п, а+п—1, .... а+1, а (а — вершина стека). Для того чтобы присвоить адреса, просматривается последовательность операций. При каждой встретившейся записи ЗАП Tj, которая открывает зону Tj, из стека берется адрес и присваивается Tj, после чего этот адрес выталкивается из стека. Для последнего чтения ЧТ Tj (которое заканчивает зону Tj) рассматриваются два случая. Если память для Tj не была отведена, то это означает, что в Tj не было записи, что является ошибкой. Если память была отведена, то адрес, который был присвоен Tj, записывается в стек S, так как содержимое этой ячейки больше не нужно.
Ниже мы иллюстрируем этот алгоритм на примере последовательности (14.2.3). В первой колонке приводится содержимое стека, во второй — присваиваемые адреса перед выполнением операции, в третьей — обрабатываемая операция.
Стек Адреса Обрабатываемая операция
Т1 Т2 ТЗ Т5
а3 а 4~ 2 а 4~ 1 а 0 0 0 0 (1) ЗАП Т1
а 4~ 3 а + 2 а 4~ 1 а 0 0 0 (2) ЗАП Т2
а 4“ 3 а 4~ 2 а а + 1 0 0 (3) ЧТ Т2
а 4- 3 а 4“ 2 а а + 1 0 0 (4) ЧТ Т1
а + 3 а 4~ 2 а а + 1 0 0 (5) ЗАП ТЗ
а 4" а а + 1 а+2 0 (6) ЧТ ТЗ
а 4~ 3 а 4“ 2 а а + 1 а+2 0 (7) ЧТ Т1
а 4~ 3 а 4~ 2 а а а + 1 а+2 0 (8) ЗАП Т5
а 4- 3 а 4~ 2 а а + 1 а+2 а (9) ЧТ Т5
а 4- 3 а 4~ 2 а а а+1 а + 2 а (10) ЧТ Т2
а 4“ 3 а 4~ 2 а а 4~ 1 а а+1 а+2 а
Заметим, что адреса в стеке могут идти и не подряд. Фактически годится любой набор адресов ячеек, которые могут использоваться как временная память.
В рассмотренном алгоритме предполагается, что мы знаем последнее чтение временной переменной. В этом случае нам, возможно, придется хранить дополнительную информацию в описателе к каждой временной переменной. Позже мы обсудим эту проблему. В действительности первоначально алгоритм Данцига и Рейнольдса [661 обрабатывал операции в обратном порядке и предполагал, что на каждую временную переменную встречается только одна запись. Таким образом, при просмотре в обратном порядке, встречая первый раз ЧТ Tj, мы выделяем ячейку, а встречая ЗАП Tj, мы ее освобождаем.
340
ГЛАВА 14
Расширение алгоритма на случай других временных переменных
Любой из приведенных методов можно легко распространить на другие временные переменные, помимо тех, которые используются внутри линейного участка. Например, мы можем расширить зону временной переменной Т, используемой для хранения значения шага, полученного в результате вычисления выражения В цикла
FOR I A STEP В UNTIL С DO <инстр>
на всю последовательность команд этого цикла. Эта зона, естественно, включает в себя зоны всех временных переменных, используемых при вычислении <инстр>.
Для условного выражения, например в контексте
... A+(IF В TNEN С ELSE D)+...
мы могли бы иметь следующее внутреннее представление:
(1) : (5) := D, , Т1
(2) BZ 5, В (6) + A, TI, Т2
(3) := С, , Т1 (7)
(4) В 6
Зоной Т1, следовательно, являются тетрады 3—6, так как для Т1 адрес выделяется сразу после генерирования команды BZ и освобождается после того, как он использовался при сложении А с Т1.
Используя программный граф и линейные участки, описанные в разд. 11.5, мы можем сформулировать следующее правило для определения зоны временной переменной, используемой на нескольких линейных участках. Зона временной переменной, используемая на нескольких линейных участках, есть минимальная область R, в которую входят линейные участки с временной переменной Т и которая обладает следующим свойством: любой путь, выходящий из R и ведущий обратно к R и к ЧТению Т, должен сначала проходить через ЗАПись в Т. На практике так искать область R неудобно, поэтому для выявления области мы будем пользоваться информацией на уровне исходной программы, как это делалось выше.
Указание о зоне в описателе временной переменной
Информацию о зонах можно хранить в описателях временных переменных в таблице символов. Мы укажем три способа хранения:
1. В описателе временной переменной содержится счетчик числа, сколько раз эта временная переменная встречается в тетрадах (он увеличивается при появлении новых тетрад, использующих данную временную переменную, и корректируется в процессе оптимизации программы). При генерации команд по тетраде счет
ОТВЕДЕНИЙ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ 34)
чик уменьшается на 1 для тех временных переменных, которые встречаются в поле операнда или в поле результата этой тетрады. Если счетчик равен нулю, то данная временная переменная больше не нужна и место, отведенное для нее, считается свободным.
2. В описателе временной переменной содержится номер последней тетрады, в которой используется эта переменная. После генерации команд для этой тетрады временная переменная больше не нужна.
3. Во время генерирования и оптимизации тетрад для каждой временной переменной строится список всех ссылок на нее, а на* чальная и конечная ссылки оставляются в описателе этой временной переменной. Например, после генерирования тетрад для (14.2.3)
получится следующий список:
(1) ЗАП (2) ЗАП Т1 (4) (6) ЧТ ТЗ(0) Т2(3) (7) ЧТ Т1 (0) Врем, пер.: Т1Т2ТЗТ5
(3) ЧТ Т2 (10) (8) ЗАП Т5 (9) Первая ЗАП: 12 5 8
(4) ЧТ Т1 (7) (9) ЧТ Т5 (0) Последнее ЧТ: 7 10 6 9
(5) ЗАП Т3(6) (10) ЧТ Т2(0) Для этого в каждой тетраде требуется дополнительное поле
для указателя на следующую тетраду в списке.
Такой список может потребоваться и для других переменных (не только временных) во время оптимизации (см. «Оптимизация циклов», разд. 18.4). Он может также использоваться и при оптимальном распределении регистров (см. «Распределение регистров», разд. 18.4). Здесь мы следующим образом используем этот список для распределения памяти временным переменным. При генерации команд в описатель временной переменной посылается номер следующей тетрады, содержащей ссылку на эту временную переменную, для которой команды еще не были сгенерированы. Если этот номер равен нулю, то временная переменная больше не нужна.
УПРАЖНЕНИЯ К РАЗДЕЛУ 14.2
1. Дается последовательность зон (Fi, Li) для временных переменных, где Fi есть номер первой ЗАПиси, a Li — номер последнего ЧТения переменной Ti. Постройте алгоритм, отводящий ячейки для Ti, который использовал бы минимальное количество ячеек. Вы можете считать, что если i<Zj, то Fi<Fj. То есть временные переменные нумеруются в порядке поступления первых ЗАПисей.
342
ГЛАВА 14
14.3. COMMON И ЭКВИВАЛЕНТНОСТЬ
Прежде чем обсуждать проблемы распределения памяти для переменных в областях COMMON и для переменных, связанных отношением эквивалентности, рассмотрим соответствующие инструкции ФОРТРАНа. Нас интересует их семантика, а не синтаксис и способ их грамматического разбора. Поэтому мы не будем здесь рассматривать все возможные вариации синтаксиса.
Следует напомнить, что подпрограммы в ФОРТРАНе не могут быть рекурсивными и что граничные пары массивов известны во время компиляции. Следовательно, область данных подпрограммы или главной программы может быть статической и содержать все переменные, задаваемые программистом, включая и массивы. Элементы в массивах располагаются по колонкам, а не по строкам. Так как граничные пары известны во время компиляции, то информационные векторы не нужны.
COMMON-области
Предположим, что А встречается в следующей инструкции ФОРТРАНа:
DIMENSION А(100),
а С определена как простая переменная. Тогда
COMMON /А1/ А, С, D(200)
специфицирует, что переменные А(1), А(2), ... , А(100), С, D(l), D(2), ..., D(200) должны располагаться в указанном порядке в подряд стоящих ячейках отдельной области данных с именем А1, так называемой А1 «COMMON-области». «/А1/» может быть опущено или заменено на «//». В этом случае область данных называется «непомеченной» COMMON-областью. Наличие компоненты D(200) в инструкции COMMON специфицирует D как массив из 200 переменных, что исключает необходимость в отдельной инструкции DIMENSION для D.
Если в программе встречается более одной инструкции COMMON с одним и тем же именем области, то каждый следующий список является продолжением предыдущего. Так, три инструкции
COMMON/A1/A, В COMMON/A1/X, Y COMMON/A1/E, D
эквивалентны одной
COMMON /А1/ А, В, X, Y, Е, D
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ
343
Один и тот же идентификатор не должен встречаться более одного раза в инструкциях COMMON, так как это означало бы, что он занимает разные места памяти в одно и то же время.
Эквивалентность
Предположим, В и С определены в инструкции
DIMENSION В(10, 10), С(10, 10).
Тогда инструкция
EQUIVALENCE (А, В(1, 1), С(11)>
означает, что переменные А, В(1, 1) и С(1,2) занимают одну и ту же ячейку. С(11) — одиннадцатый элемент массива С. Так как в ФОРТРАНе принято располагать элементы массивов по столбцам, т. е. С(1, 1), С(2, 1), ... , С(10, 1), С(1, 2), С(2, 2).С(10, 2),...
... , то одиннадцатым элементом является С(1, 2).
Эквивалентность двух элементов разных массивов приводит к эквивалентности и других элементов массивов. Если предположить, что В и С используют по одной ячейке на каждый элемент, то для нашего примера В(2, 1) и С(2, 2) располагаются в одной и той же ячейке так же, как В(3, 1) и С(3, 2), В(4, 1) и С(4, 2) и т. д.
Любая переменная может быть связана эквивалентностью с любым количеством других переменных, лишь бы при этом не возникали противоречия. Рассмотрим инструкцию
EQUIVALENCE (А, В(1, 1)), (А, С(1, 2)), (В, С).
Так как А эквивалентна В(1, 1) и С(1, 2), то все три переменные располагаются в одной ячейке. Последняя эквивалентность В с С (В(1, 1) с С(1, 1)) приводит к противоречию, так как эквивалентность С(1, 1) и С(1, 2) невозможна.
Переменная может быть связана эквивалентностью с переменной из COMMON-области. Это означает, что первая переменная и все другие, эквивалентные ей, также принадлежат COMMON-области. Такая эквивалентность уже не может изменить порядок расположения переменных в COMMON-области, она может только увеличить ее размер. Рассмотрим инструкции
COMMON X, У
DIMENSION С (5)
EQUIVALENCE (X, С)
Длина COMMON-области равна 5 в предположении, что каждая переменная занимает одну ячейку, так как С(1), ... , С(5) также входят в COMMON-область. Заметим, что Y и С(2) занимают одну и ту же ячейку.
344
ГЛАВА 14
COMMON-область не должна расширяться в другую сторону. Так, замена последней инструкции эквивалентности на EQUIVALENCE (Х,С(2)) приведет к ошибке, так как X обязана занимать первую ячейку COMMON-области.
Таблица COMMON •‘Областей и COMMON щепочки во время компиляции
Во время компиляции мы заводим таблицу COMB для COMMON-областей, используемых в компилируемой программе. Каждый элемент таблицы имеет следующий формат:
NAME DA FP IP LENGTH
где NAME — имя COMMON-области (пробел для непомеченной COMMON-области), DA — адрес, присваиваемый COMMON-области, FP и LP — указатели на элементы таблицы символов соответственно первой и последней переменных COMMON-области, LENGTH — общее число ячеек COMMON-области.
NAME COMP EQUIVP DA OFFSET
NAME — имя переменной или массива.
СОМР — 0, если переменная пока не в COMMON-области, в противном случае указывает на следующий элемент COMMON-области (или на 1-й элемент, если данный элемент последний).
EQUIVP—0, если переменная пока не связана отношением эквивалентности, в противном случае указывает на следующий элемент в кольцевой цепочке эквивалентностей.
DA — номер области данных (0, если область не отведена). OFFSET — смещение в области данных или смещение в цепочке эквивалентности.
Рис. 14.2. Некоторые поля элемента таблицы символов.
Самый простой способ задания структуры COMMON-области — это связать ее переменные и массивы цепочкой ссылок в том порядке, как они описываются в инструкции COMMON, используя для этого дополнительное поле COMP (COMMON Pointer — указатель на следующий COMMON-элемент) в каждом элементе таблицы символов. Объединим также цепочкой ссылок переменные, связанные Между собой отношением эквивалентности, используя для этого
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ 345
еще одно поле EQUIVP в элементе таблицы символов, формат которого изображен на рис. 14.2. (На этом рисунке не отмечены поля TYPE, KIND и др., поскольку они не интересуют нас при данном рассмотрении.)
Заметим, что обе цепочки закольцованы и последний элемент имеет ссылку на первый элемент. Следовательно, наличие ссылки может служить признаком того, находится ли данная переменная
NAME FP LP
А1 0 1 6 0
А2 0 3 4 0
Та0лац<ь COMB
Рис. 14.3. Пример COMMON-области и COMMON-цепочки.
в COMMON-области (связана ли она отношением эквивалентности) или нет. На рис. 14.3 изображен список COMMON-областей и COMMON-цепочки для инструкций
COMMON /А1/ А, В
COMMON /А2/ С, D
COMMON /А1/ Е, F
Цепочки эквивалентностей
Переменные, связанные эквивалентностью, также объединяются в циклический список с помощью указателей в поле EQUIVP. В отличие от COMMON-переменных порядок расположения элементов в цепочке здесь не важен, так как в любом случае им отводятся одни и те же ячейки. Мы воспользуемся этим, чтобы строить цепочку самым удобным для нас способом.
Все эквивалентные между собой переменные должны быть представлены одной цепочкой. Это означает, что мы должны иногда сливать цепочки вместе. Рассмотрим, например, инструкцию EQUIVALENCE (А, В, С), (Е, F, В). Перед тем как обрабатывается второе появление В, мы имеем две следующие цепочки:
346
ГЛАВА 14
При обработке второго В мы узнаем, что В уже участвовало в эквивалентности, и сольем две цепочки в одну
l-Д—>В—
Поле OFFSET в элементе таблицы символов указывает на положение первой ячейки переменной относительно других переменных цепочки. Если бы отношением эквивалентности связывались только простые переменные, то в этом поле не было бы необходимости. Но рассмотрим инструкцию
EQUIVALENCE (А, В(1), С(2))
и предположим, что каждый элемент массива занимает одну ячейку. Тогда А и В имеют OFFSET=0. Однако элемент С имеет OFFSET = =—1, так как массив С должен начинаться на одну ячейку раньше переменной А и массива В. Если встретилась дополнительная инструкция
EQUIVALENCE (В(2), D)
то, поскольку В(1) имеет OFFSET=0, В(2) имеет адрес 1 относительно остальных переменных в цепочке эквивалентности; следовательно, D имеет OFFSET = 1.
Общая схема реализации
В ФОРТРАНе две вещи существенно мешают нам распределить память для COMMON-областей и переменных, связанных отношением эквивалентности, за один проход. Первое — это то, что инструкция, задающая тип переменной (например, COMPLEX А), может следовать после инструкции COMMON и EQUIVALENCE, в которых встречается А. Это означает, что во время обработки инструкций COMMON и EQUIVALENCE не всегда известно количество ячеек, используемых переменной. ВторЬе — инструкция DIMENSION для некоторого идентификатора может встретиться после того, как этот идентификатор использовался в операторе EQUIVALENCE. Рассмотрим, например, инструкции:
EQUIVALENCE (А, В(1, 2)) DIMENSION В(10, 10)
При обработке инструкции EQUIVALENCE нам еще неизвестны граничные пары массива В и, следовательно, мы не можем сразу вычислить положение элемента В(1, 2) в массиве.
Это вынуждает нас при компиляции выполнять обработку за четыре шага, которые приводятся ниже. Возможен более эффективный метод, но мы используем менее эффективный в целях про
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ 347
стоты изложения тех шагов, из которых состоит обработка. После пояснения общей схемы дается более подробное описание шагов.
1. При первом просмотре исходной программы строятся цепочки для всех COMMON-переменных, т. е. для их описателей в таблице символов. Цепочки эквивалентностей не строятся только потому, что мы не можем вычислить смещение для переменных типа В(1,2), так как могут быть еще неизвестны граничные пары массива. Вместо этого мы только запоминаем операторы EQUIVALENCE в некотором внутреннем виде в отдельной таблице для последующей обработки. По окончании просмотра можно предположить, что таблица символов содержит всю необходимую информацию о типах переменных, граничных парах массивов и т. д. Затем мы переходим ко второму шагу.
2. Строятся цепочки эквивалентностей и одновременно вычисляются смещения и заполняются поля OFFSET.
3. Присваиваются адреса COMMON-переменным и всем переменным, эквивалентным COMMON-переменным.
4. Присваиваются адреса всем остальным переменным, в том числе и переменным, связанным отношением эквивалентности.
Шаг 1. Построение COMMON-цепочек
Составлять цепочку из COMMON-переменных довольно просто, и делается это на первом просмотре инструкции COMMON. Рассмотрим инструкцию вида
COMMON /А1/ А, В(100), С
с элементами А, В(100) и С. Обработка инструкции состоит в следующем:
1. В список COMMON-областей добавляется элемент с именем А1, если его там не было. Поля элемента имеют следующие значения: NAME=A1, DA = адрес следующей свободной ячейки области данных и FP=LP=LENGTH=0. Пусть Р — это указатель на элемент А1 в таблице COMMON-областей.
2. Каждый элемент списка в правой части инструкции COMMON обрабатывается следующим образом:
(а) Выполняется обычная обработка элемента таблицы символов (ищется элемент в таблице символов (если его нет, то он заводится), проверяется тип, размерность и т. д.; если элемент имеет вид <ид>(<целое>, ... , <‘целое>), то он обрабатывается как описатель массива). В указатель PS устанавливается адрес элемента таблицы символов.
(Ь) Если PS.COMP#=0, то эта переменная уже определена как COMMON-переменная. Выдается сообщение об ошибке и осуществляется переход к следующему элементу списка.
(с) Элемент таблицы символов PS добавляется к цепочке:
348
ГЛАВА 14
IF P.FP=O THEN P.FP := PS ELSE P.LP.COMP := PS; PS.COMP := P.FP;
(d) В элементе списка COMMON-областей фиксируется ссылка на последний элемент цепочки: P.LP := PS;
Шаг 2. Построение цепочек эквивалентностей
Предполагается, что исходная программа уже прошла первичную обработку и что типы и размерности всех переменных зафиксированы в таблице символов. В качестве входной информации для этого шага служат инструкции EQUIVALENCE в некотором внутреннем представлении. Например, идентификаторы представляются ссылками на элементы таблицы символов.
Эта обработка более сложная, чем в COMMON, по двум причинам: нам нужно сливать цепочки и вычислять смещения. Но нам не нужна таблица эквивалентностей наподобие COMB для COMMON-областей. Вместо этого нам нужен только указатель Р на текущий элемент формируемой цепочки и целочисленная переменная BOFFSET, содержащая текущее базовое значение OFFSET, относительно которого вычисляются OFFSET всех элементов. Вначале BOFFSET=0 и изменяется только при слиянии цепочек. Чтобы обработать инструкцию вида
EQUIVALENCE (С, D, А(5), В(1, 3))
мы устанавливаем начальные значения
Р := О, BOFFSET := 0;
после чего для каждого элемента списка в правой части инструкции эквивалентности выполняются следующие действия:
1. Пусть PS — указатель на элемент таблицы символов, a L — длина (число занимаемых ячеек) обрабатываемой переменной или длина одного элемента массива, если переменная — массив. В z получается OFFSET следующим образом:
(а) Если переменная вида <ид>, то z:= BOFFSET.
(b) Если переменная вида <ид>(1), то контролируется, что <ид> есть идентификатор массива и i лежит в допустимом диапазоне значений. Установить z := BOFFSET+L*(1—i).
(с) Если переменная вида <ид>(П, ... , in), то контролируется, что <ид> есть n-мерный массив и каждое значение индекса лежит в допустимом диапазоне. Вычисляется адрес j (см. разд.
8. 4) для элемента массива <ид>(И, .... in). Установить z := BOFFSET+L*(1— j).
2. Если PS уже участвовал в эквивалентности (PS.EQUIVP=/=0), то переход к шагу 4. В противном случае выполняется шаг 3.
3. Новый элемент PS добавляется в цепочку:
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ
349
IF Р=0 THEN Р := PS ELSE PS.EQUIVP := Р.EQUIVP; P.EQUIVP := PS; PS.OFFSET := z. Пропустить шаг 4.
4. Эта переменная (или массив) участвует в эквивалентности второй раз, так что две закольцованные цепочки нужно слить в одну.
(а) Заново вычисляются значения OFFSET в строящейся цепочке относительно OFFSET старой цепочки. При этом на каждом элементе проверяется, не пришли ли мы к элементу, с которого начали:
DIFF := z—PS.OFFSET; BOFFSET :== BOFFSET—DIFF; Q : = Р;
IF P = 0THEN BEGIN „новая цепочка еще пуста“;
Р :== PS; GOTO шаг 4(c)
END;
LOOP: IF Q = PS THEN BEGIN IF DIFF#=0
THEN сообщение об ошибке;
GOTO шаг 4(c);
END;
Q.OFFSET := Q.OFFSET —DIFF; QI := Q;
Q := Q.EQUIVP; IF Qy=P THEN GO TO LOOP.
(b) Сливаются две цепочки. Порядок следования элементов в формируемой цепочке несуществен:
QI.EQUIVP : = PS.EQUIVP; PS.EQUIVP := Р.
(с) Обработка элемента заканчивается.
Для примера рассмотрим инструкцию
EQUIVALENCE (А, В(5), С(6)), (D, В(4), Е), (F, С(2)).
На рис. 14.4 показано, как связываются между собой элементы таблицы символов после обработки каждого элемента эквивалентности в предположении, что ранее эти переменные в операторах эквивалентности не встречались. Поле EQUIVP представлено стрелками, а поле OFFSET — числами вслед за каждым именем элемента в цепочке. Заметим, что значения OFFSET могут быть как отрицательными, так и положительными.
Шаг 3. Присваивание адресов COMMON-переменным
Для каждой COMMON-области мы идем по цепочке переменных и присваиваем им адреса. Процесс временно приостанавливается, когда какая-то из переменных связана отношением эквивалентности, чтобы присвоить адреса всем элементам цепочки эквивалентности. Это значит, что переменная из COMMON-цепочки может
350
ГЛАВА 14
получить свой адрес раньше своей обычной обработки. В этом случае мы должны убедиться, что ее адрес совпадает с ранее полученным адресом. Переменная OFFS используется для хранения OFFSET для следующей переменной (вначале 0). Указатель Р содержит ссылку на текущий элемент в таблице COMB.
Шаг BOFFSET P
1 0 A L>a, o-l
Z 0 A Цд,0—
3 0 A L>A,O—»C,-5—>В,-4-*
4 0 D L>D,O-I La,0—>C,-5—
5 - 1 D Ц D, -1 —» A, 0 —>C5 —>B4J
6 -1 D L>D,-1—>E ,-1 —>A, 0 —>C5 — »В,-4-*
7 0 F Lf.0-1 Ud,-1—>E,-1 —>a,o — >C,-5—>B,-4-l
8 -4 F *->F,-4—>B,-4—>0,-1—»E,-1- ->A,0—»C,-5J
Рис. 14.4. Формирование цепочки эквивалентностей.
Во время присваивания адресов мы должны также определить число ячеек COMMON-области и занести его в поле LENGTH соответствующего ей элемента списка COMMON-областей.
Ниже приводится алгоритм, в котором «длина переменной PS» означает количество ячеек памяти, занимаемых во время счета переменной, описываемой элементом PS таблицы символов. Для массива — это количество ячеек, занимаемых каждым элементом массива, помноженное на число его элементов.
Определение полей в элементах таблицы символов смотрите на рис. 14.2.
PS :== P.FP; IF PS —0 THEN STOP; PS указывает на первый элемент OFFS := 0; Р.LENGTH :== 0; COMMON-цепочки. OFFS — очередной OFFSET.
COMMON LOOP: L : = длина пере- Это цикл по каждому элементу, менной PS;
IF PS.DA = 0 THEN • Если 0, то адрес еще не присвоен.
BEGIN IF PS,EQUIVP = 0 THEN
BEGIN
ОТВЕДЕНИЕ ПАМЯТИ ПЕРЕМЕННЫМ В ГОТОВОЙ ПРОГРАММЕ 351
PS.DA := P.DA;
PS.OFFSET OFFS
END
ELSE
BEGIN AD :=OFFS—PS.OFFSET;
Q PS;
EQUIVLOOP: Q.DA : = P.DA;
Q.OFFSET : = Q.OFFSET + AD;
IF Q.OFFSET < 0 THEN сообщ. об ошибке; LI длина переменной Q;
P.LENGTH : = MAXIMUM ( P. LENGTH, Q. OFFSET + L1); Q := Q.EQUIVP; IFQ # PS THEN GOTO EQUIVLOOP;
END END
ELSE BEGIN IF PS.DA £ P.DA OR PS.OFFSET £ OFFS
THEN сообщ. об ошибке
END;
OFFS := OFFS + L;
PS := PS.COMP; IF PS ф P.FP THEN GOTO COMMONLOOP;
P.LENGTH MAXIMUM (P.LENGTH, OFFS);
Если в эквивалентности не участвует, то присваивается адрес.
Начальные установки для последующего присваивания адресов элементам цепочки эквивалентности.
Присваивание адреса элементу.
Контроль за расширением COMMON-области в недопустимую сторону.
LI — число ячеек, необходимых для переменной Q.
Смотрим, не расширилась ли COMMON-область.
Переход к следующему элементу в цепочке эквивалентности.
Адрес уже присвоен.
Проверяем, совпадает ли старый адрес с новым.
Переход к следующему элементу COMMON-цепочки.
Шаг 4. Присваивание адресов остальным переменным
На последнем шаге просматривается таблица символов и присваиваются адреса тем переменным, которые не принадлежат COMMON-области. Если переменная связана отношением эквивалентности, то делается двойной просмотр закольцованной цепочки, в которую эта переменная входит. На первом просмотре находится значение К, равное минимальному значению OFFSET по всем элементам цепочки. На втором просмотре элементам присваиваются адреса. Если начальный адрес, присваиваемый набору эквивалентных переменных, есть OFFS, то адрес, присваиваемый каждому
352
ГЛАВА 14
элементу, равен
OFFS — К + (OFFSET элемента).
Таким образом, элементе минимальным значением OFFSET получает адрес OFFS.
Алгоритм следующий:
1. DA := номер области данных компилируемой подпрограммы, OFFS : = адрес первой свободной ячейки, PS := адрес первого элемента таблицы символов.
2. Если PS.DA^=0, то PS уже получил адрес. Переход к шагу 4.
3. Если PS.EQUIVP#=O, то PS участвует в эквивалентности и выполняется только шаг ЗЬ, в противном случае выполняется только шаг За.
(а) Вычисление длины L переменной PS;
PS.DA := DA; PS.OFFSET := OFFS; OFFS := OFFS+L.
(b) Присваивание адресов всем переменным цепочки эквивалентности.
Ы. Вычисляется минимальное смещение К:
Q := PS.EQUIVP; К := PS.OFFSET;
WHILE Q=£ PS DO
BEGIN К := MINIMUM (K. Q. OFFSET);
Q : = Q. EQUIVP END;
Ь2. Присваиваются адреса: К := OFFS—К;
LOOP:Q.OFFSET : = K+Q OFFSET;
Вычисление длины L переменной Q;
OFFS := MAXIMUM(OFFS, Q.OFFSET+L);
Q := Q.EQUIVP; IF Q=£PS THEN GO TO LOOP.
4. Если еще не все элементы таблицы символов обработаны, то адрес следующего элемента пересылается в PS. Переход к шагу 2.
Глава 15
Нейтрализация ошибок
15.1. ВВЕДЕНИЕ
Компилятор должен выявлять по возможности максимальное количество ошибок в исходной программе. Программиста следует избавить от необходимости запускать свою работу три, четыре, а то и большее число раз, прежде чем его программа будет наконец скомпилирована. Между тем лишь немногие компиляторы удовлетворяют предъявленному требованию, а статей на эту тему написано еще меньше.
Под нейтрализацией ошибки мы понимаем процесс определения того, каким образом можно продолжить анализ исходной программы после обнаружения ошибки. В разд. 15.2 мы обсудим нейтрализацию семантических ошибок, которые связаны главным образом с неправильным использованием идентификаторов и выражений. В разд. 15.3 рассматривается другая сторона проблемы — нейтрализация синтаксических ошибок в основном с точки зрения включения средств автоматической нейтрализации в алгоритмы формального грамматического разбора. При планировании процедур нейтрализации какой-то конкретной ошибки для синтаксического анализатора, в основу которого положен здравый смысл, а неформальные методы, следует представлять, как в той же ситуации показала бы себя техника автоматической нейтрализации. Знание формальных методов, если даже они непосредственно не применимы, поможет правильно подойти к проблеме и добиться в целом более стройной реализации.
Читатель должен иметь в виду, что никакая схема автоматической нейтрализации ошибок широко не испытывалась и не сравнивалась с подобной же схемой, но написанной вручную. Мы не знаем даже, насколько они хороши. Однако они., несомненно, сравнимы со многими интуитивными процедурами нейтрализации, встроенными в существующие компиляторы.
В нескольких компиляторах, среди них наиболее известны компиляторы с языков CORC (см. Конвей и Максвелл [63], Фриман [63]), CUPL и PL/С (см. Конвей и др. [70]), пытаются «исправлять» все ошибки, генерировать команды и даже выполнять полученную программу. Любая программа начинает выполняться независимо
12 д, грио
354
ГЛАВА 15
от количества обнаруженных ошибок. На первый взгляд кажется, что это приведет к потерям времени, но, поскольку компиляторы генерируют абсолютные команды для немедленного выполнения, не требуется никаких затрат на редактирование связей и загрузку. Для программиста преимущества очевидны — уменьшается коли* чество отладочных пусков на машине, поскольку независимо от количества обнаруженных синтаксических ошибок программисту предоставляется дополнительный шанс найти еще и логическую ошибку на этапе выполнения программы. Одна ошибка в пробивке не станет препятствием для выполнения программы, и с большой вероятностью она будет исправлена разумным образом.
Лишь в работе Фримана [631 подробно описывается техника исправления ошибок. Но из этой статьи трудно сделать какие-либо выводы относительно общих методов исправления ошибок1), так как в ней рассматривается исправление ошибок для довольно простого языка CORC. Единственный метод, который можно легко объяснить, — это метод исправления орфографических ошибок. Его мы и рассмотрим в первую очередь.
Осмелюсь заметить, что для исправления ошибок пригодны общие методы нейтрализации, описанные в разд. 15.2 и 15.3. Конечно, в этом случае к ним предъявляются более жесткие требования. Нейтрализация считается вполне удовлетворительной, если обеспечивается возможность продолжить анализ и не печатается много сообщений об одной ошибке. Неважно, если иногда и появится несколько лишних сообщений. При исправлении ошибки должна получиться действительно правильная программа. Например, если мы заносим в таблицу новый символ вместо символа, который был неправильно использован, мы должны гарантировать правильную установку всех атрибутов. Для найтрализации ошибки это необязательно.
Вероятно, процедура исправления ошибки должна исключить ошибочную инструкцию, а на ее место вставить инструкцию вывода, которая напечатает, что инструкция была исключена. А если ошибка исправлена, то программисту нужно точно сообщить, как она была исправлена, чтобы он мог соответствующим образом интерпретировать результаты счета. Для обычной нейтрализации ошибок в этом нет необходимости.
Исправление орфографических ошибок
Последней статьей, посвященной исправлению орфографических ошибок, является статья Моргана [70]* 2). Читателю, желающе
х) Рекомендуем читателю обратиться к статьям Лайона [74] и Вагнера [74].— Прим. ред.
2) См. также статью Вагнера [74].— Прим. ред.
НЕЙТРАЛИЗАЦИЯ ОШИБОК
355
му получить более подробные сведения и найти библиографию по этому вопросу, рекомендуем ознакомиться с этой статьей.
Существует несколько случаев, когда компилятор может сомневаться в правильности написания идентификатора. В этих случаях компилятор должен сравнить его с идентификаторами в таблице символов и попытаться определить, который из них был искажен при написании. Давайте кратко остановимся на некоторых случаях.
1. Часто во время синтаксического анализа бывает известно, что следующий символ должен быть словом из некоторого набора служебных слов языка. Если вместо него оказался идентификатор, следует проверить, не служебное ли это слово, искаженное орфографической ошибкой. Именно с этим случаем мы встречаемся в тех языках, где любая инструкция начинается с «ключевого слова». Другим примером может служить логическое выражение, в котором должны встречаться операторы типа AND, OR, GE, LE и т. д.
Можно было бы также следить за ошибочной «конкатенацией» в месте ожидаемого служебного слова. Например, если ожидается BEGIN, а встретился идентификатор BEGINA, то его надо заменить на BEGIN А.
2. Предположим, во время семантического анализа обнаружилось, что идентификатор, определенный как метка, используется в контексте, где может встретиться только имя массива. Тогда этот идентификатор скорее всего неправильно написан и его нужно сравнить с именами описанных массивов. Подобные случаи, когда из контекста определяется возможный тип идентификатора, довольно часты.
3. Нередко из-за ошибки в написании идентификатор встречается только один или два раза, и ему либо не присваивается никакого значения, либо его значение нигде не используется. Это легко обнаружить, если в каждом элементе таблицы символов имеется счетчик присваиваний и счетчик обращений к идентификатору. Когда окончен синтаксический и семантический анализ, просматривается таблица символов и все элементы, в которых один из счетчиков равен нулю, становятся кандидатами для исправления орфографической ошибки.
Далее возникает вопрос, какой из идентификаторов таблицы символов был неправильно написан. Первой работой по этому вопросу применительно к компиляторам была диссертация Фримана 1631, посвященная CORC. В методе Фримана с использованием сложной оценочной функции вычисляется «вероятность» того, что один идентификатор является искажением другого. В этой функции используется информация о количестве совпадающих букв и о количестве совпадающих букв после одной или двух перестановок букв. Учитываются также часто встречающиеся ошибки в пробивке (цифра 0 вместо буквы О или цифра 1 вместо буквы I).
12*
356
ГЛАВА 15
Метод Фримана был заменен более эффективным (но менее мощным) методом, в основу которого положен тот факт, что около 80 процентов всех орфографических ошибок попадает в один из следующих четырех классов:
1) неверно написана или пробита одна буква;
2) пропущена одна буква;
3) вставлена одна лишняя литера;
4) две соседние литеры переставлены местами.
Следовательно, большинство орфографических ошибок можно выявить проверкой только этих типов ошибок, что намного быстрее метода Фримана. Морган [70] приводит подробные блок-схемы последнего метода. В общих чертах процедура исправления орфографических ошибок будет такой:
1. В таблице символов выделяется подмножество, включающее все те идентификаторы, из которых искаженный идентификатор может получиться вследствие описки (орфографической ошибки).
2. Затем нужно определить, какой идентификатор из этого подмножества можно превратить в этот искаженный идентификатор, используя одно из четырех указанных выше преобразований.
Первый шаг позволяет ограничить общее число проверяемых идентификаторов. Для этого, как говорилось выше, можно использовать и контекст, в котором встретился ошибочный идентификатор. Очевидно, можно принять во внимание длину идентификатора. Если в ошибочном идентификаторе п литер, то его нужно сравнивать только с идентификаторами, состоящими из п—1, п и п+1 литер. Если п^2, то нет смысла искать орфографическую ошибку.
15.2. НЕЙТРАЛИЗАЦИЯ СЕМАНТИЧЕСКИХ ОШИБОК
Цель этого раздела — дать описание простого метода нейтрализации семантических ошибок в исходной программе, т. е. ошибок, связанных с неправильным использованием идентификаторов и выражений. В этом разделе мы обратим внимание на следующие основные моменты:
1. Нейтрализация ошибки состоит в замене некорректного идентификатора или выражения «корректным» идентификатором или выражением. Это делается с помощью добавления нового элемента в таблицу символов с атрибутами, получаемыми из контекста, в котором встретилась ошибка. А соответствующий указатель во внутренней исходной программе изменяется так, чтобы он ссылался на этот новый элемент.
2. По возможности следует подавлять лишние сообщения, возникающие из-за неверной или недостаточной нейтрализации.
НЕЙТРАЛИЗАЦИЯ ОШИБОК
357
3. Нейтрализацию всех семантических ошибок следует сосредоточить в одном месте, лучше всего в’программе (назовем ее ERRMES), которая печатает сообщения об ошибках (либо накапливает их в некоторой таблице для последующей печати). Это позволит отделить нейтрализацию от остальной части компилятора.
Существуют две главные проблемы, с которыми нам приходится сталкиваться,— это 1) подавление лишних сообщений из-за одной ошибки и 2) подавление повторных сообщений об одной и той же ошибке, встречающейся несколько раз.
Подавление лишних сообщений
Во многих случаях, когда неправильно используется идентификатор, достаточно напечатать сообщение об ошибке и продолжить компиляцию. Например, если анализируется инструкция А := В, где А — переменная типа REAL, а В — переменная типа BOOLEAN, то мы можем просто напечатать сообщение о несовместимости А и В в инструкции присваивания и продолжить работу, так как нет необходимости с нетерминалом Инструкция присваивания > связывать какую-либо «семантику» и, следовательно, лишние сообщения печататься не будут.
А теперь рассмотрим другой случай, например переменную с индексами A[ei,. . ., еп], когда с идентификатором связывается некоторая «структура». Предположим, что А не есть имя массива. Тогда печатается сообщение об ошибке и продолжается грамматический разбор индексов. Когда разбор индексов окончен, их число сравнивается с размерностью массива, а она, надо полагать, указывается в элементе таблицы символов для А. Так как А не имя массива, то обязательно будет второе сообщение об ошибке.
Можно довольно просто нейтрализовать такую ошибку и подавить лишние сообщения, относящиеся к данному идентификатору, если заменить его в исходной программе «корректным» идентификатором. В таблицу символов заносится новый элемент с правильными, насколько это возможно, атрибутами. Связанное с ним имя не может встретиться в исходной программе; более того, мы полагаем, что это имя можно распознать как имя, вставленное специально для коррекции ошибки. Назовем такой элемент корректирующим элементом, так как он вставляется для коррекции ошибочного идентификатора или выражения.
Конечно, мы не будем знать всех его атрибутов в момент обнаружения ошибки, и поэтому все же могут появиться лишние сообщения. Например, если встретится A lei, . . ., enh где А не есть имя массива, то в момент, когда происходит разбор А[, мы еще не знаем, сколько индексов будет у А.
358
ГЛАВА 15
Допустим, что существует программа ERRMES, которая печатает сообщения об ошибках. Для того чтобы локализовать подавление лишних сообщений, будем выполнять это подавление в программе ERRMES следующим образом:
Программе ERRMES в качестве параметра дается указатель элемента таблицы символов для идентификатора, который вызвал ошибку. ERRMES проверяет, не является ли этот элемент корректирующим элементом, вставленным для коррекции ранее обнаруженной ошибки. Если это так, то сообщение 66 ошибке не печатается.
Важно, чтобы заведение всех новых корректирующих элементов было также сосредоточено в одной программе. Поскольку так или иначе будет обращение к программе ERRMES, то ей можно поручить и эту работу. Программу ERRMES мы опишем позже.
Подавление повторных сообщений
Повторные сообщения возникают из-за того, что один и тот же идентификатор неправильно используется в нескольких местах. Это может случиться, например, из-за ошибки, допущенной в описании идентификатора. Это случается также в языках с блочной структурой, когда из-за синтаксической ошибки нарушается блочная структура программы. Например, в программе
BEGIN REAL А; ...
BEGIN BOOLEAN А; ...
BEGIM ... END;
A:—A AND B; C:=A OR B;
END
END
допущена ошибка в слове BEGIN в третьей строке, и поэтому END закроет блок, начинающийся во второй строке. Каждое использование А в четвертой строке вызовет печать сообщения: “А — переменная типа REAL, а должна быть типа BOOLEAN”.
Повторные сообщения можно легко устранить. Во-первых, если используется неописанный идентификатор, то его нужно занести в таблицу символов с атрибутами, которые можно извлечь из его контекста. Во-вторых, с элементом для каждого идентификатора можно связать список элементов, описывающих все разновидности некорректного использования этого идентификатора. Если идентификатор используется неправильно, то нужно просмотреть этот список, и если ранее встречалась такая же некорректность, то печатать сообщение не следует. Если раньше такой вид некор
НЕЙТРАЛИЗАЦИЯ ОШИБОК
359
ректного использования не встречался, то печатается сообщение об ошибке, и эта новая некорректность добавляется в список.
Эта работа также должна выполняться в программе ERRMES, подробное описание которой мы дадим чуть позже.
У программиста может возникнуть желание точно знать все места неправильного использования идентификатора, и ему неважно, сколько сообщений он при этом получит. Но количество сообщений все же можно сократить, добавив к каждому элементу списка, описывающего некорректное использование идентификатора, перечень номеров карт, где эта некорректность встречается. После того как анализ окончен, каждое сообщение можно напечатать только один раз, сопровождая его перечнем номеров карт, в которых встретилась данная ошибка.
Программа ERRMES
К этой программе обращаются при обнаружении семантической ошибки. Она должна напечатать сообщение (или подавить его, если возможно) и затем исправить ошибку. Программа имеет следующие параметры:
1. NO : Номер выдаваемого сообщения.
2. ID : Идентификатор, который явился причиной ошибки (если он есть).
3. Р : Переменная, содержащая адрес элемента, описывающего некорректный идентификатор (если он есть). ERRMES в Р запомнит адрес корректирующего элемента, который она заведет для коррекции ошибки.
4. Т : Параметр, указывающий на тип, который должны были бы иметь идентификатор или выражение (судя по контексту, в котором встретилась ошибка).
Параметр Т используется при занесении атрибутов в корректирующий элемент таблицы символов. Может потребоваться и большее количество параметров для описания атрибутов (это зависит от исходного языка и остальной части компилятора). Теперь мы можем привести общее описание процедуры ERRMES.
1. Если сообщение с номером NO есть «неописанный идентификатор», то выполнить шаг 2, в противном случае перейти к шагу 3.
2. Завести в таблице символов элемент для ID с типом Т. Адрес этого элемента занести в Р. Напечатать сообщение и выйти из ERRMES.
3. Если Р — адрес корректирующего элемента ранее встретившегося идентификатора, то выйти из ERRMES (в этом и состоит подавление лишних сообщений).
360
ГЛАВА 15
4. Если сообщение с номером NO не относится к неправильному использованию типа элемента Р, то напечатать сообщение и выйти из ERRMES.
5. Если элемент Р уже использовался некорректно в той же самой ситуации, то перейти к шагу 7. (Эта проверка осуществляется с помощью просмотра списка некорректностей элемента Р таблицы символов.)
6. Напечатать сообщение об ошибке и, если Р=/=0, добавить еще одну некорректность к списку элемента Р.
7. Если нет корректирующего элемента с типом Т, то сформировать его и занести в таблицу символов. Указатель Р изменить так, чтобы он указывал на этот корректирующий элемент с типом Т. Выход.
15.3. НЕЙТРАЛИЗАЦИЯ СИНТАКСИЧЕСКИХ ОШИБОК
На любом этапе грамматического разбора исходная программа имеет следующий вид:
(15.3.1) xTt
где х — обработанная часть, Т — следующий сканируемый символ, at — остальная часть исходной программы.
Предположим, что встретилась ошибка. При нисходящем разборе это означает, что построено частичное дерево, которое опирается на х, но его нельзя расширить так, чтобы оноопиралось и наТ. При восходящем разборе все зависит от выбранной техники разбора. Может оказаться, что либо между хвостом х и символом Т не определено отношение предшествования, либо никакой хвост х не является основой и тому подобное.
Здесь мы должны решить, как изменить программу, чтобы «подправить» ошибку. Проще всего воспользоваться одним из следующих способов (возможно, комбинацией этих способов):
1. Исключить Т и попытаться продолжить разбор. .
2. Вставить цепочку q, состоящую из терминалов, между х и Т (получится цепочка xqTt) и начать разбор, используя голову цепочки qTt. Эта вставка позволит нам целиком обработать qT, прежде чем возникнет другая ошибка.
3. Вставить цепочку q между х и Т (получится xqTt), но разбор начать с Т. (При восходящем разборе q следует занести в стек.)
4. Исключить несколько последних символов из цепочки х.
Способы 3 и 4 плохи, и их не следует применять по следующей причине. Так как цепочка х обработана, с ней, возможно, уже связана семантическая информация. Добавление q к х или выбрасывание части х означает, что необходимо соответствующим образом из
НЕЙТРАЛИЗАЦИЯ ОШИБОК
361
менить и семантическую информацию, а это сделать совсем не просто. Если не меняется содержимое стека (способы 1 и 2), то не нужно изменять и семантику. Поэтому способы 1 и 2 будут для нас главными способами нейтрализации.
Заметим, что, вставляя цепочку терминалов (способ 2), можно получить тот же эффект, который достигается с помощью способов 3 и 4. Предположим, например, что
х = . . . ТНЕМ<начало блока> Tt == ELSE . . .
и мы хотим исключить <начало блока). Исключая этот нетерминал, мы должны позаботиться о сохранении блочной структуры таблицы символов и не только об этом. Поступим иначе, а именно вставим символ END и получим
х = . . . THEN ^начало блока) Tt = END ELSE . . .
Далее обычный процесс компиляции справится с обработкой и редукцией цепочки <начало блока) END.
Казалось бы, можно добавить правила в грамматику и заранее принять меры против ошибок. Например, мы могли бы добавить правило
Присваивание) : := := Е
и, таким образом, предусмотреть случай, когда переменная в левой части присваивания опущена. Однако грамматика при этом быстро разрастается, и ее трудно будет привести к виду, который приемлем для алгоритма грамматического разбора. С этой точки зрения удобен продукционный язык, так как на нем вы действительно программируете и можете добавить любое количество продукций, учитывающих ошибки.
Нейтрализация ошибки при нисходящем разборе
Мы рассмотрим метод, предложенный Айронсом [61Ы на примере грамматики:
Р : := А;
д . ._ j ._ е
(15.3.2) Е:’:=Т{+Т}
Т : F {*F}
F : := i | (Е)
Мы предполагаем, что грамматический разбор выполняется без возвратов. Это означает, что либо параллельно выполняются альтернативные варианты разбора и отбрасываются те из них, которые привели в тупик, либо для выбора подходящего правила на каждом шаге используется контекст,
362
ГЛАВА 15
На любом шаге разбора мы имеем дело с одним или несколькими синтаксическими деревьями, в которых есть несколько неполных кустов. Например, на рис. 15.1, а сплошными линиями показано, как выглядит частично построенное дерево, а пунктирными — как можно было бы дополнить кусты с именами Р и Е.
Неполный куст U соответствует применению правила
Ри с. 15.1. Нейтрализация ошибки при нисходящем разборе, я-^момент обнаружения ошибки; ft —после исправления ошибки.
U: := Xi X,. . . Xt_tXt. . . Хп
где Xi. . . Xt_r есть построенная часть куста, а X j. . . Хп— недостающая часть куста. На рис. 15.1,а неполный куст с именем Р соответствует применению правила Р :: = А; , а«;» есть недостающая часть куста. Неполный куст Е соответствует применению правила Е : : = Т{4-Т}. Чтобы дополнить куст, необходим один нетерминал Т, за которым следует любое количество цепочек «+Т». Недостающая часть, следовательно, есть Т {+Т}.
В качестве другого примера рассмотрим правило
U : := (А | В С | D Е) (F | G)
где скобки относятся к метасимволам. Предположим, что В есть построенная часть куста. Тогда недостающей частью является С (F | G), так как или С F, или С G будут находиться в конце правой части.
Эти недостающие части кустов играют большую роль при нейтрализации ошибки. По существу они говорят нам, что может или что должно появиться далее в исходной программе.
Предположим теперь, что во время разбора возникла ошибка, т. е. никакое частично построенное дерево не может строиться дальше. Тогда выполняются следующие действия по нейтрализации ошибки:
НЕЙТРАЛИЗАЦИЯ ОШИБОК
363
1. Строится список L из символов недостающих частей неполных кустов.
2. Головной символ Т в цепочке Tt проверяется и отбрасывается (при этом каждый раз получается новая цепочка Tt) до тех пор, пока не найдется символ Т, такой, что Uz>*T . . . для некоторого UgL (либо Uz>T, либо Uz>+ Т . . .).
3. Определяется неполный куст, который на шаге 2 стал причиной появления символа U в списке L.
4. Определяется терминальная цепочка q, такая, что, если ее вставить непосредственно перед Т, то продолжение разбора привело бы к правильной привязке Т к неполному кусту, найденному на шаге 3. С этой целью исследуется неполный куст, найденный на шаге 3, и все кусты поддерева, которые он определяет. Для каждого такого неполного куста генерируется цепочка терминалов, дополняющая этот куст, а конкатенация этих цепочек дает цепочку q.
5. Цепочка q вставляется непосредственно перед Т, и разбор продолжается, начиная с головного символа цепочки q, который становится входным символом.
Рассмотрим пример грамматического разбора, изображенного на рис. 15.1,а. Ошибка была обнаружена, когда входным символом была скобка«)». Строим списокL={; ,Т, +}• Нашаге 2 пропускается символ «)». Неполный куст, вызвавший появление «;» в L, есть Р : А;. Мы должны, следовательно, вставить цепочку q, чтобы
дополнить куст Е : := Т {+Т}. Проще всего вставить идентификатор i (см. рис. 15. 1,Ь).
Рис. 15.2 иллюстрирует, как схема использует «глобальный» контекст для определения путей нейтрализации. Кажется, что ошибка в примере, представленном на рис. 15.2,а, такая же, что и на рис. 15.1,а: за «+» идет«)». Однако теперь L = {;,), +,Т}, и на этот раз скобка не выбрасывается на шаге 2. Неполный куст, вызвавший появление «)» в L, есть F: := (Е). Для того чтобы «)» была связана с этим кустом, мы должны вставить цепочку, чтобы дополнить куст Е : : = Т {+Т}, и такой цепочкой снова будет i (см. рис. 15.2,&).
Заметим, что открывающая скобка могла отстоять намного дальше от места ошибки, и все же она учитывалась бы при нейтрализации, поскольку при нейтрализации ошибки принимаются во внимание все неполные кусты.
При использовании рекурсивного спуска (разновидность нисходящего разбора, см. разд. 4.3) также хотелось бы применить описанную выше технику нейтрализации ошибки. Однако в этом случае частично построенное синтаксическое дерево явно не представлено, и поэтому прежней техникой в полной мере воспользоваться нельзя. Применим несколько иной метод.
Если рекурсивная программа обнаруживает ошибку, то она печатает сообщение об ошибке. Затем в зависимости от следующего
364
ГЛАВА IS
входного символа Т можно выбрать одну из двух альтернатив — либо что-то вставить и таким образом исправить ошибку, после чего продолжить работу, либо вернуться в вызывающую программу с указанием об ошибке. Например, если программа для правила
F : := (Е) | i
не находит«(»или«{», то она может вставить «Ь> и продолжать работу. Если она нашла «(Е», но не обнаружила закрывающей скобки,
Рис. 15.2. Другой пример нейтрализации ошибки при нисходящем разборе, а —момент обнаружения ошибки; & —после исправления ошибки.
го она может предположить, что эта скобка есть, и вернуться в вызывающую программу.
Этим мы делаем по существу то, что делает метод автоматической нейтрализации ошибки. В любой момент каждая рекурсивная процедура на данном этапе выполнения представляет неполный куст дерева. Выполняемая процедура пытается нейтрализовать ошибку, используя входной символ и неполный куст, который она представляет. Если нейтрализация невозможна, то она сообщает об этом вызывающей программе. И тогда уже вызывающая программа пытается нейтрализовать ошибку, действуя по тому же принципу.
В некоторый момент этот процесс должен прекратиться. «Особые» программы типа (инструкция > или <составная инструкция > не должны возвращаться в вызывающую программу, а должны пропускать символы исходной программы до тех пор, пока не будет возможна нейтрализация, т. е. пока не встретится END, точка с запятой или начало новой инструкции.
НЕЙТРАЛИЗАЦИЯ ОШИБОК
365
Нейтрализация ошибки при восходящем разборе
Достоинство нейтрализации ошибки при нисходящем разборе заключается в том, что частично построенное дерево несет в себе много полезной информации о символах, которые должны идти следующими в исходной программе. При восходящем разборе эту информацию получить не так просто. Все, что мы имеем, — это цепочка xTt, где х — уже обработанная часть сентенциальной фор-мы. Поскольку мы не можем с легкостью использовать такой глобальный контекст, как все неполные кусты, нам придется довольствоваться локальным контекстом, непосредственно окружающим место, где обнаружена ошибка.
Следующий метод, используемый в системе построения компиляторов XPL (см. Маккиман и др. [70]), типичен для многих автоматических анализаторов, основанных на методе восходящего разбора. По общему признанию он чрезвычайно прост.
Разработчик компилятора может в качестве начальных значений занести в массив STOPIT «особые» символы типа «;» и «END». Если обнаружена ошибка, то делается следующее:
1. Символы в цепочке Tt последовательно просматриваются и выбрасываются до тех пор, пока один из них не совпадет с каким-либо символом из STOPIT.
2. Мы получили новый символ Т. Теперь просматриваем и выбрасываем хвостовые символы цепочки х до тех пор, пока символ Т «не состыкуется правильно» с оставшимися символами х.
Заметим, что тем самым нарушается принцип раздельного хранения синтаксической и семантической информации (неизменности х). Было бы лучше вставить цепочку терминалов, обработка которой вызовет необходимые редукции в стеке. Но это сделать сложнее.
Другой метод применим при разборе с использованием матрицы переходов (см. разд. 6.4). В этом случае, если в стеке находится цепочка х = x2xx, несколько верхних символов, а именно цепочка хъ образуют голову правой части правила и позволяют определить строку i матрицы М. Входной символ Т определяет столбец j. Элемент М (i, j) есть адрес программы, которая либо заносит Т в стек и сканирует следующий символ, либо выполняет редукцию. В этой матрице обычно более половины элементов представляют недопустимые пары (xi, Т) и, следовательно, можно выявить много различных ошибочных ситуаций.
Для этой схемы нейтрализации ошибок мы предполагаем использовать конструктор, который по заданной грамматике конструирует подпрограммы нейтрализации ошибок и проставляет в элементах матрицы их имена. (Если такого конструктора нет, то разработчик компилятора должен придумать свой собственный специфический способ нейтрализации с учетом указанных ниже принципов.) Таким образом, в этих программах нейтрализации ошибок
366
ГЛАВА 15
не приходится решать, как осуществить нейтрализацию в зависимости от контекста. Они выполняют нейтрализацию заранее определенным способом, основываясь исключительно на хх и Т.
Напомним, что мы осуществляем нейтрализацию, выбрасывая Т или добавляя терминальную цепочку q между Xi и Т. Поэтому в конструкторе можно использовать следующие довольно естественные принципы выбора нейтрализации для (хх, Т):
1. Если в грамматике существует правило U ::= XizT . . ., то нужно вставить терминальную цепочку q, такую, что z=>»q.
2. Если существует правило U : := xxV ... и V=>+ zT . . ., то нужно вставить терминальную цепочку q, такую, что z=>*q.
3. Если существует правило U ::=... VT .. ., причем V=>+ . . . Wz2 и W: := xxzx есть одно из правил грамматики, то нужно вставить терминальную цепочку q, такую, что z = zx z2=>*q.
4. Если ни один из предыдущих принципов не применим, то нужно исключить Т.
Эти принципы очень похожи на те, которые использовались при нисходящем разборе, но в них учитывается меньший контекст при принятии того или иного решения. Это означает, что и нейтрализация ошибки будет выполняться менее качественно. Ниже приводится таблица, в которой мы покажем, как определяется цепочка q. Предполагается, что синтаксис похож на синтаксис языка АЛГОЛ. CS (Compound Statement) — сокращение для Составная инструкция >, a SL (Statement List) — сокращение для Список инструкций/
Случай хх Т Правила z q
1 ( ) F ::= (Е) E i
2 BEGIN : = CS :: = BEGIN SL END i SL =>* i : — E i
3 Е » ) F = (E) E =>* T T ::=T*F F i
4 ARRAY STEP (STEP исключается)
При рассмотрении этого метода, который никогда не использовался и не проверялся, мы оставили без ответа несколько важных вопросов. Какое из правил предпочесть, если можно применить более чем одно правило? Какая цепочка q из тех, для которых z=>*q, должна быть вставлена? Можем ли мы быть уверены, что некоторое вставление не приведет к бесконечной последовательности других вставлений? Тем не менее на практике этот метод успешно применялся в матрице переходов компилятора ALCOR ILLINOIS 7090 (см. Грис и др. [651).
Глава 16
Интерпретаторы
Термин интерпретатор мы используем для программы, которая осуществляет две функции:
1. Транслирует исходную программу, написанную на исходном языке (например, на АЛГОЛе), во внутреннее представление.
2. Выполняет (интерпретирует или моделирует) программу, представленную на этом внутреннем языке.
Первая часть интерпретатора подобна первой части многопроходного компилятора, и мы будем называть ее «компилятором». Внутреннее представление, в которое он транслирует исходную программу, должно выбираться так, чтобы вторая часть (собственно интерпретатор) работала максимально эффективно. Для этой цели часто выбирается польская запись, и мы ее опишем. Польская запись будет интерпретироваться способом, рассмотренным в 11.2, и читателю было бы полезно снова вспомнить содержание этого раздела, прежде чем двигаться дальше. Эта глава посвящена более детальному рассмотрению вопросов реализации интерпретаторов.
Хотя термин «интерпретатор» относится ко всей обработке в целом (к обеим упомянутым выше частям), в дальнейшем мы будем называть этим словом только вторую часть, так как именно в ней интерпретируется внутреннее представление. Работа этой второй части происходит во «время интерпретации».
С помощью интерпретатора программа выполняется намного медленнее эквивалентной программы на машинном языке. Поэтому не следует использовать интерпретатор для производственного счета, когда ббльшая часть времени машины тратится на выполнение готовых программ. Интерпретатор больше подходит к обстановке, связанной с обучением, когда ббльшая часть времени тратится на отладку программ. Как мы увидим, получить программу с хорошими средствами отладки во время счета в интерпретаторе намного легче, чем в компиляторе.
Интерпретаторы можно использовать для тех языков, в которых обычно ббльшая часть времени уходит на работу системных программ, а меньшая часть на использование собственно команд
368
ГЛАВА 16
объектной программы. Это возможно, например, в языке, предназначенном для работы с матрицами, где основная часть времени тратится для выполнения стандартных, заранее протранслированных программ матричных операций. Другим примером может служить язык символьной обработки типа SNOBOL.
Общая схема
В машине польская запись исходной программы представляется массивом целых чисел Р. Во время интерпретации р содержит индекс, указывающий на текущий обрабатываемый символ в Р (вна-
NEXT:
CASE Р(р) 1: BEGIN 2: BEGIN 3: ; 4: ; 5: ; 6: BEGIN 7: BEGIN 8: BEGIN OF P := P +1; «Занести P(p) в стек S»; END; p := p+1; «Занести P(p) в стек S»; END; «Выполнить индексирование»; END; «Выполнить присваивание»; END; i := i—2; IF S(i +1)^0 THEN BEGIN p := S(i + 2); GOTO NEXT; END;
9: BEGIN 10: BEGIN 11: BEGIN 12: BEGIN 13: BEGIN 14: BEGIN 15: BEGIN 16: BEGIN ENDCASE; i := i —1; p := S (i +1); GOTO NEXT; END; «Выполнить переход на метку»; END; «Выполнить вход в блок»; END; «Выполнить выход из блока»; END; «Выполнить описатель массива»; END; «Выполнить сложение»; END; «Выполнить умножение»; END; «Выполнить вычитание»; END;
р := р + 1; GOTO NEXT;
Рис. 16.1. Общая структура интерпретатора.
чале р = 1). Таким образом, р является «счетчиком команд». Как описывалось в 11.2, для выполнения польской записи мы используем стек S со счетчиком 1. Вначале стек пуст (i =0).
Главной частью интерпретатора является переключатель CASE, передающий управление на ту или иную ветвь в соответствии с тем или иным оператором или типом операнда польской записи.Таким
ИНТЕРПРЕТАТОРЫ
369
образом, на каждом шаге Р (р) определяет ветвь переключателя, которая выполняется. Это показано на рис. 16.1 в тех обозначениях операторов и операндов, которые использовались в 11.2 и которые мы снова здесь приведем:
1 = константа
2 = идентификатор
6 — SUBS (оператор индексирования)
7 = : = (присваивание)
8 = BMZ (переход по минусу или нулю)
9 = BR (переход)
10 = BRL (переходнаметку)
11 = BLOCK (начало блока)
12 = BLCKEND (конец блока)
13 = ADEC (описатель массива)
14 = +
15 = *
16 = —
На рис. 16.1 мы хотели изобразить только общую структуру интерпретатора, поэтому большая часть ветвей переключателя написана на обычном неформальном языке. Кроме того, на рис. 16.1 отражены два момента. Первое, 8-я ветвь осуществляет выталкивание из стека S двух операндов. Другие ветви должны делать то же самое со своими операндами и результат посылать в S, если он имеется. И второе, на каждом шаге, после выполнения ветви счетчик команд увеличивается на 1, так что на следующем шаге будет обрабатываться следующий символ. Заметим, что дополнительное прибавление 1 к р в 1-й и 2-й ветвях делается потому, что операнды в нашем представлении занимают две ячейки. Ветви, соответствующие обработке переходов, сами должны изменять значение р и уходить прямо на NEXT для обработки следующего символа, как это делает ветвь 8 при обработке BMZ.
Значения в стеке S
Допустим на время, что все переменные исходного языка только одного типа INTEGER. Проблемы, связанные с наличием различных типов и необходимостью их преобразования, будут рассматриваться позже. Предположим также, что во время интерпретации мы можем использовать таблицу символов. Тогда стек S может содержать три вида значений:
1) целое число,
2) указатель в таблицу символов и
3) адрес переменной.
Вычисление «АВ+» оставляет в стеке значение первого вида — целое число. Два других вида, например, возникают при вычисле
370
ГЛАВА 16
нии переменной с индексом, которая в польской записи имеет вид: <выр> . . . <выр> A SUBS
где А — указатель на элемент таблицы символов, соответствующий массиву А. В стеке все <выр > представляются целыми значениями. Указатель А необходим для того, чтобы SUBS мог определить количество индексных выражений и значение адреса элемента массива. Этот адрес — третий вид значения, который заносится в стек в качестве результата операции SUBS.
Каждый элемент стека должен иметь два поля, которые мы назовем KIND (вид) и VALUE (значение). S (i).KIND может быть 1,2 или 3, и в зависимости от этого S(i).VALUE есть целое, адрес элемента таблицы символов или адрес переменной. Каждый оператор перед выполнением должен проверять свои операнды и приводить их к соответствующему виду.
Например, оператор * должен выполнять следующее (его операнды S (i) и S (i — 1)):
1. Если S(i).KIND = 2, то значение переменной, описанной элементом таблицы символов с адресом, указанным в S (i)-VALUE, пересылается в S(i).VALUE. Если S (i).KIND = 3, то значение переменной с адресом S(i). VALUE пересылается в S(i) .VALUE.
2. Выполняются те же действия для S (i — 1).
3. S (i — 1).VALUE : = S(i—l).VALUE*S(i).VALUE;
S(i—1).KIND := 1. (Выполняется умножение и устанавливается вид результата.)
4. i := i—1. (Соответственно корректируется указатель стека.)
Приведенный выше метод, очевидно, требует много времени на интерпретацию. Каждый оператор должен проверить свои операнды и установить вид результата. Если компилятор может определить для каждого оператора вид операндов и результата, то мы можем осуществить более эффективную реализацию, разрешив компилятору вставлять в польскую запись операторы преобразования. Следовательно, в этом случае к моменту выполнения оператора его операнды уже будут иметь правильный вид.
Определим следующие три оператора преобразования:
1. CVPV. Преобразование операнда, лежащего на вершине стека, из «указателя на элемент таблицы символов» в «значение, описываемое этим элементом» (Pointer to Value).
2. CVPA. Преобразование операнда, лежащего на вершине стека, из «указателя на элемент таблицы символов» в «адрес значения» (Pointer to Address).
3. CVAV. Преобразование операнда, лежащего на вершине стека, из «адреса значения» в «значение, полученное по этому адресу» (Address to Value).
ИНТЕРПРЕТАТОРЫ
371
Кроме этого, все идентификаторы в польской записи мы разобьем на три категории. Напомним, что раньше идентификатор I представлялся следующими двумя ячейками:
(1, указатель на элемент таблицы символов)
Вместо этого, в 1-й ячейке мы теперь допускаем значения 2, 3 и 4, которые указывают нам на следующие три способа обработки идентификатора:
2. Занести в стек указатель на элемент таблицы символов.
Для указателя мы используем обозначение вида Р : I, где I—имя соответствующего идентификатора.
3. Занести в стек адрес значения. Для адреса мы используем обозначение вида А : I.
4. Занести в стек значение переменной, описанной элементом таблицы символов. Для значения мы используем обозначение вида V : I.
Например, предложение С := В+А (I) (в польской записи С В I A SUBS+ :=) в этой более явной записи имеет вид:
А : С Адрес С для запоминания результата.
V : В Значение В для операции сложения.
V : I Значение I для операции индексирования.
Р : А Указатель на массив А в таблице символов.
SUBS Вычисление адреса А (I) для сложения.
CVAV Получение значения А (I) для сложения.
+ Сложение значений, находящихся в стеке.
:= Занесение значения в С.
Вообще говоря, этот второй метод лучше, так как он придерживается правильного принципа: не откладывать на время интерпретации того, что можно сделать во время компиляции. Заметим также, что при этом не требуется никакого поля типа KIND, так как каждый оператор всегда знает точно, что ему следует ожидать.
Преобразование типов операндов
Два аналогичных подхода существуют и в отношении преобразования операндов из одного типа в другой: мы можем в каждом элементе стека иметь поле для указания типа и проверять его в каждом операторе, или можем задавать необходимые преобразования явно. Предположим, что в исходном языке допускаются переменные двух типов — целые и действительные, и пусть I и J имеют тип INTEGER, а А и В —тип REAL. Если мы представляем I :=A*B+J в виде
I А В * J + : =
то нам нужно поле TYPE для указания типа элемента стека. TYPE
372
ГЛАВА 16
и KIND можно представлять одним полем. Если позволяет исходный язык, предпочтительней следующее представление:
I А В »R J CVIR +R CVRI :=1
Здесь CVIR унарный оператор для преобразования операнда, лежащего на вершине стека, из INTEGER в REAL, a CVRI — аналогичный оператор преобразования из REAL в INTEGER. Заметим, что теперь для некоторых операторов исходного языка требуется по нескольку операторов в польской записи. В приведенном выше примере умножение представляется с помощью *R (умножение значений типа REAL) и *1 (умножение типа INTEGER).
Для упрощения компиляции нам потребуются также операторы CVIR2 и CVRI2, которые преобразуют второй элемент стека. Таким образом: 1: = Л-А*В можно представить в виде
I J А В *R CVIR2 +R CVRI : = I
Потребность в этом возникает из способа генерации внутреннего представления, так как мы не знаем во что нужно преобразовывать J до того момента, когда не будет сгенерировано I J А В *R.
В методе с явным заданием преобразований по сравнению с неявным заданием внутреннее представление требует больше памяти и почти удваивается общее количество операторов (если в исходном языке два типа переменных). Кроме того, от компилятора требуется дополнительная работа. Но, если тип каждой переменной и каждого промежуточного результата можно определить во время компиляции, следует выбрать метод явного задания, так как полученная программа работает быстрее.
Конечно, бывают языки, в которых тип переменных может изменяться во время выполнения (например, в языке SNOBOL). Тогда должен использоваться метод неявного задания. Кроме того, должен быть обеспечен доступ к элементам таблицы символов, чтобы можно было следить за текущим типом каждой переменной. При этом элемент таблицы символов играет роль описателя переменной.
Во многих случаях типы переменных можно определить из контекста, в котором они встречаются. Тогда нужно по возможности шире использовать явный метод, переключаясь на неявный только тогда, когда это необходимо.
Управление памятью во время интерпретации
Управление памятью во время интерпретации мало чем отличается от управления памятью, описанного в гл. 8, хотя и требуется внести некоторые поправки в соответствии с языком, на котором пишется интерпретатор. К примеру, если интерпретатор пишется на АЛГОЛе и исходный язык допускает типы INTEGER й REAL, то нужно будет завести два массива для стеков на время счета:
ИНТЕРПРЕТАТОРЫ
373
один для хранения переменных типа INTEGER, другой — для REAL. Тогда адрес переменной есть индекс одного из этих массивов. И любая работа должна вестись в терминах индексов этих двух массивов, так как в АЛГОЛе не существует указательных переменных. Если интерпретатор пишется на ФОРТРАНе, то некоторая экономия может быть получена за счет совмещения этих двух массивов с помощью эквивалентности.
Если процедуры исходного языка не могут быть рекурсивными, то текущие значения для каждой простой переменной можно хранить в соответствующем ей элементе таблицы символов. Таким образом, для переменной вообще не нужен адрес во время счета.
Дампинг таблицы символов
Одно из главных преимуществ интерпретатора перед компилятором состоит в легкости получения средств отладки для программиста. Например, довольно просто реализовать процедуру PRINTVALUE (Р), работающую во время интерпретации, которая по заданному адресу элемента таблицы символов Р печатает соответствующий ему идентификатор исходной программы и его текущее значение. Текущее значение печатается как целое, десятичное с плавающей точкой и т. д. в зависимости от типа переменной.
Для исходных языков с нерекурсивными процедурами и, следовательно, с достаточно простой организацией памяти во время счета PRINTVALUE можно использовать для выдачи дампинга таблицы символов. Всякий раз, когда во время интерпретации встречается ошибка, просматривается таблица символов и на каждом элементе, соответствующем переменной, выполняемой в данный момент процедуры, вызывается PRINTVALUE.
Здесь важно, что в момент обнаружения ошибки дампинг выдается в символьном виде в терминах исходной программы, а не в двоичном, восьмеричном или шестнадцатеричном представлении. Такой символьный дампинг можно (и должно) осуществлять также для обычных компиляторов (см. гл. 21), но для компилятора это сделать труднее.
Для языков с блочной структурой и рекурсивными процедурами осуществление символьного дампинга всех переменных и их текущих значений требует немного больших усилий. Для того чтобы его получить, используется список блоков, который представляет блочную структуру программы и указывает, где расположены элементы таблицы символов каждого блока. Кроме того, в любом месте интерпретации мы должны иметь возможность определить текущий блок. Для этого к каждому оператору BLCKEND (в польской записи) можно добавить номер блока. Тогда, чтобы найти номер блока, соответствующий символу Р (р), просматриваются символы
374
ГЛАВА 16
Р (р+1), Р (р+2), ... до тех пор, пока не встретится оператор BLCKEND.
Далее, у программы, выполняющей выдачу дампинга, должна быть возможность исследовать стек времени счета и определить, где расположена область данных выполняемой процедуры. Это нужно, чтобы найти неявные параметры процедуры.
Мы приведем схему процедуры выдачи дампинга в предположении, что этот дампинг выдается на операции Р (р). Подробную проработку оставляем читателю. Идея состоит в том, чтобы выдать на печать переменные, определенные в текущей процедуре, затем выдать переменные процедуры, которая вызвала текущую процедуру, и т. д., пока не будут напечатаны переменные главной программы.
1. Просмотреть Р (р+1), Р (р+2) , . . ., пока не обнаружится оператор BLCKEND, после чего номер блока запомнить, например, как значение переменной В.
2. Напечатать с помощью PRINTVALUE все переменные блока В.
3. Выполнить присваивание В := номер блока, объемлющего блок В.
4. Если В — обычный блок, то перейти к шагу 2, если — процедура, то перейти к шагу 5, если В=0 — блоков больше нет, то конец.
5. Напечатать значения формальных параметров процедуры В, если они есть.
6. Используя стек времени счета, найти место, где’ эта процедура была вызвана (для этого просматриваются неявные параметры). Изменить стек, как если бы был выполнен оператор RETURN. В счетчик команд р установить адрес возврата. Перейти к шагу 1.
Ряд компиляторов используют эту схему. Проблемы, связанные с выдачей дампинга в компиляторах, кратко обсуждаются в гл. 21 (см. также Байер и др. [68]). Интерпретатор SPL также использует эту схему (см. Маккиман и др. 170J) -
Другие средства отладки
Любое сообщение об ошибке во время интерпретации должно содержать номер строки исходного текста, в которой встретилась эта ошибка. Это легко делается с помощью вставления в польскую запись операторов номера строки (фактически это «пустые операторы»), каждый из которых следует за своим номером строки. Эти операторы могут использоваться аналогично тому, как использовались операторы BLCKEND при выдаче дампинга таблицы символов.
Для этой цели можно было бы также использовать номера инструкций, как это делается в компиляторе с PL/1 уровня F для IBM 360.
ИНТЕРПРЕТАТОРЫ
375
То, что таблица символов доступна во время интерпретации, облегчает введение других средств отладки. Например, можно обращаться к стандартной программе DUMP для выдачи описанного выше дампинга таблицы символов с продолжением прерванного счета. Можно также обращаться к программе PROCEDURE DUMP для выдачи только некоторой части таблицы символов, касающейся текущей процедуры.
Важным и в то же время легко осуществимым средством отладки является «трассировка». Выполнение TRACE(A) означает, что, начиная с этого момента, на каждом присваивании переменной А должно печататься ее новое значение. NOTRACE(A) выключает трассировку А.
Для осуществления трассировки в каждый элемент таблицы символов вводится дополнительное одноразрядное поле, значение которого устанавливается и сбрасывается с помощью TRACE и NOTRACE. А оператор := без труда проверяет этот разряд и, если он 1, обращается к PRINTVALUE.
Аналогично можно было бы осуществить трассировку по меткам, т. е. печатать сообщение каждый раз, когда осуществляется явный переход на указанную метку. Это можно было бы сделать с помощью той ветви переключателя CASE интерпретатора, которая обрабатывает оператор перехода BRL. Другой способ состоит в том, что обращение к программе LABEL (L, А, В, . . ., С) вызывает печать текущих значений А, В,... С при явном переходе на метку L.
Читателю предоставляется возможность создавать свои собственные средства отладки. Повторяем, главное преимущество интерпретатора состоит в том, что всегда доступна таблица символов, а также в том, что команды, осуществляющие каждое средство отладки, сосредоточены в небольшом количестве ветвей интерпретатора, осуществляющих обработку операторов польской записи с небольшой потерей эффективности интерпретации.
Обсуждение
Для того чтобы по возможности кратко и ясно описать работу интерпретатора, мы рассмотрели в основном операторы присваивания и переходов. Надеемся, что теперь читатель сможет распространить сказанное на другие типы операций. При этом следует максимально использовать стек S для хранения временных переменных. Например, непосредственно перед вызовом процедуры все неявные и явные параметры должны быть в стеке. Нет необходимости для этого заводить какую-либо другую память. В действительности для языков типа АЛГОЛ с блочной структурой и рекурсивными процедурами этот стек легко мог бы функционировать в качестве стека во время счета (см. разд, в 8.9).
376 ГЛАВА 16
Для многих исходных языков можно пренебречь таблицей символов и не обращаться к ней во время интерпретации. В конце концов если это делается во время выполнения программ на машинном языке, то это можно делать и во время интерпретации. При этом память, занимаемая таблицей символов, освобождается для другого использования, но вместе с этим теряется одно из преимуществ интерпретации перед компиляцией — легкость обеспечения хороших средств диагностики.
Не следует считать, что рассмотренные методы единственные. Без сомнения, вы сможете найти еще лучшие способы представления и преобразования различных значений в стеке для вашего конкретного языка.
Глава 17
Г енерация объектного кода
В разд. 17.1 кратко рассматриваются возможные формы объектного кода и отмечаются достоинства каждой из форм. Дается описание машинного языка, который используется в этой главе при обсуждении генерации команд. В разд. 17.2 показано, как внутренняя исходная программа, представленная в той или иной форме, преобразуется в программу на машинном языке. В этом разделе мы уделим внимание только арифметическим выражениям с простыми переменными, стремясь возможно яснее описать, как происходит генерация команд и какие проблемы возникают при использовании временных переменных. Мы предполагаем, что к любому операнду в памяти можно обращаться по абсолютному адресу (не используя индексные регистры).
В разд. 17.3 подробно рассматривается, как в машинных командах формируются адреса для операндов выражений, включая переменные с индексами, а также локальные и глобальные переменные. Предполагается, что программа написана на языке типа АЛГОЛ.
В разд. 17.4 рассматривается генерация команд и для других конструкций. Мы остановимся лишь на наиболее важных и неясных вопросах.
Одна из проблем, связанных с генерацией кода для сложного языка высокого уровня, состоит в том, что программы генерации объектного кода оказываются чрезвычайно громоздкими. В разд. 17.5 обсуждаются различные пути уплотнения информации о генерируемых командах с применением таблиц, которые можно частично интерпретировать. Наконец, в разд. 17.6 формат объектного модуля операционной системы IBM 360 описан так, чтобы, не прилагая особых усилий, читатель мог понять, как выглядит объектный модуль и почему он организован так или иначе.
378
ГЛАВА 17
17.1. ВВЕДЕНИЕ
Формы объектного кода
Возможны три формы объектного кода: абсолютные команды, помещенные в фиксированные ячейки (после окончания компиляции такая программа немедленно выполняется); программа на автокоде (ее придется потом транслировать); программа на языке машины, представленная образами карт и записанная во вторичную память в виде двоичной колоды или объектного модуля (такая программа перед выполнением должна быть объединена с другими подпрограммами и затем загружена).
Первый вариант наиболее экономичен в отношении расходуемого времени. Примерами компиляторов, которые генерируют абсолютные команды, могут служить WATFOR, PUFFT (см. Розен и др. 165]) и АЛГОЛ W. Чтобы скомпилировать небольшую программу (на 50 картах) и начать ее выполнение на большой машине, может потребоваться 1—2 секунды. Главный недостаток этого варианта состоит в том, что нельзя предварительно и независимо протранс-лировать несколько подпрограмм и затем объединить их вместе для выполнения; все подпрограммы должны транслироваться одновременно. Выигрыш во времени оборачивается проигрышем в гибкости. Компиляторы, генерирующие абсолютный код, целесообразно применять там, где через машину проходит масса мелких программ, при отладке которых многократно используется компилятор.
Проще всего получить объектную программу на автокоде. В этом случае не приходится формировать команды как последовательности битов; можно порождать образы карт, содержащие символические команды. Более того, можно генерировать макровызовы, а соответствующие макроопределения предварительно написать на автокоде. Например, на некоторых машинах, чтобы преобразовать целое число с плавающей точкой в число с фиксированной точкой, требуется три или четыре команды. Вместо генерации этих (трех или четырех) команд компилятор может генерировать одну макрокоманду, скажем, FIX, а макроассемблер позже получит макрорасширение. Это позволяет также уменьшить объем компилятора.
Несмотря на очевидные достоинства, трансляция на автокод обычно считается наихудшим из вариантов. И в самом деле, к процессу трансляции добавляется еще один шаг, и этот дополнительный шаг часто требует столько же времени, сколько длится собственно компиляция!
Большинство промышленных компиляторов вырабатывают объектную программу в виде объектного модуля или двоичной колоды, т. е. в виде последовательности образов карт, содержащих команды на машинном языке. Подробнее об этом будет сказано в разд. 17.5. Как правило, объектный модуль содержит символические имена
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
379
других программ (подпрограмм), к которым он обращается, и имена своих входных точек, к которым можно обращаться из других программ. Эта объектная программа «объединяется» с теми другими объектными программами, а затем загружается в некоторую область памяти для выполнения.
В этом варианте обеспечивается гораздо большая гибкость, и поэтому во многих системах он и принят в качестве стандартной процедуры. Следует, однако, заметить, что на объединение и загрузку также расходуется время.
Машина, используемая при описании генерации кода
Чтобы показать, как генерируются машинные команды, воспользуемся гипотетической машиной с одним сумматором, в котором выполняются все арифметические действия, и семью индексными регистрами. Машина довольно проста, и поэтому мы сможем описать генерацию команд, не встречая особых затруднений. Однако в то же время машина достаточно сложна и позволит проиллюстрировать большинство возникающих при генерации проблем.
Команды, приведенные ниже, типичны для машин средней мощности. Имеются команды: загрузить сумматор или регистр из памяти, записать в память содержимое сумматора или регистра, прибавить (вычесть и т. д.) число к сумматору. Числа в машине можно представить как в формате с фиксированной точкой, так и в формате с плавающей точкой. Конкретные сведения о форматах нас интересовать не будут. Число в любом из индексных регистров должно быть в формате с фиксированной точкой.
В команде для обращения к ячейке памяти используется абсолютное целое число к (смещение), два индексных регистра и бит для указания косвенной адресации. Обозначение k (i, j) будет использоваться как ссылка на ячейку с адресом:
к + содержимое регистра i + содержимое регистра j
Будем считать, что если i равно 0, то «содержимое регистра Ь> также равно 0. Другими словами, к (0, 0) ссылается на ячейку к. Бит косвенной адресации отмечается звездочкой: *k (i, j) ссылается на ячейку, адрес которой находится в ячейке k (i, j). В таблице команд на рис. 17.1 адрес ячейки памяти обозначается буквой М и задается так, как мы только что описали.
17.2. ГЕНЕРАЦИЯ КОМАНД ДЛЯ ПРОСТЫХ АРИФМЕТИЧЕСКИХ ВЫРАЖЕНИЙ
Программы генерации команд пользуются описанием (в таблице символов или другой таблице) каждой переменной или временного значения. В описании указан тип переменной, ее адрес во время
380
ГЛАВА 17
выполнения программы и другая необходимая информация. Однако цель этого раздела состоит в том, чтобы в общих чертах описать идеи генерации команд и показать, как и что меняется в зависимости
Команды Смысл
LOAD М Загрузить содержимое ячейки М в сумматор.
LREG i, М Занести содержимое ячейки М в регистр.
STORE М Занести содержимое сумматора в ячейку М.
SREG i, М Занести содержимое регистра i в ячейку М.
LACCR i Занести содержимое регистра i в сумматор.
LRACC i Занести содержимое сумматора в регистр i.
ADD (ADDF) M Прибавить содержимое ячейки М к сумматору.
SUB (SUBF) M Вычесть содержимое ячейки М из сумматора.
MULT (MULTF) M Умножить содержимое сумматора на содержимое ячейки М.
DIV (DIVF)M Разделить содержимое сумматора на содержимое ячейки М. При делении дробная часть результата отбрасывается.
FIX Преобразовать содержимое сумматора из формы с плавающей точкой в форму с фиксированной точкой.
FLOAT Преобразовать содержимое сумматора из
формы с фиксированной точкой в форму с плавающей точкой.
ABS Сделать знак содержимого сумматора +.
CHS Изменить знак содержимого сумматора.
В M Перейти к команде в ячейке М.
BN M Перейти к команде в ячейке М, если сумматор отрицательный (смысл других команд перехода BP, BZ и т. д. очевиден).
ADD, SUB, MULT, DIV—команды для чисел с фиксированной точкой.
ADDF, SUBF, MULTF, DIVF—команды для чисел с плавающей точкой.
Рис. 17.1. Символические команды гипотетической машины.
от формата внутренней исходной программы. Для простоты мы в этом разделе будем предполагать, что каждая переменная представлена своим символическим именем (а не указателем на описание) и что генерируются символические команды на автокоде. Для
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
381
генерации команды на автокоде с операцией X и операндом Y будет вызываться процедура GEN (X, Y), где X и Y — переменные типа STRING (например, GEN ('ADD', 'GAB')).
Рассматриваются только такие арифметические выражения, в которых используются операторы и унарный минус,
а все операнды являются простыми переменными целого типа. Мы покажем, как генерируются команды для тетрад, триад, деревьев и польской записи, используя в качестве примера выражение
(17.2.1) А*((А*В +С)— C*D)
Генерация кода для тетрад
Тетрады расположены в том порядке, в котором должны выполняться операции. Поэтому мы просматриваем их последовательно одну за другой и для каждой генерируем команды. Чтобы устранить ненужные команды LOAD и STORE, нам придется постоянно следить за содержимым сумматора, в котором при выполнении программы производятся все арифметические действия. Для этого введем глобальную переменную АСС типа STRING. Значение переменной АСС во время компиляции соответствует состоянию сумматора во время выполнения программы именно в тот момент, когда выполнится последняя сгенерированная команда. Если АСС содержит строку ' ', сумматор свободен; в противном случае в АСС содержится имя переменной или временного значения, находящегося в сумматоре (после того, как сгенерированная команда будет выполнена при работе программы).
Чтобы сгенерировать команды (если это необходимо), которые загружают во время выполнения программы переменную X или Y в сумматор, должна быть вызвана программа GETINACC(X, Y). Например, программа GETINACC будет вызвана при генерации команд для вычисления X * Y, причем один из двух операндов уже может быть в сумматоре. Некоторые операторы (такие, как X/Y) не являются коммутативными в машине и требуют, чтобы в сумматоре был первый операнд. Поэтому условимся, что в результате вызова GETINACC (X, ' ') должна генерироваться команда занесения X в сумматор. Наконец, заметим, что программе GETINACC, возможно, придется сформировать команды, которые сохранят содержимое сумматора, если в данный момент сумматор’не пуст.
Как упоминалось ранее, тетрады просматриваются последовательно и генерируются команды для каждой из них. Предположим, что счетчик i следит за последовательным перебором тетрад и что на четыре поля i-й тетрады можно сослаться с помощью QD(i). OP, QD(i).OPERl, QD(i).OPER2 и QD(i).RESULT. Ниже приводятся генераторы команд для каждого из операторов +, —, *, / и унарного минуса.
382
ГЛАВА 17
PROCEDURE GETINACC (X, Y);
STRING X, Y;
BEGIN STRING T;
IF ACC—' ' THEN
BEGIN GEN ('LOAD', X); ACC: -X; RETURN
END;
IF ACC = Y THEN
BEGIN T: = X; X:=Y;
Y:—T END
ELSE IF ACC ф X THEN BEGIN GEN ('STORE', ACC); GEN ('LOAD', X); ACC X
END; END
Генерирует команды для занесения X или Y в сумматор (X, если Y=' ') Т — временная переменная.
Если сумматор пуст, генерируется команда LOAD X и соответствующим образом изменяется глобальная переменная АСС.
Если Y уже в сумматоре, операнды меняются местами.
Если X не в сумматоре, то генерируются команды для запоминания сумматора и загрузки X.
В генераторе команд для коммутативного оператора + обратите внимание на тот факт, что, если второй операнд уже находится в сумматоре, программа GETINACC поменяет местами два операнда в i-й тетраде. В последнем генераторе для унарного минуса имеется только один операнд; следовательно, вторым аргументом при вызове GETINACC будет '
Генератор команд для тетрады + GETINACC (QD(i).OPERl, QD(i). OPER2);
GEN ('ADD', QD (i).OPER2);
ACC := QD(i).RESULT
Генератор команды для тетрады * GETINACC (QD(i).OPERI, QD (i). OPER2);
GEN ('MULT', QD (i).OPER2);
ACC := QD(i).RESULT
Генератор команд для тетрады — GETINACC(QD(i).OPERl, ' ');
GEN ('SUB', QD (i).OPER2);
ACC :== QD(i). RESULT
Генератор команд для тетрады / GETINACC (QD(i).OPERl, ' ');
GEN ('DIV', QD(i). OPER2);
ACC := QD(i).RESULT
Генерация команды занесения операнда в сумматор.
Генерация команды ADD.
Установка состояния сумматора.
Занесение операнда в сумматор.
Генерация команды умножения.
Установка состояния сумматора.
Первый операнд команды SUB должен быть в сумматоре.
Генерация команды SUB.
Установка состояния сумматора.
Первый операнд должен быть в сумматоре.
Генерация команды деления.
Установка состояния сумматора.
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
383
Генератор команд для тетрады «унарный минус»
GETINACC (QD (i).OPERl, ' '); Имеется только один операнд.
GEN ('CHS ' '); Генерация команды «изменить знак».
ACC := QD(i).RESULT Установка состояния сумматора.
В колонке 1 на рис. 17.2 изображены тетрады для арифметического выражения (17.2.1); в колонке 2 — соответствующие команды, сгенерированные для каждой тетрады; в колонке 3 показано значение глобальной переменной АСС непосредственно после генерации команд. Заметим, что хотя во время компиляции имеется описание каждой временной переменной Ti, не следует выделять ячейки памяти для тех временных переменных, которые остаются в сумматоре во время их существования.
Тетрады Сгенерированные команды ACC
(» А, В, Т1) LOAD A
MULT В Tl
(+ Tl, С, Т2) ADD c T2
(«С, D, ТЗ) STORE T2
LOAD C
MULT D T3
(— Т2, ТЗ, Т4) STORE T3
LOAD T2
SUB T3 T4
(* А, Т4, Т5) MULT T4 T5
Рис. 17.2. Генерация кода для тетрад.
Только что построенные генераторы команд могут работать неправильно, если в выражении выделены общие подвыражения. Пусть читатель попытается найти ошибку, выполняя генерацию команд для выражения А*В+А*В, если после оптимизации получены тетрады (*А, В, Tl) (+Т1, Tl, Т2). В следующем разделе мы исправим эту ошибку.
Генерация кода для триад
Тетрады весьма неудобны в том отношении, что описание каждой временной переменной хранится на протяжении всей компиляции. При работе с триадами в этом нет необходимости. Кроме того, внутренняя исходная программа получается более компактной, поскольку в каждой триаде только три поля. При использовании триад
384
ГЛАВА 17
нам все-таки требуется описание каждой временной переменной, но всякое такое описание необходимо хранить лишь до тех пор, пока генерируются команды, которые на него ссылаются. Например, когда генерируются команды для триады
(10) (* А, В)
генерируется также и описание результата. Затем после генерации команд для последней триады, которая ссылается на триаду (10), мы уничтожаем это описание.
Если зоны существования временных переменных попарно не пересекаются или вложены друг в друга (см. разд. 14.2), для хранения их описаний во время компиляции можно использовать стек; в противном случае потребуется более сложная схема выделения памяти для описаний и освобождения ее. Мы приведем пример генерации команд для первого случая. Кроме того, будем считать, что на каждое временное значение есть только одна ссылка (как в случае обычных неоптимизированных выражений).
Во время генерации команд мы храним в стеке TRIP номера триад, для которых команды уже сгенерированы, но полученные результаты еще не использовались. Параллельный стек TEMP содержит соответствующие имена Тк, присвоенные результатам. Счетчик j содержит номер текущего элемента в TRIP и TEMP.
Перед генерацией команд для триады i следует проверить оба операнда, и если какой-то из них является ссылкой на предыдущую триаду, его нужно заменить соответствующим именем временной переменной, присвоенным этой триаде. Это выполняет процедура FIXTEMP (X, У), приведенная ниже. Параметры этой процедуры: X — поле операнда, который следует проверить; Y будет при возврате содержать имя переменной или временной переменной.
После того как сгенерированы команды для триады i, следует образовать имя для описания значения, являющегося результатом выполнения этих команд. Имя и номер триады заносятся в стеки TEMP и TRIP. Поскольку результат выполнения только что сгенерированных команд находится в сумматоре, следует также изменить АСС, описывающую состояние сумматора. Эту работу выполняет процедура NEWTEMP.
При генерации команд последовательно просматриваются все триады с использованием счетчика i. Мы предполагаем, что ссылки на i-ю триаду имеют вид TR(i).OP, TR(i).OPERl и TR(i).OPER2. Генераторы команд для различных операторов похожи на те, которые использовались для тетрад. Различие состоит в том, что все операции и в том числе поиск имени, соответствующего номеру триады, исключение временных переменных из стека, образование нового имени для результата и занесение его в стек, станут более трудоемкими.
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
385
PROCEDURE FIXTEMP(X, Y)
IF X ссылается на триаду к THEN
BEGIN FOR m: STEP —1 UNTIL 1 DO
IF TRIP(m) —к THEN GOTO F;
F:Y: = TEMP (m)
END
ELSE Y: = X;
PROCEDURE NEWTEMP
T: == имя новой временной переменной;
J: = j +1;
TEMP(j):=T; TRIP(j):=i;
ACC:=T;
Если X есть ссылка на какую-либо триаду к, то ищется к в стеке TRIP и соответствующее имя из TEMP заносится в Y.
В противном случае X — имя переменной, и оно заносится в Y.
Образовать имя новой временной переменной.
Занести имя и номер триады i в стек (i — глобальная переменная).
Фиксация состояния сумматора.
Так как мы предполагаем, что зоны существования двух временных переменных не пересекаются или вложены друг в друга, то имя той временной переменной, на которую могут сослаться генерируемые в данный момент команды, обязательно находится в одном из двух верхних элементов стека. Поэтому его можно найти, проверив только два верхних элемента стека, и не просматривая весь стек. Это упрощает процедуру FIXTEMP.
Генератор команд для триады + (генератор для триады * аналогичен)
FIXTEMP(TR(i).OPERl, TI);
FIXTEMP (TR (i).OPER2, T2);
GETINACC(TI, T2); GEN ('ADD', T2); IF TR(i).OPERl ссылается на триаду THEN j:=j —1;
IF TR (i).OPER2 ссылается на триаду
THEN j:=j — 1
NEWTEMP
Занести имена операндов в TI и T2.
Генерация команд.
Если операнд ссылается на триаду, стираем его имя в стеке; оно больше не понадобится.
Фиксация нового временного имени и состояния сумматора.
Генератор команд для триады —(генератор для триады / аналогичен)
FIXTEMP(TR (i).OPERl, TI);
FlXTEMP(TR(i).OPER2, T2);
GETINACC(TI, ' '); GEN ('SUB', T2); IF TR(i).OPFRl ссылается на триаду THEN j: == j-1;
IF TR(i).OPER2 ссылается на триаду THEN
NEWTEMP
В основном совпадает с генератором для +• Единственное различие состоит в том, что так как — не коммутативен, то первый операнд непременно должен быть в сумматоре перед генерацией команды SUB .
13 д. грис
386
ГЛАВА 17
Генератор команд для унарного минуса
FIXTEMP (TR(i). OPER1, Tl);
GETINACC (Tl, ' '); GEN ('CHS', ' '); IF TR(i).OPERl ссылается на триаду THEN j: = j — 1;
NEWTEMP
•it
Занести имя операнда в TL .*
Генерация команд.
Если операнд — временная переменная, извлечь ее из стека.
Фиксация состояния сумматора.
На рис. 17.3 показана генерация команд для триад соответствующих выражению (17.2.1). Колонка 1 содержит триады; в колонке 2 показано, что получилось после замены операндов, которые ссы-
Триада После замены Команды Стек АСС
(1) (* А, В) (*А, В) LOAD А
MULT В 1, Т1 Т1
(2) (+ (1), С) (+ Т1, С) ADD С 2, Т2 Т2
(3) (*С, D) (*С, D) STORE Т2
LOAD С 3, ТЗ
MULT D 2, Т2 ТЗ
(4) (- (2), (3)) (— Т2, ТЗ) STORE ТЗ.
LOAD Т2
SUB ТЗ 4, Т4 Т4
(5) (*А, (4)) (* А, Т4) MULT А 5, Т5 Т5
Рис. 17.3. Генерация кода для триад.
лаются на триады, соответствующие именам временных переменных; в колонке 4 приводятся стеки TRIP и TEMP после обработки триады; в колонке 5 показано состояние сумматора после обработки триады. Заметим, что команды полностью совпадают с теми, которые были сгенерированы для тетрад.
Уместно сделать несколько замечаний относительно образования и исключения описаний (имен) временных переменных. Если не предполагается никакой другой обработки триад после того, как сгенерированы команды, то триаду можно заменять описанием ее результата. Это значит, что как только сгенерированы команды для триады i, можно занести в одно или в несколько полей TR(i) имя, присвоенное результату триады i. Тогда не нужен будет стек и не потребуется уничтожать описания.
Если на временную переменную может быть более одной ссылки или если зоны существования временных переменных пересекаются, то мы должны знать, где кончается каждая зона. Это необходимо не только длят исключения описания временной величины, а еще и потому, что пока ее значение продолжает использоваться в про
1
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
387
грамме, мы должны генерировать команды для его запоминания. Позднее мы вернемся к этому вопросу и рассмотрим его более подробно.
Генерация команд для дерева
Как описывалось в разд. 11.4, последовательность из п триад для одного арифметического выражения можно рассматривать как дерево с корневым кустом TR(n). На рис. 17.4 изображены триады
(D (* А, в) (2) (+ (D, с)
(3) (*С, D) (4) (- (2),(3))
(5) (* А, (4))
Рис. 17.4. Представление выражения (17.2.1) в виде дерева.
и соответствующее дерево для выражения (17.2.1). Будем теперь генерировать команды начиная с корневого узла дерева, т. е. с последней, а не с первой триады. Тогда у нас будет большая свобода в выборе последовательности, в которой будут генерироваться команды (17.2.1), и программа получится более эффективной, чем раньше.
Мы реализуем рекурсивную процедуру COMP(i), которая предназначена для компиляции команд для поддерева с корнем TR(i). Выбор тех или иных действий в процедуре COMP(i) зависит от оператора TR(i).OP и его операндов TR(i).OPERl и TR(i).OPER2. В таблицах-матрицах на стр. 388—389 имеется сводка действий, которые должны быть выполнены для различных операторов. Рассмотрим таблицу для оператора +• Если оба операнда — TR(i). OPER1 и TR(i).OPER2 являются именами переменных, генерируется команда загрузить OPER 1 в сумматор и команда прибавить OPER2 к сумматору.
Если OPER1 —переменная, a OPER2 — поддерево, корнем которого является оператор, то TR(i).OPER2 будет индексом этого корня в списке триад TR. Чтобы сгенерировать команды для этого поддерева, рекурсивно вызывается процедура COiMP. Будут сгенерированы команды, которые вычислят и оставят в сумматоре значение выражения. После возврата из СОМР генерируется команда ADD с операндом OPER1.
Если оба операнда — поддеревья, то вызывается СОМР, чтобы скомпилировать команды для первого поддерева. Затем в поле TR(i).OPERl заносится указание о том, что значение первого
13*
388
ГЛАВА 17
операнда находится в сумматоре. REPEAT означает, что для определения дальнейших действий следует снова воспользоваться той же матрицей. Теперь выполняются действия, указанные для случая, когда TR(i).OPERl = ACC и TR(i).OPER2 = поддерево. То есть генерируется новое временное имя, генерируется команда STORE для запоминания содержимого сумматора, компилируются команды для второго операнда и, наконец, генерируется команда ADD.
В приведенной ниже таблице показана последовательность действий и команды, сгенерированные в результате вызова СОМР(5)
Триада Действие Команды Действие
(5) (*А, (4)) СОМР(4)
(4) (- (2), (3)) СОМР(З)
(3) (*С, D) LOAD С
MULT D RETURN
(4) (- (2), АСС) STORE TI COMP(2)
(2) (+ (1), С) СОМР(1)
(О (*А, В) LOAD A
MULT В RETURN
(2) ADD C RETURN
(4) SUB TI RETURN
(5) MULT A RETURN
Матрица для + (матрица для * аналогична)
"\OPER2 ОРЕЮ\ ACC Переменная Целое число (поддерево)
ACC не возможно GEN (‘ADD’, TR(i). OPER2) T: = нов. врем, имя GEN (‘STORE’, Т) COMP (TR(i). OPER2). GEN (‘ADD’, Т)
переменная GEN(‘ADD’, TR(i).OPERI) GEN(‘LOAD’, TR(i).OPERl) GEN(‘ADD’, TR(i).OPER2) COMP(TR(i).OPER2) GEN(‘ADD’, TR(i).OPERl)
целое число (поддерево) не возможно COMP(TR(i).OPERl) GEN(‘ADD’, TR(i).OPER2) COMP(TR(i).OPERl) TR(i).OPERl: = ACC REPEAT
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
389
Матрица для — (матрица для / аналогична)
\OPER2 ОРЕЩХ. АСС Переменная Целое число (поддерево)
АСС не возможно GEN(‘SUB’, TR(i).OPER2) не возможно
переменная Т: —новое врем, имя GEN(‘STORE’, Т) TR(i).OPER2: = Т REPEAT GENfLOAD’, TR(i).OPERl) GENfSUB’, TR(i).OPER2) COMP(TR(i).OPER2) Т: = новое врем, имя GENfSTORE*, Т) TR(i).OPER2: = T REPEAT
целое число (поддерево) Т: = новое врем, имя GEN(‘STORE’,T) COMP(TR(i). OPER1) GEN(‘SUB’, T) COMP(TR(i).OPERl) GEN(‘SUB’, TR(i).OPER2) COMP(TR(i).OPER2) TR(i).OPER2: = ACC REPEAT
Матрица для унарного минуса
OPER1 АСС Переменная Целое число (поддерево)
GEN(‘CHS’, 4 ’) GEN(‘LOAD’, TR(i).OPERl) GENfCHS’, ‘ ’) COMP(TR(i).OPERl) GENCCHS’, ‘ ’)
для дерева, которое изображено на рис. 17.4. В колонке 1 перечислены обрабатываемые узлы, а в колонке 2 — их текущее состояние. В колонках 3, 4 и 5 приводятся действия, выполняемые перед генерацией команд, сгенерированные команды и действие, выполняемое после генерации. Так как в триаде (— (2), (3)) представилась возможность вначале сгенерировать команды для второго операнда, нам удалось сэкономить операции LOAD и STORE.
Генерация кода для польской записи
Интерпретация польской записи рассматривалась в гл. 16. Генерация команд выполняется, по существу, таким же образом. Операторы и операнды просматриваются последовательно слева направо. Но всякий раз, когда просматривается операнд, в стек заносится не его значение, а его описание (в нашей схеме — его имя).
390
ГЛАВА 17
А когда встречается (бинарная) операция, она не выполняется, но генерируются команды для ее выполнения. При этом в качестве описаний операндов используются два верхних описания в стеке; затем эти два описания заменяются описанием результата.
Заметим, что бинарный оператор всегда применяется к двум верхним операндам стека. Поэтому если в каком-либо другом элементе стека описано значение, находящееся в сумматоре, то перед генерацией команд для бинарной операции следует сгенерировать команду, которая запомнит содержимое сумматора. Это обстоятельство дает нам возможность иным способом следить за содержимым сумматора.
Теперь у нас не будет глобальной переменной АСС. Но в элементе стека может содержаться имя 'АСС', если нужно указать, что значение находится в сумматоре. Когда в польской цепочке встречается имя операнда, выполняются следующие действия:
1. Если второй элемент стека (следующий за верхним) — 'АСС' образовать новое временное имя Ti, сгенерировать команду STORE Ti и занести имя Ti в этот элемент стека.
2. Занести имя операнда в стек.
Таким образом, только в двух верхних элементах стека может оказаться описание значения, находящегося в сумматоре. Для бинарного оператора нет необходимости проверять, нужно ли освобождать сумматор. Для унарного оператора следует проверить только второй элемент, чтобы определить, надо ли запомнить содержимое сумматора.
Генерация команд в семантических программах
Если семантические программы могут генерировать тетрады или триады, из которых в том же порядке генерируются команды, то они могут с таким же успехом непосредственно генерировать команды. То есть вместо схемы
исходная программа —> тетрады —> команды имеем
исходная программа —> команды.
Конечно, семантические программы становятся значительно сложнее, но компилятор в целом получается более быстрым. При генерации команд следует иметь достаточно сведений об операндах; их описания должны быть весьма полными. Это может наложить некоторые ограничения на исходный язык, такие, например, как требование, чтобы описание идентификатора встречалось раньше, чем любое обращение к нему.
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
391
Получение более оптимального объектного кода
Одна из трудностей, с которой непременно сталкиваются при генерации кода, состоит в том, что существует немало искусных приемов, и их, казалось бы, надо обязательно использовать, чтобы сэкономить одну-другую команду в объектной программе. Эти приемы зависят от языка той конкретной машины, для которой генерируется программа, и поэтому они почти не поддаются стандартизации. Это означает, что при их реализации в каждом фрагменте программы, который генерирует команды для того или иного оператора, нужно выделять особые случаи и для каждого из них различным образом генерировать коды. В результате система генерации объектного кода становится чрезвычайно громоздкой. Достаточно привести несколько примеров.
В машине может быть команда MOVE, которая пересылает содержимое одной ячейки памяти в другую ячейку. Тогда, если нужно сгенерировать команды для тетрады (:= А, ,В) и А не находится в сумматоре, следует сгенерировать команду
MOVE А, В вместо LOAD А
STORE В
Однако заметим, что, если следующей тетрадой, будет, например, тетрада (+ А, С, Т1), следует предпочесть команды LOAD и STORE, так как значение переменной А в конечном итоге должно оказаться в сумматоре.
В некоторых машинах имеются команды «Сложение непосредственное» и «Загрузка непосредственная», где величина, которую надо прибавить или загрузить, является адресной частью самой команды. Тогда для тетрады (+ А, 3, Т1) следует сгенерировать команды
LOAD А вместо LOAD А
ADDI 3 ADD L3
где L3 — ячейка, содержащая целое число 3. Кроме экономии ячейки каждый раз при выполнении этих команд экономится обращение к памяти.
В машине может быть обратное деление INDIV (или вычитание). И в таком случае, когда делитель (или вычитаемое) находится в сумматоре, можно сэкономить команды LOAD и STORE, генерируя команду
INDIV А вместо LOAD А
DIV В
для тетрады (/ А, В, Т1), поскольку В уже находится в сумматоре.
392
ГЛАВА 17
Можно извлечь выгоду из команды LOADN (Загрузка отрицательная). Тогда для тетрады (— А,, Т1), если А не находится в сумматоре, генерируется команда
LOADN А вместо LOAD А
CHS
Некоторые функции, такие, как ABS и ENTIER в АЛГОЛе, зачастую лучше встроить в программу и не генерировать вызов подпрограммы.
17.3. АДРЕСАЦИЯ ОПЕРАНДОВ
В предыдущем разделе описывалась в общих чертах генерация объектного кода для различных форм внутреннего представления исходной программы. Для простоты изложения каждый операнд
BEGIN INTEGER N, В; PROCEDURE X;
BEGIN INTEGER P;
PROCEDURE Y;
BEGIN INTEGER M;
INTEGER ARRAY C[1S1OJ;
адрес области данных гласной, программы
адрес DA процедуры X
адрес V к процедуры Y
»« В + P + C[N] + C[NJ... END ENO
Рис. 17.5. Сегмент программы и дисплей для процедуры Y.
был представлен символическим именем. В этом разделе мы познакомимся с тем, как формируются адреса операндов в машинных командах. Эта задача может оказаться сложной для языка типа АЛГОЛ, где в любой момент выполнения программы допускается обращение к нескольким различным областям данных и где встречаются переменные с индексами.
Мы покажем, как это делается для арифметических выражений с операндами целого типа, чтобы сосредоточить внимание только на этой задаче. Внутреннее представление исходной программы — тетрады. Читатель отметит, что в главном идея генерации кода не изменяется; просто есть еще моменты, о которых не следует забывать.
Предположим, что в исходной программе на языке типа АЛГОЛ имеются описания вложенных процедур (мы уже говорили об этом в разд. 8.9). В любой момент генерации кода мы генерируем команды для тела одной процедуры. Предположим, что в соответствующий момент выполнения готовой программы адрес области данных (DATA AREA — DA) и дисплея этой процедуры (т. е. активной
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
393
области данных и дисплея) находится в регистре 1 (см. рис. 17.5).
Регистр 1 будет использоваться только для этой цели.
При генерации команд, в которых имеется обращение к переменным с индексами, мы полагаем, что это обращение выполняется с помощью информационного вектора (используя (8.4.3)). Предпо-
ложим также, что элемент таблицы символов для имени массива
LREG 2.0(1) Занести адреса DA главной программы
LREG 3.1(1) и DA для процедуры X в регистры 2, 3 для ссылки на В, Р.
LOAD В (2) Загрузить В, используя регистр 2, содержащий адрес DA главной программы.
ADD Р(3) Прибавить Р, находящееся в DA процедуры X.
LREG 4,М(1) Занести М в регистр 4.
LREG 5,С(1) Занести CONSPART для массива С в регистр 5.
ADD 0 (5, 4) Регистры 4, 5 дают CONSPART+M, поэтому к (В+Р) прибавляется С [М].
LREG 6, N (2) Для N — в DA главной программы — используется регистр 2.
ADD 0 (5, 6) Регистр 5 содержит CONSPART для массива С, а регистр 6 содержит N. Наконец, прибавляем С [NJ1
Р и с. 17.6. Программа для выражения B+P-|-C[M]-|-C[N].
содержит адресную пару (номер области данных, смещение) информационного вектора, и будем считать, что в первой ячейке информационного вектора содержится CONSPART.
Приведем пример программы, которую мы хотим получить. Рассмотрим сегмент программы на рис. 17.5. Во время работы программы, при выполнении процедуры Y, адрес активной области данных (и дисплей — на рисунке справа) находится в регистре 1. Программа, которую требуется сгенерировать для выражения B+P-f-C [М] +С [NJ, приведена на рис. 17.6. Для наглядности смещение для каждого обращения к переменной обозначается именем этой переменной.
Сперва выполняется обращение к В и Р, поэтому две первые команды загружают адреса их областей данных в регистры 2 и 3. Две следующие команды выполняют сложение В+Р. Затем, для обращения к С [М] в регистр 4 заносится М, а в регистр 5 — значение CONSPART для массива С. Команда 7 прибавляет С [М] к (В+Р). Далее, для ссылки на индекс N необходим адрес области данных главной программы, а он уже находится в регистре 2. Ана
394
ГЛАВА 17
логично значение CONSPART для массива С уже содержится в регистре 5.
Мы стремимся сгенерировать программу, в которой наилучшим образом используются регистры. Обратите внимание на то, что в примере содержимое регистров 2 и 5 используется дважды. Так или иначе, но нам придется помнить, что же содержится в каждом регистре.
В некоторых компиляторах при генерации объектного кода предполагается, что регистров R1, .... Rn сколько угодно, по крайней мере достаточно, чтобы поместить все значения, которые необходимо иметь в регистрах. Тогда на следующем проходе просматривается сгенерированный код, и эти п символических регистров отображаются на 7 реально существующих. Когда такое отображение сделано, в программу вставляются команды LREG и SREG для устранения противоречий в использовании фактических регистров. Очевидно, из всех возможных следует выбрать такое отображение, при котором минимизируется число дополнительных команд LREG и SREG.
В той конкретной реализации, которую мы здесь рассмотрим, регистры будут распределяться одновременно с генерацией программы. Чтобы регистры использовались эффективно, нам придется хранить описания регистров, очень похожие на описание сумматора (АСС) из предыдущего раздела. (Подробнее об описаниях мы будем говорить ниже.)
Постоянная обработка описаний регистров безусловно потребует времени и заметно усложнит генерацию кода. Если требуется быстрый и простой транслятор и не особенно важно качество объектной программы, то можно не вводить описания регистров. Начиная генерацию команд для любой тетрады, мы просто предполагаем, что содержимое регистров не определено (за исключением регистра 1), и распределяем регистры 2,3, ..., 7 по мере необходимости. Если бы мы так поступили при генерации команд для выражения В+Р+С1М1+С [N] (см. рис. 17.6), мы бы сгенерировали еще две команды LREG.
Изложение в этом разделе может показаться беспорядочным и сложным из-за неизбежных деталей. Ниже мы перечислим переменные и процедуры, используемые в данном разделе, снабдив их краткими описаниями. Не стоит изучать этот список сейчас; это собьет вас с толку. Используйте его как справочник при чтении различных частей раздела. Перед тем как привести список, опишем в общих чертах вопросы, которые нам предстоит рассмотреть:
1. Формат описаний переменных готовой программы в тетрадах.
2. Формат описаний регистров и сумматора и применение этих описаний. Мы назовем описание значения, находящегося в регистре или в сумматоре, операндом (OPERAND).
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
395
3. Формат адресов в готовой программе, которые заносятся в генерируемые команды для обращения к переменным при выполнении программы.
4. Процедуры для генерации команд загрузки значения в регистр и формирования адресной части команды.
5. Основной генератор команд для тетрады +.
Список переменных и процедур
1. Четыре поля тетрады i — QD (i).OP, QD (i).OPERl, QD(i). OPER2 и QD (i).RESULT. Последние три поля имеют формат, подобный формату на рис. 11.2.
2. Две глобальные ячейки INS1 и INS2, используемые для хранения адресов операндов на машинном языке дляГбинарных и унарных операторов при генерации команд для тетрады.
3. Два массива XRVALUE и XRSTATUS используются для описания текущего содержимого сумматора и регистров; в XRVALUE (0) описан сумматор, в XRVALUE (i) описан регистр i.
4. Процедура FREEACC генерирует команды (если это необходимо) для запоминания содержимого сумматора и заменяет описание сумматора на «свободно».
5. Процедура FREEREG (I). Если 1=0=0, процедура генерирует команды (если необходимо) для запоминания регистра I и заменяет его описание на «свободно». Если I = 0, процедура выбирает, какой из регистров следует освободить, основываясь на текущих описаниях регистров. Номер регистра выдается в параметре I.
6. Процедура GETINREG (OPERAND, I) генерирует команды для загрузки OPERAND в какой-либо регистр и выдает в I номер этого регистра. OPERAND не должен быть описанием переменной с индексами.
7. Процедура GETINACC (ОР1, ADD1, ОР2, ADD2), как и аналогичная ей процедура из предыдущего раздела, генерирует (если необходимо) команду загрузки одного из операндов ОР1 или ОР2 в сумматор. OPi — операнд, ADDi — соответствующий ему адрес в машинной команде (задается смещение, номера одного или двух регистров и бит косвенной адресации). Если ОР2 уже находится в сумматоре, операнды меняются местами.
8. Процедура FIXAD (OPERAND, INSTR) заносит в INSTR адрес (смещение, номера одного или двух регистров и бит косвенной адресации) для ссылки на OPERAND. Процедура выдает 0 (0, 0), если OPERAND уже находится в сумматоре и j (0, 0),если он в регистре j.
9. Процедура FIXADMEMORY (OPERAND, INSTR) подобна процедуре FIXAD, и мы предоставляем читателю написать ее. Единственное отличие состоит в том, что она должна выдать в INSTR адрес ячейки памяти. Следовательно, если OPERAND
396
ГЛАВА 17
находится в сумматоре или в регистре, но не в памяти, процедура должна сгенерировать команды для запоминания OPERAND в памяти и выдать его адрес.
Операнды в тетрадах
Поле каждого операнда и поле результата в тетраде должны иметь формат, подобный формату, описанному на рис. 11.2 в разд. 11.1. Нам не потребуются конкретные сведения о формате. Важно только знать, какую информацию содержит операнд. Заметим, что переменные с индексами имеют более сложный формат, чем другие переменные; это необходимо для генерации более эффективной программы.
Для генерации кода важное значение имеют следующие части описания операнда:
1. Поле типа (вещественный, целый, логический, процедура и т. д.). Оно определяет, какой формат в памяти будет иметь соответствующее значение во время выполнения программы. Мы предполагаем, что все операнды целого типа.
2. Поле адреса указывает номер области данных, в которой выделена память для переменной, и смещение переменной в этой области данных. Мы предполагаем, что нетрудно преобразовать номер области данных в смещение, которое необходимо для определения ее адреса в активном дисплее, и впредь не будем возвращаться к этой проблеме.
Описание временного значения переменных в таблице временных переменных должно содержать поля, указывающие зону существования этого значения. В разд. 14.2 в общих чертах описаны три способа определения зоны. В нашей схеме генерации объектного кода память для временных переменных будет выделяться во время генерации кода, а не при последующем отдельном проходе. Более того, мы не будем выделять память для временной переменной, которую не приходится запоминать (т. е. если она остается в сумматоре или в регистре на протяжении всей зоны ее существования).
Если в какой-нибудь момент содержимое сумматора или регистра нужно запомнить, то программа (только в этом случае) выделит память для этой временной переменной и сгенерирует команды, которые выполнят запоминание. После генерации команд для тетрады мы проверяем каждый операнд, не является ли он временной переменной, зона существования которой ограничивается этой тетрадой. Если это так, то выделенная для этой переменной ячейка освобождается (см. разд. 14.2).
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
397
Описания регистров и сумматора.
Массив XRVALUE содержит описания значений, которые будут находиться в сумматоре и регистрах во время выполнения программы в тот момент, когда выполнится последняя сгенерированная команда.
XRVALUE (0) описывает сумматор, XRVALUE (i) описывает регистр i для i = 1,. . . , 7. XRVALUE(i) может содержать:
1. Операнд, как на рис. 11.2 Это означает, что данный операнд находится в сумматоре или регистре.
2. Операнд, который указывает, что регистр содержит значение CONSPART массива, описанного следующим образом:
5 0 указатели па элемент таблицы символов для имени массива
3. Операнд, указывающий, что адрес области данных находится в регистре:
6 0 номер области данных
Вот такие величины, которые могут появиться в XRVALUE (i), мы называем описанием операнда (OPERAND).
Таким образом, нам известно, какое значение находилось в регистре, но нам необходимо еще знать, насколько важно, чтобы оно там и осталось. Например, регистр 1 вообще нельзя использовать в других целях, так как в нем записан адрес активной области данных. Мы воспользуемся параллельным массивом XRSTATUS, элементы которого XRSTATUS(i) могут принимать следующие значения:
1. 0 Регистр i или сумматор пусты.
2. 1 Это значение есть еще и в памяти. Значит, нет необходимости запоминать регистр, если мы хотим использовать его для других целей.
3. 2 Этого значения нет в памяти.
4. 3 Содержимое регистра не изменять.
Начиная генерировать команды для тела процедуры, мы заносим 0 в XRSTATUS (J) для J= 0, 2,.... 7 и 3 в XRSTATUS (I). Кроме того, мы помещаем в XRVALUE (1) описание:
6 0 номер области данных для этой процедуры
398
ГЛАВА 17
Такие описания сумматора и регистров заносятся каждый раз, когда из тетрады генерируются команды. В связи с этим используются две важные процедуры: FREEACC и FREEREG (I). Первая процедура проверяет описание сумматора X RVALUE (0) и XRSTATUS(O) и генерирует команды, если необходимо запомнить его содержимое:
1. Если XRSTATUS(O) = 0, то выполнить возврат (сумматор свободен).
2. Если XRSTATUS(O) = 1, сумматор содержит значение, находящееся также и в памяти. Занести 0 в XRSTATUS (0) и выполнить возврат.
3. Если XRSTATUS (0) = 2, то этого значения нет в памяти. В нашей реализации это может случиться только тогда, когда XRVALUE (0) описывает временную переменную. Выделить для нее память в активной области данных, скажем, со смещением к. Сгенерировать команду «STORE k(l)». Занести 0 в XRSTATUS (0). Возврат.
4. Случай XRSTATUS (0) = 3 невозможен при нашей реализации.
FREEREG(I) выполняет аналогичные действия: если I =/=(), то генерируются команды (если необходимо) для запоминания регистра I и изменения его описания на «свободен». Если I =0, то процедура может выбрать любой регистр, который она пожелает освободить, и выдать номер этого регистра в переменной I. Если программа выбирает регистр, то она в первую очередь должна отдать предпочтение регистру, который в данный момент свободен, во вторую очередь — регистру, содержимое которого уже находится в памяти (так что не надо генерировать команд), и в третью очередь — регистру, для которого XRSTATUS (I) — 2. Как только регистр, который должен быть освобожден, определился, выполняются действия, такие же, как в процедуре FREEACC.
В процедуре FREEREG следует учесть еще одно ограничение на выбор регистра. Однако с объяснением этого ограничения мы пока повременим.
Формы адресов операндов
При генерации кода для операции, такой, как (+А, В, Т1), мы должны знать по какому адресу следует обращаться к А и В, находящимся в памяти.
В таблице, приведенной ниже, перечислены различные операнды, которые могут встретиться во внутреннем представлении исходной программы. Во второй колонке приведены команды, которые можно сгенерировать, чтобы определить адрес операнда, тогда как в третьей колонке даются адрес и номер индексного регистра в команде,
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
399
которая в конечном счете обращается к операнду. При необходимости может быть установлен бит косвенной адресации. Первые две строки в таблице на самом деле не являются ссылками на ячейки памяти, но мы таким образом указываем, что операнд находится в сумматоре или в регистре. Мы можем это сделать, поскольку рассматривается такой случай, когда в ссылке на память используется по меньшей мере один регистр.
Операнд
1. В сумматоре
2. В регистре j
3. Ячейка в активной области даннных, смещение к
4. Ячейка в другой области даных, смещение к
5. Переменная с индексами в активной области данных. CONSPART имеет смещение к
6. Переменная с индексами в другой области данных. CONSPART имеет смещение к
Команды INSTR
0 (0, 0) «0, 0)
LREG m,адрес DA k(l) k(m)
LREG LREG j, индекс n.k(l) 0(n, j)
LREG LREG LREG j,индекс m,адрес DA n,k (m) 0(n, j)
Процедура GETINREG (OPERAND, I).
Из приведенной выше таблицы ясно, что нам придется время от времени генерировать команды загрузки в регистры индексов значений CONSPART для массивов и адресов областей данных. Следующая процедура делает это для OPERAND и заносит в I номер регистра. Единственное ограничение состоит в том, что OPERAND не может быть переменной с индексами. В процедуре используются локальные переменные j, J, D, OP и к. Читатель сможет убедиться в том, что нет никаких особых приемов в этой программе (а также почти во всех других, описываемых здесь); одно лишь скрупулезное исследование OPERAND.
1. Если OPERAND находится в регистре j, занести j в I и выполнить возврат (при проверке сравнивается OPERAND с XRVALUE (j) для j - 1, ..., 7).
2. Если OPERAND находится в сумматоре, выполнить следующее: I : = 0; вызвать FREEREG (I); сгенерировать команду «LRACC I». Переписать XRSTATUS (0) и XRVALUE (0) в XRSTATUS (I) и XRVALUE (I). Возврат.
3. Если OPERAND имеет вид (6, 0, D), то D — номер области данных и нужно занести ее адрес в регистр. Выполнить следующие
400
ГЛАВА 17
действия: I : = 0; вызвать FREEREG (I); сгенерировать «LREQ I, к (1)», где к — смещение в активной области данных для ссылки на адрес области данных D. Занести 1 в XRSTATUS (I) и OPERAND в XRVALUE (I). Возврат.
4. OPERAND — константа, временная переменная или идентификатор, описанный в некоторой таблице. Пусть D — номер области данных операнда, к — его смещение. Сформировать операнд ОР := (6, 0, D) и вызвать GETINREG (OP, J). (В результате адрес области данных окажется в регистре J. Заметьте, что это рекурсивный вызов.) Установить 1:=0; вызвать FREEREG(I); сгенерировать «LREG I,k(J)> или «LREG I,*k(J)», в зависимости от ее состояния бита косвенной адресации в OPERAND. Занести 1 в XRSTATUS (I) и OPERAND в XRVALUE (1). Возврат.
Процедура FIXAD (OPERAND, INSTR)
Для любого операнда из некоторой тетрады эта процедура формирует адресную часть команды, которая ссылается на него, и заносит этот адрес в INSTR. Результат в INSTR может также иметь вид 0(0,0) или j (0,0), если OPERAND уже находится в сумматоре или в регистре j:
1. Если OPERAND в сумматоре, занести адрес (0,0) в INSTR; возврат.
2. Если OPERAND в регистре j, занести адрес j(0, 0) в INSTR; возврат.
3. Если OPERAND описывает переменную с индексами, выполнить следующие шаги:
а) Пусть SUBSCRIPT — та часть OPERAND, которая описывает индекс. Вызвать GETINREG (SUBSCRIPT, I). Занести адрес 0(0,1) в INSTR.
b) Пусть Р — указатель на элемент таблицы символов для имени массива. Сформировать операнд ОР:=(5, 0, Р). Установить! :=0. Вызвать GETINREG (OP, I),чтобы сгенерировать команды занесения CONSPART в регистр. Приформировать адрес 0(1, 0) в INSTR;
с) Установить бит косвенной адресации в INSTR, если это требует OPERAND. Возврат.
4. OPERAND — константа, временная переменная или переменная, для которой имеется элемент в таблице символов. Значение не находится ни в сумматоре, ни в регистре. Выполнить следующие шаги:
а) Пусть D — номер области данных адреса операнда. Сформировать операнд ОР := (6, 0, D). Вызвать GETINREG (OP, I),
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
401
Ь) Пусть к — смещение для OPERAND в области данных. Занести адрес к(1) в INSTR. Установить бит косвенной адресации в INSTR, если это требует OPERAND. Возврат.
Генерация кода для арифметических тетрад
Теперь мы готовы в общих чертах описать процедуру генерации команд для i-й тетрады вида (+ А, В, Т1). Генерация команд для других тетрад аналогична, и мы предоставим читателю возможность написать соответствующие программы самостоятельно. Первая задача состоит в генерации адресов двух операндов и занесении этих адресов в две глобальные ячейки INS1 и INS2. (Далее мы объясним, почему эти две ячейки должны быть глобальными.) Итак, перейдем к генерации команд для ADD. Далее следует упрощенная схема этого генератора команд:
1. Установить INS1 := 0; INS2 := 0 (инициализация адресов операндов).
2. Вызвать FIXAD (QD (i). OPER1, INS1). (Эта процедура генерирует команды, если это необходимо, которые вычислят адрес OPERAND 1 во время выполнения программы; этот адрес в виде k (i, j) заносится в INS1.)
3. Вызвать FIXAD (QD (i).OPER2, INS2).
4. GETINACC (QD(i).OPERl, INS1, QD(i).OPER2, INS2). (Цель состоит в генерации команд (если это необходимо) занесения одного из операндов в сумматор. Каждый операнд представлен двумя значениями — собственно описанием OPERAND и его адресом в готовой программе. При выходе из процедуры первый операнд будет в сумматоре.)
5. Выполнить этот шаг только в случае, если второй операнд находится в сумматоре или в регистре. Мы хотим сгенерировать команду ADD, а для этого нужно, чтобы операнд находился в памяти. Если INS2 = 0 (0, 0) или j (0, 0), мы должны повторить вычисление адреса второго операнда, используя для этого иную процедуру; INS2 :== 0; вызвать FIXADMEMORY(QD (i).OPER2, INS2).
6. Сгенерировать команду ADD с адресом INS2. Изменить описание сумматора, чтобы указать, что в нем содержится QD (i). RESULT (занести 2 в XRSTATUS (0)).
7. Если какой-либо из операндов QD (i). OPER1 или QD (i). OPER2 является временной переменной, зона существования которой ограничена тетрадой i, выполнить следующее: если для операнда была выделена память, то освободить ее. Если операнд находится в регистре, в описании этого регистра отметить, что он свободен.
402 ГЛАВА 17
8. INS1 := 0; INS2 := 0.
Две ячейки : INS1 и INS2 — глобальные, и их следует использовать во всех программных сегментах, которые генерируют команды для бинарного или унарного оператора, по следующим причинам. Предположим, что мы генерируем адрес первого операнда и что он использует регистры 2 и 3. Тогда при генерации адреса второго операнда важно, чтобы регистры 2 и 3 оставались нетронутыми, так как они содержат величины, необходимые для обращения к первому операнду. Следовательно, FREEREG должна сама сохранить содержимое этих регистров. В программу FREEREG нужно внести упоминавшиеся при ее описании дополнительные ограничения:
если либо INS1, либо INS2 содержат ссылки на регистр j в виде j (0,0}, k (j, m) или к (m, j), этот регистр не должен освобождаться.
Обсуждение
Хотя могло показаться, что речь шла о весьма мелких деталях, в действительности мы только наметили схемы различных процедур. Многие моменты были опущены. Например, мы должны попытаться реализовать описания регистров так, чтобы работа по определению того, какое значение находится в регистре (если регистр не свободен), могла быть выполнена наиболее эффективно. Можно, например, предположить, что в каждом элементе таблицы символов имеется поле, которое указывает, находится ли значение в регистре. Или мы можем пожелать, чтобы регистры попадали в тот или иной связанный список в зависимости от их состояния (один список для свободных регистров, другой для регистров с XRSTATUS(i)-! и т. д.).
Хотя идея генерации команд для тетрад довольно прозрачна, генерация даже локально эффективной программы может оказаться достаточно сложной. В каждой процедуре предусматривается несколько особых подслучаев, и каждый из них требует индивидуальной обработки. Отладка может никогда не закончиться, так как всегда остается один последний особый случай, о котором забыли. Некоторые случаи требуют особого внимания: 1) оба операнда при сложении одновременно находятся в сумматоре (например, при оптимизации А*В+А*В), 2) значение одновременно находится в сумматоре и регистре (например, при сложении М+А[М]).
Ясно, что процесс формирования адресов операндов следует тщательно продумать и несколько раз смоделировать вручную до начала реализации.
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
403
17.4. ГЕНЕРАЦИЯ КОМАНД ДЛЯ ДРУГИХ ТИПОВ ТЕТРАД
Мы начнем этот раздел с нескольких дополнительных замечаний относительно генерации команд для арифметических выражений. Затем мы перейдем к генерации команд для других типов тетрад. Идея в основном та же: известно, какие команды мы хотим сгенерировать для каждой тетрады, и остается только разработать генератор команд, который именно эти команды порождает. Поэтому мы очень кратко обсудим генерацию команд только для нескольких операторов, касаясь лишь тех вопросов, о которых иногда забывают.
Оптимизация унарного минуса и оператора ABS
Обычно при локальной оптимизации пытаются исключить эти унарные операторы, вынося их до тех пор, пока это возможно. Так, можно заменить выражение —С*(—(A+B)4-D) на С*(А+В—D) за три шага:
— С*( —(A+B)+D) -C»(-((A + B)-D))->
---С»(А + В-D) —> C*(AH-B-D),
и тем самым исключить две операции.
Мы выполним это преобразование во время генерации кода, отведя в описании для каждой временной переменной двухразрядное поле, которое указывает, какую еще операцию нужно выполнить над этим значением: 0—+(отсутствие операции), 1=—, 2=ABS, 3=—ABS. Для тетрад (— А, ,Т) или (ABS А, ,Т) генератор команд не генерирует команд, вместо этого он просто заполняет двухразрядное поле знака в описании переменной Т в зависимости от А и в соответствии со следующей таблицей:
А: Поле знака в описа- Временная перем, со знаком Переменная исходной программы
+ — ABS — ABS
теле Т для (— А, ,Т) Т: — + —ABS ABS +
Поле знака в описателе Т для (ABS А, ,Т)‘ Т: ABS ABS ABS ABS ABS
Кроме этого, в описателе Т нужно предусмотреть указание о том, что его основное значение то же, что и А в случае, если А не находится в сумматоре или в регистре.
Теперь мы поясним, как генерируются команды для тетрады (*Т1,Т2,ТЗ), если операнды дополнены знаковыми разрядами. Предположим, .что Т1 и Т2 — временные переменные; если это
404
ГЛАВА 17
переменные исходной программы, то они автоматически имеют знаки +. Мы предлагаем читателю самостоятельно провести ту же работу для других бинарных операторов + , — и /.
Генератор команд для тетрады (*Т1, Т2, ТЗ) просматривает матрицу на рис. 17.7, чтобы определить знаковые разряды для ТЗ. Для непустого элемента матрицы генератор команд должен только сгенерировать команду обычного умножения и занести этот элемент
Т2 Н ABS —ABS В строках представлено
Т1: + — + ABS —ABS —ABS ABS поле знака В столбцах Т1. представлено
ABS —ABS поле знака Т2.
Рис. 17.7. Определение поля знака для ТЗ в (* Т1,Т2,ТЗ).
матрицы в поле знака ТЗ. Если элемент матрицы пуст, нужно сгенерировать команды, которые вычислят указанную функцию ABS от Т1 (или Т2) и запомнят полученное значение в ячейке для Т1 (или Т2) (если она имеется). Затем нужно изменить соответствующее описание, и генератор команд должен начать снова генерацию команд для преобразованной тетрады.
Откладывая программирование унарной операции, мы не всегда получим лучший код. Если временную переменную, находящуюся в регистре и имеющую поле знака, отличное от +, приходится сохранять, то может оказаться выгоднее выполнить унарную операцию до запоминания.
Тетрады Генерация с отложенными унарными операциями Обычная генерация
(+ А, В, Т1) LOAD A LOAD A
ADD В ADD В
(ABST1, ,Т2) ABS
(* C.D.T3) STORE T2 STORE T2
LOAD C LOAD C
MULT D MULT D
(+ Т2,ТЗ,Т4) STORE T3 ADD T2
LOAD T2
ABS
ADD T3
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
405
Выше в таблице в колонке 1 приведена последовательность тетрад для выражения ABS (A+B)+C*D. В колонке 2 показан результат генерации, при которой операция ABS откладывается, пока это возможно. Заметим, что при этом генерируется на две команды больше, чем в колонке 3, где команда ABS генерируется немедленно.
Генерирование команд для смешанных выражений
Предположим, что первоначальные семантические программы, которые генерируют тетрады, вставляют там, где это необходимо, операторы преобразования типа. Тогда тетрады для выражения K:=A*I+J получатся такими, как в левой колонке (переменная А — вещественная, остальные переменные — целые):
(CVIR I, , Т1) (* A, I, TI)
(*R A, TI, Т2) (+ - TI, J, Т2)
(CVIR J, ,ТЗ) ( + R Т2, ТЗ, Т4) (CVRI Т4, , Т5) (:=I Т5, , К) (: = Т2, , К)
Генератор команд для каждого оператора точно знает типы каждого операнда и результата. Так, генератор *R генерирует MULTF, не проверяя типы операндов и результата, генератор *1 —MULT, генератор CVIR — FLOAT и т. д. Это означает, что существует много различных сегментов генерации команд, но каждый сегмент довольно прост.
С другой стороны, если тетрады имеют такой вид, как в колонке справа, то генератор должен проверить для каждого оператора + , * и т. д. типы полей операнда и результата, сгенерировать, если это необходимо, команды преобразования типа и затем определить, какую операцию надо сгенерировать. При этом мы перенесли проверку преобразований типа из первоначальных семантических программ в генераторы команд. Вероятно, все же лучше сделать это раньше, в первоначальных семантических программах, поскольку сегменты генерации команд и так достаточно сложны.
Генерация команд для тетрады (:= А,, В)
Генерируются команды LOAD А и STORE В. Описание сумматора следует изменить, чтобы отметить, что В находится в сумматоре (занести 1 в XRSTATUS (0)). Таким образом можно сэкономить
406
ГЛАВА 17
команду при программировании, например, инструкций
В = . . .
IF (В) 2, 3, 2
Когда мы начинаем генерировать команды для инструкции IF, известно, что В находится в сумматоре и нет необходимости в генерации команды загрузки В в сумматор.
Следует быть внимательным в этом и в аналогичных случаях. Предположим, мы имеем
В . +В + . . .
и прежнее значение В находится, скажем, в регистре 2, как раз перед выполнением последнего присваивания В. После генерации присваивания в описание регистра 2 следует занести «свободен», так как регистр содержит старое, а не новое значение В.
Заметим, что любая тетрада, например (+ А,В,Т1), также является присваиванием Т1. Различие состоит в том, что такой временной переменной значение присваивается только один раз, и, следовательно, она не может в этот момент находиться в регистре. Временная переменная, которой присваиваются значения более одного раза, должна обрабатываться немного иначе.
Генерация команд для переходов и условных инструкций
Генерация команд перехода (BRL L) или (BR к) не представляет проблемы. Если метка или тетрада, к которой должен быть переход, еще не обработана, мы организуем связанный список всех переходов к этой метке или тетраде точно так же, как это сделано в разд. 13.3 при генерации тетрад.
До сих пор в этой главе мы генерировали команды для линейных участков, т. е. последовательности команд, не содержащие внутри себя переходов и команд, к которым есть переходы. Это позволяло нам знать точно, что находится в каждом регистре. Однако если к тетраде (или машинной команде) есть переход, то мы непосредственно перед генерацией команд для этой тетрады не знаем, что находится в сумматоре или регистрах. Следовательно, мы должны во все описания занести «свободно» (исключая описания с XRSTATUS (J) = 3). Будьте внимательны при освобождении регистров. Если в описании XRSTATUS (j) =2, то это означает, что соответствующего значения нет в памяти и нужно сгенерировать команды для запоминания этого значения.
Чтобы обнаружить тетрады, к которым есть переходы, можно, например, выделить в каждой тетраде дополнительное поле, указывающее, есть ли переход к данной тетраде или нет. Это поле будет заполняться при генерации тетрад.
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
407
Для условных инструкций (и аналогичных конструкций), если точно известно, как будут выполняться переходы, можно провести некоторую оптимизацию регистров. Для инструкции
IF <Е> THEN Sj ELSE S2
содержимое сумматора и регистров будет одинаковым, когда начинают выполняться команды для Si и для S2- Предположим, мы генерируем тетрады
(1) тетрады для Т:=<Е> (1) тетрады для Т: =<Е>
(р) (IFTEST q, Т) (Р) (BZ q+1, Т)
(р + 1) тетрады для St (р + 1) тетрады для Si
(q) (ELSE г) вместо (q) (BR, г)
(q + 1) тетрады для S2 (q + 1) тетрады для S2
(г) (ENDELSE q) (г)
для такой условной инструкции (смотри разд. 13.2). Тогда благодаря новым операторам IFTEST, ELSE и ENDELSE вовремя генерации команд нам известно, где находятся различные части инструкции. В генераторе команд для тетрады IFTEST после генерации перехода при Т = FALSE мы запоминаем текущие описания регистров XRVALUE и XRSTATUS и помещаем указатель Р на эти описания в одно из неиспользуемых полей тетрады ELSE. Затем в генераторе команд для тетрады ELSE сразу же после генерации мы с помощью Р восстанавливаем в глобальных массивах XRSTATUS и XRVALUE прежние описания регистров. Действуя таким образом, мы имеем в виду, что как перед началом выполнения Si, так и перед началом выполнения S2 содержимое регистров одинаково.
Можно, кроме того, сохранить описания регистров в Rt и в R2 после генерации команд для Sx и для S2 соответственно и использовать эту информацию для определения состояния регистров после выполнения полной условной инструкции следующим образом: для каждого регистра i если описание регистра i в Ri совпадает с его описанием в R2, то это описание используется при генерации команд для следующей тетрады; если же описания не совпадают, то в описание i-ro регистра заносится «свободен», поскольку мы не знаем, что будет в регистре i.
17.5. ЭКОНОМИЯ ПАМЯТИ ПРИ ГЕНЕРАЦИИ КОДА
Набор программ для генерации объектного кода, как правило, чрезвычайно громоздок. Существует очень много программных сегментов, различных для тетрад с разными операторами. Однако многие из этих сегментов очень схожи между собой, и имеется
408
ГЛАВА
лишь несколько различных операций, таких, как GETINACC, GETINREG, FREEACC, GEN и т. д. Следовательно, можно попытаться найти способы экономии памяти. Некоторые из них коротко описываются в этом разделе.
Интерпретация
Один метод экономии памяти состоит в том, чтобы разработать несложный язык, на котором пишутся генераторы команд для различных тетрад, и затем написать (чистый) интерпретатор для этого языка. В языке должны быть простые конструкции (примитивы) для всех обычных операций генерации команд (аналогичных GETINREG) и, кроме того, обычные инструкции перехода и условия. Создание языка облегчается в связи с тем, что в большинстве генераторов команд и в процедурах используются глобальные параметры, аналогичные QD (i) и ячейкам INS1 и INS2 и описанные в разд. 17.3.
Поясним эту идею на примере. Ниже показано, как будет выглядеть программный сегмент для тетрады + в символической и внутренней формах. Каждую операцию определяет целое число и несколько параметров. Операциями являются: INIT — установить начальное состояние (1), вызвать программу FIXAD (2), сгенерировать команды засылки операнда в сумматор (3), сгенерировать
Генератор команд для тетрады +
Символическая Внутренняя
форма форма Смысл
INIT 1 INS1 : =0; INS2 : =0.
FIXAD 1 2, 1 Вызов программы FIXAD для определения адреса первого операнда.
FIXAD 2 2, 2 Вызов программы FIXAD для определения адреса второго операнда.
GETINACC 2 3, 2 Вызов программы GETINACC для занесения одного из операндов в сумматор.
CHECKREG 2 4, 2 Обеспечить, чтобы адрес второго операнда был в INS2.
GEN 'ADD' 2 5, 1, 2 Сгенерировать команду. Эта операция — первая в таблице команд; адресная часть находится в INS2.
CHECKTEMP 1 6, I Контроль операндов; если это временные переменные, зоны существования
CHECKTEMP 2 6, 2 которых кончаются, то обработать их.
ENDSEG Конец программы,
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
409
Команду (5) и т. д. Заметим, что в такой форме для программного сегмента потребуется 20 слов вместо 50—75 команд на машинном языке. Мы могли бы также упаковать каждую операцию в слово.
Если писать компилятор на языке ассемблера или на другом языке с хорошими макросредствами, то внутренние таблицы программного сегмента можно получить автоматически из символической формы, представив каждую символическую команду в виде макровызова.
Создание более общих подпрограмм
Общий план генерации команд для любого арифметического или логического оператора состоит в том, чтобы: 1) сгенерировать команды для получения адресов операндов; 2) сгенерировать команды для выполнения необходимых преобразований типов; 3) сгенерировать команды для загрузки одного из операндов в сумматор и, наконец, 4) сгенерировать команды для операции.
Во многих случаях можно написать одну общую процедуру генерации команд, пригодную для всех арифметических и логических операторов. Параметрами для нее будут: описания операндов, требуемый тип результата, указание о коммутативности операции, указание о существовании обратной операции (например, обратное деление) и некоторые другие сведения об особенностях конкретной машины. Важным параметром является последовательность каркасных команд; она используется процедурой генерации команд (см. выше) на шаге 4.
Эта же идея (мы ее сейчас рассмотрим) используется в компиляторе IBM FORTRAN Н (хотя там схема генерации команд несколько отличается от нашей).
Шкалы
В компиляторе IBM FORTRAN Н (см. Лоури и Медлок [691) весьма искусно решен вопрос упаковки таблиц, содержащих информацию о том, как генерировать команды. Чтобы проиллюстрировать это, предположим, что каждый регистр можно также использовать как арифметический регистр (как в IBM 360).
Проход, предшествующий генерации, обрабатывает тетрады и тем самым осуществляет довольно сложную глобальную оптимизацию регистров. Для каждой тетрады (например, для (+1 Т1,Т2, ТЗ)) известно, какие из операндов уже находятся в регистрах, какие значения операндов должны оставаться в этих регистрах и т. д. Известен регистр Ri (i = 1, 2, 3), выделенный для хранения значения Ti, если это необходимо, а в регистре Bi должен храниться адрес области данных, где находится Ti. (Очевидно, если Ti в активной области данных, то Bi = 1.) Эта информация находится в
410
ГЛАВА 17
тетраде вместе с операндами. Некоторые из регистров могут совпадать. Например, если нет необходимости оставлять Т1 в регистре, полагаем R3 = R1.
Кроме того, наряду с тетрадой существует 8-разрядное поле STATUS, содержащее следующую информацию (если разряд содержит 1, то информация истинная, в противном случае справедливо обратное):
Разряд 1 2 Смысл Операнд Т1 уже в регистре R1. Значение операнда Т1 должно оставаться в регистре R1.
3 4 5 Операнд Т2 уже в регистре R2. Значение Т2 должно оставаться в регистре Т2. Адрес области данных, содержащей Т1, еще не в регистре В1.
6 Адрес области данных, содержащей Т2, еще не в регистре В2.
7 Адрес области данных, содержащей ТЗ, еще не в регистре ВЗ.
8 После операции ТЗ должно быть занесено в память.
Команды, которые могут быть сгенерированы для конкретной операции, хранятся в таблице в форме каркаса в том порядке, в котором они будут генерироваться, с каждой командой связана некоторая последовательность битов. Это иллюстрируется на рис. 17.8 для оператора +1. Процесс генерации команд происходит так: общей программе передается тетрада (вместе со всей дополнительной информацией) и таблица команд для соответствующего оператора. Программа выполняет следующие действия:
1. Первые четыре разряда 8-разрядного поля STATUS используются для выбора столбца разрядов состояния: 0000 — выбирается первый столбец, 0001 — второй и т. д.
2. В выбранном столбце все х-разряды заменяются последними четырьмя разрядами из поля STATUS. Последний х заменяется восьмым разрядом, предпоследний — седьмым и т. д.
3. Последовательно просматривается столбец разрядов, и если разряд содержит 1, генерируется соответствующая команда.
Чтобы показать, как это делается, рассмотрим 8-разрядное поле 00000011, указывающее, что ни Т1, ни Т2 не находятся в регистрах, ни один из операндов не нужно оставлять в регистре, регистры В1 и В2 уже загружены, ВЗ еще не загружен и результат следует запомнить. Первые четыре разряда выбирают столбец 1, который имеет вид хОЮхОЮхх. Заменяя все х последними четырьмя разря-
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
411
Каркасные команды Разряды состояния
0000000011111 111 0000111100001 11 1 0011001100110011 01010101010Г0101
1 LREG B1,D(1) 2 LREG R1,D(B1) 3 LREG R3,D(B1) 4 MREG R3,R1 5 LREG B2,D(1) 6 LREG R2,D(B2) 7 ADD R3,D(B2) 8 ADDR R3,R2 9 LREG B3,D(1) 10 STORE R3,D(B3) xxxxxxxx00000000 0000111100000000 Подготовить TI 1111000000000000 0000111 100001 1 11 xxxxxxxxxxOOxxOO 0100010001000100 1000101010001000 Подготовить T2 и прибавить 0111010101110111 xxxxxxxxxxxxxxxxi Запомнить результат, если хххххххххххххххх| это необходимо
MREG—пересылка из одного регистра в другой.
ADDR— прибавление содержимого одного регистра к содержимому другого.
Рис. 17.8. Шкалы для оператора +1.
дами, получаем 0010001011. Следовательно, мы генерируем (по порядку) третью, седьмую, девятую и десятую команды:
LREG R3,D(B1)
ADD R3,D (B2)
LREG B3,D(1)
STORE R3,D (B3)
Загрузить TI в R3.
Прибавить T2 к R3.. Подготовить адрес ТЗ Запомнить результат.
Смещения, обозначенные буквой D, определяются из описаний операндов; номера регистров заданы в тетрадах.
Сгенерированную программу можно сделать более эффективной, если внести в каркас дополнительные команды, в которых учитывается коммутативность некоторых операций и другие особенности.
17.6. ОБЪЕКТНЫЕ МОДУЛИ
Объектная, или двоичная, колода—это объектная программа на картах (либо образы карт во внешней памяти). Если программу можно загрузить в любое место памяти, модуль называют «пере
412
ГЛАВА 17
мещаемым»; если она обязательно должна загружаться в определенную последовательность ячеек памяти, то модуль называют «абсолютным». Перед загрузкой объектный модуль обычно можно автоматически связать с любыми другими требуемыми объектными модулями, такими, как подпрограммы ввода-вывода, стандартные функции и подпрограммы пользователя, скомпилированные в другое время.
В перемещаемом модуле все команды или значения, в которых есть ссылки на ячейки памяти в программе, должны «настраиваться», т. е. в зависимости от того, куда программа загружена, эти ссылки на память нужно соответствующим образом изменять. В машинах типа IBM 360 перемещаемость достигается легче, так как в командах при ссылках на память должны использоваться базовые регистры. В некоторых машинах, ориентированных на работу с разделением времени, эта настройка вообще выполняется с помощью оборудования, т. е. нет разницы между абсолютным и перемещаемым модулем.
Формат перемещаемого объектного модуля почти так же удобен для использования, как и формат символического языка ассемблера, однако в первом случае не требуется дополнительное время для трансляции. И все-таки мы должны обратить внимание на то, что связь и настройка объектных модулей требует времени; в тех случаях, когда время решения обычно мало и большая часть времени тратится на отладку, выгоднее генерировать абсолютную программу и немедленно выполнять ее.
По терминологии IBM OS/360 связь нескольких объектных модулей и формирование загрузочного модуля выполняется редактором связей. Окончательная загрузка (с настройкой) загрузочного модуля выполняется загрузчиком. (На 'самом деле загрузочные модули можно сохранить и позднее снова связать с другими объектными и загрузочными модулями.) В более простых операционных системах эти два шага могут быть выполнены с помощью одной программы, называемой загрузчиком связи или просто загрузчиком.
Мы опишем основной формат объектного модуля IBM OS/360. Более подробное описание можно найти в руководстве по IBM (см. ИБМ (d)) и в работе Эрмана [68]. Системы математического обеспечения на других машинах будут использовать подобный — возможно, более или менее удобный — формат. Весьма вероятно, что другой будет и терминология.
Чтобы изложение было простым и понятным, мы отчасти ограничим формат и не будем обращать внимание на некоторые тонкости. На схемах карт, представленных в этом разделе, любые неописанные колонки пусты. Колонки 73—80 можно использовать для идентификации и нумерации. Числа для удобства чтения даются в десятичной системе, хотя, вообще говоря, они должны быть представлены шестнадцатеричными цифрами.
j
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
413
Особый интерес представляют следующие вопросы:
1. Как указывается, какие внешние подпрограммы требует данный объектный модуль?
2. Каким образом указываются «точки входа» (команды или данные в модуле, на которые могут ссылаться другие подпрограммы)?
3. Как достигается перемещаемость объектной программы, т. е. возможность размещать ее в любом месте оперативной памяти?
4. Можем ли мы использовать формат объектного модуля в целях облегчения или ускорения компиляции?
Программные секции
Объектный модуль состоит главным образом из текста — команд на машинном языке и данных, которые составляют объектную программу. Модуль может содержать одну или более таких подсекций текста, называемых программными секциями (CSECT). Внутри CSECT позиция каждого байта текста (относительно начала программной секции) фиксирована, и этот порядок должен быть сохранен при загрузке программной секции в память. Порядок программных секций в памяти произволен, CSECT можно поместить в любое место памяти.
Обычно CSECT содержит:
1) команды для главной программы;
2) команды для подпрограммы;
3) область данных для главной программы или подпрограммы;
4) константы программы.
Однако нет необходимости придерживаться этих категорий; подсекцию с любым текстом можно, если это удобно, включить в CSECT.
Типы карт объектного модуля
Объектный модуль состоит из четырех частей, которые должны встречаться в модуле в том же порядке, в каком они описаны на рис. 17.9. Этими частями являются:
1. Словарь внешних символов ESD (external symbol dictionary). Словарь определяет и идентифицирует (дает единственное имя и номер) следующие объекты:
а) программные секции объектной программы;
Ь) внешние ссылки на программные секции и другие входные точки, которые используются или к которым обращаются в этом модуле, но которые не включены в него; они определяются для этого модуля посредством редактора связей;
с) точки входа — ячейки внутри данного модуля, на которые можно ссылаться из других модулей; появле
414
ГЛАВА 17
ние имени входной точки в качестве внешней ссылки в другом объектном модуле приводит к тому, что этот модуль должен быть связан с другим модулем; В OS/360 это называется определением меток;
d) непомеченные и помеченные области COMMON (используются главным образом в программах, написанных на ФОРТРАНе).
2. Текстовые карты «ТХТ». В этой части содержатся команды на подлинном машинном языке и данные для объектной пограммы.
ESD
текст
RLD
карта END
Рис. 17.9. Формат объектного модуля.
3. Словарь перемещаемых адресов RLD (relocation dictionary). В нем содержится описание перемещаемых адресов, встречающихся в тексте.
4. Карта конца модуля END. Этой картой оканчивается объектный модуль.
Словарь внешних символов (ESD)
Каждая карта ESD описывает один элемент ESD1)— программную секцию, внешнюю ссылку, входную точку или область COMMON, как это изображено на рис. 17.10. Колонки 17—24 содержат символическое имя программы или области, данное программистом (или системой для ее внутренних программ — ввода-вывода, стандартных функций и т.д.). Это имя пусто (состоит из пробелов) для непомеченной области COMMON.
Каждый элемент словаря (за исключением входной точки) имеет также единственный 16-разрядный номер, называемый ESDID (ESD identifier). Этот номер, присваиваемый при формировании модуля, используется в тексте и в RLD для ссылки на этот объект. Он используется вместо символического имени, чтобы сэкономить пространство. Входным точкам номер не присваивается, так как в
х) В конце этого раздела автор упоминает о том, что на одной карте ESD может располагаться до трех описаний элементов. Читатель несомненно обратит на это внимание, изучая рис. 17.10. Заметим еще, что в описании форматов элементов используется относительная нумерация колонок.— Прим. ред.
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
415
модуле отсутствуют ссылки на эти входные точки по их символическим именам.
Сами элементы можно различить по содержимому колонки 9, как это показано на рис. 17.10.
Какая еще информация может потребоваться? Для CSECT или области COMMON нужно указать их длину — сколько для
Карта ESQ
1 2-4 5-10 11-12 13-14 15-16 17-32 73-80
1—ESD —пробивки 12-9-2 16 (число 1— 1 элемент ESD (см. ниже) - Е SD1D для элемента, (пусто,если элемент является входной точкой) элементов на карте * 16)
Форматы элементов
1-8 9 10-12 13 14-16 элемент для CSECT или области COMMON
1—имя I—длина (число байтов) I адрес первого байта (начало) — 00 для CSECT, 05 для области COMMON
элемент для внешней, ссылки,
1-8 9 10-12 13 14-16
имя
1-8 9 10-12 13 14-16
имя
01
элемент для входной точки
I—CSECT ESDID для входной точки относительный адрес входной точки в CSECT
Рис. 17.10. Формат карты словаря внешних символов.
них выделяется байтов. Это число помещается в колонках 14—16. Мы должны также указать начальный адрес первого байта области, называемый началом, в колонках 10—12. Все адреса (относительные адреса) текста в области даются относительно этого начала. Так, если начальный адрес равен 500, то относительный адрес 500 ссылается на первый байт, 501 — на второй и т. д. Начальный адрес может быть равен 0.
Для внешних ссылок не дается никакой другой информации, кроме имени, поскольку объект с этим именем находится в программной секции, внешней по отношению к данному модулю. Для входных точек нам необходимо два вида информации. Прежде всего нам необходимо знать программную секцию, в которой определена
416
ГЛАВА 17
входная точка. Поэтому в колонки 14—16 элемента, описывающего входную точку, помещается номер программной секции (ESDID). Во-вторых, необходимо знать адрес входной точки внутри программной секции (относительно начала). Эта информация заносится в колонки 10—12.
На рис. 17.11 приведен пример словаря внешних символов, в котором описаны: программная секция с именем А (длина 100, начало 0), программная секция с именем В (длина 200, начало 501),
1-4 11—12 15—16 17—24 25 26—28 30—32
SESD 16 01 А 0 0 100
$ESD 16 02 В 0 501 200
$ESD 16 03 SIN 2
SESD 16 04 COS 2
$ESD 16 05 5 0 100
SESD 16 06 Cl 5 0 300
$ESD 16 07 Al 1 019 001
SESD 16 08 Bl 1 601 002
(Все чи< :ла i приве дены в деся' ГИЧНО1 1 с истеме)
P ИС. 17.11. Пример карт ESD.
внешние ссылки на программы SIN и COS, непомеченная область COMMON (длина 100, начало 0), область COMMON с именем С1 (длина 300, начало 0), входная точка А1 в программной секции А в 20-м байте и входная точка В1 в программной секции В в 100-м байте. Заметим, что относительные адреса этих входных точек даются относительно начал соответствующих программных секций.
Текстовые карты
Каждая текстовая карта имеет следующий формат:
1 2-4 6-8
TXT
-ЖЛила 12’9’2
11-12 13-14 15-16 17-72 73-80
L. I—текст номер программной секции, к которой ' относится текст
**часло байтое текста, на карте
адрес переоео байта, текста шносителъво начала CSECT
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
417
Заметим, что каждая карта содержит номер (ESDID) для CSECT или области COMMON, к которой относится текст, и адрес текста в CSECT относительно начала, указанного в соответствующем элементе ESD. Первый байт текста заносится в указанный байт, второй — непосредственно за ним и т. д. Если же не оказывается текста для всей программной секции или какой-то ее части, то, когда начнется счет, соответствующие байты будут неопределены.
0—4 Адрес 6-8 Число байтов 11—12 ESDID 15—16 Текст 17-72
$тхт $тхт $тхт $тхт $тхт $тхт $тхт в пр ООО 056 112 001 010 000 167 едыдущи [X I 56 56 56 2 10 2 1 ортах о пис 1 1 1 1 1 1 1 :ана так; А.. .А (А—56 раз) А...А (А—56 раз) А...А (А—56 раз) ВВ CCCCCCCCGC DD Е эя информация:
ООО DDBAAAAAAACCCCCCCCCCAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA 056 АААААААААААААААААААААААААААААААААААААААААААААААААААААААА
112 АААААААААААААААААААААААААААААААААААААААААААААААААААААААЕ
Рис. 17.12. Примеры текстовых карт.
Работа редактора связей будет более эффективной, если текстовые карты в программной секции будут размещены в порядке возрастания относительных внутренних адресов; однако такой порядок не обязателен и иногда можно сократить время компиляции, выдавая текстовые карты в каком-то ином порядке. Может также быть несколько карт с одним и тем же адресом. В этом случае последний из этих текстов «затирает» все предыдущие. Это показано на рис. 17.12. (Программисты часто «латают» колоду, чтобы сэкономить лишнюю трансляцию большой программы. Если программист обнаруживает ошибку, он перфорирует исправленные команды на картах в формате объектного модуля; их содержимое загрузится позднее и изменит ошибочные части программы.)
Имеется фиксированное число ячеек, в которых компилятор за
14 Д. Грио
418
ГЛАВА 17
поминает сгенерированную объектную программу. Если этот «буфер» переполнится, его содержимое должно быть переписано во внешнюю память. Однако в этот момент еще не вся информация может быть известна. Например, могут быть неизвестны адреса переходов вперед. Обычно эта проблема разрешается следующим образом: после окончания фазы генерации кода объектная программа считывается в память и в нее вносится дополнительная информация.
Мы можем сэкономить дополнительное чтение и запись, предоставив сделать это редактору связей. Так как редактор связей значительно меньше компилятора, он имеет возможность разместить в памяти всю объектную программу.
После того, как буфер объектной программы заполнен, образы карт TXT переписываются из буфера во внешнюю память. Затем, когда станет доступной неизвестная прежде информация, вслед дописываются дополнительные образы карт, содержащие информацию, которая при загрузке затирает неправильный текст, записанный ранее. Как уже отмечалось ранее, несколько возрастет нагрузка на редактор связей, но зато сократится время компиляции.
Так как в каждой текстовой карте указан номер программной секции, к которой относится карта, текстовые карты из разных программных секций могут быть перемешаны. Мы можем это с успехом использовать, особенно в однопроходных компиляторах, которые при первом просмотре генерируют код для главной программы, процедур и констант, используемых в программе.
Словарь перемещаемых адресов
В модуле адрес любого байта текста указывается в виде (ESDID, относительный адрес),
где ESDID — это номер программной секции или области COMMON, к которой относится байт, а относительный адрес— это адрес в области относительно ее начала (начальный адрес определяется в элементе ESD). Мы уже видели употребление такой пары в определении входной точки. Во время загрузки программы для программной секции или области COMMON будет выделена память. Загрузчик заменит затем эту адресную пару абсолютным адресом, который вычисляется по формуле
машинный адрес CSECT или области COMMON + (относительный адрес — начальный адрес, определенный в ESD)
Например, предположим, что в байтах 20—23 из CSECT 2 содержится адрес (2, 100) — относительный адрес байта 100 в CSECT 2. Предположим далее, что начальный адрес CSECT 2 равен 10
ГЕНЕРАЦИЯ ОБЪЕКТНОГО КОДА
419
и что CSECT 2 загружается, начиная с ячейки 1000. Тогда машинный адрес, помещаемый в байты 20—23, будет равен
1000+(100—10) = 1090.
Обратите внимание на сходство между адресами данных в области данных (область данных, смещение) во время компиляции, как это описывалось в гл. 8, и этими перемещаемыми адресами.
Элементы RLD (а в некоторых случаях и текст) используются для описания всех настраиваемых адресов. Какая информация должна быть в элементе RLD? Необходимо знать, во-первых, перемещаемый адрес объекта, т. е. адрес байта, на который есть ссылка, и, во-вторых, куда нужно поместить перемещаемый адрес, т. е. его место или поле в тексте. Этот адрес также задается в виде (ESDID, относительный адрес). В-третьих, необходимо знать число байтов, которые занимает перемещаемый адрес,— длину поля.
Таким образом, нам необходимы следующие пять чисел:
1. Номер секции (ESDID) объекта 1 Перемещаемый
2. Относительный адрес объекта J адрес
3. Номер секции (ESDID) поля i Куда заносится на-
4. Относительный адрес поля строенный адрес
5. Длина поля J объекта
Например, предположим, что:
1. ESDID объекта = 2
2. Относительный адрес объекта =20
3. ESDID поля =3
4. Относительный адрес поля =50
5. Длина поля =3
Если предположить, что начальный адрес для обеих секций равен 0, то байты 50, 51 и 52 в CSECT 3 должны содержать машинный адрес байта 20 из CSECT 2.
На рис. 17.13 представлен формат образа карты RLD. На каждой карте может быть указано до 7 адресов (элементов RLD). В действительности существует два различных вида элементов. Первый, внутренний элемент RLD, используется в случае, когда есть ссылка на CSECT или область COMMON, определенную в модуле. В этом случае ESDID объекта, ESDID поля, относительный адрес и длина поля определяются в элементе RLD. Куда поместить относительный адрес объекта? Для того чтобы сэкономить пространство, он помещается в текстовой карте (TXT) в поле, определенное элементом RLD.
Второй тип элемента RLD используется в случае, когда объект является внешним по отношению к модулю. В этом случае длина поля должна быть равна 4 (одно полное слово), а относительный ад
14*
420
ГЛАВА 17
рес объекта всегда равен 0. Этот второй тип необходим для организации перекрытий. Здесь эта проблема рассматриваться не будет.
73-80
t—RLD пробивки 12-9-2
^-элементы RLD каждый занимает число элементов RLD * 8- 8
1-2 2-3 5 6-8 элемент RLD ^—относительный адрес поля '-флаг (ем. справа) I—ESDID поля
—. ESDID объекта
ерлае
ЗНАЧЕНИЕ РАЗРЯДОВ
0-3: 0000 = внутренний адрес
0001 = внешний адрес
4-5: длина ноля 01 = 2 байта 10 » 3 байта 11 = 4 байта 6-7: должны быть 00
Рис. 17.13. Формат карты RLD.
Резюме
Мы оставим без внимания ряд моментов. Перечислим некоторые из них. На одной карте ESD может находиться до трех элементов, и существуют способы сократить пространство, необходимое для каждого элемента RLD. Длина одной программной секции в каждом модуле может быть указана не в элементе ESD, а в карте END; иногда это обстоятельство может оказаться полезным, но оно налагает дополнительные ограничения на порядок текстовых карт.
Мы ничего не сказали о перекрытиях, т. е. о программах, составленных из нескольких подпрограмм, которые при необходимости поочередно вводятся в оперативную память. Кроме того, что делает редактор связей, когда в двух разных модулях указаны одинаковые программные секции или области COMMON?
Формат модуля OS/360 допускает еще два типа элементов ESD, «частный код» (PC) и «псевдорегистр». Последний широко используется в компиляторе PL/1. Более подробные сведения читатель найдет в руководстве по IBM (см. ИБМ (d)) и в работе Эрмана [69].
УПРАЖНЕНИЯ К РАЗДЕЛУ 17.6
1. Разработайте и реализуйте редактор связей для связи объектных модулей, описанных выше. Заранее решите, что следует делать при появлении дубликатов областей COMMON, программных секций или входных точек и т. д.
2. Разработайте и реализуйте загрузчик. Считайте, что результат работы редактора связей имеет тот же формат, что и объектный модуль. Однако в нем не будет внешних ссылок, поскольку все связи уже отредактированы редактором связей.
Г лава 18
Оптимизация программы
Под оптимизацией программы имеется в виду обработка, связанная с переупорядочицацием и изменением операций в компилируемой программе в целях получения более эффективной объектной программы. Лучщце оптимизирующие компиляторы могут получать объектные программы для сложных фортранных и алголь-ных программ, пр качеству не уступающие программам, написанным на языке ассемблера программистами высокой квалификации, но с гораздо меньшими затратами.
Мы различаем две категории оптимизирующих преобразований: преобразования исходной программы (в ее внутренней форме), которые, следовательно, не зависят от объектного языка, и преобразования, осуществляемые на уровне объектной программы. Последние целиком зависят от объектного языка, и мы не будем подробно на них останавливаться. Краткое обсуждение и ссылки читатель найдет в разд. 18.4.
Методы первой категории применимы почти к любому алгебраическому языку — ФОРТРАНу, АЛГОЛу, PL/1 и т. д. Здесь используются четыре основных метода:
1. Свертка, т. е. выполнение операций, операнды которых известны во время компиляции.
2. Исключение лишних операций (в основном за счет однократного программирования общих подвыражений).
3. Вынесение из цикла операций, операнды которых не изменяются внутри цикла.
4. Замена сложных операций в циклах на более простые (фактически замена умножений на сложения).
Степень выполняемой компилятором оптимизации зависит от многих факторов. Не все компиляторы должны проводить максимально полную оптимизацию- Например, не следует применять очень сложные методы в компиляторах, интенсивно используемых для отладки, так как эти методы сильно изменяют порядок операций, что затрудняет поиск ошибок в полученной программе.
422
ГЛАВА IS
Поэтому мы не рассматриваем одну общую схему полной оптимизации. Вместо этого в разд. 18.1 мы начинаем с обсуждения двух простых методов, один из которых должен быть реализован в любом компиляторе. В разд. 18.2 мы рассматриваем умеренную оптимизацию FOR-циклов, которая достаточно легко реализуется. В 18.3 мы рассматриваем более сложную схему оптимизации, требующую более полного анализа структуры исходной программы. Этот раздел содержит мало сведений о деталях реализации, поскольку читатель, желающий реализовать более сложные методы, в любом случае должен будет основательно ознакомиться с литературой по этому вопросу. В разд. 18.4 приводится обзор литературы и краткий перечень ссылок на другие методы, которые не рассматривались в предыдущих разделах, включая методы, зависящие от объектного языка.
На протяжении этой главы для иллюстрации методов оптимизации мы будем пользоваться либо триадами, либо тетрадами, тем, что удобнее в каждом рассматриваемом случае. Трудно сказать, какая из внутренних форм лучше, так как никто по существу не изучал этого вопроса. Все, что мы имеем,— это мнения специалистов. В общем я предпочитаю триады или косвенные триады, так как для каждой тетрады требуется описатель временной переменной. Однако триады, как мы увидим, сложнее в обработке. Часто для большей ясности мы будем пользоваться обычной записью на АЛГОЛе вместо триад или тетрад.
18.1. ОПТИМИЗАЦИЯ В ПРЕДЕЛАХ ЛИНЕЙНЫХ УЧАСТКОВ
Как говорилось в 11.5, линейный участок — это выполняемая по порядку последовательность операций с одним входом и одним выходом (первая и последняя операции соответственно). Например, последовательность операций, соответствующих присваиваниям вида
(18.1.1) I := 1+1; I := 3; В := 6.2+1;
образует линейный участок. Внутри линейного участка обычно проводят две оптимизации: свертку и устранение лишних операций.
Свертка
Свертка — это выполнение во время компиляции операций исходной программы, для которых значения операндов уже известны, и поэтому нет нужды их выполнять во время счета. Для примера рассмотрим сегмент программы на рис. 18.1, а и его внутреннее представление в виде триад на рис. 18.1, Ь. Очевидно, 1-ю триаду
ОПТИМИЗАЦИЯ ПРОГРАММЫ
423
можно вычислить во время компиляции и заменить на результирующую константу. Менее очевидно, что можно вычислить 4-ю триаду, так как известно, что I равно 3, а это в дальнейшем позволит вычислить и 5-ю триаду. Окончательный результат свертки показан на рис. 18.1, с.
I: = 14-1; (1) + 1.1 (1):= 2,1
I: =3; (2) := (1). I (2):= 3,1
В: =6.2+1; (3) : = 3, I (3):= 9.2, В
(4) CVIR I
(5) + 6.2, (4)
(6) : = (5), В
(а) Сегмент (Ь) Триады (с) Триады после
программы оптимизации
Рис. 18.1. Иллюстрация свертки.
Свертка главным образом применяется к арифметическим операторам + , —, *, / ,так как они более часто встречаются в исходной программе. Ее также следует применять к операторам преобразования, таким, как CVIR (преобразование из INTEGER в REAL) на рис. 18.1. Проблема упрощается, если эти преобразования задаются явно во внутреннем представлении, как показано на рис. 18.1, а не подразумеваются неявно.
Процесс свертки операторов, имеющих в качестве операндов константы, понятен и не требует пояснений. Свертка операторов, значения операндов которых могут быть определены в результате некоторого анализа, несколько сложнее. Обычно свертка осуществляется только в пределах линейного участка с помощью таблицы Т (вначале пустой). В процессе свертки Т содержит пары (А, К) для всех простых переменных А, для которых известно текущее значение К. Кроме этого, каждая свертываемая триада заменяется новой триадой (С, К, 0), где С (константа) — новый оператор, для которого не нужно генерировать команды, а К — результирующее значение свернутой триады. Алгоритм свертки последовательно просматривает триады линейного участка и для каждой триады делает следующее:
1. Если операнд есть переменная, которая содержится в Т, то операнд заменяется на соответствующее значение К.
2. Если операнд есть ссылка на триаду типа (С, К, 0), то операнд заменяется на константу К.
3. Если все операнды являются константами и операция может быть свернута, то данная триада исполняется и вместо нее подставляется триада (С, К, 0), где К — результирующее значение.
424
ГЛАВА 18
4. Если триада является присваиванием А:= В значения переменной без индекса А, тогда:
а) если В — константа, то А со значением В заносится в таблицу Т (старое значение А, если оно было, исключается);
Ь) если В — не константа, то А со своим значением исключается из Т, если она там была.
На рис. 18.2 показана работа этого алгоритма на примере линейного участка, приведенного на рис. 18.1.
1 С 2 С 2 С 2 С 2 С 2 С 2
2 ••= (1),1 :=2,1 : —2, I :=2, I :=2, I : =2, I
3 :=3, I :=3,1 :=3, I :=3, I :=3, I :=3, I
4 CVIR I CVIR I CVIR I С 3.0 С 3.0 С '3.0
5 + 6.2,(4) + 6.2,(4) + 6.2,(4) + 6.2,(4) С 9.2 С 9.2
6 :=(5),В := (5),В := (5),В := (5),В :=(5),В :=9.2,В
Т: (I, 2) (I, 3) (I, 3) (I. 3) (I. 3) (В, 9.2)
Рис. 18.2. Последовательность шагов алгоритма свертки.
При обработке триад надо следить за появлением вызовов подпрограмм или функций. При компилировании с ФОРТРАНа на каждом вызове следует исключать из Т переменные, являющиеся фактическими параметрами или COMMON-переменными, так как данный вызов может изменить их значения. Для АЛГОЛа таблица Т должна полностью очищаться, если мы точно не знаем последствий вызова процедуры. Заметим также, что инструкции ввода присваивают значения переменным.
Мы должны быть уверены, что свертка не вызовет никакой ошибки во время компиляции. Например, если программист написал 1/0, то прежде чем производить деление, компилятор должен проверить, не нулевой ли делитель. К сожалению, наличие такой операции еще не означает, что объектная программа будет неправильной (хотя в большинстве случаев это так и есть). Например, если исходная программа содержит инструкцию
IF FALSE THEN А := 1/0;
это не вызовет ошибки во время счета. Лучше всего в таких случаях выдать предупреждающее сообщение, а операцию оставить несвернутой.
Мы рассматривали свертку как отдельный просмотр исходной программы, представленной в виде триад. Можно также использовать косвенные триады или тетрады. Свертку можно также выполнять в семантических программах во время получения внутреннего
ОПТИМИЗАЦИЯ ПРОГРАММЫ
425
представления или команд машины, при этом отпадает необходимость в дополнительном просмотре. Например, при восходящем грамматическом разборе программа для
Ei : := Е34-Т
должна выполнить только одну дополнительную проверку семантик Е2 и Т. Если обе константы или их значения известны, то программа их складывает и результат связывает с Ег. Здесь также можно использовать таблицу переменных с известными значениями, которая должна сбрасываться на каждой метке (или в любом другом месте, где генерируются команды, на которые возможна передача управления).
Исключение лишних операций
i-я операция линейного участка считается лишней, если существует более ранняя идентичная j-я операция и никакая переменная, от которой зависит эта операция, не изменяется третьей операцией, лежащей между i-й и j-й операциями. Например, рассмотрим линейный участок, содержащий инструкции
D := D+C»B;
(1) * С,В
(18.1.2) (2) + D,(l)
(3) := (2),D
А := D+C*B; С: = D+C*B;:
(4) * С,В (7) * С, В
(5) + D,(4) (8) + D,(7)
(6):=(5), А (9) := (8), С
Появление операции С*В во второй и третий раз лишнее, так как ни С, ни В не изменяются после 1-й триады. Может показаться, что и второе сложение D с С*В (5-я триада) лишнее, так как С*В не меняется. Но это не так, поскольку после первого сложения D с С * В 3-я триада изменяет значение D. Но третье сложение D с С* В лишнее и может быть заменено ссылкой на 5-ю триаду.
Программисты обычно умеют программировать без лишних операций, что, казалось бы, ставит под сомнение эффективность такой оптимизации. Но программирование без экономии лишних операций часто бывает легче и делает программу более легкой для чтения. Кроме того, некоторые лишние операции обычно возникают при индексировании переменных и выходят* из-под контроля программиста. Рассмотрим, к примеру, присваивание X Н, j] : = X [i, j+U в триадном представлении:
(1) * i,d2 (3) * i,d2 (5) + (4),1
(2) + (l),j (4) +(3),j (6) := X 1(2)],X 1(5)1
Ясно, что 3-я и 4-я триады лишние и могут быть исключены, так что в результате получится:
(1) * i,d2 (3) + (2),1
(2) + (l),j (4) := X 1(2)1,Х[(3)]
426
ГЛАВА 18
Алгоритм исключения лишних операций просматривает операции в порядке их появления. Если i-я триада лишняя, так как уже имеется идентичная ей j-я триада, то она заменяется триадой (SAME, j, 0), где операция SAME ничего не делает и не порождает никаких команд при генерации. Чтобы следить за внутренней зависимостью переменных и триад, мы ставим им в соответствие так называемые числа зависимости (dependency numbers) по следующим правилам:
1. Вначале для переменной А число зависимости dep(A) равно нулю, так как ее начальное значение не зависит ни от одной триады.
2. После обработки i-й триады, в которой переменной А присваивается некоторое значение, dep(A) заменяется на i, так как ее новое значение зависит от i-й триады.
3. При обработке i-й триады ее число зависимости dep(i) равно 1+ (максимальное из чисел зависимости ее операндов).
Мы используем числа зависимости следующим образом: если i-я триада идентична j-й триаде (j <i), то i-я триада считается лишней в том и только том случае, когда dep(i) = dep(j).
Приведем неформальное доказательство правильности этого метода. Из определения мы знаем, что числа зависимости операндов j-й триады меньше j. Предположим, что ни одна переменная, от которой зависит i-я триада, не изменяется между j-й и i-й триадами. Тогда i-я триада лишняя. Заметим, что во время обработки j, . . . . . . , i—1 триад числа зависимости операндов i-й триады не меняются и, следовательно, dep(i) = dep(j).
Предположим теперь, что некоторая переменная А, от которой зависит i-я триада, изменяется k-й триадой, причем j к < i. Тогда dep (А) заменяется на к, где к j. Из того, как определены числа зависимости для триад, мы видим, что dep (i) > dep (А).= = k^ji> dep(j) и, следовательно, числа зависимости различны.
Алгоритм исключения лишних операций для каждой триады делает следующее:
1. Если операнд ссылается на триаду вида (SAME, j, 0), то он заменяется на (j).
2. Вычисляется dep(i):= число зависимости i-й триады, равное 1+(максимум чисел зависимости ее операндов).
3. Если существует идентичная j-я триада, причем j<i и dep(i) — dep(j), то i-я триада лишняя и заменяется на (SAME, j, 0). (Эта проверка делается сравнением с i—1, i—2, . . . , 1 триадами. Здесь с успехом можно применить хеширование.)
4. Если i-я триада присваивает значение элементу массива В или простой переменной В, то dep (В) получает значение, равное i.
На рис. 18.3 шаг за шагом приведена работа алгоритма на линейном участке (18.1.2). На каждом шаге показаны первоначальная
ОПТИМИЗАЦИЯ ПРОГРАММЫ
427
триада, значения чисел зависимости переменных перед выполнением шага и вычисленное число зависимости для триады, а также полученная в результате триада.
При вычислении числа зависимости триады с индексируемой переменной В [Т] в качестве операнда учитываются числа зависимости и В, и Т. Кроме того, если в триаде i делается присваивание
Обрабатываемая триада i бер(переменная) А В С D dep(i) Полученная в результате триада
(1) * С, В 0 0 0 0 1 (1) * С, В
(2) + D, (1) 0 0 0 0 2 (2) + D, (1)
(3) :=(2), D 0 0 0 0 3 (3) : = (2), D
(4) * С, В 0 0 0 3 1 (4) SAME 1
(5) + D, (4) 0 0 0 3 4 (5) + D, (1)
(6) : = (5), А 0 0 0 3 5 (6) :=(5), А
(7) * С, В 6 0 0 3 1 (7) SAME 1
(8) + D, (7) 6 0 0 3 4 (8) SAME 5
(9) :=(8), С 6 0 0 3 5 (9) :=(5), С
6 0 9 3
Ри с. 18.3. Исключение ЛИШНИХ операций.
переменной с индексом В [Т], то в dep (В) посылается i. Таким образом, любая последующая ссылка на В зависит от этой триады.
Использование косвенных триад упрощает исключение лишних операций, так как идентичные триады уже были найдены. Например, представление линейного участка (18.1.2) будет следующим:
1. (1) 6. (4) (1) * С, В
2. (2) 7. (1) (2) + D, (1)
3. (3) 8. (2) (3) : = (2),D
4. (1) 9. (5) (4) : = (2), А
5. (2) (5) : = (2), С
Таблица Таблица
ОПЕР ТРИАДЫ
Теперь числа зависимости ставятся в соответствие с триадами, а не с операторами таблицы ОПЕР. Перед обработкой линейного участка dep (i) = 0 для каждой i-й триады. Число dep (i) изменяется каждый раз при обработке операции из ОПЕР, ссылающейся на i-ю триаду.
428
ГЛАВА 18
Дополнительное обсуждение свертки и исключения лишних операций
Приведенные алгоритмы не являются оптимальными. Мы можем намного их улучшить, если воспользуемся свойством коммутативности некоторых операций. Например, А*В и В* А должны считаться идентичными. Для того чтобы это делать автоматически, мы должны все операнды п-арного + (или п-арного *) располагать в некотором каноническом порядке: сначала термы, отличные от переменных и констант, затем переменные с индексом в лексикографическом порядке, затем простые переменные в лексикографическом порядке и, наконец, константы. Это можно делать для любого внутреннего представления, описанного в 11-й главе. Например, преобразование с помощью переупорядочивания термов выражений
А := 1+В+С+2; „ А := В+С+1+2;
В : = В+С+6; в В := В+С+6;
позволяет нам свернуть 1+2 и исключить второе сложение В+С. Однако это не решает всей проблемы. Переупорядочивание операндов в А : = В+С+В+С и получение А := В+В+С+С не помогает нам обнаружить тот факт, что В+С можно вычислить только один раз. Проблема нахождения всех общих подвыражений на практике так просто не решается из-за большого количества вариантов, которые могут встретиться в выражении. Дальнейшее обсуждение этой темы будет продолжено в разд. 18.4.
Можно было бы также на этом этапе обработки, а не во время генерации команд унарные операторы ABS и «—» выйести к операндам, как это объяснялось в 17.4. Это могло бы привести не только к экономии унарных операторов, но и к более полному обнаружению лишних операций. Например, обозначая унарный минус апострофом, мы могли бы следующим образом записать С := А—В; D := В—А; в виде триад:
(1) + А, В' (3) + В, А'
(2) := (1), С (4) := (3), D и затем заменить на
(1) + А, В' (3) + А, В'
(2) := (1), С (4) := (3)', D
что позволяет обнаружить идентичные операции. Признак, что операнд нужно брать с обратным знаком, часто используется даже тогда, когда исключение лишних операций не производится, так как он бывает полезен при экономии команд объектной программы на тех машинах, у которых есть операции «запись в память отрицательная» и «загрузка отрицательная».
ОПТИМИЗАЦИЯ ПРОГРАММЫ .. .42$
В первоначальном триадном представлений на каждую триаду ссылаются не более одного раза. Аналогично для тетрад, каждая сгенерированная компилятором временная переменная Т в качестве операнда используется только один раз. Это естественным образом получается при переводе обычных инструкций присваивания во внутреннее представление. Отсюда легко определяется область действия временной переменной. Заметим, однако, что после оптимизации на триаду могут быть ссылки из нескольких мест. Это делает более трудным определение области действия ее результата. Более подробно об этом говорится в разд. 14.2.
18.2. УМЕРЕННАЯ ОПТИМИЗАЦИЯ ЦИКЛОВ
Назовем операцию инвариантной в цикле, если ни один из операндов, от которых она зависит, не изменяется во время работы этого цикла. Одна из важных оптимизаций состоит в том, чтобы вынести инвариантную операцию за границы цикла. Например, если вынести одно умножение из цикла, выполняемого 1000 раз, то на этапе выполнения готовой программы мы сэкономим 999 умножений!
Второй тип оптимизаций цикла, который мы описываем здесь, называется заменой сложных операций и состоит в замене операции на более быструю. Нас главным образом будет интересовать замена умножения типа hK на сложение, где I — переменная цикла. Для иллюстрации замены сложной операции рассмотрим цикл
FOR I : =А STEP В UNTIL С DO
BEGIN . . . Tl := UK . . .END
где К инвариантна в цикле. Начальное значение I равно значению А. Внутри цикла I определяется рекурсивно, т. е. только посредством самой себя. (Единственным присваиванием I внутри цикла является ее продвижение на шаг I := I+B.) Каждый раз, когда I изменяется на В, значение 1*К(и Т1) изменяется на В* К. То есть
(1+В)*К = ик+в*к.
Следовательно, если Т1 нигде больше в цикле не изменяется, мы можем заменить сложную операцию U К, следующим образом изменяя задание цикла:
1. Перед циклом вставляются операции Т1 А*К; Т2 : = В * К, где Т2 — новая временная переменная. Это — начальная установка Т1 и вычисление приращения В*К.
2. Из цикла исключается Tl : = UK.
3. В конце цикла вставляется Tl := Т1+Т2.
В результате мы получим:
430
ГЛАВА 18
Т1:=А*К; Т2:=В*К;
FOR I := A STEP В UNTIL С DO
BEGIN ... . . . TI := Т1+Т2; END
Итак, внутри цикла мы заменили умножение на сложение. Мы предполагаем, конечно, что А и В инвариантны в цикле и I нигде не изменяется в цикле, за исключением места, где она получает приращение. (В действительности в нашей реализации переупорядочи-вание операций будет несколько иным, так что инвариантность А будет несущественна.)
Несколько слов предостережения. Мы предполагали, что В и К имеют тип INTEGER. Никогда не следует заменять умножение, если К имеет тип REAL, так как сложение с плавающей запятой неточно из-за погрешности округления. Эта погрешность имеет тенденцию накапливаться во время многократного выполнения цикла. Вообще I *К намного точнее, чем К+К+ • . • +К (I раз).
Замена умножения может быть полезна, если даже умножение работает так же быстро, как сложение, так как позволяет нам легко находить и выбрасывать несколько раз встречающиеся одинаковые операции. Этим самым в пределах цикла мы в некоторой ограниченной форме проводим исключение лишних операций. Это особенно полезно при оптимизации вычисления переменных с индексами.
Следует также помнить, что замена сложных операций не всегда приводит к оптимизации. На самом деле это может даже привести к замедлению! Ниже соответственно слева и справа приводится программа до и после замены:
TI : — 1; Т2 :=2; . .. Т10 : = 10;
FOR I: = 1 STEP 1 UNTIL 10 DO FOR I: = 1 STEP 1 UNTIL 10 DO
CASE I OF BEGIN CASE I OF
К :=1 * 1; К :=T1;
К :=1*2; К : = Т2,
К : =1 * 10;
ENDCASE;
К : = T10;
ENDCASE;
TI : = Tl + 1; ... T10 :=T10+10;
END;
В программе слева на каждом шаге цикла выполняется одно умножение. Теперь в программе справа внутри цикла нет умножений, но зато выполняются 10 сложений!
Замена сложных операций почти всегда приводит к получению более эффективной программы. Это не так только для циклов, состоящих из нескольких частей, из которых лишь немногие выпол
ОПТИМИЗАЦИЯ ПРОГРАММЫ
431
няются на каждом шаге цикла. Например, оптимизация интерпретатора, приведенного на рис. 16.1 (там цикл задан неявно), скорее всего уменьшит его эффективность.
Общая схема реализации
Мы реализуем оптимизацию за три прохода, расположенных между проходом обычного анализа, в котором получается внутреннее представление исходной программы, и проходом, генерирующим команды (см. рис. 18.4). ПРОГРАММА АНАЛИЗА ЦИКЛОВ выявляет циклы, подлежащие оптимизации, и получает
(анализ)
(синтез)
Рис. 18.4. Компилятор с умеренной оптимизацией циклов.
информацию, которая потребуется в дальнейшем. Следующий просмотр выносит за границу циклов инвариантные операции, и наконец третий просмотр осуществляет замену сложных операций.
Предположим, что исходный язык АЛГОЛ; в ФОРТРАНе благодаря более простым DO-циклам оптимизировать легче. В нашем рассмотрении мы будем использовать следующий образец цикла:
(18.2.1) FOR I := A STEP В UNTIL С DO <тело цикла>
где А, В и С — произвольные арифметические выражения. Для простоты будем считать, что В всегда положительно и не меняется во время исполнения цикла. Рассуждения очень легко распространить на случай, когда допускаются и отрицательные значения В.
Наконец, мы предполагаем, что свертка и исключение лишних операций на линейных участках осуществляются непосредственно перед или в процессе обработки инвариантных операций.
Нас главным образом будут интересовать простые переменные или формальные параметры, вызываемые по значению, и мы введем для них следующие обозначения:
432
ГЛАВА 18
(18.2.2) Определение. Величина SFVI (SFVR) п—это простая переменная или простой формальный параметр, вызываемый по значению, типа INTEGER (REAL).
Внутреннее представление циклов
Мы полагаем, что операции следуют в том порядке, в каком они должны генерироваться (если нет оптимизации). Операции могут быть представлены в виде триад, тетрад и так далее, словом в том внутреннем представлении, которое мы в данный момент имеем. Мы должны только иметь возможность распознавать различные элементы цикла по мере того, как они встречаются — иачадоцикла, I, А, В, С, <тело цикла> и конец цикла. В предположении, что оптимизации нет, мы должны были бы сгенерировать команды для следующего цикла:
INIT : I := А;
TEST : IF I > С THEN GO ТО OVER;
(18.2.3) LOOP : <тело цикла);
INCR : I := I + В; GO TO TEST;
OVER:
После оптимизации этот цикл будет иметь следующий вид:
INIT : I := А; «начальные операции»;
TEST : IF 1>С THEN GO ТО OVER;
(18.2.4) LOOP : Измененное тело цикла);
INCR : I := I+B; «операции приращения»;
GO ТО TEST;
OVER:
To есть вставляются операции, которые выполняются непосредственно перед началом выполнения цикла, а также операции, которые должны выполняться каждый раз, когда переменная цикла получает приращение. (При желании можно было бы сразу после I : = А вставить еще одну проверку «IF I> С THEN GO ТО OVER», чтобы не выполнялись начальные операции, когда цикл не работает ни одного раза. Но в этом нет необходимости, поскольку начальные операции изменяют только временные переменные, используемые в теле цикла.)
Строка с меткой INIT называется INIT-участком (initial — начальный). Строка, помеченная меткой INCR, называется INCR-участком (increment — приращение). И тот, и другой являются
х) SFV — первые буквы английских слов simple — простой, formal — фор мадьный и value — значение.— Прим, перев.
ОПТИМИЗАЦИЯ ПРОГРАММЫ
433
линейными участками — их операции выполняются по порядку, и они имеют по одному входу и одному выходу.
Так как во время оптимизации генерируются новые участки и изменяется <тело цикла), возникает желание представить программу в виде графа, вершинами которого являются линейные участки, с тем чтобы облегчить работу по добавлению или изменению линейных участков. Однако, если мы не собираемся выполнять оптимизацию, описанную в 18.3, этого не следует делать, так как это потребует организации нового вида информации. Более удобно следующее представление.
Операции исходной программы хранятся в той последовательности, в какой они появлялись, будь то тетрады, триады, польская запись или то, что мы имеем в каждом конкретном случае. Во время оптимизирующих просмотров строятся три самостоятельные таблицы: таблица, содержащая операции INIT-участков для всех циклов, таблица, содержащая операции I NCR-участков всех циклов, и таблица циклов, в которой хранится дополнительная информация к каждому циклу, в частности, переменная цикла, ссылки на INIT-или INCR-участки и тому подобное. Разумеется, генератор должен генерировать команды для основной программы (во внутреннем представлении), для INIT-и INCR-участков в должном порядке.
Заметим, что INIT-участок на самом деле не входит в цикл и выполняется только один раз. Следовательно, его можно оптимизировать так, как если бы он принадлежал объемлющему циклу. Это значит, что некоторые операции могут шаг за шагом переходить из одного цикла в другой, пока не окажутся вне всех циклов.
Мы не будем касаться внутреннего представления INIT-и INCR-участков; это, главным образом, проблема организации компилятора, и ее решение, вероятно, будет зависеть от машины.
Дополнительные требования к циклам
Для того чтобы иметь возможность выносить инвариантные операции, нам необходимо знать все величины SFVI и SFVR, которые изменяются в цикле. Для замены сложных операций должны выполняться следующие дополнительные ограничения, касающиеся переменной цикла I:
(18.2.5) I не должна изменяться в теле цикла.
(18.2.6) Ни одна переменная выражения В, задающего шаг цикла, не должна изменяться в теле цикла.
Заметим, что инвариантные операции можно выносить даже тогда, когда замена сложных операций невозможна. Но в наших рассуждениях мы будем полагать, что осуществляются либо оба вида оптимизации, либо ни одного.
434
ГЛАВА 18
В ФОРТРАНе DO-циклы проще. Поэтому условия (18.2.5) и (18.2.6) выполняются всегда. К сожалению, даже в ФОРТРАНе нельзя знать точно, какие из переменных меняются в теле цикла в основном из-за обращений к процедурам, которые могут их изменить. Следовательно, следующим шагом нам нужно более точно задать условия, которые легко проверяются, не забывая при этом, конечно, что оптимизацией мы должны охватить как можно большее число циклов.
Итак, требуется выполнение следующих условий, чтобы можно было осуществить оба типа оптимизации:
(18.2.7) В частях I, В, С и теле цикла допускаются лишь те вызовы процедур, функций и формальных параметров, вызываемых по наименованию, для которых компилятор знает, какие из величин SFVI и SFVR при этом изменятся.
То есть допускаются вызовы стандартных функций, подпрограмм ввода-вывода и других процедур, для которых сам компилятор произвел тщательный анализ. В ФОРТРАНе можно допустить все обращения к подпрограммам, если компилятор будет исходить из предположения, что все величины SFVI и SFVR в COMMON-области и все фактические параметры изменяются подпрограммой.
Для замены сложных операций должны выполняться следующие три условия:
(18.2.8) Переменная цикла I должна быть SFVI.
(18.2.9) Выражение шага В должно быть типа INTEGER и не должно содержать переменную цикла I. Операндами В должны быть константы и величины SFVI и SFVR.
(18.2.10) В теле цикла не должно быть присваиваний I или переменным выражения В (с помощью инструкций присваивания, ввода, обращений к процедурам или вызовов формальных параметров).
Для оптимизации, описываемой в этом разделе, необходимо выполнение условий с (18.2.7) по (18.2.10).
Таблица циклов
ПРОГРАММА АНАЛИЗА ЦИКЛОВ должна построить список для SFVI и SFVR, изменяемых в каждом цикле. Возможны три способа организации такого списка. В первом способе с каждой величиной SFVI и SFVR, находящейся в таблице символов, связывается список циклов, в которых эта величина изменяется. Такой список скорее всего должен быть списком со ссылками, а не последовательным списком.
ОПТИМИЗАЦИЯ ПРОГРАММЫ
435
Второй способ — это перенумеровать все величины SFVI и SFVR и построить булеву матрицу С размером nxm, где п — количество всех величин, ат — количество всех циклов. С [i, j] = = 1, если i-я переменная изменяется в j-м цикле.
Третий способ, который мы здесь используем, состоит в том, что для циклов организуется таблица, аналогичная таблице символов с блочной структурой, описанной в 9.5. Для этого нам потребуется таблица циклов, которую мы назовем LOOPTABLE. Ее i-й элемент описывает i-й цикл; циклы нумеруются в порядке появления слов FOR в программе. Вместе с этим нам потребуется таблица SFV, содержащая список самих величин SFVI и SFVR, изменяемых внутри каждого цикла. Каждый элемент LOOPTABLE содержит следующие пять полей:
LOOPVAR SURRLOOP FIRSTV LASTV BLIST
переменная цикла номер объемлю- щего цикла адрес первого элемента SFV-списка адрес последнего элемента SFV-списка указатель на список элементов SFVI шага
Все переменные в этих таблицах могут быть представлены указателями на соответствующие элементы таблицы символов. Поле LOOPVAR мы можем использовать для указания — возможна ли оптимизация цикла (если поле содержит 0, то невозможна). По причинам, которые станут понятными в дальнейшем, в LOOPTABLE должен быть нулевой элемент со значением (0, 0, 0, 0, 0).
Поля FIRSTV и LASTV указывают соответственно на первую и последнюю величины SFV, изменяемые в цикле. Несмотря на аналогию с блочной структурой, описанной в разд. 9.5, здесь есть существенное различие, облегчающее дело. В случае блочной структуры информация к разным блокам должна храниться отдельно. Здесь же информация может иметь структуру вложений, так как если переменная изменяется в цикле, то она изменяется также во всех циклах, объемлющих данный. Следовательно, список величин SFV цикла содержит также величины SFV всех внутренних циклов.
На рис. 18.5 приводится пример сегмента программы с четырьмя циклами и таблицами к ним. Каждый элемент LOOPTABLE должен также содержать поля, описывающие INCR-и INIT-участки каждого блока; мы для простоты опустили эти поля.
Программа анализа циклов
Эта программа ведет последовательную обработку операций исходной программы, выявляя циклы, подлежащие оптимизации.
436
ГЛАВА 18
Помимо этого, она строит таблицы LOOPTABLE и SFV. При этом используются следующие переменные и программы:
1. OPENLOOP. Переменная типа INTEGER, содержащий номер самого внутреннего из обрабатываемых в данный момент циклов (вначале 0).
2. LASTLOOP. Переменная типа INTEGER, содержащая число обнаруженных к данному моменту циклов (вначале 0).
FOR i := 1 STEP 1 UNTIL N DO BEGIN L1; ... END?
FOR j:=1 STEP 1 UNTIL N DO BEGIN L2:= ... ; ... END;
FOR k:=1 STEP 1 UNTIL N DO BEGIN L3:=...J ... END;
L4:=... ;
END;
FOR I := 1 STEP 1 UNTIL N DO begin L5:=...; ... end;
(1) i|о|i|бТо
(2) j|l|3|3|0
(3) k[11З]5 |0
(4) 11 ° 1 7 17 1 °
(1)
(2)
(3)
(4)
(5)
(6)
(7)
LI j L2
К
L3
L4
L5
Рис. 18.5. Пример заполнения таблицы LOOPtABLE. а —- сегмент программы; b — LOOPTABLE; с — таблица SFV.
3. OPTLOOP. Переменная типа INTEGER, содержащая номер самого внутреннего из обрабатываемых в данный момент циклов, в котором еще не нарушается ни одно из условий оптимизации.
4. СНЕСК(Р). Аргумент Р является указателем на переменную в таблице символов. К программе СНЕСК(Р) обращаются, когда обнаружено присваивание этой переменной. Если переменная есть величина SFVR или SFVI, то для всех обрабатываемых циклов (с помощью OPTLOOP и таблиц) проверяется выполнение условия (18.2.10) и, если условие не выполняется, цикл объявляется неоптимизируемым, а переменная посылается в SFV-таблицу цикла с номером OPTLOOP.
5. SURROUNDOPT. Всякий раз, когда цикл объявляется неоптимизируемым, возможно, потребуется изменить значение OPTLOOP. Это делается с помощью программы SURROUNDOPT, которая следует по цепочке объемлющих циклов, начиная с OPTLOOP до тех пор, пока не обнаружится цикл, в котором еще не нарушено ни одно условие оптимизации.
Заметим, что OPENLOOP и LASTLOOP аналогичны CURRBL и LASTBL, используемым при построении таблицы символов блочной структуры в разд. 9.5.
ОПТИМИЗАЦИЯ ПРОГРАММЫ
437
Ниже приводится краткое описание действий, которые выполняются при обработке различных частей исходной программы во внутреннем представлении:
1. Обработка FOR (переменная) := А. Так как здесь осуществляется присваивание, то происходит обращение к программе CHECK ((переменная». Для нового цикла заносится соответствующий ему элемент в LOOPTABLE. Операции, соответствующие (переменная) := А, заносятся в INIT-участок данного цикла. Если переменная есть SFVI, то номер нового цикла посылается в OPTLOOP, в противном случае в поле LOOPVAR заносится нуль, являющийся признаком того, что цикл не подлежит оптимизации.
2. Обработка выражения В, задающего шаг цикла. Каждая переменная заносится в список BLIST для этого цикла. Если переменная является переменной цикла или она не SFVI и не SFVR, то цикл объявляется неоптимизируемым, после чего следует обращение к SURROUNDOPT. Если тип В не INTEGER, то цикл также объявляется неоптимизируемым и следует обращение к SURROUNDOPT.
3. Обработка присваивания (переменная) := или инструкции ввода READ ((переменная». Следует обращение к CHECK ((переменная».
4. Обработка вызова нестандартной процедуры или функции, или каждого параметра по наименованию, не являющегося массивом. Все обрабатываемые в данный момент циклы объявляются не-оптимизируемыми и следует обращение к SURROUNDOPT.
5. Обработка конца цикла. Если дошли до конца цикла и не возникло ситуации, запрещающей оптимизацию, то сравниваются между собой списки BLIST и SFV данного цикла. Если какая-то переменная встречается в обоих списках, цикл объявляется неоптимизируемым. В OPENLOOP и OPTLOOP устанавливаются значения, соответствующие объемлющему циклу, и далее следует обращение к SURROUNDOPT.
Шаги со 2-го по 4-й следует выполнять только в том случае, когда в обработке находится хотя бы один цикл, не нарушивший условия оптимизации, т. е. когда OPTLOOP=#0.
Заметим, что мы разбили довольно сложный процесс проверки возможности оптимизации циклов на несколько элементарных шагов. Шаг 4 должен выполняться в какой-то одной программе. Вероятно, легче всего это делать в программе, которая просматривает внутреннее представление исходной программы и передает символы другим частям прохода. В любой момент, когда обнаружен идентификатор процедуры, функции или формального параметра по наименованию, эта программа должна объявить неоптимизируемыми все находящиеся в обработке циклы.
438
ГЛАВА 18
Программа обработки инвариантных операций
Операция называется инвариантной в цикле, если ее операнды не зависят от переменных, изменяющихся внутри этого цикла. Такие операции можно вынести из цикла в INIT-участок. Мы будем обрабатывать только операции типа +, —, *, BOUND и CVRI (преобразования). Мы не будем рассматривать инструкции присваивания, так как они требуют большего анализа программы, чем тот, который мы сейчас собираемся сделать. Мы предполагаем, что присваивание временным переменным Т делается по одному разу (как это обычно бывает) и имеется возможность отличать их от других переменных программы.
Этот проход просматривает последовательно операции внутреннего представления исходной программы, используя таблицы LOOPTABLE и SFV для выявления инвариантных операций. Если встречается операция из тех, которые мы условились выносить за пределы цикла, то делается следующее:
1. Предположим, что мы встретили операцию (#, А, В, TI). Если А или В не являются инвариантными в цикле (для проверки этого факта просматривается SFV-таблица), то все последующие шаги обходятся.
2. Если в INIT-участке уже существует операция (*, А, В, Т2), то осуществляется переход к шагу 4, в противном случае выполняется шаг 3.
3. Операция добавляется к INIT-участку и осуществляется переход к шагу 5.
4. Все последующие Т1 внутри цикла заменяются на Т2.
5. Операция из цикла выбрасывается. Выбрасывается Т1 из списка изменяемых переменных данного цикла (но не из списка объемлющих циклов).
Сказанное иллюстрируется на рис. 18.6,а и 18.6,Ь. Заметим, что когда мы выбрасываем Т1 из списка изменяемых переменных цикла, мы используем предположение, что каждая временная переменная изменяется в цикле только один раз. Исключение Т1 из списка позволяет нам также выносить последующие операции, зависящие от Т1. Те переменные, которые меняются более одного раза, должны быть специальным образом помечены.
Когда встречается новый оптимизируемый цикл, в его INIT-участок можно поместить присваивание ТО := В для новой временной переменной ТО (если В не константа и не простая переменная). Это можно сделать, так как для данного цикла выполняются условия оптимизации и, следовательно, все операции В инвариантны. Все ссылки на В нэ протяжении всего участка должны пониматься как ссылки на ТО.
До того момента, когда цикл будет закрыт, в INIT-участок, как будет показано ниже, могут быть вынесены несколько операций.
ОПТИМИЗАЦИЯ ПРОГРАММЫ
439
Располагается INIT-участок вне обрабатываемого в данный момент цикла и внутри объемлющего цикла. Таким образом, операции, возможно, будут вынесены еще дальше, так как при дальнейшей обработке они будут рассматриваться как часть объемлющего цикла.
INIT: I :=А INIT: I : = A T3 := J*d2 INIT: I : = A
T3 : = J*d2
TI :=I*d2
TI := l»d2
“TEST: проверка “TEST: проверка rTEST: проверка
I >N I>N I >N
LOOP: Tl: = I*d2 LOOP: Tl: = I*d2 LOOP:
T2:=T1 + J T3: = J*d2 T2: = T1+ J T2:=T1+J
T4:=T3+I T4:= T3+I T4:=T3+I
T5: = T5: = T5: =
A[T2]+A[T4] A[T2]:=T5 A [T2] + A [T4] A [T2] + A [T4]
A[T2]: = T5 A[T2]:=T5
INCR:I = I + 1 INCR: I: =1 + 1 INCR: I: =1 + 1 T1: = T1+TI
GO TO TEST GO TO TEST GO TO TEST
-OVER: -OVER: *OVER:
(а) первоначальная (b) обработка (с) замена операций
программа инвариантных операций
FOR Г. = 1 STEP 1 UNTIL N DO BEGIN A [I, J]: =A [I, J] + + A[J, I] END
Рис. 18.6. Пример обеих оптимизаций.
Программа замены сложных операций
Эта программа осуществляет последний оптимизирующий проход. Она последовательно просматривает операции каждого цикла. Встречая операцию вида (* I, К, Т1) или (* К, I, Т1), где К инвариантна в цикле, она заменяет ее на пустую операцию, после чего выполняет следующее:
1. Если операция (* I, К, ТЗ) уже есть в INIT-участке, то мы уже заменили идентичную операцию. Каждая последующая ссылка на Т1 заменяется ссылкой на ТЗ. Остальные шаги обходятся.
2. В INIT-участок добавляется (* I, К, Т1).
3. Если (* В, К, Т2) или (*К, В, Т2) в INIT-участке нет (операцию такого вида могла занести программа обработки инва
440
ГЛАВА 18
риантных операций), то генерируется новая временная переменная Т2 и в INIT-участок добавляется (* В, К, Т2).
4. В INCR-участок добавляется операция (+, Т1, Т2, Т1).
Мы предполагали, что присваивание каждой временной переменной Ti делается только один раз. Для временной переменной Т1 здесь присваивается значение в двух местах—в INIT- и INCR-участке. Но ни одно из этих присваиваний не участвует в дальнейшей оптимизации. INCR-участок мы не оптимизируем, а операция (* I, К, Т1) в INIT-участке не может оптимизироваться, так как I изменяется в цикле, в котором это присваивание осуществляется.
Обсуждение двух последних методов
На рис. 18.6,b приводится результат вынесения инвариантных операций из цикла, изображенного на рис. 18.6,а. Рис. 18.6,с показывает результат следующего шага оптимизации — замена сложных операций. Здесь существенно, что программа обработки инвариантных операций работает первой. Рассмотрим к примеру выражение (X+Y)*I, где X и Y инвариантны. Во внутреннем представлении оно имеет следующий вид:
(1) + X, Y, Т1 (2) *Т1, I, Т2
Замена операции умножения невозможна, так как Т1 не инвариантна в цикле. Но если программа обработки инвариантных операций вынесет первую тетраду в INIT-участок, то Т1 становится инвариантной.
Иногда выгоднее работать с п-арными + и * вместо бинарных. Тогда мы можем располагать операнды в каноническом порядке, например:
1) переменная цикла, внутри которого встретилась данная операция;
2) операнды, инвариантные в цикле;
3) операнды, неинвариантные в цикле.
Внутри каждого класса операнды могут быть упорядочены так, как это обсуждалось в предыдущем разделе. Заметим, что порядок зависит от цикла, в котором встречается операция. В качестве примера рассмотрим выражение Y1*X1*I*X2*Y2, где Y1 и Y2 не инвариантны, а XI и Х2 инвариантны. Если представить его в виде тетрад
(1) * YI, XI, Т1 (3) * Т2, Х2, ТЗ
(2) * Tl, I, Т2 (4) * ТЗ, Y2, Т4
то никакая оптимизация невозможна. Теперь предположим, что мы рассматриваем его в виде *Y1, XI, I, Х2, Y2, Т1 (результат по
ОПТИМИЗАЦИЯ ПРОГРАММЫ
441
сылается в Т1). После упорядочивания имеем
* I, XI, Х2, Yl, Y2, Т1
Теперь мы выносим операцию *Х1, Х2, Т2 и получаем * I, Т2, Y1, Y2, Т1. В итоге мы можем заменить умножение 1*Т2.
Очень важна «скрытая» оптимизация, которая касается переменных с индексами. Как рассматривалось в разд. 8.4, для переменной с индексами X [i, j,..., 1, ml требуется вычисление VARPART по следующей формуле:
((. . .(((i*d2)+j)*d3)+. ..) + !)* dn+m.
Если i — переменная цикла, то мы можем заменить i*d2. Для оптимизации вычисления VARPART лучше использовать формулу
i*d2*. . .*dn+j*d3*. . .*dn+. . .-H*dn-f-jn,
так как она приводит к вычислению и отдельных термов, каждый из которых может оптимизироваться независимо.
Если используются триады, то при вынесении операций за пределы линейного участка следует проявлять определенную осторожность. Ссылка на любую триаду является ссылкой на результат некоторого частного выполнения этой триады. В пределах линейного участка такая ссылка всегда указывает на последнее выполнение триады. Предположим, что на линейном участке мы имеем:
(1) (+А, В) (2)(+(1),С)
и первую триаду можно вынести из цикла. Тогда легко упустить из виду тот факт,’что ссылка (1) во второй триаде указывает на результат вынесенной триады. Гораздо лучше, если при вынесении первой триады будет сгенерирована новая временная переменная Т, а вторая триада будет заменена на (2) (+ Т, С) и в INIT-участок будут посланы следующие операции:
(k) (+А, В) (к+1) (:= (к), Т)
Обобщение метода замены сложных операций
Изложенные методы оптимизации не справляются с выражениями типа (I+K) * X, где I — переменная цикла, а К и X инвариантны в цикле. Один из способов улучшения оптимизации состоит в том, чтобы распознавать такие подвыражения, содержащие I, и преобразовывать их в I * Х+К * X. Другое решение состоит в том, что метод замены операций обобщается в двух направлениях, ни одно из которых не связано с большими усложнениями.
Первое — это заменять сложение TI := I+K следующим образом:
442
ГЛАВА 18
1. Tl := I+K заносится в INIT-участок.
2. Tl := Т1+В заносится в INCR-участок (каждый раз, когда I изменяется на В, Т1 также изменяется на В).
3. Операция Tl := I+K выбрасывается из тела цикла.
Второе — позволить другим рекурсивно определенным переменным участвовать в замене операций. Подходящими кандидатами для этого, которые не требуют дополнительного анализа исходной программы, являются временные переменные типа Т1, которые стали рекурсивно определенными на предыдущих шагах замены операций.
Ниже мы иллюстрируем это, показывая шаг за шагом процесс оптимизации тетрад для D:=(I*X+Y)*Z в цикле (показаны только INIT, INCR и LOOP участки). Оптимизируются все три операции, для каждой из которых генерируется новая рекурсивно определенная переменная.
INIT: INIT: INIT: INIT:
1:=А I :=А I := А I :=A
Т1:^ЬХ Tl:= UX T1:=I*X
Т4:=В«Х Т4:— В*Х T4:=B*X
T2:=T1 + Y T2:=T1+Y T3: —T2*Z T5:=T4*Z
LOOP: LOOP: LOOP: LOOP:
Т1:=1*Х Т2:~Т1 +Y Т2:~Т1+ Y
T3:=T2*Z ТЗ:—T2*Z T3:=T2*Z
D :=ТЗ D :—ТЗ D :=T3 D :=T3
INCR : INCR : INCR : INCR:
I:—I + B I :=1 + В I : = I + B 1 :=I+B
Tl :=Т1 + Т4 T1:='T1 + T4 T1:=T1+T4
T2:=T2 + T4 T2:=T2+T4 T3:=T3+T5
(а) замена (Ь) замена (с) замена (d) результат
ЬХ T1+Y T2*Z
Заметим, что многие тетрады в INCR-участке после оптимизации становятся ненужными, и их можно выбросить. В столбце результата (d) Т1 и Т2 нигде в цикле не используются, поэтому Т1 : = Т1+Т4 и Т2 :== Т2+Т4 можно выбросить.
Выполнение оптимизации за меньшее число проходов
На рис. 18.4 показана схема оптимизации, осуществляемой за три дополнительных прохода. Как правило, ПРОГРАММУ АНАЛИЗА ЦИКЛОВ можно объединить с семантическими программами,
ОПТИМИЗАЦИЯ ПРОГРАММЫ
443
генерирующими первоначальное внутреннее представление. Иногда также можно все оптимизации объединить с генерацией команд. Таким образом мы можем сэкономить время компиляции за счет сокращения накладных расходов, связанных с организацией трех дополнительных проходов. Поэтому здесь мы хотим кратко описать, как можно объединить оптимизацию с генерацией команд.
Хотя INIT-участок, как было описано в (18.2.4), располагается перед циклом, он не может быть окончательно построен, пока не будет пройден целиком весь цикл. Чтобы обойти эту трудность, вместо (18.2.4) мы будем генерировать следующую эквивалентную программу:
GO ТО INIT;
TEST : IF 1>С THEN GO TO OVER;
(18.2.11) LOOP: (тело цикла)
INCR : I := I+B; «операции приращения»; GO TO
TEST;
INIT : I := А; «начальные операции»; GO TO TEST; OVER:
Хотя эта программа имеет два дополнительных перехода, она позволяет нам одновременно оптимизировать тело цикла и генерировать для него команды, после чего генерировать команды для INIT-и I NCR-участков.
Внутреннее представление исходной программы, из которого затем будут генерироваться команды, складывается из трех разных источников: из таблицы основной программы, из INIT-и INCR-участков. Нужно только следить, с каким из этих источников мы в данный момент имеем дело. Мы также должны иметь возможность в любой момент включать или отключать оптимизацию, меняя значение некоторой глобальной переменной.
Генератор команд начинает свою работу с обработки основной программы в режиме, когда заблокирована всякая оптимизация, кроме свертки и исключения лишних операций. Операции обрабатываются в порядке их появления в соответствии с тем, к какому из перечисленных ниже типов они относятся. Типы операций приводятся в порядке их важности.
1. Свертываемая операция. Производится свертка операции.
2. Лишняя операция. Исключается, как было описано выше.
3. Инвариантная операция. Переносится в INIT-участок.
4. Операция, допускающая замену. Выполняется замена.
5. Операция начала цикла. Делаются подготовительные операции, открывающие новый цикл. Присваивания I := А; ТО := В; заносятся в INIT-участок. I := I4-T0 заносится в I NCR-участок. Заводится метка INIT и генерируется переход на нее. Заводятся
444
ГЛАВА 18
метки TEST и OVER и генерируются команды для
TEST : IF I >С GO ТО OVER
Заводится метка LOOP. «Указатель следующей операции» настраивается на первую операцию тела цикла. Если цикл допускает оптимизацию, то устанавливается режим оптимизации.
6. Операция окончания тела цикла. Отключается оптимизация. Осуществляется переход на новый источник входной информации — на INCR-участок данного цикла.
7. Конец INCR-участка. Генерируется GO ТО TEST. Выбрасывается INCR-участок текущего цикла, так как команды для него уже сгенерированы. Генерируется метка INIT. Объемлющий цикл делается текущим и открывается оптимизация, если он допускает оптимизацию (таким образом, INIT-участок включается в оптимизацию). Осуществляется переключение на INIT-участок только что завершенного цикла как на новый источник входной информации.
8. Конец INIT-участка. Генерируется GO ТО TEST. Генерируется метка OVER. INIT-участок только что завершенного цикла выбрасывается. Происходит переключение текущего потока входной информации на основную программу и обработка возобновляется со следующей за последней обработанной операцией этого потока.
9. Метка или операция, на которые осуществляется переход. Чистятся таблицы, используемые для свертки и исключения лишних операций. Фиксируется начало нового линейного участка.
10. Остальные операции. Генерируются соответствующие им команды.
18.3. БОЛЕЕ ПОЛНАЯ ОПТИМИЗАЦИЯ
Для описываемых здесь процедур оптимизации требуется, чтобы исходная программа была представлена в виде ориентированного графа с линейными участками в качестве узлор: Читателю было бы неплохо в этом месте еще раз просмотреть разд. 11.5. Сами операции можно было бы представлять в виде тетрад, триад или косвенных триад, отличия при этом несущественны. Мы будем пользоваться тетрадами. Подробно здесь не описывается реализация, а будут приводиться типы оптимизаций и порядок, в котором они осуществляются. Читателя же отсылаем к великолепной статье Аллен [69], из которой почерпнуты многие из описываемых здесь идей, и к работе Лоури и Медлока [69].
Прежде всего, мы предположим, что все циклы переведены в последовательность более элементарных действий — присваиваний, проверок, переходов и тому подобное. Например, два программных сегмента исходной программы
ОПТИМИЗАЦИЯ ПРОГРАММЫ
445
FORI:=1 I:=l;
STEP 1 UNTILN DO LOOP :IFI > N THEN GOTOOVER;
A [I]: =A [I] + 1; A [I]: = A [I] + 1;
I: =1 + 1; GO TO LOOP;
OVER:
на уровне внутреннего представления будут абсолютно неразличимы.
Первый шаг оптимизации состоит в том, чтобы в программном графе найти так называемые зоны, т. е. некоторые подграфы, определение которых будет дано позже. Подграфы как для обычного цикла, так и для эквивалентного ему цикла, записанного, как это было показано выше, с помощью переходов и проверок, образуют зоны. Однако понятие зоны позволяет нам находить внутри FOR-циклов другие подграфы, которые некоторым образом можно оптимизировать.
Первые четыре оптимизации, осуществляемые над зоной, выполняются в следующем порядке:
1) свертка внутри линейных участков;
2) исключение лишних операций внутри линейных участков;
3) вынесение из зоны инвариантных операций;
4) замена сложных операций в зоне.
Первые две осуществляются в точности так, как это было описано в разд. 18.1, и далее мы не будем их рассматривать. Вторые две, как вы успели заметить, применяются к зонам, а не только к FOR-циклам. Они обладают большей общностью, чем два аналогичных метода, описанных в предыдущем разделе. После замены операций далее зона подвергается следующей обработке:
5) одни проверки заменяются на другие, что позволяет нам исключить из зоны некоторые операции;
6) исключаются «вырожденные» переменные и присваивания, а также операции, от которых они зависят.
Исключение лишних операций можно было бы делать в пределах зоны, а не линейного участка, но слишком велики затраты времени в сравнении с дополнительной экономией, которую мы при этом получаем.
Зоны и список зон
Сильно связной зоной ориентированного графа называется подграф, для любой пары узлов которого существует путь, по которому можно перейти от одного узла к другому. На рис. 18.7 имеются пять сильно связных зон: (6), (3,5), (2, 3, 5, 6, 7), (2, 3, 4, 6, 7) и(2, 3, 4,
446
ГЛАВА 18
5, 6, 7). Подграф (3, 5, 6) не является сильно связной зоной, так как нет пути от 6-го узла к узлам 3 и 5. Также никакая сильно связная зона не может содержать узлы 1 и 8.
На рис. 18.8 изображен граф для обычного цикла вместе с выходом из него. Заметим, что полный цикл, исключая начальную установку I := 1, образует зону (участки 2, 3, 4, 5, 6).
Входным участком зоны называется участок, на который указывает стрелка извне зоны. На рис. 18.7 зона (6) имеет один входной
Рис. 18.8. Цикл с выходом и граф его программы.
участок — это сам 6-й участок. Зона (3,5) в качестве входного участка имеет 3-й участок.
Предшествующим участком зоны называется участок, лежащий вне зоны, из которого выходит стрелка, указывающая на входной участок этой зоны. На рис. 18.7 зона (6) имеет два предшествующих участка — 4 и 5. Зона (3, 5) имеет один предшествующий участок 2. Подобным же образом определяется последующий участок (мы еще будем называть его преемником).
Связующим участком зоны называется участок, лежащий на любом пути, который проходит внутри зоны от предшествующего участка этой зоны к ее преемнику. На рис. 18.7 участок 6 является
ОПТИМИЗАЦИЯ ПРОГРАММЫ
447
связующим для зоны (6), участок 3 — для (3,5), 2, 3, 6 и 7 —для (2, 3, 4, 5, 6, 7). Для последней зоны 4 и 5 не являются связующими участками.
Перед оптимизацией программа, представленная в виде линейных участков и графа программы, анализируется на предмет получения списка R сильно связных зон Rn R2, . . Rn, для которого верны соотношения:
1) если i=#j, то Ri#=Rj,
2) если i<j, то либо Rj и Rj не имеют общих участков, либо все участки Rj принадлежат Rj.
Зоны в списке R имеют ту же структуру, что и обычные циклы, т. е. либо они вложены друг в друга, либо вообще не имеют общих участков и таким образом «параллельны». То есть они не имеют частичного пересечения. Зоны Ri, R2, . . ., Rn оптимизируются в порядке их появления в списке. Очевидно, перед оптимизацией каждой зоны нужно проверить, допускает ли она оптимизацию, как это делалось для каждого цикла в разд. 18.2. Далее мы больше не будем говорить об этом.
Для графа на рис. 18.7 можно было бы построить следующий список зон: Ri= (6)> Ra= (3,5), R3= (2, 3, 5, 6, 7) и R4= (2, 3, 4, 5, 6, 7).
Программа на рис. 18.8 имеет две сильно связные зоны (1, 2, 3, 4) и (2, 3, 4, 5, 6). Обе они не могут быть включены в список зон, так как не выполняется второе соотношение. Тогда возникает вопрос, какую из них включить в список. Наибольшая выгода от вынесения и замены операций достигается на зонах, которые работают чаще. Опыт показывает, что обычные циклы работают часто и потому именно их разумно включать в список зон.
Но как обеспечить включение подграфов обычных циклов в список R? Один из способов, очевидно, состоит в том, чтобы как-то пометить их во внутреннем представлении исходной программы. Если же мы не хотим этого делать, то нужно найти какой-то другой способ.
Зона обычного цикла всегда имеет только один предшествующий участок, на котором делается начальная установка переменной цикла, и один входной участок, который является единственным преемником этого предшествующего участка. Это свойство поможет нам в выборе зоны, так как мы можем утверждать (здесь мы не приводим доказательства), что если две зоны пересекаются и ни одна из них полностью не перекрывает другую, то по крайней мере одна из этих зон имеет один предшествующий и один входной участок. Таким образом, если две зоны пересекаются частично, то предпочтение отдается той зоне, у которой один входной и один предшествующий участок.
448
ГЛАВА 18
Рассмотрим граф на рис. 18.9. Здесь имеются три области: (1,2), (2,3) и (1,2,3). Если мы воспользуемся приведенным правилом то получим список: Rj= (2, 3), R2= (1, 2, 3).
Р_и с. 18.9. Пример другого графа программы.
Информационные зависимости х
Для каждого участка нам потребуются сведения о том, какие из переменных используются на данном участке, каким присваиваются значения и какие из переменных используются до того, как
Рис. 18.10. Пример переменных, занятых по выходу.
им присваиваются значения. Для этого каждой переменной исходной программы и временной переменной Ti ставится в соответствие номер, а для каждого линейного участка строятся три булевых вектора.
1. REF [i] = 1, если i-я переменная используется на этом участке.
2. ASS [i] = 1, если i-й переменной присваивается новое значение на этом участке.
3. RBA [i] — 1, если i-я переменная используется до присваивания на этом участке.
Переменная занята по выходу из участка, если в конце участка она содержит значение, которое позже будет использовано. В сегменте программы на рис. 18.10 D занята по выходу из 1-го участка, а Е нет. Аналогично мы определяем переменные, занятые по выходу из зоны. Мы могли бы построить дополнительный вектор, указывающий на «занятость» каждой переменйой. Однако ту же информацию можно извлечь из REF, ASS и RBA векторов всех преемников (преемников их преемников и так далее) для данного участка.
С векторами RBA трудно работать. Ими нужно пользоваться только в том случае, если проводятся следующие две оптимизации:
ОПТИМИЗАЦИЯ ПРОГРАММЫ
449
вынесение присваиваний из циклов и исключение вырожденных присваиваний.
Из информации об отдельных участках можно получить информацию о всей зоне. Например, мы можем.определить, какие из переменных используются (или каким присваиваются значения) в зоне, логическим сложением (по ИЛИ) векторов REF (ASS) всех ее участков.
Для большой программы может получиться огромное множество векторов. Но как вы сейчас увидите, при обработке каждый раз мы имеем дело только с одной зоной, и, следовательно, нам нужны векторы только тех участков, которые входят в обрабатываемую зону.
Общая схема оптимизации
Каждый раз мы оптимизируем одну зону, которая берется в порядке ее следования в списке Ri, R2,. . ., Rn. Из этого следует,
Я1* (4,5,61 а . ь С
Рис. 18.11. Оптимизация зоны R1.
что сначала мы обрабатываем самые внутренние циклы. В процессе оптимизации создается новый участок, так называемый INIT-участок, который должен выполняться непосредственно перед входом в зону. Рассмотрим граф на рис. 18.11, а с областью Ri= (4, 5, 6).
15 д. Грио
450
ГЛАВА 18
Оптимизация Ri приводит к графу программы, изображенному на рис. 18.11, Ь. Здесь необходимо иметь два экземпляра INIT-участка, так как у Ri два входных участка. Так как участок 3 имеет одного преемника, то IN IT-участок можно поместить в конце 3-го участка, исключая тем самым необходимость в дополнительном участке.
Для ранее оптимизированной области нет нужды проводить повторную оптимизацию. Поэтому при переходе к следующей объемлющей зоне она рассматривается как один участок (см. рис. 18.11, с). Чтобы не повторять обработку, помечается, что этот участок уже прошел оптимизацию. Векторы REF, ASS и RBA для зоны легко получаются из векторов отдельных участков, как об этом говорилось выше.
Разумеется, INIT-участки принадлежат объемлющим зонам и, следовательно, подлежат дальнейшей оптимизации. Это означает, что операции самой внутренней “зоны могут выноситься шаг за шагом во все более объемлющие зоны.
В общем нам нужны три вектора только тех участков, которые входят в оптимизируемую в данный момент зону. Эти векторы можно строить в процессе свертки и исключения лишних операций на линейных участках. Заметим, однако, что по мере того, как во время оптимизации перемещаются и изменяются операции, изменяются и эти векторы. Более того, образуются новые временные переменные, которым присваиваются номера и которые добавляются к трем векторам каждого участка. (Информацию о векторах мы с равным успехом могли бы хранить в элементах таблицы символов. Это можно сделать, поскольку их использование в точности известно.) Во время обсуждения оптимизирующих процедур мы не будем больше говорить об этом, но в реальном компиляторе такая работа должна выполняться.
Полная обработка программы состоит из следующих действий:
1. Начальная установка i 1.
2. Выбор зоны Rj для оптимизации и выделение для INIT-участка места в памяти.
3. Свертка и исключение лишних операций внутри каждого линейного участка зоны Rj. Одновременно с этим формирование REF, ASS и RBA векторов. Формирование списка рекурсивно определенных в зоне величин SFVI. Эти величины могут использоваться в замене операций аналогично тому, как использовалась переменная цикла в последнем разделе.
4. Оптимизация в пределах зоны и формирование INIT-участка. Эта оптимизация может изменить векторы и породить новые временные переменные.
5. Формирование трех векторов для зоны R Р Оформление этой зоны в виде отдельного участка, не подлежащего дальнейшей оптимизации. Помещение INIT-участка в соответствующие места (на всех путях от предшествующих к входным участкам).
ОПТИМИЗАЦИЯ ПРОГРАММЫ
451
6. i := i+1. Если i^n, то переход к шагу 2, в противном случае переход к шагу 7.
7. Свертка и исключение лишних операций на всех линейных участках, которые не вошли ни в одну зону.
Далее мы продолжим описание различных оптимизаций (выполняемых на шаге 4) в том порядке, как они должны выполняться.
Вынесение инвариантных операций
Мы уже рассматривали вынесение из цикла инвариантных операций типа +, *, CVRI и так далее. Такая же обработка делается и для зоны. Кроме того, сейчас мы покажем, при каких условиях
Пщиваяват» В: =5 шгварааюпя» и может быть еыиесеяо.
После smoto а О: «В стаховвтся югеарваялшым.
Рис. 18.12. Пример вынесения инвариантных операций.
могут быть вынесены из зоны операции присваивания. Рассматриваются присваивания вида А := В или А := Т, где Т — временная переменная. Чтобы присваивание можно было вынести, требуется выполнение следующих условий:
1. В (или Т) инвариантна в зоне.
2. Участок, на котором встречается присваивание, должен быть связующим. Это гарантирует нам, что при переходе на эту зону присваивание обязательно будет выполнено.
3. В зоне нет других присваиваний А.
4. А не используется ни на каком пути от входного участка до этого присваивания.
Выполнение этих условий проверяется с помощью векторов REF, ASS и RBA на линейных участках зоны. Рассмотрим рис. 18.12. Присваивание В := 5 можно вынести. Присваивание Е : = 4 выносить нельзя, так как не выполняется условие3. Присваивание А:=3 выносить нельзя, так как не выполняется условие 2. Присваивание D := В можно вынести, если предварительно вынесено присваивание В : = 5. Присваивание С: = Е не удовлетворяет условию 1, a F : = 5 — условию 4.
15»
452
ГЛАВА 18
Замена операций
Для того чтобы можно было заменить операцию, зависящую ст рекурсивно определенной в зоне переменной I, необходимо выполнение следующих двух условий:
1. I должна быть простой переменной типа INTEGER или формальным параметром типа INTEGER, вызываемым по значению (SFVI).
2. Все присваивания I в зоне должны быть вида I := I+D, где D — инвариантное в зоне выражение типа INTEGER.
Предположим, что I рекурсивно определена при помощи п присваиваний:
I := I+Dl; I : = I+D2; . . . I I+Dn;
Тогда для операции Т1 := 1*К, где К инвариантна в области и имеет тип INTEGER, замена выполняется следующим образом:
1. В INIT-участок добавляется операция Т2 : = 1*К, где Т2 — новая временная переменная.
2. Генерируются и временных переменных TINCRi и в INIT-участок добавляются операции TINCRi := Di#K.
3. В зоне операция Т1 : = 1#К заменяется на TI := Т2.
4. После каждой I : = I+Di вставляется Т2 : = Т2 + TINCRi (для i = 1, . . ., п).
Иногда возможны некоторые улучшения. Если Di = 1, а это бывает довольно часто, то TINCRi не нужна и вместо Т2:= Т2+ TINCRi вставляется Т2 :== Т2+К- Во-вторых, если К и Di— константы, то мы можем свернуть операцию и вместо TINCRi использовать результирующее значение. В-третьих, в ситуации, которая довольно часто встречается, нам не нужна новая переменная Т2, мы можем вместо нее использовать Т1 и не вставлять операцию ТГ.= Т2. Для этого должны выполняться следующие условия: (1) в цикле Т1 не присваивается больше других значений, (2) все операции, где используется Т1, зависят только от данного присваивания и (3) ТТ не занята по выходу из области.
Для операции TI := I+K замена выполняется следующим образом:
1. В INIT-участок добавляется операция Т2 := I+K, где Т2 — новая временная переменная.
2. Т1 := I+K заменяется на Т1 := Т2.
3. После каждой I := I+Di вставляется Т2 := T2+Di (для i=l, . . п).
Заметим еще раз, что если для Т1 выполняются вышеизложенные условия, то нет необходимости генерировать новую временную переменную Т2.
ОПТИМИЗАЦИЯ ПРОГРАММЫ
453
Операции приращений Т2 := T2+TINCR1 и Т2 := T2+D1, порождаемые в результате замены операций, должны как-то помечаться, чтобы они сами больше не подвергались замене. В предыдущем разделе в этом не было необходимости, так как операции приращений входили в INCR-участок, который дальше не оптимизировался. Здесь у нас нет отдельного INCR-участка.
Обратите внимание , что Т2 рекурсивно определена и может участвовать в замене. Однако операции приращений Т2 := Т2 Ц-TINCRi не должны подвергаться замене операций.
По существу эта оптимизация та же, что и оптимизация, описанная в предыдущем разделе. Но сейчас мы допускаем замену операций для всех рекурсивно определенных переменных, а не только для переменной цикла. —
Замена проверки
На рис. 18.13, с I используется только в рекурсивном определении I := 1+1 ив проверке I. Если проверку I заменить на проверку другой переменной, то операцию I := 1+1 можно было бы вы-
|:« 1
TEST I
Т1 :=1*К1 ВТ1+К2
t:«1+1
В:-Т1+К2
|:«Н4 ,Т1 :-Т1+К1
|:=1
Т11*К1
Т2: = Т1+К2
TESTI
В:-Т2
I г= 1+1 Т1 :-Т1+К1 Т21-Т2+К1
С
Рис. 18.13. Иллюстрация замены операций.
бросить. В нашем примере для проверки можно воспользоваться переменными Т1 или Т2, но больше подходит Т2, так как операция Т1:=Т1+К1 лишняя и будет выброшена в результате последующей обработки.
Мы хотим проверку IF I > С . . . заменить на проверку
IF Т2>С2 THEN GO ТО OVER
454
ГЛАВА 18
Заметим, что Т2 определяется через I с помощью операций Т2 : = =Т1+К2=1*К1+К2. Если 1>С, то Т2>С*К1+К2 и, следовательно, для начальной установки С2 мы должны в INIT-участок вставить С2 := С*К1+К2. Мы предполагаем, что С инвариантна в зоне. Заметим также, что если приращения для I и Т2 разного знака, то О» нужно заменить на «<».
Замена проверки должна выполняться только при следующих условиях:
1. Рассматриваемая проверка имеет дело с переменной I, которая, кроме самой проверки, используется только в рекурсивном определении вида I : = I+K. I не должна быть занятой по выходу.
2. Проверка должна быть сравнительно простой для анализа (например, 1>С). С инвариантна в зоне.
3. Должна существовать другая рекурсивно определенная переменная Т, которая появилась в результате замены операции, использующей 1, т. е. определение которой зависит от I.
Эффективность этой оптимизаций сомнительна. Возможно, мы и сэкономим одно или два сложения внутри цикла, но мы затратим довольно много времени при компиляции на проверку, занята ли I по выходу. Для АЛГОЛа и ФОРТРАНа, очевидно, переменная цикла никогда не занята по выходу, так как ее значение после выхода из цикла не определено.
Исключение вырожденных присваиваний
Операция присваивания считается «вырожденной», если результат присваивания нигде не используется или если присваивание рекурсивно (типа I := 1+1) и результат используется только в этом рекурсивном определении. Такого рода присваивания и операции, от которых эти присваивания зависят, можно выбросить.
Вырожденные присваивания часто возникают в результате замены операций и замены проверки, как показано на рис. 18.13. Поэтому эту оптимизацию следует выполнять после замены проверки. Очевидно, для всех рекурсивно определенных переменных следует проверить, не стали ли они вырожденными. Однако с точки зрения затрат времени проще проверить все присваивания зоны. Так сказать, «в лоб» такую проверку для присваивания вида А : = Т можно выполнить следующим образом:
1. Последовательно просматриваются операции участка. Если встречается присваивание А, то старое присваивание объявляется вырожденным; если встречается использование А, то присваивание считается невырожденным. Если никаких ссылок на А не обнаружено, то осуществляется переход к шагу 2.
2. Предположим, что имеются векторы REF, ASS и RBA для всех участков программы. Следуем по всевозможным путям из уча
ОПТИМИЗАЦИЯ ПРОГРАММЫ
455
стка, содержащего данное присваивание. Если RBA некоторого участка указывает на использование А перед присваиванием, то А считается невырожденной и обработка прекращается. Если ASS указывает на присваивание, то этот путь можно дальше не анализировать. Если все пути приводят к такому концу или «зацикливаются», то переменная считается вырожденной.
18.4. ДОПОЛНИТЕЛЬНОЕ ОБСУЖДЕНИЕ И ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Свертка и исключение лишних операций
О переводе арифметических выражений в конкретный язык машины и осуществлении при этом некоторой ограниченной оптимизации существует несколько ранних статей. Среди них Кнут [59] и Хаски [61]. Алгоритм Флойда [61а] минимизирует количество чтений и записей в память, осуществляет свертку и исключение лишних операций. Он также распознает эквивалентные операции с учетом знака минус (например, —Ь+а=— (Ь—а)). Эти методы также рассматривает Гир [65]. Ограниченную оптимизацию последовательности присваиваний с использованием деревьев в качестве внутреннего представления обсуждает Хопгуд [70].
Более поздняя работа Брейера [69] описывает метод факторизации последовательности выражений и присваиваний, который приводит к выделению общих подвыражений. Так,
J := А+В+С+Е; К := A+B+E+F; L := A+B+D+E+F; преобразуется в
Т := А+В+Е; J := Т+С; К := T+F; L := K+D;
в то время как
(18.4.1) A*B*C+A*B*D+A*E+F преобразуется в
A*(B*(C+D)+E)+F
После того как множители определены и преобразование сделано, операции переупорядочиваются в целях уменьшения числа обращений (чтений и записей) к памяти (описание последнего метода будет дано несколько позже).
Эвристичность метода факторизации не позволяет ему достигать абсолютного оптимума, так как для того, чтобы метод имел практическую применимость, приходится сокращать количество проверяемых множителей.
Как показал Фэйтман [69], факторизация не всегда приводит к оптимальной программе. Например, выражение 5+х+х24-7х4 по методу Брейера должно быть преобразовано в 5+х*(1+х
456
ГЛАВА 18
*(1 +7*х*х)), в то время как в
TI := х*х; Т2:=Т1*Т1; RESULT :== 5+х+Т1+7*Т2; используется на одно умножение меньше.
Другой важный факт, который подметил Фэйтмен, состоит в том, что оптимальная программа для последовательно выполняемых вычислений может не быть оптимальной при параллельных вычислениях. Например, вычисление выражения в правой части (18.4.1) делается за пять шагов, в то время как на машине, способной выполнять несколько независимых операций одновременно, это выражение можно было бы вычислить за четыре шага:
Т1: = А*В Т2: = А»Е
ТЗ: = Т1*С T4: = T1»D
ТЗ: — ТЗ + Т4 T2 = T2 + F
RESULT: = ТЗ + Т2
(Здесь каждая строка соответствует одному шагу.)
Следует также помнить, что не все языки допускают такого рода преобразования выражений. Это может привести (и обычно приводит) к изменению результата, если выражение использует числа с плавающей точкой. Все это свидетельствует о том, что мы пока мало знаем, как и когда нужно оптимизировать присваивания и выражения.
' Оптимизация циклов
Гир [65] рассматривает умеренную оптимизацию цикла, приведенную в разд. 18.2, которая состоит из обработки инвариантных операций и замены операций, зависящих от переменной цикла. Он также рассматривает переупорядочивание операндов n-арных операций + и *.
Бьюзем и Энглунд [691 преследуют ту же цель: достаточно хорошая оптимизация при быстрой компиляции. Они осуществляют вынесение из цикла инвариантных операций, но замену делают только для операций, участвующих в индексировании (см. ниже). Ими был применен интересный прием для определения, используется ли переменная (или выражение) в цикле, а также было ли присваивание переменной в цикле. Для этого они формируют списки «ссылочной» структуры: список мест, где осуществляется присваивание переменной, и список мест, где она используется. Эти списки хранятся в самом внутреннем представлении исходной программы, почти в том же виде, как и цепочки ссылок «вперед» в разд. 13.3. В процессе оптимизации элемент таблицы символов для переменной содержит текущую ссылку на последнее присваивание (ASS) и использование (REF). Например, из цепочки, указанной на рис. 18.14, мы легко можем определить, что 1*5 инвариантна в цикле (фигурными скобками отмечено поле операнда, используемое для ссылки).
ОПТИМИЗАЦИЯ ПРОГРАММЫ
457
В нескольких компиляторах с АЛГОЛа применена схема Бью-зема и Энглунда для вынесения индекса из цикла; Мы не рассматривали ее подробно, так как оптимизация, описанная в 18.2, автоматически включает в себя и этот случай, мало или совсем не увеличивая при этом время компиляции. См. Гилл [62], Хакстебл [64] и Грис и др. [65]. Этот метод, названный рекурсивным вычислением индекса, был впервые предложен Замельзоном и Бауэром
10 I{50}=
20 DO 40 J = 1,N
К: =1*5
Элемент таблицы символов для I содержит 10 в поле, указывающем на последнее присваивание.
40 CONTINUE
50 I {0} =
Рис. 18.14. Формирование цепочки ссылок.
Компилятор с ФОРТРАНа IV уровня Н для IBM, описанный Лоури и Медлоком [69], и экспериментальный компилятор с ФОРТРАНа, разработанный Аллен [69], максимально используют самые сложные методы, описанные в разд. 18.3. Лоури и Медлок пользуются тетрадами, Аллен использует косвенные триады для внутренней формы программы. В обоих случаях используются лйнейные участки и строится граф программы. Статья, Аллен дает более подробное описание действительной реализации метода. Работа Кока и Шварца [70] также содержит описание этих и других методов.
Распределение регистров
Мы не рассматривали оптимизацию объектной программы, так как. она сильно зависит от машины. Здесь мы коротко остановимся на проблемах, связанных с этой оптимизацией. .
Если предположить в машине наличие нескольких быстрых регистров, которые можно использовать для хранения промежуточ-. ных результатов, то первая оптимизация, которая приходит в голову, состоит в минимизации количества используемых регистров. Эту проблему рассматривали Андерсон [64], Наката [67] и Реджи-евский (691. Основная посылка в рассуждениях следующая: если в операции вида А * В для вычисления А необходимо п регистров, а для вычисления В необходимо m (m>n) регистров, то для вычис
458
ГЛАВА 18
ления А~В потребуется ш+1 регистров, если сначала вычисляется А (дополнительный регистр требуется для хранения результата А), и только rn регистров, если сначала вычисляется В.
Пусть выражение во внутреннем представлении имеет вид дерева (см. разд. 11.4). Тогда за дополнительный просмотр этого дерева можно для каждого оператора определить количество регистров, необходимых для вычисления его операндов, и в каждом узле пометить тот операнд, который должен вычисляться первым, а при генерации команд действовать согласно этой информации.
Наката приводит эвристические правила для определения, какой-из регистров занимать, запомнив предварительно его значение, если регистров не хватает. Например, так как в большинстве машин для операций А—В или А/С требуется, чтобы А находилось в сумматоре, то регистр со значением А не следует отправлять в память. Реджиевский формулирует задачу в терминах теории графов и приводит общий алгоритм, который применяет для частного случая задачи минимизации числа регистров.
Главный недостаток этих методов состоит в том, что они не говорят нам, какой из регистров следует занимать в том случае, когда регистров не хватает. Проблема, которую мы, по сути дела, должны решить, следующая: даны п быстрых регистров, требуется минимизировать количество пересылок из памяти в регистры и наоборот при вычислении данного выражения. Для начала предположим, что нам запрещено менять порядок вычислений подвыражений и каждое значение перед использованием должно находиться в быстром регистре.
Предположим, что мы имеем п регистров Rx> Re,. Rn и в некотором месте вычислений выражения нам понадобилось значение переменной V. Тогда возникают следующие возможности:
1. Значение уже имеется в регистре R4. Тогда он используется.
2. V еще не в регистре, но существует неиспользованный регистр (или имеется регистр, значение которого нам уже не понадобится). Тогда V загружается в этот регистр.
3. V еще не в регистре и все регистры заняты. Тогда значение одного из регистров запоминается (позднее оно снова будет загружено в регистр) и V загружается в регистр.
Разумеется, возникает вопрос: какой из регистров следует запомнить в шаге 3? Интуиция подсказывает следующий ответ: (18.4.2) следует запомнить тот регистр, который в последовательности операций используется позже всех.
Этот метод распределения регистров хорошо известен и использовался в нескольких компиляторах. Биледи доказал, что при определенных условиях такое распределение регистров оптимально, т. е. приводит к минимальному количеству загрузок и запоминаний регистров.
ОПТИМИЗАЦИЯ ПРОГРАММЫ
459
Заметим, что этот алгоритм требует от нас знания для каждой переменной, где она используется в следующий раз. Для этого лучше всего иметь цепочку ссылок, связывающих элементы объектного кода.
Хорвиц и др. [66] также решили эту проблему при несколько измененном наборе исходных положений. Они предполагали, что операции должны.выполняться по порядку. Операция может обратиться к значению (которое, следовательно, должно быть загружено в быстрый регистр) и может изменить содержимое регистра. Цель та же — минимизация количества пересылок из регистров в память и из памяти в регистры. Их алгоритм сводится к нахождению кратчайшего пути между двумя узлами графа. Луччо [67] улучшил этот алгоритм так, что граф стал меньше, увеличив тем самым его практическую ценность.
Сэти и Улман [70] также предложили алгоритм минимизации числа пересылок. Исходные посылки также несколько отличаются. Они рассматривали арифметические выражения, использующие + , * и операнды, которые различаются между собой и являются простыми переменными (нет общих подвыражений). Порядок операций можно менять.
Оптимизация для параллельных процессоров
Вычислительная машина CDC 6600 имеет несколько независимых арифметических устройств, которые могут работать параллельно друг с другом. Задача состоит в генерации таких команд, которые бы максимально использовали этот параллелизм. Аллард, Вулф и Землин [64] описывают свои исследования в такого рода оптимизации арифметических выражений. Основные из применяемых методов состоят в переупорядочивании операций, исключении лишних загрузок и запоминаний и распределении регистров. Также Геллерман 166] и Сквайр [63] сообщают о многопроходных алгоритмах компиляции арифметических выражений для параллельных процессоров. Стоун [67] дает однопроходный алгоритм, который, например, A+B+C+D+E+F+G+H переводит в вид
((A+B)+(C+D))+((E+F)+(G+H)) вместо обычного
((((((A+B)+C)+D)+E)+F+G)+H.
Это позволяет параллельно вычислить А+В, C+D, E+F и G+H. См. также Бэр и Бове [68].
Прочие оптимизации
Маккиман [65] описывает «локальный» способ оптимизации, который обрабатывает объектную программу после генерации, просматривая в каждый текущий момент времени только несколько
460
ГЛАВА 18
рядом стоящих команд. Это позволяет выявлять некоторые небольшие группы команд, с тем чтобы заменять их на более эффективные команды. Например, для IBM 7090
CLA А могут . быть
CHS заменены на CLS А
Этот способ также позволяет на небольших отрезках программы находить лишние команды загрузки регистров и сумматора.
Ершов [661 рассматривает 24-проходный компилятор с языка АЛЬФА (расширение АЛГОЛа), написанный для советской машины М-20 (4096 45-разрядных слов памяти с трехадресной структурой команд). Кроме обычных оптимизаций FOR-циклов и исключения лишних операций, Ершов упоминает следующие:
1. Объединение соседних FOR-циклов с идентичными заголовками в один цикл, если это возможно (слияние циклов).
2. Минимизация числа используемых ячеек за счет распределения одних и тех же ячеек под разные переменные, если эта возможно.
3. При однократном вызове процедуры замена текста обращения на текст самой процедуры, выполняемая до оптимизации и генерации команд.
4. Замена на этапе компиляции некоторых формальных параметров процедуры на их фактические значения, если последние одинаковы для всех обращений к этой процедуре.
Вагнер в своей диссертации описывает оптимизацию выражений с массивами в качестве операндов, которая уменьшает объем памяти, используемой под временные массивы. Он также подробно излагает упомянутое выше слияние циклов. Бьюзем и Энглунд описывают, когда и где возможно слияние в один цикл вложенных циклов.
Помимо этого, можно упомянуть о следующих оптимизациях:
1. Замена деления A/В на А*(1/В), с тем чтобы вынести из цикла 1/В, а внутри цикла иметь более быструю операцию умножения.
2. Использование умножений при возведении в степень при целочисленном показателе степени. Например, Х**2 заменяется на Х*Х, a Y **7 заменяется на (Y * Y) * (Y * Y) # (Y * Y) * Y.
3. Для двоичной машины замена умножения или деления целого на степень двойки операцией сдвига, а также замена умножения на 2.0 сложением.
4. Использование в программе непосредственно команд для вычисления ABS, ENTIER и других элементарных функций.
5. Объединение пересылок смежных полей в одну команду.
6. Сокращение числа безусловных переходов за счет изменения последовательности линейных участков.
7. Исключение умножений на 1 и сложений с 0.
8. Исключение неработающих команд (экономия пространства, а . не времени).
Глава 19
Реализация макросредств
В этой главе мы хотим исследовать возможности получения средств макрогенерации в языке высокого уровня и наметить пути их реализации. В разд. 19.1, мы описываем простую схему макрогенерации и подробно показываем, как она может быть реализована. Затем в разд. 19.2 рассматривается естественное расширение схемы макрогенерации, обеспечивающее ей дополнительные возможности и большую гибкость. В разд. 19.3 описывается хорошо известный независимый макропроцессор, который не связан каким-либо из конкретных языков и может быть использован как «препроцессор» многих компиляторов с различных языков программирования. Наконец, в 19.4 приводится перечень литературы по различным вопросам, касающимся макропроцессоров.
19.1. ПРОСТАЯ СХЕМА МАКРОГЕНЕРАЦИИ
В основе идеи макрогенерации лежит текстовая подстановка, которая состоит в том, что некоторый идентификатор исходной программы заменяется строкой литер из другого потока текстовой
MAC ST VW
.макроопределегте
исх. программа
А В MAC CD at
Рис. 19.1. Простая макроподстановка.
результат
А В ST VW CD
с
информации. Эта подстановка иллюстрируется на рис. 19.1. Здесь предполагается, что существует так называемое макроопределение (рис. 19.1, а), в котором с именем МАС сопоставлена строка литер «ST VW». Во время просмотра исходной программы всякий раз, когда встречается имя МАС, оно заменяется на строку «ST VW». Таким образом, в то время как программист пишет свою программу,
462
ГЛАВА 19
как показано на рис. 19.1,6, в действительности будет компилироваться исходная программа, изображенная на рис. 19.1 ,с.
Строка литер, связанная с именем макро, называется телом макро. Имя МАС, встречающееся в исходной программе, называется макровызовом. Процесс подстановки, тела макро вместо макровызова называется макрорасширением *).
макроопределение исх. программа результат
Г S&11 &2V&1 + A F[XY, XZ] В SS A sXYttfZvXY В
а Ь с
Рис. 19.2. Макрорасширение с использованием параметров.
Дополнительное свойство макро, которое обеспечивает ему большую гибкость, состоит в том, что в макро могут задаваться параметры. Строка, которая замещает макровызов, варьируется в зависимости от задаваемых в нем параметров. Это иллюстрируется на рис. 19.2. Связанная с макро F строка имеет два так называемых формальных параметра — &1 и &2 (рис. 19.2, а). Соответственно в макровызове F имеются два фактических параметра — XY и XZ (рис. 19.2, 6). При замене макровызова на тело макроопределения вместо первого формального параметра &1 подставляется XY, а вместо &2— XZ (рис. 19,2, с).
Выше мы пользовались терминами «формальный параметр» и «фактический параметр», которые обычно используются в применении к процедурам и подпрограммам. Это связано с тем, что существует большая аналогия макровызова с вызовом процедуры или подпрограммы. Но имеется и существенное различие. Макровызов осуществляет только текстовую подстановку параметров, так как эта подстановка происходит перед тем, как компилятор производит собственно разбор программы. Можно было бы реализовать полностью независимый «макропроцессор», выходная информация которого затем поступает на вход компилятора. Мы же покажем, как провести обработку макро в сканере компилятора.
Вложенные макровызовы и макроопределения
Макровызовы часто используются внутри тела макроопределения или внутри фактического параметра. На рис. 19.3 показано использование двух макро с именами PI и ADD. Макровызов PI
Часто в этом смысле используется термин «макрогенерация», в то время как «макрорасширение» оставляется для обозначения не процесса подстановки, а ее результата» В переводе оба термина используются практически как синонимы.*— Прим, ред.
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
463
встречается в теле макро ADD (рис. 19.3, а) и во втором фактическом параметре макровызова ADD (рис. 19.3, 6). Результат расширения всех трех макровызовов приводится на рис. 19.3, с.
Макро типа PI довольно часты. Использование мнемонического имени для константы делает программу более легкой для чтения.
махроопределеиие исх, программа, результат
PI 3.14159 + ADD [2, PI *3] ss 2+3.14159*3+3.14159
ADO Л1+д2+Р1
a b e
Рис. 19.3. Вложенные макровызовы.
Кроме того, если константу по каким-либо причинам нужно изменить, то удобнее это изменение вносить в одно место — в макроопре» деление.
макроопределеяае
A MACRO 8 [XYZ] CBDBE
Рис. 19.4. Вложенное макроопределение.
Удобно использовать понятие уровня вложенности мдкровызо-ва. Если макровызова нет, то мы будем говорить, что мы находимся на нулевом уровне. Встречая макровызов во время расширения макровызова уровня п, мы переходим на уровень п+1. В примере на рис. 19.3 макровызов ADD на уровне 1, а оба обращения к PI — на уровне 2.
Внутренние макроопределения встречаются реже, но в некоторых случаях они бывают полезны. На рис. 19.4 показано макроопределение А, в теле которого содержится макроопределение В. (Мы еще не дали точного вида макроопределения. Определение MACRO В [XYZ] на рис. 19.4 связывает с именем В тело XYZ.) Вложенное макроопределение во многом играет ту же роль, что и локально описанная переменная в процедуре. Имя В внутри тела макро А ссылается на макро В, с которым сопоставлена строка литер XYZ. Вне макро А макроопределение В не действительно. Имя В попадает в «таблицу макро» (как имя макро со связанной с ним строкой литер) только тогда, когда началось расширение макровызова А. После того как А расширено, В из таблицы макро выбрасывается.
Макроопределения, которые встречаются в фактическом параметре, по существу, обрабатываются тем же способом. Они действительны только на период, когда вычисляется и вставляется в исходную программу данный конкретный параметр.
464
ГЛАВА 19
Следует заметить, что по тому, как мы здесь определили, и макроопределения, и макровызовы могут встречаться в любом месте исходной программы. Они совершенно не зависят от блочности исходного языка или структуры его инструкций, так как их обработка ведется перед компиляцией программы. Единственное условие, которое должно соблюдаться, очевидно состоит в том, что результат макрообработки должен быть с точки зрения синтаксиса и семантики правильной исходной программой.
Формат макроопределения и макровызова
Макроопределения и макровызовы используют специальные символы &, [ и ], которые, как мы предполагаем, не используются в исходном языке. Это ограничение позволяет нам четко отделить процесс макрогенерации от компиляции. В макровызовах используется символ но он может быть также символом исходного языка.
Макроопределение имеет следующий вид:
(19.1.1) MACRO (имя макро) [(строка)]
где (имя макро) — обычный идентификатор языка программирования, а (строка)—любая последовательность литер.
Заметим, что все литеры (и пробелы тоже), расположенные между двумя квадратными скобками, являются частью строки. Далее мы вводим следующее ограничение: внутри строк должно соблюдаться соответствие квадратных скобок, т. е. левой скобке [должна где-то правее найтись соответствующая правая скобка], и наоборот. Наконец, за каждым & в строке должна идти отличная от нуля цифра. &i обозначает для макро i-й формальный параметр. Ниже мы объясним его назначение.
Макроопределение с <именем макро) сопоставляет тело макро, т. е. строку. При просмотре макроопределения имя и тело макро запоминаются в таблице макро, а само макроопределение выбрасывается из исходной программы.
Макровызов может быть двух видов:
(19.1.2) (имя макро)
(19.1.3) (имя макро) [(пар), (пар),. . ., <пар>]
где (имя макро) совпадает с именем, соответствующего макроопределения.
В качестве фактического параметра (пар) может быть либо
(19.1.4) [(строка)] либо
(19.1.5) любая строка литер без запятых и квадратных скобок.
Если (пар) вида (19.1.4), то (строка) должна удовлетворять указанным выше правилам написания строки. В случае (19.1.5)
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
465
фактический параметр начинается с первой отличной от пробела литеры и заканчивается литерой, за которой следует запятая или J. Таким образом, если мы хотим впереди иметь пробел, то мы должны воспользоваться представлением (19. ГЛ).
Мы введем еще одно ограничение по двум причинам. Во-первых, мы хотим по возможности сохранить простоту реализации, чтобы вы получили достаточно ясное представление о существе происходящих процессов. Во-вторых, мы должны оставить что-то читателю для самостоятельной работы (см. упражнения 1 и 2).
Ограничение состоит в том, что в фактическом параметре нельзя задавать формальный параметр &L Это ограничение существенно сужает использование макровызова внутри макроопределения. Например, если В — имя ранее определенного макро, то в
MACRO A [B[c&ldJ]
&1 был бы ссылкой на 1-й фактический параметр макровызова А, а не В. Наше же ограничение запрещает такого вида конструкции.
Процесс расширения макровызова состоит в следующем:
1. Фактические параметры сканируются и копируются в отдельное место, а макровызов исключается из исходной программы.
2. В таблице макро, содержащей имена макро и связанные с ними <строки>, ищется самое последнее макроопределение с именем ,<имя макро >.
3. Литеры тела макроопределения одна за другой переносятся в исходную программу. Всякий раз, когда встречается формальный параметр &i, процесс переноса литер из тела макро приостанавливается и начинается перенос литер из i-ro фактического параметра (ранее скопированного). По окончании обработки параметра все макроопределения, добавленные в процессе обработки этого фактического параметра, удаляются. После чего происходит возврат к обработке тела макро.
4. Если во время выполнения шага 3 встречаются новые макроопределения и макровызовы, то они немедленно обрабатываются. Макровызов, следовательно, может быть рекурсивным. •
5. После того, как шаг 3 выполнен, все макроопределения, добавленные в список макро в процессе обработки этого макро, удаляются из таблицы макро.
Реализация простой схемы макро
Для простоты изложения в приводимых ниже программах опу? щен анализ многих ошибок и контроль за переполнением таблиц.
Для хранения макроопределений используется три массива. Тела макро запоминаются в массиве S по одной литере на каждый элемент массива. За последней литерой тела макро следует специ
466
ГЛАВА 19
альный знак #. Предполагается, что # не может быть символом исходного языка. Массив MACNAME содержит имена макро, а MACBODY содержит индексы соответствующих им тел в массиве S. Другой массив, CALLS, содержит информацию о расширяемых в данный момент макровызовах. На рис. 19.5 дается полный пере-
STRING ARRAY MACNAME (1:100); INTEGER ARRAY MACBODY(1:100); INTEGER NMAC; CHARACTER ARRAY S (1:1000); INTEGER NS; INTEGER ARRAY CALLS (1:50); INTEGER N; INTEGER INPUT; INTEGER LBSIGN; CHARACTER CHAR; STRING ID; Содержит имена макро. Содержит индексы, указывающие на тела макро в массиве S. Количество имен макро в MACNAME. Содержит тела макро и параметры макровызова (по одному элементу на каждую литеру). Количество литер в S. Содержит информацию о текущих макровызовах (работает как стек). Количество элементов в CALLS. Если 0, то ввод с карт, если не 0, то содержит индекс, указывающий на текущую литеру массива S, играющего роль другого вводного потока литер. Переменная, равная нулю,, при просмотре исходной программы, макроопределения или фактического параметра. Содержит текущую литеру вводного потока. Содержит последний набранный идентификатор.
Рис. 19.5. Описание переменных для макро.
Вначале NMAC, NS, N, INPUT и LBSIGN равны нулю.
чень используемых переменных. На рис. 19.6 приводятся таблицы для макро PI и ADD (рис. 19.3).
Все действия по обработке макро выполняются сканером. Рассмотрим кратко, как это делается. В начале просмотра обычной исходной программы значение глобальной переменной INPUT должно равняться нулю. Если в исходную программу вставляется тело макро или фактический параметр, то мы имеем другой вводной поток информации. Тогда INPUT содержит индекс, указывающий на текущую литеру тела макро или фактического параметра в массиве S. Переменная CHAR всегда содержит текущую литеру из того вводного потока, с которым в данный момент мы работаем.
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
467
В сканере очень часто используется процедура GETCHAR. Она читает следующую литеру и посылает ее в CHAR. В зависимости от INPUT следующая литера берется или из исходной программы, или из тела макро, или из фактического параметра. В двух
ADD PI
9
1
17
NS
3.14159#a1+42+PI #
S (один элемент н<ъ лилперу)
2
MACNAME MACBODY NMAC
Рис. 19.6. Иллюстрация таблиц для PI и ADD.
последних случаях символ # указывает на то, что просмотр тела макро или фактического параметра закончен. Тогда GETCHAR обращается к процедуре SWITCHBACK, которая заставляет сканер вернуться к обработке литер предыдущего потока вводной информации. Позже в этом разделе мы рассмотрим эту процедуру. Если
RETURN (ВОЗВРАТ)
Рис. 19.7. Процедура GETCHAR.
мы просматриваем текст, не являющийся ни фактическим параметром, ни телом макро, то и знак # не должен встречаться. Если же он встретился, то выдается сообщений об ошибке. Переменная LBSIGN указывает на то, разрешается ли (LBSIGN = 1) или не разрешается (LBSIGN = 0) появление в текущем потоке #. На рис. 19.7 приводится общая блок-схема процедуры GETCHAR.
GETCHAR, встречая &, как видно на рис. 19.7, обращается также к программе FORMPAR, чтобы переключиться на новый вводной поток для чтения фактического параметра.
Нам потребуются еще две процедуры. Первая, GETNONBLANK, проверяет, не содержит ли CHAR пробел и, если содержит, то повторяет обращение к GETCHAR до тех пор, пока не появится литера, отличная от пробела.
468
ГЛАВА 19
Ко второй процедуре, BUILDID, обращаются, когда встречается буква в, тот момент, когда появление буквы означает начало служебного слова или идентификатора. BUILDID (с помощью GETCHAR) добирает остальные литеры идентификатора и посылает его в ID, после чего читает следующую литеру и осуществляет возврат.
Этих вводных сведений нам достаточно, чтобы написать процедуры для обработки макро. Процедура MACRODEF вызывается, когда сканер обнаружил слово MACRO. MACRODEF просматривает имя макро. Далее это имя и индекс, указывающий в S (место, куда затем будет пересылаться тело), записываются соответственно в MACNAME и MACBODY. После этого MACRODEF вызывает процедуру GETSTRING, которая пересылает тело макро в S. GETSTRING оформлена в виде отдельной процедуры, так как то же самое действие нам нужно будет делать при пересылке фактических параметров. Заметим, что эта программа устанавливает LBSIGN=0 для того, чтобы любое появление # вызывало выдачу сообщения об ошибке. Все макроопределение целиком должно приходить к нам из одного и того же вводного потока.
PROCEDURE MACRODEF INTEGER LB;
LB := LBSIGN; LBSIGN 0;
GETNONBLANK; BUILDID;
NMAC :=NMAC+1;
MACNAME (NMAC) ~ ID;
MACBODY (NMAC) : — NS+1;
GETNONBLANK;
IF CHAR # “[” THEN ERROR;
GETSTRING;
LBSIGN :=LB;
GETCHAR;
Сохранение значения LBSIGN и установка 0 в LBSIGN, запрещающего появление 4£-
Получение имени макро.
Посылка имени макро и индекса, указывающего на место в S для тела макро, в соответствующие таблицы. Проверка наличия [ после имени макро и вызов - программы пересылки тела макро в S. . х
Восстановление прежнего значения LBSIGN и получение следующей литеры.
Процедура GETSTRING пересылает.литеру за литерой из строки текущего вводного потока в массив S. При входе в нее CHAR содержит открывающую скобку, за которой следует первый символ строки. Заметим, что начальные пробелы также пересылаются. GETSTRING должна вести подсчет открывающих и закрывающих скобок, чтобы знать, когда остановиться. Для этой цели служит локальная переменная С.
Сейчас мы приступаем к рассмотрению того, как начинается обработка макровызова. Прежде всего нужно сохранить информацию о текущем потоке, таблицах макро и массиве S. Эта информация будет восстановлена в конце обработки макровызова. Посколь-
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
469
PROCEDURE GETSTRING
INTEGER С; C:= 1;
WHILE C#0 DO
BEGIN GETHAR;
NS := NS 4-1; S (NS) : = CHAR;
IF CHAR = “[” THEN C: = C+ 1;
IF CHAR THEN C:=C—I;
END;
S(NS)
Начальная установка счетчика уровней вложенности скобок.
Литеры просматриваются и пересылаются в массив S до тех пор, пока счетчик уровней вложенности скобок не станет нулевым.
В цикле мы послали в S и последнюю}, поэтому мы заменяем ее на zft.
ку в процессе расширения одного макровызова может встретиться другой макровызов, для хранения этой информации мы должны иметь стек. Для каждого макровызова мы используем несколько элементов стека CALLS, оформленного в виде массива (см. рис. 19.5). Формат информации для каждого вызова приводится на рис. 19.8, а.
старое значение LBSIGN старое значение INPUT старое значение NMAC старое значение NS к (число параметров) индекс k-го параметра в S
индекс 2-го параметра в S индекс 1-го параметра bS
старое значение LBSIGN старое значение INPUT старое значение NMAC старое значение NS
—1
а
для макровызовов
b для вызовов параметров
Рис. 19.8. Элементы стека CALLS.
Встречая идентификатор, сканер ищет его в таблице MACNAME, просматривая ее в обратном порядке, т. е. от последнего элемента к первому. Если идентификатор найден, то индекс, указывающий на найденное имя в MACNAME, передается процедуре MACROCALL в качестве фактического параметра. Процедура MACROCALL выполняет простую работу. Помимо манипуляций со стеком, она пересылает фактические параметры в S и начинает сканирование тела макро. В LBSIGN вновь устанавливается 0, так как весь макровызов должен прийти из того же вводного потока. MACROCALL(I) предполагает, что в I стоит индекс, указывающий на соответствующее имя в MACNAME.
470
ГЛАВА 19
PROCEDURE MACROCALL (I); INTEGER I; INTEGER LB, TEMP;
TEMP :=NS;
LB := LBSIGN; LBSIGN : = 0;
N := N+1; CALLS(N) : = 0;
GETNONBLANK;
IF CHAR = “[”
THEN WHILE CHAR ф “]” DO GETPARAM;
N :=N+1; CALLS(N) : = TEMP;
N := N +1; CALLS(N) NMAC;
N := N+1; CALLS(N) := INPUT;
N := N+l; CALLS(N) :== LB;
LBSIGN := 1;
INPUT := MACBODY(I);
CHAR := S(INPUT);
Сохранить указатель на текущий элемент S, чтобы потом можно было отбросить то, что сейчас будет посылаться в S.
Установить признак, что не Должен встречаться в макровызове.
Вначале число параметров равно нулю. Прочесть 1-ю отличную от пробела литеру.
Если в макровызове есть фактические параметры, то обращаемся к GETPARAM до тех пор, пока не перешлем их все в S.
Послать в стек старые значения индексов массивов S и MACDEF (после завершения макровызова мы их восстановим).
Послать в стек указатель текущего вводного потока и запомнить в стеке старый «способ реагирования» на Так как мы сейчас начинаем просматривать тело макро, то мы можем встретить
Переключить вводной поток на тело макро и получить первую литеру.
Следующая программа, GETPARAM, используется в процедуре MACROCALL для пересылки параметра из текущего вводного потока в S. Если параметр начинается с [, то для его пересылки используется программа GETSTRING, в противном случае GETPARAM пересылает параметр сама. Эта программа оформлена / в виде отдельной процедуры, чтобы несколько упростить вид процедуры MACROCALL. Но так как к GETPARAM обращаются в одном месте, этого можно было и не делать.
К программе FORMPAR обращаются из GETCHAR при обработке формального параметра &i. Заметим, что формальный параметр является в некотором роде макровызовом без параметров, и мы трактуем его именно так. Мы добавляем в стек CALLS еще один элемент в формате, приведенном на рис. 1,9.8. При входе в FORMPAR & уже прочитан в CHAR. Единственное отличие для вызова формального параметра состоит в том, что у него нет фактических параметров. Для того чтобы отличить его от настоящего макровызова в качестве первого элемента информации в стек CALLS (см. рис. 19.8,6) отправляется «—1». FORMPAR читает
РЕАЛИЗАЦИЯ МАКРОСРВДСТВ
471
PROCEDURE GETPARAM;
CALLS(N) : = CALLS(N)+1;
N := N +1;
CALLS(N) := CALLS(N-l);
CALLS(N-l) := NS+1;
GETNONBLANK;
IF CHAR = “[” THEN
BEGIN GETSTRING; GETCHAR;
GETNONBLANK;
IF CHAR OR CHAR #
THEN ERROR
END
ELSE
BEGIN
WHILE CHAR AND
CHAR £ “]”
DO BEGIN NS NS+1;
S(NS) := CHAR;
GETCHAR;
END;
NS := NS+1; S(NS) := # END
Добавить 1 к счетчику параметров. Оставить место в стеке для адреса параметра, послать адрес и прочесть первую литеру.
Если параметр начинается с [, то вызвать программу, • пересылающую строку, и получить следующую литеру, отличную от пробела. В конце параметра должна быть либо ], либо запятая.
Здесь осуществляется пересылка фактического параметра, не содержащего запятых или скобок.
Пересылать литеру за литерой в S, пока не встретится запятая или ], завершающие параметр.
Послать заключительный символ
PROCEDURE FORMPAR;
INTEGER TEMP; GETCHAR;
IF N —0 OR CALLS(N —4)<0 OR
CHAR не цифра OR
CHAR = “0” OR
CHAR > CALLS(N — 4)
THEN ERROR;
TEMP := CALLS(N — 4);
TEMP := N —5—TEMP + CHAR;
N :=N+1, CALLS(N) 1;
N :=N+ 1; CALLS(N) NS; .
N N +1; CALLS(N) : = NMAC;
N :=N + 1; CALLS(N) := INPUT;
N := N + l; CALLS(N) : = LBSIGN;
LBSIGN := 1;
INPUT : = CALLS (TEMP)—1;
Получить номер параметра в CHAR.
В данном месте должно происходить расширение макро, а не обрабатываться фактический параметр. В CHAR должен стоять номер фактического параметра в макровызове.
Получить в TEMP значение индекса, указывающего на элемент CALLS, который содержит адрес нужного нам параметра. Затем запомнить в стеке пять элементов информации, необходимой для вызова фактического параметра (см. рис. 19.8).
Разрешить появление в фактическом параметре.
Заменить вводной поток для чтения фактического параметра и выйти' из процедуры.
472
ГЛАВА 19
цифру, следующую за &, осуществляет некоторые проверки на правильность записи &i, засылает соответствующую информацию в стек CALLS, переключает вводной поток на фактический параметр и посылает первую литеру в CHAR.
Теперь нам осталось запрограммировать действия по завершению просмотра тела макро и фактического параметра. И то и другое можно выполнить в одной и той же программе, так как эти действия идентичны. Если GETCHAR обнаруживает #, стоящий в конце каждого тела или фактического параметра в S, то она обращается к процедуре SWITCHBACK. SWITCHBACK восстанавливает информацию, сохраненную в стеке в начале обработки вызова.
PROCEDURE SWITCHBACK;
LBSIGN := CALLS(N);
INPUT := CALLS(N-l);
NMAC := CALLS(N—2);
NS := CALLS(N—3);
N := N —5;
IF CALLS(N4-1) > 0
THEN N :=N—CALLS(N +1);
Восстановить старый «способ реагирования» на
Восстановить указатель вводного потока.
Эти два присваивания, по существу, выбрасывают макро и факт, параметры, добавленные во время обработки данного макровызова.
Освободиться от элементов стека, которые использовались в течение этого вызова. Если CALLS (N+l)>0, то выбросить из стека факт, парам.
УПРАЖНЕНИЯ К РАЗДЕЛУ 19.1
1. Ранее было сделано ограничение, запрещающее в фактическом параметре использовать формальный параметр &L Объясните смысл таких формальных параметров в предположении, что это ограничение снято. С каким фактическим параметром какого вызова нужно сопоставить такой формальный параметр?
2. Измените программы, описанные в этом разделе, чтобы снять ограничение, упомянутое в 1-м упражнении.
19.2. ДРУГИЕ СВОЙСТВА МАКРО
Системы для обработки построчных текстов и текстов с фиксированным форматом полей
В той частной схеме макро, которую мы описали, исходная программа рассматривалась как непрерывная последовательность литер. Многие языки, включая автокоды и ФОРТРАН, ориентируются на карты. Каждое предложение или инструкцию разрешается писать на отдельной карте. Для автокода макроопределение могло
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
473
бы выглядеть следующим образом: MACRO
PLUS &1,&2,&3
FETCH &1
ADD &2
STORE &3
END
где PLUS — имя макро, тело макро состоит из 3-го, 4-го и 5-го предложений, a END — признак конца тела макро. Макровызов
PLUS X.Y.Z
должен породить
FETCH X ADD Y STORE Z
Такая система макро для реализации может быть проще, так как имя макровызова всегда находится в фиксированном месте, в поле операции. Общая идея реализации та же самая. Макроопределения запоминаются в отдельной области, и когда встречается макровызов, то он заменяется на тело макро с подставленными фактическими параметрами вместо формальных параметров.
Внутреннее представление макроопределения
Если макроопределение уже существует, то намного выгоднее хранить его тело в некотором внутреннем представлении, а не в первоначальном текстовом виде. При первом сканировании макроопределения оно только один раз транслируется во внутреннее представление, после чего процесс расширения макровызова проходит намного быстрее и проще. Внутреннее представление приведенного выше макроопределения PLUS могло бы быть следующим:
Тайтеца. аеяа. MMftxmjeiuemx
КАРТА СТРОКА ПОЛЕ ОПЕРАНДА ПАРАМЕТР КАРТА СТРОКА ПОЛЕ ОПЕРАНДА ПАРАМЕТР КАРТА СТРОКА ПОЛЕ ОПЕРАНДА ПАРАМЕТР КОНЕЦ ТЕЛА W- Ш СЧгО C4WW ю
474
ГЛАВА 19
Здесь в первом столбце таблицы стоят числа, обозначающие: «начало новой карты», «строка литер, не имеющая формальных параметров внутри себя», «начало поля операндов», «формальный параметр» и «макровызов». Во втором столбце помещается информация типа номера карты, количества литер в строке или номера формального параметра. Третий столбец используется в случае строки для ссылки в отдельную таблицу, где содержится фактическая строка литер.
Такое внутреннее представление много легче для обработки, так как лишние пробелы выброшены и всевозможные варианты уже рассмотрены и отсортированы. Процесс расширения макровызова есть интерпретация, во многом похожая на интерпретацию, которая обсуждалась в гл. 16. Внутренним представлением, которое нужно интерпретировать, является тело макроопределения.
Теперь мы кратко рассмотрим стандартные макровозможности, которые требуют использования переменных «времени макрогенерации», временных переменных й т. п. При этом процесс макрогенерации становится еще более похожим на интерпретацию, рассмотренную в главе 16.
Генерируемые символы
При употреблении меток в теле макроопределения, аналогичных приведенному ниже, возникают трудности.
MACRO
GREATER &1,&2,&3
FETCH &1
SUBTRACT &2 GOIFMINUS Z &3
Z: END
Каждый раз при макровызове мы генерируем метку Z, а это вызывает многократное определение Z. Большинство ассемблеров с макровозможностями решают эту проблему, тем что позволяют генерировать некоторым способом переменные. Согласно одному из способов, имя каждой переменной, которую нужно сделать уникальной, должно начинаться парой литер &&. Встречая такое имя, система генерирует переменную, отличающуюся от всех остальных. Другие системы имеют специальный системный параметр, например &MACNUM. Значением этого параметра на протяжении всего ассемблирования является номер текущего макровызова, хранящийся в виде строки литер. В макроопределениях он используется в соединении с переменной. Например, в приве-
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ -
475
денном ставить выше макроопределении GREATER мы могли бы пред-в следующем виде: MACRO GREATER &1,&2,&3 FETCH &1 SUBTRACT &2 GOIFMINUS Z&MACNUM &3 Z&MACNUM: END
Для макровызовов GREATER А,В,«STORE В»
GREATER В,A,«STORE А»
если они первыми из макровызовов встречаются в исходной программе, в результате должно получиться
FETCH А SUBTRACT В GOIFMINUS Z1 STORE В
Zl: FETCH В
SUBTRACT А GOIFMINUS Z2 STORE А Z2:
Переменные «времени макрогенерации».
Очень часто во время макрообработки бывает полезно сделать некоторые вычисления. При этом, как правило, требуются переменные для хранения результатов вычислений. Язык ассемблера для OS 360 позволяет писать в макроопределениях предложения вида
LCLA
LCLC &Y
которые определяют &Х и &Y, как локальные переменные в макроопределении арифметического и текстового типа соответственно. Следующее предложение вида
&Х SETA &Х + 1
осуществляет добавление 1 к &Х каждый раз, когда оно просматривается и выполняется. В дальнейшем мы увидим, как эти возможности реализуются в PL/I,
476
ГЛАВА 19
Условная макрогенерация
Часто во время макрообработки бывает удобно блокировать генерацию некоторых предложений или генерировать разные предложения в зависимости от тех или иных фактических параметров. Например, пусть мы хотим чтобы макро PLUS порождало
FETCH ADD STORE А В С
для макровызова PLUS A,B,C
и порождало ADD1 A
для макровызова PLUS A,1,A
где ADD1 специальная операция прибавления к ячейке 1. Нам
нужно некоторым способом сообщить препроцессору, чтобы он при генерации обошел некоторые команды. В некоторых системах перед командой ставится специальный признак, указывающий на то, что эта команда должна быть выполнена препроцессором. Например, макроопределение PLUS можно было бы записать следующим образом:
MACRO (1)
PLUS &L&2.&3 (2)
LCLB &X (3)
&х SETB (&1 NE&3) (4)
%GOIF &X,°/oZ (5)
&х SETB (&2 NE '1') (6)
%GOIF &X,°/oZ (7)
ADD1 &1 (8)
% GO %Y (9)
%Z % NULL (10)
FETCH &1 (11)
ADD &2 (12)
STORE &3 (13)
%Y % NULL (14)
END (15)
Предположим, что произошло макрообращение. Тогда просматривается тело макро. В строке 3 вводится локальная переменная
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ 477
&Х типа BOOLEAN. (LCLB является сокращением от local Boolean.) Затем в строке 4 сравнивается строка литер, составляющая первый фактический параметр, со строкой литер, составляющей третий фактический параметр. Если они не совпадают, то &Х присваивается значение TRUE, в противном случае — FALSE. В строке 5 проверяется &Х и осуществляется переход на %Z в случае TRUE. В %Z «выполняется» пустое предложение, после чего выдаются строки с 11 по 13. Если &Х в строке 5 имеет значение FALSE, то интерпретируются строки с 6 по 9.
Средства времени компиляции в PL/1
В языке PL/1 предусмотрены так называемые «Средства времени компиляции» (см. IBM (с)), большинство из которых относится к макропроцессору. Рассмотрим кратко эти средства. Рамки этой книги не дают нам возможности описать их детально.
Первый просмотр исходной программы в компиляторе с PL/1 осуществляется препроцессором, который и выполняет всю макрообработку. Мы будем говорить, что эта обработка ведется в препро-цессорное время. Части программы по мере их обработки препроцессором посылаются в некоторый буфер вывода для дальнейшего просмотра компилятором. Если никакой макрообработки не было задано, то вся программа просто копируется в буфер в неизменном виде.
В PL/1 нет макроопределений, как таковых. Но знак процента (%) перед инструкцией указывает на то, что эта инструкция должна быть выполнена в препроцессорное время, а не во время работы готовой программы. Только некоторые инструкции могут начинаться с %. Среди них DECLARE, DO, END, GOTO, IF, PROCEDURE и NULL (пустая инструкция). Ближе всего к макроопределению стоит процедура, которой предшествует %. Всякий раз, когда обнаруживается имя такой процедуры, она выполняется в препроцессорное время, в результате чего вызов заменяется результирующей строкой литер.
Поясним общую идею препроцессора на небольшом примере. Предположим, мы имеем
DECLARE I FIXFD;
DO 1 = 1 ТО 5;
A(I) = B(I)*C(I);
END;
Это обычный сегмент программы на PL/1, который просто копируется. В результате компиляции будет получен соответствующий
478
ГЛАВА 19
цикл. Однако
% DECLARE I FIXED;
%DO 1 = 1 ТО 5;
A (I) — В (I)« С (I);
% END;
порождает совершенно другую программу. Во-первых, I — пре-процессорная переменная, так как ее описанию предшествует %, и она никогда не появится на выходе препроцессора. Во-вторых, этот цикл выполняется в препроцессор ное время. Каждое исполнение цикла вызывает просмотр и выдачу предложения А(1) = =В(1)*С(1) с подставленным вместо I его текущим значением. Таким образом, на компиляцию пойдет следующий фрагмент программы
А (1)==В(1)*С(1);
А (2) = В (2) *С (2);
А(3) = В(3)*С(3);
А (4) = В (4)»С (4);
А (5) = В (5)* С (5);
Таким образом, этот цикл был расширен препроцессором. В этом примере I играет роль своего рода имени макро, телом которого является текущее значение I.
Вторым типом макроопределения является слово PROCEDURE с предшествующим ему % . Эта спецификация означает, что каждый раз, когда препроцессор встречает вызов такой процедуры, он должен немедленно ее выполнить. В результате вызов процедуры заменяется на полученную последовательность литер. На первый взгляд все вроде бы хорошо. Однако обычные предложения (типа рассмотренных выше А(1)=В(1)*С(1)) для копирования не допускаются в препроцессорной процедуре, так как препроцессорные предложения должны выполняться немедленно. Таким образом, для вывода допускаются только те строки, которые были полностью построены в препроцессорное время.
Препроцессор является интерпретатором. В первой фазе он просматривает исходную программу и транслирует препроцессорные предложения в некоторое внутреннее представление. Обычные инструкции PL/1 могут быть оставлены в их первоначальном виде. Затем во второй фазе интерпретируется информация, полученная в первой фазе, подобно тому как это описывалось в 16-й главе. Каждый раз, когда в процессе интерпретации встречаются обычные предложения PL/1, они выдаются, все препроцессорные переменные при этом заменяются их текущими значениями.
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
479
19.3. УНИВЕРСАЛЬНЫЙ МАКРОГЕНЕРАТОР GPM
GPM (General Purpose Macro Generator) — это макросистема, созданная Стречи [65], как инструмент для написания компилятора с CPL, языка типа АЛГОЛ, используемого в Математической лаборатории Кембриджского университета Англии. GPM обладает большей гибкостью, чем система, описанная в разд. 19.1, и в самом деле, эта система позволяет делать несколько весьма поразительных вещей. Мы не будем описывать реализацию этой системы, мы только укажем на некоторые трудные места ее реализации. Реализация этой системы должна бы быть интересной задачей для читателя (упражнение 1).
Макровызов
В GPM макровызов имеет вид
# <имя макро>; или
# <имя макро>, <пар>, <пар>, .... <пар>;
где <пар> — фактический параметр. Макровызовы для PI и ADD (рис. 19.3) в GPM можно написать в виде
#ADD, 2# Pl; *3;
Как и в системе, описанной в разд. 19.1, с именем макро с помощью макроопределения должно быть связано тело макро. Это тело в общем случае содержит формальные параметры &1, &2, ..., &9, вместо которых во время расширения подставляются фактические параметры. Кроме этого, добавляется еще один формальный параметр &0, вместо которого подставляется само имя макро. Пусть с именем макро PLUS связано тело
А:=&1 + &2 + &0
Тогда макровызов # PLUS, 2*Х, 5 породит
А := 2»X+54-PLUS
Заключение строки в специальные угловые скобки <и> запрещает вычисление строки — она просто копируется с отбрасыванием скобок. При этом становится возможным включить в выводной поток любой символ, кроме угловой скобки, не имеющей соответствующей парной. Например, для макровызова
# PLUS, В (1< ,>2), 5; получится А:= В (1,2)+ 5 +PLUS тогда как для
# PLUS, В(1,2), 5; будет А: = В (1 4-2)4-PLUS
Во втором случае параметр 5 в вычислениях не участвует.
480
ГЛАВА 19
Если обработка макровызова завершена, то все его фактические параметры и все макроопределения, вычисленные по ходу обработки данного макровызова, выбрасываются. Таким образом, как и в выше описанной схеме, мы можем иметь локализованные макроопределения.
Макроопределение
Возможность введения макроопределений обеспечивается специальным системным макро DEF. В обращении к DEF необходимо задать два фактических параметра — имя макро и соответствующее тело. Таким образом, для PI и ADD (рис. 19.3) мы должны написать следующие определения:
#DEF, Р, <3.14159>; и # DEF, ADD, <&1 +&2 + #Р1;>;
Подчеркнем еще раз, что макроопределение представляет собой лишь вызов другого макро. Позже мы увидим, какие новые возможности мы при этом получаем.
Расширение макро
На первый взгляд GPM выглядит так же, как простая схема макрогенерации, описанная в разд. 19.1, и отличается только несколько измененной записью. До некоторой степени это верно, и для простых макровызовов средний программист будет получать одинаковый результат на обеих системах. Однако главное различие, о чем мы еще не говорили, состоит в том, как расширяются макровызовы и какими могут быть фактические параметры. Общность системы GPM делает ее намного более гибкой и мощной. Давайте же рассмотрим алгоритм макрогенерации. Алгоритм может показаться довольно бесхитростным, если не приглядываться к нему внимательно. После описания алгоритма мы остановимся на некоторых его свойствах, которые, как правило, упускаются.
Вводной поток просматривается слева направо и копируется . на выводной поток, пока не встретился макровызов (напомним, что макроопределения — это тоже макровызовы специального макро DEF). Макровызов вычисляется. Результат вызова копируется в выводной поток, замещая при этом сам макровызов, после чего возобновляется просмотр предыдущего вводного потока. Макровызов вычисляется следующим образом:
1. Вычисляются имя макро и фактические параметры в том порядке, как они записаны. Результаты вычислений запоминаются где-то на стороне. (Если во время вычисления имени или параметра встречается макровызов, то последний также сразу вычисляется. Таким образом, обработка макровызова — рекурсивный процесс.)
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
481
2. Просматривается таблица макроопределений начиная с последнего элемента и продвигаясь к первому, который содержит системное макро DEF. При этом ищется элемент с именем, совпадающим с именем макровызова. Если такой элемент найти не удается, печатается сообщение об ошибке.
3. Тело макро, найденное при выполнении шага 2, просматривается тем же способом, что и первоначальный вводной поток. То есть любой макровызов будет расширяться сразу. Если встречается формальный параметр &i (i=0, 1, 2, 9), то вместо него под-
ставляется точная копия результата вычисления i-ro фактического параметра вызова, полученного на шаге 1. Заметим, что вместо &0 подставляется имя макро. Если i больше числа предоставленных вызовом параметров, то выдается ошибка. Обратите внимание, пожалуйста, что фактический параметр повторно не вычисляется, он только копируется без каких-либо вызовов макро при данной обработке. Выходная информация этого просмотра и является результатом макровызова.
4. По окончании обработки макровызова вычисленные ранее фактические параметры и все макроопределения, добавленные во время выполнения 1-го и 3-го шагов, выбрасываются.
5. Возобновляется просмотр предыдущего вводного потока с литеры, следующей за последней точкой с запятой данного макровызова.
Для системного макро DEF 3-й шаг работает по-другому. При этом никакое тело макро не просматривается, а первые два из вычисленных фактических параметров вызова DEF посылаются в таблицу макроопределений соответственно в качестве имени и тела макро.
Замечания к алгоритму расширения макро
Прежде всего заметим, что поскольку макроопределение есть просто вызов макро DEF, именем макро может быть не только простой идентификатор, но и любая строка литер, причем впереди и сзади строки могут стоять пробелы. В этой системе пробел, по существу, выступает как обычная литера.
Во-вторых, имя макро и фактические параметры вычисляются перед просмотром тела и даже перед поиском имени макро в таблице макроопределений. Если проводить аналогию с параметрами ал-гольных процедур, то фактические параметры в этой системе больше соответствуют параметрам, вызываемым по значению, а параметры в системе, описанной в разделе 19.1, ближе к параметрам, вызываемым по наименованию. Чтобы понять, какие удивительные последствия это может иметь, рассмотрим следующий макровызов:
# A,X,Y,# DEF,А,В;;
16 Д. Грио
482
ГЛАВА 19
То есть мы вызываем макро А с фактическими параметрами X, Y и #DEF, А, В;. Вначале мы вычисляем фактические параметры. Вычисляем X (получаем X), Y (получаем Y) и макроопределение #DEF, А, В;. В результате вычисления последнего параметра в таблицу макроопределений добавится макро А с телом В. Далее в таблице макроопределений мы ищем самое позднее макро с именем А. Это будет только что добавленное макроопределение! Значит, результатом вызова является просто литера В. Заметьте, что мы не обращались ни к одному из предыдущих макроопределений А.
Этот способ задания макроопределения в фактическом параметре можно использовать для получения своего рода условного выражения. Мы можем написать макро, являющееся эквивалентом записи
IF х=у THEN w ELSE v
где х, у, v и w —строки литер. В GPM это выглядит так:
# х, # DEF, х, <v>; # DEF, у, <w>;;
Вычисление этого вызова прежде всего порождает определение двух макро х и у с телами соответственно v и w (вычисление <v> и <w> приведет к снятию скобок и простому копированию цепочек v и w). Далее в таблице макроопределений ищется макро с именем х. Если х равно у, то в результате мы получим тело w, в противном случае у. Заметим, что в этом примере имя макро х встречается в вызове до того, как оно определено. Заметим также, что фактические параметры для х никогда не вызываются через формальные параметры. Единственная их задача — определить макро хиу. Сейчас это может казаться бесполезным, но позже мы покажем, как этим можно воспользоваться.
Другое интересное свойство состоит в том, что само имя макро может содержать формальные параметры и/или макровызовы. Предположим, что мы имеем макро PI с телом 3.14159. Тогда макровызов
#DEF, # PI; +1, 4.14159;
породит макро с именем 3.14159+1 и телом 4.14159.
В своей работе Стречи среди прочих примеров рассматривает следующий:
#DEF, SUC, <# 1,2,3,4,5,6,7,8,9,10, # DEF, 1,<&>&!;;>;
Это определение макро SUC с телом
# 1,2,3,4,5,6,7,8,9,10, #DEF, 1, <&> &1;;
Предположим, что мы имеем макровызов #SUC, 2;. При просмотре тела макро мы сразу же обнаруживаем макровызов с именем 1 и с параметрами 2, 3, 4, 5, 6, 7, 8, 9, 10 и #DEF,1 ,<&>&1;. Это приводит прежде всего к определению макро 1 с телом &2.
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
483
(Заметим, что скобки вокруг & пропадут, а вместо &1 подставится первый фактический параметр SUC, что приведет к &2). Затем вызывается макро 1. Его тело — &2, и после подстановки второго фактического параметра в результате получится 3.
В общем случае вызов # SUC, г; дает в результате г+1 для r=0,1,2,... , 9. Таким образом, макро SUC отыскивает следующий элемент (Successor) среди цифр.
Используя метод, с помощью которого мы получили выше условное выражение, можно построить макро SUCCESSOR, которое будет давать следующий элемент для чисел из двух цифр. Например, # SUCCESSOR, 2, 3; даст 2, 4, a ^SUCCESSOR, 2, 9; даст 3, 0. Тело макро для SUCCESSOR следующее:
#&2,#DEF,&2,&1«,>#SUC,>&2<;>;#DEF,
9,<#SUC,>&l<;<,>0>;;
Давайте получим макрорасширение для вызова # SUCCESSOR, i, j; где i и j цифры. В вычислении фактических параметров i и j нет макровызовов. Просматривая тело макро, мы встречаем вызов макро с именем j (второй фактический параметр). Вычисление его единственного фактического параметра приводит сначала к определению макро
j с телом i < , > # SUC, j;
и затем второго макро
9 с телом #SUC, i; < , > 0
Здесь-то и используется метод условного выражения. Мы ищем макро j, к которому мы сейчас обращаемся. Если j не равно 9, то мы используем макро j с телом i<,> #SUC, j;. Просматривая его, в результате получаем
i, к, где k=j+l.
Если j равно 9, то используется макро 9 с телом # SUC, i; <(>0, что приводит к
п, 0,. где n—i+1
Таким образом, ^SUCCESSOR,2,3 есть 2,4, ^SUCCESSOR, 2,9 есть 3, 0, a #SUCCESSOR,9,9 есть 10,0.
В последнем примере демонстрируются почти все возможности GPM: использование формального параметра в качестве имени макро; использование специальных скобок, чтобы заблокировать вычисление строки литер до момента, пока мы не пожелаем ее вычислить; использование локализованных макроопределений; использование обращения к макро, которое вначале еще не определено, и использование условных выражений.
16»
484
ГЛАВА 19
Обсуждение
Если литеры # и & , а также запятая и точка с запятой не встречаются в языке программирования х), то GPM можно использовать в качестве препроцессора для этого языка. Фактически именно так обстояло дело в отношении автокода для машины Titan (Atlas 2), на которой впервые был реализован GPM. (Правда, там применялись несколько другие символы.) Синтаксис GPM довольно ограничен, но благодаря этому его удается реализовать достаточно просто, что и описано Стречи.
Правомерен вопрос о практической ценности приведенных ранее примеров SUC и SUCCESSOR. Я сомневаюсь, что они могли бы быть использованы в какой-либо программе, зато они очень хорошо иллюстрируют возможности GPM. Практичность системы, подобной GPM, подтверждается ее фактическим использованием при написании компилятора на языке ассемблера. Реальный макропроцессор работает очень медленно, но это относится к любому достаточно сложному макропроцессору, предназначенному для универсальной обработки последовательности литер. Сам просмотр и подстановка «литера за литерой» отнимает много времени.
УПРАЖНЕНИЯ К РАЗДЕЛУ 19.3
1. Описать реализацию GPM в виде блок-схем.
2. Реализовать GPM.
19.4. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Первая реализация макрогенератора, как части ассемблера, относится к концу 60-х годов. Гринволд [59] кратко описывает использование макро для системы SHARE 709 для IBM 709 (см. также Гринволд и Кейн [59]). Как большинство языков типа автокодов, эта система ориентирована на построчную обработку текста программы. Макилрой [60] сильно расширил использование макро. В его работе рассказывается об условных макро, генерируемых переменных, об использовании списковых параметров (подсписков в списке параметров), о вложенных друг в друга макроопределениях и макровызовах. Работа Кента [69] представляет собой хороший учебник по вопросам использования макро.
Использование макро для языка высокого уровня в целях расширения этого языка впервые рассматривалось Макилроем [60]. Таким образом, сама идея не нова. Реализация АЛГОЛа на машине В5500 допускает чистую текстовую подстановку без параметров.
х) А также <и>.— Прим, перев.
РЕАЛИЗАЦИЯ МАКРОСРЕДСТВ
485
Язык FORTRAN II имел специальный тип макро с параметрами. Например, можно было бы объявить
FUNCTION F(A, B)=A*B*SIN(A)
Тогда, если написать
Q := F(2*G,H)
то компилируется на самом деле предложение вида
Q : = 2*G*H*SIN(2*G)
В разд. 19.2 показано, как некоторые макровозможности можно получить в PL/1. Инструкции времени компиляции и обычные инструкции PL/1 пишутся одинаково и отличаются лишь знаком процента впереди. Таким образом, здесь макросредства и сам язык очень тесно связаны между собой. Можно также иметь макросредства, которые полностью не зависят от языка, для которого они используются, типа GPM Стречи. Макилрой [60] приписывает эту идею Перлису. Первой работой, описывающей такой макропроцессор, является работа Стречи [65]. С тех пор разработано несколько независимых макропроцессоров — TRAC (Муерс и Дойч [65]), LIMP Вейта [67] и макропроцессор ML/1 Брауна [67]. Макропроцессор ML/1, по существу, действует по ключу, с которого начинается макровызов, но он позволяет пользователю самому определять разделители между фактическими параметрами и символ, обозначающий конец макровызова. В системе Вейта ключ не обязателен (но может использоваться). Он использует общую схему «распознавания по образцу» для обнаружения макровызова.
Халперн [64, 67 и 68] предлагает использовать развитую макросистему над автокодом в качестве основы для языка высокого уровня. Каждая программа на языке высокого уровня на самом деле является программой на автокоде. То есть каждое предложение исходного языка есть обращение к макро, определенному на автокоде. Например,
DO 10 1 = 1, N
является макровызовом для макро DO с параметрами I, 1 и N, а знак «=» и запятая являются разделителями фактических параметров.
Хотя такая система достаточно хороша для реализации некоторых языков, она остается ориентированной на построчные тексты, так как в основе лежит автокод. Возникают также трудности в реализации структур вложенных блоков алгольного типа, условных инструкций и т. п.
Более подробный обзор макропроцессоров можно найти у Брауна [69].
Глава 20
Системы построения трансляторов
20.1. ВВЕДЕНИЕ
Система построения трансляторов (СПТ)—это такая программа или набор программ, которые помогают составлять трансляторы — компиляторы, интерпретаторы, ассемблеры и т. п. Согласно этому определению, к СПТ можно отнести компилятор для продукционного языка (см. гл. 7) или конструктор алгоритма автоматического разбора. Поскольку цель СПТ — упростить задачу реализации трансляторов, то в связи с этим СПТ будет содержать конструкции (примитивы) для таких операций, которые должны выполнять большинство трансляторов.
Значительная часть работ по СПТ была направлена в основном на решение проблемы построения компиляторов. Для системы такого типа был принят термин компилятор компиляторов (КК) (см. статьи Брукера, Морриса и Рола [62], а также Брукера и др. [63]). Термин возник потому, что СПТ, разработанная для построения компиляторов, представляет собой программу, которая компилирует другие компиляторы. По аналогии, ассемблер для автокода, на котором написан компилятор, следовало бы называть ассемблером компиляторов, но мы так не говорим.
Далее, мы кратко опишем, что представляют собой большинство СПТ, и приведем их обычную классификацию. Затем мы остановимся на двух КК и опишем более подробно, как они работают. Эту главу не следует рассматривать как обзор СПТ, это всего лишь краткое знакомство с ними. Мы отсылаем читателя к работе Фелдмана и Гриса [68], которая содержит обзор и обширный библиографический материал по этой теме.
Компилятор, написанный с применением СПТ, почти наверняка потребует больше памяти и будет работать медленнее, чем аналогичный компилятор, написанный на автокоде. Так, например, Брукер, Моррис и Рол [67] смогли сократить размер компилятора в 1,6 раза и время работы в 1,7 раза благодаря тому, что переписали компилятор на автокоде. Тем не менее в конечном счете языки высокого уровня и СПТ, безусловно, заменят автокод как инструмент для написания компиляторов, точно так же, как языки высокого уровня заменили автокод в большинстве научных применений.
СИСТЕМЫ ПОСТРОЕНИЯ ТРАНСЛЯТОРОВ
487
Используя язык высокого уровня, гораздо легче сосредоточить внимание на том, что должен делать компилятор, поскольку при этом не приходится думать о многочисленных деталях программирования. Так, например, Лоури "и Медлок [69] высказали сомнение по поводу того, что они смогли бы осуществить все планы по оптимизации программы в компиляторе IBM FORTRAN IV уровня Н, если бы он был написан на автокоде, а не на ФОРТРАНе.
Общая схема СПТ
В большинстве СПТ имеются, по крайней мере, две следующие компоненты:
1. Язык для описания синтаксиса данных (исходных программ), которые должны транслироваться.
СИНТАКСИС L СЕМАНТИКА L
Часть метакомпилятора
СПТ
Транслятор для
L
Описание L
Рис. 20.1. Структура СЫТ.
2. Язык, на котором пишутся семантические программы. Это процедурный язык, такой, как автокод, АЛГОЛ, ФОРТРАН и т. д.
Транслятор состоит из описания синтаксиса и набора семантических программ. Как изображено на рис. 20.1, оба описания сначала переводятся при помощи СПТ на язык машины или в некоторую внутреннюю форму. Такая обработка описаний происходит во время метакомпиляции. Затем может выполняться полученный транслятор; это происходит во время компиляции. Результирующий транслятор выполняется под управлением синтаксического описания и исходной программы, которую он транслирует; семантические программы выполняются, как только распознаются соответствующие им синтаксические конструкции.
Значительную часть в СПТ составляет набор базисных подпрограмм, которые любой транслятор будет использовать автоматически (см. рис. 20.1). Этот набор во многих отношениях эквивалентен обычной библиотеке подпрограмм ввода-вывода, математических
488
ГЛАВА 20
функций и других стандартных программ, которые используются в алгебраическом языке. Но в данном случае программ больше, да и выполняют они другие функции, а именно те, которые необходимы в трансляторах.
Та часть СПТ, которая компилирует синтаксические описания, называется конструктором; мы уже определили этот термин в главах о синтаксисе. Входная информация обычно имеет вид, подобный НФБ, и результатом работы конструктора будет либо алгоритм разбора в виде программы, которая затем выполняется или интерпретируется, либо набор таблиц, которые при выполнении разбора используются библиотечными базисными программами.
Заметим, что на рис. 20.1 встречается термин «семантика исходного языка L». Он может ввести в заблуждение (хотя в ряде описаний СПТ этот термин используется), так как это не описание семантики в том же смысле, как описание синтаксиса, и не то описание, которое пользователь может прочесть, чтобы понять семантику языка L. Это всего лишь набор написанных на процедурном языке семантических программ, которые выполняют семантический анализ исходной программы и транслируют исходную программу в другую форму. В семантическом языке обычно имеются стандартные конструкции, которые есть и в других процедурных языках:
1. Типы данных: REAL, INTEGER, BOOLEAN, STRING.
2. Простые переменные, массивы, таблицы, возможно, структуры (записи).
3. Присваивания, условные инструкции и циклы.
4. Инструкции ввода-вывода.
Кроме того, в нем могут быть и другие конструкции, которые полезны при составлении компиляторов: указательные переменные, стеки, примитивы для занесения в таблицу и поиска по таблицам, примитивы для генерации команд и т. д.
Большинство СПТ позволяют разрабатывать лишь однопроходные компиляторы. Не следует думать, что это принципиальное ограничение; это только свидетельство того, что большинство СПТ носили экспериментальный характер и разрабатывались для проверки некоторых понятий и принципов. Есть несколько и многопроходных СПТ; в качестве примеров можно указать работу Читэма и систему AED (см. Росс [67а] и Джонсон и др. [68]).
Классификация СПТ
Одну группу СПТ образуют компиляторы компиляторов. Они предназначены для разработки компиляторов, и поэтому содержат примитивы, которые облегчают оптимизацию программы, распределение памяти и т. д.
СИСТЕМЫ ПОСТРОЕНИЯ ТРАНСЛЯТОРОВ
489
Вторая группа СПТ — это синтаксически ориентированные символьные процессоры. Они являются более общими и используются в таких задачах, как упрощение алгебраических выражений, символьное дифференцирование, трансляция с одного языка высокого уровня на другой и преобразование данных из одного формата в другой. Символьные процессоры используются и при построении компиляторов, но результатом работы такого процессора обычно является текст на автокоде, который необходимо еще раз транслировать. Как правило, их применение оправдано в тех случаях, когда структура входной информации несет основную содержательную нагрузку и когда эта структура может быть описана в терминах, близких к НФБ.
К третьей группе относится множество расширяющихся языков, т. е. таких языков, которые позволяют определять новые типы данных и новые операторы в терминах существующих конструкций. Это означает, что программист может расширить или изменить язык и тем самым приспособить его к своим нуждам. Существует несколько языков, которые допускают ограниченное расширение. Например, MAD позволяет определять новые инфиксные операторы. Истинно расширяющиеся языки позволяют добавлять новые инструкции или операции с почти произвольным синтаксисом. Такие расширения связаны с идеей макрокоманд в языках высокого уровня, которая вкратце обсуждалась в гл. 19. Компилятор Брукера и Морриса, описанный кратко в следующем разделе, можно использовать как расширяющийся компилятор, а также и как компилятор компиляторов.
20.2. ОБСУЖДЕНИЕ ДВУХ КОМПИЛЯТОРОВ КОМПИЛЯТОРОВ
Языки, подобные ФСЯ
ФСЯ (Формальный Семантический Язык) Фелдмана [661 — это система построения компиляторов, которая была реализована на машине G-20 в Университете Карнеги — Меллон и на машине ТХ-2 в Линкольновской лаборатории (МТИ). В ФСЯ имеются средства для определения сканера, очень похожие на описанные в разд. 3.4, а также продукционный язык (ПЯ, см. гл. 7) для определения синтаксиса исходного языка.
Во время компиляции синтаксический анализатор, представленный в форме программы на ПЯ, использует стек S для хранения символов. Другой параллельный семантический стек программист может использовать для хранения семантики синтаксических символов, находящихся в S. Семантическая программа, вызванная в некоторой продукции, обращается к семантическому стеку следующим образом: LI, L2, ... , L5 являются ссылками соответственно
490 ГЛАВА 20
на верхний (первый), второй, ... , пятый элементы семантического стека, если имеется в виду конфигурация стека в тот момент, когда произошло сопоставление с продукцией, но еще не было произведено преобразования стека. Точно так же Rl, R2, ... , R5 являются ссылками на элементы семантического стека, если имеется в виду конфигурация стека, которая получилась после его преобразования.
Поясним это на примере. Если в продукции
El + T ANY-^ЕЗ ANY EXEC 5
произошло сопоставление, то в семантической программе 5 L2 и L4 будут ссылками соответственно на семантику Т и Е1, тогда как R2 будет ссылкой на семантику Е2.
Основное достоинство ФСЯ заключено в механизме генерации команд, использованном в семантическом языке, который мы теперь обсудим. Напомним читателю, что мы не собираемся обсуждать сам ФСЯ; поэтому изменим обозначения и некоторые несущественные особенности, чтобы приблизить семантический язык к нестандартному АЛГОЛу.
Чтобы описать переменные готовой программы в терминах машины, для которой генерируются команды, введем новый тип данных семантического языка DESCRIPTOR (семантическое слово). В каждом компиляторе, написанном на ФСЯ, используется набор общих программ генерации команд, которые в свою очередь используют дескрипторы (значения типа DESCRIPTOR) для описания переменных в готовой программе. Эти программы генерации команд мало чем отличаются от соответствующих программ, реализованных в обычных компиляторах; они должны быть только несколько более общими.
Значение типа DESCRIPTOR состоит из нескольких компонент. Первые две, которым ниже будут даны имена, обычно заполняются разработчиком компилятора при первоначальном описании переменной. Остальные, у которых не будет имен, поскольку нам не придется ссылаться на них, изменяются и используются главным образом самой системой генерации команд, а не разработчиком компилятора. Компоненты дескриптора включают:
1. ADDRESS — целое число, задающее адрес переменной в готовой программе.
2. TYPE — целое число, задающее тип переменной в терминах машины, для которой генерируются команды (например, 1 =Р1ХЕП=число с фиксированной точкой, 2=FLOAT= число с плавающей точкой, 3=В1Т5=слово, состоящее из двоичных разрядов или целое число без знака).
3. Поле, которое определяет косвенную адресацию.
4. Поля, которые указывают, есть ли у переменной индексы или нет и если есть, то что является ее индексом.
СИСТЕМЫ ПОСТРОЕНИЯ ТРАНСЛЯТОРОВ
491
5. Поле, которое указывает, потребуется ли во время выполнения программы отрицательное значение этой переменной. (Используется при локальной оптимизации программы.) _ 6. Поля, которые указывают, находится ли описываемое значение в данный момент в сумматоре или в регистре и если находится в регистре, то в каком, и т. д.
Все поля, кроме первых двух, необходимы во время генерации команд, чтобы описать то «состояние» машины, которое будет во время выполнения готовой программы. Точное описание этих полей зависит от машины, для которой генерируются команды, а также от конкретной реализации системы генерации объектного кода.
Для того чтобы показать как дескриптор используется при генерации команд, рассмотрим семантические программы для обработки описания, идентификатора и операции умножения в каком-нибудь обычном языке, не имеющем блочной структуры. Вот правила, которые нам потребуются:
<опис> REAL <список ид>
(20.2.1) <список ид> I | <список ид>, I
F I
Т T*F
Этим правилам соответствуют продукции на ПЯ’.
LDEC: REAL —> ЕХЕС 1 SCAN GO LID
LID: <список ид>, I -> <список ид> ЕХЕС2 SCAN SCAN GO LID
I <список ид> EXEC 2 SCAN SCAN GO LID
(20.2.2) •
LF: I ANY F ANY EXEC 3 GO LT
LT: T*F ANY Т ANY EXEC 4 GO LT1
Семантическая программа 1 вызывается в продукции LDEC. Единственная ее функция — присвоить глобальной переменной Т значение, соответствующее типу идентификаторов в списке. Подобные программы должны также существовать для INTEGER, BOOLEAN и т. д.
1: Т : = FLOAT; FLOAT—переменная, значение кото-
рой имеет смысл ЧИСЛО С ПЛАВАЮЩЕЙ точкой.
Семантическая программа 2 вызывается тогда, когда верхним в стеке будет описываемый идентификатор. Ссылкой на этот идентификатор будет L1. Будем считать, что в компиляторе используется таблица символов SYMB. Программа 2 ищет идентификатор и убеждается, что его еще нет в таблице (для простоты предположим, что описание должно предшествовать использованию идентифика
492
ГЛАВА 20
тора). Тогда идентификатор вместе с его атрибутами нужно занести в SYMB.
В одном из полей элемента таблицы SYMB, а именно в дескрипторе DESCR описываются характеристики, которые переменная будет иметь в готовой программе. Используем поле TYPE, содержащееся в DESCR, чтобы указать еще и тип переменной в исходной программе: FIXED означает INTEGER, FLOAT означает REAL. В некоторых случаях в элементе таблицы символов потребуется дополнительное поле, чтобы описать тип переменной в исходной программе. Например, если и целые, и вещественные значения в машине представлены числами с плавающей запятой, то компилятору необходимо еще знать тип каждого идентификатора и выражения, чтобы он смог своевременно выполнить или сгенерировать операции преобразования.
Программа 2 формирует дескриптор и заносит тип FLOAT или FIXED в зависимости от значения глобальной переменной Т. В компиляторе есть переменная STORLOC, которая используется при присваивании адресов переменным готовой программы; ее начальное значение равно 0. В момент формирования дескриптора система автоматически заполняет «безымянные» поля соответствующими начальными значениями (они не остаются неопределенными).
2: LOOKUP(L1, Р); Поиск идентификатора — его не долж-
IF Р 0 THEN ERROR (1); но-быть в таблице.
INSERT(L1, Р); Занести его в таблицу. P.STRUC—1
P.STRUC := 1; означает, что это простая переменная.
D:= DESCRIPTOR(ADDRESS= Сформировать дескриптор переменной STORLOC, TYPE=T); и записать его в таблицу символов.
Р.DESCR := D;
STORLOC := STORLOC4-1; Увеличить счетчик адреса готовой программы.
Программа 3 вызывается в том случае, когда идентификатор I приводится к множителю F. Она ищет идентификатор в таблице и записывает его дескриптор в семантический стек, как семантику F. Проверка P.STRUC=1 позволяет убедиться, что идентификатор — простая переменная. Имена массивов, имена процедур и т. д. должны иметь различные значения в P.STRUC.
3: LOOKUP (L2, Р); Поиск идентификатора — он должен
IF Р = 0 THEN ERROR (2); быть в таблице.
IF Р. STRUC 1 THEN Он должен быть простой переменной.
ERROR (3);
R2 := Р. DESCR; Занести дескриптор в стек.
В большинстве компиляторов для генерации команд умножения вызывают генератор команд, скажем, MULT (DI, D2, D3), где D1
СИСТЕМЫ ПОСТРОЕНИЯ ТРАНСЛЯТОРОВ
493
и D2 описывают операнды для умножения в готовой программе и D3 используется для запоминания описания результата. В ФСЯ такая инструкция генерации команд имеет следующий вид:
D3 : = CODE(D1*D2);
В семантической программе 4 генерируются команды для правила Т = T*F. Как и ранее, L2 и L4 обозначают элементы семантического стека соответственно для F и Т и являются дескрипторами этих операндов. Дескриптор результата, полученный после генерации команд, запоминается в R2 — элементе семантического стека, соответствующем нетерминалу Т из левой части правила.
4: R2:= CODE (L4 * L2);
В ФСЯ внутри кодовых скобок «CODЕ(» и «)» может появиться почти любая последовательность инструкций и выражений. Когда во время компиляции выполняется такая заключенная в скобки последовательность, для нее генерируются команды. Существенным ограничением является то, что операнды, заключенные в кодовые скобки, должны быть либо дескрипторами, либо константами. Например, предположим, что А, В, С и I — переменные готовой программы, описанные во время компиляции дескрипторами DA, DB, DC и DI. Выполнение последовательности
(20.2.3) CODE(DI := DA+DB*DC)
приведет к генерации команд, которые в готовой программе выполнят присваивание: I := А+В*С.
Если в кодовые скобки заключено выражение, то результатом выполнения будет не только сгенерированная программа, но также и дескриптор результата. Этот дескриптор обычно где-то запоминается (как было сделано в семантической программе 4) для последующего использования. Приведем другой пример. Выполнение
DI := CODE(DA+DB*DC);
приведет к генерации команд для вычисления выражения А+В*С. Результат остается на сумматоре или в регистре. Дескриптор., описывающий результат, запоминается во время компиляции в переменной DI.
Система обозначений, использованная в ФСЯ для генерации команд, гораздо элегантнее и нагляднее, чем другие системы обо-^ значений, используемые для этой же цели. Вместо последовательности обращений к программам генерации команд мы обходимся одной-единственной инструкцией, которая выглядит как самая обычная инструкция, с тем лишь отличием, что она заключена в кодовые скобки.
В ФСЯ предусмотрены лаконичные обозначения для описания индексирования в готовой программе. Предположим, что мы хотим
494
ГЛАВА 20
написать семантическую программу 5 для продукции
I (Е)—>F ЕХЕС 5
где I — имя массива (его дескриптор в L4) и Е — выражение (его дескриптор в L2). Предположим, далее, что поле ADDRESS в дескрипторе для I (L4.ADDRESS) в действительности является адресом информационного вектора этого массива и что во время выполнения программы первое слово этого информационного вектора содержит значение CONSPART (см. разд. 8.4). Тогда нам необходимо сформировать дескриптор, который определит, что адрес переменной в готовой программе получается k3kCONSPART+ (текущее значение Е). Для этого нам потребуется два шага:
DI : = *L4; L4—это дескриптор. Требуется
сформировать и запомнить в D1 дескриптор, который имеет те же компоненты, что L4, с той лишь разницей, что задана косвенная адресация. Таким образом, адрес переменной в готовой программе равен значению CONSPART.
RI : = DI (L2); Сформировать и запомнить в R1 дескриптор с теми же компонентами, что в D1, с той лишь разницей, что адрес описанной переменной будет равен адресу переменной, описанной в дескрипторе D1 + (значение, описанное в Дескрипторе L2).
Таким образом, дескриптор в R1 описывает переменную с индексом. Этого достаточно, чтобы система генерации команд могла правильно сгенерировать команды для адресации элемента массива. Заметим, что обработка переменной с индексами очень похожа на обычное индексирование; только вместо обычных переменных компилятора в процессе участвуют дескрипторы. На самом деле, две предыдущие инструкции можно было бы заменить одной: R2 := *L4(L2).
Инструкции генерации команд в компиляторе ФСЯ транслируются метакомпилятором в последовательность обращений к обычным программам генерации команд. Например, инструкция (20.2.3) после трансляции на машинный язык будет выглядеть так:
MULT (DB, DC, DTI)
ADD (DA, DTI, DT2)
STORE (DT2, DI)
СИСТЕМЫ ПОСТРОЕНИЯ ТРАНСЛЯТОРОВ
495
где MULT, ADD и STORE — программы генерации команд соответственно для умножения, сложения и запоминания результата.
Не следует думать, что команды можно генерировать только в семантических программах, которые вызываются алгоритмом синтаксического разбора. В гибкой системе семантическая программа, как обычно, может генерировать некоторое внутреннее представление, а команды можно генерировать позднее из внутреннего представления, используя кодовые скобки.
ККБМ
ККБМ расшифровывается как компилятор компиляторов Брукера—Морриса (см. Брукер и Моррис [62], Брукер и др. [63] и Розен [64]). Это одна из самых ранних СПТ. Кроме того, это одна из немногих СПТ, которые продуктивно используются.
Для синтаксического анализа в ККБМ используется стандартный сканер (который разработчик компилятора может заменить своим собственным) и алгоритм нисходящего разбора. Чтобы исключить левую рекурсию, которая недопустима при нисходящем разборе, в описании синтаксиса разрешено использовать факультативные символы и повторения.^.Нет необходимости связывать с каждым правилом грамматики семантическую программу, и обычно этого не делают. В качестве примера рассмотрим следующее (неполное) синтаксическое описание для инструкций присваивания, в которой выражение справа является последовательностью арифг-метических сумм:
1. FORMAT [SS]
2. PHRASE <сум>
3. PHRASE <терм>
4. PHRASE <термы>
5. PHRASE <знак>
= <пер> := <сум>
= [<знак>] <терм> <термы>
= <пер> |(<сум>)
= <знак> <терм> <термы>|<пусто>
- + I -
Слово PHRASE (фраза), предшествующее синтаксическому правилу, указывает на то, что с этим правилом не связана семантическая программа. Запись FORMAT[SS], предшествующая первому правилу, указывает на то, что в исходной программе могут встретиться инструкции, которые имеют формат <пер> :== <сум>, и что есть семантическая программа, которая должна выполняться всякий раз, когда будет распознана инструкция такого формата.
Во время компиляции, одновременно с синтаксическим разбором исходной программы, строится синтаксическое дерево программы. (Так, нисходящий синтаксический анализатор порождает внутреннее представление исходной программы.) Во всех случаях, когда будет построено поддерево с корневым кустом, соответствующим синтаксическому правилу, которому предшествует запись FORMAT [SS] (в данном случае правилу <пер> := <сум>),
496
ГЛАВА 20
будет вызвана соответствующая семантическая программа. Построенное поддерево передается семантической программе в качестве параметра. Цель программы, как всегда, заключается в семантической обработке распознанной конструкции. Предполагается, что в этом случае программа «обходит» поддерево и генерирует соответствующую ему последовательность команд. Ниже привотчтсч примерная программа для обработки поддеревьев, построенных с использованием предыдущих правил:
1. ROUTINEISS] <пер> := <сум>
2. LET <сум> = [<знак>) <терм> <термы>
3. АС:=[<знак>] <терм>
4. LI : GOTO L2 UNLESS <терм>=<знак> <терм> <термы>
5. АС := АС <знак> <терм>
6. GOTO L1
7. L2 : STORE AC IN <пер>
8. END
В семантическом языке есть несколько инструкций для сопоставления с образцом или с деревом. Любой нетерминал в синтаксическом описании можно использовать как переменную, значением которой будет поддерево, с корнем, имеющим то же имя. Например, рассмотрим первую строку в предыдущей программе и вспомним, что синтаксическое дерево, переданное программе, имеет корневой куст, соответствующий правилу:
FORMATISS) ::= <пер> := <сум>
Помимо метки семантической программы, в первой строке указано, что переменной <пер> присваивается поддерево, принадлежащее узлу <пер> из корневого куста, а переменной <сум> присваивается поддерево, принадлежащее узлу <сум>. Так, если анализируется инструкция присваивания I := А+В, то переменная <сум> будет содержать самое левое дерево, изображенное на рис. 20.2.
Корневой куст поддерева <сум> соответствует применению правила
<сум> ::= [<знак>] <терм> <термы>
как показано на рис. 20.2. Выполнение второй строки программы присваивает дерево (Ь) переменной <терм> и дерево (с) переменной <термы>. Переменной <знак> присваивается значение <пусто>, как отсутствующему факультативному символу. Затем инструкция 3 генерирует команды, которые занесут первый <терм> на сумматор (АС). Генерация команд будет определяться поддеревом, которое в данный момент присвоено <терм>. Позднее мы еще вернемся к этой инструкции.
СИСТЕМЫ ПОСТРОЕНИЯ ТРАНСЛЯТОРОВ
497
В инструкции 4 исследуется поддерево переменной <термы>, чтобы выяснить, имеет ли оно вид <знак> <терм> <термы> (другое возможное значение — <пусто>); и если это так, то переменным <знак>, <терм> и <термы> присваиваются новые значения и выполняется следующая инструкция. В противном случае происходит переход к инструкции 7. Обе инструкции 5 и 7
<сум>
<шерм> <шермъ1>
А ।-----]---------1
<знак> <шерм> <термы> + В <пусто>
а
<терм>
А
Ъ
<термы>
<энак> <терм> <термы>
1 В - '
с
<пусио>
Рис. 20.2. Иллюстрация инструкции LET.
генерируют вполне очевидные команды на основании тех поддеревьев, которые в данный момент являются значениями <знак>, <терм> и <термы>.
Вообще говоря, нетерминал в синтаксическом описании можно использовать как переменную лишь для хранения поддерева, корень которого имеет точно такое же имя. Так как обход дерева может быть довольно сложным и может потребоваться несколько поддеревьев с одинаковым именем корня, которые надо обрабатывать в одно и то же время, система допускает массив переменных для каждого нетерминала. Для синтаксической единицы <терм> элементы массива будут называться <терм/1>, <терм/2>, ... и <терм/А>, где А — целая переменная. В нашем примере не было необходимости использовать эту возможность.
В ККБМ заслуживают внимания некоторые возможности расширения. В какой-то мере компилятор, разработанный с помощью ККБМ, является расширением самого ККБМ. Из-за расширяемости ККБМ может оказаться довольно медленным; система непрерывно строит синтаксические деревья и обходит их не только для инструкций исходного языка, но и для всех прочих.
На первом шаге составления компилятора можно разработать несколько новых инструкций, которые будут использованы при реализации компилятора. Например, можно добавить несколько инструкций генерации команд наподобие инструкций в 3-й, 5-й и 7-й строках предыдущей семантической программы. Эти три инструкции фактически не были частью ККБМ, но их добавили, чтобы облегчить составление компилятора.
Можно добавить к ККБМ новый набор базисных инструкций и тем самым сформировать расширенную версию ККБМ1. Это
498
ГЛАВА 20
делается следующим образом. Для каждой новой инструкции составляется синтаксическое описание, но в описаниях правил, связанных с семантической программой, используется
FORMATIBS1 вместо FORMATISS1.
Под BS следует понимать базисную инструкцию (basic statement), под SS — инструкции исходной программы (source program statement). Как и прежде, пишется семантическая программа, которая будет выполняться всякий раз, когда должна быть выполнена базисная инструкция с соответствующим форматом. При этом в первой строке семантической программы '
ROUTINEIBS] используется вместо ROUTINEISSJ.
Например, программа для АС := АС <знак><терм> сгенерирует команды, которые значение <терм> прибавят к сумматору или вычтут из сумматора. Если <терм> просто переменная, то будет одна команда, если же он имеет вид (<сум>), то это будет последовательность команд, зависящая от вида поддерева <сум>. В семантической программе можно использовать все инструкции ККБМ, а также любые другие, добавленные в результате расширения.
В некотором смысле выполнение инструкции АС := АС <знак> <терм> во время компиляции — это всего лишь вызов процедуры (семантической программы), но с удобным форматом вызова.
Синтаксические описания и семантические программы вводятся в ККБМ и транслируются во внутреннее представление. Это внутреннее представление объединяется с копией самого ККБМ, в результате чего получается новый метакомпилятор ККБМ 1. ККБМ1 допускает как обычные инструкции ККБМ, так и только что добавленные новые базисные инструкции.
На следующем шаге составляются синтаксические описания и семантические программы для инструкций исходного языка; при этом в инструкциях FORMAT и ROUTINE используются SS вместо BS. После введения их в ККБМ1 будет получен третий компилятор ККБМ 2, который допускает обычные инструкции ККБМ, базисные инструкции ККБМ1 и заново определенные инструкции исходного языка. И даже теперь ККБМ2 остается расширяемым компилятором и может быть расширен любое число раз. Чтобы преобразовать его в компилятор только для инструкций исходного языка, устанавливается переключатель, который указывает, что во входном потоке допустимы лишь инструкции, описанные как SS. И тогда получается компилятор, который транслирует только такие инструкции.
Глава 21
Советы разработчику компилятора
Эта глава содержит различные соображения по вопросам, которые по тем или иным причинам не вошли в предыдущие главы. Либо они слишком малы, чтобы претендовать на отдельную главу или раздел, но достаточно важны, чтобы быть растворенными среди прочего материала, либо они не подходят по своей теме к рассмотренным главам. Соображения изложены конспективно и содержат ссылки на литературу, раскрывающую соответствующие вопросы. Я предлагаю временами обращаться к этой главе и читать разделы, касающиеся тех вопросов, с которыми читатель в данный момент знакомится.
В главе следующие разделы:
Общие соображения
На каком языке писать компилятор?
Сканер может облегчить грамматический разбор Обсуждение алгоритмов грамматического разбора Совет по семантическим программам
Структура компилятора
Организация таблиц внутри компилятора Реентерабельность получаемой программы Отладка компилятора
Сообщения об ошибках во время компиляции Контроль и диагностика ошибок во время счета Раскрутка
Общие соображения
НИКОГДА НЕ ОТКЛАДЫВАЙ НА ВРЕМЯ РАБОТЫ ГОТОВОЙ ПРОГРАММЫ ТО, ЧТО МОЖНО СДЕЛАТЬ ВО ВРЕМЯ КОМПИЛЯЦИИ.
Во время компиляции всякая операция выполняется только один раз, но если ее выполнение отложить на время счета, то она, быть может, будет выполняться сотни раз. Здесь мы имеем в виду главным образом операции типа преобразования констант, проверки типа операции, операции с одними константами или значе-
500
ГЛАВА 21
ниями, известными во время компиляции, и так далее. Каждый компилятор должен проводить оптимизацию в разумном объеме. Глубина оптимизации, конечно, зависит от целей проекта, но даже небольшая забота о ней улучшает компилятор.
На каком языке писать компилятор?
Как и следовало ожидать, наметилась тенденция от автокода переходить к языкам более высокого уровня. Причины очевидны: легкость программирования, меньшее время отладки, меньшая стоимость, большее внимание к качеству проекта за счет освобождения программиста от необходимости продумывания деталей, касающихся регистров, разрядов и так далее.
Но выбор языка программирования часто зависит от того, что доступно для разработчика компилятора или к чему он привык. Компилятор с ФОРТРАНа IV уровня Н фирмы IBM написан на ФОРТРАНе, компилятор с расширенного АЛГОЛА фирмы Burroughs написан на расширенном АЛГОЛе. Я полагаю, мы будем свидетелями развития языков «системного программирования», которые станут языками высокого уровня, ориентированными на конкретные машины. Они должны позволить разработчикам компилятора лучше управлять процессом генерации команд и, таким образом, повысить эффективность получаемых программ. Другая возможность состоит в использовании языка общего назначения, типа PL/1. Это придает компилятору большую мобильность, но снижает его эффективность.
Сканер может облегчить грамматический разбор
Сканер может упростить и облегчить работу синтаксического анализатора, если возьмет на себя выполнение некоторых дополнительных функций. Например, преобразование констант может осуществляться в сканере, с тем чтобы их описание не загромождало синтаксис. Сканер может также распознавать и нейтрализовать (или исправлять) ошибки; такими ошибками могут быть, например, ошибки в константах, пробелы в символах, представляемых парой литер (типа **), или отсутствие закрывающей кавычки в константе, являющейся строкой. Эти дополнительные функции, однако, не должны слишком перегружать сканер, который должен оставаться простым и эффективным.
Часто в синтаксических описаниях несколько символов встречаются в одном и том же контексте. Например, + и — с точки зрения синтаксиса используются одинаковым способом, а символы REAL и INTEGER в АЛГОЛе могут встречаться в одних и тех же синтаксических конструкциях. Общий прием состоит в том, что сканер для всех терминальных символов одного класса выдает один синтаксический символ, а семантические программы сами
Советы разработчику компилятора
501
разбираются, какой конкретный символ за ним стоит. (Это можно сделать в ПЯ (гл. 7) с помощью описания класса (CLASS).) Например, для пользователя грамматика могла бы содержать правила:
<тип> ::= REAL [INTEGER [BOOLEAN
<'опис> ::= <тип><спис. ид.>
< Е> ::= <Т>|<Е>+<Т>|<Е>—<Т>
а грамматический разбор вместо них работал бы с правилами
< опис> ::= TYPE <спис. ид.>
< Е> ::= <Т>|<Е> ПМ <Т>
Заметим, что аналогичную вещь сканер уже делает с идентификаторами. Синтаксический символ I обозначает класс всех идентификаторов, а сематические программы различают каждый идентификатор в отдельности.
Если грамматика не подходит к частному алгоритму грамматического разбора, то часто бывает легче переложить часть функций на сканер, чем пытаться перекраивать грамматику. Например, одна из проблем, которая возникла в АЛГОЛе при использовании алгоритма простого предшествования, касается использования запятых в различном смысле — в смысле разделителей фактических параметров и в смысле разделителей граничных пар в описании массива. В сканере путем несложного анализа можно установить, что сканируется описание массива, и для разделителя граничных пар выдать совсем другой символ.
Другой пример. В ФОРТРАНе DO10I в начале инструкции может быть началом присваивания и началом DO-цикла. Сканеру можно «заглянуть» вперед, что гораздо проще, чем решать эту проблему в алгоритме формального грамматического разбора.
Обсуждение алгоритмов грамматического разбора
Сравнения нисходящих и восходящих алгоритмов грамматического разбора проводились Гриффитсом и Петриком [651. Но в действительности эти сравнения не приближают нас к знанию, какой из них работает в компиляторе быстрее. Слишком многое зависит от того, насколько аккуратно реализован каждый алгоритм и насколько он соответствует семантике. Я сомневаюсь, что можно получить значительную разницу в скорости компиляции для двух схожих компиляторов с разными алгоритмами грамматического разбора, если, конечно, один из них не будет реализован уж очень неразумным способом.
Более важными факторами являются гибкость в использовании алгоритма грамматического разбора, легкость, с какой вносятся изменения и добавляются семантические программы, и время, затрачиваемое при этом на программирование и отладку компиля
502
ГЛАВА 21
тора. С этой точки зрения, как говорилось в разд. 5.5, самым плохим методом является метод простого предшествования. Единственной причиной, по которой ему была посвящена целая глава, является то, что он самый простой, и, следовательно, с его помощью легче всего подойти к рассмотрению идеи восходящего грамматического разбора.
Если компилятор пишется на языке, допускающем рекурсивные процедуры, то, конечно, следует рассмотреть метод рекурсивного спуска, описанный в разд. 4.3. Хотя и не существует какой-либо автоматизации на этот счет, но писать процедуры, следуя грамматике, просто, а сами процедуры довольно легко отлаживаются.
Наиболее широко используемым методом восходящего разбора является метод предшествования операторов с применением функций предшествования. Большинство реализаций, в основе которых лежит такой метод, делают это некоторым интуитивным способом вместо автоматического генерирования этих функций по грамматике. Обычно используются два стека, рассмотренные в разд. 6.1. Один для операторов, с которыми связаны отношения предшествования, и другой для идентификаторов, констант и других операндов. Метод предшествования операторов часто используется именно для грамматического разбора выражений, для этой цели он и был изобретен. Ему присущи и эффективность, и гибкость.
Сказанное не означает, что всегда следует использовать алгоритм формального грамматического разбора. Заметим, что указанные два метода обычно программируются интуитивным образом. Причина, по которой одна треть книги была посвящена теории синтаксиса, состоит в том, что, как только эти формальные методы становятся понятными, программирование компиляторов и даже обсуждение их становятся легче и систематичнее. ФОРТРАН служит хорошим примером языка, который легко поддается грамматическому разбору с помощью обычных частных методов. Дать описание синтаксиса, соответствующее какому-либо из автоматических методов, трудно, в то же время структура языка довольно простая. Нет блочности, вложенных условных инструкций, переключателей и т. п. ФОРТРАН имеет построчную структуру и тип инструкции почти всегда определяется по одному или двум первым символам.
Часто бывает выгодно для разных частей исходного языка использовать разные методы грамматического разбора. Рассматривалась (еще не реализованная) идея конструктора, анализирующего грамматику, автоматически разбивающего ее на несколько частей и порождающего для каждой части самый эффективный алгоритм грамматического разбора. Эти алгоритмы должны вызывать друг друга по мере необходимости.
Конвей [63] рассматривает «разделимую диаграмму переходов» «separable transition diagram» для компилятора с КОБОЛа, где
СОВЕТЫ РАЗРАБОТЧИКУ КОМПИЛЯТОРА
503
язык разбивается на несколько секций, для каждой из которых грамматический разбор осуществляется автоматом с конечным числом состояний. Эти автоматы вызывают друг друга рекурсивно. Тиксир [67] независимо формализовал этот метод, но его формализация не была использована в реальном компиляторе.
Некоторые компиляторы разделяют анализ на две части. Например, ФОРТРАН Н (см. ИБМ(а)) использует частные методы грамматического разбора всех описаний и инструкций, а все выражения обрабатывает одной подпрограммой, использующей описанный выше метод предшествования операторов.
Совет по семантическим программам
Как правило, при программировании все, что может служить входной информацией для подпрограммы, оформляется в виде ее формальных параметров. Хотя такая практика и приводит к общности и независимости подпрограмм, для написания компилятора лучше чаще пользоваться глобальными параметрами (COMMON в ФОРТРАНе). Проиллюстрируем это одним из удачных примеров техники написания компилятора.
Каждая семантическая программа, обрабатывающая идентификатор или выражение, вероятно, обращается по крайней мере один раз к другой программе для проверки корректности типа, выдачи сообщения об ошибке, проверки возможности оптимизации и так далее. Каждая из этих подпрограмм имеет в качестве параметра указатель на описатель идентификатора или выражения. Заметим, однако, что в любом месте компиляций обрабатываются самое большее один или два операнда. Например, семантическая программа для обработки бинарной операции имеет дело с двумя операндами. Семантическая программа для обработки фактического параметра имеет дело с самим фактическим параметром и формальным параметром, которому присваивается этот фактический параметр.
Поэтому давайте условимся, что каждая семантическая программа, обрабатывающая один (или два) операнд(а), будет заносить этот (эти) операнд(ы) (или указатель на его описатель) в глобальную ячейку Р (Р1 для второго операнда). Тогда все подпрограммы, обрабатывающие операнды, будут ссылаться на глобальные ячейки Р и Р1. Перед тем как семантическая программа осуществит возврат в основной алгоритм грамматического разбора, она запомнит указатель Р (и, возможно, Р1) в соответствующем месте стека или еще где-нибудь.
Это упрощает вызовы подпрограмм, сокращает расходы и с точки зрения затрачиваемого времени, и с точки зрения занимаемого пространства. Кроме того, это приводит к «прозрачности» и стройности конструкции компилятора.
504
ГЛАВА 21
Структура компилятора
Мы рассматривали компиляцию как процесс, состоящий из четырех этапов: сканирование, анализ, подготовка генерации команд и генерация команд. Читэм (65) разбивает процесс компиляции на шесть шагов, расчленяя еще анализ на синтаксический и семантический, и генерацию команд — на начальную генерацию команд и окончательную настройку команд с одновременной выдачей.
Хотя для изучения техники написания компилятора обе эти модели хороши, они не всегда в точности совпадают со схемами реальных компиляторов. Слишком многое зависит от машины, исходного языка и целей реализации. Создатель компилятора должен чувствовать свободу в выборе структуры компилятора, но в то же время у него должны быть веские основания для принципиальных отклонений от представленных моделей, так как эти модели возникли в результате серьезного изучения данной проблемы.
Многопроходный компилятор обычно сначала получает внутреннее представление исходной программы (тетрады, триады и так далее). Затем для каждого оператора во внутреннем представлении он получает команды машины. Нужно понимать, что при некоторых ограничениях, наложенных на исходный язык, первоначальные семантические программы с равным успехом могли бы сразу получать команды машины. Главное ограничение состоит в том, что описания и спецификации переменных должны предшествовать их использованию. Это, конечно, связано с усложнением семантических программ и ухудшением готовой программы, но эти недостатки часто восполняются выигрышем в скорости компиляции.
Стремление свести к минимуму количество проходов компилятора часто обусловливается ограниченными размерами машины или соображениями, касающимися конечной цели проекта. Каждый дополнительный проход в компиляторе ведет к увеличению накладных расходов на его организацию и, вероятно, к увеличению общего времени разработки компилятора.
Организация таблиц внутри компилятора
Сведите к минимуму количество таблиц и стеков, размеры которых зависят от исходной программы. Это уменьшит вероятность переполнения одной из таблиц и ослабит ограничения на размер компилируемых программ. Для этой цели максимально используйте семантический стек (для восходящего разбора) и таблицу объектного кода. Например, адрес условного перехода вперед в инструкции IF можно хранить в элементе семантического стека, соответствующем нетерминалу <1Р-условие> (разд. 13.2),
Советы разработчику компилятора
505
а ссылки, связывающие переходы вперед в единую цепочку, можно хранить во внутреннем представлении исходной программы (разд. 13.3). То же самое относится и к FOR-циклам, CASE-инструкциям и им подобным.
Добавляя элемент в таблицу, всегда проверяйте ее на переполнение. Многие часы были потрачены на поиск ошибок, связанных с отсутствием контроля на переполнение, спустя месяцы и годы после того, как компилятор считался отлаженным.
В некоторых системах программист для своей работы может указать, сколько потребуется памяти. В таких системах компилятор начинает с опроса, сколько ему выделено памяти, и затем распределяет ее между таблицами, размеры которых зависят от размеров компилируемых программ. Сказанное относится к таблице символов, стекам, к таблицам, содержащим внутреннее представление исходной программы, и т. п. Это позволяет небольшие программы компилировать в малом объеме памяти, избавляя их от больших расходов, необходимых при трансляции больших программ.
Если все же желательно работать с множеством таблиц и стеков неопределенных размеров, то компилятор следует писать на языке, позволяющем осуществить эту работу некоторым систематическим образом. То есть во время компиляции должны существовать общая административная система управления памятью, имеющей списочную структуру, и должны существовать примитивы (элементарные операции), позволяющие добавлять к таблицам выделенные из общей области элементы и удаленные из таблиц элементы возвращать в общую область. Такая реализация приводит к некоторому замедлению из-за накладных расходов на организацию.
Для хранения таблиц по возможности обходитесь без вспомогательной памяти. Не обременяйте малые программы обменом с вспомогательной памятью. Делайте это только в том случае, когда действительно не хватает оперативной памяти. Не пишите во вспомогательную память таблицу с произвольным доступом (например, таблицу символов). Внутреннее представление исходной программы, вероятно, первый кандидат для вынесения его во вспомогательную память, так как оно и строится, и читается последовательным способом, а обмен и сам процесс компиляции в какой-то мере можно совместить. Наур [65] дает хорошее описание тщательно сбалансированного компилятора для очень малой машины.
Если вы все же вынуждены использовать вспомогательную память, то планируйте работу компилятора так, чтобы обмен совмещался с работой центрального процессора. Например, если программа во внутреннем представлении пишется на диск, то накопите первую порцию информации на буфере. Тогда во время пересылки этого буфера во вспомогательную память компилятор может про.
506
ГЛАВА 21
должать обработку и накапливать на второй буфер следующую порцию программы во внутреннем представлении.
На этапе анализа компилятор имеет дело с двумя главными таблицами: с таблицей символов и семантическим стеком. В компиляторах, написанных на автокоде, для них часто отводится большая область, и таблицу символов располагают с одного конца этой области, а стек — с другого (см. ниже рис.). Эти таблицы растут навстречу друг другу и не переполнятся до тех пор, пока не встретятся.
КОМПИЛЯТОР ТАБЛИЦЫ СТЕК ТАБЛИЦА СИМВОЛОВ
В интерпретаторах, использующих метод хеширования для работы с таблицей символов, часто много места пропадает из-за большого количества незанятых элементов. Это место можно использовать для частей исходной программы во внутреннем представлении, подготовленной для интерпретации (с дополнительными командами переходов). Это ненамного замедляет интерпретацию. Это место можно также использовать для констант и статических переменных.
Реентерабельность получаемой программы
Программа или процедура реентерабельнаг), если в процессе ее работы кто-то другой может обратиться к ней, прервав на время ее текущую работу. Это особенно полезно в системах с мультипрограммированием или разделением времени, где несколько программ могут обращаться, например, к подпрограмме SIN, являющейся реентерабельной подпрограммой. Для такой подпрограммы нужна только одна копия в памяти, независимо от того, сколько людей к ней обращаются.
По возможности компилятор должен получать на выходе реентерабельную программу. Точно так же важно (и даже более важно), чтобы сам компилятор был реентерабельным. Если это так, то независимо от того, сколько людей одновременно компилируют свои программы, необходимо присутствие только одной копии компилятора.
Реентерабельная программа должна удовлетворять следующим условиям:
1. Она не должна себя модифицировать, т. е. команды программы не должны меняться.
*) reentrant (реентерабельный) в буквальнскм переводе «повторновходимый».— Прим, перев.
СОВЕТЫ РАЗРАБОТЧИКУ КОМПИЛЯТОРА
507
2. Все переменные, которые она изменяет, должны располагаться в области данных, выделяемой персонально для каждого выполнения. Таким образом, если к программе обращаются первый раз, то либо вызывающая программа должна выделить память для ее области данных, либо это должна сделать специальная системная программа. Заметим, что административная система АЛГОЛа, рассмотренная в разд. 8.9, удовлетворяет этим требованиям.
3. Машина должна иметь фиксированный набор быстрых регистров. В одном (или нескольких) из этих регистров помещается адрес(а) области(ей) данных одной из программ. Любое обращение к переменной, находящейся в памяти, осуществляется с помощью базирования по одному из этих регистров. Во время прерывания программы система должна сохранить содержимое этих регистров и перед возобновлением работы прерванной программы — восстановить их.
Отладка компилятора
Средства отладки компилятора должны быть изготовлены на ранней стадии разработки. Должны быть написаны подпрограммы, которые выводили бы в виде текста, а не в виде восьмеричных или шестнадцатеричных цифр, следующую информацию:
1. Синтаксические и семантические стеки.
2. Элементы таблицы символов.
3. Исходную программу во внутреннем представлении.
4. Получаемые в результате команды в символьном и внутреннем представлении.
5. Последовательность шагов применения синтаксических правил в процессе грамматического разбора.
6. Последовательность обращений к семантическим подпрограммам.
Не жалейте времени на разработку этих подпрограмм, добейтесь того, чтобы вывод был в компактной и легко читаемой форме. Это облегчит отладку. Например, если получаемые команды в виде текста изображаются 20-ю литерами на каждую команду, то организуйте вывод в 3 или 4 столбца на страницу вместо одного.
Вы должны оставить возможность в любом месте включать и выключать отладочную выдачу, например с помощью управляющих карт, вставляемых в разных местах компилируемой программы. Сканер может распознавать эти карты и устанавливать соответствующие значения переключателей. Попытайтесь сделать так, чтобы можно было легко получать отладочную выдачу для отдельных частей исходной программы, чтобы не надо было делать выдачу
508
ГЛАВА 21
для всей программы только для того, чтобы посмотреть, как компилируется какая-то одна инструкция.
В общем, разные части компилятора должны программироваться и отлаживаться в их логическом порядке (сканер, синтаксический анализатор, семантические программы, программы подготовки и генерации команд). Организация работы готовой программы может довольно сильно повлиять на общий проект компилятора, поэтому она должна быть продумана в начале разработки.
Привлеките других людей, которые готовили бы тесты для вашего компилятора (во многих вычислительных центрах это делается для тестирования всех новых программ). Сами же вы, вероятно неумышленно, будете писать тесты, проверяющие только некоторые части вашего компилятора.
Каждый компилятор на первой странице листинга исходной программы должен печатать версию компилятора, дату и другую информацию, которая поможет вам разобраться в ошибках, с которыми придут к вам пользователи.
Не выбрасывайте средства отладки даже тогда, когда вы думаете, что ваш компилятор отлажен, потому что это наверняка не так.
Сообщения об ошибках во время компиляции
Сообщения об ошибках должны быть достаточно понятными, чтобы не было нужды обращаться к специальному списку за расшифровкой этих сообщений.
Часто каждое сообщение разбивают на фразы, чтобы внутри компилятора представлять его в виде последовательности указателей на эти фразы. Это позволяет не только экономить память (некоторые фразы используются очень часто), но и выдавать более сложные сообщения. Для иллюстрации предположим, что сообщения печатаются после анализа исходной программы и каждый элемент «списка сообщений» содержит четыре значения:
1. Номер сообщения об ошибке.
2. Номер карты, в которой была обнаружена ошибка (если он имеется).
3. Неправильно использованный идентификатор (0, если его нет).
4. Входной символ, на котором обнаружена ошибка.
Номер сообщения об ошибке используется для обращения к группе команд, которые и указывают, какое сообщение должно быть напечатано. Например, предположим, что для сообщения с номером 1 мы имеем следующую группу команд:
СОВЕТЫ РАЗРАБОТЧИКУ КОМПИЛЯТОРА
509
1. Печать фразы 1 1. «На карте»
2. Печать номера где фразы представляют собой
карты
3. 4. 5. 6. 7. Печать фразы 2 Печать идентификатора Печать фразы 3 Печать символа, перед которым обнаружена ошибка Печать фразы 4 следующее: 2. «идентификатор» 3. «перед» 4. «определен дважды»
Выдача сообщения в кодировке (1,20, АВС, ;) должна привести к следующей распечатке:
На карте 20 идентификатор АВС перед «;» определен дважды.
Программа, печатающая сообщение об ошибке, представляет собой простой интерпретатор. В числе компиляторов, использующих данный метод, PUFFT (см. Розен и др. [651) и ALCOR ILLINOIS 7090 (Грис, и др. [65]).
Контроль и диагностика ошибок во время счета
Если компилятор широко используется для отладок, то он должен уметь генерировать в программе пользователя различные проверки, чтобы помочь программисту отлаживать свою программу. Для большинства языков нужно контролировать:
1. Выход значения индексного выражения за допустимые границы.
2. Деление на нуль и другие некорректности арифметических операций.
3. Использование переменной до того, как ей было присвоено значение.
Такие проверки служат двум целям — максимально ранней индикации ошибок во время выполнения программы и предохранению самой системы от ошибок программистов. Эти проверки должны вставляться по желанию, чтобы, как только программа отлажена, их можно было исключить. Было бы полезно иметь возможность исключать эти проверки выборочно — для отдельных частей исходной программы.
Реализовать эти проверки довольно просто. Для этого компилятор генерирует специальные команды, выполняющие эти проверки в программе пользователя. Регистрация того факта, что переменной еще не присвоено значение,— вероятно, самая трудная
510 ГЛАВА 21
из проверок. Некоторые машины в каждом слове имеют несколько дополнительных разрядов, указывающих на «тип» слова, и слова с типом «команда» не могут быть операндами арифметического действия. Следовательно, если компилятор вначале для всех переменных проставит тип «команда», то попытка прочесть эту переменную перед тем, как ей присвоено- значение, вызовет аппаратное прерывание.
В некоторых машинах в каждом слове памяти допускается установка «разряда четности», так, чтобы чтение такого слова также вызывало аппаратное прерывание.
Для машин, в которых нет таких аппаратных средств, остаются две возможности: первая — на каждую переменную завести признак, указывающий была ли в нее запись или нет (это увеличивает расход памяти), вторая—заполнить вначале все переменные каким-либо редко встречающимся значением и при каждом чтении переменной сравнивать ее с этим значением. Компилятор IBM/360 WATFOR вначале посылает в каждую переменную X'808080...80'*) (см. Кресс и др. (69)). Это означает, конечно, что если в результате вычислений действительно получится такое число, то будет напечатано ложное сообщение об ошибке.
В языке с блочной структурой при входе в каждый блок или процедуру для всех локализованных переменных должно быть установлено значение «неопределенности».
Все сообщения об ошибках, печатаемые во время выполнения программы, должны содержать номер карты, в которой эта ошибка встретилась. Это можно сделать тем способом, о котором говорилось в гл. 16 об интерпретаторах. То есть перед командами, генерируемыми по данной карте, вставлять «пустую операцию» с номером этой карты. В случае ошибки нужно пройтись по цепочке команд от места, где была обнаружена ошибка, до ближайшей густой операции.
В PL/1 используется другой способ. Все инструкции исходной программы в листинге нумеруются, и впереди каждой группы команд, соответствующей данной инструкции, вставляется пересылка номера этой инструкции в глобальную ячейку Е. При обнаружении ошибки переменная Е содержит номер выполняемой в данный момент инструкции.
Лучшим средством отладки во время счета является символьный дампинг. Это — список всех переменных, используемых в месте обнаружения ошибки, с их текущими значениями в легко читаемом виде (не в восьмеричном или шестнадцатеричном). В 16-й гл. описывается процедура выдачи такого дампинга для интерпрераторов. Для компиляторов получить такой дампинг труднее, так как во
х) Константа в шестнадцатеричном виде, где каждая цифра представляет четыре двоичных разряда (запись на языке ассемблера).— Прим, перев.
СОВЕТЫ РАЗРАБОТЧИКУ КОМПИЛЯТОРА
511
время счета под руками нет таблицы символов и информации о расположении различных областей в памяти.
Байер и др. [67] описывают выдачу такого дампинга для программ, получаемых с помощью компиляции. Здесь мы кратко рассмотрим его способ в предположении, что язык имеет блочную структуру. Главная идея состоит в том, что компилятор формирует вторую объектную программу, называемую L-списком, которая по длине совпадает с основной программой. Каждой команде объектной программы соответствует элемент L-списка, содержащий следующую информацию:
1. Номер соответствующей карты исходной колоды.
2. Номер блока, для которого сгенерирована эта команда.
3. Информация о той части исполняемой инструкции, к которой относится команда — вызов процедуры, вычисление индекса, IF-THEN-проверка и т. д.
4. Оператор исходной программы.
5. Адрес элемента таблицы символов для операнда, с которым работает эта команда (если он есть).
Во время компиляции L-список, таблицу символов и список блоков компилятор запоминает во вспомогательной памяти. Эта информация не используется до тех пор, пока не будет обнаружена ошибка или программист не попросит ее для дампинга. Следовательно, возможность выдачи дампинга не замедляет работы программы.
При обнаружении ошибки в процессе счета вызывается процедура DUMP, которая по схеме загрузки памяти (где содержатся список загруженных подпрограмм и их расположение) находит ту подпрограмму, где была обнаружена ошибка. Если для этой подпрограммы существует L-список, то он считывается в память вместе с таблицей символов и списком блоков. Номер блока, номер карты и другая информация для выдачи дампинга, описанного в гл. 16, берутся из элемента L-списка, соответствующего ошибочной команде.
Составление L-списка может оказаться ненужным, если в самой объектной программе содержится достаточно информации, но таблица символов и список блоков должны существовать обязательно.
В некоторых системах, обладающих такими возможностями, программисты быстро «сориентировались» и стали в конце счета задавать явное деление на нуль только для того, чтобы получить дампинг.
Раскрутка
Предположим, что мы хотим получить компилятор с языка L на машину М и при этом написать его на самом языке L. L может быть языком, специально предназначенным для написания компи
512
ГЛАВА 21
ляторов, или языком высокого уровня типа ФОРТРАН или АЛГОЛ. Желание написать компилятор на том же языке вполне естественно, если нет другого подходящего языка, кроме, может быть, автокода. Здесь можно выбрать одну из двух линий поведения.
Написать компилятор на автокоде для небольшого подмножества L0 языка L. Это подмножество должно быть достаточно малым, чтобы его легко было реализовать, и достаточно большим, чтобы использовать его на следующем шаге. Следующий шаг состоит в переписывании компилятора с L0 на самом L0 и его отладке. Теперь мы попытаемся с помощью «раскрутки» (bootstrapping) шаг за шагом подняться до языка L. На каждом шаге i, i=l, ..., n, компилятор для L[i—1] расширяется до компилятора с языка Li с помощью добавления новых свойств из языка L. На каждом шаге старые части текущего компилятора можно переписать на новом языке Li, чтобы использовать его новые свойства. Главная причина расширения компилятора с L0 до компилятора с Ln=L за несколько шагов вместо одного в том, что на каждом шаге мы имеем более мощный язык Li для написания очередного расширения, что сильно облегчает работу.
Второй способ состоит в использовании существующего компилятора для языка L' на другой машине М'. Если L'=L (компилятор с этого языка есть для другой машины), то пишем на языке L компилятор, который получает объектный код машины М. Если L'#=L, то на языке L' пишем компилятор с L0, который получает объектный код машины М. Компилируя этот компилятор на машине М', получаем компилятор с L0 в командах машины М. Далее применяется раскрутках).
1) Читателю, которого интересует раскрутка, полезно познакомиться с тем, как Вирт [71] оценивает преимущества и недостатки обоих способов, основываясь на опыте, полученном при разработке компилятора с языка ПАСКАЛЬ.— Прим. ред.
Приложение
Язык программирования, используемый в книге
Язык программирования, который используется в этой книге, представляет собой расширение и разновидность языка АЛГОЛ. Мы приводим описание этого языка лишь с той целью, чтобы читатель получил представление о том, как должны выполняться программы, встречающиеся в этой книге. .Мы ограничиваемся довольно кратким описанием, предполагая, что читатель знаком с языком АЛГОЛ. Во многих отношениях оно не настолько точное, каким могло бы быть; мы полагаемся на те знания языков программирования, которыми читатель уже располагает, и не будем пополнять их очевидными и несущественными (для наших целей) подробностями. Использование указателей и структурных величин объясняется более подробно и иллюстрируется несколькими примерами.
Идентификаторы
Любой <идентификатор> имеет формат
<идентификатор> ::= <буква>{<буква>|<цифра>},
где <цифра> — это одна из литер 0, 1, ... , 9, а <буква> — одна из литер , А, В, ..., Z, а, Ь, ..., z. Идентификаторы используются в качестве имен переменных, имен процедур, и меток. Некоторые идентификаторы «резервируются» и не могут быть использованы таким способом. Это:
ARRAY, BEGIN, BOOLEAN, CASE, CAT, CHARACTER, CONTENTS, DO, ELSE, END, ENDCASE, FALSE, FOR, GOTO, GOTO, IF, INTEGER, POINTER, REAL, RETURN, STEP, STRING, THEN, TRUE, UNTIL и WHILE.
Константы
Последовательность, состоящая из одной или более литер -<циф-ра> 0, 1, ..., 9, является, как обычно, целой (INTEGER) константой. Целая константа может быть также задана в шестнадцатерич-
1 7 д. Грио
514
ПРИЛОЖЕНИЕ
ном виде. Например, шестнадцатеричная константа Х'А' эквивалентна константе 10, в то время как Х'ЗВ' эквивалентна 59.
Логическими (BOOLEAN) константами являются TRUE и FALSE.
Если Ci, с2, ... , сп — литеры в коде EBCDIC, то zCiC2 ... с' и "ел ... с"— эквивалентные текстовые (STRING) константы, состоящие из цепочки литер сп с2, ... , сп.
Константа 0 является также указательной (POINTER) константой; если она присвоена указательной переменной, то это означает, что переменная не указывает или не ссылается на какое-либо другое значение.
Типы данных и описание переменных
Основными типами данных в языке являются INTEGER (любое целое со знаком), REAL (любое вещественное число), BOOLEAN (TRUE или FALSE), CHARACTER (любая литера в коде EBCDIC), STRING (0, одна или более литер) и POINTER (адрес или ссылка на какое-либо другое значение).
Если <тип> является одним из основных типов или определен программистом как структурный тип (см. ниже), то описание D имеет формат
D <тип> <идентификатор>, <идентификатор>, ..., <иден-
тификатор >
и означает, что идентификаторы являются именами переменных, которым могут быть присвоены значения данного типа (например, REAL А, В, С5).
Кроме значений основных типов, программа может создавать, ссылаться и изменять два вида «составных» значений. Описание
D ::== <тип> ARRAY <идентификатор>
{, <идентификатор>}[И : U1, ..., Ln : Un]
определяет идентификаторы, которые должны быть именами n-мерных массивов типа <тип>. Как в АЛГОЛе, Li и Ui — выражения типа INTEGER — задают нижнюю и верхнюю границы i-ro индекса массива, <тип> может быть основным типом данных или типом структурного значения, определенным программистом. Скобки t и ] не являются метасимволами.
Структурное значение состоит из последовательности, содержащей п других значений (п>0), называемых компонентами, или полями. Каждая из компонент имеет имя и <тип>, и им могут быть присвоены значения этого типа. Например, приведенная ниже схема показывает, что В есть структурное значение, состоящее
ЯЗЫК ПРОГРАММИРОВАНИЯ, ИСПОЛЬЗУЕМЫЙ В КНИГЕ
515
из трех компонент с именами N, М и Q и имеющих соответственно типы REAL, INTEGER и POINTER
В М (REAL) М (INTEGER) Q (POINTER)
значение N | значение М | значение Q
Описание
STRUCTURE: ST(REAL N, INTEGER M, POINTER Q) может быть использовано для того, чтобы описать ST как новый <тип> структурного значения. Любое значение этого типа состоит, как указано, из трех компонент. Мы можем затем описать переменные, имеющие этот тип. Например, для того чтобы описать В как переменную этого типа (тогда В будет иметь форму, показанную на предыдущей диаграмме), используется описание
ST В.
Заметим, что можно описать массивы структурных величин.
На самом деле не будет необходимости в формальном описании структурных значений и переменных. Но всякий раз с помощью диаграмм и словесных пояснений мы укажем, каким переменным могут быть присвоены структурные величины и какими будут имена и типы компонент. Мы отсылаем читателя к разд. 8.6, где кратко рассматривается применение структурных значений в трех раз--личных языках.
Область действия идентификаторов
В этом языке для определения области действия и размещения переменных используется блочная структура (подобная той, которая применяется в АЛГОЛе). Мы будем часто говорить, что некоторая переменная А — «глобальная» для нескольких фрагментов программы. Это означает, что переменная А описана в блоке, содержащем все эти фрагменты программы. В ФОРТРАНе переменная А была бы в области COMMON.
Описания процедур
Процедуры описываются точно так же, как в языке АЛГОЛ. Синтаксис описания процедуры:
D::= PROCEDURE <заголовок>; {<спецификация>;} <тело>
17*
516
ПРИЛОЖЕНИЕ
::= [<тип>] <идентификатор> 1«пар>{, <пар>})1
::= S (любая инструкция)
::= <тип> [ARRAY]
<идентификатор> {, <идентификатор>}
<заголовок>
<тело>
<спецификация>
Каждый <пар> — это идентификатор, и он называется формальным параметром.
Если <заголовок> содержит указание <тип>, процедура является функцией, которая выдает значение этого типа. Во время выполнения процедуры имени функции должно быть присвоено значение, которое следует выдать. Спецификации описывают типы формальных параметров; в них нет необходимости, если типы очевидны из контекста или попутного обсуждения. Иногда спецификации могут появляться в самом списке параметров (это не показано в описании синтаксиса, приведенном выше). Например,
PROCEDURE X (INTEGER А, В; POINTER Р); ...
означает, что формальные параметры А, В и Р имеют типы INTEGER, INTEGER и POINTER соответственно.
Все фактические параметры вызываются по ссылке, если только они не определены иначе (см. гл. 8). Когда оканчивается выполнение тела процедуры или когда выполняется инструкция RETURN, управление передается в точку, следующую за точкой вызова.
Переменные и значения; использование указателей
1. Идентификаторы. Если идентификатор описан как имя переменной, то этот идентификатор является ссылкой на переменную:
<переменная> <идентификатор>.
2. Переменные с индексами. Пусть А — n-мерный массив. Как в АЛГОЛе, переменная с индексами А[еь е2, ..., еп) ссылается на соответствующий элемент массива. Выражение ej должно быть типа INTEGER. Мы также допускаем синтаксис
<идентификатор> (еь е...... еп).
3. Компоненты структурных величин. Предположим, что В — любая <переменная> структурного типа. Пусть компоненты В—это М, N,..., Q. Тогда В.М, B.N,..., B.Q ссылаются на переменные, которые являются компонентами. Таким образом, мы можем изменить значение компоненты, например сделать его равным 5, выполнив В.М: =5. В других языках используются другие обозначения для ссылки на компоненту М : „М OF В“ или „М(В)“. Чита
ЯЗЫК ПРОГРАММИРОВАНИЯ, ИСПОЛЬЗУЕМЫЙ В КНИГЕ
517
телю следует обратиться к разд. 8.6, где кратко обсуждаются эти понятия.
4. Подстроки. Пусть X — любая переменная типа STRING. Тогда
SUBSTR (X, еь'е,)
(где е( — выражение типа INTEGER) также переменная типа STRING, а ее значением являются литеры ei, ei+l, ...,ei + ea—1 из X. Заметьте, что литеры в X нумеруются начиная с 0. Так, если X='ABCD', то мы можем изменить X на 'A1XD' выполняя
SUBSTR (X, 1, 2) :='IX'
5. Косвенная адресация. Пусть Р — указательная переменная и Е — любое выражение. Тогда после выполнения либо
Р: = @Е, либо P:=ADDRESS (Е)
Р присваивается адрес ячейки, содержащей результат вычисления Е. Если Е — <переменная>, то Р будет ссылкой на эту переменную. Мы можем теперь ссылаться на Е, используя CONTENTS(P).
Если Е — переменная, мы можем изменить ее значение: CONTENTS(P) := 3 эквивалентно Е : = 3.
Таким образом, это не что иное, как косвенная адресация, которую можно встретить во многих машинах.
Предположим, что Р ссылается на структурную переменную В и что В имеет компоненту с именем М. Тогда можно было бы использовать Р.М как сокращение для CONTENTS(P).M .
Приведем несколько примеров. Предположим, что Р — это указатель, а В и С — структурные переменные с компонентами N, М и Q, как показано ниже:
BNMQ CNMQ
о з | о | о е | о | о '
Выполняя Р := @В; B.Q := @С, изменяем схему на
Р В N М Q с ы м q
--J 3 I О I -I—*1 6 I О | о
518
ПРИЛОЖЕНИЕ
где стрелки указывают значения указательных переменных- Р и
B.Q . Выполняя Р.М := 5, изменим схему на
Выполняя P.Q.M := 4, изменим схему на
р BNMQ CNMQ
P.Q ссылается на переменную, состоящую из компоненты Q в В; ее значение есть адрес С. Таким образом, P.Q.M ссылается на компоненту М в С, т. е. P.Q.M эквивалентно CONTENTS (CONTENTS (P).Q).M.
Выражения
Операции в выражении выполняются слева направо; как обычно, учитывается наличие скобок и приоритеты операторов. Приоритеты операторов приведены в следующей таблице (оператор в первой строке имеет наивысший приоритет):
* *
— (унарный) @
* / И
+ — (бинарный)
= ¥=<<>>
NOT
AND
01^ CAT
Любая переменная или константа является выражением. Если ei — выражение, то (ех) — тоже выражение.
1. Арифметические выражения. Пусть ei и е2 — арифметические выражения (типа REAL или типа INTEGER). Тогда ei+e2, ех—е2, —еъ ei*e2, ех/е2, ei//e2 и ех**е2 — тоже выражения. Результатом ei//e2 будет наибольшее целое, не превосходящее ei/e2. Так, 3//2=1, 4//2=2 и (—3)//2—2.
ЯЗЫК ПРОГРАММИРОВАНИЯ, ИСПОЛЬЗУЕМЫЙ В КНИГЕ
519
2. Логические выражения. Если ei и е2 — логические выражения, то
ех AND е2, ех OR е2 и NOT ег
тоже логические выражения. Эти три оператора имеют обычный смысл.
Операторами отношения являются —, ^=, >, ^, < и Если ei и е2 — выражения и R - оператор отношения, то отношение ei R е2 является выражением с очевидным значением TRUE или FALSE. Если ei — арифметическое ‘Выражение, то и е2 должно быть арифметическим выражением.
Если ei — логическое выражение, то и е2 должно быть таковым. В этом случае оператор R должен быть = или =#. Если ех — литера (CHARACTER) или строка (STRING), то таким же должно быть е2. В этом случае более короткая из строк ei и е2 дополняется пробелами до тех пор, пока они не будут иметь одинаковую длину и затем выполняется сравнение в соответствии с представлением литер в коде EBCDIC.
Если ех — указатель (POINTER), то е2 тоже должно быть указателем. Оператор R должен быть либо —, либо У=.
3. Указательные выражения. Пусть ег — любое выражение или переменная. Тогда как @ еп так и ADDRESS (ei) дают значение типа POINTER, которое является адресом или ссылкой на значение выражения или переменной. Константа 0 является таким значением типа POINTER, которое не ссылается на другое значение.
4. Структурные выражения. Пусть ST — некоторый структурный тип, состоящий из компонент Nn N2, ..., Nn, имеющих соответственно типы Rt, R2, ..., Rn. Пусть ei, е2, ..., en — выражения типов Ri, R2, ..., Rn соответственно. Тогда
(ei, е2, ..., еп)
является выражением типа ST. Значением i-й компоненты выражения будет еь
- Инструкции
Инструкции выполняются в той последовательности, в которой они написаны, если только порядок их выполнения не изменяется инструкцией перехода. В том коротком описании различных инструкций, которое приведено ниже, «S» означает «инструкция».
1. Помеченная инструкция. S ::= <метка> : S
Любая инструкция может быть помечена. <Метка> — это <идентификатор> или целое без знака.
520
ПРИЛОЖЕНИЕ
2. Пустая инструкция. S :: =
Эта инструкция обеспечивает гибкость при программировании и позволяет упростить описание синтаксиса.
3. Инструкция присваивания. S ::= <переменная> :=<выр>
Выполняется так же, как в АЛГОЛе, с обычным преобразованием типов, которое делается автоматически. Вычисляется адрес переменной, вычисляется выражение и результат выражения присваивается переменной.
4. Инструкция перехода. S ::= GOTO <метка>|ОО ТО <метка> Следующей будет выполняться инструкция, помеченная этой меткой.
5. Инструкция IF. S ::= IF <выр>ТНЕИ Si [ELSE SJ Вычисляется выражение: получается результат типа BOOLEAN : TRUE или FALSE. Если TRUE, то выполняется Si, если FALSE и если присутствует S2, то выполняется S2. ELSE соответствует ближайшему предыдущему THEN.
6. Составная инструкция. S BEGIN S {; S} END
Инструкции S выполняются по порядку. Составные инструкции используются для объединения нескольких инструкций вместе в единую инструкцию.
7. Блок. S ::= BEGIN D; {D;} S {; S} END
Так выглядит блок в языке АЛГОЛ. Должно быть хотя бы одно описание D. При входе в блок распределяется память для описанных в нем переменных. Затем по порядку выполняются инструкции. Если происходит выход из блока, память, выделенная ранее для переменных в блоке, освобождается. Такой выход может произойти вследствие инструкций перехода, возврата (RETURN) или когда окончится выполнение последней инструкции.
8. Инструкция WHILE. S ::= WHILE <выр> DO Si
Это эквивалентно инструкции
AGAIN ! IF <выр> THEN BEGIN Sr, GOTO AGAIN END
9. Инструкция FOR. S ::= FOR <переменнаЯ> := <выр> STEP <выр> UNTIL <выр> DO Si Выполняется так же, как в АЛГОЛе.
10. Инструкция CASE. S ::= CASE <выр> OF S {; S} ENDCASE |CASE <выр> OF BEGIN S S} END
Как можно видеть, имеются две эквивалентные формы инструкции CASE. Инструкция CASE выполняется следующим образом:-вычисляется <выр>, чтобы получить целое i. Выполняется i-я инструкция из списка инструкций. Затем управление передается в точку непосредственно за инструкцией CASE. Если произойдет переход к одной из подинструкций S, то, после того как окончится
ЯЗЫК ПРОГРАММИРОВАНИЯ, ИСПОЛЬЗУЕМЫЙ В КНИГЕ
521
выполнение S, управление будет передано в точку непосредственно за инструкцией CASE
11. Вызов процедуры или функции. S <идентификатор>
[«пар>, <пар>.....<пар»1
Параметры могут быть любым выражением или именем массива. Они вызываются по ссылке (см. гл. 8), если они не специфицированы иначе. Вызов выполняется, как в ФОРТРАНе или АЛГОЛе, с обычным соответствием между фактическими и формальными параметрами. Процедуры могут быть рекурсивными. Две стандартные функции, которые используются в программах, определены следующим образом:
SIGN(X)=IF Х<0 THEN—1 ELSE IF X=0THEN 0 ELSE +1 MAXIMUM (X, Y)=IF X<Y THEN Y ELSE X
12. Инструкция RETURN. S ::= RETURN
Возврат в точку вызова. Может встретиться только в теле процедуры.
СПИСОК ЛИТЕРАТУРЫ
В библиографии использованы следующие сокращения:
CACM Communications of the ACM »
J ACM Journal of the ACM
NACM Proceedings of the National ACM Conference
SJCC Proceedings of the Spring Joint Computer Conference
FJCC Proceedings of the Fall Joint Computer Conference
EJCC Proceedings of the Eastern Joint Computer Conference
WJCC Proceedings of the Western Joint Computer Conference
Ann R Annual Review in Automatic Programming, Pergammon Press
Comp J Computer Journal
IFIP Proceedings of the IFIP Congress
Если автор имеет более одной публикации, то следом за его фамилией в скобках указывается год; если же автор имеет несколько публикаций за год, то за указанием года следуют а, Ь... (звездочкой отмечены работы, включенные редакторами перевода).
Айронс [61а] (Irons Е. Т.)
A syntax directed compiler for ALGOL 60, CACM, 4 (Jan. 1961), 51—55. — [63a]
The structure and use of the syntax-directed compiler, Ann R, 3 (1963), 207—227. — [63b]
An error correcting parse algorithm, CACM, 6 (Nov. 1963), 669—673.
— [64]
«Structural connections» in formal languages, CACM, 7 (Feb. 1964), 67—72. Айронс, Ферцайг (Irons E. T., Feurzeig W.)
Comments on the implementation of recursive procedures and blocks in ALGOL 60, CACM, 4 (Jan. 1961), 65—69.
Аллард, Вулф, Землин (Allard R. W., Wolf K. A., Zemlin R. A.)
Some effects of the 6600 Computer on language structures, CACM, 7 (Feb. 19.64), 112—127.
Аллен (Allen F. E.)
Program optimization, In Ann R, 5 (1969), 239—307.
Андерсон (Anderson J. P.)
< A note on compiling algorithms, CACM, 7 (March 1964), 145—150.
Арден, Галлер, Грехем [61] (Arden В. W., Galler В. A., Graham R. M.)
. An algorithm for equivalence declarations, CACM, 4 (July 1961), 310—314. - 162]
An algorithm for translating Boolean expressions, J ACM, 9 (April 1962), 222— 239.
СПИСОК ЛИТЕРАТУРЫ
523
Батсон (Batson А.)
The organization of symbol tables, CACM, 8 (Feb. 1965), 111—112.
Бауэр, Беккер, Грехем (Bauer H., Becker S., Graham S.)
ALGOL W implementation. CS 98, Computer Science Dept., Stanford Univ.,
Белл [69] (Bell J. R.)
A new method for determining linear precedence functions for precedence grammars, CACM, 12 (Oct. 1969), 567-569.
- [70]
Quadratic quotient method: a hash code eliminating secondary clustering, CACM, .13 (Feb. 1970), 107-109.
Берман, Шарп, Старджес (Berman R., Sharp J., Sturges L.) Syntactical charts of COBOL 61, CACM, 5 (May 1962), 260.
Бернс (Berns G. M.)
Description of FORMAT, a text-processing program, CACM, 12 (March 1969), 141—146.
Биледи (Belady L. A.)
A study of replacement algorithms for a virtual-storage computer, IBM Systems Journal, 5 (1966), 78—82.
Браун [67] (Brown P. J.)
[The ML/1 macro processor, CACM, 10 (Oct. 1967), 618—623.
A survey of macro processors, Ann R, 6 (1969), 37—88.
Брейер (Breuer M. A.)
Generation of optimal code for expressions via factorization, CACM, 12 (June 1969), 333—340.
Брукер, Моррис (Brooker R., Morris D.)
A general translation program for phrase structure languages, J ACM, 9 (Jan. ' 1962), 1-10.
Брукер и др. (Brooker R. et al.)
The compiler-compiler, Ann R, 3 (1963), 229—275.
Брукер, Мрррис, Рол [62] (Brooker R., Morris D., Rohl J. S.)
Trees^and routines, Comp. J., 5 (April 1962), 33.
Experience with the compiler compiler, Comp J, 9 (1967), 345—349.
Бьюзем, Энглунд (Busam V., Englund D.)
Optimization of expressions in FORTRAN, CACM, 12 (Dec. 1969), 666—674. Бэкус (Backus J. W.)
The syntax and semantics of the proposed international algebraic language of the Zurich ACM—GAMM Conference. Proc. International Conf, on Information Processing, UNESCO (1959), 125—132.
— и др.
The FORTRAN automatic coding system, WJCC (1957), 188—198.
Бэр, Бове (Baer J. L., Bovet D. P.)
Compilation of arithmetic expressions for parallel computations, IFIP, 68, B4-B10.
Бэйер, Грис, Пол, Вил (Bayer R., Gries D., Paul M., Wiehle H. R.)
The ALCOR ILLINOIS 7090/7094 post mortem dump, CACM, 10 (Dec. 1967), 804—808.
Вагнер [68] (Wagner R. A.)
Some techniques for algebraic optimization with application to matrix arithmetic expressions. Thesis. Carnegie—Mellon Univ., June 1968.
524
СПИСОК ЛИТЕРАТУРЫ
* Вагнер [74] (Wagner R. А.)
Order-n correction for regular languages, CACM, 17 (May 1974), 265—268.
Ван дер Пол (Van der Poel L. W.)
The construction of an ALGOL translator for a small computer. In Prog. Lang, in Data Processing. 229—236. Gordon and Breach, 1963.
Вегнер [68a] (Wegner P.)
Programming Languages. Information Structures and Mechine Organization, McGraw-Hill, New York, 1968.
Вейт (Waite W.)
A language-independent macro processor, CACM, 10 (July 1967), 433—440.
*Вирт (Wirth N.)
The Design of a PASCAL Compiler. Software—Practice and Experience 1 (1971), 309—333.
Вирт, Вебер (Wirth N., Weber H.) ' .
Euler—a generalization of ALGOL and its definition. Part I, Part II, CACM, 9 (Jan., Feb. 1966), 13—25, 89—99.
Вирт, Xoop (Wirth N., Hoare C. A. R.)
A contribution to the development of ALGOL, CACM, 9 (June 1966), 413—432.
Воршалл [61] (Warshall S.)
A syntax directed generator, EJCC, 1961, 295—305.
- [62]
A theorem on Boolean matrices, JACM, 9 (Jan. 1962), 11—12
Воршалл, Шапиро (Warshall S., Shapiro R. M.)
A general-purpose table-driven compiler, SJCC, 1964, 59—65.
Галлер, Перлис (Galler В., Perlis A. J.)
A proposal for definitions in ALGOL, CACM, 10 (April 1967), 204—219.
Гарвик (Garwick J. V.)
GARGOYLE, a language for compiler writing, CACM, 7 (Jan. 1964), 16—20. Гауэр (Gowef J. C.)
The handling of multiway tables on computers, Comp J, 4 (Jan. 1962), 280—286.
Геллерман [62] (Hellerman H.)
^Addressing multidimensional arrays, CACM, 5 (April 1962), 205—207.
Parallel processing of algebraic expressions, IEEE Trans. EC—15 (Feb. 1966),
Гилл (Gill A.)
Introduction to the theory of finite-state machine. McGraw-Hill Book Co., New
York, 1962. (Есть русский перевод: Гилл А., Введение в теорию конечных автоматов, М., «Наука», 1966.)
Гинзбург [62] (Ginsburg S.)
An introduction to mathematical machine theory, Addison-Wesley, Reading, Mass. (1962).
- [66]
The mathematical theory of context-free languages. McGraw-Hill Book Company, N. Y.,1966. (Есть русский перевод: Гинзбург С., Математическая теория контекстно-свободных языков, М., «Мир», 1970.)
Гир [64] (Gear С. W.) *
Optimization of the address field computation in the ILL I AC II assembler, [Comp J, 6 (Jan. 1964), 332.
High speed compilation of efficient object code, CACM, 8 (Aug. 1965), 483—488.
*Гладкий A. В.
Формальные грамматики и t языки, М., «Наука», 1973.
СПИСОК ЛИТЕРАТУРЫ
525
Гленни (Glennie А* Е.)
On the syntax machine and the construction of a universal compiler. Techn. Rpt. № 2, Computation Center, Carnegie Inst, of Tech. (1960).
♦ Глушков В. M.
Синтез цифровых автоматов, М., Физматгиз, 1962.
Горн (Gorn S.)
Specification languages for mechanical languages and their processors, a baker’s dozen, CACM, 4 (Dec. 1961), 532—542.
* Гоулд (Gould I. H. (Ed.))
IFIP Guide to Concepts and Terms in Data Processing, North-Holland Publishing Company, Amsterdam, 1971.
Гринволд (Greenwald I.)
A technique for handling macro instructions, CACM, 2 (Nov. 1959), 21—22.
Гринволд, Кейн (Greenwald I., Kane M.)
The SHARE 709 system: programming and modification, JACM, 6 (1959), 396. Грис (Gries D.)
The use of transition matrices in compiling, CACM, 11 (Jan. 1968), 26—34.
Грис, Пол, Вил (Gries D., Paul M., Wiehle H. R.)
Some techniques used in the ALCOR ILLINOIS 7090, CACM, 8 (Aug. 1965) 496—500. ' '
Гриффитс, Петрик (Griffiths T. V., Petrick S. R.)
On the relative efficiencies of context-free grammar recognizers, CACM, 8 (May 1965), 289—299.
Гро (Grau A. A.)
Recursive processes and ALGOL translation, CACM, 4 (Jan. 1961), 10—15.
Данциг, Рейнольдс (Dantzig G. B., Reynolds G.)
Optimal assignment of computer storage by chain decomposition of partially ordered sets. Univ, of Calif., Berkeley. Operations research center Rpt. № ORC— 66—6, March 1966.
Деремер (DeRemer F.)
Simple LR(k) grammars. Computer Science Dept., Univ, of Calif, at Santa Cruz, May 1970.
• * Джермейн К- Б.
Программирование на IBM/360, М., «Мир», 1971.
Джилберт (Gilbert Р.) '
On the syntax of algorithmic languages, JACM, 13 (Jan. 1966), 90—107.
Джонсон (Johnson L. R.)
Indirect chaining method for addressing on secondary keys, CACM, 4 (May 1961), 218—222.
Джонсон, Портер, Эккли, Росс (Johnson W. L., Porter J. H., Ackley S. I., Ross D. T.)
Automatic generation of efficient lexical processors using finite state techniques, CACM, 11 (Dec. 1968), 805-813.
Дийкстра (Dijkstra E. W.)
An ALGOL 60 translator for the XI, Ann R, 3 (1963), 329—356.
Домелки (Domolki B.)
An algorithm for syntactic analysis. Computational Linguist, 3 (1964), 29—46. (Hungarian Journal).
Ершов [58] (Yershov A. P.)
On programming ©f arithmetic operations, CACM, 1 (Aug. 1958), 3—6.
526
СПИСОК ЛИТЕРАТУРЫ
- [66]
ALPHA — an automatic programming system of high efficiency, JACM, 13 (Jan 1966), 17—24.
* Ершов А. П. [67]
Альфа-система автоматизации программирования, Новосибирск, 1967.
* Ершов А. П. [71]
Универсальный программирующий процессор. В сб.: Проблемы прикладной математики и механики, М., «Наука», 1971.
Замельзон, Бауэр (Samelson К-, Bauer F. L.)
Sequential formula translation, CACM, 3 (Feb 1960), 76—83.
ИБМ (a)
FORTRAN (H) Compiler. Programming Logic Manual, Form Y28—6642. ИБМ (b)
PL/1 (F) Compiler, Programming Logic Manual, Form Y28—6800.
ИБМ (c)
An Introduction to the Compile-Time Facilities of PL/1.
Technical Publication C20—1689. IBM Corporation. August, 1968.
ИБМ (d)
Operating System/360 Assembler Language. IBM Form C28—6514.
Ингерман [61a] (Ingerman P. Z.)
Thunks, CACM, 4 (Jan. 1961), 55—58.
- [61b]
Dynamic declarations, CACM, 4 (Jan. 1961), 59—60.
— [66]
A Syntax Oriented Translator, Academic Press, New York, 1968.
(Есть русский перевод: Ингерман П., Синтаксически ориентированный транслятор, М., «Мир», 1969.)
Ихбия, Морз (Ichbiah J. D.t Morse S. P.)
A technique for generating almost optimal Floyd-Evans productions for precedence grammars, CACM, 13 (Aug. 1970), 501—508.
Каннер (Kanner H.)
An algebraic transactor, CACM, 2 (Oct. 1959), 19—22.
Кент (Kent W.)
Assembler-language programming. Computing Surveys 1 (Dec. 1969), 183—196. Клини (Kleene S. C.)
Representation of events in nerve-sets, in Automata Studies pp. 3—42. Princeton Univ. Press, Princeton, N. J., 1956.
Кнут [59] (Knuth D. E.)
Runcible—algebraic translation on a limited computer, CACMr 2 (Jan. 1959), 18-21.
- [65]
On the translation of languages from left to right, Inf. Contr., 8 (Oct. 1965), 607—639. (Есть русский перевод: см. сб. Языки и автоматы, М., «Мир», 1975, [Стр. 9—42.)
The Art of Computer Programming. Vol. 1. Addison-Wesley Publishing Company. Inc. Reading, Mass., 1968. (Есть русский перевод: Кнут Д., Искусство программирования на ЭВМ, М., «Мир», 1975.)
The Art of Computer Programming. Vol. 3. Addison-Wesley Publishing Company, Inc. Reading, Mass., 1974.
СПИСОК ЛИТЕРАТУРЫ
527
Кок, Шварц (Cocke J., Schwartz J. Т.)
Programming languages and their compilers. Preliminary notes. Courant Inst, of Math, sciences. New York, Univ., 1970.
КолМерор (Colmerauer A.)
Total precedence relations, JACM, 17 (Jan. 1970), 14^30.
Конвей (Conway M. E.)
Design of a separable transition diagram compiler, CACM, 6 (July 1963), 396— 408.
Конвей, Максвелл (Conway R. W., Maxwell W. L.)
CORC—the Cornell computing language, CACM, 6 (June 1963), 317—321.
— и др. .
PL/C. A high performance subset of PL/1. TR 70—55. Computer Science Dept, Cornell Univ., 1970.
Коэн, Готлиб (Cohen D., Gotlieb С. C.)
A list structure form of grammars for syntactic analysis. Computing Surveys 2 (March 1970), 65—81.
Кресс и др. (Cress P. H. et al.) -
Description of/360 WATFOR. Dept, of Applied Analysis and Computer Science, Univ, of Waterloo. Report № CSTR-1000.
Куно, Уттингер (Kuno S., Oettinger A. G.)
Multiple-path syntactic analyzer. Information Processing 62 (IFIP Congress), Popplewell (Ed.), North Holland Publishing Co., Amsterdam, 1962, 306—311.
*Лайон (Lyon G.)
Syntax-directed least-errors analysis for context-free languages: a practical approach, CACM 17 (January 1974), 3—14.
Лёкс (Loeckx J.)
An algorithm for the construction of bounded-context parsers. Report R99.
Manufacture Beige de Lampes et de Materiel Electron!que, March 1969.
Ливенвирт [64] (Leavenwirth В. M.)
FORTRAN IV as a syntax language, CACM, 7 (Feb. 1964), 72—80.
~ [66]
Syntax macros and extended translation, CACM (Nov. 1966), 790—793.
Линч (Lynch W. C.)
A high-speed parsing algorithm for ICOR grammars. Report № 1097, Andrew Jannings Computing Certer, Case Western Reserve Univ., 1968.
Лоури, Медлок (Lowry E., Medlock C.)
Object code optimization, CACM, 12 (Jan. 1969), 13—22.
Луччо (Luccio F.)
A comment on index register allocation, CACM, 10 (Sept. 1967), 572—574.
Льюис, Стирнз (Lewis P. M. II, Stearns R. E.)
Syntax-directed transductions, JACM, 15 (July 1968), 465—488.
Макилрой [60] (McIlroy M. D.)
Macro instruction extensions of compiler languages, CACM, 3 (April 1960), 214—220.
- [63]
A variant method of file searching, CACM, 6 (March 63), 101.
Маккалок, Питтс (McCulloch W. S., Pitts W.)
A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophysics 5, 115—333.
Маккарти (McCarthy J.)
Recursive functions of symbolic expressions and their computation by machine, CACM, 4 (April 1960), 184—195.
528
СПИСОК ЛИТЕРАТУРЫ
Маккиман [65] (McKeeman W. М.)
Peephole optimization, CACM 8 (July 1965), 443—444.
An approach to language design. CS 48, Computer Science Dept., Stanford Univ., 1966.
Маккиман, Хорнинг, Бортман (McKeeman W. M., Horning J. J., Wortman D. B.) A Compiler Generator implemented for the IBM System/360, Prentice Hall, 1970.
Макклюр (McClure R. M.)
TMG — a syntax-directed compiler, NACM, 20 (1965), 262—274.
Мартин (Martin D. F.)
Boolean matrix methods for the detection of simple precedence grammars, CACM, 11 (Oct. 1968), 685-687.
Маурер (Maurer W. D.)
An improved hash code for scatter storage, CACM, 11 (Jan. 1968), 35—38.
Мендицино, Цвакенберг (Mendicino S., Zwackenberg R.)
A FORTRAN code optimizer for the CDC 6600. UCRL-14162, Lawrence Radiation Lab. April 1965.
Морган (Morgan H. L.)
Spelling correction in system programs, CACM, 13 (Feb. 1970), 90—94.
Моррис (Morris R.)
Scatter storage techniques, CACM, 11 (Jan. 1968), 38—44.
Муерс, Дойч (Mooers C., Deutsch L. P.)
TRAC, a text handling language, NACM, 20 (1965), 229—246.
Myp (Moore E. F.)
Gedanken experiments on sequential machines. Automata Studies, pp. 129—153. Princeton Univ. Press, Princeton, 1956,
Наката (Nakata I.)
A note on compiling algorithms for arithmetic expressions, CACM, 10 (Aug. 1967), 492—494.
Hayp [63a] (Naur P. (Ed.))
Revised report on the algorithmic language ALGOL 60, CACM, 6 (Jan. 1963), 1—17. (Есть русский перевод: Алгоритмический язык АЛГОЛ-60, М., «Мир», 1965.)
— [63b]
The design of the GIER ALGOL compiler, BIT, 3 (1963), 124—140, 145—166. - [65]
The design of the GIER ALGOL compiler, Ann R, 4 (1965), 49—85.
Пардон (Purdon P. W.)
A transitive closure algorithm. Computer Sciences Technical Report it 33, July 1968. Univ, of Wisconsin.
Парик (Parikh R. J.)
Language generating devices. M. LT. Research Lab. Electron. Quart. Prog.
Report. 60, J961, 199-212. (Also in JACM 13 (Oct. 1966), 570—581, under the
title: On context free languages.) K
Петерсон (Peterson W. W.)
Addressing for random-access storage, IBM Journal of Research and Development, 1 (1957), 130.
Пласков, Шуман (Plaskow J., Schumann S.)
The TRANGEN system on the M460 Computer, AFCRL-66-516 (July 1966).
СПИСОК ЛИТЕРАТУРЫ
529
Пол (Paul М.)
ALGOL 60 processors and a processor generator, Proc, IFIP Congress, Munich, 1962, 493—497.
Пост (Post E. L.)
A variant of a recursively unsolvable problem, Bull. Am. Math. Soc., 52 (1946), 264—268.
*Поттосин И. В. [72]
О линеаризации программы и частичном ее упорядочении. В сб.: Системное и теоретическое программирование, ВЦ СО АН СССР, Новосибирск, 1972. - [73]
Оптимизирующие преобразования и их последовательность. В сб.: Системное программирование, часть II, ВЦ СО АН СССР, Новосибирск, 1973.
Радке (Radke С. Е.)
The use of quadratic residue search, CACM, 13 (Feb. 1970), 103—105.
Реджиевский (Redziejowski R. R.)
On arithmetic expressions and trees, CACM, 12 (Feb. 1969), 81—84.
Рейноладс (Reynolds J. C.)
An introduction to the COGENT Programming System, NACM, 20 (1965), 422— 436.
Ренделл, Рассел (Randell В., Russell D. J.)
ALGOL 60 Implementation. Academic Press, London, 1964. (Есть русский
перевод: Ренделл Б., Рассел Л., Реализация АЛГОЛА-60, «Мир», М., 1967.) Ришел (Rishel W. J.)
Incremental compilers. Datamation. Also in Software for Computer Systems.
College Readings, Inc. Arlington, Va. 1970.
Розен (Rosen S.)
A compiler-building system developed by Brooker and Morris, CACM, 7 (July 1964), 403—414.
Розен, Спарджен, Доннели (Rosen S., Spurgeon R. A., Donnelly J. K.)
PUFFT — the Purdue University fast FORTRAN translator, CACM, 8 (1965), 661—666.
Розенкранц, Стирнз (Rosenkrantz D. S., Stearns R. E.)
Properties of deterministic top down grammars, ACM Symposium on Theory of
Computing (May 1969), 165—180.
Росс [66] (Ross D.)
AED bibliography. Memo MAC-M-278-2, Project MAC, M. I. T., Cambridge, Mass., Sept. 1966.
- [67a]
The AED approach to generalized computer- aided design, NACM, 1967, 367— 385.
- [67b]
The AED free storage package, CACM, 10 (Aug. 1967), 481—492.
Рутисхаузер (Rutishauser H.)
Automatische Rechenplanfertigung bei programmgesteuerten Rechenmaschi-nen, Mitt. Inst, fur Angew. Math, der ETH Zurich, Nr. 3, 1952.
Сибли (Sibley R. A.) •
The SLANG system, CACM, 4 (Jan. 1961), 75—84.
Сквайр (Squire J. S.)
A translation algorithm for a multiple processor computer, NACM, 1963.
Стендиш (Standish T. A.)
A data definition facility for programming languages. Computer Science Rpt., Carnegie Inst, of Tech., May 1967.
530
СПИСОК ЛИТЕРАТУРЫ
Стирнз, Льюис (Stearns R. Е., Lewis II. Р. М.)
Property grammars and table machines. IEEE Conference record of the 1968 annual symp. on switching and automata theory, 106—119.
Стоун (Stone H. S.)
One-pass compilation of arithmetic expressions for a parallel processor, CACM, 10 (April 1967), 220-223.
Стречи (Strachey C.)
A general purpose macrogenerator, Comp. J, 8 (1965—1966), 225—241.
Сэти, Улман (Sethi R., Ullman J. D.)
The generation of optimal code for arithmetic expressions, JACM, 17 (Oct. 1970), 715—728.
Сэттли (Sattley K-)
Allocation of storage for arrays in ALGOL 60, CACM, 4 (Jan. 1961), 60—65.
Тиксир (Tixier V.)
Recursive functions of regular expressions in language analysis. CS 58. Computer Science Dept., Stanfrod Univ., March 1967.
*Трахтенброт Б. А.; Бардзинь Я- M.
Конечные автоматы (поведение и синтез), М., «Наука»,, 1970.
Тейлор, Тарнер, Вейхоф (Taylor W., Turner L., Waychoff R.)
A syntactical chart- of ALGOL 60, CACM, 4 (Sept. 1961), 393.
Уитни (Whitney G.)
An extended BNF for specifying the syntax of declarations, SJCC, 1969, 801 — 812.
Унгер (Unger S.)
A global parser for context-free phrase structure grammars, CACM, 11 (April 1968), 240—247.
Фелдман (Feldman J. A.)
A formal semantics for computer languages and its application in a compilercompiler, CACM, 9 (Jan. 1966), 3—9.
Фелдман, Грис (Feldman J. A., Gries D.)
Translator writing systems, CACM, 11 (Feb. 1968), 77—113. (Есть русский перевод в сб. Алгоритмы и алгоритмические языки, вып. 5, ВЦ АН СССР, М., 1971.)
Фишер (Fischer М. J.)
Some properties of precedence languages, Proceedings ACM symposium on theory of computing (May 1969), 181—188.
Флойд [61a] (Floyd R. W.)
An algorithm for coding efficient arithmetic operations, CACM, 4 (Jan. 1961), 42—51.
- [61b]
A descriptive language for symbol manipulation, JACM, 8 (Oct. 1961), 579— 584.
- [63]
Syntactic analysis and operator precedence, JACM, 10 (July 1963), 316—333. — [64a]
Bounded context syntactic analysis, CACM, 7 (Feb. 1964), 62—67.
— [64b]
The syntax of programming languages — a survey. IEEE Trans., EC13, 4 (Aug. 1964), 346—353.
Флорес (Flores I.)
Computer Sorting, Prentice-Hall, Inc., Englewood Cliffs., 1969.
СПИСОК ЛИТЕРАТУРЫ
531
Фриман (Freeman D.)
Error correction in CORC: the Cornell computing language. Thesis, Cornell Univ., 1963.
Фэйтман (Fateman R. J.)
Optimal code for serial and parallel computation, CACM, 12 (Dec. 1969), 694— 695.
Хакстебл (Huxtable D. H. R.)
On writing an optimizing translator for ALGOL 60. In Introduction to System Programming. Academic Press Inc., New York, 1964.
Халперн [64] (Halpern M.)
XPOP: a metalanguage without metaphysics. FJCC 1964, 57—68. - [67]
A manual of the XPOP programming system. Electronic Sciences Lab., Lockheed Missiles and Space Company, Palo Alto, California, March 1967.
- [68]
Toward a general processor for programming languages, CACM, 11 (Jan. 1968), 15—25.
Хаски, Лоув, Вирт (Huskey H. D., Love R., Wirth N.)
A syntactic description of BC NELIAC, CACM, 6 (July 1963), 367—375. Хаски (Huskey H. D.)
Compiling techniques for algebraic expressions, Comp J, 4 (1961), 10—19. Хекст, Робертс (Hext J., Roberts F.)
Syntax analysis by Domolki’s algorithm, Comp. J, 13 (Aug. 1970), 263—271. Хилл, Лангмак, Шварц, Зигмюллер (Hill V., Langmaack H., Schwarz H. R., Seegmuller G.)
Efficient handling of subscripted variables in ALGOL 60 compilers. Proc. Symbolic Languages in Data Processing Gordon and Breach, New York, 1962, 331— 340.
Холстед (Halstead M. H.)
Machine-Independent Computer Programming, Spartan Books, Washington D. C. 1962.
Хомский [56] (Chomsky N.)
Three models for the description of language, I REE Trans. Inform. Theory, vol. IT2 (1956), 113—124. (Есть русский перевод: Кибернетический сборник, 2, М., ИЛ, 1961, стр. 237—266.) - [59]
On certain formal properties of grammars. Information and Control 2, (1959), 137—167. (Есть русский перевод: см. Кибернетический сборник, 5, М., ИЛ, 1962, стр. 279-311.)
- [ВЗ]
- Formal Properties of Grammars. In Handbook of Mathematical Psychology.
Vol. 2, Luce, Bush and Galanter (Eds.) John Wiley and Sons, Inc., New York, 1963, 323—418.
Xoop (Hoare C. A. R.)
Record handling. In Programming Languages. Academic Press, 1968, pages 291—347. (Есть русский перевод: Языки программирования, М., «Мир», 1972.)
Хопгуд (Hopgood F. R. А.)
Compiling Techniques. American Elsevier. Inc., New York, 1970. (Есть русский перевод: Хопгуд Ф., Методы компиляции, «Мир», М., 1972.)
Хопкрофт, Уллман (Hopcroft J., Ullman J.)
> Formal languages and their Relation to Automata, Addison-Wesley, New York, 1969.
532 СПИСОК ЛИТЕРАТУРЫ
Хорвиц и др. (Horwitz I. Р. et al.)
Index register allocation, J ACM, 13 (Jan. 1966), 43—61.
Хорнинг (Horning J. J.)
Empirical comparison of LR(k) and precedence parsers, Memorandum, Computer research Group, Univ, of Toronto, Aug. 1970.
Циммер (Zimmer R.)
Weak precedence. Proc, of the International Computing Symposium 1970/ACM Europe, Part II (May 1970).
Читэм (Cheatham T. E.)
The TGS-II translator-generator system, IFIP, 1965, 592—593.
Читэм, Сэттли (Cheatham T. E., Sattley KO
Syntax directed compiling, SJCC, 1964, 31—57.
Шей, Спрут (Schay G., Spruth W. G.)
Analysis of a file addressing method, CACM, 5 (Aug. 1962), 459—462.
Шеридан (Sheridan P. B.)
The FORTRAN arithmetic-compiler of the IBM FORTRAN automatic coding system, CACM, 2 (Feb. 1959), 9.
Шнейдер, Джонсон (Schneider F. W., Johnson G. D.)
Meta-3; A syntax-directed compiler writing compiler to generate efficient code, NACM, 19 (1964).
IIIopp (Schorre D. V.)
META II: A syntax-oriented compiler writing language, NACM, 19(1964), page DI. 3.
Шоу (Shaw C. J.)
A specification of Jovial, CACM, 6 (Dec. 1963), 721—735.
Шоу (Shaw A.)
Lecture notes on a course in systems programming. CS 52, Computer Science Dept., Stanford Univ., 1966.
Эванс (Evans A.)
An Algol 60 Compiler, Ann R, 4(1964), 87—124.
Эйкел (Eickel J.)
Generation of parsing algorithms for Chomsky 2-type languages. Report № 6401.
Math. Onst. der Tech. Hochschule, Munich, 1964.
Эйкел, Пол, Бауэр, Замельзон (Eickel J., Paul M., Bauer F. L., Samelson K-) A syntax controlled generator of formal language processors, CACM, 6 (Aug. 1963), 451—455.
Эрли [65] (Earley J.)
Generating a recognizer for a BNF grammar. Technical Report, Carnegie Inst, of Tech., Pittsburgh, Penn., June 1965.
*—[70]
An efficient context-free parsing algorithm, CACM, 13 (Feb. 1970), 94—102.
СЕсть^русский перевод: сб. Языки и автоматы, М., «Мир», 1975, стр.
Эрман (Ehrman J.)
Q-type address constants, dummy external symbols, and pseudo registers, CGTM 66, Stanford Linear Accelerator Center, April 1969.
ИМЕННОЙ УКАЗАТЕЛЬ
Айронс (Irons Е.) 49, 124, 179, 308, 361
Аллард (Allard R.) 178, 459
Аллен (Allen F.) 294, 444, 457
Андерсон (Anderson J.) 457
Бардзинь Я. М. 105
Батсон (Batson А.) 263
Бауэр Г. (Bauer Н.) 144, 178, 218, 243, 294
Бауэр Ф. (Bauer F.) 179, 307, 457
Беккер (Becker S.) 144, 178, 218, 243, 294
Белл (Bell J.) 144, 263
Бернс (Berns G.) 14
Биледи (Belady L.) 458
Бове (Bovet D.) 459
Браун (Brown Р.) 485
Брейер (Breuer М.) 455
Брукер (Brooker R.) 124, 294, 308, 486, 489, 495
Бьюзем (Busam V.) 456, 457, 460
Бэйер (Bayer R.) 374, 511
Бэкус (Backus J.) 29, 307
Бэр (Baer J.) 459
Вагнер (Wagner R.) 354, 460
Вебер (Weber Н.) 144, 178, 308
Вегнер (Wegner Р.) 199
Вейт (Waite W.) 485
Вил (Wiehle Н.) 243, 265
Вирт (Wirth N.) 144, 178, 211, 243, 308, 512
Висотски (Vyssotsky) 263
Витни (Whitney G.) 180
Воршалл (Warshall S.) 56
Вулф (Wolf К.) 459
Галлер (Galler В.) 178
Гауэр (Gower J.) 243
Геллерман (Hellerman Н.) 243, 459
Гилл (Gill А.) 105
Гинзбург (Ginsburg S.) 64, 105
Гир (Gear С.) 455, 456
Гладкий А. В. 64
Глушков В. М. 105
Гоулд (Gould L) 6
Грехем (Graham S.) 144, 178, 243, 294
Гринволд (Greenwald I.) 484
Грис (Gries D.) 5, 24, 178, 179, 243, 265,
366, 457, 486, 509
Гриффитс (Griffiths Т.) 501
Гро (Grau А.) 124
Данциг (Dantzig G.) 338
Деремер (DeRemer F.) 179
Джермейн (Germain С.) 22
Джилберт (Gilbert Р.) 179
Джонсон Л. (Johnson L.) 263
Джонсон У. (Johnson W.) 100, 105, 488
Дийкстра (Dijkstra Е.) 307
Дойч (Deutsch L.) 485
Домелки (Domolki В.) 179
Ершов А. П. 460
Замельзон (Samelson К.) 179, 307, 457
Землин (Zemlin R.) 459
Ингерман (Ingerman Р.) 49, 220
Ихбия (Ichbiah J.) 178, 197
Кейн (Kane М.) 484
Кент (Kent W.) 484
Клини (Kleene S.) 105
Кнут (Knuth D.) 179, 241—243, 262,
263, 455
Кок (Cocke J.) 457
Колмерор (Colmerauer А.) 178
Конвей М. (Conway М.) 502
Конвей Р. (Conway R.) 353
Кресс (Cress Р.) 26, 267, 333, 510
Куно (Kuno S.) 124
Лайон (Lyon G.) 354
Лёкс (Loeckx J.) 179
534
ИМЕННОЙ УКАЗАТЕЛЬ
Линч (Lynch W.) 179
Лоури (Lowry Е.) 294, 409, 444, 457, 487
Лукашевич (Lukasiewicz J.) 281
Луччо (Luccio F.) 459
Льюис (Lewis Р.) 124, 180
Макилрой (McIlroy D.) 263, 484, 485
Маккалок (McCulloch W.) 105
Маккиман (McKeeman W.) 159, 163,
178, 209, 305, 365, 374, 459
Максвелл (Maxwell W.) 353
Мартин (Martin D.) 144
Маурер (Maurer W.) 263
Медлок (Medlock С.) 294, 409, 444, 457, 487
Морган (Morgan Н.) 354, 356
Морз (Morse S.) 178, 197
Моррис Д. (Morris D.) 124, 294, 486,
489, 495
Моррис Р. (Morris R.) 250, 263
Муерс (Mooers С.) 485
Мур (Moore Е.) 105
Наката (Nakata I.) 457
Наур (Naur Р.) 25, 36, 505
Парик (Parikh R.) 66
Перлис (Perlis А.) 178, 485
Петерсон (Peterson W.) 263
Петрик (Petrick Т.) 501
Питтс (Pitts W.) 105
Пол (Paul М.) 179, 243, 265
Пост (Post Е.) 66
Радке (Radke С.) 263
Рассел (Russel D.) 243
Реджиевский (Redziejowski R.) 457
Рейнольдс Г. (Reynolds G.) 338
Рейнольдс Дж. (Reynolds J.) 9, 124, 294
Ренделл (Randell В.) 243
Робертс (Roberts Р.) 179
Розен (Rosen S.) 124, 378, 495, 509
Розенкранц (Rosenkrantz D.) 124
Рол (Rohl J.) 486
Росс (Ross D.) 243, 488
Рутисхаузер (Rutishauser Н.) 307
Сквайр (Squire J.) 459
Стендиш (Standish Т.) 201, 215, 243
Стирнз (Stearns R.) 124, 180
Стоун (Stone Н.) 459
Стречи (Strachey С.) 479, 485
Сэти (Sethi R.) 459
Сэттли (Sattley К.) 124
Тиксир (Tixier V.) 180, 503
Трахтенброт Б. А. 105
Уллман (Ullman J.) 64, 105, 459
Унгер (Unger S.) 124
Уттингер (Oettinger А.) 124
Фелдман (Feldman J.) 5, 15, 105, 197, 264, 308, 486, 489
Флойд (Floyd R.) 124, 144, 178, 179, 197, 455
Флорес (Flores I.) 262
Фриман (Freeman D.) 353—356
Фэйтман (Fateman R.) 455, 456
Хакстебл (Huxtable D.) 457
Халперн (Halpern М.) 485
Халстед (Halstead М.) 179
Хаски (Huskey Н.) 455
Хекст (Hext J.) 179
Хилл (Hill V.) 457
Хомский (Chomsky N.) 29, 63
Хоор (Hoare С.) 211—213, 243
Хопгуд (Hopgood F.) 455
Хопкрофт (Hopcroft J.) 64, 105
Хорвиц (Horwitz L.) 459
Хорнинг (Horning J.) 179
Циммер' (Zimmer R.) 178
Читэм (Cheatham Т.) 9, 124, 504
Шварц (Schwarz J.) 457
Шорр (Schorre D.) 9, 124
Шоу (Shaw А.) 307
Эванс (Evans А.) 197
Эйкел (Eikel J.) 1.79
Энглунд (Englund D.) 456, 457, 460
Эрли (Earley J.) 197
Эрман (Ehrman J.) 412, 420
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автокод (assembler language) 17
Автомат конечный (finite state automaton) 74
----детерминированный (deterministic) 74
----недетерминированный (nonde-terministic) 76
Адрес базы (base address) 199
Алгоритм Воршалла (Warshall’s algorithm) 56
Алфавит (alphabet) 32
— входной (input) 74
Анализ (analysis) 18
— лексический (lexical) 20
— семантический (semantic) 21
— синтаксический (syntactic) 21
Ассемблер (assembler) 17
АОГ [см. грамматика аугментная операторная]
Бинарное дерево (binary tree) 256
Булева матрица (Boolean matrix) 54
Внутреннее представление (internal representation) 21, 278
Внутренняя форма исходной прог-
раммы (internal source program) 278
Входной участок (entry block) 446
Вывод (derivation) 36
— канонический (canonical) 48
— непосредственный (direct) 36
Вызов по значению (call by value) 218
----имени (by name) 220
----результату (by result) 218
----ссылке (by reference) 217
Выравнивание (alignment) 334
Выражение (expression) 518
— арифметическое (arithmetic) 518
— логическое (Boolean) 519
— регулярное (regular) 79
— структурное (structured) 519
— указательное (pointer) 519
Генерация кода (code generation) 22, 376 — команд [см. генерация кода] ----в семантических программах (in semantic routines) 390
----для дерева (from a tree) 387
--------польской записи (from Polish notation) 389
--------тетрад (from quadruples) 381
--------ТрИад (from triples) 383
Голова цепочки (head of a string) 33
----правильная (proper) 33
Грамматика (grammar) 35
— аугментная операторная (augmented operator grammar) 174
— контекстно-свободная (context free grammar) 65
— контекстно-чувствительная (context sensitive grammar) 64
— неоднозначная (ambiguous) 43
— ограниченно контекстная (bounded context grammar) 164
— однозначная (unambiguous) 43
— операторная (operator grammar) 146, 149
— предшествования (precedence grammar) 131
----операторов (operator precedence grammar) 150
— приведенная (reduced) 58
— регулярная (regular) 65
— рекурсивная (recursive) 39
— (m, n) предшествования ((m, n) precedence grammar) 163
— (1,2)(2,1) предшествования 158
— Л-свободна я (A-free grammar) 65
Граф программы (program graph) 292
Группа компонент (group of components) 269
Дампинг таблицы символов (dump of a symbol table) 373
Действия (actions) 184
Дескриптор (descriptor) 490
Диаграмма состояний (state diagram) 72, 86
536
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Дисплей (display) 201
— активный (active) 201
— глобальный (global) 226
— фактических параметров (actual parameter) 226
Длина вывода (length of a derivation) 37 — цепочки (length of a string) 32 Допвектор [см. информационный вектор]
Загрузочный модуль (load module) 412
Загрузчик (loader) 412
Замена сложных операций (strength reduction) 429
Запись активации (activation record) 199
— инфиксная (infix notation) 295
— польская (Polish notation) 281
— постфиксная (postfix notation) 281
— префиксная (prefix notation) 281 — суффиксная (suffix notation) *281 Зона (range, region) 336 , 445
Инвариантная операция (invariant operation) 429
Инструкция (statement) 519
— базисная (basic statement — BS) 498
— исходной программы (source program statement — SS) 498
— перехода (branch statement) 520
— помеченная (labeled statement) 519
— присваивания (assignment statement) 520
— пустая (empty statement) 520
— составная (compound statement) 520
— CASE 520
— FOR 520
— IF 520
— RETURN 520
- WHILE 520
Интерпретатор (interpreter) 17, 367
Инфиксная запись (infix notation) 295 Информационный вектор (information vector, dope vector) 207
Исключение вырожденных присваиваний (eliminating dead assignments) 454
— лишних операций (eliminating redundant operations) 425
Итерация множества (closure) 33 — усеченная (positive closure) 33
KA [см. автомат конечный]
Катенация, конкатенация (catenation — CAT) 33
ККБМ [см. компилятор компиляторов Брукера — Морриса]
Классификация СПТ (classification of TWS) 488
Код (code) 17
— объектный (object code) 17
Коллизия (collision) 248
Компилятор (compiler) 17
— компиляторов (compiler compiler) 18, 486
-----Брукера —• Морриса (Brooker-Morris compiler compiler) 495
Компиляторы
АЛГОЛ W 144, 178, 219, 243, 294, 378
АЛГОЛ расширенный, фирмы Burroughs 124, 484, 500
АЛЬФА 460
ККБМ (ВМСС) 124, 495—498
МЕТА 124
ФОРТРАН II 219, 307, 485
ФОРТРАН IV Н 27, 294, 409, 457, 500, 503
ФСЯ (FSL) 197, 105, 489—495
AED 100, 243, 488
ALCOR ILLINOIS 7090 24, 243,
265, 366, 509
COGENT 124, 294
CORC 353
CPL 479
CUPL 353
Gier ALGOL 25
NELIAC 179
PL/C 353
PL/1 F 243, 256, 374
PUFFT 378, 509
SHARE 7090 ALGOL 124
SPL 209, 374
WATFOR/360 26, 267, 387, 510
XPL 178, 209, 305
Компонента (component) 514
— элементарная (elementary component) 269
Конструктор (constructor) 92, 104, 145, 488
Коэффициент загрузки (load factor) 245
Куст (branch) 41
— концевой (end branch) 41
Линеаризация матрицы (linearization of a matrix) 137
Линейный участок (basic block) 292
Литера (character) 97, 101
Макровызов (macro call) 462
Макроопределение (macro definition) 461
Макрорасширение (macro expansion) 462
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
537
Матрица булева (Boolean matrix) 54 — переходов (transition matrix) 79, 170 — предшествования (precedence matrix) 127
Метакомпиляция (metacompile time) 487
Метасимвол (metasymbol) 61—63
Метаязык (meta-language) 29
Метод двойного приоритета (double priority method) 148
— помеченных границ (boundary tag method) 237
Нейтрализация ошибки (error recovery) 353
— при восходящем разборе (in bottom-up parsers) 325, 326
----нисходящем разборе (in top-down parsers) 322—325
НКА [см. автомат конечный недетерминированный]
Номер уровня (level number) 269
Нормальная форма Бэкуса (Backus ~ normal form) 36
НФБ (BNF) [см. нормальная форма Бэкуса]
Область данных (data area) 199
----динамическая (dynamic) 200
----статическая (static) 200
— действия (scope) 199, 515
— строк (string space) 209
Объектный модуль (object module) 411
----абсолютный (absolute) 412
----перемещаемый (relocatable) 412
ОГ [см. грамматика операторная]
Операнд (operand) 279
Оператор (operator) 279
Описатель (template, descriptor) 201, 264
Определение метки (label definition) 414
Оптимизация (optimization) 22
— для параллельных процессоров (for parallel processors) 459
— логических выражений (of Boolean expressions) 323
— программы (code optimization) 22, 421
— унарных операторов (of unary operators) 403
— циклов (of loops) 456
Основа (handle) 39
Отладка (debugging) 374, 507
— компилятора (compiler -debugging) 507
Отношение (relation) 49
— единичное (identity relation) 51
— предшествования (precedence relation) 125, 129, 133
— рефлексивное (reflexive relation) 50
— транзитивное (transitive relation) 50
— FIRST 52
— FIRSTTERM 151
— LAST 53
— LASTTERM 151
— SYMB 53
— WHITHIN 53
— 30, 36
— =>+ 31, 37
— =>* 37
— =4>, =$>+ 48
_>,<•, Л 125, 126
— ^>, <^, ° 150
“ O>, o<=:, o<, o>= 156, 157
Ошибка орфографическая (spelling error) 354
— семантическая (semantic error) 356
— синтаксическая (syntactic error) 360
Параметр фактический (actual parameter) 216
— формальный (formal parameter) 216
Переменные
ACC 381
ACTIVEAREA 226 .
BOOLEAN 310
BRO 110
CHAR 87
CLASS 87
CONSPART 206'
DELIM 88
FAT 109
FCHAIN 326, 329
GOAL 109
GRAMMAR 109
INTEGER 310
LABEL 310
NEXTQUAD 312
NXTSEM 306
NXTSYMB 121, 306
POINTFREE 252
QUAD 312
REAL 310
SEM 90, 195
SON 110
STACKTOP 226
SYN 90, 195
TCHAIN 326, 329
UNDEFINED 310
VARPART 206
Поддерево (subtree) 41
538
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Поиск бинарный (binary search) 246 — логарифмический (logarithmic search) 246
Поле (field) 412, 514
Польская запись (Polish notation) 281
Постфиксная запись (postfix notation) 281
Предшествующий участок (predecessor block) 446
Препроцессор (preprocessor) 477
Префиксная запись (prefix notation) 281
Правило (rule) 35
— лево(право) рекурсивное (left (right) recursive rule) 39
— подстановки (rewriting rule) 35
Предложение (sentence) 37
— неоднозначное (ambiguous) 43
Программа внутренняя (internal program) 22
— готовая (run-time program) 17
— исходная (source program) 17
— объектная (object program) 17
— реентерабельная (reentrant code) 506
— семантическая (semantic routine) 21, 295 ,
Программная секция (control section) 413
Продукционный язык (production language) 181
Продукция (production) 35, 181
Процедуры
ADD 88
binsearch 246
CHECKTYPE 312
CONVERTIR 312
CONVERTRI 312
ENTER 300, 312
ERRMESS 359
ERROR 121, 312
FILLIN 327
FREEAREA 197, 241
FREEGARBAGE 199
GC 88
GEN 381
GENERATETEMP 312
GETAREA 198
GETCHAR 88
GETINACC 381
GETNONBLANK 88
INSERT 310
LOOKUP 88, 310
LOOKUPDEC 310
MAXIMUM 521
MERGE - 327
OUT (C, D) 88
SCAN 90, 121
SIGN 521 ’
ПЯ fcM. продукционный язык]
Разбор (parse) 46
— без возвратов (parse without backup) 119
— восходящий (bottom-up) 46
— канонический (canonical) 48
— нисходящий (top-down.) 46
— слева направо (left-to-right) 46
Разделение (separation) 142
Раскрутка (bootstrapping) 511
Распознаватель (recognizer) 46
Распределение регистров (register allocation) 457
Рассеянная память (scatter storage) 249
Регулярное выражение (regular expression) 79
Редактор связей (linkage editor) 412
Редукция (reduction) 36
— непосредственная (direct) 42
Рекурсивный спуск (recursive descent) 120
Рекурсия левосторонняя (left recursion) 39, 115, 142 -
---прямая (direct) 115
— общая (general recursion) 116
— правосторонняя (right recursion) 39
— прямая (direct recur§ion) 115
Рехеширование (rehashing) 248
— квадратичное (quadratic rehash) 251
— линейное (linear rehash) 249
— сложением (add-the-hash rehash) 251
— случайное (random rehash) 250
Санк (thunk) 220
Сбор мусора (garbage collection) 241
Свертка (folding) 422
Связующий участок (articulation block) 446
Семантическое слово (semantic word) 264
Сентенциальная форма (sentential form) 37
Символ (symbol) 20, 32, 98, 102
— генерируемый (created symbol) 474
— начальный (distinguished symbol) 35
— нетерминальный (nonterminal) 35
— терминальный (terminal) 36
Синтаксис (syntax) 29
Синтаксическая единица (syntactic entity) 30
Синтаксическое дерево (syntax tree) 28, 40
Синтез (synthesis) 18
— объектной программы (of object program) 18
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
539
Система переходов (transition system) 80
Система построения трансляторов (translator writing system) 436
Сканер (scanner) 20
Словарь (vocabulary) 35
— внешних символов (external symbol dictionary — ESD) 414 .
— перемещаемых адресов (relocation dictionary — RLD) 418
Состояние (state) 72
— заключительное (final state) 74
— начальное (start state) 72, 74
Список идентификаторов (identifier list), 244
СПТ (TWS) [см. система построения трансляторов]
Стек (stack) 108
— операндов (operand stack) 146
—• операторов (operator stack) 146
— семантический (semantic stack) 302
Степень цепочки (power of a string) 33
Стратификация (stratification) 142
Структурная величина (structured va-
lue) 210, 514
Структурное значение (structured value) 210, 514
Суффиксная запись (suffix notation) 281 .
Таблица символов (symbol table) 20, 244
Текстовая карта (text card — TXT) 416
Тело макро (macro body) 462
Тетрада (quadruple) 286
Транзитивное замыкание (transitive clo-
sure) 51
Транслятор (translator) 17
Триада (triple) 289
— косвенная (indirect triple) 291
Узел (node) 41
— висячий (end node) 42
— концевой (end node) 42
Указатель (pointer) 203, 514, 517
— строки (string pointer) 209
Усеченная итерация (positive closure) 33 *
Условная макрогенерация (conditional macro) 476
Участок входной (entry block) 446
— линейный (basic block) 292, 422
— предшествующий (predecessor block) 446
— связующий (articulation block) 446
Факторизация (factoring) 62, 115, 455
Фраза (phrase) 38
— первичная (prime phrase) 151
— простая (simple phrase) 38
ФСЯ (FSL) 489
Функции предшествования (precedence functions) 137
Хвост цепочки (tail of a string) 33
-----правильный (proper) 33
Хеш-адресация (hash addressing) 247
Хеш-таблица (hash table) 252
Хеш-функция (hash functions 255
Цепочка (string) 32
— пустая (A) (empty (A) string) 32
Число зависимости (dependency number) 426
Язык (language) 37
— ассемблера (assembler language) 17
— исходный (source language) 17
— объектный (object language) 17
— продукционный (production language) 181
— расширяющийся (extendible language) 489
— системного программирования (systems programming language) 500
— существенно неоднозначный (inherently ambiguous language) 44
Оглавление
Предисловие редакторов перевода ................................... 5
Программа курса 15 «Конструирование компиляторов».................. 8
Предисловие..................................................... 11
Глава 1. Введение................................................. 17
1.1. Компиляторы, ассемблеры, интерпретаторы................ 17
1.2. Краткий обзор процесса компиляции................. . 18
1.3. Примеры структур компиляторов.......................... 24
Глава 2. Грамматики и языки....................................... 28
2.1. Обсуждение грамматик................................... 28
Упражнения к разделу 2.1.................................... 31
2.2. * Символы и цепочки .Л................................ 32
Упражнения к разделу 2.2.................................... 34
2.3. Формальное определение грамматики и языка............. 35
Упражнения к разделу 2.3.................................... 39
2.4. Синтаксические деревья и неоднозначность............* 40
Упражнения к разделу 2.4.................................. 45
2.5. Задача разбора......................................... 46
Упражнения к разделу 2.5.................................. 49
2.6. Некоторые отношения применительно к грамматикам ... 49
Упражнения к разделу 2.6................................. 53
2.7. Построение транзитивного замыкания отношений........... 53
Упражнения к разделу 2.7.................................... 56
2.8. Практические ограничения, налагаемые на грамматики ... 57
Упражнения к разделу 2.8.................................... 60
2.9. Другие способы представления синтаксиса................ 60
2.10. Краткий обзор теории формальных языков................ 63
2.11. Резюме................................................ 66
Глава 3. Сканер................................................... 69
3.1. Введение . . . ."...................................... 69
3.2. Регулярные выражения и конечные автоматы............... 72
Упражнения к разделу 3.2 ................................. 84
3.3. Программирование сканера............................... 84
ОГЛАВЛЕНИЕ
Упражнения к разделу 3.3.................................* 92
3.4. Конструирование сканеров............................... 92
Упражнение к разделу 3.4................................... 109
3.5. Система AED RWORD..................................... 100
3.6. Исторические замечания................................ 105
Глава 4. х Нисходящие распознаватели ............................ 106
4.1. Нисходящий разбор с возвратами........................ 106
4.2. Проблемы нисходящего разбора и их решение............. 115
4.3. Рекурсивный спуск..................................... 120
Упражнения к разделу 4.3................................... 124
4.4. Исторические замечания............................• . . 124
Глава 5. Грамматики простого предшествования..................... 125
5.1. Отношения предшествования и их использование......* 125
Упражнения к разделу 5.1................................... 128
5.2. Определение и построение отношений.................... 129
Упражнения к разделу 5.2................................... 134
5.3. Алгоритм разбора...................................... 134
Упражнения к разделу 5.3................................... 137
5.4. Функции предшествования............................... 137
Упражнения к разделу 5.4.................................. 141
5.5. Трудности, возникающие при построении грамматик предшествования . .............................................. . . 141
Упражнения к разделу 5.5............*...................... 144
5.6. Исторические замечания................................ 144
Глава 6. Другие восходящие распознаватели........................ 145
6.1. Предшествование операторов............................ 146
Упражнения к разделу 6.1 . ................................ 155
6.2. Предшествование более высокого порядка................ 156
Упражнения к разделу 6.2................................... 163
6.3. Ограниченный крнтекст................................. 164
6.4. Матрицы переходов ..........................х........ 170
Упражнения к разделу 6.4................................... 177
6.5. Исторические замечания................................ 178
Глава 7. Продукционный язык...................................... 181
7.1. Язык ................................................. 181
Упражнения к разделу 7.1................................... 189
7.2. Использование ПЯ ..................................... 189
Упражнения к разделу 7.2............................... • 195
7.3. Вызов семантических подпрограмм...................... 195
7.4. Исторические замечания..............................• 197
542
ОГЛАВЛЕНИЕ
Глава 8. Организация, памяти. во время выполнения программы . . . . 198
8.1. Области данных и дисплеи.............................. 199
Упражнения к разделу 8.1................................... 201
8.2. Описатели............................................. 201
8.3. Память для данных элементарных типов.................. 203
8.4. Память для массивов................................... 203
Упражнения к разделу 8.4................................... 208
8.5. Память для строк...................................... 208
8.6. Память для структур..............................* . . 210
8.7. Соответствие фактических и формальных параметров .... 216
Упражнения к разделу 8.7................................... 221
8.8. Управление памятью для ФОРТРАНа....................... 222
8.9. Управление памятью для АЛГОЛа......................... 223
Упражнения к разделу 8.9................................... 236
8.10. Динамическое распределение памяти................. 237
8.11. Исторические замечания .............................. 243
Глава 9. Организация таблиц символов............................. 244
9.1. Введение в организацию таблиц......................... 244
9.2. Неупорядоченные и упорядоченные таблицы............... 246
9.3. Хеш-адресация................................1 . . . . 247
9.4. Таблицы символов, имеющие структуру дерева............ 256
Упражнения к разделу 9.4................................... 257
9.5. Таблицы символов, имеющие блочную структуру........... 258
9.6. Истбрйчёсйие замечания . ............ . . ............ 262
Глава 10. Информация в таблице символов.......................... 264
10.1. Описатель............................................ 264
10.2. Описатели для компонент структур..................... 268
Упражнения к разделу 10.2.................................. 276
Глава 11. Внутренние формы исходной программы1................... 278
11.1. Операторы и операнды................................. 279
11.2. Польская запись...................................... 281
Упражнения к разделу 11.2.................................. 286
11.3. Тетрады ........................................... 286
Упражнения к разделу 11.3.................................. 289
11.4. Триады, деревья и косвенные триады ................ 289
11.5. Линейные участки..................................... 292
11.6. Исторические замечания............................... 294
Глава 12. Введение в семантические программы..................... 295
12.1. Перевод инфиксной записи в польскую................ 295
Упражнения к разделу 12.1 ................................ 299
12.2. Преобразование инфиксной записи в тетрады............ 299
-'Упражнения к разделу 12.2 . . .'..................... • • • 302
ОГЛАВЛЕНИЕ
543
12.3. Реализация семантических программ и стеков ....... 302
12.4. Семантическая обработка при нисходящем разборе...... 305
12.5. Исторические замечания............................... 307
Глава 13. Семантические программы для конструкций языка, подобного
АЛГОЛу.................................................... 309
13.1. Обозначения, принятые в семантических программах . . . 310
13.2. Условные инструкции.................................. 312
Упражнения к разделу 13.2.................................. 315
13.3. Метки и переходы .................................. 315
Упражнения к разделу 13.3.................................. 318
13.4. Переменные и выражения............................... 318
Упражнения к разделу 13.4.................................. 321
13.5. FOR-циклы . . . . .................................. 321
Упражнения к разделу 13.5.................................. 323
13.6. Оптимизация логических выражений . .................. 323
Глава 14. Отведение памяти переменным в готовой программе........ 332
14.1. Присваивание адресов переменным...................... 332
14.2. Отведение памяти временным переменным................ 341
Упражнения к разделу 14.2................................ 341
14.3. COMMON и эквивалентность............................. 342
Глава 15. Нейтрализация ошибок.................................. 353
15.1. Введение..........................................• . 353
15.2. Нейтрализация семантических ошибок................... 356
15.3. Нейтрализация синтаксических ошибок.................. 360
Глава 16. Интерпретаторы......................................... 367
Глава 17. Генерация объектного кода.............................. 377
17.1 Введение.............................................. 378
17.2/ Генерация команд для простых арифметических выражений 379
17.3. Адресация операндов.................................. 392
17.4. Генерация команд для других типов тетрад............. 403
17.5. Экономия памяти при генерации кода................... 407
17.6. Объектные модули................................... 411
Упражнения к разделу 17.6.................................. 420
Глава 18. Оптимизация программы.................................. 421
18.1. Оптимизация в пределах линейных участков............. 422
18.2. Умеренная оптимизация циклов......................... 429
18.3. Более полная оптимизация............................. 444
18.4. Дополнительное обсуждение и исторические Замечания . . . 455
544
ОГЛАВЛЕНИЕ
Глава 19. Реализация макросредств........................... • • • 461
19.1. Простая схема макрогенерации........................... 461
Упражнения к разделу 19.1.................................... 472
19.2. Другие свойства макро.................................. 472
19.3. Универсальный макрогенератор GPM....................... 479
Упражнения к разделу 19.3.................................... 484
19.4. Исторические замечания ................................ 484
Глава 20. Системы построения трансляторов........................... 486
20 J. Введение.............................................. 486
20.2. Обсуждение двух компиляторов компиляторов.............. 489
Глава 21. Советы разработчику компилятора........................♦ 499
Приложение. Язык программирования, используемый в книге.......... 513
Список литературы .................................................. 522
Именной указатель.............................................* . 533
Предметный указатель ............................................... 535
Д. Грис КОНСТРУИРОВАНИЕ КОМПИЛЯТОРОВ. ДЛЯ ЦИФРОВЫХ-ВЫЧИСЛИТЕЛЬНЫХ МАШИН
Редактор Л. Бабынина. Художник Н. Хмелевская Художественный редактор В. Шаповалов. Технический редактор Е. Потапенкова
Сдано в набор 22/1 1975 г. Подписано к печати 28/VII 1975’г. Бум. тип. № 2 бОхЭСИЛв.я = 17,00 бум. л. Печ. л. 34. Уч.-изд. л. 33,60 Изд. № 1/7218 Цена 2 р. 48 к.
Заказ № 2455
ИЗДАТЕЛЬСТВО «МИР» Москва, 1-й Рижский пер., 2
Ордена Трудового Красного Знамени Первая Образцовая типография имени А. А. Жданова Союзполиграфпрома при ^Государственном комитете Совета Министров СССР по делам издательств, полиграфии и книжной торговли. Москва, М-54, Валовая, 28