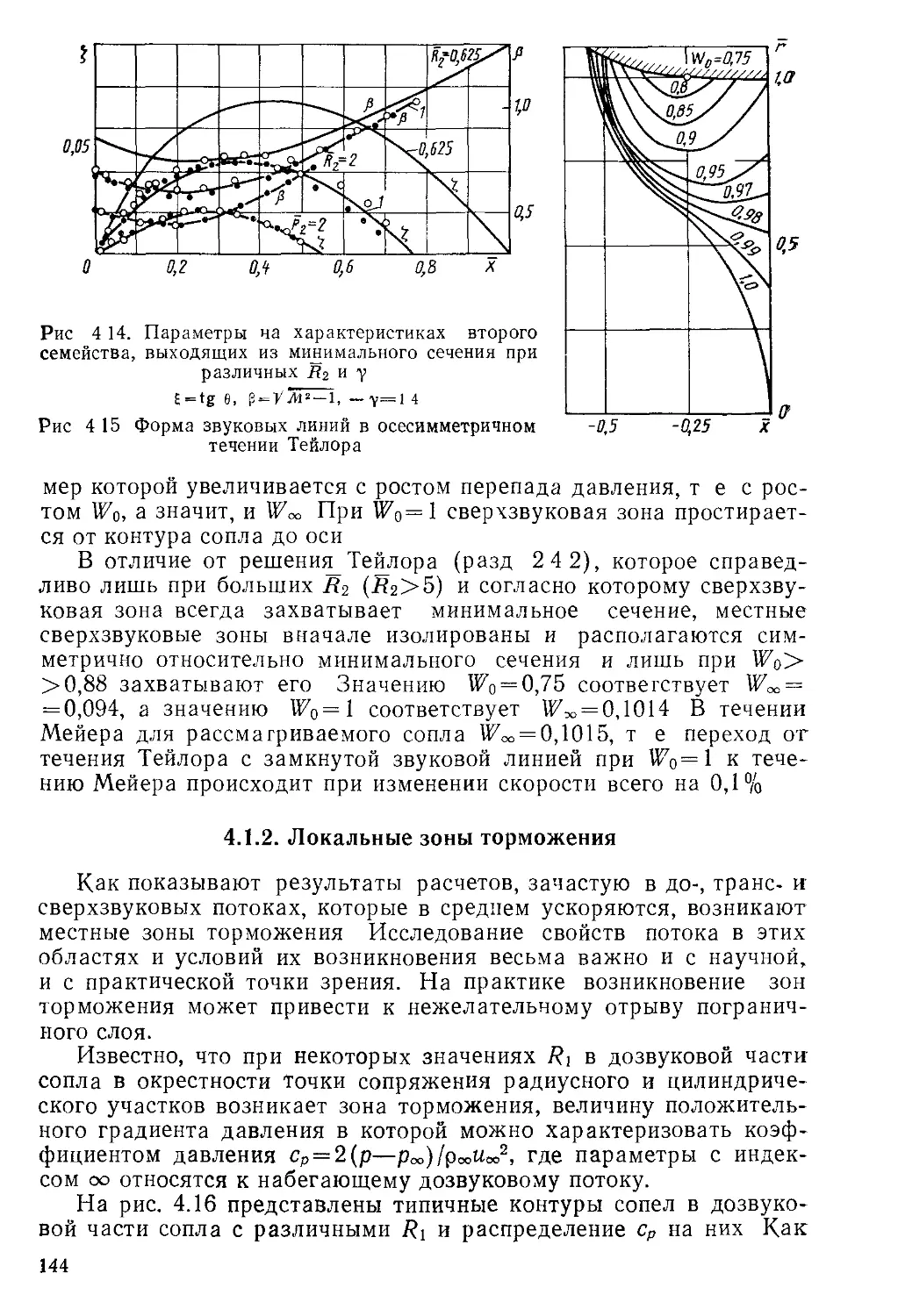
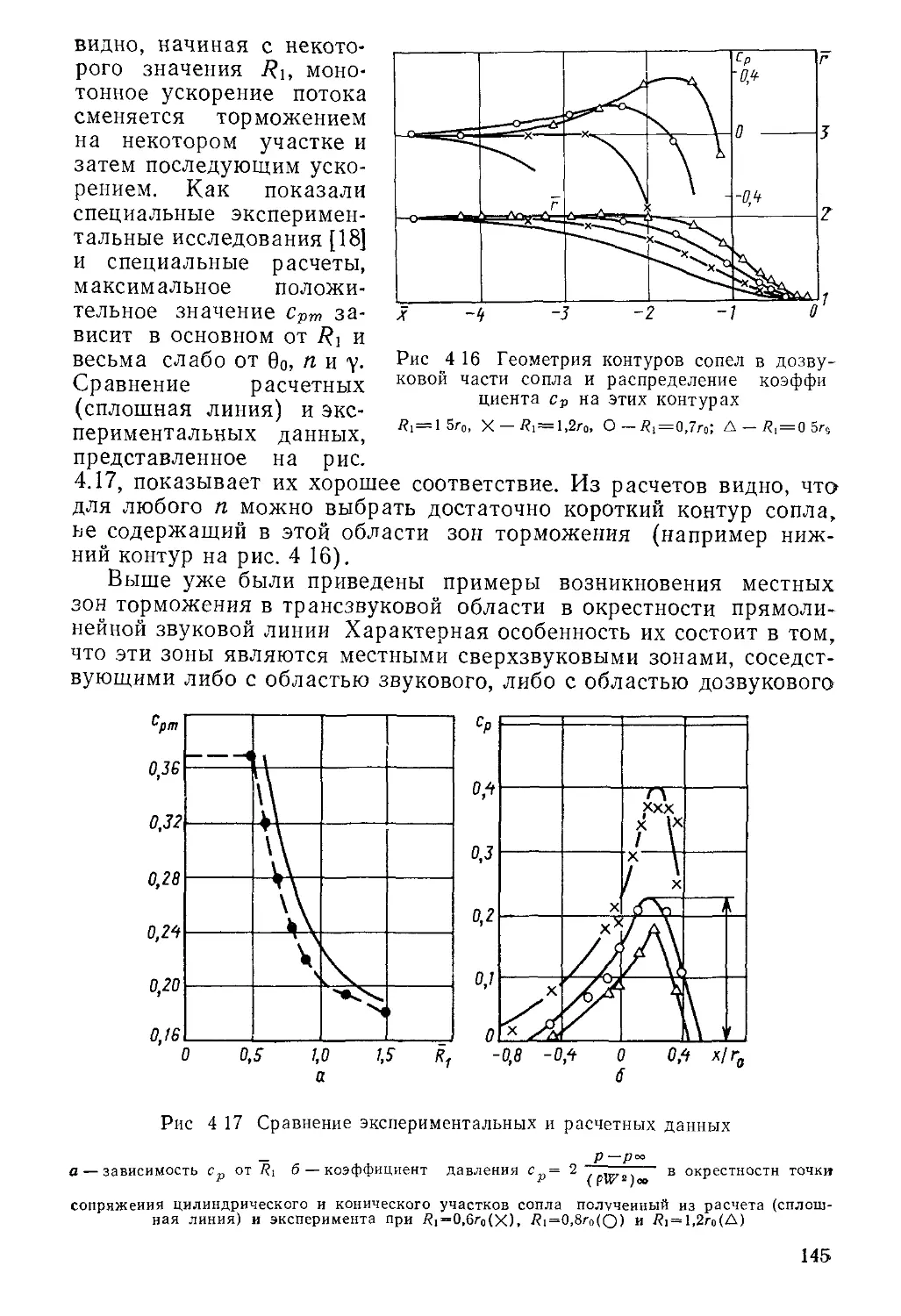
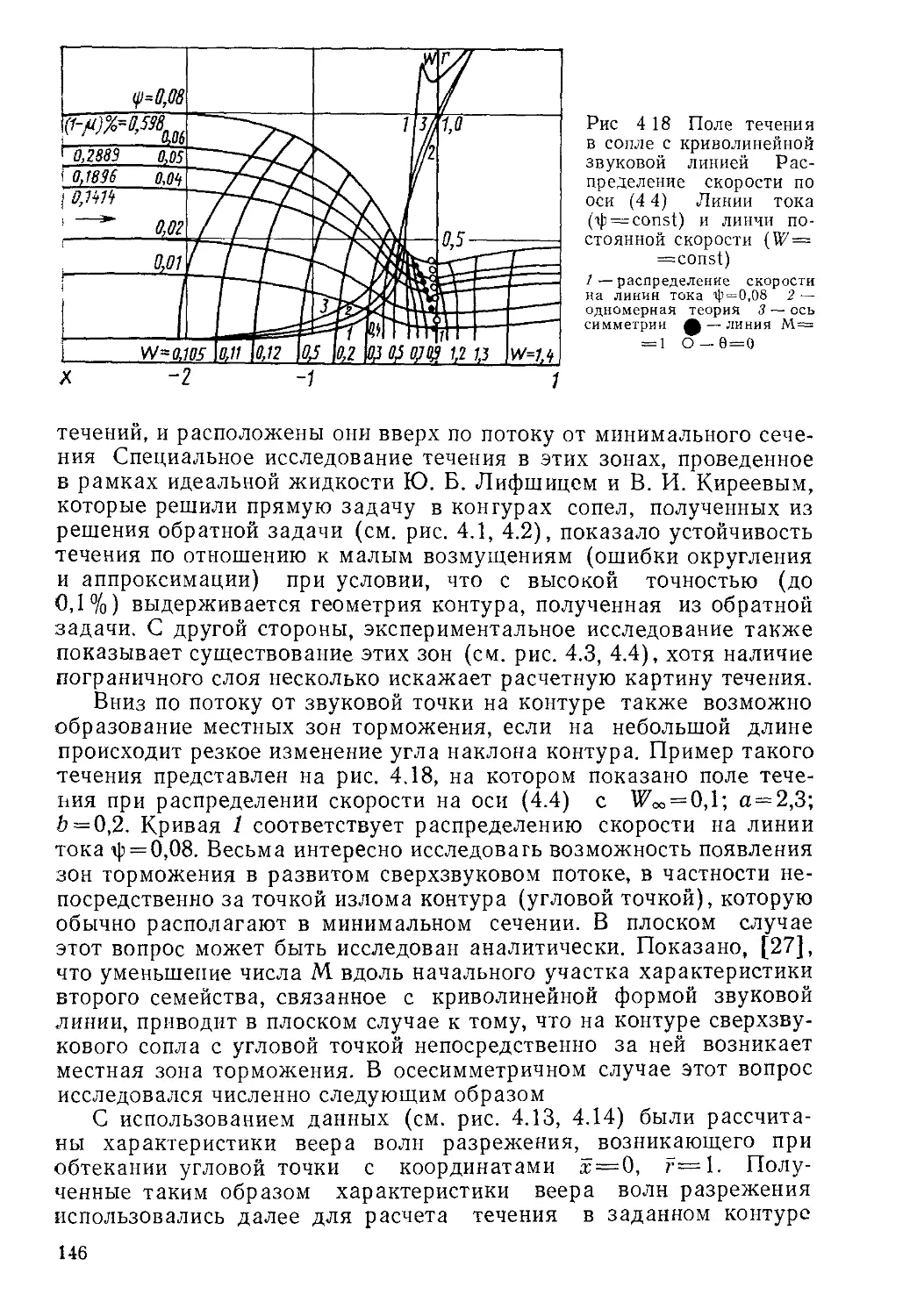
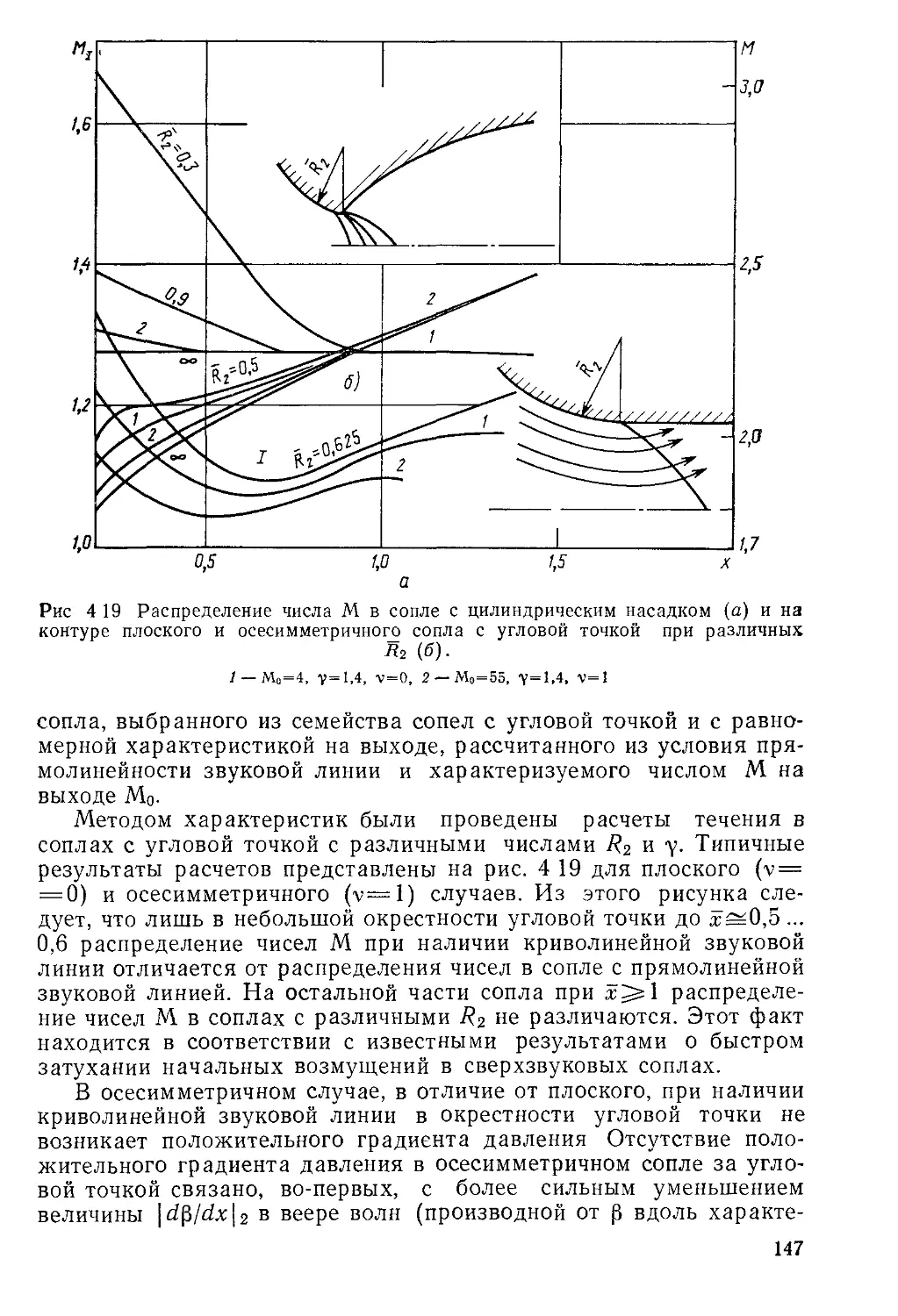
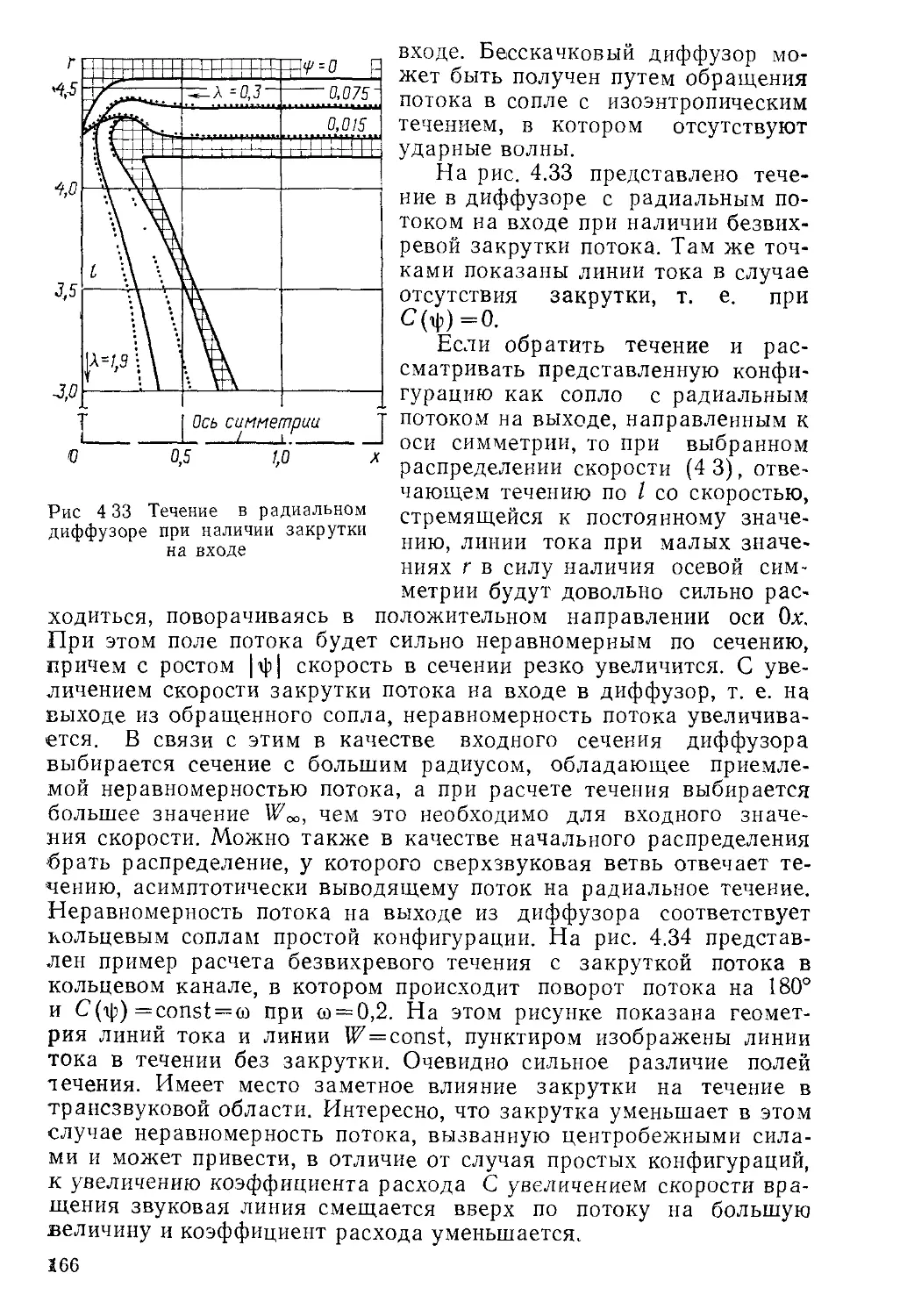
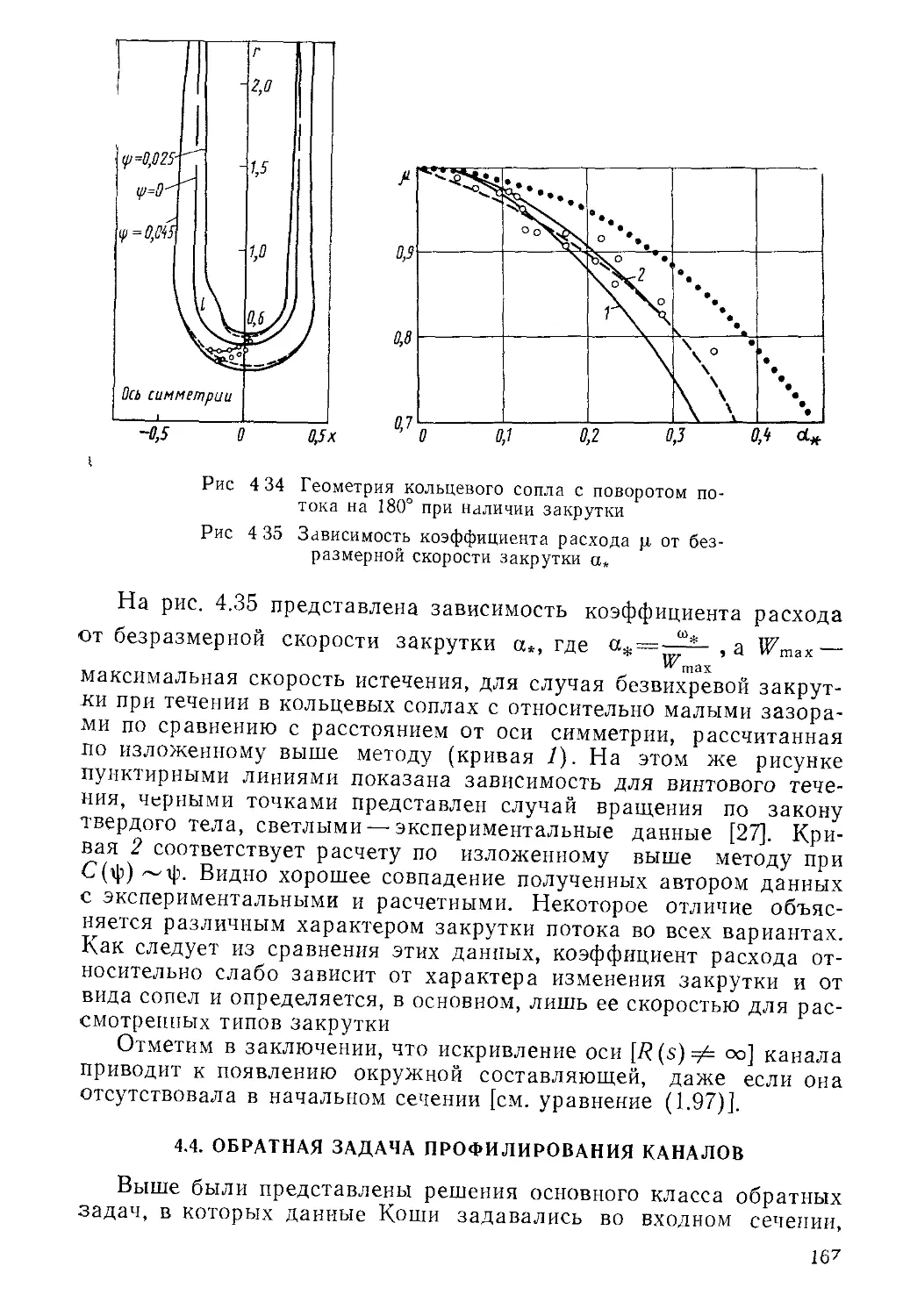
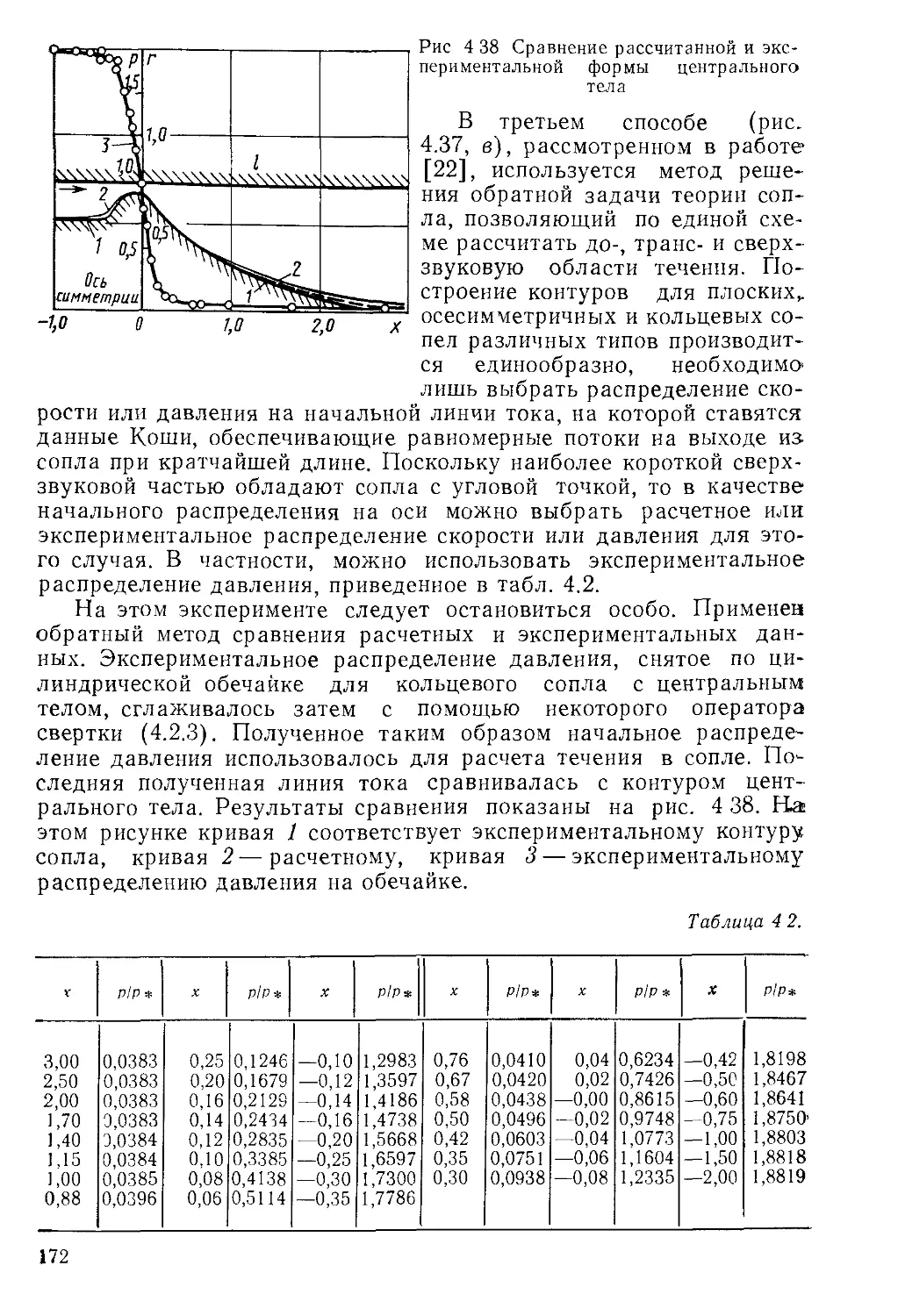
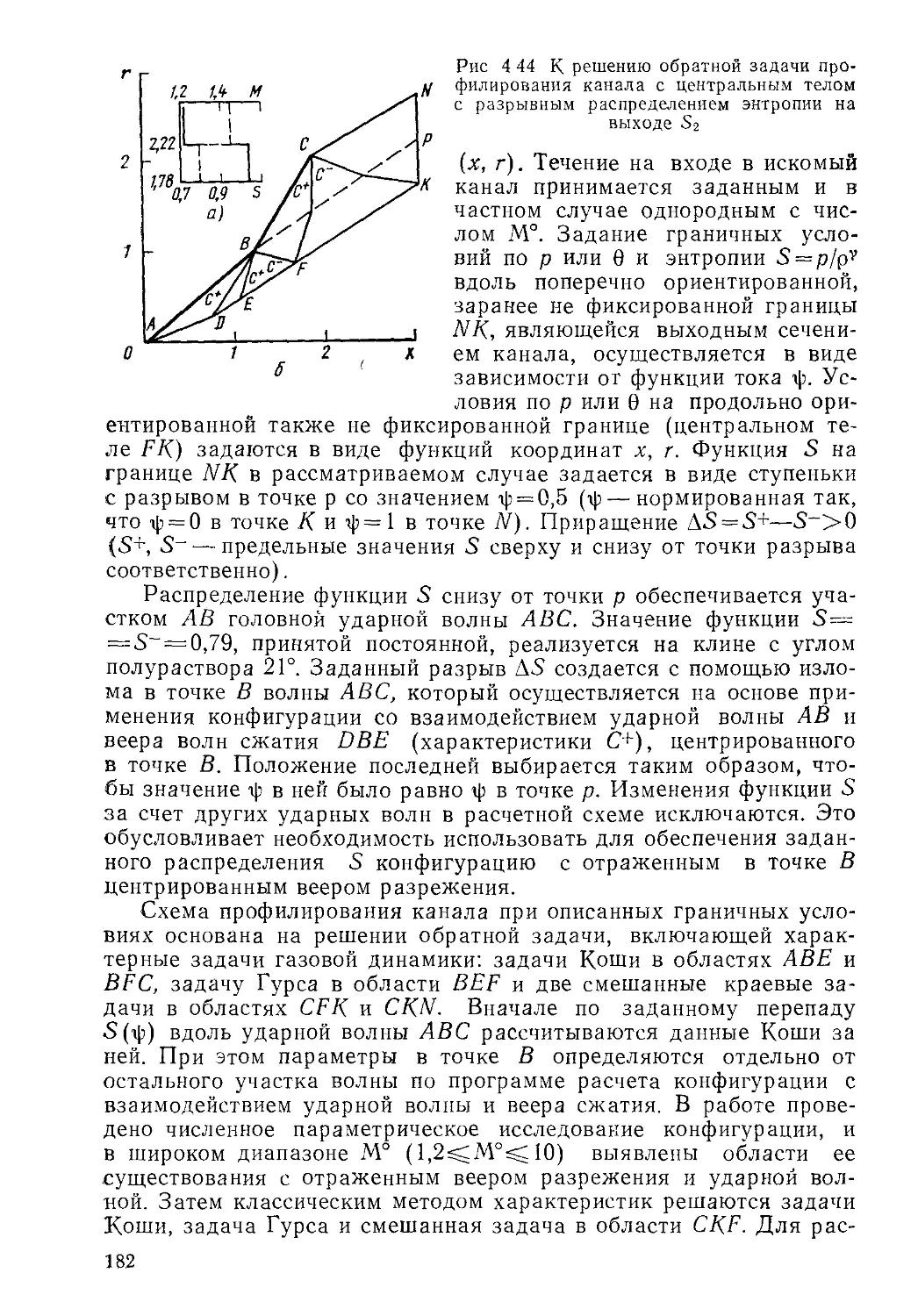
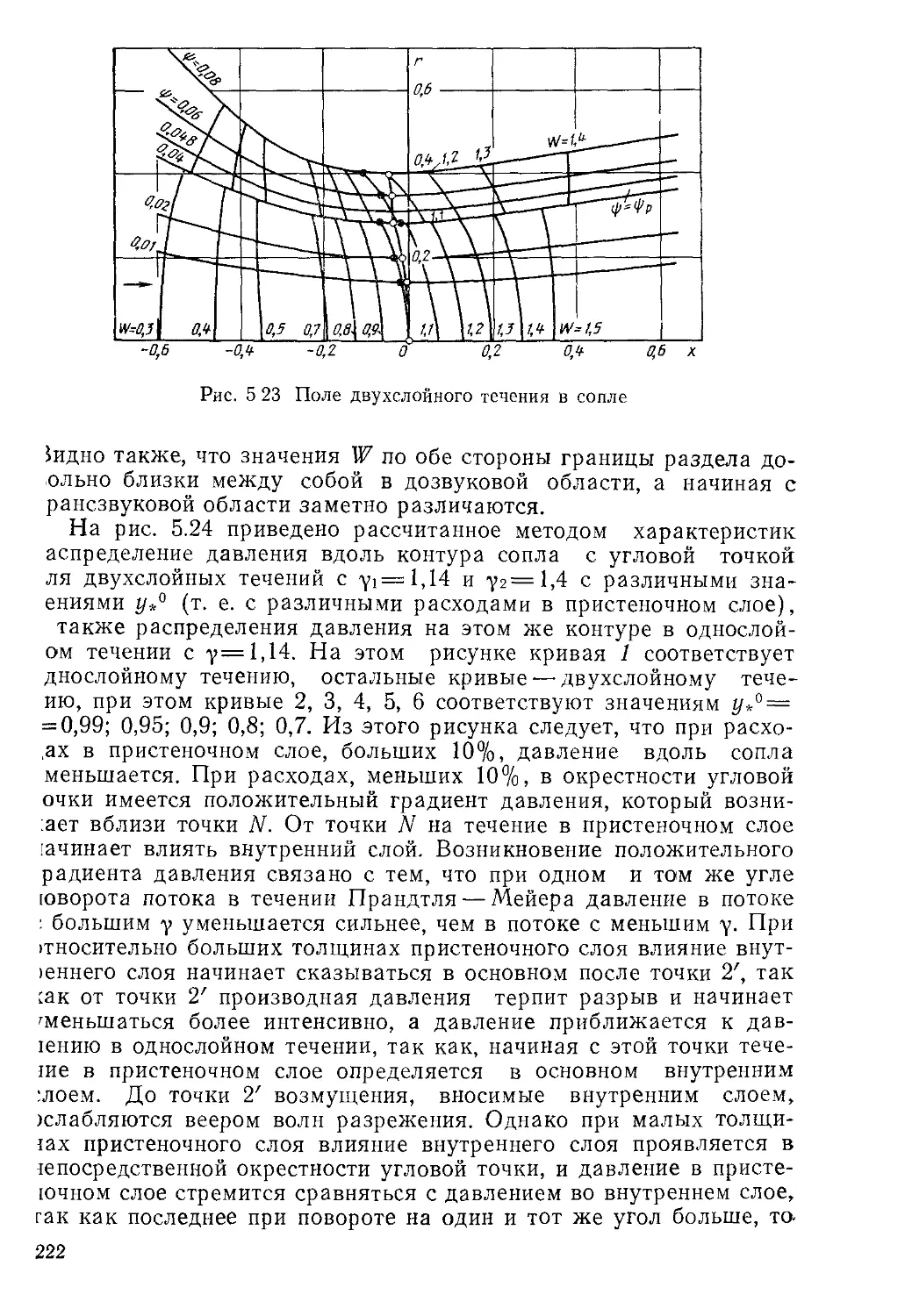
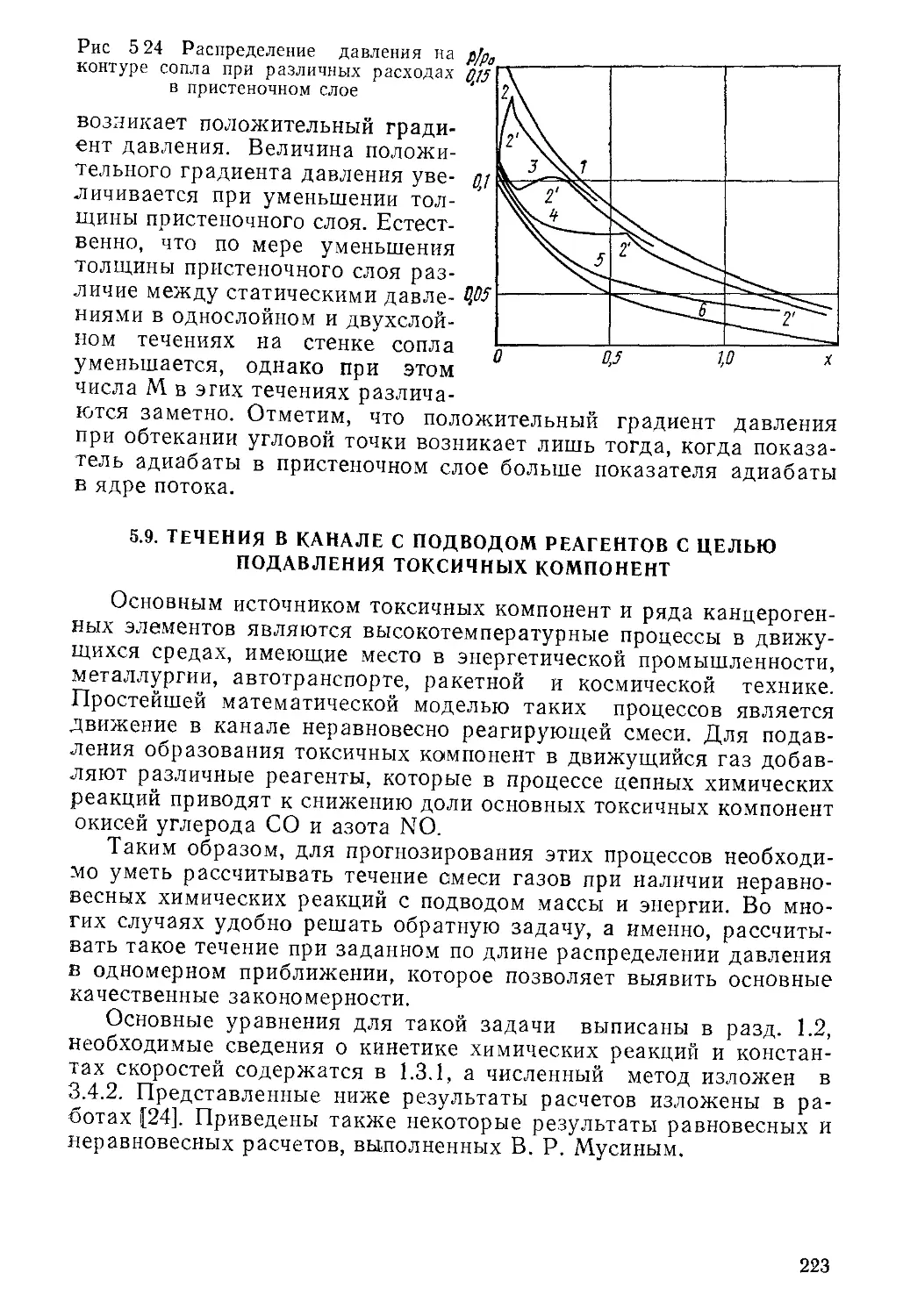
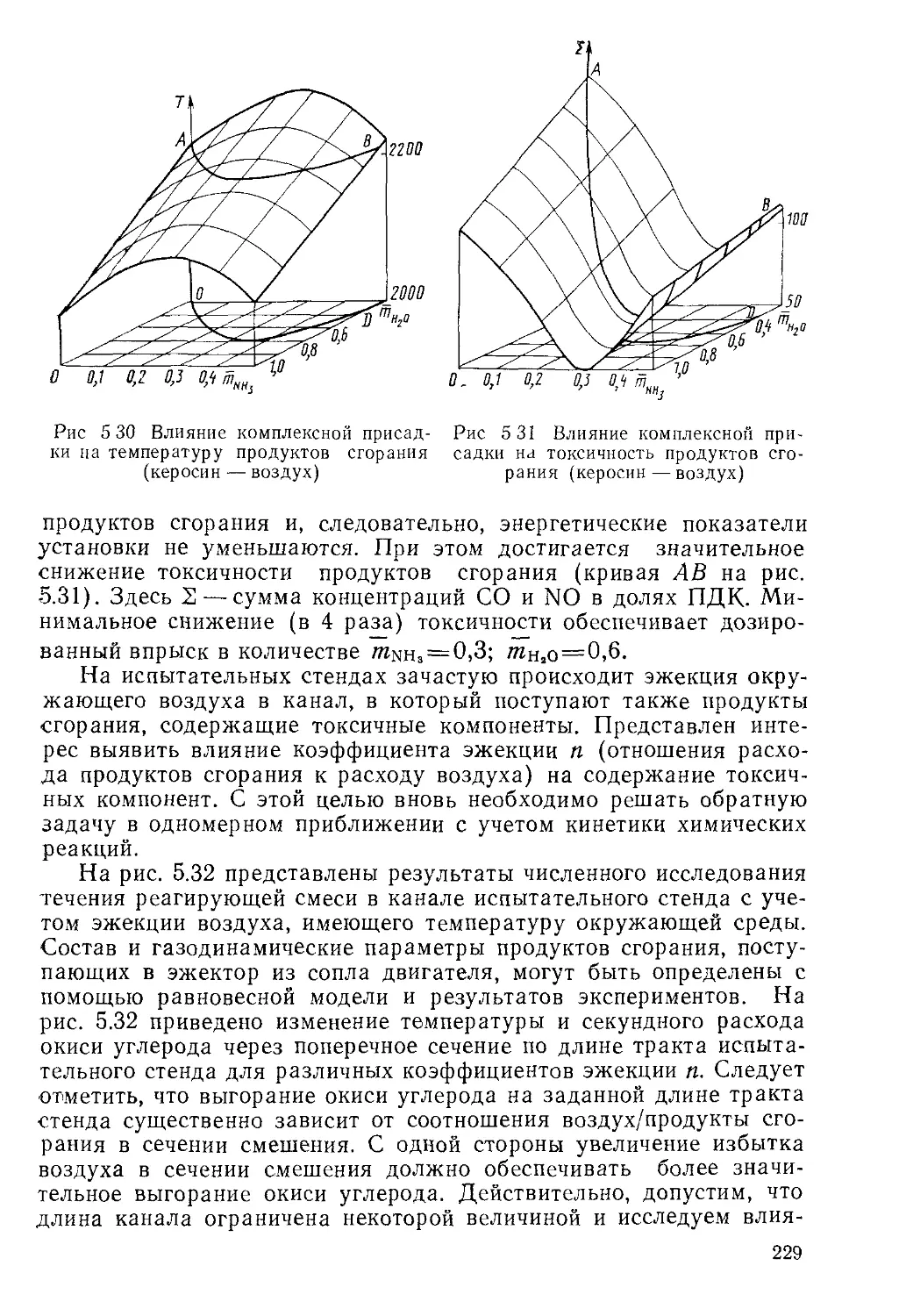
Автор: Пирумов У.Г
Теги: авиация и космонавтика летательные аппараты ракетная техника космическая техника аэродинамика теория полёта физика газовая динамика
ISBN: 5-217-00104-6
Год: 1988
У.ГПирумов
Обратная
задача
теории
сопла
УДК 629.7.015 :533.6
Обратная задача теории сопла/У. Г. Пирумов. — М.: Ма-
Машиностроение, 1988. — 240 с. — ISBN 5-217-00104-6.
В монографии рассмотрена обратная задача теории сопла для общего случая
пространственного течения, даны численные методы ее решения.
Значительное внимание уделено практическим приложениям. Приведены резуль-
результаты исследований течений в соплах, в каналах сложных форм, в каналах с под-
подводом массы и энергии. Представлены результаты решений обратной задачи про-
профилирования каналов.
Предназначена для научных работников, специализирующихся в области физи-
физической газовой динамики.
Библиогр . 33 назв. Ил. 97. Табл. 4.
Рецензент Л. Е. Стерши
3606030000 — 096 ^ .„ ,„_„
П 96—88 © Издательство «Машиностроение», 1988
038@1)-88
ISBN 5-217-00104-6
ПРЕДИСЛОВИЕ
В последние годы выполнен целый ряд исследований, посвя-
посвященных решению обратной задачи теории сопла. Значительное
внимание уделено обратной задаче профилирования сложных ка-
каналов, реализующих заданный сверхзвуковой поток на выходе из
сопла.
На основе численного метода решения обратной задачи изучен
большой класс внутренних проблем физической газовой динамики
таких, как течения в соплах реактивных двигателей, в каналах
сложных форм с поворотом потока до 180°, в каналах МГД-генера-
торов, в каналах с подводом массы и энергии.
При исследовании плоских, осесимметричных и пространствен-
пространственных течений учитывались разного рода неравновесные физико-хи-
физико-химические процессы, например диссоциация и рекомбинация, воз-
возбуждение колебательных степеней свободы, конденсация, движение
частиц в смеси газов.
Весьма эффективным оказался численный метод решения обрат-
обратной задачи, основанный на использовании трехточечных разност-
разностных схем с переменным шагом на слое.
Область приложения рассмотренных задач достаточно широка:
от авиационной техники и космонавтики до охраны воздушного
бассейна.
Возможно расширение круга прикладных задач, решаемых с
помощью обратной задачи. Это связано, в первую очередь, с соз-
созданием новых технологий, в которых требуется изучение течений
газа в каналах сложной формы с поворотом потока до 180°.
С другой стороны, возможно применение разностного метода
решения обратной задачи и для некоторого класса струйных и
внешних задач.
В то же время систематическое изложение теории, аналитиче-
аналитических методов и прикладных результатов по обратной задаче в на-
настоящее время отсутствует. Отдельные результаты содержатся в
некоторых монографиях и периодических публикациях советских и
зарубежных авторов.
В предлагаемой монографии с единых позиций изложена мето-
методология обратной задачи теории сопла, приведены аналитические
и численные методы, а также многочисленные примеры практиче-
практических приложений. Представлены новые данные по неравновесным
и двухфазным течениям.
Автор благодарит академиков Г. И. Петрова и В. С. Авдуевско-
го за постоянное внимание и стимулирование исследований, резуль-
результаты которых приведены в настоящем издании.
Автор благодарит также профессора Л. Е. Стернина за много-
многочисленные полезные замечания, а также Л. И. Анохину, А. В. Па-
насенко, М. В. Минашкину, Е. А. Чулюкову за большую помощь
при подготовке монографии к изданию.
I. ОСНОВНЫЕ УРАВНЕНИЯ И ГРАНИЧНЫЕ УСЛОВИЯ
1.1. ВВЕДЕНИЕ
В газовой динамике различают задачи прямую и обратную,
Прямая задача состоит в определении поля течения при заданной
форме канала (для внутренних задач газовой динамики) или фор-
форме обтекаемого тела (для внешних задач) и заданных на некото-
некоторых границах краевых условиях. Прямая задача сводится, в общем
случае, к краевой задаче, для которой, как правило, не доказаны
теоремы существования и единственности.
Обратная задача состоит в определении поля течения при усло-
условиях, заданных на некоторой поверхности, и условиях в начальном
сечении. При этом форма канала (или обтекаемого тела) опреде-
определяется в процессе решения. Обратная задача сводится к задаче
Коши, для которой, по крайней мере в окрестности поверхностей с
данными Коши, гарантируется существование и единственность ре-
решения.
На формулировку краевых условий при решении прямой задачи
существенным образом влияет тип уравнений, зависящий от обла-
области течения. Для стационарных течений идеального газа, которые
рассматриваются в настоящей монографии, уравнения газовой ди-
динамики являются эллиптическими при дозвуковых, параболически-
параболическими при трансзвуковых и гиперболическими при сверхзвуковых ско-
скоростях потока.
В обратной задаче формулировка данных Коши не зависит от
типа уравнений.
Численные методы при решении прямой задачи в отличие от
обратной зависят от типа уравнений газовой динамики.
Последнее обстоятельство обусловливает значительно большую
точность, быстродействие, алгоритмическую простоту и эффектив-
эффективность разностных методов решения обратных задач по сравнению
с прямыми.
Важным свойством обратных задач является возможность про-
проведения численного решения трансзвуковых задач без «вхождения»
в особые точки в окрестности звуковых линий, что существенно уп-
упрощает процесс решения и выгодно отличает их от прямых задач.
Однако при решении обратных задач, как правило, требуется
задание аналитических данных, в связи с чем рассчитываются эф-
эффективно лишь области, не содержащие поверхностей разрывов.
В то же время в рамках прямой задачи удается тем или иным ме-
4
тодом определять положение поверхностей разрывов и их интен-
интенсивность.
В настоящей монографии изучаются обратные задачи теории
сопла Лаваля. Формулировка обратной задачи дана для общего
случая пространственных течений с неравновесными физико-хими-
физико-химическими превращениями. Рассмотрены, в основном, течения иде-
идеального газа, хотя представлен пример формулировки обратной за-
задачи для вязкого и теплопроводного газа.
Выписаны уравнения газовой динамики в координатах s, ty, О,
где s — длина дуги, а г|; и 0 — функции тока. Эти координаты мож-
можно рассматривать как обобщение координат Мизеса х, -ф на про-
пространственный случай. Использование их оказывается чрезвычай-
чрезвычайно удобным при формулировке обратной задачи теории сопла и при
построении разностных схем. Помимо этого представлена запись
уравнений газовой динамики в весьма общей системе координат,
что позволяет рассматривать достаточно сложные течения в кана-
каналах.
В теории сопла можно выделить два класса обратных задач,
отличающихся заданием условий в конечных сечениях.
Общим для них является задание данных Коши на некоторой
поверхности, являющейся поверхностью тока, в частности, на оси
симметрии течения. В то же время, для первого класса обратных
задач характерно задание данных Коши в начальном сечении в
дозвуковой области, а для второго класса в выходном сечении — в
сверхзвуковой области. Второй класс задач называется задачами
профилирования сопел. В первом классе обратных задач определя-
определяется поле течения в окрестности поверхности начальных данных и
семейство линий тока, каждая из которых может быть выбрана в
качестве «жесткого» контура сопла. В монографии рассмотрен в
основном этот класс задач для одномерного, двумерного и про-
пространственного течения.
Второй класс — задачи профилирования — рассмотрены только
для двумерных (плоских, либо осесимметричных) течений на при-
примерах профилирования сопел аэродинамических труб, сопел мо-
модельных установок и сопел со специальными условиями в выход-
выходном сечении. Конечной целью задачи профилирования является по-
построение контура сопла, реализующего заданные условия в выход-
выходном сечении.
1.2. ОСНОВНЫЕ УРАВНЕНИЯ
Для определения параметров движущегося газа служит систе-
система дифференциальных уравнений газовой динамики, которая
представляет собой выраженные в дифференциальной форме фун-
фундаментальные законы сохранения массы, импульса и энергии.
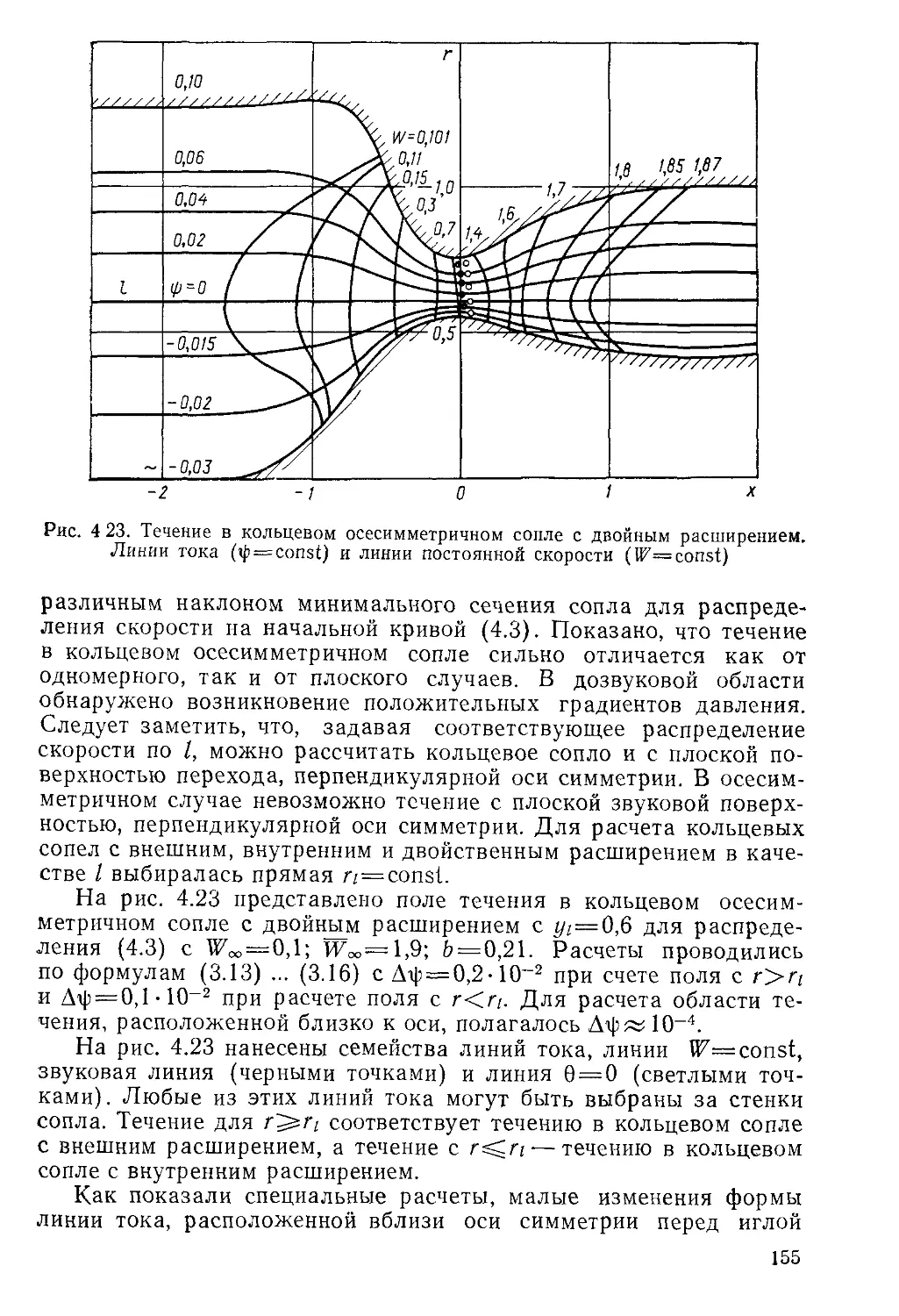
В большинстве случаев течения газа в соплах сопровождаются
разного рода физико-химическими процессами, для описания кото-
которых уравнения газовой динамики дополняются соответствующими
кинетическими или релаксационными уравнениями. Кроме того, к
уравнения вводятся дополнительные члены, учитывающие воздей-
воздействие неравновесных процессов на газодинамические параметры.
Физико-химические процессы в соплах весьма разнообразны. Наи-
Наиболее часто имеют место неравновесное возбуждение колебатель-
колебательных степеней свободы, неравновесная диссоциация и рекомбина-
рекомбинация, неравновесное движение жидких или твердых частиц, конден-
конденсация и кристаллизация, воздействие электромагнитных полей на
вид течения.
Выпишем в эйлеровых координатах дифференциальные уравне-
уравнения сохранения массы, импульса и энергии для общего случая про-
пространственного течения многофазной сплошной среды при наличии
релаксационных процессов и взаимодействия между фазами [1,
27].
Будем рассматривать гомогенные и гетерогенные смеси как
многоскоростной континуум со взаимопроникающим движением со-
составляющих и обменом массой, импульсом и энергией. Многоско-
Многоскоростной континуум представим как совокупность ./V континуумов,
каждый из которых относится к своей компоненте смеси и запол-
заполняет один и тот же объем, занятый смесью. Будем характеризо-
характеризовать каждый из этих континуумов средней плотностью рг (масса
1-й компоненты в единице объема смеси), скоростью W,-, внутренней
энергией е%, тензором напряжений П,. Помимо средней плотности
введем и истинную плотность рг°, которая представляет собой мас-
массу t-й фазы в единице объема 1-й фазы. Под компонентами будем
понимать газовые компоненты, соответствующие различным моле-
молекулам, а также различным квантовым состояниям молекул (напри-
(например, колебательным степеням свободы молекул) и частицы различ-
различных размеров с различными физическими свойствами. Тогда в каж-
каждой точке объема, занятого смесью, будет определено N плотно-
плотностей, N скоростей и т. д.
Вводятся плотность смеси р и среднемассовая (барицентриче-
(барицентрическая) скорость смеси W:
1=1 1=1
При записи дифференциальных уравнений полезно ввести субста-
циональные производные, связанные с движением t-й компоненты
dt/dt и с движением среды в целом d/dt (барицентрическая субста-
циональная производная):
где V — оператор градиента или дивергенции (применение опера-
оператора V к скалярной величине означает градиент, а к векторной —
дивергенцию). Здесь и далее произведения вида lF,mVm означают
суммирование только по верхним индексам, относящимся к коор-
координатным осям.
Ниже рассмотрим течения, в которых диффузией можно прене-
пренебречь, однако вязкость и теплопроводность надо учитывать при за-
записи уравнений Навье — Стокса в координатах Мизеса. Отметим,
что при решении обратной задачи теории сопла вязкость, как пра-
правило, не учитывается.
Примем, что возможно воздействие на поток внешних сил и ис-
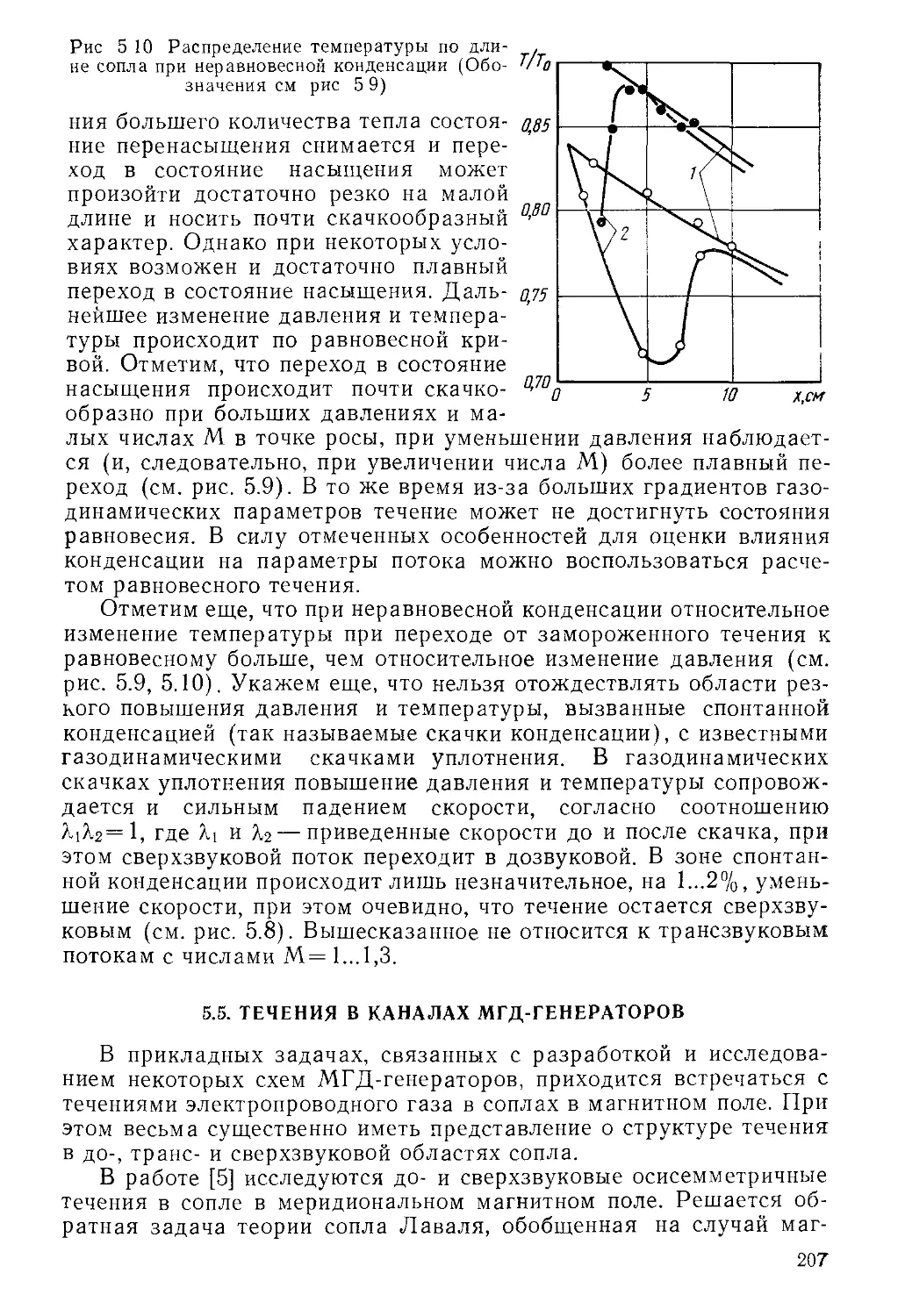
источников массы, энергии. Такого рода внешние воздействия воз-
возможны за счет электромагнитных сил, излучения, подвода массы к
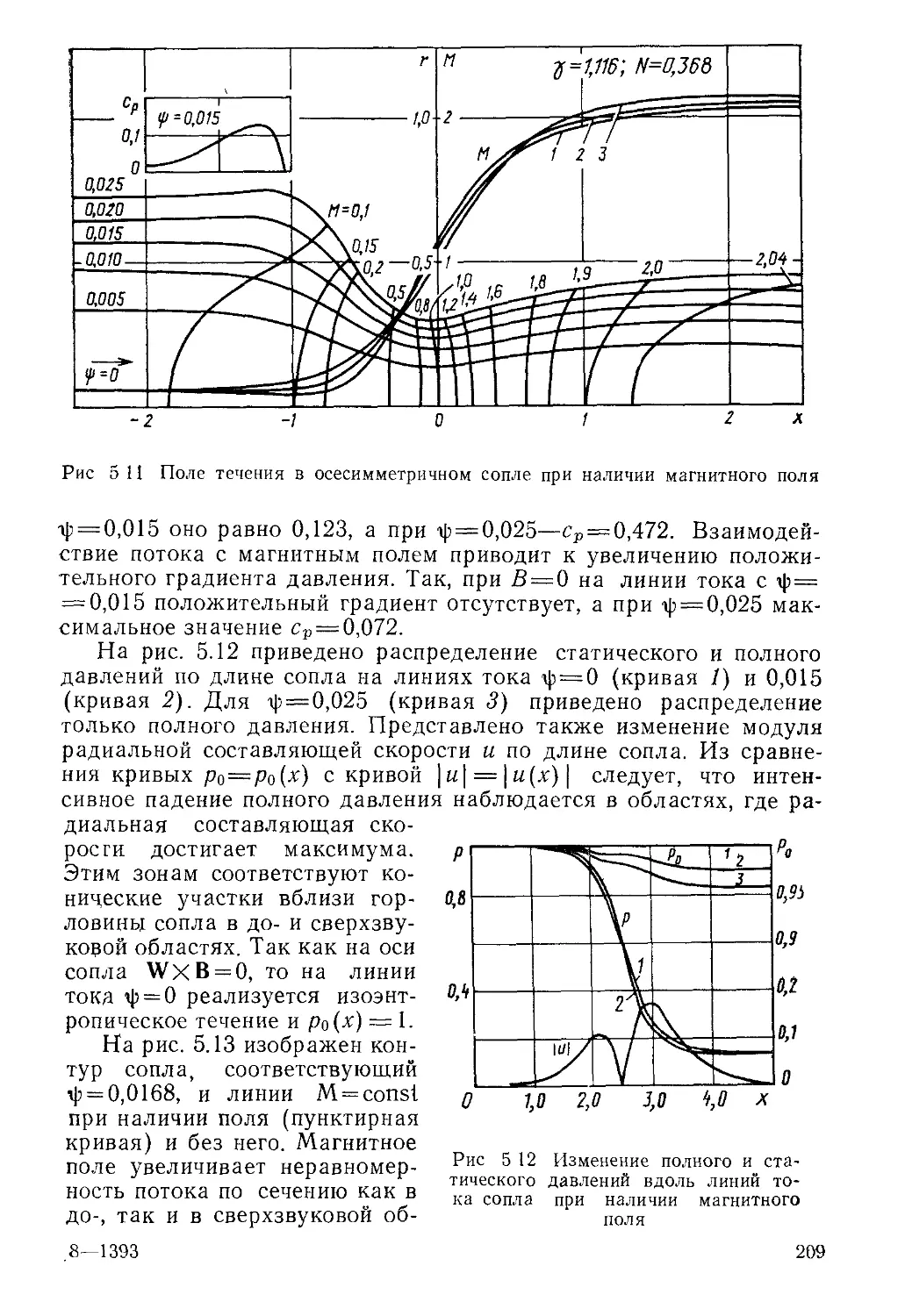
энергии при течениях в каналах испытательных станций и т. д.
Выпишем законы сохранения массы, импульса и энергии для
i-го компонента смеси. Имеем
N
A.3)
dt ' •" '
N
^[()]ii (l=h 2,..., N), A.5)
где Rlk — изменение массы i-ro компонента за счет fe-го компонен-
компонента в единице объема в единицу времени (например, из-за химиче-
химических реакций, конденсации или перехода молекул из одного кван-
квантового состояния в другое); Mi — изменение массы в единице объ-
объема в единицу времени за счет внешних источников; Р,& — измене-
изменение импульса г-го компонента за счет импульса &-го компонента в
единице объема в единицу времени; F, — вектор внешних сил;
Elk — изменение энергии г-го компонента за счет k-xo компонента;
L, — вектор внешних сил; L, —IltW,, q,— вектор потока теплоты;
Q, — приращение энергии за счет внешних источников. Кроме того,
из законов сохранения при взаимодействиях
Суммируя по i получим уравнения сохранения массы (уравнение
неразрывности), импульса (уравнение движения) и энергии для
смеси в целом:
= М; A.6)
?
A.7)
at
где
dt
A.8)
1=1 (=i
N N N
=2 p<F<; L=
N
1 = 1
Система дифференциальных уравнений A.6)...A.8) замыкается
термическими и калорическими уравнениями состояния, позволяю-
позволяющими в предположении локального равновесия, когда в каждой
точке определена температура 7\, выразить тензор напряжения Ш
,и внутреннюю энергию ес через остальные параметры смеси и неко-
некоторые физико-химические переменные. При решении конкретных
проблем необходимы также феноменологические уравнения, опре-
определяющие параметры массового Rlk, силового Pik и энергетического
Ел взаимодействия между фазами. В случае малого отклонения
от равновесия необходимые соотношения для Riu, Pik и Eik можно
получить, применяя принцип Онзагера и постулируя линейные со-
соотношения для термодинамических потоков (например, для тепло-
теплообмена, трения между фазами, интенсивности фазового перехода).
В .случае химических реакций необходимые соотношения для R,k
доставляет химическая кинетика.
Система A.6) ...A.8) представляет собой весьма общую систему
нелинейных дифференциальных уравнений в частных производных,
решение которой без упрощающих предположений чрезвычайно за-
затруднительно.
Сформулируем еще некоторые предположения, которые обычно
испрльзуются при описании течений газа в соплах. Для описания
многофазных течений в настоящее время широко используется мо-
модель двухжидкостной или многожидкостной сплошных сред, в ко-
которых реальное течение смеси газа и частиц заменяется взаимо-
взаимодействующим течением двух или более сплошных сред — собствен-
собственно газа и «газа» частиц. При этом все параметры течения представ-
представляют собой величины, получающиеся осреднением по малому объ-
объему, содержащему большое количество инородных частиц. Относи-
Относительно собственно газа делаются следующие предположения.
Газ представляет собой смесь совершенных газов, каждый из
которых подчиняется собственному термическому и калорическому
уравнениям состояния. Отклонение от свойств совершенного газа
(влияние тройных соударений, сил Ван-дер-Ваальса и др.), как
правило, не учитывается. Поступательные и вращательные степени
свободы находятся в равновесии.
Допускаются неравновесные возбуждения колебательных сте-
степеней свободы, протекание химических реакций в газовой фазе,
конденсация и пр. Предположение о равновесии поступательных и
вращательных степеней свободы молекул нарушается при истече-
истечении струй в пространство с малым давлением.
Относительно «газа» частиц делаются следующие предположе-
предположения: каждой компоненте газовой фазы, вообще говоря, может со-
соответствовать компонента «газа» частицы, для которой известны
термическое и калорическое уравнения состояния. Однако компо-
компонента «газа» частиц может и не быть связанной с какой-либо ком-
компонентой газа. Частицы имеют сферическую форму и распределены
по конечному числу групп, в каждой из которых содержатся части-
частицы Одинаковых размеров.
Расстояния, на которых характеристики течения меняются 'Су-
'Существенно, много больше расстояний между частицами.
Собственное давление «газа» частиц, обусловленное их хаоти-
хаотическим движением, мало по сравнению с давлением газа.
Система дифференциальных уравнений в частных производ-
производных A.6)... A.8) в общем случае описывает пространственное не-
нестационарное движение вязкого> теплопроводного газа с неравно-
неравновесным возбуждением различных степеней свободы молекул, не-
неравновесными химическими реакциями, фазовыми' превраще-
превращениями.
Рассмотрим некоторые частные случаи общих систем уравнений
A.2)...A.5), либо A.6)...A.8). Будем рассматривать только стацио-
стационарные течения, для которых —— = 0, где / — любая из искомых
dt
функций.
Примем, что смесь состоит только из N газовых компонент. Си-
Система A.6)... A.8) должна замыкаться термическими и калориче-
калорическими уравнениями состояния, которые при смеси совершенных га-
газов имеют вид
^f *§ A.9)
где R — универсальная газовая постоянная; МГ{ —относительная
N
молекулярная масса t-й компоненты; Mr—'S\Mr.pJp— относи-
тельная молекулярная масса смеси; е,(°ЦТ)—внутренняя энергия
i-й компоненты с учетом химической энергии и энергии поступа-
поступательных и вращательных степеней свободы; eBl(T)—энергия ко-
колебательных степеней свободы.
При наличии химических реакций система уравнений A.6)... A.8)
дополняется уравнениями типа A.3) для определения рг-.
9
В этом случае отпадает необходимость в использовании урав-
уравнений A.4) и A.5) для каждой компоненты, поскольку значения
е1 и Pi определяются по известному общему давлению, температуре
и плотности индивидуальных компонент смеси из соответствующих
уравнений состояния. Отметим еще, что вводя массовые концент-
N
рации ai==p,/p,2ai= 1 и используя A.6), уравнение A.3) мож-
можно преобразовать к виду
dai =F-(/>, T, а;-)+Ж,./р, A.10)
N
где Flip, Т, аг)=1/р
Для течений с возбуждением колебательных степеней свободы
молекул и неравновесным протеканием химических реакций систе-
система A.6) ... A.10) дополняется уравнениями для нахождения энер-
энергии колебательных мод молекул:
de
-^- = Фр(р,Т,еь,р) (р=1,2,...,Р), A.11)
где Фр — функция, характеризующая изменение колебательной
энергии молекул еШр в процессе из взаимодействия.
Нижний индекс р относится к различным возбужденным коле-
колебательным модам молекул. Очевидно, что для атомарных компо-
компонент ?9,р=0.
Пусть в потоке содержатся также частицы различных размеров,
распределенные по k групп. Придадим параметрам частиц нижний
индекс 5 и будем помечать частицы различных размеров индексом
/. Тогда движение смеси газа и частиц при неравновесном протека-
протекании химических реакций и неравновесном возбуждении колебатель-
колебательных степеней свободы описывается при сформулированных выше
предположениях следующей системой уравнений:
-*L + pvW=M; A.12)
dt
wjs
dt
10
A.14)
-=Fhp,T,a[) i=\,2,...,N; A.15)
dp
—f = Фр(р, T, ер) р=\,2,...,Р; A.16)
dt
if^i + p vWys=0 y==l, 2 fe; A.17)
^ ^ /==1,2,...,^ A.18)
где fs,- — сила взаимодействия между газом и частицами /-го раз-
размера, отнесенная к единице массы газа, qs, — тепловой поток меж-
между газом и частицами /-го размера, els=e]S(Ts) —внутренняя энер-
энергия частиц /-го размера. Система A.12)... A.18) дополняется пред-
представленными выше уравнениями состояния.
В потоке может происходить, кроме того, одновременная кон-
конденсация нескольких компонент смеси, однако, согласно правилу
фаз, число конденсирующихся компонент не должно превышать
числа независимых элементов, из которых образованы компоненты
смеси. Пусть число независимых элементов в смеси равно т, чис-
число компонент в газовой фазе N, из которых первые т конденсиру-
конденсируются. Тогда можно записать следующие уравнения материального
баланса, выражающие собой условие сохранения числа атомов в
процессе химических реакций и конденсации:
т N т
Ь^5^6»' *-1-2--»- (U9>
^5
t=l
где аи — количество атомов k-vo типа в одном моле вещества i,
bk — количество атомов k-vo типа в одном моле исходных продук-
продуктов, си — массовая доля газовой фазы, содержащей неконденсирую-
неконденсирующиеся компоненты; a.iV — массовая доля сконденсировавшейся
компоненты, а,г — массовая доля конденсирующейся компоненты.
Здесь и далее нижним индексом v обозначены параметры паров,
/ — жидкости, g — инертного неконденсирующегося газа.
Кроме уравнений материального баланса, в случае конденсации
необходимо записать также и уравнения для нахождения массовой
доли конденсирующейся компоненты и температуры частиц конден-
конденсата..
^?f}(P,Piv,T), A.20)
где функции Д° и /У определяются из кинетических уравнений не-
неравновесной конденсации. Особо подчеркнем, что при наличии не-
неравновесной конденсации в представленных уравнениях р — сум-
суммарная плотность смеси, которая равна
1=1 i-1
11
где piV — плотность i-й компоненты пара; р,; — плотность i-й ком-
Л'
поненты сконденсированной жидкой фазы; pg=~S p,- — плотность
i=m + l
неконденсирующейся газовой фазы. Энергия и удельная энтальпия
смеси при этом равна
N N
1=1 i=1
т
'Л + 2 ai'hu> ha-hiv = Li,
1=1 i=i
где Li — теплота конденсации.
Для замыкания системы необходимо записать уравнения со-
состояния:
?? ?> ( Г} 7""Ч / "| fVI •
•"ll — il \г^j * * — J- j • • •) ''*- j
bs=efs(Tfs) /= !,...,?; A.21)
P=R?T
Mrg ' 4J mtv
pg=-
Miv " <¦* Mrg '
N N
где рг=У] p,-; Pg=^, Pi- Отметим, что первые три урав-
!=m+l i = m + l
нения A.21) используются для нахождения Т и Tis по известным
е и e,s, четвертое — для определения давления, а пятое и шестое —
для определения piv и pg.
Окончательно система уравнений, описывающая течение смеси
газа и частиц при наличии неравновесной конденсации, неравновес-
неравновесного протекания химических реакций и неравновесного возбужде-
возбуждения степеней свободы молекул и внешних сил, внешних источни-
источников массы и энергии, есть система A.12)...A.21). Для решения си-
системы необходимы конкретные формулы, позволяющие определить
^/, gsj, Fi°, Fj, Фр, fi°, fil, M, F, Q. Соответствующие соотношения
получаются из химической физики, квантовой механики, статисти-
статистической механики, газовой динамики и гидродинамики, и при этом
многие физические константы, содержащиеся в них, получены экс-
экспериментально. Ниже эти соотношения будут выписаны в разд. 1.3.
В общем случае система содержит
4 + 3k + 2N+2m неизвестных р, р, Т, W, pjs, Tjs, W,-s (j=l,...,k),
at (i=m+l,...,N), aa, TiU aiv (i=m + l,... ,N) и ер (р=1,...,Р) и
столько же уравнений для их определения.
12
Итак, выписана общая система уравнений, описывающая не-
нестационарное пространственное течение смеси газа и частиц с не-
неравновесными химическими реакциями, неравновесным возбужде-
возбуждением колебательных степеней свободы и неравновесной конденса-
конденсацией.
Очевидно, что система в общем виде, как она представлена,
чрезвычайно сложна для исследования. В литературе не известны
решения для столь общего случая, хотя и содержится достаточно
большое число примеров изучения отдельно каждого неравновесно-
неравновесного процесса, протекающего в движущемся газе.
В связи с очевидной сложностью задачи используют упрощаю-
упрощающие гипотезы, позволяющие уменьшить либо размерность про-
пространства, либо число неравновесных процессов.
Выпишем соотношения для определения компонент тензора на-
напряжения П и потока тепла q,. Примем, что имеет место линейная
зависимость между касательными компонентами тензора напряже-
напряжений и тензора деформации (закон Ньютона) и линейная зависи-
зависимость потока тепла от градиента температуры (закон Фурье). Име-
Имеем тогда
я»' = ^ея.г; q.:=_X.v7\ A.22)
где я"г —касательная составляющая тензора напряжения; е"'г=
= dWn/dxr+dWr/dxn — составляющая тензора скорости деформа-
деформации; цг — динамический коэффициент вязкости 1-й компоненты; ин-
индексы г и п относятся к координатным осям; Я* — коэффициент
теплопроводности. Для нормальных компонент тензора напряже-
напряжений имеем
n?r=-p + 2v.t -i^l + CdivW, A.23)
дхГ
2
где С'=——1*/ + 1*1; где [^—коэффициент второй вязкости, кото-
О
рый в дальнейшем будет полагаться равным нулю.
Для коэффициентов вязкости можно пользоваться формулой
Сазерленда или степенной зависимостью \i от Т, а число Рг = ср\х/Х
для реальных смесей полагать равным 0,7.
Выпишем теперь важный частный случай общей системы
A.12)... A.21) для стационарного ламинарного течения вязкой, теп-
теплопроводной сжимаемой жидкости без физико-химических процес-
процессов и диффузии и при отсутствии внешних сил и внешних источ-
источников.
Запишем систему уравнений в декартовых координатах. Имеем
A.24)
A.25)
,q + ^+f+^, A.26)
dt дх ду dz
A.27)
13
где Тх, ty, xz — напряжения трения, действующие на площадки, пер-
перпендикулярные осям х, у, z, H—e + p/p+ W2/2 = h-\-W2/2 — полная
энтальпия единицы массы.
Имея в виду формулы A.22) и A.23), перепишем уравнение со-
сохранения импульса (уравнения движения) A.25) в виде
(да | да . да , ди \ др ,
dt ~ дх ~ ду ~ дг) дх~
дх [ Г дх 3 Г [дх ду дг
A.29)
у дх )\ дг [ \дх дг
р 1-U \-V \-W =
r V dt ~ дх ' ду ' ^ J
= ^.л-—Г2а —- —(х f—4- —4-—
<ty «У L ^i/ 2 Г [дх ~ ду ~ дг
' йл: L \ду дх )\~ дг 1\ дг ~ ду
р УU, \-V \-W |= — +
Ч dt дх ~ ду ~ дг) дг ~
, д Го dv 2 / ои , dv . dw \] ,
' дг [ ^ дг 3 ^ \ дх ~ ду ~ дг )\~
' дх [Г[ дх~ дг )\ ~ ду [Г \ ду ~ дг }\
где и, v, w — проекции вектора скорости W на оси декартовой си-
системы координат.
Уравнения A.28)...A.30) есть уравнения движения вязкой сжи-
сжимаемой жидкости, так называемые уравнения Навье — Стокса. Ес-
Если \i=const, то систему A.28)...A.30) можно записать в следую-
следующем векторном виде:
^ 4). A.31)
В частности, в некоторых работах приводится следующая за-
запись уравнений движения (здесь приведены уравнения для иде-
идеального газа):
ds
pW+0,
ds дп
которые используются как уравнения в частных производных, в то
время как это лишь дифференциальная связь между производны-
ми от 8, р, п по направлению вдоль линии тока и по нормали к ней,
при этом корректная запись имеет вид
+ 0;
ds ds
—+-^-=0.
ds ' dn
В этих уравнениях 0 — угол наклона вектора скорости к оси х.
Для корректной записи уравнений газовой динамики в ортого-
ортогональной системе координат, связанной с линией тока, необходимо
ввести интегрирующие множители (коэффициента Ляме), или, что
аналогично, ввести некоторый метрический тензор, который неиз-
неизвестен, если неизвестна геометрия линий тока, и для элементов ко-
которого выписываются дополнительные уравнения. Эти уравнения
должны решаться совместно с уравнениями газовой динамики.
Уравнение энергии с учетом формул A.30) и A.31) можно запи-
записать в виде
^ A.32)
p
dt
где Ф — диссипативная функция, определяемая соотношением
dw , dv \2 / ди , dw \2 2 / да , dv
В случае, если сР, Л,=const, то уравнение A.32) можно переписать
в виде
дТ , дТ , дТ \ др , др
dt ~ feT йг j дх ~ ду
Отметим, что система уравнений, описывающих движение вяз-
вязкой теплопроводной сжимаемой жидкости в произвольной криволи-
криволинейной ортогональной системе координат, выписана в [3]. Из этих
уравнений в частности могут быть получены и уравнения в так на-
называемых естественных координатах, s и п, связанных с линия-
линиями тока и нормалью к ним при соответствующем выборе коэффи-
коэффициентов Ляме.
Подчеркнем, что естественные координаты не образуют систему
координат в обычном смысле, так как линии тока не являются кри-
кривыми, вдоль которых величина п постоянна, а их ортогональные
траектории не являются кривыми, вдоль которых величина s по-
15
стоянна, при этом дифференциалы ds и dn не являются полными
дифференциалами. Поэтому записанные с их помощью дифферен-
дифференциальные уравнения в частных производных на самом деле тако-
таковыми не являются, поскольку запись частных производных в виде
лишена смысла.
ds
«—const дтъ
Уравнения, описывающие стационарные течения идеального га-
газа с физико-химическими процессами, могут быть получены из об-
общей системы уравнений A.12)...A.21), если положить в ней П=
=—р, q=0, т. е. принять, что коэффициенты вязкости и теплопро-
теплопроводности равны нулю.
Выпишем эти уравнения для случая, когда имеют место хими-
химические реакции, релаксация колебательных степеней свободы и в
потоке содержатся частицы одного размера. Имеем
A.36)
A.37)
; A.38)
dt
d
dt
dt
= ФЛр, Т, e.) /7=1,2,...,/>; A.40)
dt
TV
es=es(Ts). (
Первые три уравнения — уравнения неразрывности, движения и
энергии реагирующей смеси газа и частиц, преобразованные с уче-
учетом уравнений A.17), A.18), уравнения A.39), A.40) описывают
изменение концентраций химических компонент сц и энергии коле-
колебательных степеней свободы ер, уравнения A.41), A.42) —уравне-
—уравнения неразрывности, движения и энергии частиц и, наконец, уравне-
уравнения A.43) —термические и калорические уравнения состояния сме-
смеси и частиц.
Сделаем несколько замечаний относительно системы A.36)...
A.43), поскольку в дальнейшем в основном будем рассматривать
именно эту систему уравнений.
16
Система A.36)...A.43) записана таким образом, что в левой
части каждого уравнения находятся дифференциальные операторы,
а в правой — конечные выражения. В связи с этим при преобразо-
преобразованиях систем координат правые части этих уравнений не претер-
претерпевают изменения. Кроме того, в каждом из перечисленных урав-
уравнений в левой части содержится субстациональная производная
(оператор d/dt), которая преобразуется единообразно. Эти замеча-
замечания относятся и к приведенному ниже уравнению производства энт-
энтропии A.44) и уравнению A.45), полученному из A.37) скаляр-
скалярным умножением на вектор W. Отметим, также, что формальная
запись левых частей уравнений A.36)...A.38) одна и та же как для
течений с физико-химическими превращениями, так и для течений,
в которых такие превращения отсутствуют. Однако формулы для
определения энтальпии h существенно различаются для этих клас-
классов течений. Очевидно также, что для течений с физико-химически-
физико-химическими превращениями нельзя раздельно решать системы A.36)... A.38)
и A.39)...A.43), поскольку они взаимосвязаны.
В дальнейшем полезно получить уравнение производству энтро-
энтропии для течений с химическими реакциями.
Примем, что хотя полная система и не находится в равновесном
состоянии, тем не менее в ней существуют малые элементы массы,
которые находятся в состоянии локального равновесия, и для ко-
которых локальная энтропия является той же самой функцией Т, р и
аг, что и в состоянии полного равновесия. В частности, остается
справедливой формула равновесной термодинамики для энтропии,
элемента массы вдоль пути его центра масс, а именно
лг
rp dS de i d I 1
~dt ~ ~dt "*" P "It \~
где 5 — энтропия смеси, аддитивная по массе входящих в нее энт-
энтропии индивидуальных компонент, a Xfe — термодинамический или
химический потенциал k-я компоненты (парциальная удельная
функция Гиббса). После несложных преобразований получим урав-
уравнение производства энтропии в виде
JV N
Си—~ = ~z^i ^^(А Т, а). A.44)
>~Г ft = i
В общем случае вязкой, теплопроводной, многоскоростной среды
при наличии внешних сил и источников тепла правая часть урав-
уравнения A.43) представляет собой сумму произведений термодина-
термодинамических сил на соответствующие потоки различной тензорной раз-
размерности. Уравнение A.44) при известной зависимости энтропии от
других термодинамических параметров (например, в случае иде-
идеального нереагирующего газа S=ln(pp-T)—отношение удельных
теплоемкостей) не дает дополнительной информации по сравнению
с уравнениями A.36), A.37), поскольку оно получено с использо-
использованием этих уравнений. Поэтому при рассмотрении конкретных за-
17
дач можно использовать либо уравнения A.36), A.37), либо вмес-
вместо одного из них — уравнение A 44).
Заметим, что уравнение A 37) записано в векторном виде и со-
содержит по существу, три уравнения относительно трех составля-
составляющих скоростей вектора W. Если уравнение A 37) скалярно умно-
умножить на W, то получим следующее скалярное уравнение
dp
dt
dt
. 1 dp =FW
' p dt
p
p
j
При решении конкретных задач можно пользоваться либо тремя
уравнениями A.37), либо какими-либо двумя из них и уравнением
A.45). В дальнейшем при решении обратной задачи уравнение
A 45) будет использоваться вместо проекции уравнения A.37) на
ось х (или s), и, кроме него, будут использоваться два оставшихся
уравнения A.37) в проекциях на другие оси.
1.2.1. Уравнения газовой динамики
пространственных неравновесных течений идеального газа
в обобщенных координатах Мизеса.
Двумерные и одномерные течения
Запишем первоначально основные уравнения задачи в криво-
криволинейной системе координат, которую будем связывать с кривой
y=fo(s) в плоскости х, у (рис. 1.1). Координаты точки в этой си-
системе определяются длиной дуги s, расстоянием по нормали к этой
кривой г и углом ф. Элементар-
Элементарное геометрическое рассмотрение
показывает, что декартовы коор-
координаты х, у, z связаны с криво-
криволинейными координатами s, r, ц>
следующими соотношениями:
х= Г cosl(s)ds — rcoscp^in 8(s);
г/ = /0 (S)+r COS cp COS 8 (S); A.46)
Рис 1 1 Криволинейная ортогональ-
ная система s, г, <р
z~r sin <p,
где 8(s) —угол между касательной к кривой fo(s) и осью х. Коэф-
Коэффициенты Ламе Hi, #2, #з Для этой системы координат приведены
ниже
18
где R(s) —радиус кривизны кривой fo(s) и в формуле A.47) знак
минус соответствует вогнутым кривым fo(s), а плюс — выпуклым.
Отметим, что в плоском случае Н\= \+r/R, а #3 = 0.
Имеем следующую запись для правых частей уравнений A.36),
A.37) и оператора d/dt:
0\ ¦ дР\^Н1Н2 .
dt TPVW <tyi "r dq2 * dqz
dW L 1 nn d (JT\ дТ _J_ 1 ^ m 19 4- Л
где T =-L ^ //2m (^mJ; qm = Vm/Hm.
Тогда, вводя обозначения ql=s; q2 = r; q3 = y; Vl=u; V2 = v;
V3 = w, где и, v, w — проекции вектора скорости W на оси системы
л, г, ф, получим следующую запись уравнений A.48)...A.50). Далее
вместо одного из уравнений A 49), соответствующего проекции на
ось s, будем преобразовывать правую часть уравнения A.45) и,
кроме того, два оставшихся уравнения, соответствующих проекци-
проекциям на оси г и ф.
. d?vHiH2 I dpwHiH2 . A51)
ds "г дг "^ д?
^^-2+-^-; A.52)
dt ~ ? dt ' >'
dv , и2 cos <f w2 1 dp .-. KQ.
in , (i .oof
dt RHi H3 ' ^ ^
^te> _ m2 sin у да2 . 1 dp .. ,-д
~дТ + ~RH1 ЯГ YP# ~^" '
Здесь и, v, w — проекции вектора скорости W на оси криволиней-
криволинейной системы координат s, r, ф отнесены к критической скорости
звука а; р, р — давление и плотность, отнесены к давлению р* и
плотности р* в критическом сечении, а параметры с размерностью
длины к некоторой характерной длине г*; у== —-— —отношение
Р*
удельных теплоемкостеи в случае газа без физико-химических пре-
превращений.
Отметим, что приравняв нулю соотношения A.51)...A 54), по-
получим уравнение неразрывности и движения идеального газа при
19
отсутствии внешних сил и внешних источников массы и энергии
[см. уравнения A.36), A.37)]. Если в уравнение A.55) подставить
под знак дифференциала энтропию 5 или энтальпию Н и прирав-
приравнять правую часть нулю, то получим уравнения сохранения энтро-
энтропии или энтальпии вдоль линий тока для идеального газа.
Обратную задачу и формулировку граничных условий удобно
проводить, используя уравнения, в которых в качестве независимых
переменных взята длина дуги вдоль некоторой кривой и функции
тока [27]. Использование функций тока особенно удобно, так как
начальные условия в обратной задаче задаются обычно на поверх-
поверхности тока (жесткая стенка или ось симметрии). Выведем соответ-
соответствующие уравнения для случаев, когда в смеси присутствуют ино-
инородные частицы и допускается неравновесное протекание химиче-
химических реакций и возбуждение колебательных степеней свободы мо-
молекул.
Известно, что уравнение неразрывности, записанное в дивер-
дивергентной форме, определяет соленоидальный вектор, который может
быть записан в виде векторного произведения градиентов двух
функций; уравнение неразрывности при этом тождественно удов-
удовлетворяется. В связи с этим, для стационарных пространственных
течений могут быть введены две функции тока. Введем новую не-
независимую переменную г|? с помощью равенства, левая часть кото-
которого — скалярное произведение вектора скорости и вектора Уя|з,
и dfy v dfy | w д*\> ^
1 ' —H* ———~ ~" r~ ¦¦ — vj.
Hi ds //2 dr //3 df
A.56)
Очевидно, что поверхности ty{s, r, ф) = const являются поверхно-
поверхностями тока. Имея в виду соотношения
di? _ dr/ds _#_
A57)
ds dr/d<\> ' dr ~~\ dty ) ' dy ~~ dr/dty '
получим следующие формулы для перехода к новым переменным:
ds
г,9
д
дг
dr/ds д
dr/d<]> d<]>
d
д
s,V
dr/dy d
A.58)
Преобразования A.56)...A.58) вводят вместо независимых пере-
переменных s, r, ф новые независимые переменные s, я|з, «р. Для построе-
построения поля течения в переменных s, r, ф в случае использования но-
новых независимых переменных необходимо иметь уравнение, кото-
которое позволяло бы находить переменную г как функцию хифна по-
поверхности i|)=const.
В переменных s, -ф, ф оператор d/dt приобретает вид
Л- = Л- -L-l-J^L Л- . A.59)
dt Нл ds //4 д<?
20
.
С использованием A.57)...A.59) соотношения A.51)...A.54) можно
переписать в виде
- ; A.60)
A.61)
A.62)
A.63)
dp .
и2 cos 9 w2 i 1
, 1_ d_p_ .
dt ' о dt '
1Г
a2 sin f
RHX
ш |
dr/df
dp .
di/
dp
_dp_
dr дф
Кроме того, имеем следующее уравнение для переменной г:
#! ds ' Я3 й?
A.64)
Введем еще одну независимую переменную 9 с помощью равенст-
равенства, левая часть которого — скалярное произведение вектора скоро-
скорости и вектора V9:
и дв , w E8 ,-.
Hi ds tf3 d<f ~~ '
A.65)
Очевидно, что поверхности 0(s, ty)= const также являются поверх-
поверхностями тока и каждый из векторов V0 и Vi|j ортогонален вектору
скорости. Линии пересечения поверхностей a|)=const и 8=const яв-
являются линиями тока. Тогда из уравнения A.65) следует, что диф-
дифференциальное уравнение линии тока на поверхности i|)=const
есть
df //jk;
^s Я3а
В переменных s, -ф, 0 оператор d/dt имеет вид
_d___u d_
dt ~ Hi, ds
Используя соотношения
C9 1 dQ df/ds dH
—= , —= . =
A.66)
dfjdb
A.67)
получим следующие соотношения для перехода к новым пере-
переменным:
Ф.р
df/db db
A.68)
06
21
Используя соотношения A.67), A.68) перепишем соотношения
A.60)...A.63) в виде
D ds
где D = дг/д<Ьдф6 — ду/д<]>дг/дв;
dt ' p dt
dv . и2 cos <p w2 , \ / dp д<? dy dp \ /• 1 71 v,
~~dt ~ ~~RHX "//Г Y?> l"^F ~M W ~Wj '
_ «2 sin
Поскольку введены новые независимые переменные s, г|з, 0, то для
нахождения переменных г и ф должны быть выписаны соответст-
соответствующие уравнения. Нетрудно показать, используя A.64), A.65) и
A.67), что эти уравнения имеют вид
—= —Ях; A.73 >
ds и
ду w Я] .-. ja.
ds и Я3
Запишем, наконец, используя приведенные выше формулы A.67),
A.69)...A.74), систему уравнений A.36)...A.43) в координатах s,
г|), 8. Искомыми функциями в соответствии с вышесказанным явля-
являются и, v, w, р, р, иь ер, Ws, es, ps, r и ф. Отметим здесь лишь, что в
уравнениях неразрывности, движения и энергии частиц оператор
ds/dt действует вдоль траектории частиц и поэтому для него не-
несправедливы формулы A.59) и A.67). Итак, имеем следующую си-
систему уравнений, описывающих в координатах s, г|э и 0 течение сме-
смеси газа и частиц при наличии химических реакций и возбуждения
колебательных степеней свободы, а также внешних сил потоков
массы и энергии:
= М; A.75)
D ds
ZLT Г „ -С Wit
A.76)
(W) +
ds \ 2 l YP ds a [ p
и dv u2CCscp w2 . 1 f dp df d'f dp \
~Hl ~ds~ — lUTi r y?D [ дф дЪ d<\i db j
= Fr ^/J7 A.77)
P
и dw — u2 sin у . wv 1 1 / dr dp _ dr dp \
Hx ~ds RHi ' T ~"~ [ }~
22
A.78)
T, a,) i = \, 2,..., N; A.80)
Т,ер) i=l,2,...,P; A.81)
A.82)
qj A.83)
<L84>
fit qj
ds иг
N
л(Г)аг; h —
es=es(Ts), A.86)
где Fr7 fsr, Fф и |/5ф — проекции внешних сил и сил, действующих на
частицы на оси г и ф соответственно.
Отметим, что координаты s, -ф и 0 можно рассматривать как
обобщение на пространственный случай координат х, ар, введенных
Мизесом для двумерных течений.
Уравнение производства энтропии в координатах s, -ф, Э для те-
течений с неравновесными химическими реакциями имеет вид
N
и dS 1
Рассмотрим детально систему уравнений A.75)...A.87), проана-
проанализируем важные частные случаи и некоторые интегралы этой си-
системы.
Важно подчеркнуть, что уравнения A.75), A.76), A.79)...A.81),
A.84), A.85) и A.87) не содержат производных по гр и 0 и записа-
записаны по существу вдоль линий тока — линий пересечения поверхно-
поверхностей 1(з и 8 = const.
Отметим, что с точностью до коэффициента Ляме Я1 запись
уравнений A.76), A.79)...A.81) и A.87) одинакова для одномер-
одномерных, двумерных (плоских и осесимметричных) и пространственных
течений. Это по существу система уравнений движения A.76),
23
энергии A.79), кинетики химической и колебательной релаксации
A.80), A.81) вдоль криволинейной струи тока. Это обстоятельство
чрезвычайно важно и позволяет составить одномерные модули та-
таких уравнений для численного интегрирования вдоль струек тока
двумерных и пространственных течений, что дает возможность вы-
выписать некоторые известные интегралы общей системы, а также ис-
использовать систему при постановке обратной задачи.
Рассмотрим теперь случай, когда отсутствуют внешние силы,
внешние источники массы и энергии, а также инородные частицы,
т. е. iW=F = Q = ps = f.; = q.;=0. Кроме того, примем, что смесь яв-
является нереагирующей, т. е. .F?° —Фр=0. Тогда уравнения A.75)
A.79), A.87) могут быть проинтегрированы вдоль струек тока, что
приводит к соотношениям
= С(ф, 0); A.88)
TV7O
-^ = Я0(«1>, 9); A.89>
0). A.90).
Уравнение A.88) является аналогом уравнения расхода в од-
одномерном течении, а уравнения A.89), A.90) есть уравнения со-
сохранения полной энтальпии и энтропии вдоль линии тока в тече-
течениях нереагирующего идеального газа без внешних воздействий.
Очевидно, что если в некотором начальном сечении полные энталь-
энтальпия и энтропия постоянны, то они постоянны и во всем потоке, и
имеют место изоэнтропическое и изоэнтальпическое течения с по-
постоянной полной энтальпией.
Если в потоке происходят неравновесные процессы и нет внеш-
внешних воздействий и инородных частиц, то уравнения A.88) и A.89)
имеют место, а уравнение A.90) не выполняется.
Из уравнений A.90) и A.76) получаем вдоль линии тока интег-
интеграл Бернулли, который очевидно имеет место в случае нереагирую-
щих течений идеального газа
J^ ! +I A.91)
-1 P 2 y-1
где у — отношение удельных теплоемкостей, которое в общем слу-
случае также является функцией фив, поскольку может изменяться
при переходе от одной линии тока к другой.
Отметим, что если подвод массы и энергии производится сосре-
сосредоточенно, т. е. только в одной плоскости, то имеют место те же
уравнения A.88) и A.89), только константы С, Но и Ф° различны
слева и справа от этой плоскости.
Проведем некоторые преобразования с целью представления си-
системы A.75)...A.86) в виде, удобном для численного решения и по-
постановки граничных условий.
Выразим v из A.84) v — udr/dsHi~l и подставим в A.78). Имеем-
24
dwr _ ru sin <p i H\ I dr dp dr dp \ H\r t ps ,
Ss R y$Du \ (Э6 (Эф (Эф дв / u \ p
A.92)
Помножим A.92) на дф/д0, а A.77) на дг/dQ и вычтем одно из
другого. После некоторых несложных выкладок имеем
dwr ursmf Hi Г i j 1
(Э6
Для дальнейшего важно подчеркнуть, что уравнение A.93) не со-
содержит производных по -ф, а лишь производные по 0 и s вдоль по-
поверхностей тока.
Рассмотрим частный случай общей системы, когда подвод мас-
массы либо отсутствует, либо является сосредоточенным. Тогда в урав-
уравнении A.75) уИ=О и оно интегрируется. Не теряя общности, поло-
положим константу интегрирования С(Э, -ф) (см. 1.88) равной единице.
Имеем
j?^ J? d<f dr _ 1 A94)
д<\> дв dty d8 pur
Запишем теперь систему уравнений газовой динамики в координа-
координатах s, г|5, 9 в виде, который будет использоваться далее для поста-
постановки обратной задачи и при численном интегрировании. Для про-
простоты ограничимся случаем, когда в потоке отсутствуют частицы
(ps=0). Имеем тогда
= _i_r_L_ + JL.iq; A.95)
д<?/дв I par ' йф дв J
дР = у °(s> Ф> е> | дР/д® д<? . /19б)
(Эф гиду/дв * d<f/d6 сЭф '
4O(s, Ф, в)-^
YP дв дй
::—= — '» (^-
25
JZ-^JLh^ A.100)
ds и
*L = ^HX; A.101)
ds ru
/==1,2,...,//; A.102)
~ = Н1Фр{р, T, ep
OS
ЧхФр(р,Т,е0) i=l, 2,...,P; A.103)
р = -2?-; h=\* h.(T)a,; h, = hAT). A.104)
м, 4U
Двумерные (плоские и осесимметричные) течения
Система уравнений A.102)...A.104) может быть использована
и для расчета двумерных течений. При этом в уравнениях A.95)...
A.97) необходимо лишь положить <Э<р/д9=1 (поскольку поверхно-
поверхности тока 8 = const — плоскости), а производные dp/dQ = drjdd при-
приравнять нулю. В случае плоского течения, кроме того, необходимо
в формулах для G и Hi положить ф=0 и w = 0. Уравнения A.98)...
A.104), как уже отмечалось, сохраняют одну и ту же форму запи-
записи для всех случаев течения, хотя формулы для Hi могут разли-
различаться.
Из формул A.97) и A.101) следует, что если ЯФоо, то течение
не может обладать осевой симметрией, так как в этом случае шф
?=0 и ф=/=9, и сохраняет пространственный характер. Если /? = оо,
то течение может обладать осевой симметрией. При этом существу-
существует важный для практики случай, в котором все параметры, кроме
<р, не зависят от Э, а являются функциями только двух переменных
s и \j>. Из A.97) имеем тогда
w(s, Ф)=—
где ш0 и Го значения этих функций на начальной плоскости. Из
уравнения A.101) следует, что
— ds,
ru
s0
и следовательно, <?ф/<38=1. Описанные течения являются осесим-
метричными течениями с закруткой. Если радиус кривизны R = oo
и до = 0, то приведенная система переходит в систему уравнений
для плоского и осесимметричного случаев. При этом очевидно, что
поверхности тока -0 = const суть плоскости, и 8==<p.
В этом случае для изоэнтропических течений идеального газа,
е котором имеют место равновесные или замороженные процессы,
26
системы A.95), A.96) приобретают вид
__1 +v . др __ у dv . дг _ v
pa cty r as ds и
Здесь v=0 для плоского течения, и v=l —для осесимметричного.
Для плоского и осесимметричного изоэнтропических течений с
постоянным показателем адиабаты система A.95)...A.104) имеет
особенно простой вид
др Y_ dv_ . dr1+v _ 1 + v .dr__vm n
(^±l^А1/2. A.107)
Y—1 Y-l
Одномерное течение. Из A.106) и A.107) следуют соотношения
классической одномерной теории, в которой полагается, что пара-
параметры течения зависят лишь от одной продольной координаты s,
а скорость направлена вдоль оси сопла, т. е. и = 0. Тогда из A.106)
где i|) — некоторая константа, задающая расход газа.
Обозначая площадь поперечного сечения сопла F, расход газа,
равный массе газа, протекающего в единицу времени, через попе-
поперечное сечение сопла Q, а плотность тока /, получим следующую
запись уравнения неразрывности в одномерном течении:
?WF = jF = O. A.108)
В случае неравновесных течений к этому уравнению добавля-
добавляются уравнения A.98), A.99), A.102)...A.104), в которых для те-
течений с криволинейной осью нужно положить #i=l+/"//?, а для
течений с прямолинейной осью #i=l.
Отметим, что в гл. 2 будет дано обобщение классической одно-
одномерной теории (пригодной лишь для каналов с прямолинейной
осью) для каналов с криволинейной осью с использованием систе-
системы уравнений, записанной в ортогональных координатах (см.
1.2.2).
Двухфазные течения. В случае двухфазных течений общую си-
систему уравнений можно записать, используя в качестве независи-
сых переменных s, л|), 9 или s, tys, 8S, где tys, Qs — функции тока (тра-
(траектории) частиц. Если рассматривается полидисперсная смесь, то
в качестве tys, fls может быть выбрана функция тока какой-либо
одной частицы. Выпишем для плоского и осесимметричного случа-
случаев систему уравнений, описывающих движение двухфазной смеси
27
при наличии частиц одного размера в координатах s, -ф. Имеем для
нереагирующей смеси при /71° = Фр = 0 и при отсутствии внешних
сил F=0 и внешних источников массы и энергии следующую си-
систему уравнений:
<3/-1+v _ 1 + v _ дг _ v
di> ш ds и
Y A.109)
и J г~ ds
ds\2 Г у? ds Г ри
ри
I г'р ——(vM — ия)-\-рЛи—-—v—- N—!-?-?-= О,
. Обо
А = А(А Г); р = РТ; es = es(Ts), A.113>
где /л:, fr — проекции вектора f на оси л; и г, а все параметры при-
приведены к безразмерному виду путем отнесения к соответствующим,
критическим величинам.
1.2.2. Уравнения идеального газа
в ортогональных координатах. Характеристики уравнений
для двумерных течений в координатах х, я|5
Введенная система координат s, -ф, 0, естественно, не является
единственно возможной. Преимущество ее перед декартовой, ци-
цилиндрической и сферической системами координат в том, что гра-
границы исследуемой области в координатах s, г|), 9 обычно являются
плоскостями или прямыми линиями. Система координат s, г|>, 9 не
является ортогональной; подобные системы координат называют
нормальными. При решении прямой задачи также используются
координаты, в которых границы области переходят в плоскости или
прямые линии, что достигается соответствующей нормировкой пере-
переменных у и z.
При решении обратной задачи для сопел и каналов сложных
криволинейных конфигураций, когда контуры являются многознач-
многозначными функциями декартовых координат, удобно вместо нормаль-
нормальных систем координат типа s, rj), 9 использовать ортогональные си-
28
стемы, связанные с линиями тока. Известным примером ортого-
ортогональных координат для потенциальных течений являются коорди-
координаты г|з, Ф, где Ф — потенциал скорости.
Рассмотрим еще одну ортогональную систему координат, при-
применяемую для расчета течений газа в сложных криволинейных ка-
каналах [21]. Введем ее для течений, параметры которых не зависят
от угловой координаты ср, но в которых воможна закрутка потока
(или скос его в плоском случае параллельно оси oz). Одним се-
семейством координатных поверхностей в этой системе являются по-
поверхности т|) = const, определяемые равенством A.56). В качестве
второго семейства выбираются плоскости cp = const, проекции ли-
линий тока на которые совпадают с проекциями поверхностей а)з =
= const.
Рассмотрим теперь способ введения третьего семейства коорди-
координатных поверхностей. Пусть s — расстояние вдоль проекции линии
тока на плоскость qj = const. Запишем выражение для дифферен-
дифференциала дуги
A.114>
где и, v, V — проекции вектора скорости W на оси х, г и плоскость
Ф —const соответственно, т. е. V2 = W2—w2. В общем случае 8s не
является полным дифференциалом, а значит существует интегри-
интегрирующий множитель g такой, что
da=gbs=( — guV-^dx + l — gvV-^dr A.115)
будет полным дифференциалом. Следовательно,
guV, %gvVK -?-=0. A.116)
ох дг d<f
Нетрудно убедиться, что поверхности -ф = const, ф —const, a=
=const ортогональны. Поэтому поверхности о=const могут быть
выбраны в качестве третьего семейства координатных поверхно-
поверхностей.
В случае двумерных потенциальных течений а=const на лини-
линиях постоянного потенциала O = const, поскольку в этом случае ин-
интегрирующим множителем для длины дуги 8s является скорость.
В качестве а можно рассматривать, например, длину дуги вдоль
проекции какой-либо характерной линии тока на плоскость <р=
—const. В переменных if>, а, ф при условии, что искомые функции
не зависят от ф, но возможно существование окружной составляю-
составляющей скорости w (т. е. так называемой закрутки потока), имеем
следующую систему уравнений для течений идеального газа с у=
= const при отсутствии частиц, химических реакций, внешних сил
и внешних источников массы и энергии:
-^=—~; (i.ii8>
29
dp yg Г a /<fo . vw2 \v даЛ . r-,
r- [v \д*Г r*gV*} V
- = Л_ JLti ;
;
у—lp 2 у—1
= С (<[>); V = (W2 — w2I/2;
^ ^. A.121)
da da
Отметим, что интегрирующий множитель g неизвестен заранее, и
•определяется в процессе решения.
В ряде работ уравнения характеристик для сверхзвуковых не-
неравновесных течений записываются в координатах х, о|з. Такая за-
запись особенно удобна, поскольку уравнения, выполняющиеся вдоль
линии тока A.75), A.79), A.81), A.84), A.85) и A.87), по сущест-
существу записаны в характеристической форме. Известно, что в сверх-
сверхзвуковых стационарных течениях существуют три семейства харак-
характеристик: две линии Маха и линия тока. Характеристики опреде-
определяются уравнениями направления и уравнениями совместности.
Уравнения направления являются для линий тока уравнениями
A.84), A.85), а уравнениями совместности—A-76), A.79), A.81),
A.87).
Для линий Маха С" и С+ характеристики в двумерном (плос-
(плоском или осесимметричном) течении уравнения направления есть
-^=±tg(8 + a)^T7, A.122)
д<\> рцг1+
а уравнение совместности
—sin6sina-JV<A *± =0, A.123)
г J cos F ± а)
тде 8 — угол наклона вектора скорости к оси х; а — угол Маха; сс=
= arcsina/W (a — замороженная скорость звука); JV — некоторая
функция, связанная с исследуемым неравновесным процессом;
верхние знаки относятся к С+ характеристикам.
1.2.3. Уравнения Навье — Стокса в координатах Мизеса.
Параболизованные уравнения
Запишем уравнения Навье — Стокса в координатах х, г|5. Рас-
Рассмотрим для простоты двумерные течения. В струйных течениях
часто используются координаты Мизеса при построении разност-
разностных схем с целью разделения области на ячейки с равными расхо-
расходами газа через них. Сделаем некоторые преобразования с систе-
системой A.28), A.29), с учетом формул перехода типа A.56), A.57) и
формул A.105), A.106) и условия ш = 0.
30
Поскольку имеют место соотношения
д __ д v 1+v д д
дх дх ' dty дг
то оператор
И —+ <п—= И—. A.124)
дх ду дх
Имеем
ри
да 1 dp , ovr'1 dp , 4 Г д да д ( ., ди
дх у д* Y dty * 3 [дх дх дх \ ^ д^
f
дх
JLparpK
дх v di/X di/
^] (L125)
difj\
dv purv dp , д dv д [ dv \
дх v dty i дх дх дх { д<\> )
-iL = -JL_; A.127)
-2l=-2-. A.128)
Не будем выписывать здесь уравнения энергии в координатах
Мизеса из-за громоздкости выражений, хотя из приведенных выше
формул эти преобразования очевидны. Отметим лишь некоторые
факты. Очевидно, что уравнения A.127) и A.128) эквивалентны
соответствующим уравнениям в невязком течении, поскольку они
следуют из уравнения неразрывности и определения линии тока.
В струйных течениях и течениях в каналах используются так
называемые параболизованные уравнения Навье — Стокса, кото-
которые получаются в результате отбрасывания вторых и смешанных
производных по х, что позволяет свести краевую задачу к задаче
Коши. Если провести такую процедуру первоначально с уравнения-
уравнениями A.28, 1.29), записанными в декартовых координатах, а затем в
31
"параболизованных уравнениях перейти к координатам Мизеса, то
получим следующие параболизованные уравнения Навье — Стокса
ри —= —4— —Л-риг — (j.pKrv — ; A.129)
dx у дх у d<ty бф [ дф J
г" др , 4 д Г dv 1 ,
= — -4 rv — риг'ц. — 4-
dv
Если параболизовать уравнения A.125) и A.126), то получим
соответственно
ди 1 dp , ourv dp
r дх у
+ 4 pttr
дх у дх ' у д\> di/
di/ \ аф ,' 1
dv риг4 dp , 4 д I ^ dv \ ,
аи — = — —4 par" — рИГ —|4-
V дх у д^~ 3 V дф \ ^ )
A.132)
Сравнивая A.129), A.130) с A.131) и A.132), видим, что в этих
уравнениях совпадают лишь первые члены в правых частях. Таким
образом, вид параболизованных уравнений зависит от порядка
«параболизации». Очевидно, что более корректным является спо-
способ, в котором первоначально уравнения записываются в коорди-
координатах х, г)), а затем параболизуются уравнения A.131), A.132). От-
Отметим, что в известной литературе, однако, такой подход не реали
зуется, а используются уравнения типа A.129), A.130), которьк
получены после «параболизации» уравнений в декартовых коорди
цатах и последующего перехода к координатам х, -ф. В связи <
этим, при проведении конкретных расчетов необходимо оценить по
рядак неучтенных в уравнениях A.129), A.130) членов. Эти чле
ны, как видно из их структуры, особенно важны в тех областям
где происходит сильный разворот потока нормально оси х,
1.2.4. Граничные условия в обратных задачах
Для постановки обратной задачи теории сопла в общем случ;
пространственных течений обратимся к общей теории характер
стик для квазилинейной системы дифференциальных уравнений
частных производных первого порядка. Ниже воспользуемся эт(
.32
теорией в том виде, как она предложена Мизесом. Не излагая здесь
способа построения характеристических поверхностей и нормалей
к ним и уравнений направления, отметим лишь, что как только
компоненты этих нормалей определены, исходную систему из т
уравнений можно заменить эквивалентной системой, составленной
из линейной комбинации этих уравнений, которые разделяются на
две части, одна часть, состоящая из р уравнений (т—р — ранг
матрицы коэффициентов этой линейной комбинации), которые со-
содержат производные только вдоль характеристических поверхно-
поверхностей. Эта группа и р уравнений являются уравнениями совмест-
совместности. Другая группа из оставшихся (т—р) уравнений по терми-
терминологии Мизеса составляет систему дополнительных уравнений, со-
содержащих по крайней мере одну производную от какой-либо из ис-
искомых функций в направлении, нормальном к характеристической
поверхности, при этом те функции, производные от которых входят
в эти дополнительные уравнения, не могут претерпевать разрывов
в этом направлении. В общем случае установившегося течения га-
газа можно показать, что все поверхности, состоящие из линий тока,
являются характеристическими. Эти поверхности являются
действительными характеристиками даже для дозвукового
(если не предполагается, что течение безвихревое) и для вихревого
течения несжимаемой жидкости. Нетрудно при этом показать, что
на поверхностях тока исходная система уравнений, записанная в
декартовых координатах и состоящая из E + N + P) уравнений в
частных производных (три уравнения движения, уравнение нераз-
неразрывности, уравнение энергии и N + P релаксационных уравнений)
переходит в систему из C + N + P) уравнений совместности [урав-
[уравнения A.97)...A.99) и (N+P) уравнений A.102), A.103)] и двух
дополнительных соотношений (ранг соответствующей матрицы ра-
равен двум) A.95) и A.96). Уравнениями совместности являются
два уравнения движения A.97), A.98), уравнение энергии A.99)
и N + P релаксационных уравнений, которые не содержат производ-
лых по нормали к линии тока. Дополнительными уравнениями яв-
являются одно из уравнений движения A 96) и уравнение неразрыв-
неразрывности или уравнение, которое следует из него A.95), содержащие
производные по нормали к поверхности тока. Уравнения A.100) и
A.101) являются уравнениями направления.
В осесимметричном или плоском случаях наличие двух допол-
дополнительных уравнений позволяет элементарно разрешить обратную
задачу, сводящуюся к задаче Коши. А именно: на некоторой кри-
кривой (начальном слое я|) = const), являющейся линией тока, задается
какая-либо из компонент скорости или распределение давления
(плотности). Тогда из уравнений направления A.100), движения
A.98), энергии A.99), релаксационных уравнений и уравнения со-
состояния путем совместного численного интегрирования их по s оп-
эеделяют оставшиеся компоненту скорости (или обе компоненты,
>сли задано распределение давления или плотности), давление,
ыотность, температуру а, и ер. В случае идеального газа с посто-
шным показателем адиабаты расчет недостающих параметров на
i—1393 33
начальном слое проводят весьма просто с использованием конеч-
конечных уравнений сохранения энтропии A.107), Бернулли A.108) и
уравнения направления A.106). Для перехода на следующий слой
при решении задачи Коши (численном или аналитическом) с по-
помощью двух дополнительных уравнений A.95), A.96) на этом слое
определяют координату г и давление р, а затем путем численного
интегрирования вдоль слоя системы A.100), A.98), A.99), A.102)...
A.104) —параметры течения.
При интегрировании релаксационных уравнений A.102), A.103)
предполагается, что в начальной плоскости s = s0 при всех я|) и 9
существует некоторая связь аг=/°(р, Т), ep = f'(p, T), которая за-
задается из феноменологических соображений, например, принима-
принимается равновесие или замороженное состояние потока при s = Sq.
При аналитических начальных данных единственность и суще-
существование решения в до-, транс- и сверхзвуковой областях течения
обеспечивается теоремой Коши — Ковалевской, поскольку уравне-
уравнения газовой динамики обладают аналитическими коэффициентами
в эллиптической (дозвуковой), параболической (трансзвуковой) и
гиперболической (сверхзвуковой) областях. С другой стороны, со-
согласно теореме Веерштрасса любая непрерывная функция может
быть со сколь угодно большой точностью аппроксимирована ана-
аналитическим полиномом, и в связи с этим в качестве данных Коши
могут выбираться также и неаналитические данные.
Итак, в осесимметричном и плоском случаях обратную задачу
теории сопла, сводящуюся к задаче Коши, удается разрешить при
задании данных Коши на линии тока благодаря наличию двух до-
дополнительных уравнений несмотря на то, что эта линия является
характеристикой. Однако в плоском и осесимметричном безвихре-
безвихревом течениях линия тока является вырожденной характеристикой,
что и позволяет решить задачу Коши. Иная ситуация имеет место
в пространственном течении. В этом случае задание начальных
данных только на поверхности тока не позволяет уже разрешить
задачу Коши, поскольку поверхность тока является характеристи-
характеристической, а двух дополнительных уравнений и 3 + N + P уравнений
совместности недостаточно для определения параметров течения на
следующем слое (следующей поверхности тока), так как на этом
слое приходится решать систему уравнений в частных производных
A.97)... A.104), начальные условия для которой не заданы. Оче-
Очевидно, что при задании начальных данных (данных Коши) на ка-
какой-либо плоскости s=s0 можно получить решение задачи Коши
для этой системы уже на следующей поверхности тока.
Таким образом, обратную задачу теории сопла для общего слу-
случая пространственного течения можно сформулировать так. На по-
поверхности i|) = i|)o задана функция r = ro{s, 9) и распределение ком-
компоненты скорости u=uo(s, 6) (или распределение давления или
плотности); на плоскости s=s0 задано распределение компоненты
скорости ш = шо@, гр) и функция ф = фО@, г|з); требуется найти се-
семейство поверхностей тока и параметры течения в окрестности на-
начальной поверхности тока. Важно отметить при этом, что задание
34
на поверхности тока всех компонент скорости лишь переопределяет
задачу, поскольку наличие уравнений совместности и уравнений
направления позволяет определить эти компоненты по одной за-
заданной компоненте скорости и уравнению поверхности тока при
условии, что начальные данные заданы еще и на плоскости s=so-
Как видно, принципиальное отличие от соответствующей задачи в
осесимметричном и плоском случаях состоит в том, что начальные
данные формулируются не только на поверхности тока, но и на не-
некоторой поверхности, не совпадающей с поверхностью тока. Такая
постановка обратной задачи позволяет получить единственное ре-
решение для общего случая до-, транс- и сверхзвукового течений в
соплах и каналах переменного сечения. При этом допускается про-
протекание неравновесных процессов и переменность полной энталь-
энтальпии на линиях тока. Постановка задачи в случае пространственно-
пространственного течения в некотором смысле эквивалентна постановке обратной
задачи для вихревого плоского или осесимметричного течения.
И в этом случае некоторые данные (распределение энтропии) нуж-
нужно задавать на начальной плоскости. Итак, для пространственного
течения обратная задача расщепляется на две задачи Коши. Для
уравнений A.95), A.96) задача Коши решается в направлении а|э,
а для уравнений A.97), A.98), A.99), A.101)...A.104) — в направ-
направлении s.
В случае одномерного неравновесного течения постановка за-
задачи аналогична. На оси сопла задается либо скорость W, либо
давление, либо плотность как функции от s. Выбор функции, кото-
которую необходимо задавать, производится из условия наименьшей
чувствительности этой функции к степени неравновесности про-
процесса. Такой функцией в большинстве случаев является плотность,
и в меньшей степени скорость потока. В начальном сечении зада-
задаются все параметры течения W, р, р, Т, сц и ер. Решение задачи Ко-
Коши проводится для системы A.98), A.99), A.102)...A.104) при
этом форма струйки тока, т. е. функция F—F(s) определяется при
заданном Q из уравнения A.108).
Рассмотрим теперь постановку граничных условий в обратных
задачах профилирования сопел и каналов в сверхзвуковой обла-
области. Воспользуемся для этого теорией характеристик для сверхзву-
сверхзвуковых течений. Для случая течений идеального газа с неравновес-
неравновесными физико-химическими превращениями эта теория изложена в
[1, 11, 27], где приведены также различные численные схемы ме-
метода. Здесь лишь отметим, что при сверхзвуковом течении сущест-
существуют три семейства характеристик, два семейства линий Маха (ха-
(характеристики С+ и С~) и линии тока (характеристики Со). Каждая
из характеристик задается уравнением направления [например,
A.122)], при этом газодинамические параметры на ней связаны
уравнениями совместности [см. например, уравнения A.123) для
С+ и С~]. Отметим, что уравнение направления для линии тока
есть уравнение A.100, 1.101), а уравнения совместности — уравне-
уравнения A 98, 1 99).
2* 35
Рис. 1 2 Схема решения методом характеристик задачи Коши (а), задачи Гур-
са (б), смешанной задачи (е)
Для решения обратных задач профилирования важны извест-
известные задачи теории характеристик: задача Коши, Гурса и смешан-
смешанная задача. Рассмотрим методы их решения, предполагая, что ис-
искомыми функциями являются угол наклона скорости 8 и давление
р, которые связаны дифференциальными соотношениями совмест-
совместности.
Пусть теперь 0 и р заданы на дуге АВ некоторой кривой, кото-
которая ни в одной точке не имеет характеристического направления,
и нужно определить решение в окрестности АВ (задача Коши).
Выберем на АВ ряд точек A, a, b,...,c, CB (рис. 1.2, а) и проведем
через каждую из них характеристики обоих семейств. В точках их
пересечения d, e,...,f каким-либо численным методом (см. 3.4)
можно вычислить искомые функции. Зная решение в этих точках,
можно продвинуться еще на один «слой» и т. д., пока не вычислим
решение в точке С. Таким образом находится решение, одновремен-
одновременно строится характеристическая сетка. Аналогично определяется
решение и в характеристическом треугольнике ABD. Такая проце-
процедура возможна лишь при условии существования в области ACBD
непрерывного решения. Известно, что существование непрерывного
решения квазилинейной системы можно гарантировать лишь в ма-
малой окрестности линии начальных данных. Даже при сколь угодно
гладких начальных данных в области влияния дуги АВ (область
ACBD) могут возникать разрывы. Расчет методом характеристик
в этом случае существенно усложняется (см. разд. 3.4).
Рассмотрим задачу Гурса: на дугах АВ и АС характеристик
различных семейств заданы Вир. При этом, естественно, предпо-
предполагается, что Эйр удовлетворяют условиям совместности. Выбе-
Выберем на дугах АВ и АС последовательности точек А, аи а2,...,В и
А, Ь\, Ь2,...,С (см. рис. 1.2, б). Используя точки а\ и Ь\ в качестве
опорных, определим искомые функции в точке С\. Далее решение
можно вычислить в точке с2 и во всех остальных точках
характеристики щЕ. Затем процесс повторяется для сле-
следующей характеристики a2F и т. д., пока не будут вычислены
искомые величины на крайней характеристике BD характеристиче-
характеристического четырехугольника ABDC.
36
Рис 1 3. Постановка и схема решения
обратной задачи профилирования кана-
каналов с заданными параметрами на линии
тока L и распределениями давления или
угла наклона скорости 6 во входном 1\
и выходном Г2 сечениях
В заключение рассмотрим одну из возможных смешанных за-
задач. Пусть граничные условия заданы на дугах АВ я АС двух не-
нехарактеристических кривых, причем на АВ заданы 0 и р, а на
АС — линейная комбинация а8+|3р, и дуга АС расположена внут-
внутри угла, образованного характеристиками разных семейств, про-
проходящих через точку А (рис. 1.2, в). По данным на АВ можно вы-
вычислить 9, р в треугольнике ABD, в том числе и в точках характе-
характеристики AD (точки а, Ъ и т. д.). Для определения 6, р в точке С
используется характеристическое условие вдоль дуги АС и задан-
заданная в точке С комбинация а9 + |3р. После вычисления искомых ве-
величин в треугольнике АЕС решается задача Гурса с данными на
ED и ЕС.
Перейдем непосредственно к постановке обратной задачи про-
профилирования и опишем схему ее решения. Рассмотрим плоские или
осесимметричные сверхзвуковые течения идеального газа с посто-
постоянным показателем адиабаты. Задается кусочно-гладкая непрерыв-
непрерывная кривая L (рис. 1.3), являющаяся линией тока, и параметры на
ней FL = {p, p, W, 6}, характеризующие сверхзвуковое течение. Па-
Параметры, входящие в FL, в общем случае могут быть разрывными и
задаются из некоторых априорных условий. Эти параметры не яв-
являются произвольными. Так как линии тока обладают характери-
характеристическими свойствами, то параметры на L должны удовлетворять
характеристическим соотношениям вдоль линии тока. Слева зада-
задается кусочно-гладная, непрерывная поперечно-ориентированная
граница Гь являющаяся С~ характеристикой, с параметрами F\.
В F\ входят все параметры, описывающие сверхзвуковое течение,
которые определяются входной до- и трансзвуковой частью канала.
При неравновесной полной энтальпии потока Яо, энтропии 5 и
наличии закрутки, в F\ могут быть включены распределения этих
параметров как функции -ф. Краевые условия на L и Г\ дополня-
дополняются справа кусочно-гладкой непрерывной поперечно-ориентиро-
поперечно-ориентированной границей Г2, которая не лежит в области влияния L, с па-
параметрами F2. В качестве Г2 обычно выбирается сечение выхода.
На Г2 и F2 накладывается следующее ограничение. Г2 должна ле-
лежать в угловой области, ограниченной слева С~ характеристикой
1°, а справа — С+ характеристикой ВМ (см. рис. 1.3). В этом слу-
случае в F2 входит распределение только одного газодинамического
параметра р или р.
Следует подчеркнуть, что задание на поперечно-ориентирован-
поперечно-ориентированной границе новых граничных условий на распределения р и 8 обу-
37
словливает использование в расчете новых двухграничных смешан-
смешанных краевых задач профилирования с граничными условиями на
известной характеристике и Г2 [6]. Применение этих смешанных
краевых задач позволяет построить более широкий класс сверх-
сверхзвуковых каналов в отличие от известного, получаемого на основе
решения задачи Гурса.
В ряде случаев Г2 может совпадать с С+ характеристикой BN,
тогда F2 содержит распределения как 9, так и р.
На параметры FL, Fi и F2 не накладывается требование их не-
непрерывности, однако если на границе Ti (или L) задана ударная
волна, то необходимо, чтобы она располагалась вне области влия-
влияния Гг и L (или Г2), т. е. она должна приходить на искомый кон-
контур. В потоке требуется построить стенку канала, обеспечивающе-
обеспечивающего распределения FL, F\ и F2 на соответствующих границах. По-
Поставленная задача профилирования является трехграничной сме-
смешанной краевой задачей сверхзвуковой газовой динамики.
Рассмотрим схему решения сформулированной задачи класси-
классическим методом характеристик. Расчет осуществляется с помощью
последовательного решения задачи Коши, Гурса и отмеченных но-
новых двухграничных смешанных краевых задач профилирования.
Численное профилирование начинается с решения задачи Коши с
начальными данными на L, в процессе которого определяются об-
область влияния I (см. рис. 1.3), а также характеристики 1 и 1°. За-
Затем последовательно решаются смешанная краевая задача с гра-
граничными условиями на части ВК характеристики Г и Г2 в области
II и задача Гурса в областях III и IV. При задании в качестве гра-
границы Г2 характеристики BN вместо смешанной задачи в области
II решается задача Гурса в II + 11]. Искомый контур канала после
расчета областей I ..IV может быть определен квадратичной интер-
интерполяцией по известному полю течения.
При использовании в расчете модификации сеточно-характери-
стического метода по слоям i|) = const (см. разд. 3.4.2) линия тока
является одним из семейств разностной сетки. В связи с этим рас-
рассчитывается не вся область ABDGC (см. рис. 1 3), а ее подобласть,
ограниченная Гь Г2, L и искомым контуром канала, определяемым
в этом случае автоматически
Следует отметить, что в ряде случаев требуется обеспечить про-
прохождение контура профилируемого канала через концевые точки
С и D границ fi и Г2 одновременно Для этого необходимо, чтобы
расходы газа через Г] и Г2 были равны. Равенство расходов обе-
обеспечивается соответствующим изменением линейных размеров Т\
после решения смешанной краевой задачи в области II и опреде-
определения расхода через Г2, что обусловливает соответствующие изме-
изменения входной до- и трансзвуковой частей канала.
Рассмотрим один из возможных алгоритмов расчета левой гра-
границы Г[ при заданных граничных условиях на L и Г2. Fi рассчиты-
рассчитывается при подборе («адаптации» по терминологии работы [17]) до-
и трансзвуковой входных частей канала из условия согласования
параметров потока в ней и искомой сверхзвуковой части. Выбор
38
Рис 1 4 Решение обратной задачи профилирования каналов при подборе левой
границы Г]
входной части осуществляется из априори заданного «адаптируе-
«адаптируемого» я-параметрического семейства дозвуковых частей аналогич-
аналогичного рассмотренному в [17] В данном случае в качестве парамет-
параметров семейства можно взять размер и расположение относительно
оси симметрии критического сечения, распределение параметров
вдоль него, радиус закругления (или величину излома) закритиче-
ской части стенки канала.
Выбор искомой дозвуковой части из этого семейства осущест-
осуществляется:
1) с помощью величины расхода газа через Гг, полученного при
решении смешанной задачи в области II;
2) из условия согласования течения во входной части с гранич-
граничными условиями на L в точке А (рис 1 4, а)
Первое требование удовлетворяется выбором размера мини-
минимального сечения КС и параметров вдоль него. Затем точки К и А
соединяются гладкой кривой, что обеспечивает согласование вход-
входной и профилируемой частей канала по углу 8 После этого выбо-
выбором величины излома (при ограничениях на кривизну стенок кана-
канала, радиуса закругления закритической части) в точке А можно
обеспечить согласование течений в точке А по давлению (скоро-
(скорости) Отметим, что при проведении линии тока КА углы 8 в точке
А справа Вд+ и слева 8л~ могут не совпадать, причем при 8а+>
>8л~(9л+<8л~) должна быть задана ударная волна (волна разре-
разрежения) В этом случае волна задается по величине перепада числа
Маха ЛМ=Мл+—Ма~ Следует иметь в виду, что при реализации
в точке А ударной волны последняя должна лежать вне области
влияния Гг
После выбора дозвуковой части и образующей центрального те-
тела АК решается смешанная задача в разгонной области у и опре-
определяется искомая характеристика Fi^=CA Далее описанным выше
способом осуществляется профилирование сверхзвуковой части ка-
канала
Однако, если в постановке допускается существование ударных
волн в потоке и параметры в точке А выбраны таким образом, что
реализуется ударная волна (рис 1 4, б), то в I + III решается сме-
смешанная задача с данными на характеристике СА и L, в процессе
решения которой выстраивается ударная волна AQ. Завершается
расчет решением задачи Гурса с граничными условиями на харак-
39
Рис 1 5 Решение обратной задачи про-
профилирования каналов при задании на
Г всех параметров, определяющих
сверхзвуковое течение
теристиках ND и MN с выделением части ударной волны QE
[1,6].
Рассмотрим теперь обобщение постановки задачи профилирова-
профилирования на случай, когда на нехарактеристической границе Гг заданы
все параметры, определяющие сверхзвуковое течение. Для того,
чтобы задача была не переопределенной, необходимо, чтобы обла-
области зависимости параметров на L и Г2 не пересекались (рис. 1.5).
В этом случае после определения в процессе решения задач Коши
с данными на L и Гг областей I и II точки BeL и А^Г2 соединя-
соединяются произвольной гладкой линией BN, являющейся линией тока.
Затем решается смешанная задача в области IIIi с граничными ус-
условиями на характеристике QN и линии тока KN и определяется
С+ характеристика KQ. Далее задается некоторое гладкое распре-
распределение числа М вдоль части линии тока ВК, последовательное
решение задач Коши в 1П2 и Гурса в Шз позволяет определить С+
характеристику BR. Завершается профилирование решением зада-
задачи Гурса в области IV. Входная дозвуковая часть искомого кана-
канала может быть определена из п — параметрического «адаптируемо-
«адаптируемого» семейства описанным выше способом.
Таким образом, в этом разделе рассмотрена постановка гранич-
граничных условий для двух классов задач: обратной задачи с заданны-
заданными условиями на входе в дозвуковой части и на некоторой поверх-
поверхности \|) = const и обратной задачи профилирования сверхзвукового
канала с условиями во входном и выходном сечениях и условиями
на поверхности тока. Отметим, что в первой задаче течение рас-
рассчитывается одновременно в до-, транс- и сверхзвуковой областях
и любая из линий тока может быть выбрана в качестве стенок ка-
канала. Во второй задаче рассчитывается только сверхзвуковая об-
область потока и определяется единственная линия тока, обеспечи-
обеспечивающая заданные условия во входном и выходном сечениях.
Отметим, что постановка задачи профилирования с граничными
условиями на априори известной линии тока L является не един-
единственно возможной. Так, в ряде работ распределение некоторых
параметров задается на неизвестной образующей искомого кана-
канала Например, такой подход использован в [30] для профилирова-
профилирования дозвуковых сопел, где решается краевая задача для уравнения
Чаплыгина в плоскости годографа С помощью этого метода уда-
удается построить короткие безударные и безотрывные сопла. Однако
40
этот метод не допускает простого обобщения на случай непотен-
непотенциальных течений газа. В работе [23] предложен метод профили-
профилирования дозвуковых и трансзвуковых каналов, течение в которых
может отличаться от потенциального, а распределение скорости
(давления) может задаваться как на оси, так и на искомой стенке
канала. Метод основан на расщеплении исходной системы газоди-
газодинамических уравнений на подсистемы более низкого порядка. Ос-
Основная идея расщепления связана с выделением эллиптического
или смешанного уравнения второго порядка, для численного реше-
решения которого используется метод блочной верхней релаксации.
Для профилирования плоских и осесимметричных каналов с
заданным распределением давления вдоль искомых стенок для до-
и трансзвуковых течений в [12] применен метод установления.
Стенки канала на участках, где задано распределение давления,
предполагаются непроницаемыми и гибкими. В начальный момент
их форма определяется в соответствии с приближенной оценкой
(например, по одномерной теории) и в процессе счета изменяется
до достижения стационарного состояния. Метод достаточно просто
обобщается на трехмерный случай, однако использование метода
установления требует значительных затрат времени ЭВМ.
1.3. НЕОБХОДИМЫЕ СВЕДЕНИЯ
О ФИЗИКО-ХИМИЧЕСКИХ ПРОЦЕССАХ
В этом разделе представлены сведения по кинетике химических
процессов и выписаны реакции и константы скоростей. Описаны
возможные каналы возбуждения и дезактивации колебательных
степеней свободы и приведены данные по временам релаксации.
Приведены полуэмпирические формулы для определения коэф-
коэффициентов сопротивления частиц и формулы для нахождения чис-
числа Нуссельта, необходимые для расчета траекторий и температуры
°астиц; данные по кинетике конденсации, включающие в себя урав-
уравнения для расчета нуклеации и роста сконденсированных частиц,
а также сведения, необходимые для расчета электромагнитных воз-
воздействий при течении проводящего газа.
1.3.1. Химическая кинетика
Учесть наличие физико-химических процессов можно прибли-
приближенно, приняв скорости их протекания бесконечными или равными
нулю.
При бесконечной скорости имеет место равновесное течение, а
при нулевой — замороженное. При равновесном течении термоди-
термодинамические и газодинамические параметры определяются с привле-
привлечением соотношений термодинамики равновесных процессов Кон-
Концентрации реагирующих компонент в таких течениях определяют-
определяются из закона действующих масс; энергия колебательных степеней
свободы вычисляется по формуле Эйнштейна, парциальные давле-
давления конденсирующихся компонент — по уравнению Клапейрона —
41
Клаузиуса, а скорости и температуры частиц принимаются равны-
равными скорости и температуре газа. Энтропия в этом случае сохраня-
сохраняется неизменной вдоль струйки тока.
Другим предельным течением является полностью заморожен-
замороженное течение, когда параметры, характеризующие релаксационный
процесс, остаются неизменными в процессе движения смеси. Это
течение также является изоэнтропическим. В полностью заморо-
замороженном течении сохраняются неизменными молярные доли
различных компонент, энергия колебательных степеней свободы
молекул, скорости и температуры частиц, а процессы конденсации
вообще не происходят.
Возможны и некоторые другие модели изоэнтропического рас-
расширения, полезные для разного рода инженерных оценок. Рассмат-
Рассматривается, например, химически замороженное течение, когда все
остальные релаксирующие параметры, кроме молярных долей ком-
компонент, изменяются в соответствии с соотношениями равновесной
термодинамики. Рассматривается также течение, когда замороже-
заморожены лишь фазовые переходы, конденсация или кристаллизация. Та-
Такое рассмотрение позволяет оценить предельное влияние конден-
конденсации и кристаллизации на параметры течения. Наконец, возмож-
возможно рассмотрение замороженного двухфазного течения, когда изме-
изменение всех параметров, кроме скорости и температуры частиц, про-
происходит равновесно, а эти последние неизменны в процессе истече-
истечения.
Методы расчета равновесного и замороженного течений весьма
сложных смесей продуктов сгорания, в которых происходят пере-
перечисленные выше физико-химические превращения, изложены в
первом томе фундаментального десятитомного справочника [33].
В остальных томах этого справочника приведены таблицы пара-
параметров смеси для различных композиций, полученные в одномер-
одномерном приближении. Такого рода таблицы, так же как и h—5-диаг-
раммы, позволяют определить параметры в любой точке изоэнт-
изоэнтропического потока, если в этой точке известен один какой-либо
термодинамический параметр и параметры торможения, по анало-
аналогии со случаем одномерного течения газа с постоянным отношени-
отношением удельных теплоемкостей. Действительно, условие изоэнтропич-
ности 5=5 (р, p)=const или 5=5 (р, Т) = const доставляет связь
между давлением и плотностью (температурой), а термическое и
калорическое уравнения состояния вместе с уравнением сохранения
энергии позволяют определить температуру (плотность) и скорость,
а также молярные доли различных компонент, массовую долю кон-
конденсата и т. д.
Основные уравнения, используемые при расчете равновесного
состава, состоят из нелинейных уравнений закона действующих
масс для некоторого набора реакций и уравнений материального
баланса, выражающих условия постоянства количества атомов хи-
химического элемента в процессе химических реакций. Таким обра-
образом, для определения неизвестных парциальных давлений р,- при
заданном давлении р и температуре Т имеем систему нелинейных
42
уравнений. В настоящее время разработаны численные методы ре-
решения этой системы уравнений и созданы таблицы для многих топ-
топливных композиций [33]. По результатам этих расчетов, как отме-
отмечалось, можно получить зависимости р=/(р) и h=h(p), характе-
характеризующие данный изоэнтропический равновесный или заморожен-
замороженный процессы, которые можно использовать затем при решении об-
обратной задачи [см., например, систему A.105)].
Рассмотрим теперь неравновесные процессы. Предельные изо-
энтропические случаи, когда время физико-химического процесса
много меньше характерного газодинамического времени (равновес-
(равновесный процесс) или много больше газодинамического времени (замо-
(замороженный процесс) практически не реализуются, и имеют место
неравновесные процессы, в которых характерное время процесса
сравнимо с характерным газодинамическим временем. Рассмотрим
неравновесное протекание химических реакций. Конкретизируем
правые части уравнений сохранения массы индивидуальных ком-
компонент— функции F,°(p, T, аг) в уравнении A.80). Выпишем для
этого уравнения химической кинетики.
Пусть в газовой смеси протекают q независимых химических
реакций, каждая из которых, например, r-я, описывается химиче-
химической формулой
где vir и v/r— стехиометрические коэффициенты, показывающие,
сколько молекул вещества Л, принимают участие в прямой (v,'r)
и обратной (vjr) реакциях.
Скорость химической реакции г в прямом направлении в молях
на единицу объема и единицу времени равна
где аг и |хг — массовая доля и молекулярная масса t-й компоненты.
Коэффициент пропорциональности КГ+(Т), называемый констан-
константой скорости реакции, не зависит от концентраций индивидуальных
веществ и является функцией температуры. Скорость протекания
реакции г равна
(\ К1*
П
7
где W+ , W- , K+ , К— — скорости и константы скоростей пря-
прямой и обратной реакций соответственно.
Согласно закону Аррениуса, константа скорости реакции может
быть записана в виде
Е \
43
Коэффициент А характеризует числа эффективных соударений реа-
реагирующих частиц в секунду. Постоянные В и Е (последняя называ-
называется энергией активации химической реакции) определяются при-
природой элементарных процессов
В результате прохождения реакции г в прямом направлении об-
образуются v,r — v,r молей t-ro индивидуального вещества, следова-
следовательно, массовая скорость образования вещества с молекулярной
массой \хг в ходе реакции г равна
R[r)=(v;r - ьг) j^(+r)+(v;v - v;r) ^чк
Теперь уравнения кинетики для каждого 1-го индивидуального ве-
вещества могут быть записаны в виде
do,, r-n
—^=F°,(.p, T, au a2,...,aN)(i = \, 2,...,N),
dt
a
где Fut{p, T, a ) = — \ R.\r)— массовая скорость образования
p *A
вещества в результате всех q реакций. Система A.80) допускает
выделение конечных соотношений (уравнений сохранения вещест-
вещества), число которых равно количеству независимых компонент.
В табл. 1.1 представлены для системы С—О—Н—N элементарные
химические реакции и константы скоростей. Константы скоростей
для тримолекулярных реакций имеют размерность см6 моль~2 с'
а бимолекулярных — см3 моль^1 с"
Дифференциальное урав-
Таблица 1.1.
1
2
3
4
5
€
7
8
9
10
11
12
13
14
15
Реакция
СО + О + М — СО2+ М
Н + Н + М — Н2+ М
о + о + м —> о2+ м
ОН + Н + М — Н2О + М
о + н + м-^он + м
N + N + М —у N2+ M
N + 0 + M-^NO + M
ОН + СО — СО2+ Н
ОН + Н2 -»- Н2О + Н
он 4- он —* н2о+ о
Н2+ О —* ОН + Н
О2+ Н —¦ ОН + О
N2+ O2— NO + NO
NO + N—*N2+O
NO + 0 — О2+ N
А
3,5 1014
1,4 1020
5,5 1017
"to
3,3 1018
2,7 10ш
3,3 1015
2,5 1012
1,1 1014
1,0 1013
1,3 1013
2,2 1014
5,2 1013
3,0 1013
1,1 1013
в
1
"ел
0,87
1,0
0,5
0,5
0
0
0
0
0
0
0
0
0
Е
2100
0
0
0
0
0
0
5100
8600
1200
9860
16550
107000
200
41700
Примечание Здесь М — некоторая частица. К_^(Т)=АТ°е &т.
мерность К+(Т) — смбмоль2с—', в реакциях (8) ... A5) —см'моль-1.
В реакциях A) ... G) раз-
44
нение химической кинетики для компоненты Н2 в соответствии с
табл 1.1 имеет вид
da,.
dt
Здесь у1 = аг/|1г- Аналогично можно выписать дифференциальные
уравнения для других компонент и найти конкретные выражения
для правых частей Fl°(p, T, а) уравнений химической кинетики.
1.3.2. Колебательная релаксация
Временные релаксации колебательных степеней свободы на
один-два порядка меньше времен для химических реакций, а энер-
энергия их сравнима с химической энергией при течениях высокотемпе-
высокотемпературной смеси. Тем не менее процесс колебательной дезактивации
из-за больших градиентов газодинамических параметров может
протекать неравновесно.
Основными молекулярными компонентами продуктов, которые
рассматриваются ниже, являются N2, СО2, СО, Н2О, Н2, N0. Трех-
Трехатомные молекулы С02 и Н20 имеют три типа нормальных колеба-
колебаний и соответственно три колебательных степени свободы. Много-
Многоатомные молекулы, обладающие определенной колебательной сте-
степенью свободы, будем рассматривать как самостоятельный компо-
компонент смеси. В табл. 1.2 приведены характеристические колебатель-
колебательные температуры молекул, а также условные обозначения молекул,
которые будут использоваться в дальнейшем.
Здесь CO2(vi), H2O(vi)—молекулы, обладающие валентной
симметричной модой колебаний, CO2(v2), H2O(v2) —молекулы, об-
обладающие деформационной модой колебаний, CO2(v3, Н2О(уз) —
молекулы, обладающие валентной асимметричной модой колеба-
колебаний
В многокомпонентной смеси двухатомных и многоатомных мо-
молекул возбуждение или дезактивация колебательных степеней сво-
Таблица 1 2
Молекула
Условное
обозначение
е„, к
1
3353
>^
6
и
2
1920
-И
6
и
3
960
со
(N
О
о
4
3380
О
и
5
3084
О
X
6
5260
¦iE
О
?
7
2294
>^
О
X
8
5400
X
9
6130
О
Z
10
2700
45
боды молекул при неупругих столкновениях могут происходить
двумя путями: путем непосредственного перехода кинетической
энергии сталкивающихся частиц в колебательную энергию рас-
рассматриваемой молекулы и наоборот (процесс прямого возбуждения
или дезактивации, обычно обозначаемый символом Т—V), и путем;
обмена энергией между колебательными степенями свободы стал-
сталкивающихся молекул внутри данной молекулы (процесс колеба-
колебательно— колебательного обмена, обозначаемый символом V—V).
Для рассматриваемой смеси можно записать следующие процессы:
2. CO2 + M^CO!(v2)-f М-667 см-1;
3. СО + М^СО* + М-2143 CM-i.
4. Н2О + M^H2O*O2)-fM-1595 см;
5. Н2 + М^Н2 + М-4260 см-1;
6. NO + M^NO* + M—1876 см-1;
7. : :
8.
9. H2O*(v1) + M^H2O*Bv2) + M + 467 см-1;
10. H2O(v3)+M^H2O*Bv2)-}-M-f556 CM-i.
11. N2 + CO2^N2 + CO2(v3)-19 см-1;
12. Nj + CO^Nj + CO* —187 cm-1;
13. CO* + CO2^CO + CO!(v3)-206 см-»;
14. N2 + NO^N2 + NO*+454 см-1;
15. CO* + NO:? CO + NO* + 267 см;
16. COl(v3) + NO^CO2 + NO^+473 см-».
Кинетические уравнения, описывающие релаксацию колебатель-
колебательной энергии вследствие всех перечисленных выше процессов в сме-
смеси газов, могут быть составлены двумя способами Можно записать
систему дифференциальных уравнений для определения заселен-
заселенности каждого возбуждаемого уровня каждой колебательной моды,
используя соответствующие вероятности переходов Такой подход,
однако, в настоящее время без существенных упрощающих гипотез
оказывается весьма сложен, не только из-за значительного числа
уровней, но также из-за отсутствия надежных экспериментальных
и расчетных данных по вероятностям переходов для столь сложной
взаимодействующей смеси молекул Другой подход состоит в со-
составлении дифференциальных уравнений для определения энергии
46
каждой моды Если предположить больцмановское распределение
по энергиям внутри каждой моды и принять, что молекулы явля-
являются гармоническими осцилляторами, то релаксационное уравне-
уравнение, соответствующее приведенным выше процессам, например, для
определения колебательной энергии моды CO2(v3)—64, записы-
записывается в виде
p7^p11413+p16 = ©4(/;1 T, ер). A.134)
at Hi 05
Здесь Ф4(р, Т, ер) — правая часть уравнения A.81);
6=Ф?6 (Г10 ± б,) [,10 (,4+± в4) exp
В этих уравнениях приняты следующие обозначения: е( — коле-
колебательная энергия i-ro компонента в единице массы смеси; et° —
равновесное значение колебательной энергии при температуре га-
газа, которая согласно формуле Эйнштейна равна
', A.135)
где степень вырождения \i=l при 1^3и \з=2; г, — молярная
концентрация t-ro компонента; Ф°1} —скорость i-ro релаксационно-
релаксационного процесса, зависящая от температуры и давления газа.
Скорости релаксационных процессов определяются в зависимо-
зависимости от характера передачи энергии. При колебательно-поступатель-
колебательно-поступательном переходе энергии
ф°;=^2гА/ и=1> 2>--6; /=1»3' 4>5*7' 9> 10>' <1Л36)
где Гц — время релаксации для процесса i в случае столкновений
с молекулами сорта /. При внутримолекулярном колебательно —
колебательном переходе энергии Ф°и находятся также по формуле
A 136) при i=7, 8, 9, 10. При межмолекулярном колебательно —
колебательном обмене энергией
Ф?; = /7-^(/=11, 12, 13, 14, 15, 16; у =4, 5, 4, 10, 10, 10 соот-
соответственно),
47
где тг — время релаксации i-ro процесса. Обычно зависимости вре-
времен релаксации элементарных процессов от температуры опреде-
определяются по экспериментальным данным и коррелируются, когда это
возможно, с помощью теории Ландау — Теллера, согласно которой
имеет место линейная зависимость 1пт от Г^1/3. Аналогично выпи-
выписываются релаксационные уравнения для других мод и определя-
определяются ФР(р, Т, ер) —правые части уравнений A.81). В работе [27]
выписаны формулы для вычисления времен релаксаций. В качестве
примера приведем времена релаксации для процесса 1:
In г1>1 = 220Г-1/3- 24,81;
In хь2=240Т~У3 - 25,76;
In ть5 = 220Г-1/з_ 24,81;
In тЬ7 = 335Г-1/з_ 16,55;
In Tli9 = 86,971-1/8—19,94;
In xlilQ=223,9T~1/a - 24,96.
1.3.3. Двухфазные течения
Выпишем формулы для \s безразмерной силы взаимодействия
между газом и частицами и qs безразмерного теплового потока
между газом и частицами, входящих в формулы A.76)...A.79),
A 83) общей системы уравнений. Имеем
4?
8 psrs
Nu = Nu° A + З
где cx — коэффициент сопротивления сферы; гъ — радиус сфериче-
сферической частицы; ps° — истинная плотность материала частицы; cs —
теплоемкость частицы; Nu — число Нуссельта; Pr, St и М — числа
Прандтля, Стокса и Маха, Re — число Рейнольдса; сх — отношение
коэффициента сопротивления сх к коэффициенту сопротивления сх°
при стоксовском режиме обтекания (сх° = 24 Re). Числа Re, Pr,
St и М определяются следующим образом:
l W-Wj|/-3 • Ггс^ .
Re—
9 '
48
|W-Wf
где т|и! — коэффициенты вязкости и теплопроводности газа; W* и
г*— характерная скорость и длина; а — скорость звука.
Формулы для коэффициента сопротивления сх и число Нуссель-
та являются полуэмпирическими и учитывают инерционность и раз-
разреженность газа, обтекающего частицу.
1.3.4. Неравновесная конденсация
Конденсация может иметь место в том случае, когда парциаль-
парциальное давление одной из компонент смеси в процессе расширения ста-
становится большим его давления насыщения. Вообще говоря, при
больших степенях расширения должна последовательно происхо-
происходить конденсация всех компонент смеси, так как адиабата Пуассо-
Пуассона d\np/dt=cp/RT неизбежно пересекается в р—Г-диаграмме с
кривой, описываемой уравнением Клапейрона — Клаузиуса и даю-
дающей зависимость давления насыщенного пара над плоской поверх-
^Inp» L
ностью. Согласно этому уравнению = , где рх— дав-
ление насыщения конденсирующей компоненты, L — теплота кон-
конденсации.
На рис. 1.6 представлена р—Т диаграмма для паров воды.
Если после достижения точки насыщения А (точки росы) дальней-
дальнейшее расширение происходит термодинамически равновесно, то дав-
давление и температура пара связаны между собой уравнением Кла-
Клапейрона — Клаузиуса и процесс расширения соответствующей ком-
компоненты смеси будет уже происходить не по адиабате Пуассона АСГ
а по кривой АВ (см. рис. 1.6), при этом газовая фаза этой компо-
компоненты будет конденсироваться. Однако, как показывают многочис-
многочисленные экспериментальные данные, в действительности конденса-
конденсация в сечении, соответствующем точке Л, и на некотором участке
ниже по потоку от него не имеет места, а весь процесс следует
вдоль некоторой кривой ACD, на которой конденсация происходит
неравновесно. Неравновесные параметры течения, как обычно, яв-
являются промежуточными между параметрами равновесного расши-
расширения, соответствующего первоначально расширению по адиабате
Пуассона, а затем по кривой насыщения,
и параметрами замороженного расшире-
расширения, когда фазовые превращения не ус-
успевают произойти и расширение происхо-
происходит только по адиабате Пуассона При
равновесном процессе расширения по-
последовательно выделяется теплота кон-
конденсации; давление, температура и им-
импульс в этом случае больше, чем при не-
неравновесном течении. Эти же параметры
1105,Па
Рис 1 6 р—Т диаграмма для паров воды
1 —равновесное расширение (кривая насыщения), 2 —
замороженное расширение (адиабата Пуассона), 3 — не-
неравновесное расширение
0,25
т°с
49
при неравновесном течении, в свою очередь, больше, чем в заморо-
замороженном течении.
Изменение состояния пара вдоль АС сопровождается более ин-
интенсивным снижением температуры, чем при расширении по кри-
кривой насыщения. Таким образом, задержка конденсации в процессе
расширения сопровождается более интенсивным снижением темпе-
температуры пара, которая оказывается ниже температуры насыщения
при данном давлении. Задержка конденсации в высокоскоростных
потоках связана с тем, что в газе очень мало или вовсе отсутству-
отсутствуют центры конденсации. Однако состояние переохлажденного газа
не является устойчивым, так как малые возмущения могут переве-
перевести его в состояние насыщения, которое является абсолютно устой-
устойчивым. Состояние пересыщения может быть снято либо за счет ге-
гетерогенной конденсации на посторонних частицах, либо за счет го-
гомогенной конденсации на образующихся зародышах частиц конден-
конденсирующейся компоненты. Если примесь, находящаяся в незначи-
незначительных количествах, обладает более высокой температурой и дав-
давлением насыщения, чем основная компонента, то, хотя ее конден-
конденсация не изменяет существенно параметров, ядра конденсации, ко-
которые при этом образуются, могут стать центрами конденсации для
основной компоненты. В связи с этим конденсация последней мо-
может наступить при очень незначительном пересыщении.
Важнейшей в теории конденсации является проблема образова-
образования ядер конденсации. Этот процесс также называют нуклеацией.
Возникновение новой фазы в метастабильной исходной фазе
осуществляется в форме зародышей. Можно расширить понятие о
равновесии двух фаз Л и В таким образом, чтобы зародыши В дан-
данных размеров и формы находились в равновесии со средой А при
мегастабильном состоянии последней, т. е. при неустойчивости ее
по отношению к уже сформировавшейся фазе В, отделенной от нее
плоской поверхностью. Этот вопрос впервые был рассмотрен Том-
соном применительно к конденсации пересыщенного пара, который
показал, что давление пара, находящегося в равновесии с каплей
жидкости при заданной температуре тем больше, чем меньше ра-
радиус этой капли. Таким образом, пар, пересыщенный в обычном
смысле по отношению к капле большого размера, может оказаться
ненасыщенным по отношению к капле малого радиуса.
По Томсону имеем следующую формулу для нахождения кри-
критического радиуса:
vlpa
где а — поверхностная энергия; Ve-—объем, занимаемый одной мо-
молекулой.
В молекулярной системе могут происходить флуктуации, т. е.
отклонения от нормального состояния, переводящие систему в со-
состояние с большим термодинамическим потенциалом, т. е. менее
вероятное. Такие флуктуации приводят к появлению комплексов
(скоплений молекул) или так называемых кластеров, которые при
50
определенных условиях могут превратиться в зародыши новой
фазы.
Можно представить следующую последовательность процесса
неравновесной конденсации. В начальной стадии процесса вблизи
точки насыщения А степень пересыщения пара увеличивается, по-
поскольку капли критического размера должны быть большими, а
вероятность их образования мала. В связи с увеличением пересы-
пересыщения размер критических зародышей уменьшается, а вероятность
их возникновения растет. Ввиду быстрого убывания вероятности
флуктуации с возрастанием их размеров начало фазового перехода
определяется вероятностью возникновения зародышей именно кри-
критического размера, в связи с чем при расчете неравновесной кон-
конденсации учитывается образование только этих зародышей. Далее
за счет увеличения степени пересыщения в начальной стадии про-
процесса конденсации зародыши, которые в начальный момент имели
критический размер, через небольшое время окажутся больше кри-
критических, и их рост будет продолжаться. Скорость образования за-
зародышей критического размера велика и составляет примерно 1019
частиц в единице объема, и поэтому несмотря на их малый размер-
(гсг^10~7 см) общая поверхность, на которой происходит конден-
конденсация, достаточно велика. За счет быстрого образования зароды-
зародышей и их дальнейшего роста происходит интенсивное увеличение
массы жидкости и выделение тепла. Обычно величина L/cpT по-
порядка единицы и поэтому появление даже небольшого количества
жидкой фазы может заметно повлиять на параметры течения. Вы-
Выделение тепла не только останавливает рост пересыщения, но и
приводит к уменьшению степени пересыщения. Образование новых
зародышей, которое в сильной степени зависит от величины пере-
пересыщения, сразу же прекращается, и в дальнейшем конденсация:
идет уже на вновь образовавшихся ядрах.
Таким образом, все центры конденсации зарождаются, как пра-
правило, в самом начале процесса конденсации, когда достигнуто до-
достаточно большое пересыщение. После того как необходимое пере-
пересыщение достигнуто, переход от метастабильного состояния в со-
состояние насыщения может произойти довольно быстро и носить
скачкообразный характер (так называемые скачки конденсации).
Однако при некоторых условиях может наблюдаться и достаточно
плавный переход в состояние насыщения.
Процесс конденсации в высокоскоростных потоках можно раз-
разделить на две стадии, при этом на первой стадии определяющим
является образование ядер, на второй — процесс роста ядер, когда
нуклеации можно не учитывать. Хотя в ряде случаев одновременно
происходят оба процесса, такое разделение представляется разум-
разумным.
Согласно классической теории образования ядер конденсации
число ядер критического размера, образующихся в единице объ-
объема, в единицу времени равно
щ^у\хр
г
L
51
где dk — коэффициент конденсации, k — константа Больцмана.
На второй стадии процесса конденсации определяющим явля-
является уже рост образовавшихся ядер конденсации. Если длина сво-
свободного пробега молекул значительно больше размера капель, то
следует для нахождения массы капли (или ее радиуса) использо-
использовать формулу Кнудсена
dt k [ уЧяКТ V2nRTe
или
H_ = J*_\__Pv__ P~ У*) 1 A 14{))
dt ?e L V2nRT V~2nRTe J '
В континуальной области, когда перенос молекул пара к капле
обусловлен диффузией, следует использовать формулу Максвелла
dt [ RT
где D — коэффициент диффузии конденсирующейся компоненты.
В результате масса жидкой фазы, которая выделится при кон-
конденсации, может быть определена из следующего уравнения:
~~
J/°(т) dj^dx\ , A.142)
где первый член в правой части — приращение массы в момент т
за счет нуклеации, а второй член — приращение массы за счет ка-
капель, образованных в момент % и увеличивающихся в размере от
момента т до момента t.
Температуру капли можно определить из дифференциального
уравнения баланса энергии:
dTe
Ш
-=/Чр, Р„ Т) A.143)
1.3.5. Электромагнитные эффекты
При рассмотрении течений проводящего газа при наличии эле-
электромагнитных полей необходимо учитывать силы Лоренца и
джоулево тепло, которые можно трактовать как внешнюю силу и
внешний источник энергии в уравнениях A.7, 1.8).
Рассмотрим течение электропроводного газа при наличии ме-
меридионального магнитного поля. Если пренебречь эффектом Холла
и принять, что магнитное число Рейнольдса мало, т. е. не учиты-
учитывать индуцированное магнитное поле по сравнению с наложенным,
то в осесимметричном сопле Лаваля течение сохраняет осевую сим-
симметрию.
52
Так как предполагается, что магнитное поле создается только
внешними источниками, то оно удовлетворяет уравнению Макс-
Максвелла
rotB=0; divB = 0;
A.144)
rotE = 0,
где В — индукция магнитного поля; Е — напряженность электриче-
электрического поля. Тогда F — внешняя лоренцова сила, и Q — внешнее
джоулево тепло, связанные с электромагнитным воздействием, рав-
равны
A.145)
A.146)
где j и Е — векторы плотности электрического тока и напряженно-
напряженности электрического поля, a N— электрическая мощность, подводи-
подводимая к единице объема.
В случае присутствия в газе ионизируемой присадки с потенциа-
потенциалом ионизации / степень ионизации мала, и свободные электроны
находятся в равновесии с газом. Концентрация электронов связана
с температурой и давлением формулой Саха
- ±J(±--L)}. A.147)
2 V Т Т01)\
Поскольку поле В соленоидальное и безвихревое, то можно вве-
ввести потенциал Ф такой, что B = gradcp, при этом Ф удовлетворяет
уравнению Лапласа ДФ = 0. Аналогично для стационарных задач
уравнения Максвелла позволяют ввести электрический скалярный
потенциал ф такой, что Е =—grad ср, при этом ф для изотропно про-
проводящей среды удовлетворяет уравнению Пуассона
Acp = div(WxB). A.148)
Если известно распределение индукции магнитного поля В0(х) на
оси симметрии, то составляющие Вх и Вг в поле течения определя-
определяются выражениями
дФ Г 1 С Л
Вх — = Re — \ Bu(x-\-ircos~q)d~q ;
дх L л I J
дг я J
L о
A.149)
B0(x-\-ir cos "?)) cos тча'т] .
53
В плоском случае имеем
Bx = Re[B0(x-\-iy)]; By = R
Джоулев нагрев газа приводит к росту энтропии и уменьшению
полного давления. В связи с этим получим уравнение для вычис-
вычисления полного давления (давления торможения) р0.
Из уравнения производства энтропии после несложных выкла-
выкладок получим
d \(LW ]^ A.150)
где po, To и ро — давление, температура и плотность торможения.
2. АНАЛИТИЧЕСКИЕ МЕТОДЫ
2.1. ОДНОМЕРНАЯ ТЕОРИЯ
2.1.1. Классическая одномерная теория
идеального нереагирующего газа
Обратимся к одномерной теории сопла. Рассмотрим установив-
установившееся течение совершенного газа без релаксационных процессов
при отсутствии внешних сил, внешних источников массы и энер-
энергии. В соответствии с основной гипотезой одномерной теории будем
считать поток в любом месте сопла однородным по сечению, а ско-
скорость— направленной практически вдоль оси сопла, которая в клас-
классической одномерной теории принимается прямолинейной. Такое
предположение будет справедливым либо в случае, если площадь
и форма сечения сопла изменяются достаточно медленно в про-
продольном направлении сопла, либо если площадь струйки тока до-
достаточно мала по сравнению с характерными поперечными разме-
размерами области течения и, следовательно, поперечными состав-
составляющими скорости в первом приближении можно пренебречь. Па-
Параметры газа будут функциями только продольной координаты, и
для определения их можно применить уравнения, имеющие место
вдоль линии тока, т. е. уравнения [A.88)... A.90)]. Помимо этого,
имеем уравнение A.108)
jF=^Q. B.1)
В случае одномерного течения из этих уравнений нетрудно полу-
получить, что
где / — безразмерная плотность потока, отнесенная к р*а*;
М = число Маха; давление, скорость и плотность также отне-
отнесены к своим критическим значениям (т. е. безразмерная скорость
W совпадает с приведенной скоростью X).
Имеем также
JL^? B.3)
' W К
Соотношения B.2) показывают, что в дозвуковом течении плот-
плотность потока / возрастает по мере возрастания скорости и падения
давления, а в сверхзвуковом течении, наоборот, падает. Плотность
потока достигает максимального значения /* = р*а* в тех точках,
55
где скорость и плотность газа равны критическим значениям, и об-
обращается в нуль лри W = 0 и давлении р, равном давлению тормо-
торможения ро, а также при р = 0 и максимальной скорости, достигаемой
при истечении в вакуум. Безразмерная плотность потока / зависит
от числа М (или Я) и отношения удельных теплоемкостей у Эта
зависимость для совершенного газа имеет вид
Очевидно, что j = F*IF, где F* — площадь минимального сечения
сопла. Каждому значению относительной площади F —— соответ-
ствует два значения приведенной скорости — дозвуковое А<1 и
сверхзвуковое А>1. Из B.3) следует, что в дозвуковом потоке ско-
скорость увеличивается, а давление уменьшается в направлении умень-
уменьшения площади поперечного сечения сопла, в то время как в сверх-
сверхзвуковом потоке при увеличении площади происходит увеличение
скорости и падение давления.
Согласно B.3) критическая скорость может быть достигнута
только в минимальном сечении сопла Лаваля, где dF=0. Вниз по
потоку от минимального сечения скорость может либо продолжать
увеличиваться, либо вновь уменьшаться в зависимости от отноше-
отношения внешнего давления к давлению торможения. Если в минималь-
минимальном сечении скорость потока отлична от критической, то она имеет
экстремальное значение: максимальное (дозвуковое), если на входе
сопла скорость дозвуковая, и минимальное (сверхзвуковое), если
скорость на входе сопла сверхзвуковая. Ясно, что в рамках одно-
одномерного приближения в сужающемся канале не может быть до-
достигнута сверхзвуковая скорость, если начальная скорость дозву-
дозвуковая (это утверждение неверно, если течение носит пространст-
пространственный характер); максимальная скорость в таком канале равна
скорости звука. Сверхзвуковая скорость может быть получена лишь
в сопле, имеющем сужающуюся часть, а затем, вниз по потоку от
минимального сечения, расширяющуюся.
Максимальное значение /* достигается при критической скоро-
скорости течения Очевидно, что максимально возможное значение пол-
полного расхода для сопла заданной формы равно у'*/7*.
Важно отметить также, что одномерная теория в случае совер-
совершенного газа без релаксационных процессов позволяет определить
состояние потока в данном сечении струйки, если известен какой-
либо один параметр р, Т, р, М (обратная задача) или относитель-
относительная площадь F (прямая задача) и если известно, является поток
дозвуковым или сверхзвуковым. Абсолютный размер сопла, а так-
также форма канала вверх и вниз по потоку от этого сечения не имеют
значения, поскольку система B.1)...B.4) не содержит какого-либо
характерного размера. Аналогичный результат дает одномерная
теория для случая равновесных или замороженных течений. Напро-
Напротив, в случае неравновесного течения газа параметры потока зави-
зависят еще и от формы струйки и ее длины вверх по потоку от рас-
56
сматриваемой точки, поскольку в таких течениях появляется ха-
характерный размер —длина релаксационной зоны. Согласно одно-
одномерной теории число М в заданном сечении сопла при F/F* = const
и Y = const, также в случае замороженного [см. формулу B.4)] не
зависит от полного давления и температуры.
Приведем в заключении этого раздела формулы, позволяющие
рассчитать параметры потока в одномерном приближении, если
известна геометрия сопла, т. е. F(x) =F/F* (прямая задача).
Рассмотрим первоначально случай, когда в расширяющейся ча-
части реализуется сверхзвуковое течение и параметры вверх по по-
потоку от некоторого сечения не зависят от внешнего давления. Вос-
Воспользуемся стандартными газодинамическими функциями коэффи-
коэффициента скорости (или числа М). Тогда отношения газодинамиче-
газодинамических величин к параметрам торможения, обозначенным нижним
индексом 0, определяются следующими формулами:
^f^ B.5)
Ро V + 1 /
pMf); B.7)
Ро V Y + 1 1
z(\) = l-\-l/X. B.8)
Приведенная скорость X по заданным значениям F и у вычисляется
по формуле B.4). Если воспользоваться таблицами газодинамиче-
газодинамических функций, то в качестве независимой переменной удобно взять
q(k) =F*/F, а К и другие искомые функции находить из таблиц. Оче-
Очевидно, что задав один из параметров, (-^—, , —] (обратная
V Ро то Ро /
задача) можно в данной точке определить остальные.
Число М, скорость потока, расход газа и импульс вычисляются
по формулам
М2=—— Х2 А — I-=J- Хз4)^1; B.9)
Y+1 \ Y+1 )
T-bU/2
\ B.10)
T)Vy; B.11)
Y + l /
). B.12)
При q (X) = const (т. е. если рассматривается сопло с заданным от-
отношением площадей) с уменьшением у увеличивается Л, р{к), Т(Х)
и z(X). Это означает увеличение давления, скорости истечения и
температуры, если параметры торможения постоянны. Этот резуль-
результат физически очевиден, поскольку уменьшение у эквивалентно по-
57
следовательному увеличению числа степеней свободы молекул и
переходу их энергии при истечении в энергию поступательных сте-
степеней свободы и энергию направленного движения молекул, причем
эта энергия тем больше, чем больше степеней свободы возбуждено.
При y=1 имеем изотермическое течение, в котором Т=Т0.
J-=-E- = e~r, м==х.
Ро Ро
В случае дозвукового течения в сужающейся и расширяющейся
частях сопла Лаваля расчет параметров потока производится ина-
иначе. Обычно в выходном сечении сопла известно внешнее давление.
Так как в случае дозвукового течения давление в окружающем
пространстве совпадает с давлением в выходном сечении сопла,
то из формулы B.5) можно определить X в выходном сечении и
величину расхода, равную в этом случае Q=A(y)p0Fq(X) (RTo)
Поскольку расход во всех сечениях одинаков, из этой формулы
для каждого сечения F можно определить q{%), а затем по B.4)...
B.7) или с помощью таблиц найти Я и остальные функции. Число
М и скорость вычисляются по соотношениям B.9), B.10). Исполь-
Использование формулы B.11) в случае дозвукового течения в сопле не-
неправомерно, так как в этом случае в минимальном сечении скорость
меньше звуковой и q{k)=^=l.
2.1.2. Одномерная теория для криволинейных каналов
Для инженерных расчетов течений в криволинейных каналах:
часто используется метод вписанных кругов, который дает лучшие
результаты, чем классическая одномерная теория. Он также осно-
основан на одномерной теории с той лишь разницей, что скорость счи-
считается постоянной вдоль дуг окружностей, ортогональных стенкам.
Однако следует подчеркнуть, что как эта, так и другие известные
разновидности классической одномерной теории не дают верных
значений параметров на стенках криволинейных каналов.
Рассмотрим модификацию классической одномерной теории.
Воспользуемся для этого системой уравнений A.117)...A.121).
Из этих уравнений для плоского и осесимметричного течений
без закрутки потока (до = 0) можно получить
rv*JL = yVK, B-13)
где К — кривизна линий тока. Отсюда, предполагая в первом при-
приближении сечения a = const плоскими, имеем соотношение для оп-
определения давления вдоль нормали п к оси канала
l^^ypV^K. B.14)
дп
Для каналов с прямолинейной осью кривизна, определяемая по
среднему радиусу кривизны линий тока течения, равна нулю. И как
58
следует из B.14), давление, а следовательно и остальные парамет-
параметры поперек канала остаются постоянными в соответствии с клас-
классической одномерной теорией. В случае же криволинейных каналов
др/дпфО во всех точках, где УКфО. Таким образом, одномерная
теория в классическом виде справедлива лишь для конфигураций
с прямолинейной осью. Для криволинейных каналов она дает лишь
средние значения параметров потока.
С помощью формулы B.14) можно получить распределение па-
параметров в поперечном направлении. Для давления на стенках
криволинейного канала из B.14) имеем
р = ро ±i-YAPoA/0J(/?ori, B.15)
где р°, р°, V0 — средние значения параметров, полученные по клас-
классической одномерной теории, h — ширина канала, R°=(K)~1—
средний радиус кривизны линии тока. В этой формуле по-прежнему
все газодинамические параметры отнесены к критическим. Знаки
плюс и минус относятся соответственно к внешней и внутренней
стенкам по отношению к средней линии канала. Из рассмотрения
второго слагаемого в формуле B.15) видно, что поправка обуслов-
обусловлена действием на газ центробежных сил. При движении газа с от-
относительно большими скоростями, а также в каналах с резким по-
поворотом потока учет их необходим.
Формулу B.15) можно обобщить и на случай пространственных
течений с закруткой потока. Имеем
р = ро± J-yhpo(V2/Ri+u2/Rl) , B.16)
где Ri° и R2° — средние значения радиусов главных кривизн линии
тока.
2.2. МЕТОД ИСТОЧНИКОВ И СТОКОВ
В теории сопла метод источников и стоков может быть приме-
применен только в случае течения несжимаемой жидкости, когда в силу
линейности уравнения для потенциала и функции тока может быть
использован принцип суперпозиции. Подбором системы источников
и стоков и их интенсивностей можно построить течение в канале
заданной формы. Однако такая задача весьма сложна. Значитель-
Значительно проще обратная задача, которая позволяет по заданной системе
источников и стоков определить формы поверхностей, которые мо-
могут быть приняты за стенки сопла. Рассмотрим применение этого
метода для плоского, осесимметричного и пространственного тече-
течений [20, 27].
2.2.1. Плоское течение
Поместим на оси оу декартовой системы гоу координат 2N+1
дублетов: один дублет с моментом Мо — в центре и 2N дублетов с
59
моментами Mit M2, ...,Mn, на-
направленными в отрицатель-
отрицательную сторону оси х, симмет-
симметрично относительно центра
на расстояниях а,\, a2,...,aN
от него (рис. 2.1). При нало-
наложении поступательного одно-
однородного потока со скоростью
Uao, параллельной оси х, на те-
течение, создаваемое этой сим-
симметричной системой дублетов,
возникнет течение, симметрич-
симметричное относительно оси х. Линии
тока этого течения, например,
АВ и А'В' могут быть выбра-
выбраны в качестве стенок сопла.
Очевидно, что если интенсив-
интенсивность центрального дублета Мо
положить равной нулю, то
контуры АВ и А'В' образуют обычное сопло, а если М0ф0 —
сопло с внутренним центральным телом. Криволинейные каналы
получаются, если в качестве стенок выбирать несимметричные от-
относительно оси линии тока.
По принципу суперпозиций комплексный потенциал течения ш =
= Ф±/г|) складывается из комплексного потенциала однородного по-
потока и комплексного потенциала системы трех дублетов
Рис. 2.1. Построение контура сопла ме-
методом источников и стоков
B.17)
где
= z-
-iy. Здесь и далее y = r, z=x.
Комплексная скорость
;_„ м0 j_.Mn
at - Z2
B.18)
Разделяя действительные и мнимые части в B.17), получим по-
потенциал и функцию тока искомого течения в виде
2я
п (r2~aJ)
B.19)
B.20)
где r2 = z2 + y2, Cl = r4 + 2a2n(z2—у2) +а4и.
Линия тока г|) = 0 представляет собой, как видно из последнего
соотношения, плоскость симметрии у = 0 и контур центрального те-
тела, максимальная ширина которого R2 находится при z = 0 из ра-
60
венства
, Мо 1 Мп
Положение критической точки R\ получим из B.18) при v = 0.
,„ I Mo \ \ \ п~т~ ^1/ /О ooy
2jt R\ j aln — R{
Решая систему уравнений B.21), B.22), находим величины иско-
искомых моментов
Ж0 = 2яито[Аа, Мп= — пи^п, B.23)
где
2
Дифференцируя B.19), получим компоненты скорости
г,г_йоо+______+____ х
Г 9^2 4^2 (г2 +д^) ]
X 1 + ^-г 1 "Ч ; B.24)
L + J
Отсюда находим распределение скорости вдоль оси симметрии
B.25)
Такому распределению соответствует сопло с постоянным поджа-
тием в интервале (—оо, 0). На бесконечности поток стремится к
равномерному. Давление определяется из интеграла Бернулли для
несжимаемой жидкости.
2.2.2. Осесимметричное течение
Распространение поставленной выше задачи на осесимметрич-
ный случай дает картину обтекания овала и торообразного тела
однородным поступательным потоком, направленным вдоль оси ог.
При этом суммарный момент равномерно распределенных по ок-
окружности радиуса ап дублетов положим равным Мп. Строя стенку
61
по одной из подходящих линий тока, получим течение в осесиммет-
ри'чном кольцевом сопле.
По принципу суперпозиции, используя цилиндрические коорди-
координаты (z, r, 6) и условия симметрии, потенциал скоростей такого те-
течения запишем в виде
где
^7()v-
потенциал двойного слоя от дублетов, расположенных на окруж-
окружности, rj,Q=[z2 + r2 + a2n—2ran cos {у—8)]'>*, у — длина дуги окружно-
окружности. Нетрудно получить
B.28)
8
т/2
где K(k)=[ d\ -
0
J
0
полный эллиптический интеграл 1-го рода с модулем,
r2=W + (r + anJ- B.29)
наибольшее расстояние от исследуемой точки р до точек Q окруж-
окружности. После несложных преобразований, используя B.28), потен-
потенциал двойного слоя B.27) запишется через полный эллиптический
интеграл 2-го рода
E(k)=
i
в виде
<р„ = Jl^L. *E(k), B.30)
где
rx=Vz^{r-a^. B.31)
Так как потенциал скоростей ср удовлетворяет уравнению Лап-
Лапласа для осесимметричного течения во всей исследуемой области,
то, полагая -ф = 0 на оси симметрии oz и учитывая равномерность
набегающего потока, получим [19]
Ф=-Г (г ¦!*-)! dr+\(rJf\\ dz. B.32)
J V dz yU = -«> J \ dr y|r = const
0
€2
Выбор такого пути интегрирования сильно упрощает нахождение
функции тока. По принципу суперпозиции из B.26), B.30), B.31)
получим
Y 2 4я {zi+rif2 Гп
где
г 2и+в
¦ Г / Лч>„ \ , М„а„ д Г dv
'" J I дг ) r= const 4л дл J г 0
вклад от потенциала двойного слоя. Отсюда, учитывая B.28),
получим
E (k)-K(k)].
Y" 2пг2 [\-кЛ 2an
Линия тока ty = 0 представляет собой ось симметрии г = 0 и контур
центрального тела, максимальная ширина которого R2 находится
при z = 0 из равенства
it 1^0 1 _ Мпап 1 Г an+R2 F(h ¦. [s(u{\
где
Дифференцируя B.26) и учитывая при этом соотношения B.29)...
B.31), найдем компоненты скорости
; B.34)
я
Мо Ъгг
Отсюда при vz = 0 получаем соотношение для определения расстоя-
расстояния до критической точки R\.
1 ' 1 ' " ' B.35)
Г 2я R\ я (^Н-а^
Решая систему B.33) ...B.35), находим
А0; М„<7„ = — яи„!->п; B.36)
o=^i !-{*„ 11+-
63-
Из соотношения для скорости вдоль оси симметрии
v=u^ U Й 5^__fl + _*?i_Y| , B.37)
найденного из B.34), видно, что получающийся контур сопла ана-
аналогично плоскому случаю асимптотически выходит на цилиндриче-
цилиндрический участок. Скорость выхода ординат контура на постоянное
значение больше, чем в плоском случае. Давление определяется из
интеграла Бернулли для несжимаемой жидкости.
2.2.3. Пространственное течение
Поместим равномерно распределенные дублеты с поверхностной
плотностью момента М(х, у) на плоскости z = 0 с круговыми для
простоты отверстиями радиуса iRnm, расположенными по концент-
концентрическим окружностям радиуса ап. При наложении поступатель-
поступательного однородного потока со скоростью «оо, направленного перпен-
перпендикулярно плоскости, на поле, создаваемое этой системой дубле-
дублетов s, получим течение в пространственной системе, аналогичной
многосопельной компоновке с общей камерой. В силу принципа
суперпозиции решение задачи сводится к суммированию потенциа-
потенциалов, создаваемых дублетами, расположенными на плоскости без
отверстий, и потенциалов от частей, расположенных на месте от-
отверстий и имеющих обратный знак моментов. Решение задачи су-
существенно упростится, если потребовать постоянства поверхност-
поверхностной плотности момента Мпт по всей площади отверстия. В этом
случае в силу принципа суперпозиции достаточно записать потен-
потенциал, создаваемый лишь одним из кругов sa%R-
(x — ancosxnmJ-\-(y — ansmxnmJ^CRlm, z = 0. B.38)
В цилиндрической системе координат будем иметь
±
O-dy, B-39)
,3
тде r2PQ = ^ + r2c+l2—2rc^cos {у—9С); | и у — текущие координаты
по поверхности круга;
r^ = r2 + 4-2rancosF-tnm). B.40)
64
Нетрудно получить
R игу,
sin2 (y - 8С) ^ с A -
B.41)
где
Запишем следующие соотношения:
tdv 2
B.42)
\-d
$(-
4
—arctg
=-=^-, B.45)
где П(А, А)=
J A +Л sin2tp) у 1 — № sin2 9
о
полный эллиптический интеграл 3-го рода, k2 = 2b/ (l + b); h\ =
— 2d/(l—d); h2= — 2d/(l+d).
Подставляя B.41) в B.39) и полагая фпт=М„т/2, получим с
учетом B.43)... B.45) выражения для потенциала скоростей от
круга:
<-о — М™ Z ГП(Й2. k) /1 Лш\ , J4M) / ч | ЯптУ]
inm~ 2я С/ТТй1 1+* I В j+ 1-rf \ ^ В )]'
B.46)
Дифференцируя B.46), найдем компоненты вектора скорости
, Rnm N
= 2, г, 9; /x = ^lL; X=l, 2;
dh.
дП, ль
dht
65
<?А.
2LH dk
dk
» k \
Rum 2LN .
rc kci A + &J '
K\:
; E = E(k)\
Z,=
r — arecos(9 — trem); 7j = r;
r — ansin(9 — tnm); ^ = 6;
z~l; r\ = z;
0; 7)=r, 6;
^2; т) = л, 9.
е; 7] =
a rc, b, с, d, В, k, h% определяются из B.40), B.42), B 44).
Отсюда при z-»—оо имеем
B.48)
B.49)
Для определения поверхностей тока введем, как и ранее, две
функции тока ipi и грг- Заметим, что потенциал скоростей ср — реше-
решение уравнения Лапласа, а значит вектор Дер — соленоидальный.
Исключим из рассматриваемой области кроме точек, в которых рас-
расположены дублеты, еще и точки, где Аф = 0. Известно, что любой
соленоидальный вектор может быть представлен в виде векторного
произведения градиентов двух функций. Поэтому можно записать
Acp=[VcpiXV^2] или в координатной форме при О
B.50)
Эта система алгебраических уравнений с шестью неизвестными за-
задает ортогональную вектору скорости плоскость, в которой лежат
векторы Vi|)i и Vt|J, а также площадь параллелограмма, построен-
построенного на этих векторах. Функции тока определяются из уравнений
B.51)
'\ = bXzdz -f <М?г -f- <]>ло fltf, 1=1,2.
66
Заметим, что при tyi = x, <]4*г = 0 функция ty2 = ty{z, у) превращает-
превращается в функцию тока для плоского течения, параллельного плоскости
(г, у), а при ¦^i = avctgx/y, л|J=^(г, z) в функцию тока для осесим-
метричного потока.
Для однозначного решения системы B.50) надо доопределить
три свободных параметра ^ задав например, угол между векто-
векторами V\|)i, V\|J и модуль и ориентацию в пространстве одного из
них. В силу симметрии задачи целесообразно выбрать т|J так, что-
чтобы ф2|г=го = const было уравнением эквипотенциальной линии в
плоскости z = z0 как в плоском и осесимметричном случаях. При
этом
<РгЬ-?&г=0. B.52)
По аналогии с плоским и осесимметричным случаями положим
также
<1>1»=0, <l>ie = l. B.53)
Исключим из рассматриваемой области прямую г = 0 и точки, где
ф'г=0, и обозначим полученную область через D. Тогда из уравне-
уравнений B.50), B.52), B.53) найдем коэффициенты ty{v Интегрируя
далее по области D уравнения B 51), получим
dn
B.54)
где
Ф = ?!/(г?г)- B.55)
Пусть (lJ|(«J,o,o) = O и ф1|(г,г0,о) = 0. Условие равномерности набегаю-
набегающего потока позволяет существенно упростить нахождение функ-
функций тока i|)! и г|з2 Положим Zi =—оо, го = ап. Пусть р — число экс-
эксцентрично расположенных кругов Suxr, (т. е. ап=7^0) и Фр°° =
= lim Ф.
Z -VOO
Как следует из B.48) Ф0°° = 0.
Рассмотрим теперь случай полного заполнения слоев 1п кругами
SazRojxuoro радиуса Rnm- Учитывая соотношения"V sin (9 — tnm)=0;
m = l
ln
cos F — тлт)=0 найдем
67
sin F — xnm)
T
1 nm.
г (? - 1) - R + \^ а^Ап [(г2 - а2п) (г* + а^1 >? Г^
Л т пг
B.56)
где
;cos(8 — xnm)\
Так как при г->0 Тпт-+1 и У sin (8 — тпт)=0, то НшФ^ = 0.
"^ 0
Из B.51) следует также, что определение функций тока из
B.54) не зависит от пути интегрирования, лежащего в области D.
Поэтому в силу непрерывности подынтегральных функций в обла-
области D получим
ч-.-J-S
-dn B.57)
где фя= f r<f'rdz. B.58)
Интеграл B.58) аддитивен, так как у = ^<опт. Исключив пред-
га ,т
варительно из области D прямые гс=0, после некоторых преобразо-
преобразований найдем
y ; z = r-cos(e-t);
68
N=\-2 I Гс ^ ¦
dK dk c> __ dE dk
dk dr dk dr
остальные параметры определяются равенством B.40), B.42),
B.44) и B.48).
Давление определяется аналогично плоскому и осесимметрично-
му случаям из интеграла Бернулли для несжимаемой жидкости.
2.3. ОБРАТНАЯ ЗАДАЧА ТЕОРИИ СОПЛА
ДЛЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ
Безвихревое стационарное движение несжимаемой жидкости
описывается уравнениями
*L-*L = 0; B.59)
dr дх
J^L + -^i- + ^- ^L=0. B.60)
dxi * дг? * г dr
При решении обратной задачи на оси симметрии (при г = 0) зада-
задаются граничные условия
^ = 0; и = ио(х). B.61)
В плоском случае (v = 0) уравнение B.60) есть уравнение Лапласа,
решением которого является произвольная функция комплексного
аргумента F(x-\-ir). Из граничного условия B.61) очевидно, что
в действительной плоскости решение системы B.59), B.60) имеет
вид u = Re[uo(x + ir)]; v = Re[iuo(x + ir)]. Здесь i — мнимая единица,
а символ Re — означает действительную часть функций.
В осесимметричном случае заменой r\ = lr уравнение B.60) сво-
сводится к уравнению Дарбу, и решение системы B.59), B.60) в дей-
действительной плоскости имеет вид
= Re — \ ua(x — ir sin t)dt
L
—• I uo(x — ir sin /) sin tdt
-it/ 2
B.62)
69
Течение несжимаемой жидкости для осесимметричного случая
при распределении скорости
йЬ B-63)
на оси рассмотрено в [27]. В этом случае выражения для и, v и
имеют вид
, 2 О-О }' [{ + А (х* — у* sini t)] dt
tl = llx,-\ —
я J [1 + A (x* — ij2 sir.2 t)]2 -f- 4A?x2y2 sin2jf
0
"° л J
\ Sjn2 tdt
sin2^
0
л/2
я J [1 +Л(д:2 — у2 sin2 О]2 + 4Л2^2(/2 sin2 ^
0
Нетрудно видеть, что для этого распределения точка с координата-
координатами х = 0; г=А~'1:г является угловой, поскольку скорость в ней обра-
обращается в бесконечность. При произвольном распределении скоро-
скорости на оси угловая точка возникает в полюсах продолженной в
комплексную плоскость начальной функции. В случае сжимаемой
жидкости столь просто установить координаты угловой точки не
удается, хотя такая точка всегда существует. Для получения рас-
распределения скорости B.63) методом источников и стоков необхо-
необходимо в точке х = 0, г = А-ч* поместить начало полуплоскости, со-
состоящей из дублетов, и ортогональной оси.
2.4. РАЗЛОЖЕНИЕ В РЯД ПО ФУНКЦИИ ТОКА
В гл. 1 показано, что при решении обратной задачи теории соп-
сопла в случае изоэнтропического пространственного течения нереаги-
рующего газа нужно задавать на начальной поверхности г|)="фо
функции г—Го (s, 6) и « = «о E, 9), а на начальной плоскости s =
= s0 — функции w = w0 (9, 1|з) и ф = ф F, ф). Решение соответствую-
соответствующей задачи Коши можно получить в виде рядов. Способы пред-
представления решения в виде рядов могут быть различными: разло-
разложения в ряд по степеням декартовых координат, по отрицатель-
отрицательным степеням радиуса кривизны минимального сечения, по степе-
степеням функции тока. Отличительной особенностью является то, что
разложение в ряд производится только в трансзвуковой области.
В работе [27] решение отыскивается в виде ряда по степеням функ-
функции тока в окрестности начальной поверхности для до-, транс- и
сверхзвуковой области течения.
Ниже представлено это решение для общего случая простран-
пространственного течения, из которого следуют все известные решения для
плоского и осесимметричного течений, в том числе решения Мей-
70
ера и Тейлора, которые, по существу, являются аналитическим при-
приближенным решением обратной задачи для трансзвуковой области
сопла.
Такое решение позволяет не только качественно проанализиро-
проанализировать особенности пространственных течений, но дает возможность
убедиться в корректности постановки задачи, а также служит в
качестве исходных данных при построении численного решения в
окрестности оси симметрии.
2.4.1. Пространственный случай
Найдем решение для идеального газа с постоянным показате-
показателем адиабаты в окрестности начальной поверхности -ф = 0 в виде
рядов по функции тока. Воспользуемся для этого системой уравне-
уравнений A.95)... A.104) для идеального газа с постоянным показателем
адиабаты
dp = G(s,9,M , „ др/дв ду
дф rw(d?/dey '
pa д<\> df)
d(wr) i ur 1 ± rR—1 cosv v Г 1 dp , ^ r a ,\ dr
ds ~ R ' и((?(р/(?е)
B.66)
dr i
Г 1 <5p , n, a ,, dr 1
— + и (S, 9, f) ;
L YP дЬ дЪ J
B.
B.67)
ds и
i?_ = JL/i± -L-cos'?); B.68)
/7=pT; B.69)
a=fl±i ^_ ^(T-D/T _ V2 _ W2)lf\ B.70)
\Y- 1 Y- ¦
где
ds /
Здесь для унификации введен множитель v, который полагается
равным 0 для плоского случая, и 1 для осесимметричного и прост-
пространственного случаев.
Представим искомые функции и, v, w, р, р, ср, г в виде
N N
f E, ф, б)= ^ _/n (S, 6) фга -|-]/"ф ^ _/л E, <|))фл, B.71)
л=0 п=0
где /(s. if), 0) — любая из перечисленных функций.
71
Если ряды B.71) подставить в систему B.64)...B.70) и прирав-
приравнять коэффициенты при одинаковых степенях г|з, то получим также
систему уравнений в частных производных, но уже с двумя неза-
независимыми переменными s, Q для определения функций fn(s, 6)
и/°пE, 8).
Отметим, что в зависимости от формы начальной поверхности
т|з = О некоторые из функций fn и f°n тождественно обращаются в
нуль. Напомним, что в общем случае на начальной поверхности
г|з = О задано r=ro(s, 9) и u — Uo(s, 9), а на плоскости s = s0 заданы
w = wo(Q, г|>) и ф=фО(9, -ф).
Ниже будут выписаны системы уравнений для определения
функций fn(s, 6) и f°n(s, 9). Первоначально будет рассмотрен об-
общий случай задания начальных данных, в котором ro(s, 9) =7^=0.
Затем будут рассмотрены два частных случая, весьма важных с
точки зрения практических приложений, в которых ro = O, R=oo и
ro = O, a R=/=oo. Первый частный случай соответствует заданию на-
начальных данных на оси симметрии.
Построим решение для случая ro(s, 0)=/=О. Для определения
функций fo(s, 8) имеем систему
ds
dwQ
vo=uoA + r0 cos' %Я) -^- ; B-72)
OS
^ )-1!; B-73)
= +MobincpoAf-1+ffi)o^oKo«o(l +r0cosv
A T cos" WoR-1) (._.!._ JPo
± ^> J!l) ; B.74)
-V^r; Po = ^/T- BJ5)
Система B.72)...B.75) решается следующим образом. Нетрудно
видеть, что правые части уравнений являются функциями w0, фо,
«о, г0 и их производных по 9; при этом функции uo(s, 9) и ro(s, 8)
и их производные по 9 известны из начальных условий. Поскольку
на плоскости s = s0 заданы все искомые функции, в том числе w0 и
Фо, то систему B.73), B.74) можно проинтегрировать численно в
направлении s, используя какую-либо разностную схему, вдоль не-
нескольких плоскостей 9=const и определить на всей начальной по-
поверхности г|з = const функции wo(s, 6) и <po(s, 9), а затем из соотно-
соотношений B.72) и B.75) — функции v0, р0 и р0.
Отметим два важных результата. Во-первых, проведенный ана-
анализ показывает необходимость для корректной постановки зада-
задавать начальные данные на плоскости s = s0. Во-вторых, в результа-
72
те численного интегрирования на поверхности \J) = const определено
все поле параметров, необходимое для перехода на следующую
поверхность тока в случае численного решения обратной задачи в
направлении гр. Отметим еще, что в осесимметричном течении без
закрутки 1[/? = оо; фо = 0; w0 = 0; uo = uo(s), ro = ro(s)] задача сущест-
существенно упрощается, поскольку отпадает необходимость в численном
интегрировании системы B.73), B 74), так как <р = 6, шо = О, и функ-
функции v0, р0, р0 сразу определяются из B.72), B.75). Существенным
является также и то, что при u = uo(s), r=ro(s) и при R(s)^= oo,
даже если в начальном сечении s = s0 функции wo(so, В) и <po(so, в)
равны нулю, при остальных значениях s они становятся уже от-
отличными от нуля, поскольку при R^oo система B.73), B.74) не-
неоднородна. Это означает, что искривление оси сопла, начиная с ка-
какого-либо сечения, всегда приводит к возникновению окружной
составляющей скорости, даже если до этого сечения течение оста-
оставалось осесимметричным.
Путем простых, но громоздких выкладок можно показать, что
система уравнений для определения функций /0°(s, 8) является од-
однородной относительно этих функций, а задание в начальной плос-
плоскости Woo(so, 8) и q>°o(so, 8) определяет в этой плоскости все осталь-
остальные функции /oa(so, 8). Очевидно, что при wo° (s0, 8)=cpoo(so, 8)=0
в силу однородности соответствующей системы, все функции
fo°(so, 8) s=0. Задание при s=sQ условия Wo°(so, 8)==;cpo0(so, 9)=0
физически оправдано, поскольку трудно представить течения, име-
имеющие бесконечные производные dw/dty и <Эф/дг|) в начальной плос-
плоскости в областях, удаленных от оси симметрии.
Рассмотрим далее систему уравнений для определения функций
fi(s, 6), полагая при этом функции /o°(s, 6)==0, Имеем
д ^ Vo + Vi^1; B-76)
OS go \
drn
—
ds ' ds ' ' "
B.77)
B.78)
rouzo cos"
+Y
R
B.80)
73
= ^; uu = (Z + v4+ww) B.81)
; o1
Ро Y Ро VYPo
где LQ=\ + cosvtf0r0/?-i; Z: = r! cos vc?o—^""o sin
од<?о/дв [po«ori + /"о (Po«i
; Кx
= —w2oLQ + Yr«oCosvtp/?- + «''
+ ^ (Mo1 + ^o«i) + 2®o^i
s as
+ 2y*Wo cos» tpo^1 + y^uoR-K B.82)
В осесимметричном течении без закрутки при i? = co, ф = Э, г?>==0
соотношения B.76)... B 82) переходят в соотношения для плоского
и осесимметричного случаев (разд. 2 4.2), при этом для определе-
определения функций fi (s) необходимо дифференцировать известные функ-
функции uo(s) и ro(s). В пространственном течении, как будет показано,
по-прежнему необходимо решить задачу Коши по s и численно ин-
интегрировать систему уравнений для определения функций W\ и ерь
Действительно, нетрудно показать, что любая из функций р\, ги рь
«1 и Vi может быть представлена в виде линейной комбинации
/.(s, 0)=<xo(s, 6)+a1(s, B)w1 + a2(s, 6)?1, B.83)
где a,(s, 9)—функции известных параметров fo{s, 0) и их произ-
производных по s и 6. Представление B.83) для функций гь pi, pi и т
следует непосредственно из формул B 78), B.79) и B.81), а для
функции V\ получается после дифференцирования по 5 B.78) и под-
подстановки результата в B.76) с использованием B.82). Тогда урав-
уравнения B.77) и B 80) образуют систему Коши при условии, что на
начальной плоскости s = sQ задано w\(s, 6) и cpi(s, 8).
Таким образом, при ro(s, 8)=т^=0 показана корректность предло-
предложенной постановки обратной задачи для пространственного слу-
случая, т. е. что задание на поверхности яр = const ro(s, 8) и Uo(s, 6)
и на начальной плоскости s = s0; w = wo(Q, yp) и ф = фО(8, -ф) полно-
полностью определяет течение в некоторой окрестности поверхности я|) =
= const.
Построим решение для случая ro(s, 8)=0, R=^oo. Для опреде-
определения функций fo(s, 8); fi(s, 6) и fo°(s, 6) имеем следующую систе-
систему уравнений:
74
B.84)
о _
P° «8
г _ 1 ( ° 1 D? д(?0 1 (r°J - — { о) ¦
B.86)
B.87)
"us то ~ "о UJ)J Wo \'ШО)
О '
го
B.88)
i; ав /с /
0 0 О
"О i * О О ^0 /О QO\
Ро Y />o YPo«o
где
_,0 й^о ± "о cos foLn + 2«0«qCos ?o ~ ui sin
О0=И0 —- +
ds R
l0=~ R '
Отметим сразу, что из B.84) следует, что при го=0 uy0==yos=0.
В осесимметричном случае имеем конечные формулы для /о0, /о, /i
и /Д при этом в разложении функций г, v присутствуют лишь функ-
функции /°„ и отсутствуют функции In, а в разложении функций р, р, и
присутствуют лишь функции fn, поскольку очевидно, что в окрест-
окрестности оси симметрии нормальная составляющая скорости является
нечетной функцией г, а давление, плотность и продольные состав-
составляющие скорости — четной функцией г. Очевидно, также, что при
го=О на поверхности г]з=0, которая в этом случае вырождается в
плоскую кривую, начальная функция и есть функция только от s,
т. е. u = Uo(s).
Рассмотрим первоначально случай R = oo, т. е. случай, когда на-
начальная функция задана на прямой линии. Тогда из B.85) и B.89)
имеем рос = роо = Ио°=О- Можно показать путем простых, но гро-
громоздких выкладок, что при R = oo система уравнений для опреде-
определения функций фо°, Г\, V\, W\ является однородной и при tpo°(So, 6) =
= Wi(s0, 0)==О дает по аналогии с осесимметричным течением без
75
закрутки единственное решение (роо = Г\ = иi = W\ (s0, 0)=О, т. е. v,
w и ф в окрестности оси симметрии являются нечетными функция-
функциями <г, а р, р, и — четными.
Весьма нетривиальным оказывается построение решения для
функций vo°, ro°, р\, ф0 и wo°. Для их определения имеем уравнения
B.84), B.86), B.88). Оказалось, что уравнение B.88) можно при-
привести к виду
32 I dw°\ Г д 1 90иог°о \ то дг°0 \d/dw°0
) 2df/df) дЬ \ дЬ
ds / L ^9 \2d<to/d9) 2df0/df) дЬ \ дЬ \ ds
5,,) = 0, B.90)
2 de \ 0?0/д% J\ C8 /2d<fO/db J ds
где (Di(s, 0)—-известная функция, которая может быть вычислена
на плоскости s = const, если известны Шо°, фо и задана функция Uo(s).
На любой плоскости s = const уравнение B.90) представляет
собой обыкновенное дифференциальное уравнение второго порядка
с переменными коэффициентами, служащее для определения про-
производной dwo°/ds(Q) на этой плоскости. Чтобы найти ее, нужно чис-
численно решать краевую задачу для уравнения B.90), при этом в
силу периодичности функции шо°(8) (период ее не больше 2я) и
равенства ее нулю на плоскостях симметрии граничные условия для
dwo°/ds есть dwo°/ds = O при 0 = 0 и >8 = л/л, где п — число плоскостей
симметрии. Итак, как и во всех рассмотренных случаях производ-
производные dwo°/ds и dyo/ds на плоскости s = s0 определяются при задании
на этой плоскости функций W0°(so, 8) и фо^о, 8), а для определения
их во всей области нужно решать задачу Коши по s при условии,
что функция uo(s) задана. Однако, при г0 = 0 для определения
dwo°jds необходимо решать краевую задачу на плоскости s = const,
в то время как при гоф0 dwo/ds и dwjds определяются элементар-
элементарно по известным функциям а» (8) и ф(8) на этой плоскости.
Еще более сложно построить решение для случая ro = O, i?=/=oo.
В этом случае система B.84) ...B.88), состоящая из семи уравне-
уравнений, служит для определения восьми функций. Отметим, что соот-
соотношение B.85) позволяет определить изменение давления за счет
центробежных сил, действующих на элемент объема газа, движу-
движущийся по криволинейной траектории. Интересно, что на начальной
плоскости s = So, на которой заданы ф0, фо° и w0 из системы B.84)...
B.88) определяются остальные пять неизвестных функций vo°, ro°,
Ро°, Pi, Г\ и две производные dq>o/ds и dwo^/ds, при этом как и в слу-
случае с R = oo для определения dwo°fds приходится решать краевую
задачу. По известным производным dq>0/ds и dwo°/ds с помощью ка-
какого-либо численного метода можно определить функции ф0 и wo°
на соседней плоскости s — So + As, а затем и все остальные функции,
кроме фо и Г\ на этой плоскости. Можно показать, что для опреде-
определения их нужно привлекать дифференциальные уравнения, содер-
содержащие функции W\, Vi и их производные, при этом на каждом по-
последующем шаге численного интегрирования требуется учитывать
последовательно все функции fn и /°„, что чрезвычайно затрудняет
7fi
расчет. Итак, при го = О и ^=^=оо не удается расщепить задачу и оп-
определить первоначально функции /о0, /о и Pi независимо от f°n, fn,
как это получено в остальных рассмотренных случаях. Существен-
Существенным для дальнейшего является то, что при решении асимптотиче-
асимптотических уравнений в окрестности начальной поверхности определяются
не только искомые функции, но и производные <Эф/<Зг|5.
В общем случае решение выведенных выше нелинейных урав-
уравнений в частных производных можно получить лишь путем числен-
численного интегрирования их. Однако, при определенных предпосылках
удается получить решение в замкнутом виде. Построим первона-
первоначально методом малых возмущений приближенное решение систе-
системы B.84)... B.89) при R = oo. Представим функции <р0, ro°, vo°, wo°,
Pi в виде
?o = e + ??oi(s, 6) + s2<pO2(s, 6) + ...;
6)+...;
...; B.91)
6) + ...;
, 6)+...,
где e — некоторый малый параметр. Такая запись искомых функций
основана на физически оправданном предположении о малом отли-
отличии параметров течения в начальной плоскости от параметров осе-
симметричного течения, имеющего на оси то же распределение ско-
скорости «o(s), что и в пространственном течении. Подставив соотно-
соотношения B.91) в систему B.84)...B.89) и линеаризовав ее, можно
получить следующие уравнения:
^ 4 ^ B-92)
ds
/ о n ч 1 / ^'oi ^«oo о
(/00ЯУ01) = — 1 -— /"oo
B.93)
,.о " '
ds v ' 2 \ дЬ ds dsdb
Аналогичным образом можно получить систему уравнений для оп-
определения коэффициентов при е2.
Отметим, что формулы B.92) совпадают с соответствующими
формулами для осесимметричного случая без закрутки и позво-
позволяют определить функции rj)o(s), ¦»oo(s) и pw(s) по конечным соот-
соотношениям или путем дифференцирования известных функций uo(s)
и po(s). Важным свойством уравнений в частных производных
B.93) является линейность, что позволяет применить для решения
метод разделения переменных Фурье, с помощью которого, однако,
не удается построить решение основной нелинейной системы урав-
77
нений в частных производных. Очевидно, что из системы B 93)
можно выделить путем простых преобразований два уравнения,
служащих для определения функций Wqi(s, 6) и r<5i(s, 8).Эти урав-
уравнения имеют вид
ds Woo
<\1
\ Q ds /J
_ о W <\1 B.94)
Для решения системы B.94) применим метод разделения перемен-
переменных Фурье. Представим искомые функции в виде
к к
^ «С E) sin W; ло°1 = ^ /"о» (s) cos A6. B.95)
Подставим B.95) в B.96) и, приравняв в правой и левой частях
уравнений коэффициенты при cos ^9 и sinft0, получим
о 2 о rf / '
VOO'ZWoift) =
ds 2 [ ds
'00
?-(uo-^^-l . B.96)
ds ds \ ds J J
После простых преобразований можно получить уравнение для оп-
определения г°1к:
- = 0. B.97)
ds2 ds ds ds
Нетрудно убедиться, что уравнение B.97) с точностью до множи-
множителя v/2 есть правая часть второго уравнения системы B.96), в
связи с чем имеем
(Гnn^Olft/ =I= ^ ИЛИ ЗД'сЦй (*S)^= ^Oft ['"ОО ('S)J « (^.Уо)
rfs
Тогда из первого уравнения B.96) следует, что
—о = — I PoE)^sH о • B.99)
roo (s) 4 J гйй (so)
Непосредственной подстановкой можно выявить, что уравнение
B.97) при /"oift, определяемом из B.99), удовлетворяется.
Тогда из первого уравнения системы B.93) следует, что
^-sin?6. B.100>
78
Константы Сои и ro«(so) определяются из начальных условий, ко-
которые, согласно изложенному выше, имеют вид
к
Имеем тогда Cos=raois(so)roo(so);
— — ^
Окончательно имеем следующее решение системы:
¦yr°w(s0)wmk(s0) Cpo^s + ^oiftCSo) sin ?6;
t Л°
B.101)
к
V.
ft 0
w°o(s, 9) =
4 («о)
(so) ,D
cos A9;
гоо
где ^oift(so) и cpoift(so)— коэффициенты Фурье в разложениях на-
начальных функций wq°(sq, 0) и <po(so, 6) по sin ^Э.
Полученное решение позволяет определить форму сопла и оце-
оценить параметры течения в некоторой окрестности начальной линии
тока. Из соотношений B.101) следует, что изменения формы попе-
поперечного сечения можно достичь, варьируя начальные данные при
-s = so, т. е. величины Woik(sQ) и «pot* (s0). Если при s = sa положить
<tPoift(So)=0, то в этой плоскости поперечное сечение сопла будет
иметь форму окружности, однако при увеличении s оно уже не бу-
79
дет обладать осевой симметрией, а приобретет форму, определяе-
определяемую начальным значением Woi*(so). В то же время dro°/ds | s=So яв-
является функций В в отличие от осесимметричного случая. Очевид-
Очевидно, что если при этом Bcezyoi»(s0)=0, кроме Wqu(s0) t^O.to прост-
простр t
ранственное течение будет обладать двумя плоскостями симметрии,
а при Wou(so) фО— одной плоскостью симметрии. Существенно,
что wo°(s, 9) убывает с увеличением r°Oo(s), а из асимптотических
соотношений при s—>-оо следует, что Wq° убывает как 1/s2, в то вре-
время как cpo(s, 6) при этом стремится к некоторому конечному пре-
пределу, независящему от s. Очевидно, что формулы B.101) пригодны
для расчета как дозвуковых, так и трансзвуковых смешанных те-
течений. Для случая го = О при i?=^=oo можно построить аналогичное
решение, при этом в качестве параметра малости е можно выбрать
R~l. Можно показать, что в этом случае с точностью до величин
порядка е2 в поперечных сечениях сопло сохраняет первоначальную
форму окружности, однако ось сопла при этом криволинейна в со-
соответствии с законом изменения R = R (s).
Полученное решение для пространственного случая пригодна
для течений, удаленных от центра сопла, и позволяет рассчитывать
течение в окрестности начальной поверхности тока в до-, транс- и
сверхзвуковой областях. Оно может использоваться также для
расчета близлежащей к начальной поверхности тока, от которой
начинается численное интегрирование.
2.4.2. Плоский и осесимметричный случай
Положим R = oo и г0=0. В этом случае данные Коши на оси сим-
симметрии (г|з = 0) имеют вид u = uQ(s), ro = O и, следовательно, vo = O.
Для осесимметричного течения без закрутки потока (w = 0, <p = 8)
система B.72) ...B.81) значительно упрощается и приобретает вид
B.102)
Роцо / ds
4 V Ро « d ds
B.i04>
, 1[
Po YPo 2a0 LYPo
Нетрудно получить и выражения для р2:
^(^Ч BЛ05>
80
В плоском случае все функции f°n равны нулю; кроме того, в
силу симметрии функции fn с нечетными номерами равны нулю,
если f = p, р, и, функции fn с четными номерами равны нулю, если
f — v, r. Имеем
-; B.106)
— -1—х.'?)
'Ро 7 '
Ро«о
и,= —•
V dv\ 1
2= > Щ= —
2 ds 2ид
P2 Pi
B.107>
Po YPo
3 \ po ^o / ds ds
pt=—y-d-^-. B.108)
4 ds
Поскольку функция u=uo(s) задана, а следовательно, известны ро
и ро = Ро1/т, то формулы B.102). .B.108) позволяют определить ис-
искомые функции из конечных соотношений или путем дифференци-
дифференцирования по s известных функций.
Полученные формулы можно использовать для расчета всего
поля течения, включая до-, транс- и сверхзвуковую области Из них
как частные случаи следуют разложения; построенные Мейером и
Тейлором для трансзвуковой области.
Течением Мейера называют течение, в котором звуковая ли-
линия простирается от контура сопла до оси симметрии и разделяет
области дозвукового и сверхзвукового течений. Течением Тейлора
называют в целом дозвуковое течение с местными сверхзвуковыми
зонами, расположенными в окрестности контура сопла и ограни-
ограниченными звуковыми линиями.
Действительно, если, представить скорость на оси симметрии (в
окрестности центра сопла) для течения Мейера в виде
' + ... B.109)
(здесь s = x, поскольку 7? = оо), то нетрудно видеть, что
г°0=т/ [l+±
y B.110)
Используя формулы B.110), последовательным дифференцирова-
дифференцированием можно определить все искомые функции, входящие в форму-
формулы B.102) ...B.108), и получить, что для плоского течения
^+...; B.111)
—
6
81
Рис 2 2 Трансзвуковая область сопла Лаваля.
Звуковая линия М=1, линия 8 = 0, предельные
характеристики С_° и С+°
а для осесимметричного
B.112)
Из формул B.111), B.112) можно получить уравнения звуковой
линии (М=1), линии 9 = 0 (8 — угол наклона вектора скорости к
оси сопла) и характеристик первого (С°+) и второго (С0-) се-
семейств, выходящих из центра сопла (предельных характеристик).
Имеем
при
0
при v =
B.113)
Из этих формул следует, что звуковая линия располагается вверх
по потоку от точки х=0 на оси симметрии и смещена также вверх
по потоку от минимального сечения сопла на контуре. В точке на
оси симметрии, расположенной в той же плоскости, что и мини-
минимальное сечение, скорость меньше скорости звука (рис. 2.2).
Сравним решения, даваемые формулами B.102)...B.103), с ре-
решением Холла, в котором разложение в ряде строится по отрица-
отрицательным степеням радиуса кривизны R2 контура в минимальном
сечении (см. рис. 2.2). Выразим R2 через производные скорости, ис-
используя соотношения одномерной теории. Дифференцируя дважды
уравнение неразрывности r1+vq(K) = const, где q(k) определяется
формулой B.4), имеем в минимальном сечении
1 +v d*r
ding (I) , / d\
dl "^ {dx
dl*
B.114)
или
82
Рассмотрим отдельно течения Мейера и Тейлора. В течении
Мейера при х = 0 скорость равна скорости звука и
d\ d& " ' " * y+l \dX
а распределение скорости Uq(x) =K(x) задается формулой B.109),
Тогда из B.111), B.112), используя B.114), получим, что в плос-
плоском течении
«=1+(Y+D—f 1(т)
2+ BЛ15)
о
а в осесимметричном —
B.116)
Эти формулы получены в предположении, что плоскость х = 0 про-
проходит через минимальное сечение, ордината которого г« = 1. При
выводе формул B.111), B.112) принималось, что плоскость х=О
проходит через точку на оси симметрии, в которой скорость равна
скорости звука. Формулы B.115), B.116) точно соответствуют ре-
решению Холла.
Рассмотрим течение Тейлора. В этом течении скорость на оси
симметрии всюду дозвуковая, однако в потоке возможно возник-
возникновение местных сверхзвуковых зон. Для расчета этого течения
также можно воспользоваться формулами B.102)... B.108). Распре-
Распределение скорости на оси в этом случае имеет вид
ио=>о + ах2; Хо<1; а<0, B.117)
поскольку в течении Тейлора duo/dx = Q, если сверхзвуковая зона не
касается оси симметрии. Тогда, имея в виду, что
axz
B.118)
можно получить формулы, аналогичные B.111), B.112). Не приво-
приводя их здесь, выпишем с точностью до членов R2~~2 лишь формулы,
аналогичные B.115), B.116). В плоском и осесимметричном слу-
случаях имеем
м — \ A+У)Хр (i I~li2\ „n-1 ! l I r2D~l 1
ИХ [llTR2 +lrR2 +
, B.119)
(
83
Рис 2 3 Формы звуковой линии, линии 9=0
и предельных характеристик С+°, С_°
/ — расчет по формулам B 113) при у=\Л, А =
= 0,24, v = 0, 2 — численное решение
где
dlnq (X) 1-1
d\
Jx=o
При численном решении обрат-
обратной задачи разложения в ряд по гр
в окрестности оси симметрии ис-
используются для расчета близлежа-
близлежащей к оси линии тока, от которой
начинается численное интегрирова-
интегрирование, поскольку уравнение A.119)
содержит особенность на оси сим-
симметрии. При этом, если в осесимметричном случае эта особенность
может быть устранена путем преобразования уравнений, то в про-
пространственном случае нельзя обойтись без использования асимп-
асимптотического разложения при определении решения на близлежа-
близлежащей к оси линии тока.
До появления численных методов представленные выше соотно-
соотношения использовались для расчета течений в соплах. Доказатель-
Доказательства сходимости рядов и определения радиуса сходимости их не
имеется. В связи с этим возможность их применения устанавлива-
устанавливается сравнением с численными решениями и экспериментальными
данными, которое показывает, что разложения в ряд по ty при учете
3...4 членов ряда пригодны для описания течения в трансзвуковой
области при R^O,5г*, а также в до- и сверхзвуковых областях при
небольших поперечных градиентах параметров. Сравнения с чис-
численным решением обратной задачи теории сопла представлены
ниже.
Формулы B.111), B.112), B.115), B.116) пригодны лишь для
расчета течений в пологих соплах с R2>2r*. Однако они позволя-
позволяют получить качественное представление о структуре трансзвуко-
трансзвукового потока в окрестности минимального сечения. Кроме того, в
случае плоского и осесимметричного течений формулы B.113) с
точностью 5... 10% позволяют определить координаты всех харак-
характерных линий в трансзвуковой области даже при малых R^KRi^
;э=0,2г*), хотя параметры течения при этом рассчитываются со
значительной ошибкой (рис. 2.3).
2.4.3. Двухфазные течения
При численном решении обратной задачи теории сопла для
двухфазного течения при задании начальных данных на оси сим-
симметрии требуется построение асимптотического разложения (как
для плоского, так и для осесимметричного случаев), поскольку
уравнение системы A.109) ...A.113) содержит особенность на оси.
84
Из этого разложения на оси симметрии определяются все парамет-
параметры течения, в том числе плотность частиц и производные dv/d\p'l!,
—Yjj- . На оси симметрии задается распределение скорости, а на
плоскости s = s0 задаются us, vs, Ts, ps. Представляя в окрестности
оси симметрии функции и, us, p,
а функции v, vb и г в виде
/=/of-^ /,-/o#-v/2,
и подставляя эти соотношения в систему A.109)... A.113), получим
^ 1±1о&Ио^1; B.120)
Ро«о
Y
— /Or >
ds
B — v) rl \ ds po«Q
1
B.122)
= — —~ — I (WI 4-fl)(| B.12o)
^ B.124)
/-q ds
dvOs /
J u
os ds
To); po=poTo; eOs = es(TOs).
Система B.120)...B.125) решается следующим образом. Перво-
Первоначально численно интегрируя по s систему B.122), B.123), B.125),
(которая эквивалентна системе соответствующих уравнений нерав-
неравновесного двухфазного течения в одномерном приближении), при
заданной на оси скорости (или давления, или плотности) опреде-
определяем функции pQ, ро (или «о, р0), (или и0, р0), 70, uOs, vOs, TOs- Далее
из B.120) и B.124) последовательно определяем Го, и0 и роз- При
s = s0 обычно предполагают, что течение равновесно, т. е. uOs = uo,
Tos~TOl a pOs = po—'¦—, где z, — массовая доля i-й фракции ча-
i
стиц.
После определения всех параметров на оси симметрии по этим
формулам производится расчет параметров на ближайшей к оси
линии тока газа, с которой и начинается затем численное интегри-
интегрирование полной системы. Отметим, что в отличие от случая течения
чистого газа с постоянным показателем адиабаты, когда асимпто-
асимптотическое разложение служит в осесимметричном течении для от-
отхода от оси (из-за особенности типа v/r, которая отсутствует в плос-
85
ком течении), в двухфазном неравновесном течении это разложе-
разложение необходимо как для плоского, так и для осесимметричного те-
течений.
2.5. РАЗЛОЖЕНИЕ В РЯД В ОКРЕСТНОСТИ
ПРЯМОЛИНЕЙНОЙ ЗВУКОВОЙ ЛИНИИ
Наиболее полное исследование течения в окрестности прямоли-
прямолинейной звуковой линии в плоском случае проведено Л. В. Овсян-
Овсянниковым. В этой работе показана возможность существования пяти
различных типов течения, в том числе до- и сверхзвуковых течений,,
содержащих угловые точки. Осесимметричный случай рассмотрен
О. С. Рыжовым.
Получим разложение решения в ряд по х в окрестности прямо-
прямолинейной звуковой линии для одного из возможных типов течения,
представляющего наибольший практический интерес. Уравнения,,
описывающие безвихревое течение идеального газа, возьмем в виде
ди dv
дг дх
\дх ' [ 2 2 \дг
= 0. B.126)
В окрестности прямолинейной звуковой линии, на которой
и=\, v = 0, естественно искать решение системы B.126) в виде
После подстановки рядов B.127) в систему B.126) и приравнива-
приравнивания коэффициентов при нулевой и первой степенях х в левой и пра-
правой частях этих уравнений получим, что Ui — Vi = v2 = 0. Эти усло-
условия являются известными условиями Гёртлера, которые необходи-
необходимы и достаточны для того, чтобы звуковая линия была прямоли-
прямолинейной. Приравнивая коэффициенты при других степенях х, по-
получим
^ ^6(у+1)И0; B.128)
3г>3, +
dr dr2 r dr
dJ^=\v ^+JL^!_20(y+1)«2«3 = 0; B.129)
dr dr't r dr
^i =5v5; ^1 = 6(y+ 1)«2«4 + 3(y+ D«' + (Y+ DBY-
dr dr
+ 6D3 V5.
86
75
SO
25
Pi
^^-"" 0,3 0,
||
I
/
|
7
6 г
Пусть на оси симметрии
со стороны дозвуковой ча-
части задано распределение
скорости в виде B.109) с
Л = 0. Тогда для систем
B.128), B.129) гранич-
Рис 2 4 Функция «2(г): Рис 2 5 Схема течения в ок-
/- значения и2(г), полученные из асимптотического реСТНОСТИ прямолинейной ЗВУ-
решения B 131), 2-значения и2(/0. полученные при КОВОИ ЛИНИИ С образованием
численном интегрировании уравнения B 128) местной сверхзвуковой ЗОНЫ
ные условия при г=0 будут иметь вид
dth/dr=0; u2=B<0;
B.130)
Системы B.128), B.129) в общем случае не интегрируются в зам-
замкнутом виде. Численное интегрирование их показало, что при неко-
некотором значении г—г° функция щ{г) обращается в нуль, затем, ме-
меняя знак, становится положительной и при некотором г=г0 обра-
обращается в бесконечность. Перемена знака у функции и2 (г) означает,
что в точке г=г° возникает еще одна звуковая линия, простира-
простирающаяся вверх по потоку в сторону дозвуковой области (рис. 2.4).
Схема течения в окрестности прямолинейной звуковой линии пред-
представлена на рис. 2.5. При этом течение между прямолинейной и
криволинейной звуковыми линиями сверхзвуковое. В окрестности
точки г=г0 решение уравнения B.128) имеет вид
-roL + ... B.131)
Подставляя B.131) в B.128) и приравнивая коэффициенты при
одинаковых степенях г—г0, можно определить коэффициенты dL.
В частности.
— do- B.132)
5/п
87
0,001
Рис 2 6. Составляющие скорости к,
v в трансзвуковой области Сравне-
Сравнение численного и асимптотических
решений (х = —0,05). Разложение в
ряд по i|) = 0 (О), разложение в ряд
по \х\ в окрестности звуковой линия
(X)
Значения Го и с2 определяются из условия стыковки асимптотиче-
асимптотического решения B.131) с решением, получающимся при численном
интегрировании уравнения B.128). Такой процесс изображен на
рис. 2.4 для распределения скорости на оси B.63) с Л°=10, и<х =
= 0,1. В результате получено значение го= 0,725. Решение вида
(/¦ - ''оJ
3(Г- Г0K
B.133>
^ </—/¦„)+...]
означает, что точка х=0, г=г0 является угловой и в этой точке
имеет место течение Прандтля — Мейера. В местной сверхзвуковой,
зоне имеется волна сжатия, ограниченная некоторой характеристи-
характеристикой ОВ и характеристикой ОА, совпадающей со звуковой линией
(рис. 2.5).
Если распределение скорости на оси B.109) таково, что А =
= В = 0, то u2(r) =v$(r) =0, и выражение для всех последующих
членов ряда можно получить в аналитическом виде. Имеем
3 = C = const; v4=
4
15(Y
5
3(Y
значит
2 A + v)
Отсюда следует, что и в этом случае в окрестности прямой звуко-
звуковой линии возникает вторая звуковая линия, которая при D = 0
имеет общую точку с прямой звуковой линией на бесконечности, в
отличие от случая Л = 0, ВфО, когда эта точка находится на ко-
конечном расстоянии.
Сравним решения, полученные с помощью асимптотических ме-
методов, с численным решением обратной задачи для распределения
B.63) с Л°=10, «„0 = 0,1. На рис. 2.6, 2.7 представлены численное и
асимптотические решения, полученные в результате разложения
решения в ряд по г|з в окрестности оси симметрии, в ряд по |х|,
и г—•"=
Рис 2 7. Составляющие скорости и,
v в дозвуковой области сопла Срав-
Сравнение численного и аналитического
решений (х — —0,6). Разложение в
ряд по г)) — О Решение для не-
несжимаемой жидкости (#)
в окрестности прямолинейной звуковой линии, а также решение
обратной задачи для несжимаемой жидкости.
В окрестности прямолинейной звуковой линии асимптотическое
решение рассчитывалось по формулам
v=v3(r)x3-Jrvs(r)x5Jrv7(r)x7.
Функции и2, «4, «6, vs, v$ и и7 были получены в результате числен-
численного интегрирования системы B.128), B.129). Решение для не-
несжимаемой жидкости получено по формулам, приведенным в
разд. 2.3
Это сопоставление дает некоторое представление об области при-
применимости приближенных решений. Разложение решения в ряд по
ч|з вблизи минимального сечения правомерно лишь при небольших
значениях г (рис. 2.6). С ростом |х| результаты точного и прибли-
приближенного решений практически совпадают. Расчеты показывают, что
при малых значениях \х\, когда эффекты сжимаемости существен-
существенны, решение обратной задачи для несжимаемой жидкости не может
быть использовано для описания течения сжимаемой жидкости.
Когда скорости движения газа невелики (№<0,3), параметры те-
течения сжимаемой и несжимаемой жидкостей практически не отли-
отличаются. Сравнение точного решения с решением, полученным в ре-
результате разложения искомых функций в ряд по \х\ в окрестности
прямолинейной звуковой линии, показывает, что при х=—0,05
соответствие между точным и приближенным решением очень хо-
хорошее. При х<С—0,2 ряды расходятся.
2.6. РЕШЕНИЕ В ОКРЕСТНОСТИ БЕСКОНЕЧНО
УДАЛЕННОЙ ТОЧКИ В ДОЗВУКОВОЙ ОБЛАСТИ
Построим для системы A 106), A.107) асимптотическое реше-
решение в окрестности бесконечно удаленной точки для прямой и обрат-
обратной задач в плоском и осесимметричном случаях. Представим ис-
искомые функции и, р, р, г, v в виде
B.134)
89
N
Граничные условия имеют вид r=v = 0, K=#TO-|-V ипх~п при \|з =
п-1
= 0 — для обратной задачи и г=и = 0 при ф=0 г = г„-{-"*? fnx~n,
и-1
Л'
v/u= — 2 nfnx~ (я+1> при г|5 = -фк — для прямой задачи. Здесь
п-1
г|5к — значение расхода на контуре сопла, который должен зада-
задаваться в зависимости от режима течения и не должен превышать
критического значения, при котором течение в дозвуковой части не
зависит от противодавления. Подставляя ряды B.134) в A.106),
A.107) и приравнивая коэффициенты при одинаковых степенях х,
получим систему уравнений для определения функций gn, которая
разрешается в замкнутом виде. В частности, имеем
= vx(<!>)=0; po(ty)=const;
0=
m+vHnVU+v) l г Ф ]i/(i+
I Poo"» J У L(! + v)pooaooj
Для обратной задачи неизвестные константы р0, pi и р2 определя-
определяются из граничных условий по известным Ыоо и щ.
Имеем
/(T-i)
2
Р\=— YPooK~«r. P2 = — ^Bмтем2 + и?); B.136)
YP 2
Из формул B.135) и B.136) следует, во-первых, что первые три
члена асимптотического разложения для функции р не зависят от
¦ф (зависимость от \!р проявляется в следующих членах разложения,
которые можно получить аналогичным методом), а во-вторых, что
при уменьшении х, т. е. в направлении движения газа в окрестно-
окрестности бесконечно удаленной точки, давление на всех линиях тока
может только уменьшаться (pi<0; ра<0; если jt?i==O; и т. д.).
В прямой задаче константы р0 и pi определяются следующим
образом. При заданном грк из граничных условий и формул B.135)
находим
B.137)
90
Из B.137) следует, что в прямой задаче при заданном уравнении
контура сопла решение единственным образом определяется одним
параметром 1|эк. Это остается справедливым и в случае, если учесть
все последующие члены разложения.
2.7. АНАЛИТИЧЕСКИЙ РАСЧЕТ ПАРАМЕТРОВ СМЕСИ
В ЗОНЕ ЛОКАЛЬНОГО ПОДВОДА МАССЫ И ЭНЕРГИИ
В ОДНОМЕРНОМ ТЕЧЕНИИ
Представляет интерес расчет течения высокотемпературной
смеси в канале при наличии подвода различных химических ре-
реагентов. Такие задачи возникают, например, при определении пара-
параметров смеси в парогенераторах ТЭС, в различных дожигателях,
используемых для нейтрализации токсичных веществ, выбрасыва-
выбрасываемых из реактивных сопел при их наземных испытаниях и т. д.
Предполагается, что впрыск сосредоточенный (локальный), и после
ввода массы происходит мгновенное перемешивание ее с потоком
газа, а также испарение жидких компонент (если таковые имеются)
и установление некоторой новой температуры смеси. Эти предполо-
предположения означают, что при впрыске все химические реакции замора-
замораживаются, происходит полное перемешивание, после чего вновь на-
начинаются химические реакции. Таким образом, необходимо опреде-
определить параметры смеси, образовавшейся после впрыска, затем про-
провести расчет неравновесного течения в канале заданного сечения
или (в рамках обратной задачи) при заданном распределении ка-
какого-либо параметра (давления, плотности или скорости). Считаем,
что зону впрыска и перемешивания можно рассматривать как ка-
канал постоянного сечения, а впрыск осуществляется по нормали к
скорости потока. Тогда для определения параметров смеси в сече-
сечении впрыска имеем следующую систему уравнений, выражающих
законы сохранения массы, импульса и энергии:
= -/; B.138)
B.139)
т.
Yn + —i-
— ^-. BЛ40)
! +
Здесь индексом 1 помечены параметры смеси в сечении перед
впрыском, индексом 2 — параметры после впрыска; тг — расход
i-й компоненты впрыска, отнесенный к расходу смеси в сечении пе-
перед впрыском, те = 2тг- Систему B.138) ... B.140) можно свести
к одному нелинейному уравнению относительно температуры
f(T)= *L + 2(hu- A)_-L-J/2(fto-A) = O; B.141)
91
2
1=1
Все параметры имеют здесь индекс 2, который опущен. Для реше-
решения уравнения B.141) можно использовать любые методы решения
нелинейных уравнений, однако нужно учитывать некоторые осо-
особенности, связанные с тем, что B.141) имеет два решения. При
т = 0 это дозвуковое и сверхзвуковое решения. Таким образом, для
выделения нужного решения предпочтительно использовать методы,
имеющие двухстороннюю сходимость. Можно отметить также, что
в данной постановке удается получить решение задачи о неравно-
неравновесном течении в релаксационной зоне за ударной волной.
В случае, когда относительная величина впрыска т невелика,
значения р, р, Т, и можно найти из системы B.138) ... B.140) с по-
помощью метода малых возмущений. Подставляя формулы B.142)
в систему B.138) ... B.140) и приравнивая коэффициенты при оди-
одинаковых степенях пг, получим аналитические формулы для пара-
параметров со штрихом, при этом два первых члена разложения имеют
вид
p2=pl{\-\-p'm-\-p"m2); u.2 = ul(lJru'mJru"m2); B.142)
Г = — — ^ ; B.143)
нт {\-yM\)+Plu\
u' = 5-^-; p'=—yM\{\-\-u'), р'=1-и'. B.144)
\-yM{
Аналогично получаются выражения для Т", и", р", р". Здесь
9
2 Р1И1
hN(Tb)—индивидуальная энтальпия одного моля
Pi
впрыскиваемого компонента, \iN — его молекулярная масса (пред-
(предполагается, что впрыскивается какой-либо один компонент, обо-
обозначенный индексом N). hb\XN = hN(Tb)—h^{T\).
Во многих случаях по этим соотношениям удается получить
удовлетворительные результаты даже при ш^0,5.
2.8. РАСЧЕТ ПРОСТРАНСТВЕННЫХ ТЕЧЕНИЙ В СОПЛАХ
МЕТОДОМ МАЛЫХ ВОЗМУЩЕНИЙ
Пространственные течения имеют место либо в случае неосе-
симметричной геометрии сопел, либо в соплах, обладающих осевой
симметрией, но имеющих несимметричные начальные условия на
входе. Практический интерес к пространственным течениям в соп-
соплах связан с использованием сопел некруглого сечения в МГД-ге-
92
нераторах и двигателях специальных форм. Исследования про-
пространственных течений проводились методом малых возмущений
О. С. Рыжовым.
В окрестности центра сопла при заданной на оси составляющей
скорости и=Ах, используя метод малых возмущений, в рамках об-
обратной задачи, можно получить формулы для определения возму-
возмущений составляющих скорости и, v, w относительно поступательно-
поступательного звукового потока в цилиндрических координатах х, г, ср:
v= А2(у-\-1)xr (— — 21 cos 2w\-\-АЦу-}-1)r3 x
х(- / cos ?? +4т cos 4?); B.145)
\ 16 3 1
¦ay
y=2(Y±l) АЧхг sin 2cp-j-(y +1) A3r(—l sin 2? — Am sin А'Л .
В декартовых координатах х, у, z имеем
-4- —
3 3
В отличие от плоского и осесимметричного случаев [см. формулы
B.111), B.112)], в выражениях для и, v появляются произвольные
постоянные /, т, задавая которые можно получить сопла различной
геометрии в окрестности центра сопла. Форма звуковой поверхно-
поверхности получается из условия м=0, которое в декартовых координатах
приводит к соотношению
x=_(Y+lM|(~-/U2 + (- + /b2l- BЛ47>
Отсюда следует, что при |/|<0,25 звуковая поверхность будет эл-
эллиптическим параболоидом, при |/|=0,25 — параболическим ци-
цилиндром, при |/|>0,25 — гиперболическим параболоидом. Урав-
Уравнения поверхностей и = 0, ш = 0 (аналогичных линиям 6 = 0 в плос-
эа
ком и осесимметричном случаях) имеют в декартовых координатах
вид
16 ~*~ 3 ' j ""v 16 /
B.148)
1+4/ |Д 16
[см. также B.113)]. В общем случае эти поверхности не совпадают
между собой и могут быть эллиптическими или гиперболическими
параболоидами или параболическими цилиндрами.
Уравнения четырех характеристических поверхностей, касаю-
касающихся в центре сопла звуковой поверхности, имеют вид
B.149)
где Д1 = >/—16/; Д2 = У+ 16/. При |/|<5/16 последняя из
этих формул дает для характеристической поверхности С+° уравне-
уравнение эллиптического параболоида. По аналогии с плоским и осесим-
метричным случаями через С+° и С_° обозначаются характеристи-
характеристические поверхности, касающиеся в центре сопла звуковой линии и
простирающиеся соответственно вниз и вверх по потоку. При
|/| <0,25 первая из формул B.149) дает для поверхности С_° урав-
уравнение эллиптического параболоида, а вторая и третья — уравнения
гиперболических параболоидов. По эллиптическому CL0 парабо-
параболоиду возмущения распространяются к центру сопла. Если источ-
источники возмущений поместить внутри С_° параболоида, то вносимые
ими возмущения будут достигать поверхности перехода и влиять
на дозвуковую область течения. Как видно из B.149) С_° поверх-
поверхности существуют лишь при |/|<0,25, а С+° поверхности — при
\1\ ^5/16. Отсутствие особых характеристических поверхностей при
таких значениях / говорит о неустойчивости соответствующих сме-
смешанных течений газа. Звуковые поверхности, характеристические
поверхности для некоторых значений / изображены на рис. 2.8.
Пространственные течения в работе [27] рассчитаны лишь с
помощью асимптотических формул B.101), которые дают качест-
качественное представление о геометрии сопла и распределении парамет-
параметров, однако, возможность использования этого решения для коли-
количественного описания течения является проблематичной, хотя, как
показывают сравнения точных и приближенных решений, геомет-
•94
«=/ с!
M=1
Рис. 2 8. Форма звуковой поверхности и особых характеристических поверхностей
в пространственных течениях
рия сопла в приближенных решениях предсказывается достаточно
точно.
Результаты расчетов по формулам B.101) представлены на
рис. 2.9... 2.12. На рис. 2.9 изображено сопло, являющееся осесим-
метричным до минимального сечения и имеющее при двух плоско-
плоскостях симметрии некруглую, близкую к эллиптической, форму попе-
поперечного сечения вниз по потоку. Показана форма поперечного
сечения сопла в различных сечениях. В выходном сечении при s =
= 2 отношение полуосей равно 1,5. При расчете этого варианта бы-
было принято so=O; k=2; е = 0,0875; у= 1,4; ro=O; R = oo, при следу-
следующем распределении скорости на оси
.. ,~ч 1 . С1-"-)(«--1)(e~J/*-1)
-«.)«¦
-s/b
(«00-
где Моо=0,1; u<x>=l,9; 6^ = 3,5.
На этом же рисунке представлено геометрическое место точек
9=const, т. е. проекции на плоскость yz вторых поверхностей тока
и распределение давления в различных сечениях в зависимости
от 0. Очевидно наличие перетекания газа из плоскости 2=0 в плос-
плоскость г=0. Пунктиром изображена геометрия сопла в осесиммет-
ричном случае при том же начальном распределении скорости.
-г
-I
о
Рис. 2 9. Геометрия поперечных сече-
сечений и линий тока пространственного
сопла с двумя плоскостями симмет-
симметрии
Рис. 2 10. Геометрия поперечных се-
сечений и линий тока пространственно-
пространственного сопла с одной плоскостью симмет-
симметрии
95
Рис. 2.11. Геометрия поперечных се-
сечений и линий тока пространственно-
то сопла с двумя плоскостями сим-
симметрии
На рис. 2.10 представлены
результаты расчетов сопла, яв-
являющегося осесимметричным
до минимального сечения и
имеющего при одной плоскости
симметрии некруглую форму
выходного сечения вниз по по-
потоку. По-прежнему представ-
представлена форма поперечного сече-
сечения в различных сечениях s=
= const. При расчете этого ва-
варианта было принято So=0;
k=\; 8=0,175; Y=1'4; Го=О;
R=z oo, с тем же распределе-
распределением скорости на оси.
На рис. 2.10 изображены
те же зависимости, что и на
рис. 2.9. В этом случае перетекание газа происходит из плоскости
кр = О в плоскость ср=180. Существенно, что центр тяжести попе-
поперечного сечения при увеличении s смещается влево относительно
центра тяжести в критическом сечении, что приводит к искривле-
искривлению геометрической оси сопла и появлению боковой силы.
На рис. 2.11 и 2.12 показана геометрия сопла, имеющего в до-
дозвуковой части при so=3,5 круглое поперечное сечение, переходя-
переходящее вниз по потоку в близкое к эллиптическому, при этом сопло,
изображенное на рис. 2.11, имеет две плоскости симметрии, а на
рис. 2.12 — одну. Расчет проведен для того же распределения ско-
скорости на оси при y= 1,4 и е=0,005. На этих рисунках представлены
те же зависимости, что и на предыдущих. Существенно, однако, что
в изображенных на них соплах отклонение течения от осесиммет-
ричного начинается непосредственно из дозвуковой части, при этом
минимальное сечение также неосесимметрично.
Рис. 2.12. Геометрия по-
поперечных сечений и ли-
линий тока пространствен-
пространственного сопла с одной плос-
плоскостью симметрии
ЭБ
3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ОБРАТНОЙ ЗАДАЧИ
В этой главе описаны методы решения обратной задачи теории
сопла для течений совершенного газа с физико-химическими пре-
превращениями. Помимо детального описания основной разностной
схемы, позволяющей одновременно рассчитывать течения в дозву-
дозвуковой, трансзвуковой и сверхзвуковой областях сопла, изложены
разностные схемы, используемые для решения разного рода задач
профилирования в сверхзвуковой области.
Особое внимание уделено методам расчета релаксационных
уравнений и совместному решению уравнений газовой динамики и
кинетики, как в одномерном приближении, так и для двумерных и
пространственных течений.
3.1. ОСНОВНАЯ РАЗНОСТНАЯ СХЕМА
Первоначально рассмотрим случай совершенного газа без фи-
физико-химических превращений с постоянным отношением удель-
удельных теплоемкостей у. Примем также, что течение является изоэн-
тропическим и изоэнергетическим. Имеют место интеграл Бернулли
Ц2 j. V2 4. W2 , 1 ^ 1 Y + 1
2 y—1 2 Y—1
и условие сохранения энтропии
р = у\ C.2)
Ниже была дана постановка обратной задачи теории сопла.
Для уравнений газовой динамики A.95) ... A.104) в общем случае
пространственного течения в переменных s, "ф, 8 она заключается
в следующем. На поверхности ^=г|H задается функция r=ro(s, 8)
и компонента скорости u—uo(s, 8) (или давление, или плотность).
На начальной плоскости s=s0 задается компонента скорости w =
= ш°F, -ф) и функция ф=«р°@, г|з). Требуется определить семейство
поверхностей тока и параметры течения в окрестности начальной
поверхности тока.
Перепишем систему уравнений A.95) ... A.104) для случая
идеального газа в виде
др
у (;(s'9'^ I v dp/дб fo , . 33
4- 1393 97
(ду/дв)" \ ри
C.4)
дг и /Г> ~
v= ; C.5)
ds Hi
dwr ur sin 9 . Я] Г 1 dp . „ , „ ,. дг 1 , /О „ч
¦ = + j ^— — -4-С/ E, 6, <Ь) \ = fz'i ("J-")
as .к ud'-p/dft ]_ ур ^8 E8 J
— = — Hi=f4, C-7)
0, u . и dv , u2 cosv ф да2
(S, 9, <o)= ± !• — v .
Запишем с использованием C.1) и C.5) следующие соотношения
для давления и составляющей скорости и. Имеем
(
дг \2,1/2 VY-1 y+1
) \
1/2
. (з.9)
Покажем, что сформулированные выше данные Коши на поверх-
поверхности i|)=tJ)o и плоскости s = s0 определяют все остальные функции.
В предыдущей главе указанное свойство было продемонстрировано
с помощью асимптотических разложений. Рассмотрим случай,
когда на поверхности t|>=tyo задано распределение составляющей
скорости u=Uo(s, G). Поскольку имеет место соотношение C.8), то
в силу данных Коши на плоскости s = s0, а именно [woo = w°(Q, г|)о),
фо° = ф°(Э, tyo)], на этой плоскости известно po° = po(s, г|з0) и из
C.5) vo°=vo{s, i|H).
Тогда, интегрируя по s и Э совместно систему уравнений в част-
частных производных C.5) ... C.8), C.2) на поверхности ^ = ijH, опре-
определяем на этой поверхности недостающие начальные функции р =
=po(s, в); p = po(s, 9); v = vo(s, 6); w = wo(s, Q) и (p=<po(s, 8).
Отметим, что входящие в правые части уравнений C.6), C.7)
функции v, p и р, а также производную dv/ds можно исключить с
помощью соотношений C.5), C.8) и C.2) и получить систему двух
уравнений для определения двух функций w и ср. Однако выкладки
в этом случае чрезвычайно громоздкие и не меняют существа дела.
Если на поверхности г|з = г|H задано распределение давления
p = po(s, 6), то на плоскости s = s0 с использованием соответству-
соответствующих данных Коши определяются функции uQ°—u0(s, о|з0), vo°=
= vo(s, ipo) из соотношений C.9) и C.5). Далее при совместном
интегрировании системы C.5) ... C.7), C.9) на поверхности \|) = г|)о
определяются недостающие начальные функции u=uo{s, Э), v =
= vo(s, 8), w = wo(s, 8) и cp = cpo(s, 8). Функция p = po(s, 0) опре-
определяется сразу же из C.2).
98
Очевидно, что аналогично определяются данные Коши на по-
поверхности г|з=г|H, если задано не распределение давления, а рас-
распределение плотности, поскольку имеет место соотношение C.2).
При численном решении задачи Коши возникают определенные
трудности. В эллиптической области в общем случае задача не-
некорректна в смысле Адамара, хотя, если рассматривается класс
аналитических функций, то в ограниченной области задача стано-
становится, как показано М. М. Лаврентьевым, корректной. Тем не менее
даже при аналитических начальных данных в дозвуковой области,
где уравнения газовой динамики являются эллиптическими, при
неудачно выбранной разностной схеме при решении задачи Коши
чрезвычайно быстро возрастают ошибки округления. Поэтому для
получения устойчивого решения необходимо выбрать такую раз-
разностную схему, при применении которой ошибки округления не
превосходили бы существенно ошибок аппроксимации.
С другой стороны, в общем случае в гиперболической области
соотношение шагов в разностной схеме должно быть таково, чтобы
область влияния аппроксимирующей системы не выходила за об-
область влияния исходной системы дифференциальных уравнений,
т. е. другими словами должно быть выполнено условие Куранта —
Фридрикса — Леви. Однако в классе аналитических функций соот-
соотношение шагов в разностной схеме может быть произвольным, так
как в силу аналитичности начальных данных нельзя изменить их
на каком-либо участке, не изменив их во всей области аналитич-
аналитичности.
Ниже рассмотрены разностные методы решения сформулирован-
сформулированной задачи для пространственного, осесимметричного и плоского
случаев.
3.1.1. Пространственный случай
Опишем разностный метод, оказавшийся весьма эффективным
для решения сформулированной задачи для системы C.1) ... C.7).
Введем сетку с узлами
st = s0-{-iAs; ф;- = фо + УдФ' 0й = ?Ле;
/ = 0,1,...,/; у = 0, I У; ? = 0,1,...,/С,
обозначим fijh=f(si, ip/, 9fc). Величины шагов As, A8 в общем слу-
случае не постоянны и зависят от i и k соответственно. Пусть в узлах
слоя ф/ = const известны все параметры течения, а именно значе-
значения и, v, w, р, р, г, ф, а также дср/дф. Вычисление параметров на
слое г|з/+1 = const производится итерационным методом следующим
образом.
Очередная итерация с номером / начинается с вычисления ве-
величин rty+hk; pl'j+lik; <v\%lk\ р/,л-1,* из уравнений
r(D L + 1/A)
14* 99
_(
' \ ds
аппроксимирующих уравнения C.3) ... C.5) соответственно. Впер-
Впервой итерации (/=1) значения величин с верхним индексом 1=0
берутся с нижнего /-го слоя. Вычисление значения р\]+\,ь\ pij+i,*'
t"ij+i,k'i Vi,j+i,k используются далее при численном интегрирова-
интегрировании уравнений C.6), C.7), C.9) в направлении s для нахождения
остальных искомых величин до, ф (я=1, 2, ..., N) на слое /+1 в
1-я итерации.
Пусть для некоторого i известны /,7+i.s (k=l, ..., К), где f —
любая из перечисленных величин. Определим /}+i,y+i,ft. Этот про-
процесс также итерационный. Обозначим через т номер итерации
этого внутреннего итерационного цикла. Аппроксимируя C.6),
C.7) аналогично C.10), имеем
узл.;+1|*тУ зл+1|/+1|*1 ' ("¦"/
,U.m). „(!) , As Г// )\l'>+lkJr{fJjl^jl\k] ;
Т-1 11/2 <7,то)
(I) i Д«
,k=9i,j + l,k-j-—
ds
Отметим, что разностная аппроксимация C.10) и C.11) и соответ-
соответствующие итерационные циклы отвечают так называемой разност-
разностной схеме Эйлера с пересчетом решения систем дифференциальных
уравнений, при этом нулевая итерация — просто схема Эйлера.
Итерационный цикл по т заканчивается при достижении необ-
необходимой точности, после чего аналогично определяются величины
и, v, w, р, р, г, ф в узлах (i+2; /+1; k), k=0, 1, ..., К, и т. д. Ите-
Итерация / заканчивается, когда эти величины будут определены во
всех узлах (/+1)-го слоя. После этого, если не достигнута требу-
требуемая точность в значениях параметров на слое /+1, проводится
(/+1)-я итерация.
Центральным моментом разностной схемы является метод рас-
расчета производных dv/ds, dr/ds, dr/dQ и dp/dQ, входящих в правые
части уравнений C.10), C.11). Обратимся к разностной записи
производных dv/ds и dr/ds. На рис. 3.1 представлена типичная за-
зависимость v на контуре сопла от его длины в дозвуковой части
100
Область I
"/
У
III
Л
\
\
Рис. 3.1. Зависимость составляющей скорости v
от х в до- и трансзвуковой областях сопла
сопла. В области I, соответствующей до- 1 1 \~, \h\-\V
звуковому течению с малыми скоростями,
изменение функции v невелико, и ее про-
производные малы. Напротив, области II и
IV являются областями больших гради-
градиентов функции v. В области III в окре- х ~fo~ u
стности максимума изменение v вновь
незначительно. Естественно, в связи с
этим при замене производной разностным отношением в области
1 шаги разностной сетки в направлении оси выбирать большими
так как из-за небольших градиентов в этой области ошибки ап-
аппроксимации будут невелики; ошибки округления из-за больших
шагов разностной сетки будут также невелики. С другой стороны,
в области II и IV шаг разностной сетки должен быть достаточна
мал, чтобы ошибки аппроксимации были невелики; при этом ошиб-
ошибки округления в этой области также невелики из-за больших зна-
значении производных. В области максимума, так же как и в обла-
области 1, шаг разностной сетки должен быть выбран достаточно боль-
большим по аналогичным соображениям.
Таким образом, при расчете течения в эллиптической области
целесообразно использовать разностную сетку с переменным шагом
Использование больших шагов разностной сетки в областях с ма-
малыми градиентами приводит к тому, что рост ошибок округления
при численном решении задачи Коши для эллиптических уравне-
уравнении оказывается практически незаметным и не сказывается на ус-
устойчивости счета. J
Для проверки отмеченных фактов были проведены специальные
расчеты, в которых использовалось различное расположение точек
на слое. При использовании разностной сетки с постоянным но
мелким шагом, рост ошибок округления в области I приводил к
тому, что после небольшого числа шагов в направлении по норма-
нормали к линии тока счет становится неустойчивым. При использовании
разностной сетки с постоянным, но большим шагом, таким что рост
ошибок округления в области I становился практически неощути-
неощутимым, ошибки аппроксимации в областях II и IV становились на-
настолько значительными, что по-прежнему счет быстро становился
.неустойчивым. Только при использовании разностной сетки с ма-
малыми шагами в областях II и IV и большими в областях I и III
удавалось получить с высокой точностью устойчивое решение во
всей области течения вплоть до особой точки в трансзвуковой об-
лэсти.
Для вычисления производных dv/ds и dr/ds можно пользовать-
пользоваться различными разностными схемами. Специальные расчеты пока-
показали, что для вычисления производных наиболее устойчивой явля-
является трехточечная схема
101
df_\ = f 2y — (st+i — Si) |
ds )i ' X (s,-_i —s,-)(s,'_i —s/+1)
_|_ x 2s — E, + 1 + Sj-i) , л 2s — (S,- + 5i-l) ,g J2)
' (Si — si-x) (si — si+i) l+l(si+1 — s,-_1)(s,-+1 — s;)
При вычислении производных в крайних точках слоя s полагается
равным Si-i или Si+i для левого и правого концов соответственно.
В остальных точках слоя s = Si. Производные др/дВ и dr/dQ вычис-
лйются аналогичным образом. Однако при этом, по-видимому, це-
целесообразно использовать трехточечную схему с постоянным шагом
Д8 на плоскости s = const, который тем не менее может изменяться
от одной плоскости к другой. Очевидно, что формула C.12) полу-
получена в результате дифференцирования интерполяционного полино-
полинома Лагранжа, проходящего через точки Si-i, s,- и s,+i- Трехточечная
разностная схема при вычислении производных в сочетании с не-
неравномерной сеткой является своеобразным регуляризирующим
оператором в смысле Тихонова А. Н., который позволяет успешно
решать некорректную задачу Коши. Производная dtp/dty, входящая
в правую часть уравнений C.3) и C.4), аппроксимируется выра-
выражением (ф,,,-+\,h—фгзь)/Дгр. Изложенная разностная схема имеет
второй порядок точности по Лгр, а при постоянных шагах Д6, As —
второй порядок точности по Д8, As. Второй порядок точности обес-
обеспечивается итерациями по / и т.
3.1.2. Осесимметричный и плоский случаи
Особенно просто производится расчет в плоском и осесиммет-
ричном случаях при ш = 0, ф = 0. В этих случаях система уравнений
имеет вид A.106), A.107). Выпишем разностные уравнения, заме-
заменив s на х:
Л1) LJ+v i 1+л'Г/1/„„ч i /п.,л('-1I|<«'тг'д,|„ C.13)
JZL) +(V ff-l)W C-14)
iL ГГ ; C.15)
\ ds )i,j+\
^ ^i[fY4iI/2](l) C.16)
— i y — i ) \t,i+i
В первом приближении по C.13), C.14) определяются
(i=0, 1,... 1), при этом полагается//,°/+i = /,-у- Затем по найден-
найденным значениям г вычисляются {drjdx)\l]+\ по C.12) и определя-
102
ются v\l]+\, р,-,7+ь Utj+i' Аналогично вычисляются параметры при
следующих итерациях.
Важной особенностью предлагаемой схемы является то, что на
шаг Д\|) практически не накладывается никаких ограничений, свя-
связанных с устойчивостью, а величина его определяется лишь допу-
допустимой ошибкой аппроксимации; на шаг As ограничения наклады-
накладываются лишь в эллиптической области. Кроме того, в связи с оче-
очевидной простотой вычислительного алгоритма, особенно в плоском
и осесимметричном случаях, затраты машинного времени чрезвы-
чрезвычайно малы.
Вопрос о выборе величин шагов Дф и As решался, по существу,
эмпирическим путем. Критерием выбора служили сравнения резуль-
результатов расчетов с различными по величине шагами, а также инте-
интегральные проверки уравнений сохранения расхода и количества
движения. Шаг Д-ф выбирался равномерным, шаги по As — по су-
существу, кусочно-равномерным. Так, для определения Аг|; была про-
проведена серия расчетов с различными Aij), равными 0,2-10~'; 0,1Х
X Ю-1; 0,4-10~2; 0,2-10~2; 0,1 • 10 и 0,5-10~3. Оказалось, что с точ-
точностью 0,01% результаты расчета с тремя последними шагами сов-
совпали между собой. Этот факт означает еще, что ошибки округления
практически не сказываются на результатах расчета. При про-
проверке уравнений сохранения количества движения рассчитывалась
разность импульсов между фиксированным сечением на левом кон-
конце и некоторыми текущими сечениями, которая сравнивалась с рас-
рассчитанным вдоль линий тока интегралом сил давления. Отличие
этих величин составляло не более 0,05%. Проверка уравнения со-
сохранения количества движения проводилась как при расчетах про-
простых конфигураций, так и в случае кольцевых сопел и каналов до-
достаточно сложных форм.
Если поверхность начальных данных г|з = гро совпадает с осью
симметрии, описанный выше метод не может быть использован для
отхода от оси из-за наличия особенности в уравнениях в осесиммет-
осесимметричном течении. Для определения искомых величин на некоторой
близкой к оси симметрии поверхности -ф = const можно воспользо-
воспользоваться разложениями решения по функции тока г|з [см. 2.4 и 2.4.2].
От поверхности тока, полученной таким образом, можно вести рас-
расчет разностным методом.
При решении обратной задачи в случае течений газа в слож-
сложных каналах, когда линии тока являются многозначными функция-
функциями декартовых координат, удобно использовать уравнения
A.117) ... A.120) в переменных \р, ст, <р. Система A.117) ... A.120)
записана с учетом наличия вращения потока. Эта система может
быть решена изложенным выше методом [21]. При этом последова-
последовательность вычисления параметров может быть определена таким
образом, что расчет можно начинать непосредственно от оси сим-
симметрии.
Метод, близкий к рассмотренному для осесимметричного тече-
течения, был применен к решению обратной задачи Мортоном.
103
3.2. МЕТОДЫ РЕШЕНИЯ РЕЛАКСАЦИОННЫХ УРАВНЕНИЙ
При расчетах неравновесных течений приходится проводить
численное интегрирование дифференциальных уравнений, описы-
описывающих исследуемый неравновесный релаксационный процесс. Ки-
Кинетические и релаксационные уравнения, описывающие этот про-
процесс, вблизи равновесия являются, как правило, уравнениями
с малым параметром при старшей производной, что существенно
усложняет их численное интегрирование. К числу релаксационных
относятся уравнения: сохранения массы химической компоненты
A.15); для определения колебательной энергии A.16); для опреде-
определения скоростей и температур частиц в двухфазных потоках A.18);
для определения массы конденсата в течениях с конденсацией. Не-
Неравновесные течения в ряде случаев начинаются из состояния, где
система близка к термодинамическому равновесию. В тех же обла-
областях, где система близка к равновесию и время релаксации, а сле-
следовательно, и длина релаксационной зоны малы, возникают зна-
значительные трудности с выбором шага интегрирования. Оказывает-
Оказывается, что при использовании для численного интегрирования явных
разностных схем типа метода Эйлера, Рунге — Кутта шаг интегри-
интегрирования для проведения устойчивого счета должен быть настолько
мал, что расчет становится практически невозможен даже при ис-
использовании современных вычислительных машин.
В последние годы предложено несколько методов численного
интегрирования релаксационных уравнений. Наиболее эффективны-
эффективными и универсальными из них являются методы, основанные на ис-
использовании неявных разностных схем [8, 10, 27]. Основное требо-
требование к таким методам — возможность расчета по единой схеме с
высокой точностью как областей, где все или несколько неравновес-
неравновесных параметров близки к равновесным значениям, так и тех обла-
областей, где имеет место заметное отклонение от них. Ниже дается
обоснование выбора неявных разностных схем для расчета релак-
релаксационных уравнений. Неявные схемы позволяют на несколько по-
порядков увеличить шаг интегрирования по сравнению с явными.
В общем виде релаксационное уравнение для определения не-
неравновесного параметра at можно представить в форме
¦ = 1/т,.(й, -аг) (/=1,2,..., JV), C.17)
dt
где %i — время релаксации, являющееся в общем случае функцией
t, р, Т и всех а,; а, — условно равновесное значение <at (также функ-
функции t, p, T и всех а,), равное at при равновесном течении с постоян-
постоянной энтропией.
Действительно, уравнение A.133) можно записать в виде
daHJdt =—¦
104
То же относится к уравнениям A.137), которые можно записать
в виде
WWs),
dt xs dt
где
Таким образом, C.17) является достаточно общей записью ки-
кинетических уравнений, описывающих различные неравновесные про-
процессы.
Неустойчивость численного решения возникает из-за существо-
существования в уравнении типа C.17) произведения малой разности боль-
больших величин (а—а) на большое число т, что привносит большую
погрешность, особенно вблизи равновесия.
Из уравнения C.17), делая естественное предположение об ог-
ограниченности производной dai/dt, получаем, что при тг-М) течение
приближается к равновесному, т. е. аг-мх,-.
Рассмотрим вместо C.17) модельное уравнение, положив %¦, и
а, константами. Общее решение этого модельного уравнения имеет
вид
(^) C.18)
где нижние индексы i для простоты опущены, а ао=а@). Получим
теперь решение разностного уравнения
C.19)
ап+\ — ап
h x
аппроксимирующего дифференциальное уравнение C.17). Здесь
h — шаг интегрирования, а — параметр, O^a^l, а нижний индекс
п и л+1 приписываются параметрам в известной и искомой точках
соответственно. Используя рекуррентное соотношение
1 — иа . аи
получим следующее решение разностного уравнения C.19):
)Г+5- C-20)
Точное решение дифференциального уравнения в точке л+1, со-
согласно C.18), имеет вид
. C.21)
Из C.19), C.20) следует, что решение разностного уравнения стре-
105
мится к точному при x-vO для всех о таких, что O^a^l. Однако
точность и устойчивость решения разностного уравнения
зависят от величины этого параметра. При а=1/2 решение раз-
разностного уравнения имеет второй порядок точности. При а= 1 (яв-
(явная схема типа схем Эйлера и Рунге — Кутта) и х» 1 решения
разностного уравнения сильно отличаются от точного. Максималь-
Максимальный шаг, с которым можно численно интегрировать уравнение
C.17), равен 2т. Поэтому явные схемы позволяют численно инте-
интегрировать релаксационные уравнения вблизи равновесия, где вре-
время релаксации т мало (порядка 10^6... 10~12), лишь с очень малым
шагом (h = 2x), что делает их абсолютно непригодными даже при
использовании ЭВМ с большим быстродействием.
При а= 1/2 и х^> 1 из C.20) получаем, что решение разностного
уравнения колеблется около точного с амплитудой, не большей
|ао—а|), при увеличении шагов эти колебания затухают довольно
медленно. Тем не менее, разностная схема при а= 1/2 дает решения,
близкие к точному в тех областях, где величина |а0—а| мала по
сравнению с а. Такие области соответствуют малым значениям т и
течениям, близким к равновесию. В тех же областях, где х велико,
а течение существенно отклоняется от равновесного (например, в
угловой точке или за ударной волной), величина |a0—а| может
быть сравнима с а, и использование разностной схемы при а= 1/2
может приводить к большим ошибкам. Кроме того, как показывает
рассмотрение модельного уравнения, при а= 1/2 и больших х ошиб-
ошибка в начальных данных затухает после значительного числа шагов.
Это обстоятельство может затруднять отход от начальных точек
вблизи равновесия, особенно для многокомпонентной смеси.
Проделанный выше анализ в работе [8] обобщен на случай си-
систем релаксационных уравнений. Показано, что условия устойчи-
устойчивости разностных уравнений имеют вид
2о)Х,—1|>1 з<0,5;
|АBс-1)Х,+ 1|<1 а>0,5,
где {>,,} — множество собственных чисел матрицы \\dF/da\\\ Re^—
их действительные части. Нетрудно показать, что матрица Яко-
би системы C.17) имеет хотя бы одно собственное значение с от-
отрицательной действительной частью, так что условие устойчивости
при а>0,5 имеет вид
N -1-1
что при N=1 и ст= 1 эквивалентно упомянутому выше условию
устойчивости h «2т.
С другой стороны, при as?;0,5 множество {A.(Re/n<;0} заведомо
принадлежит области устойчивости и на шаг интегрирования огра-
106
ничения накладываются лишь в связи с ошибками аппроксимации
схемы.
В связи с этим более предпочтительными являются неявные
схемы с 0<Са<1/2, которые при х>-1 дают решения, близкие к
точному, и при использовании которых ошибки в начальных данных
быстро затухают. Применение таких схем позволяет существенно
увеличить шаг интегрирования по сравнению с явными схемами
при сохранении устойчивости. При проведении конкретных расчетов
использовалось значение а=0,4, что обеспечивало порядок точно-
точности, близкий ко второму. Проделанный анализ модельного уравне-
уравнения можно обобщить на случай, когда а является не постоянной, a
известной функцией от t.
Рассмотрим теперь конкретный алгоритм решения разностных
уравнений для сложных неравновесных систем. Пусть имеется N
неравновесных параметров ct(, для определения которых имеется N
релаксационных уравнений типа C.17) [см, например, A.80)]. Не
ограничивая общности, примем, что тг и а, суть функции только t
и а, и не зависят от р и Т. Тогда, согласно C.19), система диффе-
дифференциальных уравнений C.17) аппроксимируется следующей си-
системой разностных уравнений:
1-3)а1(я+1)] = 0, C.22)
%l = h/xi (/=1, 2,..., N)
или f(an+1)=0,
где /=(/lf /2,..., /лг).
Отметим, что каждое из уравнений C.22) получено в результа-
результате разрешения разностного уравнения типа C.19) относительно
неизвестной сцп+i)- Такое разрешение, во-первых, устраняет произ-
произведение малой разности а,—а больших величин на большую вели-
величину 1/т<, содержащееся в правой части основного уравнения, и де-
делает матрицу Якоби при вычислениях в методе Ньютона лучше
обусловленной.
Система C.22) является нелинейной системой уравнений отно-
относительно a,(n+i) (t= I, 2, .. , N). Решение ее методом простой итера-
итерации нецелесообразно, так как условия сходимости итераций приво-
приводят к ограничению на шаг h (йат), такому же, как и при исполь-
использовании явных схем. Поэтому необходимо применять какой-либо
иной метод, например, метод Ньютона с переменной матрицей Яко-
Якоби D, элементами которой являются dfi/dau- Эту матрицу удобно
находить, используя аналитические выражения для производных
dfjdk. Неизвестные a,(n+i) находятся итерациями по формуле
„0+1) „(;) п" f (rtW> \
an+i =an — ип+гт \ап+1)
107
Итерации заканчиваются при выполнении условий
и) „(Я I ^. |„(/+1) I
— Щ(п+1)\ <> ?; |а-()|
где е,, б, — заданные погрешности в компонентах решения и невяз-
невязки в уравнениях, а / — номер итерации.
Отметим, что в ряде случаев уравнения кинетики, хотя и яв-
являются уравнениями с малым параметром при старшей производ-
производной, но не имеют стандартного вида C.17). К такому числу при-
принадлежит, например, уравнение A.140), которое можно переписать
в виде
dM 1 , - ,
где т-1 = 4яг%(йBя/?7')-1/2, а p4=pm(Tt)VT/Tt.
Для численного решения их также необходимо использовать не-
неявные разностные схемы, и при конкретной реализации алгоритма
их следует включать в общую систему разностных уравнений
C.22), которая, по-прежнему, должна решаться методом Ньютона.
Предложен ряд мер, обеспечивающих быструю сходимость ите-
итераций к решению [10, 27]. При вычислениях по C.23) около 90%
времени расходуется на расчет компонент матрицы D и ее обращение.
Поэтому основная экономия может быть получена при вычислении
обратной матрицы D-1. В связи с этим матрица D-1 вычисляется
в точке л+1 только в первых двух итерациях, после чего фикси-
фиксируется, и последующие итерации проводятся с неизменной матри-
матрицей D-1. Более того, матрица D-1, вычисленная в точке л+1, ис-
используется для нахождения решения по C.23) в точках л+2,
п+3 и т. д. Вычисление «новой» матрицы D в точке л+fe произ-
производится только тогда, когда число итераций, потребовавшихся для
сходимости к решению с заданной точностью, превышает заранее
заданное число D ...6). Использование процедуры фиксирования
обратной матрицы позволяет на порядок сократить время расчета.
Известно также, что сходимость метода Ньютона к решению за-
зависит от близости начального приближения к этому решению. В свя-
связи с этим, начальное приближение в точке л+1 целесообразно за-
задавать посредством экстраполяции искомых функций с использо-
использованием их значений в предшествующих точках. И наконец, время
расчета существенно зависит от точности задания данных в началь-
начальной точке отрезка интегрирования, если эта точка находится в око-
околоравновесной области, как, например, для течений в соплах. Даже
незначительные ошибки в начальных данных (в четвертой — пятой
значащих цифрах) в силу малых значений т. могут привести к дли-
длительному счету начального участка из-за медленной сходимости
итераций. В связи с этим в начальной точке целесообразно также
решать систему C.22) методом Ньютона с переменной матрицей,
полагая второй член в левой части C.22) равным а,.
108
Таким образом, описанный алгоритм решения релаксационных
уравнений основан на: использовании неявных разностных схем;
разрешении разностного уравнения типа C.19) относительно <zn+i
с целью устранения произведения малой разности больших величин
на большую величину; решении нелинейной системы уравнений ти-
типа C.22) методом Ньютона.
В то же время отметим, что применение итерационной схемы
Ньютона для решения конечно-разностных уравнений C.22) не
обеспечивает выполнения законов сохранения на промежуточных
итерациях. В работе [8] показано, что выполнение законов сохра-
сохранения с заданной относительной точностью еще далеко не гаран-
гарантирует того, что концентрации при этом будут находиться с такой
же относительной точностью. Особенно не точно при этом могут
находиться концентрации веществ, содержание которых в смеси
мало. Но именно к таким веществам относятся, как правило, ток-
токсичные компоненты СО, N0 и др. Поэтому, чтобы гарантировать
заданную относительную точность расчета всех концентраций (в
том числе и токсичных) надо следить за тем, чтобы удовлетворя-
удовлетворялись в первую очередь те уравнения C.22), которые соответствуют
наименьшим компонентам. Кроме того, в работе [8] отмечено, что
сходимость итерационных методов, применяемых для решения
C.22), практически всегда заметно улучшается, если значения .a«+i
во всех промежуточных итерациях точно удовлетворяют законам
сохранения.
Точный расчет малых концентраций не имеет важного значения
в тех задачах газовой динамики реагирующих сред, где опреде-
определяются интегральные характеристики. Например, погрешность при
расчете малых концентраций при определении потерь удельного
импульса на химическую неравновесность при течении многоком-
многокомпонентной смеси в сопле реактивного двигателя не дает существен-
существенной погрешности в результатах исследований. В задачах же иссле-
исследования процессов образования токсичных компонент в энергети-
энергетических установках необходимо с достаточной точностью
определять концентрации токсичных веществ. Поэтому становится
очевидной необходимость разработки таких итерационных схем
решения конечно-разностных уравнений химической кинетики, в
которых обеспечивается точное выполнение законов сохранения на
каждой итерации, и, следовательно, малые концентрации вычисля-
вычисляются с заданной относительной точностью. Напомним, что законы
сохранения являются точными интегралами уравнений кинетики
A.80).
Обеспечить точное выполнение законов сохранения химических
элементов на промежуточных итерациях возможно различными
способами [8]. Один из них заключается в том, что N неизвестных
концентраций находятся в результате численного решения соот-
соответствующих им N уравнений C.22), а остальные концентрации
исключаются, т. е. их значения находятся из уравнений типа A.19).
Очевидно, что в качестве последних необходимо выбирать кон-
109
центрации тех компонент, содержание которых в смеси наиболь-
наибольшее.
Способ, предложенный в работе [8], заключается в применении
матрицы проектирования, которая вычисляется по заданному на-
набору учитываемых химических компонент единственный раз в на-
начале работы программы и в ходе дальнейших вычислений не меня-
меняется.
Поскольку применение метода Ньютона приводит к значитель-
значительным затратам машинного времени, особенно с увеличением числа
компонент, что, как отмечалось, связано с вычислением и обраще-
обращением матрицы Якоби, то в работе [10] и последующих работах этих
авторов развивается метод простой итерации для решения системы
C.22), в котором не требуется вычисления и обращения матрицы
Якоби.
Предлагаемая итерационная схема состоит из двух шагов. На
первом — промежуточном — шаге определяется значение вектора
концентраций по схеме простой итерации
О+1/2)_ (Л
где f0) — вектор невязок в уравнении C.22), а р — релаксационный
коэффициент, который выбирается так, чтобы вектор «nJ+i1/2) не
имел отрицательных компонент. Затем делается основной шаг, со-
состоящий в поиске минимума квадрата вектора невязки (скалярная
функция одной переменной) на прямой, соединяющей точки
a{/+i и v.J+11 \ Расчеты показывают, что в такой схеме удается со-
сократить время примерно в два раза по сравнению с расчетами по
методу Ньютона.
В настоящее время сохраняется необходимость в дальнейшем
совершенствовании методов решения релаксационных уравнений^
особенно в случае большого числа компонент.
3.3. МЕТОДЫ РАСЧЕТА ТЕЧЕНИЙ
С ФИЗИКО-ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ.
ОДНОМЕРНОЕ ПРИБЛИЖЕНИЕ
3.3.1. Равновесные и неравновесные течения с химическими
реакциями, колебательной релаксацией и конденсацией
Метод расчета неравновесных течений в одномерном прибли-
приближении имеет принципиальное значение, поскольку, как отмечалось,
уравнения газовой динамики в обобщенных координатах Мизеса
х, г|), 6 вдоль линий тока имеют одинаковую запись (с точностью до
коэффициента Ляме) как в одномерном, двумерном, так и в про-
пространственном течениях [см. уравнения A.76), A.79), A.80), A.81),
A.86)].
Поскольку, с другой стороны, линия тока является характери-
характеристикой, то эти же уравнения используются и в численном методе ха-
характеристик. Таким образом, модуль расчета одномерного нерав-
неравновесного течения вдоль линии тока является важным и достаточ-
достаточно
но универсальным модулем, который может использоваться как при
расчете одномерных течений, так и при стационарных и нестацио-
нестационарных пространственных течениях.
Рассмотрим первоначально течения, в которых отсутствуют
частицы, а также внешние силы и источники массы и энергии
Тогда систему уравнений, описывающих неравновесное течение,
в котором могут иметь место неравновесное протекание химических
реакций, неравновесное возбуждение колебательных степеней сво-
свободы и неравновесная конденсация в соответствии с уравнениями
A.20), A.21), A.76), A.80), A.81), A.86), A.108) при R = oo с за-
заменой и на W запишем в следующем общем виде
Q; C.24)
J- Л_!_ wA 4—L^.^0; C.25)
ds \ 2 J~ y? ds
a+-y=a0; C-26)
W ^L = Ln(p, T, yu y2,... ya) (/i= 1,..., N); C.27)
p = p(P, T, yn); C.28)
h = h{p, T, yn). C.29)
Здесь yn — релаксационный кинетический параметр, который в со-
соответствии с учитываемыми процессами может быть концентрацией
химических компонент смеси, энергией колебательных степеней сво-
свободы и массовых долей конденсирующейся компоненты. Излага-
Излагаемый ниже метод расчета применим как для случая, когда в смеси
протекают одновременно все указанные процессы, так и для слу-
случая, когда имеет место лишь один из них. Метод применим также и
в случае, когда протекают и другие процессы, описываемые систе-
системой уравнений типа C.24 ... 3.27). Конкретная запись правых ча-
частей кинетических уравнений C.27), а также термического C.28)
и калорического уравнений состояния приведена в разд. 1.3.
Ниже рассматривается обратная задача теории сопла, т. е.
принимается, что задано распределение p=po(s) или W=W0{s),
или p = po(s), а также все параметры течения в начальном сечении
s=s0. Обычно для расчета течения, начинающегося из дозвуковой
области, принимается, что при s = s0 имеет место равновесное со-
состояние и все уп определяются из соотношений равновесной термо-
термодинамики [см. разд. 1.3].
Для нахождения решения на интервале от s0 до sh (где sh —
конечное сечение) необходимо численно решить задачу Коши для
системы C.24) ... C.29). Число уравнений в этой системе может
быть очень велико (в реальных ситуациях N=10... 100) и, как от-
отмечалось в 3.2, обычно уравнения C.27) принадлежат к числу
«жестких» уравнений с малым параметром при старшей производ-
производной, для численного решения которых применяются специальные
методы.
111
Проведем некоторые преобразования с целью записи в уравне-
уравнении движения C.25) вместо производной от давления производной
от плотности. Используя C.27) ... C.29) запишем производные
dp/dx и dh/ds. Имеем
N
dp dp dp . dp dT . ^} dp .
ds dp ds dT ds
C.30)
dh _dfi_ _dp_ , dh. dT , ^T^ dh ,
ds dp ds dT ds ^шА дуп
Тогда, используя уравнение dh=\jpdp с учетом C.30), получим
м
dh I \ dp , dh dT , ^"Ч dh , п /OOU
—— -| г- > 1„ = 0. C.31)
dp р ) ds ~ dT ds Г ^ дуп
Введем замороженную скорость звука
рук [^+^[дТ1(± __Щу\ (з.32)
'Р )s'yn I dp dh/dT [ р dp )\
Тогда из C.30), C.31) и C.32) имеем
dp л $9 t ЛТП /О OQ\
= #^ ¦ biVu, iQ.Oij)
ds ds
N
лтл о / dh \—l Xk^i / dp dh dh do \ т ,о пл\
Ur / jLk \dT dyn dT dyj
n-1
Используя C.33), запишем уравнение движения C.25) в виде
dW2/2 , a2 dp N0 о о-
— . (о.оо)
ds y ds YP
Сделаем еще некоторые преобразования прежде чем переходить к
описанию разностных схем.
Уравнение неразрывности C.24) с использованием уравнений
движения и энергии можно преобразовать к следующему виду:
_L JEL^ 1 LL if. Л-JVo/a2] , C.36)
IW ds M2 — 1 j_ F ds J
где № — определяется по формуле C.34). Здесь число М определя-
определяется по замороженной скорости звука. В случае равновесного или
замороженного течений №=0 и уравнение C.36) переходит в обыч-
обычное уравнение одномерной теории [см., например, уравнение B.3) ]„
а число Маха определяется по равновесной или замороженной
скорости звука соответственно. Из уравнения C.36) следует, что-
значение М=1 (а также максимум скорости или минимум давле-
давления при дозвуковом течении) достигается не в минимальном сече-
сечении сопла, а ниже по потоку от этого сечения. Отмеченное свойство-
112
является общим свойством неравновесных течений в соплах; оно
справедливо также для двухфазных неравновесных течений. Урав-
Уравнение C.36) используется вместо C.24) при решении прямой за-
задачи, когда задается функция F=F(x).
Система C.24) ... C.29) состоит из c+iV уравнений для опреде-
определения 7-\-N неизвестных р, р, Т, W, F, h и уп и поэтому незамкну-
незамкнута. Для ее замыкания необходимо задать какую-либо из этих функ-
функций, например, F(s) или одну из функций p(s), p(s), W(s). В пер-
первом случае необходимо решать прямую задачу в одномерном
приближении, т. е. определять параметры течения при заданной
форме струйки тока F—F(s). Решение такой задачи в области,
включающей, например, дозвуковую часть сопла, весьма затрудни-
затруднительно, поскольку из-за особенности в уравнении C.36) при М= 1
приходится отыскивать единственную регулярную интегральную»
кривую, проходящую через особую точку типа седла, где М=1,
имеющую в этой точке конечную производную. Для этого необходи-
необходимо варьировать значения параметров в начальном сечении таким
образом, чтобы, с одной стороны, не попасть на дозвуковую ветвь
решения, а с другой стороны, обеспечить регулярность решения,
т. е. одновременное обращение в нуль числителя и знаменателя в-
правой части уравнения C.36). Время расчета из-за необходимо-
необходимости преодоления этой трудности значительно увеличивается.
В связи с этим решение прямой задачи в рамках одномерного
приближения при расчете разного рода неравновесных течений в
соплах и струях, в том числе и двухфазных, представляется неце-
нецелесообразным. В то же время очевидны преимущества решения
обратной задачи с заданным по длине распределением какого-либо
из газодинамических параметров р, р или W. В этом случае отпа-
отпадает необходимость использования уравнения C.36), так как
форма струйки тока не задана, а определяется из уравнения C.24),
а система C.25) ... C.29) не содержит уже особой точки. Кроме то-
того, давление, а в еще большей степени — плотность и скорость мала
отличаются от соответствующих равновесных значений и могут
быть определены из расчетов, например, двумерных равновесных
течений или измерены в эксперименте. И, наконец, отработанный
алгоритм решения системы C.25) ... C.29) с заданным распределе-
распределением p—p(s) или p = p(s) может быть полностью использован при
расчете пространственных неравновесных течений. Если неравно-
неравновесный процесс начинается в сверхзвуковой области сопла (в слу-
случае, например, неравновесной конденсации), то необходимость про-
прохождения особой точки отпадает и возможно решение как прямой,
так и обратной задачи. Отметим, что решение обратной задачи
особенно удобно при исследовании течений в струях, для которых
форма струйки F~F(s) неизвестна.
Рассмотрим теперь разностную схему решения обратной задачи.
Пусть в некотором сечении s = st заданы все параметры потока. Не-
Необходимо определить их в сечении s,-+i = Si+As, где As — шаг раз-
разностной схемы. Запишем следующую цепочку разностных уравне-
уравнений:
113
2.
!Л yp
NO \(m-l
YP
<m)
, yn J =^= /i Q |
Л + 1
i+u l iti' #« J= °~~(~2~) ' C.37)
А Го Г(т) н(тI А /^2ут).
- »i+i LPj + i. j i+u Уп J = «o— —— ,
C.38)
2. (^)+i.=(f/e), + j[?r^(p, Г, уя)\+[
i. р|?1=р[л+1, 7{;, (у.IЯ1; C_39)
P^№{+!=Q. C.40)
Здесь индекс т относится к номеру итерации, индексы i и т вы-
выбраны для соответствия с формулами C.10), C.11). В формулах
C.36) ... C.39) номер 1 соответствует случаю, когда задано рас-
распределение p=p(s), a 2 — случаю, когда задано распределение
плотности p = p(s).
Итерационный процесс строится следующим образом. В нуле-
нулевой итерации параметры в правых частях уравнений C.36) по-
полагаются равными их значениям в л-й точке, и определяется значе-
значение скорости W(iJi) в первой итерации в n-f-1-й точке. Найденное
значение скорости используется в уравнениях C.37), C.38). Си-
Система нелинейных уравнений C.37) и C.38) (заметим, что релак-
релаксационные уравнения C.38) записаны с использованием неявной
схемы) решается методами, описанными в 3.2 также итерационно
с собственным внутренним итерационным циклом по / [см. форму-
формулы C.22) и C.23)]. В результате, по завершении этих итераций
находятся значения температуры 7\+i, [f/i^^+i в первой итерации
по т, наконец, плотность p,(+i (либо давление pj+i) находятся из
C,39). Затем итерационный цикл по т повторяется с тем лишь от-
отличием, что значения параметров с индексом (т—1) в формуле
C.36) берутся из предыдущей итерации. Вычисления повторяются
до достижения заданной точности. Площадь струйки тока F опре-
определяется из соотношения C 40) после завершения итераций.
114
В представленном виде разностная схема решения близка к
схеме Эйлера с пересчетом, обеспечивающей второй порядок точ-
точности по As.
Если задано распределение скорости W=W(s), то расчет дав-
давления в точке (J+1) производится по формуле
^\Ы^)+(У?Г+^(^) 1. C.41)
2 l\ ds Ji \ ds /1+1J
Остальные параметры рассчитываются по формулам C.37.1) ...
C.39.1), в которых р,+\ берется из формулы C.41).
Отметим, что течение, близкое к равновесному (или заморожен-
замороженному), можно рассчитать, пользуясь теми же уравнениями C.36) ...
C.40), при этом в кинетических уравнениях нужно соответству-
соответствующие времена релаксации взять очень большими (или близкими
к нулю). В случае равновесного, либо замороженного течения рас-
расчет течения вдоль струйки тока в одномерном приближении суще-
существенно упрощается, поскольку такие течения являются изоэнтро-
пическими, в которых 5 = const.
Расчет равновесного течения в сопле разбивается на два эта-
этапа. Первоначально определяются все параметры в состоянии покоя,,
при этом задается давление, а температура и состав смеси нахо-
находятся из решения системы нелинейных уравнений законов дейст-
действующих масс и материального баланса с использованием заданного
значения полной удельной энтальпии. На втором этапе рассчиты-
рассчитывается непосредственно процесс расширения, при этом задается
давление в некотором сечении и условие s = s0 (s0 — энтальпия тор-
торможения), а температура и состав смеси находятся из решения
упомянутой выше нелинейной системы уравнений. В этом сечении
далее плотность находится из уравнения состояния, а скорость —
из уравнения энергии. Из результатов такого расчета могут быть
получены зависимости p=f(p) и h = h (р), соответствующие задан-
заданной sQ. Эти зависимости удобно далее использовать при расчете дву-
двумерных течений.
Методы расчета равновесного состава изложены в [33]. В ра-
работе [9] дано развитие этих методов, при этом рассмотрено два
случая: расчет равновесного состава при заданных давлении и тем-
температуре и расчет состава и температуры при заданных давлении
и удельной энтальпии смеси. Показано, что оба случая сводятся к
решению задачи безусловной минимизации выпуклых функций.
Предложен алгоритм решения этих задач, основанный на примене-
применении численных методов безусловной оптимизации и сходящийся от
любого начального приближения, что особенно важно при расчетах
новых композиций и составов.
Описанный алгоритм расчета равновесного течения сохраняется
для различных физико-химических превращений При учете диссо-
диссоциации и рекомбинации для расчета состава смеси привлекаются
уравнения материального баланса и закон действующих масс, при
учете ионизации — формула Саха, при учете возбуждения колеба-
колебательных степеней свободы — формула Эйнштейна, при учете кон-
115
денсации или испарения — уравнения Клапейрона — Клаузиуса
для кривой насыщения, при учете реальных свойств за счет межмо-
межмолекулярного взаимодействия — уравнения состояния (термическое
и калорическое) реального газа.
Расчет частично равновесного течения (при замороженном ка-
каком-либо процессе) проводится по таким же алгоритмам. К числу
таких течений можно отнести, например, течение с замороженны-
замороженными химическими реакциями, но равновесным возбуждением коле-
колебательных степеней свободы.
3.3.2. Течения с подводом массы и энергии при наличии
внешних сил
Задача расчета течений в одномерном приближении с учетом
подвода массы и энергии возникает при исследовании, например,
методов подавления токсичных компонент [24]. Учет источников
(или стоков) энергии необходим также при наличии излучения или
специальным образом организованных зон тепловыделения [13].
Запишем, имея в виду уравнения A.75) ... A.79), следующие
уравнения неразрывности движения и энергии для течений с под-
подводом массы и энергии и при наличии внешних сил в одномерном
приближении
= M(s); C.42)
ds
_4_(J_lH-| LJ^ = ,FO(S); C.43)
ds \ 2 / YP ds
ds \ 2 /
Здесь M(s), F°(s) и Q°(s) известные функции, характеризующие
внешний поток массы, внешнюю силу и внешний поток тепла. Отме-
Отметим, что в случае сосредоточенного воздействия в точке s=sc, ког-
когда M(s), F°(s) и Q°(s) есть б-функции, расчет одномерного течения
производится по формулам C.36) ... C.40) до этой точки, в точке
s = sc производится пересчет параметров и определяются новые зна-
значения расхода Q, полной энтальпии h0. Далее расчет производится
по тем же формулам C.36) ... C.40). В случае распределенного воз-
воздействия расчетные формулы и итерационный процесс сохраняют-
сохраняются теми же, с той лишь разницей, что:
1. В правую часть уравнения C.36) добавляется член
2. Правая часть уравнения C.37) заменяется следующим выраже-
выражением:
3. Правая часть уравнения C.40) заменяется следующим выраже-
выражением:
Как видно из формул A.76), A.79), учет частиц также приво-
приводит к добавлению новых членов в правую часть без изменения
алгоритма расчета уравнений движения и энергии.
3.3.3. Течения смеси газа и частиц
Пусть в потоке содержатся частицы различных фракций, рас-
распределенные по М групп. Придадим параметрам частиц нижний
индекс s и будем помечать частицы определенного размера индек-
индексом / [см. 1.21 и 1.3.3].
Выпишем в одномерном приближении уравнения, описывающие
стационарное движение многоскоростного и многотемпературного
континуума без фазовых превращений. Примем, что теплоемкости
газа ср и частиц cs постоянны. Предположим еще, что частицы суть
невзаимодействующие между собой сферы с постоянной по объему
частиц температурой; при этом давлением, которое создают части-
частицы, можно пренебречь, однако объем, занимаемый ими, учитывает-
учитывается. Будем считать также, что массовая доля частиц каждой фрак-
фракции неизменна. Имеем тогда следующие уравнения неразрывности
и движения газа и частиц, уравнение энергии смеси, уравнение
энергии частиц (или уравнение конвективного теплообмена между
газом и частицами) и уравнение состояния газа:
{\-as)Q; C.45)
s=F = djsQj, aJs=gJsas (/= 1, 2,..., My, C.46)
ds YP° ds 1 — as P°
d
W
dp , as Pr VI dWJs
1+ 2 g =° ( }
i=\,2,...,M); C.48)
м
gjs
i=~l
= ho={{\~as)cp-Lascs]To; C.49)
dTjs
ds
C.50)
117
C-51)
Здесь p, p, T, W отнесены к своим критическим значениям р», р*, Г»,
а*, теплоемкости — к yR, ax — к г*; у=а*2Р*А°*> P* = Rp*T*. Член
в правой части уравнения C.48), характеризующий обмен импуль-
импульсом между газом и частицами, равен силе, с которой газ действует
на частицы, и в соответствии с законом сохранения импульса при
взаимодействиях с обратным знаком равен силе, с которой частицы
действуют на газ. Аналогично член в правой части C.50) характе-
характеризует обмен энергией между газом и частицами.
В уравнениях C.45) — C.51) as — общая доля частиц, r]a, aJS —
радиус и массовая доля частиц /-й фракции, р, p/s — плотности га-
газа и частиц, т. е. отношения массы газа и частиц к объему, в кото-
котором они заключены, р° и ps° — истинные плотности вещества газа
и частиц, т. е. отношения массы газа и частиц к объему, занятому
только газом и только частицами, R — газовая постоянная газовой
фазы, Cxi — отношение коэффициента сопротивления сх/ к коэффи-
коэффициенту сопротивления сХ) при стоксовском режиме обтекания
(cXj—24/R%jS) , а° — коэффициент теплоотдачи, Re,-S, St/S, Nu;s
и Pr — числа Рейнольдса, Стокса, Нуссельта и Прандтля соответст-
соответственно, при этом
2f\WWj\rj 2&%а
, F.52}
Nu - 2r^° Pr—
где ц и к— кбэффициенты вязкости и теплопроводности газа. При
St,s=O течение является равновесным, поскольку инерционный
пробег равен нулю, и частица мгновенно приобретает скорость и
температуру газа. При St/S=oo течение является замороженным,
а при промежуточных значениях числа Стокса — неравновесным с
диссипацией и ростом энтропии в процессе конечного по времени
обмена импульсом и энергией между фазами.
Рассмотрим первоначально предельные режимы течения без
учета объема, занимаемого частицами. В равновесном течении
(StjS=0) скорости и температуры газа и частиц равны и, как во
всех равновесных течениях, реализуется максимальный импульс.
Путем простых преобразований, вводя газовую постоянную, плот-
плотность, удельную теплоемкость и показатель адиабаты некоторого
фиктивного газа по формулам
DO Ql\ .а V пО nl\ г/ V-1"
sh ' ' v s C.53)
I — as Cp /\ l — as
118
и принимая, что у фиктивного газа те же давление, температура и
скорость, что и у смеси, можем представить равновесное течение
смеси как течение фиктивного газа с показателем адиабаты у0, га-
газовой постоянной R0 и теплоемкостью ср° и воспользоваться для
расчета равновесного течения газодинамическими функциями. Чис-
Численное интегрирование системы C.45) ... C.51) проводится методами
решения системы, описывающей неравновесные течения с фи-
физико-химическими превращениями, изложенными в разд. 3.3.1. По-
прежнему целесообразно решать обратную задачу с заданным рас-
распределением давления p=p(s) или плотности p = p(s), а при реше-
решении релаксационных уравнений C.48), C.50) использовать неявные
разностные схемы. Имеем без учета объема частиц (вычисле-
(вычисления проводятся путем последовательных итераций в последователь-
последовательности) :
\\ YP ds )i \ YP /
X1 P" . Str1 (\J7 _ yp' • )
Л1
C.54)
A-а1)(^){-1); C.55)
l J
(y = l,2,...,M). C.56)
(y=l, 2,..., Af), C.57)
где Lwr j = JSI w>w ; л/и7,=
¦— W J W J > W J Tiy q .
LT1=NT}T; NT} =
3 Pr StjsWJscs
11-9
Итерационный метод решения системы C.54) ... C.57) анало-
аналогичен методу решения системы C.36) ... C.38). Первоначально оп-
определяется при m=l Wl+\ из C.54). Далее система нелинейных
уравнений C.55) ... C.57) решается методами, описанными в
разд. 3.2, собственным внутренним итерационным циклом. В ре-
результате после завершения полной итерации по я в точке s,+i оп-
определяются W, WJS, T и T]S из C.51) р, из C.45) —площадь струй-
струйки тока F и из C.46) —плотность конденсата pjs. Начальные дан-
данные при интегрировании системы C.54) ... C 57) задаются обычно
в дозвуковой области, при этом принимается, что в начальном се-
сечении скорости и температуры частиц и газа равны.
3.4. МЕТОДЫ РАСЧЕТА ТЕЧЕНИЙ
С ФИЗИКО-ХИМИЧЕСКИМИ ПРЕВРАЩЕНИЯМИ.
ПРОСТРАНСТВЕННЫЕ И ДВУМЕРНЫЕ ТЕЧЕНИЯ
Численные методы решения обратной задачи достаточно просто
обобщаются на случай течений с физико-химическими превращени-
превращениями. Важно при этом отметить, что запись двух основных уравне-
уравнений C.3) и C.4), которые используются для перехода на следую-
следующий слой а|) = const, одинакова как для случая течений без физико-
химических превращений с постоянным отношением удельных теп-
лоемкостей, так и для течений с физико-химическими превращени-
превращениями.
Более того, при наличии подвода массы, энергии, внешних сил
и частиц дифференциальные операторы в этих уравнениях остают-
остаются неизменными, а добавляются лишь некоторые конечные члены
в правую часть уравнения C.3).
В связи с отмеченными обстоятельствами разностная аппрокси-
аппроксимация уравнений C.3) и C.4) для случая течений с физико-хими-
физико-химическими превращениями та же, что и для идеального газа с посто-
постоянным отношением удельных теплоемкостей [см. первую и вторую»
формулы C.10) и формулы C.13), C.14)].
3.4.1. Течения с химическими реакциями,
колебательной релаксацией и конденсацией
Рассмотрим решение обратной задачи для пространственного
течения. Пусть на поверхности ip = o|5o задано r = ro(s, 0) и компонен-
компонента скорости u = uo(s, 0) (либо давление или плотность). На началь-
начальной плоскости s = s0 задается компонента скорости w = w°(Q, ij?) и
функция ф = ф°@, г|э), а также плотность р = р°F, т|э) и все парамет-
параметры г/п = г/п°@, я]}), характеризующие релаксационный процесс. Пер-
Первоначально определяются на начальной поверхности г|5 = г|H все не-
недостающие параметры. Последовательность расчетов при этом за-
зависит от задаваемого на поверхности i|) = i|3o начального распреде-
распределения.
В случае, когда задано p = po(s, 0), по формулам C.10.3),
C.11.1 и 2) и C.36.1) ... C.39.1) в общем итерационном цикле по-
120
т определяются путем численного интегрирования вдоль слоя г|50
от плоскости s = s0 на различных плоскостях 8 = const значения WQ,
vo, w0, (Уп)оро и uo=Vw^ — vl — wio.
В случае, когда задано p = po(s, 9), по формулам C.10.3),
C.11 1 и 2), C.41), C.37.2) ... C.39.2) аналогично определяются
значения v0, (w0), (tjn)o, Wo, p0, p0-
Таким образом, на начальном слое г]H определение параметров
происходит не стандартно, а зависит от типа заданной начальной
функции. Если начальная линия совпадает с осью симметрии, то
функции v, r, w тождественно равны нулю, однако, в уравнении
движения [см., например, C.3) и C.10)] при г = 0 в осесимметрич-
ном и пространственном случаях имеется особенность, которая лег-
легко устраняется путем разложения решения в ряд по г]з [см. 2.4 и
2.4.2]. Полученные в результате такого разложения параметры на
близлежащей к оси линии тока используются в качестве началь-
начальных для дальнейшего расчета.
Переход на последующий слой г|} = const и расчет параметров
на слое происходит уже единообразно следующим образом.
В итерационном цикле по / первоначально по формулам
C.10.1—3) определяются pV\ rO и и(/>. Далее от начальной плос-
плоскости s = s0 в общей итерации по т на различных плоскостях 8 =
=const вдоль слоя производится совместное интегрирование сис-
системы C.11.1, 2), C.36.1 ...3.39.1) и определяются w<l\ <p«\ W('\ у^п,
р@ и «(Z> = ]KAF2 — v2 — и;2)(' >. Далее итерационные циклы по /
и т повторяются до сходимости.
Отметим важность стандартного блока расчета одномерного не-
неравновесного течения с релаксационными параметрами уп, кото-
который постоянно используется при численном интегрировании вдоль
^иний тока пространственного течения. Расчет двумерных (плоских
и осесимметричных) течений происходит по тому же алгоритму, но
отпадает необходимость в решении системы C.11) и интегрирова-
интегрирования вдоль различных линий 0 = const. Для определения г и р на сле-
следующем слое при R = oo следует использовать формулы C.13) и
C.14), а составляющие скорости и и v находить по формулам
На каждом слое г|з = const после определения г и р по формулам
C.36.1) ... C.39.1) последовательно находятся при численном ин-
интегрировании по s, W, уп и р, а затем v я и по формулам C.58).
Отметим, что при расчете двумерных и пространственных те-
течений в формуле C.38) W необходимо заменить на и\Н\.
В случае изоэнтропического течения (равновесного или заморо-
замороженного) [см. формулы A.105)] последовательность расчета сле-
следующая: координата г и давление р определяются по формулам
C.13) и C.14). Поскольку из условия s = const известна зависи-
зависимость p = f(p), а, следовательно, из уравнений состояния h = h(p)T
121
то из этих соотношений определяются р, h и Ц7 = У^2(Л0— Л) и за-
затем из C.58) v я и.
3.4.2. Течения с подводом энергии. Многослойные течения
Рассмотрим метод расчета двумерных течений при наличии
подвода энергии. Пусть задана функция Q°(s), характеризующая
поток энергии вдоль линии тока. Примем также, что газ имеет по-
постоянное у- В этом случае первоначально определяются параметры
потока на начальном слое при заданном на этом слое r = ro(s) и
какой-либо из функций p = pQ(s), p = po(s) или u = uo(s). Пусть на
начальном слое гр = \р0 задано распределение давления p = po(s)y
а в начальном сечении s = s0 известна скорость и и плотность р. Тог-
Тогда, численно интегрируя на начальном слое уравнения A.76) и
A.79) по разностным схемам, описанным в 3.3.2 и 3.3.3, получим на
слое распределение плотности скоростей и и и и температуры. Име-
Имеем
4\ [(L Щ (±)(т') (Щ ] C.59)
Щ +() (Щ
YP ds Ji { YP j \ ds /m
C.60)
C.61)
C.62)
Представленная разностная схема является схемой Эйлера с пере-
пересчетом, позволяющая при итерациях по m в каждой точке (t+1)
определить все искомые функции на начальном слое. Действитель-
Действительно, из C.59) определяется полная скорость W, из C.60) —энталь-
—энтальпия, а затем из калорического и термического уравнений состоя-
состояния— плотность и температура (если энтальпия является нелиней-
нелинейной функцией температуры, то последняя может определяться, на-
например, с помощью метода Ньютона) и, наконец, из C.62) опре-
определяются составляющие скорости и и v.
Переход на все последующие слои осуществляется с помощью
формул C.13), C.14), позволяющих определить на слое r = r(s) и
p=p(s). Остальные параметры на слое находятся далее по форму-
формулам C.59) ... C.62). Если на начальном слое задано не давление,
а плотность или скорость, то остальные параметры определяются
по методу, изложенному в разд. 3.3.2 и 3.3.3, а метод расчета пос-
последующих слоев остается неизменным.
В координатах s, ty, 6 удобно проводить расчеты течений, содер-
содержащих поверхности тангенциального разрыва и разделяющие об-
области течения с различными физическими свойствами. Такого рода
расчеты проводятся без учета смешения слоев. При этом полная
122
энтальпия, полное давление и начальные значения концентрации
Уоп в слоях могут различаться.
Пусть до некоторой поверхности тока i[) = ajH газ имеет полную
энтальпию /ioiD>), полное давление pOi и начальные значения уОь
а от этой поверхности — полную энтальпию ho2(ty), полное давле-
давление рог и начальные значения у02. Припишем нижним параметрам
тангенциального разрыва индекс 1, а верхним — 2. Для опреде-
определения параметров с индексом 2 воспользуемся условиями равен-
равенства статических давлений Р\=р2 и равенства углов наклона ско-
скорости, которые должны выполняться на поверхности тангенциаль-
тангенциального разрыва. Тогда, интегрируя систему C.25) ... C.27), C.58) от
начальной плоскости s—s0 с использованием полной энтальпии
/гО2(г|)), полного давления р02 и начальных значений у0п2 для верх-
верхнего слоя, а также условия pi=p2, определим остальные парамет-
параметры и2, и2, рг и yn2i, Т2. После определения параметров с индексом
2 от поверхности тока а|з = г|)° может уже производиться расчет по-
поля течения при яр>гр° по аналогии с расчетом при г|з<г)H по фор-
формулам C.13), C.14), C.36) ... C.39), C.58). Особенно просто про-
производится определение параметров течения с постоянным показа-
показателем адиабаты.
3.4.3. Течение смеси газа и частиц
При численном решении обратной задачи теории сопла для
двухфазой смеси газа и частиц на оси симметрии сопла задается
распределение скорости газа, а во входном сечении — пара-
параметры газа и частиц. В результате численного интегрирования сис-
стемы уравнений, описывающих течение газа при наличии в нем
частиц конденсата, определяются параметры газа и частиц, линии
тока газа и траектории частиц с учетом взаимного влияния газа и
частиц. Одна из линий тока газа принимается за контур сопла, и
находятся предельные траектории и зона чистого газа. Описанный
ниже разностный метод позволяет по единому алгоритму рассчи-
рассчитывать до-, транс- и сверхзвуковую области течения.
В двухфазной смеси газа и частиц, в отличие от случая чистого
нереагирующего газа, необходимо решать две задачи Коши: од-
одну — в поперечном направлении для определения некоторых газо-
газодинамических параметров, другую — в продольном направлении
для нахождения остальных газодинамических параметров и пара-
параметров частиц. В результате решения обратной задачи определя-
определяются линии тока газа и траектории частиц. Линия тока газа при-
принимается за жесткую стенку сопла. В отличие от случая чистого
газа форма контура сопла, соответствующая некоторому расходу
газа, будет зависеть от параметров частиц, в частности от их раз-
размера.
Уравнения движения и энергии, описывающие течение газа при
наличии в нем частиц конденсированной фазы, отличаются от обыч-
обычных газодинамических уравнений тем, что в них в правые части
добавляются члены, учитывающие воздействие частиц на газ. К ним
123
добавляются уравнения движения частиц и теплообмена между
частицами и газом. В координатах -ф, s это система уравнений
A.109) ... A.113).
Система уравнений A.109) ... A.113) содержит 10 неизвестных
функций г, и, v, р, Т, р, us, vs, ps, Ts и является замкнутой.
Для нахождения траекторий частиц и плотностей р5 удобно
ввести функции тока для частиц o|)s по формулам
^. = purfJL_^.\^; C.63)
дх \ и us I cty
|f- = PAr. C.64>
Соотношения C.63) используются для вычисления траекторий
частиц ^s=const, a C.64) для определения плотности p(S.
Метод решения системы A.109) ... A.113) в рамках обратной
задачи аналогичен методу решения соответствующей системы урав-
уравнений в случае неравновесных течений [см. п. 3.3.1, 3.41] с той лишь
разницей, что несколько иным способом определяются начальные
данные на оси симметрии. В окрестности оси симметрии при двух-
двухфазном течении должно быть построено асимптотическое разложе-
разложение (как для плоского, так и для осесимметричного случаев), из
которого на оси симметрии определяются все параметры течения,
в том числе плотность частиц и производные (dv/dty)'12, (dus/da|))'/z
[см 2.4.3 уравнения B.120) ... B.125)].
Система B.120) ... B.125) решается следующим образом. Сна-
Сначала, численно интегрируя по х при заданной на оси скорости сис-
систему B.122), B.123), B.125) (которая эквивалентна системе со-
соответствующих уравнений неравновесного двухфазного течения в
одномерном приближении [см. 3.3.3]), определяем функции ро, ро,
^о, 7*08, «os, vas. Далее из B.120) и B.124) последовательно опреде-
определяем г0, v0, vOs и pos- Обычно предполагается, что при s = so течение
равновесно, т. е. uOs = uo, TOs = To, vOs = vo, a pos = poas/(l—as), где as —
массовая доля.
Для заданных uo(s) и у можно определить ро, То и р0 по газо-
газодинамическим функциям, а Vq из формулы B.120). Эти же началь-
начальные данные в сечении s = s0 используются и при решении полной за-
задачи с учетом того, что v=yfv0, vs—VtyvQs.
После определения всех параметров на оси симметрии по асимп-
асимптотическим формулам типа B.71) производится расчет параметров
на ближайшей к оси линии тока газа, с которой и начинается затем
численное интегрирование полной системы A.109) ... A.113). Отме-
Отметим, что в отличие от случая течения чистого газа с постоянным по-
показателем адиабаты, для которого асимптотическое разложение
типа B.71) используется лишь в осесимметричной задаче, для «от-
«отхода» от оси (из-за особенности типа v/r, которая отсутствует в пло-
плоском течении) в двухфазном неравновесном течении это разложе-
разложение необходимо как для плоского, так и для осесимметричного те-
течений.
124
Расчеты двухфазных течений в соплах можно проводить двумя
способами. Первый способ состоит в точном решении системы
A.109) ... A.113) методом, описанным ниже, в результате которого
определяются все газодинамические параметры, параметры частиц,
их траектории, зоны чистого газа с учетом взаимного влияния час-
частиц на газ. При втором (приближенном) способе первоначально ре-
решается обратная задача для чистого газа с некоторым эффектив-
эффективным постоянным показателем адиабаты у0 [см. формулу C.53)], со-
соответствующим равновесному течению смеси газа с частицами
(W=WS, T = TS), и определяются все параметры течения в до- и
сверхзвуковой областях [27]. При этом предполагается, что пара-
параметры газа, несмотря на запаздывание частиц, остаются такими
же, как и в случае равновесного течения, при котором частицы
оказывают на параметры газа наиболее „сильное" влияние. Най-
Найденные параметры газа используются далее для расчета траекто-
траекторий и параметров частиц по формулам A.18). Очевидно, что вто-
второй способ является значительно более простым.
Рассмотрим теперь численный метод решения полной системы
уравнений A.109) ... A.113). После определения всех параметров
на близлежащей к оси линии тока начинается численное интегри-
интегрирование полной системы. Для этого из системы A.109) последова-
последовательно определяются на (я+1)-м слое в первой итерации г, v и р.
Затем вдоль («+1)-го слоя, начиная от плоскости s = s0, произво-
производится численное интегрирование системы A.110) ... A.113) и после-
последовательно определяются функции W, T, us, vs, Ts, ps. В сечении
s = sQ течение принимается равновесным, т. е. параметры частиц
полагаются равными параметрам газа. При интегрировании урав-
уравнений A.112) используются неявные разностные схемы [см. разд.
3.3.3], поскольку эти уравнения имеют вблизи равновесия вид урав-
уравнений с малым параметром при старшей производной, особенно при
малых размерах частиц. Далее, как обычно, итерации повторяются
до сходимости с заданной точностью. После определения парамет-
параметров течения выделяются траектории частиц каждого размера и на-
находятся их предельные траектории, выше которых отсутствуют час-
частицы этого размера. В области выше предельных траекторий рас-
расчеты для системы A.109) ... A.113) повторяются, но уже без учета
частицы этого сорта. Выше последней предельной траектории, со-
соответствующей частицам минимального размера, рассчитывается
зона чистого газа.
Из уравнений A.109) г, р, v определяются в первом приближе-
приближении по формулам C.13) ... C.15.2). Далее, с использованием уже
вычисленных значений г, v, p система уравнений A.110) ... A.113)
интегрируется вдоль слоя, начиная от начального сечения s = s0.
При этом для аппроксимации уравнений A.110), A.111) использу-
используется разностная схема типа C.54), C.55), а при интегрировании
уравнений A.112) использовались неявные разностные схемы
[C 56), C.57)].
125
3.4.4. Течения газа при наличии электромагнитных полей
Для расчета течений газа с наложенными электромагнитными
полями используем криволинейную ортогональную систему коорди-
координат (гр, а) [формулы A.114) ... A.116)].
Имеем
*!=-2«_; C.65)
д<\> РГ2
^ C.66)
C.67)
W { ds ds ) р
NPof*, . C.68)
gp
,„7 dx
- C-70)
Система C.65) ... C.70) приведена к безразмерному виду путем от-
отнесения давления и плотности к соответствующим параметрам тор-
можения рои poi во входном сечении, скорости — к aOi—]/ Y/WPon
линейных размеров — к некоторой характерной длине L, функции
тока — к poiaOiL2, электропроводности — к о0\, индукции — к вели-
величине индукции Воо в центре цилиндрической системы координат,
электромагнитной силы — к a0iaoi^oo2- При этом параметр МГД-вза-
имодействия N, входящий в систему уравнений, определяется по
формуле 7V = aolZ.Z?oo/poi«oi-
Проекции пондермоторной силы на оси s и г|з равны
C.71)
f^^{ + xr + xr . C.72)
При численном решении обратной задачи на начальной линии
тока i|" = i|)o задается распределение давления, уравнение линии то-
тока r = ro(s), x=xo(s) и распределение индукции магнитного поля
B = Bq(x). Так же как и в случае пространственных и неравновес-
неравновесных течений, обратная задача расщепляется на две задачи Коши.
Для уравнений C.65) ... C.67) она решается в направлении тр, а
для уравнения C.68) в направлении s; при этом начальное условие
для уравнения C.68) должно задаваться в начальном сечении
126
сопла s = s0. Последовательность решения задачи следующая. При
известном уравнении начальной линии тока и распределении дав-
давления на ней из C.68) определяется полное давление ро- Это сра-
сразу позволяет оценить потери полного давления за счет джоулева
нагрева газа. Имеем
) \ [\ C.73>
gp
Все входящие под знак интеграла функции в силу граничных ус-
условий суть известные функции s. Далее из C.69) ... C.72) опреде-
определяются ро, р, W, и и и на начальной линии тока i|H. При определе-
определении величин на следующем слое в начале из уравнений C.65) ...
C.67) находятся r = r(s) x = x(s), p = p(s) с помощью, например,
разностной схемы, описанной в 3.1.2, а далее определяются все
остальные неизвестные параметры в той же последовательности,
что и на начальной линии тока. Так рассчитывается все поле те-
течения в окрестности начальной линии тока и определяется геомет-
геометрия линий тока, каждую из которых можно принять за контур>
сопла.
3.5. МЕТОД ХАРАКТЕРИСТИК
С появлением ЭВМ широкое распространение для решения за-
задач сверхзвуковой газовой динамики получил метод характеристик.
Этот метод, по-существу, является основным при профилирова-
профилировании сверхзвуковых каналов, в том числе обратным методом.
Метод характеристик обладает определенными преимуществами
перед другими численными методами, поскольку, как правило, ус-
устойчив. На характеристических линиях упрощаются уравнения, ко-
количество независимых переменных уменьшается на единицу. Гра-
Граничные точки, точки на ударной волне и свободной границе рас-
рассчитываются независимо друг от друга, и поэтому в отличие, ска-
скажем, от метода сеток здесь отпадает необходимость в использова-
использовании прогонки. Но главное преимущество метода характеристик за-
заключается в том, что в нем учитывается распространение возмуще-
возмущений; это позволяет строго учитывать такие явления, как центриро-
ганные волны разрежения, висячие ударные волны, контактные по-
поверхности. И, наконец, в методе характеристик обычно выстраива-
выстраиваются линии тока, вдоль которых интегрируются уравнения, описы-
описывающие протекающие в потоке физико-химические процессы.
Вместе с тем нельзя не отметить, что значительное усложнение
логики вычислительного алгоритма в случае образования в потоке
многочисленных поверхностей разрыва делает целесообразным при-
применение метода характеристик для таких задач газовой динамики,
в которых приходится иметь дело с относительно небольшим коли-
количеством образующихся поверхностей разрыва. К их числу относят-
относятся и задачи профилирования сверхзвуковых каналов.
В методе характеристик возможны разные способы построения
характеристической сетки. В прямой (или классической) схеме ме-
127
тода характеристик характеристические линии проводятся вперед
в направлении скорости потока в рассматриваемой точке, а узлы
сетки определяются в процессе расчета как точки пересечения ха-
характеристических линий. При такой схеме точно учитывается рас-
распространение слабых разрывов. Недостаток этой схемы состоит в
том, что узлы характеристической сетки располагаются в поле те-
течения неравномерно. Поэтому для получения нужной точности в
процессе расчета приходится перераспределять узловые точки.
Разработаны также схемы численного метода характеристик с
сеткой обратного типа (так называемый послойный или сеточно-ха-
рактеристический метод). В этой схеме расчет ведется по слоям,
причем на каждом слое узловые точки фиксированы. Характерис-
Характеристические линии проводятся в направлении, обратном направлению
скорости, т. е. от рассчитываемого слоя к предыдущему, на кото-
котором уже известны параметры течения.
При этом численное интегрирование уравнений газовой динами-
динамики осуществляется в направлении вниз по потоку. Использование
сеточно-характеристического метода позволяет проводить расчеты
без явного выделения разрывов небольшой интенсивности. Однако
для решения обратных задач профилирования использование се-
сеточно-характеристического метода по слоям -ф = const в ряде слу-
случаев невозможно (например, решение задачи Гурса в областях III,
IV и двухграничных смешанных задач в II на рис. 1 3). В связи с
этим возникает необходимость в разработке сеточно-характеристи-
сеточно-характеристического метода, приспособленного для численного профилирования
каналов. При этом вместо фиксированных слоев х = const выбира-
выбираются слои ip = const, что делает удобным использование данной
модификации для решения задач профилирования с граничными
условиями на линии тока L.
3.5.1. Классический метод характеристик
Рассмотрим уравнения характеристик для стационарных дву-
двумерных вихревых изоэнергетических течений совершенного газа.
•Определим энтропийную функцию как S = \np/p\—у^пР/рь где pi,
pi— характерные значения давления и плотности. В дальнейшем
сбудем использовать следующую сокращенную запись уравнений ха-
характеристик и уравнения для функции тока.
dy~m±dx; Ed\ + Kd% ± L±dx + QdS = 0; C.74)
dy = mddx; dS=0; C.75)
rf<|)=± U-y± dx, C.76)
чп n a ryj 0 t • m + "^ * F •
a J\\~ 111/ ^, iIV— ¦ j b )
K= ^ ; L± = v z- ; C.77)
(P ± 5) У
=Bj,).e
128
В этих формулах верхний знак соответствует характеристикам пер-
первого семейства, нижний — характеристикам второго семейства, v =
= 0,1 для плоского и осесимметричного течения соответственно.
Для дальнейшего необходимы будут также формулы для оп-
определения параметров за ударной волной. В случае совершенного
газа можно вычислить значения параметров g, р и 5 за ударной
волной по следующим формулам:
C.78)
]1/2; C.79)
C.80)
Здесь индексом 1 обозначены параметры газа перед ударной вол-
волной, б — угол поворота потока в ударной волне.
Численный расчет сверхзвукового течения методом характерис-
характеристик сводится к последовательному решению отдельных элементар-
элементарных задач, связанных с определением координат внутренних и гра-
граничных узлов характеристической сетки и параметров течения в
этих узлах. При решении этих задач узлы характеристической сет-
сетки определяются как точки пересечения отрезков прямых линий,
уравнения которых являются конечно-разностными аналогами со-
соответствующих дифференциальных уравнений направления. Этими
линиями могут быть отрезки характеристик первого или второго
семейства, линий тока или ударных волн. Параметры в искомом
внутреннем узле характеристической сетки определяются с по-
помощью условий совместности вдоль характеристик, а в граничном
узле — с помощью условий совместности и соответствующего гра-
граничного условия.
Рассмотрим элементарные задачи, которые встречаются при про-
профилировании. К ним относятся: расчет точки внутри поля течения;
;на оси или линии симметрии; на свободной границе; на линии тан-
тангенциального разрыва; в неравномерном потоке на висячей и отра-
отраженной ударных волнах. Кроме того, необходим расчет центриро-
центрированной волны разрежения, а также расчет взаимодействия расши-
расширяющейся струи и спутного потока на кромке сопла. Некоторые из
этих элементарных задач характерны для расчета и других типов
сверхзвуковых внутренних струйных и внешних течений и подроб-
подробно рассмотрены в литературе (см., например, [1, 27, 32]).
Расчет внутреннего узла. Пусть необходимо определить пара-
параметры в точке 3, лежащей на пересечении характеристик первого
A—3) и второго B—3) семейств, проходящих через точки 1 и
2 с известными параметрами (рис. 3 2, а). Заменив в C.74)...
C.76) дифференциалы конечными разностями, получим
xs=xi-\ —z — ;
5—1393 129
3 В
Рис. 3 2. Схема расчета параметров в узлах характеристиче- (
ской сетки
О — узлы характеристической сетки; ф — вспомо-
вспомогательные точки
— х2);
C.81)
Е23К13+Е13К2:
¦ [Е1гЕ23 (С2 -
Поскольку S = S(i|)), то для определения S3 линию тока можно не
строить, а найти ее с помощью квадратичной интерполяции по таб-
таблице значений S(^), которая составляется в процессе расчета при
переходе через ударные волны. В области течения без ударных
волн течение считается изоэнтропическим и 5 = const. В противном
случае, если поток в начальном сечении является неизоэнтропиче-
ским, эта таблица должна быть задана в качестве начальных ус-
условий. В формулах C.81) двойной индекс указывает, что данная
величина усреднена по значениям в соответствующих точках, на-
например mt3 = —(m.t-\-tnt).
Система C.81) решается методом последовательных приближе-
приближений, при этом в первом приближении вместо полусумм используют-
используются значения коэффициентов в соответствующих опорных точках /
или 2. Обычно приемлемая точность достигается за две — три ите-
итерации.
Если в опорных точках 1 и 2 наклон одной из характеристик
или обеих близок к л/2, т. е. величины р—? или р+? близки к ну-
нулю, то исходные уравнения характеристик и расчетные формулы
должны быть изменены во избежание больших погрешностей. На-
Например, если р—?жО, то уравнение характеристик первого семейст-
семейства и соответствующее уравнение для ip необходимо преобразовать
к следующему виду:
130
dx=m+dy;
C.82)
где m+= l/m+, a L+ и U+ получается из L+ и U+ путем замены мно-
множителя р—? на pS+1-
Всего возможно восемь вариантов расчетных формул в зависи-
зависимости от углов наклона характеристик первого и второго семейств,
что в определенной степени усложняет алгоритм расчета. В работе
[32] предложен достаточно универсальный алгоритм, независящий
от углов наклонов соответствующих характеристик.
Если точка 1 лежит на оси симметрии (см. рис. 3.2, б), то при
•у=1 расчетные формулы необходимо модифицировать, так как на
оси симметрии (г/ = ? = 0) коэффициент L+ имеет особенность типа
0/0. Устранить эту особенность можно различными способами.
Простейший способ состоит в том, что перед записью в конечно-
разностной форме условие совместности C.74) вдоль характерис-
характеристики первого семейства домножается на у. Тогда формулы для р3
и ?3 получаются аналогичными C.81), однако в них нужно поло-
положить
КК*
Z1+3=0; Qi3=±Q3. C.83)
Расчет точки на оси симметрии (при v=l), (см. рис. 3.2, в). В
этом случае г/з=Сз=1|'з=0. Для определения хъ, рз используем урав-
уравнение направления характеристики второго семейства и соответст-
соответствующее условие совместности, домножив его на у, поскольку в
этом случае в коэффициенте L~ также имеет место особенность.
Расчетные формулы имеют вид
^ [fa+LTlXa-xJ-QilSi-S!)]. C.84)
Точное значение 1))з = 0. Однако -ф3 можно вычислить также по фор-
формуле
fe = 1J2 — ?/23 (*3 — х2).
Отличие этого значения от нуля характеризует погрешность рас-
расчета.
Расчет точки на жесткой стенке. Пусть теперь точка 3 принад-
принадлежит стенке сопла (см. рис. 3.2, г), уравнение которой y = f(x).
Имеем
;
— /23
131
3=/(*3); C3=/'U3); 53=
Л13
Расчет точки на головной ударной волне в равномерном сверх-
сверхзвуковом потоке. Искомая точка 3 (см. рис. 3.2, е) лежит на пере-
пересечении ударной волны и характеристики первого семейства, прохо-
проходящих соответственно через известные точки 0 и 1. Пусть уравнение
ударной волны dyjdx = %. Расчет проводится подбором величины т3.
В первом приближении полагается тзA)=то. Координаты точки 3
определяются по формулам
C.86)
В данном случае поток перед ударной волной является равно-
равномерным и поступательным. Поэтому, положив ?i = 0, Si = 0, по фор-
формулам C.78) ... C.80) найдем ?, р и S в точке 3. Затем проверим
условие совместности на характеристике первого семейства 13.
C.87)
Для подбора величины тз, при которой удовлетворяется C.78), ис-
используется итерационный процесс.
После окончания итераций вычисляется величина
Y. + l
Расчет точки на ударной волне в неравномерном потоке.
Рассмотрим сначала алгоритм расчета точки на висячем скачке
уплотнения недорасширенной струи. Пусть рассчитана характерис-
характеристика первого семейства АВ, проходящая через точку С на висячем
скачке уплотнения, а также следующая характеристика до точки b
(рис. 3.2, е). Сначала, игнорируя наличие разрыва, характеристика
bb\ продолжается в область за скачком уплотнения. Для этого по
точкам b и с с помощью формул расчета внутренней точки рассчи-
рассчитывается точка Ь\, причем в качестве параметров в точке с, в ко-
которой имеется разрыв, естественно используются значения перед
скачком уплотнения.
Расчет как и выше, ведется подбором величины т. В первом при-
приближении xdl) = xc- Координаты точки d можно вычислить, напри-
например, по формулам C.86), если принять в качестве точек 1 и 2 точ-
точки b и с соответственно. Параметры потока в точке d перед удар-
ударной волной определяются квадратичной интерполяцией по точкам
А\, b и Ь\. Используя эти значения как параметры набегающего по-
132
тока и с помощью C.78) ... ,C.80), вычисляем параметры в точке
d за ударной волной. Затем проводим характеристику второго се-
семейства d2. Координаты точки е определяются по формулам рас-
расчета внутренней точки, а параметры потока квадратичной интер-
интерполяцией по известным точкам с, f и Ь\. Величина Га подбирается
таким образом, чтобы выполнялось условие совместности на харак-
характеристике de.
По-существу, аналогичный алгоритм используется и для расче-
расчета точки на отраженном скачке уплотнения, но здесь координаты
скачка определяются в результате пересечения линии скачка с ха-
характеристикой второго семейства, а для итераций %а используется
условие совместности на характеристике первого семейства.
Метод характеристик обобщается на случай неравновесных те-
течений, течений смеси газа и частиц и течений с электромагнитными
полями.
3.5.2. Послойный (сеточно-характеристический) метод
и его модификации
Применение классического метода характеристик сопряжено с
рядом неудобств. Одно из них заключается в том, что искомые ве-
величины вычисляются в узлах заранее неизвестной характеристиче-
характеристической сетки. На практике часто желательно знать распределения
параметров при фиксированных значениях х или я|э. При этом при-
приходится иметь дело с интерполяцией на заданные значения х или
¦ф, что усложняет программу. Иногда счет по характеристикам при-
приводит к очень неравномерному распределению узловых точек или
к сильному росту числа точек на характеристиках (например, при
расчете волны разрежения). Очевидно, что в подобных случаях не-
необходимо время от времени перераспределять точки на характе-
характеристиках, уменьшая в случае необходимости их количество. Эта
процедура также связана с интерполяцией. Наконец, следует от-
отметить, что вычислительный процесс логически сильно усложняет-
усложняется, когда течение газа сопряжено с образованием взаимодействую-
взаимодействующих друг с другом поверхностей разрывов. В этом случае целесо-
целесообразно применять так называемые методы сквозного счета (без
явного выделения поверхностей разрывов).
Послойный метод характеристик обладает свойствами методов
сквозного счета и позволяет без выделения рассчитывать ударные
волны небольшой интенсивности.
Что касается первого недостатка, то желание освободиться от
него привело к разработке так называемого послойного метода ха-
характеристик. Поясним идейную сторону метода на примере уравне-
уравнений C.74). Пусть имеется прямоугольная сетка с координатными
линиями, параллельными осям х, у. Предположим, что в узлах 5,
б, 7 слоя х—х, решение известно (рис. 3.3, а). Обозначим через 1,
2, 4 точки пересечения характеристик 1-го и 2-го семейств и линии
тока с линией x = xt и запишем C.74) в разностях. Имеем
133
Г)
Рис 3 3 Модификации сеточно-характеристического метода по слоям *=const
(а) и i|3 = const (б)
C.88)
3-51)=0; C.89)
-52)=0; C.90)
53 = 54. C.91)
Положим вначале параметры в точке 3, равными их значениям, на-
например, в точке 6; определим из C.88) координаты точек 1, 2, 4 и
вычислим в них интерполяцией по узлам 5, 6, 7 искомые функции.
Теперь из C.89) ... C 91) найдем в первом приближении |3, Рз, 53.
Далее уточним коэффициенты и повторим процесс.
Рассмотрим алгоритм построения модификации сеточно-харак-
сеточно-характеристического метода по слоям я|з = const (рис. 3.3, б). Пусть линия
тока 1|)г рассчитана, и требуется определить параметры в текущей
точке 3 следующей линии тока opt+i. С этой целью используются так
же, как и в схеме метода характеристик по слоям х=const (см.
рис. 3.3, а) уравнения линии тока, уравнения направления харак-
характеристик и условия совместности вдоль них.
Однако в отличие от метода характеристик по слоям х— const
С+ и С- характеристики (i—3 и 2—3 на рис. 3.3) выпускаются из
искомой точки 3 не вверх по потоку в противоположные по отно-
отношению к линии тока 4—3 направления (см. рис. 3 3, а), а в на-
направлении к ранее рассчитанной линии тока г|з„ в одну сторону по
отношению к отрезку 4—3 (рис. 3.3, б). Параметры в точках 1 и 2
находятся с помощью квадратичной интерполяции по узлам хп-и
хп, Xn+i. Выбор расчетных узлов на слое г|з,+1 и поперечного шага
Аг|) (или Ау) зависит от постановки конкретной задачи, вида рас-
расчетной области и требуемой точности. При этом легко строится по-
подвижная расчетная сетка по координате х. Например, производит-
производится сгущение разностной сетки по координате х около точек излома
образующей центрального тела или в окрестностях взаимодейст-
взаимодействия разрывов
134
Для разностной аппроксимации уравнения характеристик ис-
используют либо в форме C 74), C 75), либо в координатах (х, я|>)
в виде
dx=± __(ЛТ?ИФ,- = ± /±<*|>; C.92)
= 0. C.93)
Для численного расчета в переменных х, ip дифференциальные
уравнения C 92) C 93) записываются в конечно-разностной фор-
форме. Параметрам в точках 1, 2, 3, 4 будем приписывать соответст-
соответствующие нижние индексы. Тогда разностные уравнения направле-
направления характеристик C.92) для различных семейств примут вид
х3 — х1==/11зДф; -х3— Х2= — /гзДф. C.94)
Следует подчеркнуть, что при использовании переменных (х, ¦$)
формулу C.94) можно использовать в численном расчете независи-
независимо от ориентации отрезков характеристик 1—3 и 2—3 относительно
осей координат, что обеспечивает при численной реализации метода
на ЭВМ более простой алгоритм расчета в отличие от расчетных
формул при независимых переменных х, у.
Для данной модификации сеточно-характеристического метода
в переменных (х, г|з) разработан алгоритм расчета с выделением
ударной волны в потоке. При этом расчетная область разбивается
на подобласти гладкого течения, а при переходе через ударную вол-
волну используются соотношения на ней, выведенные с использовани-
использованием неравномерных параметров набегающего потока
Рассматриваемая модификация по слоям ^ = const также обла-
обладает преимуществами при решении обратной задачи профилирова-
профилирования Действительно, линия тангенциального разрыва является од-
одним из семейств разностной сетки, и выделение ее производится
автоматически Начало висячего скачка также легко определяется,
когда впервые начнут пересекаться характеристики одного семейст-
семейства, проведенные из соседних рассчитываемых точек на слое i^+i в
направлении к слою г|з(.
4. ТЕЧЕНИЕ ГАЗА В СОПЛАХ
И КАНАЛАХ СЛОЖНЫХ ФОРМ
4.1. ТЕЧЕНИЕ В ПЛОСКИХ И ОСЕСИММЕТРИЧНЫХ СОПЛАХ
4.1.1. Исследование до- и трансзвуковой областей сопел
с прямолинейной и криволинейной поверхностью перехода.
Течения Мейера и Тейлора
В рамках обратной задачи рассчитать сопла Лаваля с прямоли-
прямолинейной поверхностью перехода достаточно просто. В случае плос-
плоских и осесимметричных течений необходимо и достаточно для обес-
обеспечения прямолинейной звуковой линии задать на оси симметрии
распределение скорости, имеющее равную нулю первую производ-
производную в центре сопла (центр сопла — точка на оси симметрии, где
скорость равна скорости звука). Практический интерес к соплам с
прямолинейной звуковой линией связан с профилированием сопел
аэродинамических труб и сопел реактивных двигателей. Сверхзву-
Сверхзвуковую часть таких сопел можно профилировать независимо от до-
дозвуковой, поскольку прямолинейная звуковая линия является одно-
одновременно и характеристикой первого и второго семейств.
На оси сопла задавались следующие распределения скорости:
1 — W
W W{ur»=O,l; A=\0. D.1)
D.2)
1 +
1 — W
Здесь х заменено на s, поскольку рассматриваются плоские и
осесимметричные течения ci? = OHro = O. С распределением скорос-
скорости D.1) были проведены численные расчеты поля течения. Шаг
Аг|з = О,2-10~2, а узлы разностной сетки располагались в точках
х=0...0,16 (Д* = 0,02); 0.2..Д6 (Дх=0,05); 0,67; 0,76; 0,88; 1,00; 1,15;
1,40; 1,70; 2,00; 2,25; 2,50; 2,75; 3,00.
Результаты расчетов представлены на рис. 4.1, 4.2. На рис. 4.1
представлено семейство линий тока и линий H7=const. При W>0,2
и г|з>0,02 течение заметно отличается от одномерного. В окрестно-
окрестности прямолинейной звуковой линии, расположенной в плоскости
х = 0, при г°>0,25 в соответствии с решением разд. 2.5 возникла мест-
местная сверхзвуковая зона и вторая звуковая линия. Течение в этой
зоне изоэнтропическое. Между второй звуковой линией и прямоли-
прямолинейной звуковой линией газ первоначально разгоняется, а затем
тормозится. В окрестности звуковой линии линии тока практически
лараллельны оси.
На рис. 4.2 представлено семейство линий тока и линий W=
= const при распределении скорости D.2). Очевидно, что в окрест-
136
r,W
in
0,5
W-1
^=0,07
0,06
0,05
0,0't
__OJZ
1
tp=0,01
/
J
,105
Ц
I
1
I
0,11
^>
/
^0,12
n
r
10
0,S
0 x
-2,0
-1,0
a
Рис. 4 1 Течение в сопле с прямолинейной звуковой линией Линии тока (гр =
=const) и линии постоянной скорости (U7 = const). Распределение скорости D 1).
Распределение скорости:
1 — линия тока i|>=0,06; 2 — одномерная теория; 3 — ось симметрии; ф — эксперимент
Рис 4 2. Течение в сопле с прямолинейной звуковой линией. Распределение ско-
скорости D 2) Обозначения см рис. 4 1.
ности прямолинейной звуковой линии линии тока параллельны оси
на участке еще более протяженном, чем в предыдущем случае.
И в этом случае в поле течения возникает местная сверхзвуковая
зона, однако вторая звуковая линия имеет общую точку с прямоли-
прямолинейной звуковой линией на бесконечности, что следует также из
асимптотического решения, изложенного в 2.5.
Для экспериментальной проверки существования местных сверх-
сверхзвуковых зон в окрестности прямолинейной звуковой линии было
осуществлено измерение распределения давления на стенках сопел,
соответствующих линиям тока с г(з=О,02 и с ^ = 0,06 (см. рис. 4.1)
распределения D.1). Экспериментальное исследование течения в
этих соплах было проведено В. М. Жиравовым (рис. 4.3, 4.4) [25].
Было показано, что при наличии угловой точки в критическом сече-
сечении распределение давления в трансзвуковой области, расположен-
расположенной вверх по потоку от угловой точки, зависит от угла 0К (рис. 4.4).
Отличие измеренного распределения давления (светлые кружочки
для 6к= 12° и черные для 6к = 20°) от расчетного (сплошная кривая)
начинает проявляться при я<0,6. Распределение давления при
0к=12° отличается от расчетного при %>0,15 примерно на 5%.
При х<0,15 вблизи стенки происходит разгон потока до сверхзву-
сверхзвуковой скорости, соответствующей р/ро=ОД. Таким образом, экспе-
экспериментально показано существование зон с положительными гради-
градиентами давления и местной сверхзвуковой зоной, которые были пред-
предсказаны расчетом. Сопоставление расчетных и экспериментальных
данных для двух контуров сопел с i|5 = O,O2 и \|з = О,О6, рассчитанных
по распределению на оси D.1), показывает, что в небольшой окрест-
137
'А
0,9
0,5
¦¦»-»
\
1
\
\
v
1
-2,5 -2,0 -1,5 -1,0 -0,5
1,0 0,5
Рис. 4.3. Расчетное и эксперименталь-
экспериментальное распределение давления, отнесен-
отнесенного к давлению торможения, на кон-
контуре сопла. Распределение скорости
по оси D.1). Контур сопла соответ-
соответствует линии тока 1|э = 0,02
Рис. 4 4. Расчетное и эксперименталь-
экспериментальное распределение давления, отнесен-
отнесенного к давлению торможения, на кон-
контуре. Распределение скорости на оси
D.1). Контур сопла соответствует ли-
линии тока г]з = 0,06
ности критического сечения на распределение давления оказывает
существенное влияние наличие большого отрицательного градиента
давления на угловой точке сопла, который передается по дозвуко-
дозвуковой части пограничного слоя вверх по потоку. Кроме того, из ана-
анализа расчетных и экспериментальных данных и из данных, пред-
представленных на рис. 4.3 и 4.4, следует, что расчетные и эксперимен-
экспериментальные данные хорошо совпадают между собой в тех областях,
где влияние вязкости невелико.
В работе [27] расчеты поля течения проведены для следую-
следующих распределений скорости по оси симметрии
Г М—-г—; D.3)
arctg(ea*
D.4)
В формуле D.2) параметр Wx равен асимптотическому значе-
значению скорости в дозвуковой области на бесконечности, Woe — асимп-
асимптотическому значению скорости в сверхзвуковой области на бес-
бесконечности.
dW
Так как производная — в центре сопла отлична от нуля, то
поверхность перехода будет криволинейной, и расчет дозвуковой
и сверхзвуковой областей должен производиться совместно.
Типичный расчет поля течения в сопле Лаваля с криволиней-
криволинейной поверхностью перехода представлен на рис. 4.5. Распределе-
Распределение скорости на оси симметрии D.2) с 1^00=1,9, №оо = 0,1 и Ь = 3,5.
138
Рис. 4 5. Поле течения в сопле с кри-
криволинейной звуковой линией. Линии то-
тока (i|) = const) и линии постоянной скоро-
скорости (№ = const). Распределение_скорости
по оси D.3) при Woo =0,1, Ж» = 1,9,
&-' = 3,5. Распределение скорости:
/ — линия тока т|)"=0,06; 2 — одномерная тео-
теория, 3 — ось симметрии
На рис. 4.5 представлены линии тока, линии №=const, а также за-
зависимость скорости на линии тока i]; = 0,06, значения W, рассчитан-
рассчитанные по одномерной теории, и распределение скорости по оси, чер-
черными кружочками изображена звуковая линия, а светлыми-—ли-
светлыми-—линия 9 = 0. Основной результат этих расчетов состоит в том, что при
tj)>0,01 течение заметно отличается от одномерного как в дозвуко-
дозвуковой, так и в сверхзвуковой области, звуковая линия и линия 6 = 0
отклоняются вверх по потоку от центра сопла, так что на контуре
звуковая точка располагается вверх по потоку от минимального
сечения.
Изложим далее некоторые результаты параметрического иссле-
исследования течения в до- и трансзвуковых частях современных сопел.
Геометрию их можно характеризовать радиусом очертания линии
минимального сечения R2, углом наклона конического участка Эо,
радиусом сопряжения конического и цилиндрического участков Ri
и величиной п = го/г* (рис. 4.6). Ниже будет рассмотрено влияние
этих параметров на течение в дозвуковой и трансзвуковой областях
сопел.
Для определения течения в заданном контуре сопла (прямая
задача) можно, варьируя параметры, характеризующие распреде-
распределение скорости по оси подобрать их так, чтобы форма некоторой
линии тока полностью или частично соответствовала заданному
контуру сопла. В качестве исходного выбрано трехпараметрическое
семейство D.3).
Рассмотрим зависимости параметров течения в трансзвуковой
области от радиуса очертания критического сечения R2. Варьируя
параметры W^, Woe, b в распределении скорости D.3), можно подо-
подобрать их таким образом, чтобы окрестность критического сечения
имела форму дуги окружности с заданным значением R2. Было по-
показано, что величина R2 зависит в основном от значения первой и
второй производных в центре сопла. Отметим, что в одномерной
теории R2 зависит только от первой производной в центре сопла.
Для распределения скорости D.3) значения первой и второй произ-
производной в центре сопла равны
W40)=-b-*(W..-l)(l-W*){W~-Wa) ; D.5)
W" @)
-2 (W о
-W7oo) [2-
D.6)
139
• 1,6
* 1,65
А 1,д
A 1,31
° 1,32
x 1,33
Woo
0,2
0,15
0,1
0,09
0,08
0,07
b '
3,34
3,7
3,5
3,46
3,44
3,39
Ч -з,г -2fi -i,s -o,8 о л
Рис. 4 6. Геометрия контуров сопел в дозвуковой части
С использованием распределения скорости D.3) было рассчитано
семейство контуров сопл с у= 1,4, у которых W@) = 1,575, W" @) =
= 0, a W<x> + Wcc = 2. Полученные в результате расчетов контуры
сопел показаны на рис. 4.6. На рис. 4.6 и далее х = х\г*, г = г/г„. На
рис. 4.7 (обозначения рис. 4.6) показаны зависимости и и v транс-
трансзвуковой части сопла от R2. Из этих рисунков и результатов расче-
расчетов следует, что при варьировании 9о от 30° до 60°, Wx от 0,2 до 0,07
течение в трансзвуковой области практически не зависит от этих
параметров до значений г = 0,45, что соответствует значениям Rz~^
^0,4 г*. Зависимость от 0О и Woo (отметим, что степень поджатия
п= [<7(Woo)]~'''2) начинает проявляться при 6о^15° и W^0,3. Таким
образом, параметры течения в трансзвуковой области зависят в
основном от R2 (при i?2^0,5 г*) и слабо зависят от величины 0О и
л в диапазоне изменения Во от 30° до 60° и п от 2,5 до 6.
Для определения зависимости параметров трансзвукового те-
течения от /?2 при значениях y=M; 1.25 и 1,14 были рассчитаны кон-
контуры сопел с различными значениями #2 = 2,1; 0,5; 0,25г*. Значения
V -
1,0-0,1
0,9-
08-
-
I —
л-
a -
v;
1*
it
¦/ г
Рис. 4 7 Зависимость составляющих ско-
скорости и и о от г в трансзвуковой обла-
области
"х-0,35, V=l,4
J40
т
w
'@)
w
@)
w
@)
w
"@)
w
@)
@)
w
Таблица
/?2-0,25r*
@) W
4 1
@)
1,4 —1,5@,13) —0,35 —1,8@,185) —0,2 —2,05@,16)
1,25 —1,55@,13) —0,35 —1,85@,18) —0,2 —2,15@,18)
1,14 —1,6@,14) —0,2 —1,92@,18) —0,2 —2,35@,18)
0,2 —2,15@,15) 0,4
0,8 —2,3@,1) 0,3
0,8 — —
W @) и W"(Q), соответствующие этим величинам R2, приведены в
табл. 4.1 (в скобках указано Woo). Отметим, что указанные значе-
значения Rz получены для линии тока с if = 0,06.
На рис. 4.8 представлена зависимость давления на контуре, от-
отнесенного к давлению в критическом сечении, от относительного
радиуса г для R2 = 2ri, и различных значений Woo
Из рассмотрения этого рисунка и результатов расчетов следу-
следует, что при одинаковых W @) и W"@) форма трансзвуковой об-
области одинакова примерно до значений г= 1,15...1,2, и в этой об-
области значения р/р* практически не зависят от формы трансзву-
трансзвуковой области при г>1,2 и значений Woo. Интересно отметить, что
заметное отличие pip* от значений, рассчитанных по одномерной
теории, имеет место при Р<1,25. При 1,25<г< 1,5 р/р*, рассчитан-
рассчитанные по предлагаемому методу, не более чем на 2% превышают со-
соответствующие значения, рассчитанные по одномерной теории, а
при г> 1,5 это различие составляет не более 1 %.
Влияние показателя адиабаты на течение в дозвуковой и транс-
трансзвуковой областях также проиллюстрировано на рис. 4 8. Из этого
рисунка следует, что при одинаковой форме сопел значения при-
приведенной скорости в течениях с различными у практически не раз-
различаются, хотя значения р/р* могут различаться заметно. Таким
образом, если в сопле с заданной геометрией рассчитано поле ско-
скоростей с некоторым значением у, то результаты этих расчетов мож-
можно использовать и при других значениях у.
Проведенные расчеты позволяют построить зависимости некото-
некоторых важных газодинамических параметров от R.2 = R2lr* и у.
Из представленных на рис. 4.9 . 4.11 данных следует, что все
приведенные параметры довольно слабо зависят от у. Влияние у
несколько увеличивается при уменьшении R2.
На рис. 4.12 построены звуковые линии в соплах с различными
значениями R2. Как видно, при малых значениях R2 у звуковой
линии имеется точка перегиба, которая возникает из-за близости
угловой точки в поле течения.
В результате численного решения обратной задачи определяется
семейство линий тока и параметры на них как в дозвуковой, так и
и в сверхзвуковой областях сопла. Имея поле течения в сверхзвуко-
сверхзвуковой области, нетрудно рассчитать координаты характеристик в по-
поле течения и параметры на них. В переменных i|>, х уравнения ха-
характеристик определяются формулами A.122), A.123). По этим
141
р/р*
1fi
1,1
0,7
W
0,5
IT
•>
р/р*>.
— ¦
¦O-.
——
Dx_
M
ЦЭ9
1,5
2,0 F'
/
/
Г'1,1
/,
1,П.
У /
P-H
0,5
1,0
1,5
Рис. 4 8 Зависимость р/р* от относи Рис. 4 9 Зависимость коэффициента
тельного радиуса г=г/г, при Л2=2 и расхода [х от #2
различных Woo: эксперимент [18]
О—7 = 1,14,
X—V=1.25
— — ¦ одномерная теория
формулам были рассчитаны координаты и параметры на характе-
характеристиках 2-го семейства, выходящих из точки контура с 8 = 0, на
контурах с различными /?2 Результаты расчетов для различных R2
представлены на рис. 4.13 и 4.14. Из этих рисунков следует, что при
одинаковых R2 влияние у на форму и параметры характеристик не-
невелико, оно несколько увеличивается по мере уменьшения R2.
Немонотонность изменения ? на характеристиках, выходящих из
точки ? = 0 на контуре и приходящих на ось сопла (на оси ? = 0 в
силу симметрии) приводит к немонотонности изменения Р вдоль
характеристик. Первоначально р уменьшается, а затем начинает
расти. В плоском случае факт немонотонности изменения р очеви-
очевиден и следует из уравнения совместности, в осесимметричном слу-
случае— получен в результате численного расчета.
Предлагаемый метод позволяет рассчитывать контуры сопел в
трансзвуковой области с очень малыми R2, вплоть до таких, что
контуры сопел практически не отличаются от сопел с угловой точ-
точкой. При этом было установлено, что производная скорости в цент-
центре сопла dW/dx не превышает некоторое предельное значение
{dWjdx)*, соответствующее течению, содержащему угловую точку.
По результатам расчетов для осесимметричного случая (dW/dx)*=
^0,6...0,7, а для плоского ^0,5. Значение (dW/dx)* для осесиммет-
0,1
0
142
¦^
1,0
M L
1
1,0
1.5
°'2
0 J
i!^ Рис. 4.10. Зависимость координат звуко-
звуковой линии на контуре от Д2
О 0,5
1,5 Rz
Рис 4 11 Зависимость приведенной скоро-
скорости Кс и тангенса угла наклона скорости в
звуковой точке %„ на контур_е в минималь-
минимальном сечении от Яг
Рис 4 12 Звуковые линии в соплах с раз-
различными Лг'
/ — расчет и эксперимент при /?2 — 0,1
ричного случая находится в хорошем соответствии с эксперимен-
экспериментальными данными при измерении распределения скорости по оси,
возникающего при обтекании угловых точек.
Представленные выше результаты относятся к течению типа
Мейера, когда в потоке существует поверхность перехода через ско-
скорость звука, простирающаяся от стенки сопла до оси. Проследим
трансформацию течения в сужающейся части сопла при увеличении
перепада давления, т. е. переход от течения Тейлора к течению Мей-
Мейера. На рис. 4.15 изобра-
изображены звуковые линии в
сопле с i?2 = 2 в течении
Тейлора при задании ско-
скорости на оси сопла в виде
1 + Ах*
D.7)
где Wo — скорость в цент-
центре сопла. При таком зада-
задании скорости на оси соп-
сопла контур будет симмет-
симметричен относительно плос-
плоскости х = 0. При Wo-0,75
вблизи контура возникает
сверхзвуковая зона, раз-
г
0,5
\
ч
{\
^1=0,625'
—
о
0,2
0,1
0,6
0,8
Рис 4 13 Геометрия характеристик второго
семейства, выходящих из минимального сече-
сечения, при различных Я^ и у.
7= 1,4, О — 7=1 25 ф— 7=1.14
143
0,8
Рис 4 14. Параметры ча характеристиках второго
семейства, выходящих из минимального сечения при
различных Я2 и у
Е-tg е, р-УЛ*-1, —v=i 4
Рис 4 15 Форма звуковых линий в осесимметричном
течении Тейлора
-0,25
мер которой увеличивается с ростом перепада давления, тес рос-
ростом Wo, а значит, и Wx При Wo=\ сверхзвуковая зона простирает-
простирается от контура сопла до оси
В отличие от решения Тейлора (разд 2 4 2), которое справед-
справедливо лишь при больших Л2 (Лг>5) и согласно которому сверхзву-
сверхзвуковая зона всегда захватывает минимальное сечение, местные
сверхзвуковые зоны вначале изолированы и располагаются сим-
симметрично относительно минимального сечения и лишь при Wo>
>0,88 захватывают его Значению Wo = 0,75 соответствует Woo =
= 0,094, а значению W0=l соответствует №„, = 0,1014 В течении
Мейера для рассматриваемого сопла lFoo = 0,1015, т е переход от
течения Тейлора с замкнутой звукозой линией при W0=l к тече-
течению Мейера происходит при изменении скорости всего на 0,1%
4.1.2. Локальные зоны торможения
Как показывают результаты расчетов, зачастую в до-, транс- и
сверхзвуковых потоках, которые в среднем ускоряются, возникают
местные зоны торможения Исследование свойств потока в этих
областях и условий их возникновения весьма важно и с научной,
и с практической точки зрения. На практике возникновение зон
торможения может привести к нежелательному отрыву погранич-
пограничного слоя.
Известно, что при некоторых значениях Ri в дозвуковой части-
сопла в окрестности точки сопряжения радиусного и цилиндриче-
цилиндрического участков возникает зона торможения, величину положитель-
положительного градиента давления в которой можно характеризовать коэф-
коэффициентом давления ср = 2(р—p«.)/pooUoo2, где параметры с индек-
индексом оо относятся к набегающему дозвуковому потоку.
На рис. 4.16 представлены типичные контуры сопел в дозвуко-
дозвуковой части сопла с различными Ri и распределение ср на них Как
144
\
V
-0,4
-J
-1
о
Рис 4 16 Геометрия контуров сопел в дозву-
дозвуковой части сопла и распределение коэффи
циента ср на этих контурах
/?i=15r0, X — #i = l,2r0, O—Rl = Q,7r0; A — R, = 0 5rs
видно, начиная с некото-
некоторого значения i?b моно-
монотонное ускорение потока
сменяется торможением
на некотором участке и
затем последующим уско-
ускорением. Как показали
специальные эксперимен-
экспериментальные исследования [18]
и специальные расчеты,
максимальное положи-
положительное значение cvm за-
зависит в основном от Rx и
весьма слабо от 8о, п и y-
Сравнение расчетных
(сплошная линия) и экс-
экспериментальных данных,
представленное на рис.
4.17, показывает их хорошее соответствие. Из расчетов видно, что
для любого п можно выбрать достаточно короткий контур сопла,
ье содержащий в этой области зон торможения (например ниж-
нижний контур на рис. 4 16).
Выше уже были приведены примеры возникновения местных
зон торможения в трансзвуковой области в окрестности прямоли-
прямолинейной звуковой линии Характерная особенность их состоит в том,
что эти зоны являются местными сверхзвуковыми зонами, соседст-
соседствующими либо с областью звукового, либо с областью дозвукового
0,3G
0,32
0,28
0,20
0,1 В
\
i
V
p
0,3
0,2
0
X
X
x>"
/2
A
XXX
iП
t 1
' x
n
\
J
0,5"
1,0
а
1,5
-0,8 -Ofi
Oft x/r.
Рис 4 17 Сравнение экспериментальных и расчетных данных
а — зависимость сv от R\ б — коэффициент давления ср
в окрестности точки
сопряжения цилиндрического и конического участков сопла полученный из расчета (сплош-
(сплошная линия) и эксперимента при #i=O,6ro(X), #i=0,8r0(O) и #1=1,2г„(Л)
145
41=0,08
0,1896 ОМ
| O,Wt
~^~ 0,02
0,01
W=O,WS
f
1,0
п <г
ag
! ¦
.
—¦—
-¦ —
0,11 \0,12 \Ц5 Ш W В} О]® 1,2 у
г
^ —
W=7,4
Рис 4 18 Поле течения
в сопле с криволинейной
звуковой линией Рас-
Распределение скорости по
оси D 4) Линии тока
(i|) = const) и линчи по-
постоянной скорости (W =
=const)
1—распределение скорости
на линии тока т|) = 0,08 2 —
одномерная теория 3 — ось
симметрии ф — линия М —
= 1 0 — 8 = 0
-1
1
течений, и расположены они вверх по потоку от минимального сече-
сечения Специальное исследование течения в этих зонах, проведенное
в рамках идеальной жидкости Ю. Б. Лифшицем и В. И. Киреевым,
которые решили прямую задачу в контурах сопел, полученных из
решения обратной задачи (см. рис. 4.1, 4.2), показало устойчивость
течения по отношению к малым возмущениям (ошибки округления
и аппроксимации) при условии, что с высокой точностью (до
0,1%) выдерживается геометрия контура, полученная из обратной
задачи. С другой стороны, экспериментальное исследование также
показывает существование этих зон (см. рис. 4.3, 4.4), хотя наличие
пограничного слоя несколько искажает расчетную картину течения.
Вниз по потоку от звуковой точки на контуре также возможно
образование местных зон торможения, если на небольшой длине
происходит резкое изменение угла наклона контура. Пример такого
течения представлен на рис. 4.18, на котором показано поле тече-
течения при распределении скорости на оси D.4) с Woo = 0,\; a = 2,3;
6 = 0,2. Кривая 1 соответствует распределению скорости на линии
тока \]; = 0,08. Весьма интересно исследовать возможность появления
зон торможения в развитом сверхзвуковом потоке, в частности не-
непосредственно за точкой излома контура (угловой точкой), которую
обычно располагают в минимальном сечении. В плоском случае
этот вопрос может быть исследован аналитически. Показано, [27],
что уменьшение числа М. вдоль начального участка характеристики
второго семейства, связанное с криволинейной формой звуковой
линии, приводит в плоском случае к тому, что на контуре сверхзву-
сверхзвукового сопла с угловой точкой непосредственно за ней возникает
местная зона торможения. В осесимметричном случае этот вопрос
исследовался численно следующим образом
С использованием данных (см. рис. 4.13, 4.14) были рассчита-
рассчитаны характеристики веера волн разрежения, возникающего при
обтекании угловой точки с координатами х = 0, г=\. Полу-
Полученные таким образом характеристики веера волн разрежения
использовались далее для расчета течения в заданном контуре
146
1,2
1,0
-2,0
1,7
Рис 4 19 Распределение числа М в сопле с цилиндрическим насадком (а) и на
контуре плоского и осесимметричного сопла с угловой точкой при различных
Л2 (б).
1.4, v=0, 2 —Мо
М0=4,
55,
v=l
сопла, выбранного из семейства сопел с угловой точкой и с равно-
равномерной характеристикой на выходе, рассчитанного из условия пря-
прямолинейности звуковой линии и характеризуемого числом М на
выходе Мо.
Методом характеристик были проведены расчеты течения в
соплах с угловой точкой с различными числами R2 и у. Типичные
результаты расчетов представлены на рис. 4 19 для плоского (v =
= 0) и осесимметричного (v=l) случаев. Из этого рисунка сле-
следует, что лишь в небольшой окрестности угловой точки до ж=0,5 ...
0,6 распределение чисел М при наличии криволинейной звуковой
линии отличается от распределения чисел в сопле с прямолинейной
звуковой линией. На остальной части сопла при х~^\ распределе-
распределение чисел М в соплах с различными R2 не различаются. Этот факт
находится в соответствии с известными результатами о быстром
затухании начальных возмущений в сверхзвуковых соплах.
В осесимметричном случае, в отличие от плоского, при наличии
криволинейной звуковой линии в окрестности угловой точки не
возникает положительного градиента давления Отсутствие поло-
положительного градиента давления в осесимметричном сопле за угло-
угловой точкой связано, во-первых, с более сильным уменьшением
величины \d$ldx\2 в веере волн (производной от |3 вдоль характе-
147
ристики второго семейства), чем в плоском случае, а во-вторых, с
тем, что на начальном участке осесимметричного сопла с угловой
точкой с прямолинейной звуковой линией и равномерным потоком
на выходе угол наклона скорости первоначально увеличивается, а
затем уменьшается (в отличие от плоского сопла, у которого на
начальном участке угол остается постоянным). Отсутствие поло-
положительного градиента давления за угловой точкой в осесимметрич-
ном сопле показано экспериментально В. М. Жиравовым.
Вопрос о возможности возникновения положительного градиен-
градиента давления в окрестности угловой точки и в областях, где имеется
разрыв вторых производных на контуре, можно исследовать ана-
аналитически. Отметим, что зоны торможения возникают и в двух-
двухслойных течениях непосредственно за угловой точкой [см. гл. 5].
4.1.3. Решение прямой задачи как серии обратных
В работе [28] алгоритм решения обратной задачи приспособлен
к решению прямой задачи для до- и трансзвуковой областей соп-
сопла. В настоящее время насчитывается значительное количество
работ, посвященных решению прямой задачи [27]. Авторы этих
работ используют либо метод интегральных соотношений, либо
методы установления, либо методы разложения в ряд по величине,
обратной радиусу кривизны контура в трансзвуковой области. Ни-
Ниже описан иной метод, позволяющий, используя численный алго-
алгоритм решения обратной задачи, решать прямую задачу для всей
области до- и трансзвукового течений.
В основе этого алгоритма лежит предположение о том, что
действительные распределения скорости на оси симметрии для
двух близких контуров сопел различаются между собой пропор-
пропорционально различию соответствующих распределений скорости в
¦одномерном приближении. Тогда распределение скорости на оси,
соответствующее искомому контуру, находится по распределению
скорости для какого-либо известного контура и известным распре-
распределениям в одномерном приближении. Расчеты показывают, что
сходимость решения к искомому осуществляется после нескольких
приближений решения обратной задачи.
В работе [28] используются система уравнений в переменных
¦ф, х [см. A.106), A.107) с заменой s на х], однако для прохожде-
прохождения особых точек и уменьшения ошибок скругления к этой системе
добавляются члены типа членов искусственной вязкости и соответ-
соответствующим образом модернизируется метод расчета. Рассмотрим
детальнее алгоритм этой работы.
Чтобы уменьшить ошибки округления и добиться большей
устойчивости, особенно при больших градиентах параметров, при
счете к правым частям уравнений A.106) добавляются члены, со-
содержащие параметр сглаживания. Тогда система уравнений при-
примет следующий вид:
^i + v \z&rl+\dP= у dv jiP . 48
dif ?u "*" дх* ' <ty r" дх * дх* '
148
T-l
; р #; |
дх a v и \у - 1 у -1 У
Параметр сглаживания подбирается таким образом, чтобы ре-
решение полученной системы не сильно отличалось от решения ис-
исходной задачи, но в то же время счет становился достаточно
устойчивым.
Система дифференциальных уравнений D 8) аппроксимируется
следующей разностной системой:
Г ! +v I * +V 1 I
L
х (я+1)(.+1) ^±1) ,-1) (-+1) . D <
(ft) улФ [7 ! ^и \ i М <э« у*-1) 1 i
2 [\ ;¦' 5jc /mn \rv <?л: jm (я+ljj
П lT>mn 4- О/
Л2
; D.10)
(n + 1)
(ft) _ (ft)
(m+l) (я+l) (m—1) (л+l) tA 11\
— » (*-ll)
I/ Г
D.12)
——
OX }
„(ft). l ОГ \(ft) ц(й)
/от (я+l)
r. D.14)
Индекс (/fe) указывает номер итерации, h — шаг по х, Дг|з — шаг
интегрирования по нормали к линиям тока, fmn'=f('nh, гаДгр).
149
Расчеты по этим формулам проводятся следующим образом.
Сначала в первом приближении вычисляются в граничных точках
при т = 0, т=М Ут\п+\) и Рт\п^\) из уравнений
1Ут(п+1I = Утл "+-ДУ ——; h——Щ > С*. 10)
Рт(п+1) = Рт„ — \~г- {-—) + Т7т Г7~ Dlb)
Далее решается методом прогонки разностное уравнение
(i) ii+v 9Ги ^2 1г^(д) 12+V j ГгA)
(l)(+l)J ~ "ГД^ё7ь^оГ ("+1 +Lr(
А2 2 № Г 1 + v ,
(P«)J,0)lB+l) J
1<да<М-1. D.17)
l—o "•
При этом стоящие в правой части неизвестные величины с верх-
верхним индексом @) принимаются равными соответствующим вели-
величинам на п-м слое, после чего вычисляется производная dr/dx по
трехточечной схеме [5].
Значения pm\n+i) во всех внутренних точках (я+1)-го слоя
определяются из разностного уравнения
Р(т-1) (я+1) — 2( 1Н~о_д , 1Л _ ]Рт(п+1)-\-Р(т+1) («+!) =
I I dv\ , 1 / dv \o
(п+1)
А2
—а)
которое также решается методом прогонки После этого вычисля-
вычисляются В Первом Приближении Параметры «m^n+l). Vm\n+1)> Pm (л+1>
по формулам D.12) ... D.14) и производная |——] по трехто-
\ дх jm («+1)
чечной схеме. Аналогично вычисляются параметры во всех после
дующих итерациях.
Параметры течения в окрестности оси симметрии находятся
путем разложения решения в ряд по о|) (разд. 2 4 2).
Пусть задано в аналитическом или табличном виде уравнение
контура сопла г=г(х), при этом, как обычно, принимаем, что
г@) = 1.
Приведенные ниже примеры численного решения прямой зада-
задачи относятся к контурам, представленным на рис. 4 6, хотя разра-
разработанный алгоритм применим и для расчета сопел произвольной
формы. В качестве начального распределения скорости можно вы-
150
брать, например, распределение скорости, соответствующее одно-
одномерному приближению, при этом распределение скорости на оси
определяется из решения уравнения
I] D.19)
Согласно асимптотическому разложению в окрестности оси
сопла по i|), координата контура сопла в осесимметричном случае
при заданном распределении на оси определяется по формуле
Здесь
t Г(ХI
Г (X) dx у + 1
Их 2х(к) \ Г(Х) [ 2Х TY +
где р(А) —безразмерная функция давления.
Очевидно, что первый член в квадратных скобках соотношения
D 20) соответствует одномерной теории, второй член учитывает
уже двумерный характер течения. Как показали расчеты, контуры,
полученные по одномерной теории в дозвуковой области, распола-
располагаются ниже заданных. Это означает, что для построения распре-
распределения скорости, соответствующего истинному двумерному тече-
течению, можно подобрать некоторый контур, расположенный ниже
искомого, одномерное распределение для которого соответствует
двумерному для заданного контура. Отметим еще, что одномерная
теория позволяет достаточно хорошо «угадать» контур в трансзву-
трансзвуковой области вверх по течению от минимального сечения.
Из вышесказанного следует, что при выборе начального рас-
распределения целесообразно либо вычислять скорость по одномерной
теории для некоторого контура, расположенного ниже исходного,
либо определять скорость не из уравнения D.19), а из уравнения
D 20), считая, что левая часть есть известная функция от х. Ре-
Решать это уравнение необходимо каким-либо итерационным мето-
методом' либо методом Ньютона, либо методом хорд.
В работе [28] были использованы два способа задания
начального распределения: распределение D.3) и одномерное, со-
соответствующее некоторому контуру, расположенному ниже исход-
исходного. Последний выбирался следующим образом. Первоначально
рассчитывалось одномерное распределение, соответствующее иско-
искомому контуру, а затем координата х увеличивалась в некоторое
151
-4 -j -2-1 0 1
Рис 4 20 Распределение скорости (I) и Рис 4 21 Распределение скорости (I)
контур сопла (II) при решении прямой и контур сопла (II) при решении:
задачи как серии обратных I — одномер- прямой задачи как серии обратных,
ная теория Приближения Приближения:
X — 20 е, О — 30 е, ф — 40 е у^ — 1 е, О — 50 е
число раз без изменения скорости в точках. Такой выбор началь-
начального распределения позволял добиваться сходимости общего ите-
итерационного процесса и для крутых контуров. Корректировка
распределения скорости производилась по формуле
где
— одномерная скорость, соответствующая заданному кон-
туру, Хо — одномерная скорость, соответствующая текущему кон-
контуру, Х<2'— текущее распределение скорости на оси, ЯA) — уточнен-
уточненное распределение скорости перед проведением следующей итера-
итерации. Формула D 21) выражает тот факт, что разность между
двумя распределениями на оси, соответствующими истинным дву-
двумерным течениям, пропорциональна разности соответствующих
одномерных распределений скорости. В результате расчетов ока-
оказалось, что итерационный процесс оказался устойчивым и сходя-
сходящимся при малых ai^O.l ... 0,001. Точность расчетов заметно
повышается, если использовать разностную сетку с переменным
шагом Итерационный процесс продолжается до тех пор, пока
относительная разность между координатами исходного и текуще-
текущего контуров не станет меньше заданного числа ei
На рис 4 20, 4 21 представлены некоторые результаты расче-
расчетов. На рис 4 20 в качестве заданного контура выбран контур с
Я,= 1, R2=2, e° = 35°, го=2,5 [обозначения (см. рис 4 6)]. На-
Начальное распределение скорости на оси — растянутое одномерное.
Видна хорошая сходимость последовательных приближений в до-
и трансзвуковой областях Распределение скорости в трансзвуко-
трансзвуковой области, а также положение звуковых точек на оси и на
контуре, которые, как известно, зависят только от R%, хорошо сов-
совпадают с соответствующими значениями, полученными из решения
обратной задачи Аналогичные результаты получены и для более
крутых контуров Так, на рис 4 21 представлен контур с /?i = 0,7;
R2=\- 9°=70°; го=2,5. Здесь в качестве начального распределе-
152
ния скорости на оси выбиралось распределение D.3) с Woo = 0,1011,
? = 0,25 Видно, что и в этом случае имеет место хорошая сходи-
сходимость к заданному контуру. При больших значениях 6° и R2~l
расчет течения в рамках идеальной жидкости может оказаться не-
неправомерным, поскольку и в дозвуковой и в трансзвуковой
областях для столь крутых сопел возникает отрыв пограничного
слоя Рассмотренные выше случаи относятся к расчету осесиммет-
ричного течения Мейера, когда в потоке содержится звуковая ли-
линия, простирающаяся от стенки сопла до оси. Описанный алгоритм
был применен и к расчету осесимметричного течения Тейлора,
когда в потоке содержатся местные сверхзвуковые зоны. В этом
случае на оси распределение скорости задавалось в виде D.7).
Результаты расчетов для этого случая представлены на рис. 4.15.
В настоящее время описанный алгоритм реализован в виде
комплекса программ и позволяет рассчитывать контуры сопел в
дозвуковой области в диапазоне углов во от 10 до 50°, значений
R\jr0 от 0,3 до 2 и Rdr* от 0,25 до 3. Точность подбора координат
контура до 0,1%. В некоторой степени решение прямой задачи
приближенно может быть осуществлено с помощью табл 4 1 и
формул D 3), D 6) для распределения скорости D.3), что позво-
позволяет рассчитать контуры сопел с заданным значением R
4.2. ТЕЧЕНИЯ В КОЛЬЦЕВЫХ СОПЛАХ
И КРИВОЛИНЕЙНЫХ КАНАЛАХ
4.2.1. Течение в кольцевых соплах
Различные схемы осесимметричных сопел с кольцевым мини-
минимальным сечением (так называемые тарельчатые сопла, сопла с
центральным телом, сопла с прямолинейной верхней стенкой)
можно образовать из кольцевого сопла путем изменения отдельных
его элементов Существует три аэродинамические конфигурации
кольцевых сопел — с нулевым, положительным и отрицательным
наклонами минимального сечения (рис. 4 22, а, б, в). Кольцевые
сопла с нулевым наклоном минимального сечения подразделяются
на три группы, с внешним, внутренним и двойным (рис. 4 22, г,
д, е) расширением. Практическое использование кольцевых сопел
возможно в реактивных двигателях и в аэродинамических трубах.
Для расчета всех этих типов кольцевых сопел решается обрат-
обратная задача теории сопла (Овсянников А М, 1971 г.) Задается не-
некоторая аналитическая кривая /, являющаяся линией тока искомо-
искомого течения, на ней задается аналитическое распределение давления
(или скорости) в дозвуковой, трансзвуковой и сверхзвуковой обла-
областях, и для уравнений газовой динамики решается задача Коши.
При расчете течений в кольцевых соплах и криволинейных
каналах можно задавать в качестве кривой / одну из стенок, а
распределение давления (скорости) подбирать так, чтобы получа-
получалось требуемое течение (в качестве второй стенки выбирается под-
153
Рис 4 22 Различные схемы кольцевых сопел
АВ — звуковая линия, МО, NO, NO' — прямолинейные характеристики, NN', ММ' — харак-
характеристики веера волн разрежения
ходящая линия тока). Однако з большинстве случаев распреде-
распределение давления (скорости) бывает неизвестным и приходится для"
его оценки в первом приближении пользоваться одномерной
теорией.
Поэтому целесообразно в качестве кривой / брать линию тока
искомого течения с минимальным во всей области наклоном к ли-
линии, относительно которой ведется одномерный расчет, как имею-
имеющую наиболее близкие значения параметров неизвестного течения"
к параметрам, рассчитанным по одномерной теории.
В соответствии с изложенным выше для кольцевых сопел с
внешним и с внутренним расширением в качестве кривой / берется
цилиндрическая стенка сопла. Для расчета кольцевых сопел с
двойным расширением можно предполагать (хотя и не обязатель-
обязательно) наличие некоторой прямолинейной линии тока, параллельной
оси, и, беря ее в качестве I, строить течение в обе стороны от нее.
Выбор кривой / в случае сопел с наклонным минимальным сечени-
сечением характеризуется в основном тремя параметрами: координатами
входного и выходного сечений и углом а Течение в этом случае
также строитя в обе стороны от этой внутренней линии тока /.
Такой метод решения задачи Коши в обе стороны от начальной
поверхности предпочтителен и с точки зрения вычислительной
математики, так как позволяет рассчитывать с высокой точностью
большие области течения
Ниже приведены результаты численного расчета осесимметрич-
ного течения в дозвуковой, транзвуковой и сверхзвуковой обла-
областях кольцевых сопел с криволинейной поверхностью перехода с
154
-2
Рис. 4 23. Течение в кольцевом осесимметричном сопле с двойным расширением.
Линии тока (г|) = const) и линии постоянной скорости (W= const)
различным наклоном минимального сечения сопла для распреде-
распределения скорости на начальной кривой D.3). Показано, что течение
в кольцевом осесимметричном сопле сильно отличается как от
одномерного, так и от плоского случаев. В дозвуковой области
обнаружено возникновение положительных градиентов давления.
Следует заметить, что, задавая соответствующее распределение
скорости по /, можно рассчитать кольцевое сопло и с плоской по-
поверхностью перехода, перпендикулярной оси симметрии. В осесим-
осесимметричном случае невозможно течение с плоской звуковой поверх-
поверхностью, перпендикулярной оси симметрии. Для расчета кольцевых
сопел с внешним, внутренним и двойственным расширением в каче-
качестве / выбиралась прямая r;=const.
На рис. 4.23 представлено поле течения в кольцевом осесим-
осесимметричном сопле с двойным расширением с г/г=0,6 для распреде-
распределения D.3) с Woo = 0,\; Woc=l,9; 6=0,21. Расчеты проводились
по формулам C.13) ... C.16) с Дг|з = 0,2-10~2 при счете поля с r>rt
и Да|) = 0,Ы0~2 при расчете поля с r<ri. Для расчета области те-
течения, расположенной близко к оси, полагалось Д^» 10~4.
На рис. 4.23 нанесены семейства линий тока, линии №—const,
звуковая линия (черными точками) и линия 8 = 0 (светлыми точ-
точками). Любые из этих линий тока могут быть выбраны за стенки
сопла. Течение для r^rt соответствует течению в кольцевом сопле
с внешним расширением, а течение с rs^n — течению в кольцевом
сопле с внутренним расширением.
Как показали специальные расчеты, малые изменения формы
линии тока, расположенной вблизи оси симметрии перед иглой
155
Рис 4 24 Сравнение контуров коль-
кольцевых сопел в плоском, осесиммет-
ричном и одномерном течениях
центрального тела, практически
не влияют на течение в кольце-
кольцевом сопле с осевой симметрией, а
поэтому возможно укорочение иг-
иглы центрального тела без сильно-
сильного влияния при этом на поле те-
течения. Звуковая линия и линия
6 = 0, как следует из рис. 4.23, от-
отклоняются вверх по потоку, так
что звуковая точка на кривой I
располагается за минимальным
сечением. Причем в случае коль-
кольцевых сопел с внешним и внут-
внутренним расширением звуковая
точка на цилиндрическом участ-
участке располагается ниже по течению, чем все остальные, а отклоне-
отклонение звуковой линии вверх по потоку на внешнем контуре сопла с
двойным расширением больше, чем на внутреннем. Распределение
давления на I мало отличается от одномерного, особенно в диапа-
диапазоне скоростей от 0 до 1,6 (р>0,25).
В области малых дозвуковых скоростей, где контур практически
прямолинеен и параллелен оси симметрии, возникает зона с поло-
положительным градиентом давления. Из результатов расчета следует,
что на всех линиях тока, начиная с линий тока с i|)=0,03 и г|з =
= —0,02, имеется положительный градиент давления, увеличиваю-
увеличивающийся с уменьшением радиусов Rz, R^. Так, на линии тока с тр ====
= 0,06 максимальное значение ср=0,14, на линии тока с ^ = 0,08
оно равно 0,4, а на линии тока с г|з = 0,10 максимальное значение
Положительный градиент давления на этих линиях тока может
быть устранен, если использовать контуры, которые достаточна
плавно выходят на заданный радиус входа в дозвуковую часть
сопла. На линиях тока, расположенных в окрестности оси симмет-
симметрии, положительный градиент давления больше, и возникает из-за
наличия центрального тела. При г|)= —0,028 максимальное значе-
значение Ср = 0,36. Устранение положительного градиента давления в
этой области затруднено, так как применение более плавных пере-
переходов ведет здесь к использованию острых игл, что в области
высоких температур нежелательно.
На рис. 4.24 представлено сравнение контуров, полученных при
решении обратной задачи в осесимметричном (кривая 1), плоском
(кривая 2) и одномерном случаях (кривая 3). Координаты конту-
контуров в районе минимального сечения совпадают с точностью 1%.
Видно, что в первом приближении одномерный случай по контуру
дает неплохой результат.
Для расчета кольцевых сопел с наклонным минимальным сече-
сечением в качестве кривой I выбиралась функция, получаемая от сгла-
сглаживания ступеньки
156
1/2 (r+
х = 0;
jc<0.
D.22>
В качестве оператора сглаживания начальных данных приме-
применялся нормированный оператор свертки
D.23>
2 = 1 exp
-5
52-?2
d\.
D.24>
Из D.22), D.23) нетрудно получить угол наклона линии тока / к
оси симметрии в точке, где w= 1
9/=-arctg
(r+ — г-) е
-t
D.25>
Следует заметить, что использование оператора D.23) позволя-
позволяет в качестве начального распределения скорости (давления)
использовать кроме известных аналитических функций и распреде-
распределения, получаемые из эксперимента.
На рис. 4.25, 4.26 представлено семейство линий тока, линии
№=const, звуковая линия (черными точками) и линии 6 = 6г
Рис. 4 25. Течение в кольцевом осесимметричном сопле с двойным расширением-
с наклонным минимальным сечением
157"
-1
о
Рис 4 26. Течение в кольцевом осе-
симметричном сопле с двойным рас-
расширением с наклонным минимальным
сечением
чениями г|). Так, на линии тока с гЬ =
(светлыми точками). На рис.
4.25 кривая /, определяемая из
D.22), D.23), имеет г+=1,0;г_=
= 0,5; 9г = —13° {t = 5, 6 = 3), а
распределение скорости на / за-
задается по D.3) с Wx = 0,06;
Woa=l,9; b = 0,2\.
На рис. 4 26 кривая / имеет
г+ = 0,5; г_ = 2,0; 6г = 35° (? = 5,
6 = 3), а распределение скорости
на I рассчитано по D.3) с Wx =
= 0,1; Wx=l,9; 6 = 0,30.
Видно, что звуковая линия мо-
жег смещаться как вверх, так и
вниз по потоку, но выпукла в сто-
сторону сверхзвуковой области. На
цилиндрических участках в обоих
случаях также обнаружены поло-
положительные градиенты давления.
Их возникновение наблюдается
для верхней половины течения на
линиях тока уже с малыми зна-
01 ср = 0,08.
4.2.2. Течение в криволинейных каналах
^Течение в криволинейных каналах рассмотрено в рамках обрат-
обратной задачи в работах [21, 27]. Расчет течения проводится с исполь-
использованием уравнений, записанных в криволинейной ортогональной
системе координат [уравнения A.117) ... A.121)] по разностной
•схеме, аналогичной схеме, изложенной в разд. 3.1.2. Рассмотрим
первоначально результаты расчета радиальных сопел, в которых
происходит поворот потока на 90°.
Существуют три типа осесимметричных радиальных сопел: дис-
дисковые сопла (рис. 4.27, а), сопла с центральным телом с обычной
осесимметричной камерой (рис. 4.27, б) и кольцевые радиальные
сопла (рис. 4.27, в). Последний тип сопел является относительно
•общим случаем радиальных конфигураций. Радиальные сопла со-
состоят из двух контуров. Из технологических соображений необхо-
необходимо иметь по крайней мере один простой контур с образующей,
составленной из отрезков прямых и дуг окружностей.
Возьмем в качестве кривой /, на которой ставятся начальные
данные, кривую, составленную из дуги окружности
(х-0,3J+(г-0,75J =
г<0,75 D.26)
и полупрямых
158
= 0; г>0,75; г=0,45; х>0,3.
D.27)
Ось симметрии
а
_Ось симметрии
Рис 4 27 Геометрия радиальных сопел с поворотом потока на 90°
На этой кривой зададим распределение скорости в виде D.3) с за-
заменой в этой формуле х на ст.
Для радиальных сопел отрицательное направление криволи-
криволинейной оси 0о (направление потока) совпадает с направлением
ОСИ 0г.
В случае малых расходов возможны варианты дозвукового и
сверхзвукового разворота потока. На рис. 4.28 представлено тече-
течение в радиальном сопле с дозвуковым разворотом потока, при ко-
котором сохраняются характерные качественные особенности тече-
течений, обнаруженные в кольцевых соплах простых конфигураций
(см. предыдущий раздел). Как следует из D.3), при а=0 получим
значение скорости W=l. Эта звуковая точка на / располагалась
в месте сопряжения дуги с полупрямой, ортогональной оси сим-
симметрии, т. е. в точке с координатами х=0, у=0,75. Полагалось
также 1^ = 0,1; Woo =1,96 (т. е. на выходе М=3), 6 = 0,18.
Как и в случае кольцевых сопел с нулевым наклоном мини-
минимального сечения, звуковая линия (она изображена черными точ-
точками), смещается вверх по потоку от минимального сечения
(светлые точки) и выпукла в сторону сверхзвуковой области. На
цилиндрических участках в дозвуковой области обнаружено также
возникновение зон с положительным градиентом давления. Кроме
того, возникновение положительных градиентов давления наблю-
наблюдается и в сверхзвуковой части, что объясняется чрезмерным уско-
ускорением потока на соответствующих линиях тока. Так, на линии
тока с г|з = 0,032 имеется довольно большая область с положитель-
положительным градиентом давления при (Г>2,5. С уменьшением параметра b
в D.3), т. е. при уменьшении ускорения потока в областях выхода
скорости на постоянные значения, положительные градиенты дав-
давления, наблюдаемые в дозвуковой и сверхзвуковой областях тече-
течения, растут.
На рис 4 28 представлена также зависимость коэффициента
давления ср = 2(р—p±0o)/(pooW2ao) от х для дозвуковых областей и
от г для сверхзвуковых областей на линиях тока с г|э = 0,032 иф =
= —0,014. Максимальные значения коэффициента давления на
линии тока с г|) = 0,032 в дозвуковой и сверхзвуковой областях рав-
равны соответственно 0,13 и 0,017, а на линии тока с чр == —0,014 0,07
и 0,001.
159»
1,0
?,15
а,5
Ш,25
M=J
0,0111
0,005
1
У
о,т
Ср
0,10
0,05
О
1,0
3,5 г
L
\
V 0,032
симметрии
0,25
0,5
0,15 0,50 х
Рис 4 28 Геометрия и линии тока Рис 4 29 Геометрия и линии тока
радиального сопла с поворотом пото- радиального сопла с поворотом пото-
потока на 90° ка на 90°
В случае сверхзвукового разворота потока звуковая линия
-смещается вниз по потоку от минимального сечения и выпукла в
¦сторону дозвуковой области. Такое различие в смещении звуковой
линии объясняется разным действием центробежных сил, появляю-
появляющихся при развороте потока, что приводит к увеличению неравно-
неравномерности потока по сечению и к относительному подтормаживанию
его на линиях тока меньшей кривизны. Как показали результаты
исследования, поскольку величина центробежной силы пропорцио-
пропорциональна квадрату скорости потока, при увеличении параметра b
в D.3), т. е. с увеличением скорости дозвукового потока в области
минимального сечения, происходит более сильное относительное
подтормаживание потока на линиях тока меньшей кривизны, а зна-
значит и увеличение смещения звуковой линии. Следует заметить, что
-скорость этого смещения характеризует выпуклость звуковой линии
и зависит как от начальных данных, так и от кривизны линий тока
и значений скорости потока на них.
На рис. 4.29 представлено течение в радиальном сопле с на-
начальной кривой I, взятой в качестве стенки сопла и задаваемой, как
и выше, соотношениями D.26), D.27). Распределение скорости
задается по D.3) с параметрами W7<x,=0,3; FFcx.= l,96 (M==3); b —
160
= 0,35 и значением о=0 (W=l) при х=0, г=0,75. Из рис. 4.29
видно, что звуковая линия выпукла в сторону дозвуковой части
сопла
Как следует из формы звуковой линии, представленной на
рис. 4 29, в случае больших относительных расходов нельзя разде-
разделять сопла на варианты с дозвуковым и сверхзвуковым разворотом
потока. Само понятие критического сечения в этом случае теряет
смысл.
Как показали результаты расчетов, разрыв кривизны контура /,
имеющийся в точке сопряжения окружности с цилиндрической
частью центрального тела, не оказывает заметного влияния на
образование положительных градиентов давления. Вместе с тем с
уменьшением параметра b в D.3) область с положительным гра-
градиентом давления в окрестности точки А разрыва кривизны с коор-
координатами х=0, /-=0,75 уменьшается в поперечном течению на-
направлении. При этом уменьшается и радиус выходного сечения с
равномерными параметрами. Так, например, в случае, представ-
представленном на рис. 4.29 (при 6 = 0,35), положительный градиент дав-
давления появляется уже на линии тока с ^^0,03, а при значении
?=0,15 его появление наблюдается лишь при iJ)S^0,06. С уменьше-
уменьшением скорости в месте разрыва, что достигается увеличением га=0,
размеры области с положительным градиентом давления сокраща-
сокращаются вдоль линий тока. Если в случае, представленном на рис. 4.29
(с га=о=ГА = О,75), размеры области с положительным градиен-
градиентом давления в зоне точки А на линии тока с ар = 0,12 составляют
примерно 0,17 по длине кривой, то при r<j=o==O,87 они равны уже
0,085, т. е. в два раза меньше.
Следует заметить, что уменьшение параметра Ъ увеличивает
и минимальный радиус кривизны внешней линии тока. Уменьшение
скорости на входе Woo также уменьшает область с положительным
градиентом давления, появление которой наблюдается на более
далеких от / линиях тока. Однако в этом случае возникают поло-
положительные градиенты давления на цилиндрических участках в до-
дозвуковой части радиального сопла, что не позволяет рассчитывать
течения в соплах на большие относительные расходы.
Приближение линии / с фиксированной геометрией к оси сим-
симметрии приводит к увеличению влияния осесимметричности тече-
течения, а значит при сохранении распределения давления и к увели-
увеличению зоны с положительным градиентом давления, появление
которой наблюдается при меньших значениях г|). Увеличение же
радиуса поворота центрального тела при постоянном положении
точки А и постоянном распределении давления по / при га=о=гА
равносильно приближению линии / к оси симметрии с одновремен-
одновременным уменьшением линейного размера в D.3) в соответствующее
число раз и последующему такому же увеличению геометрических
размеров рассчитанного течения. Это увеличение радиуса поворота
сокращает размеры области с положительным градиентом давле-
давления, появление которой также наблюдается при больших значе-
значениях if.
6—1393 161
Основное требование, предъявляемое к радиальным соплам для
МГД-генераторов,— получение равномерного по сечениям радиаль-
радиального потока на выходе из сопла при достаточно малых радиусах
выходного сечения. В области входных и выходных сечений имеется
неравномерность параметров поперек сечений, характеризуемая
максимальным относительным различием давления на крайних
линиях тока. При повороте на 90° получается существенно нерав-
неравномерный по сечению поток, так что для получения равномерного
потока на выходе из сопла требуются значительные радиальные
размеры. В случае, представленном на рис. 4.29, приемлемая не-
неравномерность в 5% по давлению получается лишь при г^1,3.
Для сравнения отметим, что скорость звука на центральном теле
достигается при г=0,75. После поворота ускорение потока на
внешнем контуре меньше, чем на центральном теле.
Как показали результаты исследования большой серии ради-
радиальных сопел, с увеличением г в сечении г=const сначала дости-
достигается достаточно равномерный поток; затем равномерность дав-
давления нарушается (иногда на 7... 10%); далее в силу появления
зоны с положительным градиентом давления поток снова вырав-
выравнивается. Некоторая неравномерность давления (меньшая 3%) в
некоторых случаях остается и при г^4. При этом после мини-
минимального сечения сопло с увеличением г сначала расширяется, а
затем начинает сужаться, так как выбранное по D.3) распределе-
распределение скорости отвечает выходу потока на постоянное значение
давления.
Следует отметить, что выходное сечение сопла наиболее целе-
целесообразно выбирать в области, расположенной до зоны с положи-
положительным градиентом давления. Выбранное таким образом выход-
выходное сечение расположено немного дальше по г, чем сечение с мак-
максимальным расстоянием между стенками.
Для получения кольцевых сопел нулевой тяги необходимо
использовать симметричные радиальные течения. На рис. 4.30
представлено течение в таком кольцевом сопле нулевой тяги (обо-
(обозначения совпадают с предыдущими). Основная особенность такого
сопла состоит в том, что нулевая тяга в нем получается при всех
значениях радиуса выходного сечения независимо от степени нерав-
неравномерности потока. Однако некоторые трудности, связанные с мо-
моментом запуска и поддержанием стационарного режима течения,
говорят о том, что лучше использовать для этих целей два симмет-
симметрично расположенных радиальных сопла.
Если отсутствие ускорения потока на выходе из сопла не ст-^дь-
важно, но необходимо условие параллельности стенок на выходе,
то можно в качестве начального распределения давления (скоро-
(скорости) брать распределение, составленное из двух частей, например,
из D.3) и распределения, отвечающего сверхзвуковому плоскому
радиальному течению. Но в любом случае при выборе выходного
сечения следует учитывать и влияние пограничного слоя, если не-
неделается поправка контура.
162
-0.7 Т
О / 0,25
Ось симметрии
Рис 4 30 Геометрия и линии тока Рис 4 31. Геометрия и линии тока
радиального сопла с нулевой тягой радиального сопла с центральным те-
телом
Для расчета течений в радиальных соплах с центральным телом
с осесимметричной камерой в качестве начальной кривой / зададим
форму центрального тела и часть оси симметрии, расположенную
внутри течения.
На рис. 4.31 представлен пример течения в таком радиальном
сопле. В качестве начальной кривой / выбиралась кривая, состав-
составленная из отрезков прямых х=0, г^0,3; х^0,3; г=0 и дуги
окружности (х—0,3) 2+ (г—0,3J=0,32, соединяющей их.
На кривой / задавалось распределение скорости по D.3) с па-
параметрами: Wco=0,3; TFco=l,96 (M=3); 6 = 0,21 и значением
а=0 (№ = 1) в точке с координатами х=0, г=1,05. Использова-
Использовалась прежняя сетка. На рис. 4.31 представлен пример разворота
медленного дозвукового потока. Линия тока с г[з=0,028 довольно
близко подходит к угловой точке, образуя угол в 96°. Эта картина
показывает возможность расчета данным методом течений, близких
к течениям с угловыми точками. Следует заметить, что поджатие
потока внешним контуром в месте поворота течения на 90°
обусловлено требование непрерывного ускорения газа вдоль
части окружности на кривой /, вызванным начальным распределе-
распределением скорости. Подчеркнем, что в области, близкой к угловой
точке, точность счета существенно снижается, и подходить к ре-
результатам расчета таких течений с количественной стороны надо
особенно аккуратно.
6* 163
у////,
^7777,
r-o
r/////s
-0,020
-0,0
77777.
w
I
777T7
W=1,8
15
<Cu,,P 0,7
1,7
to г
имметр
I
r
uu
0,5
Рис 4 32 Геометрия, линии
тока и линии U7=const в
кольцевом сопле с поворо-
поворотом потока на 180°
-1,0
-0,5
0 X
Уменьшая радиус окружности центрального тела, в пределе
получим конфигурацию дискового сопла (см. рис. 4.27, а). Одна-
Однако распределение скорости по / в данном случае должно быть
другим, так как поток при подходе к плоскому экрану должен
тормозиться в окрестности оси симметрии, чтобы не было картин,
аналогичных представленной на рис. 4 31 с поджатием потока в
месте разворота. Это распределение можно брать либо из экспери-
экспериментальных данных, сглаживая его по методу, описанному выше,
либо из какого-нибудь аналитического распределения с W^(W>0)
в начале координат, отвечающего течению в требуемой конфигура-
конфигурации. В силу особенности, неустранимой даже переходом к какой-
либо другой записи основной системы уравнений, при г=0 нельзя
иметь точки торможения W=0. Но это, вообще говоря, и не тре-
требуется, так как малые изменения скорости в начале координат
слабо влияют на все течение.
Назовем линию тока, совпадающую с осью симметрии, идущую
затем по плоскому экрану дискового сопла, нулевой. Задачу о
расчете течения в дисковом сопле можно решать несколькими
способами. Наряду с описанной выше постановкой этой задачи в
координатах (ф, а) (назовем ее задачей 2), возможно решение
задачи Кеши в координатах (х, г) с начальным условием на плос-
плоском экране (назовем ее задачей У), а также с начальным услови-
условием на оси симметрии (которую назовем соответственно задачей X).
При этом целесообразно начальные данные для задач X и Y
ставить в симметричном интервале с заданием четной функции
распределения скорости или давления.
Так как при численном расчете мы имеем дело с дискретным
заданием функций, то и возможно при решении задачи Е такое
«независимое» задание распределений скорости (давления) по
плоскому экрану и оси симметрии. В самом деле, совокупности
164
дискретных точек задачи 2 отвечает другой аналитический много-
многочлен Лагранжа, нежели каждому слагаемому, являющемуся в от-
отдельности начальным условием при решении задачи Y и X соот-
соответственно.
На рис. 4 32 представлен пример течения в канале, поворот
потока в котором осуществляется на 180°. Из рассмотрения линии
W=const видно, что очень сильна неравномерность потока по се-
сечению. Интересно, что несмотря на узкие проходные сечения, на-
наличие центробежных сил при больших поворотах создает значи-
значительную неравномерность в потоке, в связи с чем использование
одновременного приближения для расчета течений в таких кана-
каналах оказывается совершенно неправомочным. Аналогичные резуль-
результаты получены также при расчете каналов, в которых дозвуковой
поток первоначально движется в направлении, перпендикулярном
оси симметрии, а затем переходит в сверхзвуковой, одновременно
поворачиваясь на 180°.
4.3. ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ С ЗАКРУТКОЙ ПОТОКА
Примем, что все параметры течения, кроме ф, есть функции
лишь двух независимых переменных (s и г|з). Будем считать также,
что R(s)= оо. Тогда из A-97) нетрудно получить, что
w(s, ф)/-E, <b)=C(<b) = wQ(sQ, <b)ro(s, а>); D.28)
St D.29)
га
где wo(so, ty) и ro(s, \р) значения функций w и г на начальной
плоскости. Уравнения A.95) ... A.104) в этом случае приобретают
точно такой же вид, как в осесимметричном течении без закрутки,
лишь в выражении для G(s, ij)) добавляется член w2/r, который
согласно D.29) является известной функцией от г, а в выражении
для W нужно учитывать и составляющую w. Уравнение D.29) слу-
служит для определения геометрии поверхностей тока. В координатах
а, \р система уравнений осесимметричного течения с закруткой
есть система A.117) . . A.121). Существенно, что если C(ij))=^=const
[см. D.28)] и <P°(iJ))^const [см. A.90)], то система A.95) ... A.104)
описывает вихревое неизоэнтропическое течение с закруткой. При
С(\|э) =const течение является безвихревым, а при Ф°(г|)) =const
еще и изоэнтропическим. В зависимости от вида функции С(г|з)
получаются различные законы закрутки' — от закона твердого те-
тела при С(']0~ у * до закона вихря при С(-ф) = const.
Ниже представлены некоторые результаты расчетов осесиммет-
ричных течений, полученных в работе [19] в рамках обратной зада-
задачи для течений в достаточно сложных каналах
Как известно, в радиальных МГД-каналах под действием лорен-
цовой силы происходит закрутка потока. В этом случае при расче-
расчете бесскачковых диффузоров необходим учет закрутки потока на
165
г
¦ffi
3,5
--ft
ш
-+Н-
III '' "
\
0,075-
0,015
! \ \
входе. Бесскачковый диффузор мо-
может быть получен путем обращения
потока в сопле с изоэнтропическим
течением, в котором отсутствуют
ударные волны.
На рис. 4.33 представлено тече-
течение в диффузоре с радиальным по-
потоком на входе при наличии безвих-
безвихревой закрутки потока. Там же точ-
точками показаны линии тока в случае
отсутствия закрутки, т. е. при
Ось симметрии
0,T 1,6'
Рис 4 33 Течение в радиальном
диффузоре при наличии закрутки
на входе
Если обратить течение и рас-
рассматривать представленную конфи-
конфигурацию как сопло с радиальным
т потоком на выходе, направленным к
—' оси симметрии, то при выбранном
Л распределении скорости D 3), отве-
отвечающем течению по / со скоростью,
стремящейся к постоянному значе-
значению, линии тока при малых значе-
значениях г в силу наличия осевой сим-
симметрии будут довольно сильно рас-
расходиться, поворачиваясь в положительном направлении оси Ох.
При этом поле потока будет сильно неравномерным по сечению,
причем с ростом \ty\ скорость в сечении резко увеличится. С уве-
увеличением скорости закрутки потока на входе в диффузор, т. е. на
выходе из обращенного сопла, неравномерность потока увеличива-
увеличивается. В связи с этим в качестве входного сечения диффузора
выбирается сечение с большим радиусом, обладающее приемле-
приемлемой неравномерностью потока, а при расчете течения выбирается
большее значение Woo, чем это необходимо для входного значе-
значения скорости. Можно также в качестве начального распределения
брать распределение, у которого сверхзвуковая ветвь отвечает те-
течению, асимптотически выводящему поток на радиальное течение.
Неравномерность потока на выходе из диффузора соответствует
кольцевым соплам простой конфигурации. На рис. 4.34 представ-
представлен пример расчета безвихревого течения с закруткой потока в
кольцевом канале, в котором происходит поворот потока на 180°
и С(г|)) =const = cu при со = 0,2. На этом рисунке показана геомет-
геометрия линий тока и линии W = const, пунктиром изображены линии
тока в течении без закрутки. Очевидно сильное различие полей
течения. Имеет место заметное влияние закрутки на течение в
трансзвуковой области. Интересно, что закрутка уменьшает в этом
случае неравномерность потока, вызванную центробежными сила-
силами и может привести, в отличие от случая простых конфигураций,
к увеличению коэффициента расхода С увеличением скорости вра-
вращения звуковая линия смещается вверх по потоку на большую
величину и коэффициент расхода уменьшается.
166
0,9
0,8
•
•
V •
\\
•
•
0,1
0,2
0,3
0,4
Рис 4 34 Геометрия кольцевого сопла с поворотом по-
потока на 180° при наличии закрутки
Рис 4 35 Зависимость коэффициента расхода ц от без-
безразмерной скорости закрутки а»
На рис. 4.35 представлена зависимость коэффициента расхода
от безразмерной скорости закрутки а*, где а*=-^*- , a Wmax —
максимальная скорость истечения, для случая безвихревой закрут-
закрутки при течении в кольцевых соплах с относительно малыми зазора-
зазорами по сравнению с расстоянием от оси симметрии, рассчитанная
по изложенному выше методу (кривая 1). На этом же рисунке
пунктирными линиями показана зависимость для винтового тече-
течения, черными точками представлен случай вращения по закону
твердого тела, светлыми —экспериментальные данные [27] Кри-
Кривая 2 соответствует расчету по изложенному выше методу при
Мг|з) ~Ф- Видно хорошее совпадение полученных автором данных
с экспериментальными и расчетными. Некоторое отличие объяс-
объясняется различным характером закрутки потока во всех вариантах
Как следует из сравнения этих данных, коэффициент расхода от-
относительно слабо зависит от характера изменения закрутки и от
вида сопел и определяется, в основном, лишь ее скоростью для рас-
рассмотренных типов закрутки
Отметим в заключении, что искривление оси [R{s)=^= оо] канала
приводит к появлению окружной составляющей, даже если она
отсутствовала в начальном сечении [см. уравнение A.97)].
4.4. ОБРАТНАЯ ЗАДАЧА ПРОФИЛИРОВАНИЯ КАНАЛОВ
Выше были представлены решения основного класса обратных
задач, в которых данные Коши задавались во входном сечении,
167
Рис 4 36 Схема профилирования
сопла с угловой точкой и равномер-
равномерным и параллельным оси потоком в
выходном сечении
расположенном в дозвуковой
области, и на поверхности тока
для до-, транс- и сверхзвуко-
сверхзвуковой областей течения. В ре-
результате решения определя-
определялось поле течения в окрестно-
окрестности начальной поверхности то-
тока и семейство линий тока,
каждую из которых можно-
принять за жесткий контур
сопла.
В этом разделе будет рас-
рассмотрен другой класс задач,
когда граничные условия зада-
задаются либо в выходном сечении, либо кроме того, еще на поверхно-
поверхности тока в сверхзвуковой области. В этом разделе рассмотрен так-
также и метод профилирования аэродинамических сопел, хотя этот
метод частично базируется на основной обратной задаче.
Методы профилирования осесимметричных сверхзвуковых:
сопел с равномерными изоэнтропическими параметрами в выход-
выходном сечении Г, основанные на использовании численного метода
характеристик, рассмотрены в [27]. Так как требуемый поток даже-
в классе плоских и осесимметричных течений можно получить,
бесчисленным количеством способов, то необходим дополнительный
критерий выбора, в связи с чем за основу был взят принцип
быстрейшего разгона потока. Это приводит к появлению точек
излома контура, если не наложено ограничение на кривизну по-
поверхности канала.
В качестве примера рассмотрим профилирование сверхзвуко-
сверхзвукового сопла с угловой точкой, в сечении ОА которого все газодина-
газодинамические параметры постоянны, а скорость равна скорости звука
(рис. 4.36, а). Требуется определить форму сверхзвуковой части
сопла, обеспечивающую равномерный и параллельный оси поток на
выходе с заданным числом М=М0.
Задача распадается на две: расчет газодинамических парамет-
параметров в области волны разрежения ОАВ (разгонный участок) и оп-
определение контура сопла АС и параметров течения в области ABC
(выравнивающий участок). Граничная характеристика АВ волны,
разрежения такова, что в точке В p=po=ctg<zo, где ао=-
= arc sin Mo. Характеристика ВС, в силу требования равномер-
равномерности потока на выходе из сопла, является прямой линией с углом
наклона ао к оси симметрии. Обратимся вначале к расчету облает»
волны разрежения ОАВ. Для отхода от звуковой линии ОА метод
характеристик не может быть использован, так как на ней харак-
характеристики обоих семейств сливаются. Для этой цели можно вос-
воспользоваться разложением решения в ряд. Для вычисления пара-
параметров течения на некоторой близкой к звуковой линии характери-
характеристике применяются разложение решения по характеристической
координате. На практике часто используется следующий простой
168
прием. Околозвуковая характеристика заменяется прямой линией,
в каждой точке которой вектор скорости параллелен оси, а числа
М постоянно и равно числу М в угловой точке. Расчеты показыва-
показывают, что если таким образом аппроксимировать характеристику,
которой в угловой точке соответствует значение М« 1,001, то обес-
обеспечивается вполне удовлетворительная точность.
Итак, пусть известны все параметры потока в точках си,
а2, ..., В\ некоторой характеристики АВ\ (рис. 4.36, б). В окрестно-
окрестности угловой точки А реализуется течение Прандтля — Мейера.
В точке А величины х=хА, У=Уа, г|з = г|ЗА постоянны, а |3 и Z,
связаны соотношением
/О) —arctgC = O. D.30>
Зная искомые величины в точке Л, соответствующие характе-
характеристике АВ\, и задавая приращение, например, др, можно найти,
используя D.30), значения р и ? в точке А, соответствующие близ-
близкой к АВ\ характеристике АВ% пучка. Теперь по известным пара-
параметрам в точках А и а\ по формулам C 81) (при 6 = const) мож-
можно вычислить все искомые величины в точке Ь\. Используя точки
«2 и Ь\ в качестве опорных, можно вычислить параметры течения
в точке b2 и т. д. При вычислении параметров в точках с\ и В2 при
v=l используются формулы C.81) с учетом C.82) и формулы
C.83). Аналогично проводятся вычисления параметров на следую-
следующей характеристике. Расчет разгонного участка продолжается до
тех пор, пока на оси сопла не будет достигнуто значение р=р0,
соответствующее заданному значению Мо па выходе из сопла.
После этого производится расчет выравнивающего участка сопла.
Зная значения параметров в точках В, а, ..., с, А граничной ха-
характеристики волны разрежения и в точке d\ прямолинейной замы-
замыкающей характеристики (вдоль этой характеристики ?=0; р =
5—1), можно последовательно вычислять параметры,
начиная с точки d (см. рис. 4.36, а), в точках характеристики вто-
второго семейства, выходящей из точки d\. Расчет ведется до тех пор,
пока в некоторой точке этой характеристики величина г|з впервые-
не превысит заданного значения i|)=i|3a. После этого квадратичной"
интерполяцией на заданное if> = i|u, используя вычисленные пара-
параметры в трех последних точках (точки е, f, g на рис. 4.36, а), опре-
определяют координаты точки А\ на контуре и значения газодинамиче-
газодинамических параметров в ней. Порядок дальнейшего расчета аналогичен.
Кроме основного контура АС с угловой точкой в процессе
расчета можно с помощью интерполяции на фиксированные проме-
промежуточные значения 0<а|)г<фА получить координаты линий тока и
распределения параметров вдоль них.
На основе аналогичного метода в классе сопел с равномерным
выходом были спрофилированы осесимметричные без центрально-
центрального тела, кольцевые, плоские симметричные и плоские несимметрич-
несимметричные каналы [27.31]. Обобщением изложенного метода явилась раз-
разработка алгоритмов, позволяющих профилировать сопла с задан-
16а-
выми неравномерными изознтропическими параметрами на выходе
J6, 7, 14, 16, 17]. В этих работах замыкающая характеристика пер-
первого семейства не является равномерной, а определяется из реше-
решения задачи Коши с неравномерными данными в выходном сечении.
В работе [16] данный метод был применен для построения сопел
модельных газодинамических установок. В [17] подробно рассмот-
рассмотрен вопрос о профилировании кольцевых сопел, в частности, зада-
задача «адаптации», т. е. согласования входного до- и трансзвукового
участков с искомым сверхзвуковым. В [6, 7] задача профилирова-
профилирования решалась сеточно-характеристическим методом при больших
леоднородностях сверхзвукового потока в выходном сечении Г.
Обобщением рассмотренных выше постановок для профилиро-
профилирования каналов с заданными изоэнтропическими параметрами на
Г является предложенная в [17] схема построения плоского сверх-
сверхзвукового канала с заданным неизоэнтропическим потоком на
выходе при изоэнтропическом течении на входе. Требуемое распре-
распределение энтропии S, которое предполагается достаточно гладким,
создается специально выстраиваемой ударной волной, расположен-
расположенной на входе в искомый канал. Однако в предложенной схеме
возникает проблема согласования входного потока с заданным
выходным, решение которой в осесимметричном случае достаточно
сложно.
Отметим, что в работах [12, 23, 30] обратная задача профили-
профилирования формулируется таким образом, что распределение давле-
давления (или скорости) задается на стенке, которая должна быть
определена в процессе решения, при этом в [30] решается краевая
задача в плоскости годографа, в [23] используется метод блочной
верхней релаксации, а в [12] — метод установления. Представляет-
Представляется, что используемые в этих работах методы являются существен-
существенно более громоздкими и требуют при расчетах на ЭВМ больших
затрат времени, чем разностный метод, описанный в 3 1.1.
Опишем возможный алгоритм решения задач, рассматриваемых
в этих работах, с помощью разностного метода 3.1.1.
Пусть на линии тока i|)==i|)K задано распределение давления, а
на оси сопла, как обычно, условие симметрии. Необходимо опреде-
определить контур сопла, обладающий заданным распределением давле-
давления. Задачу удобно решать в координатах if», х, в которых расчет-
расчетная область является прямоугольной.
Алгоритм решения такой задачи аналогичен алгоритму решения
прямой задачи как серии обратных, описанному в 4 1 3. В первом
приближении на оси сопла задается распределение давления, такое
же как и на искомом контуре, и от оси решается обратная задача
с помощью разностной схемы C 13. 3.16) до граничной линии
тока i|)=ipK. Полученное на этой линии тока распределение дав-
давления сравнивается с заданным и соответствующее различие вно-
вносится в распределение давления на оси, и решение от оси до линии
т)) = г|)к повторяется. Очевидно, что предложенный алгоритм дол-
должен достаточно быстро сходиться.
170
4.4.1. Профилирование аэродинамических сопел
Сопла аэродинамических труб по своему назначению должны
обеспечивать достаточно высокую равномерность потока в выход-
выходном сечении. В связи с этим для построения контуров аэродинами-
аэродинамических сопел тем или иным способом решается обратная задача
теории сопла, поскольку при решении прямой задачи весьма труд-
трудно «угадать» контур сопла, обеспечивающий заданную равномер-
лость потока.
Задача профилирования аэродинамического сопла распадается
на два этапа: первоначально каким-либо способом рассчитывается
в рамках идеального газа контур сопла, обеспечивающий равно-
равномерный поток в выходном сечении, а затем вносится полуэмпири-
полуэмпирическая поправка, учитывающая влияние вязкости.
Построение контура сопла, обеспечивающего равномерный
лоток в выходном сечении, возможно несколькими способами.
В первом способе предполагается наличие излома образующей в
точке А (рис. 4.37, а). Задается некоторая начальная характери-
характеристика АО и рассчитывается течение в волне разрежения ОАС.
Между характеристикой АС и равномерной характеристикой ВС,
расход через которую равен расходу через АС, решается задача
Гурса и определяется семейство линий тока, любая из которых
может быть принята за контур аэродинамического сопла. Наи-
Наименьшей относительной длиной обладает, очевидно, контур АВ.
Недостаток этого метода состоит в необходимости специально
выбирать контур сопла в трансзвуковой области вверх по потоку
от точки А, соответствующей заданной начальной характеристике
АО. Если же это условие не выполнено, то несоответствие истинно-
истинного течения в трансзвуковой области с принятым в расчете приво-
приводит к неравномерности параметров в выходном сечении.
Второй способ (рис. 4.37, б) состоит в следующем.
На участке оси сопла ОС задается некоторое распределение
скорости (определенное экспериментальным или расчетным путем)
и рассчитывается методом характеристик течение в характеристи-
характеристическом треугольнике ОВС. Контур искомого сопла AD определяет-
определяется далее в результате решения задачи Гурса между характеристи-
характеристиками СВ и CD и ОА и ОВ. При этом характеристика CD равно-
равномерная, а характеристика АО получена каким-либо способом из
расчета трансзвуковой области. Второй способ, обладая тем же
недостатком, что и первый, дает к тому же сопла слишком боль-
большой длины.
о с
а
Рис 4 37. Иллюстрация к методам профилирования аэродинамических сопел
171
Рис 4 38 Сравнение рассчитанной и экс-
экспериментальной формы центрального
тела
В третьем способе (рис.
4.37, в), рассмотренном в работе
[22], используется метод реше-
решения обратной задачи теории соп-
сопла, позволяющий по единой схе-
схеме рассчитать до-, транс- и сверх-
сверхзвуковую области течения. По-
Построение контуров для плоских,
осесимметричных и кольцевых со-
сопел различных типов производит-
производится единообразно, необходима
лишь выбрать распределение ско-
скорости или давления на начальной линчи тока, на которой ставятся
данные Коши, обеспечивающие равномерные потоки на выходе из.
сопла при кратчайшей длине. Поскольку наиболее короткой сверх-
сверхзвуковой частью обладают сопла с угловой точкой, то в качестве
начального распределения на оси можно выбрать расчетное или
экспериментальное распределение скорости или давления для это-
этого случая. В частности, можно использовать экспериментальное
распределение давления, приведенное в табл. 4.2.
На этом эксперименте следует остановиться особо. Применен
обратный метод сравнения расчетных и экспериментальных дан-
данных. Экспериментальное распределение давления, снятое по ци-
цилиндрической обечайке для кольцевого сопла с центральным
телом, сглаживалось затем с помощью некоторого оператора
свертки D.2.3). Полученное таким образом начальное распреде-
распределение давления использовалось для расчета течения в сопле. По-
Последняя полученная линия тока сравнивалась с контуром цент-
центрального тела. Результаты сравнения показаны на рис. 4 38. Н-а
этом рисунке кривая 1 соответствует экспериментальному контуру
сопла, кривая 2—расчетному, кривая 3 — экспериментальному
распределению давления на обечайке.
Таблица 4 2.
X
3,00
2,50
2,00
1,70
1,40
1,15
1,00
0,88
pip*
0,0383
0,0383
0,0383
Э,0383
3,0384
0,0384
0,0385
0,0396
X
0,25
0,20
0,16
0,14
0,12
0,10
0,08
0,06
р1р*
0,1246
0,1679
0,2129
0,2434
0,2835
0,3385
0,4138
0,5114
X
—0,10
—0,12
—0,14
—0,16
—0,20
—0,25
—0,30
—0,35
р1р*
1,2983
1,3597
1,4186
1,4738
1,5668
1,6597
1,7300
1,7786
X
0,76
0,67
0,58
0,50
0,42
0,35
0,30
р/р*
0,0410
0,0420
0,0438
0,0496
0,0603
0,0751
0,0938
X
0,04
0,02
—0,00
—0,02
—0,04
—0,06
—0,08
р/р*
0,6234
0,7426
0,8615
0,9748
1,0773
1,1604
1,2335
X
—0,42
—0,50
—0,60
—0,75
—1,00
—1,50
—2,00
pip*
1,8198
1,8467
1,8641
1,8750-
1,8803
1,8818
1,8819
172
Следует отметить, что центральное тело содержало угловую
точку, тем не менее, как видно из рисунка, при расчетах удалось
довольно близко подойти к ней. Расчетный и экспериментальный
контур хорошо совпадают между собой в до- и трансзвуковой обла-
областях, однако на концевом участке центрального тела, где толщина
пограничного слоя сравнима с толщиной тела, наблюдается замет-
заметное различие. Это различие значительно снижается, если поправить
контур на толщину вытеснения (пунктир на рис. 4.38).
Имея некоторое основное распределение давления Ро(х) на
начальной линии, можно получить набор распределений для других
чисел Мо. Пусть известно некоторое распределение давления ро(х)
и р_=Ро(—°°) и р+—ро{+ оо) —значения давления в до- и
сверхзвуковой областях на бесконечности. Тогда можно получить
следующее семейство распределений давления:
¦Р+
[ро(х)-р+],
Р- — Р+
где р'- и р'+ — новые значения давления в до- и сверхзвуковой
областях.
Если в качестве Ро(х) использовать полученное из эксперимен-
эксперимента и сглаженное распределение давления, соответствующее тече-
течению в сопле с угловой точкой, то функция р(х) позволяет рассчи-
рассчитать течение с линиями тока, достаточно близко подходящими к
угловой точке. На рис. 4.39 представлены контуры плоского, осе-
«имметричного и кольцевого аэродинамических сопел с числом
М0=3,2, полученные путем численного решения обратной задачи
с использованием в качестве начальных данных эксперименталь-
экспериментального распределения давления (табл. 4.2). На этом рисунке для
Рис 4 39. Контуры плос-
плоского (а), кольцевого (б)
и осесимметричного (в)
аэродинамических сопел
13% * 1JS 0Л%
173
ряда сечений указана неравномерность потока по давлению (в про-
процентах).
Отметим, что работа [22] содержит таблицы плоских сопел.
4.4.2. Профилирование сверхзвуковых каналов,
моделирующих заданный поток в выходном сечении
Трехграничная обратная задача профилирования, детально'
описанная в 1 2 5, состоит в определении контура канала по задан-
заданным условиям на линии тока и заданных давлениях р или угла
наклона скорости 6 во входном Г] и выходном сечениях (рис. 1 3)^
При постановке обратной задачи профилирования в 1 2.5. были
сформулированы новые двухграличные смешанные краевые задачи
с известными граничными условиями на известной характеристи-
характеристике Q и поперечно-ориентированной линией Г, на которой задается
распределение одного из газодинамических параметров либо угла
наклона скорости 0, либо давления р (см. рис. 1.3... 1 5). На
рис. 4.40 представлены различные варианты постановок этих двух-
граничных задач.
Рассмотрим подробнее постановку этих двухграничных задач
[6, 7].
В теории сверхзвуковых стационарных течений газовой динами-
динамики известны четыре характерные задачи: задача Коши с данными
на нехарактеристической кусочно-гладкой кривой или вырожден-
вырожденной характеристике, задача Гурса с данными на характеристиках
первого (С+) и второго (С~) семейств и две смешанные краевые
задачи с данными на характеристиках С+ или С~ и на граничной
линии тока, вдоль которой задано распределение одной из вели-
величин — модуля вектора скорости W (давления р) или угла 0 на-
наклона W к оси х декартовой системы координат х, г [1, 27] Для
смешанной краевой задачи, называемой ниже задачей 1, в качестве
граничной кривой задается твердая стенка с известными вдоль нее
углами 8. Для другой смешанной задачи (задача 2) вместо стенки
берется вычисляемая в процессе решения свободная поверхность с
известным вдоль нее распределением давления р. Ниже, примени-
В 8
а $
Рис. 4.40. Постановка двухграничных смешанных задач профилирования
174
тельно к двумерному стационарному сверхзвуковому в общем
случае разрывному течению внутри каналов, формулируются две
новые смешанные краевые задачи профилирования сверхзвуковых
каналов, которые для краткости будут называться смешанными
задачами 3 и 4. В качестве разрывов могут быть заданы как удар-
ударные волны, так и контактные границы Для определения рассмат-
рассматривается течение в верхней половине плоскости декартовой систе-
системы координат х, г.
Пусть заданы кусочно-непрерывная кривая Г, являющаяся С+
или (^-характеристикой, а также в общем случае разрывные газо^
динамические параметры вдоль нее F(rr) или F(г|з) (F(rr), F($>) —
вектор-столбец газодинамических параметров, гг — радиус-вектор
любой точки кривой Г, г|з — функция тока), определяющие некото-
некоторое сверхзвуковое течение, и граничная кусочно-непрерывная кри-
кривая Q, имеющая одну общую точку В с кривой Г и целиком лежа-
лежащая в угловой области, образованной характеристиками С+ и С"
(рис. 4.40, а—е). В случае, если на Г задана ударная волна L
(рис. 4.40, а), то она должна располагаться вне области влияния
данных в выходном сечении искомого канала (DCB на рис. 4.40, а
и D\C\B на рис. 4.40, б). При расчете профиля сопла с учетом
неоднородности полной энтальпии, удельной энтропии или при
наличии закрутки потока в F(^) могут быть включены распреде-
распределения этих параметров в зависимости от функции тока г|), которые
определяются течением во входной дозвуковой и трансзвуковой
областях сопла Задания исходной характеристики С" (рис
4.40, а, б) и С+ (рис. 4.40, в) для определенности ниже называют-
называются соответственно 1-й и 2-й схемой.
Другая граница смешанной области Q может быть фиксирован-
фиксированной, либо нефиксированной Рассмотрим случай, когда Q фиксиро-
фиксирована. Пусть Q имеет уравнение r=rg(s) (s — параметр) и удовлет-
удовлетворяет условию: величина производной по х в любой точке кри-
кривой Q не становится равной или меньше значения тангенса угла
наклона к оси х текущего отрезка характеристики АС+ (рис
4 40, а) или ДС~ (рис. 4.40, в), пересекающегося с Q. Это ограни-
ограничение обусловлено возможностью определения точки пересечения
ДС+(АС~) с текущим отрезком 2—3 A—3) вдоль Q. Для первой
схемы в пределе Q может быть задана как характеристика. В этом
случае вдоль нее должны быть определены все необходимые газо-
газодинамические параметры, удовлетворяющие характеристическому
соотношению, и задача профилирования сводится к решению зада-
задачи Гурса.
Кривая Q может выходить за границы потока, заданного харак-
характеристикой Г, так, как показано на рис. 4.40, а, либо заканчиваться
внутри него (рис. 4.40, б). Для второй, схемы Q в пределе может
совпадать с линией тока, и тогда смешанные краевые задачи 3 и 4
сводятся к соответствующим задачам 1 и 2. Для 2-й схемы Q мо-
может включать условно называемый ниже «особый» излом К, в
котором осуществляется переориентация Q таким образом, чтобы
верхняя часть кривой Q, обозначенная Qi, была заключена в
175
смежную угловую область, образованную характеристиками перво-
первого KKi и второго АК семейств (рис. 4.40, в).
На фиксированной кривой Q ставятся граничные условия: для
задачи 3 — 8(rq) или 6(г|з) распределение углов наклона вектора
скорости к оси х, для задачи 4 — р(тд) или р(г|)) распределение
давления. На нефиксированной кривой эти граничные условия
задаются как функции ip, 6(г|з) и p(ty). При этом имеется возмож-
возможность варьировать границу Q в текущих угловых областях, образо-
образованных С+ и С~ характеристиками. Это позволяет доопределить на
Q другой газодинамический параметр (р для задачи 3 и Q — для
задачи 4). Значения 8 или р в точке В должны быть согласованы
с соответствующими величинами на Г. На 8(rg) (9(г|))) и
Р(гч) (PC*1!')) в общем случае не накладывается требование их
непрерывности. В зависимости от положения точки В в потоке в
ряде случаев функции 8(rg) (8 (*]))) и p{rq) (р(г|>)) должны удовлет-
удовлетворять некоторым дополнительным условиям. Например, если
точка В размещена на оси х и Q перпендикулярна ей, то р'(г)|г=о
должна быть равной нулю. При указанных граничных условиях и
начальных данных требуется построить стенку канала. Поставлен-
Поставленные вдоль Q граничные условия не переопределяют задачу. Дейст-
Действительно, количество граничных условий на Q соответствует числу
отходящих от нее характеристик. Граничные условия для смешан-
смешанных задач 3 и 4 аналогичны соответственно заданию твердой гра-
границы (стенки) в задаче 1 и давления в задаче 2. Однако смешан-
смешанные краевые задачи 1 и 3, 2 и 4 не эквивалентны, так как в
задачах 3 и 4 кривая Q не является фиксированной или определяе-
определяемой линией тока, а задается поперек потока.
Рассмотрим теперь схемы профилирования каналов при реше-
решении задач 3 и 4 прямым (рис. 4.40, а, в) и послойным методами
характеристик. Порядок расчета внутренних точек расчетной об-
области классическим методом характеристик не зависит от вида
граничных условий и является обычным. Для расчета точек на
границе используется отрезок 1—3 B—3) характеристики
ДС+(ЛС-) и соотношение вдоль нее. Величины Q3 (задача 3) и р3
(задача 4) в искомой точке 3 на границе в процессе расчета опре-
определяются по 8(rg) (8(я];)) и р(г9) (р(г|))). Неизвестный параметр
в этой точке определяется из соотношения вдоль 1—3 B—3). Рас-
Расчет полной области ABD для 1-й схемы (рис. 4.40, а) и ее части
A\BDi (рис. 4.40, б) может быть организован как вдоль С+, так и
вдоль С~. В процессе расчета может быть выделена характеристи-
характеристика CD(CiDi), которая ограничивает область влияния данных на
линии BD(BDi) границы Q. Для случая, показанного на рис.
4.40, а, выделение осуществляется с использованием условия ра-
равенства текущей величины расхода газа на Q, его значению, полу-
полученному интегрированием вдоль известной характеристики Г.
Определение CD(CiDi) замыкает задачу Гурса в области
ACDF(A{CXD\D). Линия тока AD (рис. 4.40, б) после этого может
быть построена в процессе решения новой задачи в области MiD
по отрезку АА\, являющемуся частью кривой Г, и расе1 ч шой
176
характеристике AiD. Таким образом, задача профилирования
прямым методом характеристик включает несколько задач — соб-
собственно смешанную краевую задачу и задачи Гурса.
Для 2-й схемы (рис. 4.40, в), когда «особый» излом на грани-
границе Q отсутствует, смешанная краевая задача решается в области
АВК и затем выделяется нужная линия тока НК. Здесь исполь-
используется только часть характеристики АВ. В случае, когда линия Q
включает «особый» излом К, рассчитанная характеристика АК и
Qi(KD) образуют уже рассмотренную 1-ю схему. После расчета
AD и неизвестных функций на Qi можно решать задачу Коши в
области DKK\, после чего провести доопределение границы СЬ по
1-й схеме или <Эг' по 2-й схеме. Описанный процесс может быть
продолжен.
Решение смешанных краевых задач 3 и 4 для 1-й схемы более
удобно осуществлять модификацией метода характеристик по сло-
слоям a|) = const (см. 3.5.2). Это обусловлено тем, что при реализации
на ЭВМ данных задач вычисления проводятся по единому алго-
алгоритму на регулярной расчетной сетке. Существо предложенной
модификации состоит в следующем. Численный расчет проводится
в треугольной области на подвижной сетке, одно семейство которой
образуется линиями тока, а другое формируется в процессе расче-
расчета. Выбор вида последнего семейства определяется формой рас-
расчетной области и характером течения в ней.
Для большинства решенных в [6, 7] задач в качестве сеточных
принимались линии двух видов —вертикальные линии, проходя-
проходящие через точки пересечения линий тока с кривыми Г и Q, и орто-
ортогональное семейство линий, образуемое подвижными отрезками
прямых, восстанавливаемых перпендикулярно текущему отрезку
линии тока АС0, которые выходят из точек пересечения линий то-
тока с кривыми Г и Q. При численном решении интегрирование
ведется слоями, образованными линиями тока, которым соответст-
соответствуют фь г|J,..., гр,-, в направлении, поперечном к ним. Данная схема
решения в отличие от классической характеристической схемы не
накладывает жестких требований на гладкость граничных ус-
условий.
В частном случае плоского течения с равномерной начальной
характеристикой Г по аналогии с задачами 1 и 2 можно получить
аналитические решения задач 3 и 4.:
Здесь Ф3, d>4 — произвольные функции, которые могут быть оп-
определены из граничных условий.
На основе изложенной постановки и сеточно-характеристиче-
ского метода по слоям i|) = const можно профилировать новый,
более широкий по сравнению с известным класс плоских и осесим-
метричных сопел и каналов. До недавнего времени профилирование
отдельно сверхзвуковой части сопел производилось с помощью
решения задачи Гурса с использованием заданной замыкающей
характеристики (см. 4.4.1). Известны различные способы ее зада-
7—1393 177
0,7
эооор-
у"
1
м
оЗ
/7,2
Рис. 4.41. Профилирование плоского канала, реализующего на выходе те-
течение от источника
ния. Наиболее распространенный способ заключается в выборе
замыкающей прямолинейной характеристики, на которой W посто-
постоянна и параллельна оси х. Используются также симметричные и
стоковые характеристики [27]. В работах [16, 17] разработан метод
профилирования сопел, реализующих заданные неравномерные
параметры в выходном сечении, по которым с помощью решения
задачи Коши рассчитывается замыкающая характеристика.
Задачи 3 и 4 представляют новые возможности профилирова-
профилирования сопел и каналов по граничным условиям, заданным поперек
потока. Характер граничных условий в этих задачах определяется
физическими требованиями конструирования профилей сопел и
каналов. Например, задача 3 может использоваться для построе-
построения каналов с направленным отводом газов от поверхностей эле-
элементов летательных аппаратов, задача 4 — для каналов газодина-
газодинамических установок, создающих в некоторой области заданное
распределение давления в потоке, и в других случаях. При этом
семейство сопел с симметричной характеристикой на выходе полу-
получается в частном случае при решении смешанной задачи 3 с гра-
граничным условием 8 = 0, когда линия Q = Q(y).
Ниже приведены некоторые результаты численного профилиро-
профилирования сопел и каналов по заданной Г, являющейся характеристи-
характеристикой С~, и граничным условиям на границе различной формы;
Г рассчитана предварительно классическим методом характери-
характеристик, разработанным в соответствии с [16]. В качестве объекта
исследований выбирались плоские и осесимметричные сопла с
угловой точкой и радиусом скругления трансзвуковой части R2' —
= ^2/г*=18 (г, — высота или радиус критического сечения). По-
Показатель адиабаты в расчетах принимался равным 1,4.
На рис. 4.41... 4.43 приведены результаты расчетов по профи-
профилированию плоских и осесимметричных сопел и каналов, рассчи-
рассчитанных при различных формах границы Q и зависимостях рд, Qq
вдоль нее. Выбором формы границы Q, условий на ней и решением
смешанных задач могут быть спрофилированы переходные участки
178
2
г
2
7^^—
а
в
Рис 4 42. Профилирование канала, реализующего разрывные условия в выход-
выходном сечении а) ударная волна; б) контактный разрыв
сопел и каналов, реализующие преобразование одних классов те-
течений в другие. Течения, близкие к течениям источника и стока,
реализуются в сверхзвуковой части конических сопел. Известен
способ построения переходных каналов к точному течению от
источника, основанный на решении задачи Гурса по заданной
характеристике С~, определяемой формой трансзвуковой области
канала, и выходной характеристике С+ от источника B7]. Смешан-
Смешанные задачи 3 и 4 представляют другой способ профилирования
таких каналов, обеспечивающих с хорошей точностью параметры
течения от источника. При этом их длины получаются существен-
существенно короче.
Результаты расчетов для плоского течения приведены на
рис. 4.41. В качестве границы Г выбрана (^-характеристика, рас-
рассчитанная классическим методом характеристик при обтекании
угловой точки с числом М°=5 на оси. Кривая Q задана в виде
окружности с радиусом /? = г*^~(М°), проходящей через точку В.
Вдоль Q заданы распределение 9=0 (ф) по радиусу окружности
(задача 3) (ср — полярный угол) и p=p°=const (задача 4). Циф-
Цифрами / и 2 на рис. 4.41 обозначены профили каналов (рис. 4.41, а)
и распределения М(х), %(х) вдоль стенок (сплошные и штриховые
линии на рис. 4.41, б), полученные при решении задачи 4 и 3 со-
соответственно, цифрой 3 на рис. 4.41, а — контур сопла и цифрой 3
Рис 4 43 Профилирование плоских каналов, реализующих разрывные условия по
углу 6 или давлению р в выходном сечении
7* 179
на рис. 4.41, б — распределения М и \ для течения от источника.
Сплошные и штриховые линии на рис. 4.41, а иллюстрируют пове-
поведение линий M=const, рассчитанных в задачах 4 и 3. Следова-
Следовательно, граничное условие по р обеспечивает лучшее соответствие
с течением от источника. Действительно, в выходной части сопла,
начиная с лг=0,3, различие в числах М на стенках сопла 1 и 3 не
превышает 0,8%.
На рис. 4.42 приведены результаты расчетов для случая, когда
на Гь Гг заданы разрывные параметры, соответственно ударная
волна (рис. 4.42, а) и контактный разрыв (рис. 4.42, б). Характе-
Характеристика Fi получена при расчете течения с ударными волнами,
взаимодействующими с поверхностью гладкого конуса с углом
полураствора, равным 10°. Точка В кривой Fi расположена в
высокоэнтропийном слое на поверхности конуса. Это обусловливает
резкое изменение распределения М(х) в окрестности точки В,
В этом случае на Fi реализуется ударная волна с интенсивностью
pi/p2=2, расположенная вне области влияния BDC данных в вы-
выходном сечении. На Q задано 8=10°. Видно, что в месте пересе-
пересечения ударной волны 3 с линией тока AD, выбираемой в качестве
искомого контура, реализуется излом, угол которого определяется
параметрами газа до ударной волны и ее интенсивностью. Следо-
Следовательно, на стенке сопла реализуется гашение ударной волны,
что обусловлено величиной излома, зависящего от угла наклона к
оси х за ударной волной. За изломом канал расширяется и поток
разгоняется.
Рассмотрим теперь задачу 3 для двухслойного течения. Пря-
Прямая задача расчета двухслойных сверхзвуковых течений классиче-
классическим методом характеристик решена в работе [25]. Применение
сеточно-характеристического метода по слоям i|) = const для про-
профилирования сопел с двухслойными течениями является удобным,
так как позволяет естественным образом проводить выделение кон-
контактных границ.
На рис. 4 42, б приведены результаты профилирования сопел
с заданным контактным разрывом на Гг для двухслойного осесим-
метричного течения и заданным условием 6=0° на Q. Начальное
распределение чисел М вдоль оси симметрии получено классиче-
классическим методом характеристик для сопла с радиусом 7?2'=4 при
показателе адиабаты у=1,3. Это распределение использовалось
далее для определения Гг с помощью ' решения задачи Коши с
данными на оси симметрии. В рассчитанном варианте принималось,
что в ядре потока Yi=l,3, а в периферийной части его у2= 1,4- При
этом расходы газа в этих слоях выбирались равными 22 и 78%.
Полные давление и температура в обоих слоях принимались оди-
одинаковыми.
На рис. 4.42, б линиями 1 и 2 изображены контактный разрыв
и профиль стенки канала. Здесь приведены также линии уровня
М=const в поле двухслойного течения с шагом 0,1. Наблюдается
расширение потока в обоих слоях, однако в ядре потока его темп
превышает соответствующий темп в периферийной области.
180
В приложениях газовой динамики необходимо уметь получать
сверхзвуковые потоки с разрывными параметрами. Например, раз-
разрыв по 0 может быть использован для профилирования сопел экс-
экспериментальных газодинамических установок, моделирующих в
некотором сечении два потока, встречающихся под заданным
углом, а разрыв по р — для профилирования сопел газодинамиче-
газодинамических окон лазерных систем. Постановка смешанных краевых
задач 3 и 4 позволяет профилировать такие сопла.
На рис. 4.43 приведены результаты профилирования двух
плоских каналов по заданной характеристике Г и разрывным
граничным условиям по 6 и по р. Характеристика Г рассчитана
методом характеристик в течении Прандтля —Мейера на число
М°=3. В задаче 3 принят ступенчатый профиль 8, для которого
в центральной части 9=0°, а в периферийной 0= —20° (рис.
4.43, а), а в задаче 4 давление р'=р/р*а*2 задано возрастающим
в виде ступеньки от величины р/=0,0368 до р2/==0,0791 (рис.
4.43, б). На рис. 4.43, а, б показаны профили сопел и линии уровня
M=const с шагом 0,2 и 0,1 соответственно.
Анализ показывает, что разрыв граничных условий для обеих
смешанных краевых задач приводит к разрыву и других газоди-
газодинамических параметров и обеспечивается изоэнтропически с по-
помощью характеристик сжатия, фокусирующихся в точке разрыва
граничных условий. В задаче 3 граничные фокусирующие харак-
характеристики показаны штриховыми линиями 1 и 2 (рис. 4.43, а).
Числа М в точке разрыва для этих характеристик равны 1,8 и 2,7.
В задаче 4 фокусирующие характеристики 3 и 4 в отличие от
характеристик 1 и 2 являются разрывными. Вывод о фокусирую-
фокусирующем механизме создания разрыва подтверждается численными
результатами, полученными при решении соответствующих прямых
задач внутри спрофилированных сопел. Расчеты свидетельствуют
0 том, что результаты решения задач хорошо согласуются между
собой. Максимальное различие по числу М вдоль Q для задачи 3
достигается в окрестности разрыва 0 и не превосходит 2%. Пове-
Поведение линий уровня М=const показывает, что при решении зада-
задачи 3 реализуется течение разрежения в центральной части, ограни-
ограниченной характеристикой 1, и течение сжатия в периферийной ча-
части. В отличие от задачи 3 разрыв давления на Q приводит к
иному характеру течения в смешанной области. Из рис. 4.43, б
видно, что поток разделяется на три области I, II, III. В областях
1 и III реализуется течение разрежения, а в области II — течение
сжатия.
Рассмотрим решение обратной задачи построения плоского или
осесимметричного канала с центральным телом, обеспечивающего
разрывное распределение энтропии 5г на выходе при непрерывных
распределениях давления р и угла 8 наклона вектора скорости W
к оси х на выходе и вдоль профилируемых стенок [7].
Кратко сформулируем краевые условия и опишем схему рас-
расчета канала (рис. 4.44). Рассматривается верхняя половина плос-
плоскости течения в декартовой (цилиндрической) системе координат
181
2 -
иг iA
2,22
1,78,
Рис 4 44 К решению обратной задачи про-
профилирования канала с центральным телом
с разрывным распределением энтропии на
выходе S2
(х, г). Течение на входе в искомый
канал принимается заданным и в
частном случае однородным с чис-
числом М°. Задание граничных усло-
условий по р или 8 и энтропии S = p/pv
вдоль поперечно ориентированной,
заранее не фиксированной границы
NK, являющейся выходным сечени-
о J г { х ем канала, осуществляется в виде
зависимости от функции тока ф. Ус-
Условия по р или 0 на продольно ори-
ориентированной также не фиксированной границе (центральном те-
теле FK) задаются в виде функций координат х, г. Функция S на
границе NK. в рассматриваемом случае задается в виде ступеньки
с разрывом в точке р со значением гр = 0,5 (-ф — нормированная так,
что г|) = 0 в точке К и i|) = l в точке N). Приращение &S = S+—S~>0
(S+, S~ — предельные значения S сверху и снизу от точки разрыва
соответственно).
Распределение функции S снизу от точки р обеспечивается уча-
участком АВ головной ударной волны ABC. Значение функции S =
= S~=0,79, принятой постоянной, реализуется на клине с углом
полураствора 21°. Заданный разрыв AS создается с помощью изло-
излома в точке В волны ЛВС, который осуществляется на основе при-
применения конфигурации со взаимодействием ударной волны АВ и
веера волн сжатия DBE (характеристики С+), центрированного
в точке В. Положение последней выбирается таким образом, что-
чтобы значение гр в ней было равно ар в точке р. Изменения функции S
за счет других ударных волн в расчетной схеме исключаются. Это
обусловливает необходимость использовать для обеспечения задан-
заданного распределения S конфигурацию с отраженным в точке В
центрированным веером разрежения.
Схема профилирования канала при описанных граничных усло-
условиях основана на решении обратной задачи, включающей харак-
характерные задачи газовой динамики: задачи Коши в областях ABE и
BFC, задачу Гурса в области BEF и две смешанные краевые за-
задачи в областях CFK и CK.N. Вначале по заданному перепаду
5(г|}) вдоль ударной волны ABC рассчитываются данные Коши за
ней. При этом параметры в точке В определяются отдельно от
остального участка волны по программе расчета конфигурации с
взаимодействием ударной волны и веера сжатия. В работе прове-
проведено численное параметрическое исследование конфигурации, и
в широком диапазоне М° A,2^М°^10) выявлены области ее
существования с отраженным веером разрежения и ударной вол-
волной. Затем классическим методом характеристик решаются задачи
Коши, задача Гурса и смешанная задача в области CKF. Для рас-
182
чета смешанной области CKN используется сеточно-характеристи-
ческий метод по слоям i|) = const.
В результате расчета при М°=3 и постоянном значении 0 =
= 32° вдоль границы FK получен плоский канал с центральным
телом АК и обечайкой CN, реализующий разрывной профиль функ-
функции 5 (штриховая линия на рис. 4.44, а) и отклонение потока на
32°. Сплошной линией на рис. 4.44, а показан профиль функции М
на выходе, ВР на рис. 4.44, б — контактный разрыв. Интенсив-
Интенсивность веера волн сжатия DBE, характеризуемая отношением
а+/а~ (а — угол Маха), равна 0,74. Веер DBE отклоняет поток
на 11°. Изломом ударной волны ABC, составляющим величину 18е,
обеспечивается такое же отклонение потока, что обусловлено
нулевой интенсивностью отраженного веера разрежения (харак-
(характеристика BF).
При решении задач о смешении струй необходимо на малых
длинах осуществлять перемешивание двух или большего числа
сверхзвуковых неоднородных потоков, обеспечивая высокую сте-
степень однородности всех газодинамических параметров. Большая
длина перемешивания снижает эффективность широко распростра-
распространенного способа взаимодействия параллельных сверхзвуковых
струй и обусловливает необходимость использования для этой
цели струй, направленных под углом друг к другу. Однако при
реализации такой схемы в смешиваюшемся сверхзвуковом потоке
возникают существенные неоднородности, образующиеся из-за
возникающих при соударении струй сильных разрывов — ударных
волн, контактных границ, центрированных волн разрежения. Это
обстоятельство ограничивает возможность практического приме-
применения указанного способа взаимодействия.
В рамках обратной задачи профилирования можно реализовать
иную схему выравнивания параметров взаимодействующих пото-
потоков внутри переходного капала минимальной длины, реализую-
реализующего в выходном сечении однородный по р и 9 поток. Профилиро-
Профилирование канала осуществляется в идеальной постановке при реше-
решении обратной задачи двумя сеточными модификациями метода
характеристик по слоям ^=const и i|j = const. В обоих методах
используются одни и те же характеристические уравнения с иско-
искомыми функциями х, г, р, 9.
Обратная задача заключается в следующем. Пусть в декарто-
декартовой (цилиндрической) системе координат (х, г) в некотором сече-
сечении АВ, являющимся, например, выходным из решетки профилей,
заданы два плоских симметричных относительно оси х или
осесимметричных сверхзвуковых потока I и II, взаимодействую-
взаимодействующих в точке С. Пусть эти потоки в указанном сечении характери-
характеризуются различными газодинамическими параметрами: показателя-
показателями Yi. "V2, распределениями давлений Pi(r), p2(r), углов наклона
Gi (г), 9г(г), скоростей o>i(r), сог(г) (или чисел M](r), M2(r))
и плотностей р\(г), р2(г) при (в общем случае) переменных раз-
разрывных распределениях S и полной энтальпии Н°. Здесь и в по-
последующем тексте нижние индексы 1 и 2, указываемые в обозна-
183
г
2
1
С
R
i—
А .
К
¦~^"
Af__— <
——-—^
о я
/О /5 л
О
ГО
Рис 4 45. Схема решения обратной задачи профилирования каналов, реализу-
реализующих равномерный поток по давлению и углу наклона скорости в выходном се-
сечении при наличии в начальном сечении двух взаимодействующих потоков.
Профили чисел М и углов а (в)
чениях параметров, относятся к областям I, II, в которых распро-
распространяются потоки I и П. Для обеспечения разгона потока в
профилируемом канале в точке А задается положительное прира-
приращение угла 0.
На величины газодинамических параметров вдоль АВ наклады-
накладывается условие, заключающееся в том, что их значения в точке
взаимодействия С не достигают критических, при которых реали-
реализуется переход к дозвуковому течению. Кроме того, полагаем, что
интенсивность ударных волн, образующихся в точке С, не слиш-
слишком велика, а величины Нх° и Я2° одинаковы. Ограничение на ин-
интенсивность ударных волн обусловлено возможностью осуществле-
осуществления их сквозного счета послойными модификациями метода харак-
характеристик и получением достаточной для практики точности
численных результатов.
При отмеченных исходных данных и физических предположени-
предположениях требуется построить профиль переходного канала минимальной
длины AF, который обеспечивает на выходе постоянное распреде-
распределение углов 0i (г) =02 (г) =0 и, следовательно, давления pi{r) =
:=p2{f)=pl (p1 — значение р в точке пересечения характеристики
АЕ, ограничивающей область влияния данных на АВ, с осью х).
Схема профилирования выравнивающего канала состоит в
следующем. Вначале по формулам взаимодействия двух сверхзву-
сверхзвуковых потоков, приведенных, например, в [27], рассчитывается
точка С контактного разрыва CD (рис. 4.44, б). Затем по данным
Коши на АВ методом характеристик по слоям х=const рассчиты-
рассчитывается их область влияния ABE и методом характеристик по сло-
слоям ij) = const решается задача Гурса в области AEF.
Некоторые возможности разработанного подхода к проблеме
выравнивания основных неоднородностей во взаимодействующих
потоках проиллюстрированы на рис. 4.45, 4.46. В исследованиях,
184
Рис. 4.46. Контуры выравнивающих ка- ?г
налов
проведенных для трех схем взаимодействия, обозначенных Сь С2,
С3, газ в потоках 1 и II принимается с одинаковым у=\,А. При
выбранных условиях течения свойства потоков удобно характери-
характеризовать распределениями чисел М (либо давления р) и углов 6.
Профили чисел М для потоков I и II принимаются однородны-
однородными и равными Mi = 3 и Мг=2 для схем Сг и С2 (рис. 4.45, в) и
Mi=M2=3 для С3. Угол наклона касательной к стенке профили-
профилируемого канала в точке А обозначен через ц. Величины h\, /z2 ха-
характеризуют ширину потоков I и II в сечении АВ. Для схем С\
и С2 принято hi = l/3; /z2=2/3, а для C3hl=2/3; /г2 == 1/3. Угол на-
наклона 0 потоков I и II для схемы С\ принимается нулевым, а а=9°.
Для С2 и С3 распределения 0i(r) и б2(/") выбраны линейными, при-
причем в точке С для С3 0i = —18° и 02=18°, а углы \к соответственно
равны —4°, 18°. Величины последних выбирались в процессе серии
расчетов такими, чтобы во всех трех схемах взаимодействия в
потоке Е реализовались значения М'=4,17. Для С] и С3 централь-
центральные оси потоков параллельны, а для С2 ось потока I наклонена в
сторону потока II под углом 20° (штрихпунктирная линия на рис.
4.45, в).
На рис. 4.46 приведены контуры выравнивающих каналов
(сплошные линии) для Сь С2, С3, обозначенных цифрами 1, 2, 3
соответственно, а также контактные границы (штриховые линии).
Сверхзвуковым течениям внутри всех спрофилированных кана-
каналов присущ ряд одинаковых свойств. В точке С взаимодействия
встречающихся потоков реализуются контактная граница и две
ударные волны, одна из которых СК направлена от оси х, а дру-
другая CN — к оси х. Ударная волна СК, а также NM, образующаяся
в результате взаимодействия ударной волны CN с симметрично
расположенной снизу от оси х, в точках К и М соответственно
достигают верхней линии тока AF, принимаемой в качестве стенки
канала. В этих точках стенка претерпевает излом, равный углу
отклонения потока. На ударных волнах поток внутри выравниваю-
выравнивающего канала в местах отсутствия ударных волн с возрастанием х
расширяется.
Из рис. 4.46 видно, что продольные и поперечные размеры
каналов и контактных границ для схем Ct и С2 получаются доста-
достаточно близкими. Это свидетельствует о сравнительно слабом влия-
влиянии неравномерностей по углам встречи и определяющем влиянии
на указанные геометрические характеристики профилей чисел М.
Ударные волны NM и СК для обоих каналов 1 и 2 в точках их
встречи со стенкой являются весьма слабыми. Это обусловлено
185
тем, что течение на начальном участке в обоих потоках в местах
отсутствия ударных волн весьма интенсивно расширяется в обла-
области ABE влияния данных на АВ, в которой содержится веер волн
разрежения, созданный угловой точкой А.
Дадим анализ результатов профилирования канала (см.
рис 4.45), построенного для схемы С3 с одинаковыми профилями
чисел М и существенной неоднородностью по наклону W. В точ-
точке С образуются ударные волны СК и CN примерно одинаковой
интенсивности и близкие к прямолинейным. Характеристика, огра-
ограничивающая область влияния данных на АВ, обозначенная циф-
цифрой 1 на рис. 4.45, а, является достаточно искривленной. Выход-
Выходная характеристика, близкая к прямолинейной, обозначена циф-
цифрой 2 (M' = 4,17). Из рис. 4.45, а видно, что в точках КиМ стенка
канала претерпевает заметный излом. На рис. 4.45, б приведены
зависимости безразмерных давлений р'=р/р*а*2 вдоль оси х
(сплошные линии) и вдоль стенки канала (штриховые линии). Из
поведения кривой вдоль оси видно, что поток II на участке BN
интенсивно расширяется. В точке N реализуется торможение пото-
потока на ударной волне. Здесь имеет место резкое возрастание давле-
давления. Вниз по потоку от точки N осуществляется монотонное рас-
расширение потока до значения М'=4,17. Вдоль стенки канала AF
на начальном участке так же как и вдоль оси, поток расширяется.
В точках К и М, где стенка пересекается с ударными волнами СК
и NM, наблюдается скачкообразное возрастание давления. На
участках КМ и MF поток расширяется.
Из поведения р(х) вдоль стенки видно, что эффект существен-
существенного ослабления ударных волн NM и СК, отмеченный примени-
применительно к схемам С\ и Сг, для схемы С3 отсутствует. Это обяза-
обязательство обусловлено тем, что в точке А здесь нет разрыва
угла 0.
Отметим, что предложенная схема профилирования выравни-
выравнивающих каналов может найти широкое применение при разработ-
разработке сопловых решеток, сверхзвуковых диффузоров, а также при ре-
решении задач, содержащих слоистые течения.
4.5. СРАВНЕНИЕ РАСЧЕТОВ ОБРАТНЫМ МЕТОДОМ
С ЭКСПЕРИМЕНТАЛЬНЫМИ РЕЗУЛЬТАТАМИ
И РАСЧЕТАМИ ДРУГИМИ МЕТОДАМИ
Одна из особенностей внутренних течений состоит в том, что
в большинстве случаев оказывается возможным предсказать пара-
параметры течения, основываясь на одномерном приближении. В част-
частности, в современных двигателях потери удельного импульса, свя-
связанные с неравномерностью потока в выходном сечении, составля-
составляют примерно 1 ... 2%, т. е. отличие действительного потока
количества движения в выходном сечении сопла от подсчитанного
в одномерном приближении составляет 1 ... 2% • Аналогично и ве-
величина коэффициента расхода в действительном течении, харак-
характеризующая неравномерность потока в минимальном сечении, от-
186
личается от значения, подсчитанного в одномерном приближении
на 1 ...2%. В связи с этим численные методы расчета внутренних
течений, учитывающие пространственный характер течения, долж-
должны обладать точностью на порядок, превышающей указанную раз-
разницу в 1 ...2%, т. е. точность предсказания интегральных характе-
характеристик течения должна составлять 0,1%, а локальных — не менее
0,5%- Методы, не обладающие такой точностью, пригодны в луч-
лучшем случае для приближенного качественного описания течения.
Описанный выше метод расчета, как уже отмечалось, обладает
необходимой точностью. Так, при проверке уравнения сохранения
количества движения и уравнения расхода оказалось, что они вы-
выполняются с точностью, не меньшей 0,05%. Точность счета локаль-
локальных характеристик течения определялась путем расчета с различ-
различными шагами As и Аг|з и в сверхзвуковой области путем сравнения с
методом характеристик, также обладающим вторым порядком точ-
точности. Такие проверки показали точность расчета локальных пара-
параметров не меньшую 0,2 ... 0,5%.
Важной особенностью предлагаемой схемы является то, что на
шаг Аг|з практически не накладывается никаких ограничений, свя-
связанных с устойчивостью, а величина его определяется лишь допу-
допустимой ошибкой аппроксимации, на шаг Ах ограничения наклады-
накладываются лишь в эллиптической области. Кроме того, в связи с оче-
очевидной простотой вычислительного алгоритма особенно в плоском
и осесимметричном случаях затраты машинного времени чрезвы-
чрезвычайно малы В связи с этим до настоящего времени ни один из
существующих методов расчета внутренних течений в до- и транс-
трансзвуковой областях не может конкурировать с описанным выше
методом ни по точности результатов, ни по затратам машинного
времени.
Представленные выше расчетные данные в ряде случаев срав-
сравнивались с экспериментальными результатами. Такое сравнение
проводилось не с целью проверки точности метода (очевидно, что
точность метода в большинстве случаев выше точности экспери-
эксперимента), а с целью установления соответствия между истинным вяз-
вязким течением газа и предсказываемым течением идеальной невяз-
невязкой жидкости. Ниже будут описаны некоторые результаты сравне-
сравнений расчетных и экспериментальных данных.
В работе [18] представлены измерения координат звуковых
точек и коэффициента расхода. Экспериментальные данные срав-
сравниваются с расчетными на рис. 4.8, 4 9.
В. Н. Жиравов провел экспериментальное исследование рас-
распределения давления на контуре сопла, рассчитанного в резуль-
результате решения обратной задачи, для распределения D.3) с Woo =
= 1,9; Woa = 0,l и 6==3,5 при гр — 0,06. Сравнение расчетного
(сплошная кривая) и экспериментального (светлые кружочки)
распределений давлений приведено на рис 4.47. На этом же рисун-
рисунке пунктирной линией показано распределение давления, рассчи-
рассчитанное по одномерной теории. На рис. 4.3 и 4.4 дано сравнение рас-
расчетного и экспериментального распределения давления для конту-
187
—
- 1 Л
\l n a
j——+—
1 ¦—J
1
1- 1
1
I
Y
\
\
-0,3
0,2
0,1
\
\
u
V\
4
т—
V
—
-a-
-\0-3,0 -2,0 -1,0 0 1,0 2,0 3,0 x
Рис. 4 47 Сравнение расчетного и эксперимен-
экспериментального распределений давления на контуре
сопла, рассчитанного обратным методом
ров сопел, рассчитанных обратным
методом__для распределения скорости
D.1) с ^оо = 0,1 и Л = 10 при г|з = О,О2
и г|) = 0,06.
Сравнение расчетных и экспери-
экспериментальных данных по величине Срт
в зависимости от fii и коэффициенту
расхода в зависимости от степени за-
закрутки иллюстрируют рис. 4.47 и 4.35.
Анализ перечисленных выше рисунков
позволяет сделать вывод о хорошем
соответствии расчетных и эксперимен-
экспериментальных результатов в областях, где
влияние вязкости невелико. В пологих
трансзвуковых областях, где влияние
вязкости существенно, имеет место заметное различие эксперимен-
экспериментальных и расчетных данных. Существенным подтверждением до-
достоверности предложенного метода является сравнение рассчитан-
рассчитанной и экспериментальной формы центрального тела, полученного
обратным методом по заданному распределению давления (см.
рис. 4.38).
Успешное решение представленных выше задач оказалось
возможным благодаря следующим обстоятельствам. Во-первых, во
всех случаях решалась обратная задача, которая сводится к задаче
Коши, а не к краевой задаче, что значительно упрощает алгоритм
численного решения. Во-вторых, примененная разностная схема
позволяет проводить расчеты сложных течений с высокой точно-
точностью при весьма малых затратах машинного времени и практиче-
практически без ограничений, связанных с устойчивостью. В-третьих, весьма
существенным оказалось применение малоточечных (трехточеч-
(трехточечных) разностных схем с переменным шагом на слое для решения
некорректных задач Коши.
И наконец, для решения внутренних задач оказалась весьма
удачной система координат s, \|з, 8, в которой удобно решать и не-
некоторые внутренние и струйные задачи (в том числе прямые)
сверхзвуковой газовой динамики неравновесных течений. Благо-
Благоприятным обстоятельством здесь является то, что практически все
мыслимые границы областей (жесткая стенка, ось симметрии, сво-
свободная граница, линия тангенциального разрыва) являются в этой
системе координат прямыми линиями, что делает расчетную об-
область прямоугольной и значительно упрощает построение разност-
разностной схемы.
В связи с этим представляется возможным расширить класс
решенных задач.
188
В разд. 5 будут представлены многочисленные примеры реше-
решения обратной задачи с учетом разного рода неравновесных физи-
физико-химических превращений.
Можно обобщить решение обратной задачи теории сопла для
течения вязкого теплопроводного газа.
В этом случае, например, на оси симметрии необходимо задать
распределения давления и температуры, которые позволяют с
помощью асимптотических разложений (см. 2 4) определить при
численном решении задачи Коши от некоторого начального сече-
сечения вдоль оси остальные параметры течения.
Далее с использованием описанных в 3.1 2 разностных схем
можно численно определить в окрестности оси симметрии поле
течения и семейство линий тока Каждая из линий тока может
быть принята за контур сопла, на котором будет выполнено усло-
условие непротекания, но будет иметь место скольжение потока. Под-
Подбором распределения скорости на оси (см алгоритм 4.1 3) можно
добиться равенства нулю скорости на контуре сопла при задан-
заданном ф.
5. ТЕЧЕНИЯ С ФИЗИКО-ХИМИЧЕСКИМИ
ПРЕВРАЩЕНИЯМИ
В большинстве прикладных задач не удается описать течение
газа, используя лишь модель идеального газа. Реальное течение
сопровождается физико-химическими процессами, природа кото-
которых и методы математического описания существенно усложняют-
усложняются. Система уравнений и граничных условий, приведенная в 1 гл.
для многоскоростной, многотемпературной и реагирующей сплош-
сплошной среды, дает общее представление о сложности задачи описа-
описания движения такого континуума в наиболее общем случае. На
практике приходится в основном иметь дело именно с такого рода
течениями. Однако, несмотря на одновременное протекание раз-
различных релаксационных процессов, их удается разделить и изучать
независимо, поскольку взаимное влияние по существу невелико.
В частности, неравновесное возбуждение или дезактивацию коле-
колебательных степеней свободы можно изучить, используя неравно-
неравновесные значения концентраций различных компонент, полученные
в предположении равновесия поступательных и колебательных
степеней свободы. Характер неравновесного протекания химиче-
химических реакций в двухфазной среде лишь в слабой степени зависит
от динамического и теплового состояния частиц. В связи с этим в
настоящей главе будут раздельно рассмотрены неравновесные
физико-химические процессы, которые могут иметь место в соп-
соплах, в том числе неравновесное возбуждение колебательных сте-
степеней свободы, химические реакции, неравновесные двухфазные
течения.
5.1. РАВНОВЕСНЫЕ И ЗАМОРОЖЕННЫЕ ТЕЧЕНИЯ
Учесть наличие физико-химических процессов можно прибли-
приближенно, приняв скорости их протекания бесконечными или нуле-
нулевыми. При бесконечной скорости имеет место равновесное течение,
а при нулевой — замороженное. При равновесном течении термо-
термодинамические и газодинамические параметры определяются с при-
привлечением соотношений термодинамики равновесных процессов.
Концентрации реагирующих компонент в таких течениях опреде-
определяются из закона действующих масс: энергия колебательных
степеней свободы вычисляется по формуле Эйнштейна, парциаль-
парциальные давления конденсирующихся компонент — по уравнению Кла-
190
пейрона — Клаузиуса, а скорости и температуры частиц прини-
принимаются равными скорости и температуре газа. Из уравнения
производства энтропии A.44) следует, что энтропия в этом случае
сохраняется неизменной вдоль струйки тока, а из принципа мак-
максимальной работы в случае обратимых процессов следует, что
равновесное течение является предельным течением, когда удается
получить в выходном сечении сопла максимальные импульс, ско-
скорость истечения, температуру и давление по сравнению с любым
другим процессом истечения в сопле заданной геометрии и с за-
заданными параметрами заторможенного потока.
Другим предельным течением является полностью заморожен-
замороженное течение, когда параметры, характеризующие релаксационный
лроцесс, остаются неизменными в процессе движения смеси. Это
течение также является изоэнтропичсским, поскольку правая часть
уравнения производства энтропии A.44) и в этом случае обра-
обращается в нуль из-за равенства нулю скоростей соответствующих
процессов В полностью замороженном течении сохраняются неиз-
неизменными молярные доли различных компонент, энергия колеба-
колебательных степеней свободы молекул, скорости и температуры
частиц, а процессы конденсации и кристаллизации вообще не
происходят. В предельном замороженном течении в выходном
сечении сопла заданной формы и с заданными параметрами тор-
торможения получается минимальное давление по сравнению с лю-
любым другим процессом истечения, поскольку запасенная в покоя-
покоящемся газе энергия диссоциации и колебательных степеней свобо-
свободы, теплота конденсации и кристаллизации, а также тепловая
энергия частиц не передаются в поступательные и вращательные
степени свободы молекул (последние всегда предполагаются в
равновесии между собой) и, следовательно, не переходят затем в
энергию направленного движения газа.
Возможны и некоторые другие модели изоэнтропического рас-
расширения, полезные для разного рода инженерных оценок. Напри-
Например, химически замороженное течение, когда все остальные редак-
редактирующие параметры, кроме молярных долей компонент, изменя-
изменяются в соответствии с соотношениями равновесной термодинами-
термодинамики Рассматривается также течение, когда заморожены лишь фазо-
фазовые переходы, конденсация или кристаллизация. Это позволяет
оценить предельное влияние конденсации и кристаллизации на
параметры течения. Наконец, возможно замороженное двухфаз-
двухфазное течение, когда изменение всех параметров, кроме скорости и
температуры частиц, происходит равновесно, а эти последние не-
неизменны в процессе истечения
Методы расчета равновесного и замороженного течений в сопле
весьма сложных смесей продуктов сгорания, в которых происхо-
происходят перечисленные выше физико-химические превращения, изло-
изложены в первом томе фундаментального десятитомного справочни-
справочника [33] В остальных томах этого справочника приведены таблицы
параметров смеси для различных композиций, полученные в одно-
одномерном приближении. Такого рода таблицы, так же как и (h—S)
191
диаграммы, позволяют определить параметры в любой точке изо-
энтропического потока, если в этой точке известен какой-либо
один термодинамический параметр и параметры торможения по
аналогии со случаем одномерного течения газа с постоянным отно-
отношением удельных теплоемкостей. Действительно, условие изоэн-
тропичности S—S(p, p)=const или S = S(p, T)=const связывает
давление и плотность (температурой), а термическое и калориче-
калорическое уравнения состояния вместе с уравнением сохранения энергии
позволяют определить температуру (плотность) и скорость, а так-
также молярные доли различных компонент, массовую долю конден-
конденсата и т. д.
Расчет такого рода таблиц проводится, по-существу, в рамках
обратной задачи, поскольку параметры течения рассчитываются
либо при заданном давлении, либо при заданной температуре.
Если предположить замораживание химических реакций и колеба-
колебательных степеней свободы молекул, а также отсутствие фазовых
переходов, то процесс истечения может быть рассчитан по форму-
формулам B.5) ... B.12) для идеального газа с постоянным отношением
удельных теплоемкостей у=у°, которое определяется следующим
образом:
_ \-i
(=1
где ср, — теплоемкость i-й компоненты при постоянном давлении,
полученная с учетом только возбуждения поступательных и вра-
вращательных степеней свободы, а г01 — молярная доля ?-й компонен-
компоненты в камере сгорания. Для иллюстрации на рис. 5 1 представлена
зависимость удельного импульса в пустоте и температуры от отно-
относительного радиуса r=F^ для топлива с горючим — несимметрич-
несимметричным диметилгидразином и окислителем—азотным тетраксидом
[(CH3JNNH2 + N2O4] для трех предельных случаев течения: равно-
равновесного, химически замороженного и течения с замороженными
химическими реакциями и энергией колебательных степеней сво-
свободы.
Расчет двумерных или пространственных равновесных течении'
производится по-существу по тем же алгоритмам, что и расчет
т,к
Рис 5 1. Зависимость сдельного импульса в
пустоте Is (с) и температуры Г, К от г при
коэффиценте избытка окислителя а=1, дав-
давления торможения ро=1,5 107 Па
/ — равновесное течение; 2 — химически неравно-
неравновесное течение; 3 — химически замороженное те-
течение; 4 — течение с замороженными химически-
химическими реакциями и энергией колебательных степе-
степеней свободы
0480
192
течения идеального газа с у—const. Необходимо лишь иметь таб-
табличные или аналитические зависимости величин W/a*, р/ро, р/ро,
Т/То от числа М, которые можно определить независимым расче-
расчетом равновесных газодинамических и термодинамических парамет-
параметров смеси в одномерном приближении способом, описанным
выше.
5.2. ТЕЧЕНИЯ С НЕРАВНОВЕСНЫМИ ХИМИЧЕСКИМИ РЕАКЦИЯМИ
5.2.1. Одномерные течения. Расчет течения
в газовом анализаторе
Основные особенности неравновесных течений могут быть изу-
изучены в одномерном приближении. Действительно, исследование
плоских и осесимметричных неравновесных течений путем числен-
численного решения обратной задачи теории сопла, а также расчеты
вдоль струек тока осесимметричного сопла показывают, что кон-
концентрации компонент слабо зависят от формы струек тока и рас-
распределений давления вдоль них, в особенности в сверхзвуковой
области течения. На рис. 5.2 показано изменение молярной доли
водяных паров и температуры Т=Т/Т0 вдоль линий тока, получен-
полученное в результате решения обратной задачи в одномерном и осесим-
метричном течениях. Имеет место заметное различие концентра-
концентраций на различных линиях тока при равновесном течении и незна-
незначительное— при неравновесном. Кроме того, результаты расчетов
концентраций компонент в неравновесном течении в одномерном
приближении практически совпадают с результатами расчета, в
котором учтен двумерный характер течения. В то же время рас-
распределения температуры (давления) вдоль различных линий тока
заметно различаются в силу двумерности течения, при этом имеет
место также различие между равновесным, неравновесным и за-
замороженным течениями.
Отметим некоторые общие свойства неравновесных течений,
газа в соплах. Очевидно, что параметры неравновесного течения,
должны являться в большинстве случаев (хотя возможны локаль-
локальные отклонения) промежуточными между параметрами двух пре-
предельных течений — равновесного и замороженного. При этом, из-за
того, что химическая энергия в неравновесном течении выделяется
не полностью и частично не передается в активные степени свобо-
свободы и энергию направленного движения молекул, температура, ско-
скорость, давление и импульс, а следовательно, и удельный импульс
в неравновесном течении меньше, чем в равновесном (но больше,
чем в замороженном) (см. рис. 5.1). Наибольшее отличие наблю-
наблюдается в температуре и давлении (иногда на десятки процентов),
значительно меньшее — в скорости и импульсе. Плотность слабо
зависит от характера протекания процесса (будучи несколько
выше в неравновесном течении). Иногда, однако, возможны ло-
локальные превышения температуры и давления над равновесными
193
-0,05
Рис 5.2. Изменение молярной концентрации гн о и температуры вдоль различ-
различных линий тока при неравновесном (/), равновесном B) и замороженном C)
течениях. Продукты сгорания водорода в кислороде при коэффициенте избыт-
избытка окислителя а=1, давление торможения ро=5-10,5 Па:
п — номер слоя в осесимметричном течении при решении обратной задачи; 4 — расчет по
одномерной теории
значениями за счет интенсивного выделения химической энергии,
наступающего после резкого отклонения от равновесия, например,
после замораживания течения за угловой точкой.
Импульс и удельный импульс в неравновесном течении всегда
меньше, чем в равновесном. Расход газа в неравновесном течении
при заданных параметрах торможения и размере минимального
сечения больше расхода в равновесном течении, однако это разли-
различие очень невелико (не более 0,5 ... 1 %). Число М в неравновесном
течении выше, чем в равновесном, из-за значительного уменьшения
температуры, некомпенсирующего менее существенное уменьшение
скорости.
Результаты расчетов неравновесных течений вдоль струек тока
удобно представлять в виде зависимостей параметров не от длины
сопла, а от величины F=r/r*=F/2=[p*Wy (pW)]!/2 по аналогии со
случаем одномерного равновесного течения, когда параметры тече-
течения зависят только от г, а также ввиду того, что величина W
194
1,0
0,05
0,01
0,15
{
1
1
_j> .
2
.
0,315
0,3
р*
I
\ р
/ Yap
2
2
1
Рис. 5.3. Зависимости молярных концен-
концентраций /"н, гсо2> гтяо и Гц от относитель-
относительного радиуса сопла г при равновесном
A) и неравновесном B) течениях. Топ-
Топливо— (CH3JNNH2+N2O4, ct = 0,9; po =
= 5-105 Па; а„ = 100 мм
слабо зависит от характера процес-
процесса. В рамках одномерного прибли-
приближения были проведены детальные
параметрические исследования мно-
многих топливных композиций.
В [33] содержатся графические гт
материалы, позволяющие опреде-
определить потери удельного импульса,
связанные с неравновесным протека-
протеканием химических реакций.
Некоторые характерные резуль-
результаты расчетов неравновесных тече-
течений в сопле видны на рис. 5.3.
Отклонение состава и термоди-
термодинамических параметров продуктов 1 з s 7 ?
сгорания от равновесных значений
начинается в трансзвуковой области сопла, где градиенты газоди-
газодинамических параметров максимальны. При малых давлениях и
небольших размерах сопла, а также при малых температурах это
отклонение может начаться в дозвуковой части сопла. Расчеты
показывают также, что мольные доли веществ СОг, СО, N2, Ог,
Н2О и NOn в окрестности критического сечения замораживаются, и
изменение их величин вниз по потоку не превышает 5... 10%, хотя
характер изменения некоторых из них (СО2, Н2О, N2, CO) на не-
некотором участке сопла близок к равновесному. Мольные доли та-
таких компонент, как О, Н, ОН, Н2, хотя и значительно отличаются
от равновесных значений, однако вниз по потоку не заморажива-
замораживаются. В частности, мольная доля атомарного водорода имеет ми-
минимум (см. рис. 5.3), который не наблюдается при равновесном
протекании реакции. Такое изменение мольной доли водорода
связано с тем, что обменные реакции [см. табл. 1.1] довольно
близки к равновесию во всей области течения, особенно при высо-
высоких температурах, в то время как реакции рекомбинации, идущие
при тройных соударениях, в трансзвуковой области сопла резко
замораживаются.
Молекулярная масса смеси замораживается в окрестности
минимального сечения и далее остается постоянной и меньшей (на
1 ... 3%) соответствующего значения при равновесном течении.
В случае течения бинарной смеси, когда протекает лишь одна
реакция рекомбинации, а обменные реакции отсутствуют, происхо-
происходит резкое замораживание этой реакции в трансзвуковой области,
и далее вниз по потоку течение заморожено. Такой характер про-
протекания реакций, когда кинетика реакций проявляется лишь в уз-
195
кой области, послужил основой создания приближенного метода
расчета неравновесных течений, согласно которому до некоторого
сечения течение принимается равновесным, а вниз по потоку от
него — замороженным.
Параметрами, наиболее существенно влияющими на степень
отклонения течения от равновесного, являются абсолютный размер
сопла (его длина или диаметр минимального сечения dt, форма и
степень геометрического расширения сопла F (или г), полные дав-
давление ро и температура Го, а также состав газовой смеси на входе
в сопло, определяемый типом топлива и коэффициентом избытка
¦окислителя а. Изменение абсолютного размера сопла эквивалентно
изменению времени пребывания газа в сопле, уменьшение которо-
которого (при прочих равных условиях) приводит к увеличению отклоне-
отклонения течения от равновесного. Уменьшение давления р0 также при-
приводит к увеличению степени отклонения течения от равновесного,
поскольку уменьшается число эффективных соударений (особенно
для тримолекулярных высокоэнергетических реакций) и увеличи-
увеличивается исходный уровень диссоциации продуктов сгорания перед
соплом.
Изменение температуры газа влияет на степень неравновесно-
неравновесности течения как через скорости химических реакций, так и через
изменение уровня диссоциации газа перед соплом. Константы
скорости реакций рекомбинации слабо зависят от температуры,
поэтому основное влияние на скорость процесса оказывают актив-
активные радикалы, концентрации которых с ростом температуры уве-
увеличиваются. С другой стороны, с ростом температуры увеличивает-
увеличивается степень диссоциации газа перед соплом, и, следовательно, мо-
может возрасти доля энергии, теряемой из-за неравновесности
процесса. Поэтому изменение температуры может приводить как
к увеличению, так и к уменьшению степени отклонения системы от
равновесия, в зависимости от того, какой фактор окажется преоб-
преобладающим.
Для систем С—О—Н при температурах Г0<2300 К течение в
сопле является замороженным, что может приводить к большим
потерям удельного импульса (до 10%). Действительно, при таких
температурах состав продуктов сгорания в равновесных условиях
может быть в ряде случаев определен с помощью реакции водяно-
водяного пара НгО + СО^СОг + Нг. Однако в таком виде реакция в дей-
действительности не реализуется, а осуществляется через записанную
в табл. 1.1 цепочку реакций. В каждой реакции этой цепочки
должны участвовать либо радикал ОН, либо атомарные компонен-
компоненты О и Н, которые при температурах, меньше 2300 К, практически
отсутствуют. Это приводит к тому, что реакции, представленные в
табл. 1.1, не протекают и заморожены, начиная от камеры сго-
сгорания.
На степень отклонения параметров потока в сопле от равновес-
равновесных значений существенно влияет состав газовой смеси. Наиболь-
Наибольшее отклонение от равновесия имеет место при стехиометрических
газовых смесях, имеющих повышенный уровень диссоциации
196
продуктов сгорания на входе в сопло. По мере обогащения или
обеднения смеси степень диссоциации падает и степень отклонения
от равновесия уменьшается. С увеличением степени расширения
доля энергии диссоциации, которая может быть возвращена в по-
поток при равновесной рекомбинации, возрастает. Однако истинная
доля энергии диссоциации, которая успевает превратиться в кине-
кинетическую энергию потока, слабо зависит от степени расширения.
Вследствие этого увеличивается степень отклонения системы от
равновесия при увеличении г.
Расчет течения в газовом анализаторе. В настоящее время для
определения состава смеси широко используются газовые анализа-
анализаторы.
Отбор газовой пробы проводится с помощью специальных ох-
охлаждаемых зондов, вводимых в интересующие зоны течения. Если
отбор пробы производится из высокотемпературной области, то из-
изменение температуры смеси при ее течении в канале зонда сопро-
сопровождается неравновесным протеканием химических реакций. По
этой причине химический состав пробы на входе в анализатор бу-
будет отличаться от состава газа в точке отбора. В результате кон-
концентрации различных компонент газовой пробы, измеряемые в
газовом анализаторе могут не соответствовать концентрациям этих
компонент в исследуемой области высокотемпературного про-
процесса.
Рассмотрим в связи с этим следующую модельную задачу. При-
Примем, что газовая смесь в точке отбора пробы находится в состоянии
химического равновесия. Тогда ее состав может быть определен при
решении уравнений химического равновесия (см. 3.3.1). Давление
и температуру в точке отбора, а также температуру на входе в га-
газоанализатор считаем известными. Для простоты будем считать, что
закон охлаждения пробы в канале зонда является известной
функцией времени:
E.1)
где То, ТА-—соответственно температура в точке отбора пробы и
dT
на входе в анализатор; t — время; Х=-
7-Г»
будем в дальней-
dt
шем называть параметр X скоростью охлаждения. Неравновесное
протекание химических реакций между компонентами смеси опи-
описывается уравнениями химической кинетики. Таким образом, ре-
решение рассмотренной модельной задачи заключается в численном
интегрировании системы уравнений химической кинетики при за-
заданной временной зависимости температуры C.3.1).
Отметим лишь, что в этом случае решается обратная задача с
заданным распределением температуры от времени. Очевидно, что
методы расчета одномерного течения, изложенные в C.3.1), пол-
полностью пригодны и для расчета такого течения с заменой в соответ-
соответствующих уравнениях W = — .
X dt
197
0,5
о
о
о
A = Wsa \
7fl* ЛЛ
А
о
о о Та
7250
2500
1,0\ Г~\ 72 j_,„so V 7? Рис 5 4 Изменение относительных кон-
' " центраций компонент СО и NO* в га-
газовом анализаторе в зависимости от тем-
температуры ТА на входе в анализатор и
скорости охлаждения X
О — равновесные значения На оси ординат
отложено отношение относительной концент-
концентрации к концентрации начальной
Представленные ниже резуль-
тагог расчетов выполнены Муси-
Мусиным В. Р., Прохоровым М. Б. При
расчетах учитывались реакции,
приведенные в табл. 1.1.
При проведении параметриче-
параметрических расчетов варьировались сле-
следующие параметры: начальный
состав и температура отбираемой
пробы, температура пробы на входе в анализатор и скорость ох-
охлаждения в канале зонда.
На рис. 5.4 представлены зависимости содержания токсич-
токсичных компонент СО и N0* от температуры пробы на входе в анали-
анализатор. Здесь в качестве исходной смеси выбраны продукты сгора-
сгорания воздушно-керосиновой смеси при коэффициенте избытка окис-
окислителя а = 0,9; температуре Т0 = 2500К и давлении ро = О,1 Мпа.
Все кривые приведены на момент времени /=10 с после отбора
пробы. Из рис. 5.4 хорошо видно, что при Тл^1250К содержание
окиси углерода в пробе не зависит от скорости охлаждения пробы
(X) до этой температуры и определяется равновесной концентраци-
концентрацией при соответствующей температуре ТА. Если же проба охлажда-
охлаждается до температуры ниже 1250 К, то содержание СО в значитель-
значительной мере будет определяться скоростью охлаждения К, причем
здесь концентрации СО отличаются от равновесных. Такое влия-
влияние температуры на входе в анализатор ТА и скорости охлажде-
охлаждения пробы до этой температуры на содержание СО в пробе в кон-
конце охлаждения можно объяснить следующим образом.
Согласно рис. 5 4 при температурах ниже 1250 К реакции с
участием молекул СО «замораживаются», и уровень концентрации
СО, измеряемой в газовом анализаторе определяется скоростью
охлаждения пробы до этой температуры Так например, результа-
результатом охлаждения пробы (взятой при температуре 2500 К) до ком-
комнатной температуры со скоростью охлаждения в газовом анализа-
анализаторе, является заниженная величина концентрации СО на 47%
по сравнению с концентрацией в точке отбора пробы. Увеличение
скорости охлаждения в 1000 раз дает занижение на 37%, увеличе-
увеличение скорости охлаждения еще в 1000 раз (А,= 109 К/с) —на 10%.
Изменяется лишь диапазон температур, при которых реакции
с участием NO* «замораживаются». При температуре ниже 2000 К
содержание окислов азота определяется только скоростью охлаж-
охлаждения до этой температуры. Поэтому для получения достоверной
информации о содержании окислов азота в высокотемпературной
198
ri.\ .достаточно пробу охладить до 2000 К и затем, вос-
голь_ л^вн результатами проведенных предварительно числен-
ны\ иссл%зчйг.г ний, ввести поправочные коэффициенты на величи-
величину концентраций N0* в охлажденной пробе. Игнорирование выяв-
тенных закономерностей может привести к занижению истинной
концентрации N0* в высокотемпературной смеси на величину до
80%
5.2.2. Плоские и осесимметричные течения
Исследование плоских и осесимметричных течений в соплах
представляет собой значительно более сложную задачу, нежели
исследование течения в одномерном приближении, поскольку те-
теперь нужно решать систему C 36) ..C 40) вдоль линии тока не-
несколько раз для обеспечения сходимости итераций
Метод решения обратной задачи описан в 33 1. Ниже описаны
результаты расчетов, выполненные В Ф Колмогоровым, при за-
заданном на оси симметрии распределении давления
-е) , E.2)
УР\ ~ Р*>с + (Р* — Pi) о-
где а = ехр (—х/b); с=1 при хХ), а=1, с = ехр (х/b) при
ir=x/r*, р = р/ро, ри р2 — давления в начальной и конечной точках
на оси сопла, Ъ — параметр, характеризующий величину градиента
давления в трансзуковой области.
Некоторые результаты расчетов осесимметричного течения пред-
представлены на рис. 5 2, 5.5. Рассчитывалось равновесное, неравновес-
неравновесное и замороженное течения при заданном на оси симметрии рас-
распределении давления E.2) с /Ji = 0,96; р* = 0,55; р2 = 0,04 и 6 = 0,8.
Линии М= 1 и 0 = 0 как в замороженном, так и в равновесном тече-
течении выходят из одной точки на оси (х = х*) и простираются вверх
по потоку от этой точки, так что линия М=1 находится всегда вы-
выше по потоку, чем линия 8 = 0, в соответствии с общими закономер-
закономерностями поведения этих линий в осесимметричных и плоских тече-
течениях (см. 4.1.1). При неравновесном течении линии М=1, 6 = 0
также простираются вверх по потоку, однако они выходят из раз-
разных точек на оси симметрии, причем точка оси, в которой М=1,
расположена ниже по потоку, чем точка, соответствующая линии
6 = 0, поскольку в неравновесном одномерном течении происходит
смещение линии М=1 вниз по потоку относительно минимального
сечения. Внутри течения эти линии пересекаются. В неравновесном
осесимметричном и плоском течениях в зависимости от кривизны
контура в минимальном сечении скорость течения может быть мень-
меньше, равна или больше скорости звука в противоположность случа-
случаям равновесного или замороженного течений, в которых в мини-
минимальном сечении скорость всегда больше скорости звука.
В трансзвуковой области имеет место некоторое повышение тем-
температуры на линиях тока с малыми радиусами кривизны. Оно свя-
199
Рис 5 5 Звуковые линии М = 1 и линии 9 = 0 поч
неравновесном (О%) изамороженьом (АА) течениях
зано с характером протекания неравновес-
неравновесных процессов и не имеет места в равновес-
равновесном и замороженном течениях. Действи-
Действительно, высокий градиент давления в транс-
звуковой области вызывает резкое замора-
замораживание химических реакций, которые
затем начинают интенсивно осуществляться
при последующем переходе в область с
меньшим градиентом давления, что приво-
приводит к выделению тепла и повышению тем-
пературы. Другая особенность в распреде-
распределении температуры имеет место вблизи вы-
выходного сечения сопла, где при малых гра-
градиентах давления течение стремится к локальному равновесному
состоянию, что приводит к повышению неравновесной температу-
температуры на выходе из сопла и изменению концентраций компонент в-
сторону их равновесных значений.
Распределение концентраций компонент на различных линиях
тока неравновесного течения (см. рис. 5.2) характеризуется слабой
зависимостью их от формы линии тока и распределения давления
на них, что находится в соответствии с результатами расчетов в
одномерном приближении. В то же время в равновесном течении
концентрации компонент на различных линиях тока отличаются
значительно. На рис. 5.2 пунктиром показаны результаты расчета
неравновесного течения в одномерном приближении. Одномерное
приближение можно использовать с достаточной для практики
точностью при расчете концентраций компонент, однако значения
температуры определяются достоверно лишь в областях с малыми
градиентами. Потери импульса, связанные с неравновесным про-
протеканием химических реакций, с высокой точностью могут быть
определены в рамках одномерного приближения.
5.3. ТЕЧЕНИЯ С КОЛЕБАТЕЛЬНОЙ РЕЛАКСАЦИЕЙ
Времена релаксации колебательных степеней свободы на один—
два порядка меньше времен для химических реакций, а энергия их
сравнима с химической энергией при течениях высокотемператур-
высокотемпературной смеси. Тем не менее процесс колебательной дезактивации из-за
больших градиентов газодинамических параметров, особенно при
малых абсолютных размерах сопла, может протекать неравновесно.
В последние годы возрос интерес к изучению процессов колебатель-
колебательной дезактивации в сопле в связи с проблемой создания газодина-
газодинамических оптических квантовых генераторов Неравновесное
протекание дезактивации колебательных степеней свободы приво-
приводит к возникновению инверсной заселенности колебательных уров-
уровней молекул, необходимой для инициирования излучения. Метод
200
расчета неравновесных течений с колебательной релаксацией изло-
изложен в 3.3 1, а необходимые сведения о временах релаксации приве-
приведены в 1.3 2.
5.3.1. Одномерные течения
Рассмотрим влияние колебательной неравновесности на пара-
параметры течения в сопле и потери удельного импульса на примере
расширения продуктов сгорания топлива (CH3JNNH2+N2O4. На
рис. 5.6 представлены зависимости относительных колебательных
температур Tv различных компонентов от относительного радиуса
сопла r = r/r± при различных значениях параметра \|) и коэффици-
коэффициенте избытка окислителя а=1,2. Видно, что по мере уменьшения
параметра ф колебательные температуры компонентов все более
отклоняются от равновесных и при достаточно малых значениях гр
и больших степенях расширения могут даже замораживаться. Чем
меньше значение г|), тем ближе к критическому сечению происхо-
происходит отклонение колебательных температур от равновесных значе-
значений. При уменьшении %р наиболее отклоняются от равновесных
значений колебательные температуры Н2, NO, N2 и СО. Например,
если при 113 = 6,25-107 Па-мм колебательные температуры С02 и
Н20 близки к равновесным значениям, то колебательная темпера-
температура СО при ;~=10 превышает равновесное значение более чем в
J,5 раза.
0,1
0,6
0,4
€
ТА |Г=
^~—r-——
CO ^5^
t
(¦J2) 1
-700
~-вг5
10
10
Рис 5 6 Зависимость колебательной температуры T
г|> A05 Па мм):
/ — равновесная температура
S 8 10 r
Т. от г для разных
201
5.3.2. Плоские и осесимметричные течения
Плоские и осесимметричные течения в рамках обратной задачи
изучались в работах [4, 15,26].
В рамках обратной задачи в работе [4] численно решена зада-
задача расчета течения в плоском сопле при наличии неравновесной ре-
релаксации колебательных степеней свободы. Определены колеба-
колебательные температуры различных мод, установлена инверсная засе-
заселенность уровней и определен коэффициент усиления. Исследовано
влияние геометрических параметров сопла на инверсную заселен-
заселенность уровней и коэффициент усиления и продемонстрирована важ-
важность учета двумерных эффектов при их определении. На рис. 5.7, а
показаны линии M = const в плоском сопле с угловой точкой при
учете (сплошные линии) и без учета (пунктирные линии) колеба-
колебательной релаксации. Очевидно заметное изменение поля за счет
колебательной релаксации, особенно в развитой сверхзвуковой об-
области. На рис. 5.7, б представлены распределения вдоль оси сим-
симметрии (пунктирные линии) и контура сопла (сплошные линии)
числа М, коэффициента усиления К, температуры поступательных
степеней свободы Т и колебательных температур: температуры 7\
симметричной и деформационной мод СО2, температуры Т2 асим-
г, мм
№
400
Рис 5 7 Линии M = const (о), распределение температур колебательных степеней
свободы и коэффициента усиления К (б) при течении в сопле с неравновесным
возбуждением колебательных степеней свободы
202
метричного вида колебаний СО2, колебательной температуры Гз
азота. Из рисунка видно, что в дозвуковой области сопла течение
мало отличается от равновесного. В трансзвуковой области вслед-
вследствие больших градиентов газодинамических параметров прекра-
прекращается колебательно-поступательный V—Т-обмен с молекулами
азота, поскольку время релаксации этого процесса велико. Затем
тормозится V—Г-обмен между СО2 и Н2О. Инверсный и непрекра-
непрекращающийся обмен между уровнями асимметричного типа колебаний
и колебательно-возбужденным азотом обеспечивает «перекачку»
колебательной энергии от азота к третьему типу колебаний СО2.
В связи с этим величина Т2 проходит через минимум и начинает
приближаться к Т3. Ввиду малости времен релаксации V—/-обме-
V—/-обмена для молекул СО2 симметричного типа колебаний величина Тх
близка к Т. Из рис. 5.7 видно также, что изменения представленных
на нем величин вдоль оси и контура заметно отличаются, что осо-
особенно характерно для коэффициента усиления.
Важно отметить, что в рамках обратной задачи удается рас-
рассчитать контуры сопел с угловой точкой (см. рис. 5.7, а).
В работе [15] приведены результаты численного профилирова-
профилирования и анализа влияния формы сопла и газодинамических парамет-
параметров на характеристики газодинамических лазеров.
На основе исследований двумерного неравновесного течения се-
семейства подобных сопел и сопел с различным углом наклона су-
сужающейся части показана целесообразность выбора такой формы
дозвуковой части, которая обеспечивает прямолинейную звуковую
линию. Рекомендуются соотношения геометрических параметров
дозвукового и трансзвукового участка сопла, обеспечивающие без-
отрывность течения и форму звуковой поверхности, близкую к плос-
плоской. Проведено параметрическое исследование сверхзвукового
участка двух классов плоских сопел газодинамических лазеров, по-
построенных на базе равномерных и симметричных характеристик
на выходе (см. разд. 4.6.2). На основе параметрических исследова-
исследований влияния степени расширения, полного давления и температуры,
а также состава газа показано, что наименьшие потери полезной
колебательной энергии в резонаторной области обеспечивают сопла,
построенные на базе равномерной характеристики.
Эффективность преобразования тепловой энергии в энергию ко-
когерентного электромагнитного излучения существенно зависит от
геометрии сопла, определяющей свойства колебательно-неравно-
колебательно-неравновесного течения газовой смеси в рабочей части газодинамического
лазера.
Большое влияние на характер неравновесных процессов оказы-
оказывает сверхзвуковая часть сопла. В настоящее время в конструкциях
обычно используется семейство сопел с угловой точкой, построенное
на базе равномерной замыкающей характеристики. Однако данное
семейство сопел не является семейством сопел кратчайшей длины.
Более высокого темпа охлаждения газовой смеси можно достигнуть
в более коротких соплах с неравномерным распределением парамет-
параметров в выходном сечении. Поэтому в этой работе классическим ме-
203
тодом характеристик проведено параметрическое профилирование
плоских и осесимметричных сопел, обеспечивающих заданные не-
неравномерные газодинамические параметры в выходном сечении
(разд. 4.6.4). Рассмотрено, в частности, семейство, построенное на
базе симметричной замыкающей характеристики и обеспечивающее
параллельность потока на выходе и отсутствие ударных волн во
всем поле течения.
Проведено параметрическое исследование характеристик двух
классов сопел, первый из которых выстраивается на базе равномер-
равномерной замыкающей характеристики, а второй — на базе симметрич-
симметричной замыкающей характеристики. Сопла, профилируемые на базе
симметричной характеристики, имеют более высокие значения угла
наклона контура в угловой точке, что обеспечивает более интенсив-
интенсивный разгон потока как за угловой точкой, так и на всем сверхзву-
сверхзвуковом участке.
Для ГДЛ на смеси газов CO2 + N2 + H2O был проведен анализ
влияния геометрических параметров исследованных классов сопел
на величину коэффициента эффективности сопла "п.. Получено, что
для сопел второго класса средний по сечению коэффициент ц на
выходе на величину 0,04 превышает соответствующее значение ц
для сопел первого класса. Однако расчеты показали, что в выход-
выходном сечении сопел данного класса реализуются существенно нерав-
неравномерные газодинамические параметры. Продольная составляющая
скорости и числа М при удалении от оси уменьшаются, а давление
и плотность увеличиваются. Так, неравномерность по числу М со-
составляет около 60%. Наличие такой сильной неравномерности ука-
указанных газодинамических параметров на срезе сопла второго клас-
класса может привести к дополнительным газодинамическим возмуще-
возмущениям, в результате действия которых в колебательно-релаксирую-
щем потоке за срезом сопловой решетки может быть потеряна
часть колебательной энергии. Поэтому для правильного изучения
качества лазерного потока, истекающего из обоих классов сопел, в
работе проведено численное исследование релаксирующего течения
смеси газов за срезом сопел в резонаторной области.
В качестве расчетной области, моделирующей взаимодейству-
взаимодействующие потоки, принимается область, на верхней и нижней границах
которой плоскости взаимодействия заменяются эквивалентными
по граничным условиям плоскими стенками прямолинейного ка-
канала.
Смешанная задача расчета изоэнтропического потока в указан-
указанной области по данным, полученным в выходных сечениях сопел,
решается послойным методом характеристик, обладающим свой-
свойством «сквозного» счета несильных ударных волн. Расчеты, прове-
проведенные без учета влияния генерации излучения, показывают, что
неравномерность газодинамических параметров на срезе коротких
сопел оказывает сильное влияние на течение газа в резонаторной
области. Неравномерные профили газодинамических параметров в
сечениях, расположенных внизу по потоку, начинают выравниваться,
периферийная часть потока с большим давлением поджимает цент-
204
ральную часть и из-за данного поджатия появляются условия воз-
возникновения висячей ударной волны, интенсивность которой с уве-
увеличением х возрастает.
В результате из-за наличия за срезом сопла 2 ударной волны
происходит значительное уменьшение ц для сопла 2 и получаются
более низкие средние значения коэффициента усиления К. Следо-
Следовательно, поток смеси газов CO2 + N2 + H2O, истекающий из сопла,,
рассчитанного на равномерные параметры на выходе в резонатор-
ной области, имеет более высокие запасы колебательной энергии.
На основании проведенных численных исследований можно сде-
сделать вывод, что из двух рассмотренных классов сопел с точки зре-
зрения наименьших потерь колебательной энергии в резонаторной об-
области более эффективными являются сопла, построенные на базе
равномерной характеристики, которые при наличии острой кромки
на выходе из сопловой решетки обеспечивают высокую степень од-
однородности всех газодинамических параметров.
5.4. ТЕЧЕНИЯ С НЕРАВНОВЕСНОЙ КОНДЕНСАЦИЕЙ
Исследование одномерных стационарных течений в соплах по-
позволяет изучить основные особенности процесса неравновесной кон-
конденсации, являясь одновременно достаточно простым с точки зре-
зрения построения численного алгоритма и возможностей детального
параметрического исследования. Необходимые формулы и соответ-
соответствующие алгоритмы для расчета одномерного стационарного тече-
течения в соплах в случае равновесного, неравновесного и заморожен-
замороженного процесса приведены в [11]. При решении обратной задачи
вдоль оси задается распределение либо давления р = р(х), либо
плотности р = р(х), либо скорости W=W(x).
Очевидно, что при решении обратной задачи целесообразно
задавать распределение вдоль оси такого параметра, который слаба
зависит от самого процесса конденсации и может быть просто вы-
вычислен для замороженного течения. Как показали результаты боль-
большого числа параметрических расчетов одномерных и двумерных
течений в соплах [11], к числу таких параметров относятся плот-
плотность смеси р, скорость смеси W и плотность тока смеси pW. Дей-
Действительно, из результатов расчетов следует, что в неравновесном
течении, по сравнению с замороженным, плотность и скорость сме-
смеси соответственно увеличиваются и уменьшаются на 1...2%, а дав-
давление и температура—-на 15...20%. Из результатов расчетов следу-
следует также [11], что процесс неравновесной конденсации практически
не оказывает влияния на положение линий тока при двумерном те-
течении в сопле и плотность тока pW, поскольку увеличение плотно-
плотности компенсируется уменьшением скорости. Из сказанного следует,
что в рамках одномерного течения можно с высокой точностью ис-
исследовать и двумерные течения с неравновесной конденсацией Для
этого необходимо рассчитать каким-либо методом (например, мето-
методом характеристик) двумерное замороженное течение без конден-
конденсации и, получив из такого расчета распределение плотности тока
20S
Точка Вильсона
Р
PsJs
Лчка росы
и
у
W
pj
О 5
10х,см
Рис 5 8 Типичные распределения давления Рис 5 9 Распределение давления
J), температуры 7", скорости образования по длине сопла Сравнение расчет-
ядер /, числа частиц в единице объема N, ных и экспериментальных данных
массовой доли жидковой фазы ае и переох- r =1 CM q_Po=49 1O5 Па го=442 К-
лаждения s по длине сопла неравновесной /=,415 к- Л — р»=2 Ю5 Па' го°=445 К
конденсации
равновесный процесс, 2 — неравновесный, 3 —
замороженный, 4 — контур сопла
К I — равновесное течение, 2 —
неравновесное течение
вдоль различных линий тока (либо траекторий частиц в случае
нестационарного течения), рассчитать затем, уже в одномерном
приближении, процесс неравновесной конденсации с заданным по
длине распределением плотности тока. Таким образом, в рамках
одномерного течения можно изучить основные особенности процес-
процесса неравновесной конденсации как для одномерного так и двумер-
двумерного течений.
Характерные распределения параметров в процессе неравновес-
неравновесной конденсации в сверхзвуковом сопле представлены на рис.
5.8...5.10.
На рис. 5.8 показано качественное изменение основных парамет-
параметров, а некоторые количественные результаты конкретных расчетов
и экспериментов приведены на рис. 5.9, 5.10. Результаты расчетов
и экспериментов отражают развитие процесса конденсации. На
первой стадии этого процесса (см. рис. 5.8) при достижении доста-
достаточно большого перенасыщения зарождаются ядра конденсации, и
процесс зарождения ядер завершается на достаточно малой длине,
скорость их образования имеет резко выраженный максимум и до-
достигает больших значений — до 1021 частиц/см3с, после чего ско-
скорость образования снижается до нуля. Общее число ядер на пер-
первой стадии процесса конденсации также быстро растет и достигает
величины 1019 частиц/г; однако затем число ядер остается неизмен-
неизменным. Далее наступает вторая стадия процесса конденсации, в ко-
которой уже в основном происходит рост частиц на образовавшихся
ядрах и увеличение массовой доли жидкой фазы. За счет выделе-
206
Рис 5 10 Распределение температуры по дли- .
не сопла при неравновесной конденсации (Обо- '/'в
значения см рис 5 9)
ния большего количества тепла состоя-
состояние перенасыщения снимается и пере-
переход в состояние насыщения может
произойти достаточно резко на малой
длине и носить почти скачкообразный
характер. Однако при некоторых усло-
условиях возможен и достаточно плавный
переход в состояние насыщения. Даль-
Дальнейшее изменение давления и темпера-
температуры происходит по равновесной кри-
кривой. Отметим, что переход в состояние
насыщения происходит почти скачко-
скачкообразно при больших давлениях и ма-
малых числах М в точке росы, при уменьшении давления наблюдает-
наблюдается (и, следовательно, при увеличении числа М) более плавный пе-
переход (см. рис. 5.9). В то же время из-за больших градиентов газо-
газодинамических параметров течение может не достигнуть состояния
равновесия. В силу отмеченных особенностей для оценки влияния
конденсации на параметры потока можно воспользоваться расче-
расчетом равновесного течения.
Отметим еще, что при неравновесной конденсации относительное
изменение температуры при переходе от замороженного течения к
равновесному больше, чем относительное изменение давления (см.
рис. 5.9, 5.10). Укажем еще, что нельзя отождествлять области рез-
резкого повышения давления и температуры, вызванные спонтанной
конденсацией (так называемые скачки конденсации), с известными
газодинамическими скачками уплотнения. В газодинамических
скачках уплотнения повышение давления и температуры сопровож-
сопровождается и сильным падением скорости, согласно соотношению
Ai?i2=l, где Xi и Лг — приведенные скорости до и после скачка, при
этом сверхзвуковой поток переходит в дозвуковой. В зоне спонтан-
спонтанной конденсации происходит лишь незначительное, на 1...2%, умень-
уменьшение скорости, при этом очевидно, что течение остается сверхзву-
сверхзвуковым (см. рис. 5.8). Вышесказанное не относится к трансзвуковым
потокам с числами М= 1... 1,3.
5.5. ТЕЧЕНИЯ В КАНАЛАХ МГД-ГЕНЕРАТОРОВ
В прикладных задачах, связанных с разработкой и исследова-
исследованием некоторых схем МГД-генераторов, приходится встречаться с
течениями электропроводного газа в соплах в магнитном поле. При
этом весьма существенно иметь представление о структуре течения
в до-, транс- и сверхзвуковой областях сопла.
В работе [5] исследуются до- и сверхзвуковые осисемметричные
течения в сопле в меридиональном магнитном поле. Решается об-
обратная задача теории сопла Лаваля, обобщенная на случай маг-
207
нитогазодинамических течений. При построении разностных схем
используются идеи, развитые в разд. 3.4.4. Для обеспечения воз-
возможности расчета сопел сложных конфигураций использована
криволинейная ортогональная система координат (\|з, s) (s — рас-
расстояние вдоль начальной линии тока). Проведены расчеты течений
в сопле Лаваля и в кольцевых радиальных соплах. Определены
поля газодинамических параметров и потери полного давления.
Указывается на необходимость ослабления магнитного поля в
•сверхзвуковой части кольцевого радиального сопла дискового
МГД-генератора. Необходимые сведения по используемым соотно-
соотношениям для течений электропроводного газа в сопле даны в
разд. 1.3 5.
Отметим некоторые качественные закономерности течений про-
проводящего газа в сопле. Из уравнения C.73) очевидно, что с уве-
увеличением параметра взаимодействия происходит экспоненциальное
уменьшение полного давления, связанное с джоулевой диссипаци-
диссипацией энергии. Джоулев нагрев приводит также к увеличению темпе-
температуры газа, уменьшению плотности и скорости по сравнению со
случаем отсутствия взаимодействия проводящего газа и магнитно-
магнитного поля, если статическое давление газа сохранять неизменным.
Таким образом, наложение магнитного поля тормозит газ и при-
приводит к потерям давления. Эти эффекты, очевидно, возрастают с
увеличением параметра Л', в частности сверхзвуковой поток при
наложении сильного магнитного поля может перейти в дозвуковой
Приведем результаты расчетов осесимметричных течений про
водящего газа в до-, транс- и сверхзвуковой частях сопла Лавалз
и кольцевого радиального сопла. В качестве начальной криво!
выбиралась ось симметрии сопла Лаваля или контур стенки цент
рального тела кольцевого радиального сопла. На ней задавалос
распределение числа М, которое находилось из трехпараметриче
ского распределения приведенной скорости ^=W/a изоэнтропиче
ского течения — формула D.3).
На рис. 5.11 представлено поле течения для распределения т
да D.3) с Woo=0,l; Woo—1,9 и b = 3,5. Расчет проводился с пс
стоянным шагом Ai]) = 0,168-10~2 во всей области течения, включа
и область вблизи оси. На этом рисунке нанесено семейство лини
тока и линии M=const; любая из линий тока может быть выбраг
в качестве стенки сопла. Приведена также зависимость числа М (
длины сопла на оси симметрии (кривая 1) лри ^ = 0,015 и 0,05
(кривые 2 я 3 соответственно). Приведенная на рис. 5.11 завис
мость коэффициента давления ср = 2(р—poo) / (p» W^J от дли1
сопла на линии тока -ф = 0,015 свидетельствует о возникновении
области малых дозвуковых скоростей, где контур практичес
прямолинеен и параллелен оси симметрии, зоны с положительш
градиентом давления.
Из результатов расчетов следует, что положительный градие
давления имеется на всех линиях тока 1^^0,005 и увеличиваете!
уменьшением радиусов сопряжения R\ и R%. Так, на линии тс
•с ф = 0,010 максимальное значение ср —0,76-10~2, на линии ток
-2
Рис 5 11 Поле течения в осесимметричном сопле при наличии магнитного поля
1|з = О,О15 оно равно 0,123, а при г|з = 0,025—ср = 0,472. Взаимодей-
Взаимодействие потока с магнитным полем приводит к увеличению положи-
положительного градиента давления. Так, при 5 = 0 на линии тока с г|)=
= 0,015 положительный градиент отсутствует, а при г{) = 0,025 мак-
максимальное значение ср = 0,072.
На рис. 5.12 приведено распределение статического и полного
давлений по длине сопла на линиях тока ф = 0 (кривая /) и 0,015
(кривая 2). Для -ф = 0,025 (кривая 3) приведено распределение
только полного давления. Представлено также изменение модуля
радиальной составляющей скорости и по длине сопла. Из сравне-
сравнения кривых pQ=p0(x) с кривой |ы| = |м(х)| следует, что интен-
интенсивное падение полного давления наблюдается в областях, где ра-
радиальная составляющая ско-
скорости достигает максимума.
Этим зонам соответствуют ко-
конические участки вблизи гор-
горловины сопла в до- и сверхзву-
корой областях. Так как на оси
сопла WxB = 0, то на линии
тока ij) = 0 реализуется изоэнт-
ропическое течение и ро(х) = 1.
На рис. 5.13 изображен кон-
контур сопла, соответствующий
•ф = 0,0168, и линии M = const
при наличии поля (пунктирная
кривая) и без него. Магнитное
поле увеличивает неравномер-
неравномерность потока по сечению как в
до-, так и в сверхзвуковой об-
8—1393
р
0,8
О,1!
Г5
V
V
V
¦"«^
'2
3
0,9Ь
0,9
0,1
о
1,0 2,0 3,0
Рис 5 12 Изменение полного и ста-
статического давлений вдоль линий то-
тока сопла при наличии магнитного
поля
209
Рис. 5.13. Поле течения в осесимметричном сопле при наличии и отсутствии маг-
магнитного поля
ластях, а влияние на контур оказывается только в дозвуковой части.
В сверхзвуковой части отношение осевой и радиальной составля-
составляющих скорости велико, и координаты контуров отличаются не
более чем на 0,7%- Потери полного давления в этом сопле, рассчи-
рассчитанном на небольшие сверхзвуковые скорости (М~2,0), не пре-
превышают 5%. Неравномерность давления за счет воздействия маг-
магнитного поля может увеличиться в 3 ... 5 раз. Отметим, что пондер-
моторная сила направлена к оси сопла в дозвуковой части, и к
стенке — в сверхзвуковой. Из результатов расчетов и анализа
уравнений следует, что плотность газа вблизи стенок сопла сни-
снижается в большей степени, чем у оси, особенно при больших пара-
параметрах взаимодействия N. Это приводит как бы к оттеснению газа
от стенок сопла и образованию некоторого фиктивного канала с
более плавными стенками, чем у действительного сопла, в котором
и движется основная масса газа. В связи с этим происходит неко-
некоторое выравнивание линий p = const и M=const в окрестности
критического сечения. Коэффициент расхода тем не менее умень-
уменьшается за счет воздействия магнитного поля, что связано с умень-
уменьшением полного давления за счет джоулевой диссипации. Интен-
Интенсивное падение полного давления наблюдается в областях, где
радиальная составляющая достигает максимума. На оси сопла
пондермоторная сила равна нулю, и полное давление остается
неизменным. Наложение магнитного поля за счет джоулевой дис-
диссипации приводит к уменьшению импульса сопла по сравнению
с импульсом сопла в отсутствии магнитного поля. Однако это
уменьшение при реальных значениях параметра взаимодействия
невелико (~0,5%).
Рассмотрим кольцевое радиальное сопло с центральным телом.
В качестве / выбрана кривая, составленная из четверти окружно-
окружности (рис. 5.14).
(г-О.ббJ+(*-0,35J=0,352; г<0,55, х<0,35
и полупрямых
л:=0, хУ 0,55 и г=0,2, л; >0,35,
на которой задано распределение скорости вида D.3).
210
1.0
0,5
o,ms
1=1,12; N=0,092 x
M
1,5
0,5
$=1,116, N=0,366
0,5
1,0
0,5
1,0
1.5
Рис. 5.14. Поля течения в кольцевом радиальном сопле при наличии магнитного
поля (а), при наличии и отсутствии магнитного поля (б)
На рис. 5.14, а представлено семейство линий тока и линии
М— const для сопла с ^ = 0,2; Waa=l,9 и 6 = 8,0. Приведена
также зависимость полного давления и числа М от радиуса на
линиях тока я|з = О; 0,0085; 0,017 и 0,0255 (кривые 1 ...4 соответст-
соответственно) . На цилиндрическом участке в дозвуковой области, как и в
сопле Лаваля, обнаружено возникновение зоны с положительным
градиентом давления. Максимальное значение ср = 0,1. Звуковая
линия, расположенная за зоной поворота, выпукла в сторону
сверхзвуковой области, ее положение соответствует s = 0.
Джоулев нагрев газа сопровождается резким падением полного
давления в сверхзвуковой части, в выходном сечении полное дав-
давление составляет ~0,45 от давления на входе в сопло. Связанное
с диссипацией уменьшение плотности газового потока приводит к
сильному раскрытию контура второй стенки, а это в свою очередь
приводит к интенсивному ускорению газа вблизи стенки и обуслов-
обусловливает сильную неоднородность полей параметров в поперечном
сечении сопла. Так, например, неоднородность электропроводности
в выходном сечении составляет ~50%. Из сравнения распределе-
распределений М=М(г) вдоль нижней стенки для одного и того же сопла на
рис. 5.14, а в магнитном поле (кривая /) и без него (кривая 5)
видно, что в сверхзвуковой части сопла осуществляется интенсив-
интенсивное торможение газа.
При jV = 0,092 и В = 1,4 Тл скорость потока на выходе у нижней
стенки ограничена значением М~2,1. Увеличить степень МГД-
взаимодействия путем увеличения магнитного поля не удалось.
При численных расчетах внешний контур резко раскрывался, ста-
статическое давление у стенки падало до нуля и счет прекращался.
Физически это объясняется тем, что при заданных условиях поток
не может быть существенно ускорен, так как энергия его не доста-
достаточна для преодоления тормозящего действия поля. В данном
8*
211
случае удалось увеличить величину магнитного поля с 0,4 до
1,4 Тл, уменьшив скорость истечения на выходе с М=2,6 до 2,1.
Сопло изображенное на рис. 5.14, б соответствует №=0,1;
W«,= l,9; 6 = 1,75. В области поворота передзвуковой линией воз-
возникает местная сверхзвуковая зона. Положительный градиент
давления в этой зоне достаточно велик (Cj,=0,3). Линии М=const
сильно искривлены вблизи звуковой линии, что свидетельствует о
существенно двумерном характере течения в этой области. Штрих-
пунктирными линиями показаны контур сопла и линии М= const
при В=0 для того же распределения скорости на кривой I. Видно,
что влияние поля существенно сказывается в до- и сверхзвуковой
областях и значительно слабее в трансзвуковой. Так, если разли-
различие в величине максимального значения ср в зоне поворота при
наличии поля и при В = 0 не превышает 0,7%, то в дозвуковой
области достигает 12%. Различие в координатах линий М=0,1
и М=1,0 на верхней стенке составляет соответственно 2,4 и 0,6%.
Таким образом, несмотря на близость величины параметра
N к максимально возможной для рассмотренного сопла и выбран-
выбранного рабочего тела, влияние поля на геометрию и параметры по-
потока до- и трансзвуковой областей сопла незначительно. Это
позволяет с отмеченной выше точностью пренебречь влиянием
поля в этих областях и рассматривать течение как изоэнтропи-
ческое.
Представленные в дозвуковой части сопла линии s = const
поясняют расположение, узлов разностной сетки. Несмотря на сгу-
сгущение узлов на линиях тока с увеличением \|з, шаг по s сохраняет-
сохраняется постоянным, счет устойчив вплоть до пересечения двух линий
s = const.
Схема радиального кольцевого сопла дискового МГД-генера-
тора совместно с магнитной системой из трех катушек приведена
на рис. 5.15. Магнитное поле в зоне МГД-канала и сопла создается
двумя осесимметричными катушками и неоднородно по радиусу.
Поле в зоне сопла может быть ослаблено с помощью дополнитель-
дополнительной компенсирующей катушки меньшего диаметра.
Распределение индукции магнитного поля BQ(x) определяется
следующим образом. Каждая катушка заменяется эквивалентным
токовым витком, индукция магнитного поля которого на оси сим-
симметрии описывается зависимостью
где г0 — радиус витка; h — расстояние от начала координат до
плоскости витка; С — постоянная катушки.
Производя суммирование по всем катушкам, получим на оси
симметрии
212
Зона сопла
Рис 5 15 Поле течения в радиальном коль-
кольцевом сопле дискового МГД, распределе-
распределение магнитного поля
На рис 5.15 приведена геометрия
сопла, линии М = const, распределе-
распределение ро, а также Вх, Вт (в Тл) по ра-
радиусу вдоль стенок сопла. Результа-
Результаты представлены как для магнитной
системы из двух катушек (сплошная х
кривая), так и для системы из трех
катушек (шгрихпунктирная кри- 1°
вая). Параметр N равен 0,058 в
первом случае и 0,0084 во втором.
Постоянная С, входящая в выраже-
выражение E.3), равна +1,0 для основных °>s
катушек и —0,8 для компенсирую-
компенсирующей.
Компенсация магнитного поля
резко снижает потери полного дав- ^^ ^
ления и позволяет обеспечить уско-
ускорение потока до М«3,0. Неравно-
Неравномерность потока в выходном сечении сопла составляет 5% по
электропроводности и 2% по скорости при нескомпенсированном
поле и соответственно 3 и 0,6% —при скомпенсированном.
Анализ результатов показывает, что при фиксированном отно-
отношении давлений р/ро, максимальная величина скорости, до кото-
которой удается ускорить поток, уменьшается с увеличением В. Основ-
Основным путем, обеспечивающим возможность ускорения потока до
сверхзвуковых скоростей с числом М~3,0, является снижение
потерь полного давления в сверхзвуковой части сопла. Помимо
компенсации магнитного поля целесообразно по возможности
более интенсивное ускорение потока в этой области.
5.6. ТЕЧЕНИЯ С ПОДВОДОМ ЭНЕРГИИ
Течение с подводом энергии рассчитывалось в рамках обрат-
обратной задачи в работе [13]. Основные уравнения выписаны в 1.2.1, а
соответствующая разностная схема в 3.4.2.
Расчеты течения газа с зоной тепловыделения вблизи оси для
Q?=0 проводились с шагом г|з=1О~4. Предполагалось, что зона
тепловыделения расположена между линиями тока ty — О и \р-=
= 0,2¦ 10~2. Профили температуры и скорости течения на оси с
тепловыделением представлены на рис. 5.16 сплошной линией, без
тепловыделения — пунктирной. Увеличение температуры и скоро-
скорости очевидно. Максимум температуры в дозвуковой части объяс-
объясняется тем, что в области дозвукового течения, где мал продольный
градиент давления, понижение температуры газа за счет расшире-
расширения незначительно, поэтому существенен вклад в рост температу-
температуры члена с тепловыделением. Изменение параметров на оси при-
213
1,W
3,0
2,0
1,0
f
и
r
и -
/
,^-
w
w
-3,0 -2j -2,0 ¦# -7,0-/7,5 О 0,5 1,0 1,5 2,9 2,5 x
Рис. 5 16. Распределение скорости и Рис 5 17. Форма линий тока при на-
температуры на оси при наличии зо- личии зоны тепловыделения
ны тепловыделения
водит к изменению конфигураций линий тока (рис. 5.17, сплошная
линия) по сравнению с конфигурацией для Q=0 (пунктирная ли-
линия). Изменение формы линий тока в дозвуковой части объясняет-
объясняется резким повышением температуры на оси сопла, вызванным
тепловыделением. В сверхзвуковой части сопла линии тока меня-
меняются эквидистантно линиям тока для течения с Q=0, так как
профили температуры и скорости при наличии тепловыделения,
как и в случае с Q=0, в сверхзвуковой части выходят на
асимптоту.
Отсутствие теплопроводности и резкое падение тепловыделения
приводят к тому, что скорость и температура на границе тепло-
тепловыделения резко меняются и вне зоны тепловыделения наблюдает-
наблюдается течение, параметры которого хорошо согласуются с параметра-
параметрами "течения при Q=0.
Этот факт доказывает также, что распределение параметров
течения объясняется в основном тепловыделением и конвективным
сносом тепла вдоль оси, а конвективный перепое тепла поперек
сопла несуществен.
Падение температуры в сверхзвуковой части объясняется
уменьшением конвективного переноса тепла по соплу. В этом'слу-
этом'случае линии тока не имеют максимума.
Исследовалось влияние изменения области тепловыделения на
параметры течения. Область тепловыделения ограничена осью и
прямыми:
E.4)
г =-0,02252 + 0,05; _3<z<0;
г=0,0 lOOz + 0,05; 0<z<3.
При таком задании области тепловыделения часть линии тока
проходит через зону тепловыделения не по всей длине. Малый гра-
градиент температуры в дозвуковой части сопла (вне зоны тепловы-
тепловыделения) объясняется малым градиентом давления и отсутствием
214
тепловыделения. Отсутствие нивышения давления в сверхзвуковой
части сопла при входе в зону тепловыделения объясняется малой
величиной тепловыделения.
5.7. ТЕЧЕНИЯ СМЕСИ ГАЗА И ЧАСТИЦ
Основные уравнения для расчета смеси газа и частиц выписаны
в 1.2.1; в 1.3.3 представлены необходимые данные по коэффициен-
коэффициенту сопротивления и числу Нуссельта, которые должны быть ис-
использованы в соответствующих уравнениях; в 3.4.3 представлена
разностная схема для расчета течения смеси газа и частиц, как в
одномерном, так и в двумерном течении.
На основе расчетов таких течений выявлены основные качест-
качественные закономерности.
Отметим некоторые общие закономерности изменения парамет-
параметров неравновесных двухфазных потоков в соплах. Очевидно, что
скорости частиц ниже равновесной скорости и скорости газа в не-
неравновесном течении, а температура их выше. Скорость и темпе-
температура газа могут быть равны, превышать или быть меньше соот-
соответствующих параметров в равновесном течении в зависимости от
величины CslCp. Среднемассовая скорость смеси в неравновесном
течении меньше, чем в равновесном. Давление и удельный импульс
неравновесного течения при заданном отношении площадей ниже,
чем в равновесном течении, и выше, чем в замороженном. Число
М в неравновесном течении, определенное по замороженной скоро-
скорости звука, меньше числа М равновесного течения, определенного по
скорости звука фиктивного газа с у° и R0 за счет снижения газовой
постоянной в последнем. (Напомним, что в химически неравновес-
неравновесном течении имеет место обратное соотношение).
Некоторые результаты расчетов представлены на рис. 5.18.
Приведенные на этом рисунке разности скоростей и температур
газа и частиц являются типичными для неравновесных двухфазных
течений в соплах. В дозвуковой и трансзвуковой областях сопла
они увеличиваются за счет увеличения градиента скорости и для
частиц малых размеров достигают максимума в сверхзвуковой
окрестности минимального сечения (где градиент скорости макси-
максимален).
Рис 5 18 Зависимости скоростей и темпе-
температур газа и частиц от х при массовой до
ле частиц <zs = 0 3, диаметре критического
¦сечения rfx= 100 мм, р =4-106Па, 7 =
= 3200 К, 1—контур сопла
АЩг
500 6
МО 'i
200-2
If
у'
Д7^—-
,—с '
AT
й3=20мкн
!0\
г/
л-
5 10 15 х
215
Для приближенных оценок параметров газа в неравновесном
двухфазном течении иногда возможно использование газодинами-
газодинамических функций. Если отклонение от равновесия невелико и извест-
известны скорость, температура и параметры торможения, то можно,
определив число М° по равновесной скорости звука и используя
газодинамические функции, найти все остальные параметры, кото-
которые будут приближенно соответствовать параметрам неравновес-
неравновесного течения. В этом случае использование числа М, определенно-
определенного по замороженной скорости звука, может привести к большим
ошибкам в определении давления и плотности. Аналогично, по из-
известному отношению давления р/ро в точке, можно определить
остальные параметры. Из результатов расчета следует, что даже
при размерах частиц до 20 мкм и as<0,6 параметры газа в нерав-
неравновесном течении не более чем на 5. ..10% отличаются от равно-
равновесных, вычисленных с использованием показателя адиабаты у°.
Рассмотрим течения в осесимметричных и плоских соплах. Ис-
Исследования двухфазных течений, выполненные в одномерном при-
приближении, позволяют установить многие качественные особенности
таких течений. Однако при движении смеси газа с частицами дву-
двумерные эффекты играют существенную роль как из-за неравномер-
неравномерного распределения частиц в различных сечениях сопла, так и
из-за возможного выноса их на стенки в дозвуковой и сверхзвуко-
сверхзвуковой областях, что является следствием различного по величине и
знаку воздействия газа на частицы в различных точках сопла.
В результате траектории частиц отличаются от линий тока газа,
при этом вектор скорости частиц и их температура в транс- и сверх-
сверхзвуковой областях существенным образом зависят от параметров
течения в дозвуковой области. Поэтому для правильного описания
двухфазного течения в сопле необходимо проводить совместный
расчет до-, транс- и сверхзвуковой областей.
Численное решение системы A.109).. .A.113) в сверхзвуковой
части сопла удобно осуществлять послойным методом характери-
характеристик. В дозвуковой части для численного решения необходцмо ис-
использовать алгоритм решения обратной задачи (см. 3.4.3). В про-
процессе такого рода расчетов определяется все поле газодинамиче-
газодинамических параметров, параметры частиц, их траектории, зоны чистого
газа с учетом взаимного влияния газа и частиц [29]. Возможен
приближенный подход, при котором производится раздельное ре-
решение уравнений для газовой фазы и частиц [27, 29]. Предполага-
Предполагается, что параметры газа не изменяются под воздействием частиц
и могут быть определены в результате независимого расчета для
газа с фиктивным показателем адиабаты у0, т. е. параметры газа
соответствуют равновесному течению. Параметры же частиц опре-
определяются путем численного интегрирования при условии неизмен-
неизменности параметров газа. Система A.109).. .A.113) распадается в
этом случае на две независимые системы: одну — для фиктивного
|газа с ^=7° и Другую — для частиц. Первая система решается
либо путем решения обратной задачи теории сопла, либо методом
характеристик в сверхзвуковой области. В результате такого рас-
'216
г,м
щ
ш
'
-0,05
-0,2
0,2 0,4 л,м
Рис 5 19. Траектории частиц (сплошные линии) и линии тока (пунктирные ли-
линии) в соплах Лаваля при диаметре частиц d,= 10 мкм, d» = 25 мм (а) и при
d» = 2,5 мкм, d,= 100 мм (б)
чета во всех точках поля течения известны параметры газа как
функции координат. Для определения параметров частиц uts, v,s,
Tis интегрируется система A.83), при этом параметры газа счита-
считаются известными и неизменными. Обоснованием такого прибли-
приближенного подхода являются представленные выше результаты рас-
расчетов в одномерном приближении, согласно которым параметры
газа при неравновесном и равновесном двухфазных течениях от-
отличаются мало. Очевидно, что второй приближенный способ явля-
является значительно более простым.
На рис. 5.19 представлены траектории частиц для некоторых
характерных случаев при расчетах по приближенному способу.
При больших размерах частиц (ds>10 мкм) и малых диаметрах
минимального сечения сопел (d*<25 мм) траектории частиц в
сверхзвуковой части сопла близки к прямолинейным. Траектории
частиц малых размеров искривлены и при больших диаметрах со-
сопел близки по форме к линиям тока газа. Такой характер поведе-
поведения частиц различных размеров связан с тем, что запаздывание
частиц по скорости и температуре увеличивается при увеличении
размера частиц, градиента газодинамических параметров и при
уменьшении плотности газа. Линии тока газа и частиц в дозвуко-
дозвуковой части довольно близки между собой, а в трансзвуковой и
сверхзвуковой частях заметно различаются, особенно при боль-
больших диаметрах частиц и малых диаметрах минимального сечения
сопла.
Для частиц всех размеров существует траектория, которая
касается стенки сопла в дозвуковой части. Эти предельные траек-
траектории разделяют поток частиц в сопле. Частицы, траектории кото-
которых расположены выше предельной и пересекают контур сопла в
дозвуковой части, выпадают на стенку сопла. Естественно, что с
увеличением диаметра частиц и уменьшением диаметра сопла, ко-
количество частиц, выпавших в дозвуковой части сопла, увеличи-
увеличивается.
Вниз по потоку от точки касания предельная траектория явля-
является линией тангенциального разрыва, так как плотность частиц
выше этой линии равна нулю и между контуром сопла и предель-
217
ной траекторией движется чистый газ, свободный от частиц. Для
частиц с размером ds>10 мкм и сопел с d*<50 мм зона чистого
газа занимает значительную часть сечения Так, в сопле с с(* =
= 25 мм примерно 70% площади выходного сечения занято чистым
газом, т е. имеет место сепарация частиц больших размеров к оси
сопла, что связано со значительным отставанием вертикальной
и горизонтальной составляющих скоростей частиц от соответ-
соответствующих составляющих скоростей газа в трансзвуковой
области
При увеличении диаметра минимального сечения сопла зона
чистого газа на выходе из сопла уменьшается, и при некотором
значении d* = d*i предельная траектория попадает на стенку сопла
в выходном сечении. При дальнейшем увеличении d* стенку сопла
в сверхзвуковой части будет пересекать также и часть траекторий
частиц, расположенных ниже предельной. Частицы, движущиеся
вдоль этих траекторий, будут выпадать на сверхзвуковую часть
контура сопла. При этом массовая доля частиц a^i первоначаль-
первоначально увеличивается с ростом d*; точка пересечения предельной траек-
траектории со стенкой смещается внутрь сопла. Однако при дальнейшем
увеличении d» скоростное отставание частиц от газа уменьшается
настолько, что траектории частиц и газа становятся близки между
собой и, начиная с некоторого значения d* = d*2, величина a^i
начинает уменьшаться. Таким образом, имеет место немонотон-
немонотонность зависимости a°si от диаметра минимального сечения при
фиксированном размере частиц. Аналогично зависимость a;Ji от
размера частиц при фиксированном диаметре минимального сече-
сечения также немонотонна.
Остановимся теперь на результатах работы [29], в которой
проведен в рамках обратной задачи расчет до- и трансзвуковой
областей сопла с учетом взаимного влияния частиц на газ
В этой работе метод, описанный в 3 4.3, был использован для
расчета монодисперсных смесей с диаметрами частиц ds=l мкм и
dfs = 5 мкм при as=0,3. При этом на оси сопла_задавалось распре-
распределение скорости D.3) с 6 = 0,21; Woo=0,2; w»=l,8. Остальные
параметры в начальном сечении х=х0 брались из газодинамиче-
газодинамических таблиц при y=1,16.
Результаты расчетов представлены на рис. 5 20, 5.21. На
рис. 5 20 показано изменение давления и температуры газа вдоль
оси сопла. Здесь и далее введены следующие обозначения: крести-
крестиками и кружочками обозначены результаты расчетов, проведенных
с учетом взаимного влияния частиц и газа соответственно для
flfs=l мкм и ds=5 мкм; точки соответствуют случаю, когда влия-
влияние частиц на газ учитывается через эффективный показатель
адиабаты с -у=-у0== 1ДЗ, т. е. принимается, что частицы и газ нахо-
находятся в равновесии. Важно отметить, что в этом случае из уравне-
уравнений движения и энергии газа исключаются члены, содержащие
параметры частиц. И те и другие результаты получены при одина-
одинаковом распределении безразмерной скорости на оси Имеет место
218
:—**»«*=¦
0,85
-0,5
О
0,5
0,6
заметное различие меж- Р\
ду двумя рассмотренными |
случаями, особенно в
сверхзвуковой области.
На рис 5 21 представ-
представлены линии тока газа для
различных г|з, а также ли-
линии постоянного числа М.
Пунктиром показаны ре-
результаты расчетов в газе
с Y=Y°- Как видно, замет-
заметное отличие результатов,
полученных двумя мето-
методами, наблюдается в
транс- и сверхзвуковой
областях сопла. Отсюда
следует, что при расчете
сверхзвуковой области методом характеристик необходимо ис-
использовать начальные данные, полученные с учетом взаимного
влияния частиц и газа в точной постановке. Начальные данные,
полученные из расчетов в газе с эффективным показателем адиа-
адиабаты y=*Y°> как видно, могут привести к заметным ошибкам.
Такой вывод подтверждается результатами расчета величины
А— (и—u,s)/u вдоль оси симметрии для больших и малых частиц
двумя методами. Эта величина имеет максимум в трансзвуковой
области, где градиенты газодинамических параметров максималь-
максимальны, причем Д увеличивается с увеличением диаметра частиц. Не-
Рис 5 20 Изменение давления и температуры
на оси сопла в двухфазном течении
Рис 5 21 Линии тока га-
газа, линии постоянных чи-
чисел М и предельные тра-
траектории частиц Диаметр О
частиц (a) rfs = 5 мкм;
(б) ds = l мкм
-0,6
0,6
219
мотря на идентичное качественное поведение кривых наблюдается
аметное количественное их различие при расчетах двумя метода-
и; при этом разница возрастает с увеличением ds. Так, различие
А увеличивается при х=0 от 0,005 при ds=\ мкм до 0,01 при
s = 5 мкм. Этот результат представляется весьма важным. Изве-
гно, что при одинаковых начальных данных в трансзвуковой обла-
ги за минимальным сечением траектории частиц, подсчитанные
о описанному выше приближенному методу и методом характе-
истик [27], в сверхзвуковой области близки между собой. Однако
езультаты расчетов показывают, что принимать начальные дан-
ые одинаковыми при расчетах различными методами нельзя. Не-
бходимо точно учитывать воздействие частиц на газ, начиная с
озвуковой области. Различие в начальных данных может приве-
ти к различию траекторий в сверхзвуковой области и к соответст-
ующему расхождению в точках выпадения частиц на сверхзвуко-
ую часть контура.
Для сопоставления с результатами расчета методом характери-
гик определялся контур сопла и параметры в некотором сечении
=хн, расположенном в его сверхзвуковой области. С использова-
ием этих данных в сверхзвуковой области методом характеристик
ешалась прямая задача. Далее определялась предельная траек-
ория, выделялась зона чистого газа и определялись параметры на
онтуре. Результаты такого расчета по потоку от сечения х=
= хн=0,06 сравнивались с результатами решения обратной зада-
[и. На рис. 5.21 штрихпунктирными линиями показаны предель-
ше траектории, полученные в работе [29], а треугольниками — пре-
;ельная траектория, рассчитанная методом характеристик. Ре-
ультаты расчетов обоими методами достаточно хорошо совпадают
[ в сверхзвуковой области: максимальная погрешность при -^==2
^х^0,75 для ds=l мкм не превышает 0,2%. При больших х
>азличие увеличивается, что, вероятно, связано с различным ха-
>актером накопления ошибок в сравниваемых методах. Подчерк-
юм, однако, что в данном случае целью не являлось проведение
)асчетов для сверхзвуковой области с высокой точностью, а основ-
юе внимание уделялось расчету трансзвуковой части, поскольку
[ля сверхзвуковой области более предпочтительным является ме-
х)д характеристик.
Остановимся на использованных внутренних способах контроля
-очности. Были проведены расчеты при различных значениях
^>B-10^3, 10~3, 0,5-10~3) с ds=\ мкм, при этом значения А=
= {u — us)i/u для Дг|з 10~3; 0,5-10~3 различались не более чем на
),5%. Выполнение закона сохранения количества движения контро-
шровалось путем сравнения разницы в потоках импульса в сече-
ши хн и выходном сечении сопла с интегралом сил давления по !
юнтуру сопла. Для шага Аг^= 10~3 ошибка составляла не более
),5%, а для шага Дгр = 0,5-10~3 не более 0,25%. В силу того, что в
<ачестве независимой переменной была выбрана функция тока
^аза, уравнение неразрывности для газа удовлетворялось точно.
Отметим, что точность расчета параметров удалось заметно
220
улучшить за счет уменьшения шагов по х по сравнению с приня-
принятым в обратном методе традиционным расположением узлов раз-
разностной сетки. Уменьшение шага по х на порядок привело к значи-
значительному улучшению совпадения результатов с расчетами методом
характеристик, где шаг по х определялся из условия Куранта.
5.8. СЛОИСТЫЕ ТЕЧЕНИЯ
В 3.4.2 изложен метод расчета слоистых течений с использова-
использованием основной разностной схемы C.1.2). В координатах г|э, х
удобно проводить расчеты многослойных течений с различными
физическими свойствами. Такой расчет можно провести в рамках
идеальной жидкости без учета смешения слоев, при этом полные
температуры, полные давления и показатели адиабаты в слоях мо-
могут быть различны. Будем обозначать параметры ядра потока ниж-
нижним индексом 1, а -параметры пристеночного слоя — индексом 2
(рис. 5.22). Пусть до некоторой линии тока i|)=ijv газ имеет пока-
показатель адиабаты y=Yi и полное давление рои а, начиная с этой
линии тока — показатель адиабаты у—уг и полное давление рО2-
На линии тока 4j)=^P оба потока должны иметь одинаковые углы
наклона скорости и одинаковые значения статического давления.
В связи с этим на линии тока ^ = ijv должны быть выполнены
следующие соотношения:
Yl + 1
I Poll
_. _ Vi \ Y2 + 1 n H '
IW VY2-1 Y2-1
Й2 = в1_^_, ?2=р\п\ E.7)
VI
После расчета поля течения по разностным формулам C.13)...
C.16) до линии тока с i|)=i|v на этой линии по формулам E.5)...
E.7) определяют параметры с индексом 2 по известным парамет-
параметрам с индексом 1, а далее расчет продолжается по этим же форму-
формулам.
Результаты расчета двухслойного течения с распределением
скорости по оси D.3) при №„=0,1; №«,= 1,9; 6 = 3,5 и yx — \,U;
Y2=l,4; сг=1 и г))р = 0,04 представлены на
рис. 5.23, на котором показаны линии тока
рассчитанного течения (г|) = const), линии
W=const, линии 6 = 0 (светлые точки). Из
рис. 5.23 следует, что во втором слое звуко-
звуковая линия №=1 (черные точки) расположе-
расположена ниже по течению, чем в первом слое.
Рис. 5.22. Схема двухслойного течения в сопле
221
-0,6 -Ofi -0,2 ~ 0~ ' 0,2 0,* 0,6 X
Рис. 5 23 Поле двухслойного течения в сопле
5идно также, что значения W по обе стороны границы раздела до-
ольно близки между собой в дозвуковой области, а начиная с
рансзвуковой области заметно различаются.
На рис. 5.24 приведено рассчитанное методом характеристик
аспределение давления вдоль контура сопла с угловой точкой
ля двухслойных течений с yi=1,14 и 72= 1,4 с различными зна-
ениями г/*° (т. е. с различными расходами в пристеночном слое),
также распределения давления на этом же контуре в однослой-
ом течении с 7=1,14. На этом рисунке кривая 1 соответствует
днослойному течению, остальные кривые — двухслойному тече-
ию, при этом кривые 2, 3, 4, 5, 6 соответствуют значениям г/*° =
= 0,99; 0,95; 0,9; 0,8; 0,7. Из этого рисунка следует, что при расхо-
ах в пристеночном слое, больших 10%, давление вдоль сопла
меньшается. При расходах, меньших 10%, в окрестности угловой
очки имеется положительный градиент давления, который возни-
:ает вблизи точки N. От точки ./V на течение в пристеночном слое
[ачинает влиять внутренний слой. Возникновение положительного
радиента давления связано с тем, что при одном и том же угле
юворота потока в течении Прандтля — Мейера давление в потоке
: большим 7 уменьшается сильнее, чем в потоке с меньшим у. При
пгносительно больших толщинах пристеночного слоя влияние внут-
>еннего слоя начинает сказываться в основном после точки 2', так
;ак от точки 2' производная давления терпит разрыв и начинает
уменьшаться более интенсивно, а давление приближается к дав-
1ению в однослойном течении, так как, начиная с этой точки тече-
ше в пристеночном слое определяется в основном внутренним
:лоем. До точки 2' возмущения, вносимые внутренним слоем,
>слабляются веером волн разрежения. Однако при малых толщи-
толщинах пристеночного слоя влияние внутреннего слоя проявляется в
непосредственной окрестности угловой точки, и давление в присте-
ючном слое стремится сравняться с давлением во внутреннем слое,
гак как последнее при повороте на один и тот же угол больше, то-
222
0,5
Рис 5 24 Распределение давления на р/р
контуре сопла при различных расходах 015
в пристеночном слое '
возникает положительный гради-
градиент давления. Величина положи-
положительного градиента давления уве- щ
личивается при уменьшении тол- '
щины пристеночного слоя. Естест-
Естественно, что по мере уменьшения
толщины пристеночного слоя раз-
различие между статическими давле- W
ниями в однослойном и двухслой-
двухслойном течениях на стенке сопла
уменьшается, однако при этом
числа М в эгих течениях различа-
различаются заметно. Отметим, что положительный градиент давления
при обтекании угловой точки возникает лишь тогда, когда показа-
показатель адиабаты в пристеночном слое больше показателя адиабаты
в ядре потока.
5.9. ТЕЧЕНИЯ В КАНАЛЕ С ПОДВОДОМ РЕАГЕНТОВ С ЦЕЛЬЮ
ПОДАВЛЕНИЯ ТОКСИЧНЫХ КОМПОНЕНТ
Основным источником токсичных компонент и ряда канцероген-
канцерогенных элементов являются высокотемпературные процессы в движу-
движущихся средах, имеющие место в энергетической промышленности
металлургии, автотранспорте, ракетной и космической технике'
Простейшей математической моделью таких процессов является
движение в канале неравновесно реагирующей смеси. Для подав-
подавления образования токсичных компонент в движущийся газ добав-
добавляют различные реагенты, которые в процессе цепных химических
реакций приводят к снижению доли основных токсичных компонент
окисей углерода СО и азота N0.
Таким образом, для прогнозирования этих процессов необходи-
необходимо уметь рассчитывать течение смеси газов при наличии неравно-
неравновесных химических реакций с подводом массы и энергии. Во мно-
многих случаях удобно решать обратную задачу, а именно, рассчиты-
рассчитывать такое течение при заданном по длине распределении давления
в одномерном приближении, которое позволяет выявить основные
качественные закономерности.
Основные уравнения для такой задачи выписаны в разд. 1.2,
необходимые сведения о кинетике химических реакций и констан-
константах скоростей содержатся в 1.3.1, а численный метод изложен в
3.4.2. Представленные ниже результаты расчетов изложены в ра-
работах [24]. Приведены также некоторые результаты равновесных и
неравновесных расчетов, выполненных В. Р. Мусиным.
223
5,9.1. Равновесные и неравновесные течения
Ниже будет рассмотрено поведение концентраций токсичных
компонентов N0 и СО при равновесных и неравновесных процессах.
Особенно важным с точки зрения образования токсичных ком-
компонент является замораживание N0 (см. рис. 5.3). Эксперимен-
Экспериментальные измерения соответствующих концентраций N0 при тече-
-1ии высокотемпературных газов в сопле полностью подтвердили
результаты неравновесных расчетов. Следует отметить, что опре-
деление концентрации N0 по результатам равновесных расчетов
цает ошибку на 1—2 порядка в сторону занижения % N0. Замора-
Замораживание концентраций N0 экспериментально обнаружено и в-
поршневых двигателях внутреннего сгорания. Таким образом,
представленные примеры расчетов показывают важность учета
неравновесного протекания химических реакций. Как видно, равно-
зесный расчет может привести к необоснованному и опасному
прогнозу о содержании токсичных компонентов.
Большой практический интерес представляет рассмотрение
задачи течения высокотемпературного реагирующего газа в трубе
переменного сечения с подводом различных химических реагентов.
Были проведены расчеты течения продуктов сгорания топлива
кислород — керосин при коэффициентах избытка кислорода топли-
топлива а=0,76 и 1 без ввода и с вводом воздуха @,225 кг на 1 кг топ-
топлива), а также указанной смеси продуктов сгорания при <х=1 с
вводом воздуха и воды B,25 кг на 1 кг топлива) при давлении
0,4 МПа. Проведенные расчеты с учетом кинетики химических
реакций позволяют сделать общие выводы о влиянии скорости
охлаждения и коэффициента избытка окислителя на температуры
замораживания Т° окисей углерода и азота. Установлено, что
мольные доли окисей углерода и азота с некоторой температуры
превышают равновесные, а затем, через 100. ..600°, становятся по-
постоянными и соответствуют мольным долям равновесного состава
при условной температуре замораживания Т°, находящейся при-
примерно посередине указанного интервала температур.
При увеличении коэффициента избытка кислорода уменьшается
мольная доля окиси углерода и увеличивается доля окиси азота;
при замедлении скорости охлаждения уменьшаются мольные доли
окисей углерода и азота.
Следует отметить, что охлаждение высокотемпературной Среды
может осуществляться как путем расширения газа, например в
реактивном сопле или цилиндре двигателя внутреннего сгорания,,
так и путем теплоотвода в стенку или впрыска охлаждаемого
компонента. Однако в последнем случае на температуру замора-
замораживания кроме темпа охлаждения определенное влияние оказы-
оказывает химическая активность впрыскиваемого компонента.
Учитывая рекомендации о приемлемых способах нейтрализа-
нейтрализации окисей углерода и азота и полученные результаты расчетного
анализа, приходим к следующему выводу: нейтрализацию окисей
углерода и азота в высокотемпературной среде (с 7^2000 К>
224
о
0,25
0,125
„-1
т,к-юг
\
X
/
—
1,25
2,5
О
.
1
г
3
0,25 1,0
1,25
Л
Рис.5 25 Зависимость относительного Рис. 5 26. Зависимости молярных долей
массового расхода окиси углерода окиси углерода гсо, окиси азота cno и
/и°со от относительного массового температуры от коэффициента избытка
расхода впрыскиваемой воды окислителя а
необходимо осуществлять в две стадии. Вначале осуществляется
разложение окиси азота в восстановительной среде с коэффициен-
коэффициентом избытка окислителя а<1 при температурах 7=2000.. .2600 К,
а затем дожигание окиси углерода в окислительной среде с а>1
и Г= 1600... 2000 К. Обеспечение а< 1 в восстановительной зоне
достигается вводом горючего, а а> 1 — вводом кислорода или воз-
воздуха. Поддержание вышеуказанных диапазонов температур наи-
наиболее целесообразно осуществлять строго дозированным впрыском
воды. Особо следует отметить, что впрыскиваемая вода играет не
только роль охладителя, но и является химически активным ре-
реагентом, так как-образующиеся при диссоциации радикалы Н и
ОН существенно ускоряют процесс нейтрализации (см. табл. 3.1
реакция 7).
Вышеуказанные рекомендации были использованы на несколь-
нескольких объектах, выбрасывающих высокотемпературные продукты
сгорания кислородно-керосинового топлива с коэффициентом из-
избытка окислителя а=0,76. Использование дожигателя окиси угле-
углерода с тремя поясами впрыска: вода — кислород (воздух) — вода,
обеспечивающими соответственно значения температур 1800...
2000. ..1600 К и суммарное значение коэффициента избытка окис-
окислителя в смеси на выходе а=1,05, позволило снизить содержание
окиси углерода в 25 раз и практически предотвратить образование
окислов азота.
На рис. 5.25 представлена расчетная зависимость относитель-
относительного массового расхода дас°о (расход отнесен к расходу топлива)
от относительного расхода впрыскиваемой воды тн,о# Цифры 1,
2, 3 относятся к поясам впрыска, при этом в поясах 1 и 3 вводится
вода, а в поясе 2 — кислород. Отметим, что кривая 1 имеет мини-
минимум, который связан с неравновесным протеканием химических
реакций. Действительно, подвод значительного количества воды
приводит к полному замораживанию реакции, при этом уровень
СО соответствует исходному, поскольку не происходит его дожига-
225
ния. С другой стороны, при относительно малых количествах вво-
вводимой воды возникают активные радикалы, которые способствуют
дожиганию СО в процессе цепных реакций (ом. табл. 3.1). Отме-
Отметим, что на нисходящей ветви кривой 1 течение на весьма малой
длине становится равновесным. Так, при тенао = 0,1 ...0,2 равнове-
равновесие достигается на длине в несколько сантиметров, при /Wh2o=0 8
зона релаксации занимает 0,5 м, а уже при /reH,o=i,l — более
3 м. Из рис. 5.25 следует также, что для максимальной нейтрализа-
нейтрализации СО важен именно дозированный подвод воды в количестве,
соответствующем минимуму кривых 1 и 3.
Аналогичный подход был использован при рассмотрении проб-
проблемы нейтрализации токсичных компонент в парогенераторах ТЭС,
хотя в этом случае имеются некоторые отличия, в частности про-
продукты сгорания поступают в канал по нормали к стенке, что соз-
создает на начальном участке заметную неоднородность потока. Кро-
Кроме того, уровень температур и скоростей существенно ниже и, на-
наконец, при расчете неравновесного течения в канале парогенератора
необходимо учитывать теплоотвод в стенки, что может оказать су-
существенное влияние на уровень концентраций. Рассмотрим зави-
зависимость температуры, молярных долей основных токсичных ком-
компонент СО и N0 от коэффициента избытка окислителя сразу после
сгорания. Будем предполагать, что имеет место мгновенное пере-
перемешивание горючего и окислителя и равновесное протекание хи-
химических реакций.
Типичные зависимости температуры (кривая /), молярных до-
долей гсо (кривая 3) и Гно (кривая 2) от а представлены на
рис. 5.26. Отметим характерные особенности этих зависимостей.
Максимум температуры (около 2300 К) имеет место не при стехио-
метрическом соотношении а=1, а при а=0,95. Смещение макси-
максимума в сторону меньших а связано с явлением диссоциации про-
продуктов сгорания.
Из рис. 5.26 следует, что максимальное значение концентрации
гыо достигается при а=1,15, в то время как при а<0,85 (с Г<
<2000 К) NO практически отсутствует. С другой стороны, концен-
концентрация СО монотонно убывает с увеличением а и близка нулю при
а>1,1. Представляет существенный интерес рис. 5.27, на котором
с использованием данных рис. 5.26 построены зависимости от а
концентраций СО и NO в долях предельно допустимых концентра-
концентраций (ПДК) А, при этом кривая 2 — сумма концентраций СО и
NO построена в предположении равного приоритета этих токсич-
токсичных компонент при таком суммировании. Рассмотрение этой пос-
последней зависимости показывает, что минимум суммы ПДК дости-
достигается при а=0,95. Известно, что современные ТЭС работают при
<х=1,05. Поэтому переход к режиму а=0,95 приведет к увеличе-
увеличению энергосъема, экономии топлива и одновременно к уменьшению
суммарного ПДК на 10. ..15% без каких-либо конструктивных
мероприятий. Предварительные эксперименты, в которых измеря-
измерялись концентрации компонент и энергосъем, подтверждают пред-
226
„-J
Al
V / V
\f\ls
0,3
T,K
2260
2240
4-й?
-3
1,0
<*
О
esar
¦ ¦
J_
\
т,к
2180
2100
о,г о,*
*;
Рис. 5 27. Зависимость концентра-
концентраций токсичных компонент в до-
долях ПДК и температуры от а
Рис. 5.28. Зависимость концентраций ток-
токсичных компонент в долях ПДК и темпе-
температуры от количества впрыскиваемой воды
(обозначения см. рис. 5.26)—а=1,05;
а = 0,95
ставленные рекомендации. Очевидно, однако, что отмеченное сни-
снижение токсичных компонент на 10... 15% не является решающим.
Рассмотрим в связи с этим влияние ввода воды на концентрации
токсичных компонент. Будем предполагать, что вода в жидкой или
паровой фазе тем или иным способом смешивается с горючим. По-
прежнему будем предполагать, что имеет место мгновенное пере-
перемешивание горючего и окислителя и равновесное протекание хими-
химических реакций. На рис. 5.28 построены зависимости температуры
и концентрации СО и N0 в долях ПДК от т°, где т° — массовая
доля воды. Температура вводимой воды принималась равной
400 К, а подвод воды осуществлялся для составов, соответствую-
соответствующих а=0,95 и 1,05. Очевидно, что добавление воды в топливо
уменьшает температуру сгорания, но одновременно снижает и
концентрации NO и СО. Уменьшение концентрации NO связано
непосредственно с уменьшением температуры, а концентрации
СО — с увеличением окислительных элементов при подводе воды.
Из рис. 5.28 следует, что при добавлении воды в количестве т° =
= 0,45 при а=0,95 температура продуктов сгорания равна темпе-
температуре при а=1,05 и т° = 0, т. е. температуре, соответствующей
рабочему режиму современных ТЭС. При этом происходит изме-
изменение суммарного ПДК на 30%, а уменьшение концентрации NO
в 2.. .2,5 раза. Хотя в этом случае имеет место увеличение кон-
концентрации СО, однако нейтрализацию СО за счет дозированного
ввода воды можно осуществить способом, описанным выше.
Интересно проследить изменение концентраций СО и NO и тем-
температуры по длине топочной камеры парогенератора, полученное
в результате решения системы уравнений C.24), C.25), C.27),
C.44) с учетом заданного распределения теплосъема (рис. 5.29).
Видно, что значение концентрации NO практически не изменяется^
227
лю
16 20 х
Рис 5 29 Изменение концентраций токсич-
токсичных компонент по длине топочной камеры
парогенератора при наличии теплосъема
поскольку уровень температур та-
таков, что соответствующие реакции
замораживаются. С другой стороны,
эти температуры еще достаточно вы-
высоки, чтобы обеспечить почти равно-
равновесное дожигание СО при движении
смеси по тракту парогенератора,
компенсируя тем самым некоторое
повышение этой концентрации, вы-
_Пос т , званное переходом к значению а =
™™ «я образом, рекомендация по целесообразности пере-
или ВО„ГГМ Р С а = °'95 С послелУ«"Д™ введением воды
или водяного пара получила еще одно подтверждение Она
может использоваться по крайней мере в те моменты, когда нуж
но существенно уменьшить токсичность продуктов сгорания вы-
выбрасываемых в атмосферу без снижения мощности 'ГЭС
1аким образом, добавляя различные вещества в традиционное
топливо, можно добиться снижения выброса в атмосферу токсич-
токсичных компонент. Причем использование воды как присадки к раз-
различным топливам дает один эффект-это снижение токсичности
одновременно с понижением температуры продуктов сгорания Ис-
Использование же в качестве присадки метанола или аммиака на
некоторых режимах работы энергетической установки обеспечива-
обеспечивает снижение токсичности с одновременным ростом температуры
продуктов сгорания. Поэтому было бы интересно исследовать
влияние комплексных присадок на токсичность и энергетические
характеристики. Здесь под термином комплексные понимается
смесь нескольких веществ. В топливо керосин — воздух с соотно-
соотношением горючего и окислителя а=1,1 и при давлении р = 3 МПа
впрыскивалась смесь аммиака и воды. Показано, что впрыск ам-
аммиака в это топливо ведет к росту содержания окиси углерода в
продуктах сгорания. Добавка же воды несколько снижает темп
роста содержания СО в продуктах сгорания. При этом наличие во
впрыскиваемой смеси и аммиака и воды приводит к уменьшению
содержания в продуктах сгорания окислов азота. На температуру
продуктов сгорания эти два впрыскиваемых вещества оказывают
противоположное влияние. С одной стороны, есть область, где до-
добавка ведет к увеличению температуры, с другой стороны' присад-
присадка всегда уменьшает температуру. На рис. 5 30 представлена за-
зависимость температуры продуктов сгорания от массовых долей
впрыскиваемых воды и аммиака. Кривая АВ суть линия пересече-
пересечения построенной «температурной» поверхности плоскостью Т=Т0,
где То —температура продуктов сгорания «чистого» (без приса-
присадок) топлива. Кривая OD — суть проекция АВ на координатную
плоскость OmNH3fficH3OH- Таким образом, осуществляя дозирован-
дозированный впрыск смеси аммиака с водой, следуя кривой OD, температура
228
'лгао
2000
50
Ъ '%„
О 0,1 0,1 0,3 О,1/ от,
Рис 5 30 Влияние комплексной присад- Рис 5 31 Влияние комплексной при-
ки на температуру продуктов сгорания садки на токсичность продуктов сго-
(керосин — воздух) рания (керосин — воздух)
продуктов сгорания и, следовательно, энергетические показатели
установки не уменьшаются. При этом достигается значительное
снижение токсичности продуктов сгорания (кривая АВ на рис.
5.31). Здесь 2 — сумма концентраций СО и N0 в долях ПДК. Ми-
Минимальное снижение (в 4 раза) токсичности обеспечивает дозиро-
дозированный впрыск в количестве /иш3 = 0,3; /Ин2о==0,6.
На испытательных стендах зачастую происходит эжекция окру-
окружающего воздуха в канал, в который поступают также продукты
сгорания, содержащие токсичные компоненты. Представлен инте-
интерес выявить влияние коэффициента эжекции п (отношения расхо-
расхода продуктов сгорания к расходу воздуха) на содержание токсич-
токсичных компонент. С этой целью вновь необходимо решать обратную
задачу в одномерном приближении с учетом кинетики химических
реакций.
На рис. 5.32 представлены результаты численного исследования
течения реагирующей смеси в канале испытательного стенда с уче-
учетом эжекции воздуха, имеющего температуру окружающей среды.
Состав и газодинамические параметры продуктов сгорания, посту-
поступающих в эжектор из сопла двигателя, могут быть определены с
помощью равновесной модели и результатов экспериментов. На
рис. 5.32 приведено изменение температуры и секундного расхода
окиси углерода через поперечное сечение по длине тракта испыта-
испытательного стенда для различных коэффициентов эжекции п. Следует
отметить, что выгорание окиси углерода на заданной длине тракта
стенда существенно зависит от соотношения воздух/продукты сго-
сгорания в сечении смешения. С одной стороны увеличение избытка
воздуха в сечении смешения должно обеспечивать более значи-
значительное выгорание окиси углерода. Действительно, допустим, что
длина канала ограничена некоторой величиной и исследуем влия-
229
тсо,кг/с
О
—.
0,5
n=Jl5
1—¦ ^_
',5
2000
160О
120Q
800
Рис 5 32 Догорание углерода в тракте испытательного стенда при эжекции
воздуха —СО, -температура
ние величины п на расход СО в контрольных сечениях Сравнивая
расходы окиси углерода в последнем сечении л;=12 для различных
коэффициентов эжекции, например я=0,5 и п=1,5 убеждаемся,
что расход СО с ростом я уменьшается В то же время, из рис
5 32 видно, что при я=2,5 секундный расход СО через контрольное
сечение (?=12) во много раз превышает расход СО при я=1,5
Такое влияние коэффициента эжекции на секундный расход окиси
углерода в контрольном сечении может быть объяснено следую-
следующим образом. При больших значениях коэффициента эжекции я
происходит снижение температуры потока в зоне смешения до зна-
значений порядка 870 К, что приводит к уменьшению соответствую-
соответствующих скоростей реакций. Это хорошо видно из рис. 5 32, где для
п=2,5 можно отметить слабый рост температуры, а также медлен-
медленное уменьшение расхода СО по длине тракта испытательного
стенда
В результате параметрических расчетов выявлено существова-
существование оптимального значения коэффициента эжекции воздуха
(«опт), обеспечивающего максимальное выгорание окиси углерода
на заданной длине тракта стенда Зависимость расхода окиси угле-
углерода через контрольное сечение (ic=12) тракта приведена на рис
5.33. Из этой зависимости следует, что при я^Яопт расход СО
увеличивается по сравнению с расходом при я=яопт слабее, чем
При Я>ЯОпт.
Наличие минимума в зависимости расхода СО от коэффициен-
коэффициента эжекции физически аналогично минимуму в зависимости рас-
расхода СО от массы впрыскиваемой воды на рис 5 25.
230
т.
0
6
4
п
кг/с
\
\
I
1
У
1
1
о,5
1,5
2,о
Рис 5 33 Влияние коэффициента эжекции на
степень дожигания окиси углерода в тракте ис
питательного стенда
Таким образом, показано сущест-
вование оптимальных в смысле токсич-
токсичности выхлопа режимов работы испы-
тательных стендов Отметим при этом,
что в рамках равновесной модели выя-
вить такие закономерности не пред-
представляется возможным, поскольку по-
лученные зависимости являются ре-
результатом химической неравновесности
процессов, протекающих в трактах ис-
питательных стендов авиационных
двигателей.
Существенными специфическими особенностями с точки зрения
образования токсичных компонент обладают автомобильные дви-
двигатели В отличие от процессов, рассмотренных выше, в которых
течение предполагалось стационарным, течение в дизеле и двигате-
двигателях с искровым зажиганием носит существенно нестационарный
.характер, при этом полное описание картины течения требует при-
привлечения общей системы уравнений.
Действительно, течение в отдельных участках двигателя носит
существенно пространственный и нестационарный характер, при
этом важен учет как двухфазности течения, так и неравновесного
протекания химических реакций. Однако, как уже отмечалось,
даже численное решение полной системы уравнений A 112)...
A.121) весьма затруднительно, поэтому для изучения некоторых
качественных закономерностей необходимо сделать упрощающие
предположения. Так, на участке смешения горючего с воздухом
можно принять течение стационарным и одномерным, не учиты-
учитывать физико-химических превращений, но обязательно учитывать
двухфазность течения. Состав смеси после воспламенения можно
определить по соотношениям равновесной термодинамики. В то же
время при расчете параметров в цилиндре при прямом и обратном
ходе поршня необходимо учитывать нестационарность течения, не-
неравновесное протекание химических реакций, но можно принять
течение однофазным и одномерным. При истечении отработанных
продуктов сгорания через клапан течение в канале можно считать
стационарным и двумерным по аналогии с течением в кольцевых
соплах реактивных двигателей. Конечная цель исследования со-
состоит в определении концентраций токсичных компонент в отрабо-
отработанном топливе, в нахождении их, а также термодинамических па-
параметров смеси, как функций времени и таких параметров двига-
двигателя, как степень сжатия, частота вращения, коэффициент избытка
окислителя и т. д.
Ниже излагаются два подхода к решению поставленной задачи
В первом подходе (так называемом нульмерном приближении) в
предположении постоянства параметров по объему, но с учетом
231
переменного объема камеры для нахождения химических и газо-
газодинамических параметров используются интегральные законы со-
сохранения массы, импульса и энергии и уравнения химической
кинетики. На фазе всасывания и выхода учитывается наличие
подвода и отвода массы соответственно. Возможен также учет
тепла, отводимого в стенки цилиндра и поршня, путем численного
решения уравнения теплопроводности.
Во втором подходе при расчете нестационарного течения в ци-
цилиндре при движении поршня решаются одномерные нестационар-
нестационарные уравнения газовой динамики с учетом неравновесного проте-
протекания химических реакций. Закон движения поршня задается.
Расчет течения в плоскости t, х может быть проведен для всех так-
тактов двигателя. Численное решение осуществляется методом харак-
характеристик, поскольку система уравнений в этом случае является
гиперболической.
Предварительные расчеты показывают, что в процессе быстро-
быстрого нестационарного течения в цилиндре происходит замораживание
концентрации N0 по аналогии с тем, что имеет место в соплах
реактивных двигателей (см. рис. 5.3). Этот факт находится в соот-
соответствии с имеющимися экспериментальными измерениями кон-
концентрации N0 в автомобильных двигателях. Заметим еще, что
представления об уровне температур и начальном распределении
концентраций компонент в цилиндре можно получить из рис. 5.26.
Лишь для дизельных двигателей характерны значения а=1,3--.
1,4, а для двигателей с искровым зажиганием а=1. Для оценок
влияния подачи воды в топливо на энергетические характерстики
и концентрации компонент могут быть использованы данные рис.
5.26, 5.28, 5.30, 5.31.
5.9.2. Метод оптимизации массы впрыска
с целью подавления токсичных компонент
В работе [2] рассмотрена задача об оптимизации распределен-
распределенной массы впрыска. Рассматривается одномерное стационарное
течение газа в сопле с учетом неравновесных химических реакций.
Система уравнений газовой динамики и химической кинетики име-
имеет вид A.2.1., 1.3)
I; E.8)
= 0; E.9)
А 4-— W2 = Hn- E.10)
~ 2
,=/=¦«(/>, v, Т, у), t = iTlV; E.11)
232
N
2 E.13)
EЛ4)
1=1
где у», 1, N— мольно-массовые концентрации индивидуальных ком-
компонент химических реакций, у— (у,..., yN); iV —число реагирую-
dp -, dW ¦ dy,
щих компонент; /?=—*—; W = —, у, = —— •
dx dx dx
Пусть x°, x' — координаты входа и выхода из сопла соответст-
соответственно.
Заданы начальные значения на входе в сопло:
To, E.15)
На входе в сопло производится впрыск воды с целью уменьше-
уменьшения концентраций токсичных компонент (например, СО, N0) на
выходе из сопла. Необходимо определить оптимальное количество
впрыскиваемой воды, т. е. количество, при впрыскивании которого
будет достигаться минимум секундного расхода одной (заданной
заранее) токсичной компоненты на выходе из сопла. Для опреде-
определенности будем считать, что оптимизирующая компонента—¦¦уь
Наличие оптимума следует из рис. 5.25, 5.33 и получено в ре-
результате серии параметрических расчетов. В данной работе при
реализации метода сразу получается единственное значение /ганао,
соответствующее минимуму.
В результате впрыска воды на вход в сопло изменяются пара-
параметры: температуры, концентрация индивидуальных компонент
химических реакций, плотность, скорость, давление. Происходят
изменения также и в системе уравнений; уравнения E.9), E.11)...
E.14) остаются прежними, такими же как и без подвода массы,
а уравнения E.8), E.10) заменяются уравнениями:
E.16)
E.17)
соответственно, где М — массовый секундный расход воды т — —— ;
J — энтальпия единицы массы впрыскиваемой воды при темпера-
температуре впрыска.
Процесс в сопле после впрыска будет описываться уравнения-
уравнениями E.16), E.9), E.17), E.11)...E.14) с новыми начальными зна-
значениями:
233
которые являются функциями параметра т (здесь и далее вместо
М удобнее использовать величину т=—] .
Как показано в 2.7, функции р{т), W(m), Т(т), р(т) —реше-
—решения системы из четырех функциональных уравнений с четырьмя:
неизвестными. Важно, что эта система разрешима и функции
д(т), W(m), Т(т), р(т)—непрерывно дифференцируемые функ-
функции параметра m(m^O). Функции yi(m) i=l, N выпишем в явном;
виде
Y, (/») =
1 + т
где С, — некоторые неотрицательные коэффициенты. Очевидно,,
что Y«(m)—непрерывно дифференцируемые функции параметра
т (т>0).
Задача оптимизации сведена к решению краевой задачи для
системы 2N + 7 дифференциальных уравнений с краевыми усло-
условиями и уравнениями связи Краевых условий, вообще говоря, до-
достаточно для решения указанной выше краевой задачи.
При определении оптимального значения т° могут возникнуть
следующие трудности. Как известно, кроме оптимального решения
уравнениям Эйлера могут удовлетворять и неоптимальные реше-
решения, поэтому необходимо проверить полученное значение т° на
оптимальность. Эта проблема возникает всегда, когда использу-
используются необходимые условия оптимальности типа равенства нулю-
первой вариации оптимизируемого функционала-—в частности,
когда используются уравнения Эйлера и условия трансверсально-
трансверсальности.
СПИСОК ЛИТЕРАТУРЫ
1. Ашратов Э. А., Волконская Т. Г., Росляков Г. С, Усков В. И. Исследова-
Исследование сверхзвуковых течений газа в струях//Некоторые применения метода стенок
в газовой динамике Изд-во МГУ, 1974 С 241—407
2 Борисенко М. В. Метод оптимизации массы впрыска с целью подавления
токсичных компонент//Математическое моделирование процессов образования и
распространения токсичных компонентов в воздушном бассейне М МАИ, 1982
С 25—29
3 Борисов Н. Ф., Сыровой В. А. Об уравнениях вязких сверхзвуковых струй
с большой степенью нерасчетности//Изв АН СССР Сер МЖГ, 1977, № 2,
с 137—148
4 Бреев В. В., Минин С. Н., Пирумов У. Г., Шевченко В. Р. Течения смеси
газов с релаксацией колебательной энергии в плоских и осесимметричных соп
лах//Изв АН СССР Сер МЖГ, 1977, № 5 С 125—131
5 Бреев В. В., Пирумов У. Г., Шевченко В. Р. Смешанное осесимметричное
течение проводящего газа в сопле в присутствии магнитного поля — Вычислитель-
Вычислительные методы и программирование, 1977 Изд-во МГУ, вып XXVII С 81—95
6 Войновский А. С, Киреев В. И. О смешанных краевых задачах профили
рования сверхзвуковых сопел и каналов//Изв АН СССР, сер МЖГ, 1983, № 4
С 112—118
7 Войновский А. С, Киреев В. И., Минин С. П., Пирумов У. Г., Смир-
Смирнов В. С, О профилировании плоских и осесимметричных сверхзвуковых каналов,
реализующих разрывные параметры на выходе и выравнивание потока//Изв
АН СССР Сер МЖГ, 1984, № 3 С 155—159
8 Волков В. А. О некоторых особенностях систем неявных конечно-разност-
конечно-разностных уравнений химической и колебательной релаксации//Математическое моде
лирование процессов образования и распространения токсичных компонентов в
воздушном бассейне М Изд во МАИ, 1982 С 3—12
9 Волков В. А. Расчет равновесного состава смеси реагирующих газов при
заданном внешнем давлении//Математические аспекты задач охраны воздушного
бассейна М Изд-во МАИ, 1984 С 3—11
10 Волков В. А., Минин С. П., Прохоров М. Б. Метод численного решения
систем конечно-разностных уравнений при расчете течений с химической и коле-
колебательной неравновесностью//Математическое моделирование процессов образо-
образования и распространения токсичных компонентов в воздушном бассейне. М :
Изд во МАИ, 1982 С 13—20
11 Горбунов В. Н., Пирумов У. Г., Рыжов Ю. А. Неравновесная конденсация
s высокоскоростных потоках газа М Машиностроение, 1984, 200 с
12 Дзаннетти Л. Решение обратной задачи для внутренних течений методом
установления//Ракетная техника и космонавтика, 1980, № 7 С 167—172
13 Карасев С. Б., Пирумов У. Г. Расчет течений в соплах с приосевой зоной
тепловыделения//Исследование периодических движений и устойчивости механи-
механических систем, МАИ, 1983 С 67—72
14 Киреев В. И., Войновский А. С. Решение обратной задачи профилирова-
профилирования новых классов сверхзвуковых сопел и каналов сеточно-характеристическим
методом и методом С К Годунова//Численные методы механики сплошной сре-
среды, Новосибирск, 1982, т 13 № 3 С 46—82
235
15. Киреев В. И., Минин С. П., Пирумов У. Г. Влияние профиля сопла на
характеристики газодинамического лазера//Изв. АН СССР. Сер. МЖХ, 1982,
№ 6. С. 163—167.
16. Киреев В. И., Пирумов У. Г. О профилировании сопел модельных систем
//Изв. АН СССР. Сер. МЖГ, 1979. № 2. С. 187—189.
17. Крайко А. Н., Шеломовский В. В. О профилировании плоских и осесим-
метричных сопел и каналов, реализующих заданный сверхзвуковой поток в сече-
сечении выхода//Изв. АН СССР. Сер. МЖГ, 1981, № 2. С. 94—102.
18. Мельников Д. А., Пирумов У. Г., Сергиенко А. А. Сопла реактивных дви-
гателей//Аэродинамика и газовая динамика. М.: Наука, 1976. С. 57—75.
19. Овсянников А. М. Исследование влияния закрутки потока на течения в
соплах//Вычислительные методы и программирование, изд-во МГУ, 1977,
вып. XXVII. С. 65—72.
20. Овсянников А. М. Расчет течения несжимаемой жидкости в соплах мето-
методом источников и стоков//Вычислительные методы и программирование, изд-во
МГУ, 1974, вып. XXIII. С. 103—125.
21. Овсянников А. М. Исследование смешанных течений в радиальных соплах
для МГД-генераторов//Вычислительные методы и программирование, изд-во
МГУ, 1979, вып. XXX. С. 109—119.
22. Овсянников А. М., Пирумов У. Г., Плетнева Е. М., Росляков Г. С. Атлас
плоских сопел. М.: Изд-во МГУ, 1976, 108 с.
23. Осипов И. Л. Численный метод построения двумерных сопел//Изв.
АН СССР. Сер. МЖГ, 1979, № 2. С 179—183.
24. Папуша А. И., Пирумов У. Г., Прохоров М. Б. Газовая динамика про-
процессов образования и распространения токсичных компонент.— Изв. АН СССР,
сер. МЖГ, № 1, 1981. С. 98—106.
25. Пирумов У. Г. Обратная задача теории сопла и численные методы реше-
решения внутренних задач газовой динамики. Некоторые применения метода стенок
в газовой динамике. Изд-во МГУ, 1974. С. 1 —129.
26 Пирумов У. Г. Численные методы решения задач физической газовой
динамики//Гидроаэромеханика и космические исследования. М.: Наука, 1985.
С. 103—116.
27. Пирумов У. Г., Росляков Г. С. Течения газа в соплах. М.: Изд-во МГУ,
1978, 352 с.
28. Пирумов У. Г., Суворова В. Н. Прямая задача теории сопла. Вычисли-
Вычислительные методы и программирование, изд-во МГУ, 1977, вып. XXVII. С. 73—80.
29. Пирумов У. Г., Суворова В. Н. Численное решение обратной задачи тео-
теории сопла для двухфазной смеси газа и частиц //Изв. АН СССР. Сер МЖГ,
1986, № 4. С. 106—114.
30. Подсыпанина Н. А. Использование плоскости годографа при профилиро-
профилировании численным методом осесимметричного сопла Лаваля//Изв. АН СССР. Сер.
МЖГ, 1977, № 1. С. 164—168.
31. Рылов А. И. К построению сверхзвуковых несимметричных сопел//
Изв. АН СССР. Сер. МЖГ, 1977, № 3. С. 87—94.
32. Рылов А. И. Метод характеристик для плоских и осесимметричных сверх-
сверхзвуковых течений с произвольными углами вектора скорости//Численные методы
механики сплошной среды. Новосибирск, 1983, т. 14, № 3. С 140—149.
33. Термодинамические и теплофизические свойства продуктов сгорания М.:
Изд-во АН СССР. Т. 1—10, 1971 — 1981 гг.
ОГЛАВЛЕНИЕ
Предисловие 3
1. Основные уравнения и граничные условия 4
1.1. Введение 4
1.2. Основные уравнения 5
1 2.1. Уравнения газовой динамики пространственных неравновесных
течений идеального газа в обобщенных координатах Мизеса.
Двумерные и одномерные течения 18
1.2.2. Уравнения идеального газа в ортогональных координатах. Ха-
Характеристики уравнений для двумерных течений в координа-
координатах х, -ф 28
1.2.3. Уравнения Навье-Стокса в координатах Мизеса. Параболизо-
ванные уравнения 30
1.2.4. Граничные условия в обратных задачах 32
1.3. Необходимые сведения о физико-химических процессах 41
1.3.1. Химическая кинетика 41
1.3.2. Колебательная релаксация 45
1.3.3. Двухфазные течения 48
1.3.4. Неравновесная конденсация 49
1.3.5. Электромагнитные эффекты 52
2. Аналитические методы 55
2.1. Одномерная теория 55
2.1.1. Классическая одномерная теория идеального нереагирующего
газа 55
2.1.2. Одномерная теория для криволинейных каналов 58
2.2. Метод источников и стоков 59
2.2.1. Плоское течение 59"
2.2.2. Осесимметричное течение 61
2.2.3. Пространственное течение 64
2.3. Обратная задача теории сопла для несжимаемой жидкости ... 69
2.4. Разложение в ряд по функции тока 70
2.4.1. Пространственный случай 71
2.4.2. Плоский и осесимметричный случай 80
2.4.3. Двухфазные течения 84
2.5. Разложение в ряд в окрестности прямолинейной звуковой линии 85
2.6. Решение в окрестности бесконечно удаленной точки в дозвуковой
области 89
2.7. Аналитический расчет параметров смеси в зоне локального подво-
подвода массы и энергии в одномерном течении 91
2.8. Расчет пространственных течений в соплах методом малых воз-
возмущений 92
3. Численные методы решения обратной задачи 97
3.1. Основная разностная схема 97
3.1.1. Пространственный случай 99
237
3.1.2. Осесимметричный и плоский случаи 102
3.2. Методы решения релаксационных уравнений 103
3.3. Методы расчета течений с физико-химическими превращениями.
Одномерное приближение 110
3.3.1. Равновесные и неравновесные течения с химическими реакция-
реакциями, колебательной релаксацией и конденсацией 110
3.3.2. Течения с подводом массы и энергии, при наличии внешних сил 116
3.3.3. Течения смеси газа и частиц 117
3.4. Методы расчета течений с физико-химическими превращнеиями.
Пространственные и двумерные течения 120
3.4.1. Течения с химическими реакциями, колебательной релаксаци-
релаксацией и конденсацией 120
3.4.2. Течения с подводом энергии. Многослойные течения 122
3.4 3. Течение смеси газа и частиц 123
3.4.4. Течения газа при наличии электромагнитных полей 126
3.5. Метод характеристик 127
3 5.1. Классический метод характеристик 128
3.5.2. Послойный (сеточно-характеристический) метод и его мо-
модификации 133
4. Течение газа в соплах и каналах сложных форм 136
4.1. Течение в плоских и осесимметричных соплах 136
4.1.1. Исследование до- и трансзвуковой областей сопел с прямо-
прямолинейной и криволинейной поверхностью перехода. Течения
Мейера и Тейлора 136
4.1.2. Локальные зоны торможения 144
4.1.3. Решение прямой задачи как серии обратных 148
4 2. Течения в кольцевых соплах и криволинейных каналах 153
4.2.1. Течение в кольцевых соплах 153
4.2.2. Течение в криволинейных каналах 158
4.3. Осесимметричные течения с закруткой потока 165
4 4. Обратная задача профилирования каналов 167
4.4.1. Профилирование аэродинамических сопел 171
4.4.2. Профилирование сверхзвуковых каналов, моделирующих за-
заданный поток в выходном сечении 174
4.5. Сравнение расчетов обратным методом с экспериментальными ре-
результатами и расчетами другими методами 186
5. Течения с физико-химическими превращениями 190
5.1. Равновесные и замороженные течения 190
5.2. Течения с неравновесными химическими реакциями 193
5 2 1. Одномерные течения. Расчет течения в газовом анализаторе 193
5.2.2. Плоские и осесимметричные течения 199
5.3. Течения с колебательной релаксацией 200
5.3.1. Одномерные течения 201
5.3.2. Плоские и осесимметричные течения 202
5.4. Течения с неравновесной конденсацией 205
5.5. Течения в каналах МГД-генераторов 207
5.6. Течения с подводом энергии 213
5.7. Течения смеси газа и частиц 215
5.8. Слоистые течения 221
5.9. Течения в канале с подводом реагентов с целью подавления ток-
токсичных компонент 223
5 9.1. Равновесные и неравновесные течения 224
5.9.2. Метод оптимизации массы впрыска с целью подавления токсич-
токсичных компонент 232
Список литературы 235
Научное издание
Ульян Гайкович Пирумов
ОБРАТНАЯ ЗАДАЧА ТЕОРИИ СОПЛА
Редактор Л. Г. Грановская
Переплет художника А. Я- Михайлова
Художественный редактор В. В. Лебедев
Технический редактор Н. М. Харитонова
Корректор О. Ю. Садыкова
И Б № 5525
Сдано в набор 15.06.87. Подписано в печать 29.09.87. Т-14083.
Формат 60x904/i6- Бумага офсетная № 2. Гарнитура литературная. Печать
высокая. Усл. леч. л. 15,0. Усл. кр.-отт. 15,0. Уч.-изд. л. 16,0. Тираж 1700 экз.
Заказ 1393. Цена 3 р. 60 к.
Ордена Трудового Красного Знамени издательство Машиностроение
107076, Москва, Стромынский пер., 4.
Московская типография № 8 Союзполиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли.
101898, Москва, Центр, Хохловский пер., 7.